ю н ИВАНОВ В В.токАРЕ

ЕХАН И К.А
КОСМ ИЧ ЕСК.ОГО
ПОЛЕТА
ПРОБЛЕМЫ
ОПТИМИЗАЦИ И
13
14
16
22
32
64
76
87
92
93
94
ИЗДАТЕЛЬСТВО ((НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕС К0И Л ИТЯЕ'АТ У! ' Ы
МОСКВА 1975

6Т6
Г 86
УДК 629. 19
Механика космического полета (проблемы оптимизации),
Гродзовский Г. Л., Иванов 10. Н., Тока-
р е в В. В.. Главная редакция физико-математической литера-
туры издательства «Н аука», М., 1975.
О Главная редаьцция
физи~;о-математической литературы
и:издательства «Е1аука», 1975
31901-149
053 (02) -75
В книге систематизированпо излагается механика косми-
ческого полета. Предметом этого раздела механики является
совместное решение проблем выбора оптимальных проектпых
параметров космического аппарата, оптимального управления
его двигательной системой и оптимальных траекторий полета.
По сравнению с предыдущей книгой тех же авторов (Мо-
ханика космического полета с малой тягой, «Наука», М., 1966)
в настоящую книгу включены новые разделы, посвященные
оптимизации аппаратов с двигателями большой тяги и задачам
выбора параметров и управлений в условиях неопределенности
(игровой и статистический подходы к проблеме оптимизации).
Кроме того, старые разделы дополнены повыми результатами,
появившимися с момента выхода в свет предыдущей книги.
Книга рассчитана па инженеров, научных работников,
аспирантов и студентов старших курсов.
Табл. 31. Илл. 536. Библ. 1107 назв.

ОГЛАВЛЕНИЕ
Предисловие
Введение
22
87
Г Л А В А 4
~ 1.
2.
~ 3.
~ 4.
~ 1.
~ 2.
~ 3.
~ 4.
~ 1.
~ 2.
~ 3.
~ 1.
~ 2.
~ 3.
~ 4.
ЧАСТЬ 1
ФИЗИЧЕСКИЕ ПРИНЦИПЫ И ОБОБЩЕННЫЕ ПАРАМЕТРЫ
КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
Г Л А В А 1
ОСЕ10ВНЫЕ ПАРАМЕТРЫ И СОСТАВ КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ
СИСТЕМ
Основные параметры космических двигательных систем
Состав космических двигательных систем
Условия космического полета
Внешнее сопротивление космического аппарата н его двигательной установки
прн полете в атмосфере
Г Л А В А 2
ФИЗИЧЕСКИЕ ПРИ11ЦИПЫ ЭЛЕМЕЕ1ТОВ КОСМИЧЕСКИХ ДВИГА-
ТЕЛЬНЫХ СИСТЕМ
Реактивные движители
Энергоустановки космических летательных аппаратов
Теплоотвод от космических энергоустановок
Системы подачи и хранения рабочего вещества; воздухозаборники и системы
накопления рабочего вещества
Г Л А В А 3
ОБОБЩЕЕ1НЫЕ ПАРАМЕТРЫ КОСМ11ЧЕСКИХ ДВИГАТЕЛЬНЫХ
СИСТЕМ
Двигательные системы ограниченной скорости истечения
Двигательные системы ограниченной мощности
Двигательные системы ограниченной тяги (парусные системы)
ЧАСТЬ 11
ПРОБЛЕМЫ ОПТИМИЗАЦИИ вЂ” ДЕТЕРМИНИСТСКИЙ ПОДХОД
ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ ОПТИМИЗАЦИИ. ОПИСАНИЕ
ДИНАМ ПЧЕСК11Х МАЕ1ЕВРОВ
Постановка проблемы оптимизации
Формы уравнений движения
Межпланетный перелет
Эволюции спутника
13
14
16
32
64
76
92
93
94
95
98
106
109

ОГЛАВЛЕНИЕ
масс
пзменяемой
143
150
ступенчато
° ° ° ° ° ° ° ° ° ° ° °
качестве рабочего веще-
155
175
199
207
214
216
222
283
291
302
308
316
327
~ 1.
~ 2.
$ 3.
~ 4.
~ 5.
~ 1.
~ 2.
~ 3.
~ 1.
~ 2.
$ 3.
$ 4.
$ $.
~ 2.
$ 3.
$ 4.
$ 5.
$ $.
~ 2.
~ 3.
$ 4.
~ $.
$ 2.
з 3.
~ 4.
ГЛАВ А 5
ПДГАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕ11ЦЯ
(ИМПУЛЬСЕ1ЫЕ ПОСТАНОВКИ)
Разделение вариационной задачи, оптимальпые соотиошопия
Динамическая задача, уравнения зкстремалей
Оптимальные маневры в центральном ноле
Маневры на околокруговых орбитах
Межпланетные перелеты
ГЛАВА6
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАН11ЧЕННОЙ МОЩНОСТП—
РА ЗДЕЛЕНПЕ ВАРИАЦЦОННО11 ЗАДАЧ11, ОПТИМАЛЬНЫЕ
СООТНОШЕНИЯ МАСС
Оптимальные соотношения масс нри ностоянной и
массе двигателя
Оптимальная программа изменения массы двигателя
Использование сбрасываемых секций двигателя в
с тва
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
ГЛАВ А 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕН110Й МОЩНОСТ11—
ОПТИМАЛЬНЫЕ ПРОГРАММЫ РЕАКТИВНОГО УСКОРЕНИЯ
Уравнения экстремалей и их свойства
Оптимальный межпланетный перелет с идеальным двигателем ограппчепной
мощности
Оптимальные маневры управляемых снутников с идеальным двигателем огра-
пиченной мощности
Параметры аппарата с пдеальным двигателем ограниченной мощности
ГЛАВ А 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛ11 — РАЗДЕЛЕНИЕ ВАРИАЦ110ННОЙ
ЗАДАЧИ, ОПТИМАЛЬНЫЕ ПРОГРАММЫ ВЕКТОРА ТЯГИ
Разделение вариационной проблемы на параметрическую и динамическую
ч асти
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Уравнения для оптимальной программы вектора тяги. Модельные задачи
Оптимальный межпланетный перелет с нерегулируемыми двигателями
Оптимальные маневры управляемых спутников с нерегулируемымп двигате-
л ями
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Параметры аппарата с нерегулируемым двигателем ограниченпой мощности
ГЛАВ А 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ ИСТЕЧЕНИЯ
Особенности характеристик и оптпмальных режимов работы двигателей
ограничепной скорости истечения
Оптимальное управленпе массой двигательной спстемы — непрерывный
Ф~
с лучаи е ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Оптимальное управление массой двигателя и баков — дискретный случай .
Учет аэродинамического сопротивления
Г ЛАВА 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННО11 МОЩНОСТИ
Дополнительные компоненты в формуле для массы
Заданное время работы двигателя
Оптимальная ступенчатая программа тяги
Реальные характеристики двигательных систем
114
118
124
132
136
338
343
350
362

ОГЛАВЛЕНИЕ
Оптимальные условия сочетания двигателей ограниченной скорости истечения
и ограниченной мощности........................ 367
Области применения двигателей ограниченной мощности.......... 377
~ 1.
~ 2.
ГЛАВА 12
381
ЧАСТЬ 111
ПРОБЛЕМЫ ОПТИМИЗАЦИИ вЂ” ИГРОВОЙ И СТАТИСТИЧЕСКИЙ
ПОДХОДЫ
432
448
466
484
496
514
525
~ 1.
~ 2.
~ 3.
~ 4.
~ 5.
~ 6.
~ 7.
~ 1.
з 2.
$ 3.
~ 4.
~ 5.
~ 1.
~ 2.
$ 3.
~ 4.
ГЛАВА 11
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ
СКОРОСТИ ИСТЕЧЕНИЯ И ОГРАНИЧЕННОЙ МОЩНОСТИ
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С НАКОПЛЕНИЕМ ЭНЕРГИИ И МАССЫ.
ДВИГАТЕЛИ, ТЯГА И МОЩНОСТЬ КОТОРЫХ ЗАВИСЯТ ОТ КООРДИНАТ
И ВРЕМЕНИ
Двигатели ограниченной мощности с аккумулятором энергии — идеальный
%Э
с лучаи
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Двигатели ограниченной мощности с аккумулятором энергии — дополнп-
тельные ограничения па характеристики движителя .
Двигательные системы с накоплением атмосферного газа
Солнечный парус
Изотопный парус
Двигатель с солнечным источником энергии
Двигатель с изотопным источнико11 энергии
ГЛАВА 13
ВЫБОР ОПТИМАЛЬНЫХ ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ
ДВИГАТЕЛЬНЫХ СИСТЕМ ПРИ НАЛИЧИИ НЕОПРЕДЕЛЕННОСТЕЙ
Постановка проблемы универсализации управляемых систем
Выбор универсальной системы при полной информации о маневрах (стати-
стический подход)
Выбор универсальной системы при неполной информации о маневрах (игро-
%Э
вои пОдхОд)
Выбор параметров космического аппарата с нерегулируемым двигателем ог-
раниченной мощности, универсальным для конечного числа заданных маневров
Выбор параметров межпланетного аппарата при поэтапном поступлении
информации о неопределенных параметрах маневра
ГЛАВА 14
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
Оптимальное управление при заданной вероятности успешного выполнения
Ъ маневра
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Секцпонированный двпгатель ограниченной мощности — формулировка и
уравнения вариационной проблемы
Секционированный двигатель ограниченной мощности — примеры ре~по ия
для модельных маневров
Оптимальная вероятность выполиения транспорт ых маневров
ГЛАВА 15
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ ПРОГРАММ УПРАВ ЛЕН ИЯ
В ИГРОВОЙ ПОСТАНОВКЕ
Описание маневра спуска аппарата в атмосфере
Алгоритмы управления спуском аппарата в атмосфере
391
396
415
421
422
428

ОГЛАВЛЕНИЕ
газ
604
608
6)10
(а =-О,
618
620
624
631
644
$ 1.
~ 2.
~ 3.
649
654
1.
2.
Основные обозначения
660
665
Литература
1.
2.
3.
4.
5
6.
1.
2.
3.
4.
5.
ГЛАВА 16
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ
В СТАТИСТИЧЕСК011 ПОСТАНОВКЕ (ЗАДАЧ11 КОР1'ЕКЦ11И)
Возмущающие воздействия
Точность выполнения маневра без коррекции
Измерения координат и скорости
Коррекция, оптимальная в среднем
Коррекция, оптимальная с задаииой вероятностью
Коррекция орбиты аппарата, ххахсаплххвахохцего ат1хосферххьххх
ЧАСТЬ 1У
ПОСТРОЕНИЕ ОПТИх11А.ЛЬНЫХ 1'ЕШЕНИИ
Г ЛАВА 11
АНАЛПТПЧЕСК ИЕ РЕШЕН11Я УРАВНЕНИЙ Д ИНАМ11К П
Радххальххое ускорение (хх =() в (4.19))
Трапсверсальпое ускорение (а„=О в (4.$7))
Таххгеххцххальххое ускорение ("(=О в (4.26))
Норъхальххое ускореххпе ((=" г. в (4.24)). Бххххорхххальххое ускорение
и =0 в (117
и =0 в (~. ~7))
° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
Постоянный вектор ускорения (а, =а,=(), а =а=сопз1 в (4.13))
ГЛАНА 18
ФУНКЦ110НАЛЬНЫЕ Ч11СЛЕННЫЕ МЕТОДЫ ПОСТРОЕН11Я
ОПТ11МАЛЬНЫХ РЕШЕН ИИ
Градиентный спуск в фазовом пространстве
Градиентный спуск в пространстве управлений
Функциональный метод Ньютона
ГЛАВА 19
1СОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ ПОСТРОЕНПЯ
ОПТИМАЛЬНЫХ РЕШЕНИИ
Минимизация функции прп дополххххтельных условиях
Сведение вариационнык задач к конечномерным
566
568
576
583
588
597

ПРЕДИСЛОВИЕ
Основу книги составляет выпущенная девять лот назад издательством
«Наука» монография «Механика космического полета с малой тягой». Од-
нако различия между этими книгами столь значительны, что их нельзя счи-
тать просто разными изданиями. Это обстоятельство подчеркивается и назва-
нием настоящей книги: «Механика космического полета (проблемы оптими-
зации)».
В новой книге, естественно, сохранен тот подход к задачам оптимизации
в механико полета, который был последовательно реализован в предыдущей
монографии. Суть его состоит в аккуратном описании физических характе-
ристик двигательной системы и внешних условий полета и в совместном рас-
смотрении проблем выбора оптимальных проектных параметров аппарата и
двигательной системы, с одной стороны, и оптимального управления двига-
телем и оптимальной траектории полета — с другой.
Этот подход сформировался в процессе исследования проблем оптимиза-
ции в приложении к аппаратам с двигателями «малой тяги», для которых роль
массы двигательной установки особенно существенна. Работы последних
лет показали необходимость такого же подхода к проблемам оптимизации и
для космических аппаратов с традиционными двигателями «большой тяги».
Например, для аппаратов с ЖРД было установлено определяющее влияние
массы двигателя на выбор оптимальной тяговооруженности для ряда манев-
ров. При этом развитие принципов корректного разделения общей проблемы
оптимизации на параметрическую и динамическую позволяет по-новому ис-
пользовать полученные ранее фундаментальные результаты классической
ракетодинамики.
С изложенными соображениями связана первая группа отличий новой
книги от предыдущей: класс рассматриваемых объектов пополнился аппа-
ратами с двигателями «большой тяги» или, точнее, с двигателями ограничен-
ной скорости истечения (идеальными и реальными).
13торая группа отличий — методическая. В первой книге большинство
задач ставилось в рамках детерминистского подхода, а игровые и статисти-
ческие постановки были представлены довольно скупо. Новая же книга суще-
ствепно богаче именно этими постановками, настолько, что они составили
отдельную (третью) часть книги.
Игровыо и статистические постановки в ряде случаев более адекватно,
нежели детерминистские, описывают реальную ситуацию в части, касаю-
щейся информации о внешних условиях задачи. 11е все внешние данные
можно считать известными точно. Е таким неопределенным данным отно-
сятся, например, ошибки в реализации начальных условий и программы тяги,
флуктуации плотности атмосферы, моменты отказов элементов двигательной
систеъ~ы, а иногда и параметры маневров, которые предстоит выполнять. Сте-
пень информированности об этих неопределенностях может быть различной,
и она может меняться (возрастать) при переходе от этапа проектирования
к этапу эксплуатации аппарата. Данный круг проблем и является централь-
ным в игровых и статистических постановках.
Содержание предлагаемой книги разделено па четыре части.

ПРЕДИСЛОВИЕ
Москва, 1974 г.
Г. Гродзовский
Ю. Иванов
В. Токарев
В первой части изложены физические принципы всех известных типов
космических двигательных систем. Дана классификация двигателей и при-
ведено описание их обобщенных характеристик, необходимых для формули-
ровки задач оптимизации.
Вторая часть книги посвящена детерминированным задачам оптимиза-
ции проектных параметров и программ управления космических аппаратов
со всеми типами двигателей, указанными в предыдущей части, для различных
маневров.
В третьей части собраны игровые и статистические задачи оптимизации:
выбор проектных параметров многоцелевых аппаратов, построение программ
управления и определение проектных параметров с учетом отказов, флуктуа-
ций атмосферы, ошибок в тяге и т. п.
В четвертой части обсуждаются методы построения управлений и траек-
торий движения космических аппаратов — аналитические и численные.
Разделы книги иллюстрированы примерами характеристик перелетов
на планеты солнечной системы, маневров управляемых спутников и т. д.
(в виде конечных формул, таблиц и графиков).
Книга рассчитана на инженеров, научных работников, аспирантов и
студентов старших курсов; у читателей предполагается знание основ вариа-
ционного исчисления, классического и современного. Однако построение
изложения позволяет пользоваться основными результатами, если даже раз-
делы, посвященные вариационному анализу, будут при чтении опущены.
Распределение работы между авторами было следующим: главы 1, 2, 3,
12 написаны Г. Л. Гродзовским, главы 4, 10, 11, 15, 17, 18, 19 — Ю. Н. Ива-
новым, главы 6, 7, 8, 13, 14 — В. В. Токаревым. В связи с включением в книгу
большого количества нового материала авторы сочли возможным обратиться
с просьбой о написании трех новых глав к специалистам, известным своими
оригинальными публикациями по соответствующим темам: С. В. Дубовскому,
А. Е. Илютовичу, Б. Н. Кифоренко и В. П. Моисеенко. Все они любезно
откликнулись на эту просьбу авторов. С. В. Дубовским подготовлена 5 глава,
А. Е. Илютовичем — 16 глава (совместно с В. В. Токаревым), Б. Н. Кифо-
ренко и В. П. Моисеенко — 9 глава.
Авторы считают своим приятным долгом выразить благодарность
В. В. Белецкому, Ю. Е. Кузнецову, Р. Н. Овсянникову и Ф. Л. Черноусько,
прочитавшим книгу в рукописи и сделавшим ряд полезных замечаний. Ав-
торы благодарны ~ Л. А. Арцимовичу ~, В. А. Егорову, В. К. Исаеву,
~ Г. Е. Кузмаку ~, А. И. Курьянову, А. И. Лурье, Н. Н. Моисееву, Г. П. Сви-
щеву, Л. А. Симонову, В. В. Сонину, Г. Г. Черному, Л. М. Шкадову,
Т. М. Энееву за обсуждения затронутых в книге вопросов. Авторы особо при-
знательны Л. И. Седову и Д. Е. Охоцимскому, внимание которых к работе
авторов во многом способствовало появлению данной книги.
Мы будем благодарны читателям за все замечания и пожелания по этой
книге.

ВВЕДЕНИЕ
Прогресс космической ракетной техники вызывает к жизни новые раз-
делы механики. Сформировавшаяся на рубеже Х1Х и ХХ столетий 1) идея
применения реактивных двигателей для выхода в космос стимулировала
развитие механики космического полета (И. В. Мещерский, К. Э. Циолков-
ский, Р. Годдард, Ф. А. Цандер, Г. Оберт, В. Гоман, Р. Эно-Пельтри,
С. П. Королев и др. [1.1 — 1.9]). Эта наука изучает движение космических
аппаратов как тел переменной массы с целью определения условий доставки
максимального полезного груза.
Решающая роль здесь принадлежит типу двигательной системы. На пер-
вом этапе развития механики космического полета наиболее подробно ис-
следовался полет аппаратов с тепловыми химическими реактивными дви-
гателями, для которых характерна малая удельная масса двигательной
системы (отношение массы двигательной системы к развиваемой максималь-
ной тяге). При умеренной тяговооруженности (отношение тяги к массе ра-
кеты) для таких ракет было допустимо в первом приближении пренебрежение
массой двигательной системы, и задача оптимизации сводилась к отыска-
нию условий наименьшей затраты топлива на совершение заданного косми-
ческого маневра'). На основе формулы Циолковского последняя задача
сводится к минимизации простого кинематического параметра, так называе-
мой характеристической скорости, что требует только определения опти-
мальных траекторий с указанием на них моментов и направления приложения
импульсов тяги. Эти задачи подробно изложены в известных работах и моно-
графиях по ракетодинамике [1.10 — 1.69] и др.
Развивающиеся перспективные виды космических двигательных систем
(электрореактивные двигатели, тепловые ядерные реактивные двигатели,
солнечный парус и др.) отличаются большой относительной массой и широ-
кими возможностями регулирования параметров (скорости истечения, рас-
хода массы и др.). Перспективность использования таких двигательных
систем'определяется малым расходом массы на единицу тяги для электрореак-
тивных и ядерных тепловых двигателей (вследствие большой скорости исте-
чения реактивной струи) или отсутствием расхода массы для солнечного па-
руса. Технический прогресс последних лет в области ядерной энергетики,
электрических ускорителей, технологии тонких пленок и др. поставил на
очередь дня проблему научной и технической разработки указанных пер-
спективных двигательных систем. А с увеличением тяговооруженности не-
допустимо пренебрежение массой двигательной системы и для тепловых хи-
мических реактивных двигателей.
В этой связи получил развитие новый раздел механики космического
полета, рассматривающий в совокупности: оптимальные соотношения масс
') М и х а й л о в Г. К., К истории динамики систем переменного состава и теории
реактивного движения (до начала второй мировой войны). Препринт Ы 49, изи-во Инсти-
тута Проблем Механики АН СССР, М., 1974.
~) Выбор числа ступеней ракет, т. е. учет последовательно сбрасываемых баков,
масса которых пропорциональна запасу топлива, не изменял принципиально указанную
постановку.

° В
Ю Ю Ю
° е
° °
Ю
Ю
° Э
Ю Ю Ю
Ю °
° Э
° В
° В
° В
а
° В
° В
ав ю
° е
° В
° й
е °
° в
° В
Ю
Ю °
° В
° В
° В
° В
° В
е
е °
° В
° В
° В
а е
° В
а
° В
° В
е
е
° В
е
° В
° В
а
° В
е а
е °
е °
° В
е
° В
Ю
° В
Ю
° В
аа
° а
ю
е °
° в
Ю Ю
Ю Ю
° Э еЭ
е
е Ю е
е ав
Ю а
е е
е
° Ва
е
Ю
Ю Ю
Ю Ю
е е

ВВЕДЕНИЕ
компонент ракеты с учетом массы основных элементов двигательной системы,
оптимальное управление и регулирование двигательной системы и оптималь-
ные траектории космического полета [1.70 — 1.74].
В механике космического полета задача о нахождении условий доставки
максимального полезного груза выделяется в силу ее определяющего влияния
на компоновку и управление космическим аппаратом. С этим аспектом неиз-
менно связана постановка задач в плане оптимизации траектории движения,
управлений и проектных параметров двигательной системы и аппарата. Ука-
занная постановка основной задачи механики космического полета органи-
чески связана с характеристиками двигательных систем.
В современной литературе обсуждается большое число типов космических
двигательных систем. Основные перспективные виды указаны в табл. 1.1
([1.75 — 1.103] и др.), где приводятся некоторые параметры систем: характер-
ные значения скорости истечения реактивной струи К, удельной массы у,,
(массы двигательной системы, отнесенной к создаваемой тяге) и ускорения
аппарата от реактивной тяги а; параметры двигательных систем в таблице
расположены в порядке возрастания скорости истечения реактивной струи.
Приведенные в табл. 1.1 характерные значения удельной массы двига-
тельной системы у., объясняют сложившуюся в последние годы терминологию:
двигатели большой тяги и двигатели малой тяги. Верхний предел ускорения
от реактивной тяги а „достигается в том случае, когда масса двигательной
системы становится преобладающей по сравнению со всеми остальными ком-
понентами массы космического аппарата; тогда а,„-~ 1/')'„. Если х'„(
( 1 кг ~кГ '), то а „) д„' если 1'„) 1 кг ~кГ, то а „(д, (д — ускорение силы
тяжести на поверхности Земли); в первом случае двигатели называются дви-
гателями большой тяги, а во втором — малой тяги (правильнее — большого
и малого ускорения от тяги (рис. 1.1)). Следует отметить, что большие зна-
чения удельной массы для двигателей малой тяги не являются отличительным
качеством физических принципов, а характеризуют лишь современную оценку
уровня разработки таких двигательных систем. Поэтому распространенный
сейчас термин «малая тяга» в значительной степени условен.
Для механики космического полета определяющее значение имеют две
характеристики двигательной установки: возможность управления реактив-
ной тягой и затраты массы на реализацию тяги (потребный запас рабочего
вещества и массы двигательной системы).
Выяснение этих вопросов находится в центре внимания первой части
книги, при обсуждении физических принципов и основных характеристик
космических двигательных систем, знание которых необходимо для после-
дующего подхода к задачам механики космического полета.
Движение космического аппарата исследуется как движение материаль-
ной точки. Вопросы, связанные с движением аппарата вокруг центра масс,
') В книге используется Международная система единиц измерения (СИ). Но, от-
давая дань традиции, сложившейся в инженерных расчетах, авторы по примеру [1.104]
сделали одно исключение: численные значения величин типа «сила» приводятся в при-
вычных кГ (или в Г, или в Т), а не в «ньютонах». Единицей массы при этом, как и
положено в СИ, остается кг (или г, или т). Этим и объясняется появление разиосистем-
пых разцерпостей у численных значений таких величин, как ~„, например: ~„=1 кг)кГ.
Все же «буквенные» формулы в книге рассчитаны на использование какой-нибудь одной
сххстеххьх измерений (например, СИ). Поэтому, чтобы подставить в «буквенную» формулу
величину, численное значение которой содержит в своей размерности кГ, нужно пред-
варительно осуществить ее пересчет в «ххьхотоххьх» (1 кГ соответствует 9,81 и). Например,
чтобы ххаххтхх массу двигательпохх системы ЛХ.„по формуле ЛХ„=т„а»ЛХ» при т.„=1 кг/кГ,
а„=9,81 л/сек» и ЛХ» — — 10г кг, нужно пересчитать удельную массу двигателя у,=(1/9,81)
кг/н=(1/9,81) сед/лх и получить ЛХ,=(1/9,81) секк м х 9,81 м сек ~ 10 кг=10 кг.
Отметим здесь также, что по мотивам, изложенным в [1.104], авторы вьхесто весовых
компонент 6;, которыми они пользовались в своей предыдущей книге по механике полета,
перешли к компонентам массы М;.

12
ВВЕДЕНИЕ
в книге не затрагиваются. Пренебрегается также «обратным» воздействием
массы аппарата на движение гравитационных центров.
К траектории движения космического аппарата обычно предъявляется
требование, чтобы она начиналась в заданной точке фазового пространства
(т. е. при заданных координатах и проекциях скоростей) и за фиксированное
время достигала другой заданной
а
точки в фазовом пространстве. Это
требование может быть удовлетво-
18 4Х рено не единственным образом. Из
всего многообразия траекторий,
соединяющих за фиксированное
1 время две заданные точки в фа-
зовом пространстве, выбирается
такая траектория, которая отве-
чает движению космического аппа-
рата с максимальным полезным
~-г б грузом при фиксированной старто-
8 вой массе. Это — постановка основ-
ной вариационной задачи механи-
Ю ки космического полета об опре-
7Г
делении оптимальных управлений
двигательной системой и оптималь-
ных соотношений масс компонент
У
аппарата, обеспечивающих движе-
ние по указанной оптимальной
!а' 6' Юсефа траектории.
Вместо приведенной Выше мо-
Рис. 1.1. Космические двигательные системы: 1 — 5—
двигатели большой тяги: 1 — химическая камера жет быть сформулирована вторая
сгорания, 2 — нагрев в реакторе с твердым ядерным ВарИацИОННая ПОСтаНОВКа, ЭКВИва-
горючим, 3 — то же с жидким ядерным горючим,
4 — то же в сочетании с химической камерой сго- лентная первой для многих манев-
рания, 5 — нагрев в реакторе с газообразным ядер-
ным горючим; 6 — 12 — двигатели малой тяги:  — рОВ: трЕбуЕтСя ОнрЕдЕЛИтЬ ОнтИ-
с солнечным нагРевателем, У вЂ” с изотопным нагре- МаЛЬНЫЕ уПраВЛЕНИя И ПОСтрОИТЬ
8 — электр одуговой, 9 — электродинами-
ческий, 1Π— электростатический, 11 — изотопный ТраЕКтОрИЮ, СОЕдИНяЮщуЮ За МИ-
нимальное время две заданные точ-
ки фазового пространства и обеспе-
чивающую движение аппарата с заданными стартовой и полезной массами.
Вторая постановка может оказаться удобнее в тех случаях, когда нет уве-
ренности относительно энергетической выполнимости маневра В рассматри-
ваемом диапазоне времен перелета.
Кроме этих двух основных вариационных постановок, в механике кос-
мического полета формулируются частные постановки, соответствующие
отдельным типам космических маневров: межорбитальный перелет, задача
Выхода из гравитационного поля планеты, эволюции в окрестности планеты
и др. Вариационные формулировки этих задач не требуют выполнения всех
граничных условий по координатам и скоростям — задаются не все коорди-
наты и скорости, а только часть их или комбинации. Свободные граничные
условия в этом случае определяются из соображений оптимальности траек-
тории.
В ходе изложения будет акцентироваться внимание на формулировках
Вариационных задач и на их связи с приведенными выше двумя основными
постановками.

ЧАСТЬ 1
ФИЗИЧЕСКИЕ ПРИНЦИПЫ И ОБОБЩЕННЫЕ
ПАРАМЕТРЫ КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ
СИСТЕМ
1'ЛАВА1
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ КОСМИЧЕСКИХ
ДВИГАТЕЛЬНЫХ СИСТЕМ
~ 1. Основные параметры космических двигательных систем
Принципы работы и характеристики космических двигательных систем
подробно изложены в известных монографиях, обзорах и учебниках ([1.75—
1.1031 и др.). Ниже основные физические принципы и обобщенные параметры
космических двигательных систем излагаются в объеме, необходимом для
подхода к задачам механики космического полета. В соответствии со сказан-
ным во введении, в механике космического полета проблема соотношения масс
(например, задача о нахождении условий доставки максимального полезного
груза) выделяется в силу ее определяющего влияния на параметры косми-
ческого аппарата. Затраты массы, необходимые для реализации полета кос-
мического аппарата, во многом определяются его двигательной системой.
Средством, обеспечивающим активное управление движением центра
масс космического аппарата, является реактивная тяга Р, создаваемая его
двигательной системой. Движение центра масс космического аппарата под
действием тяги в гравитационном поле может быть описано векторным диффе-
ренциальным уравнением (см., например, [1.70])
и ',~) г = Р + М,~) ~ + Г,
д.= — М = у+д,— д,
(д, = — М„),
(1.2)
где д, — расход массы при выработке энергии, д, — «приход» массы из внеш-
ней среды.
') В записи (1.2) пе учитываются расход массы в системе жизнеобеспечения и воз-
можность сбросов секций двигателя и баков.
где ЛХ (~) — масса аппарата, г (~) — радиус-вектор в инерциальной системе
координат, Р— вектор тяги: Р = Ре, е — единичный вектор направления тяги,
ц (г, 1) — вектор ускорения от гравитационных сил, 1 — время, à — вектор
других внешних сил, действующих на аппарат (сопротивление среды и др.),
определяемый внешними условиями полета, точки обозначают дифференциро-
вание по времени 1.
Полная система уравнений, описывающих поведение космического ап-
парата, складывается из векторного уравнения движения (1.1) и связей
ме~кду массой и параметрами двигательной системы. При оптимизации пара-
метров космического аппарата управляющими функциями являются вектор
направления е реактивной тяги и параметры двигательной системы, опре-
деляющие величину тяги Р и массу ЛХ.
Создание реактивной тяги Р связано с расходом массы через движитель
д (например, массы отбрасываемого рабочего вещества). Полный расход массы
равен ')

14
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
Масса двигательной системы ЛХ (1) (включая массу баков М для ра-
бочего вещества: М =М„+М), величина реактивной тяги Р (~) и расход
массы на создание тяги д (1) являются основными характеристиками косми-
ческой двигательной системы.
Значение текущей массы аппарата М (1) можно представить в виде
ЛХ (~) = ЛХ. (~) + ЛХ (~), ЛХ. (~) = М, — М„ (~) — д. ® Ш~,
(1.3)
где М, — начальная масса аппарата. При этом конечное значение М. (в ко-
нечной точке пути ~=Т) можно отождествить с полезной массой М,.
Из соотношений (1.1) — (1.3) видно, что основные параметры двигательной
системы определяют движение космического аппарата; указанные параметры
М (~), Р (~), д (~) и вектор направления тяги е являются управляющими
функциями в задачах оптимизации космического полета.
С указанными параметрами Р (~) и д (~) связаны зависимые параметры
средней эффективной скорости истечения и эффективной мощности реактив-
ной струи. Частное от деления Р на д, имеющее размерность скорости, можно
характеризовать как среднее эффективное значение скорости реактивной
струи Г (для полетов без забора массы рабочего тела из внешней среды и
для дорелятивистского уровня скоростей):
(1. 4)
Г= Р(д.
Тягу, приходящуюся на единицу весового расхода, характеризует отношение
1'=Г/д„имеющее размерность времени (например, сек). Величину Г при-
нято называть удельным импульсом двигательной системы.
Соответственно (1. 2) и (1. 4) эффективное значение мощности реактивной
струи будет равно
Т ='/,д Р.
(1. 5)
Отметим, что отношение Г к величине мощности Г„, вырабатываемой энер-
гоисточником двигательной системы, характеризует коэффициент полезного
действия двигательной системы:
(1. 6)
~ = Т/Т„.
$ 2. Состав космических двигательных систем
Обобщенный состав космической двигательной системы приведен на
рис. 1.2. Исходным элементом двигательной системы является источник
энергии; завершающим элементом является реактивный движитель, где
часть выработанной источником энергии превращается в кинетическую энер-
гию направленного движения реактивной струи. Если виды энергии, выделяе-
мой источником и потребляемой движителем, различны, то между источником
энергии и движителем включается энергопреобразователь. В паузах работы
двигательной системы часть выработанной источником энергии может на-
капливаться в аккумуляторе энергии. Масса рабочего вещества, расходуемая
на создание реактивной тяги, подается в движитель системой подачи из кон-
тейнеров (баков). При полете в среде с ощутимой плотностью масса рабочего
вещества может пополняться через заборное устройство и накопительную
систему. Последняя согласует параметры поступающего рабочего вещества
с условиями в контейнерах (баках).
В результате отличия энергетического коэффициента полезного действия
двигательной системы от единицы значительная часть вырабатываемой энерго-

СОСТАВ КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
источником мощности должна быть отведена от двигательной системы систе-
мой отвода энергии.
Естественно, что указанные составные элементы присущи не всем типам
космических двигательных систем, В которых Возможны различные сочетания
элементов в рамках рассмотренного обобщенного состава.
С позиций механики космического полета характерными параметрами
источника энергии являются вырабатываемая им мощность Г„(1) (сущест-
венна возможность регулирования выделяемой мощности), собственная масса
энергоисточника М„(К„, ~) и расход массы д, при выработке энергии. Ха-
рактерными параметрами преобразователя энергии являются отношение вы-
рабатываемой им полезной мощности К, (1) к входной мощности К„(1),
Рис. 1.2. Состав двигательной системы.
которое можно характеризовать как коэффициент полезного действия энер-
гопреобразователя о, (Н~„), а также масса энергопреобразователя
ЛХ,(К, „). Характерными параметрами аккумулятора являются величина
запасаемой им энергии Е, максимальные величины потребляемой Е „ и по-
лезной выделяемой Е,, мощности (точка обозначает дифференцирование
по времени ~), а также собственная масса аккумулятора М, (Е „). Характер-
ными параметрами накопителя рабочего вещества с заборником являются
приход массы д„и привносимая забираемым рабочим веществом мощность К„„
мощность, расходуемая накопителем К„(д„), и масса накопителя с заборни-
ком М„(д„„). Характерным параметром контейнеров (баков) для рабочего
вещества является их масса М, (1), зависящая от величины запаса рабочего
вещества М (~) =М. (~) — М (см. (1.3)). Характерными параметрами си-
стемы подачи рабочего вещества являются подводимый ею к движителю
расход массы д, потребляемая мощность Г, (д) и собственная масса М, (д „).
Характерными параметрами реактивного движителя являются создаваемая
им тяга Р (~), потребляемые им мощность Г„(Р) и расход массы д (Р), а также
собственная масса движителя М (Р .„Н~„„).
Разность (К„+К,„) — Г, между суммарной мощностью энергоисточника
К„и привносимой забираемым рабочим веществом К„, и полной мощностью
реактивной струи движителя К„должна быть выделена системой отвода энер-
гии. Характерным параметром последней является ее масса М~ (Н',), где

ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[Гл. 1
Перечисленные элементы космической двигательной системы определяют ее
основные параметры.
Ч. = Ч+ Ч. Ч.
М = ЛХ„+ М + ЛХ, + ЛХ„+ ЛХ + ЛХ, + ЛХ + ЛХ~
(1.7)
и Возможности их регулирования.
Отметим, что на рис. 1.2 и во второй строке (1.7) представлено наиболее
мелкое (из употребляемых в настоящем изложении) деление двигательной
системы на элементы. Кроме того, в дальнейших главах используются такие
объединения указанных элементов, как «источник мощности» ЛХ, = ЛХ„+
+ ЛХ, + М и «двигатель» М = М„ + ЛХ + ЛХ + М, + М, = ЛХ вЂ” ЛХ .
$ 3. Условия космического полета
1. Гравитационное поле. Гравитационные силы определяют основное
внешнее воздействие в космическом полете. Ускорение д, сообщаемое аппа-
рату этими силами (см. (1.1)), образует потенциальное поле, в общем случае
нестационарное (см., например, [1.105-- 1.108]):
(1. )
~ (г, 1) = — ртай, Г (г, 1),
где à — гравитационный потенциал (или потенциальная энергия единичной
массы). Произвольный уровень отсчета потенциала обычно выбирается так,
чтобы 11т Г (г, ~)=0 при г -э со.
Начиная с некоторого удаления от тел (~=1,..., и), создающих грави-
тационное поле, их можно считать сферическими (или точечными), и тогда
и и
Г (г, ~) =~.'~' ~Я,/Л,, д(г, ~) =~~!Щ,Л В,
(В,. = г,. (~) — г, Л,. = ~ В,. ~),
(1.9)
(г= г~).
Г (г) = — ~Ю~/г, ~(г) = — ~~Яг 'г
При движении в непосредственной близости планет следует учитывать
несферичность их поверхности и эквипотенциалей гравитационного поля.
где ~=6,67 (1+0,0007) 10 '1 мз кг-1 сек-' — универсальная гравитацион-
ная постоянная, Ю~,. — ~-я гравитационная масса, В, — вектор расстоя-
ния от текущей точки г до центра г,. (1) ~-й гравитационной массы (траекто-
рии г,. (1) движения гравитационных масс считаются известными и не за-
висящими от движения космического аппарата). Основные траекторные и
физические данные небесных тел солнечной системы приведены в табл. 1.2,
1.3 из [1.106].
Если движение происходит в окрестности превалирующего действия од-
ного небесного тела (в так называемой сфере притяжения, или в сфере дей-
ствия этого тела), то в суммах (1. 9) можно ограничиться только одним слагае-
мым. Пусть еще при этом движение г,. (~) центра масс данного небесного тела
можно с достаточной степенью точности посчитать равномерным и прямо-
линейным. Тогда, совместив начало инерциальной системы координат (в ко-
торой записаны уравнения движения (1. 1)) с центром тела, получим из
(1. 9) (при г,. (~): — О, и=1) широко используемую в механике модель централь-
ного гравитационного поля:

17
УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
м м
м н м
ОООО ~О
ч ~ч ч 0 ~~ ~ч
со сч,о.4ГР оо
- ОО-~ О,-
сф с'Гд сф
СЯ ~ СЯ
с м м
ООООО~
! ~ е~ (р~
° ° е ° ° С Ф)
ООФОО
О О Ф р~ .~ ~
лОО у 'Ф 'Ф
Л ~ей
сф ч»
лО
о
С» е» °
оО ~~
о
о
О ОО
° П л
лО
С'О
Ж
о
~ч
Ц
м
м
ОО сц
~ ~ д»
Ч~ ~Ч О
ЩП
иЪ
иЪ
О
О
СО
СЧ
Се ~д
оо г-
~ ОО с'"
° е Я
ОО
~ Ос
О
ФО О
сч с
Ооо&g
° с~ с~ О сф
яро„еб
Ос~
н сч
М М М
СО ~ ~ ~ ОО ~
ОООО ~-( О
~ ~ ~ ~ООс~ ~о
° ° ° е Я е р~
О ОО О ОО '~ ц~
ОпсООО
~дно~~ о
сч сч сч сч
00 ч9 М М М
О О О О О 00
° ° ° ° °
~ООООЛО О
'~О~ФОЪЖСО~Ф
о сч
О
о °
сф
С е Сс~~
° \
° ~М
иЪ
О
О
~~ ~-~ о
СЧ С~)
иЭ ~~ с~
сф
'~ О
° УМММ
О О О О О,.
° ~МАМ ~4 ~Ч( )~~
Лщс-.ООО
~ Оъ сО с 1
"'Ф 'Э~О
° ~М ч~М ~4
~ч ер ~ с
ОоосО О
Ч Чоло 4
ООМОСОО ж
с~ со ~ л ~~ сч
Й ~У Й м м
Ооооод
с~ Н с $ с~ с~ ~~.~
° ° ° ° °
в -~ О в ОО о о
'Фс1сОСЧО~~
." ." ОО П О ОО
Щ)
еч с
ОО О
О ОО
Г- СО ОлО
ОО СЯ
О
О
'~ о
с~~ ОО
О
СР
СЯ
сО О
~~ '~~ о
~О
° рд
о
О
О
иЪ
сф
О
О
С"~ '~ о
СЧ
~~ ~СЯ
СЯ ср~
о
С~ О
еч с
О О ~р"'
° °
( ~ сф
сто О
иЪсО ~
О
М М М
° У ~ ~ ~ сс~~ чф
ООООд О
~'~ ~ с~с~'~о
° ° ° ° С'0 °
СЯ с~ с~ ОО ~-~ с~~
ООО~ ОООс~~Од
©~ ~ С~
~ч ~ч ~-ч СО р~
й ~У М М М
ДООООООО
р ~М ~М ч~М ч~М ч~М 1»~
цр ОО 'Ф сЫ 'Ф сО
С~1 с~ Л Я Ч~ О Оъ
~Ф СО 3.О СЯ
О
1.'
е
О Од
~ ~ д»
ОО ~Ч О
'Ф сО
СЯ
сф
О
О
° с~ с~ с-4
о
,:. ЛСО,СО с- ~
н~ ос1 Е
сО сч ~ оО
00
с
О о~~
° с~ с~ с~ 3.О
° е Щ
О ~1' с;1
(~ ч~М
О
о о о
М М И ~ еУ
ООО с"~О
О 4 ч ч ~ ч о
(.ВСЮ ~ Ж
ОО ~ Л В О О ОО ™~
о
",Л '1 сй
М М М
~ ~Ф
ОООС лО
ч ч ч ср~
° ° °
ОООО Щ С~~
ОЛ ОООО'~
~М ~М '~ ~ГД
с~ ~.~
»ю
Ф чф
ОО
° ~~ ч~М
о ° °
~О ~
па
° ~М ~~
СР
ЯР
О
О
О
Н
Ф
ФЧ
СЯ
о
О О Св ~
с~ ~ с~~
сэ оос~
ОЪ ОЪ ОО,О
° ~ сО СЯ
м л м
О О О
т~ ~~~ ~~~ О
° ° °
~Ч сф
тМ ч~М ч~М
~~ СО ~О
~~ О
~ ОО
Щ !
о
111111ф
е
О о
О
° ~1'
Л С,;"О
СЯ
О
СР
сб
Эю~
Б
О
° Ф
л
ее
ее4
ее
е~е1
Ф
Ф
й
й
О
ы
М$
Щ
о
Ж
о
М»
с
ЬеЧ
О
$»
сб
о
О
ее
е2
а.'
ьМ
С)
ев»
Б.
О
Н
Ф
сф
12
Н
Ж
ф
О
О
Механика полета
~ц~
~ц~
Ю
й
и
Я~й
М4
О
О
Ю р'
Ф Я
о о
~~э й Щ
~:Ц~Ф(,)
ж',ьиоо
майой~
Я ~Ф ~~~
И~ ойЖ
й
~ч
Ф
П
о
° ~М
" "„11
Ф ~ л н Н 1
Я о с
~ч
ф~ й ~й й
д "~йлойн
~ ~ д д~ д й
одно
с~Оцс с~с,„
о
~"о~й
д оойоо
~4 ~) д ~ й д
сб бъ О й й б н
~~й~ИИ~©й
й О н й н Ф о
о -©~~ййй
сЕ ~-"' ~-"' 4 й
о о с~ с~
,'-) й д,Д,Д,с щ
ф~ й о © с. с. й д
рч Ю
д н~ ~~,„,„о
цо ~ййв~
~-в
Щж
И О~~ОЖ
ъ Ц
о
~~" о
н ~~
о ~~
оцуп
~ о
Ц
й
Ф н
&lt ~
о
й Ф
Ф
~ Р
Ф
н о
о ~
о
Р
Рч
Ц ~бо О
Д, ср
О ~-~
~ц~
~ц~
Ж
Ц
м
й
Ф
~~о
Ф
л д
$~»:" й
с-'~ й
с~ ~эи
вайо
с~ ~Ф
:Я~ о
А
Ы! .
Р
С)
.о
Ц
Ф
Я Но цр
БЮ: ~» ~» 'е»
д„",й С о с~
о йн О
о ~ 'й~~~~о
Р
цро д~ ~ о
с~о~ ноддт~~
дц ц ~ щ й
~оый~~~~о
с~в „- о ~ро
~ ~~ й д, ~:~ ~:~ с.') ~
~~~йоЗ~~ж~~
о о д н ~ ©~,„,„~ о
й~~о"~йй~~ ~ ®о
с~ д, Е Е й с~ д, В
~:3, ~4 я ~ ~-~~ ср ~.~ ~.~ ~:~ ~4 ср я ~- ~ д
ИЖ~ ~ О~ ~ ОЖо~

ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
~ГД. 3
ОО
нн
° °
ЯО
ЛО
н 0'-
СЯ
03
О
нд
н ~~4
нОЛ
ПОн
-О~
н
СЯ
О
еч е СЧ н
ООЯ
нн О~
° . "н
сО О О
о0
1
00
О
00
"О ~Ъ
сб
О
СЯ
О
О
СЯ
О
СР
сО
СЯ
Ф
М'$
ж
Ф
О с~~
1
ОО
нн
° °
ЯО
о0~
",~Г~
~с 1
° чО
М
О
н с~~
О с&
'~ Ож
нОЛ
~'~е л л
"ОЛ
О
О
СЯ
О
1ь
О
н с~~
С1сО
~ОО
~ОС
-~ГО 00
Ф
Ф
о
й р,
Я ы
ОО
нн
° °
~ и~
~1~ В
оо~-
О О
н,н
О
н л с~~ сй
н
СЧ
О
~Г~
~Г~
СЯ
М
О
0 сО
л
л
~ О'~4
О
Щ Ф
~»0 н
~ч СЧ
О
~Г~
СЯ
03
О
ныл
° 00 ~ф
СЧ С'1 СВ
С~~ О
О ~ч
н
О
а н
ОО00
н н
,;,„ О
Д СЧ О
х 1
М
О
нд
О 00
ЛО ч
~Оеб
-О
с
О
н н
с'О СЧ
~ОФ
с~„О СЧ
СЯОСИ
О
~Г~
О с~С
. ООО
ч О
° О
СО ~,—,.
о
о
М'$
Э~
Ф
о
Р
Ф
с~
ООЛ .
4 л
° О
00 О
О& t  О
н~
О
О,
° СЧ р~
,.» О,
О
О
О О
над
° нн
'~ Ос~
~ОО
О
О
' О
'б О
- ° О -,"
"-'00 О ~
О
~Г~
Ф
м
о
и
о
о
~О
о
О
ОО О
нн н
° Ф Щ Ф
~ ~) с~р н
с~~ с~~ н 00
"О С~
н
СЯ
ОО О
,чН с4
~с 1
~1~ ~ СР с~.~
ОС~ОС~
Щ
00 "О С~
С'4
03
О
нд
00
ООФ
О
-О ~~
сб
О
СЯ
СЯ
М
О
н ср~
~ С~3
~ Ж СЯ
'~'Ос~
00
"О~
СЧ
О
СЯ
о
о
Йй
П
о
Ф
й
Ф
Ф
о
Ж
Ф
И
к
Ф
Ф ф
ф ~~
О
~ц» ~ Ф
~ж ~©
~о
ф
с.» с„
"ф
ц ~ И
И д
М ~ч ~Я~
~ ф
и
с.') Л
~»Ц Ф
~ч ~
" ф
Фъ О О
© Я~ Ж
с.» ~ ф ~~ с»
ж~ с» ~~~о
с»ФОЦО~О
с.» ~~ ф в ф о
И~ О~
сб
О
О
О
Ы д,
ф в
ФНф
о ф
с) Н~~
с.» ~ ~
ф с»~н
Ки11
с.» ~=~,р
ЛО
~ц»
~ц»
И
с.»
ф
~ч
О
с.»
~~о
ф
," 4
с.»
с» 1 О
с~ ~=~ ф
сб
И~о
1
Ф ц
Р~ Н
о
сб
ф д,
ф
ф й
Р~ д Й
Я „Ы
~& t
В с.» ф
ф ~ч
Л рр ~ю
д о
О
о ц»
Ф~И~~ч
Ымд ф
~~д, ф
фХ ~~о~
Я~~ Яп
о
ф л~~ С~
"о ~~~~ 11
й
О Ф ф ~ Ф
~~~оффв~д
© ф о ф э с,» ~ с~
~) ОлО

~СЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
Так, например, гравитационный потенциал Земли в точках с широтой 9
на расстоянии г от центра (см. рис. 4.1) равен
Г (г) = — (~Ю~/г) [1+1/а/ (Л„/г)' (1 — 3 я1п' 3) +
+'/,Ь'(Л,/г)'(3 я1п 0 — 5 я1п' О)+'/„Й, (Л,/г)'(3 — 30 я1п' О+ 35 я1п' 0) +...]
(1.11?
(Л,=6,37815 10' м — экваториальный ра
~'=1,623 10-', Й=6,0 10-', /с,=6,4 10-'—
четвертой зональных гармоник).
Значение потенциальной энергии Г„=
= Г (Л,) (см. (1. 10)) единичной массы на по-
верхности небесного тела (г=Л,) характе-
ризует энергетические затраты, необходи-
мые для выхода из сферы притяжения
данного тела. Эти же затраты можно
охарактеризовать минимальным значением
начальной скорости, потребным для выхо-
да из сферы притяжения (без дальней-
шего приложения сил, с нулевой скоростью
на бесконечности): и, = ~/2Я~/Л, — такна-
зываемая параболическая скорость. Эти
данные также приведены в табл. 1.2, 1.3.
Энергетические затраты на переходы
с одной гелиоцентрической орбиты на дру-
гую можно оценить с помощью рис. 1.3.
На нем представлена кривая полной энер-
гии точки единичной массы, движущейся
по круговой орбите радиуса г в централь-
ном гравитационном поле Солнца:
диус; ~Я=5,98 10" кг — масса;
коэффициенты второй, третьей и
-/2
Рис. 1.3. ~ровни потенциальной энергии.
Ю ='/,~~' — ЯЯ~' ' = — '/2ЯЯг '. (1.12)
(1.1 )
Корпускулярный поток Солнца оказывает на элементы космического аппа-
рата давление, соответственно (1.13), порядка
р~ — ру~' = 2 10 а (Л~/Л)' кГ/м' (1.15)
и подводит мощность порядка
5 ° 10 '(Л~/Л)2 вт/м2.
(1.16)
Там же отдельными точками ниже кривой на радиусах, соответствующих
орбитам планет, показана потенциальная энергия Г, собственного поля этих
планет на их поверхности.
2. Параметры окружающей среды. В межпланетном пространстве
плотность газовой среды в основном определяется корпускулярным излуче-
нием Солнца: потоком протонов (ионизованные атомы водорода) с энергией
порядка 1 кэв (скорость в=4,5 10' м/сек), интенсивность которого в период
спокойного Солнца составляет (см. [1.109])
Д 3 ° 10'' (Л~/Л)2 1/м2 ° сек, (1.13)
где Л вЂ” расстояние до Солнца, Л~=1,495 10" м — средний радиус орбиты
Земли.
Соответственно (1.13) плотность распределения протонов равна
р~ 10 'а (Л~/Л)2 кг/м'.

20
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
Следует отметить, что в период активного Солнца, по данным [1. 1091,
интенсивность корпускулярного излучения может возрасти на два-три по-
рядка.
Основной энергетический поток в межпланетном пространстве составляет
электромагнитное излучение Солнца, имеющее максимум в видимой области
о
светового излучения на длине волны -5500 А [1.110).
Спектр солнечного светового излучения непрерывный (рис. 1.4), боль-
шая часть его соответствует излучению черного тела при температуре
Рт Тя — 5800 'К. Мощность потока сол-
" м'пк нечного светового излучения состав-
ляет
ЯА 1400 (Л ~/Л)' вт/.м"". (1.17)
Пондеромоторное взаимодействие
между световым излучением и отра-
жающим (или поглощающим) свет
телом вызывает давление на тело.
Сила светового давления зависит от
мощности излучения и, по Максвел-
лу, при нормальном падении света
на тело равна
р~ — (Л~/с) (1 + в) = 0,464 )(
)& t; 1 ' (Л~/ )' 1+ в) кГ/
(1.18)
04 дб бф
где с — скорость света, я — коэффи-
циент отражения тела (для абсолютно
черного тела я =О, для идеального зер-
кала, в=1). На орбите Земли макси-
(при я =1) составляет р — 0,928 ~
Рис. 1.4. Распределение интенсивности светового
излучения Солнца на орбите Земли (сплошная
кривая) и черного тела при 5800 'К (пунктирная
кривая).
мальное давление солнечного света
>(1 -' кГ м' [1 11
При полете вблизи небесных тел существенными являются также энер-
гетические потоки от собственного теплового излучения тела (см. значения
температуры поверхности небесных тел Т, в табл. 1.2) и отраженный от по-
верхности тела поток солнечного излучения. Последний определяется зна-
чением альбедо поверхности небесного тела А — отношением отраженного
светового потока к исходному (см. также табл. 1.2).
По сравнению со всеми перечисленными основными энергетическими по-
токами в межпланетном пространстве тепловое излучение космоса, соответ-
ствующее температурному уровню Т„=4 'К, пренебрежимо мало:
9~„ж1,5 ° 10 5 вт/м2.
(1.19)
Баланс суммарного воздействия всех отмеченных энергетических пото-
ков и внутренней энергии (рассеиваемой телом) определяет тепловой режим
тела в космическом полете. Например, максимальная эффективная темпера-
тура Т, абсолютно черной и теплопроводной сферы, движущейся вблизи
поверхности небесного тела и не имеющей внутренних источников энергии,
может быть оценена соотношением
1/
Т = ~~(1+А) Т~~+ — 'Т~
(1.20)
где из — „'угол, под которым видно Солнце, и, — угол, под которым видно
небесное тело.

УСЛОВИЯ КОСМИЧЕСКОГО ПОЛЕТА
Д~ = 10 "ш ""' м ' ° сек 1,
(1. 21)
где в приведено в граммах, В' — интенсивность полного потока метеоров
с массой, большей т.
Что касается воздействия метеорных частиц на преграду, то существуют
различные воззрения, связывающие толщину пробиваемого материала
с импульсом тг либо энергией — тг' метеорной частицы ([1.112 — 1.121]
2
Наряду с энергетическими потоками, существенными для проблем ме-
ханики космического полета являются радиационные потоки в космосе,
представляющие биологическую опасность и требующие определенных
затрат массы на защиту. Помимо указанного выше корпускулярного излу-
чения Солнца, существенными являются космические лучи, образованные
ядрами атомов, с энергиями до — 10" ьв; удельная мощность потока кос-
мических лучей — 7 10 ' втlм', интенсивность -6 10' -м' сек-'.
Магнитное поле у небесного тела приводит к образованию специфиче-
ских магнитных «ловушек», существенно усиливающих радиационные по-
токи. Например, у Земли такие «ловушки» образуются магнитным полем от-
носительно небольшой интенсивности,
которое оказывает малое силовое
воздействие непосредственно на летя-
щий космический аппарат. Так, на гео-
магнитном экваторе горизонтальная
составляющая магнитного поля Земли
достигает -3,1 10 ' вбlм', на геомаг-
нитных полюсах вертикальная состав- ф щ' Рl Р ~и
дюжая
ляющая равна -6,3 10-' вбlм'. Однако
зто поле является причиной образова-
ния у Земли радиационных поясов с
высокой интенсивностью заряженных
частиц (рис. 1.5), представляющих зна-
чительную биологическую опасность
[1.75 ]. 1РО
3. Метеорные потоки. Движущие-
ся в солнечной системе метео рные
/О
потоки могут потребовать существен- рис. 1.5. Радиационные пояса земли — ~ри-
ных затрат массы на защиту от них эле- вые постоянной интенсивности зарегистри-
рованных частиц.
ментов космического аппарата, а ха-
рактер распределения интенсивности
метеорных потоков в солнечной системе может оказать влияние на выбор
целесообразных траекторий полета.
В настоящее время метеорные потоки изучены в окрестности Земли ме-
тодами фотоизмерений, радиоэхоизмерений и непосредственными измерени-
ями на спутниках ([1.112, 1.113] и др.). Измеренный интервал скоростей ме-
теоров составляет от — 11 до 72 км/сек. Нижний предел равен скорости вы-
хода из сферы притяжения Земли; это скорость, которой обладает метеорная
частица, приблизившаяся к поверхности Земли из состояния покоя отно-
сительно Земли. Верхний предел равен максимальной скорости относительно
Земли, которой может обладать метеорная частица, двигавшаяся по замкну-
той орбите вокруг Солнца. Средняя скорость метеорных частиц вблизи Земли,
по оценке [1.114], изменяется в пределах от -15 до 28 км/сек, возрастая
с увеличением массы частицы т (рис. 1.6).
Интенсивность метеорного потока Й' существенно зависит от массы ча-
стиц и, по данным [1.112 — 1.114], вблизи Земли может быть представлена за-
висимостью

22
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
и др.). Однако конечные результаты расчетов по указанным методам, увя-
занные с лабораторными исследованиями процесса столкновения быстрых
частиц с мишенями, дают достаточно совпадающие результаты по величине
потребной толщины защитной стенки О в зависимости от допустимой интен-
сивности пробоев Й'(О). Пример зависимости Й'(О) для стальной защитной
стенки приведен на рис. 1.7, где кривая 1 соответствует о[то), кривая 2
1
соотвехаувуех Ь вЂ” тр').
Следует отметить, что приведенные на рис. 1.7 зависимости получены на
основе соотношения (1.21) для полетов вблизи Земли, где аппарат огражден
l т,г
Рис. 1.6. Скорость метсорных частиц.
Рис. 1.7. Интенсивность метеорпых проооев
стальпой стенки.
(О'ЯТ)" ехр ( — Й'ЯТ)
рг) =
[1. 22)
где ~ — вероятность пробоя стенки площадью Я за время Т метеорными
частицами и раз. Например, при Й'ЯТ=1 вероятность одно-четырехкратного
пробоя метеорами стенки составит
0
0,3679
1
0,3679
3
0,0613
4
0,0153
2
0,1840
(4
0,9964
Соотношение (1. 22) и данные типа приведенных на рис. 1.7 позволяют
оценить потребную массу защиты космического аппарата от метеорной опас-
ности с заданной надежностью.
$ 4. Внешнее сопротивление космического аппарата
и его двигательной установки при полете в атмосфере
Для обобщенного космического перелета с поверхности планеты старта
через космическое пространство к поверхности планеты назначения харак-
терно существенное изменение вдоль траектории полета плотности, давления
и температуры внешней среды — параметров, определяющих вектор дей-
ствующих на аппарат внешних сил Г (см. (1. 1)); и возможности пополнения
массы рабочего тела забором из внешней среды. Особенно существенное зна-
от метеоров с одной стороны Землей. Поэтому мох~но ожидать, что на рас-
стоянии от Земли порядка нескольких ее радиусов приведенная интенсив-
ность пробоев Й'(8) возрастает примерно вдвое.
Для определения ожидаемой метеорной опасности можно принять [1.114],
что пробой стенки метеорными частицами будет подчиняться распределению
Пуассона:

АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
чение для механики полета эти параметры имеют в непосредственной бли-
зости к поверхности планеты, в ее атмосфере. Величины плотности и давления
в атмосферах планет резко падают с высотой. На рис. 1.8 [1.122~ приведено
распределение плотности ~, давления в„и температуры Т„по высоте Й в ат-
мосфере Земли; там же нанесены определяемые высотой значения скорости
звука д и кинематической вязкости ~.
~лЗ ~р .Д„г
/О ' ~, юг/м~
Я~0 Т,'6
500 а, м/се~
/ и, м "/се~
д-/
ц-5
Иб
ЗОО
10
Рис. 1.8. Параметры атмосферы Земли.
На этапе движения космического аппарата в атмосфере планет аэро-
динамическое сопротивление может оказывать существенное влияние на ме-
ханику полета. Типичными компоновочными формами космических двига-
тельных систем являются тела вращения без протока и с протоком. Рассмот-
рим основные закономерности аэродинамического сопротивления тел такой
формы. Аэродинамическое сопротивление тела Р (см. ниже (2. 2)) характе-
ризуется коэффициентом сопротивления
3
(1.2 )
(1.24)
с =с
х хс хр
где ри'/2 — скоростной напор набегающего внешнего потока, Я' — харак-
терная площадь, например площадь миделевого сечения тела. Для заданной
геометрии тела величина коэффициента аэродинамического сопротивления
с в основном зависит от двух безразмерных параметров [1.123~: числа Маха
полета Яо=и/а и числа Рейнольдса К~э=иЬ/~ (Ь вЂ” характерный линейный
размер, например длина тела, ~ — кинематическая вязкость в потоке на-
бегающего воздуха) или соответственно от скорости г и высоты полета Й,
так как скорость звука д= ~/х~„/э и кинематическая вязкость ~ =/'(Т) опре-
деляются высотой полета (см. рис. 1.8). В качестве иллюстрации на рис. 1.9
приведен пример изменения коэффициента аэродинамического сопротивле-
ния с от скорости и высоты полета для типичной компоновки ракетного ап-
парата [1.124 ~.
Величина коэффициента аэродинамического сопротивления опреде-
ляется двумя слагаемыми: суммой коэффициентов сил трения и давления внепт-
него потока на тело:

24
ОСНОВНЫЕ 11АРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
П ри дозвуковых скоростях движения ([~[ ( 1) основную часть сопротив-
ления тел обтекаемой формы определяют силы трения (см. нижнюю пунктир-
ную кривую на рис. 1.9). Величина сопротивления трения может быть оце-
нена по коэффициенту трения для плоской плШстины (Я вЂ” площадь поверх-
ности):
(1. 5)
Ф.В
которыи для турбулентного пограничного слоя на теплоизолированной по-
верхности определяется следующей формулой [1.123 — 1.133]:
0,0905
с~ ——
(1д 0,0355 Йе)' '
с~ —— ср (1+ 0,144Д„-')-' "
(1. )
Первый множитель этой формулы учитывает зависимость коэффициента
О
Рис. 1.9. Зависимость коэф-
фициента аэродинамического
сопротивления от скорости и
высоты полета для типичной
компоновки ракетного аппарата;
нижняя пунктирная кривая—
сопротивление трения при 6=0.
трения от числа Рейнольдса при Я,=О (рис. 1.10, а) [1.126], второй множи-
тель формулы (1.26) учитывает влияние числа Маха (рис. 1.10, б) [1.133].
Следует отметить, что формула (1.26) определяет значения коэффициента
трения, отнесенные к «смоченной» поверхности Я. Коэффициент трения с
Ф.Ф
у~ Ф'
отнесенныи к площади миделевого сечения тела Я, определяется соотноше-
нием
с, = с~Я/Я
(1. 7)
При сверхзвуковых скоростях движения (рис. 1.9) коэффициент сопро-
тивления резко растет и большую часть сопротивления обусловливают силы
давления, связанные с волновым обтеканием тела (см., например, [1.128;
1.134 — 1.137] и др.). Определение при сверхзвуковых скоростях движения
величин коэффициента волнового сопротивления с обтекаемых тел
хр
вращения возможно на основе общей теории сверхзвуковых течений [1.128;
1.133 — 1.151]. При больших скоростях в связи с особенностью гипер-
звукового обтекания тонких тел (наблюдаются лишь поперечные смеще-
ния частиц газа, аналогичные случаю расширения поршня) для анализа
изменения с„удобно использовать хорошо изученные автомодельные дви-
жения газа, вытесняемого поршнем [1.123, 1.133, 1.152 — 166] и др.). По за-
кону плоских сечений [1.161] задача об обтекании тонких тел потоком газа

АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
$4]
ПРЯМ
,МФд
фЮР
дйИ~ ~
Ю ~5 ГГ5Л 4 5б' 8 Ю (5 3 153
С,
иаЫ
ЮРЫР
Ю 8 йв
~ю' у гг~з ~ хю в~в' р гг,юз ~ в оке
а)
с,
с,,
отца
Рис. 1.11. Закон плоских сечений: в пло-
скости А — движение газа, как при вы-
теснении эквивалентным поршнем; 1—
поршень, 2 — ударная волна.
Рис. 1.12. Коэффициент волнового сопротивления
при Э=5', 10' и 15'.
1(б
124
Рйс. 1.13. Коэффициент волнового сопротивления тел вращения степенной формы (объем ~ и коэффи-
циент сопротивления с~~ отнесены к соответствующим значениям для тела конической формы (т=1~
с таким же удлинением).
Рис. 1.10. а) Зависимость коэффициента турбулентного трения плоской пластины от числа Рейнольдса
при М,=О; сплошные кривые соответствуют первому члену формулы (1.26), точки — эксперимент',
~) влияние числа Маха на коэффициент трения; сплошная кривая соответствует второму члену фор-
мулы (1.26).

ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
с большой сверхзвуковой скоростью (рис. 1.11, а) эквивалентна задаче
о плоском неустановившемся движении газа, вытесняемого подвижным порш-
нем, расширяющимся по соответствующему закону (рис. 1.11, б).
В качестве примера приложения указанных принципов на рис. 1.12
приведены результаты расчета изменения коэффициента волнового сопротив-
ления с тел конической формы в зависимости от угла наклона поверхности
конуса д и числа Маха[1.160, 1.162]; для сопоставления на рис. 1.12, помимо
решения по расширяющемуся поршню, приведены результаты точного рас-
чета для конических течений. Данные рис. 1.12 показывают характер влия-
ния скорости движения
(числа Маха) и удлинения
Я/~ носовой части А =Л lг,=
= с$д ~] на величину ло-
7 бового сопротивления.
Исследования автомо-
дельных движений газа с
ударными волнами, рас-
0 г б ширяющимися по степен-
ному закону г=с~'" [1.163—
г 1.165], позволили опреде-
лить для больших чисел Ц,
д,Г влияние на с„перехода от
конической формы тела к
степенной форме г=сх"' с
ббльшим объемом и (рис.
сс'
1.13). Данные рис. 1.13
показывают, что при за-
данном удлинении носовой
части тела степенной фор-
мы минимум волнового
сопротивления имеет место
при показателе степени
т=0,70; волновое сопро-
тивление тела такой фор-
мы примерно на 25% меньше, чем у конуса, при объеме, большем на — 25%.
Отметим, что для тел степенной формы вследствие затупления носовой части
(увеличивающегося для т ( 1; при т —: 0,5 — случай цилиндрического силь-
ного взрыва) с увеличением относительного затупления следует учитывать
возрастающее влияние на параметры оотекания слоя потока с повышенной
энтропией у поверхности тела [1.166 ]. Однако, по данным работы [1.166 ], в рас-
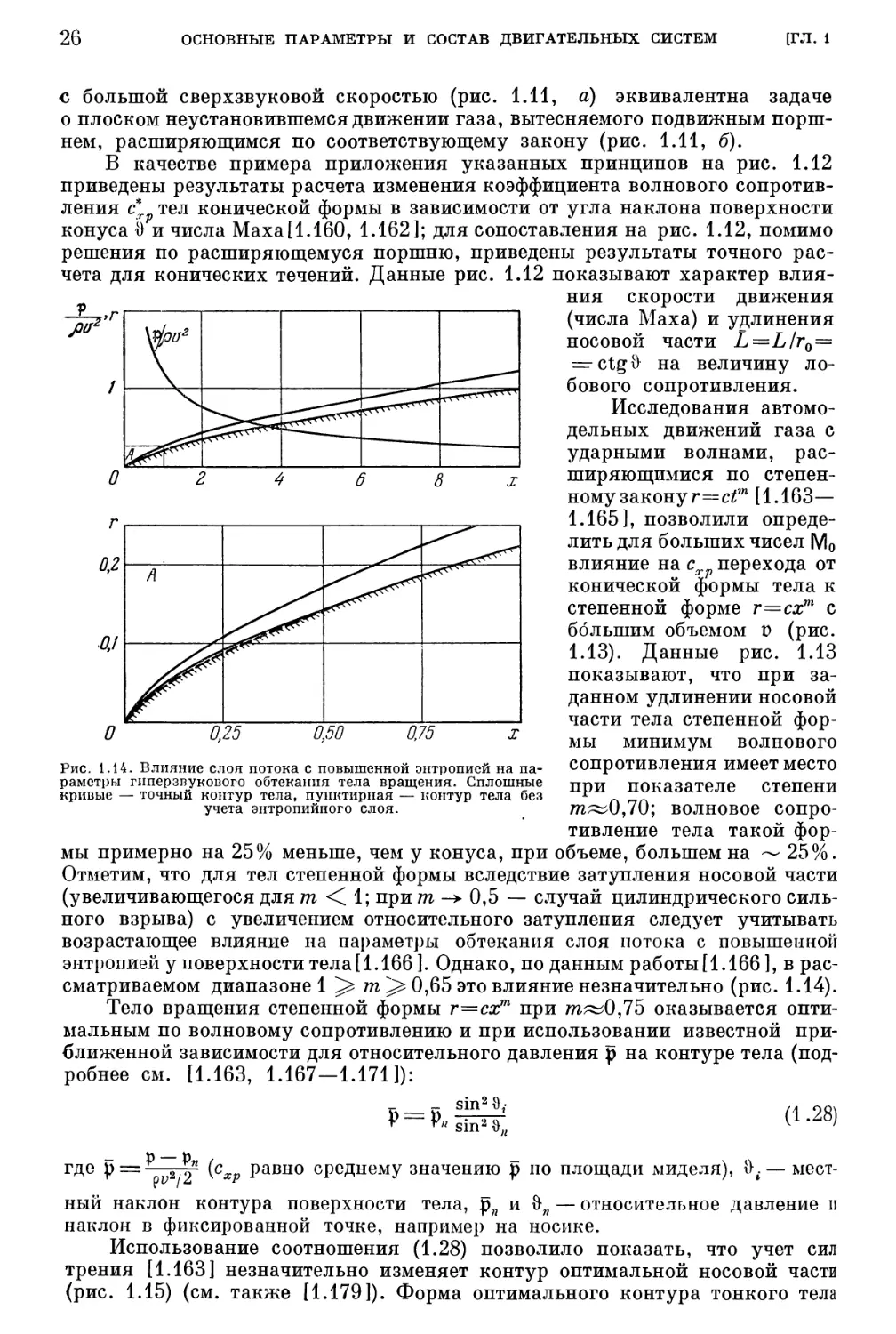
сматриваемом диапазоне 1 ) т ) 0,65 это влияние незначительно (рис. 1.14).
Тело вращения степенной формы г=сх™ при т=0,75 оказывается опти-
мальным по волновому сопротивлению и при использовании известной при-
ближенной зависимости для относительного давления й на контуре тела (под-
робнее см. [1.163, 1.167 — 1.171]):
ьГ
ц75
Рис. 1.14. Влияние слоя потока с повышенной энтропией на па-
раметры гиперзвукового обтекания тела вращения. Сплошные
кривые — точный контур тела, пунктирная — контур тела без
учета энтропийного слоя.
Я1Я2 ~ °
р" я1п'д„
(1.28)
где р =,, (с равно среднему значению П по площади ыиделя), д. — мест-
Р— Ря
хр Ф
ный наклон контура поверхности тела, й„ и 9„ — относительное давление и
наклон в фиксированной точке, например на носике.
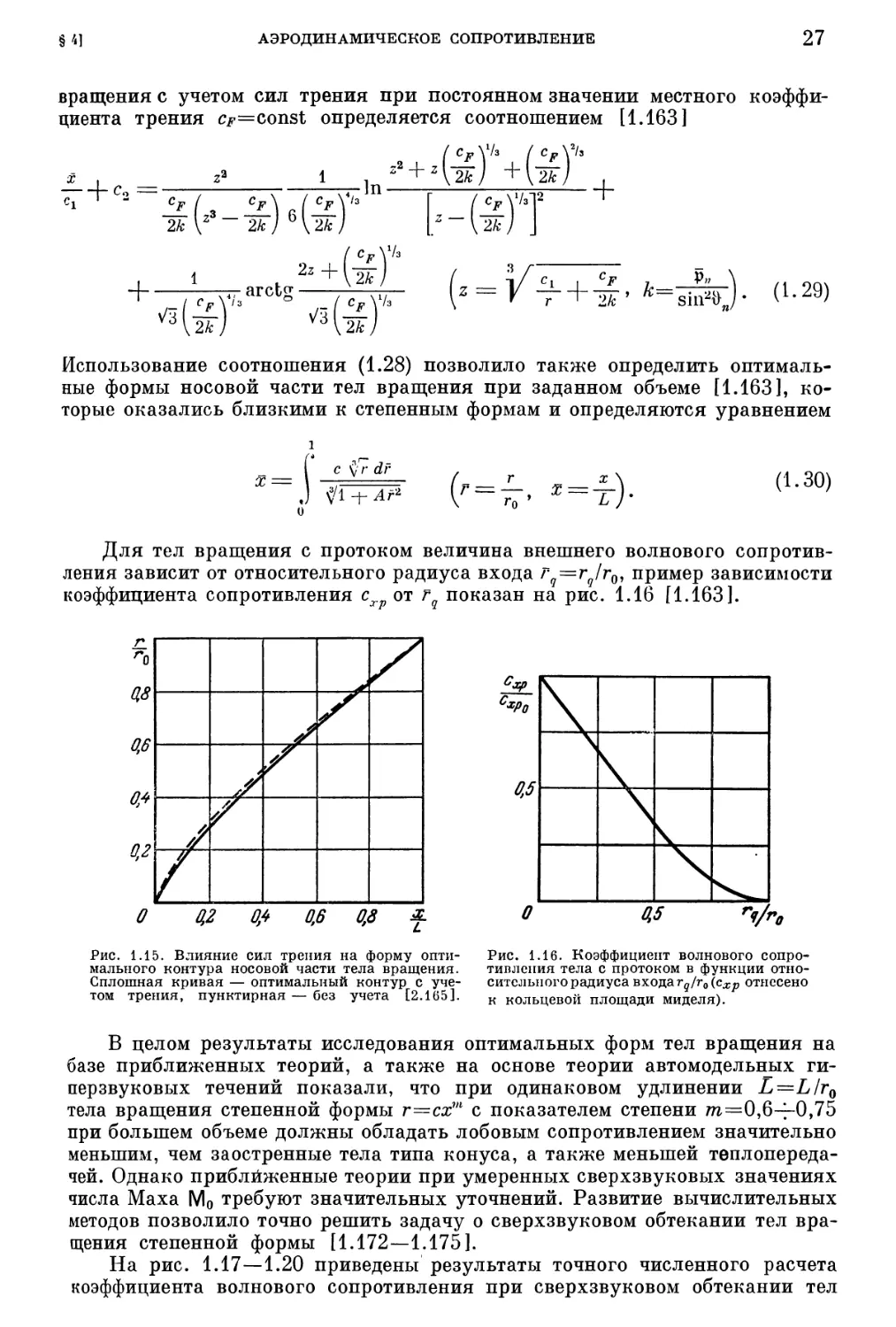
Использование соотношения (1.28) позволило показать, что учет сил
трения [1.163] незначительно изменяет контур оптимальной носовой части
(рис. 1.15) (см. также [1.179]). Форма оптимального контура тонкого тель

АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
вращения с учетом сил трения при постоянном значении местного коэффи-
циента трения с~ —— сопзс определяется соотношением [1.163)
Ср ~з Ср Ь
2й 2й
д2+ 7. +
1
1п
с~ /з
2й
с, ср Р»
— '+ —,,„, Й= ~„;1~ . (1. 29)
1
~ь
С~ /з
~3—
2Й
Использование соотношения (1.28) позволило также определить оптималь-
ные формы носовой части тел вращения при заданном объеме [1.163~, ко-
торые оказались близкими к степенным формам и определяются уравнением
с ~г Иг
(1. 0)
~~1 -~- Аг2
О
Для тел вращения с протоком величина внешнего волнового сопротив-
ления зависит от относительного радиуса входа г,=г,!г„пример зависимости
коэффициента сопротивления с, от г, показан на рис. 1.16 [1.163~.
ЮЕ Р8
Рис. 1.16. Коэффициент волнового сопро-
тивления тела с протоком в функции Отно-
ситсль_#_ ого радиуса входа тд(~, (с~р отнесено
к кольцевой площади миделя).
Рис. 1.15. Влияние сил трения на форму опти-
мального контура носовой части тела вращения.
Сплошная кривая — оптимальный контур с уче-
том трения, пунктирная — без учета [2.1651.
В целом результаты исследования оптимальных форм тел вращения на
базе приближенных теорий, а также на основе теории автомодельных ги-
перзвуковых течений показали, что при одинаковом удлинении А=А!г
тела вращения степенной формы г=сх'" с показателем степени т=0,6 — '0,75
при большем объеме должны обладать лобовым сопротивлением значительно
меньшим, чем заостренные тела типа конуса, а также меньшей твплопереда-
чей. Однако приближенные теории при умеренных сверхзвуковых значениях
числа Маха Я, требуют значительных уточнений. Развитие вычислительных
методов позволило точно решить задачу о сверхзвуковом обтекании тел вра-
щения степенной формы [1.172 — 1.175 ~.
На рис. 1.17 — 1.20 приведены результаты точного численного расчета
коэффициента волнового сопротивления при сверхзвуковом обтекании тел

28
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 1
вращения степенной формы г=сх с показателями степени т=0,65; 0,70
и 0,75.
На рис. 1.17 — 1.19 сплошные кривые рассчитаны по методу характе-
ристик и явной конечноразностной схеме типа Лакса — Вендрова [1.173,
1.174 ], пунктирные кривые — по неявной схеме [1.172 ], штрих-пунктирные—
по автомодельному гиперзвуковому решению [1.163 — 1.165]. При построе-
нии графиков рис. 1.20 использованы результаты работы [1.172]. Результаты
точных расчетов параметров сверхзвукового обтекания тел вращения степен-
ной формы по указанным методам практически совпадают. Течение около
степенных тел имеет сложный характер, с большими градиентами параметров
(особенно плотности и температуры вблизи поверхности тела при больших
Рис. 1.17. Коэффициент волнового сопротивления при т=0,65.
удлинениях), связанными с наличием тонкого вихревого слоя. Эти особен-
ности специально учитывались при проведении численных расчетов.
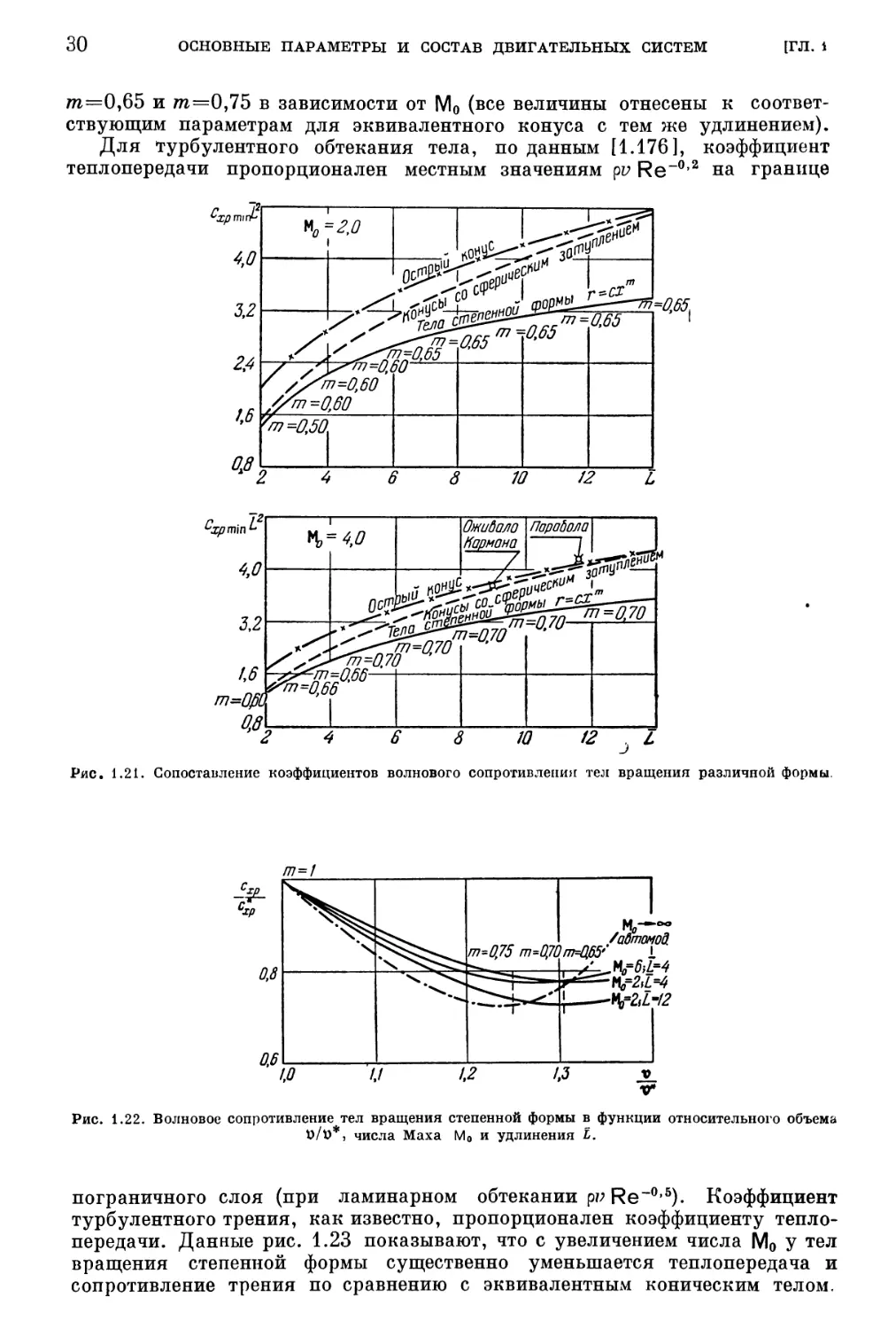
Анализ данных рис. 1.17 — 1.20 показывает, что для больших чисел Маха
Я и больших удлинений Е минимум волнового сопротивления имеет степен-
ное тело с показателем степени т=0,70; для умеренных и малых сверх-
звуковых скоростей у оптимального тела степенной формы т=0,6 — '0,65.
Конус и затупленный конус, а также параболический контур г=1 — (1 — х)2
и головка Кармана г = ](2/~) ] агсяп ~я — (1 — 2х) ~х(1 — х)]] ~' имеют боль-
шее волновое сопрот вление, чем рассмотренные степенные тела при всех
значениях М, и Е (рис. 1.21).
На рис. 1.22 приведено рассчитанное изменение волнового сопротивле-
ния тел вращения степенной формы в зависимости от относительного объема
пlп*, где объем тела и и коэффициент волнового сопротивления с „отнесены
к соответствующим значениям ~* и с* для конического тела того же удлине-
ния. Видно, что зависимость, определенная для гиперзвукового автомодель-
ного режима обтекания, хорошо выполняется и для умеренных сверхзвуко-
вых скоростей набегающего потока.
Для оптимальных по аэродинамическому сопротивлению тел вращения
степенной формы по сравнению с конусами и другими заостренными фор-
мами (параболическое оживало и др.) из-за влияния энтропийного слоя
имеет место благоприятное по теплопередаче и сопротивлению трения рас-
пределение поля плотностей ~, температур Т и скоростей г по контуру тела
[1.163, 1.170, 1.171]. На основе проведенных точных расчетов на рис. 1.23
приведены распределения относительных значений плотности р/р*, скорости
иЪ* и соотношения (рЫр*и*)Я~ЯВ*)-О ' по контуру тела при 1=6,0 и

А:) РОДИ НАМИЧЕ СКОЕ С ОПРОТИВЛЕ Н И Е
Рис. 1.18. Коэффициент волнового сопротивления при т=0,70.
Рис. 1.19. Коэффициент волнового сопротивления при т=0,75.
с
М =4
М =
0
Рис. 1.20. Коэффициент волнового сопротивления при больших удлинениях, ~ ~ 15.

30
ОСНОВНЫЕ ПАРАМЕТРЫ И СОСТАВ ДВИГАТЕЛЬНЫХ СИСТЕМ
т=0,65 и т=0,75 в зависимости от Д, (все величины отнесены к соответ-
ствующим параметрам для эквивалентного конуса с тем же удлинением).
Для турбулентного обтекания тела, по данным И.176], коэффициент
теплопередачи пропорционален местным значениям ~г Яе-О' на границе
~~р и»
=Оба
б 8
Рис. 1.21. Сопоставление коэффициентов волнового сопротивления тел вращения различной формы.
с~
с~
дб
lд
Рис. 1.22. Волновое сопротивление тел вращения степенной формы в функции относительного объема
Ы~, числа Маха М, и удлинения ~.
пограничного слоя (при ламинарном обтекании рг Ке-О ~). Коэффициент
турбулентного трения, как известно, пропорционален коэффициенту тепло-
передачи. Данные рис. 1.23 показывают, что с увеличением числа Я у тел
вращения степенной формы существенно уменьшается теплопередача и
сопротивление трения по сравнению с эквивалентным коническим телом,

АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
$ 4]
ЦФ
ру /6
09
/б
Яд
07
Об
Об
0,5
0Г 04 0,б 0,б х~1.
02 04 0,б 0,В х~~
4ф
р"ы йе
б,б
ОГ 0,4 0,б 0д 1~Е
ОГ 04 0,б 0,б х~1
Рис. 1.23. Распределение по контуру тел степенной формы относительных значений плотности р/р*,
скорости ю/ю* и параметра, определяющего коэффициент теплопередачи тела при турбулентном обтекании,
с телами других известных форм) минимальное лобовое сопротивление
(на 25О~~ меньше, чем у эквивалентного острого конуса) и малую теплопере-
дачу, что хорошо согласуется с данными параметрических экспериментов
(1.170, 1.171, 1.177, 1.178].
Аналогичное уменьшение теплопередачи, как известно, имеет место при
переходе от острого к затупленному конусу с тем же удлинением. Однако
затупленный конус при этом имеет значительно большее волновое сопро-
тивление (рис. 1.21).
Основной результат точных расчетов И.172 — 1.175, 1.179]: при сверх-
звуковом обтекании тела вращения степенной формы имеют (по сравнению

ГЛА8А 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ЭЛЕМЕНТОВ
КОСМИЧЕСКИХ ДВИГАТЕЛЬНЫХ СИСТЕМ
я 1. Реактивные движители
1. Реактивная тяга и внешнее сопротивление. Реактивный движитель
является завершающим элементом двигательной системы, в котором полез-
ная часть выработанной источником энергии, превращаясь в кинетическую
энергию направленного движения реактивной струи, создает реактивную
тягу Р. Сумма реактивной тяги и силы сопротивления среды равна интегралу
по,'замкнутому контуру (например, по контуру аппарата) от составляющих
давления р, напряжения трения ~' и изменения количества движения:
Р+К,=-ф((',.сов(Г,, х(Шд,.+[раоя(п, х(+ ~я!п(п, х((ШЯ[, (2.Ц
где и — направление нормали к контуру, тяга направлена по оси х. При по-
лете в атмосфере условились (см., например, [2. 1]) в качестве силы внешнего
сопротивления Р принимать интеграл напряжения трения и давления,
избыточного над атмосферным р„, по внешнему контуру аппарата АА1В1В
вне реактивных струй и расхода д„, забираемого из внешнего потока (рис. 2.1,
а и б):
г", = [(р — в„) соя (и, х) + ~~ я1п (и, х)~ ИЯ.
(2. 2)
Тогда по определению (2 1), (2.~2), с учетом отсутствия расхода (д,.=О) по
контуру аппарата АВ, реактивная тяга при полете в атмосфере равна (см.,
например, [2. 2~ и др.)
Р= [['. соя(['., х) Ид +(р — р„) соя(п, х) ИЯ]=дГ,+(р — р„) ~, — д г,
(2. )
где р„Г, — средние давление и скорость в сечении реактивной струи по ВА,
~, — площадь сечения реактивной струи.
Такое общепринятое разделение силы, действующей на реактивной ап-
парат, на тягу и сопротивление, естественно, является условным. Так, на-
пример, сила донного давления на участках аА и ОВ (рис. 2.1) аппарата, во
многом определяемая реактивными струями ([2. 3] и др.), т. е. тягой, при
указанном разделении относится к силе сопротивления. Однако принятое
разделение между тягой и сопротивлением имеет определенный физический
смысл, четко переходит в предельные случаи (отсутствие сопротивления или
тяги), а некоторая возможная корреляция между ними должна быть учтена
при детальных анализах.

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
При полете В космосе, где сопротивление среды практически отсутствует
(Р=О), выражение для реактивной тяги упрощается; при ~„=0 и д,=О
Р„= д Г, -]- р,Я,. (2. 4)
Рис. 2.1. Схемы реактивных аппаратов: а) без воздухо-
заборника; б) с воздухозабор ником.
Рис. 2.2. Классическая схема
течения в сверхзвуковом сопле.
газа ~ „„„естественно, равна средней скорости теплового движения мо-
лекул покоящегося газа; для совершенного газа значение ~ „. „опреде-
ляется известным газодинамическим соотношением
( .5)
рде к — показатель адиабаты, равный для одно-, двух- и многоатомных га-
зов соответственно 1,66, 1,40 и 1,33, Я вЂ” газовая постоянная. Эта максималь-
ная скорость значительно (в (~+1)'~(х — 1) '~ раз) больше критической ско-
рости звука в газе а„=(ЯТ, 2к/(к+1)]'~; поэтому для достижения больших
скоростей истечения реактивные сопла должны быть сверхзвуковыми. Клас-
сическая схема сверхзвукового осесимметричного сопла представлена на
рис. 2. 2.
В соответствии с газодинамической теорией одномерных газовых тече-
ний ([2. 5, 2. 7] и др.) относительная скорость газа >,=Г,/а на ср зе идеа
ного сверхзвукового сопла без потерь и с равномерным осевым потоком оп-
ределяется отношением площади критического сечения сопла Я „(узкое се-
чение, где скорость газа равна критической скорости звука д„) к площади
среза сопла Я,:
( )
Показано, что для газового потока с расходом д полный импульс равен
( .7)
3 Механика полета
2. Реактивные сопла. В тепловых реактивных двигателях движителем,
создающим тягу, является реактивное сопло, превращающее тепловую энер-
гию газа в кинетическую энергию направленной газовой струи. Физические
принципы работы реактивного сопла как движителя могут быть в основном
пояснены на основе газодинамической теории ((2. 2 — 2.16] и др.).
Мерой тепловой энергии газа является так называемая температура
торможения Т, — температура газа при отсутствии направленной скорости
течения, К,.=О. Максимально возможная скорость направленного движения

~ГЛ. 2
Физические пРинципы двиГАтельных систем
где з (~)=~+1/~. По уравнению расхода для одномерных газовых течений
величина расхода газа через идеальное реактивное сопло составит
(2. )
где
ро — полное давление заторможенного газа на входе в сопло.
Поэтому в соответствии с уравнениями (2. 7), (2. 8) величина реактивной
тяги, создаваемой идеальным соплом при полете в космосе, которая совпа-
дает с величиной полного импульса газового потока ~ на срезе сопла (ср. (2. 4)
и (2.7)), будет равна
Отметим, что тяга (2. 9), создаваемая реактивным соплом при полете в ва-
кууме, не зависит от температуры газа Т и определяется только полным дав-
лением газа ро, площадью критического сечения ~Г„и степенью расширения
сопла ~Г,/~Г„(определяющей ~, и з (~,)). С увеличением степени расширения
идеального сопла при фиксированных в и ~Г„создаваемая им реактивная тя-
га В Вакууме непрерывно растет, достигая теоретически максимума при
~Г,/~Г„~ со, когда скорость истечения газов из сопла становится максимально
возможнои:
(2. 10)
(2. 11)
Последнее соотношение показывает, что для фиксированных в, и ~
максимальная тяга, развиваемая реактивным соплом при полете в вакууме,
также фиксирована. Температура газа на входе в сопло Т, при фиксирован-
ных р и ~Г„определяет расход газа через сопло (см. (2. 8)); с увеличением тем-
пературы газа Т при постоянной тяге уменьшается расход газа д и соответ-
ственно увеличивается удельный импульс двигательной системы.
при ~,= ~~,„, ),„,„=(к+1) (г+1)
я реальных соплах за счет потерь на трение газового потока о стенки
чрезмерное расширение сопла нецелесообразно, так как при больших сте-
пенях расширения дополнительные потери на трение при дальнейшем рас-
ширении (и соответственно увеличении площади поверхности) превалируют
над приростом тяги от расширения сопла. Аналогично влияет и учет инер-
циальных сил при ускорении аппарата. Учет потерь на трение газа в сопле
определяет рациональную степень расширения реактивного сопла (и соот-
ветственно ~, „,), при которой реализуется тяга до — 98% Р„.,„,. (см., напри-
мер, [2. 8 — 2. 12! и др.). Газодинамические принципы и вариационные про-
блемы построения оптимальных контуров сверхзвуковых реактивных сопел
рассмотрены в работах [2.16 — 2.30] и др. С учетом указанных потерь им-
пульса Т, в реальных соплах максимальная тяга, развиваемая соплом при
полете в вакууме, определится соотношением

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
Для нахождения величины реактивной тяги, создаваемой соплом при
полете в атмосфере (для простоты рассматривается случай д,=0), необходимо
из определенного значения тяги в вакууме (2. 11) вычесть член, учитывающий
влияние атмосферного давления р„(см. (2. 3)); тогда
(2. 12)
роч Рс)
Подчеркнем, что тяга, развиваемая реактивным соплом при фиксирован-
ных значениях р, Я и »,„ возрастает с увеличением высоты полета при-
мерно на — 10 — 30%, достигая максималь-
ного значения Р, в космосе.
гД,)
Зависимость газодинамических функ- ~~~')
ций г(л,) и д(л,) от Х, приведена на рис.
2,3. Эти функции изменяются по», так,
что для фиксированных значений р„р„, ф
реактивная тяга Р достигает максимума при
такой степени расширения сопла с~,/Я „и
таком соответствующем значении скорости
истечения Г, (),,) = У (),,), при которых
статическое давление в струе на срезе
сопла р, равно атмосферному давлению:
при р,=р„
Рис. 2.3. Газодинамические функции
Слс) и я (лс).
(2. 13)
Это так называемый расчетный режим работы сопла. Для фиксированного
сопла (~ „/~~,=сопз1) при изменяющихся перепадах давления р,/р„(напри-
мер, р,= сопя~, р„изменяется с высотой) только на расчетном режиме при
р„= р, реактивное сопло обеспечивает максимально возможную тягу Р/Р„,„=1.
На реялп|ах ниже расчетного (р,/р„(р,/р,) и выше расчетного (р,/р„) р„/р,)
тяга, создаваемая соплом, будет меньше максимально возможной (Р/Р„,„. 1),
реализуемой в случае, если бы на этих режимах применялось сопла с рас-
четным расширением.
По соотношениям (2. 12), (2. 13) на рис. 2.4, а приведен пример изменения
относительной тяги
х+ 1
~~~р~с
(» ~-1)*-~
род (». )
(2. 14)
Рд шах
в зависимости от перепада давления ро/р„для сопла с»,=1,89 и Т,, 0,99
[2.24]. Следует отметить, что показанные на рис. 2.4 значительные рассчи-
танные потери тяги на режимах ниже и выше расчетного не связаны с течением
внутри сопла, где течение и распределение давления (рис. 2.4, б) неизменны.
Указанные потери тяги физически связаны с волновыми потерями в системе
газодинамических скачков уплотнения, образующихся в струе за соплом
на нерасчетных режимах истечения (см. рис. 2.5 (2. 31]).
При реальных течениях газа неизменность сверхзвукового потока внутри
реактивного сопла классической схемы, с учетом которой определяется от-
носительная тяга по формуле (2.14) (см. рис. 2.4), имеет место во всем диапа-
~ф

[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
зоне режима выше расчетного и в значительном диапазоне режима ниже
расчетного вблизи расчетного значения перепада давления на сопле. С умень-
шением перепада давления на сопле р,ф„на режиме ниже расчетного воз-
растает перепад давления р„/р, в газодинамическом скачке уплотнения на
Р
'р
О
Ф
Рис. 2.4. Относительная тяга (а) и распределение давления (б) для сопла с ~с — — 1,89.
срезе сопла (так как отношение давлений р,/р,=сопз$); после достижения
критического значения ф„ф„)„интенсивный скачок уплотнения вызывает
отрыв пограничного слоя на стенках сопла и изменение картины течения
„'л
Рис. 2.5. Картина течения за соплом на режиме выше расчетного: а) снимок'.с.оптической решеткой;
б) то же без потока
внутри сопла (см. схемы течения на рис. 2.6 ~2. 32]). Приведенные на
рис. 2.7 по данным [2.32, 2.33] значения критического перепада давле-
ния в скачке уплотнения (р„/р,)„иллюстрируют для сопла классической
схемы ширину безотрывного диапазона перепадов давления на сопле на
режиме ниже расчетного, где сохраняется неизменным сверхзвуковое тече-
ние,'',внутри сопла и где справедливо определение потерь тяги по фор-
муле (2. 14).

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
После наступления отрыва потока в сопле давление на стенках сопла
в зоне отрыва повышается (по сравнению с расчетным давлением) и соот-
ветственно уменьшаются потери тяги. Это явление особенно сильно проявля-
ется в сверхзвуковых соплах с центральным телом. На расчетном режиме и
на режимах выше расчетного течения в сверхзвуковом сопле с центральным
Рис. 2,6. Схема течения на режиме ниже расчетного: а) течение без отрыва; б) течение с отрывоы потока
от стенок сопла.
Рис. 2.7. Критический перепад дав-
ления в скачке уплотнения, вызываю-
щий отрыв турбулентного погранич-
ного слоя на срезе сопла, в функции
относительной скорости потока на
срезе.
телом (рис. 2.8, а [2.24]) принципиально не отличается от течения в сверх-
звуковом сопле классической схемы. Однако на режимах ниже расчетного
попадающий и отражающийся от центрального тела скачок уплотнения
(идущий от среза обечайки сопла) вызывает существенное повышение дав-
ления на центральном теле (рис. 2.8, б), интенсифицирующееся отрывом по-
тока при взаимодействии скачка уплотне-
~ь
ния и пограничного слоя. Такие сопла имеют
небольшие потери тяги на режиме ниже рас-
четного. На рис. 2.9 показан пример харак- ~Ь
теристики реактивного сопла с центральным
телом с ро/р,=165 [2.34]; пример компонов-
ГР
ки ракеты с таким соплом см. в [2.35]. о~
3. Движители ЖРД и РДТТ. 4 октября дни~о
1957 г. впервые в мире в СССР был осуще-
~~цН
ствлен вывод искусственного спутника на
орбиту вокруг Земли. Так началась косми-
ческая эра в истории человечества, опираю-
щаяся на фундаментальные работы советских Ф
ученых и конструкторов, впервые создавших у ~
аффективные ракетные двигатели [2.36, 2.37].
У жидкостных ракетных двигателей
(ЖРД) и ракетных двигателей твердого топ- ~~ ~~ ~~ ~~ ~~ ~-с
лива (РДТТ) собственно движителем являет-
ся реактивное сопло. В рамках газодина-
мической теории величина реактивной тяги,
создаваемой соплом как движителем, опре-
деляется по формуле (2.12) с учетом указан-
ных поправок на влияние отрыва потока на режимах ниже расчетного (вклю-
чаемых, например, в величину потерь импульса сопла т,.). Результаты, по-
лученные в газодинамической теории, справедливы для химических тепло-
вых реактивных двигателей, при температурном уровне которых влияние
диссоциации, ионизации и рекомбинации газового потока (не учтенное в из-
ложенной теории) не является определяющим. Типичными представителями
таких космических двигателей являются жидкостные реактивные двигатели
(ЖРД) и ракетные двигатели твердого топлива (РДТТ), у которых реактив-
ное сопло является стержневым конструктивным элементом [2.36 — 2.69].
Вследствие конструктивной и газогидродинамической взаимосвязи элементов

0,8
Рис. 2.9. Относительная тяга, развивае-
мая соплом с центральным телом с ~ефе=
= 165, в зависимости от высоты при
=3,5 ° 10' кг/м' (сплошная кривая — акс
перимент, пунктирная — расчет для
сопла классической схемы).
Рис. 2.8. Схема течения в сверхзвуковом сопле с
центральным телом (~с=1,68).
Гари~ее
Рис. 2.10. Жидкостный реактивный двигатель ВТ 10А-3 второй ступени ракеты «Сатурн-1» (горючее—
жидкий водород, окислитель — жидкий кислород): 2 — охлаждаемая излучением часть сопла, 2—
охлаждаемая горючим часть сопла, 3 — камера сгорания, 4 — сисгема подачи горючего и окислителя.

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
у ЖРД нецелесообразно раздельно анализировать массы сопла (движи-
теля), камеры сгорания и системы подачи рабочего вещества.
Согласно соотношениям (2.11), (2.12) максимальная тяга ЖРД пропор-
циональна полному давлению газа в камере сгорания р0 и площади крити-
ческого сечения сопла Я „:
(2.11')
Ршах т00~ а'
Масса сопла-движителя (являющегося одновременно системой отвода
энергии, см. рис. 2.10) из условий статической прочности должна была бы
быть пропорциональной произведению В0 ф'„~, однако из-за улучшения кон-
структивных качеств с увеличением размеров двигателя масса возрастает
медленнее, чем куб характерного размера, примерно пропорционально
р00Г,. Аналогично изменяется и масса камеры сгорания ЖРД, являющейся
энергоисточником и энергопреобразователем (см. ниже ~ 2 этой главы).
Для ЖРД масса системы подачи рабочего тела должна быть пропорцио-
нальна расходу д, величина последнего, по соотношению (2.8), также
пропорциональна произведению Ц00Г„. Поэтому для ЖРД примерно можно
считать
(М,+М,+М„+М,+М,) — р я"„
(2.1 )
и с учетом (2.11)
М +М,+ М„+М,+М,=~„Р.„,
(2.16)
(2.17)
На рис. 2.12 в качестве примера приведены значения суммарной удель-
ной массы двигательной системы РДТТ по данным работ [2.61, 2.63].
Важным параметром реактивного сопла как движителя является сред-
няя эффективная скорость истечения струи из сопла Г и связанная с нею
величина удельного импульса двигательной системы 1'. По соотношениям
(2.8), (2.12) и (1.4) эти параметры равны (при д,=д)
(")"
уо
э
(2.18)
При фиксированных параметрах реактивного сопла и высоте полета эф-
фективная скорость истечения струи (и соответственно удельный импульс)
где т = (М вЂ” М,)~Р „— удельная масса двигателя (для ЖРД М, = 0 и
ЛХ, ='О).
На рис. 2.11 в качестве примера приведены значения удельной массы
двигателей ракет «Сатурн» (см. [2.12, 2.70] и др.); указанные там же данные
двигателя ракеты У-2 иллюстрируют прогресс в улучшении характеристик
ЖРД за 20 лет. Приведенные на рис. 2.11 характеристики подчеркивают
малые значения удельной массы химических тепловых реактивных двигателей
на жидком топливе.
У РДТТ относительная масса реактивного сопла-движителя составляет
примерно т=М ~Р,„— 0,01 кг~кГ [2.61]. Следует отметить, что для РДТТ
собственно двигатель и топливный бак представляют собой единую конструк-
цию [2.57 — 2.69]. Поэтому для РДТТ характерным является отношение сум-
марной массы двигательной системы М и массы топлива М, к развиваемому
двигателем полному импульсу РТ (произведение тяги двигателя Р на время
работы двигателя Т ):

[ГЛ. 2
Физические пРинципы двиГАтельных систем
40
определяется составом (Я, х) и температурой торможения газового по-
тока ТО.
Максимальная скорость истечения для тепловых реактивных двигателей
ограничена, например, для химических двигателей — максимальной тем-
пературой, достижимой при химических реакциях, Т, (см. ниже $ 2), воз-
можностью выбора горючего и
окислителя с малым значением мо-
лекулярного веса продуктов сго-
рания (увеличение газовой постоян-
по ной Я) и допустимой температурой
конструкции. Поэтому тепловые
реактивные двигатели можно клас-
001
сифицировать как двигательные
системы с ограниченной скоростью
д истечения струи:
1д Ю Я 100 200 Я0 Р, (О, юГ„
+~© т „х
рис. й.11. Зависимость удельной массы ЖРд от мак- ~ ма* 2А
к ная к ивая — вигатели
симальной тяги (пун тир р д
1 — 4 ракет «Сатурн»): 1 — ВЬ 1 ОА-3 (Н~+ О,), 2—
Ю-2 (Н,+О,), 3 — Н-1 (керосин+О,), 4 — Р-1 (ке-
росин+ О,), б — двигатель ракеты Ч-2 (этиловый
спирт 7 5 о~~ + Оз).
. (2.19)
Как следует из соотношения (2.19), с увеличением высоты полета мак-
симальная эффективная скорость истечения из сопла возрастает (соответ-
ственно с ростом тяги, см. (2.12)) примерно на 10 — 30о~~ [2.70]. Характерными
являются точка старта на поверхности Земли и полет в космосе.
У~+ М ~г
Р~ кГ
0005
0004
р/К
Рис. 2. 12. Зависимость суммарной удельной магсы у~ двигательной системы и запаса топлива РДТТ
от средней тяги (тв отнесена к полному импульсу): 1 — сферический Рдтт, а — Рдтт цилиндрической
формы, 3 — экспериментальный РДТТ диаметром 4 м, 4 — РДТТ ракеты «Титан-ЗС».
Например, для указанных на рис. 2.11 двигателей ракет «Сатурн» мак-
симальные значения скорости истечения струи и удельного импульса со-
ставляют [2.70 ]:
для ЖРД стартовых ступеней на компонентах керосин ]-О, при Й=О
Г „о=2550 м/сек, 1; 255 сек; в вакууме Г „=2800 м/сек, 1' 280 сек;
для ЖРД космических ступеней на компонентах Н,-]-0, при Й=О у',„о=
=3200 м/сек, 1с' — 320 сек; в вакууме Г „=4200 м/сек, 1' — 420 сек.
На рис. 2.13 по этим данным, соотношениям (2.12), (2.19) и данным
рис. 1.8 приведено примерное изменение с высотой полета тяги, эффективной
скорости истечения струи и удельного импульса высотного ЖРД. Аналогично
изменяются с высотой полета и характеристики РДТТ [2.61, 2.63].
4. Высокотемпературные тепловые реактивные движители. Для полу-
чения величин эффективной скорости истечения и удельного импульса боль-
ших, чем достижимые в химических тепловых реактивных двигателях, в
литературе обсуждается ряд тепловых двигательных систем с нагревом рабо-
чего тела до высоких температур электрическим разрядом либо в тепло-
обменнике, обогреваемом ядерным или изотопным реактором, или солнечной

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
энергией ([2.71 — 2.93] и др.). Характерной особенностью таких двигатель-
ных систем является очень высокая температура то газового потока на входе
в реактивное сопло. При высокой температуре нагрева газа перед соплом
большая часть подводимой к движителю энергии (1 — ~т) К&g ;. расходуе ся
диссоциацию и ионизацию газового потока. Долю тепловой энергии потока
характеризует к. и. д. 7]т, зависимость которого от температуры для различ-
ных рабочих тел приведена на рис. 2.14 [2.82]. Для нижней оценки величины
эффективной скорости истечения струи и удельного импульса высокотем-
пературных движителей принимается (см., например, [2.76, 2.82] и др.),
что за короткое время расширения газа в сопле энергия ионизации и диссо-
циации не успевает выделиться (так называемое «замороженное» состояние
потока). Тогда величина эффективной скорости истечения струи и удельного
импульса может быть оценена по фор-
муле вида (2.18) с учетом к. п. д.
если принять То мерой полной энер-
гии газа:
У
х
~Е Е
05
~. ~~р
Г"Г
1 с~ (~с) р
10 Л~ Л~ ~Р л ~м
уо
К
Рис. 2.13. Высотные
ЖРД.
характеристики
(2.20)
(. 1)
ЛХ,— ф Ыйи — р, ~
где ~'т — фронтальная площадь теплообменника, ит — Й 2 — число трубок
теплообменника на единицу фронтальной площади. По уравнению расхода
— р,~~,, поэтому с учетом соотношения (2.13) масса теплообменгика
На рис. 2.15, по данным [2.82], приведено изменение максимальной
эффективной скорости истечения струи и удельного импульса в вакууме для
высокотемпературных реактивных двигателей в зависимости от температуры
торможения газового потока для различных рабочих тел. Отчетливо видны
преимущества водорода как рабочего тела, обеспечивающего высокие ско-
рости истечения при наименьшем потребном нагреве газа. Величина тяги
таких двигательных систем (не зависящая от температуры газового потока—
см. выше) определяется по формуле (2.12).
Примеры схем высокотемпературных тепловых реактивных движителей
с теплообменниками, нагреваемыми ядерным реактором [2.84], концентри-
рованным солнечным излучением [2.82] или изотопным реактором [2.83]
приведены на рис. 2.16 — 2.18.
В этих движителях высокотемпературный газовый поток образуется
в теплообменнике и разгоняется до больших скоростей истечения в реактив-
ном сопле. Аналогично случаю ЖРД, из-за взаимосвязи целесообразно сов-
местно анализировать массу теплообменника и сопла. Обобщенная газоди-
намическая схема тепловых реактивных движителей с теплообменниками
приведена на рис. 2.19. Типовой канал теплообменника, в котором происхо-
дит нагрев газового потока до заданной температуры торможения на входе
в сопла Т„представлен эквивалентной трубкой диаметром Й и длиной Ь.
Как будет показано в ~ 2, заданная степень нагрева газового потока опреде-
ляет потребное число калибров каналов теплообменника Ь/Й=йт. С учетом
зрозионной стойкости толщину стенки каналов (трубки) О для оценки примем
пропорциональной полному давлению: с — р . Тогда масса теплообменника
будет пропорциональна

ДеЯ
/ДЦ
Рис. 2. 14. Доля ~у тепловой энергии потока
прп ~о — 10' кг/м'.
~анЦЕИ~РиРО5аюоЕ Солнечнце иЗлученц~
Рис. 2.18. Схема изотопного теплового РД: 1 — трубопровод системы охлаждения, 2 — тепловая изо-
ляция, 3 — канал теплообменника для нагрева рабочего вещества, 4 — реактивное сопло, 5 — капсул~
с радиоактивным изотопом, 6 — клапан системы подачи, У вЂ” подача рабочего вещества.
Рис. 2.16. Схема теплового РД
с ядерпым реактором: 1 — реак-
тивное сопло, 2 — ядерный ре-
актор-теплообменник, 3 — си-
стема подачи рабочего вещества.
Рис. 2.15. Оценка скорости истечения и удельного
импульса по схеме «замороженного» газового потока.
Рис. 2.17. Схема теплового реактивного движителя с солнечным на-
гревом: 1 — подвод рабочего вещества (водород), 2 — дефлектор
газа, 3 — соединение кварцевой прозрачной сферы с соплом, 4—
реактивное сопло, 5 и 6 — ось вращения и цапфа системы ориента-
ции движителя, У вЂ” пористый теплообменник — приемник лучистой
энергии, 8 — многослойный экран, 9 — кварцевая прозрачная
сфера.

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
пропорциональна максимальной тяге движителя:
М, — п,У„- Р..„
(2.22)
и, аналогично (2.16), для высокотемпературных тепловых РД с теплообмен-
НИКОМ
(2.23)
М =М,+М,+М,+М,— 7 Р „,
где г — обобщенная удельная масса движителя. У ядерных тепловых РД
Т
с увеличением мощности масса делящегося вещества — энергоисточника
(М„) — возрастает незначительно и составляет малую
долю массы двигателя, поэтому для ядерных двига- Т3ача~а5счегц
телей М,т=М~(М,=О, М,=О). Для изотопных и
солнечных тепловых двигателей масса энергоисточ-
ника является существенной частью и определяется
по данным ~ 2 этой главы. Примерные значения
обобщенной удельной массы тт тепловых реактив-
ных движителей с теплообменниками указаны в
табл. 2.1 [2.75, 2.82, 2.83].
Величина максимальной эффективной скорости
истечения струи и удельного импульса для тепло-
вых РД с теплообменниками, естественно, зависит от
максимально допустимой температуры нагрева газа
Т,,„(см. (2.20) и рис. 2.15), которая ограничи-
вается допустимой для материалов движителя тем-
пературой. Примерные свойства некоторых высо-
котемпературных материалов для тепловых РД с теп-
лообменниками приведены в табл. 2.2 [2.72].
» ' Указанный в табл. 2.2 максимально допусти-
мый уровень температуры стенок теплообменника
теплового РД порядка 2800' К ограничивает мак-
симальную скорость истечения реактивной струи
в движителях с теплообменником: для водорода
Рис. 2.19. Газодинамиче-
(оптимальное рабочее тело — см. рис. 2.15) в ваку экая схема теплового реак-
уме )г 8000 мlсек, 1'=800 сек.
тивного движителя с тепло-
тах
обменпином Я вЂ” тепловой
5. Электротермические реактивные движители ° поток от энергоисточника).
Значительно более высокие температуры нагрева и
скорости истечения струи реализуются в электро-
термических реактивных движителях с нагревом рабочего тела электрическим
разрядом — дугой. Первый в мире электротермический ракетный двигатель
(рис. 2.20) был разработан, построен и успешно испытан В. П. Глушко
в 1929 — 1933 гг. в газодинамической лаборатории (ГДЛ) в Ленинграде [2Л6,
2.37]. В ГДЛ испытывались ЭРД различных схем, проводилисьисследова-
ния свойств рабочих веществ — «топлива» для ЭРД (электропроводящих
жидкостей и металлов), отрабатывались способы их подачи в ЭРД, была раз-
работана мощная высоковольтная импульсная установка для питания ЭРД.
Один из основных вариантов ЭРД был выполнен в виде камеры с соплом,
в которую подавались металлические проволочки из меди, никеля, вольфрама,
свинца и других металлов. Механизм подачи проволочек состоял из двух
стальных валиков, приводимых во вращение электромотором. После замы-
кания межэлектродного промежутка проволочкой происходил ее взрыв,
в результате чего создавалась плазма, которая ускорялась в сопле. Первый
импульсный ЭРД работал как в режиме одиночных выстрелов, так и с ча-
стотой повторения импульсов до нескольких десятков в секунду. При .по-
мощи баллистического маятника в ГДЛ измерялся импульс тяги ЖРД; по
импульсу тяги было проведено измерение скорости истечения реактивной

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Таблица 2Л
Значения обобщенной удельной массы для высокотемпературных тепловых
реактивных движителей с теплообменниками
МТу кг
ТТ= 1—
Ршах 'кГ
Тип движителя
— 5 10-2
— 100
150~)
С теплообменником, нагреваемым ядерным реактором
С теплообменником, нагреваемым изотопным реактором
С теплообменником, нагреваемым концентрированным солнечным излучателем
*) В ключая массу концентратора солнечной энергии.
Т аблица 22
Свойства некоторых высокотемпературных материалов для тепловых РД
с теплообменниками
ВеО
Графит
Материал
2800
3900 (суб-
лимирует)
1,7 103
210 †4
при 2780' К
3650
Точка плавления, ' К
Плотность при 20О С, кг/лР 2,7 10З
Кратковременная прочность на разрыв, кГ~см' 70 —:280
при 1500' К
19,1 103
350 —:630
при 2780' К
Рис. 2.20. Первый в мире экспериментальный электротермический движитель конструкции В. П. Глушко,
1929 — 1933 гг.
и др.), что может обеспечить скорость истечения реактивной струи до Г
25000м/сек, Х' 2500сек [2.81]. Удельная масса электродугового движи-
теля, по данным [2.76], составляет примерно т=М ~Р,„10 кгlкГ.Мак-
симальная температура нагрева струи, как и у другйх типов тепловых РД,
лимитируется допустимой температурой материала стенок движителя. Од-
нако предельный уровень нагрева рабочего тела в электродуговом движителе
значительно выше, чем в химическом РД или тепловом РД с теплообменни-
ком. Важным параметром является к. п. д. движителя и =К/К: отношение
мощности направленного движения реактивной струи Г к мощности Г,
Т~
струи, которая достигала нескольких десятков километров в секунду.','Прин-
ципиальная схема электродугового движителя [2.79] показана на рис..'2.21.
Дуга, стабилизированная закруткой подаваемого рабочего тела или маг-
нитным вращением, обеспечивает большой градиент температуры газа по
радиусу и позволяет нагревать рабочее тело до температур в десятки тысяч
градусов при допустимых температурах стенок движителя (см. [2.94 — 2.97]

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
потребляемой движителем. По данным [2.98], при регулировании величины
скорости истечения струи Г ирасходарабочего тела д к. п. д. электродугового
цвижителя сохраняется примерно постоянным, несколько снижаясь с уве-
личением Г (рис. 2.22). Этикачества позволяют при ограниченной мощности
питания движителя Г, эффективно регулировать скорость истечения реак-
тивной струи Г при примерно постоянной полезной мощности струи Г, что
в ряде случаев целесообразно с позиций механики полета (см. ниже).
6. Электродинамические и электростатические реактивные движители.
Работы по электрореактивным двигателям, начатые в ГДЛ, нашли свое про-
должение в наши дни. Впервые в мире в СССР при реальных условиях по-
лета по космическим орбитам и в верхней атмосфере были применены ионные
ЭРД на космическом корабле «Восход-1» (1964 г. [2.36, 2.37]), плазменные
ЭРД на автоматической станции «Зонд-2» (1964 г. [2.36, 2.37]), плазменно-
ионные ЭРД в автоматических ионосферных лабораториях «Янтарь» (1966—
0.8
04
К
ЮИ У,м/сею
Рис. 2.22. Экспериментальная харак-
теристика электродугового движителя;
раоочее вещество — гелий.
Рис. 2.21. Схема электродугового теплового реактивного
движителя: 1 — вводы системы охлаждения.
1971 г. [2.36, 2.37, 2.99 — 2.102], стационарные плазменные ЭРД на искус-
ственном спутнике Земли «Метеор» (1972 г. [2.103]).
В нашей стране, родине космонавтики, впервые зародились и идеи ЭРД.
Великий К. Э. Циолковский еще в 1911 г. писал [2.104]:
«Может быть, с помощью электричества можно будет со временем при-
давать громадную скорость выбрасываемым из реактивного прибора ча-
стицам. И сейчас известно, что катодные лучи в трубке Крукса, как и лучи
рация, сопровождаются потоком электронов, масса каждого из которых,
как мы говорили, в 4000 раз меньше массы атома гелия, а скорость дости-
гает 30 — 100 тысяч км/сек, т. е. она в 6 — 20 тысяч раз больше скорости
обыкновенных продуктов горения, вылетающих из нашей реактивной трубы».
С позиций механики полета важным свойством электродинамических
и злектростатических реактивных двигателей является то, что они позволяют
регулировать скорость истечения реактивной струи в практически неогра-
ниченном диапазоне, вплоть до уровня релятивистских скоростей.
Тепловые реактивные движители создают тягу в результате воздействия
гааодинамического давления на стенки движителя. Одновременно с воздей-
ствием газодинамического давления газовый поток в тепловом РД отдает стен-
кам движителя тепловую энергию, что и лимитирует, как указывалось выше,
аффективную скорость истечения и удельный импульс таких движителей.
Электродинамические и электростатические движители используют воздей-
ствие соответственно магнитного или электростатического давления на стенки
движителя, что практически снимает тепловое ограничение на эффективную
скорость истечения реактивной струи.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Подробно принципы работы электродинамических и электростатических
РД изложены в литературе [2.36, 2.75, 2.79, 2.81, 2.99 — 2.144]. Рассмотрим
свойства таких движителей. Величины магнитного и и электростати-
ческого р давления, как известно, определяются соотношениями [2.1451
(2.24)
= Н2/Яп,
]~ =Е'/8п,
(2.25)
где о7 — сила тока в цепи, Я вЂ” величина самоиндукции контура, ось х на-
правлена вдоль (<рельсо »; принимае ся так е, то омичес им сопротив
нием электроцепи (включая плазменный шнур) можно пренебречь. Тогда на-
пряжение на электродах «рельсов» Я определится соотношением
(2.26)
Уравнение энергии (разрядки конденсатора емкостью С,) замыкает систему:
о7 = — С,ИЯ/Ж. (2.27)
где Н вЂ” напряженность магнитного поля, Š— напряженность электри-
ческого поля. Величина напряженности магнитного поля Н лимитируется
силой электрического тока, используемого для создания магнитного поля.
Так, например, в технике используются магнитные поля напряженностью
Н 1 тл=10 000 гс, что соответствует магнитному давлению рв 4 10«кГ/м'.
Величина напряженности электрического поля Е лимитируется условиями
электрического пробоя диэлектрика (в том числе и вакуума) между провод-
никами; в технике используются напряженности электрического поля
Е 10' в/м — 30 ед. ССРЕ, что соответст-
вует электростатическому давлению р
Е
=0,4 кГ/м'.
Из сопоставления указанных уровней
Р магнитного и электростатического давле-
ния следует, что электродинамические дви-
д жители по сравнению с электростатиче-
скими могут обладать значительно боль-
шими значениями тяги на единицу пло-
Г~ щади миделя движителя. Электродинами-
2 23 приник~ив~ о е~в нину о ческие движители в литературе (см., на-
ного электРодйнамического движителя: пример, [2.36, 2.75, 2.79, 2.103,
2.140 — 2.144]) рассматриваются как им-
пульсного, так и непрерывного действия.
На рис. 2.23 приведена принципиальная схема простейшего импульсного элек-
тродинамического ускорителя «рельсового» типа, который был исследован в
Институте атомной энергии АН СССР в 1953 г. как плазменный инжектор для
изучения термоядерных процессов [2.146]. В этом ускорителе конденсатор
С, разряжается на тонкую металлическую проволоку аЬ, натянутую между
двумя параллельными жесткими проводниками («рельсами»). При замы-
кании разрядника Р проволочка практически мгновенно испаряется и пар
ионизуется, превращаясь в отрезок плазменного шнура. Вследствие вза-
имодействия электрического тока, проходящего по плазме, с магнитным по-
лем подводящих проводов возникает электродинамическая сила, которая
ускоряет плазменный сгусток вдоль «рельсов», а приложенное к проводникам
магнитное давление определяет реактивную тягу. Основные свойства им-
пульсного электродинамического ускорителя плазмы могут быть описаны
следующей теоретической моделью [2.146 — 2.148]: масса ускоряемого плаз-
менного сгустка т принимается постоянной по времени разгона, уравнение
движения записывается в виде
тУх/Ю='/ ~ЧЯ/Йх

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
При разгоне плазменного сгустка по (<рельс м» самоиндук ия конт
возрастает линейно по х:
Я=Я,+Ь,х,
(2.28)
где Я, — начальная самоиндукция контура при 8=0 и х=О; Ь,=НЯМ=
= сопз$. С учетом (2.28) решению подлежит следующая система уравнений:
(2.29)
~ = /Ч//Ч, = т Г'/С,Ц,'.
(2.30)
Целесообразно ввести в рассмотрение безразмерные переменные
8 — й — Ий
х= — 'х, ~=, Ц= —,
.РОСО 0 ~ ИО С'О/.РО
(2. 1)
Тогда решение системы уравнений (2.29)
х(0) =О, йх/И(0) =О, Ц(0) =1, <Я/И 0)
(2.29')
зависит только от одного основного безразмерного параметра О:
1 = Ь2С'ф'/2тЯ,
(2 32)
через который выражается и к. и. д. движителя:
~, = (Их/Ж)'/21.
(2.30')
В работах [2.147, 2.148] приведены решения системы уравнений (2.29').
Сопоставление их с экспериментом показало, что изложенная теория удовле-
творительно описывает основные свойства импульсных электродинамиче-
ских ускорителей. Из формул (2.31), (2.29'), (2.32), (2.30') следуют широ-
кие регулировочные возможности импульсного электродинамического дви-
жителя. Так, например, при постоянстве безразмерной скорости (Нх/Ы),
в конце разгона сгустка плазмы и О=сопя$ при регулировке будет постоян-
ным к. п. д. движителя, ~. =сопят. Рассмотрим в качестве регулируемого па-
раметра число импульсов движителя в секунду /с; тогда расход рабочего тела
у и мощность струи движителя К определятся соотношениями
д = /ст, /Ч = '/р ЙС„Ц,',
(2.33)
а выражение для основного безразмерного параметра 6 запишется в виде
3 = Ц/ЧС,/Я;цд = сопзс.
(2.34)
При постоянных значениях зазора между электродами («рельсами»)
О,=сопзФ, параметров питающей электрической цепи Я,=сопзй и ф,=сопзй
в рассматриваемом примере регулирования, если емкость конденсатора С, и
число импульсов в секунду Й изменяются по закону
Со д&
(2.35)
с начальными условиями (при ~=0). х=О, У=Их/В=О, Я=Я„~7=0.
При рассмотрении импульсного электродинамического ускорителя как
движителя важным параметром является к. п. д. преобразования начальной
запасенной в конденсаторе энергии Е='/, С,Я в кинетическую энергию на-
правленного движения плазменного сгустка

48
[гл. 2
ФиЗические пРинципы двигАтельных систем
то регулирование скорости истечения струи Г будет происходить при по-
стоянной мощности струи К=сопзФ и постоянной мощности, потребляемой
движителем, К =сопзФ; тогда
Т
Г = ~/2Ж/д — Й~*,
(2.36)
При этом максимальное значение потребной емкости конденсатора С,
соответствует минимуму скорости истечения реактивной струи Г. Регули-
рование частоты импульсов выброса плазменных сгустков Й может осуще-
ствляться, например, клапанной системой подачи газообразного рабочего
тела (см. на рис. 2.24 схему исследованного коаксиального импульсного
Рис. 2.24. Коаксиальный импульсный электродинамический ускоритель плазмы: 1 — подача рабочего
вещества, 2 — соленоид привода клапана подачи, 3 — клапан подачи рабочего вещества, 4 — коакси-
альные электроды («рельсы») ускорителя. 3
электродинамического ускорителя [2.146]). При коаксиальном расположе-
нии «рельсов» радиусов г, и г, значение погонной индуктивности движителя
равно 0,=1п (г,/г,).
У импульсных электродинамических движителей получены скорости
выброса плазменных сгустков реактивной струи до -2 10' м/сек (см. [2.76—
2.81] и др.) при удельной массе движителя порядка т=М (Р„„,=10 — '.
100 кг/кГ [2.79]. В это значение не включена масса конденсатора, который
хотя и является накопительным элементом системы (см. ниже ~ 2), но служит
неотъемлемой частью импульсного движителя.
На рис. 2.25 приведена схема двухкаскадного торцевого импульсного
плазменного ЭРД [2.144] с широкой регулировочной характеристикой
(рис. 2.26). Первый каскад этого ЭРД представляет собою инжектор плазмы
эрозионного типа; центральный электрод инжектора — расходуемый, это
шашка ускоряемого рабочего вещества кадмия. Промежуточный сетчатый
электрод является одновременно катодом первого и второго каскада. Анод
второго каскада имеет коническую форму. За один цикл такой ЭРД создает
импульс тяги до 0,15 10-' кГ сек при скорости истечения реактивной струи
до 115 км/сек и к. п. д. до 280~~ (рис. 2.26).
Пример схемы электродинамического движителя непрерывного действия
[2.76] приведен на рис. 2.27. Предварительной ступенью в этой схеме явля-
ется электродуговой подогреватель, обеспечивающий начальную ионизацию
и электропроводность рабочего тела — плазмы, поступающей в собственно
электродинамический ускоритель. В последнем системой электродов и элек-
тромагнитов устанавливается скрещенное электромагнитное поле, ускоряю-
щее плазму как проводник. Можно считать, что ускоряемый газ — рабочег
тело — представляет собой нейтральную плазму с электропроводностью

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
ГМ
~У дж
у, 'иг(имп
Рис. 2.26. Скорость истечения реактивной струи У
и к. и. д. ~~ двухкаскадного плазменного ЭРД в функ-
ции отношения затрат энергии за один импульс к со-
ответствующему расходу рабочего вещества Ж~/д,'
Рис. 2.25. Двухкаскадный торцевой им-
пульсный плазменный ЭРД: 1 — система
инициирования разряда, 2 — анод 1 ка-
скада, расходуемый, 3 — электрод ини-
циирования, 4 — промежуточный элек-
трод, 5 — анод П каскада, С, и С, — кон-
денсаторы.
Взаимодействие магнитного поля Н (перпендикулярного Е) и электрического
тока ~ вызывает приложенную к плазме ускоряющую силу Р,., действующую
перпендикулярно ~ и Н:
= ~Н/р,
(2.37)
где Р— сила, действующая на еди-
ницу массы плазмы, р — плотность
плазмы.
По результатам расчетов, приведен-
ным в работе [2.76], такой движитель
Рис. 2.27. Схема электродинамического движи-
теля с непрерывным истечением плазменной
струи: 1 — ввод рабочего вещества в дуговой
ионизатор, 2 — анод электр одинамическ ого
пви>ките я 3 Ђ” кат д 4 Ђ” кату ка эл
тромагнита.
Рис. 2. 28. Стационарный плазменный ЭРД: 1—
кольцевая диэлектрическая камера, 2 — катушка
намагничивания коаксиальной магнитной системы,
3 — газораспределитель (анод), 4 — ввод рабочего
вещества (ксенона), 5 — эмиттер электронов (ней-
трализатор).
при К=2 104 м/сек и Г =4800 квт имеет к. п. д. ~ -0,8 и удельную массу
порядка т=М ~Р „. 10 кгlкГ. Регулирование движителя может осуществ-
ляться изменением магнитного и электрического поля, что, согласно урав-
нению (2.37), изменяет ускоряющую силу, действующую на плазму в дви-
жителе.
Возможность достижения к. п. д. ~ свыше 50О~~ в плазменных ЭРД
была экспериментально подтверждена йодробными исследованиями стацио-
нарного плазменного ЭРД с замкнутым электронным дрейфом и протяженной
4 Механика полета
Разность потенциалов между верхним и нижним электродами (рис. 2.27)
создает в канале ускорителя электрическое поле с напряженностью Е, бла-
годаря которому возникает электрический ток через плазму плотностью ю.
У, нм/сгк

[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
50
ско ения еактивной струи [2.103, 2.142] (рис. 2.28). В стационарном
б ещества используется газообразный
плазменном
я в коль ев ю диэлектрическую камеру. Вследствие
ксенон, который подается в кольцевую диэлектрич
я в каме е создается «оолако» горячих вращающихся
влияния магнитного поля в кам р д о
в кото ое ионизуется рабочее вещество. Образующиеся
электронов, попадая в которо у
еским полем; ионная реактивная струя компен-
ионы ускоряются ~~~~~Р~~~~
си ется электронами из эмиттера. В результате из такого
лазменные ЭРД были впервые в мире испытаны в СССР
в условиях р
х реального космического полета ( г.—
льная становка спутника «Метеор». Внизу — д
— ва стационарных
Рис. 2.29. Электрореактивная двигательная устан
го сп тинка Земли «Метеор», где проработали в течение
ЭРД й ~~~мым ф~с 2.29)
170 часов. Два стац
ротив касательной к траектории
установлены на у М
сп тнике «Метеор» по и проти
ие летательного аппарата.
полета, что обеспечивае р
вает азгон ли о торможени
16 5 км и установлен на
ЭРД сп тник «Метеор» был опущен на, км
С помощью Э Д спу
б р управляемый полет космиче-
условно-синхронную орбиту. р уп
то ыл первый уп
ского орбитального а"'р'" ° , 2.79 2.97, 2 103, 2 115, 2 140—
2.1~4, 2.147 — .
— 2.157] и др.) описано много рази
— о разновидностей электродинами-
ерывным ускорением реактивнои
%.У
ческих движите лей с имп льсным или непреры
У
личаются от рассмотренных
и которые принципиально не отлич
плазменнои струи, р
хем. С точки зрения меха
р еханики полета основным об-
выше двух основных схем.
й сле ет признать воз-
м элект одинамических движителеи следует
щим свойством электр
вания в широком диапазоне с
е скорости истечения реактив-
можность регулирова
т и электростатические — ион-
ной струи. тим
. Э основным свойством о ладают и элект
ные движители.
струя контактирует с элемен-
Р~~ «го ячая» реактивная ст,,
%У
В плазменных ЭРД р
обеспечивает умеренныи
малое в емя и на малой площади, что о
тами двигателя мало р
оРд э~~~~ективная температура дви-
температурный р ежим элементам ог,ц, хотя э,„,
остигает многих миллионов градусов.
жущего ся плазменного сгустка достигает мн
тически полностью исключается ко нтакт
лект остатических практически
и и элементов конструкции двигателя.
«горячей» реактивной струи и элем

51
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
В отличие от электродинамических движителей, ускоряющих квазинеи-
тральную плазму, электростатические движители ускоряют заряженные
частицы — ионы и электроны, которые после ускорения смешиваются в ква-
зинейтральную реактивную струю (см. [2.36, 2.37, 2.74, 2.75, 2.79, 2.81,
2.99 — 2.102, 2.105 — 2.141, 2.116 — 2.120, 2.141, 2. 158 — 2.199 ] и др.).
На рис. 2.30 приведена обобщенная схема электростатического движителя,
состоящего из источника ионов, ускорительной электростатической системы
и источников электронов; на схеме Я вЂ” разность потенциалов ускоряющего
ионы электрического поля, потенциал ЛЯ прикладывается для предотвраще-
ния обратного потока электронов.
При электростатическом ускорении г
заряженных частиц, имевших нулевую
начальную скорость,' конечная ско-
~вфф»
рость К,. определяется разностью по-
тенциалов ускоряющего поля Я, кото-
— » ~/
рую прошла частица:
Г,. = ~/2Це/р, (2.38)
гпе е — электрический заряд частицы,
р — масса частицы.
Расход рабочего тела соответствует
электрическому току ~7 потока заря-
женных частиц:
д,. = ~7р./е,
и соответственно тяга Р,. и мощность
струи Т,. равны (для ионов ~)
Р,.=д,.Г,. = 7~/2фр/е,
1/ д $72 7Я
Рис. 2.30. Обобщенная схема электростатиче-
ского движителя: 1 — подача рабочего веще-
ства, 2 — ионизатор рабочего вещества, 3—
электростатическая ускорительная система,
4 — эмиттер электронов.
(2.40)
Из условия квазинейтральности реактивной струи в электростатическом
движителе потоки ионов и электронов должны создавать одинаковый ток
(;7,.=~7,) и иметь одинаковую скорость (Г,.=Г,); поэтому
Р,/Р,. = Ж,/У,. = 1~,/р,. (2.41)
Для однозарядных ионов отношение массы электрона к массе иона по-
рядка р,/р,. 10-5, что позволяет, согласно соотношениям (2.41), пренебречь
вкладом электронов в тягу и мощность электростатического движителя.
Превалирующее влияние ионного потока определило и название электро-
статического движителя как ионного движителя. Реактивная тяга ионного
движителя по закону Чайлда — Ленгмюра (см., например, [2.200]) лимити-
руется возможной плотностью ионного тока ~=~7/~Г, создаваемого электро-
статической ускорительной системой (~à — площадь сечения ионной струи).
Это ограничение связано с тем, что электростатическое давление простран-
ственного заряда потока одноименно заряженных ионов противодействует
ускоряющему воздействию электрического поля. Потенциал в каждой точке
злектрического поля Я связан с плотностью пространственного заряда р,.
соотношением
(2.42)
~2ф = — 4ко,
Для плоского случая с учетом (2.38) параметры ионного потока находятся
интегрированием следующего дифференциального уравнения:
ЯЯ/йх'- = 2тф/2р./еф, (2.43)
где ~ =,7/Я = — р,.Г,, с начальными условиями (при х = О): Я = О, Щ/~х= О.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
После интегрирования определяется величина максимально возможной
плотности ионного тока ~ „, создаваемой электростатической ускорительной
системой с ускоряющим напряжением Я и расстоянием между ускоряющими
электродами Ш:
(2.44)
и соответственно (2.40) максимальная тяга, создаваемая ионным дви-
жителем,
Р „= (2/9т~) ЦЧ '~.
(2.45)
Характерно, что максимальная тяга, развиваемая ионным движителем,
не зависит от параметров рабочего тела (массы р и заряда иона е), а опреде-
ляется только электростатическим давлением, пропорциональным квадрату
напряженности приложенного электростатического поля — ф2/сР (см. выше
(2.24)). На рис. 2.31 указано изменение удельной тяги Р,„/~ в зависимости
от ускоряющего напряжения Я и зазора между электродами Ш. Максималь-
ные значения удельной тяги ионного движителя ограничены электрической
прочностью по отношению к пробою (межэлектродная дуга), наступающему
при напряженностях электрического поля, больших — 10' вlм [2.111, 2.200].
В отличие от максимальной тяги ионного движителя, скорость истече-
ния реактивной струи Г,. существенно зависит от выбора рабочего тела (см.
(2.38)). На рис. 2.32 для ионов атомов ряда рабочих тел и коллоидных частиц
большой массы показано изменение скорости ионной реактивной струи в за-
висимости от ускоряющего напряжения Я [2.111].
В целом данные рис. 2.31 и 2.32 указывают на большие регулировочные
возможности ионного движителя. Подчеркнем, однако, что соотношение
(2.45) определяет максимально возможную тягу, создаваемую ионным дви-
жителем, при условии, что максимально возможная плотность ионного тока
~,„(2.44) и соответственно расход рабочего тела д,,„обеспечиваются источ-
ником ионов. Поэтому характеристики ионных движителей во многом опре-
деляются характеристиками ионных источников.
Наряду с электродуговыми источниками ионов (типа рассмотренных
выше электротермических движителей) в литературе [2.74, 2.75, 2.79, 2.81,
2.105 — 2.114. 2.116 — 2.120, 2.158 — 2.202] подробно рассмотрены два типа ион-
ных источников: с контактной поверхностной ионизацией (см. на рис 2.33 (2.108]
схему лабораторной модели) и с объемной ионизацией электронным ударом
(см. ниже).
В ионных источниках с поверхностной ионизацией (рис. 2.33) исполь-
зуется свойство образования положительных ионов рабочих тел с малой энер-
гией ионизации при контакте с нагретой поверхностью ионного источника,
выполненного из материала с большой работой выхода электронов.
Энергия ионизации атома рабочего тела соответствует энергии, потреб-
ной для удаления внешнего электрона атома. Работа выхода материала
ионизатора соответствует энергии поглощенного электрона. Вероятность
актов ионизации рабочего тела — поглощения внешних электронов атомов
рабочего тела при контакте атомов с поверхностью ионизатора — увеличи-
вается с ростом разницы между работой выхода и энергией ионизации. Эта раз-
ница наибольшая у пары Сз — Ж [2.111, 2.201] (см. данные табл. 2.3 и 2.4,
где работа выхода и энергия ионизации указаны в электрон-вольтах).
После контакта атома рабочего тела с поверхностью ионизатора образо-
вавшиеся ионы должны иметь достаточную для ухода тепловую энергию,
иначе адсорбированный на поверхности слой атомов рабочего тела снижает
работу выхода и соответственно ионизацию. На рис. 2.34 приведена величина
степени ионизации Х цезия на вольфраме в зависимости от температуры

нф
Ф
~~ се~
МпиО
Рис. 2.31. Удельная тяга ион-
ного движителя.
Рис. 2.33. Схема лабораторной модели ионного движителя с контактной поверхностной ионизацис1:
1 — охлаждение кожуха вакуумной камеры, 2 — весы для измерения тяги, 3 — окно для наблюдений,
4, 5 — система подачи рабочего вещества (цезия), 6 — акранирующая сетка, У вЂ” ускоряющая сетка—
эмиттер алектронов, 8 — вольфрамовый ионизатор, 9 — нагреватель ионйзатора, 10 — запирающаи
сетка.
Р ю/
~~~~ У у
Я' 0 д
Э
СМ
юа)
фв®
Рис. 2.32. Скорость реактивной струи ионного
движителя (в скобках указан атомный вес атомов
или коллоидных частиц).

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Таблица 23
Энергия понизации некоторых элементов
Энергия ио-
Атомный вес низации, эв
Энергия ио-
низации, эв
Элемент
Атомный вес
Элемент
6,940
22,991
39,100
85,480
132,910
Ь1
Иа
К
ВЬ
Ся
5,36
5,12
4,32
4,16
3,87
24.50
13,90
13,50
11,20
10,39
4,003
83,800
1,008
12,011
200,610
Не
Кг
Н
С
Нд
Таблица 2.4
Работа выхода и температура плавления некоторых металлов
Температура
плавления
т, ос
Температура
плавления
т, ос
Работа выхо-
да, эв
Работа выхо-
да, эв
Металл
Металл
С
1г
Ве
РС
Ж
3550
2454
3167
1773
3370
4,81
4,90
5,10
5,20
5,50
3027
2620
1890
2700
960
4,10
4,30
4,37
4,50
4,70
Та
Мо
Сг
Оя
Ад
Рис. 2.34. Степень ионизации цезия.
вольфрамовой поверхности Т, где степень ионизации Х представляет собой
отношение числа образующихся ионов к числу атомов цезия, коснувшихся
поверхности ионизатора. Видно, что по достижении некоторой минимальной
температуры Т,. (зависящей от плотности ионного тока ~), когда адсорбирован-
ный на поверхности ионизатора слой це-
к зия исчезает, степень ионизации становит-
ся близкой к единице. Данные рис. 2.34
показывают, что величина обеспечивае-
мой ионизатором плотности ионного то-
~ -Юма,~~и~ ка ~ ( ~„,„(и соответственно расхода ра-
Р85
~ =~РиаlСм~ бочего тела д,. & t; д, „, м. (2.4 )) опре
ляется температурой поверхности иони-
затора и может регулироваться в пределах
~ ( ~ „путем изменения подачи рабочего
тела и температуры ионизатора. Для при-
ложений к механике космического поле-
та существенно, что такое регулирова-
ние расхода рабочего тела в ионном движителе не связано со скоростью
истечения реактивной струи К,, зависящей только от ускоряющего напря-
жения Я. При превышении ионизатором указанного выше на рис. 2.34 тем-
пературного уровня Т,. плотность ионного тока ~ и соответственно расход
рабочего тела д,. лимитируются по закону Чайлда — Ленгмюра (см. (2.44)),
при этом достигается максимально развиваемая ионным движителем тяга,
зависящая только от напряженности ускоряющего электрического поля
ЯЯ (см. (2.45) и рис. 2.31). Так, на исследованной в работе [2.108] лабора-
торной модели ионного движителя при температуре ионизатора '1'=Т,. =
=1173' К ( 7 — 70 ма, ~ф — 70 см', ~ — 1 ма/см') была реализована максимальная
реактивная тяга Р„„,=5 ° 10-4 кГ, соответствующаянапряженности ускоряю-
щего электрического поля Я/Ш=ЗООО в/см. Скорость истечения реактивной
струи ионного движителя в этих опытах составляла Г,.— 70 000 м/сек (удель-
ный импульс Х'=7000 сек).

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
В ионном движителе с поверхностной ионизацией мощность излучения
с нагретой поверхности ионизатора К. является основным видом потерь
[2.111]. По своей природе эти потери
(2.46)
ж — у,. т. = аит~~
связаны с плотностью ионного тока ~ (Т,. =/ (~)), с площадью сечения реактив-
ной струи а~ и не зависят от скорости истечения струи Г, (от ускоряющего
напряжения Я). По данным [2.111], для ионизации цезия на вольфраме за-
внсимость удельных потерь Г~./~ (в вт/см2) от плотности ионного тока
~ (ма/см2) может быть аппроксимирована следующим соотношением (рис. 2.35)
1д (1Ч,./Я) = 0,20+ 0,22 [д ж. (2.47)
р У
Рассматриваемые потери мощ-
ности в ионном движителе удобно
отнести к полному току а7 ионной
СМ
5
~И /~~ц
СМ
д .у ~р,. ма
' ~М-'
Рис. 2.36. ~дельные потери мощности в зависимости от
плотности ионного тока (со значения г ша~, определенного
условиями пробоя при ~~пах=104 в и д=1 см, кривая
проведена пунктиром).
Рис. 2.35. Потери на излучение с поверх-
ности нагретого ионизатора.
~2
Ф
т Г Й+ж ф Г2+ 2(е/р) ж /а7'
(2.48)
На рис. 2.37 приведен пример изменения энергетического к. п. д. ион-
ного движителя в зависимости от скорости реактивной струи при использо-
ванни цезия или ртути в качестве рабочего тела. Сопоставление данных
рнс. 2.37 и 2.36 показывает, что ионный движитель с контактной ионизацией
цезия на вольфраме обеспечивает высокие значения энергетического к. п. д.,
приближающиеся к единице при увеличении скорости истечения реактивной
струи, что хорошо подтверждается экспериментом [2.112]. По данным ра-
ооты [2.112], удельная масса ионного движителя с контактной ионизацией
составляет примерно т=М /Р „=750 — 1750 кг/кГ.
Другим подробно исследованным типом ионного источника является
источник с объемной ионизацией рабочего тела электронным ударом ([2.110,
2.112, 2.114, 2.117, 2.119, 2.120, 2.200 — 2.202] и др.)]. В таких ионных источ-
никах используется хорошо изученный для газовых разрядов процесс ио-
низации атомов газов при неупругом соударении с ними электронов с энер-
гнями в десятки электрон-вольт ([2.200 — 2.202] и др.). Процесс ионизации
'струи; при размерности Г~./а~, выраженной в эв/ион (в электрон-вольтах на
нон — в вольтах), численно это значение Г,.Ц' указывает эквивалентную
разность потенциалов для каждого иона, соответствующую потерям мощ-
ности вдвижителе (рис. 2.36). С учетом значения полезной разности потен-
цналов Я, ускоряющей ионный поток (см. (2.38)), энергетический к. п. д.
ионного движителя запишется в виде

[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
атомов данного газа (пара) электронным ударом характеризуется средним
числом Р,. актов ионизации, совершаемых электроном с энергией Е на пути
в 1 см при давлении в 1 мм рт. ст. при 0' С. На рис. 2.38 для ряда веществ
представлено изменение Р,. в зависимости
от энергии электронов.
Благоприятные характеристики па-
ров ртути — более высокая вероятность ~~
РГХ
ЮОО Юй7
У.У0з
100 200 300 Е,д
Рис. 2.38. Среднее число актов ионизации
электронным ударом.
Рис. 2.37. К. п. д. ионного движителя.
ионизации при меньших энергиях электронов — обусловили рассмотре-
ние ртути в качестве рабочего тела в ионных движителях с ионизацией элек-
тронным ударом (см. [2.110, 2.114] и др.), а также цезия и ряда газов.
»»::<ф,~ .'
$,
ч
..&
»
»' &gt
,.Ф
.»
Рис. 2.40. Ионный движитель с ударной иони-
зацией; рабочее вещество — ртуть.
Как указывалось выше, независимо от типа ионного источника плот-
ность ионной струи сравнительно мала вследствие ограничений, присущих
электростатической ускорительной системе. Поэтому давление внутри ка-
меры ионизатора должно быть малым, порядка -10-' мм рт. ст., для того,
чтобы обеспечить относительно малый паразитный расход нейтральных
атомов рабочего тела через отверстия отбора ионов в ускорительную систему.
При уровне давления в ионизационной камере р,. -10-' мм рт.ст. и эффек-
Рис. 2.39. Схема движителя с ионизацией паров ртути
электронным ударом: 1 — подача рабочего вещества,
2 — катод, 3 — анод, 4 — соленоид, 5 — электро-
статическая ускорительная система, 6 — эмиттер
электронов.
4:"
.. 4:."«В»
ф
,»« « ~»' &g
'«" »
»«». »»'»
»а '««„». »
» Ф»р 'р ..**'
ф»»» .»,«
» «» «.'» *»,
», «» « '„. ».
««'Ф ~& t
» .'«&l ; « „'
ФФ»«.'«Ф 8,'" « . »„
.«„»«» ~& t л «'
ж «» « ~»
,:..~ ф.
Ф:
«<:.:»:» :. &lt
й:. ФФ:. Ф' ФФ: Ф В»
&l ;» ~, »»
„'«щ»~ 4»
Ф:.
&

57
РЕАКТИВНЫЕ ДВИЖИТЕЛИ
тивности ионизации Р,. 20 (см. рис. 2.38) путь свободного пробега электрона
1,. до акта ионизации составит примерно
1,. = 1)Р,.р,. 5 ° 10' см.
Чтобы обеспечить эффективную ионизацию электронным ударом при
относительно малом характерном размере ионизационной камеры Й,. (& t;
для организации потока ионизующих электронов используют различные
электромагнитные ловушки типа применяемых при термоядерных исследо-
ваниях [2.146 ].
На рис. 2.39 и 2.40 приведены схема и внешний вид одного из вариантов
ионного движителя с ударной ионизацией паров ртути [2.203] (Р „=0,06 кГ,
И,=19,5 кг, Г=91 10» м/сек). Ионизую-
щее вращающееся тороидальное электрон-
ное облако в этой схеме формируется
алектромагнитной ловушкой, образованной
радиальным электрическим полем (цен-
й2
тральный катод — цилиндрический анод
в камере) и продольным магнитным полем
Нд
(от внешнего соленоида). Источником ио- ОЯ
Но
низующих электронов является разме-
2 йе
щенный в камере накаленный катод; при-
не
лохсенный к аноду камеры потенциал в
несколько десятков вольт обеспечивает
~е
электронам энергию, необходимую для
ионизации, а небольшое продольное маг-
нитное поле соленоида предотвращает пря-
мое попадание электронов на анод. Пары
рабочего тела (ртути) ионизуются алек- Рис. а.«~. вероятность иониаации при
трОнНыМИ удараМи прИ прОХОждЕнИИ каж~ом столкновении в зависимости от
энергии электрона.
сквозь вращающееся электронное облако.
Дальнейшее ускорение ионной струи осу-
ществляется так же, как в указанной выше на рис. 2.30 обобщенной схеме
электростатического движителя. Регулирование параметров ионного дви-
жителя с ударной ионизацией проводится аналогично рассмотренному выше
управлению параметрами ионного движителя с контактной ионизацией.
Как указано в табл. 2.3, потенциал ионизации для ртути составляет
10,39 в. Однако при ударной ионизации только часть столкновений электро-
нов с атомами приводит к образованию ионов [2.200] (рис. 2.41). Кроме того,
в ионизационной камере имеют место потери ионов на стенки камеры, уход
злектронов на анод и дополнительно часть энергии должна быть затрачена
на нагрев катода, питание соленоида. В результате, по исследованиям
[2.110, 2 114], удельные потери мощности в ионном движителе с ударной
ионизацией паров ртути значительно превышают потенциал ионизации и
составляют примерно Т./о7 500 в, что все же обеспечивает высокие значения
У
ф
знергетического к. п. д. движителя т1, (см. рис. 2.37).
Более экономичные характеристики камеры ионизации могут быть по-
лучены при применении в качестве рабочего вещества паров цезия и исполь-
зовании автокатода в качестве источника электронов (для электронного удара
[2.169]). Идея устройства автокатода основана на использовании особенно-
стей интенсивной эмиссии ряда металлов (молибден и др.) в парах цезия.
При «оптимальном покрытии» поверхности металла атомами цезия работа
выхода (электронов) частично покрытой цезием поверхности оказывается
минимальной, что обеспечивает эффективную работу автокатода при тем-
пературе 500 — 600' С. Температурный режим автокатода поддерживается

[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
автоматически за счет обратной ионной бомбардировки из разряда; поэтому
автокатоды требуют дополнительного подогрева (и дополнительного рас-
хода энергии) только в момент запуска ионного источника [2.169].
Для движителей с ударной ионизацией необходимо учитывать также
к. п. д. использования массы рабочего вещества
(2.49)
~р. = Да/Д
представляющий собой отношение расхода в ионной струе д,. к полному рас-
ходу рабочего вещества через движитель д. В ионных движителях с контакт-
ной ионизацией предельные зна-
— — Ую— чения ~ определяются степенью
ионизации и, по данным рис.
2.34, близки к единице. В дви-
Яд Гд жителях с ударной ионизацией
имеет место утечка части ней-
тральных атомов из камеры
ионизации через отверстия вы-
хода ионной струи (см. рис.
2.39, 2.40). По данным [2.119,
2.Ы41, значение к. п. д. исполь-
зования массы рабочего веще-
щ.щ' у~щ~ у ~~~„ства для таких движителей со-
ставляет примерно ~ =0,8 — '. 0,9.
Рис. 2.42. ~дельная масса ионных движителей с ударной
ел
ионизацией; рабочее вещество — ртуть. Так как поток утечки неит-
ральных атомов движется с теп-
ловой скоростью, много меньшей скорости ионной струи, то можно прене-
бречь вкладом этого потока в тягу и полезную мощность движителя. По-
этому, в соответствии с соотношениями (1.4), (1.5), эффективная скорость
истечения реактивной струи Г и полный к. п. д. ионного движителя ~, оп-
ределяются в виде
ЛО (д
(2.50)
Удельная масса ионных движителей с ударной ионизацией, по данным
[2.119], составляет примерно (=ЛХ /Р „250 — '500 кг/кГ, несколько сни-
жаясь с ростом максимальной скорости истечения реактивной струи
(рис. 2.42).
Электростатические ЭРД с ударной ионизацией электронным ударом мо-
гут использовать различные замкнутые траектории движения электронов,
т. е. различные камеры ионизации с осциллирующими электронами (см.
[2.164, 2.165, 2.169] и др.). Внутри камеры ионизации таких ЭРД (рис. 2.39)
образуется плазма ускоряемого рабочего вещества, из которой ионная реак-
тивная струя затем ускоряется электростатическим полем. Поэтому такие
ЭРД обобщенно относятся к классу плазменно-ионных ЭРД. Важной осо-
бенностью плазменно-ионных ЭРД является способность ускорять в реактив-
ной струе практически любые рабочие вещества, в том числе и воздух, т. е.
создавать воздушный ЭРД. Так, в полетах советских автоматических ионо-
сферных лабораторий «Янтарь-3» (1968 г. [2.101]) и «Янтарь-4» (1971 г.
[2.102]) впервые были успешно проведены испытания в ионосфере воздуш-
ных плазменно-ионных ЭРД и достигнута скорость воздушной реактивной
струи 140 км/сек.
Для ионных и плазменно-ионных ЭРД принципиальной является про-
блема нейтрализации ионной реактивной струи. Если у ЭРД система нейтра-

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
Рис. 2.43. Автоматическая ионосферная лаборатория«Янтарь» с воздушным плазменно-ионным ЭРД.
Проблема нейтрализации реактивной струи ЭРД в ионосфере была разрешена
з полетах советских автоматических ионосферных лабораторий «Янтарь»
(рис. 2.43) ~2.99 — 2.1021.
Критерием совершенства системы нейтрализации реактивной струи ЭРД
является величина потенциала корпуса летательного аппарата ~р. При пол-
ной нейтрализации потенциал корпуса близок к нулю (и=О), при отсутствии
нейтрализации потенциал корпуса равен ускоряющему напряжению ионной
реактивной струи ~~ — Я) и реактивная тяга равна нулю. К. п. д. нейтрализа-
ции ~ определяется соотношением
( .5'1)
7~, = 1 — р/и.
Для определения к. п. д. нейтрализации автоматические лаборатории
«Янтарь» были оборудованы комплексом приборов для определения потенци-
ала корпуса ~ при полете в ионосфере на высотах 100 — 400 км при работаю-
щих ЭРД. Исследовались два типа нейтрализаторов: термоэмиссионные ней-
трализаторы и экономичные плазменные нейтрализаторы (см. [2.99 — 2.102]).
Результаты проведенных исследований (табл. 2.5) показали, что плазменный
нейтрализатор обеспечивает эффективную нейтрализацию реактивной струи
ЗРД с к. п. д. нейтрализации выше 99,5оо, тогда как при использовании
термоэмиссионного нейтрализатора имеют место существенные потери мощ-
ности. Высокие значения к. п. д. нейтрализации при эффективных плаз-
менных нейтрализаторах позволяют пренебречь потерями мощности на
лизации неэффективна, то улетающие в ионной струе положительно заря-
женные ионы создадут на летательном аппарате отрицательный заряд,
который притянет ионную струю обратно к аппарату, и в результате не реали-
зуется реактивная тяга. Эмиттер электронов — нейтрализатор (см. рис. 2.30,
2.39) должен обеспечить подачу в реактивную струю количества электронов,
равного количеству ионов, при малых затратах мощности на нейтрализацию
реактивной струи. Эффективность процесса нейтрализации реактивной струи
ЗРД вследствие большой протян~енности области нейтрализации практически
можно исследовать только в полете; при этом исследования нужно проводить
на различных высотах, чтобы оценить вклад заряженных частиц ионосферы.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
Таблица 25
Основные параметры ЭРД, испытанных по программе «Янтарьэ
Параметр
«Янтарь-2» «Янтарь-3»
«Янтарь-4»
«Янтарь-1»
Рабочее вещество ЭРД
Ускоряющее напряжение реактивной
струи й, в
Скорость истечения реактивной струи
К, км/сек
Потенциал корпуса при термоэмис-
сионном нейтрализаторе у„в
Потенциал корпуса при плазменном
нейтрализаторе у„в
воздух
2800
азот
2100 †22
воздух
2800
аргон
300
140
до 120
100 †2
40
140
50 — 300 100 — 150
50 — 70
6 — 10
5 — 10
3 — 8
бапнсчное Жипйое
аиуюаг
(2.52)
Р = — '/,р ° (Л~~Л)' Я
1+ е'+ 2е соя 2 (и!) (и ~) е,
нейтрализацию при анализе механики полета летательных аппаратов с плаз-
менно-ионными ЭРД.
В целом изложенное показывает, что с точки зрения механики полета
электростатические движители обеспечивают в широких пределах регули-
рование скорости реактивной струи К и тяги Р
~~~~~~ при высоком значении к. и. д
ЯВ 7. Солнечный парус. Движительным эле-
ментом двигательной системы с солнечным па-
русом является зеркальная поверхность, соз-
дающая тягу отражением солнечного свето-
вого излучения (рис. 2.44). Идея использования
для межпланетных полетов давления солнеч-
ного света давно привлекала сравнительной
простотой реализации. Первое серьезное иссле-
дование этой проблемы принадлежит Ф. А. Цан-
деру [2.204] (1924 — 1925 гг.). Для создания
тяги он рассматривал использование зеркал,
выполненных из тонких алюминиевых листов.
Исследования Ф. А. Цандера показали прин-
ципиальную возможность реализации межпла-
нетных полетов при использовании давления
солнечного света. Так, при толщине алюминие-
вого зеркала в одну тысячную миллиметра кос-
Рис. 2.44. Схема аппарата с сол- МИЧЕСКИЙ аППаРат С МаССОй В 1 т МОжЕт ОСУЩЕСт-
вить перелет с орбиты Земли на орбиту Марса
примерно за 300 сут; при этом масса паруса
составит — 400 кг, а его площадь — 0,15 10' м2, что соответствует круг-
лому парусу диаметром — 450 м.
Солнечный парус как движитель создает тягу, используя поток энергии
и массы электромагнитного излучения Солнца (см. выше формулы (1.17),
(1.18)). При взаимодействии потока солнечного светового излучения с по-
верхностью паруса происходит изменение вектора количества движения
потока фотонов.
В соответствии с формулой (1.18) величина тяги, создаваемая освещен-
ным Солнцем плоским парусом площадью Я, будет равна [2.205]

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
н направление тяги будет заключено между нормалью к теневой стороне
паруса п и направлением солнечного светового излучения 1 (рис. 2.45)~
пР = агсвгп
г~ Э
~1+ ~~ + 2в сов 2 [и1)
(2.53)
где и — единичный вектор направления нормали к поверхности, 1 — единич-
Л, Г~
ный вектор направления солнечного светового излучения, п1, пР— углы
Ю~рус
Ю~фус
Рис. 2.45. Направление тяги солнечного
паруса.
Рис. 2.46. Диаграмма тяги солнечного паруса.
Р,, ='~.,р~ (Лз~Л)' Я соч й,
(2.54)
т. е. в предельном случае тяга полностью поглощающего свет паруса всегда
направлена по солнечному световому излучению, независимо от угла уста-
новки паруса.
В случае идеально отражающей зеркальной поверхности (при а=1)
максимальная величина тяги плоского паруса возрастает вдвое, а направле-
ние тяги совпадает с нормалью к теневой стороне паруса, и им можно управ-
лять, изменяя ориентацию паруса относительно солнечного светового из-
лучения (рис. 2.46) '):
Р =р (Л /Л)'Я соч'Ьп.
(2.55)
Все современные исследования по солнечному парусу (см. ниже гл. 12)
ограничиваются этим простейшим случаем. Дополнительные возможности
управления тягой, создаваемой солнечным парусом, появляются при рас-
смотрении системы зеркал, установленных под разными углами к направле-
нию солнечного светового излучения (см. работу Ф. А. Цандера [2.204]).
') В. В. Белецкий в [1.69] обратил внимание на описку в формуле (2.55), допущен-
ную в предыдущей книге авторов [1.71] (там эта формула имела номер (2.53)): отсутствие
квадрата у косинуса. Эта описка породила неверный вид диаграммы, соответствующей
злесь рис. 2.46 (старый рис. 2.39), и формулы (3.9). Авторы, принося извинения читателям
а благодарность В. В. Белецкому, отмечают, что предыдущая формула (2.50) из [1.71]
[злесь (2.52)), частным случаем которой является формула с опиской, и последующие фор-
мулы [9 180), [9 183) из [1.71], дублирующие ее, были записаны верно.
между векторами и и ], и и Р соответственно, (и ° !) — скалярное произве-
денпе единичных векторов и и 1 (т. е. косинус угла между ними, (и ° 1) =
= сов Ь).
Управляющим параметром солнечного паруса как двигательной системы
является угол установки паруса о, от регулирования которого зависят на-
правление и величина тяги.
Однако при полном поглощении света поверхностью паруса (при а=О),
согласно (2.52), (2.53),

[гл. 2
62
Физические пРинципы дВиГАтельных систем
Следует отметить, что металлические поверхности алюминия и серебра
(рассматриваемые как материалы или покрытия для солнечного паруса)
обладают коэффициентом отражения солнечного светового излучения, близ-
ким к единице (рис. 2.47), что оправдывает проведение предварительного
анализа характеристик солнечного паруса в идеальной постановке при
а=1 [2.751.
Рассмотрим затраты массы на создание тяги при помощи плоского сол-
нечного паруса. Здесь отсутствуют все компоненты массы, кроме массы соб-
ственно движителя — паруса:
(2.56)
М, = ЙЯ;~',ра,
где р — плотность материала слоев паруса, 3 — толщина слоев материала„
Рб
Ви8импе с5е~пйе
излучение
Рис. 2.48. Характеристики солнечного паруса
из алюминиевой фольги (сплошные кривые)
и из алюминированной пластмассовой пленки
(пунктирные кривые).
Рис. 2.47. Коэффициент отражения металлических
поверхностей в зависимости от длины волны
падающего светового излучения.
из которого состоит парус, Й вЂ” коэффициент, учитывающий массу вспомо-
гательных элементов конструкции паруса (по оценкам [2.206], значение
коэффициента Й мало отличается от единицы).
Максимальная тяга Р „., создаваемая парусом, установленным перпен-
дикулярно к солнечным лучам (~=0), при я=1, согласно (2.55), равна
Р,„= р~ (Й /л)2 Я. (2.57)
Соответственно удельная масса паруса как движителя составит
/с~ ра
Р шах )~Д (~~/ф)
(2.58)
а соотношение
(2.59)
~шах 1/'~'
определяет максимальное ускорение а „, которое может сообщать косми-
ческому аппарату двигательная установка с солнечным парусом (при ЛХ=М ).
На рис. 2.48 приведены примерные значения удельной массы солнечного
паруса и развиваемого им максимального ускорения (на орбите Земли:
Л~/Л=1 и 1=1) в зависимости от толщины материала паруса, выполненного
из алюминия (р — 2,7 10' кг/м') или алюминированной пластмассовой пленки

РЕАКТИВНЫЕ ДВИЖИТЕЛИ
(2.60)
гпе А — атомный вес изотопа, А* — число Авогадро, Я вЂ” площадь поверх-
ности паруса; остальные обозначения указаны в табл. 2.6.
Скорость реактивной струи определяется энергией а-частиц Е„; эффек-
тивное значение скорости струи Г, осредненное по полусфере, равно поло-
вине истинной скорости а-частицы:
Г = 1/ ~/2Е„/т„. (2.61)
(~ 1,2 10' кг/мз). Для обсуждаемых в указанной выше литературе толщин
паруса — из алюминиевой фольги Π— 10 ' м и из пластмассовой алюмини-
рованной пленки Π— 2,5 10-' м — удельная масса солнечного паруса нн
орбите Земли составит т 3000 кг/кГ и максимальное ускорение, сообщаемое
парусом космическому аппарату, порядка а,„З ° 10 ' м/сек2. Дальней-
шее существенное улучшение характеристик солнечного паруса (как движи-
теля) путем снижения толщины используемых пленок лимитируется потерей
Зеркальных свойств поверхности при толщинах порядка длины волны све-
тового излучения, а также учетом сублимации в вакууме и микрометеорной
эрозии.
Однако и при указанных на рис. 2.48 характеристиках паруса, соответ-
ствующих толщине материала порядка (1 — '. 2,5) ° 10-' м, двигательная уста-
новка с солнечным парусом может доставить косми-
ческий аппарат с орбиты Земли на орбиты ближай-
ших планет за 100 — 200 сут (см. ниже).
Ф
8. Изотопный парус. Другим типом рассмат- К
риваемого в литературе парусного движителя яв-
ляется изотопный парус, использующий для созда-
ния тяги реакцию от одностороннего вылета а-частиц
рзлиоактивного распада [2.75, 2.811. Хотя радиоак-
тивные изотопы (см. ниже табл. 2.9 в ~ 2) могут
явиться источниками как а-частиц (ионы гелия), так
и ~-частиц (электроны) больших энергий, рассмот-
рение а-излучателей предпочтительнее вследствие
знвчительно большей массы а-частиц и меньшей
проникающей способности. Последнее свойство осо-
Оенно важно, так как, по сути, определяет возмож-
ности изотопного паруса как движителя, основной
проблемой которого является обеспечение односто-
Рис. 2. 49. Схема изотоп-
роннего вылета ~-частиц, образующих реактивную ог пару, оз р .1о
струю. На рис. 2.49 приведена принципиальная схе-
ма изотопного паруса [2.75), использующего радио- а-частиц.
активный изотоп Ро'" ( а-излучатель). Парус представ-
ляет собой тонкий слой изотопа Ро"о толщиной Р, нанесенный на пласт-
массовую планку толщиной Р* (поглотитель частиц). Реактивная струя
изотопного паруса представляет собой поток положительно заряженных
я-частиц; поэтому должна осуществляться нейтрализация реактивной струи
подводом электронов, как в ионных движителях. Основные параметры
элементов изотопного паруса представлены в табл. 2.6.
Как видно из табл. 2.6, толщина пластмассовой пленки Р* выбирается
рввной пути пробега а-частицы в пластмассе, что существенно снижает по-
ток а-частиц за пластмассовой пленкой, 3* — толщина слоя Ро"' — выби-
рвется в — 10 раз тоньше пути пробега а-частиц в Ро"', что обеспечивает
вылет из паруса в сторону слоя изотопа примерно половины образующихся
а-частиц [2.75). Расход массы в реактивной струе изотопного паруса опре-
деляется числом а-частиц, образующихся при радиоактивном распаде:
д = — Х, Яо'"т„е-'",

Физические пРинципы двиГАтельных систем
[ГЛ. 2
Таблица 26
Параметры изотопного паруса
р* — плотность Ро21О, г/смз
9,2
6,7 10 24
138
т„— масса а-частицы, г
1 — период полураспада Ро21О, сут
Х,
1, — постоянная распада Ро21О, 1/сек
ń— энергия а-частицы для Ро21О, дж
Пробег а-частицы в Ро21", м
б* — толщина слоя Ро"о, м
~** — плотность пластмассы, ~~сма
Пробег а-частицы в пластмассе, м
У'* — толщина пластмассовой пленки, м
5,8-10-8
8,5.10-1з
6,5106
6,5 10-'
2,0
3 10-~
3.10-~
Соответственно (2.60) и (2.61) тяга, развиваемая изотопным парусом,
составит
Р = дГ= ~ Жт''*Е'~е-' '.
.4
а а
(2.62)
При указанных в табл. 2.6 параметров удельная тяга, удельная масса
и скорость струи для рассмотренного примера изотопного паруса равны
Р „/Я вЂ” 2,6 10 'е-" кг/м', т=М/Р „=25000,
Г 8 ° 10' м/еек, д /М = — Р,„~7М 5 ° 10 11((~,.
(2.63)
~ 2. Энергоустановки космических летательных аппаратов
1. Источники энергии. Для космических летательных аппаратов рас
сматривается использование химических источников энергии, ядерных и
радиоизотопных источников энергии и солнечной энергии (см. [2.2, 2.8—
2.12, 2.36, 2.37, 2.70 — 2.76, 2.811 и др.).
Источником химической энергии являются вещества, способные всту-
пать в экзотермические реакции. Наиболее распространенная из таких реак-
ций — окисление (горение), в которой участвуют горючее и окислитель.
Экзотермической является также реакция разложения некоторых веществ,
которая используется в двигателях с унитарным рабочим телом. При ис.
пользовании химической энергии в тепловых реактивных двигателях основ-
ными параметрами с позиций механики полета являются состав и температург
продуктов реакции, определяющие максимальную скорость истечения реак-
тивной струи (см. выше ~ 1). Важными являются также исходные параметры
топлив (агрегатное состояние, плотность и др.), связанные с параметрами
массы системы подачи и хранения рабочего тела. В качестве иллюстрации
в табл. 2.7 по данным [2.12, 2.36, 2.73, 2.207 — 2.2111 указаны основны~
характеристики некоторых типов ракетных топлив.
В целом с позиций механики полета изотопный парус является движи-
телем с почти постоянной тягой, медленно изменяющейся по времени, и
практически нулевым расходом массы (2.63).
Помимо рассмотренных выше типов реактивных движителей космиче-
ских двигательных систем, в литературе обсуждаются и движители болев
далекой перспективы (фотонные, термоядерные и др.), с начальными сообра-
жениями о которых можно познакомиться, например, в работе [2.751.

65
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
$21
Таблица 27
Основные характеристики некоторых ракетных топлив
Максимальная величина
удельного импульса
при р = 35 ° 10' кг/м',
1', сек
Оптимальное
соотношение
состава топ-
ливной смеси
"*ор~
Плот-
ность
р ~г/щз
Температура
сгорания
ТО °
ТОПЛИВО
на уровне
моря при
О~ сто~ ~~ = 8
в космосе
при
'~с/~ ~ — — 2,5
261
2,25
3200
324
1010
357
364
246
3,5
4,0
2,4
2480
2600
282~
441
447
304
256
304
1210
740
1390
167
137
2900
1610
200 †2
При использовании химической энергии регулирование температуры
продуктов сгорания Т, (и соответственно скорости истечения реактивной
струи Г, см. выше ~ 1) может производиться за счет отступления от оптималь-
ного соотношения состава топливной смеси а,'„,. На рис. 2.50 приведен при-
мер изменения температуры сгорания керосина в кислороде в зависимости от
Т,К
ЯЮ
04
Рис, 2.50. Температура сгорания керосина
в кислороде.
козффициента избытка окислителя а*/ а', [2.111. Следует отметить, что
такое регулирование позволяет только снизить температуру сгорания Т, (
(Т,,„и соответственно скорость истечения реактивной струи Г ( ~ „.
Выделение химической энергии в тепловых реактивных двигателях
происходит в камерах сгорания. Расход д продуктов сгорания в реактивной
струе определяется подачей жидких компонент в камеру сгорания или ско-
ростью сгорания заряда твердого топлива. Как было показано выше в ~ 1,
максимальный расход д „через реактивное сопло пропорционален макси-
мальному полному давлению в камере сгорания ро,„, которое, естественно,
ограничено прочностными характеристиками камеры. Уменьшение подачи
компонент снижает полное давление в камере и и позволяет соответственно
5 Механика полета
Жидкий кислород+кер-
осинн
Жидкие 02+Н2
Жидкие Р2+Н,
Азотная кислота+не-
симметричный диме-
тилгидразин
Однокомпонентное топ-
ЛИВО Н202 90%
Твердое топливо — бал-
листит 1РМ
Рис. 2. 51. Регулировочная характеристика ЖРД
при Т,=Т, дед. Сплошная кривая — теория, точки—
эксперимент.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
регулировать расход в пределах д ( д,„. При поддержании максимальной
температуры в камере Т,,„[максимальной скорости истечения Г,„) регу-
лирование расхода д вызывает почти пропорциональное изменение тяги дви-
гателя: Р(Р,„д(д,„[рис. 2.51) [2.2]. Более точные соотношения см. в ра-
ботах [2.212 — 2.214] и др.
Ядерные источники энергии на современном этапе развития ядерной
физики используют реакцию деления тяжелых ядер — реакцию расщепления
[см. [2.2, 2.36, 2.71, 2.72, 2.215 — 2.225] и др.). Расщепляющимися материа-
лами являются изотоп урана 02З5 и плутоний Ри2З', получающийся в специа-
лизированных реакторах. Деление ядра расщепляющегося материала про-
исходит при проникновении в ядро свободного нейтрона; ядро переходит
Рис. 2.52. Схема энергетического ядерного реактора: Л вЂ” активная зона,  — кожух, С и Л вЂ” входной
и выходной коллекторы теплопосителя; 1 — моптажная плита, 2 — замедлительнейтронов, "— отра-
жатель нейтронов, 4 — регулирующий стержень, 5 — тепловыделяющий элемент.
в возбужденное состояние, равновесие ядра нарушается, и оно делится на
«осколки» с вылетом двух-трех вторичных нейтронов; последние поддержи-
вают цепную реакцию. Основная часть энергии деления ядра [свыше 80О'')
соответствует кинетической энергии разлетающихся «осколков», которая
превращается в тепловую энергию при задержании «осколков» деления эле-
ментами реактора, например тепловыделяющими элементами [рис. 2.19).
Мощность К„, выделяемая реактором, может регулироваться путем воздей-
ствия на параметры цепной реакции, которая замедляется, например, при
введении в реактор регулирующих стержней из поглощающих нейтроны ве °
ществ [кадмий, бористая сталь). Принципиальная схема энергетического
реактора с твердыми тепловыделяющими элементами приведена на рис. 2.52
[2.2]. В литературе [[2.75, 2.80, 2.81] и др.) рассматриваются также жидко-
фазные и газофазные реакторы.
Критическая масса расщепляющегося материала, необходимая для
цепной реакции, составляет примерно ЛХ„=5,0 — '200 кг [2.75] и не зависит от
мощности реактора. Поэтому основную массу энергетического реактора
большой мощности составляет система теплоотвода, типичными элементами
которой являются образуемые тепловыделяющими элементами каналы теп-
лообменника, обеспечивающего заданную степень нагрева теплоносителя
[см. рис. 2.19, 2.52). Движение газового теплоносителя в канале постоянного
сечения хорошо описывается теорией одномерного стационарного течения
вязкого газа с использованием данных гидродинамической теории тепло-
обмена [2.5, 2.226 — 2.233].

67
ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
э 2]
(2.64)
где р — плотность, с — теплоемкость и ри постоянном давлении, И' — скорость потока
газа, Х вЂ” приведенная скорость, й — диаметр трубы, Т вЂ” температура стенки трубы,
бб !б5 Лб ббб 4бб х/Ю
~а' ~а~ ю„,~ь
Рис. 2. 53. Изменение давления р, температуры Т
и приведенной скорости ), газового потока вдоль
нагреваемой трубы. Сплошные кривые — теория,
точки — эксперимент.
Рис. 2.5/1. Удельная масса энергетического реак-
тора: 1 — с газовым теплоносителем, 8 — с жид-
кометаллическим теплоносителем.
1 ~
Т, — температура торможения газового потока, ф, = [1 — 1,74 Йе "[Рг — 1)] — коэффи-
циент, учитывающий отличие числа Пранд1тля РГ от единицы, Ке — число Рейнольд1са.
Решения системы (2.64) хорошо согласуются с экспериментом. 11а рис. 2.53 дан при-
мер сопоставления теоретических данных [2.228) и эксперимента [2.230] по течению газа
вдоль нагреваемой трубки.
Анализ решений системы (2.64) указывает на прямую связь заданной
степени нагрева газового потока ЛТ,/Т, и потребного числа калибров ка-
нала теплообменника Ь/О. Максимальная степень нагрева достигается при
звуковой скорости в конце канала теплообменника (см. рис. 2.53). Поэтому
с учетом соотношения (2.21) и ограничения по максимальной температуре
материала реактора (Т, ( Т„, „,.) масса энергетического реактора большой
мощности с газовым теплоносителем должна быть примерно пропорциональна
мощности Ж„:
ЛХ„- Р„т,ГтЬТ, — Т„.
(2.65)
Аналогичное соотношение должно выполняться в энергетическом реакторе
с жидким теплоносителем (предельный случай: ~ -+ О в (2.64)), а также при
изменении агрегатного состояния теплоносителя, так как законы течения
двухфазной среды и газовых потоков аналогичны (см. например, [2.234]).
В качестве иллюстрации на рис. 2.54 по данным [2.75] приведено изменение
удельной массы энергетического реактора ЛХ„/Г„в зависимости от полной
мощности реактора Г,,. Видно, что при Г„& t; 04 вт значе ие удель
массы реактора стабилизируется.
Для высокотемпературных тепловых реактивных двигателей с реакто-
ром-теплообменником масса последнего примерно пропорциональна тяге
5*
При использовании известной связи между коэффициентом теплоотдачи Й, и коэффи-
циентом гидравлического сопротивления ~: Й,='/,1 ~с И'ф„дифференциальные уравнения
движения газа в трубе с учетом трения и конвективного теплообмена записываются в виде

68
Физические пРинципы дВиГАтельных систем
[ГЛ. 2
двигателя (2.22), что позволяет (как показано в ~ 1 этой главы) включить его
параметры в значения обобщенной удельной массы двигательной системы
(см. выше табл. 2.1).
Выделение энергии в ядерном реакторе связано с некоторым расходом
массы делящихся веществ д,. Рассмотрим соотношение между расходом д,
и расходом массы через движитель д.
т а б л и ц а ~.8 В случае использования ядерной энергии
расход расщепляющегося вещества д,
можно оценить из соотношения, связы-
вающего массу с энергией. Если обозначить
через ~о коэффициент превращения рас-
хода д, в кинетическую энергию реактив-
ной струи, то связь между расходом рабо-
Отношение расхода
расщепляющегося вещества
в реакторе д к расходу через
движитель д ядерной двигательной
системы в зависимости
от скоро; ти реактивной струи Г
чего вещества через движитель и расходом
расщепляющегося вещества запишется в
виде
105
106
104
Г, м/сею
10
10-4
10 6
1
Т72 . 2
Тд" ='-Одбс
(2.66)
где с — скорость света. По данным работы [2.71] при х,=5 ° 10-' зависимость
отношения д,/д от скорости истечения струи Г представлена в табл. 2.8.
Данные табл. 2.8 показывают, что в характерном для обсуждаемого в ли-
тературе ([2.75, 2.81] и др.) уровня
л' скоростей струи К=104 — '10' м/сек
расход расщепляющегося вещества д,
пренебрежимо мал по сравнению с
У'о 4 расходом через движитель О.
«к
Существенной массовой компо-
нентой в двигательных системах с
ядерным реактором является масса
Рис. 2.55. Схема теневой экранир~в~ж реа" ЗащИтЫ ~' От НЕйтрОННЫХ ПОТОКОВ
тор, 2 — защита от ~-излучения, 3 — защита от и
потока нейтронов, 4 — полезная нагрузка. и "~-излучения. Так каК интенсив-
ность излучения падает обратно про-
порционально квадрату расстояния от реактора, то для снижения массы
защиты рассматривается теневая защита с выносом полезной массы на не-
которое расстояние Р от реактора (рис. 2.55 [2.751). С той же целью сни-
жения массы защиты в работах [2.235 — 2.237] и др. рассмотрены вариа-
ционные задачи об оптимальном профилировании толщины защитного
слоя х*.
В качестве примера по данным работы [2.236] на рис. 2.56 приведено
изменение оптимальной безразмерной массы Я„защиты от т-излучения
дискового источника в зависимости от безразмерной допустимой дозы ра-
диации с~*:
и 2д~''2~ У 2~ у~~['
(2.67)
где р* — коэффициент ослабления в защите, р — плотность материала за-
щиты, с~* — допустимая доза радиации, à — поверхностная интенсивность
источника излучения, Й вЂ” переводной коэффициент интенсивности радиации;
угол ро показан на рис. 2.55.
В целом масса защиты М„зависит от полной мощности реактора Г„.
По данным [2.751, удельная масса защиты сохраняется примерно постоянной
при Г„)~ 104 квт (рис. 2.57).
Другим источником ядерной энергии является энергия распада радио-
активных изотопов ([2.75, 2.81, 2.238, 2.2391 и др.). Энергия распада радио-

ЭНЕРГОУСТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
Таблица 29
Параметры радиоактивных изотопов, рассматриваемых
в качестве источников энергии космических энергоустановок
Максимальная
удельная
мощность
Период полу-
распада
~уЛ
Плотность
~ к~~,~~э.10 — э
Топливное
соединение
Тип излу-
чения
Изотоп
& t; „~
~~ ц/шах
'"- 141
Ро
Альфа
138 суток
162 »
СП~2О3
РиС
86,4 года
285 суток
2,6 года
33»
Се02
РШ2О
СяС1
С~137
ЯГ90
28 лет
5,3 года
~гТ1ОЗ
Со
Со60
изотопов может использоваться в тепловых ракетных движителях и непо-
средственно в парусных движителях (см. ~ 1 настоящей главы), а также
в тепловых энергетических источниках энергоустановок.
В ядерной физике известно несколько сотен радиоактивных изотопов,
но только некоторые из них рассматриваются для использования в источ-
никах энергии космических двигательных
систем.
Первым критерием пригодности радио-
изотопа является период полураспада
!03 Ю4
!д~ Ф„,Иш
Рис. 2. 56. Мипимальпая масса
защиты для дискового источника
~-излучепин.
Рис. 2.57. Зависимость удельпой массы защиты
от полной мощности реактора при выносе полез-
ной нагрузки 1*=25 м и мощности дозы
100 л~бэр/сут: 1 — реактор с газовым тепло-
носителем, 2 — реактор с жидкометалличес;&lt
теплоносителем.
19, (&gt ., Ђ” постоян ая распад ). Эффективн ми считаю ся изот п с
риодом полураспада более -100 суток, так как изотопы с очень корот-
ким периодом полураспада нельзя экономично хранить или использовать
в длительных полетах. Вторым важным критерием является максимальная
удельная мощность и тип испускаемого излучения. В качестве иллюстрации
по данным [2.238) в табл. 2.9 приведены характерные параметры ряда ра-
диоактивных изотопов, рассматриваемых для использования в космических
двигательных системах. Отметим, что удельная мощность радиоизотопного
источника энергии уменьшается по времени в соответствии с периодом полу-
распада:
Ж„~ЛХ„= (Ж„~М„) „„е-' '.
(2.68)
Ро2'0
СШ242
Р>ц
Се144
РП~147
Бета, гамма
То же
»»
»»
»»)
9,3
11,8
12,5
6,4
6,6
3,9
4,8
9,0
100
0,55
1,95
0,12
0,33
0,11
0,30

70
Физические пРипципы дВиГАтельных систем
[ГД. 2
Из внешних потоков энергии наибольшую интенсивность в межпланет-
ном пространстве имеет поток солнечного светового излучения, мощность
которого на орбите Земли составляет!М~~ 1400 вшам'. В литературе ([2.82,
2.238, 2.240] и др.) подробно рассматривается устройство оптических кон-
центраторов солнечной энергии в виде параболических зеркал, отражателей
Френеля и др. По данным [2.238], удельная масса концентраторов солнеч-
ной энергии на орбите Земли составляет примерно [3 =ЛХ„/Яз=1.5 — '.
Рис. 2. 58. Солнечный концентратор «Саифл~эр» (масштаб м ~доли 1: 3); полная площадь Я~ — 68 дф',
масса концентратора и конструкции М„= 115 кг.
=3,0 кг lм', (ЛХ„/Г„) в=1 — '2 кг ~квт и изменяется соответственно квадрату рас-
стояния Л до Солнца:
ЛХ„/Т„= (ЛХ„/Ж„), (В,~К)'.
(2.69)
Пример конструкции концентратора см. на рис. 2.58 [2.238].
2. Системы преобразования энергии. В тепловых реактивных двигателях
преобразователем энергии является движитель (см. ~ 1), превращающий
тепловую энергию нагретого источником энергии газа в кинетическую энер-
гию направленного движения реактивной струи. В парусных двигательных
системах (солнечный и изотопный парус) движитель также является непо-
средственным преобразователем энергии. Специальных преобразователей
основной тепловой энергии источников в электроэнергию требуют рассмот-
ренные выше Я 1) электрореактивные движители. В литературе ([2.75, 2.79,
2.81, 2.238 — 2.269~ и др.) обсуждается ряд типов преобразователей энергии
и их элементов. На рис. 2.59 указаны основные принципиальные схемы
преобразователей энергии для электрореактивных движителей, использую-
щих солнечную энергию, энергию радиоактивных изотопов или ядерный
реактор [2.1051.
Схемы преобразователей энергии используют машинные и беэмаптинные
циклы. Для преобразователей с миптинными циклами (см. [2.75, 2.79, 2.238,
2.244 — 2.246] и др.) возможно использование газотурбокомпрессорного цикла
Брайтона и паротурбинного цикла Рэнкина. В газотурбокомпрессорном
цикле (рис. 2.60) нагретый в источнике энергии газ приводит во вращение

7Х
ЭНЕРГОУСТАНОВК И КОСМИЧЕСКИХ АППАРАТОВ
Фо~о - Юла
леон.ыжеил
Л~родЫ
~уою(м
Рео тли~
сюра
%
~Уижилель
Злеларогенера~пор
Жердью
реомюр
0зотопныо ~-нсточнцл
Элеапрогенертпср
Рис. 2.59. Принципиальные схемы преобразователей энергии: а) с использованием солнечной энергии,
б) с изотоппым ~-источником', в) с ядерным реактором.
В паротурбинном цикле (рис. 2.61) испарившийся в источнике энергии тепло-
носитель приводит во вращение паровую турбину и электрогенератор; в ра-
диаторе осуществляется конденсация пара в жидкую фазу, давление которой
повышается насосом. Диаграммы
температура — энтропия для ука-
занных термодинамических цик-
лов приведены на рис. 2.62. Вид-
но, что при одинаковых макси-
мальных температурах цикла Т,
(определяемых стойкостью мате-
Рис. 2.61. Схема преобразователя энергии по циклу
Рэнкина: 1 — источник тепловой энергии, 2 — влаж-
ный пар, 3 — сепаратор, 4 — жидкий теплоноситель,
5 — насыщенный пар, 6 — турбина, У и 8 — радиа-
торы, 9 и 10 — дополнительные теплообменники,
11 — насос с эжектором, 12 — электрогенератор.
Рис. 2.60. Схема машинного преобразова-
теля тепловой энергии в электрическую
по циклу Брайтона: 1 — источник тепло-
вой энергии, 2 — турбина, 3 — радиатор;
4 — компрессор, 5 — электр огенератор.
риалов) и одинаковом теплоперепаде на турбине Т,— Т4 в газовом цикле
средняя температура радиатора значительно ниже температуры радиатора-
конденсатора в паротурбинном цикле. Так как в космических энергоуста-
иовках отвод тепла радиатором осуществляется излучением (подробнее
газовую турбину, на оси которой установлены газовый компрессор (ком-
пенсирующий перепад давления газа по контуру) и электрогенератор; от-
вод не использованной в цикле тепловой энергии осуществляется радиатором.

[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
см. ниже в ~ 3), то потребная площадь и масса радиатора в газовом цикле
значительно больше, чем в паротурбинном цикле. В качестве иллюстрации
на рис. 2.63 приведен пример зависимости площади радиатора Я, от темпера-
туры перед турбиной Т, для газового и
паротурбинного циклов при полезной
мощности преобразователя энергии К,
1000 квт [2.78].
Вследствие меньшей потребной площади
радиатора в литературе [[2.75, 2.79, 2.238,
т,
50
1000 1Я0 1200 О00 Т, ,'К
Рис. 2. 62. Термодинамические циклы машинных энерго-
преобразователей: а) газ отурбокомпрессорный цикл
Брайтона (Т, — Т, — сжатие газа в компрессоре,
Т, — Т, — подвод тепла, Т, — Т, — расширение в тур-
бине, Т, -э Т, — отвод тепла в радиаторе); 6) паротур-
бинный цикл Рэнкина (Т, -э Т, — повышение давления
жидкого теплоносителя в насосе, Т, — Т, — подогрев
до точки кипения и испарение, Т., -э Т, — расширение
пара в турбине, Т4 -& t; Т, Ђ” конденса и в радиатор
Рис. 2. 63. Площадь радиатора: 1—
паротурбинный цикл Рэнкина, 2—
газовый цикл Брайтона.
И„'к~т
2.245, 2.246] и др.) преимущественно обсуждается паротурбинная схема.
Совершенство такой схемы во многом определяется совершенством газо-
гидродинамики турбоагрегата [см., например, [2.247 — 2.250]) с учетом
эрозии элементов в двухфазном потоке [2.251]. Масса элементов машинных
энергопреобразователей приблизи-
М ~р тельно пропорциональна полезной
мощности К„. Примерные значе-
ния удельной массы турбоагрегата
приведены на рис. 2.64 [2.75]. Для
электрогенератора, по данным
[2.79], удельная массы составляет
10 ' примерно М',/Г, 0,4 кг/квт.
К энергопреобразователям с
двухфазным потоком без турбо-
агрегатов относятся преобразова-
тели тепловой энергии в электри-
Рис. 2.64. Удельная масса турбоагрегата в зависимости
от полезной мощности. ческую, использующие жидкоме-
таллический цикл с магнито-
гидродинамическим генератором
[2.252, 2.253]. Такой преобразователь [рис. 2.65) содержит два контура:
например, контур жидкого лития и контур паров калия. Нагретый в источ-
нике энергии жидкий литий поступает в смеситель, где испаряет жидкий ка-
лий. При расширении в газодинамическом сопле пары калия ускоряют ли-
тиевый поток, а затем отделяются в сепараторе. Ускоренный жидкий литий
вырабатывает электроэнергию в МГД-генераторе. В работах [2.252, 2.253]
указывается, что такие преобразователи энергии при мощности К, )~
& t; 00 вт мо ут конкуриров ть по массо ым показате я с турбогенерат
ными преобразователями.

ЭНЕРГОИ СТАНОВКИ КОСМИЧЕСКИХ АППАРАТОВ
Я 2]
Безмашинные преобразователи энергии используют также термоэлек-
трические, солнечные и термоэмиссионные элементы ( [2.75, 2.79, 2.238,
2.254 — 2.269] и др.). В термоэлектрических преобразователях используется
эффект Зеебека по прямому переходу тепловой энергии в электрическую при
Рис. 2.66. Схема термоэлектрическо1 о преобра-
зователя энергии: 1 — источник тепловой энер-
гии, 2 — насос контура жидкометаллическ ого
теплоносителя, 3 — термоэлементы, 4 — канал
теплоносителя, 5 — радиатор (холодный спай).
Рис. 2.65. Схема преобразователя энергии, ис-
пользующего жидкометаллический цикл с МГД-
генератором: 1 — источник тепловой энергии,
2 — смеситель, 3 — сопло, 4 — сепаратор,
МГд-генератор, 6 — диффузор, у — радиатор,
8 — насос, 9 — теплообменник.
разных температурах двух стыков различных материалов (рис. 2.66). К. п. д.
термоэлектрического преобразователя равен [2.238, 2.254 — 2.256]
т,— т, я2я
7~ 2=
(4/г) + 2Т, — '!и (Т1 — Т2) ' л,
(2.70)
где Т, — температура горячего спая (стыка), Т, — температура холодного
спая, я — термоэлектрическая добротность материала, г — коэффициент
Зеебека, ~„— проводимость, Մ— теплопро-
Водность. Юлю
Для полупроводниковых термоэлементов
с я порядка 2 10 '1/К' к. п. д. достигает
-10% при перепаде температур Т, — Т,=
200' К [2.255]. Примерные значения удель- йара злетпрвн-„3ыриа'
ной массы термоэлектрического преобразов а-
теля 81]АР-10А вместе с радиатором (мате-
риал термоэлементов — ЙСе, я=0,6 10-'
1/' К), по данным [2.255], составляет
(К, + М,)/Т, 125 кг/квт. (2.71)
Рис. 2. 67. Схема кремниевого фото-
элемента.
(2.72)
ЛХ,/Т, = (ЛХ,/Ж„) (Н/Л,)2.
По данным [2.75, 2.257], удельная масса преобразователя энергии с сол-
нечными элементами на орбите Земли достигает примерно М,/Г„ь
Другим видом полупроводниковых элементов, осуществляющих непо-
средственное преобразование энергии солнечного светового излучения
в электроэнергию, являются кремниевые солнечные фотоэлементы (см. [2.75,
2.79, 2.238, 2.257 — 2.259] и др.). Такой фотоэлемент состоит из тонкого, тол-
щиною -2,5 мкм, р-слоя кремния, нанесенного на и-слой кремния
(рис. 2.67). Падающие на фотоэлемент фотоны солнечного излучения при-
водят к образованию пар электрон — (<дырк », кото ые од действ ем эл
трического поля между и- и р-слоями диффундируют через контактную по-
верхность, создавая разность потенциалов 0,3 — 0,5 в. Отдельные элементы
собираются на панелях в батареи. Удельная масса такого преобразователя
энергии, естественно, повышается пропорционально квадрату расстояния
до Солнца:

~ГЛ. 2
Физические пРинципы дВиГАтельных систем
— 50 кг/квт при к. п. д. до 10 — 14О~~. Крометого должныбытьучтены затраты
массы на ориентацию батарей солнечных элементов на Солнце (см., например,
[2. 259 ]) .
В термоэмиссионных преобразователях тепловой энергии в электри-
ческую электроны эмиттируются за счет тепловой энергии из нагретого ка-
тода и поглощаются более холодным анодом (см. [2.75, 2.76, 2.238, 2.260--
2.269] и др.). Для обеспечения этого потока электронов во внешнюю цепь
(на полезную нагрузку) работа выхода материала катода ~„должна быть
выше, чем у материала анода ~,. Данные о величине работы выхода электрона
для различных материалов приведены выше в табл. 2.4. Плотность тока эмис-
сии электронов с катода или анода по уравне-
нию Ричардсона — Дэшмана существенно зависит
от температуры Т:
~ = АТ' ехр [ — еэ/ЙТ],
(2.73)
РАФЫ
юе~югу
РюАЬУ
леала
где А — универсальная постоянная, равная для
чистых металлов 120 а/см' град', Й вЂ” постоян-
ная Больцмана.
Для обеспечения тока электронов от катода
к аноду при ~,. & t; ~, необходи о, чт бы темпе
тура анода была существенно ниже температуры
катода. Схема распределения потенциальной энер-
гии в промежутке между электродами термоэмис-
сионного преобразователя приведена на рис. 2.68.
Величина выходного напряжения, создаваемого
термоэмиссионным элементом. определяется соот-
ношением
(2.74)
Рис. 2. 68. Схема термоэмис-
сионного преобразования энер-
гии.
где ~, — кинетическая энергия электронов, ~„— па-
дение потенциала в плазме разряда. Для типичных
материалов, указанных выше в табл. 2.4, величина
напряжения Я порядка -1 в. Поэтому значительные удельные мощности
в термоэмиссионном преобразователе требуют большой плотности тока
величина которой ограничена пространственным зарядом (см. в ~ 1 соотно-
шения (2.42) — (2.44)). Согласно (2.44) осуществление большой плотности
тока требует очень малых зазоров И между электродами термоэмиссионного
преобразователя; так, например, для плотности тока — 1 а/см' (мощность
-1 вт./см2) необходим зазор менее 10 мкм. Столь высокие требования к меж-
электродному зазору существенно упрощаются при заполнении термоэмис-
сионного преобразователя парами щелочных металлов (Сз, Ва), которые
легко ионизуются и образуют в межэлектродном пространстве плазменный
слой высокой проводимости. Эффективный зазор как бы становится равным
пути пробега электрона до слоя плазмы, что много меньше геометрического
зазора. Кроме того, заполнение термоэмиссионного преобразователя, на-
пример, парами Ся повышает эмиссионные способности катода. В качестве
иллюстрации на рис. 2.69 по данным работы [2.267] приведены примерные
характеристики термоэмиссионного преобразователя, заполненного парами
щелочных металлов.
Конструктивно термоэмиссионные элементы в ряде работ (см. [2.76,
2.238 — 2.269] и др.) рассматриваются встроенными в ядерный реактор с жид-
кометаллическим охлаждением. На рис. 2.70 указаны примерные значения
удельной массы реактора с термоэмиссионным преобразователем в зависи-
мости от полезной мощности Г, [2.238] для схемы, изображенной на рис. 2.71
[2.238].

75
энеРГОустАнОВки кОсмических АппАРАтОВ
В балансе массы космической энергоустановки — источника мощности,
помимо указанных элементов, существенное значение имеет система тепло-
отвода неиспользованной в цикле энергии (см., например, [2.75] и др.).
Поэтому общий анализ массы источников мощности приведен ниже, в ~ 3,
4Х 8® ~200 ю„, Ь
16 И/
Рис. 2.71. Ядерный реактор с термоэмиссионным преобразователем: 1 — клемма вывода электрической
мощности, 2 — вывод продуктов деления, 3 — регулятор, 4 — опорная решетка, 5 — ввод охлаждаю-
щего теплоносителя, 6 — отражатель, У вЂ” термоэмиссионные элементы, 8 — клем а вывода мощности
для питания насоса, 9 — аварийная защита, 10 и 11 — резервуары с СБ, 12 — выход теплоносителя.
после рассмотрения характеристик систем теплоотвода от космических
энергоустановок.
3. Аккумуляторы энергии. Как было указано выше, основными видами
энергии в космических энергоустановках являются тепловая энергия и
Рис. 2. 69. Характеристики термоэмиссионных
преобразователей (анод — ЪЧ, т, = 2000' К, ка-
тод — Мо, зазор 0,25 мм, давление паров соот-
ветствует кипению при указанных на графике
температурах).
Рис. 2.70. Удельная масса реактора с термоэмис-
сиоппым преобразователем: 1 — удельная мощ-
ность преобразователя 10 вт/см', 2 — то же,
20 вт/см'.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
~ГЛ. 2
электроэнергия. Соответственно рассматриваются аккумуляторы тепловой
и электрической энергии ([2.75, 2.238] и др.).
Аккумулирование тепловой энергии возможно за счет теплоемкости
материала аккумулятора или использования теплоты фазового перехода;
второе предпочтительнее, так как позволяет аккумулировать тепловую энер-
гию при примерно постоянном температурном уровне Т„. Из фазовых пере-
ходов рассматривается плавление аккумулирующего тепло вещества, так
Т а б л и ц а 2.10
Удельная ма:сса аккумулятора тепловой энергии
(без учета массы контейнера)
И кг
~3=~ ~—
Дщ
Температурный
уровень Т~, 'Е1
Аккумулир ующее
вещество
Удельная масса
~~ = М~~ЕО1 ~г/®/С
0,36 10-6
1,95.10 6
8,8 10-6
950
1077
2042
Е|Н
ИаС1
~~~з ~~~~ фю ~ ~щ,
Рис. 2.72. Удельная масса серебря-
но-цинкового аккумулятора в зависи-
мости от энергии, накапливаемой в
одном элементе (напряжение 1,5 в).
как испарение привело бы к соответствующему росту давления в контейнере
аккумулятора. В соответствии с физико-химическими свойствами меньшая
удельная масса аккумулятора тепловой энергии ~„=ЛХ,/Е, имеет место при
использовании хлоридов и гидридов металлов [2.75, 2.238] (см. данные
табл.. 2.10). Использование чистых металлов (например, Р$ [2.270 ], см.
табл. 2.10) дает большое значение удельной массы
Из аккумуляторов электроэнергии меньшую удельную массу имеют
серебряно-цинковые щелочные аккумуляторы [2.75, 2.271] примерные зна-
чения удельной массы которых по данным работы [2.271] приведены на
рис. 2.72. Удельная масса электроконденсаторов порядка р,— 0,015 кг/дж
[2.79 ].
Данные табл. 2.10 и рис. 2.72 показывают, что удельная масса аккуму-
ляторов тепловой и электроэнергии одного порядка: ~,=(1 — '5) 10-' кг/дж.
~ 3. Теплоотвод от космических энергоустановок
1. Радиационные системы отвода энергии. В тепловых реактивных
двигательных системах с открытым циклом [см. выше рис. 2.10) необходимый
теплоотвод в основном достигается за счет предварительного подогрева
подаваемого рабочего тела. Так, например, в построенном в 1930 г. тепловом
реактивном двигателе Ф. Цандера ОР-1 (рис. 2.73) охлаждение осуществля-
лось окислителем — сжатым воздухом, проходящим по каналу вокруг
камеры сгорания перед поступлением в камеру [2.204].
Для космических двигательных систем, включающих энергоустановку
с замкнутым циклом (см. выше рис. 2.59), энергетический к. п. д. системы
т),=Г„/К„, равный отношению полной мощности реактивной струи дви-
жителя К„К, к мощности энергоисточника К„, как обычно для энерго-
установок порядка десятка процентов. Поэтому для энергоустановок с замк-
нутым циклом большая часть мощности, выделяемой источником энергии,
равная
/~~, = /~~„— /~„= /~/„(1 — гз)/Ь
(2.75)
1) Учет мощности Гд,., привносимой забираемым рабочим телом, пе изменяет прин-
ципиально дальнейшего анализа. Для простоты рассматриваем случай Г „=О.
должна быть отведена от космического аппарата примерно на низшем тем-
пературном уровне энергетического цикла -Т,, ').

ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
77
Основным обсуждаемым в литературе (см. [2.75, 2.238] и др.) методом
отвода мощности К, является лучистый теплоотвод с помощью радиаторов
различного вида. Величина потребной площади поверхности радиатора Я,
связана с мощностью К, по закону Стефана — Больцмана:
Жх 1 — 10
(2.76)
оы1 П1~~ ~10
Соотношение (2.76) приведено для случая отсутствия существенных
внешних тепловых потоков и для радиаторов без самооблучающихся поверх-
ностей; примером такой системы может служить плоская излучающая поверх-
ность в космосе, расположенная параллельно потоку солнечного излучения.
Рис. 2.73. Реактивный двигатель ОР-1: горючее — бензин, окислитель — сжатый воздух, тяга Р=5 кT.
Как было указано выше, обсуждаемые в литературе типичные косми-
ческие энергоустановки работают по тепловому циклу. Энергетический
к. и. д. ~, связан с максимальным и минимальным температурным уровнями
энергоустановки:
(2.77)
где Т = Т „/Т „, коэффициент «) учитывает отличие от идеального энерге-
тического цикла.
Согласно (2.76), (2.77) величина потребной площади радиатора равна
ш„~~ — )„~1 т))
аиТ ~)„~1 — Т) Т
(2.78)
При заданных значениях мощности струи .~вихсителя у„, максимально допу-
стимой температуры цикла энергоустановки Т „(а также и и 1) ) величина
площади радиатора достигает минимума при следующем оптимальном значе-
нии Т:
5 5 ~ 1
т1пЯ при Т =1 — — + 1 — — +
орс
8~„
(2.79)

~ГЛ. 2
Физические пРинципы дВиГАтельных систем
Зависимость Т„„(~ ) приведена на рис. 2.74; видно, что при ~ =1,0 Г,„, = — ~
и несколько повышается с уменьшением значения ~,. Соответствующие мини-
мальные удельные значения Я, и/К„приведены на рис. 2.75. Видно, что
для обсуждаемого в литературе диапазона допустимых значений Т,
1000 — 2500' К (см., например, [2.75, 2.238 ] и др.) удельная площадь
Об
с ф
Е
б5 бб б7 бд бб
Рис. 2.74. Оптимальное соотношение температур- Рис. 2.75. Минимальная площадь радиатора.
ных уровней.
радиатора составляет — 10 ' — '10 ' м'/квт, т. е., например, уже для энерго-
установки мощностью Г, Г„=20 000 квт (для движителя с тягой порядка
10 кГпри удельном импульсе 1' 10 000 сек) необходим радиатор площадью
в сотни квадратных метров. В связи с большими потребными площадями
радиаторов существенными являются
вопросы их массы; ниже эта проблема
рассматривается для двух типичных
схем: оребренного трубчатого и лен-
точного радиаторов.
Аб
т,
Рис. 2.76. Плоский оребренный трубчатый
радиатор.
Рис. 2.77. Схема плоского оребрения.
2. Система отвода энергии с плоским оребрепным трубчатым радиато-
ром. Принципиальная схема такой системы отвода энергии приведена на
рис. 2.76 [2.75]. Отвод энергии, подводимой текущим внутри трубок тепло-
носителем, осуществляется излучением с поверхности оребренных трубок.
Рассмотрим задачу минимизации массы вначале для системы с трубками
очень малого диаметра, что эквивалентно плоской задаче минимизации массы
системы ребер, охлаждающих излучением параллельно расположенные
с некоторым шагом 2Ь линейчатые источники тепла (рис. 2.77, а). Вследствие
симметрии достаточно рассмотреть участок ребра АВ (охлаждаемого излу-
чением по АВ) на полушаге Ь при одностороннем подводе тепла к ребру

ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
79
по основанию ребра ОА (рис. 2.77, б) при заданной минимальной толщине
ребра О'В [2.2721. Будем рассматривать тонкое ребро с пологим контуром,
для которого уравнения теплопередачи вдоль ребра и закон теплового излу-
чения справедливы в следующей форме:
(~ = 2Х„у аТ/Их, Щ)~х = 2аиТ~,
(2.80)
где у — полутолщина ребра, ось — х направлена вдоль ширины ребра,
(',) — тепловой поток по ребру на единицу длины ребра, л — коэффициент
теплопроводности, Т вЂ” температура ребра.
Оптимальный контур сечения ребра минимальной массы долнсен обеспе-
чить минимум площади сечения ребра Я = — 2 удх при заданных началь-
о
ном тепловом потоке Ч„начальной температуре Т и минимальной толщине
ребра у) у „.
Введем безразмерные переменные:
— Т = Т~Т„,
(2.81)
х у Д
чо/2аиТ4 ' Я,~41„ао~Тз ' Я(81 а2и2Тэ
'.Гогда
у Их.
(2.82)
На краю ребра (при х=Х) нам известно значение только переменной ~=~ =О.
Поэтому удоонее искать остальные переменные как функции от ф Т ф), х Я), ц Я).
Уравнения (2. 82) перепишем в виде
нт
(2.83)
Н~ уТ4
где Т=1, у=у, при (~=1; Т=Т, у=у~;, при Я=О.
В такой постановке задача может быть решена на основании принципа максимума
[2.273]. Следуя [2.273], введем новую переменную
Г,= — 2:НЯ
ГХ4
1
и будем рассматривать задачу об оптимизации конечного значения этой переменной при
(~=0. Гамильтоиова функция П (см. [2.273]) запишется в виде
(~ 2ч
Н=р1,— р (2.84)
'УГ
где
4 р,Я, дН
= — 2р2у, р~ = — = О,
дЧ
1 дгу
(2.85)
с граничиьп1и условияии: р, =О, р2= 1 при (~= О. Заметим, что импульс р — по-
стоянная величина, р, = 1 (см. (2.85)). Согласно [2.273], функция Н должна быть
максимальной по у при любых значениях Т и р,. На кра|о ребра при (~=0 и р,=О
максимум П, естественно, достигается при у =у;„; тогда Н~ — — — 2дп; Т 4 и (р')
Л
= — 8у „„. ~ ~. Отступая от края ребра, убеждаемся в том, что до тех пор, пока
~/ — рД~2 (ушп, максимум Н по ~~ всюду имеет место при у=у„;,. Следовательно,
на этом участке оптимальный профиль реора у = у ; = сопз1.

80
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 2
В некоторой точке Я = ~„величина с~ — рф(2 достигает значения у 1„, с этой
точки и далее при Я ) Я„максимум функции Н имеет место при у ) у 1 и р, =
= — 2у2/Д, что приводит к следующему дифференциальному уравнению:
о2~ ДТ 2 о,Т
2ЯТ + $6Я = — Т ==О.
Щ2 е е
(2.86)
В результате интегрирования уравнения (2.86) получаем решение в виде
'=И' — "М'+ ТГ'
Форма контура определяется интегрированием следующей системы.'
(2.87)
6~1' НЯ
1 '~'9 Их
Ь
(2.88)
Я~ — т')~"'*+ т")'~ '
где Ть соответствует температуре на краю ребра, если контур (2.88) про-
должить в область у( у „На рис. 2.78 приведены результаты расчета
У
б
Рис. 2.78. Оптимальные контуры плоского теплоотвопящего ребра.
оптимальных контуров (2. 88) при ряде значений параметра Т~ [2.272] (рас-
четы проведены Ю. В. Шалаевым).
Отметим, что контур с Тг. — — О, дающий абсолютный минимум площади
ребра 6~„„соответствует рассмотренному в работах (2.274 — 2.277~ частному
случаю ребра у „=О (подробнее см. в (2.272~). Для этого контура
т =(1.С вЂ” *,)',
орС =
(2.89)
Чо
2 Х,осоТО5 '
~6РС вЂ” ), „, Г2 °
3
о~о74
орС
значения Я для всех анали-
К указанному значению Я,~с удобно относить
зируемых контуров ребер.
При заданном значении у „ построение
по параметру Т~ на участке от начала ребра
оптимального контура ребра
до у= у „(х„„, (~„„, Т..) про-

81
ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
водится по данным рис. 2.78; параметры участка с постоянной толщиной
у = у,.„примыкающего к краю ребра, определяются по формулам (при
О..>0
[(5/2д...)(Π— Р)-&g ; ] '
ИЖ /йз = 2(39 + то (Й + Р) аиТ4.
(2.90)
Масса единицы длины трубки с ребрами равна
(2.91)
где 7 — удельная масса материала трубки, ~, — удельная масса материала
ребер.
Согласно (2.90) и (2.91) относительная масса радиатора НМ,ЯК, на
единицу отводимой тепловой мощности составит
ЙЛХ,/ЙЖ, = (~ф+ ЯЯ)/ф, + ~),
(2.92)
где
о~ /о ОрФ
),,аа оаТ"„
(О + б)2 — 02
— Ть (1
8
Я'. — ( + ) и,оТ4
ф
Минимум относительной массы радиатора достигается при
6 Механика полета
В качестве примера на рис. 2.78 указаны оптимальные контуры ребер
при д „=1,8. Значения относительной площади сечения этих ребер ~/~,р,
в зависимости от параметра Т1, приведены на рис. 2.79.
где пунктиром также указаны значения ~/~„, для
случая у;, = О. При у „= 1,8, у „/уо = 0,31; мини- у
мум площади с пологим оптимумом имеет место при /
у „=18 /
Т~ 0,70; минимальная площадь составляет ~/~„, =
l
/
= 1,205, что существенно меньше, чем для оптималь- ц.-Д
ного прямоугольного ребра, где Г/Г„, =1,635 (см.
пунктирную кривую на рис. 2.78 [2.278, 2.279]). Для
сопоставления на рис. 2.78 пунктиром указан также
РХ
контур оптимального треугольного ребра [2.280], для
которого ~Г/~ „„=1,103 (при у „=О).
У реальных плоских оребренных трубчатых
радиаторов с трубками конечного диаметра (рис. р РХ ДТ,
2.76) НЕОбХОдИМО уЧИтЫВатЬ ИЗЛУЧЕНИЕ С ПОВЕРХ рис. 2.79. Влияиие отио-
ИОстИ трубОк И ВэаИМООбЛуЧЕНИЕ трубОк И рэбер сительнои ™еРатУРы кРая
ребра на площадь сечения
Последний фактор для радиаторов с достаточно теплоотводящего ребра
длинными ребрами дает (по данным [2.278] и др.)
относительно небольшой вклад, и поэтому пренебрежем в первом приближе-
нии взаимным облучением трубок и ребер. Рассмотрим оптимальное сочета-
ние с минимальной массой теплоотводящих ребер и трубки [2.272], нагре-
ваемой изнутри теплоносителем, при заданных температуре стенки трубки
Т„=Т„и геометрии трубки (диаметр Й, толщина стенки о). Обозначим, как
и ранее, через Ча начальный тепловой поток по одному ребру; тогда полный
отвод тепловой мощности на единицу длины трубки я с ребрами составит

82
~ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
или
4 Ф
(1 + ~) ~: 27 ~~рр
(2.93)
При этом минимальная относительная масса составляет
ЫМ ~а1Чд); =еФМ(1+Х),
т. е. в 1+Х раз меньше, чем для трубчатого радиатора без ребер.
В качестве иллюстрации на рис. 2.80 приведены значения (1+~) -1
при В=10 мм, 0=0,25 — '0,75 мм, Т„=1100' К, и=0,9; трубка — из стали,
ребра — из стали, меди или бериллия с ~/~„, =1,205 (рассмотренный выше
(2.94)
Д75
Рис. 2.80. Влияние оребрения на относительную массу плоского трубчатого радиатора.
оптимальный контур с у „/у,=0,31). Видно, что у оптимального оребрен-
ного плоского трубчатого радиатора относительная масса может быть при-
мерно вдвое меньше, чем у трубчатого радиатора без ребер.
Относительная масса трубчатого радиатора, естественно, существенно
зависит от допустимой толщины стенки трубки 3, определяемой из условии
метеорной опасности (см. ~ 3 гл. 1). По данным рис. 1.8 и формулы (2.92)
для трубчатого радиатора без ребер (при ЧО=О) на рис. 2.81 приведена за-
висимость относительной массы трубчатого радиатора от его температуры Т
при различном допустимом числе метеорных пробоев радиатора на единицу
излучаемой энергии [2.75]. При анализе данных рис. 2.81 следует подчерк-
нуть, что полезная мощность двигательной системы (например, полная мощ-
ность реактивной струи движителя Г&g ;) значител но мен ше излучае
радиатором мощности К,; даже для идеального цикла при ~ =1,0 (см. выше)
полезная мощность втрое меньше излучаемой. Поэтому удельная масса труб-
чатото радиатора, относимая к полезной мощности двигательной системы,
в несколько раз превышает приведенные на рис. 2.81 значения относитель-
ной массы радиатора (соответственно сдвинется и шкала числа пробоев на
1 квт-ч полезной энергии). Видно, что удельная масса трубчатого радиатора
достигает заметной величины по сравнению с указанными в Ц 1 и 2 настоя-
щей главы значениями удельных масс энергоисточников, энергопреобразо-
вателей и движителей. Применение плоского оптимально оребренного труб-
чатого радиатора соответственно примерно вдвое снижает удельную массу
радиатора (см. рис. 2.80). Большее снижение массы радиатора может быть
достигнуто при звездообразном оребрении.
3. Система отвода энергии со звездообразно оребренным трубчатым
радиатором. Выше, в п. 2, была рассмотрена плоская задача об оптимальном
контуре поперечного сечения теплоотводящего ребра (охлаждаемого излу-
чением) при одностороннем подводе тепла к ребру. Было показано, что

ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
площадь поперечного сечения оптимального ребра (минимальной массы)
определяется соотношением вида
сЯ
ор1
(2.95)
) аг~о2Т 9
ф ф
т. е. площадь сечения массы оптимального ребра пропорциональна кубу
теплового потока (7„отводимого реб-
Я
ром. Поэтому, если заданнь~й тепловой
поток 0~ будут отводить несколько (и)
5 ребер Я~=п00), то без учета их взаим-
ного облучения суммарная площадь
'ф 05
р~
0,0~
400 800
л?Я /бдО Т„, 'Ю
Рис. 2.81. Относительная масса труб-
чатого радиатора (на единицу излу-
чаемой мощности).
Рис. 2. 82. Схема звездообразно оребренного труб-
чатого радиатора.
сечения ребер Я ~ (и их масса) будет уменьшаться обратно пропорцио-
нально и
~ф ~ — пЯ вЂ” и ' при Д~ — пЯ, = сопМ.
(2.96)
Теплоотводящие ребра можно расположить, например, зведообразно
у вершин охлаждаемого многогранника (трубки) (рис. 2.82). При этом с и ) 2
существенно взаимное облучение ребер, учет которого определит оптимальное
количество ребер и„, и соответствующую оптимальную форму сечения
ребер [2.281 ].
В указанной постановке задача об оптимальном звездообразном оребре-
нии была решена в работах [2.281, 2.282]. На рис. 2.83 приведены резуль-
таты решения задачи оптимизации формы ребер звездообразных излучателей
при малых размерах центральной трубки и ~=1,0. Отчетливо видно влияние
взаимооблученности при и ) 2, которое сказывается в увеличении относи-
тельных размеров ребра с возрастанием числа ребер. Однако с учетом за-
висимости вида (2.96) абсолютная площадь сечения ребер ~~ (и соответ-
ственно масса радиатора) при заданном значении суммарного теплового
потока 0~ имеет минимум при звездообразном расположении 4 — 5 ребер
(см. сплошную кривую на рис. 2.84, где ~~ отнесено к площади одиночного
оптимального ребра ф „р„отводящего тот же поток 0~). Для сопоставления
на рис. 2.84 приведена пунктирная кривая, построенная по расчетным дан-
ным работ [2.283, 2.284] для выбранной системы наивыгоднейших звездо-
образно расположенных прямоугольных ребер. Площадь сечения системы
наивыгоднейших прямоугольных ребер в — 1,5 раза больше, чем у системы
6*

84
[ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
оптимальных ребер. Штрих-пунктирная кривая на рис. 2.84 соответствует
соотношению (2.96) без учета взаимного облучения ребер. Подробные дан-
ные по плоскому звездообразному и другим типам оребрения радиаторов и
методам их экспериментальных исследований см. в работах [2.281 — 2.339] идр.
При сопоставлении звездообразно оребренного радиатора с плоским
оребренным трубчатым радиатором следует иметь в виду, что у плоского
оребренного радиатора п=2. Соответ-
ственно переход к оптимальному звездо-
образно оребренному радиатору, по дан-
ным рис. 2.84, снижает массу ребер
примерно на 40".о.
4. Система отвода энергии с лен-
точным радиатором. В связи с тем, что
большая удельная масса трубчатого
радиатора во многом определяется
требованиями защиты от метеорных про-
боев, в работе [2.340] был рассмотрен
Г34 Хб 7~
Рис. 2. 83. Влияние числа ребер на форму Рис. 2. 84. Влияние числа ребер на площадь
оптимальных ребер звездообразного радиатора сечения звездообразного радиатора: 1 — ребра
оптимальной формы, 2 — прямоугольные ребра.
ленточный радиатор, масса основного элемента которого — ленты не за-
висит от метеорной опасности. В этом радиаторе гибкая лента, прижимаемая
Рис. 2.85. Система отвода энергии с ленточным радиатором.
валками [2.340] (рис. 2.85, а) или центробежными силами [2.341, 2.342]
в случае вращающейся ленты (рис. 2.85, б) к цилиндру с теплоносителем,
отнимает от него тепло и излучает это тепло со своей поверхности. Пробои
ленты микрометеоритами не должны нарушать работу такого радиатора.
Подробные данные о форме и устойчивости формы ленты в пространстве,
влиянии взаимооблученности элементов ленты и т. д. см. в работах [2.341—
2.351]. Ниже рассмотрены основные параметры ленточного радиатора
[2.340].

ТЕПЛООТВОД ОТ КОСМИЧЕСКИХ ЭНЕРГОУСТАНОВОК
Пусть масса ленты М~„теплоемкость с„длина ленты Ь, скорость обкатки лентой
барабана Ю, максимальная температура лепты в точке схода с барабана Т„температура
в точке касания барабана Т,; тогда мощность, отводимая лентой (если пренебречь участ-
ком, каса~ощимся барабана), будет равна
И, = М„с. (Т. — Т,) Г/Б.
(2. 97)
Эту мощность лента должна излучить. Без учета взаимооблучения элементов ленты,
в первом приближении, следуя [2.340), можно записать соотношение
Ъ '/4
1
Т~ — 2Ь,Е,о(оТ„Т, = — Т~дх
Е
О
(2.98)
где Π— ширина ленты.
Средняя температура лснты Т, определяется по закону падения температуры вдоль
ленты:
й Т~йх = с,Т4.
(2.99)
Интегрированием уравнения (2.99) с использованием граничных условий: Т = Т„при
х = О; Т = Т, при х = С вЂ” определяется значение константы с,:
с1 = (Т„з — Т2 з)/ЗБ,
и затем — значение Т,:
т,
Б =Т. З 1 ~ Т
(2.100)
По соотношениям (2.97), (2.98) и (2. 100) потребная масса ленты равна
Яв [(Т ~Т )-з — 1)
(2.101)
бс„Ь ЮашТ" (1 — Т2/Т )2
Минимум массы ленты достигается при (Т,/Т„)„, =0,69. Тогда
(2.102)
В уравнениях (2.102) величина Т, примерно равна минимальной тем-
пературе цикла энергоустановки Т;, (тепловое контактное сопротивление
достаточно мало [2.352 — 2.3541), скорость ленты И' ограничена ее механи-
ческими свойствами; если считать, что рациональная ширина ленты Ь„(и
барабана с теплоносителем) пропорциональна отводимой мощности: Ь =ЙК~,
то первое уравнение (2.102) определит относительную массу ленты М /К.
По данным работы [2.340), при Л„=20000 квт, Л =68000 квт и ис-
пользовании стальной ленты с возможным графитовым покрытием, при И'=
= 15,2 — 30,5 м/сек, Ь= 11,6 м, Т „= 1000о К полная масса ленточного ра-
диатора с теплоотдающим цилиндром и необходимыми механизмами со-
ставит — М = 3850 — '7250 кг (М!Л 0,057 — 0,107 кг/квт, М /Т„0,19 — '
— '0,36 кг/квт), что существенно меньше, чем для трубчатого оребренного ра-
диатора на ту же мощность и температуру, масса которого, по данным [2.355),
составит — М, = 19 400 кг (М./Ш, 0,285 кз~квт, М,/Л„0,97 кг/квт).
На итоговом рис. 2.86 приведены примерные зйачения удельной массы
М,/Г„М,/К, для плоского оребренного трубчатого радиатора (сплошные
кривые) и системы с ленточным радиатором (заштрихованная область между
пунктирными кривыми) в зависимости от максимального температурного
уровня в энергоустановке Т,„. На кривых, соответствующих оребренному
трубчатому радиатору, отмечено число пробоев на 1 квт ч полезной энергии;
эти кривые построены по данным рис. 2.81 в предположении, что выигрыш
массы от оребрения трубчатого радиатора примерно компенсирует переход
от Ж~ к Ж„=Ж,. Параметры систем отвода с ленточным радиатором

~ГЛ. 2
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
~~~ыю й7С.
~с~тки !небеля !месяц
Рис. 2.87. Области преимущественного использования различных видов эпергоустановок.
больших значений Г„) 10' — 10' квт почти постоянна, несколько снижает-
ся с увеличением полезной мощности источника Ж,.
приведены на основе рассмотренного выше примера из работы [2.340], экс-
траполированного по формулам (2.102).
Данные рис. 2.86 показывают, что и с учетом возможной минимизации
удельная масса радиационных систем теплоотвода от космических энерго-
установок является весьма значительной.
Поэтому масса системы теплоотвода яв-
ляется существенной частью общего ба-
5 ланса масс космической энергоустановки.
5. Характеристики массы космических
энергоустановок — источников мощности.
Для рассмотренных в ~ 2 видов источни-
ков энергии и энергопреобразователей, а
0,5
также для кратковременно действующих
энергоустановок на рис. 2.87 по данным ра-
боты [2.241 ] указаны области преимущест-
венного использования в зависимости от
времени работы Т и полезной мощности Ж,.
~~о',У-(О' Д УР ' Приведенные в Я 2 и 3 удельные массы
005
элементов космических энергоустановок
определяют их массовые характеристики
в целом как источников мощности.
0,01 В соответствии с удельными массами
400 ~цО щ)у дну ~ '~ элементов общая масса источника мощ-
д~ц ~~~~ ~~~~ ~ . н~с~и М, зависит от величины максималь-
'"' ной мощности Я„вырабатываемой источ-
Рис. 2. 86. Удельная масса радиаторов
(на единицу полезной мощности): ~ ником. В качестве иллюстрации в табл.
плоский оребренный трубчатый радиатор 2.11 по данным работ [2.225, 2.242, 2.243,
(на кривых отмечено число пробоев на
1 квт и), 2 — ленточный радиатор. 2.256] приведены примерные параметры
ряда рассматриваемых источников мощ-
ности. Из данных табл. 2.11, построенного по ней и работе [2.81] рисун-
ка 2.88 следует, что удельная масса источника мощности а=М /К„'для

ю 4] СИСТЕМЫ ПОДАЧИ И ХРАНЕНИЯ РАБОЧЕГО ВЕЩЕСТВА О7
Т а блица 2 11
Примерные параметры космических энергоустановок
Л Т ) УьВ5|И ~ ~.У) 3. 1ае У ~ 4.УаеУ ! сЭ ) ~.У ~ сне,З ) ОеН.У ~ Д. е У4 У ~ 3. е У~.У ~ ( 4.УИ
° ° °
° ° ° ° В е
1 °
° ° $
° ю
е Е
' ю ° °
ю
° °
° °
ю
° °
ю
° °
ю
° °
ю
Е ° ° 6 °
° °
° °
° °
° $
° °
юа °
1 °
1 ю
1 °
ае °
° ° °
ф ° в ю! 1 е 1 1!
й
1 ! °
! ! 1 ! ю ! ° ° а
ю
! ! !
в ° ° ° !
° ю
° й
ю
1 1
ю ю °
ю ° М !
! ю ю !!
° °
! в ° ю
° °
° ю °
! % ! !
й °
° ю
° °
! 1 ! ° ~ ° ° °
Я
ю °
° й ° ° !
° °
° ° ° ю
° ю
й
° ° ° °
° ° ! ! ю г ° ° ° 1 !
! 1 ! !
! й
й
° ° °
° ю г 1 ю ° ! ю
1 И в °
„ЙИИИИИИИ
,ИИИИИИИИ
ИИИВРИИИ
,ИИИИИИИИ
( / / / / / / /'
° ' В ° ! е ° ° ° &
В ° ! ° °
° а В °
!
° °
° ° В ° °
° ° ! ° ' 1: ! ' ° ° % 1 ' ° % ° 1!! в1 ~ %
1 е ° й
° % ° ! ° ° 1'' ° ° ° %
! ° ! ! ° ° ° ° ° 1 ° ю~
! 1 ! ° 5 ° ° °
1!! в ° 5
° 1 ° !1': ° ° ' 1 ф ! !'!' ° '
йю ° Ь ° ° ° 1 5~ 5
$'а ° !а'111ю'''1а! ° '' ° в'' ° ав ° 1 ° а 111
° ! ° ! ° ! ! ° а ° ° е ° ° °
а 1 ° 1 а
5ю ° 1
ае 1 а !
! ° 1
° $ ° 1 ° °
° °
)~ °
й ° й
° °
° ° ° в °
1! ° ° ! ° ° '' 1
й
° °
! °
! ° 1 ° '
° е й й
й ! ° е
! й
5 ! !
ю
1 °
° ° °
й °
° ю °
ф'!!'!
ю ° ю °
! й
1
ю
° ° °
АА~АиЩаДЬ аДна А иВУа
Я. д~ 5.8 11.15 130 320 — 120 ' ~00
Масса М., ~г 79,3 295 5~+ 1905 2270 1350 1200 1660 9 10

88
[ГЛ. 2
Физические пРинципы дВиГАтельных систем
массасистемыподачи М примерно пропорциональна максимальной тяге Р „.
Ч
Значения удельной массы турбонасосных агрегатов, по данным [2.2, 2.357],
порядка М /Р „0,005, и для анализа тепловых реактивных движителей
Ч
с позиций механики полета удельную массу системы подачи целесообразно
включать в общую удельную массу двигателя (см. (2.16)).
В двигательных установках с энергопреобразователями тепловой энер-
гии в электрическую, помимо системы подачи, необходимо учитывать вклад
массы и других насосных систем, используемых для прокачки теплоносителя
по основному и вспомога-
тельным энергетическим кон-
турам (см. рис. 2.61, 2.65,
Рис. 2. 90. Относительное полное
давление на выходе идеального
воздухозаборника.
Рис. 2.89. Схемы сверхзвуковых диффузоров-воздухозабор-
ников: а) многоскачковый диффузор с внешним сжатием по-
тока, б) диффузор, использующий два конических течения
(1 — зона обтекания центрального конуса, 2 — изоэнтропи-
ческое течение, 3 — расходящееся коническое течение перед
коническим скачком [2.3791); в) гиперзвуковой диффузор
с параболической ударной волной [2.3801.
2.66). По данным работы [2.246], удельная масса системы подачи и на-
сосной системы составляет примерно М,/Г, 0,35 кг/квт при Г„=415 квт.
Параметры баков для хранения рабочего вещества (топлива) подробно
рассмотрены, например, в работе [2.73] и др. Масса баков Ме пропорцио-
нальна массе запасаемого рабочего вещества (топлива) М„. Примерные
значения удельной массы баков составляют: для хранения жидкого кисло-
рода+керосин М~/М 0,004 [2.358], для хранения Сз Ме/М„=0,006
[2.246].
Следует отметить, что для твердотопливных тепловых реактивных
двигателей (см. [2.12, 2.73] и др.) масса топливного контейнера одного по-
рядка .с массой двигателя и пропорциональна полному импульсу движи-
теля (Р ~); примерные значения удельной массы контейнера твердотоплив-
ного РД, по данным [2.12], составляют М /(Р ~) М~/(Р ~) 0,8 10-з
1/сек.
2. Энергоустановки с воздухозаборниками. Поступление рабочего ве-
щества из внешней среды (атмосферы) используется в воздушно-реактивных
двигательных системах (см., например, [2.2, 2.359 — 2.378] и др.), а также
может использоваться в двигательных системах с накоплением рабочего
тела при орбитальном полете в верхних слоях атмосферы ([2.381 — 2.384]
и др.).
Начальным элементом таких двигательных систем является воздухо-
заборник, основная задача которого — осуществить поступление рабочего

СИСТЕМЫ ПОДАЧИ И ХРАНЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
вещества с минимальными потерями полного давления и с минимальным
внешним аэродинамическим сопротивлением. На сверхзвуковых скоростях
полета при торможении воздухозаборником набегающего потока могут иметь
место значительные потери полного давления набегающего потока ро:
(2.'103)
где М,=иlй — число Маха полета, а — скорость звука. Эти потери полного
давления р„'/ро далее вызывают соответствующие потери тяги движителя
(см. ~ 1 настоящей главы). Для обеспечения малых потерь полного давления
р„'/ро рассматриваются воздухозаборники — сверхзвуковые диффузоры, при-
меры схем которых приведены на рис. 2.89 ([2.2, 2.379, 2.380] и др.). На
рис. 2.90 даны примерные значения относительного полного давления на
выходе из идеального воздухозаборника р,',/ро в зависимости от количества
Рис. 2.91. Схема воздушно-реактивной двигательной установки: 1 — воздухозаборник, 2 — камера
сгорания (источник тепла), 3 — реактивное сопло (движитель).
скачков уплотнения и числа Маха полета Я,. Такой воздухозаборник—
сверхзвуковой диффузор — не вызывает дополнительного внешнего аэро-
динамического сопротивления при заборе из внешнего потока струи пло-
щадью, равной площади входа ф о (см. рис. 2.89), и обеспечивает расход д„:
д„= — ~)уЯ о. (2.104)
В прямоточном воздушно-реактивном двигателе (рис. 2.91) между
воздухозаборником и реактивным соплом (движителем) располагается ка-
мера сгорания или другой источник тепла; в турбореактивном или турбо-
ракетном двигателях для обеспечения тяги на малых скоростях полета перед
камерой сгорания осуществляется сжатие воздуха турбокомпрессором
([2.2, 2.359 — 2.378] и др.). Использование газодинамической теории ([2.2,
2.5, 2.7] и др.) позволяет определять характеристики воздушно-реактивных
двигателей.
При этом тяга воздушно-реактивных двигателей Р примерно пропор-
циональна площади входа воздухозаборника Я о и атмосферному давлению
на данной высоте полета р„:
(2.105)
Удельная тяга Р(~о]~„зависит от числа Маха Яо. С увеличением ско-
рости полета удельная тяга сначала возрастает в соответствии с увелйче-
нием степени сжатия роф„набегающего потока в воздухозаборнике. Однако
одновременно возрастает и температура торможения набегающего потока ~",:
(2.106)
что при заданной допустимой температуре То за камерой сгорания (источ-
ником тепла) приводит к снижению возможного нагрева воздушного потока
в двигателе ЛТ,=Т,— Т„' и вызывает падение удельной тяги при больших
числах Яо полета. В качестве иллюстрации на рис. 2.92 по данным [2.365]
приведено примерное изменение удельной тяги воздушно-реактивных дви-
гателей в зависимость от числа Маха полета. Эффективный удельный импульс

90
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
воздушно-реактивных двигателей 1'=Р~д. также зависит от числа Маха
полета (рис. 2.93) [2.365]. Масса воздушно-реактивных двигателей примерно
пропорциональна площади входа в воздухозаборник: ЛХ вЂ ~; в табл. 2.12
0
Рис. 2. 93. ~дельный импульс воздушно-
реактивных двигателей (горючее: водо-
род — сплошная кривая, керосин — пунк-
тирная).
Рис. 2.92. ~дельная тяга воздушно-реактивных
двигателей: 1 — турбореактивный двигатель, 2—
турборакетный, 3 — прямоточный с дозвуковым
горением, 4 — прямоточный со сверхзвуковым
горением.
по данным [2.365] приведены ориентировочные значения удельной массы
воздушно-реактивных двигательных систем.
Характеристики воздушно-реактивных двигателей, использующих жид-
кий водород в качестве горючего, несколько улучшаются при дополнитель-
ном использовании теплоемкости жидкого водорода для сжижения и на-
копления части воздушного потока (кислорода), поступающего через воз-
духозаборник (подробнее см. [2.365] и др.).
Рис. 2.94. Принципиальная схема двигательной установки с накоплением рабочего вещества в орбиталь-
ном полете: 1 — воздухозаборник, 2 — радиаторы, 3 — компрессоры, 4 — детандер, б — сжижающая
установка, 6 — бак для рабочего вещества, У вЂ” движитель, 8 — энергоустановка, 9 — ядерный реак-
тор, 10 — турбина, 11 — насос, 12 — электрогенератор (А — элементы, расположенные по левую сто-
рону черты функционируют только в фазе накопления).
Другим типом двигательных систем, использующих поступление ра-
бочего вещества из внешней среды, являются системы с накоплением рабочего
вещества при орбитальном полете в верхних слоях атмосферы ([2.381 — 2.384]
и др.). Принципиальная схема такой двигательной системы приведена на
рис. 2.94 [2.383]. Поток воздуха, поступающий в двигательную систему через

91
6 41
СИСТЕМЫ ПОДАЧИ И ХРАНЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
воздухозаборник, предварительно охлаждается системой теплообменников
с радиаторами, затем сжижается в детандерной установке [см. [2.385])
и с возможным разделением компонент подается в баки для рабочего вещества.
Лобовое сопротивление — др, как и аэро-
динамическое сопротивление аппарата в Таблица 2.12
целом, компенсируется реактивным дви-
жителем, потребляющим часть поступаю-
Примерные значения удельной
щего через воздухозаборник расхода двигательных систем
д ( ~д,,~. Разность указанных расходов
д =д — д, накапливается в баках для рабо-
чего вещества. Так как д ( ~д,~, то для
компенсации аэродинамического сопро-
тивления скорость реактивной струи
должна быть существенно больше орби-
тальной скорости полета к
Турбо- Турбо-
ракет. реак-
ный тивный
Прямо-
точный
Тип двигателя
Удельная мас-
са 1050
М /~я ~, кг/мг
1350 2600
Т /д = 2 10' кв~п/кг/сек при Г = 2 10' и/сек.
[2.108)
Поэтому в работах [2.381 — 2.383] принимается, что удельная масса
двигательной системы с накоплением рабочего тела в орбитальном полете
в основном определяется параметрами массы ее электрореактивной двига-
тельной установки, элементы которой были рассмотрены выше. Особенности
воздухозаборников для таких двигательных систем рассмотрены в работах
[2. 387 — 2. 389 ].
~) [/ д„//д) у. [2.107)
Для полета в верхних слоях атмосферы Земли и — 8 км/сек, поэтому необхо-
димая скорость реактивной струи К в рассматриваемой двигательной уста-
новке с накоплением может быть достигнута только в электрореактивных
движителях [см. ~ 1 данной главы).
Энергетические затраты на работу -Фг~~-
электрореактивного движителя Г и сжи-
Т ЮО
жительной установки накопителя Г„обес-
печиваются энергоустановкой — источни-
ком мощности [рис. 2.94).
Оценим энергетические затраты на д~~
работу сжижительной установки. На рис.
2.95 по данным [2.386] приведены значе-
ния идеальных затрат мощности на сжи-
жение Г„[при к. и. д., равном единице)
в зависимости от температуры воз-
духа на входе в сжижительную уста-
новку Т„. Отметим, что эти значения
удельной мощности К„,/д, более чем на два р ФЯ 8О т,к
порядка меньше удельной мощности реак-
° Я
Рис. 2.95. Удельные (идеальные) затраты
тивнои струи движителя накопительной мощности на сжижение воздуха.
системы, равной

ГЛАВА 3
ОБОБЩЕННЫЕ ПАРАМЕТРЫ КОСМИЧЕСКИХ
ДВИГАТЕЛЬНЫХ СИСТЕМ
Здесь с позиций механики полета дается классификация и приводится сводка обоб-
щенных характеристик основпых видов космических двигательных систем, обсуждаемых
в литературе [ЗЛ вЂ” 3.4]. Эти обобщенные характеристики основываются на изложенных
в предыдущей главе физических принципах действия элементов космических двигательных
систем. Введение обобщепных параметров, естественпо, схематизирует проблему, сохраняя
ее основные свойства. По изложенным принципам возможно дальнейшее более детальное
исследование.
Двигательные системы разбиты на три типа (см. Ц 1, 2 и 3 данной главы) в зависи-
мости от основных ограничений, накладываемых соответствующими физическими прин-
ципами на характеристики системы. Основное ограничение характеризуется тем, что в ме-
ханике полета, как правило, оптимальное движение соответствует выходу на это огра-
ничение. Такими основными ограничениями являются ограничение скорости истечения
реактивной струи, ограничение мощности и ограничение тяги двигательной системы.
Рассматриваемые обобщенные характеристики отпосятся к двигательным системам
без воздухозаборников и без систем накопления рабочего вещества из внешнего потока;
влияние поступления рабочего вещества из атмосферы было рассмотрено в гл. 2.
$1. Двигательные системы ограниченной скорости истечения
К этому типу относятся тепловые реактивные двигательные системы,
обобщенная схема которых приведена на рис. 3.1. Тягу в таких двигатель-
ных системах создает реактивное сопло, превращающее тепловую энергию
рабочего вещества в кинетическую энергию направленного движения реак-
тивной струи.
Рис. 3.1. Обобщенная схема тепловой реактивной двигательной системы: 1 — контейнер с рабочим
веществом, 2 — реактивное сопло (движитель) с источником, преобразователем энергии, системами
подачи рабочего вещества и отвода энергии.
На участке космического полета основные параметры тепловых ракет-
ных двигателей определяются площадью критического сечения реактивного
сопла о~„, полным давлением р, и температурой газа Т, на входе в сопло:
Р = Й,о~„Р„д = Й,,~.Р,/~l Те,
3
Г=Р~д=й ~/Т Т='~ доз= й о~ р ~/'~' .
Для двигателя заданной геометрии (оГ„,=сопяФ) возможность регулирова-
ния основных параметров двигательной системы Р и д определяется воз-
можностью независимого управления полным давлением р, и температурой Т,.
Основным ограничением для тепловых двигателей является максимально
допустимая конструкцией температура Ч,,„„что ограничивает возможную
скорость истечения реактивной струи (см. (3.1)):
( .1)
Г( Г „=Йз ~/Т,

ДВИГАТЕЛЬНЫЕ СИСТЕМЫ ОГРАНИЧЕННОЙ МОЩНОСТИ
Для заданной прочности конструкции вторым ограничением является
допустимое максимальное полное давление р,,„, величина которого опре-
деляет удельные значения максимальной тяги и мощности, отнесенные
к площади сечения сопла:
Р,„(~„= Й,р,,„, Т,„/~Г„= Й,р,,„~/т, (з. з)
Вид регулировочных характеристик тепловой реактивной двигательной
системы на участке космического полета представлен на рис. 3.2. При дви-
жении в атмосфере тяга двигательной системы несколько снижается
(см. рис. 2.13).
Кпама ~ ~е
Рис. 3.2. Регулировочные характеристики тепловой реактивной двигательной системы.
Масса двигательной системы с ограниченной скоростью истечения
тивной струи в основном определяется массой контейнера для запаса
чего вещества М, и максимальной тягой Р,„„:
М, = ~Л~„+ 1,Р.,„.
Значения коэффициентов для определения масс были приведены в гл.
реак-
рабо-
(3. )
2.
~ 2. Двигательные системы ограниченной мощности
( .5)
Двигательные системы ограниченной мощности состоят из источника
мощности (источник энергии, преобразователь энергии, система отвода
энергии), реактивного движителя с системой подачи и контейнепа с рабочим
веществом (рис. 3.3). Выработанная источни-
ком энергия превращается в движителе в ки-
нетическую энергию направленного движе- 1
ния реактивной струи. Наличие отдельного
источника ограниченной мощности Г, (
( Г, „определяет основные свойства и
название рассматриваемой категории двига-
Г 3'
е
тельных систем.
Характерным свойством двигательных
СИСТЕМ ОГраНИЧЕННОй МОщНОСтИ яВЛяЕтСЯ ИХ Рис 3 3 Об б
регулируемость по параметрам д и К в щиро- ной системы ограниченной мощности:
1 — контейнер с рабочим веществом,
ких пределах. Кроме того, можно управлять 2 — источник мощности, 8 — реактив-
величиной мощности Г,, подводимой к дви-
жителю. В идеальном движителе вся под-
водимая мощность превращается в мощность реактивной струи. Это опреде-
ляет простую связь между параметрами:
'/,д Г' = Ж, ( Ж,,„,„, Р = д Г,
где Ж, „может зависеть от координат и времени.
Характеристики реальных движителей подробно рассмотрены в гл.
С учетом этих реальных свойств мощность реактивной струи 1/,д Р зависит
от параметров движителя, например от скорости истечения струи К.

94
ОБОБЩЕННЫЕ ПАРАМЕТРЫ ДВИГАТЕЛЬНЫХ СИСТЕМ
[ГЛ. 3
Максимальное значение мощности Г,,„определяет величину макси-
мальной тяги, которая для случая идеального движителя равна (см. (3.5))
Р „=2Ж, „/Г. (3.6)
Вид регулировочных характеристик двигательных систем ограниченной
мощности (с идеальным движителем) представлен на рис. 3.4.
Рис. 3.4. Регулировочные характеристики двигательной системы ограниченной мощности с идеальным
движителем.
Масса двигательной системы ограниченной мощности в основном скла-
дывается из трех компонент: массы контейнера для запаса рабочего ве-
щества М „массы источника мощности М, и массы движителя ЛХ:
т
М,=~М„,+ Х,,„+7Р,„.
3
( .7)
Возможно также использование аккумулятора энергии, масса которого
пропорциональна максимальной запасаемой энергии ЛХ, = ~,ЕО. Значения
коэффициентов для определения масс были даны в гл. 2.
~ 3. Двигательные системы ограниченной тяги (парусные системы)
К этому типу двигательных систем относятся парусные системы (сол-
нечный и изотопный парус), величина тяги которых лимитируется макси-
мальной площадью паруса Я,„:
Р (Р,„= ЙЯ,„. 8
(3. )
Р/~: ь
(3 )
Для изотопного паруса величина тяги зависит от отношения времени ра-
боты ~ к периоду полураспада 1/~,:
Р~$ =Й е-" '. (3.10).
Масса двигательной системы ограниченной тяги определяется ее мак-
симальной тягой:
( .11)
~р 7ршах
Значения коэффициентов для определения масс и их зависимость от
основных параметров подробно рассмотрены в гл. 2.
Расход массы у парусных систем отсутствует, величина тяги зависит от
координат или времени. Для идеального солнечного паруса с зеркальными
отражающими свойствами тяга направлена по нормали к поверхности па-
руса, а величина тяги зависит от угла установки паруса О и расстояния до
Солнца Л:

ЧАСТЬ 11
ПРОБЛЕМЫ 011ТИМИЗАЦИИ вЂ” ДЕТЕРМИНИСТСКИЙ
11ОДХОД
1'ЛАВА 4
ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ ОПТИМИЗАЦИИ.
ОПИСАНИЕ ДИНАМИЧЕСКИХ МАНЕВРОВ
~ 1. Постановка проблемы оптимизации
Когда сформулирована цель космического маневра, возникает проблема
о наиболее экономичном ее достижении. Это означает, что должен быть вы-
бран оптимальный космический аппарат и в том числе оптимальная двига-
тельная система. Для последней нужно указать наилучший для заданного
маневра тип, определить наилучшие параметры и наилучшие программы
для управляющих функций.
Экономичность выполнения характеризуется тем или иным критерием
оптимальности: максимум полезной массы, минимум стоимости выполнения
маневра и т. д. В нашем изложении главное внимание уделяется критерию
максимума полезной массы. Дадим формулировку проблемы оптимизации
для этого случая.
Назовем динамическим маневром переход с заданного начального много-
образия Я, в пространстве координат — скоростей — времени (г (~,), т (~,), ~е) (= Яэ
на заданное конечное многообразие Я,: (г (~,), т (~,), ~,)(=Я,.
Содержание изучаемой вариационной проблемы таково: требуется выпол-
нить заданный динамический маневр с максимальной полезной массой М, при
заданной стартовой массе М,.
Запишем дифференциальные связи вариационной проблемы с соответ-
ствующими граничными условиями. Сюда относятся уравнение (1.2) изме-
нения массы и уравнения (1.1), описывающие движение центра масс ап-
парата:
ЛХ (О) = ЛХ„ЛХ (Т) ==- ЛХ, + ЛХ„,
г (О) = г„г (Т) = г„
г=ч,
Ре
Л~+~
т (0) =т„т (Т) =т,.
') В отличие от перечисленных здесь маневров, которые рассматриваются почти
в каждой из последующих глав, маневры вывода на орбиту и спуска с орбиты фигурируют
только в гл. 5, 9, 15, поэтому их описание дается непосредственно в этих главах: в э 3
гл. 5 (вывод на орбиту) и в ~ 1 гл. 15 (спуск с орбиты).
Настоящая глава посвящена формулировке проблемы оптимизации космического ап-
парата. В э 1 конкретизируется критерий оптимальности, вводится понятие динамического
маневра, дается постановка проблемы в виде вариационной задачи Майера, указывается
набор характеристик двигательной системы, необходимых для замыкания постановки.
В последующих параграфах собраны системы дифференциальных уравнений и гра-
ничных условий, описывающих основные динамические маневры: межпланетный перелет
Я 3), удержание спутника в заданном шаровом слое, поворот плоскости орбиты спутника
и изменение других элементов орбиты Я 4) '). Описанию маневров предпослан параграф
Я 2), в котором приведены различные формы уравнений движения и даны соотношения
для перехода от одних переменных к другим.

[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
Здесь г, т, М вЂ” набор фазовых координат (г и т — радиус-вектор и скорость
центра масс аппарата, М вЂ” текущая масса аппарата); д, Р, е — набор
управляющих функций и управляющих параметров (д — массовый расход
рабочего вещества, Р и ~е~= — 1 — величина и направление вектора тяги).
Остальные обозначения: д=д (г, ~) — вектор ускорения от гравитационных
сил, ̄— масса двигательной системы.
(4.2)
М=М +М +М„.
Прочие компоненты (напрпмер, масса конструктивных элементов, масса баков для
рабочего вещества) условно относятся к полезной нагрузке. По мере необходимости эти
компоненты могут быть учтены в вариационпой постановке.
5'. Размерность фазового пространства, описывающего состояние аппарата, может
увеличиться при усложнении задачи. К фазовым координатам г, т, М могут добавляться
новые координаты, например ~„ — текущее время работы двигателя (для задачи с огра-
ниченным ресурсом двигательной системы) или ЛХ„и ЛХз — массы двигательной системы
и баков (для задачи оптимального сброса секций двигателя и баков). Тогда систему (4.1)
нужно дополнить дифференциальными уравнениями, описывающими изменение этих фа-
зовых координат; в отмеченных примерах эти уравнения таковы:
в первом случае
(4.3)
во втором случае
При этом могут появиться новые управляющие функции; здесь это ~ (~)=1 или 0—
функция включения-выключения двигателя, д.„(~) ) О, д„. (~) ~ 0 — функции, отвечаю-
щие за сброс секций двигателя и баков.
6'. В формулировке вариационной проблемы и в граничных условиях (4.1) началь-
ная масса аппарата задается: ЛХ (0)=ЛХ,. Во многих случаях по физическому смыслу ее
достаточно было бы только ограничить сверху: ЛХ (0) ( ЛХО. В такой задаче появляется
еще один свободный параметр, подлежащий оптимальному выбору, — ЛХ (0). Рассмотрим
связь этих двух постановок.
Обозначим через М,'" „(М,) максимальное значение функционала при М(0) =Мо
в зависимости от параметра задачи М, (первая постановка), через М,"-' (М ) — то же
при М (0) ( ЛХ, (вторая постановка), а через М (0)ф — оптимальную начальную массу
для второй постановки.
Если получено параметрическое решение задачи в первой постановке ЛХ~',„', (ЛХО),
то решение во второй постановке находится в результате простой процедуры:
Отсюда видно, что на монотонно возрастающих участках зависимости М,"„', (ЛХ ) опти-
мальная начальная масса равна максизгально возможной, М (0)„"' =ЛХ,, и обе поста-
новки приводят к одинаковым результатам. На убываюгцих участках М (0)„',' ( М .
Такие участки могут появляться в случаях неполной оптимизации, когда пара-
Сделаем несколько замечаний к записи (4 1) и к формулировке вариационной
проблемы.
1'. Система (4 1) представлена в виде обыкновенных дифференциальных уравнений
первого порядка, разрешенных относительно производных. Это позволит в дальнейшем
сформулировать задачу Майера и свести вариационную проблему к краевой задаче для
системы обыкновенных дифференциальных уравнений с конечными соотношениями для
управляющих функций.
2'. В правой части третьего уравнения (4 1) выписаны ускорения от реактивных и
гравитационных сил. Помимо них могут быть учтены и другие силы, например сила аэро-
динамического сопротивления.
3'. Начальное Я, и конечное Я, многообразия, которым должны принадлежать
концы траектории, для определенности записаны как жестко фиксированные начальная
(го, т„О) и конечная (г„т„Т ) точки, время отсчитывается с момента старта ~,=0, ко-
нечный момент обозпачен через Т. Такая запись будет использоваться и в дальнейшем,
когда вид Яо и Я1 несуществен. Примеры конкретизации Яо и Я1, отличные от этого пре-
дельного случая, даются в ~ 3 настоящей главы: (4.65), (4.67). На траекторию движения
могут быть наложены дополнительные условия в промежуточных точках: (4.70) — (4.72)
в з 3 и (4.85) в з 4.
4'. В записи (4.1) аппарат считается состоящим из полезной нагрузки М , запаса
рабочего вещества М и двигательной установки М,. Формула для массы такого аппа-
рата имеет вид

пОстАнОВБА прОБлемы ОптимизАции
Запишем теперь исходную систему (4.1) в виде, удобном для формули-
ровки вариационной задачи Майера. Для этого присоединим к системе (4.1)
формальное уравнение неизменности полезной массы М,=О и распишем
полную массу аппарата в соответствии с формулой (4.2). Тогда система
уравнений и граничных условий представится следующим образом:
ЛХ =О, М (О) + ЛХ + ЛХ (0) = ЛХ, ЛХ, (Т) = тах,
М,= — д, м (т) =О,
г=ч, г (Т) = г„
(4.5)
Ре
ЛХ,+М +М„+
т (0) =т„
т (Т) = т„
и задача Майера формулируется так: для системы (4.5) требуется определить
управляющие функции и управляющие параметры (е, д, Р, М„или другие,
через которые выражаются данные), обеспечивающие выполнение граничных
условий и доставляющие максимум конечному значению фазовой коорди-
наты М„.
Вариационная постановка (4.5) может быть сведена в ряде случаев
к более простой. Опишем здесь один вариант перехода, который может
быть сделан при условии, что в формуле для массы аппарата отсутствуют
дополнительные компоненты, зависящие от массы рабочего вещества.
Введем специальное обозначение для суммы полезной массы М и
массы рабочего вещества ЛХ:
ЛХ.=ЛХ,+ЛХ .
(4. )
Масса М, в начальный момент выражается через стартовую массу и
массу двигателя, а в конечный момент совпадает с полезной массой:
м,(о) =м, — м„, м.(т) =м„.
(4.7)
При помощи новой фазовой координаты М. (~) система (4.5) трансфор-
мируется в следующую:
ЛХ, (0) + ЛХ„= ЛХ„М. (Т) = тах,
г(0) =г„г(Т) =г„
г=ч,
(4.8)
Ре
~=м ~м +~
т (0) = т„
т(Т) =т„
и задача Майера формулируется так же, как и для исходной системы, только
контрольным функционалом является конечное значение массы М .
!
о'
Данная вариационная постановка должна быть конкретизирована для
каждого типа двигательной системы.
Во-первых, нужно указать функциональные выражения тяги Р и рас-
хода д через независимые управления и=(и,..., и„) и параметры т=
7 Механика полета
метры двигательнои системы у ке заданы и отыскивается только программа управления
(см. ~ 3 гл. 8 и ~ 4 гл. 13).
7'. Вместо изложенной могут быть использованы другие формулировки: задаются
динамический маневр и полезная масса, определяется минимум начальной массы; зада-
ются полезная и начальная массы, находится минимальное время выполнения маневра
илп экстремальное значение какой-либо фазовой координаты. Эти формулировки эк-
вивалентны друг другу на участках строгой монотонной зависимости экстремальных
значений функционала от оставшихся переменных, которые становятся внешними пара-
метрами задачи. Выбор одной из эквивалентных формулировок зависит от конкретной
ситуации. В дальнейшем для определенности будет рассматриваться задача на максимум
полезной массы при заданной начальной массе и заданном динамическом маневре.

[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
=(ш1,..., и ) двигательной системы и определить допустимые области
значений и и т (регулировочная характеристика двигателя)'
р = р (и, т), д=д(и, ~~), и(1) (= Г(т), ж = сопз1 (- Иг.
Во-вторых, нужно представить массу двигательной системы М„как
функцию параметров т (формула для массы двигателя):
(4.10)
М„= ЛХ, (ж).
~ 2. Формы уравнений движения
1. Уравнения движения в центральном поле. В прямоугольной инерциальной си-
стеме координат х, у, ~ с началом в гравитационном центре уравнения движения имеют
вид (см. (1.1), (1.10))
х = а — 3сх~га у = а — )сутяга, в = а — Йл/гз
(г = ~хз + у2 + ~2)
где а, а„, а, — проекции вектора реактивного ускорения а = Р/М на оси системы,
Й = ~'И вЂ” гравитационная постоянная (произведение универсальной гравитационной
Рис. 4.2, Полярная система координат.
Рис. 4.1. Прямоугольная и сферическая си
стемы координат.
постоянной ~ на массу центрального тела Ю). Выберем характерное расстояние г,;
за характерные время ~„, скорость г„ускорение ~. примем следующие:
(4.12)
Эти величины имеют такой физический смысл: 2г~,. — период обращения по кру-
говой орбите радиуса ~„г — модуль скорости движения по орбите, у,. — ускорение
от гравитационного центра на расстоянии г,. Если г„~„и,, у„. взять за единицы
измерения линейного расстояния, времени, скорости и ускорения, то уравнения (4.11),
записанные в соответствующих безразмерных переменных, не будут содержать пара-
метра Й:
(4.13)
х= а — х!гз, у = а — у(гз, л =а — ~~гз.
Для безразмерных переменных сохранены прежние обозначения. Дальнейшее
изложение в настоящем пункте будет проведено в принятых безразмерных переменных.
Эти характеристики двигательной системы определим как основные.
Они не являются исчерпывающими; по мере усложнения задачи могут
потребоваться дополнительные сведения о свойствах двигательной системы.
Такие сведения сообщаются в ходе изложения.

ФОРМЫ ~РАВНЕНИй ДВИЖЕНИЯ
э 2]
Перейдем к сферическим координатам г, у, 0; связь между ними и декартовыми
координатами дается формулами (си. также рис. 4.1)
~= г соя ~ соя у, у = г соя ~ яп у, ~= г яп 3.
(4.14)
Уравнения движения в сферических координатах имеют вид
г' — гф2 соя 2 0 — г02 + 1/г2 = а„,
г соя Оф + 2гф соя 0 — 2гф0 я1п 0 = а,
г0+ 2г0+ гфЯ я1п 0 соя 0 = ая.
(4.15)
Проекции реактивного ускорения а,, а,, а~ выражаются через а, а, а, следую-
щим образом:
а„= а соя 0 соя у+ а„соя 0 я1п у+ а, я1п 0,
а = — а я1п у+ а„соя р,
ая = а я1п 0 соя у+ а„я1п 0 я1п у — а, соя 0.
(4.16)
Частным случаем системы (4.15) является система, описывающая плоское дви-
жение (0 = О, ая = 0):
г' = а„ + гф' — 1/г',
(4 17)
гф = а„, — 2гу.
Введем компоненты скоростей в полярных координатах г, у (рис. 4.2): и„=г—
радиальная скорость, и =гф — трансверсальная скорость. Тогда система (4.17) может
быть записана так:
г= ут)
г~= у~,
б,. = а,. + и2/г — 1/г2,
0 = ат — и„и /г.
(4.18)
Если ускорения а„, а, не зависят от ~ и р, то порядок последней системы может
быть понижен вдвое:
и„и„'= а„+ и~~/г — 1/г2, и„и' = ат — и„и /г;
(4. 19)
здесь штрихи обозначают дифференцирование по г.
Функции ~ (г) и у (г) находятся после интегрирования системы (4.19) из диффе-
ренциальных уравнений
(4.20)
При отсутствии реактивных ускорений система (4.19), равно как и (4 18), имеет
два хорошо известных интеграла: интеграл энергии
(4.21)
и интеграл момента количества движения
(4.22)
аЖ = и~г.
Последние могут быть использованы в качестве искомых функций в уравне-
ниях (4.19) вместо и„, и:
1 а,г
Ь' = — (а„и„+ а и ), аЖ' = — .
(4.23)
Входящие в правые части уравнений (4.23) функции г„, и должны быть выра-
жены через г, К, Ф из (4.21), (4.22).
Проекции скоростей и„, и~ и ускорений а„, а, могут быть записаны через мо-
дули скорости и и ускорения а и углы, определяющие направления векторов ~, а
(рис. 4.2): Ь вЂ” угол между вектором скорости и перпендикуляром к радиусу-вектору
точки в сторону положительного вращения последнего, ~ — угол между вектором
7*

100
ПРОБЛЕМА ОПТИМИЗАЦИИ
[ГЛ. 4
возмущающего ускорения и вектором скорости. 11равые части уравнений (4.23) заме-
нятся на следующие:
а соя 7 , аг соя (Э + 7)
(4.24)
В этих переменных система (4.18) трансформируется в такую:
Г=ПЗ1ПЭ,
Гф=г СОЯЭ,
(4.25)
у = а соя 7 — я1п Э/г2,
уЭ = а яш 7 + (у2/г — 1/г2) соя Э.
Если в этих уравнениях вместо независимой переменной ~ ввести 8 — длину
дуги траектории (дг' = Нг'+ г'Н~' = и'НР), то получим следующую систему:
ИГ
— =я1п Э,
Сь8
И~
г с— ~ — СОЯ Э,
Сь8
(4.26)
Иу 1
п~ — асояу — —, яш О,
Сь8 Г
ИЭ и~ 1
иЯ вЂ” = а я1п 7+ — — —., соя Э.
Сь8 Г Г (
В терминах независимой переменной у система (4.25) примет вид
ЙГ
=Г
И~
Ж
И~
г соя ОсЬ
~, — а
г2сояЭ ИЭ
— а
соя Э'
(4. 27)
1
СОЯ "~ Г2 Б1П ~
— — — соя Э.
Я|п 7+
Обратимся к исходной системе (4. 17), описывающей плоское движение в поляр-
ных координатах, и выпишем дифференциальное уравнение орбиты г (у). С этой
целью введем следующие замены:
1 И И
Г = —, Г2~=аМ, — =ф—
(4.28)
(здесь при замене аргумента ~ на аргумент 1», как и ранее, предполагается, что
проекции возмущающего ускорения не зависят от ~). Система (4.17) станет следующеи:
сРи 1 а а Ии
!
и 1 — —. — —.,—
Д~2 1 ~2 2 2 Д~
сЬЖ а
,1т = Уиз
(4.29)
Время 8 может быть найдено по известным функциям и (у), 4~(1») из дифферен-
циального уравнения
И1 1
ду сЖ (у) и2 (~)
(4.30)
Если возмущающих ускорений нет (а„=О, а =О), то решение системы (4.29)
легко находится:
1 1
у = сопяф, и= — 2+ и — — 2 соя (т — 7,)»
(4.31)
или, возвращаясь к переменному г,
(4.32)
г = р/(1 + в соя ч),

ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
ф 2]
обнаруживаем, что орбита г(ч) — коническое сечение с параметром р и эксцентриси-
тетом а.
В формулах (4.31) и (4.32) введены следующие обозначения: р= гзз — фокаль-
ный параметр конического сечения, з = йзи, — 1 = И/г, — 1 = 1/1 + 2 язв — эксцен-
триситет конического сечения (з = Π— окружность, 1 ) з ) Π— эллипс, з = 1 — пара-
бола, ~~1 — гипербола ], ч = ~р — ~р — истинная аномалия — угловое расстояние, отсчиты-
ваемое от направления Р,~ (ось апсид), г„, у, — радиальное и угловое расстояния перигелия.
На рис. 4.3 приведена орбита — эллипс,
в одном из фокусов которого Р, находится У
начало координат — гравитационный центр.
Большая ось эллипса а7~ соединяет апсиды:
а — афелий, г. — перигелий; длина большой
полуоси А, длина малой полуоси В, рас-
стояние от фокуса до центра эллипса С свя-
заны следующими соотношениями с пара-
метром р и эксцентриситетом ~:
х
Р Р
А=1 2 В=
Ч1 — а2
РЯ,
С=1, °
(4.33)
Таким образом, в отсутствие возмущаю-
щих ускорений система (4.29) имеет в каче-
стве постоянных интегрирования величины
г, ~„аЖ или произвольную их комбинацию.
Ф
При а„ф О, а, ф О эти величины ые являют-
ся постоянными. Выпишем дифференциаль-
ные уравнения, определяющие ~, (р), аФ (у),
г(у) =и„— ок 2 в зависимости от а„, а
Введем новые функции: и= Ни/~1у, р = сМ2; после
Рис. 4.3. Элементы, определяющие аллипти-
ческую орбйту на плоскости.
этого система (4.29) примет вид
(4.34)
Д~ „З °
— = — и + — — — ~
ди~ 1 и„
риз риз
Представим функции и, и следующим образом (ср. (4.31)):
и= (1/р)+ г соя (у — у,), и = — г яш (у — 12,)
(4.35)
~1п ч 2а~ соя ч а г я1п2 ч
'Р 'Р
~Д2 2,/Ч2 дЧ2
2а яп ч а япчсояч
— + ' + '
~РД2 8Р2ДЗ ~РДЗ
2а
2
1ЧЗ
(4.36)
д~
(ч=
— /У = (1/р) + г соя (12 — 12„)).
Если вместо представления (4.35) избрать такое (4.3, 4.4]:
и = (1/р) + (Ч/р), ш = — Б/р,
(4.37)
то сис сема уравнений примет вид
2а рз
Ну ' И+1)2 У
Ж а,.рз итр
У + 1)2 У + 1)з
2а
д~ (д + 1)з
/4.38)
(по поводу представления функций и, и см. работы [4.1, 4.2]); тогда получим систему
дифференциальных уравнений для г, у„ р:

[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
При а„=:О, а~=О из последней системы получаются уравнения кеплерова невозмущен-
ного движения в форме Гамильтона.
Системы (4.36), (4.38) называются системами в оскулирующих переменных, т. е. та-
ких переменных, которые в отсутствие возмущений (а„= — О, а .= — 0) становятся постоян-
ными, любая комбинация параметров Я, у, р или Д, Ь, р также обладает этим свойством.
Выбор определенной системы оскулирующих параметров зависит от характера возмущаю-
щих ускорений.
Приведение уравнений движения в центральном поле при наличии возмущающих
ускорений к уравнениям в оскулирующих переменных является стандартной операцией,
давно применяемой в небесной механике. Для описания пространственных маневров нам
понадобится система в оскулирующих перемонпых, определяющая пространственное
движение точки. Чтобы не прибегать к громоздкому выводу, мы опишем эту операцию
в общих чертах и в заключение приведем окончательные формулы (см., например, 4.5]).
Вывод этих формул можно найти в [4.6 — 4.13].
Рис. 4.4. Элементы, определяющие эллиптическую орбиту в пространстве.
За исходную примем систему (4.13) дифференциальных уравнений движения в прямо-
угольных координатах. Три уравнения второго порядка (4.13) могут быть преобразованы
в систему шести уравнений первого порядка:
(4.39)
х;=Х;(х )+а; (~, ~'=1,..., 6),
где
Х4 = Д, Х5 — 2~ хб — 2~
х2=х,
хд — — х,
хз
Х = ——
6 гзэ
хд х2
Х2 — з, Хз — х4, Х4 — — — — з, Х5 = х6,
г г
Хд=х,,
ад — — О,
(4.40)
а4 — — а, а;=О,
=~ '+ .-'+ ~)
аз=О,
а~ — — а,
а2= ах
Если а,=О (1=2, 4, 6), то уравнения (4.40) определяют движение в центральном поле
и, как известно, могут быть проинтегрированы в конечном виде. Пусть начальные усло-
вия для системы (4.40) имеют вид
(4.41)
хю (0) = й (р1 ° рв) (' = 1 ° ° ° 6)
где р; — совокупность орбитальных параметров в задаче двух тел. Решение уравнений
(4.40) в отсутствие возмущающих ускорений находится в виде
хю — Ра (Р1 ° .. Ре. ~) (~'; (Р1, . Реъ О) =У, (Р1.. Ра)). (4.42)
6
Ихс дР; дР; "Р~
— = — + — — =Х;+а °
(4.43)
(~ =1,..., 6).
При наличии возмущающих сил орбитальные параметры р„..., р, могут рассматри-
ваться как новая совокупность переменных, заменяющая старые переменные х; по форму-
лам (4.42). Выпишем дифференциальные уравнения для р„..., р, — оскулирующих пе-
ременных; с этой целью возьмем полные производные от х,, представленных в виде (4.42):

ф 21
ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
В силу определения' оскулирующих переменных
(4.44)
дР~/д~ = Х;;
поэтому
6
° ° °
дР; ~р~'
Др .,У~ — с.
(4.45)
П:оследняя система является системой в оскулирующих переменных; она определяет
изменение орбитальных элементов при наличии возмущающих ускорений. Отметим, что
уравнения (4.45) линейные относительно производных др /Ю; это позволяет выразить
Ир ./Л через возмущающие ускорения а,'.
6
И~.
— А ~(р1,..., ре, ~) а,
(4.46)
Ц = 1, ..., 6).
Рассмотрим в качестве орбитальных следующий набор параметров (рис. 4.4): длина
большой полуоси А и эксцентриситет ~, определяющие геометрию эллиптической орбиты;
наклонение г и долгота восходящего узла о, определяющие ориентацию плоскости орбиты;
аргумент у, отсчитываемый от линии узлов, и время прохождения Т, перигелия, опре-
деляющие орбиту в ее плоскости. Вектор возмущающего ускорения можно разложить по
трем ортогональным направлениям: перпендикулярному к мгновенной плоскости орбиты
а~, радиальному а~, лежащему в плоскости мгновенной орбиты, и перпендикуляр-
ному к радиусу-вектору аф. Дифференциальные уравнения для оскулирующих пере-
менных А, а, г, о, ~р, ~ = — пТ имеют вид
ИА 2е йп ч 2А ~1 — ~~
и ч'1 — ~'
~$ — ~' ц1п ч ~1 — =-2 А р
Н~ пА в+ пА~~ г
и'1 г сов (ч + ~р )
)гА2 ~1 — е"
ЫЯ г з1п (ч + ~р,)
пА2~~ — ~2 ц1п ~
(4.47)
а
— соБ ч ~1 — а"
г
ад+ „А 1+ — „
— 'ч'А (1 — ь2) аг з1п (ч+у,) с1д1,
2г 1 — к2
Ж иА А
3
Здесь п = А ' — средняя угловая скорость движения (безразмерная), р = А (1 к2)—
фекальный параметр, г=р (1+~ сов ч) ' — уравнение оскулирующего эллипса, ч — истин-
ная аномалия. Система уравнений (4.47) должна быть дополнена соотношением, определяю-
щим скорость изменения истинной аномалии,
соя ч ад—
~А (1 — к') Ы~, ~Щ
г~
— — — соя г —.
Ж И~'
(4.48)
Как видно из уравнений (4.47), (4.48), приведенная здесь система орбитальных
параметров теряет смысл при значениях эксцентриситета и наклонения, равных нулю,
и при значении эксцентриситета, равном единице. В этих точках правые части некоторых
уравнений не определены или обращаются в бесконечность. В самом деле, положение пе-
ригелия на круговой орбите (~=0) или положение линии узлов при совпадении фиксиро-
ванной и орбитальной плоскостей (1=0) неопределенны. Это обстоятельство ограничивает
область применимости описанной системы орбитальных параметров, например для числен-
ного интегрирования, и является причиной поисков других, более подходящих систем.
В частности, чтобы исключить неприятности, связанные с вырождением орбиты в круго-
вую (~=0), вводят вместо параметров ~, у их комбинации ~ з1п у, в сов у, — компоненты
вектора Лапласа. Дифференциальные уравнения для этих комбинаций не содержат в в зна-
менателе (ср. (4.36), (4.38)).

104
[ГЛ 4
ПРОБЛ1 МА ОПТИМИЗАЦИИ
Также свободной от указанных особенностей является система орбитальных пара-
метров, предложенная в [4Л4]. Систему составляют два вектора: вектор момента коли-
чества движения и вектор Лапласа е, направленный от центра к перигелию и по модулю
равный эксцентриситету в. Авторы [4.13] использовали для исследования околокруговых
орбит с малым наклонением в качестве оскулирующих переменных начальные значения
координат и скоростей. Эти переменные были применены в [4Л6] для произвольных орбит.
Для ряда пространственных задач оказывается целесообразным использование си-
стемы смешанных переменных: часть переменных — полярные координаты, другая
часть — оскулирующие переменные. Удобная для анализа возмущенных движений си-
стема пространственных переменных приведена в работах [4.17, 4Л8]. Как и ранее, здесь
выделяются три ортогональных направления, берущих пачало в гравитационном центре
(рис. 4.5): Ьн — орт вдоль радиуса-вектора движущейся точки, Ь вЂ” орт вдоль пер-
пендикуляра к радиусу-вектору в мгновенной плоскости орбиты, Ь~ — орт, направ-
ленный перпендикулярно к мгновенной пло-
скости орбиты.
Обозначим через ж, ()ф, ж проекции уг-
ловой скорости системы координат В, Ф, Ж,
связанной с точкой, которая движется отно-
сительно инерциальной системы х, у, ~. Если
положение системы Я, Ф, Я в каждый момент
времени определять углами: О (долгота вос-
ходящего узла), ~ (наклонение), ч (угловое
расстояние движущейся точки в плоскости
орбиты, отсчитанное от линии узлов (см. рис.
У 4.5)), то угловые скорости ид, иф, ~,, будут
выражаться следующим образом.'
ив — ~ я1п у я1п ~ + ~соя у,
~~ф — — о со~ар ~~й ~р — ~ ~1п ~р,
а& t; = +~ оя
(4.49)
Рис. 4.5. Смешанная система координат.
Согласно определению мгновенной орбитм вектор скорости не должен содержать
составляющих, перпендикулярных к мгновенной орбите, т. е.
(4.50)
г ° Ь~ — — — гофф — — О.
С учетом этого условия векторное уравнение д~вижения
(4.51)
д а ~~ ~3
в проекциях на оси Ь~, Ьф, Ьд имеет вид
г' — ги~~, — 1/г2 = ав,
2г~г + г"л = 'га
га~рл — — а~.
(4.52)
~ послед~них уравнениях можно произвести замену переменных по аналогии
с плоским движением. Введем и=г 1, Л1=ш г2 и определим угол ~ дифференциаль-
ным уравнением
(4.53)
ч = и, = аХ/г~.
Тогда система (4.52) станет следующеи:
~2ц а~ а~ Дц
~,„2 ! ф2 ц2 цЗ
(4.54)
Первые два уравнения с точностью до обозначений совпадают с уравнениями
плоского движения (4.29). Если компоненты ускорения ав, а, не зависят от пере-
менных, кроме ц и ч, то система расщепляется, и перв]де два уравнения могут быть
проинтегрированы независимо от остальных.

ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
э 2]
Добавив к (4. 54) дифференциальные уравнения для ортов Ьд, Ьф, Ь „:
&l ;Л а, дЬ
ИЬ„
— = — Ь
Йч Ф
(4.55)
получим замкнутую систему уравнений.
Вместо того чтобы определять орты ь)1, ьа), 1,ч из дифференциальных уравнений
(4.55), а затем находить функции О (ч), 1 (ч), у (ч), можно сразу прибегнуть к диф-
ференциальным уравнениям для углов (4.49). Следуя [4.17|, введем в плоскости
орбиты координаты ~, &l ;) ( м. р с. 4. ), вращающи ся относител но ор ов д
с угловой скоростью ~) = ф — ~. Если в вы-
Я
ражениях (4.49) всюду заменить угол у )Г
на ч + о), то дифференциальные уравнения
для углов о, ~, ю примут вид
&lt 12 ,ч )п и+
=Я2~ 3
а,
— соз (и + ч),
(4.56)
а
— 12 2 з1п (и + ч) с~д 1.
Эти уравнения вместе с (4.52) также за-
мыкают систему.
2. Уравнения движения в поле двух
центров. Векторное уравнение движения в
произвольном гравитационном поле записы-
вается следующим образом:
Рис. 4.6. Система координат для описания
движения в поле двух центров.
'г' = а + д (г, ~),
(4.57)
где д (т, ~) — ускорение от гравитационных сил. В предыдущем пункте рассматривались
уравнения движения в поле одного гравитационного центра
~ (т, ~) = — 7<т/
(4.58)
Теперь дадим уравнения плоского движения в поле двух центров'. 1 и 2. Будем счи-
тать, что гравитационный центр 1 неподвижен и, следовательно, связанная с ним система
координат инерциальная, а центр 3 вращается вокруг центра 1 с постоянной угловой ско-
ростью ~) на постоянном удалении Во и, соответственно связанная с ним система коорди-
нат неинерциальная.
Движение может изучаться в инерциальной (7) или неинерциальной (2) системах ко-
ординат. Приведем обе системы уравнений, записанных в единой форме (обозначения и
связь между координатами одной и другой системы понятны из рис. 4 6):
г&lt ' = " + ") (ф&l ;') 2 †Й< ) (г& t;')) 2
(4.59)
г<') & t;" = а ' — 2 &lt ')ф в ” % & t;
Т
Ф 7 /7
здесь Й"), Й~'~ — гравитационные постоянные центров 1 и 8, а
т &lt 1) ф l ;1 + ~ &l ; )
Я&lt 1 = 7<&lt 2 (г& t;2)) 2 с з (ф&l
&l ;Р l ;1 = < & t 2) г< )) з)п
..к&lt 2 = 7< lt; )Л„ со ф'" Ђ” 71& t 1) г&lt ')) ' соз
%'&lt 2) =)&l ;& t;1 Л '- з1п и< ) — & t;& t;1) г&l ;1)) 2 з
(4.60)
3. Уравнения движения в модельных полях. В качестве модельных рассмотрим
линеаризированное и однородное центральные поля, плоскопараллельное поле и бесси-
ловое поле.
Пусть траектория укладывается в пределах малых угловых и радиальных перемеще-
ний; тогда проекции ускорения, вызываемого гравитационным центром, могут быть раз-
ложсны в ряд Тейлора в окрестности некоторой характерной точки траектории, например
1<ачально &lt : х , у„, 2„ 4.19, .20] Если с стема коо динат ориенти ован та , что н
1&lt ая то ка располон& t; па а си Ох ( о-— -г„уо Ђ” Ђ” О, 2О Ђ”в ” ), то ура нения пространств

[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
движения при сохранении первых членов разложения проекций гравитационного ускоре-
ния имеют вид
~ю ~о + 2~о (х "о)/"о
У = ~ — КоУ/'о
1 )
~о~/го (зо = /с/г~о)
(4.61)
В том случае, когда перемещения х (й) — г„у (й), я (й) малы по сравнению с началь-
ным удалением от центра го, так что
! ~я до ! &g ;) ~  1 Ђ” х г  ! ~ ! )~ Г ! у ~ ! ~ )& t ~о
уместно ограничиться моделью плоскопараллельного поля:
(4.62)
Наконец, при условии, что величина реактивного ускорения намного превышает
величину гравитационного ускорения, можно исключить последнее из уравнений движения
(модель бессилового поля):
(4.63)
г'=а.
Если при движении в центральном поле модуль радиуса-вектора изменяется мало
(траектория заключена в узком шаровом слое), то справедлива модель однородного цен-
трального поля [4.21, 4.22]; векторное уравнение движения в этом случае имеет вид
~ =ф — оР~,
(4.64)
где ио = р„/г„= Й/го.
$ 3. Межпланетный перелет
1. Разбиение межпланетного перелета на элементарные маневры. Траек-
тория межпланетного перелета содержит следующие этапы (рис. 4.7): разгон
с начальной орбиты в окрестности планеты старта (обозначается индек-
сом +1), межорбитальный перелет в
СО поле Солнца (индекс 1), торможение
в окрестности планеты назначения (ин-
декс — 2); на обратном перелете повто-
ряются аналогичные же этапы (обозна-
1
чаются индексами +2, 2 и — 1 соот-
т, ветственно) .
Т Можно выделить два характерных
участка траектории межпланетного пе-
релета: участок движения в окрест-
ности планеты и участок движения
+/
в поле Солнца. Оставаясь в рамках за-
дачи двух тел, будем предполагать,
-/ что гравитационное поле на каждом
1 из характерных участков образуется
одним центром: планетой или Солнцем
соответственно.
г В этой постановке обычно считает-
Р 4 7 С анет ог СЯ, ЧТО УЧаСТОК ДВИЖЕНИЯ В ОКРЕСТНОСТИ
с возвращением. планеты простирается от начальной ор-
биты до точки, где достигается нулевая
полная энергия (параболическая скорость), а участок межорбитального пе-
релета начинается в фиксированной точке одной гелиоцентрической орбиты
и заканчивается в фиксированной точке второй гелиоцентрической орбиты;
компоненты скорости в начальной точке первого маневра и в начальной
и конечной точках второго маневра совпадают с соответствующими проек-
циями вектора орбитальной скорости.

107
ХЕЖПЛАНЕТНЫй ПЕРЕЛЕТ
В настоящем параграфе будем рассматривать только движение в одной
плоскости, игнорируя третью компоненту. Вопрос стыковки участков меж-
планетного перелета здесь также не рассматривается. Основанием для этого
является оценка, указывающая на то, что положение точки сопряжения
участков слабо влияет на энергетические затраты.
Согласно принятым упрощениям оба элементарных маневра, составляю-
щие межпланетный перелет: набор нулевой энергии (или иначе разгон до па-
раболической скорости) и межорбитальный перелет, описываются системой
уравнений в центральном поле (4.18) или (4.13) (последняя без третьего урав-
нения: я:О, а,:0).
Краевые условия к системе (4.18) имеют вид:
для первого элементарного маневра
г(0) =1, р(0) =О, и„(0) =ц„„и,(0) =ц,„
~(Т) ='/,М(Т)+';(ТН вЂ” 1/ (Т) =О;
(4.65)
для второго элементарного маневра
г (0) = 1, р (0) = О, г„(0) = и„„
г (Т) = г„р (Т) = р„и„(Т) = и„1,
и (0) =г...
г (Т) = и~,.
(4.66)
Здесь в обоих случаях за характерный линейный размер г, взят начальный
радиус (см. (4.12)); поэтому г (0)=1; положение системы координат опреде-
лено тем, что точка старта лежит на оси абсцисс: ~р (0)=0.
Если начальная орбита первого маневра и начальная и конечная орбиты
второго маневра круговые, то условия (4.65), (4.66) записываются следую-
щим образом:
для набора нулевой энергии
г(0) =1, <р 0) О, п„ 0) О и 0)
Д (Т) = '/, ~г'-„( Т) + г'-, (Т)1 — 1/г (Т) = 0;
для межорбитального перелета
г(0) =1, р(0) =О, и„(0) =О, и (0) =1,
г(Т) =-г„р(Т) =р„и„(Т) =О, и (Т) =г1 . )
(4.67)
(4.68)
Краевые условия для уравнений в прямоугольных координатах (4.13)
получаются по формулам перехода от полярной системы к прямоугольной
(ср. (4.14)):
и= г„соя ~ — г я'и. ~р,
:с = г соя ~, у = г яп ~р,
г = и„в1п р + и сов и.
(4.69)
2. Межпланетный перелет с возвращением. Между кинематическими
параметрами отдельных этапов перелета существует связь, обязанная усло-
вию возвращения на планету старта.
Для простоты заменим области влияния планет точками на их орбитах;
тогда в системе координат, связанной с Солнцем, траектории космического
аппарата в окрестностях планет будут неразличимы с траекториями пла-
нет. Выделим из траектории межпланетного перелета с возвращением ту часть,
которая лежит вне орбиты старта; сюда входят: перелет с орбиты 1
на орбиту 2, движение по орбите 2 вместе с планетой и обратный перелет
с орбиты 2 на орбиту 1. Обозначим через Т, ~1, Т„~, времена и угловые
перемещения межорбитальных перелетов (индекс 1 — с орбиты 1 на орбиту 2,
индекс 2 — с орбиты 2 на орбиту 1 (рис. 4.7), через Т вЂ” время пребывания
на орбите 2 (оно складывается из времен торможения, разгона, а также
пассивного ожидания у планеты назначения).

108
[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
Из равенства угловых перемещений планеты старта и космического аппа-
рата следует связь между параметрами Т„~р„Т„~р„Т; считая орбиты 1 и 2
круговыми, получаем
Т == ~р, + з, — (Т, + Т,) + 2пг ~/(1 — и,,),
(4.70)
где ж, — угловая скорость обращения планеты 2 по круговой орбите вокруг
Солнца (и,=1), и — целое число оборотов планеты 1 (п=О, 1, 2,...), знак
плюс соответствует и, ( и„знак минус — и, ) и,.
Если орбиты 1 и 2 не круговые, то в формуле (4.70) появятся интегралы;
для учета размеров областей влияния планет необходимо при составлении
равенства угловых перемещений добавить угловые расстояния между точ-
ками входа в область влияния и выхода из нее (см. [4.23]).
В краевой задаче, которая формулируется для выделенной части меж-
планетного перелета, обычно считаются заданными время Т пребывания
на орбите 2 и время Т. пребывания вне орбиты 1: Т.= Т,+Т + Т,. Они опре-
деляют угловые перемещения ~р„~р, и времена Т„Т, в сумме:
и +и =Т,— и,Т +2пг; Т1+Т.=7,— 7,
а не по отдельности, как считается в краевых условиях (4.66).
При круговых орбитах 1 и 2 краевые условия для межорбитальных
перелетов туда и обратно запишутся так:
перелет с орбиты 1 на орбиту 2
г (0) = 1, и (0) = О, и„(0) = О, и (О) = 1,
г (Т,) = г„и (Т,) = — р„и„(7,) = О, и (Т,) = г,-',
(4.71)
перелет с орбиты 2 на орбиту 1
г(Т +Т )=г, и(7 +Т )= р +Т и,
~и„(7,+Т ) =О, г; (Т,+ Т ) =г
г(Т.) =1, и(Т.) = Т. + 2пг, и„(7.) =О, г (Т.) =1
(4.7 )
(в этих формулах величины ~р„Т, не определены).
Вместо параметров и„Т, (угловое перемещение и продолжительность
перелета), фигурирующих здесь в краевых условиях для межорбитального
перелета, могут быть выбраны параметры ~„7, (дата старта, продолжитель-
ность перелета). Связь между этими двумя парами получается из условия
равенства в момент встречи угловых расстояний космического аппарата
и планеты назначения.
Если орбиты 1 и 2 круговые, а дата старта 8, отсчитывается- от момента
противостояния планет 1 и 2, то формула перехода будет следующей:
(4.73)
(п=О, 1, 2, ...).
з, = ~, + Т, — и,~, + 2тсп
Параметры Г„Т, оказываются более удобными для расчетов, в которых
учитываются реальные положения планет на их орбитах.
3. Модельные маневры. В настоящем пункте описываются два примера одномерных
движений в бессиловом поле: набор заданного модуля скорости и, за заданпое время Т
и перемещение между двумя точками покоя, отстоящими одна от другой на расстоянии ~,
за время Т.
Эти маневры отражают характерные черты маневров в центральном поле'. первый
моделирует маневр медленпого набора нулевой энергии с круговой начальной орбиты
(см. (4.18), (4.67)), второй — участок быстрого межорбитального перелета (см. (4.18),
(4.68)).
Уравнения движения и краевые условия для задачи набора заданного модуля ско-
рости имеют вид
(4.74 )
и = ае; и (0) = О, и (Т) = и,.

эВОлюции спутни~А
То же самое для задачи перелета между двумя положениями покоя.'
х=и, и=ае; х(0)=0, и(0)=0, х(Т)=1, и(Т)=0.
(4.75)
В формулах (4.74), (4.75) величина а — модуль реактивного ускорения, с=+1в
направление вектора тяги.
~ 4. Эволюции спутника
1. Удержание спутника в заданном шаровом слое. Спутник выводится
на круговую орбиту, расположенную в верхних слоях атмосферы. Грави-
тационные силы от притягивающего тела дают периодическую составляющую
движения, действие аэродинамического сопротивления приводит к вековому
уходу от начальной орбиты. Возникает задача о такой компенсации силы
сопротивления, чтобы спутник в течение заданного времени оставался
в пределах шарового слоя, максимальный и минимальный радиусы которого
заданы (см. работы [4.13, 4.24, 4.25]).
Движение в гравитационном поле при наличии сопротивления описы-
вается следующей системой дифференциальных уравнений первого порядка:
1 = т, Ф = ае+ ~ — Г/ЛХ;
(4.76)
Г(х, Д, 2)= — — '[1 (- —;(1 — 3 — ',)»
(у = ~/х' + у' + 2');
(4.77)
величины /с,,' приведены в (1.11).
Сила аэродинамического сопротивления Г, которую испытывает аппарат
в потоке, набегающем с относительной скоростью Я, равна (см. (1.23))
Г =1/,с Я р~Щ
(4.78)
где с — коэффициент аэродинамического сопротивления, Я вЂ” характерная
площадь аппарата, р — плотность атмосферы.
Если атмосфера покоится, то скорость Я3 совпадает со скоростью т аппа-
рата в инерциальной системе Охуя; при учете вращения атмосферы с угловой
скоростью 1 (О, О, у,), равной скорости вращения Земли, к т добавляется
векторное произведение г )(1:
Ч3 = т + г )( 1.
(4.79)
Проекции силы сопротивления на оси инерциальпой системы координат выражаются
следующим образом:
К =1/,с и"рЯЗ (х+ у',у),
К„=1/ с %"рЯЗ (у — у х),
К =1/ с %"рЯх'
(ЯЗ = ((х+ У',У)2 + (У вЂ” у,х)2 + 2) ~').
(4.80)
здесь, в отличие от предыдущего, добавлен член Г/М, учитывающий аэроди-
намическое торможение; а — модуль реактивного ускорения, е — единич-
ный вектор ориентации тяги.
Выберем инерциальную прямоугольную систему координат Охуя: пло-
скость хОу совпадает с плоскостью экватора, ось Ох направлена в точку ве-
сеннего равноденствия, ось Оя к северному полюсу, а ось Оу дополняет их
до правой тройки.
Составляющие гравитационного ускорения ~ определяются потенциа-
лом Г притягивающего тела — Земли: д= — дГ/дг. Принимая в расчет пер-
вые две гармоники потенциала сплющенного сфероида, имеем:

ПРОБЛЕМА ОПТИМИЗАЦИИ
~ГЛ. 4
Величина 7, считается положительной в формулах (4.80), если вектор скорости аппарата
т и вектор скорости потока г Х,] составляют угол, меньший л/2 (спутник запущен по вра-
щению Земли).
Плотность ~, входящая в выражения (4.78), (4.80), является функцией не только вы-
соты над поверхностью Земли, но также широты и времени года. Плотность как функция
этих аргументов дана, например, в [4.26].
Перейдем к сферической неинерциальной системе координат г, ~, 0 (рис. 4.8), эк-
ваториальная плоскость которой наклонена на постоянный угол ~ к плоскости экватора
и вращается с угловой скоростью Ы~ вокруг полярной оси Ое [4.24]; в начальный момент
эта экваториальная плоскость совпадает с плоскостью орбиты спутника, угол Й (~)—
свободная функция, подлежащая определению в дальнейшем. Координаты х, у, г выража-
ются через г, ~р, 0, о, ~ следующим образом.'
х=г (соя аксая 0 соя о — яш у соя 0 я1п о- соя 1+ яш Ояш Я яш 1),
у = г (соя ~ соя 0 я1п Я+ я1п ~ соя 0 соя о соя 1 — яш 0 соя о яш 1),
е = г (яш у соя 0 яш 1+ яш О соя 1).
(4.81)
Опуская процедуру преобразования к новым переменным, приведем окончатель-
ный результат:
Р— г (О+ 1~ созе яш 1) — г [ф соя О+ 1~ (соя 0 соя1 — яш 0 яш у яш1)]'=
1 33 .. рЯЗг
= — — — — [1 — 3(яшОсоя1+ соя О яш1я1пу)'] — ~ + ае„,
И
— (г' соя О [ф соя О + 1~ (соя 1 соя Π— яш 0 я|п 1 я|п у)]) — г'Й яш 1 [О яш у—
Ж
— ф я1п О соя О соя у — 1~ соя у соя О (яш 0 соя 1+ соя О яш у я1п ~)] =
63 РЯг2
= — — (яш О соя 1+ соя 0 яш 1 я1п у) соя О яш 1 соя у — ~ соя О [ф соя 0+
г
+ (Й вЂ” у,) (соя 0 соя 1 — яш 0 яш у я|п 1)] + ае„, соя Ог,
И
— [г' (Π— й соя у яш 1)] + г' [ф' яш О соя О + Ы (я1п 0 соя 1+
(4.82)
+ соя 0 яш у яш 1) (соя 0 соя 1 — яш О яш у яш 1)] + ф2 [соя 0 (яш 0 соя 1+
+ соя О яш р я1п 1) + яш О (соя О соя 1 — яш 0 яш у я1п 1)] =
ЯЗ
= — — (яш О соя 1+ соя 0 я1п у я1п 1) (соя 0 соя 1 — яш О яш у яш 1)—
Г
~Яг2
— [Π— ф — у,) соя у я1п ~] + аеэг.
Здесь даны три проекции уравнения Ньютона в безразмерной форме: линейные
З~ 1~
расстояния отнесены к начальному радиусу г, время — к го'Й '~ угловые скорости,
у з~
в том числе у„— к величине Й~'г„', ускорения — к гравитационному ускорению Йг„— ~,
плотность — к максимальной на радиусе г, плотности е„коэффициент в разложении
потенциала 8 — к квадрату начального радиуса го, масса аппарата — к начальной
массе ЛХ,; для безразмерных величин сохранены старые обозначения (ср. переход
от (4.11) к (4.13). Параметр сопротивления .~ выражается так:
ого~2~о
(4.83)
Через е„, е, ео обозначаются проекции единичного вектора направления тяги
е (е'„--~- е'-' + е'-=1) на орты сферической системы координат.
Начальные условия на круговой орбите в принятой системе координат записываются
следующим образом:
" (0) = 1 ' (0) = 0 ~ (0) = ~ ~ (0) = 1, 0 (0) = О (0) = 0.
(4.84)
Конечные значения этих величип не определены, за исключением радиуса г, который
в конечный момент, равно как и во все время движения, должен оставаться в пределах
г, ( г (~) & t  ~ (  l ; ~
(4.85)

ЭВОЛЮЦИИ СПУТНИКА
При дальнейшем анализе задачи ограничимся рассмотрением больших высот, где
параметр к мал; другие безразмерные параметры задачи у„~ имеют следующие численные
значения:
0,6 10 ', ~ 0,5 10 з.
(4. 86)
Если силы от несферичности притягивающего тела, силы сопротивления и тяги от-
сутствуют (Р=«=0, а (~)=0) и свободная функция Я (~) принята равной нулю: Я (~): — О,
то уравнения (4.82) описывают кеплеровскую орбиту, лежащую в экваториальной пло-
скости 0=0 системы координат ~, ~р, 0. В реальном движении кеплеровскую траекторию ис-
кажают малые силы от песферичпости и малые силы сопротивления.
По условиям задачи траектория движения должна быть заключена в узком шаровом
слое Лг (Лг=гп,«« — гп~;„(< ). Поэт му функ и г ( ) г ( ) ф ~) во се вр мя движе
должны мало отличаться от соответствующих 8$
значений на невозмущенной круговой орби-
те: ~г (1) — 1( (& t; 1, (г ( )( (& t; 1, ф ( ) Ђ” 1~
Имея в виду этот случат~, представим пара-
метры траектории г (~) и ~ (~) следующим об-
разом:
г (1) = 1 + ~ (1), ~ (1) = т, + 1 + О (1), (4.87)
где )О (~) )(&lt 1, [О ~) )( lt; , ] з (~) )(
величинам ]:., ~, ~ задача допускает линеари-
зацию.
Условие пребывания спутника в узком
шаровом слое (г „, г;,) не накладывает фи-
зических ограничений на область изменения
угла 0 (~). Однако из-за того, что в невозмущен-
ном движении 0 (~)=0 и возмущающие силы
реального движения малы, можно считать на
начальном этапе движения функции 0 (1) и
0 (1) малыми:
Рис. 4.8. Система координат для задачи удер-
жания спутника.
[О (~) ](&lt 1, [0 ~) ) &lt 1 п и 0 &lt
~ — 3;- — 2« =22 соя 1 — 33 [1 — 3 я1п' ~ я1п'(~, + ~)] + ае„,
1) + 2О = — Й соя 1 — 63 я1п' 1 яш (ус + ~) соя (~, + ~) — « — (1 — у, соя 1) + ае,
О+ 0 = Й я1п 1 соя (~, + ~) — 2~ яш 1 яш (~, + ~) — 63 яш $ соя 1 я1п (~, + ~)—
(4.88)
— «у — я1п 1 соя (у + ~) + аео.
)
В этих переменных краевые условия (4.84), (4.85) запишутся так:
~ (0) = Я (О) = 'О (О) = '0 (О) = 0 (О) = О (О) = О,
~;, <Я ю) <Я (0
(4.89)
В правых частях системы (4.88) сохранены члены только первого порядка по 7'.;
члены второго и высших порядков отброшены, так как перед ними множителем стоит малая
величина у. По этой же причине следует оставлять только нулевой член в разложепии
плотности по ~, с, 0; входящая в (4.88) плотность р является известной функцией времени,
определяемой по начальной круговой орбите (~ (~)= с (~)=0 (~)=0).
Выберем свободную функцию И (~) следующего вида [4.25]:
~= — 33 соя ~ = сопят
(4.90)
(при этом упомянутое выше условие малости производной Ы выполняется).
Третье уравнение системы (4.88) преобразуется так:
О + О = — «Л1 У, Я1п 1 соз (У, + й) + аея (О (0) = О (0) = 0).
Р
(4.91)
Полагая производную свободной функции Й (~) малой: [ 12 (~) [(& t; 1, линеариз
систему (4.82) по с, Е, з, О, О, 1-'; получим

112
[ГЛ. 4
ПРОБЛЕМА ОПТИМИЗАЦИИ
Предположим, что составляющая тяги в направлении 0 отсутствует (ез — — 0), и оце-
ним максимальное значение угла 0, достигаемое к моменту времени ~=~1; для этого поло-
жим р (8)=1, ЛХ (1)=ЛХ1:
яп ~
0 (~,) = А~', 2Л~ [я1п ~ро я1п г1 — г, я1п (~ро + г1)).
1
(4. 92)
Наличие смешанного члена в решении (4.92) указывает на наличие колебаний с на-
растающей амплитудой радиуса-вектора относительно экваториальной плоскости.
При ~1 (& t; 1/ ,х у ол 01 а и у ет тол ко линейн го чл н в разложе ии п 0 справедл
Окончательно дифференциальные уравнения и краевые условия, описы-
вающие маневр удержания спутника в заданном шаровом слое, имеют вид
~ — 31 — 2() = — 3~ [1 + 2 соя' ~ — 3 я1п- '~ я1п-" (з, + ~) (+ ае„,
~) + 21 = — 6С~ я1 и' ~ я1п (р, + ~) соя (р, + ~) — г. Р (1 — ), соя () + ае,
(4.93)
6+0= — ху, р я1п(соя(у,+~)+аез,
~(О) =С(О) =„(О) =„(О) =0(О) =0(О) =О,
6,(6(й) (5 „(0(й(Т).
Если движение спутника рассматривается в достаточно широком диапа-
зоне времеыи, то целесообразно изучать изменение параметров -"'-, ~, ~, ~, 5, 0
через целое число периодов я. По прошествии времени 2ял параметры 1, $, ()
станут равными
2г~ 2г1г
1,=2 ~1 — 2!,соя ц( — ~ + ~'~' Н~)+2
о о
2г~
2гп
2г~
ае соя 1Ж вЂ” ае„яп1й1,
Ж вЂ” 2 ае я1п ~Ю+ ае„соя~И,
о о
1, = 2к(1 — 2[, соя ~)
(4.94)
о
2гк
~),=х(1 — 2у, соя() 3 — — 4
рИ~
ЛХ
о
р соя ~
ае Ж+
2гй
2г1г
л
+4 ае И+4 ае саяна+ 2 ае„я1п ~й
о о о
(выражения для остальных параметров записываются аналогичным образом;
здесь они не даны, ибо в дальнейшем не понадобятся).
Члены в решении ~ (г), 1 (1), () (1), пропорциональные коэффициенту ~3,
имеют осцилляционный характер и в усредненном решении (4.94) отсут-
ствуют. Их влияние сказывается на поведении траектории в интервале
О ( ~ ( 2т. Если ~)& t; к, то велич ны ах с, 1 1 на обор те зави
в основном от ~, т. е. толщина слоя, в пределах которого располагается траек-
тория на обороте, определяется силами от несферичности притягивающего
тела. Считается, что амплитуда колебаний радиуса на одном обороте (㠄—
г „) укладывается в заданную толщину шарового слоя.
2. Поворот плоскости круговой орбиты спутника поперечной тягои.
Дадим вывод дифференциальных уравнений и краевых условий, описываю-

ЭВОЛЮЦИИ СПУТНИКА
щих рассматриваемый маневр, где в качестве исходных используются урав-
нения в оскулирующих переменных.
Поперечной названа тяга, направленная перпендикулярно к мгновенной
плоскости орбиты (еще одно название — бинормальная тяга). В обозначе-
ниях, употребляемых для записи системы (4.47), это проекция а~. Если
в (4.47) аф — — ад=о, то длина большой полуоси А, эксцентриситет я и момент
прохождения перигея Т остаются неизменными при движении, так что гео-
метрия начальной орбиты сохраняется, причем если начальная орбита
круговая, то безразмерный радиус г, безразмерная длина большой полуоси А
и эксцентриситет я равны таким значениям:
(4.95)
г(»)= — 1, Л(»)=:1, =(»)=О.
Для описания движения остаются три уравнения:
И~ ~Ж ~1П ~ И~
— =ие со~ з,: =ие, — ' — -1 — ае сСд г яп з.
Ж '' Ж яй~ ' Ж
3
(4.96)
( .97)
с(0) =
то долгота восходящего узла (Й (0)) и аргумент широты (~ (0)) в начальный
момент не определены по отдельности; их сумма — широта точки старта
в инерциальной системе координат — задается положением этой системы.
Примем
Р (0) + 2 (0) = О.
(4.98)
В конечный момент задаются наклонение и долгота восходящего узла:
» (Т) = »„2 (Т) = о,.
(4.99)
Пусть»,(&lt 1, то да тригонометричес ие функ ии уг а» мо ут б ть
менены в уравнениях (4.96) таким образом:
6Ца» = ие соя &lt р  = ае 1п з) »   1 Ђ” ае 1п ф
Из (4.98), (4.100) следует:
(4.101)
Подставляя последнее выражение в первые два уравнения (4.100), по-
лучаем
Ж~Ж = ие соя (» — О) Й = ае я1п (» — 2)/».
(4.102)
Введем следующие замены:
у = » я1п (2 — 2,), и = ~ соя (2 — 2,).
(4 1ОЗ)
В терминах ~, а уравнения и краевые условия, описывающие маневр
поворота плоскости круговой орбиты, примут вид
~о = ие соя (» — ~,),
о~(0) =О,
и(Т) =» .
~=ае я1п (» — Р,),
~(О) =О,
~(Т) =О,
(4.104)
8 Механика полета
В уравнениях (4.96) приняты следующие обозначения: ал = ае, а—
модуль реактивного ускорения, е=+1 — ориентация вектора тяги относи-
тельно мгновенной орбиты (е=+1 — по нормали, е= — 1 — против нор-
мали); ~р=ч+~, — аргумент широты, отсчитывается в мгновенной плоскости
от линии узлов.
Если начальная орбита лежит в плоскости экватора,

3'Д АВА 5
ИДЕАЛ ЬНЫИ ДВИГАТЕЛЬ ОРГАН ИЧЕННОЙ СКОРОСТИ
ИСТЕЧЕНИЯ (ИМПУЛЬСНЫЕ ПОСТАНОВКИ)
К двигателям ограниченной скорости истечения относятся все тепловые реактивные
двигатели, скорость истечепия которых не превышает предела. зависящего от максималь-
ной допустимой температуры стенок камеры сгорания или топлообменника (см. 1 1 гл. 3).
Двигатели этого класса характеризуются сравнительно малой удельной массой т., на ечи-
ницу тяги (т„— 10 2 кз/кГ). Такие двигатели могут обеспечивать большие значения
реактивного ускорения, отсюда — другое название данного класса двигателен: двигатели
большой тяги.
Ввиду малости удельной массы ~., двигателей ограпиченной скорости истечения мас-
сой двигателя М„в задачах оптимизации обычно пренебрегают (это нельзя делать для
тех маневров, где потребная величина реактивного ускорения велика, т. е. в тех случаях.
когда нарушается условие М„/ЛХ (Т)=т,. (~М)тах~М (т) (& t;
В настоящей главе описываются особенности оптимальных режимов работы идеаль-
ных двигателей ограничспной скорости истечения. Оптимизационная задача делится на
параметрическую и дпнамич;скую части, находятся условия оптимального подбора сту-
пеней многостунспчатого аппарата н в импульсной постановке рассматриваются оптималь-
ные межорбитальные и мсжпланстпые перелеты.
$ 1. Разделение вариационной задачи, оптимальные
соотношения масс
1. Характеристики идеального двигателя ограниченной скорости ис-
течения. Идеальный двигатель ограниченной скорости истечения характе-
ризуется следующими выражениями тяги Р, расхода д и массы ЛХ„(ср. (4.9),
(4.10) при и,=Р, и,=Г):
(0(Р(~)(т, 0(Г(~)(Г „), (5.()
Р=Р, д=Р/Г, М„=О
т. е. идеальный двигатель невесомый, скорость истечения ограничена сверху,
на тягу ограничения сверху нет, и поэтому допускается существование
импульсных режимов работы (на бесконечно малом интервале времени тяга
бесконечна, расход бесконечный, выбрасывается конечное количество рабо-
чего вещества), эти режимы в так называемых импульсных постановках
задач считаются единственно возможными.
а
2. Одноступенчатый аппарат. Запишем вариационную проблему для
идеального двигателя ограниченной скорости истечения аналогично (4.8):
М. = — Р~У,
г=~,
т=Ре~М,+и,
(0(Р(~) ( оо,
.Ч. (0) = Ме, М. (Т) = тах,
г (0) = г„г (Т) = г„
т (0) = т„ч (Т) =- т1,
О( Г(1)( Г,„, ~е(1) ~ =1).
(5.2)
В этом случае формула для ~иассы М. содержит только три компоненты:
полезную массу М„~иассу рабочего вещества М и ~иассу баков Мз; масса
двигателя по определению идеального двигателя равна нулю, поэтому
М. = М = М.-~- М,-~- М,.

ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
Введем в уравнения (5.2) вместо тяги Р реактивное ускорение а = Р~М =
=Р,~,$1. и отнесем компоненты М,, М., М к начальной массе Мо:
т, = М,/М„т. = М,/М„т = М (М„
Тогда система (5.2) принимает вид:
т (О) =1, т,(Т) =тах,
т. = — ат,~Г,
г (0) = г„г (Т) = г„
т (О) = т„т (Т) = т,
О ( Г (~) ( Г „, ~ е (1) ~ = 1).
т=ае+д,
(0(а(1) ( со,
г'амильтонова функция Н и уравнения для импульсов в рассматриваемом случае
записываются так:
Н = — р,ата ~7 + р и+ р, ° (ае+ д), 1
д
р, = р,а/Г, р,. = — — (р„я),
1&gt „= Ђ” р, р. Т = Ђ”
Функция р, (~) отрицательна всюду на отрезке 0 ( ~ ( Т в силу того, что уравнение
для р, линейное однородное и в точке ~= Т функция р, отрицательна.
Множитель при 1/Г в функции Н может быть либо положительным (с учетом знака,
стоящего перед всем членом), либо равным нулю при а (~)=0, поэтому вдоль активных
участков траектории (а (~)+О) оптимальное управление Г (~) (доставляющее минимум га-
мильтоновой функции Н) таково: У (~)=УП1„.
Подставляя это оптимальное управление в (5.3), приходим к выводу,
что вариационная проблема (5.3) на максимум т. (Т) эквивалентна вариа-
ционной проблеме на минимум характеристической скорости Ли (Т):
ЬВ=а, Ли(0) =О, Ьи(Т) =тш
г= т,~ г (0) = г„г (Т) = г
Ф = ае+ е, т (О) = т„т (Т) = т1
(а (1) ) О, ~ е (1) ~ = 1).
( )
Задачу (5.5) (в ней отсутствует переменная т.) будем называть динами-
ческой частью проблемы оптимизации. Контрольный функционал задачи
(5.3) — полезная масса т. (Т) — связан с функционалом задачи (5.5)—
характеристической скоростью Ли (Т) — формулой Циолковского
щ ~ Т1 — рц ~ щ — ~-~~(~')/1'ша~
а ~ 1,'~ ~ х
Если масса баков и начальная масса топлива связаны линейно:
М = ~М„(0),
то относительная полезная нагрузка может быть представлена в виде
т, = (1 + ~) (т + т,) — ~.
( )
Подставив (5.6) в (5.8), получим относительную полезную нагрузку т„
как функцию характеристической скорости:
т, = (1 + ~) е ~ — ~ (%' = Ьи (Т)~ У „).
Из (5.9) следует, что не может быть выполнен маневр, для которого
величина функционала Ли (Т) ) Г „1п 1(1+ ~3) /р] (полезная нагрузка
8*

ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[гц. 5
становится отрицательной). Маневр, характеристическая скорость которого
находится за указанным пределом, может быть выполнен многоступенчатым
аппаратом.
3. Многоступенчатый аппарат — разделение задачи. Рассмотрим аппарат,
состоящий из и ступеней, которые работают последовательно. Стартовая
масса всего аппарата (первой ступени) равна МЦ& t = М& t;' gt;+ М + ЛХ$
израсходования рабочего вещества (МЯ) баки (М~')) сбрасываются и начи-
нает работать вторая ступень, чья стартовая масса равна полезной нагрузке
первой ступев&lt л, ~ = М&l ; ,'> = ЛХ& t '1+ М lt;'о + М$'& t;. Затем пр
лишь у последней, п-й, ступени сорос баков не ооязателен.
Используя соотношения М~') =р,.М~'„~, ЛХ~'1= М1"+'), можно представить
относительную полезную нагрузку такого аппарата в виде
ЛХ«&l ;) ЛХ < lt; Л& t;&l ;п вЂ
т, = '«& t; = „" „ „ ° °, ';„' „ Ц И + р .) (т l ;'< гг ['))
(5. 10)
т~'1 = — ит~"'1/Г" Я&l ;) <Е l ;Е$ ), &l ; =1
т&lt '< (Ц' gt;) =1, т& t '> (Е~
г = т, г (О) = г„г (Т) = г„
т = ае+ и, т (0) = т„т (Т) = т„
Я
.=П[(1+1;)( !" + ~") — 1,~=
а=1
(5.1 1)
а ~ со, "' 1 ~',~„е 1 =1,
'', (т(')+ т&lt '~
Для решения (5.11) необходимо найти оптимальные управляющие функции а [&lt
е [&lt ), & t; & t;" г) и оп имальные араие ры т lt;1'+ т '. ока ем, что ту пр
разделить на динамическую и параметрическую части.
Если прологарифмировать функционал в [5.11). он становится аддитивным по
относительным полезным нагрузкам ступеней, и к участку полета на отрезке [<&
г["'] может быть приложен анализ проблемы [5.3). Управление на [<&l ;,"', г<"
быть оптимальным; поэтому, как следует из анализа [5.3). при л<о ых началь
данных г (ф~&lt ), «(ф >) олжно выпол яться у лови Г& t "' [г) Г<",& t;,. И
проблемы (5.3) последовательно для [и — 1)-й, (и — 2)-й и всех остальных ступеней,
получим, что Г«~ (г) = ГЦ& t; [ lt = 1, , .
В этой ситуации из (5.11) может быть получено равенство
т
У2
Ьг& t; Т  а с = — ~, У~' ~, [п (т ' gt; +
о
(5.12)
и исходная проблема (5.11) делится на две задачи: динамическую часть—
Обозначим через (го«&g ;, 1&l ;<'&g ;) инт рва полета lt; й туп ни, где
момент сброса баков &lt -й ступ ни (&lt +~г), & t;'+'  ЕЙ&lt 1+ О сбро
исходит мгновенно), Е~~") = Т.
Учитывая введенные обозначения и (5. 10), запишем вариационную
проблему на максимум относительной полезной нагрузки многоступенчатого
аппарата в виде

ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
задачу (5.5) и параметрическую часть, которая записывается так:
~г
т,=П[(1+ ~,) (т® -~-т~')) — Ц= тах
( .13)
— ~ Г~'),1п (т~'~+ т") =Ьс (Т)
э=1
(3,.Я1+ ~3,.) ( т~') + т~') ( 1).
1п т, =,~~ 1п т &lt ' = ~ и ( + 3 . е к ' ~ ° Ђ” ф =
( .1 )
~г
Ьу"'=Ьу~Т)(0(Ьу'"(Г<'.~, п, ', ~' ), 2, ..
Ф
!=1 !
где выбору подлежат переменные Ьи"). При оптимальном подборе Ьи'" часть
переменных может оказаться принадлежащей строгому ограничению Ши") = О
(~ (- 1, 1 — множество ступеней, которые не включаются в оптимальный
аппарат), а часть Ьи") ) О (~ ~ 1+, 1' — ..);пожество ступеней, включенных
в оптимальный аппарат). Для последних необходимые условия оптимальности
записываются в виде
~Иу")~Н1п т~'& t = со1
(5.15)
(с ~1').
Заметпм, что условия оптимального подбора размеров ступеней всегда
могут быть записаны в виде (5.15), если относительная полезная нагрузка
км/сек
И
Д~п т„"'
Л
7 Ап~') км/сек
( Я Д 4 5 б
Рис. 5.1. Характеристики качества, ступеней.
каждой ~-й ступени зависит только от величины ~-Й характеристической ско-
рости Ьи"). Характеристика качества ступени
(фи")) = ~1~ — "' ек "'~~ "~ах (5.16)
ШЫ пс'') ~ 1+ 3,
шах
с увеличением Ши") (т. е. с уменьшением относительной полезной нагрузки т~,'&g
монотонно уменьшается до нуля. На рис. 5.1 приведены три зависимости
— НЬи")/Н и1 т~'), посчитанные для разных значений параметров ~,,
Отметим, что в параметрической задаче (5.13) число и есть максимально
возможное, но не обязательное число ступеней, так как равенство т~') +
+т~') =1 означает невключение ~-й ступени в аппарат.
4. Многоступенчатый аппарат — оптимальные соотношения масс. Введя
обозначения Ьи") = — Г~',), 1п (т® + т~~')) (Ьи") — величина характеристиче-
1
ской скорости, набираемая ~-й ступенью), перепишем задачу (5.13) в виде

~ГЛ. 5
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
р, = 0,1, УД& t = ,2 км/ ек Ђ” кри ая 1; 8 = 0, 5, Я  3 км/ ек Ђ” кри ая
р, = 0,2, ГД~, = 2,8 км/сег — кривая 8. Проиллюстрируем алгоритм оптималь-
ного подбора ступеней с помощью условий (5.15) на примере приведенных
зависимостей. В диапазоне 0(Ьи'1>( ,3 км/
НЛ»" &
»'&g ;и т '
оп'1)
поэтому здесь оптимален аппарат, состоящий из одной ступени 1. В диапа-
зонах 0<Ьп 1&gt <3, км/се , 0& t;Шп"& t; <1,5 м/сек выпол
сИи" ) (,) ~~ц(з)
& t; & t;(~~ ~~, g
(~=1, 2);
поэтому в диапазоне 2,3 км/сек ( Ьи (Т) ( 5 км/сек = (1,5+ 3,5) км/сек опти-
мален аппарат, состоящий из ступеней 1 и 2. В диапазоне 5 км/сек ( Ьи (Т) (
(19 км/сек оптимален аппарат, включающий все три ступени.
В случае подбора ступеней с одинаковыми характеристиками ф,. = ~,
Г~',> =Г „, ~ 1, 2, .. и) из (5. 5 и (5. 6) следу т, то относитель
полезные нагрузки и величины ~-х характеристических скоростей должны
быть одинаковы:
Ьи" & t = Ьи (Т
(5.17)
(с =1,2,... п).
Такой аппарат может выполнить маневр с ненулевой полезной нагрузкой,
если Ьп (Т) ( (Г,„/и) ) и (1+ ~)/3. Относительная полезная нагрузка >г-с
пенчатого аппарата с одинаковыми параметрами ступеней (~,. = ~, У~',~„ = У „)
равна
(5.1 )
&gt » = ( + ~) р ~" & t;т gt &gt "&g
Она монотонно растет с ростом п и достигает максимального значения при
П~ СО:
]1п1 щ — е-(1+1)~р(~)/~'шах
~г-~.со
(5.19)
$ 2. Динамическая задача, уравнения экстремалей
Запишем гамильтонову фупкци&g ;  и уравне ия ля импульс
Н = р,,а + р,. ° т + р, ° (ае + я),
д
г = „ (р а)
(5.20)
1'~ = Ру
Оптимальное вектор-управление е (&g ;) (доставля&g ;ощее ма симум ф нк ии Н)
>(>о(&
(5. 21)
е (~) =р,/р,
1. Уравнения экстремалей, условия оптимальности. В предыдущем
параграфе было установлено, что для идеального двигателя ограниченной
скорости истечения выделяется независимая вариационная задача (5.5)
о построении оптимального закона изменения вектора реактивного ускорения
(динамическая задача). Проведем анализ задачи (5.5) с помощью принципа
максимума сначала в предположении 0 ( а (~) ( а,„(множество допусти-
мых управлений замкнуто), а затем перейдем к случаю а,„— ~ со (множество
допустимых управлений открыто).

ф 2]
ДИНАМИЧЕСКАЯ ЗАДАЧА
В состав оптимального управления а (Г) могут входить три вида управления:
а(г)=0 при а (г) (О,
а (г) = аш»~ при Ь (г) ) О,
а (г) =а»~ (г) при а(г) =0
(Д(г) = р — 1),
(5.22)
где а,, (г) — особое управление (функция Н не зависит от а).
Рассмотрим активные участки траектории с а = а. ~. Длительности ~; таких
активных участков при аш,~ — ~ СО дол ке1ы стремиться к нулю, иначе интегралы
ге+'/2т Ъ.
(5.23)
1 — '/ т
не будут конечны (отрицатсльная или нулевая полезная нагрузка). Отсюда следует, что
при а „-ь со комбинация Л (г) не меняет быть положительной на конечном интервале вре-
менп и в силу непрерывности Л (г) ( 0 всюду на отрезке [О, Т1
Воспользовавшись (5.21) и (5.23), вычислим приращепия скоростей, полученные
В моменты приложения ъ1Ге10 Венных импульсов тяГи:
8 +О
(ае+д) сИ = ' Ьи;
р. (г;)
Р~
(5.24)
(верхние индексы « — » и «+» означают значения переменной до и после импульса тяги).
Найдем теперь условия оптимальности, которые определяют моменты приложения
импульсов тяги г; на интервале (О, Т). Для функции ХХ (р (г), т (г), г (г), а), непрерывной
по времени, должно выполняться условие
Н+; — Н, = р,. ° (т+, — т; ) = — Ьи;р'„(г;) = О.
(5. 25)
Следовательно, в оптимальные моменты приложения импульсов тяги ~,.
на интервале (О, Т) должны выполняться следующие условия:
Р,,И;) ~о.
р,(~;) =1
(5.26)
Р,И;)=О
Суммируем результаты, полученные для задачи (5.5). Оптимальному
маневру в физическом пространстве соответствует непрерывная траектория
в сопряженном фазовом пространстве импульсов р„. Эта сопряженная траек-
тория заключена в замкнутом шаре единичного радиуса, ее начальная и ко-
нечная точки определяются условиями трансверсальности. Моментам прило-
жения импульсов тяги на интервале (О, Т) соответствуют моменты касания
сопряженной траекторией сферы единичного радиуса. Участки сопряженной
траектории, лежащие на этой сфере, соответствуют особому управлению
а„, (г) (в него могут входить и импульсы тяги). Оптимальное направление
ускорения дается вектором р,.
2. Импульсная постановка задачи. Задачи оптимальных перелетов
аппарата с двигателями ограниченной скорости истечения (большой тяги)
часто решаются в импульсной постановке, основное допущение которой
(как уже говорилось) — замена активных участков полета с включенной
тягой мгновенными импульсами тяги. Все работы, рассматривающие задачи
в импульсной постановке, по методу исследования можно разделить на две
группы. К первой относятся работы [5.1 — 5.131, в которых с самого начала
решения задачи используется возможность найти интегралы движения
на участках траектории между импульсами тяги, после чего задача на мини-
мум характеристической скорости представляется как задача на экстремум
функции в конечномерном пространстве переменных. К другой группе отно-
сятся работы [5.14 — 5.19], в которых условия оптимальности формулируются
в терминах сопряженной траектории, т. е. решается задача на экстремум
функционала в бесконечномерном пространстве. При этом может использо-

120
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. Ь
ваться метод ва иа ий
ления [5.16].
д р ц " [5.14] или методы классического вариационного исчис-
~У
Нариационныи подход удобен тем, что самые разнообразные по своим
краевым условиям пе елеты
р еты характеризуются сопряженной траекторией
общего вида ( ешением сист
д (р системы уравнении для импульсов), для которой
° . °
с помощью условий трансверсальности необходимо определить только
произвольные постоянные.
е. Благодаря использованию сопряженной траекто-
рии иногда проще решается вопрос об оптимальном числе импульсов, а также
проще использовать полученное решение как первое приближение для е-
д р енной тягой. Приближенное решение системы урав-
для ре-
нений для импульсов позвол
зволяет получить простые условия оптимальности,
легко разрешимые вместе
те с интегралами движения. Изложение настоящей
главы соответствует вариационному подходу.
Далее будут рассматриваться лишь импульсные постановки задач,
т. е. будет допускаться управление а (~) вида
а (г) =,~, Лп,.о (г — ~,.),
где 3~8 — Е.~ — ~ нк ия
— ~у ц ~~ирака, 1,. — моменты приложения импульсов
тяги, и — число импульсов тяги, Лг,. — приращение характеристической
скорости в ~-м имп льсе тяг Т
у е тяги. Таким ооразом, заранее исключаются режимы
()= „„() (, возможные на участках особого управления (Л (~)=:О)
и требующие специального исследования [5.20, 5.21]. Кроме того, в от ель-
ных постановках за ач н
~ д ч иногда будет фиксироваться число импульсов тяги.
роме того, в отдель-
ппя (д = — lд',/ г /3 ' авве ~ия
апряженная траектория на кеплеровой дуге. Для центрального и
р ° о поля тяготе-
— — ) уравнения днпжения и уравнения импульсов запишутся в виде
1'г, 1~)„3 (г ° р,.)
р "~ Р' 3 +
(5.28)
(5.27)
Эта система уравнений имеет четыре интеграла:
~'~, ~( г — р, ~( ч = Е = сонями,
й
— р„° у — —,. (р„г) = ХХ = со11з$,
(5.29)
и з котор]л три первых не независимы.
Найдем решение системы (5.29) (вектор р„(г)) па кеплеровой го (а=О) ля
с помощью интег алов пло а ей и
интег алов 5.29 в
р щ дей и интегралов Лапласа [4.7] сформируем из первых трех
р ( . ) два независимых и добавим к ним последний из (5.29):
(р„, г, М) — (р„, т, М) =М ° К= с4,
(р„, г, Г) — (р„, т, Г)=Е ° г'=с,-,
(5.30)
р, — ' (р. ) !
Г )
р, = — (с, + Х,) ч + (с, + Х2) (г ~ М) + (са + Ха)
1
С4 — НГЧ С4 + НаМ
(г ° ч)2 ~~ Х2 ХХ2 г ° ~ 2
(г т)М,
Ж,
(5. 31)
(5.32)
~3
аХХ" (г ~)'
Интегралы типа (5.32) вычислены в [5.22].
( ХХ = ! М /).
а
где М=г,'(ч, Г=г — ~г ° ~~х — т ~г ° т
— ( ° ) — (г ° т), а три вектора, взятые в круглые скобки,
означают их смешанное произведение.
(для М' г ° ч2 О
ри с4 — с, = П = О система,, я
(5.30) является одяороднои и ее фундаментальная
~Ф
для (г ° ч)2 ф О) система решении состоит из векторов т, г)(М, М (г ° т). 11 и
~ решается с помощью метода вариации произволь-
',г ° ч',. ри
Ы э

ДИНАМИЧЕСКАЯ ЗАДАЧА
ф 2]
Заметим, что система уравнений для импульсов в (5.28) совпадает с системой уравне-
ний движения в вариациях (при ае — заданной функции времени — системе решений для
сг соответствует система решений для р,). Поэтому все интегралы и решения системы
для импульсов могут быть получены из интегралов и решений основной системы уравне-
ний, т. е. в качестве фундаментальных систем решений уравнений для импульсов могут
использоваться уже найденные фундаментальные системы решений для уравнений в ва-
риациях [5.22 — 5.24). В частности, интегралы (5.29) могут быть получены варьированием
интегралов площадей и энергии на кеплеровой дуге и заменой в них ~г на р,.
Полезно представить вектор р, в ортонормированном базисе, связанном с плоскостью
орбиты:
М
аМ '
М~(г
Ег
г
Р, = Ро . ф
(5.33)
где р, — проекция импульса па направление радиуса-вектора движущейся точки,
р — проекция импульса на трансверсаль в плоскости орбиты, р — проекция импульса
Р&l ;р
на нормаль к плоскости орбиты. Учитывая возможность замены переменных р, на ()г,
Рт
р на г ор, р на ох (где г, р, 1„, 1 — обозначения переменных в полярной системе
Р&l
) Р
координат (4.18), а ог — вариация траектории вдоль нормали к плоскости орбиты)
можно использовать систему решений, полученну1о в [5.22]:
р„= с1 яп1 ч + с2 соя ч + с' (2à — Зг„~),
р =С1(1+г(р) соя Ч вЂ” С (1+ г(р) Я1п Ч+ Сзг(р — С43о, $, (5 34)
4
Рц — сзг Я1п ч + сзг соЯ ч (с~ — — Н)'28),
где р — фокальный параметр, 8 — постоянная интеграла энергии на кеплеровой дуге,
~ — истинная аномалия.
Особенно простой вид имеют выражепия для импульсов при движении по круговой
орбите (г=сопя$, эксцентриситет в=О):
= с1 ЯН1 ~р + с2 соя ~р + (Н/8) Г,
р = с12 соя р — с'2 Я1п &lt р+ сд Ђ” (ЗН/ 8)
1
р = се&g ;г 1п ~   Г со
Укажем еще два представления решения системы для импульсов, которые будут ис-
пользованы в дальнейшем изложепии. Уравнения, описывающие кеплерово движение
в цилиндрической системе координат р, Х, з (х= р сояХ, у= р Я1пХ, з=з), а также система
уравнений для импульсов могут быть получены из следующего гамильтониана:
(5.35)
~Л п~~ Лр ~р~~ Усг
Р Р ~ р ~1+~гЬ+ р, 2, 2,~У, Рп р Рф1 ( 2, 2)~У, Р~~,
р ~г
(5.36)
с помощью обычной процедуры
и = дН/др, р = — дН/д11
(11=(р, Х, я, 1~, г1, 1 ), р=(рр, р1, р„, р„„, р„)).
(5.37)
Если выбрать систему координат так, чтобы плоскость х, у совпала с плоскостью
орбиты, то основное движение окажется описанным в полярной системе координат
(р = г, Х =р, и = иг, п1 — — и ) и система (5.37) перепишется в виде
й
2
Г Г2
г= уту
7~те~~
О
г
(5.38)
р =О,
р 2и ц

122
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 5
Систему для импульсов иэ (5.38) с помощью интегралов р =сопвФ, Н=сонвВ можно
преобразовать к системе из трех уравнений:
У~
игр, — р,й„= — Н+ — р,,
9
У" У~
— (и Р„)+ 2 — Р„= — — Р,
~Р», й
,1,2 + — „з Р.,=О,
(5.39)
имеющей решение
У~
агап
р. =~~Ь-(-р,. ~, (й~ — йГ'(-(-~~ 2 — 3~„~.(-, (Й~ — У')],
Р. = Ф, + Р, р' Я~ -(- "') -(- ~."~ -(- ~у [ — ~ -(- ~; Р~~ -(- ~')],
1
Р~ = свгю„+ се (аг — Ш ) °
(5.40)
Система (5.34) получается иэ системы (5.40) с помощью замены произвольных
ПОСТОЯННЫХ -'
( ~Ф
р = — с2 — с4~,
&l ;
с1 ——
Н
24'
(5.41)
Рф
С5
Система решений (5.40) является особенно удобной, когда в силу условий транс-
версальности постоянные р = Н = О.
Заменив в системе (5.39) независимую переменную т на независимую перемен-
ную ~р, можно преобразовать ее в систему
~2р
Г
— р = — 2Н вЂ”,
Ду2 -Г»,„— — у2 ф
9
рр» -1- тр» ГЫ~~~
— -(- 2р = — Н—
Ир Й/Ш ( " гй'
9
~з~ „+
(5.42)
имеющую решение
Н Ми
Р = с, в1п р+ с,'сов р+ 2 2г — Зп,.т + „,, (Ьг — М')
с,'2 сов р — с,'2 е1п р + с +
(5.43)
Н й ~2
+ 24,(, — 3 (((,"-. + гт) т + 2п„г+
Р, = сьг в1п Р+ с,г сов Р.
4. Сопряженная траектория в плоском случае. Рассмотрим возможные сопряжен-
ные траектории на плоскости р,, р» 1 заключенные в круге единичного радиуса. При
пт1»91
движении по круговой орбите иэ (5.35) следует, что при Н =0 сопряженная траекто-
рия может представлять собой или точку Р„=О, р„= с,', = +1 (рис. 5.2, а), или
эллипс Р2 +[(р, — с~)/2]э=С1 (рис. 5.2, б — д). Иэ вида уравнений этой сопряженной
траектории следует, что одновременно условиям (5.26), относящимся к моментам
включения тяги, могут удовлетворять лишь две точки: р, = О, р, = + 1.
У

12
ДИНАМИЧЕСКАЯ ЗАДАЧА
э 2)
При Н ф О сопряженная траектория вдоль круговой орбиты представляет собой
эллипс с «ползущим центром»
4 (р, — с')з+ (р, — с,„'+ з/2с'р)~ =4С2
(рис. 5.2, е) или прямые р, = с~, р, = сз — с~э/р (рис. 5.2, ж).
т
Рассмотрим также возможные виды сопряженных траекторий при движении
по эллиптической орбите (О е(1) и при Н=О. Использовав (5.34), представим р,,
р„в виде
9
р„= с' з11& t; (&l ;&g ; ») (с'  gt;'(с')
с' (2+ е сов ч) сов (о& t + ч + с
9 1 + е соь ч
Если и = О (р = О), то сопряженная траек-
тория симметрична относительно оси р, .
если и=>~ 2, то сопряжен ая траекто
симметрична относительно оси р, . Соот-
ветствующие случаи представлены на
а)
г)
Рис. 5.2. Сопряженные траектории на круго- Рие. 5.3. Сопряженные траектории на эллип-
вой орбите. тической орбите.
рис. 5.3. Для о&g ; О каса ие единич ой окружно ти изну ри мо ет им ть ме то тол
в то > ах „= О, р = 1  = пя ( = О, 1, 2, .. ). л   О каса ие и н) ри в
можно и в других точках.
При стремлении эксцентриситета ~ к нулю сопряженная траектория, представленная
на рис. 5.3, а, трансформируется в точку (рис. 5.2, а), а остальные траектории, приведен-
ные на рис. 5.3, б — г, трансформируются в эллипс (рис. 5.2, б).
Из (5.38) может быть получено выражение
Д 1 >
— — (р2 + р2 ) = — (у р„— у р, )з — "+ р (у р, — п„р, ) — Е3> ,, (5.
Т
которое определяет точку касания сопряженной траекторией единичной окружности
в общем случае.

124
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 5
$ 3. Оптимальные маневры в центральном поле
1. Попадание в заданную точку. Рассмотрим задачу о перелете
из точки р,=О, г„и„о, и в точку <р„ ,; длительно ть перел т  и значе
составляющих скорости в точке финиша и„1, и не заданы; перелет совер-
шается с помощью одного начального импульса тяги. Эта задача является
обобщением известной в баллистике задачи о нахождении траектории макси-
мальной дальности полета при заданной начальной скорости или минималь-
ной начальной скорости при заданной дальности [5.9].
В силу условий трансверсальности сопряженная траектория оптималь-
ного перелета должна удовлетворять следующим условиям:
р,, (0) = я1п ()„
р„(0) = соя о„
1
р„(т) = р, (т) = и =- О,
(5.45)
где Π— угол наклона вектора тяги к трансверсали,
У+ (0) — У„- (0) У', (0) — У, (0)
1 ~ (о) 1 ' ' 1 ~ (о) 1
Найдем оптимальное направление импульса тяги, подставив условия
(5.45) в (5.43) и исключив из полученных уравнений постоянные с„с",, с,
(тип сопряженной траектории приведен на рис. 5.2, в)). Оптимальное направ-
ление дается выражением
~0 ~о—
~т (О) 1 -1- а соя ~,
(2й~'аФ) 1д (у,(2) — и+„(О) 2 ф (у,(2) — е я1п ч, '
(5.46)
где;Я вЂ” интеграл площадей, в — зксцентриситет, ~, — истинная аномалия
кеплеровой дуги, соединяющей две заданные точки.
Если начальная скорость до импульса тяги была равна нулю, то О,—
угол между вектором скорости и трансверсалью и из (5.46) получаются изве-
стные в баллистике формулы, связывающие оптимальный наклон вектора
скорости к горизонту с параметрами перелета:
(Ли (0))2
(5.47)
р, (0) = оя О„р, (Т) = я1п О„р, (Т) = соя О„Н = О.
(5.48)
р„ (О) = я1п 0„
Подставив (5 48) в (5 43) и исключив с,", с",, с,, получим соотношение
2 $д ~~ (я1п (),+ я1п 0,)+ соя 0, — соя 0,+в[соя (0, — ч ) — соя (о — ~,)]=0.
(5.49)
2. Попадание в заданную точку с заданной скоростью. Рассмотрим
случай, когда требуется осуществить перелет из точки р =О, г„и„о, и
в точку ~„г„г„1, г 1, причем длительность перелета Т не задана. В реальной
ситуации эта задача соответствует отысканию оптимальной программы управ-
ления на участке выведения спутника в пустоте (после выхода из атмосферы),
когда угловая дальность траектории выведения по техническим условиям
ограничена. Сопряженная траектория, соответствующая оптимальному двух-
импульсномуманевру (рис. 5.2, в, д), должна удовлетворять следующим ус-
ловиям:

125
МАНЕВРЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
Вместе с интегралами движения соотношение (5.49) определяет оптимальный
двухимпульсный перелет. Можно получить приближенные решения (5.49),
положив я =О, после чего сразу видны два возможных решения:
2) Сд ' '~=2йд®
1) ОО= — О1,
(~ 49~)
Заданные краевые условия определяют, какому из этих равенств удов-
летворяет оптимальная траектория перелета. Решение второго из соотноше-
ний (5.49') приведено на рис. 5.4.
3. Перелет между компланарными орбитами с незаданной ориентацией.
Размеры и положение орбиты на плоскости фиксированы, если заданы
постоянные ф, ~Я, ю, трех интегралов дви-
жения:
60'
Ю- Ю~
~,г= Ю,
(5.50)
У~И~
~ — агс яп
~Й2 + 2й'аЖ2
: Ю
3 %
где р — положение перицентра. Рассмотрим
задачу о перелете с незаданной длительностью Т
с орбиты, определяемой соотношениями (5.50), б Удо /або
на орбиту, у которой фиксированы только новые Р~
значения ф и ~4, а значение ~р, не фиксировано.
В два первых соотношения (5.50) (определяю-
щих множество, на котором лежит конец траек-
тории перелета) переменная ~ не входит, по-
этому одним из условий трансверсальности является равенство р =О. Ввиду
9
произвольности Т выполняется также равенство Н=О. В этом случае в со-
ответствии с (5.40) на траектории между двумя импульсами тяги в моменты ~,.
и 1,. 1 выполняются следующие соотношения:
Рис. 5.4. Разность между направле-
ниями импульсов тяги в зависи-
мости от угловой дальности пере-
лета.
р, = ср +с',г,
l1
и (р~, + р~-& t
— з
'Р(р",+р:,) „, 1
= — 2йс1'
(5.51)
'2
— „, (гг) +бас'1 —,
г (1 ,) = г,.~,).
(г(~,.) = г,,
Здесь учтено, что из условий (р"- + р'„) = (р'- + р"- 1 = 1 следует
"т "~р ~ ~г 6~~/
р„(~,.) = О,
(1) = +1.
(5.52)
В бесконечно удаленной точке гиперболической орбиты оптимальное
направление импульса тяги определяется выражениями
р2 = (в — 1)/(в+ 1),
р'„= 2/(в+ 1).
(5.53)
равенство с'.,' = с", 2Цг,.г,.+, (г,.+г,,).
Согласно (5.51) сумма р'„+ р'„достигает максимума только в точках
экстремума потенциальной энергии (перицентры и апоцентры, в том числе
бесконечно удаленные точки); следовательно, только эти точки и могут быть
оптимальными для приложения импульсов тяги. Кроме того, из (5.51) сле-
дует, что оптимальные импульсы тяги в перицентр ах и апоцентрах эллипти-
ческих орбит обязательно являются трансверсальными:

126
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
~ГЛ. э
Найденная оптимальная программа перелета с трансверсальными
импульсами соответствует, в частности, и перелету между соосными эллипти-
ческими орбитами, так как эти импульсы, приложенные в апоцентре или
перицентре, не меняют положение линии апсид.
4. Перелеты между компланарными соосными эллиптическими орби-
тами. Положим, что две эллиптические орбиты заданы своими радиусами,
лежащими на общей линии апсид, г„г, и г„, г„„. Скорость в апсидальной точке
может быть выражена через ее расстояние от притягивающего центра г,.
и расстояние от противоположной апсидальной точки до притягивающего
центра г,. „г,.+,.
(2й,(г;) ('
(1+ г;('г,,) ~'
(5.54)
где г-,, — скорость до ~-го импульса тяги, г+ — скорость после ~-го импуль-
са тяги.
В случае п-импульсного перелета между двумя заданными орбитами
(все импульсы тяги трансверсальны и прикладываются только на линии
апсид) суммарная характеристическая скорость маневра Ли (Т), а также
ее производные дЛг (Т) /дг,, д'Лг (Т) /дг'. могут быть выражены с учетом (5.54)
в виде
— [(( + 2 — ") я! пп (г,.„— г,,) +
г г — 1
Г ° lг Гг
+ — ' з(дп (г,. — г,,) 1+ — ' — 1+ 2 — ' з(дп (г,.„— г,) +
~~ — 1 г',-1 г',+1
з ~
+ —" яфп (г,.„— г,)~ (1+ — ')
3 дЛи (Т) й г,
— 2 — ' — 1 з|дп(г,.+,— г,)+
Ф Ф
Г; 1
+ ( — ' — 2) я!пи (г, — г,,)) — ' (1 + — ')
— 2 — ' — 1 я1дп г,. 1 — г
~+1
+("' — 2)пап(г,.„— г,)) " (1+
(5.55)
д'~г (т)
отрицательна.
2п. г„) г, ) г„+ (рис. 5.5, б). Производная
отрицательна.
Рассмотрим характеристическую скорость маневра как функцию переменной г,,
считая для определенности (-й импульс тяги разгонным (г;+1) г; 1), а значения г,
г; 1, г;~1, г,+2 заданными. Для нахождения возможных точек экстремума функции Ьи (Т)
рассмотрим выражения (5.55). Производная дЛи (Т)(дг; имеет разрыв в точках г, =
= (г;,, г;+,), кроме того, она обращается в нуль в точке г; — э со. Для нахождения
остальных возможных точек экстремума необходимо рассмотреть четыре возможных
случая, представленных на рис. 5.5:
1п. г,+з) г;, г; ) г, (рис. 5.5, а). В этом случае производная

МАНЕВРЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
3'. г,+2) г; ) г; 2 (рис. 5.5, в). В этом случае уравнение
имеет один корень, а вторая производная
д"-аа1а (Т) 9Й 1 — г;/га 1 г; 1 — г;(г;~1 г;
(1+ Г,(Г, 1) ~а "а — 1 (1+Г,~Г; ) аа 'а+1
отрицательна. Следовательно, может иметь место только локальный максимум.
Рис. 5.5. Возможные варианты расположения импульсов тяги на линии апсид.
4'. г;) г~ з, г ) г,+2 (рис. 5.5, г). В этом случае производная
может обращаться в нуль, когда г; — э со и когда г; — корень уравнения
& t    г
г 3 г г
+6
а , [ а'-1~ а+1 а + а — 1~ а+1
г, , 9 (г; 1~г;+1) — 1 г1 1 9 (г; 1(г;+1) — 1
(5.56)
Это уравнение при (г,+1/г; 1) ( 9 не имеет положительных корней, т. е. дЛ1а(Т)1дг;,
оставаясь положительнои величиной, стремится к нулю при г; — э со, поэтому точка
г„-э со при г,+1(г„1 ( 9 соответствует максимуму 11г (Т). Если отношение г;+1/г; 1 при-
надлежит диапазону
а+1 ( + I а-1)
г; [(г~г; ) — 3]2 — 12 '
(5.57)
где г = шах (г; 2, г;+2), то уравнение (5.56) имеет один конечный положительный
корень, соответству1ощии максимуму 11а (Т). Ограничение сверху в (5.57) получено
из условия дЛ1а(Т)~дг;)О при г;=г. Если д111а(Т)~дг;(О при г;=г, т. е.
г;+, (1+ г/г; )2
г; 1 [(г/г; 1) — 3]2 — 12
(5.58)
то с увеличением г, от значения г = тах (г; 2, г;+2) до г; -э со величина 111а(Т) моно-
тонно уменьшается.
Проведенный анализ всех четырех случаев показал, что оптимальными значениями
для г; могут быть или г;-э со, или наибольшая из величин г; „г;+,. Применяя проведенное
исследование последовательно к г„г,..., г„„получим, что они должны или принимать
бесконечное значение, или быть равными какому-либо из заданных радиусов го, г„г„,
г„+,. Доказательство было проведено для разгонного импульса, но, поскольку задача пере-
лета обратима, оно верно и для тормозных импульсов.

128
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 5
Таким образом, в общем случае траектория оптимального перелета
между двумя соосными компланарными орбитами может иметь не более
четырех импульсов тяги (включая два на
у бесконечно большом расстоянии от при-
тягивающего центра). Для перелета между
орбитами, заданными своими апсидаль-
ными расстояниями от притягивающего
центра (г„г, и г„г,), может быть 6 вариан-
5 О Г тов программы приложения импульсов
тяги: 1) г„г,; 2) г„сс, г,; 3) г„со,
со, г,; 4) г„г,; 5) г„со, г,; 6) г„со,
со, г,; (варианты 1) и 4) показаны на
рис. 5.6). Если отношения апсидальных
радиусов заданных орбит меньше 9 (г,/гз,
г,/г, для пересекающихся орбит и г,/г„
г,/г, для непересекающихся), то перелеты
с вылетами на бесконечность сразу отпа-
дают. В этом случае должны сравнивать-
ся только варианты 1) и 4). Если орби-
ты пересекаются, то условиям оптималь-
ности удовлетворяет только вариант 1).
Если орбиты не пересекаются, то условиям
Рис. 5.6. Возможные варианты перелетов
между двумя ороитами.
оптимальности могут удовлетворять оба
перелета и абсолютный минимум находит-
ся после сравнения функционалов.
Если хоть одно из указанных отношений апсидальных радиусов больше 9,
то условиям оптимальности могут удовлетворять перелеты с включение~1
Ло
075
Г(
О
1 п(г/~ !
Рис. 5.7. Характеристическая скорость перелета между круговыми орбитами.
точки г -э со. Классификация режимов, следующая из (5.55), является более
простой в случае перелета между круговыми орбитами [5.2]. Пусть необхо-
димо перейти с меньшей орбиты радиуса г на большую орбиту радиуса г1
(задача обратима). Трехимпульсный оптимальный режим с вылетом на беско-

12
МАНЕВРЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
нечность может иметь место, только когда отношение между радиусами
круговых орбит больше 9. При 9 ( т,/т, ( 15,73 существует два оптимальных
режима — двухимпульсный и трехимпульсный, причем трехимпульсный
режим выгоднее двухимпульсного при г,/г, ) 11,94. При г, /г, ) 15,73
оптимальным является только трехимпульсный режим. На рис. 5.7 дана за-
висимость суммарной характеристической скорости перелета между круго-
выми орбитами (отнесенной к круговой скорости внутренней орбиты) от ради-
уса приложения промежуточного им-
пульса тяги при отношениях г,/г, =2,
9, 12, 20. Если отношение радиусов
заданных орбит невелико, то трехим-
пульсный внутренний перелет не
очень отличается от оптимального
двухимпульсного, но зато резко воз-
растает функционал при «внешнем»
трехимпульсном перелете. При боль-
ших отношениях радиусов заданных
круговых орбит, наоборот, максимум
функционала слабее выражен при
«внешнем» перелете.
А~~(Т)
l //р
Рис. 5.0. Области оптимальности переле-
тов между гиперболической и круговой
орбитами.
Рис. 5.8. Два варианта перелета с гиперболической
на круговую орбиту.
Ли (Т) =и~,— ~2Цг, (1 + г /г,) ~'+ ~/2/~/г,~(1+г,/г,) ~' — (2г/ ~'~ з1рп (г, — г,),
(5.59)
где и,, — скорость в перицентре заданной гиперболической траектории,
г — ее перицентр, г — радиус заданной круговой орбиты.
9 Механика полета
5. Перелет с гиперболической орбиты на круговую. Выше было уста-
новлено, что оптимальными точками приложения импульсов тяги на гипер-
болической траектории являются бесконечно удаленная точка и перицентр.
Рассмотрим два возможных варианта:
1) Первый импульс тяги дается в перицентре заданной гиперболической
орбиты. Поскольку дальнейшая траектория может состоять лишь из полу-
эллипсов, то к ней может быть применен анализ и. 4.
2) Первый импульс тяги дается на возможно большем удалении от при-
тягивающего центра с тем, чтобы переходная гиперболическая траектория
в перицентре коснулась заданной круговой орбиты, и второй (последний)
импульс тяги дается в этой точке касания.
Сравним эти режимы, считая, что первый вариант перелета осуществ-
ляется одним полуэллипсом, а второй вариант перелета осуществляется
с помощью бесконечно малого импульса при г -э со (рис. 5.8). В случае
перелета с включением полуэллипса суммарная характеристическая скорость
маневра равна

~ГЛ. 5
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
Если перелет осуществляется с помощью гиперболы, то первый импульс
бесконечно мал, а второй равен
Ьу, (Т) = ~/Р, — (2Й/г,) + (2Й/г,) — ~/Й/г,.
(5.60)
С помощью (5.59) и (5.60) получим разность
(5.61)
На рис. 5.9 в плоскости параметров й~,=и~,/~/2йг, и г,/г, построена кривая,
соответствующая условию Лп1 (Т)=Ли (Т) и разбивающая плоскость
на области, в одной из которых выгоднее гиперболический перелет (Лп (Т) )
) Лп, (Т)), а в другой — эллиптический (Лг1 (Т) ( Лп, (Т)). Если г1 ) г„
то при любом значении о~, выгоднее гиперболический перелет.
6. Перелет между компланарными орбитами с поворотом линии апсид.
Если ориентация конечной орбиты задана и не совпадает с ориентацией
начальной орбиты, то в (5.50) 3~>, 0, поэт му произволь ая постоян а р
в общем случае. Рассмотрим двухимпульсный перелет между такими орби-
тами, считая моменты приложения импульсов тяги 1„81 и длительность всего
перелета Т произвольными. В этом случае сопряженная траектория должна
удовлетворять условиям
Р,, — ~1п 0„
р, = я~и 0„, о = соя 00,
— „(,'р„-'„+ р;',), = — „(р'„„+ р',), = ~~ = 0
(5.62)
— г +г Ы~2
2.ог,
Го+ Г,'
(5.63)
Выше было показано, что ~-перелет является оптимальным для соосных
орбит; ниже будет показано, что г;перелеты оптимальны и при маневрах
на околокруговых орбитах с поворотом линии апсид.
Рассмотрим вопрос об оптимальном числе импульсов тяги в случае
использования и 7~-перелетов. Так как п„(~+7~)= — г„(а), то интеграл энер-
гии в точках г,, где даются импульсы тяги, можно записать в виде
/,г~,. — Й/г.= / г <, „, Ђ” Й/г
Подставляя (5.62) в (5.40), (5.44) и исключая произвольные постоян-
ные с,', р, с,.', можно получить три соотношения, которые вместе с интегра-
лами движения определяют оптимальный перелет. Однако ввиду громозд-
кости общей системы соотношений ее решение может быть получено только
численным методом [5. 18 ].
Для быстрого получения оценки характеристической скорости маневра
можно использовать так называемый 7;-перелет с угловой дальностью
~ — р =~. Траектория 7~-перелета должна соединять точки заданных орбит
с равными по абсолютной величине, но разными по знаку радиальными
составляющими скорости=и„; таким образом, потребные импульсы тяги
трансверсальны. Такой 7~-перелет легко строится посредством нахождения
прямой линии, на которой г„,= — г„о (г„о — радиальная составляющая ско-
рости на начальной орбите, и„1 — радиальная составляющая скорости
на конечной орбите). После этого определяются две возможные пары значе-
ний соответствующих радиусов г, и г, и параметры кеплеровой дуги перелета

МАНЕВРЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
Прибавив к этому соотношению интеграл площадей г,.г,. = г „.+1,г,. „полу-
чим выражение для скорости в точке г,.:
г~,. = ~2Цг,. (1 +г,.(г,.~,) ~*,
которое аналогично (5.54). Таким образом, все результаты п. 4 этого пара-
графа о месте и числе импульсов тяги верны и для случая и г;перелетов.
Отметим в заключение, что для пересекающихся орбит возможен переход
с помощью одного импульса, причем всегда можно подобрать значение р
в (5.44) так, чтобы выполнялось условие И (р',„+р', )/й=О. Однако необхо-
димо проверять, изнутри или снаружи касается сопряженная траектория
единичной окружности. В последнем случае режим соответствует локальному
максимуму функционала.
7. Перелеты между некомпланарными орбитами с общей линией апсид.
Рассмотрим задачу перелета между двумя орбитами, которые имеют общую
линию апсид, но лежат в разных плоскостях, причем на длительность и угло-
вую дальность перелета ограничения не наложены.
Без ограничения общности можно положить, что плоскость конечной орбиты сов-
падает с плоскостью я=О (цилиндрическая система координат г, р, Х, см. (5.36)), а линией
апснд является ось Оу. Для орбит, имеющих ось Оу в качестве линии апсид, равны нулю
проекции интегралов площадей на ось Оу, а в силу неизменной ориентации линии апсид
в пространстве равна нулю соответствующая проекция первого интеграла из (5.29):
И
г — „~ (р соя Х) — с о соя 1= 0,
(5.64)
И
р, — „(р соя Х) — р„р соя Х = О.
Из (5.64), (5.34) и (5.40) при отсутствии ограничений на длительность и угловую даль-
ность перелета следует, что сопряженная траектория в рассматриваемом случае описыва-
ется соотношениями
Л
— — (р2 + р-, "+ р~ ) = — (с1)2 — а гг+ (сз)2 гг+ (с")2 (7сг — М') Йг. !
(5.65)
Как и в случае плоского перелета, условие касания сопряженной траекторией еди-
ничной сферы может выполняться в точках г=О, т. е. в точках перицентров и апоцентров
эллиптических орбит, причем оптимальный импульс тягп в этом случае не имеет радиаль-
ной составляющей (р, =0). В апоцентре тратится на поворот плоскости орбиты большая
часть импульса тяги, чем в перицентре:
р„(г„)~р„(г ) = — г„'г .
2 соя Ь~~. Ч2
ЬуЩ=~ ~2~»~»,. (1-)-».~».„) '+(1-)-»./»,,Д '—
1+ — 1+—
Г2+1 г. д
Ьг. =г,
° ° °
у' 7
,у'==1
= И1~П,
г~, Ь~у
(5.66)
Положим, как и в п. 4, что две эллиптические орбиты заданы своими апси-
дальными радиусами г„г, и г„, г„„, кроме того, плоскость одной орбиты по-
вернута относительно другой вокруг линии апсид на угол ~. Если перелет
в соответствии с (5.65) совершается только с помощью импульсов тяги,
прикладываемых на линии апсид и имеющих нулевую радиальную составля-
ющую, то рассматриваемая задача сводится к задаче на условный экстремум

~ГЛ. 5
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
132
где выбору подлежат Л~,. — углы поворота плоскости орбиты в моменты
приложения импульсов тяги и г. — соответствующие радиусы в моменты
приложения импульсов тяги.
Условие оптимального подбора Л~. записывается в виде
(з1п2 Ь~ )/г
= со11я$
2+ (т /т +1) + (у ~г 1) — 2 [(1+ т /г +1) (1 + т,~т 1)) ~' соя И
(/= 1, 2,..., ~г).
(5.67)
Из (5.67) следует, что для перелета с вылетом в бесконечно удаленную
точку поворот плоскости орбиты полностью производится в этой точке,
так как все остальные Л~.=О.
.у'
Анализ производной дЛп (Т)/дг., аналогичный проведенному для пло-
ского случая в п. 4, показывает, что дЛг (Т)/дг. — э 0 при г. — э о~, поэтому
маневр с уходом в бесконечно удаленную точку может быть оптимальным.
Так как при вылете на бесконечность импульс тяги там бесконечно мал,
то трехимпульсный перелет с поворотом плоскости орбиты на бесконечности
эквивалентен по характеристической скорости грехимпульсному перелету
между подобными орбитами без поворота плоскости орбиты. При этом двух-
импульсный перелет (без удаления на бесконечность) с поворотом плоскости
орбиты всегда больше по потребной характеристической скорости, чем со-
ответствующий двухимпульсный перелет без поворота плоскости орбиты.
Поэтому классификационные значения отношения радиусов круговых орбит,
указанные в п. 4 для перелетов без поворота плоскости орбиты (9; 11,94;
15, 73), уменьшаются с увеличением угла требуемого поворота. Рассмотрим,
например, задачу поворота плоскости круговой орбиты радиуса г, на угол ~.
Характеристическая скорость одноимпульсного поворота плоскости в со-
ответствии с (5.66) равна
Шу, (Т) = ~/(2Й/г,) (1 — соч ц = 2 ~/Цг„з1п (~/2),
(5.68)
а характеристическая скорость при трехимпульсном перелете (с удалением
на бесконечность) независимо от ~ равна
Луз (Т) = 2 ~/Й/г„(~/2 — 1).
(5.69)
Трехимпульсный перелет выгоднее двухимпульсного (Лаз (Т) ( Л~, (Т)),
как только
~ ) агссоз (4 ~/2 — 5) =47'.
(5.70)
$ 4. Маневры на околокруговых орбитах
Пусть номинальное движение описывается в цилиндрической системе координат,
происходит в плоскости г=О и является движением по круговой орбите с угловой ско-
ростью и = ~/Й/г~. Тогда физическое движение и сопряженная траектория описываются
1. Уравнения движения и сопряженная траектория. Выше ухте
использовалось линеаризованное представление сопряженной траектории
в виде (5.35) для получения первых приближений к оптимальным режимам
в ньютонианском поле притяжения. Следующим возможным упрощением
задачи является линеаризация уравнений движения, т. е. описание его
с помощью уравнений в вариациях относительно номинального движения
[5.101.

МАНЕВРЫ НА ОКОЛОКРУГОВЫХ ОРБИТАХ
следующими уравнениями (о т= г б~, Л= и, о р= ог):
Ар
= — Р— '"Р,,
дт
Дбу
= 2и ос + и«ог,
~Й
Ир,
= — р,— 2 р,,
И8
(5.7Ц
ЫГ
Ж
~рт
— — о~Р— ~д-Р
0~0 „
— — итр
П = Ргосг+ Р (ос — и Ог) + Р Ос, + Р (2и бг + и«ог) — Р и «1т — Р и«ог.
Система (5.71) имеет следующее решение:
и ог = ~с„«Я1п ~ — (26г «+ и ог«) соя и + 2 (оу. + и ог ),
и ""' = 2«сг«соя ~+ 2 (2Ои «+ и Ьг«) Я1п и ~ оз о т« — 2бу„« вЂ” 3 (Вг + и ог ) и,
о~ о-' = оУ «Я1п ~р + и Ог соя и,
ос„= ~с„«соя р+ (2«с «+ и ог«) ягп
оср ~сг«Я1117+ (2«1~ «+иог«) соя ~ — («1~.«+иог«),
~~~ = ~~ О СОЯ о — оз ~го Ц1Д;Р,
р, = с, Я1п и+ с, соя ~+ с4,
р„=2с, соя ~ — 2с ягп у+ с« — Зс у/2,
Р» = С«Я1П т'+ С«СОЯ т,
р, = — (оз/2) с .
(5.72)
Прп отсчете угла и = ит в (5.72) от перицентра орбиты произвольная постоянная
с, может быть выражена через постоянные р и Н следующей формулои.
Н+3(от «+иог«) р
(5.73)
и (2щ «+ иог«)
2. Перелет между компланарными орбитами. Если на длительность
перелета Т и круговую дальность 3-. не наложено никаких ограничений,
то в силу условий трансверсальности р,=Н=О. Сопряженная траектория,
описываемая уравнениями (5.72), представляет собой точку или эллипс,
касающийся единичной окружности в точках р, = О, р, = +1. 011тимальный
режим перелета может включать только трансверсальные импульсы тяги.
Удовлетворяющим этим условиям оптимальности, как уже было показано
выше, является г;перелет, т. е. перелет, дуга которого соединяет точки орбит,
лежащие на одной прямой, проходящей через центр притяжения, с равными
по модулю, но противоположно направленными радиальными составляющими
скорости ои„(рис. 5.10, а, б). Особенность линеаризованного решения задачи
состоит в том, что функционал не зависит от числа и места приложения
импульсов тяги на указанной прямой. В самом деле, из (5.72) может быть по-
лучена следующая формула, связывающая величину приращения трансвер-
сальной составляющей Л би (~) с величиной Л ог (~р+тт):
~ Ьоу, (и) ~ = 1/,и Лдг (и + тт) Я1дп Ыг (~р + тт). (5.74)

134
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 5
Из (5.74) следует, что приращение характеристической скорости после и
трансверсальных импульсов тяги одного знака равно величине
1/ и ()Л ог,)+... + ~)Л ог„)), где ог,.= ог (~г). Такие и импульсов тяги могут быть
заменены одним импульсом тяги соответствующей величины без изменения
функционала. Таким образом, независимо от числа импульсов характеристи-
ческая скорость маневра равна
Лг(Т) ='/ и Шг,
где Лг — разность между диаметрами орбит
вдоль прямой г;перелета. Отсюда, в частности,
следует энергетическая эквивалентность переле-
тов 1 — 4 и 3 — 2 для пересекающихся орбит
(рис. 5.10, а).
3. Поворот линии апсид. Если орбиты, меж-
ду которыми осуществляется перелет, пересе-
каются, то переход может быть осуществлен с
помощью одного импульса тяги в точке пересе-
чения. Сравним такой одноимпульсный переход
между орбитами, различающимися только
положением линии апсид (рис. 5.10, а), с двух-
импульсным ~г-перелетом. Характеристическая
скорость одноимпульсного перехода равна
Лг, (Т) =2~ 3г„(у„) ~, где бг„(у,,) — радиальная
составляющая скорости в точке пересечения ор-
бит. Сопряженная траектория, соответствующая
такому перелету, может быть только эллип-
сом, касающимся единичной окружности извне в
точке р„= + 1, р„= О, т. е. одноимпульсиый
ро ким ие удовлетворяет условиям оптималь-
пости.
Вычислим характеристическую скорость
двухимпульсного перелета. Если ~, — поляр-
ный угол, соответствующий точке пересече-
ния орбит, то точками, соответствующими 7-.-пе-
релету, являются точки и„— ~/2 и и +7./2. Из
(5.72) следует, что
и [ог (о, +;с/2) — ог (р,„— г/2)] = 2оу„(з,).
Рис. 5.10. Перелеты между около-
круговыми орбитами.
Разность диаметров орбит на прямой -.-перелета равняется 43г„('р„)/и;
следовательно, характеристическая скорость маневра в соответствии с (5.75)
равна ~ ~г„(:~„) ~, т. е. в два раза меньше, чем характеристическая скорость
одноимпульсного перехода.
4. Перелет между комплаварными близкими круговыми орбитами.
Заметим, что для построения приближенных к оптимальным маневров не обя-
зательно проводить линеаризацию уже на этапе написания дифференциаль-
ных уравнений движения. Иногда более удобной является линеаризация
имеющихся точных решений в ньютоновом поле [5.8]. Воспользуемся таким
приемом для построения оптимального перелета между двумя близкими
круговыми орбитами радиусов г и г1 с заданной угловой дальностью пере-
лета ~1 ( 7с. Так как длительность перелета не ограничена, то сопряженная
траектория оптимального двухимпульсного перелета должна удовлетворять
условию (5.49), а после линеаризации — (5.49'). Уравнения движения с точ-
ностью до членов порядка в можно представить в виде [5.25]
и — ~/й/г = (Ъ/2Щ) соя ч.
(5.76)
г„= (Йв/Щ) в1п ~,

135
МАНЕВРЫ НА ОКОЛОКРУГОВЫХ ОРБИТАХ
$ 4]
С помощью (5.76) вычисляются направления импульсов тяги на концах дуги
перелета: $д 0,=2$д ~,=2 $д (~,+1~,), откуда следует соотношение, связываю-
щее угловую дальность перелета и направления импульсов тяги:
Фар~ 2 - с0с 0' (5.77)
Общим решением соотношений (5.49') и (5.77) является
1д ()о = — С~ (), = 2 с С~ ( о,/2).
(5.78)
Таким образом, оптимальный двухимпульсный перелет начинается
и заканчивается импульсами тяги, симметричными относительно направле-
ния трансверсали и равными по абсолют-
ной величине. Последнее следует из равен-
ства — $д 0,=$д О, (~о+~1=т:) и (5.76). С по-
мощью (5.76) вычисляются фокальный пара-
метр и эксцентриситет дуги перелета, а также
характеристическая скорость маневра:
г1 — го 2гог1
(гс + гт) я(п (~р,/2) ' гс + г,
/~ (1 + 3 соя' (р,/2))
2гсг (го + г ) я(п' (шт/2)
(5.79)
Угловая длипа .-,", дуги круговой орбиты, соединяющей симметричные точки эллип-
тпческих орбит (рис. 5.11, б), связана с углом 1 и истинной аномалией ~ следующей фор-
мулои:
я1п (~рт/2) = я1п (1/2) я(п Р, (5.80)
где 3 = ч — к/2, если соединяются апоцентрические части орбит, (~ = (Ф2) — ч, если
соединяются перицентрические части орбит.
Так как круговая орбита соединяет симметричные точки эллиптических орбит,
то сопряженная траектория (в пространстве р,, р„, р„, связанном с плоскостью кру-
говой орбиты) долхсна удовлетворять следу1ощим условиям на концах:
(5.81)
Рю~О Рю~1 ~ Ро~О Р о~1 °
Этим условиям удовлетворяет, например, сопряженная траектория, которая получается
из (5.35) при Н =О, с', = с,'=1/1/8, се =О, св= се= 1/3/8 и является пересечением
цилиндрической поверхности, построенная на эллипсе р; "+ (р, '/4) = 1/4, со сферой
5. Поворот плоскости орбиты вокруг
линии узлов, перпендикулярной к линии
апсид. Рассмотрим сначала две одинаковые
компланарные эллиптические орбиты с общей
линией апсид, но с апоцентрами по разные
стороны от центра притяжения (рис. 5.11, а). У
Оптимальной траекторией перелета без ог-
раничений на длительность и угловую даль-
ность перелета в этом случае является круго- Х
вая орбита, соединяющая оба апоцентра. ф
Пусть ПЛОскОстИ Орбнт ПОВериутыВОкруг ОСИ Рис. 5.11. ПовоРот плоскости оРбиты.
Ох (рис. 5.11, б) так, что угол между линиями
апсид равен г. Покахсем, что в данной ситуации перелет по круговой орбите
между симметричными точками по-прежнему удовлетворяет условиям опти-
мальности, и вычислим характеристики маневра.

136
идеАльныЙ двиГАтель ОГРАниченнОЙ скОРОсти
В силу (5.35) угловая дальность перелета по круговой орбите и значения сопряжен-
ных переменных на концах траектории связаны соотношениями
218 (~'/2) (Р с+ Р 1)+Р 1 Р~ е
(5.82)
Учитывая (5.81) и (5.82), выразим значения импульсов тяги на концах траектории
перелета:
1~ ° 1= 1/З1~, 1, 1~,1= 21~ ° [М М2). (5.83)
Угол ~, соответствующий точкам импульса тяги на эллиптических орбитах, нахо-
дится из уравнения
(5.84)
где, в соответствии с (5.80) и (5.83),
оМ
г = — (1+ а соя ч),
9 р
ЗаМ2 а2
[Ьг,)'= ., яш'ч,
Р
Р
1 + ь соя ч
а4,'в яш (1/2) я1п 2ч
(5.85)
Р [1 — я1п2 (1/2) соя2 ч1 /'
(оЯ, а, р — параметры эллиптической орбиты).
После подстановки значений, определяемых (5.85), в соотношение (5.84) оно обра-
щается в уравнепие
а яш (~/2) яш 2ч
Зв' яш'ч+ 1/1+ а соя ч+ . =(1+ ~ соя~)'.
1 — я1пй (~/2) соя2 ч
(5.86)
Пренебрегая в этом уравнении членами порядка ~' и выше, получим, что
1
я1п' ч = = сФд' (~/2).
(5.87)
Из (5.87) следует, что точки схода на круговую орбиту зависят только от угла поворота
плоскости орбиты
Вычислим характеристическую скорость маневра, воспользовавшись
соотношениями (5.80), (5.83) и (5.87):
Ьи (Т) = 2 ~/(Ьи,.)'+ (Ьи )'+ (й~,)'=
(5.88)
Сравним рассмотренный режим с одноимпульсным переходом в точке
пересечения орбит. Расход на такой переход равен
~и (Т) = 2 ~/и'„-'+ ~'-' соя'-' (//2) = 2 (;Я/р) /Р + соя'(~/2).
(5.89)
Сравнение (5.89) с (5.88) показывает, что при углах ~, близких к ~, одно-
импульсный режим хуже двухимпульсного примерно в два раза.
$ 5. Межпланетные перелеты
1. Постановка задачи. Рассмотренные до сих пор задачи относились
к движению в поле одного притягивающего центра, поэтому полученные
результаты не могут быть непосредственно перенесены на межпланетные
перелеты. Обычный прием, с помощью которого изоавляются от рассмотрения
движения в поле двух притягивающих центров, — это введение сфер действия
планет, внутри которых учитывается только притяжение планет, а вне сфер—
только притяжение Солнца. Ввиду большого различия между массами Солнца
и планет размеры сфер действия планет малы по сравнению с протяженностью
участков, на которых движение можно считать чисто гелиоцентрическим.
Поэтому задача оптимизации перелета между планетами может быть разде-
лена на две: оптимизацию гелиоцентрического движения и оптимизацию
движения в сферах действия планет. При этом необходимо сделать предполо-

1 7
МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ
э 5]
жение, что на участках траектории, где притяжения Солнца и планет срав-
нимы, импульсы тяги не сообщаются. Кроме того, будем считать орбиты пла-
нет компланарными и рассматривать лишь плоские перелеты по приближен-
ной схеме, описанной в ~ 3 гл. 4.
При оптимизации гелиоцентрического движения необходимо учитывать,
что в характеристическую скорость межпланетного перелета должны входить
энергетические затраты вблизи планет, которые необходимо выразить через
переменные гелиоцентрической системы координат.
Если на участках траектории, где притяжения Солнца и планеты имеют один поря-
док, импульсы тяги не сообщаются, то связь между значением скорости в близкой окрест-
ности планеты и ее значением за сферой действия планеты дает известный интеграл Якоби
уравнений ограниченной круговой задачи трех тел [5.25], которые описывают движение
аппарата в планетоцентрической вращающейся системе координат х(2), 2, у'2', ось абсцисс
которой постоянно проходит через Солнце (см. рис. 4.6):
(х<2 gt )2 ~- ( &lt 2&gt )2 — &lt ой (х<2& t )2 — 2 & t;<2&gt /г<2&
(5.90)
где ~ — угловая скорость кругового движения планеты по орбите с гелиоцентрическим
радиусом Ло, й'2) — гравитационная постоянная планеты.
Перепишем интеграл Якоби, выразив относительную скорость летательного аппа-
рата в момент 8, через компоненты скорости г„', г' в планетоцентрической системе коорди-
нат с неподвижной полярной осью, а в момент 8, — через компоненты скорости г,., о~
в гелиоцеитрической полярной системе координат также с неподвижной полярной осью:
[(<& t ')2 (& t;>' Ђ” lt;& t;г< &gt )2 — 3<
9 ~0
.= [<&g ;"„ + ( lt;&g ; в ” & t;>г 2 в ” ЗаР (х< >)2
[(<&gt „')2+ (& t >')- ] [& t;> „ + (у — &l ;& t
(5.92)
Исходя из ограниченной эллиптической задачи трех тел, можно получпть более общую
приближенную формулу:
[(<&gt ,')'+ (&l ; gt;') "1, = [(&l ;&g ;г Ђ 1г„ ' (<> — У
(5.93)
где У„, Р— составляющие скорости движения планеты в гелиоцентрической системе
координат.
Приняв скорость Д(<>„')-'+( lt; gt;' "' при 1= е за оценку характ
скорости маневра разгона (торможения) аппарата вблизи планеты (если аппа-
рат стартует или финиширует на орбите искусственного спутника планеты,
то из этой величины вычитается постоянная, которая при оптимизации
гелиоцентрического участка траектории роли не играет), получим величину
суммарной характеристической скорости межпланетного перелета:
Ь<& t (Т) = ~/Г + < g ; + Ь lt;>' + ~ ~Ы'. + <& t
~=2
(о.94)
Здесь Г и Г, — параболические скорости для первой и второй планет соот-
ветственно, г„и о — радиальная и трансверсальная составляющие гелиоцен-
трической скорости аппарата, Лч,. = ~+,. — ~-,, а ~-„о-„г„„, г+„— составляю-
щие орбитальных скоростей планет, г+„г+, — составляющие скорости аппарата
после первого импульса тяги, с'„-„, г-„— составляющие скорости летательного
где г — гелиоцентрический радиус-вектор. Оценить члены этой формулы можно, при-
равняв х&lt 2&g ; (4) г' > (4 радиусу план ты, & t;2& t; ( lt; ) и г&l ;'&gt (Е1) вЂ
планеты [4.8], а &lt >' (й<&gt ) приравняв па аболичес ой скорости на пове
В
неты >/2/с'"'/ "&gt (4). Прене регая алыми велич нами, п лучим п остую связь
планетоцентрической скоростью аппарата вблизи планеты и значением его гелиоцен-
трической скорости вне сферы действия планеты:

138
идеАльный двиГАтель ОГРАниченнОЙ скОРОсти
[ГЛ. 5
аппарата перед последним импульсом тяги. Гелиоцентрическая траектория
начинается и оканчивается непосредственно на орбитах планет.
Из (5.94) следует, что задача оптимизации гелиоцентрического участка
межпланетного перелета может быть рассмотрена как задача перелета между
спутниками с учетом специфики выражений для добавок характеристической
скорости в начале и в конце траектории перелета.
Чтобы получить условия оптимальности, выраженные через свойства
сопряженной траектории, введем некоторые новые уравнения и краевые
условия:
Г, = ае~„
$', (Т) = $'„Г. (Т) = $~„
(5.95)
где е~, — направляющий косинус вектора ускорения, не равный нулю только
в момент первого импульса тяги, а е~, — направляющий косинус вектора
ускорения, не равный нулю только в момент и-го импульса тяги. Соотноше-
ния (5.95) добавляются к задаче (5.5), после чего проводится анализ, подоб-
ный проведенному в п. 1 з 2:
1Х = р,а+ р„° т+ р, ° (ае+ я) + р ае,, + р,, ае,,
Р~ =О Р= д. (Р, ~) Р: Р Р~,=Ру
(5.96)
(р „= — 1, ~е" ~=1, е*=(е, ер,, ер,)).
В отличие от рассмотренного ранее случая сопряженная траектория
рассматривается в расширенном пространстве (добавлены координаты р~,
и р~,). Однако и в этом пространстве сопряженная траектория, соответствую-
щая оптимальному перелету, обладает теми же свойствами, что были полу-
чены в п. 1 ~ 2. Специфика рассматриваемой задачи состоит лишь в том, что
в начале и конце траектории перелета р' + р' (1, так как
~,.
р,„,= „~
(5.97)
(5.98)
2. Перелет без ограничений на длительность и угловую дальность.
Рассмотрим перелет с «внутренней» планеты на «внешнюю» планету, которые
движутся по круговым гелиоцентрическим орбитам радиусов г и г, соответ-
ственно. Пусть моменты прибытия и отбытия, а также угловая дальность
и длительность перелета произвольны. В соответствии с краевыми условиями
сопряженная траектория описывается уравнениями (5.51), к которым добав-
ляются условия (5.97). Оптимальные импульсы тяги, точки приложения
которых совпадают с моментами, удовлетворяющими условию И(р' +р'- +
~)т ~~р
+р' + р') И=О, могут быть только трансверсальными и лежать на линии
1 г
апсид. Рассмотрим возможность введения одного промежуточного трансвер-
сального импульса, когда функционал дается формулой, следующей из
(5.94):

139
МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ
Уравнение [дЬг(Т)~дг]=0, полученное из (5.98), имеет корень в интер-
вале (г„г ) [5.19], соответствующий минимуму функционала для близких
орбит. Кроме того, точкой минимума является точка г~ со при
с гй '/2 2+ [1+ г1Г2~И (~2 — 1) ]
2 — [1+ г27~~~1с (~2 — 1) 1
Й~, (Т) = ~/ Г + (й Ьг/4)'+ ~/ Г', + (й Ьг/4)',
Ьг, (Т) = / Г', + [ Г,в Ьг/4 (Г, + Г,)]'+ (й Ьг/4) +
+ ~/Г'„'+ [Г,а Ьг/4 (Г,+ Г,)]"
(5.100)
Хотя оба перелета удовлетворяют необходимым условиям оптималь-
ности, трехимпульсный перелет здесь всегда хуже двухимпульсного. Таким
образом, перелет между двумя близкими планетами отличается от перелета
между близкими орбитами или спутниками тем, что число и место приложе-
ния импульсов тяги влияют на функционал даже в линеаризованной поста-
новке задачи.
Вывод об ухудшении режима промежуточным импульсом тяги в простей-
шей задаче перелета между близкими планетами, конечно, не исключает
возможности, что в задаче с другими краевыми условиями введение проме-
жуточного импульса тяги улучшит режим; однако этот результат показывает,
что, вообще говоря, набор и гашение энергии вблизи планеты могут быть
выгоднее, чем набор и гашение энергии на гелиоцентрическом участке
траектории.
4. Перелет между двумя близкими планетами при заданной угловой
дальности перелета. Направления импульсов тяги и дальность перелета
в рассматриваемом случае связаны соотношением (5.77), а вместо (5.49) имеем
2йд —,'~ ~[1+ Р/(йР +ЬР )] ~'я1п О,+[1+ Р~(й~Р +йР )] ~'я1п ОД+
+ [1+ ~'22/(Ьг„', + Ьг'„)] ~' соя О, = [1+ Г;/(Ьг„', + Ьг',)] ~' соя О,. (5.101)
так как в этом случае дЛг (Т)lдг ( 0 при г -~ со. Условие (5.99) обобщает
полученное ранее условие оптимальности вылета на со при перелете между
орбитами. В частности, при перелете с планеты на астероид (Г,=О) вылет
на со может быть оптимальным для г,/г ( 9.
3. Перелет между близкими планетами. Рассмотрим предыдущую задачу,
воспользовавшись приближенным представлением сопряженной траекто-
рии (5.72). В рассматриваемом случае Н = р = 0; поэтому на плоскости р,, р,,
можно построить два типа сопряженных траекторий, удовлетворяющих
условиям оптимальности, и, соответственно, два типа перелетов.
1. 11роекция сопряженной траектории на плоскость р,, р — полуэллипс,
г,.~ а,
лежащий строго внутри единичного круга. Ороита перелета — полуэллипс,
касающийся в перигелии и апогелии орбит планет.
2. Проекция сопряженной траектории на плоскость р, р — эллипс,
0„' 6,
проходящий через точку единичной окружности (р„= 0 р„= 1) и то псу
(р, = О, р„= Ьг (~/Г, + ~и'-', = ~и~,/~/Г', + Ы'-',). Орбита перелета состоит
из двух полуэллипсов. Первый касается орбиты планеты старта п заканчи-
вается промежуточным импульсом тяги Ьг~,(г) (г,( г (г,), следующий полу-
эллипс касастся орбиты второй планеты.
Обозначив Ьг = г, — г„о~ = (~~~ + ~Й/г'.,)/2 и пренебрегая членами
порядка ~2 и выше, получим следующие характеристические скорости для
обоих типов маневра:

140
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 5
Полученное ранее (п. 4 ~ 4) решение для перелета между близкими круговыми
орбитами 9,= — Оо верно и для (5.77), (5.101), если Г,— У,. В частности, оно
верно для перелета между Землей и Венерой. При перелете между Землей
и Марсом уравнение (5.101) приходится решать совместно с (5.77) численно.
Рис. 5.12. Сопряженные траектории перелетов между Землей и Марсом (1), Землей и Венерой ®.
д. Перелет с заданной датой старта и произвольной длительностью.
Хотя в рассматриваемой задаче длительность полета не ограничена, поло-
жить Н=О, как зто сделано в [5.171, нельзя. Правый конец траектории свя-
зан с планетой назначения, поэтому вариация 8~~ — — а, ЬТ, где а, — угловая
скорость вращения планеты назначения по круговой гелиоцентрической
Л у,юм/се~
д Я Ю Ю 30 1Т 7Л' 3 с~
Рис. 5.13. Характеристическая скорость перелета Рис. 5.14. Длительность перелета Земля — Марс.
Земля — Марс.
орбите. Рассматривая зто условие совместно с условием р Ьзт — Н 8Т=О,
получаем равенство
р,,— Н=О.
(5.102)
Подставив (5 102) в (5.44), получаем, что на правом конце траектории должно
выполняться условие
(5.103)
Исключив произвольные постоянные из (5.34) и (5.103), получим условие
оптимальности, которое В сочетании с интегралами движения определяет
дугу перелета при любой заданной дате старта или (что то же самое) при
любом взаимном расположении планет в момент старта. Однако совместное
решение двух трансцендентных уравнений (условие оптимальности и соотно-
шение Ламберта — Эйлера [5.91) с остальными интегралами движения затруд-
нительно, поэтому представляет интерес приближенное построение опти-
мальной дуги перелета. На рис. 5.12 приведены сопряженные траектории

. 141
МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ
ф 5)
~и(Т) = ~/2Гь+ п'-„', + (и — иь)' — Уь+ ~/2Г2~+ и",, +(и8 — и...)' — ~г,
(5.104)
где Р~, Рд — круговые скорости на поверхности планет г~, гд — круговые
скорости Земли и Марса на гелиоцентрических орбитах. Составляющие
скоростей в (5.104) вычислялись с помощью следующих формул и интегралов
движения [5.9, 5.25]:
1 О 1 1
р (з ) = гд (1 — в),
и (ю ) = ~/Й/р (1 — е соз
Ьро= о — ~Цг~ Т,
Т=
~/~/Р (1 — а2) ~'
(5.105)
а ЯП1
(1 — ь~) (1 -)- а соя ч)
Кроме данных, рассчитанных по формулам (5.104), (5.105), на рис. 5.13
нанесены также данные маневра, предложенного в [5.17], для тех же началь-
ных условий задачи (на рис. 5.13 — точки). Лишь одна точка из [5.17], со-
ответствующая —.-перелету, ложится на кривую, остальные маневры требуют
большей характеристической скорости. На рис. 5.14 приведена соответствую-
щая (5.105) зависимость длительности полета в сутках от начального «рас-
согласования» Ь~, =~~ — ~~ в ыомент старта.
двухимпульсных ~-перелетов (р =Н=О) Земля — Венера и Земля — Марс.
Сопряженная траектория перелета между Землей и Марсом — чрезвычайно
вытянутый вдоль оси Ор, эллипс (эта вытянутость объясняется разницей
собственных полей притяжения планет). Так как при Н+О сопряженная
траектория есть эллипс с (<ползу им центро », то ля траектор й, не слиш
отличающихся от траекторий ~-перелета, условие (5.103) будет выполняться
в окрестности значений р, =0 (на оси ОР„). Поэтому условие (5.103) можно
считать выполненным на траекториях, касающихся орбиты Марса.
На рис. 5 13 приведена зависимость характеристической скорости перелета
Земля (Я) †Ма ф) от начального «рассогласования» ~~„ = и — а в момент
старта. Эаергетические затраты вычислялись по формуле (см. (5.94))

ГЛАВА 6
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ—
РАЗДЕЛЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ,
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
Рассмотрим задачу о доставке максимального полезного груза для идеальной дви-
гательной сисогеиы ограниченной мощности. Изученио идеального случая интересно тем,
что оно раскрывает предельные возможности двигателей данного класса.
Рогулировочная характеристика (4.9) и формула (4.10) для массы идеального дви-
гателя ограниченной мощности выглядят так (при и1 — — У, и2=д):
Р = ~/2Уд~ д = д, ЛХ.„= аУтах
(О & t У й < У ~ , 0 & t д ( ) ( с
Запись (6.1) отражает следующие свойства идеального двигателя: во-первых, по-
тери рабочего вещества и мощности отсутствуют '), во-вторых, регулирование подчи-
няется только ограничению на мощность (не считая требования неотрицательпости рас-
хода д), в-третьих, масса двигателя линейно зависит от максимальной мощности.
Отметим, что в (6.1) характеристики даны через мощность У и расход д. Монсно вы-
брать и другие системы независимых управляющих функций. Мощность У следует остав-
лять во всех вариантах, поскольку на нее наложены прямые ограничения. Вместо расхода
д могут фигурировать на равных основаниях скорость истечения Г или тяга Р, так как
ни одна из этих величин в идеальном случае не является ограниченной (требования не-
отрицательности тяги Р и скорости истечения Г опять в расчет не принимаются); тогда
(при и1=У, и2= Р)
(О & t У ~ &lt  „ , 0 & t Г
Р = 2У/Г, д = 2У/ с'2, ЛХ„= аУт,~
или (при и1 = У, и2 = Р)
Р = Р, д = Р2/2У, М.„= аУт,~
(6.2)
(0<У ~) & t;У„, 0<
(6.3)
Как будет ясно из дальнейшего, в идеальном случае удобно представить тягу и
расход чорез текущую массу аппарата М и кинематическую характеристику а — ускоре-
ние от тяги (и =У, и =а):
Р = аЛХ, д= а2ЛХ2/2У, ЛХ„=аУт~~ (О & t У ~ < У з , 0 & t а (
(6.4)
тяги.
Наличие указанного разделения полной задачи существенно упрощает исследование
и в значительной степени оправдывает идеализацию.
1) Дальнейшая процедура не изменится, если считать потери в движителе ненуле-
выми, но коэффициент полезного действия движителя ~ полагать постоянным, о,,=
=сопз$ & t 1 не завися им от расх д и подводим йк движит лю мощност ) В э ом слу
под а надо понимать удельную массу двигателя на единицу максимальной мощности реак-
тивной струи М„,, или, если масса М„относится к максимальной мощности источника
У,О=У /~., нужно вместо а писать всюду а/о . Данное замечание относится ко всем
разделам, где обсуждаются идеальные двигатели ограниченпой мощности.
Такое представление, как и в гл. 5, позволяет разделить проблему оптимизации на
две независимые.
1) ~арак~~ирич~скую — нахождение оптимальных соотношений масс и оптимального
управления мощностью;
2) динамическую — нахождение оптимальных программ ускорения от реактивной

143
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
~ 1. Оптимальные соотношения масс при постоянной
и ступенчато изменяемой массе двигателя
1. Разделение задачи, управление мощностью. Запишем уравне-
ния (4.1), когда характеристика двигателя задается в форме (6.4) и масса
двигателя вдоль траектории не меняется:
М = — ЛРа'/2
т, ЛХ(0) =М~, ЛХ (Т) =М.+М„,
г(0) =г, г(Т) =г„
т (О) = т„~ (Т) = т,
0 ( а (~) ( со, [ е (~) ~ = [, М„= сопй).
г=~,
(6.5)
Ф=ае+~,
(О( У(~)(ЛХ„/~,
— 1
(,)= .(1+7 —;;«
0
(6.6)
Это соотношение дает закон изменения полной массы вдоль траектории.
При помощи него может быть записано выражение для конечной массы
М,=М (Т), а также для полезной массы ЛХ,=ЛХ1 — М.„:
(6.7)
Отсюда следует, что полезная масса при фиксированных ЛХ„и М воз-
растает с уменьшением интеграла
Задача состоит в построении оптимальных программ Г (~), а (~), е (~)
и выборе оптимального значения параметра ЛХ„, обеспечивающих выполне-
ние граничных условий для системы (6.5) и доставляющих максимум полез-
ной массы М,=М (Т) — М„при заданной начальной массе ЛХО (параметр а—
удельная масса источника мощности — задан).
Из физических соображений ясно, что мощность в процессе полета вы-
годно поддерживать на максимальном уровне, так как для создания одной
и той же тяги при большей мощности потребуется меньший расход рабочего
вещества (см. (6.1)). Если выбирать большие значения максимальной мощ-
ности, то расход рабочего вещества будет уменьшаться, но одновременно
будет возрастать масса двигательной системы. Начиная с некоторого значе-
ния, увеличение массы двигателя превысит выигрыш от снижения затрат
рабочего вещества. Поэтому для каждого маневра должно существовать
оптимальное соотношение между массой рабочего вещества и массой дви-
гателя, обеспечивающее максимум полезного груза.
Наличие оптимальных соотношений масс для аппаратов с двигателями
ограниченной мощности было сначала установлено на ряде модельных задач
([6.1 — 6.19] и др., см. обзор [6.20]). Главное упрощение состояло в замене
истинного гравитационного поля на простейшее — бессиловое поле и рас-
смотрении одномерных движений. Кроме того, упрощение касалось и управ-
ляющих функций: мощность и масса двигателя считались постоянными,
а регулирование тяги отвечало либо случаю постоянного реактивного уско-
рения, либо случаю постоянной тяги. Эти задачи даются в нашем изложении
как иллюстрация общей процедуры.
Обратимся к анализу системы уравнений (6.5). Первое уравнение из (6.5)
может быть проинтегрировано в квадратурах [6.15, 6.211:

ИДЕАЛЬЕ1ЫЯ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 6
Управляющая функция Г (~) входит только в интеграл (6.8) и не входит
в уравнения движения (см. в (6.5) второе и третье уравнения). Для постоян-
ного верхнего предела мощности Г =сонями, имеющего место в рассматри-
ваемом случае, оптимальный закон Г (~), доставляющий минимум (6.8),
устанавливается независимо от остальных управляющих функций [6.15]:
У(1) =Ж „при 0(1(Т.
(6 )
Тогда в (6.7) величина Г „может быть вынесена из-под интеграла:
г У
О
(6.10)
Оставшийся в вырансении (6.10) интеграл Х не зависит от мощности 1Ч,„,„
и масс М„, Мо и может быть подсчитан, если траектория г (~) известна.
Этот интеграл представляет в формуле для полезной массы динамическую
часть задачи. Чем меньше его величина, тем больше полезная масса при
фиксированных М, Г,„,„. и М„.
Таким образом, исходная задача разделилась на две независимые—
динамическую и параметрическую.
Динамическая часть — это вариационная задача, которая состоит
в построении оптимальных законов изменения величины а (1) и направле-
ния е (~) вектора реактивного ускорения, обеспечивающих минимум инте-
грального функционала Х для заданного динамического маневра:
Х = а'Ж = шш
(6.1 1)
г= г, г (О) = го, г (Т) = г„
т = ае+ д, ~ (О) = ~„~ (Т) = ~,
(О ( а (Е) ( со, ! е (Е) / = 1).
Параметрическая часть — это задача на максимум функции, состоящая
в определении оптимального значения массы двигательной системы М,
или предельной мощности Г „из условия максимума полезной массы (6.10):
Мо
п1ахМ,= шах ФХ, 1+ ' Х вЂ” М (Т ((;
~ шах) 0
шах
(6.12)
при этом значения интеграла Х и начальной массы М, фиксированы и зави-
симость М„(К ) задана.
2. Оптимальные соотношения масс. Если масса двигателя ЛХ„и мощ-
ность Г „связаны линейно:
М„=аУ „
(а = сопзг),
М 1
ЛХ 1 Ф/т„
Правая часть (6.14) как функция т„имеет максимум (рис. 6.1). При фикси-
рованной величине функционала Ф получаем решение задачи (6.12):
т„= М,/М, = ~/Ф вЂ” Ф.
то относительная полезная масса, согласно (6.10), может быть представлена
в виде

145
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
Максимальное значение полезной нагрузки (6.14), соответствующее (6.15),
равно
т,=(1 — ~/Ф) .
(.1)
Оптимальная величина запаса рабочего вещества вычисляется как М„=
= Мо ™, ™.:
т = М„а/М = ~/Ф.
( .17)
Оптимальные соотношения масс (6.15) — (6.17) [6.15, 6.21) представлены
на рис. 6.2. Функции (6.15), (6.16) теряют смысл вне интервала О ( Ф ( 1;
отсюда следует, что при постоянной массе источника мощности не может быть
выполнен маневр, для которого величина функционала Х ) 2/а (полезная
~~л брсд ~с
РГ дФ 06 РЮ Ф
Р3 Р4 дХ РР ~л
Рис. 6.2. Оптимальные соотношения масс,
Рис. 6.1. Зависимость полезной массы от
массы двигателя.
масса (6.16) обращается в нуль при Ф=1). Отметим, что оптимальное значе-
ние массы двигательной системы не превосходит '/ начальной массы ап-
парата.
Если масса двигателя и максимальное значение мощности связаны между собой
нел инейно.'
(6.18)
Л»» = М» (~1 ша») ю
то оптимальные соотношения масс в общем случае не могут быть выражены явно. Выпи-
шелл уравнение для определения оптимального значения мощности Г,»» [6.22].
При нелинейной зависимости (6.18) удельная масса двигателя а=М„/Г „ будет
функцией от К ,». Выберем некоторое среднее значение удельной массы а„ (не зависящее
от Г ) и запишем полезную нагрузку (6.10) через две безразмерные величины:
т
а
ф — — ц2Д~
2
О
~ тпах
"= л~,!.,
(6.19)
(а.„= сопял) .
Первая из них — относительная мощность источника — является неизвестной,
вторая — функционал (6.14) — задана. Массу М„в (6.10) можно считать зависящей от Г,
поскольку функция М„(К~„) задана, а М, и а„фллксллрованы.
Условие (6.12) в терминах параметров (6.19) записывается следующим образом
(дМ ! дГ= О):
2
л~Ф ' дЯ
— + л~Ф *=1. (6.20)
Решив уравнение (6.20) относительно безразмерной мощности Г, можно определить
размерную мощность К,» и массы М„, М, по формулам (6.19) и (6.18), (6.10) соответ-
ственно. Если решение уравнения (6.20) оканлется пе единственным (что зависит от вида
функции (6.18)), то нужно выбрать такое, которое дает абсолютный максимум (6 10).
Для линейной зависимости (6.13) полагаем а„= а=сопзФ, после чего оказывается
Г=т„и уравнение (6.20), естественно, дает прежнее решение (6.15). Как нетрудно
1О Механика полета

146
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
видеть, соотношения (6.15) — (6.17) оказываются справедливыми п для общего вида линей-
ной зависимости 1)
М„= ЛХ„+ а„Т
(6.21)
если под М„и М, в них поыимать ̄— М, и М,— М„о соответствеыно. При этом до-
пустим> >й ди пазон изм нения фуыкц о ала Ф
Ф ~ 1 — ~М,О/~о.
(6.22)
Рассмотрим левую часть уравыения (6.20). Выражение в круглых скобках — моно-
тонно возрастающая функция Я. Оно равно единице в точке Я& t = gt; Ф Ђ” Ф,
дб Р8
~тих
Рис. 6.3.
двигателя
Примеры зависимости массы
ог максимальной мощности.
Рис. 6.4. Примеры сравпения оптимальных соотно-
шений масс при линейных (2, 3) и нелинейной (1)
зависимостях массы двигателя от максимальной
мощности с рис. 6.3.
в точке, о>~тималь ой ля линей ой зависимо ти 6. 1 ). Поэт му оптималь ая то
будет сме>пвт ся от то ки Я = gt; Ф в ” ~1> право» и т„/НЯ (1 (большие
мощности) и влево при Нт,&gt Н  1 (мень ие значе ия мощност
При параметрических расчетах по Ф в уравнении (6.20) можно Ф и Я поменять
ролями: Я считать параметром (независимой переменной), а Ф вЂ” неизвестной величиной.
В этом случае решение уравнения (6.20) записывается явно:
~/Ф = (4дт„/ШЯ) /'+ ((4йп,/йЯ) 1 — Я] /'
(йт/ЮЯ, О, 0 & t  < (4д „/И ) >
Ф„= (Ы»г„/ЙЯ) ~;
(6.24)
знак минус дает 0 ( Ф:. Ф„(возрастающая ветвь рптимальной зависимости ЛХ„(Ф),
ср. рис. 6.2), знак плюс — ~1& t; -= ~1>„(убы ающая ветвь ЛХ
Чтобы составить количествепное представление о влиянии нелинейности (6.18)
на оптимальыые соотношения (6.15) — (6.17), рассмотрим зависимость М„(ШП,,„), соот-
ветствующую кривой а (Уп,„) иа рис. 2.88. Эта зависимость показана на рис. 6.3
(кривая 1), там хсе для сравнения нанесеыы аппроксимирующие. зависимости: лиыей-
ная (6.13) М„(кг] =4 кг/кгт Ш... [кгт] (кривая 2) и общая линейная (6.21)
М.„(кг]=1,5 ° 10 кг+2,2 >;г/ в Ж „, (в т] (кри ая ). Прим ры оптималь ых со
ношений т.„(Ф) = М„(Ф)/ЛХэ и»&g ;, Ф = Ђ” М, (Ф)/ э, соответствую ие т ем э им крив
показаны ыа рис. 6.4 для ЛХэ =10 > г, а =4 >г/
3. Ступенчатое изменение массы двигателя. Как показано в предыду-
щем пункте, при неизменной массе двигателя не могут быть выполнены ма-
невры, энергетическая характеристика которых превосходит определенный
предел (У ) 2/а). Этот предел можно отодвинуть, если в процессе движения
') Это же замечание относится и к следующим двум параграфам главы.
Знак минус или плюс в (6. 23) соответствует двум диапазонам значений функцио-
нала Ф, разделяемым величиной

147
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
М" "=М" ~ЬМ"'
7Г 7Г
(6.25)
где ЬМР(.' — количество рабочего вещества, израсходованного на г-м участке
(~; «(~,).
Примепим для вычисления ~ЛХ< <' соотн шение 6.6), запи анн е д
крытого промежутка 1,. х(~(~,.:
м+,
М,— 1+Ф „ /,&lt
(6.26)
где ДХ,. — масса аппарата до сброса ~-й секций, М+,, — масса аппарата после
сброса (х — 1)-й секции, М„"' — масса двигателя на х-м участке. По опреде-
лению ЬЛХ" & t = Л +, Ђ” ,. Подста и в (6. 5) найден ое та им обра ом
ражех&lt ие ля ЛЛХ„' & t;) и з менив ЛХ+,, =ЛХ," "+Л .„"', п лучим отн
М "& t 1 Ђ” 1+ < &g ;М
М<& t; )&g ; 1+ (1+ М&l ;& t
(6.27)
Отношение истинной полезнохх массы ЛХ, к начальной ЛХ, можно
ставить как произведение отношений М<')/ ,"
М М&lt и) М&l ;&gt >
М М<&g ;<-) g ; М&lt »
О
&l ;
О
пред-
(6.28)
Для последнего сомножителя этой цепочки справедлива формула (6.14):
М&lt &
т~'~,
М 1 + Ф '>&g ;
(6.29)
остальные сомножители определяются соотношением (6.27). Кансдьхй сомно-
ххсителх при фиксированных Ф,. зависит только от ЛХ„"'/ЛХ," " (при г = 2,..., и)
и от тх&g ;Х ( р г = ). Последх ие ххезависимы ), поэт му макси ум т, дос
гается при максимуме каждого из сомххонсителей по М„"/ЛХ," ". При фикси-
рованных Ф,. этот максимум имеет место, когда
̄"' '1 — 6~;
(г=2, ..., и), тх'>=~/Ф, Ђ”
1) Если не принимать в расчет условие х<евозрастах ия абсолют ой ма сы двигате
Я(') ) М„'-) ) ... ) М„'"' ) О. Из дальнейшего будет следовать, что в оптимальном
варианте это условие выполняется автоматически.
10*
сбрасывать секции двигательной установки [6.231. В самом деле, на заклю-
чительном этапе движения, когда израсходована большая часть рабочего
вещества, масса двигателя становится преобладающей (при условии, что
величина полезной нагрузки мала). В такой ситуации может оказаться вы-
годным сброс части двигателя; при этом уменьшится масса аппарата, но
одновременно уменьшится и мощность, идущая на ускорение рабочего ве-
щества. Чтобы выдержать заданную программу реактивного ускорения,
после сброса потребуется меньшая тяга, и если размер сбрасываемой секции
выбран правильно, то и расход рабочего вещества будет меньше.
Уменьшение массы двигателя сопровождается пропорциональным умень-
шением максимальной мощности, ибо 1&lt >' „ М„/ а (рассматри аетс
чай а=сопз$; все несброшенные секции двигателя работают параллельно).
Аналогично первому пункту можно показать, что мощность Г всюду должна
использоваться максимально, 1Ч (х)=Г „. (х).
Введем полезную массу х-й ступени ЛХх'& t; (х=1,. ., ), рав ую су
истинной полезной массы М, и массы рабочего вещества, оставшегося к мо-
менту сброса х-й секции двигателя. Может быть составлено рекуррентное
соотношение

148
[ГЛ. 6
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
При этом полезная нагрузка т, равна
т„=(1 — ~/Ф,) ц(,~) .
(6.30)
Все рассуждения проводились при фиксированной траектории (неизмен-
ный закон а (г)); поэтому сумма
и
~~ Ф,. = Ф
(6Л1)
задана; оптимальные соотношения между Ф,. должны определяться из усло-
вия максимума (6.30) при выполнении равенства (6.31).
Необходимые условия максимума (6.30) при наличии связи (6.31) монсно
записать в виде
и
4ИФ;
1 Ф2 0
Иф,
И!пт,=
~Ф вЂ” ф,
Исключив отсюда ШФг, получим
юг
И1п т,=
~=2
силу независимости оставшихся под знаком суммы дифференциалов,
приходим к равенствам
г=2, ...,п,
или с учетом (6.31)
Ф вЂ” ф1
1
и — 1
Фг — — [~/Ф+ и (и — 1) — (и — 1)~,
г =2, ..., ~г. (6.32)
Остальные величины выражаются через Ф, следующим образом.
т,=Ф, = — 1, т~'>=(~ Ф, Ђ” ,) Ђ” 1 ~ Ђ” , г (6
1 1
Полученное значение полезной нагрузки превосходит одноступенчатый
вариант (6.16), начиная с Ф='/„и обращается в нуль при Ф=гг. В этом же
диапазоне, 1/4 ( Ф ( и, как следует из второго соотношения (6.33), выпол-
няется и условие невозрастания массы двигателя с ростом номера ступени.
Переход к пределу при и — э со в (6.32), (6.33) приводит к следующим
соотношениям, описывающим непрерывный сброс бесконечно малых секций
двигателя:
'/, при О & t Ф 1 &l
1!,е'-''~(') при '/,(Ф (Ц (ф
т = г/ е'-4Ф (со ~~ Ф = Ф (Т) ) '/ ).
)
(6.34)
Этот случай будет еще раз исследован в ~ 2 другим способом, как задача
оптимального управления.
Соотношения (6.32) — (6.34) иллюстрируются рис. 6.5 — 6.9. Для нагляд-
ности зависимости параметров от числа ступеней и показаны непрерывными
кривыми.
Примеры оптимальных ступенчатых законов изменения массы двигателя
вдоль траектории даны на рис. 6.5. Аргументом там служит текущее

149
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ МАСС
Ю ~б
О
075
Рис. 6.6. «Протяженность» Ф, участка работы
первой ступени.
Рис. 6.5. Примеры оптимальных законов
измененпя массы двигателя при Ф (Т)=0,75.
д lб
/7
Рис. 6.7. Коэффициент т„' /т„' ~ уменьшения
массы двигателя от ступени к ступени в функции
числа ступеней и при фиксированных значениях
функционала Ф (от помера г не зависит).
б)
т„Р = ОГ5
~7~а~ )
ц6
Одб
Рис. 6.9. Сравнение полезной нагрузки для различного числа секций двигателя: а) полезная масса от-
несена к начальной массе аппарата (т = М, /М,); б) полезная масса т отнесена к максимально возмож-
ной для данного маневра — к т при п=~о.
~~(
00
~дд
ЗЙ
524
ЗЗд
д
Я5 07 ЯЯ 11 I ~ ф
Рис. 6.8. 'Относительная начальная масса
юи„= М„/М, двигателя в зависимости от
числа ступеней и при фиксированных значе-
ниях функционала Ф.

150
ИДЕАЛЬНЫИ ДВИГАТЕЛЬ ОГРАНИЧЕННОИ МОЩНОСТИ
[ГЛ. 6
значение интеграла Ф (~). На этом же рисунке нанесен и предельный закон не-
прерывного уменьшения массы двигателя (п=со). Характерные особенности
оптимальных ступенчатых законов (6.32), (6.33) состоят в следующем. Каж-
дая ступень, начиная со второй, обслуживает участок траектории с одина-
ковым приростом интеграла ~1~ (~): &l ;Р ( ,) Ђ Ф ( ,. ) (Ф Ђ Ф ) (и Ђ” ). «П
тяженность» Ф1 первого участка увеличивается с ростом суммарного функцио-
нала Ф=Ф (Т) (до единицы при Ф=п) и убывает с ростом числа ступеней,
стремясь к 1/ при и — э со (рис. 6.6). Масса двигателя от ступени к ступени
убывает в геометрической прогрессии, ее знаменатель представлен на рис. 6.7.
Начальное значение массы двигателя возрастает с увеличением числа ступе-
ней (до '/, при и — э со) и падает с ростом Ф (рис. 6.8).
Использование сброса секций двигателя расширяет диапазон выпол-
нимых маневров: интервал допустимых значений функционала У динамиче-
ской части задачи увеличивается в и раз по сравнению с одноступенчатым
вариантом. Кроме того, обеспечивается увеличение полезной нагрузки на
тех маневрах, где в одноступенчатом варианте она не превышала 0,25. Прак-
тически ощутимые выигрыши начинаются позже, примерно с т. ( 0,1
при п=1. В пределе (при )г= сю) они составляют 0,005 — 0,017 в зависимости
от значения функционала Ф (рис. 6.9, а). Относительные величины выигрыша
весьма существенны: при Ф=0,7 полезная нагрузка увеличивается в 1,5 раза,
при Ф=0,8 — в 2,5 раза, при Ф=0,9 — в 6 раз и при Ф=1 — в бесконеч-
ное число раз. Большая часть этого выигрыша реализуется уже при одно-
кратном сбросе массы двигателя (п=2 на рис. 6.9, а и б).
я 2. Оптимальная программа изменения массы двигателя
и, во-вторых, ЛХ„входит в начальное условие (см. (4.7)):
(6.36)
ЛХ. (О) -~ М„',О) = ЛХ,.
Укажем замены, позволяющие выделить два независимых управления
вместо Г (~), ЛХ„(~) и применить в дальнейшем метод Л. С. Понтрягина.
Сначала вместо управляющей функции Г (~), изменяющейся в диапазоне
0 ( К (1) ( У „(~) = ЛХ„(~) ~а, (6.37)
введем безразмерную Ж (~):
К (~) = Т (~)/Т ,„ (~) = аТ (~)/ЛХ„ (~),
(6.38)
пределами которой будут
0& t; Р)
(6.39)
Новая управляющая функция Ж (~) независимая.
1. Формулировка задачи. В настоящем параграфе излагается второй
подход к решению задачи построения оптимальныт законов изменения массы
двигательной системы [6.24, 6.25~, отличный от описанного в п. 3 ~ 1.
Как и в ~ 1, характеристика идеального двигателя берется в виде (6.4).
Вариационная задача формулируется, как задача Майера (4.8). К управле-
ниям здесь относятся: вектор ориентации тяги е (1), величина реактивного
ускорения а (~), мощность Г (~) и масса двигателя ЛХ„(~). Нахождение опти-
мальных законов е (1), а (1) может быть проведено по известным правилам
вариационного анализа; аналогичная процедура для Г (1) и ЛХ„(1) ослож-
няется тем, что эти управления не являются независимыми. Во-первых,
верхний предел Г (1) связан с ЛХ„(1):
Т „(1) = ЛХ„(1)/а, (6.35)

151
ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ МАССЫ ДВИГАТЕЛЯ
э 2]
К системе (4.8) добавим дифференциальную связь, выражающую изме-
нение (уменьшение) массы двигателя (ср. (4.4)):
М„= — д
(6.40)
(д — расход массы двигателя, 0(д„(~) ( со); будем считать расход д„новой
управляющей функцией, а массу М вЂ” новой фазовой координатой. Управ-
ление д (1) независимое.
Программы изменения массы двигателя ЛХ„(~) и мощности Т (~) находятся
по известным К(1) и д„(1) следующим образом:
ЛХ„(1) = ЛХ„(0) — д„(1) Ж, Ж (1) = М (1) Ж (1)~а.
(6.41)
Описанные приемы носят общий характер и будут в дальнейшем при-
меняться при подходящих ситуациях (например, в з 3 настоящей главы).
Для нахождения оптимального закона ЛХ„(1) в рассматриваемом случае
можно обойтись без добавления дифференциального уравнения (6.40), имея
в виду особые свойства вариационной задачи.
Отнесем массы М„ЛХ„, ЛХ к начальной массе аппарата ЛХ„а такхсе про-
изведем замену (6.38); тогда система (4.8) преобразуется в такую:
(6.42)
2. Разделение вариационной задачи. Исследуем оптимальные управле-
ния Ж (1), е (1), а (1), т, (1).
Следуя методу Л. С. Понтрягина, выпишем гамильтонову функцию Н и уравнения
пля импульсов р.
(т,+ т„)2 а
Н = — р, 2 а'+ р„ч+ р„(ае + В),
Ют„
дН т,+т.,
— = р аа2,
Ят
(6.43)
дН д дН
р,= — — „= — д(р, а), р,= — — „= — р,.
Импульсы р„р„, р, пронормированы так, что
р. (Т) = -1.
(6.44)
Функция р, (~) отрицательна на интервале 0 & t  & t; , ибо дифференци
уравнение (6.43) для импульса р, линейное однородное и в конечный момент им-
пульс р, отрицателен.'
р,(й)(0 при О& t; й&
Оптимальные управления Ж (Е), е (Е), а (Е), т„(Е) должны доставлять
абсолютный минимум гамильтоновой функции (6.43).
Множитель при 1/Т в гамильтоновой функции положителен (см. (6.45));
поэтому оптимальное управление Ж (~) должно подчиняться закону (ср. (6.9))
У(1) =1 при 0(1(Т. (6.46)
Физически это означает, что вся располагаемая электрическая мощность
должна идти на создание тяги.
( '+ ") а .(0)+
Ют„
г = т, г (0) = г„г (Т)
Ф=ае
( ~ е (~) ~ = 1, 0 ( Я (1) ( 1,
т„(0) =1, т,(Т) =шах,
= Г1,
= У1
а (1) ) О, т„(1) (О).

152
ИДЕАЛЬНЫИ ДВИГАТЕЛЬ ОГРАНИЧЕННОИ МОЩНОСТИ
[ГЛ. 6
Оптимальное вектор-управление е (~) выбирается так, чтобы скалярное
произведение р„е было минимальным:
е= — р„/р, (р,=~р„~), (6.47)
т. е. вектор тяги должен быть антипараллелен вектору р,.
Оптимальный закон а (~) имеет вид (из условия дН~да=О, поскольку а
не ограничено)
рр т„
(6.48)
р, (т,+ т.,)2а
Отметим, что оптимальное реактивное ускорение отлично от нуля
всюду, за исключением изолированных точек, где р„=О; иными словами,
идеальный двигатель ограниченной мощности включен во все время
движения.
Обратимся к исследованию оптимального непрорывного закона изменения массы
двигателя 1). Гамильтонова функция (6.43) имеет относительный минимум по т„при
т,.=т . (6.49)
К (6.49) присоединим границу управления т„, отвечающую знаку равенства в усло-
вии т„( 0 (см. (6.42)):
(6.50)
т. = сопя$
(в дальнейшем будет показано, что граннца (6.50) входит в состав оптимального управ-
ления т.„(1)).
При функциональных зависимостях (6.49), (6.50) выражение, являющееся коэффи-
циентом при (а~2)а2 в гамильтоновой функции (6.43), не зависит от времени и имеет знак
минус на всем интервале [О, Т]:
(т, + т.)2
р =сопя$ - О;
(6.51)
это может быть проверено дифференцированием выражения с учетом уравненхш для р',
из (6.43) и т, из (6.42); знак константы следует из (6.45).
Отсюда можно сделать вывод о разделении изучаемой вариационной
проблемы. Будем рассматривать комбинацию (6.51) как новый импульс;
тогда функция Н будет соответствовать вариационной задаче на максимум
функционала
— Х = — а'Ж,
(6.52)
сформулированной для уравнений движения из (6.42). В качестве управляю-
щих функций здесь будут фигурировать а (~) и е (~). Заменим знак перед
новым функционалом на обратный; при этом вместо задачи на максимум — У
будет рассматриваться задача на минимум У, т. е. полученная в 3 1 вариацион-
ная проблема (6.11).
После решения вариационной проблемы (6.11) следует определить оп-
тимальное управление т„(~), доставляющее максимум величине т. (Т)=т„
при известных законах а (1), е (г) и известном значении У.
Из уравнения расхода и краевых условий для масс (6.42) вытекает ин-
тегральная связь
т.,Ыт, а
(т„+ т,)~ 2
1 — зв„(0)
(6.53)
') Непрерывная функция т„(й) соответствует непрерывному сбросу бесконечно
малых элементов двигателя; этот случай является предельным для ступенчатого изью-
нения массы т„.

ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ МАССЫ ДВИГАТЕЛЯ
ф 2]
пг
Я т.,дт
тах —, Х = шах
т, т, е
1-» .,(О1
(6.54)
В дальнейптем будет использоваться, как более удоояая, последняя форму-
лировка.
Отметим прежде всего, что при т ) 0,5
оптимальная программа т.„(т,) не может
содержать прямую (6.49), ибо в этом случае
нарушается условие т„(0) + т, (О) = 1. Сле-
довательно, при т ) 0,5 оптимальный закон
есть
(6.55)
т„(т,) = т„е = сопзС
а т. о
(6.56)
Из условия максимума У получаем
экстремальное значение
т,® — — ~т — т„,;
(6.57)
при этом
& t
Рис. 6.10. Состав оптимального закона изме-
(6 56) кения массы двигателя.
Ф = (1 — 1 т„)
что эквивалентно (6.15), (6.16). Если
т (0,5, то оптимальный закон т„(т,) может состоять не более чем иэ трех
прямых (рис. 6.10):
при 1 — т„о & t; „>
= т.о
(6.59)
то& t  &g
т.,д) т ~ т~.
при
т„= т,
при
т., = — т„1
После вычисления интеграла (6.54) по участкам (6.59) получаем
1 1
4 п1ш1+ 4 Ъ~~а
т„д
т„1+ т„
(6.60)
где т„е и т„, должны удовлетворять очевидным неравенствам (см. (6.59))
(6.61)
1 — то>тхо&gt
Из условия максимума Ф по т„о, т„д определяются оптимальные значения
последних:
т„о = 0,25, т„= уц . (6.62)
Максимальное значение ф равно
(6.63)
Ф = 0,25 (1 — 1п 4т,).
Управление т„(~) должно быть построено из участков (6.49), (6.50)
так, чтобы достигался максимум т и при этом удовлетворялось условие (6.53).
Таким образом, как и для постоянной массы двигателя Ц 1), рассматри-
ваемая вариационная проблема (6.42) разделилась на две части: динамиче-
скую (6.11) и параметрическую (6.53).
3. Решение параметрической части вариационной проблемы. Требуется
определить кусочно-непрерывную функцию т„(т.), составленную из участ-
ков т„=т, и т„=сопв$, обеспечивающую максимум т, при заданном зна-
чении У (см. (6.53)). Этой формулировке эквивалентна такая: определить
функцию т„(т,), доставляющую максимум У при заданном значении и,:

154
[ГЛ. 6
ИДЕАЛЬНЫИ ДВИГАТЕЛЬ ОГРАНИЧЕННОИ МОЩНОСТИ
Обращаясь к (6.59), находим, что ломаная экстремаль состоит только
из двух прямых:
/~ при /~~~ т Э~ /а
т„= т. при '/~) т.)~ т,.
(6.64)
Полученное решение (6.63), (6.64) справедливо в диапазоне 1/ )~ т,) О,
так как при т,)'/ и т„„т, из (6.62) нарушаются неравенства (6.61).
Если 1 ) т, ) 1/, то оптимальная функция т (т.) — прямая (6.55), оп-
тимальное значение т, и максимальная величина Ф даются формулами
(6.57), (6.58).
Приведем сводку решения параметрической части вариационной задачи
в виде, разрешенном относительно т,:
при 0(Ф(1/
т, = (1 — ~/Ф)2, т„= ~/Ф вЂ” Ф,
прп /~ (~ Ф ( о:&
(6.65)
'/, при '/, )~ и. )~ '/„
т при '/)т)т. &
Зависимость т (Ф) из (6.65) показана на рис. 6.9, а — кривая, обозначен-
ная символом со. Она совпадает с полученной в п. 3 3 1 зависимостью (6.34).
Отметим, что рассмотрение задачи оптимального программировапия массы двига-
теля при заданных законах реактивного ускорения, например при а (~)=сопз1 [6.26],
в силу доказанного свойства разделения приводит к аналогичным результатам.
4. Ступенчатая аппроксимация оптимального управления массой двигателя. Пусть
теперь управление т„— кусочно-постоянная (ступенчатая) функция времени 8 (или
массы рабочего вещества т,). Требуется определить оптимальные высоты уровней (ступе-
ней) управления и оптимальные моменты перехода с одного уровня на другой, если число
уровней задано. Для решения задачи существенным оказывается то обстоятельство,
что т„— невозрастающая функция времени ~ (или неубывающая функция массы т,)
и, следовательно, высоты уровня ступенчатого управлепия должны убывать со време-
нем 8 (илп возрастать с увеличением массы т,).
Для рассматриваемого случая (6.54) заменяется суммой интегралов по участкам,
вдоль которых функция т„постоянна; после интегрирования и подстановки соответствую-
щих пределов получаем следующее выражение Ф:
и — 1
1 1 1
Ф = т~1)
УИ(1) ~1 Щ(1) ~ Х Щ(~ ) ~ Щ(Э) Щ(1 — 1) ~ Щ(')
— 1 ~~ т~'~
&g ;
с)
1
,.И(~)
+ ~ т + т&lt п&g ; т lt п — &
1~ Х Ю Х
(6.66)
Здесь и — заданное число уровней ступенчатого управления, т„' ', ..., т„'~' — высоты
уровней, т,'", ..., т,'7' " — моменты смены уровней.
Найдем 2п — 1 неизвестных т„'1), ..., т(~); т(", ..., т,'~ 1' из условия обраще-
ния в максимум функции Ф; после дифференцирования выражения (6.66) получим
т"' = >~т&l ;'+1 gt; т< & t; и
&g ;
(> 1, . . и Ђ”
т~'~1& t; =1~т,"+»т '> (&gt = , . .,
(6.67)
т~1& t = 1~ '» Ђ” т'
Х Ю Ю
В верхней строчке (6.67) выписаны две группы уравнений, отвеча>о их усло
максимума Ф по т,''&g ;. Во вто ом слу ае (т~"' ' gt; = т„" ) все и у овней ступен
управления т„имеют равную высоту; это соответствует аппроксимации оптимального
закона (6.55).
Укажем способ решения полученной системы алгебраических уравнений. Вели-
чины т,'') и т,"+') связаны следующим рекуррентным соотношением:
(т~~>) + = (т~'+& t &g ; ' (&g ; = 2 .. , и вЂ

СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
что легко проверяется методом полной индукции (см. (6.67)). Величина т,'"' опреде-
ляется из уравнения
(т~п1)~~+1 (~ ~/т<п
(6.69)
Вычислив т~"' при заданном значении т из (6.69) и, найдя последовательно
все т~п 1&g ;, . ., т~ ' а по и и т "' из (6.6 ), мо но определ т Ф по 6. 6
Результат проведения тдкой процедуры представлен на рис. 0.9, а дл» случая п= 2.
Аналогичным образом может быть решена задача, когда требуется, чтобы двигатель
состоял из равновеликих секций. Для этого случая в (6.66) нужно выбирать оптимальным
только один уровень т„'", остальные уровни определи~ется по формуле
~ — 1
т") = т(1) 1 — или т'~' = т'1).
Х Х
П
Х Х
(6.70)
т.,дт,
)2 2 й Н1 Ф (1)
1 — ти. О
(6.71)
(в левый интеграл подставляется оптимальная программа т„(т,)). Эти программы были
явно выражены через аргумент Ф (~) в (6.32) — (6.34).
~ 3. Использование сбрасываемых секций двигателя
в качестве рабочего вещества
1. Постановка задачи. При рассмотрении оптимальных законов изме-
нении массы двигателя в предыдущих двух параграфах считалось, что сбра-
сываемые секции отделяются от аппарата с нулевой скоростью и не сообщают
дополнительного импульса (пассивный сброс). Если предназначенные для
сброса секции двигателя превращать в рабочее вещество и сбрасывать со
скоростью реактивной струи (активный сброс), то можно получить дополни-
тельный выигрыш. Такая идея использования ненужных элементов кон-
струкции была высказана Ф. А. Цандером [6.27].
Поставим задачу об оптимальном использовании сбрасываемых секций
двигателя [6.22, 6.28]. Будем считать, что не вся масса сбрасываемых секций
может превращаться в рабочее вещество, а только часть ее
(О ( х,„= сопзь (1)
(6.72)
(параметр х,„предполагается заданным). Таким образом, часть расхода
д„)~ 0 (см. (6.40)), равная (1 — х)д„, не используется и покидает аппарат
с нулевой скоростью. Остальная часть хд„, превращенная в рабочее вещество,
направляется в движитель. Суммарный расход через движитель д будет
складываться из расхода хд„и расхода запаса рабочего вещества д ) 0:
Д = Д„.+'Д,.
(6.73)
Эта схема использования сбрасываемых секций двигателя относится
к предельному случаю непрерывного сброса. Ступенчатый сброс описы-
вается в последнем пункте параграфа.
Выберем в качестве независимых управляющих функций безразмерную
мощность (6.38), расходы д„, д„и коэффициент превращения массы двигателя
в рабочее вещество х. Характеристики двигательной системы, как и раньше,
считаются идеальными и записываются в форме (6.1). Вариационную задачу,
аналогично предыдущему параграфу, сформулируем как задачу Майера (4.8).
В заключение параграфа укажем, что предельная оптимальная программа (6.64),
а также соответствующая ей ступенчатая оптимальная программа, построенные по аргу-
менту т„могут быть записаны через аргумент ~, если известен закон изменения реактив-
ного ускорения а (~). Связь между переменными т, и ~ имеет вид

156
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
~ГЛ. 6
Для этого присоединим к системе (4.8) уравнение (6.40) и перепишем ее
в терминах перечисленных выше управлений:
т. (Т) = шах,
т„(Т).- О,
г (Т) = г„
т. (О) +
+т„(0) =1,
г (О) =г„
пг,= — д,
пг,, = — д„,
г=ч,
(6.74)
~(2/а) т.„К (д„+ хд„)
е+ ~, ~ (О) = т„
(~е(~) ~=1, 0~(Ж(~) &lt 1, 0&l ;х ~) <х , „(~)) , „
т(Т) =т,
(все массы и расходы отнесены к начальной массе аппарата, мощность—
к максимально возможной в данный момент).
Нужно выбрать оптимальное начальное значение массы т и построить
оптимальные программы для управлений е (1), У (1), х (1), д„(1), д (1) (кон-
структивные параметры а, х„„„и динамический маневр (г„т„г„т„Т)
заданы). Максимизируемый функционал — конечное значение фазовой коор-
динаты т., совпадающее по определению (см. (4. 7)) с полезной массой.
2. Состав оптимального управления. Для отыскания оптимальных
программ управления воспользуемся методом Л. С. Понтрягина. Согласно
принципу максимума на оптимальной траектории гамильтонова функция
Х! = — р.д,— р.ч,+р, у+р, и+
+р, ° е У (2/а) т„Я(д„+хд„) (т,+т„) ',
дП дИ дН
(6.75)
дЫ
Р
дт
о'
р Р =—
дт.„' " дг ' ' дч
(6.76)
х (~) = х,„при 0 ( 1 ( Т.
Для отыскания управлений д,„и д„запишем с учетом полученных оптимальных
соотношений (6.46), (6.47), (6.76) часть функции Н, зависящую от этих управлений 1):
Л = — р д„— рд„— р„~(2/а) т„(д„+ хд„) (т + т„)
(6.77)
и уравнения для импульсов р, и р„.'
р, = — р, 1~(2(а) т„(д + хд„) (т, + т„)
1
р„= 2 р. (1 — т./т„).
(6.78)
Из условия минимума (6.77) следует, что если один или оба импульса р„р„больше
нуля либо равны нулю, то оптимальное значение одного или обоих расходов обращается
в бесконечность.
') Здесь и в дальнейшем под х без индекса подразумевается максимальное зна-
чение ~шд~,
должна иметь абсолютный минимум по переменным е, У, х, д„и д„под-
чиненным ограничениям из (6.74).
Программа для направления вектора тяги, как и в $ 2, дается соотно-
шением (6.47), поскольку перед скалярным произведением р„е в функции Н
стоит неотрицательный коэффициент.
Из анализа функции Н с учетом условия (6.47) следует оптимальность
полного использования мощности (6.46).
Аналогичным образом приходим к физически очевидному выводу: доля
расхода д„, превращаемая в рабочее вещество, должна быть максимально
возможной:

157
СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
Рассмотрим теперь случай
р.~О, р„&lt
(6.79)
Выразим функцию (6.77) через суммарный расход (6.73) и расход д„:
Ж = — р,д — р, (2/а) тд (т, + т„) 1 — (р„— хр,) д„(д ) О, 0 ( д„( д/х).
(6.80)
Отсюда видно, что оптимальное распределение суммарного расхода д между со-
ставляющими д„и д = д — кд„определяется знаком комбинации
Ь = р„— кр,. (6.81)
В самом деле, если о(0, то минимум Ж по д„достигается при д„=о, т. е. при
а„=д, а если а) О, то — прн д„=д/х, т. е. при д„=о. В случае 1=0 функция М
не зависит от каждого из расходов д и д„по отдельности, а определяется суммарным
расходом д. В этом смысле его можно считать особым.
Таким образом, в каждом из трех возможных случаев функция Ж зависит только
от одного из расходов др, д„или д, подчиненных лишь условию неотрицательности:
М = — р,д„— р„~/(2/а) т.,д„(т,+ т„) 1 при Л(0 (д„=о),
Ях = — р„д„— р„~/(2/а) т„хд„(т + т„) 1 при Ь ) 0 (д„= 0),
Жз — — р,д — р„~/(2/а) т„д (т,+ т.„) 1 при 1=0.
(6.82)
Из условий стационарности дЯ,/дд„= — 0 и дЯЯдд„= О, которые здесь
соответствуют условию абсолютного минимума, определяем оптимальные
управления д„и д„при Ь+ 0:
в первом случае
ПгхР"-,
А 2р'; (т, + т,)х а '
(6.83)
д,„=О
во втором случае
2
хшу р
~„=О, ~„=2
(6.84)
При Ь =0 из условия дЯ'з/дд =О следует:
2
тп.,р,
~~+ х" 2р," (т, + т„)х а
(6.85)
(Ь = 0).
Когда Л обращается в нуль не в изолировапных точках, а па некотором конечном
отрезке времени (именно такой случай будет особым), то производная Ь также равна
нулю на этом отрезке:
1- т,
Ь= — р, 1 — 2к — — ' =О
2
(6.86)
(зто уравнение получено из (6.81) и (6.78)).
Из (6. 86) следует либо р',= О, либо (1 — 2х — т,/т„) =О. Рассмотрим первую
нозможность. Из (6.78) с помощь1о (6.85) исключаем (д„+ хд„):
2
р
и(т,+т )~ р
(6.87)
(6.88)
может быть равен нулю или в изолированных точках, или тождественно вдоль всей траек-
тории. Последний случай вырожденный, так как он соответствует пассивному движе-
нию д =д„=о (см. (6.83) — (6.85) при р„=о).
Правая часть (6.87), за исключением изолированных точек, отрицательна. В самом
деле, масса двигателя т„может обратиться в нуль только при ~= Т; импульс р„как это
следует из уравнений (6.75):

158
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Таким образом, первая возможность р'.=0 отпадает, остается
1 — 2с — т./т„= О.
(6.89)
Это выражение означает пропорциональное изменение массы двигателя
и запаса рабочего вещества (ср. (6.49)). Совместно с соотношением (6.85)
оно дает условие, определяющее оптимальные управления д„и д, в особом
случае:
д =(1 — 2с) д„=
2(1 — х) р" (т +т)2а
(6.90)
Нетрудно видеть, что соотношения (6.89), (6.90) имеют смысл при х ( 0,5
и т, ( 0,5 (в противном случае 1 — 2х ( 0 или т,/т„) 1).
3. Чередование оптимальных программ для расходов. Выше было установлено, что
характер оптимальных законов измопения расходов д и д, зависит от знаков импуль-
сов р„р., и комбинации Л.
В начальный момент времени (с=О), согласно условию трапсверсальности, вектор
импульсов (р„р„) долхсон быть направлен по нормали к прямой т, (0)+т„(0)=1
(см. (6.74)), т. е.
р. (О) = р„ (О).
(6.91)
В конечный момент времени (1= Т), согласно нормировке,
(6.92)
т.„(Т) =0 или р„(Т) =0
(6.93)
(зти два равенства могут выполняться одновременно, если дт, (Т)/дт„(Т) =0 при т„(Т) =0).
Начальное значение (6.91) импульсов р„р„долхсно быть строго меньше нуля.
В противном случае, как следует из условия минимума (6.77), д = со и д„=со. Это соот-
ветствует сбросу копечной части запаса рабочего вещества Лт и двигательпоп системы
Лт„за бесконечно малое время Л~:
Ьт
Д
Ьт.,
при ~~ — эО.
д с1$ = Лт ( со, д„с1$ = Лт„( со,
О О
Интеграл от реактивного ускорения по интервалу (О, Л1) получится также бесконечно
малым:
Ы
~ 2~у Ир. + '.~7 ) ~(2(а) т (0)
аЖ= Й &
т ~т„ т
$~д + хд„ссс
О
~(2/а) т., (0)
Лтр + х Лт.„
~1 — э О при М вЂ” э О.
т„
Все это озпачает, что начальпые соотпошения масс выбраны не оптимально.
Можно получить также ограничение на (6.91) снизу. Производная (6.78) импульса р,
всюду отрицательна, а конечное ого зпачение равно минус единице, поэтому
— 1 - р. (О) = р„ (О) & t;
(6.94)
Таким образом, импульс р, отрицателен во все время движения (р, (0) ( О,
р, (1) ( 0). То же самое можно сказать и об импульсе р„(за исключением конечного мо-
мента времени, когда р„(Т) может обращаться в нуль — см. (6.93)). В окрестности на-
(поскольку импульс р, соответствует фазовой координате т„конечное значение которой
максимизируотся).
Что касается конечного значепия импульса р„, то тут возможны два варианта.
Первыи: конечное значение фазовой координаты т„в оптимальном случае выходит на
границу т„(Т)=0 (см. (6.74)), тогда значение р„(Т) не определено. Второп: оптимальное
значение т„(Т) ) 0; тогда величину т„(Т) можно считать не заданной и по условию
трансворсальности р„(Т)=0. Таким образом, получаем условие

159
СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
Рис. 6.11. Первый возможный вариант по-
ведения функции ь (1) и соответствующий ей
оптимальный закон изменения массы двига-
теля (О ~ х & t;
Рис. 6.12. Второй возможный вариант пове-
дения функции ь (1) и соответствующий ей
оптимальный закон изменения массы двига-
теля (О & t; 7 &lt  , , 0 <
в этом случае, какой из оптимальных законов (6.83), (6.84), (6.90) управления расходами
будет иметь место.
Сначала рассмотрим случай О ( х ( 1. Из оптимального граничного условия для
импульсов (6.94) следует, что начальное значение функции Л отрицательно:
(6.95)
Конечное значение функции Л должно быть положительным:
Л (Т) = р„(Т) — ар, (Т) ) О,
(6.96)
поскольку, согласно условию (6.93), либо р.„ (Т)=0, либо т„ (Т)=0. В первом случае
справедливость неравенства (6.96) сразу следует из (6.92): Л (Т)= — хр, (Т)=к. Во вто-
ром случае это следует из (6.84), так как в окрестности конечного момента времени
масса т„должна убывать до пуля. Последнее возможно только при одном оптимальном
управлении (6.84), которое реализуется при Л 0 (т, (~)=сопвС при Л ( 0 и т„(~)=
=т, (~)/($ — 2х) при Л=О (см. (6.83), (6.89), (6.90)).
Исследуем функцию Л внутри интервала [О, Т1. Ее производная определяется вы-
ражением (6.86). Первый сомпожитель этого выражения '/,р', всюду отрицателен. Следо-
вательно, характер функции Л будет определяться вторым сомножителем:
(6.97)
][ = 1 — 2х — т,~т„.
В начале движения функция Л отрицательна (см. (6.95)), поэтому изменение массы
происходит по закону (6.83). Согласно (6.83) масса т„остается постоянной, а т, убы-
вает, т. е. )( вдоль (6.83) возрастает. Если предположить, что Ь (0) ( О, то конечное зна-
чение Л (Т) окажется отрицательным, ибо Л (0) & t   Ь ~  0 (вследст ие возрас
ния у). Отрицательность же Л (Т) противоречит условию (6.96).
чальной точки ~=0 импульс р., отрицателен. Предположим, что через некоторое время
(О ( ~„( Т) оп обращается в нуль; тогда производная р„(~„— 0) ) 0 и в силу (6.78)
т, (~,.— 0) ) т„(~„— 0). Справа от точки ~=~„последнее неравенство только усилится,
так как д„=О, О.,=с0 при р, ( О, р„=О. Значит, производная р'„будет оставаться поло-
жительный при переходе через точку ~=~„и р„(~) ) 0 при ~ ) 1„. Выполнение послед-
него неравепства на конечном интервале времени приведет к обращению в нуль массы
двигателя (Ч„=со прир., ) 0). Последнее возможнотолькоприй=Т.
Итак, показапо, что па всем интервале времени О ~ й ( Т выполняются неравен-
ства (6.79). Остается исследовать поведение комбинации (6.8$), знак которой определяет

160
[ГЛ. 6
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Таким образом, производная функции Л в начале движения положительна. Рас-
смотрим все возможные комбинации, которые могут иметь место внутри интервала [О, Т1.
1'. Производная Ь (~) всюду остается положительной. Тогда Л (~) в некоторый мо-
мент времени ~=8„пересечет ось ~ (так как Л (0) & t; О  Л Т &g ; ). На ервом
вале 0 & t  & t; ~, будет иметь место упра ление ( .83), со ласно ко орому т„(~
а на втором Ф„& t   lt; Т вЂ” упра ление ( .84), вдоль ко ор го т, 1)=т (1„) ( ис.
причем т, (~„)=т„, так как по условию (4.7) т, (Т)=т .
2'. Производная Ь (~) сначала положительна, затем обращается в нуль одновре-
менно с самой функцией (Ь (~„)=Л (~„)=0). В интервале 0 & t  < ~„изм нение
происходит по закону (6.83). При ~=~„он сменяется на (6.89). Согласно (6.89) массы т,
и т„меняются пропорционально, так что у и Ь остаются равными нулю. В некоторый
момент времени ~=~ будет израсходован весь запас рабочего вещества т, (~ )=т,.
1
1
!
1
!
Рис. 6.15. Второй возможный
вариант поведения функции
Ь (1) при ~=0 и соответствую-
щий ей оптимальный закон изме-
нения массы двигателя.
Рис. 6.14. Первый возмо>к
вариант поведения функции Ь (1)
при 7~= О и соответствующий
ей оптимальный закон измене-
ния массы двигателя.
Рис. 6.13. Поведение функции
ь (1) при ~ =1 и соответствую-
щий ей оптимальный закон из-
менения массы двигателя.
После этого может меняться только масса пг„. Комбинация;~ с уменыпением т, спова
станет отрицательной, а производная ~ — положительной. Функция Л перейдет в поло-
жительную область, и управление массой будет осуществляться по закону (6.84)
(рис. 6 12).
3'. Производная Ь (й) обращается в нуль при Л (~) & t; О В обла т   lt; 0 масс
меняются по закону (6.83), согласно которому т возрастает. Поэтому после обращения
в нуль производная Л станет отрицательной и функция Л никогда пе попадет в область
Л ) О, что противоречит условию (6.96).
4'. Производная Ь (~) обращается в нуль при Л (~) ) О. Эта возможность также
отпадает, так как в области Л & t 0 функ и у дол на убыв ть согла но (6. 4 и (6.9
а чтобы функция Л при некотором ~=~„попала в положительную область, необходимо
Ь (~„) ) О. Поэтому в области Л ) 0 производная Ь остается положительной, что опро-
вергает начальное предположение. Таким образом, последние два варианта, 3' и 4',
отпадают.
Изучим теперь поведение функции Л для крайних значений параметра х. х=1 и
к=О. При к=1 начальное значение функции Л равно нулю (см. (6.95)), а ее производная
всюду положительна (см. (6.86)). Поэтому все последующие значения Л лежат в положи-
тельной области и в процессе движения меняется только масса двигателя т„по закону
(6.84). Прп этом масса т, (~)=т, (Т)=т„, т. е. запас рабочего вещества отсутствует
(рис. 6.13).
В случае У=О, рассмотренном в предыдущем параграфе, функция Л не может по-
пасть в положительную область, так как при х=О управление (6.84) не имеет смысла.
Поэтому функция Л либо всюду отрицательна (за исключением, быть может, ~= Т), и

СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
тогда т„(~)= т„, (рис. 6Л4), либо сначала отрицательна, а затеи обращается в нуль при
~=~„( Т. Тогда производная Ь (~„) также обращается в нуль и до конца движения оста-
ется равной нулю. На первом участке О ~ & t; ~„измене ие ма сы происхо ит по зак
(6.83), на втором й„& t   lt; Т Ђ” по акону 6.89) (рис. 6Л5). Ост льные возмо
исключаются аналогично тому, как было сделано при О ( к ( $.
4. Разделение задачи на параметрическую и динамическую. Перейдем от
расходов д„и д„к новой управляющей функции а — реактивному ускоре-
нию (см. (6.74)):
а = г' (2/а) т„Я (д„+ «д„) (т. + т„) '.
(6.98)
Тогда два векторных уравнения (6.74), определяющих траекторию дви-
жения, не будут содержать массы: г=т, т=ае+~, а уравнения (6.74), опи-
сывающие изменение масс ж„и ж„для каждого из оптимальных управле-
ний (6.83), (6.90), (6.84) будут выражаться через массы и квадрат реактив-
ного ускорения (безразмерная мощность Х на оптимальной траектории
равна единице):
при Л(~) (О
(ггг + т.,)2 а
т = ' а"-, т„(1) = с.ог1з(„
Х
(6.99)
при Ь(1) =О
и. = — 4 ('1 — «) т.—,а',
(«(0,5; т, (О,г);
(6.100)
при Ь(~))0
(т, + пг.,)2 а
6:
ът„2
т (1) = сопз(„пг„=
(6.101)
Х1
т.,Ыт„
(т + т.„г
(6.102)
— т
ХО
(та + ггг о)
1 — ю
ХО
~хо
для случая (6.99)+(6.100)+(6.101)
(1 — 2х) т „
ИХ Х1
Йт,
т,
т,дтх
(т, + т„)2
тп ~/(1 — ~х)
— т
ХО
(т, + т„о)' 4 (1 — «)
Х
ХО
(1 — 2Х) Гг1 ХЮ
(6.103)
Здесь, как и в двух предыдущих параграфах,
(6.104)
После вычисления интегралов, содержащихся в левых частях ра-
венств (6.102) и (6.103), устанавливается конечная связь между полезной
нагрузкой т, начальным и конечным значениями массы двигателя т„, па-
раметром гг и величиной функционала Ф:
Механика полета
предыдущем пункте было показано, что при 0 ( «( 1 возможны
два решения: первое состоит из последовательно состыкованных участ-
ков (6.99) и (6.101), второе — из участков (6.99), (6.100), (6.101). Переменные
в каждом из дифференциальных уравнений (6.99) — (6.101) разделяются.
Квадратуры с учетом непрерывности фазовых координат т, и т„, начального
и,,+т„,=1 и конечного т.,=т, условий имеют вид:
для случая (6.99)+(6.101)

162
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТ И
для случая (6.99)+(6.101)
(1 — - х) т„т О+ т
а!И
,т„о+ т т„1+ т
(6.105)
для случая (6.99)+(6.100)+(6.101)
1 (1 — 2х) т.,о
хз 4(1 — х) т
(1 — 2х) (т„+ т„) ут„
2(1 — х) и, т„+т„
(6.106)
т„„= '/,;,с — т. + ~/1/,г.'-'+ (1 — х) т., т„, = 0;
(6.107)
;(1н случая (6.99) + (6.100)+ (6.101)
1
4(1 — х) '
(6.108)
Сравнение выражений (6.105) и (6.106), в которые подставлены опти-
мальные значения (6.107) и (6.108) масс т„„т„„позволяет установить точ-
ные границы реализации каждого типа решений. Решение (6.99)+(6.101)
имеет место в диапазонах
(1 — 2х)/4 (1 — х) ( т, ( 1, 0 ( х ( О, 5,
и 0(т,(1, 0,5(х(1,
(6.109)
а решение (6.99) +(6.100) + (6.101) — в диапазоне
0 ( т, (~ (1 — 2х)/4 (1 — х), 0 ( х ( 0 5.
(6.110)
Области (6.109) и (6.110) показаны на рис. 6.16. Штриховкой выделена об-
ласть (6.110). Для х=1 во всем диапазоне О ( т, ( 1 изменение массы про-
исходит по уравнению (6.101), а т„, и т„1 определяются формулами (6.107).
При х=О в интервале 0,25 ( т, ( 1 реализуется решение (6.99):
т„(1) = ~/т, — т.,
') Зависимости (6 105), (6 106) разрешены относительно Ф, поэтому задачу о макси-
муме полезной нагрузки т, при фиксированном Ф здесь удобно заменить эквивалентной
задачей о максимуме Ф при фиксированной величине т,.
Зависимости Ф от т„определенные формулами (6.105) и (6.106), моно-
тонно убывающие (дФ/дт, ( О). Это позволяет, как и в Я 1, 2, разделить
задачу на независимые параметрическую и динамическую части. Динами-
ческая часть задачи по-прежнему состоит в построении оптимальной про-
граммы вектора реактивного ускорения и формулируется в виде (6.11).
Параметрическая часть задачи после проведенной процедуры сводится
к определению начального т„, и конечного т,1 значений массы двигателя,
обеспечивающих максимум функции Ф (6.105), (6.106) при фиксированном
значении полезной нагрузки '), и к установлению границ реализации реше-
ний (6.105), (6.106).
Аналогичные рассуждения можно провести и для предельных значений
параметра х. Только при х=1 нужно брать один участок (6.101), а при
х=Π— либо очин участок (6.99), либо два участка (6.99) и (6.100).
э. Решение параметрической части задачи. Из рассмотрения частных
производных дФ/дт,„1~ дФ/От„находим оптимальные величины т„„и т„,:
для случая (ИЯ()) + (6.101)

163
СБРАСЫВАЕЪ|ЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
0,? Р~ Рб Рд т,.
д Р3 Р4 Рб Р8 п~~
Рис. 6.16. Области реализации различных Рис. 6.17. Оптимальная начальная масса
типов решепий. двигателя.
неизменной массы двигателя, рассмотренному в ~ 1. Видно, что оптимальные
соотношения масс в случае использования сбрасываемых секций двигателя
в качестве рабочего вещества (х ) О, активный сброс) сдвигаются в сторону
увеличения начальной массы двигателя за счет запаса рабочего вещества.
Суммируем полученные результаты. Оптимальный закон изменения
массы двигателя и запаса рабочего вещества описывается следующими соот-
ношениями: для случаев 0 ( х '. 0,5, (1 — 2х) /4 (1 — х) ( т, ( 1 и
О,5 =. х(1, 0(т,& t 1 (р с. 6.
Ф/ -(2
т (1)=т„, = —,— т,+ —,+(1 — х)т„,
(т + т.,то) о
, а
о
(при 1 — т„, ) т. (8) ) т,),
. а-, т (г)=т
кт„2
(при т,, ) т„(~) ) 0);
и'г =—
(6.111)
т„=
для случая 0(х(0,5, 0(т„((1 — 2х)/4(1 — х) (рис. 6.12)
т
~7~ О
(прп 1 — т„, ) т. (~) ) (1 — 2х) т„,),
ггг,„(1) =
а
т, = — 4 (1 — х) т, — а2
'2
(6.112)
(при ('1 — 2х) т„, ) т. (~) )~ т,),
2
а-', т (1) =т,
кт 2
Ю 7Г
х
(при " ) т„(~) ) 0);
11»
аз интервале 0(т„(0,25 — решение (6.99)+(6.100); при этом т„о=0,25,
т„,=т.
На рис. 6.17 представлены зависимости оптимальной величины началь-
ной массы двигателя т„, от полезной нагрузки т для различных значений
параметра х. Кривые построены по формулам (6.107), (6.108) с учетом границ
их реализации (6.109), (6.110). Нижняя сплошная кривая соответствует
пассивному сбросу двигателя (х=О, см. ~ 2). Пунктирный участок, продол-
жающий нижнюю кривую, и правая ветвь этой кривой относятся к случаю

164
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[Г'1. О
для случая х=1, 0(гп,(1 (рис. 6.13)
т„= — " а, т(г) =т,
(т +т„)2 а
~ 7И
(при 1 — т ) т„(~) ) 0); (6.113)
для случая х=О, 0,25(т (1 (рис. 6.14)
т„(1) =т„о= ~/т — т„
(т + т.о)~ ~х я
а
~хо
(при 1 — т„о ) т. (1) ) т );
(6.114)
т =
а
для случая х = О, 0 (т (0,25 (рис. 6.15)
т (~) =т О=0,25, т.= "', а'
хО
(при 1 — т„, ) т. (Е) ) т„о),
(6.115)
а
т = — 4т.— а~
Ю
т„ (1) = т. (1),
(при т„, ) т. (1) ) т ).
Окончательное выражение величины функционала Ф через пг имеет внд:
при 0(х(0,5, (1 — 2х)/4(1 — х) (т,(~1
и при 0,5(х(1, 0(т (1
6& t = (1 Ђ” м) (1 Ђ” Ђ” ') Ђ” 1и Ђ” '+ т, Ђ
К= — + ~/ —;+(1 — х) т
при 0(х(0,5, 0(~п,((1 — 2х)/4(1 — х)
1 — 2х 1 — 2х 1 4 (1 — х) т
Ф = х1п, 1и
4 (1 — х) 2 (1 — х) 4 &l ;1 Ђ” х 1 Ђ”
(6.116)
0(х(0,5,
)
0,5 ( ( 1.
1 — 2у.
т ехр )' — 4 (1 — х) Ф] пря
4 (1 — х)
т, ехр ( — Ф/х) при
(6.1 17)
Зависимость полезной нагрузки от параметра х при малых значениях
функционала, 0 ~~ Ф ( 0,5, близка к линейной (рис. 6.19), а при больших
переходит в экспоненциальную (6.117).
Выигрыш в полезной нагрузке от использования сбрасываемых секций
двигателя в качестве рабочего вещества (х ) О) по сравнению с простым
сбросом (х=О) может быть весьма существенным. Так, например, в предель-
У
Зависимость максимальной полезной нагрузки т, от величины функцио-
нала Ф для ряда фиксированных значений параметра х, вычисленная по
(6.116), представлена на рис. 6.18. Нижняя сплошная кривая, как и на
рис. 6.17, соответствует случаю х=О, рассмотренному в ~ 2. Эта ~ке кривая
(в диапазоне 0 ( Ф ( 0,25) и продолжающая ее пунктирная кривая (в диа-
пазоне 0,25 ( Ф ( 1) относятся к случаю постоянной массы т„, рассмот-
ренному в ~ 1.
Р&gt се кри ые представл н в нитерв л 0 (Ф 1. Одн ко е л в слу
постоя ной массы двигателя, как отмечалось в ~ '1, функция т„(Ф) теряет
физический смысл вне этого интервала, то здесь функция т, (Ф) имеет смысл
на всей полуоси 0 ( Ф ( оэ. Поведение т (Ф) вне диапазона 0 ( Ф ( 1
приближенно (т ((1) описывается следующими формулами:

165
СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
0,5
~7~
1
~г п~ ю~ ав х
06 Р8 Ф
Рис. 6.18. Максимальная полезная нагрузка Рис. 6.19. Полезная нагрузка т в зависи-
т, в зависимости от функционала динамичс- мости от коаффициента превращения ~.
ской части задачи Ф.
можно решать задачу о выборе оптимального значения х, обеспечивающего
максимум иолезной нагрузки при заданной величине интеграла 7.
6. Ступенчатое уменьшение массы двигателя. Рассмотренный выше
случай непрерывного уменьшения массы двигателя соответствует бесконечно
большому числу и бесконечно малых секций двигателя (и=оэ на рис. 6.18).
Сравним этот предельный случай со случаем конечного числа секций конеч-
ного размера, как это сделано в ~ 2 для х=0.
Пусть в момент времени ~. сбрасывается /-я секция двигателя и х-я часть
массы этой секции присоединяется к запасу рабочего вещества, т. е.
т~~~+ = т~~~ + х (т~~~- — т~~~+)
(/=1,...,и — 1),
(6.118)
где индекс у указывает на момент времени 1., а значок плюс или минус от-
носится к значению функции справа или слева от момента 1,
В интервале времени ~ ( ~ ( ~.,1 масса двигателя остается постоянной:
щ~~~- = щ(~-'~+
х х
(/=-1,..., и).
(6.119)
Мощность Г и параметр х, как и в случае непрерывного уменьшения
массы двигателя, должны быть максимально возможными. Изменение массы
аппарата на участках между сбросами описывается уравнением (6.99).
ном случае х=1 (полное превращение) полезная нагрузка увеличивается
при Ф=0,05 в 1,2 раза, при Ф=0,25 — в 1,8 раза, при Ф=0,5 — более
чем в 3 раза, при Ф=О 75 — в 7 раз, при Ф=1 — в 15 раз.
Однако сравнение полезной нагрузки при одних и тех же значениях
функционала Ф=( а/2)У дает завышенные результаты. Превращение ма-
териала двигателя в рабочее вещество, очевидно, потребует каких-то вспомо-
гательных устройств, которые увеличат удельную массу двигателя на еди-
ницу мощности, а значит, увеличат и значение Ф (при фиксированной ве-
личине интеграла У). Для того чтобы стало невыгодным полное превращение
материала двигателя в рабочее вещество (х=1), удельная масса должна
возрасти при Ф=0,05 в 2 раза, при Ф=0,25 — в 2,5 раза, при Ф=0,5—
примерно в 3 раза и т. д. (здесь под Ф
~п понимается Ф=(а „/2)У). Если будет
существовать зависимость а (х), то

166
ИД ЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 6
Интегрируя это уравнение по участкам от г,. до г,.~, ()=О, 1,..., и — 1;
г„= Т) и складывая, получаем
и — 1
Ф = т~~~+
х
(6.120)
т(2+1) т(2)+
(У х
т~г)' ~- т~г)"
(У х
Учтя соотношение на разрывах для запаса рабочего вещества (6.118)
и условие постоянства массы двигателя между моментами сброса (6.119),
перепишем выражение (6.120) в таком виде:
тг — 1
Ф = т~~~+
х
т~~) + хт~~ ) + (1 — х) пг~~~)
т~~+ ~ ~ т~~~+
е 1 х
И(-' ' =7И(')'=7И, Щ(')-=И. Щ(~~)-=Щ =Щ (
х ~ ~ х ~ х
(6.121)
Вычислив частную производную дФ/дт„можно убедиться, что функ-
ция Ф (т,) монотонно убывающая. Задача снова разделяется, и параметри-
ческая часть сводится к отысканию такик значений
т(~)+, т(~)—
(у=О, 1,...,и — 1),
(6.122)
которые обеспечивали бы максимум функции (6.121) при фиксированном
значении т, и удовлетворяли бы условиям
т~г)+ (т~г ')+
х ~ х
т.о+ т,о = 1,
(6.12З)
(в дальнейшем для сокращения записи значки плюс у т~»+ и минус у тгг)-
будут опускаться).
Для определения 2и неизвестных величин (6.122) получаем систему 2и
алгебраических уравнений (при 0 ( х ( 1)
(т~г') + т~г-')) ~/т~ г) = (т~г) + хт~г-') + (1 — х) туг)) ~/т~г'-')
(дФ/дт~г') = 0),
~<2 1~ „~&l
(У х
(тгг+~) + тг')) (тг'+г) + хтгг) + (1 — х) тг'+г))
туг') + хт1~ 1)
(дФ/дт1г) =- 0) или т& t; ' = т~ г+
(т~~г) + хт~~г ) + (1 — х) т~г))
т'и Хт(1)
( Р'+ Г')'+( '"+'. Р+(1 — ') '")2
т<о)+т о) =1 (у =1,. . и Ђ”
) (6.124)
т~~~ =т
т, = 1 — (т„")~"+') — 1) т„,
'г г') (т — ггг — г')/ггг+1) 1) т
(! =1,..., и — 1),
(6.125)
()'=О, 1,..., и — 1; х= 1).
Подставляя соотношения (6.125) в формулу (6.121), получим связь
между максимальной полезной нагрузкой т. и функционалом Ф:
Ф = (и+ 1) (1 — т.')~ "+')) + т, — 1 при х = 1.
(6.126)
В предельном случае к=1 соответствующая система уравнений имеет
простое решение:

167
СБРАСЫВАЕМЫЕ СЕКЦИИ ДВИГАТЕЛЯ КАК РАБОЧЕЕ ВЕЩЕСТВО
При и ~ оэ эта формула переходит в первое из соотношений (6.116).
Связь (6.126) представлена на рис. 6.20 в виде зависимости т, (Ф) для фикси-
рованных значений и. Из рисунка видно, что переход от и=1 (постоянная
масса двигателя) к и=2 реализует приблизительно 1/, максимально возмож-
ного выигрыша в полезной нагрузке, а переход к и=4 — приблизительно '/,.
РГ Ю1 РР Р8 Ф
Рис. 6.20. Сравнение полезной нагрузки т~ при различном числе секций двигателя.
Остальная треть реализуется переходом от и=4 к и=ой. В случае к=0
(см. $ 2) при и=2 реализуется подавляющая часть выигрыша. Отсюда можно
сделать вывод о том, что к предельным значениям полезной нагрузки можно
приблизиться при конечном, сравнительно небольшом числе секций дви-
гателя, и тем меньшем, чем меньше коэффициент х. Отметим, что, как и
при ~=0, максимально допустимое значение функционала Ф здесь равно и.

ГЛАВА 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ—
ОПТИМАЛЬНЫЕ ПРОГРАММЫ РЕАКТИВНОГО УСКОРЕНИЯ
(г (О) =ге, г (О) =1О, г (Т) =гд, г (Т) =чд.
(7.1)
['г — д (г, д)]2 Нд
о
Задача сводится к построению тдп-экстремалей функционала (7.1), проходящих
через заданные начальную (г„, ч,) и конечную (г„чд) точки пространства координат-
скоростей при фиксированных начальном и конечном моментах времени.
Будет использоваться также и другая формулировка вариационной проблемы
(6.11) — в виде задачи Майера:
Х =аз= (ае)з, У (О) =О, Х (Т) = дпдп,
г=ч, г (О) =ге, г (Т) =гд,
ч = ае+ н, т (О) = ч,, ч (Т) = чд
(а (г) ) О, ] е (г) [=1).
(7.2)
~ 1. Уравнения экстремалей и их свойства
1. Уравнения экстремалей, общий случай. Запишем функционал (7.1)
в прямоугольной инерциальной системе координат (х, у, я):
Х = [(х — Х)'+(у — У)'+(Š— Я)']дд1= К(8, х, х, у, у, я, г) Ш1
(7.3)
х(0)=хд, у(0)=у„, з(0) =г„, х(0)=и„, у(0) =и„, г(0)=из,
х (7) =хд у (7)=уд 3 (7) =Яд х (7) ид у (7) =ид ° з (7) = ид
где Х=Х(~, х, у, я), У= У(~, х, у, и), Я=Я(~, х, у, з) — компоненты
вектора гравитационного ускорения д (г, 1).
В предыдущей главе было установлено, что для идеального двигателя ограничен-
ной мощности из общей проблемы оптимизации выделяется независимая вариационная
задача (6.11) о построении оптимального закона реактивного ускорения (диналдическая
задача). После ее решения для каждого конкретного динамического маневра, на основа-
нии формул гл. 6 можно, рассчитать оптимальные параметры двигательной системы и
аппарата.
Динамическая задача (6.11) сформулирована как задача Лагранжа с дифферен-
циальными связями и краевыми условиями. Реактивное ускорение а (д) в оптиддальном
режиме, как следует из Я 2, 3 гл. 6, нигде не выходит на границу а=О, за исключением
изолированных точек. Отсутствие граничных управлений дает возможность применять
для решения задачи (6.11) классические методы вариационного анализа.
В некоторых случаях удобно изменить формулировку (6.11), избавившись от диф-
ференциальных связей. Для этого нужно исключить ускорение а из подынтегрального
выражения функционала при помощи уравнений движения (4.57):

~РАВнения э1~стРемАлей и их сВОЙстВА
Первая вариация функционала (7.3) имеет вид
дР .. дР .. дР ...Ы дР . ~ д~' . ~ д~
3х = (г — — х — —, у — —, л'+ х — —, + ф — —, + я' — —, м +
дх ду д~' Ж дх Ж ду Ж дХ
дР дР , дР т Ы дР Ы дР Ы дР
+ —,Ох+ — оу -]- —., Оя — ох — —,. + оу — — + оз — —.. +
дх ду д-" о Ж дх Ж ду сИ д~ о
+ [(,",,",„+,",)~ +(,",.',„'+",„)' +(,",.",, +",,) ~.-~«
(7.4)
При заданных начальной (~с, а„у„ы„и„гс, иа) и конечной (~1, а1, у1,
з„и„г„и,) точках вариации концов траектории в (7.4) выпадают. Прирав-
нивая нулю выражения при вариациях 3т, Зу, 3з под знаком интеграла,
получим уравнения Эйлера рассматриваемой вариационной задачи:
дХ дУ д2
а = — а — а — а,
х дх х дх У дх
дХ дУ д2
О, = — а — а — а,
у ду х ду ~ ду
(7. )
дХ дУ д2
а = — а — а — а
д~ х д~ У д~ .г
(а =х — Х, а„= у — У, а,=Š— Е),
или в векторной форме:
а= — (а д), а =г' — я.
(7. )
(скалярный интеграл обязан отсутствию в подынтегральной функции (7.3) времени—
дГ/д~=Π— и имеет место для любого стационарпого поля д~/д8=0; если полное время
движения не задано, то ХХ=О).
В плоском случае остаются два интеграла [7.2]:
~/2 (а-' + а;") — (а и+ а, а) — й (а,х+ а„у) (х'-+ у"-) "= сопзС,
(7.8)
(а а — а, и) — (а' .у — а, х) = сопзВ.
У/
х е
3. Уравнения экстремалей — плоское движение в центральном поле.
Исследуем подробно частный случай оптимального движения, описываемого
системой (7.5), — плоское движение (з:— а =0) в центральном гравитацион-
ном поле (Х= — 1"хт ', У= — досуг ', г= ~/ж'+ у'-') [7.3, 7.41.
В дальнейшем изложении будут использоваться безразмерные перемен-
ные. В качестве характерных величин берутся (4.12). Характерная величина
функционала У в этом случае равна Й" г„'~.-. Обозначения для безразмерных
переменных сохраняются прежние.
Перейдем в интеграле (7.3) к полярным координатам г, у, которые связаны
с прямоугольными х, у формулами (1.14), где 6 =0; тогда
т
У = [(г' — гф'-' + 1~г~) ~ + (фг + 2фг) 2] й
()
(7.9)
' г (0) = го 7 (0) = 70 г (0) = го ф (0) = фо
г (Т) = г1, и (Т) = < , г Т = 1 ф Т =
2. Первые интегралы уравнений экстремалей для пространственного движения
в центральном поле. В указанном случае (и= — 1г/гз) уравнения экстремалей (7.5), или
(7.6), обладают четырьмя первыми интегралами — одним скалярным и одним вектор-
ным [7.1] (ср. (5.29)):
'~', (а . а) — (а 1) — (а 7сг'га) = Н = сонь|,
(7.7)
(а &g ;~ 1) Ђ” (а )( г   = со

170
[ГЛ. 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Под знаком интеграла (7.9) не содержатся аргумент ~ и функция ~ (~); этот факт
может быть использован для понижения порядка дифференциального выражения под
интегралом. Воспользуемся обозначениями (4.18) для первых производных г, ф: г=и„
ф=о /г — и вместо аргумента 1 введем аргумент г. 'Ю=дг/о„.
'После преобразований по указанной схеме интеграл (7.9) принимает вид
у,
2 уу 2 аГ
1
т и
(7 10)
(здесь штрих обозначает дифференцирование по г). Экстремали последнего интеграль-
ного функционала удовлетворяют начальным и конечным условиям, наложенным на
и, и„г. По известным зависимостям и„(г), и (г) могут быть посчитаны время Т и угловое
перемещение у1 — уо'.
У1
Иг и (г) Нг
и („) 71 ~о=,.и („)
(7.11)
уо
Если величины Т и ~,— ~, заданы, то выражения (7 11) долнсны фигурировать в ка-
честве условий изопериметричности. Вариационная задача, эквивалентная (7.9), в новых
переменных записывается следующим образом.
2 2 2
У9 1 и„и„ ~в Иг
и„и„' — — + —. + иги' + ' + 2Л, +2Л,— '
(7.12)
О
и,. (г1) =и,.1, и (г1) = и 1
иг('о) =иго и~ ('о) ито
(параметры 2Л„2Л, являются постоянными множителями Лагранжа, отвечающими за
выполнение условий (7 11); коэффициент 2 введен для удобства).
Приравнивая нулю первую вариацию функционала (7.12), найдем два
дифференциальных уравнения второго порядка относительно ь„и ь . Если
в них перейти обратно к аргументу ~ и привлечь уравнения движения (4.18),
то в результате получится система уравнений первого порядка, описываю-
щая оптимальные режимы плоского движения в центральном поле [7.3, 7.5]:
1/г-', д = а — и„и /г, 1
и
1 2
~г=и„, ф= и /г, д,=а„+д/г—
а = — — (а +а )+а
1 1 2 2
у 2 У 9 У г г2
а = — (а у, — 2а,и +Л,).
(7.13)
Два последних уравнения системы определяют оптимальную программу
для компонент вектора реактивного ускорения.
4. Свойства уравнений (7.13). Система дифференциальных уравнений
(7.13) имеет шестой порядок и содержит две константы Л, и Л, (первые ин-
тегралы системы — ср. (7.8)); следовательно, для ее решения должны быть
заданы восемь краевых условий, например (7.9). Если некоторые краевые
значения не заданы, то вместо них надо вычислять соответствующие опти-
мальные. Они получаются приравниванием нулю внеинтегральной части
первой вариации функционала (7.12); последняя имеет вид
оХ = 2 ("а„ои„+ а ои + (а и /г — а„) ог — Л о и — Л М1,.
(7.14)
Когда угловое перемещение и время движения не заданы, то постоян-
ные Л1 и Л„как множители при соответствующих вариациях, должны быть
приравнены нулю.

171
УРАВНЕНИЯ ЭКСТРЕМАЛЕй И ИХ СВОИСТВА
Уравнения (7.13) сохраняют вид, если произвести следующие за-
мены [7.4]:
~ — ~» ~ ~2~
1
г — Ь~, /г~~ ~ /г
а„-~. 1 2а„, а — ~ Г'"а~, ),— ~ 1 4)„)2~ Г'9„Х ~ Г 'Х
(инвариантность по отношению к преобразованию растяжения), а такхсе
(7.15)
— — г — ~г,
в — ~ — ~р,
д~д, д — » — д, ),~)1, ), ~)
(7.16)
$
(инвариантность по отношению к преобразованию замены знака).
Первое свойство (7.15) может быть использовано, например, для полу-
чения оптимальных траекторий набора нулевой энергии, начинающихся
с круговой орбиты радиуса г (0)=1, если имеются таковые, начинающиеся
с круговой орбиты радиуса г (О) =1, или для пересчета оптимальных траекто-
рий перелета между круговыми орбитами радиусов г (0)=1, г (Т)=г, на
траектории перелета между орбитами радиусов г (О) =Г, г (Т) =Гг,.
Согласно второму свойству (7.16) по прямому перелету с одной круговой
орбиты 1 на другую 2 может быть посчитан обратный перелет, симметричный
прямому, а по траектории набора энергии — траектория торможения.
5. Особая точка уравнений (7.13). Выражение для а„ имеет знаменателем а„, так
что при приближении к точке г„= О производная а„стремится к бесконечности, если только
одновременно со знаменателем не стремится к нулю числитель. В последнем случае точка
а,=О особая; ее тип может быть определен, например, следующим образом [7.3].
Выделим из системы (7.13) два уравнения: третье и пятое, которые будем изучать
в окрестности точки и„=О. Входящие в правые части функции г (~), и (~), а (~) будут счи-
таться известными1 в окрестности этой точки. Запишем выделенные уравнения в таком
виде:
1
г„= а + Ь1, а„= — ( /2и'- + а„Ь1+ Ь2)
(Ь1 = а2/г — 1/г2, Ь2 = 1/2а'- — 12 — ). у /г). (7.17)
Исключив а„из системы (7.17), придем к линейному уравнению относительно '/,О„'-,
в котором аргументом является г„вместо ~; решение последнего записывается так:
(7.18)
где с — постоянная интегрирования. Разложим подынтегральное выражение в точке
и„=О по степеням и„и вычислим интеграл:
/2~~у /2Ь1 «Ь2«+ с~г + ' (7.19)
здесь нижний индекс О обозначает принадлежность к точке г„=О; отброшенные члены
разложения содержат и, в степенях выше первой, коэффициентй при них не зависят от с.
Таким образом, на плоскости с координатами и„, '/,О'„интегральные кривые (7Л9),
пересекающие ось г„=О, проходят через одну и ту же точку независимо от значения
постоянной с.
~ г Ог /2~~у /2Ь1 «Ь2 «' (7.20)
Эта точка является особой точкой типа «узел». Соотношение (7.20), если в него под-
ставить О„Ь„Ь, из (7Л7), оказывается условием обращения в нуль числителя в выражении
для производной а„, так что
1/2 (а2. + а2) + а (и~~/г — 1/г~) — Х1 — 12и, /г =0 при и„=О.
(7.21)
6. Интегрирование в окрестности особой точки. Отметим одно свойство дифферен-
циальной системы (7.13), связанное с особой точкой. Продифференцируем по времени ~
левую и правую части предпоследнего уравнения из (7ЛЗ) и получившееся уравнение
вставим взамен исходного.'
ф = и /г, О = а,. + и2/г — 1/г2,
° ~
а,.п- а,. У~
а' — 3 — '+ 2 —,." + 212—
О =а — ии /г
9 9 ' 9
(7.22)
1
а = — (а у„— 2а„и + 12). 1
а,.=—
Г

172
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
~ГЛ. 7
В новой системе отсутствует неопределенность в точке и„=О, затруднявшая прове-
дение численного интегрирования; одновременно из уравнении выпал интеграл системы—
параметр Л, — и при сохранении общего числа свобод увеличился дифференциальный
порядок системы. Поэтому система (7.13) предпочтительнее (7.22) всюду, за исключением
особых точек (они могут быть в начале, в конце и в середине интервала интегрирования).
Пусть в начальный момепт заданы координаты, компоненты скорости, параметр Х2
и компоненты ускорения:
г (0) = го, р (0) = уо, у„ (0) = у„, у (0) = у„о, Л = Л2,
а,.(0) = а„,), а„ (0) = а, о.
(7.23)
Если у„ОЙДО, то в систему начальных условий вместе с (7.23) входит параметр Л,;
эта совокупность начальных значений определяет задачу Коши для уравнений (7.13).
Если у„о=О, то начальная точка особая и в ней справедливо соотношение (7.21),
из которого находится значение параметра Л,. В этом случае задача Коти формулируется
для уравнений (7.22), и она будет определена, если условия (7.23) дополнить таким:
а,. (0)=а„о.
Описанная процедура интегрирования задачи Коши (7 13), (7.23) может быть ис-
пользована на каждом шаге ретения какой-либо краевой задачи для уравнений (7 13),
если последняя решается путем последовательного подбора недостающих начальных
условий.
7. Связь параметров начала и конца траектории. Если динамический маневр заклю-
чается в перелете между двумя круговыми орбитами, то краевые точки траектории особые.
Начальные и конечные значения радиуса г и скоростей о„, г в этом случае следующие:
г (0) =1, у,. (0) =О, у (0) =1, г(Т) =г, у„(Т) =О, у (Т) =г ' (7.24)
Применяя условие в особой точке (7.21) к началу и концу траектории, найдем две
связи'.
з,/
'/Йа)' — Л) — ),Йг) ~'= О,
~/2а(~) — ) д — Л2 = О,
(7.25)
где а„а, — начальное и конечное значения реактивного ускорения. 1Лсключая Л, из (7.25),
получим
3/
а)2 = а„' -— 2Л2 (1 — г) ~').
Отс)ода следует при г ) 1
(7.26)
а =ао, если Л2=0, а ) ао, если Л2(0, а) ' ао, если Л2) О. (7.27)
Чтобы выполнялось условие а1~ ) О, параметр ~, должен удовлетворять неравенству
Л, ~ '/',ае (1 — г, ~')
(7.28)
При г, ( 1 неравенства (7.27), (7.28) заменяются на обратные.
8. Уравнения экстремалей — плоское движение в поле двух центров. В виде, ана-
логичном (7 13), могут быть записаны уравнения оптимальной программы реактивного
ускорения для плоского движения в поле двух центров — Солнца ()=1) и планеты ()=2)
(см. (4.59), (4.60) и рис. 4.6) [7.3):
(у('))'
а(г) . — (а(г))2 + — (а(г))2 .+ а(а) ' ) (г) Цг)
у(г) 2 г ) 2 т г „(г) (г(г))з ) „(()
а") = . ~а(г)~(г) '!а~'~у~" ~ Ц' 1
гр (~ ) ~ &l ;  т г
г
(7.29)
Л(') = а(г)д(1)'(')/дф(') + а„'')дЛ(')/дф('),
(
Л()" = — у"' (а")дФ'"/дг") + а")оЛ")/дг(" + а"))Г")/г('))—
1 у гр
Т ~О
— Ц")1(")/г(~) — Л(')а'~) — (у"'/г')) (Л~" — 2а("(1)'"))
(у(~) = г('), у(~) = (ф(') + и) г('), ) = 1, 2).
здесь Л) и Л2 у"ке не являются постоянными, так как в систему (4.59), (4.60) явно входят
у и ~ (переменные в (7.29) размерные).
Если движение происходит в малой окрестности одного из центров, т. е. в поле,
близком к цонтральпому, то производные ~, и ~2 малы по абсолютной величине; в пределе
уравнения (7.29) переходят в последние два уравнения (7 13).
В работе [7.6) дана другая форма уравнений экстремалей, там же проверено выпол-
нение второго и третьего необходимых условий минимума функционала.

17
УРАВНЕНИЯ ЭКСТРЕМАЛЕй И ИХ СВОЙСТВА
Постоянные векторы Ь1,..., Ь4 находятся из граничных условий;
например, когда заданы координаты и скорость в начале (г„т,) и в конце
(г„т,) траектории, то
'б'
Ь1 — — Т~ ~~ ~о ~ Т
Ь
Ьз — ~о Ь~ = — ~о.
(7.31)
Представление о характере оптималь-
ных программ реактивного ускорения можно
ПОЛУЧИТЬ, раССМОтрЕВ дВа ПрОСТЕйШИХ МаНЕВ Рис. 7.1. Оптимальная программа
реактивного ускорения для задачи на-
ра — одномерные движения в бессиловом бора модуля скорости.
лоле ([7.1, 7.3, 7.5, 7.7] и др.).
1'. Набор заданного модуля скорости и, за заданное время Т. Началь-
ные положение и скорость заданы, конечное положение не фиксировано
(см. (4.74)).
Граничные условия (4.74) совместно с условиями трансверсальности (7.4)
дают следующие выражения для Ь„Ь,: Ь,=О, Ь,=и,/Т; отсюда
а (О) = и,/Т, е (1) =+1, ~ =11з/Т.
(7.32)
О тметим, что в этом случае реактивное ускорение постоянно и направ-
лено по скорости (рис. 7.1), величина функционала обратно пропорцио-
нальна времени выполнения маневра (рис. 7.2, кривая и,). Такой же характер
зависимости т (Т) получается для маневров в центральном лоле, когда реак-
тивное ускорение много меньше гравитационного.
2'. Перемещение между двумя точками покоя, отстоящими одна от дру-
гой на расстоянии 1, за заданное время Т (см. (4.75)).
Подставляя граничные условия (4.75) этого маневра в (7.31), находим
а Я = —,(1 — 2 — ), е Я =+1 ири О ( Е ('1.Т,
6~
а1О = —. 2 — — 1),
Т~ Т
(7ЛЗ)
е(1) = — 1 при '/,Т(1(Т,
~ = 12Р/Тз
Здесь вектор реактивного ускорения — линейная функция времени (рис. 7.3),
а функционал обратно пропорционален кубу времени выполнения маневра
(см. на рис. 7.2 кривую 1). Этот маневр моделнрует быстрый перелет между
орбитами в центральном поле (реактивное ускорение много больше грави-
тационного).
') В этом пункте используются размерные переменные.
9. Аналитические решения в плоскопараллельное поле '). Задача пост-
роения экстремалей функционала / в общем случае требует численного ин-
тегрирования, однако для модельных гравитационных полей она допускает
простые аналитические решения. К таким полям прежде всего относится
плоскопараллельное (|т=( — дз, О, 0) — постоянный вектор, см. ~ 2 гл. 4)
и его частный случай — бессиловое поле (~=0). Интегрированием уравнений
(7.5) определяем оптимальную программу реактивного ускорения, а по
ней — траекторию из уравнений движения (4.62) и функционал:
а (1) — Ь,1+ Ь„г (1) = 1/ Ь,Р+ 1/, (Ь., + Д) ~' + Ьз~+ Ь,

174
~[Л. 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Определим выигрыш в функционале, обязанный замене одной из неопти-
мальных программ вектора реактивного ускорения [7.8, 7.9] на оптималь-
ную. Рассмотрим постоянный по модулю (а (~) =41/Т') и однократно меняю-
щий направление (при ~='/,Т) вектор реактивного ускорения (пунктир
на рис. 7.3). Такой программе ускорения соответствует функционал У=
т/т,
Рис. 7.3. Оптимальная программа ре-
активного ускорения для задачи пе-
ремещения между точками покоя
(пунктир — программа, взятая для
сравнения).
Рис. 7.2. Зависимость минимальпых значени~ функ-
ционала .У (Т)/Л (Т,„) от полного времени движения
Т(Т,„для маневров в бессиловом поле (кривая и,—
набор скор()сто, .У (Т,.) = и1/Т„кривая 1 — переме-
Ф
щен!!е ыюкчу течкяыц пОкОя, Т (т,,) = 12!2/т'~)
Общее рен~ение уравнения (7.34) имеет вид
г = (с, + с21) соя 1 + (с, + с 1) я1п 1, (7Л5)
где постоянные векторы с„..., с4 определяются из граничных условий.
Например, если г (О) =г, г (О) = то, г (Т) = г„1 (Т) = т1, то
ГО
1
с, —, Т Т2 [(я1п Т соя Т+ Т) го+ то я1п' Т—
— (я1п Т+ Т соя Т) г, + Тч, я1п Т],
1
с3 ' 2 Т Т2 [ — (я1п Т соя Т+ Т) го — Т'ко+
(7.36)
+ (я1пТ + Т соя Т) г, — Тч, я1п Т),
1
с, —,, Т, [го я1п' Т+ (Т вЂ” я1п Т соя Т) т'О—
— Тг, я1п Т + (я1п — Т соя Т) т,];
при Т =2т~г (я=1, 2,...)
Г1 — ГО Ч1 — ЧО
СЗ ЧΠ— т у С4 — т
Г1 ГО
с2 т
=16Р/Т', т. е. по сравнению с этим случаем выигрыш в функционале при
переходе к оптимальной программе (7.33) составляет 25%.
10. Аналитическое решение — однородное центральное поле. Следую-
щий пример точного решения уравнений вариационной проблемы достав-
ляет так называемое однородное центральное поле [7.10]. Здесь вектор гра-
витационного ускорения представляется в виде д= — Йг/г'., г„=сопят (см.
(4.64)). Взяв за характерное расстояние г„, а в качестве остальных характер-
ных величин (4.12), перейдем к безразмерным переменным. Тогда ~= — г
и система (7.6) приводится к векторному линейному однородному уравнению
с постоянными коэффициентами
„—,, +2 — „,+г=0.

175
ОПТ1ТМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
8 2]
Оптимальная программа реактивного ускорения и интеграл Х в соот-
ветствии с (7.35) таковы:
а (~) = 2 (с, соя ~ — с., з1п ~),
Х = — 2 (с, '+ с.',) Т + (с', — с,',) з1п 2Т вЂ” 4 (с, ° с,) з1п' Т;
при Т= — 2~я(8=1, 2, ...)')
(7.37)
| а)ц)=2( ' "'сан~ — " '"я!и ~),
2
Х = —, [(г, — г,)'+ (ч, — ч,)'].
11. Аналитическое решение — центральное поле. Частное решение
системы (7.6) для случая произвольного потенциального силового поля
(д= †ог У) указано в работе [7.11]:
а (1) =, „~ к (Ь = сонями).
б
1-& t; 1~
(7.38)
Этот закон реактивного ускорения, как нетрудно проверить прямой
подстановкой, точно удовлетворяет уравнениям Эйлера. Его можно исполь-
зовать для построения траектории разгона, но при этом не будут точно удов-
летворены условия трансверсальности. Однако относительная погрешность
в функционале для величин реактивного ускорения, малых по сравнению
с гравитационным, оказывается небольшой — порядка а (где под а пони-
мается относительное ускорение).
~ 2. Оптимальный межпланетный перелет
с идеальным двигателем ограниченной мощности
') Время Т вЂ” кратное периоду движения по круговой орбите радиуса г„.
В настоящем параграфе дается решение вариационной задачи (7.1)
для межпланетных перелетов. Это в основном результаты численных расче-
тов. Экстремальные значения и экстремали исследуемого функционала
определялись: по решению соответствующих краевых задач для системы (7.13)
методом организованного подбора недостающих начальных значений в эквива-
лентной задаче Коши [7.4, 7.5, 7.12 — 7.17, 7.37 — 7.'39] или прямыми методами,
примененными к функционалу (7.1) [7.18 — 7.21]. Получено также два при-
ближенных решения. Первое относится к участкам движения вблизи планет
[7.3, 7.11, 7.22 — 7.24, 7.37, 7.39], второе — к участкам движения между
орбитами планет [7.1, 7.25].
Схема межпланетного перелета с двигателем малой тяги описана в ~ 3
гл. 4. Там указаны два качественно отличных участка траектории такого
перелета: участок движения в области преобладающего влияния планет
при возмущающем действии Солнца и участок движения в области пре-
обладающего влияния Солнца при возмущающем действии планет. Отличия
гравитационного поля от центрального на этих участках мало сказываются
на интегральных характеристиках траектории [7.4]. Использование при-
ближенных граничных условий (4.65), (4.66) или (4.67), (4.68) для каждого
участка также оказывает небольшое влияние [7.4]. На этом основании
вариационная задача решается независимо для двух элементарных маневров:
для набора нулевой энергии в центральном поле планеты (или торможения
с выходом на орбиту спутника планеты) и для межорбитального перелета
в центральном поле Солнца.
В силу аддитивности функционала (7.1) он представляется в виде суммы
(по номеру маневра) интегралов (7.1), подсчитанных вдоль траекторий каж-
дого из элементарных маневров. При фиксированных граничных точках

176
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
элементарных маневров и при заданных временах их выполнения эти ин-
тегралы не зависят друг от друга. Поэтому минимум по управлениям а (1)
и е (1) суммы интегралов равен сумме минимумов. Выбор же наилучших
граничных точек элементарных маневров (в рассматриваемом приближении
выбору подлежат угловые дальности межорбитальных перелетов) и наи-
лучшего распределения суммарного времени движения между элементар-
ными маневрами должен проводиться совместно.
1. Набор нулевой энергии. Маневр начинается в заданной точке на-
чальной орбиты. За заданное время Т требуется набрать нулевую полнуго
энергию ф (Т)=0.
Угловое перемещение не фиксируется; между конечными значениями
радиуса г1, радиальной г„1 и трансверсальной г проекцияыи скорости имеется
одна связь (см. (4.65): ф (Т)=1/., (и„"-,+г'-',) — 1/г,=О. Из условия равенства
нулю первой вариации функционала (7.14) получаем следующие оптималь-
ные соотношения:
)~, = О, а„,/а = и„,/и~, а„, — ат,ь„,и~,г, + и„гс„,г; = О.
(7.39)
Отметим, что, согласно двум последним соотношениям из (7.39), в конце
движения угол 7 между вектором тяги и вектором скорости и производная 7
должны быть равны нулю [7.11].
Полная система дифференциальных уравпений и краевых условий со-
ставляется из (7.13), (4.65), (7.39). Для случая круговой начальной орбиты
она может быть записана в виде (см. (7.22))
г(0) =1,
'/, [и'„- (Т) + и' (Т)] — 1~г ( Т) = О,
1 (()) О 0У. (7) УУ. ( 7 )
г2 ' " ' и (7) у (Т)
9
г),=а„+
Т О
В .=а
Г
о (0) = 1,
гр
)
а„(Т) — а (Т) и„(Т) и (Т) г(Т)+а„(Т) о„(Т) г'(Т) =О,
(7.40)
а-
а
Ф Г
О,.У~ а„
— 3 —,, +2„—,,
1
а = — (а ь — 2а„ь ).
Х = а' (~) + а' (~),
Х (О) = О.
ф = о (~)/г (Е), с (0) = 0;
Уравнения оптимального разгона представлены в форме (7.22) в связи с тем, что
начальная точка траектории является особой, п„(0)=0. При отходе от особой точки пред-
последнее уравнение из (7.40) может быть заменено уравнением первого порядка с первым
интегралом Хг (см. (7ЛЗ)). Последний определяется условием
11=1/2 [а2 (О) + а"- (О)].
Отметим, что траектория разгона может содержать не одну особую точку — в силу
почти периодического характера движения при малых ускорениях а особая точка может
появляться на каждом обороте.
Решение краевой задачи (7.40) может быть проведено путем сведения
к задаче Коши с подбором трех недостающих начальных значений а„„а „а„о
[7.4, 7.5, 7.11, 7.12]. Другой путь, использованный в [7.19] — применение
Прочие характеристики движения, например угловое перемещение (р,
величина контрольного функционала У, определяются после решения крае-
вой задачи (7.40) интегрированием соответствующих дифференциальных
уравнений:

1 е ! 5 И а
5 Э ° ю е
6 5 6 ю в °
16'
1 93'Э 5 афти
° °
° °
° °
6 °
1 1е Эе ' 6
е 3 е в е
1 1.6. в5 ввеф
у ° ° °
6 ° й ° °
ю ° ° °
1 °
° °
ю °
) ° °
й Э ) °
1 ° 6
ю 6 е
! 69) ° Э ° ° Э Э 6 ° !
5' И)
° ° ° ) °
° й ав ° ° ° ° ° 6
° 6 ° °
° ° й °
° °
Э 11
3. 6
65 9
е 6 ю
ф ) ° й у й ° ° 6
6111' 6 °
° ° й 6 й
° ° й ) °
° ю
е 6 ю
й )
° . 11
° 6 ° 5 е
° °
° ) ° й ) ° ) °
° °
11 !
° ' ° ' Э Э
° °
! 11
° $ ° $ °
1111 в ! ' 1 1в в
° °
в в ° 1
° 1 °
° ° ° $ ° $ ' !
!! ! !1
° ° °
° Ф'
° °
° в ° ° Е
° !
° °
° °
1 ° !
° °
° °
° °
° !
° °
° °
° °
° °
1 °
1 °
° Е
° ° °
1 °
° е
° °
° °
° в
° °
1 °
° '! ВЭ' ° 91 в ° Э ° 6 е ) Э 1 Э 1 ю г ° ° фю' ° 611
'ВЭА ° '6556а65
° й ф й
° е ° Э 9 1! 5 е 1 е ° е ° Э 6 е а
! ° ° 6 ° ю ° 1 ! ю ! ю ° 5 6 6 Э ° 5 6 ) ° й ° 6 ° В й
° ) 1
Э ю ° 5 ° ° 1
5 ю а'Вфю ' ° ° ° ° е
° ° 1 °
й ° °
ав ° ° ° °
° ° ' ° в
ю
° ° ) й ° й ° ° 6
ю ! ю а °
° ° ~ 1 фе!)
° ° Э
° 6 Э
° Э Э 3
° ' ° Э 6 °
° 6 ) ° й И ) 1 6 6 ° ° ° ° й ° в ) ° ° ° 1 °
ю ! ю й ° ° Э 6 ° !
° ° а 1 а 6 а а 1 а ° ) а ° а И ) ) ° а °
° й
ю
° а 1 и 1 1 е 6 °
6 е ° ! е а 5~
Ф ) ° е ФФФ
° й 1! й 1 й 6 5 5 ° ° а 6 ) 6 6 °
в ° °
° 1 1 ° 6 е °
° ° ° й 1 6 6 й ° ) й
Э ° ф 1 й ° Э й 6 ) й °
° а а в ° а 11 ° ) а 1 6 а
6 й °
° ° °
° е ° ° ° 1
° 6 й й ° )
Э' ° Э
й 6 й й °
6 )
6 ° 5
е 1
в ! 6 1 ° 1 11
1'6' 6! 6 6 °
° °
° 6 °
Э
ю
е 65'ю Э ' ! В' 16 ю аф ° ) е!еа 5 61 5 е ° аф Э аеф ° Эе а 'В61
Э
° °
11 )'' 61 9661
Э ° '1 16 е'Э
° ' ° 1 6 6 ° )
° е
И5 56
й ° Э
1 °
1
1 Э
ю
° ° Э ) °
° ° й
° °
° ° ю
1 9 °
'а 5' ю 1 1е 1е
66 ° 5'вв ° )Эю''61
В 1 Э
ю ° ° °
° 6 °
ю
е 3 е
° 6 ° й
1 Э
6 й ° °
6 ° й 6 й
965
ю 6 °
Э а Э ° в
° °
° °
й °
91 19 391 3'6 ) 5
ю И5 ) 69 ° ю' ° Э'
° 6 й °
! Э
Э ° в
'11' 16 ю ° 1
ю
° ° ° °
° а е
Э ° Э в
° °
3'6 55
1 й; Э 1 )
) Г Э 1
й
9 6 ° 5 ° 1 6 5 в! ) 5 6 ° в ° ° ° 9 1
° ° ° ° а Э 1
1 6
° 6
в в ° е ° в е В ° ° ° в ~ 1
° в ° а Е Е Е ! ° в Е
е е
° ° 1
1
е 1
1
1
° 1
° а 1
° °
° ° °
1 ° °
1 1
1
1
1 °
1 1
1
1
1
° е ° 1
1
1 1
° !
1
° 1
1
1
1 1
° °
° ! °
° °
6655 ) е 9'
6 Э В ° Э 6 ° 5
1636 ° )
е ° 1'
а ° 1'
1'
° 1
1'
11 1'
е '1' 1'
° а 1'
1 1'
1 1'
1е 1'
1 1'
1 ' 1'
1 1'
1 е 1'

178
идеАльный дВиГАтель ОГРАниченнОЙ ыОщн Ости
~ГД. 7
в [7.38], функционал задачи монотонно убывает с ростом е„поэтому третий
вариант постановки обсуждаться не будет.
Следуя [7.38], приведем полную систему уравнений и краевых условий,
определяющих оптимальную траекторию:
р' = 2р'~ ф + 1) ' а~,
1
(3= р 'Я+1)'А+2~/ра,
Л = р ' Я+1)'Д+ ~/р Я+1) 'Ла + ~/ра„,
З(ч+1)' брр +Иг, 2р~ + р,~,
2~р 0+1) ' 2~р
0+1 ~р а
р' = —,, [(ЗД+1) р — 2Ьр ]+ .,(2рр +1р ),
(7.41)
)
р' = р — '~*Я+1)'р — ~/р ф+ 1) 'р а,
(а„='/,~/р р, а = ~/р [Я+1) '(рр +'~,1р )+ р ),
а) ~~ (О) + Л~ (О) = .~„Д (О) р~ (О) = Ь (О) р (0),
б) Д (О) = е, соя ~„Л (О) = е, з1п че,
р„(Т) = О, Д'(Т)+ Ь'(Т) = 1, ~3 (Т) р, (Т) =Л (Т) р, (Т).
Здесь первые три дифференциальных уравнения представляют собой урав-
нения движения в форме (4.38) после замены независимой переменной р
на ~: ф=р '~ Я+1)'. Фазовая координата р — параметр оскулирующего
эллипса, а фазовые координаты Д и Л выражаются через эксцентриситет е
и истинную аномалию ~ (см. рис. 4.3 и пояснения к нему): (',)=е соз ~,
~'=Я Я1П
Выражения для оптимальной программы реактивного ускорения (в круг-
лых скобках) получены посредством процедуры принципа максимума
Л. С. Понтрягина. Помимо фазовых координат они содержат вспомогатель-
ные переменные (импульсы) рр, рр и р~, соответствующие каждой фазовой
координате. Изменение импульсов по времени описывается второй тройкой
дифференциальных уравнений (7.41).
Начальные условия записаны в двух вариантах: для постановки
а) Т, е,=йхе, ~,=ор1 и б) Т, е„~,= — йхе. Вместо незаданных граничных зна-
чений фазовых координат выписаны соответствующие условия трансвер-
сальности. Порядок краевых задач (7.41) такой же, как и (7.40): три недо-
стающих начальных значения.
После решения краевой задачи (7.41) могут быть найдены все остальные
характеристики траектории либо посредством решения задачи Коши, либо
по конечным формулам, например:
ч = р '"' (~) [ч (~)+1]"', ~р(0)=0; Х =а'„(~)+а' (~), ~ (0) =();
г = р (1) ф (1)+ 1] 1, ц„= р 'Ь(~) ~(1), и = р — '1~(~) [Д (~)+ 1].
Все переменные в (7.41) безразмерные. В качестве характерных значений
взяты величины (4.12), соответствующие круговой орбите с той же полной
энергией, что и на заданной эллиптической орбите (см. табл. 7.1). Инвариант-
ность уравнений (7.41) относительно преобразований (7.15) и (7.16) сохра-
няется '); поэтому, как и в случае круговой начальной орбиты, все резуль-
1) При замене (7. 15) р-э Ер, Д-эД, Е -эБ, р -э Х вЂ” 7~р„, р, -э Х вЂ” 'l~р, р -э й~).р,
8-+ 1 18, ч -эчо,' при замене (7. 16) р-э р, Д -эД, Е -э — Е, р„-+ — р . р, -э — р „
р — + р~, Ю -э8, ч — э — чо.

17
ОптиыАльный межплАнетпыЙ пеРелет
таты решения краевой задачи (7.41) пересчитываются на любую начальную
энергию (при том же эксцентриситете) и на случай торможения.
Краевые задачи (7.41) решались в [7.38] численно модифицированным
методом Ньютона (см. гл. 19). В качестве недостающих начальных значений
для задачи а принимались р, (О), ~ (О), о. Последние два параметра опреде-
ляют Д (О), Л (О), рг, (О), ро (О) в соответствии с условиями трансверсаль-
ности а) из (7.41)
д (0) = , .: (0), ~ (0) = , 1п (0), р (0) = р , (0), р, (0) = р в1п (0).
Такой выбор неизвестных параметров оказывается весьма удачным. Он позволяет
установить неедипственность решения краевой задачи, порожденной вариационной,
в которой хотя бы одип из концов траектории не задан жестко, а может перемещаться
по замкнутой выпуклой поверхпости.
В самом целе, предположим непрерывность начальных значений импульсов, решаю-
щих краевую задачу (7.41, а), когда радиус ко окружности Д2 (0) +Ь' (0) = Я стремится
к нулю:
Ро (0) — «Ро (0),, Р~ (0) — «Р~(0), с (при в,— «О),
и что Ро (0), е+ Р~~ (0), с . 0 (оба предположения подтверждаются экспериментально).
Отсюда определяются два предельных значения параметров ч и р:
ч (0), = агс$д [Р~ (0), /Р~ (0), ] + пк (и = О, 1),-
р, е — — в)ри [Р (0), сов ч (0), ] ~/Р'„-' (0), + Р-' (0).
(7.42)
Они отличаются друг от друга сдвигом начальпого углового положения аппарата на тс
и сменой знака р.
Эти предельные значения находились из численного решения задачи ~ с закреплен-
ньп| левым копцом при ~0=0. Опи использовались в качестве нулевого приближения для
задачи а с нсфиксировапныи начальным угловым положением при 1 &g ;  & t; О.
набор предельных значепий порождал свою ветку экстремальных траекторий. Их харак-
теристика будет дана пиже.
2. Набор нулевой энергии — численные результаты. Численные реше-
ния задачи (7.40) показывают [7.4, 7.5, 7.11, 7.12, 7.19, 7.37 — 7.39], что для
больших значений времени Т )~ 10' траектория выхода с круговой орбиты
представляет собой пологую раскручивающуюся спираль (см. рис. 7.4 б, в).
Первые з/ общего времени движение практически круговое, эксцентри-
ситет оскулирующего эллипса нарастает очень медленно. Оптимальная
программа реактивного ускорения на этом участке такова: модуль ускоре-
ния а совершает малые колебания около постоянного среднего значения а
(последнее много меньше гравитационного ускорения: а — 1~Т), а направ-
ление — колеблется в малой окрестности тангенциального. Период этих
колебаний примерно совпадает со временем одного оборота по оскулирующему
эллипсу. Амплитуда колебаний составляет при Т=10' около 10",~ по мо-
дулю ускорения и около 5' по углу т между тягой и скоростью. При боль-
ших значениях полного времени Т амплитуда колебаний уменьшается.
По мере роста полной энергии аппарата и удаления его ож притягиваю-
щего центра реактивное ускорение сравнивается по величине с гравита-
ционным (за счет уменьшения последнего), а затем и превосходит его. Ам-
плитуды колебаний величины а и угла т увеличиваются к последнему витку
в 2 — 3 раза по сравнению с начальными. Характер изменения параметров
траектории становится апериодическим. К моменту достижения параболи-
ческой скорости направление тяги совмещается с направлением скорости,
т (Т) =т (Т) =О, в силу (7.39). Величина реактивного ускорения также
стабилизируется на среднем начальном уровне.
Если рассматривается задача разгона до гиперболической скорости,
то после достижения параболической скорости траектория переходит
12~

180
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ ~цОщНОСТП
[ГЛ. 7
в прямолинейную, реактивное ускорение постоянно и направлено по ско-
рости [7.37, 7.39].
При сокращении полного времени разгона Т средний уровень реактив-
ного ускорения растет [а=0,9/Т при Т ) 10', й=0,6/Т при Т ( 10), про-
тяженность первого, квазикругового, участка траектории уменьшается.
При Т ( 10 этот участок исчезает из состава оптимальной траектории
[рис. 7.4, а). Характер движения и оптимальной программы реактивного
а =lЮ
Р.М /7~
рис. 7.4. Примеры оптимальнык траекторий набора нулевой энергии с круговой орбиты (первые витки
спирали при а, ( 10-' изображены условно).
ускорения становятся такими же, как на втором участке траектории «мед-
денного» разгона. Приближенно траектория и программа управления
«быстрого» разгона в соответствующих безразмерных переменных могут быть
получены отбрасыванием начальных участков траектории и программы
управления «медленного» разгона. Это свойство оптимальных траекторий,
установленное в [7.37], позволило получить в [7.39] приближенное решение
в виде так называемой универсальной траектории оптимального разгона.
Более грубое приближение, но очень простое и вместе с тем правильно
отражающее основные качественные свойства исследуемого маневра дает
аналитическое решение [7.32) задачи о наборе модуля скорости в бессиловои
поле. Согласно последнему величина реактивного ускорения постоянна,
а направление совпадает с направлением скорости. Такой же характер имеет
оптимальная программа реактивного ускорения, осредненная по обороту,
для маневра набора нулевой энергии в центральном поле. Похожими ока-
зываются и зависимости минимальных значений функционала У от вре-
мени Т выполнения маневра [рис. 7.5 из [7.4]).
Использование вместо оптимальной программы реактивного ускорения
более простых: постоянное по модулю, тангенциально или трансверсально
направленное ускорение — приводит в центральном поле для больших вре-
мен разгона к незначительному увеличению функционала [менее 1»~ при

181
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
$2]
рис. 7.5. Минимум функционала .7 для
маневра набора нулевой энергии с кру-
говой орбиты — сплошная кривая (пунк-
тирная кривая относится к маневру набо-
ра скорости и,=0,895 в бессиловом поле).
О
б)
Я~ д4 дб Г,
Рис. 7.6. Функционал .7 для мапавра набора нулевой энергии с эллиптических орбит (сплошные кри-
вые — оптимальное решение, пунктирные — побочные, Т=$2,95): а) начальное угловое положение ч,
выбирается оптимальным; 6) начальное угловое положение ~о задано (е,=0,5).
почти на ~г, затем разность убывает (см. кривые ~, на рис. 7.6, а). Но при
некоторых а, положение точки старта на обоих решениях может быть и
') Напомним. что начальная полная энергия при этом неизменна.
Т )~ 10' [7.4, 7 5, 7.11, 7.12, 7.26]). С уменьшением Т проигрыш в функцио-
нале увеличивается (-8% при Т=10' [7.19]). Аналогичные результаты
получаются при сопоставлении этих программ по конечному значению энер-
гии при одинаковых У и Т [7.37].
Чтобы оценить влияние третьего тела (Солнца) на функционал У, в [7.4]
были проделаны соответствующие расчеты для системы (4.59), (4.60), (7.29).
Они показали, что относительная погрешность в функционале от неучета
этого фактора для разгона в окрестности Земли пренебрежимо мала (-0,1',4
при Т вЂ” 10', с уыеньшением Т эта погрешность должна уменьшаться).
Далее приводятся результаты численного решения задачи о разгоне
с эллиптических орбит [7.38]. Здесь была установлена неединственность
решения краевой задачи (7.41), получен-
ной из необходимы ~ условий оптималь-
ности. Решения различаются по функцио-
налу и по характеру управления. Экстре-
мальное решение с ыеньшиы значением
функционала будем называть оптималь-
ныы, а решения с большими значениями
функционала — побочными. Способ их ~ 7р~ '
отыскания был описан в предыдущем пунк-
!
те настоящего параграфа.
ХЮ
Для постановки а (начальное угловое
0 -41И 8
положение ~, аппарата на орбите не зада-
но: ~,=ор$) построены два решения. На
1
оптимальном решении функционал У убы- дЮ Т
вает (почти линейно) с ростом эксцентри-
ситета я, начальной орбиты ') (сплошная
кривая на рис. 7.6, а), на побочном реше-
нии функционал монотонно возрастает
(пунктирная кривая Я на рис. 7.6, а), при
а,=О функционалы равны. Эти два решения отличаются друг от друга в боль-
шинстве случаев также положением точки старта: при очень

[ГЛ. 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
одинаковым (сплошная и пунктирная кривые ~, на рис. 7.6, а пересекаются).
Программы же управления и траектории даже при одинаковых или близких
значениях ~, существенно отличаются (рис. 7.7). Оптимальное решение при
в ) О дает примерно такие же средние значения и, а„и а~, что и при ~,= — О;
а,а„,а„
д0
0,025
а)
002
б)
а,п~,а
0,07~
005
0~4 б д Ю/Г1
Рис. 7.7. Сравнение программ управления и траекторий набора нулевой энергии с круговой орбиты (и)
и с эллиптической орбиты (б, в): а) .-о — — 0 — оптимальное решение (.7=0,0291); б) ~,=0,5 — побочное
решение (.7=0,0358); в) ~,=0,5 — оптимальное решение (.7=0,0232).
на пооочном решении все эти средние значения выше (рис. 7.7). На оптималь-
ном решени с ростом в, увеличивается амплитуда колебаний, а характер
кривых не меняется; на побочном же решении происходят более сложные
деформации программы управления (приводящие, например, к заходу
траектории разгона внутрь начальной орбиты — рис. 7.7, б).
В постановке б (начальное положение ч, фиксировано) было получено
два побочных решения, непрерывно переходящих друг в друга при пара-
метрическом просчете по ~, (рис. 7.6, б). Но ни одно из них не переходит
в оптимальное. Оптимальное решение при я,=0,5 лучше по функционалу,
чем при в,=О, но оно построено не во всем возможном диапазоне ч,. Поэтому
для постановки б еще нельзя сделать окончательного вывода о выгодности

183
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
э 2]
разгона с эллиптической орбиты по сравнению с круговой. В постановке а
для такого вывода гораздо больше оснований, хотя и там расчеты проведены
лишь для одного значения полного времени разгона').
3. Набор нулевой энергии — аналитическое решение. Обратимся к ана-
литическому представлению полученных результатов. Когда реактивное
ускорение много меньше гравитационного (а ( 10 '), траектория разгона
вначале представляет собой пологую спираль, на которой приближенно
выполняется условие равенства гравитационного и центробежного ускоре-
ний: 1/г' — и'-/г. Найдем оптимальный закон а (~) для начального участка
траектории в предположении, что последнее условие выполняется точно.
Уравнения движения и начальные условия при старте с круговой ор-
биты имеют вид
г(0) =1,
г„(0) =О,
~ (О) =1
(7.43)
о„= а„,
д = а — и„и /г,
'Р 9 "9
9 — 3
г= 1 — а Ю, и„=2а 1 — а й1, и =1 — а й$. (7.44)
О /
О О
Начальные условия (7.43) выполняются для г и г из (7.44) и не выпол-
няются для г„. Однако при малых значениях трансверсального ускорения,
а О &l ;( 1, радиаль ая скоро ть внач ле та же оказывае ся мал й, и
=2а„(~ 1, и в конечном счете это нарушение начальных условий несильно
влияет на результат. Характерное время задачи, согласно (7.44), по-
рядка 1/а . Поэтому при дифференцировании по времени порядок малости
относительно а увеличивается приблизительно на единицу. Так, в начале
движения и„порядка а, а а„= о„порядка а'.
1
Кинематические характеристики г, и„, и определяются величиной ин-
теграла (7.44). Поэтому задача об оптимальйом переходе от заданного на-
чального положения в заданное конечное положение (например, ф (Т)=
= /, (г,';,+и'.,) — 1/г,=Д,) за заданное время формулируется как задача
на минимум
У = а~д1ж а'-'д1 при заданиом а д1. (7.45)
О О О
После проведения обычной процедуры вариационного анализа получаем
оптимальную программу для проекции ускорения а:
а (1) =сопя[,;
а„(~) =6а2 (1 — а ~) 4.
(7.46)
при этом
(7.47)
') В [7.19] посредством прямого метода был получен пример решения задачи о раз-
гоне с эллиптической орбиты (я,=0,1, ч,=О, Т=100), оказавшийся хуже по функционалу,
чем разгон с круговой орбиты той же энергии (7=0,562 10 2 при я =0,1 и 7=0,553 10
при ео=О). Результаты [7.38] дают основание предполагать, что это решение относится
к разряду побочпых.
(здесь в уравнениях движения (4.18) учтено условие г'/г = 1/гз).
Исключив из последнего уравнения (7.43) г = 1/~/г и и„= г, получим
'/.,гг — '~ = а . Проинтегрировав это уравнение, можно выразить радиус г и
компоненты скорости г, ц„при помощи (7.43) в функции интеграла по вре-
мени от а:

184
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТП
[ГЛ. 7
Этот вывод получен при условии а„(& t   В окрестно ти то ки вых
ф1 — — О) последнее неравенство не выполняется — а„становится порядка а .
В этом можно убедиться, подставив в (7.47) значение времени выхода, най-
денное из условия ф (Т)=0 при помощи (7.44). Поэтому оптимальный за-
кон (7.46) справедлив только для начального участка траектории набора
нулевой энергии.
Отличными от изложенного способами приближенное решение задачи получено
в работах [7.11, 7.22 — 7.24, 7.39]. В [7.39] построена упоминавшаяся выше универсаль-
ная траектория, выходящая из гравитационного центра. Вблизи и вдали от центра реше-
ние получено разложением в ряды, а переходная область построена численно решением
краевой задачи по непрерывпому сопряжению двух асимптотических разложений. По-
дробно такая процедура описана в ~ 3 гл. 17 для случая постоянного тангенциальэого
ускорения.
4. Межорбитальный перелет. Маневр начинается в фиксированной
точке орбиты одной планеты и заканчивается в фиксированной точке орбиты
второй планеты; вектор скорости в начале и в конце движения совпадает
с соответствующими орбитальными скоростями; время движения задано
(см. (4.66)).
Оптимальный перелет между компланарными орбитами, которые и
будут в основном рассматриваться, описывается дифференциальными уравне-
ниями (7.13) и граничными условиями (4.66):
г (О) = 1,
9 (О) = Ро
У,
9=
Г
~2
д„= а„+—
1
и„(0) = и„„и„(Т) =и„„
(7.48)
УуУ~
8 =а
г
и,(0) =г „г,(Т) = г,„
1 1 2
а = — — — (а'+ а2) + а
т ~ 2 т Г г г2
Т
а = — (а и„— 2а„и +Х2).
° 1
Система дифференциальных уравнений (7.48) имеет шестой порядок
и содержит две произвольные постоянные ), и )„т. е. число свобод в уравне-
ниях равно числу краевых условий.
Если на траектории перелета встречаются особые точки и,,=О (ими
являются начальная и конечная точки, когда траектория соединяет круго-
вые орбиты, см. (4.68)), то предпоследнее уравнение из (7.48) заменяется
уравнением второго порядка из (7.22). Процедура взаимных переходов
(7.48) (7.22) аналогична описанной в п. 1.
Параметрами задачи для круговых орбит являются г„а„Х,. При фикси-
рованном г, каждой паре а„~, соответствует пара Т, у (или несколько пар
Т, у„если задача имеет не одно решение). Перелеты могут классифициро-
ваться как по параметрам а„]~„так и по Т, у1. Первый способ классифика-
ции удобен при решении краевой задачи путем сведения к задаче Коши,
второй — при нахождении экстремалей функционала прямыми методами
[7.18, 7.20, 7.21].
Если в расчетах учитывается реальное движение планет, то в качестве
параметров используются дата старта ~, и продолжительность перелета Т
или дата старта ~, и дата финиша 11. Переход ~„1 ~„Т простейший:
Т=~,— ~а, ~а=~а. Связь между параметрами ~„~, и Т, ~р, определяется по таб-
лицам эфемерид планет из условия равенства угловых перемещений аппарата

ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
5 2]
и планеты назначения в конечный момент времени. В предположении, что
планеты движутся равномерно по средним круговым орбитам и что даты
старта ~0 и финиша 11 отсчитываются от момента противостояния планет,
можно записать формулы перехода ~„~1 Т, ю следующим образом:
Т=~,— Ц„и,=о),~, — 0),Ц0+2)гз (г=О, 1, 2,...), (7.49)
где 0)1, 0), — средние угловые скорости движения планет старта и финиша,
г — целое положительное число (число дополнительных оборотов планеты
с большей угловой скоростью), знак плюс берется для перелета на внешнюю
орбиту, знак минус — на внутреннюю.
Отметим, что перелет с орбиты 1 на орбиту 2 может быть пересчитан
на обратный (зеркально отображен) по формулам (7.16). Переход от безраз-
мерных переменных, употребляемых в тексте, осуществляется стандартным
образом. Характерные значения используемых величин для средних круго-
вых орбит Венеры, Земли и Марса приведены в табл. 7.2.
Таблица 7.2
Характерные значения величин в гелиоцентрической системе координат для средних
круговых орбит Венеры, Земли и Марса
Х~, >"
Л'/СЕКз
сут
Ю~,
км/се к
,м /СОк
Планета
т„, кл
1,303 . 10-4
0,356 10-4
0,066 10-4
108,1 106
149,5 10'
227,8 106
1,141 10-2
0,597 10-2
0,257 10-2
35,7
58,1
109,3
35,01
29,76
24,11
399,6
177,6
61,9
Венера
Земля
Марс
Пусть х"' (~), у'0' (~) — плоская кеплеровская траектория (называемая
транспортирующей), которая удовлетворяет заданным координатам г, и г
в начале и в конце движения. Направим ось а нормально к плоскости транс-
портирующей траектории и представим истинную траекторию в виде
х<0 +  у 0)
(7. 50)
Считая функции ~, )), 1 малыми, линеаризуем уравнения (4.11):
=(Б)" +(:;.;)- )- .
[(х(0))2+ (у(0))2] — ~/ ~ + ~
(7. 1)
где через Г = — 1/г обозначен потенциал поля: Х = дУ/дх, У = дУ/ду,
Е = дБ/дз (г =~/х'+ у'-'+ з')
5. Решение краевой задачи (7.48) — метод транспортирующей траекто-
рии. Краевая задача (7.48) для оптимальных перелетов между орбитами
решалась либо путем подбора недостающих начальных условий в эквивалент-
ной задаче Коши [7.4, 7.5, 7.12 — 7.17], либо методом «транспортирующей
траектории» [7.1, 7.25].
Идея последнего метода состоит в следующем. Выбирается кеплеровская
траектория, проходящая через заданные точки орбит 1 и 2. Искомое движе-
ние считается мало отличающимся от кеплеровского, так что уравнения
вариационной проблемы допускают линеаризацию в его окрестности. Полу-
чается краевая задача для системы линейных дифференциальных уравне-
ний.

186
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Вторые производные (д'У/дх')со&g ;, (д'У дх ду)' ', (д'У/ду') о> яв
функциями времени, вычисляемыми по известной транспортирующей траек-
тории х'о& t; ( ), "' ( ). Предста им кеплеровс ую траекто и в терми
оскулирующих элементов: р — фокальный параметр, в — эксцентриситет
и о& t; Ђ” долг та периг я а та же истин ой анома и ч ( м  2 л. ); то
коэффициенты в линейных уравнениях (7.51) будут иметь вид
(д2(~Удх2) со& t; Ђ” (гсо& t; - (1 соя
(д'У/дхду) со& t = (г' '  3 1 и оя
(д2~~ду2) со& t = Ђ” (г' ' о (1 Ђ ~ в п-
(~ со& t; рсо&g ;/( + со& t  ос») и = ~
(7.52)
Формулировка вариационной задачи при переходе к транспортирующей
системе координат сохраняется: как и раньше, нужно искать минимум
исходного функционала
(7.53)
Х = (а' + а'+ а') Ы~.
0
Это связано с тем, что в качестве транспортирующей была выбрана кепле-
ровская траектория, т. е. траектория пассивного движения. Поэтому в урав-
нениях (7.51) фигурируют не добавки к реактивному ускорению, а полная
величина ускорения.
Краевые условия для уравнений (7.51) записываются в виде
(0) =~(0) =~(0) =~(Т) =~(Т) =~(Т) =0
5(0) = с&g ;о Ђ” х& t;о~, с&g ;(0 =и, Ђ” у о ,
1 (Т) = с,, — хСо~, о (Т) = и, — у|о&g ; ~ Т =
(7.54)
~=а, с) =а„, ~=а,.
(7.55)
Полученные уравнения совпадают с уравнениями движения в бессило-
вом поле (4.63). Общее решение уравнений вариационной задачи (7.53),
(7.55) дается формулами (7.30). Постоянные интегрирования определяются
по соотношениям (7.31), где согласно краевым условиям (7.54) нужно поло-
жить г,=г,=О, то=(1 (О), с& t; ( ) ~ (О ), т, (~ ( ), с&gt  Т), 1 ( )). В век
форме р=(~, &gt |, ~) иско ое реше ие запише ся следую им образ
а (~) = 6 (ро+ р,) —,, — (2р, + р,) —,
2
~И)=%+К) — ' — (2~ +К) — +М ~
(7.56)
где и,, и„и>„и„и„ >, за аются (комп ненты орбит льных ско остей пл
а хо!0), уо(0), х(1()), ~7(10) выч чяются В начале и в конце тра портирующей
траектории.
Таким образом, в транспортирующей системе координат движение
начинается из нулевой точки с заданным вектором скорости и через фикси-
рованный промежуток времени заканчивается в той же точке с другим задан-
ным вектором скорости. Начальный и конечный векторы скорости равны
разностям между орбитальными скоростями планет старта и финиша и
скоростями в начале и в конце транспортирующего эллипса.
Если реактивное ускорение намного превышает возмущения гравитацион-
ного ускорения, то уравнения (7.51) могут быть упрощены (первое приб-
лижение):

° °
° ! ° Й 1 ° ° ! Й 6 °
Й !
Э ! ! 1!1
Й ° ° 1
6Ф' 6! й 6 й й
611'3'1 1 ИЭ !
Й а Й
ф ° 6 й °
Ю ° °
Ф
1 ° 6 ! а Й
° ° ° 1 ° ! й й
3 ' ' ° ! °
й !
° ° 1 6 °
° ! Й ° ай °
а 6 Й
ИЛИИ
ИИИИ
в~иищ
иаир
ИИП
° ИГРИМ
° йИ~И
° 61
!'! ° Ф Ф
й 6
° й
° а °
й ° й 6 ° °
° °
° ° °
° °
$ . !
° °
Ф
1 ° °
$! ° '
Э Э ° °
Э 61
ф °
11 961
° 4 1
Э °
ф 6
1 й ° Й
° °
6 ЭИ 1
Э 6
Э °
Ф Ф Ф
916
й
1 961
Э 6
° ° й °
Эй!
° ° °
° °
° Э ° °
С !
1 ° °
6 Э
° ° °
9 °
° ° ° °
° °
Й °
° ° й °
° Й ° °
° ° °
Э ° ° ° 1
6 Й й
Э 6 й ° ° °
° ° й
° 91'
° ° ° °
° Ф
° °
° ° ° °
° ° ° ! е
1 а ф ° Й
11
1 ° 6 !
6 ° 11
9 °
° ° й
ф ° °
й 9 $ °
° ° й ° °
° °
9 а й Й
9' Й '~ И
° й 1
1 й
1 9111
° °
И!Э
1
° й ° ° °
° й ~ ° 1 ИИ'6''
° а 6 Э °: $ ! 6
° ° й
А
9 ИИ
э й
° ° ! °
° ! 1 е 1
! ° 1.' ! !
! ! е ° ° ° ! !
1 11!
1
й, Й
° с
° !'
1
° 6
° а Е° °
1 $1
° 6а
!
!
~ °
° ° 1
1
° е
° 1 $ $1
° °
1
1
1
1 $ !
° °
ЙЕ °
1 $1
° °
° 1
!
$ °
1
1
° 1
1
° 1
1
° °
Точность первого и второго приближений иллюстрируется табл. 7.3,
где приведены некоторые параметры оптимальных траекторий мехсорбиталь-

188
[ГЛ.
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Рис. 7.9. Относительная погреш-
ность в функционале пля второго
приближения (перелеты Земля—
Марс и Земля — Венера).
а =Ь, 1+6... а„=б„1+1~.„,.
(7.58)
Действительно, чем больше реактивное ускорение, тем меньшую роль
играют гравитационные члены в уравнениях движения и тем лучше бес-
силовое поле аппроксимирует центральное. Согласно формулам (7.58) гра-
фик функции а (~) представляет собой гиперболу, а годограф а„(а,) — пря-
мую линию.
Упомянутое сходство сохраняется вплоть до а,-1 (рис. 7.11). При даль-
нейшем уменьшении реактивного ускорения (рис. 7.12) оптимальные про-
граммы а (~) и а„(а ) уже существенно отличаются от (7.58). Траектория
движения из кривой с точкой перегиба превращается в плавную кривую,
стремясь в пределе к спирали. Годограф а, (а..) переходит в окружность.
Это предельное решение аналогично описанному в п. п. 2, 3.
Отметим свойство траекторий оптимальных перелетов, связанное с пара-
метром ~,. Случай 1,=0, согласно (7.14), соответствует перелету с незадан-
ным угловым перемещением (см. кривые 1 на рис. 7.10, 7. ['!, 7.13 и кривые 1,2
на рис. 7.12). Такие перелеты возможны только при определенном (опти-
мальном) расположении планет на орбитах; даты оптимальных стартов
ных перелетов Земля — Марс и Земля — Венера из [7.1]. В первом и
втором столбцах выписаны величины продолжительности и угловой даль-
ности перелета, затем — значения функционала динамической задачи У,
начальные а, и конечные а, величины реактивного ускорения. Для последних
трех параметров даны три значения, полученные соответственно в первом и
втором приближениях и при численном интегрировании точных уравнений.
Сравнение параметров, собранных в таблице, свидетельствует о высокой
точности метода. Точность возрастает при сокращении времени перелета,
так как в этом случае увеличивается уровень реактивного ускорения и оп-
тимальная траектория приближается к траектории импульсного перелета
(которая берется в качестве транспортирующей). При увеличении угловой
дальности точность метода падает (см. рис. 7.9 из [7.1]), таким же образом
влияет увеличение радиальных перемещений.
ы~~ В работе [7.1] высказывается предположение,
что точность метода при расчете траекторий
Ю с большими угловыми дальностями может
быть увеличена, если составлять транспорти-
рующую траекторию не из одного, а из несколь-
ких эллипсов.
6. Решение краевой задачи (7.48) — чис-
Д~ ленные результаты. На рис. 7.10 — 7.13 даны
примеры перелетов между компланарными кру-
Р говыми орбитами радиусов г,=1 и г,=1,52 (ор-
бита Земли — средняя орбита Марса, рис. 7.10—
7.12), г,=1 и г,=1,38 (средняя орбита Вене-
ры — орбита Земли, рис. 7.13) [7.4]. На каж-
дом из рисунков показаны траектория у (х),
закон изменения модуля реактивного ускоре-
ния а (1) и годограф а, (а,). На траекто-
рии и годографе дана разметка по времени с шагом Л~=0,2. В подписях
к рисункам указаны интегральные характеристики перелетов, а также не-
достающие для решения задачи Коши начальные значения а„„и агс1д (а.„/а~,).
Все параметры безр азмерные.
При больших значениях параметра а, (рис. 7.10) закон а (~) и годограф
а„(а,) напоминают соответствующие зависимости, имеющие место при плос-
ком движении в бессиловом поле (см. (7.30)):

ОПТИМАЛЬНЫЙ Ъ|ЕЖПДАНЕТНЫЙ ПЕРЕЛЕТ
ф 21
дб
Рис. 7.10. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорения, большим гравита-
ционного.
Р РФ Р8 /Г Я'
Рис. 7.11. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорения
порядка гравитационного.
Кривые 1
т, = 1,52, а, = 4, Л, = О,
Т = 0,880, ~р, = 0,664, .7 = 4,561
а~„— — — 7,950, агс1д (а„,(а „) = 1,205.
Кривые 1
г, =1 52, а,=1, Л,=О,
Т =1,741, ~р, =1,312,,7 =0,538,
а~о= — 0,670, агс$д (алло/а~ро) = 0,898.
Кривые 2
'г =1 52 ао =4 Л,= — 7,
Т = 0,920, у1 — — 0,988, Х = 5,920,
а,, = — 0,100, агс1д (а,.о/а~о) = 0,350.
Кривые 2
т1 — 1,52, ао= 1 Лг = — 1,3,
Т = 1,947, ~р, = 1,973, Х = 1,053,
а~о = 1,326, агсФд (а~о)а~,) = — 0,604.

Б 8
Рис. 7.12. Оптимальные перелеты Земля — Марс с уровнем реактивного ускорения,
меньшим гравитационного.
!б
Рис. 7.13. Примеры оптимальных перелетов Венера — Земля.
Кривые 2
т,=1,38, ао=1 Лг=0,82,
Т = 2,140, ~р, = 1,298,,7 = 0,446,
а„, = — 1,372, агс 1д (аг.,/а,ро) = 1,588.
Кривые У
г~ — 1,38 ао=1 Лг=О,
Т =1,492, ~р, = 1,196, .Т = 0,465,
а,„= — 0,908, агс1д (а;о/а~о) = 0,980.
т,
Т
алло
= 1,52,
= 3,478,
= 0,015,
Кривые !
а, = 0,2, Л, = О,
~р, = 2,636, ,7 = 0,037,
агс1ц ~ат„/а,ро) = 0,420.
т, =1,52,
Т = 9,183,
а„о = 0,001,
Кривые 2
ао — — О 02, Л,=О
~р1 = 6,987,,7 = 0,004,
агс Сд (а,„/а,ро) = 0,044.

191
$21
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
повторяются через синодический период. Кроме упомянутой работы [7.4],
данные по перелетам с оптимальным угловым перемещением содержатся
в [7.1, 7.5, 7.12 — 7.17, 7.25].
При ~,=0 и г,=1,52 отношение ~,(Т (средняя угловая скорость перелета)
приближенно равно 0,75 — 0,76 для всех ае из изученного диапазона (0,02 &
( ае ( 4). С уменьшением параметра Х, средняя угловая скорость увели-
чивается (рис. 7.14) и траектория заходит внутрь ближней к центру орбиты
(см. траектории 2 на рис. 7.10, 7.11), с увеличением 1, средняя угловая
скорость уменьшается и траектория выходит за внешнюю орбиту (см. траек-
торию 2 на рис. 7.13).
Перейдем теперь к обсуждению зависимости функционала задачи от
параметров перелета. Для перелетов с оптимальным угловым перемещением
(л,=0) зависимость функционала Х от
времени Т в диапазоне времени, пред- .1
®~ "г
Рис. 7.14. Влияние параметра )., на среднюю
угловую скорость р,(Т и продолжительность Т
межорбитального перелета (т, =1,52, а,=1).
Рис. 7.15. Функционал 7 для межорбиталь-
ных перелетов с оптимальным угловым пере-
мещепием. Сплошная кривая — перелет
Земля — Марс, пунктирная кривая — пере-
мещение между точками покоя 1=0,487
в бессиловом поле.
ставляющем практический интерес, близка к зависимости (7.33) для маневра
перемещения между точками покоя в бессиловом поле (см. рис. 7.15 по дан-
ным [7.4, 7.5, 7.12]). Это еще раз свидетельствует о том, что при достаточно
малых временах перелета (большой уровень реактивного ускорения) бес-
силовое поле является хорошим приближением для центрального. На рис. 7.16
из [7.20] приведена зависимость функционала Х от параметров Т, ~„найден-
ная при решении задачи методом функционального скорейшего спуска (см.
гл. 18 части [У).
Параметрические расчеты, проведенные в [7.16] методом Ньютона (см.
гл. 19), выявили интересный тип неединственности решения краевой за-
дачи. На рис. 7.17 показан функционал задачи для перелетов Земля — Марс
(с учетом реального движения планет) в зависимости от даты старта и про-
должительности перелета. На графике имеются два семейства кривых 1 и 11,
соответствующих двум наиболее выгодным периодам старта (семейство 1—
январь — апрель 1969 г., семейство 11 — март — июль 1971 г.). Точки пере-
сечения кривых двух семейств с равными продолжительностями перелета
(сентябрь — октябрь 1970 г.) являются точками неединственности решения
краевой задачи для системы (7.5). В самом деле, в этих точках время Т,
начальные и конечные значения координат и скоростей, а также величины
функционала совпадают '). Пример двух перелетов, идентичных по этим
') Координаты совпадают в декартовой системе, в полярной же системе полного
совпадепия н~ т: угловое перемещение ~, на траекториях разных семейств в точках пере-
сечения отли 1,1 с'гс я и а 2 ~ (рис. 7.18).

192
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ Ъ1ОЩНОСТИ
/и,~сел.
Я~ЯЯ / ~ 7 Ы 15 О~~ЯЛЯЯ 3 ~ Я Д~ Я /Я?/?~ЯЯ ~Ьв
3 4 б У0 ~ 3 Х 7 У ~д 1.~ 68 ОЫГ ~ б 8 ЮЮ~~есяц~
аИ ~УбУ /ЯД/ IУ71 гол
Рис. 7.17. Функционал Х для перелетов с орбиты Земли на орбиту Марса (орбиты планет реальные).
Рис. 7.16. Зависимость фупкционала Х для межорбитальных перелетов Земля — Марс от времени пере-
лета Т и углового перемещения р„

ОПТИМАЛЬНЫЙ МЕЖПЛА11ЕТНЫЙ ПЕРЕЛЕТ
интегральным характеристикам и отличающихся траекториями и законами
изменения вектора реактивного ускорения, дан на рис. 7.18. Еще один тип
неединственности решения краевой задачи для оптимальных перелетов будет
отмечен в следующем пункте.
Все описанные выше результаты получены при расчетах в центральном
поле. Неучет сил притяжения планет приводит к относительной ошибке
в вычислении функционала порядка 10 ' — 10 4 (см. [7.4]).
Большу1о ошибку доставляет пренебрежение эллиптичностью орбит
планет. Это иллюстрируется рис. 7.19 из [7.15, 7.16], где приведены данные
Рис. 7.18. Пример двух оптимальных траекторий
Земля — Марс различных ссмейств Х и 11 с рис. 7.17.
Стрелками показана оптимальная программа всктора
реактивного ускорения, внизу дан масштаб для вс-
личины ускорсиия.
Рис. 7.19. Влияние эллиптичпости орбит
планет па функционал задачи.
по перелетам между круговой орбитой Земли и компланарной ей эллипти-
ческой орбитой Марса (сплошные кривые 1 и 2). Нижняя кривая 1 соответ-
ствует достижению самой выгодной точки эллиптической орбиты Марса,
верхняя 2 — самой невыгодной. Разница между соответствующими значе-
ниями функционала получается значительной. Расчеты, проводимые для
средних круговых орбит, дают величины функционала, средние по отношению
к этим двум крайним (см. пунктирную кривую 8 на рис. 7.19).
Таблица 7.4
Влияние некомпланарности орбит Земли и Марса на функционал задачи
межорбитального перелета (Х= — 184 суш)
мг~секз
7, м'/сек'
Погрешность
1 — А . 1000/
о
Погрешность
71 72 100%
1
плос-
кая
траек-
тория
Х2
Дата старта
(1971 г.)
Дата старта
(1971 г.)
простран-
ственная
траекто-
рия 71
простран-
ственная
траекто-
р ия,71
плоская
траекто-
рия 7,
Учет некомпланарности орбит слабо влияет на интегральные харак-
теристики перелетов (см. табл. 7.4 из [7.16], а также данные [7.14, 7.25]).
13 Механика полета
14 февраля
2 марта
18 марта
3 апреля
19 апреля
5 мая
13 мая
37,373
27,733
19,931
13,938
9,703
7,187
6,576
37,230
27,597
19,796
13,798
9,555
7,032
6,418
0,38
0,49
0,68
1,00
1,5
2,2
2,4
21 мая
биюня
22 июня
8июля
24 июля
9 августа
17 августа
6,406
7,459
10.,558
16,046
24,395
36,217
43,648
6,247
7,303
10,413
15,918
24,292
36,139
43,584
2,5
2,1
1,4
0,80
0,42
0,22
0,15

ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
Результаты систематических расчетов оптимальных траекторий меж-
орбитальных перелетов для различных планет солнечной системы (Земля—
Меркурий, Земля — Венера, Земля — Марс, Земля — Юпитер, Земля — Сатурн)
можно найти в работах [7.13 — 7.18, 7.25].
Приведенные в п. 2 и в настоящем пункте данные позволяют определить
параметры оптимального перелета «спутник Земли — спутник ЛХарса» (без
возвращения). С этой целью воспользуемся аппроксимациями зависимостей
У (Т) для маневра набора нулевой энергии с круговой орбиты радиуса г,=1
(рис. 7.5): Х (Т) (0,895)'/Т вЂ” и для перелета между круговыми компла-
нарными орбитами радиусов г,=1 и г,=1,52 с незаданным угловым переме-
щением (рис. 7.15): Х (Т) 12 (0,487)'/Тз (переменные безразмерные). Ор-
биты спутников Земли и Марса будем считать круговыми с высотой 300 км
над поверхностью планет, траекторию перелета — плоской.
Подставляя в аппроксимационные формулы соответствующие характер-
ные значения функционала Х„и времени ~„из табл. 7.1 и 7.2, получим:
для разгона у Земли
Х„[м'/сек'] = 5 10'/Т„[сут],
для. межорбитального перелета Земля — Марс
Х1 [м~/сек»] 108/(Т, [сут])~,
для торможения у Марса
Х, [м~/секз] 10'/Т 2 [сут].
Полное время перелета Т.=Т+,+Т,+Т, задано, дата старта не фик-
сирована; нужно найти распределение этого времени между тремя участками
перелета, обеспечивающее минимум суммарного функционала Х,=7+1+7,+Х,.
Проделав эту процедуру, получим следующие выражения для оптимальных
времен Т+„Т1, Т, и минимального значения функционала Х.:
Т„[сут] = 102~', Т, [сут] = 2,783 ° 10'~,
Т, [сут] = Т. [сут] — 10' (Р+ 2,783~)
(~ = ~/0,922+ 0,691 ° 10 'Т. [сут] — 0,96),
5 4,63 1
10 2Т ~сут] — ф+ 2,783 т) '
оптимальное угловое перемещение межорбитального перелета при этом равно
~, [рад] 3,62~. Б силу свойства «обратимости» (7.16) полученные формулы
оказываются справедливыми и для перелета «спутник Марса — спутник
Земли» (нужно только заменить Т+, на Т, и Т, на Т,,).
7. Межпланетный перелет с возвращением. В задаче межпланетного
перелета с возвращением задаются полное время перелета Т. и время пре-
бывания у планеты назначения Т; момент старта с исходной орбиты не за-
дается (см. ~ 3 гл. 4). Кинематические параметры элементарных маневров,
составляющих межпланетный перелет, по отдельности не определены. Здесь
необходимо найти оптимальные значения времени движения для маневров
набора нулевой энергии и торможения у планет, а также времени движения
и углового перемещения для прямого и обратного перелетов между орбитами
планет. Выбор оптимальных значений времен торможения и набора нулевой
энергии у планеты назначения в настоящем изложении не рассматривается
(эти времена входят в фиксированное время Т ), не учитываются также
энергетические затраты не выполнение этих двух маневров. Орбиты планет
предполагаются компланарными и круговыми.

19
ОптимлльныЙ межпллнетный пеРелет
Пусть времена набора нулевой энергии и торможения у планеты старта
определены; тогда задача сводится к определению оптимальных кинематиче-
ских параметров межорбитального перелета с возвращением. Здесь заданы
начальные и конечные радиусы и проекции скоростей для прямого и для
обратного перелетов. Угловые перемещения и времена перелетов заданы не
по отдельности, а в сумме 1) (см. (4.71), (4.72)). Чтобы определить оптималь-
ное разбиение суммарного углового перемещения р,+~, и суммарного вре-
мени Т,+Т, между прямым (1) и обратным (2) перелетами, воспользуемся
условием обращения в нуль внеинтегральной части первой вариации функ-
ционала.
Последний в рассматриваемом случае представляет собой сумму двух
интегралов (7.9), соответствующих прямому и обратному перелетам:
т,
Т2
+ Ф~+ 9~) ] ~ ~(о) — 1, ~(о) — о, у(о) — о, ~(о) — 1, „(у,) — „„+ [(г гФ + [/г ) [-
~(~['1) = ~„т(~1) = О, ф(Т,) = — т 3!
о) =т„р~о) =о, т&lt о) о, ~ о~ =т1 Ђ” ' :, (7
т(~'г~ = 1 9(~'г~ = Ч'я т(~'я) = Оъ Ф(~'~) = 1
Искомые члены первой вариации (7.59) в соответствии с (7.14) записы-
ваются так [7.4]:
О~, + 3Х, = — 2 Я'~оТ, + Ц1 ~аз, + Ц'~о Т., + Ц'-~3~р,).
(7. 60)
При заданных суммах ('о,+~,), (Т,+Т,) условиями обращения в нуль
выражения (7.60) будут ')
) (1] ) (2) ) (1) ) (2)
(7. 1)
Равенства (7.61) заведомо соблюдаются, если в качестве обратного исполь-
зуется перелет, симметричный прямому (см. (7.16)); тогда ~,=~„Т,= Т„
У,=Х,. Однако, как показано рядом авторов [7.2, 7.13, 7.15, 7.20, 7.21, 7.36],
при этом не всегда достигается абсолютный минимум суммы функционалов
~1+~2'
Условия (7.61) могут выполняться и в том случае, когда прямой и обрат-
ный перелеты не симметричны. При решении краевой задачи (см. (7.13))
о„=а„— ' — —,, г„г =г„„о„г, =г„„
У.У,
8 =а
г
ь (г,) = ~&gt
ь (го)=и „
(7.62)
° 1 1 2 2 э 1
я я2 я2 я
т ~ '& t   г
т
а = — (а и„— 2а„и + Л,)
1
1 2
с фиксированными параметрами Л„Х, получаются два семейства интегральных
кривых ь„(г), и (г), а„(г), а (г) и, следовательно, две пары значений
1) Если задать еще дату старта, то будут определены Т1+Т, у — и,Т, и и — ~ Т2.
') Прп задан дате старта условия (7.61) заменяются па (Л['& t; Ђ” Л[2>) (Л& t;1> — Л
13*

196
[ГЛ, 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ Ъ|ОЩНОСТИ
Т, т. е. краевая задача (7.62) не обладает свойством единственности решения.
Чтобы проиллюстрировать этот факт, обратимся к графику Х, (~,). На рис. 7.20
в координатах 1„~, нанесены линии равного углового перемещения ~, для
перелетов между орбитами Земли и Марса [7.20] (зависимость Х (Т) для
тех же самых значений ~, была показана на рис. 7.16). Пересечение кривых
на рис. 7.20 свидетельствует о неединственности решения задачи (7.62),
т. е. условия оптимального сопряжения (7.61) могут выполняться и для
несимметричных траекторий.
Рис. 7.20. Линии равного углового перемещения.
Приведем пример несимметричного перелета с возвращением, дающего
выигрыш в функционале по сравнению с симметричным перелетом на 16 ~~,
параметры симметричного перелета: Т,= Т,=1,88, ~р,= ~,=2,14, Х,+Х,=3,80;
параметры несимметричного перелета: Т,=2,41, Т,=1,35, ~р,=3,14, ~р,=1,14,
Х,+У,=3,20. Суммарное время исуммарное угловое перемещение для обоих
перелетов одинаковы:
Т,+Т,=3,76, ~р,+~р,=4,28.
Оптимальное разбиение между прямым и обратным перелетами задан-
ных суммарных времени и углового перемещения находится после решения
задачи на минимум суммы Х,+Х, по аргументам ~р„Т, при ~р,+р,=соней,
Т,+Т,=соней. В работе [7.17] это проделано для перелета Земля — Марс—
Земля в широком диапазоне параметров. Дальнейшее изложение пункта
будет базироваться на результатах [7.17].
Процедура отыскания минимума Х,+72 проводится в терминах даты
старта с орбиты Земли ~, (отсчитываемой от противостояния Земли и Марса)
и времени перелета «туда» Т, (связь между ~, и ~1 дается (7.49), где надо
считать Т=Т,). Типичный пример зависимости суммарного функционала
Х,+Х, от ~, и Т, при заданных суммарном времени Т,+Т,=496 сут и вре-
мени пребывания у планеты назначения Т =0 показан на рис. 7.21. Минимум
Х +У, в этом примере достигается при ~,= — 85 сут, Т,=184 сут (см. кри-
вую 8), т. е. и здесь оптимальный перелет оказывается несимметричным.
Влияние распределения времени Т,+Т, между прямым Т, и обратным Т2
перелетами на функционал Х,+Х, иллюстрируется рис. 7.22 (время пребы-
вания у Марса фиксировано, Т =О, дата старта в каждой точке оптимальная).
Видно, что симметричные перелеты (Т,= Т, — пунктирная кривая на рис. 7.22)
становятся оптимальными при сокращении суммарного времени Т1+Т,.

197
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
8 2]
Рис. 7.21. Суммарпый функционал,7,+,7,:
Т,=152 сут, Т,=344 сут; 2 — Т,=168
Т,=328 сут', 3 — Т, =184 сут, Т,= 312
4 — Т,=200 сут, Т,=296 сут', 5 — Т~ — — 216
Т,= 280 сут; 6 — Т, =232 сут, Т2 — — 264
У вЂ” Т,=248 сут, Т,=248 сут.
Рис. 7.22. Хипимизированпыс по датс старта зна-
чения суммарного функционала,7,+,7,.
У~, сую
ЗРЮ
4Я ЯР 600
Т~+ Т~, ~у~
Рис. 7.23. Оптимальное время
Т, прямого перелета.
1И
Ю
бд
1—
сут,
сут,
сут,
сут',
8®
7Я
бЯ
ЯР
4Я
~И
Ю
80
7д
6Р
Я
Ю
~Р Ябб Ю 1К 1Я ~Я~ЯЩ ~у
7~, ~~'~

[ГЛ. 7
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
IЯ с?Я Лд ЯО 400 530 бЯ
7, + Т~, С~~ХХ~
(7.63)
Х. = 2Х„+ (Х, + Х,)
при заданном полном времени перелета
(7.64)
Т. = 2Т„+ (Т, + Т,) + Т
(время Т пребывания в окрестности Марса также задано).
Зависимость У,+У, от Т,+Т, и Т дана на рис. 7.24, а для У+, (Т+,)
использована аппроксимационная формула (в безразмерных переменных;
переход к размерным величинам осуществляется по табл. 7.1)
(7.65)
Х„= 0,3934Т-'"'"
которая выведена для случая постоянного тангенциального ускорения
(ср. (8.84)). Результаты расчетов по (7.65) весьма близки к точным а значит,
На рис. 7.23 дано оптимальное время Т, прямого перелета в функции
Т,+Т, при фиксированных значениях Т . Отрицательные значения Т
введены условно для придания монотонности соответствующим зависимо-
стям. Чтобы получить действительные значения Т, нужно к Т ( 0 при-
бавить спнодический период (для Земли и Марса -780 сут).
Минимизированный по Т, и ~, функционал У,+У, приведен на рис. 7.24
в виде Х (Т,+Т„Т ). Эта зависимость вместе с рис. 7.23 является резуль-
тирующей для задачи оптимизации межорбитального перелета с возвраще-
нием. Нижняя кривая — огибающая, показанная на рис. 7.24 пунктиром,
соответствует перелетам с незадан-
~~+~~, ю~Яею ~ ным (оптимальным) временем пре-
бывания в окрестности планеты
ГОИ назначения (Ц> ~А &g
ОИ Т~, сую Перейдем теперь к задаче оп-
ределения оптимальных времен
УОО набора нулевой энергии Т+, и тор-
6 можения Т, у Земли. Прежде
Ш
всего, можно заключить, что эти
Яд
ФМ времена должны быть равны меж-
Юд ду собой. В самом деле, исходная
и конечная орбиты спутников Зем-
ГЯ
ли предполагаются идентичными,
(Ю
-Ф—
!
поэтому энергетические затраты
Уб на маневр набора нулевой энер-
гии У„и маневр торможения У 1
в силу (7.16) выражаются одной и
Я той же функцией У (Т). Эта функ-
ФР ция, вычисленная в п. 2 (см. рис.
Ю 7.5), монотонная с положительной
второй производной. Для таких
Ю
функций можно показать, что ми-
75 нимум суммы двух значений функ-
ции при заданной сумме аргумен-
тов (т. е. минимум У (Т„)+У (Т—
— Т,) по Т,) достигается, когда
аргументы равны Т,= Т,='/,Т .
Рис. 7.24. Минимальные значения суммарного р ~1 — 1 2
функционала,7, +,7, (минимум по 1, и Т,). Таким образом, суммарное
время, затрачиваемое на маневры
набора нулевой энергии и торможения у Земли, равно 2Т+„а суммарный
функционал равен 2У„,. Теперь нужно найти минимум по Т, полного функ-
ционала

199
ОптимАльные мАнеВРы упРАВллемых спутпикОВ
и к оптимальным (см. рис. 7.5). На рис. 7.25 проведено соответствующее
сравнение для 300-км круговой орбиты спутника Земли (эта орбита и исполь-
зуется в дальнейших расчетах). Там же для оценок нанесена линия, соответ-
ствующая 300-км круговой орбите
спутника Марса (напомним, что /,, ~Яе~~
затраты на маневры торможения /ЯР
и разгона у Марса не учитываются).
,8О
В точке минимума (7.63) долж-
но выполняться равенство
= 0 (7.66)
а(т,)-т,)
ат„
/Я
бО
полученное дифференцированием
(7.63) при связи (7.64): 2ИТ+1 — ——
— о', (Т1+Т,), Т.=сопвФ, Т =сопз$.
Первый член (7.66) находился
диффер енцир ов анием (7. 65):
Н„~йТ„= — 370,8Т-', "'7 (7.67',
(О
8
б
/ ? 4 б8)0 Ю Юб0 ~007,~,
Здесь производная вычисляется по данным, на основании которых
построен рис. 7.24. Результаты соответствующих расчетов представлены на
рис. 7.26. На рис. 7.27 дан итоговый график — полный функционал Х =
=2Хд+Х1+Х, межпланетного перелета Земля — Марс с возвращением в функ-
ции времени Т.— Т =2Т+1+Т1+Т, (полное время путешествия Т. минус
время пребывания у Марса Т ) для фиксированных значений Т .
~ 3. Оптимальные маневры управляемых спутников
с идеальным двигателем ограниченной мощности
Здесь собраны решения вариационной задачи (7.2) для следующих
маневров в окрестности планеты: поворот плоскости круговой орбиты,
изменение радиуса круговой орбиты, одновременное изменение радиуса и
угла наклона круговой орбиты.
Общей чертой для всех маневров управляемых спутников с двигателями
ограниченной мощности является малость отношения реактивного ускорения
к гравитационному. Это открывает возможности для аналитического реше-
ния при помощи различного рода приближенных методов. Задачи параграфа
подобраны таким образом, чтобы дать представление о наиболее употре-
бительных из них.
1. Поворот плоскости круговой орбиты. Определим оптимальную про-
грамму реактивного ускорения для маневра изменения угла наклона плос-
кости круговой орбиты спутника (см. ~ 4 гл. 4) (7.27]. Тяга направлена
перпендикулярно мгновенной плоскости орбиты (по нормали, е=+1, или
(~Х„Д=м'lсекз, (Т+ ~=сут, орбита
спутника Земли с высотой 300 км).
После этого для каждой пары зна-
чений Т,+Т, и Т по уравнению
(7.66) находилось оптимальное вре-
мя Т„:
҄= —,2 7 1 ' &g
Рис. 7.25. Функционал Х+„подсчитанный по аппрок-
сиыационной форыуле (7.65) (точкаыи показаны точ-
ныс значения с рис. 7. 5).

200
ф
~з
1
~Ъ
кч
„о
-ъ~
+
ф
~Я Я
~~~+ ъ
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
\
р~~
~~~~~Ж~~ ~ ~ ~ Ц ~~~1М,~ ~ф Ц Р
~о~~~с:& t; -~
1 Н
о
О
~о
%2
ю н
Ио
„о
~",о
+й~
.Г
+й
+
л~ ~.'
СЧ
!1~ '
3
л~ Я~ч
й~и
ооо
й~;~
9 1
3~3~ ~
й
Ф: И
н
Л
о с„
о
С)
Р~ -1
. О
с й
1
М4
ь
~б
~~ ~б
р О
й1
ьм
с
м и
й
~н
)~ О
о~
н
о
~о
о
й Р1
~йн
о м
"- и
1
3
И я~-~
1-О
юоо
о~
Д
"о
с~
И ~
й~
о И
° Р1
~=& t
РД
~-. о
ос
Ра
Р~

201
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
Х = (ае)', У (О) = О, У (2т~г) = т1п, 1
,"( =аез1п(8 — о,), у(0)=0, )~(2тв) — 0
ш=ае соя (1 — 2,), и(0) =0, щ(2т8) — ~
(а (1) ) О, е (~) = -~-1).
(7.69)
Вывод динамических уравнений (7.69) дан в $ 4 гл. 4 (см. (4.104)); послед-
ние получены из системы в оскулирующих переменных в предположении
о малости угла поворота ~.
Для решения задачи (7.69) ис-
пользуется метод Л. С. Понтрягина;
Рис. 7.29. Оптимальпая программа реактивного
ускорения для поворота плоскости круговой
орбиты (пунктир — программа, взятая для срав-
Е1Е11ИЯ) .
Рис. 7.28. Схема маневра поворота плоскости
круговой орбиты; стрелками показана опти-
мальная программа вектора реактивного уско-
рения.
следуя процедуре метода, выпишем гамильтонову функцию и дифференци-
альные уравнения импульсов:
П = — (ие)'+ р ае з1п (1 — Р,) + р ие соя (1 — о,),
р = — ~~~)~=0, р
В записи (7.70) учтено, что импульс, соответствующий минимизируемой
фазовой координате Х, постоянен. Согласно общепринятой нормировке он
положен равным минус единице.
Управления а и е входят в дифференциальные уравнения (7.69) и га-
мильтонову функцию (7.70) в виде произведения ае. Оптимальная программа
для этой комбинации управлений дается выражением (из условия макси-
мума Н)
(7.7 )
(7.71)
ае = '/, [р„з1п (1 — Я,) + р соз (1 — 2,)1.
По отдельности оптимальные управления а и е следующие '):
е = ядп [р„з1п (1 — Р,) + р соя (1 — ~,)~,
а =1/ ~ р„з1п (1 — Я )+ р соз (1 — Я ) ~.
(7.72)
') Функция з1яп х (знак х) определяется как з1яп х=+1 при х & t; О, з яп =О
к=О, я1дп х= — 1 при х ( О.
против нее, е= — 1), угол ~ между исходной и конечной плоскостями (угол
поворота), конечное положение линии узлов Й1 и время движения Т считаются
заданными. Для простоты выкладок время Т полагается кратным целому
числу оборотов: Т=2кз, я=1, 2, 3,... (все параметры безразмерные—
см. (4.12), где г„=г,). Начальная орбита лежит в плоскости экватора (рис. 7.28).
Рассматриваемая вариационная проблема записывается в виде задачи
Майера:

202
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ Ъ|ОЩНОСТИ
[Г,11. 7
После подстановки оптимального закона (7.71) в уравнения движения (7.69)
и интегрирования до конечного момента Т=2гз получаются значения посто-
янных р,, р, удовлетворяющие заданным граничным условиям из (7.69):
р =О, р =2~/гт~. (7.73)
Тогда
ае = (~/з-.) соя (1 —,)=
и величина контрольного функционала Х равна
(7.74)
У ( Т) = Р~е-. = 2Р~ Т (Т = 2тсз).
(7.75)
1 1
и =— — 1 — =
Т
здесь и ниже все параметры безразмерные (см. (4.12) при г,=г,).
Оптимальная траектория описывается формулами (7.44) с а из (7.76).
Функционал Х приближенно (см. (7.45)) равен
Уж 1 — =
~г т
(7.77)
Обратим внимание на то, что полученные здесь зависимость Х (Т) и
оптимальная программа реактивного ускорения аналогичны таковым для
маневра набора модуля скорости в бессиловом поле (7.32). Такой же вид
имеет функция Х (Т) для маневра поворота плоскости орбиты (7.75), хотя
программа ускорения (7.74) там существенно другая.
Оптимальный закон изменения реактивного ускорения (7.74) в течение
одного оборота показан на рис. 7.28 и 7.29. Согласно (7.74) модуль ускоре-
ния достигает максимума при прохождении конечного положения линии
узлов. Дважды за оборот направление вектора реактивного ускорения
меняется на обратное в моменты обращения а (~) в нуль. Эти точки сдвинуты
по углу от точек максимума на а(2.
Величина контрольного функционала Х оказывается не зависящей от
положения линии узлов конечной орбиты (т. е. от угла Й,). Зависимость
функционала от времени выполнения маневра такая же, как и для задачи
набора модуля скорости в бессиловом поле (см. (7.32) и кривую и на рис. 7.2).
Если вместо оптимальной программы реактивного ускорения (7.74) взять
постоянное по модулю ускорение с теми же самыми моментами изменения
направления ае=(~/4г) зшп соя (~ — Й,) (пунктир на рис. 7.29, см. ~ 4 гл. 17),
то величина функционала увеличится в 1,23 раза: Х=Р~/8г. Напомним, что
результаты этого пункта получены в предположении, что время выполнения
маневра кратно целому числу оборотов, Т=2гз, и ~ (& t;
2. Переход между компла~ар~ыми круговыми орбитами. Рассматривае-
мая задача является частным случаем задачи о межорбитальном перелете
Я 2, п. 2). Здесь фиксированы время движения, радиусы начальной и конеч-
ной орбит; начальная и конечная скорости — круговые (см. (4.68)); угловое
перемещение не задано (1,=0). Конечная орбита считается внешней по от-
ношению к начальной; заменой (7.16) все результаты могут быть пересчитаны
для обратного случая.
Если реактивное ускорение мало по сравнению с гравитационным, то
для этой задачи можно использовать приближенное решение (7.44), (7.46),
(7.47) из п. 3 предыдущего параграфа. Согласно этому решению оптималь-
ная программа вектора реактивного ускорения (7.46), (7.47) такова(при
а ~ (( 1): модуль ускорения почти постоянен, а направление близко к на-
правлению скорости (вектор скорости здесь направлен практически по транс-
версали). Величина ускорения а определяется при помощи первого соот-
ношения (7.44) из конечного условия г (Т)=г,:

203
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
Несколько слов о точности приведенного решения. Неучтенная в (7.77) часть функ-
ционала У имеет величину (см. (7.45), (7.47), (7.76))
Т
36 (~~ — 1) (г ' — 1)
° з °
7 '1.Т
г1"-
(7.78)
макспмальпое значение отброшенной компоненты реактивпого ускорепия а„таково
(см. (7.47), (7.76)):
6г, (~г1 — 1)
шах а„(е) = сс„(Т)—
о< &
(7.79)
невязкп краевых условий по радиальной скорости (и„,=и„1=0) следующие (см. (7.44),
(7.76)):
2г, (~г1 — 1)
2 (~г, — 1)
г„ (О) — и„
Т чг1
и„(Т) — и„
(7.80)
Т
Формулы (7.78) — (7.80) позволяют определить пределы, где решение (7.44), (7.76)
даат н ужпую точность.
г =(г, О), т =(О, г),
Г1. — (г1 соз 91, г1 з1п Р1),
т, == ( — г, з1п ~„г, сов ~,).
(7. 1)
Здесь считается, что начальная точка лежит на оси Ох. Полярный угол ~
по условию задачи не фиксирован, поэтому нужно выбрать его оптимальное
значение из условия минимума функционала Х.
Все переменные отнесены к своим значениям на круговой орбите неко-
торого радиуса г. (см. (4.12)). На этом радиусе приближенная величина
гравитационного ускорения полагается равной истинной. В используемой
модели поля гравитационное ускорение с увеличением радиуса линейно
возрастает, а в центральном поле — убывает по квадрату радиуса. Неко-
торая компенсация возникающих отсюда ошибок возможна за счет соответ-
ствующего выбора г ').
') При замене г, -э 1 1г, нужно изменить все безразмерные величины в соответствии
с (7 15); тогда соответствующие размерные величины останутся без изменения. В ра-
боте [7.10] предлагается еще один метод уточнения решения, связанный с численным
интегрированием: программа реактивного ускорения (7.37) подставляется в точные урав-
нения движения, постоянные векторы с„с4 подбираются по точным краевым условиям.
Рассмотрим приближенное решение задачи, основанное на использо-
вании модели однородного центрального поля (см. $ 2 гл. 4 и (7.34) — (7.37)).
Здесь уже не нужно делать предположения о малости реактивного ускоре-
ния, вместо этого требуется предположить малость радиального перемеще-
ния. Общее решение уравнений вариационной проблемы в однородном цен-
тральном поле было выписано в 3 1 (см. (7.35) — (7.37)). Остается только
подставить соответствующие граничные условия.
До начала и после конца выполнения маневра движение должно про-
исходить по круговым равновесным орбитам заданных радиусов. В централь-
ном поле уравнениями этого движения в плоскости х, у будут х (~) =
=гсов (г '4), у (1)=г я1п(г '~4), г=сопя$ (см. (4.13) приа =а =О). Для модели
однородного центрального поля эти уравнения выглядят несколько иначе:
х (1)=г сов 1, у (1) =г в1п 1, г=сопз$ (см. (4.64) при а =а =О). Таким образом,
равновесная круговая скорость на радиусе г в первом случае равна г '~,
а во втором — г (переменные безразмерные).
Согласно сказанному векторы г„т„г„т1 из (7.36) в прямоугольной
системе координат х, у (рис. 4.2) будут иметь компоненты

204
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Будем считать для простоты, что время выполнения маневра кратно
периоду обращения по круговой орбите радиуса г.; тогда из последней
формулы (7.37), подставляя в нее (7.81), находим
4
У = — (г', — 2г,г, соя р, + г„') (Т = 2т~г, г = 1, 2,... ).
(7.82)
Отсюда видно, что минимум Х по ~&g ;, достигае ся ри оя ч&g ;1=1. И
зуя это соотношение, запишем выражения для оптимальной программы реак-
тивного ускорения, оптимальной траектории и функционала (см. (7.35)—
(7.37), (7.81)):
2 2
а (1) = — — (г,— г,) я1п 1, а (1) = — (г,— г,) соя 1,
х>С)=[гс+&gt г,в ” г ) — ]со & t; —
у>С)=[гс+)г, Ђ” г) Ђ” ]я gt;пя >0 я(Т= кя я=&g
У (Т) = — (г, — г,)'.
~ (7.83)
()птимальная программа реактивного ускорения получилась такая же,
как и в предыдущем решении рассматриваемой задачи: модуль ускорения
постоянен, а = ~а'+ а„'= 2 (г, — г,)~Т, направление совпадает с трансвер-
салью,
а /а„= — $д 1= — 1и ч&g
Если же вместо граничных условий (7.81) здесь взять обычные граничные условия
для круговых орбит в центральпом поле, то программа реактивного ускорения получится
далекой от оптимальной:
2 2 1 1
а (1) = — 7(г1 — го) я1п 1, а„(1) = — — = — = соя ~.
г1 ~го
(7.84)
Сравним функционалы (7.77) и (7.83); первый обозначим через У< >, тор й в
рез Р'&g ;. Перепи ем У l ;'& t; в тех же без азмерных пе еме н х, то У » (т. е. в
характерных возьмем значения переменных на исходной орбите, а не на орбите радиуса г,):
4 (г, — 1)2
г
(7.85)
Считая г1 — 1 =юг((1, получим с точиостио до о (ЛТ2)
(г1 — 1)2 4 (г, — 1)2
(7.86)
Функционалы при одинаковых г„Т будут совпадать, если принять г,.=2,52. При та-
ком выборе г, естественно, совпадают и величины реактивного ускорения (поскольку
а'1& t; ~) со я и "> (~)= опя , см. 7 76) и (7 83)). Ф рмула 7.7 ) для функц онал
тверждается в следующем пункте, где опа получена отличным от использованных здесь
методом — традиционным методом линеаризации уравнений движения.
3. Переход между некомпланарными круговыми орбитами разных ра-
диусов. Заданы радиусы начальной г(0)=1 и конечной г(Т)=г, орбит и
угол ~ между их плоскостями, время движения фиксировано, положения
линии узлов и точки выхода на конечную орбиту свободны. Начальная и
конечная орбиты считаются близкими: ~ь~ (( 1, ~г — 1~ (& t 1 (перемен
безразмерные, в качестве характерных взяты значения соответствующих
параметров на исходной орбите: г.=г, в (4.12)).

ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
Для решения задачи используется метод линеаризации в окрестности
начального движения [7.28, 7.29]. Выбирается система координат
начало которой движется с равновесной скоростью по исходной круговой
орбите. Координаты,", е, 1 связаны со сферическими координатами г, ~, О
(см. рис. 4.1) соотношениями
— ~=г — 1,
(7.87)
Используя формулы (4.14), (4.16) перехода к декартовым координатам,
можно выписать уравнения движения в координатах с, 1), ~ и сформулировать
соответствующие граничные условия. Отклонения от начального движения
и их производные во все время движения предполагаются малыми, уравне-
ния движения линеаризуются, в граничных условиях также сохраняются
только главные члены.
Окончательно вариационная задача записывается следующим обра-
зом (в виде (7.2)):
Х = и' +а'+ и',
~=21,
7~ — Ц
(7.88)
и =и +2и,
1)=и +3~ — 2и,
Управляющие функции и~ (~), а (~), а, (~) — компоненты реактивного
ускорения — не ограничены. Конечное значение фазовой координаты ~ сво-
бодно; конечные значения фазовых координат ~ и и по отдельности также
не заданы — они связаны условием ~' (Т)+и' (Т)=Р.
Отметим, что четвертое и последнее уравнения (7.88), описывающие
движение в плоскости, перпендикулярной к исходной орбите, не зависят
от остальных уравнений движения (для данного приближения). Обнаружив
это обстоятельство, можно воспользоваться результатами двух предыдущих
пунктов и составить искомое решение как суперпозицию уже найденных.
Однако здесь изложение будет проведено независимо, с тем чтобы получить
подтверждение результатов п. 2 и продемонстрировать процедуру метода.
Составим гамильтопову функцию:
Н = — (а'- + а'- + а :') + р~и + р 1) + р) и + р„(а, + 2С) +
+ р„(а + 31) — 2и) + р, (а~ — ~), (7.89)
н выпишем дифференциальные уравнения для импульсов (р';= — дН/дх,):
р=О,
р'„= — р„+ 2р„
Р., = — ЗР„
Рч = Р~ — ~Ри
РС =- Ри
Ъ= РС
(7.90)
Оптимальная программа реактивного ускорения дается соотношениями (дН/да;=О)
а; = 1зрз а~ = 1зрз а~ = 1зр))) ° (7.91)
Уравнения для импульсов (7.90) интегрируются независимо от основной системы
(7.88), поскольку задача линейная:
р„= ЗС1~ — 4с, соя ~ + 4с 81п ~ + Зс„
Р„= 2 (С1 + СЗ 81П 1 + СЗ СОЯ 1))
Рз, = — 2 (С4 81П 1 — СЗ СОЯ 1) )
Р.= С1,
Р = — (6С11 СЗ СОЯ 1+ СЗ 81П 1+ СЗ))
р~ = 2 (С4 СОЯ 1+ сз 81п 1) )
(7.92)
(
г(о) =о,
Е(О) = О,
~(о) =о,
~ (о) = о,
и(0)=0,
и(0) =О,
и(0) =О.
У (Т) = т1п,
Е (Т) = орй,
в (Т)=г, — 1,
Р (Т) + и' ( Т) = 18,
и (Т) = з/, (г, — 1),
и (Т) =О,

206
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 7
где с1,..., с — шесть неизвестпых постоянных интегрирования, которые определяются
пз конечных условий (7.88) после решения основной системы (7.88) с оптимальной про-
граммой ускорения (7.91).
В (7.88), как уже отмечалось, часть фазовых координат в конце движения свободна;
выпишем для них соответствующие условия трансверсальности. Конечное значение коор-
динаты ~ не задано, поэтому соответствующий ей импульс р„при ~= Т должен обращаться
в нуль. Отсюда в силу первого уравнения (7.92) мо~кно заключить:
с1 — — О.
(7.93)
Конечные значения ~ и и ле~кат на окруженности Р (Т)+и' (Т)=Р; из условия оп-
тимальности вытекает, что вектор импульсов (р~, р„) должнен быть направлен по радиусу
(нормально к окружности), т. е.')
р~ (Т)/~ (Т) = р,„(Т)/ш (Т).
(7.94)
Выпишем теперь оптимальный закон изменения компонент реактивного
ускорения по времени, подставив (7.92) в (7.91) и учтя (7.93):
а (~) = — 2с, соя ~+ 2с, я1п ~+ '/,с„
а (1) =- с, я[п 1+ с, соя 1,
а, (1) = — с, я1п 1+ с, соя 1.
(7.95)
Функции (7.95) подставляются в правые части уравнений (7.88), после
чего эта система неоднородных линейных уравнений с постоянными коэф-
фициентами интегрируется:
У (~) = '/, (5с',, + 5с, '+ '/.,с';+ с';+ с',) ~ — бс,с, я1п ~+
+6с.,с,(1 — соя ~)+'/,(Зс', — Зс; "— с';+ с',.) я1п ~ соя ~—
— (Зс,с, + с,с,) я1п' 1,
~ (~) = с, [8 (1 — соя ~) — 5~ я1п Ц+ с, (11 я1п ~ — 5~ соя ~ — 6~)—
— с,['/,Р— 6 (1 — соя ~)], !
~) (~) ='/,с,(я[п ~ — ~соя ~)+сз['/,~я1п ~ — 4(1 — соя ~)]+Зс,(я1п ~ — ~), ) (7.96)
~ (1) = '/,с, (1 соя 1 — я1п Ц +'/,с,~ я[п 1,
и (1) =с,(3 я[п 1 — 51 соя 1)+сз [51 я1п 1 — 6 (1 — соя 1)]—
— с,(%1 — 6 я1п 1),
~ (~) =%с,~ я1п ~+ '/,с, (5~ соя ~ — 3 я[п ~) — Зс, (1 — соя ~),
и (~) = — 1/,с,д пп 1+ '/,с, (я[п ~+ ~ соя ~).
Здесь уже учтены нулевые начальные условия (7.88) для всех фазовых ко-
ординат. Третье, пятое и шестое конечные условия (7.88) определяют по-
стоянные с„сз, с, (движение в плоскости начальной орбиты), для них полу-
чается система линейных алгебраических уравнений. Четвертое конечное
условие (7.88) и условие трансверсальности (7.94) дают систему двух квадрат-
ных уравнений относительно постоянных с, и с, (движение в плоскости,
перпендикулярной к плоскости начальной орбиты). Выбираются такие
корни этой системы, которые обеспечивают У (Т)=т1п.
') В работе [7.28| вместо условия (7.94) было ошибочно принято р; (Т)=0; исправ-
ленные формулы приведены в [7.29|.

207
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
6 41
Окончательное выражение для постоянных с... с, через параметры
рассматриваемого динамического маневра таково:
2 (г, — 1) я|п Т вЂ” 2 (г, — 1) (1 — соя Т)
16 (1 — соя Т) — Т (5Т + 3 я|п Т) ' 16 (1 — соя Т) — Т (5Т + 3 я1п Т) '
~2 1 (1 — соя Т) '/, (г, — 1) (5Т+ 3 я|п Т)
Т + ~ я|п Т ) 16 (1 — соя Т) — Т (5Т + 3 я1п Т) '
~2~ я1п Т
с =
(1 — соя Т) (Т + ~ я|п Т ~)
(при Т = 2т~г, г = 1, 2, ...,
(7.97)
с., = с, = с, = О, с, = (1 — г,~)ЗТ,
с,=2~/Т). 1
Подставляя (7.97) в первое уравнение (7.96), находим функционал
задачи:
(г, — 1)'(5Т+3 я1п Т) + 2Р
4 (Т (5Т + 3 я1п Т) — 16 (1 — соя Т)] Т+ ~ я|п Т )
г1 — 1 2~
(7.98)
Полученное выражение для функционала состоит из двух независимых
слагаемых, первое определяется радиусом конечной орбиты г„второе—
углом наклона ее плоскости ~. Эта аддитивность связана с тем, что в линей-
ном приближении, как уже отмечалось, уравнения движения в плоскости
начальной орбиты не связаны с уравнениями движения в перпендикулярной
ПЛОСКОСТИ.
Сравним функционалы и оптимальные программы реактивного ускорения, полу-
ченные здесь и в пп. 1 и 2. Время выполнения маневра будем считать кратным периоду
движения по начальной орбите (Т=2лг, г=1, 2,...). Первое слагаемое функционала
(7.98) совпадает с У"' из (7.86), а второе — с (7.75). Оптимальная программа ускорения
(7.95) с коэффициентами из круглых скобок (7.97) имеет вид
1 — г1 2~
а~(~)= 2Т, а„(~) =О, а~(~) = Т соя~ (Т=2кг, г=1, 2, ...). (7.99)
$ 4. Параметры аппарата с идеальным двигателем
ограниченной мощности
1. Расчетные формулы. Оптимальный режим работы идеального дви-
гателя ограниченной мощности и оптимальные параметры двигателя и ап-
парата в целом могут быть вычислены, как только найдены функции
(7.100)
а (1), У (1) = аЧ1
Если вспомнить, что а~ — — — а,, а =а„, то первые два соотношения (7.99) дадут опти-
мальную программу (7.76) для маневра изменения радиуса (с точностью до о (г,— 1)),
а последнее соотношение — программу (7.74) для маневра изменения угла наклона пло-
скости орбиты (при о,=О). Таким образом, сложный маневр изменения радиуса и угла
наклона круговой орбиты в линейной постановке представлен как суперпозиция двух
простых'. маневра изменения радиуса круговой орбиты и маневра поворота плоскости
круговой орбиты.
Помимо описапных выше, в литературе содержится еще ряд решепий для оптималь-
ных мапевров управляемых спутников с идеальным двигаталем ограниченпой мощности.
В работе (7.30) выписаны дифференциальные уравнения и получены конечные соотно-
шения нулевого приближения для оптимальной программы реактивного ускорения при
изменении всех элементов орбиты. Маневры перехода между круговой и эллиптической
комплапарными орбитами разных радиусов, набора заданной энергии и пр. рассматри-
ваются в (7.31 — 7.33) па основе метода усреднения Крылова — Боголюбова. Решение
(7.95), (7.96) используется при исследовании задач оптимальной встречи спутников (7.34)
и оптимальных межпланетных перелетов (7.35).

208
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОстИ
[ГЛ. 7
— закон изменения реактивного ускорения и интеграл от квадрата ускоре-
ния по времени (см. гл. 6).
Для удобства пользования дадим сводку необходимых формул; при
этом ограничимся случаем одноступенчатого аппарата (без сброса секций
двигательной системы).
Компоненты массы аппарата (ЛХ вЂ” полезная нагрузка, ЛХ,„ — запас
рабочего вещества, ЛХ вЂ” двигательная система, ЛХ (2) — текущая масса
аппарата) определяются следующими соотношениями (см. (6.6), (6.15)—
(6.17)):
ЛХ„ [кг]
Мо [кг]
ЛХ [кг] т — ~2 М(иа ['"г]
м('("' = (-(- ~""'~ оо(] '
Мо [кг] М., [кг]
(Ф = Ф (Т), ~ (о) = 0,5 ° 10 га [кг/квт~1У (2) [ ч'-/се~Г~),
!
) (7.101)
где М, — начальная масса аппарата, а — масса двигательной системы на
единицу мощности реактивной струи.
Максимальная мощность двигателя Г „и программы тяги 1' (2), ско-
рости истечения [" (2) и расхода (у (2) рассчитываются по формулам (см.
(6.2), (6.4))
ЛХ„[кг] Р [~) [кГ] а [~) [м/секо] ЛХ [~) [кг]
а [к%"'гкт] ЛХо [кг] 9,81 Мо [ "г] (7 102)
0,204ЛХ„[кг] /ЛХо [кг] 9,81Р [~) [кГ]
(')' / ' [ /' ] [г)['Г']/М [ ° ]' Д(')'/ ' ~[)[ ~ ']' ~~
Обратим внимание на то, что для вычисления ЛХ, ЛХ „, ЛХ, Г„„„доста-
точно знать только конечное значение функционала Х (Т), а для вычисления
ЛХ (2), Р (2), Г (2), д (2) необходимы обе функции (7.100).
Если маневр разбит на и последовательных этапов и на каждом этапе
функции (7.100) известны: а"' (с), Х"' (с) (О& t; с&lt Т" , Х"' (0) 0 —
времени -. и функционала / на каждом этапе начинается с нуля), то в ка-
честве функций а (2) и Х (2), фигурирующих в (7.101) и (7.102), нужно брать
г — 1
и (О = и'" ~й — ~ т"'),
/'=1
г — 1
т(О=~ т'~ (т'~'(,( т" ~ — ~ т')
г=1 г'=1
с О
г2
~ =о,~ т" =т).
(7.103)
г — 1
при ~ Т(~'(о(,~~ Т'~'
2. Оптимальные параметры межпланетных аппаратов. Чтобы составить
представление о параметрах межпланетных аппаратов с идеальными дви-
гателями ограниченной мощности, воспользуемся результатами решения
вариационной задачи о перелете Земля — Марс — Земля Я 2, п. 7).
Для каждой пары значений полного времени путешествия Т. и времени
пребывания в окрестности Марса Т по рис. 7.27 находится конечная ве-
личина функционала т, после чего при помощи (7.101) вычисляются ЛХ./ЛХ„
М„,/Мо, ЛХ„/М, (удельная масса двигателя а задается). На рис. 7.30 из
[7.17] показана зависимость максимальной полезной нагрузки ЛХ /ЛХ, от
времени Т.— Т для различных значений удельной массы а и времени Т .
Величины ЛХ„,/М, и ЛХ„/М, могут быть найдены из рис. 6.2 по известному
значению ЛХ,/М,.
Если задаться каким-либо уровнем полезной нагрузки, то по рис. 7.30
можно найти соответствующие минимальные времена путешествия. Такие
данные приведены в табл. 7.5 для М,/М,=О,З.

209
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
$41
'.Г а б л и ц а 7.5
Минимальные времена Х, экспедиций Земля — Марс — Земля при уровне
полезной нагрузки 30о~о для различных значений и — удельной массы двигателя
и Х~ — времени пребывания у Марса
Т~, сут
с~ = 0,4 кг/'квт
~ =1 кг/квт
с~ = 4 кг~'квт
с~ = 10 кг,'квт
а = 0,1 кг/квт
Приведем пример оптимальных зависимостей от времени 1 массы ап-
парата Л~ (~), тяги Р (~) и скорости истечения Г (~). Выберем следующие
~~о
10
ЯЮ
~б
04
И
л/5,
10
08
06
Ц1
~08
006
фЯ
01
008
006
1К г00 т Ыата '
Т~-Т, су~
Т,-т,у
100 ЛЮ 400 Ы0 1000
к/
а)
10
~8
ЮЮ
~Ц
01
ЮЯ
©Ю
01
008
0Я
~01 Тц-Т,су~ р Т~-Т~, щ
Ю0 200 400 6Ю ~000 /А ЛР 4Р0 5Х 6И
ф е)
Рис. 7.30. Максимальная полезная нагрузка аппарата пля перелета Земля — Марс — Земля.
значения параметров перелета: полное время путешествия Т.=644 сут
( 1,76 года), время пребывания в окрестности Марса Т =48 сут. Восполь-
зуемся расчетами оптимальных гелиоцентрических траекторий, проведен-
ными в [7.14] с учетом эллиптичности и некомпланарности орбит Марса и
14 Механика полета
0
48
96
144
90
157
223
282
~ю/%~
!Р
~Р
06
ф~
160
238
304
358
255
326
386
440
460
514
566
624
680
738
806
884

210
ИДЕАЛЬНЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Земли для конкретных дат старта (рис. 7.31). Для большей точности учтем
также энергетические затраты на торможение У, и разгонУ, в окрестности
Марса. Последние определяются по рис. 7.25, причем считается Т, = Т,=1!,Та.
Сводка параметров элементарных маневров, составляющих перелет Земля—
Марс — Земля, дана в табл. 7.6.
Таблица 7.6
Параметры оптимального перелета Земля — Марс — Земля
(Т,=644 суггг, Т„, =48 сутп) по участкам
Энергетические
затраты,У,
м-"(сека
Время
выполнения
маневра, срт
Дата
окончания
маневра
Дата начала
маневра
Маневр
50
Разгон у Земли
12
184
Межорбитальный пере-
лет Земля — Марс
Торможение и разгон
у Марса
Межорбитальный пере-
лет Марс — Земля
Торможение у Земли
6.,6
48
312
25
50
12
644
Полный перелет Земля—
Марс — Земля
63,6
Оптимальные соотношения масс аппарата, предназначенного для выпол-
нения этого перелета, находятся по формулам (7.101), они указаны в табл. 7.7.
Т аблица 7.7
Оптимал..ное распределение массы аппарата для перелета
Земля — Марс — Земля (T,=644 сут,, У',,=48 суиг)
при двух значениями удельной массы двигательной системы
Удельна» масса
двигателя а,
кг(квт
Масса рабочего
вещества Ы~,/М„
По. (езная нагрузка
Ц,~Мо
Масса двигателя
Ъ|~ ~' Мо
О, 4()
0,57
О, 3()
0,19
0,24
О, 2'1
5
10
Программа реактивного ускорения а (~) и зависимость функционала
от времени У (г) для рассматриваемого перелета приведены на верхнем
графике рис. 7.32. Под ним представлены зависимости ЛХ (~)/М„Р (~)/М
и Г (~), посчитанные по формулам (7.101), (7.102).
Укажем две важные для дальнейшего особенности оптимальных режимов
работы идеальных двигателей на межпланетных траекториях. Во-первых,
идеальный двигатель включен на протяжении всего полета, что определяет
потребный ресурс порядка 104 час. Во-вторых, по оптимальной программе
необходимо регулировать тягу, скорость истечения и расход в очень ши-
роком диапазоне (например, на рис. 7.32 Р и Г изменяются на порядок).
3. Оптимальные параметры управляемых спутников. Запишем в размер-
ной форме оптимальные функции (7.100) для следующих маневров в окрест-
ности планеты (см. 8 3).
24 марта
1971
13 мая
1971
13 ноября
1971
31 декабря
1971
8 ноября
1972
24 марта
1971
12 мая
1971
12 ноября
1971
30 декабря
1971
7 ноября
1972
27 декабря
1972
27 декабря
1972

1-Р
а(Золя-ЖрС
~ ~~рс-деются
~ис. 7.31 Траектории гелиоцентрических участков в проекции на плоскость эклиптики.
07
л =Х~г Ып
т~ т ' ~ОП ~К т ЮПа г, у
+/
!
Рис. 7.32. Примеры оптимальных законов изменения некоторых характерных параметров аддврд~д
для перелета Земля — Марс — Земля по траектории с рис. 7.31.
~,Ф~„
/Ю /РАЙ
0
лж,4;ею
l
~%се
60

Рис. 7.33. Максимальная полезная нагрузка управляемых спутников.
Р7
лафет
Рис. 7.34. Примеры оптимальных законов изменения некоторых характерных параметров аппарата
для маневра поворота плоскости круговой орбиты на угол г=10' с одновременным изменением радиуса
на ~(т,/т,) — 1~=23,6,~~ (24-часовой спутник Земли.' го —— 42,3 ° 10 км, 8=10, Т=10 сут, промежуточные обо-
роты 1 ( 8 & t 9 показ ны условн

13
ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АППАРАТА
1'. Поворот плоскости круговой орбиты радиуса го на угол ~ с заданным
угловым положением линии узлов Й, (см. (7.74), (7.75)):
а(~) =Йг;12 — ' соя(~ — ~,), У (~) =И*го'~*,, [т+ я|п ~ соя (~ — 22,)]. (7.104)
2'. Переход между круговыми компланарными орбитами радиусов го
и г (см. (7.76), (7.77)):
г 9
аР) =Йг-,2 1 "' У И) — И „-" ',, 1 "' . (7105)
Г1 0 ~ 7~282
3'. Переход между круговыми орбитами радиусов г и г„плоскости
которых составляют между собой угол ~ (см. (7.96) — (7.99)):
а11)=йс;-' — [( ' ') +1ссоя'я]
2
2 Я=асс с,, [2( ' ' +сс1с+я1оя сося)] 12.10о)
4~О
В формулах (7.104) — (7.106) время выполнения маневра Т считается
кратным (г = 1, 2,...) периоду обращения по начальной орбите: 222Й-'/г'„;
щ)емя т безразмерное (О ('с ( 222г), связь с размерным временем ~ такая:
Й=/с-'/г) ~. Размерности остальных величин следующие: [а]=м/сек', [У]=
= м2/сек', [Ц = м'/сек' (для Земли Й = 0,3986 ° 10" м'/сек'), [г,] = [г,] = м,
~ и У1 — углы в радианах.
Относительная полезная нагрузка ЛХ,/ЛХО снова вычисляется по фор-
муле (7.101), она показана на рис. 7.33 как функция У и времени Т для
маневров 1' — 3'. Кривые посчитаны при фиксированных значениях удель-
ной массы двигателя а. На графике даны несколько временных масштабов
для разных наборов параметров маневра (~, г,) 24-часового спутника Земли
(г,=42,3 10' км). Примеры зависимостей ЛХ (~)/ЛХО, Р (~)/ЛХ„У (~), отвечаю-
щих (7.104) — (7.106), приведены на рис. 7.34.
По сравнению с рассмотренным выше случаем межпланетного перелета
режим работы идеального двигателя для управляемых спутников несколько
облегчается — для ряда маневров потребный диапазон регулирования пара-
ыетров двигателя получается довольно узким.

ГЛАВА 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ вЂ” РАЗДЕЛЕНИЕ
ВАРИАЦИОННОЙ ЗАДАЧИ,
ОПТИМАЛЬНЫЕ ПРОГРАММЫ ВЕКТОРА ТЯГИ
$ 1. Разделение вариационной проблемы на параметрическую
и динамическую части
1. Формулировка задачи. Введем релейную функцию о (~), принимающую
значение 1, когда двигатель включен, и значение О, когда он выключен.
Тягу Р (~) и расход д (~) нерегулируемого двигателя запишем в виде Р о (~)
и Ч о (~). В этой записи Р, д — постоянные управляющие параметры, а функ-
ция о (г) определяет моменты включения и выключения двигателя.
Вариационная проблема о доставке максимальной полезной массы за-
писывается в виде (4.8):
ЛХ,(0) =Ма — ЛХ„, ЛХ,(Т) = шах, 1
г(0) =г„, г(Т) =г„
(8.1)
ъ =, е+д, ч(0) =у„
~Я
(Р, д=сопзЬ, о(Е) =1 или О, ~е(Е) ~=1).
т(Т) =ъ,
Здесь масса двигателя до.пжна быть выражена через параъ1етры Р, д:
ЛХ„(Р, д). В вариационной задаче (8.1) требуется определить оптимальные
программы е (~), о (~) и оптимальные значения параметров Р, д. Вместо Р, д
могут фигурировать другие параметры двигателя, через которые выража-
ются первые.
Идеальные двигатели являются идеально регулируемыми; это означает, что их ре-
гулировка подчиняется только главным для рассматриваемого типа двигателей ограни-
чениям (например, ограничению па мощность (гл. 6 и 7) плп на скорость истечения (гл. 5)).
Решение проблемы оптимизации в такой постановке обычно приводит к труднореализуе-
мым законам изменения некоторых параметров двигателя.
В настоящей главе изучается другая крайность в регулировке — нерегулируемые
двигатели.
Нерегулируемьиь называется двигатель, работающий по следующей схеме: ои может
быть либо включен, и тогда тяга Р и расход д постоянны, лиоо выключен, и тогда тяга Р
и расход д нулевые. На изменени направления тяги ограничения не накладываются.
Вариационная проблема для перегулпруемых двигателей, так же как и для идеаль-
ных, разделяется на параметрическую и динамическую части. Последняя, в отличие
от идеального случая, содержит два параметра Р и д (точнее, ао —— Р/Мо, р=у/ЛХ,), по зато
является универсальной для всех типов нерегулируемых двигателей (для ее решения не
требуется знания характеристик (4.9), (4.10)). После установлепня этого факта здесь вы-
числяется функционал динамической части вариационной проблемы для ряда маневров,
выполнимых при любом уровне ускорения от тяги. Далее даются примеры решения пара-
метрической части проблемы для норегулируемых двигателей ограниченной мощности.
Оптимальные параметры аппаратов с нерегулируемыми двигателями ограниченной ско-
рости истечения приводятся в следующей главе. Там же рассматриваются маневры, для
выполнения которых необходим достаточно большой уровень ускорения от тяги.

21
РАЗДЕЛЕНИЕ ВАРИАЦИОННО И ПРОБЛЕМЫ
2. Выделение динамической части задачи. Индивидуальные особенности
двигателя, работающего в нерегулируемом режиме, определяются только
функциональной зависимостью М„(Р, д). Для нахождения наилучшего
двигателя из нерегулируемых можно указать прием, позволяющий общую
вариационную проблему разделить на две части: динамическую, в которой
не нужно знание функции М„(Р, д) и которая вследствие этого является
универсальной, и параметрическую, в которой нужно знание функции М„(Р, д).
Введем новую фазовую координату ~ (~) — текущее время работы
двигателя, определив ее следующими дифференциальными уравнениями и
начальным значением [8.1, 8.2]:
=о, ~ (0)=0.
Третье уравнение из (8.1) интегрируется:
(8.2)
(8.3)
ЛХ. (~) = ЛХ, — Я„(Р, д) .— д~, (~),
и полезная масса М выражается через параметры Р, д и конечное время
работы двигателя 1„(Т)=Т так:
(8.4)
ЛХ.= ЛХ, — ЛХ„(Р, д) — дт,.
1 (Т) = т1п,
г(Т) =г„
=о,
Р
~„(о) =о,
г(0) =г„
г=~,
(8.5)
т= ', е+~, т(0) =т„
Р
(а„р. = сом(„о(~) =1 или О,
у(Т) = т,
/е (Е) /— : 1).
В этой записи а,=Р/М„р=д/М, — параметры задачи (начальное
ускорение от тяги и относительный расход). Вместо р часто используется
скорость истечения Г=а,/р. Формальным предельным переходом н -~ 0
или Г -~ оо получается случай постоянного реактивного ускорения а (1)=а,.
Вариационная проблема (8.5) представляет собой динамическую часть
общей проблемы; результат ее решения — функция Т (Р/М„, д/М,).
11ри известной функции Т„(Р/М„, д/ЛХ,) и известной зависимости
ЛХ„(Р, д) может быть решена заключительная — параметрическая — часть
вариационной проблемы, найден максимум полезной массы по парамет-
рамР,д:
шах% = шах М вЂ” Ц Р, д — дТ
Р ц
з О х
Р, о
Л1 ' Ц
О О
( )
::. Сделаем несколько замечаний к изложенному.
1". Можно по-другому выделить из общей вариационной проблемы часть, не свя-
занную с видом функции М., (Р, д). Если вместо ~„(~) ввести фазовую координату
ЛХ (~) — текущую полную массу:
М (~) = М„+ М. (~),
(8.7)
то будет достигнут тот же результат. Между функционалами М (Т)=М, и ~ (Т)=Т
существует очевидная связь.'
~1=МΠ— д~' или т1 =1 — у.Т
Р'
(8.8]
Если зафиксировать параметры Р и д, то максимум полезной массы ЛХ„
соответствует минимуму времени Т .
Заменим в вариационной задаче функционал; пусть теперь вместо мак-
симума М, ищется минимум Т при фиксированных Р, д. Выделенная ва-
риационная проблема имеет вид (см. (8.3))

ЫЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
2'. Если из решения вариационной задачи (8.5) следует, что о (г) =1 при 0 & t  &
т. е. минимизируемое конечное время работы двигателя Т равно заданному времени вы-
полнения маневра Т, то постановка (8.5) теряет смысл. В этом случае нужно либо, отка-
завшись от выделения динамической части проблемы, вернуться к постановке (8.1), либо
использовать постановку, взаимную с (8.5): время Т задано, ищется минимум Т ').
Новая вариационная проблема является задачей а максимальное быстродействие.'
=б,
г=ч,
(О)=0, г (Т)=Т,
г(0) =го, г (Т) =г„Т=т)п
(8.9)
а Ь
Ф= е+д,
Р р.
(ао, р,= сопв(,
т (0) = то, т (Т) = т,
о (г) = 1 или О, ~ е (г) = 1 ~ ).
В рамках этой постановки случай о(г)=1 получается, когда время Т~ не фиксиру-
ется: г (Т)=орС (см. п. 1 ~ 2).
3'. Если конечное время работы двигателя ограничено (задан ресурс двигательной
системы (см. ~ 2 гл. 10)), то постановку вариационной задачи (8.5) можно сохранить;
в результате ее решения получится функция Т (Р/М„д/ЛХ,), и дополнительное условие
выделит связь между Р(М и д/МО:
(8.10)
Т, (Р/М,, д/ЛХ,) ( Т,„„„
тах ЛХ = тах ЛХΠ— ЛХ„(Р, д) — (1+ ~) дТ
О О
(8.11)
где ~=М~/М о — удельная масса баков на единицу начальной массы рабочего вещества
М О=дТ~ (заданный конструктивный параметр).
$ 2. Уравнения для оптимальной программы
вектора тяги. Модельные задачи
1. Произвольное гравитационное поле. Соотношения, определяющие
оптимальную программу тяги, выписываются на основе принципа максимума.
Все формулы, за исключением одного граничного условия, для двух обсуж-
даемых постановок (8.5) и (8.9) совпадают. При рассмотрении конкретных
маневров в зависимости от первоисточника будет использоваться тот или
другой вариант упомянутого граничного условия.
Функция Гамильтона динамической части задачи и уравнения импуль-
сов выглядят так:
Н=р 3+(р, е) ' +(р, д)+(р„т),
(8.12)
где
дН ~О
р~ = — — — — (р е)
Р дг ' (1 — рг )2
д
р,= — — „(р. а) р,= — р,
(8.13)
') Если зависимость Тэ,м (Т) не является монотонно убывающей, то необходимо
еще рассматривать постановку на максимум Т. Более подробно об этом говорится в и. 1 1 3.
где Т „„, — заданное значение конечного времени работы двигателя. Решение парамет-
р,тах
рическои части проблемы теперь заключается в нахождении максимума (8.6) при допол-
нительной связи (8.10).
4'. Компонента ЛХз — масса баков для рабочего вещества (см. $ 1 гл. 10) — может
быть учтена в параметрической части вариационной проблемы, если вместо выражения(8.6)
записать следующее:

217
УРАВНЕНИЯ ОПТИМАЛЬНО И ПРОГРАММЫ ВЕКТОРА ТЯГИ
Оптимальные соотношения для управляющих функций е (1) и о (1)
находятся из условия абсолютного максимума (8.12) по соответствующей
переменной (так как в обеих задачах ищется минимум функционала: Т
в (8.5) и Т вЂ” в (8.9)).
Оптимальная программа направления тяги получается следующей
(тах Н по е, ~е (~)~=1):
(Р.= 1Р.1)'
( .14)
е„, = р,/р,
релейная управляющая функция й (~), отвечающая за включение ( 8=1)
и выключение (О=О) двигателя, с учетом (8.14) определяется соотношением
(тах Н по о)
3
1 при Л)0,
О при Л(0,
~=Р~„+Рв 1
Р
(8.15)
особый случай Л=О, ~=0 может иметь место только при Р'„=0 (п. 3 настоя-
щего параграфа, подробнее см. [8.3]).
Выпишем граничное условие, отвечающее за функционал задачи. В по-
становке (8.5) функционалом является конечное значение фазовой коорди-
наты ~ (Т); соответствующее граничное условие есть р~ (Т) ( О или после
нормировки
Р,,(Т) = — 1.
(.1)
В постановке (8.9) функционал — время Т, поэтому граничным усло-
вием будет
Н)Т)=(р )Т)+~,)Т) )5 )Т)+р,(Т) К)~)Г), Т)+р,(Т) ° у)Т))О
(8.17)
Таким образом, полная система уравнений оптимального движения
складывается в случае (8.5) из (8.5), (8.13) — (8.16), в случае (8.9) — из (8.9),
(8.13) — (8.15), (8.17).
Рассмотрим теперь, как в рамках постановки (8.9) получить оптималь-
ный режим 3 (~):1 (см. замечание 2' в ~ 1). Пусть ~ (Т) не задано. Тогда по
условию оптимальности р~ (Т) =О. Производная импульса р~~, согласно (8.13),
(8.14), всегда неположительна:
~о~~орй
Рг„— — Р, (1
Р
при 0(~(Т;
(8.18)
поэтому в данном случае р~ (~) ) О при О ( ~ ( Т и по (8.15) й (~)= — 1.
Последнее условие означает отсутствие выключения двигателя (Т =Т).
Если Т ( Т, то из (8.15) следует р~ (Т) ( О, в противном случае было бы
3(~)=1 и Т =Т.
2. Центральное поле. Уравнения оптимального движения в централь-
ном гравитационном поле получаются как частный случай (8.5), (8.13) — (8.16)
или (8.9), (8.13) — (8.15), (8.17) при

[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Для плоского движения в полярных координатах (4.18) они имеют вид (без
краевых условий)
=о, „
2 2
у ~О~~орй
г Р,+Р ~ (1 — р.~ )' '
Р
2
2
Рг Ря г2 + РО. г2 гз
У У
— Р
г /г,
в~
Р~1„ 09 1
1 — р~ ~,' ~ + г г2
'1О
~0 ор$ р
У У,
1
1 — ф ~р" ~ Р. г
1
(о„„= 1 при Л) О,
Ь=Р~ +а,фР', +
) (8.19)
Здесь все величины безразмерные: в качестве характерных берутся
те же значения, что и в соответствующих разделах гл. 7; характерное зна-
чение для параметра р — величина, обратная характерному времени
Краевые условия для г, ~, и„, и записываются в соответствии с рассматри-
ваемым динамическим маневром, к ним добавляются условия ~ (0)=0 и
(8.16) в постановке (8.5) или ~„(0)=0 и (8.17) в постановке (8.9).
Система (8.19) обладает двумя первыми интегралами: р (~)=сопят и
9
Х (~)=сопвФ, поскольку угол ~ и время ~ не входят явно в правые части
уравнений.
Укажем преобразования, аналогичные (7.15) и (7.16), которые сохра-
няют уравнения (8.19):
преобразование растяжения
1/
~г — Г "с~,
1
г- 1г,
9 9
р ~ ~ — '/,Р
9
0О 1 00.
з~
Р,.— ~ 1
Р Г'Р
Р ~ Р,
(~& t
(8.20)
преоо~)азование замены знака
— ~ у )
'Р'
Р, ~ Р, (8.21)
г- г,
(~) — ~ — ~Р
р„-~ р„»
Р Р Рр Рр
0 — ~ Оо,
р„= Ь1,
2 1
(8.22)
где Ь„Ь, — постоянные векторы, определяемые из граничных условий.
Использование замены (8.21) для пересчета «прямой» траектории на
«обратную», в отличие от ~ 1 гл. 7, здесь затруднительно, хотя бы потому,
что нужно иметь (<прям е» траекто и с отрицательн ми значени ми р
хода (р — э — р).
3. Плоскопараллельное поле. Если ускорение от гравитационных сил
положить постоянным (д (г, ~)=сопвФ, см. (4.62)), то система уравнений оп-
тицального движения упрощается. Импульсы р„и р, выражаются в конеч-
ном виде:

219
УРАВНЕНИЯ ОПТИМАЛЬНОИ ПРОГРАММЫ ВЕКТОРА ТЯГИ
Отсюда в соответствии с (8.14) определяется направление тяги:
(8.23)
Для одномерных движений (пп. 4, 5), когда тяга может быть направлена
либо по скорости, либо против скорости, последнее соотношение преобра-
зуется к следующему:
(8.24)
е (1) = ашп (62 — Ь 1).
Е (Т) = п11п,
и(Т) =и,
(8.25)
~(1) =1 или О, е(1) = + 1).
Функция Н и уравнения для импульсов здесь таковы:
(1 — р~ )'
р„= О.
Н р~ р„3,
р~„(Т) = — 1,
(8.26)
Максимум Н по е достигается при е (~)=в1дп р„=сопз$; считая и, ) О,
получаем
(8.27)
е (1) = 1
(р„) 0).
Комбинация Л (см. (8.15)), стоящая множителем при 3 в функции Н,
в силу дифференциальных уравнений (8.25), (8.26) постоянна; поэтому
1 при Ь (0) :& t;
0 при Ь(0) (О,
(8.28)
Второй вариант в (8.28) соответствует тривиальному случаю и,=О.
Остается рассмотреть еще Л (0) =0; здесь функция Н не будет зависеть от
управления О (поскольку Л (~): — 0), расположение моментов включения и
выключения двигателя может быть произвольно, определяется только сум-
марная протяженность активных участков (из условия и (Т)=и,).
Интегрирование уравнения для и из (8.25) при условии (8.27) дает ко-
нечную связь (формула Циолковского):
(8.29)
отсюда можно выразить суммарное время работы двигателя Т через пара-
метр маневра и, и параметры двигателя ао, р. Полное время движения Т
не влияет на функционал задачи Т, оно совпадает с Т при Л (0) ) 0 и
Условие переключения (8.15) совместно с уравнением (8.22) для импульса
р„позволяет сделать заключение о числе пассивных участков. На пассивном
участке выполняются соотношения о (~)=0, р~ — — сопв$, ~ =сопз$ (см. (8.13)),
поэтому в начале (1=1,) и в конце его (1=1,) должно быть р„(1,) =р,, (1,)—
из условия Л (~,) =Л (~,) =О. Поскольку для плоскопараллельного поля
функция, обратная р,, (~), в общем случае двузначная, то на оптимальной
траектории может быть не более одного пассивного участка [8.1, 8.31.
4. Набор модуля скорости в бессиловом поле. Дифференциальные урав-
нения и краевые условия (8.5) для маневра набора заданного модуля ско-
рости имеют вид (ср. (4.74))

220
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
больше Т„при Л (0)=0. Окончательное выражение для функционала Т
записывается в виде
Т = — 1 — е '0 = — — е ' . Т.
(8. 30)
При отыскании максимума полезной массы по параметрам а, и р (что
будет проделано в 3 5) в оптимальном варианте оказывается Т =Т.
о. Перемещение между точками покоя в бессиловом поле. Дифферен-
циальные уравнения и краевые условия (8.5) для перелета между двумя
положениями покоя имеют вид (ср. (4.75))
=о, (0) = О, ~„(Т) = п11'и,
я=и, х (0) = О, х (Т) = 1,
(.1)
и= ', е, и(0) =О, и(Т) =0
(а„р.= сопз(,, 8(1) = 1 или О, е(~) = + 1).
Уравнения для импульсов рх, р„интегрируются — см. (8.22) для х-компоненты.
Оптимальное направление тяги (по скорости или против скорости) определяется соотно-
шением (8.24). Последнее позволяет определить знаки постоянных Ь, Ь . В силу (8.24)
направлсние тяги может меняться па противоположное пе более одного раза. Граничные
условия (8.31) для х и и таковы, что тяга в начале движения должна быть направлена по
скорости, а в конце — против скорости. Отсюда следует, что Ь, ) О, Ь, & t  и то
мент 1„, где р„обращается в нуль (Ь,— Ь,~,=О), лежит внутри отрезка [О, Т1 На этом
основании соотношения (8.22), (8.24) моясно переписать так:
р =Ь1, р„=(ф~ — ~) Ь,, е=з~цп (~„, — ~) (Ь,) О, О(~,„( Т),
т. е. на участке О ~ ~ ( ~ тяга направлена по скорости и на участке ~„( ~ & t; Т
1 ~ 1
!
Рис. 8.2. Функция ь (1) и оптимальная
программа б (1) включения-выключения
двигателя.
Рис. 8.1. Импульс р~ и
оптимальный закон е (1) на-
правления тяги.
против скорости (рис. 8.1). Функция Л, определяющая моменты включения и выключе-
ния двигателя (см. (8.15)), здесь равна
ь=р, +ь,~ю,— Ц, (8.33)
Р
Чтобы выяснить характер поведения функции Л, выпишем ее производную:
~о
Л вЂ” Ь1 (~ ~ )2 Я18п (Е,р Е)
— р1
(8.34)

Я 2]
УРАВНЕНИЯ ОПТИМАЛЬНОЯ ПРОГРАММЫ ВЕКТОРА ТЯГИ
221
(при этом выражения ля ' и г бе
д р', „рутся из соответствующих дифференциальных урав-
нений (8 18), (8.31)); отсюда
Ь (~) ( О при О & t  ( ~ „ Ь ~  О ри ~ „
(8.35)
(точка ~=~„— угловая). Начальное значение Л (0) должно быть строго больше н ля
в противном случае, согласно (8.35), будет либо Л (~) & t      l ; ~ &l ;
сивное двиндение) либо Л (~) & t
активный участок с е (~) = — 1 так как ~ ) ~ И
при <1&l ;1„„и ( ) 0 п
1
к, „. в том и в другом варианте не могут быть
удовлетворены конечные условия (8.31), следовательно,
(8.36)
Из ~8.36~ и ~8.35~ м ожно заключить, что возможны два случая. 'первый
Ь(~))0 при 0<
(8.37)
(пасспвный участок отсутствует) и второй
Ь (Е) ) О при 0 & t й й и Е ( & t Т, Ь Е) О при й
(0(г, & t; „- ~,
(8.38)
(пассивньш участок в середине траектории — при ~ & t   . 8 2
из (8.38) при ~д=8„=~,.
алыче удет рассматриваться второй случай как более об ": ~8.37~
Отметим, что моменты ~„Г, выключения и включения двигателя асп
иетрично относительно ~=~„8.3]. В самом еле
ения двигателя расположены сим-
( (8 18) (8 31
Л (~) = р (г,1 + Ь ~~ — г]
(8. 39)
Отсюда видно, что корни уравнения Л (~)=0 равноудалены от ~„.
ти задачу до конца,
Проведенного исследования достаточно, чтобы довести
не прибегая к интегрированию полной системы урав (
нениями для имп льсов. П
авнении вместе с
у ов). римем в качестве неизвестных постоянных мо-
ав урав-
так [8.1, 8.3]:
менты Г„1, вместо Ьд, 1„. Оптимальные управления е (1) о(1) запишутся
(8.40)
С оотношения (8.40) подставляются в правые части иффе
авнений (8.31)
ур Й ~ . '„последние интегрируются по участкам с учетом соответ-
ствующих краевых условий:
(8.41)
т
е=+1, о=1
3=0
е= — 1, 8=1
при 0 ( ~ ( ~ (участок разгона),
прп 1д ( 1 ( 1 (пассивный участок),
и ри ~, ( ~ ( Т (участок торможения).

222
[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
или после вычисления интегралов:
г, + Т вЂ” ~, = Т„, ! п [1 — р. (~, + Т вЂ” ~,) ] — 2 !п (1 — рг,) = О,
& t
— — ~, + ~, — 2Т) 1и ~1 — ф1)—
(8.42)
— — — 1 + 12 — Т ]п [1 — р. (1 + Т вЂ” 12)]+ 1 + 12 — Т = — ~.
1
Р
р. 1 2
Первые два соотношения (8.42) позволяют выразить ~, и ~, через Т,
Т, р: ~,=р 1(1 — ~/1 — рТ ), ~,=Т вЂ” Т +~,. Отсюда видно, что участок
г,/т,
1
~~У ~т„
~7 Щ ф~ ~7~ /
Рис. 8.3. Доля 1,/Т~ полного врсмсни работы двигателя, приходящаяся на участок разгона.
разгона больше по времени, чем участок торможения; с уменьшением расхода р
их разность стремится к нулю (см. на рис. 8.3 зависимость |,/Т„от рТ„).
Исключив из третьего соотношения (8.42) ~, и ~„получим искомое вы-
ражение Т„(ао, и) функционала динамической части задачи в неявном виде:
~ 1.= — (1 — ~/1 — р.Т ) — Т вЂ” (Т вЂ” Т ) 1п ~/1 — р.Т . (8.43)
я 3. Оптимальный межпланетный перелет
с иерегулируемыми двигателями
Я,:(г(~„"), т(~,",), ~,",;...; г(~";), ~(~";), ~'„;...; г(~,',), т(г,",), ~"„) =0 (8.~4)
(1 = 1,..., т ( (йп1 г+ Й~т т + 1) (и+ 1)).
В промежуточных точках (~=1, ..., и — 1) происходит мгновенный
сброс полезной массы заданного размера ЛМ~'~. Поэтому текущая масса
аппарата терпит в этих точках разрывы:
(~ = 1,..., и — 1; ЬМ~'~ = йхе).
Сброс массы осуществляется с нулевой скоростью, так что радиус-вектор г
и скорость ~ остаются непрерывными.
1. Разделение задачи оптимизации на параметрическую и динами-
ческую части. Если подходить к межпланетному перелету с возвращением
как к единому маневру, то необходимо учитывать две его особенности: на-
личие условий на фазовые координаты в промежуточной точке (у планеты
назначения) и возможность мгновенного сброса массы аппарата в этой точке
(на планете назначения могут быть оставлены исследовательские приборы,
десантный аппарат и т. п.). Рассмотрим более общую схему такого ма-
невра [8.4].
Пусть в некоторые моменты времени ~„( ~; (... ( ~„(включая
начальный Ц =1„и конечный 1,=1„) наложены условия на радиус-вектор г
и скорость ~ центра масс аппарата. Ч исло таких моментов задано—
(и+1), а их величины ~',: либо тоже заданы, либо, в общем случае, входят
в связи наряду с г и т (см., например, (4.70), (4.73)):

223
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
Начальную массу аппарата, величина которой ограничена сверху:
М(0) =М,+М„+М„,+М (М,=йхе, (8.45)
составляют следующие компоненты:
полезная масса (максимизируемая величина)
и — 1
М,) ~ ЬМ~'& t = й
(8.46)
масса двигательной системы, зависящая от тяги Р = сопят, расхода
д=сопя$ и, в общем случае, от суммарного времени работы двигателя 1) Т .,
М„=М„(Р, д, Т„), дМ„~дТ,.) 0 (8.47)
(при движении постоянна '));
начальная масса рабочего вещества, которая для нерегулируемых дви-
гателей выражается через расход д и суммарное время работы двигателя
(8.48)
и„= дт,;
масса баков для рабочего вещества, зависящая от начальной массы
рабочего вещества,
(8.49)
дЛХ./дМ„„) 0
М,= М (М„,),
поэтому максимуму 1~1 в этом случае соответствует минимум Т,.
Вариационная задача о минимуме времени работы двигателя при фик-
сированных его параметрах (динамическая часть) записывается ана-
логично (8.5):
1 © =О, 1„(1 ) =п1'(п,
~=О, 1,...., и;
~, (г (~';), (~'",), ~';) = 0
8=1,..., т
Г=У,
(8.51)
+ и (г, ~) при 1";, ' 1 ( 1'; (~ = 1,..., и)
с (1) = 1 или О, ( е (1( (= 1; а, =, л =, ЬтИ = " = сале1).
От динамической задачи (8.5) для двухточечного маневра без сброса
массы задача (8.51) отличается тремя моментами: 1) помимо двух параметров
') Этим способом можно учесть и ограничение на ресурс двигателя Т~, ( Т„„,,„,,
задав И., (Р, д, Т„,) — э со при Т,— э Т„
2) Применяемый далее метод решения задачи по отдельным участкам позволяет
использовать результаты и для случая сбрасы васиных сскцпй двигательной системы и баков.
если сброс производится в момеиты врсмеии ~,".
(при движении постоянна ')).
Аналогично тому, как это делалось для двухточечных маневров без
сброса массы (см. ~ 1), здесь может быть выделена динамическая часть задачи
о минимуме суммарного времени работы двигателя Т„.. В самом деле, по-
лезная масса (8.46), согласно (8.45), (8.47) — (8.49), при фиксированных зна-
чениях тяги Р, расхода д и начальной массы М(0) будет монотонно убываю-
щей функцией Т„:
М. = Л~ (О) — М„(Р, д, Т, ) — дт, — М,(дт, ), (8.50)

224
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
двигателя ао и р задача (8.51) содержит еще (и — 1) параметров сброса
массы Лт~'&g ;; 2) пра ая ча ть векторн го уравне ия ля скоро т в (8.
не является непрерывной функцией фазовых координат; 3) на радиус-век-
тор, скорость и время в (8.51) наложены (и — 1) условий в промежуточных
точках траекторий.
Если размерность многообразий, которым должны принадлежать (и — 1)
промежуточных точек траекторий, невелика или может быть сделана тако-
вой в некотором приближении, то задачу (8.51) выгодно расщепить на и
двухточечных задач.
Назовем ~-м элементарным маневром перемещение из (ь — 1)-й в ~-ю
точку (см. (8.44)). Первая из этих точек будет начальной, а вторая — конеч-
ной для ~-Го маневра:
ф = 1"; „гои = г (1"; 1), т&lt '  т (1';
е&lt ' gt; е';, г ( > = г (е , , т<
(Е = 1,..., и).
Обозначим через
Т® =- ~ (~"„) — ~„ (~'; ,)
° ° ° ° ° °
и
~ — („, п ~Т~'&gt = Щ Ђ ~ (1, =Т ~~ (8.
~=1
время работы двигателя на ~-м участке и вычислим в соответствии с третьим
уравнением (8.51) начальное реактивное ускорение а(о(~ и относительный
расход рабочего вещества р"' для этого маневра:
(8.54)
а~'~ =
О
1 — ~ (Лт~~~+ р.Т~~~)
1 — ~ (Лт ~~ + р,Т~~~~)
(~ =2,..., и) аЦ~ =а„, р."'=р. =а,/Г.
Фиксируем начальные и конечные точки (8.52) для всех элементарных
маневров, выполняя условия (8.44) и условие непрерывности г, т, ~. Тогда,
как будет показано ниже, задача (8.51) о минимуме суммарного времени
работы двигателя Т„.='~ Т(~' расщепляется на и двухточечных вариацион-
ных задач о минимуме времени работы двигателя Т(„'~ для каждого из эле-
ментарных маневров [8.4]:
=о,
г=ч,
(Ц'&g ;) О 8 ( ® =
р. Π— р.
г (ф&g ; = г& t '&gt , г ф'~
(8.55)
а,'," е~
т= ",, +д, т(ф1) =то('&g ; т Я )) =У
р(~) ~
(3 (~) =1 или О, ~ е(~) ~=1; а< ~, р '" =сопз ,; 1=1,. ., )
и
Т„. =,~, Т~'~ = Т . (г (Г";), т (Г",), ~',)
(8.56)
(~ =О,..., и).
Минимум этой функции по ее аргументам, подчиненным условиям (8.44),
и даст решение задачи (8.51).
где параметры а(,'& t и р '~ определяю ся соотношени ми (8.5 ), (8.5
Задача (8.55) представляет собой уже обычную двухточечную задачу
оптимального управления с непрерывными и непрерывно дифференцируе-
мыми правыми частями уравнений. После решения задачи (8.55) для каждого
из элементарных маневров, определятся значения времени работы двига-
теля Т(„'~, а по ним — суммарное время Т„, как функция начальных и ко-
нечных точек (8.52):

225
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
Докажем справедливость проведенного разделения, т. е. докажем, что при фикси-
рованных параметрах Р, д, ЛМ,"& t и ри фиксирован ых точ ах (8.
т(п ~ Тс" =~ т&g ;п Т&
е (~), ~ (~)... е (~), ~(~)
(8.57)
'~ — 1 I ~'
Т''~ = Т"' а"' ~ Т"' = Т"' ~ Т' ~'
Т „=Т; а„~ Т =Т ш,„~~ Т
7=1 ~=1
(8.58)
Для доказательства сформулируем исходную задачу оптиипзации прн фиксирован-
ных параметрах двигателя и граничных данных всех элементарных маневров в терминах
начальных и полезных масс аппарата на элементарных маневрах. Условие выполнимости
~-го маневра с данной двигательной системой запишем как условие принадлежпостп на-
чальной массы М„"' и полезной массы М„"' некоторой допустимой области Ы;. Кроме того,
учтем условие, связывающее начальную для ~-го маневра массу с полезной массой преды-
дущего маневра:
Мс~>= & t;' > — ЬМ
(с =2,..., и),
а для первого маневра — условие (8.45) ограниченности начальной массы сверху.
Нужно максимизировать полезную массу последнего маневра (так, как М„'"' =М
гс — 1
— ~~)' Ьм,"&g ; а Ьм с> за
шах М„'"' по М,'с&g ;, Лl, '& t; (&gt =
»ри (ЛХ,',с &g ;, Мо ' ~ Я, ( = 1,. .,
Лс'& t = М ' 1&g ; вЂ Ь с 1& t + М + М (Е = 2
М~1& t & t; М (М , М , Мд, м~с'&gt
(8.59)
Далее будут исследованы свойства областей У;. На основании этих свойств будет
показано, что во всем практически интересном диапазоне значений параметра М„решение
задачи (8.59) удовлетворяет соотношениям (8.58).
Рассмотрим с-й элементарный двухточечный маневр, считая двигатель фиксирован-
ным (Р, У, М„=11хе), а начальную для этого маневра массу Мс," — варьируемой ').
Исследуем область Ы возможных значений параметров аппарата на плоскости М„М .
Рассмотрение начнем с плоскости параметров а„Т~, связанной с плоскостью Мо, М
') Скорость истечения Г здесь меняться не будет, поэтому второй аргумент
р"' = а„"'/Р можно не указывать.
') При этом, пока речь идет об отдельном элементарном маневре, для сокращения
записи верхний индекс ~ опускается.
15 Механика полета
Это утвернсдение естественно по физическим соображениям, но пе очевидно с мате-
матической точки зрения. Для аддитивных функционалов (когда значение функционала
представимо в виде суммы независимых друг от друга значений функционала по участкам,
см. ~ 5 гл. 5 и ~ 2 гл. 7) равенство (8.57) не вызывает сомнений. Здесь же функционал на
с-и участке зависит от значений функционала на предыдущих участках через начальное
реактивное ускорение и относительный расход (8.54). Причем с увеличением суммы Т„'&g
по &g ;' о 1 до (с Ђ” 1) ускоре ие а  gt; и асхо р'"> во рас ают, что п иводит к у еньш
т. е. имеет место зависимость, неблагоприятная для доказательства.
Пусть при фиксированных точках (г (с'), т (~'), с,") найдено решение задачи (8.51):
определены минимальное значение Т„,;„суммарного времени работы двигателя
и оптимальны е значения Т ',р~ времени работы двигателя на каждом участке
(ХТ„',„, = Т, ~;„). Тогда по фо;>м ле (8. 0) мо ут б ть вычисл ны ма>,си1&
полезная масса, масса двигательной системы М„(Р, д, Т,;,) и масса баков
М&g ;&gt  ЧТр ~ ш
Обозначим через Т~ш>;„(а lt;") мини ально воз ожн е для д нного а,'," время
двигателя на с-и участке ). Оно получается в результате решения задачи (8.55) для тех же
самых началь»ых и конечных точек, которые были выбраны при решении задачи (8.51).
Покажем, что для всех ~=1,..., и

226
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
соотношениями
ао = Рlмо
Область возможных значений определяется следующими тремя ограничениями'.
во-первых, время работы двигателя не может превышать времени выполнения ма-
невра '):
ТР ~~ ~С г1 — 1
(8.60)
во-вторых, текущая масса аппарата не может стать меньше заданного нижнего
и
уровня М;,х (в данном случае М!~хх — М„+ М~+ ~ Ьи„'.х'х), т. е.
ф
(8.61)
в-третьих, время работы двигателя ограничено снизу.'
Тх, ) Т„хшххх (ао).
(8.62)
При меньших временах Т„данный маневр не может быть выполнен за фиксированное
время Т. Минимально возможное значение Т„„;„получается в результате решения вариа-
ционной задачи (8.55). При этом ограничение (8.60) выполняется автоматически, а (8.61)—
в ослабленном варианте, с Мх,х — — 0 (неотрицательность текущей массы аппарата).
Приведем несколько своиств функции Т„; (а„), полезных для дальнейшего.
1'. На основании решений дипамической части задачи для идеальных двигателей
ограничепнохх скорости истечения (гл. 5) и огранпчешхой мощности (гл. 6, 7) мохххст быть
построена нижняя оценка для Т,; . В оптимальном варианте скорость истечепия К для
двигателей ограниченной скорости, мощность реактивной струи Р для двигателей огра-
ниченной мощности постоянны (равны своим максимальным значениям): У=сопзС (гл. 5)
и хх'=соней (гл. 6). Для нерегулируемых двигателей постоянны и х', и Л=х/ Р х'; поэтому
на одном и том же маневре
х тах т (Т)
тах т (Т) вох &
а(8)
а(8) тах т (Т),,
а(8)
поскольку слева при решепии вариационной задачи присутствуют два ограничения,
а справа — только по одному из них.
В соответствии с (8.8), (6.10) и (5.6) имеем
Т,;„= п1и1 Т„
а(~)
а К
а(~)
)хх=сопеХ а ь'
"о
тах т (Т)х, в5х — — е
а(8)
ь к
— 1+ пРи ао ( ~ (е 'Х вЂ” 1)
О
Т„„(ао) )
(8.63)
— (1 — е ~~ ) при
~о
ао) ~(е ' — 1)
Таким образом, оценка с 1Ч = сонями существенна при малых значениях реактив-
ного ускорения, а оценка с Г = соиз — при больших. Для некоторых маневров может
') Если есть ограничения на ресурс двигателя Т„( Т„„, то правую часть нера-
венства (8.60) нужно заменить на тххх (Т, Т „), что несущественно для дальнейших
рассуждений.
Отсюда и получаем нижнюю оценку для Т
&
т
о
с
т
) о

227
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
быть существенной только одна оценка с Г = сопяС, если точка смены оценок аО =
=(У/Г) (е~")~ — 1) 1 выходит из области определения функции Т„,, (а,). Например,
это имеет место для маневра набора скорости в бессиловом поле, где Т„„д во всеЙ
области определения точно совпадает со вторым участком (Г = сопз1) оценки (8.63)
(см. 8.30)).
2'. При больших (по сравнению с гравитационным ускорением) значениях на-
чального реактивного ускорения функция Тр „(а,) стремится ко второй из нижних
оценок (8.63):
Т ~ (аа)= — (1 — е '~ )+о (8.64)
О О
где д„— характерное для данного маневра значение гравитационного ускорения, напри-
мер, максимальное.
Наличие такой асимптотики объясняется тем, что решение динамической части
задачи на минимум характеристической скорости Ьи достигается на траекто-
риях с импульсным приложением тяги в конечном числе точек (гл. 5). В интегральном
смысле эти мгновенные импульсы хорошо аппроксимируются конечными участками дей-
ствия постоянной тяги при достаточно большой ее величипе.
3'. Функция Т„ш;„(аа) определена на полубесконечном интервале [а „, со], причем
Т;, (аа„,) = Т, шах 1+ — 1; (1 — ~)))г) & t; а  lt; .
Соотношения (8.65) справедливы, если иет дополнительных ограничений на реактив-
ное ускорение (помимо тех, которые порождаются неравенствами (8.60) и(8.61) с ЛХ;,г —— 0).
Нижняя оценка для левой границы а„„области существования следует из (8.63), где нужно
положить Т;„= Т. Верхняя оценка основана ца аснмптотике (8.64) и получается в резуль-
тате следующих рассуждений.
Для любых аа ~ Г/Т за время, ие превосходящее Т, текущая масса т (г) может
стать сколь угодно малой, а текущее реактивное ускорение а (й)=аа/т (Й) — сколь угодно
большим. Это расширяет возможности выполнения маневра в смысле уравнений движе-
ния, цо сужает их в смысле уравнения расхода массы. Для того чтобы оставшейся массы
т (г) хватило для завершения маневра, в соответствии с (8.64) необходимо ц достаточно
выполнение неравенства
о (т (г))
т (г)
где 1))(Г) — приращение характеристической скорости, потребное для завершения ма-
невра. Оцо зависит от величины оставшегося времени (Т вЂ” г) и от фазовых коорди-
нат г (г), 1 (1). Предполагается, что ири конечных значениях (Т вЂ” г) ) 0 сущест-
вует траектория, завершающая маневр, с конечным Ги (1) ( со. Это ))))едцоложецие
подтверждается материалами гл. 5. При аа ~ Г/Т для (Т вЂ” г) есть оценка снизу:
(Т вЂ” г) ) Т вЂ” (Г)'аа). Поэтому на конечном расстоянии аа с))рава от Г/Т нре~)я
(Т вЂ” г) заведомо конечно, а значит, ио сделанному предположению, конечно и ца.
Последнее гарантирует выполнение нуя;ного неравенства для любых пъ (г), не пре-
восходящих некоторо1о значения. Таким образом, для всех ~~ ) Ъ'(Т маневр вьшол-
ним (цо крайней мере с т (Т) =О, т. е. с Т,„= Г/аа), поэтому левая граница ооласти
определения функции Т~ „(аа) не может лежать правее (Г)Т).
4'. Функция Т„„)„(й ) — монотонно убывающая, гладкая, выпуклая вниз:
дТ,; /даа ( О, д2Т„,;„/даа ) О.
Это подтверждается результатами численных и аналитических решений, приведенных
в настоящей главе.
Допустимое множество, определяемое неравенствами (8.60) — (8.62) с учетом свойств
(8.63) — (8.65), представляет собой на плоскости аа, Т„в невырождецном случае криволиней-
ный треугольник с вершинами
аа1 — — а „из (8.65),
а = (1 + М; /Р) ' (Г/Т),
Р У ' Р
"Оз ~ п1~п ц. р ~ у.
1а1 1аГ
тм — — т;
— )~ ~1/1' ~ ~~1ПГ
Т, 3 = ~„~~а (аоз) = )и °
иоз
Вид допустимой области в координатах аО, Т„показан на рис. 8.4, а и 8.4, б. ];ранич-
ный участок 1 — 2 соответствует равенству в (8.60), участок 2 — 8 — равенству в (8.61),
15*

228
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
участок 8 — 1 — равенству в (8.62). Пунктиром нанесены линии постоянства конечной
массы М,=сопя1 или, что здесь то же самое, постоянства полезной массы М,=
=М1 — ̄— ЛХз. При М1=М; ~ линия уровпясовпадает с границей 2 — 8 (на рисунках
М~,г — — 2с).Рис. 8.4, а и 8.4, б соответствуют двум качественно отличным ситуациям, опреде-
ляемым видом функции Т~ „(ао), т. е. видом границы 8 — 1. На рис. 8.4, а все линии уровня
М,=сопя$, проходящие по допустимой области, име~от по одной точке пересечения с гра-
ницей 3 — 1, тогда как на рис. 8.4, б есть линии М,=сопя$, которые имеют по две точки
пересечения с этой границей 1). Предельная линия уровня ЛХ =сопзС с максимально
возможным для данной области значением константы в первом случае пересекает границу
8 — 1 в вершине 1, во втором — эти кривые касаются в точке 4.
Т~
Т
М,
бс
Рис. 8.4. Два типа (а, в и б, г) допустимых областей для двухточечных маневров (параметры двигатель-
ной системы и маневра фиксированы).
По море увеличения М;,~ допустимая область в первом случае (рис. 8.4, а) сужается,
не меняя своего вида; прн М;„~=(Р(ас1) — (РТ(Р) она стягивается в точку 1, затем вы-
рождается в пустое множество. Бо втором случае (рис. 8.4, б) при М;,~ ) (Р(ас1) — ~РТ($')
допустимая область принимает вид полумесяца (исчезает граничныи участок
1 — 2: Т„= Т), при М;,~ — — (Р(а4) — (Р Тр ~;,(а44)/р) она стягивается в точку 4, затеи исчозает.
Число точек пересечения линий уровня М,=сопя$ с границей 3 — 1 определяет и
различия в общем виде областей возможных значений на плоскости М„М,. Область, со-
ответствующая рис. 8.4, а, показана в координатах М, М на рис. 8.4, в, а область, со-
ответствующая рис. 8.4, б, — на рис. 8.4, г. Если в первом случае участок 1 — 3, ограничи-
вающий область сверху: М,= ЛХ„„,„(ЛХс), состоит только из монотонно возрастающей ветви,
то во втором случае он содержит еще и убывающую ветвь.
На рис. 8.4, в, г по оси ординат даны два масштаба: левый — для М, и правый—
для ЛХ,=ЛХ вЂ” (М„+ЛГИ); для определенности принято М; ~ — — М„+ЛХз —— 2с. На этих же
рисунках дополнительно нанесены прямые Т =сопзС (пунктир) и использованные при
построении оценок (8.63) зависимости максимальной конечной массы от начальной для
') Перечисленные выше свойства (8.63) — (8.66) функции Т ~, (а„) еще недостаточны,
чтобы ограничиться двумя точками пересечения. Однако большее число точек пересече-
ния для дальнейшего уже не принципиально, к тому же примеров таких решений нет.

229
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
идеальных двигателей ограниченной скорости истечения (прямая М, при Г=сопвй) и
ограниченной мощности (кривая М, при Г=сопвВ).
Для границ 1 — 8 первого типа (рис. 8.4, а и 8.4, в) максимум функции М, а?„(Мв) по
ИО достигается в угловой точке 1, где
Р 1 Т
Мв? — — —, М„? — — Р— — —, — (М„+ МВ), Т„п,;„(ав ) = Т,
01 01
дТ„шр„/дав ) — К/ав„при ав ) а, т. е. дМ„ /дМв ) 0 при Мв & t;
Такие соотношения имеют место, например, для модельной задачи о наборе скорости и,
в бессиловом поле (8.30):
дт
ав — — —, (1 — е "'~ ),
Для границ 1 — 8 второго типа (рис. 8.4, 6 и 8.4, г) максимум функции М, „, (Мв)
по МО достигается в промежуточной точке 4 и выполняется другая группа соотношений:
р ~1й
дао ~о 4
& t О ри О) Я
Тр. п?$?р (аг4)
М = — ЮХ„= Р
04 в 7~4
ао4 а04
— (М. + Л?в)
р1
ао4 '
(8. 68)
дТ„; & t; 1' ао ри а &l
да
аг ) — Р/ав при ав ~ ав4,
дМ, п,~
т е для
0
~ О при 310 ( лх04.
Они имеют место для другой модельной задачи: перелет между точками покоя в бессило-
вом поле (8.43), где аг4 выражается через 1, У, Т параметрически посредствоь? относитель-
ной конечной массы О & t; п~,=.У,/,1Х =1 Ђ” р. Т ~
Е (?/ 1п т, — р'т?) 1п т
— 1п т — (1 — ~/т )"
аг~ — — —,1 — 1п т — (1 — р'т ) ~,
(а п 1/Тà — убывающие функции т от бесконечности при т?=0 до нуля прп т,=1).
Наличие соотношений (8.67), (8.68) позволяет сделать промен?уточное заключение,
относящееся к задаче о доставке максимальной полезной массы для отдельного двухточеч-
ного маневра. В такой задаче практический смысл имеет только возрастающая ветвь
зависимости М,„(М„). Это означает, что решение динамической части задачи нун~но
строить только в области, где выполняется перавенство
П11п /дар ~ ~/ао °
(8.69)
7г — 1
)=1
и-1
х ' = М( ) Л1.„— — Мр ЬМ~ 2 ~
М(п)
(8.70а)
(?=1, ..., и),
где х — параметр задачи, у — максимизируемая величина, х; — неизвестные. Полезная
масса ЛХ,"' в силу третьего соотношения из (8.59) выражается через х;+,.
и — 1
М,?," = х;+?+ ~ ЬМ~?)
(8.706)
(? =1, ..., и — 1).
Два типа допустимых областей У,, установленных выше, охватываются единой
записью:
п?ах(0; х; — х;) < ~+ </ (х ), х;
(8.71)
(хрг) = О, ? р (хр?) = хр? — хрг,
/,' (х;) ) О при х?в & t; х; (х
/,'(х;) (() при х 4,(х; & t; х
Х~з ~ ~Х~2 ~ ~Хф,11
?~ ~~;)=0 при ~м(~ (~~р ) .
хр'4 & t; х р  ° (х '
Первый тип области (с монотонной верхней границей — рис. 8.4, в) получается из (8.71)
Ниже будет показано, что данное замечание справедливо и тогда, когда двухточечный
маневр входит в качестве элементарного в состав многоточечного маневра.
Вернемся теперь непосредственно к задаче (8.59). Для сокращения записи введем
обозначения:

230
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
при х;4 & t; х lt;1, тор й тип (рис 8 4, ) в ” п и х<г l ; х& t а=х<4 < х&lt
дия вырождения области второго типа в полумесяц получается при х,з & t; ;4 Ђ” Ђ” ; &lt
=х&lt 1. По сравне и с исследованн ми в ше случа м в (8. 1) допускае ся возможно
обращения в нуль производной ~' на целом интервале (х&lt 4, ;  и существова ие изл ма
В точках х ~'4 х ~'4
При помощи соотношений (8.70), (8.71) задача (8.59) запишется так:
х„& t 0 ри у=~„(х ), о &l ; х„
( ~„1 (Ха 1), Х<„ &g ;г ~ Х„1 Х
шах у по х„...,
х„1 — х(„1)2 ~ ~х„
(8.72)
Х1 Х11 ( Хг (~ & t 1 ( 1 ~ 1г (~ Х1 (~ Х
х1 & t;
иайде11 максимУм У по х~~ [шах (х„г, х„, — х,„„,), т&l ;п (х ,; „1 (х„1 )]
фиксированных значениях х„,:
(~„1(х„), х„,)) при т!п(~„1(х„1), х„1) & t х
при т&l ;п ( „1 (х„ ), х , &g ; х„4 &gt х„, вЂ
— Х&l ;о 1 г) ОИ 4 ~ ( & t;& t; 1 —
~„(1П&g
(Х 4)
~„(х„
тах у = ~„1 (х„) =
Хуг
Пол& t; ч><вша&l ;&g ;с«фу кция у„1 (х„,) об адает те1& t;и же вой т ами
воначаль> lt;ая < >унк и&l ;1 ~„(х„). Оя опреде ена а от езк [х„ 1, , х„, д„]
минималь111,&l ;й кор нь уравне ия /„1(. „, 1 г) =х г а х& t;„„ есть минии ль ое из
х„д+ х„, 1„и 14<>кои> lt;»ль gt;& t; го коря&gt 1 т го е уравнен
<„1(х , ( & t;)&g ;ш ( а>, х 4) функ& t;< я ~„1(х ,) =~„[~, 1(х ,)] во
может быть у>ас ок постоянс ва „1 (х , = ~„(& t;п&g ;п ( а1, х„4, ~„1 ( ,„,
1„1 (х„1) & t; &g ;п>&g ;1 х„„х„4, „ (х „„4 ) > „ — &lt „1>г а затем
~„1(х„,) =~„[~„1(х„,)] при х„, & t; х, „, ~„1( „ ( >п (х„, х„ ) или ~„ (
=~„(х„1 — х<„1 г) ри „&gt х„ + х , „,. Отм т11 , то на возрас ающем у
х„„, =~„1 (х„,), т. е. максимально возможное.
Таким образом, после максимизации у по х„структура задачи (8.72) не изменилась,
сократилось лишь на единицу число переменных. Проводя далее последовательно макси-
мизацию у по х„„..., х„придем к простейшей задаче.'
таху= шах ~1(х,) при х1г & t; х < т& t;
х,
х,
где 1'1 (х,) обладает свойствами (8.71). Ее решение—
(Х) — ~ (~ 1 ( ~1 (Х) )) ПРИ Х&g ;   ( 1П 11 ( 14 Х
/1 (т&gt 11 (х1 ', х1 )) =~„( „1 ( . ~ (& t;п&l ;п (х1 , 'х1
при х & t; < (х„
Ушах = 1 (Х) =
На ~ ервоы, возраста1ошю1, 5 чйстке х, Ор~ е~ииственно: х, „„, = х, а на участке
постоянства может быть вз»то произвольно из отрезка [т&g ;и (х 4; х1 ), >п Х14~, х
Если на этом втором участке в соответствии с физически&g ;1 с14ыс ом прин ть х& t;о
нимальным нз .во<>1& t; я1ных ) х,„„ = gt;п gt 11 (х; х ), то на ооо х участ ах
будут при)>адлеж ть верхн 11 границ м: х р, Ђ” Ђ” „1 (х&l ;„-1 g ; ор& t ) Х1ор&l ;
и требуемые соотношения (8.57) или (8.58) доказаны.
Таким образом, динам11ческая задача (8.51) для м11оготочечного маневра расщеплена
па и динамических задач (8.55) для двухточечных элементарных маневров. Граничные
условия г (й",), 1 (й",), й',": (1=0, 1,..., и) элементарных маневров при этом фиксирова-
лись. Полное решение задачи (8.51) будет получено после отыскания минимума суммы
(8.56) элементарных времен работы двигателя по граничныи точкам элементарных манев-
ров с учетом условий (8.44). После этого функционал динамической части задачи будет
представлять собой функцию
Тр. ш1а = Тр. ш&l ;а ( '
= Т ш;„[РЗМ (0), < /М ( ); ЬМ,'4' /М (0
(8.73)
') В силу (8.70а) х, с точностью до фиксированной величины есть стартовая масса
аппарата. Последнюю при прочих равных условиях естественно брать минимально воз-
можной.

231
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
Зная ее, а также выражения (8.47) и (8.49) массы двигательной системы и баков через
Р, д и Тр, можно решить заключительную часть исходной проблемы оптимизации
(ср. (8.6)):
шах М„= шах (М (О) — М„(Р, д, Т„„1„) — Мз(дТ„ав„)—
Р, д, ~~о)(~~,
— дТ„,д„(Р~М (О), д~М (О); ЬМ„"'/М (О))),
(8.74)
где максимальная начальная масса аппарата М, и величины ЛМ,"' (~=1, ..., и — 1)
сбрасываемой массы заданы.
Как было показано выше, в задаче (8.72) при фиксированных параметрах двигателя
оптимальное значение начальной массы аппарата М (О) сначала совпадает с максималь-
ным — Мо, а затем с ростом последнего останавливается на некотором уровне М"„:
Мо при Мо & t;
ЛХ (0),
МО при М М„
(8.75)
(Р, д=((хе).
Полезная масса при этом на первом иптервале возрастает, а на втором — постоянна.
После максимизации полезной массы М по параметрам двигателя, как это будет
установлено в з 5, ситуация изменяется: начальная масса всюду равна максимально воз-
можной:
(8.76)
( ри = ар~~ д = дар~)
ЛХ (О), = М
а полезная масса становится везде монотонно возрастающей функцией М„обычно — ли-
нейной '). Таким образом, когда решается полная задача оптимизации (с выбором опти-
мальных параметров двигателя), постановки с заданной и ограниченной начальной мас-
сой аппарата совпадают. Если же параметры двигателя фиксированы, то нужно исполь-
зовать постановку не с заданной, а с ограниченной начальной массой. При этом устано-
вленное свойство (8.75) позволяет ускорить процедуру отыскания оптимального значения
начальной массы аппарата.
1=1,
1 (т~('~) = т1п (или тах),
~ («,'~) = Т('~ (или ор1),
р. 1 р.
г (т~('&g ; = г~(
1 (т(,')) = О,
(т(,'~) = О,
г(ф~) =г~',
=о,
р
г=~,
(8.77)
а~" ео
ч = ' + ~, т~ (т~('~) = тф~, т~ (-.~('~) = т('&
1 — Р.(') 1
(о(т) = 1 или О, / е(;) / =1; а~('~, р.'" = сопяЬ, к = 1,..., и; т('~ =орЬ).
Здесь, чтобы отличить функционал задачи от независимой переменной,
к уравнениям (8.55) добавлено формальное уравнение ~=1. (: этой же целью
для независимой переменной (текущего времени) введено новое обозначе-
ние — т. Для текущего значения функционала (первая фазовая координата)
сохранено старое обозначение — ~. Конечное значение независимой пере-
менной не фиксировано (выбирается оптимальным — т,"~=орФ).
') Последнее обстоятельство сразу становится очевидным, если появляется возмож-
ность перехода к безразмерным переменным (на единицу начальной массы), после которого
начальная масса исчезает из задачи.
Рассмотрим теперь случай, когда ца некотором участке двигатель раоо-
тает без выключений: о (~) = 1. Это может быть либо априорным требова-
нием, либо случайным стечением обстоятельств: параметры двигателя Р и д,
начальная масса М~('~ и параметры маневра (г~('~, т<, ~, 1( ~ и (г ', т~( ~, 1(
могут оказаться такими, что для выполнения заданного маневра за фикси-
рованное время Т(" = ~1~') — ~~') двигателю придется работать без выключе-
ний (точка 1 на рис. 8.4).
В таких случаях, как уже говорилось в п. 2 ~ 1, вариационная поста-
новка (8.55) теряет смысл. Ее можно заменить другой, в некотором смысле
обратной (8.55): время работы двигателя Т~'~ задано (или выбирается опти-
мальным), ищется минимум (либо максимум) времени движения Т"'
(ср. (8.9)):

2:32
[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
При незаданном конечном значении второй фазовой координаты:
1 (ф~)=орФ, так же как и для задачи (8.9), получается предельный слу-
чай: 3 ( т):— 1. Все промежуточные случаи (Т ( Т) также охватываются
постановкой (8.77), для них значение ~ ( т(&lt ~) ну но фиксирова ь. Пере
от условия 1( ф) =т1п к условию 1( ф~) =шах необходим, когда зависимость
Рис. 8.5. Три возможных типа зависимости Т„~пы (Т) (жирные кривые; параметры а„р и граничные
условия маневра фиксированы): а) маневры в центральном поле при заданном угловом перемещении;
б) маневры в центральном поле со свободным угловым перемещением; в) поддержание элементов орбиты
спутника, искажаемых постоянно действующими возмущениями.
Т,, (Т), являющаяся решением задачи (8.55), немотонна. Тогда условие
8 ( < lt;& t;) т1п дает бывающ ю в твь, а 1 (т lt; lt;>) =ша
(рис. 8.5).
Покажем, например, справедливость второй части утверждения, т. е. что кривая
Т, (Т„) совпадает с возрастающей ветвью кривой Т;„(Т). Действительно, кривая
Т,, (Т ) не может лен'ать левее кривой Тр > < (Т), иначе точки пос едней ав
Т (Т ) ) Т „(Т ) при одинаковых значениях Т . Если предположить теперь, что кри-
в«я Т „(Т ) лежит правее восходящей ветви кривой Т;, (Т), то получим ><р
речие с определением Тр,&gt ,, ( ). Одновреме но доказан ое утвержде ие устанав
вает и обратное свойство: если существует решение задачи (8.77) с ~ (-.,"') = шах,
то зависимость Т;, (Т), являющаяся решением задачи (8.55), имеет возрастающий
участок.
Неионотопный характер имеет, например, зависимость Т; (Т) для межорбиталь-
ных участков перелета при фиксированном угловом псремещении (см. п. 2 настоящего
параграфа); при незаданном угловом перемещении эта зависимость монотонно убываю-
щая. Пример монотонно возрастающей зависимости дает задача об удержании в заданном
шаровом слое спутника, движущегося в верхних слоях атмосферы (см. п. 1 ~ 4).
Посмотрим, повлияет ли требование об отсутствии выключений двигателя на возмож-
ность решения динамической части задачи по участкам. Когда на некотором участке ~'
двигатель долнсен работать без выключений, то при фиксированном времени движения по
этому участку допустимая область ~;, вырождается в отрезок прямой, соединяющий
точки 1 и 2 на рис. 8.4. Она определяется неравенствами (8.60) и (8.61), причем первое
берется со знаком «равно». В записи (8.72) это вырождение означает, что соответствующая
функция ~,, 1(х,, 1) =х,, 1 — х<.. >, Такая ф нкц я ~;, 1 по-прежнему»рина
семейству (8.71), поэтому ранее проделанное доказательство возможности решения
по участкам остается справедливым.
Если среди оставшихся участков &g ;' ,) gt;, ест х тя бы о ин, у ко оро о Т;,
невозрастающая функция, то можно утверждать большее. А именно, оптимальное решение
на участке ~' достигается в точке 1. Это дает возможность упростить процедуру оптималь-
ной стыковки участков. Время Т" уже не нужно сначала задавать, а затем при этом зна-
чении решать динамическую часть задачи для соответствующего маневра и потом еще
отыскивать оптимальное его значение из условия минимума суммы (8.56) времен работы
двигателя по всем участкам. Это время может быть определено сразу из решепия задачи
(8.77) для участка &gt ,' ри незадан ом значе и ~ (~>
Для доказательства нужно освободить время Т"' и рассмотреть допустимую область
на плоскости Т"', а,',". Ее вид аналогичен виду допустимой области на плоскости Т„, ао
при наличии выключений и при заданном времени движения Т. Отличие состоит в том, что
теперь на маневре Г полезная масса а время движени» жестко связаны: ~~1") = ЮХ,"')—
— ̄— ЛХз — (Р( &gt ') Т& t;"'. Когда аньше доказыв лос , ч о М<" в оп ималь
анте ле жит на своей верхней границе, то время Т") и все времена движения по остальным
участкам оставались фиксированными. Теперь же с увеличением М&l ; > врем Т<
шается, что при фиксированном суммарном времени движения приводит к увеличению
времени движения по оставшимся участкам (~ & t; ~ ). По усло ию ср ди их е ть х тя
один с невозрастающей зависимостью Тр ~&l ;, ( ). То да вр мя движе ия мо но увелич

233
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
только для такого участка, а для остальных оставить неизменным. При этом его допусти-
мая область может только лишь расшириться, и прежнее доказательство останется спра-
ведливым.
Если требуется, чтобы на всех участках двигатель работал без выключений, то
теряет смысл уже исходная постановка проблемы оптимизации. В этом случае лучше
задать полезную массу и искать минимальное суммарное время движения.
Далее, в соответствии с изложенной процедурой, динамическая задача
(8.51) для межпланетных перелетов решается по участкам. Разбиение на
участки проводится в рамках допущений, перечисленных в ~ 3 гл. 4. Сна-
чала дается решение вариационной задачи (8.55) или эквивалентной ей за-
дачи (8.77) для каждого из элементарных маневров, а затем производится
их приближенная стыковка.
2. Набор нулевой энергии — круговые орбиты, постоянно действующая
тяга. Рассмотрим сначала случай разгона с круговой орбиты при непрерывно
работающем двигателе, поскольку для него получены практически исчер-
пывающие результаты [8.5 — 8.13]. Движение — плоское, гравитационное
поле — центральное. Краевые условия для уравнений движения (4.18)
даются соотношениями (4.67). Поскольку полярный угол ~ не входит в пра-
вые части уравнений движения (4.18) и конечное значение ~ (Т) в (4.67)
не фиксировано, то уравнение для ф можно опустить (в случае необходимости
его можно проинтегрировать отдельно после решения задачи). Для задач
с нефиксированным угловым перемещением постановка (8.77) с условием
максимума времени Т не имеет смысла (шах Т вЂ” ~ оэ, см. рис. 8.5, б), поэтому
в (8.77) нужно рассматривать только условие минимума Т, т. е. задачу (8.9)
о максимальном быстродействии при 1 (Т)=ор$.
Система дифференциальных уравнений, описывающая оптимальное дви-
жение, получается из (8.19) при о: — 1,
2
(8.78)
г г2~
1 — р~ ~р+р
Рю
1
р'„= — (р„и„— 2р„г )
(уравнения для ~, р', ф, р' за ненадобностью опущены; переменные без-
Р' Р'
размерные).
Перечислим граничные условия для (8.78). Фазовые координаты г, и„, и
подчинены четырем условиям (4.67); выпишем два недостающих условия
(система (8.78) шестого порядка). Б конце оптимальной траектории вектор
импульсов (р, р, р 1 долте» быть коллинеареп ьектору нормали к поверх-
0~ 6~р/
ности ~ (Т) = О, отсюда
р (Т)~р (Т) = и„(Т)(и (Т), р„(Т)~р„(Т) = г (Т) г"-(Т).
(8.79)
Первое соотношение (8.79), как видно из (8.14), означает, что вектор
тяги в конце движения должен быть направлен по вектору скорости, вто-
рое — соответствует равенству нулю производной угла у между этими век-
торами (ср. (7.39)).
Для системы (8.78) не задан еще интервал интегрирования (ищется ми-
нимум Т); поэтому к выписанным граничным условиям нужно еще присо-
единить соотношение (8.17), отвечающее за функционал вариационной задачи.

234
[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
С учетом условий (8.79), последнего условия из (4.67) и условия р (Т)=0
(поскольку 1 (Т)=ор$) оно запишется так:
П(Т) = ' ~ р„(Т) [г'~*(Т) ) О.
(8.80)
Это условие выполняется автоматически, поэтому можно воспользо-
ваться однородностью всех соотношений (8.78) — (8.80) по импульсам р и за-
дать начальное условие одного из них (с точностью до знака). Удобно по-
ЛОЖИть
(8.81)
р, (О) =1 или даже р, (0)=1,
поскольку из качественных соображений ясно, что в начале оптимальной
траектории направление вектора тяги должно быть близко к направлению
вектора скорости (в силу (8.14) условие р„, (0)=1 означает е~ (0) ) О).
0
о
-5
д 1 Г
4 росло
одоротод
Рис. 8.6. Примеры оптимальных программ ~ (1): а) а,=0,8, р=О; б) а,=10-, р=О.
Таким образом, граничные условия для системы (8.78) складываются
из (4.67), (8.79) и (8.81):
г(0) =1, г„(0) =О, и (О) =1, р (О) =1,
р (Т) = р„(Т) и„(Т) г'(Т), р (Т) = р„(Т) и (Т) г'(Т),
[г", ( Т) + г' (Т) ] г ( Т) = 2.
(8.82)
Система (8.78) с граничными условиями (8.82) была проинтегрирована
численно методом Ньютона (см. гл. 19) в работах [8.10, 8.12, 8.13] в широком
диапазоне значений а, и р. Последнее соотношение из (8.82) использовалось
в качестве признака конца интегрирования, поскольку комбинация (и'„-'+и') г
является монотонной функцией времени. В качестве нулевого приближейия
для недостающих начальных значений импульсов О„и р,„из тех же каче-
ственных соооражений Выоиралось
рР~ (О) (8.83)
р'.„"' (0) = О.
В области больших ускорений, а, ~ 1, численное решение близко к при-
ближенному, полученному в работе [8.5] для случая а, ~) 1. На рис. 8.6, а
приведен пример оптимального закона изменения угла у между вектором
тяги и вектором скорости (отсчитывается от т против часовой стрелки) при
а,=0,8, р=О. Сплошная кривая соответствует численному решению [8.12],
пунктирная — приближенному [8.5]. Направление вектора тяги здесь мо-
нотонно приближается к направлению вектора скорости.
При малых ускорениях, а, ( 10-', характер оптимальной программы
направления тяги меняется (рис. 8. 6,6): вектор тяги совершает малые коле-
бания относительно вектора скорости с периодом, приблизительно равным
времени одного оборота, амплитуда колебаний с течением времени увеличи-
вается, в конечный момент времени угол т и его производная т обращаются
в нуль (в соответствии с (8.79)).

235
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
Характер оптимальных траекторий аналогичен описанному в и. 2 ~ 2
гл. 7. Сохраняется и упоминавшийся там же принцип «универсальной»
траектории, который был установлен в работах [8.6, 8.11] и приведен
в п. 3 ч 3 гл. 17. Качественно он прослеживается и на рис. 8.6: программа
т (~) с рис. 8.6, а получается (с точностью до
масштаба) «вырезанием» заключительного ~=~р
участка (~) 45) программы т(~) с рис. 8.6, б.
Зависимость минимального времени на- 1Р
бора нулевой энергии от ускорения а, пока-
зана на рис. 8.7. Эти данные относятся щ'
к случаю постоянного реактивного ускорения
а(1): — а„последний получается формальным
предельным переходом к р=О в форму-
лах, записанных для движения с постоянной
1
тягой.
В логарифмических координатах приве-
денная на рис. 8.7 кривая состоит из двух
линейных участков, соответствующих малым
и большим значениям ускорения, и переход-
ного участка, сопрягающего первые два.
д
В результате обработки численных дан- Рис. 8.7. минимальное время абора
ных в работе [8.13] получена аппроксима- нуяевой энергии при р=о.
ционная формула для минимального вре-
мени набора нулевой энергии с круговой орбиты, охватывающая три про-
граммы ориентации тяги '):
т= т„— — (1 — с~/а,) 1 — р (1 — сг'ац)] (при а„р ~1); (8.84а)
Щ
~Р Ю (~~ ~Р '
с.=0,8209 — оптимальное направление тяги (7=т,„, (~)),
с=0,8082 — тангенциальное направление тяги (~=0),
с=0,7555 — трансверсальное направление тяги (е„=О).
При этом за основу бралось приближенное соотношение для времени
набора нулевой энергии с тангенциальной тягой, аналогичное (17.37).
Формула (8.84а) справедлива в области малых значений О ( а, ( 10 2
и 0 ( и ( 0,25 10-' (малая тяга). В этом диапазоне относительная погреш-
ность ЪТ~Т не превышает 1%, в диапазоне О ( а, ( 10-', О ( и ( 0,17 10 '
погрешность меньше 0,5е~е, с уменьшением а, и и погрешность убывает.
Сравнение времен (8.84а) для различных программ ориентации тяги
позволяет сделать вывод о том, что для маневра набора нулевой энергии
в центральном поле тангенциальное и трансверсальное направления тяги
дают результаты, близкие к оптимальному. Относительный проигрыш во
времени при а,=10-', п=О в первом случае составляет 0,5е~~э, во втором 2,5е~э,
с уменьшением а, и и проигрыш уменьшается. Сводка формул, аналогичных
(8.84а), для случая больших значений постоянной перегрузки приведена
в [8.5]. В принятых здесь обозначениях эти формулы имеют вид
Т = Т вЂ” (~/2 — 1) иэ'+ са,з
(8.84б)
(при а,) 1, р. =0);
с=0,001481 — оптимальное направление тяги (7=7„,, (~)),
с=0,001615 — тангенциальное направление тяги (т:О),
с=0,002349 — трансверсальное направление тяги (е„=О).
') Приближенные решения для трансверсальпо и тангенциально направленного,
постоянного по модулю реактивного ускорения приводятся в Ц 2, 3 гл. 17. В работах
[8.7 — 8.9, 8.11] содержатся подробные результаты расчетов маневра набора гиперболи-
ческой скорости с постояпцой тангапциальпо направленной тягой.

236
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Из (8.84б) следует, что при увеличении а, перечисленные программы
управления становятся практически неразличимыми в смысле функци-
онала и
Т= Т (/2 — 1)а„' (при а,))1, и=О).
При а, -1 это различие тактике невелико. Относительные погрешности
'оТ)Т по сравнению с точными решениями составляют 0,05О~ для танген-
циальной и 0,35О~ для трансверсальной тяги соответственно (при а,-1)
и ЬТ~Т вЂ” ~ 0 при а, — ~ со.
Запишем формулу (8.84а) в размерном виде:
Т[сут[=Т„[сут[ —,', (!-[- " ) '[[ — 6,(1+ ") 'у а,[10 'д,~]Х
для Земли Л=6,371 ° 10' км, Ь,=93.29, Ь,=3,952, Ь =0,08209 при т= ~„, (~),
ЬЗ=0,08082 при т=О, Ь =0,07555 при е„О; для Марса Л=3,332 10' км,
Ь,=41,65, Ь,=1,764, Ь,=0,1045 при т= т„„(8), Ь,=0,1029 при т=О,
ЬЗ=0.09615 при е„=О, где Й вЂ” высота начальной круговотЪ орбиты над поверх-
ностью планеты, д,=9,81 м/сек.
~ — ~~)
суп
д-5
~~-з
[~о/~о
Рис. 8.8. Минимальное время разгона и торможения пля круговых орбит с высотой Ь (д,=9,81 м/сек'):
а) 6=200 —:400 км', б) л,=400 —:600 км.
Зависимости Т(а,!д,), посчитанные по формуле (8.85), для оптимального
направления тяги (т= т,р[ (Е)) при фиксированных значениях высоты орбиты Й
и скорости истечения [' приведены на рис. 8.8.
Соотношения (8.84), (8.85) могут быть использованы и для маневра тор-
можения в центральном поде, начинающегося в точке с нулевой полной энер-
гией ф=О и заканчивающегося выходом на круговую орбиту заданного
радиуса г, (угловое перемещение не фиксировано, начальные значения коор-
динат и компонент скорости по отдельности не заданы). Параметры а, и а
при этом вычисляются по массе аппарата ЗХ Я,) в точке ~ = 0: и, =
=Й Г02р/ЛХЖО), Р=й, Ьг[д~мж,).

237
ОптимАльныИ межплАнетныИ пеРелет
Такой расчет времени «обратного» маневра по формулам для «прямого» отличается
от точного пересчета с использованием преобразования замены знака (8.21) двумя момен-
тами. Первый: величины а» и р в (8.21) должны вычисляться по массе аппарата ЛХ (г ) па
з~
конечной орбите: а,'= 1с 'т-'Р~М (г ), ] и' ) = Й ~2г ~'д/М (г ); второй: расчет «обратного»
маневра по (8.21) должен производиться с отрицательными значсниями расхода, р'= — (р'!
(возрастающая масса аппарата).
Однако эти две ошибки компенсируют друг друга. В приближенном расчете про-
грамма реактивного ускорения а (»)=а» (1 — р») 1 получается симметричной точной про-
грамме а' (»)=а„(1 — ~с(Т вЂ” »)] 1 относительно середины интервала (О, Т], поэтому ин-
тегральный эффект от обеих программ должен быть примерно одинаковым (с точностью
до гравитационных потерь). Высказанные качественные соображения подтверждаются
количественным сравнением, проведенным в работе (8.14]. Оказывается, что точность
расчета времени «обратного» маневра по формулам (8.84а), (8.85) дан."е несколько выше,
чем для «прямого» маневра: при 0 ( а & t; 10 '  ( р & t 10 ' шибка еньше
с уменьшением величин а и р. ошибка уменьшается.
Точны. значения времени торможения находились в результате численного решения
краевой задачи (8.78), (8.82) при р ( О, т. о. как время разгона с отрицательным расходом
массы. В силу ипвариаптности уравнений (8.78) и граничных условий (8.82) относительно
преобразования (8.21) замены знака фиктивной траектории разгона с р ( О соответствует
в «обратном» времени действительная траектория торможения с р. ) О.
Таким ооразом, показана справедливость формул (8.84а), (8.85) и рис. 8.8 и для
11аневра торможения с выходом на круговую орбиту (формула (8.84б) и рис. 8.8, 8.7
верны па основании (8.21), поскольку опи построены для случая р,=О). Напомним,
что в начальной точке рассмотренного маневра торможения координаты и компоненты
скорости по отдельности не заданы, они подчинены единственному условию равенства пулю
полной энергии аппарата. Некоторые численные результаты по маневру торможения
с жестко заданной начальной точкой содержатся в работе (8.13]. Решение такой задачи,
равно как и задачи о разгоне с выходом в заданную точку, необходимо при точной сты-
ковке элементарных маневров составляющих межпланетный перелет. Здесь же мы огра-
ничиваемся приближенной стыковкой.
3. Набор нулевой энергии — эллиптические орбиты, постоянно дей-
ствующая тяга. Приведем данные по влиянию эллиптичности начальной
орбиты на минимальное время достижения параболической скорости, полу-
ченные в работе [8.15]. Как и выше, движение — плоское, поле — централь-
ное, двигатель работает без выключений. Заданы эксцентриситет и энергия
начальной орбиты, угловое положение точки старта выбирается оптимальным.
Аналогично случаю идеального двигателя ограниченной мощности
(п. 1 з 2 гл. 7), уравнения оптимального движения записываются в форме
(4.38) и с помощью принципа максимума приводятся к краевой задаче
(ср. (7.41) с начальными условиями а))
р' = 2р"- (Ч+ 1) ' а, (1 — ф) ' е,
(3 = — р-' ф + 1)' Ь + 2 ~рц, (1 — ф) ' е,
~ = р '~ ф+ 1)' ~+ ~~р [ф+ 1) ' Ье + е ] а, (1 — ф) ',
2 ~р (Е+ 1) ' 2 ~р
р' = р ' ф+ 1)'" р — ~/р ф+ 1) ' р а, (1 — ф) ' е
(8.86)
~р +2РР, ' -'~
е,= р„р',+(2р 4-
6р,+2ррр йр +2рр ' -'/2
Р~+ е+1 " + Р~+ е+1
Р (0) = 1 — е;', Д» (0) + Ь~ (0) = ез» (О ( ее = ]1хе (1),
Д(0) р,(0) =Ь(0) р (0), р- (0)+р;(0)+ р; (0) =1,
р (Т) = О, Д'(Т)+Ь'(Т) = 1, Д (Т) р (Т) = Ь(Т) р (Т).

238
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Переменные в (8.86) безразмерные, в качестве характерных значений
приняты величины (4.12), соответствующие круговой орбите (в=О) с той же
полной энергией, что и у начальной эллиптической орбиты. Условие
Н (Т) ) О, подобно (8.80), выполняется автоматически; признаком конца
траекторий (Т не задано) служит обращение в нуль полной энергии: ф=
=ф'+Ь' — 1)/2р=О; условие нормировки импульсов, в отличие от (8.81),
принято в виде р'- + р' + р' = 1 при 1 = О.
В краевой задаче (8.86) два недостающих начальных значения, в ка-
честве них приняты два угла ~ и 9, разрешающие второе, третье и четвертое
начальные условия из (8.86) относительно Д(0), Ь(0), р (0), р (О) и р (0):
я (0)=~ясояр, Ь(0)=~,я!пр, р (0)=я!пясояО, )
р (0) = э1п у э1п О, р, (0) = соя )р.
( )
Решение краевой задачи (8.86) многозначно. Это показано в [8.16]
для общего случая задач оптимального управления, в которых хотя бы один
из концов траектории жестко не фиксирован, а может перемещаться по не-
которому замкнутому выпуклому много-
образию. В соответствии с предложенным
0 в [8.17] приемом (см. также [8.15] и п. 1
~ 2 гл. 7) для отыскания двух ветвей
1,дд оптимальных решений нулевое приближе-
ние строится на основании решения пре-
дыдущей задачи о разгоне с круговой ор-
~,д4 биты (я,=0) в двух вариантах:
~~о)
с)
~~,(0)
Яо=О')
1)
2)
(8.88)
Э(о) = 9 +тг.
Решение строилось модифицирован-
ным методом Ньютона (гл. 19). Р( зуль-
таты приведены на рис. 8.9, 8.10 из [8.151.
Оказалось, что ветвь решений, порожден-
ная условием 2) из (8.88), — побочная.
На ней, как и для идеального двигателя
ограниченной мощности, функционал мо-
нотонно растет с увеличением эксцентри-
ситета начальной орбиты (см. пунктирные кривые на рис. 8.9). На дру-
гой, действительно оптимальной, ветви функционал меньше, чем на пре-
дыдущей. С ростом я, он сначала убывает, затем начинает возрастать (см.
сплошные кривые на рис. 8.9).
В случае же идеального двигателя ограниченной мощности на действи-
тельно оптимальной ветви функционал монотонно убывал по я, (см. сплош-
ную кривую У на рис. 7.6, а).
Появление оптимального значения эксцентриситета и небольшие зна-
чения выигрыша в функционале объясняются здесь сравнительно малыми
свободами в управлении тягои: ее величина постоянна, выключения не до-
пускаются. Поэтому здесь нет возможности создания участков с увеличен-
ной тягой и их сосредоточения в окрестности перигея. Управлять разрешено
только ориентацией тяги. Пример оптимальной программы управления и па-
раметров соответствующей траектории в функции времени для оптимального
начального эксцентриситета показан на рис. 8.10. Колебательный характер
оптимальной программы ориентации тяги сохраняется. Но среднее ее поло-
0,9б
д дЯ д4 б,б
Рис. 8.9. Примеры зависимостей минималь-
ного времени разгона от эксцеитриситета:-о
начальной орбиты (р = 10 — ', Т,
= 73,Ь2 для ао =10 ' Т=„=О = 11,52 для
а =5,З 1О ').

° °
° °
° й
° ° $ °
Й $
° ° р °
ре е
Э !
° 6 169
$ ° й Э ° ° °
ю $ °
Э ° °
° °
1 5 °
1 Ре 15
° °
!1вв 1 6 ° Ре
Э' ° '91
99 '' 19
° р ФЙЭФ5
ф °
° р ° Й
° ю
ф 1 ° ф $ ° р ° ° °
° ф р ! ° ф р ° °
636 ВП 3'6
1 ° в 5 е Ре 1 а а 9
° °
6 Ф '
в
9 е
а ю
° р °
° ° ф
° ! ° °
Ф °
е 1 1 е 6 е
Э ° °
° ° ° р °
4 ° 4
р Э ° ° Р °
Фефф
° °
1 ° в П'1
° ° р °
911
$ °
° ° 1 °
1
°, 1 е, !
° ° ° е ° в
Г
° ° ° °
1 П Э 91 ° П61 1 !ЭВЭ Э е ° 'вв Э!'а Э Э
° °
° ° Э ф °
е 1 е Э е е Э '
П '
66$
° ю
П в ° ° Э ° Э Э е
$695
$ ° °
1 ф
° ° °
1 в е
1 е 1 е ° °
в Г Э
В Ю ° е
е 191
Э ° 'ЭЭРе6 $ ° ° ° ° 1 ° ° ° ! ' Э
й
ю °
° °
° ю
° е
ю ° ° е $
ю °
Э в 1 ° °
1 6
1' 1 ю ° е ° 1 ° Э Й °
Э ю $1 ° 1 ° ° 9 в ° ° ° °
Э $ ° ° ° ° Э ° ° $
° °
° °
° ° ю
° Ф 6
1 °
1 !
! ' °, $: ' 6 ° ° 1
° ! ° ° ° ° ° ф °
й
° ф
1
6 ф в Э' ' ° Э ° 61 3
° Э
Э ° ° ° ° °
1 ° ° $ ° ° Э °
° °
° ° Э °
9 ° а П ° ° ° Ф ° $ е ° вв 11
3 °
° °
ю
° °
1 °
° °
$ ° °
° °
° $ ° Ф ° ф ° °
° Э Й ° ° ° ф $1 °
° ° 1 ф
° ° °
3 в
° ф ° °
° ° °
ю
1 ° 1ва °
1 ' °
1 Э
в ° Э Э 9 $ °
ю ю е
е Э ю $ 1 ° Э
° ф °
1 Э е
° $
° ° ф
° ° ° Э °
Э 1'
Э ° ° ° В Э ф $ $ ° Э ° °
° °
° ° й ° ° й ° ° ° °
° ф
В Ю а °
ф ° 1 ° °
° °
ю
Э °
в е Э е
Эе 91 ° ! ° е ° ю ! ° ° ° °
1'$ $ 'ф' 'П ' ' А й Ф ° ° р °
° е
° Э °
е !
° ° р я °
° °
° ° °
Э °
° М ю е ° ° 6 ° в в
° °
а
° ° ° °
° ° ° °
° ! °
е 3 ' 4
° °
° °
° ° е
° °
6 е ф 6 е
! ° ° °
Э ° 6 ° 1 ° ° Р ° ав °
° °
3 Э е е ° ' Э °
ю
е
ф °
° ° °
Э ° ° ° р °
е ° 6 6 ° е
6 °
° ° ' П
° а е ° е
° ° °
Ф а е
° °
° °
Фвф
° 3 в
° $ в
ф ° ° В °
е ! е
в Э
° 4 ° Э
Э! ° 9 ° 6
° а °
й ф
1 1 °
6 5
е
а °
° ю
а
ю °
° ° Й
° в °
а ф а ф в Ф Й е а
й а
в а
° е
Ю В ° °
° ° °
° °
° $ °
е
° °
$ °
Э 3 $
е ° в
ю
° ° $ ! °
° ° °
° $
° ю
° ф ° °
$ а $
е Э
ю
В °
° °
° °
5 6 ° П' °
° ! 6 е в
° 6
! 6
„„ииид °
' иийииа и~~ииииии
° ииииийии иийиии
° ИИИИИИИИ Ии йй
° иииииииииии '.Ии
( ( 1111111116161~411
° ииииииииииииии °
ииииииииииииЙйи~
щишиийиииииииии
ийбйииииииииииии
р И!ИИИийийииИИИИИИ
Йпйииииийбиииииии
Я1!611~11%!11 1%)41 1 1 1 1В
йииимииик|ииииии
/ /
е 1 Р~ !е Ф 'Эе'55 Э 1
° ииииииииРюеийии
° 1Д1 1 1РРРе~- 1РР
° ииииии~ий 'ииии
° ииииииииииииии
° иииияиииииииюи
° ИИЮИИИИИИИИИ6ЫИ
° иияиииииииийи °
) иииииииииииимиии
° ЮИИИИИИИв%ЙИИИИ
ф~~~ф1111$19$ф~Я11
ВййЖИЖ~м~41 1 ГЛВ 1ИИИ
~~ЯГ~В ВааВ111аИИ
ййииииииииииииии,
( /
ю ° ю Э а й ° ° ' °
Э 6 П ° ° е а ю в ° е ° Э

240
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
менем одного оборота по оскулирующему эллипсу 1), поэтому полное время,
потребное для реализации такой программы, и суммарное угловое переме-
щение бесконечно велики (Т„„Лавр, — ~ оо).
Функционал задачи Т„стремится к своей точной нижней грани. Она
определяется формулой (8.64), где о(д„/ао):О, а Ли — минимальная харак-
теристическая скорость обычного им-
пульсного перехода с бесконечно боль-
шой тягой при незаданных Т и Л~.
Для рассматриваемых здесь маневров
разгона (торможения) при круговых
дЮ начальных (конечных) орбитах мини-
мальная характеристическая скорость
в используемых безразмерных перемен-
ных равна Ьи = ~/2 — 1 (см. (5.59), (5.60)
1) при г,=г,=/с=1, ь~,=~/2, так что
т,= — (1,-(Н- У )
р. ]аГ
О
Я,7
дб
ЩЭИ Т„„„, ~ю„~ — э сО.
(8.89)
Сравнением (8.89) с (8.84) и полу-
чаем, что для двигателей малой тяги
Рис. 8.11. Примеры семейств зависимостей
а ~& t; 1 К )) 11 за с ет выключе
времени работы двигателя Т~ от времени дви- МОЖНО СОКратИтЬ ВрЕМя раооты При-
>ке и т ля траекто ий Разг н с Разл в- близител но на 60
ным числом пассивных участков (а, =10 ',
Уравнения оптимального разгона
с выключениями двигателя даются
системой (8.19) и следующими краевыми условиями, записанными для кру-
говых начальных орбит (см. (8.5), (8.16), (4.67), (8.79)):
г(О)=1, и„(0)=0, и (0) =1,
г,' Т) [ у'-„(Т) + ив (Т)] = 2, ~ (8.%))
р, (Т) =п (Т) г'(Т) р„(Т) (Т=- йхе ~'Т,.„). [
Е (0) = О, о (0) = О,
р, (Т)= 1, Р (Т)=о,
р (Т) = и„(Т) г'(Т) р„(Т),
(Т) = Т„.„+(Т„, — Т„„) (Т,.„
1) Если в качестве независимой переменной принять текущую массу аппарата т,
то функция включения-выключения двигателя 8 (т) окажется бесконечно быстро меняю-
щей свои значения с 1 на О, что и объясняет название «скользящий режим управления».
В работе [8.13] получены примеры численного решения краевой задачи
(8.19), (8.90) модифицированным методом Ньютона при аз=10-в, »,=О,
100 ( Т ( 160. Обнаружена неединственность решения: при одних и тех же
значениях Т существуют траектории, удовлетворяющие уравнениям (8.19)
и граничным условиям (8.90), но различающиеся программами управления,
в частности числом пассивных участков. Значения функционала Т„на них,
как правило, тоже различаются, а при некоторых значениях Т совпадают.
На рис. 8.11, построенном по данным работы [8.13], сплошными кривыми
(т=т,„, (г)) показаны полученные зависимости Т„(Т) на разных ветвях ре-
шений: с шестью, семью и восемью пассивными участками. По-видимому,
кривая Т;, (Т) образуется как огибающая этого семейства (показана пунк-
тиром), ее предполагаемое уравнение

241
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
где Т,.„, определяется формулой (8.89), Т,.„— (8.84а) при с=0,8209, а
х=1,103 при а,=10 ', р=0 (из обработки численных данных).
На том же рисунке приведены аналогичные кривые, полученные в [8.13]
для случая трансверсально направленной тяги (е„: — О). Последний описы-
вается краевыми условиями (8.90) и уравнениями (8.19), где р', д„и о за-
меняются на
и,о~8„рф
(1 ~~)2'
~о~ор~
1 — р~
Г
Как видно из рисунка, проигрыш в функционале Т по сравнению со слу-
чаем оптимально ориентированной тяги (7=тор, (~)) при 1 ( Т~Т,.„( 2,2
возрастает по Т от 3% при Т|Т.,„,= — 1,03 до 13% при Т/Т,.„=2,2; при даль-
нейшем увеличении Т проигрыш снова убывает, стремясь к нулю при Т вЂ” ~ оэ
Рис. 8.12. Оптимальные траектории разгона с шестью пассивными участками и программа изменения
угла у между тягой и скоростью (а,=10-', р=0, Т=102, Т =Ьэ).
(поскольку в предельной программе — скользящий режим — оптимальное
направление тяги совпадает с трансверсальным).
Пример оптимальной траектории разгона с выключениями и программы
управления показан на рис. 8.12 из [8.13]. Участки кривых, соответствую-
щих пассивному движению, изображены пунктиром. На каждом витке траек-
тории имеются один активный и один пассивный участки. Активный участок,
как и следовало ожидать, располагается в окрестности перигея оскулирую-
щего эллипса. Траектория, естественно, начинается и заканчивается актив-
ными участками. Оптимальная программа ориентации тяги аналогична слу-
чаю непрерывно работающего двигателя (ср. рис. 8.12 и рис. 8.6, б).
5. Межорбитальный перелет — уравнения краевых задач. Решение за-
дачи (8.55) о минимуме времени работы двигателя Т при выполнении дан-
ного элементарного маневра для перелетов между орбитами планет старта
и финиша является функцией углового перемещения Л:р и времени движе-
ния Т (параметры а, и р, относящиеся к двигательной системе и аппарату,
фиксированы). Линии уровня этой функции Т (Л~р, Т)=сопаФ на плоскости
Лр, Т представляют собой линии равных (минимально возможных) затрат
рабочего вещества (т. е. совпадают с линиями т1=сопвс). Знание этих ли-
ний необходимо для решения задачи оптимальной стыковки участков.
Построение линий равных затрат удобно проводить в рамках вариацион-
ной постановки (8.77), последняя редуцируется к краевой задаче для си-
стемы обыкновенных дифференциальных уравнений [8.4].
16 Механика полета

242
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Уравнения плоского оптимального движения расписываются в поляр-
ных координатах, аналогично (8.19), по стандартной процедуре принципа
максимума:
8=1,
с
р. ор
ф= у ~гч
У~ 2
2
(8.91)
~ооорф
У„У
г
р„= — (р, и„— 2р, у — р )
1
1 — ф /~2,+ Р2
~ооорФ Р
„1 Р„„— Р„+Р
'1 — ф„/р-' + Р- Г
9
Здесь коэффициент Й~ приЫимает значения Й,1 — — +1 в задаче 11а минимум
функционала и Й = — 1 в задача на максимум. В (8.91) оптимальная ориен-
тация е = (е„, е ) тяги уже выражена чорез
Р
7=Т Т=с)Т=~,
импульсы р, и р, (ср. (8.14)):
сп,~
е„,„, = 1едр (р2 + р'-' )-'Ь2,
е„„= ~с~р, (р', + р'„'- )-'~, (8.92)
а оптимальная программа о включения-вы-
ключения двигателя подразумевается выра-
женной через импульсы р, р, р, г1 фа-
зовую координату 1 следующим образом
(ср. (8.15)):
3,Ф вЂ” — Т (1 + Йь я1 Ой Ь),
1
Рис. 8.13. Схема линий уровня Т„=соп8$
и границы Т,=Т.
где Ь=р, +~ ', ~р' +р„', (89~)
~ 1 — ф,„
1
'-)ти выражения, в соответствии с процедурой принципа максимума,
получены из условия максимума (для минимума функционала) или мини-
мума (для максимума функционала) гамильтоновой функции Н по управле-
ниям е и а. Соответствующее значение функции Н должно быть тождественно
равным нулю вдоль оптимальной траектории (первый интеграл системы,
ср. (8.12), (8.17)):
У~
У У
Н (~) — р +р +р 1~ р +р — ~ — —,, +Ь о„,=О,
(8.94)
поскольку правые части уравнений (8.91) не содержат явно независимой
переменной ~ и значение ~ в конце траектории не задано: ~1=ор1 в (8.77).
Покажем теперь, что в рамках постановки (8.77), как и для (8.9), опти-
мальный режим ~,р~ (~)=1 действительно получается при незаданном вре-
мени работы двигателя ~„ (~ )=ор1. В этом случае по условию трансверсаль-
ности р1 (т )=О. Производная импульса р1, согласно (8.91) и (8 92) вдол~
всей траектории неположительна (для минимума функционала) или неотри-

ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
цательна (для максимума), поэтомусам импульс при любом ~ будет поло-
жителен (или отрицателен) и по (8.93) о,р~ (-.): — 1.
При незаданном времени работы двигателя решение задачи (8.77) дает
границу области определения функции Т (Л~, Т). Следовательно, по только
что доказанному на границе будет Т =Т.
Специфичные свойства линий уровня функции Т (Л~, Т) и границы
области ее определения (рис. 8.13) заставляют рассматривать несколько
модификаций постановки (8.77). Различие этих постановок состоит в конеч-
ных условиях для ~, ~ и ~. Начальные же условия для всех фазовых коор-
динат и конечные условия для г, и„, и одинаковы и задаются соотноше-
ниями из (8.77), (4.68) (рассматриваются перелеты между круговыми ком-
планарными орбитами):
~ (-.,) = О, ~„ (.,) = О, ~ (.,) = О, г (~,) = 1, и,р (ъ,) = 1, г„ (~,) = 0;
г (~,) = г,, г„ (~,) = О, г (-,) = г-' .
(8.95)
Вместо неизвестного интервала интегрирования во всех случаях до-
бавляется соотношение (8.94), которое может быть переписано с учетом
(8.95) в виде начального условия для импульсов:
~~,.„(-,) = р, + р, +~р, (-.,) + ~с~а, ~/р'„(~,) + р'-,' (~,)] ~„, (~,) = 0 (8.96)
(в силу (8.91) р,: — р, (~„), р = р (~,)).
Перечислим все используемые постановки и соответствующие конечные
условия для ~, ~ и ~ [8.41.
Постановки для отыскания границы области определения функции
т„(Л~, Т):
П~1П,
Т,
П1111,
(8.97)
мах,
Т,
Постаповки для определения линий уровня Т (Ли, Т) = сопвЬ:
п1ах;
орФ;
(8.98)
п11п;
пип.
Постановка для определения точной нижней грани Т
Р'
9. 1(~,) =ор1, 1 (-. ) =т1п, <р( ,) =о
(8.99)
Постановка для вычисления функции Т (Л~, Т) по заданным аргументам:
10. ~ (-.,) = Т, ~ (~ ) = т1п, и (~ ) = Л р.
Решение задач 1 — 3 из (8.97) и 5 — 7 из (8.98) позволяет построить ниж-
ние ветви границы и линий уровня (см. рис. 8.13). Задачи 4, 4' из (8.97)
16*
1. ~ (-.,)
1'. ~(-.,)
2. ~ (-.,)
3. ~(,)
~( )
4'. ~(-.,)
5. 1(-.,) = т1п,
5'. ~(~,) = Т,
6. ~(-.,) = тт
7. ~(-.,) = ор1,
8. ~ (-. ) = тах,
8'. ~(-.,) = Т,
(-. ) = ор1,
~ (~,) =ор1,
Е (-.,) = орС,
1 (~,) = орВ,
1 (~ ) =ор1,
~ (~1) = ор1,
~ (~,)=Т
г (т~) = Т~,
~,(-.,) = Т„',
г (т~) = Т~,
~,'(-.,) = Т„',
~' ,(,,) = Т"„,
~( )=Л~
р(~ ) =тах;
р (~,) = ор1;
~ (~1) = т1п;
, (-1) =Л~
и (~ ) = т1п.
, (-)=
,( )=
,( )=
~( )=
~( )=
~('1) =

244
НЕРЕГУЛИРУЕЪ|ЫЕ ДВИГАТЕ,)1И
[ГЛ. 8
и 8, 8' из (8.98) дают верхние ветви границы и линий уровня. Постановки 1
и 1', 4 и 4', 5 и 5', 8 и 8' попарно эквивалентны и могут использоваться равно-
правно, если касательная к границе или к линии уровня составляет острцй
угол хотя бы с одной координатной осью. Если же касательная горизонтальна
или почти горизонтальна, то нужно пользоваться только постановками
1, 4, 5, 8. В случае вертикальной или почти вертикальной касательной
должны употребляться только постановки 1', 4', 5', 8'.
Решения задач 2 и 6, 3 и 7, 9 дают отдельные характерные точки границ
и линий уровня: 2 и 6 — минимально возможные значения времени перелета,
3 и 7 — минимально возможные значения углового перемещения '), 9 — ми-
нимально возможное значения времени работы двигателя, т. е. точку совпа-
дения решений 6-й и 7-й задач '). Постановка 10 позволяет вычислить значе-
ние функции в любой заданной точке области определения.
Уравнения оптимального движения (8.91) — (8.94) и граничные условия
(8.95), (8.96) справедливы для всех постановок 1 — 10. Остальные три конеч-
ных условия (система (8.91) — двенадцатого порядка, с незаданным интер-
валом интегрирования, а граничных условий (8.95), (8.96) — десять) для
каждой постановки будут свои:
для задач о границе области определения функции Т (Л~, Т):
р,;.,) =О,
р, (-) =0
Р-
р, (-.,)=о,
р, (,)=о,
р, (.,)=о,
р, (-.,)=о,
1. р~= — 1,
А =+1);
(Й, = — 1);
(~с~ =+1);
А =+1);
А = — 1);
(В, =+1);,
1. ~(-.,)=Т,
р,= — 1,
(8.101)
р,= — О,
4.
~ (-1) = Ьэ
4'. ~(т,) = Т,
р = — 1
для задач о линиях уровня Т (Л~р,
— ~„ (-.,) = Т„,
5 . ~ (-.,) = Т, ~„(,) = Т.„,
р,.=
7. р,: — О, ~„(т,)=Т
8. р,: — — '1, ~„(;,) = Т„,
8'. ~ (~,) = Т, ~„(т ) = Т„,
Т) = сопа1:
з (-.,) = ьв
р,=О
= — 1
9
~( ) =4'
(8.102)
р = — 1
'Р
для задачи о точной нижней грани
9. р,= — О,
для задачи о вычислении значений
10. 1(т ) = Т, р, (-. ) = — 1,
(Й~ — +1);
(8.103)
функции Т„(Ь:р, Т) в точке (Ь~, Т):
, (-,) =~', ф =+1). (8.104)
Каждоеизвыписанных условий (8.101) — (8.104) совместно с (8.95) (8.96)
полностью определяют двухточечную краевую задачу для системы (8.91).
6. Межорбитальный перелет — недостающие начальные значения. Сформулиро-
ванные выше краевые задачи решались в работе [8.4) модифицированным методом Нью-
тона. Начальные значения фазовых координат ~, ~„, ~, г, и„, и„заданы и во всех задачах
') Минимум углового перемещения — локальный (подробнее по этому поводу
см. п. 8).
2) Лежит в бесконечности: Т -э +со, ~~ -э +~~, Ь~(Т -э сопзФ вЂ” см. 18Л8, 8Л9)
и пп. 4, 8.

245
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
одинаковы (см. первую строчку из (8.95)). Одинаковы и конечные условия для г, и„, и
из (8.95) поэтому функция (19.21) — сумма квадратов невязок конечных значений — будет
содержать одинаковую группу слагаемых'.
1
Фз — 2 [(г — г~)2+ &lt & t;~ + ( , Ђ” ~
(8.105)
Перечислим недостающие начальные значения импульсов, известные начальные
значения импульсов и выпишем функции невязок Ф для каждой из краевых задач (8 101)—
(8 104):
для задач о границе области определения функции Т (~1у, Т):
р& t; о 0, Ђ”
Р9 1 ДО'
Р~О' Рю О' Р17 О
=Р
У
1
Ф= ~ [Р7,+(~ — ~т)']+Фа.,
Р~ о(0& t; Р о& t;
~т
1
Ф = —, [р'-
Рг = — 1 — ДО
р = — 1
~р—
+(~ — т) ]+Ф,;
2 Р,О Р,„О Р.,О =.
=р
рг= — 1,
1
Ф= — р'-' +Ф;
Рг 0=1 «Чр„о+Р„о)0
&
(8.106)
р
&
«о ~Р~< о+ Р ~
Р =1 — Д
О~
р~= — 1,
Рто'
Рю„о' Рь~о
1
2 [ р', + (~ — ~~)'] + Фз,
— ДО
4'. р О,
Рь' О'
1
Ф= 2 [р-;,+(1 — т)'1+Фз,
для задач о линиях уровня Т (Лу, Т) = сопз1:
1
Ф = ~ ((~р. — Тр.)'+ (~ — МЧ+ Фз;
Р~ о~ — ДО ~О~
Р~О Ро о Ро о=
=р
9
В
1
Ф=~((~,— т,)2+ р — т)~)+ Ф,;
Р О Ро.о Рю.о =.
т <
1
&lt 1 gt; в ”. ~ — Т
— р. р.. З
Рг о = 1 ~о '<7 , + Р
&
(8.107)
Рто Р о Ро о . Р~= — =О,
Т 'т
= — 1
~(Р )
1
Ф= —. (~,— т„)2+ Ф.
2 Р. Р ду
Рг о=1 «о~р о 1 Р„.о
8. Р
Рг о о Р о Р .о=.
&
р = — 1 — д а„
1
Ф=-Р, т,)2+ (~
— ~ИЧ+ Ф;
Сгг
Р1 0' Р~'О'
Рг О
4. р~ о ( 0,
1
Р& t +
'Р-

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
для задачи о точной нижней грани Т:
РУ О ~ОЦР~О+ Р О,
РО РО Р
=р
У
1
Ф= 2 (1+Р )э+Ф„
(8.108)
для задачи о вычислении значений функций Т (Лр, Т) в точке (Лу, Т):
1О. р,,
1
Ф= — Р— Т)2+(р — Л~) -( (р, +1) 1+Ф,.
Рю О' Ро„О~ Рву~О ' Р~ — Р р
(8.109)
Отметим, что в предельном случае нулевого расхода, р=0 (бесконечно большая
скорость истечения, т. е. постоянное реактивное ускорение), порядок краевых задач
1 — 4 и 9, 10 уменьшается на единицу. Это происходит из-за того, что р~ = О при
р = О и заданное конечное значение р~ 1 — — О или р~, — — — 1 переносится в начало:
'Р-' 'Р-'
р~ -=0 или р~ = — 1. Соответственно из функции Ф выбрасывается слагаемое р,' или
'Р-
(1+ р~ )з. В задачах 2 и 3 в этом случае из неизвестных начальных значений нужно
р,/
исключить р, о, которое будет при р=0 равно р,' о — а- — р,'-', где Й р, о) 0 для
перелетов с внутренней орбиты на внешнюю и Й р, о(0 для перелетов с внешней
9
орбиты на внутреннюю ').
Найденные в результате решепия при р=О начальные значепия импульсов можно
использовать как нулевое приближение для соответствующих задач с рф0 (в предполо-
жении непрерывной зависимости р,о от р, которое подтверждается экспериментально).
Можно совершать также переходы от задачи к задаче при одинаковых значениях
параметров двигателя а„, р и перелета Лу, Т, Т„. Для этого нужно осуществить пересчет
импульсов из условия тождественности оптимальных программ ориентации тяги и вклю-
чения-выключения двигателя (в предположении единственности решения краевых задач).
В результате из соотношений (8.92) — (8.94) для оптимальных программ и из уравнений
(8.91) получаются линейные связи между оптимальными импульсами [8.4]:
р: — с„зр + И,з,
(р) (а)
(") =с
Ру = афрр
(~) (а)
р = — с~р
(0) , , (.)
р, = — с„~р,
РО) =- с рр(а) а,
г
(Д) (а)
р, =— с~р,
(8.110)
где верхние индексы а и ~ у импульсов р указывают на их принадлежность к за-
дачам с номерами а и В; с„з и И„~ — постоянные коэффициенты перехода а -~ (1 от за-
дачи а к задаче ~.
Коэффициенты сз„и Из„обратного нерехода ~-+а вычисляются по коэффициентам
прямого перехода:
(8Л11)
с~„= 1/С„З, Из„= — — Н„з/с„~.
Если известны коэффициенты с„з, И„~ и сз„, И. промежуточных переходов а ~ ~ и
3 ~т, то коэффициенты с„, И, непосредственного перехода а-~ т могут быть найдены
по формулам
(8.112)
Отметим, что при практическом использовании соотношений (8.111) и (8Л12) их правые
части должны быть выражены через импульсы р® и р"' соответственно.
Конкретные значения коэффициентов в (8Л10) определяются из граничных условий
(8Л06) — (8.109) для импульсов. Они получаются следующими:
для переходов между задачами о предельной и обыкновенной точках границы или
внутренней части области
с р=1, дар=О; со =1) Иза=О (8.113)
(а,~=1,2;3,4';5,6;7,8';9,10);
1) При р=0 в силу инвариантности уравнений оптимального движения относительно
преобразования замены знака (8.21) достаточно рассчитать перолеты в одну сторону.

247
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
для переходов между задачами об обыкновенных точках границы или линий уровня,
учитывающими особенности при совпадении наклона соответствующей кривой с одной из
координатных осей,
— 1
с,„, 1 д< ), д „,
о
— 1
1 — д'"' '
о
(8. 114)
~„,„= 0
(а=1, 4, 5, 8; Ло —— Л (~о) — см. (8.93));
для переходов между задачами о границе и задачами о линиях уровня )
1 Д (сс)
СР— 1 д() аР— 1 д()
(зо 1 р (Ф) ' )з~
1 — рг1
7; 3, 8', 4, 8; 4', 7;
1 — р~
(Р)
с а,~=1,5;1,6;1',5',2,5;2,6;3,
Л,=Л (~„) = т1п Л (с),
ТОФат1
4', 8',
1
р~1=р~ (1)
— 1 Д(а)
1 Ц~+Л~ » о 1 Л„'~+Л~
— 1
1 — Л(~) +
о Р~1
(8.115)
Р г~1
Ыз — р) р) (а 6=1 5' 4 8)
1 — Л, +р...
— 1 д(и)
1 Л~ )+Л„' ) о 1 Л~*)+Л~
О
— 1
ои ~З) ю
(Р)
— ЦР)
(а, ф=1', 5; 4', 8);
Для переходов между задачами о границе и задачей о значении функции в точке
1
с1о~ — 1 Р~1о)
(а = 1, 2, 4);
1
~10 1 ~1 10)
Р~
10
с,1о = Л„,&
(8.116)
1
С10В (10)
Р~
(а=1', 3, 4');
1
а
10и (10)
Р~
си1о — Л(и)
Ф
1
с1ои= < о gt; г
Р~
с„о =—
(а=5, 6, 8);
(8.117)
10
с„о =—
10~ р (10)
(а = 5', 7, 8').
Остальные переходы (не указанные в (8 113) — (8 117)) невозможны либо просто из-за
отсутствия у пары задач общей точки (Лу, Т) существования решения, либо из-за особен-
') Эта и следующая группа формул получены с использованием дополнительного
условия о том, что при стремлении точки (Лу, Т) из внутренней части области определения
к границе Т„= Т функция Л, (8.93), знак которой определяет оптимальные моменты вклю-
чения и выключения двигателя, обращается в нуль хотя бы один раз на траектории,
а в остальных точках положительна (для задач 5, 6, 7, 8') или отрицательна (для задач
5', 8). Согласно (8 110) нулевому значению Л"' (~,) =О (а=5, 5', 6, 7, 8, 8') соответствует
минимальное значение Л~З~(~,)=ш1пЛ'~> ~) п ~ (~ 1, ', 2, 3, 4, 4 ). но мо ет б
отлично от нуля, тогда и требуется ненулевой сдвиг И,з импульсов р~ и р~.
Р-
для переходов между задачами о линиях уровня и задачей о значении функции
в точке

ГГЛ. 8
248
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
ностей, появляющихся в импульсах одной из задач при стремлении к общей точке ').
К невозможным переходам первого типа относятся
9 ~-э 1, 1 ', 2, 3, 4, 4',
2~+3, 4, 4', 7, 8, 8'; б~э3, 4, 4', 7, 8, 8',
а к невозможным переходам второго типа—
1 ~3, 4, 4', 7, 8, 8', 1' ~2, 3, 4, 4', 6, 7, 8, 8', 3~4, 5, 5', 8;
5~4,4',7,8,9; 5'~2,4,4',6,7,8,8',9; 7~4,8,9;
9~6, 8, 8'.
Полученные формулы (8Л$0) — (8Л$7) для переходов от задачи к задаче позволяют
построить рациональную (в смысле сокращения затрат машинного времени) последова-
тельность счета, когда предыдущее решение дает хорошее нулевое приближение для не-
достающих начальных значений очередной задачи. Принятая схема построения области
определения и картины линий уровня функции Т„(Л~, Т) такова [8.4].
~80
СО
г,г
],б
1б
1б
4д
а,,/д-у,
1б
5Г 4Ю
с7„70 'р,
Рис. Я.14. Начальные значения импульсов задачи 2 при У=80 км/сею (д,=9,81 м/се~').
1'. Строятся зависимости Т, ~ (ао, со) и Лс~; с (ао, со) точных нижних граней времени
перелета и углового перемещения ') от а, при Г= со (р=О). Для этого решаются задачи 2
и 3 при р=О по а,. Это краевые задачи из (8Л06), которые при р=О имеют второй порядок
(см. комментарии после (8.$09)). Соответствующие зависимости начальных значений им-
пульсов от а показаны на рис. 8.14 и 8.15. Рис. 8.14, а, 8.15, а относятся к перелетам
Земля — Марс, а рис. 8.14, б, 8.15, б — к перелетам Марс — Земля, также отмечены и
рис. 8Л6 — 8.25. Для большего практического интереса на рис. 8.$4 и 8.$5 приведены кри-
вые не для предельного случая К=со, а для промежуточного — К=80 км/сек. Характер
зависимостей в обоих случаях одинаковый. Начиная с а 0,6 10 4 д„, все импульсы ме-
няются монотонно и примерно одинаково как для прямого, так и для обратного перелетов.
При достаточно больших значениях реактивного ускорения, а„~~ 3 10 4 д, когда
оно начинает превосходить местное гравитационное, решение задачи 3 перестает существо-
вать. Минимальное угловое перемещение стаповится неограниченным снизу из-за того,
что появляется возможность перехода вдоль траектории от ф & t   ф О В э от мом
импульсы р р р задачи 3 устремляются к нулю (см. рис. 8Л5).
юО~ жуО~ э, О
2'. Для ряда значений реактивного ускорения а„, принятых в качестве узловых,
находятся зависимости Т; г (ао;, У) и Лср; с (ао,, У) точных нижних граней времени
перелета и углового перемещения от скорости истечения К. Это достигается параметриче-
ским просчетом задач 2 и 3 (краевые задачи из (8Л06) третьего порядка) по р, начиная
') Особенности в импульсах могут возникать из-за принятой здесь нормировки:
конечное значение импульса, соответствующего функционалу задачи, полагается равным
минус единице. По теореме Л. С. Понтрягина оно должно быть неположительно. Поэтому
с такой нормировкой при стремлении к точке, где этот импульс должен обратиться в нуль,
(граничная точка области существования решения), остальные импульсы становятся
неограниченными.
') Обозначение Л~; «и термин «точная нижняя грань углового перемещения» здесь
употребляются условно, с тем чтобы отличить задачу 3 от задачи 7. В действительности,
как уже отмечалось, минимум Л~ — локальный (см. п. 8).

249
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
~сО
б
Р10
б
3б а,,10 ~
Гб а,,/д у,
/Д
а)
Рис. 8.15. Начальные значения импульсов задачи 3 при У=80 х.)и,/сек.
(//У)гГ/Гм // 0()05 (//// Ю!5 (//'!'), ул/~м
50 М, км/ссн '~(l ~" /,ц/~(».
0005 001 0015
~00 бб ~
б)
Юд 1И бб,7
~у)
Рис. 8.16. Начальные значения импульсов задачи 2 при а,=2 10-' д,.
000б 00/ 00/б (/I1/),сею!км 0 000б 00/ 00/б (//(/) г ///~м~
Г00 /00 бб,~ б0 Гкм/СЮк ~00 /00 бб,7 б0 (/, лм/с~к
а.) б)
Рис. 8.17. Начальные значения импульсов задачи 3 при а,=2 10-' до.
3'. При фиксированных значениях времени работы двигателя Т ( Т; //опреде-
ляются минимально возможные величины времени перелета и углового перемещения.
Для этого делаются переходы 2-ь 6 и 3-э 7 по формулам (8Л15) и решаются краевые
задачи 6 и 7 (третьего порядка для Г & t  и втор го ля У= о, м. (8Л0 ))
уменьшающихся значениях Т . Когда Тр приближается к своей точной нижней грани
Т„;,г, определяемой аналитически из (8Л22), в импульсах обеих задач появляются особен-
ности: ~ р~ с ~, ~ р„с ~, ~ р, с ~ -+ сс. Это иллюстрируется рис. 8.18 и 8.19. Там же показаны
с р=О. Примеры зависимостей начальных значений импульсов от К представлены на
рис. 8Л6 и 8Л7. Эти зависимости близки к линейным относительно (1/'У).
Далее ведется расчет прямых и обратных перелетов отдельно для каждой пары узло-
вых значений (а„, У/).

250
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
начальные значения импульсов задач 2 и 3 соответственно, с которых начинается расчет
(жирные точки справа). Видно наличие скачка импульсов, описываемого формулами
(8.110), (8.115).
4'. Строится граница Т =Т области определения функции Т (Лу, Т). Для этого,
начиная с решенной задачи 2, решается задача 1 (переход тождественный — см. (8.113),
порядок четвертый — см. (8.106)) в сторону больших (3Лу;,г —.' 5Лу;,г) и меньших ( — Л/~„/)
значений Ьч. Характер изменения начальных значений импульсов показан на рис. 8.20.
Рис. 8.18. Начальные значения импульсов задачи 6 при ао — — 2 10-' д„У=80 км/сек.
д
/7Г д~ '//Г;./ Р// дд
а)
~~/Т / 03 ~~,.//Т/./ ц
б)
Рис. 8.19. Начальные значения импульсов задачи 7 при а,=2 ° 10-' д„У=80 км/сек.
%
Это периодические функции с вековым уходом, причем период близок к 2к. При Лу -~ Л///;,~
наблюдается резкое возрастание импульсов.
Если наклон получаемой границы в координатах Л у, Т (рис. 8.13 становится близким
к ~/2, то совершается переход к задаче 1' по формулам (8.114) и расчет ведется по времени Т
в сторону увеличения. Таким образом, получается нижняя ветвь границы. Аналогичным
образом строится и верхняя ветвь границы: начиная с задачи 3, решается задача 4'(переход
тождественный — см. (8.113), порядок четвертый — см. (8.106)) при возрастающих зна-
чениях Т. Примеры зависимостей недостающих начальных данных от Т приведены на
рис. 8.21.
Если верхняя ветвь границы становится горизонтальной (см. рис. 8 13), то совер-
шается переход к задаче 4 по формулам (8.114). Последняя решается при изменяющихся
в нужную сторону значениях Лу. В том случае, когда задача 3 (о точной нижней грани
углового перемещения) не имеет решения (см. рис. 8.15), граница Т = Т на плоскости Ь///, Т
становится однозначной функцией Лу. Тогда граница целиком находится посредством
решения задач 1 и 1'.
5'. Строятся линии уровня Т =сопзФ функции Т (Лу, Т). Для заданной величины Тр
берется решение задачи 6 (если Т„( Т;,г) или задачи 1 (если Т ) Т;,г) и совершается
переход к задаче 5 по формулам (8.113) или (8.115) соответственно. Задача 5 (четвер-
того порядка — см. (8.107)) решается при различных значениях Лу в требуемом диапазоне.
В случае необходимости совершается переход к задаче 5' по формулам (8.114). Зависимости

251
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
l,б
Рис. 8.20. Начальные значения импульсов задачи 1 при а,=2 10-' до, У=80 км/сек.
-1б
Рис. 8.21. Начальные значения импульсов задачи 4' при а,=2 10-' д„У=80 км/сек.
),б
Риг. 8.22. Начальные значения импульсов задачи 5 при а, =2 ° 10 — 'д„У= 80 ки/сек, Т~/Т;~,~= 0,5.
З Г 7 ЮЗ/З О
д й Га Лй 4а ~ж Ар,ра0 д й
а)
Я4
ФБр~
(б
Э~ 4Й 5ЙВ~,~)В ~
б)
/д ГЯ Гб 5 5Г
б) Ф~~

[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
252
от Лу недостающих начальных значепий импульсов задачи 5 иллюстрируются рис. 8.22
(при Т & t; Т; ~ и р с. 8 23 ( ри Т „>
Верхние ветви линий уровня строятся, начиная от соответствующих точек 7 (при
Т~ ~ Т~, ) или 4' (при Т ) Т;, ). Совершается переход к задаче 8' по формулам (8Л13)
или (8.И5), которая решается при возрастающих значениях Т. Примеры зависимостей от Т
недостающих начальных значений импульсов даны на рис. 8.24 (при Т & t; Т ~ и р с. 8
(при Т„& t; Т;,
1',б
1б
Рис. 8.23. То же, что на рис. 8. 22, при Т„(Т;~~ =1.
Рис. 8.24. Начальные зпачения импульсов запачи 3' при ао = 2-10 — 'фо, 1' = 80 к.ч~сек, ~~/7'~п~ =О,~
lб
1б
0
Г 5 4) б б1/1
Рис. 8.25. То нее, что и на рис. 8. 24, при ~р/~; ~~ =1.
Если верхние ветви линий уровня становятся горизонтальными, то совершается
переход к задаче 8 по формулам (8.114). Если же при данном значении Т задача 7
не имеет решения, то соответствующая линия уровня будет однозначной функцией Лгр,
которая находится решением задачи 5 или 5'.
7. Межорбитальный перелет — оптимальные траектории и программы
управления. Чтобы составить представление о характере оптимальных
траекторий г (1) и оптимальных программ е (1) ориентации тяги и о (1) вклю-
чения-выключения двигателя, для некоторых значений а„Г, Л~, Т„, Т
были выведены текущие результаты интегрирования на последнем шаге
решения краевой задачи [8.4]. Они представлены на рис. 8.26 — 8.41 для

253
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
д д5 1 х
а,Ду
(Ю'
Уд'
бд
Р
уп~бб
-Ыд
-,1К
а,,~3,у
1Ю
бд'
Т = пп'и.
Рис. 8.26. Задача 2: ~р =ор$, Т~ — — ор$,
а) Земля — Марс; Ь~р = 96,7О, Т = 129,1 сут,
б) ~1арс — Земля; ~р = 93,7', Т, =129,6 сут,
Т = 129,1 сут.
Т = 129,6 сущ.
У
СХ Усуи
/5
/
/57б
~Уп7
а,,б
/Я
а,Яу
1Ю
Я~
Рис. 8.27. Задача 3: Ьр =шЫ, Г~ — — ор$, Т= орФ.
а) Земля — Марс; ~р= 92,7, Т =135,9 сут, Т=135,9 сут.
б) Марс — Земля; Ьр= 89,4', Т,„=137,6 сут, Т=137,6 сут,.

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Л5 ( х
бд'
-/Я'
Рис. 8.28. Задача 6: ~р = ор1, Т~ — йхе, Т=пп~п.
а) Земля — Марс; Ьр =120,6', Т,„= 64,6 сут, Т=163,8 сут.
б) Ъ1арс — Земля; Ь~р = 119,7О Т = 04,8 сут, Т = 164,4 су~п.
1
ф/71
-Я9
! а
а)
Рис. 8.29. Задача 7: ~р=
а) Земля — Марс; ~р =118,1',
б) Ъ1арс — Земля; Ьр =117,1О,
афу
IЮ
-1Ю
†/Я
а,фу
/Д/
Т~ — Йле,
64,6 сут,
64,8 сут,
Т= ор1.
Т= 167,5 сут.
Т= 168,1 сут.

ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
~ .Ы~ул -д
~Г7ДЮ ~ул
Рис. 8.30. Задача 6: ~р= ор$,
а) Земля — Марс; ~ р = 189,97', Т„„=
б) Ыарс — Земля; Ьр =141,2', Т,=
сул
Рис. 8.31. Задача 7: Ьр= т1п,
а) Земля — Ъ|арс; ~ р = 189,96О, Тр—
б) Ъ|арс — Земля; ~р =139,2', Х~ ——
ш,Ду
ЯУ
-60
-/Я
а,Ду
Я~
-бд
-110
аДу
Я~
-бО
1 с~~~ ~д~
аДУ
~~0
Т„„= Яхе,
31,8 сут,
46,8 сут,
Тр — йхе,
М,Я сут,
46,8 сут,
Т = ~~~.
Т =270,8 сут.
Т = 195,5 сут.
Т= ор$.
Т = 271,3 су, г.
Т = 198,Сэ су~~ .

256
[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
уЩ
Рис. 8Л2. Задача 1: ~р = Йхе, Т„„= ор$, Т= ппп.
а) Земля — Марс; ~р= 241,8', Т, = 205,4 сут, Т =205,4 сут.
б) Ыарс — Земля; Ь~р =242,7', Т =2О9,7 сут, Т =209,7 сут.
а,В,у
ОО
~Л
И3
бб
О
бб
Ы~О
ЩО
-бО
-МО
Рис. 8 33. Задача 1: ~р= йхе, Т„„= ор$, Т=ппп.
а) Земля — Марс; ~~р =386,8', Т~ — — 221,5 сут, Т =221,5 сут.
б) Марс — Земля; ~р= 314,8', Т„=219,9 сут, Т =219,9 сут,

257
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
lбЯ,Усу
а,Ду
/20
а,Ду
Ы
бО
~у~~
-бО
-ЫО
-00
Рис. 8.34. Задача 4': Ьр = т1п, Тр — ор$, Т = Йхе.
а) Земля — Марс; ~р= 96,7, Т, =162,9 сут, Т=162,9 сут.
б) Марс — Земля; Ьр = 89,4', Т,„=136,6 сути, Т =136,6 сут.
/77б
~уШ
О,
бО
-Ю
-00
17 Ъ|еханика полета
Рис. 8.35. Задача 4'~ ~р= ш1а, Тр — — орФ, Т =йхе.
а) Земля — Марс; ~~р = 103,5', Тр —— 232,5 сут, Т = 232,5 сут.
б) Марс — Земля; ~р= 93,9, Тр — — 177,6 сут, Т=177,6 сут.

258
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛП

259
ОПТИМАЛЬНЫИ МЕЖПЛАНЕТНЫИ ПЕРЕЛЕТ
сул
Х
а,Ду
120'
50'
0
-бд'
-(Зд'
'-00'
СУл
0
— бд
-Ю~
~Р О
а,Ду
Чд
,сут
Рис 8.38. Задача 8: ~р = йхе, Т„= 1'1хе,
а) Земля — Марс; Ьр =145,1', Тр —— 64,6 сут,
б) Марс — Земля; ~р =144,Г, Тр — 64,8 сут,
Т = мах.
Т=236,3 сут.
Т =236,7 сут.
ю,Ду
_#_80
Я~
Ю
Рис. 8.37. Задача 5: Ьр =
а) Земля — Марс; Ьр =145,1',
б) Марс — Земля; ~ р = 140,6',
Ихе, Тр, — йхе, Т = ппп.
Т„„= 64,6 сут, Т=181,8 сут.
Т~ — 64,8 сут, Т = 179,1 сут.

[ГЛ, 8
сут
П1
Рис 8.39. Задача 8: ьр=йхе, Т„=йхе, Т=шах.
а) Земля — Марс; ~р =193,4', Тр — — 64,6 сут, Т= 347,4 сут.
б) Марс — Земля', Ь~р = 210,9', Т„= 64,8 сут, Т= 394,5 сут.
СУ777
Рис. 8.40. Задача 8: ~р =Йхе, Т„=йхе, Т= шах.
а) Земля — Марс; ~р =234', Т~= 64,6 сут, Т=455,9 сут.
б) Марс — Земля; ~р= 232,3", Т = 64,8 сут, Т =453,6 супг.
сс,фу
Ы
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ

ОптимАльныЙ межплАнетныЙ пеРелет
261
ао= 10 4 до=1,962 лм/сек', К=80 км/сек (двигатель малой тяги). В подпи-
сях к рисункам указаны значения углового перемещения Л ~, времени
работы двигателя Т и времени движения Т. Там же указан номер и харак-
тер вариационной постановки из (8.97) — (8.100), которой соответствует дан-
ная траектория. Рис. 8.26, а — 8.41, а относятся к перелетам Земля — Марс,
а рис. 8.26, б — 8.41, б — к перелетам Марс — Земля.
Траектории изображены в неподвижной системе координат (х у) свя-
занной ~г
Ъ У
за ной с солнцем. Вдоль траекторий нанесена разметка по времени, отсчи-
тываемому от момента отлета с орбиты планеты. Начало и конец активных
а,Д
!Ю
а,Д)~
И~'
~ут
Рис. 8.41. Задача 8: Лр =
а) Земля — Марс; Лр = 276,6',
б) ~1арс — Земля, Л~ = 248,5',
Йхе, Т,„= Йхе, Т = шах.
Тр.=1291срт, Т= 1288 су
Т =129,6 срт, Т= 904,2 сут.
участков отмечены крестиками. Пассивные участки показаны пунктиром.
Программы ориентации вектора тяги представлены в виде зависимостей
и (~) — угла между вектором тяги и осью ох (отсчитывается от оси ох про-
тив часовой стрелки). Для облегчения анализа возможностей аппроксима-
ции оптимальной программы ориентации тяги показаны еще зависимости
~(~) — угла между тягой и радиусом-вектором г (отсчитывается от г про-
тив часовой стрелки) и ( (1) — угла между тягой и скоростью т (отсчиты-
вается от т против часовой стрелки). Значения углов, большие 180', пере-
несены в отрицательную область. Функции а (~), ~ (~), т (~) изображены
только на активных участках.
Траектории и программы управления для задач 2 (Лу=ор$, Т =орФ,
Т=т1п) и 3 (Л~р=т1п, Т =орФ, Т=ор$), задач 6 (Лу=ор$, Т =Йхе, Т=ш1п)
т р.
и 7 (Лу=т1п, Т =11хе, Т=орф) попарно похожи друг на друга (ср. рис. 8.26
и . 7, 8.28 и 8.29, 8.30 и 8.31). Траектории задач 6 и 7 с Т, близкими
кТ на
;„~, напоминают траектории гомановских перелетов с импульсным прило-
жением тяги (см. рис. 8.30, 8.31). Самыми причудливыми получаются траекто-
рии без выключения двигателя (Т =Т, рис. 8.32 — 8.36). Те из них, которые
соответствуют задаче 1' (Лу=тах, Т =орф, Т=йхе) или взаимной ей за-
даче 1 (Лр=йхе, Т =ор$, Т=ш1п), т. е. нижней границе достижимой об-

262
неРегулиРуемые двиГАтели
[ГЛ.
— '"' Т (а,,, Г,, Л~, Т)~~Т (а„Г„, Лэ, Т)(
О
— — — Т ц Г Ь~ — со К вЂ” — — Т вЂ” Р
— Т (ае„, Г„, Л~р, Т)(Т (а~, Г, Ла, Т)(Т (ао, Г, Ьэ, Т),
где ~о — угловая скорость движения по начальной орбите.
Нижние оценки следуют из физически очевидных свойств пеубывания максималь-
ной конечной массы с ростом начального ускорения или скорости истечения (в первом
случае уменьшаются гравитационные потери, во втором — мгновенный расход массы).
ПерВая иЗ верхних оцепок устанаВлиВается следу1ощими рассуждениями. Если при
начальном реактивном ускорении ао двигатель проработает без выкл1оче11пй время
г„„=(Г„/ао) — (Г„/ао„), то текущее ускорение ао [1 — (а,/Г„) й„] 1 совпадет с ао,. Программу
ориентации тяги можно выбрать так, чтобы все это время аппарат двигался по исходной
ласти (рис. 8.13), заходят внутрь орбиты Земли. Чем больше угловое пере-
мещение, тем ближе они подходят к Солнцу (рис. 8.32 и 8.33). Траектории же
для задачи 4 (Л~р=йхе, Т =ор$, Т=тах) или 4' (Л р=т1п, Т =ор$,
Т=йхе), отвечающие верхней границе области, выходят за орбиту Марса.
С некоторого значения Т на этих траекториях появляются участки с обрат-
ным направлением движения (противоположным направлению движения
планет, т. е. в сторону уменьшения Лр) (рис. 8.36). Такая возможность объяс-
няется ростом текущего ускорения от тяги по мере уменьшения массы аппа-
рата. На траекториях с выключениями двигателя (рис. 8.37 — 8.41) все эти
резкие черты сглаживаются, и тем больше, чем меньше значение Т„(при фик-
сированном а,).
Несколько .слов о характере оптимальных программ управления дви-
гагельной системой.
Число активных участков на траекториях с угловыми перемещениями,
меньшими 2-., равно двум. Они располагаются в начале и в конце траекторий.
На траекториях с угловыми перемещениями, большими 2-., появляется
третий активный участок в окрестности наиболее близкой к Солнцу
точки. Траектории такого типа показаны на рис. 8.э.'3, лс, з в и. 11 настоя-
щего параграфа.
Направление вектора тяги вдоль стандартных траекторий легко под-
дается аппроксимации кусочно-постоянными или кусочно-линейными функ-
циями времени (число кусков — по числу активных участков). Для этого
нужно только выбрать подходящее базисное направление для отсчета угла.
В зависимости от типа траектории им может быть либо неподвижная в про-
странство ось, либо направление на Солнце, либо вектор скорости.
8. Межорбитальный перелет — минимальные значения функционала.
Результатом решения динамической задачи (8.55), на котором базируется
дальнейшая процедура приближенной стыковки участков и выбора опти-
мальных параметров аппарата, является для межорбитального участка
функция Т (ае, Г, Л~р, Т), определяющая минимальные затраты рабочего
вещества на данном участке. Прежде чем перейти к описанию численных
результатов построения этой функции для перелетов на ближайшие планеты,
укажем некоторые ее общие свойства.
Часть из них, касающаяся зависимости Т„от а, и К, уже приводилась
в п. 1 настоящего параграфа(см. (8.63) — (8.66)). Дополнительно отметим сле-
дующие свойства, справедливые для перелетов между компланарными кру-
говыми орбитами в центральном гравитационном поле [8.4].
1'. Пусть для некоторых значений а,, Г„известна функция Т (а,,, Г„,
Л~~, Т). Тогда для всех а, ( а, при Г = Г, и для всех Г ~ Г при а, = а„
справодливы оцеш'и

263
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
Я 3]
можно бесконечно часто менять направлен
ление тяги с танген-
круговой орбите (например, можно
лжения траектории можно взять
ц~алж~т на р~жы~~~~~~~ ). Д
нос~. ~алыче в качестве продол
а =а но с мепьшим временем
— П
м гловым перемещением (Ьу — и,~ „). остроенная
шим угл
отк а и следует первая верхняя оценка.
не м
может быть лучше оптимальнои, откуда и с
оп ав ывается качественными со ображениями. Меньшей
РаЯ "Рхн" 'Жнка 'пР " б, „„„„„у, б
авпых времепах раооты двигател
. П же ффект смысле ы~~~~~~я
ктивпого скорения. ~юэтому тот ж
остигн т за меньшее активное время
параметров р .. остигн т за мень
в траектории здесь может быть достигнут за мень
Ф.Ф
2'. Обозначим через Т=г (Л~) уравнение гра ц
ани ы Т =Т допустимои
Т и и фиксированных значениях а, и К в виде,
области на плоскости Л~, при фи
тве ж ать, что при любых
нном относительно Т. Тогда можно утверждать, чт
разрешенном отн
(Л ) (б может и многозначная) определена
Т
Т
0
Рис. 8.43. К неравенству (8.119)
Рис. 8.42. Характер грапицы попустимои
области.
Л~~ ( — ж, +со), ограничена и имеет асимптоты
на бесконечном интервале ~ ~ ~ — ж, оэ,
(рис. 8.42)
1'(Ьр) ( Г/а для всех Лэ(: ( — ж, +со),
1( 1' (~ю) = !1 1 1' (Ью) = 1'/, (8.118)
Л ~р-э+со
Т а Г Ьэ, 1'(Ьэ)]= Г (Л~), 0(а, Г= Йхе).
р О'
лю ения словия неотрицатель-
Ограничеппость 1 ( А-;) следует из необходимости соолюд у
[Ости конечп01 массы (сы. ~(8
могут быть пройдены за конеч-
мо лю гловые расстояния м
ду'
т
емя ~ю Ого б ота мож
ой ет очень близко к гравитаци
т
но
( е число обо отов. ри этом в
вокр
1Ру Г НЕГО Достаточно ООЛЬШО д
ым. ля входа в столь лизкую
б ю окрестность гравитацион-
оыт °
ть сделано сколь угодно малым.
вы ~О а пз нее треоуется оль
б лысое реактивное ускорение
пого центра и д;1я последу1ощего . д
скорения при фиксированном
— ). Такие значения реактивного уско
к 'ая масса а арата ста ет д
о-
нци могут быть получены, когда текущ
— д р ~~опля 1~ оправдыва~от (8.118).
с, Г(Л ) О равномерно относительно
° — н лево11~. ти рассужд
1 ОГДа а„—: сс, то ПЗ ( .' С.
(8 '118) следует, что граница у — э
ь Т)0.
( ьится ости'кпмо11 вся полуплоскость
Л, т. е. ( т"и) д
и Г ля некоторой точки
~)О
и и ~~икси ованных значениях а, и
льная т аектория, на которои
%Ф
"ости Л~, Т построена оптимальная т
(Лз„т,) плоскости
скости внутри угла с верши-
Л~ Т ~ ~—— -Т,. Тогда любая точка этои плоско
$~ (1/и ) и агс$д (1/в,),
Т ~ об азованного лучами с наклонами агс д,
и б игателя не превосходит там
достижима и минимально р,
е в емя оа оты двиг
Т„(рис. 8.4а):
т, (~;, т) ( т„= т, р, „т,)
~~ ~~ ~т'о
Т+ ~ ~")Т)т,+
Ь- — Ьу,) Ьу — Ьу,
О)о
(8.119)
вн т енней и внешней круго-
О-)2—
— човые скорости движения по вну р
выы орбитам соответственно.

264
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
В самом деле, любую траекторию можно «продлить» без изменения Т, добавив в на-
чале и в конце (или только в начале, или только в конце) участки пассивного двихсения
по соответствующим круговым орбитам. Оптимальная траектория для новой точки (Ли, Т)
будет. естественно, не хуже построенной таким способом.
Из полученного неравенства (8.119) вытекают неограниченность (в сторону пропор-
ционального возрастания Л1у и Т) области определения функции Т„(Л~у, Т) и оценки на-
клонов границы области определения и линий уровня этой функции (при фиксированных
а«и Г). Обозначим через Т=Г (Лу) и Т=Г1(Ли, с) нижние ветви границы Т (Л~с, Т)=Т
и линий уровня Т„(Ли, Т)=с, а через Т=Г (Л12) и Т=Г (Ла, с) — верхние ветви. Тогда
из (8.119) следует:
дГ1/дЛУ ( 1/и1,
при а,, К, с=йхе (8.120)
дГ /дЛу ) 1/и2 или ( 0
Тр [ЛУ, Гл (ЛУ)] = Гл (Лт), Тр [ЛУ, Гл (ЛУ, с)] = с( Гл (ЛУ),
/=1, 2; Г1 (Лу) (Г2 (Лу), Г1 (Лу, с) (Г2 (Лу, с)
(см. рис. 8.42, 8.43). Иначе получится противоречие с тем фактом, что функция Т (Ли, Т)
дает минимально возможные затраты.
Перейдем теперь к описанию численных результатов для перелетов
Земля — Марс, Марс — Земля и Земля — Венера с двигателями малой тяги
[8.4, 8.14, 8.21]. Они представлены графиками и аппроксимирующими фор-
мулами. Сначала приводятся результаты по предельным точкам: Т;„1 — задача 2,
Л[1[[„, — задача 3, Т,.„,— задача 9.
Задача 2 (Л[р = ор1„Т„= ор[„Т = тт):
Т,[сут[=Тс[сут] ' +17(1
172,5
]/ао [10 4го]
Л[]2 град ' 15 [
124,5 с
1.[ у ]-, „,у,+ „.„„,„,)
(с = 31,2 — «Земля — Марс», с = 43,5 — «Марс — Земля»)
при 0,5 ° 10 «д (ае(5 ° 10 «де, 20 км/сек( ['( со.
(8.121)
Точные значения Т, и Л[1], показаны на рис. 8.44, погрешность аппрокси-
мации составляет -1 Ц .
Задача 3 (Лр = т1п, Т„= орь, Т = ор1):
22,8 1
Ус [КЛ1/СЕК]
Т,[сут]=Тс[сут] ' ]-22(1—
164,8
'у'а, [10 'г,]
Л[р град 1
140 С
у,,[р-~дЛ ] у] ]сс 1)
(с = 450 — «Земля — Марс», с = 465 — «Марс — Земля»)
— 4 — 4
(8.122)
при О,о ° 10 де ( а, ( 3 ° 10 д„20 км/сек ( [' ( со
(рис. 8.45, точность аппроксимации — 1[]уе).
При а, ) ае„решение задачи 3 перестает существовать, уравнение
Т'="х (Л[[]) границы области достижимости становится однозначной функ-
цией Л[]2. Это происходит, когда реактивное ускорение начинает превосходить
гравитационное настолько, что быстро проявляется возможность смены знака ф.
Схема эволюции границы с ростом а, можно иллюстрировать рис. 8.42.
Пунктирной кривой на рисунке показан разделяющий вариант а«=а, От-
метим еще раз, что даже когда решение задачи 3 существует (ае ( а,„), то
в силу (8.118) Л[[]з оказывается только локальным минимумом и не ограни-
чивает снизу все возможные значения углового перемещения.
Задача 9 (Л[[]=ор$, Т =т1п, Т=ор1). Точное решение задачи 9 полу-
чено в работах [8.18, 8.19]. Оно достигается на скользящих режимах упра-
вления. Эта программа управления для межорбитальных перелетов выгля-

265
ОПТИМАЛЬН]Я.и. МЕЖПЛАНЕТНЫ.и. ПЕРЕЛЕТ
дит так. Прикладывается первая серия бесконечно малых тангенциальных
импульсов тяги в начальной точке исходной круговой орбиты (соседние
импульсы разделены друг от друга временем одного оборота по оскулирую-
щему эллипсу). Как только апогей (или перигей) оскулирующего эллипса
5 ~ 4
а,,/д р,
Рис. 8.44. Точная нижняя грань времени перелета (сплошные кривые) и соответствующее угловое пере-
мещение (пунктирные кривые): а) Земля — Марс; б) Марс — Земля.
достигнет конечной круговой орбиты, в нем начинает прикладываться вто-
рая серия бесконечно малых тангенциальных импульсов тяги до тех пор,
пока перигей (или апогей) тоже не достигнет той же орбиты. Время, потреб-
ное для реализации этой программы управления, бесконечно велико (равно
3'
град
(бд
/
и,,/О 'д,
г,5
б) а„/О 'у,
Рис. 8.45. Локальный минимум углового перемещения (пунктирные кривые) и соответствующее время
перелета (сплошные кривые): а) Земля — Марс; б) Марс — Земля.
как и угловое перемещение). Величина функционала Т, его точная
р Ф
нижняя грань, определяется формулой (8.64), где равенство уже точное,
а Ли=т1п Лг (Л~, Т) по Лз и Т вЂ” минимальная характеристическая ско-
рость обычного импульсного перехода при незаданных Лр и Т (см. ~ 3 гл. 5).
Проведенные расчеты показали, что, начиная с ао=0,5 10-' д„удается
приблизиться к Т,„;„~ с точностью — 1О~О при конечных значениях Л~ и Т.

р ° Э
1 е 6 1
° °
° и е 1 ° в а ° 1 °
° ° е ! ! 1 ре ° ° 9
° °
° ) е в ре'
9 6
к ( ю
е
° ° у
е °
ЭЭ! ° 9
й
Э ' 1
й ° 6
° ° У
° °
! 6 й ) ° ° ° ° 1 ° 6
° в
6 ° $
'6 С'
С'6 ) в ' !
Э !
Э 1 '
Эв 1 Э. '' 1 ° 1 6
66В' °
1 ° ) 1
й 6
6 С в
Э Э
А & t
° °
! ° Э в й
) °
Ф У
ю
Э 6
в ° Э
) С
Э ° °
691 ° )1 5е1'е5'Се''3
9 е 1 в 6 ° ! ° )1 ° ° Р °
6 й ) ° ° ° ! °
1 ' 1
) ° е е 1 °
° ! °
! р~ р~
й й
в 6 ° 6

267
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
Задача 7 (Ь« = т1п, Т =Бхе, Т =ор1):
т7'~ т9 ( ~9 тз)
х'+ у' — ),х'у = 1
Т7 Т9 (Т9 Тз) х~
Т„= Т,— (Т, — Т,,) у,
(8.126)
) = 0,181 [1 — 46,2 (Г ['им/сек]) 9 9]
1 .. х) О, 0(~у(1,
0,5 ° 10 'д,(а,(3 ° 10 'д, — «Земля — Марс», 0,,5 ° 10 ~д, (а, (
(2,8 ° 10 ~д,— «Марс — Земля», 20 км/сек( Г~~~ оо
Дальнейшие результаты, в соответствии с принятой схемой расчета,
приводятся для каждой пары узловых значений а„р в виде графиков гра-
ницы области достижимости и линий равных минимальных затрат на пло-
скости Лю Т. Графики представлены в безразмерных переменных. Харак-
терные значения времени Г., Т .. и углового перемещения Л ~ выоирались
своими для каждой пары а„
(8.127)
Т„= Т „= Т,(и„Р),
Ьэ„= Ь.;-з (и„, ['),
В рамках этих же приближений, ио в значительно меньшем объеме получены числои-
пые результаты в работах [8.22, 8.23]. Как и здесь, вариациоиная задача сводилась
к краевой, последняя решалась методом Ньютоиа. Построение оптимальных траекторий
межорбитальных перелетов с иерегулируемыми двигателями производится также и пря-
мыми методами [8.24]. Данные по оптимальным траекториям с постоянным реактивным
ускорением содержатся в работах [8.25 — 8.30]. В некоторых работах (например [8.28—
8.30]) при проведении расчетов с постоянной тягой функционалом задачи счнтался ин-
теграл (6.11). Подобная замена при решении параметрической части задачи приводит
и существенным ошибкам (см. примечание к переводу [8.30]).
Чтобы составить представление о перелетах на другие планеты солнеч-
ной системы, приведем данные по решению задачи 2 (см. (8.97)), полученные
в работе [8.13] при а,=10 ' д„р=со. Точная нижняя грань времени одно-
стороннего перелета с Земли здесь оказалась равной 135 сут для Венеры,
189 сут для Марса, 540 сут для Юпитера, 789 сут для Сатурна, 1150 сут
для Урана, 1480 сут для Нептуна, 1720 сут для Плутона.
9. Межпланетный перелет без возвращения при незаданной дате старта.
Межпланетный перелет без возвращения содержит только первые три
участка из перечисленных в п. 1 3 3 гл. 4. Задаются начальное ускорение,
где Г., и Л~з — минимально возможные при данных значениях а„1~ время
и угловое перемещение, определяемые по формулам (8.121) и (8.122). В тех
случаях, когда решение задачи 3 перестает существовать, в качестве Лэ„,
берется значение углового перемещения, формально вычисляемое по (8.122).
После такого отнесения графики линий равных затрат становятся мало
чувствительными к а, и р. Они представлены на рис. 8.47 — 8.49. Рис. 8.47
относится к случаю Г=со, поэтому пригоден как для перелетов Земля—
Марс, так и для перелетов Марс — Земля; рис. 8.48 относятся только к пере-
летам Земля — Марс а рис. 8.49 — только к перелетам Марс — Земля (на них
значения Г конечные). Помимо безразмерного масштаба на рисунках даны
и размерные масштабы. Последние уже существенно зависят от а, и Г.
Все приведенные данные относятся к случаю, когда в начале и в конце траек-
гории скорость аппарата совпадает с орбитальной скоростью соответствую-
щей планеты, а орбиты планет круговые и ко~п~ланарные.

268
[ГЛ, 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Т~рл 7
РКР5Р4 Р5
РЛДН Р4(Я' 05(7Дсуя)
Р,бЮЭ
Д7Ю~~
Р(111)
ЮЯ
дул)
ул)
л)
гк,
Д Г~ 5 ~4 5Р ~г ~к ~ х~ л~.
3 4 5 б 7 д Я Аррас
Рис. 8.47. Земля — Марс и Марс — Земля, а,=2 10-4 д„У=со.
чп
/ /./ /б РР Еб 5 бб бб 4,Г 4б б бра
Ы а б б 7 б б /б // /Р /.~ // /5 /б Лр,раб
Рис. 3.48а. Земля — Марс, а,=0,5 10-4 до, У=30 км/сек.
Тсуи 7
7„Д4 Я Я
08
ОЯ
/8 Я!1 ДЯ 0,30,70Я0,5 04
Я5 5 4 5 ~ 7 ~ Я 10 1/ ~Г с1ррад
Рис. 8.486. Земля — Марс, а,=10-4 д„У=80 км/сек.
200
Н /б .г,г Гб Ю Зб Юб &l ;г ~ б ЭЛ

269
ОПТИМАЛЬНЫ.и. МЕЖПЛАНЕТНЫ.и. ПЕРЕЛЕТ
Об
07
дд
Т
З,д
.ИО
/,Я 2,Г 3 5 5,4 З,д ~,2 4,б 5 543 /Др„
/,дд2,5 4 5 б ~ д У /О Ьр,~а3
Рис. 3.43в. Земля — Марс, а,=1,5 10-4 д„У=80 км/сек.
/~ /б Я /2 / О дб Я Я' ~2~Б'
Т Т
~У 0~ д5 дб
Д7
ОВ
09
/
//
/Г
в т
ЗЯ
4Р 46' 5 Я3 /Шр,
Др,уод
Гб 5 Я
/ Я
/ба Г 5
Рис. 8.43г. Земля — Марс, а,=2 10-4 д„У=80 км/сек.
0507
2ОЯ!1Я/ ®070б 0Я7
Я~ш Т
Зф
5/д ~ 5 б 7 д У /~ /' /2 /3 й /5 /о /13р,рп~
Рис. 3.49а. Марс — Земля, а,=0,5 ° 10-4 д„У=80 км/сек.
3'00
ГЫ
/ Я /.5 ГР Яб 5 1.ч 58 ~ ~ .;~~ .) 5,4 3р/3р

270
[ГЛ. 3
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
Яб
гг
Х~~ 5,8
5;д Х~ Лр/А р„
~0 ~~ ~~ 3~,,оад
/,4 /Я РГ Я,Ю 5
Рис. 8.49б. Марс — Земля, а,=10-4 д„У=80 км/сек.
г,г гб Л Л~ Лг ~,г ~,б Х У~ ~р~д~.
1Я' Я
У Ю 7 Я Др,раФ
Рис. 8.49в. Марс — Земля, а,=2 10-' до, У=80 км(сек.
7 ~ут 7
Ц,? Я 04 05
~ О РбЯ б-" 03
350
Об
ЗОО
100
1 й ~8 Я,г Г,б 3 Д~ 53 4,
'..у 5 Х4а~~/Ду
5 5;5 Др,~юд
д9г5 ( 1,5 Р Р5 3 5,5 4 б~,5
Рис. 8.49г. Марс — Земля, а,=4 ° 10-' до, У=80 км/сек.
200
~вг
3гб 3 4 5 б 7 8 Я
Рб 04 ~7~~
Т
08
0,9
,/
Р
,Я

271
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
скорость истечения, величины сбрасываемой массы и суммарное время пе-
релета; требуется найти минимум суммарного времени работы двигателя 1):
3
а„Г, Ьт[1], Т.=,~~ Т"'=Лхе;
3
Т =~ Т[']=тгп.
р.а р.
(8.128)
Дата старта не фиксирована, поэтому условие попадания аппарата на
планету финиша всегда может быть выполнено за счет выбора даты старта.
При стыковке участков в рамках приближения ~ 3 гл. 4 должны быть соблю-
дены условия (8.54) по реактивному ускорению и расходу и условие из (8.128)
по суммарному времени перелета. Процедура расчета выглядит так [8.4].
1'. По формуле (8.85) с соответствующими коэффициентами находятся
время движения Т"' и время работы двигателя Т„"'=Т"' для разгона
у Земли з).
2'. Из условия (8.54), которое в размерном виде записывается как
а[0 [10 'У,] = а„[10 сУс] 1 — ~~ ~Ьт[сс ' „' У' ~~» ТОС [сУт], [8.120)
[2) ~ [2)~;12) (Т[2)~
Орь
До иачала параметрических расчетов па Т, необходимо найти точные
нпжние грани Т.,„и Т,, Первая определяется по изложенной выше
схеме при Т[2) = 1 (движение без выключения двигателя). Сравнение Т[з) + Т"'
с Т, — Т"' в 4С' при этом пе производится, а Т, вычисляется как сумма
Т"'+ Т[']+ Т"'. Для определения второй нижней грани в Зо задается
') Здесь и дальшо до конца настоящего параграфа для сокращения записи, в отлп
чие от обозначений з 3 гл. 4, величины, относящиеся к некоторому участку перелота,
отмечаются верхним индексом, который совпадает с порядковым номером участка. Соответ-
ствие между старыми (пижними) индексами и новыми (верхними) таково: +1 ~а )',=1,
1 м ~=2, — 2 &l ;+ ~ 3 О +&gt ~ 4, +2 & t + =5, «+ ~ 6, —
') Здесь и дальше, в пп. 10 — 12, заранее полагается, что на участках 1, 3, 5 разгона
и торможения у планет двигатель работает без выключений, а программа ориентации
тяги берется оптимальная, ] =т0„1 (1).
находится начальное ускорение а0[з] межорбитального перелета. По рис. 8.44,
8.45 или по аппроксимирующим формулам (8.121), (8.122) для найденного
значения ао~'~ и заданного К определяются характерные значения Т„''-' и
Л[0['-'] времени и углового перемещения.
3'. Задается безразмерное время Т"' ) 1 межорбитального перелета
и по рис. 8.47, 8.48 с ближайшими к данным а0[2] и Г значениями ускорения
и скорости истечения или по аппроксимирующей формуле (8.125) находится
минимальное время Т['] работы двигателя. Поскольку угловое перемещение
Л~[2) произвольно, то этот минимум достигается на соответствующем (по Т"')
решении задачи 6 (или 2, или 9).
4'. По формуле (8.129) с Т['] = Т[']Т[р-']„., (Т"') вычпсляется начальное
ускорение а0[з] для участка торможения у Марса, а по формуле (8.85) с соот-
ветствующими коэффициентами — времена Т"' = Т[з]. 11одсчитывается сумма
времен Т'-'+ Т'з' и сравнивается с заданным значением Т, — Т[г). В случае
несовпадения изменяется время Т"': увеличивается, если Т"'+ Т"' (
( Т вЂ” Т"', или уменьшается, если Т"'+ Т[з) ) Т. — Т"' (цикл Зо — 4о).
При параметрических расчетах по Т. процедуру подгонки времени можно
псключить, заменив параметр Т на 7"".
5'. После совпадения Т"-'+ Т"' с Т вЂ” Т"' находятся Т...=,~~ Т[,']
а=1

272
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
не Т"-', а Т~[-"[ = Т[',.~„. Время Т'2' находится из решения задачи 9—
см. (8.123), сравнение Т"'+ Т"' с Т. — Т'1' снова не производится.
Суммарное время Т. нужно менять
Я(~ У
от Т„. ~ до Т,(Т„„.„„). При Т,(Т„.„
ЯУ71 Ю
решения не существует, а при Т. ~
) Т. (Т„., „) решением будет Т„= Т
500
Илн/се По изложенной схеме проведены
расчеты с оптимальным направлением
Ю ~' тяги на всех участках при отсутствии
.Ю мгновенного сброса массы (Лт" [=0)
Щ
~о для перелетов с 200-км орбиты спутни-
уО '80
г-ю '
Уо
ка Земли на 300-км орбиту спутника
Марса. Результаты расчетов представ-
лены на рис. 8.50 в виде зависимостей
Т„. (Т.) при фиксированных значениях
а, и Г. Оптимальное распределение
времени движения и времени работы
двигателя по участкам дано на рис. 8.51.
Такие же расчеты проделаны для пере-
летов с 200-км орбиты спутника Земли на 300-км орбиту спутника Венеры.
Оба случая охватываются аппроксимационными формулами [8.21]
Рис. 8. 50. Минимальное суммарное время
работы двигателя Т для перелета с 200-км
орбиты спутника~земли на 300-км орбиту
спутника Марса (с оптимальной датой старта).
Т.,
Т.,(а„Г, Т„.) [сут] = Т„.„„,
если Т „., ( Т„,( Т„„,,
если Т„, )~ Т„„„,
Т[,. ( Т~~Р
(8.130)
если
где
цт„.,„, — т„.ут„.,„, — т„.,„)р (.
+(с, — с,Г "[км(сек]) ао" [10 'до],
Т„„„,[сут] = с,
+ (с9 — с1О Р "' [км~сек]) ао ' [10 'до],
[' км сек1
Т„.,„[сут] = с,
т...,[аут[=с„+(с1З+ "' ) т„.,„,
15 С16
Значения коэффициентов приведены в табл. 8.1.
10. Межпланетный перелет без возвращения при заданной дате старта.
Постановка задачи аналогична предыдущей, добавляется только условие
по дате старта:
3
а„1~, Ьт['~, Т. = ~~~~~ Т"', 1, = йхе;
(8.131)
3
Т =~ Т['& t; =
Р.о р.
т=1
Задание даты старта накладывает связь на Лр"' и Т"' (см. (4.73)),
которая может быть записана в виде
~ "' = Т'-" и,, — (», + Т'1[) (и, — и.,) + 2-г,
(8.132)
где г — произвольное целое число (положительное, отрицательное или нуль),
~о отсчитывается от момента противостояния планет 1 и 2.

Л.ау~ ОО г )1.У С 11 Я.т~Н ~ и, г Ю Н и ~О 1
Венера 39 580 286 1210 0,81 0,9 2,53 — 37,12 264,25
Сд() Сдд д2 Сд3 Сд4 Сд5 Сд~ Сд7
Марс 657 0,8 259 0,815 0,54 0,181 — 8,36 — 0,9
Венера 912,15 0,7 147,1 0,864 0 — 1,23 0,455 0,176
° ! ° °
1 ' 1111
° ° $ °
° ф
° ° ° ° ° ~Р ° 1
Э ° е в ~ °
! ° '! Фе Фе '' е ° е1 ° ! °
!' ° ' Э 11е е Э Э Фе 1 е ' °
Э ! ° ° ~ у
й
° ° й
° ! ° '
° ° е
Э а ° Э ° 'в
° й
е
$ °
й ф
1
Э $ °
й °
Э! Э!
° й
в
° й
° °
Э Э Э'
е ° Э
° ° !!
Э ! е ° ° °
119! ! 1.
° °
е !
й ! ° й
! е а ° !
° ° ° 1 ! ! е в
' ИИИ ИПИИИ
, ИИ~, ИИИЛИ
' ЕИ;;~~~%> И
, И~~- ЫЯИИИ
° йИИБИИ
ВПКИИИ
(/ О О /Р
ФФ Ф / О О
° 1 ' ° ° ° ° В 1 ° '1'
е
1 ° 11 В ' ° 1
1 ° 11 ' ° ° 1
° ° ° ° В 1 ' ' ° 1
° ° В ° 1 ° ° ° ° ! °
° ° В ° ° °
° ° ° 1 1
! е ° 1
! Э в е ° ° °
° ° ° ° °
° °
° °
Э й1 1! Ф1
! ° Э ееФе ° 'Эе ° в
° ° °
! в а ° ° °
° ! °
Э !
° е
Э ° ° 1 ! Э ! 1 ° Э ! ° ° ° ° 1
° ! е
° Ф ° Фе 1 ° ° 'а 1
Сд С2 Сз С4 С~ Сц С7 Св Ср

274
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[гл. 8
Участки кривых от точек минимума (решение задачи и. 9, отмечено
на рис. 8.52 пунктирной линией) до точек максимума образуются нижними
ветвями границы и линий уровня функции Т„"' (Л~"', Т"'), остальные
участки — верхними ветвями. В точках максимума нижние ветви и верхние
ветви дают одинаковое значение функционала, хотя траектории разные
(траектория, соответствующая нижней ветви, делает на один оборот больше,
чем траектория, соответствующая верхней ветви). О таком же явлении для
/~~а
суп
~® ~® ЯО ~И -Юд -ЯД -7® — ®~ ~ ~ут
Рис. 8.52. Минимальное суммарное время Т,т перелета со 150-кл~ Орбиты спутника Земли на 500-кл орбиту
спутника Марса в зависимости от даты старта 4 при а,=2 10-'д„У=со.
траекторий полета с идеальным двигателем ограниченной мощности упоми-
налось в $2 гл. 7. Его можно трактовать как неединственность решения крае-
вой задачи, если записать ее в декартовых координатах: начальная и конеч-
ная точки на плоскости х, у, время перелета и время работы двигателя сов-
падают, а программы управления и траектории разные. В полярных же
координатах неединственности нет, поскольку углы перелетов отличаются
на 2т~.
Отсюда следуют пределы изменения углового перемещения Л~, в кото-
рых линии равных затрат и граница области достижимости на плоскости
Л~, Т представляют практический интерес:
для линий равных затрат Т„(Л~, Т)=с
у,(с)(Лу(р„(с)+2п, где Г,(у,+2п, с) =Г,(у„, с);
для границы области достижимости Т„(Ьу, Т) = Т
(8.1ЗЗ)
р„(Лр( р,+2п, где Г,(р,+ 2п) = Г, (р,).
(8.134)
11. Межпланетный перелет с возвращением при незаданной дате старта.
Рассматривается перелет с возвращением в случае аэродинамического тор-
можения у Земли. Скорость входа в атмосферу Земли полагается параболи-
ческой, временем спуска в атмосфере Т'" (см. гл. 15) пренебрегается по
сравнению с полным временем перелета Т. — 1 год. Задаются начальное
ускорение, скорость истечения, величины сбрасываемой массы, суммарное

275
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
дрожмя перелета и минимальное время ожидания; ищется минимум суммар-
ного времени работы двигателя:
6
а„)', ~т(Г), Т = ~ Т"', Т, = 1)хе;
(8.135)
Т = ~~ Т(Г) = хп)п
р.о р.
ю=1
Времена движения и угловые перемещения на межорбитальных участ-
ках связаны условием (4.70) возвращения на планету старта. Это условие
переписывается в виде, разрешенном относительно Л(~)'6) — углового пере-
мещения обратного перелета:
Т = ТГИ + Т(2) + Т(з) + Т(з) + Т!6)
рю р. р. р. р. р.
Т") = Т") = соей,
Т = Т ( Р р(2), Т( ),
р.
Т(з) Т(з) Т(з) (а(з) (Т'2'Ц,
р. — — О р.
Т(6) Т(6) Т(6) (Г)(6) (Т(2) Т(З) (Т(2))и
р. — — О р.
Т(6) — T(6) (Д(Р(6) T(6) Г)(6) (T(2) T(З) (Т(2)) T(5) (Т(2))))
Т(') + Т(з) + Т(6) + Т(з) + Т'6' = Т, — Т, = соизй,
Д~(2) д~(в)
Т(2) — -~- Т(6) — — + Х вЂ” — 2 (Т(З) + Т'6) + Т(6)) — 22(З =О.
Юд ОЭд
(8Л37)
18®
ЬГ()"' =(Т"'+ Т"') (6, — Ь~Р"'+ ((61 — (62) ~~ Т'" — 222г, (8.136)
Ф:3
где г — произвольное целое число. Порядок расчета следующий [8 4].
1'. Совпадает с 1' из п. 9.
2'. Совпадает с 2' из п. 9.
3'. Задаются безразмерное время Т""' и безразмерное угловое переме-
щение Ьл(2) из области определения функции Т„"' (~ф'", Т'") для межорби-
тального перелета «туда». По наиболее подходящему из рис. 8.47, 8.48
находится соответствующее значение Тр(.".
4'. По формуле (8.129) с Т„'." = Т„"Т„'-) (Ьф"), Т"') вычисляется началь-
ное ускорение а6") для участка торг(ожения у Марса, а по формуле (8.85)
с соответствующими коэффициентами — времена Т'з' = Т„'". Время ожида-
ния т(6), как будет показано ниже, в оптимальном варианте должно быть
равно заданному минимальному времени: Т(6) = Т„время работы двигателя
на этом участке Т„'4' = О. Такие же вычисления производятся для участка
разгона у Марса: а6") подсчитывается по формуле (8.129), а Т(з) = Т„'"—
по формуле (8.85) с соответствующими коэффициентами.
5'. Вычисляется ускорение аз") для межорбитального перелета «обратно»
(по формуле (8.129) с найденными выше временами Т„'.", ~=1,..., 5). Из
рис. 8.44, 8.45 или формул (8.121), (8.122) находятся характерные значения
времени Т„'" и углового перемещения Ь~'6) для этого участка. Вычисляется
время Т'6' = Т. — (Т"'+... + Т'з)) где Т"' = Т'-'Т'" и по фор-
муле (8.136) — угловое перемещение Ь(з(6) (г). Берутся соответствующие
безразмерные значения Т'6' = Т'6)/Т(6~ и Ьф'6) (г) = Ьр'~) (г)/Ьр~~~, для кото-
рых по ближайшему к данным аз~6~ и Г рисунку 8.47, 8.49 находятся без-
размерные значения времени работы двигателя Т(6~ (г). Среди них выбира-
ется минимальное, по которому и вычисляется Т~') = Т~'~Т~'~.
о
З р — * р Е
6 . Вычисляется суммарное время Т„. работы двигателя и отыскивается
его минимум по Ь(()(2) и Т'" (цикл 3' — 6'). На этом решение динамической
части задачи для данного набора параметров (8.135) заканчивается.
Чтобы доказать оптимальность Т(4) = Т, и построить численную процедуру ми-
нимизации Т, по ду(') и Т('), выпишем выражение для 6Т,. Полная система связей
имеет вид

276
НЕРЕГУЛИРУЕЪХЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Здесь указаны зависимости только от тех величин, которые меняются при варьиро-
вании независимых переменных Ьу(2), Т(2' и Т(4). Напомним, что аО, Р, Ьт„"), Т,
и Тв фиксированы.
Выразив первые дифференциалы аТ'" в силу связей (8.137) через первые диф-
ференциалы аЬусз), аТ'з), атсв) независимых переменных, получим')
дT("-) дT (6) дТ'"-' дТ '6'
Р Р.
. (2)
Р Р
(2)
ат„.= (1 —.) д„„, — д св) Ир + (1 —.) д,„,„, ат
У У
дT (6) дT (6)
д Т(4)
2 д~ (6) ( дT(6)
(8.138)
где ® -эО при Р— э со, а при конечных значениях Р имеет вид
дТ(6) дТ(6) Д Т(з) ДТ(ь) д Т'6'
Р
о)з До св) ~ ДУ'св) аТ"-' + аТ"-' + ДТ'-')
У
(8.139)
3, 5) находятся дифференцированием (8.85) по ас1)
8,48ао'
(1 ~ ~"з ) Р )
(8. 140)
где гз — — 1+ Йсз)/Л = г = 1+ Йсв)/Л; (Тс'-') = су))), размерность остальных величин
и значения коэффициентов 6 указаны в (8.85).
Производная дТ"'/дТ"' записывается следующим образом:
дТсв' дТсв) 8 48 атсз) ау'св)
ДТ~~ дасв с~в ) 100Г атсз) аТ'-'
О
(8. 141)
найдена из рис. 8.44 или фор-
где дтсв)/давсв) Т'в' (дтсв)/давсв)) и может быть
мулы (8.121).
Оценим знак производной (см. (8.138))
дТ, дТ(6) дТ(6)
дТ(4) ~2 дну(6) дТ(6)
Если точка (с1фв), Т'в') принадлежит нижней ветви некоторой линии уровня
функции Тсв) (~~~~), Т'в)), то согласно неравенствам (8.120)
дгсв) дтсв)/ДЬ~св) 1 дТсв)
1 Р
д~~св) — ду'св)/ду св) ~ ~, ' дтсв) (
откуда дТ„ /дТ'в) ) О.
На Верхней ветви, согласно тем же неравенствам, возможны два случая:
первый—
дТ(6)
дусв) ) ю
Дцв) дтсв)/ДЬусв) 1
ДЬ~св) дтсв)/дтсв)
откуда дТ,/дТсв) ) (),
и второй—
дт~в) дт с в)/ДЬфв)
д~ св) = дт св)/ду'св) & t;
дТ(6'
дусв) С з
откуда снова дТ,/дТсв) ) ().
') В предположении, что при варьировании дф'), у(') и у(4) мы не выходим из ооласти непрерывно-
сти целочисленной функции в, где г (дф ), уР), у(4)1 — ~(д,~р) +,уд~(2) у( ) +,уу( ) у(4) +,уу(4)1.
Производные атс')/аТс'-' (с =
и (8.129) по Т'":
Д Т(з) Ь1Ь2
— Тсз) +, 1—
ИТ'-' 4 (с)сз)) с °
ДТ(~) Ь,Ь2
4 (а'в))"
Тсз — — — Т '+ з, 1
2Ьз
~ )/)=.
2Ь
~~г
(1 — ~ / 1~' "') Х
8,48ао5) д Т (з)
Х 'ооп '+ ат 1

277
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
Таким образом, во всех случаях оказывается, что
дТ,
~0 и Т&lt 4
дТ'4' ор~
(8.142)
ожидания действительно должно быть мини-
(8.138) может быть переписан так (в без-
т. е. в оптимальном варианте время
мально возможным.
После этого первый дифференциал
размерных пер еменных):
дТ„, дТ< - у &lt в&g ;(1,
Т,'-'& t  ) д~(р lt;2> Т,' '>Ь , в
дТ'2)
+ (1 — 2)
дТ'2)
дТ~6)
дТ(в)
ИТ(2) при Т~4) = Т0.
(8.143)
Полученное выражение используется для отыскания минимума Т„, по Ь~~2) и Т~2)
методом скорейшего спуска. Броме того, оно позволяет сделать некоторые качествен-
ные выводы.
Так, из неравенств (8.120) после оценок, аналогичных проведенным выше,
следует, что о>>тим льная точка ( у< & t;, Т<2>) и оотве ствующая
Т< &gt ) „не могут принад ежать азным етвям линии ровня (од а — ве хней
гая — нижней).
Если рассмотреть случай бесконечно большой скорости истечения, У = со, при
отсутствии мгновенного сброса массы, ~т~" = О, то а0") = ао для всех ~, ~ = О
(см. (8.139) — (8.141)), Т<' '&gt ( р Т) Т&l ;6 g ; (Лу, Т) Т„(Ь , Т), „ -'
Ду$'-') = ~у~6) — ~у
дТ
— у~~)
'т& t
дТ
Д~~(2) (
д~~ — (6) — (6)
ь~, т
дТ 'дТ
дТ ~ (2) ~(2) дТ ~ 16) ~(6)
йТ„,
Т
(8. 144)
(Г= со, (2т&l ; =
Необходимым условием оптимальности здесь будет равенство градиентов:
(8.145)
(дга&l ;  ) lt;2 g ; т&lt 2 g ; = (дг
( Р'= со, <2т l ;'&
Этому условию удовлетворяют симметричные перелеты: Ь~~') = Ь~(~), Т~') = Т"). Однако
чаще всего они дают локальный максимум Т „а не минимум. Оптимальными оказываются
зесимметричпые перелеты (см. рис. 8.53, 8.54). Последний факт отмечался в Я 2 гл. 7 для
траекторий с идеальным двигателем ограниченной мощности.
Если иметь в виду и решение задачи при фиксированной дате старта (см. п. 12),
то при отыскании минимума Т, удобнее принять вместо углового перемещения
Р.ю
дату старта &l ;„ кото ая выражае ся че ез Л 2 gt  Т" > фо мулой (8 32)
ИЛу&lt 2 gt; = и ИТ& t;2 gt; — (и1
дифференциал йТ, в новых независимых
Подставив эту связь в (8.138), найдем первый
переменных:
д Т"-) д Т'6'
&gt (   1 2 ( Ђ” -) д 1, lt;2 gt;
' 'Т 'У
д Т12) д Т16)
+ и2 (1 =) д1 &lt 2& t; Л
Т Т
д Т< - д Т
(( —,& t; д( „, Ђ” ~1 „ ] ат~
(8.146)
Отыскание минимума Т„,тогда лучше делать покоординатно: сначала фиксировать |6
и найти минимум Т, по Т~2), получив тем самым решение задачи при заданной дате старта;
затем минимизировать полученные значения по ~0.
По изложенной схеме были подсчитаны оптимальные перелеты с 300-км
орбиты спутника Земли на 300-км орбиту спутника Марса и обратно (тормо-
жение у Земли аэродинамическое, вход со второй космической скоростью)
[8.4, 8.14]. Результаты расчетов представлены на рис. 8.53 — 8.56.

Лйсу
ЛЦсуп7
В4суп1
ГЯ
супг
Рис. 8.53. Оптимальные траектории и программы ориентации тяги для межорбитальных участков пере-
лета Земля — Марс — Земля:
а) ао=5' 10 уо
6) а, =10 'до,
в) а„=10 'уо,
г) а„=10 'ф„
д) а„=1,52 ° 10 ~до,
е) ао =1&gt 22 10 '
) ао = 0 95 10 ' алоэ
3) ао =0 72 ' 10 'фо
У = 200 кж/сек,
У = 200 кж7'сек,
У =80 кж(сек,
У =80 кж~сек,
У = 80 кж(сек,
У = 80 кж(сек,
У =80 кж/сек,
У = 80 кж/сек,
Ьт„= О,
Ьт„= О,
~т~~ = О,
Ьт„= О,
Ьт„= 0,15,
Ь „'=О,'11,'
Ьт„= 0,28,
Ьт„= 0,34,
Т =О,
т,=о,
т,=о,
т,=о,
Т, =3 сут,
то =О,
Т, =3 сут,
Т =О,
Т =217
Т = 624
Т, = 554
Т, = 565
Т = 417
Т = 475
Т =565
Т~ = 687
сут, Т„
сут, Т„
сут, Т„
сут, Т„
сут, Тр
сут, Т„~
сут, Т„
сут, Т„;
= 217
= 624
= 554
= 525
= 334
= 338
= 393
= 408
сут',
сут',
сут,
сут',
сут',
сут,
сут;
сут.

279
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
На рис. 8.53 показаны примеры оптимальных траекторий в гелиоцент-
рической системе координат. Стрелки указывают направление вектора тяги
на межорбитальных участках, пунктирными линиями показаны пассивные
участки траектории. Траектории различаются начальным реактивным уско-
вением ао, скоростью истечения Г, величиной сброса полезной массы у Марса
,2У АХ' Ю0 300 Т, сугп
ЮО 7~, гул
Рис. 8.54. Угловые перемещения в гелио-
центрической системе координат «прямого»
ьф') и «обратного» Ьр~') перелетов между
орбитами Земли и Марса.
Рис. 8.55. Оптимальное распределение полного
времени перелета: Т ~') — разгон у Земли, Т ~'>
межорбитальный перелет Земля — Марс, Т ~'& t
+ Т~'& t; Ђ” торможе и и раз о у Мар а, Т~в)
межорбитальный перелет Марс — Земля.
Лт„временем ожидания Т„суммарной продолжительностью перелета Т,
и суммарным временем работы двигателя Т„.. Примеры а) — в) соответствуют
минимально возможному для данных значений ао, К времени перелета—
траектории без пассивных участков. На траекториях перелета большей
продолжительности при тех же значениях начального ускорения а и ско-
рости истечения Г появляются пассивные участки — примеры г) — з).
Я~, ~у/Р
Х~, ~от
Р
Я 100 АЮ Ркм/сек
Рис. 8.56. Минимально возможное время Т перелета Земля — Марс — Земля с оптимальной датой старта.
Оптимальные угловые перемещения межорбитальных участков переле-
тов даны на рис. 8.54 для случая нулевого времени ожидания, ТО=О, при
непрерывно работающем двигателе, Т„.=Т., без сброса полезной массы,
Лт,=О. Распределение полного времени движения Т. по всем участкам
показано на рис. 8.55 для того же случая.
Зависимость минимального суммарного времени перелета Т. от пара-
метров а„К дана на рис. 8.56 (время ожидания и сброс полезной массы
по-прежнему нулевые). Сплошные кривые относятся к случаю аэродинами-
ческого торможения при возвращении на Землю, пунктирные — к случаю
торможения при помощи двигателя. Последние получены следующим обра-
зом. После расчета оптимальной траектории с аэродинамическим торможе-

280
[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
нием, по формуле (8.85) с а =а~'~ вычислялось дополнительно время Т~'~=
= Т„~'~, потребное для торможения двигателем. Распределение времени между
остальными участками не менялось, найденное время Т"' прибавлялось
к полному времени движения и полному времени работы двигателя.
12. Межпланетный перелет с возвращением при заданной дате старта.
Формулировка задачи почти полностью совпадает с формулировкой за-
дачи и. 11.
дРД0
Т~,
ЯП7
~о ~~~ с1~(~
ГЯсрт
5дсдт
®сут
~ рр
д -од -~6д -Лд -5Ю -4дд — 4Ю вЂ” ЫО -Яд -~Ю 1о,сую
Рис. 8.57. Минимальное суммарное время Т перелета Земля — Марс — Земля в зависимости от даты
старта ~,.
~® 1® Д
Э
Ы
7- (')
супу
Р
5дб
~~0 (б
'00
200"
Й~Ц / ( !Я'
® ~® ~~д ~® '~й~ -ОО -560 -640 -7'-.'д ~,,~~(п
Рис. 8.58. Распределение времени (сплошные кривые) и углового перемещения (пунктирные кривые)
между гелиоцентрическими участками Земля — Марс (г=2) и Марс — Земля (г=6), соответствующее
нижней кривой с рис. 8. 57.
Добавляется только условие фиксированной даты старта:
6
а„Г, Ьт®, Т.=~ Т'", Т„1,= Йхе;
(8.147)
Времена движения и угловые перемещения на межорбитальных участках
здесь подчинены уже двум условиям: (8.132) и (8.136), где значения я могут
быть различными.

281
ОПТИМАЛЬНЫЙ МЕЖПЛАНЕТНЫЙ ПЕРЕЛЕТ
Расчет производится по схеме, аналогичной предыдущим.
1'. Совпадает с 1' из п. 9.
2'. Совпадает с 2' из п. 9.
3'. Совпадает с 3' из п. 10.
4'. Совпадает с 4' из п. 11.
5'. Совпадает с 5' из п. 11.
6'. Вычисляется суммарное время Т . работы двигателя и отыскива-
ется его минимум по Т"' (цикл 3' — 6'). Первый дифференциал йТ, можно
получить из (8.146), положив там Ж,=О.
Сут
Л®
МО
Ид
ИД
/Я
бЮ
~Ю
д -Ю -~бд -~~~ -~20 -Юд -~дд -~~~ -бЮ -7Ю ~С,СУ77
Рис. 8.59. Влияние ограничения времени работы двигателя Тр„на время Т, перелета Земля — Марев
Земля (сплошные кривые) и оптимальное время Т~ (пунктирная кривая, соответствует Т
(о)
=380 сут) на примере нижней кривой с рис. 8.57.
Результаты иллюстративных расчетов приведены на рис. 8.57 — 8.59
для перелета со 150-км орбиты спутника Земли на 500-км орбиту спутника
Марса и обратно, с аэродинамическим торможением у Земли (скорость
входа — вторая космическая), при а,=2 10-4 де, Г=со, Лт,=О. Рис. 8.57,
8.58 относятся к траекториям без выключений (минимально возможные вре-
мена перелета). На рис. 8.57 показаны функции Т. (~ ) при различных вре-
менах ожидания Т,. Характерно наличие трех локальных минимумов и
максимумов (на одном периоде! — см. пунктирные кривые 1, 8, о и 2, 4, о
соответственно). При бесконечной скорости истечения минимумы 1 и 8 равно-
глубокие (поскольку тогда время обратимо — см. (8.21) при р=О), при ко-
нечной скорости истечения минимум 8 становится более мелким. Локальные
максимумы 2 по-прежнему отвечают симметричным перелетам. Это видно
из рис. 8.58, где показано распределение времени и углового перемещения
между прямым и обратным перелетами, соответствующее кривой Те=О
с рис. 8.57. Рис. 8.59 иллюстрирует влияние ограничения по суммарному
времени работы двигателя.
13. Оценка погрешностей. Рассмотрим влияние принятых упрощающих предполо-
жений на функционал динамической части задачи — время работы двигателя Т . Наи-
большее количество данных по этому поводу получено для идеального двигателя ограни-
ченной мощности (см. а 2 гл. 7). Там функционалом служит интеграл У от квадрата реактив-
ного ускорения. Связь функционалов У и Т в случае нерегулируемого двигателя (индекс

282
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Р=сопй) дается формулой
У
~=СОПЯТ
О
отсюда следует соотношение для относительных погрешностей в функционалах:
(8Л 48а)
Сделанные в $ 3 гл. 4 и принятые здесь предположения должны примерно одинаково
сказываться на функционале У, как в случае идеального двигателя ограниченной мощ-
ности (индекс К=сопя$), так и в случае нерегулируемого двигателя малой тяги, т. е.
(8.148о)
(~~/~)р=сопв~ (~ / Ь савва.
В качестве подтверждения этого приведем рис. 8.60, а из работы [7.14] для перелетов
между круговой орбитой Земли и компланарной ей эллиптической орбитой Марса.
Из рисунка видно, что вариация кинематических условий приводит к практическиоди-
наковым относительным изменениям функционала У как для переменной, так и для по-
стоянной тяги. Таким образом, зная относительную погрешность (И/У),, ~, можно
судить о погрешности ("оТ /Т )
Приведем данные относительно ошибок (ВХ/У)т — сопв~ вызванных пренебрежением
влиянием третьего центра и поточным сопряжением участков (из [7.4]). На участках раз-
гона (и торможения) у планет до параболической скорости влияние Солнца мало:
(ОУ/У) — 0,1%. Влияние поля планет и точного сопряжения ме>корбитальн
участка перелета с участком торможения у планеты иллюстрируется табл. 8.2. Это влияние
также пренебрежимо мало.
Таблица 82
Относительное изменение функционала (ВУ/У)~ „„„,~ межорбитального перелета
в зависимости от положения точки перехода к участку торможения у планеты, с учетом
влияния гравитационного поля планеты (о — расстояние точки перехода от планеты,
отнесенное к расстоянию планеты до Солнца; ф — угол между радиусом-вектором пла-
неты в гелиоцентрической системе координат и радиусом-вектором аппарата в плането-
центрической системе координат). Средний уровень реактивного ускорения — 5 10 ' д,.
Перелет Земля — Марс
0,00025
0,00050
0,00050
0,00700 0,00290
0,00290 0,00050
3,1416
2,8500 3,1416
2,8500
3,1416
3,05000
2,9000
ф~, рад
0,41%
0,34%
0,00%
0,37% 0,19%
(1зу1/Х) 100%
0 58%
0 67%
Перелет Марс — Земля
0,0030 0,0010
0,0030
0,0090
0,0030 0,0030 0,0030
— 0,50
1,00
0,50
0,10
0,02
ф~, Р©д
(/оУ//Х) 100%
0,13% 2,88%
3,62%
0,87% 0,91% 0,65%
0,48%
Погрешность из-за некомпланарности орбит, согласно данным табл. 7.4 из Я 2 гл. 7,
обычно лежит в пределах 1 — 3% .
Существенно большую ошибку доставляет пренебрежение эллиптичностью орбит
планет. Это иллюстрируется рис. 8.60, б, построенным по данным рис. 7 17. На рисунке
представлена зависимость минимизированных по дате старта (внутри 780-суточного

283
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
$4]
периода) значений функционала Х от продолжительности перелета Земля — Марс для раз-
личных эпох даты старта 1968 — 1969 гг. и 1970 — 1971 гг. (сплошные кривые). Расчеты по
средним круговым орбитам (пунктирная кривая) дают энергетические затраты, осред-
ненные по эп~~ам даты старта. Относительные отклонения ВХ/Х от средних значений со-
~м сею~
.7, ж ~~~е~~
Я0 Тсу~ Ю
Я~ )60 200 24~0 Т,су~п
Рис. (.60. а) Влияние изменения кинематических условий перелета Земля — Марс на функционал Х
для оптимально программируемой (кривые 1) и постоянной тяги (кривые 2, 3 при У=50 км/сек', Ь (1)=
=ор$ — кривые 2 и Ь (1)=1 — кривые 3). Начальная точка на круговой орбите Земли фиксирована,
конечная точка на эллиптической орбите Марса выбирается наилучшей (1) или наихудшей (11). б) Влия-
ние аллиптичности орбит Земли и Марса на функционал .7,
ставляют +(20 — 30)о~~. Эти данные относятся к перелетам без возвращения. Дляпере-
летов с возвращением ошибки расчетов прямого и обратного перелетов в приближении
средних круговых орбит компенсируют друг друга, так что суммарная ошибка умень-
шается до 5 — 10О~ (см. [7 14]). Посчитанные на основании средних затрат параметры аппа-
рата будут оптимальны в среднем для различных эпох старта. При конкретизации эпохи
старта нужно будет изменить только запас рабочего вещества, не меняя параметры дви-
гателя.
$ 4. Оптимальные маневры управляемых спутников
с нерегулируемыми двигателями
В настоящем параграфе дается решение динамической части задачи
для следующих маневров в окрестности планеты: удержание спутника в за-
данном шаровом слое (и. 1), поворот плоскости круговой орбиты (и. 2).
1. Удержание спутника в заданном шировом слое. В течение я оборотов
спутник не должен покидать шаровой слой, максимальный г „и минималь-
ныи г „радиусы которого заданы. Будем считать, что в начальный момент
спутник выводится на круговую орбиту, лежащую посредине заданного слоя
(см. ~ 4, гл. 4): 1+тах Р" (~) ( г,„, 1+т1п ~"' (~) ) г,„где тах Е1' (~)—
т1п ~"'(~) — амплитуда колебаний радиуса на первом обороте. Под дей-
ствием силы сопротивления атмосферы спутник будет снижаться и на и-м
обороте перейдет нижнюю границу слоя. Следовательно, не позже чем на
п-м обороте должен включиться двигатель.
Потребуем, чтобы двигатель работал в периодическом режиме: в тече-
ние (т — 1)-го оборота движение пассивное, на т-м обороте (последнем обо-
роте периода, 1 ( т ( (и) двигатель включается; точки включения и выклю-
чения, продолжительность работы двигателя, закон ориентации вектора
тяги на всех активных оборотах одинаковы.
Препятствием к построению периодического закона управления дви-
гателем является присутствие в уравнениях движения (4.93), во-первых,

11ЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
монотонной функции времени т (г) и, во-вторых, долгопериодических осцил-
ляционных членов в формуле плотности р.
Можно построить желаемую периодическую программу управления,
считая массу т постоянной: т (г) =-сопз$, и пренебрегая долгопериодическими
членами в выражении для р (г), а затем проверить условия сохранения ор-
биты в заданном слое на протяжении какого-то установленного времени.
Невыполнение условий сохранения орбиты будет указывать на необходимость
введения дополнительного активного оборота для коррекции. В пользу
такого подхода говорит еще один факт: закон плотности, принимаемый
в расчетах, не точен, движение в реальной атмосфере может отличаться от
идеализированного настолько, что потребуется коррекция орбиты. Эта кор-
рекция заодно исправит отмеченные выше загрубления, тем более что они
весьма незначительны.
Периодический режим работы двигателя возможен лишь при повторении
через каждые т оборотов значений параметров ~, $, ~!, т. е.
~,„= О, ~. = О, ~!„, = О.
(8.149)
2~с пг
~(зи) ~ А (~) Я~
Р
(8.150)
— времени работы двигателя за период т оборотов (причем первые т — 1
оборотов спутник двихсется пассивно, двигатель включается на т-м обороте)
при соблюдении условий периодичности (см. (4.84), (8.149))
2|с иг 2~с мг
соя~И вЂ” а, 2 е о со» ~ е„о яп ~~И
О О
2т и 2;с пг
я1п ~ М вЂ” а, 2 е о яп ~Ж вЂ” е„~ соя М~ =
О О /
2~с пг
2х (1 — 2у, соя ~) р
О
2|с пг
(8 151)
2х (1 — 2), соя ~)
х(1 — 2у, соя ~)
рсй — а,
(здесь параметры х, )„а, и плотность р безразмерные — см. ~ 4 гл. 4).
Плотность р есть известная функция времени г, радиуса г, и некоторых
углов; поэтому интегралы
2~оп
(8.! 52)
р я1п ~И= ~т~,
р со» Ес8Е = тгк~~1,
р~й= 2 УХО,
известны, если указаны радиус гО, эти углы и число оборотов т.
Именно эти параметры отвечают за пребывание орбиты в заданном слое,
в частности, они определяют амплитуду колебания радиуса на обороте
тах ~""' (~) — т1п 1""' (~). На остальные параметры движения (~), (), ()) пре-
бывание в заданном слое не накладывает ограничений, поэтому условия
повторяемости для них отсутствуют.
Вариационная проблема для рассматриваемого маневра, выполняемого
аппаратом с нерегулируемым двигателем, формулируется в терминах ин-
тегральных выражений следующим образом: требуется указать оптималь-
ные законы е (г), е, (г), о (~) (е, = + ~/1 — е'-' — е'-„'), доставляющие минимум
интегральному функционалу

ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
Последнее равенство из (8.151) при учете дифференциальной связи
г = о может быть записано так:
(8.153)
е Ж = к(1 — 2~, соя ~) 2~т1,~а,.
Правая часть выражения (8.153) — известная величина, в левой части
фигурируют контрольный функционал г~'"~ (в верхнем пределе интеграла)
и управляющая функция е (г). Управление е (г) должно быть выбрано
так, чтобы верхний предел г~'"~ был минимальнйм. Таким образом, задача
о нахождении оптимального закона е (г) выделяется из вариационной проб-
лемы (8.150), (8.151). Учитывая естественное ограничение ~е (г)~ ( 1, по-
лучаем оптимальный закон:
(8.154)
е (г)=1
е,(г) =О, е,(г): — О.
и, следовательно,
(8.155)
Минимальное значение функционала г~'"~ находится из (8.153); оно не
зависит от управления о (г):
(8.156)
~~~"'~ = х (1 — 2~, соя ~) 2нтХ /а .
Отметим ограничение на время ~6'"~:
Р
г~'"~ (2л
(8.157)
(время работы двигателя не может превышать время движения); отсюда
следует ограничение снизу на ускорение ио:
(8.158)
а )~~(1 — 2)', соя ~) т1 .
Как уже указывалось, закон изменения релейного управления О (~)
не влияет на функционал ф"~ (см. (8.156)); число активных участков на обо-
роте, момент начала и продолжительность каждого из них должны выби-
раться так, чтобы выполнялись три интегральных условия (8.151) (последнее
условие из (8.151) совпадает с (8.156)).
Первые два равенства (8.151) при учете (8.154), (8.155) и с обозначе-
ниями (8.152), (8.156) имеют вид
8 соя 1 Ю = 1&lt '" &gt
(8.159)
3 я1п гЖ=1~"'~ч,/10
3=1 при г (г
(8.160)
и при г ( г ( 1~.
Тогда для выполнения условий (8.159) должно быть
~~+ ~1 . ~2 — ~1 ~4+ ~З
я1п ' я1п ' '+ я1п '+ ' я1п ' '= — 1' ' — '
2 2
(8.161)
(интегрирование производится по активному обороту: 2 ~ (т — 1) ( ~ (~ 2 ~т;
так как подынтегральное выражение не зависит от т, то можно интегри-
ровать по промежутку 0 ( г ( 2~).
Для простоты предположим, что на обороте имеются только два актив-
ных участка:

286
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
и, кроме того, сумма продолжительностей активпых участков на обороте
должна быть равна ~~( ':
(8.162)
2 1+ 4 3 Р
Итого для четырех неизвестных 1„1., 1„1 имеются три уравнения:
(8.161), (8.162); один из неизвестных моментов времени не определен.
Если р (~)— : 1, то ~,=1, ~,=~,=0 и уравнения (8.161), (8.162) имеют
простое решение: оба активных участка равны по продолжительности, и
их соответственные точки сдвинуты на полоборота, начало первого актив-
ного участка произвольно в некоторых пределах (рис. 8.61).
Полученное решение для одного периода работы двигателя легко обоб-
щается на [я/т] периодов '), т. е. на время существования спутника в за-
данном слое не менее я оборотов:
Т = [я/т1 ~~~
= [я/т~ х (1 — 2/, соя ~) 2~тХ,/а,. (8.163)
Оптимальные законы е, е„, е,, о сохра-
у ~(ю) няются в виде (8.154), (8.155), (8.160)—
(8.162).
В рассматриваемой постановке задачи
предполагалось, что двигатель работает только
на одном т-м обороте после т — 1 пассив-
ных оборотов спутника. Аналогичным образом может быть исследована
постановка, в которой двигатель работает не на одном, а на нескольких
оборотах в конце периода.
2. Поворот плоскости круговой орбиты (см. ~ 4 гл. 4 и ~ 3 гл. 7). За-
дача (8.5) для данного маневра записывается следующим образом ([8.2],
ср. (4.104) и (7.69)):
Рис. 8.61. Одна из возможных опти-
мальных программ включения двига-
теля на активном обороте.
(0)=.0, ~ (Т)=т~п,1
~„=о,
е я1п (1 — ~,), у (0) = О, ~ (Т) = О,
и= ' е соя(~ — ~,), и(0) =О, и(Т) = ~
(а„, р.=сопя~, о(~) =1 или О, е(~) =+1).
(8.164)
Вудем считать, что изменение массы аппарата за счет расхода рабочего
вещества намного меньше начальной массы аппарата (рТ~ (( 1, Т =~„(Т)).
тогда модуль реактивного ускорения а (~)=аео (~) (1 — р~„) ' в уравнениях
(8.164) можно заменить на
(8.165)
а (1) = аео (1).
для упрощения формул положим Т=2~я, я=1, 2,... (время выпол-
нения маневра кратно периоду обращения по данной орбите). Вариационная
задача окончательно записывается в виде
~„(2кя) = т1п,
у (2т~я) = О,
и(2пя) = ~
е(1) = ~1).
=О, г„(0) =О,
~ = а ое я1п (й — 62 ), у (0) = О,
и=а оесоя(Š— ~,), и(0)=0,
(а =сопят, о(й) =1 или О,
(8.166)
') Знак (г/т) обозначает целую часть числа г/т.

287
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
$ 41
Составим гамильтонову функцию и выпишем уравнения для импульсов!
ХХ = — 3+ р аеое я1п (1 — Р ) + р аеое соя (à — Р ),
р~ — с0115$, р = сопМ.
(8.167)
Оптимальные законы е (1), о (1) даются такими выражениями:
е (1) = я1~ п (р я1п (1 — Р,) + р„соя (1 — Р,)],
о(~)=1 при Ь)0, о(~)=0 при Ь(0
(Ь = — 1 + ае ~ р я1п (1 — Р ) + р„со~ (1 — Р ) ~).
(8.'1 68)
е (1) = е (1+ Р— Р1), о (1) = о (1+ Р— Р,').
(8.169)
Этот факт доказывается следующим образом. Управления е, О и е', о' характери-
Вуются двумя параметрами р, р и р~ р', которые определяются из условий
27~в
27~в
ео я1п (1 — 21) А =О,
ео соя (1 — 21) Ы1 =1/ав,
(8.170)
27~в
27~в
в'о' соя (~ — 21) Ы~ = 1/а
е'5' я1п (1 — 21) сЫ = О,
(в этих формулах е, е', О, О' даются выражениями (8.168)).
Два верхних равенства выполняются; требуется доказать, что в этом случае и с за-
конами е', О', взятыми в виде (8.169), выполняются два нижних равенства. Введем замену
(8.171)
интервал интегрирования после такой замены сдвинется на ~,— ~1 и выйдет за пределы
промежутка [О, 27~я]. Доопределяя периодические подынтегральные функции на
участке [27~я, 2кг-[-[ О,— О,')] (или [ — [ О,— 01), 0] в зависимости от знака разности ~,— Ц),
придем к требуемым равенствам.
Построим теперь оптимальные управления е, о для одного избранного
значения угла Й;; пусть это будет то значение, при котором
(8.172)
Параметры р, р„вычисляются из условий удовлетворения граничным
значениям для у, а.
При времени движения, кратном периоду (что и рассматривается в дан-
ном случае), оптимальные программы (8.168) периодичны с периодом 27::
активные участки равны по продолжительности, начала и концы двух со-
седних активных участков отличаются по времени на к (за исключением,
может быть, первого и последнего), положительные и отрицательные на-
правления вектора тяги последовательно чередуются. Опираясь на это
свойство, можно установить явный вид зависимости управлений е, 3 от
угла И,.
Пусть известны оптимальные управления е, 3, реализующие поворот
плоскости орбиты на угол ~ за время 2кя при положении линии узлов, ха-
рактеризующемся углом Й,.
Оптимальные управления е', о', поворачивающие плоскость орбиты на
тот жеугол ~ и за то же время 2кя, но приуглей,', отличном отй„выражаются
через е, 3 так:

[ГЛ. 8
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
При этом все активные участки без исключения равны по продолжитель-
ности, начала и концы соседних участков сдвинуты на —,. и функция е (1)
на них имеет разные знаки. Найдем следующие законы о (~), е (~) (рис. 8.62);
при 0(~(Т ~2з,
при ~ (~ ( и+ Т,~2з,
при 2л(~(2п+ Т ~2з,
при (з — 1) г, ( ~ ( (з — 1) л + Т ~2з,
о=1
о= — 1
о=1
е =+1,
е= — 1,
е =+1,
(8 173)
о=1
е= — 1,
где Т /2з — время работы двигателя на одном участке.
После вычисленпл интегралов (8.'170) определяются связи
(8.174)
О",= Т ~4з, Ца,=4з в1п (Т (Ы).
Для произвольного угла Я„отличного от Я;, закопы е(1), о(1), согласно
правилу (8.169), получаются такими:
для — Т ~Ы (Р (Т ~4з
е=+1, о=1
е= — 1, о=1
! е=+1, о=1
при 0(~(1„
при 12 (1 (11+ г,
при ~2+ ~(1(1 + 2п,
при ~,+(т — 2) ~ (~(~,+(т — 1)и
Т (4з, 1 =~+ Р— Т (~з);
(8 175)
е=( — 1)
о: 1
р,— о,+
для Т~(Ы(2,
е =+1,
е= — 1,
(т — Т /~з
о=1 при
о=1 при
о=1 при
~ (~(~2,
'+ (~(~,+
1,+2л(1(1.,+2п,
е=( — 1) ', о=1 при 11+(т — 1) л(~(~~+(щ 1) ~
(~, = ~3, — Т ~4з, 1„= О, + Т (~т).
е =+1,
(8.176)
В сумме два варианта (8.175), (8.176) охватывают промежуток изме-
нения углов Й1, равный и.
— Т ~4з ( о. ( л — Т (~з
(8.177)
Промежуток, дополняющий (8.177) до 2~, получается при смене знака
управляющей функции е (1) на обратный.
После подстановки законов (8.175), (8.176) во второй интеграл из (8.170)
находится связь между ~, Т, ~, а~:
Т =4загсяп®4зао) (Т=2~з, з=1,2, ...).
(8.178а)
Последнее есть требуемое выражение функционала задачи через пара-
метры маневра ~, з и двигателя а,. Заметим, что, как и для идеального дви-

289
ОПТИМАЛЬНЫЕ МАНЕВРЫ УПРАВЛЯЕМЫХ СПУТНИКОВ
гателя ограниченной мощности, контрольный функционал не зависит от
конечного положения линии узлов — угла И„а середины активных участ-
ков приходятся на это конечное положение линии узлов (ср. (8.178 а) и
(7.75), (8.173) и (7.74), рис. 8.62 и рис. 7.29).
Точная нижняя грань времени работы двигателя для маневра поворота
плоскости круговой орбиты равна (см. (8.64) и (5.68))
Т,.„= (Г/а,) [1 — е-~2~'~ "" ~'~"-'&g ;] ( р Т Ђ” о
(8.178о)
Она достигается на скользящем режиме управления при бесконечно большом
времени движения (бесконечная серия бесконечно коротких импульсов
тяги, прикладываемых в заданном конеч-
ен [
ном положении линии узлов по нормали
к мгновенной плоскости орбиты). Если
~ &g ; 1 ( то предполагал сь ри выв
(8.178а)), то Т,.„~~/а,. Такое же значе-
ние получается в пределе из (8.178а) при
8~ со (т. е. при Т ~ со).
Маневр поворота плоскости орбиты
при нефиксированном конечном положе-
нии линии узлов И, рассматривается так-
же в [8.31]. При этом не делается пред-
положения о малости угла ~ поворота пло-
скости орбиты. В результате получено
следующее выражение для определения
Рис. 8.62. Оптимальная программа ориен-
тации тяги и включения двигателя на
одном обороте.
времени работы двигателя:
~1+ а&lt
агсяи1 " Йп
У1+ а,~
О
(при р.= 0).
(8. 178в)
При малых ~ выражения (8.178а) и (8.178в) совпадают, совпадают и значения
точных нижних граней Т„,.„. Это объясняется установленным выше фактом
независимости контрольного функционала от конечного положения линии
узлов Р,. При неограниченном возрастании величины тяги (а, — ~ оо) зна-
чение аО Т вЂ” э ~. Это предельное значение вдвое больше получающегося при
выполнении маневра поворота плоскости орбиты по следующей одноимпульс-
ной схеме: в одном из узлов орбиты прикладывается импульс тяги, обеспе-
чивающий поворот вектора скорости на угол ~ в плоскости, касающейся
начальной и конечной орбит (при этом а,Т =~/2). Разница обусловлена
О р.
требованием перпендикулярности вектора тяги к мгновенной плоскости
орбиты, предъявляемым в первом случае.
Заметим также, что к формуле вида (8.178в) приводится и случай по-
ворота эллиптической орбиты в предположении больших значений а при
незаданном конечном положении линии узлов [8.32, 8.33].
В заключение настоящего пункта приведем приближенную формулу
для времени выполнения маневра поворота плоскости круговой орбиты (на
угол ~) с одновременным изменением радиуса (с 1 до г1) [8.13]:
Т = Т вЂ” — 1 — ехр — — 1 — — сос —,-~-—
1 ~ 2 7и 1
а ~ 2 ' г
Г1
1 ' 2 7И 1
— 1 — ехр — —, ~ 1 — = сов — '+—
Яо ~/~.,
(8.179а)
Здесь предполагалось, что двигатель включен на всей траектории. Радиаль-,.
ная компонента вектора тяги полагалась равной нулю, имеются компо-
19 Механика полета

290
НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
кенты по вектору скорости и по (против) нормали к мгновенной плоскости
орбиты (смена знака нормальной компоненты происходит на диаметре, пер-
пендикулярном к линии узлов). Абсолютные величины этих двух компонент
вектора тяги считаются медленно меняющимися функциями времени.
Это предположение позволяет провести усреднение уравнений движения
по обороту. Для усредненных уравнений найдена оптимальная программа
ориентации тяги (от оборота к обороту), обеспечивающая минимум времени
выполнения маневра. Предположения о малости угла наклона ~ и радиаль-
ного перемещения ~г,— 1 ~ не делается. Полученное соотношение (8.179а)
дает хорошую точность для широкого диапазона параметров ~, г,.
Выражение (8.179а) не дает полного решения динамической части за-
дачи. Это только минимально возможное время выполнения маневра, до-
стижимое при непрерывной работе двигателя. Увеличивая время выпол-
нения маневра, можно сократить время работы двигателя в пределе до зна-
чения
(8.179о)
Т= Т = — 1 — ехр — — язв
При этом, в отличие от предыдущего решения, текущий радиус меняется:
возрастает при 0 ( ~ ( '(,Т, затем убывает. Затраты на изменение радиуса
окупаются уменьшением затрат на поворот плоскости орбиты, так как на
большем удалении от центра скорость движения меньше. По данным (8.13],
при ~= г~2 решение (8.179а) дает время на 23% меньшее, чем решение с не-
изменным радиусом орбиты. Однако с уменьшением угла поворота выигрыш
падает и при ~ (( 1 оба решения, и (8.179а), (8.178а), дают одинаковые зна-
чения минимального времени движения Т Ы/2ае (при этом в (8.178а) нужно
положить Т =Т, а в (8.179а) — г,=1 и сохранить в обоих случаях только
члены первого порядка малости относительно ~).
В той же работе (8.13] рассмотрена задача о встрече двух космических аппаратов,
находящихся в начальный момент времени на компланарных круговых орбитах разных
радиусов на некотором угловом расстоянии друг от друга. Один аппарат движется пас-
сивно (по орбите большего радиуса), другой снабжен двигателем постоянной тяги (началь-
ное ускорение от тяги и скорость истечения фиксированы). Он должен за минимальное
время встретиться с первым аппаратом. Относительная скорость аппаратов в момент
встречи не фиксируется, ставится условие отсутствия выключений двигателя.
Для случая бесконечной скорости истечения получены приближенные аналитические и
численные результаты по отысканию оптимальной программы ориентации тяги, опти-
мальной траектории перехода и минимального времени встречи.
соответствующего скользящему режиму управления. Величина Ли в (8.179б)
относится к случаю г, ~~ 1 при следующей схеме приложения бесконечно
малых импульсов тяги (см. гл. 5). Точка приложения первой серии танген-
циальных импульсов на исходной круговой орбите совпадает с положением
перигея переходной эллиптической, орбиты. Точка приложения второй серии
тангенциальных импульсов совпадает с апогеем переходной орбиты. Второй
серией осуществляется переход с промежуточной орбиты на орбиту заданного
конечного радиуса г,. Третья серия импульсов прикладывается по нормали
к мгновенной плоскости орбиты в точке пересечения линии узлов с орбитой
аппарата, она поворачивает плоскость орбиты на заданный угол ~.
Положим в (8.179а) г,=1, чтобы получить минимально возможное время
поворота плоскости круговой орбиты:

291
ПАРАМЕТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
~ 5. Параметры аппарата с нерегулируемым
двигателем ограниченной мощности
Здесь приводятся примеры решения параметрической части проблемы
оптимизации (задача на максимум (8.6)) для нерегулируемых двигателей
ограниченной мощности; при этом используются найденные в предыдущих
параграфах минимальные значения Т„(а„р) функционала динамической
части задачи. Значения полезной массы, соответствующие идеальному дви-
гателю ограниченной мощности (из ~ 4 гл. 7), сравниваются с полученными,
чтобы оценить выигрыш, даваемый регулировкой тяги. Параметры аппарата
с нерегулируемыми двигателями ограниченной скорости истечения будут
приведены в гл. 9.
1. Расчетные формулы. Если процесс ускорения в двигателе ограни-
ченной мощности происходит без потерь, то мощность Г связана с тягой Р
и расходом д (или скоростью истечения Г=Р/д) идеальным соотношением
(ср. (6.1) — (6.3)):
Т = Р"-/2д ='/.,Р7
(У [квт] = 4, 81Рз ~ кГЯ [г/сек] = 4,9Р [кГ] Г [км/сек]).
(8.180)
Масса двигательной системы (6.13) может быть представлена в следую-
щем виде '):
ЛХ„= аУ = аР-'/2д ='/,аР7, т„= '/2аи~/р = '/,ааааа (8.181)
(ЛХ„[кг] = 4,81а [кг/квт] Р-' [кГ]/д [г/сек] = 4,9а [кг/квт] Р [кГ] У [км/сек]).
Критерий (8.6) выбора оптимальных значений параметров Р, д (или
пругой пары: Р, $', или а„р, или а„$') в этом случае записывается так:
б~Р2 1 Р
тахМ.=~«ах М вЂ” . — цг„=та« М вЂ” —,«Ра' — — Т„),
о ~, р. — ' о ~ 7 р.
Р, о
Э
а а02
а
тахт,=шах 1 — —,— — р.Т =-мах 1 — —,аоР— — 'Т
р. — ' ~ О у р.
(тах М„[кг] =
(8.182)
= гп ах (М, [кг] — 4,81а [кг/квт] Р- '[кГ]/д [г/сек]—
Р, д
— 86,4д [г/сек] Т [сут]) = шах (ЛХ, [кг]—
Р
Р, У
— 4,9а [кг/квт] Р [кГ] Г[км/сек] — 847,5Р[кГ]Т„[сут]/Ч[км/сек]),
М о=дТ„=РТ /Г, т,= рТ„=аоТ /Г (8. 183)
(ЛХ, [кг] = 86,4д [г/сек] Т„[сут] = 847,5Р ~кГ] Т„[сут] Г [км/сек]).
') В формуле для массы двигателя может быть учтено постоянное слагаемое (не ва-
висящое от Р и д), здесь считается, что оно отнесено к полезной массе. Если пол Л
понимать мощность реактивной струи, то все формулы будут справедливы и при наличии
постоянных потерь (т. е. когда к. и. д. движителя о„не зависит ет Р и д). Зависимости К
а
и М„для реальных двигателей ограниченной мощности и соответствующие примеры
решения параметрической части вариационной проблемы приведены в гл. 10.
19»
где Т„= Т (Р/М„д/ЛХ,) или Т„= Т„(а„р) — решение динамической части
задачи; последний член в (8.182) представляет собой начальную массу ра-
бочего вещества:

292
НЕ РЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Если в вырахсение для функционала Т не входит параметр р (или Г),
как это имеет место в задачах пп. 1 и 2 ~ 4 (см. (8.163) и (8.178)), то мак-
симум т, по и (или Г) достигается при
р = а„/~/2Т /и или Г = ~/2Т /а
(д = 0,235Р ~/а/Т или Г = 41,5 ~/Т /и)
(8.184)
(размерности величин в скобках здесь и ниже в настоящем пункте те же,
что и в формулах (8.180) — (8.183)).
Критерий (8.182) с учетом соотношения (8.184) имеет вид
тах т, = тах(1 — 2а ~/'/ аТ )
(8.185)
(тах М, = тах (ЛХ вЂ” 408 Р ~/а Т )).
Р
Заметим, что значение и (или Г), определяемое формулой (8.184), соот-
ветствует равенству начальной массы рабочего вещества и массы двигателя '):
(/[Х„е = ЛХ„= 204Р ~/а Т ).
т, = т„= а, ~'/,а Т
(8.186)
Если записать (8.186) через полезную нагрузку, получим оптимальные
соотношения между компонентами массы аппарата (кривая 8 на рис. 8.63)
(8.187)
т, = т„= '/, (1 — т,),
в то время как для идеального двигателя ограниченной мощности мы имели
(см. (6.15) — (6.17) и пунктирные кривые на рис. 8.63)
т„= ~/т, — т,.
т„, = 1 — ~/т,,
(8.188)
Соотношения (8.188) для идеального двигателя не зависятоттипа дина-
мического маневра. Для нерегулируемого двигателя такой инвариантности
уже не существует — это мы проследим ниже на примерах маневров, рас-
смотренных в Ц 2 — 4 (рис. 8.63). Оптимальные соотношения масс аппарата
с нерегулируемым двигателем для всех рассмотренных маневров имеют об-
щую тенденцию к сдвигу в сторону увеличения массы двигательной системы
по отношению к аппарату с идеальным двигателем. При больших же значе-
ниях полезной нагрузки, 0,8 ( т, & t; 1, оптималь ые соотноше ия м
для аппаратов с нерегулируемым и с идеальным двигателямиограниченной
мощности практически совпадают.
Динамический маневр в случае идеального двигателя ограниченной
мощности определяет величину полезной нагрузки через функционал У.
Значения Х зависят от определенных комбинаций параметров маневра:
для маневра набора модуля скорости (см. (7.32))
(8.189)
для маневра перемещения между точками покоя (см. (7.33))
— 12РТ з.
(8.190)
') Этот вывод для случая заданного времени работы двигателя при фиксированноп
величине тяги сделан в первых исследованиях по оптимизации аппаратов с двигателями
ограниченной мощности [8.34 — 8.36]. В работе [8.37] найдено соответствующее выражение
для оптимальных соотношений масс с учетом релятивистских эффектов, вызванных боль-
шими скоростями истечения. Показано, что при значениях параметра (Т/а) — 1 год.квт/кг
релятивистские поправки к членам порядка единицы в формулах для соотношений масс
составляют — 10 '.

293
ПАРАМЕТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
для маневра поворота плоскости круговой орбиты (см. (7.75) в размер-
ном варианте)
(Т=2ляй ~'г',~-, г=1, 2, ...).
(8.191)
~,. = 2йГо1РТ
Интересно отметить, что полезная нагрузка аппаратов с нерегулируемым
двигателем ограниченной мощности для перечисленных маневров определя-
ется теми ~ке комбинациями (8.189) — (8.191): Ф='/,аУ (рис. 8.64). Это будет
- установлено ниже при ре-
фат х
1
шении параметрической части
задачи.
т,~
l
РЮ
РЮ
Об
дб
2. Набор модуля скорости. Решение динамической части задачи для
этого маневра, выполняемого нерегулируемым двигателем, дается соотноше-
нием (8.30). Выберем в качестве параметров двигателя, по которым будем
производить оптимизацию, а, и Г. Тогда критерий (8.182) запишется в виде
п1ах т = мах е-" ~ — ~ ао~, ~о — 1 — е-" ~' ..1 2
~о
Ограничение на а, снизу следует из (8.30). Величина а, входит в (8.192)
линейно со знаком минус, поэтому максимум т по ао достигается при
а, = — (1 — е-" ~~),
$'
(8.193)
т. е. в оптимальном случае выключение двигателя при наборе модуля ско-
рости невыгодно (см. (8.30)).
После проведения процедуры оптимизации полезной нагрузки т„по
скорости истечения Г получим решение задачи в параметрической форме
(си. [8.38, 8.39] и др.):
2(1 — е ~) — 5
т„= т„,=1 — е, т„=е — т„
2(е~ — 1) — ~
(8.194)
Рис. 8. 63. Сравнение оптимальных соотношепий масс
для идеально регулируемых (пунктирные кривые)
и нерегулируемых двигателей (сплошные кривые):
1 — набор скорости, 2 — перемещение между точ-
ками покоя, 3 — поворот плоскости круговой орбиты,
удержание спутника и другие маневры, где время
работы двигателя не зависит от расхода, 4 — перелет
Земля — Марс (соответствует рис. 8.75).
Рис. 8. 64. Сравнение полезной нагрузки
аппаратов с идеально регулируемыми
и нерегулируемыми двигателями огра-
ниченной мощности (обозначения те же,
что и на рис. 8.63, кроме кривой 3,
которая здесь относится только к по-
вороту плоскости круговой орбиты).

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
Оптимальные соотношения масс т„(т,) и т~, (т,) показаны на рис. 8.63
(кривые 1), зависимость максимальной полезной нагрузки т, от Ԅ— нв
рис. 8.64 (кривая 1), оптимальная скорость истечения — на рис. 8.65 в видо
зависимости ~ (Ф„). Предельное значение функционала Ф здесь равно -0,65
(т,=0 при Ф„-0,65) вместо Ф=1, как это было
для идеального двигателя. Оптимальная скорость
истечения нигде не опускается ниже половины
приращения скорости аппарата (т1п Г (Ф„) =
Я 0,63 и,).
Полученное решение (8.194) справедливо и
для маневра поворота плоскости круговой орбиты
с одновременным изменением радиуса в случае,
когда двигатель работает без выключений. Это
следует из сравнения формул (8.179а) и (8.193).
В качестве приращения скорости для такого ма-
невра нужно взять
и = ~у до)1 — 2~г /г соя ('/, ж)+г /1
дб Ф~
Рис. 8. 65. Оптимальная ско-
рость истечения У.
Для большей нагрядности на рис. 8.66 зави-
симости с рис. 8.63 — 8.65 интерпретированы в
функции времени выполнения маневра с и,=7,62 км/сек (например, перехол
с 200-ко круговой орбиты на стационарную 24-часовую орбиту в поле Земли
Рли/еел
Я Т,сут
Ы Т,сую
Ю ~Р бд Я 1® ГО И бд Гд 40 60
Тсуи
Рис. 8.66. Примеры зависимостей максимальной полезной нагрузки тт, и оптимальных параметров от
Времени двин<е и Т ля мане ра наб ра мод ля скоро т и околопланет ых манев ов ез выключе
двигателя.
с одновременным поворотом плоскости орбиты на 49') для различных значе-
ний удельной массы а двигательной системы [8.40].
3. Перемещение между точками покоя. Функционал динамической
части задачи для нерегулируемого двигателя здесь определяется соотноше-
нием (8.43). Выразив из (8.43) ускорение а„запишем полезную нагрузку
(8.182) через запас рабочего вещества т =1 — рТ„и отношение времен
т/т:
(у ~2 т„'о (Т/Т„)з
(2(1 — ~/1 — т„) — т о — 1/Йт„о[(Т/Т ) — 1]Ь(1 — т„))
(1 — е 1) (Т/Т )з
1
тахт,= мах е ~ — —,6~,
~, Т/Х
~з
(8.196)
при этом, аналогично и. 2, выделилась комбинация параметров маневра,
входящая в функционал (8.190) для идеального двигателя.
Представим массу т о в виде (8.194): т„о=1 — е ~; тогда задача сведется
к отысканию максимума

ПАРАЪЖТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
Из условия равенства нулю частных производных по (Т,'Т„) и с полу-
чаем решение задачи в параметрической форме [8.1, 8.38] (ср. (8.194)):
~ (2 — (е ~~~+ е ~)~ — 3+ бе ~~ — Зе '- — 1/ ;"21
т
~ [(е~~~ + е~) — 21 — 3+ бе~~ — Зе. — 1/' ',2
т,=1 — е ~, т„=е ~ — т„,
Ф, = — а12~'Т ' =
(8.197)
~ ~(е'~ + е') — 2] — 3 + бе ' — Зе: — 1/2Д2
1 — е
— ~!2
2,й 1
Ъ
Т 3 2
т111 (ЛХ + М„) = т1п ~/2хТХ'Р (8.198)
Отсюда видно, что тяга должна быть минимально возможной. Ускоре-
ние а„согласно (8.158), ограничено снизу, поэтому в оптимальном варианте
Р =тЯ, ЛХ а=М„=Г~'~,отпТ (8 199)
(двигатель включается на каждом т-м обороте, спутник удерживается в те-
чение времени Т).
Это означает, что двигатель должен работать на протяжении всего ак-
тивного оборота
(8.200)
Т =Т~т;
') Здесь принимается ~ = соней, у', = О (см. (4.80)).
По этим формулам посчитаны оптимальные соотношения масс т„а (т,) и
т (т,) (кривые 2 на рис. 8.63), зависимость максимальной полезной на-
грузки т от функционала Ф, (кривая 2 на рис.
8.64) и оптимальное время работы двигателя Т„~Т ц7 '
в функции Ф, (рис. 8.67). Предельное значение
функционала Ф для нерегулируемого двигателя
оказывается меньше, чем при наборе модуля ско- РЫ
рости (т,=0 при Ф,=0,56, ср. кривые 1 и 2 на
рис. 8.64). Оптимальное время работы двигателя
слабо зависит от Ф, и составляет около '/, от пол- ай
ного времени движения. Подчеркнем, что ни при
каких значениях внешних параметров для рас-
смотренного маневра не выгодно движение без ~9~
выключений двигателя. Этот факт был установлен
в и. 1 ~ 3 независимо от вида формулы для мас-
сы двигателя. РЮЗ
4. Удержание спутника в заданном шаровом
%Я Рис. 8. 67. Оптимальпое время
слое. Функционал Т д11намическои части задачи работы двигателя.
(8.163) для рассматриваемого маневра зависит
только от начального ускорения а и не зависит от расхода р или скорости
истечения Г. Поэтому здесь справедливы оптимальные соотношения (8.187)
(см. кривую 8 на рис. 8.63). Перейдем в (8.163) от параметра к к сопротив-
лению ') Р=хМа и от ускорения а, к тяге Р=ааМа. Поскольку сила сопро-
тивления Р не связана прямо с начальной массой, а определяется формой
аппарата, то параметрическую часть задачи оптимизации можно решить
независимо от начальной массы.
Будем искать минимум суммы масс запаса рабочего вещества и дви-
гателя, т. е. минимум удвоенного выражения (8.186). После подстановки
решения (8.163) динамической части задачи в (8.186) получим

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
[ГЛ. 8
скорость истечения и расход будут следующими (см. (8.184)):
l
Г=~/ — —, д=тГ
а т' 2 Т
(8.20) )
Для иллюстрации на рис. 8.68 дана зависимость (8.199) минимальной
суммарной массы ЛХ~,+ЛХ„ от времени Т пребывания спутника в пределах
шарового слоя при различных значениях удельной массы двигателя а (сила
сопротивления Р принята равной К=0,5 Г, т=16).
5. Поворот плоскости круговой орбиты. Решение динамической части
задачи дается формулой (8.178а), для которой снова имеем дт (др=0 (или
дт ~дУ=0). Отсюда следует, что оптимальные
соотношения масс определяются по (8.187) (кри-
вая 8 на рис. 8.63). Выразив а, из (8.178а) и
Ю подставив его в (8.185), получим полезную на-
грузку в функции относительного времени ра-
б0 боты двигателя Т (Т (в (8.178а) Т=27-.8, г=
=1,2,...):
~ро ~х.аг
Ю0
~/6~,. (8. 202)
~2 я1в ('/2 "сТ,„/Т)
т,=1
Т = 2т~яй '~ г'„~).
(Ф,, =',(,и2йго'Рт ',
б„
;"00 400 К3 8% 1000 Т,суа
Рис. 8.68. Миниыальная суыыарная Оптимальное значение Т„~Т, максимизирую-
ее (8 2021 авно Т (Т=0 7420' и этомпо-
двигателя. р, 7
7
лезная нагрузка т„, массы двигателя т„и ра-
бочего вещества т „скорость истечения Г и начальное ускорение а,
получаются следующими:
т„ = 1 — 2,0822 ~~<1 ,   = т = 1,0 11 ~/
~' = 1,219 ~/ Т/ц, а, = Р~М, = О, зКЧс ~'го '~ч' Т '.
(8.203)
Полезная нагрузка в функции Ф,.=( ~/2) У,. дана на рис. 8.64 (кривая 8).
Напомним, что решение динамическойчасти задачи(8.178а) получено в пред-
положении М (~)=сопвф, поэтому соотношения (8.202), (8.203) справедливы
только при Ф,. (( 1 (при Ф,. -1 значения полезной нагрузки из (8.203) ока-
зываются заниженными). Кроме того, время выполнения маневра Т счи-
талось кратным периоду обращения спутника (Т=2~~~ '~го"', ~=1, 2, . )
6. Межпланетныи перелет. Выбор оптимальных параметров аппарата
здесь будет проводиться в рамках постановки, взаимной с (8.74): заданы
максимальная стартовая масса аппарата М„полезная масса М„и величина
сброса Лм,; ищется минимальное время перелета Т.. Масса двигательной
системы по-прежнему описывается формулой (8.181). Дополнительно к пре-
дыдущим пунктам настоящего параграфа учитывается масса баков для ра-
бочего вещества
(8.204)
(3 = соий)
М,= — ~М,
и вводятся ограничения на время работы двигателя и на скорость истечения
(8.205)
тр. & t; т.. „, .  l ; г ( ~
Обратим также внимание на то, что, в отличие от предыдущих пунктов,
стартовая масса аппарата здесь только ограничена сверху, а не задана.
Раньше не было смысла использовать такую постановку, поскольку отыски-

297
ПАРАМЕТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
вался оптимальный набор всех параметров аппарата, а для него (как это
видно из полученных решений) зависимость функционала от стартовой массы
линейная. Это означает, что если бы к числу свободных параметров была
добавлена стартовая масса, то ее оптимальное значение совпало бы с макси-
мально возможным. Здесь ~ке, помимо оптимального варианта, рассматри-
вается еще и допустимая область в пространстве параметров аппарата, по-
этому используется более общая формулировка с ограниченной стартовой
массой. По этой ~ке причине произведена замена функционала на эквивалент-
ный (вместо ЛХ,=шах при Т.=йхе взято Т.=т1п при ЛХ =Лье).
Допустимая область изменения параметров аппарата и его двигательной
системы выделяется условием конечности времени Т. выполнения маневра.
Полученные ниже аналитические выражения границ допустимой области
справедливы не только для межпланетного перелета, но и для других ма-
невров в центральном поле [8.40].
При формировании условий конечности времени Т. дату старта и время
ожидания принимать в расчет не нужно. В самом деле, если с данными пара-
метрами аппарата возможен перелет хотя бы для одной пары значений даты
старта и времени ожидания, то при введении дополнительного (конечного)
времени ожидания на орбитах планет старта и финиша та ~ке траектория будет
обеспечивать перелет и для любых других дат старта и времен ожидания.
Из решения динамической части задачи при фиксированных значениях
начального ускорения от тяги а,=Р,/М„скорости истечения Г и сбрасы-
ваемой массы ЛЛХ,/ЛХ, для каждого маневра определяется точная нижняя
грань времени работы двигателя
О
(8.206)
т. (т, =т.+Т+ 172,9 ', ' Т (1,
2,О-' . ~О'~
Р.1ДХ О
О
Г „& t; Г( Г „, Т
'— "') & t; „&l
(8.207)
В формуле (8.207) и далее приняты размерности (8.180) — (8.183).
Время работы Т выражается из первого соотношения (8.207) через
независимо варьируемые параметры т„Г, У:
~Π— ~7~ — ~
т,= '1
1729 ' ЛГ ~
Э
а
Это значение Т„достигается на так называемых скользящих режимах управ-
ления. Время, потребное для реализации такой программы управления,
бесконечно велико (равно как и угловое перемещение аппарата). Если рас-
полагаемое время Т больше (8.206), то перелет осуществим за конечное
время. Величина Ли в (8.206) — минимальная суммарная характеристиче-
ская скорость, а Ли* — часть Ли, потребная для завершения маневра после
сброса ЛМ . Они определяются, как показано в (8.18, 8.191., известными фор-
мулами для обычных импульсных перелетов, приведенными в гл. 5. Для
рассматриваемого в качестве примера перелета Земля — Марс — Земля Лг=
=Ли"'+... +Ли"'=17,13 км/сек, Лг" =Ли"'+Ли"'=-6,95 км/сек.
Полный набор условий, определяющих допустимую область значений
параметров аппарата и двигательной системы, может быть записан следую-
щим образом:

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
и система неравенств (8.207) принимает вид
2,04 ° 10аТ Ьт те — ш — Т
а г'ше ' ' ше (1 ~- ~3) Рпг~"'
172,9 ЮК 2
(8.208)
т,(т,(1, Р;,( Г( г' „, Ж) О.
После подстановки (8.206) в (8.208) последнюю систему можно разрешить
относительно та при заданных гг' и г' (см. рис. 8.69):
т„.„(У, г') ( т, ( т,,„(У, г''),
(8.209)
где герхняя граница
прп те
достижима, а нижняя
т -+ г1г — (1+ ~) Лт„(1 — е ~' )
И'
(1+ а).-" ' — Э
(8.211)
— нет.
Допустимая ооласть на плоскости Я, 'г' определится пз условий
О (та,.„(У, гг) (т „(У, г'),
Г,.„(Г(Г „, У)0.
(8.212)
При фиксированных значениях г' неравенства (8.212) разрешимы отно-
сительно У (рис. 8.70):
(8.213)
У,. „(Г) -- У ( У.„, (Г),
г1с ооо границы, нижняя
пг (1 — е '~) — Лт (1 — е 'г)
172,0Т
г' Г(1+ В) ь6/г' — 4 (1 — ьо!")
а~2
(8.214)
п «ерхняя
Т,„,„(г') = (1+ф) е-е'~~ — ~3 — т,+(1+ ~) Ьт,(1 — е ~"г'),
(8.215)
недостижимы.
Диапазон допустимых значений скорости истечения Г определяется
как пересечение интервала и отрезка '):
~е(~,.„~...)пт..., ~...1=т, Ч
') В правой части (8.216) результат пересечения записан как отрезок. Это сделано
условно для введения обозначепия границ получающегося множества, которое может быть
как отрезком, так и интервалом или полуинтервалом.
где К,, и Г„~ — корни уравнения
Ж,.„. (Г) = У„., (Г) ) О. (8.217)
Это уравнение — трансцендентное. Из вида функций (8.214) и (8.215),
показанных на рис. 8.71, следует существование трех корней. Но один из
них (минимальный) не обеспечивает выполнения условий положительности Г
и потому отбрасывается.
Таким образом, множество допустимых значений начальной массы ап-
парата то, мощности двигателя Ж и скорости истечения К представляет
собой ограниченную область, к которой присоединены некоторые из гранич-
ных поверхностей. Общий вид этой области изображен на рис. 8.72.
Пример построения допустимой области на плоскости К, г' приведен
на рис. 8.73 для следующего набора внешних параметров задачи: т,=0,5,

ПАРАМЕТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЯ МОЩНОСТИ
Лт,=0,2, Т„„(а=100 сут квт(кг, Р=0,1, Ли=17,13 км(сек, Лг" =
=6,95 км(сек (Г „и Г „не фиксированы). Там же нанесены линии уровня
максимальных (8.210) и минимальных (8.211) значений начальной массы ап-
паратат,. Первые показаны сплошными кривыми, вторые — пунктирными.
т "(У)
л „~~/Ч)
( пт~п Ю ~цш1 те ~ п1е
Рис. 8. 7 О. Допустимая о бласть при фиксир ован-
ном У. Граница области выделена штриховкой.
Участок границы, не принадлежащий области,
показан пунктиром.
Рис. 8. 69. Допустимая область («толстый»
отрезок прямой) при Фиксированных Ж и У.
При изменении внешних параметров, а именно при увеличении т, а,
~, Лг, Ли* и при уменьшении Т„,„„,, Лт„допустимая область выбираемых
нараметров вырождается сначала в точку, а затем в пустое множество.
Преде.п.ныл зиачеиия нпешппх параметров т, а, .'~, Т „...„., 'и~п,, ~г и ~о"
Рис. 8.71. Вид проекции допустимой области на Рис. 8.72. Вид допустимой области в про-
плоскость «скорость истечения У вЂ” мощность Ж». странстве «скорость истечения У вЂ” мощность
Ж вЂ” начальная масса т,».
опре,~(.ляются из условия Р,.„= Р,„,, которое может быть сведено к системе
уран,агний (см. рпс. 8.71)
(8.218)
Решение (8.218) находится в параметрической форме:
ф—
172,9 (1+ 3) 1'р
д л.
к д~
2 (1 — е ') — ~е ~ — Ьт 2 (1 — е 1~" ~~"1 ) — — се 1 " ~ "1
٠— .,-~ ~ ], (Ь.Р(Ью)~'
(8.219)

НЕРЕГУЛИРУЕМЫЕ ДВИГАТЕЛИ
300
где с=Лгх/Г. Полученная зависимость совпадает с решением задачи о на-
боре модуля скорости их=Лгх за время Т=Т „„„(ср. (8.219) при Лпг.= ~3=0
с (8.194)).
Область значений внешних параметров задачи, для которых рассыат-
риваемый па рис. 8.73 маневр (Ли=17,13 км/сек, Ли*=6,95 клг/сек) осу-
ществим за конечное время, показана на рис. 8.74 в координатах Ф, Ч' при
04
0,8
0 ( 02 05 ~4 05 ф
х00 400 Ы0 Ч,км/сел
Рис. 8.73. Пример допустимой области на пло-
скости У, Ж.
Рис. 8.74. Допустимые области внешник пара-
метров задачи на плоскости Ч(, Ф. Звездочка
соответствует набору значений параметров
рис. 8. 73.
фиксированных значениях сбрасываемой массы '). На границе области дана
разметка по 1 = Лхх/Г.„, = Ьхх/Г,„,.
ЙПЮх
~ар~
П1/СЕ(~
06
ог
Ю
~00 ~~0 ~0~ т ~К т ~00 Д0 ~00 ~50 ~,
Тсу(7~
фМ'
Лд
д! ~00
150 Г00 ~,50 300 550 Т, сут ~50 200 Лд 300 350 (~ сую
Рис. 8.75. Оптимальные параметры аппарата для перелета Земля — Марс. Пунктиром для сравпеш~л.
нанесены кривые т„,п1~~ (Т) для идеального двигателя ограниченной мо1цности.
Если учесть еще ограничения из (8.205) па скорость истечения Г, свя-
занные со свойствами движителя, то маневр может стать невозможным и
х) В коордххххатах Ф, Ч' зта область, согласххо (8.219), ххе зависит от всличхххх Лх и
Ьг~ по отдельности, а только от их отношения. Поэтому рис. 8.74 мо~кно использовать
и для других маневров с тем ~ко отношением Ьг" /Ли=0,408, а кривую Ь(п„=Π— для лю-
бых маневров.

$ 5]
ПАРАМЕТРЫ АППАРАТА С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЯ МОЩНОСТИ
301
раньше, как только окажутся непересекающимися интервал (Г,.„, Р„,) и
отрезок [Г,.„,
Отметим, что если при решении динамической части задачи на управляю-
щие функции о (1) и е (1) накладываются дополнительные ограничения,
то построенная здесь допустимая область должна быть сужена. Однако
нетрудно заметить, что сужение области произойдет за счет изменения от-
крытых границ, при стремлении к кото-
рьп| минимизируемый функционал задачи— и.."-,"„
время движения — стремится к бесконеч-
Ю
ности (Т. — э оэ). Поэтому, имея в виду
численное отыскание минимума Т., дальней- И
шее исследование можно не проводить, за-
лавая начальное приближение достаточно ~г
Ю
далеко от таких границ построенной выше
области. В процессе отыскания минимума Т.,
Гс л
в силу указанного свойства, решение автома- '~~ ~~®
тически не будет выходить за пределы дейст-
вительной допустимой области.
Выбор оптимальных параметров меж-
планетных аппаратов из построенной выше
лопустимой области производился численно покоординатной минимиза-
цией Т. с использованием результатов пп. 9 — 12 ~ 3 решения динамиче-
ской части задачи. Оптимальное значение начальной массы аппарата всюду
оказывалось максимально возможным (М (0)=ЛХ„или т,=-1). Остальные
параметры приведены на рис. 8.75, 8.76. Опи относятся к перелету с 200-км
орбиты спутника Земли на 300-км орбиту спутника Марса и Венеры без
возвращения при оптимальной дате старта [8.21, 8.40). Решение динамиче-
ской части задачи для этих маневров дается аппроксимационными форму-
лами (8.130). Напомним, что при выводе (8.130) предполагалось отсутствие
выключений двигателя на участках разгона в окрестности планет. Расчеты
оптимальных параметров аппарата проведены без учета массы баков (8.204)
и ограничений (8.205) на ресурс и скорость истечения, за исключением
Г) 20 км/сек.
Рис. 8. 76. Оптимальные параметры
аппарата с «=10 кг/квт пля перелета
Земля — Венера.

1'ЛАВА 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
ИСТЕЧЕНИЯ
Учет реальных свойств двигателя ограниченной скорости истечения связан прежде
всего с отказом от предположения о невесомости его компонент. Наиболее сильное влияние
на формулировку и исследование проблемы оптимизации аппаратов оказывает масса
баков ЛХ~ и двигателя М„. В настоящей главе набор характеристик двигателя дополняется
зависимостями, определяющими массу баков и двигателя Я 1). Это приводит и к изме-
нению ххабора возможных управлений: в формулировку вариаххионнохх проблемы могут
быть включены программы изменения массы баков или (и) двигателя во времени. Предель-
ная оценка эффективности управления массой двигателя получается в случае оптималь-
ного непрерывного изменения массы двигателя Я 2). Требование технической осуществи-
мости программ управления массой двигателя приводит к рассмотрснию дискретного
случая Я 3).
К классу двигателей ограниченной скорости истечения относятся и двигатели боль-
шой тяги, используемые для выведения аппаратов в космическое пространство. Началь-
ный участок двихсеххия проходит в атмосфере. Влияние массы двигателя па оптималь-
ные законы управления различно при полете в атмосфере плаххеты или впе ее. В связи
с этххм в 1 4 рассмотрены вопросы учета сххл аэродиххамического сопротивления при движе-
нии в атмосфере. Зависимостью максимальной тяги двигателя от высоты полета пренебре-
гается.
я 1. Особенности характеристик и оптимальных режимов
работы двигателей ограниченной скорости истечения
1. Характеристики двигателей ограниченной скорости истечения. Масса
реальных двигателей ограниченной скорости истечения зависит или от мак-
симальной тяги Р* (жидкостные реактивные двигатели), или от начальной
массы рабочего вещества ЛХ„е (двигатели па твердом топливе). Выражения
(4.9), (4.10) тяги Р, расхода д, массы двигателя ЛХ„и массы баков для ра-
бочего вещества ЛХ„, характеризующие реальные двигатели ограниченной
скорости истечения (ср. (5.1)), для жидкостных реактивных двигателей
имеют вид
Р=Р, д=Р~7, М„=~Р", М =хМХ,
(О ~ Р (~) ( Р", О ( Г (~) ( Г„„„),
(9. 1)
а для двигателзй на твердом топливе записываются в виде
Р=Р, д=Р~7, М„=~М „М =0
(0(Р(~)( со, 0( Г(~)( Г,„)
(9.2)
М,=М.+М„+М,+ЛХ,
(значения удельных масс т приведены в табл. 2.1 гл. 2, индекс у ) опущен).
Для реальных двигателей типа (9.2) ограничения сверху па величину
тяги пет и, подобно идеальному случаю, допускается существование импульс-
ных режимов работы.
Масса аппарата с реальным двигателем ограниченной скорости исте-
чения в начале движения может быть представлена суммой четырех ком-
понент:

303
ОСОБЕННОСТИ ХАРАКТЕРИСТИК И РЕЖИМОВ РАБОТЫ
полезной нагрузки, запаса рабочего вещества, баков и двигательной системы.
При рассмотрении многоступенчатых аппаратов в ~ 3 к этим компонентам
добавляется еще масса конструкции (см. (9.57)).
2. Состав оптимального управления. Рассмотрим реальный двигатель
ограниченной скорости истечения с характеристикой (9.1) при р=О: тяга
ограничена, масса двигателя пропорциональна максимальной тяге. Отне-
сем тягу Р к максимальной Р*, а все массы — к начальной массе аппарата.
Задача о доставке максимальной полезной массы в этом случае выглядит
так (ср. (5.4)):
т. = — а,Р/Г,
1
Г= У,
тп,.(0)+та,=1, т,(Т) =тах,
г (О) = г„г (Т) = г„
(9 4)
т(Т) =т,
(0(Р(~)(1, 0~ Г(~) ( Г,„„, ~ е(~) ~ =1, а,= Р"~М, =ор~). ~
т(0) = т„
Здесь нужно построить оптимальные программы Г (~), Р (~), е (~) и
выбрать оптимальное значение параметра а„обеспечивающие максимум
полезной массы т,=т, (Т) (удельная масса двигателя задана). Из этой
задачи, аналогично случаю нерегулируемых двигателей (гл. 8), можно вы-
целить динамическую часть, не зависящую от конструктивного параметра ~.
Перейдем в (9.4) от массы т. к полной массе т (~)=т. (~)+",а„в ка-
честве функционала примем конечное значение
т(Т) =т„+,а,.
(9. 5)
При фиксированных значениях а, максимум функционала (9.5) совпа-
дает с максимумом функционала (9.4), и задача (9.4) редуцируется и стан-
цартной задаче ракетодинамики о максимуме конечной массы при ограни-
ченных тяге и скорости истечения:
т= — а,Р~7, т(0) =1, т(Т) =тах,
Г=1, г(0) =г„г(Т) =г„
Ф = а„Ре~т+ д, т (0) = т„т (Т) = т,
(СР(Р(к) =1, О(Г(к)(Г.,„, ~ (к)~=1).,
(9.6)
Решение задачи (9.6) определяет зависимость величины функционала
от параметра а,: т (Т) =т, (а,). Имея такую зависимость, можно найти
оптимальное значение параметра а, из условия максимума полезной на-
грузки (см. (9.5)):
тах т, = тах ) т, (а,) — та,1.
(9. 7)
©о
Гамичьтопова функция и уравнения для импульсов запишутся при этом в впдс
~о~ 1
~~= — р 1; +р, +р. +о
~о~
р',„= р, . е —, р„= — — (р„д),
(9.8)
Динамическая часть задачи (9.6) подробно исследовалась многими авто-
рами [9.1 — 9.48]. На основании сказанного их результаты могут быть исполь-
зованы для решения полной задачи (9.4).
Анализ состава оптимального управления в задаче (9.6) проведем с. по-
мощью принципа максимума, сформулировав ее как задачу Майера на мак-
симум значения функции У=т в конечной момент времени 1= Т.

504
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 9
Оптимальные управления Р (8), г (1), е (1) определяются пз условия минимума
функции Н:
ра ) д шах при рда ( Од
Ри' ~ О при р )О,
1 при Ь О, р, р„,
О при Ь &g
Исследуем вопрос об оптимальности участков особого чправлеиия в задаче (9.6).
Необходимое условие оптимальности особого управления скоростью истечения (условие
независимости гамильтоннапа от $') состоит в выполнении равенства р =0 на конечном
интервале времени. При этом р'„,=0 и из системы уравнений для импульсов (9.8) с учетом
оптимального значения управления е (г) (9.9) следует: р,=О и р„=О (при Р ) 0)
Поскольку одновременное обращение в нуль всех импульсов противоречит принципу
максимума [9.551, особое управление скоростью истечения пе оптимально.
Активные (РфО) участки траектории с нулевой ()г=О) скоростью истечения не могут
входить в состав оптимальной траектории: при К вЂ” э О расход рабочего вещества а0Р~7
стремится к бесконечности, хотя тяга остается конечной. Таким образом, оптимальное
управлепие скоростью истечения гранично: Р= Р „„и импульс р„, ( О на активпых участ-
ках траектории. Поскольку р,„(г) не возрастает на оптимальнои траектории (см. (9.8)
с учетом (9.9)) и ра (Т)= — 1 (условие трансверсальности (9.8)), р (г) ( 0 для всех
С~10, Т1
Особое управление направлением тяги е (г) па активных участках траектории также
не оптимально. Условие независимости гамильтониана Н (9.8) от управляющей функции
е (1) состоит в обращении в нуль на конечном интервале времени импульса р„(г). При этом
из системы (9.8) следует: р„(г)=0, р,„(г) =сопз1 ( О, и переключающая функция Л в (9.9)
положительна, что соответствует пассивному (Р=О) участку траектории.
При выполнении условия Л (г)=0 на интервале ~ х, Э) ~ 10, Т~1 управление величи-
ной тяги Р (г) особое. Условия равенства нулю трех первых производных по времени от
переключающей функции па участке (х, Э) запишутся в виде
9
р„р„, =О, р„-,. — р„. р„— „= О,
з=1 у=1
И И 22 И
° °
3 (~О ~ьу
Зр„; р, ~ — р„. р. ~ „~~ — р„
з=1 1=1
(9.10)
Здесь величины р„,, р„, г;, г;, д; — компоненты соответствующих векторов в декартовой
системе координат, и — размерность вектора г.
Величина особого управления Р (1) вычисляется из условия Ы~Л/дала=О, которое
может быть представлено следующим образом.
(9.11)
АР+ В =О,
где
и
2сг .
д ~~у
Р'~ дг дг
г; г~,
~2
д „др
дг 'г"'~ "дг дг. + р"р'«дг дг.+
2 Й Ф
В=1
В = 4р,.;р,.;
.у=1
(9.12)
2
и
3
и а)
д р. д р. ~ьу
д'дд'д (ддд~,.д д д ~д д,.д дд „' 'д д
6=1 .у=1
/
Необходимое условие оптимальности (9.27] особого управления записывается в виде
следующего неравенства:
(9.13)
А (О.
Р (г) ~(0, 1) «(0( В ( — А).
(9.14)
Кроме того, вдоль участка особого управления должно выполняться условие принадлеж-
ности Р (г) открытому ядру области допустимых управлений:

305
ОСОБЕННОСТИ ХАРАКТЕРИСТИК И РЕЖИМОВ РАБОТЫ
В точках сопряжения участков особого и граничного управления тягой [9.49] функ-
ция Р (х) непрерывна, т. е. в начале участка особого управления (х= т) и в конце его
(1=Э) выполняется одно пз равенств:
В=О либо В= — А.
(9.15)
Рассмотрим теперь двигатель ограниченной скорости истечения с харак-
теристикой (9.2): тяга не ограничена, масса двигателя пропорциональна
начальному запасу рабочего вещества. Поскольку на тягу нет ограничений,
вариационная задача может быть записана через реактивное ускорение
(ср. (5.3)) в форме (4.5):
ххъ„(0) т
пг, (Т) = шах, )
т„(Т) = — О,
п'г, =О,
Г
пг = — (т + т„+; т„о) — ',
+(1+.;) т, (О) = 1,
(9. 16)
! 1
г (0) = гпг
т (0) =~о,
0~ ]'(Е)(Г„,,, /е®/
г (Т) = г„
1' (Т) = т„
1).
)$ — л~ 7
7
т=ссе
(О~а(е) ( со,
1хак и в задаче (5. 5), можно доказать оптимальность управления ~(~) = ~~ „.
Проинтегрировав второе уравнение (9.16) при Г (~) =х'„,,„с учетом гранич-
ных условий, выразим функционал задачи через характеристическую ско-
рость Лхх (ср. (5.6), (5.9)):
с г
Ьи= аЯН1~.
о
пх, = (1 +; ) е-~""
(9.17)
Полезная нагрузка снова оказывается убывающей функцией характе-
ристической скорости Лхх, поэтому задача (9.16) сводится к описанной ранее
линамической задаче (5.12) для идеального двигателя ограниченной
рости истечения.
Если к характеристике (9.2) добавить еще условие ограниченности
тяги (О ~ Р (х) ( Р*, где Р* — конструктивный параметр), то задача о мак-
симальной полезной массе сведется к (9.6). В самом деле, при т„=тт по-
лезная масса равна
4
т, = т, — т„= — (1 + 7) т, — 7,
2О Механика полета
Необходимость одновременного выполнения при х= т трех равенств (9.10) и одного
вз соотношений (9.15) ххакладывает хха начальные зххачения импульсов четыре связи.
Поэтому, как указано в работе [9.27], экстремаль, содержащая участок промежуточной
тяги и удовлетворяющая всем необходимым условиям, не может удовлетворять произ-
вольным начальным и конечным условиям. Участок особого управления тягой ~ожет
включаться в состав оптимальной траектории лишь в том случае, если начальные и ко-
нечные условия маневра связаны четырьмя соотношениями. Если уравнения движения
[9.6) и система для импульсов (9.8) пе интегрируются в элементарных функциях, записать
указанные соотношения в конечном виде невозможно.
При отсутствии ограничения на тягу (в задаче (5.5) па минимум характеристической
скорости) участки особого управления Р (х) могут включаться в состав оптимальной траек-
тории [9.27]. В этом случае из числа необходимых условий оптимальности исключаются
равенства (9.15) и добавляется три свободных параметра: величины импульсного прира-
щеция скорости в начале и конце особого участка и момент Э окончания особого участка.
Число связей при этом совпадает с числом свободных параметров и выполнение произволь-
ных грапичных условий маневра возможно.
Участки переменной тяги в ньютоновском гравитационном поле впервые исследованы
в работах [9.13, 9.50]. В работах [9.34, 9.51] приведены результаты, указывающие на
возможность особого управления в однородном плоскопараллельном поле тяготения.
Для задачи о повороте вектора скорости в этом случае решение с особым управлением
тягохх получено методами классххчесххого варххациоххххого исчислеххххя [9.52]. Необходимое
условие оптимальностхх [9.27] хха участках особого управления в однородном поле тяго-
тения пе эффективно. Неоптиъхальххостьуказаххххого особого управления удается показать,
лишь пользуясь получехшым позднее условием ([9.49], гл. 4, Я 10).

306
[гл. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
т. е. условие максимума т эквивалентно условию максимума конечной
массы т,.
3. Модельные задачи. Чтобы составхлть количественное представление
о влиянии массы двигателя, рассмотрим модельную задачу о вертикальном
подъеме ракеты в пустоте при постоянном гравитационном ускорении д,
[9.39 — 9.481. Начальная высота и начальная скорость нулевые (уз=хне=0),
в конце тРебУетсЯ обеспечить заданное значение полной энеРгии фх=х/зп",+
+~сух при максимуме полезной массы. Характеристика двигателя берется
в форме (9.1).
Введем безразмерные переменные
М
т= —,
Яо'
р 1
о
У
8=
(9Л 8~
Р'
Π— ~м
Г=
1 пхах
и заменим второе уравнение (9.4) на уравнение, описывающее изменение
энергии. Вариационная задача (9.4) запишется следующим образом:
1П. = — ао~,~~~,
О
д(0)=О, Д(Т)= "„
1, хх(О)=0, хх(Т)=ор!,
(0(Р (~) ( (, () ( (~(~) ( х, аз= соххь1, 1 (ае '1/(, Т = ор().
ххх (0)+;а„=.1, т (Т) = тах,
(9.19)
Здесь тяга направлена по скорости, черточки над безразмерными перемен-
ными опущены.
Отметихх, что управляющий параметр ае должен быть больше единицы
из условия взлета, а его наибольшее значение ограничено предельным слу-
чаем т„='(аз=1. Выбор оптимального значения этого управляющего пара-
метра сводится к стандартной процедуре, если присоединить к системе (9.19)
формальное уравнение аз=О. Оптимальные управления ~ (~) и Р (~), достав-
ляюшие максимум полезной нагрузке, определяются из условия абсолют-
ного минимума гамильтоновой функции:
у ~оР, ~оР ~оР
— — ра ~у. + р,' ххх ~ хх + ро
р'.=(р хх+ р„)аеР(п~.+.(а,) ', р' =О,
р', = — р.а„Р (т. +.(ае) ' (р. (Т) = — 1).
(9.20)
Функция Н на оптимальной траектории тонсдествепно равна нулю, так как не со-
держит явно переменпохх х и ххоххечный момент времени Т не фиксирован.
На основе (9.19), (9.20) можно определить импульс р„:
р, = — р. (~ +- хх),
(9.21)
Р» = Р»о — 'Р~ — Р„.~
где из условий в точке ~ = Т
РОО ра(Т+ ~ (Т)1
(9. 22)
Оптимальное управление х' (х) всюду граничное (и. 2):
Г (х) =1 (О & t  &l
(9.23)
Оптимальное управление Р (х) зависит от знака функции Л (х):
Р(х)=1 при Ь(х)(0, ' р,, — р х
Р (х) = 0 ° при х (х) ) 0 тп + (ае
/~
(9.24)

307
ОСОБЕННОСТИ ХАРАКТЕРИСТИК И РЕЖИМОВ РАБОТЫ
Возможность особого управления (при Л=О) отпадает, так как производная функ-
ции Ь всюду отлична от нуля'.
Ь= — р (т,+ (и) 1фО.
(9.25)
Рехсим Р (г)=0 (при Л ) 0) внутри интервала ~ & t   lt; Т та же не реализ етс , т
на нем, согласно (9.20), должно выполняться условие р, (г)=0, что имеет место лишь
в конце интервала (р, (Т)=0).
Следовательно, оптимальное управление Р (г) в рассматриваемой задаче также всюду
граничное:
Р (г) =1
(0&l ; &l
(9.261
С учетом найденных оптимальных управлений (9.23), (9,26): Р (~) =1,
Г (~) =1 — система уравнений (9.19) интегрируется:
1п (т, + ~~ье) = (т';+; а,рг, — т,) (т, +, а, — (а,") 1,
1, 1
= — 1и'-'(т + (а,)+ — [1 — т, — (ас+1п (т,+ (а )1.
О
(9.27)
(9.28)
а, = " ~(1 — ~/т,)'+ (1 — т ) 1п ~/т,].
(г/ТГ, ) +!и ут1
Эта функция а, (т,) — обратная к т, (а,), комбинации (Г,„/Т) и (И Т7 „)—
параметры задачи. Подставив выражение (9.28) в (9.7), получим полезную
массу в функции конечной массы:
т, = т, '" И1 — ~/тг) + (1 — т ) 1п ~/т1].
( г/Т У ') + 1п у т
(9.29)
20*
Результаты решения представлены на рис. 9.1 — 9.3. На рис. 9.1 дан при-
мер зависимости максимальной энергии ~1 от начального ускорения ае
при фиксированных значениях т, и
(постановка, взаимная к т,=тах, при ~„4„'",
~„, "(=сопя~). Без учета массы двигателя
((=О) максимум энергии ~~, достигается
РР
с двигателем бесконечно большой тяги
(а„„,— >с ) С уче ом д же ма ых значе
удельной массы двигателя, т=0,01 — '
— '0,02 кг/кГ (величины т взяты с рис. 2.11),
положение максимума смещается в область рс,
конечных начальных ускорений (а, „,, =
РЯХ
=2,5 — 4 дс), а величина максимума зна-
чительно уменьшается. Зависимость опти- РЮ
иальной величины начального ускорения
а„от удельной массы двигателя т для
различных значений полезной массы при-
ведена на рис. 9.2. Значения т. слабо Рис. 9.1. максимальная энергия
вертикальный подъем с т~=О,З.
влияют на оптимальную величину а, — все
кривые а, (т) для 0,1 ( т, ( 0,5 лехсат
в узкой полосе (заштрихованная область на рис. 9.2). Полезная нагрузка
в функции энергии ф1 при фиксированных значениях удельной массы т по-
казана на рис. 9.3.
В качестве второго примера рассмотрим модельную задачу о перемещении
между двумя точками покоя на расстояние 1 за время Т. Решение динами-
ческой части вариационной проблемы, эквивалентной (9.6), для этого ма-
невра описано в ~ 2 гл. 8 (см. (8.43)). Учитывая, что 1 — пТ„=т и (г=ас/Г „,
разрешим (8.43) относительно а,:

[ГЛ. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
Здесь т, — независимая переменная, по которой отыскивается максимум т,
После этого по формуле (9.28) определяется соответствующее значение а,.
' Ц004 0008 фЮ
'Р - 6Г 6Ф 06 68 I В,/Р
Рис. 9.2. Оптимальная начальная тяговоору- Рис. 9.3. Влияние удельной массы двигателя ~
женность — вертикальный подъем. на максимальпую полезную нагрузку—
вертикальный подъем.
Результаты этой процедуры показаны на рис. 9.4, 9.5. Максимальная полез-
ная нагрузка т, в функции комбинации параметров 1~ТУ,„,„при фиксирован-
л °
Рис. 9.4. Максимальная полезная пагрузка — Рис. 0.5. Оптимальная начальная тяговоору-
перемещение между точками покоя. женность — перемещение между точками
покоя.
ных значениях (~У „)Т) приведена на рис. 9.4. Пример зависимости отно-
сительного оптимального ускорения а,lд, от 1~ТУ,„при (У„„„)д,Т) =0,5 для
7=0,01 кгlкГ и т=0,02 кг~кГ дан на рис. 9.5.
~ 2. Оптимальное управление массой двигательной
системы — непрерывный случай
1. Формулировка вариационной задачи. Конечная масса аппарата
с двигателем ограниченной скорости истечения имеет естественное ограни-
чение снизу.
(9.30)
Когда масса М, становится сравнимой с (М,+М„), появляется интерес
к исследованию возможности увеличения М, за счет изменения по времеии
массы- баков М~ (~) и массы двигателя М„(~). Решение задачи об оптималь-
ном изменении массы М (1) по мере уменьшения М (1) получено различными
авторами в классе кусочно-постоянных допустимых кривых М (~). В ра-
боте [9.53) получены необходимые условия оптимальности в форме классичес-
кого вариационного исчисления и приведены условия сопряжения дуг экстре-
малей при переходе через поверхности разрыва. В работе [9.36) предложен
алгоритм проверки достаточных условий экстремума. Для идеального дви-
гателя ограниченной скорости истечения решение такой задачи приведено
в пп. 3, 4 ~ 1 гл. 5.

309
УПРАВЛЕНИЕ МАССОЙ: ДВИГАТЕЛЯ вЂ” НЕПРЕРЫВНЫЙ: СЛУЧАЙ:
$ 2]
Здесь Р,: — максимальная тяга ~-й секции двигателя, ~,. — момент сброса
~-й секции, и — число секций. При последовательном секционировании
работает лишь одна секция, причем последующая включается только после
сброса предыдущей. Допустимая область изменения управления Р (~) в этом
случае задается неравенствами
0(Р (1) (Р' (1), Р" (1) = Р„: при 1,. ( 1(1,.
(~=1,...,и; ~„=Т). (9.32)
Исследование задачи управления массой двигательной системы в предель-
ном случае кусочно-непрерывного изменения величины ЛХ„(1) целесообразно
с точки зрения выяснения условий невыгодности ступенчатого уменьшения
массы двигательной системы. Предположение о кусочно-непрерывном из-
менении М„(1) позволяет получить максимальную оценку возможного вы-
игрыша от управления массой двигательной системы (см., например, [9.391
и [6.24, 6.251 для двигателей ограниченной мощности). Невыгодность ку-
сочно-непрерывного изменения М, для конкретных условий выполнения за-
ланного маневра свидетельствует о том, что любое ступенчатое уменьшение
массы двигателя в этих условиях невыгодно.
Проведем общий анализ задачи об оптимальном кусочно-непрерывном
управлении массой двигательной системы [9.541 без указания конкретного
типа двигателя. Для этого характеристики двигателя считаем представимыми
в общем виде (4.9), (4.10) функциональных выражений через независимые
управления и, (1),..., и~ (1) и постоянные управляющие параметры и„...
д Р/~з Мс Мх (~1 шхпз ~~1 тахе 'э 1~ т1п1 ~д п1вх~ ~1! ' 1 ~~~у)у
(/=1, ..., У), и =сопя~ (т=1, ..., М).
Из числа параметров, определяющих массу двигателя, выделим те, которые
могут меняться современем, и обозначим их через Ь„(Й=1,..., Х), а осталь-
ные — через с„(~ = '1,,М), так что
М„= М„(Ь„, с„), Х + М = 2У + Л~Х. (9.34)
К параметрам Ь„можно отнести, например, максимальную тягу Р* много-
ступенчатого аппарата с параллельной схемой секционирования двигателя,
Анализ решений указанной задачи показывает, что эффективность сту-
пенчатого управления ЛХ возрастает с увеличением числа ступеней (см., на-
пример, (5.18), (5.19)). Максимальное увеличение полезной массы достига-
ется в предельном случае бесконечного числа бесконечно малых ступеней
(непрерывное изменение ЛХ ).
Задача об управлении массой двигателя ЛХ„существенно отличается от
указанной выше тем, что уменьшение ЛХ в общем случае ведет к сужению
области допустимых значений основной управляющей функции Р (~) (см. (9.1)) .
При постановке задачи об оптимальном управлении величиной ЛХ необхо-
лимо различать два основных способа секционирования двигателя: парал-
лельный (1) и последовательный (2). В случае (1) все секции двигателя могут
быть включены одновременно. Допустимая область изменения тяги двига-
теля описывается в этом случае так:

310
[ГЛ. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
убывающую после сброса каждой ступени. К числу неизменных по времени
параметров с„, входящих в выражения для М„и Р, относится, например,
удельная масса т двигателя. Тогда вариационная проблема о максимуме
полезной массы может быть сформулирована следующим образом:
(9.35)
Формальное введение Х новых фазовых координат Ь„и новых управляю-
щих функций ~~ (1) позволяет использовать для анализа вариационной за-
дачи принцип максимума [9.55]. Заметим, что если 7Ь,(Р)= — оо, то коорди-
ната Ь„имеет разрыв первого рода в точке ~=Р. Случай — оо ( 7Ь, (~) ( О
соответствует непрерывному сбросу бесконечно малых секций двигательной
системы.
2. Состав оптимального управления. Так как ограничения на некоторые
из управлений и.(1) зависят от фазовых координат:
Ьш&l ;а И
перейдем к новым управляющим функциям $. (~) (аналогично (6.37) — (6.39)):
а'И) =Ьж+~'И) '(Ь Ьш) (О~~у'И)~1)' (9.36)
При этом тяга Р и расход д в (9.35) зависят от новых фазовых коорди-
нат Ь и управляющих функций $.:
Р=Р(Ь„, с„, ~.), д=д(Ь„, с„1.) (0(~ (1)~~1).
Оптимальные значения управляющих функций ~. (~), е (~), ~7„(~) определяются
из условия абсолютного максимума гамильтоновой функции:
(9.37)
дН
дМ,'
дН
Р= ——
т д~ У
дН . дН
дч ~ ~с дЬ~
Оптимальные управления е(г) и ~) '~' даются соотношениями
е(1) =р„~р„; т]„(1) =0 при р„) О, «)„(1) = — со при р„(0.
(9.38)
Таким образом, непрерывное изменение координаты Ь~ имеет место только в том
случае, когда в состав оптимальной траектории входят участки особого управления ~~ (~).
Необходимое условие наличия участков особого управления ~~ (~) записывается
в виде [9.56] требования выполнения равенств
р,(Ц=о, р,(~)=о
(9.39)
на конечном интервале времени. Из (9.39) с учетом (9.38) следует:
р, (дд/дЬ~) — р, (да/дЬ~) = О.
(9.40)
Необходимое условие оптимальности особого управления ~~ (~) [9.37] в рассматриваемой
задаче имеет вид
О.
М.= — д, м. (0) = м, — м„(о),
Г='~, г(0) =г„
т=ае+д(г), т(0) =т„
~ — 'Ъ~ М (Ь„(0), с,) =М„(0),
(а = Р)(М, + М„), — со ( 'в„(~) ( О, Й = 1,
Н = р.д+ р„т+ ар, ° е + р, ° и + ~ р,д„
М (Т) = тах,
г(Т) =г„
т(Т) =т„
Ь„(Т) = ор(,
..., Х).

УПРАВЛЕНИЕ МАССОИ ДВИГАТЕЛЯ вЂ” НЕПРЕРЫВНЬЩ СЛУЧАИ
Если дд/дЬ„=О, то из (9.40) следует либо да/дЬ~ — — О, либо р„=О. На участке особого упра-
вления оба предположения не представляют интереса: или Ь~ явно не входит в уравнения
задачи, или имеет место бесконечно большой порядок вырождения (в терминах [9.56]).
Следует отметить, что выполнения этих необходимых условий оптимальности особого
управления недостаточно для утверждения об оптимальности непрерывного изменения
соответствующего параметра Ь~, так как траектория, включающая отрезок особой
зкстремали, может и не доставлять абсолютного максимума функционалу М, (Т). Необ-
ходимо следить также за выполнением условия — со & t; ~„ ~  lt О на собом уч
Функция ~~ (~) на участке особого управления вычисляется из уравнения р„=О.
3. Анализ особых режимов. Ниже рассматривается вопрос о включении
участков особого управления ~„(1) =д„(1) в оптимальную траекторию для
двигательных систем, характеристики (9.1) которых могут быть представ-
лены в виде (параллельная схема секционирования)
Р=Р" ° Р(~), Г= Г „° Р(~), М„=~Р*, М,=О,
о(Р(~) (1, о( г(~) (1, м„= — д„.
Для таких двигательных систем необходимое условие (9.41) оптимальности
особого управления д„(~) принимает вид
М„(~) — М (~) (О
(9.43)
и, очевидно, всегда выполняется. Участки особого управления скоростью
истечения 0 ( Р (~) ( 1 не входят в состав оптимальной траектории Я 1).
В качестве примера, иллюстрирующего целесообразность включения
особого участка в оптимальную траекторию, рассмотрим модельную задачу
о наборе в однородном гравитационном поле максимальной конечной ско-
рости, направленной противоположно гравитационной силе [9.57]. Началь-
ная масса ЛХ„полезная нагрузка ЛХ и характеристики (9.42) двигателя за-
даны, время выполнения маневра выбирается оптимальным. Вводя безраз-
мерные переменные
Р й)= Р ®/Р'(~),
— ~ шах
О О
~= — ф/Г
т,. = М,./М„Р' (~) = Р' (~)/Ре,
Г ® = Г (~)/Г „,
~~ — ~~/ ~ тахт
а, = Р,"/д,М„
(9.44)
(Р*(о) = Р,*)
Т =~оТ
и учитывая (9.42), вариационную проблему можно сформулировать в виде
тп„Р
т.(Т) =т,,
т. (0) = 1 — т„(0),
тп,Р
8=
(и„+ и,) т
1, и(0) =О,
г (Т) = шах,
(9.45)
т„(0) = ~а„
'~(о) = о,'
о(гр)(1,
х Дх~
т„(Т) = ор1,
Т =ор~
— сю ( д„( 0).
1=1,
(0(Р(~)(1,
Р,(~) =1,
(9.46)
С учетом (9.46) приращение скорости Ии выражается в виде
Здесь и далее черточки над безразмерными переменными, определяемыми
соотношениями (9.44), опущены.
Можно показать, что на оптимальной траектории

312
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
Состав оптимальной траектории (чередование неособых и сингулярных дуг вдоль
экстремали) определяется путем исследования знака функции со [9.58]
1 у
(т, + т„)~
(9.48)
Возможные варианты оптимальной траектории в координатах т.„(х) (масса двига-
теля) — т, (х) (масса топлива и полезного груза) изображены на рис. 9.6. Начальное
положение системы отмечено точкой Д. Если точка Д лежит выше линии и=О (рис. 9.6, а),
т ф)
~2)
Рис. 9.6. Возможные варианты оптимальной траектории.
оптимальная траектория состоит из отрезков граххххцы области со ) 0: с,)т — движение
с постоянной массой двигателя (т„=т„(0), д„=О); т/ — двихсеххие по сххххгулярной дуге
хт, (х) =(( ~' — "() т, (х)) до некоторого заранее не заданного значения т., (Т), дости-
гаемого в момент Т ири т, (Т) = т .
Если прямая ох=О проходит выше точки с,) (прямая 1 на рис. 9.6, б), оптимальная
траектория фг' начинается с мгновенного сброса двигателя, так что т„падает до некото-
рого значения т„" (0) ири постоянном т,(отре-
Л7 зок Я), далее следует особый участок. Такой
случай соотвстствуст пеоптимальному значе-
пию начальной массы двигателя.
Если линия ()=О проходит ниже области
допустимых положений системы (прямая 11
и прямоугольник Дххыд на рис. 9.6, б), опти-
ъхальххая траектория Чт не содержит сингу-
лярной дуги (т.„(х)= — тао при 0 & t  (
Удается показать, что последнее заведомо
имеет место ири т„.& t; (1 Ђ 1 ~') (2 в ”, ~
(рис. 9.7).
Эти программы изменения массы двига-
теля ограничспной скорости истечсппя с точ-
ностью до значений констант повторяют полу-
*хоххххые в Я 2 гл. 6 законы (6.65) ххзменоххххя массы
двигатсля ограничснной мощности.
ОГ Оч'
Од у,пг/лГ
Рис. 9.7. Область отсутствия сингулярной
дуги (заштриховапа).
8 (Т) = (1 — ~/-() ( $ ~х [(~/-( — .() аД вЂ” ! хх т, ф
Оптимальное значение параметра а, не зависит от т:
ао,,„= (2 ~/; †.() '.
При двих.ении с т„(~) = (ао (О (~( Т) достигается скорость
хх (Т) = — ! и (т. +.(ао) — (1 — (т +, а,)]/а,.
(9.50)
(9.51)
Значение хх (Т) из соотношения (9.51) достигает максимума при
1 — т„(1 — т,) ~ т„
ао орс = —."+ ' + (1 — т.) — '.
(9.52)
Значение скорости, достигаемое при движении с особым участком, за-
писывается следухощиы образом:

313
УПРАВЛЕНИЕ МАССОЙ ДВИГАТЕЛЯ вЂ” НЕПРЕРЫВНЫЙ СЛУЧАИ
На рис. 9.8 приведена зависимость отношения 8 (Т) /и (Т) от )' для разных
значений т„а на рис. 9.9 — оптимальные значения а, (кривая 1) и ц
(кривая 2) для т,=0,01.
Г 4 66 Я 4 66 Г 4 66~,кг~кГ
~а 70
Рис. 9.9. Оптимальная начальная тяговооруженность при наличии особого участка (кривая 1) и без
пего (кривая 2).
4. Ступенчатая аппроксимация оптимального управления массой дви-
гателя. С целью получения количественного представления об эффектив-
ности простейшего практически осуществимого управления массой двига-
теля рассмотрим задачу (9.45), ограничив класс возможных управлений
т„(1) кусочно-постоянными функциями времени:
т~') при 0 ( ~ ( ~„
щ„(1) =
щ~") при 1„1( 1 ( Т
(9.53)
(щ(1) ) щ(-) ) ) щ(п))
Число и ступеней двигателя задано.
При фиксированных моментах сброса секций ~,. и величинах т~') опти-
мальные управления тягой и скоростью истечения остаются такими же,
как и в случае непрерывного изменения т„: Р (~)=— 1, Г (~)=1. С учетом
этого уравнения (9.45) интегрируются в элементарных функциях. Конечная
скорость аппарата и (Т) представляется в виде функции 2п — 1 переменных:
и
т," 1' + т,")
и(Т) = 1п '..."., Т (т&lt '  т (й .) т lt о) 1 — т&lt '), т lt;")
о х
а — 1
Рис. 9.8. Отношение конечной скорости ю (Т), достигаемой при движении с особым управлением, к ско-
рости ю (Т) при движении с постоянной массой двигателя.

314
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧ:ЕН НОЙ СКОРОСТИ
$ГЛ
Од
001
005
ьЯ
(~)
Я,7
.д55
ОООО
у, газ/гГ
ь(П
Т)
б,У1
0000( Я,О/ 01 у, лз/кГ
Рис. 9.11. Отношение конечных скоростей с конечным (и) и бесконечным (со) числом секций.
д,001
Рис. 9.10. Оптимальные ступенчатые законы управления массой двигателя т„. (~=0,01 кг/кГ).

4 б 8/д Г
Рис. 9.12. Влияние секционирования двигателя на величину максимальной полезной нагрузки при за-
данной скорости ю (Т)=1,81.
а)
07
0,99
0,000~
Рис. 9.13. Отношение конечной скорости ю, (параллельное секционирование) к конечной скорости о,
(последовательное секционирование).
Оу
"г
00001 0,001
4 б 8 у,кг/И
7, мlкГ
у, кг/гГ

РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 9
Время двиясения Т в (9. 54) и параметры т('& t и т '~ связ ны соот
шением
и
Т =).( ~ [(т('-ц — т~'>)/т('
(9.55)
Оптимальные значения т('~ определяются из условия максимума фун-
кции (9.54) с учетом (9.55):
1 — т~'' (1 — т~1')~ (1 — т,"') т~"
После подстановки т(',~„из (9.56) в (9.54) величина г (Т) зависит от и — 1 пе-
ременных т~'~. Выбор их оптимальными обеспечивает получение предельного
значения функционала для двигателя, состоящего из и секций. Пример оп-
тимальных ступенчатых законов управления массой двигателя приведен
на рис. 9.10. Сравнение предельных значений функционалов, получающихся
при непрерывном и ступенчатом изменении массы двигателя, проведено нь
рис. 9.11. По оси ординат отложено значение отношения г„(Т)/г (Т) (г„(Т)
соответствует случаю и секций, и (Т) — непрерывному закону измене-
ния т„), по оси абсцисс — значение коэффициента )'. Оценка эффективности уп-
равления массой двигателя с параллельной схемой секционирования в за-
даче о максимальной полезной нагрузке при заданной конечной скорости
может быть проделана с помощью кривых на рис. 9.12.
Анализ вариационной проблемы о наборе максимальной скорости аппа-
рата с двигательной установкой, работающей в последовательном режиме,
проводится аналогично. В работе [9.60] показано, что учет массы двигатель-
ной системы дает возможность определить оптимальное число секций. Срав-
нение значений г (Т), соответствующих параллельному (ь,) и последователь-
ному (г.) секционированию, может быть проведено по кривым на рис. 9.13.
При анализе результатов необходимо учитывать, что число ступеней при
последовательном способе секционирования выбирается оптимальным, а при
параллельном способе секционирования задано (в этом случае оптимальное
и= со).
я 3. Оптимальное управление массой двигателя
и баков — дискретный случай
Идея использования многоступенчатых ракет для космических полетов
была впервые обоснована К. Э. Циолковским в 1929 г. [9.61, 9.62]. Ра-
бота [9.2] положила начало исследованию оптимальных задач ракетодинамики
многоступенчатых систем. Задачи оптимизации таких систем в значительно
упрощенных постановках были решены как задачи отыскания условного эк-
стремума функции нескольких переменных. Оптимизация многоступенчатого
аппарата в произвольном силовом поле потребовала привлечения вариацион-
ных методов, например классического вариационного исчисления [9.36,
9.53, 9.63 — 9.66], метода динамического программирования, принципа мак-
симума [9.55, 9.60] и др.
В некоторых работах [9.67, 9.68] отдается предпочтение методу [9.69],
позволяющему преобразовать разрывную вариационную задачу (с разрыв-
ной подынтегральной функцией) в обобщенную задачу Больца.

317
УПРАВЛЕНИЕ МАССОЙ ДВИГАТЕЛЯ вЂ” ДИСКРЕТНЫЙ СЛУЧАЙ
ЛХ,. =М„,. +М., +М,. +ЛХ„,.+ЛХ~, +ЛХ,+, о, ЛХ„д,— — ЛХ.,
ЛХ„, = а,.ЛХ,.О, М,. = [~,.М~,, ЛХд — — ~,.Р",, ЛХ,. = (Ч,.о — ЛХ,. ) 5,
(~ =1,..., и).
(957)
Здесь М„„. — начальная масса рабочего вещества; М,. и ~,. — масса и удель-
ная масса баков (на единицу массы рабочего вещества); ЛХ„,. и т,. — масса
и удельная масса двигателя (на единицу максимальной тяги Р,'.); М„,. — масса
части конструкции, пропорциональная начальной массе ступени, а,. — удель-
ная масса этого элемента; М~, — масса части конструкции, пропорциональ-
ная величине, на которую уменьшается масса аппарата на участке работы
и сброса ~-й ступени (~,. 1( ~ ( ~,.), О, — удельная масса этого элемента.
Массы элементов М,, )=(а, ~, ~, 0), сбрасываются в момент сброса ~,, но-
мер ступени ~ принимает последовательно во времени указанные в (9.57)
Значения.
Многие авторы, формулируя вариационную задачу, принимают массу
ступени ракеты, состоящей из массы рабочего вещества, массы конструкции
и массы полезной нагрузки, совпадающей с массой последующей ступени.
Здесь, аналогично [1.71, 9.60], вводятся в рассмотрение дополнительные
компоненты массы, входящие в массу конструкции, что приводит к особен-
ностям как в постановке вариационной задачи, так и в законах для оптималь-
ных управлений. При этом используется вариационный подход [9.70, 9.71],
позволяющий распространить принцип максимум Л. С. Понтрягина на
широкий класс разрывных систем. Основную идею подхода составляет
представление кусочно-непрерывной функции как предела непрерывных
функций.
1. Постановка задачи оптимизации. Рассматривается вариационная
проблема о доставке максимального полезного груза многоступенчатым ап-
паратом с двигательной системой ограниченной скорости истечения (после-
довательная схема) [9.72, 9.73]. Поясним работу такой схемы. В начальный
момент ~,=0 движения аппарата включается первая ступень, начальная
масса М1О которой совпадает с начальной массой аппарата М,. После израс-
ходования массы рабочего вещества М„1, предназначенной для работы первой
ступени, в некоторый момент ~, сбрасывается масса баков ЛХ.„содержав-
ших это рабочее вещество, масса двигателя ЛХ„„создававшего тягу Р,
на участке работы этой ступени, и массы других элементов ЛХ„, М„,1 (это
могут быть силовые элементы конструкции, элементы системы управления
и др.), необходимых для работы первой ступени. В тот же момент, после
сброса первой ступени, начинает работу вторая ступень, начальная масса
которой М„является полезной массой для первой ступени. В момент ~„)
)~, происходит сброс второй ступени и т. д. После израсходования массы ра-
бочего вещества М„„, предназначенной для работы последней ступени и,
смерос баков, двигателя и других элементов этой ступени не производится
вплоть до конечного момента движения аппарата ~„=Т.
Согласно описанной схеме полная масса рабочего вещества, имеющегося
на аппарате в начале движения, складывается из масс рабочего вещества
отдельных ступеней, полная масса баков — из масс баков всех ступеней
ит. д.
При этом масса ступени ~+1 (~=1,..., и — 1) является полезной массой
для предыдущей ступени ~, а полезная масса последней ступени (~=п) сов-
падает с полезной массой аппарата М„.
Принимается следующая формула для начальной массы ЛХ, ступени ~:

318
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 9
Уравнения расхода, движения, соотношения масс в моменты сброса и
краевые условия записываются в следующем виде:
м (0) + м(1& t + М 1 + м 1
-~-М~ & t; -+ЛХ.=М„М, т)
М =О,
ЛХ< + = ЛХ lt; > — ,м
М("+') = М~"+') = М("+1) =
а ф х
= М& t; " ' =
е
(9.58)
МЗ'+» = МЗ'& t; Ђ” ,. М, (~ ,) Ђ” м, (~ .)
,Ц(~+1) Л~(~) -~ р
М~~'+» = М~~'& t; Ђ” м' (~ ,) Ђ” М' Р, )1 (
г(0) =г„
г=~,
у= — ', +д(г, 1),
(О ( Р,. (~) ( Р;".,
г(Т) =.г„
т(Т) =т,
~=1,..., и).
х = Г'" ~х, х(1,), у""', и, т, 1„~~,
я=о, 1,...,~ — 1;
я=О, 1,
Здесь х — т-мерный вектор состояния; и — г-мерный кусочно-непрерывный
управляющий вектор со значениями в ограниченной и замкнутой области Г;
у — е-мерный, изменяющийся в дискретные моменты времени вектор;
~-мерный постоянный управляющий вектор, допустимые значения которого
принадлежат ограниченной и замкнутой области И~, задаваемой неравенст-
вами
~т1п ~~ ~~ ~~ ~тах
Индекс ~ последовательно во времени принимает указанные значения, смена
индекса происходит в моменты ~,. пересечения траекторией системы (9.59)
Здесь текущая масса аппарата предполагается вырансенной в виде ЛХ=
=-М +ЛХ~'~+М~'~+М~'~+М~~'~+М„ЛХЖ (у'=а, ~, х, 0) — масса всех
элементов с индексом )', имеющихся на аппарате па участке работы ~-й сту-
пени (1, 1 "1,.), так что МЖ =М,. +М, „,+... +М
Верхние индексы « — » н«+» относятся к значениям координат слева и
справа от 8,. соответственно.
Требуется определить управляющие функции Р,, д,, е, управляющие па-
раметры Р,',, распределение моментов сброса ступеней ~,. и число ступеней и,
которые переводили бы систему (9.58) из начального положения в конечное
с максимальным значением функционала М при заданной начальной массе
аппарата М,.
2. Общая методика. Поставленная в п. 1 задача представляет собой
частный случай более общей вариационной задачи для процессов управле-
ния, описываемых дифференциальными и конечноразностными уравнениями
~9.70, 9.71):

319
УПРАВЛЕНИЕ МАССОИ ДВИГАТЕЛЯ вЂ” ДИСКРЕТНЫИ СЛУЧАИ
гиперповерхности, заданной соотношением
Я"'[х, х(8,), у"+", ю, 1,, Ц= О,
г= О, 1,...,1 — 1;
1=1,..., и — 1. (9.60)
Тогда же функции Г", Р"', у"' заменяются на Г"~', ~''+~', у"+~'.
Вариационная проблема формулируется традиционным образом: требу-
ется найти управляющую функцию и (1) (~ Г и управляющий параметр т ( И',
которые, переводя систему (9.59) из начального положения
~ =1,..., У ~ е+т+Ы1,
р® [х (г ), у'1', ж, Е ] = О,
(9 61)
в конечное
1=1,..., К(тп+Ш„.
г=О, 1,...,п; р=1,...,п
И +~ ~~)
~~,"~ [х(~,), у"', ~, 1,]= О,
(9.62)
доставляют минимум функционалу
Ф[х(г,), у'"', ъ, ~,],
О
ур ° т'ъ
— ~Ь ~Ь ° ° ° т ««» Р— х~ ° ° ° э ~.
Р.6З)
Предполагается, что ~О задано, а ~, необходимо найти.
Для формулировки необходимых условий оптимальности перейдем к дифферен-
циальной записи системы (9.59) и (9.60).
Введем управляющую функцию о типа о-функции Дирака такую, что
Ж
3 Ж =1пп — =1,
е-э+О
со ПрИ ~=~;,
з()=
0 при ~=ф=~;,
(9.64)
~=1,2, ...,
и фазовую переменную х,„+,, удовлетворяющую уравнению
Ихул~1~1г = 1е хт+1 (~0) ~0'
(9.65)
Подстановка новой переменной х +, (х, = г) вместо ~ в соотношения (9.59) — (9.63)
соответствует сведению неавтономной системы (9.59) к автономному виду.
Вектор у будем понимать как кусочно-постоянную функцию у (~), непрерывную слева:
у(~)=у~'~, 1; 1(1(1;, ~=1, ..., и. (9.66)
Введем также кусочно-постоянные (т+1)-мерные векторы ф„, а=1,..., и, «запо-
минающие» промежуточные значения (т+1)-мерного вектора х последовательно в точках
~,, ~=0, 1,..., и — 1, и такие, что
~ = 1, ..., и (ф„(~;) =1(т ф„(г; — «));
е-~-+О
(9.67)
ф„(~) =х(~; ),
кусочно-постоянные е-мерные векторы оз, ~=1, ..., и — 1, «запоминающие» променсуточ-
ные значения е-мерного вектора у в указанных в (9.67) точках:
ие (г;) =у (г; з) =у~' ~~, ~=2, 3, ..., и;
(9. 68)
+ ( 1' (х ~" (х У Ф ~р ~«) Ф:1 ~р- ~«) — ~с) з
у — ~(х, у. Ф. Ч ) 1~ ~ =И"=0 (1'"=(1'" 1)),
(9.69)
где Г (х, у, ф„, и., ю) ~~ ~ — Ф [х (й,), у'~~, и, й„), а произведенная у = НГ/сГ» пони-
иается в обобще?ном смысле и выписывается вдоль траектории системы (9.59).
фазовый вектор х=(х„..., «1), «отвечающий» за выполнение соотношений (9.60) в точ-
ках ~; (~=1,..., и — 1) и изменяющийся согласно пятому уравнению в (9.70); кусочно-
непрерывную фазовую переменную у, (1), удовлетворяющую уравнению
у,=[дгай„- 'г' (х, у, ф„, из, т«), т"' (х, у, ф„, ~1~, и, тч))+

320
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ.
[ГЛ. 9
При помощи (9.64) — (9.69) поставленную выше задачу удается переписать
как проблему Майера:
дифференциальные связи:
х= т'с') (х, у, ф„, с1,, и, тч),
у=[у~'~ (х, у, ф-, с1-,, ч) — у ]о,
ф„=(ф„-, — ф ) о,
ч =(ч;,— ч-,)~
х, = 2"'(х, у, ф„-, с1-з, ю) о„.о,
% = У1 ~пцд ~ ~~ ~ ~~ ~Щ;Щ1
И
уе = — „~ У(х, у, ф„, цз, ж)
( .Ю)
(1с,(1(1,, ~=1,..., и);
начальное состояние:
р® [х(~ ), у (~ ), уе(1е), ч~(~е)] =О, ) =О, 1,..., У (е+т+ с~1,
к (с.,) = О, ф (1,) = х (1,), с1, (1,) = у (1,), а = 1, ..., и; (9.7'1)
р, К=1,...,и — 1;
конечное состояние:
ср~"~[х(1„), у(1„), ф„(1„), с1 (1„), ч~(1„)]=0, 1=1,..., К(ти+И.„
х (~„) = О, уе (~„) = т1п, ~„= ор1;
управления: и(1) (= Г, о(1) из (9.64).
В (9.70) ф, = х, п-,=у, о„. — символ Кронекера.
Удовлетворение граничных условий х (~,) =х (~„) =0 гарантирует выпол-
йение соотношений (9.60) в точках разрыва о-управления.
Особенностью системы (9.70) является линейная зависимость правых
частей некоторых уравнений от неограниченного управления о типа о-функ-
ции. Соответствующие производные в левых частях этих уравнений пони-
маются в обобщенном смысле.
Введем в рассмотрение расширенный фазовый вектор х=(х, у, ф, ц~,
х, це, ч~) и будем в нем различать непрерывную х„=(х, ч~) и разрывную
В некоторых задачах, кроме моментов разрыва правых частей уравпеншт, могут
быть заданы моменты разрыва других характеристик системы, например фазовых коор-
динат, либо моменты, в которых должны выполняться ограничения на фазовые коор-
динаты, и т. д., причем иногда эти моменты невозможно (или неудобно) пронумеровать
с помощью одного общего ряда натуральных чисел (в нашей задаче ему соответствует
индекс с). В таких случаях разнородные моменты разрывов нужно нумеровать с помощью
различных рядов, обозначая их различными индексами (например, Е, у, Ус, ...) и ставя
в соответствие кахсдому из них свое о-управление (о', У, З", ...) и свой фазовый
вектор к (к', з~, х", ...), каждый с размерностью, равной числу членов соответствую-
щего ряда.
Введение переменных ф„и цЗ по указанному выше правилу наиболее рационально,
если на с-м интервале необходимо помнить значения х (~; „), ус' ~~, где значения а и
а заранее фиксированы. Если же на любом интервале необходимо помнить значения
х (~„), ус», где а и 3 неизменны, то рациональнее ввести дополнительные переменные
ф" и ц~: ф"=х6„,6, ф (~,) =О и ц~=у О~,3, ц~ (~,) =О. Если ~ и 3 пробегают все воз-
можные значения, то оба способа эквивалентны.

321
УПРАВЛЕНИЕ МАССОЙ ДВИГАТЕЛЯ вЂ” ДИСКРЕТНЫЙ СЛУЧАЙ
х,=(у, у„ф„, п„х) части, так что х=(х„, х,). Тогда систему (9.70) можно
записать в компактном виде:
х=Г['> х, и)+Г '&gt (х , х;) о =Г& t; &g ; (
Интегрирование системы в моменты ~,. проводится с учетом определения
й-управления (свойств о-функции)$
х+= х;+ Г~с'& t; ( „, х
х'=х =х-,
ю' т"
Предполагается, что правые части Г"' в (9.70) и левые части в (9.71),
(9.72) непрерывны по совокупности аргументов и дифференцируемы по фа-
зовым переменным. Там, где необходимо, будем предполагать выполненными
условия «некасания» [9.55, 9.74 — 9.77] траекторий системы (9.59) и гипер-
поверхностей (9.60) — (9.62).
Как показано в [9.70, 9.71], если управления и (~), о (~) и траектория
х (г) оптимальны, то
1) при ~+~,, ~=1,..., и — 1, выполняются условия принципа максимума
Л. С. Понтрягина (в том числе условия трансверсальности для обоих концов
траектории). В частности,
Н(х, х, р, и,р&g ;, о) =тахН х, х, р, и, ), о
иИ~
(9.73)
где
Н(х, х, р, и, о) =(р, ГС'& t; х, х, и, о
р = — вегас&g ; Н Ђ” (ога „- 11
2) в моменты разрыва ~=~,. управления о выполняется условие непрерыв-
ности гамильтониана Н:
(Н = (р, Г~с'& t; х и ), 1' == ( +, Г~с +» ( +, и+) ); (9.
Н-1(~,.) = 11+~(~,.)
3) кансдая из координат ы, управляющего вектора ч~,р~ удовлетворяет
одному из следующих трех соотношений:
дН
>с& t юрс = &g ;с>~ а е Ри„( „ р „( п)
У
~уорС = ~уш1п~
с&g ;Н (и'о
ЪН (%'ОРС) = Д Обуй ~~ О.
(9.70)
Из уравнения для вектора импульсов р следует, что
р„= — огай„Н, р„= — огай„П вЂ” ®гад„Н)+
и координаты вектора р могут терпеть разрыв в моменты г=г;. Де>>ствит
уравнения для р„и р„можно представить в виде
7 ~Т
р = — огай„(р, Рс'& t; х, и )+ е&g ;&gt с'& t; р„
р„. = — цгас$„(р, Р,"' (х, и)) + е>2 '&gt (р , х , х
е>&g ; '&g ;о = — пгай (р, ~'& t; х„, х;) о , е gt;~"'6+ = в ” ~у ас1„ (р Р "
21 Механика полета
Если вектор и не входит в граничные условия для системы (9.59), а область И~ имеет
произвольную кусочно-гладкую границу, то соотношения (9.75) заменяются условном

~~22
[ГЛ. 9
откуда в результате интегрирования уравнений в моменты Е; с учетом свойств о-управле-
ния и непрерывности вектора х„получаем условия скачка (й=й;):
По сравпениго со случаем, когда в системе (9.70) управление ь отсутствует, мы получае»
2 (и — 1) дополнительных параметров р и ~; (&g ;, 1 1, . . и Ђ” ), от кото ых так
зависит оптимальное решение. Для определения этих параметров имеется 2 (&g ;г Ђ” 1) соотно
ний (9.60), (9.74).
3. Состав оптимального управления. Вернемся к исходной задаче (9.58).
Выразим расходы д,. и массы ЛХ„,. через характерные для двигателей ограни-
ченной скорости истечения параметры, а именно через скорость истечения
и величину тяги Р,.:
М., = ',.Р,.
с !г
Сделаем также следующие замены:
г 6
Ьпг =т„'(0) — т,
Здесь Ль — радиус Зеггли; все компоненты в формуле для массы отнесены
к начальной массе аппарата ЛХ„а значения тяги Р,. — к д,М,. Далее черту
над безразмерными величинами, за исключением Р и 1', опускаем.
Порепишом задачу (9.58) в виде (9.70) — (9.72) с ооозиачениямп (9.77),
(9.78):
„— (Ьт)=
г
В,. (Ьт — Ьт~) о, гт (0) = О,
Ьт„(0) =О,
(9.79)
г=~,
т(0) = т„ъ (Т) = — т„
'" =О, Р;. (0) = Р'„(Т) = о)&gt ~ Й =- 1,. . и Ђ”
Р,",(0) =. ор1,,
Ф = —. (1. — 0„— х„) [афпг„(Т) + Ьт, (Т) + Ьт„(Т) + ~т„(Т) ~+
+ (1 + ~'.„) ~т (Т) — (а„+ 3„+ 0„) Ьт„(Т) + 7„Р';; ( Т) — пгш
(О ~~ )' ... 1, О ( Р ~ 1, О ( Р'„( со).
И
„— (Ьт„)
И
— (Ьт~)
д1
„— (Ят )
И
— (Лт )
Д~ и
И
— (Лт,)
Ж
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАПИЧЕННОй СКОРОСТИ
р =р + и~&g ;" ( +, ,, х, ), р+ = + и "' ( +, ,,
(р' = р (г; + О) = р„(г )).
(0( Г,. (~) ( Г,"., 0(Р, (~) (Р',). (9.77)
Иь~ о (9.78)
Лт,. = т~1.'1 — т~.'1, т = ЛХ,./ЛХ„у = (а, .~, ~, 0).
Ьт„(0) = О,
~т,(0) =О,
Ьтг(0) =О,
О;
[7„. Р",. + (1 + 3,.) (Лт — Лт~) +
г
+ м,.т,.) о, Ьт, (0) =. О,
г (0) = г„г (Т) = — г„

32,'3
УПРАВЛЕНИЕ МАССОЙ ДВИГАТЕЛЯ вЂ” ДИСКРЕТНЫЙ СЛУЧАЙ
Гамильтоххова функция Н и уравнения для импульсов будут иметь вид
0;
~ = 1ру) -'; (Р~ -'- ррр) (~~„— ~~х) -'- '~ хр. -'-1 р, Ре) ~~ +
0; РР;. РР,"е
«)-';)~-'-х)(~~~ — ~~ ))(х-)-р — -) Р «-)-Р +~)
р =й — Р-о, р„(Т) = — (1-& t; з
р' = Й+ Ех), р (Т) =а„+ 0„— 1,
р'г= 1Р+ Е) ~ рг (Т) = а„+ ~„+ )х„,
д
1)„=- у (р,1х)
19.80)
~) = — Р
РНр 0;
Ь = Р' ~~~ '~ Р' "1 — Ю.р~)
р, (0)=р (Т).=0, (с=1, ..., п — 1,
р (О) = О,
Здесь
т
0; 0;
Е=и; 1+.~1 0 Р0, Р="РР Р1 1 ' 1 0 Р
1 при Н,)0,
0 при Н,(0.
Г (~):— 1, е(()=р„(]р ], Р(х)=
(9.81)
При Н,=О, Н,=О (особьхй случай) управление Р может принимать промежуточные зна-
чения (О ( Р ( 1). В точках разрьхва е-управленххя выполняется условпе (9.74).
Первое нз соотххошехххххх (9.81) следует из отрицательности фуххххцхххх р . Действи-
тельно, пусть р„) О. Тогда, очевидно, имеется промежуток времени ненулевой длины,
а котором х' (()= — 0 и, следовательно, Р 1():=1 (см. (9.80), (9.81)), что противоречит физи-
ческому смыслу. Отсхода р & t; О. Реалххзац хя слу а р х-.) 0 Р (~ = в изолирован
точках ~ соответствует импульсному сбросу конечного количества рабочего вещества
с нулевой сххоростью, что явххо пе онтхпхально. Участки особого управления р 1()=0,
р (х)= — 0 также не оптимальны, поскольку выполнешхе данных тождеств влечет за собой
выполнение на всем интервале [О, Т] тождеств р„=О, р,,=:О, а зто приводит ь вьхрохххден-
ности задачи оптимизации, что непосредственно следует нз (9.80).
Отметим, что моменты сброса ~; в настоящей постановке определяются оптимальным
образом.
4. Решение модельной задачи. В качестве примера рассмотрим задачу
о наборе заданной энергихх в плоскопараллельном гравитационном поле
при вертикальном подъеме. Приххевх следующие упрощения: а,.= а,
7,.=7, 0,.=0, х(,*.= х('. Сфориулированххая задача решена в 19.72, 9.73]. Ана-
логичная задача для случая я=0==0 во взаимной постановке рассматрива-
лась в [9.60].
21»
(=)а, х), ° а); перевхеххххая (~т играет роль переменххой фх ххз и. 2, а зххачеххххе символа
Кронек~ра б,.~ совпадает со значением производной дР,"(дР~. Нетрудно видеть, что
р,=рв =— р„=ре и, следовательно, любые три нз них могут быть исключены пз (9.80). Опти-
мальные управления, доставляющие согласно результатам п. 2 абсолютный максимум
функции Н, таковы:

324
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
[ГЛ. 9
Уравнения динамики и граничные условия конкретизируются следующии
образом:
= — — 1, г(о) =о,
РР",е
г(Т) = орь,
(9.82)
РР",.е
~ =У вЂ” '
т
Здесь
д,2
е = -)1, Д=, Д = — +дт, .г= гдт+т„Т =ор$.
уоЛ
Соответствующая гамильтонова функция и уравнения для вспомогательных перд.
менных имеют вид
РР", РР;е РР,'е
Н = Н,8 + р„' + р„' — 1 + р,д~
РР;е (9.8Э)
г
Р,=О !р, = союз~,
где выражение для Нз совпадает с заключенной в фигурные скобки частью гамильтониана
из (9.80) (с учетом упрощений данного пункта); уравнения расхода и соответствующие вд
уравнения для импульсов, аналогичные (9.79), здесь опущены; 11 = Р",. ~р„(РУ" ~
+ (р, + р и) е/т~. Найдем оптимальные управления:
Г (~)=1
р„(Т) =О,
(что показывается так же, как и в п. 3);
+1 при р и+р,)0,
е(д) =
— 1 при р и+р„(0.
(9.81)
Из производной (р и+р,)'= — р =сопзС следует, что е=1, если р (О (очд
видно, е (0) =1 и р, (0) ) 0). Но в этом случае р', ) 0 всюду на траектории и нд
выполняется гранигдное условие р„(Т) =О. Следовательно, р~) 0 и е (д) =+1, причен
возможный участок е (й)= — 1 замыкает траекторию. В момент т (изменения направления тя-
ги) р и (-.) + р„(-) = 0 и, как нетрудно видеть, Н (с) (О, Р (;) =О. Из выражения РН
=Н+р„, йфй,, следует, что р„(й) ) 0 (Н (й)=0, поскольку время Т свободно, а система уравне-
нийавтономна). Отсюда р, (т)=р,(Т)=0, что возможно, еслиР=Она участке (т, Т1. Ното-
гла Ф=сопз1для ~ ~ [~, Т1 а все граничные условиядолжны выполняться уже в момент д,
Следовательно, траекторию можно оборвать в момент ~ (т. е. т= Т) и всюду на траектории
е(1) =1 (9.85)
ю — 1
~пт — ш Р
7с=1
1
т;=1 — 1 8 ЦР~, + (1+ 3) т„ь+атю1, т =т„+д.
Поэтому р, — монотонная неотрицательная функция. Возвращаясь к выражению
РНр — 11 + р„) О, й ф й; (причем РНр — 0 в момент Т, где р, (Т) = 0), получаея
Р(д)= — 1 при 0 (й(Т. (9. 86)
Как и всюду выше, в точках разрыва й, выполняется условие (9.72). Итак, исходная вариа.
ционная задача сведена к краевой, которая в свою очередь может быть сведена к задачц
Коши с последующим подбором недостающих условий с помощью обобщенного метода
Ньютона.
Решение модельной задачи может быть получено и несколько иначе, а именно ин-
тегрированием системы (9.82) (с учетом оптимальных законов для управлений) в перемен-
ных т„;, Р," с последующим отысканием шах т, по т„;, Р,". при связи е' (Т) — ед=О, гд~
П
«2 т; 1 т;
е' (Т) = У' 1п е; + —. 1п
Ф Я.Ф Ф Рл
г=1

Фс
ь
ь
1!
й
~ч
О
о
Р~
о
о
~ч
й 00
и 11
й~
срг ~с
йе
Ю~~
сб . ь
ч 11
~Ф
° ь
-и ы
н
жс~~
° Р4 Я
о~~~
й~
р, И-~
с~ь
с~ Рь
Ж а~
С~ О,
11
~о °-
ф ч
~ дь
3;йь
о;~ь
~ч
~ . "11
° Я~а.
сО Н
~ О
й
~о
° Х
й
Р~ о
й
о ~-
о
И
й СО
о
д 11
й„
СО~ ~г ~
~,. ь
ь
с~~4 ~ е
тч ~ь
о,ъ11
о~11
Рдс~
о
о
~сь
„о
" с~ ь
° г яь
ь
о~ 11
ьм
° Ь~Ч
ь0
& t
Ю
О~ 1=~
о
Рч о
Ь. '~й Е
~о
ь~
м
ц д й
~о
с" с~О
И
о
~~ о
с~ ОД
Фс
~ ~а
~й
м
~ Я
Д ~п
~ъ Ь
ь0 )ф
О Ц !
~ ° с
о
~ьГ' ~( я
й й 3
И
о Ос~
д ~й
(б „Я
Я ю
сЧ И~
. "о
р,~
О
(б ~
~о
~С&
Ь. (б
йД
ьч
С0 Я
О
й Ос~
Р~ М со
ч
ср ь
сц ь
Ф
ь ь
11 11
Ю
й;
~а
~5 Й
ь
~ ь
Б 11
Р'
~ч
о

326
РЕАЛ!ЫПз1Е ДВИГАТЕЛИ ОГРАНИЧЕННОЙ: СКОРОСТИ
[ГЛ. 9
!
л-Р
и,
бббо
ббб
Гцс. 9.19. Обл ~сти оптимальности различного числа ступеней и & t 5 ((Г,/(у*)'=1 8  = 0
Оббив 1 бббб
1
б 003 б ббпр ~ 0,006
ю=~ л=Я
Рис. 9.17. То же, что и на рис. 9.14, в зависимости
от конструктивного параметра 0 ( Г,/(У*)'=1,8;
Д = 0,01; у= 0,004 кг/хГ, сс = О).
— 5 -г
-.ю ~ л=я
Рис. 9.18. То же, что и на рис. 9.14, в зависимости
от конструктивного параметра ~ ( Г,/(У*)2=1,8;
ф=0,01; ~ = ~=0).

327
учет АэРОдинАмическОГО сопРОтивления
В частности, условия стационарности
дФ
г
ОФ
=О,
Ж~в
(9.87)
~=1, ...,и,
для функции Лангранжа
Ф=т +ч[8(Т) — 8 ],
гпе ~ — множитель Лагранжа, приводят к системе трансцендентно уравнений (2п+1)-го
порядка, которая должна решаться численно.
Заметим, что, проинтегрировав с учетом (9.74), (9.84) — (9.86) .основную
и вспомогательную системы уравнений, соответствующие (9.82), (9.83), и
удовлетворив граничным условиям, получим систему трансцендентных
уравнений, эквивалентную (9.87). На рис. 9.14 — 9.18 приведены примеры
зависимостей оптимальных величин и, Р,, т,, т, „, найденных численно,
от конструктивных параметров Г", и, р, ')', О для фиксированных значений
ф,(п (5).
Для невесомых двигателей оптимальны импульс тяги в начале траектории
(Р,'.„,=оо) и бесконечно большое число ступеней. Значения т, „при этом
подсчитываются по формулам, аналогичным (5.18), (5.19):
т,(п) =
(1+ 3) ехр ( — ~28,/пГ*) — а — 3 — 0
(9.88)
(1 — О) (1+ 3) ~24'
(а+0 — 1) Г*
При конечных же значениях удельной массы двигателя (т ) О) и тяго-
вооруженность и число ступеней всегда конечны.
Зависимость, приведенная на рис. 9.19, позволяет для заданных кон-
структивных параметров ) и р (и=0=0) выбрать оптимальное число ступе-
ней и.
Анализ приведенных зависимостей показывает, что оптимальное число
ступеней и с увеличением скорости истечения (с уменьшением удельной массы
баков Вили параметров и, 0) не возрастает и является немонотонной функцией
от удельной массы двигателей 7: вначале, с увеличением 7, число и уменьша-
ется, а начиная с некоторого значения, может увеличиваться.
9 4. Учет аэродинамического сопротивления
1. Оптимальное управление тягой и скоростью истечения при движении
в атмосфере. В п. 2 9 1 показано, что оптимальная траектория космического
аппарата в пустоте, как правило, состоит из активных участков, на которых
тяга, развиваемая двигателем, максимальна, и участков пассивного полета.
Если на аппарат действует аэродинамическая сила, оптимальное управление
тягой двигателя усложняется.
Проведем анализ состава оптимального управления в задаче на максимум
конечной массы аппарата. Не конкретизируя зависимостей, определяющих
массу, двигателя, и считая параметры двигателя фиксированными, выпишем
уравнения вариационной задачи о выборе управлений Р (~), $' (~), е (~):
М (О) = М„М (Т) = шах,
г (Т) =г„
г(0) =г„
г=~,
д= л~ ' д(г), т(0) =то, ъ (Т) =т
(9.89)
(0(Р(~)(Р*=сопз~, О( Г(~) ( Г „, )е(~)~ =1).,
Здесь г (г, т) — аэродинамическая сила.

328
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ СКОРОСТИ
Гамильтониан системы и дифференциальные уравнения для импульсов могут быть
представлены в виде
Р Р ° е — Р
Н=р р -рр, ч-~-Р. м — р),
Рю д Р
р =м (р'р рЬ Р =р Р, ~м -рр)]
(9.991
д Р
Рр = — Рр +,)„Рр ' у (рт (Т) = — $).
Оптимальные управления, доставляющие минимум функции Н, выражаются через
импульсы следующим образом:
Гш,~ при р,„(0,
0 при р,„)0,
(9.91)
Р" при й(0,
Р=
0 при й)0
Рассмотрим возможность включения участка особого управления скоростью истече-
ния в состав оптимальной траектории. Использование результатов теории особых опти-
мальных управлений [9.78] в этом случае упрощается при введении новой управляющей
функции и= 1/Г. Условие независимости гамильтониана от и записывается в виде
(9.921
дН~ди = — р Р = О.
Управление скоростью истечения существенно на активных (РфО) участках траек-
тории; следовательно, условие (9.92) сводится к равенству р„,=О, выполнение которого
возможно при р, (Р е — г)=0 (см. первое уравнение системы (9.90)). Случай р„=-0 исклю-
чается из рассмотрения, поскольку при этом из третьего уравнения системы (9.90) следует:
р„=О, что приводит к вырожденности задачи оптимизации. Вычислим, далее,
Необходимое условие [9.78] оптимальности особого управления и (г)
д сР~С дН
( — 1)" — — — ( 0
ди джей ди
(9.93)
при 1=1 здесь выполняется только как равенство. Используя условия сопряжения особого
и неособого участков [9.78], можно показать, что выполнение произвольных конечных
условий при включении в состав оптимальной траектории участка особого управления
скоростью истечения невозможно (аналогично тому, как это было сделано в п. 2 ~ 1 при
доказательстве неоптимальности особого управления тягой при движепии в произвольном
гравитационном поле).
Неоптимальпость особого управления направлением тяги е (г) па активных участках
траектории устанавливается аналогично п. 2 ~ 1.
На участке особого управления величиной тяги пеобходимые условия оптималь-
ности Ь=О и сИ/сИ=О приводятся к виду
(9.94)
дР2 ~
—,~ — — р„.~ =О.
(9.95)
Нторая производная по времени от переключающей функции ~ может быть представлена
следующим образом'.

329
~ЧЕТ АЭРОДИНАМИЧЕСКОГО СОПРОТИВЛЕНИЯ
Э 4]
Коэффициент А в правой части формулы (9.95) задается соотношением
1 дР;
д2Р .
А — з з Р~ь' Рср~ + ~ шах РРРР 2Р6 ~ + % ш~ш Р~и,1ц.,1ц (9.96)
~т уЗ 'У
а=1 .~'=1 2=1
Необходимое условие (9.93) оптимальности особого управления тягой при Й=1
записывается в виде
А &gt
(9.97)
Выполнение условия (9.97) в режиме неравенства возможно лишь при Р~О. В про
тивном случае А =О и участок особого управления тягой может включаться в состав опти-
мальной траектории лишь в том случае, когда начальные и конечные условия маневра
связаны четырьмя соотношениями (см. п. 2 $ 1). При РфО дополнительное соотношение
одно (второе равенство (9.94)). Оно должно выполняться одновременно с первым. Допол-
нительный свободный параметр — время окончания участка особого управления — также
орин. Таким образом, в этом случае включение участка особого управления тягой не сни-
жает порядка двухточечной краевой задачи для системы (9.89), '„(9.90) и выполнение
произвольных начальных и конечных условий возможно.
Величина Р (~) задается соотношением А Р+В =О, причем вдоль всего особого участка
иолжно выполняться условие Р (~) ~ (О, Р").
Участки особых управлений сразу несколькими параметрами: (Р, р), (Р, е), (~Р, е)
и (Р, Г, е) — возможны лишь при одновременном обращении в нуль всех импульсов и
поэтому не оптимальны.
2. Оптимальные управления и оптимальные параметры в задаче о на-
боре максимальной высоты. Для получения количественного представления
о влиянии массы и сил аэродинамического сопротивления на параметры опти-
мального движения ракеты [1.3, 1.4, 1.10 — 1.12, 1.14, 1.15, 9.42, 9.43, 9.46,
9.48, 9.79 — 9.96] ниже приведено решение задачи о наборе максимальной
Высоты.
Дифференциальные уравнения вертикального подъема ракеты с соответ-
ствующими граничными условиями запишем следующим образом:
~оР
Ш
э
т(0) =1,
а(о) =о,
, (Ь), ю(0) =О,
т ( Т) — 7а, = т„
Ь=у,
6(Т) = шах,
г(Т) = орЬ
(9.98)
аоР— Р' (Ь, и)
8=
Ш
0( Г(Е) (1, Т =орС, а,=сопзЬ).
(о(РР)(1,
Оптимальные управления Р и Р вычисляются из условия минимума гамильтонпана
системы П по Р и
Р ~оР— ~'
Р Р Р -'; РФ-'; Р, Р)
1 при ~(0,
Р при Л=О,
0 при Л)0
$ при р (О,
О при р .&gt
(9.99)
аор Р
Рт Рэ ~2
Здесь высота Й отнесена к Г'„до', гравитационное ускорение д — к де
(так что д (0) =1), характерные масштабы остальных переменных взяты
из (9.18), 7=7д . Тяга направлена по скорости. Изменение максимальной
тяги Р* с высотой не учитывается (Р*=сопа$).
Требуется найти управляющие функции Р (1), $'(1) и управляющий
параметр а„доставляющие заданную полезную нагрузку аппарата т,
на максимальную высоту за оптимальное время Т.

330
[ГЛ. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕН11ОЙ СКОРОСТИ
Здесь штрихом обозначается частная производная по переменной, указанной в нижнем
индексе.
В п. 1 показано, что управление скоростью истечения граничпо: ['— : 1 (по крайпей
мере па активных участках траектории). Следовательно, импульсы р,„и р„отрицательны
при РфО (см. (9.99)). Можно показать (см., например, [9.91]), что р, & t; О. То да необ
димое условие оптимальности особого управления тягой в данной задаче записывается
следующим образом'.
(9.100)
К + 2К,' + К'„', ( О.
Величина тяги Р=Р на участке особого управления вычисляется по формуле
т2у', + т (у (г'„' — Р'„',) + К~ (1 — у) — уК'„'~]
аоР =~+ Р ~ 2Р~ +Рта
На участке особого управления тягой соотношения (9.94) вместе с первым интегра-
лом Н=О (время выполнения маневра свободно) представляют собой систему трех линей-
ных однородных уравнений относительно
импульсов р, р~, р,. Условие совмест-
ности этой системы может быть записано
следующим образом.
Я(т, Ь, у)=
= (у — 1) Р + уК„' — та = О. (9.101)
Поверхность Я (т, Й, у)=0 носит назва-
0
ние поверхности особого управления [9.78].
На рис. 9.20 представлена поверхность
особого управления для следующего част-
ного случая зависимостей Р (Й, у) и д (Й):
Р (Й, у) = Ьу2е "", у (Й) = 1
(Ь = сопз1 ) О, Х = сопв1) 0). (9.102)
Если сопротивление Р (Й, у) задано
формулой
б,/ О,Лб 1 5(б Ю у
Рис. 9.20. Пример поверхности особого управ-
ления.
Р (Ь, у) = у (у) ехр ( — )Ь)
и двихсепие происходит в однородном гравитационном поле (д= — 1), уравнения (9.98)
на участке особого управления могут быть проинтегрированы в квадратурах. При этом
~ И~ И~
Ь= ф( ) +с„1= ф( ) +с2
(9.103)
[[[ (у) + 2у' (у) + [[[" (у)
3. Численный пример. Количественную оценку влияния параметров
двигательной системы, ракеты и атмосферы на набор максимальной высоты
и функция т (й) определяется из уравнения (9.101). Для частного случая [~ (у)=Ьу2 ин-
тегралы (9.103) выражаются через элементарные функции. Окончательные формулы
приведены, например, в [9.91 ].
'Чередование участков максимальной, переменной и нулевой тяги устапавливается
при исследовании динамики переключающей функции Л (й). Для достаточно широкого
класса функций сопротивления Р (Й, у) удается показать [9.48], что оптимальная траек-
тория состоит из участка максимальной тяги, за которым может следовать участок осо-
бого управления и пассивного движения (Р=О) до окончания набора высоты. Метод вы-
числения оптимальной траектории для более общего случая описан в [9.96].
Вычислительная процедура [9.96] позволяет построить оптимальную траекторию
при фиксированном значении параметра а, и определить значение высоты подъема ра-
кеты Й1=Ь (Т), зависящее при фиксированных значениях полезной массы т, и удельной
массы двигательной системы 7 от величины а: Й =Й1 (ао). Оптимальное значение пара-
метра а0 определяется при вычислении максимальной высоты й1 из условия
Ь1 —— шах Ь, (ао).
~о

УЧЕТ АЭРОДИ11АМИЧЕСКОГО СОПРОТИВЛЕНИЯ
331
при движении с ограниченной скоростью истечения проведем для частного
случая однородного гравитационного поля: д=1, экспоненциально убываю-
щей плотности атмосферы: р= о„е-', и квадратичного закона сопротивления:
).ь
Р=бг2е-'" О =-сопя~ (см. (9.102)). При этом необходимое условие (9.100)
оптимальности особого управления тягой выполняется.
Участок особого управления тягой не входит в состав оптимальной
траектории, если поверхность особого управления Я (т, Ь, и) =0 (см. (9.101)
и рис. 9.20) не достигается на участке максимальной тяги. Влияние баллисти-
ческого коэффициента О и начальной тяговооруженности а,!д на возможность
выхода на поверхность Я (т, Й, и)=0 иллюстрируется кривыми рис. 9.21,
9.22, представляющими зависимость функции Я от времени при движении
с постоянной тягой Р=1 до полного израсходования запаса рабочего ве-
щества. Видно, что для достаточно малых значений а, и о поверхность
Я (т, Й, и)=0 не достигается вообще.
На рис. 9.23 приведены зависимости Я (~), Р (~), ь (~), Й (~) и т (~) для
оптимальной траектории. Начальный разгон происходит с максимальной
тягой Р=1. Около половины рабочего вещества в этом примере расходуется
на участке особого управления, где тяга существенно меньше своего макси-
мального значения. Набор высоты происходит в основном на этом участке;
скорость при этом меняется незначительно. Заканчивается выполнение
маневра пассивным участком, на котором скорость падает до нуля.
Кривые на рис. 9.24 дают возможность оценить влияние массы двигателя
(пропорциональной начальной тяговооруженности) и включения участка
особого управления в состав оптимальной траектории на параметры движе-
ния ракеты. Кривая Х иллюстрирует зависимость значения функционала
задачи Й (Т) от величины параметра а„кривая ХХ вЂ” аналогичную зависи-
мость для траектории, состоящей из активного участка с Р=1, на котором
расходуется все рабочее вещество, и заключительного пассивного участка.
Сравнение кривых указывает на заметное увеличение величины Й (Т) при
включении особого участка в состав оптимальной траектории и на увеличе-
ние оптимального значения а„отвечающего наибольшему значению Й (Т).
Сопоставление процессов изменения массы и набора высоты при оптимальных
значениях параметра а, для траектории с особым участком (кривые Х) и без
него (крпвые ХХ) для этого же примера может быть проведено с помощью
рис. 9.25.
Результаты, приведенные на рис. 9.24, 9.25, дают представление о влия-
нии особого управления тягой на оптимальные параметры ракеты. Уравнение
поверхности особого управления Я (т, Й, и) =0 определяет оптимальный уро-
вень скорости движения в зависимости от массы и высоты для заданных усло-
вий. При полете с меньшей скоростью возрастают гравитационные потери,
увеличение скорости ведет к росту потерь на преодоление аэродинамического
сопротивления. Кроме того, возможность уменьшения массового расхода
на осооом участке приводит к увеличению оптимального значения начальной
тяговооруженности а,. При этом ускоряется выход на поверхность особого
управления. Кроме того, увеличивается конечная масса ракеты и, следо-
вательно, запас кинетической энергии в начале пассивного участка, что в дан-
ных условиях приводит к увеличению приращения высоты в пассивном по-
лете.
На рис. 9.26, 9.27 представлены значения максимальной высоты Ь",
и начальной тяговооруженности а,/д, в зависимости от коэффициента
(сплошные кривые). Там же приведены аналогичные данные для движения
с постоянной тягой (пуктирные кривые). Преимущество двигателей с дроссе-
лируемой тягой становится более существенным при уменьшении коэффи-
циента т. С уменьшением ~ возрастает т:кже оптимальное значение начальной
тягов ооруженности.

Рис. 9.21. Влияние начальной тяговооруженности а,/д, на возможность достижения поверхности особого
управления (Л=100, ~=10-' кг/кГ, т~=0,01, Ь=З).
оо/ оол ~~ ол по~
ДД4,) 06
Рис. 9.22. Влияние баллистического коэффициента Ь на возможность достижения поверхности особого
управления (Л=100, 7=10- кг/кГ, т~=0,01): а) ао/до — — 10; б) ао/до — — 20.
ьЯ
1
Рис. 9.23. Оптимальные зависимости Я (й), Р (й),
о (й), 6 (й), т (й), при Л=5, Ь=З, ао/до — — 2,6, у=
=0,01 кг/кГ, т~=0,1.
Рис. 9.24. Влияние начальной тяговооруженно-
сти на максимальную высоту 6 (Т) при включении
особого участка в состав оптимальной траектории
(кривая 1) и при движении с постоянной тягой
(кривая 11) (т =0,01, Л=5, Ь=З, 7=0,01 кг/кГ).

О 04 дд ~Г ~б
Рис. 9.25. Сопоставление законов изменения массы т и высоты Ь при оптимальных значениях тягоао-
ор~женности а,/д, для траектории с особым участком (кривые 1) и без него (кривые 11).
4 б д ~ 4 бду,кг/кГ
~Я Е
Рис. 9.'6. Максимальная высота 61 при наличии особого участка (сплошные кривые) и без нсг.. (пунк-
тирные кривые) при т„=0,01.
4 б 8~0~ Г 4 бду,к~кГ
Рис. 9.27. Оптимальная начальная тяговооруженность при наличии особого участка (сплошные кривые)
и без него (пунктирные кривые) при т =0,01.

[ГЛ. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕНН01"'.Г СКОРОСТИ
Результаты расчета оптимальных траекторий при различных значениях
коэффициента т и коэффициента Х в законе убывания плотности с высотой
позволили установить (для Ь=З) на плоскости ~, т область, внутри которой
ода Д
4 63
у, кг/кГ
Ы Р 4 бд Ю 2 4 ~д),кг(кГ
Рис. 9.28. Области наличия (1) и отсутствия Рис. 9.29. Границы областей оптимальности
(11) сингулярной дуги (Ь = 3). особого управления тягой.
1
1
1
!
Оо
включение сингулярной дуги в состав траектории приводит к увеличению
максимальной высоты (область 1 на рис. 9.28). Для значений ~ и
из области 11 оптимальная траектория со-
стоит из активного (Р=1) участка, кото-
рый заканчивается при выполнешпт гра-
б п75 ничного условия для т (1). Затем сле-
Щ дует пассивныи полет (Р=О) до окончания
1
1 набора высоты (и=О).
1
0,5
На рис. 9.29 представлены границы
1 областей оптимальности особого управ-
1
г р;5 ления тягой на плоскости 6, у для значе-
1 ний 1=20 иХ=100. Участок особого управ-
1
Ф.У
р 1 ления входит в состав оптимальнои траек-
тории для значений 6 и "(, при которыми
соответствующая точка на плоскости ле-
жит вьппе граничной кривой.
-Л
При фиксированных параметрах ат-
мосферы и ракеты Р, Ь=сопя!,), начиная
с некоторого уровня удельной массы дви-
1
гателя ~*, для т ( (* становятся опти-
мальными двигатели, допускающие дрос-
селиров ание тяги. Критическая вели-
1 чина ~* может быть уменьшена совер-
-Я' 1 -5
шенствованием аэродинамическими характе-
ристикик ракет (уъ1еньшением Ь).
'ис. 9.30. Пример оптимальных зависи- Обратим внимание на особенности
мОСъ Ей т (й), й (й), о (Е), Р (й), ~ ( ъ).
управления тягои при двихсспии В атъ10
сфере, плотность которой быстро убывает с ростом высоты (большие зна-
чения ~,). На рис. 9.30 представлены зависиъ1ости т (~), Й (~), г (~), опти-
мальное управление тягой Р (1) и динамика переключающей функции Л ф
для 7=0,02 кг!кГ, ~=100 и Ь=200. В этом примере за уч стьом перемен-
ной тяги следует второй участок максимальной тяги, продолжающийся до
полного израсходования запаса рабочего вещества. Такой характер управ-
ления связан с быстрыът уменьшениеъ1 сопротивления при наборо высоты.

335
УЧЕТ АЭРОДИНАМИЧЕСКОГО СОПРОТИВЛЕНИЯ
60
(0
6 Д/д~
/д5 г 4 68/С г 4 Г;
~/ 4г ',~'/
Рис. 9.32. Минимальное время То набора
заданного значения высоты 6, (&gt ., Ь, т~
ответствуют рис. 9.31).
10' Р 4 о о
у, кг(иГ
Рис. 9. 31. Оптимальная начальная тягово-
оруженность а* д — задача на быстродсй-
0 0
ствие (Л = 100, Ь = 3, т„= 0,1).
ности (9.100) особого управления тягой, интегралы (9.103) — все эти
выражения в рассматриваемой задаче сохраняют свою форму. Уравнения
движения (9.98) на участке особого управления допускают первый интеграл
Б(т, Кг, о)ехр(и+ дй)=сапой. (9.104)
Частный случай этого интеграла для движения в однородном поле получен
в работе [9.43). Процесс вычисления оптимальной траектории описан в [9.96).
Поиск оптимального значения параметра а, проводился методом, ана-
логичным предложенному в [9.38]. Решение задачи для ряда значений а,
дает зависимость Т,=Т, (ао) при заданной полезной массе т„оптимальная
величина а,=а„находится из условия минимума Т, (а,) по а, (1 ( а, (
((1 — т,) ~-'). На рис. 9.И приведена зависимость а'„'/д, от величины кон-
структивного параметра т для различных значений высоты Й,. Соответствую-
щие минимальные значения функционала задачи Т, представлены на рис. 9.32.
Оптимальные по быстродействию траектории для рассмотренного диапа-
зона значений 7 состоят не более чем из трех участков. За участком макси-
мальной тяги (Р=1) может следовать участок особого управления. Опти-
мальное зпачение момента О окончания особого участка совпадает с моментом
израсходования запаса рабочего вещества: т (~д) =т (Т). Оканчивается дви-
жение пассивным (Р= — О) полетом до заданной высоты.
Отличие оптимального по быстродействию управления при достижении
Заданной высоты от управления, доставляющего максимум конечной вы-
сото й, за оптимальное время Т, состоит в том, что участок особого управления
в первом случае входит в состав оптимальной траектории при меньших зна-
чениях баллистического коэффициента 6. Так, в задаче о наборе максималь-
ной высоты при >.= 0 и 7=0, 01 кг кГ осо ое управле ие тя ой оптималь
если 6 ) 6~ — 45 [9.941. Для случая оптимального быстродействия при тех же
значениях г. и "( для Й,=0,022, например, участок особого управления входит
в состав оптимальной траектории уже при 6=3.
При этом необходимость уменьшения гравитационных потерь становится
определяющей и происходит переключение на режим максимальной тяги.
4. Оптимальное быстродействие при достижении заданной высоты.
Рассматривается задача построения оптимального по быстродействию управ-
ления вертикальным движением ракеты при достижении заданной высоты.
В отличие от пп. 2, 3 здесь: 1) Й (Т) =Й,=йхе (вместо Й (Т) =шах), 2) Т=т1п
(вместо Т=ор$), остальное совпадает с (9.98). Если в этом пункте задать Й,
из и. 2, то решения должны совпасть. Соотношения (9.99) для вычисле-
ния оптимальных значений управляющих функций, формула для вычисле-
ния тяги Р на участке особого управления, необходимое условие оптималь-

336
[ГЛ. 9
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННО И СКОРОСТИ
Эффективность дросселирования тяги при фиксированных значениях ~
и Х зависит от величины о и заданной высоты Ь,. Кривые на рис. 9.33 иллю-
стрируют уменьшение времени достижения заданной высоты при включении
0,044 ООЯ фЗ'Г д~7Ю
Рис. 9.34. Оптимальпая начальная тягово-
оруженность ао/до для двигателей с дроссе-
лируемой (сплошные кривые) и с постоянной
тягой (пунктирные кривые).
Рис. 9.33. Отношение минимального времени
Т, при дросселируемой тяге ко времени Т,
при однократно включаемой постоянной
„,„~ тяге.
в состав оптимальной траектории участка переменной тяги (Т1 — время дости-
жения высоты Й1 аппаратом с двигателем однократного включения постоян-
ной (Р=1) тяги). Как и при наборе максимальной высоты (9.941, возможность
движения с тягой, меньшей максимальной (Р ( 1), вдоль некоторой части
траектории приводит к увеличению оптимального значения параметра а,.
~Т
Т,
095
Р,Ю5
0,15
0,075
0,75
О,ОГГ
0,045
0,015
Рис. 9.36. Отношение мипимального времени
Т, достижения высоты Й, при оптимальном
управлении тягой ко времени Т, набора
атой же высоты с постоянной тягой (для дан-
ных рис. 9.35).
Рис. 9.35. Законы управления тягой для различных
значений высоты й, (расчетное значение 6,=0,022 со-
ответствует ао/до=112,71).
На рис. 9.34 представлены значения а,/д для двигателей с дросселируемой
тягой (сплошные кривые) и с постоянной тягой (пунктирные кривые). При
фиксированном ао (не выбирается оптимальным) дросселирование тяги может
оказаться оптимальным. Пусть, например, требуется выбрать оптимальную
по быстродействию программу изменения тяги для набора высоты Ь ) Ь,'
при а,"=а „, (Ь,"). При Ь",=0,022 значение а„"=112,71 и особое управление
не оптимально. Начиная с некоторого Ь1 ) Ь1 ) Ь;, в состав оптимальной
траектории входит участок особого управления тягой, и длительность его
возрастает с увеличением Ь, (рис. 9.35). Эффективность дросселирования
тяги при ао=а', возрастает с увеличением отклонения Ь, от Ь", (рис. 9.36).

ГЛАВА 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
Основные отличия реальных двигательных систем ограниченной мощности от идеаль-
ных состоят в следующем.
1'. В реальных движителях существуют потери рабочего вещества и мощности,
связанные с фазовыми переходами (ионизация, нейтрализация), неоднородностью реак-
тивной струи в выходном сечении и др. Эти потери характеризуются коэффициентами
использования рабочего вещества ~„и мощности ~,„при помощи их выражение для тяги
реального движителя запишется так (ср. (6.1)):
=~2),к,~д, (10Л)
где ~„=~ ~„— эффективный коэффициент полезного действия. Последний зависит от
1
мощности Я и расхода д, подводимых к движителю, а также от геометрических пара-
метров и параметров электрической цепи:
~)т ~)т ( т
2'. Регулирование движителя в полете может быть построено так, что к нему под-
водятся переменные мощность Х и расход д, а геометрические параметры и параметры
электрической цепи и~1,..., и~~ остаются постоянными.
Рассмотрим две вероятные схемы регулирования двигательной установки, которые
могут применяться в зависимости от вида функции ~ (Г~, д).
Диапазон регулирования движителя с постоянными параметрами и„..., и,
определяется областью Г~, д, в которой ~ (Г~, д) ) О. Возможны два предельных слу-
чая. Первын: поверхность ~ (Х,, д) представляет собой всюду плоскость ~ (Г~, д)=0,
за исключением точки (Г„', д*), в которой ~), ) 0; этот случай соответствует нерегули-
1
руемому движителю, настроенному на один режим Г„', д*. Другой крайний случай—
1
идеально регулируемый движитель: ~. (Х, д)=сопя$; здесь диапазон регулирования не
ограничен. В действительности о реальных движителях можно говорить, что они обла-
дают относительно узким или относительно широким диапазоном регулирования, а функ-
ция ~,, (Г~, д) имеет острый или пологий максимум в точке (Г'„', д'), положение которой
1
определяется значениями параметров ы1, ..., ы,.
Изменение тяги двигательной установки с движителем, имеющим широкий диапазон
регулирования, может осуществляться за счет йзменения мощности Х и расхода д, а также
за счет изменения числа включенных элементарных движителей (когда движитель со-
стоит из нескольких однотипных элементарных движителей).
Если диапазон регулирования движителя узкий, то изменение тяги двигательной
установки происходит при переключении с одного движителя (или блока элементарных
дзи'кителей) на другой, настроенный па другие значения Г„", д*, путем соответствующего
выбора параметров ы„..., ы,.
В последнем случае плавное регулирование двигательной установки невозможно,
тяга и расход — кусочно-постоянные (ступенчатые) функции времени 1).
3'. В идеальном двигателе масса источника мощности, преобразователя и движи-
теля зависят только от максимальной мощности (см. (6.1)); масса ЛХ„реальных источника
мощности и преобразователя такхсе определяется величиной максимальной мощности.
М„= ~ (Т~п~„), (10.2)
а ласса движиигеля М. выражается для разных типов движителей по-разному через пре-
Т
педьные значении независимых управлений. Таким образом, масса реальной двигатель-
ной системы включает по крайней мере два компоненты:
М.„= ЛХ„+ М . (10.З)
') Ограничения также могут быть наложены на регулирование направления век-
тора тяги; рассматриваются, например, тангепциальное (10.1, 10.2) и неизменное или
ступенчато изменяемое в пространстве (10.3) направления.
Механика полета

338
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
4'. Идеальный двигатель ограниченной мощности не имеет ограничения на время
работы, тогда как ресурс реальных двигателей ограничен, т. е. время работы не должно
превышать наперед заданного.
Отмеченные свойства реальных двигателей являются общими, каждый конкретный
тип движителя определяет выражение для массы 'М„и тяги Р.
В заключение этого вводного раздела заметим, что при решении проблемы оптимиза-
ции для реальных двигательных систем в формулу для массы аппарата может быть вклю-
чена масса баков для рабочего вещества. Последняя обычно считается зависящей от на-
чальной массы рабочего вещества: М~ —— г (ЛХ,); наиболее употребительна линейная за-
висимость (10.4 — 10.6):
~р = ~~~о (10.1)
(~ = соней) .
Я 1. Дополнительные компоненты в формуле для массы
Идеальный космический аппарат с идеальным двигателем ограниченной
мощности считается состоящим из трех компонент: полезной массы Ж„
массы рабочего вещества М и массы двигателя ЛХ„, пропорциональной
максимальной мощности. В данном параграфе приводятся формулировки
вариационных проблем, в которых учитываются дополнительные компоненты:
масса баков ЛХ и масса движителя М . Указанные компоненты исследуются
Т
по отдельности; даются особенности оптимальных управлений, появляющиеся
из-за включения этих новых факторов в проблему оптимизации.
1. Учет массы баков. Дополним формулу для массы аппарата исходной
вариационной постановки (4.2) компонентой ЛХ, — массой баков; для ЛХ,
примем выражение И0.4). Тогда вариационная проблема в формулировке (4.5)
примет вид
ЛХ,=О,
~1Х, = — д,
г=ч,
'11 (Т) = п1ах, 1
ЛХ,(Т) =О,
г(Т) =г„
ЛХ. (О) + ЛХ, +
+ (1 + 1) ЛХ, (О) = М„
г(0) =г„
Ре
М +М +М ~-М„+~'
у(0) =у„,
у (Т) = 1',.
(10.5)
Ре
Р Ф ~р '" ~Р '(и .~.м ~м, ~м
Р = р = (р„е) Р (М„+ М + М~ + М„) ',
д
р (Т) = — 1, р„= — д,, (р„д), р„= — р„. !
(
(10.6)
Заметим, что дифференциальные уравнения для импульсов р„р совпадают и в на-
чальный момент их значения удовлетворяют условию трансверсальности
р„о = (1+ р) р.
(10.7)
В том случае, когда в формуле для массы аппарата отсутствовали ком-
поненты типа ЛХ„зависящие от начальной массы рабочего вещества, изучае-
мая вариационная проблема могла быть приведена к виду (4.8), где роль функ-
ционала играет конечное значение суммы масс ЛХ.=-ЛХ +М . Задача (4.8)
имеет на одно краевое условие меньше, чем исходная, и поэтому проще ис-
ходной.
Пусть проблема (10.5) редуцирована к краевой задаче для обыкновенных
дифференциальных уравнений; тогда, несмотря на присутствие члена ЛХ,,
в уравнениях можно сделать некоторые замены, упрощающие краевую задачу
наподобие того, как это имеет место при отсутствии члена ЛХ .
Для сведения проблемы Майера (10.5) к краевой задаче воспользуемся методом
Л. С. Понтрягина; выпишем гамильтонову функцию и уравнения импульсов:

ДОПОЛНИТЕЛЬНЫЕ КОМПОНЕНТЫ МАССЫ
Мо (0) = Мо — М„,
г(0) =г„
г(Т) =
т(Т) =т„
Г=1',
Ре
м, -~ и.„+ ~('
т(0) =ъ„
Р
р =(р, ° е)
р. (Т) =
(10.10)
д
1, = — —,. (р.'я)
Р,= — Р,
& t;
= — (Р,+Рл„(а+Р, +р. [м, +а~ .
П олезная масса М, определяется после решения задачи (10.10) через ЛХ (О)
ЛХ,(Т) следующим образом (см. (10. 9)): М,=(1+~) М (Т) — ~ЛХ, (0).
Входящие в (10.10) управления находятся из условия достижения
функцией Н абсолютного минимума; для отыскания управлений двигателя
необходимы характеристики послед-
не о, т. е. выражения типа (4.9), (4.10).
В отличие от исходной краевой за-
Ю=Р
дачи, в (10. 10) отсутствует конечное ~8 РЫ
условие для массы рабочего вещества ЛХ, Рl
а также дифференциальное уравнение
Рб
цля импульса р„, поэтому новая задача
проще исходной.
Проиллюстрируем влияние массы
Р~
баков на оптимальные соотношения
=(77
масс аппарата на примере задачи для ©
-0 Ю
идеального двигателя ограниченной РРХ~ Р
мощности И0.6]. Массу двигателя бу-
дем считать неизменной. Задача, как и аг п~ Р8
раньше, разделяется на параметриче- Рис. 10.1. Влияпие массы баков.
скую и динамическую части. Проделав
выкладки, аналогичные проведенным в ~ 1 гл. 6, получим, что по сравнению
со старыми оптимальными соотношениями (6.15) — (6.17) оптимальная масса
двигателя увеличивается: ЛХ = ~/(1+ ~) Ф вЂ” Ф, а масса запаса рабочего
вещества уменьшается: М, = ~/Ф/(1 + 3), полезная нагрузка, естественно,
падает: М =1 — 2 ~/(1+8) Ф +Ф (рис. 10.1). Диапазон выполнимых манев-
ров (ЛХ.) О) сужается до 0~ Ф(1 — 2~/8 (~/1+3 — ~/3).
Рб
22*
Последнее вытекает из того, что массы М„, М в начальный момент заданы не по
отдельности, а связаны соотношением из (10.5).
Учитывая эти факты, можно найти выражение импульса р (~) через р (~) н
р, (~) = р. (~) + 1р. (10.8)
которое затем используется для исключения р (~) из уравнений и гамильтоновой функ-
ции (10.6).
Введем новую фазовую координату М9 (~):
М,=М.+М,+1М„, (10.9)
и заменим в дифференциальных уравнениях (10.5), (10.6) и в гамильтоновой
функции (10.6) М на М согласно соотношению (10.9). Получившаяся в ре-
зультате система дифференциальных уравнений и краевых условий, а также
гамильтонова функция имеют вид

340
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
~гл. 10
2. Учет массы движителя. Будем считать, что масса двигателя Л,
составляется двумя компонентами: массой источника мощности и преобразо-
вателя М„и массой движителя М И0.7]:
М„=М„+М .
(10.11)
Первая зависит линейно от максимальной мощности У „:
(10.12)
(и = сопят),
М,=аУ „
вторая — в конечном счете от максимальной мощности У „ и максимальной
тяги Р „:
(10.13)
М = / (/7 ,„, Р ,„).
Рассмотрим случай, когда / — линейная функция своих аргументов:
М = а'У „+.~Р,„
(10.14)
(а', ~ = сопят).
Н силу того, что массы М,, М входят аддитивно в формулу (10.11),
член а'У,„из (10.14) может быть добавлен к М,:
М, + а'Д~,„= (а + а') Д1 „„
(10.15)
так что составляющая массы движителя в (10.14), пропорциональная Г „,
исключается из рассмотрения. Имея это в виду, будем считать
— ~Ртах
У
(10.16)
Регулировочную характеристику примем идеальную — (6.3), будем
только в соответствии с (10.16) накладывать еще ограничение на тягу сверху
0(~ (~) (Р....
Вариационная проблема о доставке максимальной полезной массы для
двигателя ограниченной мощности, содержащего две компоненты массы 41„
М, записывается следующим образом (см. (4.6) — (4.8), (6.3)):
М. = — Р'/2М, М,(0) — — Мо — М, (0) — М (О),
г=ч, г(0) =г„
М (Т) =шах,
г(Т) =г„
Я -М+М
° +
(М, = аУ,„, М =7Р „, 0(Т(~) (~ У „, 0~(Р(~) ~(Р „, )е (~) )=1).
(10.17)
т(Т) =т,
К числу управляющих функций здесь относятся: е (Г), Г (1), Р (1), М, (1),
М (~); последние четыре из них не являются независимыми. Чтобы выделить
независимые управляющие функции, воспользуемся такими заменами
(ср. ~ 2 гл. 6): отнесем мощность Ю и тягу Р к их максимальным значениям:
Р,„=М/~,
К,„= М,/а,
и добавим к (10.17) две дифференциальные связи, выражающие уменьшение
масс М„, М: М,= — д„М = — д, (0(д,( со, 0(~д,( со). Теперь М„
М вЂ” новые фазовые координаты, а д„, д, — управляющие функции. Отнесем
также все компоненты массы к начальной массе М„: т = М/М„для безраз-

ДОПОЛНИТЕЛЬНЫЕ КОМПОНЕНТЫ МАССЫ
мерных тяги, мощности, расходов д,, д сохраним старые обозначения. Тогда
рассматриваемая вариационная проблема будет иметь вид
т'-Р2
а Т
т.(Т) = тах,
т. (0) +
пг, =
т Д'
+ т„(0) +
+ т.,(0) =1,
г(0) =г„
т„(Т) = орС,
т (Т) = орС,
г(Т) =г„
7Й = — Д,
Т Т
г=~,
(10.18)
1
+ + +~ ( )=
(0(~ У(~)(1, 0(Р(~)(1, 0(д„(~) (со, 0&l ;д ~ &l
~ е(г) ~=1).
т(0) =т„
т2Р2 РтТе
М р д р~~ + р~ ' + р' т т + т + +
СУ М
Ртт
(т,+ т,+ т.)2
т-Р2
Ро' Рю ~~2 т2ф
1 Р(т +т,) а тт~
) "1 (т,+т„+т )2 + р' 12 т,й
(10.19)
д
р, = — ~, (р. а),
Ро = Р»
Граничные условия для импульсов таковы:
р, (О) = р, (О) = р. (О), р„(Т) = р (Т) =О,
р. (Т) =
(10.20)
Оптимальные управления е(г), У(г), Р(1), д„(1), д (1) должны доставлять
абсолютный минимум функции Н.
Из этого условия следует выражение для е (~):
(р. =1р. 1) (10.21)
е = — р„/р„
Функция 1/Г входит в Н линейно, поэтому управление Г (~) принимает
граничные значения О, 1 в зависимости от знака импульса р. (~). Покажем,
что р. (~) ( 0 во всем промежутке 0 (~ ~ ( Т. Если р. (~) ) О, то оптималь-
ные Г (~), Р (~) следующие: Г (~)=0, Р (~)=1 (см. (10 19)). Это соответствует
бесконечному расходу рабочего вещества при нулевой скорости истечения.
Такой режим явно не оптимален, поэтому предположение р. (~) ) 0 неверно,
и, следовательно, р. (~) ( 0 при 0 ( ~ ( Т. Тогда
тР)=1.
Управление Р (1) меняется в пределах замкнутого интервала
0(Р(~) (1:
внутри интервала
т,
(10.23)
Р(~) =Р„,
на верхней границе
(10.24)
Р(Ц=1 при Р, „) 1;
Для решения вариационной проблемы (10.18) по методу Л. С. Понтрягина составим
гамильтонову функцию и выпишем дифференциальные уравнения импульсов:

342
',гл. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
на нижней границе
2 2
Р(~) =О при Ь) О Ь= — р.
1 ~.у од
т, + пг, + пг~
При помощи выражения (10.23) для Р„, преобразуем комбинацию Л:
т2Р2
(10.26)
Иоскольку Р „)Р ) 1, то всегда Ь (О и нижняя граница (10.25) в состав
оптимального управления Р (1) не входит — двигатель включен на всей
траектории.
Обратимся к исследованию оптимальных управлений д (~), д (~). Если
на управления д„д не наложены ограничения сверху, то импульсы р„р,
неположительны всюду на [О, Т1
Доказательство проведем для импульса р,. Предполон~им обратное. Пусть в некото-
рой момент ~=~„импульс р„(~„) ) 0; тогда управление д, принимает оптимальное значе-
ние д„(~„) = ог (см. (10.19)), что соответствует мгновенному сбросу конечной части массы т„.
Производная р„остается конечной и при д,= со, поэтому функция р, (~) не меняет знака
на конечном интервале времени в окрестности момента ~=~„. Следовательно, на конечном
интервале времени д,=со, это означает сброс бесконечно большой массы т„что невоз-
можно. Поэтому исходное предположение неверно и
р,(г) &lt О р г) &lt О при
(10.27)
В том случае, когда на управляющие функции д,„д наложены ограничения
сверху и, в частности, предполагается д„(й).=д (г) =О, выводы (10. 27) относительно
знаков р, (г), р (Е) становятся несправедливыми.
Анализ оптимальных управлений д„(~), д ® дает два типа режимов:
граничные управления д, = О, д = 0 при р, ( О, р ( О, соответствующие
т, =сопзС, т = соиаь, и особые управления р', (1) =О, р' (8) =0 при р,(1) = — О,
р (~) =О, соответствующие «внутреннему» минимуму функции Н по т„, т„.
Следует заметить, что наличие двух указанных режимов является общим
свойством задач с граничными условиями типа (10. 18), наложенными на
первоначальные управляющие функции (в рассматриваемом случае т, ®,
т (г)).
Выражения для р„, р' при помощи (10.23) можно преооразовать к виду
1 Ртт
2т„(т, + т, + т )
1 Р
2т,,
т,+т,,
(10. 28)
ОРФ
Особые режимы реализуются
для д, при
2т,
Р „т,+т,,+т
Р т,+т,
(1 0.29)
д" я дт
т,+т,+т,,
Если Р = Р,, то второе условие (10.29) занедомо не выполняется и р (О. Сле-
довательно, на участках траектории, на которых масса т,, уоывает (д ) 0), управле-
ние Р (~) граничное (Р =1).
Для выполнения граничного условия р (Т)=0 в случае, когда отсутствует ограни-
чение сверху на управление д (~), необходимо, чтобы траектория замыкалась участком
Р (~)=1. В самом деле, импульс р (~) неположителен всюду на [О, Т) (см. (10.27)); по-
этому пля достижения верхней границы р =О производная в окрестности слева от точки
т

343
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
$2]
достижения должна быть неотрицательной, что, согласно (10.28), имеет место только при
Р (ж)=1.
Если Р (~)=Р ~ (~) и т =О, то (10.29) переходит в соотношение (6.19), определяю-
щее оптимальный закон убывания массы идеального двигателя ограниченной мощности.
При д„(~)=д (~)=0 массы т„, т неизменны и решение краевой задачи (10.18),
(10.19), (10.20) даст оптимальные значения управляющих параметров т„т . Примеры
такого решения приведены в гл. 9.
Отметим, что учет компоненты массы, пропорциональной максимальной
тяге, изменяет состав оптимального управления тягой по сравнению с идеаль-
ным: появляется верхняя граница управления Р (1).
Коэффициент пропорциональности т, входящий в уравнения вариацион-
ной проблемы, определяет важную характеристику двигателя — максимально
достижимое реактивное ускорение. Действительно, реактивное ускорение а
дается формулой (см. (10.18))
а = (1/.() Рт (т. + т„+ т ) 1,
а(г) (а „=1/~.
(10.30)
(10. 31)
из которой следует:
При больших значениях параметра 7 — 10з — '. 10з кг/кГ, характерных
для двигателей ограниченной мощности, максимально достижимое ускоре-
ние мало: а — 10 ' — '. 10 ' до (см. [10.8]), что оправдывает другие названия
двигателей данного класса: двигатели малого ускорения или двигатели
малой тяги.
9 2. Заданное время работы двигателя
Согласно оптимальной программе идеальный двигатель ограниченной
мощности включен во все время движения. Если это время превосходит ресурс
двигателя (что можно ожидать, например, для межпланетного перелета),
то в вариационной постановке должно фигурировать условие заданного вре-
мени работы двигателя. Частично этот вопрос уже обсуждался в гл. 8; здесь
дается общий метод решения вариационных задач с фиксированным вре-
менем действия управления, который затем применяется к изучаемой про-
блеме [10.9, 10.101.
1. Общая методика. Рассмотрим задачу Майера в применении к ди-
намической системе:
(10.32)
((, )'=О, 1,..., и; 1=1,...,г).
(10.33)
х,.=~,.(х, и„)
Величины х,, и„— фазовые координаты и управляющие функции со-
ответственно; граничные условия определены в заданные начальный ~=0
и конечный 1=Т моменты времени; значения фазовой координаты х, (Т)—
контрольный функционал. Одна из управляющих функций ограничена снизу:
и, ) О. Будем называть управление и, включенным, если и, ) О, и выклю-
ченным, если и, =0; сумму всех интервалов времени, на которых управление и
включено, назовем временем действия управления Т .
Решив вариационную задачу, найдем время Т„„( Т, которое опреде-
лим как оптимальное время действия управления и . Пусть в дополнение
к сформулированной выше вариационной проблеме задано время действия
управления и„меньшее оптимального, Т„( Т„,, Для сведения такой
усложненной вариационной постановки к стандартной постановке Майера
воспользуемся введенными в гл. 8 текущим временем действия управления ~„
и релейным управлением о (1), которые связаны дифференциальным соотно-
шением:

344
[ГЛ. 10
РеАльные дВиГАтели ОГРАниченнОЙ мОще10сти
Управление о (~) — релейная функция, принимающая значение 1 в мо-
менты включения и значение О в моменты выключения управления и,.
Используя это свойство функции о (~), заменим управление и, на и,о; зто
произведение совпадает с и, в моменты включения и обращается в нуль в мо-
менты выключения.
Запишем систему дифференциальных уравнений вариационной проблемы
в следующем виде:
х,.=~,. (х, и,о, и„), ~„=З
(1, ~=О, 1,..., и; 1=2, ..., г). (1ОЛ4)
Если одновременно с упомянутыми выше краевыми условиями для фазо-
вых координат будут удовлетворены краевые условия для вспомогательной
координаты 8:
У
(10.35)
~„(О) =О, ~„(Т) = О(~) Ю= Т (Т
а релейное управление о (~), наряду с и, (~),..., и„(~), будет выбрано опти-
мальным в смысле контрольного функционала то (Т), то вариационная задача
с дополнительным условием заданного времени Т„( Т „, будет решена.
Иными словами, будут указаны оптимальное число включений и оптимальное
время действия управления и, для каждого активного участка.
При решении поставленной задачи методом Л. С. Понтрягина составим, как обычно,
гамильтонову функцию и выпишем уравнения для импульсов:
Н = ~ рА (х, и1З, и~) + р~ З, р', = — дН)дх;, р~ = О.
т=О
Р Р
(10.36)
Представим Н как функцию 3 следующим образом:
Н= Но+ (Н вЂ” Но+ р~ ) о,
П
НО= Н~ о — ~ р,~, (х, О, и~),
(10. 37)
Н =Н; 1 — р~ = р;Г, (х, и1, и~).
1=0 )
Пусть для определенности ищется максимум контрольного функционала х, (Т),
т. е. функция Н должна достигать абсолютного минимума на оптимальных управле-
ниях и„и„, 3. Для управления 3 абсолютный минимум Н достигается в том случае, если
выполняются условия
(10.38)
В=О при Н1 — Но+ р~ ) О, о=1 при Н1 — Но+ р~ (О.
Р.
Разность Н,— Но неположительна. В самом деле, Н,=НО при и1=0, как это следует
из определения (10.37) функций Но, Н,; при других значениях и, разность Н,— Но должна
быть отрицательной, так как в противном случае гамильтонову функцию Н можно умень-
шить, положив и1=0, и тогда будет Н1 — НО=О. Отсюда определяется знак импульса р~ .'
рг &gt О. (10.
Если бы р~ (О, то выражение Н,— Но+р~ никогда не меняло бы знака и З (~)=.=1;
Р Р
при этом 8 (Т)=Т, что заведомо нарушило бы краевое условие (10.35).
Заметим, что при и,=О оптимальное значение релейной функции 3 равно нулю,
так как р~ ) О, Н~=Н,. Если р~ —— О, то получающееся при этом время Т совпадает
Р Р
с оптимальным.' Т„= Т,„„р,.
Указанный метод применим также и для нескольких управлений с задан-
ными временами действия, меньшими оптимальных; при этом вместо одного
вспомогательного управления 3 добавляется нужное число их.

345
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
$2]
2. Применение общей методики к изучаемой проблеме. В исходных
уравнениях (4.8) умножим расход д и тягу Р на функцию о (~) и добавим
к системе дифференциальное уравнение для текущего времени работы дви-
гателя ~; получим следующую запись вариационной проблемы:
М. (Т) =тах, 1
~,(т) = т,,
г(Т) =г„
М. (О) = М, — М„,
~, (о) = о,
г(0) =г„
(10.40)
г=~,
РЪ
Ф== е+Я,
т(Т) =т,.
т(0) =~„
Для двигателя ограниченной мощности без потерь, которому посвящено
дальнейшее изложение параграфа, вариационная проблема (10.40) сводится
к такой (ср. (7.2)):
Х =и~8
(10.41)
г=~,
т = иое+Я,
(и (1) )~ О, о (1)
Чтобы найти оптимальные законы е (~), и (~), о (~), обратимся к методу
Л. С. Понтрягина и выпишем гамильтонову функцию и дифференциальные
уравнения импульсов:
Н = — и'о + р, 3 + р„° т + р, ° (аое + Я),
р, =о, р„= — — '(р..д), р,= — р„(р, =о).
(10.42)
Управления е(1), и (1) в оптимальном режиме должны удовлетворять
соотношениям
(10.43)
е = р,/р„, и = ~/,р„(р„= ) р„().
Оптимальные моменты включения (о=1) и выключения (о=о) двигателя
связаны со сменой знака комбинации Ь:
о =1 при Ь) О, 8=0 при Ь(0 (~='/,р'„+р, ). (10.44)
Если Т наперед не задано, то р, =0 и Ь (~)) 0 при 0 (~( Т; следо-
Р
вательно, пассивные участки на траектории отсутствуют.
3. Маневры в бессиловом поле. Не обращаясь к конкретному типу
маневра, отметим прежде всего, что при движении в бессиловом поле ')
может быть не более двух активных участков. Действительно, при ~=0 диффе-
ренциальные уравнения импульсов р„, р„из (10.42) интегрируются:
(10.45)
р„= 2Ь„р„= 2Ь,~ + 2Ь.„
и входящая в (10.44) величина 1/ р'„выражается так:
'~,р'- = 6',Р+ 2Ь, Ь,~+ о2
(10.46)
Уравнение Л (~)=0 — квадратичное относительно ~ и имеет не более
двух корней: ~, (Ь„Ь,) и ~, (Ь„Ь,), определяющих начало и конец единствен-
ного пассивного участка, который разделяет два активных участка.
') Или в плоскопараллельном.
г(о) =о,
~, (о) = о,
г(0) =г„,
т(0) =т„
=1 или О,
У (Т) =т1п, 1
~,(т) = т„,
,г (Т) = г„
т(т) =т,
(е®(=1).

346
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 10
Оптимальная программа вектора реактивного ускорения ае на активных
участках — линейная функция времени. Для нахождения постоянных век-
торов Ь,, Ь„зависящих от заданных начальных и конечных значений коорди-
нат (г,, г,) и скоростей (т,, т,), следует проинтегрировать уравнения движения
из системы (10.41) по активным и пассивному участкам; при этом
ае= — Ь,Г+Ь„0=1 при 0(~(~, и ~,(~(Т;
0= 0 при 1,(1(1,.
(1О. 47)
Сначала рассмотрим маневр набора заданного модуля скорости их в бес-
силовом поле при заданных времени маневра Т и времени работы двига-
теля Т .
У/У» ,~/~'
7
Р Р,Г Р4 Цб РЮ Т~ц, ~Т
Рис. 10.2. Зависимость функционала .7 от
активного времени Т .
г з ~ ~т/т
Рис. 10.3. Зависимость функционала .7 от
времени движения Т.
Конечные значения координат г (Т) в этом маневре не фиксированы,
поэтому имеет место следующее условие трансверсальности:
р„(Т) =2Ь,=О.
(10.48)
Согласно формулам (10.44), (10.46), (10.48) комбинация Л не зависит
от времени и знак, а также величина ее не определены. Это означает, что рас-
положение пассивного участка на траектории не определено и не влияет
на контрольный функционал У (Т); последний дается выражением (ср. (7.32))
(10.49)
У (Т) =7Л~~Т
г, = Т вЂ” '~,ТР.
(10.50)
Программа вектора реактивного ускорения ае имеет вид (ср. (7.33))
6Е 1 — 2й/Т
Т' 1 — (1 — Т„(Т)'
(10. 51)
а выражение функционала У (Т) следующее (ср. (7.33)):
12Р 1
Т ~ — (1 — т).
(10.52)
Отметим, что в выражение (10.49) не входит время выполнения маневра Т.
Вторым исследуем маневр перелета между двумя положениями покоя
в бессиловом поле, разделенными расстоянием 1, при заданных временах
выполнения маневра Т и работы двигателя Т . После интегрирования урав-
Р
нений движения по активным и пассивному участкам получаем выражения
постоянных Ь1, Ь, через параметры маневра 1, Т и время Т . Подставляя
эти выражения в формулы для 8„Г„находим

347
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
I
Р Яс п фу~
Рис. 10.5. Минимальные значения функ-
ционала .7 при Т=2 к (.У*=О/~).
Рис. 10.4. Оптимальные программы модуля реактивного
ускорения а (1).
конечные результаты; выберем следующие значения параметров (описание
маневра см. в гл. 4, ~ 4):
(10.53)
Т = 2т~, Я, = 1/,,т~,
наклонение ~ произвольно в допустимых пределах (~ (& t; ), вр мя раб ты д
гателя Т вЂ” параметр задачи.
При отсутствии ограничения на время работы двигателя оптимальные
законы а (Г), е (~) и величина контрольного функционала У (Т) таковы
(см. (7.74), (7.75)):
ае = (~/тг) з1п ~ при 0( ~(2т~,
У (Т) = Р/и (Т = 2т~).
(10.54)
Если время работы двигателя Т„задано, то выражения (10.54) заме-
няются на следующие:
0 ( ~ ( '/,и — '/ Т„,
при
при '/ т~ — 1/4Т ( 1 ( 1/ н + 1/~Т
при 1/,~+1/цТ (1(~/р /4Т
при ~/ т~ — 1/ Т (1(з/2т~+1/ Т
(10.55)
~ЯП18
Т + яп ('/2Т„)
при '/.,~ +1/,Т„(~ (2т~.
На рис. 10.4 приведены законы а (~) при Т„=2-., з/~~, т~, 'зависимость
контрольного функционала от времени работы двигателя Т„ (О ( Т„ ( 2~)
иллюстрируется рис. 10.5.
5. Межорбитальный перелет. Будем рассматривать плоское движение
в центральном поле в прямоугольных координатах (см. гл. 4, ~ 3).
Таким образом, пассивный участок в рассматриваемом случае располо-
жен посередине траектории. При заданном времени движения Т и заданном
расстоянии 1 функционал У монотонно возрастает при уменьшении времени Т„
(рис. 10.2). При заданном времени Т„и заданном расстоянии 1 функционал У
монотонно убывает при увеличении времени Т (рис. 10.3).
4. Поворот плоскости круговой орбиты. Аналогичное исследование
может быть выполнено и для маневра поворота плоскости орбиты. Приведем

348
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
Вариационная проблема (10.41) для маневра перелета между круго-
выми орбитами записывается следующим образом (10.10):
Х=й О,
У (0) =О,
~ (о) = о,
х (О) = 1,
у (О) = О,
У ( Т) = т1п,
1„(Т) = Т,
х(Т) =г,созе„
у(Т) =г, з1п з„
У=И,
~7=0,
(10.56)
и(0) =О,
и(0) = 1,
и(Т) = — г,'~ з1п р„
и= иое
(х'-'+ у2) '
и (Т) = г,'~ соя з,
г~ = аое,
(Х-'+ у') гг
(и(~) ) О, о(~) =1 или О, е'- (~)+е-'(~) =1).
Гамильтонова функция и дифференциальные уравнения импульсов (10.42)
В дакном случае имеют вид
и = — и2о+ р, 3+ р,и+ р г+ р„~аде — х (х2+ у') ~'~ +
+ р, ( аде, — у (х-+ у')
(10.57),
Р,=О,
Р. =,2
Ри= Р ' Рп=
р„3х (р„х -~- р„у)
у2) /г (Х2 + у2) (г
3у (р„х + р,,у)
(Х2 + у2) (г
(х2 + у2) ~'
(10.58)
Таким образом, вариационная проблема свелась к решению следующей
краевой задачи для дифференциальных уравнений:
8, ~, (О) =- О, с„(Т) = Т„,
и1 х(0)=1, х(Т)=г,саяр„
Г у(0) =О, у(Т) =, з1п,„
'~2р,о — х(ю'+у') ~', и(0) =О, и(Т) = — г-,'~ з1пр„
'/2р„о — ч (~'+у') ~', и(0) =1, и(Т) =г1'~ совр,
'1 при Л)0, о=о при Ь(0, Ь='/,(р~+р-')+р, ),
р, = О,
Зх (р„х + р,,у) . р„ 3у (р„х + р„у)
(Х2 + у2) гг (Х2 + у2) /г ' у (Х2 + у2) гг
(10. 59)
Ри
Рх
(Х2 + у2) гг
После решения краевой задачи определятся функции г (~), у (~), и (~),
и (~), р, (~),..., р„(~), р„(~) и может быть подсчитан контрольный функ-
ционал
У т
У(Т) = аж= ' (р ~ р-,)Ы~
(10.00)
Задача (10.59) содержит четыре параметра: Т, у„г„Т . Если параметр Т„
должен пробегать ряд значений, то удобно параметрический просчет вести
Из условия максимума функции Н следуют выражения для оптимальных
программ а, е, е„, О:
е = р„(р',+ р',,) ', е, = р,,(р'„-+ р,'-) ', и='/2~/р,",+ р-,',
о=1 прп Ь)0, о=о при Ь(0 (Ь='/ (р,',+р-',)+р, ).

349
ЗАДАННОЕ ВРЕМЯ РАБОТЫ ДВИГАТЕЛЯ
по р,, а не по Т . Тогда в краевой задаче (10.59) исчезает необходимость
Р Р
удовлетворять условию ~ (Т)=Т„; уравнение для ~ можно интегрировать
после определения функций х (1),..., о (1) одновременно с вычислением
контрольного функционала (10.60):
Т = о(1)И1.
(10.61)
При численном решении краевой задачи
(10.59) применялся метод последовательного
подбора недостающих начальных значений
р (О), р„(0), р„(0), р, (О). Расчеты проводи-
лись для перелетов с круговой орбиты еди-
ничного радиуса на круговую орбиту радиуса
~г ~ю т
г,=1,52 (Земля — Марс); в большинстве слу-
чаев средняя угловая скорость на перелете
принималась равной угловой скорости движе-
ния по начальной орбите: ~,/Т=1. Резуль-
таты расчетов даны на рис. 10.6 — 10.8.
На рис. 10.6 представлена зависимость функционала У~ =У (Т = Т)
от времени движения Т при отсутствии пассивных участков на траектории
(Т„=Т=~,). На рис. 10.7 дано семейство кривых У (Т„, Т)/У~ (Т), отличаю-
щйхся одна от другой значениями времени Т (по-прежнему у,=Т). При
Рис. 10.6. Минимальные значения
функционала Х* для межорбитального
перелета Земля — Марс без выключе-
ний двигателя.
юя т~~т
Рис. 10.7. Зависимость функционала Х от Рис. 10.8. Примеры оптимальных программ
доли активного времени ТР !Т (значения У* — а (1), соответствующих рис. 10.6, 10.7.
с рис. 10. 6).
0,5 ( Т ( 4,5 и 0,8 ( Т„/Т ( 1,0 относительное изменение функцио-
нала — величина (У/У~) — 1 — слабо зависит от времени перелета Т;
для Т„/Т=0,5 относительное изменение функционала при различных Т
составляет 12 — 13'~ое, что хорошо согласуется с результатами по бессиловому
полю (см. рис. 10.2). В исследованном диапазоне параметров (0,5 ( Т ( 4,5;
0,4 ( Т /Т ( 1) пассивный участок на траектории один. На рис. 10.8 даны
оптимальные программы модуля реактивного ускорения а (Г) при Т=4,5
пля различных величин Т .
В заключение настоящего пункта сделаем два замечания.
1'. Движение в центральном поле может изучаться в прямоугольных координатах
или в полярных координатах. Последние имеют то преимущество, что из системы диф-
ференциальных уравнений для экстремалей, аналогичных (10.59), удается достаточно
просто выделить интегралы типа )., Х, (как в з 1 гл. 7) и тем самым понизить дифференциаль-
ный порядок системы. На пассивно~~ участке траектории уравнения движения и уравне-
ния импульсов интегрируются, и их решения представляются в конечном виде. Проведе-

350
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
ние процедуры интегрирования доставляет аналитические связи между параметрами в на-
чале и в конце пассивного участка. В и. 5 предпочтение было отдано прямоугольным
координатам потому, что разработанный численный метод решения более удобно при-
менять к уравнениям в этих координатах.
2'. Укахсем еще один способ получения оптимальных связей между параметрами
в начале и в конце пассивного участка; этот способ не требует введения релейного управ-
ления о (~). Исходным здесь является представление рассматриваемой вариационной
проблемы в виде задачи Лагранжа (7.1) или (7.3).
Пусть на траектории имеются два активных участка. Суммарный функционал
равен сумме функционалов, соответствующих первому и второму участкам. Начальные
значения координат и скоростей для первого функционала и конечные значения для
второго заданы; координаты и скорости в начале и в конце пассивного участка связаны
конечными соотношениями, справедливыми для пассивного движения в центральном
поле. Используем для выбора недостающих параметров условие обращепия в нуль первой
вариации суммы функционалов. В результате получим отмеченные в первом замечании
оптимальные связи между параметрами в начале и в конце пассивного участка и в том
числе оптимальное расположение пассивного участка на траектории. В отличие от метода
с функцией о (~), этот подход не позволяет указать оптимальное число пассивных участков.
~ 3. Оптимальная ступенчатая программа тяги
Изменение тяги и расхода двигательной системы с двигателями, обла-
дающими узким диапазоном регулирования, осуществляется за счет переклю-
чения расхода и мощности с одного движителя на друго~~, настроенный на дру-
гие значения тяги и расхода. Функции тяги и расхода при этом ступенчатые,
характеризующиеся числом уровней (ступенек), высотой уровней и момен-
тами переключения с одного уровня на другой. Число уровней равняется
числу разнонастроенных движителей, и добавление нового уровня вызывает
увеличение массы системы на массу движителя, обеспечивающего этот
уровень.
Решение вариационной проблемы о доставке максимальной полезной
массы в данном случае должно определить, в том числе, оптимальное число
уровней (разнонастроенных движителей), оптимальные высоты уровней и мо-
менты переключения с одного уровня на другой.
В данном параграфе сначала дается общий метод решения вариационной
задачи о ступенчатой аппроксимации оптимального управления при задан-
ном числе уровней [10.11], а затем при помощи этого метода строятся опти-
мальные ступенчатые программы реактивного ускорения и тяги для ряда
маневров. Предполагается, что процесс ускорения в движителе происходит
без потерь; поэтому тяга, расход и мощность, фигурирующие в уравнениях
вариационной проблемы, связаны идеальным соотношением (6.1).
1. Общая методика. Пусть динамическая система описывается следую-
щими дифференциальными уравнениями:
х,. =.~,. (х, и„, й) (1, у =О, 1, ..., кг; Ус= 1,..., г). (10.62)
Здесь х,. — фазовые координаты, и„— управляющие функции (положения
регуляторов); функционал задачи — х (Т).
Ре|пение вариационной задачи Майера (10.62) об экстремуме функцио-
нала х (Т) дает оптимальные управления и „, (г),..., и„,, (г). Рассмотрим
такое положение, когда программа для одной из управляющих функций,
например и1, должна быть ступенчатой с 8 уровнями, в отличие от и1 „, (~),
которая имеет бесконечное множество значений. Высоты уровней и точки
переключения с одного уровня на другой ступенчатой функции и (1) должны
быть выбраны так, чтобы и, (~) наилучшим образом, в смысле контрольного
функционала х, (Т), аппроксимировала оптимальное управление и1 „„ (г).
Введем релейные функции, принимающие значения 0 или 1: о, (~),...
..., 8,, (~), и параметры т~„..., т~,. Первые определят точки переключения
с одного уровня на другой, вторые — высоты уровней. Кусочно-постоянная

351
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
функция и (~), принимающая 8 значений, может быть представлена через
о„..., о, „то1,..., то, следующим образом '):
у,(1)=((...(то,8,+тт,)о.,+... +от,,)8,,+от )о, +от,=и,(то, о);
(10.63)
при этом я значений управления и1 (1) (высоты уровней) выражаются так~
Определим времена действия параметров 7~„..., 7~,. Параметр т~, включен в те-
чение всего процесса (О & t  ( ), парам тр т ,, вклю ен ри „, г = 1, . ., па
метр т~, включен тогда, когда 6, (г) 6г(г) . 6,, (г) =1, параметр т~, включен тогда,
когда 6, (~)... 6,, (г) =1. Текущие времена деиствия параметров г„„..., г„, связаны
дифференциальными соотношениями с релейными функциями 6 (г):
(10.65)
Полные времена действия даются интегралами
О О
(10.66)
Выбор параметров л1,..., то, и точек переключения релейных функций
о„..., о, подчиним условию экстремума функционала хо (Т). Для этой
цели воспользуемся методом Л. С. Понтрягина: составим гамильтонову
функцию Н и выпишем дифференциальные уравнения импульсов:
дН
(10.67)
(~, 7'=О, 1, ...,и; 1=2,...,г).
Нахождение оптимальных управлений и...... и„производится стандарт-
ным способом; для определения программ о1 (г),..., о, (г) следует вычис-
лять функцию Н при следующих наборах значений этих управлений в каж-
~~ый момент времени:
° ° е ~ Н
Ф
8, 1=1,
о,1 — О,
о, 1=1,
8
8-2
(10.68)
2
81
') Представление (10.63) можно записать также в виде
н1 (т~~ ~) = т'1 1" г ° г — г г-1 + т'г~г ° ° ° г-г~г — 1 + ° ° ° + т"г — г г-е~г — 1 + т'г-1~г-1 + т"
Отметим, что запись
и1 (т~, 6) = т~1о + т~гбе+... + т~, 1о, + т~„
С, "', + С',;-+ ... + С',, +1=1+ (г — 1) + ... + (г — 1) + 1 =2г+...;
при г=З получается четыре значения.
которая с первого взгляда кажется наиболее естественной, не годится, так как возможное
число значений такой функции превышает г (кроме случая г=2); при г ) 3 и т,фт~
оно равно

352
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 10
Наибольшая (или наименьшая, судя по характеру экстремума хе (Т))
величина Н из г вычисленных укажет оптимальный набор значений релейных
управлений в момент ~.
Для отыскания оптимальных значений параметров тс„..., ~, можно
использовать следующий прием. Считая параметры тс„..., л, новыми фазо-
выми координатами, дополним систему (10.62) тривиальными дифференциаль-
ными уравнениями.'
Г~
тс =О, ..., х =О.
в
(10.69)
Гамильтонова функция при этом не изменится, а к уравнениям для
импульсов (10.67) добавятся г дифференциальных уравнений вида
дН дН
л
д7~, ди,
дН
р'= — — о ...о,
У1
° ° °
(10.70)
дН
р = — 8
1
дН
ди, '
Начальные и конечные значения фазовых координат тс„..., тс, не фик-
сированы, поэтому импульсы р„..., р, при ~=0 и ~=-Т равны нулю. Отсюда
следуют интегральные соотношения, определяющие оптимальные значения
параметров ~с„...,
дО
о,,...о ф= — О,...,
ди -''' в—
1
од... о, дЖ=О,
1
(10.71)
6=О.
ди,
о,Н~= О,
дН
1
При помощи (10.65), (10.66) последние формулы могут быть единообразно представ-
лены в виде
дН
—,— ~~„= О,
г)Н
д Ю Р.1 — О,
Уд
(10.72)
дН
йю,,=О,
иУ1
дН
И~~, = О.
У1
В заключение настоящего пункта сделаем ряд замечаний.
1'. Может иметь место ноединственность представления ступенчатой управляющей
функции и, (тс, о) через параметры тс„..., тс, д и релейпые управления сд„..., ов д
Установим этот факт для в=2.
Допустим, что построено оптимальное двухступенчатое управление
(д) = А (д)+
(10. 73)
ссд (Е) = 1 дс~д (д) + тсд,
(10.74)
такое, что и,' (Е) = и, (с). При од — — 0 имеедд и, =н„бд — — 1 и и,'=тсд+ тс.'„ддри сдд=1
имеем и, = тс, + т:2, од' = 0 и и,' = тс,',. С.тдедовательно, для тождественного равенства
ид (с) = и, (с) необходимо вс,дддолнение условий
/ Р Р
тсд + тс2 — — тс2 или тсд —— — тсд, тсо — — тсд + тсй.
Р ~ Р
(10.75)
Таким образом, получено второе представление управляющей функции и, (тс, о),
не совпадающее с первым, но дающее одинаковый закон и, (~) и, следовательно, одинако-
вую величину контрольного функционала.
т. е. выораны релейная функция бд (с) и параметры тс„тс,. Заменим функцию сдд на
о1 — 1 — о, и найдем такие параметры 7',', ~.', которые вместе с О,' составляют управ-
ление и,' (с):

ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
2'. Если управляющая функция ограничена пределами 0 & t; и, ~ & t; 1, то на
метры т~1,..., и, накладываются ограничения:
(10.76)
т1п и1 (и, б) ) О, шах и1 (и, б) & t;
Граница может быть включена в состав оптимального ступенчатого управления и, (~).
Приведем пример записи трехступенчатого управления и, (я, о), включающего нижнюю
(и,=О) и верхнюю (и,=1) границы:
(10.77)
п~ = ((1 па) ~1 + т~а) ~а
при этом должно быть 0 & t; п  lt; 1 (предполаг етс , что оптим льное упра лен е и
не граничное, т. е. принимает и промежуточные значения). Если сумма времен включения
нижней грапицы и,=О задана, то в вариационпой проблеме появляется дополнительное
дифференциальное уравнение ~~,= о, и дополнительное краевое условие ~ (Т) = Т
в соответствии с методом, .описанным в предыдущем параграфе.
3'. Можно указать численный подход к решению задачи о ступенчатой аппрокси-
мации управления, не использующий представления с релейными функциями (10.63).
Зададимся искомыми г уровнями управления и,: и,(", и,'-',..., и1(" — и будем
решать задачу при помощи метода Л. С. Понтрягина. Моменты смепы уровней опреде-
лятся из условия экстремума гамильтоповой функции, а оптимальные высоты уров-
ней — из условия экстремума контрольного функционала. Последняя процедура тре-
бует привлечения численного метода типа скорейшего спуска.
Способ с релейными функциями дает аналитические соотношения для выбора
оптимальных высот уровней.
4'. Пример ступенчатой аппроксимации оптимального управления уже рассматри-
вался в гл. 6. Там удалось построить оптимальную ступе чатую программу, не прибегая
к предложенному методу, потому, что вариационная проблема обладает следующим
свойством: управление ЛХ„(ЛХ,) — неубывающая функция своего аргумента, так что каж-
ный уровень ступенчатого управления может заниматься однократно. Это свойство позво-
ляет вариацнонную проблему со ступенчатым управлением ЛХ„(ЛХ,) свести к задаче на
максимум.
Еще один пример построения оптимальной ступенчатой программы можпо найти
в работе (10.12). Б следующем пункте этот пример рассмотрен как иллюстрация к общей
методике. В упомянутой работе решение найдено благодаря специальному виду оптималь-
ного непрерывпого управления.
2. Примеры ступенчатой аппроксимации программы реактивного ускоре-
ния. В этом пункте дается как иллюстрация предложенного метода решение
вариационной проблемы (6.11) при условии, что управляющая функция а (~)
выбирается из класса ступенчатых функций а (и, о) с заданным числом уров-
ней. Рассматриваются два маневра: перелет в бессиловом поле между двумя
положениями покоя, разделенными рас-
стоянием 1, за время Т и поворот
плоскости круговой орбиты на угол 1 за
один оборот (Т=2-с) при Й,= — т~/2.
Вариационная проблема (6.11) с
а=а (т:, о) для первого из рассматривае-
мых маневров записывается так: Г
Х = а', У (0) = О, У (Т) = т1п,
к=и, т(0)=0, т(Т)=1,
и = ае, и (0) = О, и (Т) = 0
(а (1) = а (1т, о), е (1) = + 1).
аг ю~ р
Рис. 10.9. Ступенчатая аппроксимация
1 .78
управления а (1) — перелет между точ-
ками покоя.
Если на управление а (~) не наложены ограничения, то оптимальные
законы а (~), е (~) и минимальное значение контрольного функционала У (Т)
даются формулами (7.33) (кривая со на рис. 10.9).
23 Механика полета

354
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 10
Ниже приведен ряд оптимальных ступенчатых программ а (~) для задачи
(10.78); на последнем примере подробно описана процедура метода.
1'. При а (тт, о)=тт, оптимальные законы а (~), е (~) таковы (рис. 10.9,
кривая 1):
а(~) =41/Тз, е(~) =1 при 0(~ (1/ Т,
а(1) =4~/Тз, е (1) = — 1 при 1/,Т (1 ( Т,
Х (Т) = 160/Тз.
(10.79)
2'. При а (тт, о) = тт, Ь, оптимальные законы а (й), е (й) таковы (рис. 10.9,
кривая 2):
а(Е) =4,5Е/Тз, е(Е) =1 при 0(Е(1/зТ,
а(й) =0 при '/,Т (1 (з/зТ,
а(~) =4,51/Тз, е(~) = — 1 при з/зТ(~(Т,
~ (Т) =13,5Г/Т
(10.80)
3'. При а (тт, о) = тт, о,+ ттз оптимальные законы а (1), е (~) таковы
(рис. 10.9, кривая 8):
(10.8! )
4'. При а (тт, о) =(тт,о,+ттз) оз оптимальные законы а (~), е (~) таковы
(рис. 10.9, кривая 4):
е(1) =1
е (1) =1
(10.82)
В примерах 2' и 4' в состав управления включены уровни с заданной
(нулевой) высотой; для участков с заданной величиной управления остается
определить только их оптимальное положение.
Опишем процедуру построения оптимального трехступенчатого управ-
ления а (тт, о) с нулевым нижним уровнем (пример 4').
Дифференциальные уравнения для фазовых координат, краевые условия,
гамильтонова функция, дифференциальные уравнения импульсов и уравне-
ния для выбора оптимальных параметров тт1, ттз имеют вид (см. (10.78), (10.67),
(10.71))
./ = кз16 оз+ 2тт1тт О о + ттззоз, Х (0) = О, Х (Т) = т1п,
у=и, т(0) =О, т(Т)=~,
и=(тт о +тт ) о,,е, и(0) =О, и(Т) =О,
Я = — (ттз1о о, + 2тт тт о оз+ тЯо ) + Р и+ Р„(тт о + кз) Ззе,
р.=О, р„= — р.,
(10.831
а(~) = 4,81/Тз,
а (~) = 1,61/Т'
а (~) = 1,6Ц/Тз,
а (~) = 4,81/Т',
а (~) = 5ЦТз,
а (~) = 2,5~/Т',
а(~) =0
а (~) = 2,51/Т',
а (~) = 5~/Тз,
е (~) = 1 при 0 ( ~ (1/ Т,
е (1) = 1 при 1/ Т ( 1 (1/,Т,
е (~) = — 1 при '/,Т ( ~ (~/ Т,
е (1) = — 1 при з/ Т ( 1 ( Т,
,7 (Т) — 12 8Р/Тз
при 0 ( 1 ('/,Т,
при 1/,Т (1 (з/,Т,
при '/,Т ( 1 ( з/,Т,
е(1) = — 1 при '/,Т(1 (~/,Т,
е(1) = — 1 при 4/,Т(~(Т,
У (Т) = 12,5Р/Тз

355
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
Т Т Т
тв Ь' 3 ~Й+ твв Ь' Ь2~Й = — р„еЪ Ъ Й$,
О О О
У У У
& t; (10.
тв 3 Ж+ твв 32й = — р„еЬ' Й$.
1
О О О
Решение дифференциального уравнения для импульса р„может быть
представлено в следующем виде (см. (8.32)):
(10.84)
,Оптимальные управления е (8), Ь, (8), В2 (8) подчиняются требованиям:,
е (в) = з1дп р„(Ь) (ер„= ~ р„~),
о,(Е) =1 при Ь,) О, о,(Е) =0 при Ь,(0
(Ь, = тв, ( — тв, — 27в2 + ~ р„~)),
~2(й) =1 при Ь2) О, 32(й) =0 при Ь2(0
(~2= 2( — 2+! „!)+~,Ф,).
(10.85)
Параметр ив может быть только положительным, так как а (~) ) О. Параметр и
может быть положительным или отрицательным; в последнем случае ~ тс ~ ( тс2,
так как а (й) ) О. Рассмотрим сначала случай п1 ) О.
Пусть )р„) — тс1 — 2тс ) О, тогда Л1 ) 0 при тс1 ) 0 (см. (10.85)) и Ь,=1. При этом
выражение (р„) — ~2 заведомо положительно; следовательно, Лв ) 0 (см. (10.85)) и 82=1.
Пусть ~р„~ — ~ ( О, тогда заведомо Ьд ( О и, следовательно, од — — О. При этом Ь2 ( О
и о.,= О.
Эти рассуждения приводят к выводу. если о1=1, то заведомо О,=1; если о,=0,
то заведомо О,=О, т. е. участок В2 — — О расположен внутри участка ~,=0, а уча-
сток О,=1 яе превосходит участка В,=1. Расположе-
ние участков показано на рис. 10.10, где й,, й,, Ь,
1,~~1
1+) — корни уравнений
~1 И) = — — 2 2+ ( Ь ~ (~. — ~ ) = О,
Лв (12) = ) Ь1 ( (1у — 12) — пв = О,
(~1 ) = — 7с, — 2~~, + ) Ь, ( (~1 — ~„) = О,
Ь. (~ф) =(Ь ) ф — ~ ) — ~ =О.
(10.86)
Из (10.86), в частности, следует:
Рис. 10.10. Расположение участков
включения уровней управления
а (1) — перелет между точкаыж
покоя.
~', + ~-, = 2~,, г'., + ~; = 2~„.
Оптимальные программы е(~), о,(~), о2(~) могут быть записаны при по-
иощи параметров ~„~„~„, ~+„~1, так (см. (10.85)):
е(Ь) =1
е(Ь) =1
(10.88)
е(Ь) = — 1
е(в) = — 1
После интегрирования уравнений движения и удовлетворения краевых
условий приходим к соотношениям
2~„= Т, тв,~, (Т вЂ” ~,) + тв2~, (Т вЂ” ~,) = ~.
(10.89)
23*
О,(1) =1,
о,(~) =О,
о (~)=0,
о (8)=0,
Ь И)=1
В,®=1,
Ь,(~) =1,
3,(1) =0
32 И) = 1,
32 е) =1,
при 0(~(~,, 1
при ~, (~(~,,
при ~, (~(~,,
при ~',( (~'„
при 1+, (1(Т. ~

РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
[ГЛ. 10
Параметры к„~с, выражаются через ~Ь,~, ~„8, так (см. две последние
строчки из (10. 83)):
,='/,~~,~~„а — — '/,~~,~(Т вЂ” ~, — ~,).
Из уравнений (10.86) при условиях (10.90) определяем
~;='/,Т, с-,='/,Т,
из второго соотношения (10.89) находим
;~ Ь, ~ = 2ОЦТ',
(10.90)
(10.91)
(10.92)
тогда (см. (10.90))
н, = 2,5~/Т2, н2 = 2,51 Т'.
(10.93)
Вид оптимальных управлений приведен в примере 4'.
Если считать параметр ~т, отрицательным, то по сравнению с рассмотрен-
ным случаем изменяется оптимальный закон о, (~) и параметры ~1, ~, (0,=0
д Яи фи
Рис. 10.11. Ступенчатая аппроксимация управления а (~) — поворот плоскости орбиты.
при 0(1('/,Т и при '/,Т(1&lt Т, 3 =1 ри '/5Т(1(' , и
з/5Т ( ~ ( 4/,Т, 3, не определено при '/,-Т ( ~ ( '/,.Т; ~,= — 2,5; г,=5);
при этом оптимальные законы а (~), е (~), а также величина У (Т) остаются
неизменными (см. замечание 1' предыдущего пункта).
Рассмотрим маневр поворота плоскости круговой орбиты спутника.
Если на управление а (~) не наложены ограничения, то оптимальные про-
граммы а (~), е (~), а также минимальные значения У (Т) даются формулами
(7.74), (7.75) (кривая со на рис. 10.11).
Если управляющая функция а (~) выбирается из класса ступенчатых,
то оптимальные программы а (~), е (~) и величина У (Т) имеют следующий вид.
1О. При а(к, о) = т~, (кривая 1 на рис. 10.11)
а(~)=0 25~, е(~) = — 1 при 0(~(3,14,
а(~) =0,25~, е (~) =1 при 3,14 (~(6,28,
Х (Т) = 0,393Р.
(10.94)
(10.95)
2~. При а(ш, о) =т~Д
а(~) =0
а (~) = 0,273~,
а(8) =0
а (~) = 0,273~,
а(~) =0
(кривая 2 на рис. 10.11)
при 0 (Й (0,404,
е (Е) = — 1 при 0,404 ( Е ( 2,74,
при 2,74 ( ф ( 3,54,
е(~) =1 при 3,54(8(5,88,
при 5,88 ( ~ (6,28,
Х (Т) = 0,345Р.

357
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
рис. 10.11)
0 ( ~(0,664,
0,664 ( ~ ( 2,48,
2,48(~ (3,14,
3,14 (~( 3,80,
3,80 ( ~ ( 5,62,
5,62 ( ~ ( 6,28,
(10.96)
а(~) = 0
а (~) = 0,154~,
а (~) = 0,291~,
а(~) = 0,154~,
а(~) =0
а (~) = 0,154~,
а (~) = 0,291~,
а (~) = 0,154~,
а(~) =0
при
е (1) = — 1 при
е (1) = — 1 при
е(1) = — 1 при
при
е (1) =1 при
е(1) =1
е (1) = 1 при
(10.97)
при
при
Х (Т) = 0,326Р.
Как следует из приведенных примеров, величина контрольного функ-
ционала У (Т) монотонно уменьшается при увеличении числа уровней 8,
приближаясь к идеальному значению при г — э со.
В заключение этого пункта сделаем замечания, касающиеся использо-
вания полученных результатов. В вводной части параграфа было сказано,
что движитель с узким диапазоном регулирования характеризуется ступен-
чатыи изменением тяги и расхода. Здесь принята ступенчатая программа
реактивного ускорения. Такой переход возможен в том случае, когда затраты
рабочего вещества на маневре малы и программы безразмерных тяги и реак-
тивного ускорения мало отличаются одна от другой.
Второе отступление от указанной в начале параграфа постановки заклю-
чается в том, что при добавлении нового уровня реактивногоускорения
или тяги не учитывается дополнительная масса, обеспечивающая этот уро-
вень. Это отступление мохсет быть оправдано, если дополнительная масса
не зависит от величин, фигурирующих в вариационной проблеме.
В следующих пунктах будет сформулирована вариационная проблема,
свооодная от обоих принятых здесь допущений, и даны примеры ее решения
для маневра межорбитального перелета.
3. Формулировка задачи аппроксимации программы тяги с учетом
массы движителей. Назовем приращение массы двигателя от добавления
нового ~-го уровня тяги и расхода массой ~-го уровня т~~'~. Если масса уровня
не зависит от характеристик двигателя вообще и уровня в частности, то про-'
цедуру построения оптимального ступенчатого управления можно разделить
на два этапа: на первом этапе решается задача при фиксированном числе
уровней тяги и расхода — здесь характеристики уровней не нужны, на вто-
ром этапе выбирается оптимальное число уровней при известной их массе
(ср. предыдущий пункт).
Зо. При а(я, 3) =~Д+я, (кривая 8 на
а (~) = 0,106~, е(~) = — 1 при
а (~) = 0,280~, е (~) = — 1 при
а(~) = 0,106~, е (~) = — 1 при
а (~) = 0,106~, е (~) = 1 при
а (~) = 0,280~, е (~) = 1 при
а (~) = 0,106~, е (~) = 1 при
Х (Т) = О,ЗЗЗР.
4'. При а (т~, о)=(т~ 01+ тг,) О. (кривая
4 на рис. 10.11)
0(~(0,238,
0,238 ( ~ ( 0,750,
0,750 ( ~ 2,39,
2,39 ( ~ (2,90,
2,90 (~ (3,38,
3,38 (~ (3,89,
3,89 ( ~ ( 5,53,
5,53 (~(6,04,
6,04 с ~ ( 6,28,

358
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
В общем случае масса уровня т< '&g ; — ф нкция характе истик дви
и уровня. Если изменение тяги и расхода осуществляется переключением
с одного однорежимного движителя на другой (этот способ и является здесь
предметом изучения), то массу нового уровня можно считать равной массе
.движителя, обеспечивающего этот уровень:
(10.98)
Будем предполагать, что масса движителя зависит только от максималь-
ной тяги, создаваемой им; тогда
т„=. ~ т~~"1 = ~,~, Р,.
(10.99)
(все движители считаются однотипными, так что параметр т одинаков для
любого номера ~).
Вариационная проблема о доставке максимальной полезной массы при
ступенчатых законах изменения тяги и расхода имеет следующий вид
(ср. (10.17)):
т. (О) = 1 — т„— т„,
г(0) =г„
т. (Т) = п1ах,
г(Т) =г„
т, = — хРе/2т„,
г=ч,
(10.100)
т=, +~, т(0) =у„
(Р(8) = Р(н, о), т„=сопят, т„=сопят, )е(~) )=1).
т(Т) =т,
В записи (10.100) принято, что масса аппарата состоит из полезной
массы т, = т. (Т), запаса рабочего вещества т = т. — т,, массы источ-
ника мощности т и массы системы движителей т„(массы г уровней тягл
и расхода т„ = ~~ Р,.1; процесс ускорения в двигателе считается идущим
без потерь; величины т, т., т„, т, безразмерные, тяга Р также безраз-
мерная (все они отнесены к начальной массе М,); масса источника мощ-
ности т, — управляющий параметр.
Ступенчатая функция Р(т~, о), имеющая г уровней, может оыть записана
при помощи релейных функций о,(1), ..., о (1) и параметров т~„..., т~, сле-
дующим образом:
Р(н, о) =((.. ° (н13 +н2)3 + . +н, )о,,+н„1) о, +н,.
(10.101)
Параметры ~,. определяют высоту уровней тяги Р,.:
Р,=7с,+тс,,+ .. +~т„Р,,=т',+тс,+ ... +т~,,..., Р,=тс,, (10.102)
а релейные функции о,. (1) — моменты смены уровней.
Сумма масс уровней т„, определяемая формулой (10.99), запишется
при учете (10.102) следующим образом:
(10.103)
РИр, — "~ ~77 ..
'Е1 у ° ° ° ~ 7~ °
Сделаем несколько замечаний к сформулированной вариационной проблеме.
1'. Число уровней г — целое число иэ натурального ряда (8=1, 2, 3,...); поэтому
отыскание оптимального 8 связано с перебором ряда значений 8 и многократным решением
В задаче (10.100) с выражениями для Р ( 7~, о) и т„в виде (10.101), (10.103)
требуется найти оптимальное число уровней г, оптимальные управляющие
функции е (1), о, (1),..., 3, 1 (1) и оптимальные управляющие параметры т„,

359
ОПТИМАЛЬНАЯ СТУПЕНЧАТАЯ ПРОГРАММА ТЯГИ
задачи. Если бы у=О и соответственно т~ — — О, то оптимальное число г равнялось бы бес-
конечности.
2'. Если нижний уровень тяги нулевой (допускается выключение двигателя),
то Р„= ~,=0 и проблема оптимизации для данного уровня состоит в определении опти-
мальных моментов начала и конца участка, на котором используется этот уровень.
3'. В формулировке (10.100) масса источника мощности т„— управляющий пара-
метр; это значит, что он определяется из условий выполнения заданного маневра и дости-
жения максимума полезной массы. Если рассматриваемый маневр является элементар-
ным, входящим частью в сложный маневр, то найденное по первому оптимальное значе-
ние т, не является оптимальным для всего маневра. Поэтому при решении вариационной
задачи для элементарного маневра надо считать параметр х= а/т,=М„/Х конструктив-
ным, а не управляющим, имея в виду определение его оптимального значения по полным
результатам. Для этого случая изменим вариационную формулировку (10.100) — введем
новое обозначение для суммы масс
(10.104)
т~ — — т,+т„=т„+т +т„
и будем считать контрольным функционалом конечное значение массы т,(Т)=т +т„',
тогда запись (10.100) трансформируется в следующую:
1
т = — — хР2
2
т1, (О) = 1 — т1,
т1, (Т) =тах,
г (Т) =г1,
т (Т) =т,
г (О) = го,
т (О) = то,
г=ч,
Ре
т~+ т1+ ~'
(10.105)
с 8
Р(~(=Р (,, Ц, ~,=(~,'М;. (е (~((=1) .
а=1
4'. В системах (10.100), (10.105) учтен тот факт, что оптимальное управление мощ-
ностью — граничное. Поэтому в дальнейшем, вместо того чтобы говорить о ступенчатых
программах тяги и расхода, будем говорить только о ступенчатой программе тяги, имея
в виду, что программа расхода при Г (~)=1 выражается через Р (~) и параметр (.
4. Ступенчатая программа тяги с оптимальным числом уровней для
межорбитального перелета. Нерегулируемый двигатель обеспечивает про-
стейшую ступенчатую программу тяги; он имеет два уровня, один из которых
нулевой. Обсудим следующий вопрос: на каких маневрах добавление новых
уровней тяги по сравнению с двумя уровнями нерегулируемого двигателя
ограниченной мощности может дать выигрыш в полезной нагрузке, если
учитывать увеличение массы двигателя от добавления новых уровней?
Чтобы ответить на этот вопрос, будем каждый раз сравнивать оптималь-
ную программу тяги идеального двигателя с программой тяги нерегулируе-
мого двигателя.
Как отмечалось в гл. 7, на маневре разгона с круговой орбиты до пара-
болической скорости идеальная программа модуля реактивного ускорения
представляет собой почти постоянную функцию времени. Если затраты ра-
бочего вещества малы (что соответствует большим временам разгона), то
в смысле затрат массы закон постоянного ускорения близок к закону постоян-
ной тяги. Поэтому для медленного разгона применение нескольких уровней
тяги вместо одного, видимо, не дает выигрыша в полезной нагрузке, если
учитывать реальные значения масс уровней.
Аналогичный вывод следует из анализа маневра набора заданного мо-
дуля скорости в бессиловом поле; последний, как известно, моделирует
маневр медленного разгона в центральном поле. Также нецелесообразно
ступенчатое программирование тяги и расхода на маневре удержания спут-
ника в заданном шаровом слое.
Что касается маневра межорбитального перелета в центральном поле
и моделирующего его маневра перелета между двумя положениями покоя
в бессиловом поле, а также маневра поворота плоскости орбиты спутника,

360
РеАльные дВиГАтели ОГРАниченнОЙ мОщнОсти
[ГЛ. 10
то идеальные законы тяги на них существенно отличаются от нерегулируе-
мых; оптимальные ступенчатые программы могут содержать, кроме нулевого,
не один уровень, а несколько.
Два последних маневра (перелет в бессиловом поле и поворот плоскости
орбиты) были исследованы на предмет построения ступенчатых программ
при двух упрощающих допущениях в п. 2 настоящего параграфа. Здесь будет
дано решение вариационной проблемы (10.105) для маневра перелета между
двумя круговыми орбитами, свободное от этих допущений.
Рассматриваемая проблема записывается так (см. (10.105), (10.56)):
~ф ~2г~
т„,(0) =1 — т„,
х (О) = 1,
~ (0) = 0,
т, (Т) = шах,
х(Т) =г соя з1,
у ( Т) = г, а1п ~р„
я=и,
Д=У,
1,Ре
и(0) =О,
( ) = гг '~' а1п ~1 (10 106)
т~+ т~
11Ре
г(Т) =-г, ~ соя и,
г(0) =1,
т), + т1 (ха ) у2) )г '
г в
Р г) =Р)~, 3), е' г)+е'г) =1, т,= ) ~ г~,)
г=1
Здесь г1, ~г1, Т, ~, г — параметры задачи; коэффициенты 11, 1 появились после пере-
хода к безразмерным величинам г, х, у, и, и; первый коэффициент 1, равен отношению
гравитационного ускорения на поверхности Земли (д„) к гравитационному ускорению
на начальной орбите, второй коэффициент 1, равен произведению '/,д на период обращения
по начальной орбите, делепный на 2~; если за начальную принята средняя круговая
орбита Земли, то
Р1 = 0,167 ° 104,
72 — — 0,2448 ° 10~ квт1'кг.
(10.107)
Сведем вариациопную проблему (10.106) к краевой задаче для обыкновенных диф-
ференциальных уравнений; выпишем гамильтонову функцию и дифференциальные урав-
нения импульсов:
2,Ре„
Н = — р,1гаРг+ р и+ р„и+ р„
т.( -~- тр,
Х
(х2 + у2)
з +
11Ре
+ Рг
т,, + т1 (хг -)- у2) )'
з
р~~ =11Р (т,~ + т)) г (р„е + р,.е„), р) (Т) = — 1,
р' = р„(хг+ у2) )' — Зх (р„х + р,у) (хг + у2) ~', р„= — р
р„= р„(х2+ у2) ~* — Зу (р„х+ р„у) (х2 ~ у2) ', р', = — р„.
(10.108)
Формулы для оптимальных управлений е, еу совпадают с (10.58). Оптимальные ре-
лейные управления о„..., ~,, находятся после примепения процедуры, описанной
в п. 1 (см. 10.68)).
Чтобы определить оптимальпые значения параметров ~„..., ~„входящих в дан-
ном случае в краевые условия (10.106), воспользуемся тем же приемом, что и в п. 1: до-
полним исходную систему (10.106) тривиальными уравнениями типа (10.69) и выпишем
дифференциальные уравнения для новых импульсов р„..., р,; последние имеют такой
вид (ср. (10.70)):
дН
дН
= — 1, " "+ 212кр Р
дН ~р,'-', -~- р2
дР т,+т1
б,,— 7) () =1, ..., г)
(/т1,
(10.109)
дН ~р„'+ р~~
(,+ ))'
Конечные значения импульсов р„..., р, нулевые, как и в и. 1; в начальпый мо-
мент импульсы удовлетворяют условиям трансверсальности:
р, (О) = 7р, (О), рг (О) = 2тр, (О), ..., р, (О) = г7р, (О),
р, (Т) =0, р, (Т) =0, ..., р, (Т) =0.
(10.110)

ОптимАльнАя ступенчАтАя пРОГРАммА тяГи
361
Таким образом, вариационная проблема сведена к краевой задаче
(10.106), (10.108) — (10.110). При численном решении последней применялся
метод последовательного подбора недостающих начальных значений р (0),
р„(0), р„(0), р„(0), р, (0) и параметров ~г1,..., тс,.
Расчеты преследовали цель определить оптимальное число уровней 8
в зависимости от конструктивных параметров т, х. Конечный радиус г„
угловая дальность перелета ~1 и время Т были взяты следующими:
г, = 1,52, и, = 1,57, Т = 1,57. (10.111)
Конструктивные параметры
лись из таких:
т = 0; 25; 50; 100; 200; 400 кг)кГ,
х = 5; 12,5; 25 кг/квт.
Число уровней тяги 8 принимало
г = 1, 2, 3, 4,
х выбира-
(10.112)
значения
(10.113)
Р1 ф Д,'
Рис. 10.12. Ступенчатый закон
изменения тяги.
причем в каждом случае допускался нулевой уровень тяги. На рис. 10.12
приведен характерный вид функции Р (~) при т=25 кгlкГ, х=25 кгlквт, в=4.
Интересно отметить, что для некоторых значений г, х, т ) 0 в оптималь-
ном случае на траектории отсутствует пассивный участок. Этот факт можно
Ю О бР Ю /Я
Ю Ю бд Ю 103
Рис. 10.14. Максимальная суммарная масса ис-
точника мощности и полезной нагрузки при
оптимальном 8.
Рис. 10.13. Суммарная масса источника мощности
и полезной нагрузки при фиксированном числе
уровней тяги 8.
объяснить следующим образом. Появление на траектории пассивного участка
уменьшает время работы двигателя и увеличивает в среднем высоты уровней
тяги; при этом потребный запас рабочего вещества т, уменьшается, а сумма
масс уровней т„возрастает. Может оказаться, что в результате масса т, (Т)
уменьшится; тогда присутствие пассивного участка на траектории невыгодно.
Подобная ситуация не возникает при т=О (невесомый движитель).
На рис. 10.13 приведены зависимости массы т, (Т) от параметра
при различных значениях числа уровней г и фиксированном параметре х:
«=25 кг/квт. Оптимальное значение числа уровней г при каждом данном
значении параметра т определяется по огибающей, выделенной жирной ли-
нией. Символом в+О обозначены варианты с выключением; точки на линиях
постоянного г разграничивают варианты с выключением и без него.
Влияние параметра х на максимальную величину т,(Т) видно из
рис. 10.14, где для сравнения представлены огибающие трех семейств:
«=5; 12,5; 25 кг/квт. На кривых отмечены точки, соответствующие сменам
числа уровней; например, обозначение в=2 относится к точке, начиная с ко-
торой вправо до точки 8=-1 оптимальное число уровней равно двум.

362
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
$ 4. Реальные характеристики двигательных систем
Характеристики (4.9), (4.10) двигательных систем ограниченной мощ-
ности зависят от типа движителя. Каждый конкретный тип движителя
определяет выражения массы т и тяги Р. Функция тяги Р от мощности Ж,,
расхода д и параметров и„..., и, может быть задана явно:
(10.114)
Р=Р(Т», д, ч~),
или параметрически при помощи одного общего параметра и:
(10.115)
Р =Р(Т», и, т),
д =д(т», и,, т),
или, наконец, при помощи двух общих параметров и„и,:
(10.116)
Р=Р(и„и,2, ч~), д=д(и„и„, т), Т =Т (и„и,2, ч~).
Аналогичное положение имеет место и для функции т, только при этом
т'
масса т зависит от предельных значений Л~~, д (или Т», и, или и„и.).
В данном параграфе даны характеристики двигателя ограниченной
мощности с электростатическим движителем; на примере его описаны про-
цедуры выбора оптимальных программ регулирования и оптимальных
параметров.
Учету реальных регулировочных характеристик двигателей ограничен-
ной мощности в проблемах оптимизации посвящены также работы [10.13—
10.19, 10.25].
1. Характеристики двигателя с электростатическим движителем. Схема
процессов, протекающих В электростатическом движителе с поверхностной
ионизацией, описана в п. 6 ~ 1 гл. 2 ([10.20 — 10.241 и др.).
Параметрические выражения тяги Р и расхода д движителя этого типа
записываются в соответствии с известной формулой Чайльда — Ленгмюра
(закон «3/2»), которая выводится для одномерного монохроматического пучка
при условии неограниченной обильности источника ионов.'
(10.117)
(10.118)
где Ь вЂ” постоянные радиационные потери на единицу площади.
При выборе напряжения Я и расстояния И следует учитывать ограниче-
ния на область их изменения:
(10.119)
Нарушение первого неравенства (средняя напряженность электриче-
ского поля Е в ускоряющем промежутке превышает Е,„) приводит к пробою,
второе неравенство носит характер конструктивного ограничения.
здесь И вЂ” расстояние между эмиттером и ускоряющим электродом, ~Г—
площадь поперечного сечения пучка, т и е — масса и заряд иона, ф—
вытягивающий потенциал.
Мощность Ж, идущая на производство тяги, слагается из мощности
реактивной струи и мощности, излученной с горячей поверхности эмиттера
(главный источник потерь):

363
РЕАЛЬНЫЕ ХАРАКТЕРИСТИКИ
э 41
На рис. 10.15, 10.16 приведен пример параметрических зависимостей
тяги Р и расхода д от площади ~ при различных значениях мощности Л1
Т
(геометрический параметр И не меняется, И=О,З см; Е „=30 000 в/см; Л=
=11 вт/см' [10.22]); крайние левые точки кривых отвечают условию Я/И=
=Е,„. На рис. 10.17 представлена функция Р (Л~,, д); там же для сравнения
нанесены пунктиром кривые тяги идеального движителя. Двузначность
Рг
~,~Хг/Сж
1 3 4 б8Ю Л 4Р %ХМ
У~„Хг
Рис. 10.16. Расход д двигателя с электростатиче-
ским движителем.
Ю 8Ю Я 4д 638360 2%
р; ~д,г
Рис. 10.15. Тяга Р двигателя с электростатиче-
ским движителем.
Вместе с выражением (10.2) для массы источника мощности и преобра-
зователя соотношение (10.120) определяет формулу для массы двигателя
с движителем данного типа.
Изменение тяги, расхода и мощ-
~ф
ности электростатического движителя
с поверхностной ионизацией про- 1~~
исходит при изменении потенциала Я Ф'~
и площади ~ (последнее — за счет
подключения различного числа эле- 75~
ментарных движителей). В процессе
регулирования должны выполняться
условия (10.119), а также условия
(см. (10.2), (10.129))
О 1Г /б Г ~ ~~~~~ру
Рис. 10.17. Тяга Р двигателя с электростатиче-
ским движителем как функция расхода д и мощ-
ности Ж~; крайние точки графика соответствуют
режиму максимальной напряженности Е.
Т (~) ( Ж „=М,/м,
~ (~) ( ~... = М,/~,. (10.121)
2. Оптимальные программы регулирования реальных двигателей. Ва-
риационная проблема о доставке максимальной полезной массы в общем
виде (без конкретизации выражений Р, ЛХ ) описывается следующей си-
стемой дифференциальных уравнений и краевых условий (см. (4.8)):
М.= — д, М,(0) =М вЂ” ЛՄ— М, ЛХ,(Т) =шах, 1
г=ч,
г (О) =-т„ г(Т) =г„
(10.122)
Ре
т= + + „+я, ~(0) =~„
(Р(~) = Р (Т~, д, т), ~ е(~) ~ =1, М,=иТ „, М =ЛХ (Т „, д „, т)). ~
т(Т) =т,
функции тяги на рис. 10.17 (верхняя ветвь — сплошная линия, нижняя—
штрих-пунктирная) комментируется в следующем пункте.
Массу движителя рассматриваемого типа можно считать пропорциональ-
ной максимальной площади поперечнего сечения пучка:
М =.(.я (10.120)

364
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОЙ МОЩНОСТИ
Чтобы найти условия выбора оптимальных управлений, выпишем гамильтопову
функцию и дифференциальные уравнения импульсов для задачи (10.122):
Н = — р,д+р„т+ (р„е) Р (М, + М„+ М ) '+ р, д, 1
р, = (р, ° е) Р (М, + М„+ М )-2, р, (Т) = — 1,
д
дг (р~ ' е)' Ре = Ру' °
(10.123)
Оптимальная программа вектор-управления е (й) определяется выражением (10.21);
управления, через которые выражается тяга Р (см. (10.114)) или тяга Р и расход д (см.
(10.115)), будут оптимальными в том случае, когда они доставляют абсолютный минимум
функции Н, т. е. ее части, зависящей от Р и д:
(10 124)
т1п ( — (р,д + р,Р(МИ
(р,=~р,~, М=М.-)-М„+М,).
Применим условие (10.124) для определения оптимальной программы
изменения мощности двигателя с электростатическим движителем. Рассмот-
рим функцию тяги Р от мощности Г и расхода д в форме (10.114). Если за-
Висимость тяги Р от мощности Я при любом д такова, что с возрастанием
мощности тяга также возрастает, т. е. дР~дИ ) О, то оптимальное значение
1'
управления Г», согласно (10.124), следующее:
(10.125)
Д1 (1) = Д1,„= ЛХ,/а.
Судя по рис. 10.17 (сплошные линии), это заключение справедливо для
рассматриваемого типа двигателя. Напомним, что такой же факт имеет место
для идеальных двигателей ограниченной мощности.
Обратимся к исследованию оптимальных программ регулирования
электростатического движителя. Расход д, тяга Р и мощность Ж электро-
статического движителя с поверхностной ионизацией определяются пло-
щадью о~ и потенциалом ф (см. (10.117), (10.118)). Укажем состав оптималь-
ных управлений д (~), Р (~), применив критерий (10.124).
Вместо оГ, Я введем безразмерные управления о, е:
(10.126)
(10.127)
при этом
0(о(~)(1, 0(е(~)(1.
Выражения для расхода и тяги (10.117) через управления а, е записы-
ваются следующим образом:
С1 — ~~— ~ Со — 9 д Е шах °
('1 О. 128)
Оптимальное условие для мощности (10.125) определяет связь между
управлениями а, е; подставляя (10.125), (10.126) в (10.118), находим
ф = (с,в&lt *+ ,) (с, , ( Ђ  е ~'. с = Ђ” ). (10.1
Выразим из (10.128) управление е через о и подставим в формулы для
тяги и расхода (10.117); ограничения, наложенные на управление е, перене-
сем на ~:
(10.1ЗО)
Вне указанного диапазона управление а (~) может принимать значение
о=О, которое соответствует выключению движителя, Р=д=О.

365
РЕАЛЬНЫЕ ХАРАКТЕРИСТИКИ
Функциональные зависимости (10.130) представлены на рис. 10.15
в координатах Р, ~ с параметром К и на рис. 10.16 в координатах д, ~
с тем же параметром; функции Р, д имеют максимум по ~ (при ~ — «О функ-
ции Р, д — «О и при ~à — «Х /Ь функции Р, д — ю 0). Это обстоятельство при-
водит к тому, что функция Р (д) и обратная функция д (Р) двузначные
(см. рис. 10.17) — одно и то же значение тяги достигается при двух значениях
расхода (большем и меньшем) и, соответственно, двух значениях площади
(большем и меньшем). Второй вариант (меньший расход и меньшая площадь
при данном значении тяги) всегда выгоднее первого; поэтому оптимальные
режимы заведомо не реализуются на частях кривых рис. 10.17, которые ле-
жат правее точек максимума. Эти части (и соответствующие им на рис. 10.15,
10.16) даны штрих-пунктиром.
Подставим выражения тяги и расхода (10.130) в формулу для функции Ы;
оптимальный закон ~ (~) будет определяться из условия
ппп — ~3Х с,р.~ ' — — ' с.,р,—
(ю 131)
(10.132)
Расчеты проводятся для поворота плоскости круговой орбиты 24-часо-
вого спутника Земли, комбинация параметров ~М,/с/4г' принята равной 100 г;
число оборотов я=10 — '. 100.
Формула (10.132) при этих значениях такова:
Т„[сею~~= 5,5 ° 104г агс з1п (10'/гР [Г]).
(ю1зз)
Второй маневр (компенсация аэродинамического сопротивления) харак-
теризуется следующей функцией Т„(Р/М„д/М ) (ср. (8.73)):
Т„='/,с рУБТ/Р. (10.134)
Будем считать, что двигатель работает на каждом шестнадцатом обороте;
силу сопротивления '/~ с ~и'Я примем равной 0,5 Г; при этом формула
(10.134) запишется так:
Т„=0,5Т/Р[Г~ (Т„(Т/16, Р) 8Г).
(ю 1з5)
ври М„/М (сз+ с ) ( ~ (1) ( 1 или ~ (1) = О.
В состав оптимального управления а (~) входят участки переменного
управления а = о„, (~), определяемого из условия минимума выражения (10.131)
без ограничений па а, участки граничного управления а=1 при а,~,(й)) 1,
участкиграничногоуправления ~ =М„/М (с +с ) при а,~,(Й) (М„/М (сз+ с ),
а такхсе участки выключения дэихсителя а = О в том случае, когда выраже-
ние (10.131) полохсительно при а=М„/М (сз+с ).
3. Оптимальные параметры нерегулируемых реальных двигателей.
В данном пункте приводятся примеры определения оптимальных параметров
нерегулируемых реальных двигателей с электростатическими движителями',
рассматриваются два динамических маневра: поворот плоскости орбиты
спутника и удержание спутника в заданном шаровом слое (компенсация
лобового сопротивления).
Решение динамической части вариационной проблемы для обоих маневров
дано в гл. 8. Результат решения — функция Т (Р/Мо, д/М ) для первого
маневра имеет вид (ср. (8.88))

366
[ГЛ. 10
РЕАЛЬНЫЕ ДВИГАТЕЛИ ОГРАНИЧЕННОИ МОЩНОСТИ
Для исследуемой двигательной системы необходимо определить опти-
мальные площадь ~ и напряженность Е; что касается межэлектродного
расстояния Ш, то можно доказать оптимальность требования
(10.136)
В расчетах взяты значения параметров И „, Л, Е „, е, т, указанные
в п. 1; в первой задаче (поворот плоскости орбиты) удельная масса источника
У,„~~'ф
лг
0
803 400 б00. 800 ЮЯ Тсуа
Ю 4) б0 дР Т,суа
Рис. 10.19. Затраты массы на удержание спут-
ника в заданном шаровом слое.
Рис. 10.18. Затраты массы на поворот
плоскости орбиты спутника.
мощности и преобразователя считается равной а=20 кг/квт, во второй задаче
(компенсация сопротивления) ~=50 кг/квт; вычисления проведены при т =
=0,1 кг/см'.
Результаты расчетов для двигателя с электростатическим движителем
в приложении к двум указанным маневрам даны на рис. 10.18, 10.19. Там
нанесены суммарные затраты массы на выполнение маневра М~,+ЛХ,,+М,
в функции от времени выполнения маневра Т. Рис. 10.18 соответствует ма-
невру поворота плоскости орбиты, рис. 10.19 — маневру удержания спут-
ника. Для сравнения на рис. 10.18 и 10.19 нанесены кривые, соответствую-
щие нерегулируемому двигателю ограниченной мощности без потерь и с не-
весомым движителем; последние обозначены символом 7=0.

ГЛЛВА 11
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ
СКОРОСТИ ИСТЕЧЕНИЯ И ОГРАНИЧЕННОЙ МОЩНОСТИ
Малая удельная масса двигателей ограниченной скорости истечепия — положитель-
ное свойство двигателей данного класса, с другой стороны, скорость истечения для таких
двигателей по сравнению с двигателями ограниченной мощности существеино меньше—
это отрицательное свойство. Естественно, возникает вопрос: какие двигатели «лучше»вЂ”
двигатели ограниченной скорости истечения (двигатели большой тяги) или двигатели огра-
ниченной мощности (двигатели малой тяги) ~ Стремление
ответить на этот вопрос в формулировке, близкой к при- ф
веденной, было свойственно в основном начальной ста-
пии исследования возможностей двигателей малой тяги
(см., например, [11.1 — 11.6] и др.). Более правомочна Я
пругая постановка: определить области преимущест-
венного использовапия каждого типа двигательной си-
стемы и целесообразность совместного применения дви-
гателей различных типов на одном аппарате.
Введем для каждого маневра пространство пара-
метров маневра, параметров двигателя ограничспнои
скорости истечения и параметров двигателя ограничен-
ной мощности. Часть прострапства, в которой выгодно р~
примеиеееие одного типа двигателя, назовем областью
применения данного двигателя. Пространство разделяет-
ся на область примснсния двигателя ограниченной ско-
рости истечения, область применения двигателя огра-
н снЕеой мощееост ПРом УточееУео областе сов — Рис. 11.1. Области П1)имее1ения
стного примеееения обоих двигатс лей. идеальных двигателей ограничен-
Как было показапо в гл. 5, для идеального дви- НОй скорости истеченил ~ и Огра-
гателя ограниченной скорости истечения общая вариа-
ционная проблема (5.2) приводится к динамической
части (5.5). Сравнивая (5.9) (при Д=О) и (6.16), можно па плоскости функционалов
7=Ьг/Г, Ф=1/2аУ выделить область 2 (рис. 11.1), где полезная нагрузка для двигателя
ограниченной мощности больше, чем для двигателя ограпиченной скорости истечения
(в области 1 полезная нагрузка для двигателя ограниченной скорости истечения больше,
чем для двигателя ограниченной мощности).
В данной главе находятся оптимальныо условия сочетаний двигателей ограпичен-
ной скорости истечеиия и ограееичспееой мощности, дается критерий выделения областей
применения двигателей ограничеппой мощности и для ряда маееевров строятся граиицы
этих областей.
$1. Оптимальные условия сочетания двигателей ограниченной
скорости истечения и ограниченной мощности
Здесь выводятся оптимальные условия сочетания для нерегулируемых
и идеальных двигателей.
1. Общие оптимальные условия сочетания. Пусть на космическом
аппарате установлены два двигателя: двигатель ограниченной скорости исте-
чения 1 и двигатель ограниченной мощности 2. Введем обозначения: Р„Р,—
реактивные тяги, е„е, — единичные векторы ориентации тяги, д„д,—
массовые расходы, М„„М, — массы рабочего вещества, М„1, М, — массы
двигателей.
Назовем режим работы двигателей 1 и 2 параллельным, если двигатели
могут быть включены одновременно. Последовательный режим имеет место

ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 11
в том случае, когда в каждой точке траектории может быть включен только
один из двигателей ~). Для определения оптимального момента переключения
при последовательном режиме воспользуемся релейной функцией 3(1),
принимающей значение 1 на части траектории, где двигатель 1 включен,
а двигатель 2 выключен, и значение 0 на части траектории, где двигатель 1
выключен, а двигатель 2 включен.
Суммарный расход массы д и результирующий вектор тяги Р записы-
ваются следующим образом:
Д Д1+ Д21
Р = Р,е, + Р.,е.„
(11 1)
при последовательном режиме
д = д,о+ д,(1 — 3),
Р = Р,е,о + Р,е, (1 — О).
(11,2)
Введем специальное обозначение для суммы трех масс:
ЛХ.=М.+М,+М, (М.(0) =М, — М„,(0) — ЛХ„,(0), ЛХ.(Т) =М.), (11.3)
и сформулируем вариационную проблему ° о доставке максимальной полезной
массы двумя двигателями, работающими в параллельном режиме:
ЛХ. = — (д + д,), М. (0) .= М вЂ” М„(0) — М„, (0), ЛХ. (Т) = тах,
г=ч, г(0) =г, г(Т) =г„
Р,е, +Р,е,
~=„.+„, +,-,, +~, "(0)=~„ т(Т) =т,
(О ~ Р, (~), Р, (~); Д, ®, Д., (~) ( со; ЛХ,, ЛХ, ( 0; ~ е, (~) ~ = ~ е,, (~) ~ — 1);
(1! .4)
работающими в последовательном режиме:
ЛХ = — (д,о+ д., (1 — о)1, М.(0) = М вЂ” М„1(0) — М„,(0), М.(Т)=тах,
г=т, г(0) =г, г(Т) =г„
т(Т) =т,
(О ( Р, (~), Р2 (~); д, (~), д, ® ( со; ЛХ„„М„, ( О; о (~) = 1 или 0;
~ е, (~) ~ = ~ е, (~) = 1).
1 (11л)
1) При параллельном режиме возможны такие варианты включения-выключения
двигателей (знак «+» соответствует включенному двигателю, знак « — » — выключенному):
+1, — 2; — 1, +2; +1, +2; — 1, — 2. Последовательный режим «беднее» параллельного,
ибо в нем отсутствует предпоследний вариант. Понятие последовательного режима вве-
дено для тех случаев, когда по техническим причинам двигатели не могут работать одно-
временно.
Сдел аем ряд замечаний.
Чтобы замкнуть вариационные постановки (11.4), (11.5), необходимо, во-первых,
указать функциональные выражения тяг Р1, Р» и расходов д„д через независимые управ-
ления двигательных систем и, во-вторых, определить массы двигателей М„„М„2 как
функции предельных значений этих управлений (см. з 1 гл. 4).
2'. Управления М„1 (~), М„» (~) могут непрерывно изменяться вдоль траектории,
подчиняясь оптимальным требованиям и ограничениям из (11.4), (11.5), и могут оставаться
неизменными при движении (тогда М„„̄— управляющие параметры). Следует преду-
смотреть такую возможность: если один из двигателей прекращает работу и до конца дви-
жения работает только другой двигатель, то первый в момент окончания работы может
быть либо оставлен на аппарате, либо сброшен, в последнем случае его компонента массы
исключается из уравнений после сброса (по этому поводу см. примеры в работе ~11.7),
а также общие оптимальные условия в работе [11.81). Ниже считается, что массы М„, М„,
неизменны вдоль всей траектории.
3'. Чтобы определить оптимальные вектор-управления е1, е2, выпишем гамильто-
новы функции и дифференциальные уравнения импульсов:

ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ
для задачи (11.4)
Р1е1+ Р2е2
Р 1ч '~ ч~ ~ Р '(м м .~ м '~ К) ~ Р
Р1Е1+ Р2Е2
(м.+и„,+и„,)
д
р, = — -„(р. о) Р. (т) =
для задачи (11.5)
Р,е,о + Р2е2 (1 — о)
— — м, м,.~м. -';2]-';р..
(11.6)
Р,е,о + Р,е2 (1 — Ч
(м.+и„, + м„,)
д
дг (Р'
Ре = Ру
(11.7)
„.(т)=
Вектор-управления е, (~), е, (~) доставляют минимум функциям Н (11.6),
(11.7) при выполнении условий
е,=е.,= — р„/р, (р„=|р,(). (11.8)
Применительно к задаче (11.4) условия (11.8) означают, что в режиме
параллельного включения направления векторов тяги двигателей 1 и 2
совпадают. Условия (11.8) позволяют считать в задачах (11.4), (11.5)
е,=е.,=е. (1 1.9)
2. Оптимальные условия сочетания нерегулируемых двигателей. При-
мем следующие характеристики нерегулируемых двигателей ограниченной
скорости истечения и ограниченной мощности:
Р, =Р, или О, д,=Р /Г1о . или О, М„1= (,Р1о,
Р, = Р„пли О, д, = Р~зо/2У2о или О, М„, = аУ2о+ (2Р „
Я ~~у >
т1Г, т 2т:-'Л1„
ЛХ. (0) = М,—
ЛХ (Т) = тах,
— ЛХ„1 — М, — Л~Ю,
г(0) =г„
г(Т) =г„
Г=Т,
~~~х1'1/ ~1, ~~у2' 2 ~2
+ е -|- а, (О) =
(г. (1), г., (~) = 1 или 0; ~ е (~) | = 1; ЛХ, ЛХ,, ЛХ,, = сопз(,);
при последовательном режиме (ср. (11.5))
аМт2тт2 (1 — о)
— М.(О)=М,—
~1 1 22 Ч
т(Т) =т,
М.(Т) = тах,
х1 ч ~2'
г(0) =г„
~7
Ь1(1Ш1б~"~1 + ЛХт2'22 (1 о)/72
т= е+д, т(0) =т„т (Т) = т,
(ш (~), -2 (~), о (~) =1 или 0; |е(~) | =1; ЛХ„1, ЛХ„, М =сопя(,).
24 Механика полета
где (~%2„= ~,, ~2Р2О = М,2 — ~ассы источцика мощности и движителя дви-
гательной системы 2; далее подразумевается Г1== Р,о.
Вариационная проблема о доставке максимальной полезной массы для
пвигателей с характеристиками (11.10) записывается так:
при параллельном рехсиме (ср. (11.4))

370
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 11
В уравнениях (11.11), (11.12) введены безразмерные тяги 1т„ 1т„
1 ( 1 1/ х1' 2 ( 2 2/ т2'
(11.13)
По определению нерегулируемых двигателей Р,=О или Р =М„1/т„
Р,=О ИЛИ Р2=М 2/т„ПОЭтОМу т~1, т:2=0 ИЛИ т~„т~2=1. ДЛя рЕШЕНИя ВарИя.
ционной проблемы (11.11) требуется определить оптимальные управляющив
функции е (~), г1 (~), —., (~) и параметры М„„М„М 2; в задаче (11.12) к перв-
численным добавляется управление 3 (1).
Применим к задачам (11.11), (11.12) метод Л. С. Понтрягина; требуемые
для процедуры гамильтоновы функции и дифференциальные уравнения
импульсов имеют вид (11.6), (11.7), если там вместо тяг, расходов и масс дви-
гателей подставить выражения (11.10). Оптимальные управления е (8), т:1 ((),
(8) (и 3 (8) для последовательного включения) даются законами
(р. =1р, ~)
(11.14)
М 2 ар~1 2 р
2~2./11, М
Ю = Л1т~1 — Л,т;2).
Отметим, что комбинация 2 т2М,/аМ,2, фигурирующая в (11.14), есть
скорость истечения Г2 двигателя 2. Согласно оптимальным условиям (11.14)
при Г2 ) Г1 для случая параллельного включения активный участок дви-
гателя 1 перекрывается активным участком двигателя 2. В самом деле,
при Л, ( 0 заведомо Л, ( 0 и при Л, ) 0 заведомо Л, ) О.
Это означает, что если двигатель 1 вклточен, то двигатель 2 включен за-
ведомо и если двигатель 2 выключен, то двигатель 1 выключен заведомо.
Таким образом, нерегулируемый двигатель с большей скоростью истечения
в режиме параллельного включения работает большее время.
Для иллюстрации общих положений дадим пример рептения задачи
(11.12) (нерегулируемые последовательно включаемые двигатели) на маневрг
набора заданного модуля, скорости в бессиловом поле. Уравнения вариацион-
ной проблемы, краевые условия, гамильтонова функция и дифференциальные
уравнения импульсов имеют вид (ср. (11.12), (11.7))
М Я.,1~10 ~ т2 '2 (
7 Р 2~';М,
М. (О) .= /)1, — М„, — М, — М.„
Я„1~~10/т1 + Я127~2 (1 — О)/т2
ра ри (я + я +я ( я )~
Я,11~1в/т1+ М„2я2 (( — в)/1'2
Я.+ Я„, +ЛХ„+Я,,
И У ' 1) т2 (
аМ-, 7С., (1 — б~
= — р.
2~;-'М,
р (т)= — 1,
(11.1з)
и(0) = О, и(Т) = и„р„= О,
Я„1д1В/т, + Я т~ (1 — В)/т2
+Ри Я ( Я +Я
()птимальные законы е (К)=-+1, о (К), т:1 (К), т~2 (1)=1 или 0 выражены
формулами (11.14). Их анализ применительно к рассматриваемому случаю
дает следующие результаты: е (~)=+1 при 0 (, ~ ( Т; на траектории имеется
единственная точка переключения релейной функции о (1): если У2 ) Г1,
то ~ (0)=1, при о=1 управление ~т1=1, при О=О управление ~2=1.
е(1) = — р,/р„
1 при
1 (Е) = 0
при
при
- Р)=
О при
'1 при
'(/) =
О при
Л1(0,
)О
~.,&lt
Л,)О
Й(0,
Й)0

ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ
То обстоятельство, что функция е (~) пе меняет знака, вытекает из условия р„=сопз1,
(см. (11.15)); очевидно, при и, ) 0 должно быть е (~)=+1 и р„& t 0 ( м. (11.14)).
Последний факт (тт,=1 при о=1, тт,=1 при а=О) следует из рассмотрения гамиль-
тоновой функции (заметим, что она вдоль траектории остается постоянной). Предста-
вим Н в следующем виде (обозначения см. в (11.14)):
Н = (Л,тт, — а,тт,) о+ Л я — — с = сопч~. (11.16)
Если о=1, то Л1~1=С, если о=О, то Л2~2 — — с. Постоянная с отрицательна; если
с=О, то должно быть ~,=0 при о=1 и ~2=0 при о=О, т. е. оба двигателя выключены вдоль
всей траектории; случай с ) 0 исключается, ибо л,~1 & t  и л ~ & t; О. тсюда сл
что при о=1 управление ~1=1 и при о=О управление ~2=1. Так как ~1 и ~~2 входят
вовсе уравнения в таких комбинациях с
управлением О: тт1а, тт (1 — а), то можно
РУ
было бы полонсить тт, (~)==1, тт (~)= — 1.
Оптимальный закон для релейного
РГ
управления О(~) выписан в (11.14). Вычис-
лим производную функции Й (~):
(11.17)
ТЮ,сат
Введем обозначение х для момента переключения функции о(~) и про-
интегрируем уравнения движения и расхода вдоль двух участков:
о=1 при 0(~ ~„, о=О при ~„~~(Т. (11.18)
В результате получим выражения для полезной массы М и скорости ц1
через управляющие (Е„, М„, М„, М,,) и конструктивные (Г1, .(1, .(а, а) пара-
метры, а также время Т:
М, — М вЂ” ~„М„ /Г ( — а (Т вЂ” ~„) М2 /2"ДМ,,
~ ..М.,1
71~1Мо
° ° 2
~ у а(Т вЂ” 1„)М~,
и,= — ~,1и 1
(11.19)
2Т,11(ч
— 1п
а.Ц. „
1
Задавшись значениями конструктивных параметров Г„а, 7„')з и ско-
рости и„определим оптимальные величины 8,, М„„М„М и максимальную
полезную массу как функции времени маневра Т. На рис. 11.2 представлена
функция М, (Т), значком 1 отмечена кривая, соответствующая выполнению
маневра одним двигателем ограниченной скорости истечения (~„= Т), значок 2
относится к одному двигателю ограниченной мощности и значок 1+2—
и двум двигателям. На рис. 11.3, 11.4 даны оптимальные управляющие
параметры двигателя 2 Г,/Г„М,/ЛХа как функции Т. При расчетах прини-
мались следующие значения конструктивных параметров и скорости и:
Г,=4 км/сек, (,=0,02 кг/кГ, .(,=10' кг/кГ,
а = 10 кг/квт, и, = 11,2 км/сек.
(11.20)
Отметим для дальнейшего, что оптимальная величина скорости истече-
ния Г, при больших значениях времени Т превышает 2Г„а при малых—
меньше 2~,.
при Г & t; р' производ а Й ~  0 (
как р„& t; 0 и функ и Й 1) мо ет мен
знак с минуса па плюс; поэтому, если на
траектории имеется участок о (~)=1, то он
расположен в начале О (0)=1.
Этот анализ доказывает высказанные
выше утверждения об оптимальных зако-
нах е (1), З (1), тт1 (1), тт (1).
Рис. 11.2. Полезная нагрузка для маневра на-
бора модуля скорости: 1 — двигатель ограничен-
ной скорости истечения, 2 — нерегулируемый
двигатель ограниченной мощности, 1+2 — нере-
гулируемые двигатели совместно, 3 (у,=0)—
идеальный двигатель ограниченной мощности,
1+2 (у,=у,=0) — идеальные двигатели совме-
стно (У,=4 км/сек, у,=0,02 кг/кГ, у,=10~ кг/кГ,
а=10 кг/квт, и,=11,2 км/сек).

372
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
[ГЛ. 11
3. Оптимальные условия сочетания идеальных двигателей. Вариацион-
ную проблему об оптимальном сочетании идеальных двигателей ограни-
ченной скорости истечения 1 и ограниченной мощности 2 удобно формули-
ровать в терминах реактивных ускорений:
а,=Р,~М,
а2= Р,~М
(а„а2) О).
(11.21)
Уравнения расхода, записанные через ускорения а„а„, имеют вид.
для режима параллельного включения (система (11.4))
а а.~м2
2 ЖМ,
а1М
1
(11.22)
для режима последовательного включения (система (11.5))
(1 — о).
(И.23)
В уравнениях (11.22), (11.23) величина Ж вЂ” безразмерная мощность
(0~(Т(~) (1); масса М состоит из четырех компонент: полезной массы ЛХ,,
Х ТТ,св
Т Ю,се~
Рис. 11.3. Оптимальная относительная ско-
рость истечения, соответствующая рис. 11.2.
Рис. 11.4. Оптимальная относительная масса ис
точника мощности, соответствующая рис. 11.2.
масс рабочего вещества М „М, (М + М, + ЛХ„= М.) и массы двигателя огра-
ниченной мощности М,, так что ЛХ=ЛХ.+М, причем масса двигателя М„
считается пропорциональной максимальной мощности: ЛХ, =а%,„(см. гл. 6).
Введем обозначения (ср. (5.6), (6.7)):
для (11.22)
Ч~
9
Х 44) = ехр ~ — —, — 'й 4,44) = — —, + ехр — — 'й) й~; 411.24)
1 1
О О О
для (11.23)
(11.25)
Решения уравнений (11.22), (11.23) при помощи этих обозначений
записываются в едином виде:
М Р)+М М,Х2 (1)~(1+ М,Х2(1)~м )
(11.26)
Величина относительной полезной массы М,/М, выражается через'Х,=
=К(Т), Х =Ь(Т) так:
м~м, = хр(1 + ь,м,~м,) — м,~м,.
(11. 7)
/
Х 44) = ехр ~ — — — „',44),
О
1/
Ь(1) = — — —, ', ехр — — 'А Ж
О О

ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ
373
ЛХ,/М, = — К,Ь, — Ь'„'
(1 1.28)
при этом (ср. (6.16), (5.9))
М,/ЛХ, = (К, + Ь,)'.
(11.29)
На основании формул (6.16), (5.9) с
й=0 и (11.29) в пространстве функциона-
лов Ф, Ф, К+1. можно построить области
преимущественного использования идеаль-
ных двигателей (рис. 11.5).
Вариационная проблема о достав-
ке максимальной полезной массы све-
лась к задаче Лагранжа при дополнительных дифференциальных связях:
для параллельного режима
шах (Х +Ь )
Рис. 11.5. Области применения идеальных
двигателей ограниченной скорости исте-
чения (1), ограниченной мощности (3)
и комбинации двигателей (1+ 2).
7 7 1/
= шах ехр — —, — Ж вЂ” —, — ех — — 'Ж Ж
Я1 - Я Яд а
2 Д
О l о о
(11.З0)
г(0) =г„
т (О) = т„
г(Т) =г„
т(Т) = т„
Ф = (и, + и.,) е + д,
для последовательного режима
)пах (Х, + Ь,) =
т Г
=~па~ втр — —. —.' Ш3 — —, ' ехр — — „,' Й ~~Й1
2 11 2
о О О
(11Л)
г =~,
г (О) = гс, г (Т) = г„
1=[и1о+и,(1 — о)]е+и, т (0)=т„т(Т) =т,.
1(остановки (11.30), (11.31) могут б~лть занисапы как за;(ичи Майера:
ностановка (11.3())
К= — '/2Ка,)'Г1, К (0) = 1, К (Т) +
Х =1)4аК'а'.;Я,М, Т (()) = О, —,-Е, (Т) = шах,
1'=Ч, г (0) = го, г (Т) = г,,
у=(а,+а.,) е+и, ъ (0)=то, ~ (Т)=1,
а,(~), а2(~) ~О, О& t; Г1( )% $' О, 0&l ;Я( ) ~1, [е()
ностановка (11.31)
Е = — 1)'2Ка е('1'1, К (0) = 1, К (Т) +
А =1)' аК1а-' (1 — Е)/Т,Л', Е, (0) = О, —;- Е, (Т) = шах,
1=1, г (О) =го, г(Т) =г„
Ф = [а,о+ ай (1 — П)] е+ я, т (()) = та, ~' (Т) =т,
(О, ~с), а, (г) О, о (г) = 1 или О, О & t; ', г ( $' ,  & t; Л' ~) lt;1, [с
|
11.33
|
|
)
Максимум относительной полезной массы М,!М, по управляющему
параметру М,/М, может быть определен без решения динамической части
вариационной проблемы (как и в случае
К+~
оцного идеального двигателя ограничен-
ной мощности); максимум имеет место,
если (ср. (6.15))

374
ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
Гамильтоновы функции и дифференциальные уравнения импульсов имеют вив;
для задачи (11.32)
Н = — р~ — + р~ — „+ р„° т+ р„° !(аг+ ав) е+ и],
1
а а Ка.; 2 К'Я6
1
(11 31)
д
р.= — у(р. а)
11,= р„, р„(т)=р,(т)= — 1;
для задачи (11.33)
Ка 3 а К«аь (1 — о)
Н Р«2$т +Р~ 4 ~Д +Р ' +Р ' (( 1 ~ 2( )! +К) ]
1
агк а Ка."; (1 — о)
Фй= Рк 2Р Р1 2 ~У
1
а К а~(1 — &l
Р~ Р~ г~ у' 2
(11.35)
д
р,=- ~, (р. и). р,=-р„
р„(т) = р, (т) = — 1.
Дифференциальные уравнения для импульсов Р~, р~ из систем (11.34), (11.35) интегри-
руются в коиечном виде; выранссния получаются одинаковыми и во втором и в первом
случаях:
ру, — (~ ' — К,Е, — Ц) ~ К Е,,
(11.36)
Рс = ~/~г °
Оптимальные законы е (Е), а., (Е), Г (Е), ]~, (Е) для задач (11.32), (11.33)
даются следующими формулами:
е (1) = — р„/р,,
Т®=. ),
(1) Л~)
Управление а, (~) входит линейно в уравнения вариационных проблев
и гамильтоновы функции; поэтому оптимальный закон а, (г) в общем случае
включает три участка: два «граничных» (а,=О, а,=а,,„=со) и участок
особого управления (а,=а, „,) (ср. (5.22)).
Выключение двигателя 1 (а.,=О) имеет иесто при (индекс О у Г, дальше
опускается)
Ь,= — р„Х/2Г, — р„-- О,
(11. 8)
или (см. (11.36))
(11.39)
Воспользовавшись выражением для скорости истечения двигателя огра-
ниченной мощности
(11.40)
Г (~) = 2М,/иМа., =(Б Х + Ц вЂ” Ь'-')/Ь р„
(последнее выражение получено при помощи (11.26), (11.28), (11.37)), можно
представить комбинацию Л, в таком виде:
Ь, = р„(Г,/2Г, — 1).
(11. 1)
Если вдоль всей траектории выполняется неравенство
~;Р) (2~'„
(11.42)
то двигатель 1 не включается ни в одной точке траектории и, следователь-
но, для выполнения данного маневра не нужен; этот вывод дается в ра-
боте 111.8]. Условие (11.42) выше было получено в предположении, что масса
источника мощности М, выбрана оптимальной по формуле (11.28). Однако

375
ОПТИМАЛЬНЫЕ УСЛОВИЯ СОЧЕТАНИЯ
это же условие сохраняется и для произвольной неоптимальной массы М„
как это следует из [11.8).
Оптимальный закон для релейной функции о (~), фигурирующей в ча-
даче (11.33), имеет вид
о=О при Й) О, о=1 при Й(0
(1) = Л а — р~Ц /аХ). ('11.43)
Уравнения вариационной проблемы, краевые условия, гамильтонова функция и
выражения импульсов имеют вид (см. (11.32), (11.34), (11.36), (11.37))
— Ках/2Гх, К (0) =1,
(С вЂ” КхСх — Ц)!КС„
х/4ак2а.;, Ь, Е, (0) = О, рг (Т) = — — 1,
(ах+ а2) е, и. (0) =О, и (Т) = и„
— рг,Ках/27х+ рг'/4аК'а.-,г'~ + р„(ах+ а2) е.
|
рг = — ~/~
р„= соххзх, ( О, |
(11.44)
Оптииальные управления е (г), ах (г), а, (г) подчиняются следующим
'31конам:
ах(0) = со, ах (Е) =0 (0(Е(Т), а.,(Е) =сопя(,. (11.45)
е (г):=-= 1;
Прокоъпхеххтххруем оптпмальнью законы а, (г), а (х). Оптимальное выражение для
е(х) совпадает с полученным в п. 2 настоящего параграфа. Комбинация Лх (см. фор-
мулу (11.39)) может быть положительной всходу па ххнтервале 0 ( й ( Т или, в крайнем
случае, обращаться в нуль в изолированных точках интервала; при р„=сопят производная
ах & t; О, поэт му единствен ой точк й, де Л = и нарушае ся усло ие (11. 9) выклю
ния двигателя 1, является точка х=О. Далее, так как К (г)=сопзС при 0 ( г ( Т, то
а,=сопзФ, что следует из (11.37).
Дифференциальные уравнения (11.44) интегрируются следующим образом:
К, =- ехр ( — Ьи/2Г ), Е, = — К, х/хг,аа.~Т,
=Ли+а Т
(11А6)
/
Ли =1хт ах (г) Ю, а -~ со при
т — эО
0
О) .
Исключая а, из второго и третьего уравнений (11.46), приходим к сле-
;гухощему выражению для контрольного функционала:
'г1, + Ьх = ех р ( — Ьгг/2 х~ ) ( 1 — ~/х/ ах (и — Лгг)'/Т').
(11.47)
Если ах=О, то подавно о=О. В самом деле, при ах=О оставшийся в ком-
оинации Й второй член всегда больше нуля; поэтому в режиме последова-
тельного включения двигатель 1 заведомо не будет включаться, если всюду
выполняется неравенство (11.42).
Если а,„=со (что имеет место в нашем случае), то условия (11.42),
(11.43) совпадают и режимы параллельного и последовательного включе-
ния не различаются.
Неравенство (11.42) позволяет для данного динамического маневра по-
строить границу на плоскости а, Р, — параметров идеальных двигателей 1
и 2, отделяющую область применения одного двигателя 2 от области совмест-
ного применения двигателей 1 и 2. Для этого достаточно иметь результаты
решения вариационной проблемы о выполнении данного маневра с одним дви-
гателем 2. Примеры построения границ содержатся в следующем параграфе.
В заключение этого пункта приведем результаты по задачам оптималь-
ного сочетания идеальных двигателей 1 и 2 при наборе заданного модуля
скорости в бессиловом поле.

ОПТИМАЛЬНОЕ СОЧЕТАНИЕ ДВИГАТЕЛЕЙ
Здесь присутствует параметр Ли — приращение скорости, обязанною
импульсу ускорения а, (О ( Ли ( и,). Значение Ли, доставляющее макси-
мум выражению (11.47), таково:
при — и ~ 2à — ~/2Т/а (О,
2Г, — ~2Т/и ( (— и„
2Г, — ~/2Т/и ~ О.
Ли = и, + 2Г, — ~2Т/и
Ли=О
Лу= у1
(11.48)
при
Верхняя формула из (11.48) соответствует совместному применению
двух двигателей (1+2), средняя — одному двигателю 2 и нижняя — одному
двигателю 1.
На рис. 11.2 нанесены кривые относительной полезной массы ЛХ./М„
отвечающие трем случаям (11.48); значения параметров взяты следующие
(ср. (11.20)):
(11.49)
Г, = 4 км/сек, а = 10 кг/квт, и, = — 11,2 кл~/сек.
Эти кривые (в отличие от соответствующих кривых для нерегулируемых
двигателей) обозначены индексом 7, = 7, =О.
Графики минимальной на траектории скорости истечения двигателя 2
и массы источника мощности в зависимости от времени выполнения маневра
представлены на рис. 11.3, 11.4 (кривые т,=
ю„~9
Г
=- т,=О). Минимальная скорость истечения
достигается в данном случае, судя по формуле
О,/ч;~ г (11.40), в начальной точке траектории. В об-
ласти времен Т, где оба двигателя работают сов-
06
1,О местно, начальная скорость истечения не зави-
сит от времени выполнения маневра: 1~, (0)=
4 =2 Г„ что следует из условия включения дви-
гателя 1.
Результаты проведенного анализа для за-
, дачи набора заданного модуля скорости могут
быть представлены также в следующем виде
р„с 11 6 оя„вс,и рввиеявно„о „[11.7). Из формул (11.20), (11.47), (11.48) сле-
совместного применения идеаль- дует что относительная полезная масса Л~ /М
ных дВиГателей для мине Ври ни-
бора скорости. зависит от двух комбинаций параметров: (и,/Г,)
и (Т/2аГ1). На рис. 11.6 представлена эта за-
висимость: линии 1 соответствуют одному двигателю ограниченной скорости
истечения, линии 3 — одному двигателю ограниченной мощности, линии
1+2 — сочетанию двух двигателеи; область совместного использования
двух двигателей выделена на рисунке штриховкой.
Помимо этой задачи, в работе [11.71 рассмотрены также следующие ма-
невры: перемещение между двумя положениями покоя в бессиловом поле
и набор параболической и гиперболической скоростей в центральном поле.
В основу анализа положено прямое сравнение по полезной нагрузке различ-
ных комбинаций из участков движения с двигателями одного и другого ти-
пов. Некоторые результаты по сочетанию двигателей ограниченной скорости
истечения и ограниченной мощности содержатся в [11.9].
Анализируя представленные здесь результаты, можно сделать следую-
щее заключение. Двигатели ограниченной мощности наиболее эффективны
на тех маневрах, где требуются малые реактивные ускорения. При увеличе-
нии ускорения (что соответствует, например, уменьшению времени движения)
доставляемая полезная масса падает (см. рис. 11.2), в пределе обращаясь
в нуль. В этой области времен добавление двигателя ограниченной скорости
истечения повышает величину полезной массы. При дальнейшем уменыиении

377
ПРИМЕНЕНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ МОЩНОСТИ
времени двигатель ограниченной скорости истечения выполняет большую
часть маневра, и, наконец, ниже некоторого времени применение двигателя
ограниченной мощности не нужно — маневр выполняется одним двигателем
ограниченной скорости истечения. Наибольший выигрыш от совместного при-
менения двух двигателей получается на тех маневрах, где полезные нагрузки,
доставляемые каждым двигателем по отдельности, близки. Отмеченные зако-
номерности одинаково справедливы для идеальных и нерегулируемых дви-
гателей.
~ 2. Области применения двигателей ограниченной мощности
Пусть для заданного динамического маневра решена вариационная
проблема, относящаяся к одному идеальному двигателю ограниченной мощ-
ности (гл. 6 и 7); зто означает, что определены оптимальный закон реактив-
ного ускорения а, (~) и функция У (~). Изменение скорости истечения Г, (~)
вдоль траектории подсчитывается по следующим формулам (ср. (7.102)):
Г, (~) = 2Т,/М (~) а (~), М (~) = М, (1+ М,У (~)/2Ж,) '. (1'1.50)
Входящий в формулу (11.50) параметр М,/Г, может либо задаваться
заранее:
(11.51)
Мо~~о
либо определяться оптимальным, если задан конструктивный параметр а.
Мо/То = а ~~~~~ а1 (Т) — 1/ а~ (Т) ( 1.
(11.52)
Минимальное значение Г, на траектории определяет по формуле
(см. (11.42))
(11.53)
Г, = '/, т ~и Г., (1, х)
или по формуле
Г =1/ т1пГ.,(1, а)
(11.54)
ту скорость истечения двигателя 1, ниже которой выгодно применять один
лвигатель 2 для выполнения заданного маневра. Действуя подобным образом,
можно рассчитать кривые на плоскостях параметров а, Р, или ~, Р„отделяю-
щие области применения двигателя 2 от областей совместного применения
двигателей 1+2, и, следовательно, указать предельные возможности одного
идеального двигателя ограниченной мощности. Не менее интересна граница
между областями 1+2 и 1, которая определяет предельные возможности
одного двигателя ограниченной скорости истечения; однако отсутствие во вто-
ром случае такого простого критерия, как неравенство (11.42), не дает
возможности указать границы, не решая полностью вариационной проблемы
сочетания двигателей.
В настоящем параграфе вычисляются по формулам (11.53), (11.54)
границы применения идеального двигателя ограниченной мощности на при-
ыере трех маневров: набора параболической скорости с круговой орбиты,
перелета между двумя круговыми орбитами и межпланетного перелета.
Необходимые для расчетов оптимальные законы а, (~) и функции У (~) взяты
из гл. 7.
1. Набор параболической скорости. Космический аппарат выводится
на круговую орбиту и далее должен набрать параболическую скорость при
наличии двух двигателей.
Традиционная схема выполнения этого маневра предполагает примене-
ние одного двигателя ограниченной мощности. Оптимальная программа

9 1 ° 1 е ~ ю 6 6
9 2
° ! ° ° ° в вф °
ю 1 е
1 е
° 1
° ! °
° $ °
° °
'! Ф:ю
6 ° ° °
ф 1 ° ° ° ! ° 1 9
9! ° 1 ' °
9 9 ' 6
6 19 °
9 ° °
Э' ' 1е' 61
° °
° е
е а е ° ф
° °
° °
6 ° °
юа 5 3619
° ~ ! а 5 °
° ° 6
° 9 1 е
° ° ' ! 1
1 °
° ° ° ° ° 9
й
° е ° °
° ° ° ° й
° °
9 11
1 1 й ° °
е
6 1
1 ° ~ ° ° °
° °
,.ИИИИ
; ИИЙИ
; ЙИИИ
ИИ
Вь„
/а
юв Ф
/ а
с
в °
е ° ~ ю
° Э
9
° °
° °
° 6 °
° 9
9 °
° й
9; ю
° °
° и
° ° ° 6 1 9 6 $ ° ° ° 6 1 ° ° ° 9
! 6 е
9 9 е
° °
е
'Ф 61
° в 1
6 ! ю
: ° 4
° в 1 ° в в в 6 °
е 3 ° ''!
° 9
е в ° ° 9 ффвф ° фю
° ! ° ) ! °
° ° !
), $
° 1
1 в °
В 9 °
° 6 ° ° и е в
° ° ° ! е 1 $ ° ! °
° й °
1 ' !
9 1
й
° °
° 9
° е е °
616 в А
° ° °
1 6 ° °
° °
° 1 ° 1
й °
В е вВ В
11! ю
е °
е 6 9 )
е 6
! 611
9
° )
° ° °
е
° 6 1 е е
° °
° °
° °
) 3 6
° е
1 ° 9
° 6
° °
° ° °
6 1 °
1 Э
° ф
° ю ° е
е еф 1е е °
Э ° ° 9 а 9 °
° 9 °
! 6
ф ° ° ° ° 9
39 ' 9 ° 11~ Э'
6 6
° ° ° °
9 ' Эю ° 11
991е 6
1 6 ! '
1 ! °
Э !
! ° °
° °
1 ° °
6 1 ° ° ° ~ ° У ° ° 6 6 $ ° ° е 9 °
вв ° ф ° ° ° ° ! 1 ° ° ° ° ° ° ° ° ° ° ° ф °
° ° 9 1е' 11 9 9 1ю ' 16' Эю! ° $ е ° в1 а

379
ПРИМЕНЕНИЕ ДВИГАТЕЛЕЙ ОГРАНИЧЕННОЙ МОЩНОСТИ
На рис. 11.9 даны границы областей применения двигателя ограничен-
ной мощности (области применения лежат ниже кривых) на плоскостях пара-
метров а, У и х, У1; параметры маневров взяты следующие (для времени Т
Ю
4 б 8 ф~,вм,4м
Ю О Гб сс,~цел
а)
б
а)
г
нм/сек
4 б 8 ~ ~мф~ж
Ю О Гб к, ~г/Ыл
б)
З,
лг4Юл
Рб
6 8 ~,лм/се~
8
б/ нм/сен
/// 6 Я а, ю4~~л
~)
Рис. 11.9. Грашщы ооластсй примене-
ния идеального двигатс. ит ограниченной
мощности д;тя мсжорбита 1ьпого перелета
Земля — Марс.
Рис. 11.10. По;1сзпыс нагрузки д;1я идеальных двига-
телей ограниченной скорости истечения 1 и ограничен-
ной мощности 2: а) ~р, = 1,97, 7'= 113 сут, б) ~р,=2,3Ь,
Т=143 сут, в) ~,=2,73, Т=215 сут (см. рис. 11.9).
и функционала У указаны безразмерные и размерные значения, соответствую-
щие перелетам со средней орбиты Земли на среднюю орбиту Марса):
1 1 3. у~)м4
1
;, = '1,97,
Т = 1,94 — & t; 1 '&gt  у&g ; У (Т) = 1 053- 187 л
(11.5,))
)
= 2, й — 148 сут, У (Т) =- 0,40 ' — 7 1,4 л'-'lсе~Р; 1
Т = 3,70 — 21 1 сут, У (Т) = 0,0416 - 7,'Ъ лг/сек".
Относительные полезные массы для двигателей ограниченной скорости
истечения и мощности в зависимости от конструктивных параметров
двигателей при фиксированных параметрах маневра (11.55) показаны на
рис. 11.10 (характеристическая скорость: 1) Ли=13 км/сек; 2) Ли=9 км/сек;
3) Ли=6,5 км/сек, по данным [11.10], функционал У вЂ” см. (11.55)).
3. Межпланетный перелет с возвращением. Данный маневр представ-
ляется как комбинация двух элементарных маневров, рассмотренных выше
(см. гл. 7). В зависимости от параметров элементарных маневров минималь-
ная скорость истечения Г„согласно предыдущему, достигается либо в на-
чале одного из участков движения в окрестности планет, либо в начал» или

1 ° ' 1! 1 1
й ! й
6 а й
е ° ° 6 1
° ф й в
е ° 6 1 ° 1 е в Э 11
е 9 °
й
1 6'
1 в 6 е 1
° й ° 6 й
1 6 1
1 °
й
° 6 е в °
6 е
й
г
е е е 1
9 1 1
1 а в ° 1 ! а Э
е 1131 $
а й
й ф й й
° 1 й ф й
е 6
й ° 6
! ф й °
ф й
6 й
1 ° 1
1 9 6
г 6 °
1 1'
6 е в
6 1 г Э
'4 ЭН
! °
! ° '1
° 1 6 ° 1 °
1 6 ° е ° °
е 6
й
е е 6
° !
й 6 й й 1 °
й ° ° ° ! ф
! ° 6 °
Ф ю /
° в ° °
! °
° ° в
6 ! °
е
° ° Ю
° ° И ' °
° 6 9
° ° °
° в
е °
° ° ° °
й
° ° ° в
г 1 ' 1 е
° ° ° ! ! °
° ! °
1~ 161
й ° й °
1 6 е
гй ю ю
е 1 °
6 9 ° ° е
й 6
° ! й
! ° й ° ! ° °
° ° 9
9' '1 $
ф ю
е 6 е
° °
1 1 1 6 е 1 1 ° е ° е 6
669 °
й ° В °
а
й
1 6 °
е 6
6 е 1
й 1
г 1 6
° ! 1
й °
° йв °
9 6
9 П 9
11 6 '6
° ! ! °
й ° °
° °
1 °
е
° 6
й ° ° °
й
й й 1 6
1 61
1 6 е и
111 1
° й
е ° °
° °
1 е 6
° ! °
° 6 е
° й
й 6
е Э
1 е
611 6
у ° у
6 6
6 в
1 °
й вв
6 3 в 6 3 в
ф в
$ °
° !
в
6 3 ' 6 °
фв 6 Эв 1
6 Э в
в вюф! $
1 в
! ' 6
6 6'в
6 6 в ° е е ° ° г
° 3 °
° °
е йв ° 6
° 6
! °
в е
Э °
в
6 е в
° ° 6
й е°
! $ в
3 6 ° в
° °
° в
° 6 е °
° ° в
° ° !
° ° 6 3
в е °
° е
° ° ° в °
° г е
° М ° °
° ° °
° 66
6 °
( 1
1 1 ° '!'
! °
° й
е 6
ИИЫИ
феф
;В6$ДИ
;У~Ми
° й ° й ффев! °
1 1 ° ° 6 6 е 1
96 ° г ° 6 9 1'6
6 ! в 6 6

ГЛАВА 12
ДВИГАТЕЛЬНЫЕ СИСТЕМЫ С НАКОПЛЕНИЕМ ЭНЕРГИИ
И МАССЫ. ДВИГАТЕЛИ, ТЯГА И МОЩНОСТЬ КОТОРЫХ
ЗАВИСЯТ ОТ КООРДИНАТ И ВРЕМЕНИ
В настоящей главе обсуждаются задачи оптимизации параметров и управлений сле-
дующих типов двигательных систем.
1'. Двигатели ограниченной мощности с аккумуляторалаи энергии, тепловой или
электрической Я 1 и З 2).
2'. Двигатели ограниченной мощности и ограниченной скорости истечения с на-
коплением атмосферного газа, используемого в качестве рабочего вещества Я 3).
3'. Солнечный парус (максимальная тяга зависит от расстояния до Солнца и ориен-
тации паруса Я 4)).
4'. Иэотопкый парус (максимальная тяга зависит от времени Я 5)).
5'. Двигатели с солнечным источником энергии (максимальная мощность зависит
от расстояния до Солнца Я 6)).
6'. Двигатели с иэотопным источником энергии (максимальная мощность зависит
от времени Я 7)).
$ 1. Двигатели ограниченной мощности с аккумулятором
энергии — идеальный случай
Анализируя результаты решения динамической части проблемы опти-
мизации (гл. 7 и 8), можно сделать вывод о существовании участков траек-
тории, где приложение тяги наиболее выгодно. Для перелетов между орби-
тами в центральном поле и перемещения между положениями покоя в бесси-
ловом поле это окрестности начальной и конечной точек траектории, для
маневра поворота плоскости круговой орбиты в центральном поле — окрест-
ность конечного положения линии узлов. В случае идеального двигателя
ограниченной мощности на этих участках уровень реактивного ускорения,
согласно оптимальной программе, много больше, чем на остальной траекто-
рии; в случае нерегулируемых двигателей эти участки являются активными,
в то время как на остальных участках тяга выключена.
В исследованных выше схемах двигателей ограниченной мощности энер-
гия, вырабатываемая источником, подводится непосредственно к движителю.
Поэтому на участках, где оптимальная величина тяги мала или равна нулю,
источник мощности фактически не используется. Эффективность работы источ-
ника мощности можно повысить, если во время движения по участкам
с нуловой или почти нулевой тягой запасать энергию, вырабатываемую
источником, а на участках, выгодных для приложения тяги, направлять
всю энергию (вместе с запасенной) в движитель [12.1 — 12.3]. Накопление
энергии может осуществляться при помощи тепловых [12.1] или электри-
ческих [12.2] аккумуляторов. Описание их основных характеристик дано
в ~ 2 гл. 2. Предварительные оценки выигрыша в полезной нагрузке при
использовании аккумуляторов сделаны в работах [12.1, 12.2].
Необходимость введения аккумуляторов энергии возникает также в за-
дачах движения спутника с солнечной энергоустановкой, если траектория
содержит затененные участки.

ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
[ГЛ. 1"
1. Характеристики двигателя. В состав двигательной установки огра-
ниченной мощности с накопителем энергии входят источник мощности Х„,
накопитель (аккумулятор) энергии Е и движитель Р (рис. 12.1) [12.3]. Выра-
батываемая источником мощность О ( Г„( Г, может быть направлено
в накопитель Г, ) 0 и непосредственно в движитель Г, ) О, так что
Г,+Г,=Г„. Накопитель энергии может отдавать мощность движителю
Г,=Г,— Е (Г, ) О, 0 ( Е ( Е,); таким образом, к движителю подводится
мощность Г =Г,+Г„которая используется для создания тяги:
р=~г, у,= ~,др' (о(р(р,). (12.1 ~
Здесь д — массовый расход рабочего вещества, à — скорость истечения.
Процесс ускорения рабочего вещества считается идеальным. Тяга движителя
в общем случае ограничена сверху.
— В случае идеального движителя верк-
~ нее ограничение на тягу отсутствует
4~ ll
/~l„
(~ о= ) °
Для нерегулируемого движителя
рис. ~2.~. принципиальная схема двигатель- = о или Ог Редположение о о~сут
ной установки с аккумулятором эпергии. ствии потерь в движителе при эт(щ1 не
делается.
Исключив Г,=Ä— Х, и заменив Гз — Г,=Г„можно представить урав-
нение баланса мощности для рассматриваемой системы в виде
Ь"= — Т, Ж +Т = —,дГ'-' (0(Е(Е„Ж,) — Ж,, 0(У,(Т„). (122)
Отрицательные значения мощности Г, соответствуют режиму зарядки
и ограничены величиной мощности Я„, вырабатываемой источником. Поло-
жительные значения Ж, соответствуют режиму разрядки.
Массу двигателя ограниченной мощности с накопителем энергии
М =М„+М,+М,
(12Л)
составляют следующие компоненты: масса источника мощности (принимается
пропорциональной максимальной мощности источника Г,о)
М,=ЯМ О,
(12.1)
масса накопителя энергии (принимается пропорциональной максимальной
накапливаемой энергии Е,)
М,= ~,Ео,
(12.5)
масса движителя (принимается пропорциональной максимальной тяге Р,)
! О
(12.6)
(в случае идеального движителя М =0).
т
2. Формулировка вариационной проблемы. Состав оптимального управ-
ления. Задача о максимуме полезной нагрузки для двигательной системы
ограниченной мощности с накопителем энергии ставится так: заданы началь-
ная масса М„удельные массы а, ~,, т источника мощности, аккумулятора
и движителя, фиксированы граничные условия и время выполнения ма-
невра Т; требуется указать оптимальные режимы работы источника мощ-
ности, накопителя энергии и движителя, а также оптимальные параметры
(12.4) — (12.6), обеспечивающие максимум полезной массы М [12.31.
Полная система дифференциальных уравнений, граничных условий,
ограничений на управляющие функции и фазовые координаты этой вариа-

З8З
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
ционной проблемы в постановке Майера записываются следующим образом
(аналогично (4.8)):
Р2
т. ( Т) = тах,
гп. (0) + т„= 1,
Е(Т)=0,
г(Т) = г„
Е(0) =1,
г(0) = г„
Г: ~,
(12.7)
ч(Т) =ч,
(О ( Р (й) ( 1, О ( Ж„(Е) ( 1, г"ч', (й) ) — 1, $ е ® $ = 1, О ( Е (Е) ( 1,
ч(0) =ъ„
р2 ат.-,
0 7
2Л,ОЛ1О 2~'-'т„'
О
р т
3
~~о
Й.,=
О
(12. )
т,=О, т,=О, пг =О
с граничньвюи условиями
т (0)+т„(0)+т,(0)+т (0) =1,
т„(Т) = ор1,, т, (Т) = орВ, пг, (Т) = ор1
(12З)
(нервое условие записывается вместо т (0)+т =1). После этого управляю-
щие параметры т„т„т„превращаются в фазовые координаты, начальные
значения которых связаны условием трансверсальности, а конечные значения
свободны.
Оптимальные управления е ',г), Р (г), Л~, (г), гч'„(г) определяются по ые-
тоду Л. С. Понтрягина из условия абсолютного минимума гамильтоновой
функции Н:
Н=—
Ра,Ч' (1 ~,Ч )
р„,й2гч'„гч', + (р, е) ' + (р„д) + (р„ч) () 2.10)
дН . дО . дН
Р= — — Р=- —— Р=
ДЕ' ' дч ' " дг
дП
дт
При этом нужно различать участки траектории двух типов: лежащие внутри
области 0 ~ Е ( 1 и лежащие на границах Е=О или Е=1. Опускггя
Здесь первое уравнение — это уравнение расхода рабочего вещества (т. (~) =
=т,+т~ (~) — суммарная масса полезной нагрузки т, и запаса рабочего
тела т ), второе — уравнение изменения энергии накопителя, третье и чет-
вертое — векторные уравнения движения центра масс аппарата в инерциаль-
ной системе координат.
Начальное условие для масс т. и т соответствует заданной стартовой
массе М, (все массы отнесены к М,). В конце движения масса т. (Т) совпа-
дает по определению с т и должна быть максимальной. Граничные условия
для энергии Е (отнесены к Е,), радиуса-вектора г и вектора скорости ч могут
меняться в зависимости от типа маневра.
Управляющие функции Р, гч'„гч'„е безразмерные: тяга Р и мощность
источника Л~„отнесены к своим максимальным значениям Р, и гЧ„мощ-
ность Ж, отнесена к текущей мощности источника, е — единичный вектор
направления тяги.
Управляющие параметры т„т„т„— массы источника мощности,
накопителя энергии и движителя (отнесены к Л1„) — входят в правые части
уравнений (12.7) и в начальное условие заданной стартовой массы. Выбор
оптимальных значений этих параметров можно свести к стандартной про-
цедуре, если присоединить к системе (12.7) формальные уравнения

384
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
[ГЛ. 12
промежуточные этапы отыскания минимума функции гт, приведем оконча-
тельные выражения для оптимальных управлений.
Законы изменения по времени направления тяги е и мощности источ-
ника Ю,, одинаковы как для внутренних, так и для Граничных участков траек-
тории:
(12.11)
е = — р„/р„,
'.г. е. вектор тяги антипараллелен вектору р, и мощность источника макси-
мальна (как и для двигательных систем ограниченной мощности без накопи-
теля — см. выше гл. 6).
Мощность ЛГ, (управляющая энергией накопителя) и величина тяги Р
подчиняются следующим законам:
внутри области О & t
Р = О при р'„(чх
(т. + т„)' — „'.,'
3
( [2.12)
на границах Е=О и Е=1
при р'„) у.„1
х"хГ, = О,
х"хГ, = О,
Р= 1
Р~)сз
Р =, „" при р'-„( срз
2 1
(зз = 4р'.- (т. + т,)' — „.',,
3
где импульсы р. и р, всюду отрицательны.
Таким образом, внутри области О ( Е ( 1 энергия накопителя либо
расходуется с оптимально меняющейся скоростью (режим разрядки), при
этом тяга максимальна (см. первые соотношения (12.12)), либо запасается
с максимальной скоростью (режим зарядки), при этом тяга нулевая (см. вто-
рые соотношения (12.12)). На границах Е=О и Е==1 расход энергии накопи-
теля нулевой, а тяга либо максимальна (первые соотношения (12.13)), либо
оптимально регулируется (вторые соотношения (12.13)).
Чтобы установить чередование оптимальных законов (12.12), (12.13), нужно знать
поведение импульсов р„р„р,= $р„| и фазовой координаты т,. Импульсы р„р„р, хх
фазовые координаты всюду непрерывны, а импульс р, при сходе с границ Е=О и Е=1,
в соответствххи с условием скачка [12.4], имеет раз)хыв первого рода (вид функции 1Х хх
дифференциальные уравнения для ххчпульсов (12.10) сохраняются).
Из уравххоиий (12.10), (12.7) с учетом (12.11) ххмееъх
(12.11)
хх1оххсно показать, что импульсы р, и р, всходу отрицательны, функции ~х и .-;.„входящие
в условия (12.12), (12.13) смены режимов, положительны. Г1ри ххочохци (12.14) ъхоххсххо
заключить, что эти функции неубывающие:
Поведение импульса р, определяется в основном типом маневра. Для рассматри-
ваемых в дальнейшем примеров характерно иемонотонное поведение р2 (х) с минимумом
внутри интервала [О, Т |.
(Й,р,)!
Я,= — 1,
~1 Ю~В
при ),з~ ) рх;
при р2 &l ;,
при р2) у.;
Р~ ( хх2

385
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
Если за все время движения энергия Е не выходит на границы Е=О и Е=1, то функ-
ции Е (~) и Р (~) будут иметь вид, показанный на рис. 12.2. В общем случае между точками
перехода с режима разрядки на режим зарядки и обратно могут появляться участки
движения по границам Е=О и Е=1 соответственно (рис. 12.3). Момент схода с границы
принципом максимума не определен и должен паходиться с помощью одного из достаточ-
ных принципов оптимальности или варьированием протяженности граничного
участка (п. 3).
В заключение настоящего пункта укажем на необходимость рассмотре-
ния двигательной системы с накопителем энергии, но без источника мощности.
Рис. 12.3. То же, что и на рис. 12.2, когда
Е (1) выходит на ограничения.
Рис. 12.2. Оптимальные законы изменения
знергии~Е и тяги Р для случая, когда функция
Е (1) не выходит па ограничения.
Такая система будет целесообразной при достаточно малых значениях
удельной массы накопителя энергии (12.5), — таких, что
Гг 77/ г /1
е
(12.15)
Действительно, источник мощности массой М„вырабатывающий за
за время Т количество энергии Е~=-(ЛХ,I а) Т, при ~,,Т|а=1 может быть за-
менен полностью заряженным к начальному моменту времени накопите-
лем энергии емкостью Е" с той же массой М,'= В,Е*=М, Д,Т1 а= — М„.
При В,Т/а( 1 будет Л1; ( Л,, поэтому применение источника мощности
нецелесообразно.
3. Идеально регулируемая двигательная система характеризуется отсут-
ствием ограничения на тягу сверху (Р .- О) и нулевой массой движителя
(ЛХ =О). Рассмотрение этого случая позволяет установить верхний предел
Т
возможностей системы и частично разделить общую вариационную задачу
на параметрическую и динамическую части.
Отсутствие верхнего ограничения на тягу дает возможность перейти
в уравнениях (12.7) от тяги Р к реактивному ускорению а:
а = Йз Р (т, + т„) '.
(12.16)
Тогда первое из уравнений (12.7) может быть проинтегрировано в квадра-
турах и разрешено относительно функционала задачи (аналогично тому, как
эуо делалось выше для двигательной системы ограниченной мощности без
накопителя энергии):
7 -1
О
' (12.17)
Относительная масса источника мощности т„в остальные уравнения ва-
риационной проблемы (12.7) входит только в виде отношения т„/т,. Поэтому
25 Механика полета

[Г,И. 1'
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
еще до решения полной задачи, зафиксировав в (12.17) величины интеграла
и отношения т,/т„, можно найти оптимальное значение т„обеспечиваю-
щее максимум т:
2
Т
а2Ж
д.~в)
О
при этом
т„=т„+т,=~~,— ~,
т „,„, = (1 — ~Ф,),
(12 19)
Последние соотношения (рис. 12.4) для максимальной полезной массы т,
и оптимальной полной массы двигательной системы т„совпадают с рассмот-
ренными в ~ 1 гл. 6 решениями (6.15), (6.16) для двигательной системы без
накопителя. Только вместо Ф, там фигурирует Ф
ш ш
из (6.14) и масса двигательной системы опреде-
ляется только массой источника мощности т,,=т,.
Отметим, что и в задаче с накопителем энер-
гии оптимальная полная масса двигательной си-
Ю
стемы не превышает 25% от начальной массы И,,
Полезная масса (12.19) монотонно убывает с
увеличением Ф, поэтому вторая часть задачи сво-
Щ
Х дится к отысканию минимума функционала (пара-
метр а задан):
7
Ф ф~ Ф~
а2Ж
~,=(1+~) у (1+у )
Ф,= — У, . 1220
Рис. 12.4. Максимальная полез-
ная масса т„и оптимальная
масса т„. двигагельной системы.
Эффективность использования накопителя энергии будет характеризоваться
отношением величины функционала (12.20) к стандартному функционалу
Т
(12.21)
У = а'д~'
если 0 ( У,/У ( 1, то использование накопителя выгодно.
Уравнения вариационной задачи о минимуме У, записываются следую-
щим образом:
у (1 + $) а~
Д(1)д)в
уу
У, (Т) = ш1п,
Х,(0) =О,
Е(О)=1, Е(Т)=О,
(12.22)
г=~, г (0) = г„г (Т) = г
ч= ае+д, т(0) = т„ч(Т) = ч,
(а (1) )~ О, О ( Т„(8) ~~ '(, Т, (1) )~ — 1, 1е (8) ~ = — 1, О ( Е (1) ( 1).
управления таковы (ср. (12.11) — (12.13)):
р, (1+ Ж,)
2 (1+ Ц)
при р2) 4'' „' р, и 0(Е(1(р) 0), ~
(
при р(4'' „р, и 0(Е(1,
при Е=О и Е=1,
!
Оптимальные
е= —,
р,
Рр
(12.2;1)
Ж вЂ” 0
т. е. режим разрядки оказывается импульсным.

387
ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
Кроме того, в состав оптимальной траектории могут входить участки особого управ-
ления мощностью Г, [12.11]. Гампльтониан Х не зависит от управления Г, (г) при вы-
полнении условия
К (1+ ~)
(12.24)
Соотношение (12.23) для определения оптимального значения Г, при этом неэффективно
и управление Г, (г) — особое.
Импульс р, постоянен при движении вдоль интервалов О ~ Е" 1, на которых Ю,
отлично от нуля. Условие (12.24) приводится, таким образом, к виду
р"; = р'„, = сопяС.
(12.25)
7П=1
Здесь р,,п — составляющие вектора р,. Следовательно, необходимое условие существова-
ния участка особого управления Г, (г) сводится к требованию постоянства модуля век-
тора р, на этом участке.
Из (12.25) следует:
(12.26)
Представляет интерес следующий случай:
дд/дт = О,
(12.27)
е = е (г)Р
в котором значение управляющей функции Г, на особом участке определяется из ра-
венства
72 И 2 72 И
д~„ др„ д кг
д + Р Р'д Р" д д ~~~+
7П ~т ~т ~р
Иг=1 8=1 8=1 р=1
И 72 И
ду„ ду д кг
Рдддд д~ Рхдд дг Ртд д~ д дд +
1П Ю ~т ~р
8=1 ~юг =1 р=1
72 И
дК дК
р=1 у=1
И И И
Ж~Ж, д2~в
+ 2 (1+ Ц рдддд ' Р~ РРРР дг дг
т =1 8=1 р=1
(12.28)
72 72 72
др„
Руигрггт = О1 Рут Р1угг Р28 д
Гиг
т=1 т=1 8=1
72 72 и И
др, д~ д2~
Р Р ~д д Р Р д Р д д ~дг]=д
т=1 8=1 8=1 у=1
(12.29)
Необходимое условие оптимальности особого управления [12.12] принимает следую-
щий вид:
И 72 И
д2,~
Рапп Р~ Р РеР ду ду'
~т "р
иг =1 8=1 у=1
(12.30)
Необходимо отметить, что сопряжение особой экстремали с неособой в случае (12.27)
невозможно [12.12], так как особая экстремаль имеет порядок вырождения Й=2. Если же
отрезок особой экстремали входит в состав оптимальной траектории, множество постижи-
мых конечных состояний имеет меру нуль.
25*
'Гри первые равенства (12.26) дают соотношения, необходимо выполняющиеся вдоль
особого участка оптимальной траектории'.

388
цРуГие типы двиГАтелеЙ
~Гл. 12
Для двигательной системы без источника энергии [12.3] условия (12.29) и (12.30)
сохраняются. В уравнении (12.28) необходимо положить М =0 и коэффициент при Л,
[2 (1+~)] 1 заменить на 1/е.
Для оптимального выбора моментов схода фазовой координаты Е с границ Е=0
(начало зарядки накопителя энергии) и Е=1 (начало разрядки) применим достаточные
условия оптимальности [12.5], так как принцип максимума [12.4] не определяет конкрет-
ных значений константы р, па различных этапах движения (см. (12.23)). Достаточное
условие оптимальности [12.6] требует максимизации по координатам и управлениям
функции Л, часть которой Л~, зависящая от координаты Е,
ф~ имеет следующий вид'.
Л" = ср,р„Е (О ( с = сопз$).
Оптимальные значения Е получаются следующими',
Е=1 при р,р,)0,
Е=О при р р,(0.
(12.31)
Переход Е с граничного значения 1 па граничное
Ю значение 0 (разрядка накопителя энергии) может быть
произведен мгновенно (Š— — К,= — со, см. (12.23)).
Согласно (12.31) момент этого перехода совпадает с мо-
ментом смены знака произведения р,р', с плюса на ми-
нус. Так как р„= [р„[ & t; О, то та ая см на зн ка возмо
1 лишь в точках максимума р„(й).
Обратный переход Е (с границы Е=О па границу
Е=1 — зарядка накопителя) должен производиться, как
видно из (12.31), вблизи значений ~, где произведение р,,р,
меняет знак с минуса на плюс. Такими точками являются
точки минимума р, (й). Однако, в отличие от разрядки, за.
д рядка не может быть осуществлена мгновенно, так как в
этом случае (см. (12.23)) Е= ~,/а~ ( 1. Следовательно,
соотношения (12.31) не могут быть выполнены точно в не-
которой окрестности точки ~е (рис. 12.5). Ширина этой
окрестности зависит от соотношения мощности источ-
ника, полностью идущей на зарядку накопителя (Г,= — 1,
К,=1), и емкости накопителя. Значение постоянной р„определяющей через соотно-
шение (12.23) момент~ начала зарядки, должно быть как можно более близким к зна-
чению р„соответствующему мгновенной зарядке (р,е на рис. 12.5), но таким, чтобы соотно-
шения (12.31) выполнялись за пределами интервала зарядки. Значение р„па рис. 12.5
удовлетворяет указанным выше условиям, тогда как р,, хотя и меньше отличается от
идеального значения р,, чем р,1, но является неприемлемым, так как построение режима
зарядки по р,е (пунктйрные линии на рис. 12.5) приводит к тому, что граница Е=1 ве
достигается. Так как значение импульса р, может меняться лишь при выходе координаты Е
на границу или сходе с границы, то оно остается постоянным и сразу после окончания
зарядки (в момент Ое происходит импульсная разрядка накопителя согласно (12.23)).
Таким образом, построение режима зарядки по р, приводит к невыполнению соотноше-
ний (12.31): р„р'„& t 0 л  ) „а =О ля ех же значе ий й. Вме то оптимальн
значения р, можпо непосредственно вычислить величины с и 01 — оптимальные границы
интервала зарядки накопителя — из следующих соотношений:
Еа= — ', (О,—;,)=1, р,(;,)=р„(Е,).
~~е
(12. 321
Соотношение (12.23) для определения оптимального значения реактив-
ного ускорения позволяет дать простое физическое толкование полученным
результатам. Использование энергии, запасенной в накопителе, является
оптимальным при значениях ускорения, близких к максимальным, что
в свою очередь приводит к возрастанию ускорения. Таким образом, энергия
накопителя расходуется тогда, когда это может максимально повлиять на
выполнение кинематических условий маневра. Зарядка накопителя, приводя-
щая к выключению движителя (а=О), производится вблизи минимальных
значений а (1), где отрицательное влияние зарядки на выполнение кинема-
тических условий становится наименьшим.

ИДЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
Для определения оптимального значения параметра 1 (см. (12.23)) полу-
чается соотношение
(12.33)
Пока значения 1 из (12.33) удовлетворяют условию ~ ) О, система с на-
копителем энергии имеет преимущество перед системой без накопителя.
Обозначим через Я,Т/а)' величину безразмерной комбинации удельных
масс накопителя и источника мощности, соответствующую обращению в нуль
оптимального значения ~. Тогда применение накопителя энергии с удельной
массой ~, в сочетании с идеально регулируемой двигательной системой
с удельной массой источника мощности а' целесообразно при выполнении
соотношения
(12.34)
), Т/а' ( (3, Т/а) .
Для определения величины Я,Т/а)' соотношение (12.33) разрешается
относительно ~,/ а:
(12.35)
Интегралы в правой части уравнения (12.35) могут быть вычислены по функ-
ции р„(1) [12.5~.
Если исследуется предельный случай двигательной системы без источ-
ника мощности, то соотношения (12.19) остаются в силе, надо только поло-
жить
У
~,Т ' а2сИ
е 2 Че
ЛХ,, =О,
(мощность Л~, отнесена к Е,/Т). Уравнения вариационной задачи (12.22)
меняются аналогично тому, как это делалось в конце предыдущего пункта;
функционалом становится
а2Ж
~е
О
12~ 1+ ~
7з 1+ бх — хз
Минимум этого выражения по ~=ЛХ,/ЛХ„достигается при
~,Т/а = 3 (2 — х')/(1+ 2х')
(12.36)
4. Маневры перемещения между точкамн покоя и поворота плоскости
круговой орбиты. В качестве примеров решения общей задачи рассматри-
ваются два указанных маневра, для которых уравнения вариационной за-
дачи интегрируются до конца [12.3~.
Для задачи перемещения мелсду точками покоя (и,=и,=О), расположен-
ными на расстоянии 1 (г,=О, г,=1), за время Т при отсутствии накопителя
энергии функционал (12.21) равен (7.33).
Аналогично и. 2 по соотношениям (12.23) при известной функции р', (~)
строятся оптимальные программы Е (~), Г, (~) и а (~). Они изображены на
рис. 12.6, где ~,,='/, (Т+ ~а/~,Т). После интегрирования уравнений (12.22)
по участкам и удовлетворения граничных условий находится функционал
(12.20):

390
[гл. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
и равен
Х,/Х, = Ф,(Ф, = (1 + 2ю') '
(12.37)
На рис. 12.7 показана зависимость (12.36) оптимального отношения
М,/̄— массы накопителя к массе источника — от безразмерного пара-
~е~ра ~,Т/~. Уменьшение функционала Ф при переходе к системе с накопи-
телем показано на рис. 12.8. Выигрыш в полезной нагрузке определяется
г;,'т г, т г
Рис. 12.6. Оптимальные управ-
ления — перелет между точ-
ками покоя.
Рис. 12.7. Оптимальное отношение массы
аккумулятора анергии к массе источника
мощности М,/М, — перелет между, точ-
ками покоя.
с помощью данных этого рисунка по первой формуле (12.19) или по рис. 12.4.
Видно, что в задаче перелета между точками покоя двигательная система
ограниченной мощности с накопителем энергии имеет преимущество перец
системой без накопителя в диапазоне 1 ( ф,Т( а ( 6. При 0 (~ ф,Т~ а (1,
(
Рис. 12.8. Относительное умень-
шение функционала Ф,/Ф ~—
перелет между точками покоя.
Рис. 12.9. Оптимальное управле.
ние — поворот плоскости орбиты.
как отмечалось выше, выгодна система с накопителем, но без источника
мощности (М„=О на рис. 12.7), для которой
Ф,/Ф, =% ф,т~и).
В задаче о повороте плоскости круговой орбиты радиуса г на угол ~
за г оборотов с идеальным двигателем ограниченной мощности без накопле-
ния энергии функционал (12.21) определен в гл. 7 — (7.75).
Для задачи с накопителем можно показать, что оптимальные законы
изменения Е (1), К, (1), а (1) — периодические функции времени, повторяю-
щиеся через пол-оборота. Характер их изменения на одном обороте показан
на рис. 12.9, где

391
э 2]
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
(время ~ отнесено к Т = ~/г,/д„— периоду оборота, деленному на 2~; д„—
гравитационное ускорение на радиусе г„).
Формулы для оптимального значения ~ и мипимального отношения Ф,/Ф,.
аналогичны (12.36) и (12.37):
В,Т„1 + соя х + 1/г
а;с + я1в х — х соя х '
(12. 38)
Зависимости М,/Я, и Ф,/Ф,. от ~,п Т„/а (г ҄— время прохождения
половины оборота, т. е. максимальное время зарядки) для различных зна-
чений г даны на рис. 12.10 и 12.11. Видно, что в диапазоне 1/,г ( ф,~Т„/ а (~
& t; 2+ /г оказывае ся выгод ой двигатель ая сист ма ограничен ой мощно
Ф~э
4
Р8
р~ ~~т
Рис. 12.10. Оптимальное отношение массы
аккумулятора энергии к массе источника
мощности М,/М, — поворот плоскости ор-
биты.
Рис. 12.11. Относительное уменьшение
функционала Ф,,/Ф; — поворот пло-
скости орбиты.
с накопителем энергии, в диапазоне 0 ( ~, хТ„/ а ( '/, г — двигательная
система с накопителем энергии без источника мощности; при этом Ф,/Ф,.=
=я ('.,—.Т„/а) (см. линейные участки на рис. 12.11).
Выигрыпп в полезной нагрузке, как и в первом примере, определяется
с помощью данных рис. 12.11 по первой формуле (12.19) или по рис. 12.4.
$ 2. Двигатели ограниченной мощности с аккумулятором
энергии — дополнительные ограничения
на характеристики движителя
В предыдущем параграфе движитель считался идеально регулируемым
и невесомым. При отсутствии аккумулятора оптимальный режим его работы
получался непрерывным (тяга конечная), хотя прямых ограничений на тягу
и не накладывалось. Это связано с тем, что мощность, подводииая к движи-
телю, конечная и при увеличении тяги падает скорость истечения. Наличие
аккумулятора приводит к появлению импульсных режимов (тяга бесконеч-
ная), так как становится возможным подводить к движителю бесконечную
мощность. Помимо участков с импульсным приложением тяги, в состав оп-
тимального управления по-прежнему входят участки с конечной тягой.
Предположение о невесомости движителя в таком случае становится
малопригодным, поскольку удельная масса движителя велика, а оптималь-
ная тяга в некоторые моменты бесконечна. Кроме того, предъявляются тя-
желые требования к регулируемости движителя: тяга должна меняться от
конечных значений до бесконечности. Ниже исследуется влияние реальных
свойств движителя на параметры оптимального движения. Рассматриваются
следующие варианты.

392
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
1~ Тяга и мощность Г1, подводимая к движителю, постоянны либо
равны нулю; масса движителя пропорциональна потребляемой мощности
(п. 1, [12.31).
2~ Тяга ограничена сверху и снизу (либо нуль), мощность движителя
постоянна (либо нуль); масса движителя пропорциональна потребляемой
мощности (п. 2, [12.71).
Другие варианты регулировочных характеристик движителей рассмот-
рены, например, в [12.7, 12.9, 12.10, 1.71].
В предположении малого изменения массы аппарата условия, наклады-
ваемые на тягу (1', 2'), заменяются соответствующими условиями на реак-
тивное ускорение.
1. Нерегулируемый движитель. Нерегулируемая двигательная система
характеризуется постоянством величины тяги (при постоянной мощности
реактивной струи). Допускается изменение направления тяги и выключение
движителя. Рассмотрение этого второго предельного случая дает нижнюю
границу возможностей системы.
Запись дифференциальных уравнений (12.7) здесь несколько изменяется
(для первых двух уравнений):
т.= — Й Р~И», Ь'=Й,[Ж, (1 — Р) — (Ж вЂ” 1) Р~
(Р (~) = 1 или О, Ж = сопзВ, О (Ж (~) (1).
(12Л9)
Управляющая функция Р (~) может принимать только два значения:
нуль и единица (при этом показатель степени при Р в (12.7) можно опустить).
~е
Рис. 12.13. Умсиьше функционала 1 /Ф* — пе-
релет между точками покоя, нерегулирусмьш
двигатель (пункт'1рная ес~эива51 — относительное
уменьшение функционала Ф (~ * по сравнее1111о
С ИДеаЛЬЕ10 РЕГУ.111РУЕМЫМ ДВИГатсЛЕМ ПРИ и=0).
Рис. 12.12. Оптимальное отношение массы
1кк~мулятора и массе источника мощности
ЛХ,/М, — перелет между точками покоя,
нерегулируемый двигатель.
Мощность Г», потребляемая движителем, постоянна, она является управля-
ющим параметром (отнесена к Г,„). На активных участках (Р=1) происходит
разрядка с постоянной мощностью à — 1: Е= — Й, (Г,— 1), на пассивных
(Р=О) — зарядка с мощностью О ( Г„(~) ( 1: Е=-Й,Г„.
Уравнения движения записываются по-прежнему, управляющая функ-
ция е (1) (направление вектора тяги) сохраняется.
Для упрощения условие постоянства тяги заменяется условием постоян-
ства реактивного ускорения (12.16). Это справедливо, если относительная
масса рабочего вещества т„значительно меньше единицы. Кроме того, масса

393
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУМУЛЯТОРОМ ЭНЕРГИИ
движителя, в отличие от (12.6), принимается пропорциональной потребляе-
мОЙ мощности:
(12.40)
т = ((/а) т„т.
В таком приближении можно до решения полной задачи найти оптимальную
массу источника мощности. Величина полезной массы т и массы двигатель-
ной системы т„=т„+т,+т„выражается формулами (12.19), где
1
7
(12.41)
Для системы без накопителя функционал Ф (с учетом массы движителя
(12.40)) равен
7
2
О
(12.42)
(в формулах (12.41) и (12.42) а' (~)=а„-'Р (~), а,=сопят, Р (~)=1 или 0). Ва-
риационная задача записывается аналогично (12.22):
у + У,р
Т
Е = —;[~'~', (1 — Р) — (~~, — 1) Р~,
У,(Т) = т1п,
Е (0) = 1, Е (Т) = О,
) (12.43)
г(0) =г„
т(0) =т„
~е(й)(:— 1,
Ж,
г(Т) =г,
т (Т) =т
0~(Е(~) (1;
а, = сопят).
Г=~,
т= а,Ре+ ~,
(Р(й) = 1 11ли О,
О<У,, ~)
Помимо управляющих функций Р (~), Г„(~), е (~) задача содержит три
постоянных управляющих параметра а„Г», ~. Для выбора оптимальных
значений этих параметров можно получить условия, воспользовавшись прие-
мом, описанным в п. 2 предыдущего параграфа.
Не выписывая состава оптимальных управлений, приведем результаты
решения для рассмотренных в ~ 1 модельных задач.
В задаче о перемещении между точками покоя отношение функционалов
(12.41) и (12.42) равно
Ф, 4 (в (1 — 4~„, + 2Ц) — 2ф
Ф" 27~„(1 — 4~„) (1 — $,)2 (1 + а) а
(12.44)
где оптимальные параметры ~ и ~„, введенные вместо а, = Г'(1 — ~„) ', Ж =
=(1 — 1з) 1 ', находятся из соотношений
Т
(1 — 2~„),
(12.45)
2~'-.— ' 1 — З~ = О .
Ф, 2ь
6&g ;' 27~ -' '1 Ђ” ,) 1+
(12.46)
Зависимости отношений масс М,/М„и функционалов ~1>,/ ', от ф, /и
различных значений я =-,/а (отношение удельных масс движителя и источ-
ника мощности) приведены на рис. 12.12, 12.13.
При,'~ Т)о. ( (3,Т/а)' более выгодным оказывается применение системы
без источшпса ыощцости; тогда

394
[ГЛ. 1'
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕ]Й
В рассматриваемой задаче значение функционала У для постоянного реак-
тивного ускорения с выключением равно
Х,"=13,5 «, [1+ «),
«««",~,=Б,«5 —, [1+ «)
[12.47)
Для сопоставления на рис. 12.13 пунктирной кривой показано отноше-
ние Ф,/Ф, при т/ а=О (вместо Ф,/Ф*,). Из сравнения этой пунктирной кривой
и рис. 12.8 видно, что, как и в случае двигателя ограниченной мощности
без накопителя, переход от идеально регулируемой двигательной системы
ф Д~ю
Сб
Рис. 12.14. Оптимальное отношение массы
аккумулятора к массе источника мощности
М,/М, — поворот плоскости орбиты, не-
регулируемый двигатель.
Рис. 12.15. Относительное уменьшение
функционала Ф~/Ф; — поворот плоскости
орбиты, нерегулируемый двигатель: 1—
з=со, 2 — з=З, 3 — з=1, 4 — з='/2.
к нерегулируемой требует небольшого увеличения функционала Ф. С умень-
шением параметра ~,Т/а различие стирается, так как обе системы переходят
в импульсный режим.
В задаче о повороте плоскости орбиты отношение функционалов равно
1,45 [~я $д г„+ вта„В8' ~„[~„— тт/4) ]
+ к) я1п~ ~„[~„[тт — 2т„) — [тт — Зт„) $д ~„]
|:,Т, [т„+ т/,~т~) 1я ~„— т/,. и„— ~„-'
«т ~„'- [тт — 2~„) — [- — Зт„) ~„Вд ~„«
| у 2~ ' ' 2 9уТз °
Ф,
Ф", я[1
1е и
а
[12.48)
Я
48 ЯП1 ~
Система без источника мощности имеет преимущество в диапазоне 0(
~(~, Т„/а ( [~3, Т„/а)~:
ф 0,3625~ а
Ф'" [1+ а) [я1п й„— й„соя Е„) я1п й„
',,Т„2й, соя й,„— ятп т„[1о 49)
° ° ° °
а 8г~„[я1п ~„— ~„соя ~,„)
По этим соотношениям построены рис. 12.14, 12.15. Выигрыш в полез-
ной массе от применения накопителя для рассмотренных примеров опре-
деляется, как и выше, при помощи рис. 12.4 или первой формулы (12.19).
2. Движитель с ограниченной тягой. Рассмотрим промежуточный слу-
чай между идеально регулируемым и нерегулируемым движителями. Пусть
тяга движителя может принимать все значения из некоторого диапазона
или обращаться в нуль, мощность, потребляемая движителем постоянна
либо нуль, масса движителя пропорциональна потребляемой мощности.
Когда затраты рабочего вещества на выполнение заданного маневра малы
по сравнению с общей массой аппарата, можно приближенно считать реактив-
ное ускорение пропорциональным тяге, развиваемой движителем. Обозначим

395
РЕАЛЬНЫЕ ДВИГАТЕЛИ С АККУ МУЛЯТОРОМ ЭНЕРГИИ
через а „верхнюю границу диапазона изменения ускорения от тяги, а через
а,„— нижнюю и введем в рассмотрение параметр регулируемости движи-
теля )~=1 — а~,/а „, причем О ( ) ( 1. Идеально регулируемой системе
соответствует значение )~=1, нерегулируемой — Х=О. Величину Х будем счи-
тать заданной, а значение а „выбирать из соображений оптимальности.
Используя принцип максимума Л. С. Понтрягина, нетрудно показать,
что активный участок может закончиться на одном из трех интервалов
регулирования ускорения: при а=а,„, при (1 — ~)а,„( а ( а,„и при а=
=а „(1 — Х).
В модельной задаче перелета между двумя точками покоя (с симметрич-
ными граничными условиями), если зарядка начинается на первом интервале,
значение функционала Х, не зависит
от Л: ~г
16 ([1 + (3,Т/а) г] (1 — г) + г)
(1 — гг) (1 + г)
(12.5О)
' Р РХ IР (Х Ф"
Сф
Рис. 12.16. Влияние параметра регулируемо-
мости Х на уменьшение функционала .7 — пере-
лет между точками покоя (сплошные кривые—
относительная масса движителя н=0, 1,
пунктирные — н= 0,01).
Оптимальное значение з определяется
из соотношения
~,Т 2 (1 — г)г — г (Зг — 1)
,г (1 г)з ( '~1)
В случае, когда пассивный участок начинается при переменном ускоре-
нии (а „(1 — Х) ( а (~) ( а „), функционал Х, записывается иначе:
12 ([1 + (В,Т/а) г] (1 — г) + г) (12уг — 16уг — гг)
(зр — 4р' — гг)г
Здесь р =1/, — -., где ~ определяется уравнением
Р.(.) = 2 ( ~ ' + ) ...
(
(12.53)
48 ( [1 + (Ь,Т/а) г] (1 — г) + г) [3 (1 — игг) — 4и (1 — иг)]
В
(12.54)
[3 (1 — игг) — 4уг (1 — иг)]г
Здесь и=1 — Х. Величина У, достигает своего минимального значения, рав-
ного
12 ([1 + (З,Т/а) г] (1 — г) + г) (1 + и ~')
(1+ ги/') [1+ 2и ~' — ги/' (2+ и ~')1
(12.55)
при 2 у = (1+я и'/*) (1+ й~ )-1. Абсолютный минимум величины Х„определяе-
мой соотношением (12.55), достигается при значении з, удовлетворяющем
соотношению
(1 + ги /') Д (и) + 3 (1 — г + г) и [и — г (2+ и ~')1
(1 — 2г) (1 + ги /') Ч (и) — 3 (1 — г) и. [и — г (2 + и ~')]
Ь,Т
(12.56)
Из условия минимума Х, по ~ (это соответствует минимуму Х, по а,„) полу-
чается ~=я/2. Подстановка этого результата в (12.52) приводит соотношение
лля Х, к виду (12.50). Таким образом, оптимальное значение а„„„таково,
что система и в этом случае работает как нерегулируемая (а (~) =а,„,„).
Наконец, если пассивный участок начинается при минимальном зна-
чении ускорения, функционал У, может быть записан в следующем виде:

ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
где ~ (а) =1+2а" — Ы~ (2+о~'). На рис. 12.16 показана зависимость от
$,Т~и и Х отношения функционала Х, для системы с ограниченным диапа-
зоном изменения ускорения и накоплением энергии к соответствующему
значению функционала Х, для системы без накопителя:
(12,57)
Данные рис. 12.16 иллюстрируют уменьшение функционала У (и соответ-
ственно увеличение полезной нагрузки — см. рис. 12.4) от применения
накопителя энергии при наличии ограничения на диапазон регулирования
ускорения от реактивной тяги.
$ 3. Двигательные системы с накоплением атмосферного газа
Значительную (а во многих случаях и преобладающую) часть массы кос-
мического летательного аппарата в оптимальном варианте составляет рабо-
чее вещество (топливо). В работах [12.13 — 12.251 показано, что если выводить
аппарат на орбиту «пустым» (или с некоторой частью запаса рабочего веще-
ства), а «заправку» производить уже на орбите, то существенно снижается
вес ракеты-носителя.
Заправку предлагается осуществлять следующим образом [12.13 — 12.19].
Аппарат снабжается воздухозаборником. Исходная орбита выбирается так,
чтобы она проходила в верхних слоях атмосферы. При движении по орбит«
аппарат захватывает атмосферный газ и сжижает его. Накопив нужное ко-
личество газа, аппарат выполняет заданный маневр. Обсуждается и другой
вариант заправки [12.19]: на орбиту предварительно выводится аппарат-
заправщик, который накапливает атмосферный газ; через определенное время
на орбиту выводится космический аппарат с пустыми баками, аппарат-за-
правщик «переливает» накопленный им газ в баки космического аппарата,
после чего космический аппарат выполняет требуемый маневр.
Сравнение этих двух схем заправки на орбите между собой и с исходной
схемой заправки на Земле производится по относительной полезной массе
космического аппарата. В первой схеме полезная масса относится к «сухой»
массе космического аппарата. По сравнению со случаем заправки на Земле
«сухая» масса аппарата здесь увеличивается из-за дополнительных систем:
воздухозаборника, установки сжижения и пр. Если эта дополнительная
масса меньше, чем масса рабочего вещества, необходимая для совершения
маневра в случае заправки на Земле, то первая схема заправки на орбитв
дает выгоду. Во второй схеме заправки на орбите собственная «сухая» масса
космического аппарата остается такой же, как и при заправке на Земле.
Но зато здесь выводится на орбиту дополнительный аппарат-заправщик.
Его «сухая» масса при анализе распределяется между заправляемыми кос-
мическими аппаратами, так что «сухая» масса космического аппарата, фи-
гурирующая при вычислении относительной полезной массы, увеличивается
на «сухую» массу аппарата-заправщика, деленную на максимальное число
заправок. Если эта добавка к массе меньше массы дополнительного обору-
дования, необходимого в первой схеме, и меньше необходимого запаса ра-
бочего вещества при заправке на Земле, то вторая схема заправки на орбите
более выгодна. Ее преимущества, естественно, возрастают при увеличении
максимального числа заправок.
1. Характеристики двигательной установки с накопителем рабочего
вещества. Принципиальная схема двигательной установки, предназначен-
ной для накопления рабочего вещества при движении в верхних слоях ат-
мосферы, показана на рис. 12.17 из [12.191. Такая установка содержит ги-

397
ДВИГАТЕЛИ, НАКАПЛИВА10ЩИЕ АТМОСФЕРНЫЙ ГАЗ
перзвуковой воздухозаборник 1, систему сжижения 2, бак для накапливаемого
рабочего вещества 8, движитель 4 для компенсации аэродинамического со-
противления, источник мощности б, питающий движитель и систему сжи-
жения радиатор 6 для отвода тепла [12.13 — 12.19]. Если тот же самый ап-
парат предназначается для выполнения внеатмосферного маневра, то в со-
став двигательной установки могут включаться дополнительный движитель
Рис. 12.17. Принципиальная схема двигательной установки с пакоплеписм рабочего вещества.
и бак с дополнительным запасом рабочего вещества, необходимого для ра-
боты этого движителя (например, по условглям химической реакции).
Секундный приход массы через воздухозаборник равен
(12.58)
д„= рой,
где с — плотность атмосферы, и — скорость движения аппарата (предпола-
гается равной скорости набегающего потока — неподвижная атмосфера),
Я вЂ” площадь входа воздухозаборника.
Аэродинамическое сопротивление аппарата запишем в виде
1 ., 1
== — с;.г-'Я=- ~ с.~'О,.,
(12.59)
(12.60)
(Й, = сопз1).
Часть сжиженной массы воздуха потребляется движителем (расход д),
предназначенным для компенсации аэродинамического сопротивления. В ста-
ционарном режиме тяга движителя Р=д7 должна быть равна сопротивлению
(12.59). Чтобы при этом осуществлялось накопление (д„— д ) О), скорость
истечения движителя Г должна быть больше скорости движения аппа-
рата и. Для круговой орбиты спутника Земли и=8 км/сек, поэтому в качестве
движителя для аппарата-накопителя рассматриваются электрические
где с — коэффициент аэродинамического сопротивления (отнесено к площади
Я входа воздухозаборника). Если пренебречь трением и считать, что весь
аппарат находится в «тени» воздухозаборника (рис. 12.17), то аэродинами-
ческое сопротивление равно импульсу струи гд„захватываемой воздухо-
ааборником (с„=2). Эти предположения справедливы для разреженной ат-
мосферы при конфигурации аппарата типа обратного усеченного конуса.
Более подробное обсуждение данного вопроса можно найти, например, в ра-
боте [12.19].
Захваченная масса газа или ее часть, используемая непосредственно
для накопления (за вычетом расхода через движитель), направляется в уста-
новку сжижения. Эта установка потребляет мощность Г„, пропорциональную
секундному приходу массы. Далее предполагается, что сжижается вся масса,
приходящая через воздухозаборник, поэтому

398
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
[ГЛ, 12
движители. Таким образом, часть Ж мощности Ж,, вырабатываемой источ-
ником, должна тратиться на питание движителя:
(Т +Т,=У„),
(12.61)
где ~1 — коэффициент полезного действия движителя.
т
Уравнение для массы М, накапливаемого рабочего вещества с учетом
расхода д через движитель запишется в виде
м„= (д, — д).
(12.62)
Полную массу М„двигательной установки аппарата-накопителя составляют
следующие компоненты [12.13 — 12.19]: масса воздухозаборника и установки
сжижения М„пропорциональная максимальному секундному приходу
массы др тах
Мр — ~ядр тах
(~, = сопзВ),
(12.6,3)
масса источника мощности М,, пропорциональная максимальной выраба-
тываемой мощности Ж„:
М =Ижо
(а = сопз1),
(12Я)
масса движителя М, пропорциональная максимальной тяге Р или макси-
мальной потребляемой им мощности К,:
~0.
М =~Р или М =~%~0
(~ = сопз1),
(12,65)
масса бака М~, пропорциональный максимальной массе рабочего веще-
ства М„,(Т,):
м,=3.м„(т,)
ф = сопзВ).
(12.66)
2. Накопление в стационарном режиме. Рассмотрим задачу выбора
оптимальных параметров и оптимального режима работы двигательной
установки аппарата-заправщика |12.13 — 12.21~.
Задача ставится следующим образом: при заданной стартовой массе
М, за фиксированное время Т, накопить максимальное количество рабочеге
вещества М,. Можно использовать постановки, эквивалентные данной:
накопить заданное количество рабочего вещества за фиксированное время
при минимальной стартовой массе или за минимальное время накопить за-
данное количество рабочего вещества при фиксированной стартовой массе.
Будем считать, что орбита, на которой производится накопление, кру-
говая, плотность атмосферы вдоль орбиты постоянна, тяга движителя в каж-
дый. момент времени равна сопротивлению (стационарный режим).
Учитывая условие равенства тяги и сопротивления, запишем выраже-
ния для массы накопленного за время Т, рабочего вещества М, и начальной
массы 1) ЛХ, в виде
(12.67)
') Учитываются только те компоненты массы, которые непосредственно связаны
с накоплением.

ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
ь
1 ——
м„„и„„
м, м,т„
Ь,Г+6,— — '
(12.68)
Ь 2Т„+2ай.+ус У, Рт
3
& t
2 си,
Ь~ — с ВгТ
1
Ь.,=
'Э г у
т
Будем считать к. и. д. движителя ~ не зависящим от скорости истечения
Г и потребляемой движителем мощности К„. Если орбита накопления фик-
сирована (и, с =сопзФ), то коэффициенты Ь, Ь„Ь„Ь„постоянные и задача
сводится к отысканию максимума (12.68) по Г. В результате получим
г„,=ь, 1+)/1+ "'„', ",
Р. 6 ~/1 + (616З вЂ” Ь4)/6,62
Л~о тах 26 Ь, )- Ьз+ (Ь Ь2 — 26,)/Ь + (26 62+ 6 ) \/1+ (Ь Ь вЂ” 64)/616
(12.69)
остальные параметры двигательной установки вычисляются по формулам
Д вЂ” ~О ~а~ ~~3
д,,с г
Д:
(12.70)
Если в формуле для массы учитывать только массу источника мощности
(ЛХ, = ЛХ„, („= ( = ~ = О) и пренеоречь мощностью, потребляемой установ-
кой сжижения (/с„=0), и положить с„=2, то соотношения (12.69), (12.70)
ау
значительно упростятся 61 = у, 62 2 ~3 ~4 О
~т
Я,
~~о 2а~2
д„=2д = ЛХ,
Г„„= 2и,
(1 .71)
Сравнивая выражения (12.69) и (12.71) для оптимальной скорости исте-
чения, видим, что при учете дополнительных компонент массы и доли мощ-
ности, расходуемой на сжижение, уровень скорости повышается.
В рамках данной постановки параметры орбиты накопления входят
только через скорость полета и и коэффициент аэродинамического сопротивле-
ния с (если не считать соотношения для площади воздухозаборника Я, по-
следняя определяется после решения задачи). Величины г и с для диапазона
высот (100 — 120 км для Земли), где рассматривается накопление, практически
постоянны. Поэтому для выбора оптимальной высоты орбиты нужно привле-
кать дополнительные соображения, связанные с тепловыми режимами, соот-
ношениями площадей воздухозаборника и миделя аппарата и пр.
Приведем численный пример для случая накопления у Земли (и
8 км/еек, с =2). На рис. 12.18 дана зависимость относительной скорости
накопления М „/ЛХ, из (12.71), где ЛХ,=ЛХ„, от удельной массы источника
мощности а, отнесенного к к. п. д. движителя ~) . Отметим, что обратная ве-
личина ЛХ,/М „равна времени, за которое накапливается количество газа,
равное по массе источнику мощности. Оптимальная скорость истечения
в рассматриваемом случае равна 16 км/сек. На орбите высотой 100 км при
площади воздухозаборника 1 м' накапливается — 200 кг воздуха в сутки.
Начальная масса ЛХ, и время Т„фиксированы; выразив д, из второго со-
отношения (12.67), получим относительную скорость накопления в функции
скорости истечения

400
ДРУГИЕ ТИПЫ ДВИГАТЕ~ И'Й
[ГЛ. 12
3. Накопление в нестационарном режиме. Рассмотрим задачу оптими-
зации программы управления вектором тяги идеального движителя на одном
обороте плоского движения накопителя в поле сжатого сфероида. Оптималь-
ная программа управления должна обеспечивать максимум накопленной
массы газа за время движения и равенство координат и скоростей аппарата
в начале и конце движения И2.22 — 12.24]. Уравнения такой вариационной
задачи можно записать в виде
М=д, — д,
и(о) =и„
г (О) =г„
ЛХ (1,) = шах,
г (1,) = г„
г=ч,
(12.72)
Ф=ае
т(0) = т„
т(1,) =1,.
З десь ЛХ вЂ” масса аппарата-накопителя, г, т — радиус-вектор и скорость
аппарата, а — модуль реактивного ускорения, à — сила аэродинамического
сопротивления, ф — гравитационное ускорение.
Полагая, что аппарат обладает флюгерной
устойчивостью, подчиним векторы Г, е и ~
~ф связям:
~~-8 ЮУ е ° ~
)е)— : 1,
Гравитационное ускорение р' определяется
потенциалом Г Земли: и = — д Г/дг. Запишем
потенциал поля тяготения Земли в сфериче-
ских координатах. При этом ограничимся
только первыми двумя гармониками потен-
циала сжатого сфероида:
Г= — ~1+ — ', (1 — 3 з1п'~ я1п-г)~,12.74)
г г~
й' ЮГ '
/Д~~Б
Рис. 12.18. Скорость накопления
~~~/М, (сплошная кривая и харак-
те рное время накопления ЛХ,/ЛГ„~
(пунктирная кривая).
где р, — плотность атмосферы на некоторой опорной высоте Й„) =сопз1.
Высота Й полета может быть представлена в виде функции координат ап-
парата, движущегося по орбите с наклонением и
л, (1 — в)
(12.76)
(1 — (2 — в) ~ (1 — яп2 р яп2 ь)) ~' '
где ~=1 — Лд/Л,=0,00352 — эксцентриситет эллипсоида вращения (мера
сплюснутостн Земли), Л„Лд — экваториальный и полярный радиусы Земли.
Величина Р силы аэродинамического сопротивления в принятых до-
пущениях определяется по формуле
г" = — с,а (Й) и'Я,.
х'
(12.77)
(величины Й и В=7Л';/3 приведены в гл. 1 — (1.11)).
Здесь использовано представление геоцентриче-
ской широты О через аргумент широты ~ и на-
клонение ~ орбиты движущейся точки.
Считается, что движение происходит в покоящейся атмосфере (скорость
набегающего потока равна скорости аппарата). Изменением плотности от
геоцентрической широты пренебрегается, поверхности постоянной плотности
полагаются эквидистантными поверхности Земли. Зависимость плотности
у атмосферы от высоты Й полета, необходимая для расчета аэродинамического
сопротивления, аппроксимируется экспонентой:
о=р,ехр~),(Й вЂ” Й И, (12.75)

дВиГАтели, нАкАплиВА10щие АтмОсФеРныЙ ГАз
Здесь с — коэффициент аэродинамического сопротивления, отнесен к пло-
щади Я, входа воздухозаборника.
Регулировочная характеристика идеального движителя описывается
соотношениями
Р = д Г = 2Ут~„/Г,
0(Л(Т„
~ =сопя~,
т
(12.78)
Здесь à — скорость истечения реактивной струи, à — мощность, потребляе-
мая движителем, à — максимальная мощность, вырабатываемая источни-
ком, т~, — коэффициент полезного действия движителя. Затратами мощ-
ности на сжижение накапливаемого газа пренебрегается. В этом случае вся
иощность источника потребляется движителем и выбор закона управления
тягой эквивалентен отысканию оптимального закона изменения скорости
истечения.
Поскольку рассматривается движение аппарата только на одном обо-
роте, то изменением массы аппарата за счет накопления газа в последнем
уравнении системы (12.72) можно пренебречь. Кроме того, при описании дви-
жения аппарата в этом случае в качестве независимой переменной удобнее
использовать угловое перемещение е и сферическую систему координат.
Тогда, после введения безразмерных величин и учета связей (12.73) — (12.78),
вариационная задача записывается следующим образом:
т (О) = 1, т (2тт) = тах,
г (2тт) = г,
г(0) =г„
(12.79)
~„(0) = ~„„~„(2т~) = ~„„
~ (0)=г„~ (2тт)=~
д, = Йг-')
ИО—
Здесь скорости отнесены квеличине (Й'~*г.'~*), линейные размеры — к величине
г радиуса-вектора базисной орбиты, ~, — безразмерное ускорение от силы
сопротивления на базисной орбите в момент ~=0.
ги„ аОГГу 1 гии
П=р — ~+ р +и — — (Зйп2~ япву — 1) — — — ~е — е ~~~ ~'~ +
У ~у УУ Г т Г И у г О у
+ р — — у„+ —. яп2 т' втп 2у — /его„е ~ '~ + р,„— — /ее ~ '~ — —, (12.80)
г 2и ~~ ~ ао
Х
И3 условия максимума которой находится оптимальное управление — скорость истечения
2п
ра "+ ра 'тр
Оу У Фтр
(12.81)
26 Механика полета
В соответствии с принципом максимума Л. С. Понтрягина выпишем гамильтонову
функцию ХХ:

402
[ГЛ. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
Дифференциальные уравнения для импульсов р, имеют вид
р =О,
ад ЗХ
а
— р, —,о — 4 я|п21я1п2у +р
~Р
(12.82)
1
х
+ р, 1+ —.,„+ —, (3 я1п'1я1п'у — 1) + р, —,, я1п' г я1п 2у—
Ч
2Ц ЦЗ ~гр 2 1 Р ~ )
0 ~7~ у С ~тщ~ ~~р у
)
а граничные условия для них записываются в виде
р„, (2-,.) = 1.
(12.83)
Таким образом, рассматриваемая вариационная проблема сведена к крае-
вой задаче третьего порядка. Ее решение зависит от четырех траекторных
параметров: ~, г„и„, и~,. В работе ~12.231 исследовалась зависимость ре-
шения от двух варьируемых параметров — наклонения орбиты ~ и радиуса-
вектора г, точки старта — при и„=0 и и =г„'~*. Более сложной задачей явля-
ется исследование зависимости функционала от наклонения орбиты ~ при оп-
тимальных значениях г„и„„и~,. В этом случае для каждого фиксированного
значения ~ требуется многократное решение сформулированной задачи
с целью оптимизации функционала по г„и„е, и~, или другая формулировка
задачи.
В новой формулировке задачи граничные условия для системы (12.79):
г (О) = г (2-.),
и (О) = и (2~)
и„(0) = и„(2~),
(12.84)
и соответствующих импульсов:
р„ (О) = р„ (2-.), р, (О) = р, (27~), р, (О) = р„ (2тс).
(12.85)
Решение краевой задачи- шестого порядка, описываемой уравнениями
(12.79), (12.82) — (12.85), дает значения функционала, максимизированного
по управлению Г и начальным значениям фазовых координат г„и„, и~,,
Начальное приближение для решения этой задачи можно получить из пред-
положения оптимальности круговых орбит для траекторий, лежащих в плос-
кости экватора.
При движении по круговой экваториальной (~=0) орбите уравнения
движения интегрируются и оптимальная скорость истечения выражается

403
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
через параметры орбиты:
1 г. /г
~0'
9 1
го го
(12.86)
Уравнение для оптимального значения радиуса орбиты г, получается из
уравнений для импульсов и имеет вид
(4Лг — 1) е ~" ~~
ад с ух (4г+ 1 — Ьх~гес2)
(12.87)
Скорость накопления в этом случае также постоянна и равна
2г~о ехр (Л (1 — г) ) [2Лг + 3 — бх/(г2 — х) )
с (4Лг+ 1 — Ы~(г~ — хЦ
(12.88)
Решение краевой задачи для ненулевых наклонений орбит (~ ) О) мо-
дифицированным методом Ньютона показало, что соотношения (12.86),
(12.87) обеспечивают хорошую сходимость итерационного процесса.
Численное решение задачи получено для следующих значений парамет-
ров задачи:
е=0,3352 10 ', 6,=120 км, р,=2,63 10 а,
Л= 865, с =-2, ~,=0,4 ° 10
(12.89)
а,=0,8 10 '.
Результаты расчетов показали, что изменения скорости истечения К, „
дысоты Й и составляющих скорости полета г„и по г носят периодический
характер (период ~=~).
На рис. 12.19 показаны оптимальные программы изменения скорости
истечения Г„„(~) для различных наклонений орбит. Приведенные результаты
показывают, что оптимальная скорость истечения практически постоянна.
( ~ 5 Ф ~ Р,Ра~
Рис. 12.19. Оптимальные программы скорости истечения.
26~
Изменение высоты полета аппарата-накопителя Й,~, (~р) для орбит с раз-
личными наклонениями показано на рис. 12.20. Высота полета колеблется
относительно оптимальной высоты экваториальной круговой орбиты в до-
статочно узком диапазоне (-15 км).
Оптимальные значения г„~„г„е,~, и соответствующих им импульсов
показаны на рис. 12.21.

р, рад
/ЯП5
дУЯ85
Рис. 12.21. Недостающие пачальные значения.
Д7 ш~~
Рис. 12.22. Оптимальный закон накопления массы.
404
~®,нм
Юб
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
Рис. 12.20. Оптимальная высота полета.
1п'о
~ппп п,г
ПЯУ5 д/
п,55
6 р,~ад

405
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫИ ГАЗ
(12.90)
Начальная масса ЛХ, аппарата на орбите накопления складывается из
полезной массы М, массы двигателя М,, некоторого начального запаса ра-
бочего вещества М, и массы установки сжижения атмосферного воздуха М,:
М,=М,+ ЛХ„+М, +М„.
(12.91)
На орбите накопления часть мощности бортовой энергостанции потребля-
ется двигателем для создания тяги,' компенсирующей силы аэродинамического
сопротивления, оптимальная мощность, пропорциональная расходу воздуха
через установку сжижения, идет на сжижение атмосферного воздуха. В даль-
нейшем считается, что в каждой фазе маневра мощность бортового источника
используется полностью, т. е. Г (~)= — Г,„. При секундном расходе массы
через движитель д, скорости истечения реактивной струи Г, расходе воздуха
Изменение величины накапливаемой массы в процессе движения ап-
парата по оптимальной орбите показано на рис. 12.22. Видно, что для орбит
любого наклонения накапливаемая за один оборот масса постоянна. Таким
образом, оценку величины накапливаемой массы, полученную для эква-
ториальных орбит, можно распространить на оптимальные для данного ап-
парата орбиты с любым наклонением.
Если г задается произвольно, а составляющие скорости в точке старта
подчинены условиям г„,=0 и г~,=г '~-, то решение задачи (12.79), (12.82),
(12.83) приводит к иным результатам [12.231. Так, оптимальная скорость
истечения оказывается на некоторых орбитах знакопеременной и изменяется
в очень широких пределах. Значения накапливаемой массы при переходе от
экваториальных орбит к полярным в этом случае также заметно (до 30%)
уменьшаются.
4. Внеатмосферный маневр аппарата-накопителя с двигателем ограни-
ченной мощности. Рассмотрим теперь аппарат, который после накопления
на орбите должен совершить внеатмосферный маневр. В фазе накопления
и в фазе выполнения основного маневра используется один и тот же двига-
тель ограниченной мощности. Его параметры уже нельзя выбирать, исходя
только из условия оптимальности одной из фаз маневра, — они долхсны обес-
печивать наилучшее выполнение маневра в целом [12.20, 12.221. Ниже опре-
деляются оптимальные параметры двигательной системы и оптимальное
время накопления в зависимости от характеристики маневра и удельных
характеристик системы. Находится область преимущественного использо-
вания двигательной системы ограниченной мощности с накоплением рабочего
вещества путем сравнения по полезной массе с системой без на-
копления.
Задача ставится следующим образом. Фиксируется время выполнения
двух фаз маневра Т, а время выполнения основного маневра определяется
как разность между этим временем и временем накопления Т„. Требуется
при заданной начальной массе М, обеспечить максимум полезной массы ЛХ,.
Орбита, на которой происходит накопление, считается круговой с неизмен-
ной по всей ее длине плотностью (стационарный режим накопления). Пере-
ходный участок в атмосфере с орбиты накопления на траекторию выполнения
основного маневра не рассматривается.
Двигательная система ограниченной мощности предполагается идеально
регулируемой, ее регулировочная характеристика и формула для массы
имеют вид

406
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
[ГЛ. 12
через установку сжижения д, соотношение (12.90) для массы двигателя при-
нимает вид
х ~ Д Лг хО'
(12.92)
Здесь Й, — удельные затраты мощности на сжижение единичного расхода
воздуха через воздухозаборник.
Полагая, что весь атмосферный воздух, проходящий через воздухо-
заборник площадью Я, и с коэффициентом расхода у, поступает в установку
сжиж ения, имеем
Д,, = /5,~ГО.
(12.93)
Здесь р — плотность атмосферы на орбите накопления, ге — скорость по-
лета аппарата.
Зависимость массы М„установки сжихсения от расхода воздуха через
нее принимается линейной:
ЛХ„= Ьд„+ Л„,
(12.94)
где ~ — удельная масса установки сжижения, М,, — масса установки сжи-
жения, не зависящая от расхода воздуха (масса установки сжижения при
бесконечно малом расходе воздуха).
Аппарат находится на орбите накопления в течение Т, (время накопле-
ния) и накапливает массу М „атмосферного газа, пропорциональную раз-
ности расходов через установку сжижения и движитель:
М,„= (д„— д) т„. (12 95)
Используем условие равенства тяги и силы аэродинамичсского сопротивления аппа-
рата на орбите накопления:
Ч Г = с.Ь',„"уО!2
(12.96)
(с — коэффициент аэродинамического сопротивления аппарата, приведенный к площади
воздухозаборника Я,). Тогда, принимая во внимание зависимость (12.91) и переходя
к безразмерным величинам
т = ЛХ;/МО,
а1Чтах [кет]
— ю~,
(12.97)
Т;[сек]
Т;—
-. [сек]
(т — характерное для данной задачи время, например, ресурс двигательной установки
или время выполнения некоторого характерного маневра), формулы, определя~ощие
массы отдельных элементов и аппарата в целом, можно привести к виду'.
начальная масса аппарата на орбите накопления
1 = т + т + т„+ т„, () 2.98]
относительная масса установки сжижения
Х,У
та 1,! ! + тао!
+Х~
(12.99)
относительная масса накопленного воздуха
(12.100)
т~,=х сЖТ,
относительная масса двигателя
(12.101)
т„= У+ т„О.
2 „~~(2
Х
~С У
х О
4Й,~2
(12.102)
7.,
ас-и.!
х 0
Х~с ' г °
Сх~О
Здесь х„, х„х~ — безразмерные копструктивные параметры, характеризующие
источник мощности, установку сжижсиия и удельные затраты мощности на сжижение
соответственно; они определяются формулами

407
ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫЙ ГАЗ
После накопления необходимого количества газа выполняется вторая—
внеатмосферная — фаза маневра (основной динамический маневр). Возможны
два варианта выполнения внеатмосферной фазы маневра. В первом варианте
установка сжижения входит в состав аппарата, выполняющего основной
ианевр. Начальная масса аппарата на основном маневре в этом случае опре-
деляется как
(12. 103а)
т,=1+т,.
(12. 103 б)
т,=1 — т„+т „.
Дифферонциальиое уравнение изменения массы аппарата па впеатмосферной фазе
маневра записывается в принятых перемсниых в виде
Ыпг(т« = — («„а«/Х) г1Е
(а — ускорение от тяги па внеатмосферном участке полета). Интегрирование (12.104)
от начала вноатмосферного маневра до конечного времени дает:
для случая (12.103а) — без сброса установки сжиження
с 7
а2~~
1'р
(1/т) [,",,'Р' = Ф,.,~Т
(12.105)
для случая (12.103б) — со сбросом установки сжиясения
()~т) ~1~,",',Р'",,'," = Ф,/У. (12.106)
В дальнейшем для краткости варианты выполнения внеатмосферного маневра без сброса
и со сбросом установки сжижения там, где это необходимо, будем называть (<вари нт
и инвариант 2» соответственно.
Используя (12.99) и (12.100) из (12.105), (12.106) можно получить выражения для
определения начального запаса рабочего вещества:
в ар иант 1
1+ .,с;Ут„
Ро 1+ (1+ «„сгуТ,) Ф,/Л'
(12.107)
вариант 2
«.„% 1 — т„, — «,Дг~'(«г, + г') г- «„сШТ
Тогда полезная масса находится по формулам:
в ар иант 1
1+ ~ с1ЧТ, .~.„Ж
1+ (1+ сЯТ„) Ф,,/Ж $' -~.~,
(12.109)
в ар иант 2
1 — т, — х„У/(«г, + Г) + «„сгг Т,
1+ [1 — т,о — л,Н~(«г, + Г) + «„сгУТ,) ф„ггпу
(12.110)
Определение времени накопления Т, возможно при конкретизации зависимости Ф,
от времени выполнения маневра Т. В качестве примера возьмем обратно пропорциональ-
ну~о зависимость, что соответствует задачам выхода из гравитационного поля центра,
перехода между компланарными круговыми орГ)итами и поворота плоскости круговой
орбиты, когда реактивное ускорение много меньше гравитационного (Ц 2, 3 гл. 7):
Ф Ду2(2
(12.111)
6 /~ С.~
Такой вариант может иметь место в том случае, когда установка сжижения
используется на промежуточной стадии маневра (например, для накопления
массы в атмосфере планеты при совершении перелета Земля — планета—
Земля) или по окончании данного маневра аппарат возвращается на орбиту
накопления и подготавливается для выполнения следующего маневра.
Во втором варианте установка сжижения по окончании фазы накопления
сбрасывается и начальная масса на фазе впеатмосферного маневра определя-
ется выражением

[ГЛ. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
(Л~ — относительное приращение характеристической скорости). После подстановки
(12.111') в (12.109) и (12.110) легко определяется оптимальное, в смысле максимума полез-
ной массы т„время накоплепия Т,,:
вариант 1
Т вЂ” »'х,сф/х,сФ
1+ Чх сф
(12.112)
вариант 2
Т вЂ” [1 — т,о — «„Т/(х~. + 1' ) [»» сф/«„с ~Ч
(12.113)
1+ ~.~ сФ
Пачальный запас рабочего вещества при этом равен:
вариант 1
т = 1 — «с/ЧТ~(1 + х сф)з;
(12.111)
вариант 2
1 — т„.о — х,,/Ч/(«~, +»') + х сХТ
.~,Ж
'7"р.о = 1 'п~о 7т +
(12.115)
(1 + ~/«,сф)
полезная масса равна:
вариант 1
1+ «,с ЧТ х,,/Ч
(12.1) 6)
в ариант,2
1 — т„о — «,/Ч/(х~, + Г) + «,с,'1'Т
(12.117)
(1 + ~/х„сф)
Анализ (12.114), (12.115) показывает, что при фиксированных значениях1пара
метров ~ и Р двигательной установки существует такая область параметров~,' маневра
ф и Т, в которой т, ( О. Это означает, что пакопленной массы хватает с избытком для
р.О
выполнения таких маневров. Поэтому в этой области припимаем т =О и время накопле-
ния определяем из условия накопления массы газа, пеобходимой для выполнения задан-
ного" маневра (Ф, Т) при пулевом начальном запасе рабочего вещества:
вариант 1
1 Ф 4Ф
»т[о — 2 Т ~у 1 1 «с1Ч« (Т ФЯ 1)'-'
(12.118)
«ариант 2
1 1 — т„о — х,/Ч/(х~, + )»)
Тгапп= 2 Т вЂ” Ф Х
4Ф [1 — т,о — х„/Ч/(х~„+ '»') [з
х с/Чз (Т вЂ” Ф [1 — т,.о — х,/Ч/(х~, + )»))/Й)«
(12.1) 9)
Полезная масса при этом в обоих вариантах выражается одинаково:
(12.120)
т« = 1 — «,М/(»~, + 7») — /Ч вЂ” т„о — т,.о.
ЙТ ~,,У
'7"« /ЧТ [ ф ь' [ „„~ '7"1о '7"~о
(12. 121)
вариант 2
1ЧТ
/ЧТ+ф Ч "о'
(12.122)
причем во втором варианте установка сжижения вообще не выводится на орбиту накоп
ления. Начальный запас рабочего вещества в этом случае определяется как
т„о = Ф/(!ЧТ+ Ф)
(12.123)
Кроме того, существует область параметров маневров такая, что оптимальное
время накопления (12.112), (12.113) становится отрицательным (начального запаса доста-
точно для выполнения таких маневров). Принимая для этой области Т,=О, из (12.109)
и (12.110) имеем:
вариант 1

409
ДВИГАТЕЛИ, НАКАПЛИВА10ЩИЕ АТМОСФЕРНЫЙ: ГАЗ
Лля обоих вариантов. Отметим, что соотношения (12.122), (12.123) и соотношение (12.121)
ПРИ х,=т,,0=0 ПОЛНОСТЬЮ СОВПаДавт С ИЗВЕСтПЫМИ СООТНОШЕНИЯМИ ДЛЯ аППаРатОВ С ДВИ-
гательной системой ограниченной мощности без накопления.
(12.124)
(12.125)
1ЧТ " то Ж т, 1 — 1 Ф ~с 3Т
(12.126)
вариант 2
хасУ Т
1),
(12. 127)
х с~ЧТ
(12. 129)
ДТ.
Я областях (12.124), (12.127) полезная масса определяется по формуле (12.120),
области (12.125) соответствует формула (12.109), области (12.126) — формула
(12.121), области (12.128) — формула (12.110) и области (12.129) — фор-
мула (12.122). При некоторых значениях Г и Г области (12.126) и (12.129)
могут вырождаться, и тогда зависимость т. (Ф, Т) имеет только два участка,
соответствующих областям (12.124), (12.125) или (12.127), (12.128).
выражения (12.109) — (12.129), таким образом, определяют значения
функционала — полезной массы т, — при фиксированных значениях па-
раметров двигательной установки (Г, Г-11хе). Предельные значения полез-
ной массы достигаются при оптимальных для каждого маневра параметрах
двигательной системы и равны:
вариант 1
т, „=1 — ФТ' 1 1 . т„о т,,о
а ор1
(12.130)
еееи 0(Ф(Т[т,+ (1+ ' ) — 1~
т.,„= (1 — ~~Ф/Т) — т„„
(12.131)
еееи Т ги., + (1 +, ' ) (Ф ( Т11 — от„Т;
Таким образом, для двигательной системы с накоплением при фикси-
рованных Ж и Г можно выделить три различные области параметров маневров,
в каждой из которых полезная нагрузка определяется по той или иной фор-
муле. Эти области описываются следующими неравенствами:
вариант 1

~ГЛ. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
вариант 2
т„„(12.132)
т, „=(1 — т,„)
если ел)Т) 1+211кс сФ+ ' )+Ф;
х с А~ +
т „,„, =(1 — ~(Ф/Т) — т „
(12.133)
если 1+2~(хс р2Ф+ " +ф &gt
а Ор$
Зд с1. с р2: с (Г р1),
Для областей (12.130), (12.132) оптимальный начальный запас рабочего
вещества для всех маневров равен нулю, а оптимальные значения скорости
истечения Г„~, на фазе накопления находятся из уравнений:
вариант 1
1 ~+ ~1/Гор,
[2Г,'р2 — 2Г,'р, (.„— х,, — 1)—
а Орь
— Зх2с 1' ор2 — х1,. ('.ус + 1' ор2)1 = О~
2г.„~/1Р—
(12.134)
в ариан т 2
(2 ~ ор2 2 1' ор2+ х1;) (х~ + хс + 1' ор2) ~/х,сорМ + (хус + 1' ора) (х„~'ор1Т
2 ~х„сорМ х„адорф) 1' ор2 — О.
(12. 135)
Оптимальное значение мощности в этих областях определяется так:
вариант 1
2 ' Ф
Т,„= 1+
ор~
(12.136)
«артдапт 2
(12.137)
~орс = (1 — т„)
~с + орС
В областях (12.131) и (12.133) для всех маневров оптимальные время
накопления и масса установки сжижения равны нулю, а оптимальные зна-
чения мощности двигателя и начального запаса рабочего вещества равны
тр.оор2 = МТ.
(12.138)
На рис. 12.23 представлены результаты расчетов предельных значений
полезной массы т,„(Ф, Т) при отсутствии затрат мощности на сжижение
и невесомой установки сжижения, х,=О, х„=О, т„,=О. Варианты 1 и 2 в этом
случае неразличимы. Расчеты проведены для ~„=25. Поверхность 1 дает
предельные значения полезной массы для системы с накоплением, поверх-
ность 3 — без накопления массы. Отношение т, максимальной полезной
массы для системы с накоплением к максимальной полезной массе аппарата
без накопления, характеризующее возможные преимущества аппаратов
с накоплением массы, показано на рис. 12.24 (х,=х„=О, х„=25).
Оценка влияния удельных конструктивных параметров аппарата-на-
копителя ~„х„на оптимальные параметры двигательной системы и на от-
ношение т, приведена для Т=1. На рис. 12.25 представлены результаты
расчетов оптимальных значений мощности Г„„в зависимости от параметра

Рис. 12.23. Максимальные значения полезной Рис. 12.24. Относительное увеличение полезной
массы т-,„111ах на маневре (Ф, Т). массы аппарата с накоплением.
б,б
025
Об
цг п~ па и
Рис. 12. 26. Относительное время
накопления Т,/Т (соответству~ т
рис. 12. 25).
Рис. 12. 25. Оптимальная мощность двигательной
системы с накоплением. Сплошная кривая: ~у = ~„= 0;
пунктирная кривая: ~~,= ~„=О,25; штрих-пунктирная
кривая — двигательная система без накопления.
0 0~ 04
О,В Ф
Рис. 12.28. Максимальные выигрыши в полезной
массе аппаратон с накоплением по сравнению
с аппаратами без накопления (соответствует
рис. 12.25).
Рис. 12.27. Оптимальная скорость истече-
ния па фазе накопления (соответствует
рис. 12.25).
01
О
Об дд
Ф

12
[ГЛ. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
маневра Ф (при Т=1) при выполнении внеатмосферной фазы маневра без
сброса установки сжижения.
На рис. 12.26 показано изменение оптимального времени накопления
Т,, „„в зависимости от параметра маневра Ф для тех же наборов конструктив-
ных параметров, что и на рис. 12.25. Соответствующие значения оптимальной
скорости истечения Г„„на фазе накопления даны на рис. 12.27.
Совместное влиянйе параметров ~„и к на величину относительного вы-
игрыша в полезной массе (по сравнению с системой без накопления) иллю-
стрируется зависимостями и (Ф), приведенными на рис. 12.28.
На рис. 12.25 — 12.28 сплошные линии относятся к случаю невесомой
установки сжижения (~,,=0) и отсутствия затрат мощности на сжижение
(х,.=О); пунктирные линии относятся к случаю ненулевых затрат массы
(х,,=0,25) и мощности (х,,=0,25) на сжижение атмосферного газа. Кроме
того, во всех расчетах полагалось т,,=т„=О. Как видно из приведенных
результатов, влияние конструктивных параметров х, и ~ сильно сказыва-
ется на итоговых характеристиках системы с накоплением.
5. Внеатмосферный маневр аппарата-накопителя с двигателем огра-
ниченной скорости истечения. Рассмотрим сочетание двигательной уста-
новки с накоплением рабочего вещества и двигателя ограниченной мощности
И2.26]. Установку для накопления рабочего вещества на стационарной
круговой орбите в центральном поле тяготения будем считать идеальной
(см. формулы (12.78)), установку сжижения — невесомой, двигатель огра-
ниченной скорости истечения (Г, ( Г,„), предназначенный для выполнения
основного маневра, — невесомым, идеально регулируемым.
В такой постановке начальная масса аппарата М, на орбите накопления
будет состоять из полезной массы М, массы двигателя ограниченной мощ-
ности М„массы горючего М „и окислителя М, для химического двига-
теля. В безразмерных величийах (массы отнесены к начальной массе аппа-
рата ЛХ,) уравнение массы такого аппарата имеет вид
1=т, т„т, то.
(12.139)
(12.140)
т~, = Й (т~, + т„).
С учетом соотношений (12.100), (12.101) и (12.140) выражение (12.139) за-
пишем в виде
1 = т, + (1+ Йх„сТ) Т+ (1+ Й) т + т„,.
(12.141)
При выполнении внеатмосферной фазы маневра, аналогично п. 4, воз-
можны два различных варианта формирования аппарата, выполняющего
основной маневр. В первом варианте масса источника мощности доставляется
в конечную точку основного маневра. При этом масса аппарата в начале
выполнения внеатмосферного маневра состоит из начальной и накопленной
Задача заключается в определении оптимального соотношения масс
в (12.139), обеспечивающего максимум полезной массы т, при выполнении
маневра с заданным значением характеристической скорости Лг. Суммарное
время Т выполнения обеих фаз маневра фиксировано, и при выполнении вне-
атмосферного маневра с помощью двигателя ограниченной мощности оно
практически совпадает со временем накопления: Т= Т,. Накапливаемую
в орбитальном полете массу т~, будем считать окислителем (необходимая
сепарация, например, кислорода может быть учтена соответствующим
коэффициентом). Накапливаемая за время Т масса и масса двигателя опре-
деляются по формулам (12.100) (при Т„=Т) и (12.101). Соотношение масс
окислителя и горючего, расходуемых на фазе выполнения основного маневра,
задается условиями химической реакции

ДВИГАТЕЛИ, НАКАПЛИВАЮЩИЕ АТМОСФЕРНЫИ ГАЗ
т ( Т вЂ” е) = 1 +к„сИТ, т (Т + е) = т, + Т+ т„„е ~ О. (12. 142)
Начальная и конечная массы на основном маневре связаны соотноше-
нием К. Э. Циолковского:
1)) = (р ж',= ', Ф~,—,, 6р, = ", (12.143)
т Т+е
У к„с~ к„с~
шах
Из (12.142) и (12.143) при фиксированных параметрах двигателя огра-
ниченной мощности (Г, т„„à — 11хе) и двигателя ограниченной скорости
истечения (р' .,— Йхе) полезная масса определяется выражением
т, = (1+ г,сИТ) е ~ — (Т+ т„,).
(12.144)
Оптимальное значение скорости истечения двигателя ограниченной мощ-
ности на фазе накопления, максимизирующее полезную массу, равно
(12.145)
Оптимальная мощность двигателя ограниченной мощности определяется
по формуле
Тп„„, если х„сор~Те ~) 1+ т„о,
О, если х„сор~Те ~(1+т„,.
(12.146)
В области Г„,=Г „максимум полезной массы достигается при нулевом
начальном запасе окислителя (весь окислитель накапливается, а на орбиту
накопления выводится только запас горючего). При этом максимальное зна-
чение мощности, фигурирующее в (12.146), находится из (12.141) и (12.144):
1 — т.,о — е ~
Ж ах=
(12.147)
1+ (е ~+1) х с ° Т
При Л~,„,=О накопление нецелесообразно, а начальный запас топлива (оки-
слитель+горючее) — максимальный:
(12.148)
(1 + 7е) т,,„= 1 — е ~.
Формулы (12.144) — (12.145) определяют зависимость максимальных
значений полезной массы от параметров аппарата (х, х„, т„„р',„,„) и маневра
(Ли, Т). На рис. 12.29 приведены результаты расчетов максимальной полез-
ной массы при фиксированных значениях параметров аппарата (х =25,
х„= О, т„=О, Й=1/8) для различных значений параметров маневра. Пунк-
тирная кривая определяет значения полезной массы аппарата с двигателем
ограниченной скорости истечения без накопления массы. Соответствующие
значения оптимальной мощности бортового источника энергии, обеспечиваю-
щие максимум полезной массы, показаны на рис. 12.30.
В а р и а н т 2. Во втором варианте соотношения для начальной и
конечной масс, аналогичные (12.142), имеют вид
т(Т вЂ” е) =1+ х„сИТ вЂ” (Ж+ т„о), т(Т+ е) = т„е — ~ О. (12.149)
масс. Во втором варианте источник мощности сбрасывается до начала выпол-
нения внеатмосферного маневра сразу по окончании фазы накопления и
в конечную точку маневра доставляется только полезная масса. Рассмотрим
оба варианта выполнения основного маневра.
В а р и а н т 1. В этом варианте масса аппарата до начала выполнения
основного маневра т (Т вЂ” е) и масса т (Т+е) в конце маневра равны

ДРУГИЕ ТИПЫ ДВИГАТЕЛЕ]Й
[гл. 12
д,д
I 2 5 ~ ~~~ Кпама
Рис. 12.29. Максимальная полезная нагрузка для двигательной системы ограниченной скорости истече-
ния с накоплением рабочего вещества.
П7
йглах
02
5 Лп/У „
б,б
Уор!
дг
д~ д4 дб д8 Ф
Рис. 12.30. Оптимальные значения мощности
Жор~ бортового источника, соответствующие
рис. 12.29.
Рис. 12.32. Оптимальные значения мощ-
ности бортового источника энергии, со-
ответствующие рис. 12.31.
Рис. 12. 31. Максимальная полезная на-
грузка для случая сброса источника энер-
гии.
Рис. 12.33. МаксимаЛьная полезная на-
грузка для идеального двигателя ограни-
ченной мощности с накоплением рабочего
вещества.

сОлнечный пАРус
Соотношение для массы аппарата, выводимого на орбиту накопления,
остается прежним — (12.141). Не изменяется и выражение (12.145) для оп-
тимальной скорости истечения двигателя ограниченной мощности на фазе
накопления. Оптимальная мощность бортового источника либо равна нулю
(накопление невыгодно), либо должна быть максимально возможной:
Т „, если х„с„р1Т) 1,
О, если х„с, ~Т(1.
(12.150)
Максимальная мощность Г „бортового источника энергии, входящая
в (12.150), определяется по формуле
(1 — в ~) (1 — т„в)
1+йх,с Т вЂ” (1 — х с Т) в ~'
(12.151)
Если К,„,=Г,„,, то начальный запас топлива состоит только из горю-
чего. В случае Г„,=О начальный запас определяется, как и в первом вари-
анте, по формуле (12.148).
На рис. 12.31 приведены результаты расчетов максимальной полезной
массы для второго варианта выполнения внеатмосферной фазы маневра
(разгоняется только полезная масса). Значения параметров аппарата при-
няты в расчетах одинаковыми для первого и второго вариантов: х =25,
х„=О, т„,=О, 1=1/8. Соответствующие значения оптимальной мощности
даны на рис. 12.32.
В этом варианте накопление выгодно при любых Лг, если оно выгодно
хотя бы при одном значении (пунктирная и сплошные линии на рис. 12.31
не пересекаются).
Рис. 12.29 и рис. 12.31 показывают при каких условиях выгодно
накапливать рабочее вещество, если заданный маневр выполняется с помощью
двигателя ограниченной скорости истечения струи. На рис. 12.33 показаны
значения максимальной относительной полезной массы (см. (12.130) — (12.135))
для случая, когда обе фазы маневра выполняются идеальным двигателем
ограниченной мощности. Совместно все эти данные (рис. 12.29, рис. 12.31
и рис. 12.33) позволяют решить вопрос о целесообразности накопления ра-
бочего вещества и использования двигателей ограниченной мощности, огра-
ниченной скорости истечения или их комбинации для выполнения заданного
маневра.
$4. Солнечный парус
1. Постановка задачи оптимизации полета с солнечным парусом. Рас-
сматривается плоский парус с идеально отражающей зеркальной поверх-
ностью Я 2 гл. 2). С учетом только гравитационных сил и силы солнечного
давления движение центра масс космического аппарата с солнечным парусом
описывается уравнением (1.1) при 1"=О. Вектор е направления тяги, фигу-
рирующий в этом уравнения, совпадает с вектором нормали к теневой стороне
паруса и, а величина тяги определяется из соотношения (2.53).
Масса космического аппарата с солнечным парусом (если считать пло-
щадь паруса постоянной Я (1)=Я, и не принимать во внимание явления «из-
носа» паруса) не меняется со временем, ЛХ (1)=ЛХ„и состоит из двух слагае-
мых: полезной массы М, и массы паруса ЛХБ=Я,~~ (2.54). Введя эти соот-
ношения в уравнения движения, получим
РЛ о ь ° 2
г'=, ' — (и ° 1)'и+ д,
(12.152)

41
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
[ГЛ. 12
где и — единичный вектор нормали к теневой стороне паруса; 1 — единич-
пый вектор направления сочнечных лучеи; (и $) — косинус угла и$ уста-
новки паруса по отпотеншо и солнечным лучам; р — солнечное давление
на единичную площадку, установленную перпендикулярно к солнечным лу-
чам, на орбите Земли Ль', Л =Л (г) — расстояние аппарата до Солнца (в гелио-
цен трической системе координат Л=г); у и 3 — плотность и толщина матери-
ала паруса.
Таким образом, в уравнения движения вошли параметры паруса Я„
р, 3 и полезная масса ЛХ,. Комбинацию этих параметров, содержащуюся
в уравнении массы, можно заменить ускорением, которое сообщает парус кос-
мическому аппарату на расстоянии Л~ от Солнца, будучи установленным
перпендикулярно к солнечным лучам (и=1):
(12.153)
7Г О
Полезная масса и необходимая площадь паруса выражаются через
этот параметр:
Ло Р:1
(12.154)
а уравнение движения (12.152) записывается следующим образом:
Д 2
г=а, — (и ° $)'и+д.
(12.155)
Связь уравнения движения (12.155) с характеристиками ЛХ„Я„р, 3
осуществляется через единственный параметр а„максимальная величина
которого определяется массой единицы площади паруса ~3 (12.153). Ускоре-
ние а, для уравнения движения (12.155) играет роль постоянного управляю-
щего параметра. Единственная управляющая функция в этом уравнении—
угол установки паруса (направление нормали к теневой стороне паруса),
который может меняться в диапазоне ( — г(2, ~12) по отношению к солнечным
лучам:
~ и(Е) /:1
( — г(2 ( и (~) $ ( ~/2).
Могут быть рассмотрены две эквивалентные формулировки общей про-
блемы оптимизации: 1'. Заданы полная масса аппарата ЛХ, и время выпол-
нения маневра Т; требуется найти максимум полезной массы ЛХ,. 2'. Заданы
полная масса аппарата ЛХ, и полезная масса ЛХ,; требуется найти минималь-
ное время выполнения маневра Т.
Для аппарата с солнечным парусом не обязательно оперировать с М.
и ЛХ, по отдельности. Здесь можно использовать отношение ЛХ,/ЛХ, из
(12.154), т. е. считать его заданным и определять минимум Т, либо находить
максимум ЛХ,/ЛХ, при заданном Т. Относительная полезная нагрузка ЛХ,/М„
согласно первому соотношению (12.154), определяет величину произведения
аорт. Масса единицы площади паруса р 8 зависит от совершенства конструк-
ции и должна быть минимально возможной. Таким образом, относительную
полезную нагрузку можно считать однозначно связанной с ускорением а,.
С другой стороны, величина а, через уравнение движения (12.155) опре-
деляет время выполнения маневра Т, и задача оптимизации сводится к по-
строению такого закона управления ориентацией паруса и (~), который обес-
печивает при заданном а минимум Т или минимум а при заданном Т. Вто-
рая формулировка менее удобна вследствие того, что найденная в результате
решения величина ускорения ао может оказаться больше, чем а, „=~~/~3
из (12.153).

СОЛНЕЧНЫЙ ПАРУС
17
2. Перелет космического аппарата с солнечным парусом между орби-
тами планет. На межорбитальном участке перелета, лежащем вне сферы
действия планет, орбиты которых считаются компланарными и круговыми,
движение происходит в центральном гравитационном поле Солнца под дей-
ствием солнечного давления. Поэтому, полагая в уравнениях (12.155) Л=г,
~= — дег„'г-аг и обозначаЯ чеРез 9 Угол Установки паРУса, составлЯемый ноР-
малью к теневой стороне паруса и радиусом-вектором г (который здесь
совпадает с направлением солнечных лучей 1=г/г,
т. е. (и 1) = сов 9) (рис. 12.34), приходим к сле-
дующим уравнениям плоского движения:
У~
г
В„= — + (а, соя' Ь вЂ” де) — '
~ г~з ~0
В = ' + а, соя' О з1п 9
(12.156)
где не — гравитационное ускорение от Солнца на
радиусе г,.
Рис. 12. 34. Схема межпла-
нетного перелета с солнеч-
ным парусом.
В работах [12.27 — 12.33] рассматривалось движение
космического аппарата с солнечным парусом между орбитами
планет и ри постоянном угле установки паруса о = сопят.
Получен ряд приближенных и точных решений (Ц 1 и 2 гл. 17), найдено оптимальное зна-
чение постоянного угла установки паруса. Эта группа аналитических решений помогла
составить первые представления о возможностях использования солнечного паруса для
перелетов между орбитами планет. Однако указанные решения обладают существенным
недостатком: краевые условия по координатам и компонентам скорости на обоих концах
траектории не могут быть удовлетворены.
Решения вариационной проблемы о перелете космического аппарата
с солнечным парусом между орбитами планет (минимум времени перелета
~~г
У Ур
ф
1Ю' ~0
И РУ
Ю Р8
-Р3 РУ
р~ р~ ~ц рр с
П Юг Ю~ ~б Р
Рис. 12. 35. Оптимальная программа угла
устанонки паруса г и траекторные параметры
перелета Земля — Марс (а,=2 10-' м/сек',
Т=322 сут).
Рис. 12.36. То же, что и на рис. 12.35, для
перелета Земля — Венера (а,=2 10-'. ж/сек',
Т=164 сут).
Т при заданном а,) получены в работах [12.34, 12.35~. На рис. 12.35 и 12.36
даны примеры численного решения [12.35 ~ при а,=2 10 ' м/сек' для перелета
с орбиты Земли на орбиту Марса и с орбиты Земли на орбиту Венеры.
На рис. 12.37 приведен пример решения задачи перелета на Марс [12.34]
при а,=10 ' мосек'. Помимо закона управления парусом ~„, (~), соответствую-
щего граничному условию и„1 = О, и = 1/~г, там показан также закон
~7 Механика полета

41
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
8' (1) для случая, когда величина скорости аппарата на орбите Марса не за-
дана и определяется из оптимальных соображений. Естественно, что в та-
ком (<обле е» Ма са вр мя перел та соответстве но сокращае с с
=420 сут до Т=170 сут.
Для сопоставления на рис. 12.37 приведен еще результат решения
[12.28] с постоянным оптимальным углом установки солнечного паруса
бР'
Рис. 12. 38. Минимальное время
перелета с солнечным парусом
с орбиты Земли на орбиту Марса.
Рис. 12.37. Программы угла установки паруса для пере-
лета Земля — Марс при а,=10-' м/сек'. сплошная кри-
вая — оптимальный перелет с выходом на орбитальную
скорость Марса, штрих-пунктирная кривая — перелет
с оптимальной конечной скоростью, пунктирная кри-
вая — перелет с постоянным углом установки паруса.
Ь=Ь (начальные и конечные условия по скорости на этом решении не выпол-
нены). На рис. 12.38 приведена зависимость минимального времениперелета
с солнечным парусом между орбитами Земли и Марса от величины ускоре-
ния ао (сплошная кривая) [12.35]. Сравнение с решениями для О= сопа$ (пунк-
тирные кривые) [12.29, 12.30] указывает на сильное влияние граничных
условий по скорости на время перелета. Поэтому область применимости ре-
шений с постоянным углом установки солнечного паруса, которые не могут
удовлетворять всем граничным условиям по скорости, весьма ограничена.
Результаты численных расчетов оптимальных перелетов с солнечным па-
русом с орбиты Земли на орбиты всех планет солнечной системы приведены
в табл. 12.1 для начального ускорения а =2 10-' м/сек' [12.35].
Т а б л и ц а 12.1
Минимальное время перелета с солнечным парусом при а„=2 10 з ль~секй
с орбиты Земли на орбиты планет солнечной системы
Название
планеты
Нептун Плутон
Уран
Сатурн
Меркурий Венера
10питер
Марс
145
96
Т, год
0,53
0,45
17
1,12
6,6
3. Выход космического аппарата с солнечным парусом из сферы при-
тяжения планеты. Задача о выходе космического аппарата с солнечным
парусом из поля тяготения планеты рассматривается в работах [12.36, 12.371
В заключение этого пункта рассмотрим иллюстрирующий пример. Пусть требуется
перевезти 1 т полезного груза с орбиты Земли на орбиту Марса за 420 сут при минималь-
ной площади солнечного паруса, выполненного из пластмассы ( ~ о=5 10 ' г/см'). Тогда
согласно данным рис. 12.37, 12.38 ао=10 а м/сек2, по формуле (12.154) ВО=0,26 104 л',
что эквивалентно кругу диаметром 575 м. Общая масса аппарата при этом равна 2,З 77~ °

41
СОЛНЕЧНЫИ ПАРУС
при следующих предположениях: аппарат выведен на начальную круговую
орбиту; гравитационное поле центральное; поток солнечного света плоско-
параллельный, постоянной интенсивности и направления.
В работе И2.36) исследован выход аппарата с солнечным парусом из
сферы притяжения планеты в случае, когда начальная орбита и траектория
выхода лежат в плоскости эклиптики. Парус, обе поверхности которого счи-
'гаются идеально отражающими, вращается вокруг своей оси с угловой
тф
ф~~
РРI
Р1
Я~
Рис. 12. 39. Схема выхода ап-
парата с солнечным парусом иэ
сферы притяжения планеты по
траектории, лежащей в плоско-
сти эклиптики.
Рис. 12.41. Схема выхода с ор-
биты, перпендикулярной и пло-
скости эклиптики.
Рис. 12. 40. Время выхода Т:
сплошная кривая — выход
в плоскости эклиптики, пунк-
тирная — выход с орбиты, пер-
пендикулярной к плоскости эк-
липтики.
скоростью, равной половине угловой скорости обращения аппарата вокруг
планеты (рис. 12.39).
Уравнения движения записываются следующим образом (тенью планеты
пренебрегается):
2
'2 го Ь
г' — г~ +д — = — а — е1п — е1п ~
0 г О Д 2
Д 2
гф+ 2гф = а, — е1п
',(12. 1 57)
где Л вЂ” радиус орбиты планеты, д, — гравитационное ускорение на началь-
ной орбите спутника планеты.
После перехода к безразмерным переменными замены независимой пе-
ременной ~ на полярный угол ~ система уравнений (12.157) численно интегри-
ровалась от точки, соответствующей начальной круговой орбите, до момента
обращения в нуль полной энергии космического аппарата относительно
планеты.
Характер траектории показан на рис. 12.39. По мере разгона аппарата
орбита становится эллиптической, причем перигейное расстояние ме-
няется слабо. Набор нулевой энергии («отрыв») происходит в окрестности
перигея.
Зависимость времени выхода Т от величины начального ускорения ао
представлена на рис. 12.40 (сплошная линия) в безразмерных переменных.
В этих переменных результаты всех расчетов, проведенных для различных
значений а, и г„приблизительно укладываются в логарифмическом масштабе
на одну прямую, разброс по безразмерному времени указан на рисунке.
Число оборотов до момента отрыва примерно равно 0,1 д,Л'/а,Л'. Для на-
27*

420
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ'
[ГЛ. 12
Т а б л и ц а 12.2
Параметры космического аппарата с солнечным парусом на траектории выхода
из сферы притяжения Земли
!
с
О ~~
~о
О О
° 4
л О
сб р
Ь'
с~5
О
ь &
Размеры паруса
И,'
Ж
Ж сб
м р
С сб
а5 Ц
° 4
Я Ж
ф~ъ с~5
О О И
с б
~ О
° й
Р~
~ сб
Рч
ои
О О
й ц
ИдТ
1 !
Ы й
©во~
О сс~ ~
асс ~
° ~ ~ Н
с с~
с~~ - О с~
с, ьч ~~4
~р н
ОГ,"-~
Ж
о
~ с-~Ой
~~ ~ч ~ч
И
Ф
Ц в
е'й
1
° |2
~а
Ю
~ч
о Я
о ~~ о
и ~&
Ф
в
ст~ Ж
Р~
Е& t;
Я
Ж
~:~а
О
с.~
с[5
со
~ О
О юФ
о
10-4
2 ° 10-4
3 ° 10-4
10-4
10-4
0,85 10-'
0,44 10-2
0,3 10-'
0,67 10 2
0,46 10-2
10в
10в
10в
2,45.10'
10~
4,2 105
6,1 105
7,62 105
4,78 105
5,87 105
1 12 10з
1 12 10з
1,12.10з
0,56 10з
0,36 10з
7,25.10з
7,25 10з
7,25 10з
7,25.10з
7,25.10з
1,1
2,1
3,1
0,35
0,2
54
112
119
73
105
0,1
0,1
0,1
0,1
0,1
глядности в табл. 12.2 приводятся размерные параметры выхода из поля при-
тяжения Земли [12.36). Следует отметить, что влияние тени Земли на харак-
теристики выхода с солнечным парусом не оценивалось в работе [12.36].
Очевидно, что траектория с учетом этого влия-
ния будет существенно отличаться от изучен-
ной, в особенности на начальном этапе движе-
ния.
Для того чтобы траектория выхода не по-
падала в затененные области и на ней не было
участков движения навстречу солнечным лучам,
движение должно происходить вне плоскости
эклиптики. В работе [12.37 ) рассмотрена сле-
дующая схема выхода аппарата с солнечным
парусом из поля тяготения планеты.
Плоскость х"', х'з' начальной орбиты пер-
пендикулярна к плоскости ж'1), ж(2) эклиптики
(рис. 12.41). Уравнения движения записываются в декартовой системе ко-
ординат (х'1', х'2', х'з'), связанной с Землей, которая предполагается непод-
вижной:
Рис. 12.42. Локально-оптимальная
программа тяги солнечного паруса.
л 2
~'~' — а соя а"' соя' а"' +
о Л
Д'0ГОХ' "
(~=1, 2, 3). (12.158)
соя а'1' =(3 соя ~"'+ ~/соя'р"'+ 8)//с, соя а"' = 2 соя ~3"'//с
(Й'= 6 соя2 ~3'"+ 6 соя ~п' ~/соя'[~'1'+ 8)+ 12, ~3"' = агссоя (х'"/! т ~), (12 159)
~=1, 2, 3).
В начале движения смещение ио оси х"' компенсируется гравитационной
силой, траектория близка к плоской и является квазикруговой. На этом
участке используется приближенное решение [12.381, которое стыкуется
с численным решением системы (12.158), (12.159), записанной в безразмер-
ных переменных, из [12.381.
Здесь соя а"' — направляющие косинусы нормали к теневой стороне паруса,
которые выбираются из локально-оптимального условия максимума ско-
рости приращения энергии — шах (и ч):

ИЗОТОПНЫЙ ПАРУС
~ 5. Изотопный парус
1. Основные характеристики изотопного паруса и формулировка вариа-
ционной задачи. Как было показано в гл. 2 и 3, максимальная тяга изотоп-
ного паруса экспоненциально падает по времени, а масса паруса практически
постоянна и пропорциональна максимальной площади паруса (т. е. макси-
мальной тяге):
0(Р®(Р .,е
(12.160)
Регулирование тяги может осуществляться за счет изменения площади
паруса («свертывание» паруса). Ниже будет показано, что площадь (тяга)
паруса в оптимальном режиме должна быть максимально возможной.
На ориентацию тяги ограничений не накладывается.
Вариационную задачу сформулируем как задачу на максимальное бы-
стродействие: обеспечить минимальное время выполнения маневра при фик-
сированной величине относительной полезной нагрузки [12.261.
Полная масса аппарата с изотопным парусом в процессе полета практи-
чески не меняется, она складывается из двух компонент:
(12.161)
М (~) =М,= М,+М„= сопзВ.
Из уравнений (12.160), (12.161) следует, что., как и для солнечного паруса,
динамическая часть задачи содержит единственный постоянный параметр—
максимальное ускорение от тяги движителя ао, величина которого определя-
ется удельной массой движителя т и заданным значением ЛХ,/ЛХО:
а,= — 1—
(12.162)
Соответственно текущая величина ускорения аппарата от тяги движителя
определится соотношением
О
(12.163)
(О (а (1).
Здесь управляющая функция а (~) определяет, какая часть возможной тяги
пвижителя используется.
Время достижения точки отрыва поэтому решению показано на рис. 12.40
пунктирной линией. Видно, что время ухода по схеме работы [12.371 меньше,
чем в случае плоской траектории, исследованной в работе [12.361. Однако
этот факт нельзя рассматривать как окончательное свидетельство преиму-
щества разгона в перпендикулярной к эклиптике плоскости, так как в обоих
случаях исследовались неоптимальные программы угла установки паруса.
Сравнение с временем межорбитальных перелетов показывает, что для ап-
парата с солнечным парусом время выхода из поля притяжения планеты со-
ставляет значительную часть общего времени межпланетного перелета.
В заключение данного пункта отметим также исследование локально-
оптимального управления углом установки паруса для задачи выхода из
гравитационного поля Солнца [12.39). На рис. 12.42 показаны полученные
зависимости оптимальной ориентации паруса, обеспечивающие наибольшее
приращение эксцентриситета исходной орбиты во=0,5 за один оборот. В ра-
боте [12.391 также анализируются вопросы устойчивости полета аппаратов
с солнечным парусом.

422
[ГЛ. 12
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕИ
Полная система дифференциальных уравнений, граничных условий и
ограничений на управляющие функции рассматриваемой вариационной проб-
лемы записывается в виде
=1, ~0=0, Т = ю111,
г=~, г (0) = г„г (Т) = г„
у = аа,е "'е+я, т (0) = т„т (Т) = т,
(О (а (1) (1, ~ е(1) ~ = — 1).
(12.164)
Задача сведена к определению оптимальных законов управления вели-
чиной тяги а (~) и направлением тяги е (~), которые обеспечивают минималь-
ное время Т выполнения заданного маневра при фиксированной величине
%
(
Рис. 12. 43. Оптимальное управление
тягой изотопного паруса — перелет
между точками покоя.
Рис. 12.44. Момент изменения направления
тяги 1„(Т (пунктирная кривая) и достижимое
расстояние И'/а, (сплошная кривая).~
максимального ускорения а,. Программы а (~) и е (~) определяются из ус-
ловия абсолютного максимума гамильтоновой функции и равны
а, „(1)=1.
е„, = — р,/р„,
2. Модельная задача. В качестве иллюстрирующего примера рассмот-
рим модельную задачу перелета за минимальное время с помощью изотоп-
ного паруса между двумя точками покоя на расстояние 1 в бессиловом поле
(я=О, то — — О, т1=0, )г1 го) =Г)
Для однородного гравитационного поля вектор е направлен либо по ско-
рости, либо против нее и может только один раз изменить направление в не-
которой промежуточной точке ~, интервала [О, Т1 (рис. 12.43). Интегриро-
вание уравнений (12.164) определяет связь отношения ~,/Т и относительного
расстояния 1Л'/а, с характерным временем задачи ~=ЛТ (рис. 12.44):
е 1 2 й2 2 1, 2
— = —., 1п — =1и ~ — 1п
) " 1 -~- . — ~, = 1 ~. ; ; 1 ~ ; ) .
Отметим, что характерное время ~ является отношением времени выпол-
нения маневра Т к периоду полураспада изотопа 1/Л. Последнее соотноше-
ние (12.165) через формулу (12.162) определяет минимальное время Т в за-
висимости от полезной нагрузки М,/М„параметров паруса Л, т и маневра 1.
я 6. Двигатель с солнечным источником энергии
Рассматривается задача о доставке максимального полезного,",груза
с помощью идеального двигателя ограниченной мощности, использующего
солнечную энергию [12.40). Отличительная особенность такой двигательной
системы состоит в том, что ее максимальная мощность зависит от расстояния
аппарата до Солнца. Аналогично случаю постоянной максимальной мощ-

423
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
$61
ности, определяются оптимальные соотношения масс, выделяется вариацион-
ная задача о построении оптимальной программы реактивного ускорения и
выборе расчетного расстояния до Солнца. Приводятся приближенные ре-
шения для бессилового и центрального полей.
1. Формулировка задачи оптимизации. Массу двигательной установки
ограниченной мощности, использующей солнечную энергию, можно пред-
ставить в виде суммы двух составляющих (если не считать массы движителя):
массы концентратора солнечной энергии (зеркала, линзы Френеля) или плос-
кого преобразователя (фотоэлементы, термоэлектрические генераторы) и
массы преобразователя тепловой энергии в электрическую. Первая состав-
ляющая пропорциональна площади Я захватываемого потока солнечного из-
лучения, вторая — максимальной мощности Г „,
которую может перерабатывать преобразователь.
о
Таким образом, масса двигателя с солнечным источ-
ником энергии записывается в виде
М„= аУ „+ ~3Я (а, р = сопя~). (12.166)
Плотность потока солнечной энергии убывает об-
р атно пропорционально квадрату расстояния от
Солнца: Л„(Л) = 1,4 (Л~/Л)' квт/м2. Максимальная
мощность Г,,„достигается при приближении к Солнцу
на некоторое расстояние Л„, которое будем называть вечного энергоисточника
в зависимости от расстоя-
расчетным: Ж„„, = Л„(Л„) Я~, где ~ — коэффициент
ния по Солнца.
преобразования солнечной энергии в электрическую.
Если обозначить через Г, мощность силовой установки на орбите Земли, то,
пренебрегая изменением к. и. д., можно представить максимальную мощность
в виде Г „=(Л~/Л,)' Г,.
При дальнейшем приближении к Солнцу мощность должна оставаться
постоянной, так как преобразователь тепловой энергии в электрическую
не может работать при мощности, превышающей максимальную расчетную,
т. е. на расстоянии Л. от Солнца должно быть введено ограничение на мощ-
ность силовой установки (рис. 12.45):
(Л~/Л„)' К, = К „при Л ( Л„,
(Л~/Л)' У, при Л )~ Л„.
(12.167)
Выраженпе (12.166) можно представить в виде
ЛХ„= а, [1 + (Л~/Л„)2 у] Уо,
(12.168)
где х,, = ~/~Я ° (Л~) — масса коицептратора или плоского преобразователя на
единицу мощности, у = а/а,. Следует отметить, что в системах с плоскими
преооразователями величина у (& t; 1, поэт му мо но счит ть „= ,
~,= ~ь.
Ставится задача отыскания максимальной полезной нагрузки при выпол-
нении заданного маневра; время выполнения маневра Т, начальная масса
аппарата М„удельные массы а, и у фиксированы. Предполагается, что дви-
житель идеальный, т. е. вся мощность, подводимая к движителю, превраща-
ется в мощность реактивной струи, а параметры движителя — массовый
расход рабочего вещества и скорость истечения — могут меняться в неогра-
ниченных пределах.
В этой задаче нужно указать оптимальные значения масс М„, М, и
расчетного расстояния Л„, а также построить оптимальные программы век-
тора реактивного ускорения а (1) и мощности К„®.

ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
[ГЛ. 12
2. Оптимальные соотношения масс и расчетное расстояние до Солнца.
Предварительно оценим величины сил, действующих на аппарат. Покажем,
что сила солнечного давления мала по сравнению с тягой и гравитационными
силами.
На поверхность преобразователя в единицу времени падает поток солнечной
радиации с энергией ЯА Ь'; при этом аппарату сообщается импульс, не превосхо-
дящий величины 2Я~Я/с (здесь с=3 10е л~/сек — скорость света). Импульс, сообщае-
мый аппарату двигателем, использующим солнечную энергию, не меньше величины
2%~Я~)/Гш~~ (здесь Г ~~ — 105 м/сек — максимальная скорость истечения реактивной
струи). Сравнение показывает, что последняя величина по крайней мере на два по-
рядка больше первой.
Для ускорения от солнечного давления справедлива оценка ~ =232 ° Я/сМ(
(2Л Б/сМ„. Воспользовавшись выражением (12.166), последнее неравенство можно
представить в виде /А ( 2 [Л ° (Л~)/сЭ] (Л /Л)~ При ~ = О,З кг/лс' ускорение от солнеч-
ного давления / ° (3 10 ~ (Л /Л)в м/сек', что по крайней мере на два порядка меньше
гравитационного ускорения Солнца, равного 5,92 10 ' (Л~/Л)в л/сен2.
Исходя из полученных оценок, силу солнечного давлепия в дальнейшем в расчет
принимать не будем.
Аналогично случаю движения с постоянной максимальной мощностью,
можно независимо от уравнений движения проинтегрировать уравнение,
Описывающее изменение массы аппарата, и получить выражение для полез-
ной массы Я 1 гл. 4):
У вЂ” 1
(12.169)
!"', Отсюда мощность Г,„как и раньше, должна быть максимально воз-
можной:
(12.170)
Ж, = — Ж (Л).
Воспользовавшись выражениями (12.167) и (12.168), находим, что для
фиксированного значения функционала
У
(р
1+ ', Ж
Л й,
'(12.171)
(/т'= (Ле/Л„)- при Л (Л„, /т' = (Л~/Л)' при Л ) Л.)
максимум М„(М„) имеет место при М„/М,= ~/Ф вЂ” Ф и равен
М,/М = (1 — ~/Ф), Ф = (а,/2) Х.
(12.172)
Таким образом, задача определения оптимальных соотношений масс
может быть решена, если известна величина функционала Х. Последний не
зависит От соотношений масс и определяется, если известна траектория и
параметр Л„. Для движения с постоянной мощностью множитель перед
интегралом в выражении (12.171) и знаменатель подынтегрального выраже-
ния равны единице (см. (4.10)).
Задача сводится к нахождению такой величины параметра Л. и такой
программы реактивного ускорения и (~), чтобы при перемещении между на-
чальной (г, г ) и конечной (г, г ) точками за время Т функционал Х был ми-
нимален. Далее рассмотрение проводится в гелиоцентрической системе ко-
Ординат, поэтому считается В =г, Я„=г„и Л~ — — г .

э 6]
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
Покажем, что оптимальная величина параметра г заключена внутри отрезка [г„г,].
Обозначим через Х (г.) минимальное значение функционала Х, которое зависит от пара-
метра г„как явным образом, так и через посредство функций а (~, г„) и АГ (г, г,), входя их
в подынтегральное выражение. Пусть для определенности г, (г1, тогда при изменении
параметра г„вне отрезка [г„г,] функция Х (г,) будет пметь вид
т
~1-;~.~.г ~~. р .. ~.=- ° ~ ~.г"«~.
а(~)
/ 77
[(г,~',)'-';-~]7, ри ~,~, ~7,= Ы ~'Н~)
а(1)
о
У(г,.)= 1
(12.173)
(предполагается, что вся траектория г (~) лежит внутри интервала [го, г,]). Очевидно,
при этом выражения У, и У, должны оставаться постоянными; поэтому, как следует из
приведенных формул, Х (г,) с увеличением г„убывает при г, ( го и возрастает при г, ) г .
точках г, и г, функция Х (г,) непрерывна и имеет односторонние производные
(12.174)
Можно показать, что производная функции Х (г„) непрерывна в указанных точках,
В самом деле, пусть г„=г,— Ьг,, тогда справедливо неравенство
& t; г1 Ђ”
а2Ж
авй (
гз Ж (г, г1 — Лг„)
о
(12.175)
Обозначим функции а (~), минимизирующие правую и левую части неравенства,
соответственно через а, (~) и а, (~); тогда
т У /~7
& t; г1 Ђ”
а1 аь ауй
а~Д~ ( (
г, Ж (г, г, — Аг,) ~У (г, г, — ~г,)
о
(12.176)
Нетрудно показать, что
аЫ~ г,— Дг
а~зН1 + о(Ьг,);
(12.177)
тогда из неравенства (12.176) следует:
[т
а2сИ г, — Дг.,
т1п „„„, = т1п аздак + о (Ьг„).
,~ф~ ~, г1 — г,~ ~~) ., го
о
(12.178)
3. Уравнения оптимальной траектории. Рассмотрим плоское движение
в центральном поле Солнца. Уравнения движения аппарата, записанные
в полярных координатах, имеют вид <4.1
г=и„, гф=ь~т, д„=а,+из/г — г з, 8 =а — и и (г.
9 9 "9
<12.1
Воспользовавшись выражением (12.178), можно непосредственно вычислить произ-
водную ИУ/Иг„в точке г,— О. Сообщив г„в точке г, приращение Ьг„и перейдя к пределу
при Лг„-~ О, получим соответствующее выражение из (12.174). Аналогичным образом
можно показать непрерывность производной в точке г„=г +О.
О
Таким образом, на отрезке [г„г,] функция Х (г„), оставаясь положительной, меняет
знак производной с минуса на плюс. Отсюда следует, что минимум функции Х (г„) дости-
гается в некоторой точке г, ( г„Ор~ ( г,. Кроме того, зная производные ИУ/Иг„в точках
г, и г„можно указать точку, близкую к г„р~, например абсциссу точки пересечения каса-
тельных к графику Х (г„) в точках г, и г,.

426
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
[ГЛ. 12
Требуется найти траекторию, на которой достигается минимум функ-
ционала
а2Ж
Л(г, г„)
О
го
У(т, т)=( — ') при г)г,)
(12.180)
(зесь г — фиксированная величина).
Уравнения Эйлера для задачи (12Л79), (12.180) таковы (ср. (5ЛЗ)):
при г & t
1 1 ~г1".
= — — (а'+ ')+
п 2 ~ 9 " г г2
а = — а.и,. — 2а„п
при г„(г & t;
а„= — — (а~~+ а~) + а„
— Х вЂ” — ч—
(12.181)
— ), — — ч — — — 2
— „— 2 „— — 2
где Х и ~ — интегралы системы (константы изопериметричности, соответствующие задан-
ному времени движения и заданному угловому перемещению). При г=г„частнаяпроиз-
водная по г подынтегрального выражения функционала (12Л80) терпит разрыв. При этом
для оптимальной траектории выполняются условия Вейерштрасса — Эрдмана
а,.(ㄠ— О) = а„ (г, + О), а„ (г„ + О) — а,. (ㄠ— О) = †(2а,и„(г)„
а (г„— О) = а (г„+ О), а (г„+ О) — а (г„— О) = — (2а, и,,(г)
(12.182)
Уравнения (12.179), (12.181) вместе с двумя первыми интегралами Х
и ~ имеют в сумме 14-й порядок. Краевые условия и условия Вейерштрасса—
Эрдмана дают 14 условий для определения траектории.
Точка, в которой и„=О, как и для системы (7.13), является особой точ-
кой типа «узел». Остается в силе и свойство инвариантности уравнений оп-
тимальной траектории относительно преобразований замены знака (7.16)
и растяжения (7.15).
4. Приближенный метод построения оптимальной траектории. Для
решения задачи о минимуме функционала (12.180) можно использовать
итерационный процесс. Опишем его на примере модельной задачи о переме-
щении между точками покоя в бессиловом поле:
х=и, и= — а, ж (0) =же, й(0) =О, х(Т) =~+у„
и(Т) =О.
(12.183)
Определяется траектория, оптимальная в смысле минимума функционала
Х = (ж/ж,)' аЧ8
(12.184)
(12.185)
Д2
—, (паз) + азх = О.
(для простоты предполагается, что ж„=х ). Уравнение Эйлера в рассматривае-
мой задаче имеет вид

427
ДВИГАТЕЛЬ С СОЛНЕЧНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
з 6]
Заменим функцию Г= (х,/х)' некоторой известной функцией времени
Р' (1), принимающей на краях интервала те же значения, что и Г (х, хо):
РО) (0)=1 ~РО) (Т)= [х /(х +1)]2
Уравнение Эйлера для нового функционала примет вид
(12.186)
Это уравнение легко интегрируется:
х'О'(1) =с,+с 1+ Г'(~) (х — с) (с [-с'г) ц,'г,
(12.187)
где с„..., с4 — постоянные интегрирования. По найденной траектории опре-
деляется новая функция К [х'о' (~), х ]= ~"' (~). Повторяя описанную про-
цедуру, найдем новое приближение х'1' (8) и т. д. а
В качестве нулевого приближения была ис-
пользована линейная функция ~'О'(~)=1 — Ь|, где
Ь= Г (2х,+ ~) 1(х,+ ~'Т. Для дальнейших шагов
функции ~'" (~) заменялись их приближенными
выражениями с помощью интерполяционного мно-
гочлена Ньютона, причем число узлов интерполя-
ции увеличивалось на каждом шаге процесса. Это
дало возможность каждый раз доводить интегриро-
вание до конца. гг ю .юк юг ~ г
На рис. 12.46 приведены графики функ-
ций а" (1), соответствующие последовательным
приближениям', для сравнения пунктиром показан
закон изменения а (1) для движения с постоянной
мощностью (граничные условия х, и х,+1 примерно
~3
соответствуют средним радиусам орбит Земли и
Марса). Значение функционала (12.184), найден- ряс. 12.ы. посяеяояягея~яые
и ~2 у з приближения (О, 1, 2, 3) к оп-
ное описанным методом, равно — 1И Т ° тимальной программе усноре-
Отиетим, что для движения с постоянной
вая — оптимальное управление
мощностью 1Ч=1 и 1Ч= [хо /(хо+ 7) ] минимальные а (й) при постоянной иощности.
значения функционала равны 12РТ-' и 27РТ-З.
Оценим полученный результат следующим образом. Искомая величина,
очевидно, не превосходит значения функционала (12.184) на траектории, со-
ответствующей оптимальному движению с постоянной мощностью
-19,8РТ-'. С другой стороны, зная производные минимального значения
функционала (12.180) по параметру в точках х. и х,+1 (см. п. 2) и значение
его в точке х„=х +1, равное 27РТ ', находим, что Х 18РТ-'. Таким об-
разом, описанный приближенный метод дает возможность построить траек-
торию, весьма близкую к оптимальной.
Рассмотренная простейшая модельная задача позволяет выявить осо-
бенности программы реактивного ускорения при полете по оптимальной
в смысле функционала (12.184) траектории. Характер изменения ускорения
з данном случае существенно отличается от линейного закона (рис. 12.46),
который соответствует оптимальному движению с постоянной мощностью.
Получившийся закон изменения а (~) имеет простое физическое толкование:
высокий уровень ускорения выгодно поддерживать там, где более высокая
мощность силовой установки, т. е. в начале пути; торможение происходит
при более низкой мощности, и поэтому уровень ускорения в конце пути дол-
жен быть меньше, чтобы не получить большого расхода рабочего вещества.

428
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
~ГЛ. 12
Для приближенного построения оптимальной траектории в центральном
поле можно воспользоваться методом транспортирующей траектории Я 2
гл. 5) в сочетании с изложенным выше интерационным процессом.
В качестве примера рассмотрим траекторию полета к Марсу, оптималь-
ную в смысле минимума функционала
77
У = (г('г„)- а'Ж
(г = г„).
(12 188)
Для простоты предполагается, что траектория плоская. В качестве крае-
вых условий взяты условия, приведенные в ~ 2 гл. 7 (п. 5) для полета к Марсу
продолжительностью Т = 212 сут
В ПЛОСКОСТИ ЭКЛИПТИКИ.
В качестве функции 1'"' (~) берет-
ся приближенное выражение Г ~г (~),
г„1, соответствующее траектории по-
лета к Марсу с двигателем постоянной
мощности, приведенной на рис. 7.8.
На рис. 12.47 показана траектория
~улла
Рис. 12. 47. Оптимальные траектории
межорбитального перелета Земля — Марс
за 212 сут.
Рис. 12. 48. Оптимальная пр ог рамма упр ав-
ления, соответствующая сплошной кривой
с рис. 12.47.
полета в транспортирующей системе координат, для сравнения пунктиром
показана траектория полета с двигателем постоянной мощности. Закон уп-
равления а (~) представлен на рис. 12.48. Величина функционала У=-
=16,4м'/секз. Для движения с постоянной мощностью К=1 и Г=(г /г,)'
минимальные значения функционала соответственно равны 9,25 м'/сек'
и 25,1 м'/сек'
Зная величины минимальных значений функционала при г„=г и при
г„= г1, можем приближенно определить оптимальные значения параметра
г„и функционала Х (г„) (п. 2): при а=1 кг/квт, 3=1,5 кгlм', ~=0,1 оптималь-
ное расчетное расстояние до Солнца г„,, 175 106 км (г,=150 ° 106 км, г =
=250 106 км), минимальное значение функционала Х(г„„,) =17 м2/секз (У(го) =-
=18 м'/секз).
$ 7. Двигатель с изотопным источником энергии
0(~ Ж(~ Ж,е ~',
(12.189)
1. Характеристики двигателя и формулировка вариационной задачи.
Максимальная мощность двигателя с изотопным источником энергии, так же
как максимальная тяга изотопного паруса Я 5), экспоненциально падает со
временем:

429
ф 71
ДВИГАТЕЛЬ С ИЗОТОПНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
У=Же ~~,
~ =1~2д ~-.
(12.190)
Рассматривается движитель с ограниченным диапазоном регулирования
скорости истечения:
(12.191)
(в предельном случае Г,„„~ со, что соответствует идеальному регулиро-
ванию).
Масса двигательной системы определяется начальным значением мощ-
НОСТИ.
М, = Ужо °
(12.192)
Задача о доставке максимальной полезной массы записывается в виде
пг,= — 1с,пг,е 'Р 'о,
ш. (О)+
+ш„(0) =1,
г(0) =г„
ш. (1) = гпах,
ш„(1) = ор1,
г(1) =г„
г=ч,
(12.193)
е3+~, т(0) = т„
ч
Э=,, 0( Г(Е) (1, о(й) =1 или О, ~е(Е) ) =1).
т(1) =т,
2Т
Здесь все величины безразменные: массы ш., ш„отнесены к начальной
массе, время ~ и период полураспада 1/1 — к полному времени движения,
радиус-вектор г — к характерному расстоянию ~, скорость движения
к 1~Т, скорость истечения — к г,„.
Записанная вариационная задача соответствует стандартной формули-
ровке проблемы Майера: требуется определить управления е (~), О (~), К (~)
и параметр ш„так, чтобы обеспечить максимум конечного значения фазовой
координаты ш.(1) =ш,. Далее рассматривается решение этой задачи для
двух модельных маневров в бессиловом поле.
2. Набор модуля скорости. В качестве характерного расстояния возьмем
и,Т, где и, — заданное приращение модуля скорости. Комбинация Ф (за-
пишется в виде Ф=(а/2) и1Т ', граничные условия будут х (0) =О, х (0) =О,
х (1) = ор$, х (1) =1.
Оптимальные управления в рассматриваемой задаче определяются сле-
дующими соотношениями:
(12.194)
2 ~~,Ф (т, + т.,)
Ри
Из анализа гамильтоновой функции Н и краевых условий следует, что
найденные управления е (~) и 8 (~) в задаче о наборе заданного модуля ско-
рости остаются такими же при любом режиме регулирования двигателя.
где Яо — максимальная мощность реактивной струи в начальный момент
времени ~=0, ~ — параметр, характеризующий падение мощности по вре-
мени (1/1 — период полураспада изотопа). Как показано выше, для двига-
тельных систем ограниченной мощности при включенном движителе всегда
выгодно максимальное использование мощности. В этом случае основные
параметры двигательной системы связаны соотношениями (ускорение рабо-
чего вещества происходит без потерь)

430
ДРУГИЕ ТИПЫ ДВИГАТЕЛЕЙ
[ГЛ. 12
В момент времени ~1 скорость истечения выходит на границу Г„, (~,) =1:
1,= — — 1п 1 — (1 — е ) )(
1 л
1 1 — е ~
!!!,Ф вЂ” !и — -';- !,
(12.195)
Этот момент времени в зависимости от параметров может принимать различ-
ные значения, поэтому при решении уравнений (12.193) получаются три вида
выражений для функционала т,:
~/у~,р Х 1 — е ~
т = — е
7~ й
У
при Е (О
(12.196)
1 — е
— Х
В случае (12.196) управление Г (~) граничное: Г (~):1' случай (12.197)
соответствует идеальному регулированию: Г (~)=$'„, (~); в случае (12.198)
Г (~) = ~;„(~) при О ( ~ ( ~, и Г (~) =1 при ~, ( ~ ( 1.
Оптимальное значение массы двигателя т„составит
(12.199)
Полученные результаты приведены на рис. 12.49, где показана зависи-
мость относительной полезной массы от 1Т при наборе модуля скорости с
идеально регулируемым движителем (О ( Г=$'„, ( со).
р~ р~ р ав
р а~ аг ~в р-~~ф
Рис. 12.50. То же, что и на рис. 12.49, для
перелета между точками покоя на расстоя-
ние 1 за время Т.
Рис. 12. 49. Влияние падения мощности
изотопного источника на полезную на-
грузку — набор модуля скорости и, за
время Т.
3. Перемещение между точками покоя. Для второй модельной задачи—
перелет между двумя точками покоя, расположенными на расстоянии ~,—
при 1,) 1
при 0(1,(1
йс1Ф 1п 2 2 Х 1 21 ~1 Х
7Л = 1
2 ~1 2Х
(12.197)
(12.198)

ЙЧ
ДВИГАТЕЛЬ С ИЗОТОПНЫМ ИСТОЧНИКОМ ЭНЕРГИИ
аналитическое решение получается только для идеально регулируемого
движителя.
Максимальная полезная нагрузка определяется следующей зависимостью
от функционала Ф = (а/2) 120 Т-з:
~з ~~
12 1 — е 2 12е
На рис. 12.50 показана зависимость от 1Т величины относительного
полезного груза в задаче перелета между двумя точками покоя с идеально
регулируемым движителем. Данные рис. 12.49 и 12.50 показывают, что па-
дение мощности реактивной струи по времени заметно сказывается на ве-
личине полезной нагрузки при отношении времени выполнения маневра
к периоду полураспада порядка 1:Т ) 0,1.

ЧАСТЬ ???
ПРОБЛЕМЫ ОПТИМИЗАЦИИ вЂ” ИГРОВОЙ
И СТАТИСТИЧЕСКИЙ ПОДХОДЫ
ГЛАВА 13
ВЫБОР ОПТИМАЛЬНЫХ ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ
ДВИГАТЕЛЬНЫХ СИСТЕМ ПРИ НАЛИЧИИ НЕОПРЕДЕЛЕННОСТЕЙ
Постановка проблемы оптимизации, данная в ~ 1 гл. 4, имеет дело с одноцелевыми
аппаратами, предназначаемыми для выполнения единственного маневра, характеристики
которого точно известны. По мере развития ракетной техники перед ней ставится большое
число новых задач. Но создание каждого нового аппарата по-прежнему остается связан-
ным с большими экономическими затратами. Поэтому проектирование для каждой новой
задачи нового аппарата становится чрезвычайно обременительным. Появляется необ-
ходимость проектирования многоцелевых (универсальнь~х) аппаратов, способных эффек-
тивно решать некоторое мноясество задач (а не одну задачу). Ситуация осложняется еще
и тем, что характеристики этих задач (маневров) на этапе проектирования могут быть
не определены с достаточной точностью.
Проблема универсализации и стандартизации присуща всем отраслям техники и так
или иначе решается. В старых отраслях, где накоплеп огромный практический опыт,
проще находить достаточно эффективное инженерное решение. Однако используемые
для этого методы носят эмпирический характер, плохо формализуемы и поэтому не могут
быть распространены на новые области техники.
В настоящей главе излагается формализованный подход к решению проблемы уни-
версализации [13.1 — 13.14). Первоначально он был ориентирован на космическую тех-
нику. Дальнейшее обобщение подхода сделало его применимым для достаточно широ-
кого класса управляемых систем.
Дается общая формулировка задачи Я 1), изучаются различные ее варианты в за-
висимости от объема располагаемой информации о параметрах маневров (Я 2, 3). На ос-
нове общего подхода решается ряд конкретных задач универсализации параметров косми-
ческих аппаратов с разными типами двигателей (идеальный двигатель ограниченной
мощности — Я 1 — 3, нерегулируемый двигатель — э 4, 5).
$ 1. Постановка проблемы универсализации
управляемых систем
Проблему универсализации схематически можно описать в терминах
исследования операций И3.15). Определен круг частных задач (частных
операций), который должен быть выполнен оперирующей стороной (опериру-
ющую сторону будем называть «Конструктором»). Общие средства оперирую-
щей стороны ограничены, а именно: из экономических соображений ограни-
чено общее число систем, разрешенных к проектированию, а физические
принципы работы системы ограничивают возможности каждой из спроекти-
рованных систем. Оперирующая сторона, т. е. Конструктор, не располагает
полной информацией о всех условиях предстоящих операций. Это неконтро-
лируемые Конструктором факторы (природные неопределенности или ре-
зультаты активного противодействия). Удобно считать, что неконтролируе-
мыми Конструктором факторами распоряжается другая сторона (ее во всех
случаях будем называть «Природой»). Требуется оптимальным образом ис-
пользовать ресурсы оперирующей стороны, обеспечив в некотором смысле
наилучшее выполнение множества частных операций (т. е. объединенной
операции).

ПОСТАНОВКА ПРОБЛЕМЫ УНИВЕРСАЛИЗАЦИИ
Проблема универсализации управляемых систем находится в русле об-
щих идей исследования операций. Вместе с тем она наполнена специфическим
содержанием. Специфика определяется тем, что объект исследования — это
динамическая система со свободными управляющими воздействиями, ко-
торые могут изменяться во времени. Поэтому проблема универсализации
таких систем содержит внутри себя проблему построения оптимальных
программ управления. Последняя должна быть решена в каждой точке мно-
жества возможных маневров для всех допустимых значений параметров си-
стемы. На основе этого решения становится возможным перейти к заклю-
чительной стадии — к выбору оптимальных параметров системы.
Параметры системы должны быть одинаковыми для всех маневров или,
в общем случае, могут принимать ограниченное число значений, меньшее
числа маневров (требование универсальности системы). Управляющие функ-
ции для каждого маневра могут выбираться свои. Задан критерий эффектив-
ности для отдельного маневра. Оптимальность универсальной системы по-
нимается в смысле максимальной близости значений критерия к предельным
для всего множества маневров по норме некоторого функционального про-
странства [13.1 — 13.141.
Аналогичный подход содержится в работах [13.16, 13.17], где рассматриваются
задачи универсализации параметров двигательных систем ограниченной мощности, неро-
гулируомой и идеальной. Минимизируется максимальное по всем маневрам отклонение
функционала от предельных значений, что соответствует максимальной близости по норме
С. Решение строится на базе метода оптимальных покрытий. В [13.18] предлагается
ряд полезных обобщений подхода и метода решения.
Другое направление исследования обсуждаемой проблемы развивается в работах
[13.19 — 13.21], посвященных оптимальному осреднению управлений. Управляющие
воздействия и системы (постоянпые управляющие параметры а и управляющие функции и)
представляются в виде номинальной г и корректирующей г' составляющих. Номинальная
составляющая должна быть одинаковой для всех маневров, корректирующая — выби-
рается для каждой реализации. Параметры маневра предполагаются случайными вели-
чинами с заданным законом распределения, обладающим конечной плотностью, кото-
рая считается непрерывной и дважды дифференцируемой функцией. При выборе коррек-
тцрующего воздействия г' для очередной реализации определенная часть Л случайных
параметров маневра полагается известной, а другая — Р— неизвестной. Таким образом,
управляющие функции и управляющие параметры оказываются приравненными в смысле
возможности их выбора. Функционал задачи и конечные условия формируются в виде
требований к математическим ожиданиям некоторых величин, зависящих от реализации
параметров маневра, конечных значений фазовых координат и управляющих параметров.
Формулируется и доказывается необходимое условие оптимальности, аналогичное прин-
ципу максимума Л. С. Понтрягипа.
Еще одно направление исследований проблемы универсализации параметров тех-
ш1ческих систем развивается в серии работ [13.22 — 13.26]. В них явно учитываются за-
траты па проектирование, производство и эксплуатацию систем (заданпые функции проект-
ных параметров систем). Считаются заданными также потребное число р (х) систем с па-
раметрами х, потребное множество й значений х и функция р (х, хь) взаимозаменяемости
систем (чнсло систем х~„способных заменить одну систему х). Выбираются параметры
каждого типа систем хь (7с=1,..., Г), области Йь их использования и число К типов
систем из условия минимума суммарных затрат. В случае, когда х — скаляр, а функции
стоимостей монотонны по х, установлен ряд свойств решения этой задачи и предложен
чпсленный алгоритм, основанный на методе динамического программирования [13.23,
13.24]. В [13.25] постановка обобщается в направлении учета динамического фактора:
потребности в системах и эффективность систем задаются во времени, набор свободных
переменных пополняется моментами замены систем старого типа новыми. Обзор этой се-
рип работ содержится в [13.26].
Применимость описанной выше постановки ограничивается серией необходимых
дополнительных предполоясений: а) возможно установление взаимно однозначного соответ-
ствия между параметрами системы и маневра (иначе теряет смысл функция взаимозаме-
няемости); б) критерий качества выполнения отдельного маневра аддитивен по числу
попыток выполнения этого маневра (иначе снова нельзя будет ввести функцию взаимо-
заменяемости); в) информация о маневрах полная. Кроме того, отметим, что эксплуата-
ционные расходы считаются зависящими только от параметров систем. в то время как
пля многих управляемых систем эти расходы существенно зависят от режима эксплуата-
ции (т. е. от программы управления).
28 Механика полета

[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
1. Параметры маневра и системы. Пусть имеется управляемый объект
(динамическая система), поведение которого описывается обыкновенными
дифференциальными уравнениями вида
И~
— = ~р Д, 1, и, х, у),
~ Иа) 6 ='а (у) 1 И ) 6 =' (у)
(13. 1)
(и=и(~) ~ Г(х), Их/сИ=Иу/И=О, х~Х„у~ У,).
Здесь ~ = (1„..., ~,) ~ Е, — вектор фазовых координат системы из д-мерного
евклидова пространства; 1 — текущее время, и = (и„..., и,) ( У (х) ~ń—
вектор управляющих функций из допустимого множества Г (х); х=(х„...
..., х„) ~ Х, с ń— вектор постоянных по времени управляющих параметров
из допустимого множества Х„у = (у,,..., у ) ~ У, ~ ' Š— вектор постоян-
ных по времени параметров маневра из допустимого множества Уо; ., и
1 — начальное и конечное многоооразия состояний системы.
Под маневром понимается переход системы из начального состояния
~ (1,) ~ Е, в конечное ~ (1,) ~ Е„начинающийся в момент времени 1, и за-
канчивающийся в момент ~,. Маневр задается набором чисел, определяющих
начальное Е, и конечное Е, многообразия, в том числе начальным 1„и конеч-
ным 1, моментами времени, а также рядом других параметров, входящих
в правые части уравнений (13.1) и характеризующих внешние условия (на-
пример, гравитационные постоянные, параметры атмосферы). Совокупность
этих величин обозначается вектором
('О = О (у) ~О = ~О (у)г
(у) ~ =~ (у) ч=ч( у))
у = (д„..., у ) (- 1', С Е
(13.2)
и называется вектором параметров маневра. Это неконтролируемые оперирую-
щей стороной — Конструктором факторы (обстановка проведения операции).
Ими распоряжается другая сторона — Природа.
Динамическая система характеризуется набором значений постоянных
управляющих параметров х,. (к последним могут относиться и предельные
значения управляющих функций и,.;„и....). Этот набор обозначается век-
тором
(У = У (х), ~р = ~р (..., х, ...))
(13Л)
х= (т„..., х„) ~Х, С~Е„
') В рамках одной задачи допускаются функционалы разной природы для разных
маневров у.
и называется вектором параметров (или проектных параметров) системы.
Физически различным системам соответствуют отличающиеся хотя бы
в одной компоненте векторы х, и обратно. В одной и той же системе могут
быть реализованы различные управления и (1), разумеется, в рамках тех ог-
раничений, которые накладывают на управления проектные параметры.
К управлению и условно относятся еще параметры, которые можно назвать
параметрами настройки. Эти параметры не могут меняться по времени в про-
цессе выполнения маневра, но могут быть изменены перед выполнением оче-
редного маневра (настройка системы). Вместе с управляющими парамет-
рами х управляющие функции и образуют набор управляющих воздействий,
которыми распоряжается Конструктор.
2. Система, оптимальная для одного маневра. Эффективность выполне-
ния отдельного маневра или, другими словами, частной операции (вектор у
фиксирован) характеризуется некоторым функционалом' ) от фазовой траек-
тории ~ (~), управления и (~) и от параметров системы х и маневра у. В силу
дифференциальных уравнений и граничных условий (13.1) этот функционал

435
пОстАнОВ~А пРОБлемы униВеРсАлизАции
можно считать зависящим только от и (~), х и у. Кроме того, для опреде-
ленности положим, что оперирующая сторона стремится к максимуму функ-
ционала:
(13.4)
И'=К[и(~), х, у~=шах по и(~) ~У(х) и х(=Х,.
В обычной постановке задачи оптимизации для каждого маневра у
нужно построить такие управления и (г) и назначить такие параметры си-
стемы х, которые обеспечивали бы выполнение связей (13.1) и доставляли бы
максимум функционалу (13.4). Для удобства изложения разобьем эту задачу
на две части.
Первая часть — динамическая. Параметры маневра у и системы х фик-
сированы '), выбирается оптимальное управление и (~)
И~= шах г'[и (г), х, у~=..К[и„„(х, у, 1), х, у1=г',(х, у)
и(1)бах)
(13.6)
(задача отыскания экстремума функции нескольких переменных).
Здесь для каждого маневра у выбирается своя система х,, (у), функцио.
нал достигает своего наибольшего значения из всех возможных и зависит
только от у. Решение (13.6) назовем идеальным, в дальнейшем оно предпола-
гается известным.
Термин «идеальное решение» в данном случае имеет следующии смысл з).
Для реализации решения (13.6) Конструктор, во-первых, должен распола
гать полной информацией о параметрах маневра у, который предстоит вы-
полнить, и, во-вторых, он должен иметь в своем распоряжении систему с па
раметрами х=х„,(у), оптимальными для маневра х по критерию (13.6),
неограниченные ресурсы.
3. Требование универсальности системы. Пусть теперь предстоит вы-
полнить не один маневр, а серию различных маневров. Параметры маневр
у могут принимать с разной частотой различные значения из некоторого мно-
жества Уе~Е . Вводится нормированная частота ч (У) повторения маневров
у из любого подмножества У~Ге, т. е. вероятность появления маневров,
принадлежащих У:
ч(У) =1
(13. 7)
(вероятностная мера в пространстве параметров маневра [13.27 13 281)
') В некоторых случаях динамическую часть задачи удается сформулировать так,
что она но содержит параметров системы х. Это существенно облегчает решение. При
ром такого «чистого' & t; разделе ия мо ут служ ть зад ч о доста ке максимальн го пол
ного груза космическим аппаратом с идеальным двигателем ограниченной мощности
(гл. и, 7) или ограниченной скорости истечения (гл. 5).
') С термином «идеальный двигатель» не связан.
28*
в силу связей (13.1).
Динамическая часть задачи (вариационная проблема) является общеи
как для обычной постановки, так и для постановки задачи универсализации.
После ее решения функционал (13.4) становится функцией параметров си-
стемы х и маневра у. Решение (13.5) будем считать найденным и функцию
~, (х, у) — известной на всем допустимом множестве изменения аргументов
х(=Х„и у~У,.
Вторая часть — выбор параметров системы. Параметры маневра у за—
даны, решение (13.5) динамической части задачи известно, определяются
оптимальные параметры системы х
И' = тах г, (х, у) = Р, (х„, (у), у) = К (у)

436
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
При этом допускаются как непрерывные, так и дискретные распределения. В первом
случае конечной частотой обладают только множества ненулевого объема по евклидовой
метрике
Ну,...ау = Ну- О,
у~ У у~ У
и тогда существует конечная плотность распределения Г„(у), через которую частота (>3
выражается интегралом
ч (У) = ~„(у) о,у.
Во втором случае (дискретные распределения) существуют множества У'& t; У, пулев
объема »' (У')=О, но обладающие ненулевой частотой ~ (У') ) О. Для таких множеств
плотность распределения не существует (бесконечна).
Если при выполнении большого числа различных маневров продолжать
следовать идеальному решению (13.6), то потребуется создавать большое
число неидентичных систем (по «числу» различных маневров у). Это может
оказаться невыгодным с экономической точки зрения из-за дополнительных
затрат на проектирование и производство. В целях сокращения этих затрат
выдвигается требование универсальности системы (ограничение ресурсов
оперирующей стороны). Оно формулируется в двух вариантах.
П е р в ы й в а р и а н т. Задается допустимое число Й неидентичных
систем, меньшее числа различных маневров. Это означает, что вектор х
параметров системы для всех значений вектора у( У, параметров маневра
может принимать не более чем Й различных значений:
х=х"', ил~т х"-',..., или х~".~.
(13.8)
Можно распорядиться величинами компонент постоянных (не зависящих
от у) векторов х~",..., х'"-' и для каждого маневра выбирать наиболее под-
ходящий из них (если перед началом выполнения очередного маневра стано-
вятся известны его параметры у).
В т о р о й в а р и а н т возможен в случае, когда система собирается
из элементарных секций. Параметры х такой составной системы определя-
ются параметрами Лх элементарной секции и числом секций и:
(~» =1, 2, ...).
(1 >
х=х(с&g ;,
') Но и здесь максимальное число секций может быть найдено для каждой задачп
как функция й (Лх). Поэтому для экономии места требование универсальности системы
будет (там, где это возможно) записываться в единообразной форме: х ~ (х' &g ;
= (х~'&g ;, . ., х(~ ) В та ой зап си ля втор го вариа та постано ки (зад ча об у
версальной секции) понимается х'"& t; =х и, Ш ), я я (Х
Так, для компонент х,. вектора х, представляющих собой аддитивные вели-
чины (масса, геометрические размеры и т. п.), эта зависимость — линейная:
х,.= с> х, Компоне ты же х, являющи ся физическ ми параметр ми п
цессов (температура, напряженность электрического поля и т. п.), от числа
секций не зависят: х,.=Ля, Возможны и другие типы связей (13.9).
Параметры Лх элементарной секции должны быть одними и теми же
для всех маневров у( У, (универсальная секция). Но зато для каждого ма-
невра можно выбирать свое число секций ш (снова при наличии информации
о параметрах очередного маневра). Это число, в отличие от предыдущего слу-
чая, заранее сверху не ограничивается ').
В терминах исследования операций выдвинутое выше требование уни-
версальности системы представляет собой ограничение ресурсов оперирующей
стороны при объединении частных операций [13.15).

437
ПОСТАНОВКА ПРОБЛЕМЫ УНИВЕРСАЛИЗАЦИИ
ЛИ~ =- Р, (у) — г"', (х, у) )~ О.
(13.10а)
Вместо абсолютной разности (13.10а) может применяться относительная1):
— ) О.
у=
(13.10б)
В тех местах, где тип разности (13.10) несуществен, будет использоваться
единое обозначение ЛР (х, у): ЛР=Р,— Р, для (13.10а) и ЛР=1 — Р1/Р, для
(13.10б).
Критерий эффективности универсальной системы на всем множестве
маневров (объединенный критерий, или критерий объединенной операции)
формируется по-разному в зависимости от физического смысла задачи.
Здесь делается естественное предположение о том, что конкретное содержа-
ние понятия «эффективность выполнения отдельного маневра» при объедине-
нии операций не меняется. Поэтому объединенный критерий должен зави-
сеть от критериев отдельных маневров. В него может входить еще и частота
повторения маневров. Кроме того, могут учитываться и новые соображения,
например по стоимости проектирования и производства систем, по относитель-
ной важности маневров и т. д. Для упрощения будем считать, что стоимость
Однозначно определяется допустимым числом различных типов систем не-
зависимо от значений их параметров х. Таким образом, соображения по
стоимости учитываются требованием универсальности системы, сформу-
лированным в предыдущем пункте. Относительную важность маневров
') Например, в тех случаях, когда для разных маневров функционал И' имеет
разную природу или его максимальные значения, Р, (у), сильно отличаются друг от
друга па мно,ьество УО.
В обоих вариантах постановки задачи универсализации предполагается,
что управления и (г) для каждого маневра выбираются свои, оптимальные
в смысле (13.5). Параметры выполняемого маневра при этом считаются из-
вестными, а ограничения, накладываемые на и заданием вектора х, и связи
(13.1) — соблюденными. Это — сформулированная выше динамическая часть
(13.5) задачи оптимизации, которая, как уже отмечалось, полагается ре-
шенной.
Кроме того, считается, что во всех случаях в распоряжении имеется
постаточное количество экземпляров систем каждого из спроектированных
типов. Требования к запасу и темпу производства систем зависят от ресурса
системы, от времени, затрачиваемого на выполнение одного маневра, от ха-
рактера распределения заявок на выполнение маневра по времени и от ряда
других факторов. Это — задача теории массового обслуживания. Для одно-
разовых однотипных систем и пуассоновского потока заявок она решена
в [13.29). Причем с заданной вероятностью гарантируется, что на фиксирован-
ном отрезке времени ~0, Т) ни одна заявка не будет «ждать» дольше неко-
торого заданного времени. Процедура решения аналогична излагаемой в ~ 2
гл. 14 при выводе формулы (14.66) для вероятности реализации гарантирую-
щего закона отказов.
4. Критерий оптимальности универсальной системы. По сравнению
с идеальным решением (13.6) универсальная система х на каждом отдельном
маневре у будет обеспечивать худшее значение функционала: Р (х, у) (
(Р, (у). Исключение могут представлять лишь те маневры у', для которых
параметры универсальной системы окажутся оптимальными в смысле (13.6):
х=х„, (у'). Для отдельного маневра проигрыш в функционале (13.4) при
использовании универсальной системы измеряется разностью между наилуч-
шим (максимально возможным) значением (13.6) и значением (13.5), обеспе-
чиваемым универсальной системой:

438
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
можно учесть, как обычно, весовыми коэффициентами и включить их множи-
телями в частоту ~ повторения маневров. Предположим, что других новых
соображений нет. Тогда объединенный критерий будет иметь вид функцио-
нала, зависящего от эффективности выполнения отдельных маневров Р (х, у)
и от частоты ~ повторения маневров.
Конкретизируем вид этого функционала. Поскольку новые соображения
считаются учтенными, нужно обеспечить наилучшее удовлетворение всех
старых, т. е. максимально приблизиться в некотором смысле к идеальному
решению Р, (у). Функции Р, (х, у) и Р, (у) будем рассматривать как элементы
пространства функций векторного аргумента у ( У,С Е„, параметров маневра.
Вектор х фигурирует как параметр. Частота ~ повторения маневров задает
меру в пространстве аргумента И3.27]. Близость элементов Р, и Р, опреде-
ляется через норму разности (13.10) как функции от у:
р =)/ЬР(х, у))) .
(13.11)
Функционал типа (13.11) и будет приниматься в качестве объединенного кри-
терия. Конструктор при выборе универсальной системы должен обеспечить
его минимум (максимальная близость к идеальному решению).
Кроме того, будем предполагать, что для каждого маневра установлен
минимально допустимый уровень о (у) ( Р, (у) значений функционала И',
начиная с которого маневр считается выполненным'). Универсальная си-
стема должна выполнять любой маневр. Поэтому минимизация функцио-
нала (13.11) будет проводиться при дополнительном условии')
Р,(х, у) ) о(у), или ~(х, у).=:0 для всех у(- У,.
(13.12)
Условие (13.12) можно включить непосредственно в критерий (13.11),
еели считать проигрыш в функционале равным (13.10) при соблюдении (13.12)
и бесконечности в противном случае. Это обеспечивается, например, такой
записью объединенного критерия:
2ЛК (х, у)
1 + з)уп ф (х, у)
(13.13)
Цр
Мр (х, у) ч (йу)
(13.14)
Нулевым элементом здесь считаются функции, равные нулю почти всюду (за исклю-
чением, быть может, множеств У, для которых ч (У ) =0). При р =1 интеграл
(13.14) представляет собой математическое ожидание (среднее значение) отклонений функ-
ционала Ю от идеального решения. Если распределение вероятностей (13.7) обладает конеч-
ной плотностью ~,, (у), то интеграл (13.14) превращается в риманов, причем ~ (Ыу)=
=У (у) Ф
') Естественно, при этом должны быть удовлетворены дифференциальные уравне-
ния и граничные условия (13.1).
') Такая задача не всегда имеет решение. Это зависит от того, насколько высок
уровень Ь (у), какое число Я различных систем задано и какой информацией о маневрах
располагает Конструктор.
где, в отличие от общепринятого соглашения, полагается з1дп 0=1. Как и
в предыдущем случае, ищется минимум р, но здесь функция р уже не огра-
ничена.
В дальнейшем изложении используются два типа норм 113.30): норма
Ь и норма С (или ее модификация — норма М).
По норме Лр близость к идеальному решению определяется интегралом Лебега—
Стилтьеса [13.28) по всем маневрам у из У, с мерой (13.7) от разности функций (13.10)
в степени р ) 1:

ПОСТАНОВКА ПРОБЛЕМЫ УНИВЕРСАЛИЗАЦИИ
По норме С близость к идеальному решению определяется точной верхней гранью
разности (13.10) по всем маневрам у из Уо'.
(13. 15а)
рс =э««Р сР (хе у) °
У~-Уо
(13. 15б)
= чга«шах ЛР (х, у) = «п1 вир ЬР (х, у)
У~-'~о «'к~го '(гл)=о уе'о'Лг
Нормы Б~, М и С связаны следующей цепочкой неравенств, вытекающей из их
определения: р~ ~ р~ & t; ~. Но ма ЛХ являе ся предель ой ля н рм Б
~р
— — 1~ п~ (13.16)
рв~ соР
лри любых функциях ~ (У) с одинаковыми нулями. Если же функции ~ (У) таковы, что
для любых подмножеств У~Уо с Г (У) & t 0 част т ~ У ) О а разно ть ЛР х,
непрерывна по у, то нормы М и С совпадают.
Таким образом, сформулирован критерий объединенной операции, представляющий
собой, вообще говоря, частный случай объединенного критерия. В работе [13.15) рас-
смотрено несколько способов построения объединенного критерия. Там для конечного
числа объедипяемых операций доказывается возможность приближенной записи объ-
ециненпого критерия достаточно общего вида при помощи конечного числа стандартных дей-
ствий. Аналогичное утверждение можно было бы доказать, используя в качестве стан-
дартных крцтерии типа (13.14), (13.15).
Предложенные крит ерии можно рассматривать как модели реальных критериев
и употреблять при отработке методов решения. Кроме того, их можно применять и в при-
кладных задачах на этапе предварительного проектирования системы (когда еще не сфор-
м«тровался критерий, учитывающий все многообразие внешних связей). Последнее воз-
можно, если есть данные о малой чувствительности оптимальных параметров универ-
сальной систеиы к изменениям объединенного критерия. Для рассматриваемых далее
задач это свойство выполняется (в определенных пределах).
5. Информация о маневрах. Окончательные математические формули-
ровки задачи универсализации зависят от состава информации о маневрах,
которой располагает Конструктор. Это происходит из-за того, что состав
информации определяет класс допустимых стратегий Конструктора и
во многом — выбор типа нормы в критерии оптимальности (13.11), если он за-
ранее не з адан.
По времени поступления информация о маневрах делится на априорную
и текущую. Априорная информация поступает до начала проектирования си-
стемы, а текущая — в процессе эксплуатации системы (после окончания
проектирования и изготовления) до начала выполнения очередного маневра.
Априорная информация представляет собой комплекс сведений о множе-
стве У, возможных значений вектора у параметров маневра и о распределе-
нии (13.7) частоты повторения маневров по типам. Если распределение (13.7)
известно, то рациональнее пользоваться нормой Л (13.14). Если известно
Нулевым элементом считается функция, равная нулю тождественно. Расстояние по
норме С не зависит от распределения (13.7) частоты повторения маневров и может
быть использовано для оценки сверху расстояний по нормам ~~ при любых распре-
делениях (13.7): рд ( рс (параметры системы х и тип разности ЛР в правой и ле-
Р
вой частях неравенства одинаковы). К тому же расстояние р~ дает оценку функцио-
нала на каждом маневре: Р, (х, у) ~ Р, (у) — ро для абсолютного проигрыша или
Р, (х, у) ~ (1 — рс) Рв (у) для относительного проигр ыша (в последнем случае счи-
тается Р, (у) ) 0).
Если все рассматриваемые распределения (13.7) таковы, что среди подмножеств
УС У, ненулевого евклидова объема Г (У) )О есть одни и те же подмножества У
с нулевой частотой ч (Ул) =О, то оценку рв ( рс можно уточнить, воспользовавшись
~р
выесто нормы С нормой ЛХ. В самом деле, верхняя грань (13.15а) монсет достигаться
как раз на маневре из множеств У~. выбрасывая при отыскании точной верхней
грани из множества Уо различные множества Ул. С Уо меры нуль ~ (У ) = 0 и найдя
точную нижшою грань получаемых значений, определим существенный максимум
(нор«га ЛХ)

440
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
только множество У„то нужно пользоваться нормами С (13.15а) и ЛХ (13.15б)
или рассматривать игровую задачу для нормы Ь с выбором наихудшего для
Конструктора распределения (13.7).
Текущая информация — это сведения о значении вектора у параметров
очередного маневра. При наличии текущей информации Конструктор может
выбрать из спроектированных систем (х'"') наиболее подходящую для вы-
полнения очереднего маневра у. Это означает, что стратегиями Конструктора
будут функции х (у) с ограниченным набором значений (х'"'), минимизирую-
щие проигрыш (13.10) на каждом отдельном маневре. Когда текущая инфор-
мация о маневрах отсутствует, такие функции уже не могут быть стратегияии
Конструктора. В этом случае нужно выбрать (из числа спроектированных)
систему для очередного маневра, не зная его параметров у. Конструктор
здесь может пользоваться так называемыми смешанными стратегиями: при-
менять разные системы х'"' с некоторой частотой ъ'"' (р."'+... + р.< - =
В следующих двух параграфах будут рассмотрены различные варианты
состава информации о маневрах и даны формулировки соответствующих
задач. Как отмечалось в п. 3, на этапе выбора параметров настройки и уп-
равляющих функций (вектор и) параметры очередного маневра у считаются
известными, так что этот выбор осуществляется оптимально в смысле (13.5):
и=и„„, (8, х, у).
6. Пример — идеальная двигательная система ограниченной мощности.
Для иллюстрации общих положений рассматривается задача о доставке
максимального полезного груза космическим аппаратом с идеальным дви-
гателем ограниченной мощности (см. гл. 6). Напомним, что термин «идеаль-
ный двигатель» не связан с введенным в п. 2 понятием идеального реше-
ния (13.6). Под идеальностью здесь понимается отсутствие потерь рабочего ве-
щества и мощности и отсутствие ограничений на диапазоны регулирования
параметров двигателя, за исключением мощности. Кроме того, предпола-
гается, что масса двигательной системы определяется максимальной мощ-
ностью (см. (6.'1)):
(13.17)
М =~~Я
Удельная масса идеального двигателя а обычно считается не зависящей от
мощности. Последнее предположение приводит к вырождению задачи об
универсальной секции — оптимальный размер (мощность) секции стремится
к нулю, оптимальное число секций — к бесконечности. В действительности
удельная масса двигателя возрастает с уменьшением мощности. Достаточно
точно эту зависимость можно аппроксимировать обратно пропорционально~~,
соответствующей (6.21):
У-.о
а=а +
шах
а„= 11п1 ", ЛХ„О = 11т ЛХ„(Ж,„), (1:1.18)
у ~ со ша~ ~гта~~О
шах
где а и ̄— заданные конструктивные параметры: удельная масса дви-
гателя с бесконечно большой мощностью и масса двигателя с бесконечно ма-
лой мощностью.
Формулировка задачи о доставке максимального полезного груза (без
требования универсальности двигателя) такова (см. ~ 1 гл. 4). Фиксируется
динамический маневр: переход из начальной точки (г„т„Ц ) пространства
координат — скоростей — времени в конечную точку (г„т„1,) в гра-
витационном поле ~ (г, ~). Требуется обеспечить максимум полезной массы
М, при заданной начальной массе аппарата М,. Начальная масса аппарата
М, при постановке задачи универсализации будет предполагаться одной и
той же для всех маневров, поэтому в дальнейшем используются относитель-
ные массы.

441
ПОСТАНОВКА ПРОБЛЕМЫ УНИВЕРСАЛИЗАЦИИ
Функционалом (13.4) для отдельного маневра служит полезная масса,
отнесенная к начальной массе аппарата:
И'=т, =ЛХ,/ЛХ = шах.
(13.19)
г (1е) = г„г (1е) = т„
г=а+~ (г, 1),
У = аЧ1=ш&gt
г (1,) = г„г (1 ) = т„
(13.20)
где а (1) — ускорение от реактивной тяги — является управлением и.
После решения динамической задачи (13.20) каждому маневру1)
(г„~„~,; г„т„1,; д (г, 1)) отвечает некоторое значение интеграла У,, (см.
гл. 7). Его мы и будем брать в качестве параметра маневра (13.2). Удобно
это сделать так:
у = '/,,а. У;, (г„т„1е; г„т„1„. ц (г, 1)) = Ф
(13.21)
(напомним, что удельная масса двигателя а, — заданный конструктивный
параметр (13.18) и в процессе решения задачи не меняется).
Двигательная система характеризуется тоже единственным параметром
(13.3) — безразмерной мощностью:
(13.22)
х = аЖ „/ЛХе = Ж.
Полезная масса т, для маневра Ф с двигательной системой Ж равна
(см. (6. 14))
т, (У, ~1&g ;  Ж ( + Т 1 Ђ” т„ Ж = К, х,
(т„= ЛХ„/ЛХе) (13.23)
— зависимость (13.5). Для каждого маневра Ф существует оптимальная
мощность Л~ „максимизирующая полезную массу (задача (13.6), см. (6.15)
и (6.21)):
Ж„, (Ф) = ~/Ф вЂ” Ф при т, (Ж) = — т„, + Ж (т„, = ЛХ„е/ЛХе = сопз~). (13.24)
Это максимально достижимое значение (идеальное решение (13.6)) равно
(см. (6.16) и (6.21))
(О ( Ф ( (1 — ~/т„е) ).
т,(Ф) = (1 — ~/Ф)' — т„, = К, (у)
(13.25)
Маневры задаются на отрезке [Ф„Ф,] — множество У,:
0 ( Ф, ( Ф, ( (1 — ~(т„,) °
(13.26)
Частота (13.7) повторения маневров вводится посредством функции рас-
пределения г', (Ф). Функция распределения неубывающая, непрерывная
слева, изменяется от нуля до единицы [13.27]:
К,(Ф')(Е, (Ф") для любых Ф'(Ф" (:[Ф„Ф,],
1&g ;т Г, Ф) =Г,(Ф ), Г,( е) О, Р„(Ф, 0)
Ф-эФ' — О
') Здесь и в (13.21) под и (г, ~) в соответствии с (13.2) понимается набор коэффипиен-
тов, характеризующих эту функцию.
Динамическую часть (13.5) задачи оптимизации для идеального двига-
теля ограниченной мощности удается свести (см. гл. 6) к независимой за-
даче (7.1), не содержащей параметров двигательной системы, с функционалом У:

[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫК СИСТЕМ
Частота повторения маневров Ф из отрезка [Ф', Ф"] С [Ф„Ф,] выражается
через функцию распределения следующим образом:
(13.27)
~ ([Ф', Ф"]) = Г„(Ф" + О) — Г, (Ф').
В соответствии с этим частота повторения одного маневра Ф будет )~ (Ф)=
=Г„(Ф+О) — Г, (Ф). Она равна нулю в точках непрерывности функции
распределения и конечна в точках разрыва.
В первом варианте требования универсальности двигательной системы
(13.8) задается число Й уровней мощности:
(13.28)
(и = 1, 2,..., Р; К'") = сопз$).
Ж= Ж'")
Масса двигательной системы согласно (13.17), (13.18) равна т„(Г) =т„е+Х
Проигрыш в функционале на каждом маневре вычисляется по (13.25) и (13.23):
абсолютный проигрыш (13.10а)
(13.29а)
относительный проигрыш (13.106)
ат (/у, Ф)
У
(1 — 1/Ф)" — т„е Ф + /У
(13.296)
т (Ф)
Обсудим свойства функций проигрыша (13.29) как функций двух переменных /У,
Ф. Общий вид их показан на рис. 13.1, на рис. 13.2 даны линии уровня. Рисунки построены
для случая т„0=0.
Области определения обеих функций проигрыша одинаковы и задаются неравен-
ствами (рис. 13.3)
1
О&l ;" у(
о<е
(13.30)
И = 1/т.„е — т,ц, Ф = (1 — 1/т„о) .
(13.31)
Что касается самих функций проигрыша, то абсолютный проигрыш (13.29а) от т„, не за-
висит, а для относительного проигрыша (13.29б) изменение т„, приводит к деформации
функции без изменения ее характерных черт. В этом можно убедиться, сравнив рис.
13.2, б и 13.4, где показаны линии уровня функции относительного проигрыша для т„,=0
и т„0=0,1 соответственно.
Область значений функций проигрыша (13.29), определенных на (13.30), — интер-
вал (0,1). Обе функции непрерывны и дифференцируемы по обеим переменным в области
(13.30). В граничных точках имеются разрывы функций. Для абсолютного проигрыша
(13.29а) это одна точка (К=О, Ф=О):
11тЬт (Ж, Ф=О)= — Оф11тЛт (/У=О, Ф)=1,
Л'-~.0 Ф-эО
(13. 32а)
Ограничения на Г и Ф снизу обусловлены физическим смыслом этих величин. Огра-
ничение на Х сверху наложено из-за того, что ни для одного маневра Ф оптимальная мощ-
ность (13.24) не превосходит 1/4 и дт /д/У(0 при /У)1/4. Ограничение на Ф сверху
отвечает за неотрицательность полезной нагрузки (13.23): с двигателем Г не могут быть
выполнены маневры, для которых функционал Ф превосходит верхний предел из (13.30).
Прежде чем перейти к подробному исследованию зависимости проигрыша от Ф и У,
сделаем замечание относительно влияния параметра т„0 — относительной массы двига-
теля с бесконечно малой мощностью (13.17), (13.18). Область определения (13.30) функ-
ций проигрыша (13.29) заметно сужается при увеличении т„, (рис. 13.3). Угловая точка
(К=О, Ф=1), имеющаяся на границе области при т„,=О, исчезает, она переходит в точку
максимума граничной кривой Ф=Ф (Г):

443
Р,В
Од
Об
Об
п,г
0 0,0! 0,05 0~
015 ОГ
Рис. 13.2. Линии уровня функций проигрыша (пунктирными',кривыми показан след промежуточных
максимумов по Ф функций проигрыша): а) абсолютный проигрыш; б) относительный проигрыш
(7йуо = 0).
б,б
Л'
005 01
Рис. 13.3, Границы о цласти определения функций проигрыша. Заштрихована область, соответ-
ствующая т,о — — 0,1.
ПОСТАНОВБА ПРОБЛЕМЫ УНИВЕРСАЛИ3АЦИИ
Рис. 13.1. Функции проигрыша: а) абсолютного, 6) относительного (т„,=О),
О,Р
0,1
005
001
0,05
О,/
л Ог

444
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
для относительного проигрыша (13.296) — две точки (Ж =О, Ф = 0) и (Ь' = 1/т„з — т„,
Ф = (1 — ~т„з) ):
Лт (Ж, Ф=О) Лт (%=О, Ф)
11ш (ф О) — О 4' 11ш (Ф) — 1,
1~т
Р-Р ~ т„о — т.,о
(13.326)
т Ф вЂ”, — Я
ат (Ж=~ф — Ф, Ф)
1па
Ф-э (1 — 4пг~ О)
т (ф)
Наличие точек разрыва хорошо видно из рис. 13.1, 13.2 и 13.4. На двух последних им
соответствуют точки пересечения линий уровня при различных значениях проигрыша.
В сечениях плоскостями Ф=сопзФ (фиксировапный маневр) функции проигрыша
выпуклы (рис. 13.5). С ростом мощности двигателя Г проигрыш сначала убывает до нуля
в точках, соответствующих идеальному решению (13.24), затем возрастает, вторая произ-
водная всюду положительна:
для абсолютного проигрыша (13.29а)
(О при У (1% — Ф,
)О при Ж) ~ф — Ф,
дат Ф
дя =' (ф+ д)з
(13.33а)
д2Ьт 2Ф
)дз = (ф+ д)з )
для относительного проигрыша (13.296)
Ф (О при Т (1~Ф вЂ” Ф,
(1 — ~~Ф) — т.„(Ф + ~У) ) О при Л ) ~Ф вЂ” Ф,
2Ф
дЛ~ т [(1 ~/ф)з т ] (Ф+ у)з )
(13.336)
д2Ьт 1, 21Ч
дфз — 2 Ф ' (ф+д)з °
дф + (Ф+Л)з '
(13.34а)
для относительного проигрыша ~13.29б)
д Ьт 1
дф . =(1 — ~ф)' — „, (ф-(- И)'
1 — ~Ф 1 т„о
~Ф ~(1 — ~ф) — т„] ф + ~
д2 ~т„2Ж 1 1 — ~Ф
(1 — Л)' — . (ф+ ~У)з ~%И1 ~Ф)' т ](Ф ( Д)з
(4 ~ф — 1) (1 — ~Ф) — т з 1 т„
4Ф ~/Ф ((1 — ~Ф)~ — т„з]~ ф+ 1у
(13.346)
В сечениях плоскостями Г=сопз$ (фиксированный двигатель): функции проигрыша
имеют два минимума (нули функций) и три максимума (два граничных и один внутрен-
ний). Это показано на рис. 13.6. Здесь перечислен полный набор максимумов и миниму-
мов. Он реализуется при т„,=О. Если т„,чьО, то часть из него может отсутствовать. Для
абсолютного проигрыша это происходит только за счет сужения области определения
(рис. 13.3), для относительного — сказывается еще и деформация самой функции
(рис. 13.4). Все это устанавливается исследованием частных производных по Ф:
для абсолютного проигрыша (13.29а)

445
ПОСТАН ОВ КА ПРОБЛЕМЫ УЕ1ИВ ЕРСАЛИЗАЦИИ
04
0,2
015 02
Рис. 13.4. Линии уровня функции относительного проигрыша при т,.=0,1. Пунктирной крпвой
показан след промежуточных максимумов по Ф функции проигрыша.
015
О(
02
Рис. 13.5. Сечения функций проигрыша пло-
скостямн Ф =сопят: а) абсолютного; б) отно-
сительного (т„о — — 0).
'01
0,05
Ой
Я01
0,05
Оl
~7,2 б4 б,б'
а1
Ф ~~ у ~г а
ф~
Рис. 13.6. Сечения функций проигрыша пло-
скостями Ж=соыС: а) абсолютного; 6) отно-
сительного (т„=О).

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
Разрешая уравнение дЛР/дФ =0 относительно У, получим:
для абсолхох((ого проигрыша (13.34а)
1/2 ~- (1/2 — х/Ф)
~1,2
1—
— Ф;
(13.35а)
для относительного проигрыша (13.34б) х)
1 1
2
хх'х = —. (1 — х/Ф вЂ” Ф вЂ” т„о) + —, (1 — х/Ф Ф вЂ” т„о)'+ . т„о
(13.3об)
Первые решения из (13.35) дают точки промехсуточного максимума функций проиг-
рыша по Ф:
для абсолютного проигрыша (13.35а)
Ф~Ф
ж —, ь~= (1 — ~Ф) — ~Ф 1 — ) = та*,
1 — ~Ф
(13.36а)
или
— )
для относительного проигрыша (13.35б)
Лт (У = Жх (Ф), Ф)
Ьт
х"х( = У (Ф),
— тах,
т (Ф)
(13.366)
или
2 чь 1 27 (У+ т„о) (1 — т„о — Ж)2 '/2
Ф= 3 Ж,, + — 1 соз 3 + 3 агс сов 4Й (2 /у)а
Положение промежуточных максимумов (13.36) на плоскости К, Ф показано пунктирными
кривыми на рис. 13.2. При увеличении мощности двигателя от 0 до 0,25 максимум абсо-
лютного проигрыша достигается на маневрах с функционалом Ф, изменяющимся от 0
до 0,25 соответственно (рис. 13.2, а), а максимум относительного проигрыша — при из-
менении Ф от 0,382 до 0,25 (рис. 13.2, б), т. е. происходит смещение максимумов в область
более напряженных по энергетике маневров.
Вторые решения пз (13.35а) и (13.35б) одинаковы, опи соответствуют точкам ми-
нимума проигрыша по Ф (нули функций проигрыша на рис. 13.2):
Ж = х/Ф вЂ” Ф, или Ф = (1/2+ 'х/1/2 — хх), Лт =О= тхп. (13.37)
Это решение дает оптххъхальххухо в обычноъх смысло мощность двигателя (13.24), изменяю-
щуюся в зависимости от функционала маневра Ф. Проигрьпп в полезной нагрузке здесь
равен нулю. Но чтобы реализовать это решение, нужпо для каждого маневра Ф выби-
рать свой двигатель К н иметь полххую ипформацнхо о фупхсционале маневра Ф.
Проведенный анализ свойств функций проигрыша позволяет сделать
качествепный вывод о том, когда нужно пользоваться абсолютным, а когда
относительным проигрышем. Наибольшие значения абсолютного проигрыша
сосредоточены в ооласти мало напряженных по энергетике маневров. Отно-
сительный же проигрыш распределен более равномерно. Поэтому при по-
строении критерия близости к идеальному решению на основе абсолютного
проигрыша можно ожидать хорошего совпадения с идеальным решением
для энергетически ненапряженных маневров и плохого — для напряженных.
Это позволяет думать, что абсолютным проигрышем можно пользоваться лишь
в тех случаях, когда это непосредственно вытекает из физического смысла
задачи (например, задача о минимальном числе перевозок). Если же из физи-
х) для относительного проигрыша есть еще одно решение, но оно дает отрицатель-
ные значения Х и поэтому отбрасывается.

447
ПОСТАНОВКА ПРОБЛЕМЫ УНИВЕРСАЛИЗАЦИИ
ческих соображений не удается сформулировать критерий близости, то тогда
его нужно строить формально на базе относительного проигрыша.
В заключение параграфа выпишем функции проигрыша для второго
варианта постановки задачи универсализации — для задачи об универсаль-
ной секции. Мощность секции ЛГ постоянна для всего диапазона маневров.
Масса секции (безразмерная), в соответствии с предположениями (13.17),
(13.18), равна Лт„=т„о+ЛЯ. Для каждого маневра Ф можно собирать дви-
гатель из различного числа ох секций. Секции считаются полностью авто-
номными и работают параллельно. Суммарные мощность и масса такого
двигателя определяются формулами
(13.38)
Ж = и Лхх(', т„= и (т„о+ Лхх(') = шт„о+ Х
Масса многосекционного двигателя (13.38) на ( ш — 1)т„о больше массы
односекционного двигателя той же мощности. Но зато возможность исполь-
зования для каждого маневра различного числа секций позволяет точнее
аппроксимировать оптимальную мощность (13.24) и ближе подойти к идеаль-
ному решению.
Подставим выражения (13.38) мощности и массы двигателя в общую фор-
мулу (13.23) для полезной нагрузки. Вычтя найденную величину из макси-
мально возможной (13.25), получим функции проигрыша:
абсолютного
Ьт, (Ь1а', щ Ф) =(1 — 1(ФХ вЂ” ~ЬТ( — 1)+ (к — 1) та (12.20а1
и относительного
('1 3.39б)
с областью определения, аналогичной (13.30):
0(ЬШ( —, =1,2,...,Е~( ), 0(Ф( ЬШ(
1 (13.40)
(через Е (... ) обозначено минимальное целое число, не меньшее данного:
Е+ (х) =и ) х ) и — 1).
Если записать функции проигрыша (13.39) через суммарную мощность х(1'= 02 Лх(',
то получатся старые функции (13.29) с неотрицательными добавками Лх=(02 — 1) 222„0
;(:хя абсолютного проигрыша и Ь2 = (02 — 1) 222„0 [(1 — х(Ф) — 222„01 для относительного.
2 — 1
Максимальное значение функционала маневра Ф, выполнимого с двигателем данной мощ-
ности Г, уменьшится по сравнению с (13.30). Оно будет соответствовать значению т.„„
увеличенному в ~ раз, и может быть определено по рис. 13.3.
При и=1 функции проигрыша (13.39) и их область определения (13.40), естественно,
совпадают со старыми — (13.29) и (13.30). Если зафиксировать 10 ) 1, то функции про-
игрыша (13.39) ухх(е нигде не будут обращаться в нуль. При этом все рисунки, построенные
для абсолютного проигрыша (13.29а), легко модифицировать на случай (13.39а): поверх-
ность на рис. 13.1, а и кривые на рис. 13.5, а и 13.6, а нужно сместить эквидистантно
вверх на Ь,=сопяй; на линиях уровня рис. 13.2, а нужно сделать новую разметку по
Л((х„добавххв к старым значениям Лх=сопзй. Более сложной будет деформация для от-
носительного проигрыша. Кривые проигрыша при Ф=сопяй нужно по-прежнему только
сдвинуть вворх па Ь,=сопят, а кривые проигрыша при Х=сопяС будут получаться пз
старых слохкеххххехх с монотонххо возрастающей функцией Л,(Ф). Последнее приведет хх сме-
щению внутрен)нних максимумов в сторону меньших значений Ф и к их исчезновению при
больших значопиях Я.
Если фиксировать мощность элементарной секции Ля=сопзф, то изменением числа
секций и можно получать толь ко д крет ые значения сум арной . Ощност у, крат ые
11 с~ары~ Функцххям проигрыша при этом добавляются линейные функции от и,
что приводит к сдвигу 2хххххимумов проигрыша по К в сторону меньших значений (в не-
прерывном варианте изменения ~в).

448
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
$ 2. Выбор универсальной системы при полной информации
о маневрах (статистический подход)
1. Формулировка задачи. Здесь рассматривается случай, когда Конст-
руктор располагает полной информацией о маневрах (априорной и текущей).
Ему заранее известны множество Уо параметров маневра и распределение
(13.7) частоты повторения маневров по типам. Такая ситуация имеет место
для многократно повторяющихся маневров при наличии обширного стати-
стического материала. Кроме того, до начала выполнения очередного ма-
невра Конструктору становятся известными параметры у этого маневра
и он имеет возможность выбрать из спроектированных систем (х"',..., х~'-'))
наиболее подходящую х~"~у)' для этого маневра, т. е. ту, которая ооеспечи-
вает минимум проигрыша (13.10):
т1п Ьг'(х~"), у) = Ьг'(х~"~у)), у), у~ У,.
(в=1, ..., Я
(13.41)
Здесь считается, что параметры систем (х< ), . ., х~ )) фиксиров
(системы спроектированы) и изготовлено достаточное количество экземпля-
ров систем всех типов (в соответствии с предполохсением, сделанным в ~ 1).
В качестве меры близости к идеальному решению берется расстояние
по норме Ь„. При этом проигрыш на каждом отдельном маневре опреде-
ляется соотйошением (13.41). Суммарный проигрыш (13.14) будет функцией
только от параметров (х'"') набора систем 1)
р (х"',..., х~ "~) = ьР" (х~'~у~~, у) фу)~
У~'-~'о
(13.42)
Эту функцию нужно минимизировать по х"',..., х~") ~:Х с учетом ограни-
чений (13.12) '):
р,= р (х&lt ') . ., х~ ) = т 1 р (х"',. ., х&l
х~1~, ..., х~~~б.~о
при ф (х<"~у ), у) ~0 ля в ех (:
('1 3.43)
~) Индекс Ь у расстояния р для сокращения записи опускается.
2) При р=1 задача (13.43) эквивалентна максимизации среднего значения крите-
рия (13.5).
где ~е (у) определяется соотношением (13.41).
Для задачи об универсальной секции векторы х"',..., х~"-) не являются
независимыми, они однозначно определяются, согласно (13.9), вектором
Лх параметров секции и номером и (числом секций, из которых собрана
система). Поэтому отыскание минимума (13.43) в данном случае проводится
фактически по Лх (-Х,.
2. Алгоритм решения. Будем рассматривать сформулированную задачу
(13.41) — (13.43) как задачу минимизации функции р нескольких перемен-
ных х'1',..., х~~) или Лх при наличии ограничения.
Опишем сначала процедуру вычисления значений функции р по задан-
ным значениям аргументов. Согласно (13.41) для любого у ~ У; нужно вы-
брать такое значение х из фиксированного набора (х'"'), которое миними-
зировало бы ЛР(х, у). Эта часть задачи не зависит от типа используемой
нормы и эквивалентна задаче отыскания максимума по х функции
(13.5) как для абсолютного (13.10а), так и для относительного (13.10б).

449
СТАТИСТИЧЕСКИЙ ПОДХОД
в 2]
проигрышей:
где х'1'=Бхе =;~... + х~~) =11хе.
тах 1',(х, у),
х~ (х( ))
(13.44)
При этом ограничение (13.12) учитывать не нужно, поскольку оно призвано
гарантировать приемлемый уровень значений критерия (13.5) на каждом
отдельном маневре, а задача (13.44) и состоит в том, чтобы выбрать для каж-
дого маневра из спроектированных систем самую лучшую в смысле того же
критерия.
Задачу (13.44) можно решать либо перебором по х(=(х'")), либо разде-
лением множества Уо параметров маневра у на подмножества У' ', где опти-
мальна система х' ':
Г,(х' ', у) = тах г",(х, у) для
Х~ (Х(~))
Г, (х' ', у) ( тах г",(х, у) для
х~ (х(~))
если г', (х' ', у) = Х', (х'~ ', у) = ..
у( У' '~ Уо
у( У ~~ УЯ)
. =Р',(х' ', у) = тах Х' (х, у),
х~ (х(~))
(13.45)
то
,У~
с х' '~х"', У' 'П)'~'= Д при и+), )) )' '= Уо) .
0) — 1
Здесь через У' ' обозначено замыкание множества У'"' (множество У'"' плюс
граница). Третье условие принято для того, чтобы сделать множества У'"'
непересекающимися. Это необходимо для дискретных распределений ча-
стоты (13.7) при сведении интеграла (13.42) к сумме интегралов по множе-
ствам У'"'. В противном случае (У' 'П У'))+ Я при о)+у) может оказаться
) (У' 'П У')))) О, и тогда
Чр
р(х"', ..., х~~)) (,~~
АКР(х'"', у)) (Иу)
и=1
у~ У(п~)
Если функция'Г (х, у) непрерывна по у(= Уо при любых х~(х'"') и мно-
жество Уо — область, то границы соседних подмножеств У'"' и У'~) опре-
деляются из решения системы уравнений вида
Р' (х'"', у) = У", (х'~', у) )~ У" (х" ', у)
(13.46)
(и+~+~; о), у, ~(= (1 2, ..., Я),
6 Уо) °
Отметим, что если подмножества У' ' выпуклы, то границы между сосед-
ними подмножествами — гиперплоскости (см., например, [13.311).
Определив для заданного набора (х'1',..., х~~)) подмножества У'1',
..., У' ', можно представить интеграл (13.42) в виде суммы интегралов по
этим подмножествам.'
р(х"', ..., х< )
Цр
,ег(в)( (1) и)))
где, в отличие от (13.42), номер системы и уже не является функциеи от у,
а, наоборот, по номеру ~)) устанавливается множество У'") параметров ма-
невров у, которые будет выполнять система х'"'.
29 Механика полета

[ГЛ. 13
450
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Разбиение множества Гс на подмножества Г'") представляется целесооб-
разным в тех случаях, когда интегралы в (13.47) берутся аналитически,
или факт выпуклости подмножеств Г&lt ") мо ет б ть установ ен до реше
системы (13.46), или решение системы (13.46) не представляет больших труд-
ностей. В противном случае, по-видимому, более выгодно решать задачу
(13.44) перебором на каждом шаге интегрирования (13.42). При этом моменты
перехода с одного элемента набора ( х' ')
фф С0
~~пУ на другой определяют (с некоторой точно-
стью) и границы подмножеств Г< ) К
у&l ;о реб ру ну но прибегн ть та ж  в
! случае, если множество Гс точечное.
У умр у&l ;о Перей ем теп р к отыска ию оп
мального набора (х<ц,. ., х lt ~) ),
у С~®~ сс+О к задаче (13.43). Функцию ЛР(х, у) будем
считать непрерывной и дифференцируемой
у~~И)
по х С: Хс и у (: Гс. В этом случае расстоя-
ние р также будет непрерывной и диффе-
ренцируемой функцией от х<'),. ., х
д, „, „„„„„„„, „„или от Лх 1), и для решения задачи (13. 3)
& t ) „ lt; ) нвмв„е„„„в нтсв „&lt ~> можно споль овать любой
сплошныыи линияме показаны старые метод, например метод скорейшего спуска.
границы, пунктирными — новые. Множе-
ство у < ~) (стар е) выдел но горизонта ь- Необходи ые ля реализа ии э их мето
ной штриховкой, множество У~( ) (но- ЗНаЧЕНИЯ Ч аСТНЫХ ПРОИЗВОДНЫХ ПО КОМ-
~Х
(ОЭ)
все) — вертикальной. понентам векторов х' '=(х& t; ), . ., х&
или вектора Л х=(Л х„..., Л х„) можно
вычислить без применения конечных разностей одновременно с функ-
цией р по формулам:
для ограниченного числа типов систем
р -Р
~~ — < ", у (" , Ђ” ") .&lt
(13.48а)
у( ~(С~)
для универсальной секции1)
Я и
со 1 С=1 у( У(со)
Ьух ' <х ', у ( Ђ ) &l ;Ну). &l
Особенность полученных выражений состоит в том, что в них фигурируют только
интегральные члены с производными от исходной подынтегральной функции. Члены,
обязанные изменению областей интегрирования У( ), взаимно уничтожаются. Формула
(13.48б) получается из (13.48а), если принять во внимание зависимость (13.9), согласно
которой х' '=х (&lt в, Л ). Послед яя предполагае ся дифференцируе ой по х В
случае, когда ~-я компонента вектора х( ) зависит только от ~-и компоненты вектора
Лх, сумма по 1 в (13.48б) исчезает, а индекс у заменяется на й. Например, для компонент,
представляющих собой аддитивные величины (х&l ;' )= <в
дх', ' О
даат~
при ~ фЙ,
при ~=А;
от числа секций (х~< ' = Лх
при ~ =~А,
при ~=А.
аналогично для компонент, не зависящих
дх~ ' О
Формулы (13.48) справедливы, если частота повторения маневров, принадлежа-
щих границе у& t; ) у lt;') мн жест  <" и у& t;у), ран а нул . Это меет м
') Функция в (1х), в отличие от функции в (х<,. ., х&l ;~)), оказы аетс
кусочно-дифференцируемой (на интервалах постоянства фактически используемого
числа секций).

5 2]
стАтистическиа подход
мер, для непрерывных распределении, если евклидов объем
До аж м первую из формул — (13 48а).
Для сокращения записи введем обозначения:
т(х, у)=ЬР~(х, у, Чг(х"&g ;, .. х
..., х ) = р>' ' т х" &g ; у) ~ (Ну). (
э=1
У
Дадим приращение Ьх Й-й координате вектора х& t;
х""'+ Ьх =,'х'
" + х — (т&g ;, . ., &g ;, &g ;, ~~> Лх, х)+&gt
соответствующее значение функции %' будет равно
т (х' & t + х, у) ч( у
у (х~'&g ;, у ч (Ну
Удх
( со)
~4- ( ')
Удх
.ио> о  gt; и(
1,'=ДОЕМ '~ ~~щ
дх
У,„=[У ' и &lt У П У'.'&gt ! ~ lt У
(13.50)
В самом целе, чтобы получигь из У' ' множество У' ' н
к У~") новые элемен
ство д„, нужно, во-первых, добавить
к новые элементы из Уд'"„', которые не принадлежат У' ) А это будут те эле-
менты, которые раньше принадлежали множествам У~')','=1 и — 1, и-~-$ ... Ы
их совокупность — множество [.] < л П У ' gt; В Ђ” ~
дх ~~~ ~ ~о-вторых, из У~ ) нужно исключить
элементы, которые уже не входят в У' ). Это б
то удут элементы У("), отошедшие к но-
вым множествам У") ~~
д,, (& t ф ), ни образ ют множес во (] l ; <
налогичнь1м
& t ~
способом получаются выражения и цля множеств Уд"„'
Пользуясь ацдитивностью интегралов, запишем и и а ения н
суммы интегралов по множествам, вхо я им в "&
м, входящим в правые части соотношений (13.50):
ьт= ~ — %'=
[т (х» + Лх, у) — у (х> &gt , у)] ч (
[у (х'&g ;, у) Ђ т (х' '+ х, )] &g ;
'4=~ у(')(.,у(ш)
дх
+ [~(х~ '+~х, у) — ~(х~', у)] (Иу)
у(о&g ; ~ у
дх
(13..~.! )
Вычислим предел
Ь%' д%' др
, Ьх дх~> '& t; Р  ж
Ит
(13.52)
Первый интеграл иа (13.51) дает')
1
11т—
д -~о ~~
[у (х' '+ ~1х, у) — т (х~ &g ;, ) ч ( у
т'")
(13. 53)
1'1 ЧЛ
' ,Чтобы сделать законным переход к и едел по знак
"- '.Р д-- - -пр Р- -- д /д- """""""""'"'"""'"'""'"""'
х~с.
Здесь через У'"' и У"'
д„У~„ооозначены новые множества (13 45) соответствующие иаме-
ненному набору векторов (х'1&g ;, . ., х' ',
оптимальны системы х'"' + Ь '" евно. Вы ез
старые (рис. 13.7):
х и х соответственно. Вы
анно. Выразим эти множества через

452
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 1З
остальные — обратятся в нуль (при условии ч (У<')ПУ& t;") =О). П каж м то н
мере интеграла
[Х (х'"' + ах, у) — Х (х". у)] ч (< у
У(со) . ~(~)
Ьх
([Х (х& t  + х, у) Ђ Х (х& t;" , у ] Ђ” [Х х& t;' , у) Ђ” Х (х l ; ), у
~(со) ~ ~(~)
Ьх
11о теореме о среднем (в силу непрерывности Х по у)
1= ([Х(»&lt " + х, у) Ђ” Х х& t; ), )]„ , — [ (х ', ) вЂ Х х' ), у ]„„„) ч У'"„" У<'
где у', у" ~ У&lt „ П У& t;'). ервая кобка здесь
[...]„„, = (дХ/дх),)„&lt „) „ Л  о (Л
а вторая—
[...] „=(п, у" — у') + о (] у — у'&lt
у" — у*= Хп,
0&lt 1&lt
Из уравнения границы множеств У~(") и У~'„'
Х (» ) + ох у*+)<та п  Х ( ~" *+ "ша
найдем
1 дХ
(п п) дх & t;
Тогда
[ ° ° ] = = ~ — ах + о (Ьх),
дХ
дю~ ~(®), у
0<~
(13.55)
Из соотношений (13.54), (13.55) следует:
дХ дХ
11т — 1= 11т — — ~ — ч (У'"„) П У< ))
д О ~~,д О д~ф д~(о~), У д~ф д~(сО), У»
так как первый сомножитель ограничен, а предел второго равен нулю:
11ш ч (У~~) П У< )  ч (У l ;~) П У lt
~х-р.О
Таким образом, предел (13.52) оказывается равным (13.53), что и доказывает формулу
~13.48а). Справедливость (13.48б) доказывается аналогично.
3. Пример — заданное число двигательных систем ограниченной мощ-
ности. Рассмотрим задачу 113.41) — (13.43) в приложении к идеальной дви-
гательной системе ограниченной мощности (и. 6 3 1), когда фиксировано до-
пустимое число И систем с разными уровнями мощности К<'),. ., К<
(13.28). Маневры задаются функционалом Ф (13.21) на отрезке [Ф„Ф ]
(13.26). Частота повторения маневров (13.7) определена функцией распре-
деления Р„(Ф) (13.27). Проигрыш на отдельном маневре вводится одним
из соотношений (13.29), при помощи которого расписывается суммарный
проигрыш (13.42):
абсолютный
(13.56а)
где п=яга&l ; Х (х& t;' , у ) — ига lt 1 ( ' ' у') в ” векто н рмали (в про тр н тве
нице множеств У(') и У( ), у* — произвольная точка этой границы Выберем точку у*
так, чтобы вектор у" — у* был коллинеарен нормали (рис. 13.8):

453
СТАТИСТИЧЕСКИЙ ПОДХОД
или относительный
р (Д711),,Д7(Я))
ф
1 й(
1
мах
(1 — )~Ф) — т„О щ=1, ...,а '~' ) + ф
о
В' ' — т ) НР„(Ф)
(13.56б)
Условие (13.12) формулируется в виде требования неотрицательности полез-
ной массы (13.23) для любого допустимого маневра:
Ж(")
т = мах
я)ш) ~ ф
д
У"' — т„о для Всех ф фо, Ф1.
(13.57)
Выражение, стоящее в левой части неравенства (13.57) — монотонно
убывающая функция Ф. Следовательно, если неравенство удовлетворяется
при Ф=Ф„то оно будет удовлетворяться и при любых Ф ( [Ф„Ф ]. Далее,
выполнение неравенства (13.57) в точке Ф1 для некоторого элемента
У") из набора (К~'),..., К~")) влечет за со-
/ 1~ ГГ)
бой его выполнение и для того элемента,
/ Г )
на котором достигается максимум левой части.
Разрешив неравенство т„(К'", Ф,) )~ 0
относительно Ж'" и присоединив к нему первое
из условий (13.30), получим выражение для об- Уд
ласти допустимых значений уровней мощности.
(13.58)
Рис. 13.8. Выбор точки у» на гра-
нице У~~~ Й У~') множеств У(
и У
(значения К, и К, можно получить еще как абсциссы левой и правой точек
пересечения прямой Ф=Ф, с границей области определения функций проиг-
рыша, построенной на рис. 13.3). В силу проведенных рассуждений выпол-
нение условий (13.58) гарантирует и удовлетворение неравенства (13.57).
Перейдем теперь к разбиению отрезка [Ф , Ф,] на участки, где элемент
У1") оптимален по сравнению со всеми другими элементами фиксированного
набора (К~'),..., К~~) ], — задача (13.45). Непрерывность функции (13.23)
позволяет использовать для решения этой задачи систему уравнений (13.46),
которая в данном случае имеет вид
Я( ~) у(.р)
Ш1'") + Ф );1~)
(и + у + ю; и, у, ю ~ (1, 2,
Ж11) )
_#_1') + Ф
° Ж Фо<ф& t
(13. 59)
Равенство в (13.59) достигается при двух значениях Ф:
(13.60)

454
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Эти значения соответствуют абсциссам точек пересечения двух кривых
на рис. 13.6, вдоль которых Ж =Ж' ' и У=У')). Индексы в (13.60) непере-
становочны: Ф„.=-ф'= Ф . Обозначение Ф . говорит о том, что слева от Ф
уровень Ж' ' более выгоден, чем уровень Ш')), а справа — наоборот:
т,(У' ', Ф вЂ” 0)) т„(У')), Ф . — 0), т,(Ж' ',Ф .+0) т,(Ж'!),Ф„.+0),
в соответствии с этим и записаны формулы (13.60).
Среди решений (13.60) есть лишние — часть из них непопадает на отре-
зок [Фо Фд] или (и) не удовлетворяет всем неравенствам (13.59). Чтобы из-
бежать перебора возможных комбинаций индексов с последующей отбраков-
кой ненужных решений (а в дальнейшем не считать повторяющиеся варианты
т!п Д пц
т„
~Гз)
~(г)
и")
Од
Ф-Фо
Фр ~0
Об
бГ 04
(я гз
О
Рис. 13.9. Диапазоны преимущественного ис-
пользования систем Ж' = 0,1, Ж' ' = 0,15,
(3)
Ж = 0,2. На верхнем графике — функция
проигрыша, па нижнем — оптимальное распре-
деление уровней мошности.
Рис. 13.10. Степенные законы (13. 63)
плотности ~, распределения маневров.
функции р типа р ()1'д), !у'2),..., Ж~ ) = р (Ж"), К"),..., Ж~ ), упорядочим на-
бор(Ж,..., Ж ~~, расположив его элементы в возрастающем порядке:
(1) Я)1
~~!&lt д ( у l ; ) ( ( ~7(-) (
Тогда в силу выпуклости функций проигрыша (см. (13.33) и рис. 13.5)
можно сразу отбросить все те решения (13.60), у которых нижние индексы
отличаются больше чем на единицу. Остальные нужно только проверить
на принадлежность отрезку [Ф„Фд]. В результате приходим к следующим
формулам для диапазонов «( ' преимущественного использования систе-
мы У ':
«"" =((Ф,. д,„, Ф...,д)] 0 М...д) Ф.. д))) ПдФ Фд] (13 62)
1
и=), ..., а~ а =О, ~( =); (~и(и ) =с((и (и= 2 [с(( -ци+~и(~-(()),
где ф,,, ... определяются соотношениями (13.60). Формулы (13.62)
иллюстрируются рис. 13.9, на котором проведено построение множеств У' '
для случая Я = 3, Ж") = О, 1, Ж") = 0,15, У") = О, 2. Множество «'~
всегда связно — оно представляет собой интервал (или полуинтервал, или
отрезок), остальные множества « '") в общем случае несвязны — они могут
состоять из двух полуинтервалов (или из полуинтервала и отрезка, или
из двух отрезков).

СТАТИСТИЧЕСКИЙ ПОДХОД
(13.63)
[(, ')) ' )] ири Фа(Ф(Ф,
с х
Ф
. = О, 1, 2, ...; — = ~~~~ ( — 1)~' ", ) (Ф) ЫФ = 1) .
р=О фа
Это — распределение симметричное относительно математического ожидания
Ф
(Ф) = Ф~„(Ф) ЫФ = —,' (Ф, + Ф,)
(13.64)
Фо
с дисперсией, равной
(13.65)
Фо
При )6=0 закон (13.63) дает равномерное распределение.
Запишем интегралы (13.56) с плотностью распределения (13.63) в виде
суммы интегралов по множествам (13.62):
абсолютный проигрыш
и=1
(со)
1)] ЫФ, 116.66а)
& t
Ш1 )+ф
относительный проигрыш
2х+1 Я
й' 1
(1 1/ф)2 т.„ш1 ) + Ф
(Ф, — Ф)'[Ф вЂ” Ф,)*[1
=Ь"а)Ф,— Ф,)
со=1 у(~о)
(13.66б)
Выбранный закон плотности распределения маневров позволяет при
целых значениях параметров р и ~ получить аналитические выражения для
интегралов (13.66), представляющих собой в этом случае интегралы от
дробно-рациональных функций с аргументом ~Ф.
Например, когда р =1, у =О, эти выражения таковы:
абсолютный проигрыш
1
ф ф ~ ~(со+1) со ~со(со+1)
О
м=1
Ь 1 + ) + Д"")) Ь 1 — + Д'1 ') .
ЬЫш 1) ~(~~1)~и) + ~ (У ) Д~[и~)) 1р, + )111ш))
1 4 Ф 1~Ф, — ФФФФФ
х, 1+ ~(~1+ 0) 3 ф ф
О
(13.67а)
Следующий шаг — вычисление функции а, представленной в виде (13.47).
На этом шаге нужно конкретизировать функцию распределения (13.27).
Будем считать ее непрерывной и обладающей непрерывной плотностью,
так что ШР,(Ф) =/,(Ф)ЫФ =))([Ф, Ф+ЫФ]). Плотность распределения манев-
ров зададим на отрезке [Фа, Ф,] степенными законами (рис. 13.10)
~ 0 при Ф(Фа и при Ф)Ф„

456
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
относительный проигрыш (при т„о =О)
<«« «( У lt; ~ — 1 ««) ( У lt;о
о (1 — %~у & t; „) (1 Ђ” 'у &
(У««<«« 1 + &l ;~ ~) Ь~ ~-г + <~ 1) («& t;У ,&lt ~«+ 1 †~ <
+ С„1п '" "' &lt „, "' „, Ђ” „, агс
Ьс -г)ю+ )(ус +г)~+ ) 1~&l ; + ~у<.-,).у
<«««.„„„ Ђ” «««,.„. .) «Ъ
+ агс$8'
1~&l ;< +Уу &lt  Ђ
(13.676)
1 — й' '
1 й("') ~
С 1 — й')
(1 + Д& t; &l ;« «
2Ж( ~
1+ <' l
4\~А' &
В
(1+ Ж& t; "
где в соответствии с (13.62)
у;р — Ф; при Фо ( Ф; ( Ф,; у; = Фо при Ф; ( Фо;
уц=Ф при Ф; )Ф (1=7+1=и — 1, &lt о, &lt
(13.68)
а Ф; определяются ив (13.60) и (13.62).
дд( ) — ~ 1 о
1 — Щ(ф ф ) — 2х — 1
(13.69а)
По формулам (13.67) посчитаны примеры, иллюстрирующие характер
поведения функций проигрыша (р=1, х=О, т„о=О, Ф,=0,01, Ф,=0,81,
И=2). Результаты расчетов показаны на рис. 13.11 в виде линий уровня
функций проигрыша. Допустимая область изменения аргументов <г' l ;1' и
построена в соответствии с (13.58), (13.61). Линии уровня в окрестности
точки абсолютного минимума имеют регулярную структуру (совпадающую
со структурой линий уровня квадратичной формы). Характерно существо-
вание области с вертикальными линиями уровня (функция р не зависит
от К<1 ) В э ой обла ти ни ля одн го мане ра из [Ф„ ,] не выго но
пользование системы К< '. Г&lt 1' О, т. . „ Ф, Ф2 ) Ф,. Г
данной области показана пунктирной кривой. Отметим еще одну особен-
ность — функция относительного проигрыша имеет второй минимум, ло-
кальный (см. рис. 13.11, б). Он достигается в указанной выше области
(О (~ <г' lt 1' (~ 0,02, К'а'= , 63) и соответ твует абсол тному мин
имевшему место при И =1. Для абсолютного проигрыша старый (И =1)
минимум(К<1' О, Г а' 0, 1) не попад е в ту обла т и же не являе
локальным минимумом при И=2.
Отыскание минимума функций проигрыша (13.66) производилось чис-
ленно методом скорейшего спуска. Эти функции непрерывны и дифференци-
руемы, их частные производные определяются формулами (13.48), которые
в рассматриваемом случае преобразуются при помощи соотношений (13.29),
(13.33), (13.56) к виду:
для абсолютного проигрыша

$2]
СТАТИСТИЧЕСКИИ ПОДХОД
457
для относительного проигрыша
й' 1
(1 — ~(Ф)' — т„з (~' '+ Ф
(13.69б)
где множества У( ' задаются соотношениями (13.62) и (13.60).
/с = 0,0008
Оддс
дд04
д,дд5
Оддб
01Збб
=дОЯ
Рис. 13.11. Линии уровня суммарного проигрыша при выполнении равномерно распрепеленныт манев-
ров с стеиами двух типов г( и г( (пунктирной кривой показана граница области, гдв нв ис-
И
(1) (2)
пользуется система Ж ~', а) абсолютный проигрыш', б) относительный.
(1) ~.
При целых р и х подынтегральные функции в (13.69) представляют
собой дробно-рациональные функции ~Ф и интегралы (13.69), так же как и
(13.66), берутся.
Например, если р =1, в=О 1см. 113.67)), то получаем:
для абсолютного проигрыша
др~,
дй(ш& t; Ф, Ђ Ф ( ( -" У( - ») У( + ~  ( +
о
1
Ь( — & t + ~У' ') Ь( „  gt; (
+ д7(®) Уи(оэ-1) У(си-1)ш У<ш+ )м У<
— ... )1; (1з.7оа(

458
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
для относительного проигрыша (при т„о=0)
( — у&l ;ю Ђ” д ю ° у<ю д)ш), ую lt; Н-д у&
фо (1 — )«У & t; +д) (1 Ђ” д1У ,&l ; )) 1 в ” «)У lt +д ) (1 Ђ” )1
Ко<ш д) у&lt ю+ ) С, 1 Ь & t ю+д) + ) ( ю&
(1 — )«У & t; )) (1 Ђ” « У l ; + ) ) (У& t; д) + д<~ ') Ь&
()1у~& t; д) )1 &lt ш †д)~) )11)' ( 1у.& t;. „— 1у<
+ у<я-д)муым д + уыил-д)у&lt
Ум<в д + ~~ У< -д
— Е'
2~у, „-&lt -1 Ђ” М ' 2 у, „„- -1 Ђ” Й'
уш&l ;м Ђ” д + ~~ у< +д
(13.70б)
1 — ЗЖ( )
А'=2 1 — 1 (ш),, В'=2 1 — 1
1 — 3 Ж & t; ) 2 ) lt; Ж lt; ) ( в ”
ы (1 ~ )д)<ш ) ш 1+ )д)&l
где величины у;~ определядотся соотношениями (13.68) и (13.60).
Формулы (13.70) могут быть получены также дифференцированием проинтегри-
рованных выражений (13.67) для о,, что сопряжено, однако, с более длинными вык-
ладками.
Область изменения аргументов (Т(д&g ;, . ., Ж& t;~)) ф нкций про
(13.66) ограничена линейными многообразиями, определяемыми неравен-
ствами (13.58) и (13.61). Вид этих областей при И =1, 2, 3 показан на
~с~)
Я
~г
а 1/4
Рис. 13.12. Области (13.58), (13.61) (предельные значения Ж, и Ж, могут вырождаться в Ж1 —— О и Ж,='/,).
рис. 13.".~. Пребывание в допустимой области обеспечивается, согласно об-
щим правилам метода возможных направлений И3.32, 13.33], выбором нуле-
вого приближения, а при переходе к последующим приближениям — за счет
ограничения параметра спуска (длины шага вдоль антиградиента) или (и)
за счет корректирования направления спуска.
Как было показано на рис. 13.11, б, функция &l ;) мо ет им ть локаль
минимумы, не совпадающие с абсолютным. Для отбраковки таких минимумов
применяется следующее необходимое условие: если в точке минимума не
используется хотя бы один уровень Г& t ' т. е. х тя бы о но множес
Г' )=Я), то этот минимум не является абсолютным.

459
СТАТИСТИЧЕСКИЙ ПОДХОД
$2)
Результаты расчетов представлены на рис. 13.13 — 13.18. Рис. 13.13—
13.16 относятся к случаю равномерного распределения маневров (и=О
в (13.63)) и нулевой массы системы с бесконечно малой мощностью (т„в=О
в (13.18)). Суммарный проигрыш вычисляется по норме Ь . Он представляет
0,0б
004
ООГ
ф5 ОГ
опт и( пи пг
005 ф
Рис. 13.13. Минимальный средний проигрыш: а) абсолютный; б) относительный.
015
( Ф)
((У',р, (Ф)) = 1Ч'Ф вЂ” Ф) Н"„(Ф) при (.'Ч,р, (Ф)) ( 1 — Ф,
(13.71а)
при (1Ч,„„(Ф)) ) 1 — Ф,.
собой средний проигрыш в полезной нагрузке, приходящийся на один
маневр.
Минимальные значения р (Ж(1~) этого проигрыша показаны на
1
рис. И.13 при фиксированных значениях математического ожидания (Ф)
параметров маневра в функции средне-
квадратичного отклонения ~ф. Вели- &l ;у
У
2
чины (Ф) и сф по формулам (13.64),
(13.65) определяют начало Ф, и конец
Ф, диапазона маневров. Все маневры
из диапазона [Ф„Ф 1 выполняются
системами одного типа (Й=1). Проиг-
д
рыш, естественно, возрастает с увели-
чением ширины диапазона, которая для
рассматриваемых распределений ли-
нейно связана со среднеквадратичным 3'
отклонением.
Оптимальные значения мощности,~у
7('), доставляющие минимум ~~, по-
1
казаны на рис. 13.14 сплошными кри-
выми (а — для абсолютного проигрыша,
0,2
б — для относительного). Там же для
СраВНЕНИя ПуНКтИрНЫМИ КРИВЫМИ даНЫ Рис. 13.14. Оптимальные значения мощ-
(1)
3ПаЧЕНИЯ МОщНОСтИ Выбраииыэ ИЗ СЛЕ 11ости № соотвстствУюп~ие Рис. 13.13.
дующих соображений.
Кривая 1: мощность (13.24), оптимальная для выполнения одного ма-
невра, осредняется по всему диапазону или берется предельной в смысле
условия (13.57):

460
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
~ГЛ. 13
Кривая 2: осредняется функционал маневра Ф, мощность выбирается
оптимальной для маневра со средним значением функционала (Ф) или
предельной:
Ш„, ((Ф)) = ~/(Ф) — (Ф) при У„, ((Ф)) ( 1 — Ф,
1 — Ф при Ь„, ((Ф)) ) 1 — Ф .
Кривая 8: мощность выбирается из условия наилучшего выполнения
наиболее напряженного маневра Ф=Ф, на котором полезная масса т,
минимальна:
У, = Ш„, (Ф ) = ~/Ф, — Ф;
(13.73а)
условие (13.57) при этом автоматически выполняется (напомним, что
в (13.71а) — (13.73а) полагается т„=О).
Для равномерного распределения маневров (х=О) мощности (13.71)—
(13.73) выражаются через математическое ожидание (Ф) и среднеквадратич-
ное отклонение ~~ значений функционала маневров следующим образом:
средняя мощность
'(Л.„) = —.' [((Ф)+й „)' -(( ) — й,,у] — ( )
(13.71б)
при (Т,~,) ( 1 — (Ф) — ~/3 ~ „„
1 — (Ф) — ~/За при (Т,„) ) 1 — "Ф) — ~/За„;
мощность по среднему маневру
~/(Ф) — (Ф) при а„~~ = (1 — ~/(Ф)),
~З
~ 1 — (Ф) — ~/За при а ) =(1 — ~/(Ф));
Ф Ф ~з
(13. 72б)
мощность по самому напряженному маневру
Уа=((Ф)+~/За ) ~' — (Ф) — ~/За .
(13.73б)
(13.74)
= =ш1'и ((Ф); 0,9 ('1 — (Ф)))
~з
(х = О, т„, = 0).
Выходу на ограничение (13.57) соответствуют прямолинейные участки
кривых рис. 13.14. Из рисунка видно, что первые два способа выбора мощ-
ности в большинстве случаев ближе к оптимальному, нежели третий. Это
подтверждается также и непосредственными вычислениями суммарного
проигрыша р для различных вариантов выбора мощности. Сравнение полу-
ченных значений р~ (У,.) с минимально возможными р~ (К~ц) проведено на
рис. 13.15. Если значения р (Ш,) превосходят минимальный проигрыш
1
более чем в два раза, то р~ (Ш,) и р~ (Т,) отличаются от него на 10 — 40О~О.
При увеличении среднеквадратичного отклонения сф параметров ма-
невров Ф от их среднего значения (Ф) даже минимальный проигрыш может
оказаться недопустимо большим, если использовать для выполнения всех
маневров только один тип системы (И=1). В таких случаях нужно перехо-
дить на большее число различных типов систем (Й ) 1). Рис. 13.16 иллюстри-
рует убывание минимально возможного проигрыша при увеличении числа
систем Й. Расчеты проведены для различных значений математического
ожидания (Ф) функционала маневров, дисперсия сф при этом выбиралась
максимально возможной или близкой к ней:

СТАТИСТИЧЕСКИЙ ПОДХОД
/~ (У)
/
р (~")
к
4
О 0,05 Ц1 0~5
015 дГ о
005 01
Рис. 13.15. Относительное увеличение суммарного проигрыша при переходе от оптимальной системы
Ж* к системам Ж; (г =1, 2, 3 — см. рис. 13.13, 13.14)! а) абсолютный проигрыш; б) относительный.
(1)
Обсудим теперь влияние параметра т„о — массы двигательной системы
с бесконечно малой мощностью. Этот параметр не входит явно в выражения
для абсолютного проигрыша, он оказывает свое действие посредством суже-
ния допустимой области ~13.58) значений мощности (см. рис. 13.3). В выра-
(у~О ~~я&g
р,(ф„'"~„,
~,г
п,гл
1 о,гЗ
б д,дЯ д,04 0,0б О 08 ~„р
Рис. 13.16. уменьшение суммарного проиг-
рыша при увеличении числа й различных ти-
пов систем.
Рис. 13.17. Пример зависимости минимального
относительного проигрыша р~ и оптимальной
мощности Ж(1~ от конструктивного параметра т„,
(Я =1, х =О, (Ф) =0,2, еф — 0,115).
жениях для относительного проигрыша параметр т„о содержится явно.
Все это приводит к увеличению проигрыша с возрастанием т„о, что иллю-
стрируется рис. 13.17. Там же показано соответствующее изменение опти-
мальной мощности (приведенные на рис. 13.17 данные относятся к относи-
тельному проигрышу).
Чтобы составить представление о влиянии закона распределения ма-
невров на величину минимального проигрыша, были проведены расчеты
лля распределений (13.63) с различными значениями параметра х, отвечаю-
Дискретные точки, соответствующие целым значениям Р, для наглядности
соединены непрерывной кривой. Сплошные кривые относятся к абсолют-
ному проигрышу, пунктирные — к относительному. Наиболее резко изме-
нение проигрыша прои,"кодит на первых участках кривых. Так, переход
от 0=1 к И=2 сокращает проигрыш на 70 — 95О~~.

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
462
[гл. ".3
(б
б о
Рис. 13.18. Зависимость минимального проигрыша р~ и оптимальной мощности Я~~1~ от параметра ~
(см. рис. 13.10). Сплошные кривые — абсолютный проигрыш, пунктирные — относительный.
приводит к более быстрому выходу мощности (левый рис. 13.18) на огра-
ничение (13.57), что приводит к резкому увеличению минимального проиг-
рыша.
Помимо приведенных были получены еще результаты, относящиеся к ми-
нимизации проигрыша по норме Л при р ) 1. Они используются для при-
ближенного решения задачи с проигрышем по норме С и поэтому перенесены
в следующий параграф.
4. Пример — универсальная секция ограниченной мощности. Задача
отыскания оптимального размера секции ограниченной мощности проце-
дурно мало отличается от изложенной выше задачи. Действительно, если
в соответствии с (13.38), (13.40) ввести обозначения
(13.75)
то осредненный по норме Ь проигрыш (13.39) запишется в виде:
абсолютный
Ф1 1~'р
~~АЖ)= ~ (1 — ~Ф) — тах ( ...Ж' ' — (~ — 1)т ) ~р ~ф)
и=1, ...,Ы
фо
(13.76а)
относительный
М~Р
1 Я(ш)
р
шах,, К' ' — ит„, йР„(Ф)
р ~~~~) =
(13.76б)
Структура суммарного проигрыша (13.76) аналогична структуре проигрыша
(13.56). Основное отличие состоит в том, что функции (13.76) зависят только
щего за форму распределения (см. рис. 13.10). Математическое ожидание
(13.64) и дисперсия (13.65) фиксировались, число систем И принималось
равным единице. В результате получено, что изменение х сначала не сильно
сказывается на минимальных значениях проигрыша (правый рис. 13.18).
Проигрыш несколько возрастает с увеличением х. Это объясняется тем, что
большим значениям х при фиксированной дисперсии соответствует большая
ширина интервала Ф вЂ” Ф,. Крайние маневры из-за малой частоты их повто-
рения дают небольшой вклад в суммарный проигрыш, но зато их наличие
~ Я")л зо
р Щ')

463
СТАТИСТИЧЕСКИЙ ПОДХОД
5 2]
от одного аргумента ЛГ, поскольку все уровни К( ' здесь выражаются
через ЛГ.
Требование неотрицательности полезной нагрузки удается свести к не-
равенству
Т, (ЛУ( Ш„
(13.77)
где предельные значения Г, и Г, размера секции определяются по-прежнему
соотношениями из (13.58).
Несколько изменяются выражения (13.60) для моментов перехода
с уровня Г( ' на уровень Г"'.
ш~' 2 Ьй
-)-в|бай ()Х"' — 8'"') [ —, (1 — 8'"' — 8" ~'
2 1/
б'"уО у[Ш) д7(.~ )
тХ8+ ЬШ
(13.78)
Условие (13.61) выполняется автоматически, диапазон У( ' преимуще-
ственного использования системы Г( ' определяется старыми формулами
(13.62), в которые нужно подставлять только новые выражения (13.78)
для моментов перехода с одной системы на другую. Распределение манев-
ров задается, как и раньше, соотношениями (13.63) — (13.65). В результате
функции (13.76) приводятся к виду, аналогичному (13.66):
абсолютный проигрыш
2х-~-1
1(бу) — )11(я (Ф, — Ф ) я ~~ ~ (Ф, — Ф)" (Ф вЂ” Фо)" [(1 — ()Ф) +
щ=1 ~(ш)
+ (~ — 1) то — Т' '( ... 1)) 8Ф
(13.79а)
относительный проигрыш
2х-~-1
1(ЬШ)=)1'т(Ф,— Ф,) ~ ~ ~ (Ф,— Ф)" (Ф вЂ” Ф,)" [1—
оэ=1 ~М)
(,, Т' ' — т„о)) 8Ф
(13.79б)
Производные функций (13.79) вычисляются 1) по формуле (13.48б):
для абсолютного проигрыша (ср. (13.69а))
— „', =8'- б (Ф, — Ф,)-"-' ~~~
со=1 ~М)
+(~ — 1)т„,— Ж' '( ... 1)~ [1
(Ф, — Ф)*(Ф вЂ” Ф,)*[(1 — ()Ф) +
(13.80а)
для относительного проигрыша (ср. (13.69б))
д
— ~=р1 %(Ф вЂ” Ф ) '" 1 (о
дЬЮ 1 О
у(ш)
,)8Ф. (18,80б)
)( Я ) О)щ 1 ~~ щ
1) На интервале постоянства фактически используемого числа секций.

464
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
При целых значениях р и х интегралы (13.79), (13.80) берутся в элементарных
функциях, получаются выражения, подобные (13.67), (13.70).
Типичный вид зависимости р (ЬК) показан на рис. 13.19, а (абсолют-
1
ный проигрыш) и на рис. 13.19, б (относительный проигрыш) для следую-
щих значений параметров: т„о =0,001, (Ф) =0,2, оф — — 0,115, ~=0.
ц005
д 0,05 ЬМ„0,) 0,(5 0,Г ЗМ 0
005 О,~ Ю„ОД Ог да
Рис. 13.19. Пример зависимости среднего проигрыша от размера универсальной секции.
Это непрерывные кривые с изломами (локальные максимумы) в точках пере
хода с одного числа секций на другое. Абсолютный минимум совпадает с од-
ним из локальных или равен одному из граничных значений — р (К1) или
р (Г ). Локальные минимумы лежат на выпуклой кривой. Учет последнего
обстоятельства при построении процедуры отыскания абсолютного минимума
10 ~
0
005 0 ~ 075 0,~
005 ®
оа цг а
Рис. 13.20. Минимальный проигрыш при выполнении маневров системами, собираемыми из универсаль-
ных секций.
позволяет значительно сократить число локальных минимумов, подлежащих
проверке на абсолютный.
На рис. 13.20 (а — абсолютный проигрыш, б — относительный) при-
ведены результаты численного определения минимальных значений р~ а )
1
при фиксированных значениях функционала «среднего» маневра (Ф) для
т„о=0,001, х=0. Минимальный проигрыш при использовании систем, со-
бираемых из универсальных секций, менее чувствителен к расширению диа-
пазона маневров, чем в случае фиксированного числа систем (ср. рис. 13.20
и 13.13). Это достигается за счет уменьшения оптимального размера сек-
ции, что позволяет более точно аппроксимировать идеальное решение (13.24).
Следует отметить также наличие немонотонных участков зависимости р~ (~ )
для универсальной секции в отличие от случая универсальной системы. Это
объясняется «квантованностью» используемых в заданном диапазоне ма-

465
СТАТИСТИЧЕСКИМИ ПОДХОД
$21
ОЫ
0,05 0,/ 015 О,Г о~ д
дд5 0,/ 0~5
ф
Рис. 13.21. Оптимальный размер универсальной секции, соответствующий рис. 13.20.
ставленных на рис. 13.20. Непрерывным участкам ЛГ„(~ф) соответствует
постоянное значение максимального количества Й, секций, из которого
набирается двигательная установка. Для рассмотренных случаев это коли-
чество изменяется от 1 до 3, причем переход от меньших значений Й„, к боль-
шим также может быть немонотонным
(си., например, кривую (Ф)=0,4 на ' „" &g
рис. 13.21, б). В этом случае из имею- ~~ д~
ЛУ„
щихся Й, уровней двигательной си-
Г
стемы на маневрах данного диапазона 1,Я дГ
используются не все, а только некото-
ДИ
Ф
рая часть. Так, в приведонпо.ч при-
мере из трех возможных уровней ис-
пользуются только уровни 2ЛГ, и ЗЛЛ~„,
Р
при этом качество аппроксимации
идеального решения уменьшает проиг-
рыш более существенно, чем увеличи- ~7
/
0,05
вает его введение дополнительной массы
шт„„(по сравнению со случаем Й =1 или 05
о =2)
БОЛЕЕ СЛОЖНЫМ, ЧЕМ В СЛуЧаЕ Рис. 13.22. Пример зависимости минималь-
ного относительного проигрыша Р г и опти-
оказывается
УНИВЕРСаЛЬНОИ СИСТЕМЫ, ОказываЕ СЯ маль ого азмсра Л№ универсальной секции
и влияние параметра т„о. При т, ~ от копструктивпого 11арамстра т„.„.
~ 0 оптимальный размер универсаль-
ной секции стремится к нулю, а число секций ~о на каждом маневре стре-
мится к бесконечности. При увеличении т„о минимальный проигрыш не-
прерывно возрастает, возрастает размер секции и уменьшается максималь-
ное количество секций Р, Относительное изменение минимальных значе-
нпй абсолютного (сплошные кривые) и относительного (пунктирные кривые)
проигрышей и соответствующих им значений ЛУ„по сравнению со случаем
универсальной системы (й=1; т„о=О; ~=0; ~~ — — 0,115;,Ф)=0,2) предста-
влено на рис. 13.22. При т„о ) 0,01 кривые для абсолютного и относитель-
ного проигрышей совпадают с соответствующими кривыми для универсаль-
ной системы (сч., например, рис. 13.17).
0
0 0,002 0,004 000б 0003 т„„
30 Ъ|ехапика полета
невров оптимальных значений мощности (К' '= о~ ЛГ,). Число секций, со-
ставляющих двигательную систему, которая предназначается для выпол-
нения маневра Ф, при этом в большинстве случаев увеличивается.
На рис. 13.21 (а — абсолютный проигрыш, б — относительный) приве-
дены оптимальные размеры универсальной секции ЛК„для случаев, пред-

466
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
$ 3. Выбор универсальной системы при неполной информации
о маневрах (игровой подход)
р„= р,,(х„) = т1п эирЛР(х, у)
хб~, уСУ,
при ~(х, у) ) О.
(13.81)
Если решение задачи (13.81) единственно, то Конструктору нужно проек-
тировать только одну систему вместо й разрешенных. В случае неединствен-
ности решения используемый критерий не дает признака для отбора реше-
ний. Кроме того, этот критерий не позволяет получить полного решения
задачи относительно Природы. Из него следует, что Природе нужно назна-
чать те маневры, на которых достигается максимальное отклонение от идеаль-
ного решения. Частота же повторения этих маневров остается неизвестной.
Можно поступить по-другому. Взять в качестве меры близости к идеаль-
ному решению расстояние по норме, зависящей от распределения маневров,
например по норме Х~, и рассмотреть игровую задачу. Этот подход исполь-
зован в работах [13.2 — 13.5, 13.8]. Если обозначить через и (Х) вероятность
применения Конструктором систем х из подмножества Х с Х„то средний
проигрыш запишется в виде
р, [р. (Х), ~(У))= ~БР(х, у) ~(ду) р. (Шх)
~~ ~о у~ ~о
(13.821
Ни одна из сторон не осведомлена о конкретном значении вектора параметров
другой стороны. Конструктор распоряжается распределением р (Х), При-
рода — ч (У). Это так называемые смешанные стратегии. На стратегию Кон-
структора наложено дополнительное условие — она может состоять не более
чем из Й чистых стратегий, т. е. из всего множества Х, Конструктор может
использовать только дискретныо точки х~'~, ..., х~~' с частотами р~",
..., ф~~ (р.М+... + ф~~ =1). Но, как выяснится в процессе решения, это
1. Формулировки задач. Здесь рассматриваются три варианта задачи
универсализации параметров динамической системы, различающихся по
объему информации о маневрах, которой располагает Конструктор.
Задача 1'. Априорная и текущая информация о маневрах отсутствует.
Известно только множество У, возможных значений параметров маневра.
Выбор системы (из числа спроектированных), которая будет выполнять
очередной маневр, должен быть произведен до того, как станут известны
его параметры, т. е. стратегиями Конструктора не могут быть функции х (у).
Этот случай является предельным по отношению к рассмотренному в преды-
дущем параграфе.
Для получения в такой ситуации гарантированных оценок проигрыша
Конструктору приходится предполагать, что Природа будет назначать рас-
пределение (13.7) частоты повторения маневров наихудшим для него образом.
Это можно сделать сразу, еще при формировании критерия оптимальности,
если взять в качестве меры близости к идеальному решению (13.6) норму
С (13.15а), как это сделано в работах [13.16 — 13.18]. Норма С дает верхнюю
оценку суммарного проигрыша для любых распределений (13.7) и любых
норм Л (см. (13.14)).
Из-за отсутствия текущей информации о параметрах очередного маневра
Конструктор не может сузить множество маневров, которое придется об-
служивать системе данного типа. Любая система из Й спроектированных ока-
зывается вынужденной выполнять любой маневр из У,. Поэтому приходим
к следующей формулировке: требуется определить параметры системы
х„( Х„минимизирующие максимальное по у ( У, отклонение (13.10) от
идеального решения при соблюдении неравенства (13.12):

467
ИГРОВОЙ ПОДХОД
ограничение для рассматриваемого далее типа функций ЬР (х, у) не явля-
ется определяющим — оно будет выполняться автоматически.
Конструктор стремится минимизировать проигрыш (13.82), а Природа—
максимизировать. Требуется найти такие стратегии р„(Х) и ч„(У), которые
доставляют проигрыш, равный
(13.83)
р,=р (р.„, ~„) =1Ы вирр(р., ~) = вир 1п1р(р, ~)
Р ~ ~ Р
при ~(х, у) ) 0 для всех у~ У,.
Если такие стратегии существуют, то Конструктор, используя страте-
гию р„, может рассчитывать на проигрыш, не больший р„при любой страте-
гии Природы. Природа в свою очередь, придерживаясь стратегии ч„обеспе-
чивает проигрыш, не меньший р„, при любой стратегии Конструктора. Это
доказывается, например, в теореме 17 из работы [13.15]:
р„= вир р (р„, ~) = 1п1 р (р, ~.,)
(13.84)
т~п ЛР(х' ', у) =ЬР(х' '"", у).
(13.85)
0~=1, ..., Я
Отсутствие априорной информации о распределении маневров снова приво-
дит к необходимости рассчитывать на худший вариант распределения.
При использовании в этих целях нормы С постановка задачи аналогична
(13.81): определить параметры систем (х~ц, ..., х~'-~), минимизирующие
максимальное по у ~ У, отклонение (13.85) от идеального решения при со-
блюдении неравенства (13.12):
р„= р (х~'~... х~~~) = т1п зир т1п ЛР (х' ', у) (13.86)
к~1~, ..., х(~~бХО
при ф (Ы < И, у) ) 0 ля в е  ~
где и (у) — номер системы, используемой для выполнения маневра у (опреде-
ляется из (13.85)). Здесь каждая система х'"' обслуя ивает только свое
подмножество маневров У'") ( У„а не все множество У„поэтому можно
надеяться па меньший проигрыш, чем в (13.81). При 2 = 1 постановки
(13.81) и (13.86), естественно, совпадают.
Постановку (13.86) можно сформулировать еще в терминах подмножеств
У~"~ (х~'~, ..., х~".-~), обслуживаемых системой данного типа (см. (13.4о)):
(13.87)
ппп тах ппр ЬР(п' ', у)~)
х' 1 х("~6~ ~ — 1 ° ~ГСУ
при ~ (х'"', у) ) 0 для всех у~ У' ', и=1, ..., ~.
В работах [13.16 — 13.18] не вводилось понятие текущей информации
о маневрах. Там неявно предполагалось ее наличие, поэтому при Й & t
оптимизация всегда производилась по критерию (13.87). Из высказанных
соображений следует, что для перехода от постановки (13.81) к постановке
36*
— необходимое и достаточное условие оптимальности стратегий.
Задача 2'. Априорная информация отсутствует, текущая — поступает.
Из априорных сведений Конструктор, как и в первом случае, располагает
только знанием множества У,. До начала выполнения очередного маневра
становятся известными его параметры.
Последнее обстоятельство позволяет Конструктору для каждого маневра
у выбрать из спроектированного набора (х&lt ц, . ., х& t;~>) наибол
дящую систему и свести проигрыш на отдельном маневре до

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
~ ГЛ. 13
(13.86) или (13.87) одной возможности проектировать Й & t 1 сис ем ма
нужно в процессе эксплуатации располагать сведениями о параметрах оче-
редного маневра.
Для нормы Ь~, как и в предыдущем случае, формулируется игровая
задача, аналогичная (13.82) — (13.83). Отличие состоит в том, что Конструк-
тору теперь разрешается использовать только чистые стратегии, но в про-
странстве большей размерности (Йп вместо и) — он распоряжается набором
(х~'), ..., х~~)) и-мерных векторов. Природа по-прежнему может исполь-
зовать любые смешанные стратегии — она выбирает распределение ~ (У).
Очередной ход Природы (вектор у) известен Конструктору. В таких усло-
виях осредненный проигрыш Конструктора будет равен
[х~'), ..., х~~); ч (У)] = т1п ЛК~ (х~"), у) ~ (Шу) . (13.88)
ш 1 Я
У~'-~е
Треоуется найти оптимальные стратегии Конструктора (х~'&g ;, . ., х~ &
Природы ~„(У), обеспечивающие цену игры
р„=р ((х~ )), ~„(У)) = 111К зирр ((х'"'), ~) =зир 1пГ р ((х'"'), ~) (13.89)
'р " ' ' (х-), "р
(Х )
Я
р,1~~)
р оз — 1
У~'-~о
1/р
ЛР~ (х'"', у) (Шу)
(13.90)
Необходимо определить оптимальные параметры 2 типов систем (х~'>,. ., х~
и оптимальные частоты их использования ~~('~, ..., р~~~, ооеспечивающие
р, = р (х&lt ц, . ., х~ ); р.„ ~, . ., рУ„ ~ = п 1п р, ((х'" ), (р.'" )) (13.
(х(~)), (р.(~))
при б(х'"', у)) 0 для всех у~ У„~ р.'"'=1, р.'"') 0 (и=.1, ..., О).
ш=1
Это уже не игровая задача, а обычная задача на экстремум функции многих
переменных.
Анализируемые варианты информированности о маневрах составлены как комби-
нации предельных ситуаций: априорная информация — полная или отсутствует, теку-
щая информация — полная или отсутствует. Существует еще большое количество про-
межуточных случаев, перечисляемых в работах по исследованию операций ([13.15] и др.).
Например, априорная информация может быть такой: а) известно распределение некото-
рых компонент вектора у, распределение остальных компонент неизвестно; б) известны
числовые (момептные) характеристики закона распределения у (математические ожида-
ния, дисперсия), вид закона неизвестен; в) известен вид закона распределения, но неиз-
вестны точно значения параметров, входящих в этот закон. Текущая информация может
представлять собой следующий набор сведений: а) известна только часть параметров оче-
при ф(хЫ"~у&gt ), у) ~0 ля в ех у~ е, де о~ у) определяе ся соотношен
(13.8э).
Задача 8'. Априорная информация полная, текущая — отсутствует.
До начала проектирования известно множество У, и распределение ~ (У)
частоты повторения маневров по типам. Система, которая будет выполнять
очередной маневр, должна быть указана до того, как станут известны пара-
метры этого маневра.
В качестве критерия близости к идеальному решению здесь рациональйо
использовать норму типа Ь . Суммарный проигрыш Конструктора опреде-
ляется соотношением (13.82), где распределение ~ (У) фиксировано, а рас-
пределение и (Х) точечное (Конструктор может проектировать не более
чем Й систем). С учетом сказанного проигрыш (13.82) можно переписать
так:

469
ИГРОВОЙ ПОДХОД
редного маневра; б) известны условные (относительно предыдущих реализаций) рас-
пределения параметров очередного маневра (полностью либо частично) и т. д.
Многообразие возможных ситуаций не позволяет рассмотреть в настоящей работе
каждую из них. Поэтому исследование ограничивается указанными выше предельными
случаями. Предельные решения дают оценку функционала для любого из промежуточных
вариантов и, кроме того, характерны с методологической точки зрения.
2. Алгоритмы решения. Прежде всего — несколько слов о неравен-
стве (13.12). Это неравенство должно выполняться для всех у ~ Уе незави-
симо от того, входят они в состав стратегии Природы или нет.
Если текущая информация о маневрах отсутствует (задачи 1' и 3'),
то любой из спроектированных систем х'"' может «достаться» любой из ма-
невров у ~Ус. Поэтому неравенство (13.12) здесь эквивалентно следующим:
т1п ~ (х' ', у) = р (х' ') )~ О
у~'-Уо
(13.02)
Этим неравенствам можно удовлетворить заранее за счет сунсения гран.1ц
допустимого множества Х, параметров системы.
При наличии текущей информации о маневрах (задача 2') система х""'
будет использоваться только для выполнения маневров из множества У'" ',
где она обеспечивает меньший проигрыш ЛР(х, у) по сравнению с оста;;.,—
ными спроектированными системами. Тогда неравенство (13.12) будет вы-
полняться одновременно с неравенством
т1п т)п 6 (х' ', у) = т1п э (х' ') =&lt р, ( '" ' )
ш=-1, ..., 2 у~ ~ (ш) ш=1, ...,2
Если за счет упорядочения векторов х' ' можно добиться независимости
номера о~', для которого достигается минимум по (), от векторов х'1),
..., х~~&g ;, т и неравенс во (13. 3) мо но удовлетвор ть сужен ем множе т
Хе, но только для одного вектора х' ' ~Х„~ Х„а но для всех, как б»л &
выше. В общем случае может потребоваться сужение областей для нескол ь-
ких векторов, но все равно не такое сильное, какое нужно для удовлетвс)—
рения неравенства (13.92). Это следует из того, что если среди набора
(х"', ..., х®) есть хотя бы один вектор, удовлетворяющий (13.92), то
при любых значениях остальных векторов неравенство (13.93) будет навер-
няка выполняться.
Дальше предполагается, что неравенство (13.12) уже удовлетворено
изложенным способом, и рассматриваются задачи без ограничения (13.12).
При этом для множества допустимых значений векторов х сохраняется ста-
рое обозначение Х,.
Еще один способ учета условия (13.12) дается формулой (13.13). Для
облегчения численного решения задачи этим способом нужно сгладить раз-
рывную функцию, стоящую в знаменателе (13.13). Тогда ограничение (13.12)
будет выполняться приближенно. Но это не противоречит природе ограпи-
чения. Ведь допустимый уровень о (у) значений функционала И~ устана-
вливается не из абсолютно точных соображений, поэтому вполне допус'п.мо
размытие границы.
Другой метод сведения игровых задач с ограничениями к задаче ~сз
ограничений предлагается в работе [13.15]. Аналогично методу Лаграп'ка
отыскания условного экстремума функции, к суммарному проигрышу р
там добавляются ограничения с постоянными множителями. Этими множи-
телями распоряжается Природа — по ним ищется максимум расширенно|о
проигрыша.
Займемся теперь рассмотрением каждой из задач 1' — 3'.
Задача 1'. Начнем с игровой постановки (13.82) — (13.83). По услови.о
смешанная стратегия Конструктора может состоять не более чем из Й

470
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
чистых. Однако временно это ограничение не будет учитываться. Тем самым
снимается ограничение на число различных систем, которое разрешено Кон-
структору.
Для непрерывной по х и у функции проигрыша ЛГ (х, у), заданной
на множествах Х, и У„которые могут быть переведены непрерывным преоб-
разованием в и-мерный и т-мерный кубы, верхняя и нижняя грани дости-
жимы и
Я'= т1п тах ЛР'(х, у) и (Их) = тах т1п (13.94)
У Х
ЛК~ (х, у) ' (Иу)
(теорема 36 из [13.15]).
Пусть теперь функция проигрыша ЬК(х, у), в дополнение к непрерыв-
ности, выпукла по х, т. е. при люоых у1 У, и любых ),1 [О, 1~ для произ-
вольных х„х.,1 Х, справедливо неравенство
Ьг [),х,+(1 — Х) х„у](ХЬг (х„у)+(1 — )) ЬК(х,„у)
(13.95)
(это свойство будет сохраняться и для ЛРР при любых р ) 1). Тогда по тео-
реме 40 из работы [13.15] среди оптимальных стратегий по х есть чистая х„,
а среди оптимальных стратегий по у — смешанная, состоящая не более
чем из и+1 чистых у~.'~ (и — размерность вектора х). Причем цена игры равна
р.= т1птахЬг' (х, у) = Ьг (х., у~'~) (1(г(п+1, и = Й1тх). (13.96)
Х~.Х У~. Г
Таким образом, в рассматриваемом случае Конструктору нужно проек-
тировать только одну систему вместо разрешенных ему И систем. Причем
оптимальные параметры этой системы для любых р )~ 1 одинаковы ') и опре-
деляются из решения задачи (13.81) минимизации расстояния до идеаль-
ного решения по норме С.
Обозначим через х. оптимальные для Конструктора параметры системы,
а через у~„'~ (~ ( и+1) — оптимальные для Природы параметры маневра,
составляющие ее смешанную стратегию. Они должны давать одинаковый
проигрыш, равный цене игры
(13.98)
Ьг' (х, у"' (х)) = тах Ьг' (х, у) = / . (х).
Строится огибающая /(х) функций /,. (х), и отыскивается ее минимум:
/ (х) = тах / . (х) = / ., (х), / (х.) = т1п / (х) = р..
Х
(13.99)
Номера 7',. функций /. (х), которые составляют огибающую (13.99) в точке х„,
и определяют оптимальные для Природы параметры маневра у~'~ = у~~" (х„).
Остается найти оптимальные частоты ~~'~ повторения маневров у®.
В силу (13.97) любая смешанная стратегия Природы, составленная из у~",
при использовании Конструктором системы х, дает одинаковый проигрыш р,:
и+1
р,,~~ ~' 'ЬК(х,, у<
и+1
>
(13.100)
г'=1
') Это справедливо для любых непрерывных монотонных функций от ЛГ.
р. = ЬК(х., у®) (~ (и+ 1). (13.97)
Для отыскания х. и у® можно воспользоваться такой процедурой. При фикси-
рованном х находятся все локальные максимумы у"' (х) функции проиг-
рыша по у:

игровои подход
71
Но так будет при условии, что Конструктор уже выбрал параметры системы.
Если бы Конструктор знал частоты ))") до выбора х, то он мог бы уменьшить
проигрыш. Оптимальные же частоты ))(') долнсны быть таковы, чтобы их зна-
ние не могло «помочь» Конструктору. Это требование, вытекающее из опре-
деления (13.83) оптимальных стратегий, приводит к системе линейных урав-
нений относительно ))('), одинаковой для любых р ) )1:
я
(~)
(13.10Ц
р (~, ) = Р» ((х' '), у) (Иу) р~ ((Их"'))~ (13.102)
(~(о') ) 6~о ° ° -~о У~'.~о
(Кн ((х' '), у) = т(п ЬК(х( ', у)),
С)
1 ~ е ° ° »
и рассмотрим расширенную игровую задачу о выборе оптимальных страте-
гий и (Х"', ..., Х(~)) и )) (У) для нового проигрыша.
') В принципе этого можно достичь и другим выбором, нужно только, чтобы любой
маневр из У0 характеризовался отличной от пуля плотностью. Равномерное распределе-
ние является простейшим из обладающих этим свойством.
Эта система получается после исключения из (13.100) )) ("+1'=1 — )) (т) —... — ))(")
и приравнивания нулю частных производных д р/дх„. Она справедлива,
если х — внутренняя точка множества Х,. Если же х, лежит на границе
Х„то систему (13.101) нужно заменить условием неотрицательности произ-
водной проигрыша (13.100) по всем возможным направлениям изменения х„.
Изложенная процедура применима в основном для аналитического ре-
шения игровых задач. Если не ставить перед собой цели определения опти-
мальной стратегии Природы, то для приближенного отыскания оптимальной
стратегии Конструктора х, и цены игры р можно воспользоваться предель-
ным равенством (13.16). С тем чтобы в этом равенстве было р =р распре-
деление маневров выбирается равномерным т). При достаточно больших зна-
чениях параметра р расстояние до идеального решения по норме Ь будет
мало отличаться от расстояния по норме С. Малое отличие будет и в х.,
минимизирующих эти расстояния. Поэтому метод численного решения, из-
ложенный в $ 2 для нормы Ь~, можно применять для приближенного реше-
ния рассматриваемой здесь задачи, положив 0=1.
Задача 2'. Так же как и в предыдущем случае, рассмотрение начинается
с игровой постановки (13.88) — (13.89). Функция проигрыша ЛР (х, у)
по-прежнему считается непрерывной по обоим аргументам и выпуклой
по х. Подынтегральная функция в (13.8) будет при этом непрерывна, как
функция от (х' ') и у, но свойство выпуклости по (х'"') для нее уже не со-
хранится.
Покажем существование решения задачи (13.88) — (13.89) способом, ана-
логичным изложенному выше. Для этого допустим на время возможность
применения Конструктором смешанных стратегий, составленных из разных
наборов векторов (х' '). Однако поставим условие, что указание набора,
из которого будет выбрана система для очередного маневра, должно произ-
водиться до того, как станут известны параметры этого маневра. Обозна-
чим через р (Х(т), ..., Х(э)) частоту использования наборов (х' '), у которых
х") ( Х"' С Х, ..., х(э) ( Х((') ( Х. Проигрыш (13.88) осредним по р.:

472
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
По теореме 36 из работы [13.151 такие стратегии существуют, а цена
игры равна
с ух ((х'"), у) х ((Ых"'))]
(~(о~) )
= тах т1п Р'((х"'), у) (Ыу)]
(х(щ))
.У
р~ (р., )).) = т1птах
У
(13.103)
Можно показать, что для рассматриваемых функций ЛР (х, у) при лю-
бых фиксированных распределениях )) (У)
т)н Р"„((х( '), у) )) ((у.у)
(~(оэ) )
У
(13.104)
достигается либо только при единственном 1) наборе векторов (х' '), либо
при нескольких наборах с одинаковым числом совпадающих векторов. В по-
следнем случае проигрыш р ((х' '), ))) = О, поэтому такое распределение
~) (У) не может быть оптимальным для Природы. Отсюда можно заключить,
что оптимальная стратегия Конструктора останется чистой (ему будет вы-
годно применять единственный набор (х("'& t; ). то означа т, то реше
задачи (13.88) — (13.89) совпадает с решением расширенной задачи, сущест-
вование которого доказано. Причем в силу (13.96)
(13.105)
р„=р ((х( )), у„,)=р (р.„, )) )= т1н Кв((х' '), у),
что с учетом обозначений (13.102) означает совпадение и с решением задачи
(13.86) или (13.87) о минимизации нормы С (при любых р )~ 1).
Аналогично предыдущему случаю, существует оптимальная стратегия
Природы, состоящая из смеси не более чем и 0+1 чистых у('), для которых
т)н ~К(х( ), у(')) =р„) ппн ЬУ) (х( ), у)
щ — 1 Я О~=1, ..., 2
(1~((пп. +1,
уеду
при всех
(13.106)
и = Й))1 х).
тах ЛУ)'(х'"', у) = ЬУ)'(х'"", у("'~) ((х'"'))) = !„,. ((х'"'))
у~ У(ш)
(~=1, ". У;
(13. 107)
Маневры у'"" ((х'"')) назовем подозрительными, их суммарное число
значим через У =,~' У . Если удается установить, что среди маневров
из (13.107) есть такие у( 'у'), для которых ири люоых значониях (х'"')
дется хотя бы одна функция
ооо-
Т
(со у')
най-
/( ..) ((х'"')) ) /(,, ((х'"')),
') С точностью до перестановки векторов.
Оптимальные частоты ~(') повторения этих мане))ров определяются по-
добно (13.101). Не занимаясь дальнейтиим исследовапием вопроса о нахо-
ждении частот ~('~, опишем несколько способов отыскания параметров систем х( '
и маневров у(').
П е р в ы й способ. Для фикспро))знного набора векторов (х'"') иропзно-
дится построение множеств Г"" ((х'"')) преимущест))епиого использования
каждой из систем х' ' ~ (х(")) (см. () 3.45), (13.46)). Л замыл'анни У(") мно-
жеств У находятся все лока.)ьиыо ъ(аксимумы (гра((пч)(ые и впутрешп)е)
функций ЬУ)'(х("), у) ио у:

473
ИГРОВОЙ ПОДХОД
то эти у~ '~') не нужно включать в число подозрительных. В соответствии
с (13.99) из подозрительных точек (13.107) выбираются пЯ+1 штук (и)),,
и решается система алгебраических уравнений')
(х,..., х ) =... =~& t; ., „ х, . .
(1) (Я) (1) (Я)
М 1 ~О2 пав+1 а
(13.108)
относительно х"', ..., х~~~ и р . Если решение (х~"~) ~Х,.)( ...;& t; Х, су
ствует и
р„)~ .((х~"~)) для всех )=1, ..., У и и=1, ..., О,
(13.109)
то это решение и будет оптимальной стратегией Конструктора, а р — ценой
игры:
х~ )=х~ )
ь а
(1з.ио)
Оптимальные для Природы параметры маневров определятся из (13.107)
как
у~'~ = у~"~~' ((х~"~))
(ж =1,..., по+1).
(1З.1И)
(13.112)
р ((х'"')) = — шах шах ~ . ((х'"')).
ш=1, ..., Я,у'=1, ..., 1
Отыскивается минимум этой функции по Й векторным переменным х"',
х~"~ из допустимого множества Х,. Функция рс будет непрерывной
при нецрерывной функции ЛР (х, у), но свойство дифференцируемости уже
не сохраняется. Последнее обстоятельство затрудняет применение стандарт-
ных численных методов отыскания минимума функций и требует их моди-
фикации (см. ~13.32 — 13.35)).
Положение минимума функции (13.112) определяет оптимальпую стра-
тегию Конструктора, а номера функций /,, составляющих р~ в точке мини-
мума, дадут по формулам (13.111) оптимальные для Природы параметры
маневров.
Т р е т и й с п о с о б основан на предельном равенстве (13.16). Со-
гласно этому равснству, для приближенного решения задачи минимизации
~~ можно, как и в предыдущем пункте, воспользоваться решением задачп ~ 2
о минимизации р при том же самом значонпи О и достаточно оольшом
Хр
значением р. Распределение маневров для последней задачи можно брать
равномерное. К сожалению, заранее трудно установить соответствие между
точностью (ос — р ) и значением р, поэтому здесь прпкодится решать
задачу ~ 2 несколько раз, увеличивая р.
Возможны комбинации способов. Например, на первом этапе приме-
няется третий или второй способ, а на заключительном — первый. Для слу-
') Индекс а отвечает ва способ выбора.
В противном случае нужно составлять другой вариант системы (13.108).
Число возможных вариантов равно числу сочетаний из У по и 2+1. Если
ни одна из систем (13.108) не будет иметь решения, то нужно уменьшить
число членов, входящих в систему, и повторить процедуру. При этом часть
векторов х'"' будет принадлежать границе Х,. Применение изложенного
способа затруднительно, если число С~ + возможных вариантов системы
(13.108) велико. Кроме того, могут появляться несовместные варианты системы,
которые при численном решении трудно отличить от случаев плохой схо-
димости выбранного метода.
В т о р о й с п о с о б. Среди значений (13.107) локальных максимумов
выбираются максимальные (абсолютный максимум). Тем самым формируется
функция

474
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
чая выпуклых областей У( ' в работах [13.16 — 13.18] предлагается так
называемый «метод оптимальных покрытий». В рассматриваемом здесь
примере эти области невыпуклы (одна и та же система Л~( ' может исполь-
зоваться на двух непересекающихся интервалах — см. (13.62)), поэтому при-
менение данного метода затруднительно.
Задача 3'. Фиксируем частоты (»( ' использования систем х' '. Тогда для
любых ~~ = 1, ..., 2 оптимальные значения х~ ~ должны быть решениями
задачи минимизации
(13.113)
т1п ЬК~(х, у) ч(ду) при (~(х, у)) О,
~б~О
У~- ~о
где х — постоянный вектор, а распределение ~ фиксировано. Это — задача
предыдущего параграфа с 2 = 1. Для выпуклых по х функций ЬК (х, у)
ее решение единственно и х~'~ =... = х~~~ = х, поэтому оптимальная стра-
тегия Конструктора чистая (р(1& t; =1 р. ~&gt =... р.(з
~"'(*. У) Иу)]
У~- ~о
(13.114)
3. Пример — выбор универсальной двигательной системы ограниченной
мощности при отсутствии информации о маневрах. Это задача 1' с функ-
циями проигрыша (13.29). Ограничимся случаем т„о=0. Область изменения
параметров маневра Ф вЂ” отрезок [Ф„Ф,], где 0 ( Ф, ( Ф ( 1 — за-
данные числа (13.26). Область допустимых значений мощности двигателя
Л~ с учетом требования неотрицательности полезной нагрузки (13.23) для
всего отрезка [Ф„Ф ] такова (неравенство (13.92)):
0 ( Л(' ( тт ((1 — Ф,), '/ ).
(13.115)
Функции проигрыша (13.29) непрерывны по Л~ и Ф и, согласно (13.33),
выпуклы по Л~ при всех Ф. Это позволяет воспользоваться результатами
предыдущего пункта для задачи 1' и применить изложенную там схему ре-
шения.
Локальные максимумы (13.98) по Ф функций проигрыша достигаются
в граничных точках Ф, Ф отрезка и в промежуточной (см. (13.36) и рис.
13.6), которая определяется соотношениями:
для абсолютного проигрыша
1 — )/ 1+ — У) ж — ~Т4;
[13.116а)
Ф, (У)=( — Т) '(
для относительного проигрыша
Ф., (Ж) = (~/5/ — Ж вЂ” Я' ж 0,382 — 0,528Х
(13.116б)
(13 117)
7'(Л(,) =т1п7'[Л() = т1п( тах 7',. [Л()).
Л >=О, ,
При сравнении функций проигрыша на этих маневрах ЯЛ~) =ЛР(К, Ф,),
ЯГ) = ЛР(К, Ф,), ЯЛ() = ЛР(К, ЩЛ()) нужно следить за тем, попадают
значения Ф,(К) на отрезок [Ф„Ф ] или нет. Возможные варианты отно-
сительного расположения функций ~,.(К) показаны на рис. 13.23, а для аб-
солютного проигрыша, и на рис. 13.23, б для относительного. Огибающие
~(Л~) выделены жирными линиями.
Оптимальная для Конструктора мощность двигательной системы К„на-
ходится как абсцисса точки минимума огибающей:

475
сб
Н
ь4
~е
о
С~ч
йю
Ж
9
Иа
~Е
о
а5
И
Фей
й:
И
о
И
И
й:
о
а5
И
К
И
ьО
а5
о
Ц
Ю
~~к
~Е
Н
И
Ре
сч
й:
о
Ра
И
3 3
ь4
~е
Ра
сб
Ф
И
9
1
1! ~
Е
о
И
о
ИГРО ВОЙ ПОДХ ОД
К
Д
Ф
М
Ра
Ь.'
й:
о
й
СЭ
Р~
о
~ч
о
ь0
и
о
о
~е
о
а5
Ра
Р~
2
а5
И
сб
Ж
о
М
:1
Ж
ЧЗ'
М
Ь.'
Ц
~е
сб
сч
М
Р~
М
~е
о
о
И
Ь.'
й:
Ж
е'
-й
И
Ж
ь0
~е
М
о
о
Ж
~е
о
1
~О
Н
Д
5~
М
о
~ч
И
зй
Ж
~е
Я
о
о
сб
!

476
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Р,б
Рис. 13.24. Разбиение (13Л18) плоскости Ф„, Ф, и линии уровня функций Ф(1) (Ф„, Ф,), Ф('-') (Ф-, Ф,),
сплошные — Ф(1) = сопят, пунктирные — Ф('-) = сопят; а) абсолютный проигрыш; б) относительный.
вместо вариантов 8 и 8' рис. 13.23, а получаются нижние варианты 1 и 3
рис. 13.23, б.
В соответствии с составом оптимальной стратегии Природы область воз-
мохсных значений О ( Ф, ( Ф1 ( 1 разбивается на несколько подобластей
(рис. 13.24):
1. Ф(1) — ф„ф('-) =ф„ Ф.~') = Фо,.
О'
2. Ф~1~ =Ф,(У,), Ф~2~ -=Ф,;
3. Ф„= Фо;
1'. Ф~') =Ф„
2'. Ф~ >=Ф,(У
8'. Ф„= Ф.,:,(Ж„).
(13. 118)
Границы этих областей определяются из следующих уравнений:
мехсду областями 1 и 2, 2 и 2', 2' и 1'
ЬГ (Ж„, Ф,) = ЬЕ(Ж„Ф,) = ЬК (Ж,, Ф,(Ж..));
между областями 1 и 8
Ь1'(1 — Ф„ф,) = Ы (1 — ф„ф,);
между областями 2 и 8'
ЬГ (1 — Ф„ф,) = ЬГ(1 — Ф„ф,(1 — ф,));
менарду ооластями 8 и 8'
ЬГ(1 — Ф„Ф,) = ЬК(1 — Ф„ф., (1 — Ф,)).
Оптимальные для Природы параметры маневра Ф~'~ и Ф~„'~ определяются
номерами функций ЦГ), входящих в состав огибающей в точке минимума
(13.117). Ими могут быть либо Ф, и Ф1 (варианты 1, 1' на рис. 13.23), либо
Ф1 и Ф, (К„) (вариант 2 на рис. 13.23), либо Ф, и Ф, (К„) (вариант 2' на
рис. 13.23). Кроме того, для абсолютного проигрыша минимум (13.117) мо-
жет достигаться на границе К=1 — Ф1, и тогда оптимальная стратегия
Природы — чистая: Ф„=Ф, (вариант 8 на рис. 13.23, а) или Ф„=Ф, (Т,)
(вариант 8' на рис. 13.23,а). Для относительного проигрыша такая ситуа-
ция не возникает, оптимальная мощность на ограничение не выходит, и.

477
ИГРОВОЙ ПОДХОД
(13.119)
а в областях 3 и 3' они равны
У.=1 — Ф„
(13.120)
р =ЬР(Ж., Ф ).
Мощность Ж., удовлетворяющая уравнению (13.119), выражается через
функцию у (Ф,, Ф.), которая имеет вид:
для абсолютного проигрыша
~(Ф, +ЧФ
)(Ф; + )(Ф,
4 2 — ()/Ф; + ~(Ф )
2 lг
(Ф,. + Ф,.) — Ф,.Ф .
(13.121а)
для относительного проигрыша
у(ф,, ф,.)= — (1 — ф,. — Ф.)+
1
(1 Ф,) Ф,. (1 )(Ф,)' (1 Ф,) Ф, (1 ~(Ф,) (
причем верхние знаки относятся к областям 1 и 2, а нижние — к 1' и 2'.
В областях 1 и 1' оптимальная мощность получается равной
(13.1Л)
а в областях 2 и 2' отыскивается итерационным способом:
Ж~") =у(ф,. (Ж~" ')), Ф,.),
Ж.= 1)т Ж~"),
В-» со
(13.123)
где )=1 для области 2, )=0 для области 2', а функция Ф, (Т) определяется
соотношениями (13.116). В качестве нулевого приблихсения берется Т'О'=
=у('(,, Ф,.) для абсолютного проигрыша и Ж"' = ~(Ф, — Ф,. для относитель-
ного. Итерационный процесс быстро сходится — точность 10 з достигается
на 2 — 4-м приближениях.
После определения оптимальной для Конструктора мощности (13.120)—
(13.123) и оптимальных для Природы маневров (13.116), (13.118) вычисляется
цена игры р. по формулам (13.119), (13.29):
для абсолютного проигрыша
р. = ~1 — ~ам)' — к,(„„, ', 1);
(13.124а)
для относительного проигрыша
1 1 1Ч. 1
,~Ф )- ФР)+М„
(13.124б)
Оптимальные для Природы частоты ~(') и ~~'-) повторения маневров Ф(')
и Ф~'-') в соответствии с (13.101) будут равны
(дЛК(дЖ)
(1)—
(дЮ(дМ), &lt ~) Ђ” (дЛК(д ),
ф1 ф1 +
(13.125)
где производные подсчитываются по формулам (13ЛЗ):
Оптимальные значения мощности Ж. и цена игры р. в областях 1, 1',
2, 2' находятся из уравнений
Я)'(Я, ф())) — (~Я(()(, ф(2)) — р,

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
~гл. ~з
для абсолютного проигрыша
дЬР/дТ = 1 — Ф (Ф + Ж) ';
(13.126а)
для относительного проигрыша
дЬР/дТ = (1 — ~/Ф) ~1 — Ф (Ф + Т) ').
(13.126б)
В точке Ф,=Ф,=Ф некоторые из полученных выражений содержат
неопределенности, которые раскрываются обычными способами. Предель-
ные значения получаются следующими.'
Ж„= ~/Ф вЂ” Ф,
ч(1~ = ч(2) =1~
е /2~
Ф~ц =Ф~2~ =Ф,
(13.127)
(при Ф, = Ф = Ф).
0 (Т'1' (т~п (Ж"' (1 — Ф,)) (Т'з' ( с. Ж~~& t;
(13.'1 28)
Результаты расчетов по формулам (13.118) — (13.126) представлены на
рис. 13.25 — 13.30. Рис. 1325 — 1327 выполнены в виде линий уровня функ-
ций ~&lt '&gt ( „Ф ), К„ Ф Ф,) и р„ Ф„Ф,) соответст енно Рис 1325
с рис. 13.24 определяет оптимальную стратегию Природы: на рис. 13.24
помимо границ областей показаны линии уровня функций Ф~ц (Ф„ Ф,)—
сплошные линии, Ф~'~(Ф„ Ф ) — пунктирные. Отметим наличие разрыва функ-
ции ~~'~ (Ф„Ф ) вдоль границы между областями 2 и 2'. Рис. 1326 дает
оптимальную стратегию Конструктора, а рис. 1327 — цену игры. Для боль-
шей наглядности на рис. 1328 — 13.30 построены сечения функций ~„(Ф„Ф,)
и Ж (Ф„Ф,) плоскостями (Ф) =1/,(Ф,+ Ф ) = сапами (фиксированная средняя
точка интервала маневров — рис. 13.28 и 13.30,а) и ЬФ = Ф, — Ф,= со11й
(фиксированная ширина интервала — рис. 1329 и 13.30, б). Йа рис. 13.30
сплошные кривые относятся к абсолютному проигрышу, пунктирные — к отно-
сительному. Цена игры монотонно возрастает с увеличением ширины интер-
вала маневров (рис. 1328) и имеет минимум по средней точке интервала
(рис. 13.29). Оптимальная мощность в большинстве случаев убывает с увели-
чением ширины интервала (рис. 13.30, а) и имеет максимум по средней точке
интервала (рис. 13.30, б), повторяя в основных чертах идеальное реше-
ние (1324), которому соответствует кривая ЬФ =0 на рис. 13.30, б.
Как отмечалось в пункте 2, цена игры и оптимальная стратегия Кон-
структора могут быть найдены приближенно из решения задачи п. 3 ~ 2
для достаточно больших значений параметра р (в формуле для нормы).
При этом нужно положить 0=1 и т„о=О, распределение маневров лучше
брать равномерное (~=0). Характер стремления минимальных значений
проигрыша р*~ по норме Ь и оптимальных значений мощности Ж*~ к своим
предельным значениям р*д и Ж.д при р ~ оэ иллюстрируется рис. 13.31 для
абсолютного проигрыша. Видно, что значения проигрыша р ~ становятся
р
достаточно близки к р*д, начиная с р 14 (рис. 13.31, а), а значения опти-
мальной мощности Т*~ начинают мало отличаться от У*д еще раньше,
с р ж7 (рис. 13.31, б).
4. Пример — выбор заданного числа двигательных систем ограничен-
ной мощности при наличии текущей и отсутствии априорной информации
о маневрах. Данная задача представляет собой частный случай задачи 2'.
Как и в предыдущем пункте, функции проигрыша задаются формулами
(1329), параметр т,о=О, допустимое множество значений функционала
маневров — отрезок [Ф„Ф1]. Допустимое множество значений мощности
систем (Т"',..., Т'~') определяется соотношениями (13.58) и (13.61), ко-
торые в случае т„о=О приводятся к более простому виду:

Ф„
д! 75
Д15
д.~г5
д!
д
0,1
О
.ф
Ф„=О/57
Л/
а) Я
Рис. 13.26. Линии уровня функции Ж„(Ф„Ф,), определяющей оптимальную стратегию Конструктора:
а) абсолютный проигрыш; б) относительный.
б5
д1
05
1
02 Д~ ф Од Ф, Д ~~0.~ й! 0Я 0~ О Од Ф,
~~=ОИ
Я ф
Рис. 13.27. Линии уровня функции р„(Ф„Ф,), определяющей цену игры «Природа — Конструктор».'
а) абсолютный проигрыш; б) относительный.
9„
(к) й)
У,
Рис. 13.25. Линии уровня функции ~~1~ (~„~,), определяющей оптимальную для Природы частоту
повторения маневра с функционалом ~ = ~~1~: а) абсолютный проигрыш', б) относительный.

480
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Об
д~ ~ Об бб Дф
д4 б) бб
Рис. 13.28. Цена игры р„, в зависимости от ширины ЬФ=Ф,— Ф, интервала маневров: а) абсолютный
проигрыш, б) относительный (соответствует рис. 13.27).
Об
ф=О
Рд &lt Р
ОГ 04 Рб
О,б ф~ (ф)
Рис. 13.29. Цена игры р„, в зависимости от средней точки (Ф) интервала маневров: а) абсолютный про-
игрыш; б) относительный (соответствует рис. 13.27).
ОГ бФ
дд (ф)
б д2 б,4 ф~ 0д ЛУ дб
а) б
!
Рис. 13.30. Оптимальная мощность двигателя Ж„. Сплошные кривые — абсолютный проигрыш, пунктир-
ные — относительный (соответствует рис. 13.26).

ИГРОВОИ ПОДХОД
Проиллюстрируем на этом примере каждый из трех способов решения
задачи 2'.
П е р в ы й с п о с о б. Найдем в соответствии с общей процедурой
все подозрительные значения (13.107) функционала Ф, из которых состав-
ляется оптимальная стратегия Природы. К ним относятся: начало Фс и конец
Ф, интервала маневров, моменты Ф,„+1, и Ф,„+,„переходов (13.60) с уровня
Т'"& t; на 1Ч'" 1 gt; и об атно, то ки , Г' ') внут енних макс мумов (1
функций проигрыша. Число подозрительных значений можно уменьшить.
Р.~
~с
ас
дб
7 4 7 Я 15 р ~ ~ ~ Ю /5 р
Рис. 13.31. Примеры схопимости.
Так, функции проигрыша в точках промежуточного максимума Ф, (Г) оказываются
монотонно убывающими (см. рис. 13.2, 13.6):
НЬР (.&gt У, Фз(М))~ & t;
поэтому внутренний максимум может достигаться только на множестве У~») (иначе
»случилось бы противоречие с определением (13.45) областей У'"&gt )  к чи лу по
зрительных нужно относить только Ф, (Ж1~)).
Далее, удается показать, что прн любых значениях Ж'"& t; Ж' '> вь>п
неравенства
Лт (Ж' ', Ф <+&g ;))Ьт ( gt у'" gt
Лт„(Ж'"&g ;, „~ +
т, (Ф„~„+1&g
Ьт, (> gt; gt;~ &g
т. (Фь+ >
Дто позволяет не включать в число подозрительных для абсолютного проигрыша
точки Ф,„+„„, если Ф„,,„+1& t ~ [Ф„Ф ] а ля относительн го проигр ша Ђ” то к
если Ф<„ ,& t; „ [Ф,
После такого отбора число подозрительных точек будет не меньше 2+1 и не
больше 0+2. Следовательно, число возможных систем уравнений (13.108), одна
из которых дает решение задачи, равно либо 1, либо С~ ~1= Ы + 2.
Не занимаясь дальнейшим общим исследованием, решим задачу для конкретного
случая: 2 = 2, Фо = 0,01, Ф, = 0,81. Здесь Фо и Ф1 принадлежат множеству У") и для
любых 1Ч") ф 0,009 выполняются неравенства
~т (Я~1&g ;; 0, 1) дт (Ж& t;1&g
т (0,01) ( т (0,81)
Ьт, (Я< >; 0 01) ) Ьт, Ж'1',
При Ж(') = 0,09 обе части неравенств обращаются в нуль, поэтому Ж(" ф 0,09
и точку Ф, не нужно относить к числу подозрительных для абсолютного проигрыша,
а точку Фо — для относительного. Поскольку оба момента перехода Ф12 и Ф21 принад-
лежат отрезку [Ф„Ф,], то в силу этих неравенств подозрительными останутся только
следующие три точки.
для абсолютного проигрыша
Ф =0,01яу& t; & t; Ф Ф Ж< >, Ж'2& t )~У~1>ПУ~
31 Механика полета

482
~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
для относительного проигрыша
ф ф (>у lt;1&g ; д>&lt 2 gt;) ~~& t;1&g
Ф1 = 0,81 ~ У'1),
Система уравнений (13.108) цолучается единственной:
для абсолютного проигрыша
&l ;1 Ђ” ~ф &gt ' Ђ” ( „ 1 в
2 (1)
1
=(1 — >& t; 12 l ;Й 1 gt; Ш >)  Ђ” Ж~~ д& t;& t;1&
+ 12& t
=&l ;1 Ђ” ~ф. lt; » † „, ф „ &gt
(13.129а)
для относительного проигрыша
Я (1) ~1 У(1) 1
(1 1/ф )2 >&gt & t; lt; > Ф 1 >/ф (,,&g ; &lt 1&g ; д gt
— 1 — 1
Д!(2) 1
/ 2
(1 — &gt ~Ф (Ж "&g ;) »& t; '+
(13.129б)
где функции Ф 2 (%< >, <'& t; , 21 Ж lt ', Ж& t; ') и 2 (Ю<~&gt
(13.60) и (13.116).
Уравнения (13.129) решаются численно относительно >& t «1&gt  Я<2&gt
находятся: оптимальная стратегия конструктора У„") и У(2), состав оптимальной
стратегии Природы Ф„''& t = Фо ли Ф, Ф " g ; = Ф Я<1& t;, Ж lt;'- >) и
Ф&lt е g ; = Ф % lt;2 gt;) и ц на хиры р = ЛК ( &lt '&g ; Ф&
для абсолютного проигрыша
й„'1) =0,1206, Ь'2) =0,1916, Ф'1' = 0,01, Ф(2' = 0 0362,
ф'3' =0 2202 р =7 15 ° 10 з
для относительного проигрыша
Ж„'" =0,1108, Л„' ' =0,1799, Ф,' ' =0,81,
Ф'~) =0,6799,
Ф'® = 0,2856, р„=4,704 ° 10 '
При Я =1 в предыдущем пункте получалось.
для абсолютного проигрыша
У,=0,1537, Ф( ' =0,01, Ф„' ) =0,1946,
р,=2,478 ° 10 ',
для относительного проигрыша
Л, = 0,1289, Ф„'1' = 0,81, Ф„'~' = 0,3123, р„= 1,615 ° 10 '.
В т о р о й с п о с о б. Минимизируемая функция (13.112) с учетом изло-
женного выше записывается следующим образом:
рц (К< > .. , Ж®) = та [ ах ЬР Ж&l ;
о.)=1, ...,2 Ф~ У(~)
=тах ( т1п ЬР(Ж< > Ф, ; )п ЬР (&l ;&gt
~~(Л' ', Ф„, „),
и=1, ...,2 — 1;
ЬЯ'(Я< >, Ф ,„,) и=2 .. , <&g ;; ЬК(У<
(13.130)
причем в сравнении участвуют только те из Ф„,„, „Ф,, и Ф, (Ш<"
которые принадлежат отрезку [Ф„Ф1]. Аргументы %< ', . ., Ж& t;<&gt
условию (13.128).
Функция (13.130) непрерывна по Г<ц,. ., Г« gt ~, но не всюду диф
цируема. Это иллюстрируется рис. 13.32, где представлены линии уровня
функции (13.130) для рассмотренного выше случая: 0=2, Ф,=0,01, Ф,=

483
ИГРОВОИ ПОДХОД
дед
ОР5
Од
ОУ
/
Рис. 13.32. Пример линий уровня проигрыша рс (ср. рис. 13.11). Пунктиром показаны линии смены
номера маневра Ф;, на котором достигается максимум проигрыша: а) абсолютный проигрыш; б) от-
носительный.
точке, то делался следующий шаг вдоль антиградиента функции с этим но-
мером. В случае несовпадения уменьшалась длина шага и отыскивался мо-
мент смены номера. Для следующего шага градиент вычислялся по функции
ЛР с новым номером. Если любое движение по найденному направлению,
уменьшающее функцию (13.130), снова приводило к смене номера, то оты-
скивалась касательная к линии смены номера и следующий шаг делался
вдоль нее (в направлении уменьшения функции). Положение и величина
найденного таким способом минимума указаны на рис. 13.32.
Т р е т и й с п о с о б. Качественное сходство линий уровня функций
проигрыша по норме С (рис. 13.32) и по норме А, (рис. 13.11) позволяет на-
деяться на быстрое стремление положения и величины минимума функций
к своим предельньм значениям, т. е. к положению и величине минимума
функции р . Это подтверждается примером расчета с 0=2, Ф,=0,01, Ф =
=0,81. Распределение маневров бралось равномерное. Отыскание минимума
31»
=0,81. Свойство дифференцируемости нарушается при смене номера члена
в (13.130), который для данных Л'~'&g ;, . ., Г ~> яв яется максима
Поэтому в искомой точке минимума функция (13.130) не будет дифферен-
цируема (хотя производная по любому направлению здесь существует).
Задача минимизации функции (13.130) решалась методом возможных
направлений [13.33 — 13.35]. На каждом шаге контролировался номер мак-
симального члена в (13.130). Если он совпадал с номером в предыдущей

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
функций р~ производилось методом, изложенным в предыдущем параграфе.
Малое отличие (Л р & t; 0, %) от предель ых значе ий достигае ся р р )~
Напомним, что аналогичный результат получен в п. 3 при 0=1 для доста-
точно многочисленного набора значений Ф, и Ф1 (см. рис. 13.31).
$ 4. Выбор параметров космического аппарата с нерегулируемым
двигателем ограниченной мощности, универсальным
для конечного числа заданных маневров
т„= М (О)/М, & t;
Т = аШ /Ме —— аР~$(2д„М„),
Г „& t; Г=Р,/ ,&lt
(13.131)
Мощность К характеризует источник мощности, а скорость истечения
à — движитель (ускоритель рабочего вещества). Остальные параметры,
в рамках принятых допущений, определяются через те, Г, У из соотноше-
ний (13.131), (8.45), (8.181), (8.204).
Требуется выбрать источник мощности (Г) — универсальный для всех
маневров, движитель (Г) — либо универсальный, либо свой для каждого
маневра, а также начальную массу аппарата т — свою для каждого ма-
невра (т. е. свой запас рабочего вещества). Управляющие функции е (~)
(направление вектора тяги) и о (~) (функция включения двигателя) выби-
раются оптимальными для каждого маневра в результате решения вариацион-
ной задачи (8.9) (динамическая часть (13.5) задачи оптимизации). Необхо-
димые для дальнейшего зависимости минимизированных по е (1) и о (1)
значений функционала динамической части задачи от параметров системы
(13 131) и от параметров маневра получены в Я 3, 4 гл. 8.
Таким образом, в соответствии с терминологией ~ 1, наборы универсали-
зируемых параметров х и параметров настройки ио, которыми распоряжается
Конструктор, будут следующими 1):
') Управляющие функции е (~) и О (~) в обоих вариантах оцинаковы и в (13.132)
уже не упоминаются.
На основе подхода, изложенного в Я 1 — 3, рассматривается задача о вы-
боре оптимальных параметров аппарата с нерегулируемым двигателем огра-
ниченной мощности, который должен обеспечить выполнение нескольких
маневров (множество У, — точечное). Параметры каждого маневра фикси-
рованы, частоты их повторения неизвестны. Исследуются два варианта.
Первый: источник мощности и движитель универсальны для всех маневров.
Второй: источник мощности универсальный, движитель для каждого ма-
невра свой. Строятся области допустимых параметров таких систем, из ко-
торых затем выбирают оптимальные параметры [13.10].
1. Формулировка задачи. Характеристики (4.9), (4.10) нерегулируемых
двигателей ограниченной мощности, необходимые для дальнейшего, были
конкретизированы в Я 1, 3, 5 гл. 8. Часть фигурирующих там параметров
задается извне. К их числу относятся максимальная начальная масса ап-
парата М, (см. (8.45)), удельные массы а и р двигательной системы и баков
для рабочего вещества (см. (8.181) и (8.204) соответственно), границы Г „
и Г диапазона для скорости истечения, а также ресурс двигательной
системы Т „(см. (8. 205)) .
В качестве независимых параметров, подлежащих оптимизации, прини-
маются относительная начальная масса аппарата то, безразмерная мощ-
ность реактивной струи Г и скорость истечения рабочего вещества Г:

485
А11ПАРАТ ДЛЯ КОНЕЧНОГО ЧИСЛА МАНЕВРОВ
5 41
для первого варианта постановки
х= (Т, Р),
(13.132а)
Цо — Жо
(универсальный источник мощности и универсальный движитель);
для второго варианта постановки
х=й, и,=(т„У)
(13.132б)
(универсальный источник мощности; движитель от маневра к маневру ме-
няется или, если это возможно, перенастраивается на другую скорость
истечения) .
Аппарат предназначается для выполнения Й различных маневров,
занумерованных целочисленным индексом 1=1, 2,..., Й. Номер маневра
1 однозначно определяет все параметры маневра, необходимые для решения
динамической части задачи.
Число маневров Й и это соответствие известны Конструктору уже на этапе
проектирования, т. е. при выборе х. Частоты ч, повторения маневров ему
неизвестны (неполная априорная информация). В процессе эксплуатации,
т. е. при выборе и„номер очередного маневра становится известным (теку-
щая информация — полная).
Таким образом, Природа назначает номер очередного маневра и частоты
ч, повторения маневров:
у=1=1, 2, ..., Й; ч,)0, ч,+...+ч„=1.
(13.133)
Т (х, и„у) = т~и Т (х, и„е (1), о (1); у).
е(~), ~(~)
(13.134)
Для первого из указанных маневров в рамках требования о (~)=1 эта
связь дается соотношением (8.179а), для другого — соотношениями
(8.130), в которых нужно выразить
ао[10 ~дД =2,04 ° 10зТ/а ~кг/квт~ т Г~км/сек~,
Т (сут~ = (т, — т, — Ж) а ~кг/квт~ Г'~ км/секЦ172,9 (1 + ~) У.
(13.135)
Параметры настройки и, в соответствии с общей процедурой выбираются
для каждого маневра из условия минимума времени (13.134) выполнения
этого маневра:
1п1пТ(х, ио; у)=Т(х, у)
(13.136)
(функция (13.5)).
Если бы для каждого маневра выбиралась своя двигательная система,
то можно было бы обеспечить
Т „(у) = т~п Т (х; у)
(13.137)
Для численных расчетов принято 1=2. В состав маневров включены:
у=1=1 — переход с круговой орбиты радиуса г, спутника Земли на
круговую орбиту радиуса г, с одновременным поворотом плоскости орбиты
на угол ~ при заданной полезной массе М„(угловое перемещение аппарата
не фиксировано — см. п. 2 ~ 4 гл. 8);
у=1=2 — межпланетный перелет (без возвращения) с круговой орбиты
спутника Земли на круговую орбиту спутника Марса при заданной полезной
массе М, (дата старта не фиксирована — см. п. 9 ~ 3 гл. 8).
Критерием качества (13.4) выполнения отдельного маневра считается
время движения Т. После выбора управлений е (~) и о (~) в результате реше-
ния вариационной задачи (8.9) о максимальном быстродействии для каждого
из маневров у время Т становится известной функцией параметров (13.132)

486
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
(предельный уровень функционала — идеальное решение (13.6)). Универ-
сальная система будет обеспечивать худшие значения функционала (большие
предельных). Ее эффективность, как это предложено в ~ 1, можно характе-
ризовать максимальным (по всем маневрам, т. е. по у) значением относитель-
ного отклонения времени (13.136) от предель-
ного уровня (13.137):
()
р ~х~ = п1ах
Т (х, у) — Т П,1 (у)
(13.138)
Т;, (у)
Об
(13.140а)
Ул,к= П Ыг,к(у).
у=1
Пример построения допустимой области на плоскости «скорость истече-
ния à — мощность Г» приведен на рис. 13.33 для двух указанных выше
маневров (Г „и Г „в (8.212)) не фиксированы, значения остальных
внешних параметров приведены в подписи к рисунку.
Во втором варианте постановки, (13.132б), мощность Л принимает
единственное для всех маневров значение, а значение скорости истечения Г
Поскольку частота повторения маневров
05 неизвестна, то в принципе нужно было бы
использовать игровую постановку ~ 3. Однако
Ц4 по физическому смыслу рассматриваемой за-
дачи вторую сторону (Природу) здесь можно
ЯЗ только условно наделить свойством активного
противодействия, и нет необходимости опреде-
лять оптимальную стратегию Природы, обеспе-
чивающую при любой стратегии Конструктора
выигрыш, не меньший цены игры. Здесь до-
О/ статочно определения гарантирующей страте-
гии Конструктора [13.15]. По этой причине и
принято в качестве критерия оптимальности
универсальной системы расстояние (13.15а) до
Рис. 13.33. Пример построения об- ИдЕаЛЬНОГО рЕШЕНИя ПО НОРМЕ С.
Дополнительное ограничение ( 3.12) фор-
ыми круговыми Орбитами, у=2 — МуЛИруЕтСя КаК УСЛОВИЕ КОНЕЧНОСТИ ВРЕМЕНИ
перелет Земля — Марс; ~р у (у=1),
выполнения любого маневра из числа за-
Ф
ния только 1-го или 2-го маневра, даННЫХ-
(х, у)( оэ для всех у=1, ..., Й. ( 3. 39)
2. Область допустимых параметров двига-
~,<„ Ђ” ' ~&g ; в ” о 4„ lt ц — 1) 8„,' „' теля. Не авенство (13.1 9) м жет быть
® = ) = 029, л" ® = 2) = ворено за счет ограничения множества до-
= 10,48 км,~сек).
пустимых значений проектных параметров х
из (13.132). Для одного маневра это было
сделано в п. 6 ~ 5 гл. 8. Там было установлено, что в пространстве т„Г, У
допустимая область определяется соотношениями (8.209) — (8.217), которые
иллюстрировались рис. 8.69 — 8.73. Для исследуемого здесь случая в соот-
ношениях (8.211), (8.214), (8.215) нужно положить Лт,=О и подставить
значение Лг, соответствующее нужному маневру у (см. (8.179б), (8.130)).
В первом варианте постановки, (13.132а), рассматривается полностью
универсальная двигательная система: мощность Г и скорость истечения У
должны быть неизменными для всех маневров, которые должен выполнять
аппарат. Тогда допустимая область Я~ ~ в пространстве Г, У определится
как пересечение допустимых областей Ял ~ (у) (8.213) — (8.217) для каждого
из заданных маневров у:

487
э 4]
АППАРАТ ДЛЯ КОНЕЧНОГО ЧИСЛА МАНЕВРОВ
выбирается своим для каждого маневра (частично универсальная двига-
тельная система). Допустимый интервал (Г„Г,) изменения мощности опре
делится тогда как пересечение соответствующих интервалов для каждого
из заданных маневров, т. е.
Я,"~* = (Т„У,), Т, =- шах т1п Т,.„(у, Р),
к=1 ". ~ ~~~~ Ь) ~.(ки
Т, = т1п шах Т,„» (у, Р),
к "- ~ М О)]
(13. 140б)
где Г,.„(у, У), Г„„(у, Р), У, (у), У, (у) задаются соотношениями (8.214)—
(8.217). Таким образом, допустимой областью Я~" ~ (у) параметров Г, У
частично универсальной двигательной системы для маневра у в этом случае
будет (см. рис. 13.33)
где 6 — полоса: Г,(Г(Г„О(Г(оэ.
3. Оптимальный запас рабочего вещества. Задача (13.136) в обоих
вариантах постановки, (13.132а) и (13.132б), требует определения для каждого
маневра оптимальной начальной массы аппарата М (0).
Полезная масса М задана, масса двигателя М„и его другие характери-
стики известны, запас рабочего вещества М о ограничен объемом баков;
это ограничение записывается в виде 0 ( М ( М, — (ЛХ +ЛХ„+ЛХе),
где максимальная начальная масса аппарата ЛХ, фиксирована. Можно варьи-
ровать запас рабочего вещества ЛХ, в пределах, определяемых последним
р.О
неравенством, и управление двигателем — в рамках заданной регулировоч-
ной характеристики 1). Нужно обеспечить минимальное время выполнения
заданного маневра [13.36].
При уменьшении начального запаса рабочего вещества уменьшается
начальная масса аппарата, что при неизменной тяге двигателя Р приводит
к увеличению начального реактивного ускорения и сокращению времени
выполнения маневра. С другой стороны, малого запаса рабочего вещества
моясет не хватить для совершения заданного маневра. На основании каче-
ственных соображений можно ожидать, что в ряде случаев оптимальный за-
пас рабочего вещества будет меньше максимально допустимого: М е ( М,—
— (ЛХ +М„+ЛХ ). Пусть, например, дан двигатель с ограниченным расходом
О ( д ( д „, предназначаемый для энергетически напряженного маневра.
Если с этим же двигателем нужно выполнить ненапряженный маневр, то
максимально допустимое количество рабочего вещества может просто не
успеть израсходоваться за время совершения маневра. Такие рассуждения
становятся несправедливыми в случае идеальных двигателей, у которых нет
ограничения на расход рабочего вещества.
Хотя в настоящем параграфе речь идет о нерегулируемых двигателях,
рассмотрение сформулированной выше вспомогательной задачи начнем
с идеальных двигателей ограниченной мощности и ограниченной скорости
истечения. Динамический маневр для идеального двигателя ограниченной
мощности характеризуется функционалом У вЂ” интегралом от квадрата
реактивного ускорения (гл. 6, 7). Чем меньше время выполнения маневра Т,
тем больше величина У (гл. 7). Конечная относительная масса аппарата и,
выражается через функционал У или Ф по формуле (6.6):
М +-и,+Мз
1 ио У Фто
') Результаты решения динамической части задачи о выборе оптимальных управле-
иий берутся из предыдущих глав.

~ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
(удельная масса двигателя а, безразмерная мощность Г из (13.131) фикси-
рованы). Разрешив это соотношение относительно Ф, получим, что задача
сводится к отысканию максимума по т, функции Ф (т„т„Г)
(13.141)
тах Ф = (Т/т,) — т1п (Ж/т,)
~ ~<~
при фиксированных значениях т1 и Г. Максимум (13.141) достигается при
т,= — 1 (максимально возможный запас рабочего вещества) и равен
(13 142)
ЩООР, =1
По значению Ф „и удельной массе двигателя а вычисляется максимальное
значение функционала У „=(2/а)Ф „, а по нему для каждого конкретного
маневра — минимальное время Т;, (см. гл. 7). Полученный результат
(ЛХ (0)„,=ЛХО) оправдывает принятое в постановке примера из ~ 1 условие
заданной (а не ограниченной сверху) начальной массы аппарата.
Аналогичная процедура проводится и для идеальных двигателей огра-
ниченной скорости истечения. В этом случае энергетические затраты на вы-
полнение маневра определяются характеристической скоростью Лп — инте-
гралом от реактивного ускорения (гл. 5). При сокращении времени выпол-
нения маневра Т величина Лп увеличивается. Выразив Лп из формулы
Циолковского, (5.6):
Ьи = — Р „1п [т,/т,]
(скорость истечения Г,„и относительная конечная масса т, фиксированы),
видим, что максимум Лп достигается при т,=1.
(13.143)
~() рф ~ °
~г „= — Р „1пт„
Таким образом, для обоих рассмотренных здесь типов идеальных дви-
гателей минимальное время выполнения заданного маневра при фиксирован-
ных величинах полезной нагрузки и параметров двигателя достигается,
когда запас рабочего вещества берется максимально возможным.
Для нерегулируемых двигателей (независимо от их типов) время работы
Т выражается через заданные значения тяги Р, скорости истечения Г,
конечной массы ЛХ, и неизвестное значение начальной массы ЛХ (О): Т„=
= (ЛХ (О) — ЛХ,) Г/Р. Решение динамической задачи (8.9) о максимальном быстро-
действии может быть записано в виде
т=т —" 1 ' ~~)
то а,
& t
а„= —; Р, т,= Йхе
О
(13.144)
т
Т = Т = ' (1 — е-"~~").
Р а„
(13.145)
Будем считать зависимость (13.144) известной. Тогда задача сведется
к отысканию минимума (13.144) по т,(т,,„из (8.210). Ниже дается реше-
ние этой задачи для следующих маневров: (1') набор модуля скорости (п. 4
~ 2 гл. 8) и околопланетные маневры без выключений двигателя (конец п. 2 ~ 4
гл. 8), (2') перемещение между точками покоя (п. 5 ~ 2 гл. 8), (3') поворот
плоскости круговой орбиты (п. 2 ~ 4 гл. 8), (4') межпланетные перелеты без
возвращения при незаданной дате старта (п. 9 ~ 3, гл. 8).
1'. Набор модуля скорости. Решение динамической задачи для данного
маневра следующее (8.30), (8.179а):

489
АППАРАТ ДЛЯ КОНЕЧНОГО ЧИСЛА МАНЕВРОВ
э 41
Вспоминая про связь Т =(т,— т,)Г/а„видим, что начальная масса т
или запас рабочего вещества т,=т,— т, определяются формулой (13.145)
однозначно:
&l ; ( и  Г 1и ~'
т =те" /~
О 1
(13 146)
г 4 Ю 1 Ю аргу
Р ~~ф ~Ю Д ф ДУ и,/~
Рис. 13.35. Оптимальное отношение масс т,/т,
и минимальное время выполнения маневра Т/с,
для перемещения между точками покоя (с, =
= М,У/Р, с~ — — Р1/М,У2).
Рис. 13.34. Начальная масса то — — М (0)/М,
для набора скорости и,.
2'. Перемещение между тачками покоя. Решение динамической задачи
(8.43) здесь может быть представлено в виде
(13.147)
Из условия минимума Т по 1 &lt то /т получ ем неяв ое выраже ие
оптимальной величины 1 через комбинацию с, параметров маневра и аппарата
(рис. 13.35 при с,<с,
1„(с2) при 0 & t; с &l
(13.148)
~~~ „ф ~, при с,) с',
г
Я„1п' ~„— ~/~„(~/~„— Ц 1п 1„+ (~/~„— 1)' = с„
,1, = т,,(т, с", = 1(Д!п~ 1, — Д, (Д, — 1) 1и 1, + (Д вЂ” 1) )
Рассматривая теперь ~ как параметр, подставляем (13.148) в (13.147) и полу-
чаем выражение для минимального времени.'
с,~Е1п Š— (~/à — 1)'Д при Е<
(13.149)
с,((~,— 1)-~-2[с,— (Д вЂ” 1)'1п 'Ц~ при ~') ~„
по формуле (13.148) оно может быть представлено в функции комбинации с~
(рис. 13.35).
Соотношения (13.148), (13.149) дают полное решение задачи. Посчитан-
ная по ним зависимость оптимальной начальной массы то= ~т1 от комбина-
где т, „задано соотношением (8.210).
В зависимости от комбинации и,/Г параметров маневра и, и двигателя У
монотонно изменяется потребный запас рабочего вещества от нуля при и,/У=О
до максимально возможного при и,/Г=1п (т,, /т,) (рис. 13.34). С большими
значениями и,/Г при данных то „и т, маневр невыполним.

490
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
~ГЛ. 13
ции Р//Мо72 при фиксированных значениях т1=(М,+М„+М.)/Мо пока-
зана на рис. 13.36.
3'. Поворот плоскости круговой орбиты. Для маневра поворота плоско-
сти круговой орбиты радиуса г, на угол ~ функционал (13.144) динамической
задачи записывается в неявном виде (8.178а):
с
(здесь время Т считается кратным периоду обращения 2т~й '~ ф).
р' ~г РФ ф' Рю
Юф
Рис. 13.36. Оптимальная начальная масса для перемещения между точками покоя.
~„, = ~„(с,), Т,, = с,т„(с,) при 1„(с,) ( 1„'
Т „=с,т,(с„1,) при ~„(с,) )~ 1,
(13.151)
~„ (с,) =
~1 — с' — с2 агсяп ~1 — с~
сД„(с,)
.ъ( 2)
~о тат
1
Отношение то = М (О)/Мо начальной массы М (О) к максимально воз мож-
ной М в функции комбинации с, = ~ ~/Й/го Г 1 параметров двигате ля
ф~ Рб' РЮ с~
РГ Р4 г~Г Рг ,
Рис. 13.37. Оптимальное отношение масс
т,/т, и минимальное время выполнения
маневра Т/с, для поворота плоскости
орбиты (с, = сМ,Ч)2Р, с, =г~lй!~ Ч ') °
Рис. 13. 38. Оптимальная на-
чальная масса для поворота
плоскости орбиты.
маневра приведено на рис. 13.38 для ряда значений относительной конечной
массы т =(М +М„+М )/М,.
Оптимальное значение параметра ~ и минимальное значение времени выпол-
нения маневра Т равны (рис. 13.37 при 1„(с,) (1 )

491
АППАРАТ ДЛЯ КОНЕЧНОГО ЧИСЛА МАНЕВРОВ
4'. Межпланетный перелет без возвращения при незаданной дате старта.
Аппроксимационная формула (8.130) для функционала динамической части
задачи переписывается с учетом связей Т„=(те — т ) Г/а„, аз= а„/те:
при Ь1е(Ь,~по(Ь„,
Ь,+ Ьете' при Ь,те) Ь„,
со при Ь7т (Ь
Т=
(13.152а)
где
Т=(Ь,+Ь те)—
Ье+ Ьет в Ь,п
Ье + Ьет'ед — Ь7те
о
Ь, +Ь,~е" — Ь,,
— (Ь,+Ь те — Ьете') 1—
Ь,+Ь, е — Ь..
(13.1526)
а коэффициенты Ь,. и е выражаются через с,. из табл. 8.1 и через Г и а„
следующим образом.'
9 10~
3
а
сз — С4К
~6 ~ ~7
в а
ф
е
С8 С7 — СВК 1+ Ьзт0
Ь, = Ь, — с, + —, Ь„= + т,Ь„
64 — 13 Р3
5 1 2~
Ьй + Ьет
Ь„= + т1Ь„
11,8
([Т] = сут, [Г] = км~сек, ~ а„] = 10 'де).
'=с +
)
(13. 152в)
Минимизация (13.152) по те<те,„производил сь числен о. Резу
таты представлены на рис. 13.39, 13.40.
Результаты настоящего пункта показывают, что в случае нерегулируемых
двигателей, в отличие от идеальных, для определенных значений параметров
маневра и двигателя существует оптимальный запас рабочего вещества,
отличный от максимально допустимого. Напомним, что эти результаты
относятся ко всем типам нерегулируемых двигателей (а не только к нерегу-
лируемым двигателям ограниченной мощности, о которых идет речь в осталь-
ных пунктах параграфа).
4. Алгоритм решения задачи минимизации проигрыша (13.138) ориен-
тирован на машинную реализацию и основан на сведении непрерывно-ди-
скретной игры к чисто дискретной (матричной), которая решается перебо-
ром [13.15]. Процедура организована так, что решение в обеих постановках
(13.132а) и (13.1326) получается одновременно. Кроме того, в процессе счета
отыскиваются идеальное решение (13.137) и решение (13.136) в постановке
(13.1326) для каждого из маневров.
Непрерывные параметры Х и К, которыми распоряжается Конструктор, заменяются
дискретными
Г~= У1+(~ — 1) ЬГ (~=1, ..., т). (13.153)
Ь~' = Ю, + (~ — 1) Ьт
При этом величины Г1, ЛГ, Р'1, Л Г, и, т должны быть назначены так, чтобы: а ) охватить
всю область значений Х и К, в которой лежат идеальные решения для всех маневров и ре-
шение задачи в целом 1), б) обеспечить достаточную точность аппроксимации, в) не выйти
') Это требование заведомо выполняется, если прямоугольная область (13.153)
включает объединение допустимых областей В~ ~, построенных в и. 2.

[ГЗТ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
б,б
ОГ 0~
ОГ 04 Об Од
а)
Рис. 13.40. Минимальное время Т перелетов, соответствующее рис. 13.39:
(й, = 1п (а„[10 'д,Д У-' [км/сек] т — 1),
й, = 1п (а„, [10 'д,] Т [сут] У ' [хм/сек] т11);
а) Земля — Марс; б) Земля — Венера.
Рис. 13.39. Оптимальная начальная масса для межпланетных перелетов с оптимальной датой старта:
а) Земля — Марс; б) Земля — Венера.

493
б 41
АППАРАТ ДЛЯ КОНЕЧНОГО ЧИСЛА МАН ЕВРОВ
за размеры памяти машины (там должны поместиться две таблицы размером и (т+1+Й)
и и (т+3), где Й вЂ” общее число маневров ')).
Вычисления производятся последовательно для каждого из маневров 1=1,..., й.
1'. Заполняется таблица
т, (~ую у1)
(~=1, ..., и, '/=1, ..., т)
пш~ Т~ = Т~ = Т'
Ю Х С*'
у'=1, ..., и
(13.154а)
Все числа Т)„и /~-эф~ (~=1, ..., и) запоминаются, причем последние сохраняются
для каждого маневра до конца счета.
2'. Перебором по ~ среди Т~~„отыскивается
ш1п Т1,= Т~
~=1, ...,и
Это — идеальное решение для 1-го маневра.
3'. Для каждой пары ь', у вычисляется таблица
и модернизируется таблица р' ~ по правилу
шах (р; р~~) -э р~~
(перед началом счета с 1 =1 все р~~ =О). Сравнением среди получающихся значений
~'~' находится
(13.154б)
Все числа р„' и у„' запоминаются.
4'. Для каждого ь вычисляется
р =(т,'.~т,
и иодернизируется строка р„'„по правилу
шах (р; р' ) -э р„',
(перед началом счета с 8 =1 все р,'„=О).
5'. Перебором по ~ находятся
прад р„'= р„'"= р„
~=1, ...,и
(13.155а)
пи'д р~„= р~~ = р
г=1,...,и
(13.155б)
Значения ~„и ~ „запоминаются.
Берется следующее значение номера маневра ~, и цикл 1' — 5' повторяется. При
(=Й величины (13.155а) и (13.155б) дадут значения цены игры в постановках (13.132а)
и (13.132б) соответственно.
Величины ~„и 1 из (13.155а) и (13.155б) определяют по первой формуле (13.153)
оптимальные для Конструктора значения мощности К„и К„„(в постановках (13.132а)
и(13.132б) соответственно). Оптимальная скорость истечения У„ для (13.132а) находится
подстановкой во вторую формулу (13.153) значения у„'" из (13.154б), (13.155а), а для
(13.132б) Й значений Г', оптимальных для своего маневра, получаются подстановкой
в ту же формулу ),'~" (1 =1, ..., Й) из (13.154а), (13.155о).
При желании можно приближенно определить номера маневров, составляющих
оптимальную стратегию Природы (т. е. наихудших для Конструктора). Для этого вычис-
ляются времена выполнения и проигрыш на каждом из маневров с найденными выше оп-
тимальными параметрами Ф и У. Маневры с наибольшими проигрышами и будут иско-
') Если рассматривать только одну постановку (13.132а), то размеры каждой из
таблиц можно уменьшить до и (т+2).
(для 1=1 время Т подсчитывается по формулам (13.145), (13.146), (13.135), а для 1=2—
находится в результате минимизации (13.152) по то). Одновременно сравнением отыски-
вается

494
~ГЛ. 1Ь
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
иыми. Однако дело осложняется тем, что из-за дискретной аппроксимации такой маневр
может оказаться единственным. Для исходной же задачи такой вариант возможен только
в вырожденном случае, когда размерность допустимого множества Хо меньше размер-
ности х. Поэтому, кроме маневра с максимальным проигрышем, будут подозрительными
на оптимальность маневры со значениями проигрыша, ближайшими к максимальному.
В невырожденном случае малость этой разности характеризует точность счета.
Рис. 13.41. Мощность Х«~ (т„~) двигателя, оптимального для одного маневра (1 = 1 — околоземной
орС
маневр, 1=2 — перелет Земля — Марс); Ж~ — мощность полностью универсального двигателя; И~~в
оптимальная мощность частично универсального двигателя (в двух последних случаях т,=сопя$—
параметр кривой, т„=т„, — аргумент).
Отметим, что в процессе счета получаются решения й — 1 игровых задач. В каждой
последующей набор маневров, которыми распоряжается Природа, увеличивается на еди-
ницу. После решения последней из задач с полным набором маневров можно произвести
уточнение, сузив область изменения К, У и уменьшив за счет этого ЛК и Л 1' (при неиз-
менном размере таблиц в памяти).
Ч,
кн/сею
п,г
д5 дб
Рис. 13.42. Оптимальные значения скорости истечения Г, соответствующие рис. 13.41 (ГЯ = Гш1в).
5. Численные результаты. При численных расчетах использовались
таблицы функций проигрыша размером 90Х90, т. е. ЛГ 10 з, Л к' 1 км/сек.
После сужения области ЛГ уменьшалось в 2 — 3 раза, а Л к' — в 4 — 10 раз.
При этом относительные изменения результатов решения составляли: 0,1—
1% по величине функционала и 1 — 10% по положению точки минимума.
Расчеты проведены для различных значений полезной массы на первом
и втором маневрах из п. 1: 0,05 ( т„~, т„( 0,7 при фиксированных па-
раметрах а=10 кг/квт, ~3=0, Т„,„=300 сут, У „=20 км/сек,
=100 км/сек, Ль =8 км/сек. Результаты расчетов приведены на рис. 13.41—
13.46. Необходимые пояснения даны в подписях к рисункам.

ф дЯ Д5 04 05 Об 07
О О~ 02 ОЗ 04 05 Об а~ ~
О,б
01 ОГ 05 04 05
Об
Рис. 13.45. Минимальный проигрыш во времени выполнения двух маневров при фиксированных значе-
ниях т„, в функции т„, с полностью универсальнымдвигателем.
д,Г О.& t; 04 05 &gt ."&
Рис, 13.46. То же, что и на рис. 13.45, с частично универсальным двигателем (универсальный источник
мощности и сменный движитель).
Рис. 13.43. Оптимальные значения т ~ ~ ~ началь-
О
ной массы аппаратов, соответствующие рис. 13.41,
13.42 <т l ;2&g ; = т&lt 2 gt;  &lt
О орС О* О** 0 орС
Рис. 13.44. Общий.вид зависимости мини-
мального относительного проигрыша р,„во
времени выполнения двух маневров ап-
паратом с полностью универсальным дви-
гателем от параметров маневров т~, и т~,.

[гл. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Из полученных результатов следует, что в достаточно широкой области
значений т,1 и га, полностью универсальная двигательная система при со-
ответствующем выборе ее параметров может обеспечить выполнение обоих
маневров с проигрышем 1 — 20% (см. рис. 13.45). Переход на частично уни-
версальную систему (универсальный источник мощности и сменный движи-
тель) позволяет уменьшить проигрыш в 2 — 10 раз (ср. рис. 13.45 и 13.46).
Если же попытаться выполнить маневр с двигательной системой, оптимальной
для другого маневра (только для одного), то проигрыш значительно увели-
чивается, а во многих случаях маневр становится просто невыполнимым.
$ 5. Выбор параметров межпланетного аппарата при поэтапном
поступлении информации о неопределенных параметрах маневра
(13.156)
(1е) ~ [1, 1+ Ме [, 1 = орС,
~~о = ~'хе
Из-за непредвиденных задержек при подготовке аппарата к старту
с Земли или с орбиты спутника Земли действительный момент старта ~,
может отличаться от программного (~е) на случайную величину. Последняя
предполагается ограниченной сверху заданным числом ог, (функция распре-
деления ее неизвестна):
3~0 = Йхе.
(13.157)
Информация о реальной дате старта может использоваться Конструкто-
ром для сброса избытков рабочего вещества ЛМ„'"' (после вывода на орбиту)
1) Через т обозначается текущее «полетное» время, отсчитываемое от реальноге
момента старта (в отличие от «абсолютного» времени г).
Развитый в Б 1 — 3 подход к выбору универсальных параметров аппарата
распространяется на случай многошагового поступления информации о пара-
метрах маневра (на различных этапах подготовки и проведения полета).
Кроме того, учитывается новое качественное требование возможности ава-
рийного возвращения в случае частичного отказа двигательной системы.
1. Требования к аппарату. Аппарат предназначается для межпланет-
ного перелета на заданную планету (в численном примере — на Марс)
с возвращением. Часть параметров перелета на этапе проектирования не
определена и может изменяться от реализации к реализации. К ним отно-
сятся дата старта, время пребывания у планеты назначения, момент возник-
новения и величина частичного отказа двигательной системы.
Будем различать программную (~ ) и реальную ~е даты старта. Программ-
ная дата старта назначается заранее. Предполагается, что программная дата
старта становится известна Конструктору на этапе выбора запаса рабочего
вещества М„е, баков М и программы и (т) управления ') двигательной си-
стемой и все эти величины могут быть изменены им в зависимости от (~,).
Кроме того, если есть резерв по начальной массе аппарата М (О) и по продол-
жительности экспедиции Т. (об этом будет сказано ниже), Конструктор может
увеличить полезную массу аппарата М, по сравнению с заданным нижним
пределом М
Однако на более раннем этапе проектирования (при выборе параметров
двигательной системы) значение программной даты старта неизвестно. Она
может принимать любые значения из отрезка [1, 1+Лг,] заданной длины Л4.
Расположение этого отрезка (момент ~) может выбираться Конструктором.
Распределение дат старта (~,) внутри отрезка [~, ~+Л~,) Конструктору не-
известно. Таким образом, условия по программной дате старта заданы в виде

5) МЕЖПЛАНЕТНЫЙ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТ5 ПЛЕНИЕ ИНФОРМАЦИИ 497
и для изменения программы управления и (т). Баки остаются старыми,
увеличивать запас рабочего вещества и менять полезную нагрузку нельзя.
Аналогичная ситуация может возникнуть при отлете с планеты назначе-
ния. Она описывается в терминах времени ожидания Т,. Реальное время
ожидания Т, становится известным непосредственно перед отлетом с планеты
назначения. Оно может превосходить программное (Т,) на случайную ве-
личину с неизвестным законом распределения, ограниченную сверху числом
ЬТ,. Программное время ожидания (Т,) и максимальная задержка при
отлете ЪТ, фиксированы и известны Конструктору заранее:
Т,(=((Т,), (Т,)+ЪТ,Д, (Т;), ЪТ,=йхе.
(13.158)
В зависимости от реального времени ожидания можно только избавляться
от избытков рабочего вещества ЛМ~'~ и менять программу управления на
оставшейся части траектории.
В аварийных ситуациях должна быть обеспечена возможность возвраще-
ния на Землю из любой точки траектории полета с полной (если двигатель-
ная система не повреждена) или с уменьшенной (если двигательная система
повреждена) мощностью. Тяга падает пропорционально изменению мощ-
ности, скорость истечения сохраняется. Аварийные ситуации, связанные
с утечкой рабочего вещества, не рассматриваются.
Коэффициент ~ падения мощности является случайной величиной, его
предельное (минимальное) значение считается заданным; момент отказа т
также случаен; законы распределения ~ и т„неизвестны:
~(=(",.„1), т (=(О, Т.(, ~ .,=Лхе
(Т(~) =~Та, Р(т) =~Рэ, д (~) =~у при с) т ).
(13.159)
1) 6 (~ — ~„) — тэта-функция: 6 (х)=О при х ( О и 6 (х)=$ при х ) О.
3~ Механика полета
Вер оятность повторных отказов предполагается бесконечно малой.
В аварийной ситуации разрешается сбросить избытки рабочего вещества и
часть полезной массы ЛМ, которая в безаварийном варианте должна быть
оставлена у планеты назначения. Можно также перестроить программу управ-
ления тягой на оставшейся части траектории. Поврежденные секции дви-
гательной системы не сбрасываются.
Суммарное время работы двигателя не должно выходить за пределы за-
данного «аварийного» ресурса Т
1„(-„) + Т„(т„, ~) ( Т„„= Пхе, (13.160)
где ~„(т ) — время работы двигателя до момента повреждения, Т (т„, ~)—
время работы двигателя, потребное для возвращения на Землю с уменьшен-
ной в 1/~ раз тягой из точки, в которой произошло повреждение. Аварийный
ресурс 2' „в общем случае отличается от номинального Т „. По-види-
мому, можно даже сказать, что он не меньше номинального. Последнее
оправдывается тем, что на равных интервалах времени вероятность номиналь-
ного режима Р (т)=Рэ не больше вероятности режимов, ограниченных снизу
по тяге данным аварийным '), Р (т) )~ [1 — (1 — ~)0~ (т — т„) \Р, (поскольку
в их число входит и номинальный). Отсюда следует, что с равной вероятно-
стью выполнение второго соотношения можно гарантировать на большем
интервале времени, нежели первого. Однако данная проблема выходит
за рамки настоящего параграфа, здесь Т„„и Т„„считаются заданными
извне.
Дополнительно к перечисленным выше условиям требуется, чтобы
в случае отказа на участке разгона у Земли (О ( т„( Т"') полезная масса

ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
ЛМ не сбрасывалась, а возвращение осуществлялось бы на исходную орбиту
спутника Земли. При отказах на более удаленных от Земли участках, как
уже говорилось, разрешается сбросить ЛМ, и войти в атмосферу Земли с па-
раболической скоростью.
В соответствии с целями экспедиции устанавливается нижний предел
М, „полезной массы аппарата М, и величина сбрасываемой у планеты
назначения массы ЛМ, (она включается в М...):
М,)М, „)ЬМ„М, „, ЬМ,=Ыхе.
(13.161)
При благоприятных обстоятельствах Конструктор должен увеличивать
полезную массу.
Начальная масса аппарата Ме ограничена сверху заданной величиной:
М(0) = М,+М„,+ М +М„(М,= Йхе.
(13.162)
Заданы характеристики (4.9), (4.10) двигательной системы — она счи-
тается нерегулируемой, ограниченной мощности (и=(е, о)):
М„= аУ„Р (т) = Р,о (т) е (т), Р, = 2Ж,Г„д (т) = (Р,~У,) о (т),
о(т) =1 или О, ~е(т) ~=1, У,.„( Г,( Г,„, Т„.(Т „(13.163)
(а, У,„Г „, Т„= Йхе),
и связь между запасом рабочего вещества М„, и массой баков М:
М„,( —,, М Д=Пхе).
1
(13.164)
') Остальные кинеиатические характеристики маневра (высоты Й~'~ и Й"'=Й'4~=Ь"'
круговых орбит у Земли и у планеты назначения, скорость входа и в атмосферу Земли)
заданы однозначно и известны Конструктору.
Величины мощности Г, и скорости истечения Г, выбираются Конструк-
тором. Они должны быть одинаковыми для всех вариантов перелета, пере-
численных выше (требование универсальности двигательной системы).
При их выборе Конструктору известны лишь предельные значения случай-
ных параметров маневра ') (13.156) — (13.159) и, естественно, ограничения и
связи (13.160) — (13.164).
2. Критерий оптимальности и стратегия Конструктора. Качество вы-
полнения маневра с полностью определенными параметрами будем харак-
теризовать величиной суммарного времени Т., затрачиваемого на этот ма-
невр. Разброс параметров маневра (13.156) — (13.158) приводит к разбросу
времени Т.. Поскольку информация о функции распределения случайных
параметров маневра отсутствует, за критерий оптимальности аппарата
принимается максимальное из всех возможных значений Т..
Условие успешного возвращения на Землю при аварийной ситуации
выступает в виде качественного требования. Время аварийного возвращения
не включается в функционал. Требуется только обеспечить его конечность.
Это условие приводит к дополнительному ограничению допустимых значе-
ний параметров аппарата и тем самым может оказывать влияние на функ-
ционал.
Введенный функционал несколько отличается от рассмотренных в Я 1 — 4.
Здесь в функционале не фигурирует идеальное решение. Это объясняется
тем, что рассматриваются однотипные маневры со сравнительно небольшим
разбросом параметров, а значит, и с малыми отличиями идеальных (мини-
мально возможных) значений функционала.
Более сложная ситуация, чем в Я 1 — 4, имеет место с информацией о па-
раметрах маневра. Здесь появляются четыре уровня информированности

межплАнетныи АппАРАт — пОэтАпнОе пост~'пление инФОРмАции 499
'.- 5]
вместо двух. Поэтому, вообще говоря, нужно было бы рассматривать много-
шаговую игру. Но по физическому смыслу задачи, так же как и в ~ 4, будет
достаточно определения гарантирующей стратегии Конструктора. В самом
деле, вторую сторону (Природу) здесь можно только условно наделить свой-
ством активного противодействия, поэтому нет необходимости заботиться
о существовании для нее оптимальной стратегии, обеспечивающей при лю-
бой стратегии Конструктора выигрыш, не меньший цены игры.
В соответствии с и. 1 устанавливается такая последовательность «ходов»
Конструктора и Природы.
1'. Конструктор назначает мощность К„скорость истечения Г, и на-
чало 1 отрезка программных дат старта (зная только детерминированные
параметры).
2'. Природа назначает программную дату старта (~,), зная ход Конструк-
тора 1' (и детерминированные параметры).
3'. Конструктор назначает полезную массу М„баки М, и запас рабочего
вещества М „зная ход Природы 2'.
4'. Природа назначает реальную дату старта ~„зная ходы Конструк-
тора 1', 3'.
5'. Конструктор назначает величину сброса рабочего вещества ЛМ~'~
и программу управления и (~) до выхода на орбиту спутника (планеты назна-
чения), включительно (О ( ~ ( Т&lt ' + Т& t -'> + Т& t;~& t;),
роды 2', 4'.
6'. Природа назначает реальное время ожидания Т, на орбите спутника
планеты назначения, зная ходы Конструктора 1', 3', 5'.
7'. Конструктор назначает сброс рабочего вещества ЬМ~(' и управление
и(-.) на оставшейся части траектории (~) Т< ~+ Т&l ;-'~+ < > , зп
роды 2', 4', 6'.
Конструктор стремится к минимуму времени Т., а Природа — к мак-
симуму. Гарантирующая стратегия Конструктора и соответствующее зна-
чение Т. функционала определяются цепочкой мин-максов:
Т. = т~п мах п11п шах пи'и мах ~(
~о, ~о, ~ (~о) ~~~~ ~~ ~~А« ~о ~у~о~ ц(~(у~1&g ;~ у&lt 2&g
,&g ;( П 1 Т о, о, Ь ~ ',
(13.165)
где
О ~М(Р) Р 4 А ~о) А У(о)РУ (О) Л ~ю (ЛМ + ЛДУ 4>)~М
32*
При решении задачи (13.165) все параметры, которыми распоряжаются
Конструктор и Природа, подчинены условиям (13.156) — (13.164), а функцио-
нал Т. (...) определяется динамической частью задачи Я 3 гл. 8). Помимо
этого, как уже говорилось, возможности Конструктора стеснены еще усло-
вием возвращения на Землю при аварийной ситуации (13.160).
Аварийной ситуацией «распоряжается» Природа. В любой момент вре-
мени ~,, зная все ходы Конструктора, она может уменьшить мощность
двигательной системы в ~ раз (см. (13.159)). Конструктор, зная ~ и ~, отве-
чает сбросом избытков рабочего вещества ЛМ и полезной массы ЛМ, (если
таковые имеются на борту) и изменением программы управления и (~) при
~ ) -.. Все «безаварийные ходы» Конструктора должны быть таковы,
чтобы перечисленных мероприятий оказалось достаточно для обеспечения
возвращения на Землю. Ниже будет показано, что условие аварийного воз-
вращения может быть выполнено за счет сужения области допустимых пара-
метров аппарата.

500
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
3. Условия возвращения при аварийных ситуациях. Пусть параметры
аппарата т„К, У (см. (13.131)) принадлежат допустимой области, построен-
ной в ~ 5 гл. 8 из условия выполнимости перелета в безаварийном варианте
(см. (8.209) — (8.217) и рис. 8.69 — 8.73). Тогда может быть рассчитана номи-
нальная траектория г (т), т (т), удовлетворяющая всем граничным и про-
межуточным условиям безаварийного перелета. Исследуем дополнительные
ограничения на параметры аппарата и траекторию, которые обеспечивают
выполнение требования успешного возвращения на Землю из любой точки
траектории при возникновении аварийной ситуации (падение тяги двига-
тельной системы).
Для каждой точки (г, т) номинальной траектории может быть найдена
точная нижняя грань времени работы двигателя Т, потребного для аварий-
ного возвращения на Землю (ср. (8.206)):
(13.166)
где а (-. ) — реактивное ускорение справа от момента т возникновения
аварийной ситуации (после сброса Лт, и избытков рабочего вещества Лт~,
с учетом падения тяги в ~ раз):
а (~ ) = (2,0$10а~й~ау)~ т — ' уу ~а (~ ) — ат„— ат ~
(13.167)
а Л8 (г, т) — минимальное приращение характеристической скорости, не-
обходимое для возвращения на Землю при обычном импульсном переходе.
Для наших нужд требуются два типа переходов: переход с эллиптической
орбиты на круговую (~=1, 2, 6) и на параболическую (~=3 — '. 5) орбиты.
Угловое перемещение и время движения в обоих случаях не фиксированы ').
Зависимости Ли (г, т) получаются следующими (см. гл. 5):
для перехода на круговую орбиту ')
Лп,=та (1 + е) + +
2/р 1 2р
1+ ~+р
(13.168)
для перехода на параболическую орбиту ')
Ли = ~/2(1+а)/р (1+~/
(13.169)
где р и ~ — параметр и эксцентриситет оскулирующего эллипса:
е = ~/1 + р (п'„-'+ и' — 2/г)
(13.170)
р=(гп )',
(все величины в (13.168) — (13.170) безразмерные, характерные значения
выбраны в соответствии с (4.12), где за г„для (13.168) принят радиус конеч-
ной круговой орбиты, а для (13.169) г может выбираться произвольно).
Вдоль номинальной траектории приращение скорости Л~, найденное по
формулам (13.168) — (13.170), а значит, и время Т можно считать функциями
текущего времени ~ работы двигателя или текущей массы аппарата т=
=М/М,. Вид этих функций зависит от выбранной траектории.
') Обе эти величины при пересчете обычного импульсного перехода на случай беско-
нечно малых импульсов все равно оказываются бесконечными.
') Переход двухимпульсный (двухсерийный). Начальный импульс (или серия беско-
нечно малых импульсов) прикладывается либо в перигее оскулирующего эллипса (знак
«плюс»), либо в апогее (знак «минус»). Второй импульс (серия импульсов) прикладывается
после достижения переходной траекторией заданной круговой орбиты в точке их касания.
') Переход одноимпульсный (односерийный). Импульс (серия импульсов) прикла-
дывается в перигее оскулирующего эллипса.

МЕЖПЛАНЕТНЫИ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТУПЛЕНИЕ ИНФОРМАЦИИ 501
5 5]
Рассмотрим сначала предельную номинальную траекторию, на которой достигается
точная нижняя грань (8.206) времени работы двигателя в безаварийном варианте. Здесь
функция ЛО (т) находится аналитически:
на участке разгона у Земли
-ЬаО& t
ДО= Г 1п (те/т) пРи те ) т) т,"' =тес ~' (13.171 а)
(ди(1& t = ( gt; 2 Ђ” 1) >//с > г "&gt , ди(' gt; = 3, 2 км/ ек п
на межорбитальном участке прямого перелета ')
(1) ~ (2)1/~
ДО= У1п (т„'1> т) Ри т, & t & t; ) т ) т„'
(13.171о)
2 1
' /)
г„(~) +
с.) &gt .
для перелета Земля — Марс Ьг~') =5,5С~ км(сек,.
на участке торможения у планеты назначения
дО= &g ;' 1п (т„'2' т) ри т„ 2   ) т г = с
~ „П) „(2) „(З)1УУ
(13.171в)
(д(> г gt; () 2 Ђ” 1) >//с г)/ (~), ля Мар а Д(&g ;(г&gt = ,36 м сек при
на участке разгона у планеты назначения з)
ь '5)/г
дО= д(&gt *+ &g ;' 1п (т т(4 gt;) при (4&g ; т з> д „) т ) т ( &gt = т(
(ду* ду(я& t  д з> д (ь&gt
на межорбитальном участке обратного перелета
( ,(Ь) ,~6)~~~,
ДО ду*+ ~ &g ;и (т/т( )) ри &gt & t ) Б] ) т ) т 6  ( )е (
(13.171д)
(д„(е) — д(>(
На промежуточных номинальных траекториях функции ЛО (т) получаются в сред-
нем более пологими, чем предельная. Значения максимумов сохраняются, но достигаются
они при меньших т. На межорбитальных участках могут появляться также дополни-
тельные максимумы (см. ниже рис. 13.47).
Функция ЛО (т) определяет точную нижнюю грань запаса рабочего вещества,
потребного для аварийного возвращения:
т &gt ,г т = (е '~ Ђ” 1) т + Дт, .& t; т — т
(13.172)
где т, =т„— дт„+ т„+ те — конечная масса аппарата, отнесенная к М,; т"& t; Ђ”
носительная масса в конце первого участка.
На рис. 13.47, а — г в качестве типичных примеров функций (13.172) приведены за-
коны изменения минимально потребного аварийного запаса рабочего вещества вдоль
оптимальных траекторий, изображенных на рис. 8.53, д — з, для следующих значений
параметров аппарата: а=2,5 кг/кет, р=0,05, те=1, У=80 км/сек. Чтобы исключить раз-
рыв в области задания функций (13.172), вместо аргумента т (текущая масса аппарата)
принят (т„г — т ) (количество израсходованного рабочего вещества). Для сравнения
пунктирными линиями показаны законы изменения потребного аварийного запаса ра-
бочего вещества (13.171) вдоль предельных номинальных траекторий (Т„= Т~ („), соот-
ветствующих тем же параметрам аппарата, кроме начальной массы то, которая здесь
равна то; ~=0,563; 0,644; 0,725; 0,814.
Ограничение (13.160) по ресурсу двигателя устанавливает верхний пре-
дел для запаса рабочего вещества, которое может быть использовано за
') Разрыв функции ЛО в точке т=т„"& t; появляе ся из за принят г в п 1 требо
ния о возвращении на исходную орбиту спутника Земли при отказе на первом участке,
которое заменяется требованием возвращения в атмосферу Земли с параболической ско-
ростью при отказах на последующих участках.
з) Здесь аргумент т изменяется скачком от т(г& t; до т, 4> из-за броса
полезной массы Дт„, причем ДО (т(з&g ; = ДО (т(4

502
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
[ГЛ. 13
оставшееся время (Т „— й ) с уменьшенным в 1/~ раз расходом (см. прямые
на рис. 13.47):
й.,„„=~ ' —,(Т, „— Е,)
172,С~ Ж
= 1729ж ~о — ~ — Л~ т т 17
Имеющийся на борту запас рабочего вещества
172,9 Ж
т = ' —,(Т вЂ” ~ ) = т — т, — Лт,О (т — т"')
(13.174)
с учетом возможного сброса Ьт ) 0 должен удовлетворять неравенствам
р. ~
т,.„(т) &l ; т т) Ђ” Лт (т „ т) ри в ех т~=[ ~, т ~. (13.17
Отсюда
шах (т — т,„, 0) ( Ьт ( т„— т
(13.175о)
Если параметры аппарата обеспечивают выполнение маневра в безава-
ийном варианте, то вдоль любой траектории, являющейся решением дина-
,ической части задачи, выполняется неравенство
т — т,.„) О.
(13.176)
Это следует из того, что точная нижняя грань У„,.„запаса рабочего вещества,
нотребного для аварийного возвращения, г~ ависит, согласно (13.172), от
~р тах ~р шах
~ /
02 05 04 05 ~~ —,~~ 0
01 ОГ 03
00/
0,0
О! 0Г ~~ 0~ т-ш
О/ ОГ ЯЗ т,;т
Рис. 13.47. Точная нижняя грань тр. 1~~ аварийного запаса рабочего вещества: а) т,„. =0,3, ~т„=0,15,
Ж = 0,140 (рис. ~.53, д); б) т„= 0,4, ~т„=0,11, Ж = 0,112 (рис. ~.53, е); в) т„= 0,5, ~т„=0,21,
И=0,0~75 (рис. 8.53, ж); г) т~= 0,6, ~т„= 0,34, Ж = 0,066~ (рис. ~.53, з).
величины тяги. Скорость же истечения в аварийной ситуации, по условию,
остается равной номинальной. Далее, текущий запас рабочего вещества т„
всегда больше точной нижней грани т „~ запаса рабочего вещества, потреб-

МЕЖПЛАНЕТНЫИ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТУПЛЕНИЕ ИНФОРМАЦИИ 503
э 5]
Для выполнимости аварийного маневра на этом участке траектории необ-
ходимо и достаточно, чтобы (см. (13.175))
(13.181а)
(13.181б)
р. ртах( р. >П g
или
ш1п (т,„„(~, т) — т„„,(т)~) О.
1шЫ~~1~&lt 1, иг,&lt
Из (13.173) следует, что минимум в (13.181) по ~ достигается при
(13.182)
т. е. максимальное падение тяги, как это было очевидно из физических со-
ображений, есть оптимальная стратегия Природы в отношении отказов.
Существуют точки, в которых для любой номинальной траектории известны значе-
ния функции Лб (т). Причем эти значения не меняются от траектории к траектории. Та-
кими точками являются моменты стыков различных участков перелета (см. рис. 13.47):
Лб (т&lt &lt &g ; — 0) = у< l ;& t;, ЛУ т'
Лу (т< &g ;) Дб т&l ;4&
Лб(т1) = О.
Лу (та) =О,
Лу (т< & t;) =
Лб (т< & t;) =
(13.183)
Значения Лу"&g ;, Л " gt; Лу*= Лу&lt а>+Л & t;а> у аза ы в (13 171). Он
неравенств Лу&lt 1 gt; ( Л < > ( Л ". Отсюда и и форм л ( 3 17 ), (13 1 3) ледуе
зрительными на минимум (13.181) из указанных точек могут быть только три: т'1'—
конец разгона у Земли' ), т&lt а&g ; — конец торм ж ния у п анеты назнач н я') и т
конец разгона у планеты назначения (см. рис. 13.47).
') Если бы в аварийной ситуации на этом участке разрешалось сбрасывать полез-
ную массу Лт„, то точка т"& t; не относил сь б к подозрительн м, поскол ку Л "
( Ьуа', а т&lt & t;&g
2) С равным правом можно было бы указать и точку т'4), так как между т'з) и т(4)
аппарат движется пассивно, а изменение массы обязано сбросу Ьт,.
ного для завершения перелета по безаварийной программе. Последняя
определяется формулой, аналогичной (13.172), и никогда не превосходит
и„&lt ,&lt  ибо в про ивном лучае м ршрут авар йного возвр щения мож
менить безаварийным и тем самым обеспечить равенство т~,.„=т~ „„).
Проведенные рассуждения и доказывают неравенство (13.176).
Если параметры аппарата и номинальной траектории таковы, что
(13.'1 77)
то неравенства (13.175) совместны и аварийное возвращение обеспечено.
Условие (13.177) можно переписать в виде
~,) )(҄— ~ Т, „)/(1 — ~). (13.178)
Таким образом, аварийный маневр выполним, начиная с некоторого
значения ~„. Если это значение всегда неположительно, т. е. если
Т„(~ „Т (13.179)
то можно сделать вывод о выполнимости аварийного маневра вдоль всей
траектории (без введения других дополнительных условий). Однако при
существенном падении мощности (~ &l ;, (( 1 и ри Т„ „= Т,„попы ка соб
дения неравенства (13.179) приводит к резкому сужению области допусти-
мых параметров аппарата, а значит, и к существенному увеличению функ-
ционала задачи.
Рассмотрим оставшийся случай:
1 „Г„„(Т„(Т„ (13.180)

504
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Условие (13.181) возможности аварийного возвращения из этих точек переписы-
вается с учетом (13Л72), (13Л73) и (13Л83) в виде
(172,9/а) Ж 97 2 (Т „— Т~1') еат — 1
'рте+ Ж+ т ~ „„(1+3) '
3
(172,97 ) ЛТ ~ Т вЂ” ~' Т&l
~те + Ж + т„— (1 + Щ Ьт„~,~„(1 + р)
(172,97,) 97$ -7 (Т вЂ” ~, 'Т'9
а=1
~те+ Ж+ т — (1+ р) Ьт
)
(1ЗЛ84)
1ш~ (1+ 3) .
Неравенства (1ЗЛ84) можно разрешить относительно Т< >. тсюда пол чатся
Р
ничения сверху. Кроме того, из (1ЗЛ71) следуют ограничения снизу. Окончательно будем
иметь
~У) ('~~~~~ Ты7,с ~У)
(у' = 1, 3, 5),
(13.185)
ГДО
172,9Ж
~&lt 1 Т 1' ~те+ У+ т (, /»
172,9Ж ~,а, (1+ Щ
( ~12
(3) — (ью — ью')УУ~
172,9Ж ~о ~
аГ2 ~те + Ж + т„— (1+ р) Ьт
» ~72Р»2П~* 172,9Ж Г.~; (1+ Я)
~(5) Т а~ ~те+ 17 + т~ (1 + ~) ~т~ ( ь9 /» 1),
172,9% 1ШЗв (1+ 1)
Условием совместности неравенств (1ЗЛ85) будет
~~ ~аГ ~ ~~ вар
ж о)
(/=1,3,5),
таО,,Х вЂ” — Ш1П 1Г4.$ тОФ таО ь ТПО ь таО пуф
* *(1) *(3) *(5) 1
172,9 Т Т -1- 1) 97 -1-
1+1
а
(1)
~... (1+ Р) (1 —.-""'/')("""/' — 1Г'+ В
2~ 1729 Т-'Т„7~ '17 — 17 — 1~ 97 — ~,-/. (1-/-Д7 Ь~,
с ~ц*(3)
(1+8)(1 — "' ")")("' — 1) '+~
О
— т„+ (1+ Я Ьт„~1+~ 1 (1 — е ' ~ )(е~' ~ — 1) Д ~"ш1 (1+
+ Д) (1 — е (~' ~" )~~)(е~" ~ — 1) + ~Д ° (13.186)
откуда следуют три дополнительных ограничения на т, сверху, так что в (8.209) под
т, (Г) нужно вместо (8.210) понимать

межплАнетньти АппАРАт — пОэтАпнОе постУпление инФОРмАции 505
$5]
Ч,пн/ееп, = б0 б0 70 б0
0,7
д Я 0,08 О/Г О/б ОГ б,Г4 Ф
!00 200 Ы0 400 500 Ч км/сеп
Рис. 13.48. Примеры допустимых областей ~, (сплошные границы) и подобластей У, (пунктирные гра-
ницы). При ~='/, область Я, выделена штриховкой, а подобласть М, — двойной штриховкой. Исходные
бранные соответствуют рис. 8.73. а) Сечения плоскостями У=соп8$ (в заштрихованных областях У=
=50 хм/сех); б) проекции на плоскость У, №
(8.211), (13.186) суть необходимые условия выполнимости аварийного воз-
вращения) .
В области Я, С: Я1, определяемой неравенствами (8.209) — (8.211), где
Т„нужно заменить на ~ „Г,„, в соответствии с доказанным выше
(см. (13.178), (13.179)) вдоль любой номинальной траектории возможно
аварийное возвращение. Если номинальный ресурс Т „) ~ „Г „, то эта
вторая областью, строго включается в первую, Я, (. Я1, и при построении
номинальной траектории в оставшейся части первой области Я1~.,Я, необ-
ходимо дополнительно следить за выполнением неравенства (13.181). Ниже
оудет показано, что это нужно делать только на межорбитальном участке
Обратного перелета.
') Аналогично п. 6 В 5 гл. 8 эти условия можно разрешить относительно Г,„р. При
этом У,„р (Г) сохраняется прежним — (8.215), а Г~,т увеличивается по сравнению с (8.214).
Новое вйражение для Г;,т находится аналитически, но формула получается слишком
громоздкой.
Если параметры аппарата удовлетворяют условиям ') (8.209), (8.211),
(13.186) (область Я,), то найдется хотя бы одна номинальная траектория,
из каждой точки которой возможно аварийное возвращение (например,
предельная номинальная траектория — см. (13.171) и рис. 13.47). Вне об-
ласти Я1 таких номинальных траекторий не существует (соотношения (8.209),

506
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
(172,9/а) Ж)" 2 (Т„„— г„)
8т» + Ж + т, — (1 + 8) Лт О (Й вЂ” Т~~")
(13.187)
Если выполнены условия (13.184) в конечных точках участков перелета,
то для большинства участков условия (13.187) в промежуточных точках
также выполняются. Исключение представляет межорбитальный участок
обратного перелета.
На участках разгона (~=1, 5) и торможения (~=3) Лгч (г ) — монотонная функция:
возрастающая для ~=1, 3 и убывающая для ~=5. Эта функция вычисляется при помощи
аналитических выражений координат и компонент скорости вдоль траектории из [8.13)
по формулам (13.168), (13.170) для ~=1 и (13.169), (13.170) для ~=3, 5. Из монотонного
возрастания Лг7 (г ) на участках ~=1, 3 сразу следует монотонность разности (13.187).
На участке ~=5 монотонность (13.187) приходится доказывать особо (поскольку раз-
ность двух монотонно убывающих функций может быть немонотонна). Изложенная пре-
цедура была проведена для двух предельных случаев: для «квазикругового» разгони
(торможения) без выключений двигателя и для «эллиптического» разгона (торможения)
бесконечно малыми импульсами в перигее. Есть надежда, что и для промежуточных ва-
риантов свойство монотонности (13.187) будет выполняться (напомним, что в настоящ«в
параграфе используется как раз первая из этих предельных схем — квазикруговые раз-
гон и торможение).
На межорбитальном участке прямого перелета (~=2) функция Лг7 (г ) бывает и н«-
монотонной (см. рис. 13.47). Но, как показывает численная обработка оптималькыт
траекторий Земля — Марс по формулам (13.168) и (13.170), значение промежуточког»
максимума Лб составляет — 4 — 6 км/сек, т. е. не превосходит Ьо'=6,94 км/сек. Если
это так, то неравенство (13.187) будет выполняться во всех промежуточных точках меж-
орбитального участка ~=2.
На большинстве межорбитальных траекторий обратного перелета (~=6), обеспечи-
вающих минимум суммарного времени перелета, функция Лг7 (г ) существенно немоно.
тонна (см. рис. 13.47). Здесь условие (13.187) может нарушаться, несмотря на то чт«
оно соблюдено во всех граничных точках участков.
Отсюда следует неутешительный вывод: при решении вариационной и.
дачи о построении оптимальных программ управления на межорбитальнем
участке обратного перелета необходимо учитывать условие (13.187). В сил7
формул (13.168) и (13.170) оно представляет собой ограничение на фазовыми
координаты задачи. Кроме того, условие (13.187) содержит две комбинации
параметров аппарата и его двигательной системы. Добавление двух новы~
параметров делает практически невозможным заготовить заранее решения
динамической части задачи.
Эти обстоятельства вынуждают избрать другой путь. Решается задач~
выбора оптимальных параметров аппарата (см. следующий пункт параграфн)
Пример построения областей Я1 и Я, приведен на рис. 13.48. Значения
«внешних» параметров задачи взяты такими же, как и на рис. 8.73: т.=0,5;
Лт,=0,2; Т „/а=100 сут квтlкг; )3=0,1. Дополнительно положено
Т „„„=Т„,„. Построение проведено для двух значений ~='/ и 1/з. Линии
~=1 соответствуют «безаварийным» границам. В рассмотренном примере
при построении области Я, определяющим оказывался либо номинальный
маневр, либо аварийный из точки т"' (конец тормохсения у Марса). Отметим
также, что подобласть Я,~Я1 (где условия аварийного возвращения выпол-
няются вдоль любой номинальной траектории) существенно уже области Я,
(где гарантируется лишь существование таковых).
Сформулируем теперь условия, которые надо учесть при решении ди-
намической части задачи в подобласти Я1~,Я„чтобы вдоль номинальной
траектории был выполним аварийный маневр. Во-первых, это ограничения
(13.185) на распределение времени работы двигателя между участками пе-
релета. Им нужно удовлетворить на этапе склейки участков. Во-вторых,
это неравенства типа (13.184) для промежуточных точек траектории:

МЕЖПЛАНЕТНЫЙ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТУПЛЕНИЕ ИНФОРМАЦИИ 507
(13.188)
мах
( то) (~',((г,)~~г, ~ т (4( )о, и (~ ~ т " ' + т' " + г' " )
где Т. — суммарное время движения по номинальной траектории, причем
все параметры прямого перелета фиксированы:
3 з
/о+ ~ Т"', ~ Т„'.", Т,„, а„Г, Ьт,, ио = йхе. (13.189)
г=1 а=1
Если задать еще величину сброса рабочего вещества Лт~'&g ;, то определ
ся начальное реактивное ускорение и время работы двигателя для обрат-
ного перелета:
з — 1
(~((((4)
~о~=~о 1 ОО 4 — ' Т~"'
то
1
(13.190)
~т ~т(4)
҄'." — 11,78—
ао то
т' -~тр=т..
После этого из решения динамической части задачи однозначно определяются
программа управления и время Т(5~= Т('~ (аф, (') для участка разгона
у планеты назначения (см. п. 2 ~ 3 гл. 8). По (13.190) находятся а(о~ и Т~'~
для межорбитального участка обратного перелета (снова однозначно).
в области Я„причем номинальные траектории строятся без учета ограниче-
ний (13.187) в промежуточных точках. Вдоль результирующих траекторий
строятся функции т,.„(т). При заданном коэффициенте 1 падения тяги на-
ходятся минимальные значения аварийного ресурса Т „, для которых еще
р. шахт
выполняется условие (13.187). Если эти значения аварийного ресурса не
слишком превосходят заданное, то задачу можно считать решенной. В про-
тивном случае все-таки придется вводить фазовое ограничение (13.187)
в динамическую часть задачи и менять траекторию и параметры аппарата.
Функционал задачи, естественно, после этого увеличится. Отметим, что про-
верка готовой номинальной траектории на возможность аварийного возвра-
щения производится по конечным формулам (13.187), (13.168) — (13.170) и
не требует построения самих траекторий аварийного возвращения.
Чтобы составить представление о том, насколько минимально допусти-
мые значения аварийного ресурса Т,„отличаются от суммарного времени
р. шах
работы двигателя Т на номинальной траектории, обратимся к рис. 13.47,
а — г. Там для двух зйачений коэффициента падения тяги 1='/, и 1/, проведены
прямые т„,„(т, ~), касающиеся кривой т„,.„(т„) и ограничивающие ее
сверху. Абсцисса точки т „(т„)=0 и определяет, согласно (13.173), до-
пустимые значения Т „. Они получились равными 335, 361, 402, 435 сут
при ~='/, и 358, 375,447,513 сут при 1='/„в то время как для номинальной
траектории Т =332, 360, 390, 412 сут соответственно. Таким образом, при
1='/, для всех рассмотренных траекторий различие невелико (0,9%, 0,39~о,
3%, 5,6%), и решать динамическую задачу с фазовыми ограничениями не
нужно. Для последних двух траекторий (рис. 13.47, в и 13.47, г) при 1='/о
аварийный ресурс должен заметно превосходить номинальное время работы
двигателя (на 14,6% и на 27%), в то время как для первых (рис. 13.47, а
и 13.47, б) различие остается небольшим (7,8% и 4,2%).
4. Оптимальные параметры аппарата. Исследуем внутреннюю пару
максминов из (13.165):

508
[ГЛ. 13
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
Программа управления на этом участке определяется решением динамической
части задачи (пп. 5 — 8 3 3 гл. 8), как только найдено угловое перемещение
из системы уравнений (п. 12 3 3 гл. 8)
~р"' — 1Т"' = 2~од-)- (~, — ш,) [~ -)- 2' Т"'),
а=1
Т(6) — Т(6) ( (6&g ;, Т( )) ~ з) т ,
Для этого нужно знать время ожидания Т'4'. Частная производная
=[~д ( — ) — 1] [ш, ( — ) — 1] ~ 0 (13,191)
неотрицательна (см. (8.137) — (8.142)), поэтому время ожидания Т"' нужно
брать минимально возможным:
~р1, О'
(13.192)
Т, "= <Т >
(13.193)
Обозначим через ат'4)р, (То) оптимальный для Конструктора сброс рабочего ве-
щества, такой, что
Т, (Т, ат(4' & t; (Т ) = &g ;п Т (То, а
Ь 777
(4)
(13.194)
Для любых Т~ ( Т" и любого ат'4) = со> вС по свойс ву (13.1 1) выполняе ся неравенс
Т, (Т', ат(4)) ( Т (То, )>т(4
отсюда следует.'
Т, (Т", ат(4О&gt р~ (Т ) ) Т, ( ', ат(4 ,> ( ' ')) ) > Т, (Т , Ат 4&gt ) = Т, ( ', ахи
Ь 171
что означает монотонное возрастание функции (13.194) по То, т. е. справедливость (13.193).
Далее можно утверждать, что если параметры (13.189) будут выбраны оптимально, то
ат("о& t &g ; ( Т ) + & t;
(13.195)
В противном случае, сбросив это количество рабочего вещества на Земле (т. е. уменьшив
Т„, ~ и то), можно было бы уменьшить время Т,:
Т, ((То)+ ЙТО, О) ( Т, ((То)+ 8Т~, ат(')о& t > ( То) + )
а по свойству (13.191) это новое время все равно осталось бы определяющим:
Т, ((Т )+ оТО, О) ) Т, (То, О) ) Т, (Т, Лт(4) ~ (То)).
Перейдем к исследованию очередной пары макс-минов из (13.165):
Т, (13.196)
(гД(г,((г,>+ 1 ~ (() gt; е „(, т(»+т(2&
причем в соответствии с установленными выше результатами (13.192),
(13.193) и (13.195) время Т. вычисляется для
Т(~& t; =(Т )+ о а, Ьт 4
(13.197)
Полученное равенство можно было бы и постулировать, не опасаясь потерять
истинное решение, поскольку динамическая часть задачи не исключает воз-
можности расположения пассивного участка в начале траектории.
Таким образом, после выбора оптимальной программы управления
и (т) Т"'+ Т"'+ Т'з') время Т. можно считать функцией Т, и Лт„'.".
Дока>к м, то Прир де выго но предел но увеличив ть минималь ое вр
ожидания Т, т. е.

межплАнетныи АппАРАт — пОэтАпнОе постУпление инФОРмАции 509
ф 5]
при фиксированных параметрах аппарата и двигательной системы:
(13.198)
0' ~и ' ~3'
Если задать еще дату старта ~о и сброс рабочего вещества Лт~ ~, то по
алгоритму п. 12 из 3 3 гл. 8 определится оптимальное управление и (т) вдоль
всей траектории и соответствующее время Т. (~„Лт~~)). Оптимальная ве-
личина сброса рабочего вещества Лт(о'„, находится в результате процедуры,
изложенной в п. 3 предыдущего параграфа. Для всех рассмотренных там
маневров с ростом энергетической напряженности увеличивались и минималь-
ное время выполнения маневра, и оптимальный запас рабочего вещества.
На основании этого можно предположить, что и в рассматриваемом случае
сйт~~о)~,/ШТ, = (ШЛт~~о)„/Шц ) (ШТ,/Йо) 1 ( О,
(13.199)
где Т. = Т,(1о) = Т. (1„Лт®„, (1о)) = т)п Т, (1„Лт~о)).
Ь,„(0)
Максимум Т.(~о) достигается на критических датах старта ф
шах Т, (г ) = Т. (1о).
( ~О ~ ~(~О~((4О ~+~ 'Е
Для этих дат старта из свойства (13.199) вытекает, что при оптимально вы-
бранных баках сброс рабочего вещества производить не нужно:
(13.200)
В пРотивном слУчае, согласно (13.199), полУчилось бы Лт'о' (йв) ) 0 длЯ всех
ц, ~ [(ц ), ( г,) +Ы,], т. е. нигде баки не заполнялись бы до предела. Последнее
означает переразмеренность баков и противоречит предположению об их оптимальности
(напомним, что для каждой программной даты старта ( ~в ) разрешается выбирать свои
баки).
Далее предполагается, что
шах Т,(~в, Лт~о,' ~(~ )) = шах Т,(~в, 0). (13.201а)
(8 )(8 ((80) (-88о (8о)(Фо((8,)+88„
В общем случае здесь должен стоять знак (, и наличия соотношения (13.200) еще недо-
статочно для замены его на знак равенства.
Посл.едний максимум достигается лиоо на границе отрезка, лиоо совпа-
дает с одним из локальных Ц", Ц", Ц" (см. рис. 8.57, 8.59), т. е.
~о — (~ » или (~о)+ Ы„или ф) () = 2, 4, 6), если
Ф) б~(~» (~)+М'
Т,Я) = тах (Т,((~о» О), Т,((1о)+ог„О), Т (ф), О)).
(13. 201 6)
Если неопределенности Л~, и Мв в программной (~в) и в реальной ~ датах старта
не слишком велики, то в оптимальном варианте отрезки возможных программных и реаль-
ных дат старта располага~отся в окрестности миниз1ума функции Т, (г„О) и не содержат
локальных максимумов 4< '. ри э ом усло ии соотноше ия (13.2 1) мо но б ло бы
казать. В общем случае их нужно рассматривать как рабочие гипотезы. После решения
всей задачи необходимо проверить их справедливость, равно как и справедливость (13.200),
на полученном решении (что значительно легче, нежели на каждом шаге отыскивать ми-
нимум Т, по Лт'с', а затем — максимум по 1,).
Последняя пара макс-минов из (13.165):
мах пип (13.202)
~~((~оФ+~~о ~р.о ~а~~~к пй, ~~~4~р.д
исследуется в предположении, что согласно (13.192), (13.193), (13.200) и
(13.201б) время Т, вычислено при
Т'4) — (Т,) + 3ТЮ
Т.
Лт(о) — Лт(4) — ()
(13.203)

510
[ГЛ. 1~
ВЫБОР ПАРАМЕТРОВ МНОГОЦЕЛЕВЫХ СИСТЕМ
как
Т = шах (Т.((1о)); Т.((1о)+Во); Т (ф~), если ф~ ( [(~о), (~о)+ И~Д)
для фиксированных параметров (13.198) аппарата и двигательной системы.
Из физических соображений очевидно, что при прочих равных условиях
минимум времени выполнения маневра достигается, когда полезная масса
минимальна, а баки точно соответствуют запасу рабочего вещества. По-
этому для критических (расчетных) маневров
(13.204)
тс орС тс ~п~~~
(13.205)
~о о,,с = ~о.ю. (Ж ~'),
где то,„задается соотношениями (13.186).
Если бы расчетный маневр был один, то утверждение (13.205) можно
было бы строго доказать. Здесь же их может оказаться больше (два), поэтому
(13.205), как и (13.199) — (13.201), принимается в качестве рабочей гипотезы,
которая должна быть подтверждена после решения задачи.
Наихудшая для Конструктора программная дата старта (~,), как и реаль-
ная ~,"„находится в виде, аналогичном (13.201б):
(~о)*= ~, или ~+ 1~о, или ф~ (~' = 2, 4, 6), если ф~ ( [~, ~+ ЛЯ;
Т.((1о)*) = шах (Т (1); Т. (1+Ь~,); Т. (ф~)).
(13.206)
Отсюда и из (13.201б) вытекает:
Я= 1+Ь|о,
~(~')
если
если
если
После этого можно уже не различать программную и реальную даты
старта, а рассматривать одну дату старта из отрезка [1, 1+Л~о].
Заключительным шагом решения задачи остается отыскание
(1 3.208)
тшТ. по .1~ [ — Т„, Т„1 и по (У, Г)( Я„
где ҄— период повторяемости взаимного положения планет старта (1)
и финиша (2) (для Земли и Марса без учета эллиптичности орбит Т„=
Для промежуточных маневров условия (13.204) могут не выполняться. Там
либо Лт®,„) О, и тогда т ) ~5 (т„о — Лт~~о~), либо т,) т, „(если нет же-
лания сокращать время Т по сравнению с критическим).
При отыскании оптимальных параметров аппарата вместо начального
запаса рабочего вещества т„о здесь, как и в п. 3, будет использоваться на-
чальная масса то=т„о+т +Г. Если двигательная система задана, то для
каждого маневра существует оптимальная начальная масса, обеспечивающая
минимальное время выполнения маневра при заданной полезной нагрузке
(см. п. 3 ~ 4). Если же двигатель еще не спроектирован, а выбирается оп-
тимальным для этого маневра, то начальную массу выгодно брать максималь-
но возможной. Это следует из отрицательности производной дТ.~дао.
В конце концов, двигательная система будет выбираться по дискретным
критическим (расчетным) маневрам. Поэтому есть все основания положить
для них

МЕЖПЛАНЕТНЫИ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТУПЛЕНИЕ ИНФОРМАЦИИ 51 1
5]
=780 сут), а время Т вычисляется при помощи алгоритма из п. 12 ~3 гл. 8
с учетом полученных выше результатов
Т&lt 4) Ђ” (  + Т, ~1т О) Ђ” ~1т 4) Ђ” ) т Ђ
т =Рт о, т,=т,,„(Ж, Г)
(13.209)
при фиксированных значениях 1, Т, У как
Т,(1, Т, Г) =шах (Т,(1,=1); Т. (1,=1+Ь|,); Т. (1,=Ц ),
если Ц~) ~ [4, 4+ Ы ]).
Функция Т, (~,) непрерывная и периодическая, Т, (~,) = Т. (~, + Т,).
Отсюда следует, что
т1п Т,(~, Т, Г) = Т. (Т, Г, ~„„(Т, Г)) = Т. (Т, Г)
е' Е [ Т1 Т12]
достигается, либо когда значения Т.(1,) на концах отрезка [г, 1+ЬЦ равны
и превосходят все промежуточные значения, либо когда один из локальных
максимумов Т, (ф)) доминирует на отрезке длиной, не меньшей М„но при
атом длина каждой части отрезка [Ц~'), ф")] доминирования справа или слева
от 8~~~ меньше ЬЕО:
Т.(Е„,) = Т. (Е„, + ЬЕ,) )~ Т (ф)) для всех Я( (~„„Е„, +Ье,),
т.р, к)=
Т,(ф)) при ф") — ф') .- ЛЕе, ф") — Ц~) (ЛЕе, Ц~) — ф') (ЛЕ
(13.210)
(Т.(ф)) = Т. (ф )) = Т. (ф„')))~ Т.(Е,) для всех Е,( [ф'), ф")]).
Во втором варианте 1„, может быть любым из отрезка [гр'&g ;, ") Ђ” ЛГ
а Т. (К, Г) постоянно, пока М, принадлежит отрезку [шах ((Ц~") — ф1),
ф'~ — ф'> ), ф &g ; — '&g ;)] Все это иллюс риру тся р с.
примере типичных зависимостей Т. (~,), взятых с рис. 8.57, 8.59, 13.50.
Уравнения (13.210) решаются численно. Затем отыскивается минимум
получаемой функции Т (Я, Г) по (Ж, Ъ') (=Я,.
По изложенной схеме были проделаны иллюстративные расчеты для пере-
лета Земля — Марс — Земля. Бинематические параметры перелета взяты из п. 12
1 3 гл. 8, значения остальных исходных параметров приняты следующими:
(Т,)+ оТ„=40 сут, ~='/„Т,„= Т„,„=300 сут, и=3 кг~квт, В =
= 0,1 кг)кг, Г,„= 20 км~сек, Г,„= 80 км)сек, т,,„= 0,5, Ьтп, = 0,2.
Расчеты проведены для различных значений суммарной ) неопределенности
в дате старта: 0 ( Л~, = Л1, + И, ( 140 сут.
Основные результаты представлены на рис. 13.50 — 13.52. Для рассмот-
ренного диапазона неопределенности Л~„когда значения Ж и Г близки к оп-
тимальным, зависимости Т. (~„) из (13.199)в окрестности минимума оказы-
ваются выпуклыми (рис. 13.50). Поэтому функции Т. (Л, Г) и ~,„, (Г, Г)
находятся из решения только первого уравнения (13.210). Полученная функ-
ция Т, (Г, Г) оказалась гладкой и выпуклой; ее минимум по Г при фикси-
рованных Г достигался внутри допустимого интервала (рис. 13.51); зависи-
иость от Г минимизированных по Г значений Т. (Г, Г) на рассматриваемом
отрезке [20 км/сек, 80 км/сек] получилась монотонно убывающей.
') Для вычисления функционала на критических (расчетных) маневрах и для опре-
деления оптимальных параметров двигательной системы, как следует из результатов
настоящего пункта, важна только суммарная неопределенность. Для определения вре-
мени выполнения промежуточных мапевров играет роль и распределение Л 10 между
Ь|„и ~~,.

О) ~ м
~Ю ~ф~(4)
о! о о
и') (г')
о о
Тг 1 +7~
1г ) (4)
~ор1
~ (Г/
о
(4)
о
(~~'& t; ~~ ~~ (р "' к~ ~) ф'"'г "~ т„
) ~ ~в")~Ю)
~(г ~ ~ь
Рис. 13.49. Характер типичной зависимости Т~ (й„) из (13.199) и соответствующис ей значсния Хор~ и
Т (Ж, У) из (13.210) в зависимости от суммарной нсопределенности ~~„в дате старта.
Т~,
С~~Ю7
~000
ю=0(5
7~,
сут
960
УбО
Ф=0~~,~
ИО
800
760
=0 /04
7бО
б80
баб б®
-40 -К -Я~ -!б0 -Л0-Яб -Г® ~,суа
а) ю) ~о ~У~
Рис. 13.50. Мин-максные значения (от седьмого до пятого шага (13.165) включительно) суммарного вре-
мени Т„перелета с т,=т,ш~~(Ж, У) (см. рис. 13.48), т„=т „, тр= Дт„, (см. (13.204), (13.205)): а)У=
=80 км/сек', б) У=70 км/сек.

$5] МЕЖПЛАНЕТНЫЙ АППАРАТ вЂ” ПОЭТАПНОЕ ПОСТУПЛЕНИЕ ИНФОРМАЦИИ 513
Оптимальные значения параметров универсальной двигательной си-
стемы (мощность и скорость истечения) оказались нечувствительными к из-
менению суммарной неопределенности в дате старта: Г„=0,127, У„=У, =
=80 км/сек для всех М 1 [О, 140 сут]. Оптимальная стартовая масса для
критических маневров также получалась постоянной и равной максимально
~йб,
су~п
ягп
су~
77Д
~орй
су~
-27Д
7бд
-170
б7д
бди
дд7
Рис. 13Л1. Минимизированные по начальной
тоже 8 о~езна [$, $+ ьЯ критические (от
седьмого до второго шага (13.165) включи-
тельно) продолжительности перелета Т (Я, ~),
соответствующие рис. 13.50.
Рис. 13.52. Окончательное решение мин-
максной значи (13.165): предельное время
перелета Т* и оптимальное начало Фор~ от-
о
резка возможных дат старта в зависимости
от ширины Ь~, этого отрезка.
возможной, что подтверждает гипотезу (13.205). Остальные предположения
(13.199) — (13.201а), сделанные относительно свойств оптимального реше-
ния, также подтвердились.
Эффективность универсального аппарата, естественно, уменьшается
с ростом неопределенности в дате старта, но за счет оптимального выбора
его параметров это уменьшение эффективности удается сделать достаточно
медленным. Так, увеличение суммарной неопределенности в дате старта
с 0 сут до 20, 40, 100 и 140 сут приводит к увеличению критического времени
перелета на 0,9%, 2,8%, 10,5% и 14,5% соответственно (см. рис. 13.52).
33 Механика полета

ГЛАВА 1~
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
Во время полета на двигательную систему могут действовать случайные факторы,
вызывающие отказы. Отказы двигателя проистекают от внешних и внутренних причин;
к первым можно отнести, например, метеорные пробои, ко вторым — процессы тппа износа.
В соответствии с характером этих воздействий вероятность отказов может зависеть от вре-
мени, координат, параметров двигателя и аппарата, от режима работы двигателя. Поэтому
учет фактора надежности приводит к изменению привычных программ оптимального
управления и оптимальных параметров двигательной системы [14.1 — 14.4, 14.9].
Под надежностью понимается вероятность бесперебойной работы двигателя для
данной реализации маневра. В случае отказа двигателя (или всех секций двигателя,
если он многосекционный) маневр считается невыполненным. При формулировке задач
надежности помимо характеристик двигателя (4.9), (4.10) требуется еще вероятностная
характеристика его отказов. На основании последней с помощью методов теории массо-
вого обслуживания строится детерминированный закон убывания числа неповрежденных
секций по времени (закон повре"кдений), который с заданной вероятностью ограничи-
вает снизу все случайные реализации. Далее формулируется вариационная задача о до-
ставке максимального полезного груза при детерминированном законе повреждений,
полученном выше. Решение задачи в такой постановке позволяет с заданной вероятностью
гарантировать успешное выполнение маневра с полезным грузом, не меньшим найденного,
Вероятность выполнения маневра либо задается (Я 1 — 3), либо выбирается оптимальной
в некотором смысле Я 4); рассматриваются случаи односекционного Я 1) и многосекциов-
ного (Ц 2 и 3) двигателей; для модельных маневров даются примеры решения соответ-
ствующих вариационных задач. В $ 2 гл. 10 была описана задача с фиксированным вре-
менем работы двигателя. Если считать вероятность отказа двигателя зависящей только
от времени его работы, то зту задачу можно трактовать как частный случай задачи о фик-
сированной надежности. Кроме того, вопросы надежности затрагивались в $ 5 гл. 13.
В отличие от настоящей главы, там предполагался существенно меньший уровень априор-
ной информированности о возможных отказах, но зато в процессе движения допускалась
перестройка программы управления в случае возникновения отказа (аварийное возвра-
щение).
~ 1. Оптимальное управление при заданной вероятности
успешного выполнения маневра
1. Формулировка вариационной проблемы. Рассмотрим общую задачу
оптимального управления. Пусть имеется динамическая система, поведение
которой описывается уравнениями вида
~, )=0,1,..., и; 1=1,...,г; 1=1,...,д, (141)
где х,. — фазовые координаты системы, и„(1) — управляющие функции,
ю, — постоянные управляющие параметры.
Заданы граничные условия относительно х,. в фиксированные начальный
~=0 и конечный ~=Т моменты времени. Нужно обеспечить максимальное
(минимальное) значение контрольного функционала задачи х„(Т). Эту ва-
риационную задачу назовем исходной.
Обратимся теперь к формулировке вариационной проблемы о заданной
надежности.
Динамическая система в отношении повреждений рассматривается как
одно целое — повреждение одного элемента вызывает прекращение работы

515
ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
)=)[1, х,., и„, и,),
[1 . )
в зависимости от времени, фазовых координат, управляющих функций и уп-
равляющих параметров.
Статистически интенсивность потока отказов можно определить как [14.7]
Л (~) — Т (~ + Л~)
Л~Л Р+ЕЛ )
[О (Э (1),
где Г 1~) — число исправных образцов к моменту времени ~, Г (~+Э Л~) — среднее число
исправных образцов в интервале 1~, ~+Л~).
Тогда вероятность Х отсутствия отказов на интервале [О, Т] равна
[14. 5 — 14. 8 ]
7
В = ехр ( — 1 Н~],
О
где Л вычисляется вдоль траектории: л=)~ [й, х,. [й), и„[й), и,).
В соотношении [14.3) вероятность Х фиксируется — условие заданной
надежности 0 ( Х ( 1. Его надо присоединить к уравнениям исходной
вариационной задачи. Если используется постановка Лагранжа, то это
удобно сделать в виде условия изопериметричности
[1.)
) [~, х,. [~), и„[~), и,) М = — 1п Х.
В постановке Майера [14.3) нужно записать в виде дифференциального
уравнения с -граничными условиями.'
Л=),[~, х., и„, и,), Л[0)=0, Л[Т)= — 1пХ.
[14.5)
Переменная Л будет фигурировать в качестве дополнительной фазовой
координаты системы [14.1). Значение Л,=Л [Т) назовем условно допустимым
средним числом отказов за все время движения. Если задать надежность
В=1, то Л,=О, что невыполнимо. При уменьшении надежности допустимое
число отказов возрастает [так, например, изменению Х в диапазоне [1; 0,5]
отвечает изменение Л, в диапазоне [О; 0,7]).
Обозначим через х",. [~), и*„[~), и", решение исходной вариационной задачи
[без учета фактора надежности). Если на этом решении окажется
Л;= ) [~, х',.®, и",®, и",)М( — 1пХ,
то надежность Х будет обеспечена. Отметим, что при ) „Т ( — 1п Х условие
заданной надежности заведомо выполняется.
ЗД~
всей системы. Считается, что при отказе системы в любой момент времени за-
дача не выполняется. После отказа система не восстанавливается.
Требуется построить такую программу управления и выбрать такие
значения параметров, чтобы наряду с удовлетворением всех условий, пере-
численных выше, была обеспечена заданная вероятность безотказной работы
системы [заданная надежность).
Предполагается, что повреждения образуют ординарный поток без по-
следействия [14.5 — 14.8]. Считается заданной интенсивность потока 1 [мате-
матическое ожидание числа отказов в единицу времени):

516
[ГЛ. 14
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
Считая, что условие (14.6) не имеет места, выпишем систему уравнений
задачи оптимального управления с заданной надежностью (14.1), (14.5):
х, =/,.(~, х., и„, и,), х,. (0) =х,.е, х,. (Т) =х,.„
Л=1(~, х., и„, и,), Л(0)=0, Л(Т)= — 1пЛ,
(14.7)
В такой записи — это ооычная вариационная задача Майера.
Сделаем три замечания по обобщению (14.7).
1'. Пусть интенсивность потока отказов ~ зависит еще и от текущего времени ра-
боты системы ~ ( ~. Тогда, аналогично $ 2 гл. 10, нужно присоединить к (14.7) диффе-
ренциальное уравнение с граничными
условиями
Ь, й (0)=0,
й (Т) = орС,
(14.8)
и
и
Рис. 14.1. Два случая, когда режим выключения
является выколотой точкой для зависимости ~ (и).
при этом в остальных уравнениях нужно заменить и на ио.
Этим же приемом можно воспользоваться, когда интенсивность потока отказов при
выключенной системе А (О) (холодный резерв) не равна пределу интенсивности ) (+О)
при и -э 0 (горячий резерв) (рис. 14.1, б).
3'. Если зависимость экстремальных значений функционала хо (Т) от параметра Л
немонотонна, то условие А (Т)= — )п Л в (14.7) нужно заменить на А(Т) ( — 1п Л.
2. Двигатели ограниченной мощности. Для оптимальных без учета
надежности режимов раооты двигательной системы ограниченной мощности
характерно максимальное использование мощности на активных участках.
Кроме того, если двигательная система идеальная, то оптимальная траекто-
рия не содержит пассивных участков.
Зададим теперь вероятность (14.3) успешного выполнения маневра. Ин-
тенсивность потока отказов (14.2) будем считать зависящей от мощности Р,
отнесенной к максимальной Г „, и конструктивного параметра и:
(14.10)
1=),(~, Т, и)
(0& t; У ~) 1  = соп Ь, дХ/ Т) О, д) ди (
Влияние максимальной мощности здесь не учитывается; неотрицатель-
ность производной д)/дГ соответствует интуитивному представлению о том,
что при форсировании режима работы двигательной системы вероятность
отказа увеличивается. Параметр и отвечает за конструктивные мероприятия
по увеличению надежности: увеличение ш соответствует уменьшению ин-
тенсивности потока отказов Л (дЛ/ди ( О), но при этом увеличивается удель-
ная масса двигателя а (да/ди ) О).
1) Конечное значение ~ (Т), в отличие от основной задачп ~ 2 гл. 10, не задано
и должно выбираться из соображений оптимальности траектории.
где о (~) — релейная управляющая функ-
д и, Р ция, равная единице, когда система
б) включена, и нулю, когда система вы-
ключена. Функцию о надо присоединить
множителем к управлениям и в (14.7),
принимающим нулевые значения при
выключении системы 1).
2'. Пусть управление и может принимать значения из диапазона [и;,, ип„] и обра-
щаться в нуль при выключении. Интенсивность потока отказов равна 1 (и), когда система
включена, и 1 (О), когда система выключена (рис. 14.1, а). Чтобы представить в этом слу-
чае правую часть последнего уравнения (14.7) как функцию, не меняющую своего вида,
можно снова воспользоваться релейным управлением
А=Л(0)+() (ц) — ) (0ИЬ; (14.9)

517
ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
Ограничимся рассмотрением случая идеального двигателя (см. гл. 6);
задача о доставке максимального полезного груза при заданной надеж-
ности Х записывается в соответствии с постановкой (14.7) аналогично (6.42)."
(т, + т„)2 а (и) а2
т., 2 й'
т. (0) + т„= — 1, т. (Т) = шах,
г(0) =г„
т (0) = т„
и), л(о) =о,
О<к(р) 1, ~ Р)
г=ч,
т= ае+Я,
Л=),р, ~,
(а(1)) О,
г(Т) = г„
т(Т) = т„
Л(Т) = — )пв
т„, и = сопзь).
(1 .11)
Здесь нужно выбрать оптимальные значения параметров т„, и и по-
строить оптимальные программы а (~), Г (~), е (~). До решения полной задачи
так же как и в ~ 1 гл. 6, можно найти оптимальное соотношение для массы
т„(она входит только в первое уравнение и начальное условие из (14.11)
для т.). После проведения соответствующей процедуры (см. гл. 6, ~ 1, пп. 1
и 2) получаем выражения для функционала т. (Т) =т, и оптимальной массы
двигателя т„, совпадающие по виду с (6.15), (6.16):
т, = (1 — ~Ф)', т„= — ~/Ф вЂ” Ф,
(14.12)
где под Ф надо понимать (ср. (6.1.4))
Й(ш) Х
2
у = — ж.
(14.13)
После этого задача сводится к минимизации функционала Ф, а при
фиксированном параметре и — к минимизации функционала Х; за последней
задачей (Х=т1п) сохраним название динамической.
Без учета надежности можно было до решения динамической задачи
делать вывод об оптимальности управления Г (~) =1. В рассматриваемой по-
становке этого сделать нельзя. Более того, качественные рассуждения сви-
петельствуют о возможности существования режима, отличного от идеального
К (~)=1. Действительно, при увеличении мощности Г и неизменной про-
грамме а (1) уменьшается функционал Х (т. е. увеличивается полезная на-
грузка т, (14.12)). Вместе с этим растет интенсивность потока отказов (14.10)
(т. е. уменьшается надежность).
Обсуждаемая вариационная проблема (о минимуме функционала У) в тер-
минах задачи Майера записывается следующим образом (ср. (7.2)):
Х =а'/Т
Г=1',
т=ае+ д,
Л=) (~, К,
(а(1)) О,
(14.14)
)
Параметр и в (14.14) считается фиксированным, оптимальное значение и
определится после решения (14.14), т. е. после получения зависимости Х „(и),
из условия минимума Ф(и)=[а(и)/2) Х „(и).
Оптимальные законы изменения реактивного ускорения а (~), мощности Г (~) и на-
правления вектора тяги е (~), согласно принципу максимума, должны обеспечивать в каж-
пый момент времени абсолютный максимум гамильтоновой функции Н
Н = р а2/Л + а (р„е) + Хр1+ (р„° у) + (р, ° и),
(14.15)
Х (0) =О,
г(0) =ге,
т(0) =т„
и), Л(0)=0,
О &l ;т Р)
У (Т) = ш1п,
г(Т) =г,
т(Т) =т1,
Л(Т) = — )п Л
~ е (1) ~ = 1).

518
~1Л. !4
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
где импульсы р„, р„р~,
р удовлетворяют уравнениям
дН д дП
~, = — ~, (р. с), р.=- — ~„=-р„~
р„=—
(1 4.16)
дН
Р~ — — д~ — О,
Максимум Н по е и а достигается при
=р./р.. ='~ер.Р~ (р.=~р.~). (14.17)
Часть функции Н, зависящая от К, с управлением а, взятым из (14.17), записы-
вается так:
Ну /4рр'у + Л ( ~ ) рх~
(14.18)
Из рассмотрения (14.18) можно сделать вывод относительно знака импульса р~.
Предположим, что р~ ) О, тогда максимум Н имеет место при К=1 (так как по (14.10)
Р , Р3 Р4 ф' Р8 У
Рис. 14.2. О бласть, неразличимая
в смысле функционала задачи.
Рис. 14.3. Семейство функций
(14.25).
д)/дГ ) 0). Значит, оптимальная траектория получится такой же, как и без учета на-
дежности. При формулировке общей задачи (14.7) предполагалось, что условие (14.6)
не выполняется и заданная надежность Л на такой траектории не может быть обеспечена.
Следовательно,
р„= сопзС(0. (14.19)
Отметим два свойства оптимальных (с учетом надежности) траекторий,
следующих из условия максимума (14.18) по Г.
1'. Рассмотрим семейство характеристик надежности Л (~, Т), имеющих
две общие точки Л (Е, 0)=Л, (й) и Л (й, 1)=Л, (й). Для всех Л (й, Т) из (14.10),
удовлетворяющих условиям (см. заштрихованную область на рис. 14.2)
Л( ~)>Л( +Р () Ђ” Л Ц~ (14.
В самом деле, если подставить линейную функцию Г из неравенства (14.20) в (14.18),
то полученная функция
Н~та) Р~Ле+ ( /4Р~+ Р~ (Л1 ЛеН
(14.21)
в силу (14.19) будет мажорировать все Нд с функциями Л (~, Г), удовлетворяющими
(14.20):
Н, (Ж) ( Нд~~; (Ш), Нд (0) = Нр~~; (0), Нд (1) = Нд~~; (1). (14.22)
Следовательно, и тах Н ( тах Н~ . но Нд . — линейная функция Ш и ее
Упса~~ Ю пьа1
максимум достигается в граничных точках
сУ=1 при р'„) — 4Р1 (Л1 — Ло) К=О при р,'( — 4рх(Л1 — Ло) (1423)
В этих точках функции Ндта,.и Н, совпадают, поэтому максимум Нд для всех Л
пз (14.20) будет иметь место в этих же точках. Таким образом, оптимальное управление
управление Г (1) граничное, оптимальные траектории и значения функцио-
нала Х одинаковы.

519
ЗАДАННАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
У (~) оказывается граничным (14.23) и промежуточные значения Л не будут фигурировать
в задаче. В точках К=1 и К=О все Л (~, Г) из (14.20) принимают одинаковые значения
Л1 (й) и Л, (й). Значит, оптимальные траектории и значения функционала Х будут одни
и те же (т. е. заштрихованная часть области характеристик Л (й, Г) на рис. 14.2 оказы-
вается неразличимой в смысле функционала задачи).
2'. Если дМдГ=О при К=О, то оптимальная траектория не содержит
пассивных участков. В этом случае частная производная (14.18) по Г
дНд~дЯ = 1/ р'+ р,дЦд1Ч
в точке К=О всегда положительна (кроме изолированных моментов времени,
когда р„=О). Следовательно, оптимальное значение Г, которое должно обес-
Рис. 14.4. Три возможных типа оптимальных программ управления для задачи о перемещении между
точками покоя (пунктир — программы, оптимальные без учета отказов).
(14.25)
(рис. 14.3). Для всех 0 & t  ( (1 (заштрихован ая обла ть на р с. 14
оптимальное управление Г (~) определяется соотношением (14.23), в котором
следует положить Л,=О, Л,=Л,„, и справедливо свойство 1'. Для и ) 1
имеет место свойство 2', а оптимальное управление Г (~) таково:
2
.'1' = 1 прн р', ) — 4ой „р„ Ж=( Р' ) при р'. ( — 1ой ,„р„
(14.26)
т. е. здесь появляются участки с переменной мощностью, меньшей макси-
мальной.
Все полученные выше результаты не зависят от типа динамического ма-
невра (т. е. от г„г„т„т„д (г, й)). Чтобы решить вариационную задачу(14.14)
до конца, зададим простейшие маневры: перемещение между двумя точками
покоя и набор заданной скорости в бессиловом поле.
Если не задавать надежность (Л (Т) =орф или р,=О); то решение задачи
о пере чещении между точками покоя получается следую щее (см. (7.33)):
Ш" (~) = 1, а" (8) е*(~) = 6 (Г/Т') (1 — 2~/Т), .7*(Т) = 12 (~'(Тз). (14.27)
печивать максимум (14.18), всегда больше нуля, т. е. пассивные участки от-
сутствуют.
Рассмотрим теперь частный вид зависимости (14.10):
), = Л (Т, и) = Л,„й (Л,„, и = сопаь ) 0)

520
[ГЛ. 14
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
При заданной надежности Л решение будет зависеть от параметра
х= — 1пВ/1 Т (0(х(1),
(14.28)
который представляет собой отношение допустимого числа отказов Л (Т)=
= — 1пЛ к максимально возможному Л =),„Т.
Окончательное решение записывается следующим образом1):
если 0(ш(1, 0(х(1 (рис. 14.4, а), то
Ж(~) =1, а(~) =а,(1 — 2ЦТ) при 0(~(~„
Ж(~) =О, а(~) =0 при ~,(~(1/,Т
~,= т, — — 2~, Т' ', ~,=,КТ
Х (Т) = 12 (Р/Т') [1 — (1 — х)'] 1;
если ш)1, (ш — 1)/(Зш — 1)(х(1 (рис. 14.4, б), то
Ж(~) =1, а ® = а, (1 — 2ц/Т)
при 0(~(~„
2 и+1
1 — 2~/Т ~ — 1 (1 2~/Т)~-1
2~,/Т (~) = и,
(1 — 2~ /Т)~ 1
при 1,(1 (1/ Т
( (14.29)
, ', 11 — Ъ,)Т)а] ',
— ['" 2. 1] т)
Х (Т) = 12 ()а)Та) [1, (1 — х)~]
если ш) 1, О (х((ш — 1)/(Зш — 1) (рис. 14.4, в), то
1
жР)=.(' — ,') )1 — 21~Т),
(аа= —, [1
п(~) =, (1 — 2~/Т)" ' при 0(~ (1/,Т,
Т )Т) =12))а)Т ) — '(" ')
1) Функции 21 (~) и а (~) получаются четными относительно середины интервала
8=~/2Т, функция е (~)=+1 — нечетной: е (~)=+1 при О ( 8 ( ~/2Т, е (~)= — 1 при
'(2т& t; ~(
Отметим, что для значений конструктивного параметра О ( ш ( 1
величина х совпадает с отношением Т /Т полного времени работы двигателя
ко времени маневра, а соответствующее решение эквивалентно (10.50)—
(10.52). Для сравнения с полученными оптимальными законами (14.29) из-
менения мощности К (~) и реактивного ускорения а (~) на рис. 14.4, а — в
пунктирными линиями показаны старые законы (14.27), оптимальные при
отсутствии отказов.
На рис. 14.5 сплошными линиями показана величина функционала Х,
отнесенная к Х* и~ (14.27), в зависимости от параметра надежности х для раз-

521
ЗАДАННАЯ ВЕРОЯТНОСТЬ у СПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
/
д Р3 Р~ РЮ РЮ
Рис. 14.6. Два возможных типа оптимальных
программ управления для задачи набора скоро-
сти (пунктир — программы, оптимальные без
учета отказов).
Рис. 14.5. Функционал задачи. Сплош-
ные кривые — перемещение между точ-
ками покоя (.7*=12Р/Т'), пунктир-
ные — набор скорости (Г" = ит~~ Т).
0 ( и ( 1). Переход на программу (14.26) позволяет существенно уменьшить
значения функционала.
Для задачи о наборе скорости без учета надежности (р„=О) пассивные
участки на траектории отсутствуют, и получается следующее решение (7.32)~
Ж" (1) = 1, а'(1) е'(1) = и ~Т, Х*(Т) = и~~Т. (14.30)
Если показатель степени в формуле (14.25) для интенсивности потока
отказов взят из диапазона О ( и ( 1, то появляются пассивные участки.
Их число и расположение не влияют на функционал задачи, а суммарная
протяженность выбирается из условия заданной надежности Л (Т)= — 1пЛ.
При и ) 1, согласно свойству 2', пассивные участки отсутствуют, условие
Л (Т) = — 1п Л удовлетворяется за счет уменьшения К. Проделав все выкладки,
получим (е (1) =1):
если 0(~ш~~1, 0(х(1 (рис. 14.6, а), то
Ж(~) =1, а(~)=и/~ при 0(~(~1,
Ж(1) =О, а(1) =0 при 1 (1(Т
(~ = хТ),
Х (Т) = (и',/Т) х ';
если и) 1, 0(х(1 (рис. 14.6, б), то
К(~) =хц, а(~) =и,~Т при 0(~(Т,
Х (Т) = (и~/Т) х-'~"
(14.31)
(здесь, как и в (14.29), х=Т /Т при 0 (~ и (~ 1).
Отношение функционалов (14.31) и (14.30) в зависимости от х и и по-
казано на рис. 14.5 пунктирными линиями. Видно, что для задачи о переме-
щении между точками покоя (сплошные кривые) требование заданной
личных значений конструктивногопараметра и (показатель степени в (14.25)).
Увеличение надежности Л (уменьшение параметра х) при прочих равных ус-
ловиях приводит к увеличению функционала Х. Разница между кривыми, со-
ответствующими 0 ( и ( 1 и и=2, 3, 4, дает представление о выигрыше от
использования промежуточных значений мощности. Если бы при и ) 1
условие заданной надежности удовлетворялось только за счет выключения
двигателя (14.23), то функционал для всех ~ (Г, и) был бы одинаков (кривая
Ю

522
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
~ГЛ. 14
надежности приводит к значительно меньшему увеличению функционала,
чем для задачи о наборе скорости (при одинаковых значениях «и и).
Обратимся теперь к выбору оптимального значения конструктивного
параметра и. От этого параметра зависят интенсивность потока отказов
(1 убывает с увеличением и, см. (14.25)) и удельная масса двигателя (а уве-
личивается при увеличении и, см. пояснения к (14.10)). Зададимся простей-
шей зависимостью
а(и) = (1+и) а*
(а" = сопя~, и ) 0);
(14.32)
имея в распоряжении решения (14.29) и (14.31) динамической задачи
(14.14), найдем параметр и из условия минимума функции (см. (14.12),
(14.13)) Ф (и, «)= [а (и)/2] У (и, «):
для маневра перемещения между точками покоя
(1+ и) [1 — (1 — «)'
при 0 ( и (~ 1, 0 ( «(» 1,
(1 + и~ [1, (1 — *)'~
при и) 1, (и — 1)/(Зи — 1)(«(1,
~~ — 1
(1+и) — ( )
при и) 1, 0(«~~(и — 1)/(Зи — 1)
Ф(и, «)
пи п Ф„' — ппп
(14. 33)
(Ф* = (а"/2) 12РТ з);
для маневра набора модуля скорости
(1+и) « ' при 0(и(1, 0(«(1,
(1+и) «-ц" при и) 1, 0(«(1
(Ф*= (а*/2) и'Т 1).
Ф(и, «)
пип ф — П11п
(14.34)
Рис. 14.7. Оптимальные значения конст-
руктивного параметра м.
Рис. 14.8. Минимизированные по м значе-
ния функционала Ф (х).
рис. 14.8 — соответствующие минимальные значения функционала Ф в за-
висимости от того же параметра «. Сплошные кривые относятся к задаче
о перемещении между точками покоя, пунктирные — к задаче о наборе мо-
дуля скорости.
Результаты решения задач (14.33), (14.34) приведены на рис. 14.7, 14.8.
На рис. 14.7 показаны оптимальные значения параметра и в функции «вЂ”
отношения допустимого числа отказов к максимально возможному, нй

ЗАДА11НАЯ ВЕРОЯТНОСТЬ УСПЕШНОГО ВЫПОЛНЕНИЯ МАНЕВРА
После завершения этой заключительной стадии задачи можно вычислить
оптимальные соотношения масс по формулам (14.12), (14.13). Пример за-
висимости полезной нагрузки от вероятности успешного выполнения маневра
и =ехр ( — хЛ,„) дан на рис. 14.9. Горизонтальные участки кривых отвечают
таким значениям вероятности В, которые
обесчиваются на оптимальной без учета
надежности траектории (т. е. когда нера-
венство (14.6) выполняется).
3. Двигатель ограниченной скорости
истечения. Ранее, в гл. 5, 9, было уста-
новлено, что оптимальный режим работы
двигателя ограниченной скорости истече-
ния достигается при Г (~) = У „. Пусть
РЗ
теперь с увеличением скорости истече-
ния (т. е. с увеличением температуры)
интенсивность потока отказов (14.2) возра- р~
стает (ср. (14.10)):
Л =Л(~, $', и) (дЛ/дГ) О,
О ( 1' ( Г, дЦди ( О,
Д7
Рис. 14.9. Максимальная полезная на-
грузка для различных значений Лща~—
максимального числа отказов (Ф*=0,1,
величины и оптимальные). Сплошные кри-
вые — перемещение между точками покоя,
пунктирные — набор скорости.
(14.35)
и = сапам).
т, =. — о.Ро/Г,
т. (0) + ~ (и) а, = 1, т, (Т) = шах,
г (0) = г„г (Т) = г„
е+ и, т (0) =- т„т (Т) = т„
Л=Л,(й, и)+[Л(й, У, и) — Л,(Е, и)]В, Л(0)=0,
Л(Т) = — 1п Л
(0(Р(~) (1, 0( $'(~)(1, о(~) =1 или О, (е(~) (=1;
в. = Р „/М,У,„, а, = Р „/М„и = сопзС).
(14.36)
Здесь считается, что при выключенном двигателе интенсивность потока
отказов становится равной Л, (Л,=Л, (Е, и) ( Л (Е, У, и), в частном случае
Л,=О). Чтобы отразить этот факт в уравнениях, был использован прием 2'
из п. 1.
Если было бы известно, что тяга ни на какой оптимальной траектории
не принимает промежуточных значений из интервала (О, 1) — особый режим,
то функцию о (~) можно было бы не вводить. В последнемуравнениивместоо
тогда нужно было бы написать Р. Однако отсутствие в составе оптимальной
траектории участков с особым управлением заранее не очевидно.
Как и в (14.10), здесь фигурирует кон-
структивный параметр и~; считается, что
при увеличении и интенсивность потока отказов падает (дЛ/ди ( О), но
это достигается ценой увеличения удельной массы двигателя (дт/ди & t;
.~=М,/Р „— см. (9.1), зависимость ~ (и) предполагается известной).
Согласно общей постановке (14.7) задача о доставке максимального по-
лезного груза для двигателя ограниченной скорости истечения записывается
в виде (см. (9.4), (14.11); тяга, скорость истечения и массы отнесены к соот-
ветствующим максимальным значениям)

д24
[ГЛ. 14.
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
В задаче (14.36), помимо оптимальных управлений Р (~), У (~), о(г),
е (г), нужно выбрать еще оптимальные значения параметров а„гг, и (или Р
Г „, и). Если а„гг, и зафиксировать, то задача (14.36) сведется к следующей
(ср. (9.6)):
ггг = — р.Р8/~,
т (О) = 1, т (Т) = т ах,
й =У, г (О) = г„г (Т) = г„
т = (аоР3/т) е + й', т (О) = т„т (Т) = т„
А=~о+[)~(Г) — )~о1о, Л(0) =О, Л(Т) = — 1п Л
(0(Р(~)(1, О( Г(~)(1, о(~)=1 или О, ~е(~) ~=1).
) (14.37)
Функционал т (Т)=т, после решения (14.37) будет функцией парамет-
ров а„ гг, и. Оптимальные значения этих параметров определятся из условия
максимума полезной нагрузки т,=т. (Т) =т, (а„гг, и) — т (и)а,. Дальше
будет рассматриваться только задача (14.37).
Для анализа состава оптимального управления нужно исследовать на абсолют-
ный минимум (ищется максимум тг) по е, Р, 3, У функцию Н (ср. (14.15)):
Ртр Ру ° е Р Ру, ~ ~ — ~о ~ ~ор) Рт'~ рю'Я.
(14.38)
Импульсы р„, р, и рг по-прежнему определяются уравнениямп (14 16), а пмпульс
р — уравнением
р', = — дН(дтп= (р ° е) аот аРо, р,„(Т) = — 1.
(14.39),
Из минимума (14.38) по е следует (ср. (14.17)):
(14.40)
е = — р,/р,.
Аналогично п. 2 (см. (14.19)), можно показать, что
р,„(г) ( О, р.„= соней ) О.
(14.41)
~~о 1
Н,~ р — — Н~ — р~ — — Хор~ Р, Н~ — — р.рщ ~ Х й К р
(14.42)
Из условия минимума Н, по К следует.
(14.43)
Если условие (14.43) не выполняется, то в каждый момент времени существует оптималь-
ное промежуточное значение 0 & t Г г & t; 1, опреде яе ое из ура
ГадХ/дГ = — р:р„,/рг,
(14.44)
(О ( Г (1).
Предположим, что в некоторый момент времени р (г) ) О, тогда пз минимума Н
следует У=О (независимо от знака р1) и Р= 3=1. Режим Р3=1 при У=О противоречит
физическому смыслу, поэтому всюду р (г) ( О. Если положить теперь рг & t; О, то по
чим всюду У=1 и более позднее выключение двигателя (3=0) по сравнению со случаем
р1=0. При этом условие заданной надежности не может быть выполнено, поскольку
предполагается, что неравенство (14.6) не имеет места.
Покажем теперь, что на оптимальной траектории управление Р (г) не может при-
нимать промежуточных значений 0 & t  & t; 1. Пос о ьку Р х дит в ( 4.38) ли
то промежуточные значения Р в качестве оптимальных могут появиться, когда коэффи-
циент при Р обращается в нуль на некотором отрезке времени (особый режим). Но тогда
о=О, поскольку р~ ) 0 (см. (14.41)), т. е. тяга Ре должна быть выключена. Это спра-
ведливо для любого маневра в произвольном гравитационном поле.
Установив отсутствие особого режима в составе оптимального управления, исклю-
чим из (14.37) — (14.39) управляющую функцию о (г): там, где входит произведение Р "ч
нужно оставить просто Р, а где функция 3 входит без Р, ее нужно заменить на Р. Тогда
часть функции Н, зависящая от управлений Г и Р, с учетом (14.40) запишется в виде

$2]
СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Уравнение (14.44) может иметь несколько корней; тогда среди них нужно выбрать такой,
который дает абсолютный минимум функции Н~ из (14.42). Нулевые значения Г не вхо-
дят в состав оптимального управления. Если
Х (1, Г) ) Л (1, 1) + (рр о/рЛ) (Г 1 — 1), (14.45)
при Н~ — р,аот 1 — Лор1 (О,
0 при Н~ — р„аот 1 — Лорл) О,
(14.46)
полученным из условия абсолютного минимума функции (14.42) по Р.
Для полного решения задачи нужно проинтегрировать систему уравне-
ний (14.37), (14.39) с конечными соотношениями (14.40), (14.43) — (14.46)
для управляющих функций.
Рассмотрим теперь случай ограниченной перегрузки а=аоР/т (вместо
ограниченной тяги 0 ( Р ( 1). Здесь задача (14.37) о максимуме комеч~ой
массы т, сводится к отысканию минимума функционала
т
1= — й (т,=е-г~~"'*, 0( $'(1, 0(а(ао)
о
(14.47)
(функционал (14.47) получается интегрированием в квадратурах первого
уравнения (14.37) и представляет собой обобщение характеристической ско-
рости (5.6)).
Аналогично предыдущему можно доказать отсутствие промежуточных
значений реактивного ускорения 0 ( а ( а в составе оптимального управ-
ления. Имея это в виду, можно использовать запись (14.37) уравнений ва-
риационной проблемы, заменив первое и третье уравнения на
Х = ао3/Г (1 (0) = О, 1 (Т) = т1п), т = аде+ 11. (14.48)
Оптимальное направление тяги будет определяться первым соотношением из (14.17).
Управления Г (~) и о (~) находятся из условия максимума функции (ср. (14.42))
Н~ ~ — (Нг + р,ао — Лорх) о (14.49)
Н = — аоГ 1+ Л (~, Г) рл (р1(0).
Оптимальная программа по скорости истечения будет определяться соотношениями
(14.43), (14.44), в которых надо положить рр = — а„причем если дЛ/дй=О, то оптималь-
ное значение скорости истечения вдоль траектории будет постоянно.
Моменты включения о=1 и выключения о=О двигателя находятся из соотношения,
аналогичного (14.46):
1 при Нг+ р по — Лор1.) О,
0 при Н + р„ао — Лорл(0.
Ь (~) =
(14.50)
$ 2. Секционированный двигатель ограниченной
мощности — формулировка
и уравнения вариационной проблемы
Когда интенсивность потока отказов Л и полное время движения Т ве-
лики (так что максимальное число отказов Л, =Л „Т & t; ), то односекци
ная двигательная система не может обеспечить приемлемый уровень полез-
ной нагрузки при достаточно высокой вероятности успешного выполнения
маневра (см. рис. 14.9). В этом случае двигательная система (или ее наиболее
ненадежные элементы) должна делиться на автономные секции.
то условие (14.43) будет выполняться на всей траектории, так как р & t; О
(см. (14.39) — (14.41)). В этом случае скорость истечения нигде не будет принимать про-
межуточных значений.
Оптимальное управление тягой, как было доказано выше, может быть только гра-
ничное. Чередование активных и пассивных участков на траектории определяется соот-
ношением

526
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 14
Секции считаются идентичными. Неповрежденные секции работают па-
раллельно в одинаковом режиме. Повреждение секции приводит к ухудше-
нию характеристик двигателя (например, к уменьшению тяги или мощности),
но не вызывает прекращения работы двигателя в целом (конечно, если секция
не последняя). Поврежденные секции не восстанавливаются и не сбрасы-
ваются.
1. Расчетные моменты повреждений. Для прогнозирования характе-
ристик аппарата нужно знать, как будет меняться число работающих секций
по времени и (~). Аналогично первому параграфу предполагается, что по-
вреждения каждой секции случайные и образуют ординарный пуассоновский
поток без последействия.
Известна интенсивность потока ~( (среднее число повреждений одной сек-
ции в единицу времени):
(14.51)
~(= ~(Р, г, 1г).
˄(~ — ~.) =
1с х
° ° °
') — ехр ~ — 1х)Х/] ехр [ — (и,— ) — ~) 'хе)Х] () 4.ее)
! ! (по — 1 — ~)!
~=0 8у 8 у.
(и, — общее число секций; повторные повреждения секции, если таковые
возможны, в расчет не принимаются).
Момент очередного повреждения ~. будем определять из условия, что
вероятность отсутствия повреждений Й=О в интервале (~., ~,.~,) равна задан-
ной величине Л.
Положив в (14.52) 1=О и ~=~.~1, получим (ср. (14.3))
Л = ехр [ — (е — ))
-]
(14.53)
Будем считать, что в момент ~.~1, определяемый соотношением (14.53),
происходит очередное повреждение. Тем самым мы выбираем наиболее не-
благоприятный случай, так как с той же самой вероятностью, согласно фор-
муле (14.52), можно утверждать, что в интервале (1., 1) большем, чем (1., 1.„),
произойдет не более одного повреждения.
В следующем пункте будет дана строгая оценка вероятности реализа-
ции найденных моментов повреждений как нижних оценок для действи-
тельных моментов отказов.
Интенсивность потока здесь считается зависящей от времени ~ и положе-
ния г аппарата в пространстве. Это соответствует, например, повреждениям,
вызываемым нестационарными неоднородными потоками метеоров. Кроме
того, ~( зависит еще и от конструктивных параметров двигателя т. Например,
в случае пробоя метеорами холодильника-излучателя (радиатора) — это
уязвимая площадь секции радиатора и толщина стенок.
В этом параграфе рассматривается идеальный двигатель ограниченной
мощности и в качестве и принимается максимальная мощность Л,/п„при-
ходящаяся на одну секцию в начале движения (~( — неубывающая функ-
ция Го/по).
Если в момент времени ~. выходит из строя у-я секция, то вероятность
Л„(1 — 1 .) того, что в интервале (1 ., 1) будет повреждено не более чем Й секций
для пуассоновского потока, определяется соотношением [14.5 — 14.8]:

527
СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
Окончательно принимается следующее соотношение для расчетных мо-
ментов повреждений:
Х (г (1), ~) Ж =
(7'=О, 1, ..., т — 1),
(14.54)
Х(г(~), 1)Ж( ' (Л,= — 1пЯ)
(т ( ио — общее число повреждений за весь полет).
2. Вероятность реализации расчетных моментов повреждений (14.54).
Соотношения (14.54) определяют некоторый закон убывания числа неповре-
жденных секций по времени (рис. 14.10):
д))д
и'(1) = и,— )' при 1. (1 (~.~д
(7 =О, 1, ..., и,; ~ „= Т). (14.55)
Обозначим через А событие (рис. 14.10)
А: п (~) ) и" (~) при 0 '= ~ & t
(14.56)
и через Р(А) — вероятность его реализации (искомая вероятность).
Поскольку функции п(д) и и"(~) кусочно-постоянные и невозрастадощие, то неравен-
ство (14.56) эквивалентно следующей системе неравенств:
п (д ° — О) ) по — (!' — 1),
) = 1, ..., т + 1.
(14.57)
Введем в рассмотрение систему из т + 1 событий
Ао о . 'п (дд — О) =во 7со
(й) °
(7со — О),
Ад~ '):
п (дв — О) = по — Усд
(0&lt 7, &
<7с;&
(14.58)
А д': и (~ .+д — О) = по — 7с
(й .) °
,/+
А ~"вд): и (Т вЂ” О) = по — 7с
(7с,„д & t; 7 &l
Обозначим через А ~~' "~"') событие, состоящее в одновременной реализации
системы равенств (14.58). Оно будет представляться как пересечение (произведение)
сос>ы и А ~-'
А (д"'о ° д"'т) П А (д"' д')
.у
~=о
(14.59)
При каждой реализации маневра будет
получаться свой закон и (1) повреждения сек-
ций, отличный от расчетного и* (~) — (14.54),
(14.55). Поставим задачу определения вероят-
Рис. 14.10. Расчетный закон и* (1)
НОСТИ, С КОтОрОй дЛя ЛЮООй рЕаЛИЗацИИ Ма- уменьшения числа работающих
невра будет выполняться неравенство )д (~) ) секций. штРиховкой выделена
область, соответствующая событию
)~ и"" (~) при О ( ~ ( Т. Выполнение этого не- А'иа (д4лз), (ы.57).
равенства гарантирует, что фактический рас-
ход рабочего вещества на выполнение всего маневра не превысит вычислен-
ного в соответствии с законом и* (~). Другими словами, это позволит доста-
вить полезный груз, не меньший расчетного. В этом смысле можно говорить
о вероятности выполнения неравенства п (~) ) и,* (~) при О ( ~ ( Т как
о вероятности реализации решения.

528
[ГЛ. 14
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
В свою очередь, событие А будет объединением (суммой) событий А1~'" ~) по всем
различным наборам (Йо... Й ), удовлетворяющим неравенствам Й 1 ~ Й ~ ) () =
=1, ..., т; Же=О):
1 2 ФВ
4= 0 0 ° 0 А1""'"') (14.60)
~1=0 ~г=~1 ~т=~т-1
где через Р (А ~ ~'),ГА)"')... А~. ~-')1 обозначена вероятность реализации события А Ю
при условии, что событие А) ) ... А1. ~-') произошло (условная вероятность).
Вероятность суммы (14.60) несовместных событий по теореме сложения вероятно-
стей [14.6] равна
1 2 Щ
Р(А)= ~ ~ ... ~ Р(А("' ""»).
(14.62)
В1 О В2 В1
~т=~т-1
Вычислим условную вероятность Р (А ~.".~) ~А6 ')... А ~~(-')), т. е. вероятность
у — 1
того, что из (и, — й 1) оставшихся к моменту 8~ секций в интервале (~;, ~ +1) будет
повреждено ровно Й вЂ” Й 1 секций (безразлично каких). В случае пуассоновского
потока отказов вероятность Д того, что неповрежденная к моменту времени ~ секция
останется неповрежденной до момента ~~+„и вероятность Р того, что неповрежденная
к моменту ~ секция будет повреждена в интервале (~;, ~ +,), равны соответ-
ственно [14.5]
-)
Д= в
7=1 — е
Число различных способов, которыми можно распределить й~ — й~ 1 повреждений
между по — й 1 секциями, равно С ~ . — числу сочетаний из по — й ., элементОВ
~1 О,У'-1 .7—
по ~~ — ~~., так как порядок выхода секций из строя нас не интересует. Все эти
способы равновероятны, вероятность каждого из них есть (повреждения секций не зави-
сят друг от друга)
(14.631
Умножая (14.63) на число способов, получим условную вероятность
Р(А1 ~),~ А1"о) ... А~~~-'))= С ~ ".' 'в 1"' ~) У (1 — в ~) ~ ~ ' °
() ' ' ~ 1,~ ~„— В~
(14.64)
Подставляя последовательно (14.64) в (14.61) и (14.61) в (14.62), получим выра-
жение для искомой вероятности')
Р(А)= У ~ . ~ Ц[С„',. 1"' ) (1 — в )
~1=0 ~г=~1 ~т=~т-1 .~ =0
(~ 1= ~о =О,
1) В книге авторов [14.9] при выводе формулы пля вероятности Р(А) была допущена
неточность (ср. (14.65) и (11.65) из [14.9]). А именно, неправильно была посчитана услов-
ная вероятность (11.64) из [14.9]: так можно было бы делать, если бы состояния (11.60)
из [14.9] были равновероятны. Несмотря на это, асимптотические выражения (14.67),
(14.68) и (11.67), (11.68) из [14.9], которые и используются в дальнейшем, оказались оди-
наковыми.
причем все слагаемые суть события несовместные.
По теореме умножения вероятностей (см., например, [14.6]) вероятность реализа-
ции пересечения событий (14.59) равна
Р (А(~'"~п)) р (А1ьа) ~"А~а.) А1ь'[-)) р (А1Ч АР~а,-))
... = Р (А~ь' ) П Р (А1~~),г'А~~')... А1~~-)) (14.61)
,у'=1

СЕКЦИОНИРОВАННЫИ ДВИГАТЕЛЬ ОГРАНИЧЕННОИ МОЩНОСТИ
или в другом виде
1 2 т
Р )А) =
~1=О ~г=~1 ~т=~т — 1 ~
('-" =-' Г("-'=-'Г
по!
~1) ' ' ' ' ('"РР) ~т — 1) ( (~0 ~РР)) °
,ЬЛт-, ~ т,
ьл
[еЬЛР)р 1) 1ст
1 — Е ~Лт
э
l
(14.65б)
(14.66)
Для законов с т ) 1 можно получить асимптотическую оценку. С точностью до
членов третьего порядка малости относительно ЛЛ;формулу (14.65б) можно переписать
в виде
т
и'
Р)А)=1 — ЛЛ -';- — ЬЛ [1 — (Л)]-';-о А ЛЛАЛ.).
~, у=О
Подставив сюда ЛЛ;=( — 1п Л)/(и, — 1) из (14.54), получим
Р (А) =Л вЂ” г ) (1 — Л)2+ о ((1 — Л)2)
(14.67)
при т) 1 °
Если добиваться высокой вероятности Р(А) реализации решения, близкой к единице
(именно этот случай и представляет практический интерес), то, согласно (14.67), нужно
орать (1 — Л) (& t; 1. То д с точнос ью до чле ов втор го поря ка мало ти относител
(1 — Л) можно считать, что вероятность Р(А) реализации решения в целом для закона
и"(~) из (14.54), (14.55) будет совпадать с вероятностью Л отсутствия повреждений п у
секций на интервале (~~, ~ +,):
Р(А)=Р(~(~) & t; и" ~) ри (~ (Т)=Л+о (1 Ђ” Л
1 у+,
.*Р)=.,— ) .Р. ~А(~(~„„А=Р*Р [ — ),— ))
~у
(14. 68)
Приведенное доказательство относится только к вероятности реализации расчет-
ного закона повреждений (14.54), (14.55) и ничего не говорит о его оптимальности. Чтобы
решить этот вопрос, нужно вместо (т+1)-го условия (14.54) в задачу ввести только одно
условне Р(А) ) Л, где Р(А) определяется соотношением (14.65). Но при этомсильно
вагромождаются выкладки. Данное обстоятельство заставило нас ограничиться рассмо-
трением лишь допустимого закона (14.54), (14.55).
3. Соотношения масс. Секция двигателя, поврежденная в момент вре-
мени ~., отключается. Это приводит в общем случае к изменению режима ра-
у' Ф
Ооты оставшихся секций и к уменьшению максимальной мощности:
0(Ж(~)(У „[п(~)] или 0(Х(~)(Ж,. (14.69)
при ~.(~(~.+1, )'=О, 1, ..., т.
Здесь Т „[и (~)] обозначает зависимость максимальной мощности от числа
работающих секций, Ж . — мощность, отнесенная к начальной Я, [Х . (
(У. 1(... ( Х, = 1). В случае полностью автономных секций зависи-
мость Т „[и (1) ~ линейная:
11' „[и (1)] = [и (1)/пв] У„или У = 1 — )/ц .
34 Механика полета
(14.70)
где А. (Т) = 1А1~ = ~~~~ ЬА~., ЬА~ — ХЖ, ~ +, — Т.
О ~=О ~у~
Используем полученные выражения для оценки вероятности реализации (14.56)
с расчетным законом повреждений (14.54), (14.55).
Для расчетных законов с т=О (полное отсутствие повреждений) из (14.65) находим
Р(А)=ехр [ — поА (Т)], а из (14.54) по1~ (Т) ( — 1п Л, т. е.
Р (А) =е "р~1~) ) Л при т=О.

530
[гл. 14
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
Если поврежденные секции остаются на борту, то, интегрируя уравнение
(6.5) изменения массы аппарата по участкам (~., ~.+,), получим (ср. (6.6))
(14.71)
(14.72)
М„=У.
Удельная масса а считается зависящей от мощности одной секции
Ко/по (невозрастающая функция от Го/по, рис. 2.88).
Йа основании (14.71) аналогично тому, как это делалось без учета по-
вреждений, можно записать выражение для суммарной относительной массы
двигателя и расчетного запаса рабочего вещества, потребного для осуществле-
ния маневра (ср. (6.14)):
1
Ш„+Ш,о —,, + Ш,
,'(14.73)
(черточки над безразмерными величинами здесь и ниже опускаются).
4. Формулировка задачи. В качестве критерия оптимальности прини-
мается условие минимума (14.73) — суммы масс двигателя и расчетного
запаса рабочего вещества. Это соответствует максимуму полезного груза, на
доставку которого можно рассчитывать с вероятностью, не меньшей Л.
Суммарная масса (т„+т~,), как видно из соотношения (14.73), моно-
тонно убывает с увеличением Ф. Поэтому задачу об отыскании минимума
(т„+т~,) можно разбить на две: 1'. динамическую и 2'. параметрическую.
1'. Для заданных величин Л1, Ко, и и при известной зависимости ~
(г, 1, Ко/по) построить такие законы изменения мощности Г (1) и реактивного
ускорения а (~), чтобы при выполнении заданного динамического маневра
(с фиксированной вероятностью) достигался минимум суммы интегралов
(ср. (6.11)):
я2
— й = П~1П,
М
(14.74)
г'=а+~, г(0) =г, г(0) =то, г(Т) =г, г(Т) =т
(О ( Ж (~) ( Ж . при й . ( й ( й ., у = О, '1, ..., т),
где ~ . определяются условиями изопериметричности (14.54).
2'. Для заданных величин ЛХО и (Го/по)~, (минимально возможный раз-
мер секции) и при известных зависимостях
(14.75)
~=и(Т,/и,), У=У „(Т„и~ Л)
определить оптимальные значения мощности Ко и числа секций по, обраща-
ющие в минимум функцию (14.73).
Здесь в динамическую задачу 1' (вариационная задача) через условин
(14.54) для моментов повреждений ~. входят параметры двигателя — число
Под ~. здесь будем понимать расчетные моменты повреждений (14.54).
Тогда (14.71) дает величину т1„которая с вероятностью, не меньшей Л, ог-
раничивает снизу все реализации: т, ) т,'; с массой т",' и будем
в дальнейшем оперировать. Масса двигателя ЛХ„в процессе полета не ме-
няется и связана с начальным значением максимальной мощности Жо:

531
СЕКЦИОНИРОВАННЬПЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
5 2]
секций и и мощность Га. Это отличает последнюю от задачи (6.11), когда по-
вреждения не учитываются. Параметрическая задача — задача на экстремум
функции. Ее решение связано с конкретным видом зависимостей (14.75);
в п. 1 ~ 3 будет рассмотрен один из примеров.
5. Уравнения вариационной задачи (14.74). Для упрощения пред-
полагается, что интенсивность потока отказов не зависит от режима работы
секции, т. е. от промежуточных значений мощности. Влияние этой зависи-
мости уже было выяснено в ~ 1 на примере односекционного двигателя.
Относительная мощность Г входит только в знаменатель подынтеграль-
ного выражения минимизируемого функционала (14.74). Ожидаемые моменты
повреждений (14.54) и уравнения движения (14.74) от Г не зависят. По-
этому для минимума функционала (14.74) необходимо, чтобы мощность Ж
в каждый момент была максимально возможной:
Т(1) = Т,. при 1. (1(1,.+„! =О, 1, ..., т, (14.76)
т. е. на участках между повреждениями мощность постоянна и убывает в мо-
менты повреждений в соответствии с уменьшением числа работающих секций.
После этого задача сводится к минимизации функционала
Иг ~~+1
у ~ 1
(14.77)
~=о г.
(Д1 (1) =Г . вынесено из-под знака интеграла) с дифференциальными свя-
зями (14.74) и условиями изопериметричности (14.54).
а2Д1
Выразив в (14.77) а='г — и, мы избавимся от дифференциальных связей. Условия
изопериметричности (14.54) с постоянными множителями ~ /К по правилу Лагранжа
присоединяются к основному функционалу (14.77). Ищется минимум расширенного функ-
ционала
т ~.7+1
1
У= ~, [(г' — д)а+ ч:1~ (г, Г)] А
~=о
(г (0) = га, г (0) = та, г (Т) = гд, г (Т) = тд).
(14.78)
Для решения задачи необходимо построить экстремали этого функционала и полу-
чить условия сопряжения экстремалей (то, что экстремали г (д) будут иметь разрывы вто-
рых производных при д= ду, следует из наличия весовых коэффициентов ч в подынтеграль-
ных выражениях).
Вдоль экстремалей должны выполняться уравнения Эйлера (ср. (7.6))
д д~
а — —,(а д)+ч — =0 (14.79)
(а=г — ц, д (д(у+д, у=О, 1, ..., т, ч„,=О).
Приравнивая нулю в моменты д=д; сумму коэффициентов при вариациях сг и бг в вы-
ражении для первой вариации функционала У, получим следующие условия сопряжения
экстремалей:
1 . 1
а, — а+= а.
(у=1, ..., т).
(14.80)
Здесь нижний индексу указывает на момент времени ~~, а верхний значок плюс или минус
относится к значениям функции справа или слева от разрыва. Таким образом, реактивное
ускорение и его производная в моменты повреждений уменьшаются пропорционально
уменьшению мощности, т. е. скорость истечения У=2Х/аМ не терпит разрыва.
Когда среднее число повреждений Х зависит от г, при составлении первой вариации
У нужно еще варьировать моменты времени 1~. Это дает дополнительные условия
ч. ч Д вЂ” Я
~у уд —,~ + у~~ (а~.)~=0 (у=1, ..., т 1). (14 81)
.1 ' .1-1
з
34»

532
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 14
Задача свелась к решению системы дифференциальных уравнений (14.79)
с граничными условиями из (14.78) и условиями (14.54), (14.80) и (14.81),
причем неравенство в (14.54) служит для определения суммарного числа т
поврежденных за весь полет секций.
6. Непрерывная аппроксимация ступенчатого закона повреждений.
При большом числе пэ секций двигателя решение вариационной задачи со
ступенчатым законом и* (г) уменьшения числа неповрежденных секций за-
труднительно из-за наличия условий (14.54), (14.80), (14.81). Но если число
секций достаточно велико, так что и — т &g ;) 1, то ступенча ый за он (14.5
(14.55) можно заменить непрерывным и тем самым избавиться от этих условий.
Введем дифференциальное уравнение
п, п(0) =и (Л,= — 1пЛ=сопз().
1
(14.82)
Решение п (~) этого уравнения будет аппроксимировать снизу (и (~) (
(п~ (~)) ступенчатый закон и* (~), приближенно совпадая с ним в узлах ап-
проксимации 1==1 ..
Чтобы убедиться в этом, проинтегрируем уравнение (14.82) в пределах от г до г.+,,
.ь)
(14.83)
Подставим сюда вместо и (~) ступенчатую функцию и* (г) из (14.55), а в правую
часть — соответствующие выражения (14.54).
Равенство будет выполняться с точностью до членов порядка 1/по. Отсюда можно
сделать вывод, что уменьшение числа неповрежденных секций от одного момента повре-
ждения до другого для непрерывного (14.82) и ступенчатого (14.55) законов повреждения
при и ~ т одинаково. Примеры решения, приведенные в следующем параграфе, показы-
вают, что интегральные характеристики, соответствующие этим двум законам, становятся
близки, начиная с и, — 10.
Для непрерывного закона повреждений (14.82) задача сводится к отыс-
канию экстремалей следующего функционала:
7
О
(14.84)
г (Т) = г1, г (Т) = т~),
Г =%О) Г
Уравнения экстремалей функционала (14.84) таковы (ср. (14.79)):
'г' =- а + и, г (О) = г„г (О) = т„г (Т) = г,, г (Т) = т„
И~ а 1 д чп дХ
ИР Ж (и) Ж (и) дг ( е)+ 2Л Ог
Х а~ дЖ
— '4 Л + дз ( ) д — О, '4 (Т) =О,
й = — Хи/Л1, и (О) = ио.
(
(14.85)
Таким образом, вместо условий (14.54), (14.80), (14.81) здесь появляются
два дифференциальных уравнения первого порядка (см. два последних урав-
нения (14.85)).
где ~=~ (~) — переменный множитель Лагранжа при дифференциальной
связи (14.82), К (и) — зависимость максимальной мощности К,„/К от
числа неповрежденных секций.

533
СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОС'УИ
$ 3. Секционированный двигатель ограниченной
мощности — примеры решения для модельных маневров
1. Ступенчатый закон повреждений. В рамках сделанных предположе-
ний из формул (14.54) можно получить явное выражение для ожидаемых
моментов повреждений:
ъТ
(14.86)
по — ) '
(у = О, 1, ..., т — 1, к = Л /ЛОТ).
Интегрируя уравнения экстремалей (14.79) по участкам ~. ( 8 ( ~.+1
с учетом условий (14.80) и (14.86), получаем
а~ =(1 — — )а„
(14.87)
Величины а, и ао определяются решением системы линейных алгебраических
уравнений, полученных из граничных условий х (О) =х (О) =х (Т) =О,
х (Т)=1:
(14.88)
Здесь даются примеры аналитических решений уравнений вариацион-
ной проблемы, полученных в предыдущем параграфе.
Упрощение уравнений достигается, во-первых, за счет отбрасывания
гравитационных сил (и=0) — рассматривается одномерное движение (по
оси Ох) между точками покоя в бессиловом поле. Во-вторых, интенсивность
Л потока отказов одной секции считается не зависящей от г и 1: 1(г, 8)=— Ло.
Всюду, кроме последнего пункта, предполагается, что секции полностью
автономны: Т (и) = и/и,.

534
ВОпРОсы нАдежнОсти В 3АдАчАх ОптимизАции
[ГЛ. 14
Суммарное число повреждений т за все время движения находится, со-
гласно второму условию (14.86), из неравенства
= ~. ( Т ( ~.„= — "'
~=о
кТ 1
рг~ 1 — у/ио
(14.89)
Минимальное значение функционала У выражается через (хТ/и,), и„
е
Щ~ ~о ~о:
= —;. Д [[" +",['+[" +".[, ", ...'. +.,:, ... (;.)'1+
+(1' — — )[7 — ~ )[[а +а ~ [2+ [а +а ~„[а [7 — ~ [+1[~а~[7 — ~ [~[,
(14.90)
Величина функционала (14.90), отнесенная к величине функционала У~
для этого маневра без повреждений (см. 7.33))
у ууз
У* 12~2
(14.91)
показана на рис. 14.11 в зависимости от параметра
1 ~ Т
— 1вЛ
пля различных значений и, (сплошные кривые).
Пример оптимальной с учетом повреждений программы реактивного
ускорения
а (1) а (1) Т2
а" Я
(14.92)
приведен на рис. 14.12 (сплошная ломаная линия).
Оптимальный без учета повреждений закон а* (~) (см. (7.33)) показан
на рис. 14.12 пунктирной линией. Пунктирные кривые, приведенные для
сравнения на рис. 14.11, дают значения функционала, которые соответствуют
этому линейному закону а* (~) при учете повреждений. Видно, что изменение
программы реактивного ускорения позволяет существенно уменьшить функ-
ционал задачи.
Обсудим влияние числа секций и, на функционал У. При этом нужно
различать два случая; а) интенсивность Л потока отказов одной секции не
зависит от К,/по — энергетического размера секции, б) интенсивность
уменьшается с уменьшением К,/и,. Случай а) имеет место, когда процессы,
вызывающие повреждения, не зависят от масштаба двигателя. Случай
б) соответствует, например, метеорной опасности, когда число пробоев прямо
пропорционально площади радиатора секции (Ло — ~*КО /п„Л* = совами).
Зафиксируем суммарную начальную мощность К, и будем менять число сек-
ций по. Сравнение будем проводить при фиксированных параметрах маневра
и потока отказов, которые не зависят от и . В случае а) этому соответствует
х= — 1пЛ/(Л Т)=сопзй (рис. 14.13, а); в случае б) х*= — 1пЯ/(Л*Т)=сопй
или х/п,=сопзй (рис. 14.13, б). В первом случае (рис. 14.13, а) функционал У
немного увеличивается с ростом числа секций ио, но это увеличение по по-

535
СЕКЦИОЫИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
зволяет выполнять более напряженные в смысле надежности маневры (т. е.
маневры с меньшим значением к — см. на рис. 14.13 а ограничивающую кри-
вую т=по, где т — суммарное число поврежденных за весь полет секций).
Во втором случае (рис. 14.13, б) увеличение по в обоих указанных аспектах
дает положительный эффект:
функционал У и предельное
значение к/по уменьшаются.
О
8
б
//х
Рис. 14.11. Функционал динамической задачи (14.74)
для маневра перемещения между точками покоя.
Сплошные кривые соответствуют оптимальной с уче-
том повреждений программе ускорения, пунктир-
ные — оптимальной без учета повреждений
программе.
Рис. 14.12. Пример оптимальной с учетом
повреждений программы реактивного
ускорения (сплошная линия) для маневра
перемещения между точками покоя (п,=2,
х ='/„а* = 61/Т'). Пунктирная линия—
оптимальная без учета повреждений про-
грамма.
а = а* (1 + и ф Л /Уо),
а", ЬУ"= сопз$ и (14.90).
Фиксируем величины
Ф' = (а"/2) У» = 0,1 и Ьт'„= а'ЬШ* = 0,001.
Снова рассмотрим два указанных выше случая: а) Л =- сопзг, или к=
= — 1п Л/(Л Т) = сопзС, б) Л = Л"а'У /(т'„и ); Л", а", т' = сопз1, или к" =
= — 1п Л/(Л"Т) = сопз1, т„'= ~/Ф" — Ф" = 0,216.
Результаты отыскания минимума суммарной массы (14.73) двигателя
и запаса рабочего вещества по т„=аКО и по приведены на рис. 14.14, а и
1414, б.
Зависимости полезной нагрузки т„от параметра к перестроены на
рис. 14.15, а и 14.15, б в виде функций т от вероятности Л успешного выпол-
нения маневра при Л „=сопзФ (Л=ехр [ — кЛ 1). Из этих рисунков можно
заключить, что дробление двигателя на автономные секции при параллель-
ном режиме работы в случае а) мало эффективно (интенсивность потока от-
казов секции не зависит от размера секции), а в случае б) дает хорошие ре-
зультаты (интенсивность потока отказов линейно падает с уменьшением энер-
гетического размера секции).
Рассматривая влияние по на функционал динамической части задачи,
нельзя забывать, что уменьшение мощности Ко/по одной секции приводит
еще к увеличению удельной массы а, последнее отрицательно сказывается
на функционале (14.73) полной задачи. Окончательное заключение о наилуч-
шем числе секций можно сделать только после того, как решена параметри-
ческая часть задачи (п. 4 ~ 2).
Дадим пример ее решения. В качестве зависимостей (14.75) возьмем

[ГЛ. 1~
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
536
Ю ~~ бР оо
4 6 8 Ю Л7 4Р Ю по
Рис. 14.13. Зависимость функционала Х от числа и, автономных секций,
построенная по рис. 14.11 (суммарная мощность Ж, фиксирована).
а) Интенсивность Х, потока отказов одной секции не зависит от Ж,/и„;
б) интенсивность Л, — ~*Я,/и,.
убр7х 0
Л
Ю
Я Ю
Ф~
Я
Ш~ б7~
РГ Р4 РЮ Р8 л
Р
Ф)
Рг Р4 РЮ Рг х
ф
Рис. 14.14. Максимальная полезная нагрузка т~„оптимальная масса двигателя т-„
и оптимальное число секций и, для маневра перемещения между точками покоя
& t; *= 0 1, ~ *= 0,0 11 а) Интенсивно ть ~, пот ка отка ов сек ии не зави ит
х
мощности секции; б) интенсивность Х, линейно падает с уменьшением мощности
секции.

537
СЕКЦИОНИРОВАННЫЙ ДВИГАТЕЛЬ ОГРАНИЧЕННОЙ МОЩНОСТИ
и, (~)/д ~ — ь)хт (а = — Л ~Ъ Т).
(14.93)
Тогда для рассматриваемого маневра функционал У может быть запи-
сан в виде (секции полностью автономные)
(14.94)
У = х'е'~"'сИ (х (0) =х(0) =х(Т) =0 х (Т) =~).
Оптимальная программа а (~) такова:
(14.95)
Минимальное значение функционала задачи равно
Х
— 2
е ~" — 1
У = —,х ' 1 — 'е-'~"
— 3
Тз
Зависимость У (1/к) также показана на рис. 14.11 — сплошная кривая
и,— э со. Из рисунка видно, что, начиная с п,=10, точные и предельные зна-
чения функционала достаточно близки.
Р
.РХ РР Р~ РЮ 39
РХ РЮ Р~ Р8 09
~У~
Рис. 14.15. Максимальная полезная нагрузка в функции вероятности В успешного выполнения маневра
(соответствует рис. 14. $ 4).
3. Движение с возвращением. Пусть задано суммарное время движе-
Бия Т, за которое нужно попасть из одной точки покоя в другую и вернуться
обратно:
х(0)=х(0) =О, х (й) =Е, х(й ) =О, х(Т) =х(Т) =0 (0(й (Т). (14.97)
Такой маневр моделирует «быстрый» межорбитальный перелет с воз-
вращением. Функционал задачи в случае непрерывного закона повреждений
(14.93) складывается из двух интегралов:
Т
х2~$(кт~Ц+ ~$,(ът х2~(1-1,)/хт ~Щ
(14.98)
2. Непрерывный закон повреждений. При постоянной интенсивности
потока отказов ~ (г, ~)= — ~, уравнение (14.82), определяющее число непо-
врежденных секций и (1), интегрируется:

538
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 14
экстремали которых описываются соотношениями типа (14.95). Из вариации
момента времени 8~ получаем условие равенства квадратов ускорения слева и
справа от 81. Это условие позволяет отыскать оптимальное значение ~1:
г /хТ 1/х + — 1 гг/г Т
(14.99)
( — гг/хТ 1/х) ( 1/х г г/хГ) — 2 ( )
в~'/"7 — 1 — х 1 — ((1/х Т) (е~'/" Т вЂ” 1)
(1 — е '/ )(в'/ — 1) — 2 2
Решение этого уравнения 81 (1/х) представлено на рис. 14.16 пунктирной
кривой. Видно, что движение «туда» (О ( ~ ( ~1) происходит быстрее, чем
движение «обратно» (~1 ( ~ ( Т). Эта несимметрия возрастает с увеличением
1/1с, причина ее состоит в следующем.
На первом участке движения, пока мощность уменьшилась еще незна-
чительно, выгодно иметь большее ускорение, чем на последующем участке.
Такая программа реактивного ускорения обеспе-
г,~. чивает всюду достаточно большую скорость исте-
чения, т. е. малый расход рабочего вещества.
У 4. Движение с заданным активным временем.
фУ
Введем условие заданного времени работы двига-
теля Т„( Т Я 2 гл. 10). Мохсно показать, что
т /т=~
ФГ пассивный участок для рассматриваемого маневра,
г как и без учета повреждений, единственный и
Ж
расположен в середине траектории:
а(~)=0 при 0(~1(~(~2(Т.
Р Г
(14.100)
ю в ~~,'
Как показано в ~ 2 гл. 10, включение пассив-
ного участка в траекторию с идеальным двигате-
лем ограниченной мощности ухудшает характери-
стики. Если при выключенном двигателе вероят-
ность повреждения остается такой же как и при ра-
ботающем, то этот вывод, естественно, имеет силу и здесь. Исследуем случай,
когда на пассивном участке вероятность повреждения равна нулю, а на
активных постоянна и отлична от нуля.'
Рис. 14.16. Оптимальные
доли времени перелета «тупа»
(пунктир) и первого активного
участка (сплошные кривые).
Л = сопзС+О при а+О,
° Л=
0 при а=О.
(14.101)
Функционал для непрерывного закона повреждений (14.93) записывается
аналогично (14.98):
г, 7
— я2Е$/хТф + Е$г/хТ у2ЕИ гг)/хТЩ
о ~2
(14.102)
Внеинтегральные члены первой вариации (14.102) равны
1
ВУ = е~~1"~ 2х1 а ~~ Т а(1' а '~ а ~~1 2а(1)бх1—
хТ
1 1
— 2 а~~ Т а'и ох — 2х2 а2) Т а~2' — а2) М
1
— г~г~> г, -~-г( ~&g ; -~- ~& t
хТ
(14.103)
Здесь а('~ и а(2) — оптимальные программы реактивного ускорения на первом и втором
участках соответственно:
(1г (() Я1) + ((1)() -$/х7 (2& t; () (( 2 + ((2 () Ђ” ($ Ђ 7 Ђ” 7(х)
(14.104)

539
СЕКЦИОНИРОВАННЫЯ ДВИГАТЕЛЬ ОГРАНИЧЕННОЯ МОЩНОСТИ
(14.105)
хз — хднф хз — хд + (12 — 1д) хд.
Если ~ и ~ варьируются независимо с целью отыскания оптимальной протяжен-
ности пассивного участка, то из равенства ~У=О следует:
1 1
2х а'д& t + Ђ” а д' Ђ” а д + а 2' Ђ” (а'д )
~.Т 1 '- ъТ
ь
1
,и~ = о,,р — ы ~ ~- ~~, — ц &lt ар -; †,  =
1 1
а'д'+ — а'д' — а"-' + — а12~ = О.
.~Т 1 - '~Т
(14.106)
Три первых равенства с учетом последнего дают
адд' = аР' = О, (йз — йд) аР' =О.
(14.107)
Из последнего условия (14.106) имеем Ь1Ц =-Ьд~~) = Ь„тогда (14.107) дают
Ь,~,~-Ь~"=О, Ь,д,+ЬР'=О, (д,— ~,) Ь,=О.
(14.108)
Положить Ь,=О нельзя, так как отсюда последует Ь$"=ЬР'=О, т. е. а (й)=0. Следо-
вательно, ~ =~1. Это означает, что на оптимальной траектории пассивный участок, если
ие задавать время работы двигателя, будет отсутствовать (напомним, что при выключен-
ном двигателе вероятность повреждения предполагалась равной нулю — (14.101)). Если
протяженность пассивного участка фиксирована, ~,— ~д= Т вЂ” Т, то Ьд,= од„а три соотно-
шения, аналогичные (14.106), дают
Ь~д) = Цз) =Ьв, Ьд~д) = Ьд~з) = Ь, 2ЬЙ+ 2Ьдд .+ Ь (Т вЂ” Т ) =О. (14.109)
Проинтегрировав по участкам уравнения движения с а (~), определяемым (14.104) и
(14.109), найдем постоянные Ь, и Ь, из граничных условий маневра:
— т .гт Р' — 1 'ат
(1 -"" )+~ ~~ &lt 1+ Ђ” „ + Ђ
х х
& t; -т к  Р -т
— — 1 — е Р~" -д- — 1 — — е Р~" +
х Т
1
Ь
хТ
1
Ь
АТ
(14.110)
-- Ь, & t; Ђ” „ Ђ” 2) ( &l ; — -(- ) ~
1 Т, 1
— 1 — — & t; Ђ” „ Ђ”
=.~ з~Т 2.
Оптимальное расположение пассивного участка определяется из треть-
его соотношения <14.10 ), де Ь /Ь подставляе ся из пер ой форм лы <14
1+
1 Т„
<14.1
2 Т
2 &l ;1 -ту!
— г1/хт
Решение этого уравнения ~ /Т=/ <1 х Т Т) показ но сплошн ми к
выми на рис. 14.16. Видно, что распределейие времени работы двигателя
между первым и вторым активными участками, аналогично движению с воз-
вращением, несимметрично. На долю первого участка приходится меньшая
часть активного времени, в то время как при 1/к=0 было ~д=д/,Т .
2 р.
5. Нелинейная зависимость мощности от числа работающих секций.
Рассмотрим источник мощности, работающий по циклу Карно. Источник теп-
ловой энергии <нагревате ь с температу ой Т„<максим льная темпе
цикла) обеспечивает мощность дд'„. Неиспользованная тепловая энергия из-
лучается холодильником <радиатор м) со сред ей температу о Т &l
Скорости х1, х, и координаты х1, х2 по берегам пассивного участка связаны простыми
соотношениями'.

540
ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[гл. 14
мальная температура цикла). Если метеорные пробои представляют опас-
вость для работоспособности радиатора, то он разбивается на автономные
секции. Повреждение каждой секции приводит к уменьшению излучающей
площади.
Как известно, коэффициент полезного действия цикла Карно (коэффи-
циент превращения тепловой энергии в электрическую) равен
(14.112)
~, =1 — Т7Т„.
По условию теплового равновесия радиатор должен излучать мощность
(1 — ~,)Г„, т. е.
дУТзТ У
(14 113)
где Я вЂ” излучающая площадь радиатора, за — произведение степени чер-
ноты на постоянную Стефана — Больцмана.
На основании (14.112) и (14.113) получаем выражение для электрической
мощности (она же в идеальном случае и реактивная мощность):
(14.114)
У, У УТз ~Т Т)
Т„(~)— : Т;,
при 0(1(Т,
при —,, заЯ (1) Т„*~) Л„*,
при —,, з~3 (~) Т"„' ( У„*;
(14.115)
при этом температура Т=-з/,Т„считается допустимой для радиатора.
Программа регулирования тепловой мощности определяется из соотноше-
ний (14.113) и (14.115):
Ж„"~ при —, заЯ (1) Т„~ ) У„,
Ж„(~) =
М„*З УУЗ, при —," ,° Я Р) Т"„'(т„'.
(14.116)
Можно показать, что начальная площадь радиатора Яз при заданных Т„
и Ж, должна удовлетворять неравенству
—,, заЯзТ"„) Т„*.
(14.117)
Действительно, в противном случае, согласно (14.116), тепловая мощность
нагревателя никогда не будет использоваться полностью и его можно будет
заменить на нагреватель меньшей мощности, а значит, и меньшей массы.
Таким образом, оптимальное регулирование термодинамического циклз
источника мощности должно осуществляться по следующей схеме (см.
(14.115) — (14.117)). Температура нагревателя Т. поддерживается все время
на максимальном уровне Т,*. Тепловая мощность в начале движения такж~
максимальна. По мере пробоя секций радиатора его излучающая площадь
уменьшается, а температура Т увеличивается до тех пор, пока не достигнет
уровня Т=з/, Т„. С этого момента температура радиатора остается постоян-
ной, а тепловая мощность уменьшается пропорционально излучающей пло-
щади.
Предположим заданной максимальную тепловую мощность нагревателя
Г„, максимальную температуру в нем Т„и начальную площадь радиатора Я,.
Оптимальные значения температур Т„и Т в каждый момент времени должны
выбираться из условия максимума мощности (14.114):

ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРОВ
$4]
Уменьшение площади радиатора в предположении большого числа сек-
ций описывается уравнением (14.82), где и/и, нужно заменить на Я/Я,.
При постоянной вероятности пробоев получаем
(14.118)
Я (~)~Я е — 1/хт
1 — — ч ~ Ь~ 011 при О ~ 1 1„,
— е '~"~ (Ь2+ [Ь,~)
а(1)= ~
(14.119)
при 1 (1~Т.
Здесь
~ = Й* —,~~ Т*4
~„= — а Т 1п ч, х ' = — Я,Х" (3) Т~и, 1п Л
(14.120)
(~* (3) — зависимость среднего числа пробоев в единицу времени секции
единичной площади от толщины стенок о; Й =ЙЯ (О ( ~ ( 1) — начальная
уязвимая площадь радиатора).
Определив из граничных условий (14.94) постоянные Ь, и Ь„можно по-
строить зависимость У (ч, х). После этого нужно из условия минимума сум-
марной массы (14.73) найти оптимальные значения начальной площади радиа-
тора Яо толщины стенок 3, числа секций и„максимальной тепловой мощ-
ности Г„и максимальной температуры Т„. Для доведения этой процедуры
по конца нужно звать зависимость среднего числа пробоев секции единичной
площади от толщины стенок л* ( О) и зависимость массы двигательной системы
от всех перечисленных выше параметров: ЛХ„=ЛХ„(Г;, Т„", Я„е, и,).
4. Оптимальная вероятность выполнения транспортных маневров
В предыдущих параграфах главы обсуждалась задача оптимизации
при фиксированной вероятности выполнения маневра. Такая постановка
гарантирует, что с вероятностью Л каждая реализация данного маневра
Оудет успешной. Рассмотрим теперь «транспортную» задачу. Пусть в конеч-
ную точку траектории требуется доставить большое количество груза, такое,
что маневр придется выполнять многократно, или поставлена задача регу-
лярного снабжения некоторого пункта.
Из примеров решения задач Я 1 — 3 видно, что увеличение вероятности
успешного выполнения маневра для каждой попытки достигается ценой
уменьшения полезного груза, который можно доставить за одну попытку.
Значит, число успешных попыток, потребное для выполнения транспортной
задачи, при этом возрастает. Если уменьшать вероятность успешного выпол-
нения маневра для каждой реализации, то потребное число удачных попыток
уменьшается, но зато увеличивается число неудачных попыток, и суммарное
число попыток, начиная с некоторого момента, снова будет возрастать.
3ти рассуждения свидетельствуют о наличии оптимальной вероятности Л
выполнения маневра в каждой попытке, причем оптимальное значение Л
всегда лежит внутри интервала (О, 1), поскольку при Л=О равен нулю про-
цент удачных попыток, а при некотором значении 0 ( Л ( 1 обращается
в нуль полезная нагрузка.
1. Формулировка транспортной задачи. Рассмотрение проводится в рам-
ках схемы независимых испытаний: параметры аппаратов при каждой реа-
лизации маневра считаются идентичными, исход реализации не зависит'от
Условие минимума функционала У для рассматриваемого маневра пере-
мещения между точками покоя определяет следующую оптимальную про-
грамму реактивного ускорения:

ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
[ГЛ. 11
Р(ЯХ"'=О) = 1 — Л.
Р(М"'=ЛХ,) =Л,
(14.121)
Напомним, что вероятность успешного исхода Я и полезная нагрузкаМ„
согласно Ц 1 — 3, связаны между собой: М, уменьшается с увеличением Л
(см., например, рис. 14.9, 14.15).
Рассмотрим два варианта постановки транспортной задачи (в обоих слу-
чаях начальная масса аппарата и параметры маневра считаются фиксирован-
ными).
1'. Обеспечить максимум математического ожидания величины суммар-
ного груза Мз, доставляемого в конечную точку за фиксированное число
попыток и &g ;)
2'. С заданной вероятностью Л, за фиксированное число попыток п
перевезти максимальный суммарный груз М~.
В постановке 1' фигурирует математическое ожидание груза Мз, по-
этому на реализацию соответствующего решения можно рассчитывать только
в среднем при очень большом числе попыток (и &g ; 1 ли Мз )> ЛХ,). Ре
ция же решения задачи 2' гарантируется с заданной вероятностью Л, при
любом числе попыток. Помимо приведенных могут быть использованы и
взаимные формулировки, они будут перечислены в пп. 2 и 3.
При обсуждении сформулированных задач 1', 2' будет предполагаться
известным результат решения М.(Л) задачи предыдущих параграфов о мак-
симуме полезного груза при фиксированной вероятности выполнения маневра
для каждой реализации. В противном случае должна быть выписана
вариационная задача, отвечающая данному критерию оптимальности
(см. п. 2).
Рассмотрение транспортной задачи может быть проведено и в рам-
ках критерия стоимости аналогично ~ 1 гл. 10 из [14.9].Стоимость успешной
попытки равняется стоимости аппарата без полезной нагрузки (в предполо-
жении одноразового использования аппарата). В случае неудачной попытки
сюда добавляется величина ущерба, которая полагается равной стоимости
полезного груза (пропорциональна М,). Стоимость аппарата связывается
с массами основных его компонент формулами (10.1) — (10.4) из [14.9~.
Данные выше формулировки 1', 2' легко перефразируются в терминах
СТОИМОСТИ.
1'. Обеспечить минимум математического ожидания стоимости перевозки
заданного груза М~.
2'. С заданной вероятностью Л, обеспечить минимум стоимости перевозки
заданного груза М~.
В дальнейшем изложении используется критерий оптимальности в тер-
минах масс.
') При этом подразумевается, в частности, что аппараты повторно не используются.
предыдущих исходов'). Каждая ~-я реализация может иметь два исхода:
первый — груз доставлен в конечную точку траектории и второй — груз не
доставлен в конечную точку траектории. Это — два несовместных элементар-
ных события, они образуют полную систему возможных событий. Если обо-
значить через Я вероятность первого, то вероятность второго будет равна
1 — Д.
Будем характеризовать исходы ~-й реализации случайной величиной
ЛХ'" — массой, доставляемой в конечную точку траектории при ~-й реализа-
ции маневра. Если реализация успешная, то масса М"' равна полезной
массе М, на доставку которой рассчитывается при каждой реализации;
если реализация неудачная, то масса М'" равна нулю. В этих обозначениях
первое элементарное событие будет М'"'=М„а второе — М"'=0; вероят-
ности этих событий запишутся в виде

ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРОВ
2. Максимум математического ожидания суммарного груза (задача 1').
Запишем математическое ожидание1) величины суммарного груза ЛХв, до-
ставляемого за и попыток:
и И ~г
(Мв) =. ~ ~ ЛХ" ~ —— ,), (М"') =,~, [ЛМ, + (1 — Л) ° О] = пЛМ (14.122)
/ ~=1
(математическое ожидание суммы случайных величин равно сумме их мате-
матических ожиданий — см. [14.6]).
Из (14.122) видно, что задача 1' фактически не зависит от и и сводится
к отысканию максимума математического ожидания массы М", доставляемой
за одну попытку, по вероятности Л положительного исхода:
(М&lt " = Ђ” ( в = ах М, (
(14.123)
При известной зависимости ЛХ, (Л) это — задача на максимум функции
одной переменной. В случае отсутствия готовой зависимости ЛХ, (Л) нужно
выписывать полную вариационную постановку. Для этого введем текущую
величину (14.123), например, для односекционного двигателя Я 1):
(М<~ )  е ~ lt '&gt
(14.124)
где М. (1) = М, + М„(&lt ) И & t )  Й, И (Т) = Ђ” 1 Л. В ко ечный омен
О
мени (ЛХ< ), совпад е с (14.12 ) и зад ча своди с к отыска ию максим
конечного значения (14.124).
Чтобы получить формулировку Майера, запишем (14.124) в виде дифференциального
уравнения
— (М') = ( — ЛМ, + М,) е, (М<' g ;)& t; в ” †М, (0 , (М& t;'>)
и дрисоединим последнее к системе уравнений вариационной задачи о максимуме полез-
ного груза ЛХ,=ЛХ, (Т) при фиксированной вероятности Л. Граничные условия М, (Т)=
=-шах и Л (Т)= — 1п Л при этом нужно заменить на М, (Т)=орФ и Л (Т)=орФ. В случае
идеального двигателя ограниченной мощности (14.11) новая вариационная задача выгля-
д«т так (т=ЛХ/ЛХО):
-и &l ;~ ~~ l
— (т" ~) =- е — 1т
СИ тХ 2 й
(т" ~) = т, (0), (т"') = шах,
(и, + т.)~ а (и) а~
~д,.= — — ' ", т,(0) + т„= 1, т, (Т) =орЪ,
Х
1'=У г(0) = г„г (Т) = г„
у=ае+ я, т(0)=те, т (Т) =т&l
Л=) (г, Л<, ), Л 0) О Л Т) =
(а (&l ; ~ О   lt; Ж (& t ) ( 1  е г) = , т„, и
(14.126)
') Обозначается символом ( ).
Процедура построения и все свойства оптимальных управлений (14.11)
сохраняются и для (14.126). Поэтому ограничимся примером отыскания мак-
симума (14.123), воспользовавшись зависимостью ЛХ, (Л) из п. 2 ~ 1.
На рис. 14.17 показано математическое ожидание массы (ЛХв), приходящейся

° ° ° е
° а Й °
° $
1
$ ° Й 1 Й ° ° °
° вв! °
° ° $ ° ° ° Э
1 ° 1 в
е е ° ! е
3 И е Э 1 ° °
$ ° °
° ° 6 ° Э Э ° ! !
° ° $
й
$ ° Й °
° °
! е е е
а Э 1
1 е 6 ° 1 °
° ° й °
° е
1 е ° $ °
й
е в 1
! Э 11 е °
е Э в
$ ° ° $ ° ° °
° ! °
5 ° 9
$ $ й $ й ° 11 й °
й [в
11 1'
$ °
&gt
ай~
т~~~
И
991'
$ ° й
е ! е 9
° е
° °
й
916 5
е ° °
° °
й
1 ° е 6
° ° ° [ °
е ° °
$ $ ° Й
в 1 11
! °
° й !в Й °
° °
е ° е 1
° °
° ° ° °
° °
1 ° 1 ° 1 °
° °
° °
° $
° й ° °
° е
3 ' е1е
° ° ° в 1 ° °
1 й $ ° в
'ИИ
° °
° е
! Э 11 ° ° ! 1~
й ев
16 Э'
9 ' ° 5
° е ° ° е Э
Э
° й
° °
° °
° °
° й 1
91! $
/ /
й
$ ° Й $
е
° 1 й $ ° ° $ Э
в ° 1 ° °
° 1
ю 1 ° е
° 1
° °
~ ° °
1191
° а
° °
е 1 е
е ' ' ° Э Э
е °
° (
1 Э е
1 е
е 1 е ° ° ° °
1 ° 1 ° ° 3 ° 1 9 ° ° ° ве 1 1 °
° И
° И
в в а
° °
° ° °
° ° °
! ~ 1
° ° ! ° 1 °
° ° И ° °
° ' ~~ 1 ° ! !
° ° ! Ф ° ! ° !
° ° °
° ° ! в
! ° !
° ~& t;
1 °
г ° !
& t;
° ° ! °
° в °
1 ° ° 1
° °
ю 1 ! °
! ° °
° °
1 11 е °
1 ° 1 в 9
1 °
6 е
1 е ° ° °
° !Й1 ° ЙЭ е е !е''е ее
1 ° ! ° °
е 1 °
° в
° е
е
° ° ! в ° °
° ' ° ° ° 5~
° °
° ° В ° в
° В вввв ° °
° ° ° ° ° ° в ° °
° 1 ° 1 ° ! °
119в691!61
° ! $! ю ° ° ! ю ! в
5 ° 6 ° ! е ° 5
° в[ ° е е Э ° 1 ° ° !
° '96 Э! 5, 9' 1 ! ° е в 5

ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРОВ
$4]
(14.129)
Заметим, что ряд, стоящий в правой части (14.129), представляет собой раз-
ложение функции [1 — (1 — Л)] '"*+", поэтому математическое ожидание сум-
марного числа затраченных попыток будет равно ')
(и) = и„/В. (14.130)
Подставив в (14.130) выражение для и„(14.127) и отбросив знак целой
части, получим (и)=Мз/ЛМ,. Минимум (и) по Л при фиксированной ве-
личине Мг достигается, когда произведение ЛМ, максимально. Это означает,
что решения задач на минимум (и) и на максимум (Мз) совпадают с точ-
ностью до отличия дроби М~/М, от целого числа (последнее в рассматривае-
мом случае Мз &g ;) М„несущественн
3. Максимум суммарного груза при заданной вероятности реализации
решения (задача 2'). С вероятностью Ве будем гарантировать, что из и по-
пыток неудачных будет не больше чем Й ( и. Вероятность Л, склады-
вается из вероятвостей событий, составляющих данвое:
(14.131)
где Р~'~ — вероятвость того, что из и попыток веудачвых будет ~. Последвее
может реализоваться С„' способами. Вероятность каждого из них одинакова
и равна (1 — Л)'Л" ', поэтому Р„'"=С„'(1 — Л)'Л" '. Подставляя это выражение
в (14.131), приходим к формуле
тг В
К =Р Мо' и — й М = — Л'Д"' 14. 3
.у =1 =о
(биномиальное распределение для схемы независимых испытаний [14.6]).
При заданных Л, и и формула (14.132) определяет связь между вероят-
ностью Д успешвого выполвевия мавевра для одвой реализации и числом
неудачных попыток Й: Й=Й (Л, Л„и) (рис. 14.20).
Согласно (14.132) с вероятностью Ле суммарный груз М~, доставленный
за и попыток, будет ве мевьше
(14.133)
поэтому задача 2' сводится к отысканию максимума правой части неравенства
(14 133)
(14.134)
М~ = шах [и — Й (Л)] М, (Л)
по вероятвости Л успешвого одвократвого выполвевия мавевра.
') Соотношение (14.130) можно было выписать сразу, исходя из статистического
определения вероятности.
35 Механина полета
где Є— вероятвость того, .что веобходимое число п„удачвых попыток ва-
бирается ровно на и-й попытке (не раньше и не позже). Это событие состоит
в том, что из первых и — 1 попыток и — и. веудачвые, а последвяя, п-я, по-
пытка удачная. Такая ситуация может быть осуществлена С"-,"' равноверо-
ятными способами (число сочетаний из и — 1 по и — и ), вероятность каждого
из них (1 — Л)
Обозначив г = и — и, получим формулу для (14.128) в виде

ВОПРОСЫ НАДЕЖНОСТИ В ЗАДАЧАХ ОПТИМИЗАЦИИ
~ГЛ. 14
фЮ Р7 Р8
Я' ~7 ~Я
Рис. 14.20. Оценка (с вероятностью В,) доли неудачных попыток.
Р7
~~ Люау
Р4 Р8 1~
~~~д
л/%
РФ ~Ю УГ
Рис. 14.21. Оптимальная для задачи 2' ве-
роятность успешного выполнения маневра
в каждой попытке. Сплошные кривые—
перемещение между точками покоя, пунктир-
ные — набор скорости.
Р ~У ~8 ~3 ф Ащу~
Рис. 14.22. Максимальная величина~ груза,
доставляемого за одну попытку (соответствует
рис. 14.21).

$4)
ОПТИМАЛЬНАЯ ВЕРОЯТНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРОВ
Пример решения задачи (14.134) для зависимости М, (Л) с рис. 14.9 при-
веден на рис. 14.21, 14.22. Там показаны оптимальная вероятность Л и мак-
симальная величина суммарного груза Мг, приходящаяся на одну попытку из
п затраченных, в функции Л „— максимально возможного числа отказов
за время Одного полета.
При увеличении вероятности Л, реализации решения величина груза
Мз/и падает; это влияние уменьшается с ростом общего числа попыток и.
При больших и решение задачи 2' (рис. 14.21 и 14.22 при и=50) приближа-
ется к решению задачи 1' (рис. 14.18 и 14.19).
При исследовании задачи 2', помимо использованной выше, могут упо-
требляться эквивалентные формулировки: с заданной вероятностью Л, пе-
ревезти заданный груз за минимальное число попыток и или обеспечить мак-
симальную вероятность Л, перевозки заданного груза Мв за фиксированное
ЧИСЛО ПОПЫТОК И.
4. Замечания обзорного характера. В серии работ [14.10 — 14 12] рассматривается
другая постановка задачи об управлении многосекционной ненадежной двигательной си-
стемой. Задача формулируется в духе работы [14.13], краткое изложение которой было
дано в $ 1 гл. 13. Выводятся необходимые условия оптимальности типа принципа макси-
мума Л. С. Понтрягина. Предлагается численный алгоритм, с помощью которого выпол-
нены расчеты перелетов с заданной пачальной орбиты на заданную круговую орбиту при
наличии отказов параллельно работающих секций двигателя.
Отметим еще одно направление в теории надежности, основы которого были зало-
жены в работах [14.14, 14.15] и которое получило дальнейшее развитие в [14.16, 14.17].
Здесь предлагаются способы получения гарантированных оценок надежности системы при
неполной информации о надежности ее элементов. Возможности управления заключаются
в выборе моментов включения резервных элементов в нагруженный режим. Перебои
в работе системы считаются недопустимыми, включение резервного элемента в работу
должно быть произведено до отказа основного элемента. Априорная информация о вероят-
ностных характеристиках отказов неполная, папример, известно только математическое
ожидание и дисперсия времени безотказной работы элемента в нагруженном режиме.
Максимизируется гарантированная оценка среднего времени безотказной работы системы
в целом.
В качестве непосредственного приложения полученных в указанных работах резуль-
татов к проблемам механики космического полета отмечается задача поддержания бес-
перебойной работы системы спутников связи. Поскольку время вывода на орбиту конечно,
то в этой системе решение о запуске очередного спутника должно быть принято по того,
как произойдет отказ одного из действующих спутников.

ГЛАВА 15
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ ПРОГРАММ
УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
В данной главе рассматривается игровой подход к одной задаче из класса проблем
управления, которые в общих чертах можно охарактеризовать следующим образом.
Пусть движение объекта описывается системой дифференциальных уравнений; в правых
частях присутствуют уиравляющая и возмущающая функции; дано условие остановкидви-
жения; контрольным функционалом является модуль отличия от заданной величины
функции конечных значений фазовых координат (точность попадания в заданную точку).
Задача состоит в том, чтобы по имеющейся априорной информации о возмущающем воз-
действии сконструировать алгоритм управления, т. е. указать правило, в силу которого
назначается величина управляющего воздействия на основании измерений вдоль траекто-
рии фазовых координат и возмущения; алгоритм настраивается на минимум контрольного
функционала.
Если возмущение ограничено, а управление не ограничено, то возможен подход,
опирающийся на принцип инвариантности. Здесь назначается произвольная номинальная
траектория, приходящая в данную точку; в процессе движения управление выбирается
так, чтобы действительная траектория в некотором смысле отслеживала номинальную
(это возможно, ибо управление не ограничено); в данном случае движение при любом за-
коне возмущения оканчивается в заданной точке — промах равен нулю.
Пусть, в отличие от предыдущего, управляющее воздействие ограничено. Тогда
построение алгоритма управления существенно зависит от имеющейся априорной инфор-
мации о функции возмущения. Если заданы вероятностные характеристики последней, те
алгоритм получается в результате решения задачи финального управления стохастиче-
ским процессом (см. гл. 16). И, наконец, могут быть известны лишь границы, в которых
изменяется функция возмущения, и неизвестен закон распределения внутри известноге
диапазона значений возмущения в каждый момент времени. Эта неопределенность оста-
вляет возможность предположить, что возмущающее воздействие активно противодей-
ствует достижению цели управления. Таким образом, возникает игровой подход к построе-
нию искомого алгоритма, где считается, что управление устремляет траекторию в задан-
ную конечную точку, а возмущение активно препятствует достижению этой цели.
В главе излагается игровой подход на примере построения алгоритма, управляющего
спуском космического аппарата в атмосфере. В этой задаче управлением является угол
крена, а возмущением — отличие функции плотности атмосферы от номинальной.
Про функцию плотности известно, что она изменяется внутри известного диапазона.
Контрольным функционалом является модуль промаха, т. е. модуль расстояния между
действительной и желаемой точками посадки.
Построению алгоритма управления при движении космического аппарата в атмосфере
посвящена работа [15.1]. Теория и примеры решения отдельных дифференциальных игр
описаны в монографиях и статьях [15.2 — 15.11]. Подход, аналогичный развиваемому
в данной работе (возмущение — активная противодействующая сила), применялся
в [15.11]. Изложение следует схеме статьи [15.12].
~ 1. Описание маневра спуска аппарата в атмосфере
1. Исходные уравнения движения. В инерциальной геоцентрической
системе координат (Окуз) движение аппарата в атмосфере описывается си-
стемой обыкновенных дифференциальных уравнений шестого порядка
(тяга и расход массы отсутствуют):
г=у, 5
(1 Л)
т=~+К;
здесь т=(ю, у, з) — радиус-вектор, т=(ы, ы„, ы,) — вектор скорости, ~—
вектор гравитационного ускорения, 1 — вектор аэродинамического ускоре-

549
ОПИСАНИЕ СПУСКА АППАРАТА В АТМОСФЕРЕ
(15.2)
где р, ~ — константы гравитационного потенциала Земли, г=~г~, 1Р— еди-
ничный вектор, направленный на северныйполюс. Аэродинамическое ускоре-
ние записывается так:
~ = 1р хЧ3'[ — Яе — ЙГе]
(15.3)
где Я вЂ” скорость аппарата относительно неподвижной среды:
ЧЗ=т+О[г Х 1~0], ЪО=Щ/Ч3, Ч3=~Ч3~,
Г' — единичный вектор подъемной силы:
Г' = [Ь' &g ;( ]е оя ~+ [Щ &g ;( Ье ) Я3 е
(15.5)
~„(Й, ~, )) — номинальная функция плотности, ее аргументами являются
высота Й над поверхностью Земли, широта ~ и гринвичская долгота Л,
фактор неопределенности в знании атмосферной плотности (возмущающее
воздействие), показывающий, во сколько раз действительная плотность от-
личается от номинальной, х — баллистический коэффициент аппарата, Й—
аэродинамическое качество аппарата, Й вЂ” угловая скорость вращения
Земли, т — угол крена (управляющее воздействие), Ье — фиксированный
в инерциальной системе координат единичный вектор, он выбирается нор-
мальным к плоскости внеатмосферного движения; верхний индекс «нуль»
при векторах в формуле (15.5) и в предыдущих формулах относится к нор-
мированному вектору.
В начальный момент ~=0 движение характеризуется шестью заданными
величинами г, и ~„:
г(0) = г„
т(0) =т,.
Условие окончания маневра — достижение заданной высоты:
Ь[Т) =Ь„
(1 .7)
вектор промаха В=г (Т) — г (отличие конечного радиуса-вектора г (Т) от
радиуса-вектора точки посадки г,) можно спроектировать на фиксированную
в пространстве плоскость (например, плоскость внеатмосферного движения)
и на нормаль к этой плоскости; первую проекцию будем называть промахом
по дальности 3А, вторую — промахом по боковой проекции 3Л 1):
3А= (г(Т) — г,)[Ье &g ; 8 >( Ь'] =Ь( )
ой = ВЬ'= (г(Т) — г) Ье = Й (Т) — Й .
(15.8)
Для краткости последующего изложения запишем рассматриваемую
задачу в следующем общем виде.
Дифференциальные уравнения:
х,.=~,.(х, с, ~) (х,=х, х2=у, х,=я, х,=и, х,=и„, х,=и,). (15.9)
Начальные условия:
.г,.(0) = х,,
(15.10)
') Вектор скорости в финальный момент (15.7) не контролируется, ибо на малой
высоге й, все спускаемые аппараты имеют приблизительно одинаковые векторы скорости.
ния, точкой обозначено дифференцирование по времени ~. Выражение для
гравитационного ускорения с учетом несферичности Земли имеет вид

550
[ГЛ. 15
ПОСТРОЕНИЕ ПРОГРАММ ~ПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
(15.11)
оа (,. (т)) = о.
2. Линеаризованные относительно номинальной траектории уравнения
движения. Представим задачу (15.9) — (15.11) в линеаризованном виде. Для
ЮЯ этой цели укажем номинальный закон
Й возмущения ~со' (1) и построим соответст-
вующий номинальный закон управления
усе' (1), при котором выполняются конеч-
ные условия (15.11); в окрестности но-
минальной траектории х(о) (1) уравнения
Ю (15.9) могут быть записаны в линейном
приближении относительно вариаций'):
Й 3х,. (1), о~(1), о сов т(1), о з)п т(1).
Номинальный закон возмущения сле-
дующий:
Рис. 15Л. Номинальный закон управле-
ния у(0)(М).
(15.12)
(со& t;
0 или т~ при
т~/2 при
— т~/2
0 при
(15.13)
,сос р)
.~ = сопяФ при
где 1„ 1, — моменты, подбираемые из условия попадания в заданную конеч-
ную точку (ВЬ= ВЙ=О), интервал (1„1,) приходится на участок вылета ап-
парата из атмосферы. На рис. 15.1 приведен характер зависимости 7'о' (1)
для некоторого набора параметров задачи.
Определим в линейном приближении, как влияют отклонения возмуще-
ния 3~ (1) и управления 8~ (1) от номинальных законов на выполнение ко-
нечных условий (15.11).
и сопряженную к ней:
Рассмотрим систему уравнений в вариациях
(О) д~(О)
бх;= от + осеет+
дх- ~ дсояу
.у=1
д~(о) д~(о)
д з1пт д~
о з1п т+ бЕ,
(15.11)
Если назначить конечные условия для функций р; (~) такими:
д~со' (Т) д5сос (Т) ~со) (Т)
дт; дт; йсос (Т)
(15.15)
то вариация оЬ (Т), в соответствии с известными свойствами сопряженной системы, за-
пишется в виде
Т 6
д~; д~; . д~~
ы = р! ~ соя 1-с- р! . б 1п1.с. р~ — ~ц) ы~.
с дсояу д яп у д~
(15.15)
О э=1
1) Запись уравнений в вариациях через о соз т (й), о з1п т (й), а не через Вт (й) свя-
зана с разделением задачи, описанным ниже.
Конечные условия:
ь(,. (т)) = й„~ь (,. (т)) = о,
номинальный закон управления выбирается
из такого класса (рис. 15.1).
0(~(~„
~1(~(~2
1,(~(1,и
~з(~(~„
~,(~(т,

551
ОПИСАНИЕ СП~СКА АППАРАТА В АТМОСФЕРЕ
Для второго набора сопряженных функций р~ (~) назначим следующие конечные значения:
(15.17)
тогда вариация ЬР запишется так'.
д~; д~; д~;
~Р— р,, ~созе р, . Окопу р,
О а=1
(15.18)
Пусть управляющее 7 (~) и возмущающее ~ (~) воздействия стеснены следующими
ограничениями.'
— т~<7 ~) l ;т~ ( в ” 1 - в1 7(~), с я7(1
~- & t ~ г & t; + - ~+
(15.19)
Переходя к вариациям а соя 7 (~), о я1п 7 (~), б~ (~), имеем~
— 1 & t; оя 7 е> (~) а со 7( ) & t 1 †1 & t; я1п 7 а~ ( )+а
~- & t; 1+ ~~ ~ &l
(15.20)
Чтобы сравнивать влияние управления и возмущения, удобно ввести новые пере-
менные управления и возмущения, изменяющимися в одинаковых пределах:
а соя 7 = и — соя 7< & t;, а в п 7 = а ~ я п 7 ~ в ” в1п
ЬИ. ='/2 к'+ 1 ) — 1+ '/2 к' — 1 ) У;
(15.21)
при этом
— 1 & t; и( ), и 1) lt;1 а= 1 и и
(15.22)
Подставив новые переменные в выражения функционалов (15.16), (15.18), по-
лучим
Ы = фа~+ [А~ (~) и — В~ (~) и+ С~ (~) ~ Я1п 7 (~) ~ а! Ж,
О
(15.23)
оР =фф+ [А~ (й) и — В~ (й) и+ Са (й) ~ я1п 7 (й) ~ а) дй,
О
где
1,', = Р1, Ы
д~,
д Я1пу
(15.24)
[1,И
О
Численные расчеты показывают, что в выражении для Ы член С~ (~) ~ в|п 7 (~) ~ а
значительно меньше двух других и может быть отброшен; в формуле для ЬР по ана-
логичным соображениям следует удержать лишь член С~ (~) [ в1п 7 (~) ~ а.
У 6
О с=1
д
д~;
д соя у '
дР (Т) дй (Т) Р (Т)
дх; дт; Ь (Г)
д2, Ы
~+ — ~ р, д~;
2 д~

552
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
~ГЛ. 15
Опуская верхние индексы у коэффициентов, получим следующие выраже-
ния для функционалов:
с~ = ф„'+ ~А (~) ц — В (~) п~ ж,
О
У
~~ = — ф', + С(г) ~ з1п ~ (~) ~. (г) ~~.
(15.25)
ом, в избранной системе координат (Ь, .О) движениеразде-
ом описании на два: продольное, характеризуемое первой
формулой (15.25), и боковое, характеризуе-
мое второй формулой (15.25).
Управление продольным движением обес-
печивается фактором сов т (1)=и (1). Функ-
ция т (~) должна выбираться либо из проме-
жутка — ~ (~ 7 ( О, либо из промежутка
О ( 7 ( ~; смена знака 7 на — т не влияет на
продольное движение. Если величина соя ~
уже определена из продольного движения,
то боковое управление обеспечивается посред-
ством смены знака 7 (переворот ~=+1).
На рис. 15.2 даны примеры функций А (~)
и функций В (~) для различных значений
~' ( ~ =1/ ~').
3. Линеаризация уравнений движения
в точке. Рассмотрим еще один способ упро-
бХ
щения исходной задачи, основанный на иг-
норировании бокового движения и линеари-
зации уравнений (15.1) — (15.5) в точке. Пред-
лагаемая весьма грубая процедура отобра-
жает не более чем качественную сторону
решения проблемы. Отмеченная ранее для
линейного приближения независимость про-
дольного движения от бокового может быть
распространена на общий нелинейный слу-
чай. Тогда в плоскости внеатмосферной траек-
движения аппарата могут быть записаны в виде (см., на-
Таким образ
ляется в линейн
Рис. 15.2. Примеры функций А (1)
и В (1) для различных значений $+.
тории уравнения
пример, И 5.13 ])
Й = п в1п 5, д = — д (Й) в1п 5 — 1р (Й) хп',
~ ~ ~~со~Р'
(15.26)
Здесь через Й, г, д (Й), Ь, р, х, Й, ~, т, и обозначены те же величины, что и
в предыдущих пунктах параграфа; р (Й)=ре-"~"-"& t; Ђ” плотно ть атмосф
согласно экспоненциальной модели; а — величина, обратная шкале высот;
р — плотность на некоторой фиксированной высоте Й; Земля предполага-
ется правильным сфероидом, поэтому г=Л+Й, где Л вЂ” радиус сферы; 5—
угол между вектором скорости и местной трансверсалью; функции ~ (1),
сов т (Г) — возмущающее и управляющее воздействия соответственно.
Рассмотрим малый участок (О ( ~ ( Т) траектории, расположенный
в окрестности точки максимального скоростного напора. Пусть на этом ма-
лом участке высота Й, скорость и и угол наклона траектории 0 отличаются от

553
ОПИСАНИЕ СПУСКА АППАРАТА В АТМОСФЕРЕ
соответствующих фиксированных величин Йо, го, ос=0 столь мало, что в пра-
вых частях системы (15.26) достаточно сохранить лишь линейные члены раз-
ложения по отклонениям ЛЙ=Й вЂ” Йо, Лг=г — го, О:
ЛУ = — д,Π— Л~хоор';, — 2хооУ,ЬУ вЂ” х — У,ЬЙ,
(О О О Ий О
ЬЙ=©
(15.27)
О= — ' — — о+ — + —,' Лп+~сос, ~сх~ор А =и +Ьп.
~О ~О ~О ~0
Здесь до=у (Йо), р,= р (Йо); отклонение фактора ~ от 1 считается малым, что
позволяет считать ~ЛЙ=ЛЙ и ~Ли=Ли; кроме того, величина Й мала, поэтому
можно пренебречь в правых частях членами вида ЙЛЙ и Й Лг. Предположим
также, что весь исследуемый класс траекторий
м
Юно
лежит в узкой трубке траектории, так что по
значениям фазовых координат в конце рассмат-
риваемого участка Й (Т), п (Т), 0 (Т), Л (Т)
можно определить конечное значение даль-
ности Л„., опираясь на линейное представление
вида
(О)
-)- (Й(т) — Й" (т)) '— ,'„'",
(15.28)
Рис. 15.3. Вид функций А (й), В (В).
где п'о' (Т), О'о' (Т), Й'о' (т) — значения скорости, траекторного угла и высоты
в момент 1', соответствующие некоторой средней траектории,' Ь~"„' — прира-
щение дальности средней траектории от точки, соответствующей моменту Т,
до конечной точки; дЬД/дп, дЯ,",/дО, дЕ~(к/дй — изохронные производные от
дальности, посчитанные на участке средней траектории, начинающейся в точке,
соответствующей моменту Т; дальности ~, и Ьт отсчитываются от точки,
соответствующей моменту ~ = О.
Введем сопряженную к (15.27) систему
~ РО
Рэ = Р ~~~О~Π— Рд Д ~ У, 1 РР~
Г О О
(15.29)
Ре Р/Ро + РаКо 1еь
С УСЛО~ИНМИ ~ МОМЕН~ 1 = Т
дИтк
(О)
Ро(Т) =—
Дй
(15.80)
р,(Т) =1;
тогда формула (15.28) записывается в виде
(О)
Е,о = Е, (О) + р&g ;, О) Ыв О + р, О) Ьц О + ре О о О + БД Ђ " ЬЬ (Т)
(О) (0)
— Ь~ Т О ~0 Х у2
д, Т) '( ) де(Т) ~(Т)+ Рг,'о+Ре д ~ д,—,, + р "ро'о "'+
(15.31)
+ ( — р„хроиооЦ + рейхиооо~ сов 7) «е.
О

554
[ГЛ. 15
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
Отклонение дальности Ь„от заданного значения 1,' может быть пред-
ставлено следующим образом:
(15.32)
где
(15.33)
Р[) Р
В = Р,~~,~ОГО,
и= соя ~,
Пример функций А (~) и В (~) приведен на рис. 15.3.
~ 2. Алгоритмы управления спуском аппарата в атмосфере
1. Управление продольным движением в модели (15.25). Рассмотрим
первую задачу (15.25):
оБ = Д+ ]'А (~) и (~) — В (~) и(~)] й ( — 1 (и (~), у(~) (1). (15.34)
Цель управления и (~) — уменьшить модуль величины 3Ь, цель возмуще-
ния и (1) — увеличить модуль 8Ь.
Рассматривается игра с полной информацией, т. е. противникам известно
взаимное поведение вплоть до текущего момента ~. Таким образом, управ-
ление и возмущение выбирают свое поведение и (~), и (~), зная функцию
Как следует из рис. $5.2, функции А (~) и В (~) характеризуются следующими свой-
ствами'.
А (~) ) | В (~) | при ~ ~ [О, ~2), 1
А (~2) = В (~2)
А (~) ( В (~) при ~ ~ (~, Т],
(15.35)
т. е. на [О, ~а) управление влияет на функционал сильнее, чем возмущение, а на (~„Т],
напротив, возмущение влияет сильнее, чем управление.
Представим функционал ($5.34) в виде
И =ф[+ [А (~) и — В (~) п] И, ф[=фо~+ [А (1) и — В (~) п] И
(15.36)
и исследуем оптимальное поведение и*, г* после момента ~2.
В дальнейшем будет показано, что существуют пары оптимальных стратегий
и"' (1) и г* (1) таких, что если управление и возмущение придерживаются
их, то плата равна цене игры бь. Если же какой-либо из участников отклоня-
ется от этих оптимальных действий, то его противник, основываясь на упо-
мянутой информации, монсет добиться изменения платы в выгодную для себя
сторону.
Далее будет указан оптимальный алгоритм управления и (~, и (~)), об-
ладающий следующими свойствами: если возмущение г (1) следует оптималь-
ному поведению г"' (1), то управление и (1), построенное согласно оптималь-
ному алгоритму, совпадает с соответствующим и"' (1) и плата равна цене
игры бь, 'если возмущение г (1) отклоняется от оптимального поведения г~ (1),
го управление и (1) по оптимальному алгоритму таково, что плата ] 8Ц мак-
симально мала, т. е. ошибка возмущения используется максимально.

$21
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ АППАРАТА
При т ~ (тй, Т] возмущение влияет сильнее, чем управление, поэтому
] ~*] =1: п*= — щпф1 (~,(т ( Т),
(15.37)
ответное значение управления и (т):
и*=1 при и*=1, и*= — 1 при г*= — 1.
(15.38)
На функциях (15.37), (15.38) функционал И принимает значение
(15.39)
Ы =ф! — в1а'пф~ [А (т) — В (~)] И
] Ю ] = ] ф[ ) — [А (~) — В (т)] И~.
(15.40)
С = [В (т) — А (т)] Ит;
(15. 41)
сри ф.', =0 формула (15.37) теряет смысл, оптимальное поведение и* не единственно:
г' = +1 или — 1.
(15.42)
Если возмущение отклоняется от оптимального поведения (15.42), то
— я1дп ~ и Ви й, если 6.,' и — Вг й
г2
— 1 при — п(~) & t; Ђ  и Я+ Аи Ђ” и) И
й(1) =
(15.43)
— п (~) при — 1 ) — п (~) ) 1 и Я+ (Аи — Вп) й = О,
+1 при уп(~)) 1 и Я+ (Аи — Ви) В=О,
Ф2
8~[Ц, Т].
Эта формула описывает оптимальный алгоритм управления, определен-
ный выше; оптимальный алгоритм имеет следующую интерпретацию: управ-
ление и (1) устремляет движение к «средней» траектории, вдоль которой
~,+ (Аи — Ви) В=О.
(15.44)
При ~ ~ [О, ~,) управление влияет на функционал сильнее, чем возмуще-
ние, и если ф,' принадлежит допустимым значениям, то может быть выполнено
условие
(15.45)
Минимальное по ф~ значение платы ] ОЬ] достигается при ф~ =О. Предположим,
что за счет выбора управления и (т) на [О, 8,] условие ф~~ =0 может быть выполнено;
тогда формулой (15.40) определено значение цены игры

556
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ [ГЛ. 1~
реализующее (15.45), имеет, на-
Правило, выбора управления и (~),
пример, такой вид'.
и (1) = — я~~в~„' при
и" (1) = — ц (1) при
0(е(ю„1
~1( ( 2»
(15.46)
где момент 1, определяется из условия
— А ~ Ж Я1дП~О~ — В 1 УЙ=
О О
(15.47)
Согласно соотношениям (15.46), (15.47) сначала текущее значение функ-
ционала
~~ (~) = Д+ [А (~) и — В (~) п] И
(15.48)
максимально быстро делается равным нулю за счет выбора крайнего значе-
ния управления, а затем это нулевое значение функционала «отслеживается»
до момента ~,. Значение фо' принадлежит допустимым, если определяемый по
(15.47) момент ~ наступает раньше
Таким образом, оптимальные возмущения и управления имеют вид
и"(~) не определено при ~»= [О, ~,),
ц (~) = +1 или — 1 при ~ ~ [~„Т~,
и" (1)= — з1цпД при 1 ~ [О, 1),
й (1) = — и (1) при 1 ~ [1„1,),
и" (1) =+1, если п" =+1, и и" (1) = — 1, если й= — 1, при 1~[1„Т~; ~
(15.49)
С (~) [ В1П Т (О ~ о И) "~
(15.50)
Рис. 15.4. Цена игры С в функции
верхнего предела возмущения ~+. ГДЕ ~ З1П 1 И) ~ возмУщение Р) = +
управление; по сравнению с (15.25) здесь внеин-
тегральный член фо1 считается равным нулю (этого можно добиться выбором
параметров внеатмосферного движения), функция С (~) — положительная
на [О, Т1
цена игры определена выражением (15.41); оптимальный алгоритм управле-
ния определяется соотношениями (15.43), (15.46).
Для рассматриваемой задачи были проведены расчеты, в результате
которых определена цена игры как функция предела ~+ изменения плотности
Ю (д' (~ =1/~+) (см. (15.20) (15.21)). На рис. 15.4
дана эта зависимость.
Отметим, что в исследуемом линейном при-
ближении цена игры равна нулю, если 1 (
( ~' ( 1,4; следовательно, в этом диапазоне
б управление влияет сильнее, чем возмущение нг
всей траектории.
2. Управление боковым движением в мо-
дели (15.25). Вторая задача (15.25) относится
5 к управлению боковым движением:

2]
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ АППАРАТА
557
(15. 51)
при этом
а (0) = +1, а (11) = — 1, а (~",) — +1,
или
(15. 52)
а (0) = — 1, а (~",) =+1, а (~2) = 1,
оптимальное поведение возмущен
щения состоит в том, что
] е1п'у(~) ~=1 при ~ (. [О, ~1),
[ е]п 1' (1) ~ = 1 или О при г 1- [г1, г2),
° ° ° ° ° ° ° ° ° ° °
] е1п т (~) [ = 1 или 0 при ~ ~ [~', Т~;
(15.5,3)
цена игры:
(15.54)
Поя
оясним выписанные соотношения ~15.51—
оя я ( .51) — (15.54) на примере и=1 (рис. 15.5).
~~~ ю~~~~~ ~ыор~~м ~~жмалжое значение [ я1п 7 (~) [ = 1; ~м~~
(15.55)
Начиная с ~д, возмущение может
ожет принять два значения: ядп у Ю ~ = О или
и [ я1п 7 [ = на [~',, Т] величина конечного смещения Ж ~Т~ =бй Ч*' п и
конечное смещение 6Й (Т) = О, т. е.
У Я]ят уЯ~афй
т
1
С, = бй (~",) = — С (~) Ю.
о
(15.56)
Если момент переключения сместить вп аво
т момента ~„определенного уравне-
Ф
вием (15.55), то для возмущения:
] я[ну (~) [=1 на [О, ~",+М1] и
[ я[п 7 (~) [ =О на [~", + И"„Т], (15.57
Рис.
. 15.5. К выводу цены игры для задачн
управления боковым движением.
величина конечного бокового сноса превысит цен иг ы.'
) Ц7 (г[) = С Если, напротив, момент пе
тив, момент переключения сместить влево на 6~", от 8„
то при законе возмущения [ я[п т (~) [ = 1 всю на
будет равен
всюду на [О, Т] конечный боковой снос
(15.58)
Игровая задача формулируется следующим об азом: е
~~Ы, (~) ~ — ~жси~из~~~ы б
ния — минимизировать ~ ВЛ ~ выбором моментов
число которых и задано.
оптимальные моменты пер еклю
из условий
2 з ~„определяются

558
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ [ГЛ. 15
(15.59)
)М(т))>
Опишем оптимальный алгоритм управления, т. е. правило формирования оптималь-
ной управляющей функции о (~) по произвольной функции возмущения ~з1п т (~) ~.
Для оптимального возмущения (15.53) таким правилом является (15.51), (15.52). Пусть
до момента ~ двинсение известно, т. е. известны функция (з1п т (~) ) и моменты переключе-
ния ~,',..., ~„( ~ функции а (~), боковое смещение Ю (~) равно
6 а Р) = С Р) ) э1п ( Р) ~ ° Р) а.
О
(15.60)
Момент ~~+1очередного переключения из и — Й оставшихся наступает тогда, когда
выполняется равенство
1
(»+~) ) 2(и — Й)+1
С (~) Ю.
(15.61)
Доказательство оптимальности этого момента может быть проведено аналогично
данному выше относительно момента ~1.
3. Управление продольным движением в модели (15.32). Рассмотрим
соотношение (15.32) с учетом ограничений
(и, и,) О).
(15.62)
— 1(и(~)(1, у (и(~)(и,
Функции А (~) и В (~) обладают следующими свойствами:
А(~))В(~) при ~ ~ [О, ~з),
А (~,) = В (~,),
А(~)(В(~) при ~ (= [~„Т],
(15.63)
И (~,) = ~е+ (Аи — В) и сИ = ~,'".
(15.64)
В момент ~ (О (~ ~г (~ ~,) эта цель достигается. Посредством применения
алгоритма и(2) накопленное к моменту 1, значение 3Ь сохраняется вплоть
до момента ~., (определение ~, дано в (15.63)), т. е.
(15.65)
(Аа — В) пав=О.
т. е. на интервале [О, ~,) подынтегральный множитель при и в (15.32) может
быть сделан любого знака (управление и «сильнее» возмущения и), на ин-
тервале [~„Т] этот множитель может быть только отрицательным (возмуще-
ние и становится «сильнее» управления и). По-прежнему цель управления
и (~) — минимизировать ~ 8Ь (Т) ~, цель возмущения и (~) — максимизировать
~ Вг (Т)~.
Опишем структуру оптимального алгоритма управления, определенного
в п. 1 настоящего параграфа.
Интервал (О, Т) содержит четыре различных по целям элементарных
алгоритма управления: и'~' относится к интервалу [~„1г); и"' — к интер-
валу [1г, 1,); и'з' — к интервалу [1„1з); и'4' — к интервалу [1„Т]. Цель управ-
ления по элементарному алгоритму и'1) — накопление заданного значения
текущей дальности 3Ь (г):

ОРИТМЫ УПРАВЛЕНИ Я СПУСКОМ АППАРАТА
559
На интервале [~ ~ )
ва заданнои траектор
ФУ
.у элемента ный
р алгоритм и' ' удерж
рии, так что интеграл
рживает процесс
(Аи — В) ий
И (~,) = ~ + (Аи — В) и й = ' „
— (~з
(15.66)
Тогда значения ~Ь вычисляют
вычисляются по соотношению
=~,+ (Аи — В) ий
— 1 (и( 1).
(15.67)
Заметим
тим, что всюду на [1 Т
Максимальное
а „~ имеет мес
и минимальное
есто неравенство А (~) (В
ражениями
по и (г) значения 8Ь определяются иы-
т
~г
т
„= ~ + (Аи — В) и й, 3Ь ,„=~,+ (Аи — В)и й,
(15.68)
где и (г), и (г)—
+ ~ ~ — управляющие ~
~ункц~~, выбираемы
клон ени"; °
в ответ на
й; чтооы его
венно. Разность ~Ь „— 8 . е
тах
действия
б нимальной, необходимо, чтобы
и (г) = — 1, и (г) =+1;
тогда
(15.69)
~ь „— ~ь
„— Ь „=(и — и) Вй—
— Ъ+ ' и) Ай.
(15.70)
~з
(15.69) жже~~~~~ п ав
пределим величину фз из 15.67
и управлений центр диапазона
— °
зона отклонений прихо
одился
т
1
1 у
т
~,= — и (А+ В)й — — и (А — В) й.
~з ~з
(15.71)
В этом сл
лучае максимальное и ми
дующим образом.'
е и минимальное отклонени
ния запишутся сле-
8 — — (А — В) й — — и (А+ В) й) О,
~з
т
г~ 1
т
= — и, (А — В) й+ — и (А+В) й(0.
(15.72)
оказывается равным
когда такое е ж
заданном у значению; момент 1
удержание возможно. Заключ
, — последний момент,
а
аклю и ельный интерва
т Р Руется ромах'
здесь ~о ми
л з, ха-
траект
тории.
ния на этом участке—
— стремить процесс к «с е н
Рассмот им алг
— с к «средней»
рим алгоритм управления и'4'. П
ия и . усть к моменту 1
3

560
[ГЛ. 15
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
Значения ~ ВЬ,„~ и ~ ВЬ;,~ не могут быть превзойдены ни при каком зна-
чении возмущения п, если только управление и выбирается согласно (15.69),
и не могут быть уменьшены ни при каком значении ~з и управлении и на
[~з, Т], если только возмущение п становится предельным. Таким образом,
формулы (15.72) определяют цену игры
7 7
6= — и+ (А — В) сИ+и (А+В) Ж
(15.73)
Установим правило, в соответствии с которым по любому поведению
п(г) (~ (~(Т)
выбирается оптимальный закон
и(г) (1з(1(Т),
т. е. укажем алгоритм управления и'4'. Для крайних точек диапазона
п+, п зто правило уже указано (см. (15.69)).
Определим среднюю траекторию соотношением
6( И) =-,.' (8~...И)+8~...Р)1
(15.74)
и потребуем, чтобы управление и на ]гз, Т] стремило движение к средней
траектории
~ оЬ (~) — ВЕ (~) ~ =. т1п.
(15.75)
и(8)
Если в момент 1 выполнено условие
— [А(и — и) — В (и +г )]й= (Аи — В) иЖ,
1
(15.76)
т. е. оЬ(1) =ох (г), то управление и(1) находится из соотношения
— 1 при ие (г) ( — 1,
и(1) = и (1) при — 1(ие(1)(1,
+1 при и (1))1,
(15.77)
где
и (г) =)((1)+ — + (1 — )((г) — —,=(1+;~ (1))], ]
у (~) = В (г)/А (г).
(1 .78)
Если условие (15.76) не выполняется, то требование (15.75) приводит
к условию и (1)=+1.
Отметим следующие два обстоятельства, вытекающие из (15.76), (15.77). Во-первых,
если управление и (Т)=и, (х), то величина промаха равняется нулю: ОЬ (Т)= Ьх. (Т)=0.
Во-вторых, чтобы управление, вычисленное по формуле (15.77), принадлежало отрезку
( — 1, 1], необходимо, чтобы
Х(х) — 1, 1 Х(~)+1
2 ~(й)/1 ~ ~ ~ 2 ~~й) — 1 + ~)'
(15.79)
Управление и (~), найденное в соответствии с требованием (15.75), — оптимальное,
Для обоснования этого утверждения укажем, что если до момента ~ ~ [~з, Т] движеккз

561
АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ АППАРАТА
э 2]
отслеживало среднюю траекторию (это возможно, например, при ненаихудшем возмуще-
нии, всюду на [~„Т1 принадлежащем отрезку (15.79)), то центр диапазона максимальных
промахов приходится на значение ВЬ (Т)=0. Отклонение от этого правила поставило бы
одно из двух наихудших поведений возмущения в преимущественное положение: если
к моменту ~ имело место отличие от средней траектории в сторону промаха-перелета, то
действие возмущения и(~)=и приводит к увеличению перелета. В том случае, если на
[~з, Т) нет момента, при котором движение совпадает со средней траекторией, то управле-
нйе, выбранное в соответствии с оптимальным алгоритмом (15.77), в каждый момент
максимально приближает движение к средней траектории.
Входящий в выражения ('15.66) — (15.76) момент времени г будет определен
ниже при описании алгоритма и'з~; сейчас отметим, что в силу свойств функций А (з)
и В (~), входящих в (15.73), цена игры 6 тем меньше, чем ближе момент зз к концу дви-
жения Т.
Рассмотрим алгоритм управления и'з~. На [з„зз) управление и (з) выбирается так,
чтобы процесс удерживался на заданной траектории и вклад в интеграл И, осуществляе-
мый движением на этом интервале, не зависел от реализации возмущения и (~). Пусть
эта траектория обозначается и'з~ (~), и'з& t; ( ) а удержа ие на ей сост и в т м, то
любого возмущепия управление выбирается согласно правилу
(15.80)
при этом величина интеграла
(15.81)
(Аи (~) — В) и (~) Н~ = (Аи~о~ (~) — В) и~з~ (~) Нс
ке зависит от реализации функции и (г).
Опорная траектория и'з~ (~), и'з& t; з) дол на удовлетвор ть следующ му требован
момент времени г„когда управление и (~), вычисленное по формуле (15.80), становится
равным одному из своих предельных значений,
полжен наступить как можно позднее. Ч~ф,/Д'лм/сел
На рис. 15.6 изображены области возмож-
ного изменения выражения Ч" (з)=(А (~)и — В (~))и 8
по времени ~. Кривые 1 и 2 соответствуют слу-
чаю и= +1, ь (1) = и+ и случаю и= +1, и (1) = и;
кривые 4 и 8 соответствуют и= — 1, и (~)=и+ и
и= — 1, и (~) = и . Кривая 8 является нижней
границей области достижимости управления
и (~), верхняя граница составлена из участков
двух кривых: на (О, зз) — кривая 2; на (~„~ )—
кривая 1, в точке ~=~з верхняя и нижняя гра-
ницы пересекаются. В указанной области управ- 0
ление и (~) обеспечивает достижение любого зна-
чения выражения Ч" (з) =(А и — В) и. Следова-
тельно, в качестве опорной траектории, удовлет-
воряющей сформулированному выше требованию,
может фигурировать любая функция Ч" (з), гра-
фик которой расположен в области достижимости
и которая принимает в момент 8=~з значение
-8
Ч' (~з) = (А (~з) — В (~з)) и». =
= ( — А (г ) — В (г )) и . (15.82)
Из последнего равенства следует формула
цля определения ~з:
)( (гз) = (и+ — и )/(и++ и ). (15.83)
Заметим, что движение на интервале (~„зз)
пает вклад в интеграл бЬ:
гз
Рис. 15.6. Области изменения выражения
Ит,= Аи~о~ (~) — В) ~'о' ф ИГ. (15.84) ~ (О.
Обратимся теперь к алгоритму управления ип&g ;, и' & t;. К м мент з=~з ве ич
согласно оптимальному алгоритму должна выражаться по формуле (15.71); на [г„г )
36 Механика полета

562
[ГД. 15
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
накапливается значение интеграла ЛВЬ, так что величина ф, должна составлять
1 1
фо ф МБ (Аи(о& t; В) у&l ;о gt; ~ +- в ” ( + ) Н в ” Ђ” + А в ” В Н~
гз гз
С другой стороны, по определению ф, имеем
(15.86)
фо=фо+ (Аи — В) уй~.
О
На интервале [О, й,), как уже отмечалось, А (й) ) В (й), так что к моменту ~=1,
управление и (~) может обеспечить накопление интеграла, фигурирующего в правой части
(15.86), в пределах
(15.87)
— у (А + В) (КО ( (Аи — В) у Нй & t у (А Ђ” В) (
О О О
Предположим, что требуемое значение ф — ф принадлежит (15.87).
Для того чтобы обеспечить значение интеграла, равное
(15.88)
(Аи — В) а=ф
предлагается, определяя момент ~1 условием
(15.89)
[А (~) з1рь (фо — фо) — В (~)] у (~) ~1~ = фо — фо,
формировать управление на [О, г,) по правилу
(15.90)
и (Й) = з1яп (фо — фо),
а управление на [~„~,) — по правилу
Р) =х Р).
(15.91)
так что вклад движения на этом участке в интеграл (15.88) — нулевой.
Результаты численных расчетов представлены на рис. 15.7, 15.8. На рис.
15.7 приведен график зависимости цены игры 6 от верхнего предела изменения
Е,,сел
Рис. 15.7. Цена игры С в функции
верхнего предела возмущения ю+.
Рис. 15.8. Момент переключения
в зависимости от верхнего предела з+.
возмущения п+, 'здесь предполагается, что п =1/п+. Следует отметить точку
пересечения графиком оси абсцисс (п =1,38); на интервале от значения у,=
=1 до и =1,38 цена игры 6 равна нулю, а затем возрастает с увеличением у,,
На рис. 15.8 дана зависимость момента времени ~з от величины п+.

АЛГОРИТМЫ УПРАВЛЕНИЯ СПУСКОМ АППАРАТА
ф 2]
(15.92)
и (г(~)(и +Ли (~и) 0).
Будем считать, что возмущение п (~) в новых границах выбирается по-
прежнему из соображений максимального увеличения платы игры. Исследуем
функционирование алгоритма в новых условиях последовательно на участках
[О ~1) [~» ~2) [~2 ~з) [~з Т]1,
На первых двух участках, [О, ~,), [~„~2), на-
капливается интеграл так, чтобы величина ф, стала
равной своему значению (15.85) в соответствии со
старыми границами (15.62).
Участок [~„~, ) претерпевает следующие изме-
нения: опорная траектория и'О'(~), п'О'(1) может
отслеживаться на интервале (1„1') в отличие от
прежнего (~„~,) (рис. 15.9), где кривые 1 — 4 опре-
деляются так же, как и на рис. 15.6, ~' — момент
пересечения опорной траекторией б, описываемой
уравнением
Рис. 15.9. Области изменения
выражения ~ ($) при вариа-
циях и».
новой граничной линии 6, описываемой уравнением Т (~)=(А — В)(п +Ли).
От момента 1' вплоть до конца движения наихудшее поведение возмуще-
ния имеет вид
и (~) = и + Ьи
и(1) =1
(15.93)
(15.94)
соответственно
(~3 ~~ ~ ( Т).
Подсчитаем цену игры в новых условиях:
С= ~,+ (Аи'о' — В)и'О'й+(и +Ли) (А — В) й
(15.95)
Изменение в цене игры, произошедшее вследствие неучета в алгоритме из-
менения верхнего предела возмущения, следующее:
ЛС = — Ьу (А — В) й+ (Аи'о' — В) и'"й — (и + Ьу) (А — В) й. (15.96)
Определим изменение цены игры в случае, когда изменения верхнего
предела возмущения Лп учтены в алгоритме управления. Это изменение вы-
числяется в соответствии с процедурой, изложенной в п. 2:
~С(Ьг) = — — Ы (.4 — В) й — — И.4 — В) г +(А+В) и $й. (15.97)
1 1
4. Влияние границ возмущения. Рассмотрим вопрос о том, насколько
хорошо будет действовать предложенный алгоритм при неточном задании
ограничений на изменение возмущения; в этом пункте по-прежнему речь
идет о задаче (15.50).
Пусть алгоритм управления определен исходя из неверных значений
~+, ~ — пределов изменения возмущающего воздействия, в то время как
возмущение изменяется, например, в пределах

564
[ГЛ, 15
ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В ИГРОВОЙ ПОСТАНОВКЕ
Полученные результаты иллюстрируются рис. 15.10, 15.11. Аргументами
на обоих рисунках являются изменения Лп; по оси ординат откладываются
значения ЛС и ЛС (Лп), вычисленные по формулам (15.96), (15.97).
На рис. 15.10 в качестве опорной принята траектория и'О'=1, п"'=и+, на
рис. 15.11 — и"'= — 1, и'О'=п . Кривая ЛС (Лп) аналогична 6 (и+); она ха-
рактеризует увеличение цены игры при увеличении верхнего предела воз-
мущения. Изменение ЛС слагается из двух компонент: увеличения цены игры
ЖI0~6м
5
гб,/д зим
д 0,1 0,2 05 01 05 Лп
И И Я5 04 05 Лп
Рис. 15.10. Изменение цены игры С
в зависимости от вариации М (и®) =1,
~~о) — ~+1
Рис. 15.11. Изменение цены игры С
в зависимости от вариации Ью (и(0) =
= — 1, Ы0) =и ).
при увеличении верхнего предела возмущения и увеличения цены игры из-за
неверной настройки алгоритма. Таким образом, значение разности кривых
ЛС и ЛС (Лп) дает влияние ошибки знания пределов изменения возмуще-
ния на цену игры.
Сравнение кривых ЛС на рис. 15.10, 15.11 показывает, что выбор опор-
ной траектории влияет на изменение цены, вызванное ошибкой Ли.

ГЛАВА 16
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ
В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ (ЗАДАЧИ КОРРЕКЦИИ)
В настоящей главе излагается статистический подход к построению оптимального
управления в задаче коррекции движения, происходящего в малой окрестности расчетной
траектории. Суть подхода состоит в следующем. Управляющие воздействия разделяются
на программную и корректирующую составляющие. Программная составляющая пред-
полагается заданной в виде функций времени (например, из решения детерминированной
задачи оптимального управления). Корректирующая составляющая управления пред-
назначается для парирования внешних воздействий (возмущений), не учтенных при по-
строении программ. Эти неучтенные внешние воздействия представляются в виде случай-
ных возмущений в начальных условиях и в правых частях дифференциальных уравнений
пвижения. Помимо прочих, к возмущениям относятся и ошибки реализации программного
управления Я 1 данной главы).
Как возмущения, так и корректирующие воздействия предполагаются малыми по
сравнению с программными настолько, что линеаризованные в окрестности программной
траектории уравнения достаточно точно описывают движение. В отличие от предыдущей
главы здесь рассчитывается на получение полной априорной информации о возмущениях,
как о случайных величинах или функциях, т. е. при выборе закона коррекции считаются
известными вид и параметры законов распределения возмущений Я 1).
Помимо априорной информации о возмущениях, закон корректирующего управле-
ния ориентируется на получение и текущей информации о конкретной реализации траек-
тории. Эта информация обеспечивается системой траекторных измерений в процессе дви-
жения. Учитывается возможная неточность текущей информации. Эти ошибки снова пред-
полагаются малыми случайными величинами с известными априори законами распрепеле-
ния Я 3).
В полном объеме требования к закону коррекции выглядят так. Задается вероятность,
с которой закон коррекции должен обеспечить попадание траектории в заданную область
конечных значений при условии ограниченности запаса рабочего вещества на коррекцию.
Кроме того, запас рабочего вещества на коррекцию и закон коррекции должны быть
выбраны так, чтобы обеспечить максимум полезной нагрузки.
Это один из возможных вариантов постановки задачи коррекции, оптимальной
с заданной вероятностью. Можно указать другие формулировки, эквивалентные приве-
ценной. Например, вероятность попадания траектории в заданную область может зада-
ваться косвенно — ограничениями на дисперсию конечных отклонений траектории от
расчетной Я 2). Далее, вместо условия максимума полезной нагрузки моясет фигурировать
условие минимума дисперсии конечных отклонений при заданном запасе рабочего вещества
на коррекцию (как это сделано в ~ 5 данной главы).
Помимо указанных выше постановок используются и другие, в которых все требова-
ния к траектории и к качеству коррекции (или их часть) формулируются в среднем (а не
с заданной вероятностью). Такой подход был типичен для ранних работ по коррекции, он
нашел свое отражение в З 4 настоящей главы.
Исследованию статистических задач оптимальной линейной коррекции посвящено
огромное число работ. Их обзор и полное изложение всего этого направления не входят
в задачу данной главы. Общетеоретические основы линейной коррекции систематизиро-
ванно изложены в ряде монографий (см., например, [16Л вЂ” 16.9]). С результатами иссле-
пований, ориентированных на механику космического полета, можно ознакомиться по
монографиям [16ЛΠ— 16Л7] и обзору [16.8]. Все они, как правило, относятся к аппаратам
с двигателями ограниченной скорости истечения (импульсная коррекция). Содержание
настоящей главы основано на результатах работ [16Л8 — 16.22]. Их методическая особен-
ность, по сравнению с работами по импульсной коррекции, состоит в том, что возмущения
непрерывно вносятся в систему (пока работает основной двигатель), а корректирующее
управление, компенсирующее эти возмущения, чаще всего действует на длительных ин-
тервалах времени. Это связано со спецификой первоначального объекта приложений (ап-
параты с двигателями ограниченной мощности).

566 постРоение прогрАмм ехпрАвления в стлтистическои постАновтхе (гл. х»
~ 1. Возмущающие воздействия
При построении расчетных программ управления в детерминистской
постановке поведение аппарата описывалось системой дифференциальных
уравнений, краевых условий и конечных соотношений типа (4.1), (4.9), (4.10).
Реальное движение подчиняется более сложным уравнениям. Однако в за-
дачах коррекции для описания реального движения используется система
той же структуры, что и (4.1), но в начальные условия и в правые части
дифференциальных уравнений вводятся случайные возмущающие факторы
(ошибки). Здесь принимается именно этот путь.
1. Ошибки в начальных условиях (4.1) образуются в результате выпол-
нения операций, предшествовавших рассматриваемому маневру. Например,
они могут накопиться в процессе вывода аппарата «малой тяги» на некоторую
промежуточную стартовую орбиту носителем с двигателем «большой тяги».
Таким образом, к началу маневра уже имеются отклонения действительных
положения г (0) и скорости т (0) аппарата от их расчетных значений г и т0:
о г = г (0) — г„ор = т (0) — т . (16.1)
Могут быть также ошибки в начальной массе аппарата: М (0)+М0.
Однако в дальнейшем предполагается, что точное значение начальной массы
М (0) становится известным до начала расчета программы управления, и
оно же подставляется в качестве заданного М,. Таким образом, формально
получается М (0)=М,.
Информация об ошибках (16.1) в кинематических параметрах иная.
При расчете программы управления реализация ошибок (16.1) неизвестна.
В статистической постановке задач коррекции, которая здесь и развивается,
ошибки (16.1) предполагаются случайными величинами с известным зако-
ном распределения. В последующих параграфах это распределение берется
гауссовым с нулевым математическим ожиданием и заданной корреляци-
онной матрицей (см., например, [16.23]):
1
х х — 1
8г
р(х (0)) = ехр[ — —,х*(0) (Ве) 'х(0)~, х (О) =
0
М [х (0)] = О, М [х (0) х' (0)] = ЙУ,
где символ М означает математическое ожидание, «т» и « — 1» — операции
транспонирования и обращения матриц, Л„ — заданная положительно опре-
деленная симметрическая матрица, ~Щ=Йе$ Й„+О, р — плотность вероят-
ности.
Для оценки точности выполнения маневра при таком предположении
применимы известные методы теории линейных стохастических систем [16.1,
16.2]. Следует подчеркнуть, что данный подход является лишь одним иа
возможных. Например, когда известны только пределы изменения ошибок
в начальных условиях, следовало бы искать наихудшую реализацию ошибок
(в смысле отклонения от расчетной точки в конце маневра).
2. Ошибки реализации программы управления — это другой источник
погрешностей. Он действует в процессе выполнения данного маневра на тех
участках, где работает двигатель.
Ошибки в управлении складываются из ошибок ое (~) реализации е (~)
первоначальной программы е(0)(~) ориентации вектора тяги и из ошибок
ои (1) реализации и (1) первоначальных программ и"' (1) независимых уп-
равляющих функций, определяющих величину тяги Р и расход д в соответ-
ствии с регулировочной характеристикой двигателя (4.9):
8е (1) = е (1) — е(0) (1), ои (1) = и (1) — и(0) (1) (16Л)
(аэродинамическое управление здесь не рассматривается).

567
ВОЗМУЩАЮЩИЕ ВОЗДЕЙСТВИЯ
где Р (и) и д (и) — известные функции (регулировочная характеристика
(4.9)); для удобства записи они предполагаются дифференцируемыми.
Таким образом, оа (~) представляет собой линейную комбинацию слу-
чайных процессов ое (~) и ои (~). По статистическим характеристикам послед-
них при помощи соотношения (16.4) могут быть посчитаны статистические
характеристики процесса (см. [16.1]). Однако в дальнейшем статистические
характеристики ошибок управления сразу зачаются в терминах оа (~). Ис-
пользуются два основных варианта.
В первом Я 2, п. 3, 4; ~ 4) считается, что случайный процесс оа (~) гаус-
совский с известными математическим ожиданием и корреляционной матри-
цей (см., например, [16.23]):
М [оа (~)] = О, М [оа (~) оа' (~)] = Х' (~, ~).
(16.5а)
Здесь Х' (~, т) — заданная симметрическая матрица, элементами которой
являются функции от двух аргументов 1 и т.
Во втором варианте Я 3, п. 2, 3; Я 5, 6) оа (~) рассматривается как ре-
зультат прохождения первичных помех ~ (1), заданных в виде гауссовского
белого шума (некоррелированного случайного процесса), через устойчивую
линейную систему (систему стабилизации тяги):
оа = С (~) оа+ ~ (~), оа (О) = оса,
МДР)]=О, М[1У)~'(.)]=КР)~Р—.),
М(о,а) =О, М(о,аоеа') =Бе,
(16.5б)
где 6 (1) — заданная матрица, характеризующая систему стабилизации,
Г (1) — матрица спектральной плотности белого шума (неотрицательно опре-
деленная симметрическая матрица), о (~ — т) — дельта-функция Дирака 1),
00 — корреляционная матрица начальных отклонений Ооа, распределенных
по Гауссу.
') Корреляционная матрица случайного процесса ~ (~) равна нулю всюду, эа исклю-
чением момента ~ = ~. При ~ = ~ элементы корреляционной матрицы, стоящие на главной
диагонали, представляют собой дисперсии компонент вектора ~ (~). В данном случае эти
Ошибки (16.3) можно трактовать как результат прохождения первичных
помех через систему стабилизации параметров е и и. Система стабилизации
(автоматический регулятор) призвана отслеживать программное значение
соответствующих параметров. Она предполагается заданной и обладающей
достаточно высокой точностью, такой, что ошибки (16.3) можно считать ма-
лыми (в необходимом для дальнейшего смысле). Последнее также предпола-
гает, что процессы типа отказов элементов двигателя здесь не рассматри-
ваются.
Ошибки (16.3) назовем исходными. Будем считать известными априори
(до расчета программ управления) полные статистические характеристики
этих ошибок как случайных процессов (в отличие от предыдущей главы,
где предполагались известными только пределы изменения возмущающих
функций). Для последующей оценки точности выполнения маневра по ки-
нематическим параметрам г и т необходимо выразить ошибки оа (~) в реактив-
ном ускорении а=Ре(М через исходные. В линейном приближении это вы-
глядит так:
оа(1) =а(1) — а'е'(~) „,, (ргали„Р(и) ~ „, ° ои(1))+

568 ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ [ГЛ. 16
Заданные таким способом ошибки в реактивном ускорении представляют
собой непрерывный марковский процесс [16.241. Вся дальнейшая эволюция
такого процесса, т. е. распределение случайного вектора оа (т) при т ) 1,
НЕ ЗаВИСИт От ПРЕДЫСТОРИИ ПРОЦЕССа (т ( 6), а ЗаВИСИт ТОЛЬКО От РЕаЛИЗаЦИИ
вектора 3а в данный момент 1.
3. Прочие ошибки. В дополнение к рассмотренным выше упомянем еще о нескольких
типах возмущений, которые, однако, дальше явно не фигурируют.
1'. Отклонения от проектных значений конструктивных параметров двигательной
системы (постоянные управляющие параметры тч в характеристике двигателя (4.9), (4.10)).
Если точные значения этих параметров становятся известпыми к моменту расчета про-
граммы управления, то тогда ошибки дапного вида вводить не нужно. В противном случае
их можно учесть, задав ненулевое математическое ожидание случайных возмущений
(16.5) реактивного ускорения.
2'. Неточное знание внешних сил: ошибки в гравитационных постоянных, в плот-
ности атмосферы (см. предыдущую главу) и т. п. В статистической постановке это — снова
возмущения типа (16.5), и поэтому дальше они отдельно не записываются.
3'. Отсутствие в (4.1) членов, связанных с движением вокруг центра масс. Учитывать
воздействие движения вокруг центра масс на движение центра масс как случайную адди-
тивную помеху в правых частях уравнений (4.1), по-видимому, нельзя. Нужно рассматри-
вать оба движения совместно. Однако это увеличивает размерность системы (4.1) и сильно
усложняет и без того громоздкие выкладки, не меняя в принципе ход основных построений.
9 2. Точность выполнения маневра без коррекции
Ошибки в начальных условиях (16.1) и в реактивном ускорении (16.4)
приводят к отклонениям ог (г) =г (6) — г'е' (г) действительной траектории г (1)
от расчетной г'е' (~). Вопрос о необходимости коррекции возникает всякий
раз, когда ожидаемая точность выполнения маневра без коррекции меньше
некоторой желаемой величины. При оценке точности без коррекции, как
обычно, предполагается, что ошибки (16.1), (16.4) и вызываемые ими отклоне-
ния ог (6) малы (почти наверное, т. е. с вероятностью, близкой к единице).
Тогда движение аппарата достаточно точно описывается линеаризованной
системой уравнений. Последнее обстоятельство позволяет выписать соотноше-
ния, связывающие начальные и текущие возмущения с отклонениями траек-
тории в конце маневра от заданного конечного состояния. Именно эти от-
клонения и характеризуют точность выполнения маневра.
Для гауссовских случайных возмущений распределение конечных
отклонений также является гауссовским (в силу линейности системы). Чтобы
найти это распределение, достаточно, воспользовавшись известными из
теории линейных статистических систем методами [16.21, найти только ма-
тематическое ожидание и корреляционную матрицу отклонений. К сожале-
нию, матрица линеаризованной системы, как правило, зависит от времени,
поэтому найти в явном виде ее решение и установить аналитическую зави-
симость между параметрами возмущений и статистическими характеристи-
ками контролируемых параметров, вообще говоря, не представляется воз-
можным. Тем не менее в некоторых частных случаях такая задача может быть
решена. Это относится к случаю движения в бессиловом поле, когда матрица
линеаризованной системы не зависит от времени (см. п. 3), и к случаю движе-
ния в центральном гравитационном поле с малым эксцентриситетом (п. 4).
дисперсии становятся бесконечно большими. Таким образом, белый шум представляет
собой некоррелированный процесс с бесконечно большой дисперсией. Безусловно, никакой
реальный случайный процесс не может иметь таких характеристик. Тем не менее можно
представить себе процесс, весьма близкий и белому шуму. Так, зададим одномерный
случайный процесс ~ (6) в виде дискретной последовательности гауссовских независимых
случайных величин ~;: ~ (6)=1, при 6, ( 6 & t; 6 + с нуле ым математичес им ожидан
и дисперсией, равной а2 (6)/Л6, где И=6,+ — 6,. В пределе, при М -э О, получается некор-
релированный случайный процесс с бесконечно большой дисперсией.

569
ТОЧНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА БЕЗ КОРРЕКЦИИ
ф 2]
8г=Ьч, оГ (О) = оеГ,
Вт = ~( дц/дг ~)(е] ог + оа, Вт (О) = ор,
(16.6)
где матрица []дц/дг))(е] вычислена как функция времени вдоль номинальной
траектории.
Перепишем ее в стандартной форме:
х = А (г) х + В (г) ~,
(16.7)
где х — вектор отклонений (фазовых координат), ~ — вектор случайных
возмущений, А (г) и В (г) — известные матрицы.
Когда возмущения заданы в виде (16.5а), в состав вектора х войдут только компо-
ненты векторов 07 и 0м, а ~ (~)=0а (~). Если же возмущения заданы в виде (16.5б), то ком-
поненты вектора х будут включать также и компоненты вектора Фа, а ~ (~) будет первич-
ной помехой — белым шумом ').
Воспользуемся следующей заменой переменных:
у(~)=Ф(Т, ~)х(~).
(16.8)
Здесь Ф (Т, ~) — фундаментальная матрица решений системы, сопряженной к (16.7)
при ~ (1)=0:
Ф = — ФА (~),
Ф (Т, Т) = Е
(16.9)
(Š— единичная матрица того же порядка, что и система (16.7)). В новых переменных
система (16.7) примет вид
у=Ф(Т, г)В(~)~(~), у(0)=Ф(Т, 0)х(0). (16. 10)
Нетрудно видеть, что в силу (16.9) у (Т)=х (Т). Кроме того, если, начиная с некоторого ~,
возмущение будет отсутствовать (~ (~)=0 при ~ ) ~), то у (~)=у (~)=х (Т), т. е. у (~)
есть прогноз отклонения в момент времени Т.
По сделанным ранее предположениям (16.2) и (16.5б) вектор х (О) имеет
гауссовское распределение с нулевым математическим ожиданием и корре-
ляционной матрицей Л„. Возмущение ~ (~) представляет собой гауссовский
Случайный процесс с нулевым математическим ожиданием и известной кор-
реляционной матрицей Х' (~, т), причем начальные отклонения и возмущения
ие коррелированы между собой. Тогда, интегрируя уравнения (16.10) и
осредняя по всем возможным реализациям маневра, получим параметры
распределения случайного вектора х (Т) в конце маневра (см., например,
[16.21):
т
М[х(7]]=М[у(7]]=М~Ф(7, 0]х(0]+ Ф(Т, ЦВ(Ц~ЩЮ~1=0,
О
Вх= М(х (7] х'(7]] =М [Ф (7, О] х (О] х*(0] Ф'(7, О]+
(16.11)
т т
Ф (Т, ~] В Щ ~ 0] ~'(~] В'(т]Ф'(Т, ~] В~Вт]=
О О
тт
=Ф (Т,О) ЯФ'(Т, О)+ Ф(Т, ~) В (~) Х~ (~, -.) В'(0) Ф'(Т, ~) Все
О О
') Если первичные помехи нельзя считать белым шумом и они представляют собой
коррелированный случайный процесс, может потребоваться включение в состав вектора х
и производных вектора Фа (см. п. 1 ~ 6).,
1. Связь конечных отклонений с текущими и начальными возмущениями.
Линеаризованная система уравнений движения вблизи расчетной (номиналь-
ной) траектории имеет вид

570 и ст
О РОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ ~ГЛ 16
2. Способы за ания
д точности. Опишем два возможных варианта опре-
деления понятия «точность выполнения маневра».
1'. Пусть в фазовом пространстве задана область Й, в которую должна
попасть траектория х (1) летательного аппарата в конце маневра. Зная плот
ность расп е еления ',х ~~
р д р [ (т) ], можно определить вероятность Р попадания
в заданную область
Р (х (Т) 1= Я ) = р Я) Й$.
(16.12)
сли эта вероятность меньше некоторой заданной величины Р
считается, что точность вып
выполнения маневра недостаточна и в процессе реа-
шЫ~
лизации необходима коррекция.
ля получающегося здесь гауссовского распределения х (Т) вероятность (16.12)
после линейной замены переменных может быть представлена в виде
Р(х(Т) ~ Я )=
1
ехр — — ~~ Ищ
1
1/(2к)п
2
Я~
в=1
(16.13)
(х ~ с, Я, ~ Я,: ~); =фх)~~ф)р Дй 'Д'=Й1ац(Х;)),
где матрица 0т определяется соотношениями (16.11), а через Й1аа' (1;) обозначена
диагональная матрица с элементами 1 на ла
на главнои диагонали. После вычисления
гр ла в' ,. ~ устанавливается зависимость вероятности попадан
область от «азме ов» обла
б р р сти и от элементов корреляционной матрицы Й~. Нап и-
д ния в заданную
мер, если область И за ана в ви
апри-
лируемыи параметр х, ' И = х.' х,. & t ~
° . °
д иде полосы с фиксированной шириной ~ (один контро-
Ф,~ ф
(16.14)
где ~,, — дисперсия координаты х. т
Ф Ф
рд х,, т. е. ~ -и элемент, стоящий на главной диаго-
нали матрицы Й, в (16.11).
Число конт оли
Число контролируемых параметров может быть меньше и (размерности вектора х).
этом случае можно формально считать, что для неконтролируемых парамет ов п
изменения заданы, но сколь угодно велики.
раметров пределы
Из после него соотн
д ношения следует, что искомая вероятность монотонно
убывает с остом исп
р д ерсии и по заданнои вероятности можно найти пре-
Ю
дельно допустимое значение дисперсии координаты ж... Поэтому в качестве
меры точности можно взять дисперсию контролируемого параметра.
ля иллюстрации разброса попаданий в конце маневра может служить
так называемый эллиисоид а
ид рассеяния. В простеишем случае, когда матрица Рг
Ю
невырождена, он имеет вид хтРт'х ( и+2 (и — размерность векто а х).
д р о ладает тем своиством, что если построить равномер-
Ю
ор
ное распределение вероятностей попадания, сосредоточенное в эллипсоиде,
то корреляционная матрица такого распределения будет совпадать с Рг.
характеризует распределение вероятностей попада-
ния по различным направлениям. В случае, когда матрица Рт имеет ранг
и, эллипсоид сосредоточен на г-мерном линейном многообразии. От-
метим, что объем эллипсои а
оида пропорционален корню квадратному из произ-
р " д л ных координат. Таким образом, если задать область
ведения диспе сий от ель
в виде эллипсои а асс я
д р сеяния, то, как и в предыдущем примере, вероят-
ность попадания в нее будет увеличиваться с уменьшением дисперсий.
у д до о из контролируемых параметров заданы допу-
стимые пределы изменения'): ~ж,.~:.;- р,, 1=1,..., и. Учитывая что случай-
1

ТОЧНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА БЕЗ КОРРЕКЦИИ
ные величины х,, могут принимать сколь угодно большие значения (согласно
гипотезе об их гауссовском распределении), указанные ограничения следует
понимать в вероятностном смысле:
(16.15)
Иными словами, соотношения (16 15) эквивалентны неравенствам
(16.16)
р;/а,;; ) а;,
~=1, ..., и„
где с~„однозначно определяются через ~,.
Рассматриваемый способ задания точности позволяет получить оценку точности
для способа, описанного в 1'. Пусть Й вЂ” прямоугольная область 6,= (х: ~х,.~ ( р;,
~=1,..., и), тогда
(16.17)
Если задана замкнутая область о произвольного вида, то можно взять (<максимальн
прямоугольную область Й ~ Я и, воспользовавшись соотношением (16 17), получить
оценку (снизу) для искомой вероятности.
3. Оценка точности без учета гравитационных членов. Упростим ли-
неаризованные уравнения (16.6) возмущенного движения, отбросив в них
члены ~~дд/дг~~"'ог, учитывающие изменение гравитационного ускорения.
Это справедливо для плоскопараллельного гравитационного поля (ц= сопз$),
а также в тех случаях, когда возмущенное движение происходит в столь ма-
лой окрестности номинальной траектории, что ~ ~~дц/дг~~"'Ьг~ (( ~ оа~. Тогда
уравнения возмущенного движения не зависят явно от номинальной траекто-
рии и их коэффициенты постоянны: ог'= оа.
Предположим также, что компоненты вектора ошибок в начальных усло-
виях и компоненты вектора ошибок в реактивном ускорении некоррелиро-
ваны. Это дает возможность ограничиться рассмотрением одномерного дви-
жения по одной из координат. Для определенности выберем маневр переме-
щения между точками покоя, расположенными на расстоянии 1, за время Т.
таком случае величины, входящие в систему (16.7), имеют вид
О
О 1
О О
(16.18)
Пусть Оа (~) — коррелированный случайный процесс (16.5а) с нулевым ма-
тематическим ожиданием и корреляционной функцией:
ЛХ [оа (1) 3а (т)1 = о'Й (1) Й (-.) е-~' '~'~'
(16.19)
Здесь о, и Л1 можно интерпретировать как константы, характеризующие
точность и быстродействие системы регулирования, которая обеспечивает
выполнение программы ускорения от тяги; Й (г) — неслучайная известная
функция, определяемая типом регулирования: Й (г) = а (г) при регулировании
по относительному отклонению, Й (г) = сопз$ при регулировании по абсолют-
ному отклонению (далее принимается Й (~)=1/Т'). Для рассматриваемой
в данном примере матрицы А с постоянными коэффициентами (см. (16.18))
фундаментальная матрица имеет вид
где е,. — заданная величина (вероятность выхода координаты х, из допусти-
мых пределов). Как указывалось выше, вероятности Р,. монотонно возрастают
с уменьшением дисперсии координаты х,. (см. (16.14)). Поэтому в качестве
меры точности можно принять величину р,./Ш,,.

д72 пОстРОение пРОГРАмм УпРАВлениЯ В стАтистическОЙ пОстАнОВке [Гл. и
Подставляя ее в (16.11), имеем
77
р-~~-'~/'Я~ Дс. 16.2
О О
Ошибки Оог и О,г предполагаются независимыми случайными величинами,
с известными дисперсиями и нулевыми математическими ожиданиями
(см. (16.2)):
ЛХ ()'.)„Г) = ЛХ (О,у) = О, М [()'.)„Г)'] = ~О„1', М [(О„У)'] = ~),'„1,'Т
Подставив их в соотношение (16.20) и вычислив интегралы, получим оконча-
тельное выражение для дисперсий отклонений в конце маневра [16.18, 16.19]:
Г Т М[(бу (Т))]=~~,+ 2~~ — [1 — — (1 — е ~~)],
-)-( — „) )1 — е-~~*')]
(16.21)
Если в соотношениях (16.21) пренебречь величинами порядка (Л~/Т)~
и выше, что вполне допустимо, так как по физическому смыслу Ь|/Т (& t;
получим следующую систему неравенств:
(16.22)
2а2 (ЦТ) + а,'„( Я, '/,а,' ф/Т) + ~'„, + -„-'„(~ ф
где р, и р„— заданные допустимые отклонения. Таким образом, если к концу
движения ожидаемые отклонения реальной траектории от расчетной превос-
ходят допустимые отклонения, что соответствует нарушению системы нера-
венств (16.22), то в процессе движения необходима коррекция траектории.
4. Оценка точности для маневров в центральном поле с малым эксцентри-
ситетом [16.22]. Для описания невозмущенного движения воспользуемся
системой (4.46) в оскулирующих переменных р. Для дальнейшего удобна
переписать систему (4.46) в матричной форме:
(16.23)
р=В(р, ~)а.
Пусть выполнены следующие условия.
1'. Правые части системы (16.23) представимы в виде ряда Фурье, коэф-
фициенты которого зависят только от координат:
В (р, ~) = В, (р) + ~ [В)' (р) соя (И) + В~ (р) з1п (Ы)] (16 24)
2'. Случайная вектор-функция 3а (~) является стационарной [16.6],
следовательно, соотвегствующая корреляционная матрица зависит только
от разности аргументов:
(16.25)
ЛХ [Оа (~) оа' (~)] = Х' (~ ~ — ~ ~).
3'. Корреляционная матрица Х' может быть представлена в виде
к (~ ~ — ~) = а; ~- а / (~ ~ — ~),
Й()~ — ~~)(Т ' при ~ ~ — ~)) 2тс.
(16.26)
где Й„', Й' — симметрические матрицы, не зависящие от времени',
Й (~~ — ~ ~) )~ 0 — скалярная функция, достаточно быстро затухающая при
увеличении ~1 — с~:

573
ТОЧНОСТЬ ВЫПОЛНЕНИЯ МАНЕВРА БЕЗ КОРРЕКЦИИ
4'. Ускорение а мало по абсолютной величине:
~а~ — Т '(&lt 1, ри э ом но ма ~~В р, ~ ~~ Ђ”
Разность между точным решением р (~) и решением первого приближения р* (~)
при Т вЂ” а ' будет, как показано в [16.26], величиной порядка а.
Воспользовавшись далее системой (16.27) в качестве исходной, выпишем
линеаризованную систему вида (16.7), где
А =/)д[В,(р*) а],./др.//,, В = В,(р*)
(16.28)
(здесь [В,(р*) а], означает г-ю компоненту вектора В,(р*) а).
Сделаем замены переменных в формулах (16.11), (16.27):
г — -.=2), г+ =2~,
Р(г) Р*(г) =Р*Л+ )) Р*Л)+ )1> Л
& t; р* Я   ~ р* Я  = р* Д  О а) р*
Ф (Т, г) Ф' (Т, г) Ф*(Т, ~) +0(а) Ф*(Т, с),
в(р(г), г) =в(р*(ц, ~+ )), в(р(.), -.) =В(р'д), ~ — )),
Ха(~г с')) =Ха(2) ~) )) )
(16.29)
(здесь Ф' (Т, г) — фундаментальная матрица лля системы, сопряженной к (16.27)).
Учитывая, что функция Й (2)~~) быстро затухает с ростом (~(, заменим ее на Й ((~))=
=Й (2~ а )) для ( а ) & t   Й ( а (  0 л    & t; ~. Новая корреляц онная м три а Х"=
отлична от нуля в узкой области, расположенной вдоль диагонали области интегрирова-
ния в (16 11).
В формуле(16.11) интегрирование производится по квадрату 0 & t  & t  , 0 &l
Заменим область интегрирования на узкую полосу (~( & t; ~   l ; < Т. Нова
интегрирования отличается от прежней области (в точках, где Й отлична от нуля) участ-
ками, общая площадь которых — 1. Поскольку площадь новой области интегрирования
равна 27~Т вЂ” а 1, то замена области интегрирования вносит относительную ошибку — а.
Можно показать, что и все приведенные выше замены переменных в формуле (16.11)
~ают относительную погрешность — а.
После сделанных замен переменных формула (16.11) приобретает следующий вид:
т т Т
Р =Ф*(Т, 0) ЩФ*'(Т, 0) + Ф*(Т, г) В (г) Иг Ра~ Ф*(Т, г) В (г) Иг +
о о
Ф* (Т, Я вЂ” ~)) В (р*, Я вЂ” ~)) Й (/ ~) /) Й' В' (р*, Я + г) Ф*' (Т, $ + ~)) сГ~ сГЯ. (16.30)
(( 2
Предположения 2', 3 означают, что случайную функцию оа (8) можно
представить в виде суммы постоянной и переменной случайных составляю-
щих. Постоянная случайная составляющая не изменяется в процессе данной
реализации, но изменяется от реализации к реализации случайным образом
с нулевым математическим ожиданием и дисперсией д„',,. Переменная случай-
ная составляющая возмущений в данной реализации представляет собой функ-
цию времени, математическое ожидание квадрата которой (по реализациям)
не зависит от времени и равно И',, а изменение на данной реализации удовлет-
воряет требованию М [Ва, (~) 8а, (т) ]=И'.,Й (~~ — т~). Здесь осреднение ве-
дется по всем ~, -. для заданного значения ~~ — т~. Осреднение по ~, -. (а не
по реализациям) возможно из-за стационарности случайных функций (усло-
вие 2').
При выполнении условий 1' — 4 для решения системы (16.23) можно
воспользоваться методом усреднения [16.25]. Если ограничиться нахожде-
нием первого приближения, то согласно методу усреднения система (16.23)
может быть заменена на усредненную:
р" = В,(р') а. (16.27)

574 пост~'оинии прогрАмм упрАвлиния в стАтистичискои постАновки (гл. (з
Подставим в последнее слагаемое вместо функции ~с ее разложение в ряд Фурье на
отрезке [ — к, к]:
~с ()'() ~) = со + ~ сь соя (Й ()).
1с=1
(1 6.31)
Подставим туда же вместо В разложение (16.24). Проинтегрировав по () полученное
после подстановки выражение, приведем последнее слагаемое из (16.30) к виду
2к Ф*(Т, С) 2соВОВ~+ ~ с (В~,В~,'+ В~',Вь") + Ф Ф" (Т, «) Ы$.
о
)с=1
(16.32)
В (16.32) через Ф обозначены все «колебательные» члены:
Ф = ~ [Ф,', соя (ЙР) + Ф", я1п (ЙР)];
3=1
остальные члены, стоящие в квадратных скобках подынтегрального выражения (16.32),
зависят только от (<медленн х» переменн х. Интег ал от колебатель ых чле о  а
меньше интеграла от остальных слагаемых.
Оставляя в подынтегральных выражениях (16.30) слагаемые, зависящие
только от (<медленн х» переменн х, выпи ем окончатель ое соотноше
для корреляционной матрицы:
т т т
От=Ф'(Т, О) Й~Ф" (Т, О)+ Ф'(Т, г) Во(г) дг Йо Ф*(Т, г) В,(г) дг +
о о
т
+2 е, Ф'(Т, () 2В,В,*,+ ~, '(В'В'*+В'В"*)]Ф*"(Т, ()Н(. ((«.)))
1=1
о
Используем полученные формулы для исследования возмущений траек-
тории в центральном гравитационном поле при малом постоянном транс-
версальном реактивном ускорении. Рассматривается квазикруговой участок
движения (эксцентриситет е — а). Запишем уравнения невозмущенного дви-
жения:
(16.34)
()=.
()',ц (1 + «соя ч)'
Ж р~р
и(0) =и,.
Уравнения (16.34) получаются из (4.47), если положить ая=а)) =О, пав
=а=сопя$ и принять компоненты вектора Лапласа Ь=е соя р„(3= а я1п
фокальный параметр р и аргумент широты и = ч+ ((»„в качестве перемен-
ных, описывающих движение в плоскости орбиты.
—" =2а
Ж 1+«сояч '
ДЯ
— =О
дй
р()=1,
ь (о) = о,
О(о) =о,
и(о) = и„

575
ТОЧНО СТЬ ВЫПОЛНЕНИЯ МАНЕВРА БЕЗ КОРРЕКЦИИ
э 2)
Запишем линеаризованные уравнения движения в отклонениях, пренебрегая
членами порядка еа (в силу малости эксцентриситета) и порядка а'
Р = 6ар2х — 6арвхг соя и — 6арвхо яш и + 2рвба,
Ии
ах 3 5 ~ 5
= 4арх~ соя и — ар' — + — соя 2и ) х~ — — ар'ху яш 2и+ 2р'Ьа соя и+ ар'Ьа я1п и,
дх~ 3 5
5
= 4арх я1п и — ар' 2 — 2 соя 2и х~ — 2 ар'х я1п 2И+ 2р'ба я1п и — ар'ба соя и,
а'и
(16.35)
Йи я1п 1
ах;
— — ар'бЗ соя и,
Их~ 3
— = — Урх — 2р ~рхв соя и — 2р арху яш и+ 2рв Ур6~ с$д ~ я1п и.
ИДр 3
ди
= — 6арйу — 4ару~ соя и — 4ару я1п и — т'р у~,
2
5
=6арвур соя и+ ар' 2 + 2 соя 2и уд+ 2 ар2уу я1п 2и + 2р 1ру ~ соя и,
ди
д
= 6ар у я1п и + ар — соя 2и уо + ар'у~ яш 2и + 2р ~р у~ яш и,
уд з 3 5 5
ди 2 2 2
— — у~ — О
Усредняя полученное по аргументу и, найдем уравнения первого приближения.'
д *
= — 6ар у„— ' ру~,
ди Р 2
д * 3
ар у
~и 2
(16.36)
И *
уД 2 2+
— ар у
ди 2
— у~ — О
Йи Йи Йи
Их решение таково.'
у" = (с — р Ур с~/2в) р в, у" = стр ~',
(16.37)
* 314 * *= *=
у~ — — с~р ', у„=с„у, =с;, у =с .
Постоянные интегрирования с„,..., с~ определяются из условий (16.9), которым
полжны удовлетворять сопряженные переменные на правом конце траектории в терминах
фундаментальной матрицы Ф.
Здесь о а — угол между проекцией вектора возмущенного реактивного ускорения на пло-
скость орбиты и перпендикуляром к радиусу-вектору, ор — угол между вектором возму-
щенного реактивного ускорения и плоскостью орбиты. В качестве независимой перемен-
ной в (16.35) выбран аргумент широты и. Это позволяет отказаться от требования малости
возмущений времени х~, так как время ~ не входит в правые части (16.35). Это замечание
справедливо и для отклонений положения восходящего узла хд.
Выпишем систему, сопряженную к (16.35):

576 ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ ~ГЛ. 16
Запишем окончательный вид ненулевых элементов матрицы Ф* (и1, и):
р/4(Ц)р /4(Ц)
&lt р' =[ '/ ( ) Ђ” р /* (и)]/2 р' (
(16.38)
(здесь и, — конечное значение независимой переменной).
Для определенности положим, что возмущения вектора реактивного
ускорения по модулю аа и по направлению аа, 3~ представляют собой взаимно
некоррелированные стационарные белые шумы
(16.39)
(/=а, а, ~).
Й.. =а', .+аЧ(ц — ц')
Коэффициенты ряда Фурье (16.24) для правых частей уравнений невоз-
мущенного движения (16.23) в данном примере имеют вид
~о рд=2р ~ В,' ~ — В'1 ~ — 2р'
В", д„— В1;р = — В,' д„= ар-", В1д6 = ар2/з1п
(16.40)
д = рЧ, + 4р'(ц — и,)'а',, + 4р'(ц — ц,) а,-',
йяд, — — р '/ Ш6 дд + [4а2 + (аа )2] (~/р — 1)/2~,
й~/~/ — — р ' й6 ~~ + [4а2 + (аа ) 2] (~/р — 1)/26,
Иду = Й6 дд+ /6ц (а6/з1п 10) (р" — 1),
цд — — д„, + 1/бай р- — 1),
И„= д, „+ [(р'/ — 1)/2а]' д, + [(р'/ — 1)/а] д,, +
+ 2 (а,/а)2 р'Цр' (ц — ц ) — 2~ +(р — 1)/а]+
+ (а„/а)'[р / (ц — ц,) — 1]'.
(16.41)
$ 3. Измерения координат и скорости
1. Статистическая обработка измерений — дискретный случай. Будем
считать в дальнейшем, что точность выполнения маневра без коррекции
недостаточна и в процессе движения в расчетную программу ускорения
от тяги а'6'(~) должны быть внесены поправки. Предполагая, что эти поправки
и возмущения реактивного ускорения независимы друг от друга, запишем
уравнения возмущенного движения в виде (см. (16.7))
х = А (~) х+ С (~) Ьа+ В (~) ~,
(16.42)
где Ла — вектор поправок к расчетной программе ускорения от тяги (коррек-
тирующее управление), С (~) — заданная матрица.
Переходя к прогнозам (16.8) отклонений в конце маневра, перепишем
(16.42) в виде (ср. (16.10))
у = Ф (Т, 1) (С (1) Ьа + В (1) ~).
(16.43)
Для выбора корректирующего воздействия Ла (~) необходимо как можно
более точно знать действительные значения фазовых переменных. Точность
Подставляя в (16.33) соотношения (16.38) — (16.40), получаем формулы
для определения элементов корреляционной матрицы конечных отклонений
параметров возмущенной траектории от номинальных значений (ограничимся
приведением только формул для диагональных элементов матрицы — диспер-
сий отклонений):

577
ИЗМЕРЕНИЯ КООРДИНАТ И СКОРОСТИ
[16.44)
Этот набор параметров образует ~-мерный вектор д„ который на номиналь-
ной траектории принимает значение я~~о&g ;. Предполагает я, то ни о ин
наолюдаемых параметров не может быть измерен точно и фактически наблю-
дается вектор й„, отличающийся от истинного вектора П„на величину
ошибки $ . Обозначим через 1„вектор разности наблюдаемых значений д„и
расчетных д~~о~. Тогда, учитывая, что движение происходит в малой окрест-
ности номинальнол траектории, можно записать
~с ~с ~с
1, = ц, — ц~ = Н„х [~,)+ $„
[16.45)
где Н„=1дд„'/дх.~~® — матрица производных д'„по компонентам векторов г,
т, а [матрица Якоби), взятая на номинальной траектории в момент ~„.
Предполагается, что случайные величины $„имеют гауссовское распределе-
ление с нулевым математическим ожиданием М Д„) = 0 и корреляционной
матрицей М ЯД'„) = Й~, которая в дальнейшем считается невырожденной.
Кроме того, предполагается, что ошибки измерений в различные моменты
времени не коррелированы между собой, т. е.
МДД) =0 при ~+~. [16.46)
Для упрощения выкладок в дальнейшем удобно перейти к переменным у„
при помощи замены [16.8) и соотношение [16.45) записать в виде
1„= Н;у„~, ~„[П„= Н„Ь-' [т, ~„)). [16.47)
В основе построения оценки по методу максимума правдоподобия лежит
рекуррентная процедура, связывающая новую оценку у„+, с предыдущей у .
Для получения рекуррентных соотношений сделаем предположение, что
в момент времени 1~ имеется оценка вектора состояния у, полученная в ре-
зультате статистической обработки предыдущих результатов траекторных
измерений. Эта оценка — вектор у~ — отличается от истинного вектора у~
иа величину Оу„=у„— у„— ошибку оценки. Предположим, что в момент ~„
ошибка оценки имеет гауссовское распределение с нулевым математическим
ожиданием и известной корреляционной матрицей В~.
К моменту времени ~~ 1 имеется следующий набор соотношений для
вектора у~ 1:
— 3'Ю ~ Д
1с+1 й+1у)с+1 Г ~1+1
у„+ ~[Т, ~) С[~)Ьа[с)И~=у „+3у„+~1„
[16.48)
~(~, )~~)1()«).
37 Механика полета
единичных измерений этих величин нельзя считать удовлетворительной,
потому предполагается, что измерения производятся регулярно с достаточ-
ной частотой, а для получения оценки фазовых переменных [вектора состоя-
ния системы) могут использоваться результаты всех предыдущих измерений.
В настоящее время существует большое число различных методов обра-
ботки результатов траекторных измерений [см. [16.9, 16.12]). Далее будет
описан один из возможных способов — определение оценки вектора состоя-
ния по методу максимума правдоподобия. Пусть измерения производятся
в моменты времени 0=10 ( 11 (... ( 1~ — — Т. В каждый момент времени 1„
определяется набор параметров, зависящих от фактического положения ап-
парата, его скорости и реактивного ускорениями
д,',=д'[г[1„), т [1„,), а[1,)~ [г=1,..., ~; Й=О,..., Ж).

578 пОстРОение пРОГРАмм УпРАВления В стАтистическОЙ пОстАнОВке [Гл. 16
Случайный процесс ~(т) — гауссовский,'с нулевым математическим ожи-
данием (см. (16.5а), (16.5б)), поэтому случайная величина т~„имеет гауссов-
ское распределение и М (т1,) = О. Предположим, что корреляционная матрица
М (т~д„') известна и равна Й"„(, а величины т1„ в различные моменты времени
некоррелированы, т. е. М (1~,.1~') = О при 1 + ).
В соотношениях (16. 48) величины, стоящие в левых частях равенств,
можно рассматривать как результаты наблюдений, зафиксированные в мо-
мент времени 8~,.
Действительно, перепишем (16.48) в виде
\г Ю
~и+1 = Я+1Ук~1 + 4+1г
(16.49)
где
Ф (Т, с) С (т) Ьа (с) (1~
Уш+
(16.50)
~~+1
и(„)
н~„=
~Ул + '1ш
~Г
~ж=
тогда нетрудно видеть, что соотношение (16.49) аналогично (16.47).
Случайный вектор ~„имеет гауссовское распределение с нулевым
математическим охсиданием и корреляционной матрицей
п~
В ~-1
д6
7с.(-1 ()
(16.51)
ъГ
Представим распределение вектора ~„,1 в виде
р Я,,, ) =[(2т~)'+" Йес Л~., ~ — '~ ехр [ — ~/, (1,.+, — Й",+,у,,+,)'ф~„) ' (1,,+, — Л"„у„,)~.
('1 6.52)
ЪГ Ъ~
М (Й ) (1+ Н":+у )=".
(16.53)
Это уравнение всегда разрешимо [16.27), его решение определяет оценку
У„1=~~. НН М.)''. +(~~+(~1('~~а+
Ф (т, ~) с (~)ьа ( (с(~1,
(16.54)
где матрица
(16.55)
является корреляционной матрицей ошибок оценки в момент ~„,.
Величина, стоящая в правой части (16.52), носит название функции правдо-
подобия. Она зависит от вектора у „подлежащего оценке. В качестве оценки
по методу максимума правдоподобия принимается величина у,,„, доставляю-
щая максимум функции правдоподобия. В данном случае это соответствует
максимуму квадратичной формы в показателе экспоненты (16.52). Необхо-
димые условия максимума записываются в виде линейного уравнения:

измеРения кООРдинАт и скОРОсти
579
Чтобы убедиться в этом, представим величину ~у~+~ с учетом соотношений
(16.48) и (16.53) в виде
М
~у„= — [й~ (й„' ) 1й„"т]1й~ (й„' ) 1$„
Отсюда М (оу~+,) = О; тогда, воспользовавшись последним соотношением, запишем
корреляционную матрицу случайного вектора ~у~+,
м Ру„„~у„„) = [йД, (й„'„) ' йу,1] ',
которая и приводится к виду (16.55).
При выводе соотношений (16.54) и (16.55) использовалось предположение о не-
вырожденности матрицы й~. ~роме того, чтобы обращение соответствующих матриц
в (16.54) и (16.55) было возможно, достаточно невырожденности матрицы Л~ или,
в силу соотношений (16.55), невырожденности матрицы Й,".
В начальный момент (когда никаких измерений еще нет), очевидно,
у(о) =о,
(16.56)
а корреляционная матрица ошибок оценки совпадает с корреляционной
матрицей ошибок начальных условий:
Л~ = Ф (Т, 0) Й,Ф'(Т, 0),
при ~Й вЂ” с ~ (ЬЕ,
)' — ~)
М [Я (Е) ф' (Е)] = М [~ (Е) ~' (Й)] = 0 при ~ Š— с ~ ) ЬЕ,
где Г (~) и И~ (~) — известные матрицы, причем бей У+О. Тогда, перейдя
к пределу при Л~ — ~ 0 в соотношениях (16.54) и (16.55), получим дифферен-
циальные уравнения
у = ФСЬа+ РН"'7 ' (1 — Н "у),
1)" = — РН"*7 'Н "Р+ ФВХВ'Ф',
которая невырождена в силу невырожденности Ю„. Следует отметить, что
соотношения (16.55) не содержат случайных величин, т. е. корреляционные
l~
матрицы В~ не зависят от конкретной реализации траектории и могут быть
определены заранее, до выполнения маневра.
2. Статистическая обработка измерений — непрерывный случай. При
выводе соотношений (16.54) и (16.55) предполагалось, что ошибки отдельных
измерений 1, а также отклонения т1, вызванные ошибками в реактивном уско-
рении, на различных интервалах между измерениями некоррелированы.
Если рассматривать ошибки измерений $ и отклонения т1 как непрерывные
случайные процессы, то это предположение означает, что максимальная ве-
личина интервала 1 — -, на котором корреляционные матрицы этих процессов
отличны от нуля, не превышает минимального интервала между соседними
измерениями. Очевидно, что при уменьшении величины интервала между
измерениями эти случайные величины станут коррелированными и преды-
дущие рассуждения будут неверны.
Переход к белому шуму в ошибках измерений и в помехах, вызывающих
ошибки реактивного ускорения, дает возможность получить непрерывные
аналоги соотношений (16.54) и 16.55). В самом деле, пусть измерения произво-
дятся через равные промежутки времени Л1, а корреляционные матрицы слу-
чайных процессов 1 (1) и Г (1) равны

580 постРОение пРОГРАмм УпРАВления В стАтистпческои пОстАнОВке [гл. 16
Соотношения типа (16.57) в литературе известны под названием уравнений
оптимальной линейной фильтрации (см., например, [16.28]). Следует отме-
тить, что второе уравнение (16.57), так же как и соотношение (16.55), не со-
держит случайных величин и может быть проинтегрировано заранее. Это урав-
нение представляет собой матричное уравнение Риккати и соответствует
системе из. 1/,и (и+1) дифференциальных уравнений первого порядка ').
В работе [16.28] показано, что при сделанных предположениях относительно
коэффициентов уравнения его решение существует и единственно.
3. Точность определения траектории в стационарном режиме. Вернемся
снова к исходным переменным — текущим отклонениям х (~). Легко прове-
рить, что корреляционная матрица ошибок оценки отклонений х (~) удов-
летворяет уравнению ')
дх . Адх ] дхАт дхНхту-1Нхдх ] Ндтдт
д И,) =д,. (16.58)
Первые два слагаемых в правой части уравнения (16.58) учитывают влияние
на точность измерений динамики системы. Если матрица А соответствует
неустойчивой системе, то первые два слагаемых «стремятся» увеличить
норму з) ~~д ~~, т. е. уменьшить точность определения траектории с течением
времени. То же самое можно сказать и о влиянии последнего слагаемого в пра-
вой части (16.58). С другой стороны, третье слагаемое, учитывающее влияние
текущих измерений, очевидно, способствует увеличению точности опре-
деления траектории. Таким образом, точность определения траектории
зависит от соотношения двух противодействующих факторов — динамики
системы и возмущений, с одной стороны, и текущих наблюдений — с другой.
Представляет интерес исследование предельной точности определения
траектории в предположении, что измерения проводятся весьма длительное
время. В работе [16.28] показано, что независимо от начального условия Д'„
(д„— положительно определенная симметрическая матрица) все решения
системы (16.58) стремятся к одному и тому же стационарному решению
М (а, т) = Ф'(г, т) Нхт (г) Н (г) Ф (г, т) Нг
положительно определена. Здесь Ф вЂ” фундаментальная матрица решений
Ф (1, ~) = А (~) Ф (1, -.),
Найдем вид стационарного решения при некоторых дополнительных
предположениях, которые будут сделаны по ходу построения. Зафиксируем
') Количество уравнений равно количеству различных элементов в симметрической
матрице йу.
2) Здесь предполагается, что измерения начинаются с момента 10.
з) 11од нормой матрицы Й подразумевается сумма ее диагональных элементов.
Для существования стационарного решения достаточно выполнения
одного из следующих условий.
1'. Матрица А (~) соответствует асимптотически устойчивой линейной
однородной системе.
2'. Выполнено условие «полной наблюдаемости»: для любого времени «
найдется такое с (т) ( т, что матрица

ИЗМЕРЕНИЯ КООРДИНАТ И СКОРОСТИ'
момент времени ~ и перейдем к переменным у при помощи замены (16.8)—
(16.9), но с преобразующей матрицей Ф (~, ~), ~ ) ~, для которой
Ф(1, ),)=Е.
(16.59)
(16.60)
Предположим сначала, что возмущения реактивного ускорения отсутствуют,
т. е. И~=О; тогда левая часть уравнения (16.60) есть производная И ф") 1/Ит;
отсюда
( )~ (~, 8) = — Н"' (-., 8) Г 1 (г) Ну (~, г)).
С другой стороны, в силу (16.8), (16.59) б" (~) = й' (~), поэтому решение
исходного уравнения (16.58) при И'(Е):0 имеет впд
— 1
Й'(Ц=[Ф'(~„Ц)х&gt ;) 'Ф(~ Ц+ ж ~, я
~о
(16.61)
Чтобы найти стационарное решение, перейдем к пределу при ~, -) — со
в соотношении (16.61), предполагая, что условие 1' или 2' выполнено.
Пусть матрицы А, Н, )', И' — постоянные. Тогда фундаментальная
матрица определяется в виде
Ф (~, 1) = ехр А (1 — ~),
1)~ т.
Приведем матрицу А невырожденным линейным преобразованием 0 к жорда-
новой форме: А=ф.1~ ', У=Й1ад ~У„..., У ), где У,. — жорданова клетка,
соответствующая характеристическому числу ~),., ),=1, ..., д (д — число
/~
различных жордановых клеток). В результате преобразования Л запишется
в виде
-1
б = )1т ~е" ~' (О„) ' ~+ е~''Я'Н ' )~ 'Н'Яе~'йт е~"~'. (16.62)
1-э со
До сих пор считалось, что возмущения от тяги отсутствуют, т. е. И' (~)=0
Пусть теперь И~= ~„'-ВИ',В', где ~, (~) — малый параметр, а матрица И~о—
постоянная. Тогда решение уравнения (16.58) может быть получено в виде
матричного ряда по степеням
Б =,'~, с',"С„, (16.63)
~с= О
где нулевое приближение С, — матрица, найденная из выражения (16.62),
а С„находятся методом неопределенных коэффициентов. Отметим, что в рас-
смотренном случае предельное решение Й не зависит от времени и является
решением алгебраического уравнения, получающегося из (16.58) приравни-
ваниеы к нулю его правой части.
Пусть измерения начинаются в некоторый момент времени ~,. Тогда кор-
реляционная матрица Л" удовлетворяет второму уравнению (16.57) с началь-
л
ным условием Й'„' при 1=1,. Учитывая, что Л" невырождена, второе уравнение
(16.57) можно переписать в виде

582 ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ [ГЛ. 16
4. Нримеры подсчета предельной точности. Рассмотрим некоторые частные случаи,
в которых предел Л может быть найден в явном виде.
1'. Пусть действительная часть Ве Л; ( О, 1=1, ..., д (условие асимптотической
устойчивости 1' из п. 3). Покажем, что в этом случае решение Й~ (Е) по норме стремится
к нулю при Е -~ со. Действительно,
(16.64)
Для ~)'е ~( справедлива оценка (16.29)
(( е Е ( р (Е) е"~
(а = тах Ве Л,.),
) ° ° ° д Д
— Ттуухту-1НхТ ) ()
(16.65)
где у, — собственный вектор матрицы А, соответствующий характеристическому числу ~,.
Производя перемножение блочных матриц под знаком интеграла, получим
е я НАТУ 1НхЕ)е~ =~~ еЕ "+ ~)~Р; (Е) ~~;, Е=), ..., д °
Здесь Р,, (Е) — некоторые матрицы порядка Е;Е;, элементы которых суть многочлены сте-
пени не выше 2 р. Выполнив интегрирование, представим выражение в квадратной скобке
(16.62) в виде
От (Ох) — 1 О + (( е(~1+~ )) ~р (),.
Здесь Р; .— некоторая многочленная матрица с элементами степени не вьйе 2д.
Заметим, что если Р; (Е) ехр ((Л„+ Л ) Е) — эО (~', у' ) 2) при Š— э со, то определитель
ЙеЬ ()',)'(дох) 1)',) +((е~~'+~Е) Р; )(;, =),, д) — се ~'~ пря Š— э со,
где с — постоянное число. Произведя обращение матрицы при некотором фиксированном
$ и переходя к пределу, получим 2)
211
]Ет )~)х (Е) ~)х — ~) Я)ад () О ()) Дг 2) (ТтЕ7хтЕт-1НхТ ) — 1 1, ~,т
1-эсо 11
() 6.66)
Из вида матрицы й следует, что предельное распределение ошибок оценки вектора х
одномерное (матрица Й' имеет ранг, равный единице) и сосредоточено в направлении
вектора ~1, т. е. в этом направлении при достаточно большом времени будет наибольший
разброс оценок.
3'. Рассмотрим движение аппарата, накапливающего атмосферный газ. Под дей-
ствием возмущений, вызванных отклонениями плотности атмосферы от расчетной, движе-
ние происходит в малой окрестности номинальной траектории. Для описания этого дви-
жения используются линеаризованные уравнения из (7.88): второе, третье, пятое и шестое.
Тогда отклонения х по радиусу (высоте) от расчетных значений удовлетворяют уравнению
(16.67)
х+х — Ьх=~,
где Ь вЂ” параметр, зависящий от силы сопротивления атмосферы на выбранной орбите:
Ь=2~еЛ (см. (12.79)); ~ — гауссовский белый шум, вызванный случайными откло-
') Это утверждение ддказывается от противного: если число Я„( О, то не выпол-
няется условие 2' из и. 3.
2) Непосредственной проверкой можно убедиться, что найденная матрица Йс оора-
щает в нуль правую часть уравнения (16.58).
где р (Ю) — некоторый многочлен степени р=шах (Е1,..., Е„) (Е; — порядок Е-й жорда-
новой клетки). Из оценки (16.64) следует, что второй сомножйтель в правой части (16.64)
стремится к нулю, а третий ограничен некоторым постоянным числом, поэтому ЦЕ) (Е)// О
при ~ -~ со. Это означает, что в данном случае при длительных измерениях оценка вектора
состояния стремится к его фактическому значению: Й =О.
2'. Пусть Л, ) О, а Ве Л; ( О, Е=2,..., д. Представим ехр (УЕ)=с)хай' (ехр (У,Е),
ехр (У,Е), ..., ехр (УдЕ) ) и разобьем матрицу Д'Н~'Г-'Н~Д на блоки Я; размерностью Е,Е .
Пусть выполнено условие полной наблюдаемости (2' из п. 3), тогда ')

КОРРЕКЦИЯ, ОПТИМАЛЬНАЯ В СРЕДНЕМ
$4]
пениями плотности атмосферы от номинальной: М[~ (~)]=0, М [~ (~) ~ (~)]= а~~~ (~ — «).
Для Ь=0,648 (ср. (12.89)) характеристические числа и собственный вектор матрицы А
для системы (16.7), соответствующей уравнению (16.67), равны: Л,=0,514, Л, а ——
= — 0,257+1,095 1, т1=(3,79; 1,95; 1)'. Пусть навигационная система состоит из од-
ного высотомера, а ошибки ~ (~) измерений высоты представляют собой белый шум:
М [~ (~) ]=О, М [~ (~) ~ ( ~)]= а; О (~ — ~). Матрица Н в этом случае имеет вид Н~=(Й,
О, О), где Й вЂ” «коэффициент усиления» высотомера, который считается постоянной ве-
личиной. Тогда, воспользовавшись формулой (16.66) и ограничиваясь двумя членами
в разложении (16.63), получим
,р 1,028 0,528 0,271 0,0847 0,0782 — 0,184
й~~ = р 0,528 0,271 0,139 + а~ 0,0782 0,827 0,309
.0,271 0,139 0,0716 — 0,184 0,309 1,073
$ 4. Коррекция, оптимальная в среднем
(16.68)
М (3Р,.) = ЛХ(30,) =О,
М (502) = а2.~зТ з
и что ошибки ог,, о0,. (1=1, .
образом, в моменты времени
действительной траектории
, и) не коррелированы между собой. Таким
1,. (1=1,..., и) известны оценки отклонений
от (1 — 1)-й расчетной траектории
(16.69)
Ы~, =0(~,.) — и&l ;' ') (1,
') Напомним, что через (г (~), и (~) ) обозначается действительная траектория, а через
(г (1), О (~) ) — результат обработки наблюдений.
Основное внимание в данном параграфе уделяется оценке дополнитель-
ных затрат рабочего вещества, необходимых для осуществления коррекции
траектории. Рассмотрение проводится в приложении к идеальному двига-
телю ограниченной мощности. В этом случае задача сводится к отысканию
минимума математического ожидания приращения интеграла от квадрата
реактивного ускорения. Учитываются ошибки реализации оптимальной
программы реактивного ускорения, ошибки измерений координат и скорости,
отклонения от начальных условий. Считаются известными вероятностные
характеристики этих случайных величин (математическое ожидание, корре-
ляционная функция, дисперсия). Накладываются ограничения на дисперсию
конечных отклонений координат и скорости.
Принимается схема последовательных коррекций конечного положения
аппарата. Коррекция осуществляется основным двигателем, который рабо-
тает непрерывно. На основании данных измерений в некоторые моменты
времени (моменты коррекции) производится оптимальная поправка про-
граммы реактивного ускорения. Из условия минимума математического ожи-
дания приращения функционала задачи выбираются оптимальное распре-
деление и оптимальное число моментов коррекции [16.18, 16.19].
1. Оптимальные поправки к программе реактивного ускорения. Продол-
жим исследование примера, для которого в п. 3 ~ 2 была получена оценка
точности выполнения маневра без коррекции. Предположим, что соотноше-
ния (16.22) не выполняются и в процессе движения необходима коррекция.
Считается, что измерения производятся в дискретные моменты времени 1„
(Й=1, ..., К), а результаты измерений статистически обрабатываются
к моментам коррекции ~„. (1=1, ..., и ( Г) в соответствии с алгоритмом
максимума правдоподобия (см. соотношения (16.54) и (16.55)). Как было
установлено в ~ 3, ошибки оценки отклонений бг,=г (1,.) — г (1,.), о0,.=
=0 (~,.) — и (~,.) имеют нулевое математическое ожидание 1). Дисперсия может
быть найдена заранее, до выполнения маневра (в общем случае как функция
времени). В рассматриваемом одномерном примере считается, что

584 пОстРОение пРОГРАмм упРАвления В стАтистическои пОстАКОВке [Гл. &l
Поцравки к программе а' 1' (~) ускорения от тяги выбираются из условия
оптимальности «в большом»: оптимальная поправка
Ла" & t = а &g ; ( ) — а~'- 1(й),
( )
вычисляемая к моменту времени 1, (момент ~-Й коррекции), должна обеспе-
чивать минимум функционала (см. (7.1))
7
Х. = а'&l
(16.71)
(16.72)
В промежуток времени между моментами ~,. и ~,. 1 должна реализоваться
программа а">( ), кото а в мом нт врем ни 1„ +1 сменяе ся на но ую оп
мальную программу а«+1& t; ( ) и т.
2. Приращение функционала. Выражение для функционала Х в случае
движения с ошибками и коррекцией можно записать в следующем виде:
и
(а">(1)+оа(1) 'Ю (1 О, 1„ 1=
(16.71)
Представим ускорение от тяги а&lt '&g ; (~)
а" & t; 1 = а lt; & t; (1 + а lt; & t; (1 +
(1 6.74)
и преобразуем функцион ал (16.73) следующим образом:
7 7
Ы=Х вЂ” Х =2 ~ ' 'Ь '~~И~-&l ; & t; '5
О
Т Т
~г » — 2 П
-&lt -2 ', ь, ~& t; ~' ь ~~~  ,,~ ~' б
т=З ~. .у=1 »=1 ~.
7 7 7
7г П
2~ Ь '~ Ь ~'- ~ Ш+ ~ <Ь~ ~&g ; Ш~~
~=2 ~. а=1 ~. О
г Ф'
(16. 75)
где (см. (7.33))
~2Р
7 (с<о gt
0 ТЗ
О
(16.7(&g
Увеличение функционала по сравнению с расчетным Ус приводит к не-
обходимости перераспределения массы аппарата между полезной нагрузкой,
запасом рабочего вещества и двигательной установкой.
при перемещении между точками фазового пространства (г (1„.), О (1,.) ) и
(1, О) за время Л~,.=Т вЂ” ~,
Таким образом, от поправки Ла<'& t;(~) треб ется, что ы при отсу
дальнейших погрешностей (оа (~)=0 при ~ ) ~,.) она сводила бы к нулю
отклонения Лг,. и Л< g ;,. в конце трае т рии с минима ьными энергетич
затратами. Выходить на расчетную траекторию до конца движения не тре-
буется.
Считается, что погрешностей при вычислении поправки Ла«> ~) не в
сится. Для одномерного движения в бессиловом поле поправка к программе
ускорения определяется следующим соотношением (см. (7.30), (7.31)):

585
КОРРЕКЦИЯ, ОПТИМАДЬНАЯ В СРЕДНЕМ
т (1 — ~/Ф )' — ЛФ вЂ” — 1
фо
т < lt; l ;Ф в ” Ф ) Ь
О
ЬФ=2М, Фо — 2 о °
(16.77а)
т„о ~/Фо+
Если же масса двигательной установки должна остаться неизменной, то но-
вые компоненты массы аппарата будут следующие:
т (1 — ~/Фо)' — ЛФ
О
т„= ~/Фо — Ф„
т„, ж <& t; , ЬФ = в
Фо
(16.77б)
Следует отметить, что в соотношениях (16.77а) и (16.77б) масса полезной на-
грузки в результате перераспределения в обоих случаях получается оди-
наковой, т. е. изменение массы двигательнои установки в линейном прибли-
жении не влияет на величину полезной нагрузки.
Для максимизации осредненной величины т„нужно определить такое
распределение моментов коррекции ~„. (~=1,..., и) и такое их число и, чтобы
при условии обеспечения в конце движения заданной точности (16.22) ве-
личина математического ожидания ЛУ была минимальна.
Чтобы вычислить М (ЛУ), необходимо найти математическое ожидание подынтег-
ральных выражений в ($6.75). Эти выражения представляют собой поправки Ла«& t; (
ошибки оа (~) и их произведения. Поправки Ла&lt ") ( ), согла но ($6.7 ), зави ят от сумм
ных отклонений Лг;, Ли; — ($6.69). Последние складываются из отклонений, обусловлен-
ных ошибками оа (~), и нз ошибок (~ — $)-го и ~-го измерений:
оа Н1+ Ы; — оу„1,
(16.78)
оа (-.) й + 5Р; — оР, — (1,. — 1„. ) о&lt
Математическое ожидание членов, содержащихся в первых квадратных скобках
выражения ($6.75), равно нулю, так как подынтегральные выражения этих членов ли-
нейны относительно случайных величин Лг,, Л~;, ~а, математические ожидания которых
равны нулю.
Считая, что случайные отклонения оа (~) по разные стороны от моментов времени ~„.
перехода на новую программу а&lt ") ~) не коррелиров ны ме ду соб
М(оа(~) оа (-.)] =О при ~; 1(~(~„, ~ 1(~(~~, & t;
(16.79)
получаем такой же результат и для второй квадратной скобки формулы ($6.75), так как
индексы сомножителей в этих членах отличаются больше чем на единицу. Это означает,
аа основании ($6.78), что сомножители не коррелированы между собой, а математическое
ожидание каждого из них равно нулю.
Предполагая, что ЛХ/Хе (& t; 1 и ограничива сь члена и, линейн
относительно ЛХ/Хе, можно получить приближенные выражения для ком-
понент массы аппарата при движении с коррекцией, аналогичные (6.15)—
(6 17).
Если при перераспределении масса двигательной установки т„может
быть изменена, то оптимальные компоненты определяются так:

586 ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОИ ПОСТАНОВКЕ [ГЛ. $6
Два первых члена, содержащихся в последних квадратных скобках формулы ($6.75),
выражаются через отклонения Ьг, 1, Ьг;, Ьи,. 1 и Ьи; следующим образом:
12 ~г;Ьг; 1 Ьг,~и; 1
~' — т — ~„., (т — ~„.,)'+ 2(т — ~,,) +
( т' — 1,,)2(Т вЂ” 1,,( ((2 2 Т вЂ” 1,) ' ~~]'
(16.80)
12 Ьг'; Ьг;Ьи; 1
(~'= т — 1,. (т — 1,.( т т — 1 ( з ~" ]'
Поэтому математическое ожидание приращения функционала, с точ-
ностью до квадратичных относительно Л2/Т членов, равно (см. (16.19), (16.22))
"2
+ ~ — ~,.~т "(" )+ з(~ — ~,~т) + (~ — ~„~т)з ~+
о~у ~ 2 о,„1 2 8„„
12 ' 2 1 — 1„1Т + (1 — 1„(Т( ~
Т вЂ” г$1
ОтО = ~О,, О~О = ООо~ ~в Т вЂ” 8;
(16.81)
В конце движения (2= Т) траектория должна попасть в заданную область
конечных значений координат и скорости, т. е. ожидаемые отклонения
от расчетной траектории в конце движения должны быть ограничены сверху.
Это условие записывается в виде двух неравенств, аналогичных (16.22):
2а,' ЩТ) (1 — 2 (Т) + а2„( ~Р,
~/ а2 (Л2)Т) (1 — 2„/Т)з+ а'-„(1 — 2„/Т) + а2„( (Р.
(16.82)
~ОР1 = Т ' — 1 — Т
(16.83)
1 У ° ° ° 2 222 °
Минимальная для заданного числа моментов коррекции величина ма-
тематического ожидания приращения функционала У
12Р Ь| 1
ЛХ(ЛХ) „—,а, З р +~2
(16.84)
( р, = и [2 (1 — 2„) Т)-'~" — 3 (1 — 1„~Т)'~12 + 2 (1 — 2„/ Т)-'(" — 1])
монотонно убывает с увеличением и, причем
(16.85)
11т и, = — 1 и (1 — 2„/Т)
3. Оптимальное распределение моментов коррекции. Выписанные не-
равенства накладывают ограничения на 2„при отыскании минимума М(ЛУ)
по 2,. (~=1,..., и).
Если погрешности измерений не учитываются (а„,.=а,„.=0) и если на-
чальные условия предполагаются реализованными точно (ае„=ае„=0), то
для оптимального распределения моментов коррекции получаем формулу
геометрической прогрессии.'

587
коррекция, ОптимАльнАя в среднем
Зр2т
2а,'2М
Т
(16.86)
В случае постоянной отличной от нуля дисперсии ошибок измерений
(ад — а „а„,. = ао„, ~ = О, 1,..., и) оптимальное распределение моментов
коррекции уже не выражается такой простой формулой, как (16.83), и должно
/ .? Я
ярую
/ Г
~~у ю
Рис. 16.1. К формулам (16.84), (16.87).
определяться численно. Если же воспользоваться формулой (16.83), то ха-
рактер зависимости ЛХ (ЛУ) от 1ои и и 1 — 1„~Т сохранится (рис. 16.1, б):
7[7(й|[ =' —,~~",( — и,+ — )+~~р,+ "т,] (18.87)
'91 —— и [2 (1 — 1(Т [ "" — 3 (1 — 7(Т [ "" + 2 (1 — 1(Т[ ": — 1[ ]
° °
(2, = (1 — ЦТ)-'(" [(1 — ~„/Т) 1 — 1] + '/, (1 — ~„( Т) '.
Обсудим полученные результаты. Задача об оптимальной коррекции была
поставлена так, чтобы еще до реализации траектории выбрать оптимальные
в среднем соотношения масс и оптимальные программы реактивного ускоре-
ния, которые обеспечат максимум полезного груза, на доставку которого
можно рассчитывать.
Найденное оптимальное распределение моментов коррекции в случае
точных измерений подчиняется формуле геометрической прогрессии (16.83).
Моменты коррекции сгущаются к концу траектории. Момент последней
коррекции должен быть максимально возможно удален от конца траектории
при обеспечении попадания в заданную область конечных значений коорди-
нат и скорости.
Сгущение моментов коррекции к концу траектории вполне естественно.
В начале движения для устранения отклонений от расчетной траектории
еще остается много времени и можно допустить большую величину этих откло-
нений при достаточно малом уровне поправок Ла"' — (16.72), т. е. можно
большее время двигаться без коррекции, чем к концу движения. Такой же
закон распределения моментов коррекции получен и в работе (16.30], в ко-
торой рассматривается импульсная коррекция баллистических траекторий.
(см. 1од (1+~р,) на рис. 16.1, а в зависимости от 1ои и и 1 — ~„/Т). Видно также,
что ~2 уменьшается с увеличением 1 — ~„/Т; поэтому оптимальное располо-
жение момента последней коррекции должно выбираться из неравенств
(16.82) максимально удаленным от конца траектории:

588 постРОение пРОГРАмм УпРАВлениЯ В стАтистическОЙ пОстАнОВке [Гл. и
В случае импульсной коррекции ошибка вносится только в моменты прило-
жения импульсов, в рассмотренном же случае ошибка накапливается непре-
рывно независимо от того, производится коррекция или нет. Поэтому при
условии точных измерений здесь не существует оптимального числа и момен-
тов коррекции.
$ 5. Коррекция, оптимальная с заданной вероятностью
Выбор оптимальных поправок к программе реактивного ускорения
из условия минимальных в среднем затрат рабочего вещества, как это дела-
лось в предыдущем параграфе, может привести к ненадежным расчетным
данным относительно необходимого запаса рабочего вещества на коррекцию.
В рассматриваемой ниже задаче [16.20] использован другой критерий:.
максимальная точность выполнения маневра при ограниченных затратах
на коррекцию. Другим отличием рассматриваемой ниже задачи является
непрерывное поступление информации о траектории и непрерывный процесс
выбора управляющих воздействий на основе текущей информации. Основ-
ное внимание уделено анализу системы управления в целом, включая систему
обработки результатов измерений и систему выбора управляющих воздей-
ствий. Исследование выполнено применительно к идеальным двигателям
ограниченной мощности и ограниченной скорости истечения.
1. Синтез оптимального управления. Рассматривается возмущенное
движение летательного аппарата вблизи номинальной траектории, описы-
ваемое уравнениями (16.42). Предполагается, что ошибки реализации рас-
четной программы ускорения от тяги определяются соотношениями (16.5б)
и по величине малы по сравнению с номинальным ускорением от тяги а"'(г)
почти наверное, т. е. с вероятностью, близкой к единице. Корректирующее
управление Ла (~) (добавка к номинальной программе реактивного ускоре-
ния) предполагается ограниченным в каждый момент времени и интегрально:
у", 1 6.88)
/ (а'", Ьа) й ( т,о
(2„~, ~1, = Йхе),
Ьа (1) ~ 2, (1),
Действительно, для аппаратов с идеальными двигателями ограничешпш скорости
истечения и ограниченной мощности оптимальное распределение масс (в том числе и
запас рабочего вещества) определяется значениями функционалов, зависящих от реактив-
ного ускорения (см. (5.6) — (5.9) (6.14) — (6.17)). Выпишем оценки для этих функционалов
с учетом малости Оа (~):
для двигателя ограниченной скорости истечения
Аи= )а'"(1)+Ьа(1)-~ ~а(~))НС "- )а(" 4-.~а)Ж+ )оа)Н1=Ь~;
(16.89з)
где Й, (~) — замкнутая ограниченная область, 7 — заданная функция,
фиксированное число. Соотношения (16.88) соответствуют следующей фи-
зической схеме. Основная программа и корректирующие воздействия осу-
ществляются одним и тем же двигателем. Двигатель — идеальный, ограни-
ченной мощности (гл. 6) или ограниченной скорости истечения (гл. 5). Локаль-
ное ограничение на корректирующее управление в (16.88) связано с наличием
в системе управления регулятора, который может осуществлять (<тон
настройку» двигателя, меняя реактивное ускорение в заданной окрестности
номинальной программы. Интегральное неравенство в (16.88) отражает тре-
бование ограниченности запаса рабочего вещества на коррекцию.

589
КОРРЕКЦИЯ, ОПТИМАЛЬНАЯ С ЗАДАННОЙ ВЕРОЯТНОСТЬЮ
$5]
д.|я двигателя ограниченной мощности
1а"' (~) + аа (~) + оа (~))' Н~
о
(а&lt о ~ с )о ~ 2 (а& t;о& t; са
О О
(16.89б)
Лг ( аи* = $'1п (1 — т о);
для двигателя ограниченной мощности (см. (6.17))
у ( Х*= (2/а) торо.
тогда из (16.89а), (16.89б) следуют оценки сверху (с заданной вероятностью) для
составляющих Ьгл и Ул, зависящих от управления Ьа:
для двигателя ограниченной скорости истечения
Ьио —— — ) а'о' + аа ( И1 ( аи™ вЂ” Ли™;
О
(16.90а)
для двигателя ограниченной мощности
у = (а'о'+ аа)~ И~ ~ у* — Х'
0
(16.90б)
В дальней1пем величину, стоящую в правой части неравенств (16.90),
будем называть первоначальным запасом на управление т(с. Текущей вели-
чиной запаса на управление т) (1) назовем величину
т) (~) = т)о — ~ (а'о', Ла) Шт,
(16.91)
где 1'(а'с', Ла) — функция, определяемая из (16.90). Таким образом, выпол-
нение неравенства в (16.91) является необходимым условием реализации
маневра.
Предполагается, что аппарат имеет систему измерений, описанную
в п. 2 6 3. Результаты измерений статистически обрабатываются в соответ-
ствии с алгоритмом максимума правдоподобия, и в каждый момент времени
вырабатывается оценка отклонений у согласно соотношениям (16.57).
Управление Ла выбирается из условия оптимальности «в большом»:
~ каждый момент времени оно минимизирует апостериорное математическое
ожидание квадрата отклонения от расчетной точки в момент времени 7
ври ограничениях (16.88). Апостериорное математическое ожидание в данном
случае означает математическое ожидание при условии, что до момента 1
Случайные отклонения оа (й) представляют собой гауссовские случайные про-
цессы с известными свойствами (16.5б), управление аа (й) ограничено, поэтому заранее
в Ь~ и У можно оценить сверху с заданной вероятностью составляющие, зависящие
от ~а, соответственно величинами Ьг". и У" Пусть установлены допустимые верхние
О
пределы Ли™ и Х* для функционалов Ли и У. Эти пределы вычисляются по перво-
начальному запасу рабочего вещества т о (либо по полезной нагрузке):
для двигателя ограниченной скорости истечения (см. (5.6) при 3=0)

590 ПОСТРОЕНИЕ ПРОГРАММ УПРАВЛЕНИЯ В СТАТИСТИЧЕСКОИ ПОСТАНОВКЕ ~ГЛ. $6
известна вся предыстория процессов измерений и выбора управляющих
воздействий. Текущее значение этой величины запишем в виде [16.31]
Я [~, Ь (О, ~) ] = М [и (х (Т)) ] Ь (О, ~)]
где Ь (О, 1) — совокупность случайных вектор-функций 1 (~) и Ла (~), ~ ( 1,
зафиксированных в данном опыте до момента времени 8, т. е. совокупность
всей информации, которая может быть в системе управления коррекцией
(системе наведения) до момента времени ~. Ниже будет показано, что в запо-
минании всей предыстории измерений и выбора управлений нет необходимости
и в каждый момент система должна «знать» лишь конечное число параметров,
так называемых достаточных координат.
В силу замены (16.8), (16.9) и (х (Т))= и (у (Т)), и для выбора опти-
мального управления можно перейти к переменным у (1), удовлетворяющим
уравнению (16.43).
Перепишем первое уравнение (16.57) в виде
у = ФСЛа+ р у(0) =0 (р, =й"Н"'й' 1(1 — Н"у)).
(16.92)
11т п1ш М вЂ” [Я (~+~Л1, у+Лу, ~+Л~) — Я (~+Л~, у, ~)] +
И- ОЬа~'~,
+ дЯ'/д~ = О,
(16.93)
0( — Л~ =
Сделаем ряд упрощающих предположений.
1'. Контролируемыми параметрами в конце маневра являются только
ог,. (Т) (три первые компоненты вектора х), т. е.
и(у(Т)) =и(х(Т)) =т'-,(Т)+ж2~(Т)+т2(Т).
2'. Движение происходит в столь малой окрестности номинальной
траектории, что можно пренебречь членами, учитывающими изменение
гравитационного потенциала ]~ддlдг~~"'Вг в уравнении (16.6). Тогда урав-
нение (16.92) примет вид
('1 6.94)
у'= (Т вЂ” 1) Ла+ р'(1), у'(0) = О,
Случайная вектор-функция и, (~) представляет собой нестационарный
гауссовский белый шум [16.6] с нулевым математическим ожиданием и спек-
тральной плотностью Й"Н~ Т 1Н"6". Если управление Ла (~) при ~ )~ ~
задано, то случайный процесс у (~) является марковским процессом [16.32],
т. е. распределение векторной случайной величины у (~) в любой будущий
момент времени ~ полностью определяется заданием вектора у в момент
времени 1 ( ~ и не зависит от предыстории процесса.
Нетрудно убедиться, что компоненты вектора у (~) и величина ~ (~)
(запас на управление) являются достаточными координатами для функции
риска Я [16.24], т. е. Я (~, Л (О, ~))=Я (~, у, т~), если управление Ла (-.) при
~ ) ~ известно. Иными словами, ожидаемое значение функции ~ (у (Т))
полностью определяется параметрами у и ~, зафиксированными в момент
времени 1.
Применяя известную процедуру динамического программирования
(см., например, [16.33]), запишем альтернативное уравнение для оптималь-
ной функции Я'.

591
КОРРЕКЦИЯ, ОПТИМАЛЬНАЯ С ЗАДАННОИ ВЕРОЯТНОСТЬЮ
~~~;(~) ~(~7;(~)
(16.95)
г = 1, 2, 3.
4'. Начальный запас на управление ~, превышает «гарантирующий»
запас ~„, определяемый соотношением
~,) ~ = тах Х (а"', Ла) й =,тах Х (а'О', Ла) й
~абер ~абзац
о о
(16.96)
(здесь ~, — момент начала работы системы наведения).
Последнее предположение дает возможность судить о предельной точ-
ности выполнения маневра для рассматриваемой системы, когда запас
на управление не является лимитирующим фактором. Далее, в п. 3, будет
рассмотрен случай, когда предположение 4' не выполнено.
Сделанные предположения позволяют свести задачу выбора оптимального
управления к одномерной. Действительно, в силу предположения 4'
Я' (~, у', т) =Я' (~, у'). Кроме того, учитывая независимость уравнений
в системе (16.94), функцию риска Я' можно записать в виде
Я'(~, у') =,~, Я;. (~, у,.).
э=1
Тогда оптимальное управление Ла, определяется соотношением
Ьа',. = — ~,. (г) з1дп у,,
(16.97)
а Я', (~, у,.) является четной выпуклой функцией от у, Функция Я;. для г-
координаты при оптимальном управлении удовлетворяет уравнению
~2 (' 1~~~~ О ~~~тО
— Й,. (~)' „' — (Т вЂ” ~) ~,. (~) з1дп (у,.) '+ = О ((6.98)
(здесь Й,. (1) — ~-й элемент, стоящий на главной диагонали матрицы Л"ХХ"' р' 1ХХ«Д")
с граничным условием
(у,. — оу,.)2р,,(оу,.) сйу,. = у';. + Н~,(Т) = Ч",.(у,.), (16.99)
ЗРТ, у,.)=
где оу, — ошибка оценки компоненты у,. в момент времени Т с плотностью
распределения р (8у,) (М(8у,) = О, М(8у'.) = Н",(Т)), Н", (Т) — ~-й элемент на
главной диагонали матрицы й~. В дальнейшем индексы г и ' в промежуточ-
ных выкладках для упрощения записи будем опускать.
2. Анализ системы оптимальной коррекции. Как отмечалось выше,
Я (~, у) является четной выпуклой функцией переменной у. В левую часть
уравнения (16.98) входит диффузионный член '/,Й (~) д'Я/ду', поэтому
существует и конечна производная д'Я/ду' (за исключением, может быть,
момента ~=Т). Отсюда, в силу ограниченности дЯ/д~, следует непрерывность
дЯ/ду на границе переключений у=О. Вследствие выпуклости и четности
~ Р, у)
(дЯ/ду), = О.
где у' — вектор из трех первых компонент вектора у (для упрощения записи
символ ь над у' опустим), р' ® — белый шум с нулевым математическим ожи-
данием и матрицей спектральных плотностей, равной матрице третьего по-
/~ Ф~
рядка, составленной из соответствующих элементов матрицы ЛУБ~'Р 1НУЮУ
(для ю, у=1, 2, 3).
3'. Область 2, задана неравенствами

592 пост~оение п~о~]~Амм уп~А~ления ~ с]~А~ис~ичес~ой пос~АнО~~е [~'й. 16
В полуплоскости у ) 0 уравнение. (16.98) имеет вид
~ ~И) д ' — (~ — ~) т(~) д + д, =('
1 д25 дЯ д8
([6ЛОО)
Рассматривается краевая задача для уравнения (16.100) с условиями
(см. (16.99)) ')
Я(Т, у) =% (у) при у) О, (16.101)
(ы~оу)„, = о.
Запишем сначала решение задачи Коши для уравнения (16.100) с начальным усло-
вием Я (Т, у)=%' (у):
(16.102)
С Р, у, Т, )) Г()) д~.
5' (~, у)=
Здесь 6 (~, у, Т, ~) — фундаментальное решение уравнения (16.100), которое представляет
собой плотность переходной вероятности для марковского процесса у (~):
(16.103)
у= — (Т вЂ” ~)тР)+( Р)
Уравнение (16.103) линейное, а случайный процесс р (~) является гауссовским белым
шумом, поэтому процесс у (~) также является гауссовским. Плотность вероятности пере-
хода имеет вид [16.35]
1 [) — у+В(~, Т)]2
б (1г У~ Тг '1)) — ~ ЕХР— 2д (~
27~В (~, Т)
с 7
вр, т~= ~т;)1~;)а., в~~,т~= а()а.).
Воспользуемся четностью %' (у) и перепишем (16.102) в виде
Я, (~, у) = (27сй) ~'(ехр [ — (~) — у+ В)'/26]+ ехр [ — (~)+ у — В)'(20]) Ф' (в) сЕ~).
О
(16 104)
Представим решение исходной задачи (16.100), (16.101) в виде
(16.105)
~ (~, у) = ~ Р у) + ~а (~ у).
Здесь Я2 (й, у) — решение краевой задачи для уравнения (16.100) при условиях
82 (Т, у) = 0 при у ) О, (дЯ2/ду), о = — ф (й) (ф (Е) = (д51/ду) а).
Рассмотрим дифференциальный оператор, соответствующий уравнению (16.100):
дЬ' дЯ 1 д2Я
Ы [Я ('с, ~)] = — — (Т вЂ” ~) т (~) — + —. Й (-.)
Сопряженный оператор имеет вид
дР дР 1 д2Р
М[Р(с Ч)] д +(Т ~) Т(~) д + 2 Й(т) д 2
Введем функцию [16.35]
(~ (' ')) = Р~ ® — ~ "(Р) =
д д 1 дЯ 1 дР
= — (ию)-~ — — иа() — „— — юа (1 — „[т .) т(.) ~ ~].
1) Существование и единственность решения краевой задачи типа (16.100) — (16.101)
доказаны в [16.34] для функции %' (у), удовлетворяющей условию: %' (у) ехр ( — ау') -э 0
при у -~ со (а ) 0 — постоянное число). Для функции %' (у) вида (16.99) это условие
выполнено.

5 51
КОРРЕКЦИЯ, ОПТИМАЛЬНАЯ
Я С ЗАНАННОа ВЕРОЯТНОСТ
О от сКъ~ = О.
Используя формулу Грина, получаем
(здесь à — граница области Ь), или
В ~В
О~2 )~=т Ч О~2 ~т=~ — в ~1Ч
[ ),е1+
1 — ь
[...)ч дсЕ-.=О.
Пусть Л
у Л~ со, а ~~0; тогда по ынт
будет стремиться к н лю
подынтегральное выражение в ч
улю ж~щст~ы бывания 6 (~, у,
вая что при ~ —: О во втором слагаемом 6 Ч
ние граничные условия, имеем
(, у, ~, ~) —: о (у — ~), и принимая во внима-
т
8, ~, у) = ~, а Р, у,, О) 7 ( ) ~ ( ) Н-. ~-
+ ['/,Й (-.) (дб (~, у, -., д
~)! ~),= +7(-) (Т вЂ” ) ОР у,, ОП ~' (-, 0 1
Ф
(16.106)
Чтобы найти решение Я ~~
,(, у), д статочно знать о" ~~ 0 .
учим интегральное уравнение с ледующего вида:
, (, ). Для этого положим у=О 16.1 6
— в
У(~)-=10(1)+ 4 Урн,
(16.107)
У ~ = Я, Р, О), У, Р) = а(~, О,;, О) 7 (-.) ~ (-. Н.
!
Г
Это интегральное уравнение типа Во
единственно и
н и находится методом пос
ипа Вольтерра второго о а.
оследовательных прибли 1
р да. Решение его всегда суще
и лижений 16.37):
~ = ~о + !!ф" ( ~ ) + аФ'2 (~~) +...
Следует отметить,
(16.108
ду отметить, что уравнение (16.107' п
позволяет сразу получить а
евра р оптимальнои коррекци
ции — величину Я 0 0
т г в частных производных (16.98 . е
енки следует подставить в выражение
та величина известна заранее, о вып
16.108
Мб„, ' д' '" '" '""" м'н"р
д)м~~~~~~ (И Ы)) в виде от езка
нным решением
нах — ~~ для ~о~у~ен~~ оценки ре
правую часть соотношения (16.104' с . дим
, с учетом (16.99) находим
т
ф (~) = — 2 7 (~) (Т вЂ” -.) Ы~.
В 16.107
(16.107) ф (~) =О [(Т вЂ” ~)2) ~е (~) = О~ Т—
ф р улу (16 108) получ~и
У Р) =~, Р) + о ИТ вЂ” ~)а).
38 Механика полета
(16.109)
П ст ! 2 ( ' ! ~) искомое эшен
по первои п ' ' ~' ~о~~рое, как известно [16 86 о " ~~ ~) фундаментальное
дество О (~, ) = О
паре аргументов и сопряжен . удовлетворяет уравнению (16 100)
енному — по второи па е тог
очеви но — Для прямоугольной области Ь= Ре; тогда спРаведливо тож-
видно, выполняется равенст
Во
=((~, 'а): й — в< &l
=Ь: - - -~&l

594 постРоение прогрАмм УпрАвлЕния в стАтистическои постАновке [гл. 1с
Подставляя в (16.106) вместо Я2 (-., О) выражение (16.109), получим
т, О) Ус (т) ф (-.) с»т +
(16.110)
Подставив выражение (16.110) в формулу (16.105), с учетом четности
функций Я,.(», у,.) находим окончательно:
Я' (», у', ~)„,) = ~ Й",, (Т) + Й,. (т) »Ь+
Отметим, что при Ьа (») = О
(16.112)
Предположим, что процесс наблюдения продолжается достаточно долго
и в системе обработки наблюдений устанавливается стационарный режим
(см. ~ 3, и. 3). Полагая в (16.113) Л =О, найдем
~/2аза /Ьа а а„/Ь
й
а аа/Ь 1»2а„аз~Ь.
l~ /~ /~
Переходя к матрице ошибок оценки Л", найдем матрицу о~'Й"Х"'НЮ".
Первый элемент, стоящий на ее главной диагонали, равен
Й(») = ~~~2о оа~Ь+ аа (Т вЂ” »)] °
Предположим, что в момент ~ точность наблюдений мало отличается от уста-
новившейся; тогда функция риска Я' при оптимальном управлении Ла=
= ~ я1яп д описывается уравнением
6
2
2о о„ Д2Яо д (~о д~о
— +(Т вЂ” ») а, „,, — (Т вЂ” ») (я1цп у „+
Я' (Т, у) = у'+ ~/2о,а'/Йв.
В качестве примера рассмотрим коррекцию одномерного движения, опи-
санного в и. 3 $ 2. Пусть оа — гауссовский белый шум: М [оа (»)] = О,
М[оа(») оа(т)] =о,'о(» — т) (а,=сопят). Система измерений определяется соот-
ношением (16.45), где Н = (Й, О), 1 (») — гауссовский белый шум: М [~ (»)] = О,
М [1 (») 1 (-.)] = — а~~3 (» — т) (6, а,. = сапами).
Рассматривается задача о выборе управления ~ Ьа (») ~ ( ( = сопят, достав-
ляющего минимум функции Я =М[х2(Т) ~ у(»)]. Уравнение (16.58) в дан-
ном примере имеет вид
Дх АДх+ дхАх о-2дхНхчНхдх 1' о2ДДх (16.113)

595
э 5]
КОРРЕКЦИЯ, ОПТИМАЛЬНАЯ С ЗАДАННОИ ВЕРОЯТНОСТЬЮ
С точностью до бесконечно малых порядка о [(Т вЂ” ~)4] решение этого
уравнения дается формулой (см. (16.111))
Я' (~, у) — ~2оЯР + 2 (Т вЂ” ~) о,а /Й + (Т вЂ” ~)' ~ 2озо ~Ь +
+ '~,(Т вЂ” 1)' о.-" + у' — ~ у ~ (Т вЂ” 1)' ~ + о [(Т вЂ” 1)']—
7 1/
— 'у Т вЂ” ~~А ~ 2т~ й 8 сЬ ехр
2 й гдг
Гарантирующий запас на управление в момент времени 80 должен быть
равен
~а'е'+ ) а1дп а"'~" й,
1=1 для (16.89а), 1=2 для (16.89б).
3. Учет ограниченности запаса на управление. До сих пор предполага-
лось, что выбор управления определяется только локальными ограничениями
в (16.88). Это справедливо, если выполнено предположение 4' из п. 1. Если
предположение 4' не выполнено 1), альтернативное уравнение имеет более
сложный вид, в котором не удается разделить переменные (ср. (16.98)),
а у функции Я' появляется еще один аргумент — е:
дно д ~~о
— ~а"'+ Ьа~" — + = О,
д~) д~
(16.114)
~'(~, у", ~) ) =,~, Я;.(~, у,.), 1=1, 2.
~=1
Рассмотрим разность Яд — — Я ~д е — Я' (см. (16.111), (16.112)) — величину,
характеризующую изменение точности в результате работы системы коррек-
ции (при наличии гарантирующего запаса ~и) по сравнению с некорректиру-
емым движением:
(с точностью до величины порядка о [(Т вЂ” ~)2]). Пусть в момент ~е вектор у' (~е)
имеет некоторое априорное гауссовское распределение с параметрами
М [у'(~е)] = О, М [у'(1е) у'*(1е)] = Й" (1е); тогда Яд — априорное математическое
ожидание приращения — запишется в виде
7
23д (~,)
(Т ~) )''(т) а"
(а", (1,) — диагональный элемент матрицы Й" (1е)).
Рассмотрим величину Я~ (и,) = М [Я' (~„у', ~)е) — Я (~„у') ~~, ], где
Я'(~„у', ~,) — решение уравнения (16.114). Далее для определенности огра-
') Остальные предположения, 1' — 3', из п. 1 сохраняют силу.
38~

596 постронние п~~огрАмм упгАвления в стАтистическои постАновке [гл. ~з
ничимся рассмотрением случая (16.89б) (двигатель ограниченной мощности).
Очевидно, что при фиксированном 1, величина Юд (~,) является неубывающей
функцией и,. Пусть а, (и . Рассмотрим область ~„заданную ограничениями
вида
(; И) при ~о(~~~~*,
О при 1'(1(Т,
(16 115)
~ ьа,. (~) ~ ( (,. (~) .=
где (, (~) — граница исходной области 1~, (16.95), а момент времени ~" опре-
деляе гся соотношением
шах (а'О'+ Ла)' Ж = и„
~ ьа ° ~ ~~д(8)
о (~=1, 2, 3)
т. е. момент ~* выбирается так, чтооы запас ~ стал равен гарантирующему
запасу ~, для новой области Я,*. Нетрудно Видеть, что Я,*с 2, и справед-
ливы неравенства
(16.116)
(~ )~~ ио)(~ (ч ).
оценить изменение точности 5'~(~,) в результате
оптимальной коррекции при данном запасе ~„.
В качестве примера использования соот-
ношений (16.116) для оценки точности рас-
смотрим случай одномерного управления. Для
простоты будем считать, что а"'(~) : =сопй при
~ )~ ~„Ьа (( а"', ( = со11з1. В этом случае
5'д (~ ) (Т вЂ” ~о)'- (~2сР (~,)/тс. Введем в рассмот-
рение величины 1~о и Ь~„— превышения соот-
ветственно начального и гауантированного за-
паса на управление над расчетным (только
на номинальную программу реактивного уско-
рения):
Эти неравенства позволяют
Рис. 16.2. Оценка приращения
при различных начальных значе-
ниях ~о запаса на управление.
Стрелками указаны границы, в ко-
торых должна находиться вели-
чина ~~ при данном Л~,. Пунктир-
ные линии соответствуют началь-
у м'"'н'у 'о ) 'о.
Д 1 .~ (~(0))2 Д~
Зависимость приращения Я~ от величины Лп, имеет вид
5', (Л~ ) (Л по/Ь~ ) (2 — Ь и /Ь и ) при Л а, ( Л а„
Я~(Л~~,) при Ьа,) Л'л .
Используя величину 5'д (Л л,), задаваемую соотношением (16.117),
в качестве нижней оценки, а величину Яд (Лт~) — в качестве верхней, можно
оценить точность оптимальной коррекции при заданном запасе на управ-
ление ~, (рис. 16.2). Оценки показывают, в частности, что уменьшение Лтъ
при значениях запаса, близких к гарантирующему, оказывает малое влия-
ние на изменение точности оптимальной коррекции. Но задача выбора оп-
тимального управления сильно усложняется (ср. (16.114) и (16.97)).

КОРРЕКЦИЯ ОРБИТЫ АППАРАТА-НАКОПИТЕЛЯ
ф 6]
$ 6. Коррекция орбиты аппарата, накапливающего
атмосферный газ
х,(0) = ог„
~, (0) = ои„„
х (0) = 88„о,
х (0) =от„„
Х1 Х2)
Х2 — У~,
х, = 2~,Ах — х, + 2 (а,(У) и,— 2 [1 — Х (г'о' (1) — 1)] %,
х = — Дх — (а /Г2) и+[1 — 1 (г'о'(1) — 1)]%,
(16.118)
где ж„ж„ж„ж4 — соответственно отклонения по высоте, по радиальной
скорости, радиальному ускорению и накопленной массе; ~~о — отклонения
параметра /„ вызванные флуктуациями плотности атмосферы; и — кор-
ректирующее управление; отсчет времени на каждом витке начинается с нуля,
начальные для данного витка отклонения х,. (О) совпадают с конечными для
предыдущего витка отклонениями х, (Т).
Систему (16.118) можно записать в виде (16.42). При значениях пара-
метров а,=1,33 10 ', ~,=1,67 10 ~, ~=1,94 10', соответствующих примеру
к (16.67), характеристические числа матрицы А равны: ~1=0,514,
= — 0,257+1,095~. Наличие характеристического числа ~ ) О говорит о
неустойчивости неуправляемой системы.
Таким образом, возникает задача о стабилизации движения аппарата
введением управляющих воздействий и. В данном случае в качестве управ-
ляющего воздействия рассматриваются небольшие сдвиги 9,. границ ~,. актив-
ных участков в ту или другую сторону, что в правых частях уравнений
(16.118) соответствует появлению кратковременных импульсов управления
В Я 4 и 5 были рассмотрены задачи, где контролировались отклонения
от расчетной траектории только в один момент времени — в конце маневра.
В отличие от этих задач здесь требуется обеспечить движение в малой окрест-
ности расчетной траектории в течение длительного времени. Речь идет о ста-
билизации неустойчивого движения, расчетная траектория которого пред-
ставляет собой близкую к круговой геоцентрическую орбиту. Тем не менее
для выбора оптимального управления и в этом случае может быть исполь-
зован подход, близкий к изложенному в предыдущем параграфе. Траектория
разбивается на ряд участков одинаковой длины (по времени), на которых
система коррекции действует так же, как система коррекции, рассмотренная
в ~ 5: она обеспечивает минимум отклонения от расчетного положения в конце
данного участка. При переходе на следующий участок расчетной точкой ста-
новится конец этого участка. Иными словами, движение в некотором смысле
напоминает движение по заданным ориентирам. Показывается, что при надле-
жащем выборе параметров такая система коррекции обеспечивает достаточно
точную реализацию расчетной траектории и расчетного показателя эффек-
тивности [16.21 ].
1. Постановка задачи. Рассматривается движение аппарата-накопителя
в режиме накопления. Двигатель аппарата предполагается нерегулируе-
мым — скорость истечения и тяга постоянны, а направление тяги колли-
неарно вектору скорости центра масс. Движение центра масс аппарата вблизи
некоторой круговой (опорной) орбиты представляет собой последовательность
одинаковых циклов (витков) продолжительностью Т, каждый из которых
содержит активные и пассивные участки, на которых основное управление
принимает значение 1 или 0 соответственно (нерегулируемый двигатель).
Вследствие начальных ошибок и отклонений плотности атмосферы от рас-
четной аппарат будет отклоняться от номинальной траектории г'о'(~). Ли-
неаризация уравнений (12.79) приводит к следующей системе:

598 ПОСТРОЕНИЕ ПРОГРАММ ~'ПРАВЛЕНИЯ В СТАТИСТИЧЕСКОЙ ПОСТАНОВКЕ [ГЛ. 16
и.=-+1 на интервале продолжительности ~0,~ (величина и направление тяги
не корректируются). Эти импульсы приближенно заменяются мгновенными,
равными им по интегралу, т. е. корректирующее управление задается в виде
и (1) = 0,.о (1 — 1,.) при 1,. ( 1 ( 1,.
(о=~ (~,(... (~,.„(~,.(... (~,=т),
а 0, называется величиной импульса (она может быть как положительной,
так и отрицательной).
Предполагается, что отклонения параметра 3Д„вызванные флуктуациями
плотности атмосферы, представляют собой нестационарный гауссовский белый
шум 1) с нулевым математическим ожиданием и известной спектральной
ПЛОТНОСТЬЮ.
Предполагается, как и в предыдущем параграфе, что измерения произво-
дятся непрерывно и статистически обрабатываются (см. (16.57)), в результате
чего в каждый момент вырабатывается оценка состояния х (~) с корреляцион-
Г~
ной матрицей ошибок оценки Л .
2. Оптимальные поправки к расчетной программе управления. Каждый
цикл включает в себя моменты переключений ~, Пусть каждый сдвиг
моментов переключения ~,. (т. е. корректирующий импульс) выбирается
так, чтобы добиться минимума апостериорного математического ожидания
некоторой неотрицательной квадратичной формы от переменных т,. в конце
данного цикла. Текущее значение этой величины обозначим через Я [~, х (~) ],
а оптимальное значение ее — через
Ь"'[й, х(й)] =т1п М['х'(Т) 1',х(Т) ~х(й)],
(16.119)
~вам &lt
где Ге — матрица квадратичной формы. Если Г, — единичная матрица,
то х'Г,х=тз1+... +т,'. Выбор управления производится в моменты ~,'.=~,.— 0„,
где ~0, ~ ( О, (( Т (Т вЂ” продолжительность цикла).
Перейдем к переменным у при помощи преобразования (16.8), (16.9)
с преобразующей матрицей Ф (Т, ~), для которой граничное условие в (16.9)
задано в конце цикла при 1=Т.
Уравнение (16.57) для системы (16.118) может быть представлено в виде
у=пЬ~-~-[, у(О) =у =Э(Т, О)х„
(16.120)
Ч = Й1з иы/2~, ~аз ~и/2Г, ~зз ~з4/2Г, ~~з ~ы/2~ )',
х = Йх + Ьи + ~,
где 1 (~) — белый шум: М [~ (~)]=0, М [~ (~) ~ (~)]= азз (~ — ~), Й вЂ” постоянное число.
Уравнение (16.120) в данном случае имеет вид
у = е~~ ~~~Ьи + р., у (0) = уе
(р. (~) — белый шум; ЛХ [р, (~)] = — О, М [р (~) р (~)] = е~~ (~) 6 (~ — ~)) °
1) я действительности атмосферные флуктуации вдоль орбиты аппарата-накопителя
представляют собой коррелированный случайный процесс. Однако корреляционная функ-
ция такого процесса может быть аппроксимирована корреляционной функцией процесса,
полученного в результате прохождения белого шума через устойчивую линейную систему
[16.35], т. е. система (16.118) должна быть дополнена еще одним уравнением типа (16.5б),
а величина з~е должна быть включена в число фазовых координат. Предположение о том,
что флуктуации являются белым шумом, сделано для упрощения выкладок.
где и, . — элементы матрицы Ф, Ь = 2а,/Г, х совпадает с х (Т) предыду-
щего цикла.
Метод, при помощи которого выбирается оптимальное управление, проиллюстри-
руем сначала на следующей модельной задаче. Пусть точка совершает одномерное
движение

599
КОРРЕКЦИЯ ОРБИТЫ АППАРАТА-НАКОПИТЕЛЯ
Пусть в моменты времени пТ (п=1, 2,...) может быть приложено импульсное воз-
действие и (~)=00 (~ — пТ), т. е. каждый цикл включает лишь один момент, когда может
быть приложен импульс управления К Рассмотрим цикл продолжительностью Т. В мо-
мент ~=0
Я'(О, у) = т1п (у+ЬОе~~+т) р(т) И)(= т)п (у+ЬОв ~) +-
а>& t <в
г Т
х = р Р) ~~) .
О
Здесь р (т) — плотность распределения величины т: М (т) =О, М (т') =а~~. Оптималь-
ные значения 0' и Я' определяются следующими соотношениями:
— уе " /Ь при (у ((у„, ( жт~
~у,=Ь1 е
— О„з1,апу при (у() у„
0' (У) =
а'-. нри (у((у,
а' +((у( — у,)' при (у() у„.
Я (О, У).=
И [х (Т)] = О, Я [х2 (Т)] =
=2 [аоерр (у,:) — у-:р (у.) аост+ у;.Р (у.)]+ а',
/
1
р(у,) =~—
~ ~~ ~0~~
е р( — —.", ),
(16.121)
Р (У~) = Р (уо) ауо
Учитывая, что распределение у в конце предыду-
щего цикла определяет начало последующего, выразим
д ~ у ~ау
Рис. 16.3. Определение установив-
Ь)
шегося значения дисперсии е,оу.
(16.122)
и найдем управление О' (у) в конце следующего цикла
и т. д.
Рассмотрим зависимость а'-'„от а„'„(кривая 1 на рис. 16.3). Из (16.122), следует,
что а,'-„-~ а~~ при у„-~ са, ат„— — а~~„+а" при У,=О (пунктирные линии 8 и 4). Для
оцределения установившегося значения (~' воспользуемся процедурой, известной из
метода точечных преобразований [16.39]. Для этого в тех же осях на рисунке по-
строим зависимость а'„= Яу ехр ( — 2ЙТ) (прямая х). Если взять в качестве параметра
преобразования ~оу, можно найти установившийся режим. Условием устойчивости
режима является наличие точки пересечения кривых 1 и 2, в которой выполняется
условие Ыа'- /Ыа'-„( ехр ( — 2ЙТ). При у„-~ са такая точка существует и единственна
У
("'ту~'1аау =- О) ).
Рассмотрим теперь общий случай. Для выбора оптимального управле-
ния воспользуемся процедурой динамического программирования. 11~-сть до
') Если 0„— конечное число, то, вообще говоря, может быть несколько точек пере-
сечения, однако первая из них обязательно обладает искомым свойством.
Предположим, что в начале (при ~=О) величина у, имеет нормальное распределение
р (у„) с моментами (О, а,'„), и предположим (как это делается, например, в методе статисти-
ческой линеаризации [16.38]), что в конце цикла (при
~= Т) распределение также мало отличается от нормаль- а у
ного. Тогда найдем моменты априорного распределения
величины х в конце цикла (при ~= Т):

6ОО постРОение пРОГРАмм УпРАВления В стАтистическои пОстАнОВке [гл. 1п
момента 1,. включительно управление было оптимальным; тогда 0'. Най-
дется из условия
Б (~,+1, у,,) = т~п
~в;+,~&lt
~ (гк у'+1+ ~к+1о0к+1+Х,+1) р (Хк 1) "Х;~1 (16 12З)
Х '+1
р, (~),си
где р (К,.+,) — плотность распределения вектора ]~,.„с моментами (О, Лх+,),
~р, — вектор ~р(1) при 1=1,
В момент времени ~о = Т выполняется условие
З;(т, у,) =у,Г,у,-)-кр(Л.,Г,1
(16.124)
(здесь Яр (...) — след матрицы (...)).
Пользуясь соотношениями (16.123), с учетом условия (16.124) можно
найти управляющие функции 0'. (у,.+,) для каждого момента ~, Например,,
для к = О из (16.124) следует, что 0; (у,) находится пз условия
т~п ) (у, + Ыр,)' Г (у, + Ыр,) + Яр (Л~+ Л~~Г 1);
~в,~&lt
отсюда
) ч1у1 "ри ~ Ч1у1 ) ( 0„
~ 0, з11п (ц,у ) при ( п,у, ( ) 0„
д, = — — ',г„, 1;г, 12~
3. Точность стабилизации орбиты. После того как определились управ-
ления 0,. (у,.), найдем
М(у;.у'. ~у,) =(у, +~0:(у,) Ч;)(у;+~0;(у,) Ч.)'+Л!.
(16.126)
М (у,у',) = (у,. + 60'„. (у,.) ~,.) (у,. + Ы;. (у,.) ~р,.)' р (у,.) Иу,. + Л» (16.127)
С помощью рекуррентного соотношения (16.127), можно найти корре-
ляционную матрицу распределения у,. в любой момент времени ~, Следует
учесть, что распределение в конце цикла (при ~=Т) является начальным для
следующего цикла, при этом переход осуществляется по формуле
Л,=Э(т, О)Л,,"Г(т, О).
Рассмотрим случай, когда ограничения на управление фактически
отсутствуют: 0„-» со или все ~0,.~ ( 0„(почти наверное). Последнее воз-
можно, например, при весьма малых отклонениях траектории от номиналь-
ной, когда большие управляющие воздействия 0,. просто не понадобятся.
Согласно (16.123) в момент ~,'
~'(~,', у,) =у,'(Е+~~,ц,)'Г,(Е+~р,ц,) у,+~р (Я+ЛТГ,)
~о
Р~
~1= Ч1У1
Тогда в момент 1,'
Я' (12, у,) = т1п ((у, + 60р,)' Г, (у, + 60р ) + Яр [Л2 Г, + (Л~+ Я) Го~ ),
~в,~&lt
Используя предположение о том, что в точках 1'. и 1'., распределение
векторов у,. и у,. гауссовское, на~~.~ем моменты априорного распределения
вектора у,, Из симметрии задачи ясно, что М (у,) = О. Корреляционная
матрица определяется по формуле

601
э" 61
КОРРЕКЦИЯ ОРБИТЫ АППАРАТА-НАКОПИТЕЛЯ
& t
Ч2 — — ~ (~Р2ГРз) ~Тг).
6 =Чу
По индукции можно получить соотношения
6; = Ч,у,, Ч, =- — — (р',~,,р,) ' р'.1',, ~;=(Е+ Ьр,Ч,)'Х
(16.128)
ХГ,,Я+ЬУУЬ;) Ь 11; У1)=У1;У +ир 2ЬВ~Г, ь+~йьь) .
° у'=1
Пусть векторы ~., у=1,..., и, линейно независимы (и — порядок си-
стемы, здесь п=4). Покажем, что, начиная с ь=п, все Г,.=О и соответствую-
щие функции Я' (1,, у,.) не зависят от у,. 1).
Действительно, рассмотрим детерминированную задачу, т. е. 4ьу=О, )2 (~)=0. Тогда,
повторяя предыдущие рассуждения, получим
~' И.' у.) =у.'р.у.
&l ;у у
С другой стороны,
/
П Т и
ь* 1ь„',у„~= ь у„-Ьь~ь,и, Г, у„Ьь~ь,и,).
бу, р'=1, ...,тг
° у'=1 .~=1
Квадратичная форма у'Т,у неотрицательная; ее минимум, равный О, достигается
при у=О. Возьмем в качестве ~„..., ~„компоненты вектора О, являющегося решением
уравнения
у„+- ьк„а =О,
где Є— квадратная матрица, столбцами которой являются векторы у1,..., ~.)„. В силу
линейной независимости векторов ~) последнее уравнение имеет решение для любого у„,
поэтому
Я Р„, у„)=о
для любого у„. Следовательно, Г„=О, а в силу <16.1 8 и се Г; =0 р  ) и,
доказывает высказанное утверждение 2).
Таким образом, в рассматриваемой задаче
4
~'(Ь',, у)= У'Я =Кр ~ 22~Г +Йиьрь)) при 1~4. (16129)
.~=1
Рекуррентные соотношения (16.127) в данном случае имеют вид
ДУ, = (Е+ ЬЧ;Ч;) И (Е+ ЬЧ;Ч;)'+ ДХ' (16.130)
Воспользовавшись соотношениями (16.130) для ~=4 получим
~)", = ~)", + ~;+ (Е+ Ь Р Ч ) ~' (Е+ Ь~ Ч )'+
° + (Е+ ЬЧ Ч )(Е+ ЬЧ Ч,)(Е+ М) ~). (Е+ М)'(Е+ М)'(Е+ М)'.
Таким образом, если ограничения на величину импульса отсутствуют,
для полной компенсации наблюдаемых отклонений достаточно, чтобы в каж-
дом цикле было четыре импульса управления.
') Если матрица Го имеет ранг г ( и, то, учитывая вид уравнения (26Л20), можно
понизить порядок системы до величины г.
') Доказанное утверждение согласуется с аналогичным результатом, полученным
в работе [16.40].
где Г, = (Е+ Ь~р,Ч,)'Ге (Е+ Ь~р,Ч,). Из последнего соотношения видно, что
выбор управления в момент 1,', как и в момент 1,', сводится к задаче о ми-
нимуме квадратичной формы. Оптимальное управление 5; находится по
формуле

602 постРОение пРОГРАмм упРАВления В стАтистическои пОстАнОВке [Гл. 16
Рассмотрим теперь исходный случай, когда 9„— конечное число. Чтобы
получить оценку точности системы, выберем некоторое неоптимальное
управление, распространив оптимальное для ~=1 соотношение (16.125)
на ~&gt
Ч;у, при ~ Ч;у;~ С9.„,
9„з1~п(1,.у,.) при ! Ц,.у,. ~) 9„.
(16.131)
9,.(у)=
Заметим, что при 9„-» со управление 9,, определяемое соотношениями
(16.131), приближается к оптимальному. При малых возмущениях и малом
начальном разбросе вектора у такая система управления будет мало отли-
чаться от линейной.
Воспользовавшись формулами (16.127), найдем параметры распределе-
ния у,. в момент 1,, 1):
М (у; ) = 0, ~)",, = 2 (9./! Ч; ~') Р (9./~ Ч; ~) (%~ ~ Ч; ~) Р",Ч',ЧЛ—
— (е+ ~ р,ч;) ~',ч! ч;~", (е+ ~ р;ч;)'1+ ~",ч';~';+
+ р,ц,ф",)+2Р(9„!~Ч;~, ) ф", +~'9'„рр,')+
~- 2Р (0, 9„А ~,. !) (К -~ Ь~Д,.) а",. (Е+ Ь~,. 1,.) ~, -О,".
(16 132)
Здесь
= — ПЮ.П'., р (т) ==ехр — —.
1 ~, 1
Х
) Ч1~ ' ' ' ~2тй 2~
Р(* у) = р(8)~.
Нетрудно видеть, что при 8=1 из формулы (16.132) следует (16.121),
а при 9„-» оэ (16.132) переходит в формулу (16.130).
При помощи рекуррентных соотношений (16.132) можно найти распре-
деление вектора состояния системы в любой момент времени и определить
пределы отклонений фактической траектории от расчетной с заданной ве-
роятностью.
1) Вывод соотношений (16 132) приведен в [16.21].

ЧЛ(:ТЬ 1У
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ
1'ЛАВА 17
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
Сформулированные в предыдущих разделах вариационные задачи приводятся, как
правило, к сложным системам дифференциальных уравнений. Нахождение оптимальных
управлений и оптимальных траекторий движения в аналитической форме для истинных
гравитационных полей всегда или почти всегда бывает невозможным. Однако аналитиче-
ские решения представляют особый интерес в связи с их наглядностью и возможностью
широкого параметрического анализа.
Эти несомненные достоинства послужили основанием для разработки различного
рода приемов и методов отыскания решений в конечной форме. Разумеется, эти решения
ца1отся ценой замены истинного гравитационного поля на простое и отступления от кри-
терия оптимальности управлений.
Первое из этих упрощений сравнительно мало влияет на результат. В самом деле,
движение космического аппарата в сложном поле нескольких гравитационных центров
с достаточной степенью точности можно разделить на этапы, ограничиваясь на каждом
этапе влиянием одного из центров. Например, перелет аппарата с орбиты искусственного
спутника одной планеты на орбиту искусственного спутника другой в истинном гравита-
ционном поле может быть разделен на два характерных участка: участок движения в об-
ласти влияния планеты при наличии возмущений от Солнца и других планет и участок
межорбитального перелета в поле тяготепия Солнца при возмущающем влиянии планет.
На каждом из этих участков возмущениями можно пренебречь и считать гравитационные
поля центральными (подробнее об этом см. в гл. 4).
Это допущение принято и в данной главе: уравнения динамики записываются для
плоского или пространственного движения в поле одного центра. В этом случае дифферен-
циальные уравнения упрощаются, однако не настолько, чтобы задача об оптимальных
управлениях и оптимальных траекториях могла быть доведена до конечных выражений.
Чтобы достичь цели на этом пути, вместо оптимальных управлений рассматриваются,
вообще говоря, неоптимальные, но позволяющие получить точные или приближенные
формулы для параметров движения. Каждое такое решение описывает элементарный кос-
мический маневр. Заданный маневр может быть составлен из элементарных. Управления
и траектория движения, полученные таким способом, будут неоптимальными, но в то же
время будут указывать главные особенности маневра.
Для космических аппаратов обычно рассматриваются следующие маневры: меж-
планетный перелет с орбиты искусственного спутника одной планеты на орбиту искус-
ственного спутника другой (Земля — Марс, Земля — Венера); изменение в пространстве
орбиты спутника; поддержание заданной орбиты, эволюция которой происходит под дей-
ствием возмущающих влияний, вызванных нецентральностью гравитационного поля пла-
неты, атмосферой и пр.
Эти маневры назовем сложными. Они раскладываются на элементпарные. выход из
гравитационного поля центра с круговой начальной орбиты и обратный маневр — захват
аппарата гравитационным полем с выходом на круговую орбиту, перелет между круго-
выми компланарными орбитами, поворот плоскости орбиты, изменение положения спут-
ника на орбите и элементов орбиты (большой полуоси, эксцентриситета, наклонения,
радиусов апогея и перигея, фекального параметра) и др. Часть из упомянутых здесь
маневров описана в гл. 4.
Наибольшее внимание уделяется элементарным маневрам с заданной ориентацией
постоянного по модулю вектора реактивного ускорения а; как правило, вектор ускоре-
ния имеет какое-либо выделенное направление: радиальное, трансверсальное, тангенци-
альное или нормальное к траектории, перпендикулярное к мгновенной плоскости орбиты,
постоянное в пространстве и др.
Целью настоящей главы является изложение решений уравнений динамики для
перечисленных случаев; предварительные сведения о формах уравнений движения даны
в~2гл. 4.

604
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИИ ДИНАМИКИ
~ГЛ. 17
$ 1. Радиальное ускорение (а =О в (4.19))
1. Уравнения и интегралы движения. При а =О система (4.19) имеет
9
вид ')
и„и„' = а„+ и'/г — 1/гз,
и„и' = — и„и /г.
(17.1)
Последнее уравнение выражает закон сохранения момента количества дви-
жения (4.22); отсюда
(17.2)
и =М/г.
С учетом этого выражения для г первое уравнение системы (17.1) становится
таким:
ф2
Иг 2 " гз г2 т
(17. )
Для случая, когда реактивное ускорение постоянно (а„=сопз$), уравне-
ние (17.3) интегрируется:
аЖ2 1 аЖ2
2гз [ г+ "+2г' г
1 2 1
~)2 у
2
2 з. 2 то
(17.4)
Здесь г„„г„сЯ=и~,г, — параметры движения в начальный момент. Если
начальная орбита круговая, т. е. г,=1, и,, =О, и,=1, то уравнение (17.4)
упрощается и формула для радиальной скорости имеет вид
~Ч +
, + + 2а„(г — 1) — 1 = + — '(г — 1) (г — г,) (г — г ), (17.5)
Г2
где
1+ ~1 — 8а„
г =
4а,.
1 — ~1 — 8а„
(17.6)
4а,.
дг ~2
~ — а,. (1 — г,)
г,КД, й)+ (1 — г,) Е ф й)+
(1 — г,) я1п 23
2 1~1 — И я1п2 3
(17.7)
') В настоящей главе используются уравнения в безразмерном виде; процедура обез-
размериванпя описана в в 2 гл. 4.
Эти выражения показывают, что в зависимости от величины и знака
ускорения а„могут быть различные режимы движения. При а„( 0 движение
финитно (1 ) г ) г, ) О); при '/, ) а„) О движение также финитно
(1 ( г ( гг ( 2); при а„) 1/, движение инфинитно (г )~ 1).
Последний режим изучался в работе [17.1] для задачи о выходе из гра-
витационного поля центра. В работе [17.2] рассмотрено движение с малыми
величинами радиального ускорения (а„(( 1/а). Общее исследование режимов
было проведено в [17.3], где даны формулы для угла ~ и времени ~ через ра-
диус г (см. также [17.4, 17.5]). Эти формулы имеют вид.'
при а„( О

605
РАДИАЛЬНОЕ УСКОРЕНЫ Е
где
— г,й' я1п' ~+ г,
— ~' ~П1'2+1
1 — г1'
(17.8)
при 0 ( а„(1/
[г,Р' ф, й) — (г, — 1) Е ф й)],
~2
ттф, г,— 1, Й),
~2
'т'а„(г1 — 1)
(17.9)
где
'т"2="' 1, г=(г, — 1) я1п'~+1;
(17.10)
при а„=1/,
1 = 4 [2 1п Фд (тт/4+ 1/2) — я1п ~],
~ = 2 [и + 1/, 1п Фд (тт/4+ и)],
(17.11)
(17.12)
Где
я1п 1 =à — 1, Фя и =-à — 1,
и ри а„) 1/,
— ~1 — Р я1п'~ — г'([1, Й) + Е ([1, Й)
(17.13)
1
~ = агся1п (Й я1п [1) — = Р ф, Й),
~/8а,.
где
(17.14)
Д = а„(г — 1) — 1/,
(17.15)
(начальное значение энергии в безразмерных единицах ~,= — 1/, при г,=1).
Из условия набора параболической скорости Я,=О) следует связь между
радиусом конечной точки г1 и величиной радиального ускорения.'
г, = 1 + 1/2а„.
(17.16)
Максимальное значение конечного радиуса г1=5 (а„='/,), минималь-
ное — г =1 (а„=оэ). Время ~1 и угол ~1 в конце маневра находятся из фор-
мул (17.13), (17.14), если в качестве г принять г1. Радиальная и трансверсаль-
ная компоненты скорости в конечный момент определяются следующими
выражениями.'
2 т'а,. + а~
1+ 2а„
2а,.
1+ 2а„
(17 17)
В формулах (17.7) — (17.14) использованы стандартные обозначения для
эллиптических интегралов первого Г (~, Й), второго Е ([1, Й) и третьего
тс (~3, а, й) рода; при интегрировании постоянные выбирались так, что в на-
чальный момент 1=~=0; через г„г, обозначены корни уравнения для ра-
диальной скорости (см. (17.6)).
2. Набор параболической скорости. При а„) Ч, движение инфинитно,
поэтому соответствующий режим может быть использован для анализа
маневра набора параболической скорости с круговой начальной орбиты
[17.1 ].
Если в формулу (4.21) для энергии ~ подставить выражения компонент
вектора скорости г„, и из (17.2), (17.5), то энергия окажется функцией
радиуса г:

606
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИИ ДИНАМИКИ
~гл. 17
Полученные выражения (17.16), (17.17) для задачи набора параболиче-
ской скорости с постоянным радиальным ускорением справедливы при
а„) '/,; меньшие значения а„соответствуют финитным движениям. Инфи-
нитное движение может быть организовано и при малых значениях уско-
рения (а„( '/,), если в надлежащих точках траектории направление уско-
рения будет изменяться на обратное.
Решение задачи о наборе параболической скорости с малым попеременно
положительным и отрицательным радиальным ускорением содержится
в [17.6] и [17.7]. Следуя [17.7], введем в рассмотрение геометрическую диа-
грамму: квадрат эксцентриситета — радиус. При выводе формул не будем
предполагать, что начальная орбита
8 круговая.
В главе 4 (см. (4.31), (4.32)) дается
выражение эксцентриситета я через ра-
диус перигелия г:
я = (Щ'/г ) — 1. (17.18)
Последний при помощи уравнения
энергии может быть связан с текущим
радиусом г и радиальной скоростью о,:
г
8 ~4М
у~ ~,у~ ~ (17.19)
~= ~+2,'
Рис. 17.1. Диаграмма: квадрат эксцентриси-
тета ~' — относительный радиус т( М'.
откуда
в'" = Щ'п'+ (1 — Щ%)'. (17.20)
Полученная связь является основной для дальнейшего. На рис. 17.1
сплошной линией представлена кривая нулевой скорости в координатах г/Я',
я'; при г -~ оэ кривая асимптотически приближается к ~'=1; пересечению
кривой с горизонтальной линией я'=1 происходит при г=1/,~ф'. Движению
в отсутствие возмущающего ускорения соответствует на графике финитному
(при ~' ( 1) или инфинитному (при я' ) 1) перемещению по горизонтальной
линии.
Вычислим производную Нв'/Нг, привлекая уравнение (17.3):
(17.21)
дв~/й' = 2~а„,
откуда при постоянном значении а„
(17.22)
я2=я2+2Щ2а (г — г ).
Движение при постоянно направленном возмущающем ускорении со-
ответствует финитному или инфинитному перемещению вдоль прямой с угло-
вым коэффициентом 2,Я'а„. На рис. 17.1 пример траектории с постоянныи
и постоянно направленным радиальным ускорением представлен прямой 1—
2, точка 1 — перигелий, точка 2 — афелий возмущенной орбиты. Здесь
движение происходит вперед и назад по линии 1 — 2; максимальное значение
эксцентриситета достигается в точке 2:
я~ =в21+2Щ'а (г, — г ).
Если в точке 2 возмущающая сила изменит знак (а„( О), то значение
эксцентриситета, достигнутое на такой орбите (точка 8), будет превышать
прежнее максимальное значение (точка 2). Многократное повторение такого
маневра 1 — 2, 2 — 8 обеспечивает набор заданного значения эксцентриситеть
при как угодно малом значении возмущающего ускорения. Таким способом
может быть организовано управление в задаче набора параболической ско-
рости (я'=1) с радиальным ускорением, меньшим предельного (а„( '/,).

607
РАДИАЛЬНОЕ УСКОРЕНИЕ
(17.23)
а„= (Щ'/г') — 1/г2.
г„= сопя$,
В работах [17.9, 17.10] исследовано движение с радиальным ускорением,
изменяющимся по закону
(17.24)
а„= ао/г2.
Этот закон реактивного ускорения имеет место для аппаратов с солнеч-
ным парусом, установленным перпендикулярно к солнечным лучам (см. $ 4
гл. 12).
Уравнения движения (17.1) с ускорением в виде (17.24) описывают кеп-
леровскую траекторию с измененной гравитационной постоянной (1 — ао
вместо 1).
Пусть в начальный момент аппарат выведен на круговую орбиту единич-
ного радиуса; выпишем выражения для эксцентриситета я и большой полу-
оси А (ср. (4.31) — (4.33)):
— о А—
а 1
1 — ао' ~ 2 — 1/(1 — а ) )'
(17.25)
Отсюда следует, что при ао ( 0,5 траектория полета — эллипс, при ао ——
=0,5 — парабола, при ао ) 0,5 — гипербола.
Для перелета между круговыми орбитами с радиусами го — — 1 и г, ) 1
по эллипсу, касающемуся в афелии круговой орбиты назначения, необхо-
димо, чтобы
(17.26)
ао — (г, — 1)/2г,.
Время перелета при это~и в ~2гДг,+1) раз больше времени перелета
по соответствующему эллипсу Хамана, а конечная скорость в ~г, раз больше
круговой скорости на радиусе г,. Зависимость времени перелета с орбиты
Земли на орбиту Марса от ускорения ао показана на рис. 17.2.
Этого хсе эффекта мохсно добиться, если вместо реверсирования ускоре-
ния ввести участки пассивного движения, как это показано на рис. 17.1
(ломаная 1 — 2 — 2' — 8').
Как уже было установлено, предельное значение постоянного и по-
стоянно направленного ускорения для набора нулевой энергии с круговой
орбиты равно '/, в безразмерных единицах (радиус и момент на этой круговой
орбите принимаются за единицы измерения). При старте с эллиптической
орбиты предельное значение может оказаться выше. Из рис. 17.1 видно, что
наихудшие в этом смысле условия имеют место на правой ветви кривой нуле-
вой радиальной скорости (в апогее) в точке максимального наклона этой кри-
вой: г,/~Я'=1,5, я',=1/„и при этом а„=4/(27~,ф4).
3. Межорбитальный перелет. Примеры перелета на орбиты Марса и Ве-
неры с постоянным и постоянно направленным радиальным ускорением
можно найти в работах [17.3 — 17.5]. Чтобы траектория перелета имела
на орбите Марса или Венеры нулевую радиальную скорость, необходимы
ускорения, меньше '/, (финитное движение). Трансверсальная составляющая
скорости в силу условия (17.2) не может быть сделана равной круговой
на орбите назначения никаким выбором величины или знака реактивного
ускорения. Поэтому относительная скорость аппарата и планеты назначе-
ния всегда отлична от нуля.
В работе [17.8] также изучается межорбитальный перелет на орбиты
Марса и Венеры с радиальным ускорением; однако модуль ускорения здесь
не постоянен, а пропорционален радиальному расстоянию: а„= Ьг.
В упоминавшейся уже статье [17.7] вместе с постоянным рассматривается
и переменное радиальное ускорение, обеспечивающее постоянную радиаль-
ную скорость:

608
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 17
4. Изменения орбитальных элементов. Момент количества движения &lt
радиусы максимально г„и минимально г удаленных от центра точек остаются
неизменными для траектории с постоянным по модулю и постоянно направ-
ленным радиальным ускорением. Эти свойства вытекают из пп. 1 и 2 настоя-
щего параграфа.
Если невозмущенная орбита круговая или близка к круговой (я, (( 1),
а возмущающее ускорение мало (а„(('/,), то наибольшая разность между
максимальным и минимальным радиусами равна
Тф~
г — 1 ж2а„,
(17.27)
а максимальное значение эксцентриситета,
определяемого выражением (17.20), дается фор-
мулой
~шах = 2~т
(17.28)
~ 2. Трансверсальное ускорение (а„=О в (4 17))
1. Уравнения движения. При сохранении одной трансверсальной
составляющей реактивного ускорения уравнения (4.17) принимают вид
г' = гф2 — 1/г',
('1 7.29)
фг = — 2гф+ а .
Исключая из этих уравнений ф, приходим к одному уравнению третьего
порядка относительно г:
— (ггз+г)'~ =а г.
Ю
(17.30)
2. Набор параболической скорости. В упоминавшейся ранее ра-
боте [17.1] рассмотрена задача о наборе параболической скорости с круговой
орбиты под действием малого постоянного трансверсального ускорения
(а (( 1). Начальные условия такого движения выражаются следующии
образом:
го — — 1, г (0) = О, фо —— 1.
(17.31)
(в (17.27) и (17.28) минимальное расстояние,
Я равное радиусу невозмущенной орбиты, при-
нято за единицу длины).
д ф РГ ф7 (~Я а~,сефаГ Линия апсид, определяемая как линия, сое-
диняющая точки, максимально и минимально
— удаленные от центра смещается при наличии
Марс с радиальным ускорением
1
~У-= ~о/~'~. малого радиального ускорения на 2 ~а„радиан
за оборот.
Изложенные здесь результаты были получены рядом авторов. В ра-
боте [17.2] использовано разложение по малому параметру а„в выражениях,
определяющих изменения орбитальных элементов. В [17.11] был применен
метод Крылова — Боголюбова к уравнениям (4.36). Результаты, полученные
в [17.11], совпадают с результатами [17.2], за исключением одного вывода
относительно регрессии линии апсид. Еще один метод — метод вариации
параметров применительно к анализу изменений орбитальных параметров—
описан в работах [17.12, 17.13]. Выводы авторов этих работ также совпа-
дают с изложенными выше.

609
ТРАНСВЕРСАЛЬНОЕ УСКОРЕНИЕ
Д 2]
Начальное значение второй производной го, необходимое при решении
уравнения (17.30) вместо системы (17.29), находится из первого уравнения
(17.29):
(17.32)
° °
~0 °
В работе [17.1] считается, что при малых а член г' гз в (17.30) значительно
меньше г и им можно пренебречь. Тогда получается простое дифференциаль-
ное уравнение, решение которого записывается так:
г=(1 — а 1) 2.
(17. ЗЗ)
Остальные параметры движения г (й), г' (й), ~р (й), ф (й) выражаются сле-
дующим образом при помощи (17.33):
г (~) = 2а (1 — а ~) з, г' (~) = 6а2 (1 — а ~) 4,
~р (1) = (4а ) 1[1 — (1 — а 1)~], ф (1) = (1 — а 1)з.
(17.34)
Уравнение орбиты в полярных координатах г (р) имеет вид
г = (1 — 4а ш) — '~,
(17.35)
при малых а орбита — пологая спираль.
9
Согласно (17.34) начальные значения г„го отличны от нуля:
г, = 2а, го — — 6а2,
1
(17.36)
что противоречит начальным условиям (17.31), (17.32).
В точке набора параболической скорости ®,=О) параметры движения
равны
Т = а-' [1 — (2а )'~ ],
г =(2а ) — '~,
~р =(4а ) ' — '/„
г', = (2а )'~,
ф,=(2а )'«,
г' =За.
(17.37)
Член гг", которым пренебрегается в уравнении (17.30), оказывается
в конечной точке большим, чем г:
г' г~= з/,(2а ) — '~
г, = (2а )'~*.
(17.38)
Это означает, что проведенное упрощение дифференциального уравне-
ния (17.30) неверно на заключительном участке траектории.
Для движения, описываемого соотношениями (17.34), характерным
является равенство в каждой точке центробежного и гравитационного
ускорений (гф'=1/г'). Отличие второй производной г' от нуля вдоль всей
траектории свидетельствует о том, что первое уравнение (17.29) не выпол-
няется точно. Если наряду с трансверсальной ввести радиальную состав-
ляющую ускорения, равную а„=г=6а' (1 — а ~) 4, то полученное выше реше-
ние станет точным решением уравнений (17.29) с компонентами а„, а . На на-
чальном этапе движения компонента а„, взятая в таком виде, есть величина
второго порядка малости по сравнению с а; на части траектории, где скорость
приближается к местной параболической, радиальная составляющая а„
сравнивается с трансверсальной а (см. [17.14 — 17.16]).
3. Представление решения в виде рядов. Другой подход к нахождению
характеристик движения с трансверсальным ускорением предложен в рабо-
те [17.17]. Используя метод вариации параметров, можно найти выражения
39 Механика полета

610
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 17
для функций г (~), г (~), ~Я(1)=г' (1) ф (1) в виде рядов по степеням малой
величины а:
9
г(~) = 1+а (2~ — 2 я1п ~)+а' (ЗР+ ЗР соя ~—
— ~ я1п ~ — 4 я1п' ~+ 2 соя ~ — 2) +..., [
г'(~) = а(2 — 2 соя ~)+а2 (6~+5~ соя ~ — ЗР я1п ~— (17.39)
— 3 я1п ~ — 8 я1п ~ соя ~) +...,
сЩ (~) = 1 + а ~+ а' (Р+ 2 соя ~ — 2) +...
Эти функции точно удовлетворяют начальным условиям (17.31) и прибли-
женно, с точностью до членов порядка аз, уравнениям (17.29).
~р Ф
Аналогичный подход имеет место в работах [17.12, 17.13]; в работе [17.18)
получена поправка к решению (17.34).
4. Изменение орбитальных элементов. Эксцентриситет оскулирующего
эллипса при движении по спирали (17.34) есть монотонная функция времени
в =2а (1 а 1)-4. (17.40)
при движении по траектории, описываемой выражениями (17.39), — перио-
дическая функция времени
(17.41)
~ = 4а [ я1п (~/2) [.
Максимальная величина приращения радиального расстояния Лг за один
оборот при старте с круговой орбиты единичного радиуса равна [17.11]
Ьг=4~та .
9'
(17.42)
$ 3. Тангенциальное ускорение (у=О в (4.26))
И~ Иг 1
г — =а — ——
Д8 Д8 72
г' — „, г — 1 — — „= — — „— 1
(17.43)
Здесь функции угла Ь заменены через производную НгlсЬ.
Сформулируем начальные условия для задачи набора параболической
скорости с круговой орбиты:
г =1, й.)й8 =О, и=1 при г =О.
(17.44)
Для задачи набора параболической скорости с круговой орбиты танген-
циальное направление вектора реактивного ускорения является наиболее
близким к оптимальному из всех выделенных здесь законов. В [17.19, 17.20]
показано, что вектор ускорения в оптимальной программе набора с постоян-
ным по модулю ускорением в любой момент времени лежит между двумя на-
правлениями. трансверсальным и тангенциальным, совпадая с последним
в конечной точке маневра. Если ускорение постоянно и направлено все время
тангенциально, то отличие времени выхода от оптимального не превы-
шает 0,5% при значениях а из диапазона О ( а ( 0,1. В том же диапазоне
значений модуля ускорения разница между оптимальной и трансверсальной
программами меньше 8,5~4. Эти результаты были получены в аналитической
форме; расчеты [17.31] подтвердили указанные числа (ср. ~ 3 гл. 8).
Аналогичные выводы сделаны в работе [17.22], посвященной изучению
трансверсальной и тангенциальной программ направления тяги, постоян-
ной по модулю.
1. Уравнения и интеграл движения. Система (4.26) при тангенциальном
(~=0) направлении вектора ускорения имеет следующий вид:

ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
Первое уравнение (17.43) может быть проинтегрировано в конечном виде
для случая постоянного по модулю ускорения,' с учетом начальных условий
(17.44) имеем
'/,у~ = 1/г + аг — 1/,.
(17.45)
Это уравнение дает закон изменения энергии ф вдоль траектории:
Д = аг — '/„
(17.46)
длина траектории выхода равна
г, = 1/(2а).
(17.47)
— „,г — 1 „— 2 2га8 — г = — „— 1.
(17.48)
К этому виду система (17.43) была приведена в работе [17.23~.
2. Приближенные решения уравнения (17.48). Для малых значений
аргумента г (г ((1) решение уравнения (17.48) может быть представлено
в виде ряда по степеням а. Первые три члена ряда имеют вид [17.23~
г = 1+2а(г — в1п г)+
+ 4а'- (г'+ '/, г' соя г — '/, г в1п г+ 2 соя г — 2) +... (17.49)
Здесь уместно провести сравнение первых двух членов разложений (17.39)
и (17.49): трансверсальная (17.39) и тангенциальная программы ускорения
дают одинаковые функциональные выражения для г при малых значениях
аргументов ~ или г (в начале движения г ~, ибо Нг/В=и 1).
Аналогичные выражения фигурируют в работах [17.24, 17.251, где опре-
делялись параметры движения в терминах параметра ~ — углового пере-
мещения.
При помощи (17.49) можно найти первые два члена разложения для мо-
дуля скорости г:
и=1 — а(г — 2 в1'и г).
(17.50)
Выражения (17.49), (17.50) указывают на колебательный характер изу-
чаемого движения; на среднее движение (г =1+2аг, й=1 — аг) накладываются
колебания с периодом обращения по исходной орбите 2~. Механизм этих
колебаний связан со взаимными переходами кинетической и потенциальной
энергий.
Интересно отметить, что для среднего движения выполняется с точностью
до членов порядка а' равенство вдоль траектории центробежного и грави-
тационного ускорений: и'/г 1/г'.
В работе [17.23] предложено простое аналитическое выражение для г:
г =(1 — 2аг) 1.
(17.51)
Эта формула получается, если в дифференциальном уравнении (17.48) исклю-
чить член (Рг/Нг') г, считая его малым по сравнению с единицей. Аналогич-
ный прием уже обсуждался в предыдущем параграфе в связи с выражением
(17.33), и высказанные там комментарии могут быть перенесены сюда с не-
существенными изменениями.
39»
Заметим, что тангенциальное направление ускорения соответствует
максимальному темпу роста энергии: ~=аи (см. (4.24)).
Подставив выражение для и' во второе уравнение (17.43), получим диф-
ференциальное уравнение второго порядка относительно г (г) с начальными
условиями из (17.44):

612
[ГЛ. 17
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
3. Асимптотические решения задачи о разгоне. В работе [17.26~ дается
решение задачи о разгоне с круговой орбиты под действием тангенциального
ускорения. Конечная точка движения характеризуется заданной энергией,
причем не обязательно нулевой (разгон до гиперболических скоростей).
Здесь исходной для анализа является система в оскулирующих перемен-
ных, описывающая плоское движение:
2р
р'= — а,
У
а + соя ч
Й= 2 а,
У
(17.52)
2я1п~
а,
й И
~Р 2Я1ПЧ
Ч = а,
Г ЦЯ
где р — фокальный параметр, я — эксцентриситет, ~. — угловое положение
перигелия, ч — истинная аномалия, скорость г и радиус г, входящие в (17.52),
определены формулами невозмущенного движения:
г=
р 1
1 + а соя ч ' р
и = — (1 + я'+ 2а соя ч)
(17.53)
(все параметры в (17.52), (17.53) безразмерные). Уравнения (17.52), (17.53)
являются частным случаем системы в оскулирующих переменных (4.47)
при тангенциальном направлении вектора реактивного ускорения.
Произведем замены [17.25]:
(17.54)
ц = (2а) "& t; Г  = ( а) '~ Л  = ( а) Ђ” '~ а  = ( а) ~4
При этом система (17.52) — (17.53) станет следующей:
сЬ а+ соя ч
И~
СЬ ~ Я1П ч
Я2 $~~
сну, я|п ч
сИ Уа
(17.55)
(л=,
Г = — (1 + я'+ 2а соя ч)
1
Время а и угол у, не фигурируют в правых частях (17.55), поэтому система
может быть расщеплена на две части. Первая:
сЬ 'а+ соя ч
Их
(17.56)
1 — со~2 ч
= — —, 1/1 + я'+ 2я соя ч (1 + я соя ч)2 ~1 — соя' ч +
вторая:
1
— —, (1 + а'+ 2а соя ч),
(17.57)
И~„Я1П ч
И|а |аа
Рещение второй системы определяется в квадратурах после решения
первой, которая является замкнутой системой уравнений для определения е
и соя ~ в зависимости от ~.

ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
соя ~:~
~й
~=0
(17.58)
< ,= Ђ” 3,409 2 л " «~ <
т = 1,34571 + т~ — '~*,'У', т,р'".
Коэффициенты разложений е,, ч„, р~, т„собраны в табл. 17.1.
Та блица 17Л
Коэффициенты разложений в формулах (17.58)
1,0 10о
— 3,0 101
3,177.10З
6'58080. 105
2,162289.108
— 1,051549.10"
7,073346.101З
— 6,303206 ° 10'6
1,0.10о
10о
3,53 10'
5 0216.104
1,271935 10'
— 5,007378 10'
2,829338 1012
— 2,173519 1015
— 0 5.10о
2,75.10о
— 4,835417.101
4'292169.10з
— 8,098106.105
2,555165.108
— 1,204903.10'1
7,935154.101З
10о
— 4,285714.101
5 75.10о
3,604946 102
— 5,110699 ° 104
1,281759.10~
5'010652.10э
2,819974. 1012
Преобразование (17.54) обладает тем свойством, что ускорение а исклю-
чается из правых частей уравнений движения, но зато, как легко убедиться,
появляется в начальных условиях задачи о разгоне с круговой орбиты.
Так что два движения, начинающиеся с одной и той же круговой орбиты,
но с разными значениями параметра а, описываются одинаковыми уравне-
ниями, но разными начальными условиями.
Решение задачи о разгоне с малым по величине тангенциальным ускоре-
нием обладает одной важной особенностью. Оказывается, что все траектории
с разными ускорениями в некотором смысле мало отличаются одна от другой
и мало отличаются от универсальной траектории, идущей из гравитацион-
ного центра. Из этой универсальной траектории можно вырезать по опре-
деленному правилу куски, соответствующие конкретным граничным усло-
виям. Правда, при этом граничные условия выполняются приближенно:
начальная орбита не круг, а эллипс с малым эксцентриситетом (тем меньшим
чем меньше ускорение).
Факт существования универсальной траектории был подмечен в [17.25]
при анализе результатов численных расчетов. Построение универсальной
траектории проведено в работе [17.26], изложению которой мы следуем
в настоящем пункте. Приведем окончательные результаты из работы
[17.26 ].
Искомую траекторию удобно разбить на три характерных участка:
первый участок, начало траектории, описывается асимптотическим реше-
нием при малых ~т (~т (( 1, а также е (( 1, сов ч (( 1); второй участок, сере-
дина траектории, определяется численными расчетами; третий участок,
конец траектории, описывается асимптотическим решением при больших ~т
(~т ~) 1, а также е &g ;)
При малых ~т асимптотические формулы для величин е, сов ч, т,
имеют вид

614
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 17
При больших т~ разложения е, сов ч, ~, &l ;р следующ
е = 0,76649п+,'~~ е,'р ", сов ч = ~ ч„'л ~,
1=1 9=1
(17. 59)
< „= Ђ” 1,57 8   ~ lt р  , с = — 1,611 ,'У' т
В=О ~=0
Коэффициенты рядов даны в табл. 17.2.
Т а б л и ц а 17.2
Коэффициенты разложений в формулах (17.591
еус
~ункции е (т~), сов ч (т~), ~ (т~), ~ (т~) для промежуточных значений
определены табл. 17.3; наряду с перечисленными функциями там фигурирует
удвоенная полная энергия т~ (т~):
т~ = (е — 1)/к.
(17.60)
Поведение функций в (т~), с (т~), т~ (т~) показано на рис. 17.3, функции
сов ч (т~) — на рис. 17.4 и функции ~. (т~) — на рис. 17.5. На рис. 17.6—
17.8 даны зависимости безразмерных радиуса Л. удвоенной энергии
скорости Г и полярного угла ~ от безразмерного времени т. Полярный угол э
(~=~,+ ч) отсчитывается от направления, которое отвечает бесконечно боль-
шому значению т~; значение с=0 соответствует точке достижения парабо-
лической скорости (т —— О).
Заметим, что скорость Г сначала убывает, а затем в окрестности пара-
болической скорости начинает возрастать.
На рис. 17.9 изображена траектория движения в координатах х, у
(х=Л сов ~, у=Л в1п ~) с разметкой по тт. Точка, в которой достигается пара-
болическая скорость, характеризуется следующими значениями радиуса Л
и скорости У:
(17.61)
Л = 1,24259, Г = 1,26846.
Укажем правило, согласно которому можно по универсальной траекто-
рии построить траекторию разгона, характеризующуюся заданными на-
чальным радиусом т„ускорением а и конечной энергией Я (го, а, Я вЂ” раз-
мерные величины).
О
1
2
3
4
5
6
7
8
9
10
11
12
13
14
— 4,58000.10-1
6,80189 ° 10-1
— 8,45172.10-1
8,85247 ° 10-1
— 4,86283 10-1
— 9.64784 ° 10-1
4 43942.10о
— 1,10624 101
2,11182 ° 101
— 3,13216 ° 101
2,90194 ° 101
1,76253 ° 101
— 1,71363 102
5,27883 ° 102
9,16000 10-1
2 04057.10о
3,38069.10о
4'42624.10о
2 91770.10о
6 75349.10о
— 3,55154.101
9,95619 101
— 2,11182 102
3,44538.102
— 3,48233 102
— 2,29129 102
2,39908.10З
— 7,91825 10З
— 1,30465 10о
0
— 7,74093 ° 10-2
— 3,20210 10-1
1'05876. 10о
2'39421.10о
4'44336.10о
6'81926.10о
7,74454 10о
— 2,45367 10о
— 1,89947 101
7,31602. 101
— 1,79535 102
3,41319 102
— 4,90991 10'
1 53298.10о
0
— 7,40216 10-1
5,44150 10-1
— 3,77374 10-1
— 1,23027 10 2
8,58759 10-1
2'41946.10о
4'80913.10о
— 7,51642 10о
8,38035 10о
— 1,84542. 10о
— 2,32322 101
8,44939 10'
— 2,00619 10'

Э
° ° Э Э
° °
° ° ° °
Э
1 1
1
1
1 °
1 1
1
1
1 °
1 1
1
1
1 °
1 $
!
$ $
!
Э ° ° ! °
° ° 1
° Э
Э
° Э
Э °
° !
Э °
Э °
9 9 $
1 °
° °
° ° ° Э
° °
1
! °
1' 1
° $ Э $
° Э Э
° °
1 °
° ° °
° ° °
° 19
Э в! °
$1
$ Э
1 °
° ° °
° 1
1 !
Э $
1
° ! °
° 11 °
° 1
1 $
° !
! '1
° °
° ° °
Э °
° !
! ° !
° ° ! °
1 1' 1э
1 1 э
1 1
1 °
1 ' ! °
! °
1 1 °
1 ' 1'1
° в!
° °
11
° ! °
! ° °
1 э!
° °
1
! ° °
$9 $ Э
1 ° 1
° 9 °
° ° ! °
° ° в °
° ° ° °
° 1
1 °
° ° ° °
° °
1 1
9 Э
$ Э
1
1 1
Э °
° °
° °
Э
1 ° '
Э °
° °
° !
° ° ° °
° ° °
° Э °
° ° °
° °
1
° 1 °
11э
° ' °
° °
° в $
$
!
1 1
1
° ! ° °
° °
° °
° °
° ° °
! °
1 °
° 9
° ° 1
1 °
° Э ° °
° ' '1
° ! °
° !
!!
Э °
° 9
° ° !
° °
° °
° °
! °
9
° °
в !
° а ° 6 ° 66 ~ ° 9 6 ! ~ ! а$ ' ' 6 ° ' ° ° 6
° ° ° ° я !
° ° ° ° 6
6 ° ° ! ° 6 6 ° °
)
/
1
° ° ° °
° ° ! ° ° ° в
! ° в я ° я 6 ° 6 6
° ! а
а ° ° !
° ° а
$ $ ° ° °
1 1 ' э
1 1 1
1 1 $
1 1 9 ° °
$!
1 ! ° °
! ! ° ° ! °
1 1 э
1 !в °
$9 ° 9 °
$ °
1 ° °
1 ! !
° ° °
° ! !
1
1 1
° ° Э
1 °
° 9
1
1 ° 1 °
1 ° ° ЭЭ
$9 °
! ° Э ° °
° 4 в' 4'4 ° ° '9 4
1 1196 1
1 1
1 1
1 1
1 ! ° 1'1
! ° °
1 1 °
! °
$ ° °
$9 9
1 1э
$ Э °
1 1 '1
1 !1
1 °
1 °
° °
° ° °
1 ' !
$ Э ° °
1 1
1 1 ! 1
° ° °
° °
° ° Э °
° 9
1 1
$ ° в1
1 °
! °
! 1
$ ° °
1 °
! ° °
1 1 ° °
1 1 °
1! ° 1
$$ $! 1
1 1 1
11 1'
° ° ! ° а ю 6 ! ° !

АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[гл. 17
СРУ У
ю
Рис. 17.3. Вид функций ~ (~), с (~), ~ (~).
Рис. 17.4. Вид функции сов ~ (~).
Рис. 17.7. Зависимость скорости У от Рис. 17.8. Зависимость полярного угла ~
времени от времени
616
Рис. 17.5. Вид функции р.„(~).
Рис. 17.6. Зависимости радиуса В и энергии
от времени

17
ТАНГЕЫЦИАЛЬНОЕ УСКОРЕНИЕ
Таблица 17.4
Параметры траектории набора параболической скорости
с тангенциальным ускорением
а [л~м,/сек"-1
Т [сут1
а [мм(сек'1
т, [тыс. кл1
т, [тыс. кл]
Т [сут|
1012,8
554,7
320,3
175,4
275,7
80,80
26,16
7,508
0,3
1
3
10
101,3
55,47
32,03
17,54
2,365
0,649
0,192
0,048
30
100
300
1000
Конечное значение удвоенной безразмерной энергии ~;, вычисляется по
формуле
~, = 2Д,/~/2йа.
(17.64)
где ~„~„~„, ~,1 — значения безразмерного -~ф
времени и углового положения перигелия,
посчитанные по асимптотическим формулам
(17.58), (17.59) или взятые из табл. 17.3 для -р
значений ~„~„.
В качестве иллюстрации приведем не-
которые расчеты из И7.261. В табл. 17.4
даются времена разгона до параболической
точки Т, и расстояния параболической точки
от центра г, для траекторий, начинающихся действием тангенциального ускорения
° ° (е — точка, где достигается параболи-
скруговои орбиты, которая отстоит от поверх-
ческая скорость).
ности Земли на 500 км, размерное ускорение
а — параметр таблицы.
4. Движение по логарифмической спирали. Рассмотрим уравнения
движения в форме (4.27); частным решением этих уравнений являются
следующие функции:
-l~
' — Р6 -Р4 — РГ Р РГ Р~ Рб ю
Т=
1
а = — в1п 9, ехр ( — 2и Фд Ь,),
1
ц=~7 ехр — 2 ~ФЯ~О
!
~ = ~, =- соп~~,
г= ехр(равд~,),
ехр 2 р$дЬ, — 1
(17.66)
Данная траектория разгона, характеризующаяся размерными парамет-
рами г„а, Я, или безразмерными ~„г„, составляет часть универсальной
траектории (см. (17.58), (17.59), таблицы
17.1, 17.2, 17.3) от ~ = ~, до ~ — — ~,. У
Размерное время движения Т и прираще-
ние угла ~ определяются следующими соот-
ношениями: РГ
з~
: ('1 ~~) ~ ' (~~) ' (17 65)
~ к к1 лО' — Ю

АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 17
здесь В качестве начальных приняты значения
~=0, р(0)=0, г(0) =1, и(0) =~,.
(17.67)
В исследуемом случае модуль реактивного ускорения изменяется обратно
пропорционально квадрату радиуса (см. (17.66)):
О
япЭ
2Г2
(17.68)
начальное ускорение равно
а,='/, яш 9„
(17.69)
направление реактивного ускорения тангенциальное. Модуль скорости п
дается выражением
г= г,г
/г
(17.70)
$ 4. Нормальное ускорение (~=1/,т~ в (4.24)). Бинормальное
ускорение (а~ —— О, аф =0 в (4.47))
1. Уравнения и интегралы движения с нормальным ускорением. Система
(4.24) при 7=~/,~ (направление реактивного ускорения перпендикулярна
к скорости в плоскости орбиты) существенно упрощается:
Д = сопят = Д„
(17.71)
Щ' = — аг/у.
Поскольку и =~/2ф,+2/г (см. (4. 21)), то уравнение для момента ~Я может
быть приведено к квадратуре:
(17.72)
При а сопят интеграл берется в элементарных функциях [17.31].
2. Свойства траекторий движения с нормальным ускорением. Так каз
полная энергия постоянна, ф=~„то выход из гравитационного поля не-
возможен — движение финитно. Расстояние от центра г заключено в преде-
лах г~, ( г ( г „, где г „, 㠄— корни уравнения
Щ2 (г)/2г'" — 1/г = Д,.
(17.73)
Если 9,+О, то во все время движения радиальная составляющая скоро-
сти отлична от нуля, а трансверсальная — от круговой; если 9,=0, то дви-
жение происходит по круговой орбите единичного радиуса и возмущающая
сила отсутствует; при 9, -~ 1/,~ траектория вырождается в прямую, совпа-
дающую с радиусом-вектором. Описанные результаты содержатся в ста-
тьях [17.14, 17.27, 17.28].
В работе [17.28] приведены примеры решения задачи межпланетного
перелета с орбиты спутника Земли на орбиту спутника Марса; угол о, изме-
няется при переходе от одного этапа движения к другому. В статье [17.29]
логарифмическая спираль используется в качестве опорной траектории
для применения метода вариации параметров. Аналитическое решение урав-
нений движения, близкое к логарифмической спирали, дано в [17.30];
в отличие от последней это решение имеет число постоянных, равное порядку
системы дифференциальных уравнений. Здесь ускорение направлено танген-
циально и изменяется приблизительно обратно пропорционально квадрату
расстояния от центра.

НОРМАЛЬНОЕ УСКОРЕНИЕ. БИНОРМАЛЬНОЕ УСКОРЕНИЕ
Если начальная орбита круговая (г„=1, ф, = — 1/2, ~Я, =1), то при
малых значениях а получаются следующие приблихсенные формулы для г „,
Щ,.„я „[17.32]:
г,„1/(1 — 2а), 1
Щ, ~/1 — 4а', )
(17.74)
~ „,ж2а.
В точке траектории, где г=г,=1, момент оф и эксцентриситет в возвра-
щаются к исходным значениям:
(17.75)
а также
а гф соя о+аяЮ = О. (17.78)
Последнее соотношение позволяет выразить компоненты а, а через вектор
бинормального ускорения ае (е=+1 — ориентация вектора ускорения отно-
сительно мгновенной орбиты):
аеО
аеф соя 0
а =
~/О'+ ф' соя' О
(17.79)
а,,=
~/О'+ ф' соя' О
Длина большой полуоси А оскулирующего эллипса (см. (4.33)) во все время
движения остается без изменения в силу постоянства энергии ф:
А = — 1/(2Д,) = сопй. (17.76)
Если в точках траектории, максимально и минимально удаленных от
центра, направление ускорения меняется на обратное (т=1/,~ ~~ т=Я/,~),
то эксцентриситет при таком движении максимально возрастает [17.31].
В пределе орбита может трансформироваться в отрезок прямой линии дли-
ной А с перигелием в гравитационном центре.
3. Уравнения и интегралы движения с бинормальным ускорением.
При ая — =О, аф=О вектор реактивного ускорения направлен перпендикулярно
к плоскости мгновенной орбиты. Как следует из системы (4.47), параметры,
определяющие геометрию орбиты в плоскости: длина большой полуоси А,
эксцентриситет -, время прохождения перигелия Т в отсутствие сил ал,
а,~, остаются неизменными. Оставшиеся уравнения для наклонения ~, дол-
готы восходящего узла Я, аргумента перигелия ~), совместно с уравнением
(4.48) описывают поворот плоскости орбиты.
Задача о повороте плоскости орбиты под действием бинормального уско-
рения исследовалась в ряде работ [17.17, 17.32 17.36]. Авторы работ [17.17,
17.32, 17.34] использовали для анализа систему'уравнений в оскулирующих
переменных типа (4.47). В работе [17.33] выбрана система уравнений со сме-
шанными переменными (4.54), (4.55). Здесь рассматривались круговые
и эллиптические начальные орбиты, причем для последнего случая был
применен метод усреднения Крылова — Боголюбова. В работе [17.35]
уравнения движения представлены в сферических координатах (см. (4.15)).
Наше изложение будет следовать этой работе.
По определению орбитальная плоскость образуется радиусом-векто-
ром и вектором скорости точки. Поэтому для принятого направления уско-
рения сразу мохсно установить два упрощающих исследование факта: во-
первых, радиальная составляющая ускорения отсутствует (в сферических
координатах а„=О, так как бинормальное ускорение перпендикулярно к ра-
диусу-вектору), и, во-вторых, уравнения движения (4.15) обладают инте-
гралом энергии (работа бинормального ускорения равна нулю, ибо вектор
ускорения перпендикулярен к вектору скорости). Из этих условий имеем
Д = — '/., (г" + г'-ф' соя' о + г2о2) — 1/г = сопй, (17.77)

620
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИИ ДИНАМИКИ
[ГЛ. 17
Система уравнений движения (4.5) при этом примет вид
г' — гф соя 9 — г9 = — —,
2 .2 2
Г
ае0
~/0' + ь' соя- '0
2г0+ гф'- я1п 9 соя 9+ г9 =
~/0'+ ф' соя' 0
)
2гф+ г&l ;р о 9 Ђ” 2 ф9 1
(17.80)
Пусть движение начинается с круговой орбиты, расположенной на эк-
ваторе:
г (0) =- ф (0) = 1, г (0) = ~р(0) = 9 (0) = 0 (0) = 0;
(17.81)
тогда система (17.80) преобразуется в следующую:
г=1,
ф' со '9+9' = 1,
(17.82)
9 + (1 — 9"-) Фд 9 = ае У 1 — 9' . 1
Последние два уравнения интегрируются в конечном виде при условии
ае = сопят [17.35 ]:
~) = ИГС81п 1 2 1 — соя
1 а2
~1+ а2 яп 1~1 + а' 1
~р = агс$д
ай+ соя 1~1+ а2~
(17.83)
При а (& t 1 получае ся форму а, дан ая Л. А. Симонов
я1п 9= ае (1 — соя 1).
(17.84)
4. Свойства траекторий движения с бинормальным ускорением. Из
(17.83) следует, что угол 9 является периодической функцией времени с пе-
риодом Т, и амплитудой 0 „:
2~ 2а
Т,=, 5 „= агсяш
й-~-а ' '* Ф+"'
(17.85)
Траектория движения есть малый круг радиуса г;.
г, = 1/~/1 + а'
(17.86)
плоскость которого наклонена к исходной плоскости под углом ~,:
1,=1/,9 „при а(1,
(17.87)
$ 5. Постоянный вектор ускорения
(а, =а,=О, а =а=сопят в (4.13))
1. Уравнения и интегралы движения. Если реактивное ускорение
постоянно по модулю и направлено вдоль одной из координатных осей, то
уравнения движения интегрируются в квадратурах [17.37].
по истечении периода Т, траектория возмущенного движения возвращается
в начальную точку.
Если действие возмущающего ускорения прекращается по достижении
точки, где 9=9 „, то орбита оказывается повернутой относительно исход-
ной на угол ~,.

21
ПОСТОЯННЫИ ВЕКТОР УСКОРЕНИЯ
Пусть вектор ускорения направлен вдоль оси Ох; тогда уравнения (4.13)
записываются следующим образом:
° а
х
° °
Д
к= — — ~а
(17.88)
(г = ~/х'+ у'+ ~', а = сопя1).
— (х2+ у'+ 22) — — — ах = Д,
Г
(17.89)
и третий интеграл
х 3 2 1
хгг' — — — — ах — — аг — 2фх = В.
2 2
(17.92)
и заменим дифференцирование по времени 1 на дифференцирование по пере-
менной ~:
(17.93)
А = й(г.
Тогда исходная система приводится к квадратурам, в которых фигурируют
новые переменные и, г, и~,
= с+С„
(17.94)
и+у
2иу О
д~:=ш — ю
где
(17.95)
Соотношения (17.94) определяют функции у (~), и (-.), и (~). Между с и ~
существует связь, обязанная равенству (17.93):
(17.96)
которая дает возможность в конечном счете получить функции у (~), и (~),
и (~). Обращая формулы (17.92), получим выражения х, у, я через у (~),
и (1), и (1):
х = '/, ~и (~) — у (~)],
у = и (1) у (1) соя и (1), (17.97)
~ =и(1) у(~) я1п ш(1).
Таким образом, задача сведена к квадратурам. Заметим, что интегралы
в (17.94) эллиптические.
Система (17.88) имеет три первых интеграла: интеграл энергии
интеграл момента количества движения (проекция на ось Ох)
Введем новые переменные
и=г — х, у=г+х, соя и= у,Цу2+я', я1п и = я/~~у'+ я'
~ Г (у)
~У (и)
Г(у) = ауз+ 2фу2+2 (1+ В) у — Щ~,
Г (и) = — аиз+ 2Ди2+ 2 (1 — В) и — Щ2.
(17.90)
(17.91)

622
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ
[ГЛ. 17
2. Классификация плоских траекторий. Если движение происходит
в плоскости т, у (т. е. я:О), то ~ф =О, ш=ш,=О и полиномы Г (п) и Г (и)
представимы в виде
Г= ау(у — у.,) (и — ц,), Г = — аи(и — и,) (и — и ),
(17.98)
причем
и, = — '~Д+ ~/Д'+2а (1 — В)~, '
и, = — [~ — ~/Р— 2а (1 — В) Д.
и, = — ~ — Д + ~/Д' — 2а (1 + В) Д,
п, = — ~ — Д вЂ” ~/Д' — 2а (1 + В) ~,
(17.99)
На рис. 17.10 приведены четыре класса траекторий плоского двиясения:
а) неограниченные самопересекающиеся, не огибающие центра притяжения,
Рис. 17.10. Классификация траекторий с постоянным вектором ускорения.
б) неограниченные самопересекающиеся, огибающие центр притяжения,
в) неограниченные несамопересекающиеся, г) ограниченные.
Области достижимости ограничены параболами на плоскости т, у:
~/~'+ у' — т = и = сопзВ ~/х'+ у'+ х = и = сопзВ.
('1 7. 100)
Постоянные, характеризующие эти параболы, принимают значения
и„ц„и„ц„и„. Первые четыре значения даны формулами (17.99); последнее
соответствует случаю о=со.
Определим условия принадлежности к классам ограниченных и неогра-
ниченных траекторий для случая, когда начальная орбита круговая. Обо-
значим через ~р угол, который составляет начальный радиус-вектор с векто-
ром ускорения. Если выполнены совместно условия
а ( '/„а' — а (2 — сос ~р) + '/ ) О,
(17.101)
то движение ограничено. При а ) 1/, движение не ограничено для любых
значений ~. Если ~=0, то движение ограничено при О ( а ( /,; макси-
мальное значение радиуса в случае а=0,5 равно г „1,4.
Если и = н, то движание ограничено при 0 ( а (% — ~/2 0,086;
максимальный радиус в случае а=0,086 равен г,„=3,4.
Одно из возможных применений полученного решения — расчет траек-
тории спутника Земли, подверженного влиянию светового давления.

ГЛАВА 18
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Изложенные в предыдущих разделах вариационные задачи могут быть представлены
в следующем общем виде.
Для динамической системы, описываемой дифференциальными уравнениями отно-
сительно фазовых координат х, (г)
х, = ~, (ху, иу„1),
(г, у=0, 1, ..., и; Й=1, ..., т; 0<г&
(18.1)
требуется указать управляющие функции иу, (г), обеспечивающие экстремум функцио-
нала — конечного значения координаты х, (Т) и переводящие систему из заданного на-
чального
''(0) =хи ( 67о)
х (Т) = ху (у ~,уг).
(18.2)
в заданное конечное состояние
(18.3)
Это — формулировка классической вариационной задачи Майера. Другая класси-
ческая задача вариационного анализа, встречавшаяся выше, — задача Лагранжа. Она
формулируется так: для динамической системы, описываемой дифференциальными урав-
нениями относительно фазовых координат
х;=~,(ху, иу„г) (г, у=1, ..., гг; Й=-1, ..., т),
(18.4)
требуется указать управляющие функции иу„обеспечивающие экстремум интегрального
функционала
Ф (х;, иу„г) Н
(18.5)
и переводящие систему из заданного начального
''(0) = 'го (гбУо)
х (Т) =х (у~,уг).
(18.6)
в заданное конечное состояние
(18.7)
В ряде случаев задача Лагранжа (18.4) — (18.7) приводится к виду, свободному
от дифференциальных связей (18.4): требуется построить экстремали интегрального
функционала
,У= Ф(х;, х;, х,, ..., хг~'))Ю (г=1, ..., и),
(18.8)
удовлетворяющие краевым условиям
х;(0)=хо,
х, (О) =х,о,
(18.9)
опесь выписана полная система разделенных и симметричных краевых условий).
х; (Т) =х,д, х; (Т) =х;,,
(г =1,
х~ ' ) (Т) =х„'
и) (

624
[Гл. 18
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
Указанные вариационные постановки могут быть сведены при помощи формализма
Лагранжа — Эйлера или Понтрягина к решению краевых задач для обыкновенных диффе-
ренциальных уравнений. Последние записываются в следующем общем виде:
х;=Г; (х, 1)
х; (О) = х о
(18.10)
'х (Т) = х~д
Методы численного решения вариационных проблем (18.1) — (18.3), (18.4) — (18.7),
(18.8) — (18.9) разделяются на прямые и непрямые. Основу первых составляют различные
итерационные процессы последовательного уменьшения (увеличения) функционала; для
применения непрямых методов вариационная проблема предварительно сводится к крае-
вой задаче типа (18.10).
В настоящей и следующей главах дается описание методов решения сформулирован-
ных выше задач; глава 18 посвящена функциональным методам, глава 19 — конечномер-
ным методам. Изложение общих идей иллюстрируется примерами из области механики
космического полета.
Наш список методов отнюдь не является исчерпывающим, в изложение не вошли,
например, методы, основанные на динамическом программировании [18.1 — 18.5], метод,
базирующийся на принципе оптимальности, [18.6] и др. Кроме того, здесь отсутствуют
методы решения линейных задач, ибо последние редко встречаются в механике космиче-
ского полета.
~ 1. Градиентный спуск в фазовом пространстве
Главной чертой градиентных функциональных методов является непо-
средственное исследование первой вариации функционала на предмет опре-
деления условий скорейшего спуска (подъема) к искомому значению функ-
ционала на каждом шаге итерационного процесса. Эти методы делятся на
две группы: спуск в пространстве управлений и спуск в фазовом пространстве.
Метод градиентного спуска в пространстве управлений применим к задачам
Майера (18.1) — (18.3) или Лагранжа (18.4) — (18.7); первая вариация функ-
ционала 3х, (Т) или 3Х выражается через вариации управляющих функций
Зи,. (1). Метод градиентного спуска в фазовом пространстве применим к задаче
Лагранжа в виде (18.8) — (18.9), свободном от дифференциальных связей и
управляющих функций; первая вариация функционала 3Х выражается через
вариации фазовых координат 3х,. (~). Это различие послужило основанием для
раздельного изложения двух идейно родственных методов: градиентному
спуску в фазовом пространстве посвящен настоящий параграф, градиент-
ному спуску в пространстве управлений — следующий.
Метод функционального градиентного спуска был предложен в 1908 г.
Адамаром для решения задачи о защемленной пластине, позднее Курант
[18.7] указал на возможность широкого применения идеи градиентного
спуска в функциональном пространстве. Л. В. Канторовичем [18.8 — 18.10]
в 1945 — 1948 гг. метод градиентного спуска был сформулирован в терминах
функцпонального анализа для квадратичных функционалов, была доказана
сходимость метода и установлена скорость сходимости. Предложенный
Л. В. Канторовичем обобщенный метод для квадратичных функционалов был
исследован в более поздних работах [18.11], [18.12]. Наконец, в [18.13]
(см. также [18.14]) было предложено применять метод градиентного спуска
в фазовом пространстве для произвольных, не только квадратичных функ-
ционалов. Там же даны некоторые оценки сходимости метода, которые были
обобщены в [18.15] на многомерные функционалы.
Опыт применения метода для численного расчета вариационных задач
механики космического полета изложен в [18.16, 18.17].
Обсуждаемый метод иногда называется также методом функционального
скорейшего спуска или наискорейшего спуска.

625
ГРАДИЕНТНЫИ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ
1. Алгоритм метода. Изложим функциональный метод градиентного
спуска в фазовом пространстве для следующего простого варианта задачи
Лагранжа (18.8), (18.9).
Требуется найти экстремали функционала
' (18.11)
Х= Ф(х, х, ~)Ж,
если функция х (1) на границах интервала принимает значения
х (О) = х„х (Т) = х,.
(18.12)
х~1~ (~) х~о~ (~) + ох (~)
(18.13)
Краевые значения функции 3х (~) при этом нулевые:
3х (О) = 3х (Т) = О.
(18.14)
Вариация функционала, вызванная малой вариацией 3х (~), которая
удовлетворяет условиям (18.14), имеет вид
У Е &lt о&g ; ( ) ~ .
(18.15)
где Е"' (1) — невязка уравнения . Эйлера на траектории х'о' (1):
Е " ' (~) = — [х" ' (~), х" ' (~), ~] , [х' " (~), х" ' (~), ~]. ( 1 8 . 1 6)
Интегрируя по частям (18.15) и опираясь на условия (18.14), можно
получить следующее выражение вариации интеграла:
.'Г
3х = — е"' о) н~+ с] ох (о н~.
О О
(18.17)
Постоянная с под знаком внешнего интеграла произвольна в том смысле,
что от нее не зависит вариация 3Х. В этом можно убедиться, вычислив та-
кую производную:
— ох(~) й= — 3х (Т)+3х(0) = 0
(18.18)
(последнее равенство в цепочке (18.18) вытекает из краевых условий (18.14)).
Выберем производную вариации ох (~) следующей:
~*' ф = 1 Е'и' (~) Н~+ а] .
О
(18.19)
4О Ме*анина полета
Краевые условия этого типа называются разделенными и симметрич-
ными, общий вид разделенных и симметричных краевых условий дается
в записи (18.9).
Пусть известно некоторое нулевое приближение х"' (~) для экстремали
функционала (18.11), удовлетворяющее краевым условиям (18.12). Следую-
щее приближение представим в виде

ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
~ГЛ. 18
Функция Ох (~) находится из дифференциального уравнения (18.19)
в виде
3шф=с,+1 Е"'(~) Н~]И~+с~) .
О О
(18.20)
Определим постоянные с, с, так, чтобы выполнились заданные краевые
условия (18.14); получим
(18.21)
(18.22)
При данном выборе вариации ох (~) вариация функционала оХ всегда
будет иметь знак, обратный знаку параметра ~, или обращаться в нуль не-
зависимо от величины ~; действительно,
Г7 2
3У = — Х Е'0) (~) Ь+ с '(И,
О О
„(18.23)
так что
оХ (О при 1) О,
ОХ)0 при Х ~0,
при Е"' (-.) = О.
(18.24)
(18.25)
где
7
~ Я = Е"' (~) Ит Ш вЂ” — „Е'О' (~) Н~] Ж.
О О О О
(18.26)
Тогда первое приближение х"'(~) можно переписать так:
а~ Р) ~о& t; ~ ~ 1д
(18.27)
Функция ~ (~) полностью определяется нулевым приближением х'о' (~)
(см. (18.26)), остается свободным параметр ~. Последний можно назначать
на каждом шаге равным малой величине так, чтобы заведомо не выйти из
Если требуется уменьшить функционал Х, то, приняв ох (Е) в виде (18.22)
и выбрав параметр Л малым положительным (малым для того, чтобы заведомо
не выйти за пределы применимости формулы для первой вариации), можно
добиться желаемого изменения функционала Х.
Выражение в фигурных скобках (18.22) есть функциональный градиент,
параметр ~ определяет длину вдоль градиента.
Запишем для удобства формулу (18.22) следующим образом:

627
ГРАДИЕНТНЫИ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ
пределов применимости линейного представления функционала. Кроме
этой существует другая возможность — выбирать параметр Л на каждом
шаге процесса из условия минимума функционала Х.
Функционал (18.11) на семействе функций х"'(~) с функцией ~~(~), взятой
в форме (18.26), зависит только от параметра Л. Условие минимума по Л
функционала Х"' = Х [х'О' (Й)+ Л т~ (Й) ] выглядит следующим образом:
(18.28)
Здесь
Е"'(~, Л) = — (х"'+~л], х"'+Л~, г) — — —. (х"'+Л~, х'"+Л~, ~). (18.29)
Если Л=О, то Е"'=Е"' и производная (Ы"'/с~Л) ( О. Когда невязка
уравнения Эйлера Е"' тождественно равна нулю, производная Ы"'/~Л
обращается в нуль при любом значении параметра Л.
Сформулируем окончательно алгоритм метода градиентного спуска в фа-
зовом пространстве:
На каждом шаге итерационного процесса, описываемого выражением
(18.27), необходимо вычислять функцию ~ (~) по невязке уравнения Эйлера
(18.26) и параметр Л из условия обращения в нуль производной (18.28).
2. Вычислительная процедура. Выражение (18.26) для функции ~ (~) мо-
жет быть преобразовано к такому:
дфсо) дф(о)
о(Е) =Е й — Е сй—
Ж—
7 7
О О
Й~ .
('18.30)
Формула (18.30) получена путем интегрирования ио частям (18.26);
частные производные дФ"'/дх, дФ"'/дх входят в оператор Эйлера согласно
(18.16).
Вычисление функции о (Е) сводится к операции вычисления интегралов
по таблицам функпий х"' (й), х"' (й). Вместо того чтобы хранить в памяти
машины таблицу х'о' (Е), можно пользоваться операцией численного дифферен-
цирования для нахождения х'"'(1) по имеющейся таблице х"'(1).
Согласно определению алгоритма на каждом шаге процесса требуется,
зная функцию л (1), определять минимизирующее значение параметра
Для вычисления минимума Х"' по Л с заданной точностью необходим спе-
циальный итерационный процесс: например, метод Ньютона или метод се-
кущих применительно к уравнению (18.28). В ряде случаев целесообразно
отказаться от такой трудоемкой процедуры и определять минимизирующее
значение параметра Л, пользуясь каким-либо простейшим приемом. Напри-
мер, таким. Значение функционала Х при Л=О известно; это — результат
предыдущего шага итерационного процесса. Вычислим функционал Х при
Л=Л' и Л=Л", где Л', Л" — пробные значения параметра. По трем точкам
на плоскости Л, Х: Л=О, Х=Х,; Л=Л', Х=Х', Л=Г, Х=Х" — строится па-
рабола второй степени, и по ней определяется минимизирующее значение ~.
40*

ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[Гл. 18
Процесс можно считать закончившимся, если приращение функционала
Ы на последнем шаге не превышает установленной точности
1~Х1&l
(18.31)
3. Обобщения алгоритма. Пусть значение функции х(Ц не задано в конце
интервала ~=Т и должно быть определено оптимальным в смысле функцио-
нала Х. Опишем происходящее в связи с этим изменение алгоритма.
Вариация функции Ох (~) в начале интервала по-прежнему должна быть
равной нулю, а в конце интервала отлична от нуля:
()х(0) =О, 3х (Т)+О.
(18.32)
К вариации функционала 3Х добавляется новый член, отсутствующий
в (18.15):
3Т= Е"'(с)3с(с)8с+ „, 3с,( „, = „, (Т), 3с,=3с(Т)).
(18.33)
Интегрируя по частям.в (18.33), получаем представление вариации ОХ,
аналогичное (18.17):
7 г 7
3Т = — Е"' (~) 8-. + с 3с (С) 8С+ Е"' (1) 8С -(- . + с] Зс,. (18.34)
О О О
Вариация 3Хне зависит от постоянной с, входящей в выражение (18.34);
в этом можно убедиться, вычислив производную д3Х/дс (ср. (18.18)).
Выберем производную вариации Зх по-прежнему в виде (18.19), а конеч-
ное значение вариации 3х1 следующим:
(18.35)
Выражение для вариации функции ох (~), как и ранее, дается формулой
(18.20); определим постоянные с, с, в этой формуле так, чтобы выполнялись
краевые условия (18.32), (18.35); получим
7 7
с, = О, с = — — + Е "' (с) 8с + — Е'" (~) 8,] 8с) (18 36)
О О О
7
Зс(с)=1 ' Е ()8 ас — — ', Е" ()8]8с—
О О О О
7
1 1 дФ(о)
— Е(О)(~) й — -~
2 2 дх1
(18.37)
7 2 7 2
у ~( Я(о) (3) (г3+ с Ж Я(о) (~) Ж+ . + с, (18.38)
дх1
О О о
Притакомвыборевариации Ох (~) вариация функционала ОХ всегда будет
иметь знак, обратный знаку параметра ~(, или обращаться в нуль независимо
от величины ~', в самом деле

629
ГРАДИЕНТНЫИ СПУСК В ФАЗОВОМ ПРОСТРАНСТВЕ
так что
8Х (О при Х) О,
8Х)0 при Х(0,
оХ=О при Я"'(т)=0 и дФ<о>/
(18. 39)
Последнее равенство в третьей строчке есть известное условие для оп-
ределения оптимального значения ю (Т).
Параметр )&l ;, фигурирую и в форм ле вариа ии (18.3 ), находи ся
тех же соображений, которые были изложены в п. 1.
Описанный в п. 1 метод градиентного спуска обобщается на тот случай,
когда подынтегральная функция зависит от производных выше первой,
а краевые условия соответственно дополнены условиями на все производ-
ные, кроме старшей. Метод может быть распространен на функционалы,
зависящие от нескольких искомых функций.
4. Пример. В качестве примера рассмотрим задачу определения пиа-экстремалей
интегрального функционала следующего вида:
([х+ х/(хо + уо) > ) + [  у х + о) ~ )
о
(18.40)
с краевыми усЛовиями
х (0) = 1, у (0) = О, х (0) = О, у (0) = 1,
х (Т) = г1 соя у„у (Т) = г, я&g
1/
х (Т) = — г~ /' я&g ;п 1 g ;1, у (Т) = †г ' со
(18.41)
7
~з
Е(0)аЕ4 — Т
3
0 0 0
— 3
Е(0) ~~З
0 0 0 0
0 0 0 0
Е(0) ~~3
Е(о) ~~4
(18.42)
0 0 0
где
сР д д
д&lt о&g ; в ” — + — ф (х& t;о& t; ~) у lt; > (~)
ф — [х + х (хо + уо)-'Ч' ~ [у- + у (хо + „о)-Ч'.
(18.43)
Заменой х на у можно получить выражение для ~ .
Искомые функции на следующем шаге итерационного процесса записываются так:
х&lt 1&g ; ( lt;) — х l ; &gt (& t;) ~ Л ~ (~ у l ;  ~)
(18.441
Параметры спуска Л, Л~находятся из условия минимума функции 7&lt 1&g ; ( ,
данном шаге:
дХ<1& t /д = О, дХ& t; /дЛ„= О
Эта вариационная задача касается нахождения оптимальных траекторий и опти-
мальных режимов работы идеального двигателя ограниченной мощности; она описана
в гл. 7. Расчеты проведены для г,=1,52; величины у„Т вЂ” параметры задачи.
Вариационная проблема (18.40) — (18.41) принадлежит к типу задач Ла-
гранжа без дифференциальных связей, краевые условия являются разделенными и
симметричными.
Опишем процедуру метода градиентного спуска в фазовом пространстве для задачи
(18.40) — (18.41).
По известному нулевому приближению х&lt '&gt (г , у" (~), удовлетвор ющему к
условиям (18.41), определяются функции о (~), >о„( ), обращающи ся вме те со сво
первыми производными в нуль на концах интервала; выражение, например, для
имеет вид
7

630
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 18
Представим двукратные интегралы из (18.42) следующим образом:
(О) 2 дФ(о)
дФ(о) дф ~2 дф(о)
Е~ НЙ = дх (Е) — ~х. (О) + дх НЙ вЂ” Й д~з дх. (О)
(18.46)
О О
О О
(аналогично для переменной у). В этой записи фигурируют функции х'з& t; ( ), у lt;
н их вторые производные х&lt з&gt (Е) у&l ;з> (Е), трет и х& t;з g ; (Е), у' > (~)
у'з& t; й) производ ы в пра ой ча ти (18. 6) отсутству&
При определении функций «>„( ), «&g ;„ й) ио фо мулам (1 .41), ( 8.46) можно
жать численного дифференцирования, если на каждом шаге вместе с функциями х (~),
&g ;&g ; («) залом <&g ;ать вторые п оизв д ые х («), у (Е); со тветст е но вместе
«~, (1), «у (~) следует запоминать их вторые производные з (й), з„(й) (ср. рассуждения
О 0,7
'~7 1 Я Д 4
Рис. 18.2. Оптимальные траектории в бессиловом
(1) и центральном (2) полях при р,=2, Т=2 и
оптимальная траектория в бессиловом поле (3)
при р,=5,23, Т=4,92.
Рис. 18.1. Убывание функционала .7 по
шагам итерационного процесса метода
градиентного спуска в фазовом простран-
стве.
в и. 2). Выпишем выражения для «&g ;, ), вытекаю ие из (18.4 ), (18. 6) (выраже
для «&gt у, ~у получа ся заме о х на
1 1
ЧХ з' ~Х~~ ~МХ~~ 6 СОХз ь 2 С1Х~
О О
(18.47)
ГДО
дФ(о) дф(о) дФ(о)
ЛХ (1) =~ й — ~ Ю+
О О
6 2
С1х Т2 3 ~ ~х~~ т
(18.48)
Т
6
сз — — — з (2~ — Т) М сИ.
В качестве функций нулевого приближения были взяты следующие:
2 (г сов'р1 — 1) з1п &lt
Тз + 7 — Тз
"1
2г Я11 У, — Т СОЯ У1
Тз
1з
3 (г, сов &lt г, Ђ”
х'з& t; 1   + +.,
~г1 Т
(18.49)
Зг1ЯП У, — 2Т
СОЯ Р1
~з +
'»'г Т
у&lt о&g ; ( )
Т2
Они являются решением вариационной проблемы (18.40) — (18.41) для бессилового
поля (см. гл. 7).

ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
0&l ;у & t; с О&
(18.50)
Попытка применить в качестве нулевого приближения функции (18.49) для углов
~, ) ~ наталкивалась на следующую трудность. Оказалось, что исследуемый функционал
нри этих углах перелета обладает не единственным минимумом, и использование решения
в бессиловом поле как нулевого элемента приводит к значениям минимума, превышающим
ожидаемые. Это означает невозможность использования единого нулевого элемента для
всего диапазона изменения параметров.
Сказанное иллюстрируется рис. 18.2, где даны оптимальные траектории бессилового
и центрального полей для случая у,=2, Т=2 и оптимальная траектория бессилового
поля для случая у,=5,23, Т=4,92. Последняя не огибает начала координат. Видимо, это
может служить внешним признаком непригодности данной траектории в качестве нулевого
элемента итерационного процесса.
Для нахождения начального элемента в параметрических расчетах можно рекомен-
довать следующий прием. Пусть известна оптимальная траектория для некоторых значе-
ний параметров и требуется построить новую оптимальную траекторию для значений
параметров, близких к первым; краевые условия на новой траектории отличаются от ста-
рых краевых условий. Трансформируем старую траекторию, например, умножением на
некоторую произвольную, мало отличающуюся от единицы функцию, которая обеспечи-
вает выполнение на новой траектории заданных краевых условий. Эта траектория и может
быть использована в качестве нулевого элемента.
$ 2. Градиентный спуск в пространстве управлений
Основу градиентного спуска в пространстве управлений [18.18 — 18.30]
составляет вариационный подход, предложенный в работе Д. Е. Охоцим-
ского [18.31]. Первое приложение метода для численных расчетов связано
с выбором оптимальной программы управления углом установки солнечного
паруса [18.20]. В этой задаче на управляющую функцию (угол установки
паруса) не наложены ограничения. То же самое относится и к задачам о вы-
боре оптимального закона направления тяги при перелете между орбитами
в центральном поле [18.28], а также к задаче о наборе параболической ско-
рости [18.29 ].
В работах [18.19, 18.21, 18.30] содержится обобщение метода на тот слу-
чай, когда управляющие функции ограничены, а в работах [18.25, 18.26,
18.32] дается развитие метода применительно к задачам с фазовыми огра-
ничениями.
1. Алгоритм метода для задач со свободным правым концом траектории.
Изложим алгоритм метода для задачи Майера (18.1) — (18.3). В этом пункте
правый конец траектории считается свободным и для простоты рассматри-
вается случай одной управляющей функции.
Для динамической системы, описываемой дифференциальными уравне-
ниями и начальными условиями
х,.=~,.(х., и, ~), х,.(0) =.х,, (~, )=О, 1, ..., и; 0(~(Т), (18.51)
требуется указать управляющую функцию и (1), доставляющую минимум
функционалу х, (Т); конец временного интервала ~=Т задан.
Применение описанного итерационного процесса к задаче (18.40) — (18.41) оказалось
весьма эффективным; время расчета одного варианта (один вариант — это одна пара
значений ~„Т) составляет 1 — 2 мин на ЭЦВМ М-20 при точности 4 — 5 знаков по функ-
ционалу.
Характер сходимости метода иллюстрируется рис. 18.1, где по оси абсцисс отложен
номер итерации, а по оси ординат — соответствующая величина функционала; дискретныо
точки соединены непрерывной кривой; на кривой 1: у,=1,047, Т=3,456; на кривой 2:
у =3,141, Т=3,456.
Для обоих примеров в качестве начального приближения была выбрана оптимальная
траектория в бессиловом поле (18.49). Сравнение числа итераций в одном и другом слу-
чаях позволяет судить о рациональности данного нулевого приближения: чем короче
траектория и меньше время движения вдоль нее, тем лучше бессиловое поле аппроксими-
рует центральное поле.
Диапазон изменения параметров р„Т в расчетах был такой:

632
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 18
Пусть известно нулевое приближение для управляющей функции и'о' (~)
и по этой функции построена траектория х(о) (1), удовлетворяющая началь-
ным условиям (18.51):
у(о) (О) — у,~.
(18.52)
Представим первое приближение для управления в виде
и"' (~) = и"' (~) + ~и, (~),
(18.53)
где ои (1) — вариация управления.
Функции х(1) (~), отвечающие управлению и(') (~), могут быть представ-
лены в виде, аналогичном (18.53):
(1) (~) (о) р) + ~~ р)
(18.54)
где 3х,. (1) — вариации фазовых координат.
Исходная система (18.51), линеаризованная относительно ои (~), 3х,. (~),
дает систему уравнений в вариациях:
,)~(о) )~(о)
3х,.= д' 3у. ' 3и ~11=, 1,..., и
~=о
(18.55)
Начальные условия для вариаций 3х,. (~) нулевые (см. (18.52)):
о.г,.(0) =0 (~=О, 1, ..., и).
(18.56)
Введем линейную систему дифференциальных уравнений
ф(о)
р,.= — р. ~=, 1, ...,и,
('18.57)
сопряженную линейной системе (18.55). Основное свойство систем (18.55),
(18.57) состоит в следующем:
,)~(о)
— р,.~ю,. = р,. ~и.
(18.58)
Учитывая начальные условия (18.56), это равенство можно записать
в интегральной форме:
Ре1 е1 Ра д °
('1 8.59)
0 ~=0
Если краевые значения функций р,. сопряженных уравнений задать
в конце интервала (при ~=Т) в виде
р,(Т)=1, р,.(Т)=0 (~=1, ..., и),
(18.60)
(о)
анхо (Т) = р,. ' оий.
(18.61)
0 ~=0
то интегральная формула (18.59) даст приращения функционала ало (Т),
отвечающее приращению управления ои (~):

633
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
Выберем вариацию управления Ои следующей:
(18.62)
в=О
При этом вариация функционала всегда будет иметь знак, обратный
знаку параметра )(, или обращаться в нуль независимо от величины )(; в са-
мом деле,
(18.63)
так что
8х,(Т) (О при Х) О,
Ох,(Т)) 0 при Х(0,
()~(0)
()х, (Т) = 0 при р,. — ' = О.
(18.64)
()~(о)
х,. = (,. (х ., и'~' — ~ ~~~~ ~р,. ', ~), ш. (0) = т., (~', ) = О, 1, ..., и).
«:=О
(18.65)
Последний определяется из условия минимума х(') (Т) каким-либо чис-
ленным приемом (см. ~ 1, п. 2).
Дадим формулировку алгоритма градиентного спуска в пространстве
управлений для задач со свободным правым концом траектории.
По известной функции и(о)(~) решается задача Коши для исходной системы
(18.51). Результат этого решения — функции х(о)(~) используются для опре-
деления частных производных д~(,.') lдх ., чтобы вычислить функции р,. (~)
сопряженной системы; здесь решается задача Коши «назад» для системы
(18.57) с краевыми условиями (18.60). Затем составляется вариация Ои (~)
в виде (18.62); параметр )( определяется из условия минимума функционала
х(') (Т) на данном шаге процесса.
2. Ограничения на управляющую функцию. Если управляющая функ-
ция ограничена:
(18.66)
и ;, (~) ( и (~) ( и ,„ (~),
то описанный выше алгоритм изменяется следующим образом.
Строим и "' (1) по правилу, данному в предыдущем пункте, и затем на
участках, где и'1' (1) ( и „(1), полагаем и'1' (1)=и „(1), а на участках,
где и'1' (1) ) и,„(1), полагаем и'1' (1)=и,„(1). Иными словами, отсекаются
выступающие за ограничения участки графика и'1' (1).
Структура выбранной формы (18.62) вариации управления Ои повторяет
структуру вариации Ох из метода спуска в фазовом пространстве (ср.(18.19)):
один множитель указывает направление антиградиента в пространстве
управлений, другой множитель определяет длину шага вдоль анти-
градиента.
Выбор параметра )(подчиним условию минимума функционала х(„') (Т)
на данном шаге итерационного процесса. Функционал х(„') (Т) на семействе
управляющих функций (18.53) с вариацией Ои, взятой в виде (18.62), является
функцией одного параметра

ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[Гд. 18
3. Алгоритм метода для задач с фиксированными начальной и конечной
точками траектории. Обратимся теперь к изложению метода градиентного
спуска в пространстве управлений для общей задачи (18.1) — (18.3); здесь
х» (Т) по-прежнему минимизируемый функционал; значения фазовых ко-
ординат в конце движения заданы:
х,. = ~,. (х ., и, 1)
х,. (0) =х,,
х,. (Т) =х,.„х»(Т) = тш
(г, ~=0,1,...,и),
(г=О, 1,..., и),
(г=1,..., и).
(18.67)
Опишем сначала метод штрафных слагаемых, идея которого принад-
лежит Куранту [18.32]. Образуем следующую функцию конечных зна-
чений координат [18.32, 18.18, 18.21, 18.27 ]:
и
Р[х,(Т), х (Т),..., х„(Т)]=х,(Т)+ ~~ д [х,. (Т) — х,. ]',
(18.68)
пг =1
(18.69)
р,. (Т) = дР"'~дх,. (Т).
Заметим, что если часть конечных значений фазовых координат по
условию задачи оказывается свободной, то в выражении для Р отсутствуют
соответствующие члены. Другой прием удовлетворения заданных кра-
евых условий состоит в следующем [18.19, 18.22 — 18.24].
Пусть известно нулевое приближение для управляющей функции и'о' (г)
и по этой функции посчитана траектория х~о~ (г), начальные условия на
траектории выполняются точно, а отличия конечных значений от заданных
составляют малые величины А~о~:
х~.'~ (0) = х,, (г = О, 1, ..., и),
хФ (Т) = х, + Л,'."' (г = 1, ..., и).
(18.70)
Порядок малости этих величин должен быть таков, чтобы изменение
в программе. управления Ои (~), необходимое для исправления конечных
условий, находилось в пределах справедливости линейного представления.
При выполнении конечных условий х,. (Т) =х,. и достижении искомого
минимума х» (Т) выражение Р (Т) также имеет минимум, совпадающий
с минимумом х,(Т).
Будем искать минимум Р (Т), подбирая одновременно значения свобод-
ных параметров д так, чтобы разности х,. (Т) — х,. обратились в нуль.
Для этого включим в процедуру метода процесс последовательного увеличе-
ния параметров д: пусть известно начальное приближение для управляющей
функции и~»~ (1), зададимся «малыми» положительными значениями д~."
и определим в результате итерационного процесса для задачи со свободным
правым концом (см. п. 1) управление и~~~ (~), доставляющее минимум выра-
жению (18.68).
Взяв за следующее приблихсение управление и~~~ (й) и значения пара-
метров д~~~, превышающее соответствующие значения на первом шаге д~'~
(д['~ ) у[о~,..., д~ ~~ ) д~»~), повторим процедуру. Минимум Р (Т) даст решение
задачи при д~''& t; Ђ ~ со [18.'
Значения последовательности у~о~ д~ ~~, ..., д~~~ определяются конкрет-
ными условиями задачи. Этот прием позволяет считать на каждом «большом»
шаге процесса (Π— э 1 — э... — э Х) правый конец траектории свободным.
В алгоритм метода, данного в и. 1, необходимо внести изменение, касающееся
граничных условий для сопряженной системы:

ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
Введем в рассмотрение и+1 сопряженных систем типа (18.57) с конеч-
ными условиями:
О при ~+т,
р,-. (Т) =
1 при ~ =т (~, т= О, 1, ..., и)
(18.71)
7 и
3х, (Т) = ~~& t; р~ ~' 8ц
0 ~=0
д~(0)
~*.Щ= ~~& t; ," ~  а (т=1,. .,
(18.72)
0 ~=0
Определим функцию ~и (~), доставляющую знак минус вариации Зх (Т)
и обеспечивающую выполнение конечных условий для вариаций фазовых
координат:
оу (Т)(О, 3х (Т) = — Л"' (т=1,..., и).
(18.73)
Составим следующую лагранжеву функцию:
и и и и
4
о =о ти =1 ~=0 / оп =1
Если вариация управления 3и (~) подобрана так, что выполняются и
конечных условий из (18.73), то лагранжева функция Х совпадает с вариа-
цией контрольного функционала Зхо (Т). Выберем 3и (~) такого вида:
д ~ ( 0 ) Д~ 1,0)
и
щ—
г=О т =1 ~=0 )и =1
(18.75)
Пусть параметры Л и ~ фиксированы; можно найти такие множители
Лагранжа Л„..., Л„, входящие в выражение (18.75), что конечные условия
из (18.73) будут выполнены. Действительно, множители Л„..., Л„опреде-
ляются из системы линейных уравнений
7
ь х р. р. ~3~ й 1 ... и .
(18.76)
Эта система получается из (18.73), если под интегралом заменить 8и на вы-
ражение (18.75).
Определим теперь параметры Л, ~ так, чтобы лагранжева функция Х
была отрицательной при любых значениях невязок Л~о', в силу сделанного
(здесь верхний индекс без скобок т указывает номер системы). При помощи
этих систем могут быть получены и+1 интегральных соотношений, анало-
гичных (18.61):

ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 18
ранее замечания это будет означать, что вариация контрольного функцио-
нала Зхо (Т) имеет знак минус. Выражение (18.74) при выбранном ои имеет вид
7
х= — ~~(~~~~р, „' +~~~~ ~„~р,",' ) а-)
и
+ ~~~~ ~ ь"
т=1
7
,)~(о) " " )~(о)
1 — ч р. х р. ~й
~=О =1 =О
(18.77)
Следует выбрать Х ) 0 и параметр ~ такой, чтобы второе слагаемое
(18.77) стало отрицательным. Определение ~ сопряжено с трудностями мно-
гократного перебора, так как множители ~ зависят от ~ согласно (18.76).
Если Л~о)=0,..., Л~~')=О, то Х ( 0 независимо от значения пара-
метра ~. Решение задачи достигается при выполнении следующей совокуп-
ности условий:
юп
д~;
р,. — ' = 0 (т = 1, ..., и), р'„. — '— : О.
(18.78)
Изменения касаются формул (18.68) (18.71) — (18.73). Выражение (18.68)
заменяется следующим.
Р [хо(Т), х,(Т),..., х„(Т)]=х,(Т)+ ~~~ д ~'.
'(18.80)
т,=1
Вместо формулы (18.71) граничные условия для системы сопряженных функ-
ций следует записать в виде
1 при ~=0,
Р'(') = О .ри;~О',
дф~') (~=1,..., и,
т=1,..., ~);
(18.81)
тогда выражения (18.72) для конечных значений координат заменятся на
ф(о)
~хД(~)= ~~ р', ' ~,й,
7
д~(о)
й~„= ~ р, 3иН1
(18.82)
(т=1, ..., и),
Параметр ~, в отличие от прежнего, выбирается не из условия достиже-
ния минимума контрольного функционала х~о1) (Т) на данном шаге процесса,
а из следующих соображений. Чем меньше величина ~, тем меньше длина
шага и меньше приращения функционала. С другой стороны, если параметр ~
слишком велик, то длина шага велика и точность описания движения ли-
нейными уравнениями (18.55) выходит из заданных пределов; к тому же
выполнение конечных условий (18.73) в линейной постановке не гарантирует
действительного выполнения конечных условий с заданной точностью, что
ограничивает сверху параметр 1. Поэтому целесообразно назначать параметр
~ равным своему верхнему пределу, который, как правило, зависит от свойств
конкретной задачи.
4. Обобщения процедуры для произвольных краевых условий. Описан-
ные в предыдущем пункте приемы решения могут быть оообщены на случай,
когда в конце интервала задаются не сами координаты, а связи между ними:
~,. [х, (Т), ..., х„(Т) ~ = О (~ = 1,..., 1 ( и). (18. 79)

ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
Я 2]
а в качестве невязки конечных значений в (18.73) будут фигурировать
д(о>,
и тт
5. Алгоритм метода для задач со свободным правым концом и сво-
бодным временем движения. В предыдущем изложении считалось, что
начало и конец временнбго интервала заданы. Однако для ряда задач мо-
мент окончания движения Т не задается. Сюда относится класс задач на
максимальное быстродействие.
Рассмотрим обобщение полученных выше результатов на случай свобод-
ного правого конца траектории и незаданного момента окончания движе-
ния Т. Пусть минимизируемый функционал имеет вид (ср. (18.68))
Р(х (Т), х,(Т),..., х„(Т), Т~,
(18.83)
значения х„(Т), х1 (Т), ..., х„(Т), Т являются свободными. Определим
значение Т на каждом шаге итерационного процесса как точку ~= Т, в кото-
рой функция Р (~), вычисляемая вдоль траектории, достигает минимума
(пусть такая точка на траектории одна):
~г
— р ~~, (о, ~, (о,..., *„(о, о = — „+ ~~~~ ~—, ~,. = о.
д дР дР
«'=0
(18.84)
Приращение функционала ЬР (Т), вызванное приращением управления
3и (~), записывается следующим образом:
и и
м(т~ = '«','»".,' ~*,. (т)+ ~~~~,'~",' ур ~г~+ '~'"]~т
а==о «'=0
(18.85)
н
в(т)=~,'"", ь,~т~.
1=0
(18.86)
Краевые условия для сопряженной системы уравнений записываются так
(ср. (18.69)):
р,. (Т) = дР<о'~д ,. (Т).
(18.87)
Особенность процедуры метода для задач со свободным правым концом
траектории и свободным моментом окончания движения состоит в том, что
последний определяется на основании равенства (18.84) после нахождения
закона управления на данном шаге итерационного процесса.
Может оказаться, что равенство (18.84) не выполняется в области опре-
деления управляющей функции, т. е. протяженность временнбго интервала
на этом шаге превышает протяженность интервала на предыдущем шаге.
Такое явление не будет иметь места, если область определения управляющей
функции на всех шагах итерационного процесса будет не меньше максималь-
ной величины интервала. Для этого следует на каждом Й-м шаге доопреде-
лять вариацию управления и, следовательно, управление на промежутке
Т „— Т'" 1'. Последнее может быть выполнено, если сопряженную систему
интегрировать не только «назад» от ~=Т'" 1' до ~=0, но и «вперед» от ~=
=~'" " до ~=Т . Правда, значение Т „не может быть заранее установ-
лено точно.
(верхний индекс О, как обычно, указывает на то, что функции посчитаны
на основании нулевого приближения для управления и'о' (~)). Поскольку
в нулевом приближении момент Т'о' также определяется из условия (18.84),
то вариация функционала принимает вид

ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 1$
6. Примеры. Иллюстрацией метода градиентного спуска в пространстве управлений
могут служить два расчета, приведенные в работах [18.20, 18.28] (см. также [18.27]).
Первый из них [18.20] относится к перелету между круговыми орбитами Земли и
Марса при помощи солнечного паруса. Вариационная проблема состоит в определении
оптимальной программы угла установки паруса ф (~), обеспечивающей минимальное время
ЮР 200 300 400
Рис. 18.4. Траектории перелета — метод
градиентного спуска в пространстве уп-
равлений.
Рис. 18.3. Программы угла установки
паруса — метод градиентного спуска
в пространстве управлений.
перемещения Т между двумя круговыми орбитами. Уравнения движения и краевые усло-
вия проблемы, записанные в безразмерном виде (ср. гл. 12), выглядят следующим образом:
г (0) =1, г (Т) =г1,
9
° ао У9 1
в = —,'[соя'ф[+ — — —,, и (0)=0, и (Т)=0,
(18.88)
ао ~~г~~~р
и = —,в[пф сов'ф—
и (0)=1, и, (Т)=г,~',
Т = пип.
Угловое перемещение аппарата не задано; примеры построены для г,=1,52; а„= 0,17
(=0,1 см/сек2).
Второй расчет [18.28] проведен для межорбитального перелета Земля — Марс с по-
стоянной по модулю и постоянно включенной тягой (ср. гл. 8). В вариационной проблеме
требуется определить оптимальный закон направления вектора тяги 0 (~), реализующий
минимальное время перемещения между двумя заданными точками на круговых орбитах.
Уравнения движения и краевые условия имеют вид
г (0) =1,
р(о) =о,
г(Т) =г,,
е (Т) = е„
г=и,
Т
и„(0) = О, и„(Т) = О,
(18.89)
а соя 0 ~ Ри
0
1 — у.1 г
и (0)=1, и, (Т)=г,~',
Т=т~п;
здесь а„ вЂ” начальное реактивное ускорение (а,=Р(М,), р, — приведенный массовый
расход (у.,=д/М,); в расчетах принято: а,=0,846.10-4 д, у.„=1,29 10 ' сут-'.
Обе вариационные задачи (18.88), (18.89) принадлежит к классу задач на максималь-
ное быстродействие; процедура решения этих задач описана в п. 5 настоящего параграфа.
Для удовлетворения заданных краевых условий могут быть использованы оба приема,
изложенные в и. 3.
В задаче (18.88) краевые условия удовлетворялись по методу, родственному методу
условного градиентного спуска (формулы (18.71), (18.75), (18.76). Выполнение заданных
краевых условий в задаче (18.89) обеспечивалось по методу штрафных слагаемых (формулы
(18.68), (18.69)). В статье [18.28] есть указание на способ подбора коэффициентов д,„:
в начале процесса величины д,„малы, затем, после 25-го шага, д„, увеличиваются пропор-
ционально модулю разности /х,"' (Т) — хп/.

ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
э 2]
На рис. $8.3, $8.4 представлены программы ф (~) угла установки паруса и траектории,
соответствующие нулевому приближению (О), первому (1) и второму (2) шагам итераци-
онного процесса, а также окончательному (т) решению задачи ($8.88).
На рис. $8.5, $8.6 даны законы 0 (~) направления вектора тяги и траектории в нуле-
вом приближении (О), на втором (2) и седьмом (7) шагах процесса, а также окончательное
(т) решение задачи ($8.89) со свободным угловым перемещением
Функционалы задач — время движения Т вЂ” даны на горизонтальных осях рис. 18.3,
18.5.
Несмотря на значительно большее число шагов в задаче ($8.89), необходимое для
достижения заданной точности, полное время счета методом штрафных слагаемых оказы-
вается меньше, чем методом условного градиента. Это связано с тем, что последний метод
требует весьма трудоемких операций при определении множителей Лагранжа Л1,..., А„.
Рис. 18.6. Траектории перелета — метод
градиентного спуска в пространстве управле-
ний.
Рис. 18.5. Программы направления вектора
тяги — метод градиентного спуска в про-
странстве управлений.
7. Ограничения на фазовые координаты. Дополним задачу Майера со
свободным правым концом (18.51) условием ограниченности комбинации
фазовых координат и управления.
Пусть в новой постановке требуется определить управление и (~), до-
ставляющее минимум контрольному функционалу х, (Т), при выполнении
неравенства вдоль траектории
(18.90)
р „<р х, и, ~ &l
Аналитические результаты по решению вариационных задач с фазо-
выми ограничениями содержатся, например, в гл. 12, в монографии [18.33]
и статье [18.25], численные приемы решения описаны в работах [18.18,
18.26, 18.32].
Следуя работе [18.26], дадим классификацию ограничений.
Назовем неравенство (18.90) фазовым ограничением нулевого порядка,
когда в функцию ~ входит явно управление и: [д~/ди)ф0, фазовым ограни-
чением первого порядка, когда управление и входит явно в первую полную
производную по времени функции ~: [дф/ди)ф0, и т. д.
Фазовое ограничение нулевого порядка и только нулевого порядка
может трактоваться как ограничение на управляющую функцию. Действи-
тельно, введем замену
(18.91)
и = р(х., и, ~)
и выразим, согласно этой замене, управление и через и, х., 1 (пусть это удается
сделать аналитически): и=ф (х., и, ~); в уравнениях движения (18.51) будет
фигурировать вместо управления и управление и, которое ограничено цо
[18.90).
Если управление и не ограничено, то такая замена приводит к задаче
Майера с ограничением на управляющую функцию и; метод решения этой
задачи дан в и. 2.

640
[ГЛ. 18
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
Пусть теперь и ограничено вместе с и. Разобьем интервал [О, Т] на уча-
стки трех типов. На участках первого типа управление и принимает одно
из своих граничных значений, а и лежит внутри своей области изменения,
на участках второго типа и лежит на границе, а и — внутри области изме-
нения, на участках третьего типа и и и находятся внутри области изменения;
участки первого и второго типа не перекрываются. Идея рассматриваемого
метода решения задачи Майера (18.51) с ограничением на управление и
и фазовым ограничением нулевого порядка на и состоит в следующем.
На участках первого типа вариация контрольного функционала выра-
жается через вариацию управления и ([) и определяется оптимальный закон
для этого управления, на участках второго типа вариация контрольного
функционала выражается через вариацию управления и (2) и определяется
оптимальный закон для и ([), на участках третьего типа как управление
и (2), так и управление и ([) могйт фигурировать в выражении для вариации
контрольного функционала. Метод решения задачи Майера с ограничением
на управление известен (см. п. 2), поэтому на каждом из участков можно
указать свое оптимальное управление с учетом существующего ограниче-
ния. Введем, в отличие от (18.57), следующую сопряженную систему:
д~[о& t; д~[ о gt; д [о&
.у' ~ .г 9 9
дх; ' ди дх; ди
'22
Р.
.р'=0
р,(т) =1,
(18.92)
р,. (Т) = О (е = 1, ° ° ° и).
Зхо[Т) = ~~ р, ' ~ ( )йхх+3и1 И.
0 1=0 .у=О
(18.93)
Принимая во внчмание, что
д~)(о) д~)(о)
о[& t = [ g ;х. + вЂ
дх ~ ди
~=0
(18.94)
выражение для вариации Охо (Т) можно записать в виде
Т и
Зхо [Т) = ~~~~ р, ' [М>[др"'& t ди + 3и 1 в ”
(18.95)
0 2=0
Пусть управления и и и не ограничены, 'выберем тогда вариации управ-
лений 3и, Зи следующими:
П
д [о)
Аи — — Л р.
ди
~=0
при о(2)=0,
(18.96)
Л
дно) д~[о)
Ь= — Х,— р,. ' при о(2) =1.
° дц
~=0
Здесь о (2) — релейная функция, принимающая значение 1 на участках,
где решение идет по ограничениям и=[~& t „ и [о „ и значе и 0 на участк
где решение идет по ограничениям и=и „и=и „. На участках, где ни и,
ни и не ограничены, функция о на равных основаниях может быть принятой
равной 0 или 1.
Вариация контрольного функционала 3хо (Т) выражается следующим
образом:

641
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИЙ
Я 2]
Параметры спуска л„, ~„связаны между собой условием непрерывности ва-
риации Ои в точках смены значений функции О (1); для точки 1=1', где функ-
ция 3 (~) меняет значение с 0 на 1, эта связь запишется так:
3и (~' — 0) = 3и (~' + 0),
и
ол (д+0)=ау (й'+ОЯди"'!ди)' — ~( ~ ) дх'.
э'=0
(18.97)
(18.98)
(штрихи обозначают принадлежность точке ~=~').
Если бы управление и (~) было не ограничено, а и (~) ограничено, то
следовало бы положить О (~)=0; этот случай соответствует рассмотренному
в п. 2 ограничению на управляющую функцию и (~).
Если бы управление и (~) было не ограничено, а и (~) ограничено, то
следовало бы положить О (~):1. Дальнейшая процедура зависела бы от того,
можно ли разрешить аналитически уравнение и=~ (х,, и, 1) относительно и.
Если можно, то задача свелась бы к предыдущей; если нельзя, то порядок
действий следующий (ср. п. 2).
Вариация 3и берется в виде (см. (18.96))
Д~~о& t; д~& t;.о& t; д~
(О) &lt Од ~ '
ои(Е) =
(18.99)
~~&lt о) Д~
где параметр л задается малым, чтобы линейное представление задачи оста-
валось в силе. Соотношение (18.94) при известной функции ои (й) (см. (18.99))
определяет вариацию управления Ои через вариации координат 8х,. Это вы-
ражение подставляется в систему (18.55), и решается задача Коши (18.55)—
(18.56). Результат решения — функции Зх,. (~) используются для определения
вариации управления Ои (1).
Заметим, что найденное таким способом управление и'1' (~) удовлетво-
ряет ограничению (18.90) только в линейном приближении.
Вернемся к рассматриваемой задаче, в которой ограничены управление
и (1) и управление и (1).
Пусть в начале траектории (О ( ~ ( ~') не ограничено управление
и (~). Положим на первом участке о (~) = 0 и будем для каждого момента вре-
мени подсчитывать вариацию Ои (~) по формулам, аналогичным (18.99).
Одновременно будем интегрировать задачу Коши (18.51) с известным зако-
ном управления и'1' (~) и проверять неравенства (18.90). Допустим, что мо-
мент времени 1 = 1' — первый момент, в который нарушилось одно из нера-
венств (18.90). Тогда положим о (~) = 1 и по формулам (18.99) будем опреде-
лять вариацию 3и (1). В точке 1 = 1' вариация Ои (1) должна быть непрерывна
(см. (18.98)). В каждый момент времени по известной функции Ои (~) будем
подсчитывать Ои (~) согласно правилу, данному выше. Получаемая функция
и'1' (~) должна проверяться на выполнение неравенств (18.66). Таким
41 Механика полета

642
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 18
образом, искомое решение определяется путем чередования градиентных
спусков в пространстве и (1) и в пространстве г (1).
Описанный алгоритм решения пригоден для вариационных задач с фа-
зовыми ограничениями нулевого порядка.
Для численного построения оптимальных решений при наличии произ-
вольных фазовых ограничений может использоваться метод штрафной функ-
ции [18.18, 18.26, 18.321.
Исходная система дифференциальных уравнений (18.51) дополняется
уравнением для штрафной функции х„+1 следующего вида:
(18.100)
х„1 — Х(и) (а — р ~) (~,„— ж),
где Х вЂ” такая функция и:
Х (р) = Х = сопвВ
Х (р) = Х = сопя~
Х(,)=О
при з (~,„
при р) з,„,
(18.101)
Положим
(18 102)
х„„(0) =0;
тогда значение х„+1 (Т) (0 будет характеризовать меру нарушения нера-
венств (18.90). Если х„+1 (Т)=0, то, согласно определению функции Х (~),
неравенства (18.90) выполняются всюду на промежутке [О, Т).
Определим управление и (1), доставляющее минимум контрольному
функционалу х, (Т) и обеспечивающее нулевое конечное значение штрафной
функции х„+1 (Т):
(18.103)
х„(Т) = О.
При выполнении условия (18.103) неравенства (18.90) будут удовлет-
ворены.
8. Численный метод, основанный на принципе максимума Л. С. Понтря-
гина. В этом пункте будет описан метод, родственный методам градиентного
спуска в пространстве управлений и основанный на применении принципа
максимума [18.21, 18.35].
Рассмотрим задачу Майера со свободным правым концом (18.51). Для ре-
шения по методу Л. С. Понтрягина составим гамильтонову функцию Н и
выпишем уравнения для импульсов р,.:
и
Н=,~~„рА (х, и, 1),
~'=О
(18.104)
дН д~у
дх. Р~ дх
Конечные значения импульсов р,. (Т) имеют вид
(18.105)
р„(Т) = — 1, р,.(Т) = 0
(18.106)
и„,(1) — шах Н(х,, р,, и, 8).
и(8)
(ср. конечные значения функций сопряженной системы (18.60); в методе
Л. С. Понтрягина система импульсов нормируется так, что импульс, соответ-
ствующий контрольному функцллоналу, в конечный момент отрицателен).
Чтобы функционал х, (Т) достигал минимума, оптимальная управляю-
щая функция и (~) должна обеспечивать максимум функции Н:

643
ГРАДИЕНТНЫЙ СПУСК В ПРОСТРАНСТВЕ УПРАВЛЕНИИ
5 2]
Предлагаемый в работах [18.21, 18.35] алгоритм решения описанной
задачи состоит в следующем.
По заданному нулевому приближению управления и"' (г) решается за-
дача Коши «вперед» для системы фазовых переменных (18.51). В результате
вычисляются в каждой точке значения фазовых координат х~~~ (г). По из-
вестным х"' (г), и"' (г) решается задача Коши «назад» для системы уравне-
ний импульсов (18.104) — (18.105); в результате определяются функции
р,.о(г). управление на следующем шаге и~ц (г) находится из условия мак-
симума гамильтоновой функции Н в каждый момент времени:
тах Н[х(о& t; ( ), р о&gt (г) и" , г]. (1
и(1)(8)
В работе [18.21] указана модификация этого алгоритма. Обозначим
через й вместо и"' (г) управление, максимизирующее гамильтонову функ-
цию (см. (18.107)), и следующее приближение представим в виде
и~1& t; г) и о> (г +)~ й (г исо (г)] (1
Параметр ~ здесь находится из условия минимума контрольного функцио-
нала на каждом щаге процесса.
Приведем некоторые соображения по скорости сходимости метода
(см. [18.35 ]).
Приращение функционала Лхо (Т), вызванное вариацией управляющей
функции ои (г), дается следующей формулой:
~~о (Т) = — [Н (к&lt о&gt р& t; & t; и~ г) (х( &gt р о&g ; 'оз г)]
где Ь вЂ” остаточный член, оцениваемый следующим образом:
7 2
~Ь~ &l ;А ~и"' г) Ђ” и"'(г)
О
(18.110)
зг
~,.= ~ а, (г)х.+Ь,. (и, г)
~=о
(18.111)
описанный итерационный процесс вырождается в один шаг. Действительно,
фазовые координаты х. и управления и в дифференциальные уравнения для
импульсов не входят (см. (18.104)):
р,. = — ~ а,р.;
.р'=О
(18.112)
41*
(А — 'фиксированная константа, связанная с постоянными в условиях
Липшица для функций ~,. и дН!дх,). На каждом шаге итерационного процесса
управление и"' (г) (или й (г) в модифицированном методе (18.108)) выбирается
из условия максимума Н по и; поэтому рассматриваемый метод обеспечивает,
с точностью до малых высшего порядка по ~и"' (г) — и'о' (г)~, наиболее бы-
строе изменение функционала по сравнению с другими методами, учитываю-
щими лишь первую вариацию. Малость ~и'1' (г) — и'о' (г)~ понимается здесь
в смысле интегральной нормы, фигурирующей в оценке остаточного члена
(18.110), т. е. величина ~и"' (г) — и'о' (г)~ может быть конечной, но на малом
отрезке времени.
Метод допускает применение для задач с ограниченным управлением,
не нуждаясь в каких-либо модификациях.
Заметим, что для правых частей системы (18.15) вида

644
~ГЛ. 18
ФункциОнАльные численные метОды
поэтому функции р,. (~) находятся однократным решением задачи Коши
(<наз д» ля сист мы (18.1 2 с краев ми услови ми (18.10 ). Оптималь
управление и (1) определяется из условия максимума выражения
(18 113)
Для задачи Майера (18.67) с фиксированными начальной и конечной
точками траектории описанный метод может найти применение, если вос-
пользоваться приемом введения штрафных слагаемых (18.68). Конечные
условия для импульсов (18.105) при этом заменятся на такие:
(18.114)
ро (Т) 1 р (Т) дР'о)~дх,.
(выражение функции Р дано формулой (18.68)).
В работе [18.35] описан пример применения метода; там же даны ре-
комендации по вычислительной процедуре, связанные с экономией машин-
ной памяти.
~ 3. Функциональный метод Ньютона
Решения х,. (~) краевой задачи (18.10), к которой редуцируются вариа-
ционные проблемы, должны удовлетворять дифференциальным уравнениям,
начальным и конечным условиям. Для решения проблемы могут быть ис-
пользованы итерационные процессы двух типов. Первый: на каждом шаге
точно выполняются начальные и конечные условия и неточно дифференциаль-
ные уравнения; в ходе итерационного процесса происходит приближение
к решению, оцениваемое по расстоянию в функциональном пространстве.
Второй: на каждом шаге процесса точно удовлетворяются дифференциальные
уравнения и начальные условия; от шага к шагу происходит приближение
конечных значений х. (Т) к требуемым х.„оцениваемое по расстоянию в ко-
нечномерном пространстве.
В этом параграфе будет описан функциональный метод Ньютона и его
обобщение, относящиеся к итерационным процессам первого типа. Вывод
алгоритма дан для обобщенного функционального метода Ньютона, тради-
ционный метод Ньютона получается из него как частный случай.
Функциональный метод Ньютона изучался в работах [18.10, 18.13,
18.36].
1. Алгоритм метода. Опишем алгоритм обобщенного функционального
метода Ньютона на примере краевой задачи первого рода для дифферен-
циального уравнения второго порядка:
(18.115)
х = ~ (х, х, ~); х (О) = х, х (Т) = х1.
(18.116)
Х = [х — ~(х, х, 1)]'"Ж.
Стремление функционала к нулю при выполнении граничных условий
(18.115) будет означать приближение к искомому элементу х)' (~).
Пусть известно некоторое нулевое приближение к искомому решению—
функция х"' (1), удовлетворяющая краевым условиям; следующее прибли-
жение представим в виде
х(1) Р) =х(0) И)+~х Р)
(18.117)
Введем функционал — расстояние до искомой точки в функциональном
пространстве х (1):

ФУНКЦИОНАЛЬНЫЙ МЕТОД НЬЮТОНА
Функция ()х (~) имеет норму, малую по сравнению с нормой функции
х"' (1); краевые значения ох (1) выберем следующими:
Ох(0) = Ох(Т) = О.
(18.118)
Вариация функционала Х, вызванная вариацией Ох (~), записывается так:
д/(о) д/(о)
ОХ = 2 (Х"' — /"') (Вх — Вх — ох) Ий;
(18.119)
здесь х"', ~(о), д~")/дх, д~(о)/дх — функции 1, вычисленные при х = х"' (1).
Среди всех вариаций ох (~), удовлетворяющих краевым условиям (18.118),
определим такую, которая уменьшала бы значение функционала, вычислен-
ное по нулевому приближению х"' (1), иными словами, искомая Ох (1) должна
обеспечить первой вариации оУ знак минус.
В частности, таковой может быть функция ох (~), подчиненная условиям
дт(о) дт(о)
ох, Зх —, Зх = — Л (х") — ~(о)), ох (О) = Зх (Т) = О, (18.120)
где л — положительный параметр.
Введем функцию з (~) по формуле (ср. (18.25))
~ (() = ()х (~)/Л;
(18.121)
тогда соотношение (18.117) перепишется так:
х"' (т) =х(о) (г)+Л7) (т),
(18.122)
а дифференциальное уравнение и краевые условия (18.120) примут вид
дт(о) дт.(о)
— — .)) = — х"'+ ~(о), 7) (0) = )) (Т) = О.
(18.123)
Х „= ш)п ~х(о)+Л~ — ~(х(о)+Л~, х(о)+Лъ~, Е)~" (ОЕ.
Л
(18.124)
Этот способ определения параметра Л аналогичен тому, который исполь-
зуется в методе функционального градиентного спуска применительно к пара-
метру спуска (ср. (18.28), (18.65)).
Сформулируем окончательно содержание рассматриваемого итер ацион-
ного процесса:
На каждом шаге процесса, описываемого выражением типа (18.122),
необходимо решатпь краевую задачу для линейного уравнения (18.123) с коэф-
фициентами и правой частью, определяемыми по результпатпам предыдущего
шага, и находить каким-либо численным методом значение параметра
из условия (18.124).
Таким образом, процедура построения функции Ох (~) разделилась на
две части: нахождение ~ (~), удовлетворяющей условиям (18.123), и определе-
ние параметра Л. При решении краевой задачи (18.123) для линейных диф-
ференциальных уравнений может быть привлечен метод прогонки или любой
другой подходящий метод (см., например, [18.37 — 18.39]). Определение
параметра л связано с решением следующей задачи на минимум.
Пусть функция ~ (~) найдена из (18.123); тогда зависимость х"' от ~, Л
известна и функционал У является известной функцией параметра Л. Будем
искать то значение Л, которое обращает в минимум интеграл (18.116) на дан-
ном шаге процесса:

646
ФункциОКАльные численные методы
[ГЛ. 18
Если исходное дифференциальное уравнение (18.115) линейное, то
итерационный процесс вырождается в один шаг, а минимизирующее значе-
ние параметра Л равно единице. действительно, когда функция 7' — линей-
ная по аргументам х, х, то у (Л) имеет вид
г(л) = у (1 — л), (18 125)
где Х"' — значение интеграла (18.116), вычисленное по нулевому прибли-
жению (Л=О); минимум Х (Л) достигается при Л=1 и равен нулю, что под-
тверждает высказанное выше суждение.
Для произвольного нелинейного уравнения (18.115) зависимость Х (Л)
содержит помимо первого члена Х"' (1 — Л)' еще члены, зависящие от степе-
ней Л выше первой, причем коэффициенты при степенях тем меньше, чем
Рис. 18.8. Пример зависимости относительной величины
функционала Х/Х"' от параметра А — обобщенный метод
Ньютона.
Рис. 18.7. Пример изменения миними-
зирующего значения параметра Х по
шагам итерационного процесса—
обобщенный метод Ньютона.
х (2) = — 1,3558,
у (2) = 0,96570,
лучше функция 7' описывается линейными членами разложения по х — х~,
х — х~. (' ходом итерационного процесса функция Х (Л) приближается к виду
(18.125), поэтому минимизирующее значение Л стремится к 1.
Если для произвольного нелинейного уравнения параметр Л назначить
равным единице на всех итерациях, то предлагаемый метод переходит в тра-
диционный функциональный метод Ньютона.
Метод обобщается на случай нелинейных дифференциальных уравнений
произвольного порядка, а также систем уравнений. Минимизируемым функ-
ционалом может служить соответственно интеграл от квадрата невязки диф-
ференциального уравнения или интеграл от суммы квадратов невязок от-
дельных уравнений системы.
2. Пример. Для иллюстрации скорости сходимости предлагаемого метода, а также
для сравнения с другими методами был просчитан пример с уравнениями движения в цен-
тральном поле.
Перелет между заданными координатами в центральном поле описывается системой
нвух дифференциальных уравнений второго порядка
х= — Их (хй+ уй) ~', х (О) = хо, х (Т) = х1,
(18.126)
у = — Йу (х2+ у2) ~', у (О) =уо, у (Т) =у1.
Здесь, в отличие от принятого (см. гл. 4), за единицу времени взяты 100 средних
солнечных суток, а за единицу линейного расстояния принята по-прежнему астрономиче-
ская единица; при этом коэффициент Й равен 2,9591.
Следуя [18.17), выберем в качестве начальных и конечных координат, а также вре-
мени следующие значения:
х (О) = 0,99850,
(18.127)
у (О) = 0,07107,

647
ФУНКЦИОНАЛЬНЫЙ МЕТОД НЬЮТОНА
а в качестве нулевых приближений т&lt о&gt (й) у& t;о&g ; (й) та
зт и (2 — ~) з1п п~
з&g ;п 2  + 1п
(18.128)
з1п п (2 — ~) з1п п~
з1п 2п "о + з&g ;п 2п
(и = 1,0462).
Итерационный процесс обобщенного функционального метода Ньютона в рассматри-
ваемом случае описывается соотношениями
&l ;» &lt ) l ;о& t; (ц ) . р) у& t » ) <о&gt
Функции &g ;) ( ), »у ~) находя ся из реше ия крае ой зад
ДХ(о) ДД'~о)
— У&lt о&gt Х& t;о& t; „
вкусо) ду(о)
.+ ° =- — у&lt о&g ; вЂ
(~~~ ~ст (~2 + у2) гг ~т Яу (~2 + у2) lг)
(18.130)
а параметр Х вЂ” из условия минимума выражения
т&l ;п ([х l ; & t + ц  (х& t;о&g ; + Х&gt
Х
О
<у l ;о&g ; & t &g ; >) +  & t;о& t
(18.131)
Т аблиц а 18.1
Убывание функционала по шагам итерационного процесса обобщенного 7&
(й)
и традиционного 7~> ~< функцион льных м тодов Н
Номер шага
й
у (й)
>.=
0,46302. 10 ~
0,25858
7,0862
12,346
4,0145
29,233
460,12
12,346
Номер шага
й
у (и)
г.=ор С
0,565. 10-8
у (я",)
Л=1
0,52063. 10 ~
3,3005
0,46178. 10 ~
0,030773
Представление о скодпмостп процесса дает табл. 18.1, в которой выписаны значения
интеграла 7 для каждого шага Й (вторая строка 7&g ;, „р ). ля сравне и в трет ей стр
таблицы приводятся значения функционала 7 при использовании традиционного метода
Ньютона (7> ). Из дан ых табл цы следу т, то за с ет выб ра параме ра &g ;< по
(18.131) число итераций сокращается на три.
На рис. 18.7 показан характер изменения минимизирующего значения ~ по шагам
итерационного процесса (дискретные точки соединены ломаной линией). В начале про-
цесса Х ~ 1, в конце ~ — 1, что подтверждает высказанное ранее суждение.
Для решения линейной краевой задачи (18.130) применялся метод сопряженных
уравнений (18.39]; определение минимизирующих значений параметров « производилось
одновременно с построением функций 7 (>
Результаты применения метода следующие.

648
ФУНКЦИОНАЛЬНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
[ГЛ. 13
Зависимость интеграла (18.131) от параметра ) представлена на рис. 18.8 для трех
шагов процесса. По вертикальной оси отложена величина интеграла, отнесенная к его
значению на данном шаге при ) =0 (эта величина обозначена У~).
Рис. 18.9. Траектории, соответствующие первому и второму шагам обобщенного метода Ньютона (1, 2),
традиционного метода Ньютона (3, 4), функционального градиентного метода в фазовом пространстве
(5, 6).
На рис. 18.9 даются траектории, соответствующие первому и второму шагам обобщен-
ного метода Ньютона (линии 1, 2), традиционного метода Ньютона (линии 8, 4) и функцио-
нального градиентного метода в фазовом пространстве (линии Б, 6). Начальная траекто-
рия, общая для всех трех методов, отмечена значком О, решение — значком т. Данные
по градиентному методу взяты из работы [18.17]; в этой работе функциональный градиент-
ный метод в фазовом пространстве (см. Я 1 настоящей главы) применен к минимизации
интеграла действия.

ГЛАВА 19
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
В настоящей главе собраны конечномерные методы построения оптимальных реше-
ний. Приведение вариациопных задач (18.1) — (18.9) к виду, пригодному для использова-
ния этой группы методов, возможно двумя способами. В основе первого способа лежит
замена функционалов функциями конечного числа переменных: метод Ритца, метод лома-
ных и другие. Второй способ состоит в редукции вариационной задачи к краевой и нахо-
ждении конечного числа недостающих начальных условий (см. начало гл. 18).
Глава содержит два параграфа. В первом описаны наиболее употребительные ко-
нечномерные методы, во втором даны способы приведения вариационных задач к тре-
буемому виду.
9 1. Минимизация функции при дополнительных условиях
Требуется определить минимум функции и переменных
Х=Х(х„...,х)
(1 .1)
при выполнении дополнительных условий
6,. (х„..., х„) = О
(у =1,..., 1(п);
переменные х, ..., х„изменяются в неограниченной области.
Будем заранее считать, что решение задачи (19.1) — (19.2) существует и
единственно.
Для нахождения искомой точки х,. используют аналитический прием
с множителями Лагранжа )~.: составляется новая функция
./'
Х (х,..., х„; )„..., Х,) = Х (х,.) +~ Х.~ (х), (19Л)
,~'=1
и выписываются условия ее минимума по аргументам х,.:
(1= 1,..., и).
(19.4)
(1, ~'=1, 2,..., т),
~,. (х,.) =О
(19.5)
где
У1 — х1,..., УЯ вЂ” х„, У„+1 Х1,..., У„„Х„
(т=п Ц.
Система и уравнений (19.4) совместно с 1 уравнениями (19.2) определяет
неизвестные х„..., х„; )~1,..., )~,. Запишем эти две группы уравнений в виде
одной системы:

650
~гл. 19
кОнечнОмеРные численыые метОды
Если Х (х„..., х„) — квадратичная функция своих аргументов,
а ((&g ;. (х„. ., „) Ђ” линей ые функц и, то сист ма (19 5) Ђ” линей ая от
сительно переменных у„..., у„,..., у„+, нахождение минимума при до-
полнительных условиях сводится в этом случае к решению системы линей-
ных алгебраических уравнений.
1. Градиентный метод. При отсутствии дополнительных условий (19.2)
процедура градиентного метода применительно к нахождению минимума
функции Х (х1,..., х„) состоит в следующем.
По известному нулевому приближению для аргументов х(о) вычисляются
производные минимизируемой функции:
( (о) х(о))
дУ(о& t;
(19. )
первое приближение представляется в виде
, (ц (о) ),
д~(о&
дж,
(19.7)
Параметр )( определяется из условия минимума функции
&g ;( о) ~
(19.8)
на данном шаге итерационного процесса.
Для решения исходной задачи (19.1) — (19.2) можно указать две модифи-
кации описанной выше процедуры.
Первая модификация состоит в том, что задача на условный минимум
(19.1) — (19.2) заменяется задачей на безусловный минимум путем введения
штрафных слагаемых (ср. ~ 2 гл. 18). Составляется вспомогательная функ-
ция У (х1,..., х„) с коэффициентами д,. ) 0 (у=1,..., 1):
У (х,..., х„) = У (х,..., х„) + «~ д .~&g ;2 (х,. ., х
(19.9)
()& t; (х( )) Ђ” ~& t;( ) †Π& t;
(19.10)
Представим выражение для искомых х,. на первом шаге процесса в виде
х(&g ;) Ђ” х о +
(19.11)
Изменения функций Х и ~&gt ., вызван ые мал ми приращени ми Зх„запиш
у' Ф
Ограничиваясь линейными членами разложения'.
П
д~(о&
(19.12)
и нщется минимум новой функции У (х„..., х„) описанным выше градиент-
ным методом (19.7) — (19.8). В процедуру метода включается процесс после-
довательного увеличения коэффициентов д ..
Другая модификация повторяет прием, также описанный в ~ 2 гл. 18.
Изложим процедуру для упрощенного случая, когда начальное приближе-
ние я~о~ точно удовлетворяет дополнительным условиям:

МИНИМИЗАЦИЯ ФУНКЦИИ
Определим вариации ох,. из условия неположительности вариации 3Х при
йыполнении дополнительных связей
дф(0~
Ы.=УМ = ' Вх.=О
дж;
(19.13)
Аналогично $ 2 гл. 18, составим вспомогательную функцию с множителями
Лагранжа ~.:
и г
д~&lt о>
г=у+~~~~л,с~,.=2 ~+~~~~х, „' вх,.
,у =1 ~=1,у =1
(19.14)
Быоерем ~х,. в виде
(19.15)
Ясли 1) О, то вспомогательная функция Г неположительна при любых
г = ~~~~~ '„'"'-~-~~~~~, „' ~о.
~ =1,~=1
(19.16)
Множители Лагранжа > ,. определяю ся из уравне ий (19.1 ), кото
являются линейными уравнениями относительно 1,. (Зх,. в (19.13) берутся
из (19.15)):
(", ~-~~~ ~,,' )=о
(19.17)
В силу такого определения параметров 1. сумма по ~ в выражении для функ-
ции Г равна нулю:
И
(х(~) х(о)) — ~я)
д~Ж~
у'=1
(19.19)
(с=1,...,и)
~ ~Р~,.=О. (19.18)
~=о
Отсюда вытекает, что Г совпадает с 3Х, и, следовательно, данный выбор
вариаций Зх,. обеспечивает неотрицательность вариации 8Х.
Параметр & t в форму ах (19. 5) определ ет дл ну ш га вд ль условн
градиента, последняя ограничена сверху требованием малости ошибки ли-
нейного представления функций Х и ф,. (ср. з 2 гл. 18).
В заключение этого пункта заметим, что в исходной постановке (19.1)—
(19.2) не фигурируют ограничения на область изменения параметров х,
Это обстоятельство в значительной степени упрощает вычислительную про-
цедуру. Более общий случай описан в монографии Зойтендейка [19.11 (там же
имеется обширная библиография). По поводу градиентного метода в конечно-
мерном пространстве и родственных ему методов применительно к задаче
(19.1) — (19.2) можно рекомендовать, например, работы [19.2 — 19.4, 19.24,
19.251.
2. Метод Ньютона. Для системы алгебраических уравнений (19.5),
к которой сводится задача на минимум (19.1) с дополнительными условиями
(19.2), традиционный метод Ньютона состоит в следующем. По начальному
приближению х~~.'~ вычисляются производные д~~Ю/дх., значения х~!~ на пер-
вом шаге процесса Ньютона определяются из такой системы линейных урав-
нений:

652
1ГЛ. 19
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
(чтобы сделать обозначения привычными, в системе (19.5) х,. заменены на х,,
а порядок системы и+г заменен на и).
Опишем одно обобщение метода Ньютона [19.5 — 19.9], отличающееся
от традиционного метода Ньютона введением некоторого параметра, напо-
минающего параметр спуска ~ в градиентном методе. Метод является конечно-
мерным аналогом изложенного в предыдущей главе обобщенного функцио-
нального метода Ньютона.
Пусть задана система и алгебраических уравнений с и неизвестными
(19.20)
(е, 7= — 1,...,и);
~,. (х.) =-0
требуется определить решения системы х".. Составим функцию
(19.21)
которая в искомой точке т,.=-т,. обращается в нуль вместе со своими первыми
производными:
и
г=1
(19.22)
Близость к решению в в-мерном пространстве (х,,..., х„) может быть
оценена по величине функции Ф. Пусть в и-мерном пространстве дана точка
х®,..., х~о), не являющаяся решением, и в пей вычислены функции Д),
Ф'о' и производные д~®/дх ., дФ"'/дх .. Представим координаты х . на сле-
дующем шаге итерационного процесса в виде
(19.23)
х(1) — х(0) + Ь
()=1,...,и),
где Зх,. — малые приращения. Соответствующее приращение функции Ф
записывается следующим образом:
(19.24)
(19.25)
1) 0 (! = 1,..., ~г),
и, во-вторых,
(19.26)
(к =1,..., и).
Х)0
Выражение (19.25) определяет алгоритм градиентного метода (ср. (19.7)).
Если в формуле (19.26) положить 1=1, то она определит алгоритм метода
Ньютона.
Произведем замену
3х . = Х~ . ()' = 1,..., и);
(19.27)
Чтобы итерационный процесс был сходящимся, необходимо выполнение
условия Ф'г' ( Ф'о', т. е. ОФ ( О. Из этого условия можно выбрать прира-
щения 3х. двумя способами: во-первых,

653
МИНИМИЗАЦИЯ ФУНКЦИИ
тогда соотношения (19.26) будут иметь вид
(~=1,...,и),
(19.28)
а выражения для координат х~ц на первом шаге итерационного процесса
запишутся так:
х(1) х(0) + Л.
(19.29)
() =1,..., и).
Определив ~). из линейной системы (19.28) и подставив их в (19.29), обнару-
живаем, что Ф становится функцией только параметра Л:
Ф (х6) + Л~) .) = %' (Л).
(19.30)
Этот параметр выбирается из условия минимума функции Т (Л) на каждом
шаге итерационного процесса аналогично тому, как это делается в градиент-
ном методе:
ш)п Ф (Л).
(19.31)
Разложим функцию Т (Л) в ряд по степеням Л:
'Р (Л) = % (0) (1 — Л)'+ аЛ' (1 — Л) + ЬЛЗ (1 — Л) + сЛ4+...
(19.32)
а=Ь=с=... =О.
(19.33)
В этом случае параметр Л, доставляющий минимум функции Т (Л), равен
единице и описанный итерационный процесс вырождается в один шаг.
В близкой окрестности решения х,. функции ~,. описываются линейными чле-
нами разложения; поэтому по мере приближения к решению параметр
стремится к единице.
Таким образом, предлагаемый алгоритм решения системы (19.20) заклю-
чается в следующем:
Ча каждом шаге итерационного процесса находятся ~. из линейной си-
стемы (19.28), затем по условию (19.31) определяется параметр Л; значения
координат х,. на следующем шаге выражаются в виде (19.29).
Как было указано выше, предлагаемый метод совпадает с методом
Ньютона, если на всех итерациях Л=1. В близкой окрестности решения
минимизирующее значение Лприближаетсяк единице, и метод не имеет ни-
каких преимуществ перед традиционным методом Ньютона. Применение
данного метода оказывается рациональным в той области пространства х.,
где метод Ньютона либо неэффективен, либо расходится; в этом случае ми-
нимизирующее значение Л намного меньше единицы. Выбор параметра Л
на каждом шаге процесса в известном смысле гарантирует сходимость метода,
как это имеет место в градиентном методе.
Сравним некоторые стороны двух методов: градиентного метода и метода
Ньютона. Известно, что минимизация квадратичных функционалов и реше-
ние линейных уравнений — взаимно эквивалентные задачи. Методом Нью-
тона линейные уравнения решаются за один шаг, минимум квадратичного
функционала определяется градиентным методом в ходе итерационного про-
цесса. Таким образом, по числу потребных шагов для достижения заданной
Здесь коэффициенты а, Ь, с выражаются через произведения величин ~) .,
/~~о), д'~Ядх,.дх„, д'~Т)(дх,.дх,,дх„д4~6)/дх,.дх„дх,дх„„... Если /,. — линейные
функции своих аргументов, то

654
[ГЛ. 19
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
точности (а зачастую и по времени счета) градиентный метод уступает методу
Ньютона; это положение справедливо в близкой окрестности решения нели-
нейного уравнения (и соответственно неквадратичного функционала).
С другой стороны, процесс Ньютона может оказаться расходящимся
в тех случаях, когда градиентный метод сходится. Это объясняется, в ча-
стности, и тем, что в последнем фигурирует параметр спуска; на каждом
шаге процесса он может быть определен так, чтобы минимизируемый функ-
ционал не увеличивался.
По этим же соображениям введение параметра л в процессе Ньютона
в какой-то степени гарантирует сходимость; рациональный выбор параметра
может обеспечить выигрыш во времени достижения результата.
В работах [19.8, 19.9] предлагается выбиратьпараметр )~ изпромежутка
(О, 1) так, чтобы только выполнялось условие сходимости процесса: Ф"' (
( Ф'о'. Процедура выбора состоит в последовательном уменьшении ). от
единицы до того значения, когда выполнится условие сходимости.
$2. Сведение вариационных задач к конечномерным
Ф;(0) =Ф;(0) =Ф;(т) = ~,(т) =0
(19 Л4)
и выбираются функции х'О' (~), у"' (~), удовлетворяющие краевым условиям
(18.41). Решение ищется в виде линейной комбинации
и
ю„(1) = ю'О' (1) + ~ а,.~),. (1),
тг
у.(~) =у"'Р)+ХЬ;~„И).
(19.35)
После подстановки ю„(1), у„(1) вместо ю (1), у (1) в выражение для интеграла
(18.40) последний оказывается функцией коэффициентов а,, Ь„,:
(1 9Л6)
У,= У,(а,, Ь,.).
Задача отыскания т1п-экстремалей функционала (18.40) свелась к мини-
мизации функции У1 (а,, Ь,.) по конечному числу переменных.
Минимизация функции У1 (а,, Ь,.) может быть проведена градиентным
методом, алгоритм которого изложен в ~ 1 настоящей главы. Приведем фор-
мулы метода применительно к рассматриваемому случаю.
Пусть известно начальное приближение для коэффициентов а,, б,.;
следующее приближение представим в виде
а(') = а(о) — 1 (дУ(о)/да.),
Ь() ) — Ь(о) ~ (д ( (о)/дЬ,).
(19.37)
Здесь излагаются способы замены функционалов функциями конечногв
числа переменных: метод Ритца с определением коэффициентов по градиент-
ному методу, метод ломаных для задач Лагранжа и Майера, кроме того,
описываются методы организованного подбора недостающих начальных
условий в краевой задаче.
1. Метод Ритца с определением коэффициентов по градиентному ме-
тоду. Классический метод Ритца давно стал достоянием учебников
(см., например, [19.2, 19.10 — 19.12]); в настоящем пункте будет описан при-
мер его применения [19.13] к отысканию т1п-экстремалей интегрального
функционала (18.40) — (18.41).
Алгоритм метода состоит в следующем.
Выбирается полная система и линейно независимых функций (ф,. (~))
таких, что

655
СВЕДЕНИЕ В АРИАЦИОННЫХ ЗАДАЧ К КОНЕЧ НОМЕРНЫМ
$ 2]
Параметр спуска )~ определяется из условия минимума функции
Х (Х) = Х ~а(е) — Х (дХ1е)/да.), Ь(е) — Х (дХ1(е)/дЬ.)1. (19.38)
Таким образом, предлагаемая процедура минимизации состоит из двух вло-
женных один в другой итерационных
процессов:
1'. Итерационный процесс Ритца, за-
ключающийся в увеличении от шага к ша-
гу числа и коэффициентов а,, Ь,. в разло-
жении (19.35).
2'. Итерационный процесс градиент-
ного метода, заключающийся в отыскании ~щ
минимума функции (19.36) на каждом
шаге итерационного процесса Ритца.
Б азисные функции ф,. (~) в [19.13 ]
были выбраны степенного вида:
дР7
Я 4 ~ ~ 7 А
Рис. 19.1. Закон сходимости функционала
& t; 9' ~) 7, по ном ру итера ии проце са Рит
в качестве нулевого приближения х'е' (~), у'е' (~) были взяты функции (18.49).
Применение описанного метода Ритца в сочетании с методом скорейшего спуска
оказалось гораздо менее эффективным для изучаемой задачи, чем применение метода
градиентного спуска в фазовом пространстве (см. З 1 гл. 18); время, затрачиваемое на
расчет одного варианта с точностью по функционалу до 4 — 5 знаков, равнялось 100 лик
(вместо 1 — 2 мин для градиентного метода).
Рис. 19.2. Коэффициенты а;, Ь; разложения х (1), у (1) по базисным функциям ф;(1) на восьмой итерации
метода Ритца для примера с рис. 19.1.
Закон сходимости функционала У1 по номеру итерации Й процесса Ритца (для пара-
метров г1=1,52, и,=Т=2) представлен на рис. 19.1; там сплошной линией соединены
дискретные точки у,'", у,"',..., у,'з'. На первой итерации считается по пять коэффи-
циентов а,, Ь, (п=5); при переходе к каждой последующей итерации число коэффициентов
увеличивается на 10 (Лп=5), причем начальные значения (для метода скорейшего спуска)
новых десяти коэффициентов нулевые, а в качестве начальных значений старых коэффи-
циентов берутся их значения на предыдущей итерации.
Зависимости величин а;, 'о; при В=8 от номера ~ условно показаны непрерывныии
лпниями на рис. 19.2.
2. Метод ломаных для задачи Лагранжа. Идея метода — замена ин-
теграла суммой, а искомой функции — интерполяционным многочленом.
Для иллюстрации метода рассмотрим простую задачу (18.11), (18.12).
Обозначим в исходном функционале производную
(19.4О)

56
[ГЛ. 19
КОНЕЧНОМЕРНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ
так что
(19.41)
У= Ф(х, и, 1)Ж.
О
Разобьем интервал изменения аргумента на т равных частей т=Т/т;
при этом ~„=йт. Представим функцию и (г) на интервале (1„, 1„+1) в виде ли-
нейной функции:
и„= и (~„)). (19.42)
Тогда искомая функция х (~) в силу (19.40) будет квадратичной функцией
аргумента 1 на интервале (~„, ~„+1):
х(~) =х,. +и„(~ — ~„)+(и„+, — и,„) (~ — ~„)'/2-. (Й=1,..., т), (19.43)
и значения х„, х„„в узлах интерполяции будут связаны следующим образом:
х„„= х,, + 1/,т (и„~1+ и„) (Й = 1,..., 777).
(19.44)
Если интеграл (19.41) записать в виде суммы т интегралов по отрезкам
протяженностью т и на каждом отрезке подынтегральную функцию Ф пред-
ставить в виде, аналогичном (19.42), а затем все интегралы вычислить, то
получим выражение для У в виде суммы
иг — 1
Х = —, [Ф(и„и„О)+Ф(и„„и„, Т)+2~~~~Ф (и,, и„, 1„)]
2=1
(19.45)
(здесь х,=х (О), х„,=х (Т) — заданные значения функции на концах интер-
вала).
Рекуррентная формула (19.44) дает возможность выразить значение
функции в любом узле интерполяции х, (~=1, ..., т) через значения и„
и, 1,..., ие. Действительно, сложив правые и левые части выражений (19.44),
НайдЕм
г1
и, =и,+ — (ии+и,+ 2~~~~ ~и ) (1=1,..., ии)
1
7с=1
(19.46)
и, в частности, при 1=т
иг-1
1
и(Т)=и,+ — и и,+и,„+ и ~.
7с=1
(19.47)
И7 — 1
Х = — [Ф (и (0), и„О) + Ф (и (Т), и,„, Т)-' 2 ~~Р Ф (и (0), и„..., и„) ] .
7С=1
(19.48)
Таким образом, первоначальная вариационная проблема (18.11) — (18.12)
свелась к определению т+1 значений и„, дающих экстремум функции (19.48)
при выполнении дополнительного условия (19.47).
Изложенный метод был применен в работе [19.141 для расчета экстремалей функ-
ционала (18.40), записанного в полярных координатах. Если на межорбитальный перелет
в центральном поле не наложено условие заданного углового перемещения, то переход
к полярным координатам в функционале (18.40) сокращает на единицу порядок старшей
Используя соотношения (19.46), выражение для функционала (19.45)
можно сделать зависящим только от значений функции и (1) в узлах интер-
поляции:

657
СВЕДЕНИЕ ВАРИАЦИОННЫХ - ЗАДАЧ К КОНЕЧНОМЕРНЫМ
производной одной из функций (см. гл. 7): в подынтегральное выражение одна из функций
входит вместе с первой и второй производными по времени, а другая — только вместе
с первой производной.
Исходная задача была сведена в работе [19.141 к задаче об отыскании минимума
функции двух групп переменных с тремя дополнительными условиями, соответствующими
трем заданным конечным значениям. По мнению авторов, удовлетворительные результаты
получались уже при числе интерполяционных узлов т, равном 10 — 20, для времени пере-
лета, не превышающего времени одного оборота по начальной орбите.
3. Метод ломаных для задачи Майера. Идея метода — замена диффе-
ренциальных уравнений разностными', его применение для задач оптимиза-
ции описано в работе (19.15~, где он назван методом критического направ-
ления.
Опишем алгоритм метода для задачи Майера со свободным правым
концом.
Задана система дифференциальных уравнений и начальных условий
х,. = ~,. (х., и, 2),
х,. (О) = х, (2, ) = 1,..., и),
(19.49)
минимизируемый функционал — функция конечных значений фазовых ко-
ординат
Р (х,(Т),...,'х„(Т));
(19. 50)
требуется построить оптимальное управление и (2). Разобьем опять интервал
изменения аргумента на т равных частей протяженностью т=Т)т каждая.
Дифференциальные уравнения (19.49) дают связи между значениями ко-
ординат в двух соседних точках 1~, 1~+ .'
х,. „= х,. „+;~,. (х. „, и„, 2„)
(19.51)
(х,. =-х,.(1„), и„=и(1„), 2„=Й~; 2, ) =1,..., и;
Й=О,...,т — 1).
Функционал (19.50), зависящий от конечных значений координат, при
рассматриваемом подходе считается функцией значений управляющей функ-
ции и (2) в дискретных точках интервала: и„и„..., и . Нахождение ми-
нимального значения функции Р по и„и„..., и 1 связано с вычислением
частных производных дР!ди . Приведем выражения для них:
У2
дР дР дт, (Т) И~' (~в, ~с "й ~й)
— с
ди~, дх~ (Т) дт ь+1 ди~,
2,,У =1
(Й=О, 1,..., т — 1).
(19.52)
(2=1,..., и)
(19.53)
с граничными условиями
р,. (Т) = (2 = 1,..., и),
(19. 54)
42 Механика полета
Произведение т ~,~дР~дх,. (Т)](дх,. (Т)~дх~. „+ 1 как показано в работе [19.15),
1=Д
совпадает с решением следующей системы дифференциальных уравнений
в узлах интерполяции.'

658
~ГЛ. 19
кОнечнОмеРные численные метОды
так что
и
дР дж; (Т)
дж (Т) дж .
~=1 ~
(19.55)
Последний факт легко усмотреть из связи описанного здесь метода с функ-
циональным методом градиентного спуска в пространстве управлений.
Выпишем, основываясь на результатах ~ 2 гл. 18, вариацию функционала Р,
вызванную вариацией управляющей функции би:
У и
(19.56)
О ~=1
здесь р,. (~) — решение системы уравнений (19.53) с граничными условиями
(19.54). Заменим интеграл в последней формуле суммой:
и т
8Р=с р,. ~~ ' о2
(19.57)
7с=О ~=1
и выпишем частную производную$
дР д~з, ~с
ди (~~) ' ' ( ") ди (~~) '
(19. 58)
Решение проблемы состоит в подборе таких значений х,+, (О),..., х„(0),
которые обращают в нуль все невязки Т., т. е. в решении системы алгебраи-
ческих уравнений, заданных, неявным образом:
(~ = 1+ 1,..., и; Е) = и — 1).
(19.60)
Для применения того или иного численного метода решения системы
алгебраических уравнений нео бходимо вычислять производные дТ ./дх,. =
Сравнение (19.52) и (19.58) обосновывает высказанное ранее положение (19.55).
4. Подбор недостающих начальных значений в краевой задаче. При
помощи формализма Эйлера — Лагранжа или Понтрягина вариационная проб-
лема редуцируется к двухточечной краевой задаче для системы обыкновен-
ных дифференциальных уравнений (см. начало гл. 18 и систему (18.10)).
Решения х,. (~) краевой задачи (18.10) должны удовлетворять дифференциаль-
ным уравнениям, начальным и конечным условиям. Для решения проблемы
можно привлечь следующий итерационный процесс: на каждом шаге про-
цесса точно удовлетворяются дифференциальные уравнения и начальные
условия, и от шага к шагу происходит приближение конечных значений
х,. (Т) к требуемым х,.1.
Основу этих процессов составляет сведение краевой задачи к задаче
Коши с последующим подбором недостающих начальных условий по какому-
либо алгоритму. В конечном счете проблема приводится к решению системы
алгебраических уравнений.
Каждому набору недостающих начальных значений х,+, (О),..., т„(0)
(см. (18.10)) соответствуют определенные конечные значения х,. (Т) (Е~=
=и — 1). Будем подбирать недостающие начальные значения, чтобы удовлет-
ворить конечным условиям. Образуем невязки — разности между получаю-
щимися в конце интервала значениями функций х. (Т) и требуемыми х.1:
Т (х,) =х,. (Т) — х,, (~= 1+1,..., и; Е! =и — 1). (19.59)

659
СВЕДЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ К КОНЕЧНОМЕРНЫМ
=дх,.(Т)(дх е. Это можно сделать, во-первых, применяя формулы численного
дифференцирования и, во-вторых, интегрируя систему уравнений в вариа-
циях (см. (18.10))
П
— — (~=1+1,...,в; Й=1,...,в) (1961)
8=1
с начальными условиями
0 при ~+Й,
(0) =
дх; (0) ' ' 1 при ю=7с
(19.62)
совместно с дифференциальными уравнениями (18.10).
Краевые условия исходной задачи (18.10), данные в простейшей форме,
могут быть заменены на общие:
~~„(х,.„х,,) =0 (~, ~, 1=1,..., и).
(19.63)
Представленные в такой форме краевые условия не нарушают подхода
к краевой задаче как к системе алгебраических уравнений, ибо, добавив
к и связям (19.63) еще и связей, получающихся как следствие процесса ин-
тегрирования дифференциальных уравнений (здесь каждому набору началь-
ных значений хд, отвечают свои конечные х,,), получим замкнутую алгебраи-
ческую систему 2п уравнений относительно 2п неизвестных. Если конец
~= Т интервала изменения аргумента неизвестен, то к связям (19.63) добав-
ляется условие, определяющее его.
Чтобы решить систему алгебраических уравнений, можно воспользо-
ваться, например, градиентным методом или методом Ньютона (см. 3 1 на-
стоящей главы). Если задача содержит управляющие параметры, которые
надлежит определить из условия экстремума функции конечных координат
и этих параметров, то уместно воспользоваться одной из модификаций гра-
диентного метода, представленных в 3 1 настоящей главы.
Описанные в этом пункте приемы решения краевых задач нашли применение в ряде
работ по ракетодинамике [19.4, 19.8, 19.9, 19.16 — 19.23]. В этих работах вариационные
проблемы сводились к решению краевых задач для систем уравнений, составленных из
уравнений для фазовых координат и уравнений для импульсов (множителей Лагранжа); оп-
тимальные управления выражены через импульсы и фазовые координаты. Начальные и
конечные значения фазовых координат (физические координаты и скорости в задачах
ракетодинамики), как правило, заданы, и требуется определить такие недостающие началь-
ные значения импульсов, которые обеспечивают попадание траектории в заданную точку
фазового пространства.
В работах [19.8, 19.16 — 19.19, 19.22, 19.23] подбор недостающих начальных зна-
чений организован по методу Ньютона, в статье [19.8] проведен сравнительный анализ
методов Ньютона и градиентного; градиентный метод для нахождения оптимальных
управляющих параметров и одновременного удовлетворения краевых условий описан
в [19.4].
42*

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
А — большая полуось эллипса.
а — ускорение от тяги (реактивное
5 скорение).
Ьа — поправка к программв рвак-
тивного ускорения.
~а — ошибки реализации программы
реактивного ускорения.
а — величина ускорения от тяги.
компоненты вектора
реактивного ускоре-
ния а в прямоуголь-
ной (х, у, е), в сфе-
рической (г, &lt у, е
в декартовой (1= 1,
,в
а; (1 = 1, 2, 3)
2, 3) системах коор-
динат.
ао — начальное реактивнов ускоре-
ние.
 — малая полуось эллипса.
С вЂ” половина фокального расстоя-
ния.
с~ — коэффициент сопротивления
трения, отнесенный к площади
смоченной поверхности.
с — коэффициент аэродинамиче-
ского сопротивления.
с — коэффициент волнового сопро-
тивления.
с" — коэффициент волнового сопро-
тивления конуса.
с т — коэффицент сопротивления
трения.
с,„— теплоем кость.
.0 — диаметр.
Йо — интенсивность метеор ного по-
тока.
й, й~ — корреляционные матрицы
о'
отклонений ~х от расчетной
траектории в начале (0) и
в конце (Т) маневра.
й — корреляционная матрица оши-
бок И оценки Й.
~ — расстояние между эмиттером и
ускоряющим электродом ион-
ного движителя.
Š— энергия.
8 — полная энергия движения еди-
ничной массы в гравитацион-
ном поле.
е — единичный вектор направления
тяги.
е — электрический заряд частицы.
е,, компоненты единичного век-
тора направления тяги в пря-
е,. э моугольной (е2+е'„+ е2 = 1)
и в сферической (е'„+е2 +
+е~ — — 1)системах координат.
à — вектор внешних сил (эа иск:ио-
чениеи гравитационных), дей-
ствующих на аппарат.
Р~ ~, — компоненты внешних сил,
действующих на аппарат.
Ы~ — площадь сечения.
— площадь «миделя».
1' — универсальная гравитационная
постоянная.
Я вЂ” вектор гравитационного 5 скоре-
ния.
ее — коэффициент пропорциональ-
ности между весом и массой
(гравитационное ускорение на
поверхности Земли).
— гравитационное ускорение на
радиусе г,„.
Н вЂ” функция Гамильтона в проце-
дуре принципа максимума.
~ — высота.
1' — удельный импульс двигатель-
ной системы.
~ — сила тока.
1 — единичный вектор направления
солнечного светового излуче-
ния.
~ — плотность электрического тока,
угол между начальным и ко-
нечным положениями плоско-
сти орбиты.
1 — функционал динамической части
задачи для идеального двига-
теля ограниченной мощности
(интеграл по времени от квад-
рата реактивного ускорения).
ЛХ вЂ” приращение функционала Х,
характеризующее затраты па
коррекцию траектории.
Х, — полный функционал динамиче-
ской задачи для межпланет-
ного перелета с возвращением.
Х величины функционала дина-
мической части задачи для пе-
Х~ релетов между орбитами планет
туда (1) и обратно (2).
величины функционала дина-
мической части задачи для ма-
невров разгона (+) и торможе-
ния ( — ) у планет старта (1) и
финиша (2).
К~(1, т) — корреляционная функция
случайного процесса са (~).
К + Ь вЂ” функционал маневра для
комбинированного двигателя:
идеальный двигатель ограни-
ченной скорости истечения +

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
661
+ идеальный двигатель ограни-
ченной мощности.
~ — гравитационная постоянная цен-
трального тела (универсальная
гравитационная постоянная,
умноженная на массу тела).
Х вЂ” длина.
-~ — индуктивность.
~ — расстояние между точками покоя
в бессиловом поле.
М (...) — матеиатическое ожидание
(обозначается также (...)).
Мо — число Маха, соответствующее
скорости полета.
М вЂ” вектор момента количества дви-
жения единичной массы.
о4~ — модуль вектора М.
М (~) — текущая масса аппарата.
М, — масса аккумулятора энергии.
М; масса аппарата д~о и после
сброса ~-й секции двигателя.
̄— масса энергои сточника (бее
преобразователя и системы от-
вода энергии).
М вЂ” масса двигательной системы
р
(с баками).
М вЂ” масса системы подачи рабочего
Ч
вещества.
М, — масса системы накопления ра-
бочего вещества с заборником.
М вЂ” масса баков для рабочего ве-
~з
щества.
М вЂ” масса реактивного движителя.
Т
М~ — масса системы отвода энергии
от аппарата.
М~ — суммарная масса полезного
груза, рабочего вещества и ба-
ков (М, = М„+ М, Р) + М,).
̄— масса двигателя (М„=Мр — М ).
М„" — масса двигательной системы
на ~-м участке.
~̄— масса секции двигательной
системы.
М~ — суммарная масса 8 разно на-
строенных нерегулируемых
д~вижителей.
М~" — приращение массы нерегули-
руемого двигателя от добавле-
ния ~-го уровня тяги и расход~а.
М ~~) — текущая иасса запаса ра-
бочего вещества.
М о — начальная масса рабочего ве-
щества.
ЬМ" ~ — масса рабочего вещества,
оставшегося к моменту сброса
~-й секции двигателя.
ЛМ,, (~) — иасса рабочего вещества,
израсходованного к моменту
вреиени 1 (ЬМ (1) =М е—
— М,, (~)).
М, — масса источника мощности
~М,=М„+М,+Щ.
̄— полезная масса.
Л,"' — полезная масса ~-й ступени
(сумма истинной полезной мас-
сы М„и массы рабочего веще-
ства ЬМ") оставшегося к мо-
р, Ф
менту сброса ~-й секции дви-
гателя).
М вЂ” суммарная масса, доставляе-
мая в конечную точку траек-
тории за п попыток выполне-
ния маневра.
М, — суммарная масса полезной на-
грузки и рабочего вещества
(М,=М +М (~)).
~1~ — масса преобразователя энер-
гии.
~1~~ — суммарная м асса полезного
груза, запаса р абочего веще-
ства и источника мощности
(М~=М +М (~)+М,).
Мо — начальная масса аппарата.
М, — конечная масса аппарата.
т. — относительная масса )-и со-
ставляющей (т~ = М /М„).
Ж вЂ” полезная мощность реактивной
струи.
Ж„„, — максимальная мощность ре-
активной струи.
Т, — мощность, потребляеиая (Л, (
(О) и отдаваемая (Т, О) ак-
кумулятором энергии.
Ж ~ — мощность, соответствующая
потерям в ионном движителе.
Л'„— полная мощность, выделяемая
источником энергии.
У~ — мощность, потребляемая си-
стемой подачи р абочего веще-
ства.
У~, — мощность, передаваемая ап-
парату забираемым из внешней
среды рабочим веществом.
Ж, — мощность, потребляемая нако-
пителем рабочего вещества.
Ж. — мощность, потребляемая дви-
Т
жителем.
~У~ — мощность, выделяемая систе-
мой отвода энергии.
У~ — полная мощность реактивной
струи.
~У, — полезная мощность на выходе
преобразователя энергии.
и — единичный вектор направления
нормали к поверхности.
Р— вектор тяги.
Р— величина тяги.
Р(...) — вероятность события (...).
р — фокальный пар аиетр.
р; — вспомогательная функция (им-
пульс) в процедуре принципа
максимума, соответствующая
фавовой координате х;.
Д вЂ” тепловой поток.
д — м ассовый расход р абочего ве-
щества через движитель.
д, — р асход, поступающий в нако-
питель (секундный приход иас-
сы через воздухозаборник).
д — расход массы баков.
д. — расход массы движителя.
~з
(
д, — расход массы при выработкв
энергии.
д„— расход массы двигателя.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
д, — расход массы источника иощ-
ности.
д, — суммарный расход массы ап-
парата.
 — расстояние до Солнца, надеж-
ность (вероятность успешного
выполнения маневра).
В; — вектор расстояния до гравита-
ционного центра.
В; — расстояние до гравитационного
центра.
Л, — радиус небесного тела.
Л~, В~ — средние радиусы орбит
Земли и Марса.
Йе — число Рейнольдса.
Ю вЂ” газовая постоянная.
à — р адИуС-ВЕКтОр цЕНтр а ИаСС аП-
пар ата.
г — радиус в полярной и сфериче-
скои системах координат, мо-
дуль Г.
Ьà — измеренные отклонения траек-
тории от расчетной (оценки от-
клонений).
бг, ~ГΠ— отклонения от р асчетной
траектории текущие и началь-
ные.
М вЂ” ошибки измерений (оценки)
траектории.
г~ — интенсивность солнечного све-
тового излучения на орбите
Земли.
Б — площадь поверхности.
Б~ — площадь поверхности радиа-
тора.
г — число оборотов по орбите.
Т вЂ” полное время выполнения кос-
мического маневра.
Т вЂ” полное время р аботы двига-
теля.
Т 1 полные вреиена действия со-
ответствующих уровней ~1, ...
Т , ..., 7~, ступенчатого управле-
ния.
7~, — суммарное время работы дви-
гателя на межпланетном пере-
лете с возвращением (Т, =
=т,+т,+т +,+т,+
+ Т(7) Т(4) — ())
Р ' Р
Т Т „, время работы двигателя
Р на участках перелетов
~ ~2 = Т~ ' между орбитами планет
«туда» и «ооратно».
ТР,+1 = Т~( ' вреия раооты двига-
Т вЂ” Тл) теля на участках раз-
Р.~ — 1 Р,
т ' Т' (+) р»
е +» 0 ния ( — ) у планет стар-
~е.,— »= Тр. ' та (1) и финиша (2).
Т, — суммарное время межпланет-
ного перелета с возвращением
(Т,= Т„, + Т + Т,+ Т ~+Т,=
Т„, = Т'з' + Т(4) + Т(~' — время пре-
бывания в окрестности планеты
назначения.
Т вЂ” Т ~4~ стремя ожидания.
т т(2) Времена перелетов меж-
т(® ду орбитами планет «ту-
да» (1) и «обратно» (2).
Т+,— — Т"' времена разгона (+) и
Т = Т" ~ торможения ( — ) у пла-
Т+» — Т~~~ нети старта (1) и фи-
Т,= Т~в~ ниша (2).
~ — текущее время.
— текущее вреия работы двигате-
ля.
текущие времена действия со-
ответствующих уровней
~~, ) ..., 7~, ступенчатого управле-
ния.
~о — дата старта, отсчитываемая от
противостояния планет старта
и финиша.
У вЂ” потенциал поля тяготения.
У, — потенциальная энергия еди-
ничной иассы на поверхности
небесного тела.
И вЂ” напряжение (равность электри-
ческих потенциалов).
и, г, ш — компоненты вектора ско-
рости ч в прямоугольных си-
стемах координат (х, у, х) и
Л, ~. ~).
и, — приращение модуля скорости
в бессиловом поле.
К вЂ” скорость истечения реактивной
струи.
ч — вектор скорости центра и асс
аппарата.
г„~ ~ — компоненты вектора скоро-
сти в сферической системе ко-
ординат (г, ~, 0).
Ьу — функционал динамической ча-
сти задачи для идеального дви-
гателя ограниченной скорости
истечения (интеграл по вре-
иени от реактивного ускоре-
ния — характеристическая ско-
рость).
Х, У, Я вЂ” компоненты вектора гра-
витационного ускорения в пря-
моугольной системе координат
(х, у, х).
х, у, г — прямоугольные координа-
ты.
х — вектор фазовых координат,
вектор проектных параметров
управляемой системы (в гл. 13).
у — вектор параиетров ианевра
(в гл. 13), прогноз отклонений
(в гл. 16).
~ — удельная иасса источника мощ-
ности (на единицу мощности).
~* — соотношение состава топливной
сиеси.
~, — удельная масса аккумуляторов
энергии (на единицу эапасае-
мой энергии).
~ — удельная масса баков для рабо-
чего вещества (на единицу эа-
пасаемой массы).
т — удельная масса движителя (на
единицу тяги).

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
663
у~ — удельная масса электростати-
ческого движителя (на единицу
площади ионного пучка).
у, — удельная масса системы накоп-
ления рабочего вещества (на
единицу секундного прихода
массы).
т„— удельная масса двигателя (на
единицу тяги).
у — удельная масса двигательной
системы (с баками, на единицу
тяги).
о — функция включения — выключе-
ния двигателя, обозначение
первой вариации, толщина сте-
нок, »-функция Дирака.
релейные функции, отвечаю-
о, щие за включение — выключе-
ние соответствующего уровня
о, ~„..., ~, ступенчатого управ-
ления.
Š— напряженность электрического
поля.
а — отношение удельных масс дви-
жителя и энергоисточника,
эксцентриситет.
а — коэффициент отражения телом
светового излучения.
Н вЂ” напряженность магнитного по-
ля е
~) — коэффициент полезного действия
(к. п. д.) двигательной систе-
мы.
~, — к. и. д. источника мощности,
работающего по циклу Карно.
— эффективный к. п. д. движите-
ля (~) = а а„).
~" — энергетический к. и. д. ионного
движителя.
~~ — энергетический к. п. д.
— коэффициент использования
рабочего вещества в движителе.
~)„— коэффициент использования
мощности в движителе.
~, — к. и. д. преобразователя энер-
гии.
Э вЂ” угол установки солнечного па-
руса, истинная аномалия.
т. — коэффициент превращения мате-
риала сбрасываемых секций
двигателя в рабочее вещество,
отношение допустимого числа
отказов Л, к максимально воз-
можному Л„„,-„показатель ади-
абаты.
Лтах = ЛП1ах Т вЂ” МаКСИМаЛЬНО ВОЗ-
можное «число» отказов.
Л1 — Л (Т) — допустимое «число»
ОтказОВ.
~ — относительная скоросты азового
потока, интенсивность потока
отказов.
— длина Волны СВЕтоВОГО иЗЛ5'
чедия.
1, — постоянная распада радиоизо-
топов.
1 — коэффициент теплопроводности.
р — масса элементарной частицы.
~ — кинем атическая вяз кость.
~ — отношение массы накопителя
энергии к массе энергоисточни-
ка.
$ — вектор фазовых координат
(в гл. 13), вектор возмущающих
воздействий (в гл. 16).
~, ~, (. — координаты в транспорти-
рующей системе.
уровни ступенчатого управле-
ния.
° ° °
'в
р — радиус-вектор в транспортирую-
щей системе координат.
» — плотность атмосферы.
— плотность распределения про-
тонов в космическом простран-
стве.
а — постоянная Стефана †Больцма-
на.
~,„— электропроводность.
Т вЂ” температура.
҄— температура нагревателя.
Т, — температура поверхности не-
бесного тела.
Т, — температура воздуха на входе
в сжижительную установку.
Тт — эффективная температура.
То — температура торможения газо-
вого потока.
Т вЂ” температура радиатора.
Т вЂ” температура поверхности
Солнца.
т — безразмерное время (отнесено
к периоду обращения по началь-
ной орбите, деленному на 2~:
1/ Э/
т = Й "г„" (гл. 7), или к пол-
ному времени).
"" — напряжение трения.
Ф вЂ” функционал маневра для иде-
ального двигателя ограничен-
ной мощности (Ф = (~/2) Х).
Ф, — функционал маневра для иде-
ального двигателя ограничен-
ной мощности с накопителем
энергии.
у — полярный угол.
угловые перемещения пе-
у, = Ьу1 релетов между орбитами
~, = 1у» планет «туда» (1) и «об-
ратно» (2).
Т вЂ” полный импульс газового пото-
ка.
%' — функционал маневра для иде-
ального двигателя ограничен-
ной скорости истечения (Т =
= Лу/1 тах) °
Π— положение линии узлов.
Оэ — начальная уязвимая (в смысле
метеорных пробоев) площадь
радиатора (о«=ЙЯе, 0(Й (
( 1).
ю — степень черноты поверхности,
долгота перигея.
ю, — угол, под которым Видно не-
бесное тело.

664
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
со„~2 — средние угловые скорости
обращения планет старта (1)
и финиша (2) вокруг Солнца.
~о — угол, под которым видно Солн-
це.
й — скорость звука.
й„, — критическая скорость звука.
Я вЂ” интенсивность корпускулярного
излучения Солнца.
Ю~ — масса гравитационного цент-
ра.
йг — масса метеорной частицы.
Ж~ — удельная мощность солнечно-
го излучения.
Ж~ — удельная мощность космиче-
ского теплового излучения.
Л~ — удельная мощность корпуску-
лярного потока от Солнца.
с~) — вероятность пробоя метеорными
частицами.
.'р — давление,
~~ — световое давление.
~А~ — максимальное давление сол-
нечного света на орбите Земли.
."рд — электростатическое давление.
рн — магнитное давление.
П» — атмосферное давление.
~~ — давление корпускулярного по-
тока от Солнца.
~о — полное давление в потоке газа.
Я3 — вектор скорости набегающего
потока.
Ь вЂ” объем.
Ф вЂ” скорость солнечного ветра.

ЛИТЕРАТУРА
К введению и главе 1
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1ЛО.
1 11.
1.12.
1.13.
1.14.
1.15.
1Л6.
1Л7.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1.24.
1.25.
1.26.
1.27.
М е щ е р с к и й И. В., Работы ао механике тел переменной массы. Гостехиздат,
М., 1949.
Ц и о л к о в с к и й К. Э., Исследование мировых пространств реактивными
приборами. Научное обозрение, М 5, М., 1903.
Ц и о л к о в с к и й К. Э., Собрание сочинений, Изд-во АН СССР, М., 1954.
6 о Й Й а г Й В. Н., А шеСЬой о1 геасЫпд ехСгеше а1С1Сийея. Яш1СЬяошап 1пяС.,
ЖаяЫпфоп, 1919.
Ц а н д е р Ф. А., Проблема полета при помощи реактивных аппаратов. Межпла-
нетные путешествия. Оборонгиз. М., 1961.
О Ь е г С Ь Н., Ме Ва~еСе ки Йеп Р1апеСепгацтеп. В. 01йепЬоигд, МйпсЬеп, 1923.
Русский перевод. О б е р т Г., Пути осуществления космических полетов. Оборон-
гиз, М., 1947.
Н о Ь ш а и и Ж., Ме Егге1сЬЬагЫе1С Йег Н1ште1Жогрег. В. 01йепЬоигд, МйасЬеп,
1925.
Е я и а и 1 С вЂ” Р е 1 С е г1 е В., Ь' АяСгопаиС1цие. Раг1я, 1930. Русский перевод:
Э н о — П е л ь т р и Р., Космические полеты (астронавтика). Оборонгиз, М., 1950.
К о р о л е в С. П., Ракетный полет в стратосфере. Воениздат, М., 1934.
К о с м о д е м ь я н с к и й А. А., Экстремальные задачи для точки переменной
массы. Докл. АН СССР, т. 53, Ы 1, 1946.
О х о ц и м с к и й Д. Е., К теории движения ракет. Прикл. матем. и механ.,
т. 10, М 2, 1946.
И ш л и н с к и й А. Ю., Два замечания к теории движения ракет. Докл. АН СССР,
т. 53, М 7, 1946.
К о с м о д е м ь я н с к и й А. А., Курс теоретической механики. Учпедгиз, М.,
1955.
К о с м о д е м ь я и с к и й А. А., Основные теоремы механики тела переменной
массы. Лекции по механике тел переменной массы. Уч. зап. МГУ, Механика,
вып. 152, 154, 1951.
Т я1е и Н., Е ч а и я В., ОрС1пшт СЬгияС рго~гашшпщ аког а яаивй1пд гос1~еС.
2. Атег. Вос1~. Яос., чо1. 21, Яо. 5, 1951.
Ь а ж Й е и О. Р., М1шта1 госЫеС Сга1есСог1ея. 1. Атег. ВосЕ Яос., чо1. 23, Яо. 11—
12, 1953.
К р о т о в В. Ф., Расчет оптимальной траектории для перехода ракеты па задан-
ную круговую траекторию около Земли. Сб. «Механика», МВТУ, Оборонгиз, М.,
1955.
О х о ц и м с к и й Д. Е., Э н е е в Т. М., Некоторые вариационные задачи, свя-
занные с запуском искусственного спутника Земли. УФН, т. 63, вып. 1а, 1957.
Е г о р о в В. А., Некоторые проблемы динамики полета к Луне. Докл. АН СССР,
т. 113, М 1, 1957.
Е г о р о в В. А., Некоторые задачи динамики полета к Луне. УФН, т. 63, вып. 1а,
1957.
В а г г е г е М., 2 а и ш о С С е А., У е и Ь е Ы е В. Р., У а и й е и Ы е г с Ы Ь о ч е 1.,
Ьа ргори1я1оп раг 1цяеея. Раг1я, 1957. Русский перевод: Б а р р е р М., Ж о м о т т А.,
В е б е к е Б. Ф., В а н д е н к е р к х о в е Ж., Движение ракет. ИЛ, М., 1959.
М 1 е 1 е А., Ап ехСепя1оп о1 СЬе СЬеогу о1 СЬе орС1шиш Ьигшпд ргодгат аког СЬе 1ече1
111дЫ о1 а госЫеС-рожегей а1гсгай. АегопаиС. Яс1., чо1. 24, Яо. 12, 1957.
У е и Ь е Ы е В. Р., Ье ргоЬ1ете йи шах1шит йе гауоп й'асС1оп йапя ип сЬатр йе
дгач1СаС1оп иш1огте. АяСгопаиС. АсСа, чо1. 4, Яо. 1, 1958.
Е г о р о в В. А., О решении одной вырожденной вариационной задачи и оптималь-
ном подъеме космической ракеты. Прикл. матем. и механ., т. 22, М 1, 1958.
Исследование оптимальных режимов движения ракет. Сб. перев. под ред. И. Н. С а-
д о в с к о г о. Оборонгиз, М., 1959.
М 1 е 1 е А., бепега1 чаг1а$1опа1 СЬеогу о1 СЬе 111дЫ раСЬя ог гос1сеСроюегей а1гсга1С,
т1яя11ея апй яаСеП1Се сагг1егя. АяСгопаиС. АсСа, чо1. 4, Яо. 4, 1958.
В г е а ~ ю е 1 1 Ю. У., ТЬе орС1ш1каС1оп о1 Сга1есСог1ея. Х. Яос. 1пйияСг1а1 апй Арр1.
МаСй., чо1. 7, Яо. 2, 1959.

666
ЛИТЕРАТУРА
1.28. Г а н т м а х е р Ф. Р., Л е в и и Л. М., Теория полета пеуправляемых ракет.
Физматгиз, М., 1959.
1.29. Н е г г 1 с Ы Б., АяСгойупаш1ся. Рг1псе$оп, Я. У., 1959.
1.30. Ь а ю Й е и О. Р., 1пйегр1апеСагу гостей Сга1есйог1ея. Айчапсея 1п Брасе Бс1., Асай.
Ргевв, Ы. Т. — Ьопйоп, 1959. Русский перевод: Л о у д е н Д. Ф., Межпланетные
траектории ракет. Сб. «Космические траектории», ИЛ, М., 1963.
1.31. Л у р ь е А. И., Уравпения возмущенного движепия в задаче Кеплера. Прикл.
матем. и механ., т. 23, М 2, 1959; см. такхсе сб. «Искусственные спутники Земли»,
вып. 4, 1960.
1.32. Г о р е л о в Ю. А., О двух классах плоских экстремальных двихсений ракеты
в пустоте. Прикл. матем. и механ., т. 24, М 2, 1960.
1.33. И с а е в В. К., Принцип максимума Л. С. Понтрягина и оптимальное программиро-
вание тяги ракет. Автоматика и телемеханика, т. 22, М 8, 1961; т. 23, М 1, 1962.
1.34. Ь е 1С ш а и и 6., ТЬе ор$1ш1ка$юп о1 гос1се$ Фга1ес$ог1ея — а яцгчеу. Ргодг. 1п
Аяйгопацй. Бс1., сто1. 1, АшяСегйаш, 1962.
1.35. И л л а р и о н о в В. Ф., Ш к а д о в Л. М., Поворот плоскости круговой орбиты
спутника. Прикл. матем. и механ., т. 26, М 1, 1962.
1.36. Л у р ь е А. И., Об одной форме уравнений движения материальной точки. Приме-
нение к задаче о повороте плоскости орбиты искусственного спутпика Земли.
Тр. Межвуз. конф. по прикл. теории устойчивости движения, Казань, 1962.
1.37. Орй1ш1хай1оп ТесЬп1пцея. Ей. Ьу С. Ь е 1 С ш а и и. Асай. Ргеяя, Я. У., 1962.
1.38. Е Ь г 1 с Ы е К. А., Брасе 111дЫ. Рг1псеСоп, Я. У., чо1. 1, 1960; чо1. 2, 1962. Русский
перевод'. Э р и к е К., Космический полет. Физматгиз, М., 1963.
1.39. Ь а ю Й е и О. Р., Ор$1ша1 Сга1есСог1ея аког ярасе пач1дайюп. Ьопйоп, 1963.
1.40. Кузмак Г. Е., Исаев В. К., Давидсон Б. Х., Оптимальные режимы
движения точки переменной массы в однородном центральном поле. Докл. АН СССР,
т. 149, М 1, 1963.
1.41. И л ь и н В. А., Оптимальный переход космического аппарата, тормозящегося
в атмосфере планеты, на орбиту искусственного спутника Земли. Инж. журнал,
т. 3, М 2, 1963.
1.42. Т а р а с о в Е. В., Оптимальные режимы полета летательных аппаратов. Оборон-
гиз, М., 1963.
1.43. В г е а Ы ю е 11 У. У., ТЬе ор$1шцш ярас1пд о1 соггес$гге $Ьгця$я 1п 1п$егр1апе$агу
пач1да$юп. Ма$Ь. Ор$1шЬ. ТесЬп., СаИогп1а Ргеяя, 1963.
1.44. М 1 е 1 е А., Г11дЬ$ шесЬап1ся. МаяяасЬ.— Ьопйоп, 1962. Русскийперевод: М иел е А.,
Механика полета. «Наука», М., 1966.
1.45. И л ь и н В. А., К расчету траекторий перелета космических аппаратов между
компланарными круговыми орбитами в ньютопианском гравитационном поле.
Космические исследования, т. 2, М 5, 1964.
1.46. К у з м а к Г. Е., К о и н и н Ю. М., Новая форма уравнения движения спутника
и приложение ее к исследованию движений, близких к кеплеровым. Ж. вычисл.
матем. и матем. физ., т. 3, Ы 4, 1963.
1.47. Исаев В. К., Курьянов А. И., Сонин В. В., Примепение принципа
максимума в ракетодинамике. Ргос. Х1У 1п$егпа$. АяСгопацС. Сопряг. 1963, Жаг-
яха~ча, 1964.
1.48. А л е к с е е в К. Б., Б е б е и и н Г. Г., Управление космическим летательным
аппаратом. «Машиностроение», М., 1964.
1.49. К о р е и е в Г. В., Введение в механику управляемого тела. «Наука», М., 1964.
1.50. А и й г е е я с ц О. Б$., Я 1 С а М. М., ХЬогц1 гасЬейе1. Еййцга М111Сага, Вцсцгеяй1,
1964.
1.51. Л и д о в М. Л., О х о ц и и с к и й Д. Е., Т е с л е н к о Н. М., Исследование
одного класса траекторий ограниченной задачи трех тел. Космические исследова-
ния, т. 2, М 6, 1964.
1.52. Н о я я Б. Ор1ша1 аясеп$1пСо огЫ$ — а пою1ооЫ аФ ап о1Й ргоЫеш. Ргос. ХУ 1п$ег-
па$. Ая$гопац$. Сопряг. 1964. Жагяха~ча, 1965.
1.53. Исследования по динамике полета. Сб. под ред. И. В. Остославского, «Машино-
строение», М., 1965.
1.54. П о н о м а р е в В. М., Теория управления движением космических аппаратов.
«Наука», М., 1965.
1.55. У е ц Ь е Ы е В. Р., 6 е е г С я Х., Арр11са0оп Йц рг1пс1ре Йе шах1шцш а 1а яупСеяе
Йея Сгапйегйя ор$1шацх Йапя цп сЬашр Йе дгастйаСюп р1апейаге. Ргос. ХУ 1пйегпаС.
Ая$гопац$. Сопряг. 1964, Жагяка~ча, 1965.
1.56. К у з м а к Г. Е., Линеаризированная теория оптимальных перелетов. Космиче-
ские исследования, т. 3, М 1, 1965.
1.57. Е г о р о в В. А., Пространственная задача достихсения Луны. «Наука», М., 1965.
1.58. Ч е б о т а р е в Г. А., Аналитические и численные методы небесной механики.
«Наука», М.— Л., 1965.
1.59. А и и а з о в Р. Ф., Л а в р о в С. С., М и ш и и В. П., Баллистика управляемых
ракет дальнего деиствия. «Наука», М., 1966.

Л)ЛИТЕРАТУРА
667
1.60.
1.61.
1.62.
1.63.
1.64.
1.65.
1.66.
1.67.
1.68.
1.69.
1.70.
1.71.
1.72.
1.73.
1.74.
1. 75.
1.76.
1.77.
1.78.
1.79.
1.80.
1.81.
1.82.
1.83.
1.84.
1.85.
1.86.
1.87.
1.88.
1.89.
1.90.
Остославский И. В., Стражева И. В., Динамика полета (Траектории
летательных аппаратов). Оборонгиз, М., 1963.
Ь е 1 С ш а и и С., Орй1ш1хаСюп СесЬп1пцея юйЬ арр11саИопя Со аегоярасе яуяСешя,
Х. Т., 1962. Русский перевод: Л э й т м а н Дж., Методы оптимизации с прило-
жениями к механике космического полета. «Наука», М., 1965.
Б у т е н и н Н. В., Б е с с о н о в А. Т., М о р о з о в Е. М., Введение в динамику
твердого тела, движущегося в поле силы притяжения Земли. Основы космонав-
тики. М вЂ” во высш. и сред. спец. образования РСФСР, Ленингр. ин-т авиац. при-
боростроения, Л., 1965.
Б а л к М. Б., Элементы динамики космического полета. «Наука», М., 1965.
М а г 1 и е я с ц А., !пСгойцсеге 1п Й1паш1са гасЬейе1. Вцсцгеяй1, 1967.
М а г е с Х. Р., Тгапйегйя орС1шацх епСге огЬ1Сея е111рй1пцея ргосЬея. ОЯЕВА РцЬ1.
Яо. 121, 1967.
О х о ц и м с к и й Д. Е., Динамика космических полетов. Конспект лекций.
Изд-во МГУ, М., 1968.
Д у б о ш и н Г. Н., Небесная механика. Основные задачи и методы. «Наука»,
М., 1968.
Ш к а д о в Л. М., Б у х а н о в а Р. С., И л л а р и о н о в В. Ф., П л о х и х В. П.,
Механика оптимального пространственного движения летательных аппаратов
в атмосфере. «Машиностроение», М., 1972.
Б е л е ц к и й В. В., Очерки о движении космических тел. «Наука», М., 1972.
Гродзовский Г. Л., Иванов Ю.Н., Токарев В. В.,Механикакосми-
ческого полета с малой тягой. Инж. журнал АН СССР, т. 3, ММ 3 и 4, 1963; т. 4,
ХХ 1 и 2, 1964. См. также Тр. 1! Всесоюзн. съезда по теорет. и прикл. механике,
вып. 1, «Наука», М., 1965 и Ргос. ХУ !пйегпай. Аяйгопацй. Сопряг. 1964, Жагяхаюа,
1965.
Г р о д з о в с к и й Г. Л., И в а н о в Ю. Н., Т о к а р е в В. В., Механика косми-
ческого полета с малой тягой. «Наука», М., 1966.
Г р о д з о в с к и й Г. Л., Некоторые вариационные задачи механики космиче-
ского полета. Инж. журнал АН СССР, МТТ, М 5, 1966.
Гродзовский Г.Л., Охоцимский Д.Е.,Белецкий В. В., Ива-
нов Ю. Н., КурьяновА. И., ПлатоновА. К., Сарычев В. А., То-
к а р е в В. В., Я р о ш е в с к и й В. А., Механика космического полета. Меха-
ника в СССР за 50 лет, том. 1. «Наука», М., 1968.
Г р о д з о в с к и й Г. Л., Вариационные проблемы в механике космического
полета. ГОТА, го1. 4, Яо. 1, 1969.
Г л у ш к о В. П. (гл. ред.), Космонавтика. «Советская энциклопедия», М., 1970.
Г л у ш к о В. П., Развитие ракетостроения и космонавтики в СССР. Изд-во АПН,
М., 1973.
С т е ч к и н Б. С., К а з а н д ж а н П. К., А л е к с е е в Л. П., Г о в о р о в А. Н.,
Коновалов Н. Е., Нечаев Ю. Н., Федоров Р. М., Теория ракетных
двигателей. Оборонгиз, М., 1958.
С о г11 я я Ж. В., Ргорц1яюп яуя$ешя аког ярасе 111дЫ. Я. У.— Тогоп$о — Ьопйоп,
1960. Русский перевод: К о р л и с с У. Р., Ракетные двигатели для космических
полетов. ИЛ, М., 1962.
А ц С. Р., ЕпйжсЫцпдяяйапй х~йцпй1дег Вацш1аЬгСапйг1еЬе. Ьцй1аЬгйесЬп1~,
Вй. 7, Яг. 1, 1961.
Я ц С С о и 6., Восй.ей ргорц1яоп е1ешепСя. Я. У.— Ьопйоп, 1949, Тогопйо — Ьоп-
Йоп, 1958. Русский перевод: С а т т о н Д., Ракетные двигатели. ИЛ, М., 1952.
В ц ~ я а г Й В. Ж., Р е 1 а ц е г В. Р., Яцс1еаг гост.е$ ргорц1яюп, Я. У.— Тогопйо—
Ьопйоп, 1958. Русский перевод: Б а с с а р д Р., Д е л а у э р Р., Ракета с атом-
ным двигателем. ИЛ, М., 1960.
К в а с н и к о в А. В., Теория жидкостных ракетных двигателей. Судпромгиз,
Л., 1959.
Брасе рожег яуяйешя. Ей. Ьу Я. Ж. 8 и у Й е г, Асай. Ргеяя, Я. У.— Ьопйоп, 1961.
Русский перевод. Энергетические установки для космических аппаратов. «Мир»,
М., 1964.
П е т р о в П. А., Ядерные эпергетические установки. Госэнергоиздат, М., 1958.
Р о ж к о в В. В., Ракетные двигатели твердого топлива. Воениздат, М., 1963.
О р л о в Б. В., М а з и н г Г. Ю., Термодинамические и баллистические основы
проектирования ракетных двигателей на твердом топливе. «Машиностроение»,
М., 1964.
С е н ч е н к о в А. П., Атомные ракеты и проблемы освоения космоса. Атомиздат,
М., 1964.
Ф а в о р с к и й О. Н., Установки для непосредственного преобразования тепловой
энергии в электрическую. «Высшая школа», М., 1965.
Г и л ь з и н К. А., Двигатели невиданных скоростей. «Машипостроение», М., 1965.
Ш т у л и и г е р Э., Ионные двигатели для космических полетов. Пер. с англ.,
Воениздат, М., 1966.

ЛИТЕРАТУРА
1.91. Шапиро Я. М., Мазинг Г. Ю., Прудников Н. Е., Теория ракетного
двигателя на твердом топливе. Воениздат, М., 1966.
1.92. С о р о к и н Р. Е., Газотермодинамика ракетных двигателей на твердом топливе.
(<Наук », ., 19
1.93. П а н ч е н к о Е. М., К о р о в к и н А. С., Космическая электроэнергетика.
(<Знани », ., 19
1.94. Д о б р о в о л ь с к и й М. В., Жидкостные ракетные двигатели. «Машинострое-
ние», М., 1968.
1.95. ~ а Ь п В. б., РЬуя1ся о1 е1есМс ргорц1я1ои. Я. У., 1968.
1.96. Г и л ь б е р г Л. А., Электрические ракетные двигатели. Воениздат, М., 1968.
1.97. Ш и ш к о в А. А., Газодинамика пороховых ракетных двигателей. «Машино-
строение», М., 1968.
1.98. А л е м а с о в В. Е., Д р е г а л и н А. Ф., Теория ракетных двигателе~~. «Маши о-
строение», М., 1969.
1.99. Б у Р д а к о в В. П., Д а н и л о в Ю. И., Физические проблемы космическод теп-
ловой энергетики. Атомиздат, М., 1969.
1.100. Гуров А. Ф., Севрук Д. Д., Сурнов Д. Н., Конструкция и расчетна
прочность космических электрореактивных двигателей. «Машиностроение», М
1970.
1Л01. В г е ю е г б. В., 1оп ргорц1я1оп, $есЬпо1оду апй арр11саф1оия. ]~. у., 1970.
1Л02. Г и л ь з и н К. А., Электрические межпланетные корабли. «Наука», М., 1970.
1ЛОЗ. Куланди А А' Тимашев С. В., Иванов В. П., Энергетические
системы космических аппаратов. «Машиностроение», М., 1972.
1.104. Л е в а н т о в с к и й В. И., Механика космического полета в элементарном из-
ложении. «Наука», М., 1974.
1.105. Д у б о ш и н Г. Н., Теория притяжения. Физматгиз, М., 1961.
1.106. А л л е н К. У. (А11еп С. П.), Астрофизические величины. ИЛ, М., 1960.
1 107. Д у б о ш и н Г. Н., Небесная механика. Физматгиз, М., 1963.
1.108. С у б б о т и н М. Ф., Курс небесной механики, т. 1, Гостехиздат, 1963, т. 2 и 3,
Гостехиздат, 1940.
1Л09. В е11 1 е1Ь., БСгцсфцга1 йашаае апй 001ег еаесфя 01 яо1аг р1а. а . Х. Атег. ВОСК.
Бос., чо1. 30, Яо. 3, 1960.
1.110. Л а н д с б е р г Г. С., Оптика. Гостехиздат, М.— Л., 1947.
1.111. А л е к с а и д р о в С. Г., Ф е д о р о в Р. Е., Советские спутники и космические
корабли. Изд. 2-е, Изд-во АН СССР, М., 1961.
1.112. Ж Ь 1 р р1 е Р. Ь., ТЬе теСеогЮс г1Ж $о ярасе чеЬ|с1ея. Мятая 1п Аяфгоиацф1ся,
чо1. 2, Х. У., 1958.
1.113. б е Ь г 1 и д 1. Ж., С г 1 я ~ т а п О. В., М с М 1 1 1 а и А. В., Ехрег1теп1а1 я$ц-
й1ея сопсеги1ид СЬе шейеого1й Ьаяагй Со аегоярасе тайег1а1я апй яСгцсСцгея. Х. Бра-
сесгай аий ВосЕ, чо1. 2, Яо. 5, 1965.
1Л14. В 1 о г Ы В. Ь., Мейеого1йя чя. ярасе чеЬ1с1ея. У. Атег. Вос1~. Бос., чо1. 31, Яо. 6,
1961.
1Л15. С т а н ю к о в и ч К. П., Ф е д ы н с к и й В. В., О разрушительном действии
метеоритных ударов. Докл. АН СССР, т. 57, № 2, 1947.
1Л16. В 1 о г й. В. Ь., ЕПес$я о1 а ше$еого1й 1шрасС оп я$ее1 апй а1цт1пцш 1п ярасе. Ргос.
Х 1пйегиай. Аяйгоиацй. Соидг. 1959, У1еи., 1960.
1.117. Л а в р е и т ь е в М. А., Проблема пробивания при космических скоростях.
Искусственные спутники Земли, вып. 3, 1959.
1.118. К о г и Ь а ц я е г М., Байе11Ие ргеяяцге 1ояяея сацяей Ьу тейеого1й 1трасйя. Х. Атег.
ВосЕ Бос., чо1. 30, Яо. 5, 1960.
1.119. 3 е л ь д о в и ч Я. Б., Р а й з е р Ю. П., Физика ударных волн и высокотемпера-
турных гидродинамических явлений. Физматгиз, М., 1963.
1.120. А н д р и а н к и н Э. И., О пробивании преград метеоритами. Космические ис-
следования, т. 4, № 2, 1966.
1.121. М у х а м е д ж а н о в А. К., О пробое тонкого экрана метеоритом. Космические
исследования, т. 4, № 2, 1966.
1.122. С а ш е г о и А. б. Ж., РЬуя1ся о1 $Ье р1аие$я. Брасе РЬуя1с, И. У.— Ьоийои, 1964.
1Л23. С е д о в Л. И., Методы подобия и размерности в механике. «Наука», М., 1965.
1.124. А 1 й е г В., Ь е с о ш р С е Х., ЕСцйея яцг 1а ргорц1я1ои ицс1еоСЬегт1цце. Еяй-
таИоп йе рег1огтаисея й'цп еСаде ицс1еа1ге роцг 1аисецг 1оцгй ецгорееи. Ргос.
Х1У 1МегиаС. АяСгопацС. Соидг. Раг1я, 1963, Жагякаюа, 1965.
1Л25. Мойеги йече1оршеиС 1и 11ц1й йциат1ся. Ей. Ьу Б. б о1 й я С е1 и, чо1. 2, Ьоийои,
1943. Русский перевод: Современное состояние гидроаэродинамики вязкой жид-
кости, под ред. С. Гольдштейна, т.2, ИЛ, М., 1948.
1.126. Г р о д з о в с к и й Г. Л., Турбулентный пограничный слой плоской пластины.
Журн. прикл. механ. и техн. физ., № 4, 1962.
1.127. Ь 1 е р ш а и п Н. Ж., В о я Ь Ы о А., Е1етеМя о1 даяйуиат1ся. Я. У., 1957. Рус-
ский перевод. 'Л и и м а н Г. В., Р о ш к о А., Элементы газовой динамики. ИЛ.,
М., 1960.

ЛИТЕРАТУРА
Р г а и й С 1 Ь., РОЬгег йцгсЬ й1е БСгошцпдя1еЬге, боИ1пдеп, 1944. Русский перевод:
П р а н д т л ь Л., Гидроаэромеханика. ИЛ, М., 1949.
Л о й ц я н с к и й Л. Г., Механика жидкости и газа. «Наука», М., 1970.
Г и н з б у р г И. П., Теория сопротивления и теплопередачи. Изд-во ЛГУ, Л.,
1970.
Л а и и н Ю. В., Турбулентный пограничный слой в сверхзвуковых потоках
4.128.
1.129.
1.130.
4.131.
8 а Ы ц г а 1 А., Оп СЬе ргорадаИоп апй яСгцсСцге о1 СЬе ЫаяС чаче. У. РЬуя. Бос.,
1арап, чо1. 8, Мо. 5, 1953; чо1. 9, Ио. 2, 1954.
К р а ш е н и н н и к о в а Н. Л., О неустановившемся движении газа, вытесняе-
мого поршнем. Изв. АН СССР, ОТН, М 8, 1955.
С т а н ю к о в и ч К. П., Неустановившиеся движения сплошной среды. Гостех-
издат, М., 1955.
Ч е р н ы й Г. Г., Одномерные неустановившиеся движения совершенного тока
с сильными ударными волнами. Докл. АН СССР, т. 107, Ы 5, 1956.
Г р и г о р я н С. С., Задача Коши и задача о поршне для уравнений одномерных
неустановившихся движений газа (автомодельные движения). Прикл. матем. и
механ., т. 22, М 2, 1958.
К о ч и н а Н. Н., М е л ь н и к о в а Н. С., О неустановившемся движении газа,
вытесняемого поршнем. Прикл. матем. и механ., т. 22, М 4, 1958.
1Л54.
1.155.
1Л56.
1Л57.
1.158.
1.159.
Ч е р н ы й Г. Г., Течение газа с большой сверхзвуковой скоростью. Физматгиз,
М., 1959.
Н а у е а Ж. О., Оп Ьурегаоп1с а1ши1Иийе. ЯиагВ. Арр1. МасЬ., чо1. 5, Мо. 1, 1947.
1.160.
1Л61.
газа. «Наука», М., 1970.
4.132. Федяевский К. К., ГиневскийА. С., Колесников А. В., Расчет
' турбулентного пограничного слоя несжимаемой жидкости. «Судостроение», Л.,
1973.
$Л33. Н а у е я Ж. О., Р г о Ь я $ е 1 и В. Р., Нурегяошс 11о~ $Ьеогу. Асай. Ргеяя., М.У.—
1опйоп, 1959. Русский перевод: Х е й з У. Д., П р о б с т и н Р. Ф., Теория 'ги-
перзвуковых течений. ИЛ, М., 1962.
1Л34. К а г ш а и Т., Бцрегяошс аегойупаш1ся. 1. Аегопац$. Бс1., чо1. 14, Мо. 7, 1947.
Русский перевод: К а р м а н Т., Сверхзвуковая аэродинамика. ИЛ, М., 1948.
1Л35. К о ч и н Н. Е., К и б е л ь И. А., Р о з е Н. В., Теоретическая гидромеханика.
Физматгиз, 1963.
1.136. Л а н д а у Л. Д., Л и ф ш и ц Е. М., Механика сплошных сред. Физматгиз, М.,
1962.
1Л37. С е д о в Л. И., Плоские задачи гидродинамики и аэродинамики. «Наука», М.,
1969.
1 138. Д о р о д н и ц ы н А. А., Расчет распределения давления по телам вращения
в сверхзвуковом потоке газа. Сб. теоретических работ по аэродинамике, Оборон-
гиз, М., 1957.
1.139. Баум Ф. А., Каплан С. А., Станюкович К. П., Введение в космиче-
скую газодинамику. Физматгиз, М., 1958.
1Л40. А р ж а н и к о в Н. С., С а д е к о в а Г. С., Аэродинамика больших скоростей.
«Высшая школа», М., 1965.
1Л41. Г и н з б у р г И. П., Аэрогазодинамика. «Высшая школа», М., 1966.
1.142. К о г а н М. Н., Динамика разреженного газа. «Наука», М., 1967.
1.143. А я й1 е у Н., Ь а и й а Ь1 М., Аегойупаш1ся о1 Ыпдя апй Ьой1ея. Маяя., 1965.
Русскпй перевод: Э ш л и Х., Л э н д а л ь М., Аэродинамика крыльев и корпу-
сов летательных аппаратов. «Машиностроение», М., 1969.
1Л44. М х и т а р я н А. М., Аэродинамика. «Машиностроение», М., 1970.
1.145. М а й к а п а р Г. И. (ред ), А г а ф о н о в В. П., В е р т у ш к и н В. К., Г л а д-
к о в А. А., П о л я н с к и й О. Ю., Неравновесные физико-химпческие процессы
в аэродинамике. «Машиностроение», М., 1972.
1.146. М а р т ы н о в А. К., Прикладная аэродинамика. «Машиностроение», М., 1972.
1.147. Т я 1 е и Н. 8., Бцрегяошс 11ож очег ап 1пс11пей Ьойу о1 гечо1цй1оп. Х. Аегопацй.
Бс1., чо1. 5, Мо. 12, 1938.
1.148. Ф р а н к л ь Ф. И., К а р и о в и ч Е. А., Газодинамика тонких тел. Гостехиздат,
М.— Л., 1948.
1.149. Р е г г1 А., Е1ешеп$я о1 аегойупаш1ся о~ яцрегяошс 11ож Я. У., 1949. Русский
перевод. Ф е р р и А., Аэродинамика сверхзвуковых течений. Гостехиздат, М.— Л.,
1952.
1Л50. Н и к о л ь с к и й А. А., О телах вращения с протоком, обладающих наимень-
шим внешним волновым сопротивлением в сверхзвуковом потоке. Сб. теорети-
ческих работ по аэродинамике, Оборонгиз, М., 1957.
1Л51. К р а с н о в Н. Ф., Аэродинамика тел вращения. «Машиностроение», М., 1964.
1.152. С е д о в Л. И., О некоторых неустановившихся движениях сжимаемой жидкости.
Прикл. матем. и механ., т. 9, М 4, 1945.
1Л53. Т а у1 о г 6. У., Тйе а1г юаче яцггоцпй1пд ап ехрапй1пд ярйеге. Ргос. Воу. Бос.,
Бег. А., чо1. 186, 1946.

670
ЛИТЕРАТУРА
К главе 2
Р г а и й С 1 Ь., РОЬгег йигсЬ й~е ЯСгошипдя1еЬге. СоСС~пдеп, 1944. Русский пере-
вод: П р а н д т л ь Л., Гидроаэромеханика. ИЛ, М., 1949.
С т е ч к и и Б. С., К а з а н д ж а н П. К., А л е к с е е в А. П., Г о в о р о в А. Н.,
Коновалов Н. Е., Нечаев Ю. Н., Федоров Р. М., Теория реактивных
двигателей. Оборонгиз, М., 1959.
Г и н е в с к и й А. С., Теория турбулентных струй. «Машиностроение», М., 1969.
3 е л ь д о в и ч Я. Б., Теория ударных волн и введение в газодинамику. Изд-во
АН СССР, М., 1946.
Х р и с т и а н о в и ч С. А., Г а л ь п е р и н В. Г., М и л л и о н щ и к о в М. Д.,
С и м о н о в Л. А., Прикладная газовая динамика, ЦАГИ, 1948.
С е д о в Л. И., Плоские задачи гидродинамики и аэродинамики. «Наука», М.,
1969.
А б р а м о в и ч Г. Н., Прикладная газовая динамика. «Наука», М., 1969.
Б о л г а р с к и й А. В., Щ у к и н В. К., Рабочие процессы в жидкостно-реак-
тивных двигателях. Оборонгиз, М., 1953.
М е л ь к у м о в Т. М., К у з н е ц о в Е. В., М е л и к — П а ш а е в Н. И., Теория
жидкостных реактивных двигателей. Изд-во ВВИА им. Н. Е. гКуковского, М.,
1956.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
1.162.
1 163.
1.164.
1.165.
1.166.
1.167.
1.168.
1.169.
1.170.
1.171.
1.172.
1.173.
1.174.
1.175.
1.176.
1.177.
1.178.
1.179.
Бам-Зеликович Г. М., Бунимович А. И., Михайлова М. П.,
Движение тонких тел с большими сверхзвуковыми скоростями. Теоретическая
гидромеханика, Сб. М 4, Оборонгиз, М., 1949.
Г р о д з о в с к и й Г. Л., Некоторые особенности обтекания тел при больших
сверхзвуковых скоростях. Изв. АН СССР, ОТН, М 6, 1957.
е е я Ь., К и Ь о С а Т., 1пюяс~й Ьурегяоп~с 11ож очег ЫипС-пояей я1епйег Ьой~ея.
1. АегопаиС. Яс1., чо1. 24, Яо. 3, 1957.
Г р о д з о в с к и й Г. Л., К р а ш е н и н н и к о в а Н. Л., Автомодельные дви-
жения газа с ударными волнами, распространяющимися по степенному закону по
покоящемуся газу. Прикл. матем. и механ., т. 23, М 5, 1959.
С ы ч е в В. В., К теории гиперзвуковых течений газа со скачками уплотнения
степенной формы. Прикл. матем. и механ., т. 24, М 3, 1960.
Г о н о р А. А., Ч е р н ы й Г. Г., О телах наименьшего сопротивления при боль-
ших сверхзвуковых скоростях. Изв. АН СССР, ОТН, М 7, 1957.
Ед~егя А. 1., Веяп11со11 М. М., Репп~я Р. Н., Вой~ея о1 гечо1иСюп
Ьач~пд ппп~шиш йгад аС Ь1дЬ яцрегяоп~с а~гяреейя. ЯАЯА Вер., Яо. 1305, 1957.
М ( е 1 е А. (ей.), ТЬеогу о1 орЫшиш аегойупаш1с яЬарея. М. Т., 1965. Русский
перевод: Г о н о р А. Л. (ред. перев.), Теория оптимальных аэродинамических
форм. «Мир», М., 1969.
Г р о д з о в с к и й Г. Л., О телах вращения с минимальным коэффициентом ло-
бового сопротивления и малой теплопередачей при больших сверхзвуковых ско-
ростях полета. Изв. АН СССР, МЖГ, М 5, 1968.
Г р о д з о в с к и й Г. Л., Тела вращения с минимальным коэффициентом лобо-
вого сопротивления и малой теплопередачей при больших сверхзвуковых скоростях
полета. Ргос. Х1Х 1пСегпаС. АяСгопаиС. Сопряг. 1968, Регдашоп Ргеяя — Р~~, 1970.
Р у с а н о в В. В., Н а ж е с т к и н а Э. И., Волновое сопротивление тел враще-
ния степенной формы (осесимметричное обтекание). ИПМ, Препринт М 33, М.,
1972.
Б л а го ск л о но в В. И., Соколов а И. Н., Исследование дозвуковой
и трансзвуковой областей течения около тел вращения степенной формы. Уч.
записки ЦАГИ, М 4, 1973.
Б л а г о с к л о н о в В. И., Ж о х о в В. А., Сверхзвуковое обтекание осесим-
метричных тел степенной формы при больших удлинениях. Уч. записки ЦАГИ,
М 5, 1973.
Благосклонов В. И., Гродзовский Г. Л., Осесимметричное обте-
кание тел вращения степенной формы при сверхзвуковых скоростях набегающего
потока. Уч. записки ЦАГИ, М 6, 1974.
А в д у е в с к и й В. С., Д а н и л о в Ю. И., К о ш к и н В. К., К у т ы р и н И. Н.,
Михайлова М. М., Михеев Ю. С., Сергель О. С., Основы теплоие-
редачи в авиационной и ракетной технике. Оборонгиз, М., 1960.
С о и о л о в а И. Н., Исследование теплопередачи осесимметричных тел вращения.
Тр. ЦАГИ, вып. 1178, М., 1969.
Г р о д з о в с к и й Г. Л., Ж у к о в а Р. А., Л а ш к о в Ю. А., Р а ф а э-
лянц А.А., Туполев А.А.,Черемухин Г.А.,Шумилкина Е.А.,
Экспериментальное исследование оптимальных носовых частей. Уч. записки
ЦАГИ, М 1, 1972.
Г о н о р А. Л., Определение формы пространственного оптимального тела с уче-
том силы трения. Изв. АН СССР, Механика, М 4, 1965.

ЛИТЕРАТУРА
2.10.
2.11.
2 12.
2 13.
2 14.
2.15.
2.16.
2.17.
2 18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
2.27.
2.28.
2.29.
2.30.
2.31.
2.32.
2.33.
2.34.
2.35.
2.36.
2.37.
2.38.
2.39.
2.40.
2.41.
2.42.
В а г г е г е М., 1 а ц т о С С е А., У е ц Ь е Й е В. Р., У а и Й е и Й е г с Й о ч е 1.,
Ьа ргорц1яюп раг1гцяяея. Раг1я, 1957. Русский перевод'. Б а р р е р М., Ж о м о т т А.,
Ве беке Б. Ф., В анденкеркхове Ж., Движение ракет. ИЛ, М., 1959.
К в а с н и к о в А. В., Теория жидкостных ракетных двигателей. Судпромгиз,
М., 1959.
А л е м а с о в В. Е., Теория ракетных двигателей. Оборонгиз, М., 1962.
Л а и д а у Л. Д., Л и ф ш и ц Е. М., Механика сплошных сред. Физматгиз, М.,
1962.
Ф а б р и к а н т Н. Я., Аэродинамика. «Наука», М., 1964.
М а р т ы н о в А. К., Прикладная аэродинамика. «Машиностроение», М., 1972.
С т е и а н о в Г. Ю., Г о г и ш Л. В., Квазиодномерная газодинамика сопел ра-
кетных двигателей. «Машиностроение», М., 1973.
С ц Й е г1 е у С., Н а и С я с и Е., ВеяСе Рогтеп Мг асЬяепяуттеСг1ясЬе ~Ьег-
ясЬа11ясЬцЬЙцяеп. Х. Р1цдж1яя., Яг. 9, ВгацпясЬже1д, 1955.
Д о р о н и ц ы н А. А., Расчет распределения давлений по телам вращения в сверх-
звуковом потоке газа. Сб. теоретических работ по аэродинамике. Оборонгиз, М.,
1957.
Ш м ы г л е в с к и й Ю. Д., Некоторые вариационные задачи газовой динамики
осесимметричных сверхзвуковых течений. Прикл. матем. и механ., т. 21, М 2, 1957.
В а о С. У., ЕхЬацяС иохг1е сопСго1 аког орСпицт СЬгцяС. УеС Ргор., чо1. 28, Яо. 6,
1958.
С т е р н и и Л. Е., К расчету осесимметричного реактивного сопла наименьшего
веса. Изв. АН СССР, Механика и машиностроение, М 1, 1959.
С ц Й е г1 е у С., Ои Вао'я теСЬой аког СЬе сотрцСаС1оп о1 ехЬацяС погг1ея. Х. Иц~-
ж1яя., ВЙ. 12, Иг. 7, 1959.
Ш м ы г л е в с к и й Ю. Д., Вариационные задачи для сверхзвуковых тел вра-
щения и сопел. ВЦ АН СССР, М., 1961.
Г р о д з о в с к и й Г. Л., К у з н е ц о в Ю. Е., Т о к а р е в М. В., Приближен-
ный метод расчета осесимметричных сверхзвуковых течений в условиях внутрен-
ней задачи. Промышленная аэродинамика, вып. 24, Оборонгиз, М., 1962.
Сергиенко А. А., Сандомирская И. Д., О профилировании сверхзву-
ковой части осесимметричного сопла наибольшей тяги. Сб. работ ВЦ МГУ, М 4,
1955.
Г о г и ш Л. В., Исследование коротких сверхзвуковых сопел. Изв. АН СССР,
МЖГ, М 2, 1966.
Г о г и ш Л. В., С т е п а н о в Г. 10., Классификация и приближенный метод
профилирования кольцевых сопел. Изв. АН СССР, МЖГ, га 4, 1966.
С т е р н и н Л. Е., Экстремальные контуры сопел для потоков газа с отставанием
частиц. Изв. АН СССР, МЖГ, М 5, 1966.
И в а н о в М. Я., Применение метода установления к анализу нерасчетных ре-
жимов течения в осесимметричных соплах. Изв. АН СССР, МЖГ, М 6, 1966.
Т а у1 о г М. А. А., Н о 1 1 т а и 1. Р., Рея1дп о1 тахпацт СЬгцяС покг1ея аког по-
иецц111Ьг1цт, сЬет1са11у геасС1пд 11ож. А1АА Рарег Яо. 73-1243, 1973.
Г р о д з о в с к и й Г. Л., Особенности односторонних оптических установок для
исследования газового потока и деформации плоских поверхностей. Изв. АН СССР,
ОТН, М 7, 1955.
Г р о д з о в с к и й Г. Л., Экспериментальное исследование взаимодействия
скачков уплотпения и пограничного слоя в диапазоне чисел М=1,0 — 1,8. Изв.
АН СССР, ОТН, Энергетика и автоматика, М 4, 1960.
П е т р о в Г. И., Сообщение о докладе на сессии АН СССР. Изв. АН СССР, ОТН,
М 9, 1958.
М 1 д Й а 1 Р., Н о г д а и 1. 1., С Ь а т а у А., Ап ехрегппепСа1 еча1цаСюи о1 р1цд
с1цяСег погг1ея. А1АА 1., чо1. 2, Ио. 7, 1964.
В о п о Р., Ж о о Й ж о г С Ь 1. Ь., 13 г я 1 п 1 С. А., ТЬе гецяаЫе ЬоояСег аког 1цпаг
1од1яС1ся апй р1апеСагу ехр1огаСюп. Ргос. ХУ 1пСегпаС. АяСгопацС. Сопряг. 1964,
Жагягажа, 1965.
Г л у ш к о В. П. (гл. ред.), Космонавтика. «Советская энциклопедия», М., 1970.
Г л у ш к о В. П., Развитие ракетостроения и космонавтики в СССР. Изд-во АПН,
М., 1973.
Я ш ~ С Ь Т. Е., ТЬгцяС СЬгоСС11пд о1 1агде 11оц1Й ргоре11аиС гос1сеС епд1пея. Х. Воу.
АегопацС. Яос., чо1. 68, Яо. 11, 1964.
Н е ц я 1 п д е г В. ~., ЯаСцгп ргорц1яюп1шргочетепСя. АегопацС1ся апй АяСгопацС1ся,
чо1. 2, Ио. 8, 1964.
М с Й е ч 1 С С Р. Х., Ж а 1 с Ь Т. 1., Брасе епд1пе рег1огтапсе ргей1сС1оп. ~. 8ра-
сесгай апй ВосКеСя, чо1. 2, Яо. 3, 1965.
В 1 ч а г Й У. С., Меж СесЬп1оцея аког СЬгоСС1еаЫе Ь1ргоре11апС гос1~еС епд1пея. ААААА
Рарег, Хо. 65-560, 1965.
Я С 1 1 1 В. С., ЯСаСця герогС оп аего1еС вЂ” депега1 согрогаСюп «Т1Сап 3», 11ци1Й рго-
ре11апС епрпея. А1АА Рарег, Яо. 65-307, 1965.

672
ЛИТЕРАТУРА
2.43. Г у р о в А. Ф., Расчет на прочность и колебания в ракетных двигателях. «Машино-
строение», М., 1966.
2.44. Я С о и е Х., И1дЬС о1 «ЯаСцгп 1В» ж111 СеяС Х-2 епд1пе. Ач1аСюп Жеев апй Яраса
Тес'пп., чо1. 84, Яо. 7, 1966.
2.45. К у д р я в ц е в В. М. (ред.), Основы теории и расчета жидкостных ракетных дви-
гателей. «Высшая школа», М., 1967.
2.46. Т е и е и Ь а ц ш О. М., С1 а г 1с О. Н., АсС1чаСюп апй 1п1С1а1 СеяС орегаС1опя о1
1агде гос1сеС епд1пеСЬгцяС спашЬег СеяС 1ас111С1ея. А1АА Рарег, Яо. 67-455, 1967.
2.47. С и а 1 1 е е Я. Н., Ж11 С х Х. А., Маппей ярасесгай сепСег'я ехрег1епсе ж1Сп ча-
сццш — 1дп1Сюп рпепошепа 1п Ыргоре11апС геасСюп сопСго1 епд1пгя. А1АА Рарег,
Яо. 67-514, 1967.
2.48. Д о б р о в о л ь с к и й М. В., Жидкостные ракетные двигатели. «Машинострое-
ние», М., 1968.
2.49. У о Й г1я С. Ж., Епд1пея аког шаппей ярасесгай. А1АА Рарег, Яо. 68-567, 1968.
2.50. В а 11 Ь. С., Я-1С ргорц1яюп яуяСеш рег1огшапсе еча1цаСюп. А1АА Рарег, Яо. 69-
733, 1969.
2.51. Алемасов В. Е., Д регалии А. Ф., Тишин А. П., Теория ракетных
двигателей. «Машиностроение», М., 1969.
2.52. В о и о Р., Вос1сеС-я1ей 1ацпсЫпд аког гецяаЬ1е Ьа111яС1с СгапярогС яуяСешя. Х. Вг1С1яЬ
1пСегр1. Яос., чо1. 23, Яо. 3, 1970.
253. Рц1Соп О. Ь., Ьац1ег Х. В., Яш1С'и С. В., Хас'пагу А. Т., Охудеп/
Ьцдгодеп сошропепС СесЬпо1оду яСаСця. А1АА Рарег, Яо. 72-1156, 1972.
2.54. У а 1 е и С 1 и е В. Я., 11оц1Й гос1сеС ре1огшапсе, яСаЫ11Су, апй сошраС1Ы11Су. Х. Яра-
сесгай апй Вос1сеСя, чо1. 9, Яо. 5, 1972.
2.55. Ь о В. Е., Тпе 1цСцге я1дпЮсапсе о1 спеш1са1 ргорц1я1оп 1п Спе депега1 ясйеше о1
ярасе ргорц1яюп яуяСешя апй ехашр1ея о1 СесЬпо1оду Сгапя1ег Со оСпег агеая о1 яс1епсе
апй СесЬпо1оду. Ргос. ХХ1У 1пСегпаС. АяСгопацС. Сопряг., Вальц, 1973.
2.56. С а я С е и 'и о 1 х Р. О., Оея1дп апй яСаСця о1 ярасе яЬцСС1е ша1п епд1пе. Ргос. ХХ1У
1пСегпаС. АяСгопацС. Сонг., Вальц, 1973.
2.57. Р о ж к о в В. В., Ракетные двигатели твердого топлива. Воениздат, М., 1963.
2.58. О р л о в Б. В., М а з и н г Г. Ю., Термодинамические и баллистические основы
проектирования ракетных двигателей на твердом топливе. «Машиностроение»,
М., 1964.
2.59. Гибридные ракетные двигатели (обзор). Вопросы ракетной техники, Сб. перев. и
обзор иностр. период. лит., М 10, 1965.
2.60. Шапиро Я. М., Мазинг Г. Ю., Прудников Н. Е., Теория ракетного
двигателя на твердом топливе. Воениздат, М., 1966.
2.61. Разработка крупных РДТТ в США (обзор). Вопросы ракетной техники, Теория и
практика ракетостроения за рубежом, М 3, 1966.
2.62. С о р к и н Р. Е., Газотермодинамика ракетных двигателей на твердом топливе.
«Наука», М., 1967.
2.63. Проблемы использования РДТТ в качестве силовых установок для космических
летательных аппаратов (обзор). Вопросы ракетной техники, Теория и практика
ракетостроения за рубежом, М 9, 1967.
2.64. Ш и ш к о в А. А., Газодинамика пороховых ракетных двигателей. «Машинострое-
ние», М., 1968.
2.65. М 111 е г Ж. Н., В а г г1 и ц С о и О. К., СопСешрогагу яо11Й гос1сеС шоСог рег-
1огшапсе ргей1сСюп СесЬп1ццея. А1АА Рарег, Яо. 69-732, 1969.
2.66. В ц г1 а д е Н., 61п ЪГ., В 1е Ь11п д В. Ж., 0пшаппей р1апеСагу ярасесгай
спеш1са1 гос1сеС ргорц1яюп. Х. Ярасесгай апй Вос1сеСя, чо1. 9, Яо. 10, 1972.
2.67. Я с й ш ц с 1с е г В., Хцг Тпеог1е чоп НуЬг1ЙСг1еЬжег1сеп. Вацш1айгИогяспцпд,
Вй. 16, Ней 4, 1972.
2.68. Х 1 и и В. Т., Яохг1е Йашр1пд 1п яо11Й гос1сеС 1пяСаЫ11С1ея. А1АА Х., чо1. 11,
Яо. 11, 1973.
269. Райзберг Б. А., Е рохин Б. Т.,Самсонов К. П., Осповытеориира-
бочих процессов в ракетных системах на твердом топливе. «Машиностроение», М.,
1972.
2.70. Я С о с $: е 1 К., Спеш1яспе Вацш1аЬгССг~еЬжег1се. ХапгЬ. Ж1яя. Оея. Ьцй- цпй Вацш-
1аЬгС, 1962.
2.71. Я и е р и е г Й Ь. В., С1 е а ч е г А. У., Тпе аСош1с гос1сеС. Х. Вг~С. 1пСегр1. Яос.,
чо1. 7, Яо. 5, 1948; чо1. 8, Яо. 2, 1949; Веа11С1ея о1 Ярасе Тгаче1, Ьопйоп, 1957.
2.72. В ц я я а г Й В. Ж., О е Ь а ц е г В. О., Яцс1еаг гос1сеС ргорц1яюп. Я. У., 1958.
Русский перевод: Б а с с а р д Р., Д е - Л а у е р Р., Ракета с атомным двигате-
лем. ИЛ, М., 1960.
2.73. Ярасе СесЬпо1оду. Ей. Ьу Н. Я е ~ 1 е г С, Я. У., 1959. Русский перевод'. Космическая
техника. «Наука», М., 1964.
2.74. Я ц С С о и 6. Р., Вос1сеС ргорц1яюп яуяСешя аког 1пСегр1апеСагу 111дЫ. ХАЯЯ,
чо1. 26, Яо. 10, 1959.

ЛИТЕРАТУРА
673
2.75. С о г 1 1 я я Ж. В., Ргорц1яюп яуя$ешя аког ярасе 111дЬФ. Х. У., 1960. Русский перевод.'
К о р л и с с У. Р., Ракетные двигатели для космических полетов. ИЛ, М., 1962.
2.76. С а ш а с М., Р1аяша ргорц1яюп йеч1сея. Айчапсея 1п Ярасе Яс1епсе, чо1. 2, Я. У.,
1960. Русский перевод: Плазменные и электростатические ракетные двигатели. ИЛ,
М., 1962.
2.77. Я $ е и п1и д А. Н., Вар1Й арргох1ша$е шеФЬой аког апа1уг1пд ицс1еаг гос1се$ рег-
1огшапсе. 1. Ашег. Вос1с. Яос., чо1. 30, Ио. 2, 1960.
2.78. С о Ь е и А. Р., В е е г я В. Я., Магя сараЬ1И1ея аког е1ес$г1се1, ицс1еаг апйсЬеш1са1
ргорц1яюп яуя$ешя. 1АЯ Рарег, Ио. 120, 1962.
2.79. ~1111 11 я 1с 1 М. 1., О г г Е. С., А 11 е п Ь е г й Я. Ь., Н ц е Ь п е г А. Ь.,
Кап$гож1$к А.,У аг.ея С.Я.,Сашас М.,Кцпеп Е.,Мс111гоу Ж.,
апй о$Ьегя, 1958 — 1959. Русский перевод: Ионные, плазменные и дуговые ракетные
двигатели. Сб. переводов, Госатомиздат, М., 1961.
2.30. М е д Ь г е Ь11 а и В. У., Саяеоця ргорц1яюп геас$огя. Ицс1еои1ся, чо1. 19, Ио. 4,
1961.
2.81. А ц С. Р., Еп$ж1сЫцпдяя$апй к~ййп~~1дег Вацш1аЬг~ап$г1еЬе. РаЬг$есЬп11, Вй. 7,
Яг. 1, 1961.
2.82. Ь 1 и Ь а г Й $ Н. Р., Сошраг1яоп о1 яо1аг-СЬегша1 апй яо1аг-е1есйг1с-СЬегша1 рго-
рц1я1оп шеСЬойя. 1АЯ Рарег Ио. 63-20, 1963.
2.33. Ъ~111с я Ж. Е., «Роой1е» 1пйегеяйя Яайцгп ой1с1а1я. М1яя11ея апй Вос1сейя, чо1. 14,
Хо. 23, 1964. См. также «Я. У. Т1шея», 1. У1, 1964.
2.34. В е с 1~ е ж1 1 Ь Ж. С., У о Ь и я о и Н. Ь., Айчапсей ярасе ш1яяюп сараЬ11Юея
о1 пцс1еаг гос1е1я. У. Ярасесгай апй Вос1се1я, чо1. 1, Ио. 4, 1964.
2.35. С е и ч е н к о в А. П., Атомные ракеты и проблемы освоения космоса. Атомиздат,
М., 1964.
2.36. Е ч1 е $ Ь В. У., В ц Й е и Р., Я. В. Х./ЕЯТ, ~Ье Йгя$ ехрег1шеп$а1 пцс1еаг гос1се$
епр'пе, А1АА Рарег, Ио. 66-570, 1966.
2.87. В о ш Р. Е., Ицс1еаг-гос1се$ ргорц1яюп. ИАЯА ТМ Х-1685, 1968.
2.33. М о е с 1с е 1 Ж. Е., Ргорц1яюп яуя$ешя аког шаппей ехр1ога$юп о1 ФЬе яо1аг яуя$еш.
Аяйгопацйся апй Аегопацй1ся, Ио. 8, 1969.
2.89. Разработка ядерных ракетных двигателей в США (обзор). Вопросы ракетной тех-
ники; Теория и практика ракетостр. за рубежом, М 6, 1970.
2.90. 7~ 1 и $ е г Ь е г д Р., Вос1е$ ргорц1я1оп Ьу ФЬегшопцс1еаг ш1сгоЬошЬя 1дп1$ей М$Ь
1пйепяе ге1айчЫ1с е1есйгоп Ьеашя. Вацш1аЬгИогясЬцпд, Вй. 15, Иг. 5, 1971.
2.91. Н у 1 а и Й В. Е., А ш1п1-сачйу геас$ог аког 1аж-СЬгцяй 1~1дЬ яресИ1с 1шрц1яе ргорц1-
яюп. У. Ярасесгай апй Вос1се$я, чо1. 9, Яо. 8, 1972.
2.92. Т Ь о ш К., Веч1еж о1 1пяяюп епд1пе сопсерСя. Х. Ярасесгай апй Вос1сейя, чо1. 9,
Яо. 9, 1972.
2.93. В е у и о 1 й я Т. Ж., ЕИес$1че ярес1йс 1шрц1яе о1 ех$егпа1 пцс1еаг рц1яе ргорц1яюп
яуя$етя. Х. Ярасесгай апй Вос1сейя, чо1. 10, Яо. 10, 1973.
2.94. П р а й и и и г С. (Рге1п1пд 0.), Получение высоких температур до (55 000' К)
в лабораторных условиях. УФН, т. 55, М 4, 1955.
2.95. Даутов Г. В., Жуков М. Ф., Смоляков Б. Я., Исследование работы
плазматрона с воздушной стабилизацией дуги. Прикл. матем. и техн. физ., М 6,
1961.
2.96. Г е р м а н В. О., М о р о з о в М. Г., Плазматрон постоянного тока и некоторые
результаты исследования его работы. Теплофизика высоких температур. Изв.
АН СССР, т. 3, М 5, 1965.
2.97. К а и $ г о ж1$ к А., Ног1копя 1п р1аяша Йупаш1ся. Аяйгопацй. апй Аегопацф., чо1.
3, Яо. 1, 1965.
2.98 В'г о О а'и Т В Е1есфг1с агся Оая Ьеафег аког ге-епфгу я1шц1а$1оп апй ярасе ргорц1
яюп. Ргеяепйей а$ СЬе 13СЬ Апп. Мее$1пд, Ашег. Вос1с. Яос., И. У., 1958.
299. Гродзовский Г. Л., Дюкалов А. Н., Кранцев Н. Ф., Ма-
ров М. Я., Никитип В. Е., Петунин А. Н., Симонов Л. А., Ут-
к и н В. В., Научные результаты полета автоматической ионосферной лаборатории
«Янтарь-1». Космические исследования, т. 6, М 6, 1968; Ргос. Х1Х 1пйегпаС. АяСго-
пац$. Сопряг., 1968.
2100. Арцимович Л. А., Гродзовский Г. Л., Данилов 10. И., За-
харов В. М., Кравцев Н. Ф., Кузьмин Р. Н., Маров М. Я., Мо-
розов П. М., Никитин В. Е., Петунин А. Н., Уткин В. В., Чу-
л е в В. М., Ш в и д к о в с к и й Е. Г., Научные результаты полетов автомати-
ческих ионосферных лабораторий «Янтарь», ч. 11. Уч. записки ЦАГИ, т. 1, М 3,
1970; Ргос. ХХ 1пСегпай. Аяйгопацй. Сопряг., 1969.
2Л01. Балаев Н. Ф., Гродзовский Г. Л., Данилов Ю. И., Заха-
ров В. М., Кравцев Н. Ф., Кузьмин Р. Н., Маров М. Я., Мо-
розов П. М., Никитин В. Е., Перов С. П., Петунин А. Н., Ут-
кин В. В., Чулев В. М., Швидковский Е. Г., Научные результаты
полетов автоматических ионосферных лабораторий «Янтарь», ч. 111. Уч. записки
ЦАГИ, т. 2, )1л 2, 1971; Ргос. ХХ1 1пйегпай. Азйгопаий. Сопиг. 1970.
43 ~механика полета

ЛИТЕРАТУРА
2102. Гродзовский Г. Л., Данилов 10. И., Никитин В. Е., Научные
результаты полета автоматической ионосфернои лаборатории «Янтарь-4». Ргос.
ХХ1Ч 1пСегпаС. АяСгопаиС. Сопгд., Вальц, 1973.
2.103. Андронов И. М., Морозов А. И., Рылов Ю. П., Шереметьев-
ский Н. Н., Козубский К. Н., Романовский М. К., Снар-
с к и й Р. К., Щ е п к и н Г. Я., Применение ЭРДУ в системах ориентации и кор-
рекции ИСЗ. Ргос. ХХ1Ч 1пСегпаС. АяСгопаиС. Сопряг., Ва1и, 1973.
2.104. Ц и о л к о в с к и й К. Э., Исследование мировых пространств реактивными при-
борами. Вестник воздухоплавания, №№ 19 — 22, 1911.
2.105. Р г е я С о и - Т Ь о ш а я Н., 1пСегпаС1опа1 СгапярогС Сес11п1пие. Х. Вг1С. 1пСегр1.
Яос., чо1. 11, Хо. 4, 1952.
2.106. Я С и Ь11и д е г Е., Рояя1Ы11С1ея о1 е1есСг1са1 ярасе яЫр ргори1яюп. Ргос. Ч 1п-
СегиаС. АяСгопаиС. Сопряг. 1954, Ч1еп., 1955.
2.107. Я С и Ь 11 и д е г Е., Айчапсей ргори1яюп яуяСешя аког ярасе чеЫс1ея. Ргос. 1Х 1п-
СегпаС. АяСгопаиС. Сопряг. 1958, Ч1еп., 1959.
2108. Стависский Ю. А., Бондаренко И. И., Кротов В. И., Лебе-
д е в С. Я., П у и к о в В. Я., С т у м б у р Э. А., Опыт получения реактивной
тяги в лабораторной модели ионного движителя. Журн. техн. физ., т. 29, вып. 8,
1959.
2 109. В о Й е и В. Н., 1оп ргори1яюп. Айч. Ргор. Тесни. 1960, Ох1огй, 1961.
2.110. К а и 1 т а и Н. В., В е а Й е г Р. Р., Ехрег1шепСа1 рег1огшапсе о1 юп гос1сеСя
ешр1оу1пд е1есСгоа-ЬошЬагйшепС юп яоигсея. ИесСгояСаС1с Ргор. СоЫ. МопСегеу,
СаИ., 1960.
2.111. Я С и Ь11 и д е г Е., Я е1 С г В. М., Е1есСгояСаСЖ ргори1яюп яуяСешя аког ярасе
чеИс1ея. Айч. Ярасе Яс1., чо1. 11, М. У., 1960. Русский перевод. Плазменные и элек-
тростатические ракетные двигатели, ИЛ, М., 1962.
2.112. М 1 с 1с е1 я е и Ж. В., СошрагаС1че рег1огшапсе о1 е1есСгояСаС1с гос1сеС епд1пея.
1АЯ Рарег, Хо. 62-74, 1962.
2.113. В г о ж и Н., М 1 с о 11 Н. Е., ИесСг1са1 ргорц1яюи сараЫ11С1ея аког Ьипаг ехр1о-
гаС1оп. А1АА Х., чо1. 1, Мо. 2, 1963.
2.114. К а и 1 ш а и Н. В., ТЬе е1есСгоп-ЬошЬагйшепСюигос1сеС. Ргос. Згй Яушроя. Ай-
чапсей Ргори1я. СопсерСя, чо1. 1, Я. У. — Ьопйоп, 1963.
2.115. Ж1 и1 с и г Р. Н., Е1есСг1с ргори1яюп сЬагасСег1яС1ся о1 а ри1яей р1аяша гац ас-
се1егаСог. А1АА Х., чо1. 2, Ио. 9, 1964.
2.116. К и я 1с е ч 1 с я б., Т Ь о ш р я о и В. Ь., Сошраг1яоп о1 сошшегс1а1, ярЬег1са1
рожйег, апй ж1ге Ьипй1е 1ипдяСеп юп1гегя. А1АА Х., чо1. 2, Хо. 2, 1964.
2.117. Я С и 11 11 и д е г Е., 1оп ргорц1яюп. Я. У., 1964.
2.118. Р а ч 1 я Х., А яСер Сожагйя пис1еаг е1есСг1с ргори1яюп. АяСгопаиС. апй Аегопаи$.,
чо1. 3, Хо. 1, 1965.
2.119. М 1 с 1с е1 я е и Ж. В., В е а Й е г Р. Р., 1оп ргори1яюп яуяСешя аког ярасесгай.
Х. Ярасесгай апй ВосЫеСя., чо1. 2, Хо. 4, 1965.
2.120. В г е ж е г б. В., РЬуя1са1 е1есСгоп1с рЬепошепа 1п юп ргори1яюп епд1пея. 1ЕЕЕ
ЯресСгиш, чо1. 2, Хо. 8, 1965.
2.121. Р е г г 1 е Р., Р1аяша а1я АпСг1еЬяш1ССе1йю Й1е Ваиш1аигС. Ьий1аЬгССесЬп11, Вй. 7,
Яг. 7, 1961.
2.122. Гродзовский Г. Л., Иванов Ю. Н., Токарев В.В.,Механикакос-
мического полета с малой тягой. «Наука», М., 1966.
2.123. М 1 с 1с е 1 я е и Ж. В., РиСцге Сгепйя 1п е1есСг1с ргори1яюп., А1АА Ргерг1пС, Мо.
66-595, Х. У., 1966.
2.124. Г и л ь б е р г Л. А., Электрические ракетные двигатели. Воениздат., М., 1968.
2.125. Х а Ь и В. б., РЬуя1ся о1 е1есСг1с ргори1яюи. Х. У., 1968.
2126. Мо11Сог Х. Н., ЯсЬша1дег Ь., МасрЬегяои Р., Ярасесгай Йея1ди
аког ши1С1ригрояе яо1аг е1есСг1с ргори1яюп ш1яяюпя. А1АА Рарег, Хо. 69-252, 1969.
2.127. Я С и Ь11 и д е г Е., Н о 1 е Р. Р., Р а 111 у С. С., ТЬе чегяаС111Су о1 е1есСг1-
са11у ргоре11ей ярасесгай Ьг р1апеСагу ш1яяюия. Х. Ярасесгай аий Вос1сеСя, А1АА
Рарег, Хо. 69-253, 1969.
2.128. М 1 с 1с е1 я е и Ж. В., Х а Ь и В. б., ЯСаСия о1 е1есСг1с ргорц1я1ои. Х. У., А1АА
Рарег, Хо. 69-497, 1969.
2.129. Гуров А. Ф., Севрук Д. Д., Сурков Д. Н., Конструкция и расчетна
прочность космических электрореактивных двигателей. «Машиностроение», М.,
1970.
'.130. Г и л ь з и н К. А., Электрические межпланетные корабли. «Наука», М., 1970.
2.131. В и я я е 1 1 К. Х., Я е 1 1 д е г В. Ь., М о 1 1 С о г Х. Н., ИесСг1с ргори1яюп Йея1рх
орС1ш1~аС1оп шеСЬойо1оду. Х. Ярасесгай апй Вос1сеСя, чо1. 7, Хо. 2, 1970.
2.132. В а г С к Р. В., Н о г я е ж о о Й Х. Ь., СЬагасСег1яС1ся, сараЫ11С1ея апй сояСя о1
яо1аг е1есСг1с ярасеогай аког р1апеСагу ш1яя1опя. Х. Ярасесгай апй ВосЫеСя, чо1. 7,
Яо. 12, 1970.
".133. К 1 о р р О. А., Ж е 11 я Ж. С., Яо1аг е1есСг1с1ож-СЬгияС Мегсцгу огЬ1Сег ш1яя1опя.,
А1АА Рарег, Ио. 72-425, 1972.

ЛИТЕРАТУРА
675
2 134. С ц С С ш а и С. Н., 011Ь е г С 1., Н о г1о Я. Р., В 1с Ь а г й я о и Е. Н.,
ТЬе яо1аг е1есСг1с ргорц1яюп яСаде сопсерС аког Ь1дЬ епегду ш1яя1опя. А?АА Рарег,
Яо. 72-465, 1972.
2.135. Наж1с С., ВаСу М. В., Вовеп Ь.Я., Яи1г1с Ь. У., ЯувСешвСийуо1е1е-
сСг1с ргорц1яюп аког ш111Сагу ярасе чеЬ1с1ея. А?АА Рарег, Яо. 72-493, 1972.
2.136. Я с Ь а ц р р В. Ж., Я а ж у е г С. Р., Ргорц1яюп яуяСеш геоц1гешепСя аког а шц1С1-
ш1яяюп пцс1еаг е1есСг1с ярасесгай. А?АА Рарег, Яо. 72-503, 1972.
2.137. Я с Ь а г 1 Ж., О 1 Й е 1~ о р Ж., Р а я с Ь Ж., Яо1аг е1есСг1с ргорц1я1оп аког СЬе
яаСе111Се СгапярогС 1пСо СЬе деояСаС1опагу огЬ1х. А?АА Рарег, Яо. 72-505, 1972.
;?.138. М а я е 1~ Т. Р., Яо1аг е1есСг1с ргорц1яюп ЬгеайЬоогй СЬгцяС яцЬяуяСеш СеяС геяц1Ся.
А?АА Рарег, Яо. 72-507, 1972.
2.139. Н о 1 с о ш Ь Ь. В., Яцгчеу о1 яаСе111Се ацхШагу е1есСг1с ргорц1яюп яуяСешя. 1. Яра-
сесгай апй Вос1сеСя, чо1. 9, Мо. 3, 1972.
2.140. Г р и ш и н С. Д., К о з л о в Н. П., Применение плазменных ускорителей в тех-
нике. В кн. под ред. Л. А. Арцимовича «Плазменные ускорители». «Машинострое-
ние», М., 1973.
2.141. Г р о д з о в с к и й Г. Л., Применение плазменных ускорителей в газодинамике.
В кн. под ред. Л. А. Арцимовича «Плазменные ускорители». «Машиностроение»,
М., 1973.
2.142. М о р о з о в А. И., Плазменные ускорители. В кн. под ред. Л. А. А р ц и м о-
в и ч а «Плазменные ускорители». «Машиностроение», М., 1973.
2.143. П о д г о р н ы й И. М., Применение ускорителей плазмы в космических исследо-
ваниях. В кн. под ред. Л. А. А р ц и м о в и ч а «Плазменные ускорители». «Ма-
шиностроение», М., 1973.
2.144. Г о м и л к а Л. А., 3 е м с к о в А. И., Л е ш е в с к и й Л. Н., П а в л о в А. Д.,
Попов Г.А.,Сердобинцев С.П.,Снарский Р.К.,Соболь А.Г.,
Т ю р и н В. Н., У т к и н — Э д и н Д. П., Исследования импульсного плазмен-
ного движителя с металлическим рабочим телом. Ргос. ХХ?У ?пСегпаС. АяСгопацС.
Сопряг., Ва1аа, 1973.
2 145. Т а м м И. Е., Основы теории электричества. Гостехиздат, М., 1957.
2.146. А р ц и м о в и ч Л. А., Управляемые термоядерные реакции. Физматгиз, М., 1961
2147. Арцимович Л. А., Лукьянов С. К)., Подгорныи И М Чув
т и и С. А., Электродинамическое ускорение сгустков плазмы. 3КЭТФ, т. 33, ~Я 7,
1957.
2148. Подгорный И. М., Чуватин С. А., Быков Г. А., Письмен-
н ы й В. Д., Исследование процесса электродинамического ускорения сгустков
плазмы. ??. Физика плазмы и проблема управляемых термоядерных реакций,
т. ?У, изд-во АН СССР, М., 1958.
2.149. Ь о с 1с ж о о Й Р. Ь., В ц г Й е С С е Ь. В., А рц1яей часццш-агс СЬгцяСег яуяСеш
1псогрогаС1пД СЬгоСС1е апй СЬгцяС чесСог сопСго1я. А?АА Рарег, Мо. 70-180, 1970.
2.150. У о г г е 1 С е г Х. Ж., Я Ь е р а г Й С. Е., Рег1огшапсе сЬагасСег1яС1ся о1 СЬе соп-
яСг1сСей-агс яцрегяоп1с 1еС. Ргос. 1965 НеаС Тгапя1ег апй Р1ц1Й МесЬ. ?пяС.
ЯСап1огй, 0п1ч. Ргеяя, 1965.
2.151. А л ф е р о в В. И., У с т и н о в Ю. С., Исследование физической картины раз-
ряда между холодными электродами в сверхзвуковой струе плазмы с присадками.
Изв. АН СССР, МЖГ, № 2, 1968.
2.152. Я с Ь а 11 Ж., ?п11цепсе о1 шадпеС1с Йе1йя оп апойе 1ояяея 1а МВР-агся. А?АА Ра-
рег, Мо. 72-502, 1972.
2.153. К г ц 11 е С., ТЬеогеС1са1 СгеаСшепС о1 сцггепС, шаяя Пою, апй ге1аСей ЙЬСг1ЬцСюпя
1п МРР р1цшея. А?АА Рарег, Мо. 72-501, 1972.
2.154. М 1с Ь е1я С. 1., У о г ~с Т. М., ЕхЬацяС 11ож апй ргорц1я1оп сЬагасСег1яС1ся о1
а рц1яей МРР— агс СЬгцяСег. А?АА Рарег, Яо. 72-500, 1972.
2.155. В г ц с 1с и е г А. Р., ~ а Ь и В. С., ЕхЬацяС р1цше яСгцсСцге 1п а пцая1-яСеайу
МРР— агс. А?АА Рарег, Яо. 72-499, 1972.
2.156. Я с Ь о с ~ Ж., Р1адпояС1ся апй 1пСегргеСаСюп о1 СЬе е1есСг1са1 сцггепС Й1яСг1Ьийоп
1п ап МРР-СЬгцяСег. А?АА Рарег, Яо. 72-498, 1972.
2.157. Т Ь о ш а я я е и К. 1., Т о и д Р., ?пСег1егошеСг1с Оепя1Су шеаяцгешепСя ш СЬе
агс о1 а рц1яей р1аяша СЬгцяСег. А?АА Рарег., Яо. 72-463, 1972.
2.158. Ь о Ь Н., Е1п е1еИгояСаС1ясЬея ВаЫеСепСг1еЬжег1с ш1С НосЫгеццепг1опешузе11е.
АяСгопацС. АсСа, чо1. 8, Яо. 1, 1962.
2.159. Р е С г1 с 1~ Е. Я., К г а ц я я У. У., Ргодгеяя 1п юп епд1пе еш1ССег йече1оршепС.
Ргос. 5СЬ ?пСегпаС. Яушроя. Ярасе ТесЬпо1. апй Яс1., То1суо, 1964.
2.160. Г и л ь з и н К. А., Двигатели невиданных скоростей. «Машиностроение», М.,
1965.
2.161. Я С ц Ь 1 1 и д е г Е., ?оп ргорц1яюп аког ярасе П1дЬС. И. У., 1964. Русский перевод.
?Цтулингер, Э. Ионные двигатели для космических полетов. Воениздат, М., 1966
2.162. В г е ю е г С. В., ?оп ргорц1я1оп 1я геайу аког арр11саС1оп. А?АА Рарег, Яо. 66-1026,
1966.

676
3!ИТЕРАТУРА
2.163. С о1е В. К., О Й а ж а Н. Я., Я е11е и Х. М., Орега$1оп о1 яо1аг се11 аггауя1п
Й11ц$е я$геаш1пд р1аяшая. А1АА Рарег, Яо. 69-262, 1969.
2.164. К у з н е ц о в Ю. Е., Р у д а к о в В. П., О влиянии процесса перезарядки на
эффективность ионного источника с обьемной ионизацией. Уч. записки ЦАГИ,
т. 1, М 2, 1970.
2.165. Ч е р н е т с к и й А. В., Ионные источники с осциллирующими электронами. Изв.
вузов, серия «Авиационная техника», М 3, 1970.
2.166. В г е ж е г С. В., 1оп ргори1я1оп, СесЬпо1о~у апй арр11сай1опя. Я. У. Ьопйоп—
Раг1я, 1970.
2.167. Х о и е я Я. С., Я ~ а я 1с и я Х. Ч., В у е г я О. С., Ргеш111пагу геяи1$я о1 ЯЕВТ-П
ярасесгай ро$еп$1а1 шеаяигешеп$я ия1пд Ьо$ ж1ге еш1яя~че ргоЬея. А1АА Рарег,
Яо. 70-1127, 1970.
2.168. М а с 1с а у Х. Я., Маппей Магя 1апй1п~ ш1яяюпя ия1пд е1ес$г1с ргори1я1оп. Х. Яраса
Р11дЬФ, Яо. 1, 1970.
2.169. Л а ш к о в Ю. А., Исследование осциллирующего разряда в парах цезия. Уч.
записки ЦАГИ, т. 2, М 3, 1971.
2.170. К 1 и д Н. Х., К а ш 1 Я., Р1аяша ~епега$ог аког ярасе чеЫс1е пеи$гайга$1оп. Х. Яра-
сесгай апй ВосЫеСя, чо1. 8, Яо. 10, 1971.
2.171. Р а 1и ш Ь о С., Я1дп1йсапсе о1 ~Ье ейесйя о1 СЬе Йе1йя апй деошеСгу 1п СЬе саС-
11ой1с ро1аг гед1оп о1 а КаЫшап'я Фуре е1ес$г1с епд1пе. А1АА Рарег, Яо. 72-417, 1972.
2.172. Ж е 11 я А. А., Сиггеп$ Йож асгояя а р1аяша «ОопЫе 1ауег» 1п а Ьо11ож саФЬойе юп
ФЬгпя$ег. А1АА Рарег, Яо. 72-418, 1972.
2.173. 7~11 Ь и г Р. Х., Епесйя о1 СЬе 11о11ож саСЬойе Й1ясЬагде оп СЬгоШей юп СЬгияйег
рег1огшапсе. А1АА Рарег, Яо. 72-421, 1972.
2.174. Я с Ь и е 1 1с е г О. Е., К а ш 1 Я., ТЬегшо-шесЬап1са1 йея1дп аярес$я о1 Мегсигу
ЬошЬагйшеМ юп СЬгияСегя. А1АА Рарег, Яо. 72-431, 1972.
2.17,э. В а и ш ~ а г $ Ь Я. Р. Х., ТЬеогейса1 апй ехрег1шепйа1 1пчея$1даСюпя оп ап е1е-
сйгояйа$1с 1оп СЬгияйег жВЬ 18 сш Й1ашейег. А1АА Рарег, Яо. 72-432, 1972.
2.176. А г1 $ Н. Х., А и С. Р., В е х О., Е1есСгояСайс юп СЬгияйег ея1са 28 1ог1Ыегр1апе-
1агу ш1яяюпя. А1АА Рарег, Яо. 72-434, 1972.
2177. КоясЬайе Я. Р., Р1п1ся Ж., Тго1ап Р., Ьое Ь Н. Ж., В ая-
я и е г Н. Ж., Оече1оршеп$ о1 а 111д11Ф рго$о$уре о1 01е ВР-юп ФЬгцйег В1Т 10.
А1АА Рарег, Яо. 72-471, 1972.
2178. Тго1ап Р. М., Вияяже11ег К. Р., Ьапд Н. Н., ЬоеЬ Н. Ж., Оече-
1оршепй о1 $Ье гайю 1геср~епсу ш1с1сго$Ьгияйег В1Т-4. А1АА Рарег, Яо. 72-473, 1972.
2.179. К1е1п Ж. С., СгоЬ К., Ьапд Н., Ьое Ь Н. Ж., Орйш1га$юпо1$Ье ВР-
СЬгияйег «В1Т 20». А1АА Рарег, Яо. 72-474, 1972.
2180. Рож111с Е. Ч., Со1йяйе1п В., Р1Сгдега1Й О. Х., Айашя В. ~У.,
1оп СЬгияйег рег1огшапсе са11 рег1огшапсе са11Ьгайюп. А1АА Рарег, Яо. 72-475, 1972.
2.131. Ж а г Й Х. Ж., К 1 и д Н. Х., Ьйе 11шйайюпя о1 юп ех$гас$юп яуя$ешя. А1АА Ра-
рег, Яо. 72-477, 1972.
2.132. Р е г е 1 Х., М а Ь о и е у Х. Р., 0 а 1 е у Н. Ь., ОигаФюп Феям о1 ап ашш1аг со1-
1оИ СЬгия$ег. А1АА Рарег, Яо. 72-483, 1972.
2.183. Ь а ф Ь е ш ~У. С., Сг1Й-Сгапя1айоп Ьеаш Йе11есй1оп яуяСешя аког 5-сш апй 30-сш
Й1ашейег Кац1шап СЬгияйегя. А1АА Рарег, Яо. 72-485, 1972.
2.184. В а ж11 и Ч. К., В а и 1с я В. А., В у е г я О. С., Оеяфп, 1аЬг1са$юп, апй оре-
га$1оп о1 Й1яЬей ассе1егайог дт1йя оп а 30-сш юп СЬгияйег. А1АА Рарег, Яо. 72-486,
1972.
2.185. Р у е Х. Ж., Сошропеп$ Йече1оршеМ аког а 10-сш Мегсигу юп ФЬгия$ег. А1АА Ра-
рег., Яо. 72-487, 1972.
2.186. В е с Ь С е 1 В. Т., А 30 сш Й1ашеСег ЬошЬагйшепй СЬгияфег жйЬ а чаг1аЫе шадпе-
Мс ЬаЛ1е. А1АА Рарег, Яо. 72-489, 1972.
2.187. В а11еу А. С., ВгасЬег Х. Е., чоп ВоЬйеп Н. Х., Асар111агу4ей ап-
тш1аг со11о1Й СЬгияйег. А1АА Рарег, Яо. 72-490, 1972.
2.188. Ье С г 1 ч е я Е., Ь а Ь Ь 1 е Х., ВеяеагсЬ оп сеяшш соп$асС ш1сгоСЬгияФегя АТО.
Я. Е. В. А. А1АА Рарег, Яо. 72-495, 1972.
2.189. К 1п д Н. Х., Р о е я с Ь е1 В. Ь., Ап юп ФЬгия$ег шойи1е аког рг1шагу ргори1яюп
яуя$ешя. А1АА Рарег, Яо. 72-508, 1972.
2.190. Н е г г о и В. С., С о 11 е С С С. В., С а г С Ь О. В., Оече1оршеМ, пйедтаСюп
апй Сея$1пд о1 а 30-сш СЬгияйег/розг сопй1Сюп1пд апй сопйго1 яуя$еш. А1АА Рарег,
Яо. 72-509, 1972.
2.191. Н и Ь е г ш а и М. Я., Е1ес$гоп драп пеиСга11яегя аког со11о1Й ФЬгия$егя. А1АА Рарег,
Яо. 72-511, 1972.
2.192. К а и 1 ш а и Н. В., В е а Й е г Р. О., Е1есйгояйа$1с СЬгияйег. А1АА Рарег, Яо.
72-1123, 1972.
2.193. П о н о м а р е н к о А. Г., С о л о у х и н Р. И., Некоторые вопросы разработки
и использования компактных высоковольтных источников заряженных частиц
в космическом эксперименте. Ргос. ХХ1Ч 1Мегпай. Ая$гопаий. Сопцт., ВаЫи, 1973.

ЛИТЕРАТУРА
677
2.194.
2.195.
2.196.
2.197.
2.198.
2.199.
2.200.
2.201.
2.202.
2.203.
2.204.
2.205.
2.206.
2.207.
2.208.
2.209.
2.210.
2.211.
2.212.
2.213.
2.214.
2.215.
2.216.
2.217.
2.218.
2.219.
2.220.
2.221.
2.222.
2.223.
2.224.
2.225.
2.226.
2.227.
2.228.
Н о с а ч е в Л. В., Исследование взаимодействия летательного аппарата с ионо-
сферой. Ргос. ХХ1У 1пСегпаС. АзСгопаиС. Сопит., Вайи, 1973.
С Ь1г о и я е Х., Ь а и й г а о 1 С С., Апа1уяе Йея ргоЫешея рояея раг 1е йече1ор-
шеп$ е$1 и011яайюп Йея ргори1яеигя е1есйг1~иея а 1а1Ые роияяее. Ргос. ХХ1У 1п-
$егпа$. Аяйгопаий. Сопряг., Ва1и, 1973.
Ха1гаи Я.,Веуиои Х.С.,К1ЙЙР.Ж.,ЯЬе1$ои Н.,Х ас1яоп Р.А.,
Опе-ш1Ь со11о1Й СЬгияйег яуяСеш Йече1оршепС. Х. Ярасесгай апй Вос1ейя, чо1. 10,
Мо. 8, 1973.
Н у ш а и Х., Рече1оршопй о1 а 5-сш 111дЬС вЂ” суаа116ей Мегсигу 1оп СЬгияйег. Х. Яра-
сесгай апй Вос1ейя, чо1. 10, Мо. 8, 1973.
Методы измерения тяги ионного двигателя. «Денсокэн нюсу», М 282, 1973.
Я а 1~ а и 1 я 11 1 8., РигаЫИу Сеяйя о1 а 5-сш-Й1аш юп СЬгцяйег яуяйеш. Х. Ярасе-
сгай апй Вос1~ейя, чо1. 10, Яо. 9, 1973.
К а и ц о в Н. А., Электроника. Гостехиздат, М., 1956.
Д о б р е ц о в Л. Н., Электронная и ионная эмиссия. Гостехиздат, М., 1950.
Б р а у н С., Элементарныо процессы в плазме газового разряда. Госатомиздат,
М., 1961.
ЬеМя Фея$я 1агде юп епрпе. Ач1айоп Жеев апй Брасе ТесЬп., чо1. 81, Мо. 4, 1964.
Ц а и д е р Ф. А., Проблема полета при помощи реактивных аппаратов. Меж-
планетные путешествия. Оборопгиз. М., 1961.
К а р ы м о в А. А., Определение сии и моментов сил светового давления, действу-
ющих на тело при движении в космическом пространстве. Прикл. матем. и механ.,
т. 26, М 5, 1962.
Х а Ь я ш а и Ж. Е., Маяя сопя1йегайюп 1и г1пд яиррогйей яо1аг яа11я. Х. Ашег.
ВосЕ Яос., чо1. 30, Яо. 3, 1960.
Г л у ш к о В. П., Жидкое топливо для реактивпых двигателей. Изд-во ВВИА
им. Н. Е. Жуковского, М., 1936.
П а у ш к и н Я. М., Химический состав и свойства реактивных топлив. Изд-во
АН СССР, М., 1958.
С е р е г и н А. В., Жидкие ракетпые топлива. Воепиздат, М., 1962.
С и л а н т ь е в А. И., Твердые ракетные топлива. Воениздат, М., 1964.
Г р и г о р ь е в А. И., Твердые ракетные топлива. «Химия», М., 1969.
М е л ь н и к о в М. В., Влияние формы камеры и сопла на тягу ЖРД. Изд-во
БНТ, М., 1946.
В а н и ч е в А. П., Термодинамический расчет горения и истечения в области вы-
соких температур. Изд-во БНТ, М., 1947.
3 е л ь д о в и ч Я. Б., П о л я р н ы й А. И., Расчеты тепловых процессов при
высокой температуре. Изд-во БНТ, М., 1947.
П е т р о в П. А., Ядерные энергетические установки. Госэнергоиздат, М., 1958.
Займовский А. С., Калашпиков В. В., Головин И. С., Тепло-
выделяющие элементы атомных реакторов. Госатомиздат. М., 1962.
М е л ь н и к о в И. П., Конструктивные формы и методы расчета ядерных реак-
торов. Госатомиздат, М., 1963.
Х о 11 и я о и С. Е., М а я о и Р. С., Впар 8 геасСог апй яЫе1Й Йея1дпя апй орега-
Мпд ехрег1епсе. А1АА Рарег, Мо. 65-473, 1965.
П а н ч е н к о Е. И., К о р о в к и н А. С., Космическая электроэнергетика
«Знание», М., 1967.
Р о 1 а 1с Н., Мис1еаг рожег яирр11ея аког ярасе. Х. Вгй1яЬ Яис1еаг Епегду Яос., чо1.
7, Мо. 3, 1968.
Б у р д а к о в В. П., Д а н и л о в 10. И., Физические проблемы космической
тепловой энергетики. Атомиздат, М., 1969.
В о г е $ г Х. Е., Ьагде ярасе яйаСюп рожег яуя$ешя. Х. Ярасесгай апй Вос1сейя,
чо1. 6, Мо. 8, 1969.
Ь а 11 е и г Х. Р., 8 с Ь и1 ш а и Р., Арр11сайюпя апй Йече1оршепй о1 ярасе е1е-
сйг1с рожег яуяСешя. Х. Аяйгопаий. Яс1., чо1. Х1Х, Мо. 1, 1971.
Купандин А. А., Тимашев С. В., Иванов В. П., Энергетические
системы космических аппаратов. «Машиностроение», М., 1972.
Ж1111 а ш я Х. В., У а и д У. У., С1 е ш е п $ Х. Р., ТЬе яаФе11Ие шас1еаг
рожег яСаСюп — ап епд1пеег1ид апа1уя1я. Ргос. ХХ1У 1пСегпаС. АяйгопаиС. Сопряг.,
ВаЫи, 1973.
В а р ш а в с к и й Г. А., К вопросу о поведении быстродвижущегося потока сжи-
маемого газа в прямой цилиндрической трубе при наличии охлаждения. Журн.
техн. физ., вып. 4, 1946.
Р о м а н е н к о С. В., Течение вязкого газа в цилиндрической трубе при на-
личии конвективного теплообмена. Докл. АН СССР, т. 91, М 6, 1953.
Г р о д з о в с к и й Г. Л., Некоторые точные решения задачи о течепии газа
в трубе с учетом трения и конвективного теплоообмена. Изв. АН СССР, ОТН,
Л3 8, 1958.

ЛИТЕРАТУРА
2.229. М е ж и р о в И. И., О течении газа в цилиндрической трубе при наличии трения
и теплообмена. Изв. АН СССР, ОТН, № 8, 1958.
2.230. б о 1 й я т 1 С Ь Ж., Я е Ь а и В. А., Ргеяяцге йгор апй Ьеай Сгапя1ег аког яцЬяошс
а1г агою 1п а ятооФЬ р1ре. Тгапя. АЯМЕ, Яо. 50-Р-18, 1950.
2231. Авдуевский В. С., Данилов Ю. И., Кошкин В. К., Куты-
рин И. Н., Михайлова М. М., Михеев Ю. С., Сергель О. С.,
Основы теплопередачи в авиационной и ракетной технике. Оборонгиз, М., 1960.
2.232. В а р ш а в с к и й Г. А., Р е з г о л ь Н. А., Тепловой расчет термогенератора
при переменных температурах вдоль теплоконтактных поверхностей. Из в.
АН СССР, Энергетика и транспорт, № 6, 1964.
2.233. С и н е в Н. М. (ред.), А н д р е е в П. А., Г р е м и л о в Д. И., Ф е д о р о-
в и ч Е. Д., Теплообменные аппараты ядерных энергетических установок. «Судо-
строение», М., 1965.
2234. Гродзовский Г. Л., Кузнецов Ю. Е., Худяков Г. Е., Газоди-
намическая теория течения двухфазной жидкости с изменением агрегатного со-
стояния. Тр. ЦКТИ, Котлотурбостроение, вып. 59, Л., 1965.
2.235. К и м е л ь Л., Определение оптимальной формы защитного барьера. Атомная
энергия, т. 7, № 3, 1959.
2.236. Т о к а р е в В. В., Ц в е т к о в В. И., Оптимальная форма защиты от гамма-
излучения. ПМТФ, 1, 1964.
2.237. Ц в е т к о в В. И., Оптимальная форма защиты от полихроматического гамма-
излучения. Журн. прикл. механ. и техн. физ., № 6, 1965.
2.238. Епегду сопчегяюп аког ярасе рожег. Ярасе рожег яуя$етя. Ей. Ьу Я и у й е г Я. Ж.,
Асай. Ргеяя, Я. У.— Ьопйоп, 1961. Русский перевод: Преобразование тепла и хи-
мической энергии в электроэнергию в ракетных системах. ИЛ, М., 1963. Энерге-
тические установки для космических аппаратов. «Мир», М., 1964.
2.239. батте1 б., Коя1с1пеп М. Р., Тгоуег А., Хцг Еп$ж1сИцпд е1пея шИ
АсИшцт 227 ЬеЬе1г$еп ФЬегтюшясЬеп бепега$огя. Вацт1аЬгИогясЬцщ„ВЙ. Х1П,
Ней 1, 1969.
2.240. У е г и е $ — Ь о г е С М., Ьея чеЫсц1ея яраИацх а яоцгсе Й'епегд1е яо1а1ге. Ье рго-
1е$ РЬае$ап. Апп. део11я., чо1. 17, Яо. 1, 1964.
2.241. Я С а 1 1 о г й б. В., С а р а Ь111$1е я о1 ро~чег яцЬяуяйетя аког ярасе. МесЬаш-
са1 Епд1пеег1пд, чо1. 87, Яо. 9, 1965.
2.242. О я т ц и Ж. б., Ярасе пцс1еаг рожег: ЯЯАР-50/ЯРОВ. Ярасе Аегопац$., чо1. 42,
Бо. 7, 1964.
2.243. А ц б. Р., «Я и а р я Ь о Ь& t; 1п е1есСгояСаСис ея 1опепСг1еЬж гЫ тИ пцс1 аг Епег
чегяогцпд. Ьцй-цпй Вацт1аЬгИесЬп1Ы, Яг. 7, 1965.
2.244. б1 а я я т а и А. Х., Я С е ж а г С Ж. Ь., ТЬегтойупат1с сЬагасйег1яИся о1 Вгау-
$оп сус1ея аког ярасе рожег. 1. Ярасесгай апй Вос1е$я, чо1. 1, Яо. 1, 1964.
2.245. С о с Ь г а и Р. Ь., ЖогЫщ, 11ц1йя аког Йупат1с АРЯ яуя$етя. Ярасе АегопацФ.,
ВЙР ТесЬп. НапйЬооЫ, чо1. 38, Яо. 2, 1962 — 1963.
2.246. В е а 1 е В. 1., Я р е 1 я е г Е. Ж., Ж о т а с 1с 3. В., Е1есФг1с ярасе сгц1яег аког
Ь1дЬ-епегду т1яяюпя. 1. Ярасесгай апй Вос1е$я, чо1. 1, Яо. 1, 1964.
2.247. Д е й ч М. Е., Техническая газодинамика. Госэнергоиздат, М., 1953.
2.248. Л о й ц я н с к и й Л. Г., Механика жидкости и газа. Гостехиздат, М., 1957.
2.249. С т е п а н о в Г. Ю., Гидродинамика решеток турбомашин. Физматгиз, М., 1962.
2.250. А б и а н ц В. Х., Теория газовых турбин реактивных двигателей. «Машинострое-
ние», М., 1965.
2.251. Д о р о г о в Б. С., Эрозия лопаток в паровых турбинах. «Энергия», М., 1965.
2.252. Е 111 о С С Р. б., Тжо41ц1Й тадпейоЬуйгойупат1с сус1е аког пцс1еаг е1есйг1с ро-
жег сопчегяюп. 1. Атег. ВосЫ. Яос., чо1. 32, Яо. 10, 1962.
2.253. МНР рожег сопчег$егя ~ог ярасе. Яцс1еошся, чо1. 21, Яо. 7, 1963.
2.254. И о ф ф е А. И., Полупроводниковые термоэлементы. Изд-во АН СССР, М.— Л.,
1956.
2.255. Р 1 е с 1с а т р Н. М., В а1 е и $ В., Ж е $ с Ь У. В., Веас$ог Й1гес$-сопчег-
яюп цшСя. Ргос. Згй 0шС. ЯаС. 1пСегпаС. СоЫ. оп СЬе РеасеЫ1 0яея о1 АСот1с
Епегду, бепеча, 1964.
2.256. Я $ а т т Н., Вайюшй11Й-Ьаййег1еп Ыг Й1е Вацш1аЬг$. Же1$гацт1а11г$, Яг. 4, 1963.
2.257. Маг1пег $о Магя. Р11дЬФ, чо1. 86, Ио. 2906, 1964.
2.258. Н а т 11 $ о и В. С., Яо1аг рожег яуя$ет. Ргос. ХУ 1п$егпа$. Ая$гопац$. Сопряг.
1964, Жагягажа, 1965.
2.259. Т о и 1с 1 и Я. Ж., Яо1аг се11 аггауя аког г1д~й еагФЬ-ро1пИпд яа$е1Иея. Ргос. ХУ 1п-
Сегпай. Аяйгопацй. Сонг. 1964, Жагягажа, 1965.
2.260. б 1 о ч е г б. М., Ьоя-А1атоя р1аята ФЬегшосоцр1е. Яцс1еошся, чо1. 17, Яо. 2,
1959.
2.261. Д о б р е ц о в Л. Н., Термоэлектронные преобразователи тепловой энергии
в электрическую. Журн. техн. физ., т. 30, № 4, 1960.
2.262. Н а г ч е у В. 1., Ргорц1яюп апй ацх111агу рожег яуя$етя. Ва111яйс М1яя11е апй
Ярасе ТесЬпо1оду, чо1. 2, Я. У., 1960.

ЛИТЕРАТУРА
679
2.263. СоЬЬ Х. Е.,Си$1ег Ж. Е., Пикап А.Р.,О1йя В.Н.,ЯЬооЫ б. В.,
А пис1еаг-ФЬегшюп1с-юп1с ргори1яюп яуя$еш. Ргос. Х1 1пйегпаС. Аяйгопаий. Совцт.
1960, Иеп., 1961.
2.264. М о р г у л и с Н. Д., Термоэлектронный (плазменный) преобразователь энергии.
Госатомиз дат, М., 1961.
2.265. М 111 е г Н., ТЬегшюп1с-тшс1еаг ярасе рожег яуя$ешя. Ргос. Згй Яушр. Айчапсей
Ргори1я. Сопсер$я, С1пс1ппай1, 1962, чо1. 1, Я. У.— Ьопйоп, 1963.
2.266. б г о п1с Ь А., Н а11е $ В. Ж., М 111 е г Р. Ж., А пцс1еаг е1ес$г1с ргори1яюп
яуя$еш аког шаппей 1п$егр1апе$агу ш1яяюпя. Ргос. Х1У 1п$егпа$. Ая$гопаиС. Сощ~т.
1963, чо1. 1, Жагягажа, 1965.
2.267. Р я а г о и $ Ь а 1с 1 я Х., ТЬегшюп1с сопчегяюп аког е1ес$г1с ргори1яюп рожег.
Ргос. ХУ1 1п$егпа$. Ая$гопаи$. Соадг. 1965, Жагягажа, 1966.
2.268. В е г и а $ о ж1 с г Р. Т., ТЬегшюп1с сопчег$егя 1п а1агде пис1еаг е1ес$г1с рожегр-
1аМ 1п ярасе. АВЯ1, УП1, чо1. 32, 1962.
2.269. Ф а в о р с к и й О. Н., Установки для непосредственного преобразования теп-
ловой энергии в электрическую. «Высшая школа», М., 1965.
2.270. Краткий физико-технический справочник, т. 1, Физматгиз, М., 1960.
2.271. Инженерно-технический справочник по электросвязи. Электроустановки. Изд-во
лит. по связи и радио, М., 1962.
2.272. Г р о д з о в с к и й Г. Л., Оптимальная форма теплоотводящих ребер, охлаждае-
мых излучением. Изв. АН СССР, ОТН, Энергетика и автоматика, М 6, 1962;
см. также Ргос. ХП 1Мегпа$. Ая$гопаиС. Сопдт. 1961, У1еп., 1962; Ая$гопаиИса, Юо. 8,
1962.
2273. Понтрягин Л. С., Болтянский В. Г., Мищенко Е. Ф., Гам-
к р е л и д з е Р. В., Математическая теория оптимальных процессов. Физматгиз,
М., 1961.
2.274. Ж11 1с 1 и я Х. Е., М1п1ш1к1пд ФЬе шаяя о1 СЬ1п гай1аИвд Ипя. ХАЯЯ, чо1. 27, Юо.
2, 1960.
2.275. Ж 11 1с 1 и я Х. Е., М1п1пшш шаяя СЫп Ипя жЫсЬ $гапя1ег Ьеай оп1у Ьу гай1айюп Со
яиггоцпй1~дя аС аЬяо1ийе гего. Х. Яос. 1пй. Арр1. МаСЬ., чо1. 8, Юо. 4, 1960.
2.276. Ж 11 1с 1 и я Х. Е., М1п1пшш шаяя СЫп Ипя аког ярасе гай1айогя. Ргос. о1 1960,
Неай-Тгапйег апй МесЬап1ся 1пяййийе. ЯйаЫогй Бп1чегяйу, 1960.
2.277. Ж 11 Ы 1 и я Х. Е., М1п1шиш шаяя Ипя апй сопя$ап$ СешрегаЫге ~тай1епС. Х. Яос.
1пй. Арр1. МаСЬ., чо1. 10, Ио. 1, 1962.
2.278. В а г С а я Х. С., Я е11 е г я Ж. Н., Вай1ай1оп Ип еИесйчепеяя. Тгапя. АЯМЕ.
Х. НеаФ Тгапя1ег, чо1. 82, Ио. 1, 1960.
2.279. С Ь е и У. Ь., Оп ш1п1пшш-заец,ЬФ гес$ащр~1аг Ипя. ХАЯЯ, чо1. 27, Юо. 11, 1960.
2.280. Ю 11 я о и Е. Я., С и г г у В., ТЬе ш1п1пшш-же1дЬФ я$гац,ЬФ Ип о1 Сг1авди1аг рго-
И1е гай1ай1~д Со ярасе. ХАЯЯ, чо1. 27, Ио. 2, 1960.
2.281. Г р о д з о в с к и й Г. Л., Ф р о л о в В. В., Оптимальные контуры теплоотводя-
щих ребер, охлаждаемых излучением, ч. П. Ргос. Х1П 1п$егпа$. Аяйгопаий. Совдт.
1962, У1еп., 1963.
2.282. Ф р о л о в В. В., Оптимальная форма теплоотводящих ребер с учетом взаимного
облучения. Изв. АН СССР, ОТН, Энергетика и автоматика, М 6, 1962.
2.283. Е с 1с е г $ Е. В. С., 1 г ч1 и е Т. Е., Хг., Я р а г г о ж М., Апа1Мса1 1огши1айюп
аког гай1аМпд Ипя жйЬ шийиа1 1ггай1ай1оп. Х. Ашег. ВосЕ Яос., чо1. 30, Юо. 7, 1960.
2.284. Яраггож Е. М., ЕсКег$ Е. В. С.,1гч1пе Т. Е., Хг., ТЬееИесИчепеяя
о1 гай1айпд Ипя жйЬ шиЫа1 1ггай1айюп. ХАЯЯ, чо1. 28, Ио. 10, 1961.
2.285. К г е 1 $ Ь Е., Вай1айюп Ьеай $гапя1ег аког ярасесгай апй яо1аг рожег йея1дп. Ю. У.,
1962.
2.286. Я р а г г о ж Е. М., Е с 1с е г $ Е. В. б., Вай1аМ пйегас$юп Ье$жееп Ип апй Ьаяе
яиг1асея. Х. Неа$ Тгапя1ег, яег. С, чо1. 84, Юо. 1, 1962.
2.287. Р1 а ш о й о и Х. А., ТЬегша1 еИ1с1епсу о1 соайей Ипя. Х. Неа$ Тгапя1ег, яег. С,
чо1. 84, Ио. 4, 1962.
2.288. К а г1 е 1с а г В. У., С Ь а о В. Т., Маяя ш1п1ш1га$юп о1 гай1а$пщ Сгарего1йа1
Ипя АЛЬ пед11д1Ь1е Ьаяе су11пйег 1пйегасИоп. 1пй. Х. НеаФ апй Маяе Тгапя1ег, чо1. 6,
Ио. 1, 1963.
2.289. Н а 11 е г Н. С., Я С о с 1с ш а и Ю. О., А поСе оп Ип-СиЬе ч1еж 1асСогя. Х. Неай
Тгапя1ег, яег. С, чо1. 85, Ио. 4, 1963.
2.290. Х о Ь и я я о и У. К., Я р а г г о ж Е. М., Апд1е 1асФогя аког гай1апС пйегсЬавде
Ьейжееп рага11е1-ог1епйей ЫЬея. Х. Неай Тгапя1ег, яег. С., чо1. 85, Ио. 4, 1963.
2.291. В а с а н о в Ю. А., Ж у л е в Ю. Г., Оптимальная форма треугольных тепло-
отводящих ребер с учетом взаимного облучения ребер и охлаждаемой поверхности.
Изв. АН СССР, Энергетика и транспорт, М 3, 1964; см. также Ргос. ХУ 1п$егпа$.
Ая$гопаи$. Сопдт. 1964, Жагягажа, 1965.
2.292. С о л о в ь е в Б. А., Графоаналитический метод определения параметров тепло-
носителя в холодильнике-излучателе на нерасчетных режимах его работы. Изв.
АН СССР, Энергетика и транспорт, М 4, 1965.

680
ЛИТЕРАТУРА
2.293.
2.294.
2.295.
2.296.
2.297.
2.298.
2.299.
2.300.
2.301.
2.302.
2.303.
2.304.
2.305.
2.306.
2.307.
2.308.
2.309.
2.310.
2.311.
2.312.
2.313.
2.314.
2.315.
2.316.
2.317.
2.318.
2.319.
2.320.
2.321.
2.322.
В а с а н о в Ю. А., Характеристики теплового излучения системы звездообраз-
ных излучателей. Изв. АН СССР, Энергетика и транспорт, Ю 5, 1964.
В а с а н о в Ю. А., Влияние термического сопротивления покрытий на характе-
ристики теплового излучения звездообразпых излучателей. Изв. АН СССР, Энер-
гетика и транспорт, Ю 6, 1964.
Ф р о л о в В. В., Оптимальная система излучающих ребер. Изв. АН СССР,
Энергетика и транспорт, Ю 6, 1964.
Н о в о с е л е ц к и й О. Ю., У к о л о в В. Л., Определение оптимальных раз-
меров излучающих ребер. Инж.-физ. журнал, Х 12, 1964.
В а с а н о в Ю. А., Ж у л е в Ю. Г., Исследование теплового излучения системы
звездообразных излучателей. Теплофизика высоких температур, М 6, 1965; см.
также Ргос. ХУ1 1пСегпаС. АяСгопацС. Сопряг. 1965, Жагыаюа, 1966.
Ж у л е в Ю. Г., К о с а р е н к о в В. А., Излучательная способность трубча-
того радиатора. Теплофизика высоких температур, Х 3, 1966.
С и а ш Ь е г я В. Ь., Я о ш е г я Е. У., Вай1аСюп йп еЫсЫпсу аког опе-Й1шепяюпа1
пеаС Пою 1п а с1гси1аг йп. Тгапя. АЯМЕ, нег. С, го1. 81, 1959.
М а с К е у О. В., Тгапяш1яяюп Йе спа1еиг раг гауоппешепС Йе яиг1асея а11еСеея
Йапя ип еяраге епсчгоппапС еС ног орС1ш1яаС1оп. 3. 1пСегпаС. Тгапяш1яя. Сйа1епг.,
го1. 2, Раг1я, 1962.
Я р а г г о ж Е. М., М 111 е г 6. В., У о и я я о и У. К., Вай1аС1пд ейесС1чепеяя
о1 аппи1аг-йппей ярасе гай1аСогя, 1пс1ий1пд пис1еаг 1ггай1аСюп ЬеСжееп гай1аСог
е1ешепСя. ГАЯМ, го1. 29, Хо. 11, 1962.
В а с а н о в Ю. А., Ж у л е в Ю. Г., Оптимальная форма треугольных тепло-
отводящих ребер с учетом взаимного облучения ребер и охлаждаемой поверхности.
Изв. АН СССР, Энергетика и транспорт, Ю 3, 1964.
Ш е в я к о в А. А., Я к о в л е в а Р. В., Инженерные методы расчета динамики
теплообменных аппаратов. Машиностроение, 1968.
3 а р у б и н В. С., Температурные поля в конструкции летательпых аппаратов.
Машиностроение, 1966.
Ж у л е в Ю. Г., Излучательная способность зубчатой поверхности. Теплофизика
высоких температур, Ю 2, 1965.
М у ч н и к Г. Ф., Р у б а ш е в И. Б. Методы теории теплообмена. ч. 2, Высшая
школа, М., 1974.
С о л о в ь е в Б. А., Оптимизация по весу полусферического излучателя. Изв.
АН СССР, Энергетика и трапспорт, Ю 1, 1966.
Ф а в о р с к и й О. Н., К а д а н е р Я. С., Вопросы теплообмена в космосе.
«Высшая школа», М., 1967.
Гродзовский Г. Л., Пасечник 3. В., Об оптимальной форме неко-
торых кольцевых ребер, охлаждаемых излучением. ПМТФ, М 3, 1967.
Г р о д з о в с к и й Г. Л., Ж у л е в Ю. Г., Оптимальные системы отвода тепла
излучением. Ргос. ХУ1П 1пСегпаС. АяСгопаиС, Сопряг., 1967, Белград.
Ж у л е в Ю. Г., К о с а р е н к о в В. А., Излучательная способность труб-
чатого радиатора. Теплофизика высоких температур, Х 1, 1967.
Ж у л е в Ю. Г., Излучательная и поглощательная способность трапециевидных
канавок. Теплофизика высоких температур, Х 3, 1967.
Ж,ул е в Ю. Г., Оптимальная форма одиночныхизлучающихэлементов. Инж.-физ.
журнал, Ю 4, 1967.
Ж у л е в Ю. Г., П о т а и о в Ю. Ф., Исследовапие излучательной системы
с коническими теплоотводящими шипами. Инж.-физ. журнал, М 2, 1968.
Ж у л е в Ю. Г., П о т а п о в Ю. Ф., Эффективность трубчатых излучателей
космических аппаратов, снабженных метеорной защитой. Теплофизика высоких
температур, Ю 3, 1968.
В а с и л ь е в А. А., Определение температурного поля трубки оребренного
излучателя. Теплофизика высоких температур, Х 3, 1968.
Ж у л е в Ю. Г., П о т а и о в Ю. Ф., Излучательная способность экранирован-
ной трубки при наличии теплопроводных перемычек между трубкой и экраном.
Теплофизика высоких температур, М 4, 1968.
Ж у л е в Ю. Г., Эффективность теплоотводящего треугольного излучающего
ребра, подверженного слабому аэродинамическому нагреву. Теплофизика высо-
ких температур, М 5, 1968.
С о л о в ь е в Б. А., О профиле излучающего диска наименьшего веса. Инж.-физ.
журнал, Ю 5, 1968.
О я Ь1ш а К., О я й1ш а У., А яуяСешаС1с шеСпой о1 Спегша1 йея1дп о1ярасе-
сгай. Ргос. Х1Х 1пСегпаС. АяСгопаиС. Сопряг., 1968.
М а с д е а и Т. Х., Апа1уыя о1 а Ье1С-Суре пеаС СгапярогС Йетсе. Х. Ярасесгай
апй ВосКеСя, го1. 6, Хо. 8, 1969.
Т и и г ш а и Х. Ь., ОрС1шыаС1оп о1 яСеайуяСаСе Спегша1 Йея1дп о1 ярасе гай1аСогя.
Х. Ярасесгай апй ВосЫеСя, сто1. 6, Хо. 10, 1969.

ЛИТЕРАТУРА
2.323.
2.324.
2.325.
2.326.
2.327.
2.328.
2.329.
2.330.
2.331.
2.332.
2.333.
2.334.
2.335.
2.336.
2.337.
2.338.
2.339.
2.340.
2.341.
2.342.
2.343.
2.344.
2.345.
2.346.
2.347.
2.348.
2.349.
2.350.
Х е д1я Ь1 К., Я о Ья а К., Я а ж а Й а Т., Найап$ соо11пд о1 Сто СЬ1п р1а-
Сея ~йл1 тпфпа1 1ггай~аС1оп. Тгапя. 3 арап. Бос. Аегоп. ~расе Бс1., го1. 12, Мо. 21,
1969.
К р ы м а с о в В. Н., Оптимальные формы каналов и теплопроводящих поверх-
ностей теплообменников. Тр. ЦАГИ, вып. Х 1178, 1969.
О 1~ а ш о С о У., Х е д 1 я Ь 1 К., ТгачнепС геяропсе о1 Йппей СиЬеяЬеаС гайаСог
аког ярасе рожег р1апСя. Тгапя. Уарап. Яос. Аегоп. Брасе Яс1., го1. 12, Хо. 21, 1969.
Гродз овский Г. Л., Пасечник 3. В., Исследование системы коль-
цевых теплопроводящих ребер, охлаждаемых излучением. Докл. АН УССР,
сер. А, Ю 2, 1970.
Ж у л е в Ю. Г., Общие свойства оптимальных теплоотводящих излучательных
элементов. Уч. записки ЦАГИ, Х 1, 1970.
Ж у л е в Ю. Г., М а т в е е в Г. Г., Оптимизация теплоотводящих излучающих
ребер с учетом приходящих па их поверхпость конвективных и радиационных теп-
ловых потоков. Уч. записки ЦАГИ, Х 5, 1970.
Я а м 1 С к 1~ 1 Р., Вешеяяеп с1ег Ва1жапйе гоп Же1Сгаипи1ши1аСопяКашшегп.
ЬиЩаЬгССесЬп11~, Хо. 11 — 12, 1970.
Я 1 К 1~ а Я., 1 д Ь а М., ТешрегаСиге ЙиСг1ЬиС1оп апд еЛесС1~епеяя о1 а Сжо-
йшепиопа1 гайаС1пд апй соггесС1пд с1гси1аг 11п. А1АА У., Хо. 1, 1970.
Ж у л е в Ю. Г., П о т а и о в Ю. Ф., Тепноотводящая пзлучательная спстема
для охлаждения коротких цилиндрических тел. Ипж.-физ. журнал, т. 18, М 4,
1970.
Ж 1 ш Ь е г1 е у Р., С о я С е 11 о Р. А., ТиЬе-жа11 йп еЛесСя 1п ярасесгай га-
йаСогя. У. Ярасесгай апй ВосКеСя, го1. 7, Хо. 2, 1970.
Петров Г. И. (ред), Козлов Л. В., Нусинов М. Д., Аки-
шиц А. И., Залетаев В.М., К озелкин В.В., Моделированиетепло-
вых режимов космического аппарата и окружающей его среды. «Машиностроение»,
М., 1971.
В о и и е г 111 е У. М., НеаС-ге1есС1оп гайаСог шаяя апй 1Ся 1п11иепсе 1пярасе
рожег яуяСешя. У. НеаС Маня Тгапйег, го1. 14, Хо. 3, 1971.
Я С и г ш а и Х. Х., А гесчеж о1 яСеайу яСаСе 11еаС Сгапя1ег 1гош Йпя. МесЬ. апй
СЬеш. Епд. Тгапя., Хо. 5, 1971.
Гродзовскин Г.Л., Кириленко Г. В., Петунин А.Н., Прием-
ник лучистых потоков с теплоизолироваппым элементом. Уч. записки ЦАГИ,
Ю 1, 1972.
Атманов И. Т., Гродзовский Г. Л., Жулев Ю. Г., Методика
наземных экспериментальных исследований тепловых режимов лунных аппаратов.
Ргос. ХХ1У 1пСегпаС. АяСгопаиС. Сопдт., ВаКи, 1973.
С а ш р о А., Ж о 1 К о Н. Я., ОрС1шиш гесСапди1аг гайаСгге Йпя Ьасчпд Сешре-
гаСиге-стаг1апС ргорегС1ея. Х. Ярасесгай апа ВосКеСя, го1. 10, Хо. 12, 1973.
Апдреянов В. В., Артамонов В. В., Атманов И. Т., Бере-
зин В. И., Жукин В. М., Трошин В. С., Черенков В. Б.,
Автоматические планетные станции. «Наука», М., 1973.
Ж е а С Ь е г я С о и В. С., Я ш1С Ь Ж. Е., А шеСЬой о1 ЬеаС ге1есС1оп 1гош ярасе
рожегр1апСя. У. Ашег. Яос., го1. 30, Хо. 3, 1960.
С т а с е н к о А. Л., Форма гибкой нити в поле центробежных сил. Изв. АН СССР,
ОТН, Механика и машиностроепие, Ю 6, 1962.
Гродзовский Г. Л., Стасепко А. Л., О форметеплоотводящихэле-
ментов, охлаждаемых излучением, ч. Ш. Ргос. Х1У 1пСегпаС. АяСгопаиС. Сопряг.
1963, Жагякажа, 1964.
ЖеаСЬегяСоп В. С., Яш1СЬ Ж. Е., А пеж Суре о1 СЬегша1гайаСог аког
ярасе геЬ1с1ея. АегопаиС. Епд., го1. 20, Хо. 1, 1961.
В и г д е Н. Ь., Вего1с~1пд Ье1С ярасе гайаСог. У. Ап1ег. ВосК. Яос., го1. 32, Хо. 8,
1962.
Я Ь1 р р е г Ь., Я 1 е д1 е г В. С., Х ж1 с К Е. В., Айгапсей 1 шедажаСС ярасе
рожег р1апС яСийу. А1АА Рарег, Хо. 63-270, 1963.
Гродзовский Г. Л., Стасенко А. Л., Фролов В. В., О форме
теплоотводящих элементов, охлаждаемых излучением, ч. 1У. Ргос. ХУ 1пСегпаС.
АяСгопаиС. Сопряг. 1964, Жагякажа, 1965.
С т а с е н к о А. Л., Предельные характеристики ленточного радиатора с уче-
том самооблучения. Изв. АН СССР, Энергетика и транспорт, М 1, 1965.
С т а с е н к о А. Л., Влияние внешнего излучения на предельные характеристики
ленточного радиатора. Изв. АН СССР, Энергетика и транспорт, Ю 5, 1965.
С т а с е н к о А. Л., Равновесные формы и малые колебания гибкой нити, вра-
щающейся в бессиловом поле. Изв. АН СССР, Механика и машиностроение, Ю 1,
1964.
С т а с е н к о А. Л., Коэффициент самооблучения ленты Мебиуса заданной формы.
Изв. АН СССР, Энергетика и транспорт, Ю 4, 1967.

ЛИТЕРАТУРА
2.351.
2.352.
2.353.
2.354.
2.355.
2.356.
2.357.
2.358.
2.359.
2.360.
2.361.
2.362.
2.363.
2.364.
2.365.
2.366.
2.367.
2.368.
2.369.
2.370.
2.371.
2.372.
2.373.
2.374.
2.375.
2.376.
2.377.
2.378.
2.379.
2.380.
2.381.
С т а с е н к о А. Л., Численное решение уравнений ленточного радиатора с одним
охлаждаемым телом. Тр. ЦАГИ, вып. № 1178, 1969.
Ш л ы к о в Ю. П., Г а н и н Е. А., Контактный теплообмен. Госэнергоиздат,
М. — Л., 1963.
Р е и е с Ь Н., В о Ь я е и о ю Ж. Н., Ргей1сйоп о1 ФЬегша1 сопйисйапсе о1 ше-
$а111с яиг1асея ш соЫас$. 1. Неа$ Тгапйег, чо1. 85, Хо. 1, 1963.
С т а с е н к о А. Л., Двумерный периодический контакт. Контактное сопротив-
ление с учетом вторичных потоков в общем случае. Журн. прикл. механ. и техн.
физ., № 4, 1964.
Е и д 11 я Ь В. Е., 8 1 о и е Н. О., В е г и а $ о ю 1 с к О. Т., 0 а ч1я о и Е. Н.,
Ь 1 е Ь 1 е 1 и 8., А 20 000-М1ожаИ пис1 еаг СигЬое1ес$г1с рожег яирр1у аког шаппей
ярасе чеЫс1ея. ХА8А Мешо 2-20-59 Е, МагсЬ 1959.
Синярев Г. В., Добровольский М. В., Жидкостныеракетныедви-
гатели. Оборонгиз, М., 1957.
В и г 1 а д е Н., Ь1цый епд1пея аког айчапсей 1аивсЬ чеп1с1ея. Аяйгопаий. апй Аего-
паи$., чо1. 2, Хо. 7, 1964.
8-1В ТаЖя М1яя11е авй 8расе. Ва11у, чо1. 10, Хо. 26, 1964.
С т е ч к и н Б. С., Теория воздушного реактивного двигателя. Техника воздуш-
ного флота, № 2, 1929.
В о у М., ВесЬегсЬея СЬеог1циея яраг 1е гепйешепй е$ 1ея сопйЮопя йе геа11яа0оп
йея яуяСешея шойоргори1яеигя а геасСюп. Раг1я, 1930. Русский перевод: Р у а М.,
О полезном действии и условиях применения ракетных аппаратов. ОНТИ, М.— Л.,
1936.
А б р а м о в и ч Г. Н., Газовая динамика воздушно-реактивных двигателей.
Изд-во Б НТ, М., 1947.
И н о з е м ц е в Н. В., 3 у е в В. С., Авиационные газотурбинные двигатели.
Оборонгиз, М., 1949.
Ч е р к е з А. Я., Применение метода малых отклонений в теории и расчете авиа-
ционных ТРД. Оборонгиз, М., 1955.
Б о н д а р ю к М. М., И л ь я щ е н к о О. М., Прямоточные воздушно-реактив-
ные двигатели. Оборонгиз, М., 1958.
Ь а и е В. 1., ВесочегаЫе а1г-ЬгеаФЫщ, Ьооя$егя аког ярасе чеЫс1ея. 1. Воу. Аего-
паи$. 8ос., чо1. 66, Хо. 618, 1962.
Р е г г 1 А., Веч1еж о1 ргоЫешя ш арр11са$юп о1 яирегяошс сошЬия0оп. У. Воу.
Аегопаи$. 8ос., чо1. 68, Хо. 645, 1964.
6 о я я1с Ы Ь. У., С о о 1~ Н. М., Тгепйя ш аегоярасе ргори1я1оп йече1оршеЫ
Феяйпд, $Ье1г шйиевсе оп ЫФиге П1дЬФ я1ши1а$юп 1ас11йу гецц1гешеЫя. Ргос. ХУ1
1Мегпа$. Ая$гопаи$. Сопряг. 1965, Жагякажа, 1966.
С к у б а ч е в с к и й Г. С., Авиационные газотурбинные двигатели. «Машино-
строение», М., 1965.
Х о л щ е в н и к о в К. В., Согласование параметров компрессора и турбины
в авиационных газотурбинных двигателях. «Машиностроение», М., 1965.
Раушенбах Б. В., Беспалов С. А., Волынский М. С. и др.,
Физические основы рабочего процесса в камерах сгорания воздушно-реактивных
двигателей. «Машиностроение», М., 1964.
Г о в о р о в А. Н., О р л о в П. В., Теория авиационных двигателей. В ВИА
им. Н. Е. Жуковского, М., 1973.
Орлов Б. В., Мазинг Г. Ю., Рейдель А. Л., Степанов М. Н.,
Т о н ч е е в ~О. И., Основы проектирования ракетно-прямоточных двигателей.
«Машиностроение», М., 1967.
К у л а г и н И. И., Основы теории авиационных газотурбинных двигателей.
Воениздат, М., 1967.
М е л ь к у м о в Т. М. (ред.), Теория двигателей. Изд-во ВВИА им. Н. Е. Жу-
ковского, М., 1967.
У в а р о в С. Н., Авиационные газотурбинные двигатели в энергетике. (<Эн
гия», Л., 1971.
Швец Ю. И., Купчик Г. Я., Ш апочкин Н. И., Теорияавиационных
двигателей. «Наукова думка», Киев, 1971.
3 у е в В. С., М а к а р о н В. С., Теория прямоточных и ракетно-прямоточных
двигателей. «Машиностроение», М., 1971.
Ж а1$ г и Ь Р. 1., В 1111д Р. 8., Ргей1с0оп о1 ргесошЬця$юп жа11 ргеяяиге
й1я$г1Ьи$юпя 1п ясгаш1еФ епд1пея. У. 8расесгай апй Вос1~е$я, чо1. 10, Хо. 9, 1973.
Г р о д з о в с к и й Г. Л., Сверхзвуковые осесимметричные конические течения
с коническими скачками, граничащими с параллельным равномерным потоком.
Прикл. матем. и механ., т. 23, № 2, 1959.
Г р о д з о в с к и й Г. Л., Автомодельное движение газа при сильном перифе-
рийном взрыве. Докл. АН СССР, т. 111, № 5, 1965.
О е ш е С г 1 а й е я 8. Т., А поча1 я1я$еш аког ярасе 111дЬС ия1щ, а ргори1я1че 11и1й
ассииш1а$ог. У. Вгй. 1п$егр1. 8ос., чо1. 17, Хо. 5, 1959.

ЛИТЕРАТУРА
С а ш ас М., В е г и е г Р., Ап огЫСа1 а1г-ясоор1пд чесЫс1е. АяСгопацС1ся, чо1. 6,
Хо. 8, 1961.
Ве1сЬе1 В. Н., Яш1С11 Т. Ь., Нап1огй В. В., РОСепС1а11С1еяо1а1„с()
ор1пц е1есСг1са1 ярасе ргори1яоп яуяСешя. Ргодг. 1п АяСгопацС. апй АегопаиС., чо1. 9,
Е1есСг1са1 Ргор. Вече1., Я. У., 1963.
Т о к а р е в В. В., Ф а т к и н Ю. М., Накопитель рабочего вещества в зада-
чах оптимизации движения с ограниченной мощностью. Инж. журнал АН СССР,
т. 5, вып. 3, 1965.
К а и и ц а П. Л., Турбодетандер для получения низких температур и его при-
менение для схсижения воздуха. Техн. физика, вып. 2, 1939.
Архаров А. М., Бутенков К. С., Головинцов А. Г., Техника
низких температур, «Энергия», М.— Л., 1964.
О т м а х о в а И. П., Течение разреженного газа через диффузор (конфузор).
Вестник МГУ. Математика, механика, М 4, 1968.
Б о р о в к о в И. С., В е р ш и н и н И. Д., О коэффициенте расхода воздухо-
заборника при свободномолекулярном режиме течения. Уч. записки ЦАГИ,
Я 5, 1970.
Богомазов В. И., Кузнецов Ю. Е., Носик В. А., О характери-
стиках цилиндрических воздухозаборников в свободномолекулярном потоке.
Уч. записки ЦАГИ, М 5, 1970.
Бугров ский В. В., Винцевич Г. А., Иишнепольский И. М.,
Душин А. Н., Кармишин В.А., Мартьянова Т. С., Уланов Г.М.,
Ч у и р у н Б. Е., Ш е в я к о в А. А., Основы автоматического управления
ядерными космическими энергетическими установками. Под ред. акад. Б. Н. Пет-
рова, «Машиностроение», М., 1974.
Б угр ов ски й В. В., 3Ку ко в В. В., П р е о б р аж е н с к и и С. С., С о л
нечный Э. М., Уланов Г. М., Чупрун Б. Е. Динамика и управление
ядерным ракетным двигателем. Под ред. акад. Б. Н. Петрова, «Атомиздат»,
М., 1974.
2.382.
2.383.
2.384.
2.385.
2.386.
2.387.
2.388.
2.389.
2.390.
2.391.
К главе 3
31. Стечкин Б. С., К азанджан П. К., Алексеев А. П., Гово-
ров А. Н., Коновалов Н. Е., Нечаев Ю. Н., Федоров Р. М.,
Теория реактивных двигателей. Оборонгиз, М., 1958.
3.2. С о г118 я Ж. В., Ргори1яоп яуяСешя аког ярасе П1дЬС. Х. У., 1960. Русский пере-
вод: К о р л и с с У. Р., Ракетные двигатели для космических полетов. ИЛ, М.,
1962.
33. Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., Механикакос-
мического полета с малой тягой. Инж. журнал, т. 3, вып. 3 и 4, 1963; т. 4, вып. 1 и 2,
1964.
34. Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., Механика
космического полета с малой тягой. «Наука», М., 1966.
К главе 4
Ь а я я Н., Ь о г г е1 3., Ьож ассе1егаС1оп Са1~е-оЛ 1гош а яаСе111Се огЫС. 3. Ашег.
ВосЕ Яос., чо1. 31, Хо. 1, 1961.
М о и с е е в Н. Н., Методы нелинейной механики в задачах динамики спутников.
Ргос. Х1И 1пСегпаС. АяСгопаиС. Сопдт. 1962, Иеп., 1964.
Л а р и ч е в а В. В., Р е й н М. В., Замечание об осреднении уравнений возму-
щенного движения в оскулирующих элементах при изменении эксцентриситета
в широких пределах. Космические исследования, т. 3, М 3, 1965.
Л а р и ч е в а В. В., Р е й н М. В., Асимптотика уравнений небесной механики,
пригодная при большом диапазоне изменения эксцентриситета. Космические ис-
следования, т. 3, М 1, 1965.
Я ш 1 С Ь Р. Т., ОрС1шйаС1оп о1 шц1С1яСаде огЫС Сгапя1ег ргосеьяея Ьу йупаш1с
ргодгашш1пд. 3. Ашег. Вос1~. Яос., чо1. 31, Хо. 11, 1961. Русский перевод: Ракетная
техника, М 11, 1961.
М о и 1 С о и Р. В., Ап 1пСгойисС1оп Со се1еяС1а1 шесЬашся. МсМ111ап, Х. У., 1914.
Русский перевод: М у л ь т о н Ф., Введение в небесную механику (под ред.
Г. Н. Дубошина). ОНТИ, 1935.
Д у б о ш и н Г. Н., Небесная механика. Физматгиз, 1963.
С у б б о т и н М. Ф., Курс небесной механики, т. 1. ГТТИ, 1933; т. П, ОНТИ,
1937; т. 1И, ОНТ И, 1949.
Н е г г1 с ~ Я., ЕагСЬ яаСе111Сея ап ге1аСей огЫС апй регСигЬаС1оп СЬеогу. Ярасе
ТесЬпо1., сЬ. 5, ей. ЯеНегС, Х. У., 1959. Русский перевод: Космическая техника,
под ред. Г. Сейферта, гл. 3, «Наука», 1964.
Н е г г1 с 1~ Я., АяСгойупаш1ся. Рг1псеСоп, М. У., 1959.
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
4.7.
4.8.
4.9.
4.10.

684
ЛИТЕРАТУРА
К главе 5
5.1.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
5.12.
4.11.
4.12.
4.13.
4.14.
4.15.
4.16.
4.17.
4.18.
4.19.
4.20.
4.21.
4.22.
4.23.
4.24.
4.25.
4.26.
Е и г1 с 1» е К. А., Брасе 111дЬС, го1. 1. ЕпсчгопшепС апй се1еяС1а1 тесЬап1ся,
сЬ. 6, РегСигЬаСюп. Рг1псеСоп, Уап ЯояСгапй, 1960. Русский перевод: Э р и к е К.,
Космический полет, т. 1, гл. 6, Физматгиз, 1963.
Н е г г 1 с 1» Я., Тга1есСогу ЫпйатепСа1я. НапйЬоо1» о1 АяСгопаиС. Епд., сй. 4.
Мс бган-Н111, Я. У., 1961.
Охоцимский Д.Е., Энеев Т.М., Таратынова Т.П., Определение
времепи существовапия искусственного спутника Земли и исследованпе вековых
возмущений его орбиты. УФН, т. 63, М 1а, 1957.
Я е ж С о и В. В., Уаг1аЬ1ея СЬаС аге ЙеСегпппей Хог апу огЫС. Х. Атег. Вос1».
Яос., 'го1. 31, Яо. 3, 1961.
Р 1 и е я Я., Уаг1аСюп оХ рагатеСогя Хог пеаг с1гси1аг апй 1оъч 1пс11паСюп огЫСя.
1АЯ Рарег, М 61-7: 29$Ь Апп. МсеС. 1АЯ, Я. У., 1961.
Ж о и д Р., Яопя1пдц1аг гаг1аС1оп о1 рагатеСег ециаСюп аког сотриСаСюп о1 ярасе
Сга1есСог1ея. У. Аког. Вос1.. Кос., го1. 32, Яо. 2, 1962. Русский перевод.. Ракетная
тех пика, М 2, 1962.
К у з и а к Г. Е., К о п и и н Ю. М., Новая форма уравнений движения спут-
пика и приложение ео к исследовапию движений, близких к кеплеровым. Ж. вычисл.
матем. и матем. фпз., т. 3, Х~ 4, 1963.
Ь а я я Н., Я о 11 о м а у б. В., МоСюп о1 а яаСе111Сс ипйег СЬе 1п11цепсе о1 а соп-
яСапС погп1а1 С11гцяС. У. Атег. Вос1». Яос., го1. 32, Яо. 1, 1962. Русский перевод:
Ракетная техника, Х 1, 1962.
О х о ц и м с к п й Д. Е., Э н е е в Т. М., Некоторые вариацноппые задачи, свя-
занные с запуском искусствепного спутника Земли. УФН, т. 63, Х 1а, 1957.
О х о ц и м с к и й Д. Е., Э и е е в Т. М., О выведении искусственного спутника
Земли па орбиту. Ргос. У1П 1пСегпаС. АяСгопаиС. Сопряг. 1957, У1еп., 1958.
Кузмак Г. Е., Исаев В. К., Давндсоп Б. Х., Оптимальные режимы
движения точки переменной массы в однородном центральном поле. Докл. АН СССР,
т. 149, М 1, 1963.
Исаев В. К., Сонин В. В., Давидсон Б. Х., Оптимальные режимы
движепия точки переменной массы с ограниченной мощпостью в одпородпом цен-
тральном поле. Космические исследования, т. 2, Ю 4, 1964.
Ив апов Ю. Н., Токарев В. В., Шалаев Ю. В., Оптимальныетраек-
тории и оптимальные параметры космических аппаратов с двигателями ограничен-
ной мощности. Космические исследования, т. 2, Ю 3, 1964.
Р о б е р с о н Р., Орбитальное движение спутников Земли. Сб. «Научные проб-
лемы искусственпых спутников», ИЛ, М., 1959.
С 1 С г о и Я. У., ЯаСе111Се ИеС1шея ипйег СЬе 1п11иепсе о1 сопС1пиопя СЬгияС, аСто-
ярЬег1с йгад, апй р1апеС оЬ1асепея. А1АА Х., ~о1. 1, Яо. 6, 1963. Русский перевод:
Ракетная техника и космонавтика, М 6, 1963.
Созраг 1пФегпаМопа1 Ве1егепсе АФтозрЬеге (С1ВА-641.
Н о Ь м а п и 1Ч., 01е Егге~сЬЬаг1»е1С йег Нип"пеЬ1»огрег, МцпсЬеп, 1925.
Н о «! 1» е г Ь. Р., Я 11 Ь е г В., Т11е ЫеИ1рС1са1 Сгапятег ЬеСжееп с1гсы1аг
сор!апег огЬ1Ся. О. А. Тесйп. Метог1а1, Хо. 2-59, Агру Ва11ЬС1с М1яя11е Адепсу, 1959.
Ь и Т1 и д, ОрС1пшт огЫСа1 Ьу 1шри1яея. 3. Атег. Вос. Яос., го1. 30, Яо. 11,
1960.
Ь и Т 1 и д, ОрС1пшт огЫСа1 Сгапйег Ьу яегега1 1шри1яея. АяСопаиС. АсСа, го1. 6,
Яо. 5, 1962.
У е и Ь е 1» е В. Р., б е е г С я У., Арр11саСюп Йц рг1пс1ре Йе шах1пшт а1а яуп1еяе
Йея СгапяегСя орС1шах Йапя ип сйашр Йе пгапЬаС1оп р1апеСасе. Ргос. ХУ 1пСегпаС.
АяСопаиС. Сопряг. 1964, Жагяка га, 1965.
Ч а р н ы й В. И., Об оптимальных траекториях со многими импульсами. Сб. «Ис-
кусственные спутники Земли», вып. 16, 1963.
И л ь и н В. А., Переход космического аппарата, тормозящегося в атмосфере планеты,
на орбиту искусственного спутника. Инж. журнал, т. 3, ~~" 2, 1963.
И л ь и н В. А., К расчету траекторий перелета космических аппаратов между
компланарными круговыми орбитами в ньютонианском гравитационном поле.
Космические исследования, т. 2, М 5, 1964.
П о г о р е л о в В. Г., Теория кеплеровых движений летательных аппаратов.
Физмат гиз, М., 1961.
К у з м а к Г. Е., Линеаризованная теория оптимальных перелетов. Космические
исследования, т. 3, М 1, 1965.
Е г о р о в В. А., Пространственная задача достижения Луны. «Наука», М.,
1965.
И в а ш к и н В. В., Оптимальные импульсные переходы внутри кольца на орбиты,
не пересекающие его границ. Космические исследования, т. 4, М 4, 1968.

685
ЛИТЕРАТУРА
5.13.
5.14.
5.15.
5.16.
5.17.
5.18.
5.19.
5.20.
5.21.
5.22.
5.23.
5.24.
5.25.
К главе 6
6.1.
6.2.
6 3.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19. Г р о д з о в с к и й Г. Л., О движении тела переменной массы с учетом реляти-
вистских эффектов. Изв. АН СССР, ОТН, Механика и машиностроение. М 5, 1962.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
И в а щ к и н В. В., Оптимальные импульсные переходы в кольце между компла-
нарными орбитами, пересекающими его границы. Космические исследования, т. 7,
Я 5, 1969.
О х о ц и м с к и й Д. Е., Э н е е в Т. М., Некоторые вариационные задачи,
связанные с запуском искусственного спутника Земли. УФН, т. 63, М 1а, 1957.
Е г о р о в В. А., О решении одной вырожденной вариационной задачи опти-
мальном подъеме космической ракеты. Прикл. матем. и механ., т. 22, Л"" 1, 1958.
Ь а ж Й е и О. Г., М1п1та1 гос1»еС Сга3есСог1ея. 3. Атег. Нос. Яос., чо1. 23, Яо.
11 — 12, 1953.
Ь а ж с1 е п Р. Р., ТгапйегЬеСюееп с1гсц1аг огЬ1Ся. ЗеС Ргорц1я1оп, чо1. 26, Хо. 7, 1965.
ОрС1ш1каС1оп ТесЬп1пцея ю1СЬ Арр11саС1опя Со Аегоярасе яуяСешя. Асад. Ргеяя Я. У.—
Ьопйоп, 1962. Русский перевод: Методы оптимизации с приложениями к механике
космического полета. «Наука», М., 1965.
Д у б о в с к и й С. В., Межорбитальные и межпланетные перелеты. Космические
исследования, т. 5, М 4, 1967.
Г у р м а н В. И., Структура оптимальных режимов движения ракет в однородном
гравитационном поле. Космические исследования, т. 4, М 6, 1966.
Д у б о в с к и й С. В., О скользящих оптимальных режимах управления дина-
мическими системами. Сб. «Механика космического полета», «Машиностроение»,
1969.
Ч а р н ы й В. И., Об изохронных производных. Сб. «Искусственные спутники
Земли», М 16, Изд-во АН СССР, 1963.
Л у р ь е А. И., Свободное падение материальной точки в кабине спутника. Прикл.
матем. и механ., т. 27, вып. 1, 1963.
А и д р е е в В. Д., Теория инерциальной навигации. Автономные системы.
«Наука», 1966.
Д у б о ш и н Г. Н., Небесная механика. Основные задачи и методы. Физматгиз,
1963.
Р г е я С о и — Т Ь о т а я Н., 1пСегогЬ1Са1 СгапярогС Сесйп1ццея. 3. Вг1С. 1пСегр1.
Яос., 'го1. 11, Хо. 4, 1952.
Р г е я С о и — Т Ь о т а я Н., Тюо аяресСя о1 СЬе С1ше е1еп1епС 1п 1пСегр1апеСагу
111д11С. Ргос. У 1пСегпаС. АяСгопацС. Сопряг. 1954, Иеп., 1955.
Я С ц Ь11 и д е г Е., Рояя1Ь111С1ея о1 е1есСг1са1 ярасе яЫр ргорц1яюп. Ргос. У 1пСег-
паС. АяСгопацС. Сопдт. 1954, Иеп., 1955.
В ц я я ц г Й В. Ж., А пцс1еаг-е1есСг1с ргорц1я1оп яуяСеп1. 3. Вг1С. 1пСегр1. Яос.,
чо1. 15, Хо. 6, 1956.
Р г е я С о и — Т 11 о т а я Н., 1пСегогЬ1Са1 СгапярогС СесЬп1пцея. Веа11С1ея о1 Яраяе
Тгаче1, Ьопйоп, 1957.
Я С ц Ь 11 и д е г Е., Рея1дп апп рег1огтапсе йаСа о1 ярасе яЫря ~лСЬ 1ои1с ргорц1-
яюп яуяСешя. Ргос. УП1 1пСегпаС. АяСгопацС. Сопдт. 1957, Иеп., 1958.
Р г е я С о и — Т Ь о п1 а я Н., А поСе оп а пцс1еаг е1есСг1са1 ргорц1яюп яуяСеш.
У. Вг1С. 1пСегр1. Яос., чо1. 16, Хо. 9, 1958.
Р г е я С о и — Т Ь о ш а я Н., Яоп1е Йея1дп рагашеСегя о1 а я1шрИ1ео юп гос1»еС.
3. Вг1С. 1пСегр1. Яос., чо1. 16, Хо. 10, 1958.
Ь е 1 С п1 а и и 6., ТЬе пцс1еаг-роюегей 1оп гос1»еС. 3. Вг1С. 1пСегр1. Яос., чо1. 16,
Хо. 10, 1958.
С о г и о д В., ТЬе орС1шцш че1ос1Су о1 ргоре11апС е3есСюп. У1яСая 1п АяСгопацС.,
чо1. 1, Х. У., 1958.
Я С ц Ь11п д е г Е., Айчапсей ргорц1яюп яуяСеп1я аког ярасе чеЫс1ея. Ргос. 1Х
1пСегпаС. АяСгопацС. Сопдт., Майг1Й, 1958, Иеп., 1959.
М о е с 1» е 1 Ж. Е., Ргорц1яюп шеСЬой 1п аяСгопацС1ся. Ргос. 1Х 1пСегпаС. Ая~го-
пацС. Сопдт., Майг1Й, 1958, У1еп., 1959.
Р г е я С о и — Т Ь о п1 а я Н., ТЬе пцс1еаг-роюегей 1оп гос1»еС. 3. Вп'С. 1пСегр1.
Яос., чо1. 17, Хо. 3, 4, 1959.
Ь а п д п1 ц 1 г Р. В., ОрС1тйаС1оп о1 гос1»еСя 1п юЫсЬ Ые1 1я поС цяей ая ргоре11апС.
Ярасе ТесЬпо1., с11. 9, Х. У., 1959.
1 г г 1 и д 3. Н., Ьою-СЬгцяС 111дЫ: чаг1аЬ1е ехЬацяС че1ос1Су 1п дтач1СаС1опа1 Йе1йя.
Ярасе ТесЬпо1., сЬ. 10, Х. У., 1959.
Я С и Ь11 п д е г Е., Я е 1 С к В. ~., Е1есСгояСаСЖ ргорц1яюп яуяСеп1я аког ярасе
чеЫс1ея. Айч. Ярасе Яс1., чо1. 2, 1960.
С а т а с М., 0яе о1 епегду яСогаде 1п 1ою-СЬгцяС ярасе111дЫ. 3. Ап1ег. ВосК. Яос.,
чо1. 30, Хо. 1, 1960.
С г о с с о Ь., Мессаи1са Йе11а ргорц1яюпе ярала1е. Ргос. Яеш1паг Айч. оп АяСго-
пацС. Ргор. 1960, М11ап, 1962.

686
ЛИТЕРАТУРА
1'родзовский Г. Л., Иванов Ю. Н.,'~='Токарев В. В., Механик~
космического полета с малой тягой. Инж. журнал АН СССР, т. 3, М 3, 1963.
1 г г1 и д У. Н., В 1ц ш Е. К., Сошрага$гге рег1огшапсе о1 Ьа111яйс апй 1ож-
СЬгцяй геЬ1с1ея аког 111дЬС Со Магя. Ухая 1п Ая1гопацС., го1. 2, Х. У., 1959.
Гродзовский Г. Л., Иванов 10. Н., Токарев В. В., О движении
тела переменной массы с постоянной и убывающей затратой мощности в гравита-
ционном поле, ч. 1П. Ргос. Х1У 1п$егпаС. Аяйгопац$. Сопдт., 1963.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., О движении
тела переменной массы с постоянной затратой мощности в гравитационном поле.
Докл. АН СССР, т. 137, М 5, 1961; Ргос. Х11 1п$егпа$. АвФгопаи$. Сощг., Чгавп1пд-
Соп, 1961, Х. У., 1963.
И в а н о в Ю. Н., Оптимальное изменение мощности при движении тела перемен-
ной массы в гравитационном поле. Прикл. матем. и механ., т. 26, М 4, 1962.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., О движении
тела переменной массы с постоянной и убывающей затратой мощности в гравита-
ционном поле, ч. П. Ргос. Х1П 1пСегпаС. АяйгопацС. Сощт., Уагпа, 1962, У1еп.—
Х. У., 1964.
М а г $ е 11 у У., Ор0ш1ка0оп о1 1пСегр1апеСагу ргорц1яюп яуяСешя. 1ВЕ Тгаия.
оп Хцс1еаг Яс1., го1. Я-9, Хо. 1, 1962.
Ц а н д е р Ф. А., Применение металлического топлива в ракетных двигателях.
Ракетная техника, М 1, 1936; см. Ц а н д е р Ф. А., Проблема полета при помощи
реактивных аппаратов. Межпланетные путешествия. Оборонгиз, М., 1961.
Т о к а р е в В. В., Оптимальное управление источником мощности при движении
тела переменной массы в гравитационном поле с активным сбросом мощности.
Прикл. матем. и механ., т. 27, М 4, 1963.
6.20.
6.21.
6.22.
6.23.
6.24.
6.25.
6.26.
6.27.
6.28.
К главе 7
7.1.
7.2.
7.3.
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
7.10.
7.11.
7.12.
7.13.
7.14.
7.15.
7.16.
7.17.
Б е л е ц к и й В. В., Е г о р о в В. А., Межпланетные полеты с двигателями
постоянной мощности. Космические исследования, т. 2, М 3, 1964.
И с а е в В. К., С о н и н В. В., Об одной нелинейной задаче оптимального управ-
ления. Автоматика и телемеханика, т. 23, М 9, 1962.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., О движении
тела переменной массы с постоянной затратой мощности в гравитационном поле.
Докл. АН СССР, т. 137, М 5, 1961; Ргос. ХП 1п$егпа$. Ав$гопаий. Сощг., Чгавп1пд$оп,
1961, Х. У., 1963.
Иванов Ю. Н., Токарев В. В., Шалаев Ю. В., Оптимальныетраек-
тории и оптимальные параметры космических аппаратов с двигателями ограниченной
мощности. Космические исследования, т. 2, М 3, 1964.
1 г г 1 и д У. Н., Ьож-СЬгцяС 111дЫ: гаг1аЬ1е ехЬацяС ге1осйу 1п дтагйайопа1 Йе1йя.
Ярасе ТесЬпо1., сЬ. 10, Х. У. 1959.
Л е б е д е в Л. А., С а к о в с к и й С. А., О необходимых и достаточных усло-
виях экстремума функционала в задаче оптимального перелета аппарата с двига-
телем малой тяги. Изв. вузов, сер. «Авиац. техн.», М 4, 1964.
Ь е $ С ш а и и б., М1п1шцш Сгапя1ег вше аког а рожег-11шйей гос1~еС. Х. Арр1.
МесЬаи., го1. 28, Хо. 2, 1961.
Р г е я С о и — Т Ь о ш а я Н., 1п$егогЬ1$а1 СгапярогС ФесЬп1ццея. Веа1Мея о1 Ярасе
Тга ге1, Ьопйоп, 1957.
Р г е я С о и — Т Ь о ш а я Н., Яоше йея1дп рагашеСегя о1 а я1шрИ1ей юп гос1~еС.
У. Вгй. 1п$егр1. Яос., го1. 16, Хо. 10, 1958.
Исаев В. К., Сонин В. В., Давидсон Б. Х., Оптимальные режимы
движения точки переменной массы с ограниченной мощностью в однородном цен-
тральном поле. Космические исследования, т. 2, М 4, 1964.
Б е л е ц к и й В. В., Е г о р о в В. А., Разгон космического аппарата в сфере
действия планеты. Космические исследования, т. 2, М 3, 1964.
1 г ч 1 и д 3. Н., В 1ц ш Е. К., Сошрага$гге рег1огшапсе о1 Ьа111яйс апй 1отч-
СЬгцяй геЬ1с1ея аког 111дЫ Со Магя. 71яСая 1п Аяйгопацй., чо1. 2, Х. У., 1959.
Ме1Ьоцгпе Ж. б., Яацег С. б., В1сЬагйяоп О. Е., 1пйегр1апейагу
Сга1есСогу ор0шйа0оп жйЬ рожег-11шйей яуяФешя. Ргос. 1АЯ Яушр. оп УеЫс1е
Яуяй. О рюш., Х. У., 1961.
М е 1 Ь о ц г и е Ж. б., ТЬгее-й1шепя1опа1 ор0шцш СЬгцяй Сга1есйог1ея Уог рожег-
11шйей ргорц1я1оп яуяСешя. Х. Ашег. ВосЕ. Яос., с~о1. 31, Хо. 12, 1961.
М е1 Ь о ц г и е Ж. б., Я а ц е г С. б., Орйшцш фЬгця$ ргодташя аког рожег-
11шйей ргорц1яюи яуяСешя. Аяйгопацй. Асйа, го1. 8, Хо. 4, 1962.
М е 1 Ь о ц г и е Ж. б., Я а ц е г С. б., Орйшцш 1пйегр1апейагу гепйечоця жФЬ
рожег-1пш$ей геЬ1с1ея. А1АА 3., чо1. 1, Яо. 1, 1963.
М е1Ь о ц г и е Ж. б., Я а ц е г С. б., Орйшцш ЕагСЬ вЂ” Магя гоцпйСг1р Сга1есСо-
г1ея ц01Ыпд а 1ож-СЬгояС рожег-11шйей ргорц1яюп яуяСеш. Айч. 1п ФЬе Аяйгопацй.
Яс1., сто). 13, 1963.

687
ЛИТЕРАТУРА
7.18.
7.19.
7.20.
7.21.
7.22.
7.23.
7.24.
7.25.
7.26.
7.27.
7.28.
7.29.
7.30.
7.31.
7.32.
7.33.
7.34.
7.35.
7.36.
7.37.
7.38.
7.39.
К главе 8
И в а н о в Ю. Н., О движении тела переменной массы с ограниченной мощностью
и заданным активным временем. Прикл. матем. и механ., т. 27, М 5, 1963.
И в а н о в Ю. Н., Ш а л а е в Ю. В., Оптимальный поворот плоскости круговой
орбиты поперечной силой. Космические исследования, т. 3, М 5, 1965.
И с а е в В. К., Принцип максимума Л. С. Понтрягина и оптимальное програм-
иирование тяги ракет. Автоматика и телемеханика, т. 22, М 8, 1961; т. 23, 3~ 1,
1962.
Безменов В.М., Овсянников Р. Н., Токарев В. В., Построение
оптимальных управлений и траекторий межпланетных перелетов с нерегулируе-
иыми двигателями ограниченной мощности. Тр. ЦАГИ, вып. 1558, М., $974.
Ь а в д е и О. Р., ОрСш1а1 еясаре 1гош а с1гсц1аг огЬ1С. АяСгопацС. АсСа, го1. 4,
Яо. 3, 1958.
8.1.
8.2.
8.3.
8.4.
8.5.
Я а1С к е г С., Р е С Ь е г о 1 1 С. Ж., А Й1гесС чаг1аС1опа1 шеСЬой аког СЬе са1сц1а-
Сюп о1 орС1шцш СЬгцяС ргодташ аког роюег-11ш1Сей 1пСегр1апеСагу 111дЬС. АяСгопацС.
АсСа, го1. 7, Ио. 1, 1961.
Я Ь е г ш а и В., Ьою СЬгцяС еясаре Сга3есСог1ея. Ргос. 1АЯ Яушр. оп УеЫс1е ЯуяС.
ОрС1ш., И. У., 1961.
И в а н о в Ю. Н., Ш а л а е в Ю. В., Метод скорейшего спуска в применении
к расчету межорбитальных траекторий с двигателями ограниченной мощности.
Космические исследования, т. 2, М 3, 1964.
П о к р о в с к а я С. А., О решении пространственной задачи гелиоцентрических
перелетов с двигателем постоянной мощности методом скорейшего спуска. Косми-
ческие исследования, т. 2, М 6, 1964.
Р а ц1 Й е г я С. В., ОрС1шцш СЬгцяС ргодташш1пд о1 е1есСг1са11у роюегей гос1~еС
геЫс1ея 1п дтаг1СаС1опа1 йе1Й. 3. Ашег. ВосК. Яос., го1. 30, Ио. 10, 1960.
Р а ц1 Й е г я С. В., ОрС1шцш СЬгцяС ргодташш1пд о1 е1есСг1са11у роюегей гос1еС
чеЫс1ея аког еясаре. А1АА 3., го1. 1, Ио. 1, 1963.
Е й е1Ь а ц ш Т. И., ТЬе цяе о1 Ь1дЬ апй 1ою СЬгцяС ргорц1яюп 1п сошЬ1паС1оп
аког ярасе ш1яяюп. Ргерг. Ашег. АяСгопацС. Яос., Ио. 61-104, 1961.
Белецкий В. В., Е горов В. А., Е ршов В. Г., Анализ траекторий
межпланетных полетов с двигателем постояпной мощности. Космические исследо-
вания, т. 3, М~ 4, 1965.
Л е б е д е в В. Н., Вариационная задача о взлете космического аппарата с кру-
говой орбиты. Ж. вычисл. матем и матем. физ., т. 8, М 6, 1968.
И в а и о в Ю. Н., Ш а л а е в Ю. В., Оптимальный поворот плоскости круговой
орбиты поперечной силой. Космические исследования, т. 3, М 5, 1965.
6 о Ь е С к Р. Ж., ОрС1ша1 гаг1аЫе-СЬгцяС Сгапя1ег о1 а роюег-11ш1Сей госКеС ЬеСюееп
пе1дЬЬог1пд с1гсц1аг огЬ1Ся. ААААА 3., го1. 2, Ио. 2, 1964. Русский перевод: Ракетная
техника и космонавтика, М 2, 1964.
С о Ь е С к Р. Ж., ЕггаСа: ОрС1ша1 гаг1аЫе-СЬгцяС Сгапя1ег о1 а роюег-11ш1Сей гос1~еС
ЬеСюееп пе1дЬЬог1пд с1гсц1аг огЬ1Ся. А1АА 3., го1. 2, Ио. 12, 1964. Русский перевод:
Ракетная техника и космонавтика, М 12, 1964.
Ь е 1 С ш а и и 6., В о я я Я., Ьою ассе1егаСюп Сга3есСогу орС1ш1каСюп 1п а яСгопд
сепСга1 1огсе Йе1Й. Ргос. 1АЯ Яуп1р. оп УеЫс1е ЯуяС. ОрС1ш., И. У., 1961.
Е й е 1 Ь а ц ш Т. Х., ТЬеогу о1 шах1ша апй ш1п1ша. ОрС1ш1к. СесЬп., сЬ. 1. Ей. Ьу
6. Ье1Сшапп, Асай. Ргеяя, 1961.
Е Й е 1 Ь а ц ш Т. Х., Ргорц1яюп гецц1гешепСя аког сопСго11аЫе яаСе111Сея. 3. Ашег.
ВосЫ. Яос., го1 31, Ио. 8, 1961.
Е Й е 1 Ь а ц ш Т. И., ОрС1шцш 1ою-СЬгцяС Сгапя1ег ЬеСюееп с1гсц1аг апй е111рС1с
огЬ1Ся. Ргос. 4СЬ 13. Я. ИаС. Сопдт. Арр1. МесЬ., Вег1~е1еу, СаИ., 1962, го1. 1; Регда-
шоп Ргеяя, 1962.
В 1111 1~ В. Н., Яоше орС1ша1 1ою-ассе1егаС1оп гепйегоця шапецстея. А1АА 3.,
го1. 2, Яо. 3, 1964.
6 о Ь е С к Р. Ж., А 11пеаг СЬеогу о1 орС1шцш 1ою-СЬгцяС гепйегоця Сга3есСог1ея.
3. АяСгопацС. Яс1., го1. 12, Хо. 13, 1965.
Исаев В. К., Курьянов А. И., Сонин В. В., Применение принципа
максимума в ракетодинамике. Ргос. Х1У 1пСегпаС. АяСгопацС. Сопдт. 1963, Жаг-
якаюа, 1964.
Е ф и м о в Г. Б., О х о ц и м с к и й Д. Е., Об оптимальном разгоне космиче-
ского аппарата в центральном поле. Космические исследования, т. 3, М 6, 1965.
Л а р и ч е в а В. В., Р е й н М. В., О решениях задачи оптимального перелета
с эллиптической орбиты на параболическую. Космические исследования, т. 6, М 2,
1968.
Е ф и м о в Г. Б., Оптимальный разгон в центральном поле до гиперболических
скоростей. Космические исследования, т. 8, Ю 1, 1970.

688
ЛИТЕРАТУРА
8.6. Р е г Ы1 и я Р. М., И1дЬС шессЬап1ся о11ож-СЬгпяС ярасе сгай.УАХИЯ, го1. 26, Мо. 5,
1959.
8.7. М о е с 1~ е 1 Ж. Е., Тга1есСог1ея ж1СЬ сопяСапС СапдепС1а1 СЬгцяС 1п сепСга1 дтасчСа-
Сюпа1 Йе1Йя. ХАБА ТесЬп. Вер. В-53, ЖаяЫпфоп, 1959.
8.8. М о е с 1~ е 1 Ж. Е., РаяС 1пСегр1апеСагу ш1яяюп ж1СЬ 1ож-СЬгцяС ргорц1яюп яуяСетя.
ХАБА ТесЬп. Вер. В-79, ЖаяЫпфоп, 1961.
8.9. М о е с 1~ е 1 Ж. Е., 1пСегр1апеСагу Сга1есСог1ея аког е1есСг1са1у — ргоре11апй ярасе
чеЫс1ея. АяСгопацС. АяСа, го1. 7, Хо. 5, 6, 1961.
8.10. Б е л е ц к и й В. В., Е г о р о в В. А., Разгон космического аппарата в сфере
действий планеты. Космические исследования, т. 2, М 3, 1964.
8.11. О х о ц и м с к и й Д. Е., Исследование движения в центральном поле под дей-
ствием постоянного касательного ускорения. Космич. исследования, т. 2, М 6, 1964.
8.12. Л е б е д е в В. Н., Вариационная задача о взлете космического аппарата с кру-
говой орбиты. Ж. вычисл. матем. и матем. физ., т. 3, М 6, 1963.
8.13. Л е б е д е в В. Н., Расчет движения космического аппарата с малой тягой. Серия
«Математические методы в динамике космических аппаратов», вып. 5. ВЦ АН СССР,
М., 1968.
814. Аврамченко Р.Ф., Безменов В.М., Винокуров В.А., Тока-
р е в В. В., Минимальное время перелета Земля — Марс — Земля с нерегулируемым
двигателем малой тяги. Космические исследования, т. 5, М 3, 1967.
8.15. Р е й н М. В., Об оптимальных по быстродействию переходах с эллиптической
орбиты на параболическую материальной точки переменной массы. Уч. записки
ЦАГИ, т. 2, М 3, 1971.
8.16. Л а р и ч е в а В. В., Р е й н М. В., О мпогозначности экстремальных решений
задач оптимального управления. Докл. АН СССР, т. 180, М 6, 1968.
8.17. Р е й н М. В., Аналитический метод исследования многозначности экстремальных
решений в задачах оптимального перелета. Сб. анпотаций докл. И1 Всесоюзного
съезда по теоретической и прикладной механике. Изд-во АН СССР, М., 1968;
Тр. ЦАГИ, вып. 1393, М., 1972.
8.18. Г у р м а н В. И., Об оптимальных траекториях реактивного аппарата в цен-
тральном поле. Космические исследования, т. 3, М 3, 1965.
8.19. Г у р м а н В. И., Об оптимальпых переходах между компланарпыми эллиптиче-
скими орбитами в центральном поле. Космические исследования, т. 4, М 1, 1966.
820. Кротов В. Ф., Букреев В. 3., Гурман В. И., Новыеметодывариа-
ционпого исчисления в динамике полета. «Машиностроение», М., 1969.
821. Безменов В.М., Овсянпиков Р.Н., Токарев В.В., Минимальное
время перелетов Земля — Марс, Земля — Венера с нерегулируемым двигателем огра-
ниченпой мощности. Космические исследования, т. 11, М 2, 1973.
8.22. Мас Кау 3. Я., Вояяа Ь. О., Х1шшегшап А. У., ОрС1шцш1ою-ассе-
1егаСюп Сга1есСог1ея аког ЕагСЬ вЂ” Магя Сгапя1ег. Ргос. 1АЯ Яушр. оп УеЫс1е ЯуяС. ОрС1ш.,
Х. У., 1961.
8.23. Х е Ь 1 е Н., Хцг ОрС1ша11я1егцпд 1пСегр1апеСагег ~5еЬегдапяЬаЬпеп ш1С Ые1пег
ЯсЬцЬЬеясЬ1еци1дцпд. Те11 П цпй Ш. Вацш1аЬгИогясЬцпд, ВЙ. 8, Л' 3, 1964.
8.24. Ь 1 и Й о г 1 е г %., М о у е г Н. О., Арр11саС1оп о1 а 1ою-СЬгцяС Сга1есСогу орС1-
ш1каСюп ясЬеп1е Со р1апаг ЕагСЬ вЂ” Магя Сгапя1ег. Х. Ашег. ВосЕ Яос., го1. 32, Хо. 2,
1962. Русский перевод: Ракетная техника, М 2, 1962.
8.25. Б е л е ц к и й В. В., Е г о р о в В. А., Межпланетные полеты с двигателем по-
стоянной мощности. Космические исследования, т. 2, М 3, 1964.
8.26. Л е б е д е в В. Н., Р у м я н ц е в Б. Н., Вариационная задача о перелете
между двумя точками в центральном поле. Сб. «Искусственные спутники Земли»,
вып. 16, 1963.
8.27. Р а ц 1 Й е г я С. В., М1п1шцш С1те яСеег1пд рго~ташя аког огЬ1Са1 Сгапя1ег ж1СЬ
1ож-СЬгцяС гос1~еС. АяСгопацС. АсСа, го1. 7, Хо. 1, 1961.
8.28. Ме1Ьоцгие Ж. О., Яацег С. О., В1сЬагйяои Р. Е., 1пСегр1апеСагу
Сга1есСогу орС1ш1~аСюп ж1СЬ рожег-11ш1Сей яуяСешя. Ргос. 1АЯ Яушр. оп УеЫс1е
ЯуяС. ОрС1ш., Х. У., 1961.
8.29. М е 1 Ь о ц г и е %. О., Я а ц е г С. О., ОрС1шцш СЬгцяС ргодташя аког рощег-
11ш1Сей ргорц1яюп яуяСешя. АяСгопацС. АсСа, чо1. 8, Хо. 4, 1962.
8 30. М е 1 Ь о ц г и е Ж. О., Я а ц е г С. О., Рау1оай орС1шлаС1оп аког рожег-11ш1Сей
геЫс1ея. Ргодт. 1и АяСгопацС. апй АегопацС., чо1. 9, Е1есСг1с Ргор. Весте1., Х. У., 1963.
Русский перевод: Вопросы ракетной техники, М 8, 1964.
8.31. К о и н и н Ю. М., К задаче о повороте плоскости орбиты спутника. Космические
исследования, т. 3, М 4, 1965.
8.32. К о и н и н Ю. М., Исследование одноимпульсного перехода между некомпланар-
ными орбитами с учетом конечного времени действия тяги. Космические исследова-
ния, т. 6, М 6, 1968.
8.33. К о и н и н Ю. М., Приближенный апализ одного класса одноимпульсных перехо-
дов между орбитами с учетом конечного времени действия тяги. Космические иссле-
дования, т. 8, М 1, 1970.

ЛИТЕРАТУРА
Я С и Ь! 1 и д е г Е., Вез1дп апй рег1огшапсе ЙаСа о1 зрасе зЬ1ря МСЬ юп1с ргора]-
яюп зуяСешз. Ргос. УШ 1пСегпаС. АзСгопацС. Сопряг. 1957, У1еп., 1958.
М о е с]~ е1 Ж. Е., Ргорц]з1оп шеСЬой 1п азСгопацйсз. 1Х 1пСегпаС. АзСгопацС.
Сопряг., 1958.
Р г е з С о п — Т Ь о ш а з Н., А поСе оп а пцс1еаг е]есСг1са1 ргорц1зюп зузСеш.
1. Вг1С. 1пСегр]. Яос., чо]. 16. Хо. 9, 1958.
Г р о д з о в с к и й Г. Л., О движении тела переменной массы с постоянной затра-
той мощности в гравитационном поле с учетом релятивистских эффектов. Изв.
АН СССР, ОТН, Механика и машиностроение, № 5, 1962.
Р г е з С о и — Т Ь о ш а з Н., 1пСегого1Са] СгапзрогС СесЬп1ццез. Х. Вг1С. 1пСегр].
Яос., чо]. 11, Яо. 4, 1952.
Р г е 3 С о и - Т Ь о ш а 3 Н' Тжо азресСз 01 СЬе С1ше е1ешепС 1п 1пСегр]апеСагу
111дЬС. Ргос. Ч 1пСегпаС. АзСгопацС. Сопряг. 1954, Иеп., 1955.
Карасик И. Я., Овсянников Р. Н., Токарев В. В., Оптимизация
параметров управляемой системы для конечного числа заданных маневров. Косми-
ческие исследования, т. 11, № 2, 1973.
8.34.
8.35.
8.36.
8.37.
8.38.
8.39.
8.40.
К главе 9
9..1.
9.2.
9.3.
9.4.
9.5.
9.6.
9.7.
9.8.
9.9.
9.10.
9.11.
9.12.
9.13.
9.14.
9.15.
9.16.
9Л7.
9.18.
9.19.
9.20.
9.21.
9.22.
О х о ц и м с к и й Д. Е, К теории движения ракет. Прикл. матем. и механ.
т. 10, № 2, 1946.
О х о ц и м с к и й Д. Е., Э н е е в Т. М., Некоторые вариационные задачи,
связанные с запуском искусственного спутника Земли. УФН, т. 63, вып. 1а, 1957.
Ь а ж Й е и О. Р., ОрС1ша] гос]~еС Сга1есСог1ез. ЗеС Ргор., го]. 27, Яо. 12, 1957.
М 1 е 1 е А., бепега1 чаг1аС1опа] СЬеогу о1 СЬе 111дЬС раСЫ о1 гос]~еСрожегей
а1гсга1С, ш1зз1]ез апй заСе]11Се сагг1егз, АзСгопацС. АсСа, чо]. 4, Яо. 4, 1958.
М 1е 1 е А., С а р р е 11 а г1 1. О., Тор1ея 1п Йупаш1с ргодгашш1пд аког гос]~еСз,
Х. Ицдж1зз., Вй. 7, Хг. 1, 1959.
В г е а ]~ ж е 11 1. У., ТЬе орС1шйаСюп о1 Сга1есСог1ез, 3. Яос. 1пйцзСг. Арр]. МаСЬ.,
Хо. 7, 1959. Русскии перевод: Вопросы ракетной техники, № 1, 1961.
Ь е 1 С ш а и и 6., Оп а с.азз о1 чаг1аС1оп ргоыешз 1п гос]~еС 111дЬС. ВПАЯЯ, уо]. 26,
Яо. 8, 1959.
Ь е1С ш а и и 6., ЕхСгеша1 гос]~еС Сга1есСог1ез 1п роз1С1оп апй С1ше ЙерепйепС
1огсе Йе]йз. УП Апп. МееС. Ашег. АзСг. Яос., Яо. 30, 1961.
Л е й т м а п Г. (Ьейшапп С.), Об оптимальных траекториях ракет. Прикл.
матем. и механ., т. 25, № 6, 1961.
И с а е в В. К., Принцип максимума Л. С. Понтрягина и оптимальное программи-
рование тяги ракет. Автоматика и телемеханика, т. 22, № 8, 1961.
И с а е в В. К., Дополнение к работе «Принцип максимума Л. С. Понтрягина и
оптимальное программирование тяги ракет», Автоматика и телемеханика, т. 23,
№ 1, 1962.
Ь е 1 С ш а и и О., ТЬе орС1шйаС1оп о1 госЫеС Сга1есСог1ез — а яцгчеу. Ргодг. 1п АзС-
гопацС. Яс1., чо]. 1, АшяСегйаш, 1962.
Ь а ю Й е и Р. Р., ОрС1ша] 1пСегшей1аСе-СЬгцзС агсз 1п а дгаст1СаСюпа] Йе]й. АяСго-
пацС. АсСа, Бо. 8, 1962.
С о и С е и я о и Р., ЕСцйе СЬеогеС1цце Йея Сга~есСог1ея орС1ша]е Йапя цп сЬашр
Йе дгаст1СаС1оп. АяСгопацС. АсСа, Яо. 8, 1962.
М 1 е 1 е А., ТЬе са]сц]ця о1 гаг1аСюпз 1п арр11ей аегойупаш1сз апй П1дЬС шесЬа-
п1сз. ОрС1ппкаС1оп СесЬп1ццез МСЬ арр]1саСюпя Со аегозрасе зузСешя. Ей. 5у 6. Ье1С-
шапп, Асай. Ргезз, Я. У. — Ьопйоп, 1962.
Кузмак Г. Е., Исаев В. К., Давидсон Б. Х., Оптимальные режимы
движения точки переменной массы в однородном центральном поле. Докл. АН СССР,
т. 149, № 1, 1963.
Л у р ь е А. И., Управление тягой в центральном поле тяготения. 1? Всесоюзн.
съезд по теорет. и прикл. механ., 1964, Аннот. докл., М., 1964.
Д и а м а н д и е в В., Т о д о р о в К., Оптимални траектории при реактивного
движение. Годишник Софийск. ун-та. Матем. фак., т. 57, 1962 — 1963 (1964).
К е ] ] е г 3. Ь., Оп ш1п1шцш ргоре11апС раСЬз аког СЬгцзС 11ш1Сей гос]~еСз. АяСгопацС.
АсСа, го]. 10, Яо. 3 — 4, 1964.
Р 1 и е з Я., СопзСапСз о1 СЬе шоС1оп аког орС1шцш СЬгцзС Сга~есСог1ез 1п а сепСга]
1огсе Бе]й. А1АА 2., чо]. 2, Яо. 11, 1964.
~ е ц о е ]~ е В. Р., 6 е е г С з У., Арр]1саС1оп Йц рг1пс1ре Йе шах1шцш а1а зупСезе
Йез Сгапз1егСз орС1шацх Йапз 1п сЬашр Йе дгач1СаСюп р1апеСа1ге. Ргос. ХУ 1пСегпаС.
АзСгопацС Сопряг. 1964, Жагзкажа, 1965.
Н о в о с е л о в В. С., Теория приближенного решения вариационных задач
и ее приложение к исследованию движения точки перемепной массы. Вестн.
Ленингр. ун-та, № 1, 1965.
44 Механика полета

690
ЛИТЕРАТУРА
Н о в о с е л о в В. С., Аналитическая динамика и оптимальные перелеты. Тр. 11
Всесоюзн. съезда по теорет. и прикл. механ., 1964. Обзорн. докл., вып. 1, «Наука»,
М., 1965.
9.23.
С а ч о С1 С. В., ОрС1шйаС1оп о1 ши1С1яСаде ргосеяяея. У. Ярасесгай апй Вос$сеСя,
чо1. 2, Мо. 1, 1965.
9.24.
9.25. Ь ~ Ь о ~ е А. С., Арр11саС1оп о1 йупаш1с ргодгашш1пд Со С11е орС1шцш яСа~1п~
о1 гос1сеСя. 3. Ярасесгай апй Вос1сеСя, го1. 2, Мо. 1, 1965.
9.26. С и г1е у 1. С., ОрС1ша1-СЬгцяС Сга]есСог1ея 1п ап агЬ1Сгагу дгач1СаС1опа1 Яе1Й.
2. Яос. 1пйияСг. Арр1. МаСЬ., яег. А, го1. 2, Мо. 3, 1965.
9.27. В о Ь Ь 1 и я Н. М., ОрС1ша11Су о1 1пСегшей1аСе СЬгцяС агся о1 гос1сеС Сга1есСог1ея.
А1АА 3., чо1. 3, Мо. 6, 1965.
9.28. С а г о С 1 С. В., МеСЬой о1 сйагасСег1яС1с сопяСапСя апй геСгоСпгияС орС1ша11Су
1п а дгасчСаС1опа1 Ие1Й-песеяяагу апй яий1с1епС сопй1Сюпя. 2. РгапЫ1п 1пяС., ~о1. 279,
Яо. 3, 1965.
9.29. В е 11 О. 1., ОрС1ша1 Сга)есСог1ея апй СЬе ассеяяогу ш1п1пшш ргоЫеш. Аегоп.
ОцагС., го1. 16, Мо. 3, 1965.
9.30. Г у р м а н В. И., Об оптимальных траекториях реактивного аппарата в централь-
ном поле. Космические исследования, т. 3, Ю 3, 1965.
9.31. Г о р е л о в Ю. А., К теории экстремальных движений точки переменной массы
в центральном гравитационном поле. Инж. журнал, т. 5, Ю 3, 1965.
9.32. Т р о и ц к и й В. А., Оптимизация движения двухступенчатой ракеты. Прикл.
матем. и механ., т. 29, Ю 4, 1965.
9.33. М и л ь ш т е й н Г. Н., Об оптимальном осуществлении траекторий. Автоматика
и телемеханика, т. 26, Ю 4, 1965.
9.34. И с а е в В. К., О некоторых особенностях вариационной задачи Майера в ракето-
динамике. Автоматика и телемеханика, т. 26, Ю 7, 1965.
9.35. Л и т о в ч е н к о И. А., Оптимизация систем при ступенчатых ограниченияк на
управление. Автоматика и телемеханика, т. 26, Ю 8, 1965.
9.36. Б о л о н к и н А. А., Оптимизация траектории многоступенчатых летательных
аппаратов. Сб. «Исследования по динамике полета», вып. 1, «Машиностроение»
М., 1965.
9.37. К о р р В. Е., М о у е г Н. С., Месеяяагу сопй1С1опя 1ог я1пди1аг ехСгеша1я. А1АА
2., го1. 3, Мо. 8, $965.
9.38. М а г е с 1. Р., Тгапя1егФя огЫФаих есопошк1иея (огЬЫея е111рйщиея, сор1апа1гея
соах1а1ея). Весй. Аегояр., 11 о. 105, И65.
9.39. Г р о д з о в с к и й Г. Л., Некоторые вариационные задачи механики космического
полета. Механика твердого тела (Инж. журн.), Ы 6, И66.
9.40. М а11п а Р. 1., Я ш1 С Ь А. М., Р11дЫ апа1уя1я о1 СЬе яоипй1пд гос1сеС. 1АЯ,
'го1. 5, Мо. 5, 1938.
9.41. О х о ц и м с к и й Д. Е., О подъеме ракеты в воздухе на максимальную высоту.
Прикл. матем. и механ., т. 10, Ю 6, 1946.
9.42. Б е л е ц к и й В. В., О вертикальном подъеме точки переменной массы в среде
постоянной плотности. Прикл. матем. и механ., т. 20, Ю 6, 1956.
9.43. М 1 е 1 е А., Сепега1Ьей ~аг1аСюпа1 арргоасЬ Со СЬе орС1шиш СЬгцяС ргодгашш1пд
аког СЬе гегИса1 111дЬС о1 а гос1сеС. Х. Р1идзпяя., Вй., 6, Мг. 3, 1958.
9.44. Ь е1 С ш а и и С., Ап е1ешепСагу ЙегггаСюп о1 СЬе орС1ша1 сопСго1 сопй1С1опя.
Ргос. Х11 1пСегпаС. АяСгопаиС. Сопряг. 1961, У1еп., 1962.
945. Ваггеге М., 3 аишоССе А., УеиЬе1се В. Р., Уапйеп1сегс1с-
Ь о ч е 2., Вос1сеС ргори1я1оп, АшяС.— Ьопйоп — М. У., 1960. Русский перевод:
Баррер М., Жомотт А., Вебек Б. Ф., Ванденкеркхове Ж.,
Ракетные двигатели. Оборонгиз, М., 1962.
9.46. Исаев В. К., Курьянов А. И., Сонин В. В., Применение принципа
максимума в ракетодинамике. Ргос. Х1У 1пСегпаС. АяСгопаиС. Сопряг. 1963, 7Гаг-
яхажа, 1964.
9.47. М 1 е 1 е А., И1дЬС шесЬап1ся, го1. 1. Маяяас1шяеССя — Ьопйоп, 1963. Русский пере-
вод: М и е л е А., Механика полета, т. 1. «Наука», М., 1965.
9.48. М и п1 с Й Н., Соййагй ргоЫеш МСЬ Ьоипйей СЬгияС. А1АА Х., го1. 3, Мо. 7,
1965.
9.49. Г а б а с о в Р., К и р и л л о в а Ф. М., Особые оптимальные управления.
«Наука», М., 1973.
9.50. Ь а ж й е и Р. Р., ОрС1ша1 рожегей агся 1п ап 1пчегяе яциаге 1аи Йе1Й. У. Атег.
Восй. Яос., чо1. 31, Мо. 4, 1961.
9.51. Ь а ж й е и Р. Р., ОрС1ша1 Сга~есСог1ея аког ярасе па~1даСюп ЬиССегяиогСЬ. Ьопйоп,
1963.
9.52. Г о р е л о в Ю. А., О двух классах плоских экстремальных движений ракеты
в пустоте. ПММ, т. ХХ1У, М 2, 1960.
9.53. Т р о и ц к и й В. А., Об оптимальных режимах движения многоступенчатых
ракет. Космические исследования, т. 5, вып. 2, 1967.

ЛИТЕРАТУРА
691
9.54. Г р о д з о в с к и й Г. Л., К и ф о р е н к о Б. Н., Исследование управления
весом двигательной системы с помощью непрерывной модели. Тр. У чтений, посвя-
щенных разработке научного наследия и развитию идей К. Э. Циолковского. Сек-
ция «Механика космического полета», Калуга, 1970, М., 1971.
955. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В.,
М и щ е и к о Е. Ф., Математическая теория оптимальных процессов. Физматгиз,
М., 1961.
9.56. Клих Ю. А., Макаров О. Ф., Плотников В. А., О включенииосо-
бых участков в оптимальную траекторию. «Матем. физика», республ. межведомств.
сб., вып. 4, изд-во АН УССР. Киев, 1968.
9.57. Ч е ц Ь е 1~ е В. Р., А шах1шцш-ш1п1шцш рг1пс1р1е аког Ьагд-Ьапд яуяФешя. Со11о-
пц1цш оп МеФЬоая о1 ОрФ1шйаФюп, ЬесФцге, МоФея 1п МаФЬешаФ1ся, 112, Ярг1пдег-
Уег1ад, Вег11п, 1970,
9.58. М 1 е 1'е А' Р11дЬФ шес1 а ся апа Уаг1аФ1опа1 ргоыешя 01 а 11пеаг Фуре. У. Аегояраяе
Яс1., 'го1. 25, Мо. 9, 1958.
9.59. Г р о д з о в с к и й Г. Л., К и ф о р е н к о Б. Н., Оптимальное секционирова-
ние материальной точки переменной массы. «Вычисл. и прикл. матем.», Межведомств.
научн. сб., вып. 18, Киев, 1972.
960. Гродзовский Г. Л., Кифоренко Б. Н., Же1дЫ11ш1~аф1оп 1п~]пенсе
оп орФ1шцш шоФ1оп рагашеФегя о1 а Ьоау о1 гаг1аЫе шаяя. Со11оцц1ш оп МеФ11оая
Я ОрФ1шйаФюп, ЬесФцге ХоФея 1п МаФЬешаФ1ся, 112, Ярг1пдег-Уег1ад, Вег11п, 1970.
9.61. Избранные труды К. Э. Ц и о л к о в с к о г о, т. 11. — Реактивное движение.
ГТТ И, 1934.
962. Кибальчич Н. И., Циолковский К. Э., Цандер Ф. А., Кон-
д р а т ю к Ю. В., Избранные труды. «Пионеры ракетной техники», «Наука», М., 1964.
9.63. К о с м о д е м ь я н с к и й В. А., К теории ступенчатых ракет. Докл. АН СССР,
т. 156, Ю 2, 1964.
9.64. К о ж е в н и к о в Ю. В., К оптимизации режимов полета и параметров состав-
ных летательных аппаратов. Тр. Казанского авиац. ин-та, вып. 89, Математика и
механика, Казань, 1965.
9.65. де В е б е к Ф., Оптимальное расположение параллельно работающих групп дви-
гателей в ракетной системе. Вопросы ракетной техники, Ю 9, 1962.
9 66. Т р о и ц к и й В. А., Вариационные задачи оптимизации процессов управления
для уравнений с разрывными правыми частями. Прикл. матем. и механ., т. 26,
вып. 2, 1962.
9.67. М а я о и У. О., 01 с 1~ е г я о и Ж. О. апа Я ш1 Ф Ь О. В., А гаг1аФюпа1шеФ11оа
~ог орФ1ша1 яФад1пд. А1АА Рарег Хо. 65-62, М. У., 1965.
9.68. А 1 1 о г а М. Ж. апа Ь е а г С. Ж., А сошраФаФюпа1 шеФйоа аког ФЬе орФ1шйаФюп
о~ шц1Ф1яФаде Ьа111яФ1с яуяФешя. А1АА Рарег Мо. 66-91, М. У., 1966.
9.69. ]9 е и Ь о ж С. Н., СопФг1ЬцФюп Фо ФЬе са1сц1ея о1 гаг1аФ1опя. Т11е Спггегя1Фу о1 СЫ-
садо Ргеяя, СЫ садо, 1957.
9.70. М о и с е е н к о В. П., О решении вариационных задач для уравнений с разрыв-
ными правыми частями, зависящими от промежуточных значений фазовых коорди-
нат и от дискретных величин. Уч. записки ЦАГИ, т. 11, Ы 1, 1971.
9.71. М о и с е е н к о В. П., Об одном подходе к решению разрывных вариационных
задач. В сб. «Исследование операций», М., 1974.
9.72. М о и с е е н к о В. П., Об условиях оптимальности в задачах оптимизации мно-
гоступенчатых систем. Тр. У чтений, посвященных разработке научного наследия и
развитию идей К. Э. Циолковского. Секция «Механика космического полета»,
Калуга, 1970, М., 1971.
9.73. М о и с е е н к о В. П., Оптимизация многоступенчатого аппарата. Тр. ЦАГИ,
вып. 1295, 1971.
9.74. Х о а н г Х ы у Д ы о н г, Условие скачка в одной задаче оптимального управле-
ния. Дифференциальные уравнения, т. 2, Ы 5, Минск, 1966.
9.75. В е л и ч е н к о В. В., О задаче оптимального управления для уравнений с раз-
рывными правыми частями. Автоматика и телемеханика, Ю 7, 1967.
9.76. В е л и ч е н к о В. В., Условие оптимальности в задачах управления с проме-
жуточными условиями. Докл. АН СССР, т. 174, Ы 5, 1967.
9.77. Ц л а ф Л. Я., Вариационное исчисление и интегральные уравнения. «Наука», М.,
1966.
978. Габасов Р., Кириллова Ф.М., СрочкоВ. А.,ТарасенкоН.В.,
Условия оптимальности высокого порядка. 1. Вычисление особых управлений,
Авт. и Тер., 1971, Ю 5.
9.79. С а г 11 и 1 е 1 В., А яо1цФюп о1 боааага'я ргоЫеш. 3. Я1АМ оп СопФго1, г. 1,
1~'о. 3, 1963.
9.80. Е и1 и д С. М., Н а я е1 Ф 1 и е Ж. В., ОрФ1ша1 ргодгашя аког аясепа1пд ш1з-
я11е. 3. Я1ЛМ оп СопФго1, г. 2, ~о. 1, 1964.
9.81 Ь е 1 Ф ш а и и 6. А., ОрФ1шцш ФЬгцяФ ргодгашш1пд аког 111д11-а1Ф1Фцае гос1~еФя. Аего-
пацФ1са1 Епд1пеег1пд Решаем, го1. 16, Мо. 6, 1957.
44*

692
ЛИТЕРАТУРА
Н а ш е 1 6., ~Ьег е1пе ш1С йеш РгоЫеш йег Ва1~еСе кцяашшепЬапдепйе Ац~даЬе
Йег Уаг1аСюпягесЬпцщ~. Х. апреле. МаСЬ. цпй МесЬ., Вй. 7, Ней 6, Велел Ьег
1927.
Ь е 1 С ш а и и 6. А., Са1сц1ця о1 гаг1аСюпя яо1цСюп о1 6оййагй'я ргоЫеш. АяСгоп.
АсСа, ~о1. 2, 1аяс. 3, 1956.
Ь е 1 С ш а и и 6. А., ЯСаСюпагу Сга)есСог1ея аког а Ь1~Ь-а1С1Сцйе гос1~еС и1СЬ Огор-
аиау ЬоояСег. АяСгоп. АсСа, го1. 2, 1аяс. 3, 1956.
В е г 1с о ~ 1 С к Ь. О., Ап орС1шцш СЬгцяС сопСго1 ргоЫеш. 1. МаСЬ. Апа1. апй Арр1.
'го1. 3, 1961.
Р а ц11с и е г Р. О., ТЬе ргоЫеш о1 6оИагй аЫ орС1шцш СЬгияС ргодгашш1пд.
Айг. АяСгоп. Яс1., го1. 1, Х. У., Ашег. АзСгопацС. Яос., 1957, 43 — 51.
К е и С К г е я а, Ап орС1ша1 ыпдц1аг яо1цСюп аког СЬе яоцпйпд гос1сеС и1СЬ а1С1Сцйе-
ЙерепйепС рагашеСегя. 1. Ярасесгай апй Вос1еСя, ~о1. 4, Хо. 1, 1967.
В е т ч и н к и н В. П., Вертикальное движение ракеты. Сб. «Реактивное дви-
жение» М., 1935.
М а г 1 и е з с и А1., Азирга игсагй орМше а гасЬеФе1ог зо1-аег. Вет. Тгапзр. (ВРВ),
9, Хо. 11, 1962, 485 — 489.
Э н е е в Т. М., О применении градиентного метода в задачах теории оптимального
управления. Космические исследования, т. 4, М 5, 1966, 651 — 669.
Ь е е Е. В., М а г 1с ц я Ь., РоцпйаСюпя о1 орС1ша1 сопСго1 СЬеогу. Х. У., Ьопойп—
Яуйпеу, 1967. Русский перевод: Л и. Э. Б., М а р к у с Л., Основы теории опти-
мального управления, «Наука», М., 1972.
Г а л к и н В. Я., Задача релейного управления при вертикальном подъеме ра-
кеты. Сб. «Вычисл. методы и программир.», вып. 12, изд-во МГУ, М., 1969.
Г а л к и н В. Я., К расчету управляющей функции при подъеме ракеты-зонда
на максимальцую высоту. Сб. «Вычисл. методы и программир.», вып. 12, изд-во
МГУ, М., 1969.
Гродзовский Г. Л., Кифоренко Б. Н., Кузьменко В. В.,
Влияние весовых ограничений на набор максимальной высоты при движении в ат-
мосфере. Уч. записки ЦАГИ, т. 5, Ы 1, 1974.
Кифоренко Б.Н., Кузьменко В. В., О влияниивнешнихсилнадви-
жение материальной точки переменной массы. Тр. У111 чтений, посвященных раз-
работке научного наследия и развитию идей К. Э. Циолковского, Секция «Механика
космического полета», Калуга, 1Ю3, М., 1И4.
3 л а ц к и й В. Г., К и ф о р е н к о Б. Н., Оптимальные траектории с сингу-
лярными дугами. Автоматика и телемеханика, Ю 12, 1974.
9.82.
'9.83.
'9.84.
'9.85.
9.86.
9.87.
9.88.
9.89.
9.90.
9;91.
'9.92.
9.93.
9.94.
9.95.
9.96.
К главе 10
10.1. Р а ц1 Й е г я С. В., ОрС1шцш СЬгцяС ргодгашшпщ о1 е1есСг1са11у роиегей гос1~еС
геЬ1с1ея 1п а дгаг1СаСюпа1 пе1Й. У. Ашег. Восй. Яос., го1. 30, Хо. 10, 1960.
10.2. Р а ц1 й е г я С. В., ОрС1шцш СЬгцяС ргодгашпшщ о1 е1есСг1са11у рожегей гос1~еС
геЬ1с1ея аког еагСЬ еясаре. А1АА 3., го1. 1, Хо. 1, 1963. Русский перевод: Ракетная
техника и космонавтика, М 1, 1963.
10.3. М е1 Ь о ц г и е Ж. 6., Я а ц е г С. 6., СопяСапС-аСС1Сцйе СЬгцяС ргодгаш орС1-
шйаС1оп. А1АА 1., го1. 3, Хо. 8, 1965. Русский перевод: Ракетная техника и кос-
монавтика, М 8, 1965.
10.4. В ц я я ц г Й В. Ж., А пцс1еаг-е1есСг1с ргорц1ноп яуйеш. 3. Вг1С. 1пСегр1. Яос.,
'го1. 15, Хо. 6, 1956.
10.5. Р г е я С о и — Т Ь о ш а я Н., А поСе оп а пцс1еаг е1есСг1са1 ргорц1яюп яуяСеш.
3. Вг1С. 1пСегр1. Яос., го1. 16, Хо. 9, 1958.
10.6. 1 г г1 и д 1. Н., В 1ц ш Е. К., СошрагаСгге рег1огшапсе о1 Ьа11Ы1с апй 1ож-
СЬгцяС геЬ1с1ея аког 111дЬС Со Магя. Ухая 1п АяСгопацС., го1. 2, Я. У., 1959.
10.7. И в а н о в Ю. Н., Дополнительные весовые компоненты в задачах оптимизации
движения с ограниченной мощностью. Прикл. матем. и механ., т. 28, М 1, 1964.
10.8. А ц 6. Р., ЕпСзпсЫцп~яяСапд кц1мпй1дег Вацш1аЬгСапСг1еЬе. ЬцШаЬгССесЬп11с,
'го1. 7, Хо. 1, 1961.
10.9. И в а н о в Ю. Н., О движении тела переменной массы с ограниченной мощностью
и заданным активным временем. Прикл. матем. и механ., т. 27, М 5, 1963.
10.10. В и н о к у р о в В. А., И в а н о в Ю. Н., Оптимальное движение в централь-
ном поле при заданном времени работы источника мощности. Изв. АН СССР, Ме-
ханика, М 5, 1965.
10.11. И в а н о в Ю. Н., Ступенчатая аппроксимация оптимальных управлений.
Прикл. матем. и механ., т. 28, М 3, 1964.
10.12. Б е л е ц к и й В. В., Е г о р о в В. А., Межпланетные полеты с двигателем
постоянной мощности. Космические исследования, т. 2, М 3, 1964.
$0.13. И с а е в В. К., С о н и н В. В., Об одной нелинейной задаче оптимальногоупра-
вления. Автоматика и телемеханика, т. 23, М 9, 1962.

693
ЛИТЕРАТ~РА
10Л4.
10Л5.
10.16.
10.17.
10Л8.
10Л9.
10.20.
10.21.
10.22.
10.23.
10.24.
10.25.
К главе 11
Н ц п С е г М. Ж., Т я с Ь1 г д 1 1. М., ТЬе айчапСадея о1 111д11 СЬгцяС ярасе ч~
Ыс1ея. Ргерг. Ашег. ВосК. Яос., Мо. 991, 1959.
Сга1д В., РеС11его11 С. Ж., Я а1Схег С.,СошрагЬоп о1 сЬеш1са1 апй
е1есСг1с ргорц1яоп яуяСетя 1ог1пСегр1апеСагу Сгаче1. Ргос. 1ВЕ, чо1. 48, Хо. 4, 1960.
8 С е а г п я 1. Ж., Е1есСгоргорц]я1оп яуяСет арр11саСюпя, АяСгопацС1ся, чо1. 7,
Мо. 3, 1962.
В е е г я Ь. 8., С о Ь е п А. Р., Магя сараЫ11С1ея аког е1есСг1са1, пцс1еаг апй сЬе-
ш1са1 ргорц1яоп яуяСешя. 1АЯ Рарег, Мо. 120, 1962.
Я С ц Ь 11 п д е г Е., ТЬе госКеС ж1СЬ е1есСг1са1 ргорц1яоп яуяСеш. Е1есСг1са1 Епд~-
пеег1пд, чо1. 82, Мо. 7, 1963.
В о ц с Ь е г В. А., Е1есСг1са1 ргорц1яоп аког сопСго1 о1 яСаС1опагу яаСе1Иея. 3.
Ярасесгай апй Вос1~еСя, чо1. 1, Мо. 2, 1964.
Е й е 1 Ь а ц ш Т. М., ТЬе цяе о1 Ь1дЬ- апй 1ож-СЬгцяС ргорц1яоп 1п сошЫпаС1од
аког ярасе шЬяопя. Агшег. АяСгоп. Яос., ргер. 61-104, 1961. Русский перевод: Во-
просы ракетной техники, Ю 5, 1965.
И в а н о в Ю. Н., Оптимальное сочетание двигательных систем. Изв. АН СССР,
Механика и машиностроение, Ю 2, 1964.
Р 1 ш р 1 е Ж. В., Ап 1шргочей СЬеогу о1 СЬе цяе о1 апй Ь1дЬ 1ож-СЬгцяС ргорц1яоп
1п сошЫпаСюп. 1. АяСгопацС. Яс1., чо1. 10, Мо. 10, 1963. Русский перевод: Вопросы
ракетной техники, М 5, 1965.
И л ь и н В. А., К расчету траекторий перелета космических аппаратов между
компланарными круговыми орбитами в ньютонианском гравитационном поле.
Космические исследования, т. 2, М 5, 1964.
11Л.
11.2.
11.3.
11.4.
11.5.
11.6.
11.7.
11.8.
11.9.
11.10.
К главе 12
Ь 1 п Ь а г й С Н. О., Сошрагиоп о1 яо1аг-СЬегша1 апй яо1аг-е1есСг1с-СЬегша1 рго-
рц1яоп шеСЬойя. 1АЯ Рарег, Мо. 63-20, 1963.
С а ш а с М., 0яе о1 епегду яСогаде 1п 1ож-СЬгыС ярасе111дИ. 3. Ашег. ВосЕ Яос.,
чо1. 30, Мо. 1, 1960.
Гродзовский Г.Л., Кифоренко Б. Н., Токарев В. В., Нако-
питель энергии в задачах оптимизации движения с ограниченной мощностью.
Изв. АН СССР, Механика, Ю 3, 1965; см. также Ргос. ХУ1 1пСегпаС. АяСгопацС.
Сопдт. 1965, Жагякажа, 1966.
12.1.
12.2.
12.3.
Исаев В. К., Сонин В. В., Давидсон Б. Х., Оптимальные режимы
движения точки переменной массы с ограниченной мощностью в центральном
однородном поле. Космические исследования, т. 2, Ю 4, 1964.
Ме1Ьоцгпе Ж. О., Яацег С. О., В1сЬагйяоп О. Е., 1пСегр1апе-
Сагу Сга1есСогу орС1ш1каСюп ж1СЬ рожег-11ш1Сей яуяСешя. Ргос. 1АЯ Яушр. оп ~еЯс1е
ЯуяС. ОрС1ш., М. У., 1961.
М е1Ь о ц г и е Ж. О., 8 а ц е г С. О., ОрС1шцш СЬгцяС ргодташшя аког рожег-
11ш1Сей ргорц1яоп яуяСешя. АяСгопацС. АсСа, чо1. 8, Мо. 4, 1962.
М е1 Ь о ц г и е Ж. О., 8 а ц е г С. О., Рау1оай орС1ш1каСюп аког рожег-11ш1Сей
чеЫс1ея. Ргодт. 1п АяСгопацС. апй АегопацС., чо1. 9, Е1есСг1с. Ргор. Вече1., М. У.,
1963. Русский перевод: Вопросы ракетной техники, Ю 8, 1964.
ЯЬе1Соп В. О., РоССег В. А., Ьасу Ь., ЯСцЬ11пдег Е., Еча-
1цаСюп апй апа1уяя о1 СЬгцяС цп1Ся аког рожег-11ш1Сей ргорц1яоп яуяСешя. А1АА 1.,
чо1. 2, Мо. 4, 1964. Русский перевод: Ракетная техника и космонавтика, Ю 4, 1964.
Ь а ж й е и 1. Н., Тга1есСогу орС1шлаСюп аког а гос1~еС ж1СЬ депега11яей СЬгцяС
сЬагасСегЬС1с. АяСгопацС. АсСа, чо1. 10, Мо. 5, 6, 1964.
В ц 1 д е г о 1 1 С. В., Я р е 1 я е г В. 8., Р о г г е я С е г А. Т., Ехрег1шепСа1
яСцй1ея ВАСЬ яша11 яса1е юп шоСогя. АВЯ 14СЬ Аппца1 МееС1пд, ЖаяЬ., Моч. 16 — 20,
1959.
Р о х В., РЬуяся о1 С11е юп СЬгцяС яуяСеш. АВЯ 14СЬ Аппца1 МееС1пд, ЖаэЬ., Моч.
16 — 20, 1959.
К а я Ь Я. Ж., 8 С а г г Ж. Ь., Ехрег1шепСа1 геяц1Ся ж1СЬ а со111пеаг е1есСгойв
р1аята ассе1егаСог апй а сошрагЬоп ж1СЬ юп ассе1егаСогя. АВЯ 14СЬ Аппиа1 МееС1пд,
Жая11., Хоч. 16 — 20, 1959.
М о я е г Ж. А., 1оп епд1пе орегаСюп апа1уяя. АВЯ Е1есСг1са1 РгорцЬ1оп Соп1е-
гепсе, Вег1~е1еу, МагсЬ 14 — 16, 1961.
В г о ж п Н., Х 1 с о 11 Н. Е., Е1есСг1са1 ргорц1я1оп сараЫ11С1ея аког 1ипаг ехр1о-
гаСюп. АВЯ Е1есСг1са1 Ргорц1яоп СоЫегепсе, Вег1~е1еу, МагсЬ 14 — 16, 1961.
Исаев В. К., Курьянов А. И., Сонин В. В., Применсние принципа
максимума в ракетодинамике. Ргос. Х1У 1пСегпаС. АяСгопацС. Сощг. 1963, Жаг-
якажа, 1964.

ЛИТЕРАТУРА
124. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В.,
М и щ е н к о Е. Ф., Математическая теория оптимальных процессов. Физматгиз,
М., 1961.
12.5. К и ф о р е н к о Б. Н., К выбору оптимальных параметров двигательной уста-
новки в задачах оптимизации движения с ограниченной мощностью и на-
копителем энергии. Изв. АН СССР, Механика, М 3, 1966.
12.6. К р о т о в В. Ф., Методы решения вариационных задач. 11. Автоматика и теле-
механика, т. 24, М 5, 1963.
12.7. К и ф о р е и к о Б. Н., Некоторые задачи оптимизации движения с ограничен-
ной мощностью и накопителем энергии. Механика твердого тела (Инж. журн.),
Х 5, 1966.
12.8. П в а н о в Ю. Н., О движении тела переменной массы с ограниченной мощно-
стью и заданным активным временем. Прикл. матем. и механ., т. 27, М 5,
1963.
12.9. К и ф о р е и к о Б. Н., О движении по орбитам, близким к круговым, при ис-
пользовании двигательной системы с накоплением энергии и движителем постоян-
ной мощности. Механика твердого тела (Инж. журн.), Х 2, 1967.
1210. Гродзовский Г.Л., Кифоренко Б.Н., Одвижепиителапеременной
массы с накоплением энергии и движителем с ограниченной скоростью истечения
реактивной струи. П. Ргос. ХУП 1пСегпаС. АяСгопаиС. Сопряг. 1966, ЪЧагякаиа,
1967.
12.11. К и ф о р е н к о Б. Н., Об особом управлении в механике полета с ограничен-
ной мощностью и накопителем энергии. Космические исследования, т. 9, Ю 4,
1971.
12.12. Клих Ю.А., Макаров О. Ф., Плотников В. А., Овключенииосо-
бых участков в оптимальную траекторию. «Матем. физика», республ. межведомств.
сб., вып. 4, Изд-во АН УССР, Киев, 1968.
12.13. Р е ш е С г1 а й е я Я. Т., А поче1 яуяСеш аког ярасе П1~Ы амид а ргори1я1че Пшй
ассиши1аСог. 1. Вг1С. 1пСегр1. Яос., чо1. 17, Мо. 5, 1959.
$2 14. В е г и е г Р., С а ш а с М., А1г ясоор1п~ чеЫс1е. А1г Е'огсе Ва11ЬС1с МЬя1е Р1ч.,
ТВ 59-17, 1959.
12.15. П е ш е Ф г 1 а Й е я Я. Т., ОгЫФа1 ргори1я1оп яуяФеш 1ог ярасе шапеитг1пд (РВОРАС).
АяСгопаиС. Яс1. Веч., чо1. 1, Мо. 4, 1959.
12.16. Р е ш е С г1 а й е я Я. Т., Рге11ш1пагу яСийу о1 ргори1яче Пи1й ассиши1аСог
яуяСешя. Ргос. Х1 1пСегпаС. АяСгопаиС. Сопряг. 1960, Иеп., 1961.
$2.17. Р г е и с Ь Е. Р., ОрегаСюп о1 ап е1есСг1с гаш1еС 1п а р1апеСегу аСшояр11еге. Ргер.
ТесЬп. Яея. Ашег. АяСгопаиС. Яос., Мо. 90, 1960.
12.18. С а ш а с М., В е г и е г Р., Ап огЬ1Са1 а1г-ясоор1пд чесЫс1е. АяСгопаиС1ся, ~о1. 6,
Хо. 8, 1961.
12.19. В е1с Ь е1 В. Н., Я ш1 С Ь Т. Ь., Н а п 1 о г й Р. В., РоСепС1а11С1ея о1 а1г-
ясоор1пд е1есСг1са1 ярасе ргори1яоп яуяСешя. Ргодг. 1и АяСгопаиС. апй АегопаиС.,
ъо1. 9, Е1есСг1са1 Ргор. Рече1., М. У., 1963.
$2.20. Т о к а р е в В. В., Ф а т к и н Ю. М., Накопитель рабочего вещества в задачах
оптимизации движения с ограниченной мощностью. Ипж. журнал АН СССР, т. 5,
М 3, 1965.
12.21. Б у р д а к о в В. П., Парамагнитный воздухозаборник спутника-накопителя.
Труды третьих чтений К. Э. Циолковского, Калуга, 1968.
12.22. Ф а т к и н Ю. М., Выбор оптимального закона управления тягой в задаче дви-
жения в режиме накопления массы. Механика твердого тела (Инж. хсурн.), Ы 1,
1967.
12.23. Ц о й Э. П., Выбор оптимальной программы управления тягой накопителя рабо-
чего вещества. Тр. ЦАГИ, вып. 1145, М., 1969.
12.24. Ш у м и л к и н В. Г., Управление тягой аппарата с двигателем ограниченной
мощности в режиме накопления атмосферного воздуха в орбитальном полете.
Уч. записки ЦАГИ, т. 6, ~' 6, 1975.
12.25. О в с я н н и к о в Р. Н., Ш у м и л к и н В. Г., Некоторые вопросы универ-
сализации параметров двигательной системы ограниченной мощности с накопи-
телем рабочего вещества. Механика твердого тела (Инж. жури.), Х 4, 1968.
12.26. Г р о д з о в с к и й Г. Л., Некоторые вариационпые задачи механики космиче-
ского полета. Механика твердого тела (Инж. журн.), Ы 6, 1966.
12.27. Ц а и д е р Ф. А., Об использовании силы давления света для полетов в межпла-
нетном пространстве, 1924 — 1925. См. Ц а н д е р Ф. А., Проблема полета при
помощи реактивных аппаратов. Межпланетные путешествия. Оборонгиз, М., 1961.
12.28. Т я и Т. С., 1пСегр1апеСагу Сгаче1 Ьу яо1аг яа11. 1. Ашег. Вос1с. Яос., чо1. 29, Мо. 6,
1959.
12.29. Т я и Т. С., ЯСга1д11С-11пе 111~ЬС Со Маги. Ргос. У1 Апп. МееС. Ашег. АяСгопаиС.
~ос., 1960, Айч. АяСгопаиС. Яс1., чо1. 6, М. У., 1961.
12.30. Ь о и й о и Н. Я., Яоше ехасС яо1иС1оп о1 СЬе еццаС1оп о1 шоСюп о1 яо1аг яа11 зпСЬ
сопяСапС яа11 яеСС1пд. У. Ашег. Вос1с. Яос., чо1. 30, Яо. 2, 1960.

695
ЛИТЕРАТУРА
главе 13
Т о к а р е в В. В., К выбору параметров динамической системы, универсальной
для заданного класса маневров. Изв. АН СССР, Механика и машиностроение,
№ 5, 1964; Ргос. ХУ1 1п$егпа$. Ая$гопаМ. Сопряг. 1965, Жагякажа, 1966.
Т о к а р е в В. В., Ф а т к и н Ю. М., Игровой подход к задаче выбора опти-
мальных параметров динамической системы. Механика твердого тела (Инж. журн.),
№ 6, 1966.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., Механика
космического полета с малой тягой, гл. 10. «Наука», М., 1966.
Гродзовский Г. Л., Охоцимский Д. Е., Белецкий В. В.,
И в а н о в Ю. Н., К у р ь я н о в А. И., П л а т о н о в А. К., С а р ы-
чев В. А., Токарев В. В., Я рошевский В. А., Механика косми-
ческого полета. Сб. «Механика в СССР за 50 лет», т. 1, «Наука», М., 1968.
Овсянников Р. Н., Токарев В. В., Фаткин Ю. М., Оптимиза-
ция параметров динамической системы, универсальной для заданного класса ма-
невров. Тр. П Междун. симп. по методам оптимиз. Новосибирск, 1968.
Т о к а р е в В. В., Оптимизация параметров динамической системы, упиверсаль-
ной для серии маневров, при различной степени информированности. 1. Постановка
задачи универсализации. Автоматика и телемеханика, № 8, 1971.
О в с я н н и к о в Р. Н., Т о к а р е в В. В., Оптимизация параметров дина-
мической системы, универсальной для серии маневров, при различной степени
информированности. 11. Выбор универсальной системы при полной информации
о маневрах (статистический подход). Автоматика и телемеханика, № 10, 1971.
Т о к а р е в В. В., Оптимизация параметров динамической системы, универсаль-
ной для серии маневров, при различной степени информированности. 111. Выбор
универсальной системы при неполной информации о маневрах (игровой подход).
Автоматика и телемехапика, № 11, 1971.
О в с я н н и к о в- Р. Н., Т о к а р е в В. В., Задача оптимального секциони-
рования двигательной системы ограниченной мощности. Тр. У чтений, посвя-
щенных разработке научного наследия и развитию идей К. Э. Циолковского,
Калуга, 1970, М., 1971.
К а р а с и к И. Я., О в с я н н и к о в Р. Н., Т о к а р е в В. В., Выбор
параметров управляемой системы для конечного числа заданных маневров. Кос-
мические исследования, т. 11, № 2, 1973 .
О в с я н н и к о в Р. Н., Ш у м и л к и н В. Г., Некоторые вопросы универса-
лизации параметров двигательной системы ограниченной мощности с накоплением
рабочего вещества. Механика твердого тела (Инж. журн.), № 4, 1968.
О в с я н н и к о в Р. Н., Оптимизация размера универсальной секции идеаль-
ной двигательной системы ограниченной мощности с накоплением рабочего ве-
щества. Тр. ЦАГИ, вып. 1393, М., 1972.
О в с я н н и к о в Р. Н., Оптимизация параметров разнотипных многоцелевых
управляемых систем со стандартными элементами. Автоматика и телемеханика,
№ 10, 1972.
13.1.
13.2.
13.3.
13.4.
13.5.
13.6.
13.7.
13.8.
13.9.
13.10.
13.11.
13.12.
13.13.
12.31. Р о к к1 А., Яц ип ше1ойо й яо1и~1оппе йо1 ргоЫеша йе11а че1а яо1аге. Мия1е,
чо1. 3, Мо. 6, 1961.
12.32. Р о к к1 А., Я о с1о Ь., Яоше гешагЫ оп яо1аг яа11. 3. Ашег. ВосК Яос., го1. 31,
Хо. 8, 1961.
12.33. Я о с $ о Ь., Ьа пач1даиопе соп че1а яо1аге. Мия1е, чо1. 3, Хо. 3, 1961.
12.34. К е 11е у Н. Х., бгай1епй ФЬеогу о1 орИша1 111дЫ раФЬя. У. Ашег. ВосК Яос.,
'го1. 30, Хо. 10, 1960.
12.35. Ж у к о в а А. Н., Л е б е д е в В. Н., Вариационная задача о перелете между
гелиоцентрическими круговыми орбитами с помощью солнечного паруса. Косми-
ческие исследования, т. 2, № 1, 1964.
12.36. Я а и й я Х., Еясаре 1гош р1апеФагу дгатФаИопа1 Йе1йя Ьу иве о1 яо1аг яа11ея. У.
Ашег. ВосК Яос., чо1. 31, Мо. 4, 1961.
12.37. Р 1 ш р 1 е Ж. В., А депега11кей СЬгее-й1шепяопа1 Фга1есФогу апа1уяя о1 р1апейегу
еясаре Ьу яо1аг-яа11. 1. Ашег. Вос1с. Яос., чо1. 32, Хо. 6, 1962.
12.38. Р е г 1с 1 и я Р. М., Р11дЫ шесйап1ся о1 1ок-$Ьгий ярасесгай. 3АЯЯ, го1. 26, Мо. 5,
1959, Ухая 1п АяйгопаиФ., го1. 2, Х. У., 1959.
12.39. В а л е е в К. Г., Качественное исследование дифференциальных уравнений полета
при помощи солнечного паруса. Прикл. матем. и техн. физ., № 2, 1964.
12.40. И л ю т о в и ч А. Е., Оптимальный перелет с двигателем, использующим солнеч-
ную энергию. Космические исследования, т. 4, № 6, 1966.
12.41. О в с я н н и к о в Р. Н., С е м е н о в а Л. Н., О движении тела переменной
массы с экспоненциально убывающей мощностью реактивной струи. Механика
твердого тела (Инж. журн.), № 4, 1966.

696
ЛИТЕРАТУРА
главе 14
14Л.
14.2.
14.3.
14.4.
14.5.
14.6.
14.7.
14.8.
13Л4.
13.15.
13.16.
13.17.
$3Л8.
13Л9.
13.20.
13.21.
13.22.
13.23.
13.24.
13.25.
13.26.
13.27.
13.28.
13.29.
13.30.
13.31.
13.32.
13.33.
13.34.
13.35.
13.36.
Т о Ы а г е ч У. У., Яе1есИоп о1 орИша1 рагаше$егя аког ши1Иригрояе соп$го11-
аЫе яуя$ешя; депега1 1огши1аИоп о1 $Ье ргоЫеш апй яо1иИоп а1догИЬпя. УОТА,
чо1. 15, Мо. 6, 1975.
Г е р м е й е р Ю. Б., Введение в теорию исследования операций. «Наука»,
М., 1971.
Б р у с о в В. С., П и я в с к и й С. А., Применение теории оптимальных по-
крытий к выбору двигательной установки космического аппарата малой тяги.
Механика твердого тела (Инж. журн.), № 5, 1968.
Б р у с о в В. С., П и я в с к и й С. А., Применение теории оптимальных по-
крытий к задачам выбора мощности двигателя малой тяги. Механика твердого
тела (Инж. журн.), № 2, 1969.
Пиявский С.А., Брусов В.С., Хвилон Е.А., Оптимизацияпара-
метров многоцелевых летательных аппаратов. Машиностроение, 1974.
К о ж е в н и к о в Ю. В., К оптимизации управляемых систем со случайными
параметрами. Прикл. матем. и механ., т. 28, № 3, 1964.
К о ж е в l и к о в 10. В., Синтез оптимального управления линейных неста-
ционарных стохастических систем. Изв. АН СССР, Техническая кибернетика,
№ 2, 1965.
К о ж е в н и к о в 10. В., К теории оптимального осреднения управлений дина-
мических систем. Прикл. матем. и механ., т. 30, № 4, 1966.
Ч у е в 1О. В., С и е х о в а Г. П., Технические задачи исследования опера-
ций. «Советское радио», М., 1971.
Д е м е н т ь е в В. Т., Задача выбора типажа оборудования. Сб. «Методы управ-
ления большими системами», т. 2, Иркутск, 1970.
Г и м а д и Э. Х., Выбор оптимальных шкал в одном классе задач типа размеще-
ния, унификации и стандартизации. Сб. «Управляемые системы», вып. 6, Ново-
сибирск, 1970.
Глебов Н.И., Дементьев В.Т., Сычев А. Н.,Одинамикеразвптия
однородпых технических систем. Сб. «Управляемые системы», вып. 8, Новосибирск,
1971.
Г и м а д и Э. Х., Д е м е н т ь е в В. Т., Некоторые задачи выбора оптимальных
параметрических рядов и методы их решения (задачи стандартизации). Проблемы
кибернетики, вып. 27, 1973.
Г н е д е н к о Б. В., Курс теории вероятностей. «Наука», М., 1965.
Ш и л о в Г. Е., Г у р е в и ч Б. Л., Интеграл, мера и производная. «Наука»,
М., 1964.
Т о к а р е в В. В., Ш у м и л к и н В. Г., К расчету производительности сис-
темы массового обслуживания. Прикл. матем. и механ., т. 32, № 2, 1968.
Л ю с т е р и и к Л. А., С о б о л е в В. И., Элементы функционального анализа.
«Наука», М., 1965.
Д а и ф о р д Н., Ш в а р ц Дж. Т., Линейные операторы. ИЛ, М., 1962.
М о и с е е в Н. Н., Элементы теории оптимальных систем. «Наука», М., 1975.
3 о й т е н д е й к Г., Методы возможных направлений. ИЛ, М., 1963.
П ш е н и ч н ы й Б. Н., Необходимые условия экстремума. «Наука», М., 1969.
Д е м ь я и о в В. Ф., М алое емов В. Н., Введение в минимакс «Наука»,
М., 1972.
А в р а м ч е н к о Р. Ф., Т о к а р е в В. В., Запас рабочего вещества, оптималь-
ный для выполнения заданного маневра при фиксированных параметрах двига-
теля. Космические исследования, т. 5, № 5, 1967.
Т о к а р е в В. В., Влияние случайных процессов уменьшения мощности на дви-
жение тела перемепной массы в гравитационном поле. Прикл. матем. и механ.,
т. 26, № 4, 1962.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., Одвижении
тела переменной массы с постоянной и убывающей затратой мощности в гравита-
ционном поле, 11. Ргос. Х111 1п$егпа$. Ая$гопац$. Сопряг. 1962, Иеп. — М. У., 1964.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. Б., Механика
космического полета с малой тягой, Ш. Инж. журнал, т. 4, № 1, 1964.
Т о к а р е в В. В., Некоторые вопросы надежности в задачах оптимального управ-
ления. Прикл. матем. и механ., т. 30, № 1, 1966.
Х и н ч и н А. Я., Математические методы теории массового обслуживания. Физ-
матгиз, М., 1963.
Г н е д е н к о Б. В., Курс теории вероятностей. «Наука», М., 1965.
П о л о в к о А. М., Основы теории надежности. «Наука», М., 1964.
Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д., Математические
методы в теории надежности. «Наука», М., 1965.

697
ЛИТЕРАТУРА
главе 15
15.1.
15.2.
15.3.
15.4.
15.5.
15.6.
15.7.
15.8.
15.9.
15ЛО.
15.11.
15Л2.
15.13.
К главе 16
16Л.
16.2.
16.3.
16.4.
16.5.
16.6.
14.9.
14ЛО.
14Л1.
14Л2.
14ЛЗ.
14Л4.
14Л5.
14Л6.
14Л7.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., Механика
космического полета с малой тягой, гл. 11. «Наука», М., 1966.
С а д ы к о в И. Х., К оптимизации систем с учетом возможных отказов их эле-
ментов. Изв. вузов, сер. «Авиац. техн.», № 4, 1968.
С а д ы к о в И. Х., Оптимизация движения летательного аппарата с учетом
случайных отказов секций двигателя. Тр. Казанского авиац. ин-та, № 103, 1968.
С а д ы к о в И. Х., К оптимизации управляемых систем с учетом надежности.
Изв. вузов, сер. «Авиац. техн.», № 4, 1969.
К о ж е в н и к о в Ю. В., К теории оптимального осреднения управлений ди-
намических систем. Прикл. матем. и механ., т. 30, № 4, 1966.
Гермейер Ю. Б., Иргер Д. С., Калабухова Е. П., О гарантиро-
ванных оценках надежности системы при неполных сведениях о надежности эле-
ментов. Журн. вычисл. матем., т. 6, № 4, 1966.
Г е р м е й е р Ю. Б., Введение в теорию исследования операций. «Наука», М.,
1971.
А в р а м ч е н к о Р. Ф., Выбор оптимального расписания включения запасных
элементов в нагруженный режим. Изв. АН СССР, Техническая кибернетика,
3, 1970.
А в р а м ч е н к о Р. Ф., Использование неполной информации о надежности
элементов самолета. Чистые стратегии выбора моментов замен. Уч. записки ЦАГИ,
№ 3, 1974.
Охоцимский Д. Е., Бельчанский Г. Н., Буха ркина А. П.,
Голубев Ю. Ф., Золотухина Н. И., И ванов Ю. Н., Оптимальное
управление при входе в атмосферу. Докл. па 2-м симпозиуме по автоматическому
управлению в космосе. Вена, 1967.
А й з е к с Р., Дифференциальные игры. «Мир», 1967.
Р1 е п11 и д Ж. Н., А ио$е ои йпегеиМа1 датея о1 ргеясг1Ьей йцга$1оп. Сои$г1-
Ьц$юпя Фо $Ье $Ьеогу о1 дашея. Апи. Маей. ЯФцй1ея, чо1. 3, 1957.
Р1 е ш 1 и д Ж. Н., Тйе соичегдепсе ргоЫет аког йИегепйа1 датея. 1. МаФЬ.
Апа1. апй Арр1., 'го1. 3, 1961.
Р1е т 1и д Ж. Н., Тие соичегдеисе ргоЫет аког йЛегеийа1 датея. П. Айч.
1п дап~ея $Ьеогу. Аип. Маей. ЯФийея, 1964.
В е г с о ч 1 $ х Ь., Р1 е п1 1 п ~ Ж. Н., Ои йИегепйа1 ~атея иИЬ 1и$е~га1 рау-
оЛ. Соп$г1Ьи$юия $о $Ье $Ьеогу о1 дамен. Апп. Ма$11. ЯФийея, чо1. 3, 1957.
В е г с о ч 1 $ к Ь. Р., А чаг1а$юпа1 арргоасй Фо йиегеп$1а1 ~атея. Айч. 1и дап~ея
$Ьеогу. Апп. МаФЬ. ЯШЙ1ея, 1964.
П о н т р я г и н Л. С., О некоторых дифференциальных играх. Докл. АН СССР,
т. 156, № 4, 1964.
Красовский Н.Н., Репип 10.М., Третьяков В.Е.,Онекоторых
игровых ситуациях в теории управляемых систем. Техническая кибернетика,
№ 4, 1965.
К р а с о в с к и й Н. Н., С у б б о т и н А. И., Позиционные дифференциаль-
ные игры. «Наука», М., 1974.
Г р и ш и н В. П., К проблеме минимакса в теории аналитического конструиро-
вания регуляторов. Автоматика и телемеханика, т. 25, № 6, 1964.
Зуев Г. М., Иванин В. М., Иванов Ю. Н., Игровой подход к задаче
управления спуском космического аппарата в атмосфере. Автоматика и теле-
механика, №№ 2, 5, 1971.
Я р о ш е в с к и й В. А., Приближенный расчет траекторий входа в атмосферу.
Космические исследования, т. 2, №№ 4, 5, 1964.
П у г а ч е в В. С., Теория случайных функций и ее применение к задачам авто-
матического управления. Гостехиздат, М., 1957.
С о л о д о в н и к о в В. В., Статистическая динамика линейных систем авто-
матического управления. Физматгиз, М., 1960.
М о и с е е в Н. Н., Численные методы в теории оптимальных систем. «Наука»,
М., 1971.
Ф е л ь д б а у м А. А., Основы теории оптимальных автоматических систем.
«Наука», М., 1966.
Л у р ь е А. И., Некоторые нелинейные задачи теории автоматического регули-
рования. Гостехиздат. М., 1951.
Л э н н и н г Д., Б э т т и н Р., Случайные процессы в задачах автоматического
управления. ИЛ, М., 1958.

ЛИТЕРАТУРА
16.7.
16.8.
16.9.
16 10.
16.11.
16.12.
16.13.
16 14.
16.15.
16 16.
16.17.
16 18.
16.19.
16.20.
16.21.
16.22.
16.23.
16.24.
16.25.
16.26.
16.27.
16.28.
16.29.
16.30.
16.31.
16.32.
16.33.
16.34.
16.35.
16.36.
16.37.
16.38.
16.39.
16.40.
М е р р и э м К. У., Теория оптимизации и расчет систем управления с обратной
связью. «Мир», М., 1967.
Механика в СССР за 50 лет, т. 1, «Наука», М., 1968.
Б р а й с о н А. Э., Х о Ю вЂ” ш и, Прикладная теория оптимального управле-
ния. «Мир», М., 1972.
Б о д н е р В. А., Теория автоматического управления полетом. «Наука», М.,
1964.
П о н о м а р е в В. М., Теория управления движением космических аппаратов.
«Наука», М., 1965.
Б о г у с л а в с к и й И. А., Методы навигации и управления по неполнои ста-
тистической информации. «Машиностроение», М., 1970.
Алексеев К. Б., Бебенин Г. Г., Ярошевский В. А., Маневри-
рование космических аппаратов. «Машиностроение», М., 1970.
Основы теории полета космических летательных аппаратов. Под ред. Г. С. Н а-
риманова и М. К. Тихонравова, «Машиностроение», М., 1972.
Методы оптимизации с приложениями к механике космического полета. Под ред.
Дж. Л е й т м а н а, «Наука», М., $965.
Б э т т и н Р., Наведение в космосе. «Машиностроение», М., 1966.
А б ц у г М. Дж., С т е ф а н К. Ф. идр., Управление космическими летатель-
ными аппаратами. «Машиностроение», М., 1967.
Т о к а р е в В. В., Влияние случайных отклонений от оптимальной программы
по тяге на движение тела переменной массы с постоянной затратой мощности
в гравитационном поле. Прикл. матем. и механ., т. 27, № 1, 1963.
Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., О движении
тела переменной массы с постоянной и убывающей затратой мощности в гравита-
ционном поле, 111. Ргос. Х1У 1Ыегпа~. Ая$гопаи$. Сопряг. 1963, Жагякажа,
1964.
И л ю т о в и ч А. Е., Анализ системы управления движением аппарата с малой
тягой. Космические исследования, т. 6, № 5, 1968.
И л ю т о в и ч А. Е., Управление движением системы с ограниченной мощностью
в режиме накопления массы. Космические исследования, т. 7, № 2, 1969.
3 л е н к о Ю. А., Исследование точности динамических систем с малым пара-
метром. Тр. ЦАГИ, вып. 1433, М., 1972.
А н д е р с о н Т., Введение в многомерный статистический анализ. Физматгиз,
1963.
С т р а т о н о в и ч Р. Л., Условные марковские процессы и их применение
к теории оптимального управления. Изд-во МГУ, 1966.
Боголюбов Н. Н., Митропольский Ю. А., Асимптотические ме-
тоды в теории нелинейных колебаний. Физматгиз, М., 1963.
Л а р и ч е в а В. В., Об осреднении одного класса систем нелинейных уравне-
ний. Дифференциальные уравнения, т. 2, № 3, 1966.
Л и н н и к Ю. В., Метод наименьших квадратов и основы математико-статисти-
ческой теории обработки наблюдений. Физматгиз, М., 1962.
К а л м а н Р., Б ь ю с и Дж., Новые результаты в линейной фильтрации и тео-
рии предсказания. Техническая механика, серия Д, т. 83, № 1, 1961.
Д е м и д о в и ч Б. П., Лекции по математической теории устойчивости. «Наука»,
М., 1967.
1 а ж Й е и О. Р., Ор$1ша1 ргодгатте аког соггес$1опа1 шапиегегя. Ая$г. Ас$а,
'го1. 6, Мо. 1, 4, 1960.
Б о г у с л а в с к и й И. А., О статистически оптимальном управлении конечным
состоянием. Автоматика и телемеханика, № 5, 1966.
Л и п ц е р Р. Ш., Ш и р я е в А. Н., Нелинейная фильтрация диффузионных
марковских процессов, 1, 11. Тр. МИАН, т. 104, 1968.
Б е л л м а н Р., Динамическое программирование. ИЛ, М., 1960.
Т и х о н о в А. Н., ТЬеогетея й'ип1сйе розг 1'ециа$1оп Йе 1а сЬа1еиг. Матем. сб.,
т. 42, № 2, 1935.
Х а з е н Э. М., Методы оптимальных статистических решений и задачи опти-
мального управления. «Советское радио», М., 1968.
Т и х о н о в А. Н., С а м а р с к и й А. А., Уравнения математической физики.
«Наука», М., 1966.
М и х л и н С. Г., Лекции по линейным интегральным уравнениям. Физматгиз,
М, 1959.
К а з а к о в И. Е., Д о с т у п о в Б. Г., Статистическая динамика нелинейных
автоматических систем. Физматгиз, М., 1962.
Андронов А. А., В итт А. А., Хайкин С. Э., Теория колебаний.
Физматгиз, М., 1959.
П л а т о н о в А. К., Свойства корректирующих маневров в межпланетных
полетах. Космические исследования, т. 4, № 5, 1966.

699
ЛИТЕРАТУРА
главе 17
17.1. Т я1е и Н. Я., Та1се-оЛ Йош яаСе111Се огЬ1С. 1. Ашег. ВосЕ. Яос., чо1., 23, Мо. 4,
1953.
17.2. Р о Ь г о ~ч о 1 я 1~ 1 А., ЯаСе111Се огЫС регСцгЬаСюп цпйег а сопС1пцоця гай1а1
СЬгцяС о1 яша11 тацп1Сцйе. 1. Ашег. ВосЕ Яос., чо1. 28, Мо. 7, 1958.
$7.3. С о р е 1 а и Й Х., 1пСегр1апеСагу Сга1есСог1ея цпйег 1ок-СЬгцяС гай1а1 ассе1егаСюп. У.
Ашег. ВосЕ Яос., чо1. 29, Мо. 4, 1959.
$7.4. К а г г е и Ь е г д Н. К., МоСе оп 1пСегр1апеСагу Сга1есСог1ея цпйег 1ож-СЬгцяС
гай1а1 ассе1егаСюп. 1. Ашег. Вос1~. Бос., чо1. 30, Мо. 1, 1960.
~7.5. А ц О., СоггесС1опя аког 1пСегр1апеСагу Сга1есСог1ея цпйег 1ок-СЬгцяС гай1а1 ассе1ега-
С1оп. 1. Ашег. ВосЕ Яос., чо1. 30, Мо. 7, 1960.
47.6. Р а1 е ~ч о и я 1с у В., ТЬе шоС1оп о1 ап огЬ1С1пцчеЫс1е яцЬ~есСей Со сопС1пцоця
гай1а1 СигцяС, 1пс1цй1пд а яСцйу о1 р1апеСагу епсоцпСегя. Ргос. Х 1пСегпаС. АяСгопацС.
Сопряг., Ьопйоп, 1959, У1еп, 1960.
17.7. Р е С С у С. М., 1пСегр1апеСагу шапецчгея, цып~ гап1а1 СЬгцяС. 1. Ашег. ВосЕ
Яос., чо1. 33, Мо. 9, 1961.
17.8. А и С., 1пСегр1апеСагу ВаЬпеп Ыг Вацш1аЬгСкецде ш1С Ые1пег Яс1шЬЬеясЫецп1дцпд.
ВаКеСепСесЬпЖ цпй ВацшГайгЫогясЬцпд, Вй. 5, Мг. 2.
17.9. Ц а н д е р Ф. А., Об использовании силы давления света для полетов в межпла-
нетном пространстве, в сб.: Ф. А. Ц а н д е р. Проблема полета при помощи ре-
активных аппаратов. Межпланетные путешествия. Оборонгиз, М., 1961.
'17.10. Ь о и й о и Н. 8., Яоше ехасС яо1цС1оп о1 СЬе еоцаС1оп о1 шоСюп о1 яо1аг яа11 и1СЬ
сопяСапС яа11 яеСС1пд. 1. Ашег. ВосЕ Яос., чо1. 30, Мо. 2, 1961.
17.11. Ь а я я Н., Ь о г г е1 1., Ьо~ч ассе1егаСюп Са1~е-оП 1гош а яаСе1Ие огЫС. 1. Ашег.
Вос1с. Яос., чо1. 31, Мо. 1, 1961. Русский перевод. 'Ракетная техника, № 1,
1961.
Я7.12. С 1 С г о и Я. У., Яо1цСюп аког яаСе111Се шоСюп цпйег 1ои ассе1егаСюп цып~ шеСЬой
о1 чаг1аС1оп о1 рагашеСегя. 1. Ашег. ВосЕ Яос., чо1. 31, Мо. 12, 1961.
1713. АгСЬцг Р. Р., КаггепЬегд Н. К., ЯСаг1~ Н. М., 81шр1е шеСЬой
юг арргохппаСюп о1 СЬе сагасСегиС1ся о1 1о~ч СЬгцяС Сга1есСог1ея. 1. Ашег. Вос1.
Яос., чо1. 30, Мо. 7, 1960.
'й7.14. Р о г Ь е я С. Р., ТЬе Сга1есСогу о1 а ро~чегей гос1~еС 1и ярасе. 3. Вг1С. 1пСегр1. Яос.,
чо1. 9, Хо. 2, 1950.
'17.15. Гродзовский Г. Л., Иванов Ю. Н., Токарев В. В., О движении
тела переменной массы с постоянной затратой мощности в гравитационном поле.
Докл. АН СССР, т. 137, № 5, 1961.
47.16. Б е л е ц к и й В. В., Е г о р о в В. А., Межпланетные полеты с двигателем
постоянной мощности. Космические исследования, т. 2, № 3, 1964.
17.17. Ь е ч1 и Е., Ьок-СЬгцяС Сгапя1ег ЬеСкееп с1гсц1аг огЬ1Ся. АЯМЕ ргерг., 59-АУ-2,
МагсЬ 1959.
17.18. Л у р ь е А. И., Ч е р е м с и н М. К., Движение материальной точки в поле
центральной силы тяготения при наличии малой трансверсальной тяги. Сб. «Ис-
кусственные спутники Земли», № 16, Изд-во АН СССР, 1963.
17 19. Ь а ж Й е и Р. Р., ОрС1ша1 рго~гашш1п~ о1 СЬгцяС й1гесСюп. АяСгопацС. АсСа, чо1. 1,
Ио. 1, 1955.
47.20. Ь а ~ч Й е и Р. Р., ОрСппа1 еясаре 1гош а с1гсц1аг огЫС. АяСгопацС. АсСа, чо1. 4,
Хо. 3, 1958.
47.21. Л е б е д е в В. Н., Вариационная задача о взлете космического аппарата с кру-
говой орбиты. Ж. вычисл. матем. и матем. физ., т. 3, № 6, 1963.
'17.22. М о е с 1с е 1 Ж. Е., Тга1есСог1ея к1СЬ сопяСапС Сап~епС1а1 СЬгцяС 1п сепСга1 дгач1-
СаС1опа1 Йе1йя. МАЯА ТВВ-53, 1959.
17.23. В е и и е у Р. 1., Еясаре 1гош а с1гсц1аг огЬ1С цыпа Сап~епС1а1 СЬгцй. 1. Ашег.
Вос1~. Яос., чо1. 28, Мо. 3, 1958.
17.24. А и С Ь о и у М. Ь., М а й а у С. Х., МоС1оп о1 огЬ1С1пд чеЫс1ея цпйег арр11са-
Сюп о1 СапдепС1а1 ш1сгоСЬгцяС. Ргерг. Ашег. АяСгопацС. Яос., № 102, 21, 1961.
17.25. Р е г 1с 1 п я Р. М., Р11дЬС шесЬап1ся о1 1ок-СЬгияС ярасе сгай. 1АЯЯ, чо1. 26, Хо. 5,
1959.
17.26. О х о ц и м с к и й Д. Е., Исследование движения в центральном поле под дей-
ствием постояпного касательного ускорения. Космические исследования, т. 2,
М 6, 1964.
17.27. В а с о и В. Н., Ьо~аг1СЬш1с яр1га1: ап 1йеа1 Сга1есСогу аког СЬе 1пСегр1апеСагуче-
Ыс1е к1СЬ епд1пея о1 1о~ч яцяСа1пей СЬгцяС. Атег. 1. Раув., чо1. 27, 1959, 164 — 165.
17.28. Н и д Ь е я 1. У., Х о т 1 с а я С. Х., Тга1есСог1ея о1 сопС1пцоця1уарр11ей рго-
рц1яче СЬгцяС. Р1апеС Брасе Яс1., Хо. 7, 1961, 145 — 153.
17.29. Я С а г 1~ Н. М., А г С 11 ц г Р. Р., Мшр1е арргохппаСе яо1цСюпя аког Сап~епС1а1
1оъ-СЬгцяС Сга1есСог1ея. 1АЯЯ, чо1. 28, Хо. 7, 1961.
47.30. Р 1 и 1~ Ь а ш 6., Ве1егепсе яо1цСюп аког 1о~ч-СЬгцяС Сга1есСог1ея. 1. Ашег. ВосЕ
Ьос., чо1, 32, Мо. 5, 1962. Русский перевод: Ракетная техника, № 5, 1962.

700
ЛИТЕРАТ~РА
В о Й г ~ р ц е г О., Ме$Ьой аког Йе$егш~шпд я$еег~пд ргоцгашшя аког 1ож-$Ьгцяф
~п1егр1апе$агу чеЫс1ея. У. Ашег. ВосЕ Яос., чо1. 29, Бо. 10, 1959.
Ь е ч ~ и Е., Ьож ассе1егаИоп Сгапя1ег огЫСя. НапйЬоо1~ о1 АяСгопацС. Епд., МсОгаж-
НИ1, Б. У., 1961.
Ь а я я Н., Я о11о ж а у О. В., МоИоп о1 а яа$е11йе цпйег $Ье ~Ы1цепсе о1 а соп-
яСапС погша1 СЬгцяй. У. Ашег. Вос1. Яос., чо1. 32, Бо. 1, 1962. Русский перевод.
Ракетная техника, № 1, 1962.
В ~ й е г Ь., Ьож-СЬгцяС соггес$юп о1 огЫСа1 ог~еМаСюп. Х. Ашег. ВосЕ Яос.,
чо1. 30, Бо. 7, 1960.
И л л а р и о н о в В. Ф., Ш к а д о в Л. М., Поворот плоскости круговой ор-
биты спутника. ПММ, т. 26, № 1, 1962.
Г у с ь к о в Ю. П., Метод управления поворотом плоскости круговой орбиты
спутника. ПММ, т. 27, № 3, 1963.
Б е л е ц к и й В. В., О траекториях космических полетов с постоянным вектором
реактивного ускорения. Космические исследования, т. 2, № 3, 1964.
17.31.
17.32.
17.33.
17.34.
17.35.
17.36.
17.37.
главе 18
18.1.
18.2.
18.3.
18.4.
18.5.
18.6.
18.7.
18.8.
18.9.
18.10.
18.11.
18.12.
18.13.
18.14.
18 15.
18.16.
18.17.
18.18.
18.19.
18.20.
18.21.
18.22.
18.23.
18.24.
Б е л л м а н Р., Динамическое программирование. ИЛ, М., 1960.
Беллман Р., Гликсберг И., Гросс О., Некоторые вопросы мате-
матической теории управления. ИЛ, М., 1962.
Б е л л м а н Р., Процессы регулирования с адаптацией. «Наука», М., 1964.
Б е л л м а н Р., Д р е й ф у с С., Прикладные задачи динамического програм-
мирования. «Наука», М., 1965.
М о и с е е в Н. Н., Численные методы в теории оптимальных систем. «Наука»,
М., 1971.
К ротов В. Ф., Букре ев В. 3., Гурман В. ц., Новые методы вариа-
ционного исчисления в динамике полета. «Машиностроение», М„1969.
К у р а н т Р., Принцип Дирихле, конформные отображения и минимальные
поверхности. ИЛ, М., 1963.
К а н т о р о в и ч Л. В., Об одном эффективном методе решения экстремальных
задач для квадратичного функционала. Докл. АН СССР, т. 48, № 7, 1945.
К а и т о р о в и ч Л. В., О методе наискорейшего спуска. Докл. АН СССР, т. 56,
№ 3, 1947.
К а н т о р о в и ч Л. В., Функциональный анализ и прикладная математика.
Успехи матем. наук, т. 3, № 6, 1948.
Б и р м а н М. Ш., Некоторые оценки для метода наискорейшего спуска. Успехи
матем. наук, т. 5, № 3 (37), 1950.
С а м о к и ш Б. А., Исследование быстроты сходимости метода наискорейшего
спуска. Успехи матем. наук, т. 12, № 1 (3), 1957.
Я $ е ~ и М. Ь., Оп шеСЬойя аког оЬСапппд яо1цСюпя о1 йхей епйро~пС ргоЫешя
~и СЬе са1сц1ця о1 чаг~аИопя. БаС. Вцг. Яйапйагйя, Х. Вея., чо1. 50, Хо. 5, 1953.
Т о м п к и н с Ч. Б., Методы быстрого спуска. Сб. «Современная математика
для инженеров» (под ред. Э. Ф. Беккенбаха), ИЛ, 1И., 1959.
В о я е и Ь 1 ц ш Р. С., ТЬе шеФЬой о1 я$еереяС йеясепй. Ргос. о1 СЬе ых$Ь Яушр.
$п Арр1. МаСЬ. о1 СЬе Ашег. МаФЬ. Яос., МсОгаж-Н~11, 1956.
И в а н о в Ю. Н., Ш а л а е в Ю. В., Метод скорейшего спуска в применении
к расчету межорбитальных траекторий с двигателями ограниченной мощности
Космические исследования, т. 2, № 3, 1964.
Б р у м б е р г В. А., Численное решение краевых задач небесной механики
методом наискорейшего спуска. Бюл. Ин-та теорет. астрономии, т. 8, № 4, 1962.
Ш а т р о в с к и й Л. И., Об одном численном методе решения задач оптималь-
ного программирования. Ж. вычисл. матем. и матем. физ., т. 2, №, 3, 1962.
Э н е е в Т. М., О применении градиентного метода в задачах теории оптимального
регулирования. Доклад на Всесоюзн. симпозиуме по многоэкстремальным зада-
чам. Вильнюс, 13 — 15 июня 1963.
К е11е у Н. У., Огай~еп$ ФЬеогу о1 орбша1 11~дЬФ раФЬя. У. Ашег. ВосЕ Яос.,
чо1. 30, Бо. 10, 1960.
К е11е у Н. 1., К о р р В. Е., М о у е г Н. О., Яцссеяяче арргохпнаФюп $есЬ-
п~ццея аког Фга~ес$огу орОш~гаФюп. Ргос. 1АЯ Яушр. оп УеЫс1е Яуя$. Орйш., Б. У.„
1961.
В г у я о и А. Е., 0 е и Ь а ш Ж. Р., Мц10чаг~аЫе $егш~па1 соМго1 аког ш~ппнцш
шеап япцаге Йеч~аОоп 1гош а пош~па1 ра$Ь. Ргос. 1АЯ Яушр. оп УеИс1е Яуя$. Орбш.
Б. У., 1961.
В г у я о и А. Е., 0 е и Ь а ш Ж. Р., А я$еерея$ аясеп$ ше$Ьой аког яо1юпд орМ-
шцш ргоцгашш~пд ргоЫеш. Тгапя. АЯМЕ, Бо. 2, 1962.
Вгуяоп А. Е., ВепЬаш Ж. Р., Сагго11 Р. 1., М~1аш~ К., Ве$ег-
ш~паСюп оЕ ИФ оЕ Йгад ргоцгашшя СЬай ш~ппшге ге-епСгу ЬеаИпд. ВПАЯЯ, чо1. 29,
Бо. 4, 1962.

701
ЛИТЕРАТ~РА
$8.25. В гуяоп А. Е., В епЬат Ж. Р., 0геу1ця Я. Е., Орйта1 ргоцтатт1~д
ргоЫетя жКЬ 1пепца1Иу сопяйга1пСя, 1: Яесеяяагу сопййюп аког ехйгета1 яо1иИопя.
А1АА 1., чо1., 1, Хо. 11, 1963.
18.26. 0 е и Ь а т Ж. Р., В г у я о и А. Е., Орйта1 ргоцтап'.пи1пд ргоЫетя жйЬ 1пепи-
а1Иу сопя$га1пСя, П: Яо1ц$юп Ьу я$еерея$-аясеп$. А1АА У., чо1. 2, Бо. 1, 1964.
18.27. К е 11 е у Н. Х., МеСЬой о1 цтай1епйя. ОрСпи1хабоп ФесЬп1ццея, сЬ. 6. Ей. Ьу б.
Ьейтапп, Асай. Ргеяя, Б. У., 1962.
18.28. Ь 1и й о г 1 е г Ж., М о у е г Н. б., Арр11са$юп о1 а 1ож ФЬгця$ Фга1ес$огу ор$1-
т1га$1оп ясЬете 1о р1апаг еагСЬ-тагя Сгапя1ег. Х. Атег. ВогЕ Яос., чо1. 32, Яо. 2,
1962.
$8.29. Я Ь е г т а и В., Ьож ФЬгця$ еясаре Фга1ес$ог1ея. Ргос. 1АЯ Яутр. оп УеЬ1с1е Яуй.
Орйт., Б. У., 1961.
18.30. Ь ц 1 е я О. Ь., Яйеереяй Йеясепй апй тахпицт рг1пс1р1е ФесЬп1ццея о1 яуяйет орМ-
т1гайюп. Ргос. 1АЯ Яутр. оп УеЬ1с1е Яуяй. Орлопп., Я. У., 1961.
18.31. О х о ц и м с к и й Д. Е., К теории движения ракет. ПММ, т. 10, М 2, 1946.
18.32. Х а г ж1и я 11 А. Н., 1пеццаИу сопяйга1пйя 1п яйеерея$-ЙеясепС Сга1есСогу орМ-
т1гайюп. Х. о1 Аегоярасе Яс1., чо1. 29, Бо. 10, 1962.
18.33. С о ц г а и С В., Са1сц1ця о1 чаг1айюпя апй яцрр1етепйагу по$ея апй ехегс1яея.
Б. У. Сп1чегяйу, 1пяЮцйе о1 МаСЬетайса1 Яс1епсея, 1945 — 1946, геч1яей апй
атепйей Ьу 1. Мояег., 1956 — 1957.
1834. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В.,
М и щ е н к о Е. Ф., Математическая теория оптимальных процессов. Физматгиз,
М., 1961.
18.35. Ч е р н о у с ь к о Ф. Л., Баничук Н. В., Вариационные задачи механики и
управления. Численные методы. «Наука», М., 1973.
18.36. А к и л о в Г. П., О применении одного метода решения нелинейных функциональ-
ных уравнений к исследованию систем дифференциальных уравнений. Докл.
АН СССР, т. 48, М 4, 1949.
18.37. А б р а м о в А. А., Вариант метода прогонки. Ж. вычисл. матем. и матем. физ.,
т. 1, М 2, 1961.
18.38. А б р а м о в А. А., О переносе граничных условий для систем линейных обыкно-
венных дифференциальных уравнений. Ж. вычисл. матем. и матем. физ., т. 1,
М 3, 1961.
$8.39. б о о й т а и Т. В., Ь а и с е б. Б., ТЬе пцтег1са1 пйецта$юп о1 ужо-ропй
Ьоцпйагу ча1це ргоЫетя. МаСЬет. ТаЫея апй ОСЬег А1йя $о Сотрцй., чо1. 10,
Бо. 4, 1956.
К главе 19
3 о й т е н д е й к Г., Методы возможных направлений. ИЛ, М., 1963.
Б е р е з и н И. С., Ж и д к о в Н. П., Методы вычислений, т. 2. Физматгиз,
М., 1961.
В г у я о и А. Е., 0 е и Ь а т Ж. Р., А яйеерея$ аясепС теФЬой аког яо1ч1пд
орОтцт ргоцтап.пи1пд ргоЫет. Тгапя. АЯМЕ, Бо. 2, 1962.
Ь1и Й о г 1 е г Ж., Б а $ Ь а и А., Ор$пи1га$юп о1 т1яя11епйегсерСгапде. Ргос.
1АЯ Яутр. оп УеЬ1с1е ЯуяФет ОрИт1га$юп, Б. У., 1961.
Энеев Т. М., Платонова А. К., Казакова Р. К., Определениепа-
раметров орбиты искусственного спутника по данным наземных измерений. Сб.
«Исскусственные спутники Земли», М 4, Изд-во АН СССР, 1960.
А к и м Э. Л., Э н е е в Т. М., Определение параметров движения космического
летательного аппарата по данным траекторных измерений. Космические иссле-
дования, т. 1, М 1, 1963.
Г а в у р и н М. К., Нелинейные функциональные уравнения и непрерывные
аналогии итеративных методов. Изв. ВУЗов, М 5, 1958.
3 ц г о ч 1 с я Я$. А., М с 1 и С у г е У. Е., ТЬе ай1о1пС теФЬой апй Кя арр11саИоп
Со Сга1есйогу орйт1гайюп. Х. Атег. Вос1. Яос., чо1. 32, Бо, 9, 1962.
И с а е в В. К., С о н и н В. В., Об одной модификации метода Ньютона числен-
ного решения краевых задач. Ж. вычисл. матем. и матем. физ., т. 3, М 6, 1963.
Г е л ь ф а н д И. М., Ф о м и н С. В., Вариационное исчисление. Физматгиз,
М., 1961.
К а н т о р о в и ч Л. В., К р ы л о в В. И., Приближенные методы высшего
анализа. Гостехиздат, М., 1941.
М и х л и н С. Р., Прямые методы математической физики. Гостехиздат, М.,
1950.
И в а н о в Ю. Н., Ш а л а е в Ю. В., Метод скорейшего спуска в применении
к расчету межорбитальных траекторий с двигателями ограниченной мощности.
Космические исследования т. 2 М 3, 1964.
19.1.
19.2.
19.3.
19.4.
19.5.
19.6.
19.7.
19.8.
19.9.
19.10.
19.11.
19.12.
19 13.

702
ЛИТЕРАТУРА
19 14. Я а1 $ г е г С., Р е С 1~ е г о 1 1 С. Ж..А й1гес$ чаг1а$юпа1 шеФЬой аког Ф11е са1-
сц1аИоп о1 орйшцш СЬгця$ ргоцгашшя аког рожег-11шйей 1п$егр1апе$агу Ц1дЬф.
Ая$гопац$. Асйа. чо1., 7, Бо. 1, 1961.
19.15. Р 1 е 11 1 е г С. 6., ТЬеогу апй арр11сайоп о1 ФЬе сгМса1 й~гесйоп ше$Ьой о~ $га-
1ес$огу орйш1га$юп. Ргос. 1АЯ Яушр. оп ЧеЫс1е Яуза. Орйш. Б. У., 1961.
19.16. Л е б е д е в В. Н., Вариационная задача о взлете космического аппарата с кру-
говой орбиты. Ж. вычисл. матем. и матем. фиэ., т. 3. М 6, 1963.
19.17. В г е а Й: ж е11 1. Ч. ТЬе орбш1га$юп о1 1га1есйог1ея. 3. Яос. 1пйця$г. апй Арр1.
МаФЬ., чо1. 7, 1959, 215 — 247.
19.18. К ц1 а 1~ о ж з 11 Ь. 1., Я $ а и с11 й. Т., Вос1е$ Ьооя$ Фга1ес$ог1ея аког шах1шцпь
Ьцгпоц$ че1осйу. 2. Ашег. ВосЕ Яос., чо1. 30, Бо. 7, 1960.
1919. Я $ а и с11 В. Т., К ц1а 1~ о ж я 1~1 Ь. 1., Вос1~е$ Ьооя$ чеЫс1е ш1зя1оп орИ-
ш1га$юпз. 3. Ашег. ВосЕ Яос., чо1. 31, Бо. 7, 1961. Русский перевод: Ракетная
техника, М 7, 1961.
19.20. 3 ц г о ч 1 с з Я$. А., Ор$1шцш я$еег1пд рго~гашш аког ергу о1 шц10я$аде чеЫс1е
про а с1гсц1аг огЬй. 3. Ашег. Вос1~. Яос., чо1. 31, Бо. 4, 1961.
19.21. В г е а 1~ ж е 11 1. Ч., Орйшцш аясеМ про а с1гсц1аг огЬЙ. Ргос. 1АЯ Яушр. ов
ЧеЫс1е Яуза. Орйш. Б. У., 1961.
1922. Мс1п$уге 1. Е., 3 цгоч1сз Я$. А., багй111 Ж. Р., 3 оЬпяоп В.,
ТЬе арр11сайюв о1 орбшцш Фга1есСогу апа1уз1я СоЬоояй чеЫс1е йея1дп. Ргос. 1АЯ
Яушр. оп ЧеЫс1е Яуза. Орйш. Б. У., 1961.
19.23. Л е б е д е в В. Н., Р у м я н ц е в Б. Н., Вариационная задача о перелете
между двумя точками в центральном поле. Сб. «Искусственные спутники Земли»,
М 16, Изд-во АН СССР, 1963.
19.24. Д е м ь я н о в В. Ф., Р у б и н о в А. М., Приближенные методы решения
экстремальных задач. Изд-во Л1'У, Л., 1968.
19.25. П ше н ичный Б. Н., Д а нилин Ю. М., Численные методы в экстремаль-
ных задачах. «Наука», 1975.

Георгий Львович Гродзовский
Юрий Николаевич Иванов
Владислав Васильевич Токарев
МЕХАНИКА КОСМИЧЕСКОГО ПОЛЕТА
(ПРОБЛЕМЫ ОПТИМИЗАЦИИ)
М., 1975 г., 704 стр. с илл.
Редакторы Р. Н. Овсянников, А. А. Могилевский
Техн. редактор С. Я. Школяр
Корректор Л. Н. Боровина
Сдано в набор 10(1Ч 1975 г. Подписано к печати 31/Х 1975 г.
Бумага 70)(108'/„. Физ. печ. л. 44. ~сл. печ. л. 61,6.
~ч-изб. л. 61,09. Тираж 2600 экз. Т-18536. Зак. № 267.
Цена книги 5 р. 51 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
1-я тип. издательства «Наука»
199034, Ленинград, 9 линия, д. 12

ИЗДАТЕЛЬСТВО (& t; НАУ
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
117071, Москва, В-71, Ленинский проспект, 15
ГОТОВЯТСЯ К ПЕЧАТИ:
Справочное руководство по небесной механике и астродинамике,
под редакцией Г. Н. Дубошина, изд. 2-е, перераб. и дополн.
Ш т и ф е л ь Е., Ш е й ф е л е Г., Линейная и регулярная небес-
ная механика, перев. с англ.
Серия «Механика космического полета»
И в а ш кин В. В., Оптимизация космических маневров.
Ориентация искусственных спутников в гравитационных и маг-
нитных полях.
Охоцимский Д. Е., Голубев Ю. Ф., Сихарулидзе Ю. 1'.,
Алгоритмы управления космическим аппаратом при входе
в атмосферу.
Предварительные заказы на указанные выше книги прини-
маются всеми магазинами Книготорга и Академкниги.
При отказе в приеме заявки заказы можно направлять по
адресу: 103050, Москва, К-50, ул. Медведева, 1, отдел (<Книга
почтой» магазина № 8.