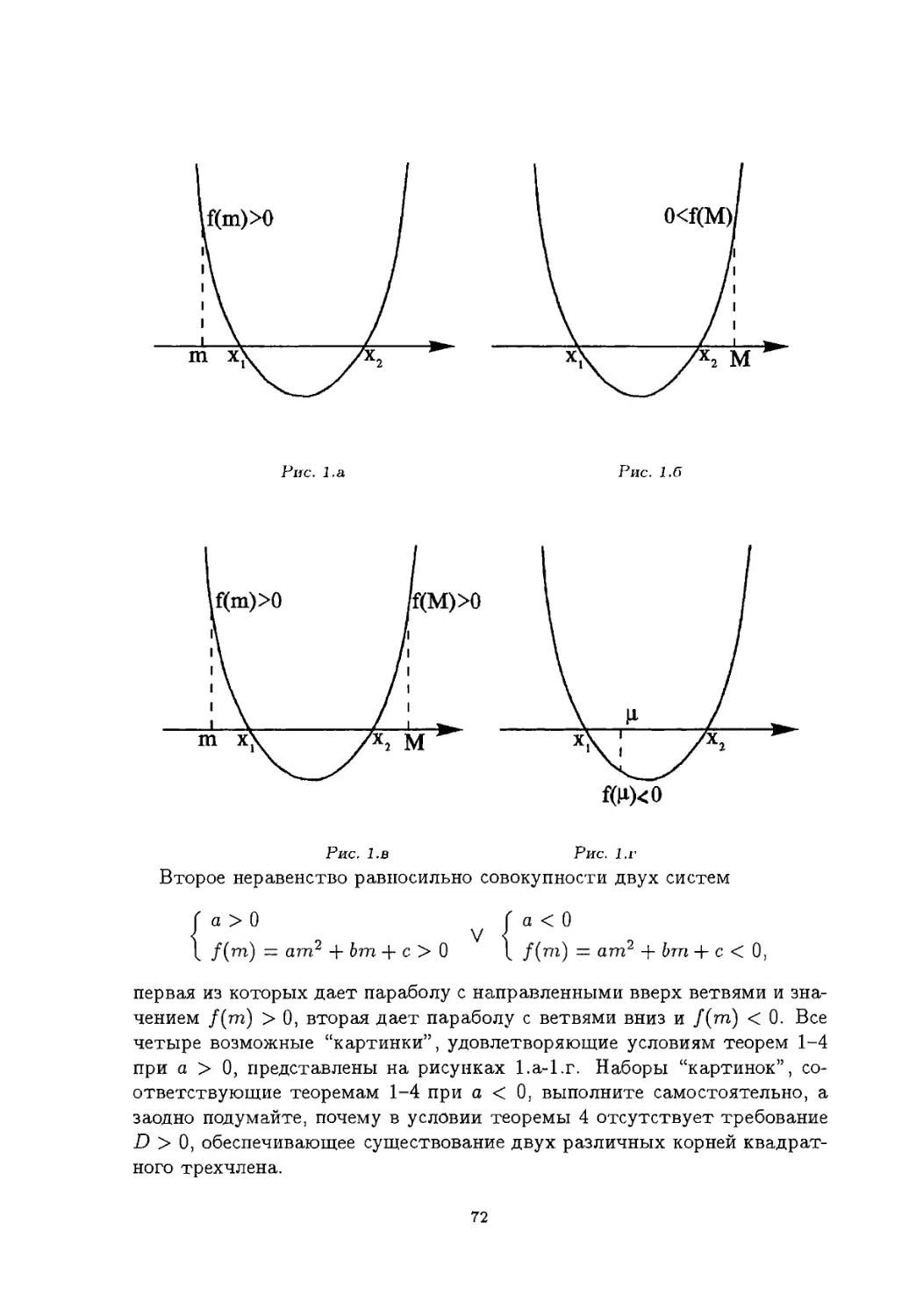
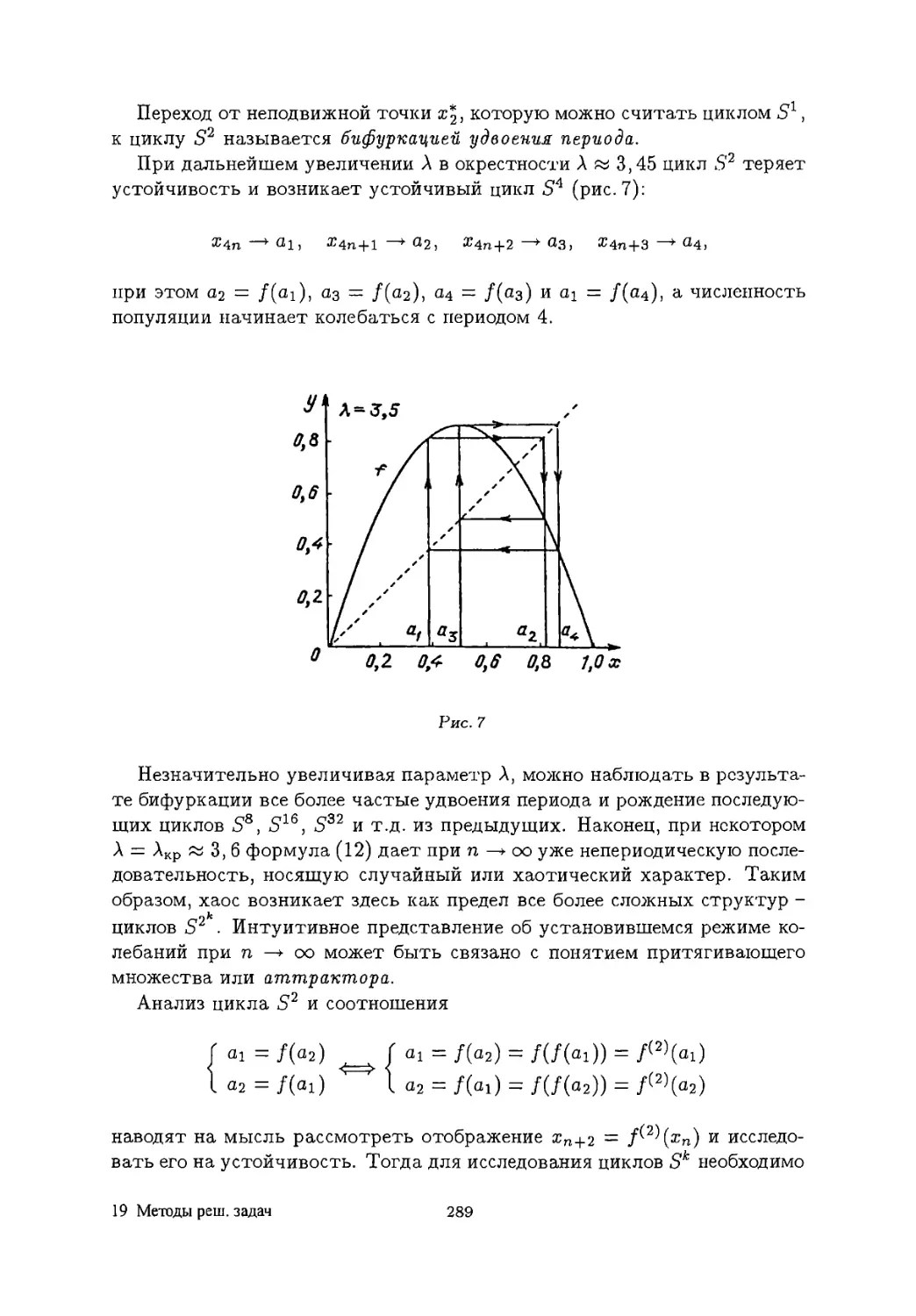
Author: Натяганов В.Л Лужина Л.М.
Tags: математика элементарная математика задачи с параметрами
ISBN: 5-211-04680-3
Year: 2003
Text
В.Л. Натяганов Л.М. Лужина
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ
УЧЕБНОЕ ПОСОБИЕ
Издательство Московского университета 2003
УДК 51 ББК 22.10 НЗЗ
Рецензент: кандидат физико-математических наук, доктор педагогических наук, заведующий кабинетом методики преподавания элементарной математики МГУ им. М.В. Ломоносова И.И.Мелъников
Натяганов В.Л., Лужина Л.М.
НЗЗ Методы решения задач с параметрами: Учеб, пособие. — М.: Изд-во МГУ, 2003. - 368 с.
ISBN 5-211-04680-3
Данное пособие посвящено задачам с параметрами, которые для абсолютного большинства абитуриентов традиционно являются задачами повышенной трудности.
В пособии основное внимание уделено классификации методов, основанных на использовании различных свойств функций (ограниченность, монотонность, периодичность, четность и т.д.), симметрии переменных, применении производной, а также специальных приемов решения задач с параметрами, требующих глубокого знания школьной математики и высокой логической культуры, что подкреплено большим количеством примеров из вариантов вступительных экзаменов в Московский государственный университет за последние 40 лет.
Для учащихся и учителей средних школ, гимназий, лицеев и колледжей, абитуриентов, руководителей математических кружков, преподавателей и слушателей подготовительных отделений и курсов.
УДК 51
ББК 22.10
ISBN 5—211—04680—3 © В.Л.Натяганов, Л.М. Лужина, 2003
© Издательство Московского
университета, 2003
ПРЕДИСЛОВИЕ
— Что толку в книжке, — подумала Алиса, — если в ней нет пи картинок, ни разговоров?
Л.Кэрролл. Алиса в стране чудес
На. протяжении ряда лет на вступительных экзаменах в Московский университет регулярно предлагались так называемые задачи с параметрами: уравнения, неравенства и системы уравнений и неравенств, содержащие параметры. Интерес к этим задачам возрастает с каждым годом: если до начала 60-х годов задачи подобного рода эпизодически встречались лишь на механико-математическом факультете, то в 60-х годах они стали регулярно предлагаться на физическом факультете, а с середины 60-х годов и на других факультетах МГУ, где есть письменный экзамен по математике, а также в других вузах.
Все возрастающая популярность задач с параметрами далеко не случайна. Теоретическое изучение и математическое моделирование многообразных процессов из различных областей науки и практической деятельности человека часто приводят к достаточно сложным уравнениям, неравенствам или их системам, содержащим параметры.
1 Необходимой частью решения подобных задач является исследование характера и конечного результата процесса в зависимости от значений параметров, причем часто оказывается, что решение зависит не от каждого параметра в отдельности, а от некоторого их характерного комплекса. В подобных случаях становится невозможным разбиение исходной задачи со многими параметрами на совокупность задач с одним из параметров. Такие задачи требуют глубокого понимания сути процесса, свободного владения различными математическими методами и скрупулезного анализа.
Можно сказать, что задачи с параметрами, предлагающиеся на конкурсных экзаменах, являются упрощенным прообразом подобных важных научно-исследовательских задач, которые предстоит решать будущим научным сотрудникам. Именно поэтому задачи с параметрами занимают важное место в числе задач на вступительных экзаменах в Московский университет.
Конкурсные задачи с параметрами чрезвычайно многообразны: задачи на исследование квадратичной функции и систем линейных уравне
1*
3
ний, задачи на делимость многочленов, задачи па минимум и максимум, геометрические задачи с параметрами, так называемые “логические” и “нестандартные” задачи и т.д.
Нельзя отрицать, что для того, чтобы успешно решать задачи с параметрами, часто требуется, говоря словами известного немецкого математика и популяризатора науки Ф. Клейна, “хотя и не слишком изощренное, но все-таки трюкачество”.
Авторы ставят своей целью в учебном пособии “Методы решения задач с параметрами” дать некоторую классификацию подобного типа задач и указать возможные пути подхода к их решению, предварительно ознакомив читателей с характерным набором специальных “трюков”.
Разумеется, в одном пособии невозможно разобрать все типы задач с параметрами и осветить в общем виде большинство вопросов, возникающих при решении подобных задач. Поэтому там, где это возможно, будет приведена краткая теория вопроса (исследование квадратичной функции и линейных систем из двух или трех уравнений). Однако большинство методов решения задач с параметрами будет проиллюстрировано на конкретных примерах из числа задач, предлагавшихся на вступительных экзаменах в МГУ на различные факультеты, и будет сопровождаться необходимыми пояснениями.
Следует подчеркнуть, что получить высокую оценку на конкурсном экзамене по математике при поступлении в МГУ, не умея решать задачи с параметрами, становится все труднее. А решить задачу с параметрами - это значит установить, при каких значениях параметров задача имеет решения, и найти эти решения в зависимости от параметров, т.е. решение подобного типа задач должно сопровождаться своего рода исследованием. Как правило, именно необходимость проводить исследование значительно осложняет решение задач с параметрами, так как требует от абитуриентов глубоких знаний различных разделов школьной программы и высокой логической культуры.
Кроме того, для успешной подготовки к конкурсным экзаменам решение некоторого количества однотипных задач является не менее важным, чем расширение знаний за счет решения задач разных типов. Поэтому в данном пособии после каждой главы даны задачи с ответами для самостоятельного решения, а в приложении приведены конкурсные задачи с параметрами разных типов, предлагавшиеся на различных факультетах МГУ в разные годы. Решение части этих задач является необходимым для успешной сдачи вступительных экзаменов по математике.
Авторы надеются, что пособие “Методы решения задач с параметрами” будет полезно слушателям и преподавателям подготовительных курсов и отделений, будущим абитуриентам и учителям средних школ, колледжей и гимназий, а также послужит основой специальных курсов для студентов педагогических вузов и университетов, специализирующихся в области элементарной математики.
При подготовке пособия авторы использовали свой опыт работы на подготовительном отделении Московского университета, в ФМШ № 18 имени академика А.Н. Колмогорова при МГУ (ныне специализирован
4
ный учебно-научный центр при МГУ) и в Московоском городском центре образования № 654.
В заключение авторы считают своим долгом выразить благодарность и восхищение всем безымянным составителям конкурсных задач с параметрами, без творческих идей и кропотливого труда которых появление данного пособия было бы проблематично. Особенно авторы признательны В.В.Вавилову и И.И.Мельникову, взявшим на себя труд прочитать рукопись и сделавшим ряд ценных замечаний.
Идея о необходимости создания пособия по решению задач с параметрами возникла у авторов во время их работы в ФМШ № 18 при МГУ. Именно поэтому авторы посвящают эту книгу всем преподавателям и выпускникам школы-интерната физико-математического профиля имени академика А.Н. Колмогорова.
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ:
N множество натуральных чисел;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество действительных чисел;
0 - пустое множество;
{а, Ь, с} - множество, состоящее из элементов а, Ь, с;
[а, Ь] - отрезок, или замкнутый промежуток с началом а и концом 6;
(а, 6) - открытый промежуток, или внутренние точки отрезка [а, 6];
a G М - элемент а принадлежит множеству М;
b М - элемент b не принадлежит множеству М\
=> - знак следствия: А => В, когда из А следует В;
<=> - знак равносильности, или эквивалентности: А <=> В, когда из
А следует В и, наоборот, из В следует А;
U - знак объединения;
П - знак пересечения;
V - логический знак “или”: А V В <=> истинно хотя бы одно из А или В\
Л - логический знак “и”: А Л В <=> истинны и А, и В;
| - знак системы: <=> А Л В;
[ - знак совокупности: <=> А V В;
?! - условный знак, акцентирующий внимание на
полученном противоречии.
В тексте встречаются сокращения:
- УФ МГУ - филиал МГУ им.М.В.Ломоносова в г. Ульяновске;
- ПО ОП - подготовительное отделение МГУ, общий поток, куда входят подготовительные отделения факультетов биологического, географического, химического, почвоведения и психологии;
- механико-математический факультет, ИП - вечернее отделение факультета для лиц с высшим образованием (инженерный поток).
5
ГЛАВА 1
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОГО
ИССЛЕДОВАНИЯ В ЗАДАЧАХ С ПАРАМЕТРАМИ
— По-моему, они играют совсем не так, — говорила Алиса. — Справедливости никакой... правил нет, а если есть, то никто их не соблюдает...
Л.Кэрролл. Алиса в стране чудес
Поскольку перечень теоретических вопросов, возникающих при решении задач с параметрами, достаточно широк, кратко остановимся на основных моментах их исследования. Более подробно изучить соответствующий материал можно по учебникам, справочникам и пособиям.
Как уже отмечалось в предисловии, необходимой частью решения задач с параметрами является исследование. Поэтому для того чтобы заострить внимание читателей на основных вопросах, которые возникают при решении задач с параметрами, а также показать, из каких элементов складывается решение подобных задач, рассмотрим сначала отдельные элементы исследования и проиллюстрируем их простейшими примерами.
Из школьных учебников и многочисленных пособий абитуриентам должны быть хорошо известны следующие понятия:
- область допустимых значений (ОДЗ);
- область значений, или область изменения функции (ОИФ);
- условие равносильности, или эквивалентности преобразований (УРП);
- необходимые и достаточные условия (ПДУ);
- четность, периодичность, непрерывность, монотонность функций, симметричность систем уравнений и неравенств относительно всех или некоторых переменных.
Все вышеперечисленные и некоторые другие понятия и факты могут быть полезны при решении задач с параметрами, и их учет представляет собой отдельные элементы исследования этого класса задач.
Основные определения и обозначения, а также стиль изложения материала близки к принятым в известных пособиях по элементарной математике [1-3].
7
Бесспорно, что для большинства абитуриентов на конкурсных экзаменах по математике задачи с параметрами часто вызывают серьезные трудности. Некоторые абитуриенты вообще не могут понять, что же от них требуется. Причин тому несколько. Первая - недостаточное внимание к подобным задачам при изучении школьной программы, причем следует отметить, что любой заинтересованный учитель в состоянии дать элементарное понятие о решении задач с параметрами, объясняя многие разделы именно школьной программы и используя при этом школьные учебники. Вторая причина более существенна. Она состоит в том, что основной стратегией математического образования в средней школе является развитие умений и навыков решения ограниченного ряда типовых задач, как правило, связанных с определенным набором стандартных алгебраических преобразований. Таким образом, в средней школе гораздо большее внимание уделяется тому, КАК надо решать ту или иную конкретную задачу определенного типа, а не тому, ПОЧЕМУ ее нужно решать именно ТАК. Поясним сказанное подробным разбором простейших примеров.
Пример 1. При всех значениях параметров а и b решить уравнение
ax + b = 0.
(1)
Решение. Если бы в условии задачи не было последней фразы с упоминанием о параметрах а и Ь, то многие абитуриенты сразу написали бы ответ: х = —b/а. Однако слово “параметр” должно бы насторожить и заставить думать. Проанализируем алгоритм решения уравнения (1). Первый шаг алгоритма заключается в вычитании из обеих частей исходного уравнения числа Ь (или переносе числа Ь с обратным знаком в правую часть уравнения). Подчеркнем, что для любого числа Ъ это преобразование дает равносильное уравнение ах = —Ь. Второй шаг заключается в делении обеих частей полученного уравнения на число а, откуда и получается уже знакомый результат: х = —b/а. Однако делить можно, если только а 0! Следовательно, необходимо отдельно рассмотреть особый случай, когда а = 0. При этом возможны две существенно разные ситуации.
1. а = 0, но b ф 0. Тогда уравнение принимает вид 0 • х = —6?! Очевидно, что решений оно не имеет.
2. а = b = 0. Тогда уравнение принимает вид 0 • х = 0, которое справедливо при всех х € R.
Грамотный абитуриент мог бы записать решение этой задачи вообще без каких-либо пояснений в следующем виде:
ах + 6 = 0 <=+ ах = —Ь <=>
8
Ответ: при а ф 0 и любом b - единственное решение х = —Ъ/а\
при а = 0, 6^0- решений нет;
при а — b = 0 решениями являются все действительные числа. Возможна и сокращенная запись ответа:
при а ф 0, b Е R Xi = —Ъ/а\
при а = 0, b ф 0 х Е 0;
при а = Ъ = 0 х Е R
Здесь индекс “1” при неизвестном х в случае а ф 0 указывает на
единственность решения.
Пример 2. Для каждого значения параметра а решить неравенство
1ойа (я + З)2 > 0.
(1)
Решение. Вспомнив, что для логарифмической функции выполняются следующие условия:
— выражение, стоящее под знаком логарифма, должно быть положительно, т.е. (ж + З)2 > 0 <=> х ф —3;
— основание логарифма должно быть положительно и отлично от 1, т.е. 0 < a 1;
— логарифмическая функция монотонно возрастает при а > 1 и убывает при 0 < a < 1;
и не забыв о знаке модуля при выносе четной степени из-под знака логарифма, решение неравенства (1) можем без всяких дополнительных пояснений записать в следующей форме:
Ответ: при а О, а = 1 х Е 0;
при О < а < 1 х Е [—4; —3) U (—3; —2];
при а > 1 х Е (— оо; —4] U [—2; +оо).
Пример 3. Найти все значения параметра а, при каждом из которых уравнение
Зах2 - 2(3а - 2)х + 3(а - 1) = 0 (1)
имеет хотя бы один положительный корень.
Решение. При а/0 уравнение (1) является квадратным и имеет корни а?! ого, если его дискриминант неотрицателен:
D = 4(3а - 2)2 - 4 • За • 3(а - 1) = 4(4 - За) 0 <=> а 4/3.
По теореме Виета сумма и произведение корней приведенного квадратного уравнения x2+px + q — 0 связаны с его коэффициентами посредством формул
2(3а — 2) а —1
+ х2 = -р = ---7----, хх • х2 = q = -----.
За а
Существование двух положительных корней 0 < х^ х2 задается системой
а <С 4/3
а < О V а > 2/3
а < О V а > 1
а Е (—оо; 0) U (1; 4/3]. (2)
Существование одного положительного и одного отрицательного корня Х{ < 0 < х2 задается системой
D > 0 Г а < 4/3
х2 < 0 I -—- < 0 4 а
а < 4/3
0 < а < 1
0 < а < 1.
Случай наличия нулевого корня соответствует условию х± • х2 = q = О а — 1
<=> -----= 0 <=> а = 1 => Zi + х-) = — р = 2/3 > 0, т.е. второй
а
корень при а = 1 является положительным. Поэтому один положитель-
ный корень у квадратного уравнения (1) существует при а Е (0; 1].
При а = 0 степень исходного уравнения (1) понижается, оно становится линейным и приобретает вид 4х — 3 = 0 <=> х = 3/4 > 0,
10
т.е. имеет единственный корень, который оказывается положительным. Следовательно, исходное уравнение имеет положительный корень при a G [0; 1]. Объединение полученного множества с множеством (2) дает ответ задачи:
а е (-оо; 0) U [0; 1] U (1; 4/3] = (-оо; 4/3].
Ответ: а Е (—оо;4/3].
Замечание. На вступительных экзаменах чаще всего встречаются две постановки задач с параметрами:
1) для каждого значения параметра а решить уравнение (неравенство или систему);
2) найти все значения параметра а, при каждом из которых решения уравнения (неравенства или системы) удовлетворяют некоторым заданным условиям.
Отметим, что во втором случае не требуется находить сами решения (в общем случае зависящие от параметра).
Подчеркнем еще раз, что приведенные примеры вполне могли быть рассмотрены в качестве иллюстрации при изучении соответствующих разделов школьной программы. Никаких специальных методов и приемов решения задач с параметрами здесь не использовалось. Специальные “трюки” или не совсем стандартные методы и подходы к решению задач этого класса, но вполне доступные достаточно упорному абитуриенту, будут изложены ниже.
1.1. ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ И НЕИЗВЕСТНЫХ
— А, может, здесь и нет никакой морали, — заметила Алиса. — Как это нет? — возразила Герцогиня. — Во всем есть своя мораль, нужно только уметь ее найти!
Л.Кэрролл. Алиса в стране чудес
Области определения многих элементарных функций ограничены, поэтому и ОДЗ неизвестных и параметров для ряда задач оказывается ограниченной. Как правило, нахождение ОДЗ сводится к формулировке и
11
решению системы неравенств, определяющих допустимые значения неизвестных и параметров для отдельных функций и алгебраических выражений, входящих в условие задачи. Поскольку решения отдельных неравенств системы могут зависеть от параметров, совмещение этих решений для нахождения общего решения системы требует исследования взаимного расположения на числовой оси границ областей решений каждого из неравенств в зависимости от параметров. Только после того как эта работа выполнена, становится возможным правильный выбор границ ОДЗ неизвестных для каждого значения параметра. Следует подчеркнуть, что встречаются случаи, когда при некоторых значениях параметра ОДЗ не включает ни одного значения неизвестного, т.е. исходная задача не имеет решений. Таким образом, часто только формулировка условий, определяющих ОДЗ неизвестного, позволяет определить и значения параметра, при которых задача может иметь решение.
Задача 1 (экономический факультет, отделение политэкономии, 1985). Укажите все а, при которых уравнение
log2 х + loga х + log4 х - 1 (1)
имеет решения, и найдите эти решения.
Решение. Так как логарифмическая функция определена при положительном, отличном от единицы основании и только для положительных выражений, стоящих под знаком логарифма, то ОДЗ параметра а и неизвестного х определяется условиями
( 0 < a 1,
[ х > 0.
Использовав формулы перехода к основанию 2, перепишем уравнение (1) в следующем виде:
Если 2 + 31og2 a = 0 <£=> a = 2-2/3, то уравнение (2) и равносильное ему уравнение (1) решений не имеют. Если 24-3 log2 a 0, т.е. a 2-2/3, то уравнение (2) можно представить в эквивалентной форме
1ог х = 21°g3fl = 2I°g2a 4log2 a/ log2 4a3
2 2 4- 3 log2 a log2 4a3
Ответ: при 0 < a / 1; 2-2/3 ж — 4bg2 a/iog2 4a3
12
Задача 2 (географический факультет, 1987). Найдите все натуральные значения Ь, при каждом из которых выражение 1/(х 4- у 4- 3) имеет смысл для всех таких пар чисел (ж; у), где х < 0 и у < О, что выражение 1g (ту — Ъ) также имеет смысл.
Решение. Требуется найти множество значений JVi натурального параметра Ь, при которых выполняется система
х < 0, у < О < ту > b £ N
(1)
< х 4- у 4- 3 ф 0.
Заметим, что искомое множество TVi значений параметра 6 совпадает с множеством значений этого параметра, для которых система
х < 0, у < 0
< ху > b £ N
< х 4- у 4- 3 = 0
(2)
не имеет решений.
Действительно, если через N* обозначить множество значений параметра Ь, для которых выполняется подсистема системы (1), составленная без учета последнего соотношения, т.е. без учета значения суммы х4-т/4-3, то множество N* = Ni U Nz, причем для любого b Е N* возможны лишь два случая:
а?4-у4-3^0и тогда b Е Ni,
т4-2/4-3 = 0и тогда b Е N2 •
При b — 1 и b = 2 система (2) совместна, так как для х = у = —3/2 имеем ху = 9/4 > 2.
Докажем, что при b 3 система (2) несовместна. Действительно, так как х < 0 и у < 0, то |а?| • |т/| = х у > 0, но из известного соотношения между средним арифметическим (|ж| 4- |г/|)/2 и средним геометрическим урЁ||г/| двух положительных чисел |®| и |у| следует
= УИ • М •
Возводя обе части этого неравенства в квадрат и используя условия системы (2), получаем противоречие:
з<х.у=н.ыцжыу=^у = 2>25 ?!
13
Следовательно, при натуральных b 3 система (2) несовместна, а система (1) имеет решения.
Ответ: 3 b £ N.
Разумеется, далеко не всегда условия, определяющие ОДЗ параметров и неизвестных, можно достаточно просто разрешить. В ряде случаев решение неравенств, определяющих ОДЗ, бывает значительно более сложным, чем непосредственное решение задачи. Если задача состоит в решении уравнения, то в таких ситуациях удобно бывает сначала решить уравнение, а затем проверить, при каких значениях параметра для каждого из корней выполняются условия, определяющие ОДЗ. Однако при решении большинства задач с параметрами проверка становится настолько сложной, что выполнить ее практически невозможно. Именно поэтому использование методов, позволяющих устранить посторонние решения, не прибегая к проверке, приобретает большое значение. Кроме того, реализация условий, определяющих ОДЗ, часто избавляет от необходимости выполнять большой объем ненужных вычислений, которые все равно могут привести к посторонним решениям.
В любом случае формулировка условий, определяющих ОДЗ, и сведение исходной задачи к равносильной ей системе уравнений и неравенств полезны, так как позволяют избежать ряда возможных ошибок и выбрать оптимальный путь решения задачи в каждом конкретном случае.
1.2. ОБЛАСТЬ ИЗМЕНЕНИЯ ФУНКЦИИ
А мораль отсюда такова: думай о смысле, а слова придут сами.
Л.Кэрролл. Алиса в стране чудес
Область значений многих элементарных функций или (не путать с ОДЗ неизвестных и параметров!) область изменения функций (ОИФ) тоже может быть ограничена. Поэтому выражения, составленные из подобных функций, также могут изменяться в некоторой ограниченной области.
Задачи с параметрами, в условиях которых фигурируют ограниченные функции, при некоторых значениях параметров могут не иметь решений. Поэтому к числу условий, из которых определяются возможные значения параметров, относятся и условия ограниченности функций, входящих в условие задачи.
Задача 3 (факультет ВМиК, 1970). Определить все действительные
14
значения параметра а, при каждом из которых уравнение
sin4 х + (а — 4) sin2 х — 3(а — 1) = О
(1)
имеет решения, и найти эти решения.
Решение. Сделаем замену z = sin2 ж, тогда уравнение (1) сведется к квадратному уравнению
z2 + (а — 4)z — 3(а — 1) = О
(2)
21,2 = 2 - - ± (а + 2)2 = 2 - - ± -|а + 2|.
Так как для любого х справедливо неравенство 0 | sin х| <С 1, то
О z 1. Тогда при а — 2 выполняется |а + 2| = —(а + 2) и
21,2 = 2 - =F + 2) = 2 - =F =F 1 = (1 - а); 3.
При а —2 имеем |а + 2| = a + 2 и
21,2 = 2- -±-(а + 2)-2--±-±1=3; (1 - а).
Следовательно, для любого а уравнение (2) имеет единственный корень zi = 1 — а, удовлетворяющий условию 0 zi 1, при 0 a 1.
Тогда относительно переменной х при a Е [0; 1] получаем уравнение
sin2 х = 1 — a
sin х = ±-\/1 — a.
Ответ: при a Е (0; 1) х = iarcsinл/1 — а + тгтг;
7Г при a = 0 х — — + 7гп; при a = 1 х = тгп, n Е Z .
Задача 4 (факультет почвоведения, 1983). Найдите все значения а, которые удовлетворяют условию 2 < а < 5 и при которых уравнение
(1)
относительно х имеет хотя бы одно решение, удовлетворяющее условию 2 <С х <С 3.
Решение. Заметим, что при любом х
cos (тех — — < 1
\ 6/1
— 1 < COS ( 7ГХ — — I < 1, X 6/
15
| sin az| 1 ==> (3 — | sin az|) 2 €=> log2 (3 — | sinaz|) 1.
Поэтому уравнение (1) может иметь решение лишь только в том случае, когда только левая и правая его части одновременно принимают соот-
ветственно свое минимальное и максимальное значение, равное единице. В этом случае уравнение (1) будет эквивалентно системе
log2 (3 — | sin ах|) = 1 cos (тгх — 7г/6) = 1
3 — | sin ах| = 2
тех — тг/6 = 2тгп, п £ Z
sin ах = ±1
т = 1/6 + 2n, п Е Z
ах = 7г/2 4- тгт, т £ Z х — 1/6 4- 2n, п £ Z.
По условию задачи надо найти решение, удовлетворяющее условию 2 < х < 3, т.е. 2 < 1/6 4- 2п < 3 п = 1 => х = 13/6, и найти параметр а £ (2; 5). Следовательно, для определения параметра а имеем
неравенство
л 1.3 7Г
2 < —а = —|- тгт < 5
6 2
m = 1; 2 => а =
9 15
13^ iT
Ответ: 9тг/13; 15тг/13.
Задача 5 /экономический факультет УФ МГУ, 1992). чения параметра а, при которых система уравнений
( 26 2
3х 4- — COS у = а2 4- а
L 1з
3 — cos у = — 1
3 У имеет хотя бы одно решение.
Найти все зна-
(1)
Решение. Система (1) элементарными преобразованиям приводится к следующей эквивалентной системе:
Г 13 cos у = а2 4- а 4- 1
t 3 • Зг = а2 4-а — 2. U
Так как 3х > 0 при всех х и | cos у\ 1 при всех у, то для того, чтобы система (2) имела хотя бы одно решение, необходимо и достаточно, чтобы выполнялась система:
|а2 4- а 4- 11 13
а2 4- а — 2 > О
а2 4- а 4- 14 О а2 4- а — 12 <1 О о2 4- а — 2 > 0.
Первое соотношение последней системы выполняется при любом а, a
два оставшихся дают систему
Г -4 а 3
[ а < — 2 V а >1 Ответ: а £ [—4; —2) U (1; 3].
а £ [—4; —2) U (1; 3].
16
Задача 6 (факультет почвоведения, 1988). При каких значениях параметра р система
х2 + 2рх + 4р2 — 5р + 3 4 sin у — 3 cos у
О у 2%
(1)
имеет единственное решение?
Решение. Выделив полный квадрат в левой части первого неравенства и применив метод введения дополнительного аргумента для правой части, систему (1) можно привести к виду
(х + р)2 + Зр2 — 5р + 3 5 sin
. 3 у — arcsin -У 5
(2)
О у 2%.
Так как в левой части неравенства (2) стоит квадратичная функция, график которой представляет собой параболу с направленными вверх ветвями, то ее ОИФ С [Зр2 — 5р + 3; +оо), а ОИФ правой части заключена в отрезке [—5; 5]. Следовательно, для выполнения условий задачи необходимо, чтобы наименьшее значение Зр2 — 5р+ 3 левой части при х = —р совпадало с наибольшим значением правой части на отрезке у 6 [0;2тг], т.е. должно выполняться соотношение
Зр2 — 5р + 3 = 5 <=> Зр2 — 5р — 2 — 0 <=>
Р1,2 =
5±7
И
Заметим, что это соотношение является и достаточным, так как условием 0 у 2тг гарантируется существование единственного максимума для правой части первого неравенства исходной системы, представляющей собой периодическую функцию с периодом 2%. Если бы множество значений переменной у было меньше полного периода, то это не гарантировало бы достижения максимума, а если больше периода, то максимум мог быть не единственным.
Ответ: —1/3; 2.
2 Методы реш. задач
17
1.3. УСЛОВИЯ РАВНОСИЛЬНОСТИ ПРЕОБРАЗОВАНИИ
А мораль отсюда такова: хорошая мина при плохой игре — самое главное!
Л.Кэрролл. Алиса в стране чудес
Как было показано выше, формулировка условий, определяющих ОДЗ, позволяет в большинстве случаев сводить первоначальную задачу с параметрами к равносильной системе уравнений и неравенств. Однако в процессе решения полученной системы не всегда удается ограничиться только равносильными преобразованиями. В ряде случаев возникает необходимость выполнять и неравносильные преобразования, как правило, расширяющие ОДЗ. При выполнении подобных преобразований среди полученных решений могут оказаться такие, которые не удовлетворяют ОДЗ исходной задачи и, следовательно, будут посторонними.
Эквивалентность перехода в таких случаях можно обеспечить формулировкой дополнительных условий равносильности преобразований (УРП), учет которых наряду с ОДЗ исходной задачи позволяет довести решение до конца.
УРП тесно связаны с понятием равносильности на множестве.
Определение. Уравнение (неравенство или система.) А равносильно системе В на множестве М, если все решения А из множества М удовлетворяют системе В, а все решения системы В из множества М удовлетворяют А.
Таким образом, при необходимости выполнения неравносильных в целом преобразований все множество М ОДЗ параметров и неизвестных разбивается на ряд подмножеств М^ \
М = Mi им2 и.. .имп,
которые попарно не пересекаются и на каждом из которых первоначальная система будет равносильна новой системе, а на всем множестве М она будет равносильна совокупности этих систем.
Подобный прием часто необходим при решении иррациональных уравнений и неравенств, когда поиск решения требует применения операции возведения в квадрат.
Подчеркнем, что переход от исходной задачи к равносильной ей совокупности систем является очень удобным приемом решения, так как все вспомогательные задачи, из которых могут быть найдены решения исходной задачи, формулируются одновременно, что уменьшает вероятность пропуска какой-либо возможной ситуации.
18
Поясним изложенные выше общие соображения подробным разбором конкретных примеров.
Задача 7 (механико-математический факультет, устный экзамен). Найти все такие значения параметров a, b и с, при которых уравнение
у/х + а д/г + b + у/х = с (1)
имеет бесконечно много решений.
Решение. ОДЗ исходного уравнения определяется системой
х О
х + ay/х + b 0.
Тогда на ОДЗ уравнение (1) будет равносильно совокупности систем
с — у/х О
х + ay/х + b = (с — у/х)2
(с — у/х < О
V <
L х G 0
О у/х <С с
(а + 2с)у/х = с2 — Ь.
(2)
Уравнение системы (2) может иметь бесконечно много решений лишь в том случае, если
a + 2с = с2 — b = 0 <=> d = —2с, Ъ = с2, где с 0.
Подставляя полученные выражения для параметров а и b через параметр с в уравнение (1), получаем
(3)
Уравнение (3) при с < 0 решений не имеет, при с = 0 имеет единственное решение х = 0, а при с > 0 равносильно неравенству
с — у/х ':> 0 <=> у/х с => 0 х с2,
т.е. имеет бесконечно много решений х Е [0;с2].
Ответ: a = —2с, b = с2, с > 0.
2:
19
Задача 8 (факультет психологии, 1989). При каждом значении параметра а найдите все решения неравенства
х + 2а — \/Зая 4- 4а2 > 0.
Решение. Условие неотрицательности подкоренного выражения дает следующую ОДЗ параметра а и неизвестного х:
а(3з? 4- 4а) 0.
Решение неравенства (1) требует применения операции возведения в квадрат. Однако эта операция осуществляет равносильный переход лишь в том случае, если обе части исходного неравенства, переписанно
го в виде
з? 4- 2а > \/а(Зх 4- 4а),
будут неотрицательны.
Поскольку в зависимости от х и а левая часть этого неравенства может иметь разные знаки, необходимо рассмотреть каждый из этих случаев отдельно.
Итак, получаем, что исходное неравенство будет равносильно совокупности систем
< п(3.г 4-4а) 0
х 4- ‘2а > у/а(3х 4- 4а)
а < 0
< 3z 4- 4а 0
х 4- 2а > >/а(31' 4- 4а)
х — 4а/3
х 4- 2а 2а/3
< '2а/3 > \/а(Зж 4- 4а)
( а < 0
! ж <С —4а/3
[ 0 <$ у/а(3х 4- 4а) < 2а/3 < 0 ?!
а. < 0
х 6 0
а 0
< а(3х 4- 4а) 0
х 4- 2а > у/а(3х 4- 4а)
а 0
< Зх 4- 4а 0
х 4- 2а > у/а(3х 4- 4а)
' а 0
х —4а/3
х + 2а 2а/3
< 2а/3 > д/а(3.т 4- 4а)
а 0
< х —4а/3
(х 4- 2а)2 > а(3х 4- 4а)
Г а > 0
1 z € [—4а/3; —а) U (0; ос).
а < 0
а < 0
а = 0
х > 0
Ответ: при а < 0 х Е 0,
20
при а — О при а > О
х £ (0; оо),
х £ [—4а/3; —a) U (0; оо).
Замечание. В данном примере подробно излагались все переходы. В дальнейшем объяснения уже встречавшихся и достаточно простых фактов будут сведены к минимуму.
Задача 9 (физический факультет, 1990). Определите, при каких a уравнение
^2х + а = 2 (1)
имеет решение, и найдите эти решения.
Решение. Заметив, что основание логарифма и подлогарифмическое выражение возведены в одну степень, уравнение (1), опустив знаки квадратного корня, можно представить в следующей равносильной форме:
1оё(2 _ ж) (2* + °) = log(2 _ ж) (2 - ^)2
0 < 2 - х ф 1
2х + a > 0
(2 — ж)2 = 2х + a
— a/2 < ж < 2
х ф 1
ж2 — 6ж + 4 — а = 0 V
a <
х £
-5
0
V < £i = 3 + л/5 + а
—а/2 < х < 2
/ £2 = 3 — л/5 + а
5 — а/2 < х < 2
V
-5
0
Ж1 = 3 + л/5 + а
< / 1
— (3 И- а/2) < \/5 Ч- а
< л/5 + а < — 1
Х2 = 3 — а/5 + а
Х2 / 1
3 + а/2
а < —5
х £ 0
а —5
г £! = 3 + л/5 + а
а £ 0, х £ 0
-4 < а / -1
£2 = 3 — \/5 + а
a
х
€
V
V
f а < -4 Г — 4 < а 1
< V < \______
( х Е 0 ( х = 3 — у5 + а.
Ответ: х = 3 — л/5 + а при —4 < а 7^ — 1.
21
1.4. НЕПРЕРЫВНОСТЬ И МОНОТОННОСТЬ ИЗМЕНЕНИЯ ФУНКЦИЙ
А мораль отсюда такова: всякому овощу — свое время.
Л. Кэрролл. Алиса в стране чудес
В предыдущих двух примерах для решения иррациональных неравенств потребовалась операция возведения в квадрат с учетом УРП на подмножествах ОДЗ. Необходимость проводить исследование неравенств н в зависимости от результата делать определенные выводы и выбирать соответствующий путь решения возникает и в ряде других задач. Часто выполнение очередных преобразований требует использования свойств непрерывности и монотонности входящих в условия функций.
Задача 10 (физический факультет, 1967). Для каждого действительного значения параметра а найти все 0 < х < кудовлетворяющие неравенству
xsinx-a>l. (1)
Решение. Заметим, что х = 1 не является решением исходного неравенства при любом значении параметра а. Далее, так как возрастание или убывание показательной функции зависит от величины основания в сравнении с единицей, то неравенство (1) равносильно совокупности двух систем неравенств
( 0 < д < 1 ч f 1 < х < 7Г/2
(2) V . 7 (3)
t sin х — а < 0 L sin х — а > 0.
В силу монотонного возрастания функции sinz при х £ (0; тг/2) первые неравенства систем (2) и (3) можно представить в виде
0 < х < 1 <=> 0 < sin х < sin 1,
1 < х < тг/2 <=> sin 1 < sin х < 1.
Тогда совокупность систем (2) и (3) будет равносильна совокупности систем
( 0 < sin х < sin 1 f sin 1 < sin x < 1
• . V • (5) t sin x < a t sin x > a.
Рассмотрим решения этих систем на различных подмножествах параметра а. Совокупность систем (4) и (5) будет иметь следующие множества решений:
22
при а О х Е 0 V 1 < х < 7г/2;
при 0 < а sin 1 <=> О < arcsin а 1
О < х < arcsin а V 1 < х < тг/2;
при sin 1 < а < 1 <=> 1 < arcsin а < тг/2
О < х < 1 V arcsin а < х < тг/2;
при а 1 О < х < 1 V х Е 0.
Объединение полученных решений дает нужный ответ.
Ответ: при а 0 х Е (1;тг/2);
при 0 < а sin 1 х 6 (0; arcsin a) U (1; тг/2);
при sin 1 < а < 1 х Е (0; 1) U (arcsin а; тг/2);
при а 1 х Е (0; 1).
Задача 11 (филологический факультет, отделение прикладной лингвистики, 1971). Определить, при каких а неравенство
1°6а/(а + 1) (х + 2) > 1 (1)
выполняется при любом х.
Решение. Так как х2 + 2 > 0 для всех х, то ОДЗ параметра определяется условиями
0< -----^1 <=> a G (—оо; — 1) U (0;+оо).
а + 1
Если a < —1, то а/(а + 1) > 1 и логарифмическая функция в (1)
является монотонно возрастающей. Если а > 0, то а/(а + 1) < 1 и ло-
гарифмическая функция является монотонно убывающей. Поэтому неравенство (1) равносильно совокупности систем
( а < — 1 ( а > 0 t z2 + 2 > а/(а +1) t х2 + 2 < а/(а + 1). )
Так как эти системы должны выполняться при любом х, а для всех х справедливо неравенство х2 0, то системы (2) и (3) можно переписать в виде
Г а < — 1 Г 1 0 < (а + 2)/(а +1) 1 ( а < — 1 f <=> V [ а < — 2 V а > — 1 1 а > 0 0 > (а + 2)/(а -f- 1) а > 0 -2 < а < -1
а < -2 V аЕ 0 а < -2.
Ответ: а < —2.
23
Задача 12 (факультет психологии, 1990). Считая известным, что при любом a > 0 уравнение
2х3 4- х2 — х — a — 1 — О (1)
имеет единственный положительный корень хо (зависящий от a), найдите все a > 0, при которых
12^о — 7жо > ба 4- 1.
Решение. Из уравнения (1) имеем
a = f(x) = 2z3 4- х2 — х — 1.
Поэтому задача сводится к нахождению всех положительных значений параметра а как функции a = для которых имеет решение следующая система относительно переменной х;
f(x) = 2х3 4- х2 — х — 1
/(я) > О
12i’3 — 7х > 6f(x) 4- 1
х > О
/(гг) = 2х3 4- х2 — х — 1
/(я) > О
О < х < 5/6.
Так как /(0) = — 1 < 0, а /(5/6) = 1/54 > 0 и /(х) - непрерывная функция, то на множестве х G (0; 5/6) она принимает каждое из значений, принадлежащих интервалу (—1; 1/54), в том числе и все положительные значения от 0 до 1/54. По условию каждое свое положительное значение a > 0 непрерывная функция /(гг) принимает при единственном хо > 0, следовательно, никаких других положительных значений при х G (0; 5/6) она не принимает. Тогда все положительные значения ОИФ a = /(х) или все искомые значения параметра а > 0 составляют интервал (0; 1/54).
Ответ: (0; 1/54).
Замечание. Ответ в предыдущем примере можно получить и с помощью понятия производной, если увидеть, что /(0) = /(1/2) = — 1 и /(х) < 0 при х Е (0; 1/2), а производная /'(х) — 6х2 4- 2х — 1 > 0 при х Е [1/2; 5/6]. Поэтому функция a = f(x) является монотонно возрастающей на множестве (1/2; 5/6). Следовательно, ОИФ a = f(x) при х Е (1/2;5/6) является интервал (— 1; 1/54), а положительные значения параметра а при 0 < х < 5/6 составляют множество a Е (0; 1/54).
Использованию понятия производной для решения задач с параметрами будет посвящена часть гл. 6.
24
1.5. ЧЕТНОСТЬ ФУНКЦИЙ И СИММЕТРИЧНОСТЬ ПЕРЕМЕННЫХ
А мораль отсюда такова: это птицы одного полета!
Л.Кэрролл. Алиса в стране чудес
В некоторых задачах с параметрами неизвестные могут входить в условия лишь четным образом, т.е. через четные функции. Так как значения четных функций зависят только от модуля аргумента, а не от его знака, то при замене неизвестной х на —х условия задачи не меняются.
Аналогичным образом симметрические относительно неизвестных х и у системы уравнений или неравенств не изменяются при замене переменной х на у и наоборот.
В ряде задач с параметрами использование свойств четности функций (ЧФ) и симметричности переменных (СП) может существенно облегчить решение.
Задача 13 (филологический факультет, отделение прикладной лингвистики, 1984). Найти все значения параметра а, при каждом из которых система неравенств
Г у^х2 + 2а t х у2 + 2а имеет единственное решение.
Решение. Пусть пара (хъ\уо) - некоторое решение системы (1), тогда в силу СП системы пара (г/о;^о) тоже является ее решением. Для единственности решения необходимо, чтобы хо = уо-
При х = у система (1) эквивалентна неравенству
х2 — х + 2а 0, (2)
которое имеет единственное решение
хо - “ За) = |(1 + V1 ~ 8а) = i при а =
2 2 2 о
Пусть а = 1/8, тогда из системы (1) следует неравенство
1 / 1\2/ 1 \2
х + у^>х2+у2 + - Иг- -] + N--J
которое действительно имеет единственное решение xq = уо = 1/2.
Ответ: 1/8.
25
Задача 14 (ИСАА, социально-экономический факультет, 1991). При каких значениях параметра b система уравнений
х2 + у2 = 2
М - х = Ь
(1)
имеет ровно три решения?
Решение. Пусть пара (xiji/i) - решение системы (1). Так как неизвестная у входит в условие задачи только через четные функции у2 и |у|, то пара ?/i) - тоже решение системы. Следовательно, для любого yi 0 существуют два различных решения. Тогда три решения система (1) может иметь лишь в случае, когда решением задачи является пара вида (а?о;0). При у = 0 система (1) принимает вид
х2 = 2
—х = b
Следовательно, равенства b = ±у/2 являются необходимым условием существования у системы (1) нечетного числа решений (в том числе и трех).
Проверим достаточность этих условий для существования ровно трех решений.
При b = — \/2 система (1) будет равносильна системе
х2 4- у2 = 2 Г 2х(х — л/2) = О
Ы = х - у/2 ( Ы = х - \/2
Хо = \/2 ( Х\ = 0 __ f £о — \
М = 0 V t |г/| =-л/2 ?! I у = О,
т.е. система. (1) при b = — -/2 имеет единственное решение (х/2; 0). При b = \/2 система (1) будет равносильна системе
2х(х + х/2) = 0 |j/| = х + \/2
26
т.е. система (1) при b = у/2 имеет три решения.
Ответ: у/2.
Замечание. В данном примере необходимые условия на значения параметра были найдены использованием лишь ЧФ по переменной у. Решение исходной системы при b = — \/2 оказалось единственным, а при Ь = у/2 система (1) имеет три решения. Таким образом, лишь b = у/2 явилось не только необходимым, но и достаточным условием для существования именно трех решений. Часто проверка достаточности необходимых условий представляет наиболее трудную часть задачи. Более подробно задачи на необходимые и достаточные условия будут разобраны в главе, посвященной так называемым логическим и нестандартным задачам. Здесь лишь подчеркнем, что проверка достаточносгги условий является обязательной частью решения подобных задач.
Задача 15 (механико-математический факультет, 1990). Найти все значения параметра а, при которых уравнение
х2 — 2а sin (cos х) + a2 = 0 (1)
имеет единственное решение.
Решение. Так как х2 и cosz - четные функции, то левая часть уравнения (1) тоже является четной функцией переменной х. Поэтому единственным решение может быть лишь в случае х = 0. Но для того, чтобы х = 0 было решением уравнения (1), необходимо, чтобы выполнялось условие
a2 — 2asinl = 0 <=> а — 0 V a = 2sinl.
Проверим достаточность этих условий.
Пусть а = 0, тогда уравнение (1) принимает вид
х2 = 0 <=> х — 0,
т.е. имеет единственное решение.
При а = 2sinl уравнение (L) равносильно уравнению
х2 + (2 sin I)2 = 4 sin 1 sin (cosz),
где левая часть не меньше, а правая - не больше (2sin I)2, причем достигается это значение левой и правой частями одновременно только при х = 0. Таким образом, и при а = 2sinl исходное уравнение имеет единственное решение х = 0.
Ответ: 0; 2sin 1.
27
Задача 16 (экономический факультет, отделение политэкономии, 1977). Найти все значения параметра а, при каждом из которых неравенство
25г/1 2 + —- а? - аа?г/+ г/- 25а?2 (1)
выполняется для любых пар чисел (х',у), таких, что
И = Ы-
(2)
Решение. Пусть o,q - некоторое значение параметра, удовлетворяющее условию задачи. Из равенства (2) следует
|г/| = И <=> У = х V у——х.
Таким образом, неравенство (1) должно выполняться при любом х при замене в нем у как на х, так и на —х:
(ао + 50)а?2 — 2а: + tj-qq 0, (3)
(50 - ац)х~ + 0. (4)
Очевидно, что неравенство (4) выполняется при любом х, если
50 — aQ 0 <=> а0 50.
Неравенство (3) выполняется при любом х, если ао —50, а дискриминант квадратного трехчлена, стоящего в левой части этого неравенства, неположителен:
4
4 - —(50 + а0) < 0 <=> а0 50.
Таким образом, необходимым условием выполнения условия задачи является равенство а = 50.
При а = 50 исходное неравенство (1) имеет вид
25г/2 + х - 50а?у + у - 25а?2
9 1 1
(5а? + 5г/) - 2(5а? + 5г/) • — + — °
1 2
<=> (5а? + 5г/— —) 0.
28
Это неравенство выполняется для любых х и у.
Следовательно, значение параметра а = 50 является единственным решением задачи.
Ответ: 50.
Замечание. В разобранном примере для нахождения необходимых условий на значения параметра использовались свойства симметричности и четности по обеим неизвестным х и у. В некоторых примерах СП может быть не по всем неизвестным, а только по некоторым из них.
Задача 17 (биологический факультет, 1991). Найти все значения параметра а, при которых система
z cos (х — у) + (2 + ху) sin (ж 4- у) — z — 0
< х2 + (у — I)2 4- z2 = a 4- 2х (1)
(х 4- у + a, sin2 z)[(l — a) In (1 — ху) 4- 1 ] = 0
имеет единственное решение.
Решение. Заметим, что второе уравнение системы (1) можно привести к симметричному виду относительно переменных х и у:
(х - I)2 4- (у - I)2 4- z2 = a 4- 1.
Отсюда и из вида остальных уравнений системы (1) следует, что если упорядоченная тройка чисел (xqУо; ) является решением исходной системы, то и тройка (т/о! го) будет ее решением. Действительно, cos (х — у) = cos (у — х) в силу четности косинуса, а комбинации х • у и х 4- у являются симметричными относительно переменных х и у.
Таким образом, необходимым условием единственности решения системы (1) является равенство xq = уо.
При х = у система (1) равносильна системе
(2 4- ж2) sin 2 а? = 0
< 2(z - I)2 + г2 = а 4- 1
k (2х 4- а sin2 z)[(l — а) In (1 — х2) 4- 1] = 0.
(2)
Поскольку из ОДЗ логарифма следует, что |х| < 1, то из первого уравнения получаем х = 0, так как система
Г (2 4- х2) sin 2х = 0
t |я| < 1
f х = тгп/2, n G Z
I kl < 1
sin 2х = 0
И < 1
29
имеет единственное решение.
При х = 0 система (2) принимает вид
( z2 = а — 1
1 ’ 2 А 3
[ asm2 z = 0.
Из ЧФ z2 и sin2 z следует, что единственным решением системы (3) может быть только z = 0, т.е. должно выполняться равенство а = 1.
Таким образом, единственным решением исходной системы (1) может быть только решение хц = уо = zq = 0 и для этого необходимо, чтобы выполнялось условие a = 1.
Проверим достаточность этого условия.
При а = 1 система (1) равносильна системе
{z cos (х — у) + (2 + ху) sin (х + у) — z = 0
(х - I)2 + (у - I)2 + z2 = 2 х + у + sin2 z = 0 z cos (х — у) + (2 + ху) sin (rr + у) = z
<=> < X2 + у2 + z2 - 2(х + у) = 0
х + у = — sin2 z
{z cos (а? — у) + (2 + ху) sin (х + у) = z
X + у = — sin Z х2 + у2 + z2 + 2 sin2 z — 0 <=> х = у = z = 0,
т.е. исходная система действительно имеет единственное решение при a = 1.
Ответ: 1.
Подведем предварительные итоги. В разобранных задачах этой главы в различных комбинациях были использованы те отдельные элементы исследования, или, по Клейну, “трюки”, о которых говорилось в предисловии.
Так, определяющие ОДЗ условия формулировались в задачах 1, 2, 7-9, 11. Кроме того, в процессе решения трех последних из перечисленных задач использовались УРП на подмножествах параметра и неизвестной переменной, а в задаче 11 - еще и условия возрастания-убывания логарифмической функции. Монотонность синуса, арксинуса и показательной функции использовалась в задаче 10, а непрерывность - в задаче 12. Условия ограниченности функций формулировались в задачах 3-6, причем решение двух из этих задач стало возможным лишь после сравнения
30
max и min выражений, стоящих в разных частях уравнения или неравенства. А для полного решения задачи 6 потребовались еще и свойства периодической функции. Использование в различных сочетаниях свойств ЧФ и СП в задачах 13-17 позволило сформулировать необходимые условия на значения параметров. При решении этих задач было обращено особое внимание на проверку достаточности необходимых условий.
Подчеркнем, что полное осознание изложенных в данной главе “трюков” является необходимым условием для понимания материала последующих глав.
1.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
— Это все чепуха по сравнению с тем, что я могла бы сказать, если бы захотела, — ответила польщенная Герцогиня.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (географический факультет, 1987). Найти все отрицательные целые числа а, при каждом из которых выражение l/(j/ —ж + 3) имеет смысл для всех пар чисел (х;у), где х > 0, у < 0, для которых выражение 1g (а — ху) также имеет смысл.
Задача 2 (экономический факультет, 1985). Определить все а, при которых уравнение
log3 х + 3 loga х + log9 х = 5
имеет решения, и найти эти решения.
Задача 3 (факультет ВМиК, 1974). Найти все действительные значения а, при которых каждое решение неравенства
log0i5 х2 1оёо,5 (я + 2)
является решением неравенства
49а?2 -4а4 < 0.
31
Задача 4 (факультет ВМиК, 1970). Определить все действительные значения а, при каждом из которых уравнение
cos4 х — (а + 2) cos2 х — (а 4- 3) = О
имеет решения, и найти все эти решения.
Задача 5 (факультет почвоведения, 1983). Найти все значения параметра а из интервала (5; 16), при каждом из которых существует хотя бы одно число х из отрезка [1; 2], удовлетворяющее уравнению
f ох Зтг
1 + cos2 — + —
\ Z О
I \ I COS 7ГХ — sin XXI
37
Задача 6 (филологический факультет, 1970). Найти все х, для которых |х| 3 и которые при всех а 5 удовлетворяют неравенству
:а _ х2) (х - 2ах) > 1.
Задача 7 (биологический факультет, 1973). а) Найти все значения параметра с, для которых неравенство
1 4- log5 (х2 + 1) log5 (сх2 + 4х + с)
справедливо при всех х.
Ь) Найти все значения параметра с, для которых неравенство
( 7\
1 + 1°ё2 ( 2х2 4- 2х + - 1 > log2 (сх2 4- с)
имеет хотя бы одно решение.
Задача 8 (экономический факультет УФ МГУ, 1992). Найти все значения параметра а, при которых система уравнений
4 sin х 4- 2У = a 4- 2
4 sin х — 3 • 2У = a2
имеет хотя бы одно решение.
Задача 9 (механико-математический факультет, 1993). Найти все значения а, при которых уравнение
4х 4- (а2 4- 3) 2х + 25 - а2 = О
не имеет решения.
32
Задача 10 (филологический факультет, 1971). Определить, при каких а неравенство
1оё1/(а 4- 1) О2 + 21а1) > 0
выполняется при любом х.
Задача 11 (физический факультет, 1967). Для каждого действительного значения параметра a > 0 решить неравенство
\7a-\- х 4- \/а — х > а.
Задача 12 (факультет психологии, 1989). При каждом значении параметра а найти все решения неравенства
х 4- 2a — 2\/3ax 4- а2 > 0.
Задача 13 (факультет почвоведения, 1984). Найти все значения параметра а, при каждом из которых уравнение
у а 4- л/а 4- sin я = sin х
имеет решение.
Задача 14 (факультет психологии, 1990). Считая известным, что при любом a > 0 уравнение
х3 — х2 — 2a — 1 = О
имеет единственный положительный корень хо (зависящий от а), найти все a > 0, при которых
4х3 — Xq — 2хо > 8а 4- 9.
Задача 15 (ИСАА, социально-экономический факультет, 1991). При каких значениях параметра а система уравнений
х2 + у2 = 1
У - к| - а
имеет ровно два решения?
3 Методы реш. задач
33
Задача 16 (физический факультет, 1981). Найти все значения параметра а, при каждом из которых система уравнений
( х2 + у2 -- 1
I х + у = a
имеет единственное решение.
Задача 17 (механико-математический факультет, 1990). Найти все значения параметра Ь, при которых уравнение
b2x2 — b tg (cos х) + 1 = 0
имеет единственное решение.
Задача 18 (экономический факультет, 1977). Найти все значения параметра. а, при каждом из которых неравенство
16х2 + аху - у х - 16у2 -
выполняется для любых пар чисел (х; у), таких, что |х| = |j/|.
1.7. УКАЗАНИЯ И ОТВЕТЫ
1. а —3, a G N.
2. х = 3101°ёз a/3(log3 а + 2) При 0 < а # 1/9; 1.
3. а , а л/7.
4. х = ± arccos л/а + 3 + тгк, к £ Z при — 3 а — 2.
5. 9тг/5, 17тг/5, 5%.
6. х G (—3;—1).
7. а) с 6 (2; 3].
Ь) с G (0;8].
8. a G (—1; 2).
9. а G [—5; 5].
10. a G ( —1;—1/2).
11. При а 6 (0; 2) — а х а-, при а = 2 — 2 < к < 2;
при a G (2;4) - ^^а(4 - а) < х < ^\/а(4 - а); при а 4 решений нет.
12. При а < 0 решений нет;
при а = 0 х > 0;
при а > 0 х 6 [—а/3; 0) U (8а; 4-оо).
13. -1/4 а 0.
14. а > 23/54.
15. а G {-л/2} U (—1; 1).
16. ±л/2.
17. ctgl.
18. 32.
3*
35
ГЛАВА 2
ЭЛЕМЕНТЫ ГРАФИЧЕСКОГО ИССЛЕДОВАНИЯ В ЗАДАЧАХ С ПАРАМЕТРАМИ
2.1. МЕТОД СЕЧЕНИЙ
- А еще они рисовали всякую всячину... все, что начинается на М... мышеловки, месяц, математику, множество... Ты когда-нибудь видела, как рисуют множество? — Множество чего? —- спросила Алиса. — Ничего, •— отвечала Соня. — Просто множество!
Л.Кэрролл. Алиса в стране иудее
Для успешного применения графических методов решения задач необходимо уметь строить графики элементарных функций и выполнять графически простейшие операции над ними. Не уделяя внимания обоснованию правил преобразования графиков, напомним основные положения, без понимания которых дальнейшая работа будет крайне затруднена.
1. График функции у = /(к) + а получается из графика функции у = f(x) путем параллельного переноса на величину а вдоль оси Оу.
2. График функции у = f(x — а) получается из графика функции У — /(ж) путем параллельного переноса на величину а вдоль оси Ох.
3. График функции у = к • f(x) получается из графика функции у — /(ж) путем растяжения в к раз по оси у при к > 1 и путем сжатия в \/к раз при 0 < к < 1.
4. График функции у = f(k х) получается из графика функции у = /(ж) путем сжатия в к раз по оси х при к > 1 и путем растяжения в 1 /к раз при 0 < k < 1.
5. График функции у = —f(x) получается из графика функции у = f (#) зеркальным отражением относительно оси х.
6. График функции у — f(—x) получается из графика функции у — /(т) зеркальным отражением относительно оси у.
37
Графики многих функций, в том числе и таких, как у = |/(х)| и у = /(|х|), можно построить, последовательно применив изложенные выше правила.
Заметим, что содержание данной главы тесно связано с некоторыми идеями Ф.Клейна о преподавании математики, изложенными в его книге “Элементарная математика с точки зрения высшей”.
Предположим, что уравнение (или неравенство), содержащее параметр, удалось привести к виду /(ж) — д(х,а) (или /(а?) д(х, а)), где /(а?) и д(х, а) - достаточно изученные функции, графики которых легко построить. Тогда соотношение у^ = /(а?) определяет на координатной плоскости XOY некоторую кривую, а соотношение у2 = с/(ге, а) - целое семейство кривых, в котором каждому допустимому значению параметра а соответствует одна кривая. При этом в зависимости от величины параметра а кривые семейства у2 = д(х, а) могут занимать принципиально различные положения относительно кривой yi = /(х). Изучая сечение кривой yi(х) семейством кривых у2 = д(х,а) при соответствующих им значениях параметра а, мы получаем возможность исследовать вопрос о количестве решений уравнения /(а?) = д(х,а) в зависимости от параметра, правильно выбирать эти решения и использовать их для нахождения решений неравенств вида У(х) д(х,а\ Типичными критическими значениями параметров оказываются те, которые соответствуют точкам касания графиков. При этом удобно исходить из соображения, что наклонная прямая у = кх + I касается параболы или гиперболы у = <£>(х) (у = <р(х) - соответствующая квадратичная или дробно-линейная функция), если уравнение <р(х) = кх-Д имеет единственное решение (отметим, что полученное уравнение сводится к решению квадратного уравнения!)
Рассмотрим применение этого метода к решению конкретных задач, когда сечение производится семейством
- прямых, ломаных;
- парабол, гипербол, окружностей;
- логарифмических кривых.
Задача 1 (физический факультет, 1965). Для каждого действительного значения параметра а решить уравнение
х | х + 11 + a = 0.
Решение. Рассмотрим функции д(х, а) = — а и
/(х) = х\х + 1| =
х2 + х, х — 1;
—х2 — х, х < —1; (х + 1/2)2 - 1/4, -(х + 1/2)2 + 1/4,
х -1;
х < —1.
38
График функции /(а?) будет состоять из части параболы (х + |)2 — | при х — 1 и части параболы — (а? + |)2 + | при х < —1.
Функция д(х,а) = —а задает семейство прямых, параллельных оси ОХ.
1. При —а < —1/4 (т.е. а > 1/4) исходное уравнение будет иметь вид
—х2 — х + а = О,
и будет иметь единственное решение вида
-1 - VTT4R з?1 = ----------.
2
2. При —а = —1/4 (т.е. а = 1/4 ) будет два решения:
— 1 — х/2 9
•Д1 — ------ (меньший корень уравнения — х — х + 1/4 = 0)
и
Х2 = —1/2 (корень уравнения х2 + х + 1/4 = 0).
3. При —1/4 < — а < 0 (т.е. 0 < а < 1/4) получаем три решения:
-1 - л/1 + 4а -1±х/1-4а
*> =-------2----, х2,з =-------2-----'
4. При — а = 0 (т.е. а = 0) вновь два решения:
а?1 = 0, Х2 = -1.
39
5. При — а > 0 (т.е. а < 0) имеем одно решение - наибольший корень уравнения х2 + х 4- а = 0:
-1 + х/1-4а
Ответ: при при при
при
при
-1 + УГ^4а
а < 0 х\ = -----------:
2
а = 0 xj_ = 0, х2 = —1;
„ ,. — 1 — л/1 + 4а
0 < а < 1/4 = ------------, х2
-1 - л/2
а = 1/4 хг = -------, х2 = —1/2;
— 1 —л/Г+Ча
а > 1/4 X! = ------------.
-1 ± х/1 -4а 2
Задача 2 (физический факультет, 1964). Для каждого значения параметра а решить неравенство
х2 + ах 4- 1 > 0.
Решение. Рассмотрим функции f(x) = х2 4- 1 и д(х,а) = —ах. Графиком функции f(x) является парабола, ветви которой направлены вверх, с вершиной в точке (0; 1). Функция д(х, а) порождает семейство прямых, проходящих через точку (0; 0), не параллельных оси OY.
В зависимости от значения параметра а возможны три случая:
1) прямая не пересекает параболу;
2) прямая касается параболы;
3) прямая пересекает параболу в двух точках.
40
Найдем, при каких значениях параметра а уравнение х2 + 1 + ах = О имеет единственное решение. Это имеет место тогда и только тогда, когда дискриминант уравнения равен нулю, т.е.
а2 — 4 = 0 <=> а = ±2.
Следовательно,
1) при |а| < 2 парабола находится выше прямой д(х,а) = —ах и исходное неравенство выполняется при любом ж;
2) при |а| = 2 парабола касается прямой и неравенство выполняется при всех х, кроме тех, которые отвечают точкам касания, т.е. при х 5/: — 1 (если а = 2) и х ф 1 (если а = —2);
3) при |а| > 2 исходное неравенство будет выполняться при х > х^ и х < х 1, где
—а — \/а2 — 4 —а + -\/а2 — 4
х 1 = ------------- и ж о = -------------7-------
2 2
- корни уравнения
х2 + ах + 1 = 0.
Ответ: при |а| > 2 при а — ±2 при |а| < 2
—а — \/а2 — 4 —а + л/а2 —
х Ф т1> х е R.
Замечание. Гораздо более естественно было бы решать эту задачу, анализируя дискриминант квадратичного выражения
F(x, а) = х2 + ах + 1
и рассматривая соответствующее семейство парабол. Но предложенное выше решение очень поучительно и представляет интерес с точки зрения применения данного метода в других задачах.
Задача 3 (физический факультет, 1965). Для каждого действительного значения параметра а решить неравенство
1 ах > — .
х
Решение. Рассмотрим функцию f(x) = 1/х и семейство прямых д(х, а) = ах. Их графики будут иметь вид
41
1. При а > 0 неравенство /(ж) < д(х,а) выполняется при < х < 0 и
х > Х2, где a?i, а?2 “ корни уравнения
1 ах = —
х
2. При а 0 неравенство /(ж) < д(х,а) выполняется при х < 0.
Ответ: при а > 0
1 а 1
-т= < х < 0 V х > —j= /а у/а
при а 0 х > 0.
Задача 4 (геологический факультет,- 1991). При всех значениях параметра а решить уравнение
|а? + 2| + а\х — 4| = 6.
Решение. Перепишем уравнение в виде
|а? + 2| — 6 = —а|ж — 4|
и рассмотрим ломаную f(x) = |а? + 2| — 6 и семейство ломаных д(х, а) = — а\х — 4|.
42
График ломаной /(ж) = |а? + 2| — 6 имеет вид, указанный на рис. 1,
Рис. 1
и проходит через точку (4,0). Все ломаные семейства д(х, а) = — а\х — 4| имеют “вершину” именно в этой точке. Поэтому
1) при а < — 1 графики семейства д(х, а) = — а\х — 4|
Рис. 2
располагаются как на рис. 2, и решение исходного уравнения дает только “вершина” семейства, откуда получаем единственное решение х = 4;
2) при а = — 1 части правых ветвей ломаной /(а?) = |а? + 2|—6 и ломаных
43
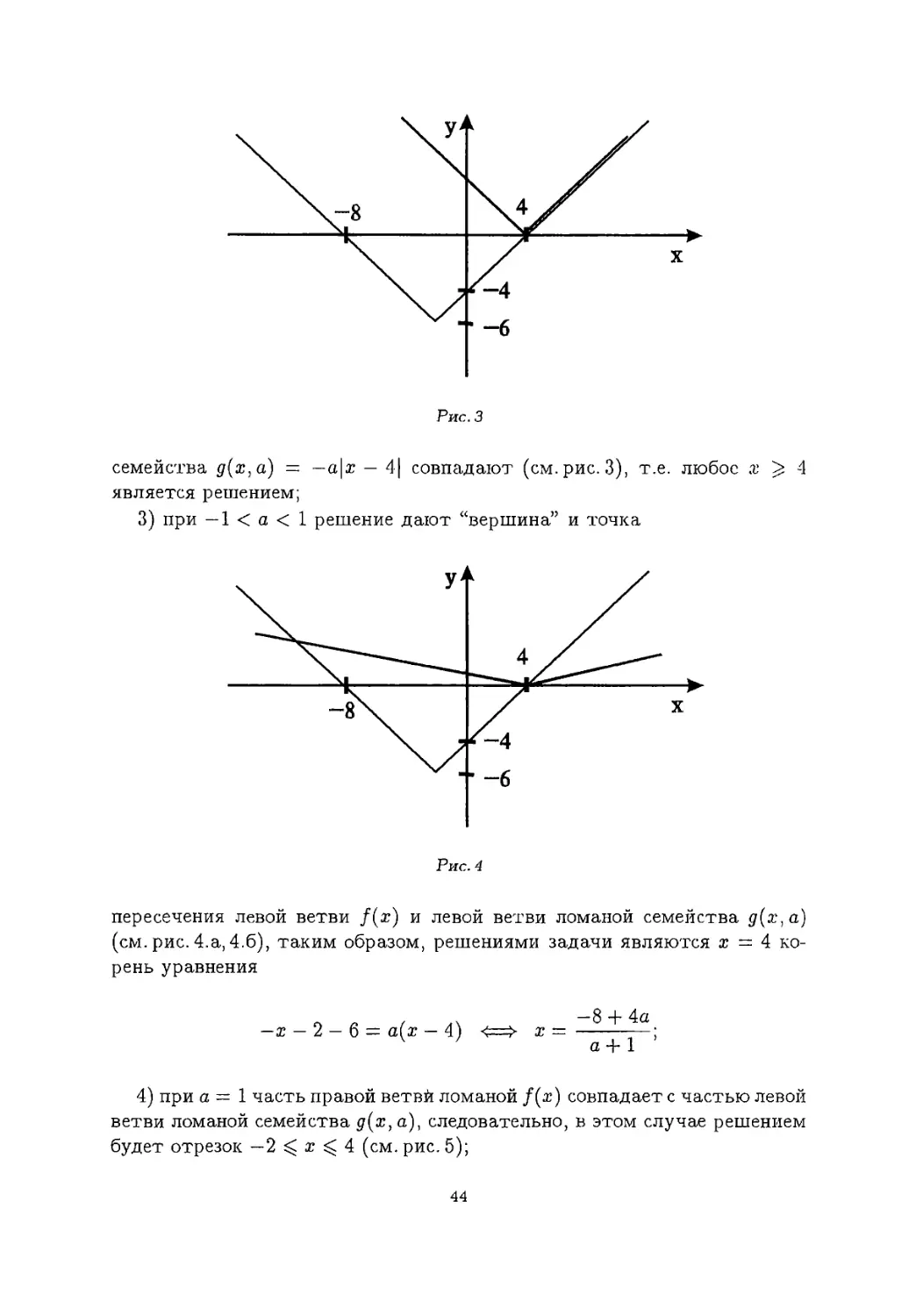
семейства д(х,а) = — а|т — 4| совпадают (см. рис. 3), т.е. любое х 4 является решением;
3) при — 1 < а < 1 решение дают “вершина” и точка
пересечения левой ветви /(т) и левой ветви ломаной семейства д(х,а) (см. рис. 4.а, 4.6), таким образом, решениями задачи являются х = 4 корень уравнения
—х — 2 — 6 = а(т — 4)
-8 + 4а а + 1
4) при а = 1 часть правой ветвй ломаной /(я) совпадает с частью левой ветви ломаной семейства (/(ж, а), следовательно, в этом случае решением будет отрезок — 2 х 4 (см. рис. 5);
44
Рис. 5
5) при а > 1 графики семейства ломаных д(х,а) будут симметричны относительно оси Ох графикам ломаных этого семейства при а < — 1 и также будут иметь единственную общую точку х = 4 с графиком /(т) = |т + 2| — 6.
Ответ: при а < — 1 х = 4;
при а = — 1 х 4;
. , и 4а - 8
при — 1 < а < ] х — 4 V х = ------;
а 4" 1
при а = 1 — 2 <С т <С 4;
при а > 1 х = 4.
Задача 5 (механико-математический факультет, устный экзамен). Определить, при каких значениях параметра a > 1 уравнение
|т2 — 6т + 8| + 2 = logG х
имеет единственное решение.
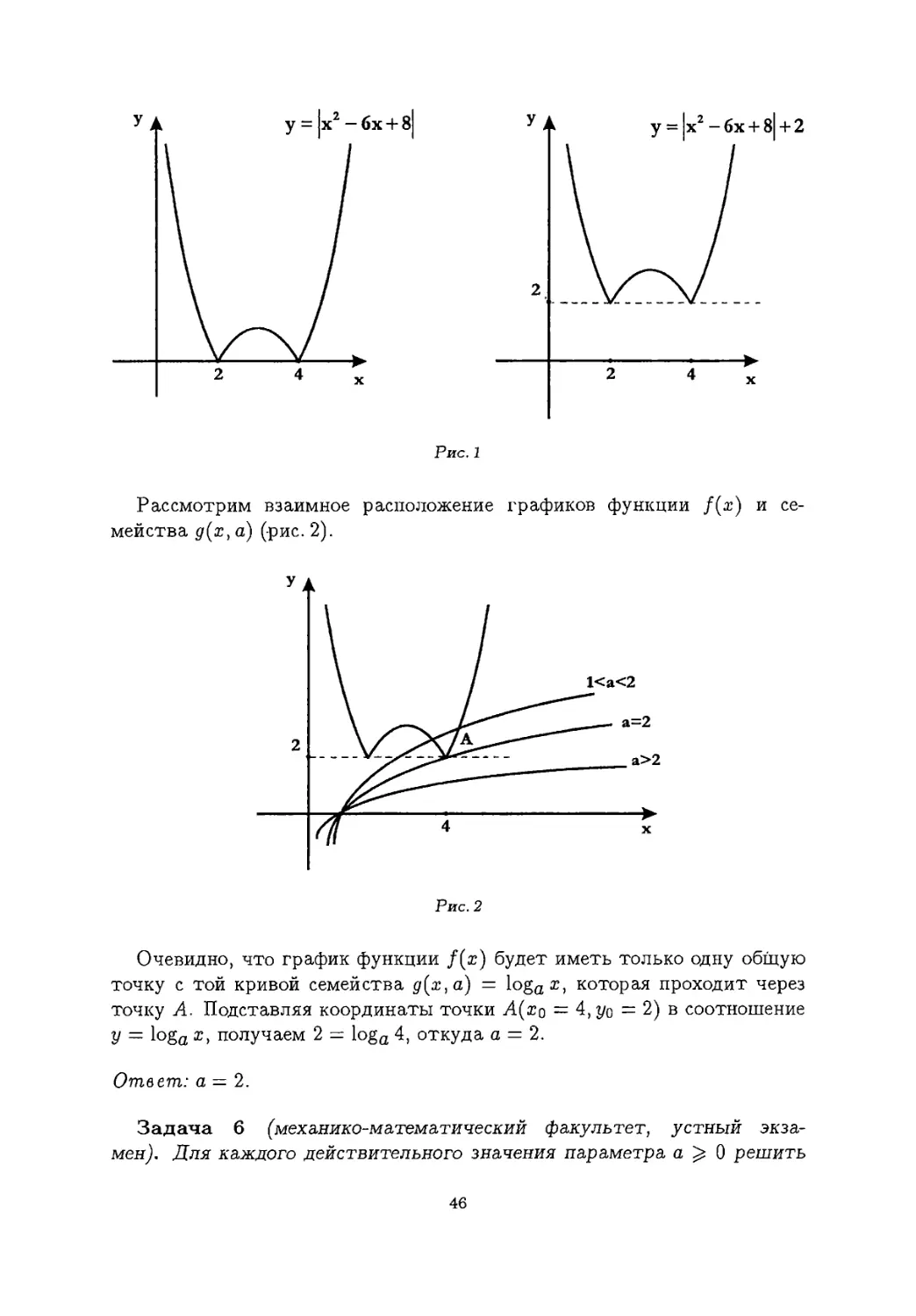
Решение. Рассмотрим функции /(т) = |т2 —6т + 8| + 2 и g(x, а) = logG х и построим их графики. График функции f(x) = |т2 — 6а? + 8|4-2 строится с помощью графика функции у = т2 — 6т + 8 путем применения серии простейших операций (см. рис. 1).
45
у = |х2 -6х + 8| + 2
2 4
Рис. 1
Рассмотрим взаимное расположение графиков функции /(я) и семейства д(х, а) (рис. 2).
Очевидно, что график функции f(x) будет иметь только одну общую точку с той кривой семейства д(х,а) = loga х, которая проходит через точку А. Подставляя координаты точки А(з?о = 4,t/o = 2) в соотношение У ~ 1°£а х> получаем 2 = loga 4, откуда а = 2.
Ответ: а — 2.
Задача 6 (механико-математический факультет, устный экзамен). Для каждого действительного значения параметра а 0 решить
46
неравенство
уо2 — х2 > х + 1.
Решение. Рассмотрим функцию f(x) = х + 1 и семейство функций д(х,о) = \/а2 — х2. График функции у = у/a2 — х2 совпадает с частью геометрического места точек, задаваемого уравнением
2 2 2
у = а — х
(1)
и расположенного выше оси Ох.
Уравнением (1) определяется семейство окружностей с центром в начале координат, радиусы которых равны а. Следовательно, семейство д(х,а) представляет собой семейство полуокружностей в верхней полуплоскости. В зависимости от величины параметра а график функции д(х, а) может занимать следующие положения относительно графика функции f(x) (см. рисунок).
1. График функции д(х, а) проходит не выше точки А (точки касания графиков /(т) и д(х,а) с координатами xq и уо).
Соответствующее значение параметра легко найти из уравнения
а2 — х2 = х2 + 2х + 1
при условии D — 0, где D - дискриминант полученного квадратного уравнения, откуда а = \/2/2 и xq = — 1/2. В этом случае, определяемом условием 0 а %/2/2, исходное неравенство решений не имеет.
2. График функции д(х,а) проходит выше точки А, но ниже точки Е с координатами (0; 1), которой соответствует а = 1. В этом случае, определяемом условием \/2/2 < а < 1, исходное неравенство выполняется
47
при xi < х < Х2, где ^1 и ^2 - соответственно меньший и больший корни уравнения
а2 — х2 = х2 + 2а? + 1 (2)
(точки В и С). Следовательно,
-1 - V2a2 - 1 -1 + д/2а2 - 1
-------------- < х < --------------.
3. График функции д(х,а) проходит через точки D и Е. Неравенство д(х,а) > /(ж) выполняется при — 1 < х < 0.
4. График функции д(х,а) проходит выше точки Е, т.е. а > 1. Неравенство д(х,а) > f(x) выполняется при —а х < а?з, где а?з - больший корень уравнения (2)
-1 + V2a2 - 1
ГГо = ------------
(точка AQ.
Ответ: при 0 а л/2/2 решений нет;
л -1 — л/2а2 - 1 — 1 + у/2а2 — 1
при у 2/2 < а < 1 -------------- < х < -------------
при а = 1 — 1 < а? < 0;
-1 + х/2а2 - 1
при а > 1 а х < ----------------.
Задача 7 (механико-математический факультет, 1967). Для каждого действительного значения параметра а решить уравнение
2 |lg аа?| • logj, 10 = (41g a - 3) loga,2 10 - 11g x.
Решение. Область допустимых значений переменной определяется условиями
х > 0 и х 1.
Кроме того, очевидно, что при а <С 0 уравнение решений не имеет.
Преобразуем исходное уравнение к следующему виду:
2| Iga + lgx|j+j = (4 Iga — Ig®-
Полагая 4 lg а = b и 41g а? = и, получаем уравнение
|и + 6| — Ъ + 3 + и2/16 _
~ U
<=> |д + 6| — 6 + 3+ —и2 — 0
48
(и — 1g х 0, так как х 1).
Рассмотрим функцию /(и) = —и2/16 — 3 и семейство ломаных </( м, 6) = |и + Ъ\ — Ь. Заметим, что график последней функции получается из графика функции </?(u) = |и| параллельным переносом, при котором вершина, ломаной переходит из точки (0,0) в точку (—6; Ь). Найдем точки пересечения прямой u(u) = и и параболы /(и) = —и2/16 — 3:
1 9
— и +и + 3 = 0 <=> щ = —12, и2 = —4, 16
при этом = —12 и /(ui) = —4.
В зависимости от величины параметра может быть пять различных случаев взаимного расположения параболы и ломаной.
1. При —Ь > —4 <=> b < 4 задача решений не имеет.
2. При — Ь = —4 -<==> b = 4 парабола и ломаная имеют единственную общую точку А, при этом ui = —4.
3. При —12 < — Ъ < — 4 <=> 4 < b < 12 задача имеет два решения, одно из которых щ = — 4 , а второе - и2 = 8 — 4д/1 + 2Ь - меньший корень уравнения — -^и2 — 3 = —и — 2Ь.
4. При — b = —12 <=> b = 12 парабола и ломаная имеют две общие точки Av, В, при этом щ = —12, и2 = —4.
5. При — b < —12 <==> Ь > 12 задача имеет те же два решения, что и в п.4.
Вернемся к исходным обозначениям.
1. При b = 41g а. < 4 -<==> 0 < а < 10 исходная задача решений не имеет.
2. При b — 41g а = 4 <=> а — 10 получаем
Ui=41gz = — 4 <=> IgT = —1 <==> х = 10-1.
4 Методы реш. задач
49
3. При 4<fe = 41ga<12 <=> 10 < а < 1000 получаем = 10 1
и U2 = 41g ж = 8 — 4д/1 + 26 <=> Х2 = 102 — 8 а
4, 5. При b = 41gа 12 <=> а 1000 получаем два решения Х\ = 10-1 и Х2 : 10-3.
Ответ: при а < 10 решений нет;
при а = 10 Ж1 = 10“1;
при 10 < а < 1000 хг = 10“1, х2 = Ю2 “ + 81&а;
при а 1000 ху = 10“1, Х2 = 10-3.
Задача 8 (УФ, физико-технический факультет, 1991). При каком значении параметра к уравнение
а?2 (4а? + 6) — 2 |ж |л/4ж + 6 — 3 = Зк
имеет два корня?
Решение. Используя соотношение |а?| = у/х2, перепишем исходное уравнение в виде
а?2 (4а? + 6) — 2\/а?2(4а? + 6) — (Зк + 3) = 0.
Обозначим <р(а?) = ^/а?2 (4а? + 6) 0. Тогда уравнение примет вид
Д^) = р2 - 2^ - (Зк + 3) = 0.
Разрешим полученное квадратное уравнение относительно </?:
Да?) — \/х2(4х + 6) = 1 ± А, где А = у/4 + Зк 0.
Рассмотрим графики функции Да?) и семейства параллельных прямых у = 1 ± А. График функции </?(а?) строится с помощью графика функции F(x) — х2(4х + 6) (рис. 1,2):
50
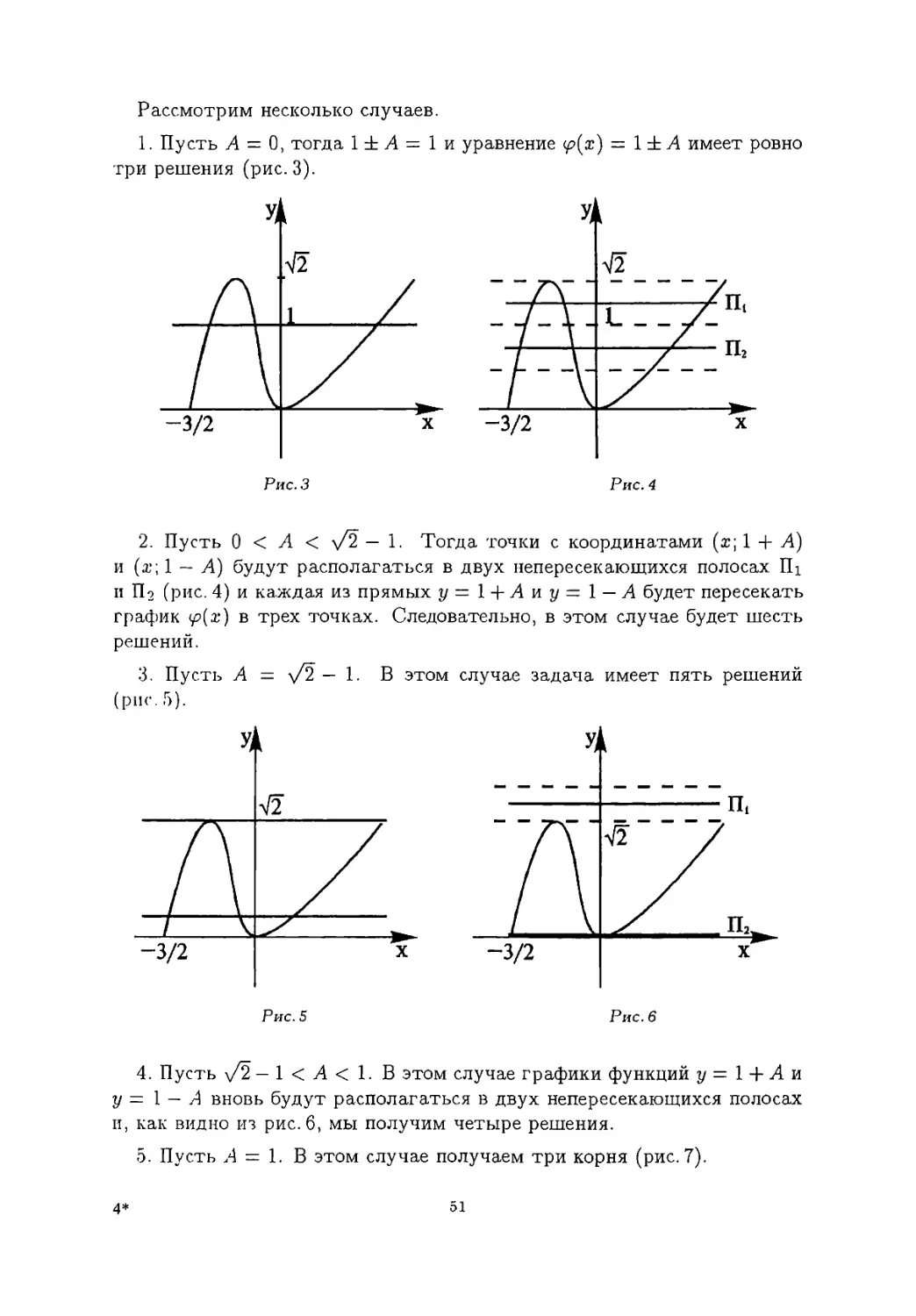
Рассмотрим несколько случаев.
1. Пусть А = 0, тогда 1 ± А = 1 и уравнение <£>(z) = 1 ± А имеет ровно три решения (рис. 3).
2. Пусть 0 < А < а/2 — 1. Тогда точки с координатами (а?; 1 + А) и (ж; 1 — Л) будут располагаться в двух непересекающихся полосах Щ и Щ (рис. 4) и каждая из прямых у = 1 + А и у = 1 — А будет пересекать график у?(аг) в трех точках. Следовательно, в этом случае будет шесть решений.
3. Пусть А = \/2 — 1. В этом случае задача имеет пять решений (рис. 5).
4. Пусть \/2 — 1 < А < 1. В этом случае графики функций у = 1 + А и у = 1 — /4 вновь будут располагаться в двух непересекающихся полосах и, как видно из рис. б, мы получим четыре решения.
5. Пусть ,4 = 1. В этом случае получаем три корня (рис. 7).
51
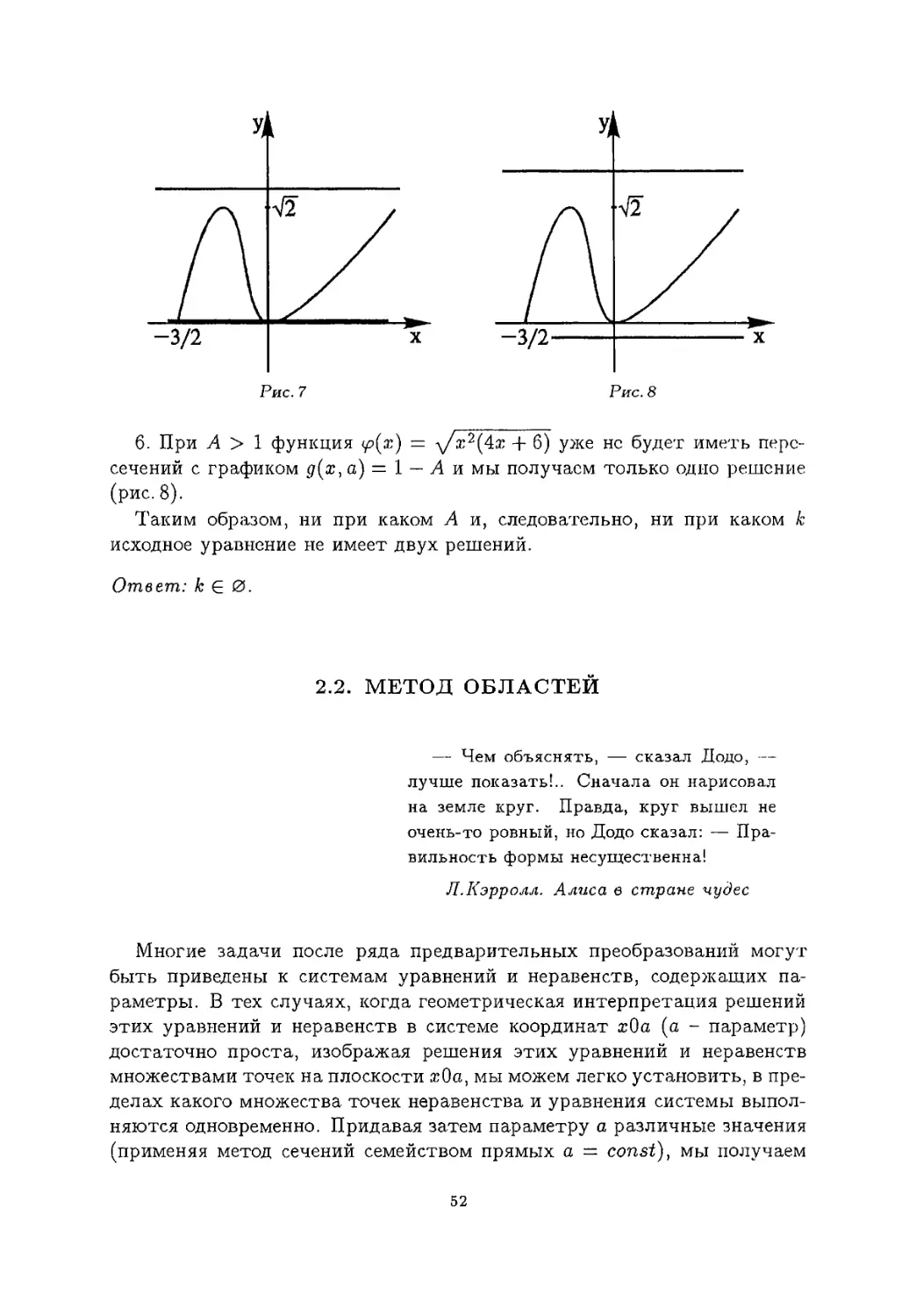
б. При А > 1 функция у?(ж) = л/д2(4д + б) уже нс будет иметь пересечений с графиком д(х, а) = 1 — А и мы получаем только одно решение (рис. 8).
Таким образом, ни при каком А и, следовательно, ни при каком k исходное уравнение не имеет двух решений.
Ответ: к £ 0.
2.2. МЕТОД ОБЛАСТЕЙ
— Чем объяснять, — сказал Додо, — лучше показать!.. Сначала он нарисовал на земле круг. Правда, круг вышел не очень-то ровный, но Додо сказал: — Правильность формы несущественна!
Л.Кэрролл. Алиса в стране чудес
Многие задачи после ряда предварительных преобразований могут быть приведены к системам уравнений и неравенств, содержащих параметры. В тех случаях, когда геометрическая интерпретация решений этих уравнений и неравенств в системе координат дОа (а - параметр) достаточно проста, изображая решения этих уравнений и неравенств множествами точек на плоскости дОа, мы можем легко установить, в пределах какого множества точек неравенства и уравнения системы выполняются одновременно. Придавая затем параметру а различные значения (применяя метод сечений семейством прямых а = const), мы получаем
52
возможность найти решение задачи для каждого значения параметра.
Задача 9 (экономический факультет, отделение политэкономии, 1977). Найти все значения параметра а, при каждом из которых неравенство
3 — |ж — а| > х2
имеет хотя бы одно отрицательное решение.
Решение. Раскроем знак модуля и получим, что исходное неравенство эквивален тно совокупности двух систем
х — а > 0 ( х — a < О
х2 -Ь ж — а — 3 < 0 [ж2 — х + a — 3<0
а х ( a > х
a > (х + 1/2)2 - 3| V I а <-(ж-1/2)2 + 3|.
Рассмотрим графики полученных парабол и прямой a = х.
3
Точки пересечения парабол, а также каждой из них с прямой a = х совпадают.
Рассмотрим часть полученного множества, содержащую точки (ж; а), для которых выполнено х < 0. В этой части параметр а удовлетворяет условию — 3 4 < a < 3. V q
Ответ: — 3| < а < 3.
Следующая задача уже была рассмотрена в предыдущей главе, посвященной аналитическим методам исследования. Здесь она иллюстрирует применение графических методов исследования к задачам с параметрами.
53
Задача 10 (факультет психологии, 1989). При каждом значении параметра а найти все решения неравенства
х + 2a — \/3ax 4- 4а2 > 0.
Решение. После ряда эквивалентных преобразований получим, что исходное неравенство равносильно системе
Зах + 4а2 0 ( а(3х + 4а) О
< х 4- 2а 0 <=> < а — х/2
Зах 4- 4а2 < х2 4- 4а2 4- 4ах [ х(х 4- а) > 0,
которая в свою очередь равносильна совокупности систем
' а V 1 н to W V 1 к о W V 1 к to а —х/2
а о а 0 а 0 а 0
Зх 4- 4а 0 V < а — Зх/4 V < а — Зх/4 V < а —3z/4
X > 0 х < 0 х > 0 х < 0
< х 4- а > 0 х 4- а < 0 х 4- а > 0 х 4- а < 0
' а — х/2 — р V 1 н to ' а—х/2 р V 1 н to
а 0 а 0 а 0 а 0
=> < а — Зх/4 V < а —Зх/4 V < а — Зх/4 V < а — Зх/4
а > —х а < —х а > —х а < —х
< х > 0 < х < 0 < х > 0 < х < 0.
1. Рассмотрим первые две системы. Неравенства имеют простейший вид, поэтому легко получаем следующую “картинку”.
54
2. Рассмотрим вторую пару систем. В этом случае решений нет, так как третье и четвертое неравенства в третьей системе, а также первое, четвертое и пятое неравенства в четвертой системе противоречат друг другу.
Ответ: при а < О при а = О при а > О
х G 0;
х 6 (0; +оо);
х G [~4а/3; —a) U (0; +оо).
Задача 11 (механико-математический факультет, ИП). Определить, при каких действительных значениях параметра а минимум функции
/(а?) = х2 4- 2|а? 4- a - 1| + (a + I)2
меньше трех.
Решение. Функция f(x) без знака абсолютной представлена следующим образом:
/] (.-Г) = х2 4- 2а? 4- 2(а - 1) 4- (а 4- I)2 /j(;r) = х2 — 2х — 2(а — 1) 4- (а 4- I)2
величины может быть
при х 4* а 1>
при х 4- а 1.
(1)
Тогда задача, сводится к нахождению тех значений параметра а, при которых имеет решение совокупность систем
Г ж 4- О 1 Г а? 4- а 1
t fx(x) <3 V t /2(я) <3
a I — x f a 1 — x
(x 4- I)2 4- (a 4- 2)2 < 9 V [ (a? - I)2 4- a2 < 1-
На координатной плоскости a?0a системе (2.1) соответствует множество точек кругового сегмента, лежащих внутри круга радиуса = 3 с центром в точке ОЦ —1; —2) и на или выше хорды АВ, задаваемой уравнением х 4- а = 1 (см. рис. 1).
Координаты точек А и В находятся из решения системы
а = 1 — х Л (1-^2/2:72/2) ,
(х 4-I)2 + (а 4-2)2 = 9 В (1 + V2/2; -V2/2) ,
т.е. система (2.1) имеет решение при a 6 (—д/2/2; л/2/2).
55
Аналогичным образом можно проанализировать систему (2.2) и получить, что точки А и В имеют координаты А (1 — л/2/2; \/2/2) и В (1 + \/2/2; — д/2/2), а соответствующая область представляет собой нижнюю часть полукруга (рис. 2) с минимальным значением ординаты а = —1. Поэтому система (2.2) имеет решение при a G (— 1.; л/2/2), а совокупность систем (2.1) и (2.2) имеет решение при
a G (-л/2/2;л/2/2) U (-1;л/2/2) <=> а G (-1; л/2/2) .
Ответ: a G (—Г, д/2/2).
Замечание. Данную задачу можно решить, рассмотрев взаимное расположение двух парабол у = fi(x) и у = /2(2) и точку их пересечения. В этом случае задача сводится к решению совокупности из трех систем (доказать самостоятельно!)
J а < О f 0 а 2 Г а >2 1/(1) <3 V t/(l-a)<3 V t /(—1) < 3.
Задача 12 (экономический факультет, 1992). Найти все значения параметра q, при каждом из которых число целочисленных решений неравенства
х2 — 5(z — 1) 4- 3|z — g| — q 0 (1)
максимально.
Решение. Исходное неравенство (1) равносильно совокупности систем
56
На координатной плоскости xOq эти две системы задают область, ограниченную частями двух парабол
(х — 4)2 11
q= 2 + Т
(ж - I)2
+ 1,
и
Q =
4
включая их границы. Эти параболы пересекаются в двух точках А( 1; 1) и В(5; 5). Ветви первой параболы направлены вниз, а вершина находится в точке С(4; 11/2). Ветви второй параболы направлены вверх, а ее вершина совпадает с точкой А (рис. 1).
Таким образом, рассматриваемую область можно вписать в прямоугольник, координаты которого задаются неравенствами
10^5 и 1 О П/2.
Для целочисленных решений х G [1; 5] неравенства (1) из совокупности систем (2) имеем:
1 / 1 q
при X = 1 <
11^9
( 2 q при х = 2 <
I 7/2 g
при х = 3 f q
I 5^g
, S 4 д при х = 4 <
. / 5 q при х = 5 <
I 5 q
1 q 1 я 2^q Ь/4: q 3^? 2<? 4^9 13/4 q b^q 5 0
5 = 1,
5/4 q^ 7/2,
2 ^<7^5,
13/4 g 11/2,
<=> q = 5.
57
Отметим на числовой оси полученные значения параметра q и соединим концы соответствующих отрезков (рис. 2).
. I ' I________________
1 1 о 13 7. < 11 q
1 4 Z 42 2
Рис. 2
Тогда всем значениям параметра q, принадлежащим только одному из полученных отрезков, соответствует единственное целочисленное решение х G [1; 5] исходного неравенства. Значениям q = 1 и q = 5 также соответствуют целочисленные решения. Окончательно получаем, что неравенство (1) не имеет целочисленных решений при q G (1; 5/4); имеет одно целочисленное решение при q G {1} U [5/4; 2) U (5; 11/2]; два решения при q G [2; 13/4) U (7/2; 5) и три решения при q G [13/4; 7/2] U {5}.
Ответ: q G [13/4; 7/2] U {5}.
Замечание. Геометрическая интерпретация решений уравнений, неравенств и систем на координатной плоскости очень полезна при решении задач в области комплексных чисел, изучение которых раньше входило в школьную программу. Некоторые задачи с параметрами в комплексных числах будут рассмотрены в главе, посвященной “разным” задачам.
А в заключение этой главы приведем достаточно тонкую по замыслу и математически красивую задачу, В'условии которой требуется изобразить множество решений на координатной плоскости.
Задача 13 (механико-математический факультет, 1967). На координатной плоскости указать все точки, координаты (х; у) которых таковы, что выражение
^2 cos t 4- cos x cos y'j cos x cos у 4- 1 4- cos x — cos у 4- cos 2i
положительно при всяком значении t, и изобразить область, образуемую этими точками.
58
Решение. Для исходного неравенства справедлива следующая цепочка равносильных преобразований:
2 cos t 4- - cos х cos у J cos x cos у 4- 1 4- cos x — cos у 4- cos 2t > 0
2 cos2 /4-2 cos x cos у cos t 4- cos2 x cos2 у 4- cos x — cos у > 0
/ 1 \2
21 cos / 4- - cos x cos у I 4- cos x — cos у > 0.
(1)
Для любых x и у найдется такое /, например
( 1 А
t — arccos I — - cos x cos у I,
при котором
cos t 4- - cos x cos у — 0.
Следовательно, неравенство (1) будет выполняться при всех значениях t только тогда, когда
cos х — cos у > 0
. ху . х — у
sin —-— • sin —-— < 0.
2 2
(2)
Неравенство (2) равносильно совокупности двух систем
4тгА; < х 4- у < 4тгк 4- 2тг 4тг/ — 2тг < х — у < 4тг/
С 4тгт — 2тг < х 4- У < 4тгт V
( 4тгп < х — у < 4тгп 4- 2тг,
где к, l,m,n G Z и независимы друг от друга. Заметим, что неравенство
4тг& < х 4- у < 4тгк 4- 2тг
при каждом конкретном к £ Z на координатной плоскости (х',у) задает полосу, параллельную биссектрисе второго и четвертого квадрантов. Так, на рис. 1.а представлены полосы для к = 0; ±1;—2. Множество всех полос, задаваемых неравенством (За) для всех целых к, образует на
59
плоскости (а?; г/) бесконечную “зебру” - прямолинейные полосы с угловым коэффициентом —1.
Аналогичным образом неравенство
4тг/ — 2тг < х — у < 4тг/, I G Z
(36)
на координатной плоскости дает прямолинейные полосы с угловым коэффициентом 1, т.е. перпендикулярные полосам первой “зебры” (рис. 1.6).
Система неравенств (За) и (36) задает на координатной плоскости своеобразное бесконечное поле для игры в “крестики-нолики” и пустое множество, получаемое наложением двух “зебр” (рис. 1.в). Причем ответ дают лишь квадратики (без границ), которые для наглядности закрашены черным цветом.
Можно показать, что неравенства
4тгт — 2тг < х 4- у < 4тгт, т G Z,
4тгп — 2-тг < х — у < 4тгп + 2тг, п G Z,
(Зв)
(Зг)
задают своеобразный “негатив” соответственно первой и второй “зебры” (т.е. окраска полос каждой “зебры” меняется на противоположную). Тогда система неравенств (Зв) и (Зг) также дает “негатив” рис. 1.в, т.е. белые клетки на рис. 1.в станут черными клетками, а черные клетки -чисто белыми. Тогда совокупность систем (3) или неравенство (2) задает на координатной плоскости (а?; г/) бесконечную “шахматную доску” (рис. 1.г), получаемую наложением друг на друга рис. 1.в и его “негатива” , причем итоговым ответом, являются только черные квадраты (без их границ). Диагонали квадратиков этой “шахматной доски” равны 2тг и параллельны осям координат.
60
В качестве заключения к данной главе подчеркнем два момента.
1. Графические методы делают решение наглядным и позволяют в ряде случаев с большей по сравнению с аналитическими методами легкостью отсортировать правильные пути, ведущие к решению задачи, от тупиковых, которые приводят к посторонним решениям или вовсе не дают решения. Часто это избавляет от необходимости выполнения определенного объема вычислений при исследовании тех возможностей, которые в конечном счете все равно не дадут положительного ответа.
2. Однако ссылки на “картинки”, используемые при графических методах решения, должны быть подкреплены вычислениями и явной формулировкой соответствующих теорем и свойств графиков используемых функций, изучаемых в рамках школьной программы. Без этого одни “картинки” решением являться не будут!
В подтверждение последнего утверждения может быть приведен классический пример, вошедший уже в школьные учебники и построенный более четверти века назад в ФМШ № 18 при МГУ.
Зададимся вопросом: “Сколько решений может иметь уравнение ( 1 V
— = logi/i.6 х Даже очень тщательно выполненная “картинка”
\ 16/ '
с вероятностью, близкой к единице, даст одну общую точку, лежащую на биссектрисе первого координатного угла (ибо сообразительный абитуриент увидит равенство двух взаимообратных функций в этом уравнении). Однако хорошо образованный абитуриент должен знать, что это уравнение имеет еще два решения: х = 1/2 и х = 1/4. Зная ответ, попытайтесь теперь нарисовать картинку с тремя общими точками! И подсчитайте при этом количество попыток. Заметим, что подобных примеров, когда
61
графические методы приводят к ошибкам, можно привести достаточно много. Поэтому для уверенности в правильности выводов, полученных из “картинки”, необходимо эти выводы подтверждать аналитически.
Общей основой аналитического исследования графиков функций является понятие производной, однако это понятие в настоящее время исключено из программы вступительных экзаменов в МГУ им. М.В.Ломоносова.
Логическим продолжением данной главы является следующая, посвященная исследованию квадратичной функции.
2.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1 (физический факультет, 1964). Для каждого действительного значения параметра а решить неравенство
а) х2 + 2ж + a > 0;
б) ах2 — |ж — 1| > 0;
в) ж4 — ах2 + 1 < 0;
г) ах2 + |ж| + 1 > 0.
Задача 2 (механика-математический факультет, 1967). Для каждого действительного значения параметра а решить уравнение
logioo z2 = logy7 Ю • (lg 10а - |lg I) .
Задача 3 (факультет ВМиК, 1982). Для каждого значения параметра а найти все значения х, удовлетворяющие уравнению
а) |ж + 3| — а|ж — 1| = 4;
б) а|ж + 3| + 2|ж + 4| = 2;
в) 3|ж - 2| - а|2ж + 3| = 21/2.
Задача 4 (экономический факультет, 1983). Найти все значения параметра а, при каждом из которых уравнение
а) х — a = 2 12|ж| — а2|;
б) х — а/3 = 9 |9|ж| — а2|
имеет три различных корня, и найти эти корни.
62
Задача 5 (механико-математический факультет, ИП). Определить, при каких значениях параметра а минимум функции f(x) = 3|z — а| + |х2 + х — 2| меньше двух.
Задача 6 (механико-математический факультет, устный экзамен). При всех значениях параметра а решить систему
f х2 + 4х + 3 + а<0
а) <
[ 2х + a + 6 > 0;
[ х2 — 2х — 3 + а > 0
б) S о
[ х2 — 4х + 3 + a < 0.
Задача 7 (экономический факультет, 1996). Найти все значения параметра а, при которых фигура, заданная на координатной плоскости условием
|у| — |z|) + arcsin (sin (а — |z|)),
представляет собой а) четырнадцатиугольник; б) двенадцатиугольник.
Задача 8 (ИСАА, 1991). При каких значениях параметра а система уравнений
( х2 + у2 = 1
а) < имеет ровно два решения;
( у - |z| = a
( х2 + у2 = 2
6) < имеет ровно три решения?
I |г/| - х = a
Задача 9 (физико-технический факультет УФ МГУ, 1991).
1. При каком значении параметра I уравнение
х2(х - 3) - 2|х|л/2^6 = 2(1 + 1)
имеет два корня?
2. При каком значении параметра m уравнение
х2(2х — 3) — |г|л/4г — 6 = - + m
имеет три корня?
3. При каком значении параметра п уравнение
х2(х + 3) — 2\х^х?2х + 6 = 6п
имеет один корень?
63
Задача 10 (географический факультет, 1992). Найти все значения параметра с, при которых уравнение
а) \х2 — 1| + |z2 — х — 2| = х2 — Зх + с;
б) |z2 — 2а? | + \х2 — Зх + 2| = х2 — 4х + с
имеет ровно три различных решения.
Задача 11 (механико-математический факультет, 1996). Найти все значения к, при каждом из которых хотя бы для одного числа b уравнение
1) |z2 — 1| + kx = |z2 — 8z + 15| + Ь;
2) |z2 — 2х | — kx — |z2 — 10z + 24| — b
имеет: а) более 5 корней; б) ровно 5 корней.
Задача 12 (механико-математический факультет, 1967). На координатной плоскости указать все точки, координаты (z; у) которых таковы, что выражение:
a) sin2 (t + z) + sin (t + у) + sin (t + 2z — y) + 1/4 положительно при всяком значении t, и изобразить область, образуемую этими точками;
б) sin21 cos2 z + cos2 t sin2 z + - sin 2z • sin 2t + 2(cos 2z + cos y) отрицательно хотя бы для одного значения t, и изобразить область, образуемую этими точками.
Задача 13 (экономический факультет, 1977). Найти все значения параметра а, при каждом из которых неравенство
3 — |z — а| > z2
имеет хотя бы одно отрицательное решение.
Задача 14 (экономический факультет, 1977). Найти все значения параметра а, при каждом из которых неравенство
2 > |z + а| + х2
имеет хотя бы одно положительное решение.
64
2.4. УКАЗАНИЯ И ОТВЕТЫ
I. а) При а < 1 х Е (—сю; — 1 - ч/1 - a) U (-1 + а; оо);
при а = 1
при а > 1 х Е R
б) При а 0 х Е 0;
/ —1 — л/1 4- 4а \ / —1 + л/1 + 4а \
при а > 0 х G I -оо;-------------U ----------------; оо .
\ 2а J \ 2а J
в) При а 2 х Е 0;
п ( /а 4- л/а2 — 4 /а — у/а? - 4\
при а > 2 х Е I -у-------------; -у---------- I U
г) При а 0 х Е В.;
А / 1 + д/1 - 4а -1 - х/1 -4а\ при а < 0 х 6 I ---------;-------------- .
у 2а 2а J
2. При а < Ю1-^ х Е 0;
при а = Ю1-^ х = 101-х//3;
при < а < IO"1/2 х = Ю1^, х = ю^+4Т^-1.
при а = 10-12 х - 10-1/2;
при 10“1/2 < а < Ю1^ х = 101'А х = lox/s+^g"-1;
при а 101+у/з х = io1"б) 5?7'43, х = lO^5?7’43.
3. а) При а = 1 при а = -1 при |а| < 1 при |а| > 1
х Е [1; оо);
ж Е [-3; 1];
7 + а
х = ------х = 1;
а — 1
х = 1.
б) При а = 2
х Е [-4; -3];
при а = —2
при |а| < 2
при |а| > 2
х Е [—3; оо);
х — —3, х = — х = —3.
За 4~ 10
2 4- а
в) При а = 3/2 х Е (—оо; —3/2];
при а = —3/2 при |а| < 3/2
х Е [-3/2; 2];
х = —3/2, х =
ба 4- 33
6-4а ’
5 Методы реш. задач
65
при |а| > 3/2 х = —3/2.
4. а) а = —2, а = —1/2;
при а = — 2 х = —2, х = 6/5, х = 10/3;
при а = —1/2 х = —1/5, х = 0, х = 1/3.
б) а = -3, а = -1/27;
при а = — 3 х = —1, х — 41/40, х = 40/41;
при а = -1/27 х = -1/3321, х = 0, х = 1/3240.
5. а е (-8/3;-1) U (0; 5/3).
6. а) При а <С — 8 х G 0;
при —8 < а 0 хе (—(а + 12)/2; —2 + л/1 — а);
при 0 < а < 1 хе (—2 — л/1 — а; —2 + г/1 — а);
при а 1 х Е 0.
б) При а < 0 х е (1 + л/4 — а; 2 + г/1 — а);
при а О х е 0;
7. а) а е (5тг/2; 7тг/2].
б) a е (Зтг/2; 5тг/2].
Указание. Построить график функции у = f(x), где /(ж) = х + arcsin (sin х). В силу четности исходного неравенства по х и у построение части требуемого n-угольника можно проводить только в первой четверти при условиях 0 х <С а, 0 у /(а — ж), а затем отразить полученные “картинки” относительно всех осей. Анализ сводится к использованию нечетности функции У, в силу чего /(а —ж) = —/(ж —а), и упомянутым выше преобразованиям графика функции f. При увеличении параметра а n-угольник проходит следующие фазы:
при а = 0 - точка;
при 0 < а <С тг/2 - ромб;
при тг/2 < а <С Зтг/2 - выпуклый 6-угольник;
при Зтг/2 < а 5тг/2 - невыпуклый 12-угольник;
при 5тг/2 < а <С 7тг/2 - невыпуклый 14-угольник и т.д.
8. а) а е {-72}и(-1;1).
б) а = л/2-
9. 1) 1е (-2;-1];
2) те 0;
3) п > 0.
10. а) с = 2, с — 10/3.
66
б) с - 4, с = 19/4.
LI. 1) а) Ат = —8, б) к G (-8;-4л/3);
2) а) А = 8, б) к е (4л/3;8).
1.2. а) Указание. Свести задачу к неравенству, которое задает на координатной плоскости “зебру” полос с угловым коэффициентом 1 (см. рис. 1).
б) Указание. Свести задачу к неравенству, равносильному совокупности двух систем, которая задает на координатной плоскости “картинку” в виде косоугольной “шахматной доски”, составленной из ромбов, диагонали которых параллельны осям координат и равны тг вдоль оси Ох и 2тг вдоль оси Оу (см. рис. 2).
13. а £ (-13/4; 3).
14. a G (-9/4; 2).
5*
67
ГЛАВА 3
КВАДРАТИЧНАЯ ФУНКЦИЯ
3.1. КРАТКАЯ ТЕОРИЯ КВАДРАТНОГО ТРЕХЧЛЕНА
--- Вернись! — закричала Гусеница ей вслед. •- Мне нужно сказать тебе что-то очень важное.
Это звучало заманчиво — Алиса вернулась.
Л.Кэрролл. Алиса о стране чудес
Множество экзаменационных задач после ряда преобразований сводится к исследованию квадратного уравнения или неравенства при некоторых ограничениях на значения его корней. Поэтому для решения задач с параметрами очень важным является знание свойств квадратичной функции и зависимости этих свойств от возможных соотношений между ее коэффициентами.
Приведем основные факты, относящиеся к теории квадратичной функции (квадратного трехчлена).
Уравнение вида
ах2 + Ьх + с = 0, (1)
где а, Ь, с - числа, причем а 0, называется квадратным уравнением.
Дискриминантом квадратного трехчлена называется число
D =-Ь2 — 4ас.
Если D < 0, то уравнение (1) не имеет действительных корней.
Если D > 0, то уравнение (1) имеет два различных корня:
и тогда
-b-VD
X1 ~ Та
х2 =
-ь + Тр
2а
ах2 + Ъх + с = а(х — я1)(я — х2).
(2)
69
Если D = 0, то уравнение (1) имеет один корень (кратности два)
Ь ~ > 2а
и тогда
ах2 + Ьх + с — а(х — Zi)2. (3)
Представление квадратного трехчлена ах2 4- Ьх ф с в виде (2) или (3) называется его разложением на линейные множители.
Это разложение позволяет сформулировать известную теорему Виета, которая устанавливает следующие соотношения между корнями и коэффициентами квадратного трехчлена:
Ь с
ф х2 = -- , Z1Z2 = - • а а
С помощью теоремы Виета можно, не вычисляя самих корней, устанавливать их знаки, вычислять по коэффициентам уравнения различные выражения, зависящие от корней, решать системы вида х ф у = А, ху = В и т.д.
Выделение полного квадрата, т.е. представление квадратного трехчлена в виде
2 , ( Ь \ Ь2
ах + Ьх + с = a z ф — ф с------,
\ 2а/ 4а
позволяет найти координаты вершины параболы (графика функции у = ах2 ф Ьх + с)
Ь 4ас — Ь2 D
Х° = = ~~4а~ = ~4а '
Из школьного курса известно, что знак коэффициента при х2 определяет направление ветвей параболы (при а > 0 ветви направлены вверх, при а < 0 - вниз), знак D определяет количество корней, и каждый случай однозначным образом может быть представлен некоторой “картинкой” на координатной плоскости XOY.
Однако для целого ряда задач требуется определить взаимное расположение на числовой оси корней квадратного трехчлена и каких-либо заданных чисел. Это позволяют сделать следующие теоремы.
Теорема 1. Корни квадратного трехчлена действительны и оба больше данного числа m тогда и только тогда, когда выполняется система
D — Ь2 — 4ас О
< а/(т) = а(ат2 ф Ьтп ф с) > О
т ф Ь/2а < 0.
70
Данную теорему можно, используя знак эквивалентности (<=>), записать с помощью символов в следующем виде:
( D = Ь2 — 4ас О
т < xi Х2 <=$ \ а/(т) = а(ат2 + Ьт + с) > О
[ т + Ь/2а < 0.
Остальные теоремы сформулируем только в символьной форме.
Теорема 2.
{D = Ь2 — 4ас 0
а/(М) = а(аМ2 + ЬМ + с) > 0
М + Ь/2а > 0.
Теорема 3.
т < Xi Х2 < М <=>
/ D = Ь2 - 4ас 0
af (М) = а(аМ2 + ЬМ + с) > 0
а/(т) = а(ат2 + Ьт + с) > 0
т + Ь/2а < 0
< М + Ь/2а > 0.
Теорема 4.
xi < /а < Х2 = а(ар,2 + Ьр, + с) < 0.
Заметим, что каждой из теорем однозначным образом соответствует набор некоторых “картинок” на координатной плоскости XOY, т.е. теоремы могут быть истолкованы геометрически, что существенно помогает при решении ряда задач, так как “картинки” выполнить и проанализировать проще, чем запомнить формулировки теорем.
Для примера представим “картинки” при а > 0 ко всем теоремам, введя для удобства обозначения:
/(ж) = ах2 + Ьх 4- с - квадратичная функция,
f(x*) = ах2 + Ьх* + с - значение этой функции при х = х*.
Остальные обозначения (D, xi, Х2, хо, Уо} введены выше.
Тогда знак величины х* + 6/2а определяет положение вершины параболы хо относительно точки х = х*, а знак /(ж*) - положение точки параболы у = f(x) при х = х* относительно оси Ох.
Последнее неравенство теоремы 1 однозначно указывает, что точка х — т лежит левее абсциссы вершины параболы хо = —Ь/2а. Первое неравенство допускает две ситуации: при D > 0 парабола пересекает ось Ох в двух различных точках и вершина параболы лежит между ними, т.е. существуют два различных корня и xi < хо < Х2', при D = 0 парабола касается своей вершиной оси Ох и Xi = Х2 = Xq.
71
Рис. 1.Г
f(H)<0
Второе неравенство равносильно совокупности двух систем
а > 0 f а < О
V
У(тгг) = ат2 + Ьт + с > 0 [ f(m) — ат2 + Ьт + с < О,
первая из которых дает параболу с направленными вверх ветвями и значением Дт) > 0, вторая дает параболу с ветвями вниз и Дт) < 0. Все четыре возможные “картинки”, удовлетворяющие условиям теорем 1-4 при а > 0, представлены на рисунках 1.а-1.г. Наборы “картинок”, соответствующие теоремам 1-4 при а < 0, выполните самостоятельно, а заодно подумайте, почему в условии теоремы 4 отсутствует требование D > 0, обеспечивающее существование двух различных корней квадратного трехчлена.
72
3.2. ЗАДАЧИ НА ИССЛЕДОВАНИЕ КВАДРАТИЧНОЙ ФУНКЦИИ
— Глупости! —• рассердилась мышь. — Как я от них устала! Этого просто не вынести'.
— А что нужно вынести? — спросила Алиса. — Разрешите, я помогу!
Л.Кэрролл. Алиса в стране чудес
Задача 1 (факультет ВМиК, 1980). Найти все значения параметра а, при каждом из которых уравнение
(2a — 1)х2 + ах + 2а — 3 = 0 (1)
имеет не более одного корня.
Решение. При а = 1/2 уравнение (1) становится линейным и имеет один корень х = 4. При а ф 1/2 уравнение (1) является квадратным и имеет не более одного корня при
(2)
D = а2 - 4(2а - 1)(2а - 3) < 0 <=> 15а2 - 32а + 12 О 16 — 2^/19 16 + 2V19
<=> а < --------- V а > ---------.
'15 15
, , /0= /16-2719 16 + 2У19\ „
Заметим, что а = 1/2 Е --------; ------- . Поэтому оба полу-
\ 15 15 /
интервала (2) целиком входят в ответ.
„ 16 — 2719 16 + 2719
Ответ: а < ---—-----: а = 1/2 ; а > -—----.
15 ' 15
Задача 2 (механико-математический факультет, 1989). При каких значениях с выражение (xi + 2x2)(x2 + 2xi), где х^, х? - действительные корни квадратного трехчлена х2 + сх + с + 1/5, принимает наименьшее значение?
Решение. По теореме Виета для корней Xi, х% квадратного трехчлена х2 + сх + с + 1/5 (1)
выполняются два соотношения: Xi + Х2 = — с и Х1Х2 = с + 1/5. Поэтому (a?i + 2х2)(х2 + 2x1) = 2х2 + 2х% + 6x1X2 = = 2(xi + х2)2 + xix2 = 2с2 + с + 1/5.
73
Эта квадратичная относительно параметра с функция принимает минимальное значение при с = —1/4, так как
2с2 + с + 1/5 = 2(с + 1 /4)2 + 3/40.
Внимание! Проверим, что при с = —1/4 существуют корни квадратного трехчлена (1), т.е. его дискриминант
D = с2 - 4(с + 1/5) = 21/80 > 0.
Ответ: —1/4.
Задача 3 (факультет психологии, 1981). Найти все значения параметра а, при каждом из которых наименьшее значение квадратного трехчлена
4ж2 — 4ах + а2 — 2а + 2 (1)
на отрезке 0 х 2 равно 3.
Решение. Выделим в (1) полный квадрат и обозначим
/ д \ 2
/(®) = 4^--J — 2(а — 1).
Функция f(x) убывает при х а/2 и возрастает при х а/2.
Тогда справедливы следующие утверждения:
1) если а/2 0, т.е. а 0, то f(x) возрастает при х 0. Следователь-
но, при 0 х 2 выполняется min f(x) = /(0) = а2 — 2а + 2;
2) если 0 < а/2 < 2, т.е. 0 < а < 4, то f(x) убывает при 0 х а/2 и возрастает при а/2 х 2. Следовательно, при 0 х 2 выполняется min/(z) = /(а/2) = —2(а — 1) = 2(1 — а);
3) если а/2 2, т.е. а 4, то f(x) убывает при х 2. Следовательно,
при 0 х 2 выполняется min/(ж) — /(2) — а2 — 10а + 18.
Таким образом, min/(ж) на отрезке 0 х 2 равен
а2 — 2а + 2,
minf(x) = < 2(1 — а),
а2 — 10а + 18,
при а 0,
при 0 < а < 4, при а 4.
Поэтому решение задачи сводится к совокупности систем
( а< 0 ( 0 < а < 4 Г а > 4
< V < V <
( а2 - 2а + 2 = 3 ( 2 - 2а = 3 ( а2 - 10а + 18 = 3
<=> а — 1 — л/2 V а Е 0 V а = 5 + \/10
<=> а = 1-^2 V а = 5'+ У10.
Ответ: 1 — \/2; 5 + э/10.
74
Задача 4 (филологический факультет, отделение лингвистики, 1980). Найти все значения а из промежутка [1; оо), при каждом из которых больший из корней уравнения
х2 — 6х + 2ах + а — 13 — 0 (1)
принимает наибольшее значение.
Решение. При a = 1 уравнение (1) принимает вид
х2 — 4х — 12 = 0 <=> £1 = — 2 V Х2 = 6.
Докажем, что для всех a Е (1; оо) уравнение (1) не имеет корней при х 6. Так как верно равенство
х2 — 6х + 2ах + а — 13 = (а — 1)(2ж -Ь 1) 4- (х — 6)(ж + 2), то при а > 1 и х 6 выполняется х2 — 6ж -Ь 2ах -Ь а — 13 > 0.
Следовательно, больший корень уравнения (1) принимает наибольшее значение х = 6 при а = 1.
Ответ: 1.
Замечание. Решите эту задачу “в лоб”, отыскивая наибольшее значение функции
Х2 = f(a) = 3 — а -Ь а/я2 — 7а -Ь 22
при a G [1; оо) с помощью производной. Покажите, что /'(а) < 0, т.е. шах/(а) = /(1) = 6.
[1;оо)
Задача 5 (химический факультет, 1981). Найти все значения параметра а, при каждом из которых неравенство
(а3 + (1 - У2) а2 - (з + \/2) а + 3^) х2 + 2 (а2 - 2) х + а > -J2 (1) выполняется для любого х > 0.
Решение. Перепишем неравенство (1) в виде f(x) = Ax2+Bx + C>Q, (2)
где
А = а3 + (1 - У2) а2 - (з + л/2) а + 3^ =
а — л/2) (а2 + а — 3) —
Я = 2 (а2 - 2) = 2 (а - V2) (а + ,
С — а Т д/2.
75
Имеем
D = В2 - 4АС = 4 (а2 - 2)2 - 4 (а2 - 2) (а2 + а - 3) = = —4(а - 1) (а - (а + 72) .
Рассмотрим случай А = 0.
1. а = а/2, тогда А = В = D = 0, а неравенство (2) принимает вид 2\/2 > 0, что справедливо для всех х, в том числе и для х > 0.
д/13 + 1
2. а =-------, тогда из (2) получаем
(з+7Н).г + 72-Л1+2>0
713 + 1 - 2д/2 2(>/13 + 3)
>0,
X
следовательно, это значение параметра не удовлетворяет условию задачи, / 713 + 1 - 2л/2 \
так как множество х Е ----7—7=--;—; +оо не содержит множество
2(713 + 3) )
х G (0; +оо).
„ 713-1
3. а = ---- тоже не удовлетворяет условию задачи, так как в этом
т VI3-1+272
случае неравенство (2) эквивалентно неравенству х < - -----—.
2 (713 — 3)
В случае А < 0 неравенство (2) имеет множество решений в виде конечного интервала (см. “картинку” к теореме 1) или не имеет решения. В любом варианте при А < 0 множество решений (2) не содержит множество .1! > 0.
Рассмотрим случай А > 0.
1. Л > 0, D > 0, тогда множество решений неравенства (2) состоит из двух полубесконечных интервалов
в + 7в -B + y/D х <-----—---- И X > ----—----
2А 2А
и содержит множество х > 0, если только
/(0) = С^0 и А>0
(см. теорему 2 и Ваши “картинки” к ней!).
Таким образом, нужно решить систему
( . / f , 713 + iA ( 713-1\ .
А = - 72J I а +------ 11а--------- I > 0
< В = 2(а-Т2)(а + Т2)>0
С = а + 72 0
< D = -4 (а - 1) (а - 72) (а + 72) > 0.
76
Методом интервалов можно установить (сделайте это!), что данная система решений не имеет.
2. А > О, D = —4 (а — 1) (а — \/2) (а + \/2) = 0. Данным условиям удовлетворяют только два значения параметра а = —у/Ъ и а = 1.
При а = —л/2 неравенство (2) равносильно неравенству
2д/2 (1 + у/2^ х2 >0,
которое справедливо для всех г 0, в том числе и для х > 0, т.е. а = — \/2 удовлетворяет условию задачи.
При а = 1 неравенство (2) равносильно неравенству
(ж - 1 - л/2)2 > 0,
которое справедливо для всех х =4 1 + у2. Ио х = 1 + у/2 > 0, т.е. а = 1 не удовлетворяет условию задачи.
3. Л > 0, D = В2 — 4АС < 0, тогда неравенство (2) выполняется для всех х, в том числе и для х > 0. Решим полученную систему относительно параметра а:
<=> —л/2 < а < 1 V у/2 < а < оо.
Итоговый ответ — объединение полученного множества с особыми случаями, когда А = 0 при а = у/2 и А > 0, D = 0 при а = —д/2-
Ответ: а Е [—л/2; 1) О [д/2;оо).
Задача 6 (биологический факультет, 1977). Найти все те значения параметра s, при каждом из которых корни уравнений
? Зх ? 12х
х2 4----Ь 2s = 0 и х --------------s = 0
s s
не перемежаются, т.е. оба уравнения имеют по два корня и между двумя корнями одного из уравнений нет ни одного корня другого уравнения.
Решение. Обозначим
«/ . о Зх п / \ 2 12х
Дх) = х2 + — + 2s, g(x) = х2 + —------s,
77
#1 < хз — корни уравнения f(x) = О,
Х2 < %4 — корни уравнения д(х) = О,
9 — 8s3
Di = ----5-----дискриминант уравнения /(ж) = О,
s2
144 + 4s3
D2 = ----5-----дискриминант уравнения д(х) = 0.
Так как оба уравнения имеют по два корня, то
9 - 8s3 > О 144 + 4s3 > О
s / О
' s3 < 9/8 s3 > -36 s / О
(1)
Условие задачи будет нарушено, если корни перемежаются, что возможно только в следующих двух ситуациях:
Ж1 < Г2 < Хз < Х4 ИЛИ Х2 < Х± < Х4 < Х3.
В этих случаях числа /(;г2), /(24) отличны от нуля и имеют разные знаки, т.е. /(а^) • /(ж4) < 0- (См. теорему 4 и “картинки” к ней!)
Поэтому условие задачи будет выполнено в противном случае, когда /(®s) • Л®4) 0.
Так как т2, х4 - корни уравнения д(х} = 0, то
9 12 2 12
.То = S--------Х2 И Х4 = S--------------Х4,
s s
а /(ж->) = s-----------Х2 ) 4—Х2 + 2s — 3s-----------Х2.
\ s J s s
Аналогично /(гг4) = 3s — 9x4/s.
По теореме Виета для квадратного трехчлена д(х) имеем
12
х2 + х4 =----, х2х4 = -S.
S
Тогда
/ 9 \ ( 9
/(ж2) • /(®4) = (3s - -Х2 ) (3s - -х4
81
= 9s2 - 27(я2 + ж4) + х2х4 =
м2 12 81 м 2 243
= 9s2 + 27---------= 9s2 +-------
S S S
s < 0 ( s > 0
s3 £ -27 V 1 s3 > -27
0.
(2)
78
Сравнивая (1) и (2), получаем, что
s G U (О; ^9/2) .
Ответ: s Е -^36; — 3j (J (О; fy'9/2^.
Замечание. Следует подчеркнуть, что многие абитуриенты неверно понимают условие задачи, исключая из рассмотрения некоторые случаи, в частности
< Х-2 < Х4 < Х% И Х2 < < Х$ < Ж4.
Первое из этих неравенств соответствует ситуации, когда между корнями уравнения д(х) = 0 нет ни одного корня уравнения /(ж) = 0, а второе описывает противоположный случай, т.е. оба неравенства удовлетворяют условию задачи!
3.3. ЗАДАЧИ, ПРИВОДИМЫЕ К ИССЛЕДОВАНИЮ КВАДРАТИЧНОЙ ФУНКЦИИ
— Прежде всего нужно принять прежний вид, — сказала Алиса, пробираясь меж деревьев. — А потом — найти дорогу в тот чудесный сад. Так я и поступлю — лучше плана не придумаешь!
Л.Кэрролл. Алиса в стране чудес
Задача 7 (экономический факультет, 1983). Для каждого неотрицательного значения параметра а решить неравенство
а3х4 + 6а2ж2 — х -|- 9а + 3 0. (1)
Решение. Представим полином четвертой степени
Д(ж) = а3х4 -I- 6а2ж2 — х + 9а + 3
в виде произведения двух квадратных трехчленов методом неопределенных коэффициентов или следующим рядом последовательных преобразований:
/4 (ж) = а(а2х4 + бах2 + 9) — х + 3 = а(ах2 + З)2 — х + 3 =
= а [(аж2 + З)2 — ж2] 4- аж2 — ж 4- 3 =
= а(аж2 — ж + 3)(аж2 4- ж 4- 3) 4- (аж2 — ж Ч- 3) =
= (аж2 — ж + 3)(а2ж2 4- ах 4- За 4- 1).
79
Дискриминант второго сомножителя = —а2(12а+3) < 0 для каждого а > 0. Следовательно, а2х2 + ах + За + 1 > 0 для всех х при а > 0. Поэтому при а > 0 неравенство (1) равносильно неравенству
ах2 — х + 3 0.
(2)
Дискриминант квадратного трехчлена неравенства (2) равняется D\ = 1 — 12а. При а 1/12 О1^0и решением (2) является вся числовая ось. При 0 < а < 1/12 D\ > 0 и множество решений неравенства (2) состоит из двух полубесконечпых промежутков:
1 - yi - 12а' ’ Та
1 + х/1 - 12а 2а
При а = 0 из неравенства (1) получаем х 3.
Ответ: при а = 0 х € (—оо; 3];
при 0 < а < 1/12
( 1 - VI - 12а 1 Г1 +71 - 12а \
х G -оо;------------- U --------------; +оо ;
\ 2а J [ 2а /
при а 1/12 х 6 R.
Задача 8 (биологический факультет, 1987). Найдите все значения а, при которых система
( 9х2 — бху + у2 + 6г — 13?/ + 3 = 0
[ 13.г“ + б;г у + 10?/2 + 16.г — '2у — 4ах — бау + а2 — 2а + 3 = 0
имеет хотя бы одно решение.
Решение. Систему (1) можно привести к виду
Г и2 = Зг t а2 + (г — 6)2 = 2, где и = Зх — у + 2, v = 2ж + Зу + 1/3, Ь = а — 2/3. Для существования решения системы (2) необходимо и достаточно, чтобы уравнение
Зг + (г — 6)2 = 2 +=> г2 + (3 - 26)г + Ь2 - 2 = 0 (3)
имело хотя бы один неотрицательный корень, так как в противном случае первое уравнение системы (2) решений не имеет.
Возможны три случая:
1) уравнение (3) имеет нулевой корень, тогда
Ь2 - 2 = 0 <=> b = ±х/2;
80
2) уравнение (3) имеет один отрицательный и один положительный корень, тогда (см. теорему 4)
г»1 < 0 < г»2
62 - 2 < О
3) уравнение (3) имеет два положительных корня, тогда (см. теорему 1) должна выполняться система
D = (3 - 26)2 - 4(62 - 2) 2 Г 126 17
Ь2 - 2 > О J |6| > х/2 ^6 G 0
3 - 26 < О I 26 > 3.
Таким образом, получаем ответ:
2
2 а - 2/3 <$ V2
Ответ: a G [2/3 — л/2; 2/3 + д/2].
Задача 9 (механико-математический факультет, 1991). Найдите все пары чисел р и q, при которых неравенство
\х2 + рх + д| >2
(1)
не имеет решений на отрезке [1; 5].
Решение. Обозначим f(x) = х2 + рх + q, тогда хо = —р/Ъ - абсцисса вершины параболы. По условию требуется найти такие числа р и q, чтобы система
Г I/WI > 2
| 1 х 5
была несовместна, т.е. для любого х 6 [1; 5] должно выполняться противоположное неравенство:
I/И 2
-2 f(x) = х2 + рх + q 2.
(2)
На координатной плоскости (х,у) это означает, что график функции у = /(ж) целиком должен лежать в полосе — 2 у 2 при х G [1; 5]. Вспоминая теоремы 1-4 и “картинки” к ним, получаем, что пара (х,у)
6 Методы реш. задач
81
удовлетворяет условию задачи лишь тогда, когда она является решением совокупности трех систем:
{Х0 < 1
/(1)^-2
/(5) < 2
V /(1) 2
. /(5) £ -2
(1 а?о 5
Л1) 2
/(5) $ 2
Дх») -2
р > — 2 ( р < —10
1 + Р + 9 -2 V < 1 + р + q < 2 V <
5(5 + р) + q < 2 [ 5(5 + р) + g ~2
-10 О -2 1 +р + 0. 2 5(5 + р) + q 2 q — р2/4 У -2
1 + Р + Q 2
1 +р+ g -2
р >-2
р -5
-10
Р <
!—10 Р С -2
1+ р + q< 2
26 + 6р + 2g ^4 р2/2 — 2g 4.
Первые две системы несовместны, а из двух последних неравенств третьей системы получаем квадратное неравенство относительно р:
р2/2 + 6р+ 18 < 0 р2 + 12р + 36 = (р+ 6)2 < 0,
которое выполняется при единственном значении р = —6. Тогда g = —7 -единственное значение, которое не противоречит последней системе.
Ответ: р = — 6, g = 7.
Задача 10 (физический факультет, 1988). При каких значениях a система
Г аху + х - у + 3/2 = 0
( х + 2р + ху + 1 = 0 имеет единственное решение?
Решение. Непосредственной проверкой можно убедиться, что а = 0 не удовлетворяет условию задачи. Умножим второе уравнение системы (1) на а 0, вычтем из результата первое уравнение и получим, что система (1) равносильна системе
Г а?( 1 - а) - р(2а + 1) + 3/2 - а = 0 t ху + X + 2р + 1 — 0.
При а = 1 и а = —1/2 система (2) имеет единственное решение
х = —4/5
У = -1/6
х = -8/3
У = -5/2
82
соответственно. При других значениях а можно выразить из первого уравнения х через у (или наоборот), тогда для у получим квадратное уравнение
(2а + l)t/2 + (а + 3/2)?/ - 1/2 = О,
которое имеет единственное решение только в том случае, если
D= а2 + 7а+17/4= О,
-7 ± 4х/2 т.е. при а = -------.
z. , ~7±4х/2
Ответ: —1/2; 1; --------.
Задача 11 (факультет психологии, 1977). Найти все значения параметра а, при каждом из которых имеется хотя бы одна пара чисел (ж; у), удовлетворяющая условиям
Г х2 + (т/ + З)2 < 4
1 у = 2ах2.
(1)
Решение. Система (1) имеет решение только в том случае, если решение неравенство
х2 + (2ах2 + З)2 < 4.
Обозначим z = х2 и рассмотрим квадратный трехчлен
г/ \ /п о\2 л л 2 ( 1 + 12а \ 64а2 + 24а + 1
/(z) = (2az + 3) + z — 4 = 4а 6+-^“)-------------
имеет
(2)
• (3)
Неравенство (2) будет иметь решение, если /(z) < 0 при z 0.
Если а = 0, то /(z) = z + 5 и /(z) 5 при z 0, т.е. а = 0 не
удовлетворяет условию задачи.
Если а ф 0, то график /(z) представляет собой параболу, ветви которой направлены вверх, а вершина имеет координаты
1 + 12a , . 64a2 + 24a + 1
(4)
При z0 0 <=> 1 + 12а 0 функция f(z) монотонно возрастает на
множестве z 0, следовательно, min/(z) = /(0) = 5 > 0, т.е. а —1/12 не удовлетворяют условию задачи.
При zq > 0 <=> 1 + 12а < 0 <=> а < —1/12
r/ \ 64a2 + 24a + 1
min/(z) = ftz0) =----. --6д2----
6*
83
достигается в вершине параболы.
Следовательно, все искомые значения параметра а являются решением системы
а < —1/12
64а2 + 24а + 1 > О
V
-З + а/5
16
а >
Ответ: а <-----——.
Задача 12 (геологический факультет, 1988). Найдите все действительные значения параметра а, при каждом из которых область значений функции
sin х + 2(1 — а)
У ~---------2--
а — cosz х
содержит отрезок [1;2].
Решение. Введем обозначения b = 1 — а и sin х = z, |z| <С 1. Тогда cos2 х = 1 — г2, и задачу можно переформулировать следующим образом: найти все значения параметра Ь, при которых для каждого у 6 [1;2] уравнение
f{:-) = yr-z-b(y + 2) = 0 (1)
относительно переменной г имеет хотя бы один корень, удовлетворяющий условиям |г| <С 1, с2 / Ь.
Заметим, что с2 = b приводит к системе
=>4b2 = b b = 0 V 6=1/4.
I г = — 26
При 6 = 0 уравнение (1) или исходное уравнение у = (z + 2b)/(z2 — 6) для каждого у 6 [1; 2] имеет корень z — 1/у 6 [1/2; 1]. При 6 = 1/4 существует корень z = \/у — 1/2 6 [0: 1/2]. Поэтому 6 = 0 и 6 = 1/4 удовлетворяют условиям задачи.
Квадратное уравнение (1) имеет при всех у 6 [1;2] корни, если его дискриминант
D = 1 + 4by(y -h 2) = 46г/2 + ЗЪу +1^0
(2)
для каждого у 6 [1; 2].
84
Рассматривая D как квадратичную функцию относительно переменной у:
D(y) = 4Ь(у + I)2 + 1 - 46
с абсциссой вершины соответствующей параболы уо = —1, можно показать, что условие D(y) 0 для всех у 6 [1;2] эквивалентно системе (вспомните идею доказательств теорем 1-4 и “картинки” к ним!)
D(l) = 126 + 1 О
D(2) = 326 + 1 О
6 -1/12
6 -1/32
6 -1/32.
(3)
Подчеркнем, что условие (3) обеспечивает выполнение неравенства (2), т.е. существование корней уравнения (1) при всех у G [1; 2]. Найдем теперь условия, при которых корни уравнения /(z) = О принадлежат отрезку [—1;1]. При у £ [1; 2] ветви параболы /(z) = yz2 — z — b(y + 2) направлены вверх, а абсцисса ее вершины zq = 1/2 6 [1/4; 1/2]. Следовательно необходимым и достаточным условием существования корня — 1 z 1 уравнения (1) является выполнение хотя бы одной из систем (см. теоремы 1-4 и “картинки” к ним):
6 —1/32 Г 6 -1/32
/(-1) = г/+ 1 - 6(2/+ 2) О V t /(1) = 2/- 1 - 6(2/+2) О
' 6 -1/32 ( 6 -1/32
<=> Hl V < у - 1
I 2/ + 2 I г/ + 2
У + 1
=> —1/32 6 ----- для всех у 6 [1; 2],
У + 2
причем первая система обеспечивает существование одного корня, принадлежащего отрезку [—1; 1], а вторая - двух корней. Так как при »е[1;2]
!/+1] , ( 1 1 , 1 2
------ > = 1 — шах < -- > = 1--------— = -
У + 2 J \у + 2) mm {г/+ 2} 3
достигается в точке у = 1, то
-1/32 < 6 = 1 - а < 2/3 1/3 а 33/32.
Ответ: a G [1/3;33/32].
85
Задача 13 (ПО ОП, 1990). Найти все значения параметра а, при каждом из которых уравнение
(4х' _ 2х — a2 + a) (cos х — 3 + а) = О
(1)
имеет единственное решение, и найти это решение.
Решение. Уравнение (1) имеет бесконечно много решений, если второй сомножитель обращается в ноль, т.е. когда существуют решения уравнения cos х = 3 — а, что имеет место при
|3- а| 1
-1 < 3 - а < 1 <=> 2 < а < 4.
Пусть а [2; 4], тогда cos х ф 3 — а и уравнение (1) заменой z — 2х > О сводится к квадратному
z2 — z — а24-а = 0
(2)
4,2 = 1/2±|а-1/2|,
которое при а = 1/2 имеет кратный корень z± = z? = 1/2 > 0, т.е.
2‘г = 1/2 <=> х = — 1 - единственный корень уравнения (1).
Если меньший корень уравнения (2) неположителен, т.е.
ci = 1/2- |а - 1/2| < 0 |а — 1/2| 1/2 <=> а<0 V О 1,
то уравнение (1) гарантированно имеет одно единственное решение х = logo где zn = 1/2 4- |а — 1/2| > 0 - больший корень уравнения (2).
Так как при а <С 0 г2 = 1/2 4- |а — 1/2| = 1 — а, а при а 1 и а £ [2; 4] Z2 = 1/2 4- |а — 1/2| = а, то уравнение (1) имеет единственное решение
х = log2 (1 — а) при а 6 (—оо; 0],
х = log2 а при а 6 [1; 2) U (4; оо).
Ответ: х = log2 (1 — а) при а 6 (—оо; 0];
х = — 1 при а = 1/2;
х = log2 а при а 6 [1; 2) U (4; оо).
Замечание. Хотя дискриминант уравнения (2) является полным квадратом, и, следовательно, в формуле для его корней можно опустить знак абсолютной величины, в подобных ситуациях иногда лучше этого не делать. Запись с модулем сильно упрощает решение получаемых неравенств и, соответственно, анализ единственности решения исходного уравнения.
86
Задача 14 (биологический факультет, 1989). Числа x,y,z таковы, что х2 + Зр2 + z2 = 2. Какое наибольшее значение может принимать выражение 2х + у — z ?
Решение. Основная трудность при решении этой задачи состоит в гом, чтобы увидеть, что в ее условии “зашифрована” задача на исследование квадратичной функции.
Введем параметр/? = 2х + у — z. Тогда переменная z выражается через переменные х, у и параметр р посредством соотношения z = 2х + у — р. Подставив это выражение в уравнение х2 + Зр2 + z2 — 2 и сгруппировав подобные члены, получим квадратичное относительно х, у и р уравнение 5ж2 + 4.(у - р)х + 4у2 - 2ру + р2 - 2 = 0. (1)
Теперь исходную задачу можно переформулировать следующим образом: найти наибольшее значение параметра/?, при котором уравнение (1) имеет решение.
Рассмотрим уравнение (1) как квадратное относительно переменной х с коэффициентами, зависящими от параметров у и р. Это уравнение имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
Dr > 0 -16?/2 + 2р//-р2 + 10 0 16р2 — 2р?/+/?2 —10 0. (2)
Рассматривая полученное неравенство (2) как квадратное относительно переменной у, получим что его дискриминант также должен быть неотрицательным, а именно
о 2 ™ Л 2 32 /32 /32
П2 > 0 « —З/?2 + 32 0 р « -ууО^уу-
Отсюда следует, что наибольшее значение параметра р — 2х + у — z
Замечание. Задачи такого вида допускают очень короткое решение, если использовать понятия длины вектора и скалярного произведения векторов.
В заключение этой главы рассмотрим три задачи, стоящие несколько в стороне от основной темы исследования квадратичной функции, однако чрезвычайно важные с методической точки зрения.
87
3.4. РЕШЕНИЕ ОТНОСИТЕЛЬНО ПАРАМЕТРА
И вправду, план был замечательный — такой простой и ясный. Одно только плохо: Алиса не имела ни малейшего представления о том, как все это осуществить.
Л.Кэрролл. Алиса в стране чудес
Метод решения относительно параметра часто оказывается эффективным, когда степень искомой переменной в уравнении или неравенстве относительно высока, а степень параметра не превосходит двух.
Основным признаком этого метода является своеобразный взаимообмен ролями неизвестной и параметра, когда исходную задачу трудно или невозможно сразу решить относительно искомой переменной, но достаточно легко разрешить относительно параметра.
Поясним сказанное подробным разбором приводимых ниже задач.
Задача 15 (биологический факультет, факультет фундаментальной медицины, 1994). Найти все такие значения величины х, при которых неравенство
(4 - 2а)а?2 + (13а - 27)я + (33 - 13а) > 0 (1)
выполняется для всех а, удовлетворяющих условию 1 < а < 3.
Решение. Исходное неравенство является квадратным по неизвестной .г и линейным по параметру а. Попытка получить ответ традиционным способом решения неравенства (1) относительно х крайне затруднена условием “для всех а 6 (1;3)”. Поэтому неравенство (1) представим в виде
?/(а) = k(x) • а + Ь(х) > 0, (2)
где параметр а играет роль новой независимой переменной, а угловой коэффициент k(x) = -2ж2 + 13гс—13 и свободный член Ь(х) = 4х2 — 27а?+33 зависят квадратичным образом от неизвестной х, рассматриваемой далее в качестве нового параметра.
На координатной плоскости аОу уравнение Z?(a?) • а + Ь(х) = 0 задает семейство прямых линий (зависящих от нового параметра я), отрезки которых в полосе 1 < а < 3 должны лежать в верхней полуплоскости (соответствующие “картинки” нарисуйте самостоятельно!). Поэтому выполнение неравенства (2) для всех а Е (1; 3) равносильно выполнению
88
системы
( ?/(1) О Г k(x) + Ь(а?) О
1 2/(3) > О t 3/г(а?) + Ь(х) О
2х2 - 14х + 20 О Г (х - 2)(х - 5) О
—2х2 + 12z - 6 0 t (х-+ л/6 — 3)(ж — л/6 — 3) < О
<=> х G [3 — >/б; 2] U [5; 3 + ч/б].
Подчеркнем, что при решении этой системы необходимо было исключить особый случай 2/(1) = 2/(3) = 0, который, как видно из приведенного выше решения, не реализуется пи при одном значении х.
Ответ: [3 — >/б; 2] U [5; 3 + л/б].
Задача 16 (механико-математический факультет, 1992). Найти все значения х, удовлетворяющие неравенству
(а + 2)ж3 — (1 + 2а)а?2 — 6х + (а2 + 4а — 5) > 0
хотя бы при одном значении а, принадлежащем отрезку [—2; 1].
Решение. Исходное неравенство является кубическим по неизвестной х (общие способы решения этого неравенства школьникам неизвестны) и квадратным по параметру а. Поэтому представим его в виде
/(а, а?) = а2 + 6(а?)а + с(ж) > 0, (1)
где коэффициенты Ь(ж) = х3 — 2х2 + 4 и с(т) = 2т3 — х2 - 6a? — 5 зависят от неизвестной х как от нового параметра.
На координатной плоскости аОт/ графики функции у = f(a, х) при различных х представляют собой семейство парабол с направленными вверх ветвями. Поэтому условию задачи удовлетворяют всевозможные положения этих парабол относительно полосы — 2 а 1, кроме тех случаев, когда параболы пересекают ось новой переменной а, причем корни Я1 < «2 уравнения f(a, х) = 0 находятся по разные стороны от этой полосы, включая ее границы (соответствующую “картинку” нарисуйте самостоятельно!).
Таким образом, исходная задача может быть кратко переформулирована следующим образом: найти все значения х за исключением тех, при которых противоположное (1) неравенство f(a,x) 0 выполняется для каждого а G [—2; 1]. В силу теоремы 4 это исключительное множество значений х задается решением системы
/(-2) = 3(х2 - 2х - 3) <С 0 Г — 1 < х < 3
/(1) = За?(а?2 — х — 2) 0 (i^-lV0^r^2
<=> х G {-1} U [0; 2]. (2)
89
Следовательно, ответом исходной задачи являются все значения ж, за исключением множества (2), т.е.
ж 6 (—оо; —1) U (—1; 0) U (2; +оо).
Ответ: х 6 (— оо; —1) U (—1; 0) U (2; +оо).
Задача 17 (механико-математический факультет, ИП). При каждом значении параметра а решить уравнение \/a + у/a + х = х.
Решение. Исходное иррациональное уравнение равносильно системе
( 0 х; 0 а + а? ( 0 х; а х2
I a + л/а + ж — х2 I a + х = (х2 - а)2
Г 0 < ж; а х2
1 ж4 — 2аа?2 — х + а2 — а = 0.
Уравнение системы (1) является уравнением четвертой степени относительно переменной х и второй степени относительно параметра а. Поэтому представим его в виде
а2 — (2а?2 + 1)а + (а?4 — а?) = 0 (2)
и решим относительно параметра а.
Дискриминант квадратного трехчлена относительно параметра а уравнения (2) зависит от переменной а? и равен
Z?(a?) = (2а?2 + I)2 - 4(а?4 - а?) = 4а?2 + 4а? + 1 = (2а? + I)2.
Следовательно, корнями уравнения (2) будут выражения, зависящие от переменной а?:
а12 = ^(2i’2 + 1 ± |2а? + 1|) <=> = х2 — а? V а2 = х2 + а? + 1.
Тогда уравнение (2) можно записать в виде разложения на линейные относительно параметра а множители:
(а — а?2 + а?)(а — х2 — а? — 1) = 0.
Отсюда следует, что система (1) будет равносильна совокупности систем
90
о
х — a = x
x 0
' x2 — a = — (a? 4 1)
< x < — 1 ?!
k x 0
a < —1/4
V
x G 0
— 1/4 < a < 0
1 4 -/1 4 4a
xi,2 --------5------
( a > 0
V 1 4 лЛ + 4a
I zi - 2 ’
решение которых и дает ответ задачи.
Ответ: при a < —1/4 х Е 0,
,,. . п 1 ± vT+^E
при -1/4 < а <С О Х1,2 = -g’
, ,л n 1 + л/1 + 4a при а = —1/4 и a > 0 х^ = -----.
Замечание. Условие приведенной выше задачи изменено: на самом деле требовалось решить уравнение
а + х = х
(3)
при каждом значении параметра а.
Предполагалось, что при наличии трех радикалов желание возводить обе части уравнения (3) в квадрат три раза достаточно быстро пропадет и будет найден другой путь решения этого уравнения.
Второй способ решения этой задачи основан на следующей теореме (вообще говоря, выходящей за рамки школьной программы, однако легко доказываемой методом от противного).
Теорема. Для монотонно возрастающей функции f(x) уравнения
= х и /(/(. ./(а?)...)) = х
п раз равносильны.
Тогда для решения уравнения (3) достаточно убедиться, что функция /(ж) = у/a 4 х является монотонно возрастающей в своей области определения (что можно сделать с помощью производной, так как Г(х) = -/== > 0). a 4 х
Следовательно, уравнение (3) равносильно уравнению
(Л®))) = х 4=> /(а?) = х <=> y/a-Рх = х,
которое фактически уже было решено выше.
91
3.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
— Это все? — спросила, Алиса, стараясь пе сердиться. — Держи себя в руках! — сказала Гусеница.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (географический факультет, 1990). Найти все значения параметра а. при ко торых уравнение
(а 4- 1).т~ 4- (| а 4- 21 — | а 4- 101)х 4~ а — 5
имеет два различных положительных корня.
Задача 2 (ИСА А, 1989). При каких значениях параметра а сумма S квадрачов корней уравнения
j‘~ 4- 2аз? 4” 2а2 -|- 4а 4-3 = 0
является наибольшей? Чему равна эта сумма?
Задача 3 (физический факультет, 1989). При каких значениях m уравнение
(2.и)2 - 4.г (m3™)1/2 4- 3w+] + m - 3 = 0
имеет корни и каковы знаки корней при различных значениях т?
Задача 4 (факультет ВМиК, 1988). Найдите все значения параметра а. при которых уравнение
[(2г 4- a) \/22« - 4а2 - 24 - 2 (х2
х . 1. / 36а — 9а2\
+ *М ig ( 35 )
= о
имеет по крайней мере два корня, причем один неотрицателен, а другой не превосходит — 1.
Задача 5 (биологический факультет, 1986). Найдите все значения Ь, при каждом из которых система уравнений
Г 2х2 - 2ху 4- W2 = b4 - 663 4- 9Ь2 - 19 4- л/85
1 х2 4- 2ху — Зу2 = 4
имеет хотя бы одно решение.
92
Задача 6 (физический факультет, 1985). При каждом а решить уравнение
4Г — 2а(а + 1)2Г-1 + а3 = 0.
Задача 7 (факультет почвоведения, 1985). Пусть a - больший из корней уравнения
,т2 + (Заб + За — 2)х + 5ab + 5а — 17 = 0.
Найти наибольшее значение хо при a 1, b 0.
Задача 8 (факультет ВМиК, 1983). Для каждого значения параметра а найти все значения х, удовлетворяющие уравнению
(ж - 3)(z + 1) + 3(х - 3)а/-—- = (а - 1)(а + 2),
V х — 3
н найти все значения параметра а, при каждом из которых уравнение имеет только один корень.
Задача 9 (химический факультет, 1982). Найти все значения параметра с, при каждом из которых уравнение
[(ж — с — I)2 — 2] (ж — с — I)2 = с2 — 1
имеет больше положительных корней, чем отрицательных.
Задача 10 (факультет психологии, 1981). Найти все значения параметра а, при каждом из которых наибольшее значение квадратного трехчлена
—х2 + 2ах — (а2 — 2а + 3)
на отрезке 0 х 1 равно —2.
Задача 11 (экономический факультет, 1980). Найти все целые значения параметра к, при каждом из которых уравнение
5 — 4 sin2 х — 8 cos2 — = 3k
2
имеет решения. Найти все эти решения.
Задача 12 (биологический факультет, 1978). Найти все значения параметра а, при каждом из которых уравнение
х|х -|~ 2а| -f- 1 — а — О
имеет единственное решение.
93
Задача 13 (геологический факультет, 1977). Найти все значения параметра к, при каждом из которых существует хотя бы одно общее решение у неравенств х2 + 4kx 4-ЗА?2 > 1 + 2к и х2 + 2кх Зк2 — 8к + 4.
Задача 14 (географический факультет, 1978). Найти все значения параметра а, для каждого из которых существует только одно значение х, удовлетворяющее системе уравнений
Г |з?2 — + 4| — 9з?2 — Ьх + 4 + 10ж|ж| = О
t з?2 — 2(а — 1)з? + a(a — 2) = О.
Задача 15 (экономический факультет, 1977). Найти все значения параметра а, при каждом из которых уравнение log2 (41 — а) = х имеет два решения.
Задача 16 (географический факультет, 1993). При каких значениях параметра а четыре корня уравнения
х4 + (a — 5)а?2 + (а 4- 2)2 = О являются последовательными членами арифметической прогрессии?
Задача 17 (геологический факультет, 1988). Найти все действительные значения параметра а, при каждом из которых область значений функции a — cos х у — -------------------------------------
2a + sin2 х — 1 содержит отрезок [1/5; 1/3].
Задача 18 (факультет психологии, 1993). Уравнение
(а — 1)х2 — (а + 1)я 4- 2а — 1 = О
имеет действительные корни х^, х^.
1. Найти все значения параметра а, при которых оба корня меньше единицы.
2. При a 1 найти все значения параметра Ь, чтобы выражение (xi — Ь)(х2 — Ь) не зависело от параметра а.
Задача 19 (механико-математический факультет, ИН). Найти все значения а, при каждом из которых уравнение \/а — у/а 4- х = х имеет решения, и найти эти решения.
Задача 20 (механико-математический факультет, ИН). Решить ( х3 4- 2х2 + 2х = у
систему уравнений < у3 4- 2,у2 4-2?/ = z
z3 4- 2z2 4- 2г = х.
94
3.5. УКАЗАНИЯ И ОТВЕТЫ
I. а£ (5;7).
2. а = —3, S = 18;
3. При т = 0 х = 0; при т G [3; оо) оба корня положительны.
4. {3/2} U {5/3} U [2; 4).
5. Ъ £ (—оо; — 1] U [4; оо).
(>. х = 21og2 (—а) при а < 0; х 6 0 при а = 0;
xi = log2 а, Х2 = 2 log2 а при а > 0.
7. 3.
8. 1 - У(а - I)2 + 4, 1 + У(а + 2)2 + 4 при а G (-оо; -2);
1 - У(а - I)2 + 4, 1 - У(а + 2)2 + 4 при a G [-2; -1/2) U (-1/2; 1];
—3/2 при а — —1/2 (единственный корень);
1 + д/(а - I)2 + 4, 1 - У(а + 2)2 + 4 при а G (1; оо).
9. с £ [0; оо).
10. 1/2; 2 + х/2.
11. 2тгп, 7г/2 + тгт, п, т 6 Z при к = —1;
12. a G
±2тг/3 + 2тг/, I G Z при к = 0;
1 - %/7
± arccos —------h 2тгр, р G Z при к = 1.
Ъ- 1\ ч
——I U(l;oo).
13. к Е (-оо; 1/2) U (3/2; оо).
14. а е {—1} U (1; 3) U (4; 6].
15. а £ (-1/4; 0).
16. -5; -5/13.
17. а£ [—2; 0) U (0; 4/3).
2) 1/2-
19. При а = 0 х = 0; при а 0
20. (0; 0; 0), (—1; —1; —1).
-1 + У4а -3
95
ГЛАВА 4
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
4.1. КРАТКАЯ ТЕОРИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
— Образование мы получили самое хорошее, — продолжал Черепаха Квази. — И немудрено — ведь мы ходили в школу каждый день...
Л.Кэрролл. Алиса в стране чудес
Результаты исследования вопроса о существовании и числе решений системы линейных уравнений приведем на примере линейной системы двух уравнений с двумя неизвестными
оцх + а^У =
021Х + «222/ = &2,
(1)
где 011,012,021,«22, ^1,^2 “ численные коэффициенты, причем
ан "Ь a2i 7^ 0 и а12 + а22 ф 0.
Основными методами решения системы (1) являются метод последовательного исключения неизвестных (метод Гаусса), метод подстановки и метод определителей.
Метод Гаусса. Предположим, что численные коэффициенты при неизвестных величинах х и у в системе (1) отличны от нуля. Умножая первое уравнение на «21, а второе на йц, получаем равносильную систему
ацй21Ж + 012(3212/ — «21 ^*1 ац(121£ + а11а22У — а\\^2
(211(221^ + <212(2212/ — «21 &1 (<211(222 — (221 а12)2/ — <211^2 — а21^1-
(2)
7 Методы реш, задач
97
Если обозначить А = (дцД22 — <з-21<з-1з) и Ау = (ац&2 — ^2161), то при А ф 0 из второго уравнения системы (2) находим
<21162 ~ <22161 Ау у — -------------------— —~-
<211<322 — <121^12 А
Подставляя это значение у в первое уравнение системы (2), получаем
Д22^1 — <3-12^2 Ах
аца22 - а21а12 А
где введено обозначение Ах = (22261 — <21262-
Если А = 0, а Ау 0, то второе уравнение системы (2), а следовательно и исходная система (1), решений не имеет.
Если А — Ау = 0, то второе уравнение системы (2) справедливо для любого значения у* 6 R. Тогда и система (1) имеет бесконечно много решений вида
61 — Д12У* D
2? =-----------, у = у* £ R
аи
(при ап ф 0).
Метод подстановки продемонстрируем ниже на конкретном примере, а основное внимание уделим методу определителей, который в настоящее время, к большому сожалению, не входит в обязательную школьную программу.
Метод определителей. Введем сначала понятие матрицы для системы (1): прямоугольные таблицы
А =
<211
<221
<3-12
0-22
<2ц <212 61
021 022 62
(4)
И
составленные из числовых коэффициентов системы (1), называют соответственно основной и расширенной матрицами системы (1).
Коэффициенты aij матрицы А называются ее элементами, первый индекс г указывает на номер строки, в которой находится элемент матрицы, а второй индекс - j - на номер столбца. Если число строк и число столбцов совпадают, то такая матрица называется квадратной. Для квадратной матрицы М = (тгу) существует понятие определителя (или детерминанта), который обозначается одним из следующих способов:
detM = |7И | = \rriij |.
Для основной матрицы А = (aij) системы (1) определителем называется выражение
detA — | А| =
<3ц <212
<121 а22
= <211^22 — <3-21*312 =
98
которое равно разности произведения элементов главной диагонали и произведения элементов второй диагонали.
Тогда в соответствии с формулами (3)
д
у
bi
«12
«22
— Ь1«22 — ^2«12j
«п
«21
&1
Ъ2
— &2«11 — &1«21,
^2
где определители Дд. и Ду являются определителями квадратных матриц, получаемых из расширенной матрицы А системы (см. (4)) путем замены коэффициентов при неизвестной соответственно х или у на столбец свободных членов.
Исключив методом Гаусса из второго уравнения системы (1) неизвестную х, мы получили эквивалентную систему (2), где второе уравнение можно (с учетом введенных обозначений) записать в виде Д • у = Ду.
Аналогичными преобразованиями можно было бы из первого уравнения исключить неизвестную у и получить Д • х = Дж (проделайте это самостоятельно!).
Тогда при ненулевых коэффициентах «ц, «21; «12> «22 можно показать, что
f апх + а12у = Ьг (Д-х = Дх
< <=> < (5)
( «21 х + а22у = Ь2 I Д • у ~ Ау.
Заметим, что при произвольных коэффициентах ci{j система (5) является следствием системы (1). Однако все изложенные ниже выводы, основанные на эквивалентности этих систем в случае aij ф 0, остаются в силе (попытайтесь это доказать самостоятельно!).
Таким образом, метод определителей и установленная эквивалентность систем (1) и (5) позволяют сформулировать условия совместности исходной системы (1) через ее коэффициенты и свободные члены.
Для системы (5), а следовательно и для системы (1), возможны следующие случаи.
1) Д ф 0, тогда система (1) имеет единственное решение, которое определяется формулами Крамера
х =
а= д-
Если коэффициенты ф 0, то
д/0 2110 2И
(6)
7*
99
2) A = Ax = Ay = 0, тогда система (1) имеет бесконечно много решений, а связь между неизвестными х и у задается одним из уравнений системы (1). При aij 0,b2 ф 0
А = Дх = Ау = 0
Д11 _ Д12 _
а21 а22 i>2
т
3) А = 0, но хотя бы один из определителей Аг или Ау не равен нулю, тогда система (1) несовместна, т.е. не имеет решений. При 0, Ь2 ф 0
А = 0, Ах ± 0 (А = 0,Ау^0)
Д11 _ Д12
Д'21 Д‘22 Ъ2
(8)
Заметим, что при несоблюдении требований + а21 ф 0 или а12 + а22 7^ 0 из условия А = Ах = Ау = 0 не следует, что система (1) имеет бесконечно много решений (постройте пример самостоятельно).
Все три разобранных случая поведения системы двух линейных уравнений с двумя неизвестными имеют простую геометрическую интерпретацию. Действительно, каждое из уравнений системы (1) задает линейное соотношение между переменными х и у, которое в прямоугольной системе координат на плоскости XOY определяет некоторую прямую. Пусть первому уравнению системы (1) соответствует прямая li, а второму - прямая 12. Тогда при А 0 прямые /[ и 12 пересекаются в единственной точке L = Д Л 12 с координатами х = Д.х/А, у = Ау/А (см. рис. 1).
Рис. 2
При А = Ах — Ау = 0 прямые и 12 совпадают, т.е. Zj Л Z2 = Zj. = h (см. рис. 2), и система (1) имеет бесконечно много решений.
При А = 0 и Дг 0 (или Ау ф 0) прямые li и 12 параллельны, т.е. 11 Л 12 — 0 (см. рис. 3), и система (1) решений не имеет.
юо
Подчеркнем, что рис. 1---3 соответствуют соотношениям (6)-(8).
’Заметим, что с помощью метода определителей можно решать системы из п линейных уравнений с п неизвестными, хотя проще при п 3 для систем без параметров использовать метод Гаусса.
Рассмотрим для примера систему трех линейных уравнений с тремя переменными
' ацХ + 012?/ + G13Z = bl
< a2ix + а22у + а2з? = Ь2 (9)
k аз1Я + аз2У + a33z = b3)
которая имеет следующие
основную и расширенную матрицы:
/ Оц 012 013
А = 1 O21 022 023
\ O31 032 озз
Оц
021
«31
012
022
032
013
023
033
bl ^2 Ьз
1) Если определитель этой системы
Д — det/l — аца22а33 + 012023031 + 013032021 — — (013022031 + 012021033 + 011023032) / О,
то система (9) имеет единственное решение, определяемое формулами Крамера
Д X х= д’’ Д« Д.. z~ д ’ (10)
где
bl 012 013 оц bl 01з
Д.т = i>2 O22 O23 > A-у = 021 Ь2 023
Ьз 032 033 О31 Ь3 Озз
101
ап а12 by
«21 а22 Ь2
«31 <*32 Ьз
Правило вычисления определителя квадратной матрицы третьего порядка можно графически сформулировать следующим образом: трехчленные произведения элементов aij берутся со знаком плюс, если они “параллельны” главной диагонали (см. матрицу А и прямые линии, соединяющие ее элементы), и со знаком минус, если они “параллельны” второй диагонали.
Со знаком Со знаком
Каждое из уравнений системы (9) в координатном пространстве XYZ определяет плоскость 71,72 и 73 соответственно. Разобранный случай единственного решения системы (9), задаваемого формулами (10), соответствует ситуации, когда все три плоскости 71,72 и 73 различны, а линии пересечения li2 = 71 П 72, /13 = 71 С 7з имеют одну общую точку L — /12 А Сз (см. рис. 4).
Рис. 5
2) Если Д = 0, но хотя бы один из дополнительных определителей Да;, Ду или Дг 0, то система (12) несовместна. В этом случае возможна
102
ситуация, когда две плоскости пересекаются по прямой I, параллельной । ретьей плоскости (на рис. 5 - плоскости 73).
Рис. 6
3) Если Д = Д.г = Ду = Дг = 0, то система (9) может быть несовместной или иметь бесконечно много решений. Во втором случае возможны ситуации, когда все три плоскости пересекаются по одной прямой / = 71 П 72 П 7з (см. рис. 6) и когда все три плоскости совпадают.
Однако если все три плоскости параллельны друг другу (см. рис. 7), причем две из них могут и совпадать, система (9) несовместна, хотя все определители в этом случае равны нулю. Попытайтесь построить пример подобной системы самостоятельно.
В заключение заметим, что более строгая и подробная классификация множества решений системы (9) основана на понятии ранга матрицы, что существенно выходит за рамки школьной математики.
4.2. ЗАДАЧИ НА РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
— Времени у меня не было — подтвердил Грифон. — Зато я получил классическое образование... Мы с моим учителем, крабом-старичком, уходили на улицу и целый день играли в классики. Какой был учитель!
— Настоящий классик! — со вздохом сказал Квази.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (физический факультет, 1981). Найти все значения параметра Ь, при каждом из которых система уравнений
юз
r bx + у = 1
t 4х — 2у — Ь
имеет бесконечно много решений.
Решение. Система (1) имеет бесконечно много решений при Д = Дх = — Ду — 0. Так как
д = b 1 4 - 2 = -26- 4 = 0 6 - —2,
дх = 1 1 b - 2 = -2-6 = 0 С => 6=-2,
ду = b 1 4 b = 62 - 4 = 0 6 = ±2,
то Д = Дх = Ду : 0 при b = —2.
Ответ: —2.
Задача 2 (географический факультет и отделение почвоведения биолого-почвенного факультета, 1970). При каких значениях параметра а система уравнений
ax — 4у = а + 1
2х -|- (д Т 6)?/ — а Т 3
(1)
не имеет решений?
Решение. Система (1) не имеет решений, если Д = 0, но Д^ ф 0 или Ду 0. Найдем соответствующие определители:
а + 1 —4
д Т 3 а Т 6
Д
X
— д2 Т 11 а + 18 — 0 \ -z a\t2 — —9", —2;
Д
у
Д Д Т 1 о, п-1
q д+д — 2 — 0 <=> ait2 — —2; 1.
При а = — 2 Д = Да; = Ду = 0 и система (1) имеет бесконечно много решений. При а = — 4 Д = 0, но Дг 0 и Ду ф 0, следовательно система (1) не имеет решений.
Ответ: —4.
104
Задача 3 (биолого-почвенный факультет, отделение биологии, 1970). Числа а и b таковы, что система
( a2x — ay = 1 — а
1 Ьх + (3 — 2Ъ)у = 3 + а
(О
имеет единственное решение х = 1, у = 1. Найти числа а и Ь.
Решение. Система (1) имеет единственное решение, если 0. Тогда должно выполняться соотношение
Так как по условию х — у = 1 является решением системы (1), то должны выполняться следующие условия:
a2 — а = 1 — а
b -|- 3 — 26 — 3 Т а
а = 1 ( а = — 1
V S
ъ = -1 0 = 1.
Г а2 = 1
[ — Ь = а
Проверим условие (2) для каждой пары значений параметров а и Ь.
Пусть а = 1 и b = — 1, тогда Д = 4 0. Следовательно, эта пара
является решением задачи.
Пусть а = —1 и b = 1, тогда Д = 0 и система (1) не может иметь единственного решения.
Ответ: а = 1, Ъ = — 1.
Задача 4 (механико-математический факультет, ИП). Для всех значений параметра а решить систему
( ax + (а — 1)?; — 1
I tv )J
I (а + 1 )а? + (За - 5)у = а.
Решение. Решим эту задачу методом подстановки (читателю предлагается решить эту задачу с помощью определителей и сравнить объем вычислений и логические трудности в том и другом случае).
Пусть а. = 0, тогда система (1) примет вид .
-У = 1
х — бу = О
х = — 5
У = -1-
105
Если а 0, то из первого уравнения системы (1) можно выразить х через у.
х _ 1+ (1 - а)у а
Подставив это выражение во второе уравнение, получим
(2а2 — 5а + 1)г/= а2 — а — 1. (2)
5 ± -\/17
Если 2а2 — 5а + 1 = О <=> ах ,2 = --------, то уравнение (2) не вы-
m г , 5±У17
полняется, тогда и система (1) не имеет решении. Если cii 2 7= ---,
то
_ а2 — а — 1 _ —а2 + 4а — 5
V 2а2 — 5а + 1 ’ 2а2 — 5а + 1
Заметим, что при а = 0 из формул (3) можно получить уже найденное решение х = — 5, у = — 1.
Ответ: при а = (5 ± л/17)/4 решений нет;
/Ръ/л -а2 4-4а-5 а2 - а - 1
при а * (5 ± л/17)/4 * = 2а2 _ 5а + j • У = Г5а +Т
Задача 5 (факультет ВМиК, 1975). Решить систему уравнений ( ctg(2y - cos2 z) = 1
t бу — 15 cos2 x — Зтг/4 — 1.
Решение. Вспомнив решение простейшего тригонометрического уравнения ctg (р = а <=> <р = arcctg а+ nk, к £ Z, где Z - множество целых чисел, получим, что система (1) равносильна системе
2у — cos2 z = тг/4 + 7Г&, к € Z бу — 15 cos2 х — Зтг/4 — 1.
(2)
Система (2) является линейной системой относительно переменных у и t = cos2z. Необходимо определить, при каких целочисленных значениях параметра к эта система имеет решения, и найти эти решения. Здесь метод определителей применять нецелесообразно, легче разрешить эту систему относительно у и t = cos2 х с учетом соотношения 0 t 1. Тогда система (2) будет равносильна системе
2у — t = тг/4 + кк бу - 15/ = Зтг/4 - 1
О < t < 1, к ez
7Г 15тг k + 1
8 + 24
ЗтгАт + 1
12
О < t < 1, к £ Z.
У =
106
Разрешая неравенство 0 t =
Зтг А; + 1
——— 1 относительно к, получаем
Г -±<£<11
< Зтг "" "" Зтг => к = 0; 1.
[ kez
При к = 0 имеем
i + Зтг 2 I ГТ
W=-2^, * = cos x=-=>coSa! = ±y-,
х — ± arccos \l — + 7гп, п £ Z.
При к = 1 имеем
] + 18тг 2 1 + Зтг /1 + Зтг
у = ---------, t = COS X = => COS X — ± А /---------,
У 24 ’ 12 V 12
। /1 + Зтг
х = ± arccos у ——-----1- тгп, п g Z.
/а Л П~ г, 1 + Зтг\
Ответ: ±arccos а/— +тгп, ,
\ V 12 24 /
/ /1 + Зтг 1 + 18тгЛ
I ± arccos а / ——---h тгп, п £ Z; ——— I .
Задача 6 (философский факультет, отделение социологии, 1989).
Найти все пары значений (а;/3), при каждой из которых система уравнений
( (& + (3)х + 26г/ = 2
t 8>х + (а2 — а/? + 132)у = 4 имеет бесконечно много решений.
Решение. Система (1) имеет бесконечно много решений при А = Аг = = Ау = 0. Так как
а + /3 . 26
8 а2 — а/3 + /З2
= (а + /?)(а2 — а/3 + /?2) - 8 26 = 0
Л э п .9 =2(а2-а/? + /?2)-4-26 = 0
4 а2 -а/3+ /32 к }
Ду
= 4(а + /?) - 16 = 0,
107
то получаем
а + /3 = 4
а2 — aft + fl2 = 52 <=>
(а + /?)(а2 — а/? + /?2) = 208
/? = 4 — а ( /3 — 4 — а
а2 — 4а — 12 = 0 \ а = 2 ± 4
а = —2 f а = 6
V S
/? = 6 1/? = -2.
а + /3 = 4
а2 — а(3 + /?2 = 52
Следовательно, система (1) имеет бесконечно много решений при ai = — 2, Pi = 6 и a2 = 6, ft? = — 2.
Ответ: (—2; 6), (6;—2).
Задача 7 (ПО, биологический факультет, факультет психологии, 1992). Найти все значения параметров а и 6, при которых системы уравнений
f ax + 2у =26+1 f 2ж + ?/= a2 + 2
t1) и , о о (2)
t х + у = 3 t х + Зу = 3
равносильны.
Решение. Найдем определители обеих систем:
a 2
1 1
Ai
= a — 2 => Ai = 0 при a = 2,
Д-lr —
26 + 1
3
26+ 1 3
= 26 — 5 => Д^ = 0 при 6 =
5
2’
= За — 26 + 1 => = 0 при
а = 2
6 = 5/2.
Л u
т
2
1
Таким образом, система (1) при о, ф 2 имеет единственное решение, которое выражается формулами Крамера
Ala: 26 — 5 А1„ За — 26 — 1
~Д ~~п д п О
А.1 а — z А.1 а — z
Система (1) имеет бесконечно много решений при а = 2и 6 = 5/2, когда Д1 = Д1 х = Aiy = 0, и система (1) несовместна при a = 2 и 6 / 5/2.
108
Для системы (2) имеем
2
1
Дг
3 =5^0’
причем ^2у = 4 — а2 — 0 при а = ±2.
Так как основной определитель Д2 0, то система (2) имеет единственное решение
Д2.Т 3(й2 + 1) Д21/ 4 И2
Д2 5 Д2 5
Следовательно, необходимым условием эквивалентности систем (1) и (2) является равенство координат точек пересечения:
С — Х2 ( 3(а — 2)(а2 + 1) = 5(26 — 5)
I У1 — У2 I —(а — 2)(а2 — 4) = 5(3а — 26 — 1)
Г З(а3 - 2а2 + а - 2) = 106-25 t 3(а3 - 2а2 - 4а + 8) = 15 + 306 - 45а Г З(а3 - 2а2 + а - 2) = 106-25
I 3(а - 2) = 9а - 46 - 8
Г (а - 2)(а2 + 1) = 5(а - 2)
t 26 = За - 1
Г а = 2 Г а — —2
(6 = 5/2 V ( b = —7/2.
Но при а = 2, 6 = 5/2 систем'а (1) имеет бесконечно много решений, а система (2) - только одно, следовательно эта пара не является решением задачи. При а = —2, 6 = —7/2 обе системы имеют единственное решение и эти решения совпадают:
= Ж2 = 3, У1 = XJ2 = 0, т.е. при а = —2, 6 = —7/2 системы равносильны. Ответ: а = —2, 6 = —7/2.
109
Задача 8 (экономический факультет, 1978). Найти все значения параметра Ь, при каждом из которых система уравнений
Ъх + 2у = b + 2
26ж+(6 + 1)г/ = 26 + 4
(1)
имеет хотя бы одно решение.
Решение. Система (1) может иметь единственное решение, бесконечно много решений или не иметь решений вообще. Необходимо найти все значения параметра b за исключением тех, когда система (1) несовместна.
Найдем определители системы (1):
Да;
Ау
Ь 2 26 6+1
= 6(6-3),
6 + 2 2
2(6 + 2) 6 + 1
= (6 + 2)(6 - 3),
6 6 + 2
26 2(6 + 2)
- 0.
А =
При А ф 0 <=+ 6 ф 0 и 6 ф 3 система (1) имеет единственное решение.
При А — А^ — Ау = 0 система (1) имеет бесконечно много решений. Так как Ау = 0, то А = А^ = 0 одновременно при 6 = 3.
Таким образом, система (1) имеет хотя бы одно решение при всех 6, кроме 6 = 0. Действительно, при 6 = 0 А = 0, Ау = 0, но А^ / 0 и система (1) не имеет решений.
Ответ: 6^0.
Задача 9 (механико-математический факультет, ИП). Найти все пары значений (a',b), при каждой из которых система уравнений
ах + у = а ay + z = b
(1)
х + (а + 1)?/ + az = 6(6 — 1)
1) имеет единственное решение,
2) имеет бесконечно много решений,
3) не имеет решений.
110
Решение. Система (1) является линейной системой трех уравнений относительно трех неизвестных. Для ее исследования воспользуемся методом определителей для квадратных матриц третьего порядка:
А ——
О
1
а 1
О а
1 а+ 1
— а3 — 1 — а(а + 1) =
а
= (а + 1)(а2 — а + 1) — а(а + 1) = (а + 1)(а — I)2.
Поэтому А = 0 при а = ±1.
1
а
а -|- 1
Аг
Ау
Д.
а b b(b-V)
а а
О b
1 6(6-1)
О
1 = а3 + b(b — 1) — а(а + 1) — ab, а
— а2Ь + а — а6(6 — 1),
а 1 а
О а 6
1 а + 1 6(6 — 1)
= а26(6 — 1) + 6 — а2 — а6(а + 1).
Система (1) имеет единственное решение при А 0 <=> а ±1 и любом 6. При А = 0 дополнительные определители будут равны:
а = — 1 : Аг = Ау = Аг = 6—1 = 0 при 6 = ±1,
<7=1: Ад. = — Ау = Аг = 62 — 26 — 1 = 0 при 6 = 1 ± \/2.
Система (1) не имеет решений
при а = -1, 6 ф ±1, когда А = 0, А^ = Ау = Аг = 62 — 1 ± 0,
при а = 1, 6 ф 1 ± \/2, когда А = 0, Аг = —Ау = А2 = 62 — 26 — 1 0.
Необходимым условием существования бесконечного множества решений системы (1) является равенство нулю всех определителей:
Проверьте самостоятельно, что это условие будет и достаточным.
Ответ: 1) единственное решение при любом 6 и а ф ±1;
2) бесконечно много решений при а = — 1, 6 = ±1 и а = 1,
6 = 1 ± ч/2;
3) не имеет решений при а — — 1, 6/±1иа = 1, b 1 ± \/2.
ill
4.3. СМЕШАННЫЕ ЗАДАЧИ НА ЛИНЕЙНЫЕ СИСТЕМЫ И КВАДРАТНЫЙ ТРЕХЧЛЕН
— А долго у пас шли занятия? — спросила Алиса, торопясь перевести разговор.
— Это зависело от нас, — отвечал Черепаха Квази. — Как все займем, так и кончим.
— Займете? — удивилась Алиса.
Л.Кэрролл. Алиса в стране чудес
Задача 10 (механико-математический факультет, 1986). Найти все значения а, при каждом из которых для любого значения b система.
‘2Ьх + у = a
(1 — b)x + by = z2 + z
(1)
имеет хотя бы одно решение (х, у, z).
Решение. Заметим, что система (1) состоит из двух уравнений, но содержит три неизвестных, т.е. в общем случае является недоопределенной; если неизвестное z рассматривать в качестве дополнительного параметра,™ система (1) является линейно!! относительно неизвестных х и у. Найдем ее основной определитель:
А =
26 1-6
= 262 + 6 — 1.
Тогда при А ф 0 <=> 6 ф —1 и 6 ф 1/2 система (1) относительно переменных х и у имеет единственное решение для любого значения переменного z и параметра а.
При 6 = — 1 А = 0 и система (1) будет иметь бесконечно много решений, если (см. формулу (7) из пункта 4.1)
Z -|- Z -|- CL — 0.
(2)
Квадратное уравнение (2) имеет решения относительно переменной z, если его дискриминант
А = 1 - 4а О
1
4
a <
112
Аналогичным образом при b = 1/2 условие совместности системы (1)
имеет вид 1 а о а ,. ч = — <=> z2 + z = 0. (4) 1/2 z2 + z 2 V J
Уравнение (4) имеет корни при
1 D% — 1 + 2а + 0 <++> а . (5)
Тогда система (1) совместна для любого значения Ь, в том числе и для I) = — I V 6=1/2 <=> Д = 0, если только параметр а одновременно удовлетворяет требованиям (3) и (5), т.е. при —1/2 <С а <С 1/4.
Ответ: a. G [—1/2; 1/4].
Задача 11 (химический факультет, 1988). Найти все значения параметра а, при которых равносильны системы уравнений
х + 2у = 2 — a
— х У ay — a — 2а2
(1)
х2 — у4 — 4т + 3 = О
2х2 + у2 + (а2 + 2а — 11)т + 12 — 6а = 0.
Решение. ('истема (1) равносильна системе
Дг
Д • X = Дд;
Д • у = Ду,
где Д =
(3)
2- а 2 а — 2а2 а
= За2, Ду
1 2 —а
— 1 а — 2а2
= 2(1 - а2).
— а Т 2,
Пусть Д / 0 <=> а ф — 2, тогда системы (3) и (1) имеют единственное решение:
За2 2(1 — а2)
х =------, у = -----------
а + 2’ У а + 2
Если Д = 0 <=> а = —2, то Д^ = 12 / 0, Ду = — 6 / 0, следовательно система (1) не имеет решений.
При а = —2 система (2) будет эквивалентна системе
у4 = х2 — 4х + 3
у2 = —2х2 + 11т — 24.
(5)
8 Методы реш. задач
113
Но квадратный трехчлен —2ж2 + 11ж — 24 < О для любого х, поэтому система (5) решений не имеет. Тогда по определению системы (1) и (2) при а = —2 равносильны.
Рассмотрим случай а ф —2. Так как при а — 2 система (1) имеет единственное решение, то и система (2) должна иметь единственное решение. Пусть (я?о; !/о) ~ некоторое решение системы (2), тогда (жо;— уо) тоже является ее решением (в силу четности по у входящих в систему (2) функций). Поэтому для единственности решения системы (2) необходимо, чтобы соблюдалось условие уо = —уо = 0. В силу требования равносильности систем (1) и (2) необходимо, чтобы решение (4) системы (1) тоже давало у — 0, т.е.
2(1-а2) п
у = < = 0
J а + 2
а = ±1.
Проверим эти значения параметра а на достаточность.
Если а = 1, то А = 3 и система (1) имеет единственное решение ж = 1, у = 0.
При а = 1 система (2) равносильна системе
у4 — х2 — 4ж + 3 — (ж — 1)(ж — 3) у2 = — 2(т2 — 4ж + 3) = —2(т — 1)(ж — 3),
т.е. имеет два решения: х = 1, у = 0 и х = 3, у = 0. Поэтому при а = 1 системы (1) и (2) неравносильны.
Если а = -1, то А = 1 и система (1) имеет единственное решение х = 3, у — 0, а система (2) равносильна системе
у4 = х2 — 4ж + 3 — (ж — 1)(т — 3) у2 = —2(ж2 — 6х + 9) = —2(х — З)2,
т.е. имеет единственное решение х = 3, у = 0.
Поэтому при а = — 1 системы (1) и (2) будут равносильны.
Ответ: —2; —1.
Задача 12 (факультет ВМиК, 1993). Точка М(х,у), декартовы координаты которой удовлетворяют условиям а2х — у = 2а2 — 2Ь, х — by = 2 — 2а2, лежит на прямой у = 2 — х. При каких а и b эта точка наиболее близко расположена к точке N (3; —1)?
Решение. Так как по условию точка М лежит на прямой у = 2 — х, то искомое расстояние равно
\MN\ = у/(х -ЗУ + (y+ iy = У2(г - З)2 = л/2|я - 3|.
114
Поэтому задача состоит в определении параметров а и 6, для которых функция /(ж(а, 6)) = \/21х — 3| достигает своего минимума при соблюдении условий
(1)
а2х — у = 2а2 — 26 х — by = 2 — 2а2 х + у = 2.
Наиболее короткий путь заключается в непосредственном решении системы (1), которую можно представить в виде
( ж(1 + а2) = 2(а2 — 6+1) я(1 + 6) = 2(1 - а2 +6)
[ у = 2 - х
6 / — 1, у = 2 — х
_ 2(а2 — 6+1) ( 6 = —1, у — 2 — х
1 + «2 V 2(а2 + 2) 2
_ _ 2(1 - а2 + 6) I 1+а2
6^—1, у = 2 — х
2(а2 - 6+ 1)
х —-----;---5---
1 + а2
(1 + 6)(а2 - 6 + 1) = (1 + а2)(1 - а2 + 6)
Г а = 0, b = -1 V <
I х - 4, у -- —2.
При b ф — 1 из первой системы получаем уравнение, связывающее параметры а и Ь:
b2 + b = а2(а2 + 1). (2)
Рассматривая уравнение (2) как квадратное относительно параметра Ь, получаем
<=> 61 = а2 V 6г = —(1 + а2).
При 6 = а2 0 для первой координаты точки М получаем х = 2/(1 +а2),
тогда
/(z) = л/2
+ а2
2а2
1+а2
2
2
1 +
Очевидно, что min/(z) = у2 при а = 6 = 0 и достигается он в двух точках: (4;—2) и М2 (2;0).
8*
115
При b = —(1 + а2) ф —1 => а ф 0 получаем х = 4, у = —2, т.е. точку Mi (4;—2), являющуюся к тому же еще и решением второй системы при а = О, b = — 1! Поэтому эти два случая можно объединить в один, который реализуется при b = — (1 + а2) и любом а Е R-
Ответ: а = b = 0; b = — (1 + а2), а Е R.
Замечание. Читатель, знакомый с основами информатики и программирования, может увидеть, что нахождение min/(ж) при ограничениях (1) является частным случаем задачи параметрического линейного программирования, которая в случае двух переменных х и у допускает сравнительно простое графоаналитическое решение. Такое решение и подробный анализ основаны на изложенном выше методе определителей для подсистемы из первых двух уравнений системы (1) и дальнейшем учете последнего уравнения.
4.4. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
— Занятия почему так называются? — пояснил Грифон. — Потому что на занятиях мы у нашего учителя ум занимаем... А как все займем и ничего ему не оставим, тут же и кончим. В таких случаях говорят: “Ему ума не занимать”.
Л.Кэрролл. Алиса в стране иудее
Задача! (факультет ВМиК, 1975). Решить системы уравнений:
cos (2ж + 6 sin2 у) = 1 З.г — 3 sin2 у = —10; tg(3?/ — 5 cos2 х) = 1 Ъу — 10 cos2 х = — 1;
sin (2х + sin2 у) = 0 х — 3 sin2 у = —2.
Задача 2 (УФ МГУ, 1994). При каких значениях параметра b не существует арифметической прогрессии щ, а-z, аз, сц, для которой выполнены условия
(6 + 2)ai — 2аз — b + 1, —ba% -|- (b -|- 4)й4 — 2b -I- б.
116
Задача 3 (биолого-почвенный факультет, отделение биологии, 1970). При каких значениях а система
( а2х + (2 — а)у — 4 + а3
1 ах + (2а — = а5 — 2
не имеет решений?
Задача 4 (биологический факультет, 1970). При каких значениях параметров а и b система
{a2x — by = а2 — b
Ъх — Ь2у = 2 + 46
имеет бесконечно много решений?
Задача 5 (биолого-почвенный факультет, отделение биологии, 1970). Числа a, b и с таковы, что система
{ax — by = 2а — b
(с + 1)т + су = 10 — а + 36
имеет бесконечно много решений, причем х = 1, у = 3 - одно из этих решений. Найти числа a, b и с.
Задача 6 (экономический факультет, 1978). Найти все значения параметра а. при каждом из которых система уравнений
( 2т + (9а2 — 2)у = 6а — 2
I х + у = 1
не имеет ни одного решения.
Задача 7 (философский факультет, отделение социологии, 1989). Найти все пары значений (а;/?), при каждой из которых система
( 8т + (а2 + а(3 + /?2)у = 4
( (а — /?)т + 26у = 2
имеет бесконечно много решений.
Задача 8 (механико-математический факультет, 1986). Найти все значения а, при каждом из которых для любого значения 6 система
f 6т — у - az2 = 0 f т — by + аг2 = 0
а) < Ь) s
I (6 — 6)т + 2by — 4z = 4; ( 26т + (6 — 6)у — 8z = 8
имеет хотя бы одно решение (т; у, z).
117
Задача 9 (механико-математический факультет, ИП). Определить, при каких значениях параметра, а для любого значения Ъ найдется такое значение параметра с, что система
{Ьх — у = ас2
(b — 6)z + 2by = 1 + с имеет хотя бы одно решение.
Задача 10 (химический факультет, 1988). Найти все значения параметра а, при которых равносильны системы уравнений
( ах + Зу — 6а — 4 [ х2 — 2т/4 — бх 4- 8 = О
< и <
х 4- у — 2а х2 4- у2 — (2а 4~ 4^х 4~ 2(а2 4~ а 4~ 2) — 0.
Задача 11 (ПО, биологический факультет, факультет психологии, 1992). Найти все значения параметра а, при каждом из которых системы уравнений
{ах + у = a [ ах 4- у = |а|
, и 1 ?
х 4- ау = 1 х 4- ау = а
будут равносильны.
Задача 12 (ПО, географический факультет, факультет почвоведения, 1992). Определить все тройки значений параметров а, Ъ и с, при которых уравнение ax + Ъу = с имеет решение х = 4, у = 1, а система уравнений
( ax + by = с [ 5х 4- 7у = 15 решений не имеет.
Задача 13 (механико-математический факультет, ИП). Найти все пары значений (a;b), при каждой из которых система
{ах 4- у = а ay + z — b х + az = b(b — 1) имеет хотя бы одно решение.
Задача 14 (механико-математический факультет, ИП). Найти все пары значений а-, Ь, при каждой из которых система уравнений
{х + у+ z = О
2х 4- Зу + z = 1 х 4- 2у 4- az — b 1) имеет единственное решение;
2) имеет бесконечно много решений.
Найти эти решения.
118
Задача 15 (факультет ВМиК, 19УЗ). Точка М(х,у), декартовы координаты которой удовлетворяют условиям
а2х + у = 26 — а2, х + 2by — а2 — 1,
лежит на прямой у — х + 1. При каких а и Ь эта точка наиболее близко расположена к точке N (—3/2; —1/2)?
4.5. УКАЗАНИЯ И ОТВЕТЫ
х = —5/2, у = ± arcsin уб/6 + тгп, п G Z; тг+10 , . /10-Зтг
х —--------—, у = ± arcsin у ——------h тгп, n G Z.
х = ± arccos \/1/5 + тгп, n £ Z, у — 1/3 + тг/24;
х = ± arccos
+ тгп, п £ Z, у = 1/3 + Зтг/4.
с) х = — 2/7, у = ± arcsin 2/л/7 + тгп, п G Я;
2 + Зтг /4 - Зтг
х =---------—, у = ± arcsin у —------------(- тгп, п G Z.
2. 6 = -4. V
3. a = 1.
4. (-1; 1), (1;-1), (-1;-2), (1;-2).
5. a = b : 0, с — 9/4 и a = 2, 6 = —1, с - 1.
6. a = -2/3.
7. а=6, /3 = 2 и а = —2, = —6.
8. a) a 6 [-1/4; 1/3];
6) а G [—1/2; 2/3].
9. a 6 [-1/16; 1/12].
Указание: если А = 262 + b — 6 / 0, то система имеет единственное решение, если А = 0 <=> b = Ъ/2 или Ь — —2, то для существования решений системы необходимо выполнение условий (8) из п. 4.1, которые при этих значениях Ь дают два квадратных уравнения относительно параметра с. Условие неотрицательности их дискриминантов позволяет получить ответ.
10. a = 2 и a = 3.
11. a = 1.
12. a = г, b = Чт/Ь) с = 27т/Ь, 0 / г £ R.
13. a / —1, b - любое и a = —1, b = ±1.
14. 1) При b € R, а / 0 х = (2(1 —6) —а)/а, у = (a + b— 1)/а, z = (6—1)/а; 2) при а = 0, 6 = 1 х = —(1 + 2г), у = 1 + г, z — г, г £ R.
15. а = 6 = 0; 6 = —(1 + а2)/2, a 6 R.
119
ГЛАВА 5
ЭКСТРЕМУМЫ
5.1. РАЗНЫЕ ЗАДАЧИ НА МИНИМУМ И МАКСИМУМ
— Боюсь, что не сумею вам все эго объяснить, — учтиво промолвила Алиса. — Я и сама ничего не понимаю. Столько превращений... хоть кого собьет с толку.
Л.Кэрролл. Алиса в стране чудес
Достаточно широкий и чрезвычайно важный класс задач составляют так называемые задачи на экстремумы, в которых надо найти максимум или минимум некоторой функции одной или нескольких переменных. Экстремальные задачи очень разнообразны по содержанию, форме и методам решения. Большое количество задач на решение уравнений или неравенств с параметрами сводится к экстремальным задачам, если удается доказать, что min/i тахД, где Д и Д - выражения, стоящие в разных частях уравнения или неравенства.
Ниже будут рассмотрены задачи на минимум и максимум только для функций нескольких переменных, включая параметры, что существенно усложняет решение. Однако можно отметить некоторые элементарные приемы (без использования понятия производной) частного и общего характера, позволяющие решать задачи на минимум и максимум. Это анализ ОДЗ и ОИФ, в частности, ограниченности тригонометрических функций у — sin х и у = cos ж, использование монотонности и периодичности, экстремальных значений квадратного и биквадратного трехчленов, следующих свойств модуля чисел:
IH - Ml |я + г/| < И + М, Ikl- Ml k-j/l kl + М,
|z + г/| = |ж| + |г/| <=> ху О,
|z + s/| = Ikl- Ml <=> ХУ “ У\ = И + М
(1)
ху < О,
121
а также неравенства между средним арифметическим и средним геометрическим п неотрицательных чисел:
ai + аг + . .. + ап ---------------------
у ' ^2 * • • j
(2)
где знак равенства возможен лишь при условии
Gt 1 — Gt2 — • • • — G>fi •
Неравенство (2), которое можно доказать методом математической индукции, и условие обращения его в равенство будем далее называть теоремой о средних, из которой можно получить два важных следствия:
1) произведение п положительных чисел с постоянной суммой достигает максимума, когда все эти числа равны между собой;
2) сумма п положительных чисел с постоянным произведением достигает минимума, когда все эти числа равны между собой.
Рассмотрим конкретные примеры на применение этих приемов.
Задача 1 (механико-математический факультет, устный экзамен). Доказать, что если a,b,c - длины сторон произвольного треугольника, а S - его площадь, то
. „ ab + ас + Ьс
а) S<--------------;
а2 + Ь2 + с2
Решение. 1. Обозначим углы треугольника, противолежащие сторонам a, b и с, через a, /3 и у соответственно. Тогда
1 1 1
3S = -absiny + -ас sin + -Lesina
< - (ab + be + ac) ==>
ab + ac + be О
6
так как в треугольнике лишь один угол может быть прямым, а синусы двух других углов строго меньше единицы.
2. По теореме о средних имеем
а2 + Ь2 а2 + с2
—2------- а^> —2------ аС’
Ь2 + с2
2
122
Тогда из предыдущего результата получаем
ab + ас + Ьс < 6
1 / а1 2 -Ь Ь2 а2 + с2 Ь2 + с2 \ а2 + Ь2 + с2
6 \ 2 + 2 + 2 J = 6
а2 + Ь2 + с2
Ь< 6
что и требовалось доказать.
Задача 2 (географический факультет, 1985). Найдите все числа Ь, удовлетворяющие условию — 1 b 1, для которых выражение
1 — 2\/4а?2 + 4Ьху 4- г/2 + 8г/ + 18
принимает наибольшее значение лишь при одной паре чисел (я; г/).
Решение. Введем обозначения
f(x, у) = 1 - 2у/д(х,у), д(х, у) = 4ж2 + 4Ьху + у2 + 8у + 18.
При 6 = ±1
д(х, г/) = (4а?2 ± 4ху+ у2) + 8г/ + 18 = (2х ± у)2 + 8г/ + 18, следовательно, максимум f(x) равен
max f(x, г/) = 1-2 min (2я ± г/)2 + 8г/ + 18 = 1
и достигается при А = 8г/ + 18 О, В = (2х ± г/) = ±л/—А не для единственной пары чисел (х;у).
При b Е (—1; 1) подкоренное выражение можно привести к виду
д(х, у) = 4х2 + 4Ьху + г/2 + 8г/ + 18 =
= (2х + б!/)2 + (1 - Ь2)у2 + Sy + 18 =
= (2х + б!/)2 + +(i8__^_).
Тогда f(x, у) = 1 - 2у/А + В2 + С2, где
1 — о2
В = 2а? + by
>--------- 4
123
При А < 0 maxf(x,y) = 1 — 2тт\Л4 + В2 + С2 = 1. Максимум достигается при условии В2 + С2 = —А, выполнение которого можно обеспечить различными способами, например:
В=О ГС=О
С = ’ ЬЦ В = ’
с)£ = С = ±^С|.
Заметим, что в каждом случае за счет знаков перед радикалами мы получим по крайней мере две различные пары чисел (х\у\.
При А > 0 <=> Ь2 1/9 -1/3 ^6^1/3
max f(x, у) = 1 — 2 min \/ А + В2 + С2 = 1 — 2\/А,
когда
26
X ~ T^b2
4
У ~ “ 1 - 62 ’
т.е. при единственной парс значений (ж; у).
Ответ: b 6 [—1/3; 1/3].
Задача 3 (геологический факультет, 1986). При всех значениях раметра р 9 найдите решения уравнения
па-
Т --- Sill X-------— га 5
3t\ . /2т . о 3т\
5.|.smlTs,n г + л1 +
9 / 5т
+ cos (14
т \ ( т . 2т \
— cos 2х = 6 tff — sm х --— р
7 J 6V15 5 J
(1)
на отрезке [0; 2 т].
Решение. Введем обозначения:
т a = — sm
15
5т t
p =---------cos 2x -
14 7
2т
Т
2т . 2
— sin X
7
Т Зт
— sm х-----= a — т,
15 5
Зт Т. „ ч Зт
+ —= -(1-c°s2x) + —= Д
Тогда уравнение (1) можно преобразовать к виду
sin2 (3 + Зл/Stg a sin (3 + 6tg 2 a = p + 1
<=> ^2V3tg a - sin (73tg a — sin /?) = p + 1. (2)
В = 0
С = 0
124
ТГ 7 тг
—; — , то в силу монотонности tga на 3 15
тг . 2тг
Так как а = — sin х + — € 15 5
7Г у—
[0; тг/2] имеем tga tg — = уЗ.
Аналогичным образом можно показать, что
ЗТГ ТГ 14’ 2
=> sin /5 G
. Зтг
Sln14;1
тогда
2у/3tg а — sin (3 2y/3tg ^-1 = 5, у/Зtg а - sin /5 у/З tg ^-1 = 2.
О
Следовательно, левая часть уравнения (2) нс меньше 10, а правая часть при р 9 не больше 10. Отсюда следует, что решение существует лишь при р = 9 и в случае выполнения системы
tg а = уЗ, sin/5 = 1
ТГ 7тг
— С Qi < —
3 15
Зтг Л^тг
14 2
7Г . 2тг 7Г
15 ЯП1 + Т = 3
5тг 2тг тг
---------cos 2ж = —
14 14 2
0 < х < 2тг
sin ж = — 1
cos 2х = — 1
0 х < 2тг
х - —7г/2 + 2тгп, п 6 Z 2х = тг + 2тг£, к G Z 0 х < 2тг
<=> х = Зтг/2.
Ответ: при р < 9 х G 0, при р — 9 х = Зтг/2.
Задача 4 (механико-математический факультет, устный экзамен). Найти наибольшее и наименьшее значения функции
f(x) = a sin2 х + b sin
+ c cos2 (% — x)
для любых значений параметров a, b и с.
Решение. По формулам приведения имеем
\ / Зтг \
J = cos ж, cos I — + X 1 — sin X, cos (тг — ж) = — cos ж.
125
Поэтому функцию /(ж) можно представить в виде /(а;) — a sin2 х 4- b sin х cos х + с cos2 х =
1 — cos 2х b . 14- cos 2х
= а--------------4- - • sin 2х 4- с----------
n 4” е 1 г/ \ _
= —-------F - [(с — a) cos 2х 4- b sin 2а;] =
_ а 4- с \Д2 + (с — а) (с — а) cos 2х 4- b sin 2х
2 2 /, 2 I ( \2
л/о 4- (с — а)
а 4- с \Д2 + (с“ а)2 / • .
= —-------1----------------(sin a cos 2a; 4- cos a sin 2a;)
а 4- с \/ь2 4- (с - а)2
<=> Л*) = -у- + “--------------j---— sin (2a; 4-а) (1)
или
а с \/Ь2 4- (с — а)2
Л*) = -у- + -----------j---------cos (2a? - /3), (2)
где вспомогательные аргументы а или (3 при необходимости можно определить из уравнений
sin а = cos /3 —
с — а
или
cos а- = sin /3 =
b
Из (1) и (2) видно, что
Г/ Ч 1 max fix) = - <
при
sin (2а; 4- а) = 1
(или cos (2х — /3) = 1),
• г/ ч 1 mm/(а;) = -
а
при
sin (2а; 4- а) = — 1
Ответ: max/(а;) — а 4- с 4-min/(a;) = i а 4- с -
(или cos (2а; — (3) = —1).
126
Задача 5 (факультет ВМиК, 1986). Найдите значения а и Ь, при которых наибольшее значение функции
9 5Г + - 2 3
4 ‘ 6х + 5~х + 2 + 2
5х - 1 о
—----- + 2а + b
(1)
на отрезке [— 1; 1] является наименьшим.
3 Решение. Обозначим p = a — b,q = 2a + b,z=--
9 52г - 2 • 5® + 1 52г - 2 • 5®
5® - 1
------, тогда
5Г + 1
+ 1
г2 =____________________ ____________
4 52х + 2 • 5Г + 1 52г + 2 • 5Г + 1
и = f(z) = z2 +pz + q ==> у(х) = |/(z)| .
3 5r — 1
Заметим, что при х G Г— 1; 11 областью значений функции z = - • ---
2 о37 + 1 тоже является отрезок [—1; 1]. Квадратный трехчлен f(z) = z2 + pz + q в точках z — 0, z — ±1 принимает значения /(0) = q, /(—1) = 1 — р + q, /(1) = 1 + р + ?•
Максимальное значение модуля
max |/(z)| = max < |1 ± р + q\;
р2 q-т
для любого z Е [—1; 1], следовательно, для всех z0,zi,Z2 6 [—1; 1]
max |/(z)| i [(|/(Z1)| + |/(20)|) + (I/(^)I + l/Oo)l)]
> | -Ж)1 + l/W -/Wil
> 5 [/(*1)-/(*<>) +/(*2)-/(*o)b
Если ВЗЯТЬ Zo = 0, Z1 = — 1 И Z2 = 1, TO
1 1 max|/(z)| > - [(1 - p) + (1 + p)] = -,
причем равенство достигается лишь при р = 0.
Таким образом, min (max |/(z)|) = 1/2 при р = 0, т.е. /(z) = z2 + q. Тогда min (max |/(z)|) = 1/2 при p = a—b — 0 достигается, когда q = 1/2. Легко проверить, что при q < —1/2 и q > —1/2 max|/(z)| > 1/2. В итоге получили систему для определения искомых значений параметров а и Ь:
р = а — Ъ = 0 q = 2а + b = —1/2
а = b = —1/6.
Ответ: а = Ъ = —1/6.
127
Задача 6 (факультет психологии, 1988). Найдите наибольшее значение величины Ь, при котором неравенство
/ b 2
- ж1 2 - 16) + --ъ~хЪ\ СО8 7Гж|
8ж — х1 — 16 3
(1)
имеет хотя бы одно решение.
Решение. ОДЗ неравенства (1) имеет вид
b 0, х 4.
Заметим, что при b = 0 неравенство (1) выполняется при любом х ф 4. При b > 0 неравенство (1) можно преобразовать к виду
(2)
Используя условие | со5 7гж| 1и второе следствие из теоремы о средних о минимальном значении суммы двух взаимно обратных чисел, из неравенства (2) получаем
2х/б^ \/р _ 4)2 _|_
1
Ь(х — 4)2
< - Ь I COS 7Гж| < - Ь.
3 1 1 3
Отсюда следует, что если неравенство (2) имеет решение, то
9
Q,y/b^ <; - ь о
При максимально возможном значении 6^1/9 неравенство (2) выполняется при
b(x — 4)2 = 1 х — 4 = ±3 <=> Xi = 1 V Х2 = 7.
Ответ: bmax = 1/9.
Задача 7 (биологический факультет, 1990). Найти все пятерки чисел a,b,x,y,z, для которых справедливы соотношения
1 + tg(bz) sin2 (ху) + cos (2ху) [cos х 4- sin (аг/)] • | sin 2жг/|
2 + 2x/tg(6z) • cos [Ь(у + z)] + cos [26(г/ + ж)] = 0.
128
Решение. Уравнение исходной системы заменой t = cos [Ь(ж + т/)] сводится к квадратному
2i2 + 2x/tg(6z) - i + 1 = 0. (2)
Для существования искомой пятерки чисел и решения уравнения (2) необходимо, чтобы его дискриминант удовлетворял условию
D = 4 [tg (fcz) — 2] 0 <=> tg (bz) 2.
Для левой части неравенства системы (1) имеем
1 + tg (6z) • sin2 (ху) + cos (2ху) = [tg (bz) — 2] • sin2 (xy) + 2^2,
а для правой
[cos х + sin (ау)] • | sin (2жт/)| 2.
Поэтому неравенство системы (1) равносильно системе
[tg (bz) — 2] • sin2 (ху) = 0
[cos х + sin (ат/)] • | sin (2ху) | = 2
(3)
cos х = 1
sin (аг/) = 1
| sin (2хт/)| = 1
tg(6z) = 2
COS Ж — 1
sin (ay) = 1 , 4
I /9 M 1 36
| sin (2xy) | = 1
k sin (xy) = 0.
Так как | sin (2ггт/)| = 2j sin(a?T/)| • | cos (я?т/)|, то последняя система несовместна, а исходная система (1) равносильна уравнению (2) и системе
9 Методы реш. задач
129
(За), откуда последовательно находим х, у, a, b,z-.
1)
2)
3)
4)
х — 2тгк, к £ Z;
7Г
sin 2ху = ±1 <=> 4тгку = — + тгп, п £ Z
<=> у = (1 + 2п)/8А:, 0 к G Z\
. , х . 1 + 2п 7г(1 + 4т7г)
sin (at/) = 1 <=> а - -----------
1 + 4m
<=> а — 4тг -----—к’.
1 4~ 2п
2 + 2л/2 cos [Ь(ж + г/)] 4- cos [2Ь(ж + у)] = О
<=> (л/2 • cos [6(ж + ?/)] + I)2 = О х/2 cos [b(x + т/)] = ——
Зтг
<=> b(x + t/) = ±— + 2тгр, р е Z , 8р±3 .
Ь 1СтгР+2п+Г
t.g (bz) = 2 <=> bz = arctg 2 + тгд, q £ Z 16тг&2 + 2n 4- 1 . .
2= 2rt(8P±3)' (arCtg2 + ’r’)’
cos х = 1
2
Ответ: x = 2тгк\
1 4- 2n
У = Sk
а = 4тг& •
b = 2тгк
1 + 4772
1 + 2п ’
8р ± 3
1 бтгАт2 4- 2п + 1 ’
16тгХс2 + 2п + 1 .
—————— • (arctg 2 + 7гд); 0 к, п, m, р, q G Z.
Z7r/u(op ± 3)
130
5.2. ИСПОЛЬЗОВАНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
Потом она сползла с гриба и скрылась в траве, бросив Алисе на прощанье: — Откусишь с одной стороны — подрастешь, с другой — уменьшишься!
Л.Кэрролл. Алиса в стране чудес
Многие задачи на минимум и максимум могут быть решены с помощью производной. Напомним основные факты, которые могут быть полезны при решении таких задач.
Теорема Ферма (необходимое условие локального экстремума). Если функция f(x) определена, на. интервале (а; Ь) и точка этого интервала является точкой локального экстремума (min или max), то производная этой функции f'(x) в точке Жц или равна нулю, или не существует.
Напомним, что точки, в которых производная равна нулю или не существует, называются критическими.
Используя связь между возрастанием-убыванием функции и знаком ее производной, можно сформулировать достаточное условие локального экстремума непрерывной функции в точке жо посредством таблицы:
Знак пре Ж < Жо шзводной ж > Жо Вывод Ж = Жо
+ + не явл. экстремумом
+ — локальный max
— + локальный min
— — не явл. экстремумом
При решении ряда задач могут быть полезны следующие теоремы.
Теорема Ролля. Если функция /(ж) непрерывна на отрезке [а; Ь], дифференцируема на интервале (щЬ) и f(a) = f(b), то существует по крайней мере одно значение с € (а; 6), такое, что f'(c) = 0.
Теорема Лагранжа. Если функция /(ж) непрерывна на отрезке [а; 6] и дифференцируема на интервале (а; 6), то существует по крайней мере
9*
131
одно значение с G (а; 6), такое, что
Задача 8 (факультет почвоведения, 1991). Для каждого отрицательного числа а найдите наименьшее значение функции
на промежутке 0 х <С 1.
Решение. Найдем критические точки данной функции из уравнения у'(х) = 0 (х — а)2 — (ж — а) = О
<==> (ж — a)(x — а — 1) = 0 <=> Xi = а V жг = а+1.
Анализ изменения знака производной показывает, что (см. рисунок) в точке Ж1 = а функция у(х) имеет максимум, а в точке ж2 = а + 1 -минимум.
При а < 0 возможны два случая взаимного расположения отрезка [0; 1] и критических точек Ж1 = а, ж2 = а 4- 1.
1. При — 1 а < 0 только точка ж2 = а 4-1 G [0; 1], в ней функция у(х) имеет минимум. Поэтому
min у(х) = 7/(ж2) О Z о
2. При а < — 1 обе критические точки лежат левее отрезка [0; 1] и функция у(х) возрастает при 0 ж 1. Поэтому
(_ 3 _ 2 \ /Л 1 \
CL CL \ / Q, 1 \
V + V = ~а Q + 9 •
о 2 / у о 2/
Ответ: при а <
при —1
, . о(а 1\
-1 mint/ = -az I - + - )
n 1
< а < 0 min у = —.
У 6
132
Задача 9 (механико-математический факультет, устный экзамен). Найти наибольший член последовательности
an = n1/n, n Е N. (1)
Решение. Рассмотрим непрерывный аналог формулы общего члена последовательности (1), а именно функцию /(х) = х1^ при х 1, и исследуем ее на минимум и максимум. Так как /(г) = e~®£, то при х > 1
имеем
г// \ 1П-£
f (х) = е t
1 \ х2 )
In X е х = —-у- (1 — In яг) х£
Следовательно,
/'(х) = О /'(х) > О /'(х) < о
при
при
при
х = е,
1 < х < е,
х > е.
Поэтому /(х) при х — е имеет максимум, при 1 < х < е возрастает, при х > е убывает. Так как 2 < е « 2.72... < 3, то достаточно сравнить между собой только два соседних члена аг = \/2 и аз = -у^З. Возведением в шестую степень легко доказывается, что -у^З > д/2 и, значит,
_ 3/9
maxan = аз = уЗ.
Ответ: аз = -у^З.
Замечание. Аналогичный переход к непрерывным переменным и более общим функциональным неравенствам часто бывает полезным при сравнении двух чисел и доказательстве неравенств, например:
е* > 7ге, (х/2)75 < (л/3)Л 19921"3 > 19931"2 и т. д.
Эти неравенства докажите самостоятельно.
Задача 10 (факультет ВМиК, 1977). Найти все значения параметра a (0 а тг/2), при каждом из которых наименьшее значение функции
f(x) = Зх4 + 4x3(cos a — sin a) — 3x2 sin 2a
на отрезке — sin a x cos a принимает наименьшее значение.
Решение. Найдем критические точки и интервалы возрастания-убывания дифференцируемой функции /(х).
f (х) — 12х3 + 12x2(cos a — sin a) — 6ж sin 2a, f'(x) = Q <=> £i = 0 V X2 = sina V хз = — cos a.
133
Обозначим f*(a) = min/(г) при х £ [— sin a; cos а]. Рассмотрим следующие случаи взаимного расположения критических точек Х1,%2,хз в зависимости от параметра а £ [0; тг/2].
а) а = 0 => х 1 = х2 = 0, хз = — 1 и отрезок [— sin a; cos а] совпадает с отрезком [0; 1]. В этом случае ни одна из критических точек не является внутренней точкой интервала (0; 1), но функция /(ж) непрерывна и f'(x) сохраняет знак при х £ (0; 1). Поэтому
ЛИ = Ulin {/(0); /(1)} = /(0) = 0. (la)
b) о = тг/2 => xi = з?з = 0. х= 1 и отрезок [— sin a; cos а] совпадает с отрезком [—1; 0]. Аналогичным образом можно показать, что при а = тг/2
АП = min Дх) = rnin{/(0); Д-1)} = ДО) = 0. (1Ь)
xG[-l;0]
с) 0 < а < 7г/4 => 0 < sin а < cos а => хз < Ху < х2 и Xi, Х'> £ (—sin а; cos а). Анализ распределения знаков производной /'(х) и промежутков возрастания-убывания функции /(ж) (нарисуйте соответствующую “картинку”) показывает, что
Д(а) = min/(x) = min {/(— sin a); /(sin а)} =
= f(— sin а) — 7 sin3 a(cos a — sin a) > 0,
(1c)
так как /(sin a) — /(— sin a) = 8 sin3 a(cos a — sin a) > 0 при a £ (0; тг/4).
(1) t/4 < о- < тг/2 => 0 < cosa < sina => X3 < Xi < X-2 и
•t‘i • <’з € (— sin a; cos о). Аналогичным образом можно показать, что
Л (a) = min {/(— cos a); /(cos a)} = /(cos a) = = 7 cos4 a — 10 sin a cos a,
(Id)
так как /(—cosa) — /(cosa) — —8cos3a(cosa — sina) > 0 при a £ (тг/4; тг/2).
e) a = тг/4 => —\/2/2 — хз < x^ = 0 < x2 — л/2/2, а отрезок [— sin a; cos a] совпадает с отрезком [—л/2/2; \/2/2] и Xi £ (—>/2/2; \/2/2). Следовательно, при a = тг/4
/ л/2 \ / л/2 \ / а/2 \
/Да) = min < / I —— I ; ДО); / I — I 7 = / ( ±у- i • (1е)
Из (1а)-(1е) заключаем, что /-(а) можно записать в виде
( 7 sin4 a — 10 sin3 a cos a
( 7 cos4 a — 10 sin a cos3 a
при a £ [0; тг/4];
при a £ [я-/4; тг/2].
(2)
134
По условию требуется найти min Л(Л) при a G [0; тг/2]. Однако из фор-(7Г \
— — a j при a G [0; тг/4]. Тогда достаточно найти
min A(°0 = min (7 sin4 а — 10 sin3 a cos а).
<*€ [О;тг/4] ае[0;тг/4]
На интервале а 6 (0; тг/4) имеем
Л (а) = 28 sin3 ct cos а — 30 sin2 ct cos2 ct + 10 sin4 а =
= | sin2 2a(5tg2a + 14tga — 15) = 0 <=>
r « -7 ±2^31
5tg2 ct + 14tg ct — 15 = 0 <=> tgcvi2=-----z----
' 5
x - 7 + 2л/31 ai = arctg------------1- 7гп, n G Z
-7-2^31 »2 = arctg------------1- 7гп, n G Z.
5
Однако a G (0; тг/4) <=> tga G (0; 1), следовательно, только от при п = 0 удовлетворяет этому условию, т.е.
0 2х/31- 7 / 7г\
aj = arctg--------G (0; -) .
Так как A(a) < 0 при ct G (0; а°), Л (а) > 0 при ct G (а°;тг/4) и
Л(<*) = Л - <*?)> то
min Л И = Л(<*?) = A - »1) о€[0;тг/2] \ 2 /
только при двух значениях параметра ft G (0; тг/2):
о 2а/ЗТ-7 % о 7г 2V31-7
ai = arctg------ ил= — — = — — arctg-------
2а/Л-7 7г х 2л/31-7
Ответ: arctg-------; — — arctg-----
5 2 5
Задача 11 (химический факультет, 1987). Стороны треугольника лежат на осях координат и на касательной к графику функции у = х2+2х+1
135
в точке, абсцисса а которой удовлетворяет условию — 1/2 а 0. Найдите значение а, при котором площадь треугольника будет наибольшей.
Решение. Общий вид уравнения касательной, проведенной к графику функции у = /(г) в точке с координатами xq = а, уо = выглядит следующим образом:
у - f(a) = f'(a)(x - а).
По условию задачи
/(ж) = х2 + 2х + 1 = (г + I)2, /(а) = (а + I)2, Г(д) = 2(Ж+1), Да) = 2(а+1).
Тогда уравнение касательной имеет вид
у = 2(а + 1)(д — а) + (а + I)2 = (2х + 1 — а)(а + 1),
а координаты точек А(д*;0) и В(0;у*) пересечения этой касательной с осями координат находятся из систем
( х - 0 ( у - (2ж + 1 — а)(а + 1)
1 у = (2х + 1 - а)(а +1) [ у = 0
I у* = 1 -а2 [ у = 0.
Полученный треугольник является прямоугольным, поэтому его площадь равна
5=^|ЛО||ОВ| = ||1-а2|Ц^ =
= l|(l-a2)(a-l)|=i(l-a2)(l-a)
S = т(°3 — °2 ~ a + 1)’
так как |1 — a2| = 1 — а2, |а — 1| = 1 — а при a G [—1/2; 0]. Найдем значение a G [—1/2; 0], при котором функция S(a) имеет максимум:
S'(a) = ^(3a2 — 2a — 1) = 0 <=> a = — V a " 1.
Учитывая, что только a = —1/3 E [—1/2; 0] и производная S'(о) при a = —1/3 меняет знак с плюса на минус, заключаем, что
шах S(a} = S [ — - | = 8.
ае[—1/2;0] \ 3/
Ответ: —1/3.
136
Задача 12 (экономический факультет, 1979). Найти все значения параметра a 1, при каждом из которых площадь фигуры, лежащей в полуплоскости х 0 и ограниченной прямыми у = 1, у = 2 и кривыми у — ах2, у = ах2/2, будет наибольшей. Найти эту площадь S.
Решение. При фиксированном значении параметра а 1 на рисунке изображена криволинейная трапеция ABCD, максимальную площадь которой и надо определить.
Координаты точек А, В, С и D определяются соответственно из решения систем
2 у = axz
2 у = ах£
{у — ах2/2 ( у = ах2/2
у = 2 V < у = 1 ж > О I х > О
Так как точки В и D имеют одинаковые абсциссы, то криволинейная
трапеция ABCD состоит из двух частей:
1) прямоугольного треугольника ABD с криволинейной гипотенузой
АВ, лежащего под кривой у = ах2 и над прямой у = 1 при х €
2) прямоугольного треугольника BCD с криволинейной гипотенузой CD, лежащего над кривой у = ах2/2 и под прямой у = 2 при
137
X-G
V a y/a
Используя геометрический смысл определенного интеграла, для площади трапеции ABCD получаем следующее выражение:
Легко заметить и без производной, что рассматриваемая функция
S(a.) = - { --2а/2 | при а 1 монотонно убывает. Поэтому
а \ 3 J
maxS(a) = S(l) = — 2л/2
а^1 3
достигается при наименьшем значении а — 1.
Ответ: a = 1, Smax = 10/3 — 2 >/2-
Задача 13 (геологический факультет, 1977). Найти все значения параметра a > 0. при каждом из которых площадь фигуры, ограниченной параболой
х'2 4- 2az 4- За2 у= —7-7-4— 4- л4
и прямой
a2 — ах
у = 1.4’ 1 + а4
будет наибольшей.
Решение. При фиксированном значении параметра a > 0 абсциссы точек пересечения кривых находятся из уравнения
х2 4- 2аж 4- За2 _ а2 — ах
1 4-а4 “ 1 4- а4
т2 4- Зах 4- 2а2 = 0 <=> zi = —2а V х? = —а.
Тогда ординаты точек пересечения будут иметь вид
3/1 =
За2
2а2
1 4-а4
138
Следовательно, полученная фигура представляет собой сегмент параболы, стянутый хордой, проходящей через точки А (—2а;За2/(1 + а4)) и В (—а; 2а'2/(1 + а4)) , и лежащий над параболой
х2 + 2ах + За2
У “ ---—4------
1 + а4
и под прямой
а2 — ах
У= 1 А'
1 + а4
при х G [—2а;— а].
Используя геометрический смысл определенного интеграла, для площади этого сегмента получаем выражение
5(a)
— а
// 2
/ а — ах
\ 1 + а4
-2а
х2 + 2ах + За2 \ .
---------;---- dx
1 + а4 J
— 2а
1 f X3 3 2 2
—т-------И -аг + 2а х
h а4 V 3 2
— а
_ q3
-2а = 6(1 +а4)’
Надо найти те значения a > 0, при которых функция 5(a) имеет максимум. Найдем критические точки этой функции:
, 1 За2(1 + а4) — 4а3 • а3 а2(3 — а4)
о (а) — ~ ’ о — — О
6 (1 + а4) (1+а4)
<=> ао = О V Qi = №>.
Учитывая, что только ai — >
О, и производная S' (a) > 0 при
О < a < ^3 (т.е. 5(a) возрастает), и 5'(а) < 0 при а > (т.е. 5(a)
убывает), а также то, что 5(a) непрерывна при а = л/З, получаем
шах 5(a) = 5 ("^з) ПРИ a = ^3-
Ответ: -^3
139
5.3. УСЛОВНЫЕ ЭКСТРЕМУМЫ И ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ
Вслух же она спросила:
— Скажите, пожалуйста, куда мне отсюда идти?
— А куда ты хочешь попасть? — ответил Кот.
— Мне все равно... — сказала Алиса.
— Тогда все равно, куда и идти, — заметил Кот.
Л.Кэрролл. Алиса в стране чудес
В последние годы на вступительных экзаменах в МГУ стали встречаться задачи на определение экстремума функции, зависящей от нескольких переменных величин, которые связаны между собой дополнительными соотношениями.
Например, требуется исследовать функцию z = f(x\y) на максимум или минимум, причем переменные х и у не являются независимыми, а связаны дополнительным условием вида д(х-,у) = 0. Экстремумы такого типа называются условными. При определении условных экстремумов одна из переменных на некотором этапе решения принимается за основную, а другая играет роль параметра.
Вообще говоря, функция z может зависеть от трех и более переменных величин, связанных не одним, а несколькими условиями, которые могут быть представлены и в виде системы неравенств. В высшей математике подобные задачи называются вариационными и решаются методами вариационного исчисления. Однако ряд задач можно решить с помощью разобранных выше элементарных приемов.
Задача 14 (экономический факультет, отделение планирования и экономической кибернетики, 1985). Среди всех решений (x\y,z\v) системы
х2 + у2 = 4 z2 4- V2 — 9 xv + yz 6
(1)
найдите такие, при которых выражение х + z принимает наибольшее значение.
Решение. Уравнение х2 + у2 = 4 задает на координатной плоскости (х-,у) окружность с центром в начале координат и радиусом R = 2. По-
140
этому можно ввести угол а, такой, что
х — 2 cos a, y = 2sina.
Аналогичным образом можно ввести угол (3, такой, что
z = 3 cos /3, v = 3 sin /3.
Тогда неравенство системы (1) можно переписать в виде
xv + yz = 6(cos a sin /? + sin a cos /?) = 6 sin (а + /?) ^ 6.
Откуда следует, что
sin (а + /?) = 1
а + (3 = + 2-7Г72, п € Z.
Тогда
/ 7Г \
x + z = 2 cos a + 3 cos (3 = 2 cos a + 3 cos — — a j — = 2 cos a + 3 sin a — /22 + 32 sin (a + у?) = /Тз sin (a + cp),
2
где дополнительный аргумент <р = arcsin Следовательно, v 13
13 max [sin (a + </>)] = /ТЗ
при
7Г
2
7Г . 2
— — arcsin ____:.
2 /13
Тогда
. / . ' 2
х = 2 cos а — 2 sm arcsin —=
\ /13
/ . 2
у = 2 sin а = 2 cos arcsin —-=
\ /13
4 /тг 6 /Тз’
n ( • 2
= 3 cos arcsin .____
\ /13
\ . ( . 2
v = 3 sin 0 = 3 sm — — a = 3 sin arcsin —= \2 J V /13,
/ 7Г z = 3 cos (3=3 cos
9 /ТГ 6 /Тз ’
141
Выше использовались формулы
sin arcsin а = a, cos arcsin а = v 1 — а2.
4 6 9 6
Ответ: х = .____, у = —=. z = —, v --
л/13 У13 Vl3 л/ТЗ
Замечание. Гораздо более короткое решение этой задачи можно получить, если использовать понятие скалярного произведения векторов, которое было включено в программу вступительных экзаменов в 1996 г.
Действительно, если первое уравнение системы рассматривать как выражение для квадрата длины первого вектора, а второе уравнение -для квадрата длины второго вектора, то левая часть последнего неравенства системы (будьте аккуратны!) в точности дает выражение для скалярного произведения этих векторов. Однако знак неравенства меняется с на что позволяет сделать вывод о коллинеарности этих векторов.
Остается найти условия, при которых достигается максимум выражения, представляющего собой сумму первой компоненты первого вектора и второй компоненты второго вектора.
Задача 15 (механико-математический факультет, 1989). Найдите наименьшее из значений х, для которых существуют числа у, z, удовлетворяющие уравнению
х2 + 2у2 + z2 + ху — xz — yz = 1. (1)
Решение. Рассмотрим соотношение (1) как квадратное уравнение относительно переменной z:
z2 - (х + y)z + х2 + 2у2 + ху - 1 = О,
где х и у играют роль параметров. Для существования решения этого уравнения необходимо и достаточно, чтобы его дискриминант удовлетворял условию
D\ = (х + у)2 — 4(х2 + 2г/2 + ху — 1) = 4 — Зт2 — 1у2 — 2ху О
<=> 7у2 + 2жу + Зя2 — 4^0.
Рассматривая полученное неравенство как квадратное относительно переменной у, где х - параметр, получим, что оно имеет решение тогда и только тогда, когда его дискриминант удовлетворяет условиям
7
D2 = 4 (28 - 20ж2) > 0 <=> х2 -
Л
142
Откуда следует, что min х =
Ответ:
Замечание. Попробуйте решить эту задачу, используя понятие скалярного произведения векторов.
Задача 16 (географический факультет, 1986). Для каждого значения а, удовлетворяющего условию 0 < а < 1, найдите наименьшее значение выражения
(х2 + Z/2) - а(ж - у)
при условии
sin (яху) = 0.
Решение. Наименьшее значение выражения
/(я; у) = | (я2 + у2) - а(х -у) = |(ж - у)2 - а(х - У) + ХУ =
1 1 п2
1 -/ \ 12 Gt 1 г/ \ 12 О-
= 2^ “ У) ~ aJ “ у + ХУ = “ У’ ~ + n ~ Т
при п 0 достигается при х — у=аип = 0и равно
• р/ ч а2 mm f(x; у) =
При п < 0 (т.е. когда х и у имеют разные знаки) и х — у > 0 по теореме о средних получим
так как 0 < a < 1, 0 > п 6 Z и
/(ж; г/) = (ж - у) f - а
143
Таким образом, при ху = п < 0 минимум /(ж) равен
min /(ж; у) = 1 — 2а
и достигается при условии равенства средних арифметического и геометрического чисел х > 0 и (—у) > 0, т.е.
Следовательно, . Г а2 1
min f (х; у) = min < 1 — 2а; — — >.
0<а<1Jv 1 2 J
Так как 1 — 2а —а2/2 <==> 2 — л/2 а 2 + %/2, то
а2 г
min/(z; у) = при 0 < а 2 - V2, min /(ж; у) = 1 — 2а при 2 — д/2 а < 1.
Ответ: —а2/2 при а 6 (0; 2 — \/2)j
1 - 2а при а G (2 - л/2; 1).
Задача 17 (биологический факультет и факультет фундаментальной медицины, 1992). Найти наименьшее значение величины
1 / За Ь \
с \vT^2 + ’
где a,b,c,t,u - положительные числа, удовлетворяющие условиям
at + bu с, а2 + 2bcu b2 + с2, /2 - ?/2 Ь2 —7---h с2 26са.
Z2 — 1
Решение. Докажем следующее утверждение: если существуют положительные числа a,b,c,t,u, удовлетворяющие условиям задачи и определено выражение
f _ i ( За Ь
~~с' IvT^2 +
1,
144
то существует и треугольник АВС, такой, что ВС = а, АС = Ъ, АВ = с, где ABAC = a, /АВС — (3, 0 < cr,(3 < тг/2 и cos а = и, cos (3 = t.
Действительно, если построить ДЛВС по двум сторонам АВ = с, АС — Ъ и острому углу а между ними, то по первому признаку равенства треугольников такой /\АВС можно построить единственным образом. Пусть в ДАВС сторона ВС = clq, /АВС = (3q. Докажем, что тогда а0 = а, /Зо = /3 < тг/2.
Входящие в условие задачи неравенства с учетом замены и = cos а и t = cos (3 можно записать в виде
a cos/? + b cos а с (1)
д2 Ь2 + с2 — 26с cos аг, (2)
» 9 9 л» » 9 SIB Ct
b2 + с2 — 26с cos сх Ь2 ——-.
sinp
(3)
Предположим, что угол /?о в ДАВС не является острым, тогда проекция стороны АС на сторону АВ равна b cos а с, что противоречит неравенству (1), так как в силу неравенств а > 0 и 0 < t = cos/? < 1 имеем 0 < /?о < тг/2. Следовательно, угол /?о - острый, т.е. О < /?о < тг/2 и cos /?о > 0.
По теореме косинусов для А АВС имеем
а2 — Ъ2 + с2 — 26с cos а.
(4)
Из неравенств (2) и (4) получаем, что
а до-
Неравенство (3) с учетом соотношения (4) и теоремы синусов для ЛАВС
sm a sin /?о
где R - радиус описанной вокруг ДАВС окружности, можно представить в виде
• 2 • 2 а -2
? ,9 9 . >9 sm a sin /?о 7 sin а
а/ = Ь2 + с2 - 26с cos а < 6Z —~--------А— = Дп —
sin2/?0 sin2/? sin2/?
<=> sin2/? ^ sin2/?о <=> /? < /?о,
так как /? и /?о - острые углы.
10 Методы реш. задач
145
Из неравенства (1) с учетом неравенств а ао и cos/? cos/?o <=> /? ^ /?о Л 0 < /?; /?о < тг/2 получаем
с a cos /3 + b cos cv ао cos (3 + b cos cvao cos (3q 4- b cos cv = c (5)
как сумма проекций сторон ао и b на сторону с.
Из цепочки неравенств (5) следует, что всюду стоит знак равенства, следовательно, а — ао и cos (3 = cos /3q <=> (3 = /3q.
Таким образом, установлено соответствие между всеми условиями задачи и существованием ААВС с двумя острыми углами а и /3. Тогда по теореме синусов искомый min f приобретает простой геометрический смысл:
f = - (зА—+А—] = фз-2Я+2Я) = —.
с \ sin ar sm (3 J с с
Для всех треугольников с 2R, причем равенство с = 2R достигается в прямоугольном треугольнике [А АС В = тг/2), отсюда
8Я А
2R ~ ’
. 8R 8R mm j - min — = ----
с max с
что и требовалось найти.
Ответ: 4.
Замечание. Разобранная выше задача на условный экстремум является редким исключением, так как при решении сводится к геометрическим соотношениям и теоремам. Чаще бывает наоборот - геометрические задачи на минимум и максимум решаются алгебраическими методами. Подчеркнем, что наиболее общий метод решения экстремальных задач с геометрическим содержанием состоит в следующем: величина, экстремальное значение которой требуется найти, записывается в виде функции какого-либо геометрического параметра, удобного для данной задачи. Затем эта функция исследуется на экстремум с учетом некоторых ограничений, вытекающих из условий конкретной задачи.
Ниже будут рассмотрены лишь так называемые изопериметрические задачи. Подобными задачами в узком смысле этого слова называются задачи о нахождении геометрической фигуры некоторого класса (треугольники, четырехугольники и т.д.) с максимальной площадью при заданном периметре. Например, еще в Древней Греции знали, что окружность является решением задачи о форме замкнутой кривой заданной длины, ограничивающей максимальную площадь.
В настоящее время изопериметрическими задачами называется значительно более общий класс задач на условный экстремум функции нескольких переменных при наличии так называемых изопериметри-ческих условий, когда некоторая комбинация этих переменных равна постоянной величине. Поясним сказанное конкретными примерами.
146
Задача 18 (механико-математический факультет, устный экзамен). Из всех треугольников с заданным периметром найти треугольник <• максимальной площадью.
Решение. Обозначим стороны искомого треугольника через a, b и с, а И- b И- с
тогда по условию имеем р = ------- = const. Площадь треугольника
выразим по формуле Герона:
S = \/р(р- а)(р - Ь)(р-с).
Так как р = const, то max S' достигается при
П1ахП “ тах [(? — а)(Р “ &)(Р ~ C)L
По сумма сомножителей произведения равна
(р — а) + (р — 6) + (р — с) : - Зр — (а + b + с) = р = const.
Тогда по первому следствию из теоремы о средних тах]^[, а следовательно и max S', достигается при равенстве всех сомножителей произведения между собой:
2р
(р — а) = (р — 6) = (р — с) <=> а = b — с — —.
Поэтому из всех треугольников с заданным периметром 2р наибольшую площадь
имеет равносторонний треугольник.
Замечание. Для рассмотренной выше изопериметрической (в узком смысле слова) задачи может быть сформулирована
Обратная задача. Какой из всех треугольников с данной площадью S имеет наименьший периметр?
Подчеркнем, что общим приемом решения взаимообратных задач является их сведение к прямым изопериметрическим задачам методом от противного, хотя в некоторых случаях возможно непосредственное решение (например, прямое использование второго следствия из теоремы о средних).
10*
147
Задача 19 (механико-математический факультет, устный экзамен). Из всех треугольников с данным углом а и площадью S найти тот, у которого наименьшее значение имеет:
а) сумма двух сторон, заключающих угол а;
Ь) сторона, противолежащая углу а;
с) периметр треугольника.
Найти соответствующие экстремальные значения.
Решение. Пусть a,b,c - длины сторон треугольника ABC, a - угол, лежащий против стороны с, тогда
5 = - ab sm a <=> ab = ---, (1)
2 sin or v 7
т.е. произведение двух сторон, заключающих угол от, есть величина постоянная.
При решении задачи воспользуемся теоремой о средних и соотношением (1).
Имеем
a + b /—г / 2S
1. —-— Vab = \ , причем равенство двух средних достигается
2 V sin а
лишь в равнобедренном треугольнике, когда a — b. Следовательно,
min (a + 6) = 2а/о6 = 2\/ —-.
V sin a
2. Из теоремы синусов и соотношения (1) получаем
с2 = a2 + b2 — 2а6 cos а = а2 + b2 — 4S ctg а.
Тогда
min с2 = min (а2 + b2 — 4S ctg аг) -
-- min (а2 + 62) — 4S ctg а =
1 — cos аг , „ а
= 2ab — 4S ctg а = 4S —:---= 4Stg —
sin аг 2
«=> c^ystg|, (2)
причем знак равенства в соотношении (2) опять достигается в равнобедренном треугольнике, когда а = Ь.
148
3. Поскольку (а + 6) и с достигают своего минимума лишь в равнобедренном треугольнике, то и минимум периметра, равный
min 2р = min (а + Ъ + с) — 2
/ 2S
V sin а
достигается при а = Ь.
Ответ: минимумы достигаются в равнобедренном треугольнике, когда а = Ь, и равны:
а 5tg-;
25 Л . а\ ----- 1 + sin - . sin а \ 2 /
Задача 20 (механико-математический факультет, устный экзамен). Найти наименьшее значение выражения
111
(3, Т) ~: у Т ~ Д" Т ~ у >
sm | gm £ sin I
где a,/3, у - углы треугольника.
Решение. По теореме о средних при п = 3 имеем
1 1 1
/(а, /?, у) = —+ —j + sm f sm f sm f
зя/ .1
у sin j sin sin ’
причем равенство имеет место, если только
. а . (3 .у sm — = sin — = sm —
2 2 2
(1)
(2)
Преобразуем знаменатель подкоренного выражения в соотношении (1):
, . a . /3 . у \ . у ( a - в а + /3
a — sm — sm — sm — — - sm — cos--------cos------
2 2 2 2 2 \ 2 2
Так как по условию a + (3 + у — тг, то
а + /3 тг у a + (3 .у
—д— — тг — тг => cos —— = sm —.
2 2 2 2 2
149
Тогда
, 1 • 7 ( ос - /3 7^ , 1 Л • 7\ • 7
а — - sin — cos —-----------sin — < - 1 — sin — sin —,
2 2 \ 2 2/ 2 \ 2/ 2
(3)
где равенство выполняется только при
cos
а — (3 2
а — /3 = 4тп, п Е Z
= 1
п = О
<=> ct - /3,
поскольку для углов любого треугольника 0 < а; (3 < 2тг. Из соотношения (3) можно получить, что
, 1 IV1 • 7\ • 71 1
шаха = - max 1 — sin - sin - =
2 L\ 2/ 21 8
поскольку по
произведения
/ 1 * ' I
— Sill — J ножителей:
второму следствию теоремы о средних максимум • 7\ • 7
1 — sin —J sin — при постоянной сумме сомножителей
7
+ sin - = 1 достигается при выполнении равенства этих сом-
sin - = sin -2/ 2
• 7 1
sin - = -
2 2
Тогда из соотношений (1) и (2) получаем
min Да,/3,7) = 3 \/—-—: = 3^8 = 6 V шаха
при
. а . /3 .у
sin — = sin — — sin —
2 2 2
1
2
7Г
<=> ос = (3 = 7 = -,
О
т.е. в равностороннем треугольнике.
Ответ: б.
Замечание. Соотношение (4) предыдущей задачи можно было полу-
чить из неравенства
. а . (3 . у 1
sin — sin — sin - < -
2 2 2 8
(4*)
и другим путем (без использования теоремы о средних). Действительно, из теоремы косинусов для £±АВС получаем
а2 = 62 + с2 — 2bc cos а — (Ь — с)2 + 26с (1 — cos а) = = (6 — с)2 + 46сsin2 у ==> а 2\/6csin
150
причем равенство выполняется только при b = с, т.е. в равнобедренном треугольнике.
Аналогичным образом для других сторон имеем
b 2x/acsin
2’
2у/аЬ sin .
с
Разрешая полученные неравенства углов, находим
относительно синусов половинных
— % —т=, sm — < ——==, sm — < —j=, 2 2л/Ьс 2 2д/ас 2 (2у/аЬ
откуда и следует неравенство (4*). При этом знак равенства в (4*) имеет место только при а = b = с, т.е. в равностороннем треугольнике.
В заключение заметим, что большой интерес представляют аналогичные задачи изопериметрического характера (в широком смысле) для объемных тел с экстремальными значениями их поверхностей и объемов. Здесь эти задачи рассматриваться не будут. Приведем лишь некоторые интересные выводы.
1. Из всех призм с равновеликими основаниями и равными высотами наибольшую поверхность (полную и боковую) имеет прямая правильная призма.
2. Из всех призм с одним и тем же основанием и равными высотами наименьшую поверхность (полную и боковую) имеет прямая призма.
3. Из всех тетраэдров с данной полной поверхностью наибольший объем имеет правильный тетраэдр.
4. Из всех параллелепипедов с дайной полной поверхностью наибольший объем имеет куб.
5. Из всех призматических и цилиндрических тел с данной полной поверхностью наибольший объем имеет прямой круговой цилиндр, диаметр основания которого равен высоте.
6. Наибольший объем из всех тел с заданной поверхностью имеет шар.
Как и в случае плоских изопериметров, верны выводы, взаимообрат-ные по отношению к перечисленным, формулировать которые здесь, на наш взгляд, нет необходимости.
Музыкант в данном случае сказал бы, что тема уже хорошо прозвучала и развивать ее дальше - значит ослабить впечатление от нее. Математик (словами Л.Кэрролла) мог бы сказать, что Чеширский Кот уже появился и исчез, но его улыбка еще долго парила в воздухе...
151
5.4. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
...Только бы попасть куда-нибудь, — пояснила Алиса.
— Куда-нибудь ты обязательно попадешь, — сказал Кот. — Нужно только достаточно долго идти.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (географический факультет, 1985). Найти все числа а, удовлетворяющие условию —1 < а < 1, для которых выражение
1 + \/а?2 - 2аху + р2 - 6р + 10
принимает наименьшее значение лишь при одной паре чисел (л; у).
Задача 2 (геологический факультет, 1986). При всех значениях параметра р 5 найти решения уравнения
„ , ? { л 7тг\ л 9 (1 Зтг
54t# -cos2z + — +p = 8sm —— \ О 24 / \ OU
• 2 5тг\ ( тг . 47тг\
+42 tg — sm х — — • cos — sin x + ——
6 \4 12/ \20 60 J
при x E [— 2тг; 0].
Задача 3 (факультет почвоведения, 1988). При каких значениях параметра р система
х2 + 2рх + Зр2 + Зр + 3 3 sin у — 4 cos у
0 у 2-тг
имеет единственное решение?
Задача 4 (факультет психологии, 1988). Найти наибольшее значение величины а, при котором неравенство
>—/ 2 г» -1 \ у/& . 4/ o' I . 7ГЖ I
a^(x -2х+.1)+х2_2х + 1^ vV .jsin т |
имеет хотя бы одно решение.
152
Задача 5 (механико-математический факультет, 1983). Найдите все значения параметра а, при которых система уравнений
к
cos —— 5
/. 7г(ж - 2у - 1)
= 11 — А / sin -----------------
имеет хотя бы одно решение.
Задача 6 (факультет ВМиК, 1986). Найти значения end, при которых наибольшее значение функции
У =
3х + 3"* - 2
3х + 3-х + 2
+ (с + 2о!)
3х - 1
3* + 1
4- 2с И- d
на отрезке [—1; 1] является наименьшим.
Задача 7 (факультет почвоведения, 1991). Для каждого положительного числа а найти наибольшее значение функции
у(х) = - а)3 + (л - а)2
на промежутке — 2 х 0.
Задача 8 (факультет ВМиК, 1977). Найти все значения параметра a (тг/4 а тг/2), при каждом из которых наибольшее значение функции
f(x) = х4 — 2л2 sin2 a — 2(1 + cos а)3
на отрезке —(1 4- cos а) х 1 4- cos а принимает наименьшее значение.
Задача 9 (химический факультет, 1987). Стороны треугольника лежат на осях координат и на касательной к графику функции у = —х2 4- 6х — 9 в точке, абсцисса b которой удовлетворяет условию 0 Ь 5/2. Найти значение Ь, при котором площадь треугольника будет наибольшей.
Задача 10 (экономический факультет, 1979). Найти все значения параметра а 2, при каждом из которых площадь фигуры, лежащей в полуплоскости х 0 и ограниченной прямыми у = 1, у = 2 и кривыми у = у/ax, у = у/ох/Т., будет наибольшей. Найти эту площадь S.
153
Задача 11 (геологический факультет, 1977). Найти все значения параметра a > 0, при каждом из которых площадь фигуры, ограниченной параболой у — (1 4- а2)2 х2 и прямой у = а, будет наибольшей.
Задача 12 (геологический факультет, 1977). Найти все значения параметра a > О, при каждом из которых площадь фигуры, ограниченной параболами
4а2 — 2ах — х2 х2
У ~ ---73—4------- и У = 73—4 ’
1 + а4 1 4- а4
будет наибольшей.
Задача 13 (географический факультет, 1986). Для каждого значе-
ния а, удовлетворяющего неравенствам О < a < 2, найти наименьшее
значение выражения х2 4- у2 — 2а(ж 4- у) при условии cos
~ 1.
Задача 14 (экономический факультет, 1985). Среди всех решений (а,Ь,с,сГ) системы
( а2 4- Ь2 = 9
< с2 4- d2 — 16
I ad 4- be 12
найти такие, при которых выражение b + d принимает наименьшее значение.
Задача 15 (механико-математический факультет, 1989). Найти наибольшее из значений z, для которых существуют числа х, у, удовлетворяющие уравнению
2z2 4- 2т/2 4- z2 4- ху 4- xz 4- yz = 4.
Задача 16 (биологический факультет, 1989). Числа x,y,z таковы, что
х2 4- Зг/2 4- z2 - 2.
Какое наибольшее значение может принимать выражение 2х + у — z?
Задача 17 (биологический факультет, 1989). Числа а, Ь, с таковы, что
2a2 4- Ь2 4- с2 = 3.
Какое наибольшее значение может принимать выражение а — 26 4- с?
154
Задача 18 (механико-математический факультет, ИП). Используя функцию
/(л) = (1 + х)а • ( 1 + - ) ,
для любых положительных чисел a, b, с, d доказать неравенство
(1)
В качестве следствий из неравенства (1) получить неравенства о среднем арифметическом и среднем геометрическом, Гсльдера, Коши-Буняковского.
Задача 19 (механико-математический факультет, устный экзамен). Для углов а, /3,у произвольного треугольника доказать:
а)
Ь)
с)
cos a + cos /? + cos у <C
cos a • cos • cos у <C sin2 a + sin2 /3 + sin2
В каких случаях достигается равенство?
Задача 20 (механико-математический факультет, устный экзамен). Доказать, что во всяком треугольнике отношение радиуса вписанной окружности к радиусу описанной окружности не больше 1/2.
Задача 21 (механико-математический факультет, устный экзамен). Три окружности с центрами в точках А, В и С попарно касаются друг друга внешним образом в точках К, L и М. Найти максимально возможный радиус окружности, описанной около треугольника KLM, если сумма радиусов трех первых окружностей равна постоянной величине р.
Задача 22 (факультет ВМиК, 1991). Три круга с центрами в точках Р, Q и R попарно касаются друг друга внешним образом в точках А, В и С. Известно, что величина угла PQR равна 2 arcsin (1/3), а сумма радиусов всех трех кругов равна 12л/2. Какую наибольшую длину может иметь окружность, проходящая через точки А, В и С?
155
Задача 23 (биологический факультет и факультет фундаментальной медицины, 1992). Найти наименьшее значение величины
Г \ u v'l - v2
где p,q,r,u,v - положительные числа, удовлетворяющие условиям:
pv + g\/l — u2 г, р2 + 2gr\/l — u2 q2 + г2,
г------- 2 1 — v2 — и2
2qrу/1 - u2 + q2-----5------
vz — 1
Задача 24 (экономический факультет, 1978). Найти все а, при которых функция
f(x) — sin 2 ж — 8(а + 1) sin х + (4а2 + 8а — 14)ж
возрастает и не имеет критических точек.
Задача 25 (механико-математический факультет, 1996). При каком значении а сумма различных корней уравнения
cos х — sin 2х + sin 4ж — a(ctgx + 2 cos Зж),
принадлежащих отрезку
Зтг 22тг
, максимальна?
4 ’ 3
Задача 26 (экономический факультет, 1997). Найти все значения параметра а, при которых периметр фигуры, заданной на координатной плоскости условием
1оё2-|ау| 2д2 > °’
будет наименьшим.
156
5.5. УКАЗАНИЯ И ОТВЕТЫ
2. х = —3/2-тг при р = 5; х G 0 при р > 5.
3. —2; — 1/2.
4. 1/6.
5. ai = 6k — 1, а2 = 6/ + 3, аз — 6m, а$ = 6п + 2, к, l,m,n G Z.
6. с = -1/3, d = 1/6.
7. 4/3 при а 2, —а3/3 + а2 при а < 2.
8. 7г/3.
9. 1.
10. а = 2, 5=7/2.
11. 7з.
12. ^3.
13. —а2 при 0 < а 4 — 2д/2; 8(1 — а) при 4 — 2л/2 а < 2.
14. а = -12/5; b = -9/5; с = -12/5; d = -16/5.
15. z = >/5.
16. 4д/б/3.
17. —х/66/2.
19. а = /3 = 7 = 7г/3.
а . (3 7
20. Указание: докажите, что г = 47?sin — sin — sin —, где г и R - радиусы вписанной и описанной окружностей.
21. Указание: докажите, что окружность, описанная около ДКЬМ, является вписанной в ДАВС. Тогда искомый радиус г = S/p, где S - площадь, а р = 7?i + Т?2 + 7?з = const - полупериметр ДАВС. Далее см. изопериметрическую задачу 18 из п. 5.3.
22. 67Г.
23. 5.
24. а < —2 — у/б, а > у/б.
25. а = -у/Ъ/2.
26. а = ±у/2.
157
ГЛАВА 6
“НЕСТАНДАРТНЫЕ” И “ЛОГИЧЕСКИЕ” ЗАДАЧИ
6.1. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
— Так бы и сказала, — заметил Мартовский Заяц. — Нужно всегда говорить то, что думаешь. — Я так и делаю, — поспешила объяснить Алиса. — По крайней мере я всегда думаю то, что говорю..., а это одно и то же... — Совсем не одно и то же, — возразил Болванщик.
Л.Кэрролл. Алиса в стране чудес
Как показывает многолетний опыт проведения вступительных экзаменов, у поступающих в МГУ наибольшие затруднения возникают при решении так называемых “нестандартных” и “логических” задач с параметрами.
Как следует из самого названия подобного типа задач, получить их решение стандартными методами, к которым привыкли школьники, как правило, не удается. Такие задачи требуют индивидуального подхода, высокой логической культуры рассуждений, хорошего уровня математической подготовки в рамках школьной программы и применения нестандартных приемов решения.
Однако именно низкий уровень логической культуры и достаточно поверхностное владение школьной программой и являются самым слабым местом в подготовке большинства абитуриентов.
Заметим, что в общем виде решение любой задачи состоит в том, чтобы построить цепочку утверждений, с помощью которых будет получен окончательный ответ. При построении такой цепочки утверждений возможны два пути:
1) от условия к заключению (метод синтеза);
2) от заключения к условию (метод анализа).
159
При применении метода синтеза, составляя разные комбинации из условий задачи, получают ряд вытекающих друг из друга суждений. В результате последовательного повторения этого приема и решения возникающих при этом задач в конечном итоге получают ответ.
Идея и техника применения метода анализа иная. При решении задачи на каждом этапе формулируется суждение типа “задача будет решена, если справедливы следующие условия...”, т.е. поставленная задача заменяется последовательностью нескольких более простых обратных задач. Это повторяется до тех пор, пока сформулированные вспомогательные задачи не удается решить непосредственно с помощью условий исходной задачи. Разумеется, построенная цепочка рассуждений должна быть логически безупречна! Малейшая неточность, и почти построенное здание рухнет, как карточный домик (или радужный шарик лопнет, как мыльный пузырь)!
Для того чтобы на основании одного суждения уметь делать вывод о справедливости или отрицании другого суждения, надо хорошо разбираться в вопросе о взаимоотношении суждений, их достаточных и необходимых условиях (или признаках).
Прекрасной иллюстрацией логической путаницы между понятиями “необходимо" и “достаточно" является эпиграф из “Алисы..." к данной главе и дальнейшее продолжение разговора в “Безумном чаепитии”.
С точки зрения анализа причинно-следственных связей и взаимоотношений между необходимыми и достаточными условиями еще более поучительной является вся сцена суда в последней главе “Алисы..." Заметим, что различие между судебным процессом по привычной схеме (сначала доказательства, потом приговор) и обратной схемой Кэрролла (сначала приговор, потом доказательства) по существу представляет собой различие между двумя методами: синтезом и анализом.
Вообще, почти вся “Алиса..." - это своеобразная, чрезвычайно интересная и сложная борьба логики здравого смысла реального мира с логикой “наоборот” обитателей Страны Чудес. Подчеркнем, что часто “сумасшедшая" логика героев Кэрролла близка и созвучна логике развития современных физических теорий, сочетающих в себе “безумные идеи" (по Бору) и “математическую красоту" (по Дираку).
Схеме “сначала приговор - потом доказательства" еще в большей степени следует математика. Достаточно упомянуть геометрию Лобачевского, уравнения электродинамики Максвелла, теорию множеств Кантора, знаменитую теорему Ферма, квантовую механику и фрактальную геометрию.
Однако пора вернуться к необходимым и достаточным условиям и взаимоотношениям между суждениями.
Пусть А и В - некоторые суждения, связанные между собой. Охарактеризуем эту связь следующим образом.
Суждение В называется необходимым условием суждения А, если из А следует В (А ==> В\
Суждение В называется достаточным условием суждения А, если из В следует А (В ==> А).
160
Если из В следует А и, наоборот, из А следует В, то В является необходимым и достаточным условием А [В <=> А).
Заметим, что взаимоотношение суждений напоминает причинно-следственные связи и равносильность уравнений.
Пусть В - необходимое условие А (А => В). Подчеркнем, что отрицание А (обозначается А) не влечет за собой отрицание В (А Ф- В), так как В может быть справедливым и тогда, когда А неверно. Однако из отрицания необходимого признака А следует отрицание самого А (В =>Х).
Пусть В - достаточное условие А (В => А). Можно доказать, что отрицание достаточного условия А не влечет за собой отрицание А (В Ф А), тогда как из отрицания А следует отрицание его достаточного условия (А => В).
При решении ряда логических задач бывают полезны правила логического отрицания суждений, содержащих знаки (кванторы) 3 (существования) и V (всеобщности).
В формализованном виде эти правила можно записать следующим образом:
1) не {Заз € М : А(т)} {Vz G М : А(т)},
2) не {Vx £ М : А(т)} <==> {Зт £ М : А(т)}.
В словесной форме первое из этих правил читается так: суждение “не существует х, принадлежащих множеству М, чтобы выполнялось условие А(т)” эквивалентно суждению “для каждого х, принадлежащего множеству М, выполняется противоположное условие А(т)”.
Подчеркнем, что при логическом отрицании конкретного суждения кванторы 3 и V взаимозаменяются, а суждение изменяется на свое отрицание.
В предыдущих главах уже встречались задачи, где использовались понятия о необходимых и достаточных условиях. Здесь лишь подчеркнем, что в логических задачах с параметрами чаще всего используется тот факт, что отрицание необходимого признака некоторого суждения влечет за собой отрицание данного суждения.
В качестве самопроверки найдите в предыдущих главах задачи, при решении которых правила логического отрицания в словесной форме уже применялись, и запишите их в формализованном виде.
Таким образом, если в процессе решения задачи удается получить необходимые условия для параметра, то все те значения параметра, которые не удовлетворяют этим условиям, являются посторонними для данной задачи. Это позволяет ограничить множество значений параметра, в пределах которого находится решение задачи. Часто такого ограничения бывает достаточно, чтобы довести решение задачи до конца. В частности, если необходимым условиям удовлетворяет лишь несколько конкретных значений параметра, то задача сводится к непосредственной проверке всех этих значений.
11 Методы реш. задач
161
6.2. “...ХОРОШАЯ ДОГАДКА - ПОЛОВИНА РЕШЕНИЯ!”
Она совсем забыла о Герцогине и вздрогнула, когда та сказала ей прямо в ухо:
— Ты о чем-то задумалась, милочка, и не говоришь ни слова. А мораль отсюда такова... хорошая догадка — половина решения!
Л.Кэрролл. Алиса в стране чудес
В ряде логических задач удачный выбор нескольких конкретных значений параметра (или неизвестной величины), при которых задача легко разрешима, позволяет сразу определить необходимые условия.
Задача 1 (механико-математический факультет, 1966). Найти все
значения а, при которых система
2&х + (а + l)6j/2 = а2 (а - 1>3 + у3 = 1
(1)
имеет хотя бы одно решение для любого значения Ь.
Решение. Так как по условию исходная система должна иметь решения для любого значения Ь, то сначала выберем такое значение Ь, при котором система (1) существенно упрощается. При 6 = 0 имеем
2° = а2
(а - 1)я3 + у3 = 1
а2 = 1
(а — 1)а?3 + у3 = 1
Таким образом, для того чтобы система (1) имела хотя бы одно решение для любого значения Ъ (в том числе и для Ь = 0!), необходимо, чтобы параметр а = ±1. Проверим достаточность этих условий.
При a = — 1 система (1) принимает вид
х = 0
< У = 1
b = г G R
2&х = 1
-2а?3 + у3 = 1
{х = г G R у = tyl + 2r b = 0,
т.е. для любого значения b имеет по крайней мере одно решение х = 0, у = 1. Следовательно, a = — 1 удовлетворяет условию задачи.
162
При а = 1 система (1) принимает вид
Г 2Ьх + 26г/2 = 1 Г У = 1
[ у3 = 1 I 2bx = 1 - 26.
Полученная система будет иметь решение лишь при 1 — 26 > 0 <=> 6 < 1/2. Следовательно, а = 1 не удовлетворяет условию задачи.
Ответ: —1.
Задача 2 (факультет психологии, 1978). Найти множество всех пар чисел (ct.b), для каждой из которых при всех значениях х справедливо равенство
a(cos х — 1) + 62 = cos (az + 62) — 1. (1)
Решение. Пусть (а; 6) - пара чисел, удовлетворяющая условию задачи. Тогда равенство (1) справедливо для всех х = г £ R, в том числе для х = те и х = 2тг. Тогда из равенства (1) при х — к и х = 2тг получаем систему для определения а и 6
( —2a + 62 = cos (тга + 62) — 1
t 62 = cos (2тга + 62) — 1, из последнего уравнения которой следует, что
62 0 <=> 6 = 0, так как cos (2тга + 62) 1
для любых а и 6. Но это означает, что
соз2тга=1 <==> a = n 6 TV U {0}.
Из первого уравнения системы (2) при 6 = 0 получаем
cos та = 1 — 2а => —1^1 — 2а <С 1 <=> 0 С а = n 1.
Следовательно, необходимым условиям задачи удовлетворяют только две пары чисел:
a = 0, 6 = 0 и a = 1, 6 = 0.
Проверим достаточность этих условий.
Пусть a = 6 = 0, тогда равенство (1) выполняется для всех х = г G R.
При a = 1, 6 = 0 равенство (1) принимает вид равенства cosz = cosz, которое также выполняется для всех х = г G R.
Ответ: (0; 0), (1; 0).
Замечание. Иногда задачи подобного типа лучше решать с помощью производной. Тогда не нужно угадывать “хорошие” значения переменной, при которых получаются необходимые условия на значения параметров.
11*
163
Задача 3 (механико-математический факультет, устный экзамен). Найти все такие пары чисел (а; Ь), где a > О, b О, что для всех х > О выполняется равенство
a In х + b = In (ax + b).
(1)
Решение. Введем обозначения:
/i(z) = a • In x + b и A(z) = In (ax + 6).
По условию задачи требуется найти такие пары чисел (а;6), чтобы при всех х > 0 эти функции совпадали, т.е.
А(*) = А(*) => f[(x) = f'2(x) <=>
a a
x ax + b’
(2)
так как из равенства функций на каком-то множестве следует равенство их производных (но не наоборот!).
При a > О, b 0 из равенства (2), справедливого для всех х > О, получаем необходимые условия на параметры: a = 1, b = 0. Непосредственной проверкой убеждаемся, что условия a = 1, 6=0 являются и достаточными для выполнения равенства (1) при всех х > 0.
Ответ: (1;0).
Задача 4 (факультет ВМиК, 1990). Найдите все значения параметра а, при которых для любых значений параметра b неравенство
fx\ /10а + 36 + 31\ 2 /Л,2 п,
1оёб (хт) + --------Z-------- х - (962 + 96 + 1)
\3о/ \ о /
log6 (—я2 — (66 + 2)z + 962 + 156 + 3 (1)
\ х J \ 5 /
имеет хотя бы одно решение.
Решение. Неравенство (1) имеет вид |А| А и поэтому эквивалентно двойному неравенству
—/2 fl А или системе
А - А о
А + А о,
(2)
где
f —1 ( х \ Юа + 36 + 31 2 о/912 । Qi , 1 \
А — 1°ёб ( хх ) Н-----ё х ~ 3(3& +36+1),
\ 00 / о
А = — log6 х + ——— ^—2?2 + 2х2 — 2(36 + 1)2? + 962 + 156 + 5.
164
Из первого неравенства системы (2) получаем условие log6 х х2 — (36 + 1)ж + (36 + 2)2, которое справедливо при всех х > 0 в силу выполнения неравенств log6 х < х и х а?2 — (36 + 1)ж + (36 + 2)2
Второе неравенство системы (2) приводится к виду 10а + 36 + 36 _ (36 + х + + 0
о
и должно иметь хотя бы одно положительное решение для любого значения параметра 6. В частности, при 6 — —1/3 из неравенства (3) для х > 0 следует
(2а + 7)а?2 0 <=> а -7/2.
Проверим достаточность этого условия.
При а — 7/2 неравенство (3) приводится к виду
—-—(а? — 5a?+5)^U <=> 5
36 + 1 0 Г 36 + 1 0
9 V S 9
а?- — 5а? + 5 0 ( а? — 5а? + 5 0.
Последняя совокупность систем для любого значения параметра 6 имеет по крайней мере два решения а?ц2 = (5±>/5)/2, т.е. все значения а —7/2 удовлетворяют условию задачи.
Ответ: а —7/2.
Задача 5 (экономический факультет, отделение кибернетики, 1978). Найти все значения параметра а, при каждом из которых функция
у(х) = Sax — a sin 6а? — 7а? — sin 5а?
возрастает и не имеет критических точек на всей прямой.
Решение. Так как данная функция при каждом фиксированном значении параметра а является дифференцируемой при любом х и по условию возрастает, то ее производная
г/(а?) = 8а — 6а cos 6a? — 5 cos 5a? — 7
165
неотрицательна: у!(х) 0. Кроме того, по условию функция т/(ж) не
имеет критических точек, т.е. у’(х) 0 для всех х. Тогда у'(х) > 0 для
любого значения х = т Е R, т.е.
8а — 6а cos 6х — 5 cos 5х — 7 > 0
<=> 6а cos 6х + 5 cos 5х < 8а — 7.
(1)
Поскольку неравенство (1) должно выполняться при всех х, то при х = 0 имеем
6а + 5 < 8а — 7
а > 6.
Проверим достаточность этого условия.
При а > 6 неравенство (1) с учетом ограниченности косинуса можно переписать в виде неравенства
6а cos 6х + 5 cos 5z 6а + 5 < 8а — 7,
которое выполняется при всех х.
Ответ: а > 6.
Задача 6 (механико-математический факультет, 1989). Найти все такие значения параметра а, что при любом с система
2(с2 + 2с + 2)^ + (1 + 4х4)а = 3
х3у3 + (с + + а2 — а = 6
имеет не менее одного решения (а?; у).
Решение. Найдем такое значение параметра с, при котором система (1) существенно упрощается. При с = — 1 она принимает вид
2-:Р + (1+4я)а = з х3у3 + а2 — а = 6
а ф 0
х = 0
6 + а — а2 = 0
( (1 + 4z)a = 1
1 2j3j/3 — = 6 + а — а2
а = 0
х = г Е R => а = 0; —2; 3
х3у3 = 6
- необходимые условия на значения параметра а.
Проверим достаточность этих условий.
При а = 0 из первого уравнения системы (1) для любого значения с имеем
(с2 + 2с + 2)У = 1 => у = 0,
166
но тогда из второго уравнения получаем 0 = 6?!— противоречие. Следовательно, а = 0 не удовлетворяет условию задачи. При а = —2 V а = 3 система (1) имеет решение х = у = 0 для любого значения с.
Ответ: —2; 3.
6.3. “КВАЗИЭКВИВАЛЕНТНОСТЬ” УРАВНЕНИЙ И НЕРАВЕНСТВ
— Объяснись, — сказал Черепаха Квази.
— Нет, сначала приключения, — нетерпеливо перебил его Грифон. — Объяснять очень долго.
Л.Кэрролл. Алиса в стране чудес
В сложных словах приставка
“квази-” (quasi - латынь) <==> “псевдо-” (pseudos - древнегреческий)
означает “мнимый” или “ложный”, т.е. ненастоящий. В чем конкретно состоит мнимая эквивалентность в приводимых ниже задачах, предлагаем разобраться читателю самостоятельно.
Задача 7 (механико-математический факультет, 1968). Найти все те числа а, при каждом из которых всякий корень уравнения
sin 3z = a sin х + (4 — 2|a|)sin2 х (1)
является корнем уравнения
sin 3z + cos 2х = 1 + 2 sin х cos 2х (2)
и, наоборот, всякий корень второго уравнения является корнем первого уравнения.
Решение. Использовав формулы для тройного и двойного аргументов, исходные уравнения можно записать в виде
4 sin3 х + (4 — 21а|) sin2 х + (а — 3) sin х = 0, (1*)
2 sin2 х — sin х = 0. (2*)
167
Второе уравнение имеет два решения относительно переменной z = sin х, о 1 z - О V z - -.
2
При z = sin х = 0 уравнение (1*) выполняется при всех а Е R.
При z = sin а? = 1/2 уравнение (1*) дает необходимое условие для параметра а;
|а| — а а 0.
Уравнение (1*) относительно переменной z имеет три решения: о 1 а-3
zi = 0, z2 = z3 =
Для выполнения условий задачи необходимо и достаточно, чтобы третий корень гз = (а — 3)/2 совпадал с одним из первых двух:
1—1 = 0 V 1=1 2 2
| <=> а = 3 V а = 4,
либо уравнение sin а? = гз = (а — 3)/2 не имело решений при а 0, т.е.
1Q-31
2 а О
|а — 3] > 2
а О
<=> 0 а < 1 V а>5.
Ответ: 0 а < 1; а = 3; а = 4; а > 5.
Задача 8 (экономический факультет, отделение кибернетики и планирования, 1988). Найдите все значения параметра а, при которых любой корень уравнения
a(2a — 1) sin3 х + 3 cos3 х — 2а2 sin х = О
(1)
является корнем уравнения
logi/2 - 1) - l°g2 (Mgz + 1) - log1/x/2 (5 - tgx) = 1 (2)
и, наоборот, любой корень второго уравнения является корнем первого уравнения.
Решение. ОДЗ второго уравнения задается системой
3tg х — 1 > О
3tg х + 1 > О
5 — tg х > О
х тг/2 + кп, n Е Z
Г 1/3 < tgz < 5
[ х тг/2 + кп, n Е Z.
(3)
168
Переходя во втором уравнении к одному основанию, получаем, что
/Г _ , х2
1062 (9tg2J —1) = 1 (tgI “5)2 = 2(9tg2* ' J)
27
<=> 17tg2х + lOtg х — 27 = 0 <=> tg гс = — — V tgге — 1.
Тогда, с учетом ОДЗ в соответствии с системой (3) второе уравнение будет равносильно простейшему тригонометрическому уравнению
tg а? = 1 <=> х = + тгАг, к 6 Z. (4)
Подставив (4) в уравнение (1), получим необходимые условия для параметра а:
3
2а2 + а — 3 = 0 а = — - V а = 1. (5)
Проверим достаточность условий (5).
Пусть а = — 3/2, тогда уравнение (1) будет равносильно уравнению
4 sin3 х + 2 cos3 х — 3 sin х = О,
которое с помощью соотношения
sin х = sin a;(sin х + cos х)
можно привести к виду
(sin х — cos a?) (sin2 х — 2 cos2 х + sin 2а?) = О
<=> tg х = 1 V sin 2х — 3 cos 2х = 1
<=> х = тг/4 + тгк, k^Z V sin (2х + 921) = 1/\/10. (6)
Второе уравнение совокупности (6) с дополнительным аргументом <pi дает вторую серию решений, отличных от (4). Поэтому а = —3/2 не удовлетворяет условию задачи.
При а — 1 уравнение (1) равносильно уравнению
sin3 х + 3 cos3 х — 2 sin х = О,
которое аналогичным образом можно привести к виду
(cos х — sin a?)(sin2 х + 3 cos2 х + | sin 2а?) = О
tg х = 1 V sin 2а; + 2 cos 2х = —4
<=> х = тг/4 + тгк, к £ Z V sin (2а; + <£>2) = —4/д/5. (7)
169
Однако второе уравнение системы (7) с дополнительным аргументом не имеет решения, так как —4/>/5 < — 1. Поэтому при а = 1 каждое из уравнений (1) и (2) имеет единственную серию решений х = тг/4 + irk, k Е Z, т.е. а — 1 удовлетворяет условию задачи.
Ответ: 1.
Задача 9 (механико-математический факультет, 1972). Даны три уравнения:
х2 — (а + Ъ)х + 8 = 0 х2 — b(b + 1 )х + с = 0 х4 — b(b + 1)ж2 + с = 0.
(1)
(2)
(3)
Каждое из них имеет по крайней мере один корень. Известно, что корни первого уравнения больше единицы и являются корнями третьего уравнения, а хотя бы один корень первого уравнения удовлетворяет второму уравнению. Найдите числа a, b и с, если b > 3.
Решение. Из условия задачи следует, что все три уравнения имеют по меньшей мере один общий корень xq. Поэтому для уравнений (2) и (3) имеем систему
( х2 - Ъ(Ь + 1)а?о + с = 0
I х4 - Ъ(Ъ + 1)а?§ + с = 0,
из которой следует, что — x'q удовлетворяет уравнению (2), причем Xi ф х*о, т.е. хо и Xi = х2 - различные корни уравнения (2).
Действительно, если хо и а?! = х2 один и тот же корень уравнения (2), то х2 = Хо <=> Хо = 0 V Xq = 1. Но Хо = 0 просто не удовлетворяет уравнению (1), a Xq = 1 не подходит условию, что все корни уравнения (1) больше единицы.
Используя четность биквадратной функции, стоящей в левой части уравнения (3), получаем, что это уравнение имеет наряду с корнем xq > 1 еще и корень — xq. Сводя биквадратное уравнение (3) заменой z — х2 к квадратному уравнению, получаем еще два его решения: £3,4 = ±д/жо. Из условия задачи следует, что Х3 = у/хо > 1 является также корнем уравнения (1), поэтому по теореме Виета для уравнений (1) и (2) при условии b > 3 находим, что имеет место следующая система:
' хОу/х^ = 8
Хо + у/хо - а. + b
< 2?q — С
х0 + х2 = 6(6 + 1)
< b > 3
с = 64
х0 = 4
* а + Ъ — 6
6(6+1) = 20
< 6 > 3
хо = 4 а = 2
6 = 4
с = 64.
170
Непосредственной проверкой убеждаемся, что все условия задачи при а = 2, 6 — 4 и с = 64 выполняются.
Ответ: а = 2, b = 4 и с = 64.
Задача 10 (факультет психологии, 1992). При каких значениях параметров а и b найдутся два различных корня уравнения
х3 — Зх2 + 7х = а, которые будут также корнями уравнения х3 - 8х + 6 = 0 ?
Решение. По условию задачи необходимо найти такие пары значений параметров (а; 6), чтобы система уравнений
х3 — 5х2 + 7х = а
Ч п С1)
х3 — 8х + Ь = О
имела не менее двух различных решений.
Система (1) будет равносильна системе
х2 = Зх —
х3 — 8х + b ~ О
5х2 — 15х + а + b = О
/ а + b х Зх--------—
\ 5
3 Зх —
х2 = Зх--------
5
х(х2 — 8) + Ь = О
а + b
5
х2 = Зх-------—
5
Зх2 = (—F 8^ х — b
V 5 /
9 ci “|“ b
X2 = Зх-------~
5
5
(а + b — 5)х = 2Ь — За
х2 — Зх-Ь ——~—— = 0.
5
Последняя система может иметь не менее (но и не более) двух различных решений тогда и только тогда, когда дискриминант квадратного уравнения положителен, а коэффициенты линейного уравнения обращаются в нуль, т.е. когда выполняется система
а + 6-5 = О
26 — За = О
9- 4(а + Ь)>0
5
а = 2
Ъ = 3.
Ответ: а — 2, 6 = 3.
Замечание. Попытайтесь решить эту задачу с использованием обратной теоремы Виета (см. гл. 7).
171
Задача 11 (механико-математический факультет, 1965). Найти все пары чисел а и Ь, для которых всякая пара чисел (ж; у) (х тг/2 4- тгтг, у тг/2 + тгт, n, m G Z), удовлетворяющая уравнению
хфу = а, (1)
удовлетворяет также уравнению
tgx+tgy + tgx- tgy = b. (2)
Решение. Поскольку любое решение уравнения (1), кроме чисел х, у = тг/2 4- 7гп, должно удовлетворять уравнению (2), то рассмотрим два решения уравнения (1):
(a?i; 2/1) = (0; а) и (ж2; t/2) = а -
Подставляя эти решения во второе уравнение, получаем необходимые условия для параметров а и Ь:
tg а — b
2tg (а — тг/4) -- b — 1
tg a = b
tga = 1
tga = b (tga~ I)2 tga + 1 tga = 1 b= 1
a = тг/4 + irk, k £ Z b -1.
(3)
Проверим достаточность этих условий. Пусть выполняется система (3), тогда из уравнения (1) для всех х тг/2 4- ттп получаем у = тг/4 4- тгк — х, где к, n G Z. Подставив эти значения для у в уравнение (2), получим
(тг \ (тг \
tg ж + tg - zj 4- tg я • tg - xj = 1
1 — tg X ,Л ч
ITTiT(1 + tsl) = 1-tgI'
т.е. верное равенство для всех допустимых значений х. Поэтому условия (3) являются необходимыми и достаточными.
Ответ: a — тг/4 + тгк, к £ Z, b = 1.
172
Задача 12 (химический факультет, 1987). Найдите все значения р, при каждом из которых множество решений неравенства
(р - х2)(р + х - 2) < О
не содержит ни одного решения неравенства х2 1.
Решение. По условию задачи требуется найти все такие значения параметра р, чтобы система неравенств
( (Р~ х2)(р + х- 2) < О
t х2 1 U
не имела решений, т.е. для всех х 6 [—1;1] должно выполняться противоположное неравенство
(р - х2)(р + х - 2) 0. (2)
В частности, при z = 0 и z = -1 получаем систему для определения необходимых условий для параметра р:
Р(Р - 2) О
(Р- 1)(р — 3) О
<=> р О V р 3.
(3)
Проверим достаточность этих условий.
При р <С 0 р — ,т2 0, р + ж — 2 — 1 при х G
[— 1; 1] и неравенство (2)
выполняется.
При р^З р — z2 2, р + х — 2^0 при х G [—1; 1] и неравенство (2)
также выполняется.
Следовательно, условия (3) являются необходимыми и достаточными условиями, чтобы система (1) не имела решений.
Ответ: р G (—оо; 0] U [3; +оо).
Задача 13 (механико-математический факультет, 1978). Найти все значения параметра а, при каждом из которых система неравенств
Г х2 + 2жр — 7у2 -—-
1+а (1)
[ Зя2 + Южр — 5р2 —2
имеет решение.
Решение. Умножив первое неравенство системы (1) на —2 и сложив его со вторым, получим, что
х2 + бху + 9 у2 = (х + Зр)2 С -т—— => а < -1, (2)
1 + а
173
т.е. условие (2) является необходимым для решения задачи. Докажем его достаточность. Заметим, что
1 — а
1 ± а
-1
----< 0 <=> а < — 1 V а>0 1 +
Следовательно, при а < — 1 выполнено условие (1 — а)/(1 + а) > —1 и поэтому достаточно доказать, что имеет решение система уравнений х2 + 2ху — 7у2 = -1
За?2 ± 1Оа?г/ — 5т/2 — —2
х2 + 2ху — 7у2 = — 1 Г х = -Зу Г я? = =рЗ/2
(х±Зт/)2 = 0 t 4т/2 = 1 [у = ±1/2.
Таким образом, при а < —1 система уравнений (3), а следовательно и система неравенств (1), имеет решение.
Подчеркнем, что логический переход от системы (1) к системе уравнений (3) при выполнении необходимого условия (2) на значения параметра а для большинства абитуриентов оказался далеко не очевидным.
Ответ: а £ (—оо; — 1).
6.4. ЛОГИЧЕСКИЕ ЗАДАЧИ НА ИСПОЛЬЗОВАНИЕ СВОЙСТВ ЧЕТНОСТИ И СИММЕТРИЧНОСТИ
— Что это ты выдумываешь? — строго спросила Гусеница. — Да ты в своем уме?
— Не знаю, — отвечала Алиса. — Должно быть, в чужом...
Л.Кэрролл. Алиса в стране чудес
Задача 14 /механико-математический факультет, 1965). Найти все значения а и Ъ, при которых система
' ху - 1
< ху ± 1
. х2 ± у2 = Ь, х > О
(1)
имеет только одно решение.
Решение. Заметим, что при замене у вид. Действительно,
на — у система (1) сохраняет свой
х~у - 1
х~у ± 1
1/хУ - 1
1'/хУ ± 1
1 - хУ
1 ± ху
Ху - 1
хУ ± 1
174
и (—у)2 = у2. Следовательно, система (1) является четной по переменной у. Тогда для единственности решения (то; t/о) необходимым условием является равенство
г/о = О
а = О V х2 = Ъ > 0.
Проверим достаточность этих условий.
При а = 0 и b > 0 система (1) имеет вид
ху = 1
т2 + у2 = Ь b > О
' у = О
< х = ±Vb
х = 1
У2 = Ь - 1
b > 0
У = О х = ±\/б Ъ > 0
х — 1
V < у = ±д/6 — 1
b > 1
( х = 1
V S
I УЕ 0.
(2)
Заметим, что согласно ОДЗ показательной функции основание должно быть положительным, т.е. х > 0. Тогда первая система совокупности (2) дает для любых b > 0 единственную пару: х = у/Ъ, у = 0. Вторая система при 6=1 дает ту же пару х = 1, у = 0, а при b > 1 дает две пары с различными значениями у = ±д/6 — 1, при 0 < b < 1 решений нет. Таким образом, исходная система (1) имеет единственное решение (\/б; 0) при а = 0 и b 6 (0; 1].
Ответ: а = О, b 6 (0; 1].
Задача 15 (филологический факультет, 1992). Найти все значения параметра а, при которых система уравнений
ax2 + 4ах — y + 7a + l = Q ay2 — х — 2ау + 4а — 2 = 0
(1)
имеет единственное решение.
Решение. Система (1) выделением полного квадрата по квадратичным переменным преобразуется к виду
( а(х + 2)~ — (у — 1) + За = 0 ( аи2 — г? + За = 0
| а(у - I)2 - (х + 2) + За = 0 I аг>2 — и + За = 0,
где и = з? + 2, v = у — 1. Если система (2) имеет единственное решение, то в силу симметричности относительно переменных и и v единственное
решение должна иметь и система
аи2 — v av2 — и
п — v
Т За — 0
4- За = 0
аи2 — и + За = 0 и = V.
(3)
175
Система (3) имеет единственное решение при а = 0, когда первое уравнение превращается из квадратного в линейное, и при
2 J_
12
“-±2УЗ’
когда дискриминант квадратного уравнения равен нулю. Непосредственной проверкой можно убедиться в достаточности условий а = О V а = ±1/2л/3 для единственности решения системы (1).
Ответ: 0; ±1/2л/3-
Задача 16 (механико-математический факультет, 1966). Найти все значения а, при которых система
ж3 - ay3 = | (а + I)2 re3 + ах2у + ху2 = 1
(1)
имеет хотя бы одно решение и всякое ее решение удовлетворяет уравнению
x + y = Q. (2)
Решение. По условию каждое решение системы должно удовлетворять уравнению (2), т.е. у = —х. Использовав это условие антисимметричности переменных, систему (1) при у — —х можно переписать в виде
z3(l + a) = |(1 + а)2 z3(2 — а) = 1
( a = 2
V S
I x G 0
{a 7^ —1 V a 2
, а + 1 1
= --- — ---
2 2 —a
Из последней системы получаем a = 0 V а = — 1.
Таким образом, необходимым условиям для решения задачи удовлетворяют три значения параметра а: 0; ±1.
Проверим достаточность этих условий.
Пусть а — 0, тогда система (1) имеет вид
х3 = 1/2
ГЕ3 + Ху2 = 1
X = 1/-^2 г/2 = 1/^4
х = 1/-^2
у = ±1/^,
т.е. имеет два решения, а условию (2) удовлетворяет только одно из них.
176
При а = -1 система (1) равносильна системе
( х3 + у3 = О Г (ж + 2/)(®2 - ху + У2) — О
[ а?3 — х2у + ху2 = 1 [ х(х2 — ху + у2) = 1
Г х = 1/7з t 3/ = -1/7з, т.е. имеет одно решение, которое удовлетворяет условию задачи. При а = 1 система (1) равносильна системе
Г х3 - у3 = 2 Г х3 - у3 = 2
[ х3 + х2у + ху2 = 1 [ 2х(х2 + ху + у2) = х3 — у3
Г (я - У)(х2 + ху + у2) = 2
I (ж + у)(х2 + ху + у2) = О ( х3 — у3 — 2 ( х = 1
I х = -у I у = -1,
т.е. имеет одно решение, которое удовлетворяет условию задачи. Таким образом, из трех значений параметра а только а = ±1 являются решением задачи.
Ответ: ±1.
Задача 17 (экономический факультет, 1990). Найдите все значения параметра а, при которых система
( (3 - 2у/2)У + (3 + 2у/2)У - За = х2 + б® + 5
< у2 — (а2 — 5а + б)®2 = 0 (1)
[ — б х О
имеет единственное решение.
Решение. Исходная система является четной по переменной у, так как
(з - 275) ’’ = ----1—У =------- г , = (з + 275)’,
' (3 - 2у/2)у (3 - 272) (3 + 2^2) ' '
аналогичным образом получаем
(з + 275) ’ =------!—у = (з - 2л/2У
7 (3 + 272)’ \ /
и (~УУ — У2- Поэтому для единственности решения (®о;?/о) системы (1) необходимым условием является равенство уо = 0.
12 Методы реш. задач
177
При у = 0 система (1) имеет вид
х2 + 6х + 3(1 + а) = О
(а2 — 5а + 6)ж2 = О
—6 х О
{а2 — 5а + 6 = О
х2 + 6х + 3(1 + а) = О
—6 х О
а = —1 ( а = 2 f а = 3
V <; V
х — О [ ® = — 3 [ х Е 0.
Проверим достаточность при а = — 1 иа = 2. При а = 2 система (1) имеет вид
———+ (3 + 2л/2) — х2 + 6ж + 11 Г х — -3
< (3 + 2у 2) <=> <
к У2 = о, -6 X О I 2/ = °.
т.е. имеет единственное решение.
При а = — 1 система (1) имеет вид
/ (idw+(3+w=x2+Sx+2
[ у2 = 12ге2, —6 х 0.
(2)
В левой части системы (2) стоит сумма двух положительных взаимо-обратных чисел, которая по неравенству о среднем арифметическом и среднем геометрическом для всех у не меньше двух, причем
-—^-=^ + (3 +W = 2<^(3 + 2vz2)±’ = 1^!Z = 0.
(3 + 2у2)
В правой части этого же уравнения стоит квадратичная функция
/(ж) = х2 + 6х + 2,
для которой при всех х Е [—6; 0] выполняется неравенство f(x) 2, причем f(x) = 2 при х = — 6 и х = 0. Поэтому первое уравнение системы (2) может иметь решение на множестве х Е [—6; 0] только при у = 0 и х = — 6 V х = 0. Непосредственная проверка показывает, что только единственная пара х = 0, у = 0 является решением.
Ответ: —1, 2.
178
Задача 18 (механико-математический факультет, 1966). Найти все
значения а и Ь, при которых система
xyz + z = a
< xyz2 + z = b
x2 + у2 + z2 — 4
(1)
имеет только одно решение.
Решение. Заметим, что если (я?о; Уо', го) ~ решение данной системы, то (—х0; —г/о; го) также является решением системы (1). Поэтому единственным решением системы (1) может быть только (0; 0; го). Но при х = у = 0 исходная система имеет вид
z = b
<=> z = a = b = 2 V z — a — b — —2.
Проверим достаточность этих условий. При a — b = 2 система (1) приобретает вид
xyz + z = 2
< xyz2 + z = 2 (2)
х2 + У2 + z2 = 4
и имеет более одного решения: например, при z = 1 из системы (2) получаем
ху = 1
х2 + У2 = 3
У = 1/х
х4 — Зх2 + 1 = 0
т.е. четыре различных решения. Поэтому a = b = 2 не удовлетворяет условию задачи.
При a = b = — 2 система (1) принимает вид
xyz + z — — 2 xyz2 + z = —2 re2 + у2 + z2 — 4
xyz + z = —2
z2 + z — 2 = 0
V z = 1.
(3)
=+ z = -2
x2 + y2 + z2 = 4
12*
179
При z = — 2 получаем систему
ху — О з?2 + у2 = О
<=> х - у = О,
которая имеет единственное решение (0;0;— 2).
При z — 1 система (3) принимает вид
ху = — 3 ( ху = — 3 Г z £ 0
z2 + у2 = 3 ' t (z + у)2 = — 3 ?! t у £ 0.
Поэтому только при а = b = — 2 система (1) имеет единственное решение х = у — 0, z = —2.
Ответ: а — b — —2.
Задача 19 (экономический факультет, отделение кибернетики, 1977). Найти все значения параметра а, при каждом из которых система уравнений
Г z2 + у2 = 2(1 + а)
t (я + у)2 = 14
имеет два решения.
Решение. В силу четности и симметричности уравнений по переменным х и у для каждого решения (zq>; г/о) системы (1) пары чисел (—z0;- Уо), (уо',хо) и (—г/о; также будут являться решениями. Заметим, что решения (zo; Уо) и ( — £о; ~Уо) должны быть различны, так как в противном случае zq = уо = 0 и второе уравнение системы (1) не удовлетворяется. Различными должны быть и решения (zq; г/о) и (—уо',~ zo), иначе zq + уо = 0, что опять противоречит второму уравнению системы (1). Поэтому система (1) имеет только два решения лишь в том случае, если пары (—zo;— уо) и (—уо',— zo) совпадают, т.е. при zq = уо-При z = у система (1) имеет вид
z2 = 1 + a 4z2 = 14
a = 5/2
z = ±772,
т.е. необходимым условием является равенство a = 5/2. Проверим достаточность этого условия.
При a — 5/2 исходная система принимает вид
х2 ± у2 = 7
(z ± у)2 - 14
х2 ± у2 = 7
(z - у)2 = О
180
у=х
х = ±УТ/2, то есть имеет именно два решения.
Ответ: 5/2.
Замечание. Напомним, что некоторые задачи на использование свойств четности функций и симметричности переменных были разобраны в п. 1.5 первой главы.
6.5. ЛОГИЧЕСКИЕ ЗАДАЧИ НА КОЛИЧЕСТВО РЕШЕНИЙ
— На что мне безумцы? — сказала Алиса.
— Ничего не поделаешь, — возразил Кот. — Все мы здесь не в своем уме — и ты, и я.
Л.Кэрролл. Алиса в стране чудес
Задача 20 (экономический факультет, отделение политэкономии, 1984). Найти все значения параметра а, при каждом из которых ровно одно решение неравенства
\/dA + а2 — а — 1 х3 — \/а3 + а2 • х2 + \/а4 — а2 • х — а2 0 (1)
удовлетворяет условию
а х 2а + 1. (2)
Решение. ОДЗ параметра а задается системой
а3 + а2 — а — 1 0 (а — 1)(а + I)2 <С О
а3 + а2 0 < а2(а+1)^0
а4 — а2 0 а2(а — 1)(а + 1) <С О
а = — 1 V а > 1
<=> а = — 1 V а 1. (3)
а — О V а <С — 1 V а 1
Проверим достаточность условий (3). При а = — 1 неравенство (1) принимает вид — 1 <С О, которому удовлетворяет любое х. Однако в этом
181
случае условие (2) дает — 1 <С х <С — 1 <=> х = — 1 — единственное значение. Следовательно, а = — 1 удовлетворяет условию задачи.
При а > 1 справедливо равенство а = у/а2, а неравенство (1) можно
переписать в виде
x2Va + 1 [ху/а2 — 1 — а) + а [ху/а2
1 - а) < О
<=> (х\/а2 — 1 — а) (а?2\/а + 1 + а) О
<=> (ху/а2 — 1 — а) <С О <=> х <С (4)
\ / Va^T к ’
По условию задачи должно существовать единственное х, удовлетворяющее неравенству (4) и условию (2), что возможно лишь в том случае, когда правый конец полуинтервала (—оо; а/д/а2 — 1] совпадает с левым концом отрезка [а; 1 + 2а], т.е. когда справедлива система
При а = 1 из неравенства (1) получаем \/2 • х2 —1, что справедливо для всех х, а условие (2) дает: 1 х 3, т.е. последнему условию удовлетворяет бесконечно много решений неравенства (1).
Ответ: —1; у/2.
Задача 21 ('механико-математический факультет, 1987). Найти все пары значений а и Ъ, для которых система
Г х2 - у2 + а(х + у) = х - у + а
[ х2 + у2 + Ъху —1 = 0
имеет не менее пяти решений (х;у).
Решение. Исходную систему можно привести к виду
(ж - У + а)(ж + у - 1) = 0 х2 4- у2 + Ьху —1 = 0
У = х + а
(Ь + 2)z2 + а(Ъ + 2)а? + (а2 — 1) = 0
У = 1 - х
(2 — Ь)х2 + (Ь — 2)а? = 0.
(2)
182
Для того чтобы система (1) имела не менее пяти решений, необходимо, чтобы хотя бы одна из систем совокупности (2) имела не менее трех решений. А это возможно только при выполнении равенств
Ь + 2 = а(Ь + 2) = а2 - 1 = 0 b = -2, а = ±1 (3)
или 2 — b — b — 2 = 0 <==> b = 2, а = г Е R, (4)
когда квадратные уравнения в совокупности (2) превращаются в тождества 0 = 0 для всех х.
Проверим достаточность условий (3) и (4). При b = — 2 и а = ±1 система (1) равносильна системе
( (х — у ± 1)(ж + у — 1) = 0 Г х = Г1 Е R
1 (х — у — 1)(ж - у + 1) - 0 [ у = х ± 1,
т.е. имеет бесконечно много решений.
При b = 2 и а = г Е R система (1) равносильна системе
( (х - у + г)(я + у - 1) = 0 Г X = 7’2 Е R
I (х + у + 1)(к + у - 1) = 0 1 у = 1 - х,
т.е. тоже имеет бесконечно много решений.
Ответ: (а = — 1; b = —2), (а = 1; b = — 2), (а = г; b = 2)r Е R-
Задача 22 (химический факультет, 1986). Найдите все значения а, при каждом из которых система
Г х/|у + з| = 1 - л/вд
1 16а — 9 — бу = 25ж2 + у2
имеет ровно четыре различных решения.
Решение. С помощью замены переменных и = 0 и
v = yj\y -|- 3| 0 приведем систему (1) к симметричному виду:
U + V = 1
< и4 + v4 = 16а
(2)
и 0, v 0.
Подчеркнем, что каждой паре строго положительных значений и > 0, v > 0 соответствует ровно четыре различные пары значений исходных переменных х, у:
и2 „9
а? = ± —, y = -3±v,
6
183
Поэтому если при некотором значении параметра а исходная система (1) имеет ровно четыре решения, то симметризованной системе (2) не может удовлетворять ни одна пара (и; и), для которой
и > О, -у > 0 и и v,
(3)
так как в противном случае симметричной паре (и; у) соответствовало бы еще четыре решения системы (1) в исходных переменных. Поэтому искомые значения параметра а должны обеспечивать такие решения (и; и) системы (2), для которых нарушались бы условия (3), т.е. выполнялось хотя бы одно из равенств:
и = 0 либо v = 0, либо и = v > 0.
(4)
Из равенства и = 0 или v = 0 и системы (2) следует, что должно выполняться условие а = 1/16. При и = v > 0 необходимо, чтобы выполнялось условие а = 1/128.
Проверим достаточность условий, вытекающих из равенств (4), т.е. а = 1/16 V а = 1/128.
При а = 1/16 система (2) имеет только два решения (1;0) и (0; 1), которым соответствует ровно четыре решения системы (1):
Других решений система (2) иметь не может, так как при u,v Е (0; 1) выполняется и4 + и4 < и -f- v и равенства
и4 + v4 = 16а = 1 = и + v
184
невозможны.
При а = 1/128 система (2) имеет единственное решение (1/2; 1/2), которому соответствует ровно четыре различных решения исходной системы (1). Других решений система (2) иметь не может, так как для любого симметричного решения системы (2) вида и — v величина z = и — 1/2 = 1/2 — v должна удовлетворять условию
IV /1 V 1 о 2 4
z 4- - ) 4-1— — z) — — 4- 3z z z — 0.
2 / \ 2 J о
Таким образом, при а = 1/16 и а = 1/128 система (1) имеет ровно четыре различных решения.
Ответ: 1/16; 1/128.
Задача 23 (факультет ВМиК, 1972). Найти все значения параметра а, при которых неравенство
tg2 (sin д/Этг2 — х2} — 2а tg (sin а/9тг2 — 4- a 4- 2 0 (1)
имеет и притом конечное число решений. Для каждого такого а указать все решения неравенства.
Решение. ОДЗ неизвестной х задается неравенством
9тг2 — х2 0 |л| <С Зтг —Зтг <С х <С Зтг.
Абсолютная величина синуса при этом не превышает единицы:
|sin \/9тг2 — z2| 1 —1 sin \/9тг2 — х2 1,
а значения тангенса удовлетворяют двойному неравенству
-tg 1 tg (sin ’у/Э71'2 — z2) 1-
Введем новую переменную z = tg (sin л/9тг2 — х2), тогда неравенство (1) будет равносильно системе
z2 — 2az 4- a 4- 2 0 ___ f а — y/D <С z а 4- VD
-tgl^z^tgl t- tgl^z^tgl,
где дискриминант квадратного трехчлена D должен быть неотрицателен, т.е.
D = а2 — а — 2^0 a <С — 1 V а 2. (3)
185
Неравенства (3) являются необходимыми условиями для существования решения системы (2) или исходного неравенства (1). Проверим их достаточность.
Рассмотрим сначала случай, когда дискриминант
D = О а = — 1 V а = 2.
При а = 2 имеем
z = tg fsin л/9тг2 — а?2) = 2
sin д/Этг2 — а?2 = arctg 2 4- тгп, n Е Я.
Докажем, что последнее уравнение не имеет решений при всех п Е Z. Так как arctg - возрастающая функция, то верны цепочки неравенств
arctg 2 > arctg \/3 = тг/З > 1 при п = О
и arctg 2 — тг < тг/2 — тг = —тг/2 < — 1 при п = — 1,
что и доказывает отсутствие корней приведенного выше уравнения (так как остальные значения п, очевидно, не годятся в силу ограниченности синуса).
При а = — 1 имеем
z = tg ^sin х/9тг2 — а?2) = — 1
sin л/9тг2 — я2 = —7г/4 4- тг&, к Е Z.
Очевидно, что к = 0 => sin л/9тг2 — а?2 = — тг/4, и поэтому последнее уравнение будет равносильно уравнению
х/9тг2 — х2 = (—l)n+1 arcsin — 4- тт, т Е Z,
4
которое в силу ОДЗ и неотрицательности арифметического корня имеет решения только при т = 1 и т = 2:
х = ±v 9тг2 — {тг 4- arcsin —
V \ 4>
\/9тг2 — х2 = 2тг — arcsin —
4
/ ( .It
х = ±1/ 9тг2 — ( 2тг — arcsin —
V \ 4
186
Таким образом при а = — 1 неравенство (1) имеет четыре решения, г.е. конечное число.
При D > 0 <=> а < — 1 V а > 2 из системы (4) следует следующий вывод: чтобы неравенство (1) относительно х имело конечное число решений, необходимо, чтобы система (4) имела единственное решение. Это возможно лишь в случае, когда отрезки [а — \/Z); а 4- и [—tg 1; tg 1] имеют только одну общую точку, т.е. необходимо, чтобы выполнялось одно из двух равенств:
а. - SD = tg 1 или а + y/D = — tgl.
(4)
Заметим, что первое из соотношений (4) может выполняться лишь при а > 0, а второе - при а < 0.
Проверим достаточность полученных условий.
Решение первой системы имеет вид
а — у/а2 а>2
. _ tgal + 2
2tgl-l’
а — 2 = tg 1
так как для всех a G (0; тг/2) выполняется
а —2=—
2tgl - 1
При а — (tgJl + 2)/(2tg 1 — 1) получаем уравнение
z — tg Г sin х/Этг2 — а?2] -= tg 1 <=>
sin v9tf2 — х2 = 1
л/9тг2 - а?2 = | + 2%/, I G Z,
которое имеет решение только при I = 0 и I = 1:
х/Этг2 — а?2 — 7J-
х/9тг2 - а?2 -
Вторая система будет равносильна системе
а + \/а2 — а — 2 = — tg 1 а < —1
_ tg 21 + 2
а ~ 2tg 1 + 1
а < —tg 1 < —1,
187
которая решений не имеет, так как полученное значение
tg2l + 2
а = — ——> — 1 (докажите это самостоятельно!).
Ответ: при а = — 1
/ / \ тг \ 2 / ' тг \ 2
х = ±\ 9т2 — тг + arcsin — ) , х = ±\ 9тг2 — 12% — arcsin — ) ;
V х 4/ V х 4/
л/32 л/ГТ
при а = (tg2l + 2)/(2tg 1 — 1) х = ±—— %, х = ±—— тг.
Задача 24 (механико-математический факультет, 1980). Найти все значения параметра а, при каждом из которых неравенство
log1/a (\/;г2 + шт + 5 + • log5 (х2 + ах + 6) + loga 3^0 (1)
имеет одно решение.
Решение. ОДЗ параметра а задается соотношением 0 < а / 1. Поэтому исходное неравенство можно записать в виде
log3(v^+ 1) •log5(u+ 1) - 1 < 0
log3 а
где и = х2 + ах + 5 0.
При 0 < a < 1 неравенство (2) на множестве и 0 равносильно неравенству
log3 (у/й + 1) • log5 (и 4-1) 1.
Заметим, что функция
f(u) = log3 (у/й + 1) • log5 (и + 1)
на множестве и 0 определена и монотонно возрастает, так как каждый из ее множителей неотрицателен и также монотонно возрастает. Кроме того, /(4) = log3 3 • log5 5=1, поэтому при и 0 неравенство
/(и) /(4) <=> и = ж2 + аа?-|-5^4
<=> х2 + ах + 1 0,
а последнее неравенство имеет бесконечно много решений для любого a G (0;1).
188
При а > 1 неравенство (2) равносильно неравенству
log3 (д/й + 1) • log5 (и + 1) 1,
которое с учетом ОДЗ (и 0) и свойств монотонности функции /(и) в свою очередь равносильно двойному неравенству
Система (3) может иметь решения лишь при условии неотрицательности дискриминанта второго уравнения, т.е. при
D2 = а2 - 4 0 а > 1
Проверим достаточность этого условия.
При а > 2 различные корни
второго неравенства системы (3) удовлетворяют и первому неравенству, так как
.т2 + axi + 5 = (х2 + ахг 4-1)4-4 — 4>0 и з?2 + ах2 + 5 = (а?2 + ах2 + 1) + 4 = 4 > 0.
Следовательно, система (3) (и исходное неравенство (1)) при а > 2 имеет по крайней мере два решения a?i и а?2-
При а = 2 второе неравенство системы (3), а значит сама система и исходное неравенство (1), имеет единственное решение х = — 1.
Ответ: 2.
189
6.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
— Откуда вы знаете, что я не в своем уме? — спросила Алиса.
— Конечно, не в своем, — ответил Кот.
— Иначе как бы ты здесь оказалась?
Л.Кэрролл. Алиса в стране чудес
Задача 1 (экономический факультет, отделение кибернетики и планирования, 1988). Найти все значения параметра а, при которых любой корень уравнения
3 sin3 х 4- (а — 2)(2а — 5) cos3 х — 2(а — 2)2 cos х = О является корнем уравнения
logs (Zctgx + 3) - log1/5 (6 - ctgx) - i logys (Sctgx + 2) = 1
и, наоборот, любой корень второго уравнения является корнем первого уравнения.
Задача 2 (механико-математический факультет, 1968). Найти все те числа а, при каждом из которых всякий корень уравнения
2 sin7 х = (1 + sin тга) sin х + a sin3 х
является корнем уравнения
(a — 1)(1 + cos2 z) + 2 sin6 х = 2 sin2 х + 2(а — I)3
и, наоборот, всякий корень второго уравнения является корнем первого уравнения.
Задача 3 (химический факультет, 1987). Найти все значения q, при каждом из которых множество решений неравенства
(д — x2)(q + 2а? — 8) < О
не содержит ни одного решения неравенства
х2 < 4.
190
Задача 4 (механико-математический факультет, 1992). Найти все значения параметра Ь, при каждом из которых система неравенств
Ьх2 — 4ху 4- 2у2 3
< п 7 о ? 26 - 1
7z2 4- 4ху 4- 2у2 - -
26 4- 5
имеет решение.
Задача 5 (филологический факультет, 1992). Найти все значения параметра Ь, при которых система уравнений
( Ьх2 4- 2,Ьх 4- у 4- 36 — 3 = О t by2 4- х — 6by 4-1164-1 = 0
имеет единственное решение.
Задача 6 (экономический факультет, 1990). Найти все значения параметра а, при которых система
(2 - л/3)1 4- (2 4- л/З)* - 5 = a - 2у 4- у2
< х2 4- (2 — a — a2)y2 = О
. О^т/^2
имеет единственное решение.
Задача 7 (биологический факультет, 1991). Найти все значения параметра т, при которых система
1(х 4- 2)2 4- 2(т 4- 2у) 4- у2 4- z2 = О
2 4- (т 4- 2}xyzyJ 1 — 2ху (msin2 z4-i4- у) = О
(ху 4- l)tg(z 4- у) 4- cos (х - у) = 1
имеет единственное решение.
Задача 8. (Механико-математический факультет, 1980). Найти все значения параметра а, при каждом из которых уравнение
4-|г-а| 1оёуз (х2 - 2х 4- 3) 4- 2-2+2х . log1/3 (2|х - а| 4- 2) = О имеет три решения.
Задача 9 (химический факультет, 1986). Найти все значения а, при каждом из которых система
г 1 -
I 49?/2 4- х2 4- 4а = 2а? — 1
имеет ровно четыре различных решения.
191
Задача 10 (механико-математический факультет, 1987). Найти все пары значений а и Ь, для которых система
Г 6z(2z - у) + (у - l)(2z - у) = Ьх + у - 1
[ 4ж2 + у2 + аху — 1 = 0
имеет не менее пяти решений (т;у).
Задача 11 (факультет ВМиК, 1972). Найти все значения параметра а, при которых неравенство
у/Зтг — 2|х| • [ctg2(cos х) + a ctg(cos х) + О
имеет и притом конечное число решений. Для каждого такого а указать все решения неравенства.
Задача 12 (экономический факультет, отделение кибернетики (старая программа), 1978). Найти все значения параметра а, при каждом из которых неравенство
а2 + 2а — sin2 х — 2а cos х > 2
выполняется для любого числа х.
Задача 13 (факультет психологии, 1978). Найти множество всех пар чисел (a;b), для каждой из которых при всех значениях х справедливо равенство
1) аех + 6 = еах +
2) a sin х + b = sin (ах + 6).
Задача 14 (экономический факультет, отделение кибернетики (новая программа), 1978). Найти все значения параметра а, при каждом из которых функция
f(x) = sin 2х — 8(6 + 2) cos х — (462 + 166 + 6)ж
является убывающей на всей числовой прямой и при этом не имеет критических точек.
Задача 15 (механико-математический факультет, 1966). Найти все значения а, при которых система
( (х2 + 1)“ + (62 + if = 2
I а + Ьху + х2у — 1
имеет хотя бы одно решение для любого значения 6.
192
Задача 16 (факультет ВМиК, 1990). Найти все значения параметра Ъ, при которых для любых значений параметра а неравенство
/х\ 7а + 106 — 11 9 п 9
log4 (77)-------=------х2 - 4$a2 + 21а - 1 <
\ 16/ 5
, /1б\ 7а+106-21 2 л 2 nr
log4 —-----------------х2 + (14а — 2)z + 49а2 — 35а + 3
\ х ) 5
имеет хотя бы одно решение.
Задача 17 (механико-математический факультет, 1989). Найти такие значения 6, что при любом значении а система
2(1 + |т/|)6 + (а2-2а + 2)2 = 3
zy(z + a — 1) = 262 — 36 + 1
имеет не менее одного решения (?/; z).
6.7. УКАЗАНИЯ И ОТВЕТЫ
1. 3.
2. 1; 2.
3. q 0, q 12.
4. 6 < -5/2.
5. 0; ±1/272.
6. -3; —2.
7. -2.
8. 1/2; 1; 3/2.
9. -1/32; -1/4.
10. а = —4, 6 = г G R] а = 4, 6 = 2.
11. При а = —2ctg 21 • (1 + 2ctg 1) х = 0;
при а = 2 х = ± arccos (—тг/4), х = ± (2тг — arccos (—тг/4)).
12. а < (2 + Тб) , а > 2.
13. 1) а = 1, 6 = 0.
2) а = 1, 6 = 0; а = —1, 6 = 0; а = 0, 6 = 0.
14. 6 < (з + Уз), 6 > 7з- 1.
15. 1.
16. 6 < 3/2.
17. 1/2; 1.
13 Методы реш. задач
193
ГЛАВА 7
РАЗНЫЕ ЗАДАЧИ
7.1. ПАРАМЕТРЫ В ТРИГОНОМЕТРИЧЕСКИХ ЗАДАЧАХ
— Опять о чем-то думаешь? — спросила Герцогиня и снова вонзила свой подбородок в Алисино плечо.
— А почему бы мне и не думать? — отвечала Алиса.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (физический факультет, 1968). Для каждого числа а найти все решения уравнения
। Iсts2 т “I- actsх 1 /1\
I COS Ж | & 0=1. (1)
Решение. ОДЗ уравнения (1) задается системой неравенств
sin 2х О sin х / О
2х тгп, п Е Z х тгк, к Е Z
<=> х тгп/2, п Е Z.
Поэтому уравнение (1) равносильно совокупности систем
cos х = ±1
ctg2х + actgх = г E'R
х тгп/2, п Е Z
{cos х О
ctg 2х + actg х = О
х ф тгп/2, п Е Z
( cos 2х + 2a cos2 х = О V
t х / тгп/2, п Е Z
х — тгк, к Е Z
< х тгп/2, п Е Z
ctg 2х + actg х = г Е R
( (1 + a) cos 2х + a = О
<=> 160 V , ,
( х тгп/2, п Е Z.
13
195
Заметим, что а 7^ — 1 в силу несовместности ОДЗ и уравнения cos 2х = 1. Поэтому уравнение системы (2) можно записать в виде
а
cos 2х =---------
а + 1
,1 / а \ _
х = ±- arccos----------- + 7гю, к G Z,
2 у а + 1J
при
Ответ:
1 при а --
1
при а > —-
х £ 0,
1 ( а \
х — ±- arccos----------+ тг&, k G Z.
2 \ a + 1J
Задача 2 (филологический факультет, 1985). Для каждого значения b решите уравнение
3 cos х sin 6 — sin х cos b — 4 cos b = ЗУЗ. (1)
Решение. Использовав общую схему введения дополнительного аргумента, уравнение (1) цепочкой тождественных преобразований можно привести к виду
3 cos х sin b — sin x cos b — 4 cos b = ЗУЗ <=>
3 sin b cos b ЗУЗ + 4 cos b
—у ----- cos x . = sin X = —. =
vl + 8sin26 v 1 + 8 sin2 b vl + 8sin26
, ч ЗУЗ + 4 cos b
<=+ cos (x + = __ (
V 1 + 8 sin2 b
где дополнительный аргумент <p определяется одним из соотношений:
(2)
cos b 3 sin b 1 ,
W = 7 cos^ = =, tgy> = -ctgb.
vl + 8sin2b vl + 8sin26 3
Правая часть уравнения (2) положительна при любых значениях параметра 6, поэтому это уравнение имеет решение, если только выполняется неравенство
Зл/З + 4 cos b \/1 + 8 sin2 b
1 <=> ^Зл/З + 4 cos б)
1 + 8 sin2 b
<=> 24 cos2 b + 24^3 cos 6+18^0 <=> (2\/б cos b + Зл/^ 0
196
<=> cos b
При b = 5тг/6 + 2тгп
л/ 3 тг
<=>6 = ±^ + 27гп, nEZ.
2 о
sin b = 1/2 и уравнение (1) равносильно уравне-
нию
V3 1 .
— COSI+ jSinx = 1
cos
x = —|- 2тг&, к E Z.
6
При b — —5тг/6-|-27гп sin 6 = —1/2 и уравнение (1) равносильно уравнению
л/3 1 .
cos X — - sin X = — 1
(
cos z + — ) = -1 \ б /
<=> x = — + 2тг&, к E Z. о
Ответ: при b ±---------1- 2тгп, п Е Z хЕ0,
6
, 5тг Л тг
при b = — + 2тгп х — — + 2тгю, n, к Е Z, 6 б
5тг 5тг
при b = —— + 2тгп х —--------1- 2тг&, п, к Е Z.
6 6
Задача 3 /механико-математический факультет, устный экзамен). При каких значениях параметра а уравнение
1 + sin2 ax = cos х
(1)
имеет единственное решение?
Решение. Так как 1 + sin2 ax 1 для любых а и х, а — 1 cosz 1, то уравнение (1) может иметь решение, если только оно равносильно системе
1 + sin2 ax = 1
cos х — 1
{sin2 ax = 0 f ax = тгп, n E Z
cos x = 1 [ x = 2rk, k E Z.
Тогда тгп — 2тг&, n,k E Z => a = т.е. при рациональных значениях параметра а уравнение (1) имеет бесконечно много решений. Единственное решение исходное уравнение будет иметь при a 2n/k, n,k Е Z, т.е. когда a - любое иррациональное число.
Ответ: a - иррациональное число.
197
Задача 4 (экономический факультет, 1991). Найдите все значения' параметра q, при которых уравнение
i
sin2 х + (q — 2)2sin х + q(q — 2)(g — 3) = О (1)
имеет на отрезке [0; 2т] ровно три корня.
Решение. Замена переменной sin г = z, |z| 1 приводит уравнение (1)
к квадратному уравнению относительно z. Пусть z^ и z2 - корни этого уравнения, тогда по теореме Виета имеет место система
' Z! + z2 - ~(q - 2)2
< 2^2 = q(q - 2)(g - 3) (2)
ч -1 zi; z2 1.
Если корни z\ и z2 удовлетворяют неравенству 0 < |zi|, |z2| < 1, то каждому значению z± и z2 по общей формуле
£1,2 = (~1)П arcsin (21,2) + тгп, n Е Z,
соответствует ровно два значения х Е (0;2тг), т.е. четное число корней уравнения (1).
Поэтому на отрезке [0; 2тг] исходное уравнение может иметь три корня только в случаях, когда z^ = sin г = 0; ±1.
При ci = 0 из системы (2) получаем
q(q — 2)(g — 3) = 0 <=> q = 0 V g = 2 V q = 3.
При q = 0 или q — 2 уравнение (1) равносильно уравнению sin г = 0, которое на отрезке [0; 2тг] имеет ровно три корня:
П =0, х2 = т, хз -- 2т.
При q = 3 уравнение (1) равносильно уравнению
sin х (sin х + 1) = 0 <=> sin х = 0 V sin г = — 1,
т.е. имеет на отрезке [0; 2т] четыре корня.
При zi = 1 из системы (2) получаем
z2 = -1 - (q - 2)2 < -1 при q / 2,
т.е. уравнение (1) имеет единственный корень Хх = т/2 Е [0;2т].
198
При zi = — 1 из системы (2) получаем
22 = -q(q - 2)(g - 3) = 1 - (q - 2)2 = (q - 1)(3 - q)
q = 3 V
Как было показано выше, q = 3 не З-л/5
q = —-— не удовлетворяет условию
удовлетворяет условию задачи, а
|z2| < <=> q2 - 4g + 2^0 <=> 2-У2^д^2 + \/2. (3)
и 3 +
Непосредственная проверка показывает, что q = —-— удовлетворяет условию (3), поэтому при этом значении параметра q уравнение (1) имеет три корня на отрезке [0; 2тг].
3 4- \/5
Ответ: 0; 2; —-—.
Задача 5 (геологический факультет, 1979). Найти все значения параметра а, при каждом из которых уравнение
о 6 ж 9л/3
г2 + -== 4- 4-36 = 0
V sin a cos a
(1)
имеет единственное решение.
Решение. ОДЗ параметра а задается системой
Г cos а Г а тг/2 4-7rfc, k£Z
[ sin a > 0 I 2тгп < a < тг 4- 2тгп, n Е Z.
Для всех а, удовлетворяющих системе (2), уравнение (1) имеет единственное решение, лишь когда его дискриминант
о=^__звЛ_ 4 36 = 0 sm a cos а
<=> cos а — \/3 sin a — 4 cos а sin а = 0
• /7Г \
<=> sin-----а — sin 2a = 0
\6 /
(тг За\ / % cv\
12 - Tj C0S (12 + 2) = °
тг 2тг, , _ 5% _
<=> a = —- 4- — fc, к E Z V а = — 4- 2тгп, n E Z.
18 3 6
199
Очевидно, что для этих a cos a 0. Полагая k = 3m, k = 3m + 1 и k = 3?n + 2, m E Z, первую серию решений (3) разбиваем на три подгруппы:
т 13т 25т
«1 = — + 2тт, а2 = —— + 2тт, а3 = —— + 2тт. 1о io 1о
Так как для любого т Е Z имеем
т 13т Л . . 25т
sin от — sin — > 0, sin а<2 — sin —- > 0, sin а3 = sin —- < 0, 18 18 18
то условию задачи удовлетворяют серии а = 5т/6 + 2тп, cvi и а2.
_ 5т т 13т , ,
Ответ: — + 2тп, — + 2тт, -jg~ + 2тк, к,т, п £ Z.
Задача 6 (экономический факультет, отделение политэкономии, 1988). Найдите все значения параметра а, при которых неравенство
|3 sin2 х + 2а sin х cos х + cos2 х + а| 3 (1)
выполняется для любых значений х.
Решение. Функция, стоящая под знаком модуля, может быть преобразована к виду
/(г; а) = 3 sin2 х + a sin 2r + cos2 x + a —
= a sin 2x — cos 2x + a + 2 —
= \/a2 + 1 sin(2r — 99) + a + 2,
где дополнительный аргумент может быть определен одним из соотношений
a . 1 1
cos^ = sin 99 = , , tg9P =
ya2 + 1 va2 + 1 a
Тогда неравенство (1), которое должно выполняться при всех х, можно переписать в виде
—3 min f(x; a) max f(x; a) 3
a T 2 — \/a2 T 1 —3
а T 2 T \/a2 t"-1" 3
—5 < a < 1
a -12/5
a < 0
—7" C a 0
5
так как min f(x\a) достигается при sin (2z — 99) = —1, a max/(x; a) - при sin (2x — 99) = 1.
Ответ: a E [—12/5; 0].
200
Задача 7 (химический факультет, 1975). Найти все значения параметра Ь, при которых система
cos (?/ — &)— 2 cos х = О
log2 (by - у2) = 21og4 (-ж) - log1/2 (Зу) имеет нечетное число решений.
Решение. ОДЗ параметра b и переменных х и у задается системой
1 1 V н о V ND О V Л 'S' О О | V Л S Л о а V Л Л Н -о S
(2)
При выполнении системы (2) второе уравнение системы (1) можно записать в виде
bg2 (by ~ У2) = log2 (-Зху)
<=> у(Ь - у) + Зет/ = 0 <=> у = Зе + Ь. (3)
Тогда из первого уравнения системы (1) получим, что
cos Зг = 2 cos х <=$ 4 cos3 х — 5 cos х = О
/ 2 5\
COS Е COS Е------ = 0 <=> COS Е = О
\ V
7Г
Е = — + ТГП, п G Z. (4)
Так как согласно (2) х < 0, то в выражении (4) п < 0. Подставляя найденные значения х в выражение (3) для у, получаем
У = b + + Зтгтг, п < 0, (5)
но из (2) следует, что у > 0, а это возможно лишь при b > 0.
Рассмотрим отрицательные числа an = Ътг/Ч + Ътт, где n G Z и п < 0. Если в соответствии с формулой (5) положительные значения параметра Ь выбирать согласно одному из условий
Зтг 9тг 15тг , 21тг
—- < b < — или —— < b < ——
2 2 2 2
либо в более общем виде 3 тг 9 тг
— + 6тг& < b < — + бтгАт, 0 к G Z, то в каждом случае найдется только нечетное количество целых чисел п < 0, при которых з/ = 6 + ап>О,т.е. исходная система (1) будет иметь нечетное количество решений.
Зтг 9тг ,
Ответ: — + бтгАг < b < — + 6тг&, 0 <С к 6 Z.
201
Задача 8 (геологический факультет, отделение геофизики, 1974). Определить, при каких целых значениях к система
(arcsin х)3 + (arccos у)3 = 7Г3(А: + 1) arcsin х + arccos у = тг имеет решения, и найти эти решения.
Решение. В соответствии с определением обратных тригонометрических функций
[ТГ 7Г 1
— —; —j , (3 = arccos у Е [0; 2тг]
и
sin a = х => |х| 1, cos /? = у ==> |?/| ^ 1.
Поэтому исходную систему (1) можно записать в виде
( a3 + (З3 — 7Г3(& + 1)
[ а + (3 = тг
Г (а + /?) (о2 - а(3 + /?2) - тг3(к -ь 1)
( а + (3 = тг
( а + /3 = тг С а -Р /3 = тг
t (а + /?)2 — За/? = 7г2(& +1) t а/? = —тг2Лг/З.
Так как а Е [—тг/2; тг/2] и /3 Е [0; тг], то —тг2/2 а/3 тг2/‘2 и для цело-
численного параметра к возможны только три значения: к = 0; ±1.
При к — — 1 из системы (2) и теоремы Виета получаем, что а и (3 должны являться корнями квадратного уравнения 2 тг2 z - TTZ + — = 0, О
которое, однако, не имеет действительных корней.
При к = 1 аналогичное квадратное уравнение имеет вид о 7Г2 ТГ Л
2-_„__ = 0 Ч2=г(1±^-
Однако полученные корни не являются решением задачи, так как тг Л М
maxzli2= - (1 + Уз/ >’•
При к = 0 из системы (2) получаем, что а = 0, (3 = тг ( arcsin х = 0 ( х = 0
[ arccos у = тг [ у = — 1.
Ответ: при k = 0 х = 0, у = О', при к ф 0 решений нет.
202
Задача 9 (факультет психологии, 1991). При каждом значении пара-1
метра а — найдите все корни уравнения 2тг
/ 2г + а \ ( 2х — а \
COS I ~—7 -----------—гГ-;'' | = COS I ——7 ~—Г) , 1 .
\2х2 + 2ах + 5а2/2/ \2г2 — 2ах + 5а2/2/
(1)
Решение. Введем обозначение f(z) = -т-----т-, тогда
zl + а2
2х + а _ х + а/2 _f( а\
2х2 + 2ах + 5а2/2 (г + а/2)2 + а2 \ + 2/ ’
2х — а х — а/2 „ ( а\
--------------- — ----------------- — fix — — ) 2х2 - 2ах + 5а2/2 (г - а/2)2 + а2--%'
а уравнение (1) можно записать в виде
. f (х + а/2) + f(x - а/2) . f (х + а/2) - f (х - а/2)
sm--------------------------- sin--------------------
2 2
f (х + а/2) + f (х — а/2) = 2тгп, n G Z, f (ж + а/2) — f (х — а/2) = 2тг/с, k Е Z.
Функцию f(z) при z ф 0 можно записать в виде
р/ ч _ z _ 1 _ 1 Р , а\-1
f (z) — —2 — /"/—;—гл — ~ ।—)
zl + az a(z/a + a/z) a \a z)
В силу следствия теоремы о средних
причем
203
Поэтому для совокупности уравнений (2) имеем
к +± f ~ I к 0е+DI+к 0е - I< а 2т’
тогда в совокупности уравнений (2) п = к — 0, т.е.
/ а\ / а\
f (х + -) ± f (х - -) = О
+ а2
= О
= О
= о
„ . av5
<=> х = О V х = ±——.
Ответ: 0; ±----.
2
Задача 10 (механико-математический факультет, 1988). Найдите все значения а, при которых система
sin х sin у = 1/z2
< cos х cos у = — (х + у)2/{a — тг)2 sin (х — у) = 2(х + у)/(а — тг)г
имеет одно решение, удовлетворяющее условиям
z>0, О С у <
(1)
(2)
Решение. Введем новые переменные
и = sin х cos у, v = — cos х sin у.
Тогда
uv = — sin х sin у cos у cos х =
(g + z/)2 z2(a — тг)2
204
и
. . . 2(х + у}
и + v = sm х cos у — cos х sm у — sm (х — у) = —)-----
. \ 2
и + V \
2 /
2
Т2 = uv
и = V.
Следовательно,
и — v = sin х cos у + cos х sin у = sin (х + у) = О
<==> х + у = тгп, п £ Z. (3)
В силу условия (2) имеем sin у 0, поэтому из первого уравнения системы (1) следует, что
sin х > О
2тгт < х < тг + 2тгт, т £ Z. (4)
Из сравнения (3) и (4) и условия 0 у тг/2 получаем, что п = 2т + 1, т £ Z.
Так как z > 0, то с учетом первого и третьего уравнений системы (1) получаем, что
1 п х + у
sm х = sm у = — > 0, cos у = — cos х =-------------.
z а — тг
Следовательно, необходимо найти все значения а, при которых система
( х + у ( 7г(1 + 2т)
cos у =------- cos у ~ —----------------------------------------
а — тг I а — тг
х + у = 7г(1 + 2m), meZ ] 0 тг/2
< 0 7Г/2 I х = 7г(1 + 2m) — у, т £ Z
имеет единственное решение, т.е. неравенство
0 7Г(1 + 2m) 1
а — тг выполняется только при одном целом т.
При а > тг из неравенства (5) получаем 1 а
— - < т < ----]
2 2т
Аналогично при а < тг получаем
(5)
2тг < а < 4тг.
—2тг а < 0.
Объединяя эти неравенства, получаем ответ а £ [—2%; 0) U (2тг; 4тг].
Ответ: а £ [—2%; 0) U (2тг; 4тг].
205
7.2. ПАРАМЕТРЫ В ЛОГАРИФМИЧЕСКИХ ЗАДАЧАХ
— Обдумайте свое решение! — сказал Король присяжным.
— Нет, нет, — торопливо прервал его Кролик. — Еще рано. Надо, чтобы все было по правилам.
Л.Кэрролл. Алиса е стране чудес
Задача 11 (экономический факультет, отделение планирования и экономической кибернетики, 1977). Найти все значения параметра а, при каждом из которых уравнение
log3 (9Ж + 9а3
(1)
имеет два решения.
Решение. ОДЗ уравнения (1) определяется неравенством
Г а О
[ х = г G R.
9Ж + 9а3 > О
а < О
х > log9 (—9а3)
(2)
На ОДЗ исходное уравнение равносильно системе
а > 1/736
z £ 0
z2 - z + 9а3 = О z = Зж > О
а 1/736
z = (1 ± д/1 - 36а3) /2
а>1/736 Г а=1/736 Га<1/736
з; £ 0 V[x = - log3 2 V t Зж = (1 ± 71 - 36а3) /2.
Поэтому два решения может иметь только последняя система при а < 1/736. Однако при а 0 (1 — 71 — 36а3) <С О и существует только одно решение исходного уравнения. При a G (б; 1/73б) 1 ± 71 — 36а3 > 0, следовательно, последняя система и исходное уравнение имеют два решения:
Х1
= log3 |(1- л/1 - 36а3)
Г1
которые удовлетворяют ОДЗ. Ответ: 0 < а < 1/736-
206
Задача 12 (филологический факультет, отделение прикладной лингвистики, 1970). Найти все х, для которых |а?| 3 и которые при всех
а 5 удовлетворяют неравенству
log/on _ (х ~ 2ах) > г I Z/U> I
(1)
Решение. ОДЗ неравенства (1) при а 5 и |ж| 3 определяется систе-
мой
( а 5
I kl < 3
ж(1 — 2а) > О
к 0 < 2а — х2 ф 1
к 2а — ж2 1
а 5
< -3 х < О 2а — х2 -ф- 1,
(2)
которая должна выполняться при всех а 5, поэтому х — 3 => 2а — х2 > 1. Тогда общая ОДЗ, задаваемая системой (2), распадается на ОДЗ параметра а: а 5, и ОДЗ переменной х: — 3 < х < 0.
Исходное неравенство (1) на ОДЗ параметра равносильно системе
—3 < х < 0 ( —3 < х < 0 f —3 < х < 0
о <=> s V <
х2 + (1 — 2a)z — 2a > 0 [ 0 < 2a < z — 1
<=> х € 0 V —3 < х < — 1 <=> —3 < х < —1,
так как при а 5 корни соответствующего квадратного трехчлена будут равны:
2a-l±|2a + l| 2a-l±(2a-f-l)
zi,2 =-------------1 =-------= -1; 2a > 0.
Ответ: —3 < х < —1.
Задача 13 (механико-математический факультет, 1967). Указать все значения а, при которых уравнение
loga х + log^ a • |a + loga z| = a log^ a
имеет решение, и найти все соответствующие решения.
Решение. ОДЗ параметра и неизвестного определяются из условий
0 < а ф 1, 0 < х ф 1.
207
На ОДЗ исходное уравнение равносильно уравнению
1^ „л. 2 |а 4- loga я?| а
loga х 4---;---------1------— О
loga х loga х
<=> loga£ + 2|a + logaz| - а = 0, (1)
так как loga х 0 => х 7^ 1. Иначе из уравнения (1) следует
2|а| — а = 0 <=> а = О,
что противоречит ОДЗ параметра.
Заменой z = loga х 0 уравнение (1) приводится к совокупности двух смешанных систем:
f z2 + 2z + а = 0 ( z2 — 2z — За — О
> n v L (2)
l^a + z^O a + z < 0.
Квадратное уравнение первой системы имеет решения
zi = — 1 — л/1 — а и Z2 = — 1 + л/1 — a
при Pi = 1 — а 0 => 0 < а < 1 (с учетом ОДЗ параметра а).
Используя теоремы 1-4 из главы о корнях квадратного трехчлена и соответствующие им “картинки”, можно показать (проделайте это самостоятельно!), что случай
—а < zi < Z2 <=> a > 1 невозможен, а реализуется только случай, когда
< — а < Z2 <=> 0 < a < 1.
Тогда первая система совокупности (2) имеет единственное решение
z = л/1 — a — 1 <=> Zi = ~~ а ~~
при 0 < a < 1.
Аналогичным образом можно показать, что для второй системы случай
zi = 1 — л/1 + За < Z2 = 1 + \/1 + За < —а а < —1 также невозможен, а реализуется лишь случай
z\ < —a < Z2 <=>- 0 < a < 1.
Тогда вторая система совокупности (2) имеет единственное решение
z = 1 - л/1 + За <=> х2 = а1 ” ^1 + 3а.
Ответ: при а 6 (0; 1) ~ а ~ Ц Х2 = а^ ~ + За;
при а (0; 1) х 6 0.
208
Задача 14 (физический факультет, 1967). Для каждого значения параметра а решить уравнение
lo8|sinx|24in2I3 = ‘2'
Решение. Учитывая, что sin2 х = |sinrr|2, получаем ОДЗ исходного уравнения
О < | sin гг | 1 <=>
sin х ф О
( Sin Ге| 1
sin х ф О
sin х ±1
f х ф тгп, n G Z 7Г
<=> <=> х± -k, kez.
[ х тгт/2, т G Z 2
Используя формулу перехода к основанию 2, можно показать, что уравнение (1) на ОДЗ будет равносильно уравнению
1 2 I • I 3
log2 sinrr = —--------
2а
(2)
a > 0 ( a > О
, ... /ь^з v < ... (3)
log2 |sini| = ( log2 |sinz| =
Так как левая часть уравнения (2) на ОДЗ положительна, то а > 0; при а <С 0 г 6 0.
При х ф тгАт/2, к G Z log21 sin гг| < 0, тогда первая система совокупности (3) решений не имеет, а из второй системы получаем
| sin ГЕ I = 2_^(log2 3)/2а <=> sin X - ±2-^/(1оё2 3)/2а
х — (—l)n arcsin (±2 0°&2 3)/2а\ z,
так как для всех a > 0 справедливо неравенство
±2-\/(log2 3)/2а
= 2~^/(1оё2 3)/2а < 1 <=> -x/(log23)/2a < 0.
Ответ: при а <С 0 х Е 0,
при a > 0 х = (—1)л arcsin f±2—\/(^оё2 3)/2аА n z.
14 Методы реш. задач
209
Задача 15 (механико-математический факультет, ИП). Решить систему уравнений
Г (az)lga = (6?/)lg6
1 fclg* = a!gy
при всех возможных значениях параметров а и Ь.
Решение. ОДЗ задачи определяется неравенствами
О < а, 0 < Ь, 0 < х, 0 < у.
(2)
Логарифмируя уравнения системы (1), получаем на множестве (2) равносильную систему
lga(lga + Igz) = lgb (1gb 4- 1gy) 1g b • 1g x = 1g a • 1g у
1g а — 0 ' 1g а ± 0
lg b • 1g х = 0 V < 1 lg6 1 lgy = г— ’lg® а (3)
ч lg b (lg b 4- 1g у) = 0 *о ** < (1g2 а ~ 1g2 Ь} (1g а 4- 1g х} = 0.
Первая система совокупности (3) равносильна совокупности двух
систем < — \ н р II II b = 1 > о, п eR v < — \ Н Р II II b = г > 0
у = 1/6 (4)
k У = п > 0, Г-2 eR г 6 R.
Вторая система совокупности
(3) равносильна совокупности трех
систем
Г lg а = 1g 6 ± О
I 1g ж = 1g у
X — Г2 > О
ч Г-2 £ R
lg b = - lg a 0 О
1g У = -1g У
х = г-2 > О
г-2 € R
V < 1g ж = — 1g а О
. 1g У = - lg ъ
' lg a ± О
a = ri > 0 1 а = П > 0
а 1
b — 1/а b = г2 > 0
a = b = ri > 0 V < V т / (5)
х = г2 > 0 х = 1/а
х = у = г2 > 0
. у= 1/х < У =
где Г1, го - любые положительные числа.
Из сравнения, совокупностей систем (4) и (5) получаем итоговый ответ.
210
Ответ: при а = b = 1 х = г^, у = г2, при а = b = и 1 х — у — г2, при а = Г1 1, b = 1/а х = г?, у = 1/г2, при а = Г1 ф 1, b = Г2 х = 1/а, у - 1/6, где Г1, Г2 - любые положительные числа.
7.3. ЗАДАЧИ НА ДЕЛИМОСТЬ МНОГОЧЛЕНОВ
— Я изучал только обязательные предметы, — вздохнул Черепаха Квази... — А потом принялись за четыре действия Арифметики: Скольжение, Причитание, Умиление и Изнеможение.
Л.Кэрролл. Алиса в стране чудес
К сожалению, в последние годы делимость многочленов и теорема Безу не входят в обязательную программу средней школы. Поэтому ниже приводятся краткие сведения о делимости многочленов.
Определения. 1. Многочленом п-й степени относительно переменного х называется выражение
Pn(x) — anxn 4- an_iKn-1 4- ... 4- a2x2 + сцх + a0,
где an 0, an_i,..., a2, ai, ao ~ коэффициенты многочлена.
2. Делением многочлена Рп(х) степени п на многочлен Pm(x) степени m называется тождественное представление Рп(х) в виде
Рп(х) = Рт(х) Sn-m(x) 4- Rk(x),
где Sn-m(jP) ~ многочлен степени n — m, называемый частным от деления, а Rk(x) - многочлен степени k < т, называемый остатком.
3. Число Xi называется корнем многочлена, если оно является решением алгебраического уравнения n-й степени Рп(х) = 0:
Xi - корень многочлена Рп(х) <=>
Pn(xi) = anXi 4- an-i^i-1 4-... 4- ai^i 4- a0 = 0.
Теорема Безу. Многочлен Рп (х) при делении на (х — с) дает остаток R, равный значению данного многочлена при х — с, т.е. Pn(c) = R.
Действительно, так как Pn(x) = (х — c)Pn-i(x) 4- R(x), то при х = с получаем Рп(с) = R.
14*
211
Следствие. Для того чтобы многочлен Рп(х) делился без остатка на выражение (х — с), необходимо и достаточно, чтобы при х = с исходный многочлен обращался в нуль; т.е. число с должно быть корнем многочлена.
Представление многочлена n-й степени в виде
Рп(х) = an(x - xif1 • (х - Хг/2 •••••(£- x3)ks , Ч* ^2 Ч* • • • к3 = п,
где xi, Х2, • • •, х3 - корни многочлена, а к\, къ, -.. > к3 - кратности соответствующих корней, называется разложением на линейные множители. Подчеркнем, что подобное разложение всегда осуществимо над множеством комплексных чисел (см. следующий параграф), тогда как над множеством действительных чисел попарные произведения части линейных множителей дадут квадратные трехчлены с отрицательным дискриминантом.
Для корней г’1, хз,.. ., х3 многочлена Рп(х) (здесь каждый корень взят ; столько раз, какова его кратность) имеет место обобщенная
Теорем:а Виета. j
Х1 Ч" Х2 Ч" • • • Ч" 2'п—1 Ч" З'п — Я^_ 1/Яп
•Е 1 «Е 2 Ч” «Е1 «Ез 4“ • • • 4“ З'п — 1 ®п — Лп — з/Лп
Ч" 1 24 Ч" • • • Ч" «Еп—2*Ел— 1 — 3/Яп.
\ 2 j X 2Хз . . . Хп — | tCfi — ( 1) Я0 /Яп
Задача 16 (механико-математический факультет, устный экзамен). Один из корней уравнения
х2 Ч- рх Ч- q = 0 (1)
равен 1 + \/3. Найти р и q, если они рациональны.
Решение. Пусть Xi = 1 Ч-д/З и х2 - корни квадратного уравнения (1). Тогда по теореме Виета имеем
mi Ч- Х2 = -р
х\Х2 = q
( х2 = - (р Ч- 1 Ч- л/3)
1 g = - [р ч- 4 ч- \/3(р ч- 2)] .
Последнее соотношение можно переписать в виде
\/3(р Ч- 2) = -(р Ч- q Ч- 4).
(2)
212
Поскольку р и q - рациональные числа, то рациональными будут также выражения, стоящие в равенстве (2) в круглых скобках. Если р + 2 0 и
p+q+4 ф 0, то приходим к противоречию: рациональное число — (р+?+4) равно иррациональному числу д/3(р + 2). Противоречия не получаем, если выполняется система
( р 4- 2 = 0 ( р = — 2
1р+?+4=0 I ? — — 2.
Непосредственной проверкой можно убедиться, что при р = q = —2 второй корень уравнения (1) есть г2 = 1 — а/З.
Ответ: р = q = —2.
Замечание. В предыдущей задаче квадратное уравнение с рациональными коэффициентами по условию имело иррациональный корень Xi = 1 + л/З. В результате решения было показано, что тогда з?2 = 1 — л/З является вторым корнем исходного уравнения. В общем случае справедлива следующая теорема.
Если алгебраическое уравнение п-й степени Рп(х) = 0 с рациональными коэффициентами имеет корень вида Xi = a + by/c, где a, b и с -рациональные числа, причем Ь^О, с>0исне является квадратом рационального числа, то это уравнение имеет и корень вида х? = a — Ьу/с. (Попробуйте доказать эту теорему самостоятельно.)
Задача 17 (ПО, ОП, 1978). В уравнении
х4- + ах3 + Ьх2 + 6г + 2 = 0 (1)
один из корней равен 1 + л/З. Найти остальные корни уравнения, если a и b - рациональные числа.
Решение. Если число п = 1 + л/З является корнем уравнения (1), то многочлен
Pt(x') = х4 + ax3 + bx2 + 6х + 2
при х = 1 + л/3 обращается в нуль:
Р^ ^1 + л/З^ = ^1 + л/З^ + а ^1 + \/3^ + b ^1 + л/З^ + + б(1 + Тз) 4-2=0,
откуда получаем равенство
18 +5а+ 26 = —д/3(11 + За + 6). (2)
213
Так как а и b - рациональные числа, то из равенства (2) следует система
5а + 26 4* 18 — О
За + 6+11 = 0
а = —4 6= 1.
Сформулированная выше теорема или непосредственная проверка позволяет утверждать, что число х2 = 1 — УЗ тоже будет корнем исходного уравнения. Тогда многочлен Р^х) = х4 + ах3 + Ьх2 + 6х + 2 должен делиться на квадратный трехчлен
(ж — Zi)(z — х2) = (х— 1
- Уз) (z - 1 + Уз) =
х2 — 2z — 2.
Разделив “углом” [1] многочлен A(z) = х4 — 4z3 + х2 + 6z + 2 на квадратный трехчлен = %2 — 2х — 2:
х4 — 4z3 + х2 + 6z + 2
х4 — 2х3 — 2х2
- 2х3 + 3z2 + 6z
- 2z3 + 4z2 + 4z
- x2 + 2z + 2
- z2 + 2z + 2
0,
x2 — 2x — 2
x2 — 2z — 1
в качестве частного получим квадратный трехчлен Pz(x) = х2 — 2х — 1, КОРНЯМИ КОТОРОГО ЯВЛЯЮТСЯ ЧИСЛа £3,4 = 1 ± У2.
Ответ: х2 = 1 — УЗ, £3,4 = 1 ± У2.
Задача 18 (факультет ВМиК, устный экзамен). Найти действительные значения а и 6, при которых многочлен Pi(x) = х4 + 1 делится на многочлен Pz(x) = х2 + ах + 6.
Решение. Если многочлен Р^х) = х4 + 1 делится на трехчлен = х2 + ах + 6, то имеет место тождественное представление
Р^(х') = х4 + 1 = Рз(х) • (х2 + сх + d) = = (х2 + ах + 6)(z2 + сх + d) = = £4 + (а + c)z3 + (6 + ас + d)x2 + (ad + bc)x + bd.
Если два многочлена тождественно (т.е. при всех z) равны друг другу, то у них равны все коэффициенты при одинаковых степенях неизвестного.
214
Таким образом, получаем систему
а -|- с - 0 ( с — ~а
b 4- ас + d = О I d—1/b
be 4- ad = 0 | а (1/6— 6) = О
bd = 1 [ b — а2 4- 1/6 = О
{а = с = О
d=l/b V
62 4- 1 = 0 ?!
с = —а
d= 1/b
62-а26 4- 1 = 0
k а (1 — 62) = О
|с = —а
d= 1/b
62 = 1
а26 — 2
а = с = О < d = 1/6 k 6 £ 0
Ответ: а = ±>/2; 6=1.
Задача 19 (факультет психологии, 1970). Найти все действительные числа а, при которых уравнение
х8 4- ах4 4-1 = 0 (1)
имеет ровно четыре действительных корня, образующих арифметическую прогрессию.
Решение. Заменой z = х4 0 сведем исходное уравнение (1) к квадратному:
z2 4- az 4- 1 — 0 <=> 21,2 — а ± \/а2 — 4^ при |а| 2,
каждому значению корня которого соответствует ровно два значения х при а 0:
Следовательно, при а — 2 исходное уравнение (1) имеет ровно четыре корня:
215
которые образуют арифметическую прогрессию с разностью d, если
а?2 — = 3?1 — Х_у — Х-1 — Х-2 — d
Х-! = -X!, Х_2 - -Х2
Х2 — 3X1
<=> —40а - 41\/а2 — 4
। । 82
|а|=у
С учетом неравенства а — 2 получаем, что а = — = — 9|. Непо-
средственное решение уравнения (1) при этом значении параметра показывает, чаю действительно оно имеет ровно четыре корня (кратность каждого равна двум):
уЗ л/З
Х_2 = -V3, Х-1 = - —, Х1 = =
3,
которые образуют арифметическую прогрессию.
Ответ: —9|.
Задача 20 (механико-математический факультет, ИП). При каких значениях параметра а многочлен Рз(х) = х3 + 2х2 + а имеет кратные корни?
Решение. Пусть Рз(х) имеет один корень кратности три Xi = Х2 = Х3. Тогда, по обобщенной теореме Виета имеем систему
3xi — —2
Зх2 = 0
3 __ Л
3/1 — a
Xi G 0.
Пусть Рз(х) имеет один корень кратности два xi = Х2 и корень хз ф Хр Тогда по теореме Виета получаем систему
2xi Т хз — —2 х2 + 2х1Хз = 0 ?
х^хз — —а
хз - -2(1 + xi) xi(xi + 2х3)
2
х^хз = —а
xi — 0
< Хз = -2
а = 0
xi — 0 хз = -2 а — 0
2хз = — xi
2xi + хз = —2 х3 — 2а
' xi = -4/3
< х3 = 2/3
k а = -32/27.
216
Следовательно, многочлен Рз(х') имеет корни кратности два при а = 0 и а = -32/27.
Ответ: 0; —32/27.
Замечание. Использование понятия производной позволяет без применения обобщенной теоремы Виета отобрать кратные корни (если они есть) уравнения Рп(х) — 0 в соответствии со следующим алгоритмом [3]:
1) найти производную Рп(х);
2) найти НОД (наибольший общий делитель) многочленов Рп(х') и
3) найти корни НОД многочленов Рп(х) и P4(x‘)i тогда каждый корень этого НОД является корнем многочлена Рп(х) причем кратность корня Рп(х) на единицу больше его кратности в НОД. Если НОД равен постоянной, то уравнение Рп(ге) = 0 не имеет кратных корней.
Задача 21 (механико-математический факультет, ИП). При каких значениях параметра а уравнение х3 + ах + 2 = 0 имеет корень кратности два?
Решение. Рассмотрим многочлен Рз(х) = х3 + ах + 2. Его производная равна Р^х) = Зх2+а. Найдем НОД многочленов Рз(ге) и Рз(х)- Для этого разделим многочлен Рз(ге) на Рз(ге) с остатком:
з п 1 2 \ 2а / 3\
xd + ах 4- 2 = - х(3хг + а) + — I х -|— .
3 3 \ а /
Далее, разделим Рз(ге) на (х + 3/а), т.е. на полученный выше остаток, взятый с точностью до постоянного множителя:
Для того чтобы первый остаток (х + 3/а) был НОД Рз(ге) и -Рз(я), необходимо, чтобы остаток от второго деления обращался в нуль:
27 а -|—7 = 0 <=> а3 = —27 <=> а = —3.
а2
Таким образом, при а = —3 НОД Рз(ге) и Рз(ге) равен (х — 1), т.е. х = 1 является корнем кратности два уравнения Рз(ге) = 0. Непосредственная проверка показывает, что при а = —3 Рз(ге) = ж3 — Зге + 2 = — (х — 1)(ге2 + х — 2) = (гс + 2)(ге — I)2, т.е. действительно х = 1 является кратным корнем многочлена Рз(х).
Ответ: —3.
217
7.4. ЗАДАЧИ С ПАРАМЕТРАМИ
НА МНОЖЕСТВЕ КОМПЛЕКСНЫХ ЧИСЕЛ
— Что ты знаешь об этом деле? — спросил Король.
— Ничего, — ответила Алиса...
— Это очень важно, — произнес Король, поворачиваясь к присяжным.
Л.Кэрролл. Алиса е стране чудес
Изучение комплексных чисел входило в школьную программу в конце 60-х - начале 70-х годов. Сейчас эту тему проходят только в некоторых специализированных школах физико-математического профиля. Поэтому здесь будут даны лишь краткие сведения о комплексных числах, необходимые для решения приводимых ниже задач. Более подробно с теорией комплексных чисел можно ознакомиться по пособиям [1], [5].
Определения. 1. Множество, состоящее из выражений вида z — a + ib, где а и b - действительные числа, а мнимая единица i определяется условием г2 = —1, называется множеством комплексных чисел.
2. Действительная и мнимая части комплексного числа z — a-\-ib обозначаются соответственно
Re z = a, Im z — b.
3. Два комплексных числа Zi = ai + ib и z? = а 2 + ib называются равными, если равны их действительные и мнимые части:
*1 =- z2 <=> Д1 - а2 A bl = 62-
Заметим, что из других знаков сравнения: ф, <, ^, >, ^ - в множестве комплексных чисел имеет смысл лишь знак ф:
z\ ф Z1 <=> 0,1 ф (12 V 61 ф Ь2.
4. Комплексное число z = a + ib при b = 0 считается совпадающим с действительным числом а: а + г’0 = а <=> z = Rez. Комплексное число z = а + ib при а = 0 называется чисто мнимым и обозначается
2 = ib <=> 2 = ilm z <=> Re 2 = 0.
5. Над множеством комплексных чисел операции сложения, вычитания, умножения и деления определяются соответственно следующими
218
правилами:
Z\ + Z2 — (di + i^l) + (&2 "I" ^2) — (al "I" ^2) "I" ^(&1 "I" ^2))
Zi - z2 = (ai + 261) - (a2 + ib2) = (ai - a2) + i(&i - b2),
zx • z2 = (ai + i6i) • (a2 + ib2) = (axa2 - bxb2) + i(axb2 - a2bx),
zi _ ai + ibx _ (ai + ibi)(a2 - ib2) _
z2 a2 + ib2 (a2 + ib2)(a2 - ib2)
_ aya2 4- 61 b2 .<12^1 — aib2
a% 4- 62 Z a2 + ^2
Из этих определений арифметических действий над комплексными числами следует, что их можно проводить по правилам действий над многочленами относительно мнимой единицы г, заменяя г2 на — 1 и объединяя отдельно члены, содержащие и не содержащие мнимую единицу.
6. Для числа z — a-\-ib число z — a — ib называется сопряженным. Для операции сопряжения имеют место равенства
zr ± z2 = zT±z^, zx • z2 = z{ -z^, (zx/z2) = z^/z^.
Величина z~z = a2 + b2 есть квадрат неотрицательного числа \/a2 + b2, которое называется модулем комплексного числа z и обозначается
|z| = л/zF = \/a2 4- Ь2.
Замечание. Для действительного числа z <=> z = Re z <=> Imz — 0 понятие модуля комплексного числа совпадает с понятием абсолютной величины.
7. Тригонометрической формой записи комплексного числа z = a 4- ib 7^ 0 называется запись
z — г (cos р + i sin р),
где г = |z| = у/a2 + b2 - модуль, а угол <р 6 [0; 2тг) называется главным значением аргумента комплексного числа: <р = argz. Величина этого угла р может быть найдена из системы
a Л о
Sin<p = . . COStP — 0 < 09 < Z7T.
ч/a2 + Ъ2 Va2 + b2
8. Тригонометрическая запись комплексных чисел часто бывает полезна при операциях умножения и деления:
Zx -z2 = ТхТ2 [cos + ^2) + i sin (^1 + ^2)], — = — [cos (^1 - p2) + i sin (^1 - ^2)] •
219
Заметим, что в этих формулах углы <pi ± <р2 необязательно лежат в пределах от 0 до 2тг. Такие значения аргумента комплексного числа обозначаются
Arg z = arg z + 2тгк, к 6 Z.
В качестве следствия из правила умножения комплексных чисел в тригонометрической форме можно получить теорему Муавра
(cos <р + i sin <£>)n = cos n<p + i sin n<p.
Задача 22 (факультет психологии, 1966). Где расположены комплексные числа z — a + ib, для которых
loga|z| + loga(|z| + l) < loga (2|z|+ 5), (0 < a < 1) ? (1)
Решение. В силу условия a 6 (0; 1) модуль |z| = \/a2 + 62 > 0 и нера-
венство (1) равносильно неравенству
которое на комплексной плоскости задает множество точек, лежащих вне окружности радиуса л = ------- с центром в начале координат.
„ 1 + У21
Ответ: вне окружности радиуса--------с центром в начале координат.
Задача 23 (физический факультет, 1966). Для каждого вещественного числа а 0 найти все комплексные числа z, удовлетворяющие равенству
z\z\ + az 4- i = 0. (1)
220
Решение. Исходное равенство можно представить в виде
z (12г| + а) 4- i = О <=> z (|z| 4-а) = —г.
(2)
Гак как |г| 4- а является действительным числом, то для выполнения равенства (2) комплексное число z должно быть чисто мнимым. Пусть z — iy, тогда получим уравнение относительно действительной переменной у
J/|j/| 4- ау 4- 1 - 0 <=>
У О
у2 4- ау 4- 1 = О
VS,
I -у2 4- ау 4- 1 = О
У < О
у2 - ау - 1 = О
У =
2
так как при а 0 г/2 4- аг/ 4- 1 > 0, а второй корень уравнения у2 — ау — 1 — О У2 = (а 4- \/а2 4- 4)/2 > 0. Поэтому z = i(a — \/а2 4- 4)/2.
Ответ: i(a — \/а2 4- 4)/2.
Задача 24 (механико-математический факультет, устный экзамен). Используя понятие мнимой части комплексного числа и формулу Муавра, решить систему уравнений
sin х 4- sin у = sin /3
sin 2аз 4- sin 2у — sin 2/?
(1)
для любого значения действительного параметра /3.
Решение. Рассмотрим следующие комплексные числа:
z\ = cos х 4- i sin x, z% = cos у 4- i sin y, z3 = cos /3 4- i sin /3.
По формуле Муавра соответственно имеем
z2 = cos 2х 4- i sin 2х, z$ = cos 2y 4- i sin 2y, z^ — cos 2/3 4- г sin 2/3.
Комплексные числа z\,z3,z3 и их квадраты таковы, что соответствующие мнимые части
Im (zi 4- z2) = sin x 4- sin у, Im (z2 4- z%) = sin 2x 4- sin 2y, Im z3 = sin /3, Im z% = sin 2/3
равны какому-либо члену уравнений, образующих исходную систему. То есть систему (1) можно записать в виде
Im(zi 4- г2) = Imz3
Im (z2 4- z2) — z3
221
Рассмотрим систему уравнений с
комплексными неизвестными z\
и z2 и
комплексным параметром /з
-*1 + z2 = z3
„2 I 2 _ 2
z2 — z3
Zi+ Z2 = Z3
Z1 • z2 = 0
zi = 0
*2 = *3
V / 21 = 23
I z2 — 0.
(3)
Тогда решение системы (2) и исходной системы (1) получается из решения системы (3) простым выделением мнимой части:
Im zi = 0
Im z2 = Im z3
sin x — 0
sin у — sin /3
x = 7ГП
у = (—V)k/3 + тгк
{Imz2 = 0
Imzi = Imz3
( sin и = 0
v {
t sin x = sin (3
{ у — irk
X — (—l)n/? + 7ГП,
где параметры n и k независимо друг от друга принимают любые целые
значения.
Ответ: х^ = тгп, у\ — (—1)к /3 + тгк, п,к Е Z, х2 = (~1)п/3 + 7ГП, у2 = тгк, n,keZ.
Задача 25 (физический факультет, 1966). Для каждого вещественного числа a 1 найти все комплексные числа z, удовлетворяющие равенству
z + a|z-|-l|-|-i = 0. (1)
Решение. Представим комплексное число z в виде z = x + iy, где х 6 R, у 6 R. Тогда исходное равенство (1) можно записать в виде
х + ay (х + I)2 + у2 + i(y + 1) = 0
У + 1 = 0 С у = —1
х + ad(х + I)2 + у2 [ х + ad(х + I)2 + у2.
Так как по условию а 1, то корнями уравнения х + ау (х+1)2-Ь 1 = 0 могут быть только отрицательные значения х. Для их определения имеем систему
ayj(х + I)2 + 1 ~ -х х < 0
а2(х2 + 2х + 2) = х2 х < 0
222
(a2 — 1)ят2 + 1a2x 4- 2a2 = 0
x < 0
f a = 1 f a> 1, i<0
S V <
t x = — 1 [ (a2 — l)ir2 4- 2a2z 4- 2a2 = О
z = —(1 4- г), при 1 < а \/2
Таким образом, при а — 1
( а2 ± ал/2 — а2
*1,2 = - ---------2---:----4- г
I а2 — 1
при а > \/2 z £ 0.
Ответ: при а — 1 z = — (1 4- г);
1 л? / а2 ± ал/2 — а2 \
при 1 < а V2 zi э = - ---------5--:-----h г ;
\ а ~ 1 / при а > \/2 z £ 0.
Задача 26 (факультет психологии, 1968). При каких действительных значениях а хотя бы одно комплексное число z = x-\-iy, удовлетворяющее равенству
|z 4-л/2| = а2 -За 4-2, (1)
удовлетворяет одновременно и неравенству
\z 4- гд/21 < а2 ? (2)
Решение. Для того чтобы хотя бы одно комплексное число удовлетворяло равенству (1), необходимо, чтобы выполнялось неравенство
а2 — За 4- 2 0, <=> a 1 V а 2.
Кроме того, а О, так как при a = 0 неравенство (2) не выполняется ни при каких z. Следовательно, допустимыми для параметра а являются значения
0^a^lVa^2. (3)
Геометрическим местом точек комплексной плоскости, удовлетворяющих равенству (1), является окружность у1 с центром в точке Ci (—0) и радиусом Ri = а2 — За 4- 2, которая при a = 1 и a = 2 стягивается в
223
точку C'i. При а^О все точки, удовлетворяющие неравенству (2), лежат внутри окружности 72 с центром в точке С2 (0; —л/2) и радиусом R2 = а2 > 0. Требуется найти те значения параметра а, удовлетворяющие условиям (3), при которых хотя бы одна точка окружности 71 лежала внутри окружности 72. Легко видеть, что это возможно в двух случаях: либо когда эти окружности пересекаются (см. рис. 1), либо когда окружность 71 целиком лежит внутри окружности 72 (см. рис. 2).
Рис. 1 Рис. 2
Определив из треугольника CiOC2 длину линии центров С1С2:
G СЧ = -^)2+(</1 - и)2 == у(-75) 2 + (л)2 = VI = 2,
можно составить систему неравенств, которыми описывается каждый из этих двух случаев.
Для первого случая (рис. 1) точка А соответствует внешнему касанию окружностей 71 и 72, когда 7?i + R2 = С\С2. Тогда В и D соответствуют внутреннему касанйю окружностей 71 и 72, когда |Кх — йг| = CiC2. Поэтому окружности 71 и 72 пересекаются при выполнении системы
|Я1 - Я2| < 2 Г |2 - За| < 2
7?i + R2 2 \ 2а2 — За 4- 2 > 2
-2 < За - 2 < 2 Г 0 < а < 4/3
а(2а — 3) > 0 ( а< 0 V а > 3/2
которая не имеет решений даже без учета допустимых значений (3) для
224
параметра а. Во втором случае с учетом соотношений (3) имеем
Т?2 — 2
О ф а 1 V
а > 2
За - 2 > 2
О ф а 1 V а 2
а > 4/3 а > 2
<=> а > 2.
Ответ: а 2.
Задача 27 (механико-математический факультет, ИП). Для каждого значения параметров ntNnO^aCR решить в комплексных числах уравнение
(z + a)n = zn. (1)
Решение. Так как по условию а ф 0, то уравнение (1) не имеет корня z = 0, поэтому оно равносильно уравнению
(2)
Это означает, что число 1 + a/z является корнем n-й степени из 1. Тогда, исходное уравнение имеет (п — 1) корней z\,... ,zn_\, определяемых из равенств
а 2тгАг . . 2тгАг , , Л
1 Н----— cos-----h г sin----, я=1,2,...,п — 1.
Zk n n
Откуда получаем, что
2тгАг , . . 2тгАг
cos---------1 + г sin------
п п
( 2тгк . 2тгк\ a cos------1 — г sin-
\ n nJ
2 тгк
— cos------
п
а А . 2тт&\
- i + г dig ,
X }
т.е.
а А . 2тг&\ , , Л ,
Zk = — - 1 + г ctg----- , к = 1,2,... ,п — 1 Е N.
2 \ n J
a ( 2ттк\
Ответ: = —- I 1 + г ctg--------- , к = 1, 2,..., п — 1 G N.
15 Методы реш. задач
225
Замечание. Подчеркнем, что переход от исходного уравнения путем извлечения корня п-й степени к уравнению z + а = z не дал бы ни одного решения исходного уравнения при а / 0, так как равенства z = w и y/z = aJ/w, где z и w - некоторые комплексные числа, не являются равносильными. В комплексных числах равенство y/z = y/w означает лишь, что для каждого значения y/z найдется равное ему значение y/w и наоборот.
7.5. “СОВСЕМ РАЗНЫЕ” ЗАДАЧИ
— Зачем читать всю эту ерунду, — прервал ее Квази, — если ты все равно не можешь ничего объяснить?
Л.Кэрролл. Алиса в стране чудес
Задача 28 (факультет психологии, 1985). Найдите все значения а, при каждом из которых существует единственная пара целых чисел х и у, удовлетворяющая уравнению
Зх2 + Пху + Юг/2 = 7 (1)
и двум неравенствам
х + у > 0 и 4а2х — Зау < 0.
Решение. Исходное неравенство (1) можно привести к виду
(х + 2г/)(3г + 5г/) = 7.
Поэтому целочисленная пара (ж+2г/; Зж +5у) совпадает с одной из четырех пар (1; 7), (—7; —1), (—1; —7) и (7; 1). Следовательно, исходное уравнение имеет четыре целочисленных решения (х; у): (9;—4), (33;—20), (—9; 4) и ( — 33; 20), среди которых только первые два удовлетворяют неравенству х + у > 0. Поэтому осталось найти все значения параметра а, при которых выполняется только одно из неравенств
4 • 9а2 + 3 • 4а < 0 <=> 12а(3а + 1) < 0 <=> —- < а < 0,
О
5
4 • 33а2 + 3 • 20а < 0 12а(11а + 5) < 0 <=> -— < а < 0.
226
Следовательно, а должно удовлетворять двойному неравенству
5 1
----< а <----.
11 3
( 5 Л
Ответ: а Е I---— - I .
\ *!• /
Задача 29 (географический факультет, 1993). Найти все значения параметра а, при каждом из которых уравнение
111С-<-|-5|-2| + 1| = 3
(1)
имеет ровно три корня.
Решение. Обозначим выражение, стоящее под внешним знаком абсолютной величины, через А (г):
/1(я?) = |||я2 - а| - б| - 2| + 1.
Тогда по определению абсолютной величины уравнение (1) будет равносильно совокупности систем
Л(х) = 3 V/1(х) =-3 <=> fi(z) = ±3
Г ||к2 - а| - 5| - 2| = 2 Г|к2 - а| - 5| - 2 = ±2
' ||к2 — а| — 5| — 2| = —4 '' х Е 0
|к2 — а| — 5| = О к2 - а| - 5 = О
' |к2 — а| — 5| = 4 к2 — а1 — ^ = ±4
< => к2 — а| = 5 V к2 - ^1 = 1 V к2 — а| = 9
< => х2 — a = ±5 V х2 — a — ±1 V х2 — a = ±9
< => х2 — a i 5 V x2 — a i 1 V x2 a i 9.
Каждое положительное значение a ± b, где 6 = 1,5 или 9, даст два различных корня исходного уравнения: ^1,2 = ±\/а ± Ь. Нечетное количество корней уравнение (1) может иметь лишь в случае, когда при одном из значений b выражение a ± b = 0. Поэтому исходное уравнение будет иметь ровно три корня, когда лишь одно из возможных значений а± b > 0, второе равно нулю, остальные отрицательны. Это выполняется только при а = — 5, когда последняя совокупность из шести уравнений будет равносильна совокупности
х2 = -14 < 0 V х2 = -10 < 0 V ? = -6<0V V х2 = —4 < 0 V х2 = 0 V х2 = 4
<=> х Е 0 V х = 0 V х = — 2 V х = 2.
Ответ: —5.
15*
227
Задача 30 (геологический факультет, отделение геофизики, 1967).
Указать все действительные а, при которых не существует ни одного действительного х, одновременно удовлетворяющего неравенствам
(х — a)(ax — 2a — 3) О,
(1)
ах > 4.
Решение. Заметим, что значение а = 0 удовлетворяет условию задачи.
При а < 0 задачу можно переформулировать следующим образом: для любого значения х 4/а должно выполняться неравенство, противоположное исходному неравенству (1), т.е.
(2д । 3 \
х------] > 0. (2)
а )
С учетом условия х <С 4/а неравенство (2) будет выполняться при
4 4 2а+ 3
-< а V - < -------
a cl а
откуда при а < 0 можно получить, что
а2 <4 V 4 > 2а + 3 -2 < а < 0.
При а > 0 для всех х 4/а должно выполняться неравенство
\ < \ ( 2а + 3 \
]\х) — (х — а) х------------< 0.
\ а J
Однако при
f 4 2а+ 3
х > max < а; -----
а>о I а а
выполняется противоположное неравенство f(x) > 0. Следовательно, положительные значения параметра а не удовлетворяют условиям задачи.
Ответ: a G (—2; 0].
Замечание. Решение этой задачи допускает интересную геометрическую интерпретацию на координатной плоскости хОа. Уравнение (х — а)(ах — 2а — 3) = 0 распадается на уравнение, задающее прямую I (х — а = 0), и уравнение, задающее гиперболу 71 (а(х — 2) = 3) (см. рисунок).
Уравнение а = 4/х задает гиперболу 72, которая пересекается с гиперболой 71 только в одной точке (8; 1/2). Прямая I делит координатную
228
плоскость на две полуплоскости, при этом в верхней выполняется неравенство х — а < 0, а в нижней - неравенство х — а > 0.
Неравенства а(х — 2) > 3 и ах > 4 верны для всех внутренних точек гиперболы 71 и 72 соответственно. Две гиперболы и прямая делят всю координатную плоскость на одиннадцать областей (см. рисунок), но только для областей бд и (?ц, включая их границы, выполняются неравенства:
ах 4, а(х — 2) 3, х а.
Из рисунка видно, что только для значений а* 6 (—2; 0] на прямой а = а* не существует ни одной точки (ж; а), координаты которой удовлетворяли бы приведенным выше неравенствам.
Задача 31 (экономический факультет, отделение экономической кибернетики, 1970). Найти хотя бы один такой многочлен третьей степени
РзС1) = az3 + Ьх2 + сх + d,
чтобы при 0 х 1/2 выполнялось неравенство
1-х/2 Рз^ <0’02’
Решение. Если заметить, что при х £ [0; |] выражение
*?(х) =
1 — ж/2 1 + 2 + 4 + 8 + 16 '' ‘
229
является суммой бесконечно убывающей геометрической прогрессии с первым членом ai = 1 и знаменателем q — х/Ч 6 [0; 1/4], то становится понятно, что справедлива следующая цепочка равенств:
(2 3 4
1 + ? + Т + Т + • • •
2 4 о lo
/рЗ / 2* д»2 2»3 д,4 \
= l + T + T + ’8’A1 + 2 + T + T+i6";
T3 X2 X4 1
- Т + Т + * + Т ' 1 - z/2‘
Считая теперь, что в искомом полиноме
Р3(а?) = ах3 + Ьх2 + сх + d
а = 1/4, 6=1/2, с = 1, d = 0, легко получаем при 0 х 1/2 цепочку неравенств
Рз(*)
х4
Т
1 -z/2 96 < °’02'
Следовательно, выбранный таким образом полином действительно удовлетворяет условиям задачи.
5?3 X2
Ответ: Рз(г) = — + — + х. 4 2
Задача 32 (факультет психологии, 1983). Найти все значения параметра а, при каждом из которых система уравнений
' 2 cos х + a sin у — 1
logz (sin у) = (log2 a) • loga (2-3 cos z)
I ( 1 \
loga z + 1оёа I ~ 1 ) = 0
(1)
имеет хотя бы одно решение. При каждом таком значении а найти все решения.
Решение. системой
ОДЗ параметра а и неизвестных системы (1) определяется
' 0 < а ф 1
О < z ф 1 sin у > О
2 — 3 cos х > О < l/2a — 1 > О
' 0 < a < 1/2
О < z/ 1 sin у > О „ cos х < 2/3.
230
Последнее уравнение исходной системы можно записать в виде
l0goz = logoJ^ (2)
С учетом ОДЗ получим, что
п Ъа , л п 11 1
0<T^2Z#1 *=* 0<о<4 V 4<а<2'
Использовав формулу перехода к другому основанию, второе уравнение можно переписать в виде
logz(sin у) = logz(2 — 3 cos ®) <=> sin г/ = 2 — 3cos®.
Подставляя значение sin г/, выраженное через cos®, в первое уравнение системы, получаем, что
I”20 • 1 /44
cos® = ---— и sin и = --------. (41
2-За у 2-За V ’
Учитывая ограниченность тригонометрических функций cos®, sin у и ОДЗ, получаем, что должны выполняться следующие неравенства:
1 Г а < 2/3
0 < 7—гг" < 1 <=> 5 , , а < 1/3
2 - За ( а 1/3 V а > 2/3
1 1 -2а 2 Г а 3/5 V а > 2/3 о 1с
2-За <3<==>(а<2/3 ^а^/>
причем в ОДЗ параметра а эти неравенства будут иметь место в случае выполнения системы
1
3’
1 1
4 V 4
I 1 3
1^3’°^5
При этих значениях параметра а из соотношений (2) и (4) можно найти решение исходной системы (1):
1-2° ,
® — ± arccos -—h 2тгй;, к G Z,
2 — За
у = (-1)” arcsin 1 + тгп, п G Z,
2 — За
2а
Z = 1 - 2а ‘
Ответ: при a G (0; 1/4) U (1/4; 1/3) ® = ± arccos + 2тг&, к G Z\ 2 — За
f 1 \П • 1 , 2°
У = (-1) arcsin ----— + 7ГП, п G Z; z - ---—.
2 — За 1 — 2а
231
Задача 33 (механико-математический факультет, 1992). Найти все значения х, для каждого из которых неравенство
(2 - а)а:3 - За:1 2 + (а - 5> + 2(5 + 4а - а2) < О (1)
выполняется хотя бы при одном значении а, принадлежащем отрезку
Решение. При a = — 1 неравенство (1) равносильно неравенству
х3 — х2 — 2х < 0 <=> а:(а: + 1)(ж — 2) < О
х < -1 V 0 < х < 2. (2)
При a = 2 неравенство (1) равносильно неравенству
х2 4- х — б > 0 <=> х < —3 V х > 2. (3)
Объединение решений (2) и (3), т.е. множество решений исходного неравенства (1) при a = —1 и а = 2, имеет вид
х 6 (—оо; — 1) U (0; 2) U (2; 4-оо). (4)
При х = 2 неравенство (1) равносильно неравенству
а2 — а — 2 > 0 <=> a < — 1 V а > 2,
т.е. а [— 1; 2]. Следовательно, дальнейшее решение задачи состоит в том, чтобы установить, имеет ли при a G (—1;2) неравенство (1) решения х G [—1; 0].
Введем обозначение
/(х) = (2 — о)х3 — За:2 + (а — 5)х + 2(5 4- 4а — а2) =
= (2 — a)x2(x + 1) + (а — 5)a:(a: + 1) — 2(а 4- 1)(а — 5)
и исследуем функцию f(x) при х Е [—1; 0] на минимум и максимум с помощью производной
f'(x) = 2(2 — а)х2 — 6х 4- а — 5.
Так как при а Е (—1; 2) коэффициент при х2 в выражении для f'(x) равен 3(2 - а) > 0 и /'( —1) = 7 - 2а > 0, /'(0) = а - 5 < 0, a /'(a?) = 0 при
1 ± л/(а2 -7а+ 13)/3
Ti = ---------------------
232
то меньший корень уравнения f'(x) = О
1 - У(а2 - 7а+ 13)/3
Поэтому при х 6 [— > 0 и функция f(x) возрастает; при
ж G (a?i; 0] f'(x) < 0 и функция /(ж) убывает; при х = a?i f'(x) = 0 и
/(ж) имеет максимум.
Так как минимальное значение функции f(x) при a G (—1;2) и х 6 [—1; 0] равно
/(-1) = /(0) = -2(а + 1)(а - 5) > 0,
то для всех а е ( — 1; 2) и х G [— 1; 0] f(x) > 0, т.е. неравенство (1) решений не имеет.
Таким образом, множество (4) является итоговым ответом.
Ответ: х G (—оо; —1) U (0; 2) U (2; +оо).
Замечание. Задачу можно было решить и без помощи производной, если представить функцию /(ж; а) как квадратный трехчлен относительно переменной а с коэффициентами, зависящими от параметра х. Переформулируйте задачу для подобной замены и решите ее самостоятельно.
7.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
— Я тебя честно предупреждаю, — закричала Королева и топнула ногой. — ...Решай сейчас же — нет, в два раза быстрее!
Л.Кэрролл. Алиса в стране чудес
Задача 1 (физический факультет, 1968). Для каждого действительного числа а найти все действительные решения уравнения
sin х 4- cos (а + а?) + cos (а — а?) = 2.
Задача 2 (физический факультет, 1968). Для каждого действительного числа а найти все действительные решения уравнения
sin х + v2sin (а — а?) = 1.
233
Задача 3 (филологический факультет, отделение структурной и прикладной лингвистики, 1985). Для каждого значения а решить уравнение
4 cos х sin a + 2 sin x cos a — 3 cos a = ‘ly/l.
Задача 4 (экономический факультет, 1991). Указать все значения параметра с, при которых уравнение
cos2 х — (с + 2)2 cos х — с(с + 2)(с + 3) = О
имеет на отрезке [—тг/2, Зтг/2] ровно три корня.
Задача 5 (геологический факультет, 1979). Найти все значения параметра о, при каждом из которых уравнение
) 1 п /-х + —. +------4- 2V2 = О
vsina cosa
имеет единственное решение.
Задача 6 (экономический факультет, отделение политической экономии, 1988). Найти все значения параметра а, при которых неравенство
|5 sin2 х + 2a sin х cos х 4- cos2 х 4- a 4- 11 6
выполняе тся для любых значений х.
Задача 7 (химический факультет, 1975). Найти все значения параметра а, при которых система
sin (a — г/) 4- 2 sin х = О f л/з\
2 logie (a - У) + 4 logi/4 у = log2 — +31og64z
\ У )
имеет четное число решений.
Задача 8 (химический факультет, 1975). Найти все значения параметра Ь, при которых система
{cos (6 — г/) — 3 cos х = О
2 log9 (by - г/2) = log3 (Зг) - log1/9 у
имеет нечетное число решений.
234
Задача 9 (химический факультет, 1975). Найти все значения параметра а, при которых система
( sin (За — Зр) 4- 3 sin х = О
I 2 log4 (а - у) + 2 log4 (2^) = log2 у/у + +3 log8 (2т) имеет четное число решений.
Задача 10 (геологический факультет, отделение геофизики, 1974). Определить, при каких целых значениях k система
{ (arctgх)2 4- (arccos г/)2 = тг2к
arctg х + arccos у — тг/2
имеет решения, и найти эти решения.
Задача 11 (геологический факультет, отделение геофизики, 1974). Определить, при каких целых значениях к система
{arccos х + arcsin у = &7г2/4 (arcsin у)2 • arccos х = тг2 /16
имеет решения, и найти эти решения.
Задача 12 (геологический факультет, отделение геофизики, 1974). Определить, при каких целых значениях k система
( (arccos х)2 + (arctgу)2 4- arccos х arctgу = тг2к
( arccos х + arctg у = тг/2 имеет решения, и найти эти решения.
Задача 13 (факультет психологии, 1991). При каждом значении параметра а 1/2тг найти все корни уравнения
/ Зх + 2а \ / Зт — а \
\3т2 4- 4ах 4- 13а2/3/ \3т2 — 2ат 4- 10а2/3/
Задача 14 (механико-математический факультет, 1988). Найти все значения Ь, при которых система
( 1
cos т sin у =-X
* Z2
4(т - у)2
< cost/smx =
(Ь 4- тг)2
, . 4(т — и)
cos (т 4- у) = 77-г1
k (Ь4-7г>
имеет одно решение, удовлетворяющее условиям 0^t^7t/2hz>0.
235
Задача 15 (экономический факультет, отделение планирования и экономической кибернетики, 1977). Найти все значения параметра а, при каждом из которых уравнение
log2 (4Ж - а) = х
имеет два решения.
Задача 16 (филологический факультет, отделение прикладной лингвистики, 1970). Найти все х, для которых 1/2 < х < 5/2 и которые удовлетворяют неравенству
при всех а из промежутка 0 < a < 2.
Задача 17 (филологический факультет, отделение прикладной лингвистики, 1970). Найти все х < 1, удовлетворяющие неравенству
/ \
'“Ml + a) + 9 < '
3
при всех а, для которых 1/2 < а < 2.
Задача 18 (филологический факультет, отделение прикладной лингвистики, 1970). Найти все х > 1, которые при всех Ь, удовлетворяющих условию О < b <С 2, являются решениями неравенства
logz2 (х + 2^- х) < L b
Задача 19 (механико-математический факультет, 1967). Указать все значения а, при которых уравнение
2 11g (аж)[ loga» 10 = (41g a — 3)log 2 10 — 1g ar
имеет решение, и найти все соответствующие решения.
Задача 20 (механико-математический факультет, 1967). Указать все значения а. при которых уравнение
log7^ a |loga 11 = loga2 2 ’ 1оёУж д2 “ loga
имеет решение, и найти все соответствующие решения.
236
Задача 21 (механико-математический факультет, 1967). Указать все значения а, при которых уравнение
logioo х2 = logy^ 10 (lg 10а - |lg I)
имеет решение, и найти все соответствующие решения.
Задача 22 (механико-математический факультет, 1967). Указать все значения а, при которых уравнение
“2 |loga2 II + log“ х = '°V 4 ' l°^a
имеет решение, и найти все соответствующие решения.
Задача 23 (механико-математический факультет, 1967). Указать все значения а, при которых уравнение
loga х| logz a - log2 а| = log^ (ат) - log2 а2 + loga x • log2 a
имеет решение, и найти все соответствующие решения.
Задача 24 (физический факультет, 1967). Для каждого вещественного а решить неравенство
^sin х - а > ।
при условии, что 0 < х < тг/2.
Задача 25 (факультет психологии, 1970). Найти все отличные от нуля действительные значения а, при которых уравнение
х& 4- ат4 + а4 = 0
имеет’ ровно четыре действительных корня, образующих арифметическую прогрессию.
Задача 26 (факультет психологии, 1970). Найти все действительные значения а, при которых уравнение
х(х12 4- ат6 4- 1) = 0
имеет ровно пять действительных корней, образующих арифметическую прогрессию.
237
Задача 27 (факультет психологии, 1970). Найти все отличные от нуля действительные значения а, при которых уравнение
ж(ж12 — ах6 + а4) = О
имеет ровно пять действительных корней, образующих арифметическую прогрессию.
Задача 28 (факультет психологии, 1966). Где расположены комплексные числа z = а 4- Ы, для которых
1 к — И + 4 ?
gl/2 3|z — 1| ~2 > ’
Задача 29 (факультет психологии, 1966). Где расположены комплексные числа z = а + Ы, для которых
logi/2\z - 2| > log1/2 |z| ?
Задача 30 (факультет психологии, 1966). Где расположены комплексные числа z = a + Ы, для которых
|z|2 - |z|+ 1
log^ 9хЫ <2?
Задача 31 (физический факультет, 1966). Для каждого вещественного числа а 0 найти все комплексные числа z, удовлетворяющие равенству
\z\2 — c2Az 4- 2а(1 4- г) = 0.
Задача 32 (физический факультет, 1966). Для каждого вещественного числа а 0 найти все комплексные числа z, удовлетворяющие равенству
2|г| — 4az 4- 1 4- га = 0.
Задача 33 (факультет психологии, 1968). При каких действительных значениях а любое комплексное число z = х + iy, удовлетворяющее равенству
\z — г\/2| = (а 4- I)2,
удовлетворяет одновременно и неравенству
\z — >/2| > а2 — 4а ?
238
Задача 34 (факультет психологии, 1968). При каких действительных значениях а хотя бы одно комплексное число z = x + iy, удовлетворяющее равенству
\z — аг| = a + 4,
удовлетворяет одновременно и неравенству
|г-2|<1?
Задача 35 (факультет психологии, 1968). При каких действительных значениях а любое комплексное число z = х + iy, удовлетворяющее равенству
\z — аг‘| — 2a,
удовлетворяет одновременно и неравенству \z — 1| > - ?
Задача 36 (факультет психологии, 1985). Найти все значения а, при каждом из которых существует единственная пара целых чисел х, у, удовлетворяющая уравнению
— 15х2 + 11ху-2у2 = 7
и двум неравенствам
х < у, 2а2х + За?/ < 0.
Задача 37 (геологический факультет, 1967). Указать все действительные а, при которых не существует ни одного действительного х, одновременно удовлетворяющего неравенствам
ах2 + (а — 3)я + 2/а — 2а 0, ах а2 — 2.
Задача 38 (геологический факультет, 1967). Указать все действительные а, при которых не существует ни одного действительного х, одновременно удовлетворяющего неравенствам
а2х + 2а
----------- 0, ах + а > 5/4.
ах - 2 + а2
Задача 39 (геологический факультет, 1967). Указать все действительные а, при которых не существует ни одного действительного х, одновременно удовлетворяющего неравенствам
(1 — а)х — а х — 2(1 — а)
>0,
х — 8 ах.
239
Задача 40 (экономический факультет, отделение экономической кибернетики, 1970). Найти хотя бы один такой многочлен третьей степени
Р3(х) = ах3 4- bx2 + сх + d,
чтобы выполнялось неравенство
х — 1
х + 1
Рз(х) $ 5
при |ж| 1/2.
Задача 41 (факультет психологии, 1983). Найти все значения параметра а, при каждом из которых система уравнений
1(а — 2) sin х + cos у = 1
l°ga (2 cos У) = (loga logz (1 + 7 sin х)
logz () = 1 у О — /
имеет хотя бы одно решение. При каждом таком значении а найти все решения.
Задача 42 (факультет психологии, 1983). Найти все значения параметра а, при каждом из которых система уравнений
' a cos у + sin х + 1 = О
< logz (-1 - 4 sin х) = (log2 a) loga (1 + 2 cos у)
. , /4 — a\
loga z + loga ----- = 0
v \ a /
имеет хотя бы одно решение. При каждом таком значении а найти все решения.
Задача 43 (факультет психологии, 1983). Найти все значения параметра а, при каждом из которых система уравнений
' a sin х + (1 — 2a) cos у = 2
I loga (1 - 2 sin x) = (loga z) logz cos у
logz f 77?—-) = 1
\ 10 — a/
имеет хотя бы одно решение. При каждом таком значении а найти все решения.
Задача 44 (механико-математический факультет, 1992). Найти все значения х, удовлетворяющие неравенству
(а + 2)х3 — (1 + 2а)х2 — бх + (а2 + 4а — 5) > О хотя бы при одном значении а, принадлежащем отрезку [—2; 1].
240
УКАЗАНИЯ И ОТВЕТЫ
ТГ ТГ
1. При-------h тгк а — + тгк
6 6
2
х = —у? + (—l)n arcsin . = + тгп, п, к Е Z, где tgy? = 2 cos а;
V1 + 4 cos2 а
при других а решений нет.
„ тг „ , 7тг „ ,
2. При —|- 2тг£ < а < ——h 2тгАг
4 4
х = — arccos (1 — 72COS а) + (—l)n arcsin
при других а решений нет.
тт 2 тг
3. При а = arcsm —-= + — + 2тгп, п 6 Z,
V 7 2
2 тг
при а = — arcsin —= — — + 2тгп, п Е Z.
у/Ч 2
при других значениях а решений нет.
— + тгп, п, к Е Z;
V 3 — 2 >/2 cos а
х =---------F 2тгк, к Е Z\
6
5тг „ , , г,
х — —— + 2тгАг, к Е Z \ 6
4. с = 0, —2, (—3 — л/5) /2.
Зтг п г-, тг . . __
5. -|- 2тгп, п Е Z\ — 4- 2тгк, к Е Z.
24
6. —— а 0.
5
7. бтгт < а < Зтг(2т +1), т = 0,1,2,....
8. Зтг/2 + бтгт < b <С Зтг/2 4- Зтг(2т + 1), m = 0,1, 2,....
9. 2тгт < а тг(2т + 1)> т = 0,1, 2,....
, А тг(1-г/7) тг(1 + г/7)\
10. к = 1 (аг, у) = I tg----------, cos----------- I.
11. к = 2 (х,у) = (cos7t2/4, ±1).
io ь i \ ( тг(1 + У5) 7г(-1 + л/5)\
12. к = 1 (х, у) = I cos----------, tg ----------- I.
„ „ а а : у/б
13. Xi = — ж2 з = — - ± —— а. 6’ ’ 6 2
14. [—8тг; —4тг) U (0; 4тг].
15. -1/4 < а < 0.
16. х =
2
17. 0 < х < 1.
25тг 17тг 7тг Птг
18. X! = —, х2 = —, хз = У2. *4 = -п-.
19. При 0 < а < 10 решений нет;
при а — 10 Xi = 1/10;
16 Методы реш. задач
241
при 10 < а < 1000 ц = 1/10, 12 = 102-^1+81go;
при а 1000 «1 = 1/10, 12 = 1/1000.
20. При 0 < а 1 решений нет;
при 1 < а < -^2 ii = а4;
при а = У2 xi = 2;
при а > -У2 xi = сг~2+2>/1+21Qgo 2.
21. При а < Ю1-^ решений нет;
при а = Ю1-^ xi = 101-А
при lO1-^ < а < Ю-1/2 а?! = 101-А х2 — io^3+41ga-1;
при а = 10-1/2 Ki = 101-А
при IO"1/2 < а < 101+78 a?i = Ю1-75, х2 = 10^’3+418а-1;
при а - 101+v/8 хх = 101-А i2 = 101+А
при а > 101+v/8 ху = 101-А х2 = .
22. При 0 < а 1 решений нет;
при 1 < а < \/2 Xi = а2;
при а = Xi = 2;
при а > л/2 Xi = а>/1+41о8а 2-1
23. При 0 < а 1 Xi = а(2(1о§2 « “ I))"1 (log2 а + ^/log2a — 21og2a i2 — а '
при 1 < а < 2 Xi = </2(1оВ2 а-1)) \
при а = 2 решений нет;
при 2 < а < 4 Ж1 = c/2(log2 а-1)) 1.
при а = 4 а?1 = 2.
(log2 а + ^log2 а — 2 log2 а при а > 4 11 = а '
24. При а sin 1 0 < х < arcsin а, 1 < х < тг/2;
при sinl<a<l 0 < 1 < 1, arcsin а < х < тг/2; при а 1 0 < 1 < 1.
242
27. a =
65
28. Вне окружности с центром в точке (1;0) и радиусом 10
или внутри окружности с центром в той же точке (1;0) и радиусом,
равным 2/3.
29. В той полуплоскости от прямой а = 1, где лежит точка (2;0).
30. Внутри окружности радиуса 5 с центром в начале координат.
31. При 0 а л/2 — 1 z = а 4- i (— 1 ± — 2а — а2);
при а > — 1 решений нет.
32. При 0 < а 1/2 решений нет;
/Г1 4а 4- \/4а2 + 3 , i
33.
34.
35.
36.
37.
38.
39. Ни при каком а.
при а > х/z z = ----г--
4(4а2 - 1) 4
(1 — \/3 \
/-21 5\
Л л/13 - 2\ ( ЛЗ + 2 \
i 6 /\б /
-13/3 < а -19/5.
Ни при каком а.
каком а.
40. 2(ж3 — х2 + ж) — 1.
41. 2 < а < 5/2, 5/2 < а < 5;
(—l)fc arcsin „ —(- тгк, ± arccos --° - + 2тгп, ——— ) , п, к 6 Z.
’ 3 + 2а 3 + 2а ’ 5 - а) ’ ’
42. 3/2 < а < 2, 2 < а < 4;
(—l)fc arcsin ---— 4- 2тгАг, ± arccos —---h 2тгп, —-—| , п, к £ Z.
k 7 2а-1 1 — 2а ’ 4-aJ
43. 4 < а < 5, 5 < а < 10;
. .г .14-2а . 4 —а а \ _
( — 1) arcsin ----- 4- тгк, ± arccos - —h 2тгп, —---- , п, к G Z.
5а — 2 2 — 5а 10 - а /
44. (-оо; -2) U (0; 1) U (1; 4-оо).
16*
243
ПОСЛЕСЛОВИЕ
С КОММЕНТАРИЕМ К НАГЛЯДНОМУ МАТЕРИАЛУ
И ИСТОРИКО-ЛИТЕРАТУРНЫМИ ОТСТУПЛЕНИЯМИ
Этот раздел мы с загадки начнем — Лаже Алиса ответит едва ли: Что остается от задачи потом — После того, как ее разобрали 1
В.Высоцкий. “Песня Кэрролла’’ (выделенные курсивом слова изменены)
Естественно, некоторые из разобранных в данном пособии задач могли быть решены иначе. Но авторы не стремились, особенно в первых главах, к поиску оптимального пути решения каждой задачи, а часто выбирали тот или иной способ решения для демонстрации конкретного “трюка" пли особенностей именно данного метода. Например задачи №2 и № 14 первой главы намного проще можно решить графическими методами. Однако достаточно заумный и логически сложный способ решения первой из этих задач был специально выбран для того, чтобы показать, как теорема о средних может быть использована для отрицательных чисел. А задача № 14 третьей главы с помощью понятия скалярного произведения векторов, включенного в программу вступительных экзаменов в МГУ лишь в 1996 году, вообще решается в три-пять строчек! Попробуйте это сделать самостоятельно...
Авторы, исходя из собственного опыта, обращают внимание учителей и преподавателей подготовительных курсов и отделений на то, что последовательность изложения материала может быть иной. Для классов и групп не математического профиля целесообразно начинать с систем линейных уравнений (глава 4), затем переходить к задачам на исследование квадратичной функции (глава 3), а уж потом решать задачи из первых двух глав, изучая специальные “трюки” и основные методы графического анализа. Заметим, что полный объем данного пособия с добавлением некоторого числа задач из других источников может составить основу для двухгодичного факультатива. При этом каждую задачу, если она это
245
допускает, желательно решать разными способами, предваряя решение анализом возможной последовательности общих методов и специальных “трюков”.
Например, при решении задачи № 6 первой главы подобный предварительный анализ может выглядеть следующим образом.
1. Первое неравенство имеет вид: Дацр) h(y), где f - квадратичная функция, h - тригонометрическая, а так как общих подходов к решению задач нет => единственной надеждой является прием, когда max одной функции равен min другой.
2. График функции /(ят;р) представляет собой параболу с направленными вверх ветвями => min f реализуется в вершине параболы => для функции h(y) скорее всего надо искать max.
3. Для нахождения ОИФ и max Л естественно использовать метод введения дополнительного аргумента, желательно в урезанной форме, ограничившись фразой “где у? - некоторый дополнительный аргумент” .
После реализации намеченного алгоритма возникают два вопроса.
1) Почему функции f и h зависят от разных аргументов, т.е. какой здесь заложен смысл или подвох?
2) Какую роль играет второе неравенство?
Ответы на эти вопросы естественным образом приводят к проверке достаточности полученных необходимых условий для существования именно единственного решения. Заметим, что доказательства достаточности нет ни в одном из пяти известных авторам других пособий, где разобрано решение этой задачи.
Подобная практика преподавания методов решения параметрических задач с предварительным анализом и наводящими вопросами показала свою эффективность на подготовительном отделении МГУ и в старших классах эколого-географического профиля Городского центра образования № 654.
P.S. Ответ на поставленный в эпиграфе вопрос будет дан в конце приложения II.
Комментарий к наглядному материалу
Авторы выражают глубокую признательность академику РАН Анатолию Тимофеевичу Фоменко за любезное разрешение использовать в данном пособии в качестве наглядного материала его замечательные рисунки из монографии “Наглядная геометрия и топология: математические образы в реальном мире” (изд-во Московского университета, 1988г.).
Краткие комментарии к этим рисункам частично взяты из этой монографии (что далее будет обозначаться буквой Ф), частично написаны
246
авторами (что будет отмечаться буквой А). Заметим, что выбор рисунков обусловлен либо эпиграфом к последующей главе, либо содержанием самой главы, либо некоторыми ассоциациями авторов, связанными, как правило, с их научными интересами в области математического моделирования физических явлений.
К главе 1, стр. 6 (А). Схематичная перестройка тора в дважды скрученный тор, изображенный в центре рисунка, имеет отношение к объяснению магнитного поля Земли и заключается в доказательстве качественной возможности самовозбуждения геомагнитного поля при движении проводящей среды.
Согласно этому механизму начальное тороидальное магнитное поле "вморожено” в проводящую среду жидкого тора. Конвективные движения при наличии кориолисовой силы создают из тора “петли”, которые скручиваются в “восьмерку”, а полный прогиб “талии восьмерки” приводит к совмещению ее половинок и слиянию в один тор, подобный исходному, но с удвоенным магнитным потоком. Если подобная деформация происходи'!' п раз, то магнитное поле увеличивается в 2П раз. Аналогичный сценарий может лежать в основе одного из объяснений возникновения турбулентности через процедуру бифуркации удвоения периода (см. Приложение I и ссылку [3] к нему, что далее будет обозначаться как (Пр.1 [3]).
К главе 2, стр. 36 (Ф). Условно показано покрытие многообразия не-пересекающимися’шарами (кругами в R2) таким образом, чтобы дополнение к объединению шаров имело нулевой объем (нулевую площадь). ...Аналогичные процессы возникают в теории фракталов (Пр.1 [34]). С этой точки зрения фракталом является “белое множество”, т.е. дополнение к объединению черных шаров (кругов).
К главе 3, стр. 68 (Ф). Известно, что текстовая и зрительная информация часто избыточна... Из зрительного образа можно удалить многие фрагменты, и тем не менее объект будет узнаваем. Конечно, желательно удалять лишь малосущественные детали, сохраняя главное... Именно это и делают гомеоморфизмы и гомотопии. Подчеркнем, что на этом принципиальном факте узнавания объекта лишь по отдельным штрихам основаны многие современные статистические методы распознавания образов. Главной проблемой в разработке соответствующих методик является обнаружение инвариантых характеристик объекта. Решение этой задачи чаще всего нетривиально... См. рисунок, являющийся одновременно символом зодиакального созведия Скорпиона.
(А). Для тех читателей, которые там больше ничего не увидели, советуем перевернуть рисунок “вверх ногами”... Аналогичным образом при решении задач с параметрами часто бывает полезно посмотреть на условие с разных сторон и даже “вверх ногами!”. Метод решения от
247
носительно параметра и диалог Алисы с Белым Рыцарем в Зазеркалье служат хорошим подтверждением этому:
— Как это вы можете говорить вниз головой, да еще так спокойно? — спросила Алиса...
Рыцарь, казалось, очень удивился ее вопросу.
— Неважно, где находится мое тело, — сказал он.
— Мой ум работает, не переставая.Чем ниже моя голова, тем глубже мои мысли!
Если же и стояние “вверх ногами” ничего не дает, то это - плохо, ибо может означать синдром болезни папаши Вильяма, проявившийся у него еще в молодости:
— В ранней юности, — старец промолвил в ответ, —
Я боялся раскинуть мозгами,
Но, узнав, что мозгов в голове моей нет,
Я спокойно стою вверх ногами...
Если говорить серьезно, то в последние 2-3 года авторы данного пособия с удивлением обнаружили, что многие абитуриенты не умеют двигать по координатной плоскости параболу у = ах2 + Ьх + с и решать элементарные задачи с использованием теорем 1-4 третьей главы. Для читателей, которым задачи этой главы покажутся чрезмерно сложными, рекомендуем сначала поупражняться на простых примерах из других пособий.
К главе 4, стр. 96 (Ф). На рисунке показана схема локальнотривиального расслоения пространства. Вверх уходят слои (каждый из которых гомеоморфен некоторому стандартному слою, условно показанному в виде некоторой фигуры в центре). Слои опираются на базу -изогнутую дугу на рисунке.
(А). Авторам к этому добавить нечего, ибо они уже все сказали словами Л.Кэрролла в эпиграфах к параграфам этой главы.
К главе 5, стр. 120 (Ф). Изображена схема выворачивания наизнанку в классе гладких погружений двумерной сферы S2 в трехмерном пространстве R3. Справа внизу под номером I показано стандартное вложение сферы. Двигаясь вверх, мы видим последовательные стадии ее деформации, занумерованные римскими цифрами от I до IX. Описывать процесс деформации словами здесь чрезвычайно трудно. Поэтому снова вспомним средневековых геометров, которые иногда вместо логического доказательства говорили: “Смотри...”. Положение IX (самая сложная часть всей конструкции) соответствует гладкой деформации сферы, переводящей ее в окрестность поверхности Боя без изломов и других особых точек, но с несколькими линиями самопересечения, которые организованы в петли. Далее, применяя процесс встречного проталкивания
248
листов деформированной сферы, мы меняем местами ее внутренность и внешность. После выворачивания меняется лишь окраска зон (белая -в черную и черная - в белую). Затем начинаем обратный процесс, двигаясь от положения IX вплоть до положения I. В результате получаем вывернутую наизнанку сферу.
Заметим, что аналогичная задача о выворачивании сферы S1 в R2 (т.е. окружности в плоскости) неразрешима в классе гладких погружений. Более того, сфера Зп выворачивается наизнанку в Rn+1 лишь при п = 2 и п = 6.
К главе 6, стр. 158 (Ф). На рисунке изображена сфера - поверхность постоянной средней кривизны, образованная мыльной пленкой (т.е. мыльный пузырь). Эта система устойчива (пока вода не испарится), однако при быстром прокалывании пузыря он лопается, т.е. мгновенно разрушается. Если пузырь прокалывать очень осторожно и медленно, то его можно проткнуть насквозь, не разрушая...
(А). Сферическую форму часто имеет и одно из самых загадочных явлений природы - шаровая молния. Общепризнанной физико-математической модели шаровой молнии, которая объясняла бы большинство загадок и парадоксов ее поведения, нет до сих пор... И это в наше время, когда физики, похоже, знают, что творилось в первые мгновения существования Вселенной, что происходит в еще не открытых черных дырах, из каких субэлементарных частиц состоят элементарные вроде бы еще вчера частицы?
Перечислим три основных парадокса, подчеркнутых в книге И.II.Стаханова “О физической природе шаровой молнии”.
1. Шаровая молния излучает видимый свет несмотря на низкую температуру ее вещества (шаровую молнию можно даже иногда “подержать в руках”, т.е. медленно поднести к ней ладонь, не опасаясь получить при этом ожог).
2. Шаровая молния часто сопровождается разнообразными электромагнитными эффектами, в том числе и сильными импульсами тока (так что ловить ее голыми руками небезопасно и лучше вообще держаться от нее подальше).
3. Шаровая молния состоит из вещества с характерной плотностью для газов, а имеет поверхностное натяжение, характерное для жидкостей (известны случаи, когда шаровая молния проникала в закрытые помещения через микротрещины в оконном стекле, восстанавливая после очень больших деформаций свою сферическую форму; в других случаях ее в буквальном смысле выметали из помещений на улицу веником или метлой, а в одном случае выстрел дробью с расстояния 15 м шаровая молния даже не “почувствовала”. Заметим, что предложенная одним из авторов данного пособия электрокапиллярновихревая модель
249
шаровой молнии объясняет некоторые загадки и парадоксы ее поведения, но вопросов пока больше, чем ответов...
К главе 7, стр. 194 (А). На рисунке изображен смерч типа торнадо в зрелой стадии развития. Смерч - одна из возможных форм вихревых движений, наблюдаемых в атмосфере. От ураганов смерчи отличаются более высокой плотностью концентрации энергии: если ураган как бы “размазан” на тысячи километров, а скорости в нем редко превышают 50 км/ч, то размеры смерча обычно не превышают сотню метров, однако скорости в нем часто порядка звуковых, т.е. до 300 м/с! Возникновение ураганов связано с перемещением больших масс воздуха за счет разности температур у поверхности Земли и в атмосфере на больших высотах. Тогда как смерчи обычно порождаются грозовыми облаками, а точнее, спиральными вихрями в их нижней части. За счет наличия разности электрических потенциалов эти спиральные вихри вытягиваются из грозового облака к поверхности Земли в виде некоторой “сосульки”. В разрезе эта “сосулька” (или “хобот”) представляет собой коническую воронку, т.е. два вложенных друг в друга соосных конуса с общей вершиной и разным углом раствора. В момент, когда хобот касается земли, начинается разрушительная “работа” смерча, сосулька заполняется пылью, мусором, обломками разрушенных строений и становится отчетливо видимой. В стенках конической воронки протекает спиралевидный электрический ток, который генерирует магнитное поле. Взаимодействие этого тока с собственным магнитным полем порождает электромагнитную вихревую силу, которая обеспечивает относительную устойчивость смерча (на рисунке эта сила схематично изображена в виде рук, обхватывающих хобот смерча) и объясняет многие другие интересные эффекты.
К послесловию и приложению I (Ф). Эти рисунки посвящены попытке современного геометрического преломления некоторых научных идей, волновавших еще средневековых ученых и художников (в частности, Леонардо да Винчи, Босха, Брейгеля, Дюрера и др.). Все они интересовались геометрической теорией перспективы, разрабатывали принципы правильного изображения объектов, нащупывали математические механизмы оптических иллюзий и т.п. Творчество многих авторов тех времен находилось, естественно, под влиянием специфического (и очень интересного) научного мировоззрения, которое отражалось в графике и живописи той эпохи. Поэтому казалось любопытным синтезировать в нескольких графических работах немного странные средневековые образы и современные математические концепции бесконечности, деформации, непрерывности... На рисунках изображены как многие символы и образы средневековой науки (геометрические и астрономические приборы, химические принадлежности и т.д.), так и сугубо современные предметы
250
(оптические линзы, часы, радиоаппаратура и т.п.). Однако эта смесь -не механическая, а наследственная, поскольку рассматривается глазами современного зрителя, чувствующего связь между глубокими математическими исследованиями нашего времени, и тем своеобразным научным мышлением, которое населяло тогдашний окружающий мир странными фантастическими образами.
(А). Обращаем внимание читателей на сидящую к ним спиной фигуру с книгой в руках, изображенную на переднем плане в нижнем левом углу рисунка к этому разделу. В книге явно читаются имена Босха и Дали, что перекидывает дополнительный мостик из средневековья в уходящее XX столетие. Испанец Дали и голландец Эшер уже в этом веке продолжили тот синтетический подход, заложенный еще вышеперечисленными средневековыми художниками, где причудливым образом переплелись реальность и грезы (некоторые называют это бредом), математика и искусство. Дали всю свою полную экстравагантностей жизнь интересовался новейшими достижениями науки, что находило порой очень странное отражение в его неординарных работах.
Его восхищали тайна и красота двойных спиралей ДНК, корпускулярно-волновой дуализм поведения элементарных частиц, загадки оптических иллюзий и голография, парадоксы многомерной геометрии и топологии, а в последние годы он увлекся эстетической простотой = красотой математических образов теории катастроф. Последняя картина Сальвадора Дали называется “Ласточкин хвост” (май 1983 г.) в честь одной из шести в то время известных метаморфоз из теории катастроф.
С другой стороны, его возмущало и ужасало использование последних достижений науки в целях разрушения, особенно - атомная бомбардировка американцами городов Японии.
Про творчество С.Дали и М.Эшера (см. дальше) можно рассказывать бесконечно и написать еще не одну диссертацию, однако лучше хотя бы полистать альбомы с репродукциями их интереснейших работ...
Заметим, что второй рисунок, предваряющий Приложение I, является своеобразной вариацией на тему известной гравюры Брейгеля “Алхимики”. Подобный выбор рисунка был сделан авторами специально, чтобы еще раз обратить внимание читателей на слова Михаила Васильевича Ломоносова, которые были сказаны еще 250 лет назад, но как современно они звучат и сейчас на рубеже тысячелетий!!!
Энциклопедичности интересов, познаний и свершений М.В.Ломоносова, универсальности его таланта посвящены многие научные статьи и книги, но лучше всего об энциклопедическом характере ломоносовского гения сказал А.С.Пушкин: “Он создал первый университет. Он, лучше сказать, сам был первым нашим университетом... Историк, ритор, механик, химик, минералог, художник и стихотворец, он все испытал и все
251
проник”.
Лучше не скажешь и добавить тут нечего, но авторы рискуют лишь поставить под сомнение избитую фразу о том, что А.С.Пушкин - родоначальник современного русского литературного языка. Однако еще в 1760 г. А.П.Шувалов (двоюродный племянник И.И.Шувалова - первого куратора Московского университета, внесшего огромный вклад в реализацию мечты М. В. Л омоносов а об открытии внесословного университета именно в Москве) писал: “Ломоносов - гений творческий, он отец нашей поэзии... Он открыл нам красоты и богатства нашего языка, дал нам почувствовать его гармонию, обнаружил его прелесть и устранил его грубость...”
Спустя почти столетие это же подтвердил Н.В.Гоголь, написав, что Ломоносов “стоит впереди наших поэтов, как вступление впереди книги”. Ф.М.Достоевский в статье “Анна Каренина” как факт особого значения” высказался шире и еще определеннее: “Бесспорных гениев, с бесспорным “новым словом” во всей литературе нашей было всего только три: Ломоносов, Пушкин и частью Гоголь”. Следует подчеркнуть, что под литературой здесь подразумевается не только поэзия, но и проза. А в первичном своем значении проза М.В.Ломоносова - это либо научное сочинение (хотя большинство своих научных работ им было опубликовано на латыни или немецком языке), либо деловая записка, либо частное письмо.
Авторы настоящего пособия сочли своим долгом привести фрагменты трех естественно-научных сочинений М.В.Ломоносова, чтобы читатель сам оценил красоту слога и глубину мысли основателя Московского университета.
Явление Венеры на Солнце, наблюденное в Санкт-Петербургской Императорской Академии Наук майя 26 дня 1761 года
26 мая - 4 июля 1761 г.
Нередко легковерием наполненные головы слушают и с ужасом внимают, что при таковых небесных явлениях пророчествуют бродячие по миру богаделенки, кои не токмо во весь свой долгий век о имени астрономии не слыхали, да и на небо едва взглянуть могут, ходя сугорбясь. Таковых несмысленных прорекательниц и легковерных внимателей скудоумие ничем, как посмеянием презирать должно...
Итак, идолопоклонническое суеверие держало астрономическую Землю в своих челюстях, не давая ей двигаться, хотя она сама свое дело и божие повеление всегда исполняла. Между тем астрономы принуждены были выдумывать для изъяснения небесных явлений глупые и с механикою и геометриею прекословящие пути планетам, циклы и эпициклы (круги и побочные круги).
252
Жаль, что тогда не было таких остроумных поваров, как следующий: Случились вместе два астронома в пиру,
И спорили весьма между собой в жару.
Один твердил: Земля, вертясь, круг Солнца ходит;
Другой - что Солнце все с собой планеты водит;
Один Коперник был, другой слыл Птолемей.
Тут повар спор решил усмешкою своей.
Хозяин спрашивал: - Ты звезд теченье знаешь?
Скажи, как ты о сем сомненье рассуждаешь?
Он дал такой ответ: - Что в том Коперник прав, Я правду докажу, на Солнце не бывав.
Кто видел простака из поваров такого,
Кто бы вертел очаг вокруг жаркого?
Коперник возобновил, наконец, солнечную систему, коя имя его ныне носит, показал преславное употребление ее в астрономии, которое после Кеплер, Невтон и другие великие математики и астрономы довели до такой точности, какую ныне видим в предсказании небесных явлений, чего по земностоятельной отнюдь достигнуть невозможно.
P.S. (А). В сугубо научном отношении прохождение Венеры по диску Солнца 26 мая 1761г. было интересно тем, что его заранее точно рассчитали. Большинство ведущих астрономов мира (112 человек) наблюдали это редкое явление более чем в 40 различных точках земного шара. Это позволило более точно определить расстояние между Землей, Венерой и Солнцем, тем самым уточнить масштаб для всей Солнечной системы. Наблюдал это явление и М.В.Ломоносов с помощью телескопа-рефрактора. усовершенствованного прибора на основе его же оптических работ. В ходе этого коллективного эксперимента, поставленного самой природой, М.В.Ломоносов был единственным в мире, кто установил, что на Венере есть атмосфера. Интересно отметить, что даже сегодня в иностранных астрономических руководствах пишут, что это открытие было сделано лишь в 1882 году (через 121 год после открытия М.В.Ломоносова!), когда Венера уже в следующий раз проходила через солнечный диск.
Насколько приведенный отрывок из сочинения М. В. Л омоносов а (особенно его начало) злободневен и сейчас - судить читателю, однако не мешает вспомнить многочисленных астрологов, гуру, пророков и т.д., каркавших с газетных полос и экранов телевизоров о конце света в период появления кометы Галлея, “парада планет” Солнечной системы и в конце 1999 года (или, если цифры перевернуть, в 6661 году, т.е. в первый год “эры сатаны”). Да и сегодня в книжных магазинах научно-популярных книг по астрономии не найти, а вот прекрасно изданного бреда под названием “Астрология” сколько угодно...
253
Слово о явлениях воздушных, от электрической силы происходящих... май - октябрь 1753 г.
...Ясно, что ни полков, ни городов надежно укрепить, ни кораблей построить и безопасно пустить в море, не употребляя математики; ни оружия, ни огнедышащих махин, ни лекарств поврежденным в сражении воинам без физики приготовить; ни законов, ни судов правости, ни честности нравов без учения философии и красноречия ввести, и, словом, ни во время войны государству защищения, ни во время мира украшения без вспоможения наук приобрести невозможно...
Того ради часто в свободные часы, смотря па небо, не без сожаления привожу на память, что многие главы натуральной науки и в малейших частях весьма ясно истолкованы, но знание воздушного круга еще великою тьмой покрыто...
Правда, по сие время еще я почитаю за доказанную многими доводами по возможности истину, что причина теплоты состоит в движении материи тел собственной, которая их составляет...
Посему вероятно весьма, что подобным движением посторонняя электрическая материя сперва побуждается к произведению других движений и разных явлений. Ибо теплота и электрическая сила происходят от трения; теплота требует сильного к движению грубых, электрическая сила - нежного к побуждению тончайших частиц, чтобы около центров своих вертелись...
Древних историй сказания и недавних очевидных свидетелей известия в том уверяют, что из громовых туч огонь на землю падает. Сей огонь по не весьма стремительному движению за особливый и от молнии разный почитать должно. Итак, здесь довольно явствует, что жирные пары, падением в кучу собравшись и загоревшись, на землю опускаются и чудным сим явлением рассуждениям моим соответствуют.
Господина профессора Рихмана рок не во много разных обстоятельствах случился...
Подобное сему утверждено в нынешние веки от плавающих по океану, под жарким поясом разливающемуся, что опускается из облака как бы столп некоторый к морской поверхности, которая ему встреть, как холм, подымается; в приближении кипит; тощий облачный (т.е. возникший из облака, о чем Ломоносов говорил выше, ссылаясь на сочинение Плиния) столп внутре наподобие винта вертится... Опущение облачного столпа происходит от стремления верхнего погружающегося воздуха; ...водяной холм, который выше морской поверхности восходит к облачному столпу, также суда разбитые кверху взметает,- все сие происходит от “притягивания крепкой электрической силы...”
P.S. (А). М.В.Ломоносов готовился к назначенному на 6сентября
254
1753 г. выступлению на собрании Академии, где ему предстояло быть оппонентом-содокладчиком Рихмана. Трагическая гибель последнего от удара шаровой молнией 26 июля во время проведения экспериментов по изучению атмосферного электричества вначале дала повод многочисленным противникам материалистической идеи М. В. Л омоносов а о природе электрических явлений вообще отменить этот доклад и урезать средства на проведение дальнейших исследований. И только после многочисленных ходатайств М.В.Ломоносова и благодаря поддержке графа Разумовского (президента Академии), который после горячих споров решил, что “дабы господин Ломоносов с новыми своими произведениями между учеными в Европе людьми не опоздал и через то труд его в учиненных до сего времени электрических опытах не пропал” - этот доклад состоялся 26 ноября, спустя 4 месяца после гибели Рихмана. Подчеркнем, что работы М.В.Ломоносова о природе атмосферного электричества более известны стали в Европе не по своим новым и революционным для того времени научным гипотезам и конкретным результатам, а из-за трагической смерти его сподвижника.
Заметим, что в силу указанных выше причин М.В.Ломоносов был вынужден много места уделить в начале доклада роли Петра I - основателя Академии и “рачителя наук в государстве Российском”, а также, говоря современным языком, агитации о пользе развития наук вообще, о чем и свидетельствует первый абзац.
Второй абзац является пророческим. Происхождение атмосферного электричества М.В.Ломоносов связывал с восходящими и нисходящими потоками воздуха, которые всегда сопровождают грозовые тучи. Этот взгляд и по сей день считается правильным, но полностью механизм возникновения заряда облаков до сих пор не изучен, так что еще не вся тьма развеяна...
Третий абзац фактически является ссылкой на более раннюю работу М.В.Ломоносова “Размышления о причине теплоты и холода” (1744г.), где было развито учение о теплоте как о молекулярном движении, опередившее современную ему науку на столетие. Следует заметить, что в этой работе он сформулировал закон сохранения материи (а чуть позже - и движения). Экспериментальное доказательство закона сохранения материи М.В.Ломоносов провел в 1756г. (на 17 лет раньше Лавуазье!). Одно это ставит М.В.Ломоносова в ряд крупнейших ученых мира.
Четвертый абзац в комментариях не нуждается. Далее у М.В.Ломоносова следует именно научная часть доклада, посвященная различным явлениям атмосферного электричества в природе и опытах, попутно он объясняет причины частых ударов молний в кресты церквей (но говорит о железных флюгерах и шпилях на высоких домах!), чем очень тонко опровергает бытовавшие суеверия и слухи то ли о “божьей каре”, то
255
ли о “происках сатаны”, вдруг возобновившиеся даже в Академии после гибели Рихтера.
Последние два абзаца посвящены двум загадочным явлениям: шаровой молнии и атмосферным смерчам или торнадо, о которых мы уже говорили.
Слово о пользе Химии...
(май - август 1751г.)
“Бесполезны тому очи, кто желает видеть внутренность вещи, лишаясь рук к отверстию оной. Бесполезны тому руки, кто к рассмотрению открытых вещей очей не имеет. Химия руками, математика очами физическими по справедливости назваться может. Но как обе в исследовании внутренних свойств телесных одна от другой необходимо помощи требуют, так, напротив того, умы человеческие нередко в разные пути отвлекают. Химик, видя при всяком опыте разные и часто нечаянные явления и произведения и приманиваясь тем к снисканию скорой пользы, математику, как бы только в некоторых тщетных размышлениях о точках и линеях упражняющемуся, смеется. Математик, напротив того, уверен о своих положениях ясными доказательствами и, чрез неоспоримые и беспрерывные следствия выводя неизвестные количеств свойства, химика, как бы одною только практикою отягощенного и между многими беспорядочными опытами заблуждающего, презирает и, приобыкнув к чистой бумаге и к светлым геометрическим инструментам, химическим дымом и пеплом гнушается. И для того по сие время сии две, общею пользою так соединенные сестры, столь разномысленных сынов по большей части рождали. Сие есть причиной, что совершенное учении химии с глубоким познанием математики еще соединено не бывало. И хотя в нынешнем веку некоторые в обоих науках изрядные успехи показали, однако... некоторые, с немалою тратою труда своего и времени, пустыми замыслами и в одной голове родившимися привидениями натуральную науку больше помрачили, нежели свету ей придали.”
P.S. (А). Этот фрагмент непосредственно следует за словами М.В.Ломоносова, вынесенными в эпиграф к Приложению I. Насколько эти мысли актуальны сегодня, и говорить не надо. Тем более, что за прошедшие четверть тысячелетия узкая специализация в науке достигла такого предела, что математик не понимает физика, химик - биолога, тем более, гуманитарий - естественника. В более широком смысле конфликт между “физиками и лириками” поднял на международном уровне английский писатель и физик по образованию Ч.Сноу в своей, наделавшей много шуму, лекции “Две культуры и научная революция” (Кембридж, 1959г.). Основной смысл конфликта он увидел в том, что увеличивается взаимное обособление науки и искусства, которое ведет к образованию двух
256
самостоятельных культур - “научной” и “художественной”. Опасность заключается в том, что традиционная культура не способна воспринять новейшие достижения науки и поэтому, якобы, неизбежно будет скатываться на путь антинаучности. С другой стороны, научно-технический прогресс без учета культурных ценностей приведет к антигуманности, а то и гибели цивилизации.
С тех пор, несмотря на огромное число научных конференций, где обсуждались пути выхода из этой тупиковой ситуации, положение лишь ухудшилось. Теперь уже не редкость, когда выпускники одного факультета, но обучавшиеся на разных кафедрах, не понимают друг друга. Подтверждением этого служат слова ректора МГУ, академика РАН В.А.Садовничего: “От чего мы страдаем? Мы страдаем от того, что очень рано студенты, разбившись на кафедры, перестают понимать друг друга. Теряется междисциплинарная связь, студент как будущий научный работник быстро погружается в очень узкие и очень сложные математические задачи. Сейчас требуется профессионал-математик математический эрудит, универсал, который хорошо видит не только обширный математический мир, но и мосты, которые наведены или могут быть наведены с другими мирами знаний.” (Пленарный доклад “Математическое образование: настоящее и будущее” на Всероссийской конференции “Математика и общество. Математическое образование на рубеже веков.” г. Дубна, 19 сентября 2000г.).
Разрозненных попыток засыпать все углубляющуюся пропасть или хотя бы навести мосты между “двумя культурами” (т.е. между логическим и образным мышлением, между прагматизмом и верой в неограниченные возможности науки и новейших технологий, с одной стороны, и основанными на ограничениях морально-экологическими принципами типа гип-пократовского “Не навреди!” - с другой) можно привести много, в частности, прекрасную книгу А.В.Волошинова “Математика и искусство”. Однако, по мнению авторов, системный подход к решению этой проблемы (а, в более узком смысле, и обсуждаемой реформе математического образования) заключается в следующих словах В.А.Садовничего из уже цитировавшегося выше доклада: “...Я предлагаю сосредоточить внимание на “ничейной земле”, той математике, которая располагается где-то между границами школьной и университетской.” Поэтому авторы убеждены, что необходимо для всех первокурсников во всех вузах в рамках обязательного спецкурса “Дополнительные главы “ничейной” математики” ввести разделы “Математическое природоведение” и “Математическое обществоведение” (все названия условны) на базе программы курса средней школы.
В этом спецкурсе должны быть три главные содержательные линии: математическая, естественно-научная и историко-гуманитарная, объ
17 Методы реш. задач
257
единенные общей методологической основой. Акцент на ту или иную составляющую этой триады зависит, в конечном итоге, от профиля вуза и специализации студента. Введение такого курса позволит решить три главные задачи:
1) без особых усилий существенно сузить нейтральную полосу между школьной и вузовской математикой;
2) на конкретных и простых примерах показать будущим естественникам и гуманитариям, что “математика - язык науки” или (что кому больше нравится) “математика - царица наук” с непременным добавлением “и как хорошая царица она должна заботится о своих подданных”}
3) проследить в историческом контексте эволюцию благотворного взаимовлияния естественно-научного и гуманитарно-художественного мышления.
Это позволит уже на базе средней школы развеять миф о непреодолимых различиях между “двумя культурами” и показать, что культура -едина, просто у нее две стороны, как у медали, как у Януса - два лица, как у мозга - два полушария (по последним исследованиям как раз и отвечающих за последовательно-логическое и одномоментно-образное мышление).
Частными примерами, которые подтверждают последний тезис о единстве двух сторон культуры, служат энциклопедичность гения М.В.Ломоносова, ...и многогранность таланта А.Т.Фоменко. Авторы вместо многоточия подразумевают целый список имен других великих ученых: Пифагора, Л.да Винчи, И.Кеплера, И.Ньютона, Л.Эйлера, А.Пуанкаре, М.В.Келдыша, А.Н.Колмогорова... - и оставляют за читателем право этот ряд дополнить.
В заключение этого и так уже достаточно длинного историко-литературного отступления необходимо заметить, что М.В.Ломоносов в своей неоконченной “Древней Российской истории” и, особенно, отзывах на диссертацию Миллера “Происхождение имени и народа российского” и план работы Шлецера, а также нескольких докладных и объяснительных записках явно обвинил последних не только в научной недобросовестности (ошибаться может каждый), но и в целенаправленном искажении фактов, финансовой нечистоплотности и попытке воровства древних рукописей из библиотеки Академии... Поэтому Рукописи не только горят, но изымаются из научного оборота разными способами (от цензуры до воровства) и целенаправленно уничтожаются. Вышеупомянутые Миллер и Шлецер являлись креатурами Тауберта - врага М.В.Ломоносова в стенах Академии и проводниками скалигеровской версии исторической хронологии, против непогрешимости которой так упорно выступает сегодня в серии книг по “новой хронологии” академик РАН А.Т.Фоменко с соавторами.
258
Интересно, что Скалигер - “основоположник современной хронологии как науки” - опубликовал в свое время книгу, в которой утверждал, что он решил задачу о квадратуре круга (одну из трех знаменитых задач древности, которые не имеют решения!). Математики пытались ему доказать, что его рассуждения неправильны, но Скалигер (как и философ Гоббс) и его сторонники... отвечали лишь руганью и презрительными эпитетами, а в конце концов... объявили всех математиков (в том числе и Виета!) совершенными профанами в геометрии. К сожалению и сегодня, когда не хватает серьезных аргументов или необходимого минимума специальных знаний, крик и ругань часто их заменяют...
К приложению II и последней странице обложки (А). Здесь авторы сделали исключение и решили поместить несколько известных графических работ знаменитого голландского художника Мариуса Эшера (J898-1972). Он досконально изучил законы сочетания орнаментальносимметричных элементов и широко использовал разработанный им принцип динамической симметрии в своих картинах для достижения художественного эффекта. Эшер первым перешел от “евклидовых” равноповторяющихся орнаментов к “неевклидовым” равноизменяющимся. Лучшим подтверждением использования Эшером в своем творчестве последних достижений математической мысли может служить даже беглый сравнительный анализ раскрашенной в два цвета модели Пуанкаре неевклидовой геометрии Лобачевского на круге (слева вверху) и знаменитый “Предельный круг - IV” Эшера (справа вверху). Этот предельный круг можно условно назвать “Рай и Ад” по центральным фигурам ангелов и чертей, которые в процессе приближения к границе круга в пределе превращаются в бесконечное множество голубей и летучих мышей. О философском контексте этой картины авторы предлагают читателю подумать самостоятельно. Заметим лишь, что “Предельный круг - I”, нарисованный Эшером за полтора года (ноябрь 1958г.) до “Рая и Ада”, еще более похож на модель Пуанкаре.
Все четыре “Предельных круга”, а также “Предельный квадрат” и некоторые другие работы Эшера являются не только художественным осмыслением идей деформации пространства и бесконечности с точки зрения неевклидовой геометрии, но 'и гениальным предчувствием основных свойств самоподобия фрактальной геометрии до ее рождения в компьютерных программах Мандельброта.
Днем рождения неевклидовой геометрии следует считать 23 февраля 1826 г., когда Николай Иванович Лобачевский на заседании физико-математического отделения Казанского университета сделал доклад "Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных линиях”. Однако гениальное открытие Н.И.Лобачевского о независимости пятого постулата о параллельных
17*
259
прямых в геометрии Евклида и построение новой геометрии на базе отказа от этого постулата было настолько революционным, что научная мысль того времени была абсолютно не готова к этому. Спустя ровно 30 лет после рождения неевклидовой геометрии Н.И.Лобачевский скончался почти всеми забытым и непризнанным, а его труды так никто и не понял за исключением великого Гаусса. Последний прочитал написанную Лобачевским в 1840 г. на немецком языке небольшую книгу “Геометрические исследования по теории параллельных линий”. После этого 63-летний Гаусс два года изучал русский язык, чтобы прочитать в оригинале остальные труды Лобачевского! Перефразируя В.Маяковского, можно сказать: “Он русский выучил только за то, что на нем писал Лобачевский!” Именно по предложению Гаусса в 1842 г. Лобачевский был избран членом Геттингенского научного общества, уже тогда имевшего статус Академии наук. Это было единственным научным признанием, которого был удостоин еще при жизни создатель неевклидовой геометрии с постоянной отрицательной кривизной. В 1868 г. была опубликована лекция Римана “О гипотезах, лежащих в основании геометрии” (1854г.), где был построен пример неевклидовой геометрии с постоянной положительной кривизной на простой двумерной сфере. В том же 1868г. итальянский математик Бельтрами построил поверхность вращения, реализующую геометрию Лобачевского и названную впоследствии псевдосферой. Однако только модель Пуанкаре, неожиданно увиденная им во время работы над аналитическими вопросами теории функций комплексного переменного и полученное спустя целое десятиление “физическое обоснование” этой модели на основе оптического принципа Ферма в некоторой гипотетической среде, позволили на достаточно простом уровне ознакомиться с геометрией Лобачевского всем интересующимся математикой. Сам Пуанкаре относительно этой физической интерпретации сказал: “Я описал воображаемый мир, обитатели которого неминуемо должны были бы прийти к созданию геометрии Лобачевского”.
В качестве окончания краткого экскурса в историю создания геометрии Лобачевского авторы еще раз возвращаются к уже сформулированной выше идее о необходимости введения обязательного для студентов всех специальностей спецкурса “Дополнительные главы “ничейной” математики”, в рамках которого всего за 3-4 лекции можно рассказать о комплексных числах и их основных свойствах, геометрии Евклида на базе линейных функций и модели Пуанкаре геометрии Лобачевского в верхней полуплоскости на основе (всего-то!) дробно-линейных функций комплексной переменной.
О какой культуре в начале III тысячелетия можно говорить, если большинство школьников понятия не имеет о комплексных числах и азах теории вероятностей, зато их садистски мучают (а без теории пределов
260
это именно так!) вроде бы подсчетом производных и, особенно, интегралов. Более того, во многих вузах технического, педагогического и даже физико-математического профиля о геометрии Лобачевского в программе по математике нет ни слова!
В заключение и так уже растянувшегося послесловия авторы чистосердечно признаются, что не смогли преодолеть соблазн поместить на последней странице послесловия автопортрет Ч.Л.Доджсона (с характерным для Л.Кэрролла комментарием: “Вот как я выгляжу, когда читаю лекции!”) в змеино-колчужную рамку работы Эшера.
261
ПРИЛОЖЕНИЕ I
КОНКУРСНЫЕ ПРИМЕРЫ С ПАРАМЕТРАМИ КАК АНАЛОГИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ ПРИКЛАДНОЙ МАТЕМАТИКИ
Не такой требуется математик, который только в трудных выкладках искусен, но который, в изобретениях и доказательствах привыкнув к математической строгости, в натуре сокровенную правду точным и нспоползповенным порядком вывесть умеет.
М.В.Ломоносов.Слово о пользе химии...
В предисловии уже говорилось, что теоретическое изучение и математическое моделирование многообразных процессов из различных областей науки, техники и практической деятельности человека часто приводит к достаточно сложным уравнениям, неравенствам или их системам, содержащим параметры.
Необходимой частью решения подобных задач является исследование характера и конечного результата процесса в зависимости от значений параметров.
Сложность решения параметрических задач заключается в том, что при изменении параметров меняются не только коэффициенты, но и целый ряд других важных характеристик рассматриваемой задачи: область допустимых значений, степень и даже тип уравнений, непрерывность, монотонность, периодичность, четность и другие свойства входящих в условие функций. Обычно это приводит к тому, что при разных значениях параметра приходится использовать различные методы и приемы решения.
Следует подчеркнуть, что с точки зрения высшей математики решение любой задачи с параметрами представляет собой исследование функции как минимум от двух неизвестных: независимого переменного и параметра. Иногда в процессе решения необходимо несколько раз менять ролями зависимые и независимые переменные, а также параметры.
263
Причем часто в задачах с несколькими параметрами оказывается, что решение зависит не от каждого параметра в отдельности, а от некоторого их характерного комплекса. В подобных случаях становится невозможным разбиение исходной задачи на совокупность задач с одним из параметров. Такие задачи требуют глубокого понимания сути процесса, свободного владения различными математическими методами и скрупулезного анализа.
Можно сказать, что задачи с параметрами, предлагающиеся на конкурсных экзаменах, являются упрощенным аналогом подобных важных научно-исследовательских проблем, которые предстоит решать будущим научным сотрудникам. Именно поэтому задачи с параметрами занимают важное место в вариантах вступительных экзаменов по математике в Московский университет.
Целью данного приложения является конспективное изложение подобных многочисленных аналогий между конкурсными задачами с параметрами и некоторыми проблемами прикладной математики.
1. Исследование квадратичной функции с тремя параметрами является одним из важнейших разделов в курсе математики средней школы, который представляет собой почти идеальную модель по отработке многих навыков решения задач с параметрами и, кроме того, глубокое понимание которого необходимо при изучении высшей математики.
Так, тип квазилинейного уравнения в частных производных [1] вида
Д^РхХ ”Ь 2В<рху Сфуу - 0, (1)
где А,В,С - известные функции а?, у, <р, ipx и <ру, определяется квадратичной формой Ат]2 + 2Вт?£ + С£2, которая имеет тот же знак, что и квадратный трехчлен At2 + 2Bt + С (t — т]/0- Смена знака квадратного трехчлена определяется его дискриминантом D = В2 — АС, поэтому уравнение (1) является
1) эллиптическим, если D < 0 (квадратичная форма знакоопределенная);
2) гиперболическим, если D > 0 (квадратичная форма знакопеременная);
3) параболическим, если D = 0 (квадратичная форма знакопостоянная).
Система уравнений газовой динамики [2;3] для плоских установившихся безвихревых течений идеального газа приводится к одному квазилинейному уравнению
(а — Рх^РхХ ~ ^РхРуРху + (а — р>у}(руу = 0, (2)
где <р - потенциал течения, и = у>х, v = ipy - компоненты скорости движения газа, а - скорость звука.
264
Чрезвычайно важным обстоятельством является тот факт, что уравнение (2) может менять свой тип, так как его дискриминант
D — u2v2 — (а2 — ц2)(а2 — v2) = a2(V2 — а2)
при дозвуковых скоростях V = у/и2 v2 < а <=> D < 0, а при сверхзвуковых скоростях V > а <=> D > 0.
Смена типа уравнения (2) при V = а принципиально меняет свойство его решений и это отражает тот факт, что характер движения в сжимаемых средах резко меняется при переходе через скорость звука. Некоторые характеристики течения при этом заменяются прямо противоположными, в частности при дозвуковых режимах расход (произведение плотности среды на скорость) растет при увеличении скорости, а при сверхзвуковых - падает. Скачком меняется подъемная сила и сопротивление. Легко понять, как важно это и аналогичные ему обстоятельства для пилота самолета с околозвуковой скоростью, ведь одинаковые действия при дозвуке и сверхзвуке могут давать противоположные результаты!
Особенно простой вид уравнение (2) имеет в плоскости годографа (и,и), записанное в полярной системе координат (V"; 0)
V (w = V cos 9, v = V sin0) через функцию тока и число Маха М — —
1-М2 , д (V \ п
Эта форма записи называется уравнением Чаплыгина, а тип уравнения определяется одним безразмерным параметром М (эллиптический при М < 1 - дозвук, гиперболический при М > 1 - сверхзвук). Подчеркнем, что разрывные решения могут возникать лишь при М > 1.
Заметим, что уравнение (2) в околозвуковом приближении при |М — 1| <С 1 с помощью замены г) = 2k(u — а), £ = 2kv, к = const > 0 и стандартной процедуры перемены ролей зависимых и независимых переменных (вспомните метод решения относительно параметра) приводится к линейному уравнению Трикоми [2]: т) • — 0, которое являет-
ся одним из простейших уравнений смешанного типа. В полуплоскости т] < 0 оно эллиптическое (дозвук), а при т] > 0 - гиперболическое (сверхзвук). При этом линия вырождения типа есть ось г) = 0 <=> и = а, т.е. является звуковой линией.
Аналогичная ситуация возникает в задачах обтекания тел потоком не-ныотоновской жидкости, где соответствующее уравнение имеет вид [4]
(1 — к2\фхх 4- -фуу + ikzz = Re rpx. (3)
Здесь Re - число Рейнольдса, a к = V/V* - отношение характерной скорости течения к “естественной” скорости называется вторым упругим
265
числом. В докритическом случае (к < 1) уравнение (3) является эллиптическим и допускает непрерывные решения, позволяющие получить силу сопротивления для тел простейшей формы (сфера, цилиндр) в явном виде. В закритическом случае (k > 1) уравнение (3) является гиперболическим и имеет решения с разрывами вдоль волновых фронтов, а для силы сопротивления получены лишь оценки нижней и верхней границ.
Сходная картина встречается в задаче кручения стержней, когда имеет место так называемая “падающая диаграмма”. При этом кривая связи между углом сдвига и тангенциальным напряжением сначала возрастает, а потом, проходя через максимум, убывает. Заметим, что многие упруго-пластические задачи являются гиперболо-эллиптическими.
Но в отличие от предыдущих случаев здесь в отдельных областях (зоне упругости и пластичности с неизвестной границей между ними) приходится иметь дело не только с уравнениями разных типов, но разных порядков и даже видов интегродифференциальных операторов.
Прямой аналогией этого являются конкурсные задачи с параметрами и функциями fag, которые относятся к существенно разным видам. Как правило, единственной надеждой на решение подобных задач является условие: min/ = max<7 па заранее неизвестной границе областей изменения этих функций.
В аэродинамике нестационарных пограничных слоев встречаются по-раболические уравнения второго порядка со сменой направления пара-боличности, которые также требуют постановки дополнительных граничных условий на подвижной и заранее неизвестной границе. Лишь совсем недавно на основе обобщенного преобразования функций и координат система уравнений данного класса получила единообразное описание, где учет пестационарности внешнего потока и формы тела происходит в результате изменения управляющих параметров.
Из параболо-эллиптических задач упомянем исследования на устойчивость 'гонкой пластины в окрестности отверстия и течений вязкой жидкости на основе уравнений Навье-Стокса. Указанные примеры не исчерпывают даже малой доли проблем, когда приходится иметь дело с уравнениями разных типов в отдельных областях, занятых сплошной средой [5]. Подчеркнем лишь, что их решение требует применения ряда современных математических методов.
Большинство задач МГД-обтекания тел [6] сводится к нахождению фундаментального решения уравнения вида
д д2 \
А2 - Re —А - Н2—- Ф = 0, (4)
дх дх2 J
где А - оператор Лапласа в пространстве двух (для цилиндрических тел) или трех измерений, Н - число Гартмана, Re - число Рейнольдса, х -координата, вдоль которой направлено внешнее магнитное поле.
266
Для эффективного нахождения решения этого уравнения требуется разложить дифференциальный оператор четвертого порядка в произведение двух неравных и коммутирующих операторов второго порядка. На “школьном языке” это означает, что квадратичное выражение
А2 - Re • q • А - Н2 • g2
относительно переменных Аид надо разложить в произведение линейных по А и g множителей. Проще всего это сделать, найдя корни квадратного трехчлена относительно параметра р = &./q
2 о rr-2 Re ± ,
р2 - Re • р - Н2 = 0 <=> рХ‘2 = ------------
А - qpx V А = qp2 <=> (А - gpi)(A - gp2) = 0.
Таким образом, левая часть уравнения (4) представима в виде произведения двух операторов типа Озеена:
/. д \ ( д д \ ,
А - pi • — • А - р-2 • — Ф = 0, \ ox J \ ох )
фундаментальные решения которых хорошо известны.
Заметим, что безразмерная сила сопротивления сферы в МГД-приближении Озеена содержит радикал У Ле2 + 4Я2 (несмотря на то, что в уравнение (4) Re входит линейным, а Н квадратичным образом) и оказывается равной
F = бтг [1 + | уе22+2Я22] б7г[1 + ^Re + Я)],
L 8 УЯе2 + 4Я2] L 8V 'J)
т.е. не сводится к простому суммированию классических поправок Озеена и МГД-приближения Стокса.
Заинтересованный читатель без особого труда среди конкурсных задач с параметрами найдет соответствующие аналоги разобранным выше примерам из различных разделов механики сплошных сред. В менее очевидных случаях авторы такие задачи будут стараться указывать явно.
2. В теориях устойчивости и колебаний [7] большое число задач после ряда математических преобразований сводится к квадратным, биквадратным и другим степенным уравнениям или их системам, аналоги анализа которых можно найти среди конкурсных задач с параметрами.
В качестве примера можно привести модельные задачи о явлении антирезонанса в системе с двумя степенями свободы, устойчивости трубопровода, частотном анализе собственных колебаний автомобиля, устойчивости горизонтального полета и различных видах флаттера самолета [8-10].
267
Флаттером называют явление динамической неустойчивости конструкции под действием аэродинамических, упругих сил и сил инерции. Ниже рассматриваются две достаточно простые модели флаттера крыла самолета.
Первая модель представляет собой упруго закрепленную по краям пластину, положение которой характеризуется двумя координатами: углом поворота </?(£) и вертикальным перемещением ?/(/) ее центра тяжести (см. рис. 1). Уравнения баланса сил и моментов приводят к системе дифференциальных уравнений, которая может быть записана в виде
mS ij = R + Y
mSb2
12
<р = М + Y
?/ + аиН Д12У? = о ip + а21у + Д22<Р = о,
(5)
г. Pv2 dkf
где подъемная сила Y = срЬ • -т- • -у2-; приведенная реакция опор R 2 da
и момент М выражаются через координаты y(t), y?(Z), размеры b и I пластины и коэффициенты жесткости упругих опор ci и Со; S = b • I и
т - площадь и погонная масса пластины; р и v - плотность и скорость
натекающего потока газа; kf =
dkt
—— ср - коэффициент подъемной силы, da
который считается пропорциональным углу атаки а = ср, а параметры
a{j однозначным образом выражаются через размерные характеристики
пластины и потока.
Рис. 1. Схема сил, действующих на отклоненную пластинку, и схема перемещений профиля крыла при флаттере
Если решение однородной системы дифференциальных уравнений (5)
268
2
- (Д11Д22 - Д12«21)- (6)
2 Сц + Д22 .
= —2—±
искать в виде у — Aexp(iwt), ip — Вехр(гсЛ), то для определения амплитуд А и В получаем однородную систему линейных уравнений. Эта система может иметь не только тривиальное решение лишь в том случае, если ее определитель равен нулю, что приводит к биквадратному уравнению относительно частоты сэ:
А(ац — а>2) + Ва-^2 — 0 оц — ш2 012 _ g
Aa2i 4- В(о22 — w2) = 0 ^21 022 — w2
'£=> а>4 — (оц + O22)^2 + (fll 1^22 ~ ^12^21) = 0
Д11 + ^22 2
Для устойчивости системы необходимо, чтобы все четыре значения ш были действительными, следовательно оба полученных значения ш2 2 должны быть положительными. Откуда следует, что
(. / Oil + 0.22
0; (---------
Критическим состояниям соответствуют границы этого интервала, т.е. равенства
ОцО22 — 012021 ИЛИ (Оц — О2г)2 + 4al 2а21 = 0.
Первое из этих равенств, записанное в размерных переменных, дает некоторое значение критической скорости потока, которое при wi = 0 соответствует статическому пределу устойчивости. Второе равенство дает именно скорость флаттера крыла самолета, т.е. динамический предел устойчивости
И _ 2 /с* ~ (ci ~ CjC2 + с$)(2у - 1)^
кр 27 — 1 У 2>p-dkj/da
где 7 = а/Ъ, а с* = ус\ — (1 — 7)02 - приведенная жесткость системы. При скорости полета v > UKp подкоренное выражение в (6) становится отрицательным, следовательно 7m(a>) 0 и амплитуды колебаний растут по
экспоненте, что практически мгновенно приводит к разрушению самолета.
Второй моделью флаттера является жесткий профиль крыла при наличии демпфера с сухим трением и упругой связью (см. рис. 2). Уравнение движения можно записать в виде [10]
тх — Ьх + сх + р sign(x) = 0. (7)
269
Рис. 2. Модель флаттера, крыла в аэродинамической трубе (1 - демпфер с сухим трением, 2 - профиль крыла, 3 упругая пружина) и фазовый портрет уравнения (1 - полуустойчивый предельный цикл, 2 - “зона застоя").
Дифференциальное уравнение фазовых траекторий при переходе к безразмерным переменным с сохранением их прежних обозначений имеет вид
dy = y-signy-e^ k2 = cm/b2 dx у
При малых значениях безразмерного параметра к2 на фазовой плоскости получается полуустойчивый предельный цикл с зоной застоя по оси абсцисс, характерной для систем с сухим трением [7]. Спирали, находящиеся внутри цикла, соответствуют траекториям с убывающей амплитудой, вне - возрастающей. При возрастании параметра к2 предельного цикла не возникает и колебания исчезают, в отсутствие сухого трения (у = 0) фазовый портрет является неустойчивым узлом.
Подчеркнем, что приближенное построение фазовых траекторий по методу Льенара [7] вполне доступно для понимания старшеклассников, ибо опирается на простейшие построения и геометрический смысл производной.
Обычно метод Льенара широко используется для построения фазовых портретов автоколебательных систем с различными законами нелинейности, особенно для нахождения устойчивых предельных циклов - замкнутых фазовых траекторий.
В свое время, до появления в ФМШ № 18 при МГУ персональных компьютеров и ЭВМ, этот и аналогичные ему методы применялись для выполнения ряда задач математического практикума [11].
270
Подробное изложение теории флаттера не только крыльев, но и других частей самолета можно найти в [8], а в [12] представлены более сложные модели флаттера в сверхзвуковом потоке ионизованного газа с учетом электромагнитных сил.
Несмотря на кажущуюся экзотичность эти исследования очень актуальны, ибо МГД-генераторы и реактивные двигатели самолетов и ракет имеют в качестве рабочего тела потоки высокотемпературной плазмы. Кроме того летательные аппараты при скоростях в “несколько Махов” (т.е. в несколько раз быстрее звука) движутся не только в магнитном поле Земли, но и в ионизованном ударной волной газе. А современные тенденции развития авиационной и ракетной техники свидетельствуют о все более жестких требованиях к маневренности самолетов, зенитных и крылатых ракет при расширении диапазона скоростей полета за счет увеличения Vmax.
Подчеркнем, что учет электромагнитных сил в явлениях флаттера чрезвычайно усложняет задачу по многим причинам. Так, в проводящем газе существуют три скорости распространения слабых разрывов: альфвеновских, медленных и быстрых магнитозвуковых волн, зависящих к тому же от направления магнитного поля (тогда как в непроводящем газе существует лишь одна скорость звука).
Однако природа часто идет навстречу пытливым исследователям и в магнитной газодинамике при больших сверхзвуковых скоростях имеет место так называемый “закон плоских сечений” [2], который позволяет в ряде важных случаев существенно упростить расчеты. Как правило [12], в конечном итоге задача сводится к характеристическому уравнению второй, третьей или четвертой степени, коэффициенты которого зависят от упругих, аэродинамических и электромагнитных параметров задачи.
Так как общих методов аналитического решения степенных уравнений пет, то для выяснения устойчивости обычно применяется критерий Гурвица [13], дающий необходимые и достаточные условия отрицательности действительных частей всех корней многочлена n-ой степени через его коэффициенты.
Более подробный анализ устойчивости многих систем показывает, что неприятности могут возникать и в случаях, когда характеристическое уравнение для определения частот имеет кратные корни или когда значения собственных частот образуют арифметическую прогрессию. В первом случае происходит слияние двух частот и в решении могут возникнуть так называемые вековые или секулярные члены типа t sin(o^), медленно растущие с течением времени. Во втором случае для нелинейных систем за счет так называемого перекрытия резонансов [7] могут возникнуть очень сложные, практически хаотические колебания с весьма большими амплитудами, что также часто приводит к разрушению.
271
Однако не всегда подобные свойства корней характеристических уравнений являются нежелательными. Рассмотрим задачу о собственных вертикальных колебаниях автомобиля, когда случай равных частот повышает его комфортабельность.
Рис. 3. Динамическая схема автомобиля и собственные колебания при p2=ab
На рис. 3 представлена упрощенная динамическая схема автомобиля с двумя степенями свободы, где за обобщенные координаты и q2 приняты вертикальное перемещение центра тяжести автомобиля массы m и угол поворота вокруг центра тяжести. При этом осадки упругих опор равны qi + aq2 для задней и q± — bq2 для передней опоры.
Выражения для кинетической и потенциальной энергий системы имеют вид
1 1
Е = 2+ т^2Й]; и = 2 Ы?1 +а^2 +С2^1 _ ^2)21 >
тогда из уравнений Лагранжа получаем уравнения движения системы
Г mq\ + (ci + c2)?i + (aci - bc2)q2 = О
I mp2q2(aci - 6c2)gi + (a2ci + b2c2)q2 = 0.
Решения этой системы будем искать в виде qk = Ak • sin (wkt + <рь), что позволяет получить однородную систему алгебраических уравнений относительно частоты и
Г —Л177гш2 + Xi (ci + с2) + A2(aci — 6с2) = 0
t — A2mp2w2 + Xi(aci — 6с2) + А2(а2С\ + 62с2) = 0.
272
Из равенства нулю определителя этой системы следует частотное уравнение
4 (ci+c2 a2ci + 62с2\ 2 , cic2(a + 6)2 у m трл J тл
которое, как правило, имеет различные корни. Каждому значению корня соответствует свое соотношение между амплитудами вида
А1 _ аС} bc2 (gs
А2 771W2 — ci — с2
Наиболее просто анализируется частный случай, когда р = у/ab, т.е. радиус инерции системы р является средним геометрическим между расстояниями а и Ь. Тогда частотное уравнение имеет не равные между собой корни
2 _ С1(а + Ь) 2 _ с2(а + 6) — и — ~~ > то та
при подстановке которых в соотношение (9) получаем очень простую связь для амплитуд колебаний:
Ai = ЬА2 при о>2 = о>2 и Ai + аА2 = 0 при о>2 = о^.
Особенностью таких колебаний является их независимость друг от друга, т.е. колебания одной подвески не передаются другой, что повышает комфортабельность автомобиля.
В другом частном случае, когда aci = bc2, уравнения системы (8) становятся независимыми, что означает возможность чисто вертикальных колебаний без поворотов (подпрыгивание) или чисто угловых колебаний (галопирование) при неподвижном центре тяжести автомобиля. В случае
л / п л п 2 ^1 “Ь С2
подпрыгивания имеем Ai А О, А2 = 0, /А = ------, в случае галопиро-
т
9 a2Ci 4- b2Ci
вания - Ai = О, А2 А 0, wl = ----9---, т.е. частоты этих колебаний,
трл
как правило, различны.
Можно доказать, что при одновременном выполнении двух условий \ л /ci + с2
р = v ab и aci = bc2 частота собственных колебании а>о = \ -----
V т
Подчеркнем, что совпадение частот не приводит в этом случае к появлению секулярных членов и росту амплитуды колебаний, так как при одинаковой частоте колебания
qi = Ai sin(woi + и q2 = A2 sin (w0Z + <p2) могут отличаться лишь фазами.
18 Методы реш. задач
273
3. Уделив столько внимания явлению флаттера самолета, авторы считают своим долгом привести краткую историческую справку [14] о вкладе ученых механико-математического факультета МГУ нс только в решение этой проблемы, но и в приближение Великой Победы советского народа в Отечественной войне 1941-1945 гг.
Интенсивная научная деятельность ученых МГУ в области аэродинамики накануне и в годы войны способствовала качественному скачку в развитии советской авиации. Невиданные ранее в истории темпы производства первоклассных боевых машин в годы войны (истребителей Яковлева и Лавочкина, штурмовиков Ильюшина, бомбардировщиков Петлякова) стали возможны благодаря не только трудовому подвигу конструкторов, инженеров, рабочих и строителей, но и оперативному использованию теоретических разработок ведущих советских ученых. Большую роль в совершенствовании важнейших достоинств боевого самолета (маневренности и скорости) сыграли исследования различных характеристик основной части самолета - крыльев. Работы С.А.Чаплыгина (первый Герой Социалистического Труда среди ученых страны), В.В.Голубева (зав. кафедрой аэромеханики, декап механикоматематического факультета МГУ в 1944-1952гг.), М.А.Лаврентьева и Л.И.Седова (зав. кафедрой гидродинамики) в этой области во многом определили дальнейшее развитие аэродинамики и авиационной техники. А “кривая Христиановича” для выбора формы крыльев при больших околозвуковых скоростях по результатам испытаний на малых скоростях была известна всем советским конструкторам боевых самолетов.
В борьбе за скорость самолетов существенное значение имела разгадка нашими учеными тайны флаттера. С середины 30-х годов именно флаттер стал самым серьезным препятствием на пути увеличения скорости полета. В сжатые сроки М.В.Келдыш (президент АН СССР в 1961-1975 гг.) совместно с сотрудниками ЦАГИ провел ряд экспериментов в аэродинамических трубах и на испытательных стендах, по результатам которых была разработана не только математическая теория флаттера, но и предложен комплекс практических мер, исключающих это явление [8]. За научные работы в этой области уже в 1942г. М.В.Келдыш был удостоен Государственной премии, а в 1946г. ему была присуждена вторая Государственная премия за решение проблемы “шимми переднего колеса” самолета [8], которое часто при посадке не хотело катиться ровно, а начинало сильно колебаться, что нередко приводило к аварии. Заметим, что свою научную деятельность В.В.Голубев и М.В.Келдыш начинали как чистые математики, а в механике они, как говорят, нашли свою звездную дорогу.
Важное значение имели работы по изучению способов выведения самолета из штопора, повышению устойчивости движения самолета при
274
вынужденных посадках на землю (Н.Г.Четаев), исследованию аэродинамических свойств и надежности парашютов.
В отчете МГУ за 1940 г. о научных исследованиях работа Х.А.Рахматулина (зав. кафедрой газовой и волновой динамики) по аэродинамике парашюта была названа в числе выдающихся. В кратчайшие сроки эти исследования были завершены, что позволило в годы войны наладить производство нескольких новых видов парашютных систем различного назначения. Кроме того, Х.А.Рахматулиным были разработаны математические теории деформации гибкой нити при поперечном ударе и открыты волны разгрузки, возникающие при ударе в твердом теле за пределами упругости при быстром спаде высокого давления, которые теперь в мировой научной литературе известны под названием “волн Рахматулина”. Первая теория во время войны нашла свое применение при создании противовоздушных заграждений советских городов из связанных тросами аэростатов, что было особо отмечено при награждении Х.А.Рахматулина медалью “За оборону Москвы”. Вторая теория вместе с исследованиями А.А.Ильюшина (зав. кафедрой теории упругости) по упруго-пластичным деформациям позволила в несколько раз увеличить производство боеприпасов, так как существенно упрощала технологию изготовления корпусов артиллерийских снарядов из сталистого чугуна вместо ранее употреблявшейся высокопрочной стали. За научные работы военных лет Х.А.Рахматулин был удостоен Ломоносовской (1945 г.) и Государственной (1949 г.) премий, А.А.Ильюшин - Государственной премии (1948 г.).
Результаты многих исследований коллектива кафедры теории упругости нашли применение в оборонной промышленности, кроме того, именно здесь решалась задача о прочности ледового покрытия “Дороги жизни” по льду Ладоги во время героической обороны блокадного Ленинграда. Исследования А.А.Ильюшина по теории пластичности легли в основу новой технологии изготовления стволов артиллерийских орудий; Н.Г.Четаев решил сложные задачи по определению оптимальной крутизны нарезки орудийных стволов и устойчивости снарядов и мин при полете. В 1943 г. они были избраны чл.-корр. АН СССР, а в 1947г.--членами Академии артиллерийских наук при Министерстве обороны одновременно с М.А.Лаврентьевым (лауреат Государственных премий 1946 и 1949 гг.) и А.А.Космодемьянским.
Перед самой войной А.А.Космодемьянским был выполнен цикл работ по механике тел переменной массы и реактивной динамике, имеющих прямое отношение к первым пороховым ракетам, в частности, к снарядам легендарных “катюш”. Дальнейшие исследования А.А.Космодемьянского нашли приложения в ракетной технике и космонавтике.
18*
275
В середине войны на полях танковых сражений появились немецкие “Тигры”, лобовую броню которых из наших противотанковых пушек пробить было невозможно. В сжатые сроки М.А.Лаврентьеву на основе теории соударения жидких струй (!) удалось построить математическую модель так называемого кумулятивного снаряда, применение которых повергло фашистов в шок. Лишь спустя много лет после войны нашим ученым и конструкторам удалось найти противоядие кумулятивным снарядам и противотанковым ракетам в виде комплекса так называемой активной защиты. Для этого необходимо специальным образом обложить танк специальной взрывчаткой. Все гениальное - просто, когда уже сделано, а вот как до этого додуматься ?!?
Следует подчеркнуть, что оборонной тематикой в годы войны занимались и “чистые” математики. Так, Л.А.Люстерник (зав. кафедрой функционального анализа) был одним из авторов таблиц для определения местоположения кораблей по радиопеленгу, сотрудники кафедры теории вероятностей выполнили исследования по оптимальному рассеиванию снарядов при стрельбе по площадям (академик А.Н.Колмогоров) и по бомбометанию с малых высот при малых скоростях самолетов (Б.В.Гнеденко и А.С.Монин).
Интересно отметить, что составленные по этим исследованиям рекомендации и таблицы очень повысили (особенно в ночное время) эффективность действий женских легкобомбардировочных авиаполков, личный состав которых преимущественно состоял из добровольцев - студенток и аспиранток механико-математического и физического факультетов МГУ, Московского авиационного института. На вооружении этих полков находился знаменитый “небесный тихоход” - самолет По-2, который широко применялся в народном хозяйстве в довоенное время, а во время войны стал грозным оружием - ночным “ангелом смерти” для фашистов. Недаром уже в 1942г. за каждый сбитый По-2 гитлеровских летчиков награждали “железным крестом”, однако деревянных крестов наши девушки “подарили” захватчикам во много раз больше.
Важное значение для решения ряда оборонных задач имела работа номографического бюро при НИИ математики МГУ, которым руководил известный геометр Н.А.Глаголев. Номограммы, подготовленные в этом бюро, применялись в военно-морском флоте, в частности, при веерных атаках конвоев противника с подводных лодок и торпедных катеров; частях зенитной артиллерии; истребительной авиации для оптимального перехвата бомбардировщиков противника, совершавших налеты на наши города. В частности, осенью 1941г. Н.А.Глаголев решил задачу по оптимальному размещению зенитных батарей вокруг Москвы, а С.В.Бахвалов разработал теорию приборов управления артиллерийским огнем.
276
4. Построение номограмм для конкретных функциональных зависимостей позволяет не только исследовать их качественный характер, но и практически мгновенно находить приближенные решения, отвечающие заданным критериям.
Для начала рассмотрим семейство приведенных квадратных трехчленов вида ж2±ра?±д, где р и q - действительные параметры. Заметим, что излагаемый ниже материал может рассматриваться как отдельный параграф главы III, посвященной исследованию квадратичной функции, и как интересная иллюстрация к обобщению метода решения относительно параметра.
Каждому трехчлену этого семейства х2 +р*х + q* с конкретными параметрами р* и q* на некоторой фазовой плоскости тг с декартовыми координатами (р; q) поставим в соответствие точку с координатами (р*;д*). Тогда равенство q = р2/4 определяет в плоскости тг дискриминантную параболу, все точки которой соответствуют трехчленам, имеющим совпадающие (или кратные) корни. “Внутри” параболы при q > р2соответствующие трехчлены не имеют действительных корней; область “вне” параболы при q < р2/4 соответствует трехчленам, имеющим два различных корня. Прямая g ± ар ± а2 = 0 на плоскости тг (р, q - переменные, а - фиксированный параметр) называется корневой, так как точки этой прямой соответствуют трехчленам х2 ± рх ± q, которые в качестве своего корня имеют число а. Простым вычислением можно убедиться, что прямая будет корневой тогда и только тогда, когда она касается дискриминантной параболы:
( g = p2/4 ( q = p2/4 ( q = а2
t q ± ар ± а2 = 0 1 р2 + 4ар ± 4а2 = О I Р — —2а,
т.е. корневая прямая является касательной к дискриминантной параболе в точке (—2а, а2). Следовательно, через любую точку дискриминантной параболы проходит ровно одна корневая прямая; из любой точки “внешней” области параболы к ней можно провести две различные корневые прямые; а из “внутренней” - ни одной. Если на плоскости тг провести много корневых прямых, придавая параметру а значения
0; ±0.5; ±1; ±1.5; ±2; ±2.5;...,
то получившаяся “сеть” из прямых называется сетчатой номограммой для решения приведенных квадратных уравнений. Например, уравнению х2 ± х — 3 = 0 на плоскости тг соответствует точка (1; —3), принадлежащая четырехугольнику ABCD (см. рис. 4). Это уравнение должно иметь два различных корня, причем a?i £ (—2.5; —2) и х2 Е (1; 1-5), а за их приближенные значения можно взять средние арифметические
—2.5 — 2 1 ± 1.5 о
з?1 --------— —2.25 и х2 ~ —-— = 1.25.
277
Рис. 4. Сетчатая номограмма приведенного квадратного уравнения
Для нахождения приближенных решений уравнений с кратными корнями можно соответствующим образом проградуировать и дискриминантную параболу, вспоминая отмеченную выше роль точек (—2а; а2). Заметим, что “сетка” корневых прямых имеет сгущение у дискриминантной параболы и как бы автоматически ее “вычерчивает”, в силу чего дискриминантную параболу называют огибающей множества корневых прямых. Если по определению принять, что огибающая семейства корневых прямых является геометрическим местом точек (р, q), каждая из которых соответствует уравнению с кратными корнями, то возможно обобщение изложенного здесь метода построения сетчатых номограмм для приведенных степенных уравнений вида x3+px+q = 0, х4+рх + q = О или д4 ± х2 + рх + q = 0 [15,16].
В качестве самопроверки попробуйте:
1) на фазовой плоскости 7Г нарисовать “картинки”, соответствующие теоремам 1-4 гл.III, задавая числам m, М и р конкретные значения;
2) вывести уравнения огибающих для приведенных уравнений:
ч (Р\3 (Ч. \2
х +px-\-q-Q в виде (-) + (- ! = 0;
у ч 4
j \ 3
х + рх + q = (J в виде q = 3 I - I ;
278
4 „ f р= ±2а(1±2а2)
х ± х + рх + q = 0 в параметрической форме < „ „
( q = cr(3a2 ± 1).
(Со знаками разберитесь самостоятельно!)
Изложенный выше материал доступен для школьников старших классов и созвучен идеям Ф.Клейна [17] о целесообразности геометрического подхода к решению степенных уравнений с двумя и более параметрами.
Каждая номограмма строится для определенной функции в заданных пределах изменения переменных, значения переменных обозначаются точками или линиями. Множество таких точек, зависящее от одной переменной, называется шкалой, зависящее от двух переменных - бинарным полем. Широко известным примером бинарного поля является сетка из параллелей и меридианов на географической карте, а нанесение на карту еще и горизонталей (значений высот от уровня моря) дает пример сетчатой номограммы. В [15] для уравнения Ван дер Ваальса (р+1 /У2)(У — 1) = Т, где р, V,T - безразмерные давление, объем и температура газа, построена в плоскости (V, р) сетчатая номограмма изотерм 7' = const, которая позволяет сразу по двум заданным параметрам из трех р, V и Т определить значение третьего.
Заметим, что сетчатые номограммы отражают практически любую зависимость с тремя переменными F(x,y,z) = 0.
Одним из недостатков этого вида номограмм является наличие трех семейств линий, наложенных друг на друга, что в некоторых случаях делает затруднительным их использование. Однако это можно устранить, преобразуя сетчатую номограмму в номограммы из выравненных или равноудаленных точек [18]. В качестве примера рассмотрим фактически школьную задачу, решение которой привело к созданию в первые месяцы войны очень важной номограммы из выравненных точек с тремя бинарными полями [19].
Задача. Точка S движется прямолинейно с постоянной скоростью v. Направление движения характеризуется углом <р, образуемым вектором скорости с вертикалью. В начальный момент времени точка S находилась в точке В, об этом было получено сообщение в другой точке А, отстоящей от В на расстояние I, причем прямая АВ составляет с вертикалью угол 9. Через промежуток времени т из точки А начинает прямолинейное движение со скоростью w точка J. Вектор скорости w составляет с вертикалью угол -ф. Требуется определить ф по данным значениям I, т, <р, 0, v, и w из условия, что точки S и J должны встретиться и все происходит в одной плоскости.
Решение. Пусть t - время встречи точек S и J в точке С, тогда стороны ААВС будут равны: АВ — I, АС = wt, ВС = (t + r)v. Проектируя стороны треугольника на вертикальную и горизонтальную оси, получаем
279
систему уравнений
( I cos 0 + v(t + г) cos 99 = wt cos ф !
[ I sin 0 + v(t + r) sin <p = wt sin ф. 1
Исключая t/т и введя обозначение l/т = и, приходим к уравнению:
и cos 0 + v cos 99 _ и sin 0 + v sin 99 w cos ф — v cos 99 w sin ф — v sin 99 ’
из которого можно найти т/’ по заданным значениям 0, 99, и, v и w. Его, аналитическое решение достаточно громоздко и требует много времени: для вычисления. Так как в этом уравнении 6 переменных, то удобно; построить для его приближенного решения номограмму из выравненных! точек с тремя бинарными полями: '
( х\ - v cos 99 ( Х2 = w cos ф ( хз = —и cos 0
[ yi = v sin99; [ У2 = wsini/’; I Уз = — usin0.
Откуда сразу получаем
x2 + yl = v2, z% + yl = w2, ^з + Уз = и2-
Таким образом, номограмма состоит из семейства прямых (линии углов 99 и ф) и семейства концентрических окружностей (линии величин и, г, w) с началом координат в точке А.
Эта номограмма позволяла практически мгновенно определять азимут вылета наших истребителей для перехвата фашистских бомбардировщиков на дальних подступах к Москве. На основе этой номограммы позднее был создан И КО (индикатор кругового обзора) радиопеленгатора и весь процесс автоматизирован, а автор номограммы И.Н.Денисюк награжден орденом Ленина.
Заметим, что почти аналогичные вычисления возникают при расчете задач обтекания клина и конуса сверхзвуковым потоком. И если в первом случае из алгебраических соотношений на ударной волне, следующих из законов сохранения массы, количества движения и энергии, прямая задача о построении ударной поляры [2;3] решается практически методами школьной геометрии (с использованием подобия треугольников и теоремы о пересекающихся хордах), то в случае конуса необходимо предварительное построение фактически сетчатой номограммы. Эта номограмма в плоскости годографа состоит из яблоковидной кривой и семейства интегральных линий, соединяющих точки кривой с ударной полярой [2], и фактически позволяет решать прямую задачу обтекания конуса методом обратной задачи.
280
Другие конкретные примеры и теоретические принципы построения номограмм разных типов можно найти в [18].
Аналогией сетчатых номограмм для рассмотренных выше приведенных степенных уравнений на фазовой плоскости параметров (р, q) является для уравнения Матье
сРу
+ (р - 2g cos 2т)р = О атл
(10)
диаграмма Айнса-Стретта (см. рис. 5), которая является симметричной относительно оси р в силу четности по переменной q, что следует из замены т на
Большое количество механических и электрических систем может испытывать параметрически возбуждаемые колебания, которые во многих случаях описываются уравнением (10). Диаграмма Айнса-Стретта [9,20] полностью освобождает от исследования на устойчивость решения уравнения Матье в каждом конкретном случае. Достаточно просто найти значения параметров системы р и q и диаграмма сразу даст ответ на этот вопрос.
Каждой системе, характеризуемой параметрами р и q, соответствует точка с координатами (р, д) на диаграмме: если точка попадает в заштрихованную область, то система устойчива, в противном случае - система неустойчива. По определению система называется устойчивой, если ее колебания ограничены, и неустойчивой, если колебания возрастают. Для практических целей наибольшее значение имеют границы между областями устойчивых и неустойчивых решений. Из диаграммы
281
Айнса-Стретта явно видно, что неустойчивость при сколь угодно малых q появляется вблизи точек р = п2, п Е N. В [20] доказано, что в каждой’ окрестности точек (п2, 0) существуют как устойчивые, так и неустойчивые решения.
Одним из простейших примеров параметрически возбуждаемых систем является маятник на жестком стержне с колеблющейся точкой подвеса. Парадоксальная потеря его устойчивости в нижнем положении и еще более ошеломляющая устойчивость в верхнем доступны для понимания учащимися старших классов. Тем более, что предложенная выдающимся советским физиком П.Л.Капицей экспериментальная установка [9] может1 быть собрана в физическом кабинете любой школы. Предварительное знакомство с построением номограмм приведенных степенных уравнений существенно облегчает восприятие диаграммы Айнса-Стретта. А изучение номограмм степенных уравнений входило в задачи математического практикума ФМШ № 18 при МГУ [11] и других специализированных школ, что способствовало развитию исследоватсльских навыков еще до поступления в вуз.
5. Кроме квадратичной функции существует еще один раздел школьного курса математики, посвященный системам линейных уравнений с квадратной матрицей, который допускает проведение исследования вопроса о существовании и числе решений в достаточно общей постановке методом определителей. К большому сожалению этот метод, довольно несложный для понимания, сейчас не входит в школьную программу. Однако следует подчеркнуть, что в случае двух неизвестных подобное исследование может быть проведено на основе пропорций, составленных из коэффициентов линейных систем. Аналоги конкурсным примерам на решение систем линейных уравнений и неравенств с параметрами можно найти среди задач газовой и волновой динамики, а также среди прикладных вопросов линейного и параметрического программирования [21], имеющих важное значение для решения многих экстремальных задач по оптимальной организации производственно-экономической деятельности.
Заметим, что метод определителей был уже выше использован при изучении флаттера и получении других характеристических уравнений в задачах устойчивости. В высшей математике метод определителей часто применяется в комбинации с другими приемами решения задач с параметрами, где используются свойства симметричности переменных или четности функций, а также разные модификации метода решения относительно параметра.
В прикладных вопросах радиофизики и электроники характеристическое уравнение часто получается в виде pA(i/) + qB(i/) + C(z/) = 0, где р, q - действительные параметры, а А, В, С - комплекснозначные
282
функции комплексной частоты у. Если один из корней этого уравнения является чисто мнимым, т.е. v — iw, то для него справедливо уравнение
pA(iu>) + qB(iu>) + C(iw) = 0.
Выделяя в функциях А, В и С действительную и мнимую части
A(?w) = ReA. + iJmA = Ai(w) + iA2(w) B(icA) = ReB + iJmB = Bi(w) 4- 7.B2(A) C'(iu’) = ReC + iJmC = Ci(u') + 26'2(0;),
получаем из характеристического уравнения систему линейных уравнений относительно переменных р и q:
pAi(w) + qBi(u>) = -Ci(w) pA2(w) + = -C2(w),
где коэффициенты Ai, В] и Сг - четные, а А2, В2 и 64 нечетные функции параметрам.
Если основной и дополнительные определители этой системы
Ai
Л2
Bi
В2
#0,
Л1 = -
С2
В1
В2
А2 —
Ai С\
А2 С2
то формула Крамера р = Aj/A, q = А2/А дает параметрическое уравнение некоторой кривой на фазовой плоскости (р, q) - границу так называемого D-разбиения. Заметим, что р и q являются четными функциями параметра м, так как определители A, Ai и А2 - нечетные функции м. В случае линейной зависимости уравнений системы при некоторой частоте м = мд формулой Крамера пользоваться нельзя, а особая граница D-разбиения будет являться прямой рА1(мд) + qBi(m0) + Ci(mq) = 0. Определения порядка неустойчивости и правил его нахождения с помощью D-разбиения касаться здесь не будем, однако подчеркнем, что проектирование и эксплуатация многих радиофизических приборов без подобного анализа были бы проблематичны.
Для систем линейных уравнений, в которых число уравнений не совпадает с числом неизвестных, метод определителей не пригоден. И, как указывалось в конце §4.1, более строгая классификация множества решений подобных систем с основной матрицей размера п х т основана на понятии ранга матрицы. Это понятие и применение его к исследованию разрешимости общих систем линейных уравнений (так называемая теорема Кронекера-Капелли) были независимо открыты несколькими авторами. Причем первая публикация (1867 г.) этой теоремы принадлежит профессору математики оксфордского колледжа Христовой церкви
283
Ч.Л.Доджсону, т.е. Л.Кэрроллу - автору знаменитых во всем мире книг “Алиса в стране чудес” и “Алиса в Зазеркалье”. К сожалению, история распорядилась так, что его имени нет в названии теоремы, однако очень многие взрослые люди могут цитировать “Алису...” целыми страницами. Среди этих людей много математиков, в том числе и авторы этого пособия.
6. Достаточно часто на вступительных экзаменах в МГУ встречаются иррациональные уравнения и неравенства с параметрами, а многие задачи высшей математики также содержат иррациональные выражения различных видов. Одним из эффективных методов решения подобных задач является применение рационализирующих подстановок. Наиболее известны и доступны для понимания тригонометрические подстановки, когда заменой переменной можно избавиться от иррациональности и свести задачу к тригонометрической [22]. При этом полезными могут оказаться следующие подстановки:
1) ж = as'mt или х = a cost, если в условие входит радикал у/а2 — х2',
2) х = а/sin I или х = а/ cost, если в условие входит радикал у/х2 — а2',
3) ж = atgt или х = aetgi, если в условие входит радикал д/а2 + ж2.
В задачах с дробно-л инейной иррациональностью часто оказывается полезным некоторый аналог теоремы Чебышева об интегрируемости биномных дифференциалов, а в задачах с квадратичным радикалом Vах2 + Ьх + с иногда бывают полезны подстановки Эйлера, широко известные из курса интегрального исчисления [23]:
1) \/ах2 + Ьх + с = t ± Ху/а при а > О,
2) \/ц.г2 + 6т + с = xt ± у/с при с > О,
3) у/ах2 + Ьх + с = l(x — Xi) при D = Ь2 — 4ас > 0, когда ах2 + Ьх + с =
а(х — Ж1)(т — Т2), где х^ - корни квадратного трехчлена ах2 + Ьх + с.
Заметим, что основная идея всех подстановок Эйлера заключается в том, чтобы для определения х получить линейное уравнение. Тогда и радикал у/ах2 + Ьх + с выражается через новую переменную t квадратичнорациональными функциями вида
у = у/ ах2 + Ьх + с =
At2 + Bt + C
Dt2 + Et + F’
где параметры А, В, С, D, Е и F однозначным образом определяются через а, Ь, с и корни Xiв случае третьей подстановки Эйлера.
Подчеркнем, что при А ф 0 и D 0 существует всего 15 топологически различных видов графиков квадратично-рациональных функций, которые различаются по числу особых точек и типу особенностей, количеству локальных экстремумов и характеру асимптот. При этом полная классификация графиков этих функций возможна без привлечения понятия производной на основе лишь элементарных преобразований (см.
284
начало гл.II) графиков функций 1/1,2 = t ± - [24]. Интересно, что за-k
мена переменных вида у = х ± — часто позволяет эффективно решать возвратные уравнения [22] путем понижения степени вплоть до получения квадратных уравнений.
Многочисленные приложения интегралов с квадратичными радикала
ми для подсчета длин кривых, площадей фигур, объемов тел вращения и различных физико-механических величин (моментов инерции, например) можно найти в [23]. Там же рассматриваются интегралы, содержащие квадратные корпи из многочленов 3-й или 4-й степени, которые уже не
выражаются, как правило, в конечном виде через элементарные функции. При подсчете подобных интегралов достаточно проанализировать лишь общий случай многочлена 4-й степени. Ибо для кубического многочлена всегда существует хотя бы один действительный корень я?1, т.е.
Р3(ж) = ах3 + Ьх2 + сх + d = а(х — а?1)(ж2 + рх + 7)
и тогда замена х — xi = ±/2 осуществляет приведение ^/Р3(ж) к y/Pift), интегралы от которых выражаются в конечном виде через элементарные функции и всего лишь три стандартных эллиптических интеграла 1-го, 2-го и 3-го рода.
Заметим, что в ряде прикладных задач переход в интегралах от х/Рз(х) к 5/^4(Z) не всегда оправдан. Так, при изучении автомодельного МГД-течения в плоском диффузоре для безразмерной радиальной скорости v можно получить дифференциальное уравнение второго порядка
+ (4 - H2)v + Re v2 + С = 0.
Решение этого уравнения выражается через интеграл
dv
VPM’
где Р3(д) = -
з 3(4-Я2) 2 3CZ
’ +^ + D) '
Если представить P3(v) = (^1 — v')(y — ^г)(^ — ^з)> где vi _ корни
многочлена Р3 (ситуации комплексно сопряженных корней ъ’г.з касаться с х ъ 3(Я2-4)
не будем), то по теореме Биета + V3 = п ------ и возможны два
2 Re
основных случая:
Я2 - 4
1) 0 < v < V3 < ——— или 2) 0 < v < vi, V2 С 0. 2Яе
Полный анализ вида решения представляет собой достаточно трудоемкую задачу высшей математики с параметрами Я, Re и а - углом раствора диффузора.
285
Заметим, что кроме отмеченной способности рационализировать квадратичные радикалы подстановки Эйлера имеют и наглядный геометрический смысл.
Рассмотрим невырожденную кривую второго порядка у(х') = = ±Уаж2 + 6ж + с или у2 = ах2 + Ьх + с, которая при а > 0 является гиперболой, а < 0 - эллипсом, особые случаи а ~ — 1 и а = О соответствуют окружности и параболе. Возьмем на этой кривой произвольную точку (жо; Уо) так, что у% = «Жу+Ьжу+с. Тогда проходящая через эту точку секущая у — уо = /(ж — жо) пересечет кривую еще только в одной точке (ж»;!/*). Очевидно, что, надлежащим образом изменяя переменный угловой коэффициент t в уравнении секущей, можно заставить вторую точку (ж*;у») описать всю кривую. Поэтому текущие координаты (ж;у) второй точки дальше будем писать без “звездочки”. Исключив у из уравнений кривой и секущей, получим выражение ж через квадратично-рациональную функцию переменной t:
x^t2 — 2yol + clxq + b
Х = ~ /2 - а ’
следовательно, и текущая координата у второй точки пересечения выражается через рациональные функции переменной t.
Тогда зависимость л/аж2 + Ьх + с — уо = 1/х — жо) и определит соответствующую рационализирующую подстановку. Если аж2 + Ьх + с = а(ж — Ж1)(ж — жг), то кривая пересекает ось ж в точках (ж].; 0) и (Ж2; 0). Взяв, например, первую из них за точку (жу;г/о), получим третью подстановку Эйлера Уаж2 + 6ж + с = /(ж — жг). При с > 0 кривая пересекает ось у в точках (0;±\/с), взяв одну из них за точку (жу; г/о), получим вторую подстановку Эйлера: у/ах2 + Ьх + с ± у/с = tx. Если при а > 0 за точку (жу; у0) взять бесконечно удаленную точку кривой, которая в данном случае будет являться гиперболой, и пересекать ее прямыми у = i ± Жл/п, параллельными асимптоте у = ±Жл/а и проходящими через бесконечно удаленную точку, то получим первую подстановку Эйлера: у/ах2 + 6ж ф с = I ± Ху/а.
Авторы надеются, что внимательного читателя не может не восхитить глубокая взаимосвязь различных проявлений квадратичной функции, конспективно изложенная выше, а также геометрически-естественный переход к другой очень важной теме: общей теории кривых второго порядка.
С точки зрения авторов сейчас эта тема излагается в средней школе очень фрагментарно, без взаимосвязи с другими предметами. Тогда как все кривые второго порядка и их канонические уравнения можно ввести в старших классах единообразно и достаточно строго, используя метод координат, понятие геометрического места точек и фокальные свойства
28А
этих кривых [25]. Такой подход способствует не только единству школьных курсов алгебры и геометрии, но и позволяет существенно расширить межпредметные связи с физикой и астрономией через оптические свойства конических сечений, вывод траекторий движения тел в поле силы тяжести и законы Кеплера [26], [27].
В качестве завершения краткого экскурса по кривым второго порядка и интересной иллюстрации к графическим методам решения задач с параметрами можно проанализировать линейную, параболическую и гиперболическую модели боевых действий [28-30], которые появились еще во время первой мировой войны и больше известны даже в отечественной литературе под названием “уравнений Ланчестера”, хотя впервые были предложены в 1915 г. Осиповым.
Дальнейшее развитие математическое моделирование военных операций (особенно в связи с прогрессом вычислительной 'техники) получило при создании пространственно-временных моделей [30], допускающих изучение протекания боевых действий не только во времени, но и в пространстве. Э'го позволяет рационально выбирать боевые порядки войск, тактику применения различных средств поражения и защиты, схему подвода резервов и т.д. Заметим, что соответствующая система уравнений очень похожа на уравнения газовой и волновой динамики [2;3], где кривые второго порядка, особенно гиперболы, играют важную роль во многих задачах с ударными волнами.
7. Кроме задач на перечисленные выше традиционные 'гемы школьного курса математики соответствующие аналоги научно-исследовательских задач можно найти и для уравнений вида
/(/.../(ж)...) = ж, описывающих многие итерационные процессы в различных областях науки и техники.
Рассмотрим модель роста популяции какого-то вида организмов, заполняющих определенную экологическую нишу с ограниченным воспроизводством ресурсов. Пусть zq - начальная численность популяции, а zn - ее численность через п жизненных циклов (часов, суток, недель или лет). Считая, что zn+i = f(zn,b), где b - некоторый параметр, при различных видах функции f получаем разные результаты.
В простейшем случае zn+\ = bzn (& > 1) приходим к мальтузианской модели экспоненциального роста популяции, что возможно при избытке ресурсов. Но если ресурсы ограничены и допускают существование не более N особей популяции, то коэффициент прироста k = b — 1 не может оставаться постоянным. Поэтому часто используется зависимость с переменным коэффициентом b(zn) = b(N — zn), тогда процесс задается итерационной формулой:
^п+1 — b(N ^72)^72 - z з-n+i — Ax/j(l Лп.), (И)
287
где А = bN, 0 < < 1.
Из (11) следует, что функция f = А.тп(1 — жп) при 0 < А 4 задает отображение единичного отрезка [0; 1] в себя. Однако поведение последовательности хп при п —► оо будет существенно разным в зависимости от величины параметра А.
При 0 < А 1 парабола у = Аж(1 — ж) лежит ниже прямой у = х и хТ1 —+ 0 при п —+ оо независимо от выбора xq G [0; 1].
При 1<А<Зиго^0жп-> х* = const, где х* можно найти из уравнения
X* = /(ж*) X* = Аж*(1 - ж*) ®;=0V4 = ^i.
Подчеркнем, что при А < 1 существует один неотрицательный корень ж* = 0, а при А > 1 - два. Все точки, удовлетворяющие уравнению /(ж) = х, называются неподвижными точками функции f. При А = 1 происходит бифуркация: неподвижная точка т* = 0 теряет устойчивость, а новая точка становится устойчивой.
Отметим, что бифуркацией называется изменение числа и устойчивости решений уравнения.
Рис. 6
При дальнейшем увеличении параметра А поведение системы изменится: неподвижная точка х% потеряет устойчивость и при п —» оо •Е2п+1 -- 01 (А), х2п —> 02(A), где ai = /(a2), a2 = /(ai) (рис. 6). В этом случае отображение (12) имеет устойчивый цикл S'2 с периодом Т = 2, а неподвижные точки aii2 находятся из формул
1 “‘.2-2
288
Переход от неподвижной точки х'?, которую можно считать циклом S1, к циклу S2 называется бифуркацией удвоения периода.
При дальнейшем увеличении А в окрестности А « 3,45 цикл S2 теряет устойчивость и возникает устойчивый цикл S4 (рис. 7):
•^4п * aj, ^4п + 1 * а2, ^4n+2 * ^3 > ^4п+3 ► ^4>
при этом а2 = аз = /(а2), 04 = /(аз) и ai = /(04), а численность
популяции начинает колебаться с периодом 4.
Незначительно увеличивая параметр А, можно наблюдать в результате бифуркации все более частые удвоения периода и рождение последующих циклов S8, S16, S32 и т.д. из предыдущих. Наконец, при некотором А = Акр «3,6 формула (12) дает при п —► оо уже непериодическую последовательность, носящую случайный или хаотический характер. Таким образом, хаос возникает здесь как предел все более сложных структур -циклов S2 . Интуитивное представление об установившемся режиме колебаний при п —> оо может быть связано с понятием притягивающего множества или аттрактора.
Анализ цикла S2 и соотношения
ai = /(аг) ; Г ai = /(а2) = /(/(ai)) =
аг = /(ai) I а2 = /(aj = f(f(a2)) = f(2)(a2)
наводят на мысль рассмотреть отображение хп+2 = и исследо-
вать его на устойчивость. Тогда для исследования циклов Sk необходимо
19 Методы реш. задач
289
рассмотреть отображения
у = А).
к раз
Заметим, что для итерационного процесса (11) каскад удвоения периодов для циклов S'2 заканчивается в окрестности Л « 3,6..., а при А = 3,83 возникает устойчивый колебательный цикл периода 3 с последующим удвоением периода до 6,12,24... и превращением в хаос при А ~ 3,85. Однако полный, а не структурированный хаос возникает при А = 4, что следует из теоремы Шарковского [31].
Более подробную информацию об итерационных процессах можно найти в [32 34], а в [35] сделана попытка более подробно рассказать о некоторых затронутых здесь понятиях современной математики на элементарном языке исследования квадратичной функции, зависящей от одного параметра.
Заметим, что возрождение всеобщего интереса к итерациям началось с работы [36], где впервые были экспериментально получены каскады удвоения периодов при моделировании наблюдаемых на практике двухгодичных колебаний улова горбуши. Последующий бум в изучении итерационных процессов принес много неожиданностей.
Так, для целого класса одномерных итерационных процессов фундаментальным свойством является следующий факт: если через Ai, А2, A3,.. . обозначить возрастающую и ограниченную последовательность тех значений параметра А, при которых происходят бифуркации удвоения периодов, то существует предел, называемый числом Фейгенбаума,
lim Лп+1 ~ лп = ~ 4, 669201660 ...
п-ч-ос Ап+2 — Ап + 1
Подчеркнем, что это число является такой же универсальной характеристикой сценария удвоения периодов, как и число % для отношения длины любой окружности к ее диаметру!
Математики все еще пытаются понять эту фундаментальную универсальность. Однако более важно, что появилась надежда на систематизацию нелинейных явлений.
В 1976 г. биолог Р.Мей писал: “...Это уравнение можно изучать феноменологически, итерируя его на калькуляторе или даже вручную. Его изучение даже не требует... понятий, какие используются в элементарном анализе... Для всех нас было бы лучше, чтобы не только в научной работе, но и в повседневной политической и экономической жизни как можно больше людей поняло, что простые нелинейные системы не всегда обладают простыми динамическими свойствами”.
290
Рис. 8. Множество Мандельброта,
В 1980 г. Бенуа Мандельброт в результате изучения на компьютере в комплексной плоскости итерационного процесса zn+i = J\zn) = z? + с обнаружил множество, носящее теперь его имя (рис. 8). Все необходимые пояснения по фракталам можно найти в прекрасной книге [34], где высокий научный уровень математической монографии соседствует с мистической красотой компьютерных рисунков. С этой книгой по глубине и единству эстетического и математического содержания может конкурировать лишь монография [37], где великолепные рисунки выполнены не машиной, а человеком*. Здесь лишь подчеркнем, что фрактальная геометрия изучает множества с дробной или хаусдорфовой размерностью, т.е. объекты, занимающие промежуточное положение между точками и линиями, линиями и поверхностями, поверхностями и телами... Подобные структуры привлекали внимание чистых математиков и раньше, но казались абсолютной абстракцией, не имеющей никакого отношения к реальным вещам. Однако международные конференции и лавинообразный рост числа публикаций по применению фракталов в прикладных вопросах свидетельствуют об обратном [37]. Может быть, именно на этом пути некоторого симбиоза механики сплошных сред с фрактальной геометрией будет найдено решение важной практической задачи по увеличению
* Академик РАН А.Т.Фоменко известен не только как один из крупных математиков современности и оригинальный художник, но и как автор смелых исторических гипотез и исследований.
19*
291
отдачи нефтегазовых пластов, которые во многих случаях имеют фрактальную структуру.
В качестве заключения к этому разделу заметим, что итерационные процессы известны в математике с древнейших времен. Так, алгоритм Евклида для нахождения наибольшего общего делителя двух натуральных чисел (или наибольшей меры длины двух соизмеримых отрезков) основан на итерационном процессе деления с остатком. Это естественным образом приводит к представлению любого рационального числа в виде конечной цепной дроби [38]. Тогда иррациональным числам соответствуют бесконечные цепные дроби. Кроме теории цепных дробей, имеющих прямое отношение к вопросу о решении в целых числах уравнений вида ах2 * * * * * В + Ьху + су2 = d, итерации бесконечных радикалов [39] позволяют на достаточно элементарном уровне установить ряд далеко не очевидных фактов из теории чисел.
В частности, справедливо следующее утверждение: для каждого а > О при п оо имеют место равенства
1 + х/1 + 4д 2
При а = 2 имеем 2 = у 2 + + л/2 + ..?, отсюда вытекает знамени-
тая формула Виета
2 _ л/2 >/2 + л/2 \/2+ л/2 + х/2
? - ~2 2 2
для приближенного вычисления числа тг, а дробная часть цепной дроби
\/5 — 1
при а = 1 дает число —-------известное “золотое сечение”.
8. Возникновение устойчивых колебаний и более сложных аттракторов не только в дискретных отображениях типа (12), но и описываемых непрерывными функциями вызывает в последнее время огромный интерес в разных разделах науки и техники [3,7,33,40,41].
В теории колебаний и физике волн до недавнего времени основой классификации колебательных процессов являлись количественнокинематические признаки: периодичность, амплитуда и форма. Для строго периодических процессов должно выполняться соотношение f(t + Т) = /(£), справедливое для любого момента времени t, где Т - период колебаний, z/ = 1/Т - число периодов в единице времени или частота колебаний, ш = 2 л г/ - круговая частота.
292
Особое значение имеет простейший вид колебательного процесса -гармоническое колебание
х — f(t) = А ’ sin(w£ + ^>1), (12)
где А - амплитуда колебаний, u>t + <f>\ - мгновенная фаза колебаний.
Заметим, что уравнение (12) на координатной плоскости (ж, /) представляет собой хорошо известную синусоиду, однако часто это уравнение полезнее рассматривать как проекцию движущейся по окружности радиуса А с угловой скоростью ш некоторой точки или радиус-вектора на фиксированную ось абсцисс.
Такое представление позволяет складывать гармонические колебания с одинаковой частотой. Пусть xi = Ai sin(o4 + </>i) и ж 2 = Аг sin(wt + </?г), тогда результирующее колебание
х = a?i + ж2 = Asin(wi + 0),
где А = у/А? + А% + 2А1А2 cos<S, £ = у>2 ~ ~ разность начальных фаз,
а начальная фаза результирующего колебания 0 находится из уравнения
, . Ai sin^i + A2sin<p2
tg 0 — -----------------—.
Al COS </?i + A2 cos (f>2
7Г
Из этих выражений при = 0, </>2 — сразу следует метод введения дополнительного аргумента, часто используемый при решении тригоно
метрических задач с параметрами.
Подчеркнем, что самые общие колебания на плоскости, которые могут возникать при анализе линейных автономных систем, имеют вид
x(t) = Ai sin(wt + 9?i), ?/(£) = A2 sin(wi + ^2)-
На фазовом портрете этому соответствуют замкнутые эллиптические траектории.
В динамике популяций существует много примеров, когда изменение их численности имеет колебательный характер. Однако такие колебания существенно отличаются от гармонических и для их моделирования необходимы нелинейные дифференциальные уравнения. Одним из самых простейших и известных примеров является нелинейная модель Лотка-Вольтерра для систем типа “хищник - жертва” [40], [41]:
х — (а — Ьу)х, у = (—с + dx^y. (13)
Легко можно проверить, что система (13) имеет первый интеграл в виде произведения двух функций от х и у:
h(x, у) = xce~dx yae~by = hi(x) • h2(y\
293
Наибольшее значение функция h(x,y) принимает в точке х = c/d, у = а/b, а ее линии уровня являются замкнутыми кривыми вокруг этой точки. Заметим, что фазовые траектории системы (14) совпадают с этими линиями уровня, а точка (c/d\a/b} является центром.
Известно, что система (13) является структурно неустойчивой [40], т.е. добавление малых нелинейных членов £ii2(^i у} в уравнения системы приводит к вырождению центра в устойчивый фокус (численность обеих популяций с течением времени стабилизируется в равновесии) или неустойчивый фокус (амплитуды колебаний численности обеих популяций возрастают и система идет в разнос вплоть до исчезновения одного из видов). Однако наиболее интересен случай, когда на фазовой плоскости возникает устойчивый предельный цикл, что отвечает колебаниям с неизменной амплитудой, которая зависит от начального состояния системы. В [40-42] можно найти многочисленные примеры математических моделей реальных явлений из различных областей знаний, где возникают предельные циклы.
Заметим, что предельные циклы Пуанкаре в течение полувека оставались без приложения, но когда потребности развития радиотехники выявили необходимость математической теории нелинейных автоколебаний, то оказалось, что нужный аппарат был уже математиками фактически создан [43]. В настоящее время наблюдается возрождение интереса к качественной теории дифференциальных уравнений, .что обусловлено открытием в последние десятилетия колебательных явлений в сложных физических, химических и биологических системах [40-45].
В химии наиболее известна, но все еще полностью не изучена колебательная реакция Белоусова-Жаботинского. Причина этого состоит в том, что динамическое поведение этой королевы колебательных реакций чрезвычайно многообразно, а число ее вариантов с разными реагентами весьма велико. Интересна и история открытия этой реакции.
Автоколебательную реакцию окисления лимонной кислоты броматом в присутствии ионов цезия Б.П.Белоусов экспериментально открыл в 1951 г., однако первая публикация об этом появилась лишь в 1959 г. в ведомственном сборнике. Ибо рецензенты ведущих химических журналов отклоняли рукопись, считая, что такая реакция противоречит законам термодинамики и здравому смыслу, а наблюдаемые колебания окраски раствора - какой-то хитрый фокус. На основе многочисленных экспериментов к середине 60-х годов А.М.Жаботинским была предложена схема этой автоколебательной реакции, включающая более 20 промежуточных стадий, а затем - и упрощенная математическая модель для концентраций всего двух веществ.
К этому времени вспомнили о математических работах Колмогорова-Петровского-Пискунова (1937 г.), Зельдовича и Фр анк-Каменецкого
294
(1938, 1941гг.), Винера-Розенблюта (1946г.), Тьюринга (1952г.) и “реабилитировали” колебательную реакцию иодат-пероксид водорода, попытки опровергнуть открытые Оже и Бреем периодические изменения в которой продолжались почти полвека! Ибо экспериментаторы, обнаружив в химической реакции колебания, обычно отказывались от их исследования, ссылаясь на случайные помехи, примеси и нечистоту эксперимента. Однако к 70-м годам пришло понимание, что автоколебания в сложных химических и биологических системах могут являться отражением самой сути таких систем. Это стимулировало объединение усилий математиков, физиков, химиков и биологов по взаимообогащению двух развивавшихся практически независимо направлений: экспериментальному исследованию автоволн в конкретных системах и математическому моделированию автоволновых процессов (оба термина предложены советским физиком, ректором МГУ в 1973-1978 гг. Р.В.Хохловым). Что явилось, пожалуй, первым большим шагом к практическому ответу на известный вопрос М.В.Ломоносова: “Здесь, уповаю, еще вопросить пожелаете, чего ради по сие время исследователи естественных вещей в сем деле столько не успели? На сие ответствую, что к сему требуется весьма искусный химик и глубокий математик в одном человеке”.
Рис. 9. Схема интерференции при столкновении двух обычных волн и “глаза совы’’ при столкновительной аннигиляции двух автоволн
Квазидвумерная реакция Белоусова-Жаботинского в тонком слое раствора оказалась чрезвычайно удобной системой для экспериментального исследования свойств автоволн, ибо они легко различимы невооруженным глазом и проявляются в смене красного цвета раствора на синий при прохождении фронта волны. Кроме круговых автоволн от ведущих центров и их аннигиляции при столкновении (см. рис. 9) в этой реакции были открыты и предсказанные ранее при математическом моделировании спиральные волны с различным топологическим зарядом или многорукие ревербераторы (см. рис. 10). Заметим, что спиральные волны и
295
более сложные виды автоколебаний были обнаружены не только в химически активных средах, но и биологических системах: популяциях коллективных амеб, тканях сердечной мышцы, сетчатке глаза, мозге [40,44].
Рис. 10. Многорукие ревербераторы по [44]; интервалы между кадрами: а — 4 мин, б - 15 с
Подчеркнем, что простейшую математическую модель образования и распространения спиральных волн в возбудимых средах можно построить на основе известного школьникам принципа Гюйгенса и графических методах исследования задач с параметрами. Для этого необходимо лишь уметь стоить огибающую семейства равных окружностей, центры которых распределены вдоль заданной кривой.
Интересно, что совсем недавно в так называемой “цилиндрической вертушке” Ревуженко-Шемякипа при проведении экспериментов по исследованию сложного нагружения сыпучих и вязких сред была получена картинка спиралей, аналогичная многоруким ревербераторам. Математическое моделирование подобных процессов в сферических объемах способно дать ответ, как влияют поля тяготения (в первую очередь Луны и Солнца) на внутреннюю структуру строения Земли и природу геомагнитного поля [46], происхождение и поведение которого до сих пор таит много загадок!
Бурное развитие вычислительной техники в последние годы способствовало значительному расширению фронта исследований автовол-новых процессов в трехмерных системах. Причем это не привело к доминированию таких количественных характеристик колебаний, как период или амплитуда, а лишь подчеркнуло важность качественных методов и аспектов исследования, в частности бифуркационного анализа и возможности появления устойчивых предельных циклов, а также более сложных
296
аттракторов в фазовом пространстве.
Заметим, что много вопросов осталось и для “чистых” математиков. Так, один их них относится к 16-й проблеме Гильберта о числе предельных циклов у системы
х = Р(х-,у), У = Я(х-,у),
где Р и R - произвольные многочлены второй степени. Известны конкретные системы с тремя циклами, но может ли их быть больше?
С развитием вычислительной техники связано и другое важное открытие XX в.: изучение свойств солитонов - уединенных волн в нелинейных консервативных средах без диссипации и внешнего подвода энергии. Свойство солитонов сохранять свою форму, амплитуду и скорость роднит их с автоволнами. Однако, если все свойства конкретного вида автоволн в возбужденной среде однозначно определяются лишь характеристиками самой среды, то солитон в одной и той же среде может двигаться с разной скоростью и амплитудой. Конкретные значения этих характеристик солитона зависят от начальных условий, приведших к его образованию. Элементарное введение в теорию солитонов на уровне школьной физики и графических методов решения задач с параметрами, а также описание многих интересных свойств этих полуволн-получастиц можно найти в [47]. Здесь лишь заметим, что преобразования Беклунда, применение которых в последние годы к солитонным уравнениям sin-Гордона, Кортевега - де Фриза и Шредингера привело к возрождению группового анализа дифференциальных уравнений и методу обратной задачи, являются глубоким обобщением приема использования свойств симметричности переменных в широком классе конкурсных задач с параметрами.
9. В заключение данного приложения отметим, что соответствующие аналоги при желании можно найти и для отдельных, экзотических на первый взгляд, конкурсных задач. В качестве примера приведем лишь три задачи из вариантов вступительных экзаменов на механикоматематический (1967 г.), биологический (1989 г.) и географический (май 1996 г.) факультеты МГУ.
Аналогом последней задачи являются возникающие в ряде приложений интегралы от произведений трех бесселевых функций вида
ОО
/dt 2П-1 • S2n-1
Jn(at)Jn(bt)Jn(cP} —у = I, где 1=-----------
о (аЬс)пГ( | jrfn + | j
если a, b, с - длины сторон треугольника площади S'; если же из а, Ь, с нельзя составить треугольник, то I = 0.
297
Еще более интересную аналогию для этой задачи можно найти в диссертации [48], посвященной квазиклассическому приближению в квантовой механике, где достаточно сложные понятия объясняются с помощью тетраэдра, т.е. неравенств для сторон четырех треугольников, образующих его грани.
Совсем недавно методом, фактически идентичным способу решения второй задачи, в работе [49] (естественно, после ряда преобразований исходной системы уравнений в частных производных) рассмотрен возможный механизм образования природных алмазов в кимберлитовых трубках. Интересно, что в процессе анализа критических условий образования алмазов от удара комет или крупных метеоритов с Землей, в этой работе ровно три раза пришлось решать квадратичное по многим параметрам уравнение и каждый раз выяснять физическую суть обращения в нуль соответствующего дискриминанта. Работа [49] и последующая серия статей исходят из концепции академика Е.И.Шемякина, что кимберлитовые трубки являются следом встречи Земли с крупным космическим телом [50]. Ибо опыт показывает, что кимберлитовые трубки алмазоносны, если они привязаны к месторождениям природного газа. Поэтому исходным материалом для кристаллизации алмаза может быть природный газ в порах горных пород, а приводит к этому следующая цепь превращений при высокоскоростном ударе: природный газ -- углерод -алмаз.
Рис. 11. Схема образования полос непропускания
‘'Шахматные доски” и “зебры” из последней задачи второй главы в качестве промежуточных результатов возникают в целом ряде задач механики композитов, при создании оптических фильтров и лазеров. Для работы лазера нужны зеркала, от которых свет отражался бы многократно, но с очень малыми потерями. Полированные алюминиевая или серебря
298
ная пластины отражают соответственно около 97% и 99% падающего света. Однако при большой мощности поглощение 1-3% приводит к прожиганию зеркал. Но если на поверхность напылить определенным образом
полосы из алюминия и серебра, то такое слоистое зеркало может отражать до 99,99% света. Принцип действия подобного слоистого материала
основан на взаимодействии пространственных гармоник бегущей волны
f(z, 2) = А cos (art — kz + <р), и возникновении полос непрозрачности или непропускания света (см. рис. 11). Поскольку волна периодически повто-
ряется, когда (art — kz + 92) изменяется на 2тг, то волна с фазовой посто-, , , 2тгп
яннои к не отличается от волны с фазовой постоянной кп = к -|—— ,
где L - длина волны. На рис. 11 штриховыми линиями представлены V-
образные ломаные - пространственные гармоники с вершинами в точках
, 2тгп
к = ——, где п 0.
Li
Ломаная, выходящая из начала координат и зада-
ваемая уравнением типа ш = а|А?|, является основной волной, или модой.
Огибающие этой косоугольной “шахматной доски”, построенные в полосе —ir/L < к < тг/L сплошной линией, и приводят к появлению полос непропускания. Ибо в частотных интервалах (0,u>i), (u>2,^3), (^4>^б) и т.д. невозможно распространение света без затухания.
Рис. 12. Схема образования свободных зон в кристалле
Аналогичные построения возникают и при нахождении энергетических зон в кристалле, т.е. областей энергий, в которых электроны могут свободно перемещаться (см.рис. 12). Качественно это можно объяснить исходя из представления о связанных волнах. Известно, что электроны ведут себя в некоторых отношениях как частицы, а в других - как волны, которые описываются уравнением Шредингера. Для электрона в вакууме без внешних электромагнитных полей соотношение между h и ш имеет
299
квадратичную зависимость и> = 7г/г2/4тгт, где h, - постоянная Планка, т - масса электрона. Построив по этой формуле основную моду, а сдвигом на 2тгп/Л, где L - расстояние между атомами в слоистом кристалле, и соответствующие пространственные гармоники штриховыми линиями, мы получаем сетку из парабол. Огибающие к этой сетке в полосе — тг/L < k < ir/L и дадут энергетические зоны в интервалах (0,u>i), (<Д2,^з) и т.д., без знания которых работа приборов на транзисторах была бы невозможна.
Авторы выражают признательность сотрудникам МГУ А.В.Аксенову, В.В.Вавилову, В.М.Гендугову, Д.Б.Гнеденко, А.В.Звягину, Б.В.Куксен-ко, В.Ф.Максимову, Н.П.Смирнову, Е.А.Сагомонян и аспирантке Е.В.Шиврипской (механико-математический факультет), Г.А.Беляковой (биологический факультет) и В.А.Мамонтову (химический факультет) за полезное обсуждение многих затронутых выше аналогий, И.И.Мельникову и И.Н.Сергееву за саму идею подобных аналогий, а также Е.Ф.Гавриковой за помощь в оформлении рисунков.
Литература
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1966.
“2. Черный Г.Г. Газовая динамика. М.: Наука, 1988.
3. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988.
4. Астарита Дж., Марруччи Дж. Основы гидромеханики неньютоновских жидкостей. М.: Мир, 1978.
5. Седов Л.И. Механика сплошной среды. Т. 1,2. М.: Наука, 1973.
6. Натяганов В.Л. О фундаментальном решении задач МГД-обтекания тел при малых числах Рейнольдса // Вопросы механики сплошных тел. М.: Изд-во МГУ, 1993.
7. Мигулин В.В. и др. Основы теории колебаний. М.: Наука, 1988.
8. Келдыш М.В. Избранные труды. Механика / Под ред. К.И.Бабенко и др. М.: Наука, 1985.
9. Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем. М.: Наука, 1987.
зоо
10. Ишлинский А.Ю. Механика: идеи, задачи, приложения. М.: Наука, 1985.
11. Колмогоров А.Н., Вавилов В.В., Тропин И.Т. Физико-математическая школа при МГУ. М.: Знание, 1981.
12. Амбарцумян С.А., Багдасарян Г.Е., Белубекян М.В. Магнитоупругость тонких оболочек и пластин. М.: Наука, 1977.
13. Эльсголъц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
14. Московский университет в Великой Отечественной войне. М.: Изд-во МГУ, 1985.
15. Колмогоров А.Н. и др. Летняя школа на Рубеком озере. М.: Просвещение, 1971.
16. Вавилов В.В. Сетчатые номограммы // Квант. 1978, № 9.
17. Клейн Ф. Элементарная математика с точки зрения высшей. Т. 1. М.: Наука, 1987.
18. Хованский Г. С. Основы номографии. М.: Наука, 1976.
19. Денисюк И.Н. Номограмма с тремя бинарными полями // Номографический сборник. М.: Изд-во МГУ, 1951. С. 77-79.
20. Якубович В.А., Стпаржинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения. М.: Наука, 1972.
21. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986.
22. Олехник С.Н., Потапов М.К., Пасиченко П.И. Нестандартные методы решения уравнений и неравенств. М.: Изд-во МГУ, 1991.
23. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. М.: Наука, 1969.
24. Энциклопедия элементарной математики / Пол ред. П.С.Александрова, А.И.Маркушевича, А.Я.Хинчина. Т. 3. М. -Л.: Гостехиздат, 1952.
х^5 . Лурье М.В., Александров Б.И. Пособие по геометрии. М.: Изд-во МГУ, 1984.
26. Мар куш ев и ч А.И. Замечательные кривые. М.: Наука, 1978.
27. Амелькин В.В. Дифференциальные уравнения в приложениях. М.: Наука, 1987.
301
28. Осипов М. Влияние численности сражающихся сторон на их потери // Военный сборник. 1915, № 6-9.
29. Татарченко П.Н. и др. Математические модели боевых действий. М.: Сов. радио, 1969.
30. Чуев Ю.В. Исследование операций в военном деле. М.: Воениздат, 1970.
31. Шарковский А.Н. Сосуществование циклов непрерывных преобразований прямой в себя // Укр. мат. журнал, 1964. T.XIV, № 1.
32. Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988.
33. Каданов Л.П. Пути к хаосу. М.: Мир, 1985.
34. Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993.
35. Аксенов А.В., Лужина Л.М., Натяганов В.Л., Шивринская Е.В. Итерационные процессы, бифуркации решений, странные аттракторы и уравнения вида /(/ ... /(ж)...) = х // Труды IV Международной конференции женщин-математиков. Т.4, вып.2. Н.Новгород, 1997.
36. Шапиро А.П. Математические модели конкуренции // Управление и информация. Владивосток: ДНЦ АН СССР, 1974. Т. 10.
37. Фоменко А.Т. Наглядная геометрия и топология: математические образы в реальном мире. М.: Изд-во МГУ, 1998.
38. Хинчин А.Я. Цепные дроби. М.: Наука, 1978.
39. Вавилов В.В. Радикалы правые, левые и нейтральные. Препринт СУНЦ МГУ, 1995.
40. Николис Г., Пригожин И. Самоорганизация в неравновесных системах. М.: Мир, 1979.
41. Томпсон Дж.М.Т. Неустойчивости и катастрофы в науке и технике. М.: Мир, 1985.
42. Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения: качественная теория с приложениями. М.: Мир, 1986.
43. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Физматгиз, 1959.
44. Васильев В.А., Романовский Ю.М., Яхно В.Г. Автоволновые процессы. М.: Наука, 1987.
45. Гарел Д., Гарел О. Колебательные химические реакции. М.: Мир, 1986.
302
46. Шемякин Е.И. О деформации вращающихся планет // Вести. Моск, ун-та. Сер. 1. 1993. № 3.
47. Филиппов А.Т. Многоликий солитон // Биб-ка “Квант”. Вып.48. М.: Наука, 1986.
48. Крошилин А.Е. Дис. на соискание ученой стерени к.ф.-м.н. МГУ, механико-математический ф-т, 1976.
49. Гендугов В.М. О механизме и критических условиях образования природных алмазов. В печати.
50. Шемякин Е.И. О происхождении алмазных трубок (физико-математическая гипотеза) // Вести. Моск, ун-та. Сер. 1. 1995. №2.
ПРИЛОЖЕНИЕ II
ЗАДАЧИ ПОСЛЕДНИХ ЛЕТ
— Отгадала загадку? — Спросил Бол-ванщик, снова поворачиваясь к Алисе.
— Нет, — ответила Алиса. — Сдаюсь. Какой же ответ?
•— Понятия не имею, — сказал Болван-тик.
— Ия тоже, — подхватил Мартовский Заяц.
Л.Кэрролл. Алиса в стране чудес
Задача 1 (механико-математический факультет, май 1995, 3(6)). Найти вес числа k, при которых функция
7/(.т) = A?(2sin х + cos2 х + 1)
не принимает значений больше 3.
Задача 2 (механико-математический факультет, май 1995, 3(6)). Найти все числа k, при которых функция
у(х) = k(2 sin2 х — 2 cos х — 1)
не принимает значений больше 3.
Задача 3 (механико-математический факультет, май 1995, 6(6)). Пусть Xi - наибольший отрицательный корень уравнения
л/З sin х — 3 cos х =- 2а — 1,
а х-> - наименьший положительный корень уравнения
2 cos2 х — 2 sin2 х = a.
Найти все значения а, при каждом из которых
kil ^2-
20 Методы реш. задач
305
Задача 4 (механико-математический факультет, май 1995, 6(6)). Пусть xi - наибольший отрицательный корень уравнения
4 cos2 х — 4 sin2 х = a,
а х 2 - наименьший положительный корень уравнения
у/З sin х + 3 cos х = 1 — a.
Найти все значения а, при каждом из которых
|®1| х2.
Задача 5 (механико-математический факультет, июль 1995, 6(6)).
Найти все значения параметра а из отрезка [0; 2тг], при которых система
Г х2 + у2 + 2г(ж + у + z) — sin a = 0
t (x + 1) sin2 у + y2y/x + ci2\fz + sin = 0
имеет хотя бы одно решение.
Задача 6 (механико-математический факультет, июль 1995, 6(6)). Найти все значения параметра а из отрезка [—тгО; %], при которых система
( х2 + у2 + 2z2 — 2z(a; + у) + sin a = 0
t (г/ + 1) cos2 у + z2y/y + oc2y/x — cos = 0 имеет хотя бы одно решение.
Задача 7 (факультет ВМиК, предварительный экзамен, 1995, 4(6)). Для каждого значения параметра а решить неравенство
ж + 2а .
х
Задача 8 (факультет ВМиК, предварительный экзамен, 1995, 4(6)). Для каждого значения параметра а решить неравенство
— + 2а х
Задача 9 (факультет ВМиК, основной экзамен, 1995, 1(6)). Найти все целые числа тип, для которых
2mn + п = 14 и пт 9.
306
Задача 10 (факультет ВМиК, основной экзамен, 1995, 1(6)). Найти все целые числа тп и п, для которых
Зп2 + 2пт = 11 и п + 2т^>10.
Задача 11 (физический факультет, март 1995, 7(8)). Найти минимальное значение произведения ху, где х и у удовлетворяют системе уравнений
( ж-]-г/ = За-1
[ х2 4- у2 = 4а2 — 2а + 2.
Задача 12 (физический факультет, июль 1995, 7(8)). Для всех значений а решить неравенство
ж 1 >2^ —
Задача 13 (физический факультет, июль 1995, 7(8)). Для всех значений m решить неравенство
------- /. \ 1 - m Qy/i — х . (2 ।
Задача 14 (химический факультет, предварительный экзамен, 1995, 5(5)). Найти все пары целых чисел m и п, удовлетворяющие уравнению
тп2 + amn — bn2 = О,
где а = 1953100, b = 1995100.
Задача 15 (химический факультет, предварительный экзамен, 1995, 5(5)). Найти все пары целых чисел тп и п, удовлетворяющие уравнению
т2 amn— bn2 — О,
где а = 174350, b = 199550.
Задача 16 (химический факультет, основной экзамен, 1995, 5(5)). Найти множество пар действительных чисел (х;у), удовлетворяющих системе
( 2~ху4 -2у2 + 2х
I 8Ж - у4 + 2х - 1 = 0.
20*
307
Задача 17 (химический факультет, основной экзамен, 1995, 5(5)). Найти множество пар действительных чисел (х;т/), удовлетворяющих системе
Г 3“ V - 2т/2 + Зж О t 27ж - у4 - Зж - 1 = О.
Задача 18 (биологический факультет, 1995, 6(6)). Найти все значения параметра а, при которых уравнение
(х2 — б|т| — а)2 + 12 (х2 — 6Ы — а) + 37 = cos -1-'^-а
имеет ровно два корня.
Задача 19 (биологический факультет, 1995, 6(6)). Найти все значения параметра а, при которых уравнение
9 I G ТГ
(х2 — б|ж| + а) +10 (х2 — 6|ж| + а) + 26 = cos-
имеет ровно два корня.
Задача 20 (факультет почвоведения, предварительный экзамен, 1995, 5(6)). Определить область значений параметра а, при которых уравнение
2 cos 2х — 4а cos х + а2 + 2 = 0
не имеет действительных решений.
Задача 21 (факультет почвоведения, предварительный экзамен, 1995, 5(6)). Определить область значений параметра Ь, при которых уравнение
cos 2у + 4b cos у + 2b2 + 1 = 0
не имеет действительных решений.
Задача 22 (факультет почвоведения, основной экзамен, 1995, 5(5)). При каких значениях параметра b система уравнений
( 4у = 4b + 3 — х2 + 2х
[ х2 + у2 = 2х
имеет два действительных решения?
Задача 23 (факультет почвоведения, основной экзамен, 1995, 5(5)). При каких значениях параметра а система уравнений
( х2 + 4а = 4у — 2х — 5
[ х2 + 2х + у2 = 0
имеет два действительных решения?
308
Задача 24 (геологический факультет, предварительный экзамен. 1995, 7(9)). Пусть
f(x) = \J х2 —4х + 4 — 3, g(x) = у/х — a,
a - параметр. Решить относительно х неравенство f{g(x)') 0.
Задача 25 (геологический факультет, предварительный экзамен 1995, 7(9)). Пусть
f(x) = \/х2 — 6х + 9 — 2, g(x) = у/х — a,
a - параметр. Решить относительно х неравенство f(g(x)) 0.
Задача 26 (геологический факультет, предварительный экзамен 1995, 8(9)). Изобразить фигуру, образованную всеми точками (х;у) декартовой плоскости Оху, координаты которых удовлетворяют неравенству
х2 + у2 + б (к - |г/|) < 0.
Найти площадь этой фигуры.
Задача 27 (геологический факультет, предварительный экзамен 1995, 8(9)). Изобразить фигуру, образованную всеми точками (ж; г/) декартовой плоскости Оху, координаты которых удовлетворяют неравенству
х2 + У2 + 4 (х - |г/|) < 0.
Найти площадь этой фигуры.
Задача 28 (геологический факультет, предварительный экзамен 1995, 9(9)). Для каждого а решить систему
( log2 (|а|х2 - Зх + 4) _ |х|+ 1)2
log2(—Зх + 4) -5
[ X 1.
Задача 29 (геологический факультет, предварительный экзамен 1995, 9(9)). Для каждого а решить систему
( log3 (|а|х2 — 4х + 5) = 2_|х((ж + з)2
< log3 (-4х + 5)
[ х 1.
309
Задача 30 (геологический факультет, основной экзамен, 1995, 8(8)).
Найти все значения параметра а, при которых неравенство
9х <20 3х + a
не имеет ни одного целочисленного решения.
Задача 31 (геологический факультет, основной экзамен, 1995, 8(8)).
Найти все значения параметра а, при которых неравенство
16ж < 30 -4х -а
не имеет ни одного целочисленного решения.
Задача 32 (географический факультет, предварительный экзамен, 1995, 6(6)). Найти все значения параметра а, при каждом из которых функция
у(х) = log25_a2 (cos х + л/8sin х — a) определена при всех значениях переменной х.
Задача 33 (географический факультет, предварительный экзамен, 1995, 6(6)). Найти все значения параметра а, при каждом из которых функция
у(х) = loga2_a_2 (4 sin х + a cos x + 5)
определена при всех значениях переменной х.
Задача 34 (географический факультет, основной экзамен, 1995, 5(5)). Сколько корней на отрезке х G [—тг; тг] имеет уравнение
х2 + a = 3b cos х,
если параметр b есть наименьшее возможное значение суммы квадратов корней квадратного трехчлена
х2 — х\/5 — Зе2 + | — с2 ?
Задача 35 (географический факультет, основной экзамен, 1995, 5(5)). Сколько корней на отрезке х G [—тг; тг] имеет уравнение
2 36
х — a = — cos х, если параметр b есть наименьшее возможное значение суммы квадратов корней уравнения
х2 — ху/Зс2 — 1 + с2 — 1 = 0 ?
310
Задача 36 (экономический факультет, отделение экономики, 1995, 5(6)). Найти все х Е [-3; 1], для которых неравенство
х (тг(т + 1) — 4arctg (3m2 + 12m +11)) >0
выполняется при любых целых т.
Задача 37 (экономический факультет, отделение экономики, 1995, 5(6)). Найти все х Е [-7; 2], для которых неравенство
х (тг(.г + 2) — Sarctg (2m2 + 12m + 17)) > 0
выполняется при любых целых т.
Задача 38 (экономический факультет, отделение экономики, 1995, 6(6)). Найти наименьшее значение выражения а2 + (b - I)2 среди тех а и Ь, для которых уравнение
||ж — 4| — 2| — ах + 4а — b = 0
имеет ровно три различных корня. Указать, при каких а и b достигается это наименьшее значение.
Задача 39 (экономический факультет, отделение экономики, 1995, 6(6)). Найти наименьшее значение выражения а2 + (6 + I)2 среди тех а п Ь, для которых уравнение
| |.г + 2| — 2| + ах + 2а + b = 0
имеет ровно три различных корня. Указать, при каких а и b достигается это наименьшее значение.
Задача 40 (экономический факультет, отделение менеджмента, 1995, 6(6)). Найти все значения параметра р, при которых уравнение
х - 2 = у/-2(р+ 2)х + 2
имеет единственное решение.
Задача 41 (экономический факультет, отделение менеджмента, 1995, 6(6)). Найти все значения параметра Ь, при которых уравнение
х-2 = у/2(Ь- 1> + 1
имеет единственное решение.
311
Задача 42 (факультет психологии, 1995, 5(5)). Найти все значения параметра а, при которых неравенство
л —г х2 + 9
cos х — 2у я2 + 9 -----------a
a + cos х
имеет единственное решение.
Задача 43 (факультет психологии, 1995, 5(5)). Найти все значения
параметра а, при которых неравенство
л л гт,----------- х + 10
cos 2х + а 2 v х2 + 16--------—•
a + cos lx
имеет единственное решение.
Задача 44 (Институт стран Азии и Африки, 1995, 6(6)). Найти все значения параметра а, при которых неравенство
х2 + 4х + 6а|х + 2| + 9а2 О
имеет не более одного решения.
Задача 45 (Институт стран Азии и Африки, 1995, 6(6)). Найти все значения параметра а, при которых неравенство
х2 — 6х + 4а\х — 3| + 4а2 О
имеет не более одного решения.
Задача 46 (механико-математический факультет, март 1996, 4(6)). При каких значениях а уравнение
\/3sin ^22гг-а:2) = а- 2cos2 (s2*-3"2-1)
имеет хотя бы одно решение?
Задача 47 (механико-математический факультет, март 1996, 4(6)). При каких значениях а уравнение
2cos2 (22з:-з:2) = а + 73sin (s23^41)
имеет хотя бы одно решение?
Задача 48 (механико-математический факультет, март 1996, 5(6)). Какое наибольшее число членов может содержать конечная арифметическая прогрессия с разностью 2 при условии, что квадрат ее первого члена в сумме с остальными членами не превосходит 160?
312
Задача 49 (механико-математический факультет, март 1996, 5(6)).
Какое наибольшее число членов может содержать конечная арифметическая прогрессия с разностью 4 при условии, что квадрат ее первого члена в сумме с остальными членами не превосходит 100?
Задача 50 (механико-математический факультет, май 1996, 4(6)).
При каком значении а сумма различных корней уравнения
cos х — sin 2а: + sin 4х = a(ctgx + 2 cos За?),
принадлежащих отрезку [Зтг/4; 22тг/3], максимальна?
Задача 51 (механико-математический факультет, май 1996, 4(6)).
При каком значении а сумма различных корней уравнения
sin а? + cos 2а? + cos 4а? = a(tgx + 2 cos За1),
принадлежащих отрезку [4тг/3; 31 тг/4], максимальна?
Задача 52 (механико-математический факультет, май 1996, 6(6)). Пайти все значения k, при каждом из которых хотя бы для одного числа b уравнение
|а?2 — 1| + kx = |а?2 — 8а? + 151 + b
имеет: а) более 5 корней; б) ровно 5 корней.
Задача 53 (механико-математический факультет, май 1996, 6(6)).
Найти все значения k, при каждом из которых хотя бы для одного числа b уравнение
|а?2 — 2а? | — kx — |а?2 — 10а? + 24| — b
имеет: а) более 5 корней; б) ровно 5 корней.
Задача 54 (механико-математический факультет, июль 1996, 4(6)). Решить систему
' log3 18 sin а? - log3 Зу + |log3 cos а? - log3 Зу| = 1
< 1 / 7Г \ 2 1
. 4 Г 4/ + V
Задача 55 (механико-математический факультет, июль 1996, 4(6)).
Решить систему
log2 18 sin а? — log2 2у + |log2 cos а? — log2 2у | = —2
313
Задача 56 (механико-математический факультет, июль 1996, 6(6)). При каких значениях параметра а уравнение
(а?2 — х + a2 + 1)2 = 4а2 (ба?2 — х + 1)
имеет ровно 3 различных решения?
Задача 57 (механико-математический факультет, июль 1996, 6(6)). При каких значениях параметра а уравнение
(х2 — х + а2 + 2)2 = 4а2 (2а?2 — а? + 2)
имеет ровно 3 различных решения?
Задача 58 (факультет ВМиК, предварительный экзамен, 1996, 5(6)). Найти все целочисленные решения уравнения
14а?4 - 5г/4 - За?2?/2 + 82г/2 - 125а?2 +51 = 0.
Задача 59 (факультет ВМиК, предварительный экзамен, 1996, 5(6)). Найти все целочисленные решения уравнения
10а?4 - 2г/4 + х2у2 + 29г/2 - 113а?2 + 171 = 0.
Задача 60 (факультет ВМиК, основной экзамен, 1996, 3(6)). При всех значениях параметра а решить уравнение
25х - (а - 1) • б1 + 2а + 3 = 0
и указать, при каких а оно имеет единственное решение.
Задача 61 (факультет ВМиК, основной экзамен, 1996, 3(6)). При всех значениях параметра а решить уравнение
9х + (а + 2) • 3* + | + 3 = О
и указать, при каких а оно имеет единственное решение.
Задача 62 (физический факультет, предварительный экзамен, 1996, 7(8)). Для любого допустимого значения а решить неравенство
2-loga (а? — 3) < logaa?.
314
Задача 63 (физический факультет, май, 1996, 8(8)). Для любого значения а решить уравнение
(log5 2)^+а+2 = (log4 25)V:r2-3a-5.
Задача 64 (физический факультет, июль 1996, 8(8)). Для каждого значения а найти число решений уравнения
a ctgx — 1 = cos 2х,
принадлежащих промежутку 0 х 2тг.
Задача 65 (химический факультет, основной экзамен, 1996, 5(5)). Решить уравнение
11 + cos (тгл/х) | + |х2 — 15ж + 441 = 15ж — х2 — cos (тгл/ir) — 45.
Задача 66 (химический факультет, основной экзамен, 1996, 5(5)). Решить уравнение
| — 1 + cos (тг tyx) | + |ж2 — 16z + 551 = 16ж — х2 + cos (тг \[х) — 56.
Задача 67 (биологический факультет, 1996, 5(5)). Найти все пары натуральных чисел удовлетворяющие одновременно двум нера-
венствам
18? > 2р+ 2q2 + 27 7р + 10 4?.
Задача 68 (биологический факультет, 1996, 5(5)). Найти все пары натуральных чисел (т; тг), удовлетворяющие одновременно двум нера-
венствам
2m + 2п2 < 24тг — 63 5тг 12m + 11.
Задача 69 (факультет почвоведения, предварительный экзамен, 1996, 6(6)). Определите площадь фигуры, расположенной на координатной плоскости и состоящей из точек (х;у), удовлетворяющих неравенству l
l°g(x2+y2) (z + $/) > I-
315
Задача 70 (факультет почвоведения, предварительный экзамен, 1996, 6(6)). Определите площадь фигуры, расположенной на координатной плоскости и состоящей из точек (х',у), удовлетворяющих неравенству
~ У) > Г
Задача 71 (факультет почвоведения, основной экзамен, 1996, 6(6)). Определите, при каких значениях а решения неравенства
\/х + а х
образуют на числовой прямой отрезок длины 2|а|.
Задача 72 (факультет почвоведения, основной экзамен, 1996, 6(6)).
Определите, при каких значениях а решения неравенства
у/2х — 4a х
образуют на числовой прямой отрезок длины 3|а|.
Задача 73 (геологический факультет, предварительный экзамен, 1996, 7(8)). Решить уравнение
sin 51 гг | = sin —3.
Задача 74 (геологический факультет, предварительный экзамен, 1996, 7(8)). Решить уравнение
sin 21 а: | = — sin 1.
Задача 75 (геологический факультет, предварительный экзамен, 1996, 8(8)). Найти все значения а, для которых неравенство
ax2 + 1 > 4х — За
выполняется для всех х из интервала ( — 1; 0).
Задача 76 (геологический факультет, предварительный экзамен, 1996, 8(8)). Найти все значения а, для которых неравенство
ах2 — 3 > 2(2 — а)х — 4а
выполняется для всех х из интервала (—2; —1).
316
Задача 77 (геологический факультет, июль 1996, 8(8)). Найти все действительные значения параметра Ь, при которых для любого действительного а уравнение
cos (a + ab + ax) + 4 cos (a2x) = 5b2 имеет хотя бы одно решение.
Задача 78 (геологический факультет, июль 1996, 8(8)). Найти все действительные значения параметра а, при которых для любого действительного b уравнение
cos (6 + ab + bx) + 2 cos (b2x) = За2 имеет хотя бы одно решение.
Задача 79 (географический факультет, предварительный экзамен, 1996, 6(6)). Найти все значения параметра р, при каждом из которых уравнение
х3 + (р - 6)х2 — 7рх — р2 = О
имеет три различных корня, которые являются длинами сторон некоторого треугольника.
Задача 80 (географический факультет, предварительный экзамен, 1996, 6(6)). Найти все значения параметра d, при каждом из которых уравнение
х3 — (4 + d)x2 + 6dx — d2 = О
имеет три различных корня, которые являются квадратами длин сторон некоторого неостроугольного треугольника.
Задача 81 (географический факультет, основной экзамен, 1996, 5(5)). Даны два вектора
и = {~р(ч + 2); —2р —3;р(д+ 2)} и v = {-q - 2;р + 2,q + 2}.
1) Найти все значения параметров р и q, при которых эти векторы будут коллинеарны, но не равны.
2) В случае р = q найти все значения параметра q, при которых эти векторы взаимно перпендикулярны.
Задача 82 (географический факультет, основной экзамен, 1996, 5(5)). Даны два вектора
и — {—b(a — 2); 1 — 26; — b(a — 2)} и v = {а — 2; b — 2; 2 — а}.
1) Найти все значения параметров р и q, при которых эти векторы будут коллинеарны, но не равны.
2) В случае р = q найти все значения параметра q, при которых эти векторы взаимно перпендикулярны.
317
Задача 83 (экономический факультет, отделение экономики, 1996, 6(6)). Найти все значения параметра а, при которых фигура, заданная на координатной плоскости условием
представляет собой четырнадцатиугольник.
Задача 84 (экономический факультет, отделение экономики, 1996, 6(6)). Найти все значения параметра а, при которых фигура, заданная на координатной плоскости условием
представляет собой двенадцатиугольник.
Задача 85 (экономический факультет, отделение менеджмента, 1996, 6(6)). При каких значениях параметра р площадь фигуры, заданной на координатной плоскости условием
|2ж + у\ + |ж - у + 3| р,
будет равна 24?
Задача 86 (экономический факультет, отделение менеджмента, 1996, 6(6)). При каких значениях параметра q площадь фигуры, заданной на координатной плоскости условием
|2ж + у\ + |ж - у - 3| q,
будет равна 54?
Задача 87 (факультет психологии, 1996, 5(5)). Пусть ti и £2 - действительные корни квадратного уравнения
t2- (56 — 2)t — 362 - 76+1 = 0.
Найти все значения параметра Ь, при каждом из которых для любого значения параметра а функция
f(x) = cos (атгж) • cos ((tf _|_
является периодической.
318
Задача 88 (факультет психологии, 1996, 5(5)). Пусть ti й+2 - действительные корни квадратного уравнения
t2 - (36 + l)i + Ь3 - 1162 + 6-7 = 0.
Найти все значения параметра Ь, при каждом из которых для любого значения параметра а функция
/(ж) = cos (атгж) • cos ((^ +t3) тгж)
является периодической.
Задача 89 (Институт стран Азии и Африки, 1996, 6(6)). При каких значениях параметра а неравенство
(sin х — л/3 cos х — a — 4 \ -----------г---------- > °
5 / выполняется для любых значений х ?
\) Задача 90 (Институт стран Азии и Африки, 1996, 6(6)). При каких значениях параметра а неравенство
(sin х + л/З cos х + a — 5 \ ------------г---------- > 0
5 /
выполняется для любых значений х ?
Задача 91 (механико-математический факультет, март 1997, 3(6)). ('читая х и у целыми числами, решить систему уравнений
{?х2-2ху+1 _ z . зу2-1 cos (5ttz) = —1.
Задача 92 (механике-математический факультет, март 1997, 3(6)). Считая х и у целыми числами, решить систему уравнений
Г 4з;2 + 2г2/ + 1 _ _|_ 2) . 71у I -1
t sin = 1.
Задача 93 (механико-математический факультет, март 1997, 5(6)). Решить систему
( + 2| — 2 х
t (2*+i + 21-1 + 21-з:) sin ^-+ cos (тгж) = 3 + 22r-1.
319
Задача 94 (механико-математический факультет, март 1997, 5(6)). Решить систему
+ 1| — 1 х
(2х + 2Х~2 + 22~х) cos + cos (тле) + 3 + 22а7~3 = 0.
Задача 95 (механико-математический факультет, май 1997, 6(6)).
Найти все значения а, при каждом из которых среди решений неравенства
л/(а — ж2) (х2 + a) + a > х
есть ровно два различных целочисленных решения.
Задача 96 (механико-математический факультет, май 1997, 6(6)).
Найти все значения Ь, при каждом из которых среди решений неравенства
\/(6 — ж2) (ж2 + 6) > х + b
есть ровно два различных целочисленных решения.
Задача 97 (механико-математический факультет, июль 1997, 5(6)). Для всех значений параметра а решить уравнение
Задача 98 (механико-математический факультет, июль 1997, 5(6)). Для всех значений параметра а решить уравнение
Задача 99 (факультет ВМиК, предварительный экзамен, 1997, 5(6)). Найти все значения х, для которых неравенство
\/х2 2х + b > Ьх2 + (1 — 6)(2ж — 1) — 2
выполняется для всех b из отрезка [—2; 0].
Задача 100 (факультет ВМиК, предварительный экзамен, 1997, 5(6)). Найти все значения х, для которых неравенство
х2
—---х + a > ax2 + (2a — 1)(ж 4- 2) — 3a
выполняется для всех а из отрезка [—3; 0].
320
Задача 101 (факультет ВМиК, основной экзамен, 1997, 6(6)). Найти все значения параметра а, при которых уравнение
\/ж3 — ОАх2 4- 118ят 4- 7 = 5\/7ж — ж2 4- \/а2 — 11а + 18
имеет единственное решение.
Задача 102 (факультет ВМиК, основной экзамен, 1997, 6(6)). Найти все значения параметра а, при которых уравнение
>/—Зж3 4- 8а?2 4- 47ж — 52 = 6\/бж — ж2 — 5 4- \/а2 — 10а 4- 21
имеет единственное решение.
Задача 103 (физический факультет, март 1997, 7(8)). Найти все зна
чения а, при которых неравенство
1оёа + 4) > 1
выполняется для всех значений х.
Задача 104 (физический факультет, март 1997, 7(8)). Найти все значения Ь, при которых неравенство
logj (ж2 4- 3) > 1
выполняется для всех значений ж.
Задача 105 (физический факультет, май 1997, 7(8)). Найти все зна
чения а, при которых неравенство
ж — 2а — 4
ж 4- За — 2
О
выполняется для всех х из промежутка 1 ж 3.
Задача 106 (физический факультет, май 1997, 7(8)). Найти все зна
чения а, при которых неравенство
х 4-'2а — 3
ж — За — 4
выполняется для всех х из промежутка 2 ж 4.
Задача 107 (физический факультет, июль 1997, 7(8)). Для любых значений а решить неравенство
a — 2 < (а — 1)л/ж 4- 1.
21 Методы реш. задач
321
Задача 108 (физический факультет, июль 1997, - 7(8)). Для любых значений а решить неравенство
5 — a > (4 — а)л/я — 3.
Задача 109 (химический факультет и Высший колледж наук о материалах, предварительный экзамен, 1997, 6(6)). Найти все пары целых чисел (z; у), удовлетворяющие уравнению
(х1 2 + у2) (х + у - 3) = 2ху.
Задача 110 (химический факультет и Высший колледж наук о материалах, предварительный экзамен, 1997, 6(6)). Найти все пары целых чисел (тгг, п), удовлетворяющие уравнению
(т2 + п2) (т 4- п — 5) = 2тп.
Задача 111 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1997, 6(6)). Найти наибольшее и наименьшее значения выражения х2 + 2г/2, если х2 — ху + 2 г/2 = 1.
Задача 112 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1997, 6(6)). Найти наибольшее и наименьшее значения выражения х2 + Зг/2, если х2 — 2ху + Зг/2 = 1.
Задача 113 (биологический факультет и факультет фундаментальной медицины, 1997, 6(6)). Найти решения системы
Задача 114 (биологический факультет и факультет фундаментальной медицины, 1997, 6(6)). Найти решения системы
1 / х2
20 vsinz
322
Задача 115 (факультет почвоведения, предварительный экзамен, 1997, 6(6)). Найти наибольшее и наименьшее значения выражения
л /1 —cos 2х Г
—За/----------F у 2 — v3 cosх — 1
1 — 2 cos 2у
2
4- у 11 — v 3 cos у 4- 1
Задача 116 (факультет почвоведения, предварительный экзамен, 1997, 6(6)). Найти наибольшее и наименьшее значения выражения
л /1 — cos 2ж Г \ /1 — 2 cos 2у Г Z , \
—2д /-----------Н у 3 —1/2 cos х — 1 1 I -----------1- у 7 — 1/2 cos у 4- 1 1.
У Z / \ /
Задача 117 (факультет почвоведения, основной экзамен, 1997, 6(6)). Для каждого значения параметра а решить неравенство
\/а2 — х2 a 4- 1.
Задача 118 (факультет почвоведения, основной экзамен, 1997, 6(6)). Для каждого значения параметра с решить неравенство
\] с2 — х2 2 — с.
Задача 119 (геологический факультет, предварительный экзамен, 1997, 7(8)). Стоимость изготовления п банок пропорциональна 24 4- 4п 4- п2. Определить количество банок, при котором стоимость изготовления одной банки минимальна.
Задача 120 (геологический факультет, предварительный экзамен, 1997, 7(8)). Стоимость изготовления m коробок пропорциональна 17 4- 5m 4- m2. Определить количество коробок, при котором стоимость изготовления одной коробки минимальна.
Задача 121 (геологический факультет, предварительный экзамен, 1997, 8(8)). При каких а система
а(х - 4) = 3(у 4- 2) у 4- у/х - О
имеет два различных решения?
21*
323
Задача 122 (геологический факультет, предварительный экзамен, 1997, 8(8)). При каких /3 система
Г /3(х - 9) = 4(2/4- 3)
I у + у/х = О
имеет два различных решения?
Задача 123 (геологический факультет, основной экзамен, 1997, 8(8)). При каких значениях а уравнения
ха2 — а — (ж3 — 5ж2 + 4) = О,
(ж + 1)а2 4* (ж2 — ж — 2)а — (2ж3 — Юж2 4- 8) = О
не имеют общего решения?
Задача 124 (геологический факультет, основной экзамен, 1997, 8(8)). При каких значениях а уравнения
а2 4- (ж2 — ж — 1)а — (ж3 — 6ж2 4* 5) = О, (3 - ж)а2 + (Зж2 - Зж - 2)а - (2ж3 - 12ж2 4- 10) = О
не имеют общего решения?
Задача 125 (географический факультет, предварительный экзамен, 1997, 6(6)). Найти все значения параметра а, при каждом из которых множество точек пространства с координатами (x;y;z), удовлетворяющих уравнению
|ж - а| 4- |ж 4- а| 4- \у - 2а| 4- \у 4- 2а| 4- \z - 2а| 4- \z 4- 2а| = а2 4- 9,
1) содержит два одинаковых шара радиуса г = к/3;
2) имеет ненулевой объем и содержится в сфере радиуса R= тг.
3) Найти rmax и Rmin и соответствующие им значения параметра а.
Задача 126 (географический факультет, предварительный экзамен, 1997, 6(6)). Найти все значения параметра а, при каждом из которых множество точек пространства с координатами (x-,y,z), удовлетворяющих уравнению
|ж - 2а| 4- |ж 4- 2а| 4- |1/ - 2а| 4- |г/ 4- 2а| 4- |.z - а| 4- |.z 4- а| = а2 4- 9,
1) содержит два одинаковых шара радиуса г = тг/2;
2) имеет ненулевой объем и содержится в сфере радиуса R= тг.
3) Найти rmax и Rmin и соответствующие им значения параметра а.
324
Задача 127 (географический факультет, основной экзамен, 1997, 4(6)). Найти все значения параметра а, при каждом из которых единственное решение имеет система
ах2 4* 4ах — т/4-7а 4-2^0 ау2 — х — Чау 4- 4а — 1 0.
Задача 128 (географический факультет, основной экзамен, 1997, 4(6)). Найти все значения параметра Ь, при каждом из которых единственное решение имеет система
by2 4* 4by — Чх 4- 7b 4- 4 0
Ьх2 — Чу — ЧЬх 4- 46 — 2 0.
Задача 129 (географический факультет, основной экзамен, 1997, 6(6)). На координатной плоскости построить Г.М.Т. (геометрическое место точек), координаты (х,у) которых соответствуют существованию тупоугольного треугольника с длинами сторон Ч, у — х, х + у. Построение обосновать, уравнения границ Г.М.Т. выписать в ответ.
Задача 130 (географический факультет, основной экзамен, 1997, 6(6)). На координатной плоскости построить Г.М.Т. (геометрическое место точек), координаты (х\ у) которых соответствуют существованию остроугольного треугольника с длинами сторон 1, |х|, у/—у. Построение обосновать, уравнения границ Г.М.Т. выписать в ответ.
Задача 131 (экономический факультет, отделение экономики, 1997, 5(6)). Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4 и на промежутке — 2 х 0 ее значения вычисляются по правилу f(x) = Чх(х 4- 2). Решить уравнение
2/(-3 - ат) - 3
+ 1)-^
Задача 132 (экономический факультет, отделение экономики, 1997, 5(6)). Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4 и на промежутке —2 х 0 ее значения вычисляются по правилу f(x) = 3z(z 4- 2). Решить уравнение
3/(5 —д:) —5
#й+1У- л
325
Задача 133 (экономический факультет, отделение экономики, 1997, 6(6)). Множество точек, расположенных внутри фигуры F, задано на координатной плоскости условием
/ Юг/— 24 — г/2 \
к 850 Ж и‘
Множества F(t) получаются из F поворотом вокруг начала координат против часовой стрелки на угол t. Найти площадь фигуры, образованной точками, каждая из которых при некотором t G [0; тг] принадлежит множеству F(t).
Задача 134 (экономический факультет, отделение экономики, 1997, 6(6)). Множество точек, расположенных внутри фигуры G, задано на координатной плоскости условием
, /ж2 + 1994\ п
°6(^) к 1997 J > ’
Множества G(P) получаются из G поворотом вокруг начала координат против часовой стрелки на угол t. Найти площадь фигуры, образованной точками, каждая из которых при некотором t 6 [0; тг] принадлежит множеству G(t).
Задача 135 (экономический факультет, отделение менеджмента, 1997, 5(6)). Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4 и на промежутке 0 х 2 ее значения вычисляются по правилу f(x) = 1 — |х — 1|. Решить уравнение
2f(x) f(x - 8) + 5f(x + 12) + 2 = 0.
Задача 136 (экономический факультет, отделение менеджмента, 1997, 5(6)). Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4 и на промежутке 0 х 2 ее значения вычисляются по правилу f(x) = |х — 1| — 1. Решить уравнение
2f(x + 4) f(x) - 5 f(x -16)4-2 = 0.
Задача 137 (экономический факультет, отделение менеджмента, 1997, 6(6)). Найти все значения параметра а, при которых периметр фигуры, заданной на координатной плоскости условием
будет наименьшим.
326
Задача 138 (экономический факультет, отделение менеджмента, 1997, 6(6)). Найти все значения параметра Ь, при которых периметр фигуры, заданной на координатной плоскости условием
будет наименьшим.
Задача 139 (факультет психологии, 1997, 4(6)). При каких действительных р уравнение
4Т + 2^+2 + 7 _ Р _ _ 2.21-®
имеет решение?
Задача 140 (факультет психологии, 1997, 4(6)). Найти все действительные значения параметра Ь, при которых уравнение
36х-2 + З3^2+3 _ 36 _ 5 _ 9 . 33^2+1 _ 36а;2
имеет решение.
Задача 141 (факультет психологии, 1997, 6(6)). Найти все значения параметров а и Ь, при которых система уравнений
( х2 4* у2 4- 5 = Ь2 + 2х — 4у
t х2 4* (12 — 2о)х + у2 = 2ay 4- 12а — 2а2 — 27
имеет два решения (х^-, yi) и (.t^; 2/2), удовлетворяющие условию
xi ~ х2 _ у! 4- У2
У2 - У1 X! +х2'
Задача 142 (факультет психологии, 1997, 6(6)). Найти все значения параметров р и q, при которых система уравнений
х2 + у2 + 2р2 = (10 — 2р)у 4- 2рх 4- Юр — 21
х2 4* у2 4- 52 = q2 — 8х — 12т/
имеет два решения (x’i; 3/1) и (х2-, у2), удовлетворяющие условию
^1 - х2 _ У2 ~ У1
У1 +У2 +х2'
327
Задача 143 (социологический факультет, 1997, 6(6)). Укажите все неотрицательные значения параметра а, при которых уравнение
sin (2а) • sin2 (аж) + 1 = (1 + sin (2а)) sin (аж)
имеет ровно 4 решения на отрезке [—тг; тг].
Задача 144 (социологический факультет, 1997, 6(6)). Укажите все неотрицательные значения параметра Ь, при которых уравнение
sin (26) + 1 = sin (26) • (sin (6ж) + cos2 (6ж)) + sin (6ж)
имеет ровно 4 решения на отрезке [—тг; тг].
Задача 145 (Институт стран Азии и Африки, 1997, 5(7)). Найти площадь фигуры, заданной на координатной плоскости условием
{у д/4 — ж2 у |ж - 1| - 3.
Задача 146 (Институт стран Азии и Африки, 1997, 5(7)). Найти площадь фигуры, заданной на координатной плоскости условием
( у л/9 — ж2 t у |ж + 2| - 5.
Задача 147 (Институт стран Азии и Африки, 1997, 7(7)). Найти все пары целых ж и у, удовлетворяющих уравнению
Зху — 14ж — 17?/ + 71 = 0.
Задача 148 (Институт стран Азии и Африки, 1997, 7(7)). Найти все пары целых ж и у, удовлетворяющих уравнению
Зху + 16ж + 13?/ + 61 = 0.
Задача 149 (механико-математический факультет, март 1998, 6(6)).
Найти все значения а, при каждом из которых уравнение
(ж2 + (1 - а)ж - 3(а + 2)) • log(a._a) (ж - 2а - 1) = 0
имеет хотя бы один корень на отрезке [—2; 1], а вне этого отрезка корней не имеет.
328
Задача 150 (механико-математический факультет, март 1998, 6(6)). Найти все значения а, при каждом из которых уравнение
(х2 - (а + 1)х - 2(а + 3)) • log(;c_a_i:) (х - 2а - 2) = О имеет хотя бы один корень на отрезке [—1; 2], а вне этого отрезка корней не имеет.
Задача 151 (механико-математический факультет, май 1998, 4(6)). Найти все значения k, при которых хотя бы одна общая точка графиков функций
2 2
у = — - — arcsin х и у = — - — 2arctgkx
имеет положительную ординату.
Задача 152 (механико-математический факультет, май 1998, 4(6)). Найти все значения k, при которых хотя бы одна общая точка графиков функций
X
2 2 п
у —----arcsin х и у —--------2arctgkx
5 ' 5
имеет отрицательную ординату.
Задача 153 (механико-математический факультет, май 1998, 6(6)). Фигура задана на координатной плоскости системой
Г (у2 - X2)2
[ t/ > 1 - X.
Сколько интервалов на прямой у = 2 — х образует ортогональная проекция этой фигуры на указанную прямую?
Задача 154 (механико-математический факультет, май 1998, 6(6)). Фигура задана на координатной плоскости системой
Г (х2 - У2)2 - 6 (х2 - у2) - (х - у)2 - 7х + 5у + 1 < О
( у > 1 + X.
Сколько интервалов на прямой у = х — 3 образует ортогональная проекция этой фигуры на указанную прямую?
Задача 155 (механико-математический факультет, июль 1998, 5(6)). При каких значениях параметра а система
( cos2 (кху) — 2 sin2 (тле) — 3 sin2 (тг?/) — 2 + tg (тга) = О
3 <31
J cos (тгозг/) — - sin2 (тле) — 2sin2 (тг?/) — - + -tg(ivct) = О
ТГ \ 2 2\ 1
— — X— у < -16/ У J 2
/ • 9 / 7Г Сб
к log2 + 4 sin имеет ровно четыре решения?
329
Задача 156 (механико-математический факультет, июль 1998, 5(6)). При каких значениях параметра а система
' cos2 (тгжт/) + 3sin2 (тгж) + 6 sin2 (тг?/) — tg (2тга) = О
1 1
cos (тгж?/) — sin2 (тгж) — 2 sin2 (тг?/) + - + - tg (2тго?) = О
I . (-1 л 9 (ТГ СИ ТГ \ q n \ 1
( log3 (1+4 cos"
\ \ 2 16/ / 3
имеет ровно четыре решения?
Задача 157 (факультет ВМиК, предварительный экзамен, 1998, 5(6)). Найти все значения параметра а, при которых уравнение
2х /j;2 _ |\ 5
2 i+r7 + a • cos ( ------ I + a2 — - = О
\ x J 4
имеет единственное решение.
Задача 158 (факультет ВМиК, предварительный экзамен, 1998, 5(6)). Найти все значения параметра а, при которых уравнение
2
. ( Тг(ж" + X + 1)
1+г - а • sin —-----------------
к 2ж
11
Т
= О
2
имеет единственное решение.
Задача 159 (факультет ВМиК, основной экзамен, 1998, 5(6)). Найти все значения параметра а, при которых существуют (х;у), удовлетворяющие системе неравенств
max(2 — 3?/,?/Н-2) 5
< у a2 + £ arccos у/1 — х2 — 16 — arcsin х (тг + 2 arcsin ж) . У2 + 2а?/ + 7.
Задача 160 (факультет ВМиК, основной экзамен, 1998, 5(6)). Найти все значения параметра а, при которых существуют (ж; у), удовлетворяющие системе неравенств
max (4 + у, 3 — 3?/) < 6
< у a2 + arcsin л/1 — ж2 — 4 — arccos ж • (^ + arccos ж) . У2 + ^ау + 3.
ззо
Задача 161 (физический факультет, март, 1998, 8(8)). При каких значениях а система уравнений
log3 (г/ — 3) — 2 log9 а? = О (х + а)2 — 2у — 5а = О
имеет хотя бы одно решение?
Задача 162 (физический факультет, май, 1998, 7(8)). Найти все значения а, при которых неравенство
logi (х2 + ах 4- 1) < 1
выполняется для всех х из промежутка х < 0.
Задача 163 (физический факультет, основной экзамен, 1998, 7(8)). Для любых допустимых значений а решить неравенство
loge (Заг - 5) < х + 1.
Задача 164 (биологический факультет и факультет фундаментальной медицины, 1998, 5(5)). Найти все решения системы
{27
cos 1 Оа? — 2 sin 5а? 3 • 4Z — 3 • 2*+2 + —
(2- х/З)4*-h (2 + ч/3)4<+ 2 + 14 log2 (cos 10a?) + 6 cos 5a? (2/ + I)3/2.
Задача 165 (биологический факультет и факультет фундаментальной медицины, 1998, 5(5)). Найти все решения системы
79
бл/3соз41’ — 3 cos 8а? 415-< — 25-* + —
£
. 7(72+Уз)^‘+(Л — \/2) 4<+2 +10 log2 (cos 8a?)+4\/2cos4a? (t+3).
Задача 166 (факультет почвоведения, предварительный экзамен, 1998, 6(6)). Определите, при каких значениях а имеет хотя бы одно решение (х,у) следующая система:
\/—у2 — 2а? = аа? у 2, 5 + а.
331
Задача 167 (факультет почвоведения, предварительный экзамен, 1998, 6(6)). Определите, при каких значениях а не имеет решений (х, у) следующая система:
{\/4у — х2 + ay = О
а? + а + 4, 5 < О.
Задача 168 (факультет почвоведения, основной экзамен, 1998, 6(6)). Определите,
а) при каких значениях а существует такое число Ь, что уравнение
5 cos х + sin х + cos (х — Ь) = a
имеет решения,
б) при каких значениях а это уравнение имеет решения при любом значении Ь.
Задача 169 (факультет почвоведения, основной экзамен, 1998, 6(6)). Определите,
а) при каких значениях а существует такое число Ь, что уравнение
cos х 4- 4 sin х + sin (х — b) = a
имеет решения,
б) при каких значениях а это уравнение имеет решения при любом значении Ь.
Задача 170 (геологический факультет, предварительный экзамен, 1998, 8(8)). При каких а для любого Ь 2 неравенство
(b - 1)а? + 2х/1-(Ь-1)-2 < (- Ь + 1
выполняется для всех х < 0 ?
Задача 171 (геологический факультет, предварительный экзамен, 1998, 8(8)). При каких а для любого b 0 неравенство
(6 + 1)х + 2^1 - (6 + 1)-2 < (2—1 -6-1)1
\ Ь + 1 / х
выполняется для всех х < 0 ?
Задача 172 (геологический факультет, основной экзамен, 1998, 8(8)). При каких значениях а уравнение
х2 — 4ах + 4а2 + 1 х — 2а
+ х2 — 2a? — 1 = О
имеет хотя бы одно решение?
332
Задача 173 (геологический факультет, основной экзамен, 1998, 8(8)). При каких значениях а уравнение
имеет хотя бы одно решение?
Задача 174 (географический факультет, 1998, 6(6)). Найти все пары целых чисел (х;?/), удовлетворяющих уравнению
Зх = 5?/2 + 4у - 1,
и доказать, что для каждой такой пары сумма х3 + у3 является нечетным числом.
Задача 175 (географический факультет, 1998, 6(6)). Найти все пары целых чисел (х;у), удовлетворяющих уравнению
бу — 2х2 — 7х 4- 3,
и доказать, что для каждой такой пары разность х2 — у2 является нечетным числом.
Задача 176 (факультет психологии, 1998, 6(6)). Найти все целые значения параметров а и b, при которых уравнение
arcsin
у/b2 — х2
- ‘lab
имеет не менее 10 различных решений.
Задача 177 (факультет психологии, 1998, 6(6)). Найти все целые значения параметров тип, при которых уравнение
1 / / х2 \
— arccos (1/1------о “ m • 2sin С™*)-
m \ V m? I
— arccos m
л» " \
1----------- + m • 2sin + 2mn = 0
тп / I
имеет не менее 10 различных решений.
ззз
Задача 178 (филологический факультет, 1998, 6(6)). При каких значениях параметра а уравнение
sin2 (а? + 6) — (а — 1) sin (а? + 6) • sin тга? + (а — 1) sin2 тга? = О
имеет единственное решение?
Задача 179 (филологический факультет, 1998, 6(6)). При каких значениях параметра а уравнение
sin2 (а? — 5) — (а — 2) sin (а? — 5) • sin тга? + (а — 2) sin2 тга? = О
имеет единственное решение?
Задача 180 (химический факультет и Высший колледж наук о материалах, предварительный экзамен, 1998, 6(6)). При каких а уравнение
^\/ а?2 — 2аа? + 7 + л/a?2 — 2аа? + 5^ +
+ а?2 — 2аа? + 7 — д/а?2 — 2аа? + 5^ = 2(\/2):и
имеет единственное решение?
Задача 181 (химический факультет и Высший колледж наук о материалах, предварительный экзамен, 1998, 6(6)). При каких а уравнение
(\/ а?2 — Заа? + 8 + \/а?2 — Зах + б) +
+ а?2 — Заа? + 8 — \/х2 — Зах + б) = 2(х/2)т
имеет единственное решение?
Задача 182 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1998, 6(6)). Решить уравнение
log2 (4а? + 1) log5 (4а? + 4) + log3 (4а? + 2) log4 (4а? + 3) = = 2 log3 (4а? + 2) log5 (4а? + 4).
Задача 183 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1998, 6(6)). Решить уравнение
log2 (За? + 1) log5 (За? + 4) + log3 (За? + 2) log4 (За? + 3) =
= 2 log3 (За? + 2) log5 (За? + 4).
Я.Я4
Задача 184 (институт стран Азии и Африки, 1998, 7(7)). При каких значениях параметра а система
( х4 — (а — 1)\/а 4- 3 у 4- а4 4- 2а3 — 9а2 — 2а 4- 8 = О
[ у — л/а 4- За?2
имеет ровно три различных решения?
Задача 185 (институт стран Азии и Африки, 1998, 7(7)). При каких значениях параметра а система
( у4 — (а — 3)л/а 4- 1 а? 4- а4 — 6а3 4- За2 4- 26а — 24 = О
[ а? = Уа 4- It/2
имеет ровно три различных решения?
Задача 186 (механико-математический факультет, март 1999, 5(6)).
Найти все значения а из промежутка [—2; 1], при каждом из которых расстояние на числовой оси между любыми различными корнями уравнения
sin 2а? 4- |2а 4- 1| sin х 4- |а| = 2|а| cos х 4- sin х 4- |2а2 4- а|
не меньше, чем тг/2.
Задача 187 (механико-математический факультет, март 1999, 5(6)).
Найти все значения а из промежутка [— 1; 2], при каждом из которых расстояние на числовой оси между любыми различными корнями уравнения
sin 2а? 4- 2|а| cos а? 4- sin а? 4* |а| = [2а — 1| sin a? 4* |2а2 — а|
не меньше, чем тг/2.
Задача 188 (механико-математический факультет, май 1999, 5(6)).
Найти все значения а, при каждом которых множество решений неравенства
a 4- 2 — 2х-2 5а 4-5
а 4- 3. 2(2® 4- За 4- 3)
содержит какой-либо луч на числовой прямой.
Задача 189 (механике-математический факультет, май 1999, 5(6)).
Найти все значения а, при каждом из которых множество решений неравенства
2 - 2а 3(3* + 4а - 8)
З*"1 - а 4-1 5а - 15
содержит какой-либо луч на числовой прямой.
335
Задача 190 (механика-математический факультет, основной экзамен, 1999, 5(6)). Найти все значения а, при каждом из которых сумма длин интервалов, составляющих решение неравества
х2 + (2а2 + 6)а? — а2 + 2а — 3 а?2 + (а2 + 7а — 7)х — а2 + 2а — 3 ’
не меньше 1.
Задача 191 (механико-математический факультет, основной экзамен, 1999, 5(6)). Найти все значения а, при каждом из которых сумма длин интервалов, составляющих решение неравества
х2 + (2а2 + 2)а? — а2 + 4а — 6 а?2 + (а2 + 5а — 5)а? — а2 + 4а — 6 < ’
не меньше 1.
Задача 192 (факультет ВМиК, предварительный экзамен, 1999, 5(6)). При каких значениях параметра а уравнение
^x2-f-2ax-j-4a — 3 __ 2 __
а — 2 х + a
имеет ровно два корня, лежащих на отрезке [—4; 0]?
Задача 193 (факультет ВМиК, предварительный экзамен, 1999, 5(6)). При каких значениях параметра а уравнение
/ / । \ ат24-4аг+4а —2 \
12а — 1| ( ( 2 ) — 1 1 = |а? + 2а|
имеет ровно два корня, лежащих на отрезке [—2; 1]?
Задача 194 (факультет ВМиК, основной экзамен, 1999, 5(6)). Решить уравнение
tg!4x + 3ctgl4a? + sin 6а? — 2\/2sin
/ тг\
(За? + — ) х 4/
4
х/3 + f
Задача 195 (факультет ВМиК, основной экзамен, 1999, 5(6)). Ре-
шить уравнение
6 tg 13а? + etg 13а? — x/2sin 12а? — 4sin
6а? —-
X 4/
20
2л/3 + л/2
336
Задача 196 (физический факультет, предварительный экзамен, март 1999, 7(8)). Для любых допустимых значений а решить уравнение
loga (а?2 - За) = loga (а2 - Зж).
Задача 197 (физический факультет, предварительный экзамен, март 1999, 7(8)). Для любых допустимых значений а решить уравнение
^/^-3a _ ig _ у/^-Зх _
Задача 198 (физический факультет, предварительный экзамен, май 1999, 7(8)). При каких значениях а уравнение
cos 2ж 4- 2 cos х — 2a2 — 2a + 1 = О
имеет ровно одно решение на промежутке 0 х < 2тг?
Задача 199 (физический факультет, предварительный экзамен, май 1999, 7(8)). При каких значениях а уравнение
cos 2х + 2(2a — 1) sin х — 2а2 + 2а — 1 = О
имеет ровно три решения на промежутке 0 х < 2%?
Задача 200 (физический факультет, основной экзамен, 1999, 8(8)). Для любого допустимого значения а решить неравенство
log2a (log3 х2) > 1
и найти, при каком значении а множество точек х, не являющихся решениями неравенства, представляет собой промежуток, длина которого равна 6?
Задача 201 (физический факультет, основной экзамен, 1999, 8(8)). Для любого допустимого значения m решить неравенство
log4m (1°ё5 Ж2) > 1
и найти, при каком значении m множество точек х, не являющихся решениями неравенства, представляет собой промежуток, длина которого равна 10?
22 Методы реш. задач
337
Задача 202 (химический факультет, предварительный экзамен, 1999, 6(6)). Для всех значений параметра а, принадлежащих отрезку [—1; 0], решить неравенство
1оё^+а (х2 - (а + 1)ж + а) > 1.
Задача 203 (химический факультет, предварительный экзамен, 1999, 6(6)). Для всех значений параметра а, принадлежащих отрезку [0; 1], решить неравенство
iogz-a (ж2 + (а -1)я - а) 1.
Задача 204 (Высший колледж наук о материалах, предварительный экзамен, 1999, 5(5)). Знаменатель бесконечно убывающей геометрической прогрессии отрицателен. Найти все целые т, при которых сумма ее членов с нечетными номерами больше суммы ее членов с четными номерами на величину, равную произведению ее второго члена и числа вида m2 + 10m + 20.
Задача 205 (Высший колледж наук о материалах, предварительный экзамен, 1999, 5(5)). Знаменатель бесконечно убывающей геометрической прогрессии положителен. Найти все целые п, при которых сумма ее членов с нечетными номерами больше суммы ее членов с четными номерами на величину, равную произведению ее второго члена и числа вида 6п — п2 — 15/2.
Задача 206 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1999, 6(7)). Найти все значения параметра а, при которых уравнение
x(2z - 1) 2* + 1
2а
— a2 + 1.
имеет нечетное число решений.
Задача 207 (химический факультет и Высший колледж наук о материалах, основной экзамен, 1999, 6(7)). Найти все значения параметра а, при которых уравнение
х(Зх- 1) 3* + 1
— 2а
= а2 + 1.
имеет нечетное число решений.
338
Задача 208 (биологический факультет и факультет фундаментальной медицины, 1999, 5(6)). Найти все значения у, удовлетворяющие условию у > 1/2, такие, что неравенство
16у3 + 6у3х — 4у3х2 — 50у2 — 11з/2ж 4- 102/2ж2+
+52г/ + 4?/а? — 8?/а?2 — 18 + х + 2х2 > О
выполняется при всех х из интервала 1 < х < 2у.
Задача 209 (биологический факультет и факультет фундаментальной медицины, 1999, 5(6)). Найти все значения у, удовлетворяющие условию у > 1/3, такие, что неравенство
\2у3х2 - 21у3ж - 42?/3 - 28т/2ж2 + 43?/2ж + 111?/2+
+20?/а?2 — 23?/а? — 96?/ — 4а?2 + х + 27 < О
1 я
выполняется при всех х из интервала ± < х < т-у.
Задача 210 (факультет почвоведения, предварительный экзамен, 1999, 6(6)). Найти все значения параметра (3, при которых уравнение
(х2 + а?)(а?2 + 5г? + 6) = /3
относительно х имеет ровно три корня.
Задача 211 (факультет почвоведения, предварительный экзамен, 1999, 6(6)). Найти все значения параметра а, при которых уравнение
(а?2 — а?)(а?2 — 5а? + 6) = a
относительно а? имеет ровно три корня.
Задача 212 (факультет почвоведения, 7(7)). Для каждого значения параметра b носительно х)
у/х2 — 1 --------о.
х
Задача 213 (факультет почвоведения, 7(7)). Для каждого значения параметра а носительно х)
у/х2 — 4 -------< а.
основной экзамен, 1999, О решить неравенство (от-
основной экзамен, 1999, О решить неравенство (от-
х
22*
339
Задача 214 (географический факультет, предварительный экзамен, 1999, 5(6)). При каких значениях параметра а система
(у2 — (2а 4- 1)?/ + а2 + а — 2 = 0
t у/(х- о)2 + у2 + у/(х - а)2 + (у- З)2 = 3
имеет единственное решение?
Задача 215 (географический факультет, предварительный экзамен, 1999, 5(6)). При каких значениях параметра а система
( х2 — (2а — 2)а? + а2 — 2а — 3 = 0
t у/(у - а)2 + х2 + у/(у - а)2 + (а? - 4)2 = 4
имеет единственное решение?
Задача 216 (географический факультет, основной экзамен, 1999, 4(6)). Найти все значения параметра а, при которых среди корней уравнения
sin 2х + ба cos х — sin х — За = 0
найдутся два корня, разница между которыми равна Зтг/2.
Задача 217 (географический факультет, основной экзамен, 1999, 4(6)). Найти все значения параметра а, при которых среди корней уравнения
sin 2а? + 4а sin х — cos х — 2а = 0
найдутся два корня, разница между которыми равна Зтг/2.
Задача 218 (экономический факультет, отделение экономики, 1999, 7(7)). Найти все значения Ь, при каждом из которых система
( b sin 12z| + log5 (x y/2 — 5a?8) + b2 = 0
l ((т/2 — 1) cos2 z — у sin 2z + 1) (1 + у/тг + 2z + у/тг — 2z) = 0
разрешима и имеет не более двух решений; определить эти решения.
Задача 219 (экономический факультет, отделение экономики, 1999, 7(7)). Найти все значения а, при каждом из которых система
J а| cos 2z| + log3 (а? 1v/2 — За?12) + a2 = 0
I ((т/2 — 1) sin2 z — у sin 2z + 1) (1 + y/z + -/тг — z) = 0
разрешима и имеет не более двух решений; определить эти решения.
340
Задача 220 (экономический факультет, отделение менеджмента, 1999, 6(6)). Для каждого значения b найти все пары чисел (х;у), удовлетворяющие уравнению
b sin 2у + log4 (з? \/1 — 4з?8) = Ь2.
Задача 221 ("экономический факультет, отделение менеджмента, 1999, 6(6)). Для каждого значения а найти все пары чисел (з?;г/), удовлетворяющие уравнению
a cos 2з? + log2 (у 1\/1 — 2 г/12) = а2.
Задача 222 (факультет психологии, 1999, 4(6)). Найти все значения параметра р, при каждом из которых множество значений функции
/м = 3*+р х2 + 5х + 7
содержит полуинтервал (—1; 3]. Определить при каждом таком р множество значений функции f(x).
Задача 223 (факультет психологии, 1999, 4(6)). Найти все значения параметра а, при каждом из которых множество значений функции
\ 4х — a /(г) = ^-4х + 7
содержит полуинтервал (—4/3; 1]. Определить при каждом таком а множество значений функции f(x).
Задача 224 (факультет психологии, 1999, 6(6)). Найти все значения параметра а, при каждом из которых ровно пять различных наборов (я; у, г) натуральных чисел х,у, z удовлетворяют системе условий:
( 12з?2 — 4х — 2ху + Зг/ — 9 = О [ ayz 4- axz 4- axy > xyz.
Задача 225 (факультет психологии, 1999, 6(6)). Найти все значения параметра р, при каждом из которых ровно четыре различных набора (х\ у, г) натуральных чисел x,y,z удовлетворяют системе условий:
( 48г/2 4- 20г/ — 4з?у 4- Зз? — 67 = 0
[ pyz 4- pxz 4- рху > xyz.
341
Задача 226 (социологический факультет, 1999, 6(6)). При каких значениях параметра а неравенство
l°ga^+2a^+i V 16 arcsin 4 (я + За)
l°gaa;2+2a2i:+i у 16 arcsin 4 (ж + За)
не имеет решений на отрезке [—5; 6]?
Задача 227 (социологический факультет, 1999, 6(6)). При каких значениях параметра а неравенство
loSa^+a^+i у 16 arcsin 4 (z + 2а) <
ioga^+a^+l V 16 arcsin 4(:Е + 2а)
, не имеет решений на отрезке [—7; 4] ?
Задача 228 (институт стран Азии и Африки, 1999, 7(7)). Решить систему неравенств
х2 + 2у+2 у4 - 4 я + 13 я2 - у2 4 - 2у+1.
Задача 229 (институт стран Азии и Африки, 1999, 7(7)). Решить систему неравенств
2х2 — log2 (г/л/2 + 6)3 — 16 у4 — Зя — у2 х2 - у2 log2 (з/л/2 + 6) + х + 1.
Задача 230 (механико-математический факультет, Олимпиада “Абитуриент-2000”, март, 5(6)). При каких значениях параметра а уравнение
2J 5 \2J 5
имеет хотя бы одно решёние и каждое его решение является целым числом?
342
Задача 231 (механико-математический факультет, Олимпиада “Абитуриент-2000”, март, 5(6)). При каких значениях параметра а уравнение
имеет хотя бы одно решение и каждое его решение является целым числом?
Задача 232 (механико-математический факультет, Олимпиада “Абитуриент-2000”, май, 5(6)). Найти все а, при которых уравнение
(2а + 4)а?2 + (5а + 10)a? + a + 10 = 0
имеет два корня и между этими корнями расположен ровно один корень уравнения
(а — 1)а?4 — (а — 1)а?3 — (а — 7)а?2 + (10а + 5)а? — a + 12 = 0.
Задача 233 (механико-математический факультет, Олимпиада “Абитуриент-2000”, май, 5(6)). Найти все а, при которых уравнение
(2a + 6)а?2 — (5а + 15)а? + a + 11 = 0
имеет два корня и между этими корнями расположен ровно один корень уравнения
(а + 1)а?4 + (а + 1)а?3 + (3 — а)х2 — (10а + 20)а? — а + 9 = 0.
Задача 234 (механико-математический факультет, основной экзамен, 2000, 5(6)). Найти все а, при которых уравнение
(|а| — 1) cos 2а? + (1 — |а— 2|) sin 2х + (1 — |2 — a|)cosa? + (1 — |а|) sin х = 0
имеет нечетное число решений на интервале (—тг; тг).
Задача 235 (мех ан и ко-математический факультет, основной экзамен, 2000, 5(6)). Найти все а, при которых уравнение
(|а| — 2) cos За? + (2 — |a — 4|) sin За? + (2 — |4 — a|) cos 2з? + (2 — |a|) sin 2а? = 0
имеет нечетное число решений на интервале (—тг; тг).
343
Задача 236 (факультет ВМиК, Олимпиада “Абитуриент-2000”, апрель, 5(6)). Для каждого значения параметра а найти все решения системы уравнений
' у2 — Зг/ log2 (4ж2 + (14а — 10)ж + 8а — 8)4-4-2 log2 (4ж2 4- (6 - 2а)ж 4- 4а2 — 8а + 4)2 = О 5г/2 — 8г/ log4 (4ж2 + (6 — 2а)ж 4- 4а2 — 8а 4- 4)24-
к +3 log2 (4ж2 + (14а — 1О)ж 4- 8а — 8) = О.
Задача 237 (факультет ВМиК, Олимпиада “Абитуриент-2000”, апрель, 5(6)). Для каждого значения параметра а найти все решения системы уравнений
4г/2 — бг/logi (ж2 4- (И — 14а)ж + 18 — 30а)+
4- log 1 (ж2 + (3 4- 2а)ж + 16а2 — 14а 4- 6)2 = О
< 4
г/2 4- 4j/log± (ж2 4- (3 + 2а)ж 4- 16а2 — 14а 4- 6)2 —
-5logl (ж2 + (И - 14а)ж + 18 - 30а) = 0. ' 2
Задача 238 (факультет ВМиК, основной экзамен, 2000, 5(6)). Найти наибольшее значение выражения
4ж2 + 80ж 4- у + 43
при условии, что
6х2 + 32ж + у 4- 283 0 и ж2 4- 86ж + г/ + 202 0.
Задача 239 (факультет ВМиК, основной экзамен, 2000, 5(6)). Найти наименьшее значение выражения
9ж2 — ЗОж + у + 40
при условии, что
Зж2 + 42ж + г/110 и 18ж2 4- 6ж 4- у 98.
Задача 240 (физический факультет, Олимпиада “Абитуриент-2000”, март, 7(8)). При каких значениях Ъ уравнение
25® - (26 + 5)5Я7-1/:г + 106 • 5-2/® = 0
имеет ровно два решения?
344
Задача 241 (физический факультет, Олимпиада “Абитуриент-2000”, март, 7(8)). При каких значениях а уравнение
4~х - (а + 2)2~х+1/х + 2а • 22^ = О
имеет ровно два решения?
Задача 242 (физический факультет, Олимпиада “Абитуриент-2000”, май, 7(8)). Для каждого допустимого значения а решить неравенство
a\a - l)r - 2ax+1 - (а - 1)г + 2а < О
и найти, при каких значениях а множество решений неравенства представляет собой промежуток длины 2.
Задача 243 (физический факультет, Олимпиада “Абитуриент-2000”, май, 7(8)). Для каждого допустимого значения а решить неравенство
ax(a - 3)* - ar+1 - (a - 3)* + a О
и найти, при каких значениях а множество решений неравенства представляет собой промежуток длины 2.
Задача 244 (физический факультет, основной экзамен, 2000, 7(8)). При каких значениях а неравенство
(х2 — (a + 2)х — 2a2 + 4а) у/1 — х О
имеет единственное решение?
Задача 245 (физический факультет, основной экзамен, 2000, 7(8)). При каких значениях а неравенство
(~х2 — (a + 6)z + 6а2 + 12а) Vz + 2 <С О
имеет единственное решение?
Задача 246 (факультет почвоведения, Олимпиада “Абитуриент-2000”, 6(6)). Пусть f(x) - периодическая функция с периодом 8, такая, что f(x) = Зх—х2 прих G [0; 8]. Решите уравнение f(2x+16)+23 = 5/(ж).
Задача 247 (факультет почвоведения, Олимпиада “Абитуриент-2000”, 6(6)). Пусть f(x) - периодическая функция с периодом 1, такая, что f(x) = х2 при х G [0; 1). Решите уравнение f(2x + 5) + 2f(x) = 1.
345
Задача 248 (факультет почвоведения, основной экзамен, 2000, 7(7)). Найдите все значения параметра а, при которых при любых значениях параметра Ь уравнение
|яг — 2| + Ь|2з? + 1| = a
имеет хотя бы одно решение.
Задача 249 (факультет почвоведения, основной экзамен, 2000, 7(7)). Найдите все значения параметра а, при которых при любых значениях параметра b уравнение
Ь|3з? — 1| + |з? 4- 1| = а
имеет хотя бы одно решение.
Задача 250 (геологический факультет, Олимпиада “Абитуриент-2000", 7(8)). Найти все значения а, при которых каждое решение неравенства х2 4- а <С 0 удовлетворяет неравенству (з? 4- 2а)^/3 — х <С 0.
Задача 251 (геологический факультет, Олимпиада “Абитуриент-2000”, 7(8)). Найти все значения а, при которых каждое решение неравенства х2 — а <С 0 удовлетворяет неравенству (а — Зх)у/х 4- 5 0.
Задача 252 (географический факультет, Олимпиада “Абитуриент-2000", 2(6)). Найти все значения параметра а, при каждом из которых уравнение
loga_6,5 (®2 + 1) = loga-6,5 ((a - ЭД
имеет два различных решения.
Задача 253 (географический факультет, Олимпиада “Абитуриент-2000”, 2(6)). Найти все значения параметра а, при каждом из которых уравнение
loga-5,5 (х2 + 1) = loga_515 ((а - 4)я)
имеет два различных решения.
Задача 254 (географический факультет, основной экзамен, 2000, 6(6)). Даны функции
f(x,y) = |г/| 4- 2|а?| - 2 и д(х, у, а) = х2 4- (г/ - а)(у 4- а).
а) При каком наименьшем положительном значении параметра a система уравнений
Г f(x, у) = О
[ д(х, у, а) = О
346
имеет ровно четыре различных решения?
б) При этом значении параметра а найдите площадь фигуры, координаты (х, у) всех точек которой удовлетворяют неравенству
0
С7(ж,у,а) "
Задача 255 (географический факультет, основной экзамен, 2000, 6(6)). Даны функции
f(x,y) = |т/| + 3|яг| - 3 и g(x,y,a) - у2 + (ж - а)(ж + а).
а) При каком наименьшем положительном значении параметра a система уравнений
f f(z,y) - О
I g(z,y,a) = О имеет ровно четыре различных решения?
б) При этом значении параметра а найдите площадь фигуры, координаты (х, у) всех точек которой удовлетворяют неравенству
ЛХ’У) 0
5(ж,у,а) "
Задача 256 (филологический факультет (отделение прикладной лингвистики), 2ООО, 5(6)). Найти все значения параметра а, при каждом из которых уравнения
(2а — 1)ж2 + бах + 1 = 0 и ах2 — х + 1 = О
имеют общий корень.
Задача 257 (филологический факультет (отделение прикладной лингвистики), 2000, 5(6)). Найти все значения параметра а, при каждом из которых уравнения
(2а + 1)ж2 + бах —1 = 0 и ах2 + х — 1 = О
имеют общий корень.
Задача 258 (социо логический факультет, 2000, 6(6)). Найти все значения параметра а, при каждом из которых отношение решений квадратного уравнения
(а2 + 1)ж2 + 4х Н-= О
а + 1
является целым числом. Кратные корни учитываются дважды.
347
Задача 259 (социологический факультет, 2000, 6(6)). Найти все значения параметра а, при каждом из которых отношение решений квадратного уравнения
(2а2 + 2а + I)®2 + 2х + — — = О
4(а+1)
является целым числом. Кратные корни учитываются дважды.
Задача 260 (Институт стран Азии и Африки, 2000, 5(7)). Найти все значения параметра а, при которых неравенство |ж2 —2а? + а| > 5 не имеет решений на отрезке [—1; 2].
Задача 261 (Институт стран Азии и Африки, 2000, 5(7)). Найти все значения параметра а, при которых неравенство |ж2+4ж —а| > 6 не имеет решений на отрезке [—3; 0].
Задача 262 (механико-математический факультет, Олимпиада “Абитуриент-2001”, март, 6(6)). Найти все значения а, при которых система
( (а — 1)ж2 + 2аж + а + 4 0
1 ах2 + 2(а + 1)ж + а + 1 0
имеет единственное решение.
Задача 263 (механико-математический факультет, Олимпиада “Абитуриент-2001”, март, 6(6)). Найти все значения а, при которых система
( ax2 — 2(а + 1)ж + а + 5 О
( (а + 1)ж2 — 2(а + 2)ж + а + 2 0
имеет единственное решение.
Задача 264 (механико-математический факультет, Олимпиада “Абитуриент-2001”, май, 6(6)). Найти все значения параметра а, при каждом из которых графики функций
Зж -р 1 4ж -р За — 7
У = ----- и У = ----------------:-
х ax — 1
разбивают координатную плоскость ровно на пять частей.
Задача 265 (механико-математический факультет, Олимпиада “Абитуриент-2001”, май, 6(6)). Найти все значения параметра а, при каждом из которых графики функций
4х + 1 (7а + 4)ж + За
У = ----- и У = -------------------
х ax — i
разбивают координатную плоскость ровно на пять частей.
348
Задача 266 (механико-математический факультет, основной экзамен, 2001, 5(6)). Найти все числа, которые не могут быть корнями уравнения
4у/2х4 + х3 = а \/4 — а4 (х + 4ж2 — 8)
ни при каком значении параметра а.
Задача 267 (механико-математический факультет, основной экзамен, 2001, 5(6)). Найти все числа, которые не могут быть корнями уравнения
За/Зж4 — 2z3 = a ^6 — a4 (х — Зз?2 + 6)
ни при каком значении параметра а.
Задача 268 (факультет ВМиК, Олимпиада “Абитуриент-2001”, апрель, 5(6)). Для каждого значения параметра а решить неравенство
За - 1 - (8а - 5) • 3"2^“ i°gei (*3+б*+э) ца + 2) • |з? + 3|2\/log|x+3| i.
Задача 269 (факультет ВМиК, Олимпиада “Абитуриент-2001”, апрель, 5(6)). Для каждого значения параметра а решить неравенство
2а + 3 - 2(а - 1) • 2 2\/21оЧ|а; 4| (За + 7) . - 8х + 16)V4 log|x-4|2.
Задача 270 (физический факультет, Олимпиада “Абитуриент-2001”, март, 7(8)). Для любого значения параметра а решить неравенство
3(2з? — а) + 5а>/2з? — а — 2а2 > 0.
Задача 271 (физический факультет, Олимпиада “Абитуриент-2001”, март, 7(8)). Для любого значения параметра а решить неравенство
2(а — х) — ау/а — х — а2 > 0.
Задача 272 (физический факультет, Олимпиада “Абитуриент-2001 ”, май, 7(8)). Для каждого целого значения m найти все решения уравнения
1о£(”£+;с2) (Зя)”*41 = m2 + 1.
349
Задача 273 (физический факультет, Олимпиада “Абитуриент-2001”, май, 7(8)). Для каждого целого значения п найти все решения уравнения
о I „2 1°ё(п2+4:г2) (Зя) + — 1-
О Т **'
Задача 274 (физический факультет, основной экзамен, 2001, 7(8)). Для каждого целого значения а найти все решения уравнения
cos 2ж + 2 sin2 (ж + а) + 2 — sin a = О,
принадлежащие промежутку тг <С х <С 2-тг.
Задача 275 (физический факультет, основной экзамен, 2001, 7(8)). Для каждого целого значения а найти все решения уравнения
cos 2ж + 2 cos2 (ж + а) — 4 — cos a = О,
принадлежащие промежутку ж
УКАЗАНИЯ И ОТВЕТЫ
1. к е [-3; 1].
2. к Е [-1; 3].
3. аЕ [-10/9; —2/3] U {2}.
4. a G [1 - 2л/3; -2] U {4}.
5. 0, тг, 2тг.
6. —7Г, 0, 7Г.
7. При a < — 1 ж G (0; — a — л/а2 — 1] U [—а + \/а2 — 1; —а + л/а2 + 1];
при а — 1 ж £ (0; — а + л/а2 + 1].
8. При а < — 1 ж Е [а + л/а2 + 1; —а — л/а2 — 1] U [—а + >/а2 — 1; +оо);
при а — 1 ж Е [а + л/а2 + 1; +оо).
9. п = —14, m = —1.
10. п = —И, m = 16.
11- ®2/min = -9/10.
12. При а < 1 ж —1;
350
при а 1 х > ((а — 1) log3 2)2 — 1.
13. При т < 1 х 1;
при т 1 х < 1 — ((m — 1) log2 З)2.
14. (0;0).
15. (0; 0).
16. (0; 1), (0;-1).
17. (0; 1), (0; —1).
18. -3, 9.
19. —4, 8.
20. а Е (-оо; -2) U (2; +оо).
21. b Е (—оо; — 1) U (1; +оо).
22. b Е (-2; 0).
23. а Е (—оо; —2) U (0; +оо).
24. 0.
25. При а < —5 решений нет; при — 5 а 1 (а + 5)2;
при а > 1 (а — I)2 х (а + 5)2.
26. При а < — 5 решений нет;
при — 5 а — 1 0 х (а + 5)2; при а > 1 (а + I)2 х (а + 5)2.
26. 27% + 18.
27. 12%+ 8.
28. При а = 0 х = 0 или х = —1; при а ф 0 х = 0.
29. При а = 0 х = 0 или х — —3; при 0 х = 0.
30. а Е (—оо; —99].
31. и Е [224;+оо).
32. а е (-5; -д/24) U (-\/24; -3).
351
34. При а Е (—оо; —1 — тг2) U (1; 4-оо) корней нет;
при а Е [—1 — тг2; 1) - два корня;
при а = 1 - один корень.
35. При а Е (—оо; —1) U (тг2 + 1; +оо) корней нет;
при а Е [—1; тг2 + 1) - два корня;
при а = тг2 + 1 - один корень.
36. —3 х < —2, х = 1.
37. —7 х < —4, х = 2.
38. Наименьшее значение равно | и достигается при а = ±|, Ь = |.
39. Наименьшее значение равно | и достигается при а = ±|,Ь = —|.
40. р -3/2.
41. b 3/4.
42. 2.
43. 3.
44. а 2/3.
45. а 3/2.
46. (2;3].
47. [-1; 2).
48. 14.
49. 8.
50. -ч/3/2.
51. ^2/2.
52. а) -8; б) (-8;-4^3).
53. а) 8; б) (4>/3; 8).
54. {(arctg |; г/)}, где у (з (1 - | (J - arctg |)2))
55. {(arctg г/)}, где у (2 Г1 - (f - arctg |)2}}
352
V19 4-2
56. ±1; i-^.
57. ±Л;
4
58. (2; 3), (2;-3), (-2;-3), (-2; 3).
59. (3; 1), (3; -1), (-3; -1), (-3; 1).
_ , с, ,оч . а — 1 + \/а2 — Юа — И
60. При а Е (—оо; —3/2) х = log5------------------
при а Е [—3/2; 11) решений нет;
при а = 11 х = 1;
, а - 1 ± л/а2 - 10а - И при а Е (11;+оо) zi>2 = log5------------------;
Единственное решение при а Е (—оо; —3/2) U {11}. „ , „I 1 —а — 2 + -\/а2 + 2а — 8
61. При а Е (—оо;—6] х = log3-------------------;
. п . — а — 2 ± л/а2 + 2а — 8
при а Е (—6; -4) х х>2 = log3------------------;
при а = —4 х = 0;
при а Е (—4; +оо) решений нет;
2
Единственное решение при а Е (-оо; —6] U {—4}.
62. При 0 < а < 1 3<х<3 + 7^+^;
3 +V9+4a2 при а > 1 х > -
, -1±л/5 63. При а / ------
— 1 — л/5 при а = -------
решений нет;
х
при а = --------
64. При а < — 1, а — 0,
2 -3-У5
Х ~ 2
а > 1 - два решения;
при а = ±1 - четыре решения;
при —1 < а < 1,а^0 - шесть решений.
65. 9.
66. 8.
67. (1; 5), (1; 6), (2; 6).
68. (1;5),(1:6), (1;7), (2;7).
23 Методы реш. задач
353
69. 1.
70. ^ + 2^3.
72. 2/9, -6.
, /3( —l)n + 1 + 7Гп\ d n
73. x = i I ------------- I , n = 1, 2,....
\ 5 J
/ f —l)n + 1 7Г71 \
74. x = ± I -------------] , n = 1, 2,....
75. a -1/3.
76. a -1/3.
77. b = -1.
78. a = -1.
79. (—6; —5) U (—5; 2 (1 — \Z10)).
80. (6-2x/5;2V5-2]U{4}.
q =—2
P ± -5/3
или
P 6 {—1; —3} q G R
ч f a = 2
82. 1) < , или
b = -1 a G R
83.
84.
3 ± \/7 2
85. p = 6.
86. q = 9.
87. 2/5.
88. -1/3.
89. a G (—00; —11) U (—7; —6.5).
90. a G (7.5; 8) U (12;+00).
91. (1; 1; 1), (-1;-1; 1).
92. (1; — 1; — 1), (—1; 1; — 1).
3S4
93..1.
94. 2.
95.
96.
97.
[-15;-5) и {1}.
{-1} U (5; 15].
При а < — 1 решений нет;
/2 — а
при — 1 а 0 х — ±\/—-—, ж = ±
6 ’
, , 2 — а х = ±
при 0 < а < 1/2
6
, / 2 — а х = ±
98.
99.
6 ’ 1-0;
при а > 2 х = 0.
При а < —1/2 решений нет;
... п /1 — 2а
при —1/2 а 0 х = ±\ —-—, V о г"! 2д~
при 0 < а < 1/6 х = ±1/—-—;
V д
. _ I л /1 2 а
при 1/6 а 1/2 х = ±1/—-—
V 3
при а > 1/2 х = 0.
х
х = О;
7 + ^22
3
100.
X £
101.
a G
102.
а £
И- л/77 п
2 ’ 2
5 - 2л/3; 3) U (7; 5 + 2л/3].
103. 1 <
104.
105.
106.
-3/2, а > 1/3.
-2/3, а 1/2.
107.
а — 2^
а — 1)
х — 1;
/ о\2
/ а — z \
при а 2 х > ----------- — 1.
\ а — 1)
При а < 1
2
-1;
23*
355
г \ 2
а — 4 /
108. При а < 4 3
при 4 а < 5
/ к\2
г [ а — 5 \ _
при а > 5 х > --------- + 3.
\а - 4J
109. (2; 2), (0; 3), (3; 0).
110. (3; 3), (0; 5), (5;0).
111.
112.
113.
114.
2л/2 2л/2
2л/2 — 1 ’ 2-/2 + 1 л/3 л/З
Уз- 1’ л/3 + 1‘
7г\
2/
7г\
’117Г IT’ ’117Г "24”’ 2
115.
10-
116. 6 — л/2; - (
При а < — 1
117.
при а > —1/2 решений нет.
118. При с 2 — с <J х <J с;
при 1 а < 2 —л/с — 1 х л/с — 1;
при с < 1 решений нет.
119. тг = 5.
120. т = 4.
121. а Е [-3/2; -3/4) U (—3/4; 0).
122. /3 Е [-4/3; -2/3) U (-2/3; 0).
123. а Е (-оо; -4/5) U (-4/5; 0) U (0; 1) U (1; +оо).
124. а Е (—оо; —5/6) U (—5/6; 0) U (0; 1) U (1; +оо).
125. 1) а = ±9;
2) а = ±1;
3) T’max — При Q, — i9( -^min — 3 при О, — il.
356
126. 1) a = ±9;
2) a = ±1;
3) rmax = 9 при a = ±9; Kmin = 3 при a = ±1.
127. —1/2.
128. 1/3.
129. xy = ±1; x2 + y2 = 2; x = ±1; у - 1.
130. у = -(x2 + 1); у = ±(z2 - 1).
131. x = + 8k, к G Z.
132. x = + 8k, к G Z.
133. 112тг — 12^3.
134. бтг — л/З-
135. — | + 4m, m G Z; — |+4n, n G Z.
136. — | + 4m, m G Z; — |+4n, n G Z.
137. a = ±V2 (Pmin =8л/2).
138. b = ±V2/2 (Pmin = 8a/2).
139. p 17.
140. b 17.
141. a = 4; л/45 — 3 < |61 < д/45 + 3.
142. p = 2; УЙ7 - 2 < |g| < УП7 +2.
145. S = 2л- + 7.
146. S= Jtt + 17.
147. (4; 3), (6; 13), (14;-5).
148. (—6; —7), (—4; 3), (4; —5).
149. {-4} U [—3;—1].
150. {-4} U [-3;-!].
357
152. 153. ( 2 cos2 | ’ 2.
154. 2.
155. a = | + 4n, n G Z.
156. a= l + n, 7 G z.
157. a = -3/2.
158. a = 7/2.
159. a G (—oo; — \/13] U [11/3; +oo).
160. a G (—сю; — y/2] U +oo) .
161. -7/3 < a < 6.
162. a < y/2.
163. Если 0 < a < i. X < 1оёазЪ’>
если 1 < a < 3, loga | < X < loga 3^
если a 3, C > loga I-
7Г 27ГП „
164. 165. t = 1; x = — - + —, nez. 7Г 7ГП „
t = —1; x = 24 + T’ ”eZ'
166. a G (—сю; - 2] U [-1/2; 0).
167. aG[-4,5;0)U[^±^;+oo).
168. a) |a| < a/27+%/104;
6) |a| < V21 r-x/104 (x/27±a/I04= a/26± 1
169. a) |a| \/18 + a/68;
6) |a| \/1Ё - л/68 (yi8±x/68 = a/17± 1J.
170. a G (—сю; 0].
171. a G (—сю; 2].
172. a = 0; a -- 1
173. ci — 3 < a —
174. у = 4к + 2, х = 15fc2 + 24fc + 9, k G Z.
175. x = 5к + 3, у — 10fc2 + 5k, к G Z.
358
176. ( —1;&), k G N, k 3; (—2;n), n G N, n 4.
177. n = 1, m = 3,4,5,...; n = 2, m = 4,5,6,....
178. a £ (1;5).
179. a G (2; 6).
180. a e (-\/5;\/5).
181. a G (-2x/6/3;2>/6/3).
182. 1/4.
183. 1/3.
184. a = 2.
185. a = 4.
186. — 2; 0; 1; x/2/2; [—1 — x/2/2; -1].
187. 2; 0; -1; —x/2/2; [1; 1 + ^/2].
188. a e (-oo; -3) U {1} U [3; +oo).
189. a G (-oo; -3] U {1} U (3; +oo).
190. a G (—oo; 3] U [4; +oo).
191. a G (—oo;2] U [3;+oo).
192. a G [1; 2) U (2; 3].
193. a G [0; 1/2) U (1/2; 3/4].
2тг „ 7Г „
194. — + 2ttZ, I G Z; — + 2тгт, m G Z.
195. —I- 7rk, k G Z.
6
196. Если 0<а<1, l<a^3, x = — a — 3;
если a > 3, Xi = — a — 3,^2 = a.
197. Если — 1 < a < 4, x = ~a — 3;
если a —1, a 4, Xy = —a — 3, x% — a.
198. a - —2, a = 1.
199. a = 0, a = 1.
200. 1) Если 0 < a < 1/2, -3a < x < -1, 1 < x < 3a;
если a > 1/2, x < — 3a, x > 3a.
359
2) При а = 1.
201. 1) Если 0 < т < -1/4, -52m < х < -1, 1 < х < 52т; если т > 1/4, х < —52т, х > 52т.
2) При т — 1/2.
202. Если а = 0, х G [2; +оо);
если —1/2 < а < 0, х G (1; 1 — a) U [а + 2; +оо);
если а = —1/2, х G (1; 3/2) U (3/2; +оо);
если —1 < а < —1/2, х G (1; а + 2] U (1 — а; +оо);
если а -- —1, х G (2; +оо).
203. Если а = 0, х 6 [2; +оо);
если 0 < а < 1/2, х G (1; 1 + а) U [2 — а; +оо);
если а = 1/2, х G (1; 3/2) U (3/2; +оо);
если 1/2 < а < 1, х G (1; 2 — а] U (1 + а; +оо);
если а = 1, х G (2; +оо).
204. п е {-6;-5;-4}.
205. п = 3.
206. ±1.
207. ±1.
208. [5/6; 1) U (1; 3/2].
209. [53/99; 1) U (1; 2].
210. 9/16.
211. 9/16.
212. При 6^—1, х G (—сю; —1] U [Г, +оо);
при — 1 < 6 < 0, х G-т ; — 1
\ л/1^62
U [1; +оо).
213. При а 1, х G (—оо; —2] U [2; +оо);
при 0 а < 1, х G (—оо; —2] U
214. a G [-2; 1) U (1; 4].
’ л/1 — а2
215. a G [—1; 3) U (3; 7].
360
216. ±1/6; ±ч/2/6.
217. ±1/4; ±ч/2/4.
218. При b = единственное решение (-^;0;0);
при 6 = -| ± У| два решения: (-^=; 1; и (-^=; -1; -f ) .
219. При а = — | ± единственное решение (~ф=; 0; у) ;
при а = - два решения: (-ф=! 1; j) и (“ф=! ”1; •
220. При b = решение ± , k £ Z;
при Ь = | решение (-^=; | ± тгк^, к £ Z;
при Ъ ф ±| решений нет.
221. При а = решение (j ± irk', , к G Z;
при а = | решение ^тгЛг; ~^=^> к G Z;
при а ±| решений нет.
222. р = 9; [—1; 3].
223. а = 9; [-4/3; 1].
224. (5/11;6/13].
225. (4/9; 5/11].
226. a G (-оо; -1] U {0} U (2; ±оо).
227. a G (-оо; -1] U {0} U (4; ±оо).
228. (2; — 1).
229. (3; л/2).
230. 1; 5/2.
231. 2; 5/2.
232. (—оо; —3) U (6; ±оо).
233. (—оо;—4) U (5;±оо).
234. [0; 1) U (1; 2) U {3}.
235. [0; 2) U (2; 4) U {-2}.
г х -
236. При а £ (-оо; |) U ±оо) < 4
и v 37 V5 7 I y = log2(15a2-26a±7)-2;
361
при а £
У - 1°ё2 (-За2 + 4а - 1) + 1;
при ае (1;6) y = log2(_5o2 + 12o_7) + i;
( х = Ъ, где b £ (-оо; -1) U (0; +оо) при а — 1 | log2^2 + 4^. при а = | и при а = | - решений нет.
237. При а в (-оо; £) и (|; +оо) { ’ = + + 2.
х = 4а — 3
у ~ — log2 (-20а2 + 16а - 3) — 1;
при а £ (|;|) — log2 (—12а2 + 16а - 5) - 1;
Г х = Ь, где 6 £ (—оо; —3) U (—1;+оо)
ПРИ а t У = -log2(62 +46 + 3); при а = и при а = | - решений нет.
238. 30.
при а 6
239. 30.
240. а Е (0; 1) U (4;+оо).
241. ае(0;^)и(¥;+оо).
242. 1) При a £ (1; 2) х £ (-оо; log^ 2а] U [0; +оо);
при а — 2 х £ [0; +оо); приаб(2;+оо) х Е [0;log£X_1 2а].
2) При а = 2 + д/З.
243. 1) При а Е (3; 4) х Е (-оо; loga_3 а] U [0; +оо);
при а = 4 х Е [0; +оо);
при а Е (4; +оо) х Е [0; loga_3 а].
2) При а = 7+^.
244. а Е [|; 1].
245. ае
246. 1 + 8п, 7 + 8тг, п Е Z.
247. + тг, | + тг, п £ Z.
248. а =
362
249. a = |.
250. a e {0} U [-9; -1].
251. a G {0} U [9; 25].
252. a G (7;^) U (^;+oo).
253. aG (6;^) u(^;+oo).
254. a) 6) 4- |тг.
255. a) 6) 6-Д7Г.
256. 0, |.
257. —- 0 -
258. a= t±y/t2-±4t.— } где t = 16 n = -5,-4,-3,-2
2 + (n + l/n)’
2
или n = 1,2,..., 17.
i - 2 ± \Л2 + 4/ - 4 J 16 c . o n
259. a = ---------------------, где i = ----------—, n — —5, -4, —3, —2
2+(n + l/n)’
2 или n — 1,2,..., 17.
260. [-4; 2].
261. [-6; 2].
262. -3/4; 4/3.
263. -7/4; 1/3.
264. a G [0; 1].
265. a G [—1; 0].
266. x G (—oo; —8/7) U (—1/2; 0) U (8/9; 4-oo).
267. x € (-oo; -6/7) U (0; 2/3) U (6/5; +oo).
268. При a G (-oo; 1/4] x G [-3 - l/x/3; -3) U (-3; -3 + l/x/3];
при a G (—1/4; 1/10) x G (—4; —3 — y?(a)] U [—3 — l/x/3; —3)U
U(—3; -3 + l/x/3] U [-3 + ^(a); -2);
при a =1/10 x G (-4; -3) U (-3; -2);
при a G (1/Ю; 1/3) x G (—4; -3 - l/x/3] U [-3 - y>(a); -3)U
U(—3; -3 + y>(a)]U; [-3 + l/x/3; -2);
при a G [1/3; +oo) x G (-4; -3 - l/\/3] U [-3 + 1//3; -2).
363
Здесь принято обозначение у>(а) = 3 1 за
269. При a G (-оо; -3/2] х Е (3; 4 - 1/ч/2] U [1/4 + ч/2; 5);
при а Е (—3/2; —1) х G (3; 4 — л/2] U [4 — у>(а); 4)U
и(4;4+^(а)]и(4+1/ч/2;5);
1ОК2 57+3
приа = -1 х G (3; 4) U (4; 5);
при a G (-1; -2/3) х Е (3; 4 - у>(а)] U [4 — 1/ч/2; 4)U
U(4; 4 + 1/ч/2) U [4 ± у>(а); 5);
при a G [-2/3;+оо) х Е (-4 - 1/ч/2; 4) U [4; 4 ± 1/ч/2).
Здесь принято обозначение у>(а) =
270. Если а < 0, х > 2а2 ± а/2; если а 0, х > (а2 ± 9а)/18.
271. Если а < 0, х < а — а2/4; если а 0, х < а — а2.
272. т = 0, х = 3; т = ±1, х = ±(3 ± 2л/2)/2; т = ±2, х = (3 ± д/5)/2;
т = ±3, х — ±3/2.
273. п = 0, х = 2; п = ±1, х = ±(2 ± з/3)/2; п — ±2, х = 1.
274. Если а — тг/2 ± 2тгп, n EZ, х = Зтг/2; при других а решений нет.
275. Если а = тг + 2тгп, п Е Z, х = 2тг; при других а решений нет.
P.S. Алиса вздохнула.
— Если вам нечего делать, — сказала она с досадой, — придумали бы что-нибудь получше задачек без решений...
Л.Кэрролл. Алиса в стране чудес (выделенные курсивом слова изменены)
ЛИТЕРАТУРА
I.,1 Вавилов В.В., Мельников И.И., Олехник С.В., Васиченко В.И. Задачи по математике. Алгебра. М.: Наука, 1987.
'2.1 Вавилов В.В., Мельников И.И., Олехник С.В., Васиченко В.И. Задачи по математике. Уравнения и неравенства. М.: Наука, 1987.
3. Марков В.К. Метод координат и задачи с параметрами. М.: Изд-во Моск, ун-та, 1970.
(4. Дорофеев Г.В., Потапов М.К., Розов В.Х. Пособие по математике для поступающих в вузы. М.: Наука, 1976.
5. Моденов В.В. Пособие для подготовки к устному экзамену по математике. М.: Изд-во Моск, ун-та, 1973.
6. Вестеренко Ю.В., Олехник С.В., Вотапов М.К. Задачи вступительных экзаменов по математике. М.: Наука, 1986.
7. Вавилов В.В., Мельников И.И., Олехник С.В., Васиченко В.И. Задачи по математике. Начала анализа. М.: Наука, 1990.
< 8. Мельников И.И., Сергеев И.В. Как решать задачи по математике на^вступительных экзаменах. М.: Издат. отдел УНЦ ДО МГУ, 1994.
9. Вотапов М.К., Олехник С.В., Нестеренко Ю.В. Конкурсные задачи по математике: справочное пособие. М.: Столетие, 1995.
Й., Горнштейн В.И., Волонский В.Б., Якир М.С. Задачи с пара-ами. Киев: Евроиндекс, 1995.
'11. Амелькин В.В., Рабцевич В.Л. Задачи с параметрами: справочное пособие по математике. Мн.: Асар, 1996.
(12. Мельников И.И., Олехник С.В., Сергеев И.В. Математика. Задача вступительных экзаменов с ответами и решениями (1993-1997). Изд. 3-е, исправл. и дополн. М.: ИзДат. отдел УНЦ ДО МГУ, 1998.
13. Моденов В.В. Грани математики: координатно-параметрический мёТ'бд. М.: Издат. отдел УНЦ ДО МГУ, 1999.
14. Шестаков С.А., Юрченко Е.В. Уравнения с параметром. М.: Слог, 1993.
15. Справочники для поступающих в Московский университет 1958— 2002 гг.
365
ОГЛАВЛЕНИЕ
Предисловие................................................ 3
Глава 1. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОГО ИССЛЕДОВАНИЯ В ЗАДАЧАХ С ПАРАМЕТРАМИ ................................. 7
1.1. Область допустимых значений параметров и неизвестных ..................................... 11
1.2. Область изменения функции..................... 14
1.3. Условия равносильности преобразований......... 18
1.4. Непрерывность и монотонность изменения функций ... 22
1.5. Четность функций и симметричность переменных . 25
1.6. Задачи для самостоятельного решения .......... 31
1.7. Указания и ответы ............................ 35
Глава 2. ЭЛЕМЕНТЫ ГРАФИЧЕСКОГО ИССЛЕДОВАНИЯ В ЗАДАЧАХ С ПАРАМЕТРАМИ ................................ 37
2.1. Метод сечений ................................ 37
2.2. Метод областей................................ 52
2.3. Задачи для самостоятельного решения .......... 62
2.4. Указания и ответы ............................ 65
Глава 3. КВАДРАТИЧНАЯ ФУНКЦИЯ ............................ 69
3.1. Краткая теория квадратного трехчлена ......... 69
3.2. Задачи на исследование квадратичной функции... 73
3.3. Задачи, приводимые к исследованию квадратичной функции ......................................... 79
3.4. Решение относительно параметра ............... 88
3.5. Задачи для самостоятельного решения .......... 92
3.6. Указания и ответы ............................ 95
Глава 4. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ...................... 97
4.1. Краткая теория систем линейных уравнений ..... 97
4.2. Задачи на решение систем линейных уравнений ..103
4.3. Смешанные задачи на линейные системы и квадратный трехчлен..............................112
4.4. Задачи для самостоятельного решения ..........116
4.5. Указания и ответы ............................119
Глава 5. ЭКСТРЕМУМЫ ......................................121
5.1. Разные задачи на минимум и максимум...........121
5.2. Использование производной при решении экстремальных задач .............................131
366
5.3. Условные экстремумы и изопериметрические задачи .. .140
5.4. Задачи для самостоятельного решения ...........152
5.5. Указания и ответы .............................157
Глава 6. “НЕСТАНДАРТНЫЕ” И “ЛОГИЧЕСКИЕ” ЗАДАЧИ .. 159
6.1. Необходимые и достаточные условия .............159
6.2. “...Хорошая догадка - половина решения!” ......162
6.3. “Квазиэквивалентность” уравнений и неравенств .167
6.4. Логические задачи на использование свойств четности и симметрии ...........................174
6.5. Логические задачи на количество решений .......181
6.6. Задачи для самостоятельного решения ...........190
6.7. Указания и ответы .............................193
Глава 7. РАЗНЫЕ ЗАДАЧИ ....................................195
7.1. Параметры в тригонометрических задачах.........195
7.2. Параметры в логарифмических задачах............206
7.3. Задачи на делимость многочленов ...............211
7.4. Задачи с параметрами на множестве комплексных чисел ..........................................218
7.5. “Совсем разные” задачи ........................226
7.6. Задачи для самостоятельного решения ...........233
7.7. Указания и ответы .............................241
Послесловие с комментарием к наглядному материалу и историко-литературными отступлениями ......................245
Приложение I. КОНКУРСНЫЕ ПРИМЕРЫ С ПАРАМЕТРАМИ КАК АНАЛОГИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ ПРИКЛАДНОЙ МАТЕМАТИКИ ................263
Приложение II. ЗАДАЧИ ПОСЛЕДНИХ ЛЕТ ...................305
Указания и ответы ..................................348
Литература ................................................365
Учебное издание
Владимир Леонидович Натяганов Любовь Михайловна Лужина
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ
Зав. редакцией Г. С. Савельева Редактор Р.А. Бунатян Художественный редактор Ю.М. Добрянская Корректор В.А. Ветров
Подписано в печать 02.10.2003.
Формат 60x90 1/1б- Бумага офс. № 1.
Офсетная печать.
Усл. печ. л. 23,0. Уч.-изд. л. 22,3.
ТиражЗ 000 экз. Заказ №2072
Изд. № 7430
Ордена “Знак Почета” Издательство Московского университета 125009, Москва, ул. Б. Никитская, 5/7
Тел.: 229-50-91. Факс: 203-66-71
Тел.: 939-33-23 (отдел реализации)
E-mail: kd_mgu@rambler.ru
В Издательстве МГУ работает служба «КНИГА—ПОЧТОЙ» Тел.: 229-75-41
Отпечатано в ГУП Московской типографии № 2 Министерства Российской Федерации по делам печати, телерадиовещания
и средств массовых коммуникаций (МПТР России). Тел.: 282-24-91. 129085, Москва, пр. Мира, 105.