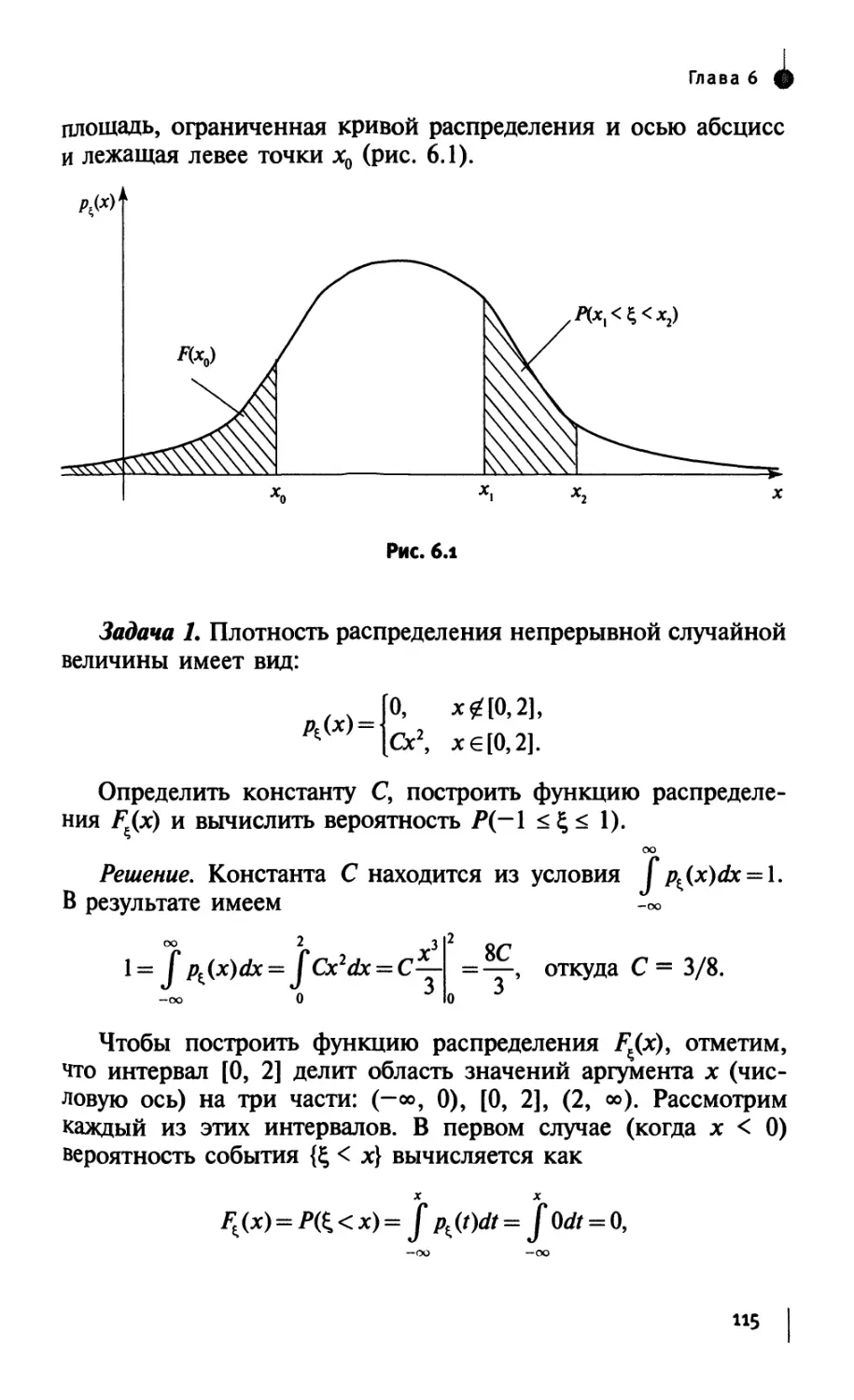
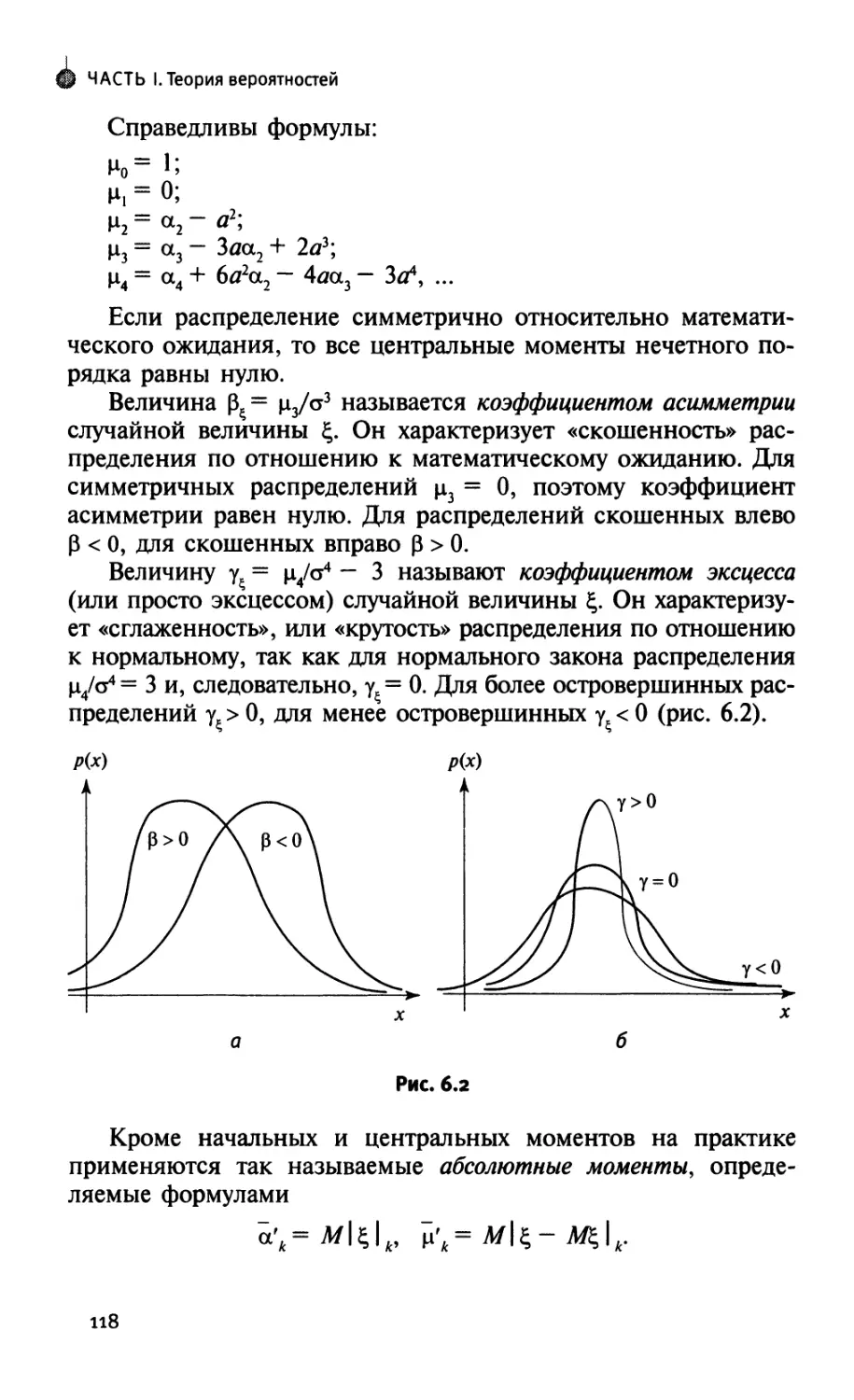
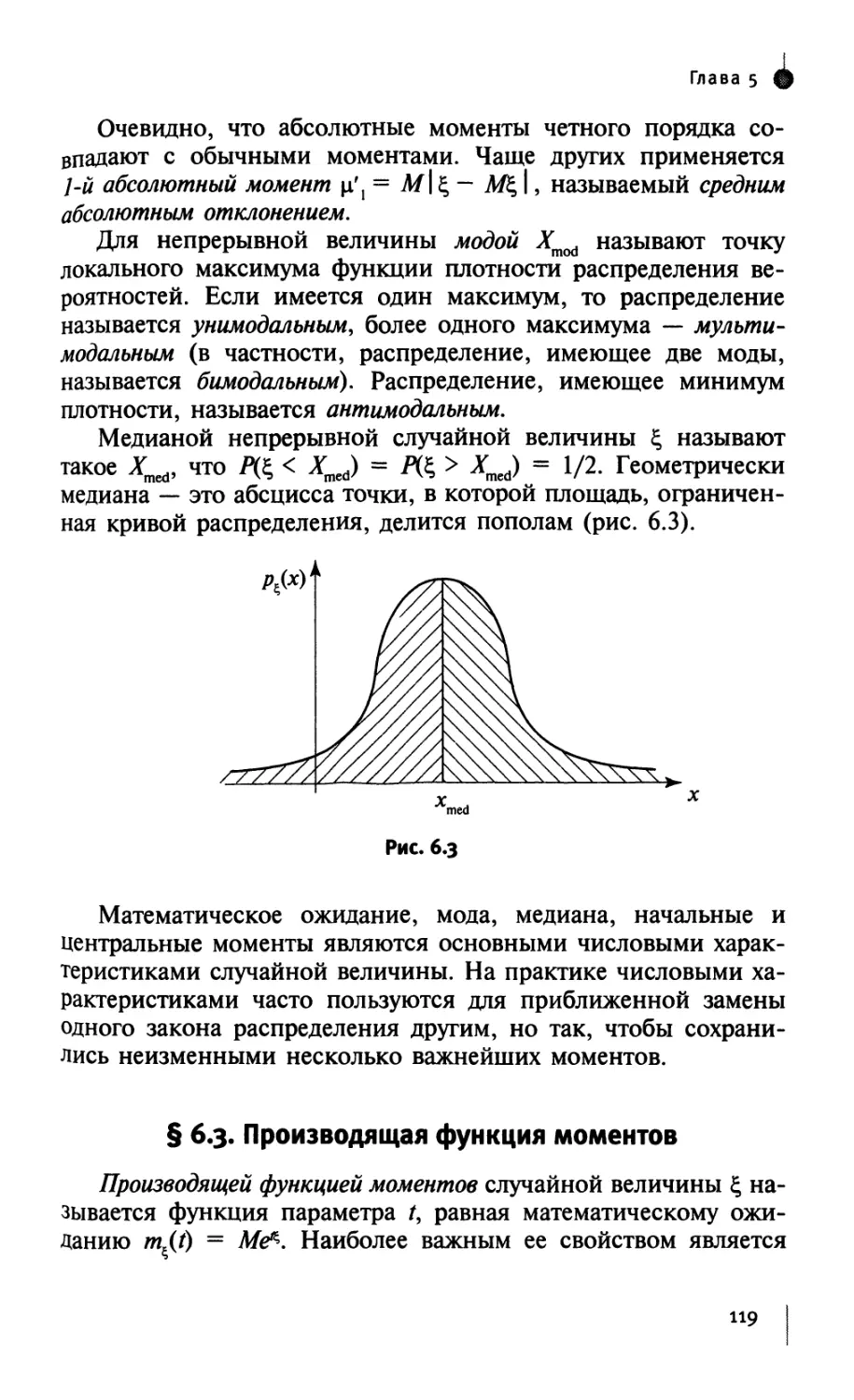
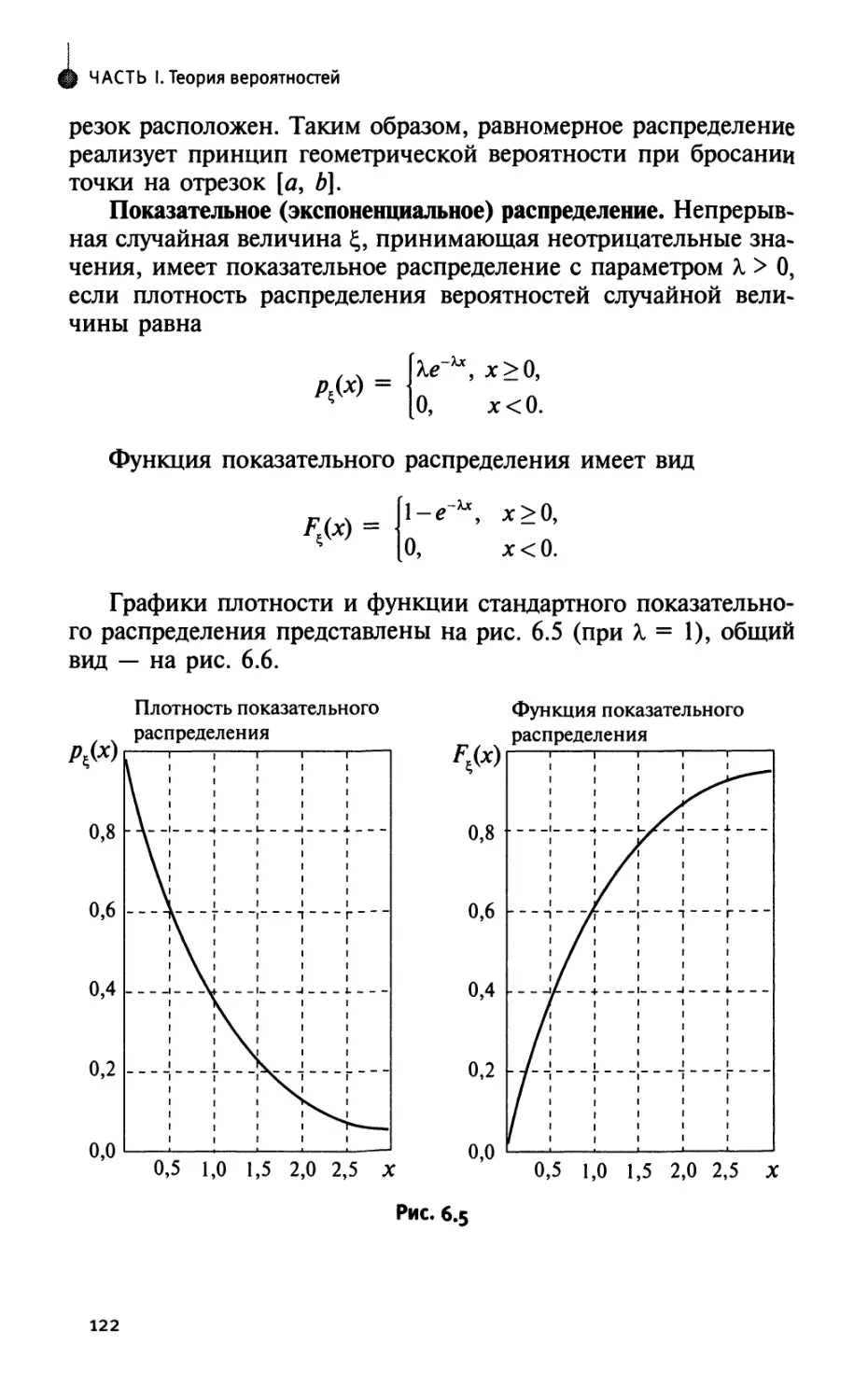
Author: Лебедев А.В. Фадеева Л.Н.
Tags: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 978-5-699-35345-3
Year: 2010
Text
э.
I НОВОЕ
ЭКОНОМИЧЕСКОЕ
ОБРАЗОВАНИЕ
Л. Н. ФАДЕЕВА
А. В. ЛЕБЕДЕВ
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
и математическая статистика
учебное пособие
Под редакцией Л. И. Фадеевой
2-е издание, переработанное и дополненное
Допущено
УМО по классическому университетскому образованию
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению 080100 «Экономика»
Москва эксмо 2010
УДК 519.2
ББК 22.171
Ф 15
Об авторах:
Фадеева Л.Н. — кандидат физико-математических наук, доцент
кафедры математических методов анализа экономики
экономического факультета МГУ им. Ломоносова
Лебедев А.В. — кандидат физико-математических наук, доцент кафедры
теории вероятностей механико-математического факультета
МГУ им. Ломоносова
Фадеева Л. Н.
Ф 15 Теория вероятностей и математическая статистика : учеб.
пособие / Л. Н. Фадеева, А. В. Лебедев ; под ред. Л.Н.
Фадеевой. — 2-е изд., перераб. и доп. — М. : Эксмо, 2010. — 496 с. —
(Новое экономическое образование).
ISBN 978-5-699-35345-3
Книга представляет собой учебно-методический комплекс,
объединяющий теоретический материал, задачи и краткое руководство
к разработке методов принятия решений в условиях
неопределенности; рекомендации и выводы на основе анализа статистических
данных, научно обоснованного прогнозирования случайных
явлений и их взаимосвязи, построения математических моделей
реальных экономических ситуаций.
Учебное пособие подготовлено в соответствии с Федеральным
государственным образовательным стандартом высшего
профессионального образования.
Для студентов и преподавателей экономических вузов и
факультетов.
УДК 519.2
ББК 22.171
ISBN 978-5-699-35345-3
© Л.Н. Фадеева, А.В. Лебедев, 2009
© ООО «Издательство «Эксмо», 2009
Оглавление
Предисловие 7
Часть I
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ГЛАВА 1. Элементы комбинаторного анализа 11
§ 1.1. Основные понятия и теоремы комбинаторики 11
§ 1.2. Упорядоченные совокупности (последовательный выбор) ... 13
§ 1.3. Неупорядоченные совокупности (одновременный выбор) ... 16
§ 1.4. Разбиение множества на группы 18
Задачи для самостоятельного решения 19
ГЛАВА 2. Классическая вероятностная модель. Геометрическая
вероятность 23
§ 2.1. Частотная интерпретация вероятности. Свойство
устойчивости частот 23
§ 2.2. Пространство элементарных исходов. Событие
и его вероятность 25
§ 2.3. Статистики Бозе-Эйнштейна, Ферми-Дирака,
Максвелла-Больцмана 32
§ 2.4. Геометрическая вероятность 33
Задачи для самостоятельного решения 37
ГЛАВА 3. Основные формулы теории вероятностей 41
§ 3.1. Операции над событиями 41
§ 3.2. Теоремы сложения вероятностей 44
§ 3.3. Условная вероятность и теорема умножения 46
§ 3.4. Независимость событий 48
§ 3.5. Формула полной вероятности 50
§ 3.6. Формула Байеса 53
§ 3.7. Аксиоматическое построение теории вероятностей 54
Задачи для самостоятельного решения 58
ГЛАВА 4. Повторные независимые испытания. Теорема Бернулли 65
§ 4.1. Испытания Бернулли 65
§ 4.2. Наивероятнейшее число успехов 67
§ 4.3. Предельные теоремы и приближенные формулы 70
§ 4.4. Полиномиальные испытания 74
§ 4.5. Полиномиальные испытания 74
Задачи 76
ГЛАВА 5. Дискретные случайные величины 81
§ 5.1. Случайная величина и закон ее распределения 81
§ 5.2. Функция распределения 83
3 I
Содержание
§ 5.3. Случайный вектор в дискретном вероятностном
пространстве 85
§ 5.4. Совместная функция распределения случайного вектора. ... 90
§ 5.5. Числовые характеристики дискретных случайных величин... 92
§ 5.6. Основные дискретные распределения и их характеристики ... 96
§ 5.7. Ковариация. Коэффициент корреляции 97
§ 5.8. Условное распределение и условные математические
ожидания (дискретный случай) 102
Задачи для самостоятельного решения 105
ГЛАВА 6. Непрерывные случайные величины 113
§ 6.1. Плотность и функция распределения непрерывной
случайной величины 113
§ 6.2. Числовые характеристики непрерывной случайной величины . .116
§ 6.3. Производящая функция моментов 119
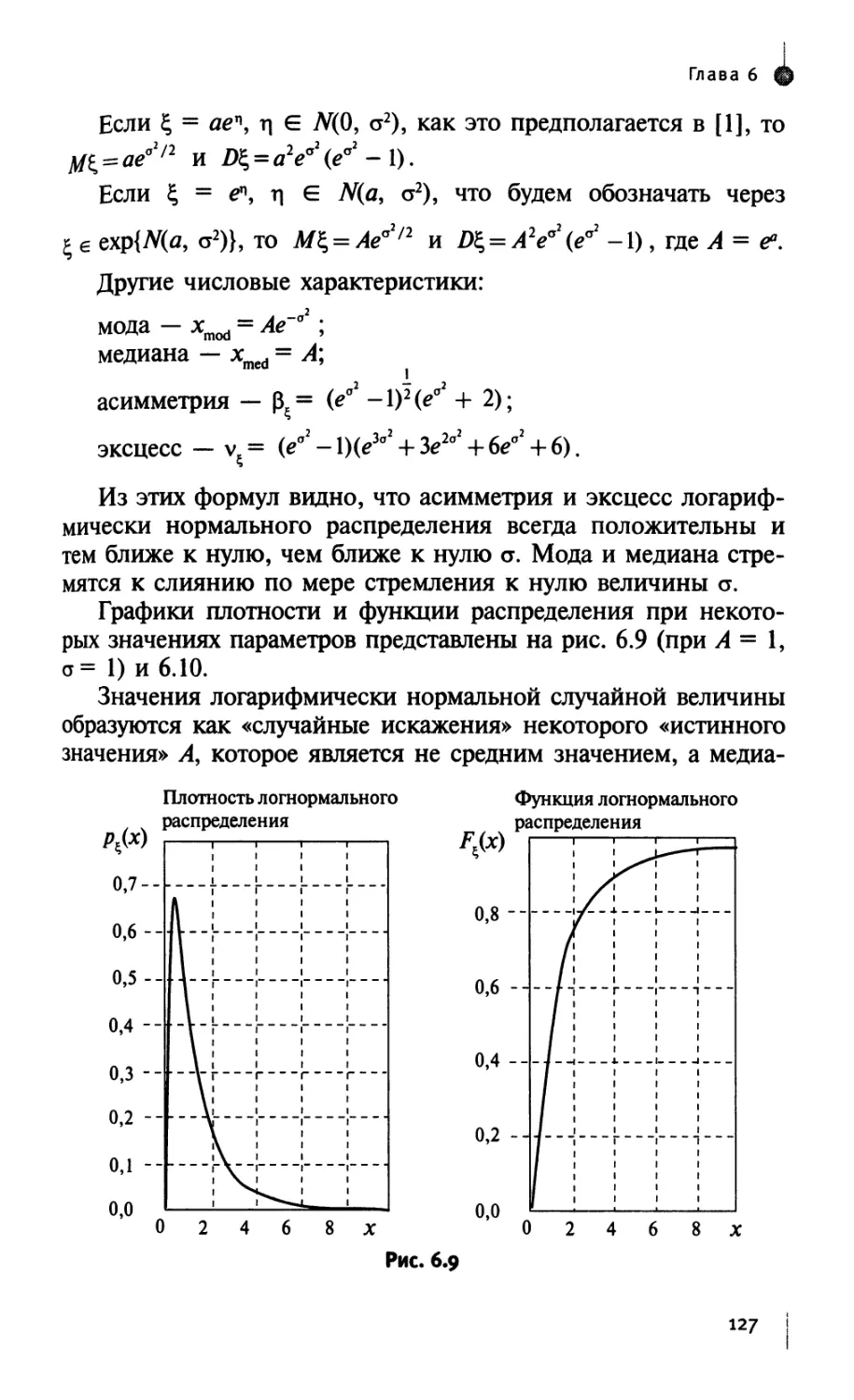
§ 6.4. Примеры непрерывных случайных величин 120
Задачи для самостоятельного решения 133
ГЛАВА 7. Функции от случайных величин. Непрерывный
случайный вектор 137
§ 7.1. Функции от случайных величин 137
§ 7.2. Совместный закон распределения непрерывных
случайных величин 139
§ 7.3. Плотность суммы двух непрерывных случайных
величин 144
§ 7.4. Условные распределения и условные математические
ожидания (непрерывный случай) 146
Задачи для самостоятельного решения 149
ГЛАВА 8. Закон больших чисел. Центральная предельная теорема .... 153
§ 8.1. Неравенство Чебышева 153
§ 8.2. Закон больших чисел 155
§ 8.3. Центральная предельная теорема (ЦПТ) 158
Задачи для самостоятельного решения 162
ГЛАВА 9. Цепи Маркова 167
§ 9.1. Основные понятия 167
§ 9.2. Цепи Маркова с конечным числом состояний
и дискретным временем 168
§ 9.3. Цепи Маркова с непрерывным временем. Системы
массового обслуживания 173
Задачи для самостоятельного решения 177
Часть II
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ГЛАВА 10. Основные понятия и задачи математической статистики ... 183
§ 10.1. Генеральная и выборочная совокупности 183
§ 10.2. Графическое представление статистических рядов 187
4
Содержание
§ 10.3. Эмпирическая функция распределения 192
Задачи для самостоятельного решения 196
ГЛАВА 11. Точечные оценки параметров законов распределения 201
§ 11.1. Выборочные характеристики и точечные оценки 201
§ 11.2. Статистическая устойчивость основных выборочных
характеристик 203
§ 11.3. Асимптотически нормальный характер основных
выборочных характеристик 209
§ 11.4. Эффективность оценок. Неравенство Рао—Фреше—Крамера . .210
§ 11.5. Оценки математического ожидания по неравноточным
наблюдениям 216
Задачи для самостоятельного решения 218
ГЛАВА 12. Функции и распределения в математической статистике . . . 226
§ 12.1. Бета- и гамма-функции 226
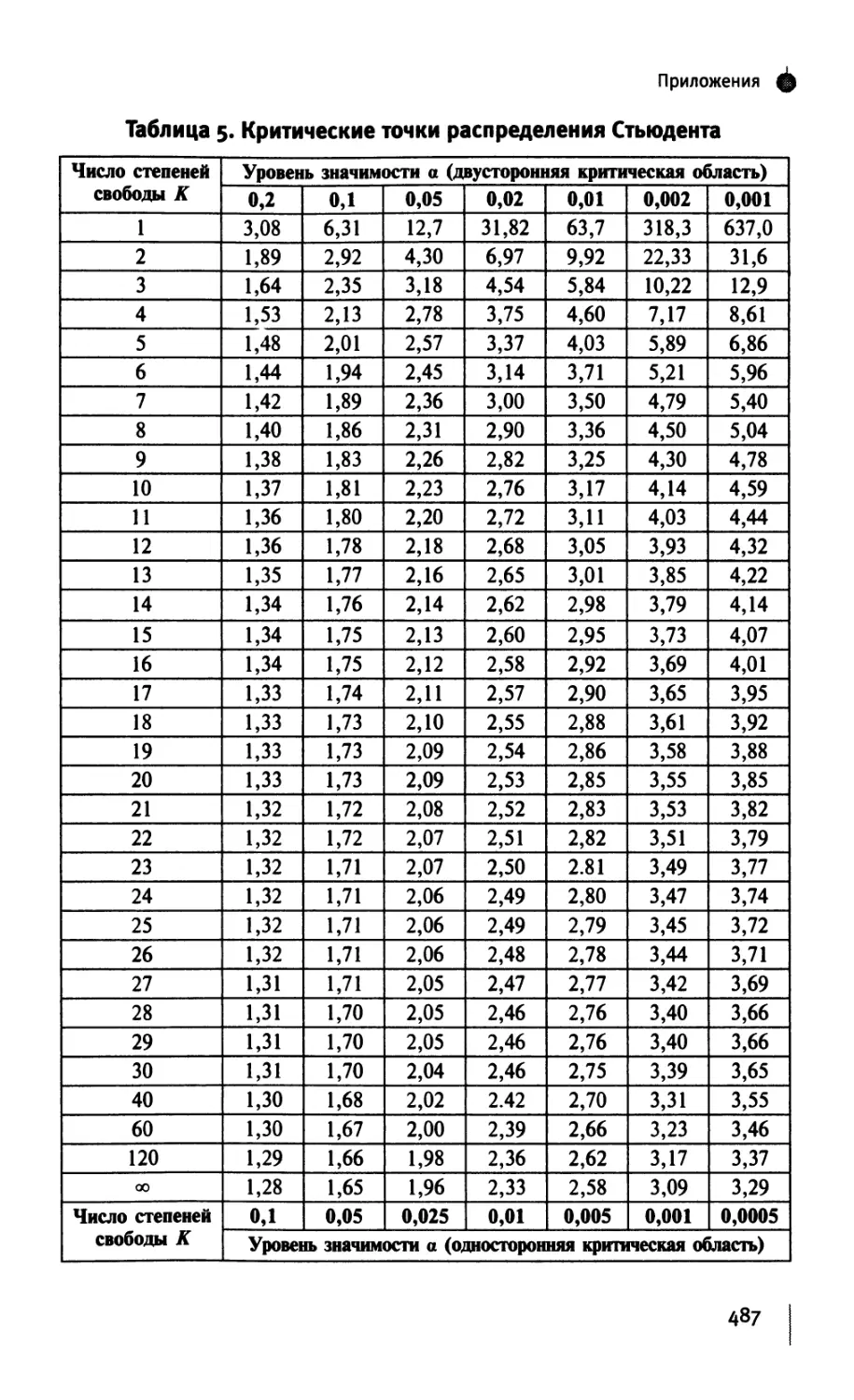
§ 12.2. Квантили, процентные и критические точки 230
§ 12.3. Распределение хи-квадрат (закон Пирсона) 233
§ 12.4. Распределение Стьюдента 236
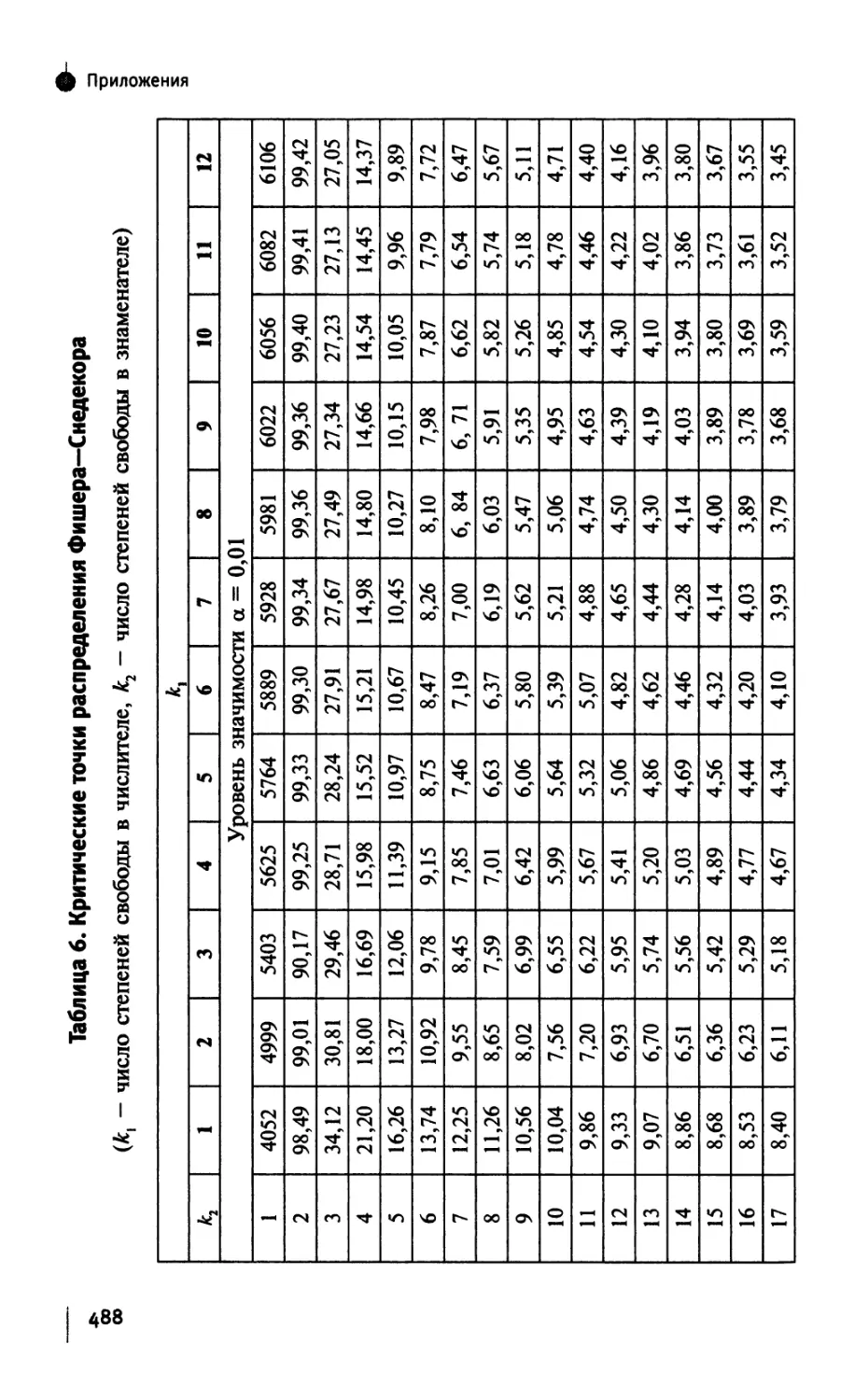
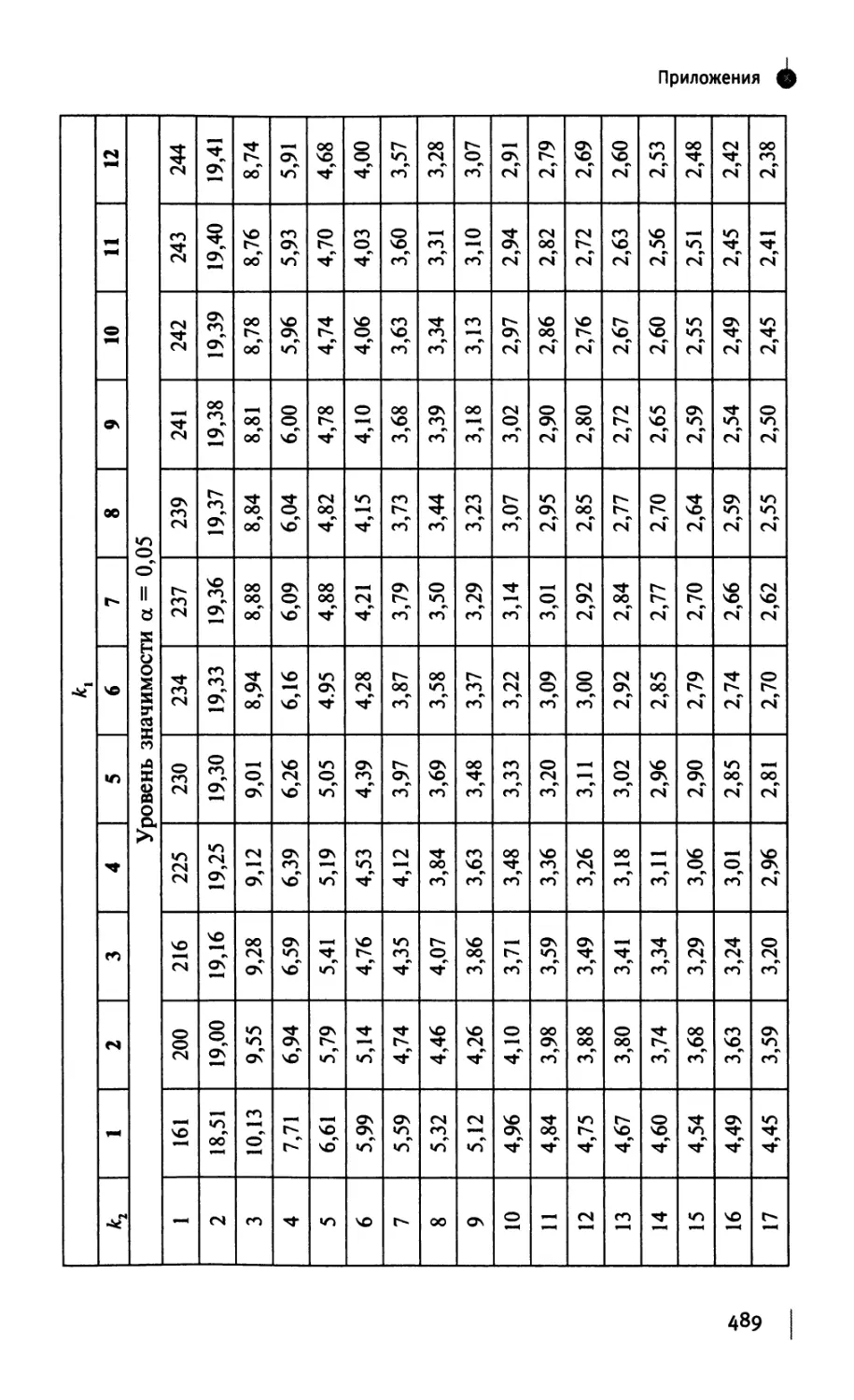
§ 12.5. Распределение Фишера 238
§ 12.6. Гамма-распределение 240
§ 12.7. Бета-распределение 246
§ 12.8. Приложения распределений в математической
статистике. Теорема Фишера 248
Задачи для самостоятельного решения 253
ГЛАВА 13. Методы построения оценок 257
§ 13.1. Метод моментов 257
§ 13.2. Метод максимального правдоподобия 262
§ 13.3. Метод наименьших квадратов. Линейная регрессия .... 270
Задачи для самостоятельного решения 278
ГЛАВА 14. Доверительные интервалы 294
§ 14.1. Основные определения 294
§ 14.2. Точные доверительные интервалы 295
§ 14.3. Асимптотические доверительные интервалы 300
§ 14.4. Интервальная оценка коэффициента корреляции 304
Задачи для самостоятельного решения 306
ГЛАВА 15. Проверка статистических гипотез 313
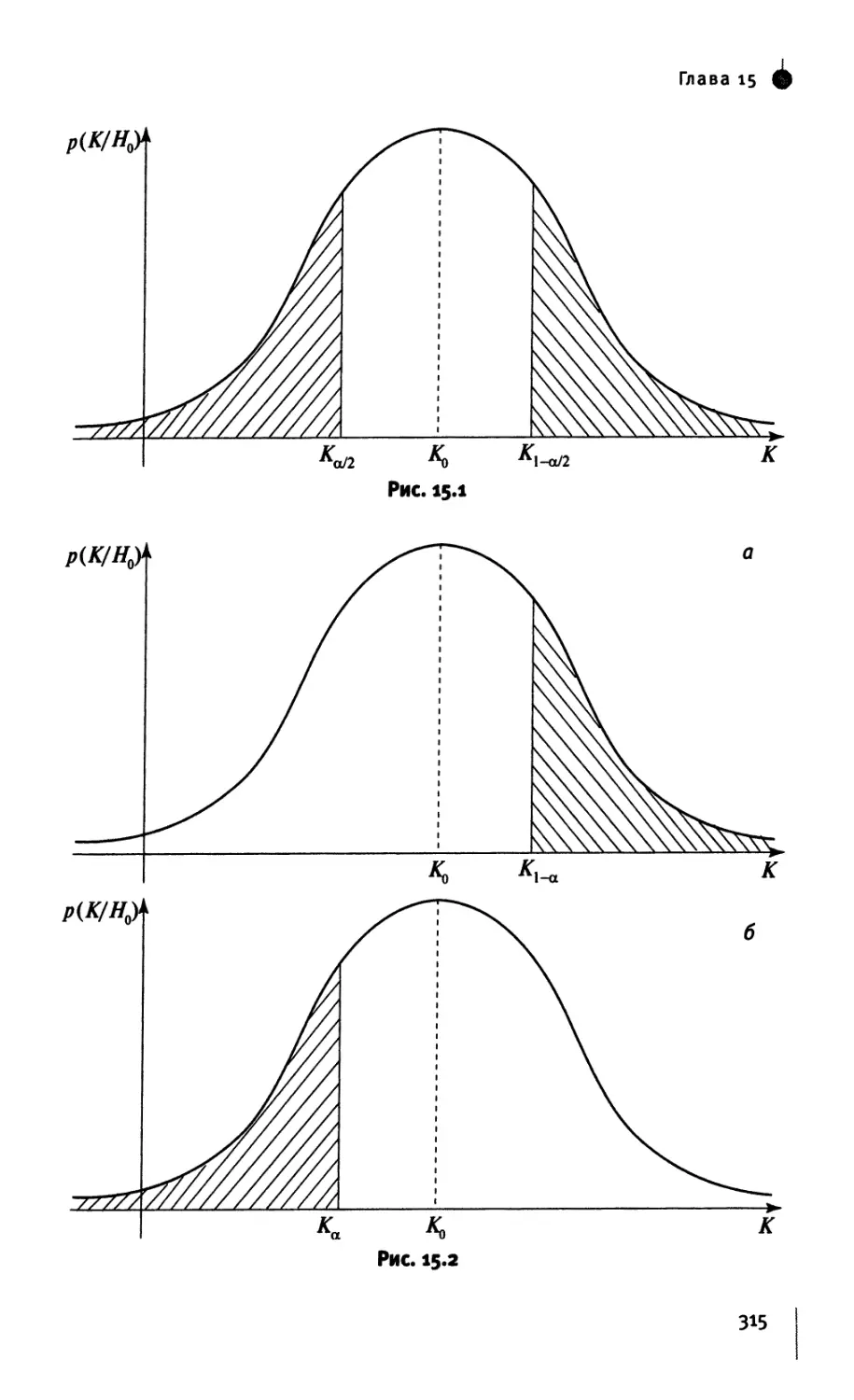
§ 15.1. Основные определения 313
§ 15.2. Критерий отношения правдоподобия 316
§ 15.3. Проверка гипотез для одной выборки 320
§ 15.4. Проверка гипотез для двух выборок. Зависимые выборки:
парные наблюдения 328
§ 15.5. Проверка гипотез для двух выборок. Независимые выборки . .329
§ 15.6. Проверка гипотез о равенстве дисперсий для нескольких
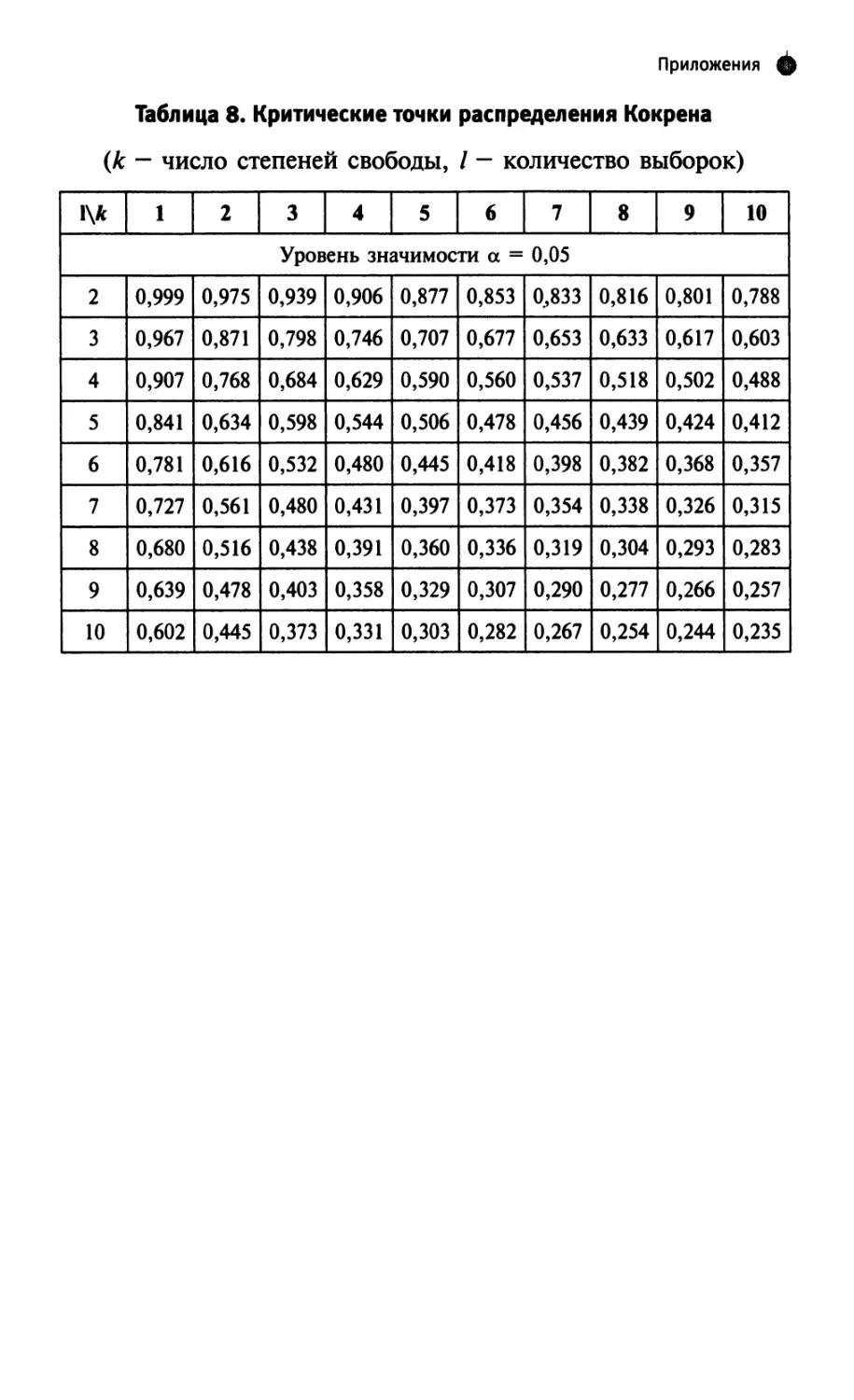
выборок. Критерии Бартлетта и Кокрена 337
Задачи для самостоятельного решения 339
* I
Содержание
ГЛАВА 16. Критерии согласия 353
§ 16.1. Критерий согласия Пирсона и Фишера (хи-квадрат) .... 353
§ 16.2. Критерий согласия Колмогорова 363
Задачи для самостоятельного решения 368
ГЛАВА 17. Элементы анализа временных рядов 373
§ 17.1. Основные понятия в анализе временных рядов 373
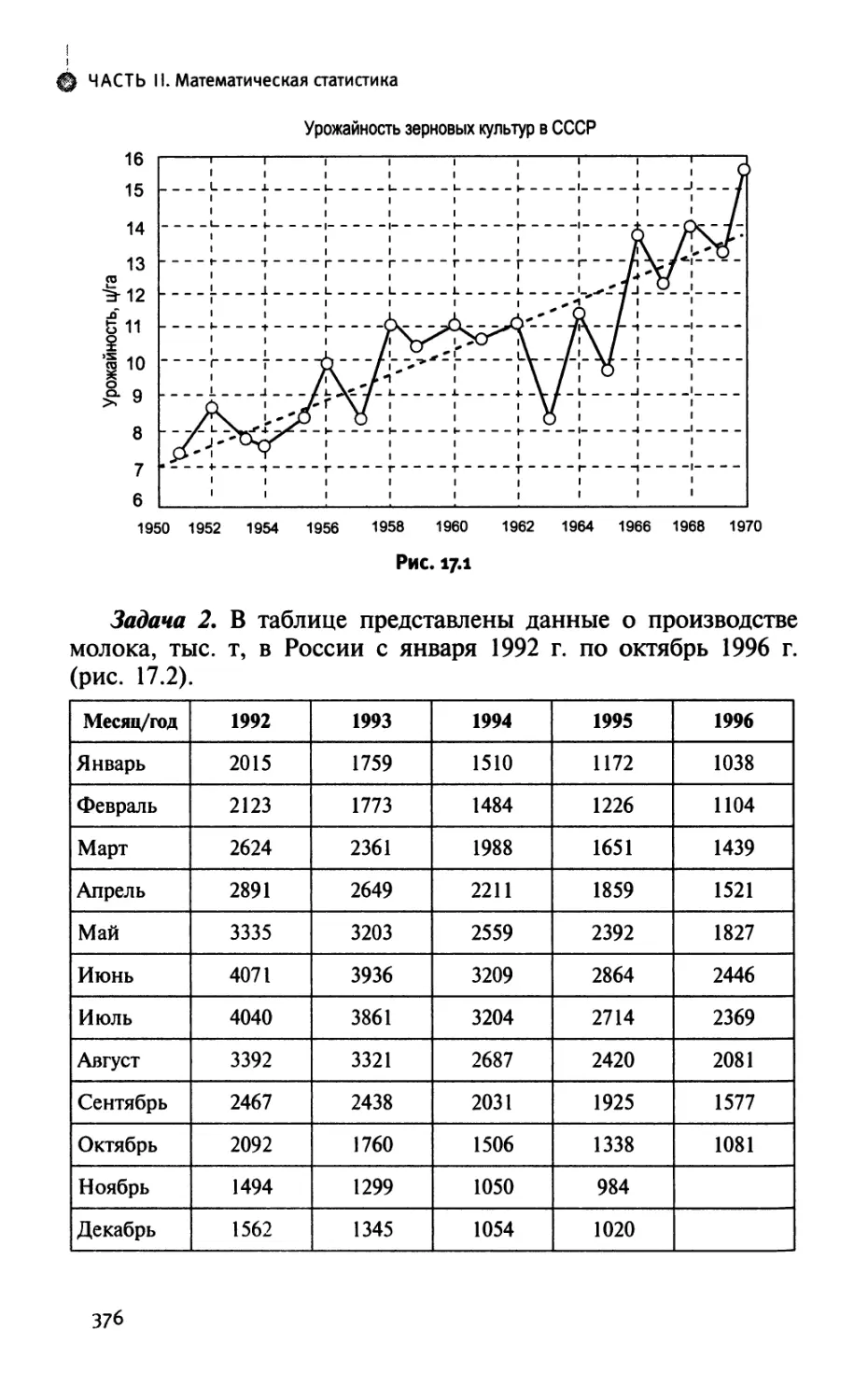
§ 17.2. Простые методы анализа и прогнозирования временных
рядов 375
§ 17.3. Стационарность. Автокорреляция. Периодограмма 379
§ 17.4. Модели авторегрессии и скользящего среднего 382
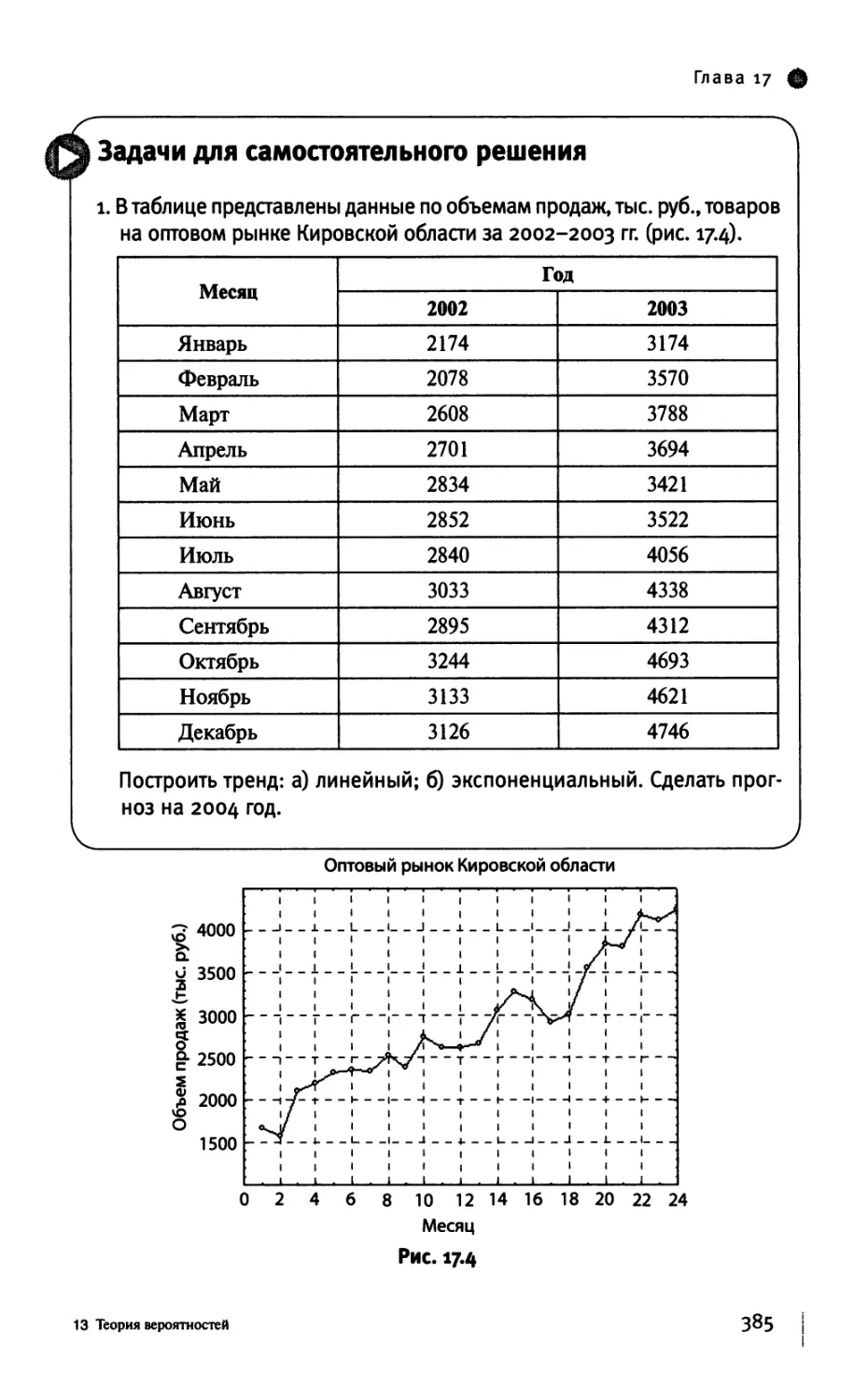
Задачи для самостоятельного решения 385
ГЛАВА 18. Элементы линейного регрессионного и корреляционного
анализа 390
§ 18.1. Функциональная, статистическая и корреляционная
зависимости 390
§ 18.2. Регрессионные модели как инструмент анализа
и прогнозирования экономических явлений 393
§ 18.3. Выборочные коэффициенты корреляции
и их применение 395
Задачи для самостоятельного решения 399
ГЛАВА 19. Элементы дисперсионного анализа 401
Задачи для самостоятельного решения 404
Ответы и указания 406
Приложения
Приложение 1 432
Приложение 2 479
Литература 492
Предисловие
Курс теории вероятностей и математической статистики
входит в цикл фундаментальных дисциплин, изучение которых
является обязательным для студентов экономических
факультетов государственных университетов.
Одной из важнейших сфер приложения теории
вероятностей и математической статистики является экономика. В
настоящее время невозможно себе представить исследование и
прогнозирование экономических явлений без использования
эконометрического моделирования, регрессионного анализа,
трендовых и сглаживающих моделей и других методов,
опирающихся на закономерности, которые изучаются в курсах теории
вероятностей и математической статистике.
Настоящая книга является учебником для студентов
экономических факультетов университетов и вузов, в которых
изучаются курсы «Теория вероятностей» и «Математическая
статистика». Материал книги соответствует программе
университетского курса и представляет собой цикл лекций, которые
авторы читают на экономическом факультете Московского
государственного университета им. М.В. Ломоносова.
Книга состоит из двух частей: «Теория вероятностей» и
«Математическая статистика», каждая из которых разбита на
главы, состоящие из отдельных параграфов.
Чтобы облегчить восприятие и запоминание достаточно
сложного материала, все определения, утверждения и доказа-
Предисловие
Авторы
тельства сопровождаются многочисленными примерами,
причем большинство задач учебника содержит конкретный
экономический материал. С целью закрепления полученных
знаний к каждой главе прилагается большой список задач для
самостоятельного решения. Они состоят из теоретических и
вычислительных задач. Упражнения, предлагаемые для
самостоятельного решения, дают возможность студенту овладеть
основными методами обработки и анализа статистических
данных, получить навыки построения экономических моделей
вероятностно-статистическими методами, научиться
пользоваться статистическими пакетами прикладных программ для
проведения конкретных вычислений, уметь интерпретировать
результаты анализа и строить на них научные прогнозы.
К теоретической части учебника прилагается большой пакет
контрольных и экзаменационных работ, а также теоретические
тесты для контроля знаний, полученных студентом. В рамках
образовательных программ третьего поколения,
ориентированных на экономистов и менеджеров, с 2010 года вводится новая
система обучения студентов, которая предполагает организацию
самостоятельной работы студентов и применение стандартной
и прозрачной методики оценивания их работ.
Основное достоинство этого учебника состоит в том, что он
соответствует новым программам и представляет собой учебно-
методический комплекс, объединяющий теоретический
материал и краткое руководство к решению задач.
Цель данного учебника - помочь изучающим теорию
вероятностей и математическую статистику в усвоении
необходимых теоретических знаний и приобретении практических
навыков для квалифицированного использования статистической
информации в целях принятия правильных решений в
вопросах управления и прогнозирования.
Часть I
Теория
вероятностей
ГЛАВА l
ЭЛЕМЕНТЫ
КОМБИНАТОРНОГО
АНАЛИЗА
Одной из основных задач комбинаторного анализа
(комбинаторики) является подсчет числа элементов
конечных множеств, заданных каким-либо описательным
условием. Для этого разработаны различные формулы и
правила.
§ 1.1. Основные понятия и теоремы
комбинаторики
Пусть имеется к групп Av Av Ак , причем /-я группа
содержит п. элементов. Тогда справедливы следующие правила.
^ Теорема умножения (основная формула комбинаторики).
Общее число N способов, которыми можно получить
упорядоченную совокупность (др д2, ... ак), где а. Е Ар т.е. выбрать по
одному элементу из каждой группы и расставить их в
определенном порядке, равно
Это правило распространяется и на ситуации, когда новые
группы образуются в процессе выбора элементов, если
численности этих групп не зависят от того, какие именно элементы
были выбраны.
it
? ЧАСТЬ I. Теория вероятностей
^ Теорема сложения. Если один элемент из группы А. можно
выбрать п. способами и при этом любые две группы А. и А. не
имеют общих элементов, то выбор одного элемента или из Av
или из Av или из Ак можно осуществить
N = ц +п2+... + пк
способами.
Как правило, рассматриваются следующие три типовые
ситуации, которые являются частными случаями общей схемы выбора
элементов из некоторой конечной совокупности Ц, av ...ап}9
называемой генеральной совокупностью. Будем называть их схемами
последовательного выбора с возвращением, последовательного
выбора без возвращения и одновременным выбором.
Последовательный выбор с возвращением. Эксперимент
состоит в том, что из генеральной совокупности объема п
последовательно выбирают к элементов, и каждый отобранный
элемент перед отбором следующего возвращается в генеральную
совокупность. Тогда общее число способов, которыми это мож-
—к —к
но сделать, обозначается Ап и равно Ап = пк.
Последовательный выбор без возвращения. Эксперимент
состоит в том, что из генеральной совокупности последовательно
выбирают к элементов, и каждый отобранный элемент в
генеральную совокупность уже не возвращается. Число
способов, которыми можно выбрать последовательно к элементов
из генеральной совокупности объема п без возвращения, равно
/ лк л!
числу размещении из п по к: Ап = -——.
Одновременный (неупорядоченный) выбор. Эксперимент
состоит в том, что выбирают элементы без учета порядка и без
возвращения. И все возможные наборы из к элементов
отличаются друг от друга хотя бы одним элементом. Число различных
по составу наборов по к элементов из п равно числу сочетаний
из п по к: С = •
* к\(п-к)\
В следующих параграфах изучим эти модели подробнее.
Задана 1. В группе 30 студентов. Необходимо выбрать
старосту, заместителя старосты и профорга. Сколько существует
способов это сделать?
12
Глава i ф
Решение. Старостой может быть выбран любой из 30
студентов, заместителем — любой из оставшихся 29, а профоргом —
любой из оставшихся 28 студентов, т.е. я, = 30, п2 = 29, я3 = 28.
По правилу умножения общее число N способов выбора
старосты, его заместителя и профорга равно N = л, х п2 х п3 = 30 х
х 29 х 28 = 24 360.
Задана 2. Два почтальона должны разнести 10 писем по
10 адресам. Сколькими способами они могут распределить
работу?
Решение. Первое письмо имеет пх = 2 альтернативы — либо его
относит к адресату первый почтальон, либо второй. Для второго
письма также есть п2 = 2 альтернативы и т.д., т.е. пх— п2 = ... =
= nlQ = 2. Следовательно, в силу теоремы умножения общее число
способов распределений писем между двумя почтальонами
N = л. «2... ц0 = 2х2х...х2 = 210 = 1024.
ю
Задана 3. В ящике 100 деталей, из них 30 деталей 1-го
сорта, 50 — 2-го, остальные — 3-го. Сколько существует способов
извлечения из ящика одной детали 1-го или 2-го сорта?
Решение. Деталь 1-го сорта может быть извлечена л, — 30
способами, 2-го сорта — п2 = 50 способами. По теореме
суммирования существует N = л, + п2 = 30 + 50 = 80 способов
извлечения одной детали 1-го или 2-го сорта.
§ 1.2. Упорядоченные совокупности
(последовательный выбор)
Пусть имеется некоторая конечная совокупность элементов
{я,, а2ап), называемая генеральной совокупностью, и п —
объем этой совокупности. Пусть эксперимент состоит в том,
что из генеральной совокупности последовательно выбирают
к элементов и располагают их в порядке выбора. Возможны
две ситуации.
Размещения без повторений. Отобранный элемент перед
отбором следующего не возвращается в генеральную
совокупность. Такой выбор называется размещением к элементов из п
(или последовательным выбором без возвращения).
ф ЧАСТЬ I. Теория вероятностей
Размещения — это упорядоченные совокупности к
элементов из л, отличающиеся друг от друга либо составом, либо
порядком элементов.
Пример 1. Пусть имеется множество {а9 Ъ9 с} из трех
элементов. Тогда все размещения двух элементов из трех таковы:
ab9 Ъа9 ас9 са9 Ъс9 cb.
> Теорема 1. Число различных способов, которыми можно
произвести последовательный выбор без возвращения к элементов из
генеральной совокупности объема п, равно
Доказательство. Очевидно, что первый элемент можно
выбрать я, = п способами, и поскольку отобранный элемент не
возвращается в генеральную совокупность, то следующий
элемент выбирается из совокупности, объем которой на один
элемент меньше, т.е. п2 = п - 1, и т.д., так что nk = п — (к — 1).
Тогда по теореме умножения общее число способов равно
N= п(п- 1) ... (п — (к — 1)) = п\/(п - к)\
В частном случае, когда выбирают все элементы
генеральной совокупности, т.е. когда к = п9 размещения называются
перестановками. Их число обозначается Рп.
Перестановки — это упорядоченные совокупности,
отличающиеся друг от друга только порядком элементов.
Следствие. Число всех перестановок множества из п
элементов равно Рп =п\
Пример 2. Все перестановки множества {а9 Ь9 с} из трех
элементов устроены так: abc9 bac9 cba9 acb9 саЪ9 Ьса и Ръ = 3! = 6.
Размещения с повторениями. Если каждый отобранный
элемент перед отбором следующего возвращается в генеральную
совокупность, то такой выбор называется размещением с
повторениями (или последовательным выбором с возвращением).
14
Глава i ф
^ Теорема 2. Общее число различных способов, которыми можно
произвести выбор с возвращением к элементов из генеральной
совокупности объема п, равно Акп — пк.
Доказательство. Так как каждый раз отобранный элемент
перед отбором следующего возвращается в генеральную
совокупность, то выбор на каждом шаге производится из
совокупности объема л, и можно считать, что выбор производится из
к групп и все группы состоят из одинакового числа элементов
л. = п2 = ... = пк = п. Тогда, в силу основной теоремы
комбинаторики, число таких способов выбора равно N = пк.
Пример 3. Все размещения с повторениями двух элементов
из множества с тремя элементами {а, Ъ, с}: аа, ab9 ас, ba, bb,
be, са, cb, сс.
Задана 4. Расписание одного дня состоит из 5 различных
уроков. Определить число вариантов расписания при выборе
из 11 дисциплин.
Решение. Каждый вариант расписания представляет
набор 5 дисциплин из 11, отличающихся от других
вариантов как составом, так и порядком их следования, поэтому
# = А5. = —^— = — = 7x8x9x10x11 = 55440.
11 (11-5)! 6!
Задана 5. В конкурсе по 5 номинациям участвуют 10
кинофильмов. Сколько существует вариантов распределения
призов, если по каждой номинации установлены различные
премии?
Решение. Каждый из вариантов распределения призов
представляет собой комбинацию 5 фильмов из 10,
отличающуюся от других комбинаций как составом, так и их
порядком. Поскольку каждый фильм может получить призы как
по одной, так и по нескольким номинациям, одни и те же
фильмы могут повторяться. Поэтому число таких
комбинаций равно числу размещений с повторениями из 10
элементов по 5: W = Z) = 105 =100000.
15
ЧАСТЬ I. Теория вероятностей
§ 1.з« Неупорядоченные совокупности
(одновременный выбор)
Сочетания без повторений. В результате одновременного
неупорядоченного выбора к элементов из генеральной совокупности
объема п получаются комбинации, которые и называют
сочетаниями из п элементов по к.
Сочетания — это неупорядоченные совокупности
элементов, различающиеся только составом элементов.
Пример 4. Все сочетания без повторений двух элементов из
множества {а, Ь9 с}:
{а9 b}9 {а9 с}9 {Ь9 с}.
> Теорема 3. Число сочетаний из п элементов по к равно
Доказательство. Среди Акп размещений без повторений
имеется по к\ наборов каждого состава (представляющих
собой всевозможные перестановки из к элементов этого состава).
Поэтому Скп=Акп/к\
Свойства числа сочетаний:
Числа С* называют также биномиальными коэффициентами,
поскольку они участвуют в разложении бинома Ньютона:
{n-k)\k\
сй°=с;=1;
п 1 п п+\ '
c°n+cl+c2„+...
+ ... + С™ = 2";
п
{а + ЬУ =Y,Cknak»
,n-k
k=Q
16
Глава i
Сочетания с повторениями. Если в сочетаниях из п
элементов по к некоторые из элементов или все могут оказаться
одинаковыми, то такие сочетания называются сочетаниями с по-
вторениями из п элементов по к.
> Теорема 4. Число сочетаний с повторениями из п элементов
по к равно
Пример 5. Все сочетания с повторениями двух элементов из
множества {а, Ь, с}:
{а, а}9 {а9 Ь}9 {а, с}, {b, Ь}, {6, с}, {с, с}.
Задана 6. В шахматном турнире участвуют 16 человек.
Сколько партий должно быть сыграно в турнире, если между
любыми участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 16
и отличается от других только составом пар участников, т.е.
представляет собой сочетания из 16 элементов по 2. Их число
п1 16! 15x16 _
равно С,, = = = 120.
16 14!2! 1x2
Задана 7. В условиях задачи 5 определить, сколько
существует вариантов распределения призов, если по каждой
номинации установлены одинаковые призы?
Решение. Если по каждой номинации установлены
одинаковые призы, то порядок фильмов в комбинации 5 призов
значения не имеет, и число вариантов представляет собой число
сочетаний с повторениями из 10 элементов по 5, определяемое
л. т;5 ^5 -5 10x11x12x13x14 -ЛЛ-
по формуле Со = С150+5_1 = С,54 = 1х2хзх4х5 = 2002*
Задана 8. Порядок выступления 7 участников конкурса
определяется жребием. Сколько различных вариантов
жеребьевки при этом возможно?
Решение. Каждый вариант жеребьевки отличается только
порядком участников конкурса, т.е. является перестановкой из
7 элементов. Их число равно Рп =7! = 1x2x3x4x5x6x7 = 5040.
17
|j| ЧАСТЬ I. Теория вероятностей
пх\п1\...пк\
Доказательство. Пусть в первую группу могут попасть
любые я, элементов из имеющихся п элементов первоначально.
Это можно сделать СЯЛ| способами. Вторую группу надо
заполнить п2 элементами из оставшихся п - пх элементов. Это можно
сделать С^2_щ различными способами. Продолжая эту процедуру
и используя основную формулу комбинаторики, получаем, что
число способов, каким можно разместить п элементов по к
групп, равно
N=QCnn\...Cnnkn „ = - х—^Z!h)l—х...х
п я.щ п-пх-..-пк_х П1\(П_П{)1 rh\(<n_rh_n2)\
х (п-п1-...-пк_1)\_ п\
пк\0\ п, In,\...пк\
т.е. Nn(n]9n2,...,nk) = —^ .
щ\п2\...пк\
Пример 6. Перечислим разбиения множества из 4 элементов
а, Ь, с, d на 2 группы по 2 элемента (6 разбиений): [{а, Ь), {с,
</}], [{а, с}, {Ь, </}], [{а, </}, {Ь, с}], [{с, </}, {a, b}], [{b, d\, {а, с}],
[{А с}, {a, d}].
Задача 9. Сколькими способами можно разбить группу из
25 студентов на три подгруппы по 6, 9 и 10 человек
соответственно?
18
§ 1.4. Разбиение множества на группы
Пусть множество из п различных элементов разбивается на
к групп так, что в первую группу попадают пх элементов, во
вторую — п2 элементов, в к-ю группу — пк элементов, причем
п\ + п2 + — + пк = п- Такую ситуацию называют разбиением
множества на группы. Заметим, что порядок элементов при
разбиении на группы не важен, а вот порядок групп (какую из них
мы считаем первой, какую — второй и т.д.) существенен.
> Теорема 5. Число разбиений равно
Глава i
4
Решение. Здесь п = 25, к = 3, я, = 6, я2 = 9, я3 = 10. Согласно
формуле Л^я(л„/12,...,/1А) = ——-1—-, число таких разбиений
tf25(6,9,10) = - 251
6!9!10!
Задача 10. Сколько существует семизначных чисел,
состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза,
а цифры 5 и 6 — по 2 раза?
Решение. Каждое семизначное число отличается от
другого порядком следования цифр, при этом фактически все семь
мест в этом числе делятся на три группы: на одни места
ставится цифра 4, на другие места — цифра 5, а на третьи
места — цифра 6. Таким образом, в нашем случае множество
состоит из 7 элементов (я = 7), причем п{ = 3, п2 = 2, я3 = 2, и,
следовательно, в силу теоремы 5 таких чисел
ЛШ;2;2) = —— = 210.
7 3!2!2!
о
Задачи для самостоятельного решения
1. В ящике 5 красных и 4 зеленых яблока. Сколькими способами
можно выбрать три яблока из ящика?
2. Монету подбросили 3 раза. Сколько различных результатов
бросаний можно ожидать?
3. Сколькими способами можно вытащить две карты пиковой масти
из колоды в 36 карт?
4. Десять человек при встрече обмениваются рукопожатиями. Сколько
всего рукопожатий будет сделано?
5. Доступ к файлу открывается, только если введен правильный
пароль - определенный трехзначный номер из нечетных цифр.
Каково максимальное число возможных попыток угадать пароль?
6. Сколькими способами можно расположить на шахматной доске две
ладьи так, чтобы одна не могла взять другую? (Одна ладья может
взять другую, если она находится с ней на одной горизонтали или
на одной вертикали шахматной доски.)
19
ф ЧАСТЬ I. Теория вероятноаей
7. Сколькими способами можно расположить на полке ю томов
энциклопедии?
8. Сколькими способами можно расположить на полке ю томов
энциклопедии так, чтобы девятый и десятый тома рядом не стояли?
9. Группу из ю человек требуется разбить на две непустые подгруппы.
Сколькими способами это можно сделать? Подгруппы считаем
различными.
ю. Группу из ю человек требуется разбить на две подгруппы так, чтобы
в первой группе было 6 человек, а во второй — 4 человека.
Сколькими способами это можно сделать?
11. Группу из 16 человек требуется разбить на 3 подгруппы, в первой
из которых должно быть 5 человек, во второй — 7 человек, в
третьей — 4 человека. Сколькими способами это можно сделать?
12. Сколько существует двузначных чисел, кратных либо 2, либо 5,
либо тому и другому числу одновременно?
13. Из бригады в 14 врачей ежедневно в течение 7 дней назначают
двух дежурных врачей. Определить число различных расписаний
дежурства, если каждый человек дежурит один раз.
14. Сколько четырехзначных чисел, составленных из нечетных цифр,
содержит цифру 3 (цифры в числах не повторяются)?
15. Шесть групп занимаются в 6 расположенных подряд аудиториях.
Сколько существует вариантов расписания, при которых группы i
и 2 находились бы в соседних аудиториях?
16. Восемь мешков постельного белья доставляются на 5 этажей
гостиницы. Сколькими способами можно распределить мешки по
этажам? В скольких вариантах на пятый этаж доставлен один мешок?
(Мешки принимаем различными.)
17. Два наборщика должны набрать 16 текстов. Сколькими способами
они могут распределить эту работу между собой?
18. Поезд метро делает 16 остановок, на которых выходят пассажиры.
Сколькими способами могут распределиться между этими
остановками юо пассажиров, вошедших в поезд на конечной остановке?
19. Акционерное собрание компании выбирает из 50 человек
президента компании, председателя совета директоров и ю членов
совета директоров. Сколькими способами можно это сделать?
20. Из фирмы, в которой работают ю человек, 5 сотрудников должны
уехать в командировку. Сколько может быть составов этой группы,
если директор фирмы, его заместитель и главный бухгалтер
одновременно уезжать не должны?
ч )
20
Глава l ф
21. В телевизионной студии работают з режиссера, 4
звукорежиссера, 5 операторов, 7 корреспондентов и 2 музыкальных редактора.
Сколькими способами можно составить съемочную группу,
состоящую из одного режиссера, двух операторов, одного
звукорежиссера и двух корреспондентов?
22. В группе из 25 студентов нужно выбрать старосту и трех членов
студкома. Сколькими способами это можно сделать?
23. Шесть студентов, переведенных с других факультетов, следует
распределить по трем группам. Сколькими способами это можно
сделать?
24. Лифт останавливается на 7 этажах. Сколькими способами могут
выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
25. Восемь авторов должны написать книгу из 16 глав. Сколькими
способами можно распределить материал между авторами, если два
человека напишут по три главы, четыре - по две и два - по одной
главе книги?
26. Из цифр 1, 2, з, 4, 5, 6, 7, 8, 9 составляются всевозможные
пятизначные числа, не содержащие одинаковых цифр. Определить
количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
27. Сколько существует пятизначных чисел, в которых есть цифры i и 2
(считаем, что число может начинаться с нуля)?
28. Семь яблок и три апельсина надо положить в два пакета так, чтобы
в каждом пакете был хотя бы один апельсин и чтобы количество
фруктов в них было одинаковым. Сколькими способами это можно
сделать? Пакеты считаем различными.
29. Байт — это машинное слово, состоящее из восьми бит, каждый бит
равен либо о, либо 1. Сколько символов можно закодировать с
помощью байта?
30. Автомобильный номер состоит из трех букв и трех цифр.
Сколько различных номеров можно составить, используя 30 букв и ю
цифр?
31. Садовник должен в течение трех дней посадить ю деревьев.
Сколькими способами он может распределить по дням работу, если будет
сажать не менее одного дерева в день?
32. Из ящика, в котором лежат ю красных и 5 зеленых яблок,
выбирают одно красное и два зеленых яблока. Сколькими способами это
можно сделать?
21
ЧАСТЬ I. Теория вероятностей
33. Десяти ученикам выданы два варианта контрольной работы.
Сколькими способами можно посадить учеников в два ряда,
чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих
друг за другом был один и тот же вариант?
34. Студенческую группу в 24 человека (12 девушек и 12 юношей)
разбивают на две равные подгруппы так, чтобы в каждой подгруппе
юношей и девушек было поровну. Сколькими способами это
можно сделать?
35. Группа, состоящая из 25 человек, пишет контрольную работу, в
которой три варианта. Сколькими способами можно выбрать 5
человек из группы так, чтобы среди них оказались писавшие все три
варианта?
36. Лифт, в котором находится 9 пассажиров, может останавливаться
на ю этажах. На одном этаже выходят два человека, на другом -
три, и еще на одном - четыре. Сколькими способами пассажиры
могут выйти из лифта?
37. Сколькими способами можно расставить группу из ю человек
в очередь так, чтобы между двумя студентами А и Б было два
человека?
38. Есть з билета в различные театры. Сколькими способами они
могут быть распределены среди 25 студентов группы, если каждый
студент может получить только один билет?
39. На группу из 25 человек выделены 3 пригласительных билета на
вечер. Сколькими способами они могут быть распределены (не
более одного билета в руки)?
40. Имеются 7 билетов: 3 в один театр и 4 — в другой. Сколькими
способами они могут быть распределены между студентами группы
из 25 человек?
Ч )
ГЛАВА 2
КЛАССИЧЕСКАЯ
ВЕРОЯТНОСТНАЯ МОДЕЛЬ.
ГЕОМЕТРИЧЕСКАЯ
ВЕРОЯТНОСТЬ
§ 2.1. Частотная интерпретация
вероятности.
Свойство устойчивости частот
Теория вероятностей — это наука о закономерностях
случайных событий. Под случайным событием в теории вероятностей
понимается всякое явление, которое может произойти или не
произойти (случайным образом) при осуществлении
определенного комплекса условий. Каждое такое осуществление
будем называть испытанием, опытом или экспериментом.
События можно подразделить на достоверные,
невозможные и случайные.
Достоверным называется событие, которое обязательно
произойдет при испытании.
Невозможным называется событие, которое заведомо не
произойдет при испытании.
Случайным называется событие, которое в результате
эксперимента может либо произойти, либо не произойти (в
зависимости от случайных обстоятельств).
23 I
4J) ЧАСТЬ I. Теория вероятностей
Такое определение событий можно назвать эмпирическим.
Более строгие, математические (теоретико-множественные)
определения будут даны позже.
Предметом теории вероятностей являются закономерности
массовых случайных событий, где под массовостью мы
понимаем многократную повторяемость.
Рассмотрим несколько событий:
1) А — появление герба при бросании монеты;
2) В — появление трех гербов при трехкратном бросании
монеты;
3) С — попадание в цель при выстреле;
4) D — выигрыш по билету денежно-вещевой лотереи.
Очевидно, что каждое из этих событий обладает какой-то
степенью возможности. Для того чтобы количественно
сравнивать между собой события по степени их возможности, нужно
с каждым событием связать определенное число.
Вероятность события есть численная мера степени
объективной возможности этого события. В качестве единицы
измерения вероятности принята вероятность достоверного события.
Вероятность невозможного события равна нулю. Вероятность
любого случайного события обозначается Р(А) и изменяется в
диапазоне от нуля до единицы: 0 < Р(А) < 1.
Пусть проведена серия из п испытаний (п называют
длиной серии), в каждом из которых может произойти или не
произойти событие А. Подсчитаем, сколько раз в этой серии
эксперимент заканчивался наступлением события А, и
обозначим это число через п(А). Поделив его на общее число п всех
повторений эксперимента, получим величину Р(А) =^1^, ко-
" п
торая называется относительной частотой события А. При
небольшом числе экспериментов относительная частота события
носит случайный характер и может заметно меняться от одной
группы опытов к другой. При увеличении числа экспериментов
случайные обстоятельства, свойственные каждому отдельному
эксперименту, в массе взаимно погашаются, и частота Рп(А)
проявляет тенденцию стабилизироваться, приближаясь к
некоторой средней величине.
Этот эмпирический факт называется свойством
статистической устойчивости частот: по мере неограниченного увеличения
24
Глава 2
числа однородных и независимых испытаний относительная
частота события А стремится к некоторой постоянной величине.
Если данное свойство выполняется, то число, к которому
приближается относительная частота события при
неограниченном увеличении числа экспериментов, можно принять за
вероятность события А. Таким образом, частотная
интерпретация вероятности состоит в том, что относительную частоту
события принимают за приближенное значение вероятности
этого же события.
Частота события А отличается от вероятности этого события
тем, что вероятность величина детерминированная, а частота —
величина случайная и до опыта неизвестная.
В качестве примера укажем на опыт Бюффона, в котором
симметричная монета подбрасывалась 4040 раз, а герб выпадал
2048 раз. Частота появления герба в данной серии наблюдений
равна 2048/4040 = 0,507, что близко к интуитивно ожидаемому
значению вероятности 0,5.
Следует отметить, что приближение частоты события к его
вероятности не является обычной сходимостью к пределу (как
в математическом анализе). В разных сериях испытаний это
может происходить по-разному. Различные виды сходимости в
теории вероятностей и математической статистике будут
рассмотрены позже.
К сожалению, частотная интерпретация вероятности
несовершенна как с логической, так и с практической точки зрения.
Далеко не всегда возможно или желательно провести большое
количество экспериментов, а кроме того, существует
необходимость в предсказании вероятностей событий, которые еще
не происходили. Поэтому далее мы рассмотрим другие
определения.
§ 2.2. Пространство элементарных исходов.
Событие и его вероятность
Для того чтобы формально описать некоторый
эксперимент1, нужно прежде всего указать все возможные
варианты исходов, которыми этот эксперимент может закончиться.
1 Под экспериментом имеем в виду не обязательно научный
эксперимент, а любое действие или наблюдение либо их последовательность.
2* I
^ ЧАСТЬ I. Теория вероятноаей
: 26
Предполагается, что эксперимент может закончиться одним и
только одним исходом.
Множество Q всех возможных исходов эксперимента
называют пространством элементарных исходов, а каждый его
элемент — элементарным исходом, или элементарным событием.
Если все возможные исходы можно перечислить, то
пространство элементарных исходов называют дискретным
(конечным, или счетным):
Q = {(Dp со2, ... соя}, или Q = {сор со2, ...}.
Пример 1. При бросании симметричной монеты возможны
два исхода — выпадение решки или герба, и пространство
элементарных исходов имеет вид Q = {Р, Г}, где буквами Р и Г
обозначены решка и герб соответственно.
Пример 2. При одновременном бросании двух монет исходы
представляют собой упорядоченные пары, состоящих из
символов Р и Г. Первый элемент этой пары - результат, выпавший
на первой монете, второй элемент — результат на второй
монете. Очевидно, что таких пар - четыре:
Q = {РР, РГ, ГР, ГГ}.
Пример 3. В случае бросания игральной кости может
выпасть любое из чисел 1, 2, 3, 4, 5, 6. Поэтому пространство
элементарных исходов Q = {1, 2, 3, 4, 5, 6}.
Пример 4. При одновременном бросании двух игральных
костей элементарные исходы представляют собой пары (х, у),
где х — число очков, выпавшее на первой кости, а у — число
очков на второй кости. Всего таких пар - 36:
й = {(х, у): х = 1, 6, у = 1, 6}.
Кроме элементарных событий, рассматривают так
называемые сложные события, состоящие из более чем одного исхода.
Например, событие А — выпадение четного числа очков на
игральной кости — имеет вид А = {со2, со4, со6}.
Событием в случае дискретного пространства элементарных
исходов называется любое подмножество А = {со/р со/2, со/1(, ...}
этого пространства: >4cQ. Говорят, что «событие А произошло»,
если эксперимент закончился одним из элементарных исходов
со G А.
Глава 2
Вероятность в дискретном пространстве вводится
следующим образом. Поставим каждому элементарному исходу со. в
соответствие неотрицательное число р. > О, называемое его
вероятностью, такое, что сумма (конечная или бесконечная)
вероятностей всех элементарных исходов равна единице:
п оо
]Г>,=1 (или ?д=1).
/=1 /=1
Вероятностью события А называют сумму вероятностей всех
элементарных исходов, входящих в А, т.е. Р(А) = Х^(ч). Из
этого определения следует, что всегда выполняется неравенство
О < Р(А) < 1, а также:
1) P(Q) = 1, где Q — пространство элементарных исходов;
2) Р(0) = 0, если 0 — пустое множество.
Простейшим пространством элементарных исходов является
так называемая классическая модель, в которой пространство
конечно и все исходы эксперимента:
1) равновозможны;
2) взаимно несовместны (никакие два исхода не могут
произойти одновременно);
3) образуют полную группу событий, т.е. никакие другие
исходы, кроме перечисленных, не могут произойти.
Такое пространство называют симметричным.
Если Q = {©,, ю2, ... ©я} — симметричное пространство,
то вероятности элементарных событий равны между собой:
Дю,) = Pi = Р Для любого /=1,2, п и
Отсюда р1=р=- и вероятность события А = {со., со,, ... со }
п
по определению равна
P(A)=^P(&i) = m(A)~^
щ*А " п
где п = |Q| — число элементов во множестве Q, которое обычно
называют общим числом исходов, а т = \А\ —- число элементов во
множестве А, называемое числом исходов, благоприятствующих
событию А.
* I
ЧАСТЬ I. Теория вероятностей
28
Итак, в случае симметричного пространства вероятность
события А определяется как отношение числа случаев,
благоприятствующих событию А, к общему числу случаев:
п
Это «классическое» определение вероятности события —
результат принятия гипотезы о равновероятности
элементарных исходов.
Указанное равенство используется для вычисления
вероятности события А в случае, когда вероятность
противоположного события известна или легко может быть найдена. Тогда
Р{А) = \-Р(А).
Таким образом, для вычисления вероятности в каждой
задаче важно определить, в чем состоит эксперимент, правильно
построить соответствующее пространство элементарных
исходов Q и выделить в нем требуемое событие А. Затем, используя
методы комбинаторики, подсчитать число элементов в Q и А.
Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу
выбираются 3 фрукта. Какова вероятность, что все три фрукта —
апельсины?
Решение. Элементарными исходами здесь являются
выборки, включающие 3 фрукта. Поскольку порядок здесь
безразличен, будем считать выборки неупорядоченными (и разумеется,
бесповторными). Общее число элементарных исходов п = |Q|
равно числу способов выбрать 3 элемента из 9, т.е. числу
сочетаний С93. Число благоприятствующих исходов т = |Л| будет
равно числу способов выбора трех апельсинов из имеющихся 5,
т.е. числу сочетаний трех элементов из 5, или С]. Тогда
искомая вероятность
5!
^) = f = ^ = 0,12.
3!6!
Задача 2. Преподаватель предлагает каждому из трех
студентов задумать любое число от 1 до 10. Считая, что выбор
каждым из студентов любого числа из заданных равновозмо-
Глава 2
жен, найти вероятность того, что у какой-то пары из них
задуманные числа совпадут.
Решение. Вначале подсчитаем общее количество исходов.
Первый из студентов выбирает одно из 10 чисел и имеет пх = 10
возможностей, второй тоже имеет п2 = 10 возможностей,
наконец, третий также имеет пъ = 10 возможностей. В силу
основной теоремы комбинаторики общее число способов будет
равно: п = пх х п2 х пг = 103 = 1000, т.е. все пространство содержит
1000 элементарных исходов.
Подсчет количества благоприятствующих исходов более
сложен. Заметим, что совпадение задуманных чисел может произойти
у любой пары студентов (или даже одновременно у всех троих).
Чтобы не разбирать отдельно все эти случаи, удобно перейти к
противоположному событию, т.е. подсчитать количество тех
случаев, когда все три студента задумывают разные числа. Первый из
них по-прежнему имеет т] = 10 способов выбора числа. Второй
студент имеет теперь лишь т2 = 9 возможностей, поскольку ему
приходится заботиться о том, чтобы его число не совпало с
задуманным числом первого студента т2± тх. Третий студент еще
более ограничен в выборе — у него всего тъ = 8 возможностей.
Из 10 возможных для тъ исключаются два числа: m3*mv тъ ф т2.
Поэтому общее количество комбинаций задуманных чисел, в
которых нет совпадений, равно в силу той же основной теоремы
/w = 10 х 9 х 8 = 720. Остальные 280 случаев характеризуются
наличием хотя бы одного совпадения. Следовательно, искомая
вероятность совпадения равна Р = 280/1000 = 0,28.
Задача 3. Найти вероятность того, что в 8-значном числе
ровно 4 цифры совпадают, а остальные различны.
Решение. Событие А = {восьмизначное число содержит 4
одинаковые цифры}. Из условия задачи следует, что в числе
пять различных цифр одна из них повторяется. Число
способов ее выбора равно числу способов выбора одной цифры
из 10 цифр. Эта цифра занимает любые 4 места в числе, что
возможно сделать С84 способами, так как порядок здесь не
важен. Оставшиеся 4 места занимают различные цифры из
неиспользованных девяти, и так как число зависит от порядка
расположения цифр, то число способов выбора четырех цифр
равно числу размещений А%. Тогда число благоприятствующих
29
§ ЧАСТЬ I. Теория вероятноаей
где все элементарные исходы равновероятны. Событие А =
{первый студент взял «счастливый» билет} имеет вид
а событие В = {второй студент взял «счастливый» билет} имеет
Q = /2): /, = 1,25, /2 = 1,253
% /2):/, = 1,5, /2 = 1,25, /, ^/2},
вид:
^ = {ft,f2):^=l,...,25, /2=1,...,5, h*i2}.
исходов |у4| = 10С8%4. Всего же способов составления 8-значных
чисел |Q| = 108. Искомая вероятность
|Q| 108 4!4! 5! 107
Задача 4. Шесть клиентов случайным образом обращаются
в 5 фирм. Найти вероятность того, что хотя бы в одну фирму
никто не обратится.
Решение. Рассмотрим противоположное событие А, состоящее
в том, что в каждую из 5 фирм обратился клиент, тогда в какую-
то из них обратились два человека, а в остальные 4 фирмы — по
— 5x6»
одному клиенту. Таких возможностей \А\ = 5N6(291,1,1,1) = щцц^, •
Всего же способов распределить 6 клиентов по 5 фирмам
|Q| = 56. Отсюда Р(А)= 1ц!щ!2;^' = 0,1152, следовательно,
Р(А) = 1-Р(А) = 0,8848.
Задача 5. Среди 25 экзаменационных билетов имеется
5 «счастливых» и 20 «несчастливых». Студенты подходят за
билетами один за другим по очереди. У кого больше вероятность
вытащить «счастливый» билет: у того, кто подошел первым,
или у того, кто подошел вторым?
Решение. Пусть «счастливые» билеты имеют номера 1, 2,
3, 4, 5. Обозначим через /, номер билета, взятого первым
студентом, через /2 — номер билета, взятого вторым студентом,
тогда элементарным исходом будет пара (/,,/2), а пространство
элементарных исходов
I
Глава 2 i|
Каждое из событий А и В содержит | А \=\ В \= С\с\А = 120
элементов, а все пространство Q имеет | Q | = С]25С124 = 600
элементов. Следовательно, Р(А) = Р(В) = 1/5. Вероятность не зависит
от того, кто подошел первым, кто вторым и т.п.
Задача 6. Пусть в урне имеется N шаров, из них М белых и
N — М черных. Из урны извлекается выборка объема п. Найти
вероятность того, что в этой выборке будет ровно т белых шаров.
Решение. Поскольку порядок элементов здесь
несущественен, число всех возможных выборок объема п из N
элементов равно числу сочетаний CnN. Число испытаний, которые
благоприятствуют событию А — «т белых шаров, п — т
черных», равно C%CnN~"M, и, следовательно, искомая вероятность
равна Р(А) = м Nn~M . Описанная ситуация представляет
собой пример «урновой модели». Говорят также, что случайное
число белых шаров в выборке здесь имеет гипергеометрическое
распределение.
В общем случае предположим, что имеется N = пх + п2 + ...+ пк
различных частиц, причем я, частиц первого типа, п2 — второго
типа, пк — к-ю типа. Случайным образом из этих TV частиц
выбирается m частиц. Найдем вероятность события А,
состоящего в том, что среди выбранных окажется ровно тх < пх частиц
первого типа, т2< п2 — второго типа, тк< пк — к-го типа,
так что т = тх + т2 + ... + тк.
Поскольку порядок выбора несущественен, при определении
общего числа исходов и числа благоприятных исходов
необходимо пользоваться числом сочетаний. Общее число элементарных
исходов равно С™. Далее, тх частиц первого типа можно выбрать
С^1 способами, т2 частиц второго типа — С^2 способами, тк
частиц к-то типа — С"к способами. При этом любой выбор частиц
определенного типа комбинируют с любыми выборами частиц
остальных типов и, следовательно, число благоприятствующих
событию А исходов равно С"1С?...С™к. Поэтому вероятность
N
m-m
P(A) = P(mx,m2,...,mk) =
31
^ ЧАСТЬ I. Теория вероятностей
32
§ 2.3. Статистики Бозе—Эйнштейна, Ферми—Дирака,
Максвелла—Больцмана
Предположим, что п неразличимых частиц распределяются
по т ячейкам. Различными и равновозможными считаются
распределения частиц по ячейкам, отличающиеся только числом
частиц, попавших в каждую ячейку. Такое распределение
носит название статистики Бозе—Эйнштейна. Найдем общее
число элементарных исходов в статистике Бозе—Эйнштейна. Если
считать «белый» элемент частицей, а «черный» —
перегородкой, то существует взаимно однозначное соответствие между
способами выбора т - 1 «черного» элемента и размещениями
частиц в статистике Бозе—Эйнштейна. Для этого рассмотрим
последовательность из п + т — 1 элементов и выберем из них
т — 1 «черный» элемент.
1 2 3 т-1
о#ооо##о... о •
1 2 3 4 5 6 7 л + /и-1
РИС. 2.1
Так, на рис. 2.1 в первую ячейку попала одна частица, во
вторую — три, третья оказалась пустой и т.д., последняя, /и-я
ячейка, также оказалась пустой. Поэтому общее число
размещений равно С"~хт_х. Найдем вероятность того, что в
фиксированную ячейку попало ровно к частиц (событие А). Заметим, что
если в этой фиксированной ячейке уже находится к частиц, то
остальные п — к частиц должны быть распределены по
оставшимся т — 1 ячейкам, а это можно сделать C™+~J^_,_, = С™~*_к_2
способами. Следовательно, искомая вероятность
Р(А)= "+mf-2 .
В статистике Ферми—Дирака п неразличимых частиц
распределяются по т ячейкам (п < т), однако в каждой ячейке
не может находиться более одной частицы. Число различных
элементарных исходов совпадает с числом способов,
которыми можно выбрать п занятых ячеек из общего числа ячеек т,
I
Глава 2 ф
и так как порядок выбора несущественен, то число способов
равно Спт. Найдем вероятность того, что заняты к
фиксированных ячеек. Пусть событие А — заняты фиксированные к ячеек
(к <п). Тогда оставшиеся т - к ячеек должны быть заполнены
п - к частицами, а это можно сделать Спт~_\ способами. Поэтому
искомая вероятность
Предполагая, что п различных частиц распределяются по т
ячейкам без ограничений на число попавших в каждую ячейку
частиц, получаем статистику Максвелла—Больцмана. Поскольку
каждая из п частиц может попасть в любую из т ячеек, то
общее число элементарных исходов равно тп. Событие А
заключается в том, что в первую ячейку попало я, частиц, во
вторую — nv в т-ю — пт частиц (пх + п2 + ... + пт = п). Число
благоприятных для события А исходов равно числу разбиений
множества п на группы объема nv п2, пт:
Таким образом, искомая вероятность
Статистика Максвелла—Больцмана представляет собой
частный случай так называемой полиномиальной схемы (см. гл. 4).
Рассмотрим я-мерное вещественное пространство Rn. Пусть
в какую-то ограниченную область Q с Rn наудачу бросили
точку. Слово «наудачу» означает, что в таком эксперименте все
точки области Q «равновозможны». В этом случае вероятность
попадания этой точки в какую-то подобласть А с й
определяется формулой
Р(А) =
п\ 1
«1Ч '-"J ni
§ 2.4. Геометрическая вероятность
Р(А) =
V(A)
2 Теория вероятностей
33
ЧАСТЬ I. Теория вероятностей
где V(A) и V(Q) — л-мерные объемы областей А и Q
соответственно. Здесь элементарными исходами называются точки
множества Q (которое играет роль пространства элементарных
исходов), а благоприятствующими исходами — точки
множества А.
Задача 7. Точку наудачу бросили на отрезок [0; 2]. Какова
вероятность попадания этой точки на интервал [0,5; 1,4]?
Решение. Здесь пространство элементарных исходов — весь
отрезок Q = [0; 2], а множество благоприятствующих исходов
А = [0,5; 1,4], при этом длины этих интервалов равны /(Q) = 2
и 1(A) = 0,9. Поэтому вероятность попадания брошенной точки
Задача 8. На отрезок [0; 2] бросили наудачу и поочередно
две точки. Какова вероятность, что первая точка лежит правее
второй точки?
Решение. Обозначим получившиеся координаты точек через
х и у. Элементарным исходом в таком бросании двух точек
будет пара (х, у), а пространством элементарных исходов —
квадрат Q = {(х, у): х, у е [0; 2]}. Событие А = {первая точка
лежит правее второй точки} равносильно условию х > у,
следовательно, А = {(х,у):х9уе[0; 2],х>^}, т.е. представляет собой
треугольник (рис. 2.2). Площади квадрата и треугольника
равны соответственно S(Q) = 4 и S(A) = 2, а потому вероятность
в указанный интервал Р(А) =
Р(А) =
S(A) 2
= т = 0Д
5(П) 4
РИС. 2.2
I 34
Глава 2 ф
Задача 9. Стержень (рис. 2.3) разламывается на две части в
случайной точке, равномерно распределенной по длине
стержня. Найти вероятность того, что меньший обломок имеет
длину, не превосходящую одной трети длины стержня.
Ox L
РИС. 2.3
Решение. Обозначим длину стержня L, а расстояние точки
разлома от одного (например, левого) конца стержня — х.
Тогда описанное событие произойдет при условии, если
х < у либо х>?у. Искомая вероятность равна отношению
к+к
Р(А) = 1—2l=-.
L 3
Задача 10 (задача о встрече). Два лица А и В условились
встретиться в определенном месте между 12 и 13 часами.
Пришедший первым ждет другого в течение 20 минут, после чего
уходит. Чему равна вероятность встречи лиц Аи В, если приход
каждого из них может произойти наудачу в течение указанного
часа и моменты прихода независимы?
Решение. Обозначим моменты прихода лица А через х и лица
В через у. Для того чтобы встреча произошла, необходимо и
достаточно, чтобы I х — у I < 20. Изобразим х и у как
координаты на плоскости, в качестве единицы масштаба выберем
минуту. Всевозможные исходы представляются точками квадрата
со стороной 60, а благоприятствующие встрече располагаются
в заштрихованной области. Искомая вероятность равна
отношению площади заштрихованной фигуры (рис. 2.4) к площади
всего квадрата: р = (602 - 402)/602 = 5/9.
Задача 11 (задача Бюффона). Плоскость разграфлена
параллельными прямыми, отстоящими одна от другой на
расстоянии 2а. На плоскость наудачу бросается игла длиной 21
(I < а). Найти вероятность того, что игла пересечет какую-
нибудь прямую.
2*
Ill ЧАСТЬ I. Теория вероятностей
У
60
20
20
60
х
Рис. 2.4
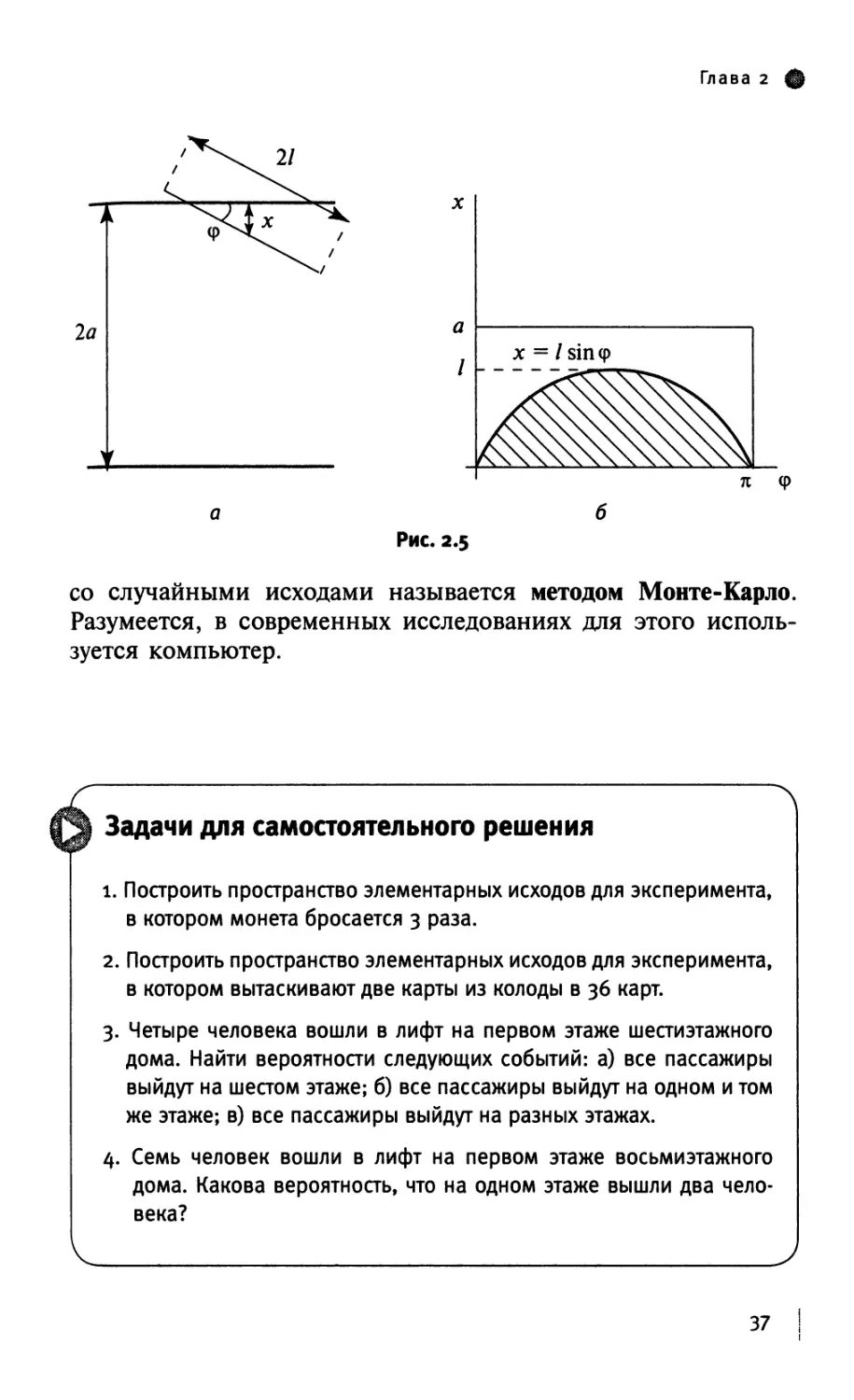
Решение. Если игла бросается с достаточной высоты и ее
начальное положение случайно, то под словом «наудачу»
подразумевается, во-первых, что центр иглы наудачу попадет на
отрезок длиной 2а, во-вторых, что угол ф между прямой и
иглой равномерно распределен на отрезке [0; п] и, в-третьих,
что на величину угла не влияет расстояние от центра до
прямой. Поэтому изобразим результат бросания точкой с
координатами (ф, х), лежащей внутри прямоугольника со сторонами а
и к, где х — расстояние от центра иглы до ближайшей прямой.
Из рис. 2.5а видно, что пересечение иглы с прямой происходит
тогда и только тогда, когда х < Isiny. Искомая вероятность
равна отношению площади заштрихованной области А к площади
прямоугольника на рис. 2.56:
Отметим, что полученную формулу можно применить для
приближенного вычисления числа п. Действительно,
получаем: я = 21/(аР(А)). Проводя многократные эксперименты
(бросания иглы), можно приблизить вероятность Р(А)
относительной частотой Рп(А) и, соответственно, найти приближенное
значение яя= 21/(аРп(А)). Подобное вычисление
детерминированных величин с помощью последовательности испытаний
I зб
Глава 2 ф
2а
Рис. 2.5
со случайными исходами называется методом Монте-Карло.
Разумеется, в современных исследованиях для этого
используется компьютер.
Задачи для самостоятельного решения
1. Построить пространство элементарных исходов для эксперимента,
в котором монета бросается з раза.
2. Построить пространство элементарных исходов для эксперимента,
в котором вытаскивают две карты из колоды в 36 карт.
3. Четыре человека вошли в лифт на первом этаже шестиэтажного
дома. Найти вероятности следующих событий: а) все пассажиры
выйдут на шестом этаже; б) все пассажиры выйдут на одном и том
же этаже; в) все пассажиры выйдут на разных этажах.
4. Семь человек вошли в лифт на первом этаже восьмиэтажного
дома. Какова вероятность, что на одном этаже вышли два
человека?
ф ЧАСТЬ I. Теория вероятноаей
38
С ^
5. Бросают две игральные кости. Чему равна вероятность того, что
сумма очков, выпавших на обеих костях, не превзойдет 5?
6. Какова вероятность того, что в 4 бросаниях кости хотя бы один раз
выпадет «единица»?
7. Найти вероятность того, что дни рождения 12 человек приходятся
на разные месяцы года.
8. В урне 5 белых.и 4 черных шара. Из урны наугад вынимают два
шара. Какова вероятность того, что это будет: а) два белых шара;
б) два черных шара; в) один черный и один белый.
9. Пять клиентов случайным образом обращаются в 4 фирмы. Какова
вероятность, что хотя бы в одну фирму никто не обратится?
ю. На остановке ю человек случайным образом выбирают один из
ю вагонов поезда. Найти вероятность того, что ровно в один вагон
никто не войдет.
11. В каждой упаковке товара имеется одна из 5 различных наклеек
(равновероятно). Какова вероятность собрать их все, купив 7
упаковок товара?
12. Шесть шаров случайным образом раскладывают по 3 ящикам.
Найти вероятность того, что во всех ящиках будет разное число шаров.
13. Найти вероятность того, что в 6-значном номере 3 цифры
совпадают, а остальные различны (считаем, что номера могут начинаться
с нуля).
14. Семь человек становятся случайным образом в очередь один за
другим. Какова вероятность того, что два определенных человека,
А и Б, встанут рядом?
15. В очередь в булочную случайным образом встали 8 женщин и
2 мужчин. Какова вероятность того, что между мужчинами будут
стоять 2 женщины?
16. В очередь в кассу стоят 9 человек (3 мужчин, 4 женщины и 2
детей). Какова вероятность, что между некоторыми двумя
мужчинами будут стоять 2 детей и одна женщина?
17. В партии из 8 изделий 3 изделия — высшего качества. Найти
вероятность того, что среди отобранных (без возвращения) 4
изделий — ровно одно изделие высшего качества.
18. Из ю проданных за день холодильников 4 имеют скрытые
дефекты. Найти вероятность того, что среди выбранных наудачу 5
холодильников будет ровно 2 без скрытых дефектов.
Ч J
Глава 2 ф
19. Шесть шаров случайным образом раскладываются по 3 ящикам.
Найти вероятность того, что в первом ящике лежит 4 шара.
20. На шахматную доску случайным образом поставлены 2 ладьи.
Какова вероятность того, что они не будут бить друг друга?
21. Группа из 18 студентов пишет контрольную работу из 3
вариантов (по 6 человек в каждом). Найти вероятность того, что
среди случайно выбранных 5 студентов есть писавшие каждый
вариант.
22. На группу из ю человек предоставлено для производственной
практики 6 мест в лаборатории № i и 4 места — в лаборатории
№ 2. Какова вероятность того, что при случайном распределении
мест двое неразлучных друзей из этой группы попадут на практику
в одну лабораторию?
23. В трех студенческих группах 72 человека (по 24 человека в
группе: 12 юношей и 12 девушек). Наудачу выбраны 5 человек.
Какова вероятность того, что среди них будут девушки из всех трех
групп?
24. Из колоды в 36 карт выбираются наугад 4 карты. Найти
вероятность того, что среди них окажется хотя бы один туз.
25. В лотерее из 50 билетов 5 выигрышных. Какова вероятность того,
что среди первых 5 наугад выбранных билетов 2 будут
выигрышными?
26. Работа каждого из 4 студентов заочного отделения может
проверяться одним из 4 преподавателей. Какова вероятность, что все
4 работы проверены разными преподавателями?
27. Найти вероятность того, что в пятизначном числе имеются 2
четные цифры и з нечетные, при условии, что все они различны
(принимаем, что число может начинаться с нуля).
28. В ящике находятся 5 белых, 3 красных и 2 черных шара. Наудачу
выбирают 6 шаров. Найти вероятность того, что выборка будет
содержать 3 белых, 2 красных и i черный шар, если: а) выборка
производится без возвращения (все 6 шаров отбираются сразу);
б) выборка производится с возвращением (фиксируется цвет
выбранного шара, после чего он возвращается в ящик).
29. Какова вероятность того, что дуэль состоится, если каждый из
дуэлянтов приходит на место дуэли в случайный момент времени
между 5 и 6 часами и ждет противника в течение 5 минут?
v .
39
ф ЧАСТЬ I. Теория вероятностей
30. Две подруги договорились встретиться в условленном месте в
промежутке от 17 до 19 часов. Пришедшая первой ждет другую не
более 15 минут. Какова вероятность, что подруги не встретятся?
31. На отрезок [2; 5] наудачу бросают две точки. Какова вероятность
того, что расстояние между ними меньше 2?
32. На отрезок [-1; 2] наудачу брошены две точки. Какова вероятность
того, что расстояние между ними больше 1?
33. Точку бросают случайным образом на квадрат площадью юо см2.
Какова вероятность того, что координаты х, у этой точки
отличаются между собой не более чем на i см?
34. Два теплохода должны подойти к одному и тому же причалу. Время
прихода обоих теплоходов независимо и равновозможно в
течение данных суток. Найти вероятность того, что ни одному из
теплоходов не придется ожидать освобождения причала, если время
стоянки первого теплохода — i час, а второго — 2 часа.
35. Студент может добраться до факультета либо на автобусе,
интервал движения которого составляет 7 минут, либо на троллейбусе,
интервал движения которого составляет ю минут. Найти
вероятность того, что студенту, пришедшему на остановку в случайный
момент времени, придется ждать не более 3 минут.
36. Наудачу взяты два положительных числа/и V, каждое из которых
не превышает единицы. Найти вероятность того, что сумма х+ Уне
превышает 1, а произведение xy не меньше 0,09.
37. Найти вероятность того, что из 3 наудачу взятых отрезков длиной
не более L можно построить треугольник.
38. В точке С, любое положение которой на телефонной линии АВ
длиной ю км равновозможно, произошел разрыв. Определить
вероятность того, что точка С удалена от точки А, где находится
ремонтная станция, на расстояние, не меньшее i км.
39. На плоскость с нанесенной сеткой квадратов со стороной а
брошена монета радиуса г [г < а/2). Найти вероятность того, что монета
не пересечет ни одну из сторон квадрата.
40. Найти вероятность максимального выигрыша в «Спортлото»
(угадать 6 цифр из 49).
41. В пачке юоо лотерейных билетов, из которых ю выигрышные.
Какова вероятность выиграть хоть что-нибудь, имея: а) 3 билета;
б) юо билетов?
V J
ГЛАВА з
ОСНОВНЫЕ ФОРМУЛЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
§ 3.1. Операции над событиями
Одной из основных задач теории вероятностей является
вычисление вероятностей различных событий, когда известны
вероятности каких-то других событий. Это возможно в том
случае, если эти новые события можно выразить через исходные с
помощью различных операций.
Суммой (или объединением) двух событий А и В называется
событие АиВ (А + В), заключающееся в том, что произойдет
хотя бы одно из событий А или В (либо событие А, либо
событие В, либо А и В одновременно).
Произведением (или пересечением) двух событий А и В
называется событие АпВ (или АВ), состоящее в одновременном
появлении и события А, и события В.
Отрицанием (или противоположным событием) для события
А называется событие А, которое происходит тогда и только
тогда, когда не просходит событие А.
Симметрической разностью событий А и В называется
событие С = AS/В, в которое входят те элементарные события,
которые входят или в А, или в В, но не входят в их пересечение:
AVB = (А\В) и (В\А).
Поскольку все события рассматриваются как
подмножества пространства элементарных исходов Q, то и операции
над ними — это соответствующие операции над множествами
(объединение, пересечение, дополнение). Все пространство Q
соответствует достоверному событию (поскольку эксперимент
41 I
ф ЧАСТЬ I. Теория вероятноаей
А\В AVB
Рис. зл
Пример 1. Бросают две игральные кости. Пусть А —
событие, состоящее в том, что сумма очков нечетная, В — событие,
заключающееся в том, что хотя бы на одной из костей выпала
двойка. Опишем события А и В и А п В.
42
всегда заканчивается каким-то элементарным исходом), а
пустое множество 0 — невозможному событию (поскольку в нем
нет ни одного возможного исхода).
Справедливы следующие соотношения:
1. AuQ = Q, Au0 = A, AuA = А
2. AnQ = A, An0 = 0, AnA = А
3. А = А, Q = 0, 0 = Q
4. АПВ = АиВ, АиВ = АпВ (принцип двойственности, или
формулы де Моргана)
5. АиВ = ВиА, АслВ = ВпА (коммутативность операций
объединения и пересечения)
6. Akj(BuC) = (AkjB)uQ An(BnQ = (АпВ)г\С
(ассоциативность операций объединения и пересечения)
7. Аи(ВпС) = (у4и5)п(ЛиС) (дистрибутивность операции
объединения относительно пересечения)
8. Лп(5иС) = (AnB)v(AnQ (дистрибутивность операции
пересечения относительно объединения)
Для наглядности соотношений между событиями используют
графическую модель, называемую диаграммой Вьенна (рис. 3.1).
Глава з @
Пространство элементарных исходов может быть
представлено в виде: Q = {(1, 1), (1, 2), (2, 1),..., (6, 6)}; |Q| = 36.
Согласно условию задачи, события А и В состоят из
следующих элементарных исходов:
А = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (6, 1), (6, 3),
(6, 5)};
В = {(1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (5, 2), (2, 5),
(2, 6), (6, 2), (2, 2)}.
Объединение А и В представляет собой событие, состоящее
в наступлении хотя бы одного из событий А и В, т.е. событие
А и В означает, что либо сумма выпавших очков нечетна, либо
на одной из костей выпала двойка:
А и В = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6), (6, 1), (6, 3), (6, 5)}.
Пересечение А п В представляет собой событие, состоящее
в одновременном наступлений событий А и В, т.е. в том, что
на одной из костей выпала двойка, а на второй — нечетное
число очков:
А п В = {(1, 2), (2, 1), (2, 3), (3, 2), (2, 5), (5, 2)}.
События А и В называются несовместными
(непересекающимися), если они не могут произойти одновременно: АпВ = 0.
События Av Av Ап образуют полную группу событий, если
они несовместны и в сумме образуют все пространство П, т.е.
i=\
Это означает, что в результате эксперимента обязательно
произойдет одно из данных событий, и только одно.
Пример 2. Бросают одну игральную кость: Q = {1, 2, 3, 4,
5, 6}. События А = {1, 2}, В = {3, 4}, С = {5, 6} несовместны
и образуют полную группу событий. События А и В
несовместны, но не образуют полную группу событий. События А,
В и D = {3, 5, 6} в сумме образуют все пространство Q, но не
образуют полную группу событий.
43 |
ф ЧАСТЬ I. Теория вероятностей
44
§ 3.2. Теоремы сложения вероятностей
Пусть заданы вероятности некоторых событий и требуется
найти вероятности их объединения.
> Теорема 1 (теорема сложения вероятностей несовместных
событий). Вероятность объединения двух несовместных событий
равна сумме их вероятностей, т.е. если АпВ = 0, то Р(АиВ) =
= Р(А) + Р(В).
Доказательство проведем для случая конечного числа
исходов. Пусть пространство элементарных событий Q = {сор со2,
юл} содержит п элементарных исходов, из них пх
благоприятствуют событию А и п2 благоприятствуют событию В, т.е.
Р(А) = р(®^ и = 11, P(®k)> и нет исходов, благо-
гю/ ?а Лю^еЛ
приятствующих одновременно А и В, так как события
несовместны. Отсюда следует, что событию ЛоВ благоприятствуют
пх+ п2 исходов и вероятность этого события вычисляется по
формуле
Р(АиВ) = ? = + Е'Ю = pW + pw-
a>jeaub <о,еа Mk^b
Доказательство без труда переносится на случай счетного
пространства Q = {со,, со2, ю3, ...}, когда вместо конечных сумм
рассматриваются суммы со счетным числом слагаемых —
сходящиеся ряды.
Следствия
1. Методом математической индукции эту теорему можно
распространить на любое конечное число слагаемых, т.е.
если все события А. несовместны, то
P([J А) = Р(А{) + Р{А,) + ... + Р(Ап).
i=\
2. Если события Av А2, Ап образуют полную группу
событий, то сумма их вероятностей равна единице. В
частности, поскольку противоположные события
несовместны и в сумме образуют Q, отсюда следует формула:
Р(А) = 1-Р(А).
3. Если А с В , то Р(А) < Р{В).
Глава з ф
^ Теорема 2 (теорема сложения вероятностей произвольных
событий). Для любых событий А и В верно равенство: Р(А и В) =
- + + Р(В) - Р(А п В).
Доказательство. Для любых событий А и В событие А и В
наступит тоща, когда наступит одно из несовместных событий
А п В, А п В или А п В. По теореме сложения для
несовместных событий
Р(А и В) = Р(А пй) + Р(А п5) + Р(А п 5).
Событие А наступит, если наступит хотя бы одно из двух
несовместных событий: А п В или А п В. Тогда вероятность
события А по теореме сложения для несовместных событий равна
Р(А) = Р(А п В) + п 5). Аналогично событие В наступит,
если наступит хотя бы одно из несовместных событий А п В
или А п В, и вероятность события В равна Р(В) = Р(А п В) +
+ Р(А п В). Отсюда получаем:
Р(АиВ) = Р(А) + Р(Ап В) + Р(АпВ) - Р(А п В) =
= Р(А) + Р(В) - Р(А п 5).
Следствия
1. Вероятность пересечения любых двух событий А и В
вычисляется по формуле Р(А п В) = + - Р(Л и В).
2. Вероятность суммы любого числа событий вычисляется
по формуле включения-исключения:
P<4U...U4) = ?P<4)-^
/=1 Ы]
3. Из теорем 1 и 2 для любых событий А и В следует, что
Р(А и В)< Р(А) + Р(В).
Задача 1. В ящике 10 красных и 5 синих пуговиц.
Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы
будут одноцветными?
Решение. Событие А = {вынуты пуговицы одного цвета}
можно представить в виде суммы А = Ах + Av где события Ах и А,
означают выбор пуговиц красного и синего цвета соответствен-
45 |
i
ф ЧАСТЬ I. Теория вероятностей
46
С2
но. Вероятность вытащить две красные пуговицыР(АХ) = -у-,
С2
а вероятность вытащить две синие пуговицы Р(А2) = —у*. Так
как события Ах и А2 не могут произойти одновременно, то в
силу теоремы сложения
10! 5!
Р{А)=С^ = Щ^ = №.
2ЙЗ!
Задача 2. Среди сотрудников фирмы 28% знают английский
язык, 30% — немецкий, 42% — французский; английский и
немецкий — 8%, английский и французский — 10%, немецкий
и французский — 5%, все три языка — 3%. Найти вероятность
того, что случайно выбранный сотрудник фирмы: а) знает
английский или немецкий; б) знает английский, немецкий или
французский; в) не знает ни один из перечисленных языков.
Решение. Обозначим через А, В и С события,
заключающиеся в том, что случайно выбранный сотрудник фирмы
владеет английским, немецким или французским соответственно.
Очевидно, доли сотрудников фирмы, владеющих теми или
иными языками, определяют вероятности этих событий. Получаем:
а) Р(А и В) = Р(А) + Р(В) - Р(АВ) = 0,28 + 0,3 - 0,08 =
= 0,5;
б) Р(А и В и О = Р(А) + Р(В) + P(Q - (Р(АВ) + ДАС) +
+ P(BQ) + P(ABQ = 0,28 + 0,3 + 0,42 - (0,08 + 0,1 + 0,05) +
+ 0,03 = 0,8;
в) 1 - Р(А и В и С) = 0,2.
§ 3.3. Условная вероятность и теорема умножения
Говорить о вероятности Р(А) как о мере возможности
появления случайного события А имеет смысл только при
осуществлении определенного комплекса условий эксперимента,
в рамках которого событие может произойти. При изменении
условий эксперимента, вообще говоря, изменится и
вероятность события А. Поэтому помимо обычной (безусловной) ве-
Глава з ф
П4
= Р(А{)Р(А21 А{)Р{Аг 144).../>(4,144-4м)-
Для условной вероятности выполняются следующие
свойства:
1) 0 <_Р{А \В)<\;
2) Р(А\В)=\- Р(А | В);
3) Р(А \А) = 1;
4) Р(Ци^) \В) = Р(А1\В) + Р(А\\В) - Р(А1пА2\В);
5) если А п В = 0, то Р(А \ В) = 0;
6) если А <= В, то Р(В \ А) = 1.
В случае, когда имеем дело с пространством равновозмож-
ных исходов (гл. 2), условную вероятность можно найти по
формуле
47
роятности события А рассматривают так называемую условную
вероятность события А, вычисляемую при условии, что
произошло некоторое событие В.
Условной вероятностью события А при условии, что
произошло событие В (Р(В) > 0), называется число Р(А\В), которое
вычисляется по формуле
Р(А1В)=^1.
Р(В)
Аналогично определяется условная вероятность события В:
Р(В\А) = ^-, Р(А)>0.
Р(А)
Из определения условной вероятности вытекает следующая
теорема.
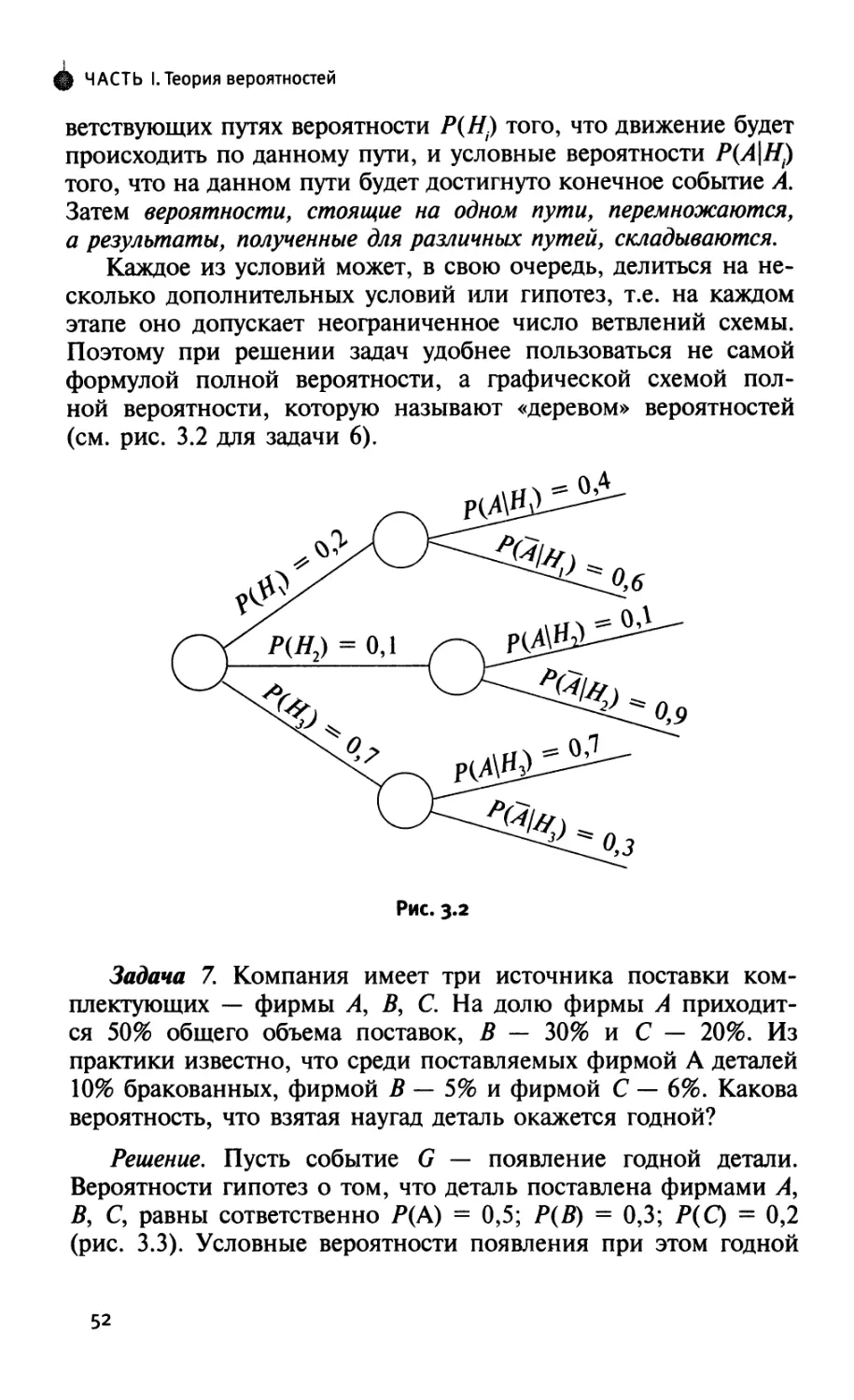
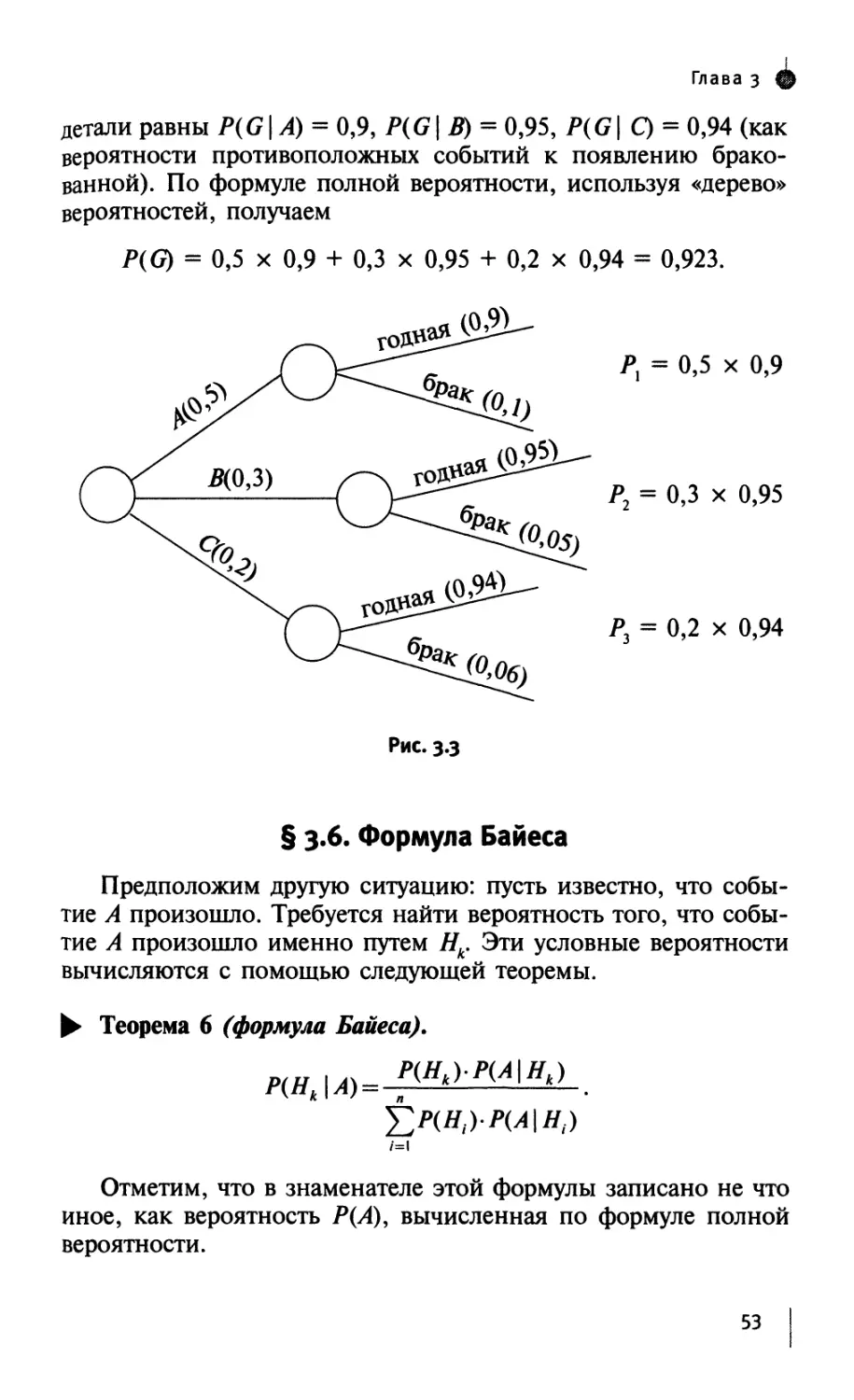
^ Теорема 3 (теорема умножения).
Р(АВ) = Р(В)Р(А\В) или Р(АВ) = Р(А)Р(В\А).
Несмотря на тривиальность доказательства этой теоремы,
она имеет огромное практическое значение, так как
используется для построения сложных вероятностных моделей.
Следствие. Для пересечения произвольного числа событий
верно равенство
ф ЧАСТЬ I. Теория вероятностей
48
Задана 3. В семье двое детей. Какова вероятность того, что
старший ребенок — мальчик, если известно, что в семье есть
дети обоего пола?
Решение. Пусть А = {старший ребенок — мальчик}, В = {в
семье есть дети обоего пола}. Будем считать, что рождение
мальчика и рождение девочки — равновероятные события. Если
рождение мальчика обозначить буквой М, а рождение
девочки — Д, то пространство всех элементарных исходов состоит
из четырех пар: Q = {ММ, МД, ДМ, ДД}. В этом пространстве
лишь два исхода (МД и ДМ) отвечают событию В. Событие
АВ означает, что в семье есть дети обоего пола. Старший
ребенок — мальчик, следовательно, второй (младший) ребенок —
девочка. Этому событию АВ отвечает один исход — МД. Таким
образом, \АВ\ = 1, \В\ = 2 и
P(^|5) = i^i = i = 0,5.
Задача 4. Мастер, имея 10 деталей, из которых 3 —
нестандартные, берет и проверяет детали одну за другой, пока ему не
попадется стандартная. Какова вероятность, что он проверит
ровно две детали?
Решение. Событие А = {мастер проверил ровно две детали}
означает, что при такой проверке первая деталь оказалась
нестандартной, а вторая — стандартная. Значит, А = AXA^, где
Ах = {первая деталь оказалась нестандартной} и А2 = {вторая
деталь — стандартная}. Очевидно, что вероятность события Ах
равна /^Л,) = 3/10, кроме того, Р(А2 | Д) = 7/9, так как перед
взятием второй детали у мастера осталось 9 деталей, из
которых только 2 нестандартные и 7 стандартных. По теореме
умножения
Р(А) = Р(АХА2) = Р(АХ)Р(А21 Ах) = А 1 = 7 /30.
§ 3.4. Независимость событий
Событие А не зависит от события В, если появление В не
меняет значения вероятности события А, т.е. условная
вероятность равна безусловной: Р(А\В) = Р{А). Тогда из теоремы
умножения Р(А\В) = Р(А)Р(В\А) = Р(В)Р(А\В) в предполо-
Глава з
жении, что Р(А) > О, получим, что условная вероятность
события В равна его безусловной вероятности Р(В/А) = Р(В).
Следовательно, события Aw В независимы, если появление
одного из них не меняет вероятности появления другого.
Из определения независимости двух событий следует
^ Теорема 4. Два события А и В независимы, если
справедливо равенство
Р(АВ) = Р(А)Р(В).
Это равенство используется как критерий при практической
проверке независимости двух событий.
Понятие независимости обобщается на любое конечное
число событий.
События Av Av Ап называются независимыми в
совокупности, если для любого их набора Al9Ai9...,Ai имеет место
равенство
РЦ4)...4а) = РЦ)/>(42).../>(^)
для любых к от 1 до п и любых несовпадающих номеров /,,
/2, ik.
События Ах, Ап называются попарно независимыми, если
для любых / /, j е {1, п) события А. и А. независимы.
Из данных определений следует, что из независимости в
совокупности следует попарная независимость, но из попарной
независимости не следует независимости в совокупности.
Пример Бернштейна. На плоскость бросается правильный
тетраэдр (треугольная пирамида), три грани которого
покрашены в цвета: красный, синий и зеленый, а на четвертую грань
нанесены все три цвета. Событие А — при бросании выпала
красная грань, событие В — синяя грань, событие С — зеленая
грань. Вероятности этих событий равны между собой:
Р(А) = Р(В) = P(Q = 2/4 = 1/2.
Найдем вероятности их попарных произведений:
Р(АВ) = 1/4 = 1/2 х 1/2 = Р(А)Р(В)\
P(AQ = P(A)P(Q = 1/4 = 1/2 х 1/2.
Отсюда следует, что они попарно независимы. Однако
вероятность появления всех трех цветов
P(ABQ = 1/4 * Р(А)Р(В)Р(С) = 1/2 х 1/2 х 1/2 = 1/8,
49 I
ЧАСТЬ I. Теория вероятностей
§ 3.5. Формула полной вероятности
Пусть событие А может быть реализовано только при
условии появления одного из событий Я., / = 1, п. Предположим,
что события Я. образуют полную группу и вероятности их до
опыта известны. Такие события Я. называются гипотезами.
> Теорема 5 (формула полной вероятности). Вероятность
события А вычисляется по формуле
P(A) = ^P(Hi)P(A\Hi)t
/=i
Доказательство. Поскольку гипотезы Я., / = 1,2, ... к,
несовместны, то несовместны и их пересечения с событием А, т.е.
несовместны комбинациии А п Я. и А п Я при i ф j. Обозначим
п
Я = [JЯ,. Так как Я,, Нк образуют полную группу событий,
/=i
50
т.е. вероятность произведения всех трех событий не равна
произведению вероятностей этих событий и, следовательно, они
зависимы в совокупности.
Задача 5. В одном ящике 3 белых и 5 черных шаров, в
другом ящике — 6 белых и 4 черных шара. Найти вероятность
того, что хотя бы из одного ящика будет вынут один белый
шар, если из каждого ящика вынуто по одному шару.
Решение. Событие А = {хотя бы из одного ящика вынут
белый шар} можно представить в виде суммы А = Ах + А,, где
события Aj и ^ означают появление белого шара из первого
и второго ящика соответственно. Вероятность вытащить белый
шар из первого ящика равна Р(АХ) = 3/8, а вероятность
вытащить белый шар из второго ящика Р(А^ = 6/10. Кроме того,
в силу независимости Ах и А, имеем:
Р(АХА2) = Р(АХ)Р(А2) = ± ^ = 9/40.
По теореме сложения получаем:
Р(А) = Р(Ах+А2) = Р(Ах) + Р(А2)-Р(АхА2) = 3/% + 6/10-9/40 = 3/4.
Глава з ф
Р(А) = Р
АП
= />
и^ПЯ,) = ?/>(ЛПЯ,).
Применяя теорему умножения вероятностей для каждого
слагаемого, получаем окончательный результат:
Р(А) = ?/>(ЛпЯ,) = ^ГР(Н;)Р(А\Н{).
Задача 6. Три экзаменатора принимают экзамен по
некоторому предмету у группы в 30 человек, причем первый
опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента
(выбор студентов производится случайным образом из списка).
Отношение трех экзаменаторов к слабо подготовившимся
различное: шансы таких студентов сдать экзамен у первого
преподавателя равны 40%, у второго — только 10%, у третьего —
70%. Найти вероятность того, что слабо подготовившийся
студент сдаст экзамен.
Решение. Обозначим через Я,, Я2, Я3 гипотезы, состоящие
в том, что слабо подготовившийся студент отвечал первому,
второму и третьему экзаменатору соответственно. По условию
задачи
Р(Я,) = 6/30 = 0,2; />(#2) = 3/30 = 0,1; Р(Н3) = 21/30 = 0,7.
Пусть событие А = {слабо подготовившийся студент сдал
экзамен}. Тогда в силу условия задачи
p(A\Ht)=0A, р(а\н2)=ол, адя3)=о,7.
По формуле полной вероятности получаем
Р(Л) = 0,4х0,2 + 0,1х0,1 + 0,7х0,7 = 0,58.
Для решения задач такого типа удобно использовать так
называемое «дерево» вероятностей. Из формулы полной
вероятности следует, что для вычисления вероятности события А
необходимо осуществить перебор всех путей, ведущих к
результирующему событию А\ вычислить и расставить на соот-
51
то Я = Q и его вероятность равна единице: Р(Н) = 1. Из
теоремы сложения получаем Р(А п Я) = Р(А) + Р(Н) - Р(А и Я) =
= Р(А) + 1 - 1 = Р(А), или
ЧАСТЬ I. Теория вероятностей
РИС. 3.2
Задача 7. Компания имеет три источника поставки
комплектующих — фирмы А, В, С. На долю фирмы А
приходится 50% общего объема поставок, В — 30% и С — 20%. Из
практики известно, что среди поставляемых фирмой А деталей
10% бракованных, фирмой В — 5% и фирмой С — 6%. Какова
вероятность, что взятая наугад деталь окажется годной?
Решение. Пусть событие G — появление годной детали.
Вероятности гипотез о том, что деталь поставлена фирмами А,
В, С, равны сответственно Р(А) = 0,5; Р(В) = 0,3; P(Q = 0,2
(рис. 3.3). Условные вероятности появления при этом годной
52
ветствующих путях вероятности Р(Н) того, что движение будет
происходить по данному пути, и условные вероятности Р(А\Н)
того, что на данном пути будет достигнуто конечное событие А.
Затем вероятности, стоящие на одном пути, перемножаются,
а результаты, полученные для различных путей, складываются.
Каждое из условий может, в свою очередь, делиться на
несколько дополнительных условий или гипотез, т.е. на каждом
этапе оно допускает неограниченное число ветвлений схемы.
Поэтому при решении задач удобнее пользоваться не самой
формулой полной вероятности, а графической схемой
полной вероятности, которую называют «деревом» вероятностей
(см. рис. 3.2 для задачи 6).
Глава э
Рис. з-з
§ з.б. Формула Байеса
Предположим другую ситуацию: пусть известно, что
событие А произошло. Требуется найти вероятность того, что
событие А произошло именно путем Нк. Эти условные вероятности
вычисляются с помощью следующей теоремы.
> Теорема 6 (формула Байеса).
Р(Нк\А)= ,
?/>(#,.)• ад я,)
Отметим, что в знаменателе этой формулы записано не что
иное, как вероятность Р(А), вычисленная по формуле полной
вероятности.
53
детали равны P(G | А) = 0,9, P(G | В) = 0,95, P(G | С) = 0,94 (как
вероятности противоположных событий к появлению
бракованной). По формуле полной вероятности, используя «дерево»
вероятностей, получаем
P(G) = 0,5 х 0,9 + 0,3 х 0,95 + 0,2 х 0,94 = 0,923.
jjfc ЧАСТЬ I. Теория вероятностей
и аналогично
Р(Я2Й) = ^М = 0,214, Р(Н3\А)=^^
v 21 ' 0,42 31 0,42
Отсюда следует, что, вероятнее всего, слабо
подготовившийся студент сдавал экзамен третьему экзаменатору.
§ 37. Аксиоматическое построение теории
вероятностей
Ограниченность «классического» определения
вероятностей заложена в предположении равной возможности исходов.
Многие реальные случайные эксперименты не укладываются
также в рамки дискретной модели с конечным или счетным
пространством Q. Не всегда может помочь и геометрическая
интерпретация. Кроме того, возникают различные парадоксы.
Например, можно построить так называемые неизмеримые
множества, при попытке определить вероятность которых мы
приходим к противоречию.
Пример Вители. Пусть точку наудачу бросают на
окружность. Положение точки на окружности определяется углом
(от 0 до 2я). Выберем иррациональное число а > 0 и поставим
в соответствие каждой точке х класс точек Ах, получаемых из
54
Доказательство. По определению условной вероятности
Р(Н li)=P(AnHk) = P(Hk)P(A\Hk)
*' Р(А) Р(А)
где вероятность Р(А п Нк) найдена с помощью теоремы
умножения.
Задача 8 (см. задачу 6). Пусть известно, что студент не сдал
экзамен, т.е. получил оценку «неудовлетворительно». Кому из
трех преподавателей вероятнее всего он отвечал?
Решение. Вероятность получить «неуд» равна Р(А) = 1 —
- Р(А) = 1 - 0,58 = 0,42. Требуется вычислить условные
вероятности P{Hi | A), i — 1, 2, 3. По формуле Байеса получаем:
1 Р(А) 0,42
Глава з
нее поворотами на угол 2жхл, п = 0, 1, 2, ... Поскольку а
иррационально, у нас никогда не получится целое число оборотов,
а значит, все точки класса различны.
Для различных точек х классы Ах могут либо совпадать
(когда одна точка переходит в другую поворотом вида 2жхя), либо
не пересекаться нигде. Возьмем все непересекающиеся классы,
выберем из каждого по одной точке и объединим эти точки в
одно множество В0. Обозначим через Вп множество,
получающееся из В0 поворотом на угол 2жхя. Тогда множества Вп, п = О,
1, 2, ... не пересекаются, а их объединение дает всю окружность.
Следовательно, они образуют полную группу событий. Понятно,
что вероятности Вп равны между собой. Если предположить, что
они равны нулю, то в сумме получается ноль, хотя должна быть
единица. Если предположить, что они больше нуля, в сумме
получается бесконечность, что также неверно.
Поэтому в случае бесконечного пространства Q построение
современной теории вероятностей базируется на подходе,
предложенном великим русским математиком А.Н. Колмогоровым.
Основная идея подхода заключается в том, что не все
подмножества пространства Q рассматриваются как события.
Предполагается, что события — это некоторые подмножества
из пространства элементарных исходов Q, совокупность
которых замкнута относительно операций конечного или счетного
числа объединений и пересечений.
Пусть Q — произвольное пространство элементарных
исходов, а 3 — некоторый класс подмножеств множества Q.
Алгеброй событий 3 называется любая непустая система
подмножеств пространства Q, удовлетворяющая следующим
аксиомам:
1) если подмножество А принадлежит 3 (является
событием), то его дополнение А также принадлежит 3 (также является
событием);
2) если подмножества А и В принадлежат 3 (являются
событиями), то и их объединение А и В принадлежит 3 (также
является событием).
Поскольку любую из операций над подмножествами можно
получить, используя формулы де Моргана, с помощью только
двух операций дополнения и объединения
АГ)В = АиВ, А\В = АПВ = АиВ,
55 I
ЧАСТЬ I. Теория вероятностей
пересечение и разность двух событий также будут событиями:
А п В е 3, А\В е 3 при любых А е 3, В е 3. Отсюда следует,
что Q е 3 и 0 = Q\Q е 3 тоже события.
Алгебра событий 3 называется с-алгеброй, если объединение
счетного числа элементов из 3 также является элементом 3, т.е.
оо
из того, что Ап е 3, п = 1, 2, ... , следует (J Ап е 3.
Таким образом, а-алгебру событий 3 можно определить
как систему подмножеств пространства элементарных
исходов П, замкнутую относительно счетного числа теоретико-
множественных операций. Тривиальная а-алгебра событий
состоит из полного и пустого множеств: 3 = {0, Q}. Любая
а-алгебра событий является одновременно и алгеброй событий.
Обратное, вообще говоря, неверно, т.е. существуют алгебры
событий, не являющиеся ст-алгебрами.
Теперь, согласно аксиоматике Колмогорова, можно ввести
общее понятие вероятности события.
Вероятностью события, или вероятностной мерой, называется
числовая функция, заданная на а-алгебре событий 3, которая
каждому событию А е 3 ставит в соответствие число Р(А) так,
что выполняются следующие четыре аксиомы:
1. Аксиома неотрицательности: Р(А) > О для всех А е 3.
2. Аксиома нормированное™: P(Q) = 1.
(
3. Аксиома конечной аддитивности: Р
ил = Е^л) для
V/=i ) /=1
любых AinAj= 0, / *j\ и А. е 3 для любого /=1,2, п.
' 00 1 оо
4. Аксиома счетной аддитивности: Р (J4 =^Р(Д), если
,/=1 J /=i
события Л в последовательности Av А2, Ап, ... несовместны,
т.е. для любых А.пА.= 0, / фу, А. е 3 для любого / = 1, 2, ...
Очевидно, что вероятность, определенная в дискретном
вероятностном пространстве условием Р(А) = ^ /Чс^.), является
счетно-аддитивной. ,(й'€А
Заметим также, что введенные аксиомы в случае
дискретного пространства превращаются в доказуемые утверждения.
Конечно-аддитивная вероятность Р(Ап), заданная на
а-алгебре множеств 3, называется непрерывной, если для любой
I 56
Глава з ^
Р(В) = Р
(J*, +Р (J В, =^/>(5/) + Р(4),
откуда
JTP(Bi) = P(B)-P(An)->P(B) = P [JB,
i=\
n —> oo,
что и означает счетную аддитивность.
Докажем теперь, что из счетной аддитивности следует
непрерывность. Пусть последовательность Ап удовлетворяет условиям
аксиомы непрерывности. Введем события С = А^Ап+х. Тогда эти
события несовместны, причем допустимы представления:
4\л=Ск л=0сг
По теореме сложения получаем
Р(Ах) = Р(Ах\Ап) + Р(Ап) = р\()с\ + Р^
57
убывающей последовательности множеств Ляс 3, л = 1, 2, ...
оо
такой, что Ап+1 с Ля, имеющих пустое пересечение р|Л= 0>
имеет место равенство lim Р(А) = 0.
п—>оо
Аксиома непрерывности
?с/ш последовательность событий Ар А2... такова,
что каждое последующее вложено в предыдущее, а пересечение
всех событий Ап пусто, то P(AJ -> 0 при п -> оо.
> Теорема 7. Аксиома счетной аддитивности равносильна
аксиоме непрерывности.
Доказательство. Докажем сначала, что из непрерывности
следует счетная аддитивность. Рассмотрим последовательность
оо
несовместных событий Вп, и пусть B = [JBr Введем события
оо /=1
вида Ап= (J Д, тогда они удовлетворяют условиям аксиомы
/=л+1
непрерывности и Р(Ап) -> 0 при п оо. По теореме сложения
получаем
л-1
ЧАСТЬ I. Теория вероятностей
о
Задачи для самостоятельного решения
Теоретические задачи
1. Пусть А9 В9 С — три произвольных события. Найти выражение для
событий, состоящих в том, что: а) произошли все три события;
б) произошло хотя бы одно из событий; в) произошли хотя бы два
события; г) произошло ровно два события; д) произошло ровно
одно событие; е) ни одно событие не произошло; ж) произошло
не более двух событий.
2. Прибор состоит из трех блоков первого типа и четырех блоков
второго типа. Событие А. = {исправен /*-й блок первого типа},
/ = 1, 2, з; В. = {исправен у-й блок второго типа}, / = 1, 2, 3, 4.
Прибор работает, если исправны хотя бы один блок первого типа и
не менее трех блоков второго типа. Найти выражение для события
С, которое соответствует рабочему состоянию прибора.
3. Бросают две игральные кости. Пусть А — событие, состоящее в
том, что сумма очков четная; В — событие, заключающееся в том,
что хотя бы на одной из костей выпала единица. Составить
пространство элементарных событий Q, связанное с данным опытом,
и описать событие А Г)В.
4. Событие А — хотя бы одно из трех изделий бракованное, В — все три
изделия качественные. Что означают события: а) АиВ ; б) АПВ?
5. Рабочий обслуживает три автоматических станка. События А, В, С
заключаются в том, что первый, второй или третий станок
соответственно потребует внимания рабочего в течение часа.
58
откуда
л-1 ( оо
P(A„) = P(A1)-J2P(CI) = P ус, -^Р(С()^0, я-оо,
/=1 \i=\ J /=1
так что аксиома непрерывности выполняется.
Тройка (Q, 3, Р), где Q — пространство элементарных
событий, 3 — а-алгебра подмножеств Q, называемых событиями,
Р — вероятностная мера, определенная на событиях,
называется вероятностным пространством.
Далее будем всюду неявно предполагать, что любые
рассматриваемые множества относятся к некоторой а-алгебре 3,
а вероятность удовлетворяет всем необходимым аксиомам.
Глава з ф
Что означают события: _ _ _ _ _ _
а)ABC; 6)А + В+ С; в) АпВпС + АГ1ВГ1С + АпВпС;
г) ЛПЯПС+ЛПЯПС+ЛПЯПС; д) ЛПЯПС?
6. Страховые компании интересуются распределением возрастов
супругов. Пусть/означает возраст мужа, a y— возрастжены. Каждое
наблюдение дает пару чисел (X, V). В качестве пространства
элементарных событий Q берем i-й квадрант, т.е. любая точка % y),
x > о, y > о — элементарное событие. Событие а — мужу более
40 лет, событие в — муж старше жены, событие С — жене более
40 лет. Что означают события: а) а п в; б) а п в; в) а п С; г) >А и С;
д)^иб;е)8пС? Изобразить эти события графически.
Вычислительные задачи
7. Рабочий обслуживаеттри независимо работающих станка. Событие
А, = {/-й станок в течение часа потребует наладки}, р(а) = о,2; / = 1,
2, 3. Выразить события: а) ровно два станка потребуют наладки;
б) не более двух станков потребуют наладки; в) хотя бы один
станок потребует наладки. Найти вероятность события в).
8. Стрелок делает три выстрела, при этом он поражает цель с
вероятностью о,6 при одном выстреле. Событие At = {/-я пуля попала
в цель}, /' = 1, 2, 3. Выразить события: а) было хотя бы одно
попадание; б) было ровно одно попадание; в) было не менее двух
попаданий. Найти вероятность события в).
9. В коробке 4 детали. Мастер извлекает детали до тех пор, пока не
вытащит годную (или пока они не кончатся). Событие А = {/-я
извлеченная деталь является годной}, р(а) = 0,9, / = 1, 2, 3, 4. Выразить
события, состоящие в том, что мастер сделал: а) ровно одно
извлечение; б) ровно 2 извлечения; в) не менее двух извлечений.
Найти вероятность события б).
ю. В пакете с леденцами лежат 4 красных, 5 желтых и 6 зеленых
конфет. Найти вероятность вынуть наудачу подряд 3 конфеты одного
цвета.
11. В партии из 20 изделий 4 бракованных. Найти вероятность того,
что в выборке из 5 изделий не более одного бракованного.
12. В лифт девятиэтажного дома на первом этаже входят 6 человек.
Для каждого равновероятен выход на любом из остальных 8
этажей. Известно, что все вышли на разных этажах. При этом
условии найти вероятность того, что на первых трех этажах (из восьми)
вышли два человека.
v
59
ЧАСТЬ I. Теория вероятностей
13. Три пассажира садятся в поезд, случайно выбирая любой из 6
вагонов. Какова вероятность, что хотя бы один из них сядет в первый
вагон, если известно, что все они сели в разные вагоны?
14. В ящике 12 красных, 8 зеленых и ю синих шаров. Наудачу
вынимаются два шара. Какова вероятность, что вынутые шары разного
цвета, если известно, что не вынут синий шар?
15. Шесть шаров случайным образом раскладывают в три ящика.
Найти вероятность, что во всех ящиках окажется разное число шаров
при условии, что все ящики не пустые.
16. Двое шахматистов равной силы играют 4 партии (без ничьих).
Найти вероятность, что в результате победил первый, если известно,
что в процессе игры каждый выиграл хотя бы один раз.
17. В лифт на цокольном этаже входят 5 человек. Считая для каждого
человека равновероятным выход на любом из 9 этажей, найти
вероятность того, что двое из них выйдут на одном этаже, а
остальные — на разных.
18. Известно, что все цифры 5-значного номера телефона разные.
Какова при этом условии вероятность, что среди них ровно одна
цифра четная (считаем, что номер может начинаться с нуля)?
19. Пять человек случайным образом (независимо друг от друга)
выбирают любой из 7 вагонов поезда. Известно, что ровно 2 вагона
остались пустыми. При этом условии найти вероятность того, что
первый и второй вагоны заняты.
20. В урне 5 белых и ю черных шаров. Извлечены 6 шаров (с
возвращением). Известно, что среди них есть белые шары. При этом
условии найти вероятность того, что среди них будет также не
менее двух черных шаров.
21. Семь пассажиров случайным образом выбирают один из 9
вагонов поезда. Известно, что они сели в разные вагоны. При этом
условии найти вероятность того, что в первых трех вагонах поезда
будут ехать два человека.
22. Пять шаров распределены по трем ящикам. Известно, что нет
пустых ящиков. При этом условии найти вероятность того, что в
первом ящике лежит один шар.
23. В четырех группах учится юо человек (по 25 человек в каждой).
На олимпиаду отобрано 5 человек. Какова вероятность того, что
среди них будут представители всех групп?
24. Сколько раз надо бросить игральную кость, чтобы не менее чем
на 95% быть уверенным в том, что хотя бы при одном бросании
появится «шестерка»?
V J
60
Глава з ^
25. Известно, что в пятизначном числе все цифры разные. Найти
вероятность того, что среди них есть цифры i и 2 (считаем, что число
может начинаться с нуля).
26. Бросают три кубика. Какова вероятность того, что хотя бы на одном
из них выпадет «шестерка», если известно, что на всех кубиках
выпали разные грани?
27. Фирма участвует в 4 проектах, каждый из которых может
закончиться неудачей с веростностью 0,1. В случае неудачи одного проекта
вероятность разорения фирмы равна 20%, двух — 50%, трех —
70%, четырех — 90%. Найти вероятность разорения фирмы.
28. Два аудитора проверяют ю фирм (по 5 фирм каждый), у двух из
которых имеются нарушения. Вероятность обнаружения
нарушений первым аудитором равна 8о%, вторым — 90%. Найти
вероятность, что обе фирмы-нарушителя будут выявлены.
29. В первой урне лежат i белый и 3 черных шара, а во второй урне —
2 белых и 1 черный шар. Из первой урны во вторую
перекладывается, не глядя, один шар, а затем один шар перекладывается из
второй урны в первую. После этого из первой урны вынули один
шар. Найти вероятность, что он белый.
30. В прибор входит комплект из двух независимых деталей, для
которых вероятность выйти из строя в течение года соответственно
равна 0,1 и 0,2. Если детали исправны, то прибор работает в
течение года с вероятностью 0,99. Если выходит из строя только
первая деталь, то прибор работает с вероятностью 0,7, а если только
вторая — то с вероятностью о,8. Если выходят из строя обе детали,
прибор будет работать с вероятностью 0,1. Какова вероятность,
что прибор будет работать в течение года?
31. Электроэнергия поступает в город через три электролинии, каждая
из которых может быть отключена с вероятностью 0,1. Если
отключена одна электролиния, город испытывает недостаток
электроэнергии с вероятностью 0,2. Если отключены две электролинии,
недостаток электроэнергии ощущается с вероятностью 0,5. Если же
отключены все три электролинии, то недостаток электроэнергии
наступает с вероятностью 1. В случае, когда работают все
электролинии, недостатка энергии нет. Какова вероятность того, что город
испытывает недостаток электроэнергии?
32. Фирма нарушает закон с вероятностью 0,25. Аудитор
обнаруживает нарушения с вероятностью 0,75 (если они есть). Проведенная
им проверка не выявила нарушений. Найти вероятность того, что
на самом деле они есть.
61
ЧАСТЬ I. Теория вероятностей
33. Изделие имеет скрытые дефекты с вероятностью 0,2. В течение
года выходит из строя 75% изделий со скрытыми дефектами и
15% изделий без дефектов. Найти вероятность того, что
изделие имело скрытые дефекты, если оно вышло из строя в течение
года.
34. Из урны, где было 4 белых и 6 черных шаров, потерян один шар
неизвестного цвета. После этого из урны извлечены (без
возвращения два шара, оказавшиеся белыми. При этом условии найти
вероятность того, что потерян был черный шар.
35. Производственный брак составляет 4%. Каждое изделие
равновероятным образом поступает к одному из двух контролеров,
первый из которых обнаруживает брак с вероятностью 0,92,
второй — 0,98. Какова вероятность, что признанное годным изделие
является бракованным?
36. В центральную бухгалтерию корпорации поступили пачки
накладных для проверки и обработки. Удовлетворительными были
признаны 90% пачек: они содержали 1% неправильно оформленных
накладных. Остальные ю% накладных были признаны
неудовлетворительными, так как они содержали 5% неправильно
оформленных накладных. Какова вероятность того, что взятая наугад
накладная окажется неправильно оформленной?
37. Известно, что проверяемая фирма может уходить от налогов с
вероятностью 40% и выбрать для этого одну из трех схем
(равновероятно). Найти вероятность того, что фирма уходит от налогов
по третьей схеме, если при проверке по первым двум схемам
нарушений не обнаружено.
38. Стрелок а поражает мишень с вероятностью о,6, стрелок Б — с
вероятностью 0,5 и стрелок в — с вероятностью 0,4. Стрелки дали
залп по мишени, и две пули попали в цель. Что вероятнее: попал
стрелок В в мишень или нет?
39. Имеются три партии по 20 деталей в каждой. Число стандартных
деталей в первой, второй и третьей партиях соответственно
равно 20, 15 и ю. Из наудачу выбранной партии извлечена деталь,
оказавшаяся стандартной. Деталь вернули в партию и вторично
из той же партии наугад извлекли деталь, которая оказалась
стандартной. Найти вероятность того, что детали были извлечены из
третьей партии.
62
V )
Глава з ф
63
v )
40. На заводе установлена аварийная сигнализация, которая в случае
аварии срабатывает с вероятностью 99%. Однако в 0,1% случаев,
когда аварии нет, сигнал также может возникнуть. Найти
вероятность того, что случилась авария, если сигнализация сработала.
Вероятность аварии 0,005.
41. В продукции птицефабрики 70% яиц стандартных, 20% большего
объема и ю% двухжелтковых. С какой вероятностью среди 5
случайно выбранных яиц найдутся хотя бы одно большего объема и
хотя бы одно двухжелтковое (вместе)?
42. Студент в состоянии решить 25 задач из 30 в первом туре экзамена
и 18 из 24 — во втором. Найти вероятность сдачи им экзамена,
если в каждом туре дается четыре задачи и достаточно решить три
из них.
43. Из ю лотерейных билетов 3 выигрышных. При подготовке вечера
2 билета потеряли, и было решено добавить i выигрышный. Какой
стала вероятность вытянуть выигрышный билет?
44. Фирма А занимает 20% рынка электронной техники, фирма Б —
50%, фирма В — 30%. Доля мобильных телефонов в поставках
фирмы А составляет 20%, в поставках фирмы Б — 40%, в
поставках фирмы В — 70%. Покупатель приобрел мобильный
телефон. Какова вероятность того, что этот телефон произведен
фирмой А?
45. В магазине было проведено исследование продаж некоторого
товара. Выяснилось, что этот товар покупают 25% женщин, ю%
мужчин и 20% детей. Среди покупателей магазина 6о% женщин,
30% мужчин и ю% детей. Найти вероятность того, что случайный
покупатель приобретет этот товар.
46. Есть две упаковки орешков, в каждой из которых 5 орехов с белой
глазурью и 4 — с черной. Из первой упаковки достали 2 орешка,
после чего ее смешали со второй упаковкой. Какой стала
вероятность достать орех с белой глазурью?
47. В компании 70% менеджеров работают в центральном офисе,
30% — в региональных. Вероятность того, что менеджеру
центрального офиса потребуется консультация специалиста, равна
0,3, менеджеру регионального офиса — 0,5. Одному из
менеджеров потребовалась консультация. Какова вероятность того, что он
работает в центральном офисе?
ф ЧАСТЬ I. Теория вероятностей
48. Фирма занимается строительством домов по одному из двух
типовых проектов. При строительстве по первому проекту нарушение
технологий происходит с вероятностью 0,3, а по второму — 0,2.
При этом дома первого и второго типа составляют
соответственно 40 и 50% общего объема строительства. Какова вероятность
того, что случайно выбранный дом построен с нарушением
технологии?
49. К системному администратору обращаются пользователи. Среди
них начинающих — 6о%, опытных — 40%. Вероятность того, что
за помощью обратится начинающий пользователь — 8о%,
опытный — ю%. Найти вероятность того, что очередной пользователь,
обратившийся за помощью, окажется начинающим.
50. Среди клиентов туристической фирмы 30% ездили в Турцию,
20% — в Египет, ю% — в Грецию; в Турцию и Египет — 12%, в
Египет и Грецию — 5%, в Турцию и Грецию — 6%, во все три
страны — 4%. Найти вероятность того, что случайно выбранный
клиент: а) ездил в Турцию или Египет, б) ездил в Египет или Грецию,
в) ездил в Турцию, Египет или Грецию, г) не ездил ни в одну из
перечисленных стран.
I ЧАСТЬ I. Теория вероятностей
Число всех комбинаций такого рода равно числу способов,
какими можно из п элементов одновременно выбрать т
элементов, соответствующих т появлениям события А, т.е. числу
сочетаний С". Вероятность каждой такой комбинации
(каждого слагаемого) по теореме умножения независимых событий
равна pmq"~m, а так как составляющие событие Вт являются
несовместными событиями, то согласно теореме сложения
несовместных событий Р(Вт) = Рп (т) = С" pmqn~m.
Задача 1. Игральная кость брошена 6 раз. Найти
вероятность того, что ровно 3 раза выпадет «шестерка».
Решение. Шестикратное бросание кости можно
рассматривать как последовательность независимых испытаний с
вероятностью успеха («шестерки»), равной 1/6, и вероятностью
неудачи — 5/6. Искомую вероятность вычисляем по формуле
66
Эта формула называется формулой Бернулли.
Схему испытаний Бернулли называют также биномиальной
схемой, а соответствующие вероятности — биномиальными, что
связано с использованием биномиальных коэффициентов С*.
Доказательство. Каждое испытание Бернулли описывается
пространством элементарных исходов Q = {У, Н}, состоящим
из двух элементов: У (успех) и Н (неудача), а также их
вероятностями Р(У) = р, Р(Н) = q, р + q = 1. Примем успех в
испытании за событие А.
Составной эксперимент (серия из п испытаний) задается
пространством Qn, каждый элемент которого представляет
собой упорядоченный я-мерный набор конкретных результатов
этих испытаний. Обозначим через Вт событие, состоящее в том,
что в п опытах событие А появилось ровно т раз. Разложим
событие Вт в сумму произведений событий, состоящих в
появлении и непоявлении события А в отдельных опытах, при
этом обозначим через А. появление события А в /-м опыте и
Ai — непоявление А в /-м опыте. Тогда каждый вариант
события В состоит из т появлений события Ак п - т непоявлений
т
события А, т.е.
Глава 4 ф
Задача 2. Монета бросается 6 раз. Найти вероятность того,
что герб выпадет не более 2 раз.
Решение. Искомая вероятность равна сумме вероятностей
трех событий, состоящих в том, что герб не выпадет ни разу,
либо один раз, либо два раза:
Р(А) = Р6(0) + Р6(1) + Р6(2) =
чО
г
6
(4
т5
-\ +cl
\Ш
[2)
2 6
Задача 3. Аудитор обнаруживает финансовые нарушения у
проверяемой фирмы с вероятностью 0,9. Найти вероятность
того, что среди 4 фирм-нарушителей будет выявлено больше
половины.
Решение. Событие состоит в том, что из 4 фирм-нарушителей
будет выявлено три или четыре, т.е.
Р(А) = Р4(3) + Р4(4) =С430,93 • 0,1 +С440,94 = 0,93(0,4 + 0,9) = 0,9477.
§ 4*2. Наивероятнейшее число успехов
Число /и, при котором биномиальные вероятности Рп(т)
достигают своего максимального значения (при
фиксированном числе испытаний л), называют наиболее вероятным (наи-
вероятнейшим) числом успехов. Справедливо следующее
утверждение.
^ Теорема 2. Наивероятнейшее число успехов т * в серии из п
независимых испытаний Бернулли (с вероятностью успеха р в одном
испытании) определяется соотношением пр - q < т* < пр + р,
причем:
1) если число пр — q — дробное, то существует одно
наивероятнейшее число т*;
2) если число пр — q — целое, то существует два наивероят-
нейших числа:
т* = пр — q, т* - пр + р\
3) если пр — целое число, то наивероятнейшее число т* = пр.
67 j
ф ЧАСТЬ I. Теория вероятноаей
Рп(т*) (m* + l)q
Рп(т*) _(п-т* + 1)р
Pn(m*-l) m*q
>1 получаем т* < пр + р. Таким
образом, получаем, что т* лежит в интервале единичной длины
пр — q < т* < пр + р, причем, обозначив через т* = [пр — q]
целую часть числа пр — q, получим:
1) если число пр — q — дробное, то имеется единственное
целое число т - (т* + 1), принадлежащее промежутку [пр — q\
пр + р], для которого вероятность Рп(т) достигает своего
максимального значения: Рп(т* + 1) = max Рп(т)9 т = 0, 1, п\
2) если число пр — q — целое, то имеются две точки
максимума т* = пр — q и т* + 1 = пр + р:
maxP(m) = Рп(т*) = Рп(т* + 1), т = О, 1, п.
Последнее равенство следует из непосредственной проверки
Рп(т*+\) (п-т*)р
того, что отношение — = - — равно единице, если
заменить т* на пр — q9 a q на 1 - р\
3) если пр целое, то наивероятнейшее число т* = пр.
Действительно, если пр — целое, то в промежутке пр — q < m < пр + р9
длиной единица (р + q = 1), содержится единственное целое
число — пр.
68
Доказательство. Рассмотрим отношение двух соседних
с РЛ(т + \) (п-т)р
вероятностей. Если отношение — = - — больше
Рп(т) (m + \)q
единицы, то последующая вероятность Рп(т + 1)
превышает предыдущую Рп{т). Если же Рп(т + 1) < Ря(т)9 то отно-
Рп(т + \) (п-т)р тт
шение — = - — меньше единицы. Для нахождения
Рп(т) (m + \)q w
наивероятнейшего числа т* надо уловить тот момент, когда
отношение, большее единицы, станет меньше единицы, т.е.
найти такое /я*, для которого одновременно выполняются не-
равенства — <1, —- >1. Тогда из неравенства
Рп(т) ~ Рй{т-1)~
" - - < 1 получаем т* > пр — q, а из неравенства
Глава 4 Ф
т
0
1
2
3
ад
1/8
3/8
3/8
1/8
Из таблицы видно, что наиболее вероятными значениями
являются числа 1 и 2 (их вероятности равны 3/8). Этот же
результат можно получить и из теоремы 2. Действительно, п = 3,
р = 1/2, q = 1/2. Тогда
Зх---<т <3х- + -, т.е. \<т<2.
2 2~ " 2 2' " "
Задача 5. Вероятность получения удачного результата при
производстве сложного химического опыта равна 3/4. Найти
наивероятнейшее число удачных опытов, если общее их число
равно 10.
Решение. В этом примере п = 10, р = 3/4 = 0,75, q = 1/4 =
= 0,25. Тогда неравенство для наиболее вероятного числа
успехов имеет вид: 10 х 0,75 - 0,25 < т* < 10 х 0,75 + 0,75 или
7,25 < т* < < 8,25. Существует только одно целое решение этого
неравенства, а именно т* = 8.
Задача 6. В результате каждого визита страхового агента
договор заключается с вероятностью 0,1. Найти наивероятнейшее
число заключенных договоров после 25 визитов.
Решение. Имеем п = 10, р = 0,1, q = 0,9. Неравенство для
наиболее вероятного числа успехов принимает вид: 25 х 0,1 — 0,9 <
й т* < 25 х 0,1 + 0,1 или 1,6 < т* < 2,6. У этого неравенства
только одно целое решение: ая* = 2.
69
Задача 4. Монета подбрасывается 3 раза. Найти наиболее
вероятное число успехов (выпадений герба).
Решение. Возможными значениями для числа успехов в трех
рассматриваемых испытаниях являются т = О, 1,2 или 3. Пусть
Ат — событие, состоящее в том, что при трех подбрасываниях
монеты герб появляется т раз. По формуле Бернулли легко
найти вероятности событий А .
ф ЧАСТЬ I. Теория вероятностей
Поскольку при больших п верно пр « X, то можно считать,
Хт^
ml
что X = пр. Предельные вероятности Рп(т) « —j— называются
пуассоновскими.
Формула Пуассона выражает закон распределения Пуассона
вероятностей массовых (п велико) и редких (р мало) явлений.
Отсюда название закона Пуассона — закон редких явлений.
Закон Пуассона широко применяют в теории информации,
в теории массового обслуживания при изучении потока
событий.
70
§ 4.3. Предельные теоремы
и приближенные формулы
При больших значениях п непосредственное нахождение
вероятностей Рп(т) по формуле Бернулли сопряжено с
трудностями вычислительного характера, поэтому в таких случаях
используют различные варианты приближенных формул,
основанных на предельных теоремах Пуассона и Муавра—Лапласа.
А. Приближенная формула Пуассона используется в том
случае, когда число испытаний п велико, а вероятность успеха в
отдельном испытании мала (р < 0,1) и при этом пр невелико
(пр < 10).
^ Теорема Пуассона. Пусть п -»00, р -> 0, пр -> X = const Тогда
\т
Р(т)->—е-\
т\
Доказательство. По формуле Бернулли, после умножения
числителя и знаменателя на пт и некоторых преобразований,
получаем
РЙМ = СЙУГ = п(п-\)...(п-т + \)рт {х_р)п.т =
ml
= n(n-l)...(n-m + l)nm пр =
- т\пт(\-р)т п
ml п (\-р)т ml F
Глава 4 ф
1) Лооо(З) * jf
-5.
2) Pim(m>3) = 1 -Pim(m < 3) = 1 -[Pim(0)+Pim(l) + Pim(2)] *
* 1 - ^2—e~5> и по табл. 3 приложения 2 находим Р{т(3) «0,14;
Р1т(т > 3) « 0,875.
Б. Приближенные формулы Муавра-Лапласа. Предположим,
что в схеме независимых испытаний Бернулли число
испытаний п велико, а вероятности «успеха» и «неудачи» не малы
(например, 0,1 < р < 0,9) или пр не мало (пр > 10),
> Локальная теорема Муавра-Лапласа. Пусть р = const, л -»оо,
тогда
РЛт)*Щ, х = ^,
Jnpq 4npq
1
где ф(х) = -г=е 2 .
л/2тг
Функция ф(х) — четная, и для положительных значений х
составлена таблица ее значений (приложение 2).
71
В силу определенной «симметричности» понятий «успех» и
«неудача» приближенная формула Пуассона может
использоваться в схеме независимых испытаний Бернулли при больших
п также и в случае, когда р близко к единице, т.е. при q < 0,1
и nq < 10:
л т
;(л-/я) = Сп р q =Спр q &—е , X = nq.
Задача 7. Известно, что процент брака для некоторой
детали равен 0,5%. Контролер проверяет 1000 деталей. Какова
вероятность обнаружить ровно три бракованные детали? Какова
вероятность обнаружить не меньше трех бракованных деталей?
Решение. Имеем 1000 испытаний Бернулли с вероятностью
«успеха» р = 0,005. Применяя пуассоновское приближение с
X = пр = 5, получаем:
р ЧАСТЬ I. Теория вероятностей
у <х
4ш
J e~2dz,
где т — число успехов для любого числа х.
Отсюда следует, что для вычисления вероятности Рп(тх, т2) =
= Р(тх<т <т2) события, состоящего в том, что число успехов
т в п испытаниях Бернулли окажется заключенным в пределах
от тх до mv можно использовать приближенную формулу
Рп (Щ, 1Щ ) = Ф0 (хх) - Ф0 (х2),
-п -п Iх-—
где хх = m'r—Р , х2 = т2_а_р ? а Ф0(х) = -= fe2dz~ функция
Лапласа.
Функция Ф0(х) равна 0 при jc = 0. Ф0(—х) = ~Ф0(х) для всех
х, т.е. функция нечетная. Для функции Ф0(х) составлены
специальные таблицы при некоторых положительных значениях
аргумента (табл. 2 приложения 2). При х > 5 можно считать, что
Ф0(*) = 0,5.
Задача 9. Страховая компания заключила 40 000 договоров.
Вероятность страхового случая по каждому из них в течение
года составляет 2%. Найти вероятность того, что таких случаев
будет не более 870.
72
Задача 8. Вероятность покупки при посещении клиентом
магазина составляет р = 0,75. Найти вероятность того, что при
100 посещениях клиент совершит покупку ровно 80 раз.
Решение. В данном случае п = 100, т = 80, р = 0,75, q = = 0,25.
„ . 80-100x0,75 ллс _ - -
Найдем х = . =1,16, и по табл. 1 приложения 2
^/100x0,75x0,25
определяем ср(х) = 0,2036, тогда искомая вероятность Р100(80) =
= 0.2036 =
7100x0,75x0,25
^ Интегральная теорема Муавра-Лапласа. Пусть р = coaw/,
п -юо, тогда
1
Глава 4 ф
емся интегральной теоремой Лапласа:
Р(0 < т <
870-800
Р(0<т< 870) = Ф0(х2) - Ф0(дс.), где х, = =-28,57 и
28
28
- = 2,5.
Находим по таблице значений функции Лапласа:
Рф < т <l 870) = Ф0(х2) - Ф0(х.) = Ф0(2,5) - Ф0(-28,57) =
= 0,4938 + 0,5 = 0,9938.
Следствие (интегральной теоремы Муавра-Лапласа)
Вероятность того, что относительная частота появления
успеха в п независимых испытаниях Бернулли (т.е. число т/п)
отклонится от вероятности успеха не более чем на е > 0, может
быть найдена по формуле
т
Р
<е«2Ф0
п
J
Доказательство получаем из следующей цепочки очевидных
равенств:
т
= Р р—е < — </> + е = P(np-ns<m<np + ns)z
*Фп
пр + пг-пр
yfnpq J °[ 4т )
пр-пе-пр
= Ф„
Ф,
-8
= 2Ф
Задача 10. Вероятность появления события в каждом из 400
независимых испытаний равна 0,8. Найти такое
положительное число е, чтобы с вероятностью 0,99 абсолютная величина
отклонения относительной частоты появления события от его
вероятности не превышала е.
Решение. В этом примере р = 0,8, п = 400. По условию задачи
р
т
Р
< 8
= 0,99 = 2q>
п
>
. Следовательно, ф0
п
\ pq
= 0,495.
73
Решение. По условию задачи п = 40 ООО, р = 0,02, пр = 800,
yfnpq = 28. Для вычисления вероятности Р(т < 870)
воспользуф ЧАСТЬ I. Теория вероятностей
§ 4.4. Полиномиальные испытания
От схемы независимых последовательных испытаний с
двумя исходами (схема Бернулли или биномиальная схема) можно
перейти к полиномиальной схеме, т.е. к схеме последовательных
независимых испытаний, в каждом из которых возможны к ис-
к
ходов, к > 2, с вероятностями pv pv pk, 0 < pt< 1, YlPi~
/=1
В этом случае пространство элементарных событий содержит к1
таких событий, а вероятность того, что из п испытаний т]
закончатся первым исходом, т2 — вторым исходом, тк — к-м
исходом, равна
щ ищ!... тк!
Эта формула также описывает полиномиальный закон
распределения.
74
По таблице для функции Лапласа определяем г I— = 2,58; и
значит, б = 0,0516. Р^
Приближенную формулу можно использовать и в
следующей «урновой» схеме: из генеральной совокупности объема
N, содержащей М белых и N— М черных шаров,
осуществляется последовательный выбор п элементов без возвращения.
Вероятность того, что в полученной выборке окажется ровно
m белых шаров, вычисляется по формуле
Если объем генеральной совокупности и число белых шаров
достаточно велики (N -> оо, М -> оо, M/N ->р = const), то «урно-
вую» схему можно приближенно заменить схемой Бернулли
^v(>">")~W> где Рп(т) = Сутд"-т.
Далее, при необходимости, можно использовать формулы
Пуассона и Муавра—-Лапласа.
Глава 4 ф
Полиномиальную схему можно трактовать как обобщение
статистики Максвелла—Больцмана на случай, когда
вероятности попадания каждой частицы в различные ячейки
различны.
Задана 11. Шесть рукописей раскладываются случайным
образом в пять папок. Какова вероятность, что ни одна папка
не останется пустой?
Решение. На раскладку 6 рукописей в папки можно смотреть
как на серию шести полиномиальных испытаний с 5 исходами
(попадание в /-ю папку — это /-й исход). Вероятности исходов
(папок) совпадают и равны р{ = р2 = ... = рк = 1/5. Событие
А = {ни одна папка не останется пустой} означает, что в одну
папку попадут 2 рукописи, а в остальные папки — по одной
рукописи. Следовательно, вероятность того, что в первую папку
попадут 2 рукописи, а в остальные папки — по одной
рукописи, равна
/>(2,1,1,1,1) =
6! [1]
(If
Г
1
(If
Y
2! l!l!l!l!(5j
Ы
,5,
-5,
а вероятность искомого события А (для которого неважно, в
какую из 5 папок попадают две рукописи) равна
Р(Л) = 5Р6(2,1,1,1,1) = 5х| 1 = | 1 = 0,1152.
Задана 12. Курс акции за день может подняться на 1 пункт
с вероятностью 50%, опуститься на 1 пункт с вероятностью 30%
и остаться неизменным с вероятностью 20%. Найти вероятность
того, что за 5 дней торгов курс поднимется на 2 пункта.
Решение. Возможны только следующие два варианта
развития событий:
1) курс растет 2 дня, ни разу не падает, не меняется 3 дня;
2) курс растет 3 дня, падает 1 день, не меняется 1 день.
Таким образом,
Р(А) = />(2, 0, 3) + Р5(3,1,1) = ^|^0,52 х 0,3° х 0,23 +
+ —^- 0,53х 0,3^0,^= 0,02 + 0,15 = 0,17.
ф ЧАСТЬ I. Теория вероятностей
Задачи для самостоятельного решения
1. Ежедневно новая сделка совершается с вероятностью о,2 (но не
более одной в день). Какова вероятность того, что за 5 дней будет
совершено 3 сделки?
2. В результате каждого визита страхового агента договор
заключается с вероятностью 1/4. Какова вероятность того, что из ю визитов
страхового агента 5 закончатся заключением договора?
3. Вероятность поражения мишени стрелком равна 0,9. Найти
вероятность того, что он поразит мишень ровно два раза, сделав 5
выстрелов.
4. Для вычислительной лаборатории приобретено 9 компьютеров,
причем вероятность брака для одного компьютера равна 0,1.
Какова вероятность того, что придется заменить более двух
компьютеров?
5. Зачетная работа по предмету состоит из 6 задач, при этом зачет
считается сданным, если студент решил хотя бы 3 задачи. Студент
Иванов может решить каждую задачу с вероятностью о,6. Какова
вероятность того, что он сдаст зачет?
6. Тест по теории вероятностей состоит из ю вопросов. На каждый
вопрос в тесте предлагается 4 варианта ответа, из которых надо
выбрать один правильный. Какова вероятность того, что,
совершенно не готовясь к тесту, студенту удастся угадать правильные
ответы по крайней мере на 6 вопросов?
7. Статистика аудиторских проверок компании утверждает, что
вероятность обнаружения ошибки в каждом проверяемом документе
равна 0,1. Какова вероятность того, что из ю проверенных
документов большинство документов будет без ошибок?
8. Два равносильных противника играют в шахматы. Что вероятнее:
а) выигрыш одной партии из двух или двух партий из четырех;
б) выигрыш не менее двух партий из четырех или не менее трех
партий из пяти? Ничьи во внимание не принимаются.
9. Мастер и ученик играют шахматный матч. Мастер побеждает в
матче, если он выиграл все партии, ученик побеждает в матче, если
он выиграл хотя бы одну партию. Из какого числа партий должен
состоять матч, чтобы шансы на победу у мастера и ученика были
равны, если вероятность победы мастера в одной партии равна
0,9, а ученика — 0,1?
V j
Глава 4 ф
ю. Испытание состоит в подбрасывании трех кубиков. Сколько раз
нужно провести испытание, чтобы с вероятностью не менее 0,95
хотя бы один раз появились три «единицы»?
11. В некотором многочисленном сообществе 5% левшей. Каков
должен быть объем случайной выборки, чтобы вероятность встретить
в ней хотя бы одного левшу была не менее о, 95?
12. В коробке 4 детали. Вероятность, что деталь стандартная, равна 0,9.
Сколько надо взять коробок, чтобы с вероятностью не менее 0,99
среди них нашлась хотя бы одна коробка, не содержащая брак?
13. Сколько раз надо двукратно подбросить монету, чтобы с
вероятностью не менее 0,95 хотя бы один раз появилось событие «один
герб и одна решка»?
14. Вероятность хотя бы одного попадания при двух выстрелах равна
0,96. Найти вероятность трех попаданий при четырех выстрелах.
15. Проводится 12 независимых испытаний с вероятностью успеха,
равной 0,4. Найти наиболее вероятное число успешных испытаний.
16. Сколько надо сделать выстрелов с вероятностью попадания в цель
0,7, чтобы наивероятнейшее число попаданий в цель составило 15?
17. Система состоит из 6 независимо работающих элементов.
Вероятность отказа элемента равна 0,3. Найти: а) наивероятнейшее число
отказавших элементов; б) вероятность наивероятнейшего числа
отказавших элементов системы; в) вероятность отказа системы, если
для этого достаточно, чтобы отказали хотя бы 5 элементов.
18. Игральная кость бросается 16 раз. Найти наивероятнейшее число
бросаний, в которых выпало число очков, кратное трем, и
вычислить его вероятность.
19. Сколько раз надо бросить игральную кость, чтобы
наивероятнейшее число появлений четного числа очков составило 6?
20. Сколько надо сыграть партий в шахматы с вероятностью победы
в одной партии, равной 1/3, чтобы наивероятнейшее число побед
было равно 5?
21. Каждый из юо компьютеров в интернет-кафе занят клиентами в
среднем в течение 8о% рабочего времени. Какова вероятность
того, что в некоторый момент клиентами будет занято: а) от 70 до
90 компьютеров; б) не менее 8о компьютеров?
22. Известно, что вероятность «зависания» компьютера равна о,6%.
Какова вероятность того, что из 200 компьютеров «зависнут»:
а) ровно 6 компьютеров; б) не более 5 компьютеров?
77
v )
ф ЧАСТЬ I. Теория вероятностей
23. При наборе текста наборщик делает ошибку в слове с
вероятностью 0,001. Какова вероятность того, что в набранной книге,
насчитывающей 5000 слов, будет не более 5 ошибок?
24. Страховая фирма заключила ю ооо договоров. Вероятность
страхового случая по каждому в течение года составляет 2%. Найти
вероятность того, что таких случаев будет не более 250.
25. Сборник задач содержит 400 задач с ответами. В каждом ответе
может быть ошибка с вероятностью 0,01. Какова вероятность, что
для 99% всех задач сборника ответы даны без ошибок?
26. В партии из 768 арбузов каждый арбуз оказывается неспелым с
вероятностью 0,25. Найти вероятность того, что число спелых
арбузов будет находиться в пределах от 564 до боо.
27. Известно, что вероятность выпуска дефектной детали равна 0,02.
Детали укладывают в коробки по юо штук. Чему равна
вероятность того, что: а) в коробке нет дефектных деталей; б) число
дефектных деталей не более двух?
28. Вероятность того, что в партии из 8 изделий имеется хотя бы одно
бракованное, составляет 57%. Найти вероятность того, что в
партии не более одного бракованного изделия.
29. Найти вероятность того, что в серии из юо бросаний монеты
числа «орлов» и «решек» совпадают.
30. В коробке з детали, вероятность брака для каждой из них равна
0,1. Какова вероятность того, что среди ю коробок будет не менее
8 не содержащих бракованных деталей?
31. Производители калькуляторов знают из опыта, что в среднем 1%
проданных калькуляторов имеет дефекты. Аудиторская фирма
купила 500 калькуляторов. Какова вероятность того, что придется
заменить ровно 4 калькулятора?
32. Вероятность того, что в партии из юо изделий имеется брак,
составляет 63,2%. Найти вероятность, что в партии не более 3
бракованных изделия.
33. На научную конференцию приглашены юо человек, причем
каждый из них прибывает с вероятностью 0,7. В гостинице для гостей
заказано 65 мест. Какова вероятность того, что все приезжающие
будут поселены в гостинице?
34. Вероятность того, что брокер продаст ценную бумагу, равна о,6.
Сколько необходимо попыток, чтобы с вероятностью 0,99 можно
было надеяться, что доля проданных бумаг отклоняется от о,6 не
более, чем на 0,05?
78
Глава 4 0
35. На выборах кандидата в мэры поддерживает 40% населения. При
изучении общественного мнения было опрошено юоо человек.
С какой вероятностью можно утверждать, что доля избирателей из
этой выборки, поддерживающих кандидата, отличается от
истинной доли не более, чем на 0,05?
36. Каждый из 900 посетителей оптового рынка случайным образом
обращается в один из ю ларьков. В каких границах с
вероятностью 0,95 лежит число клиентов отдельно взятого ларька?
37. Производится 500 подбрасываний симметричной монеты. В каких
пределах будет находиться отклонение частоты выпадения герба
от 0,5 с вероятностью 0,99?
38. Доля населения региона, занятого в промышленности, равна 0,4.
В каких пределах с вероятностью 0,95 находится число занятых в
промышленности среди ю ооо случайно отобранных людей?
39. По экспертной оценке, доля р населения данной социальной
группы равна 0,25. Каков должен быть объем п выборки, чтобы с
вероятностью не менее 0,99 погрешность в оценке р составляла не
более 0,005?
40. Вероятность того, что случайно взятая деталь окажется второго
сорта, равна 3/8. Сколько нужно взять деталей, чтобы с
вероятностью, равной 0,995, можно было ожидать, что доля деталей
второго сорта отклонится от вероятности менее, чем на 0,01?
41. Шесть рукописей случайно раскладывают по пяти папкам. Какова
вероятность, что ровно одна папка останется пустой?
42. Пять яблок раскладываются в четыре ящика. Какова вероятность,
что в двух ящиках будет по два яблока, в одном — одно яблоко и
один ящик будет пустой?
43. Пять клиентов случайным образом обращаются в 5 фирм. Найти
вероятность того, что ровно в одну фирму никто не обратится.
44. Два шахматиста, А и Б, встречались за доской 50 раз, причем
15 раз выиграл А, ю раз выиграл в и 25 партий закончились
вничью. Найти вероятность того, что в матче из ю партий между этими
шахматистами 3 партии выиграет/\, 2 партии выиграет в, а 5
партий закончатся вничью.
45. В магазине висит один костюм второго роста, два костюма
третьего роста, три костюма четвертого роста. Костюм второго роста
спрашивается с вероятностью 0,2, костюм третьего роста — с
вероятностью 0,3, костюм четвертого роста — с вероятностью 0,5.
В магазин обратились три покупателя. Найти вероятность того, что
хотя бы один из них ушел без покупки.
7. |
ЧАСТЬ I.Теория вероятностей
46. Лифт начинает движение с 7 пассажирами и останавливается на ю
этажах. Найти вероятность того, что 3 пассажира вышли на одном
этаже, 2 — на другом этаже и еще 2 — на еще одном этаже.
47. В некоторой лотерее каждый сотый билет выигрышный. Сколько
нужно купить билетов, чтобы с вероятностью 0,95 быть уверенным
в том, что хотя бы один билет окажется выигрышным?
48. В среднем 5% рекламных листков дают отклики (т.е. привлекают
клиентов). Выпущено 500 рекламных листков. Найти
наивероятнейшее число откликов и вероятность того, что число откликов
будет отличаться от него не более чем на ю.
49. Фонд инвестирует средства в три компании. Вероятность
получения прибыли от каждой из компаний равна 0,7. Фонд
зарабатывает деньги, если хотя бы две компании дают прибыль. Известно,
что фонд оказался в выигрыше. Какова вероятность того, что при
этом условии вложения во все три компании оказались
прибыльными?
50. Консалтинговая фирма обслуживает 120 компаний. Каждая
компания обращается в эту фирму в среднем 4 раза в год. Какова
вероятность того, что в следующем месяце фирме придется
обслужить более 50 компаний?
51. На ежегодную вечеринку приглашены 12 человек, причем каждый
из них может прийти с вероятностью 0,7 независимо от других.
Найти наиболее вероятное число гостей и его вероятность.
52. Курс акции за день равновероятно растет или падает на i пункт.
Найти вероятность того, что за ю дней торгов курс упадет на
4 пункта.
53. Курс акции за день может подняться или опуститься на i пункт
либо остаться неизменным (все три случая равновероятны).
Найти вероятность того, что за 5 дней торгов курс повысится на
2 пункта.
54. Курс акции за день может подняться на i пункт с вероятностью
50%, опуститься на i пункт с вероятностью 30% и остаться
неизменным с вероятностью 20%. Найти вероятность того, что за
5 дней торгов курс: а) поднимется на 3 пункта; б) упадет на
2 пункта.
55. В люстре з лампы. Вероятность того, что они перегорят в течение
года, составляет о,8%. Найти вероятность того, что в течение года
перегорит ровно одна лампа.
V . j
ГЛАВА 5
ДИСКРЕТНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 5-1. Случайная величина и закон ее
распределения
Случайной величиной § называется любая действительная
функция1 § = ?(со), о) € Q, определенная на пространстве
элементарных событий Q. Если множество значений функции
конечно или счетно, то такую случайную величину называют
дискретной.
В результате опыта случайная величина может принять то
или иное значение, причем заранее неизвестно, какое именно.
Примерами случайных величин являются: колебания курсов
валют или цен товаров, прибыль или убытки фирмы, время
выполнения работы, ожидания транспорта и т.д.
Пример 1. При двукратном подбрасывании монеты возможны
следующие исходы: ых = РР, со2 = РГ, ю3 = ГР, со4 = ГГ, т.е.
пространство элементарных событий имеет вид Q = {со,, со2, со3, а>4},
причем каждый элементарный исход имеет вероятность 1/4.
Пусть — число выпадений герба при двукратном
бросании монеты, тогда ?(со,) = 0, ?(со2) = 1, ?(со3) = 1, ?(со4) = 2.
Зная вероятности для элементарных исходов, можно вычислить
1 В аксиоматике Колмогорова требуется, чтобы функция была
измеримой, т.е. все события вида < t} принадлежали а-алгебре 3 вероятностного
пространства (W, 3, Р) (см. § 3.7). Далее будем считать это условие
выполненным по умолчанию.
81
ЧАСТЬ I. Теория вероятностей
0
1
2
р
1/4
1/2
1/4
Такая таблица уже не содержит информацию о том, на
каком вероятностном пространстве определена случайная
величина, в ней приведены лишь значения случайной величины
(в первой строке) и их вероятности (во второй строке).
Законом распределения случайной величины называется
всякое соотношение, устанавливающее связь между возможными
значениями случайной величины и соответствующими им
вероятностями.
Простейшей формой закона распределения дискретной
случайной величины является ряд распределения.
Рядом распределения дискретной случайной величины ?
называется следующая таблица, в которой перечислены все
возможные значения х} х2,..., хп этой случайной величины и
соответствующие им вероятности р. = Р(% = х).
х1
Х2
\
р
р,
Рг
Рп
При этом ^2р.=1. Если множество значений случайной
величины счетно, то эта таблица является бесконечной справа,
оо
а суммой вероятностей является ряд J*)p, =1.
/=1
Задача 1. В связке из 3 ключей только один ключ подходит
к двери. Ключи перебирают до тех пор, пока не отыщется под-
82
вероятности для соответствующих значений случайной
величины §:
/Ч$=0) = /Чец) = 1/4;
Р( 1) = PC®!,©,) = 1/4 +1/4 = 1/2;
Р(^=2) = Р(а>4) = 1/4.
Полученные вероятности можно свести в следующую
таблицу (в первой строке перечислены значения случайной
величины, а во второй — их вероятности).
I
Глава 5 ф
5
1
2
3
р
1/3
1/3
1/3
§ 5.2. Функция распределения
Функцией распределения случайной величины ? называется
функция F?x)9 определенная для любого действительного х и
выражающая вероятность того, что случайная величина ?
примет значение, меньшее х:
F?x) = Р& < х).
Функция распределения обладает следующими свойствами:
1. Для любого х G R справедливо неравенство 0 < F%(x) < 1.
2. Функция распределения является неубывающей
функцией, т.е. если х2< х{9 то F^(xx) < F^(x2).
3. Вероятность того, что случайная величина примет
значение из полуинтервала [х{9 х2), равна разности значений
функции распределения на концах интервала, т.е.
Р(хх<^<х2) = = F%(x2) - Ffa).
4. Справедливо равенство: Р(?> > х) = 1 — F^(x).
5. Справедливы следующие предельные соотношения:
lim FAx) = 0, limiv(jc) = l.
6. Функция распределения непрерывна слева, т.е.
Ит Д(х) = = F(e).
83 I
ходящий. Построить закон распределения для случайной
величины ? — числа опробованных ключей.
Решение. Число опробованных ключей может равняться 1,
2 или 3. Если испытали только один ключ, это означает, что
этот первый ключ сразу подошел к двери, а вероятность такого
события равна 1/3. Итак, Р(% = 1) = 1/3. Далее, если
опробованных ключей было 2, т.е. \ = 2, это значит, что первый ключ
не подошел, а второй — подошел. Вероятность этого события
равна 2/3 х 1/2 = 1/3, т.е. Р{^ = 2) = 1/3. Аналогично
вычисляется вероятность Д? = 2) = 1/3. В результате получается
следующий ряд распределения случайной величины.
ЧАСТЬ I. Теория вероятностей
184
Доказательство. 1) Очевидно, поскольку это вероятность
события.
2) Представим событие, состоящее в том, что случайная
величина примет значение, меньшее х2, в виде суммы
несовместных событий
{со: ?(со) < х2} = {со: ?(со) < х,} и {со: х, < ?(со) < х2}.
По теореме сложения для несовместных событий: F(x2) =
= Р&((0) < х2) = Р(§(©) < х,) + Р(хх < §(cd) < х2) = Г(хг) +
+ Р(х, < §(©) < х2),
и так как вероятность Р(х, < ?(©) < х2) > 0, то получаем
неравенство F?x2) > ^(х,).
3) Свойство вытекает из равенства
F%(x2) = F%(xx) + Р(хх < 4(со) < х2).
4) Событие {со: ?(со) > х} является противоположным
событию {со: ?(со) < х} и, следовательно, Р(? > х) = 1 — Р(?> < х) =
= 1 - F?x).
5) Рассмотрим убывающую последовательность ап -» — оо и
множества Ап = {со: ?(со) < ап}. Они удовлетворяют условиям
аксиомы непрерывности (см. § 3.7), так что F^an) = Р(Ап) -> О,
п —> со. Для возрастающей последовательности ап -> +оо и
множеств Ап = {со: ?(со) > ап} получаем F^(an) = 1 - /ЧД) -> 1, п -» оо.
6) Рассмотрим возрастающую последовательность ап < а,
ап -> а и множества Ап = {со: ая < ?(со) < а}. Они удовлетворяют
условиям аксиомы непрерывности, и поскольку F(fl) = F(a ) +
+ Р(Ап), то /;(ал) = ^(я) - Р(Ап) -> F(a), #!->«>.
Таким образом, каждая функция распределения является
неубывающей, непрерывной слева и удовлетворяющей
условиям F(—co) = 0 и F(+aa) = 1 функцией. Верно и обратное:
каждая функция, удовлетворяющая перечисленным условиям,
может рассматриваться как функция распределения некоторой
случайной величины.
Функция распределения является универсальным законом
распределения случайной величины. Все ее свойства остаются
верными и когда пространство элементарных событий не
является дискретным.
Функция распределения любой дискретной величины
разрывна, возрастает скачками при тех значениях х, которые
являются возможными значениями Величина скачка функции
F(x) в точке х. равна рг
f
FAx) =
0, х < 1,
1/3, 1<х<2,
2/3, 2<х<3,
1, х>3.
§ 5.3. Случайный вектор в дискретном
вероятностном пространстве
Пусть на дискретном вероятностном пространстве Q задано
несколько случайных величин ?,(ю), ^2(со), ?„(со), где со е Q.
Такой упорядоченный набор называется многомерным
случайным вектором, или я-мерной случайной величиной, и
обозначается ?(со) = (§р ?2, у.
Рассмотрим случай п = 2, т.е. когда на дискретном
пространстве элементарных исходов заданы две случайные величины §
и г|, принимающие значения х. (/ = 1, 2, ...) и уу (/ = 1, 2, ...)
соответственно. Упорядоченная пара (?, л) называется
двумерным случайным вектором, или двумерной случайной величиной.
Сами величины ? и г| называются в этом случае составляющими
[компонентами) случайного вектора.
85
Задача 2. Построить функцию распределения F^(x) для
случайной величины ? из задачи 5.1.
Решение. Случайная величина § имеет три значения 1, 2, 3,
которые делят всю числовую ось на четыре промежутка: (—оо, 1],
(1, 2], (2, 3], (3, +оо). Если х < 1, то неравенство § < х
невозможно (левее х нет значений случайной величины §) и значит,
для такого х функция F%(x) = 0.
Если 1 < х < 2, то неравенство § < х возможно только если
4 = 1, а вероятность такого события равна 1/3, поэтому для
таких х функция распределения F^(x) =1/3.
Если 2 < х < 3, неравенство § < х означает, что или § = 1, или
§ = 2, поэтому в этом случае вероятность Р(^ < х) = Р(? = 1) +
+ />($= 2) = 2/3, т.е./;(х) = 2/3.
И наконец, в случае х > 3 неравенство ? < х выполняется
для всех значений случайной величины поэтому Р(? < х) =
= />(^ = 1) + Р& = 2) + />($ = 3) = 1, т.е. /;(х) = 1.
Итак, мы получили следующую функцию:
Глава 5 ^
ЧАСТЬ I. Теория вероятностей
Геометрически совокупность двух случайных величин
можно рассматривать как случайную точку с координатами (§, г|)
на плоскости АО У или как случайный вектор, направленный
из начала координат в точку (?, г|), составляющие которого
случайные величины ? и г|. Совокупность трех случайных
величин изображается случайной точкой или случайным вектором
в трехмерном пространстве, совокупность п случайных
величин — случайной точкой или случайным вектором в
пространстве п измерений.
Любое соотношение между возможными значениями
случайного вектора и их вероятностями называется совместным
законом распределения.
Совместный закон распределения вероятностей
дискретных величин \ и г| задается набором вероятностей р..
одновременного осуществления событий = х.} и {г| = у), т.е.
Pg=Pfe = xl9y\ = yj}9 и представляется в виде таблицы.
л
Ух
Уг
Ут
*|
Р„
Рп
Рп
Рп
Р„х
Р„2
Рпт
Первый столбец таблицы содержит все возможные значения
составляющей § а первая строка — все возможные значения
составляющей г\. В соответствующей клетке таблицы указана
вероятность того, что двумерная случайная величина приняла
значение (х, у). Поскольку события ? = хр ц = у^ образуют
полную группу событий, сумма вероятностей, помещенных во всех
клетках таблицы, равна единице: ^Г^Р(?> = хп ц = jr) = = 1 •
/ J i J
Такая таблица называется рядом распределения вектора (§, г|).
Вероятность события типа {(§, г|) G В} — «случайная
точка (§, г)) попадает в область В — вычисляется по формуле
Р((?, ц) е В) = 2 Р (5=xi»Л -У])> гДе суммирование происходит
ix„yj)eB
86
Глава 5
по всем возможным парам (х/5 у) значений случайных величин
4 и л, для которых случайная точка (х/? у) входит в область В.
Частным законом распределения случайной величины §
называется набор вероятностей событий = х;.}. Если задан
совместный закон распределения, то частный закон
распределения для ? можно получить с помощью формулы
р^) = Р{^ = х{}^Р{^ = хпц = у.}=^рг
j j
Действительно, событие {со: § = х) может появиться с одним
из событий = хр л = Ух), = хр л = У2}> = хр л = Ут}9
которые несовместны и их объединение равно событию {а>: ? = х;),
т
т.е. = х.} = (J {?, = Хр ?>2 = у). Отсюда в силу теоремы сложе-
т
ния несовместных событий следует, что Р(? = х;.) = ^ру .
Аналогично частным законом распределения л называется
набор вероятностей событий {л = у), которые также можно
вычислить с помощью формулы.
Таким образом, распределение каждой случайной величины
восстанавливается с помощью совместного закона
распределения вероятностей.
Пример 2. Совместное распределение пары (§, л) задано
таблицей.
-1
0
1
Л
-1
1/16
1/8
1/16
1/4
1
3/16
3/8
3/16
3/4
1/4
1/2
1/4
1
Частные законы рассчитаны суммированием по строкам и
по столбцам.
87
^ ЧАСТЬ I. Теория вероятноаей
5
л
1
2
-1
1/16
3/16
0
1/16
3/16
1
1/8
3/8
Вычислить частные законы распределения составляющих
величин § и т). Определить, зависимы ли они. Вычислить
вероятность Р{$ + г}>2}.
Решение. Частное распределение для § получается
суммированием вероятностей в строках:
Р{^ = -1}=Р{^ = Ч,л = 1}+/>{^ = -1,Л = 2}=1/16 + 3/16 = 1/4;
Р{^ = 0}=Р{^ = 0,л = 1}+Р{^ = 0,л = 2}=1/16 + 3/16 = 1/4;
Р{^ = 1}=Р{^ = 1,Л = 1}+Р{^ = 1,Л = 2}=1/8 + 3/8 = 1/2.
Случайные величины § и г| называются
независимыми, если для любых множеств А и В выполняется условие:
PfeeA, г\еВ} = Р{$еА}Р{цеВ}, т.е. независимы события
{?еЛ} и {г|е2?}. Справедлива следующая теорема.
> Теорема. Дискретные случайные величины ?> и ц независимы
тогда и только тогда, когда события {^-х)и{х\—у^
независимы для всех значений х{ и у. .
Доказательство. Пусть Р($ = xt, ц = у) - Р(? = х)Р(ц = j>y)
для всех значений xt и у; тогда получаем
Р$еА9ЦеВ}= ? = Л = I />{*в*/Ип = )>,}=
= ItP{^ = xi}YiP{y] = yJ}=P{^A}P{y]BB}.
xteA yjSB
Задача 3. Совместный закон распределения случайных
величин § и г] задан с помощью таблицы.
88
Глава 5 щ
1
2
h
-1
1/16
3/16
1/4
0
1/16
3/16
1/4
1
1/8
3/8
1/2
р.
1/4
3/4
1
Теперь ответим на вопрос о независимости случайных
величин \ и т). С этой целью для каждой клетки совместного
распределения вычислим произведение Р{?> = х1}Р{т\ = у]}, т.е. сумм по
соответствующей строке и столбцу, и сравним его со значением
вероятности Pfc = xi9r\ = yj} в этой клетке. Например, в клетке
для значений § = -1 и л = 1 стоит вероятность 1/16, а
произведение соответствующих частных вероятностей 1/4 х 1/4 = 1/16, т.е.
совпадает с совместной вероятностью. Это условие так же
проверяется в оставшихся пяти клетках, и оно оказывается верным
везде. Следовательно, случайные величины § и л независимы.
Заметим, что если бы наше условие нарушалось хотя бы
в одной клетке, то величины следовало бы признать
зависимыми.
Для вычисления вероятности P{^ + rj>2} отметим клетки,
Для которых выполнено условие ? + л>2. Таких клеток всего
три, и соответствующие вероятности в этих клетках равны 1/8,
3/16, 3/8. Их сумма 11/16, это и есть искомая вероятность.
Вычисление этой вероятности можно записать так:
Р?+т^2}=Р? = 1, Л = 1}+^{^ = 0, Л = 2}+Р? = 1, л = 2}=
= 1/8 + 3/16 + 3/8 = 11/16.
89 I
Аналогично получается частное распределение для tj:
Р{т| = 1}=1/16 + 1/16 + 1/8 = 1/4;
Р{л = 2}=3/16 + 3/16 + 3/8 = 3/4.
Полученные вероятности можно записать в ту же таблицу
напротив соответствующих значений случайных величин.
ЧАСТЬ I. Теория вероятностей
Л '
X
шшш
У %
Рис. 5.1
90
§ 5.4. Совместная функция распределения
случайного вектора
Рассмотрим вероятностное пространство Q, на котором
определен вектор (§, г|). Обозначим через < х, л < у}
множество тех элементарных событий ю, для которых одновременно
выполняются эти неравенства.
Совместной функцией распределения вероятностей случайных
величин ? и л или случайного вектора (\, г\) называется функция
двух аргументов F(x, у), равная вероятности Р(\ < х, л < у) =
= F(x, у).
Это общее определение верно как в дискретном, так и в
непрерывном случаях.
Частными функциями распределения называют функции
распределения составляющих § и r\: F^(x) и F(x).
Многомерные функции распределения обладают
аналогичными свойствами, что и одномерные:
1) 0 < F(x, у) < 1;
2) F(x, у) есть неубывающая функция по каждому из
аргументов;
3) Дх, у) непрерывна слева по каждому из аргументов;
4) Дх, у) удовлетворяет соотношениям: F (+оо, +оо) = 1 и
Fix, -00) = Д-оо, у) = Д-оо, -оо) = 0.
Геометрически функция распределения 7^(х, у) = Р(?{ <х, ?2 <у)
определяет вероятность попадания случайной точки в
бесконечный угол с вершиной в точке (х, у), не включая его границы
(рис. 5.1).
Геометрическая интерпретация функции распределения
Дх, у) позволяет дать простое пояснение предельным свой-
Глава 5
ствам функции распределения: если х -> — оо (или у -> -оо)
правая граница (верхняя граница) бесконечного квадранта
неограниченно смещается влево (вниз), то вероятность попадания
случайной точки в квадрант стремится к нулю. При х -> +оо и
у -» +оо бесконечный квадрант превращается во всю плоскость
XOY и попадание случайной точки в эту плоскость является
достоверным событием.
Если один из аргументов равен +оо, то функция
распределения вектора превращается в функцию распределения
случайной величины, соответствующей другому аргументу: Дх, +оо) =
= ^(х), Д+оо, у) = FJy). Действительно, поскольку событие
{со: 4(со) < +00} достоверно, Дх, +оо) определяет вероятность
события {со: ?(со) < х}, т.е. представляет собой функцию
распределения составляющей Аналогично, Д+оо, у) = F(y).
Геометрически функция распределения составляющих есть
вероятность попадания случайной точки в полуплоскость,
ограниченную прямой X = х, для Дх, +оо) = /^(х), или прямой Y = у для
Д+«>, у) = Fft) (рис. 5.2).
Л '
У
ж
ж
Рис. 5.2
Используя геометрическую интерпретацию функции
распределения F^(x9 у), можно вычислить вероятность попадания
случайного вектора (?(со), ц(со)) в прямоугольник П = {(х, у):
х е К, Ьх], у е \av b2]}. Действительно (рис. 5.3), Р[(?, л) е П] =
= 1\\ < Ь{9 л < Ь2) ~ Щ < Ь{9 л < а2) + Щ < а{9 л < а2) -
- Р?< а19 ц<Ь2) = Щ9 Ь2) - Щ9 а2) - F(av Ь2) + Дя„ я2).
91
ЧАСТЬ I. Теория вероятностей
Рис. 5.3
Если вектор непрерывный, то эта формула верна для
любого интервала, полуинтервала или отрезка, так как вероятности
точек и прямых в этом случае нулевые.
В многомерном случае приведенных четырех свойств
недостаточно, чтобы функция F(x, у) была функцией распределения.
Необходимо еще, чтобы при любых ai и bi следующее выражение
было неотрицательно:
Р(ах<^< Ь19 я2<л< Ь2) = т> л) € П] =
= Щ, Ь2) - Щ9 а2) - F(av Ъ2) + F(av а2) > 0.
Из определения независимости случайных величин § и т|
следует, что их совместная функция распределения равна
произведению функций распределения составляющих: Дх, у) =
= F^FJy). Справедливо и обратное: если Дх, у) = F^x)Fn(y)
верно для любых х и у, то случайные величины независимы.
Все свойства, доказанные для функции распределения
двумерной случайной величины, остаются справедливыми и для
функции распределения Дхр xv хп) в случае п аргументов.
§ 5.5. Числовые характеристики
дискретных случайных величин
Пусть ? — дискретная случайная величина со значениями
хр х2, хп и их вероятностями р. = Р(?, = х,.), /=1,2, я.
Математическим ожиданием (средним значением)
дискретной случайной величины ? называется число
92
/=1
Глава 5
Если множество значений случайной величины §
бесконечно, т.е. счетно, то математическое ожидание определяется как
бесконечный ряд
/=1
в случае, когда он абсолютно сходится. Если ? — дискретная
величина и ф(х) — некоторая функция, то математическое
ожидание величины г| = ф(?) можно вычислить по формуле
= !>(*,)/>,
при условии, что ряд абсолютно сходится.
Если заданы совместное распределение вероятностей
случайных величин § и г| и функция ф(х, у) двух аргументов, то
ij
Математическое ожидание обладает следующими
свойствами:
1) МС = С (С — константа);
2) М(С?) = СМЬ> для любой константы С;
3) Mfc + л) = + МЛ;
4) Л/(?л) = CM?)(Mi), если % и л независимы.
Доказательство (дискретный случай).
1) Константу С можно рассматривать как случайную
величину, принимающую единственное значение С с вероятностью
единица, так что МС = С х 1 = С.
2) Случайная величина С% принимает значения Ос, вместо
х. с вероятностями р., таким образом, сумма увеличивается в
С раз.
3) Используя ранее введенные обозначения, получаем
ма+ц)=5j<*<+ум=
Лу / У У /
= 2 *, д (х,) + 2^ ) = А/6, + Л/л.
' У
4) Аналогичным образом получаем
'.У /.У ' У
93
ЧАСТЬ I. Теория вероятностей
94
Методом математической индукции можно доказать, что
математическое ожидание суммы п случайных величин §р §2, ..., \
равно сумме их математических ожиданий:
м% + ?2+ ... + у = щ2+ ... + щп.
Дисперсией случайной величины § называется число =
= Af(4 - А^)2. Величина а = у[щ называется средним квадра-
тическим отклонением.
Из определения дисперсии вытекают формулы для
вычисления дисперсии дискретной случайной величины:
/=1
если случайная величина принимает конечное число значений
¦^р Хп9 ^
оо
/=i
при условии сходимости ряда. В общем случае вычисляют
дисперсию по другой (эквивалентной) формуле
Щ= Щ2- (Щ)2
Доказательство. Из свойств математического ожидания
получаем
Щ= М(\- Щ)1 = М(? - 2\Щ + (Л^)2) =
= Щ2- 2(Щ)2+ (Щ)2= Щ2- (Щ)2
(разумеется, при условии существования конечных Щ2 и Щ).
Для дисперсии справедливы следующие свойства:
1) DC — О (дисперсия постоянной равна нулю);
2) D(C%) = ОЩ;
3) Щ + Q =
4) если случайные величины % и г\ независимы, то D($ + г\) -
= D% + Dx\.
Доказательство.
1) DC = М(С - MQ2 = М(С - Q2 = МО = 0.
2) D(CQ = M(G,-M(0$)2= М(СЕ, - СЩ)2= Щ)2 =
= СЩ.
3) D(&+ 0 = Щ&+ Q-M&+ Q)2= М(&+ С)-(Щ+ 0)2 =
= М{\- Щ)2= Щ.
Глава 5
4) + Л) = М(& + Л) - М($ + л))2= М((?- + (л - Мл))2 =
= + 2М(($ - Щ)(у\ - Мл)) + Dr],
где Щ? ~ Лф(л " Мл)) = М($л - 4Мл - цЩ + Л^А#п) = М(?л) "
- 2А/^Мл + ЩЩ = 0.
Методом математической индукции можно доказать, что
если §2, ?я попарно независимы, то дисперсия их суммы
равна сумме дисперсий:
D(SX + $2 + ... + у = + Д2 + ... +
Модой случайной величины называют ее наиболее вероятное
значение. В частности, наивероятнейшее значение числа успехов
в схеме Бернулли — это мода биномиального распределения.
Медианой случайной величины § называют число xmed,
такое, что Щ < xmJ = Щ > xmJ = 1/2. Для дискретной
случайной величины § это число может не совпадать ни с одним
из значений Поэтому медиану дискретной случайной
величины определяют как любое число xmed, лежащее между
двумя соседними возможными значениями х. и такими, что
F{x) < 1/2; Дхж) > 1/2.
Задача 4. Пусть случайная величина § имеет следующий
закон распределения.
-1
0
2
р
1/4
1/4
1/2
Вычислить математическое ожидание Щ, дисперсию Щ и
среднеквадратическое отклонение а.
Решение. По определению математическое ожидание §
равно
ЛЛ- = ?х,д =-1x1/4 + 0x1/4 + 2x1/4 = 1/4.
/=1
Далее:
М^2=^Л=(-1)2х1/4 + 02х1/4 + 22х1/4 = 5/4,
а потому
^ = М^2-(М^)2 =5/4-1/16 = 19/16.
95 |
ЧАСТЬ I. Теория вероятностей
§ 5-6. Основные дискретные распределения
и их характеристики
Распределение Бернулли (биномиальное распределение)
определяется как закон распределения случайной величины, равной
числу успехов в п испытаниях Бернулли. Эта случайная величина
\ может принять любое из значений 0, 1,2, я, а их
вероятности определяются формулой Бернулли: если р — вероятность
успеха, q — вероятность неудачи, то
РЦ = т) = Рп(т) = Cmnpmqn~m9 т = О,1,п.
Для распределения Бернулли М% = пр, D\ = npq.
Распределение Пуассона. Случайная величина,
распределенная по закону Пуассона, может принять любое из значений О,
1, 2, ... (счетное множество значений), а их вероятности
задаются формулой
л т
Р^ = т) = ^-е-\ щ = О, 1, 2, Х>0.
ml
Для распределения Пуассона Щ = X, D\ = X.
Геометрическое распределение имеет случайная величина
равная числу испытаний Бернулли до первого «успеха» (включи-
96
Среднее квадратическое отклонение а = = Vl9 / 4.
Задана 5. Для пары случайных величин из задачи 3
вычислить Л/(?п).
з
Решение. Воспользуемся формулой M?> = ^2xipr А именно, в
/=1
каждой клетке таблицы выполняем умножение соответствующих
значений х. и ур результат умножаем на вероятность и все это
суммируем по всем клеткам таблицы. В итоге получаем
M(^) = -lxlxl/16 + (-l)x2x3/16 + 0xlxl/16 + 0x2x3/16 +
+ 1x1x1 /8 + 1х2хЗ/8 = -1/16~3/8 + 1/8 + 3/4 = 7/16.
Глава 5 $
§ 5.7. Ковариация. Коэффициент корреляции
Ковариацией случайных величин ? и л называется число
cov($, л) = МО; ~ Щ(г\ - Мл)]
(в предположении существования всех математических
ожиданий).
Ковариацию можно вычислить по более простой
эквивалентной формуле
covft, л) = А«Кл) " (Щ)(Мц).
Действительно,
cov(^, л) = М[(4 ~ Щ)(г\ - Мл)] = М(^л - ^Мл - г\Щ +
+ ЩМц) = М(^л) ~ 2ЩМг\ + ЩМц = М(^л) - (М^)(МЛ).
4 Теория вероятностей
97 !
тельно) с вероятностью «успеха» в одном испытании, равной р.
Такая случайная величина § принимает значения 1, 2, 3,
а их вероятности задаются формулой
P(i = m) = pqm-\ т = 0, 1, 2, 0</><1, q = l-p.
Для геометрического распределения Щ = Z>? = ^/р2.
Гипергеометрическое распределение возникает, например, в
задаче о выборке деталей. Пусть имеется N деталей, из которых
М — стандартные. Делается выборка из п деталей. Случайная
величина \ определяется как число стандартных деталей в
такой выборке. Оно может равняться любому числу от 0 до п,
но, конечно, не больше, чем М. С другой стороны, число
нестандартных деталей в выборке не больше, чем N- М, поэтому
число стандартных не меньше п - (N - М). Вероятности этих
значений определяются гипергеометрической формулой
Р(^ = т)= м Nn~M , т = max(0, n-N + M)9 ...,тт(п, М).
Для гипергеометрического распределения Щ = пр, Dl> -
= (N - n)npq/(N - 1), где р = M/N, q = 1 - р.
^ ЧАСТЬ I. Теория вероятноаей
[ 98
Из определения ковариации вытекают следующие ее
свойства:
1) если \ и л — независимые случайные величины, то
cov (?, л) = 0;
2) cov(?, л) = cov(ti, ?);
3) cov(Q, л) = Ccov(^, л); cov(^, Сл) = С cov(?, л);
4) cov(^ + $2, л) = cov(^, л) + cov(^2, л); cov(4, л, + Л2) =
= cov(^, л,) + cov(?, л2);
5) cov($, Q = Щ;
6) если случайные величины ^ и ?2 имеют конечные
дисперсии Щх и Z)?2, то дисперсия суммы этих случайных величин
существует и равна
А^+У = Д2+2соу(^, у;
7) ~^i^2 <соу(^Л2)<^1^2 ;
8) равенство cov(^ %2) = ±У[5§1~Ш^ достигается тогда и
только тогда, когда случайные величины и ?2 линейно зависимы.
Доказательство.
1) В случае независимых случайных величин M(fyc\) -
- (Щ)(Мц) = 0, так как М(^г\) = (Щ)(Мг\).
2) От перемены мест сомножителей произведение не
меняется.
3) cov(Q, л) = Щ(&> - ЩО0)(ц ~ Щ)] = - СЩ)) х
х (л - Мг\)] = СА/[(? — Щ)(г\ — Мл)] = Ccov(?, л). Аналогично
для л-
4) Воспользуемся свойством математического ожидания:
covfc, +t2,Ti) = +^2)-^fti +^аЖл-^л)) =
= M(ft1 -М^) + (^2 -М^2))(л-Мл)) =
= Af (ft, - М?, )(л - Мл)) + М(Ц2 - )(л - Мл)) =
= соу(^,л) + соу(^2,л).
Аналогично для л! и лг
5) Получаем по определению дисперсии.
6) щх + у = мъх + у^ _ + у)2 = M(^2 + 251§2 +
+ у) - (^ + М?2)2 = Щ* + 2Щ&+ Щ22~ (Щх)2- 2ЩХЩ2-
~(Щ2У= Щ2+2соч($х, д.
Глава 5 ф
7) Найдем дисперсию случайной величины г\х =х^ -?2, где
х — произвольное число. По свойствам дисперсии получим
Dt\x = ^ - 2xcov(^, у + Я$2.
Как функция от х, дисперсия />пх представляет собой
квадратный трехчлен. Но дисперсия любой случайной величины
не может быть меньше нуля, так что Dr\x > О для любого х.
Поскольку В?>х > О, то дискриминант уравнения Dr\x = 0 должен
быть неположителен, т.е.
[covft,, у]2 - D^D$2<Q или |cov(§|f yl < V^W-
8) Предположим, что дискриминант равен нулю, тогда
уравнение
хЩ{ - 2xcov(^, у+ 1^=0
имеет решение х0 и /)т|Хо = 0. Это означает, что = с, т.е.
величина постоянная, и° случайные величины §, и ?2
связаны линейной функциональной зависимостью ?2 = х?{ — с,
причем если коэффициент пропорциональности х0
положителен, то cov(^,i2) = y]DtblDi2, а если jc0 отрицателен, то
cov(t,^2) = -V^i^2-
Свойствами 1—5 удобно пользоваться при вычислении ко-
вариации от сложных выражений. Например:
cov(2? + ti, 3?-4t))=2cov(?, 3?-4ti) + cov(t),3?-4ti) =
= 6cov(6„ ?)-8cov(?, t]) + 3cov(ti, 6,)-4cov(ti, ti) =
= 6Di-5cov(^ t))-4Z)t].
Итак, ковариацию можно считать мерой зависимости
случайных величин, так как для независимых случайных величин
ковариация равна нулю. Существенным недостатком ковариа-
ции является то, что ее размерность совпадает с
произведением размерностей случайных величин. Естественно, желательно
иметь безразмерную характеристику зависимости. Таковой
является коэффициент корреляции.
Коэффициентом корреляции случайных величин § и г| (с
положительными дисперсиями) называется число
covfe п)
4*
ф ЧАСТЬ I. Теория вероятностей
Коэффициент корреляции является одной из важных мер
зависимости случайных величин. Как следует из свойств ко-
вариации, он принимает значения от -1 до +1, отражая как
силу зависимости (по абсолютной величине), так и характер
(положительная или отрицательная).
Чем ближе I р I к единице, тем с большим основанием
можно считать, что и ?2 находятся в линейной зависимости, т.е.
коэффициент корреляции характеризует не всякую зависимость,
а только так называемую линейную вероятностную зависимость,
которая заключается в том, что при возрастании одной
случайной величины другая имеет тенденцию изменяться по
линейному закону. Можно сказать, что коэффициент корреляции р
отражает степень линейной зависимости случайных величин.
С возрастанием случайная величина ?2 имеет тенденцию к
увеличению при р > 0 и к уменьшению при р < 0. Поэтому при
р > 0 говорят о положительной корреляционной зависимости и
§2, при р < 0 — об отрицательной.
Для независимых случайных величин коэффициент
корреляции равен нулю. Если р = 0, то случайные величины
называются некоррелированными. Из независимости случайных величин
следует их некоррелированность, но наоборот — не всегда.
Для линейно зависимых величин, т.е. в случае г| = а% + Ь,
где а и b — константы, коэффициент корреляции равен +1 при
а > 0 и -1 при а < 0.
Итак, для независимых случайных величин р = 0, для
линейно зависимых |р| = 1, а в остальных случаях он находится
в интервале -1 < р < 1.
Задача 6. Для пары случайных величин из задачи 3
вычислить ковариацию cov(?, г|).
Решение. В предыдущей задаче уже было вычислено
математическое ожидание Щх\ = 19/16. Осталось вычислить Щ и
Мц. Используя полученные в решении задачи 3 частные законы
распределения, получаем
Д#? = -1х1/4 + 0х1/4 + 1х1/2 = 1/4; Мг\ = 1x1 /4 + 2x3/4 = 7/4;
и значит,
covft,ri) = JI/(^)-^-AfTi = 7/16-1/4x7/4 = 0,
чего и следовало ожидать вследствие независимости случайных
величин.
I 100
Глава 5 ф
Задача 7. Случайный вектор (?, г|) принимает значения
(О, 0), (1, 0), (-1, 0), (0, 1) и (0, —1) равновероятно (рис. 5.4).
Вычислить ковариацию случайных величин § и г|. Показать,
что они зависимы.
if
of
-1
-1 о
Рис. 5.4
Решение. Поскольку Р($ = 0) = 3/5, Р(? = 1) = 1/5, Р($ = -1) =
= 1/5; Р(Л = 0) = 3/5, Р(Л = 1) = 1/5, Р(ц = -1) = 1/5, то
^=3/5x0+1/5x1 + 1/5 (-1) = 0 и Л/л = 0;
M(fy\) = 0x0x1/5+1x0x1/5-1x0x1/5 + 0x1x1/5-
-0x1x1/5 = 0.
Получаем cov(^, л) - ~ ЩЩ = 0, и случайные
величины некоррелированы. Однако они зависимы. Пусть ? = 1, тогда
условная вероятность события {л = 0} равна Р(л = 0 | ? = 1) = 1
и не равна безусловной Р(г\ = 0) = 3/5, или вероятность
совместного появления (^ = 0, л = 0) не равна произведению
вероятностей: Р($ = 0, л = 0) = 1/5 * Р($ = 0)/>(л = 0) = 9/25.
Следовательно, \ и л зависимы.
Задача 8. Случайные приращения цен акций двух
компаний за день § и л имеют совместное распределение, заданное
таблицей.
-1
+1
-1
0,3
0,2
+1
0,1
0,4
Найти коэффициент корреляции.
101 I
ф ЧАСТЬ I. Теория вероятностей
Решение. Прежде всего вычислим Щт\ = 0,3 - 0, 2 - 0,1 +
+ 0,4 = 0,4. Далее находим частные законы распределения § и г\
-1
+ 1
р\
-1
0,3
0,2
0,5
+1
0,1
0,4
0,5
А,
0,4
0,6
1,0
Определяем Щ = 0,5 - 0,5 = 0; Щ = 0,6 - 0,4 = 0,2; Д- = 1;
Dx\ = 1 - 0,22= 0,96; cov(?, ц) = 0,4. Получаем
0,4
Р =
« 0,408.
Задача 9. Случайные приращения цен акций двух
компаний за день имеют дисперсии = 1 и Dx\ = 2, а коэффициент
их корреляции р = 0,7. Найти дисперсию приращения цены
портфеля из 5 акций первой компании и 3 акций второй
компании.
Решение. Используя свойства дисперсии, ковариации и
определение коэффициента корреляции, получаем
Z)(5^ + 3ri) = 52/^ + 32Z)Ti + 2x5x3pV^V^:n =
= 25xl + 9x2 + 30x0,7xlxV2«72,7.
Замечание. Дисперсия приращений цены портфеля акций
часто используется на практике как мера риска вложений: чем
больше дисперсия, тем больше риск. Поэтому оценка данной
величины имеет важное значение для инвесторов.
§ 5.8. Условные распределения и условные
математические ожидания (дискретный случай)
Пусть на одном и том же пространстве элементарных
исходов Q заданы две случайные величины ?>и ц.
Условным законом распределения случайной величины § при
условии т| = у называется любое соотношение, ставящее в со-
102
Глава 5 ф
ответствие значениям случайной величины ? условные
вероятности ИХ ПРИНЯТИЯ При УСЛОВИИ x] = у.
Рассмотрим здесь случай дискретных случайных величин §
и л> принимающих значения х. (/ = 1, 2, ...) и у. (j = 1, 2, ...)
соответственно. Тогда условное распределение % при условии
Л = у} ставит в соответствие значениям xi вероятности
^(xi\yj) = P(i = xi\y] = yj) =
P(r\ = yj)
При этом предполагается, что Р(г\ = ур > 0.
Если случайные величины независимы, то их условные
распределения совпадают с исходными, и значение одной
величины не влияет на распределение другой.
Условной функцией распределения случайной величины § при
условии л = У называется функция, ставящая в соответствие
любому числу х условную вероятность события < х} при
условии л = У- В дискретном случае получаем
Fb(x\yj) = РЦ<хЫ = У]) = *^=П)У,)'
Условным математическим ожиданием случайной
величины § при условии л == У называется математическое ожидание
условного распределения ? при условии л = У- В дискретном
случае получаем
Аналогичным образом можно определить условную
дисперсию и т.п.
Функцией регрессии случайной величины § по л называется
функция, ставящая в соответствие числу у условное
математическое ожидание § при условии л = У-
%ц(У) = М?\г] = у).
Функция регрессии определена только на области
возможных значений л-
На практике обычно невозможно точно предсказать
значение одной случайной величины на основе знания другой,
однако можно сделать это «в среднем». Функция регрессии
как раз и характеризует среднее значение одной (неизвестной)
юз I
^ ЧАСТЬ I. Теория вероятностей
Задача 10. Распределение двумерной случайной величины
задано таблицей.
л
1
3
4
8
3
0,15
0,06
0,25
0,04
6
0,30
0,10
0,03
0,07
Найти условное распределение и условное математическое
ожидание г| при § = 1.
Решение. Условное математическое ожидание равно
M(r{\i = xl) = У]Р^(ух1хх) + у2/>,ч0ъ I*i)•
Из условия задачи найдем распределение составляющих г| и
5 (последний столбец и последняя строка таблицы).
ц
1
3
4
8
л
3
0,15
0,06
0,25
0,04
0,50
6
0,30
0,10
0,03
0,07
0,50
л
0,45
0,16
0,28
0,11
1,00
Ю4
величины при известном значении другой. В случае если
разброс возможных значений не очень велик, это может принести
большую пользу.
Условным математическим ожиданием ? по л называется
случайная величина, равная ф4|п(л)> которая обозначается М(?|л).
Условное математическое ожидание обладает следующими
свойствами:
1) A/(ch)-c;
2) М(а$ + Ь\ц) = аМ($\х)) + Ъ\
3) + гул) = МУл) + МУл);
4)Щ=М[М(Ш
5) МА$Жл)1л] = А(л)М/Ю1л], где/(^) и А(л) -
произвольные функции от случайных величин § и г|;
6) А/(?|л) = М(%), если § и г| независимы.
Глава 5 ф
Так как 7>(х,) = P(xvyx) + P(xvy2) = 0,15 + 0,30 = 0,45, то
условные вероятности находятся по формулам
. (v|x) **рУ.) 0,15 1 ¦ P(xt,y2) 0,30 2
V* w " o,45 " 3 ' W |X,)~ />(*,) " 0,45 ~ 3 '
а искомое условное математическое ожидание равно
Л/(лК = 1) = Зх| + 6х| = 5.
О
Задачи для самостоятельного решения
Теоретические задачи
1. Докажите, что для случайной величины распределенной по
закону Пуассона с параметром X, математическое ожидание M^ = Xf
а дисперсия DZ, = X.
2. Докажите, что для случайной величины распределенной по
закону Бернулли с параметрами п и р, математическое ожидание
М? = яр, а дисперсия D6, = яр(1 - р).
3. Докажите, что для случайной величины распределенной по
геометрическому закону с параметром р, математическое ожидание
к**- 1 1-/?
Af? = —, а дисперсия М; = —f-.
/> />
4. Случайная величина ? имеет математическое ожидание а и
дисперсию а2. Найти математическое ожидание и дисперсию случайной
величины г| = - .
Вычислительные задачи
5. Монету подбросили з раза. Найти распределение вероятностей для
числа появлений герба.
6. Три стрелка с вероятностями попадания в цель при отдельном
выстреле о,7, о,8 и о,9 соответственно делают по одному выстрелу.
Найти распределение вероятностей для общего числа попаданий.
. У
Ю5
ЧАСТЬ I. Теория вероятностей
7. Вероятность того, что лотерейный билет окажется выиграшным,
равна o,i. Покупатель купил 5 билетов. Найти распределение
вероятностей для числа выигрышей у владельца этих 5
билетов.
8. Стрелок поражает мишень с вероятностью 0,7 при одном
выстреле. Стрелок стреляет до первого попадания, но делает не более
трех выстрелов. Найти распределение вероятностей для числа
выстрелов.
9. Два станка выпускают детали с вероятностями брака 0,01 и 0,05
соответственно. В выборке одна деталь выпущена первым станком
и две — вторым. Найти закон распределения для числа
бракованных деталей в выборке.
ю. Прибор комплектуется из двух деталей, вероятность брака для
первой детали — од, а для второй — 0,05. Выбрано 4 прибора.
Прибор считается бракованным, если в нем есть хотя бы одна
бракованная деталь. Построить закон распределения для числа
бракованных приборов среди выбранных 4 приборов.
11. С конвейера поступили 4 детали. Вероятность брака для каждой
детали равна од. Детали проверяют одну за другой, пока не
наберут две годные (или пока они не кончатся). Найти распределение
вероятностей для числа проверенных деталей.
12. Два стрелка поражают мишень с вероятностями о,8 и 0,9
соответственно (при одном выстреле). Найти распределение
вероятностей для общего числа попаданий в мишень, если первый стрелок
выстрелил один раз, а второй — два раза.
13. Каждая из 5 лампочек имеет дефект с вероятностью од.
Дефектная лампочка при включении сразу перегорает, и ее заменяют
новой. Построить закон распределения для числа опробованных
ламп.
14. Среди 5 ключей два подходят к двери. Ключи пробуют один за
другим, пока не откроют дверь. Найти распределение вероятностей
для числа опробованных ключей.
15. Монету подбрасывают до тех пор, пока герб не выпадет два раза,
но при этом делается не более 4 бросаний. Найти распределение
вероятностей числа подбрасываний.
16. Среди ю деталей три — нужного размера. Детали извлекают
поочередно, пока не найдут 2 детали нужного размера, но при этом
делается не более 4 проб. Найти распределение числа
извлеченных деталей.
106
V )
Глава 5 ф
17. На станцию обслуживания заявки поступают случайно в
соответствии с распределением Пуассона с параметром X = 2. Мощность
станции позволяет обслуживать не более 2 заявок в единицу
времени. Найти вероятность того, что в течение данной единицы
времени: а) станция не справится с потоком заказов и образуется
очередь; б) станция обслуживания будет простаивать или работать
не на полную мощность; в) на станции обслуживания не
образуется очередь.
18. В процессе производства изделие высшего качества удается
получить только с вероятностью 0,2. С конвейера берут наугад детали
до тех пор, пока не взято изделие высшего качества. Найти
математическое ожидание числа проверенных изделий.
19. Экзамен по математике сдается до получения положительного
результата. Шансы сдать экзамен остаются неизменными и
составляют 20%. Найти математическое ожидание числа попыток сдачи
экзамена.
20. ОТК должен проверить юо комплектов, состоящих из 4 изделий
каждый. Найти математическое ожидание числа комплектов,
состоящих из стандартных деталей, если каждая деталь может быть
стандартной с вероятностью о,8.
21. Игральная кость подбрасывается до: а) второго; б) третьего
появления грани с номером 3. Найти среднее число подбрасываний.
22. Найти математическое ожидание и дисперсию суммы выпавших
очков при бросании 4 игральных костей.
23. В шестиламповом приемнике перегорела одна лампа. Лампы
проверяют одну за другой, пока не найдут неисправную.
Найти математическое ожидание и дисперсию числа проверенных
ламп.
24. Стрелок стреляет по движущейся мишени до первого попадания
в нее, причем успевает сделать не более 4 выстрелов. Найти
математическое ожидание и дисперсию числа сделанных выстрелов,
если вероятность попадания при каждом выстреле равна о,6.
25. В каждой упаковке товара имеется одна из 5 различных наклеек
(равновероятно). Сколько в среднем упаковок понадобится
купить, чтобы собрать их все?
26. Курс акции в течение дня может подняться или опуститься на
один пункт либо остаться неизменным (все три варианта
равновероятны). Найти распределение изменения курса акции за
2 дня.
107
ф ЧАСТЬ I. Теория вероятностей
27. В телеигре игроку задают вопросы. Если игрок правильно
отвечает на вопрос, ему задают следующий; если неправильно, то
игрок выбывает из игры. Всего задается не более трех вопросов.
Вероятность ответить на первый вопрос равна 0,9; на второй —
0,3; на третий — 0,1. Найти: а) распределение числа правильных
ответов; б) математическое ожидание выигрыша, если за один
правильный ответ платят юо руб., за два — 400 руб. и за три —
юоо руб.
28. В офисе проводится собеседование с 4 кандидатами на
некоторую должность (по очереди). Если подходящий человек найден
(принято решение о приеме его на работу), то с оставшимися
кандидатами собеседование не проводится. Вероятность того,
что кандидат подходит, равна 0,2. Найти распределение числа
кандидатов, с которыми беседовали, и его математическое
ожидание.
29. В экзаменационном билете три задачи. Вероятность правильного
решения студентом первой задачи равна о,8, второй — 0,7 и
третьей — 0,3. Построить закон распределения для числа правильно
решенных задач и найти его математическое ожидание.
30. В игровом автомате три окошка, в которых случайным образом
появляются цифры от о до 9 независимо одна от другой. Если две
цифры совпали, игрок получает ю руб., если все три — юо руб.
Чтобы начать игру, он платит 5 руб. Найти математическое
ожидание выигрыша игрока.
31. Бросают две кости. Пусть и ?2 — число очков на 1-й и 2-й
кости соответственно, а г| — максимальное из двух выпавших чисел:
г| = max {?1, ?2}. Найти совместное распределение и х\.
32. Совместный закон распределения пары (?, ti) задан таблицей.
п
S
-1
0
1
0
1
1
1
10
5
5
1
1
1
1
1
5
10
5
Найти распределение вероятностей случайной величины ? - т| и
вычислить cov(? + т|, ^ - г|). Исследовать вопрос о зависимости
^ случайных величин % и ту
I ю8
Глава 5 ф
33. Совместный закон распределения пары (?, г|) задан таблицей.
л
-1
0
1
-1
1
12
1
4
1
6
1
1
4
1
12
1
6
Найти закон распределения вероятностей случайной величины fy\
и вычислить cov(2? - зг|, ? + 2т]). Исследовать вопрос о
зависимости случайных величин % и т].
34. Совместный закон распределения пары (?, т|) задан таблицей.
1
л
0
1
2
-1
1
9
1
6
1
3
1
1
9
1
18
2
9
Найти закон распределения вероятностей случайной величины
\ + л и вычислить cov(2ti + г| + у. Исследовать вопрос о
зависимости случайных величин \ и г\.
35. Совместный закон распределения пары (?, г|) задан таблицей.
4
Л
-1
0
2
0
1
8
1
6
1
6
1
1
1
3
12
12
8
Найти закон распределения вероятностей случайной величины
? + г] и вычислить cov(? - т), 2^ + г|). Исследовать вопрос о
зависимости случайных величин ? и г|.
J
109 |
Ф ЧАСТЬ I. Теория вероятностей
36. Совмеаный закон распределения пары (?, л) задан таблицей.
п
-1
1
2
-1
1
6
1
6
1
6
1
1
18
1
18
7
18
Найти закон распределения вероятностей случайной величины ?п
и вычислить cov(2? + г|, з? - т|). Исследовать вопрос о
зависимости случайных величин \ и х\.
37. Закон распределения случайной величины ? имеет вид:
0
1
2
3
р
1/8
3/8
3/8
1/8
Найти функцию распределения случайной величины вычислить
ее математическое ожидание, дисперсию и среднее квадратиче-
ское отклонение. Вычислить вероятность P{-i < % < 3/2}.
38. Закон распределения случайной величины % имеет вид:
-1
2
3
5
р
1/4
1/2
1/8
1/8
Найти функцию распределения случайной величины вычислить
ее математическое ожидание, дисперсию и среднее квадратиче-
ское отклонение. Вычислить вероятность Я5/2 < ? < 5}.
39. Закон распределения случайной величины ? имеет вид:
%
0
1
3
4
Р
1/9
2/9
1/6
1/2
Найти функцию распределения случайной величины вычислить
ее математическое ожидание, дисперсию и среднее квадратиче-
ское отклонение. Вычислить вероятность P{i/2 < ? < 7/2}.
v j
110
Глава 5 &
40. Закон распределения случайной величины ? имеет вид:
4
-2
-1
1
3
р
1/7
3/7
2/7
1/7
Найти функцию распределения случайной величины вычислить
ее математическое ожидание, дисперсию и среднее квадратиче-
ское отклонение. Вычислить вероятность Р{-з/2 < ? < 2}.
41. Случайные приращения цен акций двух компаний за день ^ и т|
имеют совместное распределение, заданное таблицей.
4
-1
+1
-1
0,2
0,1
+1
0,2
0,5
Найти коэффициент корреляции.
42. Случайные приращения цен акций двух компаний за день ? и ц
имеют совместное распределение, заданное таблицей.
ч
-1
+1
-1
0,4
0,1
+1
0,1
0,4
Найти коэффициент корреляции.
43. Случайные приращения цен акций двух компаний за день имеют
дисперсии D\ = 1,21 и Dr\ = 2,56, а коэффициент их корреляции
р = 0,5. Найти дисперсию приращения цены портфеля из: а) 4
акций первой компании и 6 акций второй компании; б) 7 акций
первой компании и 3 акций второй компании; в) 9 акций первой
компании и 1 акции второй компании.
44- Случайные приращения цен акций двух компаний за день имеют
дисперсии DZ> = 2 и Dr\ = 3, причем они некоррелированы.
Инвестор намеревается приобрести ю акций. Сколько акций каждой
компании он должен купить, чтобы минимизировать риск
вложений, т.е. дисперсию приращения цены портфеля?
Ц ЧАСТЬ I. Теория вероятностей
45. Случайные приращения цен акций двух компаний за день имеют
дисперсии 0? - 1 и От] - з, причем они некоррелированы.
Инвестор намеревается приобрести 12 акций. Сколько акций каждой
компании он должен купить, чтобы минимизировать риск
вложений?
46. По таблице совместного распределения из задачи 32: а) найти
условное распределение § при условии г| - о; б) найти условное
распределение тг\ при условии § = о; в) функцию регрессии % по г\;
г) функцию регрессии г| по
47. По таблице совместного распределения из задачи 33: а) найти
условное распределение % при условии r\ = -i; б) найти условное
распределение г\ при условии § -1; в) функцию регрессии % по ту,
г) функцию регрессии г| по §.
48. По таблице совместного распределения из задачи 34: а) найти
условное распределение ? при условии rj = 2; б) найти
условное распределение г| при условии % = -i; в) функцию регрессии
§ по г|; г) функцию регрессии г\ по
49. При условиях задачи 31 найти: а) условное распределение и
условное математическое ожидание ^ при условии г| = 4; б) условное
распределение и условное математическое ожидание ц при
условии ^= 2.
50. Две независимые случайные величины ^ и ?2 имеют
распределения Пуассона с параметрами \ и Х2 соответственно. Найти
условное распределение ^ при условии, что т| = ^ + ?2 = л, /7 > о, и
функцию регрессии ? по т].
v ; j
ГЛАВА 6
НЕПРЕРЫВНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 6.1. Плотность и функция распределения
непрерывной случайной величины
Случайная величина ? называется непрерывной, если ее
функция распределения F%(x) = < х) непрерывна. Множество
значений непрерывной случайной величины несчетно и
обычно представляет собой некоторый промежуток (конечный или
бесконечный). Функция распределения непрерывной
случайной величины обладает теми же основными свойствами, что и
в дискретном случае (§ 5.2).
Случайная величина § называется абсолютно непрерывной,
если существует неотрицательная функция р%{х) такая, что при
любых х функцию распределения F%{x) можно представить в
виде интеграла
F^x) = P^<x)=] p^t)dt.
-оо
Функция р%(х) называется плотностью распределения.
Имеют место следующие свойства рЛх):
1. р%{х) > 0.
2. В точках непрерывности плотность распределения равна
производной функции распределения: рк(х) = F^(x).
3. Интеграл по всей числовой прямой от плотности распре-
оо
Деления равен единице: Г p^(x)dx = \.
113
ЧАСТЬ I. Теория вероятностей
114
4. Плотность распределения определяет закон
распределения случайной величины, так как определяет вероятность
попадания случайной величины на любой полуинтервал [а, Ь)\
ь
P{K&[a,b)}=P{a<%<b}=FK(b)-F%(a) = J p,(t)dt.
а
5. Вероятность того, что непрерывная случайная
величина примет конкретное значение а, равна нулю: = а) = 0.
Поэтому справедливы следующие равенства:
P{a<i<b}=P{a<i<b}=P{a<i<b}=P{a<i<b}=FK(b)-FK(a).
Доказательство.
1) Следует из определения.
2) Следует из взаимосвязи между производной и
интегралом.
ОО X
3) ГpAx)dx — lim 1 pAx)dx = lim FAx) = l.
J * x->+ooJ 4 x-»+oo ^
-00 -00
4) Используем формулу Ньютона—Лейбница.
5) Представим событие А = {ю: ?(ю) = а} в виде произведе-
оо
ния р| {а < § < а + 1/п} и воспользуемся аксиомой непрерыв-
ности (§ 3.7), тогда
а+-
я
Р(А) = Р& = а) = lim Р(а < ? < а + 1/я) = lim Г а(*)Л = 0.
я-»оо я—»оо J
а
Заметим, что плотность может быть разрывна в некоторых
точках, где ее можно определить произвольным образом: это
никак не повлияет на функцию распределения и другие
числовые характеристики.
Можно считать, что множество значений случайной
величины совпадает с промежутком, на котором плотность
распределения отлична от нуля.
График плотности распределения называют кривой
распределения. Площадь, ограниченная кривой распределения и осью
абсцисс, как следует из свойства 3, равна единице. Тогда
значение функции распределения F^x) в точке х0 геометрически есть
Глава 6
площадь, ограниченная кривой распределения и осью абсцисс
и лежащая левее точки х0 (рис. 6.1).
Рис. 6.1
Задача 1. Плотность распределения непрерывной случайной
величины имеет вид:
О, *0[О,2],
Ос2, хе[0,2].
Определить константу С, построить функцию
распределения F~(x) и вычислить вероятность Р(—1 < ? < 1).
оо
Решение. Константа С находится из условия J* /^(х)Лс = 1.
В результате имеем
оо i 3
1 = J pK{x)dx = fCx2dx = C—
откуда С = 3/8.
Чтобы построить функцию распределения F%(x), отметим,
что интервал [0, 2] делит область значений аргумента х
(числовую ось) на три части: (-оо, 0), [0, 2], (2, оо). Рассмотрим
каждый из этих интервалов. В первом случае (когда х < 0)
вероятность события < х} вычисляется как
X X
F^x) = P(i<x)= J pK(t)dt= J 0Л = 0,
«5
ф ЧАСТЬ I. Теория вероятностей
* X
FK(x)= J pK{t)dt= J p^t)dt+f Pi(t)dt = 0+-ft2dt =
-oo -oo 0 0
Наконец, в последнем случае, когда х > 2,
X U L л л L
FK(x)= j pK(t)dt = J p%№ + J p%(t)dt + f P^t)dt = 0+-J t2dt =
-оо -oo 0 2 0
= 0 + 1 + 0 = 1,
так как плотность р%(х) обращается в нуль на полуоси (2, оо).
Итак, получена функция распределения
[0, х<0,
FK(x) =
хг
—, 0<х<2,
8 - - '
[1, х>2.
Следовательно, Р{-1 < ? < l}= F(l) - F(-1) = 1 / 8 - 0 = 1 / 8.
§ 6.2. Числовые характеристики
непрерывной случайной величины
Математическое ожидание для непрерывно распределенных
случайных величин определяется по формуле
Л/?= J* xp^(x)dx.
При этом интеграл, стоящий справа, должен абсолютно
сходиться.
Пусть ? имеет плотность р(х) и \у(х) — некоторая функция.
Математическое ожидание случайной величины \|/(^) можно
вычислить по формуле
.ТО
Afy(S)= / V(x)p(x)dx9
—оо
если интеграл, стоящий справа, абсолютно сходится.
116
так как плотность ? на полуоси (-оо, 0) равна нулю. Во втором
случае
Глава 6 ф
о -2 оо Л 412
3 г 7 , . г Л, 3 х
А/^= J* xp^(x)dx= J xQdx + -Jxx2dx + J x-0dx = -~
-oo -oo 0 "
Далее
Mi2 = J x2Pi(x)cbc = lfx2-x2dx = ~?j
Ц 8 5
12 (3)2
12
= —, и значит,
о
^ = M^2-(M02=y-^j =0,15
В качестве других характеристик, описывающих свойства
распределения случайной величины, используются начальные
и центральные моменты.
Начальным моментом к-го порядка называется
математическое ожидание к-п степени случайной величины, что
обозначается ак = Щк.
Очевидно, что Щ = а,.
Центральным моментом к-го порядка \хк называют
математическое ожидание к-й степени отклонения случайной величины
от ее математического ожидания: \х.к = Л/(? - Щ)к.
Из определения следует, что ц2 = М(?> — Щ)2 = D^.
117
Дисперсия непрерывной случайной величины § вычисляется
по формуле
оо
Щ = J (x-MQ2p(x)dx,
—оо
а также, как и в дискретном случае, по формуле
оо
Di = Mi2-(Mtf, где Mi2 = Jx2p{x)dx.
-оо
Все свойства математического ожидания и дисперсии, кова-
риации и коэффициента корреляции, приведенные в гл. 5 для
дискретных случайных величин, справедливы и для
непрерывных случайных величин.
Задача 2. Для случайной величины § из задачи 1 вычислить
математическое ожидание и дисперсию.
Решение.
ЧАСТЬ I. Теория вероятностей
а
|i3 = а3 — Заа2 + 2аъ\
ц4 = а4 + 6я2а2 — 4яа3 - За4, ...
Если распределение симметрично относительно
математического ожидания, то все центральные моменты нечетного
порядка равны нулю.
Величина р^= ц3/а3 называется коэффициентом асимметрии
случайной величины Он характеризует «скошенность»
распределения по отношению к математическому ожиданию. Для
симметричных распределений ц3 = 0, поэтому коэффициент
асимметрии равен нулю. Для распределений скошенных влево
Р < 0, для скошенных вправо (J > 0.
Величину у% = [xja4 — 3 называют коэффициентом эксцесса
(или просто эксцессом) случайной величины Он
характеризует «сглаженность», или «крутость» распределения по отношению
к нормальному, так как для нормального закона распределения
ц4/а4= 3 и, следовательно, у4= 0. Для более островершинных
распределений у^> 0, для менее островершинных у^< 0 (рис. 6.2).
рис. 6.2
Кроме начальных и центральных моментов на практике
применяются так называемые абсолютные моменты,
определяемые формулами
и8
Справедливы формулы:
Ц,= 0;
I I = Л* /72
Глава 5
Очевидно, что абсолютные моменты четного порядка
совпадают с обычными моментами. Чаще других применяется
7-й абсолютный момент \i\ = М\ъ>— Mt, I, называемый средним
абсолютным отклонением.
Для непрерывной величины модой Xmod называют точку
локального максимума функции плотности распределения
вероятностей. Если имеется один максимум, то распределение
называется унимодальным, более одного максимума — мульти-
модальным (в частности, распределение, имеющее две моды,
называется бимодальным). Распределение, имеющее минимум
плотности, называется антимодальным.
Медианой непрерывной случайной величины § называют
такое Xmtd, что < Хтсй) = Д? > XmJ = 1/2. Геометрически
медиана — это абсцисса точки, в которой площадь,
ограниченная кривой распределения, делится пополам (рис. 6.3).
х
Рис. б.з
Математическое ожидание, мода, медиана, начальные и
Центральные моменты являются основными числовыми
характеристиками случайной величины. На практике числовыми
характеристиками часто пользуются для приближенной замены
одного закона распределения другим, но так, чтобы
сохранились неизменными несколько важнейших моментов.
§ 6.3. Производящая функция моментов
Производящей функцией моментов случайной величины §
называется функция параметра /, равная математическому
ожиданию m^t) = Наиболее важным ее свойством является
119
ф ЧАСТЬ I. Теория вероятностей
§ 6*4* Примеры непрерывных случайных
величин
Равномерное распределение. Непрерывная случайная
величина \ имеет равномерное распределение на отрезке [а, Ь], если
плотность распределения рАх) сохраняет постоянное значение
на этом промежутке:
/\(*) =
1
, хе[а9Ь],
Ъ-а
О, х?[а,Ь].
График плотности равномерного распределения показан на
рис. 6.4.
120
то, что производящая функция m^t) содержит в себе
сведения обо всех начальных моментах («производит» моменты).
Действительно, т^(0) = Ще*>[ = 0 = Щ = <хр и вообще для
любого к получаем т^к)(0) = Щке*>[ т Q = ак, т.е. к-я производная
от производящей функции при / = 0 равна начальному моменту
к-то порядка, а любой центральный момент можно выразить
через начальные моменты.
Свойства производящей функции следующие:
1. m^a(t) = Ме*« + *= m^ct)e«.
2. Производящая функция суммы независимых случайных
величин равна произведению производящих функций этих ве-
личин. Действительно, пусть ? = ^6,,, тогда
/=i
rn^it) = Л/ехр fix) = ^ПехР Ю = ПМехР (Ь) = ГК О-
V /=1 ) /=1 /=1 /=1
По производящей функции можно определить функцию
распределения, содержащую все сведения о случайной
величине. В этом смысле производящая функция и функция
распределения являются эквивалентными обобщающими
характеристиками случайной величины. К сожалению, производящая
функция моментов может быть определена не при всех
значениях параметра (или вообще определена только в нуле).
Глава 6
1
О1 a
—>
К N
а с
d b
Рис. 6.4
Функция распределения F^x) равномерно распределенной
случайной величины имеет вид
[о,
х — а
х<а,
, а<х<Ь,
Ь-а
1, х>Ь;
математическое ожидание и дисперсия — соответственно:
2 12
В силу симметричности равномерного распределения
относительно математического ожидания асимметрия равна нулю,
^med= Щ» а моду равномерное распределение не имеет.
Для определения эксцесса вычислим четвертый
центральный момент: ц = —— Г(x-^^fdx = ———. Отсюда эксцесс
^4 b-aJ 2 80
а
Равен у = Hi - 3 = -1,2.
* а4
Вероятность попадания случайной величины § на отрезок
k d\ с [а, Ь] равна Р(с < § < d) = - /Хс) = ^—^, т.е. зави-
сит только от длины отрезка и не зависит от того, где этот от-
121
i
ЧАСТЬ I. Теория вероятностей
резок расположен. Таким образом, равномерное распределение
реализует принцип геометрической вероятности при бросании
точки на отрезок [а, Ь].
Показательное (экспоненциальное) распределение.
Непрерывная случайная величина принимающая неотрицательные
значения, имеет показательное распределение с параметром X > О,
если плотность распределения вероятностей случайной
величины равна
Хе~и, jc>0,
О, х<0.
Функция показательного распределения имеет вид
1-е-**, х>0,
О, х<0.
Графики плотности и функции стандартного
показательного распределения представлены на рис. 6.5 (при X = 1), общий
вид — на рис. 6.6.
Плотность показательного
распределения
Функция показательного
распределения
0,5 1,0 1,5 2,0 2,5 x
0,5 1,0 1,5 2,0 2,5 x
Рис. 6.5
122
Глава 6
Рис. 6.6
Математическое ожидание и дисперсия равны
Действительно, имеем
оо I оо
Щ= j &e-"dt = \lt= z, dz = Xdt\= - J ze'^z =
0 ^ 0
1 00 1
D\ = Щ2 - (Mi,)2 = J fileMdt - -i- = -LJ *2<?_zd*
1 1 1
1
о
= 2-
. 2 *
Можно показать также, что ц3 = —, асимметрия Р4 = 2,
эксцесс у = 6, J!fmod = 0, ХтеЛ= —In2. Производящая функция
моментов показательного распределения описывается форму-
31
лой m^(t) = при t < X (в противном случае производящей
функции не существует).
Нормальное распределение (распределение Гаусса).
Непрерывная случайная величина называется распределенной по нор-
мольному закону с параметрами а и с2, если ее плотность
распределения
р$(х)-
1
(х-а)2
~ 2а2
Множество случайных величин, распределенных по
нормальному закону с параметрами а и а2, обозначается через
123
J) ЧАСТЬ I. Теория вероятностей
Плотность нормального Функция нормального
Рис. 6.7
124
N(a, а2). В частном случае, когда а = 0 и с2 = 1, нормальное
распределение называется стандартным, и класс таких
случайных величин обозначается N(0, 1).
Функция распределения нормально распределенной
случайной величины
1 х c-fl)2
/г<д) = —' Г е" 2°2 dt.
Графики плотности и функции стандартного нормального
распределения представлены на рис. 6.7, в общем случае — на
рис 6.8.
Глава 6
1
Параметры нормального распределения суть
математическое ожидание Щ = а и дисперсия Щ = а2.
Плотность нормального распределения симметрична
относительно х = я, поэтому Xmcd = A"mod = Л/% = я. Асимметрия и
эксцесс нормального распределения равны нулю.
Плотность стандартного распределения
1 -—
а функция распределения
X /2
ф(х) = -4= Г e~Jdt.
Такой интеграл невычислим аналитически, но функция Ф(х)
связана с функцией Лапласа
1 *г
Ф0(х) = -== е 2Л
соотношением
ф(х)=|+ф0(х).
В случае же произвольных значений параметров а и а2
функция распределения F%(x) случайной величины \ ? iV(a, о2)
связана с функцией Лапласа с помощью соотношения
Отсюда вероятность попадания нормально распределенной
случайной величины ? G N(a, а2) на полуинтервал [с,, с2)
можно вычислять по формуле
/»(С1<4<С2)=ф„(^)-ф„(^).
Напомним, что значения функции Лапласа затабулированы
в табл. 2 приложения 2.
Задача 3. Пусть задана случайная величина ? Е 4).
Вычислить вероятность Р(0 < § < 3).
125
i
ЧАСТЬ I. Теория вероятностей
Решение. Здесь а = 1 и с = 2. Согласно указанной выше
формуле
/>(0<$<3)=ФС
3-1
¦фо[^1 = фо(1)-фо(^5) =
= Ф0(1) + Ф0(0,5) = 0,3413 + 0,1915 = 0,5328.
Важными свойствами нормального распределения являются
следующие:
1) Если л = А\ + Д где § € 7У(я, <*2), то л € + Д ^о2).
В частности, случайная величина § € а2) может быть
представлена в виде § = а + а?0, где ?0 € #(0, 1).
2) Сумма двух независимых нормально распределенных
случайных величин имеет нормальный закон распределения. При
этом их математические ожидания и дисперсии суммируются.
Производящая функция моментов нормального распреде-
ления имеет вид m^(t) = e 2 (существует при любом значении
параметра /).
Для центральных моментов любого порядка нормально
распределенной случайной величины можно вывести
рекуррентное соотношение
\ik = (к - 1)а2|^_2,
позволяющее выражать моменты высших порядков через
моменты низших порядков. Поскольку ц, = 0, все нечетные
моменты нормального распределения равны нулю. Для четных
моментов получаем следующие выражения:
ц0= 1, ц2 = а2, ц4= Зет4, \i2k = (2к - 1)!!а2*.
Отсюда асимметрия равна р^ = n/a3 = 0, эксцесс равен
П=Ц4/а4-3 = 0.
Логарифмически нормальное (логнормальное) распределение
случайная величина § имеет в том случае, когда ее логарифм
имеет нормальное распределение. Соответственно § может быть
представлена как показательная функция от нормально
распределенной случайной величины. Для описания логнормального
распределения используется различная параметризация и,
соответственно, по-разному выражаются математическое ожидание
и дисперсия.
126
Глава 6
Если 4 = л G N(09 а2), как это предполагается в [1], то
Mi = ae°2/2 и DZ, = a2ea\e°2 -\).
Если ? = еп, л G 7У(д, а2), что будем обозначать через
5 б ехр№, ст2)}, то Л/? = Ле°2/2 и Щ = А2е*(е** -1), где Л = е*.
Другие числовые характеристики:
мода - хтой = Ае~°2;
медиана — xmed = А;
асимметрия — р% = -l)1^ + 2);
эксцесс - v^= (^2-1)(в3аЧз^2ст2 + 6^2 + 6).
Из этих формул видно, что асимметрия и эксцесс
логарифмически нормального распределения всегда положительны и
тем ближе к нулю, чем ближе к нулю о. Мода и медиана
стремятся к слиянию по мере стремления к нулю величины а.
Графики плотности и функции распределения при
некоторых значениях параметров представлены на рис. 6.9 (при А - 1,
о= 1) и 6.10.
Значения логарифмически нормальной случайной величины
образуются как «случайные искажения» некоторого «истинного
значения» А, которое является не средним значением, а медиа-
Плотность логнормального
распределения
Функция логнормального
распределения
Рис. 6.9
127
ЧАСТЬ I. Теория
вероятностей
а = 0,7, ст2 = 1
-^Л \ я = 0,7,а2 = 0,3
О
х
Рис. 6.10
ной. Значения логарифмически нормальной случайной величины
оказываются характерными для многих конкретных физических
и социально-экономических ситуаций (размеры и вес частиц,
образующихся при дроблении; заработная плата работника;
доход семьи; размеры космических образований; долговечность
изделия, работающего в режиме износа и старения, и другое).
Распределение Лапласа задается плотностью
(двусторонняя показательная плотность).
Функция плотности распределения симметрична
относительно нуля, т.е. четна, и поэтому математическое ожидание
М% = 0. Дисперсия в два раза больше дисперсии случайной
величины, распределенной по показательному закону: Щ = —•
Действительно,
Симметричная унимодальная функция плотности этого
закона с острым максимумом в точке ноль иногда используется
для описания распределений остаточных случайных компонент
(ошибок) в моделях регрессионного типа.
В силу симметрии имеем Хтед = Хтод = 0, (3^ = 0. Эксцесс
равен у = 3.
Графики плотности и функции стандартного распределения
Лапласа представлены на рис. 6.11 (при X = 1), общий вид
плотности — на рис. 6.12.
•оо < x < оо
128
Глава 6
pJLx)
Плотность распределения
Лапласа
Функция распределения
Лапласа
-3-2-10 1 2 x -3 -2 -1 0 1 2 x
РИС. 6.11
Распределение Вейбулла может быть задано плотностью
{Хах^е-^, х>0,
Р^(х) =
[0, х<0,
Функция распределения имеет вид
а>0.
РЛх) =
0,
х<0.
Графики плотности и функции распределения Вейбулла при
некоторых значениях параметров представлены на рис. 6.13
(<х= 2, Х = 1) и 6.14.
5 Теория вероятностей
129
ЧАСТЬ I. Теория вероятностей
, . Плотность распределения Функция распределения
Вейбулла ffi) Вейбулла
Рис. 6.14
Распределению Вейбулла подчиняется время безотказной
работы многих технических устройств. В задачах этого профиля
важной характеристикой является интенсивность отказа
(коэффициент смертности) X(t) исследуемых элементов возраста /,
определяемый соотношением X(t) = t ^f\t)' '^ЛЯ ^acn^e^CJie"
ния Вейбулла этот показатель принимает достаточно простой
вид степенной функции: X(t) = Xata~\
130
Глава 6 ©
Если а = 1, то распределение Вейбулла превращается в
показательное распределение, а если а = 2 — в так называемое
распределение Рэлея.
Математическое ожидание распределения Вейбулла Щ =
1
г(1+А)
-г!
fi+i)
, где
1 <¦)
1 aJ
= Х -Г 1+- и дисперсия D$ = X0a
Т(а) — гамма-функция Эйлера: Г(у) = Jxy~le~xdx9 которая обла-
0
дает следующими свойствами:
1) Г(у + 1) = уГ(у);
2) Г(/|) = (п — 1)! для целых п.
[О, а<1;
Мода имеет вид Хто6 =
-I 1 I
^0а(1-—)а, а>1;
а
fln2)
1/а
медиана Хтсд = =
В различных задачах прикладной статистики часто
встречаются так называемые «усеченные» распределения. Например,
налоговые органы интересуются распределением доходов тех
лиц, годовой доход которых превосходит некоторый порог с0,
установленный законами о налогообложении. Эти
распределения приближаются распределением Парето.
Распределение Парето задается функциями распределения и
плотности (рис. 6.15, с0= 1, а = 2)
4W-l-(4[i *«-$Г
где а > 0, a х > с0 Функция плотности имеет вид монотонно
убывающей кривой, выходящей из точки (с0, а/с0).
Основные числовые характеристики этого распределения
существуют не всегда, а лишь при соблюдении определенных
требований к значению параметра а:
математическое ожидание Щ = ~^Z\ существует при а > 1;
дисперсия Щ =
ас:
(а-1)2(а-2)
существует при а > 2;
131 I
ЧАСТЬ I. Теория вероятностей
рЛх)
Плотность распределения
Парето
Функция распределения
Парето
1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 x 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 x
Рис. 6.15
мода xmod = с0 и медиана xmed = с02а существуют всегда;
момент fc-го порядка Щк = —— существует при а > к.
а-к
Распределение Коши задается функцией плотности
распределения
*(х)=п(с>+(х-а)>)'
где о 0 - параметр масштаба и а — параметр сдвига,
определяющий значение моды и медианы. Функция распределения
задается формулой
F(x)=-+—arctg .
2 71 с
Стандартное распределение Коши соответствует случаю а = 0,
с = 1.
Для параметров а = 0, с = 1 графики приведены на рис. 6.16.
Отметим два важных свойства (самовоспроизводимости)
распределения Коши.
1) Если случайная величина 4 имеет распределение Коши
с параметрами с и а, то любая линейная функция b0 + bfi
132
Глава 6 ф
имеет распределение того же типа с параметрами d = | Ьх \ с и
2) Если случайные величины §р ?2, ?л независимы и
имеют одинаковое распределение Коши, то среднее
арифметическое ? = (4, + ?2 + ... + ?п)/я имеет то же распределение
Коши, что и
Плотность распределения
Коши
Функция распределения
Коши
3-2-10 1 2 x
Задачи для самостоятельного решения
Теоретические задачи
1. Случайная величина % имеет нормальное распределение с пара-
метрами а и а2. Показать, что величина —^— нормально
распределена с параметрами о и i.
2. Случайные величины ?t, ?2,... ?п независимы и имеют одинаковую
функцию плотности распределения
ае'™ х>0
[0, х<0.
133
ЧАСТЬ I. Теория вероятностей
Найти функцию и плотность распределения величин:
a) r\t ш min{^ , ^2... б) л2 = тах{^... у.
3. Случайные величины ^, §а>?п независимы и равномерно
распределены на отрезке [а, Ь]. Найти функции распределения и
плотности величин у\х = min{^, ?2, ... у и т|2 = max{^,
Доказать, что M(r\x + r\2) = a + Ь.
а. Случайная величина распределена по закону Коши р(х)= а ,.
Найти: а) коэффициент а; б) функцию распределения; в)
вероятность попадания на интервал (-1, i). Показать, что математическое
ожидание ? не существует.
5. Случайная величина подчинена закону Лапласа с параметром X
{X > о): р(х) = ае~^. Найти коэффициент а, математическое
ожидание Щ и дисперсию 0^, вероятности событий {|?| < у[Щ } и {|^| <
б. Найти Р(\^-М^\<Зу1Щ), если ? имеет: а) нормальное
распределение с параметрами а и а2; б) показательное распределение с
параметром X; в) равномерное распределение на отрезке [-i; i].
7. Случайная величина ? подчинена закону Симпсона на отрезке
[-о, а], т.е. график ее плотности распределения имеет вид,
показанный на рис. 6.17.
Написать формулу для плотности распределения, найти /И? и
8. Случайная точка Д имеет в круге радиуса R равномерное
распределение. Найти математическое ожидание и дисперсию расстояния
р точки до центра круга. Показать, что величина р2 равномерно
распределена на отрезке [о, Я2].
134
Глава 6 ^
9. Найти производящую функцию моментов для: а) равномерного
распределения на отрезке [а, Ь]; б) распределения Лапласа с
параметром X.
ю. Доказать, что для распределений: а) логнормального; б) Вейбулла
с а < 1; в) Парето — производящая функция моментов определена
только при t < о; г) для распределения Коши — только при t - о.
А(*) =
Вычислительные задачи
11. Плотность распределения случайной величины % имеет вид
С(х + 1), х€[-1;2],
О, х?[-1;2].
Вычислить конаанту С, функцию распределения F(x), М% и
вероятность Р%2<1}
12. Плотность распределения случайной величины ? имеет вид
С(5-х), хе[-2;1],
О, х0[-2;1].
Вычислить константу С, функцию распределения F(x), /И? и
вероятность Р{0<?<3}.
13. Плотность распределения случайной величины \ имеет вид
С(х-2), хе[3;5],
О, х0[3;5].
Вычислить константу С, функцию распределения F(x), /И? и
вероятность Р{4 < $ < 6}.
14. Плотность распределения случайной величины % имеет вид
С(х + 1Г3/2, х>0,
О, х<0.
А(*) =
/\(*) =
Вычислить константу С, функцию распределения F(x), /И?, 0? и
вероятность Р{|?-1/3|<1}.
15. Плотность распределения случайной величины ? имеет вид
С(1-х2), |х|<1,
О, |х|>1.
Вычислить константу С, функцию распределения F(x)f 0? и
вероятность Р{К-1/2|<1/4}.
/\(*) =
135
ЧАСТЬ I. Теория вероятностей
16. Плотность распределения случайной величины % имеет вид
JCV, х<0,
[О, х>0.
Вычислить константу С, функцию распределения F(x), Mi„ D? и
вероятность Р{-2<?,<1}.
17. Случайная величина % имеет функцию распределения
F(x) =
х<0,
1 X
l-^"x,jc>0.
Вычислить плотность случайной величины, математическое
ожидание, дисперсию и вероятность Р{-1 < ? < 3}.
18. Проверить, что функция F(x) =
0, х<0,
2х-х2, 0<jc< 1,
1, х>1
может быть функцией распределения случайной величины. Найти
числовые характеристики этой величины: и D?.
19. Случайная величина равномерно распределена на отрезке [2; 6].
Выписать плотность распределения. Найти функцию
распределения. Найти вероятность попадания случайной величины на
отрезок [2; 5] и на отрезок [5; 7].
20. Пассажир приходит в случайный момент на остановку, где может
сесть на автобус или троллейбус (смотря что придет раньше).
Автобус ходит с интервалами в 15 минут, троллейбус — ю минут
(независимо один от другого). Найти функцию распределения времени
ожидания и его среднее значение.
21. Стержень длиной 24 см ломают на две части; будем считать, что
точка излома распределена равномерно по всей длине стержня.
Чему равна средняя длина большей части стержня?
22. Отрезок длиной 12 см случайным образом разрезается на две
части. Точка разреза равномерно распределена по всей длине
отрезка. Чему равна средняя длина малой части отрезка?
ГЛАВА 7
ФУНКЦИИ ОТ СЛУЧАЙНЫХ
ВЕЛИЧИН. НЕПРЕРЫВНЫЙ
СЛУЧАЙНЫЙ ВЕКТОР
§ 7.1. Функции от случайных величин
Пусть задана функция плотности р(х) случайной
величины ? и монотонная дифференцируемая функция у = \|/(х). Тогда
плотность распределения случайной величины t| = равна
dy
Здесь — функция, обратная к функции у = \|/(х).
Доказательство. Пусть \|/(лс) — возрастающая функция,
тогда обратная ей функция также возрастающая, и функцию
распределения случайной величины r| = можно представить в
виде F^(x) = ^(\|/_1(х)), так как
Ffi) = /tyft) < = Р(§ < уЧх)) = /^г!<*)).
Дифференцируя, получаем
rfV-'(Jc)
flbc
>0.
Пусть теперь — убывающая функция, тогда обратная
ей также убывающая, и
FJx) = < х) = > v-'(x)) = 1 -
137
ЧАСТЬ I. Теория вероятностей
Отсюда получаем
/>„(*) = Fj(x) = (1 - F^-'ix))' = -
ч,_ dF^-\x)) dy~\x)
= -р%(у->(х))
dy-\x)
dy-\x)
dx '
dx
причем здесь т <0.
dx
Объединяя формулы, полученные в случаях возрастающей и
убывающей функции \|/, получаем исходное утверждение.
Если плотность р^(х) отлична от нуля на некотором
промежутке (конечном или бесконечном), то границы
соответствующего промежутка для р(у) находятся подстановкой исходных
границ в функцию у. Заметим, что порядок следования границ
может меняться, когда у — убывающая функция.
Задача 1. Случайная величина % равномерно
распределена на отрезке [0; 2]. Найти плотность случайной величины
Решение. Из условия задачи следует, что
[0, х?[0;2],
РЛх) =
\, *€[0;2].
Далее, функция у = -у/х+1 является монотонной и
дифференцируемой функцией на отрезке [0; 2] и имеет обратную функ-
цию х = у 1 (у) = у1 -1, производная которой равна
Кроме того, \|/(0)=-1, v|/(2) = ->/3. Следовательно, dy
¦ = 2у.
Рг,(У) = Р^'1(у))\
= 2\у\
Значит, рчО>)=
<Л|Г'0>)
dy
рЛу-\у))-2\у\=
0, у*[->/3;-1],
0, y<?[S;-l],
-у, уе[-Л;-Ц.
138
Глава 7 Ц
§ 7.2. Совместный закон распределения
непрерывных случайных величин
Пусть на вероятностном пространстве Q заданы две
непрерывные случайные величины ? и г|. Тогда упорядоченная пара
(?, г|) определяет «случайную» точку на плоскости и называется
двумерным случайным вектором, или двумерной случайной
величиной, так же как в дискретном случае.
Совместной функцией распределения непрерывных случайных
величин ? и ц называется функция F(x,y) = {^<x,r\<y},
определяющая вероятность попадания случайного вектора (?, г|) в
бесконечный угол на плоскости с вершиной в точке (х, у),
лежащий ниже и левее этой точки. Это общее определение верно
как в дискретном, так и в непрерывном случаях, и свойства
совместной функции распределения для дискретных величин
остаются справедливыми и для непрерывных случайных
величин. Напомним, если случайные величины % и г\ независимы,
то совместная функция распределения равна произведению
функций распределения составляющих: F(x, у) = F^xjFJy), и
наоборот: если выполнено равенство F{x, у) = F^F^iy), то
случайные величины ? и т| независимы.
Случайный вектор называется непрерывным, если его
совместная функция распределения непрерывна. Случайный
вектор называется абсолютно непрерывным, если существует
такая неотрицательная функция Р^ц(х, у), называемая совместной
плотностью распределения случайных величин \ и г| (или
вектора), что имеет место равенство
X У
F(x, у)= J j p^(u,v)dudv.
—оо —оо
Смысл определения совместной плотности распределения
заключается в следующем. Вероятность того, что «случайная
точка» (?, л) попадет в область BQR2 на плоскости, вычисляется
как объем трехмерной фигуры — «криволинейного» цилиндра,
ограниченного поверхностью z = У) и плоскостью z = О,
основанием которого является множество В. Аналитически этот
факт записывается с помощью двойного интеграла:
Р{(Ъч))еВ}= ffp^(x,y)dxdy.
в
139 I
ЧАСТЬ I. Теория вероятностей
Совместная плотность распределения обладает также
следующими свойствами:
1) р(х, j>)>0;
+00+00
2) J f p(x,y)dxdy = l;
—00-00
3) p(x9y) = F^(x9y).
Простейшим примером совместного распределения двух
случайных величин является двумерное равномерное
распределение на множестве А. Пусть задано ограниченное множество А
с площадью S(A) Тогда указанное распределение определяется
как распределение пары (?, л)> задаваемое с помощью
следующей совместной плотности:
[О, (х9у)#А,
1
S(A)9
(х,у)еА.
Задана 2. Пусть двумерный случайный вектор (?, л) равномерно
распределен внутри треугольника Д = {(х, у): х > О, у > О, х + у < 2}.
Вычислить вероятность неравенства ? > г\.
Решение. Площадь указанного треугольника А равна S(A) = 2
(рис. 7.1). В силу определения двумерного равномерного
распределения совместная плотность случайных величин \> ц равна
[О, (х,д>)0Д,
\, (х,у)еА.
Событие > г\} соответствует множеству В = {(*, у): х > у}
на плоскости, т.е. полуплоскости. Тогда вероятность
Р(В) = Р{а,ц)еВ}= ff PiJx,y)dxdy.
Рис. 7.1
140
Глава 7 ф
На полуплоскости В совместная плотность Р^чЦ(х9 у) равна
нулю вне множества А и 1/2 — внутри множества А. Таким
образом, полуплоскость В разбивается на два множества Вх = В п Д
и В2 = ВпА. Следовательно, двойной интеграл по множеству В
представляется в виде суммы интегралов по множествам Вх и
В2, причем второй интеграл равен нулю, так как там совместная
плотность равна нулю. Поэтому
Р{(^)еВ}= ff p^(x,y)dxdy = ff\dxdy + ff Odxdy =
в я, в2
2 17 2 2
Если задана совместная плотность распределения Р%п(х, у)
пары (§, л), то плотности р%(х) и р^у) составляющих § и г\
называются частными плотностями и вычисляются по формулам:
оо
-оо
оо
-оо
Для непрерывно распределенных случайных величин с
плотностями р%(х), рц(у) независимость означает, что при любых х и
у выполнено равенство
Р^(х^У) = Рк(х)Рц(У)'
Задача 3. В условиях предыдущей задачи определить,
независимы ли составляющие случайного вектора ? и ц.
Решение. Вычислим частные плотности рЛх) и р (у). Имеем:
О,
2-*
х?(0;2),
jyy, xg(0;2) :
/\(*)= J pKJx,y)dy =
—оо
Аналогично
оо
/>„(*)= j P%,^,x,y)dy =
О, *?(0;2),
*€(0;2).
О, у^(0;2),
2-у
, у 6(0; 2).
141 j
f
0 ЧАСТЬ I. Теория вероятностей
2 2-х 2
М^\ = ff xy^dxdy = ^f xdx f ydy = ^f xdx
2-х
У
2—' 2J J 2*
Д 0 0 0
= lfx(2-x)2dx = ±
Важную роль в приложениях играет двумерное
нормальное распределение. Пусть ц, и т)2 — независимые случайные
величины, имеющие стандартное нормальное распределение.
Ц2
Очевидно, что в нашем случае pir)(x,y)^ р%(х)р^(у)9 и
потому случайные величины 4 и Л зависимы.
Числовые характеристики для случайного вектора (?, ц)
можно вычислять с помощью следующей общей формулы. Пусть
^п(х, у) — совместная плотность величин ? и t|, a у) —
функция двух аргументов, тогда
+00+00
Л/<р(^л) = J J y(x,y)p^(x,y)dxdy.
—оо—оо
В частности,
+оо +0о
M%=JJ xp%Jx,y)dxdy;
-00-00
+оо +оо
Mt)=JJ yp^(x,y)dxdy;
—оо —оо
+00+00
Mt,t)= J Jxyp^(x,y)dxdy.
-oo -oo
Задача 4. В условиях предыдущей задачи вычислить Щг\.
Решение. Согласно указанной выше формуле имеем
+оо +оо
Mtn= J fxypKn(x,y)dxdy = JJ xy.\dxdy.
—oo —oo Д
Представив треугольник А в виде
Д = {(*,}0:0<х<2;0<;у<2-;с},
двойной интеграл можно вычислить как повторный:
,2|
Глава 7 0
х2+х2
р(х19х2) = ^-схр
По определению, случайная величина % = ?2) имеет
двумерное нормальное распределение, если ее можно представить
в виде
S = а + А|,
где а = (av а2) — вектор математических ожиданий, 5 —
некоторая матрица.
В случае, когда коэффициент корреляции р = р(?р ?2)
отличен по модулю от единицы, распределение имеет двумерную
нормальную плотность:
р(хх,х2) = - 1
хехр
1
((*,-«,)2
2(1-р2)
1 «?
2тю]р2^-
2p(x]-ai)(x2-a2) | (дСз-О;)
а, а,
При этом составляющие имеют нормальные
распределения:
^еЩа^о2), $2eN(a2,o22).
Двумерное нормальное распределение обладает рядом
полезных свойств, например:
1) если р = 0, то и \2 независимы;
2) любая линейная комбинация с,?, + с2\2 имеет нормальное
распределение;
3) условные распределения каждой составляющей по другой
также нормальны;
4) функции регрессии составляющих линейны.
Поэтому на практике если исследуется пара случайных
величин, каждая из которых имеет нормальное распределение, то
можно предположить, что их совместное распределение
является двумерным нормальным распределением.
143
Тогда двумерная случайная величина л = (лР Л2) имеет
стандартное двумерное нормальное распределение. Его совместная
плотность
Л ЧАСТЬ I. Теория вероятностей
Рис. 7.2
Переходя от двойного интеграла к повторному, получаем
—оо\ —оо ,
и далее, дифференцируя под знаком интеграла,
+оо
P^(z) = F^(Z) = J* p%Jz - y,y)dy.
-00
Поскольку величины § и л независимы, рКл(х9у) = pi(x)p1](y).
144
§ 7.3. Плотность суммы двух непрерывных
случайных величин
Пусть ^ и г| — независимые случайные величины с
плотностями р(х) и рл(у). Плотность случайной величины § + ц
вычисляется по формуле свертки
оо
Р^(х)= J Pi(x-y)p1](y)dy.
-00
Доказательство. Используем представление совместной
функции рспределения через двойной интеграл:
F^(z) = Р{$ + л < Z) = //P^{x,y)dxdy,
где множество 1)^= {(*, у): * + .У < (рис 7.2).
///////. .
У///////Л .
////////Л/-
Глава 7
Подставляя последнее равенство в полученное выражение
ддя плотности суммы, приходим к формуле свертки (с
точностью до обозначения аргумента)
оо
-оо
Разумеется, в силу симметрии справедлива также формула
оо
Рк+п(у)= J pK(x)p^y-x)dx.
—оо
Задана 5. Пусть § и т| — независимые случайные величины,
распределенные по показательному закону с параметром X = 2.
Вычислить плотность суммы § 4- т).
Решение. Поскольку \ и г| распределены по показательному
закону с параметром X = 2, их плотности равны
А(*) = А(*) =
2<Г2*, х>0,
О, х<0.
Следовательно,
рЛх-у)--
2е~2{х-у\ х>у,
О, х<у.
Поэтому
оо оо
/Vm(*)= J Р^х-у)Рц(у)^у = f P^x-y)2e~2ydy.
-оо О
Если (х - у) < 0, то в этой формуле аргумент функции
Р$(х - у) отрицателен, и поэтому р(х — у) = 0. Следовательно,
/\+л(х) = 0. Если же (х - у) > 0, то имеем
оо X
= / ^(x-j>)-2e-2'<fy = J 2e-1(x-")-2e-2"dy =
о о
х х
= 4J e-2ix-y)-e-2ydy = 4e-2,c f \dy = 4xe-2x.
о о
Таким образом, получен ответ:
[0, jc<0,
4хе
х>0.
145
|j| ЧАСТЬ I. Теория вероятностей
§ 7.4. Условные распределения и условные
математические ожидания
(непрерывный случай)
Пусть на одном и том же пространстве элементарных
исходов Q заданы две случайные величины ?и г|.
Условным законом распределения случайной величины ? при
условии л = у (так же как и для дискретных случайных
величин), называется любое соотношение, ставящее в соответствие
значениям случайной величины ? условные вероятности их
принятия при условии г\ = у.
В общем случае условную функцию распределения
случайной величины ? при г| = у также естественно было бы
определить формулой
Однако это невозможно, поскольку для непрерывной
случайной величины Р(у\ = у) = 0. Поэтому вместо события {г| = у}
рассматривают событие {у < г\ < у + Aj;} и переходят к пределу
по Ау -> 0. Таким образом, получаем формулу
]imP(i<x,y<^<y + Ay) = F^yl
д^о Р(у<ц<у + Ау) р^у)
Наиболее важен для приложений случай, когда вектор {%, ц)
представляет собой двумерную непрерывную случайную
величину с совместной плотностью распределения р%ч(х, у)- Тогда
Тогда условная функция распределения имеет
производную по х, т.е. существует условная плотность распределения ?
при условии т| = у, равная
дх рп(у)
Условное математическое ожидание непрерывной случайной
величины вычисляется по формуле
МЦЫ = у) = Jxp^lx I y)dx = Jx^'^dx
146
Глава 7 {j)
Р^(х9у) =
О, (*;>>) 0Д,
1 йй6д и
О,
2-У
у* №2),
У€(0;2).
Поделив первую плотность на вторую, получаем условную
плотность:
[О, х0(О;2-у),
1
2-у
хе(0;2-у).
Таким образом, речь идет о равномерном распределении на
промежутке (0, 2 - у). Функцию регрессии вычисляем как
математическое ожидание равномерного распределения. Получаем
%ц(у) = (2 - у)/2, О < у < 2.
Задана 7. Точку бросают случайным образом в круг радиуса
R с центром в начале координат. Найти условную плотность
распределения случайной величины ? — абсциссы точки
падения — при условии, что ордината л приняла значение у.
Решение. Естественно, поскольку точка не может попасть
за пределы круга, то р^ц(х, у) = 0 при х2 + у1 > /Р. Для каждой
области внутри круга вероятность попадания пропорциональна
площади этой области. Поэтому р л(лс, у) = А при х2 + у2 < /Р, т.е.
плотность внутри круга постоянна. Определим константу А:
оо оо
/ / Pjx, y)dxdy = ff Adxdy = nAB?= 1.
-оо -оо x2+y2<R2
и называется функцией регрессии % по t|.
%1](у) = М($\ч = у)9
Функция регрессии определена на области возможных
значений л при А,0>)>0.
Задана 6. Двумерный случайный вектор (§, ц) равномерно
распределен внутри треугольника Д = {(х,у): х > О, у > О, х + у < 2}.
Найти условное распределение ? при т) = у и функцию
регрессии ф^ОО.
Решение. Как уже было показано (см. задачи 2 и 3),
^ ЧАСТЬ I. Теория вероятностей
Отсюда А = V(nR2) и плотность совместного
распределения
О, x2+y2>R2,
^x2+y2<R2'
О, \x\>ylR2-y2,
1 .H^V^V;
рп(у)=
о,
2^
яЛ2
яЛ2
\y\>R,
, \y\<R,
и при \у | ^ Л получаем условную плотность
[О, \x\>jR2-y2,
Р^(х\у) =
1
2^
2 2
, \x\<yJR2-y2
Таким образом, случайная величина i; при условии г\ = у
равномерно распределена на отрезке [-yJR2-y2\ + ^R2-у2]. Ее
условное математическое ожидание тождественно равно нулю.
Интересно отметить, что условная плотность распределения
случайной величины ? при условии г\ = у равномерна, в то
время как безусловная плотность ? таковой не является. И в этом
примере случайные величины i и ц зависимы между собой.
В заключение отметим, что в таком важном для
приложений случае, когда случайная пара ? = ?2) имеет двумерное
нормальное распределение
1
p(xvx2)-
хехр
1
[(*,-я.)2
20-р2)
1 «?
2яст,а2^/1 —р2
(х{-а{У ^(Xi-qXX;-^) | (х2-а2)2
функции регрессии оказываются линейными и имеют вид:
Ф5А(*|) = а2 +Р—(*i Ф5,15г(х2) = 0| +Р—(*2 -«г).
что также можно вывести из представленных формул.
« 148
!
Глава 7
I Задачи для самостоятельного решения
Теоретические задачи
1. Найти плотности распределения: а) суммы; б) разности; в)
произведения; г) частного двух независимых случайных величин,
имеющих равномерное распределение на [о; а].
2. Случайные величины %х и ?2 независимы и имеют нормальные
распределения с параметрами ai9c* и а2, о\ соответственно. Доказать,
что ^ + ?2 имеет нормальное распределение, и найти его
параметры.
3. Показать, что если ? имеет непрерывную функцию распределения
F(x) = Р(? <*)»то случайная величина г| = F(q имеет равномерное
распределение на отрезке [о, 1].
Вычислительные задачи
4. Плотность распределения % равна
[О, х<1.
Найти постоянную С, плотность распределения л = i/? и
вероятность Р(о,25 < т| < 0,64).
5. Случайная величина ? равномерно распределена на отрезке [1,3].
Найти плотность распределения случайной величины т| = ^2 + 1.
6. Случайная величина ? равномерно распределена на отрезке
[-1, 1]. Найти плотность распределения случайной величины
Л = -1п(? + 2).
7. Случайная величина ? равномерно распределена на отрезке [о, 3].
Найти плотность распределения случайной величины т| = 10 — ?2.
8. Случайная величина ? распределена по показательному закону с
параметром А. = 2. Найти плотность распределения случайной
величины r\ = ei —\.
9. Случайная величина ? распределена по нормальному закону с
параметрами а = 2 и а2 = 4. Найти плотность распределения
случайся) =Сх 2> *>!>
ной величины л = (?-2) .
149
ЧАСТЬ I. Теория вероятностей
ю. Случайная величина § имеет функцию распределения
0, х<0,
х2, 0<х<1,
1, х>1.
F(x) =
Найти функцию распределения случайной величины т]= *
11. Случайная величина ? имеет стандартное нормальное
распределение (с параметрами а = о и а2= i). Найти плотноаь случайной
величины ц = ?2.
12. Случайная величина ? имеет показательное распределение с
параметром X. Найти функции плотности распределения случайных
величин:
а)Л1 = Ц;б)л2 = ^;в)л3= г) л4 = 1-*"^.
13. Случайная величина § равномерно распределена на отрезке [о, 1].
Найти плотности распределения случайных величин:
а) цг = 2^ + 1; б) л2 - -ln(i - Q; в) л3 - tgjicj§-| .
14. Найти плотность распределения суммы двух независимых величин
5 и г|, равномерно распределенных на отрезках [1, 3] и [о, 1]
соответственно.
15. Случайные величины ? и х\ независимы и равномерно
распределены на отрезках [о, 2] и [3, 4] соответственно. Найти плотность
распределения суммы ? + г\.
16. Случайные величины § и т| независимы и равномерно
распределены на отрезках [о, 4] и [1, 2] соответственно. Найти плотноаь
распределения суммы % + х\.
17. Случайные величины ^ и г| независимы и равномерно
распределены на отрезках [1, 3] и [2, 4] соответственно. Найти плотноаь
распределения суммы ? + т].
18. Случайные величины независимы и имеют показательное распре-
\е~\ х>0,
деление с плотноаью р(х) =
пределения их суммы.
л Найти плотноаь рас-
0, х<0.
I 150
Глава 7
19. Найти распределение суммы независимых случайных величин % и
т|, где \ имеет равномерное на отрезке [о, 1] распределение, а х\
имеет показательное распределение с параметром X.
20. Совместное распределение ц является равномерным в квадрате
(1 1 ^
К = {(*, у)- И + М ^ 2Ь Найти вероятностьР\ "
Являются ли ? и л независимыми?
21. Пара случайных величин ? и г) равномерно распределена внутри
треугольника К - {(х9у):х + у<1,х>0,у>0}. Вычислить
плотность ? и г). Являются ли эти случайные величины независимыми?
Найти вероятность Р(? < 1/2).
22. Случайные величины ? и г| независимы и равномерно
распределены на отрезках [о, 1] и [-1,1]. Найти вероятность Р(^г\<\ /2).
23. Двумерная случайная величина (?, л) равномерно распределена
в квадрате с вершинами (2; о), (о; 2), (-2; о), (о; -2). Найти
значение совместной функции распределения в точке (i; -1).
24. Случайный вектор (?, л) равномерно распределен внутри круга
радиуса 3 с центром в начале координат. Написать выражение для
совместной плотности распределения. Определить, зависимы ли
эти случайные величины. Вычислить вероятность />(б>>0,т]>0).
25. Пара случайных величин ? и г| равномерно распределена внутри
трапеции с вершинами в точках (-6; о), (-3; 4), (3; 4), (6; о).
Найти совместную плотность распределения для этой пары случайных
величин и плотности составляющих. Зависимы ли ? и г|?
26. Случайная пара (?, л) равномерно распределена внутри
полукруга К = ^х,у): (х -I)2 + у2 < U У > О}. Найти плотности ? и л,
исследовать вопрос об их зависимости.
Р(х9у) =
27. Совместная плотность двух случайных величин ? и л равна
4е2у9у<09х<09у<х-9
О, иначе.
Найти плотности Л- Исследовать вопрос о зависимости ? и т|.
28. Случайная пара (?, л) равномерно распределена на множестве
К = {(х9у):х>0'91>у>х}. Найти плотности ? и г\9 исследовать
вопрос об их зависимости. Найти М(^ц).
151
ЧАСТЬ I. Теория вероятностей
29. Случайные величины ? и г| независимы и распределены по
показательному закону с параметром X = 2. Найти + < 2}.
30. Дана совместная плотноаь случайных величин % и 11:
^sin(x-h^), 0<х<^;0<^<~;
О, иначе.
Найти: а) коэффициенте; б) совместную функцию распределения;
в) частные плотности и функции распределения; г) условную
плотноаь распределения § при условии т| - у.
31. Случайная пара (?, л) равномерно распределена в единичном
квадрате К = {(х,у):0<х<1; 0<у<1}. Пуаь р — расаояние
от точки (?, ti) до нуля. Найти функцию условного распределения
р при условии ? = х, о * х * 1.
32. Пара случайных величин % и г| равномерно распределена в
треугольнике с вершинами в точках (о; о), (i; 1), (2; -1). Найти: а)
функцию регрессии % по ту, б) функцию регрессии т| по
33. Две независимые случайные величины ^ и cj2 имеют
показательное распределение с параметром X. Найти условное
распределение ?t при условии, что Т] = ^ + ?2 = tf t > о.
ГЛАВА 8
ЗАКОН БОЛЬШИХ ЧИСЕЛ.
ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ
ТЕОРЕМА
§ 8л. Неравенство Чебышева
> Теорема 1 (неравенство Маркова). Пусть случайная величина ?
имеет М\^\, тогда для любого г > 0 верно
Доказательство. Проведем доказательство раздельно в
дискретном и в абсолютно непрерывном случае.
Пусть ? — дискретная случайная величина и Щ = х) = р.,
/ = 1, 2, п. Тогда вероятность Р{ I ? | > е) равна сумме
вероятностей рр для которых х. находятся вне промежутка (—е, е).
kl
Очевидно, для таких xt имеет место неравенство — >1.
Учитывая это неравенство, получаем 8
Р(\$\>г) =
= Е л < Е^л < Е^л + Е^л =±±Ыл =^1-
|х,|>е |х,|>е ь |х,|>е b |х,|<е b fc /=1 fc
Пусть ^ — абсолютно непрерывная случайная величина с
плотностью распределения р^(х). Тогда вероятность Р( I % I > е)
равна сумме интегралов от плотности распределения по про-
153 |
i
ЧАСТЬ I. Теория вероятностей
\х\
межуткам (—оо, —е) и (е, +<х>). На этих промежутках — >1.
8
Воспользовавшись формулой для математического ожидания,
получаем неравенство
-е оо - -е
P(UI >е) = J p%(x)dx + jp^x)dx <- J \x\p%(x)dx +
—oo e ^ —oo
+-J\x\p^(x)dx <-f \x\pfx)dx +-J \x\pjx)dx +
^8 ^ -oo ^ -8
1 oo - oo 1
+ - f \x\pAx)dx=- f \x\p.(x)dx = -M\%\.
8 —oo
В общем случае подобное доказательство проводится с
использованием интеграла Лебега, что не входит в программу
настоящего курса.
Следствие. Если случайная величина § имеет Щ2, то для
любого е > 0 верно
i>(M>e)<i?
Доказательство. Заметим, что событие {со: I ^ I > е}
равносильно событию {ш: ??> е2}, и применим неравенство Маркова
к случайной величине 42.
> Теорема 2 (неравенство Чебышева). Пусть случайная
величина ? имеет математическое ожидание Щ и дисперсию Тогда
для любого е > 0 верно
Р^-Щ\>г)<^.
Доказательство. Применяем следствие неравенства Маркова
к случайной величине |§ - Щ\, замечая, что " Щ)2 = Щ-
Неравенство Чебышева часто используют в виде
Щ
82
р{5-м§|<в)>1-?.
154
Глава 8 ф
р. Теорема 3 (неравенство Колмогорова). Если независимые
случайные величины \v \п имеют математические ожидания
Щ. и дисперсии то для любого е > 0 верно
, 1 п Iя
<е
> 1-
Доказательство. Применяем неравенство Чебышева к слу-
чайной величине С, = —, которая имеет Mt^ = M$t и
п /_1 п ;_|
1 - "
DC, = — Y^^i (согласно свойствам математического ожидания
и дисперсии).
Задача 1. В 400 испытаниях Бернулли вероятность успеха в
каждом испытании равна 0,8. С помощью неравенства
Чебышева оценить вероятность того, что разница между числом успехов
в этих испытаниях и средним числом успехов будет меньше 20.
Решение. Число успехов в этих испытаниях распределено
по закону Бернулли, поэтому среднее число успехов равно
Щ = пр = 400 х 0,8 = 320, а дисперсия К> = npq = 400 х 0,8 х
х 0,2 = 64. Тогда в силу неравенства Чебышева имеем
P(fe-320|<20)>1-^ = 1- — = 0,84.
^ч 1 7~ 202 400
Вычислим эту же вероятность с помощью приближенной
(интегральной) формулы Муавра—Лапласа (см. гл. 4):
Р (|§ - 320| < 20)= Р ([§ - пр\ < е)= Р
{ 20 )
е ?> — пр 8
= 2ФП
= 2Ф,
(V64J
1 Jnpq Jnpq yjnpq)
= 2Ф0 (2,5) = 2 х 0,4938 = 0,9876
Последнее вычисление показывает, что неравенство
Чебышева дает довольно грубые оценки вероятностей.
§ 8.2. Закон больших чисел
^ Теорема 4 (закон больших чисел). Пусть задана бесконечная
последовательность независимых одинаково распределенных
случайных величин ?2, \п, для которых существуют мате-
155 I
ф ЧАСТЬ I. Теория вероятноаей
ПтР
1 п
П /=1
>6
= 0.
Доказательство. Применяем неравенство Чебышева к слу-
Iя 1 я
чайной величине С,,=-]ГХ' Km°P** имеет Л/Ся=-Е^/==в
1
>е
= ^(KJ>b)<-
> 0, п —> оо.
Суть закона больших чисел состоит в том, что при
возрастании числа слагаемых (одинаково распределенных случайных
величин) среднее арифметическое этих слагаемых мало
отличается от математического ожидания а. Иначе говоря, любое
положительное отклонение среднего арифметического случайных
величин от числа а становится при достаточно большом числе
слагаемых маловероятным.
Закон больших чисел может выполняться и в случае по-
разному распределенных случайных величин.
> Теорема 5. Пусть \v ?>п, ... — последовательность
независимых случайных величин, для которых существуют
математические ожидания Щ. и дисперсии Z>?., удовлетворяющие усло-
1 "
вию — ]Г0, п оо. Тогда для любого г > О справедливо
pari ,=i
венство
ПтР
п—юо
\ П 1/1
" 1=1 " /=!
<е
= 1.
Доказательство. В силу неравенства Колмогорова имеем
1-
1
1я Iя
<i.
156
матическое ожидание Щ. = а и дисперсия = <*2 • Тогда для
любого е > 0 верно
Глава 8
i
Переходя к пределу в неравенстве при п ¦+ оо, получаем
утверждение теоремы.
В общем случае сходимость случайной последовательности
Хп к пределу X вида
\\тР(\Хп-Х\>г) = 0
п—>оо
для любого б > 0, называется сходимостью по вероятности и
обозначается как
Пример 1. Пусть §2, §я, ... — последовательность
случайных величин, каждая из которых равна числу успехов в
одном испытании Бернулли (т.е. 1 в случае успеха и 0 — в
случае неудачи). Закон распределения каждой такой случайной
величины имеет вид:
0
1
р
я
р
Тогда математическое ожидание Щ{ = р и дисперсия
- 1
равно частоте
D^^pq. Среднее арифметическое х = —
п /=1
успехов в п испытаниях, и закон больших чисел утверждает, что
эта частота успехов стремится к вероятности успеха р, когда
число слагаемых (т.е. число испытаний) неограниченно возрастает.
На самом деле справедливо и более сильное утверждение,
чем закон больших чисел, однако его доказательство является
существенно более сложным.
^ Теорема 6 (усиленный закон больших чисел). Пусть задана
бесконечная последовательность независимых одинаково
распределенных случайных величин ?2, для которых
существует математическое ожидание Щ. = а, тогда
' Ъ.1
lim
л—юо
— а
= 1.
В общем случае сходимость случайной последовательности
Хп к пределу X вида
P(limXn=X) = l
157
^ ЧАСТЬ I. Теория вероятноаей
§ 8.3. Центральная предельная теорема (ЦПТ)
> Теорема 7 (центральная предельная теорема). Пусть ?2,
\п, ... — независимые одинаково распределенные случайные
величины с Mt)i = а и Dt,. = a2, i = 1, 2, ... п, ... 7Ъгдя для любого
числа х верно:
ПтР
Оу/п
<Х
1 г --
= Ф(х) = -= / е 2rfy.
Смысл центральной предельной теоремы заключается в
п
том, что сумма 5*я==]Г^. случайных величин при надлежа-
щем линейном преобразовании с увеличением числа слагаемых
(п -> оо) ведет себя почти как случайная величина со
стандартным нормальным распределением N(0, 1). Вероятность
попадания в любой интервал имеет следующий предел:
limP
S„-na
у\/п
-<с,
1 °2
е 2^ = Ф(с2)-Ф(с,) = Ф0(с2)-Ф0(с,),
откуда следует приближенная формула
(В-па)
P(A<S„<B)*<i>0
Syfn
Ф,
А-па
^ J
которой имеет смысл пользоваться, если А и В не очень далеки
от па.
Центральная предельная теорема может оставаться
справедливой и в случае, когда случайные слагаемые не являются
одинаково распределенными.
^ Теорема 8 (Ляпунова). Пусть \р \2,..., — независимые
случайные величины, имеющие конечный третий абсолютный
центральный момент, и пусть ak = Щк, ак2 = D^k, с\ = А/|^ - ак\3,
158
называется сходимостью с вероятностью единица (или почти
наверное) и обозначается как
Из сходимости с вероятностью единица следует сходимость
по вероятности, обратное верно не всегда.
Глава 8
jln = Y^uk , B*=Y^c2k , С] =Y^cl. Если при n -> oo отношение
Д.
k=\ k=\ k=\
> 0, то для любого числа x верно
limP
1 г
= Ф(х) = —= I е 2 dy
y/2nJ
В общем случае сходимость случайной последовательности
Хп к пределу (случайной величине) X вида
ПтР(Хп<х) = Р(Х<х)
п—*оо
в точках непрерывности функции распределения X называется
сходимостью по распределению и обозначается как
х„-^х.
Из сходимости по вероятности следует сходимость по
распределению, обратное верно не всегда (но верно в случае
сходимости к константе).
Пример 2. Пусть §2, §л, ... — последовательность
случайных величин, удовлетворяющая условиям предыдущего
примера 8.1. В этом случае сумма Sn = + ?2 + ... + \п есть число
успехов т в п испытаниях Бернулли. Из ЦПТ следует, что
limP
л—>оо
т — пр
yfnpg
„2
е~2ах = Ф0(с,)-Ф о (е.),
1 г --
где Ф0(х) = -= I е 2 dy — функция Лапласа.
V2nJn
Тогда вероятность того, что число успехов заключено между
/и, и т2, равна
Р(/и, <т<т2) = Р
щ-пр ^ /н-я/> < щ-пр
{ л/йй -Jnpq J
<Фл
т^ — пр
-Ф
пц-пр
Этот результат называется интегральной теоремой Муавра-
Лапласа и уже встречался нам раньше (см. § 4.3).
159
ЧАСТЬ I. Теория вероятностей
Задача 2. В продукции цеха детали отличного качества
составляют 50%. Детали укладываются в коробки по 200 шт. в
каждой. Какова вероятность того, что число деталей отличного
качества в коробке отличается от 100 не более, чем на 5?
Решение. Пусть — случайное число деталей отличного
качества в i-Pi коробке, тогда при п = 200, p = q = - получим:
Р(95<т<\05) = Р
5 <т-пр < 5
л/50 V50J
<Ф0(0,71)-Ф0(-0,71)«0,52.
Задача 3. Используя условия задачи 2, указать, в каких
границах с вероятностью 0,997 находится число деталей отличного
качества в коробке.
Решение. По табл. 2 приложения 3 при условии
т-пр
yfnpg
<и
; 0,997 находим и = 3, и следовательно, S лежит
в пределах np±3yfnpq, т.е. число деталей отличного качества в
коробке с вероятностью 0,997 находится в пределах 100 ±21.
Задача 4. Используя условия задачи 2, определить, сколько
деталей надо положить в коробку, чтобы с вероятностью, не
меньшей 0,99, можно было утверждать, что число деталей
отличного качества в коробке не менее 100.
Решение. Обозначим н = ^=^. Используя нормальное
приближение, получаем
\m-np
yfnpq
Р(т>\00) = Р
>и
npq
а-Ф(1/) = ~Ф0(и)>0,99.
Отсюда Ф0(и) < —0,49, а из табл. 2 приложения и свойств
функции Лапласа получаем неравенство и < —2,32. Обозначив х = л/л > 0,
с учетом р — q = ^ , приходим к квадратному неравенству
х2 —2,3х — 200 > 0, решая которое получаем п > 236.
Можно предложить и другой метод. Пусть — число
деталей, которые пришлось перебрать, чтобы найти /-ю деталь
отличного качества (включая ее саму). Случайные величины
имеют геометрическое распределение с параметром р = 1/2.
i6o
Глава 8
Можем вычислить Щ = 1/р = 2, D% = (1 -p)lf = 2. Используя
цПТ, получаем неравенство
Гл —2001
Р(51(Ю<л) = Ф
/1-100-2) 1
, V2V100 ]~2+Ф°
{ 14,14 J
>0,99,
откуда следует п > 200 + 14,14 х 2,32 = 232,8, или, округляя,
п > 234.
Результаты получаются близкие, но первый метод более
точен и потому предпочтительней. Вторым методом лучше
пользоваться, если нужно определить границы, в которых лежит
неизвестное число деталей.
Задача 5. Доходы (в месяц) жителей города имеют
математическое ожидание 10 тыс. руб. и среднее квадратическое
отклонение 2 тыс. руб. Найти вероятность того, что средний
доход 100 случайно выбранных жителей составит от 9,5 до
10,5 тыс. руб.
Решение. Переформулируем условие задачи для суммарного
дохода: он должен составлять от 950 до 1050 тыс. руб. Используя
ЦПТ, получаем:
Р(950<5100<1050) = Ф0
(1050-100x10
2л/100
Фп
f950-100x10)
2V100
= 2Ф0(2,5) = 0,9876.
Задача 6. Срок службы электрической лампы имеет
показательное распределение с математическим ожиданием 1000 час.
Найти вероятность того, что средний срок службы для 100 ламп
составит не менее 900 час.
Решение. Примем для простоты 1000 час. за единицу
времени. Вспомним числовые характеристики показательного
квадратическое отклонение совпадает с математическим
ожиданием (и оба они здесь равны единице). Переформулируя
условие задачи для суммарного срока службы и используя ЦПТ,
получаем:
распределения: Щ= — , DE= -7 . Отсюда следует, что среднее
Р(5100>90) = 1-Ф
6 Теория вероятностей
161
^ ЧАСТЬ I. Теория вероятностей
о
Задачи для самостоятельного решения
Теоретические задачи
1. Пусть задана последовательность независимых случайных величин
4М ?,п, имеющих следующий закон распределения.
-4~п
0
р
1/п
1-1
п
1-1
п
Применим ли к этой последовательности закон больших чисел?
2. Пусть задана последовательность независимых случайных величин
?2, имеющих следующий закон распределения.
—п
п
р
1/2
1/2
Применим ли к этой последовательности закон больших чисел?
3. Доказать закон больших чисел в «обобщенной форме»: пусть
?>х, \v \nf ... — последовательность независимых случайных
величин, у которых существуют математические ожидания и
дисперсии D^.t причем все дисперсии ограничены сверху одной
константой С > о. Тогда для любого е > о
limP
я-»оо
1я Iя
п /=1 п /=i
:0.
4. Пусть случайная величина ? имеет нормальное распределение с
параметрами Щ = a, D? = а2. Найти вероятности Р(|§-д|>а)
и P(j§-e|>3a), пользуясь таблицами функции Лапласа. Затем
оцените те же вероятности с помощью неравенства Чебышева.
5. Пусть случайная величина ? имеет распределение Лапласа, т.е.
ее плотность равна />(*) = — Х>0. Найти вероятности
Р(|^|<ст) и Р(|^|<За), где а — среднее квадратическое
отклонение, и сравнить их с оценками, получаемыми с помощью
неравенства Чебышева.
162
Глава 8 0
случайная величина т],. =
6. Будет ли выполнен закон больших чисел для последовательности
независимых случайных величин ?г, §2,... ?л,... если:
а) Р?п=Г) = ± />((;„ =-2")=Д;
6 />(^ = 2л) = 2-(2я+1), Р(^я = 0) = 1-2-2я, Р(^=-2я) = 2-(2,,+1).
7. Пуаь некоторая величина а измеряется прибором без
систематической ошибки, но со средним квадратическим отклонением а.
Это означает, что результат измерения можно считать случайной
величиной ? с М$ - a, DZ, = а2. Какова вероятность при юо
измерениях получить для среднего арифметического отклонение от
величины а более, чем на 0/4? Дать оценки этой вероятности с
помощью неравенства Чебышева и ЦПТ.
8. Пусть ?lf ?2,... ... — независимые, одинаково распределенные
случайные величины с функцией распределения F(x). Пусть задана
1, ъ<х,
О, Ь>х.
Выполняется ли для последовательности т^т^,... rj.,... закон
больших чисел?
9. Пусть для последовательностей {^п} и {rin} случайных величин
существуют числа а и Ь такие, что lim Р(\^п - а\ > е) = О,
lim Р(|г|я - b\ > е) = 0 для любого е > о. Доказать, что:
л-юо ' " '
а) ИтРф;Л-д|<е, \ц„-Ь\<г) = 1;
л->оо iiii
б) если Дх, у) непрерывна в некоторой точке (а, Ь), то для любого
6 > о
\imP(\f(^4n)-f(a,b)\<e) = \.
л—юо 1 1
ю. Последовательности ^ ?2, ... и т]2, ... случайных величин
таковы, что ИтР(кя|<8) = 1 для любого е > о и существует функция
распределения F(x), для каждой точки непрерывности которой
выполняется соотношение lim P(r\n < х) = F(x). Доказать, что
л—>оо
для каждой точки непрерывности F(x) справедливо равенство
limP(j)n+in<x) = F(x).
163
ф ЧАСТЬ I. Теория вероятностей
Вычислительные задачи
11. Средний размер вклада в отделении банка равен бооо руб. Оценить
вероятность, что случайно взятый вклад не превысит ю ооо руб.
12. Среднее количество вызовов, поступающих на АТС завода в
течение часа, равно 300. Оценить вероятность того, что в течение
следующего часа число вызовов на коммутатор: а) превысит 400;
б) будет не более 300.
13. По статистическим данным в среднем 87% новорожденных
доживают до 50 лет. С помощью неравенства Чебышева оценить
вероятность того, что из юоо новорожденных доля доживших до 50 лет
будет отличаться от вероятности этого события не более чем на
0,04 (по абсолютной величине).
14. Среднее изменение курса акции компании в течение биржевых
торгов составляет 0,3%. Оценить вероятность того, что на
ближайших торгах курс изменится более чем на 3%.
15. Отделение банка обслуживает в среднем юо клиентов в день.
Оценить вероятность того, что сегодня в отделении банка будет
обслужено: а) не более 200 клиентов; б) более 150 клиентов.
16. Вероятность сдачи в срок всех экзаменов студентом факультета
равна 0,7. С помощью неравенства Чебышева оценить
вероятность того, что доля сдавших в срок все экзамены из 2000
студентов заключена в границах от о,66 до 0,74.
17. В среднем ю% работоспособного населения некоторого
региона — безработные. Оценить с помощью неравенства Чебышева
вероятность того, что уровень безработицы среди обследованных
ю ооо работоспособных жителей города составит от 9 до 11%
(включительно).
18. Опыт страховой компании показывает, что страховой случай
приходится примерно на каждый пятый договор. Оценить с
помощью неравенства Чебышева необходимое число договоров,
которые следует заключить, чтобы с вероятностью 0,9 можно было
утверждать, что доля страховых случаев отклонится от 0,2 не
более чем на 0,01 (по абсолютной величине). Уточните ответ с
помощью следствия из интегральной теоремы Муавра—Лапласа.
19. Дисперсия каждой из 3500 независимых случайных величин
равна 5. Оценить вероятность того, что отклонение среднего
арифметического этих случайных величин от среднего арифметического
их математических ожиданий не превысит 0,25.
164
Глава 8 0
20. Ежедневно новая сделка заключается с вероятностью о,2 (но не
более одной в день). За сколько дней с вероятностью 0,9 можно
ожидать заключения не менее 50 сделок?
21. В продукции цеха детали отличного качества составляют 8о%.
В каких пределах будет находиться с вероятностью 0,99
число деталей отличного качества, если взять ю ооо деталей? Дать
оценку с помощью неравенства Чебышева и с помощью теоремы
Муавра—Лапласа.
22. Театр, вмещающий юоо человек, имеет два разных входа. Около
каждого из входов имеется свой гардероб. Сколько мест
должно быть в каждом из гардеробов для того, чтобы в среднем в 99
случаях из юо зрители могли раздеться в гардеробе того входа,
через который они вошли? Предполагается, что зрители приходят
парами и каждая пара независимо от других выбираете
вероятностью 0,5 любой из входов. На сколько можно будет сократить
число мест в гардеробе, если зрители будут приходить поодиночке и
также независимо друг от друга с равной вероятностью выбирать
любой из входов?
23. Аппаратура состоит из юо одинаково надежных и независимо
работающих элементов, каждый из которых может отказать в
течение суток с вероятностью 0,01. На обнаружение отказавшего
элемента и его замену требуется 20 минут, в течение которых
аппаратура простаивает. Найти: а) вероятность того, что время
простоя составит не более 40 минут в сутки; б) среднее время простоя
аппаратуры в сутки.
24. В поселке 2500 жителей. Каждый из них примерно 6 раз в месяц
ездит на поезде в город, выбирая дни поездок по случайным
мотивам независимо от остальных. Какой наименьшей вместимостью
должен обладать поезд, чтобы он переполнялся в среднем не чаще
одного раза в юо дней (поезд ходит раз в сутки)?
25. На заводе юоо станков, каждый из которых в среднем в течение
24 дней в месяц потребляет электроэнергию независимо от
других станков с интенсивностью ю единиц в день. Какое количество
электроэнергии необходимо заводу ежедневно, чтобы недостаток
электроэнергии наблюдался в среднем не чаще двух раз за юо
дней?
165 |
V )
ЧАСТЬ I. Теория вероятностей
26. Предприятие выпускает 30% изделий стоимостью юо руб., 30%
изделий стоимостью 200 руб. и 40% изделий стоимостью 300 руб.
Какова вероятность получить за юоо случайно отобранных изделий
не менее 215 тыс. руб.?
27. Известно, что 1/3 всех деталей, сходящих с конвейера,
подвергается выборочному контролю на основании некоторого случайного
признака. Пусть через контроль прошло юо деталей. В каких
границах с вероятностью 0,99 лежит общее число деталей, сошедших
с конвейера?
28. Для проверки эффективности новый метод стимулирования роста
производительности труда был введен на юо предприятиях. При
этом на 32 предприятиях введение нового метода вызвало
снижение производительности труда, а на 68 — повышение
производительности труда. Какова вероятность того, что чисто случайные
колебания вызовут не меньшее отклонение от числа 50 (половины
общего числа предприятий)?
29. Изготовление детали занимает случайное время, равномерно
распределенное от ю до 15 минут. Найти вероятность того, что на
изготовление юо изделий понадобится не менее 20,5 ч.
30. Число посетителей магазина (в день) имеет распределение
Пуассона с математическим ожиданием 289. Найти вероятность того,
что за юо рабочих дней суммарное число посетителей составит от
28 550 до 29 250 человек.
31. Вес яблока имеет математическое ожидание 200 г и среднее ква-
дратическое отклонение 50 г. Найти вероятность того, что в юо кг
окажется не менее 490 яблок.
32. Вес арбуза имеет математическое ожидание ю кг и среднее ква-
дратическое отклонение 2 кг. Найти вероятность того, что в i тонне
окажется не более 105 арбузов.
ГЛАВА 9
ЦЕПИ МАРКОВА
§ 9.1. Основные понятия
Случайным процессом называется функция двух переменных
?(/, со), где / е Т — время, со е Q — элементарный исход. Время
может быть непрерывным или дискретным (целочисленным).
Случайный процесс ставит в соответствие каждому моменту
времени / е Г случайную величину §(/) = со) как функцию от
со е Q. Поэтому процесс обычно для краткости обозначают ?(/).
Пусть заданы моменты времени 0 <tx< t2< ... < tn< tn+{< ... <
< tn+m, я, m > О, и А — любое событие (утверждение),
относящееся к случайным величинам ?(/,), ?(/„_,), В —
относящееся к §(/я+1), Wn+J* с — относящееся к &п). Говорят, что
процесс обладает марковским свойством, если для него всегда
выполняется равенство
Р(В\АС) = Р(В\С),
или (в эквивалентной форме):
Р(АВ\С) = Р(А\С)Р(В\С).
Марковское свойство означает, что будущее поведение
процесса не зависит от его прошлого при условии, что известно
настоящее (т.е. текущее значение процесса).
Марковским процессом называется случайный процесс,
обладающий марковским свойством.
Пространством состояний S случайного процесса называется
множество всех возможных значений функции ?(/, со).
Цепью Маркова называется марковский процесс, для
которого выполнено хотя бы одно из следующих двух условий:
167 I
I
|^ ЧАСТЬ I. Теория вероятноаей
§ 9.2. Цепи Маркова с конечным
числом состояний и дискретным временем
В этом параграфе рассмотрим цепи Маркова:
а) с пространством состояний S из конечного числа
элементов т\
б) с дискретным временем п, принимающим значения 0, 1,
2 и т.д.
Обычно полагают, что элементы S занумерованы числами
1, 2, /я.
Для таких цепей марковское свойство может быть записано
в форме
Pfc(n + l) = i.+l\l(n) = iM9 i(n-l) = in_l9..., m = i0) =
= Р(«л + 1) = /я+1К(я) = /.>
Однородными называются цепи Маркова, для которых
условные вероятности Р(^(п + 1) = j \ ?(я) = /) не зависят от п.
Таким образом, однородная цепь ведет себя с любого момента
так же, как с начала (п = 0). Далее будем рассматривать только
однородные цепи Маркова.
Вероятности р„= Щ(п + 1) =j | = /) называются пере-
ходными вероятностями, а составленная из них матрица Р —
матрицей переходных вероятностей:
Ри
hi
Р22
Р\т
Plm
[Рт\ Рт2
Поскольку в каждой строке матрицы записаны
вероятности всех возможных переходов из выбранного состояния
(в том числе и вероятности того, что система останется в нем),
168
а) пространство состояний конечно или счетно;
б) время дискретно.
Далее будем изучать цепи Маркова с конечным или
счетным числом состояний, как с дискретным, так и с
непрерывным временем.
Глава 9 ф
эти переходы образуют полную группу событий. Поэтому для
т
каждой строки имеет место равенство $^/fy=l для ЛК)бого
/ = 1, 2, т. 7=1
Распределение ?(я) задается вектором р(п) = (р,(я),Рт(п)),
где рЦп) = Pfc(/i) = /).
По формуле полной вероятности получаем
р(п + 1) = р(п)Р.
Начальным распределением цепи Маркова 4 называется
распределение 4(0)» заданное соответствующим вектором р(0).
Зная начальное распределение, можно найти р(п) при любом
п > 0, последовательно вычисляя /?(1) = р(0)Р9 р(2) = /?(1)Р
и т.д. В общем случае получаем формулу
р(п) = р(0)Р\
Отсюда следует, что вероятности Р..(п) перехода из
состояния / в состояние j за время п можно найти как элементы п-й
степени матрицы Р, т.е. (P,(w)) = Рп.
Говорят, что из состояния / можно перейти в состояние
у, если существует п такое, что Р..(я) > 0. Если из состояния
/ можно перейти в состояние j такое, что обратно вернуться
нельзя, то состояние / называют несущественным', в противном
случае — существенным. Если из состояния / можно перейти
в у, а из j — в /, то такие состояния называют сообщающимися.
Все существенные состояния цепи разбиваются на классы
сообщающихся состояний (внутри каждого класса все состояния
сообщаются между собой, но не сообщаются с состояниями
других классов).
Класс называется периодическим с периодом d, если для
любого состояния / из этого класса возможные времена
возвращения в него (т.е. такие п, что Р/7(я) > 0) кратны некоторому числу
d > 2. В противном случае класс называется апериодическим.
Эргодической называется цепь Маркова, для которой
существует предельное распределение я = (яр ... пт):
т
п. = ИтР(я), Гя- =1.
J л—юо —Г
Если имеется лишь один класс сообщающихся состояний, и
он апериодический, то цепь Маркова является эргодической.
169
ф ЧАСТЬ I. Теория вероятностей
Предельное распределение имеет важное практическое
значение, однако найти его из приведенной формулы
затруднительно, поэтому используется иной подход.
Стационарным распределением цепи Маркова называется
такое распределение, которое, будучи задано в качестве
начального, в дальнейшем останется неизменным. В таком случае
говорят, что система находится в стационарном режиме.
Для эргодических цепей Маркова стационарное
распределение существует и единственно, а самое главное — совпадает
с предельным. Таким образом, если система изначально не
находится в стационарном режиме, она со временем (при п -»оо)
выходит на него.
Стационарное распределение я = (яр пт) легко найти из
системы уравнений:
т
71 = 7гР, XX =1.
7=1
Следует отметить, что это система из т + 1 уравнений с т
неизвестными, так что одно из уравнений (любое из первых т)
можно исключить.
Пример 1. Простейшая форма контроля качества
продукции с переменным планом заключается в следующем. Задается
т различных объемов выборок (планов), в порядке убывания:
пх > п2 > ... > пт, т > 2. Если в выборке из партии изделий
обнаружено хотя бы одно дефектное, партия бракуется. Схема
контроля производства строится по следующему алгоритму. Первая
партия изделий проверяется выборкой максимального объема
пг Если она оказалась принятой, делается вывод о нормальном
ходе производства, и для следующей партии переходят на
выборку меньшего объема я2; в противном случае объем остается
максимальным. При контроле партии выборками
промежуточного объема пк, 1 < к < т, в случае приемки партии переходят
на выборку меньшего объема пк+]\ в случае отбраковки — на
выборку большего объема пк_у При контроле партии выборкой
минимального объема пт в случае приемки этот объем
сохраняется, в случае отбраковки переходят на выборку объема пт_у
В рассматриваемой модели номер используемого плана
(объема выборки) образует цепь Маркова, так как при
известном текущем значении его следующие значения не
зависят от предыдущих. Пространство состояний в данном случае
I 170
Глава 9 ф
S = {1, 2, т). Обозначим через г вероятность отклонить
партию при объеме выборки пр 1 < i < т. Тогда переходные
вероятности принимают вид:
Заметим, что если вероятность е дефекта изделия мала, то
г,* ей.. Поэтому для простоты далее будем полагать г.= ей..
Задача 1. На производстве используется система
приемочного контроля с переменным планом, где я, = 20, п2 = 10,
б = 0,01. Построить матрицу переходных вероятностей и найти
стационарное распределение для номера плана.
Решение. Здесь S = {1, 2}. Вычисляем ^ = 0,2; г2 = 0,1.
Матрица переходных вероятностей имеет вид
Решаем систему уравнений для вектора я = (я,,я2):
я = яР, я, 4- я2 = 1,
или, более подробно,
Решая первое (или второе) уравнение совместно с третьим,
получаем я = (1/9, 8/9).
Задача 2. В городе Ромашкино каждый год 1% жителей
переселяются в пригород, а 4% жителей пригорода — в город.
Найти стационарное распределение в предположении, что
общая численность населения остается постоянной.
Решение. Будем считать, что живущий в городе находится в
состоянии 1, а живущий в пригороде — в состоянии 2. Матрица
переходных вероятностей имеет вид
г„ у = /-1, />1;
г„ У = / = 1;
l-r*,> j = i = m.
Р =
0,2 0,8
,0,1 0,9
я, =0,2я, +0,1я2
я2=0,8я,+0,9я:
я, +я2 =1.
Р =
0,99 0,01
0,04 0,96
!71 !
ф ЧАСТЬ I. Теория вероятноаей
Решая систему уравнений
[я, =0,99^+0,04*2,
я2=0,01я,+0,96я2,
я, + я2 = 1,
получаем я = (0,8; 0,2). Таким образом, в стационарном режиме
80% живут в городе, 20% — в пригороде.
Задача 3. Магазин электротоваров торгует холодильниками.
Случайный спрос на холодильники за неделю имеет
распределение, заданное таблицей
Спрос
0
1
2
р
0,2
0,5
0,3
Если холодильники заканчиваются, делается заказ на 2
штуки, который прибывает на следующей неделе. Построить
матрицу переходных вероятностей. Найти стационарное
распределение числа холодильников в магазине.
Решение. В данном случае будем нумеровать состояния от
нуля (по числу холодильников), так что S = {0, 1, 2}. Матрица
переходных вероятностей имеет вид
0 0 1
Р= 0,8 0,2 0
0,3 0,5 0,2]
Предполагаем, что неудовлетворенный спрос пропадает и
не переносится на следующую неделю (т.е. если он составлял
2 штуки, а в магазине был только один холодильник, то
система переходит в состояние 0, без каких-либо последствий).
Решая систему уравнений
я0 =0,8я, +0,3я2,
я, =0,2я, + 0,5я2,
я2=я0 +0,2я2,
я0 + я, + я2 = 1,
получаем я « (0,330; 0,258; 0,412). Следует отметить, что
используемая в данном случае политика пополнения запасов не
выглядит эффективной. Действительно, 33% времени товар
отсутствует, и магазин упускает возможную прибыль от продаж.
1172
Глава 9 ф
173
§ 9.3. Цепи Маркова с непрерывным временем.
Системы массового обслуживания
В этом параграфе рассмотрим цепи Маркова:
а) с пространством состояний S из конечного или счетного
числа элементов;
б) с непрерывным временем t > 0.
Обычно полагают, что элементы S занумерованы числами
1, 2, ...
Как и ранее, будем рассматривать только однородные цепи
Маркова, свойства которых не зависят от времени.
Интенсивностью перехода из состояния / в состояние j (i ф j)
называется число X такое, что вероятность перехода из
состояния / в состояние j за промежуток времени At равна XAt + o(At)
при At -> 0. Предполагается, что вероятность более чем одного
перехода за это время составляет о(А/) при At -> 0.
Определим также формально величины
хИ=-]ГХ-,
имеющие смысл полных интенсивностей выхода из
соответствующих состояний.
Тогда для вероятностей /?,.(/) = P{tfJ) = /) имеет место
система дифференциальных уравнений, называемых уравнениями
Колмогорова:
at t=i
Эти уравнения могут быть решены, исходя из начального
распределения р(0).
Определим матрицу Л = (А,), называемую матрицей
интенсивностей переходов, тогда уравнения перепишутся в виде
/>'(/) =/КОЛ.
Как и ранее, нас будут интересовать эргодические цепи Маркова
и предельные (стационарные) распределения. Поскольку в
стационарном режиме распределение не меняется (и производные равны
нулю), оно может быть найдено из системы уравнений:
т
тгЛ = 0, 5>у=1.
Если в цепи Маркова с непрерывным временем есть только
один класс сообщающихся состояний, а стационарное распре-
ф ЧАСТЬ I. Теория вероятностей
1 На практике эти условия выполняются далеко не всегда. Однако
получаемые при указанных предположениях результаты можно использовать
в качестве предварительных грубых оценок показателей работы системы.
174
деление существует и единственно, то такая цепь оказывается
эргодической, и ее предельное распределение совпадает со
стационарным.
Типичной областью применения цепей Маркова с
непрерывным временем является теория массового обслуживания,
занимающаяся изучением систем массового обслуживания, т.е. таких
систем, в которых, с одной стороны, возникают массовые
требования на выполнение каких-либо услуг, а с другой —
происходит удовлетворение этих требований (по мере возможности).
Система массового обслуживания включает в себя источник
требований (внешний или внутренний) и обслуживающие
приборы (каналы обслуживания).
Эту терминологию не следует понимать буквально. Так, в
качестве требований могут выступать люди, предметы,
документы, файлы и пакеты данных и др.; в качестве обслуживающих
приборов — люди, станки, организации, компьютеры и др.
Простейшим потоком событий называется такая
последовательность событий (в непрерывном времени), когда
интенсивность наступления очередного события постоянна. Иначе
говоря, существует такое X, что вероятность наступления
события за промежуток времени At равна XAt + о(А/) при At -> 0.
Предполагается, что вероятность наступления более чем одного
события за это время составляет о(А/) при At -» 0. Отсюда
получается, что время до наступления события распределено
показательно с тем же параметром X. Верно и обратное.
Таким образом, если требования поступают в систему через
показательно распределенные промежутки времени и времена
обслуживания требований также показательно распределены,
причем параметры остаются постоянными во времени, то
данную систему можно описать цепью Маркова1. Далее будем
полагать все случайные времена показательно распределенными
по умолчанию.
Пример 2. Машина требует наладки в среднем один раз в 9
единиц времени. Наладка занимает в среднем т единиц
времени. Требуется найти стационарное распределение вероятностей
застать машину в рабочем (1) и нерабочем (0) состоянии.
Глава 9
Перейдем к интенсивностям: X = 1/0, ц = 1/т. Переход из
состояния 0 в состояние 1 (наладка) имеет интенсивность ц, а
переход из состояния 1 в состояние 0 (поломка) —
интенсивность X. Матрица интенсивностей переходов имеет вид
получаем
х т ц е
Яп = = , Я, = = .
X+V т+е а,+ц т+е
В общем случае, если выходят из строя или обслуживаются
параллельно несколько объектов, соответствующие
интенсивности суммируются.
Пример 3. В систему из п обслуживающих приборов
поступает поток требований с интенсивностью X. Средняя длительность
обслуживания равна т единиц времени. Если при поступлении
требования все приборы заняты, оно становится в очередь.
Состояния будем нумеровать по числу требований,
находящихся в системе (как в очереди, так и на обслуживании).
Пространство состояний S = {0, 1,2, ...} в данном случае
бесконечно и счетно.
Введем интенсивность обслуживания ц = 1/т и величину
р = X/\i = Хт, называемую загрузкой системы. Она описывает,
сколько в среднем новых требований поступит за время
обслуживания одного. Если р > п, то очередь требований растет до
бесконечности, если же р < я, то система выходит на
стационарный режим.
Интенсивности переходов имеют вид
Для данной системы рассчитаны, в частности, следующие
показатели:
1) вероятность того, что все приборы свободны
Решая систему уравнений
яЛ = 0, я0 + я, = 1,
X У = / + 1,
min(/,/i)ii, у = /-1, />0.
я.
'О
к\ я!(1-р//|)
175 |
Глава 9
3) средняя длина очереди
*=«+i к=п+\П п1(т-к)\
Задачи для самоаоятельного решения
1. На производстве используется система приемочного контроля с
переменным планом, где пг = 20, п2 = ю, пз = 5. Найти
стационарное распределение, если: а) е = 0,01; б) е = 0,02.
2. Трудоспособное население (постоянной численности) делится
на работающих и безработных. Вероятность потерять работу в
течение месяца составляет 2%, а вероятность ее найти — 16%.
Определить стационарный уровень безработицы. Во сколько раз
сократится доля безработных, если благодаря государственной
программе занятости вероятность найти работу в течение месяца
увеличится вдвое?
3. Рабочие города Молотково трудятся на трех заводах. Вероятности
ухода с каждого завода в течение месяца составляют 1, 6 и 9%
соответственно. В случае ухода с одного завода рабочий
переходит на один из двух других равновероятно. Найти стационарное
распределение. Общая численность рабочих предполагается
постоянной.
4. Решить уже рассмотренную задачу о холодильниках в
предположении, что вводится дополнительное правило: если в магазине
остается один холодильник, делается заказ на еще один.
5. Мебельный магазин торгует шкафами. Случайный спрос на шкафы
за неделю имеет распределение, заданное таблицей.
спрос
0
1
2
р
0,3
0,6
0,1
Если шкафы заканчиваются, делается заказ на 2 штуки, если
остается один — на 1 штуку. Заказы прибывают на следующей неделе.
Найти стационарное распределение числа шкафов в магазине.
177
v . )
ЧАСТЬ I. Теория вероятностей
2) вероятность того, что в системе находится ровно к
требований
к к
Ч =ттяо ПРИ ^ ^к<п\ кк = ,р. я0 при к > п\
к\ п\п
3) вероятность того, что все приборы заняты
п\(1-р/п)
4) средняя длина очереди
1 =
рП>п _ P'
п-р п\п(1-р/п)
яп.
2 '"О
Пример 4. Бригада из п рабочих обслуживает т станков
(п < т). Каждый станок требует наладки в среднем один раз в
8 единиц времени. Наладка занимает в среднем х единиц
времени. Если все рабочие заняты, наладка станка откладывается
(ставится в очередь).
Состояния будем нумеровать по числу требований (т.е.
требующих наладки станков). Пространство состояний
S = {0, 1, 2, т) в данном случае конечно.
Как и ранее, положим X = 1/0, ц = 1/т, р = X/\i = т/0.
Интенсивности переходов имеют вид
Х{}
(m-i)X, У = / + 1, Km,
min(/,«)|i, у = /-1, />0.
Для данной системы рассчитаны, в частности, следующие
показатели:
1) вероятность того, что все станки исправны
ял =
Й*!(т-*)Г ktf+lnk-nn\(m-k)\
2) вероятность того, что в системе находится ровно к
требований
я, =
т\
к k\(m-k)V 0
р*я0 при 1 йк <п\
я, =-
пк-пп\(т-к)\
р*я0 при к > п\
V6
ЧАСТЬ I. Теория вероятностей
0,7
0,2
0,1'
0,4
0,5
0,1'
а)
0,3
0,6
0,1
; б)
0,1
0,7
0,2
0,1
0,7
0,2
0,6
0,2
0,2
Найти стационарное распределение объема сбыта фирмы.
10. Продуктивность фермерского хозяйства в каждом году
оценивается как хорошая (1), удовлетворительная (2) или плохая (3).
Матрица переходных вероятностей имеет вид
0,3
0,6
0,1
0,3
0,5
0,2'
а)
0,1
0,6
0,3
; б)
0,2
0,6
0,2
«Л
0,4
0,5
0,1
0,5
0,4
Найти стационарное распределение продуктивности хозяйства.
178
С ^
6. В городе Традицино каждый взрослый мужчина имеет одну из трех
профессий А, Б и В. Сыновья сохраняют профессии отцов с
вероятностями 3/5, 2/3 и 1/4 соответственно или выбирают любую
из двух других равновероятно. Найти: а) распределение по
профессиям в следующем поколении, если в нынешнем профессию
А имело 20%, Б — 30%, В — 50%; б) стационарное распределение
по профессиям. Предполагается, что у каждого отца ровно один
сын.
7. Торговец из города Олино ездит продавать товар в города Алино
и Валино. Выехав из Олино, он направляется в Алино с
вероятностью 40%, в Валино — с вероятностью 6о%. Продав товар, он
возвращается в Олино. Найти стационарное распределение
вероятностей застать предпринимателя в каждом из городов.
8. Решить предыдущую задачу в предположении, что, посетив Алино
или Валино, торговец возвращается в Олино с вероятностью 8о%
или едет в другой из двух городов (продавать оставшийся товар)
с вероятностью 20%.
9. Фирма оценивает недельный объем сбыта как
удовлетворительный (1), хороший (2) или отличный (з). Матрица переходных
вероятностей имеет вид
V )
Глава 9
г л
11. В процессе ежемесячного погашения кредита клиент банка может
оказаться в одном из следующих состояний:
а) ежемесячный платеж погашен в срок в полном объеме;
б) ежемесячный платеж погашен в полном объеме, но с
временной задержкой;
в) ежемесячный платеж погашен в срок в неполном объеме,
с переходом остатка долга на следующий месяц;
г) ежемесячный платеж погашен с временной задержкой и в
неполном объеме, с переходом остатка долга на следующий месяц.
Матрица переходных вероятностей имеет вид
а)
г0,3
0,4
0,1
0,2'
0,5
0,3
0,2
0
0
0,2
0,5
0,3
;б)
0
0,4
0,4
0,2
0
0
0,4
0,6
0
0
0,3
0,7
0
0
0
1
0
0
0
1
Вычислить вероятности состояний через три месяца, если в
начале клиент находился в состоянии а).
12. Машина требует наладки в среднем один раз в 2 часа. Наладка
занимает в среднем 15 мин. Найти стационарное распределение
вероятностей застать машину в рабочем (1) и нерабочем (о)
состоянии.
13. Есть 2 станка, каждый из которых требует наладки в среднем один
раз в 2 часа. Наладка занимает в среднем ю мин. Найти
стационарное распределение числа работающих станков.
Предполагается, что станки требуют наладки и обслуживаются независимо один
от другого.
14. Машина состоит из трех узлов, каждый из которых отказывает с
интенсивностью X = 2. Интенсивность восстановления отказавшего
узла равна ц = 3. Найти стационарное распределение числа
работающих узлов.
15. Машина состоит из трех узлов. Среднее время безотказной работы
каждого узла составляет 20 час, а среднее время ремонта узла —
5 час. Найти среднюю производительность машины, если при трех
работающих узлах она равна юо%, при двух — 50%, а при одном
или менее машина вообще не работает.
179 I
V )
ЧАСТЬ I. Теория вероятностей
16. В ремонтной мастерской трудятся 5 мастеров. В течение дня на
ремонт поступает в среднем ю изделий, а каждый мастер успевает
отремонтировать в среднем 2,5 изделия. Предполагая, что
мастерская работает в стационарном режиме, найти: а) вероятность того,
что все мастера свободны; б) вероятность того, что все мастера
заняты; в) среднюю длину очереди; г) среднее число мастеров,
свободных от работы.
17. В ремонтную мастерскую, где работает 3 мастера, поступает в
среднем 4 заказа в час. Среднее время выполнения заказа составляет
полчаса. Определить среднее число заказов, ожидающих начала
выполнения.
18. Рабочий обслуживает группу из 3 автоматов. Каждый автомат
требует обслуживания в среднем раз в полчаса. Обслуживание занимает
в среднем 12 мин. Найти: а) стационарное распределение числа
неисправных автоматов; б) среднее число автоматов, ожидающих
обслуживания; в) среднее число простаивающих автоматов.
19. Двое рабочих обслуживают машину, состоящую из 4 блоков.
Каждый блок требует обслуживания в среднем один раз в 2 часа.
Обслуживание занимает в среднем 15 мин. Найти: а) стационарное
распределение числа работающих блоков; б) среднюю длину
очереди; в) среднее число занятых рабочих.
20. В кассу обращаются клиенты, в среднем по одному за ю мин.
Сколько в среднем времени должно занимать обслуживание
одного клиента, чтобы средняя длина очереди в стационарном режиме
не превышала: а) 2 человека; б) 5 человек?
21. В конторе три сотрудника принимают посетителей в порядке
общей очереди. В среднем обращается по 5 человек в час,
обслуживание каждого занимает в среднем 18 мин. Найти: а) вероятность
того, что все сотрудники свободны; б) вероятность того, что все
сотрудники заняты; в) среднюю длину очереди.
21. На железнодорожную сортировочную станцию поступает в
среднем 2 состава в час. Обслуживание (расформирование) состава
занимает в среднем 20 мин. В парке прибытия станции есть два
пути, на которых производится обслуживание; если оба пути
заняты, составы ожидают на внешних путях. Найти: а) вероятность того,
что все пути свободны; б) среднюю длину очереди.
V j
I
Часть II
Математическая
статистика
ГЛАВА ю
ОСНОВНЫЕ ПОНЯТИЯ
И ЗАДАЧИ
МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
§ юл. Генеральная и выборочная
совокупности
Генеральной совокупностью называется множество объектов
произвольной природы, обладающих признаками, доступными
для наблюдения и количественного измерения.
Например, в случае социально-экономических
исследований это может быть население какого-то города, региона или
страны, а измеряемыми признаками могут служить доходы,
расходы или объем сбережений отдельно взятого человека. Если
какой-то признак имеет качественный характер (например,
пол, национальность, социальное положение, род деятельности
и т.п.), но принадлежит к конечному множеству вариантов, он
может быть также закодирован числом (как это часто делают
в анкетах).
Объекты, входящие в генеральную совокупность,
называются ее элементами, а их общее число — ее объемом.
Пусть число элементов генеральной совокупности равно N.
Примем каждый из них за элементарный исход со
некоторого вероятностного пространства Q и припишем всем исходам
одинаковую вероятность 1/N. Тогда соответствие между объ-
183 I
^ ЧАСТЬ II. Математическая аатиаика
ектами и значениями какого-либо их признака задает
случайную величину ? = ?(оо), как функцию на вероятностном
пространстве (согласно аксиоматике А.Н. Колмогорова). Числовые
характеристики введенной формально случайной величины
отражают важные свойства совокупности исследуемых объектов.
В частности, ее математическое ожидание Щ равно среднему
значению признака, а функция распределения F%(x) = Д? < х)
показывает долю объектов, для которых значение признака
меньше х.
Например, в социально-экономических исследованиях нас
могут интересовать средний доход на душу населения, доля
людей с доходами меньше прожиточного минимума и т.п.
Распределение ? часто называют распределением генеральной
совокупности (говорят, например, о нормально распределенной
или просто нормальной генеральной совокупности).
Будем последовательно извлекать из генеральной
совокупности ее элементы, выбирая их случайным образом (наудачу),
измерять и записывать значения некоторого признака для них:
xv xv хп. Эти значения называются наблюдениями
(признака), их набор — выборкой, а число сделанных наблюдений —
объемом выборки л. Понятно, что наблюдения представляют
собой случайные величины, в силу случайности нашего
выбора объекта. Они заданы уже на другом вероятностном
пространстве — на множестве всех вариантов выбора п элементов
из генеральной совокупности. Полученные данные называют
наблюдениями случайной величины а также говорят, что
случайная величина § «принимает значения» xv xv хп.
Основная задача математической статистики — сделать
научно обоснованные выводы о распределении одной или более
неизвестных случайных величин или их взаимосвязи между
собой.
Выборочным методом называется метод решения этой задачи
посредством анализа выборки, полученной в результате
многократных наблюдений.
Для того чтобы характеристики случайной величины,
полученные выборочным методом, были объективны, необходимо,
чтобы выборка была репрезентативной, т.е. достаточно хорошо
представляла исследуемую величину. В силу закона больших
чисел можно утверждать, что выборка будет репрезентативной,
если ее осуществить случайно, т.е. все объекты генеральной со-
| 184
!
I
Глава io
вокупности имеют одинаковую вероятность попасть в выборку.
Для этого существуют различные виды отбора выборки.
1. Простым случайным отбором называется отбор, при
котором объекты извлекаются по одному из всей генеральной
совокупности (случайным образом).
2. Механическим называется такой, при котором
генеральную совокупность делят на столько частей, сколько объектов
должно войти в выборку, и из каждой группы случайным
образом отбирают один объект.
3. Серийным называется отбор, при котором объекты из
генеральной совокупности отбираются «сериями», которые
подвергаются сплошному обследованию.
4. Стратифицированный (расслоенный) отбор заключается в
том, что исходная генеральная совокупность объема N
подразделяется на подсовокупности (страты) Nv Nv Nk, так что
Nx + N2 + ... + Nk = N. Когда страты определены, из каждой из
них извлекается простая случайная выборка объема nv nv nk.
Частным случаем стратифицированного отбора является
типический отбор, при котором объекты отбирают не из всей
генеральной совокупности, а из каждой типической ее части.
Комбинированный отбор сочетает в себе сразу несколько
видов отбора, образующих различные фазы выборочного
обследования. Существуют и другие методы организации выборки.
Выборка называется повторной, если отобранный объект
перед выбором следующего возвращается в генеральную
совокупность. Выборка называется бесповторной, если отобранный
объект в генеральную совокупность не возвращается. Для
конечной генеральной совокупности случайный отбор без
возвращения на каждом шаге приводит к зависимости отдельных
наблюдений, случайный равновозможный выбор с
возвращением—к независимости наблюдений.
На практике обычно имеют дело с бесповторными
выборками. Тем не менее, когда объем генеральной совокупности N во
много раз больше, чем объем выборки п (например, в сотни или
тысячи раз), зависимостью наблюдений можно пренебречь.
Таким образом, можно считать, что наблюдения х{9 xv
хп являются просто независимыми случайными величинами с
одинаковым распределением — тем же, что и у исходной
случайной величины
185 I
ЧАСТЬ 11. Математическая статистика
*1
Х2
W2
186
Иногда рассматриваются по-разному распределенные
наблюдения (например, в случае неравноточных измерений), а
иногда — и зависимые наблюдения, но все эти случаи
оговариваются особо.
Бывают ситуации, когда затруднительно или невозможно
описать объекты, чьи признаки мы наблюдаем. Речь идет об
измерении какой-либо величины, которая меняет свое
значение случайным образом от одного наблюдения к другому. Это
могут быть, например, колебания в ценах акций, курсах валют,
случайные ошибки измерения и т.п. В качестве «объекта»
выступает некоторое стечение обстоятельств, которые в принципе
могли сложиться различным образом. В этих случаях, тем не
менее, все равно применяют изложенную выше статистическую
модель, хотя «выбор» здесь осуществляется без личного участия
исследователя, какими-то внешними силами.
Как уже было отмечено, случайная величина § имеет
определенную функцию распределения F^x) и другие числовые
характеристики, которые будем называть теоретическими, в
отличие от выборочных, которые определяются по наблюдениям.
Ряд наблюдений, упорядоченных по возрастанию, называют
вариационным радом. Его члены обычно обозначают jc(1), х{2) ... х(п).
Наименьшее и наибольшее значения (минимум и максимум)
обозначают xmin и хтах и называют их крайними членами
вариационного ряда. Различные значения признака, появившиеся в
процессе наблюдения, называют вариантами.
Когда мы наблюдаем дискретную случайную величину, она
может принимать одни и те же значения по много раз. Поэтому
для экономии места и времени каждое значение записывают
только один раз, с указанием, сколько всего раз оно появилось.
Число п., показывающее, сколько раз появилось значение х,в
п наблюдениях, называют частотой данного значения, а
отношение wt — п/п — относительной частотой. Число к различных
значений в п наблюдениях всегда конечно, и к <п. Очевидно,
к к
имеют место равенства ^/if-=/i и ]Г^ = 1. Результаты можно
записать в таблицу. /=1 ,=1
Глава io
В случае непрерывной случайной величины на практике
часто применяют группировку. Это означает, что весь интервал
наблюдаемых значений разбивают на к частичных интервалов
[с0, с,), [с,, с2), ... [сы, ск] равной длины А и затем подсчитыва-
ются числа попаданий наблюдений в эти интервалы, которые
принимают за частоты п. (для некоторой новой, уже дискретной
случайной величины). В качестве новых значений вариант х.
обычно берут середины интервалов (либо в таблице указывают
сами интервалы). Группировка может применяться и в случае
дискретных случайных величин, если шаг, с которым меняются
их значения, кажется нам слишком мелким.
Согласно формуле Стерджеса, рекомендуемое число
интервалов разбиения к « 1 + log2w, а длины частичных интервалов
* = (xmax"~ xmin)/^ Предполагается, что весь интервал имеет вид
Понятно, что группировка связана с потерей части
полезной информации, заключенной в выборке. Однако она имеет и
свои преимущества. Оценим величину экономии, например, для
п = 106 наблюдений. Рекомендуемое число интервалов к = 21,
и от нас требуется сохранить и обработать лишь 2к = 42 числа
вместо миллиона!
Набор вариант х. (или частичных интервалов) и их
относительных частот w. называют статистическим радом. Графически
статистические ряды могут быть представлены в виде полигона,
гистограммы или графика накопленных частот (рис. 10.1).
Полигоном частот называют ломаную линию, отрезки
которой соединяют точки (xv пх)9 (х2, я2), (хк9 пк). Полигоном
'min' max-
§ Ю.2. Графическое представление
статистических рядов
РИС. 10.1
187
^ ЧАСТЬ II. Математическая статиаика
*1
2
3
5
6
п,
10
15
5
20
п1
25
20
15
10
5
0 1 2 3 4 5 6 7 xi
РИС. 10.2
Решение. Отложим на оси абсцисс (рис 10.2) варианты хр а
на оси ординат — соответствующие им частоты п., затем
соединим последовательно точки \хр п).
Гистограммой относительных частот1 (или просто
гистограммой) называется ступенчатая фигура, состоящая из
прямоугольников, основанием которых служат частичные
интервалы длиною Л, а высоты равны w/h. Гистограмма обычно
служит для изображения выборки в случае непрерывных
случайных величин. Площадь гистограммы равна единице
(рис. 10.3).
Поэтому гистограмму можно рассматривать как график
эмпирической (выборочной) плотности распределения рп(х). Если у
теоретического распределения F существует конечная плотность,
1 На практике гистограммами также называют ступенчатые фигуры с
высотами м>.(без деления на h) как на рис. 10.3.
188
относительных частот называют ломаную, отрезки которой
соединяют точки (jc,, Wj), (х2, w2), (х^, w^). Полигоны обычно
служат для изображения выборки в случае дискретных
случайных величин.
Задача L Построить полигон частот по заданному
распределению выборки.
Глава ю
то эмпирическая плотность является некоторым приближением
для теоретической. В этом и состоит практическая польза
гистограммы.
При построении гистограмм в реальных исследованиях
следует понимать, что формула Стерджеса (как и любая другая)
для числа интервалов разбиения к дает лишь рекомендацию, а
не строгое правило. Проблема выбора этого числа заключается
в следующем. При слишком малых к гистограмма
получается слишком грубой, «смазанной», плохо отражающей свойства
распределения. При больших к гистограмма становится
«колючей», и в конце концов распадается на отдельные «иглы» (узкие
столбцы) вперемешку с пустыми интервалами. Оптимальное
значение в общем случае неизвестно — оно зависит как от
типа распределения, так и от конкретной выборки. Что
касается концов интервалов и значений вариантов, то для
человеческого восприятия удобнее, чтобы они выражались более или
менее «круглыми» числами.
Поскольку гистограммы теперь строят не вручную, а на
компьютере. Исследователь легко может варьировать
параметры гистограммы (нижнюю и верхнюю границы интервала,
число частичных) и в конечном счете выбрать тот вариант, при
котором, по его мнению, график выглядит лучше всего.
Графиком накопленных частот называется фигура,
строящаяся аналогично гистограмме с той разницей, что для расчета
высот прямоугольников берутся не простые, а накопленные отно-
сительные частоты, т.е. величины wf =Х1м;у Эти величины не
7 = 1
убывают, и таким образом, график накопленных частот имеет
вид ступенчатой «лестницы» (от 0 до 1). График эмпирической
функции распределения проходит через правые верхние углы
прямоугольников, т.е. точки вида (c,,wf).
График накопленных частот и эмпирическая функция
распределения на практике используются для приближения
теоретической функции распределения (рис. 10.4).
Задана 2. Анализируется выборка из 100 малых
предприятий региона. Цель обследования — измерение коэффициента
соотношения заемных и собственных средств (х) на каждом /*-м
предприятии. Результаты представлены в табл. 10.1.
189
4^ ЧАСТЬ II. Математическая статистика
Таблица юл
Коэффициенты соотношений заемных и собственных
средств предприятий
5,56
5,45
5,48
5,45
5,39
5,37
5,46
5,59
5,61
5,31
5,46
5,61
5,11
5,41
5.31
5,57
5,33
5,11
5,54
5,43
5,34
5,53
5,46
5,41
5,48
5,39
5,11
5,42
5,48
5,49
5,36
5,40
5,45
5,49
5,68
5,51
5,50
5,68
5,21
5,38
5,58
5,47
5,46
5,19
5,60
5,63
5,48
5,27
5,22
5,37
5,33
5,49
5,50
5,54
5,40
5.58
5,42
5,29
5,05
5,79
5,79
5,65
5,70
5,71
5,85
5,44
5,47
5,48
5,47
5,55
5,67
5,71
5,73
5,05
5,35
5,72
5,49
5,61
5,57
5,69
5,54
5,39
5,32
5,21
5,73
5,59
5,38
5,25
5,26
5,81
5,27
5,64
5,20
5,23
5,33
5,37
5,24
5,55
5,60
5,51
Требуется построить гистограмму и график накопленных
частот.
Решение. Построим группированный ряд наблюдений.
1. Определим в выборке xmin = 5,05 и хтах= 5,85.
2. Разобьем весь диапазон [xmin xmJ на к равных
интервалов: к » 1 + log2100 = 7,62; к * 8, отсюда длина интервала
д _ *max ~ *min _ 5,85 — 5,05 _ q j
Таблица 10.2
Сгруппированный ряд наблюдений
Номер
интервала
Интервал
Середина
интервала х}
<
1
5,05-5,15
5,1
0,05
0,05
0,5
2
5,15-5,25
5,2
0,08
0,13
0,8
3
5,25-5,35
5,3
0,12
0,25
1,2
4
5,35-5,45
5,4
0,20
0,45
2,0
5
5,45-5,55
5,5
0,26
0,71
2,6
6
5,55-5,65
5,6
0,15
0,86
1,5
7
5,65-5,75
5,7
0,10
0,96
1,0
8
5,75-5,85
5,8
0,04
1,00
0,4
190
Глава io
Гистограмма
¦<-
О
5,0 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8 5,9
Наблюдения
Рис. ю.з
На рис. 10.3 и 10.4, построенных по данным табл. 10.1 с
помощью статистического пакета STATISTICA, представлены
гистограмма и график накопленных частот. Кривые
соответствуют плотности и функции нормального распределения,
«подобранного» к данным.
График накопленных частот
5,0 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8 5.9
Наблюдения
Рис. 10.4
191
ЧАСТЬ II. Математическая статистика
192
§ ю.з. Эмпирическая функция распределения
Эмпирической функцией распределения (или функцией
распределения выборки) называют функцию Fn(x), определяющую
для каждого числа х относительную частоту события § < х, т.е.
Fn(x) = пJn, где пх — число наблюдений, меньших х, п — объем
выборки, т.е. долю из п наблюдений, меньших х.
Иначе говоря, эмпирической функцией распределения
называют функцию, определяющую для каждого числа х долю из
п наблюдений, меньших х.
Из определения следует, что значения эмпирической
функции распределения при каждом х являются случайными
величинами. В отличие от эмпирической функции распределения
функцию распределения F^(x) генеральной совокупности
называют теоретической функцией распределения. Эмпирическая
функция распределения обладает всеми свойствами обычной
функции распределения, а также некоторыми специфическими:
l.O<Fn(x)<l.
2. Fn(x) — неубывающая функция.
3. Fn(x) непрерывна слева.
4. Fn(x) = О при х < xmin, и Fn(x) = 1 при х > хтах.
5. Р( lim sup| Fix) — F(x) | = 0) = 1 (теорема Гливенко-Кан-
телли).
Доказательство теоремы Гливенко-Кантелли является
довольно сложным, поэтому докажем следующий ее упрощенный
вариант.
> Теорема 1. При любом г > 0 верно lim Р( \ Fn(x) — F{x) \ < г) = 1
для любого х. "~*00
Доказательство. По определению F (х) = —, где п — число
п п х
наблюдений, меньших х. Рассмотрим наблюдения как п
независимых испытаний Бернулли, в каждом из которых возможны
два исхода: {хк<х} или {хк>х}. Вероятности этих событий
равны р = Р(^ < х) = F(x) и q = Р(? >х) = 1 — F(x) соответственно.
Событие {хк < х} можем называть успехом, тогда пх — число
успехов в п независимых испытаниях Бернулли. Следовательно,
математическое ожидание Мпх = пр, и дисперсия Dnx = npq.
Отсюда
MFn(x) = -Mnx=^- = F(x);
п п
Глава ю ^
Л п п
В силу неравенства Чебышева для любого г > 0 верна оценка
8
поэтому
ix\Fn(x)-m\±t)±F{m-F{x)) -^о,«^оо,
откуда следует утверждение теоремы.
Смысл теоремы Гливенко-Кантелли заключается в том, что
при увеличении объема выборки п у эмпирической функции
распределения исчезают свойства случайности и она
приближается к теоретической функции распределения. Эмпирическая
функция распределения служит оценкой функции
распределения генеральной совокупности.
График эмпирической функции распределения есть
неубывающая ступенчатая кривая со скачками, равными 1/п в
точках вариационного ряда (если значения не совпадают). Если п.
точек вариационного ряда совпадают и равны хр то скачок в
точке х. равен п/п.
Задача 3. Пусть задана таблица наблюдений случайной
величины
*/
2
3
5
п1
75
20
5
wf
0,75
0,2
0,05
100
ад
Тогда эмпирическая функция распределения имеет вид
да*
0, если х<2, !
0,75, если 2<х<3, 0,95
0,95, если 3<х<5, 0,75
1, если х > 5.
Ее график представлен на
рис. 10.5.
7 Теория вероятностей
193
^ ЧАСТЬ II. Математическая статистика
Задача 5. Построить гистограмму частот по заданному
распределению выборки.
Номер
Частичный
Число наблюдений, попавших
интервала i
интервал
в интервал, ni
1
2-7
5
2
7-12
10
3
12-17
25
4
17-22
6
5
22-27
4
Решение. Найдем сначала плотности частот, т.е. величины
n/h. Для данного примера h = 5.
Получаем:
Номер интервала i
Плотность частоты n/h
1
1
2
2
3
5
4
1,2
5
0,8
194
Задача 4. Пусть х{, xv хп — выборка независимых
наблюдений из непрерывной генеральной совокупности с функцией
распределения F(x) и плотностью распределения р(х). Найти
функции распределения и плотности распределения крайних
членов вариационного ряда: xmin и х^.
Решение. Из определения функции распределения следует, что
*L (У) = Р(хтах <У) = Р(х, <у, х2 < у,хп < у) = Pn(Xi <у) = F{(y).
Тогда Px^{y) = [Fx_(y)\ = [F^y)\ = nF^\yyFl (y) = nFf\y).ф).
Аналогично
Г*ть <Л = ^min < У) = 1" F(Xmin * У) = 1 " Р{ХХ >у,Х2>у9...,Хп>У) =
=1-[1-^0>)Г.
Отсюда получаем функцию плотности
Глава io ф
Отложим на оси абсцисс (рис. 10.6) интервалы длиной
h = 5 каждый, а затем проведем над ними отрезки,
параллельные оси х, на расстояниях от нее, равных соответствующим
значениям плотности частоты (ось ординат).
п./п
5
12
17 22 27
Рис. 10.6
Задача 6. Построить гистограмму относительных частот по
заданному распределению выборки.
Номер
Частичный
Число наблюдений,
интервала i
интервал
попавших в интервал, л,
1
10-15
2
2
15-20
4
3
20-25
8
4
25-30
4
5
30-35
2
Решение. Найдем относительные частоты и плотности
относительных частот.
Частота w,
Плотность относительных частот w/h
wj = njn = 2/20 = 0,1
wjh = 0,1/5 = 0,02
w2 = njn = 4/20 = 0,2
wjh = 0,2/5 = 0,04
w3 = njn = 8/20 = 0,4
wjh = 0,4/5 = 0,08
w4 = V = 4/20 = °>2
wjh = 0,2/5 = 0,04
w5 = njn = 2/20 = 0,1
wjh = 0,1/5 = 0,02
7*
iJl ЧАСТЬ II. Математическая статистика
10 15 20 25 30 35 X
Рис. Ю.7
Задачи для самостоятельного решения
1. Построить полигон частот по следующему распределению
выборки.
*1
15
20
25
30
35
"i
10
15
30
20
25
2. Построить гистограмму частот по следующему распределению
выборки.
Номер
интервала /
Частичный
интервал
Число наблюдений,
попавших в интервал, л,
1
3...5
4
2
5...7
6
3
7...9
20
4
9...11
40
5
11...13
20
6
13...15
4
7
15...17
6
V j
j 196
Построим на оси абсцисс (рис. 10.7) частичные интервалы
h = 5, затем проведем параллельно им отрезки, отстоящие от
оси х на соответствующие значения плотности относительной
частоты.
0,08 т 1
Глава ю ф
3. Построить гистограмму относительных частот по следующему
распределению выборки.
Номер
Частичный
Число наблюдений,
интервала /
интервал
попавших в интервал, п.
1
2...5
6
2
5...8
10
3
8...11
4
4
11...14
5
4. Построить полигон относительных частот по следующему
распределению выборки.
2
4
5
7
10
wi
0,15
0,2
0,1
0,1
0,45
5. Для изучения распределения заработной платы работников
определенной отрасли обследовано юо человек. Результаты
представлены в следующей таблице.
Зарплата
Число
Зарплата
Число
в долларах США
человек
в долларах США
человек
190...192
1
200...202
19
192... 194
5
202...204
11
194...196
9
204...206
4
196...198
22
206...208
1
198...200
28
208...210
0
Построить гистограмму и график накопленных частот.
6. В OTK были измерены диаметры 300 валиков из партии,
изготовленной одним станком-автоматом. Отклонения измеренных
диаметров от номинала, нм, даны в таблице.
Границы
отклонений
Середина
интервала
Число
валиков
Границы
отклонений
Середина
интервала
Число
валиков
-30..-25
-27,5
3
0...5
2,5
55
-25...-20
-22,5
8
5...10
7,5
30
-20...-15
"17,5
15
10...15
12,5
25
-15...-10
-12,5
35
15...20
17,5
14
-10...-5
"7,5
40
20...25
22,5
8
-5...0
-2,5
60
25...30
27,5
7
^ Построить гистограмму и график накопленных частот. J
197 \
ф ЧАСТЬ II. Математическая статиаика
*1
0
1
2
3
4
5
6
7
8
9
10
п1
146
97
73
34
23
10
6
3
4
2
2
Построить гистограмму и график накопленных частот.
8. В таблице представлены данные о месячном доходе жителя
региона, руб., по выборке из юоо жителей.
х1
Менее
500
500-1000
1000-1500
1500-2000
2000-2500
Свыше
2500
ni
58
96
239
328
147
132
Построить гистограмму и график накопленных частот.
Указание. В качестве верхней границы последнего интервала
использовать 3000.
9. В таблице представлены данные об удое юо коров на молочной
ферме за лактационный период, центнеры.
*1
4...6
6...8
8...10
10...12
12...14
14...16
16...18
18...20
20...22
22...24
24...26
1
3
6
11
15
20
14
12
10
6
2
Построить гистограмму и график накопленных частот.
ю. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетителей,
посетивших сайт в течение данного часа. Результаты исследования
представлены в таблице.
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
57
7
139
1
203
8
45
2
383
9
27
3
525
10
10
4
532
11
4
5
408
12
1
6
273
14
1
Построить гистограмму и график накопленных частот.
198
с : : ~гл
7. В таблице представлены данные по числу сделок на фондовой
бирже за квартал для 400 инвесторов.
Глава io @
11. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетителей,
посетивших сайт в течение данного часа. Результаты исследования
представлены в таблице.
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
12
7
103
1
108
8
24
2
316
9
13
3
551
10
2
4
632
11
0
5
492
12
0
6
273
14
0
Построить гистограмму и график накопленных частот.
12. Построить гистограмму и график накопленных частот по данному
распределению выборки.
Номер
интервала /
Частичный
интервал
Число наблюдений,
попавших в интервал, л,
1
2...7
5
2
7...12
10
3
12...17
25
4
17...22
7
5
22...27
5
Результаты исследования прочности 200 образцов на сжатие
представлены в виде интервального статистического ряда в таблице.
Номер
интервала /
Частичный
интервал
Число наблюдений,
попавших в интервал, л,
1
190...200
10
2
200...210
26
3
210...220
58
4
220...230
64
5
230...240
30
6
240...250
14
Построить гистограмму, полигон и график накопленных частот.
199 |
ЧАСТЬ II. Математическая статистика
14. Построить гистограмму, полигон относительных частот и график
накопленных частот по заданному распределению выборки.
Номер
Частичный
Число наблюдений,
интервала /
интервал
попавших в интервал, п.
1
10...15
2
2
15...20
4
3
20...25
8
4
25...30
5
5
30...35
3
V J
ГЛАВА и
ТОЧЕЧНЫЕ ОЦЕНКИ
ПАРАМЕТРОВ ЗАКОНОВ
РАСПРЕДЕЛЕНИЯ
§ пл. Выборочные характеристики
и точечные оценки
Выборочными характеристиками называются функции от
наблюдений, приближенно оценивающие соответствующие
числовые характеристики случайной величины. В случае
равноточных измерений в качестве оценок математического ожидания,
дисперсии, начальных и центральных моментов используются
следующие выборочные характеристики:
1 п
1) выборочное среднее — х = —У^х,;
2) выборочные дисперсии — а2 = —-х)2;
3) выборочные начальные моменты k-го порядка —
4) выборочные центральные моменты к-то порядка —
k=~J2(xi-x)k.
п /=1
201
ф ЧАСТЬ 11. Математическая статистика
202
В качестве других используемых на практике выборочных
характеристик можно назвать выборочную моду xmod, равную
значению варианты с наибольшей частотой, и выборочную
медиану xmed, равную значению, стоящему в середине
вариационного ряда (либо полусумме двух значений, с номерами к и
к + 1, при четном числе наблюдений п = 2к).
Иногда рассматриваются такие числовые характеристики
распределения, как коэффициент вариации V = а/Щ,
асимметрия р = ц3/а3и эксцесс v = |i4/a4-3. Им также соответствуют
выборочные характеристики: выборочный коэффициент
вариации V = s/x, выборочная асимметрия р = ц3Д3, выборочный
эксцесс v = H4A4-3.
Все эти характеристики не совпадают с
соответствующими характеристиками генеральной совокупности, поскольку
являются случайными величинами. Распределение указанных
случайных величин однозначно определяется распределением
генеральной совокупности.
Заметим также, что вычисление выборочных характеристик
для какого-либо набора полученных в исследовании данных
может быть полезно даже без предположения, что наблюдения
представляют собой независимые и одинаково распределенные
случайные величины.
Точечными оценками параметров распределения называются
функции от наблюдений, предназначенные для
приближенного оценивания этих параметров. Если распределение
параметризуется какими-то числовыми характеристиками (например,
нормальное распределение однозначно задается своими
математическим ожиданием и дисперсий), то соответствующие
выборочные характеристики являются их точечными оценками.
Чтобы статистические оценки давали «хорошие»
приближения оцениваемых параметров, они должны удовлетворять
определенным требованиям. Эти требования заключаются в
том, что оценка должна быть состоятельной, несмещенной и,
желательно, эффективной.
Оценка ёя называется состоятельной, если при
неограниченном увеличении выборки она сходится по вероятности к
оцениваемому параметру: \imP(\Qn-0|<е) = 1 для любого е > 0.
Глава ii ф
Свойство состоятельности — асимптотическое, оно может
проявляться и при столь больших объемах выборки, которые
на практике не встречаются.
Оценка 0Я называется несмещенной (оценкой без
систематической ошибки), если ее математическое ожидание при
любом п равно оцениваемому параметру: MQn = 0. Несмещенность
оценки характеризует ее «доасимптотические» свойства, т.е.
является показателем ее «хороших» свойств при любом конечном
объеме выборки.
Оценка называется эффективной (в некотором классе
оценок), если она имеет минимальную дисперсию в этом классе.
Задана 1. Найти выборочное среднее по выборке объема
п = 20.
*1
2560
2600
2620
2650
2700
ni
2
3
10
4
1
Решение. Для упрощения расчетов перейдем к условным ва
риантам щ = х, — 2620.
-60
-20
0
30
80
ni
2
3
10
4
1
Тогда и = (2(-60)+3(-20)+10 х 0 +1 х 80) / 20 = 1
и х = 2620 + й = 2621.
Замечание. В качестве числа, которое вычитается при
переходе к условным вариантам (условный нуль), обычно
выбирается варианта, стоящая в середине ряда, либо та, для которой
частота максимальна (выборочная мода). В данном примере
они совпадают.
§ ii.2. Статистическая устойчивость
основных выборочных характеристик
На практике важно знать, насколько выборочные
характеристики отличаются от истинных значений характеристик
генеральной совокупности.
203
Ц ЧАСТЬ II. Математическая статиаика
Пусть ? имеет характеристики Щ — ау D\ — а2, Щк = а^,
А/(§ - М;)* = ц^, F(x) = Р(? < х). Соответствующими
выборочными характеристиками будут х, а2, 6сл, Д , ^„(*).
Докажем, что х является несмещенной и состоятельной
оценкой математического ожидания. При этом воспользуемся
известным неравенством Чебышева
Р(|Л-Мл|>8)<^1,
8
справедливым для любой случайной величины г\ (имеющей
математическое ожидание и дисперсию) и любого
фиксированного е > 0.
Вычислим математическое ожидание и дисперсию
выборочного среднего:
Мх = М
1^ 1^, па
\ntt ) nf\ п
так как Mxt = Щ, т.е. выборочное среднее является
несмещенной оценкой математического ожидания.
_ (1 " ^ 1 " пс2 а2
Dx = D -Yx, =—У Dx =—— = >0 при л —> оо,
так как Dx. = Z>?.
Отсюда в силу неравенства Чебышева для любого
фиксированного 8 > О
Dx о2
Р(\х-а\>е)<—г = —- -> 0 при п -> оо.
8 я8
Итак, среднее арифметическое выборки х сходится по
вероятности к математическому ожиданию случайной величины,
т.е. является состоятельной оценкой математического
ожидания. Аналогично доказывается состоятельность оценок других
начальных моментов ак.
Вычислим математическое ожидание выборочных
начальных моментов: Мак = M[-Yxk ] = -УЛ/х* = —^- = а, .
Следовательно, выборочные начальные моменты являются
несмещенными оценками теоретических начальных моментов.
Очевидно, что для любого к справедливо равенство
Щ*) = М(??) - (Щк)2= а2к- а/.
204
Глава li ф
Учитывая, что х. независимые случайные величины,
получим соотношение
Dak =D(-txf) = \tDx" = ац "а* ->0 при п -> оо,
что является достаточным условием для сходимости по
вероятности. Действительно, в силу неравенства Чебышева для
любого фиксированного е > О
Р(\ак " aj >?)<^ = ^Ц^ ->0 при
8 №
т.е. выборочный начальный момент а* ^"го порядка является
состоятельной оценкой начального момента ак генеральной
совокупности. ^ п _
Покажем, что выборочная дисперсия о2 =-У(х;. -х)2 явля-
л/=|
ется смещенной оценкой дисперсии D?> = а2 генеральной
совокупности.
Поскольку выборочная дисперсия, как и теоретическая, не
изменяется от прибавления к значениям случайной величины
фиксированного числа, то для любого числа b выборочную
дисперсию можно записать в виде
°2=-Х(*/-*)2-(*-6)2.
Действительно, доказательство утверждения вытекает из
следующей цепочки равенств:
^ = -2>/ "*>2 -Ь)-(х-Ь)]2 =
= -*>2 ~2<*/ -*)(*-*) + (*-*)2] =
п /=1
= -?(х/ -*)2 -2(x-Z0-$>, -Ь) + -?(х-Ь)2 =
= 1У (х. - *)2 -—[2У х - 2я6 - их + =
= 11(^ -*)2 -—[2?х,. -^-?х,] =
= -?(*,-Ь?-<*-А)[±2>, = -Ь?-(х-Ь)\
205 |
ф ЧАСТЬ 11. Математическая статистика
А/а2 =М
- М(х - а)2 = - ? M(xt - a)2 -Dx =
"/=1
2 _2
_ па а _ л-1 2
п п п
Отсюда следует, что с2 является смещенной оценкой
дисперсии.
J п _
Несмещенной оценкой дисперсии будет s2= ]?(*,-х)2,
так как п ~ *ы
Ms2=M
Afa2 = a" =er
-a
-2 Jl
я-1 n-\ n
Поэтому оценку a2 (при получении которой сумма
делится на п) называют смещенной, или неисправленной выборочной
дисперсией, а оценку s2 (при получении которой сумма делится
на п — 1) называют несмещенной, или исправленной выборочной
дисперсией. Выборочным средним квадратическим отклонением
(исправленным или неисправленным) называют положительный
корень из соответствующей выборочной дисперсии. Эта оценка
теоретического среднего квадратического отклонения a = V#?,
к сожалению, в обоих случаях является смещенной. Далее по
умолчанию мы будем иметь в виду исправленные оценки.
Обычный закон больших чисел неприменим к
центрированным величинам, так как после центрирования они становятся
зависимыми. Однако с помощью теоремы Слуцкого можно
доказать, например, что выборочная дисперсия сходится по
вероятности к теоретической дисперсии, если последняя существует.
> Теорема 1 (теорема Слуцкого). Пусть функция f(x,y)
непрерывна в точке (а,Ь) и случайные последовательности Хпи Yn
сходятся по вероятности соответственно к числам а и Ь. Тогда
f(Xn, YJ сходится по вероятности к f(a, b).
206
Следствие. Если Щ = а есть среднее генеральной
совокупности, то
° = -?(х(-а)2-(х-а)2.
Вычислим математическое ожидание выборочной дисперсии:
Глава ii 0
Доказательство. Если fix, у) непрерывна в точке (а, Ь), то
для любого б > 0 существует 8 > 0 такое, что при \х — а\< 8
и | у — b | < 8 выполняется неравенство \f(x, у) — f(a, b)\< е.
Тогда, если | Яде, у) - fa, b) \ > с, то справедливо хотя бы одно из
неравенств: [х — а \ > 8 или | у - 61 > 8. Рассмотрим событие
{о: !/(*„, Гя) - /(а, Л) | > 6} е {со: | ^ - л | > 8} и {а>: | УЛ - * | > 8}.
В силу теоремы сложения получаем
P(\f(Xn, Yn)-Да, Ь)\>в)<Р({\Хп-а\ >6}u{| Yn~ Ь\>Ь}) =
= Р{\Х- а\ >8) + Р(\Y-Ь\ >8) - Р(\Хп-а\ >Ъ,\?-b\ >8) <
±Р(\Хп- а\ >8) + P(\Yn- Ь\>8),
причем Р( | Хп - а \ > 5) -» 0 и Р( \ Yn - b I > 5) -> 0 при «->•».
Следовательно, вся сумма стремится к нулю, т.е.
ШР(\АХп, Yn) - -Да, Ь)\ >е) = 0 илиДЛ;, Ги) Да, Ь).
П—>оо
Для доказательства сходимости по вероятности выборочной
дисперсии к теоретической достаточно рассмотреть функцию
J[x, у) = х — у1, положив
Iя _
Хп = -]Гх2 -хх2 = а2 + а2, Г = х -> я (при я-»оо),
и применить теорему Слуцкого, поскольку выборочная
дисперсия представима в виде
а2 =!?(*,-х)2 = ±±х?-х\
Конечно, сходимость выборочной дисперсии можно
доказать и проще. Однако подобным образом доказывается
сходимость по вероятности всех выборочных центральных моментов
\хк —\хк, если существует \хк = Af(? - а)к. Действительно, из
сходимости по вероятности случайных величин ^.(п) к
некоторым постоянным числам а. следует, в силу теоремы Слуцкого,
сходимость по вероятности любой рациональной функции
ф(^(«), ?2(л), ?к(л)) к ее значению в точке (av а2, ак), т.е.
если Цп)-^->ар то ф(^(л), Цп), ?>к(п))^^>фр а2, ак) при
П -> оо.
Поскольку все выборочные центральные моменты (а также
некоторые их модификации — асимметрия, эксцесс и т.п.)
являются рациональными функциями от наблюдений, они схо-
207
р ЧАСТЬ II. Математическая аатиаика
Доказательство. Пусть 0я — несмещенная оценка
параметра 0, т.е. Л/0я = 0. Тогда для любого г > 0_из неравенства
I л I DQ
Чебышева получаем Р(\ Qn — 9 I ? е) ? 1— —f-.
По условию DQn ->0 при п -» оо и, следовательно, при
каждом фиксированном е > 0 limP(
0-0
< е) = 1. Теорема доказана.
Задача 2. Найти неисправленную выборочную дисперсию
по выборке объема п = 50.
18,4
18,9
19,3
19,6
«1
5
10
20
15
Решение. Перейдем к условным вариантам и.= 10(х- 19,3).
щ
-9
-4
0
3
ni
5
10
20
15
Тогда a2(w) = 100a2(x).
Найдем выборочную дисперсию для новой варианты и:.
1 4
a2(«)=^>,2 - Z^L
л /=1 V /=1 п
= —(5(-9)2+10(-4)2+20х02+15х32) -
50
- ((-45 - 40 + 0 + 45)/50)2 = 13,36.
208
дятся по вероятности к соответствующим теоретическим
значениям.
Справедлива следующая теорема
> Теорема 2. Если 0я - несмещенная оценка параметра 0 и ее
дисперсия стремится к нулю, D( 0я) -> 0 при п -> оо, то оценка
состоятельная.
Тогда, переходя к первоначальной варианте xt
а2(х) = д2(и)/100 = 13,36/100 = 0,1336.
Задана 3. По выборке объема п = 50 найдена смещенная
оценка а2 = 9,8 теоретической дисперсии. Найти
несмещенную оценку дисперсии генеральной совокупности.
Решение. Несмещенная оценка дисперсии связана со
смещенной следующей формулой:
*2=а2х— = 9,8 х 50/49 = 10.
п-1
Глава 11
§ н.э. Асимптотически нормальный характер
основных выборочных характеристик
Свойства выборки объема п зависят от распределения
генеральной совокупности, но по мере увеличения п (п -> оо)
выборочные характеристики начинают вести себя одинаковым
образом независимо от специфики генеральной совокупности.
Поэтому характер поведения выборочных характеристик
следует рассматривать в двух вариантах: при фиксированном п
(ограниченном объеме выборки) и при п -> оо (асимптотические
свойства выборки). При фиксированном п свойства выборок
будут различны для разных типов генеральной совокупности
(нормальной, экспоненциальной, равномерной, пуассоновской
и т.д.). В условиях асимптотики (п -> оо) общий характер
поведения числовых характеристик практически не зависит от типа
анализируемой генеральной совокупности. Введем следующее
определение.
Случайная последовательность §2, §я, ... называется
асимптотически нормальной, если существуют числовые
последовательности Av Ар ... и В{9 Bv ... (В.> 0 для всех i) такие, что
1 Х 2
->Ф(х) = -= [e~^2dt при п ->оо.
Здесь Ф(х) — функция стандартного нормального
распределения. Числа А. и В. называются параметрами асимптотически
<х
209
ЧАСТЬ II. Математическая статистика
' 2 ц4-о-
о ,
п
210
нормально распределенной случайной величины Условие, что
последовательность §2, §я, ... асимптотически нормальна,
записывается в виде е у N(A., В).
Используя введенный термин, центральную предельную
теорему можно сформулировать следующим образом: пусть r\v
ti2, г|л, ... — независимые одинаково распределенные
случайные величины с конечными моментами первого и второго
порядков: Mr\i = а; Ог){ = о2. Тогда если Sn = г|у + х\2 + ... + г\п то
Sn е > N(na, па2), я-»оо.
> Теорема 3. Если распределение генеральной совокупности
имеет конечные математическое ожидание а и дисперсию а2, то при
п -» оо основные выборочные характеристики являются
асимптотически нормальными:
1) x-^N
з, вд^№),™'в-№>>).
Другими словами, при больших объемах выборки все
основные выборочные характеристики можно считать практически
нормально распределенными.
§ 11.4. Эффективность оценок.
Неравенство Рао—Фреше—Крамера
Для одних и тех же параметров распределения
существует бесконечно много различных оценок, сходящихся к ним
по вероятности, т.е. состоятельных. Среди них также
бесконечно много несмещенных. Поэтому важной задачей
является сравнение их между собой и поиск наилучшей среди них.
Естественным критерием такого поиска является дисперсия,
как мера разброса вокруг среднего. Предпочтительней те
оценки, дисперсия которых меньше, а наилучшей оценкой является
Глава ii
та, чья дисперсия минимальна. Получая ту или иную оценку,
нужно иметь возможность определить, обладает ли она
минимальной дисперсией из всех возможных. С этой целью
вводится понятие эффективности оценки и используется неравенство
Рао—Фреше—Крамера.
Информацией Фишера о неизвестном параметре 6,
содержащейся в одном из независимых наблюдений случайной
величины называется величина
1(0) = М
50
где в качестве р(х, 0) берется либо плотность в точке х (для
непрерывных случайных величин), либо вероятность принять
значение х (для дискретных случайных величин).
> Теорема 4 (Рао—Фреше—Крамера).
Пусть плотность р(х, Q) удовлетворяет следующим условиям
регулярности:
1) область Gn = fx: p(x,Q) > 0} возможных значений случайной
величины, где плотность отлична от нуля, не зависит от 0;
+00 +00
2) в тождествах jxp(x,Q)dx s М\ и jp(x9Q)dx = l допустимо
-00 -00
дифференцирование по 0 под знаком интеграла;
3) информация Фишера 1(в) конечна и положительна.
Тогда для произвольной несмещенной оценки 0Я выполняется
неравенство (Рао—Фреше—Крамера)
ЯО >—— •
" «/(0)
Доказательство. Пусть 0„ — несмещенная оценка
параметра 0, т.е.
Мвп = } вп(Х)ЛХ, WX= 0, (15.1)
-00
где X = (х{9 х2, хп) и р(Х9 0) — плотность распределения,
так что
J р(Х9 Q)dX= 1. (15.2)
211
^ ЧАСТЬ II. Математическая аатиаика
<[ l(Q„(X)-Q)2p(X,Q)dX]x[ jldlnf^'e)]2p(X,Q)dX],
50
или
1</>9хЛ/' 5,П^9^
ae
Учитывая независимость и одинаковый закон
распределения наблюдений х,, х2, хп, можно записать, что
mSlnf(X,B))2=nM{8W(Xi,Q))2=nm
50 50
Подставляя это выражение в последнее неравенство, окон-
1
чательно получаем утверждение теоремы: D 0„ > .
я/(0)
Теорема верна и в дискретном случае, если в условии 2
заменить интегралы на суммы (по всем возможным значениям
случайной величины).
Заметим, что информацию Фишера можно также
представить в виде
\ 6Q
\ ( я2 1_ „/к л\Л
и I(Q) = -M
д'\пр($, в)
592
212
Дифференцируя по 0 равенства (15.1) и (15.2), получим
]5(А)Ф(^0)^=1и ц
i 50 ] 90
Умножим второе равенство на 0 и вычтем его из первого:
1= ] (в.(Л)-в) Щ^-dX (15.3)
-оо ^
По условию на множестве Gn плотность р(Х, 0) > 0, поэтому
можно записать, что =— /?(Jf,0).
50 50
Подставим полученное выражение в равенство (15.3) и,
используя неравенство Коши—Буняковского, находим
\ = [)mX)-Q)dln^Q)p(X,Q)dXf <
J 50
Глава
ii Ф
Обозначим правую часть неравенства Рао—Фреше—Крамера
через Ал = —^—. Эта величина является нижней гранью всех
возможных дисперсий оценок параметра 0 (возможно,
недостижимой).
Эффективностью (по Рао—Фреше—Крамеру) несмещенной
оценки 0Л называется
D0n nI(Q)DQn
Отсюда следует, что эффективность любой несмещенной
оценки удовлетворяет неравенству 0 < e(Qn) < 1, и чем ближе
она к единице, тем лучше оценка.
Несмещенная оценка 0Я называется эффективной, если
е(в„) =1.
Асимптотической эффективностью оценки называется предел
е0(ё) = Ите(ё,,),
если он существует.
Оценку называют асимптотически эффективной, если
*о(0) = 1.
Кроме того, для асимптотически нормальных оценок
понятие асимптотической эффективности иногда трактуется более
широко. А именно, для асимптотически нормальной оценки
0„ е >N(Q,a2/n) при п -» со полагают
Задача 4. Доказать, что выборочное среднее является
эффективной оценкой математического ожидания нормального
распределения, когда дисперсия известна.
Решение. Выпишем функцию плотности для нормального
распределения:
р(х,а) = —=е 2о
стл/2я
213
ЧАСТЬ II. Математическая статистика
да 2а2 с2 9 { да ) а4
Отсюда найдем информацию Фишера
V да
= \м(х-а)2=\.
Получаем значение Ап=с2/п. С другой стороны, Dx=a2/n,
так что Dx = An.
Таким образом, оценка является эффективной.
Из доказанного следует, что чем больше дисперсия
нормальной случайной величины, тем меньше информации о значении
среднего этой величины заключено в одном наблюдении.
Задача 5. Доказать, что относительная частота успеха в
качестве оценки неизвестной вероятности 0 в схеме Бернулли
является эффективной оценкой.
Решение. Оценкой неизвестной вероятности является отно-
сительная частота успеха 0 = — Ух,, где х — успех (1) или не-
удача (0) в /-м испытании. Покажем, что оценка несмещенная:
MQ = -М(х, + х2 +... + хп) = -Y Мх, = М$ = 0.
п п /=1
Дисперсия имеет вид
DQ = D
Гл п
1 хг«
^ ^ 1 DZ, 0(1-0)
Найдем информацию Фишера, причем в данном случае
наблюдаемая величина принимает всего два значения: 0 и 1 с
вероятностями Р(0\ 0) = 1 - 0 и Р(\\ 0) = 0.
214
Прологарифмировав ее, получим
In р(х, а) = In—J= - ,
при этом производная будет равна
д\пр(х,а) 2(х-а) х-а (д\пр(х,а)Л2 _(х-а)2
Глава
дв)=
д\пР(0;д)
Р(0;Э) +
dlni>(l;0)
л2
50
i>(i;0)=
1
1-е
Таким образом, е(в„) =
(1-0)+
1^
16.
0 = -
1
0(1-0)
1
и/(0)Д0я)
= 1.
Задача 6. Пусть выборка xv х2, хп произведена из
генеральной совокупности с равномерным распределением на ин-
л + 1
тервале (0; 0). Проверить на эффективность оценку 0= хтах
для неизвестного параметра 0. п
Решение. Функция распределения F^x) максимума хтт
задается формулой
Fmax{x) = Р(хтш<х) = Р(хх <х,...,х„<х) = Р(х{ <х)...Р(х„ < *) = (|
на отрезке 0 <, х <0. Отсюда получаем
и+Г
MQ = —[nx—dx = Q.
п \ 0я
Значит, оценка 0 несмещенная. Найдем дисперсию этой
оценки:
Мв2 =
И + П2вГ 2 X"
П + 1 Г 2
= \ПХ
\ п i
0я
-dx =
№ = Мв2-(Мв)2 =
(п + 1)2
п(п + 2)
02
в2;
п(п + 2)
Видно, что дисперсия оценки 0„ при п -» оо убывает как \.
п
Такая оценка оказалась лучше эффективной, поскольку
дисперсия эффективной оценки имеет порядок убывания только
—. Разгадка парадокса в том, что для данного семейства рас-
п
пределений не выполнены условия теоремы Рао—Фреше—
Крамера. А именно, область значений случайной величины
зависит от параметра 0.
Подобные оценки называют сверхэффективными.
215
{j) ЧАСТЬ II. Математическая статистика
216
§ 11.5. Оценка математического ожидания
по неравноточным наблюдениям
Ранее предполагалось, что все наблюдения равноточны, т.е.
имеют одинаковую дисперсию (и среднее квадратическое
отклонение). Однако на практике встречаются и ситуации
неравноточных наблюдений. А именно, пусть выполнено
Мхх = Мх2 = ... = Мхп = a; Dx] = af, Dx2 = g22 , Dxn = a*,
и надо найти наилучшую (в каком-то смысле) оценку для а.
Классом линейных несмещенных оценок параметра 6
называется класс оценок вида 0„ = сххх + + ... + спхп, для которых
М0„=0.
Числовые коэффициенты с,, с2, ... сп называются весами
наблюдений. Из требования несмещенности оценки следует, что
должно выполняться равенство сх + с2+... + сп= 1. Чтобы получить
эффективную оценку (в классе линейных несмещенных оценок),
надо минимизировать дисперсию Dan = cxg2 + с2о22 + ... + с2па2п.
Действительно, из требования несмещенности оценки
Л п п п
Ма„ = М^см = ]?сДМх/) = я]Гс/ =а
/=1 /=1 /=1
п
получаем, что оценка будет несмещенной, если ]Гс,. =1.
/=1
По определению, оценка будет эффективной, если она
имеет минимальную дисперсию. Коэффициенты с{ надо
определить так, чтобы дисперсия была минимальна, но при условии,
" л
что 2/,=1. Вычислим дисперсиюDan:
/=1
Dan = D±ciXl = 2>,2(?Ц) = tcfo1,
/=1 /=1 1=1
поскольку случайные величины х. независимы и дисперсия
суммы равна сумме дисперсий.
Задача свелась к нахождению таких коэффициентов е., при
п
которых функция f(c) = ^c2c2 имеет минимум при условии
п /=1
g(c) = ^ci-1 = 0. Это задача на условный экстремум. Функция
/=1
Глава
Лагранжа имеет вид L(c) = f{c) — Xg(c). Для определения
коэффициентов приравниваем к нулю производные:
— = 2с,а,2-Я = 0,
дс,
8L
= -*(с) = -
= 0;
с, =
2о?'
с, =
X.
2о?'
1 = 2
с, =-
2»Г
^ /=1 о,
Из этих условий получаем значения для коэффициентов
с;=а:2/^ат2. Таким образом, веса наблюдений должны быть
обратно пропорциональны их дисперсиям (менее точные
наблюдения, имеющие большую дисперсию, входят с меньшим
весом, более точные — с большим). В результате эффективной
оценкой математического ожидания оказывается
средневзвешенное значение, имеющее вид
V 1
п 1
с дисперсией, равной ^ял=1/]Го/.
У=1
Если дисперсии всех наблюдений равны (т.е. наблюдения
л 1 я
равноточные), то с. = 1/п для любого /=1,2, л и а„ =—Ух »
т.е. среднее арифметическое выборки является эффективной
оценкой математического ожидания в классе линейных
несмещенных оценок (при любом распределении, имеющем
конечные математическое ожидание и дисперсию).
217
ЧАСТЬ 11. Математическая статистика
о
Задачи для самостоятельного решения
Теоретические задачи
1. Доказать состоятельность выборочного коэффициента вариации
(в случае М% > о), выборочных коэффициентов асимметрии и
эксцесса.
2. Пусть ха, х2,хп, yt, у2,ут — случайные выборки объема п и т
из нормально распределенной генеральной совокупности N(a, а2)
с исправленными выборочными дисперсиями s2x, s*. Доказать,
что
П + ТП — L
является несмещенной оценкой параметра о2.
3. Вывести формулы, связывающие третий и четвертый центральные
моменты с начальными моментами. Построить соответствующие
формулы для выборочных моментов и доказать их
состоятельность.
4. Доказать, что если MQn ->9 и DQn -»0, то 0„ — состоятельная
оценка параметра 0.
5. В случае п независимых наблюдений xt, х2, хп за
показательно распределенной случайной величиной ? с заданной функцией
плотности
/<*,0) =
1 --
-е\ х>09
|0, х<0,
доказать, что выборочное среднее является эффективной
оценкой параметра 0.
6. Доказать, что выборочное среднее является эффективной оцен-
Хк
кой параметра X в распределении Пуассона: Р(^ = к) =—е \
к\
7. Доказать, что эмпирическая функция распределения Fn(x) является
эффективной оценкой теоретической функции распределения F(x)
при каждом х.
8. Пусть F(x) = е*,х< 0. Построить несмещенную оценку на основе хтах
и доказать ее сверхэффективность.
218
Глава ii
9. Пусть F(x) = (х/0)р, о <х<, р > о. При известном значении р
построить несмещенную оценку 0 на основе хтах и доказать ее
сверхэффективность.
ю. В случае распределения Парето
\l~(jc/0)-2, jc>0
оценивается параметр 0. Проверить эффективность оценки х .
Вычислительные задачи
ii. Из генеральной совокупности извлечена выборка объема п = 6о.
*1
1
3
6
26
"i
8
40
10
2
Найти выборочное среднее.
12. Найти направленную выборочную дисперсию по выборке объема
п = 50
*1
0,1
0,5
0,6
0,8
"i
5
15
20
10
13. В итоге четырех измерений некоторой величины одним прибором
(без систематических ошибок) получены следующие результаты: 8,
9, ii, 12. Найти: а) выборочное среднее результатов измерений;
б) смещенную и исправленную выборочные дисперсии ошибок
прибора.
14. С помощью измерительного прибора, не имеющего
систематической ошибки, было сделано 8 независимых измерений некоторой
величины.
Номер
измерения
1
2
3
4
5
6
7
8
*i
2504
2486
2525
2495
2515
2528
2492
2494
Найти несмещенные оценки математического ожидания и
дисперсии.
219 I
i
^ ЧАСТЬ II. Математическая статиаика
15. В ОТК были измерены диаметры 300 валиков из партии,
изготовленной одним станком-автоматом. Отклонения измеренных
диаметров от номинала, в нм, даны в таблице.
Границы
отклонений
Середина
интервала
Число
валиков
Границы
отклонений
Середина
интервала
Число
валиков
-30...-25
-27,5
3
0...5
2,5
55
-25...-20
-22,5
8
5...10
7,5
30
-20...-15
-17,5
15
10...15
12,5
25
-15...-10
-12,5
35
15...20
17,5
14
-10...-5
"7,5
40
20...25
22,5
8
-5...0
-2,5
60
25...30
27,5
7
Найти выборочное среднее, выборочные дисперсии, выборочную
моду.
16. В таблице представлены результаты наблюдений х. случайной
величины Найти выборочное среднее х, исправленную
выборочную дисперсию s2, выборочное среднее квадратическое
отклонение s.
а) % — число сделок на фондовой бирже за квартал; п = 400
(инвесторов);
*1
0
1
2
3
4
5
6
7
8
9
10
п1
146
97
73
34
23
10
6
3
4
2
2
б) § — месячный доход жителя региона (в руб.); п = юоо
(жителей);
Менее
500
500... 1000
1000...1500
1500...2000
2000...2500
Свыше
2500
п1
58
96
239
328
147
132
Указание. В качестве верхней границы последнего интервала
использовать 3000;
в) § — удой коров на молочной ферме за лактационный период,
центнеры ; п = юо (коров).
*1
4...6
6...8
8...10
10...12
12...14
14...16
16...18
18...20
20...22
22...24
24...26
"i
1
3
6
11
15
20
14
12
10
6
2
V _J
220
Глава ii
17. В таблице приведено распределение 50 рабочих по
производительности труда § (единиц за смену), разделенных на две группы:
30 и 20 человек.
Прошедшие техническое обучение
(группа I)
Не прошедшие техническое
обучение (группа II)
85
34
96
102
103
63
69
83
89
106
»,
2
5
11
8
4
2
6
8
3
1
Вычислить общие и групповые выборочные средние и дисперсии.
18. Расстояние до цели определено двумя способами. Точность
первого способа характеризуется средним квадратическим
отклонением сг = 30 м, результат измерения хг = 1480 м; точность
второго — средним квадратическим отклонением а2 = 40 м, результат
измерения х2 = 1560 м. Определить приближенное значение
расстояния до цели и оценить его точность.
19. Диаметр втулки определен четырьмя способами, точность которых
of = 1,6 мм2, <j22 = 2 мм2, а] = 2,5 мм2, а24 = 3 мм2. Результаты
измерений: хх = 19 мм, х2 = 18 мм, хз = 20 мм, х4 = 21 мм. Определить
приближенное значение диаметра втулки и оценить его точность.
20. При измерении диаметра детали одним прибором установлен
средний диаметр Зс, = ю мк, пг = 8. При измерении другим
равноточным прибором — х2 = 12 мк, п2 = 16. Определить наиболее
точную оценку диаметра по измерениям двух приборов.
21. Трое исследователей провели выборочное обследование доходов
населения. Первый обследовал ю семей и определил средний
годовой доход 2400 у.е., второй — 25 семей и 2350 у.е., третий —
15 семей и 2450 у.е. Построить наиболее точную оценку среднего
годового дохода.
22. Для изучения распределения заработной платы работников
некоторой отрасли обследовано юо человек. Результаты представлены
в следующей таблице.
Зарплата
Число
Зарплата
Число человек
в долларах
человек
в долларах
190...192
1
200...202
19
192...194
5
202...204
11
194... 196
9
204...206
4
196...198
22
206...208
1
198...200
28
208...210
0
Найти несмещенные оценки математического ожидания и
дисперсии зарплаты.
221
ЧАСТЬ II. Математическая статистика
23. Производство зерна в России в 1996-2002 гг. представлено таблицей.
Год
1996
1997
1998
1999
2000
2001
2002
Производство,
млн т
69,3
88,6
47,9
54,7
65,5
85,2
86,6
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную медиану, крайние члены
вариационного ряда.
24. Производство пшеницы в России в 1995-2001 гг. представлено
таблицей.
Год
1995
1996
1997
1998
1999
2000
2001
Производство,
млн. т
30,1
34,9
44,3
27,0
31,0
34,5
47,0
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную медиану, крайние члены
вариационного ряда.
25. Урожайность зерновых культур в России в 1992-2001 гг.
представлена таблицей.
Год
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Урожайность, ц/га
18,0
17,1
15,3
13,1
14,9
17,8
12,9
14,4
15,6
19,4
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную медиану, крайние члены
вариационного ряда.
26. Численность населения городов России с числом жителей более
1 млн чел. на 2002 г. представлена таблицей.
Город
Население, тыс. чел.
Волгоград
1013
Екатеринбург
1293
Казань
1105
Москва
10 358
Нижний Новгород
1311
Новосибирск
1426
Омск
1134
Пермь
1000
V j
222
Глава ii
Город
Население, тыс. чел.
Ростов-на-Дону
1070
Самара
1158
Санкт-Петербург
4669
Уфа
1042
Челябинск
1078
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную медиану, крайние члены
вариационного ряда.
27. Решить предыдущую задачу, исключив из выборки Москву и Санкт-
Петербург как города федерального значения.
28. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения (в граммах):
49>i; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1; 49,7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную медиану, крайние члены
вариационного ряда.
29. В таблице приведены сгруппированные данные о коэффициентах
соотношения заемных и собственных средств на юо малых
предприятиях региона.
Номер
интервала
Интервал
Середина
интервала х1
1
5,05...5,15
5,1
5
2
5,15...5,25
5,2
8
3
5,25...5,35
5,3
12
4
5,35...5,45
5,4
20
5
5,45...5,55
5,5
26
6
5,55...5,65
5,6
15
7
5,65...5,75
5,7
10
8
5,75...5,85
5,8
4
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения.
223 j
ЧАСТЬ II. Математическая статистика
30. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице.
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
57
7
139
1
203
8
45
2
383
9
27
3
525
10
10
4
532
11
4
5
408
12
1
6
273
14
1
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную моду.
31. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице.
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
12
7
103
1
108
8
24
2
316
9
13
3
551
10
2
4
632
11
0
5
492
12
0
6
273
14
0
Найти выборочное среднее, выборочные дисперсии, средние ква-
дратические отклонения, выборочную моду.
V )
224
i
Глава ii ф
32. В таблице приведены результаты измерения (в сантиметрах) роста
случайно отобранных юо студентов.
Рост
154... 158
158... 162
162... 166
166... 170
170... 174
174... 178
178...182
Число
студентов
10
14
26
28
12
8
2
Найти выборочное среднее, выборочные дисперсии, выборочную
моду.
33. Найти несмещенные оценки математического ожидания и диспер
сии по данным выборки.
*1
1250
1275
1280
1300
»i
20
25
50
5
34. Для определения точности измерительного прибора,
систематическая ошибка которого равна нулю, было произведено 5
измерений. Результаты их даны в таблице.
Номер
1
2
3
4
5
измерения
*i
2781
2836
2807
2763
2858
Найти несмещенную оценку дисперсии ошибок измерительного
прибора, если значение измеряемой величины: а) известно и
равно 2800 м; б) неизвестно.
35. Даны результаты 8 независимых измерений одной и той же
величины (длины протяжки) прибором, не имеющим систематических
ошибок: 369, 378, 315, 420, 385, 401, 372, 383 см. Определить
несмещенную оценку дисперсии ошибок измерения, если: а)
номинальная длина протяжки известна и равна 375 см; б) номинальная
длина протяжки неизвестна.
36. Трое исследователей провели независимые выборочные
обследования доходов населения. Первый определил средний
годовой доход 3200 у.е. с точностью at= 100 у.е., второй — 2900 у.е. с
о2= 50 У-е., третий — 3000 у.е. с о3= 40 у.е. Построить наиболее
точную оценку среднего годового дохода и найти ее дисперсию.
8 Теория вероятностей
ГЛАВА 12
ФУНКЦИИ И РАСПРЕДЕЛЕНИЯ
В МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
§ 12.1. Бета- и гамма-функции
Бета-функцией, или интегралом Эйлера первого рода,
называется интеграл вида B(a,b)= jxa~\l-x)b~ldx, где параметры а > О,
о
Ъ > 0.
Введенный интеграл сходится для любых положительных
значений параметров.
Свойства бета-функции:
1. В(а, Ь) = В(Ь, а).
2. %4)=-^-%*-1), 1) = 1.
a + b-l
Отсюда, в частности, следует, что В(т9п)=-
3. B(a,b)= f У° hdy.
оо а-\
В частности, В(а, \-а)= \——dy= п .
*l + y sinan
Гамма-функцией, или интегралом Эйлера второго рода, на-
оо
зывается функция вида Г(а)= jxa~le~xdx, где интеграл сходится
о
для любого значения параметра а > 0.
I 226
Глава 12 ф
Свойства гамма-функции:
1. Г(а + 1) = аТ(а), откуда следует
Г(а + п) = (о + п - + и - 2)...(а + 1)Г(а).
2. Г(1) = 1.
3. Г(л + 1) = и!
4. Г(1/2) = Vit.
Г(а)Г(Ь)
5. Я(а,6) =
Г(в+*)
6. Г(я)Г(1-я) = (формула дополнения).
sinan
хЛ
7. Г(х + 1)«-
>/2ях, х->ао (формула Стирлинга).
Докажем свойства 1-4.
оо
1) Вычислим интеграл Г(а + 1) = Jx^dbc, интегрируя по
о
00 I
частям. Получим Г(а + 1) = j x?e~xdx = —х?е~х\ъ +
+ а J X*'xerxdx = аГ(а).
о
2) Очевидно,
Г(1) = ] e~xdx = 1.
о
3) Применим принцип математической индукции.
Утверждение верно для п = 0. Пусть оно выполнено для п = к - 1: Г(к) =
=(к ~ 1)! Тогда по свойству 1: Т(к + 1) = кГ(к) = к(к- 1)! = \д.
4) Вычислим интеграл методом замены переменной
(у = х1/2) :
00 00 +00
Г(1/2) = \xme-xdx = l\e-yidy= \е* =7^ (интеграл
О 0 -оо
Эйлера—Пуассона).
Поскольку гамма-функция не выражается через
элементарные функции, ее значения табулированы. Обычно в таблицах
представлены значения Г(х) для 1 < х < 2, и этого достаточно
для вычисления функции при любых х > О (с помощью
свойства 1).
8*
227 |
I
(fa ЧАСТЬ II. Математическая статистика
График гамма-функции
О и
На рис. 12.1. представлен график гамма-функции на отрезке
[0,01; 5].
Примеры:
1. Г(3/2) = Г(1 + 1/2)
2 \2) 2
2. Г(4,7) = 3,7 х 2,7 х 1,7 х Г(1,7) = 3,7 х 2,7 х 1,7 х 0,9086 =
= 15,43;
3. Г(0,7) = Г(1,7)/0,7 = 1,298;
4. Пользуясь свойствами гамма-функции, можем вычислить:
5 3 1г(1,
-х —х—Г — х
2 2 2 U
Г(5)
т.
5x3x1 5п
= гп = -г-
4!х24 27
Задана 1. Доказать формулу, связывающую бета- и гамма-
функции:
B(a,b)=W>>.
Г(а + Ь)
228
Гамма-функция стремится к бесконечности при х
при х -> +оо.
Глава 12 ф
о
х у
у = , тогда х = -^— и
1-х 1 + у
4оо а-\
- У
В(а, Ь)= [—i г 1— Ц-4у= f^- тф.
Для доказательства равенства преобразуем гамма-функцию,
сделав в интегральном выражении для Г(а) замену х = ty, тогда
¦МО +00
Г(а)= JxaVdc= \ta-xy*-xe-»tdy.
о
+00
Отсюда следует равенство ^~^= jV V'rfy. Заменим в по-
* о
лученном равенстве г на / + 1 и положим а= а + Ь. Получим
r(fl + 6) = 1 у<«+*Не-<-+'»</у
(1 + /Г* oJ
Умножив это равенство на г~х и проинтегрировав по / от О
до +оо, получим следующее равенство:
+оо а-\ +00 +оо
о vl + '/ О о
+00 +00 +00 Т(п\
Г(а + Ь)В(а,Ь)= \y{a+b)-{e'ydy J/-1e"°'A= Jy*+'He-^.?S^:
ООО -у
+00
= Г(в) J/V'rfp = r(e)r(A).
о
Задача 2. Вычислить интегралы:
1. Г^=Л= \хт е-хах = Г - = >/я.
+оо +оо
2. JjcV*A= Jx5-Vxfl^ = r(5) = 4! = 24.
229
Решение. По определению бета-функция равна интегралу
B(a9b)= рсв"! (1—jc)*"1 dbc. Сделаем замену переменных, положив
ЧАСТЬ II. Математическая статистика
3. jx3(l-xfdx = ре4-' (1 - ж?'1 dx = В(4,3) =
Г(4)Г(3) 3!х2! 1
Г(7)
I 5
4. jx2(l-x)2dx =
г\7-\г
(3)
5
3
1
Г Г
ИЛ
— X
— X
Г
-Г
UJ
2
2
2
12,
12 1
,2j
О
2 5
Г(5) 4!
1 5
6! 60
5я
128'
5. ^(2-хМ = |х = 2д>, dx = 2dy\= j(2y)2(2-2yf2dy =
о
- 4 1 - — (1 \
= 2? \у2(\-у)Ыу=22В\^, 4 :
О \* j
f 13 ^ '
Г|у + 4
13
22
хЗ!
11
2
9
2'
7 5 3
2'2Y
2
222
19
17
15
13
11
9 7 5
19x17x5
2
' 2
' 2 '
2
2
'2Y2
2 2Г
Задача 3. Найти В
7 3
2'2
2 2
53
222
ч
1 5
Решение. By-,|j = pc^d-x2*fc =
IrfiVrf']
2 V2J2 v2j_5x3xl
7 Зл
2 2
Г(5)
5я
4!х24 27
§ 12.2. Квантили, процентные и критические точки
Квантилью уровня р или /ьквантилыо непрерывной
случайной величины ? с функцией распределения ^(х) называется
такое возможное значение хр этой случайной величины, для
которого вероятность события ?> < хр равна заданной величине
р: Р($ < хр) = 0 < р < 1, т.е. из определения следует, что
х есть решение, по предположению единственное, уравнения
Пхр)=р,0<р< 1.
Глава 12 @
Геометрически хр есть такое значение случайной величины
5, при котором площадь криволинейной трапеции,
ограниченная графиком плотности распределения и осью абсцисс и
лежащая левее х, равна р (рис. 12.2).
Pixy
<
р а
РИС. 12.2
Процентной точкой уровня q или 0%-ной точкой (при 0 <
< q < 100) для непрерывной случайной величины ? с
функцией распределения F(x) называется такое значение vq случайной
величины, что вероятность события § > v равна #/100, т.е.
1 - F(vg) = Р& > vq) = 9/100.
Геометрически #%-ная точка — это значение случайной
величины, при котором площадь криволинейной трапеции,
ограниченной графиком плотности распределения, осью абсцисс и
лежащая правее v, равна q/100.
На рис. 12.3 показана квантиль уровня 0,8 (20%-ная
точка) для стандартного нормального распределения (на графиках
плотности и функции распределения).
К понятию процентной точки близко понятие
критической точки, широко используемое в задачах проверки гипотез.
Критические точки для заданного распределения определяют
границы, за пределы которых случайная величина выходит
достаточно редко. Например, если нас интересуют большие
положительные значения случайной величины то критическая
точка / может быть определена из условия Р(% > /кр) = а, где а
мало. Если же нас интересуют значения, большие по
абсолютной величине (положительные или отрицательные), то можно
определить критическую точку из условия Р(\?\ > / ) = а.
231 |
^ ЧАСТЬ II. Математическая аатистика
Плотность нормального Функция нормального
распределения распределения
РИС. 12.3
Нижней критической границей ца и верхней критической
границей йа, соответствующей заданному уровню значимости а,
называются значения случайной величины, для которых
выполнены условия
Pft < Mj = F(\) = а/2;
Р(ца<$< \) = F(\) - FQO = 1 - а;
Р(^>1/а) = 1 -^а) = а/2.
1
а
а \
2
0
а
2
Рис. 12.4
232
Глава 12 ф
§ 12.3. Распределение хи-квадрат (закон Пирсона)
Распределением хи-квадрат с п степенями свободы
(обозначается %1) называется распределение суммы квадратов п
независимых случайных величин со стандартным нормальным рас-
пределением, т.е. %2п = ]Г?2, если е N(0, 1).
/=1
Такое же распределение будет иметь величина
г\ = Х^^-.если ЬеЩа,о>).
Плотность распределения случайной величины %2„ с и
степенями свободы имеет вид
р(х) =
1
22Г
О,
х>0,
х<0.
Функция распределения:
1
I-
X П j t_
22Г
О,
х>0,
х<0.
Основные числовые характеристики распределения %] сле~
дующие:
математическое ожидание - М%] = п\
дисперсия - D%2n = 2л;
233
Между критическими границами и квантилями для
симметричного распределения существуют следующие соотношения
Яа=ха; иа=х_а (рис. 12.4).
2
Конкретные значения критических точек для различных
распределений и уровней значимости можно найти в таблицах.
Эмпирическими аналогами теоретических квантилей будут
члены вариационного ряда.
|j| ЧАСТЬ II. Математическая статистика
Pyi(x) Плотность распределения хи-квадрат
0,16
0,14
0,12
0,10
0,08
0,06
0,04
0,02
0
L
J А
L
_ \_
1 J
L
1 j
L I
l
г 1
I
1 1
г х.—
1 '
L 1
L 1
_ j
L
2 4 6 8 10 12 14 16 18
Рис. 12.5
Плотность xl распределения зависит от одного параметра
п — числа степеней свободы. При п < 2 функция плотности
убывает, а при п > 2 имеет единственный максимум в точке
xmod= я ~ 2. С ростом числа степеней свободы п распределение
%2п приближается к нормальному со средним п и дисперсией 2п
(в смысле асимптотической нормальности). Общий вид
графика представлен на рис. 12.6.
Заштрихованная область соответствует вероятности а и
определяет квантиль уровня а распределения хи-квадрат.
Задана 4. Доказать асимптотическую эффективность
несмещенной оценки генеральной дисперсии в случае нормального
распределения.
Решение. Как известно, несмещенная оценка
генеральной дисперсии и ее дисперсия выглядят следующим образом:
*2=— У^-Зс)2, Ds2=—.
234
асимметрия — (3^2 =
эксцесс — vx2= 12/л.
На рис. 12.5 представлен график плотности распределения
хи-квадрат с 5 степенями свободы.
Глава 12 ф
4 Х2а 8 12 16 20 24 х
рис. 12.6
Для того чтобы доказать эффективность оценки,
необходимо найти информацию Фишера. Выпишем функцию плотности
нормального распределения:
j (*-<о2
/?Дх,а2) =—j=e 2ty2 , и прологарифмируем ее:
а>/2я
\np^x,c2) = \n—j=-y / = -1п>/2я--1па2-4 / .
а>/2я 2а 2 2а
Продифференцируем по параметру 0 = а2:
49 " 29+ 2Э2 '
tfln/^(x, 0)
= -^((х-я)2-0)2
404
Тогда информация Фишера равна
т~М(($-а)> -0)2 =^Щ-а? -±рв\
494
404 49"
402^' 202 2а4'
так как случайная величина
.л/в J
л2
= Х, имеет распределение
хи-квадрат с одной степенью свободы, и тогда Z>xf = 2. Отсюда
235
ЧАСТЬ II. Математическая статистика
получим Л_ . С другой стороны, Ds2 , и в результате
я я-1
к 2а4
имеем —V = л—>1 при я ->ао.
Л2 2а4
я-
я-1
Таким образом, несмещенная оценка генеральной
дисперсии является асимптотически эффективной.
§ 12.4. Распределение Стьюдента
Пусть я + 1 случайных величин ?0, %п независимы и
имеют стандартное нормальное распределение: е iV (О,1). Пусть
г] = ./-У^2 Случайная величина / = — называется безразмер-
ной дробью Стьюдента, а ее распределение — распределением
Стьюдента с п степенями свободы.
Плотность распределения tn имеет вид
/я + Г
Г
#(*)= г
Г
- л/яя
2)
л+1
' x2V-
1+—
я
-оо<Х<+оо.
Плотность распределения Стьюдента зависит от одного
параметра — числа степеней свободы. С ростом числа степеней
свободы распределение Стьюдента сходится к стандартному
нормальному.
Основные числовые характеристики:
1) мода и медиана равны математическому ожиданию и
равны нулю, т.е. распределение унимодально и симметрично
относительно точки х = 0;
2) дисперсия — Dtn= п /(я - 2) и существует только при
п > 2;
3) асимметрия — р = 0;
4) эксцесс - vn = 6/(я — 4).
На рис. 12.7 представлен график плотности распределения
Стьюдента с тремя степенями свободы.
Плотность распределения Стьюдента зависит от одного
параметра я — числа степеней свободы. Общий вид кривой
распределения представлен на рис. 12.8.
! 236
Глава 12 ф
-3-2-10 1 2 3 t
Рис. 12.7
Рис. 12.8
Заштрихованным областям (слева и справа)
соответствуют вероятности по а/2, в сумме дающие вероятность а и
определяющие критические точки распределения Стьюдента
для двусторонней области.
237
Плотность распределения
Pit) Стьюдента
Р ЧАСТЬ II. Математическая аатиаика
р, п + тл
г(«]гГ
п2т2х2 л
—, *>0.
(ях + т) 2
Распределение Фишера определяется двумя параметрами: я
и /я, называемыми числами степеней свободы.
Основные числовые характеристики:
1) математическое ожидание MF— существует только
при т > 2; т"2
лч п 2я22(я + Я2-2)
2) дисперсия Z) = —г — существует только при
т > 4; п(т-2) (т~4)
3) мода xmod - т(п-2) ПрИ п > j.
я(/я + 2)
4) асимметрия р/г= . v при w > 6;
(я!—6)у я(я + Я! — 2)
3(m-6)(2 + ip2f)
5) эксцесс v = - 3, при т > 8.
/и-8
238
§ 12.5. Распределение Фишера
Если %1 и х2т независимые случайные величины,
распределенные по закону х2 с числами степеней свободы пит
соответственно, то случайная величина
г2 In
F(n,m) = ^
имеет распределение, которое называют распределением Фишера-
Снедекора (F-распределением) с числами степеней свободы пит,
или распределением дисперсионного отношения.
Функция распределения и функция плотности имеют вид
(п + тЛ „ „
r i ^ I 2 ) х{п2т2и2' л
К Л*) = / \ , ч du;
' (п\ (т\) 5+«
Глава 12 0
Из этих формул следует, что .F-распределение всегда имеет
модальное значение, меньшее единицы, и среднее значение,
большее единицы, а также положительную асимметрию.
На рис. 12.9 представлен график плотности распределения
Фишера с числами степеней свободы п = 10 и т = 15.
р {х) Плотность распределения Фишера
0 0,5 1 1,5 2 2,5 3 3,5 х
Рис. 12.9
Общий вид графика плотности распределения Фишера при
различных значениях параметров представлен на рис. 12.10.
РИС. 12.10
239
ЧАСТЬ II. Математическая статистика
§ 12.6. Гамма-распределение
Двухпараметрический закон гамма-распределения случайной
величины 4 е у(а, X) описывается функцией плотности:
/>(*) =
Да)
1о,
х>0,
х<0,
где Г(а) — гамма-функция Эйлера, а > 0 — параметр «формы»,
к > О — параметр «масштаба». Если А. = 1, случайная величина
у (а, 1) зависит от одного параметра а и подчинена однопараме-
трическому закону гамма-распределения.
Основные свойства гамма-распределения следующие:
1. Если случайная величина имеет гамма-распределение
? G у(сх, X), то с? G у(а, к/с), в частности М; Е у(а, 1).
Доказательство. Действительно, пусть х\ = с?. Найдем
функцию распределения F(y). По определению имеем
F(y) = P(y]<y) = P(d,<y) = P
= \cx = u,cdx = du\^\\±\ е
и
Г(а)Дс
с Г(а) q
oJHa)
Следовательно, функция плотности случайной величины
г| = имеет вид
А,О0 =
>>>0,
Да)
[О, у<0.
Отсюда следует, что если с = X, то А? е у(а,1).
2. Сумма любого числа независимых гамма-распределенных
случайных величин с одинаковым параметром масштаба А. и
параметрами формы ар а2, ая также подчиняется гамма-
распределению с параметрами a = а{ + а2 + ... + ал и А..
Доказательство. Рассмотрим случай, когда % к ц являются
однопараметрическими гамма-распределенными случайными
величинами с параметрами аир соответственно (а > 0, р > 0),
240
Глава 12 ф
*[0,оо)
ляемая соотношением
°У [О, х*Д
Отсюда следует, что
[1, 0<z-x<+oo,_ fl, x<z,
[О, z-x<0 ""[О, х>*.
Таким образом, получаем
+оо 1 1
n+n 0JT(a) Г((3) |ад
^[0,+оо)(? *)""
- 'f хаЧ (z - xf-xe~ldx =
r(a)r(p)J
— = u,dx = zdu\
z
a+P-1 1
1 1 7<*+P-i 1
r(a)r(p)JV r(a)r(P)J
Г(а)Г(р)
Г(а)Г(Р) Г(а + Р)'
241
т.е. А. = 1. Покажем, что если ? и rj независимые случайные
величины, то случайная величина т = ? + г\ подчиняется гамма-
распределению с параметром а + р.
Пусть ? е у(а, 1) и г\ е у(Р, 1). Функции плотностей
распределения случайных величин ? и г| соответственно равны
рЛх) = — xaVx, /> (х) = — хм«Гх, х > 0.
^v Г(а) ^v Г(Р)
Поскольку § и г] независимы, совместная плотность
распределения равна произведению функций плотностей
сомножителей: р(х, у) = р^(х)рц(у), и функция плотности суммы
вычисляется с помощью свертки
+оо +00
P^(z) = \p(x,z-x)dx=\p^x)pA(z-x)dx.
-оо -оо
Подставляя в последнюю формулу выражения для
плотностей составляющих, получим
где /ГОвЛ — индикаторная функция множества DcR1, опреде-
1, хеД
Р ЧАСТЬ II. Математическая статистика
2 2 а<л у 2 2
Доказательство. Достаточно подставить параметры а = 1
1 2'
Я. = - в формулу плотности гамма-распределения и сравнить с
формулой плотности распределения хи-квадрат.
Основные числовые характеристики случайной величины
у (а, X) следующие:
1) математическое ожидание — М= —;
X
2) мода - xmod = ~ при а > 1;
3) дисперсия — D = ;
X
2
4) асимметрия — Р = —j=\
У у/а
5) эксцесс — v = —.
242
Поэтому функция плотности распределения суммы ? + т|,
равная
п+тЛ Г(а + р)
соответствует гамма-распределению с параметром а + р, т.е.
^ + л е у(а + р, 1).
Из первого свойства следует, что = — § е у (а, X) и т), =
1 Х
= — Л е у(р, X). Тогда в силу доказанного получаем, что случай-
X
ная величина + т), = — (§ + ti) е у(а + р, А,).
А.
По индукции теперь можно доказать, что сумма любого
числа независимых гамма-распределенных случайных величин
с одинаковым параметром масштаба X и параметрами формы
а,, а2, ап также подчиняется гамма-распределению с
параметрами а = а, + а2 + ... + ал и X.
3. Распределение %] является частным случаем гамма-рас-
п , 1 2 (п П
пределения с параметрами а = -, А, = -, т.е. %п =у\ -, - I.
Глава 12 @
(О, х<0.
Найти константу С, математическое ожидание Щ и дисперсию
ПЬ-
Решение. По свойству плотности распределения имеем
\p(x)dx = C jxaVxrfx = CT(a) = l, a>0.
-00 О
Отсюда получаем, что С=—^—.
Г(а)
Вычислим числовые характеристики распределения.
М\ = lxp(x)dx = 1—xae-xdx = J—lx{a+l)-Vxdx = Г(а + 1) = a.
i ojha) r(a)J Г(а)
Для нахождения дисперсии вычислим второй начальный
момент.
=lx>p(x)dx = — +|х(а+2н^Л = П^±2) =
s i Г(а) J Г(а)
(а + 1)аГ(а) t |ч
= - —— = а(а + 1).
па)
Тогда дисперсия равна
D\ = М% - (Mtf = a(a +1) - a2 = a.
Общий вид графика плотности гамма-распределения при
различных значениях параметров представлен на рис. 12.11.
На рис. 12.12 представлен график плотности гамма-
распределения при a = 3 и X = 1.
243
Гамма-распределение иногда используют при
моделировании реальных ситуаций; с его помощью описывается,
например, распределение доходов или сбережений населения в
некоторых определенных случаях.
Задана 5. Пусть случайная величина § имеет плотность
распределения вида
\Сха-]е'\ х>0,
(j) ЧАСТЬ II. Математическая статистика
А
Плотность гамма-распределения
Задача 6. Пусть случайная величина г| подчиняется
стандартному нормальному закону распределения: г) е N(0, 1). Най-
л2
ти функцию плотности случайной величины ^ = ~у- К какому
параметрическому семейству распределений относится ??
Решение. Поскольку случайная величина г| е N(09 I), ее
плотностью распределения будет функция рЛх) =
1 ~
Найдем
функцию распределения случайной величины
2
FJx) = />(4 < х) = < х) = Р(г|2 < 2jc) =
I 244
I
Глава 12 ^
дано плотностью р(х,а9Х) =
О,
х<0.
Найти константу С, математическое ожидание и
дисперсию
+оо +оо
Решение. Поскольку | p(x)dx = 1, имеем
-оо О
Сделаем замену, положив Хх = и, Xdx = Л/, получим
-!(-) e-udu = —lu«-]e-udu = —r(a) = l.
Отсюда следует, что С =
Г(а)
Вычислим теперь
математическое ожидание:
+оо л а +оо
Хх = и,ах = —I
X
1
_г
Г(а)"г
+оо
\uae-du =
Г(а + 1)_а
Г(аЯ
245
|>(|r||<V2Jc), х>0, п/ рг- ,— ^ , 4J
= -Д= f ехр(--)Л = — = и; t2 = 2и; ltdt = 2du; dt = — = =
J2n $ 2 2 t J2u
>/2я о V2w >/я о
Из этого равенства получаем плотность распределения
случайной величины ^ в виде
1 -!
л/я
а эта функция является плотностью однопараметрического гамма-
распределения с параметром, равным а = 1/2, т.е. у(1/2, 1) =
= Yd/2).
Задача 7. Пусть распределение случайной величины ? за-
ЧАСТЬ II. Математическая статистика
Для вычисления дисперсии аналогично находим второй
начальный момент
+оо л а
Л/$2= [х2р(х)ах = — Гха+,Л!х = |
du,
Xx = u, dx = —I
X.
1 {.^.-л. г<а+ 2) а(а + 1)
—- и е аи = — = —.
Г(а) Ха+2 i Г(а)Х2 X2
Тогда дисперсию находим по формуле
Д!- = М§2-(Щ) =
2 а(а + 1) а2 а
§ 12.7. Бета-распределение
Случайная величина ? е р(я, 6), подчиняющаяся закону
бета-распределения (В-распределение) с параметрами а > О и
b > 0, имеет плотность распределения
Р^х)-
Г(а + Ь)ха-](1-х)
0<х<1,
ШПЬ)
[О, х€[091].
Основные свойства бета-распределения следующие:
1. Если е у(ар Х)и^2е у(а2, X) — две независимые гамма-
распределенные случайные величины, то отношение г| = —-—
имеет бета-распределение с параметрами ах и a2: r| е р(ар а2).
2. Случайная величина р(1, 1) распределена равномерно на
отрезке [О, 1].
3. Функция распределения квадрата стьюдентовской
величины t2m связана с функцией распределения случайной
величины р соотношением
FAx) = F
Л т
\2' 2,
т + х
4. Функция распределения случайной величины Дя, т)
связана с функцией распределения случайной величины р
соотношением
пх
F„lx) = F
п т
т + пх
246
Глава 12 ^
5. Между функцией распределения случайной величины р и
биномиальным распределением существуют соотношение
П к к к
А:=т
6. Имеет место симметрия:
/W)<x> = ^м*1 " *> и = = 1 " Fma)<<1 " *)•
Основные числовые характеристики случайной величины
№ *)'• а
1) математическое ожидание (среднее) — МтЬ) = •
2) мода - xmod =
д + 6
а + й-2
3) дисперсия - Dmb) =
при а > 1, * > 1;
(л + й)2(л + й+1) '
4) асимметрия
2(6-g)Vfl + 6+l
р (a + b + 2)Jab
5) эксцесс — v =
_ 3(д + й+1)[2(л + й)2-г-а6(а + 6-6)]
-3.
ab(a + b + 2)(a + b + 3)
Бета-распределение используется для описания некоторых
реальных распределений, сосредоточенных на отрезке [0,1],
например, для описания распределения величин субъективных
вероятностей, полученных в ходе экспертного опроса.
На рис. 12.13 представлен график плотности
бета-распределения с а = 3, b = 5.
Плотность бета-распределения
>> = beta (х; 3; 5)
Р(х)\
247
щ ЧАСТЬ II. Математическая статистика
у2 + у] +... + у2п = YTY = (СХ)Т(СХ) = ХТ(СТС)Х = X1 X =
Поэтому
= х2 + х2 + ... + х2.
Pyiyv У) =
е2а =[[ , =е 2а
kg
откуда следует независимость и нормальное распределение
У,еМ0, о2).
248
§ 12.8. Приложение законов распределения
в математической статистике.
Теорема Фишера
При построении экономико-математической модели
особенно важным является исследование свойств конечной
выборки при фиксированном я, когда выборка xvxv хп сделана из
нормальной генеральной совокупности N(a, а2). Справедлива
теорема Фишера, описывающая доасимптотические свойства
оценок. Предварительно рассмотрим следующие леммы.
Лемма 1. Если xv xv хп — независимые одинаково
распределенные нормальные случайные величины: х{ е N(0, а2), и
yv yv уп получены из х,, х2, хп ортогональным преобразо-
п
ванием у = ?с/лхл ,/=1,2, п, где С = (с.) ортогональная
матрица, то yv yv уп независимые, одинаково
распределенные нормальные случайные величины: у. е N(09 а2).
т
Доказательство. Пусть х. е 7V(0, а2) и у= ^ckixk, / = 1, 2,я,
где матрица С ортогональна. Тогда существует обратная
матрица С"1, тоже ортогональная и, следовательно, IdetC"1! = 1.
В векторной форме это преобразование можно записать в виде
Y = СХ и обратное преобразование X = C~lY = Д У).Функция
плотности случайного вектора Убудет равна py{yv yv уп) ==
= px(xx(Y), х2(У), л:л(У)) I det JI, но так как преобразование
Х^> К линейное, легко видеть, что якобиан J = С~х Кроме того,
квадратичная форма инвариантна относительно
ортогонального преобразования
Глава 12
Лемма 2 (Фишера). Пусть задано некоторое число р < п
линейных функций yv yv урот х,, xv хп: у= спх{ + с(7х2 + ... +
+ cinxn, i = 1, 2, />, где строки матрицы С = (су) удовлетворяют
п {l,i = k '
условию ортогональности Хс//С*/ =bik =< . Если х,, х2, хя
y_i [0, / ^ Л
независимые одинаково распределенные нормальные случайные ве-
п Р
личины х;. е N(0, а2), то случайная величина ?> = ^х2 -^у?
распределена по закону ох с п — р степенями свободы, причем §
и у2 + у\ +... + у\ взаимно независимы.
Доказательство. Известно, что для прямоугольной матрицы
С^п) с ортогональными строками можно подобрать
дополнительно п — р строк и дополнить ее до квадратной
ортогональной матрицы С(ях||). Если к вектору X применить
преобразование СХ9 то получим вектор Y, у которого первые р компонентов
совпадают с заданными случайными величинами yv yv у 9
и так как квадратичная форма инвариантна относительно орто-
п п
тонального преобразования, получим ^х2 = ^у? • Отсюда сле-
п р п
дует, что ^ = Тах* ~Цу? = Z у? и $ как Функция °т yp+v уп
/=1 /=1 i=p+\ р
не зависит от у{9 yv у , т.е. не зависит от суммы ^у2.
/=i
В силу леммы 1 случайные величины yv yv у имеют
нормальное распределение у. е N(0, а2), а сумма квадратов
нормально распределенных случайных величин имеет х2-распределение:
X (—)2 еК2п-Р ' следовательно, ? у2 ео2%2п_р. Лемма доказана.
i=p+\ о i=p+l
> Теорема Фишера. Пусть хп и s2n соответственно
выборочное среднее и выборочная дисперсия, построенные по выборке
х,, х2, хп из нормальной генеральной совокупности N(a9 а2).
Тогда при любом фиксированном объеме выборки п их совместный
закон распределения описывается следующим образом:
1) хп распределено по нормальному закону хп е N(a, о2/п);
2) статистика ^п 1^ распределена по закону %2 с п — 1
о
степенями свободы;
3) случайные величины хп и s] статистически независимы.
249 I
ЧАСТЬ II. Математическая статистика
Доказательство. Пусть xv xv хп — случайная выборка из
нормальной генеральной совокупности N(a, а2). Нормальность
распределения выборочного среднего хп вытекает из факта
нормального распределения любой линейной комбинации
нормально распределенных случайных величин.
Введем случайную величину z. = х. — а. Тогда Afe. = О,
Dz= = Dx= а2. Отсюда следует, что s\ =s2x, т.е. без
ограничения общности можно полагать а = 0.
Итак, zr х - а е N(0, а2) и s2x = s2z = —(?z2 -nz2). Так
a = 0, имеем /=1
как
—2
X =
1 п
Отсюда получим пх =
^1 j Z2 i
л/я л/я yfn)
Обозначим ух = yfnxz = -j=+-j=+.т.е. случайная ве-
>/Я >/Я у/п
личина ух представлена в виде линейной функции
Ух = си*1 + ci2^2 + - + CiA> ™e Си=-^>
\1п
1 ^
удовлетворяет ус-
а С2 + С22+... + С2Л =1, т.е. строка
ловию ортогональности. Применяя лемму Фишера к yx=y[n*z,
при р = 1 получаем, что y2=nz и случайная величина
?> = (n-l)s2z = ^z2 - у2 в случае выборки из нормальной гене-
ральной совокупности независимы, причем ух = yfnxzeN(0,c2)
И (я-1)5 60 Хя-р
- ет2
Таким образом доказано, что xeN(a,—),
(я-1)52 2
я а'
Следствие 1. Дисперсия исправленной выборочной дисперсии s2,
построенной по случайной выборке объема я из нормальной
генеральной совокупности Ща, с2), определяется формулой
Ds2 =
2 2а4
я-1
250
Глава 12
= 2(11-1),
то
= ^#^ = 2(„-1).
Поскольку
9 4
Поэтому Ds2 = —— •
л-1
Следствие 2. ?с/ш х w s2 соответственно выборочное среднее
и дисперсия, построенные по выборке из нормальной генеральной
совокупности N(a, о2), то статистика
s
распределена по закону Стьюдента с п — 1 степенями свободы.
Для доказательства достаточно представить статистику Т в
виде —
х. —а
а
\(п-
-Ds2
Do2
, (п-
-IK2
и так как ?—^-4п е N (0, 1), v" 7~я е%„_р то по определению
с а
статистика Г имеет распределение Стьюдента с п — 1 степенями
свободы.
Следствие 3. Пусть случайная выборка х{, х2, хп
произведена из нормальной генеральной совокупности N(ap с2), а выборка
yv yv ут — из генеральной совокупности N(a2, cs\) и эти
выборки независимы. Тогда
х-у eN
ах-а2,-±- + -^-
п т
В частности, если обе выборки взяты из одной и той же
а2), то
генеральной совокупности (я, = av с{
х-у eN
0,а2
1 1
— + -
Поскольку линейная комбинация независимых нормально
распределенных случайных величин распределена нормально,
то для доказательства достаточно вычислить математическое
ожидание и дисперсию разности независимых случайных
величин хи у.
251
t
П~Т hn-\)sx2Hm-l)s22 '
\п т\ п+т-2
где s2 us2— исправленные оценки дисперсий,
имеет распределение Стьюдента с (п + т - 2) степенями свободы.
Из следствия 3 вытекает, что
Л, = (x-?-^-aJ е МО, 1).
V п т
По теореме Фишера -—^е^.,, -—г-2-^.,, причем
а а
52, 522 независимы. Следовательно,
л = (n-\)sx2 (m-\)s22 2
а а
так как по свойству ^-распределения сумма xL+xL
распределена тоже по закону %2 с т + я — 2 степенями свободы. Тогда
случайная величина . 1 по определению распределена
_Jk_
\л + /я-2
по закону Стьюдента сй + /и-2 степенями свободы.
Следствие 5. Пусть случайная выборка хх, х2, хп
произведена из нормальной генеральной совокупности N(av с2), а выборка
ух, у2, ут из генеральной совокупности N(a2, g\) и эти выборки
независимы. Тогда при одинаковых (возможно, неизвестных)
дисперсиях а2 =а]= о2 случайная величина
•>2
252
Следствие 4. Пусть случайная выборка хх, х2, хп
произведена из нормальной генеральной совокупности N(av о2), а выборка
ух, у2, ут из генеральной совокупности N(av g\) и эти выборки
независимы. Тогда при одинаковых (возможно, неизвестных)
дисперсиях а2 =<з]= а2 случайная величина
Т^ (х-у)-(ах-а2)
^ ЧАСТЬ II. Математическая статистика
Глава 12 ф
о
Задачи для самостоятельного решения
1. Доказать свойства 1-3 бета-функции.
2. Пусть §lf ?2,?п и tilf л2» —» Лт — независимые, нормально
распределенные случайные величины — е Л/(о, a2); е Л/(о, а2).
Найти закон распределения случайной величины у =
„15?
1 т
3. Доказать, что в случае нормального распределения N(a, а2)
неисправленная выборочная дисперсия имеет дисперсию
^ = 2а>-1)
л2
4. Докажите, что сумма двух независимых х2*РаспРеделенных
случайных величин подчиняется распределению %2* а именно
5. Найти математическое ожидание и дисперсию распределения %2п.
6. Доказать, что если §t е уЦ, X) и ?2 € y(a2, X) — две
независимые гамма-распределенные случайные величины, то отношение
71 = —21— имеет бета-распределение с параметрами at и а2:
Л б Р(а1? а^.
253
распределена по закону Фишера с п — 1 и т — 1 степенями
свободы.
Доказательство вытекает из того факта, что случайные
величины
а а
распределены по закону %2 и независимы, так как независимы
соответствующие выборки.
ЧАСТЬ 11. Математическая статистика
7. Пусть ?0, ?lP^п — независимые, нормально распределенные слу-
чайные величины,
1 я
,1, § € Л/(0, ст2), / = о, 1, 2 П и Т1 = л "У^?-
Найти распределение случайной величины t = —.
Л
8. Доказать, что распределение %] сходится к нормальному закону
со средним п и дисперсией 2п при п -> оо (в смысле
асимптотической нормальности).
9. Вывести формулу для дисперсии распределения Стьюдента при
п > 2.
ю. Пусть случайная величина ? имеет распределение Стьюдента с п
степенями свободы. Какое распределение имеет случайная
величина Т| = ?2?
11. Пусть даны две независимые случайные величины т| е у(л; X).
I
Найти распределение случайной величины —.
Л
12. Найти моду случайной величины, имеющей гамма-распределение
У (а, X).
13. Найти математическое ожидание и дисперсию случайной
величины, имеющей бета-распределение р(а, Ь).
14. Найти моду случайной величины, имеющей бета-распределение
Р(0, Ь).
15. Доказать, что распределение Стьюдента с ростом числа степеней
свободы сходится к нормальному.
16. Определить, к какому распределению сходится распределение
Фишера F(n, т) при т -> оо.
17. Вычислить дисперсию и эксцесс распределения Стьюдента.
18. Вычислить математическое ожидание, моду и дисперсию
распределения Фишера.
19. Пусть xt, х2,xn, уг, у2,ут - случайные выборки объема пиш
из нормально распределенной генеральной совокупности Л/(а, о2)
с исправленными выборочными дисперсиями s2x, . Доказать,
у п+т-2 у
является эффективной в классе всех линейных несмещенных
оценок параметра s2, построенных по наблюдениям s\, s2y.
254
Глава 12 ф
20. Пусть имеется М случайных выборок объемов пг, п2,пм из
нормально распределенной генеральной совокупности Л/(а, а2) с
исправленными выборочными дисперсиями _>5^ . Построить
эффективную оценку (в классе всех линейных несмещенных
оценок) для дисперсии а2.
21. Доказать, что смещенная выборочная дисперсия нормального
распределения является асимптотически эффективной (согласно
определению для асимптотически нормальных оценок).
22. Для показательно распределенной случайной величины
заданной функцией плотности р%(х,Х) = Хе~**, х>0, доказать несме-
„ j
щенность и асимптотическую эффективность оценки х = —=^
паях
раметра X.
23. Для оценивания параметра а нормального распределения Л/(о, а2)
с v4
намереваются использовать оценку вида a*=~2Jx|. Найти кон-
п /=i
станту с, при которой оценка а* является несмещенной.
Вычислить ее эффективность.
24. Для оценивания параметра а нормального распределения Л/(о, а2)
намереваются использовать оценку вида о = cns, где s -
исправленное выборочное среднее квадратическое отклонение. Найти
последовательность чисел сп, при которых оценка а является
несмещенной. Проверить ее на асимптотическую эффективность.
25. Пусть хг, х2,xn, yt, у2,ут — случайные выборки объема пит
из нормально распределенной генеральной совокупности Л/(а, а2)
с исправленными выборочными дисперсиями s2, s2. Доказать,
что оценка
Цг[(А1-1К2+(/«~1)^]
является эффективной в классе всех линейных несмещенных
оценок параметра а2, построенных по наблюдениям s2, s2y.
26. Пусть имеется М случайных выборок объемов пх, п2,пм из
нормально распределенной генеральной совокупности N(a, а2) с
исправленными выборочными дисперсиями 52,52,...,5^.
Построить эффективную оценку (в классе всех линейных несмещенных
оценок) для дисперсии а2.
255
ЧАСТЬ 11. Математическая статистика
27. Доказать, что смещенная выборочная дисперсия нормального
распределения является асимптотически эффективной (согласно
определению для асимптотически нормальных оценок).
28. Для показательно распределенной случайной величины за-
данной функцией плотности fJx9\) = Xe **, х > о, доказать не-
п — 1
смещенность и асимптотическую эффективность оценки Х = -^^
пх
параметра А,.
29. Для оценивания параметра а нормального распределения
* с п
Л/(о, а2) намереваются использовать оценку вида а*=—У|х, |.
Найти константу с, при которой оценка ст* является несмещенной.
Вычислить ее эффективность.
30. Для оценивания параметра а нормального распределения N(a, а2)
намереваются использовать оценку вида а = cns, где s —
исправленное выборочное среднее квадратическое отклонение. Найти
последовательность чисел сп, при которых оценка а является
несмещенной. Проверить ее на асимптотическую эффективность.
ГЛАВА 13
МЕТОДЫ ПОСТРОЕНИЯ
ОЦЕНОК
§ 13.1. Метод моментов
Метод моментов, предложенный английским статистиком
Карлом Пирсоном в 1894 г., заключается в приравнивании
определенного числа выборочных моментов к
соответствующим теоретическим, которые являются функциями
неизвестных параметров 0Р 02, Qk. Рассматривая количество
моментов, равное числу к неизвестных параметров, подлежащих
определению, и решая полученные уравнения относительно
этих параметров, получаем искомые оценки. Иначе говоря,
оценки параметров 0Р 02, Qk являются решениями систем
уравнений а/(0„02,...,вА) = а, или ц.(01,02,...,0л) = ц/ для
некоторых / = /,, /2, ... ik.
Метод моментов содержит неопределенность, поскольку
можно получить уравнения для неизвестных параметров 0,, 02,вк
используя как начальные, так и центральные моменты, а также
некоторые их модификации типа асимметрии или эксцесса.
Пример. Функция
задает плотность распределения Рэлея случайной величины
представляющей собой расстояние от точки на плоскости до
9 Теория вероятностей
ЧАСТЬ 11. Математическая статистика
начала координат, при условии, что координаты этой точки
независимы и имеют стандартное нормальное распределение.
Требуется оценить параметр 0 по выборке х,, х2, хп.
Найдем оценку параметра 0, приравнивая начальные
выборочные и теоретические моменты. Первый начальный момент
имеет вид: ^ = <JnQ/2. Приравнивая, получаем первую оценку
, _ л 2х
параметра: yjnQjl^x, откуда 0„ = .
Приравнивая вторые начальные моменты, можем получить
л 1 »
другую оценку: 0„ = —Ух\, а из уравнения, которое получит-
ся при использовании второго центрального момента (диспер-
сии), — третью оценку: 0Я = .
4-я
Часто полагают, что для нахождения оценки одного
параметра следует брать первый момент, для двух — первые два
момента и т.п. По возможности, действительно имеет смысл
поступать так, поскольку это проще всего. Однако такой
подход годится не всегда. Он не проходит, например, если
некоторые моменты равны нулю или не зависят от нужных
параметров.
В общем случае система уравнений для моментов может не
иметь решения в элементарных функциях (и тогда можно
искать решение приближенными методами) или вообще
оказаться неразрешимой (несовместной).
Оценки, полученные методом моментов, часто оказываются
смещенными. К достоинствам метода моментов следует
отнести его простую вычислительную реализацию, а также то, что
оценки являются функциями от выборочных моментов.
В силу теоремы Слуцкого любая непрерывная функция от
выборных моментов сходится по вероятности к постоянной,
получаемой подстановкой в эту функцию теоретических
моментов, если они существуют и если получаемая таким
образом постоянная конечна. Для определенности рассмотрим
функцию Я(ар а2) от двух моментов (начальных или
центральных), хотя ее можно обобщить на любое конечное число
аргументов, в том числе и на случай, когда Н зависит только
от одного аргумента.
| 258
Глава 13
Теорема 1. (Крамера). Пусть в некоторой окрестности точки
(а,, а2) функция Я(ар а2) непрерывна и имеет непрерывные
частные производные первого и второго порядка. Обозначим
_ дН(аха2) _ дН(ах,а2) _
Я'~ —з^-' Щ и Я°~~ Я(а" ^
л л
Тогда случайная величина #(си,а2) ассимптотически
нормальна при п оо со следующими параметрами:
МЯ = Я0 + 0(1/л);
Я(а1,а2)^->ЛГ(Я0,/)а1Я12+2Я1Я2соу(а1,а2) + /)а2Я22). (1)
Иногда оценки, получаемые с помощью метода моментов,
принимаются в качестве первого приближения, по которому
можно построить другими методами оценки более высокого
качества.
Оценки метода моментов используются также, когда
существует необходимость оценить не сами параметры
распределения (которые часто представляют собой некие абстракции), а
определенные практически значимые показатели, зависящие от
этих параметров функционально: G = g(0p 02, 0к). Самый
простой (хотя и не самый точный) способ такого оценивания —
подставить полученные оценки в соответствующую функцию:
С = ^(01,02,...,0Л).
Если распределение определяется одним параметром, то для
построения оценки один теоретический момент приравнивают к
одному эмпирическому моменту того же порядка (обычно первого).
Задача 1. Случайная величина ? (число появлений события
А в т независимых испытаниях) подчинена биномиальному
закону распределения с неизвестным параметром р. Далее
приведено эмпирическое распределение числа появлений события
в 10 опытах по 5 испытаний в каждом (в первой строке указано
число х. появлений события А в одном опыте; во второй строке
указана частота п. — количество опытов, в которых
наблюдалось столько появлений события А).
xi
0
1
2
3
4
"i
5
2
1
1
1
9*
^ ЧАСТЬ II. Математическая аатистика
0,3
0,5
0,7
0,9
1,1
1,3
1,5
1,7
1,9
2,2
2,3
Я/
6
9
26
25
30
26
21
24
20
8
5
Найти методом моментов точечные оценки неизвестных
параметров а и а нормального распределения. Оценить долю
изделий с отклонением менее 1,5 мм в генеральной
совокупности, используя нормальное приближение.
Решение. Для нахождения двух неизвестных параметров
необходимо два уравнения. Первое получаем, приравняв
начальный теоретический момент первого порядка к
начальному эмпирическому моменту первого порядка, а второе —
приравняв центральный теоретический момент второго порядка к
центральному эмпирическому моменту второго порядка:
я*=х, (а*)2=52.
| 2бО
Найти методом моментов точечную оценку параметра р
биномиального распределения. Оценить вероятность р0 = = 0).
Решение. Математическое ожидание биномиального
распределения известно: Щ = тр. Приравняв математическое
ожидание к выборочному среднему, получим уравнение: тр = х,
откуда р = х/т. Для рассматриваемого примера имеем:
х = (0-5 + Ь2 + 2-1 + 3-1 + 4-1)/10 = Ц;
Р = 1,1/5 = 0,22; >0=(1 - 0,22)5«0,29.
Если распределение определяется двумя параметрами, то для
построения их оценок два теоретических момента приравнивают
двум соответствующим эмпирическим моментам тех же порядков
(обычно первым двум).
Задача 2. Случайная величина X (отклонение
контролируемого размера изделия от номинала) подчинена нормальному
закону распределения с неизвестными параметрами а и а.
Далее приведена таблица наблюдаемых отклонений от номинала,
подвергнутых группировке, для п = 200 изделий. В первой
строке указаны середины интервалов отклонений хр мм; во второй
строке приведена частота я. — число наблюдений, попадающих
в данный интервал.
Глава 13 @
Найдем величины х и а2 по данным выборки:
1 11
х= =(0,3x6 + 0,5x9 + 0,7x26 + 0,9x25 + 1,1x30 + 1,3x26 +
200 /=|
+1,5х21 + 1,7х24 + 1,9х20 + 2,2х8 + 2,3х5)/200 = 1,266.
Для нахождения выборочной дисперсии перейдем к
условным вариантам u.t = 10х.:
/- 1 п V
= (6x9 + 9x25+26x49+25x81 +
-2 1 11 ( 1 11
200?? l200tT
+30xl21 + 26xl69 + 21x225 + 24x289 + 20x361 + 8x484 + 5x529)/200~
-l,2662x 100 = 24,72;
a2(x) = a2(w)/100 = 0,2472; *2=y^<*2 = 0,2484 (при больших
л исправленная и неисправленная выборочные дисперсии мало
различаются); s = 0,498.
Таким образом, получаем: а « 1,27 (мм); а* « 0,5 (мм).
Оценим долю изделий с отклонением менее 1,5 мм как
вероятность для нормальной ?:
^1,5-1,27^1
Р = Р&< 1,5) = Ф
0,5
* 0,68.
Замечание. Эту долю можно оценить также непосредственно
по таблице: поскольку значение 1,5 мм делит соответствующий
интервал пополам, получается, что 122 из 200 изделий имеет
отклонение меньше заданного, что дает близкую оценку 0,61.
Задача 3. Предполагается, что выполнение некоторой
работы занимает случайное время с распределением Симпсона на
отрезке [а, Ь]. Хронометраж 20 испытаний дал среднее время
работы 30 мин и исправленную выборочную дисперсию 24 мин2.
Определить параметры а и b методом моментов. Оценить, за
какое время работа будет выполняться с вероятностью 98%.
Решение. Для распределения Симпсона (плотность которого
имеет вид равнобедренного треугольника с основанием на
заданном отрезке) имеем
2 24
261 !
^ ЧАСТЬ II. Математическая аатистика
Параметры распределения можно выразить через
математическое ожидание и дисперсию:
а = М$-у1Щ; Ь = М$+.]Щ.
Подставляя вместо теоретических моментов выборочные,
получаем оценки
д = х->/бУ ; 6 = х + л/бУ,
откуда я =18 (мин), Ъ = 42 (мин).
Функция распределения Симпсона имеет вид
0, х<а;
\2(x-a)2/(b-a)29 а<х<(а + Ь)/2;
W |1-2(*-х)2/(*-я)2, {а + Ь)/2<х<Ь\
1, х > Ь.
Решая уравнение Дх) = 0,98, находим искомое время
Г= 6-0,1(?-я).
Подставляя полученные оценки в формулу вместо
теоретических параметров, получаем Т = 42 - 0,1(42 - 18) =
= 39,6 (мин).
§ 13.2. Метод максимального правдоподобия
Одним из основных методов получения оценок параметров
генеральной совокупности по данным выборки является
метод максимального правдоподобия, предложенный Р. Фишером.
Основу метода составляет функция правдоподобия,
выражающая плотность вероятности (либо вероятность) совместного
появления результатов выборки xv xv хп.
Результаты выборки рассматривают как одну из возможных
реализаций я-мерной случайной величины (§|S ?2, ?Л),
компоненты которой независимы и имеют одну и ту же функцию
распределения.
Совместное распределение этих величин задается в виде
произведения частных распределений (поскольку
предполагается, что наблюдения независимы) и, следовательно, функция
правдоподобия имеет вид
Цх{9 х29 хп9 6) = flP(xi9Q)
i=l
I 262
Глава 13 ф
в случае дискретного распределением, заданного
вероятностями Р(х9 0), и
п
L(xv xv х, 0) = Пр(хпд)
/=i
в случае непрерывного распределения с плотностью p(x,Q).
Из определения функции правдоподобия следует, что чем
вероятнее (правдоподобнее) набор значений (хр xv хп)
случайной величины ? при фиксированном 0, тем больше
значение функции правдоподобия. Поэтому в качестве оценки
неизвестного параметра 0 принимается такое значение 0Я, которое
максимизирует функцию правдоподобия.
Если параметр 0 е Q, где Q — замкнутая область
допустимых значений параметра, то получаем задачу математического
программирования:
найти такое 0„, чтобы Дх,,...,хи, 0„) = maxL(x,,...,x„,0).
Поиск оценки упрощается, если максимизировать не саму
функцию правдоподобия, а ее логарифм, потому что
максимумы ЦХ9 0) и 1пЦХ9 0) достигаются при одном и том же
значении параметра 0. Функцию /л(хр хл, 0) = In ДА", 0) называют
логарифмической функцией правдоподобия.
Если максимум функции /я(хр хя, 0) достигается внутри
допустимой области Q, то в точке максимума 0Я выполняются
необходимые условия экстремума:
5/„(хр...,х„,0) = 0 любого / = ! 2, к.
50,.
Полученная система уравнений называется уравнениями
правдоподобия. Решения этой системы могут соответствовать
максимуму, минимуму функции Цх{9 хп9 0), а также являться
точками перегиба. Необходимо проверить, что полученное решение
есть точка максимума функции правдоподобия.
Отсюда следующий алгоритм для отыскания оценки
параметра 0: решают уравнение или систему уравнений
правдоподобия, получаемых приравниванием производной (частных
производных) по параметру (параметрам) 0 к нулю: ^L =0.
50
Затем отбирают то решение, которое соответствует именно
максимуму, функции InZ,, т.е. вторая производная в данной
2б3 j
i
ЧАСТЬ II. Математическая статистика
точке должна быть отрицательной: д ^ < 0. Иногда функция
30
правдоподобия имеет несколько максимумов, и приходится
искать наибольший из них.
Бывают также случаи, когда этот алгоритм не действует,
поскольку функция правдоподобия достигает максимума не во
внутренней точке, а на границе некоторой области, либо
когда она просто недифференцируема в точке максимума. Такие
случаи называют нерегулярными.
Достаточные условия регулярности (в одномерном случае)
следующие.
1. Область Gn- {х:/?(х,0)>О} возможных значений
случайной величины не зависит от параметра 0.
00
2. Тождество jp(x, Q)dx = 1 можно дважды дифференциро-
—оо Л ГЛ
вать под знаком интеграла, а соотношение mq„ = J &„(х)р(х>
можно один раз дифференцировать под знаком интеграла по
параметру 0.
3. Математическое ожидание 7(0) = М
положительно.
fdln/(S,0)Y
1 1 конечно и
50
Интегралы в условии 2 могут быть многомерными.
> Теорема 2. Если для выборки (хр х2, xj объема п выполнены
условия регулярности 1—3, то:
1) решение 0Л уравнения правдоподобия единственно;
2) 0Я — состоятельная оценка параметра 0;
3) распределение оценки 0Я асимптотически нормально и
предельное распределение имеет математическое ожидание 0 и дис-
1
персию ;
4) оценка максимального правдоподобия асимптотически
эффективна.
Если для оценок максимального правдоподобия выполнены
условия теоремы Рао—Фреше—Крамера (см. § 11.4), то
справедлива следующая
264
Глава 13 $
^ Теорема 3. Если эффективная (по Рао—Фреше—Крамеру)
оценка существует, то она является оценкой максимального
правдоподобия.
Однако это не означает, что любая оценка максимального
правдоподобия эффективна. Но если эта оценка оказывается
неэффективна, это значит, что эффективных оценок вообще
нет, хотя при этом могут существовать оценки с дисперсией,
сколь угодно близкой к Дя.
Следует также отметить, что метод максимального
правдоподобия иногда дает те же оценки, что и метод моментов,
а иногда — другие. Бывает, что ни один из этих методов
не дает хороших оценок, и приходится использовать другие
методы.
Задача 4. Найти методом максимального правдоподобия
оценку вероятности «успеха» 9 в схеме испытаний Бернулли.
Решение. Рассмотрим случайную величину
тогда функция вероятностей случайной величины § запишется
Логарифмическая функция правдоподобия для одного
испытания будет иметь вид
, , т>, fine, х = 1;
/,е) = 1пР(х, е)= '
1 [1п(1-0), х = 0.
Для п испытаний и т «успехов» в п испытаниях получаем
/я (0) = т 1п9 + (п - т) 1п(1 - 6).
Отсюда /' (0) = —-п т = 0 и 0„ = —. Проверим знак
л е 1-е п
второй производной: /я(0) = ~^Г~^ 9)2 <
Таким образом, относительная частота появления события
является оценкой вероятности «успеха» в одном испытании
А. Дискретные распределения
1, в случае «успеха»,
О, в случае «неудачи»,
в виде
265
ф ЧАСТЬ II. Математическая статистика
*1
0
1
2
3
4
5
6
7
ni
199
169
87
31
9
3
1
1
Найти методом максимального правдоподобия точечную
оценку неизвестного параметра X распределения Пуассона.
Решение. Выпишем функцию правдоподобия
L = Р(хх, X) Р(х2; X) ... Р(хп; X) = —-| лю+~+*.е-*.
Найдем точку максимума логарифмической функции
правдоподобия, для чего приравняем к нулю ее первую
производную по X:
In L = (?х,) Ш - пк - 1п(х,! х2! ... х„!), ^ = f ?х, -и = 0.
/=1 иХ X /=1
Имеем X* = х. Убедимся, что полученное значение X
является точкой максимума. Для этого найдем вторую производную и
a2ini 1 а
проверим ее знак в точке X : — = —j^xr ^сли в послеД"
дХ X i=\
нее уравнение подставить Х* = Зс, то вторая производная будет
отрицательна, значит, х является точкой максимума.
Найдем значение X* для рассматриваемого примера:
X* = -Y«,jc,. =(169 + 2- 87 + 3 31 + 4- 9 + 5- 3 + 6 + 7)/500 = 1.
п /=1
266
Бернулли, найденной методом максимального правдоподобия.
Поскольку Л/0Л = 6, то оценка 0Я является несмещенной
оценкой вероятности.
Задана 5. Случайная величина ? (число поврежденных
стеклянных изделий в одном контейнере) распределена по
закону Пуассона с неизвестным параметром X. В таблице
приведено эмпирическое распределение числа поврежденных изделий в
500 контейнерах (в первой строке указано число х. поврежденных
изделий в одном контейнере, во второй строке указана частота
п. — число контейнеров, содержащих xt поврежденных изделий).
Глава 13 ф
Б. Непрерывные распределения
Задана 6. Найти методом максимального правдоподобия по
выборке xv xv хп точечные оценки параметров а и а
нормального распределения, плотность которого
/>(*) =
1
(х-аУ
' 2о2
Решение. Выпишем функцию правдоподобия:
Дх,х2,...,хяя,а)=-
1
-ехр
1 я о
2а /=i
Логарифмическая функция правдоподобия имеет вид
lnZ- = -«lna-/ilnv2jt гХ^*' ~°)2-
Найдем точку максимума, решив систему из двух
уравнений, получающихся приравниванием первых двух частных
производных по неизвестным параметрам к нулю:
dhiL 1 А, . л
да а м
dlnL и 1А, ч2 п
-т—=—+—2>,-«) =0
ост ст ст м
2>,-а) = 0,
1 = М
I(^-a)2
fl = -2>/>
ст2Л?(*(-х)2.
Проверим, является ли точка (а, ст2) точкой максимума
функции правдоподобия:
а21п! и
се2 а2'
до ст ст (=|
d2lnL_ 2^(т _
дадст ст3 м '
267
ф ЧАСТЬ II. Математическая статистика
А =
Отсюда
. а <=1 а а |=!
\ =-4 < о;
п ЗиЛ. >2 4 Л, ч
о а /=1 а V/=j
л Зл2 Л
+—-0=
а а
2л2
>0
Следовательно, точка (я, о ) — действительно точка
максимума, и полученные оценки являются оценками
максимального правдоподобия.
Задача 7. Найти оценку максимального правдоподобия для
параметра сдвига 9 распределения Коши, заданного
плотностью р(х) = =-, по выборке из двух наблюдений, если:
я(1 + (х:-0)2)
а) хх = -1, х2 = 1; б) хх = -2, х2 = 2.
Решение. Функция правдоподобия для двух наблюдений
имеет вид
Д0) =
1
1
Введем функцию Л(0) =
ла+Ос.-б)2) тг(1 + (;с2-е)2)
1
я2Д0)
. Тогда задача максимизации
функции правдоподобия эквивалентна задаче минимизации R(<8):
а) если х,= -1, х2= 1, то Л(е) = (1+(1 + 9)2)(1+(0-1)2) = в4+4.
Функция R достигает минимума в точке 0=0, так что это и
есть оценка максимального правдоподобия;
Как известно из математического анализа, чтобы
функция /?(jCj, jc2, хп) достигала максимума в некоторой точке,
достаточно, чтобы матрица второго дифференциала функции
(Pf в этой точке была отрицательно определена. По критерию
Сильвестра для этого необходимо и достаточно, чтобы ее
главные миноры чередовались по знаку, а именно А, < О, А2 > 0.
Рассмотрим матрицу производных
( п гп \
~2 —L<*/-fl>
Глава 13 ф
б) если х. = -2, х2 = 2, то Л(0) = (1+(2 + 0)2 )(1+(0 - 2)2) = 04 - 602 + 25,
и производная имеет три нуля: в точках 0 = 0 и 0 = ±y[i. При
этом точка 0=0 оказывается точкой максимума функции R.
Точкам 0 = ±>/з соответствует минимум функции R9 причем
в обеих этих точках величина R одинакова. Таким образом, оба
значения ±>/з являются в данном случае оценками
максимального правдоподобия.
Замечание. Ни метод моментов, ни метод максимального
правдоподобия не могут дать хороших оценок для параметра
сдвига распределения Коши. Тем не менее существует простая
оценка для него — выборочная медиана: 0Л = xmed, поскольку
Д0) = 1/2.
В. Нерегулярные случаи
Задача 8. Найти методом максимального правдоподобия
оценки параметров а и Ь равномерного закона распределения:
1
р(х; а, Ь) =
, хе[а9Ь]9
Ь-а
0, х*[а9Ь].
Решение. Для равномерного закона не выполняется одно из
условий регулярности. А именно, область возможных значений
исследуемой случайной величины, в которой р(х; 0) > 0,
зависит в данном случае от параметра 0, где 0 — оцениваемый
параметр. В подобных ситуациях оценку следует искать другим
способом.
Выпишем функцию правдоподобия для равномерного
распределения:
Цх19 х29 хп) = 1 , если все х.е [а9 Ь];
(о-а)
L(xv х2, хп) = 0 в остальных случаях.
Условие, что все наблюдения принадлежат отрезку [а9 Ь]9
можно выразить через неравенства для крайних членов
вариационного ряда: а < xmin, b > xmax. При фиксированном значении
а функция правдоподобия убывает по b при b > xmax и,
следовательно, принимает максимальное значение при Ъ = х . При
269
fl ЧАСТЬ II. Математическая статистика
Д0) = —ехр|
V /-1 )
Логарифмируя, получаем:
1пДв) = -и1п2-][]|дс/-в|.
Заметим, что эта функция недифференцируема во всех
точках хр х2,..., хя, а в остальных точках производная имеет вид:
de е>х,.
Отсюда следует, что функция правдоподобия возрастает, если
слева от значения 0 находится меньше членов вариационного
ряда, чем справа, и убывает в противном случае. Следовательно,
максимума она достигает посередине вариационного ряда. Если
п = 2к + 1, то это происходит в точке х(к). Если п = 2к, то
функция постоянна на интервале (х(к)9 где принимает
наибольшее значение, и в качестве оценки можно взять середину этого
интервала. Таким образом, оценкой максимального
правдоподобия оказывается выборочная медиана: 9Я = xmed.
§ 13.3. Метод наименьших квадратов.
Линейная регрессия
Метод наименьших квадратов заключается в том, что оценка
определяется из условия минимизации суммы квадратов
отклонений выборочных данных от определяемой оценки. Метод
наименьших квадратов получил самое широкое распростра-
фиксированном значении Ъ функция правдоподобия возрастает
по а при а < xmin и, следовательно, принимает максимальное
значение при а = х..
Таким образом, оценками максимального правдоподобия
будут крайние члены вариационного ряда: а = xmin и b = хтах.
Задача 9. Построить оценку методом максимального
правдоподобия параметра сдвига 6 для распределения Лапласа с
плотностью р(х) = ~exp(-|x - 0|), - оо < х < оо.
Решение. Функция правдоподобия имеет вид
j г п \
| 270
Глава 13 ф
где С =
Д0) =
Г 1
е 1
<тл/2я
е 2° '-' = Се~*т,
А = -^>0, Г = ?(дс(-в)2
^О /=1
Следовательно, функция правдоподобия имеет максимум
я
тогда, когда Г = ^(х/~0)2 достигает минимума. Если на пара-
/=1
метр 0 не накладываются ограничения, то оценка, полученная
методом наименьших квадратов, совпадает с оценкой
максимального правдоподобия для нормального распределения: 0 = х.
В более общем случае пусть Y — некоторый экономический
показатель, объективный закон которого описывается
функциональной зависимостью Y= у(Х, 0), где 0 = (0Р 02, вк) —
параметр; X — многомерная неслучайная переменная. Пусть в
результате /-го наблюдения мы получили значение у. функции
q>(Xj, 0) со случайной ошибкой гР т.е. у. = ср(х., 0) + е.. Требуется
по наблюдениям (х,, у,), (хя, уп) оценить значения
параметров в,, 02, 0Л.
Если в результате наблюдений получено п пар значений
(х., у), где х. — значение аргумента, a yt — значение функции,
то параметры (0,, 02, вк) аппроксимирующей функции
выбираются так, чтобы обратилась в минимум сумма
s= 2>,-ф<*р в)р.
/=1
Обоснование метода следующее. Пусть измерения
независимы и распределение ошибок нормальное: е. € N(09 а2).
Величина у, как сумма постоянной величины ф(х/5 0) и
случайной величины б;. является случайной величиной, и ее рас-
271
нение в практике статистических исследований, так как, во-
первых, не требует знания закона распределения выборочных
данных, во-вторых, достаточно хорошо разработан в
отношении вычислительной реализации.
Первоначально метод был разработан для обработки данных
с нормальными ошибками. В простейшем случае речь идет о
данных вида х,.= 0 + гр где е. е N(0, а2). Оценка 0 строится
методом максимального правдоподобия. Функция правдоподобия
для нормального распределения равна
fi> ЧАСТЬ II. Математическая аатиаика
272
пределение также нормальное: у. € N(<p(xp 9), а2). Плотность
распределения у{ будет иметь вид
1 (ц-Ф(*„е))2
с\12п
Функция правдоподобия для наблюдаемых значений
>>2> ^ бУДеТ РаВНа
ДГ,9) = -т- е*«
Отсюда функция правдоподобия 1(9) при изменении 9
имеет максимум тогда и только тогда, когда статистика
2>,-<P<*„ б)]2
достигает минимума.
Задача свелась к задаче математического
программирования: найти такое значение 9Я, которое минимизировало бы
квадратичную форму
гя(в.) = т1п Zto-rt*/.©)]2.
в,,- .,в4 /=1
где (*,, у,), (х2, >>2), (хя, д>я) — случайная выборка. Так как
9„ = (9,, 92,вк) является точкой минимума статистики Гя(0),
то приравнивая к нулю ее частные производные
щ
получаем систему нормальных уравнений, решения которой и
являются оценками (91592,...,9Я) неизвестных параметров,
найденными методом наименьших квадратов.
Система нормальных уравнений всегда имеет решение, так
как положительный квадратичный многочлен всегда достигает
минимума. Однако решение не обязательно является
единственным. Может случиться, что нормальные уравнения однозначно
разрешимы лишь для некоторых определенных линейных
комбинаций параметров 9,, 92,9к, а относительно самих
параметров однозначного решения нет. Такие линейные комбинации
индийский статистик Рао назвал допускающими оценку.
На практике метод применяется теперь гораздо шире, в
частности, если об ошибках е. известно лишь, что Me. = 0 и
Глава 13 ф
2яа,о2^1-р2
1
хехр^ =-
1 2(1-р2)
(х,-ах) (хх-ах)(х2-а2) (х2-а2)
.2 Р _ _ 2
а, о,Ол а0
функции регрессии оказываются линейными и имеют вид
Однако на практике модель линейной зависимости между
величинами используется гораздо шире, без предположения
нормальности совместного распределения.
Линейной регрессией называется сведение наблюдаемой на
опыте зависимости некоторой переменной (зависимой или
объясняемой) от одной или более других переменных (независимых
или объясняющих) к линейной (в предположении, что строгая
линейная зависимость между ними нарушается случайными
ошибками). Для проведения линейной регрессии часто
используется метод наименьших квадратов.
В простейшем случае речь идет о двух переменных. Пусть
х — независимая переменная, у — зависимая, и между ними
существует следующая связь:
у = а + ЬхЛ гр
где а и Ъ — числовые коэффициенты, е, — случайные ошибки,
Me. = 0 и Dz. < оо. Задача состоит в том, чтобы по имеющимся
273
Def < оо. Бывает, что метод применяется даже в случаях, когда
об ошибках нельзя сказать, что они являются случайными
величинами, независимыми и одинаково распределенными.
Одной из основных задач математической статистики
является исследование зависимости между двумя или несколькими
переменными. Строгая функциональная зависимость
реализуется редко, так как одна или обе величины подвержены еще и
воздействию случайных факторов. Статистической называется
зависимость, при которой изменение одной из величин влечет
за собой изменение распределения другой.
Поскольку обычно невозможно точно предсказать
неизвестное значение одной величины при известном значении другой,
это желательно сделать хотя бы «в среднем». Поэтому
естественно использовать функции регрессии (см. § 7.4). Например,
в случае двумерного нормального распределения с плотностью
р(хх,х2) = - 1
ЧАСТЬ II. Математическая статистика
274
наблюдениям (хр ух), (х2, у2)9 (хя9 уп) построить оценки для
а и Ь.
Согласно методу наименьших квадратов, необходимо
решить следующую математическую задачу:
/=1
Решим задачу, вычислив частные производные суммы
квадратов по каждому из коэффициентов и приравняв эти
производные к нулю. Получим систему нормальных уравнений:
^ = -2?<У/-в-Лх,) = 0,
да м
^- = -21(У,-«-^К=0.
оо /=1
Решая данную систему относительно параметров а и Ь,
получим оценки:
Л п In
4 = ?(Я->0(*/-Ю/?(*/-*)2; а = у-Ьх.
/=1 / /=1
Уравнение вида у = а + Ьх называется уравнением линейной
регрессии, а получаемые из него значения yi=a-^bxi —
предсказанными значениями, в отличие от наблюдаемых значений
уг Заметим, что уравнение линейной регрессии часто бывает
удобно записать в виде у = у + Ь(х-х). Соответствующая
прямая всегда проходит через точку выборочных средних (х,у).
Числитель и знаменатель в формуле оценки параметра b можно
вычислять по следующим эквивалентным формулам:
п п п п
?(>>, -У)(х, -х) = J^xtyt -пху; -х)2=^х2-пх2.
/=1 /=1 /=1 /=1
Здесь также можно перейти к условным вариантам и = х-с,
v. = yf - d, и оценка Ъ от этого не изменится.
В некоторых случаях, например, когда величина у (по
смыслу) представляет собой некую долю от х, рассматривают более
простой тип линейной зависимости:
Глава 13
т.е. полагают а = 0. В этом случае оценка Ь методом
наименьших квадратов имеет вид
/=1 / /=1
Важным и практически значимым результатом линейной
регрессии является то, что она позволяет «предсказывать»
значения зависимой переменной даже для таких значений
независимых, которые не наблюдались реально. Таким образом,
например, можно строить прогнозы на будущее.
Задана 10. Затраты х на развитие производства и у —
величина годовой прибыли фирмы в течение 5 лет представлены в
условных единицах следующей таблицей.
x
6
3
7
5
10
у
33
27
32
28
42
На величину прибыли влияют случайные факторы.
Предполагается, что имеет место линейная зависимость у.= а + Ьх.+ е.
между затратами х и прибылью у. Среднее значение е. равно
нулю, и дисперсия конечна. Каждый год случайное влияние не
коррелировано с предыдущими годами. Оценить параметры а
и Ъ. Оценить годовую прибыль в том случае, если на развитие
производства будет затрачено 12 у.е.
Решение. Перейдем к условным вариантам ui = xi - 6, v. =
= J>-33.
и
0
-3
1
-1
4
v
0
-6
-1
-5
9
Получаем й = (0-3+1-1+ 4)/5 = 0,2; v = (0 - 6 -
- 1 - 5 + 9)/5 = -0,6.
Отсюда х = 6,2; у = 32,4.
Далее вычисляем следующие суммы:
5>v, -iiSv = ((-3) (-6) + 1 (-1) + (-1) (-5) + 4 х 9) - 5 х
х 0,2 (-0,6) = 18 - 1 + 5 + 36 + 0,6 = 58,6.
275 I
^ ЧАСТЬ 11. Математическая статистика
1 1
1 1
1 1
1 1
! 1 .
1
*
1 ~ 1 "
1 1
1 1
1 1
1 1 s
*
*
" " " \~ "
Л 'f
У о
1
—
с
?.
1 1 1 "1
1 1 1
1 1 1
1 1 1
h 1
—
2 3 4 5 6 7 8 9 10 11 у.е.
Расходы
Рис. 13.1
Замечание. На самом деле по столь небольшому числу точек
нельзя делать серьезные выводы на будущее.
Задача 11. В таблице представлены данные о годовых
доходах и расходах на личное потребление (в долл. США) для
10 семей.
Годовой доход
Расходы на личное потребление
2508
2406
2572
2464
2408
2336
2522
2281
276
^uf-nu2 = (0 + (~3)2+ 12+ (-1)2+ 42) - 5 х0,22= 9 + 1 +
/=|
+ 1 + 16 - 0,2 = 26,8.
Получаем b = 58,6/26,8 * 2,187; а = 32,4 - 2,187 х 6,2 *
* 18,843.
Имеем у (12) « 45 (у.е.).
На рис. 13.1 представлены данные задачи и прямая
линейной регрессии.
Зависимость между расходами на развитие и прибылью
Глава 13 ^
Продолжение табл.
Годовой доход
Расходы на личное потребление
2700
2641
2531
2385
2390
2297
2595
2416
2524
2460
2685
2448
Провести линейную регрессию расходов по доходам в виде
у = Ъх. Оценить параметр Ь. Оценить величину расходов для
семьи с годовым доходом 2500 долл. США.
Решение. Суммируем доходы хр расходы yi и делим одно
Л я In
на другое. Получаем значение параметра * = 2^^/Хх/ =
= 24 134/25 435 « 0,949. м 1 ых
Для семьи с доходом 2500 долл. США получаем оценку
расходов в 2372 долл. США.
На рис. 13.2 представлены данные задачи и прямая
линейной регрессии.
Зависимость расходов от доходов
долл.
| 2600
х
ё
& 2500
x 2400
си
5 2300
I
Ри 2200
1
...... iZ.
1" ~
, 1 ->
1
1
' 1
_ _/-ч
?
О
1 ' 1
о оу
J
г ¦> г
°:
1
1
1
1
1
{J
*
*
с
7
о
1
1
«
1
2300
2400
2500 2600
Доходы
РИС. 13.2
2700
ДОЛЛ.
277
ЧАСТЬ II. Математическая статистика
о
Задачи для самостоятельного решения
Теоретические задачи
1. Найти методом моментов оценку параметра X распределения
Пуассона.
2. Найти методом моментов оценку параметра р (вероятности
«успеха») для геометрического распределения.
3. Найти методом моментов оценку параметра 9 для геометрического
распределения с вероятностью «успеха» р = i/(i + 9), 9 > о. Доказать
ее несмещенность.
4. В случае сдвинутого показательного распределения р(х,9,ц) = -е 6 ,
9
х > ц (0, ц > о) с помощью метода моментов найти оценки 9 и ц
параметров 9 и ц соответственно.
5. Найти методом моментов оценку параметра а
гамма-распределения
О, х<0,
va-l
х>0.
р(х,а) =
[ЦаУ
Исследовать полученную оценку на несмещенность и состоятельность.
6. Для гамма-распределения y(a, X) методом моментов найти оценку
параметра а при известном X. Доказать ее несмещенность и найти
дисперсию этой оценки.
7. Найти оценку для числа степеней свободы г распределения %2Г
методом моментов. Доказать несмещенность и найти дисперсию этой
оценки.
8. Найти оценку для числа степеней свободы г распределения
Стьюдента методом моментов. При каких г это возможно?
9. Пусть случайная величина ? равномерно распределена на отрезке
[о, 9]. Найти методом моментов оценку для параметра 9.
ю. Пусть случайная величина % равномерно распределена на отрезке
[а, Ь]. Найти методом моментов оценки для а и Ь.
11. Пусть случайная величина ^ равномерно распределена на
[c-\[d\c + 4d]. Найти методом моментов оценки для с и d.
Доказать их несмещенность.
278
Глава 13
12. В случае равномерного распределения на отрезке [0t, 0t + 0J с
помощью метода моментов найти оценки 0, и 02 для параметров
13. Случайная величина § равна сумме двух независимых случайных
величин, имеющих показательное распределение с параметрами
\ и Х2 соответственно. По наблюдениям случайной величины ?
оценить параметры Хг и Х2 методом моментов, в предположении,
что Хг< Х2.
14. По наблюдениям случайной величины с распределением Парето
При каких значениях параметра а это возможно?
15. По наблюдениям случайной величины с распределением = хР,
о < х < 1, оценить параметр р методом моментов.
16. По наблюдениям логнормальной случайной величины ? е
е ехр{Л/(а, а2)} найти оценки параметров о и а2 методом
моментов.
17. Найти оценку методом моментов для параметра X распределения
X
Лапласа, заданного функцией плотности р(х) = — е~хы.
18. Найти по выборке xlf х2,хп методом максимального
правдоподобия точечную оценку параметра р геометрического
распределения: Р(? = к) = p(i - р)к\k>i.
19. Найти методом максимального правдоподобия оценку параметра
0 для геометрического распределения с вероятностью «успеха»
р = 1/(1 + 0), 0 > о. Доказать ее несмещенность.
20. В урне находится неизвестное число шаров N. Все шары
пронумерованы соответственно от i до N. Производится выборка длины п с
возвращениемxifx2, ...хп, гдех. — номер /-го шара. Найти с помощью
метода максимального правдоподобия оценку для N. Является ли
эта оценка несмещенной или асимптотически несмещенной?
21. По выборке xlf х2, хп в случае биномиального распределения
P(?> = m) = C%pmqN~m при известном N методом максимального
правдоподобия найти оценку параметра р. Совпадает ли эта
оценка с оценкой, полученной с помощью метода моментов?
Исследовать оценку на несмещенность и состоятельность.
е, и е2.
оценить параметр а методом моментов.
279
ЧАСТЬ II. Математическая статистика
22. По выборке х1#ха, ...,х„ в случае равномерного распределения на
отрезке [о, 6] методом максимального правдоподобия найти
оценку параметра 9. Вычислить математическое ожидание полученной
оценки и построить несмещенную оценку на ее основе.
23. Случайная величина равномерно распределена на [9,29], 9 > о.
Найти оценку параметра 9 методом максимального правдоподобия.
24. Случайная величина равномерно распределена на [1 - 9,1 + 9],
о < 9 < 1. Найти оценку параметра 9 методом максимального
правдоподобия.
25. Найти методом максимального правдоподобия оценку параметра
а для распределения, заданного следующей функцией плотности:
fl, айх<а + 1,
Р(Х) \о, хе[л,в + 1].
Построить несмещенную оценку на основе оценки максимального
правдоподобия.
26. Найти оценку методом максимального правдоподобия для
параметра X распределения Лапласа, заданного функцией плотности
27. Оценить с помощью метода максимального правдоподобия
параметр сдвига 9 в сдвинутом показательном распределении, задан-
\е-(х-*\ х>0,
ном плотностью р(х) = <
[О, х<0.
28. Пусть случайная величина % имеет функцию распределения
\ех~\ х<9,
F(x) = \
[О, х>9.
По известным наблюдениям х1# х2, хп методом максимального
правдоподобия оценить параметр 9.
,/ч (g(x)-a)2
29.РаспределениеКэптейнаимеетплотностьвида р(х) = -^=е 2°2 ,
а>/2я
где д(х) — дифференцируемая функция. Найти методом
максимального правдоподобия точечную оценку параметра а, если параметр а
известен.
280
Глава 13
30. Для распределения Кэптейна найти методом максимального
правдоподобия точечную оценку параметра а, если параметр а
известен.
31. Случайная величина подчинена гамма-распределению, плотность
которого определяется параметрами а > о и Ь > о и функцией
xfl_1 --
плотности р(х) = е ъ, х > о. Найти методом максимального
ЬТ(я)
правдоподобия оценку Ь (при известном значении а).
32. По результатам независимых наблюдений х4, х2, хл за
случайной величиной распределение которой задано плотностью
1 ~
р(х) = —е ц, где х > о, jn > о, найти методом максимального прав-
доподобия оценку параметра ц.
33. Функция распределения случайной величины % имеет вид
__е_
F(x) = e *2 , х > о, 0 > о. Найти оценку параметра 0 методом
максимального правдоподобия.
34. Для сдвинутого показательного распределения с плотностью
р(х) = —е е , х > ц, 0 > о, ц > о, методом максимального правдо-
6 л л
подобия найти оценки 0 и ц параметров 0 и ц соответственно.
35. По наблюдениям случайной величины с распределением Парето
вида
О, х<1,
FM" [1-хЛ х>1,
оценить параметр а методом максимального правдоподобия.
36. По наблюдениям случайной величины с распределением F(x) =)Р,
о < х<1, оценить параметр р методом максимального
правдоподобия.
37. По наблюдениям логнормальной случайной величины ? е
е ехр{Л/(о, а2)} найти оценки параметров а и а2 методом
максимального правдоподобия.
281
ЧАСТЬ II. Математическая аатиаика
38. По наблюдениям случайной величины, равномерно
распределенной на отрезке [а, Ь], найти оценки параметров а и Ь методом
максимального правдоподобия. Вычислить их математическое
ожидание и построить несмещенные оценки.
39. Доказать эффективность оценки, полученной методом
максимального правдоподобия, для параметра G гамма-распределения
(с фиксированным параметром а), параметризованного в виде
/>(х,а,0) =
уа-1
- е-х1\
х>0.
9аГ(а)
40. Доказать, что оценка методом моментов для параметра р
биномиального распределения P(?> = m) = C%pmqN~m является
эффективной (при известном N).
41. Доказать, что не существует эффективных оценок для параметра X
показательного распределения /^(х,Х) = Хе~**, х>0.
42. Доказать, что не существует эффективных оценок для параметра
X гамма-распределения (с фиксированным параметром а),
параметризованного в виде
/(х,а,0) = ^г^,
Г(а)
х>0.
43. Доказать, что не существует эффективных оценок для параметра
а2 нормального распределения N(a, а2).
Вычислительные задачи
44. Случайная величина ? (число семян сорняков в пробе зерна) рас-
X1
пределена по закону Пуассона: Р(/) = — е к. Ниже приведено
распределение семян сорняков в п = юоо пробах зерна (в первой
строке указано количество х, сорняков в одной пробе; во второй
строке указана частота п. — число проб, содержащих х, семян
сорняков).
*1
0
1
2
3
4
5
6
ni
405
366
175
40
8
4
2
Найти методом моментов точечную оценку параметра X. Оценить
вероятность того, что в пробе зерна не будет сорняков.
282
Глава 13
45. Случайная величина ? (срок службы изделия) имеет показательное
распределение Дх) ¦ Хе** (х> о). В таблице приведены
сгруппированные данные по срокам службы (в часах) для п = 200 изделий.
2,5
7,5
12,5
17,5
22,5
27,5
п,
133
45
15
4
2
1
Найти методом моментов точечную оценку неизвестного
параметра X показательного распределения. Оценить время, которое
изделие прослужит с вероятностью 90%.
46. Случайная величина ? (уровень воды в реке по сравнению с
номиналом) подчинена гамма-распределению, плотность которого
Ваха~1
определяется параметрами аир, р(х) = - е~*х (а > о, р > о,
х> о).
В таблице приведены сгруппированные данные по уровням воды,
см, для п = 45 паводков.
37,5
62,5
87,5
112,5
137,5
162,5
187,5
250
350
и,
1
3
6
7
7
5
4
8
4
Найти методом моментов точечные оценки неизвестных
параметров аир рассматриваемого гамма-распределения.
47. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
57
7
139
1
203
8
45
2
383
9
27
3
525
10
10
4
532
11
4
5
408
12
1
6
273
14
1
283
ЧАСТЬ II. Математическая статистика
В предположении, что случайное число посетителей описывается
распределением Пуассона, оценить параметр X методом
моментов. Определить вероятность того, что в течение часа на сайте не
будет ни одного посетителя.
48. Проведено исследование посещаемости популярного интернет-
сайта. Много часов подряд регистрируется число посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице.
Число
посетителей
Время, час.
Число
посетителей
Время, час.
0
12
7
103
1
108
8
24
2
316
9
13
3
551
10
2
4
632
11
0
5
492
12
0
6
273
14
0
В предположении, что случайное число посетителей
описывается биномиальным распределением с числом испытаний т = ю,
оценить параметр р методом моментов. Определить вероятность
того, что в течение часа на сайте будет не более одного
посетителя.
49. В поселке Червонцево все жители имеют доход не менее юо тыс.
руб. в месяц. Выборочное обследование доходов ю человек дало
средний доход 200 тыс. руб. В предположении, что случайная
величина дохода имеет распределение Парето вида
[0, х<х0,
[l-(x/x0)~a, х>х0,
где хо= юо (тыс. руб.), оценить параметр а и средний доход
жителей методом моментов. Определить долю жителей с доходами
свыше 500 тыс. рублей с использованием метода моментов.
284
Глава 13
50. Известно, что некоторая работа занимает время, состоящее из
обязательного периода \х и случайной задержки, распределенной
показательно со средним 0. Хронометраж рабочего времени в ю
испытаниях показал среднее время 37 мин при исправленной
выборочной дисперсии 49 мин2. Оценить параметры ц и 0 методом
моментов. Определить срок, за который работа будет выполнена с
вероятностью 99%, на основе оценки методом моментов.
51. Прибор состоит из двух блоков: основного и резервного. Если
основной блок выходит из строя, включается резервный.
Времена службы блоков показательно распределены со средними
значениями 0г и 02. Выборочные испытания для ю приборов показали
средний срок службы 35 час. и среднее квадратическое
отклонение 25 час. Оценить среднее время службы основного и
резервного блоков методом моментов в предположении, что 0t> 02.
52. В группе людей, имеющих доходы с логнормальным
распределением ехр{А/(а, о2)}, проведено выборочное обследование. По
выборке из ю человек получен средний доход 5000 руб. при среднем
квадратическом отклонении 300 руб. Найти оценки параметров а
и а2 методом моментов. Оценить долю людей с доходами от 4500
до 5500 рублей на основе оценок методом моментов.
53. В таблице приведены сгруппированные данные о коэффициентах
соотношения заемных и собственных средств на юо малых
предприятиях региона.
Номер
интервала
Интервал
Середина
интервала xt
ni
1
5,05-5,15
5,1
5
2
5,15-5,25
5,2
8
3
5,25-5,35
5,3
12
4
5,35-5,45
5,4
20
5
5,45-5,55
5,5
26
6
5,55-5,65
5,6
15
7
5,65-5,75
5,7
10
8
5,75-5,85
5,8
4
Оценить долю малых предприятий с коэффициентом не более 5,5
на основе оценок методом моментов (используя нормальное
приближение) и непосредственно по таблице.
Ч J
285
ЧАСТЬ II. Математическая статистика
54. В ОТК были измерены диаметры 300 валиков из партии,
изготовленной одним станком-автоматом. Отклонения измеренных
диаметров от номинала, нм, даны в таблице.
Границы
отклонений
Середина
интервала
Число
валиков
Границы
отклонений
Середина
интервала
Число
валиков
-30...-25
-27,5
3
0...5
2,5
55
-25...-20
-22,5
8
5...10
7,5
30
-20...-15
-17,5
15
10...15
12,5
25
-15...-10
-12,5
35
15...20
17,5
14
-10...-5
"7,5
40
20...25
22,5
8
-5...0
-2,5
60
25...30
27,5
7
Оценить долю изделий, для которых отклонение не превосходит
15 нм по абсолютной величине, с применением метода моментов
(используя нормальное приближение) и непосредственно по
таблице.
55. В таблице представлены данные по числу сделок на фондовой
бирже за квартал для 400 инвесторов:
0
1
2
3
4
5
6
7
8
9
10
"i
146
97
73
34
23
10
6
3
4
2
2
В предположении, что случайное число сделок описывается
распределением Пуассона, оценить параметр X методом моментов.
Определить вероятность того, что число сделок за квартал будет
не менее двух, применяя метод моментов, и непосредственно по
таблице.
56. Для изучения распределения заработной платы работников
определенной отрасли обследовано юо человек. Результаты
представлены в таблице.
Зарплата,
долл. США
Число
человек
Зарплата,
долл. США
Число
человек
190... 192
1
200...202
19
192... 194
5
202...204
11
194... 196
9
204...206
4
196...198
22
206...208
1
198...200
28
208...210
0
286
Глава 13
Определить долю работников с зарплатой менее 200 долл. США
на основе оценок методом моментов (используя нормальное
приближение) и непосредственно по таблице.
57. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения, г:
49Д; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51.6; 49.8; 50,1; 49.7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Определить долю батончиков с весом менее 49 г на основе оценок
методом моментов (используя нормальное приближение) и
непосредственно по их доле в выборке.
58. Пассажир, приходящий в случайные моменты времени на
автобусную остановку, в течение 5 поездок фиксировал свое время
ожидания автобуса: 5,1; 3,7; 1,2; 9,2; 4,8 мин. Известно, что автобус
ходит с интервалами по 0 минут. Оценить 0 методом моментов.
59. В июне ежедневный спрос на мороженое в киоске составляет в
среднем 700 порций со средним квадратическим отклонением
50 порций. Оценить количество порций, удовлетворяющих
потребность на один день, с вероятностью 95% (используя
нормальное приближение).
60. Ежедневный спрос на некоторый товар имеет распределение
Симпсона на отрезке [а, Ь]. За 25 рабочих дней спрос составлял в среднем
юо кг с исправленной выборочной дисперсией 54 кг2. Определить
параметры а и Ь методом моментов. Оценить, сколько нужно
товара, чтобы удовлетворить ежедневный спрос с вероятностью 92%.
61. Рукопись проверяют два редактора, независимо друг от друга.
Один нашел 70 ошибок, другой — 50, причем 25 найденных
ошибок были одни и те же (т.е. обнаружены обоими редакторами).
Оценить число ошибок, которых они еще не нашли.
62. Известно, что доля возвратов по кредитам в банке имеет
распределение F(x) = х^, о й х * 1. Наблюдения показали, что в среднем
она составляет 90%. Методом моментов оценить параметр (3 и
вероятность того, что она опустится ниже 75%.
63. Известно, что некоторая работа занимает время, состоящее из
постоянного периода и случайной задержки, распределенной
показательно. Хронометраж рабочего времени показал, что работа
занимает в среднем 45 мин со средним квадратическим
отклонением 15 мин. С помощью метода моментов оценить вероятность,
что работа будет закончена за i час.
\ j
287
ф ЧАСТЬ II. Математическая статистика
0
1
2
3
4
5
6
7
ni
2
3
10
22
26
20
12
5
Найти методом максимального правдоподобия точечную оценку
неизвестного параметра р биномиального распределения.
68. Случайная величина % (время безотказной работы изделия) имеет
показательное распределение: р(х) = Хе~**, гдех> о. В следующей
таблице приведены сгруппированные данные по времени работы
(часов) для юоо изделий.
5
15
25
35
45
55
65
365
245
150
100
70
45
25
Найти методом максимального правдоподобия точечную
оценку неизвестного параметра X показательного распределения.
Оценить вероятность того, что изделие может прослужить более
6о часов.
ч )
288
- \
64. Ежедневный спрос на некоторый товар имеет равномерное
распределение на отрезке [а, Ь]. За период наблюдения спрос
составлял в среднем юо кг с исправленной выборочной дисперсией
192 кг2. С помощью метода моментов оценить, сколько нужно
товара, чтобы удовлетворить ежедневный спрос с вероятностью 90%.
65. Срок службы некоторого изделия имеет распределение Вейбулла
с параметром а = 2. Наблюдения показали, что в среднем он
составляет юоо ч. Найти вероятность того, что изделие прослужит
более 1500 ч.
66. Случайные относительные изменения цены акции за день
описываются распределением Лапласа. Наблюдения показали, что
среднее квадратическое отклонение составляет 1%. Найти границы, в
которых относительное изменение цены акции за день находится
с вероятностью 90%.
67. Случайная величина ? (число появлений события Asm
независимых испытаниях) подчинена биномиальному закону
распределения с неизвестным параметром р. В таблице приведено
эмпирическое распределение числа появлений события А в юо
наблюдениях (в первой строке указано число х. появлений события
в одном опыте из т = ю испытаний, во второй строке дана частота
п. — число опытов, в которых наблюдалось столько появлений
события А).
Глава 13 ф
69. В поселке Полтинниково все жители имеют доход не менее 50 тыс.
руб. в месяц. Выборочное обследование доходов ю человек дало
следующие результаты: 54; 6о; 59; 79; 71; 92; 53; 54; 78; 56 тыс. руб.
В предположении, что случайная величина дохода имеет
распределение Парето вида
гдехо= 50 тыс. руб., оценить параметр а и средний доход жителей
методом максимального правдоподобия. Вычислить долю жителей
с доходами свыше юо тыс. руб. на основе оценки максимального
правдоподобия.
70. Известно, что некоторая работа занимает время, состоящее из
обязательного периода ц и случайной задержки, распределенной
показательно со средним значением 9. Хронометраж рабочего
времени в ю случаях дал следующие результаты: 32; 30; 37; 35;
42; 39; 34; 32; 31; 35 мин. Определить параметры jli и 0 методом
максимального правдоподобия. Найти срок, за который работа
будет выполнена с вероятностью 99%, на основе оценки
максимального правдоподобия.
71. В группе людей, имеющих доходы с логнормальным
распределением ехр{Л/(а, а2)}, проведено выборочное обследование. По
выборке из ю человек получены следующие результаты: 4722; 2907;
4974; 2763; 3659; 5493; 3*6i; 3175; 4521; 3698 руб. Найти оценки
параметров а и а2 методом максимального правдоподобия.
Вычислить долю людей с доходами от 4000 до 5000 руб. на основе
оценок максимального правдоподобия.
72. Пассажир, приходящий в случайные моменты времени на
автобусную остановку, в течение 5 поездок фиксировал свое время
ожидания автобуса: 5,1; 3,7; 1,2; 9,2; 4,8 мин. Известно, что автобус ходит
с интервалами по 6 мин. Оценить параметр 9 методом
максимального правдоподобия. Определить несмещенную оценку.
73. Ежедневный спрос на некоторый товар равномерно распределен
на отрезке [а, Ь]. За 6 рабочих дней спрос составлял: 104; 8о; 96;
120; 113; 82 кг. Вычислить а и Ь, используя несмещенные оценки
на основе оценок максимального правдоподобия. Определить,
сколько товара нужно для удовлетворения ежедневного спроса с
вероятностью 90%.
х<х.
х>х(
'О'
10 Теория вероятностей
289 i
ЧАСТЬ II. Математическая статистика
74. Известно, что некоторая работа занимает время, состоящее из
постоянного периода и случайной задержки, распределенной
показательно. Хронометраж рабочего времени показал, что работа
занимает, как минимум, 30 мин, а в среднем — 45 мин. С помощью
метода максимального правдоподобия оценить вероятность, что
работа будет закончена за i час.
75. Случайные относительные изменения цены акции за день
описываются распределением Лапласа. Наблюдения показали, что
выборочное среднее абсолютное значение (модуль) составляет 1%.
Оценить границы, в которых относительное изменение цены
акции за день находится с вероятностью 90%.
76. В таблице представлены данные о производстве электроэнергии в
России за 1998-2003 гг.
Год
1998
1999
2000
2001
2002
2003
Производство,
млрд кВт-ч
827
846
878
891
891
915
Провести линейную регрессию производства по годам и сделать
прогноз на 2004 г.
77. В таблице представлены данные о производстве всех зерновых
культур и производстве пшеницы в России за 1998-2002 гг.
Год
1998
1999
2000
2001
2002
Производство зерновых,
млн т
47,9
54,7
65,5
85,2
86,6
Производство
пшеницы, млн т
27,0
31,0
34,5
47,0
57,7
Провести линейную регрессию и сделать прогнозы на 2003 г, для:
а) производства зерновых по годам; б) производства пшеницы по
годам.
78. В условиях предыдущей задачи провести линейную регрессию
производства пшеницы по производству всех зерновых культур в
виде: а) у = а + Ьх; б) у = Ьх (а = о).
В обоих случаях оценить производство пшеницы, если
производство всех зерновых составит 90 млн т.
290
Глава 13 0
79. В таблице представлены данные о годовых доходах и расходах на
личное потребление, долл. США, для ю семей.
Годовой доход,
долл. США
Расходы на личное потребление,
долл. США
2435
2311
2354
2278
2404
2240
2381
2181
2581
2408
2529
2379
2562
2378
2624
2554
2407
2232
2448
2356
Провести линейную регрессию расходов по доходам в виде у « Ьх.
Оценить параметр Ь. Определить величину расходов для семьи с
годовым доходом 2600 долл. США.
8о. В таблице представлены данные об урожайности зерновых
культур, ц/га, в СССР за 1951-1970 гг.
Год
Урожайность 1 Год
Урожайность
1951
7,4
1961
10,7
1952
8,6
1962
10,9
1953
7,8
1963
8,3
1954
7,7
1964
11,4
1955
8,4
1965
9,5
1956
9,9
1966
13,7
1957
8,4
1967
12,1
1958
11,1
1968
14,0
1959
10,4
1969
13,2
1960
10,9
1970
15,6
Провести линейную регрессию урожайности по годам.
10*
291
^ ЧАСТЬ II. Математическая статистика
8i. В таблице представлены данные о производстве молока, тыс. т, в
России с января 1992 по октябрь 1996 г., по месяцам.
1992
1993
1994
1995
1996
Январь
2015
1759
1510
1172
1038
февраль
2123
1773
1484
1226
1104
Март
2624
2361
1988
1651
1439
Апрель
2891
2649
2211
1859
1521
Май
3335
3203
2559
2392
1827
Июнь
4071
3936
3209
2864
2446
Июль
4040
3861
3204
2714
2369
Август
3392
3321
2687
2420
2081
Сентябрь
2467
2438
2031
1925
1577
Октябрь
2092
1760
1506
1338
1081
Ноябрь
1494
1299
1050
984
Декабрь
1562
1345
1054
1020
Провести линейную регрессию производства молока по годам для
следующих месяцев: а) март; б) июнь; в) сентябрь. Построить для
них прогноз на 1997 г.
82. Годовые прибыли фирмы, тыс. долл. США, за 5 лет представлены
в таблице.
Год
1-й
2-й
3-й
4-й
5-й
Прибыль
99
112
120
135
144
Провести линейную регрессию и дать прогноз на следующий год.
83. В таблице представлены данные за ю лет о трудоемкости
производства 1 т цемента (нормо-смен).
Год
1-й
2-й
3-й
4-й
5-й
6-й
7-й
8-й
9-й
10-й
Трудоемкость
7,9
8,3
7,5
6,9
7,2
6,5
5,8
4,9
5,1
4,4
Провести линейную регрессию и дать прогноз на и-й год.
V ' )
1292
ч
Глава 13 0
84. В таблице представлены средние цены на растительное масло и
сахар-песок в 12 городах Центрального района России на июнь
1996 г.
Город
Цена на масло, руб.
Цена на сахар, руб.
Брянск
7726
3410
Владимир
7880
3183
Иваново
6182
3209
Калуга
8237
3400
Кострома
8750
3600
Москва
И 024
4418
Орел
8456
3634
Рязань
9172
4033
Смоленск
8320
3909
Тверь
7083
3416
Тула
8259
3486
Ярославль
7991
3938
Провести линейную регрессию цены на масло по цене на сахар.
85. В таблице представлены средние цены на говядину и белый хлеб в
12 городах Центрального района России на июнь 1996 г.
Город
Цена на говядину, руб.
Цена на хлеб, руб.
Брянск
12 500
4875
Владимир
13 857
7125
Иваново
14 150
4998
Калуга
12 697
5170
Кострома
13 000
5476
Москва
14 120
6466
Орел
10 678
4200
Рязань
12 163
4720
Смоленск
12 833
4354
Тверь
14 400
5440
Тула
12 083
5140
Ярославль
14 397
5283
Провести линейную регрессию цены на говядину по цене на белый
хлеб.
j
ГЛАВА 14
ДОВЕРИТЕЛЬНЫЕ
ИНТЕРВАЛЫ
§ 14.1. Основные понятия
Точечная оценка неизвестного параметра, найденная по
выборке объема л, не указывает, какую ошибку допускают,
принимая вместо точного значения параметра 6 его
приближенное значение. Поэтому вводят интервальную оценку, которая
определяется двумя числами — концами интервала, внутри
которого с определенной вероятностью находится неизвестное
значение параметра 0, причем границы интервала не должны
зависеть от искомого параметра.
Доверительным интервалом, или интервальной оценкой,
называется интервал (0Р92)> который покрывает неизвестный параметр
6 с заданной доверительной вероятностью 0 < у < 1 (ее называют
также надежностью доверительного интервала). Часто
доверительный интервал может быть представлен в виде (0-6, 6+5),
тогда величина 8 (половина длины интервала) называется
точностью оценки (точностью доверительного интервала). При
заданном значении у точность 8 зависит от объема выборки п.
Понятно, что чем меньше длина доверительного интервала, тем
точнее оценка.
Однако сама интервальная оценка конструируется вокруг
точечной оценки, вид которой определяется законом
распределения случайной величины, который зависит от неизвестного
параметра, т.е. границы доверительного интервала зависят от
значения неизвестного параметра и, следовательно, пользо-
i 294
1
Глава 14 ф
ваться такими границами нельзя. Существуют два подхода к
преодолению этой трудности.
1. Классический метод состоит в искусственном подборе ста-
тистик 0, = Ql(xl9x29...,xH)9 02 = в2(х,,х2,...,хя), не зависящих от
неизвестного параметра и таких, что <02 при любых хр х2,
хй9 е, и />(е1<е<ё2)=у.
2. Метод, основанный на асимптотических свойствах
оценок (как правило, на асимптотической нормальности). Поэтому
такой метод дает приближенные результаты и пригоден только
при достаточно больших объемах выборок.
В обоих случаях бывает, что границы доверительных
интервалов, построенных формально из каких-то теоретических
соображений, выходят за рамки возможного (например,
становятся отрицательными для положительных по смыслу величин).
В таких случаях их «округляют» до разумных пределов.
§ 14.2. Точные доверительные
интервалы
Точные доверительные интервалы строятся, как правило,
в предположении нормальности данных. Следует понимать,
что реальные данные, на основании которых мы строим эти
интервалы, могут совсем не выглядеть нормальными
(например, это целые положительные числа, в то время как
нормальное распределение непрерывно и рассредоточено по всей
действительной прямой). Тем не менее широкое практическое
применение описываемых методов дает неплохие результаты
(это объясняется, в частности, асимптотической
нормальностью оценок), и такое несоответствие не должно нас смущать
в дальнейшем.
Предположим, что наблюдается случайная величина § е N(a, о2).
Для параметров строятся следующие точные доверительные
интервалы.
1) Для неизвестного среднего а при известной дисперсии о2:
_ а _ а
х—i=u <а<х + —j=u ,
где w определяется из соотношения Ф0(и) = у/2.
295
В ЧАСТЬ II. Математическая статистика
2 -~ - 2 ,
Ха , X. а ,
где Хя-1 ~~ критические точки х2-распределения с л — 1
степенями свободы и соответствующими уровнями значимости,
а = 1 — у.
Доказательство. 1) По теореме Фишера (см. § 12.8)
имеем xeN(a,c2/n). Случайная величина у] = ^—^-у/п тогда имеет
а
стандартное нормальное распределение N(0, 1) и
Р(\у] | < и) = Р(-и < л < и) = Ф(к) - Ф(-к) = Ф0 (и) - Ф0 (-и) = 2Ф0 (и).
Выбирая иу из соотношения Ф0(иу) = у/2, получаем,
что Р(\у\\<иу) = у. Таким образом, с вероятностью у верно
<wy, откуда следует
_ а _ а
х—j=u <а<х +—f=u.
у/п у/п
У
2) По следствию 2 из теоремы Фишера (см. § 12.8)
статистика T = ^—^-yfn имеет распределение Стьюдента с п - 1 степе-
s
нями свободы. Заметим, что критическая точка распределения
Стьюдента (для двусторонней области) определяется таким
образом, чтобы выполнялось Р(\Т\ > / ) = а. Выбирая а = 1 — у,
получаем Р(\Т\ < / ) = у. Таким образом, с вероятностью у вер-
но
<t , откуда следует
$ $
х—j=t <a<x+—=t .
у/п у/п
1 296
2) Для неизвестного среднего а при неизвестной
дисперсии а2:
$ $
х—j=t <a<x+—j=t.
у/п у/п
где t — критическая точка распределения Стьюдента (для
двусторонней области) с п — 1 степенями свободы и уровнем
значимости а = 1 ~ у.
3) Для неизвестной дисперсии а2:
(n-\)s2 2 (n-l)s2
Глава 14 $
W, <Г<г\ >W>x. ,)-W>x; )=i-0 ,
2 2 2 2
Таким образом, с вероятностью у верно %2 а < -—j— < %2а
(n-l)s2
i—-"-1 а2 "т'Л-1'
откуда следует 2 w г
^2 j*i-qf2
— <а <— •
Х-а , %, а ,
Можно также по выборке xv xv хп построить
доверительный интервал для следующего (и + 1)-го наблюдения (т.е.
определить границы, в которых оно будет лежать с заданной
вероятностью у). А именно, имеем
X-S/v Jl + — <Хя+1 <X+tfYJl + — .
V Yt V ft
Понятно, что это может быть полезно в качестве прогноза
на будущее.
Доказательство. Заметим, что случайные величины хя+1 и
х независимы, причем хя+1 еЛГ(а,а2)и xeN(a, а2/я),
следовательно, хя+1-Х€ЛГ
х — X
. Тогда величина "+1 имеет
а\ 1+-
стандартное нормальное распределение 7V(0, 1)
Введем статистику
,2 *
аЛ 1 + -
V п
Поскольку ^п |^ е xl-\> статистика Т имеет распреде-
сг
ление Стьюдента с п - 1 степенями свободы. Рассуждая как
297
3) По теореме Фишера имеем ^п e%2n_v Заметим, что
с
критические точки распределения %2р п_{ определяются из
условия Р(%2 >%2р,п-\) = Р- Выбирая а = 1 - у, получаем
2
= 1 — а = у.
ф ЧАСТЬ II. Математическая статистика
ранее в доказательстве 2, получаем, что с вероятностью у верно
V п
< /7, откуда следует х - stn
л 1
1 + -<х„
п
tfnl+-.
7V п
Задача 1. Найти минимальный объем выборки, при
котором с надежностью 0,925 точность оценки математического
ожидания нормально распределенной случайной величины (по
выборочному среднему х) равна 8 = 0,2, если известно среднее
квадратическое отклонение ет= 1,5.
Решение. Формула, определяющая точность оценки
математического ожидания по выборочному среднему, выглядит
слезет
дующим образом: 8 = -^. Отсюда следует п = — 2
(при этом
обычно п округляют в большую сторону для надежности). По
таблице функции Лапласа находим иу для данного примера,
учитывая, что функция принимает значение Ф0(и) = 0,925/2 =
= 0,4625. Таким образом, и= 1,78. Подставив данные
задачи, получим искомый объем выборки: п-
Принимаем округленно п = 179.
1Дх1,У
0,22
; 178,22.
Задача 2. Из генеральной совокупности извлечена выборка
объема п = 12.
Варианта xi
-0,5
-0,4
-0,2
0
0,2
0,6
0,8
1
1,2
1,5
Частота п.
1
2
1
1
1
1
1
1
2
1
Оценить с надежностью 0,95 математическое ожидание а
нормально распределенной случайной величины с помощью
доверительного интервала.
Решение. Найдем выборочное среднее Зс и исправленное
выборочное среднее квадратическое отклонение s. Пусть щ = 10х,
тогда
_ 1 10 _ ц
и = —У^п.х. =4,2; х = — = 0,42;
П-l
ю W ю
/=i
;0,52.
Находим для уровня значимости а = 0,05 и числа степеней
свободы п - 1 = 11 по таблице распределения Стьюдента кри-
298
Глава 14 ф
тическую точку f = 2,23 и определяем границы доверительного
интервала:
Таким образом, искомый доверительный интервал
-0,04 < а < 0,88.
Задача 3. Для отрасли, включающей 1200 фирм,
составлена случайная выборка из 19 фирм. По выборке оказалось, что
исправленное среднее квадратическое отклонение для числа
работающих на фирме составляет s = 25 человек. Построить
90%-ный доверительный интервал для среднего квадратическо-
го отклонения числа работающих на фирме по всей отрасли.
Решение. Доверительный интервал для параметра а имеет вид
где х« и X2 а находят по таблице критических точек рас-
1-7-1
пределения хи-квадрат. По таблице определяем для данного
примера Хп ,05:18 — 28,9; yd 95;i8 =9,39. Подставив в формулу
необходимыевеличины, получаем искомый доверительный интервал:
25^/18/28,9 < а < 25^18/9,39, откуда 19,74 < а < 34,61 (человек).
Задача 4. За последние 5 лет годовой рост цены актива А
составлял в среднем 20% со средним квадратическим
отклонением (исправленным) 5%. Построить доверительный интервал
с вероятностью 95% для цены актива в конце следующего года,
если в начале года она равна 100 денежных единиц.
Решение. Рассмотрим величины относительного прироста
цены актива за год. Будем пользоваться нормальным
приближением1. Применяем формулу
1 Такое приближение и соответствующие оценки являются довольно
грубыми. На практике распределение относительного прироста цены
обычно далеко от нормального и, к сожалению, не описывается ни одной из
классических формул.
299
ф ЧАСТЬ II. Математическая аатиаика
la? а2, - -
Х~У~\ + — иу <а]-а2<х-у-\-
п т 1
/а2 а2
V п т 1
где иу определяется из соотношения Ф0(и) = у/2.
Доказательство основано на следствии 3 теоремы Фишера
(см. § 12.8).
2) При неизвестных, но равных дисперсиях
- ^ Un-l)s2xHm-l)s2
\п + т
V пт у
Х-У-Л п + т-2 <й] ~а2<х-У +
(n-l)s2x+(m-l)s2y \п + т ^
V А7™ 7'
пЛ-т-2 V пт
где ty — критическая точка распределения Стьюдента (для
двусторонней области) с« + /и-2 степенями свободы и уровнем
значимости а = 1 — у.
Доказательство основано на следствии 4 теоремы Фишера.
§ 14.3. Асимптотические доверительные интервалы
Асимптотическим доверительным интервалом при оценивании
параметра 0 называется такой интервал (0,, 02), что Р(0, < 0 < 02) -> у
(при п -> оо).
Предположим, мы решили учитывать тот факт, что наши
наблюдения имеют распределение, отличное от нормального.
Пусть это распределение зависит только от одного параметра 0,
300
где ty находим из таблицы критических точек распределения
Стьюдента (для двусторонней области): / = t(0,05; 4) = 2,78.
Получаем 0,2-0,05-2,78VU<x6 < 0,2 +0,05-2,78VU, откуда
0,05 < х6 < 0,35. Таким образом, цена актива в следующем году
составит от 105 до 135 денежных единиц.
Помимо случаев построения доверительных интервалов для
параметров одной выборки, иногда рассматривают и случай двух
выборок. Например, когда имеются две выборки xv xv хп
и yv yv ут из распределений N(av а2) и N(av о])
соответственно, и надо построить доверительный интервал для разности
средних.
1) При известных дисперсиях
Глава 14 @
для которого надо построить доверительный интервал, а также
известно, что оценка 0Я асимптотически нормальна и верно
0—^—>./У(0,а2(0)/л) при п -> оо. Приведем два метода
построения асимптотических доверительных интервалов.
1) Подстановка оценки параметра в формулу для дисперсии.
Получаем:
<е<ё+о<е>
yjn у/п
где иу определяется из соотношения Ф0(и) = у/2.
2) Использование функционального преобразования.
Определим функцию
#(к)= Г~тт' тогДа веРН0 Я(в)—^-»^(я(0),1/л) при я ->оо.
J cr(w)
Следовательно, можно использовать асимптотическое
неравенство
S(e)-^<g(e)<g(e) + ^L.
Решая его относительно 0, получаем асимптотический
доверительный интервал.
Например, доверительный интервал для вероятности
«успеха» р в п испытаниях Бернулли обычно строится первым
методом. Поскольку Щ = р и Z>? = р(1 — р), то из ЦПТ получаем
w—^-+N(p,p(l-p)/n), и доверительный интервал имеет вид
где w — относительная частота события.
Асимптотические доверительные интервалы рекомендуется
применять, когда объем выборки достаточно велик (порядка
сотен и более).
Доказательство (обоснование метода функционального
преобразования). Если оценка 0Л асимптотически нормальна и
верно 0 е >JV(0, а2(0)/л), то для любой функции g, гладкой в
окрестности 0, верно g(0)—^AXs(0),(s'(0))V(0)//O.
Чтобы дисперсия не зависела от 0, необходимо функцию g
подобрать так, чтобы выражение a(0)g40) было постоянным,
например, положив а(0)^(0) = 1.
3d |
i
р ЧАСТЬ 11. Математическая статистика
302
Задача свелась к выбору такой функции g, чтобы она
являлась решением дифференциального уравнения g(d) = 1/а(0).
Решение этого уравнения имеет вид g(0) = Г, при этом про-
J а(6)
извольная постоянная в неопределенном интеграле выбирается
из соображений простоты окончательного выражения и обычно
полагается равной нулю. Тогда получается g(0)—^-+N(g(Q),l/n)
при л —> оо.
Задача свелась к построению доверительного интервала для
математического ожидания нормально распределенной
случайной величины при известной дисперсии с заданной
надежностью у. Согласно ранее доказанному, такой интервал имеет
вид
g(Qn)—LUy <g(0)<g(0j+-Lw
у/П у/П
Задана 5. Произведено 300 испытаний, в каждом из которых
неизвестная вероятность р появления события А постоянна.
Событие А появилось в 250 испытаниях. Найти доверительный
интервал, покрывающий неизвестную вероятность р с
надежностью 0,95.
Решение. Число испытаний п = 300 достаточно велико,
поэтому можем воспользоваться следующими формулами для
границ доверительного интервала:
/w(l — w) lw(l — w)
Значение w находим из соотношения Ф0(и) = у/2 = 0,475
по таблице функции Лапласа, в данном случае и = 1,96.
Относительная частота события А составляет w = 250/зб0 * 0,83.
Подставим это значение w в формулы для рх и р2\
л gl iQ, /0,83x0,17 п _л л пл * /0,83x0,17 л ОП
Р\ = 0,83-1,96J——— «0,79; р2 = 0,83 +1,96J ' «0,87.
Итак, получаем искомый доверительный интервал: 0,79 < р <
< 0,87.
Задача 6. Построить доверительный интервал для
вероятности «успеха» в испытаниях Бернулли методом
функционального преобразования.
Глава 14 0
Замечание. Очевидно, первым способом получается гораздо
более простой и удобный в применении доверительный
интервал, хотя и менее точный.
Задача 7. Построить асимптотический доверительный
интервал для параметра X показательного закона распределения
(двумя способами).
Решение. В данном случае удобно перейти к новому
параметру 0 = 1Д. Эффективной оценкой для него является
выборочное среднее 0 = х. Имеем M0 = 0, DQ = Q2/n, откуда
ст(0) = 0.
зоз
Решение. Необходимо построить функцию g(u) = Г, где
J <r(w)
Для рассматриваемого случая имеем
= 2arcsin/ = 2arcsin V/>.
С учетом вида функции g(p) асимптотическое неравенство
примет вид
2arcsin Vw --j= < 2arcsin Vp < 2arcsin Vw +-т=.
Для функции у = g(x) - 2arcsin Vx при 0 < х < 1 обратной
функцией будет х = g~l(y) — sin2(j>/2), где 0 < у < я. Поэтому
если выполняются неравенства
2arcsin Vw - > О, 2arcsin Vw + -^L < 7r,
V« у/П
то, применив обратное преобразование g~\ получим
доверительный интервал
sin2(arcsin Vw —~=) < р < sin2(arcsin Vw Н——=).
2V« 2Vw
^ ЧАСТЬ II. Математическая статистика
Первым способом, подставляя оценку в формулу для
дисперсии, получаем
_ х _ х
х—j=u <9<х Н—j=ru.
у/П у/П
Возвращаясь к параметру А. = 1/9, приходим к неравенству
1+л
X
1_Л
I Я)
Вторым способом, определив функцию g(u) = J— = lnw,
получаем асимптотическое неравенство и
_ и _ и
lnx —~г < 1п0 < 1пх н—рг,
у/П у/П
откуда следует
хехр
га
<9<хехр
—ехр
х
га
< X < —ехр
х
Заметим, что по ходу решения задачи получены
доверительные интервалы для математического ожидания 9
показательного распределения. Этот результат имеет и самостоятельную
ценность.
В дальнейших задачах асимптотические интервалы по
умолчанию строятся методом функционального преобразования
(кроме задач на вероятности «успехов»).
§ 14.4. Интервальная оценка коэффициента
корреляции
Пусть (jc,, ух)9 (х2, у2)9 (хя9 уп) — независимые наблюдения
над двумерной нормальной случайной величиной. Построим
асимптотический доверительный интервал для коэффициента
корреляции р, соответствующий надежности у.
304
Глава 14
Точечной оценкой методом моментов для коэффициента
корреляции является выборочный коэффициент корреляции
1л — —
п (=\
Известно, что оценка асимптотически нормальна со
следующими параметрами:
Р,
ai—>00 .
Отсюда следует, что а(р) = 1 - р2 и
g(9) - /Т
dp _ ltJ + P _
= -ln^-^- = arth p.
Получено так называемое z-преобразование Фишера для
коэффициента корреляции. Это преобразование хорошо
исследовано, и для него известны следующие соотношения:
MarthPj *arthp+—В—, Z>(arthPw) =
2(я -1) л2 — 3
Построим доверительный интервал для arth р. Заменив п на
п - 3 и пренебрегая в математическом ожидании при
достаточно большом п величиной
2(п-\)
, получаем
P(arthP„ - -т=^«7 < arth р < arthP, + -4^=4) = у.
Функция thx =
V«^3
ех-е
ех+е~
(гиперболический тангенс),
обратная функции arth х, существует, однозначна и монотонно
возрастает, поэтому после преобразования доверительный
интервал имеет вид
th(arthp
1 ,и)<p<th(arthp +- 1
-wy),
V^3~y/ ^г ~"х-п ' V^3
где иу определяется соотношением Ф0(иу) = у/2.
Найденный приближенный доверительный интервал
настолько мало отличается от истинного, что может применяться
уже для выборок объема п > 10.
305
ЧАСТЬ 11. Математическая статистика
Задачи для самостоятельного решения
Теоретические задачи
1. Построить асимптотический доверительный интервал для параме-
Хк
тра X распределения Пуассона: Р(% = к) =—е х .
к\
2. Построить асимптотический доверительный интервал для
параметра 9 случайной величины равномерно распределенной на
отрезке [о, 9]. Точечную оценку параметра 9 найти методом
моментов.
3. Построить асимптотический доверительный интервал для
неизвестного параметра X при известном а, если случайная величина ?
имеет гамма-распределение: ? е у(а, X). Указание: перейти к новому
параметру 9 = а/Х.
4. Построить асимптотический доверительный интервал для
неизвестного параметра а при известном X, если случайная величина %
имеет гамма-распределение: ? е у(а, X).
5. Построить асимптотический доверительный интервал для числа
степеней свободы распределения хи-квадрат.
6. Построить асимптотический доверительный интервал для
вероятности р при наблюдениях биномиальной случайной величины с
известным числом испытаний т: Pm{k) = Cn\pk(\-р)т~к (двумя
способами).
Вычислительные задачи
7. Станок-автомат штампует валики. По выборке объема п = юо
вычислено выборочное среднее диаметров изготовленных
валиков. Найти с надежностью 0,95 точность 8, с которой выборочное
среднее оценивает математическое ожидание диаметров
изготовляемых валиков, зная, что их среднее квадратическое отклонение
а = 2 мм. Предполагается, что диаметры валиков распределены
нормально.
8. Найти минимальный объем выборки, при котором с надежностью
о»975 точность оценки математического ожидания а по
выборочному среднему равна 8 = 0,3, если известно среднее квадратическое
отклонение а = 1,2 нормальной генеральной совокупности.
v j
306
Глава 14
9. Случайная величина § имеет нормальное распределение с
известным средним квадратическим отклонением а = 3. Найти
доверительный интервал для неизвестного математического ожидания а
по выборочному среднему, если объем выборки п = 36 и задана
надежность оценки у = 0,95.
ю. Фирма коммунального хозяйства желает на основе выборки
оценить среднюю квартплату за квартиры определенного типа с
надежностью не менее 99% и погрешностью не более ю денежных
единиц (д.е.). Предполагая, что квартплата имеет нормальное
распределение со средним квадратическим отклонением, не
превышающим 35 д.е., найдите минимальный объем выборки.
ii. Из генеральной совокупности извлечена выборка объема п = ю.
Варианта х.
-2
1
2
3
4
5
Частота п.
2
1
2
2
2
1
Оценить с надежностью 0,95 математическое ожидание а по
выборочному среднему при помощи доверительного интервала.
12. Для отрасли, включающей 1200 фирм, составлена случайная
выборка из 19 фирм. По выборке оказалось, что в фирме в среднем
работают х = 77,5 человек при среднем квадратическом
отклонении s = 25 человек. Пользуясь 95%-ным доверительным
интервалом, оцените среднее число работающих в фирме по всей отрасли
и общее число работающих в отрасли. Предполагается, что число
работников фирмы имеет нормальное распределение.
13. По данным 16 независимых равноточных измерений некоторой
величины найдены среднее арифметическое результатов измерений
и исправленное среднее квадратическое отклонение, равные
соответственно 42,8 и 8. Построить доверительный интервал для
истинного значения измеряемой величины с надежностью у = 0,999.
14. По данным выборки объема п из нормальной генеральной
совокупности найдено исправленное среднее квадратическое
отклонение 5. Найти доверительный интервал, покрывающий среднее
квадратическое отклонение а с надежностью 0,95, если: а) п = ю,
s = 5,1; б) п = 30, s = 14.
15. По данным выборки объема п = 16 из нормальной генеральной
совокупности найдено исправленное среднее квадратическое
отклонение 5 = 1. Найти доверительный интервал, покрывающий среднее
квадратическое отклонение а с надежностью 0,95.
307
ЧАСТЬ II. Математическая статистика
16. Произведено 12 измерений некоторой физической величины одним
прибором (без систематической ошибки), причем исправленное
среднее квадратическое отклонение случайных ошибок измерения
оказалось равным о,6. Найти точность прибора с надежностью 0,95.
Предполагается, что результаты измерений распределены нормально.
17. По выборке из 25 упаковок товара средний вес составил 101 г с
исправленным средним квадратическим отклонением 3 г. Построить
доверительные интервалы для среднего и дисперсии с
вероятностью 90%.
18. Исправленное среднее квадратическое отклонение ежесуточного
дохода случайно выбранных ю киосков некоторой фирмы
оказалось равно юо д.е. Построить доверительный интервал для
среднего квадратического отклонения. Предполагается, что доход —
нормально распределенная величина.
19- Производитель автомобильных шин заинтересован в получении
оценки средней износоустойчивости шин особой модели. Он
произвел случайную выборку объемом ю шин и подверг их специальному
испытанию. Средняя износоустойчивость по данным выборки
оказалась равна 22 500 миль с неисправленным средним квадратическим
отклонением 3000 миль. Построить доверительный интервал с
вероятностью 99% для средней износоустойчивости всего выпуска шин
этого типа. Генеральная совокупность распределена нормально.
го. Импортер упаковывает чай в пакеты с номинальным весом 125 г.
Известно, что наполняющая машина работает со стандартным
отклонением а, равным ю г. Выборка 50 пакетов показала средний
вес 125,8 г. Найти доверительный интервал для среднего веса в
генеральной совокупности с вероятностью 95%. Найти объем выборки
л, при котором с вероятностью 95% точность интервала составила
бы 2 г. Генеральная совокупность распределена нормально.
21. За последние 9 лет годовой рост цены актива Д составлял в среднем
22% со средним квадратическим отклонением (исправленным) 6%.
Построить доверительный интервал с вероятностью 90% для
средней цены актива в конце следующего года, если в начале она равна
2оо единицам.
22. Бухгалтер компании решил предпринять выборочную проверку и
выбрал 18 из 1200 компонент, продававшихся в прошлом месяце.
Стоимость отобранных компонент 82, 30, 98,116, 8о, 150, 200, 88,
70, 90,160, юо, 86, 76, 90,140, 76, 68 д.е. Найти оценку средней
стоимости всех компонент и построить для нее доверительный
интервал с надежностью 0,95. Какой объем выборки необходим для
достижения точности интервальной оценки, равной 5 = 3 д.е.?
Ч_ j
308
i
Глава 14 ®
23. Среднее время сборки изделия было 90 мин. Инженер предложил
новый метод сборки этого изделия. При испытаниях
продолжительность сборки ю изделий новым способом составила: 79,74,112, 95,
83. 96, 77. 84, 70, 90 мин. Построить доверительный интервал для
нового среднего времени сборки с надежностью 95%.
24. Производство зерна в России в 1996-2002 гг. представлено
таблицей.
Год
1996
1997
1998
1999
2000
2001
2002
Производство,
млн т
69,3
88,6
47,9
54,7
65,5
85,2
86,6
Построить доверительные интервалы для среднего и для
следующего наблюдения с надежностью 95%, используя нормальное
приближение.
25. Производство пшеницы в России и 1995-2001 гг. представлено
таблицей.
Год
1995
1996
1997
1998
1999
2000
2001
Производство,
млн т
30,1
34,9
44,3
27,0
31,0
34,5
47,0
Построить доверительные интервалы для среднего и для
следующего наблюдения с надежностью 95%, используя нормальное
приближение.
26. Урожайность зерновых культур в России в 1992-2001 гг.
представлена таблицей.
Год
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Урожайность, ц/га
18,0
17,1
15,3
13,1
14,9
17,8
12,9
14,4
15,6
19,4
Построить доверительные интервалы для среднего и для
следующего наблюдения с надежностью 95%, используя нормальное
приближение.
27. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения, г:
49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49.7; 51,6; 49,8; 50,1; 49.7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Построить доверительный интервал для среднего веса с
надежностью 90%.
309
ЧАСТЬ II. Математическая статистика
28. В таблице приведены сгруппированные данные о коэффициентах
соотношения заемных и собственных средств на юо малых
предприятиях региона.
Номер
интервала
Интервал
Середина
интервала х,
я,
1
5,05-5,15
5,1
5
2
5,15-5,25
5,2
8
3
5,25-5,35
5,3
12
4
5,35-5,45
5,4
20
5
5,45-5,55
5,5
26
6
5,55-5,65
5,6
15
7
5,65-5,75
5,7
10
8
5,75-5,85
5,8
4
Построить доверительные интервалы для среднего и для
следующего наблюдения с надежностью 95%, используя нормальное
приближение.
29. Для установления срока службы испытано на продолжительность
непрерывной работы юо изделий. Выборочный средний срок
службы оказался равным 19,5 месяцев, а исправленная выборочная
дисперсия составила 2,25. При этих условиях:
а) с вероятностью 0,683 определить, в каких пределах находится
теоретический средний срок службы изделия;
б) с какой вероятностью можно утверждать, что модуль отклонения
эмпирического среднего от теоретического не превысит 0,3 (месяца);
в) сколько нужно произвести испытаний, чтобы модуль отклонения
не превысил 0,5 (месяца) с вероятностью 0,9973?
30. Производятся независимые испытания с одинаковой, но
неизвестной вероятностью р появления события А в каждом испытании.
Найти доверительный интервал для р с надежностью 0,99, если в
юо испытаниях событие А появилось 6о раз.
31. Изготовлен экспериментальный игровой автомат, который должен
обеспечить появление выигрыша в одном случае из юо бросаний
монеты в автомат. Для проверки пригодности автомата произведено
400 испытаний, причем выигрыш появился 5 раз. Построить
доверительный интервал, покрывающий неизвестную вероятность
появления выигрыша с надежностью у = 0,99.
I 310
V . )
Глава 14 ф
32. В 360 испытаниях, в каждом из которых вероятность появления
события одинакова и неизвестна, событие Л появилось 270 раз. Найти
доверительный интервал, покрывающий неизвестную вероятность
р с надежностью 0,95.
33. При испытаниях юоо элементов зарегистрировано юо отказов.
Найти доверительный интервал, покрывающий неизвестную
вероятность р отказа элемента с надежностью: а) 0,95; б) 0,99.
34. В случайной выборке из 300 аспирантов, специализирующихся по
управлению предприятиями, составленной по нескольким основным
университетам, 180 человек оказались сыновьями бизнесменов.
Оценить долю аспирантов в обследованных университетах (построить
доверительный интервал), отцы которых являются бизнесменами, и
число таких аспирантов среди 2000 аспирантов с надежностью 90%.
35. Среди юо электрических ламп в течение юоо час. вышло из строя
36 штук. Построить доверительный интервал с вероятностью 95% для
генеральной доли ламп, которые прослужат не менее юоо час.
36. Согласно социологическому опросу среди юо человек 20%
пользуются стиральным порошком фирмы а. Сколько еще людей надо
опросить, чтобы с вероятностью 99% получить результат (долю людей,
пользующихся этим стиральным порошком) с точностью до 1%?
37. Фирма разослала юоо новых рекламных каталогов и получила 120
заказов. Построить доверительный интервал для эффективности
рекламы (вероятности отклика) с надежностью 95%.
38. Проведена случайная выборка заемных счетов в банке. Из юоо
отобранных счетов 6о оказались с задолженностью по возврату
ссуды сроком до трех месяцев. Найти доверительный интервал с
вероятностью 90% для доли счетов в банке, которые имеют
задолженности до трех месяцев.
39. В ходе аудиторской проверки была проведена случайная выборка
записей по счетам. В выборке из 500 записей ю содержали
некоторые ошибки в самой записи или процедуре. Найти доверительный
интервал для доли ошибок во всей генеральной совокупности с
надежностью 0,95. Определить объем выборки, которую надо
произвести аудитору, чтобы оценить долю ошибок с точностью до 0,5% и
надежностью 95%.
40. За юо рабочих дней в магазин обращалось в среднем 256 человек
в день. Известно, что число покупателей в день имеет
распределение Пуассона. Построить доверительный интервал для генерального
среднего числа покупателей с вероятностью 99%.
311
V . )
ЧАСТЬ II. Математическая статистика
41. В выборке из 400 изделий средний срок службы составил 2000 час.
Известно, что срок службы изделия имеет показательное
распределение. Построить доверительный интервал для генерального
среднего срока службы изделия с вероятностью 95%.
42. По выборке из юо изделий нашли, что средний срок службы
изделия равен юоо час Построить доверительный интервал для
генерального среднего срока службы изделия с вероятностью 90%.
Время службы изделия распределено по показательному закону.
43. В заданных условиях была проверена сила анодного тока 300
однотипных радиоламп, причем у 6о она оказалась выше
гарантированной паспортом. Найти с надежностью 0,95 границы интервала,
содержащего долю таких радиоламп среди всех радиоламп данного типа.
44. В таблице представлены данные по числу сделок на фондовой
бирже за квартал для 400 инвесторов.
0
1
2
3
4
5
6
7
8
9
10
*1
146
97
73
34
23
10
6
3
4
2
2
В предположении, что случайное число сделок описывается
распределением Пуассона, построить доверительный интервал для
параметра X с надежностью 90%.
45. Случайная величина % (число семян сорняков в пробе зерна)
распределена по закону Пуассона. Далее приведено распределение
семян сорняков в п = юоо пробах зерна (в первой строке указано
количество х. сорняков в одной пробе; во второй строке указана
частота п. — число проб, содержащих х; семян сорняков).
*|
0
1
2
3
4
5
6
ni
405
366
175
40
8
4
2
Построить доверительный интервал для параметра X с надежностью
95%.
46. Анализ выборки из юо заказов в интернет-магазине показал, что
в среднем делается по 1,8 покупки. Построить доверительный
интервал для генерального среднего 0 с надежностью 95% в
предположении, что число покупок в заказе имеет геометрическое
распределение. Решить задачу методом подстановки.
47. По выборке из 50 наблюдений двумерной нормальной случайной
величины получен выборочный коэффициент корреляции 0,5.
Построить доверительный интервал для коэффициента корреляции с
надежностью 90%.
Ч )
ЧАСТЬ II. Математическая статистика
314
При проверке гипотез могут быть ошибки двух типов.
Ошибка первого рода состоит в том, что основная гипотеза
отвергается, хотя на самом деле она верна. Ее вероятность
обозначают обычно а.
Ошибка второго рода состоит в том, что основная гипотеза
принимается, хотя на самом деле она неверна. Ее вероятность
обозначают обычно р.
Часто вероятности ошибок называют для краткости просто
ошибками (первого и второго рода).
Вероятность а совершить ошибку первого рода называют
также уровнем значимости или размером критерия. Вероятность
1 - р не совершить ошибку второго рода называют мощностью
критерия.
Критерий называется наиболее мощным, если из всех
возможных критериев с заданным уровнем значимости а он
обладает наибольшей мощностью.
Пример 1. Пусть определена статистика критерия К и пусть
функция плотности вероятностей выборочной статистики К
при условии истинности нулевой гипотезы Я0 равна р(К\Н0),
медиана К равна К0. По заданному уровню значимости а
определяют квантили К^2 и Кх_ы2 из условия
ка
P(K<KJ= j p(K\H0)dK= а/2;
Р(К > К{_а/2) = J p(K\H0)dK = а/2,
¦-т
где а полагают достаточно малым, чтобы попадание случайной
величины К за пределы интервала (А^; АГ1а/2) можно было
считать маловероятным событием. Область (Кы2, Кх^2) и является
областью допустимых значений, т.е. областью принятия
нулевой гипотезы. Промежутки (-оо; К^) и (А^,^; +оо) образуют
критическую область критерия, при попадании в которую
наблюдаемого значения ? нулевую гипотезу отвергают. Точки,
отделяющие критические области от области принятия гипотезы,
называются критическими точками (рис. 15.1).
Критическая область называется двусторонней, если она
располагается слева и справа от медианы К0 (см. рис. 15.1),
правосторонней, если Р(К > Кх_ ) = а, и левосторонней, если
Р(К<Ка) = а (рис. 15.2).
р ЧАСТЬ 11. Математическая статистика
§ 15.2. Критерий отношения правдоподобия
Основным методом построения наиболее мощных
статистических критериев (по теореме Неймана—Пирсона) является
метод отношения правдоподобия, суть которого заключается в
следующем: пусть ? — непрерывная случайная величина, имеющая
плотность распределения р0(х) при условии истинности нулевой
гипотезы Я0 и р^х) при выполнении гипотезы Я,. Функции
правдоподобия в точке х соответственно равны
Zt)(jc) = p0(x1)p0(x2)...p0(x/,); 1л(х) = р1{х])р1(х2)...р1(хя).
О правдоподобии выборки в отношении гипотез Я0 и Я,
будем судить по отношению правдоподобия Ц/Ц (Ц* 0): чем
правдоподобнее выборка в условиях истинности гипотезы Я0,
тем меньше L{ по сравнению с 10, и тем меньше отношение
^ Теорема 1 (Неймана—Пирсона). Критическая область S паи-
более мощного критерия имеет вид
х:Ц(х) = 0и^>С, Ц(х)*0
Ц\Х)
316
Итак, основной принцип проверки статистической
гипотезы можно сформулировать так: если наблюдаемое значение
статистики критерия принадлежит критической области,
нулевую гипотезу отвергают; если наблюдаемое значение
принадлежит области допустимых значений, нулевую гипотезу
принимают.
Заметим также, что можно установить связь между
задачами проверки гипотез и задачами построения доверительных
интервалов (см. гл.л14). Например, пусть построен
доверительный интервал (01982)для параметра 6 с надежностью у. Тем
самым утверждается, что истинное значение параметра лежит
в интервале с вероятностью у, а вне этого интервала — с малой
вероятностью а = 1 - у. Таким образом, если мы проверяем
гипотезу Я0: 0 = 90 против какой-либо альтернативной
гипотезы, то в качестве критерия можно взять S = {x:Q0g(Ql,Q2)}.
Уровень значимости в этом случае будет равен а. Однако такой
критерий не обязательно будет оптимальным.
Глава 15
где константа С = С(а) является решением уравнения
„(А<*).
>С\Н0
= а.
Подобный метод построения критической области,
использующий отношение правдоподобия, дает нам критерий
отношения правдоподобия. В дискретном случае построение проводится
аналогично (только вместо плотностей берутся вероятности).
Статистика критерия здесь имеет вид K = Ll/L0 (при Z0= О
полагаем К = +оо), тогда критическая область 5 = {К > Q, а
область допустимых значений S = {К < Q.
Задача 1. Пусть случайная величина § € N(a, а2), причем
значение параметра а неизвестно, а дисперсия а2 известна.
Требуется на уровне значимости а проверить нулевую гипотезу Я0:
а = а0, если альтернативная гипотеза Нх: а = ах > а0. Построить
критерий отношения правдоподобия. Вычислить объем выборки
я, необходимый для достижения ошибок второго года аир.
Решение. Если верна гипотеза Я0, т.е. § е #(я0, а2), то
функция правдоподобий в точке х = (х,, х2, хя) равна
1
(ал/2я J
ехр
Е^.-Яо)2
2сг
Если же верна гипотеза Нх, т.е. § е iV(tf,, а2), то функция
правдоподобия
А(*) =
1
ехр
/=1
2сг
Отношение правдоподобия имеет вид
f(a,-fln)(2x-g1 -д0)я
~ = ехр
А)
2а2
Поскольку ах > а0, это отношение является монотонно
возрастающей функцией от х, и поскольку L0(x) ф О, неравенство
LX/L0>C равносильно неравенству х>С, где С и С —
некоторые константы. Поэтому критическая область имеет вид
5 = {х:х>С}, где Р(х>С\Н0) = а.
317
ЧАСТЬ 11. Математическая статистика
При условии истинности нулевой гипотезы Я0 имеем
х е N(a09 —), поэтому
а = />(х>С|#0)=1-Ф
^4~п
1-ф
_1_ф
— ~ 0
а
2
а
_ 1
-а..
~ 2
Отсюда Ф0
Обозначим через иа решение уравнения Ф0(иа) = 1/2 - а,
тогда константа имеет вид С = а0 +иа-^=. Заметим, что величина иа
у/п
является квантилью уровня 1 - а для стандартного нормального
распределения и выступает здесь в качестве критической точки.
Значение ее можно найти по таблице функции Лапласа.
Итак, наиболее мощным критерием проверки гипотезы Я0:
а = а0 при альтернативной Н,: а = я, > а0 оказывается
следующий:
если х <а0 +wa-^L, то Я0 принимается;
у/п
если х>а0+иа-^=9 то Я0 отклоняется (и принимается Нх).
у/п
По определению ошибки второго рода имеем
Р = Р(х<С\Нх) = Ф
^4~п
Отсюда Ф
=i-p.
Получаем, что должно выполняться
f a a
\}П у/П
Решая уравнение относительно п, получаем
(и. +«р)2 ,
/1 = г- a .
(я,-Яо)
Полученное значение обычно округляется до целого в
большую сторону для уменьшения вероятностей ошибок.
Мощность критерия в данном случае составляет
1-р = Ф
=ф
й1 ~°о Г
уП — U
a
{ о "J
I 318
Глава 15 ф
н 1 20
= Ф(1,35) = ^ + Ф0(1,35)«0,91.
Отсюда вероятность ошибки второго рода р » 0,09.
3) Используем формулу для необходимого объема выборки.
Для этого найдем квантили иа и ир с помощью таблицы
функции Лапласа и получим
(1,95 + 1,65)2 20* =51,84, откуда п = 52.
100 J
319
Задана 2. Крупная торговая фирма желает открыть в
новом районе города филиал. Известно, что фирма будет работать
прибыльно, если средний месячный доход жителей района
превышает 400 долларов. Также известно, что среднее
квадратическое отклонение дохода с составляет 20 долларов. Проводится
выборочное обследование населения по величине доходов,
чтобы принять решение об открытии филиала.
1) Определите правило принятия решения, с помощью
которого, основываясь на выборке п = 100 человек и уровне
значимости а = 0,05, можно установить, что филиал будет работать
прибыльно.
2) Рассчитайте вероятность того, что при применении
правила принятия решения, полученного при ответе на вопрос
п. 1, будет совершена ошибка второго рода, если в
действительности средний доход достигает 406 долларов.
3) Считая альтернативное значение генерального среднего
месячного дохода равным 410 долларов, рассчитайте объем
выборки, при котором ошибка первого рода не превысит 2,5%,
а ошибка второго рода не превысит 5%.
Решение. 1) Фирма не откроет филиал, если средний доход
жителей не превысит 400 долларов. Поэтому будем считать, что
Я0: а = а0= 400, а Я,: а = ах > 400. Значение дисперсии а2
дохода известно. Находим иа по таблице функции Лапласа, исходя
из равенства Ф0(«а) = 1/2 - а. Поскольку а0= 400 и иа= 1,65,
то Я, принимают и, следовательно, филиал открывают, если
средний месячный доход 100 жителей
x>400+-JLl,65 = 403,3.
у/Ж
2) Вероятность ошибки второго рода р можно легко найти,
зная мощность критерия, которая равна 1 - р. Получаем
406-400 /77^ , ,Л _ 1
ЧАСТЬ II. Математическая статистика
320
Замечание. Приведенная формула может давать слишком
малые значения п, так как основывается на строго нормальном
распределении. На практике п должно быть достаточно велико,
чтобы пользоваться асимптотической нормальностью оценок.
§ 15.3. Проверка гипотез для одной выборки
Рассмотрим простые методы проверки параметрических
гипотез в случае нормального распределения (которые являются
формально точными), а также гипотезы о вероятности
«успеха» в испытаниях Бернулли (на основе асимптотической
нормальности). Как и ранее, нас не будет смущать тот факт, что
реальные данные, по которым проверяются гипотезы, могут
совсем не выглядеть нормальными (например, это целые
положительные числа, в то время как нормальное распределение
непрерывно и рассредоточено по всей действительной прямой).
Тем не менее широкое практическое применение описываемых
методов дает неплохие результаты (это объясняется, в
частности, асимптотической нормальностью оценок).
Следующие три типа гипотез проверяются для нормальных
данных: ? е N(a, о2).
1. Гипотезы о неизвестном среднем а при известной
дисперсии <т2
Основная гипотеза Я0: а = а0, альтернативная гипотеза Нх
может быть трех видов: а) а ф а0; б) а > д0; в) а < а0. Во всех
трех случаях для проверки используется статистика критерия
В случае а) критическая точка икр выбирается из условия
Ф0(и ) = (1 - а)/2. Если \U\ < икр, гипотеза Я0 принимается,
если \U\ > икр — отвергается. Таким образом, в данном случае
имеет место двусторонняя критическая область.
В случаях б) и в) критическая точка икр выбирается из
условия Ф0(икр) = 1/2 - а.
В случае б), если U < икр, то гипотеза Я0 принимается, если
U > икр — отвергается.
В случае в), если U > -икр, то гипотеза Я0 принимается, если
U < —и — отвергается.
Глава 15 ф
2_("-1)*2
Для проверки берутся критические точки распределения хи-
квадрат с п - 1 степенями свободы (и различными уровнями
значимости).
11 Теория вероятностей 3^1 I
Здесь имеют место односторонние критические области
(правосторонняя и левосторонняя соответственно).
Замечание. Этим методом можно пользоваться и в случае
неизвестной дисперсии при больших объемах выборки
(порядка сотен), когда оценку дисперсии можно принять за ее точное
значение.
2. Гипотезы о неизвестном среднем а при неизвестной
дисперсии о2
Основная гипотеза Я0: а = а0, альтернативная гипотеза Я,
может быть трех видов: а) а * а0; б) а > а0; в) а < а0. Во всех
трех случаях для проверки используется статистика критерия
s
Для проверки берутся критические точки / распределения
Стьюдента с п — 1 степенью свободы и уровнем значимости а,
причем в случае а) — для двусторонней критической области, в
случаях б) и в) — для односторонней критической области.
В случае а), если |Г| < / , то гипотеза Я0 принимается, если
\Т\ > t — отвергается.
В случае б), если Т < t , то гипотеза Я0 принимается, если
Т > t — отвергается.
В случае в), если Т> —икр, то гипотеза Я0 принимается, если
Т < —ип — отвергается.
кр
3. Гипотезы о неизвестной дисперсии о2
Обычно предполагается, что хотя дисперсия неизвестна, но
дана ее несмещенная оценка s1. Основная гипотеза Я0: а2 = а02,
альтернативная гипотеза Нх может быть трех видов: а) а2 * а02;
б) а2 > а02; в) а2 < а02. Во всех трех случаях для проверки
используется статистика критерия
i
ф ЧАСТЬ II. Математическая статистика
[ 322
В случае а), если %1а/2.п_х <%2 <Xa/2,*-i> то гипотеза Я0
принимается, иначе она отвергается. Заметим, что границы
области несимметричны относительно оценки s2.
В случае б), если %2<%2а;п_1, то гипотеза Я0 принимается,
иначе отвергается.
В случае в), если %2>%2_а.п_19 то гипотеза Я0 принимается,
иначе отвергается.
Следующая гипотеза проверяется приближенно, на основе
асимптотической нормальности оценки.
4. Гипотеза о неизвестной вероятности «успеха» в испытаниях
Бернулли
Основная гипотеза Я0: р = р09 альтернативная гипотеза Нх
может быть трех видов: а) р ф р0; б) р > р0; в) р < р0. Во всех трех
случаях для проверки используется статистика критерия
у-пр* г
U= . М=у1п, где w — относительная частота «успехов» в
п наблюдениях.
Далее критические точки и области для проверки
выбираются так же, как и при проверке гипотезы о неизвестном
среднем при известной дисперсии.
Замечание. Этим методом можно пользоваться только при
больших объемах выборки (порядка нескольких десятков или
сотен).
Доказательство. 1) Если нулевая гипотеза справедлива,
статистика критерия U = -——4п имеет стандартное нормальное
a
распределение N(0, 1).
В случае справедливости гипотезы а) эта статистика может
стремиться как к +оо, так и к —оо, в зависимости от того, а > а0
или а < а0. Поэтому область принятия гипотезы Я0 следует
ограничить с двух сторон, справа и слева. Логично это сделать
симметричным образом, в силу симметрии нормального
распределения. Имеем P(\U\ < и) = 2Ф0(и), поэтому выбирая и из условия
фо("кр) = О - а>А получаем P(\U\ <икр)=\-аи P(\U\ > uj =
= а, что обеспечивает уровень значимости а.
В случае справедливости гипотезы б) а > а0 статистика U
стремится к +оо, так что область принятия гипотезы Я0
следует ограничить справа. Имеем P(U < и) = Ф(и) = 1/2 + Ф0(и),
Глава is ф
Таблица 15.1
Предположения
Статистика
критерия
н\
Область принятия Я0
а =а0
а2
а> а0
V< VW= !/2-а;
известно
?/ = *_а°^
а< а0
U>-UKp,0o(uJ=l/2-a;
а
а*а0
|U|< V Ф0(Ич))=(1-а)/2
323
поэтому, выбирая икр из условия Ф0(икр) = 1/2 - а, получаем
P(U < икр) =1 — а и P(U> u^) = а, что обеспечивает уровень
значимости а.
В случае справедливости гипотезы в) а < а0 статистика U
стремится к —оо, так что область принятия гипотезы Н0 следует
ограничить слева. Имеем P(U > - u) = 1 - Ф(-и) = 1/2 + Ф0(и),
поэтому выбирая икр из условия Ф^и^) = 1/2 - а, получаем
P(U> — и^) = 1 — а и P(U< —w^) = а, что обеспечивает уровень
значимости а.
2) Если нулевая гипотеза справедлива, статистика критерия
Т=*——у[п имеет распределение Стьюдента с п — 1 степеня-
s
ми свободы. Критическая область выбирается в зависимости
от альтернативной гипотезы из тех же соображений, что и в
случае 1.
3) Если нулевая гипотеза справедлива, статистика критерия
2 (n-l)s2 t
X = -—т— имеет распределение хи-квадрат с п — 1 степенями
свободы. Далее рассуждаем аналогично.
4) Если нулевая гипотеза справедлива, из центральной
предельной теоремы (см. гл. 8) следует, что относительная
частота успехов w асимптотически нормальна, с математическим
ожиданием р0 и дисперсией р0(\ — р0)/п, так что статистика
U = .w пр° сходится по распределению к стандартной
нормальной величине при п -> оо. Значит, при достаточно
больших п можно считать, что она имеет стандартное нормальное
распределение. Далее рассуждаем, как в случае 1.
Описанные критерии проверки гипотез можно представить
в виде табл. 15.1.
|j| ЧАСТЬ II. Математическая статистика
Продолжение табл. 17.1
Но
Предположения
Статистика
критерия
Нх
Область принятия Я0
а2 не
известно
т=*-а»4п-
S
а>а0
а<а0
а*а0
Г < /кр(а, п - 1) для
односторонней области;
Г > ~/кр(а, л - 1) для
односторонней области;
\T\<tJa,n- 1)для
двусторонней области
а не
известно
о2>а02
X < Ха;л-1 '
"о
о2<а02
X > Xl-a;/i-l '
2 2 2.
Xl-a/2;w-l < X < Ха/2,я-1 >
Р = Ро
п порядка
нескольких
десятков
или сотен
и- 4~п,
VPoO-Po)
где w = пг/п
Р > Ро
Р<Ро
Р*Ро
^>-^фо(мкр)=1/2-а;
М < V фо(«кр) = 0 - а)/2
Задача 3. Из нормальной генеральной совокупности с
известным средним квадратическим отклонением a = 5 извлечена
выборка объема п = 100 и по ней найдено выборочное среднее
26,5. Требуется на уровне значимости 0,05 проверить гипотезу
Н0: а = а0 = 25 против альтернативной гипотезы Нх\ а * 25.
Изменится ли результат, если заменим альтернативную
гипотезу на Нх: а > 25?
Решение. Найдем значение статистики критерия:
^ = 26^^щ = 3
При проверке гипотезы Нх: а ф 25 из соотношения Ф^и^) =
= 0,95/2 = 0,475 находим икр= 1,96, и \U\ > икр, так что
основная гипотеза отвергается. При проверке гипотезы Нх\ а > 25 из
соотношения Ф0(икр) = 0,45 находим икр = 1,65, и U > икр, так
что основная гипотеза отвергается. В обоих случаях результат
одинаков.
| 324
Глава 15 ф
0,01
Альтернативной гипотезой в данном случае является Я,:
По таблице находим критическую точку распределения хи-
квадрат: Хо,05;24 = 36>4'
Поскольку 48 > 36,4, то основная гипотеза отвергается.
Следовательно, станок не обеспечивает необходимой точности.
Задача 6. Из нормальной генеральной совокупности
извлечена выборка объема п = 31. В следующей таблице
представлены сгруппированные данные.
Вариант х.
10,1
10,3
10,6
11,2
11,5
11,8
12,0
Частота п.
1
3
7
10
6
3
1
325
Задача 4. По выборке объема п = 16, извлеченной из
нормальной генеральной совокупности, найдены выборочное
среднее, равное 12,4, и исправленное среднее квадратическое
отклонение, равное 1,2. Требуется при уровне значимости 0,05
проверить нулевую гипотезу Я0: а = 11,8 при конкурирующей
гипотезе Я,: а ф 11,8.
Решение. Найдем наблюдаемое значение статистики критерия:
(х-<0>? = (12,4-11,8)-4 = 2
s 1,2
Поскольку конкурирующая гипотеза имеет вид а ф а0,
искомая критическая область двусторонняя. По таблице
критических точек распределения Стьюдента найдем по уровню
значимости а = 0,05 и числу степеней свободы п - 1 = 15
критическую точку /кр= /кр (0,05; 15) = 2,13.
В силу того что 171 < t, нет оснований отвергнуть нулевую
гипотезу.
Задача 5. Точность работы станка-автомата проверяется по
дисперсии размеров изделий, которая не должна превышать
а] = 0,01 (мм2). По выборке из 25 изделий получена
исправленная выборочная дисперсия s2 = 0,02 мм2. На уровне
значимости 0,05 проверить, обеспечивает ли станок необходимую
точность.
Решение. Найдем значение статистики критерия:
!
Требуется на уровне значимости 0,05 проверить нулевую
гипотезу Я0: а2= 0,18, приняв в качестве конкурирующей
гипотезы Нх: с2> 0,18.
Решение. Перейдем к условным вариантам ui = lQx, -ПО.
щ
-9
-7
-4
2
5
8
10
ni
1
3
7
10
6
3
1
Получаем:
и-1
7 if 7
1=1 л
30
822-
26_2^
31
; 26,67;
^«0,27; ,2=^= 30x027 =45
х 100 * от* 0,18
По таблице критических точек распределения хи-квадрат
по уровню значимости а = 0,05 и числу степеней свободы к =
= п - 1 = 30 находим х2кр(°'05; 30> = 43'8-
Поскольку 45 > 43,8, основная гипотеза Я0 отвергается.
Задача 7. Партия изделий принимается, если доля брака
составляет не более 2%. Среди случайно отобранных 500
изделий оказалось 13 бракованных. Следует ли принять партию
(на уровне значимости 0,05)?
Решение. Относительная частота брака составляет w = 13/500 =
= 0,026.
Найдем значение статистики критерия
^= 0,026-0,02^^
^0,02x0,98
Альтернативной гипотезой в данном случае является Я,:
Р > Ро-
Из соотношения Ф0(икр) = 0,45 находим икр= 1,65 и
получаем U < икр, так что основная гипотеза принимается. Таким
образом, партию изделий можно принять.
Задача 8. Торговец утверждает, что он получает заказы в
среднем, по крайней мере, от 30% предполагаемых клиентов.
Можно ли при 5%-ном уровне значимости считать это
утверждение неверным, если торговец получил заказы от 20 из 100
случайно отобранных потенциальных клиентов?
! 326
ф ЧАСТЬ II. Математическая статистика
Глава is ф
Решение. В данном случае нулевая гипотеза будет выглядеть
как Я0: р = р0 = 0,3, а конкурирующая — как Я,: р < 0,3.
Найдем значение статистики критерия, учитывая, что
относительная частота для данной задачи равна w = 20/100 = 0,2:
и (w-Pohfc (0,2-0,3)х10 01Я
и = -—===== = . —^ —2,10.
Vft(l-A) л/0.3 х 0,7
Из соотношения Фо^) = 0,45 находим икр = 1,65, и ?/< -и ,
так что нулевая гипотеза отвергается и с утверждением торговца
согласиться нельзя.
Задача 9. По выборке объема я, извлеченной из нормальной
генеральной совокупности с известным средним
квадратическим отклонением а, найдено выборочное среднее. При уровне
значимости а требуется найти функцию мощности критерия
проверки нулевой гипотезы Я0: а = а0 при конкурирующей
гипотезе Н{: а = ах ф а0.
Решение. Поскольку конкурирующая гипотеза имеет вид а ф а0,
критическая область двусторонняя. Она определяется
неравенством: \U\ > и , где и находится из соотношения Ф0(и ) =
= 1/2 - а.
Найдем мощность рассматриваемого критерия, что по
определению есть вероятность попадания статистики критерия
в критическую область при допущении, что справедлива
конкурирующая гипотеза:
\(х-Оо)у1п\
1-(3=Л
Преобразуем выражение, стоящее под знаком модуля:
(х-а0)у/п ^(x-a^yfn | (о,-а0)у[п =b | ^
(x-a^Jn
где Ь = ! ,
а
Х =
(я,-а0Ь/л
Используя данные соотношения, найдем мощность
критерия:
1 - р = Р(\Ь + Х\> икр) = Р(Ь + Х> и ) + Р(Ь + Х <-nJ =
= Р(Ь > икр - X) + Р(Ь < - и„- X) = [1 - />(/> < wKD- X)] +
327
@ ЧАСТЬ II. Математическая статистика
+ 1(* < -Ukp- X) = [1/2 - Ф0(и - X)] + [1/2 + Ф0(-Ич) - X)} =
= 1 " Ф0(«кр " ^> " фо(«кР +
Поскольку каждому значению будет соответствовать свое
значение мощности критерия (в силу того, что X есть функция
от я,), то мощность критерия также является функцией от ау
Обозначив мощность критерия через тс, получим:
п(ах) = 1 - [Ф0(икр - X) + Ф0(ккр + А.)].
§ 15.4. Проверка гипотез для двух выборок.
Зависимые выборки: парные наблюдения
Под случаем «зависимых выборок» обычно имеют в виду
ситуацию, когда речь идет об одном и том же наборе объектов
до и после какого-либо воздействия на них. Предполагается,
что воздействие может повлиять на признаки, сдвинув их
средние значения в большую или меньшую сторону, и это
необходимо проверить.
Вначале признаки объектов принимают значения хр после
воздействия — значения уг Такие наблюдения называются
парными. Вычислим их разности di = yt — jc . Тогда ставится
следующая задача: по наблюдениям dv dv dn проверить гипотезу
о равенстве нулю генерального среднего (Я0: ad= 0) при
неизвестной дисперсии оД Предполагается, что случайные
изменения признаков распределены нормально. Тогда гипотезу можно
проверить, как это описано в предыдущем параграфе.
Задача 10. Физическая подготовка 9 спортсменов была
проверена при поступлении в спортивную школу, а затем после
недели тренировок. Итоги проверки в баллах приведены в
таблице (в первой строке указано число баллов, полученных
каждым спортсменом при поступлении в школу; во второй
строке — после обучения).
76
71
57
49
70
69
26
65
59
У,
81
85
52
52
70
63
33
83
62
Требуется на уровне значимости 0,05 проверить,
существенно ли улучшилась физическая подготовка спортсменов
(используя нормальное приближение).
328
Глава 15 ф
Решение. Вычислим разности d. = у. — х..
4
5
14
-5
3
0
-6
7
18
3
Получаем
f^d, = 5 +14- 5 + 3- 6 + 7+ 18 + 3 = 39;
/=i
?Х = 25 + 196 + 25 + 9 + 36 + 49 + 324 + 9 = 673.
/=i
Отсюда находим выборочное среднее и исправленное
среднее квадратическое отклонение:
1
Проверяем гипотезу Я0: ad= 0 против Я,: ах > 0.
Найдем значение статистики критерия:
Г = ^ = ^33х3^
sd 7,94
По таблице критических точек распределения Стьюдента
для односторонней области по уровню значимости 0,05 и числу
степеней свободы к = п - 1 = 8 определяем С(0,05; 8) = 1,86.
Поскольку Т < t , нет оснований отвергнуть нулевую гипотезу.
Таким образом, нельзя утверждать, что подготовка
спортсменов существенно улучшилась.
§ 15.5. Проверка гипотез для двух выборок.
Независимые выборки
Пусть имеются две независимые выборки: хр х2, хп и yv
yv ym, имеющие нормальное распределение с параметрами
(ах, ах2) и (ау, о,2) соответственно. Обычно ставится задача
проверки их однородности, т.е. равенства обоих параметров, либо
надо проверить равенство параметров по отдельности.
П 1 [ п
/=1 п\м
673-169
8
*7,94.
329
ЧАСТЬ II. Математическая статистика
1. Гипотеза о равенстве дисперсий двух выборок
Предположим, что известны исправленные выборочные
дисперсии для обеих выборок — s2 и sy2. Проверяем гипотезу Я0:
g2 = а2. Альтернативная гипотеза Нх может быть трех видов:
а) с2 * ъ2\ б) a2 > g2; в) и2 < с2, однако случай в) сводится к
б) перестановкой х и у и не будет рассматриваться отдельно.
В случае а) делят большую выборочную дисперсию на
меньшую:
с2
I? max
^min
Обозначим через пт.т объем выборки с меньшей
выборочной дисперсией и через ятах — с большей. По таблице для
распределения Фишера находим критическую точку с уровнем
значимости а/2 и числами степеней свободы птах- 1 и nmin- 1.
Если F < FKp9 то основная гипотеза принимается, иначе
отвергается.
В случае б) делят первую выборочную дисперсию на вто-
рую: F = ~r.
По таблице для распределения Фишера находим
критическую точку с уровнем значимости а и числами степеней
свободы п — 1 и т — 1. Если F < Fvn, то основная гипотеза при-
кр
нимается, иначе отвергается.
2. Гипотеза о равенстве средних при известных дисперсиях
Проверяем гипотезу Я0: ах = ау. Альтернативная гипотеза Я,
может быть трех видов: а) ах * ау\ б) ах > ау\ в) ах < ау, однако
случай в) сводится к б) перестановкой х и у и не будет
рассматриваться отдельно. Во всех случаях вычисляют статистику
критерия
В случае а) критическая точка икр выбирается из условия
Ф0(икр) = (1—а)/2. Если \ U\ < икр, гипотеза Я0 принимается, если
\U\ > икр — отвергается.
330
Глава 15 ф
В случае б) критическая точка икр выбирается из условия
Ф0(икр) = 1/2 - а. Если U < икр, то гипотеза Я0 принимается,
если U > м — отвергается.
кр
Замечание. Гипотеза о средних обычно проверяется таким
образом и в случае неизвестных дисперсий для больших
выборок (объемом порядка сотен), когда оценки дисперсий можно
принять за их точные значения.
3. Гипотеза о равенстве средних при неизвестных равных
дисперсиях
Проверяем гипотезу Н0: ах = ау. Альтернативная гипотеза Нх
может быть трех видов: а) ах ф ау; б) ах > ау\ в) ах < ау9 однако
случай в) сводится к б) перестановкой х и у и не будет
рассматриваться отдельно. Во всех случаях вычисляют статистику
критерия.
Величина s? является объединенной оценкой дисперсии
(общей для выборок).
Эту же формулу можно представить в виде
Для проверки берут критические точки t распределения
Стьюдента c« + /w-2 степенями свободы и уровнем
значимости а, причем в случае а) — для двусторонней критической
области, в случае б) — для односторонней критической области.
В случае а), если \ Т\ < t 9 то гипотеза Я0 принимается, если
\7] > t — отвергается.
В случае б), если Т < t , то гипотеза Я0 принимается, если
Т > t — отвергается.
Замечание. Поскольку для проверки гипотезы требуется
равенство дисперсий у двух выборок, сначала необходимо
проверить гипотезу о равенстве дисперсий. В противном случае
данный метод применять нельзя.
Т =
х-у
где s =
2_(n-l)s2x+(m-l)s2y
n + m-2
ф ЧАСТЬ II. Математическая статистика
4. Гипотеза о равенстве вероятностей «успеха» в двух сериях
испытаний Бернулли
Гипотеза проверяется на основе асимптотической
нормальности относительных частот, так что данный метод может
применяться только при больших объемах выборок (порядка
нескольких десятков или сотен). Пусть в одной серии из пх
испытаний получили тх «успехов», в другой серии из п2
испытаний получили т2 «успехов». Проверяем гипотезу Я0: рх = р2.
Альтернативная гипотеза может быть трех видов: а) рх * р2\
б) рх > р2\ в) рх < pv однако случай в) сводится к б)
перестановкой индексов и не будет рассматриваться отдельно.
Во всех случаях вычисляют статистику критерия
В случае а) критическая точка икр выбирается из условия
Ф0(икр) = (1 — а)/2. Если \U\ < икр9 гипотеза Я0 принимается,
если \U\ > икр — отвергается.
В случае б) критическая точка икр выбирается из условия
Ф0(икр) = 1/2 - а. Если U < икр, то гипотеза Я0 принимается,
если U > икр — отвергается.
Доказательство. 1) Если основная гипотеза справедлива, то
по следствию 5 теоремы Фишера (см. § 12.8) статистика F = ^
имеет распределение Фишера с числами степеней свободы п — 1
и т — 1.
Если справедлива гипотеза б), то Устремится к +а>, так что
область принятия нулевой гипотезы следует ограничить
справа. Критические точки распределения Фишера определяются из
условия: P(F > FKp) = а. Выбирая соответственно критическую
область, получаем уровень значимости а.
Если справедлива гипотеза а), то F может стремиться как
к +0О, так и к 0, так что область принятия нулевой гипотезы
следует ограничить и справа, и слева. Но условие -^l < С эк-
и =
где w =
min
! 332
Глава 15 ф
1 5?
вивалентно — < -у < С при О 1. С учетом того, что для рас-
С s
1
пределения Фишера верно F(n,m) = , получаем, что
/;_«("*, л)
при выборе критической точки F 9 соответствующей уровню
значимости а/2, будет выполняться Р
max
>F^
Л " кр
так что
достигается нужный нам уровень значимости а.
2) Если основная гипотеза справедлива, то по следствию 3
х — у
теоремы Фишера статистика U = , • имеет стандартное
п т
нормальное распределение. Далее рассуждаем так же, как при
проверке гипотезы для одной выборки (см. § 15.3).
3) Если основная гипотеза справедлива, то по следствию 4 те-
гп х — у \пт(п + т — 2)
оремы Фишера статистика Т — '
lnm(n-
имеет распределение Стьюдента с« + /и-2 степенями
свободы. Далее рассуждаем так же, как при проверке гипотезы для
одной выборки.
4) Если основная гипотеза справедлива, то из центральной
предельной теоремы следует, что относительные частоты wx и w2
асимптотически нормальны с одинаковым средним р = рх — р2
и дисперсиями р{\ — р)/пх и р(\ — р)/п2. Кроме того, они
независимы. Следовательно, их разность w, — w2 асимптотически
нормальна с нулевым средним и дисперсией р{\ - р)(1/пх + 1/я2).
Однако р неизвестно. Наилучшей оценкой (несмещенной,
состоятельной, эффективной в классе линейных несмещенных
оценок) для р является w = ———. Заменяя р на и>, получаем,
что распределение статистики
w(l - w)
1+1
сходится к стандартному нормальному распределению при
п -> со. Далее рассуждаем так же, как при проверке гипотезы
для одной выборки.
333 |
I ЧАСТЬ II. Математическая статистика
Таблица 15.2
Н0
Предположения
Статистика критерия
H,
Область принятия H,
II
сх2 и а/
известны
и-
V я т
и<икр,Ф0(и^=\/2-а;
U>-UKp,0o(uJ=l/2-a;
м < v фо(«кр) - a - «)/2
ах2 и
а/ не
известны,
но равны
Т= х~у ,где
\я /я
^_(n-l)slHm-l)s2y
n + m—2
<>,< "у
°x*ay
Г < 'кр(а> я + /я - 2) для
односторонней области;
Г > -tj.a, п + m -2) для
односторонней области;
1Л < У», и + « - 2)
для двусторонней области
V
II
V
ахИ ау
не
известны
F = -f, где si >s2y
sy
a2> a2
x у
F<FJfi,n-l,m-\);
F<Fjia/2,n-l,m-l)
«с
н
и, и п2
порядка
нескольких
десятков
или сотен
Li_w)fi+i|
где w = — -
/>,>/>2
Л < /»2
Pi* Pi
и<и<ч>,Ф0(и1Ч)=\/2-а;
и>-и1ф,Ф0(икр)= 1/2-а;
М < «„р, Ф0(и«р) = (1 " «)/2
Задана 11. По выборке объема я = 30 найден средний вес
изделий, равный 130 г, изготовленных на первом станке; по
выборке объема m = 40 найден средней вес изделий, равный
125 г, изготовленных на втором станке. Генеральные дисперсии
известны: о2 = 60 г2, оу2 = 80 г2. Требуется на уровне
значимости 0,05 проверить нулевую гипотезу Я0: ах = ау при
конкурирующей гипотезе Я,: ах*ау. Предполагается, что случайные
величины распределены нормально и выборки независимы.
j 334
Описанные критерии проверки гипотез можно представить
в виде табл. 15.2.
Глава 15
Решение. Найдем значение статистики критерия:
Ц= =™~П5=2,5.
По таблице функции Лапласа найдем критическую точку
из равенства Ф(«кр) = (1-а)/2 = 0,475, получаем икр = 1,96. Так
как \U\ > икр, гапотеза Н0 отвергается. Таким образом, нельзя
утверждать, что средние значения веса изделий двух станков
совпадают.
Задана 12. По двум независимым выборкам, объемы
которых п = 9 и т = 16, извлеченным из нормальных генеральных
совокупностей, найдены исправленные выборочные дисперсии
5^=34,02 и s2, =12,15. На уровне значимости 0,01 проверить
нулевую гипотезу Я0: о2 = су2 против конкурирующей гипотезы
Н- а? > а/.
Решение. Рассчитаем значение статистики критерия:
F=4=H02
s] 12,15
Числа степеней свободы кх = п — 1 = 8, к2 = т — 1 = 15. По
таблице критических точек распределения Фишера—Снедекора
по заданному уровню значимости а = 0,01 и числам степеней
свободы находим i710,01; 8; 15) = 4. Поскольку F< F. нуле-
кр кр
вая гипотеза принимается.
Задана 13. Реклама утверждает, что из двух типов
пластиковых карт «Русский Экспресс» и «Супер-Понт» богатые люди
предпочитают первый. С целью проверки этого утверждения
были обследованы среднемесячные платежи п = 16 обладателей
«Русского Экспресса» и т = 11 обладателей «Супер-Понта».
Выяснилось, что платежи по картам «Русский Экспресс»
составляют в среднем 563 долл. с исправленным средним
квадратическим отклонением 178 долл., а по картам «Супер-Понт» —
в среднем 485 долл. с исправленным средним квадратическим
отклонением 196 долл.
Предварительный анализ законов распределения месячных
расходов как среди обладателей «Русского Экспресса», так и
335
ф ЧАСТЬ II. Математическая статиаика
среди обладателей «Супер-Понта» показал, что они достаточно
хорошо описываются нормальным приближением.
Проверить утверждение рекламы на уровне значимости 0,1.
Решение. В данном случае речь идет о проверке гипотезы о
средних при неизвестных дисперсиях (объемы выборок малы).
Поэтому прежде всего необходимо проверить гипотезу о
равенстве дисперсий, а лишь затем двигаться дальше. Имеем
*L= 1962 =38416
-2 1782 31684
«1,21.
По таблице критических точек распределения Фишера—
Снедекора по уровню значимости а/2 = 0,05 и числам
степеней свободы кх - птах - 1 = 10 и к2 = птХп — 1 — 15 найдем
критическую точку /\ = 2,55. Так как 1,21 < 2,55, принимаем
гипотезу о равенстве дисперсий двух выборок.
Теперь можем воспользоваться критерием Стьюдента для
проверки гипотезы о равенстве средних. Имеем
2 10x38416 + 15x31684 1>ir7lCQ. 1С<- л
s -— = 34376,8; s « 185,4.
Вычисление статистики критерия дает:
Т= 56^485 «1,074.
185,471/11 + 1/16
Из таблиц критических точек распределения Стьюдента
(для односторонней области) по уровню значимости а = 0,1 и
числу степеней свободы 25 находим t = 1,32.
Поскольку Т < t , принимается основная гипотеза (о
равенстве средних). Таким образом, утверждение рекламы не
подтверждается имеющимися данными.
Задана 14. В партии из 500 деталей, изготовленных первым
станком-автоматом, оказалось 60 нестандартных; из 600
деталей второго станка — 42 нестандартных. На уровне значимости
а = 0,01 проверить нулевую гипотезу Я0: рх = р2 о равенстве
вероятностей изготовления нестандартной детали обоими
станками против конкурирующей гипотезы Нх\ рх *р2.
Решение. Имеем wx = 60/500 = 0,12; w2 = 42/600 = 0,07; w =
= (60 + 42)/(500 + 600) » 0,09.
I 336
Глава 15
Найдем значение статистики критерия
°9x0,91|-i- + -^-
1500 600
Найдем критическую точку из соотношения: Ф0(икр) = 0,495,
откуда икр= 2,57. Поскольку \U\ > икр, нулевая гипотеза
отвергается. Значит, вероятности изготовления нестандартных деталей
на двух станках различны.
§ 15.6. Проверка гипотез о равенстве дисперсий для
нескольких выборок. Критерии Бартлетта и Кокрена
Пусть генеральные совокупности XVXV ... Хм распределены
нормально. Из этих совокупностей извлечены независимые
выборки объемов nv nv По выборкам найдены
исправленные выборочные дисперсии 5,2,522,...,^. Требуется на уровне
значимости а проверить нулевую гипотезу о равенстве
дисперсий для всех выборок, т.е. Я0: а2 = а2 = ... =с2м (против
гипотезы, что какие-то из дисперсий не равны).
Опишем критерий Бартлетта, позволяющий проверить
такую гипотезу.
Введем обозначения: пусть к. = п. — 1 — число степеней
свободы sf\
м
к = ^2к{ - сумма чисел степеней свободы;
1 м
s2 =—^2к^ —- среднее арифметическое исправленных дис-
к /=1
персий, взвешенное по степеням свободы;
V = klns2-±ki]ns2; с = 1+-1—(?14).
3(М-1)
It?*, к)
Статистикой критерия Бартлетта является величина B-V/C.
При условии, что нулевая гипотеза верна, эта статистика
распределена примерно как хи-квадрат с М - 1 степенями
свободы. Для применения критерия необходимо, чтобы все п. > 4.
Если В < Ха;л/-1> то #о принимается, иначе отвергается.
337
ЧАСТЬ II. Математическая статистика
338
Иногда нет необходимости вычислять величину С. А
именно, если оказывается, что V < х1,м-\> то этого достаточно для
выполнения В < х1,м-\> поскольку С > 1.
В случае, когда размеры выборок одинаковы,
предпочтительнее использовать критерий Кокрена. Статистикой критерия
Кокрена является отношение максимальной исправленной
выборочной дисперсии к их сумме:
s2
Q max
~si2+522+... + 4 "
В предположении, что нулевая гипотеза верна,
распределение этой статистики зависит только от числа степеней свободы
к = п - 1 и числа выборок М.
По таблице критических точек распределения Кокрена
находят критическую точку GKp = GKp(a; к; М). Если G < <7кр, то
Я0 принимается, иначе отвергается.
Если гипотеза о равенстве дисперсий у всех выборок
принимается, то в качестве оценки этой общей дисперсии можно
использовать величину s2.
Задача 15. По четырем независимым выборкам, объемы
которых п{ = 17, п2 = 20, п3 = 15, я4= 16, извлеченным из
нормальных генеральных совокупностей, найдены исправленные
выборочные дисперсии, соответственно равные 2,5; 3,6; 4,1; 5,8.
Требуется: 1) на уровне значимости 0,05 проверить гипотезу о
равенстве дисперсий; 2) оценить генеральную дисперсию.
Решение.
1) Вычислим вначале числитель К критерия Бартлетта:
4 4
V = klns2-J2kilnsf, где * = Х>, =16 + 19 + 14 + 15 = 64.
/=i /=1
Имеем
s2 =|&5/2 =^-06х2,5 + 19хЗ,6 + 14х4,1 + 15х5,8) = 3,95.
к ;=1 64
Следовательно, V= 64 х 1пЗ,95 — (16 х 1п2,5 + 19 х 1пЗ,6 +
+ 14 xln4,l + 15 xln5,8)) * 2,79.
По таблице критических точек распределения хи-квадрат для
уровня значимости 0,05 и числа степеней свободы М — 1 =
3 находим критическую точку %2Kp = 7,8. Так как V < х2^, то
Глава 15
В = = V/C < у2, и принимаем нулевую гипотезу о равенстве
средних.
2) При условии равенства дисперсий в качестве оценки
генеральной дисперсии принимаем среднее арифметическое
исправленных дисперсий, взвешенное по числам степеней
свободы: s2 = 3,95.
Задача 16. По четырем независимым выборкам одинакового
объема п = 17 найдены исправленные выборочные дисперсии:
0,21; 0,25; 0,34; 0,40. Требуется: 1) на уровне значимости 0,05
проверить гипотезу о равенстве дисперсий; 2) оценить
генеральную дисперсию.
Решение.
1) Находим значение статистики критерия Кокрена:
0 4
G = — « 0,33.
0,21 + 0,25 + 0,34 + 0,4
По таблице критических точек распределения Кокрена по
уровню значимости 0,05, числу степеней свободы 16 и числу
выборок 4 находим <7р= 6^(0,05; 16; 4) = 0,437. Поскольку G < GKp,
нулевая гипотеза принимается.
2) При условии равенства дисперсий в качестве оценки
генеральной дисперсии принимают среднее арифметическое
исправленных дисперсий:
j2 0,21 + 0,25 + 0,34 + 0,4 = Q3
4
Задачи для самостоятельного решения
Теоретические задачи
1. Пусть случайная величина ? е N(a, а2), причем значение параметра
а известно, а дисперсия а2 неизвестна. Требуется на уровне
значимости а проверить нулевую гипотезу Но: а = а0, если
альтернативная гипотеза Н: о = at> a0. Построить критерий отношения
правдоподобия.
339
v )
{jl ЧАСТЬ II. Математическая статистика
2. Пусть имеется последовательность независимых испытаний
Бернулли с неизвестной вероятностью «успеха» р. Требуется на уровне
значимости а проверить нулевую гипотезу Но: р = ро, если
альтернативная гипотеза Нг: р = рг>ро. Построить критерий отношения
правдоподобия, используя нормальное приближение для числа успехов.
Вычислить объем выборки л, необходимый для достижения
заданных ошибок первого и второго рода аир.
3. Пусть случайная величина имеет распределение Пуассона с
параметром X. Требуется на уровне значимости а проверить нулевую
гипотезу Но: X = А.0> если альтернативная гипотеза Ht: X = Xt > А,0.
Построить критерий отношения правдоподобия, используя
нормальное приближение. Вычислить объем выборки п, необходимый
для достижения заданных ошибок первого и второго рода аир.
4. Пусть случайная величина имеет показательное распределение с
параметром X. Требуется на уровне значимости а проверить
нулевую гипотезу Но: X = Хо, если альтернативная гипотеза Wt: X = Хг>Х0.
Построить критерий отношения правдоподобия.
5. Проверяется нулевая гипотеза о том, что случайная величина
равномерно распределена на отрезке i] против гипотезы, что она
имеет нормальное распределение Л/(о, а2). Построить критерий
отношения правдоподобия в общем виде и в частном случае при
п = 2, а < я/4.
Вычислительные задачи
6. По выборке объема п = 9, извлеченной из нормальной
генеральной совокупности с известным средним квадратическим
отклонением ст = 4, на уровне значимости а = 0,05 проверяется нулевая
гипотеза Но: а = оо= 15. Требуется: 1) найти мощность критерия для
проверки гипотезы Я: а = аг = 17; 2) найти объем выборки пг, при
котором мощность критерия равна о,8.
7. По выборке объема п = 25, извлеченной из нормальной
генеральной совокупности с известным средним квадратическим
отклонением а = ю, найдено выборочное среднее, равное 18. При уровне
значимости 0,05 требуется: 1) найти критическую область для
проверки нулевой гипотезы Но: a = ao=i6 при конкурирующей гипотезе
Я: а = at > 16 и провести проверку; 2) найти мощность критерия
при аг = 20.
340
V )
Глава 15 ©
8. Крупная торговая фирма желает открыть в новом районе города
филиал. Известно, что фирма будет работать прибыльно, если
средний месячный доход жителей района превышает 300 долл. Также
известно, что среднее квадратическое отклонение дохода а
составляет 50 долл. Проводится выборочное обследование населения по
величине доходов, чтобы принять решение об открытии филиала.
1) Определите правило принятия решения, с помощью которого,
основываясь на выборке п = юо (человек) и уровне значимости
а = 0,05, можно установить, что филиал будет работать прибыльно.
2) Рассчитайте вероятность того, что при применении правила
принятия решения, полученного при ответе на вопрос п. 1, будет
совершена ошибка второго рода, если в действительности средний доход
достигает 310 долл.
3) Считая альтернативное значение генерального среднего
месячного дохода равным 320 долл., рассчитайте объем выборки, при
котором ошибка первого рода не превысит 2,5%, а ошибка второго
рода не превысит 5%.
9. Путем выборочного опроса проверяется гипотеза о том, что
стиральным порошком фирмы а пользуется 30% населения, против
гипотезы, что им пользуется только 20%. Оценить объем выборки,
необходимый для проверки гипотезы с ошибкой первого рода не
более 5% и второго рода — не более 2,5%.
ю. Выборочные испытания ю изделий показали, что их средний срок
службы составляет 950 час В предположении, что срок службы
изделия распределен показательно, проверить гипотезу о том, что
генеральное среднее составляет юоо час (против гипотезы, что оно
меньше) на уровне значимости 5%.
11. По выборке объема п = 36, извлеченной из нормальной
генеральной совокупности с известным средним квадратическим
отклонением а = 6 на уровне значимости а = 0,01 проверяется нулевая
гипотеза Но: а = ао= 15 при конкурирующей гипотезе И: а * ао.
Найти мощность двустороннего критерия проверки рассматриваемой
гипотезы для аг = 12.
12. Из нормальной генеральной совокупности извлечена выборка
объема п = 17, и по ней найдена исправленная выборочная дисперсия
s2 = 0,24. Требуется на уровне значимости 0,05 проверить нулевую
гипотезу Но: а2= а02= 0,18, приняв в качестве конкурирующей
гипотезы И: а2 > 0,18.
341
ЧАСТЬ II. Математическая статистика
13. В результате длительного хронометража времени сборки узла
различными сборщиками установлено, что дисперсия этого времени
ао2 = 2 мин2. Результаты 20 наблюдений за работой новичка
приведены в таблице (х — время сборки одного узла в минутах, середины
интервалов; п. — частота).
*1
56
58
60
62
64
п1
1
4
10
3
2
Можно ли на уровне значимости 0,05 считать, что дисперсия
затрачиваемого им времени существенно не отличается от дисперсии
времени остальных сборщиков?
14. Независимому статистику поручено проверить информацию
маркетинговой службы некоторого туристического бюро о том, что 70%
клиентов выбирают в качестве формы обслуживания
полупансион. Статистик провел опрос 150 случайно выбранных туристов, из
них полупансион предпочли 84 человека. К какому выводу
пришел статистик при проверке гипотезы Но: р = 0,7 при альтернативе
Н\ р ф 0,7 на уровне значимости критерия а = 0,05?
15. По юо независимым испытаниям найдена относительная частота
w = 0,15. На уровне значимости 0,05 проверить нулевую гипотезу
Но: р = 0,17 при конкурирующей гипотезе Нг: р * 0,17.
16. Статистику необходимо проверить экспертную оценку того, что 75%
отечественных предприятий уклоняется (частично) от уплаты налогов. По
результатам неофициального опроса руководителей предприятий 140
из 200 случайно отобранных директоров подтвердили, что используют
различные схемы для ухода от уплаты налогов. Можно ли при уровне
значимости 0,05 согласиться с приведенной экспертной оценкой?
17. Партия изделий принимается, если вероятность того, что изделие
окажется бракованным, не превышает 0,03. Среди случайно
отобранных 400 изделий оказалось 18 бракованных. Можно ли
принять партию на уровне значимости 0,05?
18. Фирма разослала юоо новых рекламных каталогов и получила 120
заказов. Можно ли утверждать (на уровне значимости 0,05), что
эффективность рекламы повысилась, если ранее она составляла в
среднем ю%?
19. Средний доход фирмы в день составлял 1020 единиц. После
реорганизации выборочный средний доход в день за 30 рабочих дней
составил 1070 единиц с выборочным средним квадратическим
отклонением (исправленным) 90 единиц. Можно ли утверждать (на
уровне значимости 0,05), что реорганизация привела к увеличению
среднего дохода?
342
Глава 15
20. Средний дневной объем продаж в магазине составлял 500 единиц.
После реорганизации выборочный средний дневной объем продаж
за 25 рабочих дней составил 520 единиц с выборочным средним
квадратическим отклонением (исправленным) 40 единиц. Можно
ли утверждать (на уровне значимости о,ю), что реорганизация
привела к увеличению среднего дохода?
21. Инвестор считает вложения в активы с дисперсией доходности
более 0,04 слишком рискованными. За последние ю лет выборочная
дисперсия (исправленная) доходности актива а составила 0,06.
Следует ли делать вложения в актив Д принимая решение на
уровне значимости 0,05?
22. Рафинированный сахар упаковывается в пакеты с номинальным
весом 1,0 кг со средним квадратическим отклонением, равным
0,01 кг. Случайная выборка п = 16 пакетов готовой продукции
выявила средней вес 1,01 кг. При уровне значимости 0,05 проверить
нулевую гипотезу о том, что средний вес пакета соответствует
номиналу.
23. Штамповочный пресс делает отверстия в металлических шайбах с
нормативным размером 4,00 мм и средним квадратическим
отклонением а = 0,20 мм. Случайная выборка п = 25 шайб показала, что
средний размер 3,88 мм. На уровне значимости о,ю проверить
нулевую гипотезу о том, что средняя величина отверстия
соответствует нормативу.
24. Среднее время сборки изделия было 90 мин. Инженер изобрел
новый метод сборки этого изделия. В результате время сборки ю
изделий новым способом составила 79, 74,112, 95, 83, 96, 77, 84,
70, 90 мин. Можно ли утверждать, что среднее время сборки
сократилось на уровне значимости 0,05?
25. В селе Сидорово проведено выборочное обследование доходов
жителей. По выборке из 16 человек получено среднее 2620 руб. и
среднее квадратическое отклонение 150 руб. Можно ли утверждать
на уровне значимости о,ю, что средний доход жителей составляет
более 2500 руб.?
26.В селе Петрово проведено выборочное обследование доходов
жителей. По выборке из 25 человек получено среднее 2380 руб. и
среднее квадратическое отклонение 90 руб. Можно ли утверждать
на уровне значимости 0,05, что средний доход жителей составляет
менее 2500 руб.?
343
{J) ЧАСТЬ II. Математическая статистика
27. В книжном магазине проведено исследование продаж детективов
писателя Горшкова «Хромой против Косого». В течение 16 рабочих
дней роман продавался ежедневно в среднем по 57 экземпляров со
средним квадратическим отклонением 12 экземпляров. Можно ли
утверждать на уровне значимости о,ю, что этот роман расходится
лучше, чем предыдущий роман автора «Хромой против Слепого»,
если тот расходился в среднем по 50 экземпляров в день?
28. В книжном магазине проведено исследование продаж
фантастического романа писателя Бурьяненко «Танцы в пустоте». В течение 25
рабочих дней роман продавался ежедневно в среднем по 64
экземпляра со средним квадратическим отклонением ю экземпляров.
Можно ли утверждать на уровне значимости 0,05, что этот роман
расходится хуже, чем предыдущий роман автора «Звездная жуть»,
если тот расходился в среднем по 70 экземпляров в день?
29. По выборке из 25 упаковок товара средний вес составил 101 г с
исправленным средним квадратическим отклонением 3 г. На уровне
значимости 0,05 проверить гипотезу о том, что генеральный
средний вес составляет юо г.
30. Партия изделий принимается, если дисперсия размеров не превышает
0,2. Исправленная выборочная дисперсия для 30 изделий оказалась
равна 0,3. Можно ли принять партию на уровне значимости 0,05?
31. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения, г:
40,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1; 49,7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Согласуются ли полученные данные с номиналом (на уровне
значимости о,ю)?
32. Старая наполняющая машина работала со средним квадратическим
отклонением веса упаковки 1,5 г. Были проведены испытания новой
машины. По выборке из 30 упаковок товара получено выборочное
среднее квадратическое отклонение о,8 г. Можно ли утверждать на
уровне значимости 0,05, что для новой машины среднее
квадратическое отклонение меньше?
33. В таблице приведены данные по годовым поступлениям в
региональные бюджеты доходов от налогообложения субъектов малого
предпринимательства (юридических лиц) до и после введения в
рассматриваемых регионах единого налога на вмененный доход,
млн руб.
Ч )
344
Глава 15
Год «до»
32
25
42
35
50
40
38
19
15
Год «после»
35
35
25
19
40
40
75
45
18
Требуется установить на уровне значимости 0,05, существенно ли
изменились объемы поступлений в региональные бюджеты в
сторону увеличения (используя нормальное приближение).
34. На двух весах в одном и том же порядке проведено взвешивание
ю проб вещества. Через х и у. обозначены результаты /-го
взвешивания, мг, на первых и вторых весах соответственно.
25
30
28
50
20
40
32
36
42
38
У1
28
31
26
52
24
36
33
35
45
40
На уровне значимости 0,01 установить, существенно ли
различаются результаты (используя нормальное приближение).
35. В таблице представлены месячные объемы продаж в денежных
единицах в магазинах фирмы до и после проведения ее
рекламной кампании.
Магазин
1
2
3
4
5
6
7
Объем продаж:
до рекламы
10
15
12
13
14
11
15
после рекламы
17
20
13
11
16
10
18
Можно ли утверждать на уровне значимости о,ю, что рекламная
кампания привела к существенному увеличению объемов продаж?
36. В таблице представлены данные о производительности труда
группы сотрудников фирмы до и после обучения на курсах повышения
квалификации.
Сотрудник
1
2
3
4
5
6
7
Производительность
труда:
до обучения
20
18
15
16
20
14
17
после обучения
26
27
20
23
19
22
28
Можно ли утверждать на уровне значимости 0,05, что обучение
привело к существенному увеличению производительности труда?
345
V )
ЧАСТЬ II. Математическая статистика
37. В таблице представлены данные о числе аварий на автомобильной
дороге по месяцам в 1983 и 1985 гг.
1983
1985
Январь
125
85
Февраль
150
80
Март
80
85
Апрель
50
40
Май
40
45
Июнь
43
40
Июль
80
42
Август
75
43
Сентябрь
80
50
Октябрь
65
36
Ноябрь
50
78
Декабрь
95
83
В 1984 г. значительные средства были вложены в увеличение
безопасности дорожного движения. Можно ли утверждать на уровне
значимости 0,05, что число аварий в результате существенно
снизилось?
38. За последние 5 лет выборочная дисперсия доходности актива А
составила 0,04, актива Б — 0,05. Есть ли основание утверждать, что
вложения в актив А менее рискованны, чем в Б? Уровень
значимости 0,05.
39. За последние 7 лет выборочная дисперсия (исправленная)
доходности актива А составила 0,05, актива Б — 0,08. Есть ли основания
утверждать (на уровне значимости 0,05), что вложения в Б более
рискованны, чем в А?
40. По выборке объема п = 50 найден средний размер диаметра
валиков, изготовленных автоматом № 1, равный 20,1 мм; по выборке
объема т = 50 найден средний размер диаметра валиков,
изготовленных автоматом № 2, равный 19,8 мм. Генеральные дисперсии
известны: стх2 = 1,750 мм2, ау2= 1,375 мм2. Требуется на уровне
значимости 0,05 проверить нулевую гипотезу Но: ах= ау при
конкурирующей гипотезе Я: ахф ау. Предполагается, что случайные величины
распределены нормально и выборки независимы.
346
v )
Глава is ®
41. По двум независимым выборкам с объемами п = ю и т = ю,
извлеченным из нормальных генеральных совокупностей, найдены
выборочные средние, равные 14,3 и 12,2 соответственно. Генеральные
дисперсии известны: ах2 = 22, ау2= 18. На уровне значимости 0,05
проверить нулевую гипотезу Но: ах= ау при конкурирующей гипотезе
Н;.ах>ау.
42. По двум независимым выборкам с объемами п = 50 и т = 50,
извлеченным из нормальных генеральных совокупностей, найдены
выборочные средние, равные 142 и 150 соответственно. Генеральные
дисперсии известны: ах2 = 28,2, с2 = 22,8. На уровне значимости
0,01 проверить нулевую гипотезу Но: ах= ау при конкурирующей
гипотезе Н: ах <
43. В таблице представлены сгруппированные данные о расходе сырья
на одно изделие для двух различных технологий изготовления.
Показатель
Старая технология
Новая технология
Расход сырья
304
307
308
303
304
306
308
Число изделий
1
4
4
2
6
4
1
В предположении, что расход сырья как при старой| так и при новой
технологии имеет нормальное распределение, выяснить, влияет ли
изменение технологии на средний расход сырья на одно изделие.
Принять а = 0,1.
44. По двум независимым выборкам с объемами п = ю и т = 8,
извлеченным из нормальных генеральных совокупностей, найдены
выборочные средние, равные 142,3 и 145,3» и исправленные
выборочные дисперсии, равные 2,7 и 3,2 соответственно. На уровне
значимости 0,1 проверить нулевую гипотезу Но: ах= ау при
конкурирующей гипотезе Н: а* ау.
45. По двум независимым выборкам с объемами пх и nyt извлеченным
из нормальных генеральных совокупностей, найдены
исправленные выборочные дисперсии sx2 и sy2. При уровне значимости а
проверить нулевую гипотезу ах2= ау2 против конкурирующей гипотезы
Hi: ах2>аЛ если:
а) пх= ю; пу= 16; sx2= 3,6; sy2= 2,4; а = 0,05;
б) пх= 13; пу= 18; s/= 0,72; sy2= 0,20; а = 0,01.
347
ф ЧАСТЬ II. Математическая статиаика
46. Для сравнения точности двух станков-автоматов взяты две пробы
(выборки), объемы которых п = ю и т = 8. В результате измерения
контролируемого размера отобранных изделий получены
следующие результаты.
x.
1,08
1,10
1,12
1,14
1,15
1,25
1,36
1,38
1,40
1,42
У,
1,11
1,12
1,18
1,22
1,33
1,35
1,36
1,38
Можно ли считать, что станки обладают одинаковой точностью, если
принять уровень значимости а = 0,1 и в качестве конкурирующей
гипотезы взять Ht: ах2* сту2?
47. Для оценки качества изделий, изготовленных двумя заводами, взяты
выборки по nt= 200 и /?2= 300 изделий. В этих выборках оказалось
соответственно mt= 20 и т2 = 15 бракованных изделий. При уровне
значимости 0,05 проверить нулевую гипотезу Но: pt = р2 о равенстве
вероятностей изготовления бракованного изделия обоими
заводами при конкурирующей гипотезе Я: рг> р2.
48. Из юо выстрелов по цели каждым из двух орудий зарегистрировано
соответственно 12 и т2 = 8 промахов. На уровне значимости 0,05
проверить нулевую гипотезу Яо: рх=Р2о равенстве вероятностей
промаха обоих орудий при конкурирующей гипотезе Я: р± р2.
49. Компания по производству сахарного песка имеет две
производственные линии для наполнения пакетов сахарным песком по i кг.
Среднее квадратическое отклонение веса пакетов, поставляемых
с первой линии, с^ = 0,02 кг, а со второй линии — а2= 0,04 кг.
С первой линии была взята случайная выборка объема п1 = ю
пакетов и найден средний вес Зс, = 1,018 кг. Подобная выборка
п2 = 12 пакетов была взята со второй линии и найден средний вес
х2 = 0,989 кг. Есть ли основание считать, что средний вес
пакетов первой и второй линий различаются? Проверить гипотезу при
уровне значимости 0,01.
50. Аудиторы компании интересуются системой обработки счетов
доходов. Они взяли случайную выборку объема /7t= 50 законченных
счетов, в которой 4 счета оказались дефектными. Тогда аудиторы
предложили некоторые модификации в процедуре и через
определенное время провели случайную выборку п2 = бо завершенных
счетов, где обнаружили 3 дефектных счета. Имеется ли основание
предполагать на уровне значимости 0,05, что новые процедуры
уменьшают ошибку?
348
V )
Глава 15
' 51. Компания «Рекс», производящая батарейки, утверждает, что в ^
среднем период службы их батареек дольше, чем батареек их
конкурента — компании «Полкан». Ассоциация потребителей взяла
случайную выборку п = ю батареек производства компании «Рекс», и,
испытав их, определила средний срок службы х = 198 час. с
исправленным средним квадратическим отклонением sx= 8,7 час. Такая же
проверка продукции компании «Полкан» для выборки объема т =
15 дала величины у = 194 и sy= 5,8 час. Подтверждают ли эти
результаты заявление компании «Рекс»? Уровень значимости — 0,1.
52. В течение юо рабочих дней магазин А посещало в среднем 198
человек в день, магазин Б — 202. Есть ли основания утверждать на
уровне значимости 0,05, что магазин Б более популярен, чем А,
если числа покупателей в день имеют дисперсии, равные 256?
53. В течение 64 дней в фирму А обращалось в среднем 87 человек в
день, в фирму Б — 93. Есть ли основания утверждать (на уровне
значимости 0,05) , что фирма Б более популярна, чем фирма А, если
числа клиентов в день имеют дисперсии 124 и 132 соответственно?
54. Для исследования качества определенного вида полимера были
сделаны выборки по ю единиц из двух серий и определен процент
вещества в каждой выборке. Для первой серии процент составил
х = 68,2% с исправленным выборочным средним квадратическим
отклонением sx = 0,70%; для второй серии у = 67,0% с
исправленным выборочным средним квадратическим отклонением sy= 0,74%.
Имеются ли основания предполагать, что две серии содержат
разный процент химического вещества? Уровень значимости — 0,1.
55. В селах Сидорово и Петрово проведены выборочные обследования
доходов жителей. По выборкам из ю человек получены следующие
результаты: в Сидорово средний доход 2620 руб., среднее
квадратическое отклонение 150 руб.; в Петрово средний доход 2380 руб.,
среднее квадратическое отклонение 90 руб. Можно ли утверждать
на уровне значимости 0,1, что в Петрово живут в среднем беднее,
чем в Сидорово?
56. В городах Сковородкино и Кастрюлино проведены выборочные
обследования доходов жителей. По выборкам из 200 человек
получены следующие результаты: в Сковородкино средний доход
5230 руб., среднее квадратическое отклонение 250 руб.; в
Кастрюлино средний доход 5180 руб., среднее квадратическое отклонение
190 руб. Можно ли утверждать на уровне значимости 0,05, что в
Сковородкино живут в среднем богаче, чем в Кастрюлино?
349
ч )
ЧАСТЬ II. Математическая статистика
57. В городах Усатово и Полосатово проведены выборочные
обследования доходов жителей. По выборкам из юо человек получены
следующие результаты: в Усатово средний доход 4050 руб., среднее
квадратическое отклонение 105 руб.; в Полосатово средний доход
3970 руб., среднее квадратическое отклонение 85 руб. Можно ли
утверждать на уровне значимости 0,05, что в Усатово живут в
среднем так же, как и в Полосатово?
58. В книжном магазине проведено исследование продаж детективов
писателя Горшкова «Хромой против Косого» и «Рябой против
Глухого». В течение ю рабочих дней первый роман продавался
ежедневно в среднем по 57 экз. со средним квадратическим
отклонением 12 экз.; второй роман — в среднем по 62 экз. со средним
квадратическим отклонением 15 экз. Можно ли утверждать на уровне
значимости 0,1, что второй роман расходится лучше первого?
59. В книжном магазине проведено исследование продаж
фантастических романов писателя Бурьяненко «Ночной досмотр» и
«Дневной просмотр». В течение 12 рабочих дней первый роман
продавался ежедневно в среднем по 70 экз. со средним
квадратическим отклонением 14 экз.; второй роман — в среднем по 63
экз. со средним квадратическим отклонением и экз. Можно ли
утверждать на уровне значимости 0,1, что второй роман
расходится хуже первого?
60. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения, г:
49.1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51.6; 49,8; 50,1; 49,7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Согласуются ли полученные данные с номиналом (на уровне
значимости 0,1)?
61. Урожайность зерновых культур в России в 1992-2001 гг.
представлена таблицей.
Год
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Урожайность,
ц/га
18,0
17,1
15,3
13,1
14,9
17,8
12,9
14,4
15,6
19,4
Можно ли утверждать, что урожайность в 1992-1996 гг. и 1997-
2001 гг. была в среднем одинаковая (на уровне значимости 0,1)?
350
Глава 15
62. Производство пшеницы в России в 1995-2002 гг. представлено
таблицей.
Год
1995
1996
1997
1998
1999
2000
2001
2002
Производство,
млн т
30,1
34,9
44,3
27,0
31,0
34,5
47,0
57,7
Можно ли утверждать, что производство пшеницы в 1992-1998 гг.
и 1999-2002 гг. было в среднем одинаковое (на уровне
значимости 0,1)?
63. Можно ли воспользоваться критерием Бартлетта для проверки
гипотезы об однородности дисперсий по выборкам объема пг = 15,
п2= 25, а?з= ю, /?4= з? Дайте пояснения.
64. По трем независимым выборкам, объемы которых пг = 9, п2 = 13,
пз = 15, извлеченным из нормальных генеральных совокупностей,
найдены исправленные выборочные дисперсии, равные 3,2; 3,8;
6,3 соответственно. Требуется: 1) на уровне значимости 0,05
проверить гипотезу о равенстве дисперсий; 2) оценить генеральную
дисперсию.
65. Требуется сравнить точность обработки изделий на каждом из трех
станков. С этой целью на первом станке было обработано 20, на
втором — 25, на третьем — 26 изделий. Отклонения X, V, 1
контролируемого размера от заданного оказались следующими (в десятых
долях миллиметра).
Отклонения для изделий первого станка
2
4
6
8
9
Частота п1
5
6
3
2
4
Отклонения для изделий второго станка
у,
1
2
3
5
7
8
12
Частота п.
2
4
4
6
3
5
1
Отклонения для изделий третьего станка
2
3
4
7
8
10
14
Частота п.
3
5
4
6
3
2
3
Можно ли считать, что станки обеспечивают одинаковую точность
на уровне значимости 0,05 (в предположении, что отклонения
распределены нормально)?
351
ЧАСТЬ 11. Математическая статистика
66. Инвестор имеет данные по доходности актива А за 5 лет, актива
Б — за 7 лет, актива В — за ю лет. Исправленные выборочные
дисперсии доходности равны 0,01; 0,02 и 0,03 соответственно. Можно
ли утверждать на уровне значимости 0,05, что риск вложений в эти
активы одинаков?
67. Инвестор имеет данные за ю лет по доходности активов А, Б, В и Г.
Исправленные выборочные дисперсии равны 0,012; 0,021; 0,025;
0,032 соответственно. Можно ли утверждать на уровне значимости
0,05, что риск вложений в эти активы одинаков?
V )
ГЛАВА 16
КРИТЕРИИ СОГЛАСИЯ
Критерии проверки гипотезы о предполагаемом виде закона
распределения случайной величины называют критериями
согласия.
Следует понимать, что проверяют не то, что случайная
величина действительно имеет определенный закон распределения
(например, нормальный), а лишь достаточно ли хорошо
наблюдаемые данные согласуются с некоторым законом
распределения, чтобы можно было использовать этот закон для
прогнозирования поведения рассматриваемой случайной величины.
Гипотезы могут быть как простыми, так и сложными.
Гипотеза называется простой, если проверяется соответствие
некоторому закону распределения с заданными параметрами.
Гипотеза называется сложной, если проверяется соответствие
некоторому закону распределения с произвольными
параметрами. В этом случае параметры оценивают по выборке.
Наиболее часто используемые критерии согласия — это
критерии Пирсона и критерии Колмогорова.
§ 16.1. Критерий согласия Пирсона
и Фишера (хи-квадрат)
Критерий согласия Пирсона (хи-квадрат) идеально
подходит для проверки гипотез в полиномиальной схеме.
Пусть проводится п независимых испытаний, каждое из
которых может иметь г различных исходов Ах, Аг,... Аг. Требуется
проверить гипотезу о том, что вероятности этих исходов равны
Рр Pv Рг> если в последовательности испытаний они
встретились тх, т2, тг раз.
12 Теория вероятностей
353
ЧАСТЬ II. Математическая статистика
^ Теорема 1 (Пирсона). Если основная гипотеза верна, то рас-
пределение статистики хи-квадрат
х2=у("*,-лл)2
при п -> оо стремится к распределению хи-квадрат с г — 1
степенями свободы.
В противном случае эта статистика стремится к
бесконечности.
Отсюда получаем критерий (применимый при больших п):
если x2<Xa,r-i, то основная гипотеза принимается, иначе
отвергается.
Проведем краткое обоснование критерия Пирсона.
Будем считать наступление события А. успехом, а его
ненаступление — неудачей.
Тогда т. — это число успехов в п испытаниях Бернулли,
т./п — относительная частота события Ар которая является
асимптотически нормальной, несмещенной и состоятельной
оценкой вероятности этого события. Поскольку М
f I'*
при больших п можно считать справедливым приближенное ра-
т, т (гг\ 1Щ тг^
венство — » р„ т.е. вектор частот — = —>—>•••>— является
п *1 п \п п п )
оценкой гипотетических вероятностей р = (р{9 pv р).
В качестве меры расхождения гипотетической и
теоретической вероятностей рассматривается сумма квадратов
отклонений
/=1
т,
Pi
где у. — веса отклонений. Например, в методе наименьших
квадратов принято у, = 1, но согласно теории ошибок Гаусса
каждое слагаемое должно входить в сумму со своей точностью.
Пирсон показал, что если положить у. = п/рр то полученная
статистика критерия будет иметь известный закон
распределения. Действительно
т,
Pi
_^ п (щ-прЛ =^(от,.-пр,У
п ) ы\ пр,
354
Глава i6 ф
т. -пр;
величина у. = ' : - также асимптотически нормальна и
у/Щ
у. g ) МО. 1). Если бы yt были независимы, то случайная вели-
г
чина х2 = имела бы предельное распределение %2Г. Однако
между случайными величинами yi для различных / существует
линейная зависимость. Действительно, поскольку
2W А л = Z—г— = -p2/w/ " "л)="г(л " л)=°'
/=1 м yjnPi у/П /=1 у/П
т. - npt
то у. = //—Г линейно зависимы, причем их связь описывает-
ся всего одним уравнением. С учетом этого факта, при п -> оо
г
случайная величина %2 = имеет распределение х2 с г — 1
степенями свободы. /=1
Если вероятности />,, />2, рг зависят от неизвестных
параметров 0,, 02, Qk, которые можно оценить по mv т2,... тг, то
их оценивают методом максимального правдоподобия,
получают соответствующие оценки pv pv рг и так же вычисляют
статистику хи-квадрат, но в этом случае ее предельное
распределение имеет уже г — к - 1 степеней свободы. Тогда, если
х2<Ха,г-*-Р, то гипотеза принимается, иначе отвергается.
Критерий хи-квадрат для простой гипотезы, т.е. в случае
известных параметров, называют также критерием хи-квадрат
Пирсона, а критерий хи-квадрат для сложной гипотезы (с
оцениванием параметров) — критерием хи-квадрат Фишера.
Критерий хи-квадрат можно применять и в более общей
схеме, для проверки распределений случайных величин. В этом
случае в качестве исходов Av Av ... 4г берут попадания
наблюдений в некоторые множества Ар ... Аг. Для дискретных
величин это могут быть отдельные значения или их объединения.
Для непрерывных величин используют обычную группировку,
т.е. подсчитывают числа попаданий в некоторые интервалы.
Если распределение не ограничено слева или справа, то
крайние интервалы продолжают до бесконечности. Если числа
попаданий в какие-то интервалы слишком малы (например,
меньше 5), то такие интервалы объединяют с соседними ин-
12*
ф ЧАСТЬ II. Математическая аатиаика
тервалами. Всего желательно иметь не менее 50 наблюдений в
выборке.
В результате есть множества А,, ... Аг, находят числа mv
mv ... тг попаданий наблюдений в эти множества и
теоретические вероятности pt = е А)9 i = 1, 2, ... г, после чего
применяют критерий хи-квадрат.
Рассмотрим более подробно следующие случаи.
I. Пусть х,, х2, ... , хп — независимые наблюдения некоторой
случайной величины х с неизвестной функцией распределения
F(x). Требуется по выборке xv xv ... , хп проверить нулевую
гипотезу о том, что генеральная совокупность имеет функцию
распределения F0(x)9 если известны значения параметров
закона распределения, т.е. имеет место простая гипотеза.
Для проверки этой гипотезы область наблюдаемых
значений хр х2, ... , хп случайной величины ? произвольным образом
разбивают на г непересекающихся областей Д., / = 1, 2, г.
Обычно это последовательность непересекающихся интервалов
и полуинтервалов вида (-оо, С,); [Ср С2); ... [С^,, +оо); С0= —оо;
С = +00.
Если справедлива основная гипотеза, т.е. случайные
величины хк имеют своей функцией распределения функцию F0(x),
то можно найти теоретические вероятности попадания
случайной величины в частичные интервалы из условия
A=/4CM^§<C/) = F0(C/)-F0(Cw)> где р, > О, 1>,=1.
Со случайными величинами xv х2, ... , хп естественно
связана полиномиальная схема с п испытаниями, в которой
результатом ?-го испытания является попадание значения хк в
какой-либо интервал. Обозначим через т. = m.(xv х2, ... , хп)
число значений среди хр х2, ... , хя, попавших в промежуток
* = [СН1,С).
По теореме Пирсона получаем, что если xv х2, хп —
выборка из генеральной совокупности с функцией распреде-
ления FQ(x)9 то статистика х2= j]—¦—^— имеет при п оо
/«I Щ
(т.е. при достаточно больших п) распределение хи-квадрат с
г - 1 степенями свободы, если основная гипотеза верна. В
противном случае статистика стремится к бесконечности. Поэтому
в качестве критической области выбирают область больших
значений.
Глава i6 0
Поскольку односторонний критерий более «жестко»
отвергает нулевую гипотезу, чем двусторонний, построим
правостороннюю критическую область, исходя из требования, что
вероятность попадания критерия в эту область в предположении
истинности нулевой гипотезы должна быть равна принятому
уровню значимости а: Р(%2> х2а^_,) = а.
Алгоритм проверки гипотезы следующий.
1. Из генеральной совокупности производят выборку
объема п (п > 50).
2. Составляют сгруппированный статистический ряд.
3. Весь диапазон наблюдаемых значений разбивают на г
частичных интервалов (в каждом из которых должно быть
минимум 5—8 наблюдений, иначе интервалы объединяются; хорошие
результаты получают при пр. > 10)
4. На основании гипотетической функции распределения
F0(x) вычисляют вероятности попадания случайной величины §
в частичные интервалы:
р = Р(СН1 < % < С) = FJLC) - F0(CM), I = 1, 2, г.
5. Умножая полученные вероятности р. на объем выборки,
получаем теоретические частоты прр т.е. частоты, которые
следует ожидать, если нулевая гипотеза справедлива.
6. Вычисляют статистику хи-квадрат: х2 = У\——•
м Щ
7. По таблице критических точек распределения хи-квадрат
по заданному уровню значимости а и числу степеней свободы
г — 1 находим критические точки х2а ^г
8. Сравнивая наблюдаемые значения критерия х2 с
критическим значением Xa,r-i, принимаем одно из двух решений:
а) если х2 > xl,r-i» то нулевая гипотеза отвергается в пользу
альтернативной, т.е. считается, что гипотетическая функция
распределения не согласуется с опытными данными;
б) если х2 < Xo,r-i» то нет основания для отклонения
нулевой гипотезы, т.е. гипотетическая функция F0(x) согласуется с
опытными данными.
II. Если значения параметров гипотетической функции
распределения F0(x) неизвестны, то имеем сложную гипотезу.
Основная гипотеза Н0 заключается в том, что функция
распределения имеет вид FQ(x) = F{x, 0,, ... , 0^) при некоторых
357 !
ЧАСТЬ II. Математическая статистика
неизвестных значениях параметров 0,, 02, ... , Qk. В этом случае
вероятности pv pv ... рх также зависят от параметров.
Выборочный критерий проверки истинности нулевой
гипотезы имеет вид
х2= ^(^-^.(9ре2,...е,))2
/-I npi(Ql,Q2,...9Qk)
При известных значениях параметров имел бы место первый
случай. Но так как истинные значения 0Р 02, 0^ неизвестны,
то, подставляя их оценки, найденные методом максимального
правдоподобия, получаем статистический критерий %2 с
меньшим числом степеней свободы, а именно v = г — к - 1, где
г — число интервалов, на которые разбит весь диапазон
наблюдаемых значений, к — число параметров гипотетической
функции распределения.
Сравнивая наблюдаемое значение критерия х2 с
критическим значением х1чГ-к-\ > по приведенной схеме делаем
заключение об истинности нулевой гипотезы: гипотеза принимается,
если х2 < Xa,r-*-i' и отвергается в противном случае.
Задача /. В следующей таблице представлены данные о
числе сделок, заключенных на фондовой бирже за квартал, для 517
инвесторов.
/
0
1
2
3
4
5
6
7
т.
112
168
130
68
32
5
1
1
В первой строке приведено число сделок, во второй — число
инвесторов, заключивших указанное число сделок за квартал.
Проверить, используя критерий Пирсона на уровне
значимости а = 0,05 число сделок, заключенных одним инвестором
за квартал, распределено по закону Пуассона с параметром X
= 1,5.
Решение. Поскольку распределение Пуассона дискретно, в
качестве различных исходов здесь можно принять сами
значения случайной величины. Заметим, что два последних
значения (6 и 7) встретились слишком мало раз, поэтому их
следует объединить с предыдущим (5). Кроме того, распределение
Пуассона не ограничено справа, и следует учесть все
значения, превышающие число 7 (которые не встретились ни разу).
358
Глава 16 ф
Таблица 16.1
1И,
пр,
mi - npi
(iw, - пр)2/(пр)
0
112
115,34
-3,34
0,10
1
168
173,04
-5,04
0,15
2
130
129,77
0,23
0,00
3
68
64,88
3,12
0,15
4
32
24,35
7,65
2,40
>5
7
9,62
-2,62
0,71
Суммируя значения в последнем столбце, получаем
значение статистики хи-квадрат (х2= 3,51).
По таблице критических точек распределения хи-квадрат при
уровне значимости а = 0,05 и числе степеней свободы г — 1 — 5
находим критическую точку х2кр = ИД. Поскольку %2 < х2кр>
можно считать, что число сделок, заключенных одним
инвестором за квартал, распределено по закону Пуассона с параметром
Х = 1,5.
Замечание. Если бы значение параметра X = 1,5 было
оценено по самой выборке, следовало бы задать число степеней
свободы г — 2 = 4. Тогда имеем х2кр = 9,5, следовательно, гипотеза
тоже принимается.
359
Таким образом, в качестве множеств А. выберем значения {0},
{1}, {2}, {3}, {4}, [5, +00). Здесь г = 6.
Найдем теоретические вероятности по формуле
распределения Пуассона:
Р($ = Л~е-\ 7 = 0,1,2,...
у!
При Л. = 1,5 получаем:
р0 = Д$ = 0) « 0,2231; />3 = ^ = 3) * 0,1255;
= ЯК = 1) « 0,3347; />4 = = 4) * 0,0471;
р2 = Я? = 2) » 0,2510; />5 = > 5) * 0,0186.
Умножим эту величину на число инвесторов п = 517 и
составим таблицу (табл. 16.1).
ЧАСТЬ II. Математическая статистика
Задача 2. В табл. 16.2 приведены сгруппированные данные
о коэффициентах соотношения заемных и собственных средств
на 100 малых предприятиях региона.
Таблица 16.2
Номер
интервала
Интервал
Середина
интервала
Число наблюдений
в интервале
1
5,05-5,15
5,1
5
2
5,15-5,25
5,2
8
3
5,25-5,35
5,3
12
4
5,35-5,45
5,4
20
5
5,45-5,55
5,5
26
6
5,55-5,65
5,6
15
7
5,65-5,75
5,7
10
8
5,75-5,85
5,8
4
На уровне значимости а = 0,05 проверить гипотезу о том, что
коэффициенты можно описать нормальным распределением.
Решение. В рассматриваемом случае параметры распределения
явно не заданы, их следует оценить по сгруппированным
данным. Находим выборочное среднее (5,46) и выборочную
дисперсию (0,03).
Теоретические вероятности оцениваем по формуле:
¦хч
/ = 1,2,...,8.
Следует продолжить крайние интервалы и положить с0 = —оо,
с8 = +оо, поскольку нормальное распределение не ограничено
с обеих сторон.
С учетом полученных значений строим таблицу (табл. 16.3).
Таблица 16.3
А/
т.
пр.
т. ~ пр.
(т. - пр)2/(пр)
<5,15
5
3,67
1,32
0,47
5,15-5,25
8
7,59
0,41
0,02
I 360
Глава 16 ф
Продолжение табл. 16.3
щ
пр.
Щ ~ пр.
(т. - пр)2/(пр)
5,25-5,35
12
15,00
-3,00
0,60
5,35-5,45
20
21,43
-1,43
0,09
5,45-5,55
26
22,14
3,86
0,67
5,55-5,65
15
16,53
-1,53
0,14
5,65-5,75
10
8,93
1,07
0,13
> 5,75
4
4,70
-0,70
0,10
Суммируя значения в последнем столбце, получаем
значение статистики хи-квадрат (х2 = 2,22).
С помощью таблицы критических точек распределения хи-
квадрат по уровню значимости а = 0,05 и числу степеней
свободы г — 1 — Л = 8 — 1 — 2 = 5 находим критическую точку
Х2кр= 11,1. Поскольку х2< Х2кр> можно считать, что
коэффициенты хорошо описываются нормальным распределением.
Замечание. В принципе здесь можно было бы объединить
крайние интервалы с соседними. Вычисления показывают, что
и в этом случае гипотеза принимается.
III. Экономисты также используют критерий х2 в качестве
критерия однородности.
Пусть имеется к > 2 независимых выборок, содержащих
соответственно я,, я2, пкнезависимых наблюдений: (хрх2,...,дс );
Гипотеза об однородности предполагает, что генеральные
совокупности, из которых извлечены выборки, одинаковы (или
все выборки произведены из одной генеральной совокупности)
и им соответствуют одинаковые функции распределения.
Наиболее часто в приложениях встречается случай, когда
к = 2. Пусть есть два ряда наблюдений некоторого признака,
и каждый ряд разбит на г групп по значениям этого признака.
Сгруппированный ряд имеет вид:
пх: тх т2 ... т{ ... тг
I- /, /2 ... /, ... /г
361 j
ф ЧАСТЬ II. Математическая статистика
Пусть т. и /. — число выборочных значений в i-й группе
соответственно для первого и второго наблюдений. Тогда
статистический критерий для проверки истинности нулевой
гипотезы принимает вид
\?
.1
"2,
и в случае истинности основной гипотезы при п -» оо он имеет
предельное распределение xVi с г — 1 степенями свободы.
Критическими точками, соответствующими уровню значимости
а, будут Ха.г-i, и проверка гипотезы проводится по общей схеме:
если %2 <х2;г_,, то нулевая гипотеза принимается, в противном
случае отвергается.
, то формулу мож-
т,
Если положить w =
1 ^+'/
и w= ——
но представить в виде, часто более удобном для практических
расчетов:
х2 = (А±п2У
(
.2 Л
1
w(l - w)
Задана 3. Распределение доходов среди рабочих и служащих
согласно шведской переписи 1930 года приведено в таблице.
С помощью критерия Пирсона проверьте гипотезу об
одинаковости распределения доходов у двух возрастных групп для
заводских мастеров и всех рабочих и служащих.
Доходы,
1000 крон
Все рабочие и служащие
в промышленности
Заводские мастера
Возрастные группы
Возрастные группы
wi
т,
/.
wi
40-50
50-60
40-50
50-60
0-1
7831
7558
0,508869
1
54
0,568000
1-2
26 740
20 685
0,563837
430
324
0,570291
2-3
35 572
24 186
0,595267
1072
894
0,545269
3-4
20 009
12 280
0,629784
1609
1202
0,572394
4-6
11 527
6776
0,629787
1178
903
0,566074
> 6
6919
4222
0,621039
158
112
0,585185
362
Глава 16 ф
Решение. Рассматривается гипотеза однородности: обе
выборки (по возрастным группам) извлечены из одной
генеральной совокупности. Статистика критерия при проверке
основной гипотезы имеет вид
:n\"2i2—„
т,
1
«2
/11,+/,
Для заводских мастеров получаем %2 = 4,27. Отсюда
X2 < Хо,о5;5 = 11,1 и можно считать, что две выборки извлечены
из одной генеральной совокупности. Но если сравнить
распределение доходов у возрастных групп всех промышленных
рабочих и служащих, то получаем у} = 840,62, что указывает
на очень высокую степень различия между распределениями.
При этом видно, что числа wi имеют тенденцию возрастать с
ростом доходов.
§ i6.2. Критерий согласия Колмогорова
Критерий согласия Колмогорова применяют для проверки
гипотез о законах распределения только непрерывных
случайных величин. Проверяем гипотезу Н0: Дх) = F0(x) против
альтернативной Нх: F{x) ф F0(x).
Критерий основан на том факте, что распределение
супремума разности между теоретической и эмпирической
функциями распределения Dn = sup|F (х) — Дх)| одинаково для любой
Дх). Величину Dn называют статистикой Колмогорова.
При малых п для статистики Колмогорова существуют
таблицы критических точек DKp. Если Dn < ?>кр, то гипотеза Я0
принимается, иначе отвергается. При больших п используют
предельное распределение Колмогорова. Имеет место следующая
теорема.
> Теорема 2 (Колмогорова)
оо
P(yfcDn < х) -> Q(x) = 1 + 2]Г(-1)* е~2кv, п -> оо.
Для распределения Колмогорова Q(x), предельного для
статистики X = 4nDn, также существуют таблицы критических
Збз I
ф ЧАСТЬ II. Математическая статистика
-O0</<00
364
точек X . Практически их используют уже при п > 20. Если
К < КР> то гипотеза Я0 принимается, иначе отвергается.
Покажем, что распределение статистики Колмогорова Dn не
зависит от вида неизвестной функции распределения Дх).
Рассмотрим преобразование t = F(t), 0 < f < 1. Можно
предположить, что F(t) — строго возрастающая функция. Тогда
существует обратное преобразование / = F~l(t'). Разность
функций распределения равна
F(ft - Fn(t) = t'- Fn{F\t')\
где Fn(F-l(f)) = число *i<F~\t') Однако из неравенства х.< F\f)
п
следует, что Дх.) < V. Пусть Дх,.) = т|. и обозначим через Ф„(г*)
выборочную функцию распределения для г)р x\v г\п.
Теоретическая функция распределения для т| следующая:
Ф(Г) = />(Л/< V) = P(F(x) < Г) = Р(х< F-*(f)) =
= F(F*(f)) =
и в силу свойств вероятности можно записать
'0, >'<0,
Ф(0 = t\ 0</'<1,
1, Г>\
Следовательно, Ф(/') является функцией распределения
равномерной случайной величины, заданной на отрезке [0, 1],
т.е. Дх;.) имеет равномерное распределение на отрезке [0, 1].
Тогда статистика
D= max | Д/) - Fit) | = max \f - FlF\f) I = max | Г - Ф(Г) \
" -ОО<Г<00 " 0</'<l " 0</'<l "
имеет ту же величину, но уже для известного (равномерного)
распределения. Таким образом доказано, что распределение
статистики Dn не зависит от вида неизвестной функции
распределения Дх).
Функция распределения Дх) может быть и разрывной, хотя
она может иметь разрывы только первого рода, являющиеся
скачками, и поэтому выборочную статистику Dn в общем случае
определяют с помощью точной верхней границы (sup):
Dn = sup [Fn(x) - F0(x)].
Глава i6 ф
Введем также статистики Dn = sup [F0(x) - Fn(x)] и
-00</<00
D+„ = sup [Fn(x) - F0(x)] тогда D = max[D„,D;}.
-00<f<00
Статистики D~, D* называют статистиками Смирнова.
На практике статистику Колмогорова можно считать по
формуле
1
D„ =max
п \<i<n
F(x
+ 2n
где x(/) — члены вариационного ряда.
Заметим, что критерий Колмогорова, строго говоря, нельзя
применять в случаях сгруппированных данных при
неизвестных параметрах распределения. Тем не менее, его иногда
применяют на практике и в подобных ситуациях. Однако при этом
статистики критерия получаются заниженными, что увеличивает
ошибку первого рода. В таких случаях предпочтительней
пользоваться критерием хи-квадрат Пирсона.
Проверка гипотезы однородности с помощью критерия
Колмогорова-Смирнова состоит в следующем. Пусть х,, х2, ... , хп и
У\$ У2> — ' Уп — выборки из двух генеральных совокупностей.
Требуется проверить нулевую гипотезу Н0 о совпадении
законов распределения генеральных совокупностей, из которых
произведены выборки.
Определим эмпирические функции распределения Ff"0 и
F^. Для проверки гипотезы вводятся статистики:
2>;Л2= sup (F}*\x)-F**\x));
-CO<jc<00
D-nih= sup (/^>(x)-/**>(*));
-00<jc<00
A,* = sup(Z>* ,/>")= sup|^>(x)-^>(4
Пусть л,, n2 -» oo, n "\"г и предельные функции Fx(x) и
F2(x) непрерывны. Тогда в условиях истинности нулевой
гипотезы статистика имеет в пределе распределение Колмо-
365
ф ЧАСТЬ II. Математическая аатистика
горова. Критической областью является область больших
значений, т.е. основная гипотеза отклоняется, если Dn ^yfc > Ха, —
критическая точка распределения Колмогорова, соответствующая
уровню значимости а.
Задана 4. Пассажир, приходящий в случайные
моменты времени на автобусную остановку, в течение пяти
поездок фиксировал время ожидания автобуса: 5,1; 3,7; 1,2; 9,2;
4,8 мин. Проверить гипотезу о том, что время ожидания
равномерно распределено на отрезке [0; 10] на уровне
значимости а = 0,05.
Решение. Составим вариационный ряд: 1,2; 3,7; 4,8; 5,1; 9,2.
С учетом того, что в данном случае F0(x) = х/10, 0 < х < 10,
построим таблицу.
I
Х(0
(2/ - 1)/(2л)
\F0(xin) - (2/ - 1)/(2л)|
1
1,2
0,12
0,1
0,02
2
3,7
0,37
0,3
0,07
3
4,8
0,48
0,5
0,02
4
5,1
0,51
0,7
0,18
5
9,2
0,92
0,9
0,02
Таким образом, значение статистики Колмогорова
составляет D5 = 0,18 + 0,1 = 0,28.
По таблице критических точек при а = 0,05 и п = 5 находим
An= 0>56. Поскольку D < D. нулевая гипотеза (о равномер-
ности распределения) принимается.
Замечание. На самом деле по таким небольшим выборкам,
конечно же, нельзя делать далеко идущие выводы.
Задача 5. Выборка из 10 наблюдений приведена в таблице.
Проверить с помощью критерия Колмогорова гипотезу о том,
что эта выборка из генеральной совокупности, равномерно
распределенной на отрезке [0, 1]. Уровень значимости а = 0,05.
j 366
Глава i6 ф
Решение. Пусть F(x) =
/
Х(0
w4
ад = ',•
ь
1
0,01
0,1
0,01
0,09
0,01
2
009
0,2
0,09
0,11
-0,01
3
0,1
0,3
0,1
0,2
-0,1
4
0,25
0,4
0,25
0,15
-0,05
5
0,33
0,5
0,33
0,17
-0,07
6
0,35
0,6
0,35
0,25
-0,15
7
0,52
0,7
0,52
0,18
-0,08
8
0,73
0,8
0,73
0,07
0,03
9
0,76
0,9
0,76
0,14
-0,04
10
0,86
1
0,86
0,14
-0,04
Из таблицы получаем DlQ = 0,25.
По заданному уровню значимости а = 0,05 находим
критическую точку DKp = 0,41. Поскольку Dl0 < Х>кр, то гипотеза
принимается.
Задача 6. В таблице приведены условные данные о
заработной плате пх = 100 и п2 = 100 служащих двух отраслей
народного хозяйства. Проверить с помощью критерия Колмогорова
гипотезу о том, что распределение заработной платы служащих
первой отрасли (Fx(x)) совпадает с распределением заработной
платы служащих второй отрасли (F2(x)). Уровень значимости а
= 0,05.
Решение.
Зарплата
i
Зарплата
Fx{xJ - F2(x(i)
130...150
4
1
1
150
0,04
0,01
0,03
150...170
4
1
2
170
0,08
0,02
0,06
170...200
15
8
3
200
0,23
0,10
0,13
200...250
51
43
4
250
0,74
0,53
0,21
250...300
22
34
5
300
0,96
0,87
0,09
300...350
3
7
6
350
0,99
0,94
0,05
350...400
1
3
7
400
1,00
0,97
0,03
400...500
—
3
8
500
1,00
1,00
0,00
367
ф ЧАСТЬ II. Математическая статистика
Используя значения эмпирических функций распределения
в правых концах интервалов, получаем данные для расчета
критических статистик. Получаем
X = Aoo,ioo>/50 = 0,21V50 «1,4849,
так как
„o=JVL = ^ = 50.
0 ц+я2 2
По таблице критических точек распределения Колмогорова
содим Хкр
отвергается.
находим А, = 1,36. Поскольку X > X. гипотеза однородности
кр кр
Задачи для самостоятельного решения
Теоретические задачи
1. В городе 17 036 семей имеют двоих детей. В 4529 семьях — два
мальчика, в 4019 — две девочки, в 8488 семьях — мальчик и
девочка. Можно ли на уровне значимости 0,05 считать, что число
мальчиков в семьях с двумя детьми имеет биномиальное распределение с
вероятностью рождения мальчика 0,515?
2. Проведено исследование посещаемости популярного интернет-
сайта. Долгое время регистрируется число людей, посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице.
Число посетителей
Часы
Число посетителей
Часы
0
57
7
139
1
203
8
45
2
383
9
27
3
525
10
10
4
532
11
4
5
408
12
1
6
273
14
1
На уровне значимости а = 0,05 проверить гипотезу, что
посещаемость сайта можно описать распределением Пуассона.
368
Глава i6
3. Проведено исследование посещаемости популярного интернет-
сайта. Долгое время регистрируется число людей, посетивших сайт
в течение данного часа. Результаты исследования представлены в
таблице.
Число посетителей
Часы
Число посетителей
Часы
0
12
7
103
1
108
8
24
2
316
9
13
3
551
10
2
4
632
И
0
5
492
12
0
6
273
14
0
На уровне значимости а = 0,05 проверить гипотезу, что
посещаемость сайта можно описать биномиальным распределением с
числом испытаний т = ю.
4. В ОТК были измерены диаметры 300 валиков из партии,
изготовленной одним станком-автоматом. Отклонения измеренных диаметров
от номинала, нм, даны в таблице.
Границы
отклонений
Середина
интервала
Число
валиков
Границы
отклонений
Середина
интервала
Число
валиков
-30...-25
-27,5
3
0...5
2,5
55
-25...-20
-22,5
8
5...10
7,5
30
-20...-15
-17,5
15
10...15
12,5
25
-15...-10
-12,5
35
15...20
17,5
14
-10...-5
-7,5
40
20...25
22,5
8
-5...0
"2,5
60
25...30
27,5
7
На уровне значимости а = 0,05 проверить гипотезу, что
отклонения диаметров от номинала можно описать нормальным
распределением.
v j
369
ф ЧАСТЬ II. Математическая статистика
5. В таблице представлены данные о числе сделок л., заключенных на
фондовой бирже за квартал, для 400 инвесторов.
X.
0
1
2
3
4
5
6
7
8
9
10
ni
146
97
73
34
23
10
6
3
4
2
2
На уровне значимости а = 0,05 проверить гипотезу о том, что число
сделок, заключенных инвестором за квартал, имеет распределение
Пуассона.
6. В таблице представлены данные о месячных доходах х., руб.,
жителей региона для юоо жителей:
*1
До 500
500... 1000
1000... 1500
1500...2000
2000...2500
Свыше
2500
"i
58
96
239
328
147
132
На уровне значимости а = 0,05 проверить гипотезу, что доходы жи
телей региона можно описать нормальным распределением.
7. В таблице представлены данные об удоях х., ц, коров на молочной
ферме за лактационный период для юо коров.
4...6
6...8
8...10
10...12
12...14
14...16
16...18
18...20
20...22
22...24
24...26
п,
1
3
6
И
15
20
14
12
10
6
2
На уровне значимости а = 0,05 проверить гипотезу, что удои коров
можно описать нормальным распределением.
8. В таблице приведены сгруппированные данные по срокам службы
х для юоо изделий:
х., час.
0-10
10-20
20-30
30-40
40-50
50-60
60-70
365
245
150
100
70
45
25
На уровне значимости а = 0,05 проверить гипотезу, что срок службы
изделия имеет показательное распределение.
370
Глава i6
9. В таблице приведены данные о числах покупок, сделанных в
магазине (в первой строке — интервалы для чисел покупок, во второй —
число покупателей, сделавших такое число покупок).
*1
1
2
3
4
5
6
7
8
ni
298
152
77
35
20
11
4
3
На уровне значимости а = 0,05 проверить гипотезу, что число
покупок для одного покупателя имеет геометрическое распределение
с параметром р = 1/2.
ю. В таблице приведены сгруппированные данные о моментах прибытия
машин к бензоколонке в течение ю час. наблюдений (с 8 до 18 час).
Интервал, час.
Число машин
8-9
12
9-10
40
10-11
22
11-12
16
12-13
28
13-14
6
14-15
11
15-16
33
16-17
18
17-18
14
На уровне значимости а = 0,01 проверить гипотезу, что моменты
прибытия машин распределены равномерно.
ii. При измерении веса 20 шоколадных батончиков (с номинальным
весом 50 г) получены следующие значения, г:
49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1; 49,7; 48,8;
51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
На уровне значимости а = 0,05 проверить гипотезу, что вес
батончиков имеет нормальное распределение со средним 50 г и
дисперсией 1 г2.
371
V )
i
ЧАСТЬ II. Математическая статистика
12. За 6 рабочих дней спрос на некоторый товар составлял: 104; 8о;
96; 120; 113; 82 кг. На уровне значимости а = 0,1 проверить гипотезу
о том, что спрос равномерно распределен на отрезке [75; 125].
13. В поселке Полтинниково все жители имеют доход не менее 50 тыс.
руб. в месяц. Выборочное обследование доходов ю человек дало
следующие результаты: 54; 6о; 59; 79; 71; 92; 53; 54; 78; 56 тыс. руб.
На уровне значимости а = 0,05 проверить гипотезу, что случайная
величина дохода имеет распределение Парето вида
fo,
F(x) =
х<х0,
1-(х/х0)~а, х>х0,
гдехо=50 тыс. руб., а = з.
14. Урожайность зерновых культур в России в 1992-2001 гг.
представлена таблицей.
Год
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Урожайность,
ц/га
18,0
17,1
15,3
13,1
14,9
17,8
12,9
14,4
15,6
19,4
Проверить на уровне значимости а = 0,1 гипотезу, что урожайность
можно описать нормальным распределением с параметрами а = 16,
а = 2 ц/га.
ГЛАВА 17
ЭЛЕМЕНТЫ АНАЛИЗА
ВРЕМЕННЫХ РЯДОВ
§ 17л. Основные понятия в анализе временных рядов
Временным рядом называется ряд наблюдений некоторой
величины, сделанных в последовательные моменты времени
(обычно через равные интервалы). В экономических
приложениях это могут быть, например, объемы производства или
продаж каких-либо товаров, колебания цен акций, курсов валют
и т.п. Данные могут регистрироваться ежегодно, ежемесячно
или ежедневно, а учитывая современные компьютерные
технологии — даже ежечасно и ежеминутно.
Основными целями анализа временных рядов является
выявление присущих им закономерностей и прогнозирование на
будущее (с учетом этих закономерностей).
Существует великое множество методов анализа временных
рядов, которым посвящена обширная литература. Эти методы
могут применяться каждый в отдельности, в различных
комбинациях и в разной последовательности. В зависимости от этого
могут получаться различные результаты. Однако для «хороших»
временных рядов они будут не очень сильно различаться между
собой.
В этой главе рассмотрим методы, не требующие углубления
в теорию и в то же время удобные для расчетов.
Предполагается, что временной ряд можно разделить на три
составляющие:
1) тренд, т.е. некая общая закономерность роста или
убывания;
373
ЧАСТЬ II. Математическая статистика
* 374
2) сезонная (циклическая) компонента;
3) случайная компонента (шум).
В качестве тренда обычно берут достаточно простую
функцию. Наиболее часто встречаются линейный и
экспоненциальный тренды. Первое означает, что величина в среднем растет
или убывает в арифметической прогрессии (на столько-то в
единицу времени), второе — что она меняется в
геометрической прогрессии (во столько-то раз или на столько-то
процентов в единицу времени). Иногда рассматривают и более
сложные тренды, например полиномиальные и другие.
Линейный тренд легко построить с помощью линейной
регрессии, применяя метод наименьших квадратов к исходным
данным. Экспоненциальный тренд можно построить, если
перейти к логарифмам наблюдаемых величин, провести
линейную регрессию для них, а затем взять экспоненту от
полученной линейной функции.
Сезонной (циклической) компоненты во временном ряду
может не быть совсем, их может быть несколько или одна.
Например, во временном ряду из ежемесячных данных, скорее
всего, будет сезонная компонента с периодом 12 (годичный
цикл). В ряду ежедневных наблюдений могут быть
компоненты с периодом 7 (неделя), около 30 (месяц) и 365 (год) и т.д.
В ежегодных наблюдениях могут присутствовать многолетние
циклы (например, экономические циклы Кондратьева).
Сезонная компонента может быть аддитивной (когда ее
амплитуда относительно «среднего» значения остается в среднем
постоянной) и мультипликативной (когда колебания
происходят пропорционально текущему «среднему», и их амплитуда
может расти или убывать со временем согласно тренду). Для
описания сезонной компоненты часто используют сезонные
индексы, показывающие, насколько (или во сколько раз)
значение в данной точке цикла отличается от некоторого «среднего»
значения.
Следует отметить, что существуют временные ряды с
ложными трендами и ложными циклами, когда закономерности,
выявленные на одном отрезке наблюдений, не подтверждаются
на других. Однако здесь такие ряды рассматривать не будем.
Общая схема анализа временного ряда обычно такова, что
выявленные в нем закономерности исключают путем
некоторых преобразований и далее изучают получившиеся величины,
Глава 17
называемые остатками, пытаясь выявить закономерности уже
в их поведении, и т.д. Так продолжают до тех пор, пока не
останутся чисто случайные колебания (независимые случайные
величины).
§ 17.2. Простые методы анализа и прогнозирования
временных рядов
Рассмотрим некоторые простые методы анализа и
прогнозирования временных радов, не требующие глубокой теории,
на примере нескольких практических задач.
Задача 1. В таблице представлены данные об урожайности,
ц/га, зерновых культур в СССР за 1951-1970 гг.
Год
Урожайность
Год
Урожайность
1951
7,4
1961
10,7
1952
8,6
1962
10,9
1953
7,8
1963
8,3
1954
7,7
1964
11,4
1955
8,4
1965
9,5
1956
9,9
1966
13,7
1957
8,4
1967
12,1
1958
ИЛ
1968
14,0
1959
10,4
1969
13,2
1960
10,9
1970
15,6
Построить линейный тренд.
Решение. Методом наименьших квадратов находим
tr(t) = 6,97 + 0,34(/-1950), где t — год наблюдения. На рис. 17.1
изображен график урожайности и линейный тренд. Видно, что
в поведении остатков (отклонений от тренда) не проявляется
какой-либо закономерности, и их можно считать чисто
случайными.
375
0 ЧАСТЬ 11. Математическая статистика
1950 1952 1954 1956 1958 1960 1962 1964 1966 1968 1970
Рис. 17.1
Задача 2. В таблице представлены данные о производстве
молока, тыс. т, в России с января 1992 г. по октябрь 1996 г.
(рис. 17.2).
Месяц/год
1992
1993
1994
1995
1996
Январь
2015
1759
1510
1172
1038
Февраль
2123
1773
1484
1226
1104
Март
2624
2361
1988
1651
1439
Апрель
2891
2649
2211
1859
1521
Май
3335
3203
2559
2392
1827
Июнь
4071
3936
3209
2864
2446
Июль
4040
3861
3204
2714
2369
Август
3392
3321
2687
2420
2081
Сентябрь
2467
2438
2031
1925
1577
Октябрь
2092
1760
1506
1338
1081
Ноябрь
1494
1299
1050
984
Декабрь
1562
1345
1054
1020
376
Урожайность зерновых культур в СССР
Глава 17 @
Производство молока в России
О 10 20 30 40 50 60
Месяц
Рис. 17.2
Построить линейный тренд, вычислить сезонные индексы
по данным 1992—1995 гг. Сделать прогноз на 1996 г. и сравнить
его с реальными данными.
Решение. Методом наименьших квадратов получаем
tr(t) = 2899,9 -26,64/, где / — номер месяца (от 1 до 24).
Производство молока имеет тенденцию к уменьшению,
обусловленную сокращением поголовья молочного скота, и
подвержено сильным сезонным колебаниям с максимумом летом
и минимумом зимой. При этом величина сезонных колебаний
пропорциональна среднему уровню производства.
Вычислим значения x(t)/tr(t), выразим их в процентах, а
затем усредним для каждого месяца за 1992—1995 гг., и таким
образом получим сезонные индексы.
Месяц/год
1992
1993
1994
1995
Сезонный индекс
(среднее)
Январь
70,13
68,88
67,59
61,22
66,96
Февраль
74,58
70,16
67,23
64,95
69,23
Март
93,05
94,43
91,16
88,71
91,84
377
^ ЧАСТЬ II. Математическая статистика
Продолжение табл. 17.1
Месяц/год
1992
1993
1994
1995
Сезонный индекс
(среднее)
Апрель
103,50
107,09
102,64
101,34
103,64
Май
120,54
130,89
120,29
132,32
126,01
Июнь
148,57
162,62
152,75
160,80
156,18
Июль
148,89
161,29
154,47
154,69
154,83
Август
126,25
140,30
131,23
140,06
134,46
Сентябрь
92,74
104,17
100,50
113,16
102,64
Октябрь
79,44
76,06
75,52
79,90
77,73
Ноябрь
57,31
56,79
53,37
59,71
56,80
Декабрь
60,54
59,49
54,30
62,91
59,31
Теперь, чтобы построить прогноз для какого-либо
месяца последующих лет, надо умножить значение, получаемое из
тренда, на соответствующий сезонный индекс. Для 1996 г.
получаем таблицу (результаты округлены до целых).
Месяц
Тренд на 1996 г.
Прогноз на 1996 г.
Реальные данные
Январь
1595
1068
1038
Февраль
1568
1085
1104
Март
1541
1415
1439
Апрель
1515
1569
1521
Май
1488
1875
1827
Июнь
1461
2282
2446
Июль
1435
2221
2369
Август
1408
1893
2081
Сентябрь
1381
1418
1577
Октябрь
1355
1053
1081
Видно хорошее согласие прогноза с реальными данными в
первые 5 месяцев — относительная погрешность не превышает
3%. В последующие 4 месяца прогноз ниже реальных данных
на 6-10%. Относительная ошибка за октябрь не превышает 3%.
Заметим, что наибольшие различия прогноза с реальными дан-
378
Глава 17
ными наблюдаются в летние месяцы, сезонный индекс которых
подвержен наибольшим колебаниям. Эти колебания из года в
год имеют порядок 10-20%. С учетом этого можно признать в
целом хорошее согласие прогноза с реальными данными.
Задача 3. Годовые прибыли фирмы, тыс. долл., за 5 лет
представлены в таблице.
Год
1-й
2-й
3-й
4-й
5-й
Прибыль
99
112
120
135
144
Построить экспоненциальный тренд и сделать прогноз на
следующий год.
Решение. Построим временной ряд из логарифмов y(t) =
= In x(t):
Год, /
1-й
2-й
3-й
4-й
5-й
y(t)
4,60
4,72
4,79
4,91
4,97
Проведя линейную регрессию, получаем линейный тренд:
= 4,52+ 0,09/.
Возвращаясь к исходным величинам, получаем
/гх(/) = ехр(4,52 + 0,09/).
В качестве прогноза на следующий год имеем trx(6)& 157,6,
тыс. долл.
§ 17.3. Стационарность. Автокорреляция.
Периодограмма
Временной ряд можно рассматривать как
последовательность наблюдений некоторого случайного процесса X(t), t > 0,
в целочисленные моменты времени.
Случайный процесс X(t) называется стационарным в узком
смысле, если для любого s > 0 и любых 0 < /, < t2 < ... < tn
распределение многомерного вектора (Д/,), Д/2), X(tn))
совпадает с распределением вектора (Д/. + s), X(t2+ s), X(tn+ s)).
Таким образом, стационарный в узком смысле случайный
процесс ведет себя с любого момента так же (в статистиче-
379 |
ЧАСТЬ II. Математическая аатистика
ском смысле), как и с начала. Однако проверить это условие
на практике бывает затруднительно.
Определим характеристики случайного процесса: функцию
математического ожидания m(t) = MX(t) и ковариационную
функцию B{U s) = соу(д/), X(s)), и s > 0.
Отсюда можем выразить дисперсию DX(t) = B(t, t) и среднее
квадратическое отклонение o(t) = ^[ШЩ = ^[Щi).
Корреляционной функцией называется
R{U s) = B(t, s)/(a(t) х а(5)).
Случайный процесс X{t) называется стационарным в широком
смысле, если для него m(t) = const и B(tx + s, t2 + s) = B(tv t2)
для любых tx 2, s > 0. Это условие уже проще проверить
статистическими методами. Из него также следует, что R(tx + s, t2 + s) =
= /?(/,, t2) для любых txv s > 0.
Автокорреляционной функцией стационарного случайного
процесса называется функция r(t) = R(s, s + t), где s > 0 — любое.
Пример 1. Пусть Ar(/) = c^cos(w/ + 9), где w > 0 — число,
? е 7V(0, 1), а ф равномерно распределено от 0 до 2л, и эти
случайные величины независимы. Данный процесс стационарен
как в широком, так и в узком смысле, причем r(t) = cos(Mtf).
Действительно, поскольку Щ = 0 и Щ2 = 1, то m{t) = 0 и
B(tx , >2) = MX(tx )X(t2) = M&2 cos(wtx + <|>)cos(w/2 +ф)} =
2л
= fcos(w/, +w)cos(w/2 +u)— =
2n
12n du
= - J{cos(w(f, -/2))+cos(w(^ + t2)+2u)^ =
0
2it
= ^cos(w(>, -/2))+-Uin(w(f, +/2)+2m)|
2 4л
= ^cos(w(/,-f2)),
так что + s, t2 + 5) = 2?(/p /2) для любых 2, 5 > 0. Кроме
того, a(r) = v5(/,0 = l/V2 и Д(>р f2) = 2?(fp /2) = cos(w(^ - /2)),
откуда следует г(/) = cos(w/).
В случае временных рядов имеем дело с
автокорреляционной функцией от целых чисел, т.е. г(к). Ее можно оценить
статистически следующим образом.
380
Глава 17
Выборочной автокорреляционной функцией называют
п-к
?(*,-*)(*,+*-*)
г(к) = ^-п .
х><-*>2
/=1
Этой формулой имеет смысл пользоваться только при
достаточно больших размерах п (не менее 50). Отметим, что
точность приближения снижается с ростом к, поэтому на
практике обычно ограничиваются изучением ограниченного числа
первых значений г(к) (как правило, не более л/4). Кроме того,
полученная оценка оказывается смещенной (со смещением
порядка 1/я).
График выборочной автокорреляционной функции
называют коррелограммой.
Построение коррелограммы для реальных временных рядов
может давать различные результаты.
Если все значения выборочной автокорреляционной
функции достаточно велики и испытывают слабую тенденцию к
убыванию, это может свидетельствовать о наличии тренда (или
общей нестационарности ряда).
Если после удаления тренда и анализа остатков получаем
коррелограмму, похожую на график периодической функции,
это может свидетельствовать о наличии одной сезонной
(циклической) компоненты с соответствующим периодом.
Если после удаления тренда и сезонной компоненты корре-
лограмма имеет хаотический характер, причем значения
выборочной автокорреляционной функции малы и попадают (все или
почти все) в 95%-ный доверительный интервал -l/w±2/Vw , это
свидетельствует о том, что остатки можно считать за «белый
шум» (последовательность независимых одинаково
распределенных случайных величин).
Некоторые другие случаи поведения коррелограмм будут
рассмотрены в следующем параграфе.
Бывают ситуации, когда временные ряды содержат
несколько циклических компонент с разными периодами, которые
накладываются одна на другую и создают сложную картину. Для
их анализа можно применить следующий метод, предложенный
А. Шустером в 1898 г. Введем функции
381
@ ЧАСТЬ II. Математическая аатиаика
382
A(X) = -Yxkcos—9 *<X) = -V>4sin—, 52(*) = Л) + 2?2(Х).
/itr| X nf^i X
График функции S*(X) называют периодограммой.
Построенная функция должна принимать большие
значения (иметь локальные максимумы — пики) для тех
значений X, которые являются периодами имеющихся у временного
ряда циклических составляющих. На практике, в силу наличия
случайности временного ряда, это не всегда так, и некоторые
максимумы могут не иметь отношения к реальным периодам.
Поэтому к анализу периодограммы следует подходить с
осторожностью. В настоящее время разработаны также другие,
более точные и более сложные методы.
§ 17.4. Модели авторегрессии и скользящего среднего
До сих пор предполагалось, что случайная компонента
временного ряда представляет собой «белый шум»
(последовательность независимых одинаково распределенных случайных
величин). Однако на практике это может оказаться не так, и
величины могут быть зависимы. Эта зависимость может
возникать и в результате каких-то преобразований ряда, что также
необходимо учитывать. Для описания этих явлений
используются, в частности, следующие модели.
Процессом скользящего среднего порядка р называется
процесс вида
ВД=^+е^_1+...+ед,_,,
где 0^ — некоторые коэффициенты, а \к образуют
последовательность независимых одинаково распределенных случайных
величин. Определенный таким образом процесс всегда является
стационарным.
В коррелограмме процесса скользящего среднего
достаточно велики только значения г(к) при к от 1 до р (те, для
которых коэффициенты вк отличны от нуля), а остальные малы и
хаотичны.
Процессом авторегрессии порядка q называется процесс
вида
Глава 17
где ук — некоторые коэффициенты, а %к образуют
последовательность независимых одинаково распределенных случайных
величин. Такой процесс является стационарным только при
дополнительном условии: все корни характеристического
уравнения
Хр =q>1A/-1+~- + Ф,
должны быть по модулю меньше единицы.
Коррелограмма процесса авторегрессии имеет вид
экспоненциального убывания или затухающих колебаний (при р > 1).
В простейшем случае, при р = 1, автокорреляционная
функция представляет собой просто геометрическую прогрессию:
r(*) = <pf.
Как правило, рассматриваются процессы скользящего
среднего и авторегрессии небольших порядков (первого или
второго).
В случае, когда применяется модель авторегрессии первого
порядка, т.е.
X(k) = ^X(k-m^k9
можно также провести линейную регрессию Х(к) по Х(к - 1).
Пример 2. Временной ряд описывает значения выхода 70
последовательный партий продукта в химическом
производственном процессе (данные расположены по столбцам).
47
71
51
50
48
38
68
64
35
57
71
55
59
38
23
57
50
56
45
55
50
71
40
60
74
57
41
60
38
58
45
50
50
53
39
64
44
57
58
62
49
59
55
80
50
45
44
34
40
41
55
45
54
64
35
57
59
37
25
36
43
54
54
48
74
59
54
52
45
23
383
^ ЧАСТЬ II. Математическая статистика
384
Выборочное среднее значение выхода продукции составляет
51,13 единицы, а выборочное среднее квадратическое
отклонение — 11,91 единицы. Тренд и циклические компоненты
отсутствуют.
Видно, что в ряду имеется отчетливая тенденция к
чередованию «вверх-вниз», однако невозможно предсказать точно
выход следующей партии. Проведем линейную регрессию Х(к)
по Х(к - 1). Результат представлен на рис. 17.3.
90
80
70
60
50
40
30
20
20 30 40 50 60 70 80 90
Х(/с-1)
Рис. 17.3
В качестве оценки коэффициента <р, (как автокорреляции)
получаем ср, « -0,4. Подобная отрицательная зависимость часто
наблюдается в данных о выпуске продукции и является
следствием эффекта «переноса». В данном примере высокий выход
цикла производства приводил к получению дегтярных остатков,
которые не полностью устранялись из емкости и отрицательно
влияли на выход следующего цикла.
Глава 17 0
Задачи для самостоятельного решения
1. В таблице представлены данные по объемам продаж, тыс. руб., товаров
на оптовом рынке Кировской области за 2002-2003 гг. (рис. 17.4).
Месяц
Год
2002
2003
Январь
2174
3174
Февраль
2078
3570
Март
2608
3788
Апрель
2701
3694
Май
2834
3421
Июнь
2852
3522
Июль
2840
4056
Август
3033
4338
Сентябрь
2895
4312
Октябрь
3244
4693
Ноябрь
3133
4621
Декабрь
3126
4746
Построить тренд: а) линейный; б) экспоненциальный. Сделать
прогноз на 2004 год.
v j
Оптовый рынок Кировской области
О 2 4 6 8 10 12 14 16 18 20 22 24
Месяц
Рис. 17.4
13 Теория вероятностей
ЧАСТЬ II. Математическая статистика
2. В таблице представлены данные по продажам, руб. в день,
мороженого «Пломбир» фирмой в Нижнем Новгороде за два года
(рис. 17.5.)
Месяц
Объем продаж
Месяц
Объем продаж
Июль
8174,40
Июль
8991,84
Август
5078,33
Август
5586,16
Сентябрь
4507,20
Сентябрь
4957,92
Октябрь
2257,19
Октябрь
2482,91
Ноябрь
3400,69
Ноябрь
3740,76
Декабрь
2968,71
Декабрь
3265,58
Январь
2147,14
Январь
2361,85
Февраль
1325,56
Февраль
1458,12
Март
2290,95
Март
2520,05
Апрель
2953,34
Апрель
3248,67
Май
4216,28
Май
4637,91
Июнь
8227,57
Июнь
9050,33
Построить экспоненциальный тренд и вычислить сезонные
индексы. Сделать прогноз на следующий год.
Продажи мороженого «Пломбир»
8 10 12 14 16 18 20 22 24 26
Месяц
Рис. 17.5
386
Глава 17 ф
3. В таблице представлены данные по розничной торговле бензином,
млн долл., в США в 1991-1995 гг. (рис. 17.6).
Месяц
1991
1992
1993
1994
1995
Январь
11 297
10 508
10 839
10 966
11 981
Февраль
10 064
10 071
10 498
10 652
11 443
Март
10 883
10 725
11 476
И 800
12 790
Апрель
11 052
10 885
11 684
11 842
12 701
Май
11 960
11 836
12 346
12 491
13 937
Июнь
11 846
11 874
12 291
12 835
14 210
Июль
12 091
12 225
12 638
13 207
14 013
Август
12 406
12 218
12 418
13 710
14 186
Сентябрь
11 350
11 569
11 679
12 854
13 213
Октябрь
11 678
12 002
12 237
12 983
13 190
Ноябрь
11 360
11 418
11 806
12 647
12 650
Декабрь
11 308
11 619
11 785
12 880
12 931
Построить линейный тренд и вычислить сезонные индексы.
Розничная продажа бензина в США
Рис. 17.6
13*
387
ф ЧАСТЬ II. Математическая статистика
4. В таблице представлены данные по месячным перевозкам, тыс.
человек, пассажиров на международных авиалиниях в 1954-1958
гг. (рис. 17.7).
Месяц
1954
1955
1956
1957
1958
Январь
204
242
284
315
340
Февраль
188
233
277
301
318
Март
235
267
317
356
362
Апрель
227
269
313
348
348
Май
234
270
318
355
363
Июнь
264
315
374
422
435
Июль
302
364
413
465
491
Август
293
347
405
467
505
Сентябрь
259
312
355
404
404
Октябрь
229
274
306
347
359
Ноябрь
203
237
271
305
310
Декабрь
229
278
306
336
337
Построить экспоненциальный тренд и вычислить сезонные индексы.
Перевозки пассажиров на международных авиалиниях
Месяц
Рис. 17.7
V j
I 388
Глава 17 ?
( ^
5. В таблице представлены данные о производстве электроэнергии
в России за 1998-2003 гг.
Год
1998
1999
2000
2001
2002
2003
Производство,
млрд кВт-ч
827
846
878
891
891
915
Построить тренд: а) линейный; б) экспоненциальный. Сделать
прогноз на 2004 г.
ГЛАВА 18
ЭЛЕМЕНТЫ ЛИНЕЙНОГО
РЕГРЕССИОННОГО
И КОРРЕЛЯЦИОННОГО
АНАЛИЗА
§ i8.i. Функциональная, статистическая
и корреляционная зависимости
Для описания, анализа и прогнозирования явлений и
процессов в экономике применяют математические модели в
форме уравнений или функций. Модели экономического объекта,
отражая основные его свойства и абстрагируясь от
второстепенных, позволяют судить о его поведении в определенных
условиях.
Одной из основных задач математической статистики
является исследование зависимости между двумя или несколькими
переменными. Две переменные X и Y могут быть
независимыми или связанными функциональной либо статистической
зависимостью. Строгая функциональная зависимость
реализуется редко, так как хотя бы одна из переменных подвержена
случайным факторам.
Статистической зависимостью называется такая зависимость,
при которой изменение одной из величин влечет за собой
изменение распределения другой.
Если при изменении одной из величин изменяется среднее
значение другой, то в этом случае статистическая зависимость
| 390
I
Глава i8 0
является корреляционной. Корреляционной зависимостью между
двумя переменными величинами называется функциональная
зависимость между значениями одной из них и условным
математическим ожиданием другой.
Основная цель изучения зависимостей между случайными
величинами заключается в прогнозировании с данной
вероятностью области значений одной случайной величины на
основании наблюдаемых значений другой случайной величины.
На практике при исследовании зависимости между
случайными величинами X и Y часто ограничиваются
исследованием зависимости между X и условным математическим
ожиданием Y.
Напомним, что зависимости такого рода называются
регрессионными зависимостями. Функцию
<p(x) = *]yp(y\x)dy = M(Y\X = x)
-00
называют функцией регрессии первого рода (или модельной
функцией регрессии) Yno X, а ее график — линией регрессии Y
на *(см. § 7.4).
Аналогично функцию
<p(y) = *]xp(x\y)dx = M(X\Y = y)
-СО
называют функцией регрессии X по Y
Например, уравнение регрессии У по X двумерной
случайной величины (X, У), распределенной по нормальному закону,
имеет вид
ф) = ау+г^-(х-ах),
т.е. функция является линейной и график ее имеет вид
прямой линии, проходящей через центр распределения С(ах, ау).
Аналогично линией регрессии X по Y будет прямая
Ф) = ах+г?±(у-а).
Уравнение регрессии У = ц>(х) делает возможными точечные
предсказания значений условных математических ожиданий
составляющей Y двумерной случайной величины (X, Y) по зна-
391
ф ЧАСТЬ II. Математическая статистика
чению составляющей X = х. Однако для такого прогноза
необходимо знать закон распределения двумерной случайной
величины (X, У)> который на практике, как правило, неизвестен.
Поэтому исследование зависимости случайной величины
от ряда неслучайных и случайных величин приводит к
моделям регрессии на базе выборочных данных. В качестве оценок
условных математических ожиданий принимаются условные
средние, которые находятся по данным выборки (х/5 у), i = 1,
2, п объема п.
Условным средним ^называется среднее арифметическое
наблюдавшихся значений у, соответствующих значению X = х.
Например, если при х = 2 величина у принимает значения
5 + 6 + 10 + 8 = 29
4 " 4 "
ух = 5, у2 = 6, уъ = 10, уА = 8, тогда ух =
Условным средним ху называется среднее арифметическое
наблюдавшихся значений X, соответствующих Y = у.
Если результаты выборки представить в виде точек (х., у),
/=1,2, п в декартовой системе координат, то получим
точечную диаграмму, называемую корреляционном полем (рис. 18.1.).
Рис. i8.i
• М(У|Х = х)
1 х
Оценку функции регрессии называют эмпирической
регрессией, или функцией регрессии второго рода. Поскольку
функции регрессии обладают свойством минимальности, т.е. среднее
квадратическое отклонение случайной величины Y от функции
ф(х) является наименьшим, то для нахождения эмпирических
уравнений регрессии )> = ф(х, а, с) применяется метод
наименьших квадратов (см. § 13.3).
Регрессионный анализ — это анализ функций регрессии
первого и второго рода. Перед проведением регрессионного
анализа необходимо по статистическим данным выбрать
общий вид эмпирической функции регрессии. На практике ча-
392
Глава 18 ф
сто считают, что функция регрессии — это линейная
функция: у = Ьх + а9 где к = р — коэффициент регрессии у по х.
Проверка этой гипотезы основывается на результатах оценки
коэффициента корреляции.
Если установлено, что зависимость между некоторыми
наблюдаемыми величинами существует, то на практике важно
знать, какая она: сильная или слабая, положительная или
отрицательная. Для выяснения этих обстоятельств используется
корреляционный анализ.
Корреляционный анализ — это анализ оценок
коэффициента корреляции. Он позволяет ответить на вопрос: существует
ли линейная функциональная зависимость между случайными
величинами Хи Y9 и позволяет измерить степень близости
статистической зависимости к функциональной.
§ 18.2. Регрессионные модели
как инструмент анализа и прогнозирования
экономических явлений
В случае применения регрессионных моделей результат
действия экономической системы или объекта в виде одного
или нескольких выходных показателей можно представить как
функцию влияющих на него факторов. Некоторые из них
оказывают существенное влияние на результат, другие — весьма
незначительное. Как правило, существенных факторов мало,
в то время как несущественных — достаточно много, поэтому
пренебрегать полностью ими нельзя.
К числу основных факторов при изучении экономического
объекта обычно относятся настоящий труд (или трудовые
ресурсы) и прошлый труд (энергия, сырье, материалы, оборудование,
здания, сооружения и т.д.). Вместе с тем труд прилагается при
определенном состоянии внешней среды, т.е. при определенных
экономических и природных условиях. Поэтому
соответствующие факторы также должны найти отражение в модели.
В процессе производства и распределения продукции
имеют место массовые многократно повторяющиеся события.
Несмотря на развитие экономики и ее отдельных частей, на
протяжении относительно небольших временных периодов и
в пределах отдельных экономических подсистем имеет место
стабильность в условиях совершения массовых событий. Так,
393
^ ЧАСТЬ II. Математическая статистика
394
прежде всего в процессе прогнозирования подразумевается
возможность многократного повторения производственной
ситуации, при наличии других существенных и несущественных
факторов, однако при относительно стабильном комплексе
внешних условий.
Таким образом, приходим к следующей
теоретико-вероятностной схеме. Результирующий показатель у является
функцией существенных (хр х2, хк) и несущественных факторов
(в,, е2, ея): у = F{x{9 хк, б,, ея).
Несмотря на инертность поведения экономических систем,
особенно больших, возможно их резкое изменение в связи с
достижениями научно-технического прогресса. В новых
условиях, вообще говоря, следует рассматривать другую функцию.
Однако исходя из предположения эволюторности поведения
экономической системы на относительно небольшом
временном интервале и при сравнительно малых изменениях
переменных, в принципе, с помощью полиномов можно с высокой
степенью приближения описать любую эволюторную функцию.
В случае же невозможности линеаризировать функцию
(разлагая в ряд или преобразуя ее) при небольшом числе
коэффициентов используют методы нелинейного оценивания.
Линейная регрессия двух переменных и ее различные
экономические приложения более подробно разобраны в §13.3.
§ 18.3. Выборочные коэффициенты корреляции
и их применение
Основными характеристиками, описывающими степень
связи между составляющими Хи К двумерной случайной величины
(X, У), являются ковариация cov(*, Y) = \хху = М(X-ах)(Y-ау) и
коэффициент корреляции р = ^ , который является мерой
а а
х у
линейной зависимости между X и Y
Так как в случае статистических данных закон
распределения двумерной случайной величины неизвестен, для оценки
тесноты связи применяется эмпирическая (или выборочная)
1 я _ _
ковариация vxy=-Y.(xi-x)(yi-y) и эмпирический (или выбо-
рочный) коэффициент корреляции.
Глава 18 ф
Выборочным коэффициентом корреляции для выборки вида
(*р У{)> (*2> У^ • •> У г) называется выборочная
характеристика
п
YjLx,-x){y,-y)
г= ,
V /=1 /=1
Выборочный коэффициент корреляции может принимать
значения от -1 до +1. Он сходится к теоретическому
коэффициенту корреляции соответствующих случайных величин, если
тот существует. По абсолютной величине и знаку
коэффициента можно судить о степени зависимости (сильная или слабая) и
характере (положительная или отрицательная).
Выборочный коэффициент корреляции обычно
используется в предположении нормального закона распределения
данных (нормальность данных). Как известно, в этом случае из
равенства нулю теоретического коэффициента р следует
независимость случайных величин (в более общем случае это
неверно). В случае нормального распределения можно проверить
гипотезу р = 0. Пусть
Если гипотеза р = 0 верна, то Т имеет распределение
Стьюдента с п — 2 степенями свободы. При уровне
значимости а выберем критическую точку / = /кр(а; п — 2) для
двусторонней области. Если 171 < / , гипотеза р = 0 принимается,
иначе — отвергается.
В случае, когда нормальность данных нарушается,
применение выборочного коэффициента корреляции может вести к
ошибкам: либо «не заметим» зависимость между величинами,
либо получим ложную корреляцию. Существуют
коэффициенты и методы, свободные от предположения о
нормальности.
Наблюдения всегда можно упорядочить по возрастанию
какой-либо переменной (х или у). Рангом наблюдения
называется его номер в таком ряду. Если какое-то значение
переменной встречается несколько раз, ему приписывается средний
395
4J| ЧАСТЬ И. Математическая статистика
ранг. Обозначим ранги наблюдений по возрастанию хи у через
г.и ^.соответственно. Пусть
/=1
Выборочным коэффициентом ранговой корреляции Спирмена
называется величина
Этот коэффициент также может принимать значения от —1
до +1. Аналогичным образом он отражает силу и характер
зависимости между величинами. Для проверки гипотезы о
независимости случайных величин существуют специальные таблицы
критических точек. Однако при больших п можно проверять
гипотезу так же, как для обычного выборочного коэффициента
корреляции.
Заметим, что с помощью коэффициента Спирмена можно
анализировать и ситуации, когда некоторый признак объекта
(«качество», «привлекательность» и т.п.) нельзя строго выразить
численно, но можно упорядочить объекты по его возрастанию
или убыванию, т.е. проранжировать их.
Задача 1. В табл. 18.1 представлены средние цены (руб.), на
растительное масло и сахар-песок в 12 городах Центрального
района России на июнь 1996 г. (рис. 18.4).
Таблица 18.1
Город
Цена на масло
Цена на сахар
Брянск
7726
3410
Владимир
7880
3183
Иваново
6182
3209
Калуга
8237
3400
Кострома
8750
3600
Москва
11 024
4418
Орел
8456
3634
Рязань
9172
4033
Смоленск
8320
3909
! 396
i
Глава 18 ф
Продолжение табл. 18.1
Город
Цена на масло
Цена на сахар
Тверь
7083
3416
Тула
8259
3486
Ярославль
7991
3938
4600
4400
4200
4000
3800
3600
3400
3200
3000
Цены на масло и сахар
в городах Центральной России
о
•Чэ о -»¦ -о-
5000 6000 7000 8000 9000 10000 11000
Цены на масло, руб.
Рис. 18.4
Вычислить выборочный коэффициент корреляции между
ценами на растительное масло и сахар. Проверить нулевую
гипотезу на уровне значимости а = 0,1.
Решение. Выборочный коэффициент корреляции г = 0,82.
Имеем Г = -^Е^*4,53, в то время как / (0,1; 10) = 1,81.
Vl-0,822 Р
Таким образом, нулевая гипотеза отвергается. Связь между
ценами на растительное масло и сахар оказывается довольно
сильной и положительной.
Задача 2. Два эксперта проранжировали 11 фирм в порядке
их привлекательности для инвестиций. Получены следующие
последовательности рангов фирм.
1
1
2
3
4
5
6
7
8
9
10
11
si
1
2
3
5
4
9
8
11
6
7
10
397
ф ЧАСТЬ II. Математическая статистика
Задачи для самостоятельного решения
1. В таблл8.2 представлены средние цены, руб., на растительное
масло, сахар-песок, говядину и белый хлеб высшего сорта в 12 городах
Центрального района России на июнь 1996 г.
Таблица 18.2
Город
Цена
на масло
Цена
на сахар
Цена
на говядину
Цена
на хлеб
Брянск
7726
3410
12 500
4875
Владимир
7880
3183
13 857
7125
Иваново
6182
3209
14 150
4998
Калуга
8237
3400
12 697
5170
Кострома
8750
3600
13 000
5476
Москва
11 024
4418
14 120
6466
Орел
8456
3634
10 678
4200
Рязань
9172
4033
12 163
4720
Смоленск
8320
3909
12 833
4354
Тверь
7083
3416
14 400
5440
Тула
8259
3486
12 083
5140
Ярославль
7991
3938
14 397
5283
V j
398
Проверить с помощью коэффициента Спирмена, насколько
согласуются мнения экспертов. Проверить нулевую гипотезу на
уровне значимости а = 0,05.
Решение. Вычисляем 5= 12 + 12 + 32 + 12 + 32 + 32 + 32 + 12 =
= 40, отсюда гд =1- в'*^«0,82. Для проверки нулевой гипо-
0 82\/9
тезы вычисляем Т= ' у =г«4,29 и /кп(0,05; 9) = 2,26, поэто-
Vl-0,822 Р
му нулевая гипотеза отвергается. Мнения экспертов достаточно
хорошо согласуются между собой.
Глава i8
Вычислить выборочные коэффициенты корреляции между
ценами на:
а) масло и говядину;
б) масло и хлеб;
в) сахар и говядину;
г) сахар и хлеб;
д) говядину и хлеб.
В каждом случае проверить нулевую гипотезу на уровне значимости
0,05. Сделать вывод о зависимости цен.
2. Решить предыдущую задачу, вычислив выборочные коэффициенты
ранговой корреляции Спирмена для цен на товары.
3. Два эксперта проранжировали 9 проектов реорганизации фирмы
по их предполагаемой эффективности. Получены следующие
последовательности рангов.
1
2
3
4
5
6
7
8
9
si
4
1
5
3
2
6
9
8
7
Проверить с помощью коэффициента Спирмена, насколько
согласуются мнения экспертов. Проверить нулевую гипотезу на уровне
значимости а = 0,1.
4. В таблице представлены данные о производстве всех зерновых
культур и производстве пшеницы в России за 1996-2002 гг.
Год
1996
1997
1998
1999
2000
2001
2002
Производство
зерновых, млн т
69,3
88,6
47,9
54,7
65,5
85,2
86,6
Производство
пшеницы, млн т
34,9
44,3
27,0
31,0
34,5
47,0
57,7
Вычислить выборочный коэффициент корреляции и выборочный
коэффициент ранговой корреляции Спирмена между
показателями.
399
ЧАСТЬ 11. Математическая статистика
5. В табл. 18.3 представлены данные о годовых доходах и расходах,
долл., на личное потребление для ю семей.
Таблица 18.3
Годовой ДОХОД
Расходы на личное потребление
2508
2406
2572
2464
2408
2336
2522
2281
2700
2641
2531
2385
2390
2297
2595
2416
2524
2460
2685
2448
Вычислить выборочный коэффициент корреляции и выборочный
коэффициент ранговой корреляции Спирмена между
показателями.
ГЛАВА 19
ЭЛЕМЕНТЫ
ДИСПЕРСИОННОГО
АНАЛИЗА
Предположим, что имеется к выборок с объемами nvnv ... пк,
N = пх + п2 + ... + пк, и наблюдения можно представить в виде
х.. = dj + е., где / - номер наблюдения в выборке; у - номер
выборки; а.} - групповые математические ожидания; г.. —
случайные ошибки с Мг..= О, о которых предполагается, что они
независимы и одинаково распределены.
Подобная ситуация возникает, когда существует некий
фактор, принимающий к различных значений (называемых
уровнями), и каждая группа объектов, чьи признаки мы измеряем,
подвергается воздействию определенного уровня этого фактора.
Методы математической статистики, изучающие воздействие
одного фактора на объекты и их признаки, называют в
совокупности однофакторным анализом.
Предположим, что ошибки нормально распределены:
е.. € N(0, а2). Тогда можно изучать влияние фактора, вычисляя
дисперсии некоторых величин. Совокупность этих методов
называют однофакторным дисперсионным анализом.
Основной гипотезой, нуждающейся в проверке, является
гипотеза о равенстве групповых средних Я0: ах = а2 = ... = аг
Иными словами, проверяют гипотезу о том, что фактор во-
обще не влияет на наблюдения. В случае нормальных ошибок
ее можно проверить, вычислив две разные оценки дисперсии
а2, а именно:
401 |
ЧАСТЬ II. Математическая статистика
Задана 1. Банк имеет по четыре отделения в трех
городах. Текущие объемы денежных вкладов (в условных единицах)
представлены в следующей таблице.
Отделение
Город
1
2
3
1
38
20
21
2
36
24
22
3
35
26
31
4
31
30
34
402
где через x9j обозначены групповые выборочные средние.
Первую величину называют остаточной дисперсией, а вторую —
факторной.
При нарушении гипотезы Я0 оценка а2** имеет тенденцию
к возрастанию, тем большему, чем больше отклонение от Я0.
Проверить гипотезу можно с помощью дисперсионного
отношения Фишера: F = c2**/a2\ которое должно иметь
распределение Фишера с к — 1 и N — к степенями свободы. При
заданном уровне значимости а можно найти критическую точку
Fп = F(a; к - 1; N — к). Если F < F. то нулевая гипотеза
принимается, иначе отвергается. Заметим, что если F < 1, то
следует сразу принять гипотезу Я0, поскольку F всегда больше
единицы.
Если гипотеза о равенстве средних не подтверждается,
имеет смысл оценивать величины а по отдельности. Получаем для
них следующие доверительные интервалы (с надежностью у):
ylnj yjnj
где ty — критическая точка распределения Стьюдента с N — к
степенями свободы и уровнем значимости а = 1 — у (для
двусторонней области): / = / (1 — у; N — к).
Существуют и более сложные методы однофакторного
анализа, не требующие предположения о нормальности
наблюдений. Однако здесь будем придерживаться классического
дисперсионного анализа.
Глава 19
Можно ли утверждать на уровне значимости а = 0,05, что
в среднем дела идут одинаково хорошо во всех трех городах?
Построить доверительные интервалы для средних по городам с
надежностью 90%.
Решение. Вычисляем групповые средние х. = 35, хт2 = 25,
хв3 = 27 и общее среднее х = 29. Затем вычисляем оценки
дисперсий: а2** = 112, а2* «22,67. Получаем F*4,94. По
таблице находим критическую точку: /^(0,05; 2; 9) = 4,26. Имеем
F > FKp, следовательно, групповые средние различаются. Чтобы
построить доверительные интервалы, находим а*» 4,76 и ty =
= fKp(0,l; 9) = 1,83. Точность доверительных интервалов во всех
группах составляет a'tjyfc «4,36, отсюда 30,64 < ах < 39,36;
20,64 < а2< 29,36; 22,64 < аъ< 31,36. Таким образом, лучше
всего дела идут в первом городе, с явным отрывом от двух других,
где ситуация примерно одинакова (доверительные интервалы
перекрываются).
Задача 2. В цеху работает четыре бригады по семь рабочих.
Выработка каждого (в условных единицах) представлена в
следующей таблице.
Рабочий
Бригада
1
2
3
4
1
51
52
56
54
2
59
58
56
58
3
53
66
58
62
4
59
69
58
64
5
63
70
70
66
6
69
72
74
67
7
72
74
78
69
Можно ли утверждать на уровне значимости а = 0,05,
что все бригады работают в среднем одинаково?
Решение. Вычисляем групповые средние х%{ = 60,9; хт2 = 65,9;
х#3= 64,3; х#4= 62,9 и общее среднее х = 63,5. Затем вычисляем
оценки дисперсий: а2** = 31,67; а2* «60,25. Получаем ^ < 1,
так что следует принять гипотезу о равенстве групповых
средних. Все бригады работают в среднем одинаково.
403 I
ЧАСТЬ II. Математическая статистика
Задачи для самостоятельного решения
1. Фирма имеет по пять филиалов в четырех регионах страны. Прибыли
за отчетный период (в условных единицах) представлены в таблице.
Филиал
Регион
1
2
3
4
1
36
56
52
39
2
47
61
57
57
3
50
64
59
63
4
58
66
58
61
5
67
66
79
65
Можно ли утверждать на уровне значимости а = 0,05, что дела во
всех регионах идут в среднем одинаково?
2. Фирма имеет 13 магазинов в трех округах Москвы: 4 - в Северном
округе, 6 - во Южном, 3 - в Восточном. Объемы продаж за
отчетный период (в условных единицах) по каждому магазину
представлены в таблице.
Филиал
Регион
Северный округ
Южный округ
Восточный округ
1
37
60
69
2
47
86
100
3
40
67
98
4
60
92
5
95
6
98
Можно ли утверждать на уровне значимости а = 0,01, что продажи
во всех округах идут в среднем одинаково? Построить
доверительные интервалы для средних по округам с надежностью 95%.
3. В целях изучения влияния материального вознаграждения на
производительность труда проведено обследование четырех групп
рабочих по 5 человек, упорядоченных по величине вознаграждения
(от меньшей к большей). Выработка (в условных единицах)
представлена в таблице.
Ч )
404
Глава 19
Группа
1
2
3
4
1
8
12
12
24
2
10
17
15
16
3
16
14
16
22
4
13
9
16
18
5
12
16
19 .
20
Можно ли утверждать на уровне значимости а = 0,05, что
вознаграждение влияет на производительность труда?
4. В продуктовом магазине продается четыре вида соков - яблочный,
апельсиновый, персиковый и ананасовый (за одну цену). Данные о
продажах, л, за пять рабочих дней представлены в таблице.
День
Сок
Яблочный
Апельсиновый
Персиковый
Ананасовый
1
18
28
26
20
2
24
31
28
29
3
25
32
30
32
4
29
33
29
30
5
34
33
40
33
Можно ли утверждать на уровне значимости а = 0.05, что спрос на
разные виды соков в среднем одинаковый?
5. Изучается популярность еженедельной передачи у трех
возрастных групп населения. Рейтинги, %, за 4 недели представлены в
таблице.
Неделя
Молодежь
Средний возраст
Пожилые
1
27
24
22
2
23
20
21
3
29
26
36
4
29
30
37
Можно ли утверждать на уровне значимости а = 0,05, что передача
пользуется одинаковой популярностью у всех трех групп
населения?
Ч j
405
Ответы и указания
Глава 1
1. 84. 2. 8. 3. 36. 4. 45. 5. 125. 6. 3136. 7. 10! 8. 9!-8. 9. 1022.
10. 210. 11. 12. 54. 13. 14- Л4-Л4 =96. 15. 5 -2 -4! =
5!7!4! 27 ^ 4
= 240.16. 58; 8 • 47.17. 2'6.18. 16100.19. 50• 49• СЦ. 20. С,50-С72 =231 .
21. 2520. 22. 50 600. 23. З6. 24. 76. 25. —^-. 26. 1800. 27. 14 670.
2!4!1!6
28. 210. 29. 256. 30. ЗОЧО3. 31. С92 =36. 32. 100. 33. 2 (5!)2.
34. (С,62)2. 35. ЗС93ОД+ЗС92С92С; =55404. 36. Л30ЛГ9(2,3,4)~.
37. 14 -8! 38. у4235 =13800.. 39. С235 =2300. 40. С35С42 =16824500.
Глава 2
1. РРР, РРГ, РГР, РГГ, ГРР, ГРГ, ГГР, ГГГ. 2. Пространство
элементарных исходов состоит из неупорядоченных пар {х, у)
(сочетаний), где х = 1, 36, у = 1, 36. 3. а) 1/54; б)
1/53; в) 24/53. 4. 0,994. 5. 5/18. 6. 0,52. 7. 8. а) 5/18; б)
3/18; в) 5/9. 9. 0,765. 10. 0,0163. 11. 0,215. 12. 0,66. 13. 0,1008.
14. 2/7. 15. 0,155. 16. 0,0476. 17. 0,43. 18. 0,238. 19. 0,082. 20.
49/63. 21. 0,725. 22. 0,47. 23. 0,17. 24. 0,39. 25. 0,067. 26. 0,094.
27. 25/63. 28. а) 2/7; б) 0,135. 29. 1 - (11/12)2. 30. 49/64. 31. 8/9.
32. 4/9. 33. 0,19. 34. 0,88. 35. 0,6. 36. 0,2. Указание: запишите
условие задачи в виде неравенства, изобразите графически
события и вычислите площади с помощью интегралов (1п9 « 2,2).
37. 0,5. Введите пространственную систему координат.
Возможные значения х, у, z — от 0 до L. События,
благоприятствующие условию задачи, х < у + z, у < х + z, z < х + у. 38. 0,9.
39. p = (fl-2r> . 40. 0,00000007. 41. 0,03. Можно использовать
приближенную формулу (1 + *)"« 1 + пх для малых х.
406
Глава з
Ответы и указания
Теоретические задачи
1. а) ЛЯС; б) Л + Я + С;в)ЛЯ+ЯС+ЛС;г) АВС+АВС+АВС;
Д) Л.5.С+7.5С+7.5.С;; е) МС;ж) Ж.
2. (Л, иЛ2 и^ХОДД, vBxB2B4vBxB3B4vB2B3B4).
3. На одной из костей выпало четное число очков, а на
другой — нечетное, большее единицы.
4. а) П; б) 0.
5. а) Все три станка потребуют внимания рабочего в течение
часа; б) хотя бы один станок потребует внимания рабочего в
течение часа; в) только один станок потребует внимания
рабочего; г) два станка потребуют внимания рабочего; д) ни один
станок не потребует внимания рабочего.
6. а) АпВ — мужу больше 40 лет и он старше жены; б) АслВ —
мужу больше 40 лет, но не старше жены; в) АпС- каждому
из супругов больше 40 лет; г) AkjC— хотя бы одному из
супругов свыше 40 лет; д) АиВ— либо мужу свыше 40 лет, либо
он старше жены; е) ВглС — муж старше жены и жене больше
40 лет.
Вычислительные задачи
7. а) АХА2А3 + АХА2А3 +АХА2А3\ б) А^ -А1 -А3; в) AiA2A3, р =
= 0,488. 8. а) ~АХ-~А2-~А3\ б) Ах -А^-А^+~АХ-~А2-АЪ +~АХ>А2-~Аг ;
в) АХА2А3, р = 0,784. 9. а) \ \ б) ~АХА2 \ в) Jx ; р = 0,09. 10. 0,075.
11. 0,75. 12. 0,535. 13. 0,5. 14. 0,51. 15. 0,67. 16. 2/7. 17. 0,512.
18. 0,099. 19. 0,476. 20. 0,98. 21. 0,5. 22. 7/15. 23. 0,25. 24. п > 17.
25. 2/9. 26. 0,5. 27. 0,085. 28. 0,722. 29. 0,328. 30. 0,9148.
31. 0,2089. 32. 0,077. 33. 0,55. 34. 0,75. 35. 0,00207. 36. 0,014.
37. 0,182. 38. Стрелок В попал в мишень с вероятностью 10/19
и не попал с вероятностью 9/19. Более вероятно, что он
попал. 39. 0,138. 40. 0,83. 41. 0,2499. 42. 0,66. 43. 17/45. 44. 4/45.
45. 0,2. 46. 5/9. 47. 7/12. 48. 0,22. 49. 12/13. 50. а) 0,38; б) 0,25;
в) 0,41; г) 0,59.
407
{j) Ответы и указания
Глава 5
Теоретические задачи
00 А,*
1. Воспользуйтесь разложением У— = ех. 2. Воспользуйтесь
tiki
представлением ? = +... + ?„, где ?,=0 в случае неудачи в /-м
испытании, и =1 в случае успеха. 3. Воспользуйтесь тем, что
пр"'1 = (/>")'. 4. Mi= 0; Dr\ = 1.
408
Глава 4
1. 0,05. 2. 0,058. 3. 0,0081. 4. 0,05. 5. 0,82. 6. 0,019. 7. 0,998.
8. а) Вероятнее выиграть одну партию из двух; б) вероятнее
выиграть две партии из четырех. 9. п = 7. 10. п > 645. 11. п > 58.
12. п * 5. 13. п Z 5. 14. 0,4096. 15. 5. 16. 21. 17. а) 2; б) 0,324;
в) 0,0109. 18. 5; р = 0,2078. 19. л = 11, 12, 13. 20. п = 14, 15, 16,
17. 21. а) 0,9876; б) 0,5. 22. а) 0,00125; б) 0,998 (воспользоваться
формулой Пуассона). 23. 0,616 (формула Пуассона). 24. 0,981
(интегральная формула Муавра—Лапласа). 25. 0,195 (формула
Пуассона). 26. 0,8185. 27. а) 0,135; б) 0,676. 28. 0,813. 29. 0,079.
30. 0,463. 31. 0,175. 32. 0,981. P{m>l}=l-P(0) = l-e~x =0,632.
Отсюда Х*1 и P{m<3}=P(0) + P(l)+P(2) + P(3) = 099Sl
(формула Пуассона). 33. 0,1379. 34. 440. 35. 0,998. 36. От 73 до 107.
37. е = 0,057. 38. от 3904 до 4096. 39. п > 49 923. 40. п > 18 507.
41. 0,4992. 42. 0,35. 43. 0,384. 44. 0,08505. 45. 0,131. Указание:
рассмотреть полиномиальную схему: три испытания (три
покупателя) с тремя исходами (требуемый размер костюма),
выписать все возможные запросы, соответствующие событию, что
ни один покупатель не ушел без покупки. 46. 0,00756. 47. 300.
Указание: вычислить вероятность хотя бы одного выигрыша.
Обозначив через п число купленных билетов, найдите п из
неравенства для вероятностей. Решая неравенство, удобно
воспользоваться приближенным соотношением 1п(1 — х) * х (для
малых х) и тем, что е3» 20. Это дает практически точный ответ.
48. 25; 0,96. 49. 7/16. 50. 0,38. 51. 9; 0,24. 52. 15/128. 53. 10/81.
54. а) 0,14375; б) 0,0612. 55. 0,384.
Ответы и указания
Вычислительные задачи
5.
0
1
2
3
р
1/8
3/8
3/8
1/8
%
0
1
2
3
Р
0,006
0,092
0,398
0,504
0
1
2
3
4
5
Р
0,59049
0,32805
0,0729
0,0081
0,00045
0,00001
9.
1
2
3
р
0,7
0,21
0,09
\
0
1
2
3
р
0,893475
0,103075
0,003425
0,000025
10.
11.
12.
13.
14.
15.
16.
0
1
2
3
4
р
0,53439
0,36251
0,0922
0,0104
0,00044
%
2
3
4
Р
0,81
0,162
0,028
0
1
2
3
Р
0,002
0,044
0,306
0,648
\
1
2
3
4
5
Р
0,9
0,09
0,009
0,0009
0,0001
\
1
2
3
4
Р
0,4
0,3
0,2
0,1
\
2
3
4
Р
0,25
0,25
0,5
%
2
3
4
Р
1/15
7/60
49/60
17. a) P{t,>2}=\-P{Z,<2}=l-P(0)-P(l)-P(2) = l-5e-2 =0,323;
409
Ответы и указания
б) < 1}= Р(0)+Р(1) = Ъе~2 = 0,406;
в) />{4<2}=5е-2=0,677.
18. 5 (геометрическое распределение).
19. 5 (геометрическое распределение).
20. 40,96. 21. а) 12; б) 18. 22. Л/$ = 14; Я$ = 35/3.
23. Щ = 7/2; 0^ = 35/12. 24. Л/^ = 1,624; Z>4 = 0,811. 25. 15.
27.
28.
29.
0
1
2
3
р
0,1
0,63
0,243
0,027
1
2
3
4
р
0,2
0,16
0,128
0,512
; 187,2 (руб.).
; 2,952.
0
1
2
3
р
0,042
0,284
0,506
0,168
; 1,8. 30.-1,3 (руб.)
31.
1
2
3
4
5
6
1
1/36
1/36
1/36
1/36
1/36
1/36
2
0
2/36
1/36
1/36
1/36
1/36
3
0
0
3/36
1/36
1/36
1/36
4
0
0
0
4/36
1/36
1/36
5
0
0
0
0
5/36
1/36
6
0
0
0
0
0
6/36
32.
-1
0
1
2
р
1/5
2/5
1/5
1/5
; % и х\ - зависимы;
cov(4+ti, 4-ti) = -0,44.
33.
-1
5/12
0
1/3
1/4
; 4 и т| — зависимы;
соу(2$-Зл, $+2л)=-13/6.
410
Ответы и указания
34.
35.
36.
4+л
-1
Т/9
1/6
4/9
1/18
2/9
; ^ и г] — зависимы;
cov(2ti + S, л + 4) = -49/81.
S + Л
-1
1/8
О
1/4
1/12
1/6
3/8
; \ и т1 — зависимы;
cov(i;-Ti, 2^ +л) = -913/288.
4л
-2
-1
1
2
р
1/6
2/9
2/9
7/18
; % и т| — зависимы;
cov(2S+ti, 3?-л)=406 / 81.
37. А/^ = 3/2; /^ = 3/4; о = Л/2; <^<3/2}= 1 /2;
ад=
0, х<0,
1/8, 0<х<1,
1/2, 1<х<2,
7/8, 2<х<4,
1, х > 4.
38. Щ = 7/4; /^ = 55/16; о*1,854; Р{5/2<^<5}=1/8;
0, х<-1,
1/4, -1<х<2,
F(x) = -3/4, 2<х<3,
7/8, 3<х<5,
1, х>5.
39. Щ = 49/18; Z)$*2,312; а*1,52; Р{1 /2<^<7/2}= 7/18;
0, х<0,
1/9, 0<х<1,
/•(х)=1/3, 1<х<3,
1/2, 3<х<4,
1, х>4.
411
g) Ответы и указания
46. а)
в)
47. а)
в)
48. а)
в)
49. а)
X
0
1
2/3
1/3
У
-1
0
1
2/3
1/3
1/2
X
-1
1
У
х|-1)
-1
1/4
0
3/4
1
Фил
j
1/2
с
-1/5
-1
! 0'
1
У
х|2)
0
3/5
1
2/5
2
Ф51п
0 -1/2 •
-1/5
;б)
|;г)
;б)
У
-1
0
1
0,2
0,4
0,4
X
0
1
0,2
0
У
-1
0
1
1/2
1/6
1/3
X
-1
1
1/6
-1/6
;б)
|;г)
У
0
1
2
2/11
3/11
6/11
X
-1
1
15/11
9/7
X
1
2
3
4
1/7
1/7
1/7
4/7
У
2
3
4
5
6
1/3
1/6
1/6
1/6
1/6
; M(§,h = 4) = 22/7;
Т^;М(л|41=2) = 11/3.
412
40. Л/? = 0; ?>4 = 18/7; о*1,604; />{-3/2<4<2}=5/7;;
0, х<-2,
1/7, -2<хй-\,
= < 4/7, -1<х<1,
6/7, 1<х<3,
1, х > 3.
41. 0,356.
42. 0,6.
43. а) 153,76; б) 119,29; в) 116,41.
44. 6 акций первой компании и 4 акции второй компании.
45. 9 акций первой компании и 3 акции второй компании.
Ответы и указания
X
50. Биномиальное распределение с параметрами п и р = —1
Х»| "Ь Х2
кХ
функция регрессии %\ц(к) = —, к = 0, 1, 2, я.
Глава б
Теоретические задачи
1. Воспользоваться формулой для плотности функции от
случайной величины.
2. а) /Чл. <*) = 1 -*х,$2 >х,...,?„ >х) = 1 **)>" = 1 -е"вйХ;
б) Р(ц2 <х) = Л$, <*,$2 <*.-Л. <х) = (/>($<*))" =<1-е-"Г.
3. Найти функции распределения для г\1 и г\2 методом,
использованным в задаче 2, и вычислить их математические
ожидания.
4. а) а = -\ б) F(x) = -+-arctgx; в) Р{-1<?<1]}=1/2.
я 2 я
5. я=4; Л/§ = 0,Д$=Д; />{|^|< V^} =1-*^ =0,75;;
Р{| ^ |< 2>4Щ) = 1 -е-ъГг = 0,98. •
6. а) 0,9974; б) 0,9817; в) 1.
7. />(*) =
1-1
, |х|<а; Щ= 0; Д; =
О
8. Воспользоваться методом геометрической вероятности:
ях2 х2
P(p<x) = P(^W<x2) = ^ = ^;xe[0,R];Mp = ^R,Dp = ^.
9. а) /^(0 =
яЛ2 Л
КЬ-а)9 9 б) ^(0 = -^, \t\<X.
1, / = 0;
18
10. Указание. Изучить соответствующие интегралы на
сходимость.
413
4^ Ответы и указания
Вычислительные задачи
fo,
11. C = 2/9,F(x) = -
х<-1,
(х + 1)2
, -1<х<2; Л/^ = 1;/>{42<1}=4/9,
1,
х>2;
12. C = 2/33;F(x) = \
fO, х<-2,
-х2+10х + 24
33
1,
Р{0<^<2}=3/11
fo,
13. C = l/4;F(x) = -
х -4х + 3
8
1,
, -2<х<1, = -7/11;
дс>1;
х<3,
3<х<5, Л/$ = 25/6;
х>5;
P{4<$<6}=5/8.
14. C = l/2;F(x) = |°'
' [1-(х + 1)-,/2, х>0;
ожидание не существует; />{1^-1/3|<1}=1-(7/3)"1/2.
х<0,
математическое
15. C = 3/4;f(x) =
х<-1,
-(Зх-х3 + 2), -1<х<1,
4
[1, х>1;
Jl/$ = 0;Z)$ = l/5;P{U-l/2|<l/4}=35/128.
16. С = 1;/•(*) = j**' MZ, = -l,D$ = \;P{-2<S<l}=
= 1-е"2 =0,86.
П. Р(х) = \1_,х ~ ' ЛЯ; = 0, DZ, = 2; i»{-l < % <3}=0,79.
I 414
!
Ответы и указания ф
18. р{х) = \1 2Х> Хе[^> Л/$ = 1/3,^ = 1/18.
[О, хе[0,Ц;
19. Р(2<^<5) = ^; Р(5<^<7) = 1
4 4
20. F(x) =
О,
х<0,
X X
, 0<х<10, Среднее время ожидания —
[1, х>10;
3,89 минуты.
21. Указание: доказать, что случайная величина
г| = тах(?,24-?) распределена по равномерному закону
на [12; 24]. Ответ: 18 см.
22. Указание: доказать, что случайная величина r| = min(?,12-?)
распределена по равномерному закону на [0; 6]. Ответ:
3 см.
Глава 7
Теоретические задачи
1. а) р(х)=<
0,
х/а\
х<0,
0<х<а,
(2а - х)1 а2 ,а < х < 2а,
0 х > 2а.
б) р(х) = \
0, х < -а,
(а + х)/а2 9-а<х<0,
(а-х)/а2,0<х<а,
0, х>а;
1 а2
в) р(х) =—1п—, 0<х<а; г) р(х) =
0, х<0,
<1/2, 0<х<1,
[1/(2jc2), jc>1;
2. Достаточно доказать это свойство для «центрированных»
случайных величин, т.е. для тех, у которых Af^ = 0.
Воспользоваться формулой свертки, учитывая соотношение
[-
(а
3. Рассмотреть функцию распределения для г|.
415
© Ответы и указания
4. С = |, р(х) = -^= при х6(0,1]; Д0,25 < л < о,64) = 0,3.
2 2Vx
5. />(*) = —-jL= при хе[2;10].
4vx-l
6. р(х) = ^е~х при хе[-1пЗ; 0].
7. р(х) = — 1 при хе[1; 10).
6V10-X
_2_
(* + l)J
8. />(*) = -—ту при х>0.
1 -М2/3
9. /?(*) = /_| 2/3е 8 при х*0.
6л/2т^|х|2
2 Г П
10. /?(х) = — 1— при х>1.
хЧ
11. p(x) = —jL=e~xn при х>0.
v2tcx
Указание: вычислить функцию распределения для г| и
продифференцировать ее.
12. а) р(х) = е~х при х>0;
X
б) р(х) = —=e~kyIx при х>0;
2у]х
в) р(х) = 2Ххе~Хх2 при х>0;
г) равномерное распределение на отрезке [0; 1].
13. а) равномерное распределение на отрезке [0; 1];
б) показательное распределение с параметром X = 1;
в) стандартное распределение Коши.
I 416
Вычислительные задачи
Ответы и указания ф
14. ^+ч(х) =
О, х<1,
х-1
-, 1 < х < 2,
z
1/2, 2<х<3,
4-х
15. Р^(х) =
16. ^+nW =
О,
О,
х-1
3 < х < 4,
х>4.
х<1,
, 1<х<2,
1/4, 2<х<5,
6-х . ,
, 5 < х < 6,
4
О, х > 6.
О, х < 3,
х-3
-, 3 < х < 4,
1/2, 4<х<5,
^ *, 5<х<6,
О,
х>6.
17. /W*) =
О, х < 3,
х-3
4
7-х
О,
18. ^+ч(х) = хе-х, х>0. 19. />4+л(х) =
, 3<х<5,
, 5<х<7,
х>7.
х<0,
0<х<1,.
Го,
1
(^-1)^, х>1.
20. 1/32, случайные величины зависимы.
21. />4(х) = 2(1-х),хе[0,1], рц(у) = 2(1 -у),уе[0,1]; случайные
величины § и г| зависимы, Р{?<3/4}=15/16.
22. 0,92. 23. 1/8. 24. р^ц(х,у) = 1/(9п) внутри круга, случайные
величины § и Ti зависимы, Р> 0,г| > 0}= 1 /4.
25. />4>Т1(х,>0 = 1/36 внутри трапеции, #=(х) =
f0, у* [0,4],
Л,О0 =
0, хе[-6,6],
х + 6 ,
-, -6 < х < -3,
27
1/9, -3<х<3,
6-х - ,
-, 3<х<6;
27
8 - у случайные величины § и т| зависимы.
, 3>е[0,4],
24
14 Теория вероятностей
417
Ответы и указания
26. pJx) = -Jl-(x-l)29xe[092)9 А^ = ->/1^,УМ0,1], случай-
s я 1 я
ные величины ^ и г| зависимы
27. />4(л:) = 2е2дс, х<0, д,О0 = -4>*2'> д><0, случайные величины ?
и т| зависимы.
28. р^(х) = 2(1-х)9хе[091]9р1](у) = 2у9уе[091]; случайные
величины ? и т| зависимы; Af(?r|) = l/4 .
29. /> = (1-<Г2)2.
30. а) А = 1/2; б) F(x^)=SinX+Sin^SinU + >;);
_ч „. . 1-cosx+sinx . . sinx + cosx
б) ^(х) = ; рь(х)= ;
х€[0, л/2]; случайная величина т| распределена так же;
в) Р,ы(х\у)= sin<*+^ , хе[0,я/2], уе[0,я/2].
s" siny+cos^
31. F^x\y) = ylx2-y2, xe\y,J?7i].
[Ъ-ly
32. а) Ф5|Ч(у)=
5
2j>+3
, -1<у^0,
б) <P4B(*)=
I 5
, 0<у<1;
х
4*
6-5х
I 4
0^х<1,
33. Равномерное распределение на отрезке [0, /].
Глава 8
Теоретические задачи
1. Да, применим. Проверить условия применимости закон
больших чисел Чебышева.
! 418
Ответы и указания ?
Пусть е < 1. Тогда вероятность Р
. 1 п 1 л
л /=1 п /=1
[п 1=1 л J
т.е. не стремится к нулю.
3. Применить неравенство Чебышева к случайной величине
1 п
4. Неравенство Чебышева дает оценки: Р{|^-д|>а}<1,
Р{|?-я|>За}<1/9 = 0,11. Непосредственное вычисление этих
вероятностей дает Р{|?-д|>а} = 0,3174, Р{\$-а\>За} = 0,0027..
15
5. М$ = 0, а = ^;; />^1«*}=1-е^ =0,75 ; P{Ul<3a}=
= 1-е~3>^ =0,98. Неравенство Чебышева приводит к
оценкам: Р{|?|<а}>0; P{Ul<3a}>0,89.
6. a) Af = 0, D^n = 22я. В силу независимости случайных
величин Р($я =2Л, §я_, =2"",) = ^. Поэтому, например, при е< 1
получим
г\
р
1 л 1 п
п /=1 Л /=1
>е
1 я
2я-1+2"^
>Р(^=Г, 4я-1=2Л-1) = 1,
т.е. не стремится к нулю. Закон больших чисел не
выполняется;
б) закон больших чисел выполняется.
7. Из неравенства Чебышева Р
получаем 0,0124.
8. Выполняется.
j 100
ЮО ?
Л
а
> —
4
<0,16. Из ЦПТ
419
2. Нет, закон больших чисел Чебышева не выполняется.
М% = О, D\ = п2. В силу независимости Р {?л = и, §я_, = л -1}= 1/4.
^ Ответы и указания
Вычислительные задачи
11. Р{?<10000}>0,4. Применить неравенство Маркова.
12. Применить неравенство Маркова. Р{?>400}<0,75. Это
неравенство дает несодержательную оценку для второй
вероятности: Р{?<300}>0.
13. Р{|/и/я-0,87|<0,04}>0,93. Применить неравенство
Чебышева.
14. Р{?>3}<0,1. Применить неравенство Маркова.
15. а) Р?<200}>0,5; б) />?>150}<2/3.
16. Р{|т/л-0,7|<0,04}>0,934.
17. P{|/w/«-0,l|<0,0l}>0,91.
18. Неравенство Чебышева дает оценку п > 16 ООО, а следствие
из интегральной формулы Муавра—Лапласа п > 4356.
19. Р
л1 п 1 -
<0,25
> 0,9771.
20. п > 294.
21. Р(\т-пр\<х) = 0,99, отсюда по таблицам нормального
распределения x^2,51yjnpq «103. Величина т находится в
пределах 8000 ± 103 по ЦПТ и 8000 ± 400 по неравенству
Чебышева.
22. 558; 541.
23. а) 0,92; б) 20 мин.
24. 547.
25. Более 8310 единиц.
26. 0,0287.
27. От 237 до 363 деталей. Указание: применить ЦПТ, учитывая,
что на каждую подвергнутую контролю деталь приходится
геометрически распределенное (с р = 1/3) число деталей с
конвейера.
28. В предположении, что метод является нейтральным, не
влияющим на производительность труда, положим
вероятности «успеха» и «неудачи» равными -. Получаем
420
Р(]/я-50|>18) = Р
т-50
Ответы и указания ф
«0,0004. Следовательно, на-
. ^3,6
блюдаемое отклонение маловероятно. Предположение
следует отвергнуть, и можно признать, что вероятность
«успеха» больше -.
29. 0,9177. 2
30. 0,9606.
31. 0,9649.
32. 0,9927.
Глава 9
1. а) (0,0065; 0,0523; 0,9412); б) (1/28, 3/28, 6/7).
2. Доля безработных - 1/9. Сократится в 17/9 * 1,89 раза.
3. (18/23, 3/23, 2/23).
4. (0,079; 0,658; 0,263).
5. (1/31, 20/31, 10/31).
6. а) (143/400, 171/400, 86/400); б) (15/41, 18/41, 8/41).
7. (0,5; 0,2; 0,3).
8. (4/9, 13/54, 17/54).
9. а) (25/54, 23/54, 1/9); б) (4/15, 42/75, 13/75).
10. а) (1/8, 17/32, 11/32); б) (7/36, 5/9, 1/4).
11. а) (0,027; 0,076; 0,217; 0,68); б) (0,125; 0,183; 0,242; 0,45).
12. (1/9, 8/9).
13. (1/169, 24/169, 144/169).
14. (8/125, 36/125, 54/125, 27/125).
15. 70,4%.
16. а) 0,013; б) 0,554; в) 2,216; г) 1,001.
17. 8/9.
18. а) (0,282; 0,339; 0,271; 0,108); б) 0,49; в) 1,2.
19. а) (0,00046; 0,00729; 0,05837; 0,31129; 0,62259); б) 0,00821;
в) 0,44353.
20. а) не более 7,32 мин.; б) не более 8,54 мин.
21. а) 0,211; б) 0,237; в) 0,237.
22. а) 1/2; б) 1/12.
Глава ii
Теоретические задачи
3. М{%-М^ = М^-ЪМ^М% + 2{М^)г; ц3 =а3-За23с + 23с3;
421
ф Ответы и указания
1+—,
9. в = |
10. Оценка неэффективна, ее дисперсия бесконечна.
Вычислительные задачи
11. Зс = 4.
12. 5* = 0,035.
13. Зс = 10; а2 = 2,5; s2 =3,33.
14. Зс = 2504,88; 5* = 254,41.
15. Зс = -0,4; л» = 128,85.
16. а) Зс = 1,535; л»= 3,39, 5 = 1,84;
б) Зс = 1653; s2 = 446037, s = 667,86;
в) Зс = 15,6; = 19,9; 5 = 4,38.
17. В группе I: Зс = 96,17; s>= 30,49;
в группе II: Зс = 88,75; ? = 25,99;
общие: Зс = 93,2; ** = 41,59.
18. а = 1508,8; о = 24 (м).
19. а = 19,31; а= 0,73 (мм).
20. а = Ц,33 (мк).
21. а = 2390 (у.е.).
22. Зс = 198,96; *»= 9,45.
23. Зс = 71,11; j»= 264,52; 5 = 16,26; xmed = 69,3; х„.п= 47,9;
^=88,6.
24. Зс = 35,54; s2 = 55,45; 5 = 7,45; xmed = 34,5; xmin = 27;
х =47
25. х = 15,85; 5» = 4,69; s = 2,17; xmed = 15,45; xmin = 12,9;
422
ц4 = а4 - 4а33с + 6а23с2 - 33с4.
8. e=xmax+i.
Ответы и указания
rt-2
" V 2
.2
ски эффективна.
Оценка неэффективна, но асимптотиче-
Г
423
26. 5с = 2127,46; j»= 7 078 286; 5 = 2660,5; xmed = 1134; х^ 1000;
27. х = 1148; 5»= 18937,16; s = 137,61; xmed= 1105; xmin= 1000;
*U»1426.
28. х = 50,01; s> = 1,05; s = 1,02; xmed = 49,9; xmin = 48,1;
^„=52.
29. x = 5,46; ? = 0,03; s = 0,17.
30. x = 3,87; ^= 3,69; s = 1,92; xmod= 4.
31. x = 3,99; s* = 2,48; 5 = 1,57; xmod= 4.
32. x = 166; s2 =33,44; xmod =168.
33. x = 1273,75; s2 = 168,88.
34. a) s2 =1287,8 (м2); 6) s2 =1508,5 (м2).
35. a) s2 =814,87 (см2); 6) s2 =922 (см2).
36. a = 2982,22 (y.e.); a2= 888,89
Глава 12
2. Распределение Фишера—Снедекора F(m, it).
7. Распределение Стьюдента с п степенями свободы.
10. Распределение Фишера—Снедекора F(l, я).
11. Распределение Фишера—Снедекора F(2n, In).
16. Сходится к гамма-распределению у^, ^
20. *2=^^?>,.-1)52,где # = f>,..
23. c=<Jri/2; e(a*)=—^«0,88. Оценка неэффективна.
Ответы и указания
Глава 13
Теоретические задачи
1. i = x. 2. Р = Ух. 3. 0 = Зс — 1. 4. 9 = 5,ц = Зс-5 . 5. а = 3с.
6. а = АЗс,/)а = а/я. 7. r = x9Dr = 2r/n. 8. r = -^— ,r>2. 9. 0 = 2x .
10. a = x~s\l3, й = х + 5>/3. 11. c = x, df = 3s2.
12. 0,=x-W3, 92=2>/35. 13. ^1)2=г
x±yJ2s2-x2
14. а = —, а>1. 15. Р = т^=.
х-1 1-х
16. я = 21пх-^1па2, а2 =1па2-21пх. 17. X = >j2/s . 18. /? = 1/х .
19. 0 = х-1. 20. ЛГ = хтах. Оценка смещенная, асимптотически
несмещенная. 21. p = x/N. Оценка несмещенная,
состоятельная. 22. 0 = хтЯ?. Несмещенная оценка: 0 =
Л + 1
23. 0 = хтах/2. 24. 0 = тах(1 - xmin, хтах -1). 25. Оценкой
максимального правдоподобия является любое число на интервале
(*тах ~Ъ xmin)- Несмещенная оценка — середина интервала:
Tijl 1-1
^ = (^max+^in-D/2. 26. Х =
• 27. e=xmin. 28. e=*max.
29. e = -5>(*,). 30. а= i?(g(;c()-a)2. 31. b = x/a. 32. ? =
и /-i V Л '=1
33. 0 =
(\ « 1 V1
• 34. ^ = xmi„,e = x-xmin. 35. а =
Л « V1
ЧЛ (=1
36. P = -|-Xlnx,| .37. a = -Jlnxf ; сг2 =-?(1пх,.-о)2.
38- a = xmin,b = x,
X — х
. Несмещенные оценки: й = xmin ————
max ^ nun Л —1
v — V .
Ь — X _j_ _ max ^min
и-1
44. A. = 0,9; p0 = 0,41. 45. X = 0,2
f =11,51 (часа). 46. a = x2/s2 = 3,97;р = ЗсД2 =0,024. 47. X = 3,87
424
Ответы и указания ф
р0 = 0,02. 48. р = 0,4; рй1 = 0,05. 49. а = 2; средний доход —
200 тыс. руб.; доля жителей 4%. 50. ц = 30; 9 = 7; Т = 62,24 (мин).
51. 9, = 20; 92 = 15 (часов). 52. а = 8,156; о2 = 0,003; доля
людей 92%. 53. На основе оценок методом моментов — 59%, по
таблице — 58%. 54. На основе оценок методом моментов —
81%, по таблице - 82%. 55. X = 1,535. На основе оценки
методом моментов — 46%, по таблице — 39%. 56. На основе
оценок методом моментов - 63%, по таблице - 65%. 57. На
основе оценок методом моментов - 16%, по доле в выборке - 20%.
58. 9 = 9,6 (мин). 59. 783 порции. 60. а =82; S =118 (кг);
товара нужно 110,8 кг. 61. 45 ошибок. 62. 9; 0,075. 63. 1 - е'2«
* 0,86. 64. 119,2 (кг). 65. 0,17. 66. ±1,63%. 67. р = 0,4.
68. X = 0,05; "р = 0,05. 69. а = 3,94. Средний доход -
67 тыс. руб.; доля жителей 6,5%. 70. ц = 30; ё = 4,7; Т =51,64
(мин). 71. я = 8,244; а1 = 0,059; доля людей 29%. 72. ё = 9,2;
ё = 11,04 (мин). 73. а = 72; b = 128 (кг); товара нужно 122,4 кг.
74. 1-е"2* 0,86. 75. ±2,3%. 76. у = 866,27 + 16,8(х - 2000);
"у (2004) = 933,47. 77. а) у = 67,98 + 10,79(х - 2000); у (2003) =
= 100,35; б) "у = 39,44 + 7,74(х - 2000); у (2003) = 62,66.
78. а) "у = -7,26 + 0,69х; у (90) = 54,84; б) "у = 0,58х;
"у (90) = 52,22. 79. у = 0,943х; } (2600) * 2452. 75. "у = 10,37 +
+ 0,34(х - 1960). 76. а) у = 2012,6 - 308(х - 1994); у (1997) =
= 1088,6; б) у = 3305,2 - 432,2(х - 1994); у (1997) = 2008,6;
в) у = 2087,6 - 229,3(х - 1994); у (1997) = 1399,7; 77. "у =
= 88,1 + Ц,3х; у (6) = 155,9. 78. у = 8,81 - 0,43х; у (11) =
= 4,08. 79. у = -1153,5 + 2,59х. 80. у = 8625 + 0,84х.
1.
IX -
2>/й
<Х<
Vx +—w
24п
Глава 14
2. 2хехр
г и Л
т
>/ЗЙ,
<9<2хехр
где Ф0Ц) = ^.
4ьУ
425
ф Ответы и указания
3. —ехр
х
иу I 1 а I
—Р= <л<—ехр|
\1ап) х
' и ^
У
4.
2^i
\2
<а<
Vx—-_ I
\2
<r<
\2
/v(l-v) /v(l-v)
;-w . </><v + w, ;
T\ mn T\ mn
sin
arcsinVv ^= < /? < sin2
, 2\/mn J
f
arcsinvv +
2yfmn )
, где v = —.
m
Вычислительные задачи
7. 8 = 0,39 (мм). 8. n = 81. 9. 4,02 < a < 5,98. 10. я = 82.
11. 0,28 < a < 3,72. 12. 65,46 < a < 89,54 (человек на фирме);
78 552 < N < 107 448 (человек в отрасли). 13. 34,66 < а < 50,94.
14. а) 3,51 < ст < 9,31; б) 11,24 < ст < 18,85. 15. 0,74 < ст < 1,55.
16. 0,43 < ст< 1,02. 17. 99,97 < а < 15,65 (г); 5,93 < ст2< 15,65 (г2).
18. 72,98 < ст < 164,4. 19. 19 250 < а < 25 750. 20. 123,03 < а <
< 128,57 (г); я = 96. 21. Цена актива от 220,5 до 276,5 д.е.
22. 80,11 < а < 119,89 (д.е.); я = 792. 23. 77,04 < а < 94,96 (мин).
24. 56,05 < а < 86,17; 28,52 < х < 113,7 (млн т). 25. 28,64 < а <
< 42,44; 16,03 < х <55,05 (млн т). 26. 14,3 < а < 17,4; 10,71 < а <
< 20,99 (ц/га). 27. 49,53 < а < 50,49 (г). 28. 5,43 < а < 5,49;
5,12 < х < 5,8. 29. а) 19,35 < а < 19,65 (мес); б) 0,9544; в) я = 81.
30. 0,47 < р < 0,73. 31. 0 < р < 0,03. 32. 0,71 < р < 0,73.
33. а) 0,08 < р < 0,12; б) 0,08 < р < 0,12. 34. 0,55 < р < 0,65.
35. 0,55 < р < 0,73. 36. я = 10 551 (человек). 37. 0,1 < р < 0,14.
38. 0,05 < р < 0,07. 39. 0,01 < р < 0,03; я = 3012 (записей).
40.251,89 < X < 260,14 (покупателя). 41.1813,3 < 9< 2205,93 (часа).
42. 847,89 < в < 1179,39 (часа). 43. 0,15 < р < 0,25. 44. 1,44 < X <
< 1,64 (сделки). 45. 0,84 <Х< 0,96 (сорняки). 46. 1,56 < 0< 2,04
(покупки). 47. 0,3 < р <0,6.
426
Ответы и указания
Глава 15
Теоретические задачи
1. 5= *:Л1<*/-*>2>?.
I <*о w J
2. 5={дс:5с>/?0+«аЛ//?0(1-/?0)/л}; Ф0(«а) = 1/2-а; Ф0Ц,) = 1/2-р;
_(waV/;o(1-Po)+wpV/?i(1-A)j
п = -
(Ро-Рх)
3. 5 = {х:х>Л,0+маЛ/А,0/л}; п = -
4. 5 = |x:?i0|jx/<xL,2W|-
5. В общем виде: 5' = {x:|x|max>l}u|x:|jx/2<с|;
В частном случае: S = {| х, |> l}u {| х2 |> 1}и |х,2 + х22 < -^а|.
Вычислительные задачи
6. а) Мощность критерия 0,44; б) п = 25. 7. а) х > 19,3.
Нулевая гипотеза принимается; б) мощность критерия 0,6368.
8. а) х > 308,25; б) р = 0,36; в) п = 81. 9- п = 237. 10. Нулевая
гипотеза отвергается. И. Мощность критерия 0,66. 12. Нулевая
гипотеза принимается. 13. Нет. 14. Нулевая гипотеза
отвергается. 15. Нулевая гипотеза принимается. 16. Да. 17. Нет.
18. Да. 19. Да. 20. Да. 21. Да. 22. Нулевая гипотеза отвергается.
23. Нулевая гипотеза отвергается. 24. Да. 25. Да. 26. Да. 27. Да.
28. Да. 29. Нулевая гипотеза принимается. 30. Нет. 31. Да.
32. Да. 33. Нет. 34. Нет. 35. Да. 36. Да. 37. Да. 38. Нет. 39. Нет.
40. Нулевая гипотеза принимается. 41. Нулевая гипотеза
принимается. 42. Нулевая гипотеза отвергается. 43. Да. 44. Нулевая
гипотеза отвергается. 45. а) Нулевая гипотеза принимается;
б) нулевая гипотеза отвергается. 46. Да. 47. Нулевая
гипотеза отвергается. 48. Нулевая гипотеза принимается. 49. Нет.
427
^ Ответы и указания
Месяц
Прогноз (линейный)
Прогноз (экспонента)
Январь
4690
4770
Февраль
4793
4915
Март
4897
5064
Апрель
5001
5219
Май
5104
5378
Июнь
5208
5541
Июль
5312
5710
428
50. Нет. 51. Да. 52. Да. 53. Да. 54. Да. 55. Да. 56. Да. 57. Нет.
58. Нет. 59. Да. 60. Да. 61. Да. 62. Да. 63. Нет. 64. 1) Нулевая
гипотеза принимается; 2) s2 = 4,69. 65. Да. 66. Да. 67. Да.
Глава i6
1. Да. 2. Да. 3. Да. 4. Да. 5. Нет. 6. Да. 7. Да. 8. Нет. 9. Да.
10. Нет. 11. Да. 12. Да. 13. Да. 14. Да.
Глава 17
1. а) г = -0,18; зависимости нет; б) г = 0,24; зависимость
есть; в) г = 0,01; зависимости нет; г) г = —0,05; зависимости
нет; д) г = 0,61; зависимость есть. 2. а) rs — 0,43; б) rs = 0,07;
в) г = -0,1; г) г = -0,18; д) rs = 0,62. 3. rs = 0,73. Мнения
экспертов достаточно хорошо согласованы. 4. г = 0,90; г5 = 0,89.
5. г = 0,78; г5= 0,76.
Глава 18
1. Да. 2. Нет. 29,61 < ах< 62,39; 69,62 < я2< 96,38; 69,05 < аъ<
< 108,95. В Северном округе дела идут хуже, чем в Южном и
Восточном (где примерно одинаково). 3. Да. 4. Да. 5. Да.
Глава 19
1. a) trx(t) = 2098 + 103,67/, где t - номер месяца (от начала
наблюдений); б) Ггх(/) = ехр(7,72 + 0,03О. Прогнозы на 2004 г.
представлены в таблице.
Ответы и указания щ
Продолжение табл.
Месяц
Прогноз (линейный)
Прогноз (экспонента)
Август
5415
5884
Сентябрь
5519
6063
Октябрь
5622
6248
Ноябрь
5726
6438
Декабрь
5830
6634
2. frx(0 = exp(8,2024 + 0,0070, где t - номер месяца (от начала
наблюдений).
Месяц
Сезонные индексы, %
Прогноз
Июль
224
9725
Август
138
6042
Сентябрь
122
5362
Октябрь
60
2685
Ноябрь
90
4046
Декабрь
78
3532
Январь
56
2554
Февраль
34
1576
Март
59
2725
Апрель
76
3513
Май
108
5016
Июнь
208
9788
Здесь и далее сезонные индексы, как и прогнозируемые
значения, округлены до целых.
429 I
{j) Ответы и указания
3. trx(t) = 10836 + 39,285/, где / - номер месяца (от начала
наблюдений).
Месяц
Сезонные индексы, %
Январь
94
Февраль
89
Март
97
Апрель
97
Май
105
Июнь
105
Июль
106
Август
107
Сентябрь
100
Октябрь
102
Ноябрь
98
Декабрь
99
4. /гх(/) = ехр(5,44 + 0,01/), где t - номер месяца (от начала
наблюдений).
Месяц
Сезонные индексы, %
Январь
92
Февраль
87
Март
101
Апрель
98
Май
99
Июнь
114
Июль
128
430
Ответы и указания щ
Продолжение табл.
Месяц
Сезонные индексы, %
Август
125
Сентябрь
107
Октябрь
92
Ноябрь
80
Декабрь
89
5. а) /гх(/) = 815,87 + 16,8/, где f — номер года (начиная с 1998-го).
Прогноз: 933,5.
б) /гх(0 = ехр(6,7 + 0,02г). Прогноз: 934,5 (млрд кВт-ч).
ПРИЛОЖЕНИЯ
Приложение i
Примеры вариантов контрольных работ
по теории вероятностей
Контрольная работа № 1. Случайные события
Вариант 1
1. Определения пространства элементарных исходов,
события. События несовместные, противоположные, образующие
полную группу событий, и их свойства.
2. Вероятность изготовления стандартной детали на
автомате равна 0,95. Изготовлена партия — 200 деталей. Найти
наивероятнейшее число стандартных деталей в этой партии и его
вероятность.
3. Электроэнергия поступает в регион с некоторой
постоянной интенсивностью по трем электролиниям. Каждая
электролиния может быть отключена в течение дня с вероятностью
0,1. Если отключается только одна электролиния, то регион
испытывает недостаток электроэнергии с вероятностью 0,2, если
отключается 2 электролинии, то с вероятностью 0,5 , если 3 —
то с вероятностью 1. Какова вероятность, что в день проверки
регион испытывает недостаток в электроэнергии?
4. Шесть шаров случайным образом раскладываются по 3
ящикам. Найти вероятность того, что во всех ящиках будет
разное число шаров.
5. В коробке 3 детали. Событие А. состоит в том, что /-я
деталь дефектна, Р{А) = 0, 1, / = 1, 2, 3. Выразить события:
1) все детали годные, 2) имеется только одна годная деталь,
3) годных деталей не менее двух. Найти вероятность второго
события. Сколько надо взять коробок, чтобы с вероятностью не
менее 0,999 получить годную деталь? Какова вероятность того,
что среди 10 коробок будет ровно 5 коробок, не содержащих
дефектные детали?
432
Приложения ф
Вариант 2
1. Схема последовательного выбора без возвращения и схема
одновременного выбора (описать соответствующие
пространства элементарных исходов и найти их объемы). Показать, что
/w-кратный последовательный выбор элементов без
возвращения из совокупности объема N эквивалентен схеме т
независимых испытаний с уменьшающимся числом равновозможных
(в рамках одного испытания) исходов; построить
вероятностную модель, воспользовавшись и доказав следующую теорему
умножения: P(ABCD) = P(A)P(B/A)P(C/AB)P(D/ABQ.
2. Семь частиц распределяются равновероятным образом по
6 ячейкам. Найти вероятность того, что нет пустых ячеек.
3. Фирма участвует в 4 проектах, каждый из которых
может закончиться неудачей с вероятностью 0,1. В случае
неудачи одного проекта вероятность разорения фирмы равна 20%,
двух — 50%, трех - 70%, четырех — 90%. Найти вероятность
разорения фирмы.
4. Страховая фирма заключила 10 000 договоров. Вероятность
страхового случая по каждому в течение года составляет 2%.
Найти вероятность того, что таких случаев будет не более 250.
5. Сколько надо произвести опытов по 3-кратному
подбрасыванию монеты, чтобы с вероятностью 0,9 получить хотя бы
один раз ровно 2 выпадения герба?
Вариант 3
1. Операции над событиями. Формулы де Моргана. Теоремы
сложения. Построить вероятностную модель для «-кратного
независимого повторения игры с тремя исходами («выигрыш»,
«проигрыш», «ничья»), вероятности которых остаются
неизменными в разных играх. Вывести формулу для подсчета
вероятности числа выигрышей.
2. Известно, что в пятизначном номере телефона все цифры
разные. Найти вероятность того, что среди них есть цифры 1
и 2.
3. В лифт 9-этажного дома на 1-м этаже входят 6
человек. Для каждого человека равновероятен выход на любом из
8 этажей. Известно, что все вышли на разных этажах. Какова
при этом условии вероятность того, что на первых трех этажах
вышли 2 человека?
4. Известно, что проверяемая фирма может пытаться уйти
от налогов с вероятностью 40% и выбрать (равновероятно) для
15 Теория вероятностей
^ Приложения
j 434
этого одну из 3 схем. Найти вероятность того, что фирма
уходит от налогов по третьей схеме, если по первым двум
нарушения не обнаружены.
5. С вероятностью 0,8 орудие при выстреле поражает цель.
Произведено 1600 выстрелов. Какова вероятность того, что при
этом произошло не менее 1200, но не более 1300 попаданий?
Вариант 4
1. Показать, что я-кратный последовательный выбор
элементов с возвращением, осуществляемый из совокупности
объема N, эквивалентен схеме п независимых испытаний, каждое
из которых имеет N равновозможных исходов (построить
вероятностную модель). Доказать теорему умножения и формулу
Байеса (дать при этом все необходимые определения).
2. Распределяются случайным образом 5 шаров по 3
ящикам. Известно, что нет пустых ящиков. При этом условии
найти вероятность того, что в первом ящике лежит один шар.
3. Каждый из 900 посетителей оптового рынка случайным
образом обращается в один из 10 ларьков. В каких границах
с вероятностью 0,95 лежит число клиентов отдельно взятого
ларька?
4. Поставки некоторого продукта в город могут
производиться из трех областей, соответственно в соотношениях 20,
30 и 50%. Доля продукта высшего сорта в поставках
соответственно равна 40, 50 и 20%. Какова вероятность купить продукт
более низкого качества? Были приобретены 2 коробки продукта
в разных магазинах. Какова вероятность того, что среди них
будет продукт более низкого качества?
5. Вероятность того, что случайно взятая деталь
окажется второго сорта, равна 3/8. Сколько нужно произвести
испытаний, чтобы с вероятностью, равной 0,995, можно было
утверждать, что частота отклонится от вероятности менее чем
на 001?
Вариант 5
1. Дать определение условной вероятности события А при
условии В. Как изменится вероятностная модель дискретного
случайного эксперимента, если дополнительно известно, что
произошло событие В. Доказать формулу полной вероятности.
Приложения ф
2. Известно, что у пятизначного номера телефона все
цифры разные. Какова при этом условии вероятность того, что
среди них ровно одна четная (0 считаем четной)?
3. Известно, что 96% продукции удовлетворяют
стандарту. Упрощенная схема контроля признает годной стандартную
продукцию с вероятностью 0,98 и нестандартную - с
вероятностью 0,05. Определить вероятность того, что изделие, принятое
по упрощенной схеме, удовлетворяет стандарту.
4. Сколько надо произвести независимых испытаний с
вероятностью появления события в каждом испытании, равной
0,4, чтобы наивероятнейшее число появления события в этих
испытаниях было равно 25?
5. В магазине вывешены один костюм 2-го роста, два
костюма 3-го роста и три костюма 4-го роста. Костюм 2-го роста
спрашивается с вероятностью 0,2, костюм 3-го роста - с
вероятностью 0,3, костюм 4-го роста — с вероятностью 0,5. В
магазин обратились 3 покупателя. Найти вероятность того, что хотя
бы один из них ушел без покупки.
Вариант 6
1. а-алгебра и вероятностная мера на ней. Сформулировать
аксиомы конечной и счетной аддитивности. Доказать, что если
неотрицательная нормированная конечно-аддитивная мера
является счетно-аддитивной, то она обладает следующим
свойством непрерывности: lim Р(Ап) = Р(С) для любой последова-
л->оо оо
тельности вложенных событий Вх d52 з...,С = Р|5/.
/=i
2. Рабочий обслуживает три независимо работающих
станка. Событие А.( состоит в том, что /-й станок в течение часа
потребует наладки, Р(А) = 0,2, / = 1, 2, 3. Выразить события:
1) ровно 2 станка потребуют наладки, 2) не более 2 станков
потребуют наладки, 3) хотя бы 1 потребует наладки. Найти
вероятность события 3. Найти вероятность того, что в течение
7 часов работы будет не менее 2 часов, когда наладки
потребуют все три станка.
3. Товаровед осматривает 24 образца товаров. Вероятность
того, что образец годен к продаже, равна 0,6. Найти
наивероятнейшее число образцов, которые товаровед признает годными
к продаже.
4. Найти вероятность того, что у 6-значного номера
телефона совпадают ровно 3 цифры.
15*
i
? Приложения
j 436
5. Вероятность наступления события в каждом отдельном
испытании равна 0,2. Произведено 900 испытаний. Найти
вероятность того, что относительная частота появления события
отклонится от его вероятности не более чем на 0,04.
Вариант 7
1. Сформулировать и доказать теорему Бернулли. Найти
наивероятнейшее число появления события в п независимых
испытаниях. Сформулировать теоремы Пуассона и Лапласа, а
также следствие из интегральной теоремы Лапласа.
2. Телеграфное сообщение состоит из сигналов «точка» и
«тире». Статистические свойства помех таковы, что
искажается в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире».
Известно, что среди передаваемых сигналов «точка» и «тире»
встречаются в отношении 5:3. Определить вероятность того,
что принят передаваемый сигнал, если: а) принята «точка»;
б) принято «тире».
3. Сколько раз надо провести опытов «трехкратное
подбрасывание кубика», чтобы с вероятностью 0,95 хотя бы один раз
появилось ровно 2 единицы?
4. Шесть рукописей случайным образом раскладывают по
5 папкам. Какова вероятность того, что некоторая папка
останется пустой?
5. Прядильщица обслуживает 1000 веретен. Вероятность
обрыва нити на одном веретене в течение одной минуты равна
0,004. Найти вероятность того, что в течение одной минуты
обрыв произойдет на 5 веретенах.
Контрольная работа № 1 «Случайные события»
(специальность «Экономика»)
Вариант 1
1. Основные правила комбинаторики. Сочетания,
размещения, перестановки. Разбиение множества на группы. Дискретное
пространство элементарных исходов. Простые и сложные
события. Классическое определение вероятности.
2. В урне 9 белых шаров, 7 красных и 4 черных. Найти
вероятность извлечь (без возвращения) три шара разного цвета.
3. Два аудитора проверяют 8 фирм (по 4 фирмы каждый), у
трех из которых имеются нарушения. Вероятность обнаружения
Приложения ф
нарушений первым аудитором равна 0,6, вторым - 0,9. Найти
вероятность того, что все фирмы-нарушители будут выявлены.
4. В цехе работают 7 мастеров и 3 ученика, производящие
одинаковое число изделий. Мастер допускает брак в 1%
случаев, а ученик — в 5% случаев. Изделие оказалось бракованным.
Найти вероятность, что его сделал ученик.
5. Деталь является бракованной с вероятностью 2%. Сколько
деталей надо взять, чтобы с вероятностью 99% среди них
оказалась хотя бы одна бракованная? Найти наивероятнейшее число
бракованных деталей в этом случае.
Вариант 2
1. Сигма-алгебра и аксиомы вероятности. Доказать
эквивалентность счетной аддитивности и монотонности.
Геометрическая вероятность.
2. В партии из 30 изделий 5 бракованных. Найти
вероятность, что в случайной выборке из 10 изделий содержится не
более одного бракованного.
3. В одной коробке 4 красных шара и 6 синих, а во
второй ~ 8 красных и 2 синих. Из первой во вторую переложили
два шара, а затем извлекли из второй два шара без
возвращения. Найти вероятность того, что последние оказались одного
цвета.
4. На заводе установлена система аварийной сигнализации,
которая при наличии аварии срабатывает с вероятностью 99%.
Однако в 0,2% случаев, когда аварии нет, сигнал также
может возникнуть. Найти вероятность того, что случилась авария,
если сигнализация сработала. Вероятность аварии 0,007.
5. Страховой агент при каждом визите заключает с
вероятностью 30% договор. При каком числе визитов
наивероятнейшее число договоров будет равно 10?
Вариант 3
1. Независимые испытания Бернулли. Формула Бернулли
и неравенство для наивероятнейшего числа успехов (с
доказательствами).
2. Шесть клиентов равновероятно обращаются в 3 фирмы.
Найти вероятность того, что ровно в одну фирму обратятся
2 клиента.
3. Из продукции птицефабрики 75% яиц стандартные, 20% —
большего объема и 5% - двухжелтковые. С какой вероятностью
437 |
ф Приложения
среди 3 случайно выбранных яиц одновременно окажутся хотя
бы одно большего объема и хотя бы одно двухжелтковое?
4. К системному администратору обращаются за помощью
пользователи. Среди них 60% начинающих, 40% опытных.
Вероятность обращения начинающего пользователя 85%,
опытного — 15%. Найти вероятность того, что очередной
пользователь, обратившийся за помощью, окажется начинающим.
5. Стиральным порошком фирмы А пользуется 25%
населения. Сколько людей надо опросить, чтобы получить эту долю
с точностью 0,05 с вероятностью 0,95?
Вариант 4
1. Условная вероятность. Полная группа событий. Формула
полной вероятности и формула Байеса (с доказательствами).
2. Студент в состоянии решить 20 задач из 25 в первом туре
экзамена и 15 из 20 - во втором. Найти вероятность сдачи им
экзамена, если в каждом туре дается 3 задачи и достаточно
решить хотя бы 2 из них.
3. Фирма участвует в четырех независимых проектах,
вероятности успеха которых составляют 0,5; 0,6; 0,7 и 0,8
соответственно. Найти вероятность того, что хотя бы два проекта
увенчаются успехом.
4. В город поступают товары трех фирм в соотношении 2:3:5.
В поставках первой фирмы 60% товара высшего качества,
второй - 40%, а третьей - 20%. Куплен товар высшего качества.
Найти вероятность того, что он изготовлен второй фирмой.
5. Вероятность того, что пассажир опоздает к поезду, равна
0,005. Найти наиболее вероятное число опоздавших, если всего
билеты купили 600 человек, и вероятность того, что их будет
именно столько.
Вариант 5
1. Операции над событиями. Формулы де Моргана.
Независимость событий. Вероятность противоположного события.
Теоремы сложения и умножения вероятностей (с
доказательствами).
2. В каждой упаковке товара фирмы «Том» имеется одна из
букв Т, О, М равновероятно. Какова вероятность собрать все
буквы, купив 5 упаковок товара?
3. В урне 7 красных шаров и 9 синих. Извлекли три шара
(без возвращения), затем положили их обратно и добавили в
j 438
Приложения @
урну два шара того цвета, который оказался в большинстве
среди извлеченных. С какой вероятностью два шара, вынутых
после этого, окажутся синими?
4. Мимо бензоколонки проезжают легковые и грузовые
машины. Среди них грузовых машин 75%. Вероятность того, что
проезжающая машина подъедет заправиться, для грузовой
машины равна 0,1, для легковой — 0,2. Найти вероятность того, что
очередная машина, подъехавшая на заправку, окажется грузовой.
5. К 5 менеджерам обращаются 400 клиентов фирмы. В
каких границах с вероятностью 0,95 лежит число клиентов
отдельно взятого менеджера?
Вариант 6
1. Теорема Муавра—Лапласа и следствия. Теорема Пуассона
(с доказательством).
2. Группа из 27 студентов пишет контрольную из 3
вариантов (по 9 человек в каждом). Найти вероятность того, что
среди случайно выбранных 5 студентов есть писавшие каждый
вариант.
3. Фирма имеет 3 поставщиков, каждый из которых
надежен с вероятностью 0,8. В случае отказа одного поставщика
вероятность разорения фирмы равна 0,25, двух - 0,75, трех -
0,95. Найти вероятность разорения фирмы.
4. Из урны, где было 10 красных, 6 белых и 4 синих шара,
вынут один шар. После этого из урны извлечены (без
возвращения) 2 шара, оказавшиеся красным и белым. При этом условии
найти вероятность того, что сначала был вынут синий шар.
5. Страховая фирма заключила 2500 договоров. Вероятность
страхового случая по каждому в течение года составляет 2%.
Найти вероятность того, что число таких случаев не превзойдет
наивероятнейшее число более чем на 2.
Контрольная работа № 1 «Случайные события»
(специальность «Менеджмент»)
Вариант 1
1. Дискретное пространство элементарных исходов. Простые
и сложные события. Классическое определение вероятности.
2. В каждой упаковке товара фирмы «Рекс» вложена одна
из букв Р, Е, К, С (равновероятно). Найти вероятность собрать
все буквы, купив 6 упаковок товара.
439 |
ф Приложения
! 440
3. Из урны, где было 5 белых и 2 черных шара, переложен
вынутый наудачу шар в урну, содержащую 3 белых и 4 черных
шара. Найти вероятность вынуть после этого из второй урны
белый шар.
4. Магазин производит закупки некоторого продукта у трех
производителей в долях 25, 35 и 40% соответственно. Доли
продукта высокого качества в поставках равны 50, 60 и 80%
соответственно. Куплен продукт высокого качества. Найти
вероятность того, что он поставлен первым производителем.
5. В партии из 400 арбузов каждый арбуз оказывается
неспелым с вероятностью 0,2. Найти наивероятнейшее число спелых
арбузов и вероятность того, что реальное число спелых арбузов
в указанной партии будет в пределах от 300 до 350.
Вариант 2
1. Основные правила комбинаторики. Сочетания,
размещения, перестановки. Разбиение множества на группы.
2. Из 15 проданных за неделю телевизоров 3 имеют
скрытые дефекты. Найти вероятность того, что среди выбранных
наудачу 5 телевизоров (из числа проданных) окажется не более
одного со скрытыми дефектами.
3. В магазине было проведено исследование продаж
некоторого товара. Выяснилось, что этот товар покупают 25%
женщин, 10% мужчин и 40% детей. Среди покупателей магазина
65% женщин, 20% мужчин и 15% детей. Найти вероятность
того, что наудачу выбранный покупатель приобретет данный
товар.
4. На заводе, изготовляющем болты, машины А, В и С
производят 20, 30 и 50% всех изделий соответственно. В их
продукции брак составляет 5, 3 и 1% соответственно. Случайно
выбранный болт оказался дефектным. Какова вероятность того,
что он был произведен машиной А?
5. При наборе текста наборщик делает ошибку в слове с
вероятностью 0,003. Найти наивероятнейшее число ошибок в
тексте из 1300 слов и вероятность того, что оно не будет
превышено.
Вариант 3
1. Независимость событий. Независимые испытания
Бернулли. Формула Бернулли. Наивероятнейшее число успехов.
Приложения ф
2. Шесть клиентов случайным образом обращаются в 4
фирмы равновероятно. Найти вероятность того, что в какие-то две
фирмы обратятся по два клиента, и в две - по одному.
3. Электроэнергия поступает в город по трем линиям, каждая
из которых может быть отключена с вероятностью 0,05. Если
отключается одна, две, три линии, то город испытывает недостаток
электроэнергии с вероятностями 0,3; 0,6; 1. Если работают все
линии, то недостатка электроэнергии нет. Какова вероятность
того, что город будет испытывать недостаток электроэнергии?
4. Первый стрелок поражает мишень с вероятностью 0,5,
второй стрелок — с вероятностью 0,3 и третий стрелок — с
вероятностью 0,7. Стрелки дали залп по мишени, но только одна
пуля попала в цель. Какова вероятность, что третий стрелок
попал в цель?
5. Изделие является годным с вероятностью 0,96. Какова
вероятность того, что в партии из 100 деталей будет не более
3 бракованных?
Вариант 4
1. Условная вероятность. Полная группа событий. Формула
полной вероятности. Формула Байеса.
2. Шесть клиентов случайным образом обращаются в 3
фирмы равновероятно. Найти вероятность того, что во все фирмы
обратится разное число клиентов.
3. Из урны, где было 7 белых и 3 черных шара, переложен
извлеченный наудачу шар в урну, содержащую 5 белых и 2 черных
шара. Найти вероятность извлечь из второй урны черный шар.
4. Фирма нарушает закон с вероятностью 0,15. Аудитор
обнаруживает нарушения (если они есть) с вероятностью 0,8.
Проведенная им проверка не выявила нарушений. Найти
вероятность того, что на самом деле они есть.
5. Страховая фирма заключила 10 000 договоров. Вероятность
страхового случая по каждому в течение года составляет 2%.
Найти наивероятнейшее число страховых случаев и
вероятность того, что реальное число случаев отклонится от него не
более чем на 30.
Вариант 5
1. Операции над событиями. Формулы де Моргана.
Вероятность противоположного события. Теоремы сложения и
умножения вероятностей.
441 |
I
ф Приложения
I 442
2. Слово МЕНЕДЖМЕНТ разрезано на буквы, и они
перемешаны. Какова вероятность вновь собрать слово при
случайном расположении букв?
3. Фирма участвует в трех независимых проектах,
вероятности успеха которых составляют 0,7; 0,8 и 0,9. Найти вероятность
того, что по крайней мере два проекта увенчаются успехом.
4. Изделие имеет скрытые дефекты с вероятностью 0,1.
В течение года выходит из строя 80% изделий со скрытыми
дефектами и 5% изделий без дефектов. Найти вероятность того,
что изделие имело скрытые дефекты, если оно вышло из строя
в течение года.
5. Известно, что в среднем 1% деталей имеет дефекты.
Сколько деталей надо проверить, чтобы с вероятностью 95%
среди них оказалась хотя бы одна с дефектами? Найти
наивероятнейшее число деталей с дефектами в этом случае.
Вариант 6
1. Предельные теоремы Пуассона и Муавра-Лапласа.
Следствия.
2. Известно, что в лотерее из 50 билетов имеется 4
выигрышных. Найти вероятность того, что среди купленных 10
билетов окажется хотя бы один выигрышный.
3. Два аудитора проверяют 8 фирм (по 4 каждый), у двух из
которых имеются нарушения. Первый аудитор обнаруживает
нарушения с вероятностью 0,7; второй — с вероятностью 0,8. Найти
вероятность того, что обе фирмы-нарушители будут выявлены.
4. К системному администратору обращаются за помощью
пользователи. Среди них 70% начинающих, 30% опытных.
Вероятность обращения начинающего пользователя 80%,
опытного - 10%. Найти вероятность того, что очередной
пользователь, обратившийся за помощью, окажется начинающим.
5. При визите страхового агента вероятность заключения
договора составляет 20%. Найти наивероятнейшее число
заключенных договоров после 10 визитов и вероятность того, что
их будет заключено не больше найденного числа.
Контрольная работа № 2. «Случайные величины.
Законы распределения»
Вариант 1
1. Два станка выпускают некоторую деталь соответственно с
вероятностями брака рх = 0,01 и р2 = 0,05. В выборке одна де-
Приложения ф
таль, выпущенная первым станком, и две — со второго станка.
Найти распределение вероятностей случайной величины ^ —
числа бракованных деталей в выборке.
2. Двумерная случайная величина (?, л) равномерно
распределена на множестве {(х, >>)|х:2+ у*< 1, у > 0}. Найти плотность
распределения составляющих ? и г| и ответить на вопрос о
зависимости ? и т| (ответ обосновать).
3. Плотность распределения случайной величины ? имеет
, , /С(х + 1), хе[-1,2],
вид р^(х) = <
0,
х*Н,2].
Найти С, функцию распределения Дх), Я(?2< 1)5 Л/(4 + 2)1/2.
4. Совместная плотность распределения пары (?, г|) задана
таблицей.
ч
-1
0
1
-1
1/16
1/8
1/16
1
3/16
3/8
3/16
Найти распределения вероятностей ? + л; cov(? — л, 4 + л);
ответить на вопрос о зависимости случайных величин ^ и л
(ответ обосновать).
5. Случайная величина равномерно распределена на отрезке
[1, 3]. Найти плотность распределения вероятностей л = ?2+ 1.
Вариант 2
1. Двумерная случайная величина (?, л) равномерно
распределена в квадрате с вершинами (-2, 0), (0, -2), (2, 0),
(0, 2). Найти значение функции совместного распределения
F{x, у) в точке (1, -1).
2. Плотность распределения случайной величины ^ имеет
вид ^(jc) = Jc(x + 1)"1, *^0,
[0, х<0.
Найти С, функцию F(x), Р(\$ - 1/31 < 1) и Щ1.
3. Случайные величины ? и л независимы и имеют
показательное распределение с параметром X = 2. Найти Р(? + л ^ 1).
4. Совместное распределение пары (?, л) задано таблицей
443
Приложения
ч
-1
0
1
-1
1/8
1/8
1/8
1
3/8
1/8
1/8
Найти распределение 2? + tj; cov(? - т|, ц); ответить на
вопрос о зависимости ? и г| (обосновать).
5. Два стрелка поражают мишень соответственно с
вероятностями 0,7 и 0,8 при одном выстреле. Найти распределение
вероятностей числа попаданий, если первый стрелок выстрелил
один раз, а второй — два раза.
Вариант 3
1. Двумерная случайная величина равномерно распределена
в треугольнике (0, 4), (4, 0) и (4, 4). Найти плотность
распределения составляющих § и г\ и ответить на вопрос о зависимости
случайных величин ? и т| (ответ обосновать).
2. Плотность распределения случайной величины § имеет
fC(l-x2), |х|<1,
вид рЛх) = \
* [0, |х|>1.
Найти С, функцию распределения F(x), Р(\$ - 1/21 < 1/4),
Affl- + 1),/2.
3. Совместный закон распределения пары (?, г|) задан
таблицей.
-1
0
1
-1
1/10
1/5
1/5
1
1/5
1/10
1/5
Найти распределение вероятностей § - х\\ cov(^ + ti; § — т|);
исследовать вопрос о зависимости § и г|.
4. Случайная величина § имеет равномерное
распределение на отрезке [-1; 1]. Найти плотность случайной величины
Л = tg(n§/2).
} 444
Приложения
5. Среди 5 ключей два подходят к двери. Ключи пробуют
один за другим, пока не откроют дверь. Найти распределение
вероятностей ? — числа опробованных ключей.
Вариант 4
1. Случайная величина ? имеет равномерное распределение на
отрезке [—1, 1]. Найти плотность распределения г) = —In(2 + ?).
2. Плотность распределения случайной величины § имеет
fC(l-|x|), |х|<1,
вид *w=jo, М,1.
Найти С, функцию распределения Дх) и Щ.
3. Совместный закон распределения пары (?, л) задан
таблицей.
ц
-1
0
1
-1
1/12
1/6
1/4
1
1/4
1/12
1/6
Найти закон распределения вероятностей ?л;
cov(? — л, ? + л), исследовать вопрос о зависимости случайных
величин ? и л (ответ обосновать).
4. Случайная пара (?, л) имеет равномерное распределение
на множестве {х, у: I х I + | у \ < 2}. Найти плотности
распределения ? и л- Являются ли они зависимыми? (Ответ обосновать.)
5. С конвейера поступили 4 детали. Вероятность брака для
каждой детали р. Детали проверяют одну за другой, пока не
наберут 2 доброкачественные. Найти распределение вероятностей
числа § проверенных деталей.
Вариант 5
1. Случайная величина ? равномерно распределена на
отрезке [—х, х]. Найти плотность распределения случайной вели-
. я?
чины л = sin—.
2
445 [
ф Приложения
К(х) =
1 ,
Г'
4-
х>0.
Найти математическое ожидание Щ9 дисперсию D\ и
вероятность Р(—\ < ? < 3).
3. Совместный закон распределения пары (?, г\) задан
таблицей.
s
-1
0
1
-1
1/16
1/16
1/8
1
3/16
3/16
3/8
Зависимы ли ^ и г| (ответ обосновать)? Найти закон
распределения ?2 + г|, cov(? ~ т), 4 + л)-
4. Случайная пара (§, л) равномерно распределена на
множестве {х, у: \х\ + \у\ < 1; у > 0}. Найти плотности
распределения ? и т|. Ответить на вопрос о зависимости ? и г\ (ответ
обосновать).
5. Прибор комплектуется из 2 деталей, вероятность брака
для первой детали 0,1, а для второй 0,05. Пусть § — число
бракованных среди 4 приборов. Найти распределение случайной
величины 5 и ее математическое ожидание.
Примеры вариантов экзаменационных работ
по теории вероятностей
Вариант 1
1. Пространство элементарных исходов. События (простые
и сложные). Операции над событиями. Формулы де Моргана.
Классическое определение вероятности.
2. Ковариация. Коэффициент корреляции и его свойства.
3. Группа из 20 студентов пишет контрольную работу из
4 вариантов (по 5 человек в каждом). Найти вероятность того,
что среди случайно выбранных 5 студентов есть писавшие
каждый вариант.
I 446
I
2. Случайная величина ? имеет функцию распределения
Приложения ф
\Сеъ\ х<0,
"to, х>0.
Найти константу С, функцию распределения Дх),
вероятность Р(—2 < \ < 1), математическое ожидание Щ и плотность
Л = 42+1 .
Вариант 2
1. Непрерывная случайная величина. Плотность
непрерывной случайной величины и ее свойства. Совместная плотность
распределения двумерной случайной величины. Условия
независимости случайных величин.
2. Нормальный закон распределения. Функция
распределения нормально распределенной случайной величины. Правило
трех сигм. Вычислить математическое ожидание и дисперсию
нормально распределенной случайной величины.
3. Семь клиентов случайным образом обращаются в 5 фирм.
Найти вероятность, что хотя бы в одну фирму никто не
обратится.
4. Найти плотность распределения суммы независимых
случайных величин ^ и л» если они равномерно распределены на
отрезках [0, 2] и [1, 4] соответственно.
5. Плотность случайной величины § равна
\Сех-\ х<2,
* [0, х>2.
Найти константу С, функцию распределения Дх),
вероятность Р(\ < ? < 4), математическое ожидание Щ и плотность
1
Вариант 3
1. Независимость событий, попарная и в совокупности.
Независимые испытания Бернулли. Теорема о распределе-
447
4. Двумерная случайная величина (4, л) равномерно
распределена на множестве |0<^<4-х2}. Проверить величины ? и л
на независимость, найти их плотности.
5. Плотность случайной величины ? равна
ф Приложения
Найти константу С, функцию распределения F(x),
вероятность Р(0 < ? < 4), плотность Л = 7—г, математическое
ожидание Мг\.
Вариант 4
1. Полная группа событий. Формула полной вероятности,
формула Байеса (с доказательством).
2. Дать определение распределения Бернулли. Вычислить
математическое ожидание и дисперсию.
3. Фирма нарушает закон с вероятностью 0,25. Аудитор
обнаруживает нарушение с вероятностью 0,75. Проведенная им
проверка не выявила нарушений. Найти вероятность, что на
самом деле они есть.
4. Найти плотность распределения суммы независимых
случайных величин 4 и г|, если § равномерно распределена на
отрезке [0, 1], а г| показательно распределена с параметром к = 2.
5. Плотность случайной величины § равна
Найти константу С, функцию распределения Дх), вероят-
2
ность Р(-\ < § < 1), плотность r| = -^f—^, математическое
ожидание Мг\.
*е[0,2],
хе[0,2].
| 448
нии вероятностей числа успехов в п независимых испытаниях
Бернулли. Формула Бернулли. Наивероятнейшее число
успехов.
2. Дать определение показательного распределения.
Вычислить математическое ожидание и дисперсию.
3. Найти вероятность, что в 8-значном числе ровно 3 цифры
совпадают, а остальные различны (число может начинаться с
нуля).
4. Двумерная случайная величина равномерно распределена
на множестве |0<^<4-(х-1)2}. Проверить величины § и ц на
независимость, найти их плотности.
5. Плотность случайной величины ? равна
Приложения ф
Вариант 5
1. Определение вероятности события. Вероятность
противоположного события. Условная вероятность. Теоремы сложения
и умножения. Теорема умножения для независимых событий.
2. Дать определение распределения Пуассона. Вычислить
математическое ожидание и дисперсию.
3. Курс акций за день растет или падает на 1 пункт
равновероятно. Найти вероятность того, что за 10 дней торгов курс
акций упадет на 4 пункта.
4. Двумерная случайная величина (?, л.) равномерно
распределена на множестве {(х-2)2 +у2 <9,>>>0 j. Проверить величины
4 и г\ на зависимость, найти их плотности.
5. Плотность случайной величины § равна
fCx"5, х>1,
[0, х<1.
Найти константу С, функцию распределения F(x),
вероятность Р(0 < § < 2), плотность Л = л/?-1, математическое
ожидание Мг\.
Вариант 6
1. Неравенство Чебышева. Закон больших чисел в форме
Чебышева. Теорема Бернулли как частный случай теоремы
Чебышева. Формулировка центральной предельной теоремы.
2. Случайная величина и ее законы распределения. Функция
распределения случайной величины и ее свойства.
3. Два аудитора проверяют 8 фирм (по 4 фирмы каждый),
у двух из которых есть нарушения. Вероятность обнаружения
нарушений первым аудитором равна 0,8, вторым - 0,9. Найти
вероятность того, что все фирмы-нарушители будут выявлены.
4. Найти плотность распределения суммы независимых
случайных величин ^ и т|, если они показательно распределены с
параметрами \=1, \=2 соответственно.
5. Плотность случайной величины % равна
[ОГ(*+,), х>-1,
х<-1.
449
Приложения
Найти константу С, функцию распределения F(x),
вероятность Р(?? < 1/4), математическое ожидание Щ и плотность
Примеры вариантов контрольных по математической статистике
Контрольная работа № 1. Точечные оценки
Вариант 1
1. По выборке хр х2, хп методом моментов найти оценки
параметров равномерного распределения на отрезке [а, Ь].
2. Доказать состоятельность, несмещенность и
эффективность оценки функции распределения.
3. Пусть случайная величина ? подчиняется стандартному
нормальному закону распределения: § е N(0, 1). Найти функ-
?2
цию плотности вероятностей случайной величины r\ = -у. К
какому параметрическому семейству распределений относится х\>
4. Докажите, что сумма двух хи-квадрат-распределенных
случайных величин имеет хи-квадрат-распределение.
5. Ежедневный спрос на некоторый товар имеет
равномерное распределение на отрезке [а, Ь]. За период наблюдения
спрос составил в среднем 150 кг с исправленной выборочной
дисперсией 243 кг2. С помощью метода моментов оценить,
сколько потребуется товара, чтобы удовлетворить ежедневный
спрос с вероятностью 95%.
Вариант 2
1. По выборке х,, х2, хп методом максимального
правдоподобия найти оценку для параметра 0 в показательном законе
распределения
Исследовать оценку дисперсии на состоятельность и
несмещенность.
2. Известно, что хр х2, хп — случайная выборка из
генеральной совокупности с геометрическим распределением веро-
Л = ($ + 2)2.
/(*,©) =
1 --
-е 6
0
0,
х>0
х<0
450
Приложения ©
п + т — L
являются несмещенными оценками параметра а2.
4. Пусть 5Р ?2, —> 4Я независимые нормально
распределенные случайные величины: \ € N(09 а2). Найти плотность рас-
п
пределения ц = ]Г ?2.
/=i
5. Известно, что некоторая работа занимает время,
состоящее из постоянного периода и случайной задержки,
распределенной показательно. Хронометраж рабочего времени показал,
что работа занимает как минимум 30 минут, а в среднем — 45
минут. С помощью метода максимального правдоподобия
оценить вероятность того, что работа будет закончена за час.
Вариант 3
1. В случае известного математического ожидания а при
§ е N(a9 а2) методом максимального правдоподобия найти
оценку дисперсии и исследовать ее свойства.
2. Доказать несмещенность, состоятельность и
асимптотическую нормальность выборочных начальных моментов.
3. Случайная величина задана функцией плотности
распределения
\Схв'1е'кс9 х>0,
р(х9а9Ь) = <
[0, х<0.
Ъ°
Доказать, что С = и найти Щ и Z)?.
Г(а)
4. Пусть х{9 х29 хп - выборка независимых наблюдений из
непрерывного распределения с функцией плотности р(х) и
функцией распределения F(x). Найти функцию распределения и
функцию плотности крайних членов вариационного ряда: xmin и х^.
451
ятностей = к) = (1 - p)pfc~\ к = 0, 1, 2, .... Методом
моментов найти оценку параметра р и доказать ее состоятельность.
3. Пусть х,, х2, хп9 >>р >>2, ут — случайные выборки
объема лит, извлеченные из нормально распределенной
генеральной совокупности N(a9 а2). Доказать, что
^ Приложения
4. Вывести формулу, связывающую гамма-функцию и бета-
функцию.
5. В поселке Полтинниково все жители имеют доход не
менее 50 тыс. руб. в месяц. Выборочное исследование отразило
средний доход 200 тыс. руб. В предположении, что случайная
величина дохода имеет распределение Парето Дх) = 1 — (х/х0)"а,
х > х0, где х0= 50 тыс. руб., оценить параметр а методом
моментов и долю жителей с доходами свыше 400 тыс. руб.
Вариант 5
1. Доказать эффективность оценки математического
ожидания, найденную по неравноточным наблюдениям.
2. В случае биномиального распределения методом
максимального правдоподобия найти оценку параметра р и
исследовать ее свойства (состоятельность, несмещенность,
эффективность).
3. Пусть 52 выборочная дисперсия, построенная по выборке
Хр х2, х из нормальной генеральной совокупности N(a, а2).
Доказать, что статистика г—2- распределена по закону % с
а
п — 1 степенями свободы.
452
5. Известно, что доля возвратов по кредитам в банке имеет
распределение F(x) = jfi, 0 < х < 1. Наблюдения показали, что
в среднем она составляет 80%. С помощью метода моментов
оценить параметр (3 и вероятность того, что доля возврата
опустится ниже 70%.
Вариант 4
1. По выборке хр х2, хп методом максимального
правдоподобия найти оценки параметров равномерного
распределения на отрезке [а, Ь].
2. Доказать состоятельность, несмещенность и
эффективность среднего арифметического как оценки математического
ожидания.
3. Пусть ?0, 5р §2, %п - независимые нормально распре-
деленные случайные величины е N(0, о2), / = 0, 1, 2, и
Приложения ф
4. Найти методом моментов точечную оценку параметра р
геометрического распределения = т) = р (1 - р)т, где р —
вероятность появления события в одном испытании.
5. Трое исследователей провели независимые выборочные
обследования доходов населения. Первый определил средний
доход 3100 у.е. с точностью а1 = 80 у.е., второй - 2950 у.е. с а2 =
= 50 у.е., третий - 3050 у.е. с а3 = 40 у.е. Построить наиболее
точную оценку среднего годового дохода и найти ее
дисперсию.
Контрольная работа № 2. Доверительные интервалы.
Статистическая гипотеза
Вариант 1
1. Проверить гипотезу о равенстве дисперсий при
неизвестных средних.
2. Для параметра X пуассоновского распределения по
выборке хр х2, хп построить асимптотический доверительный
интервал. Точечную оценку параметра X найти методом
максимального правдоподобия.
3. Импортер упаковывает чай в пакеты. Известно, что
наполняющая машина работает со стандартным отклонением а, равным
10 г. Выборка 50 пакетов показала средний вес х = 128,5 г. Найти
доверительный интервал для среднего веса в генеральной
совокупности с вероятностью 95%. Генеральная совокупность
распределена нормально. Найти объем выборки я, чтобы с вероятностью
95% точность доверительного интервала была бы равна 2,0 г.
4. Среди 100 электрических ламп в течение 1000 часов
вышло из строя 36 штук. Построить доверительный интервал с
вероятностью 95% для генеральной доли ламп, которые
прослужат не менее 1000 часов.
5. Партия изделий принимается, если дисперсия размеров
не превышает 0,2. Исправленная выборочная дисперсия для
30 изделий оказалась равной 0,3. Можно ли принять партию
при уровне значимости 5%?
Вариант 2
1. Проверить гипотезу о равенстве средних при неизвестной
дисперсии.
453
ф Приложения
454
2. Построить асимптотический доверительный интервал для
параметра 0 равномерного распределения на отрезке [0, 0]
случайной величины Точечную оценку параметра 0 найти
методом моментов.
3. Производитель автомобильных шин заинтересован в
получении оценки средней износоустойчивости шин особой модели.
Он провел случайную выборку объемом 10 шин и подверг их
специальному испытанию. Средняя износоустойчивость по
данным выборки оказалась равна 22 500 миль со стандартным
выборочным неисправленным отклонением S = 3000 миль. Найти
доверительный интервал с вероятностью 99% для средней
износоустойчивости всего выпуска шин этого типа. Генеральная
совокупность распределена нормально.
4. Можно ли две независимые нормальные выборки
(хр х2, хп) и (ур yv ут) считать одинаково
распределенными, если х = 2,7; s2 =0,36; у = 3,5; s] =0,64; п = 10; т = 10;
s2- несмещенные оценки дисперсии? Проверить гипотезу на
уровне значимости 10%.
5. За последние 5 лет годовой рост цен акции А составил в
среднем 20% со средним квадратичным отклонением
(исправленным) 10%. Построить доверительный интервал с
вероятностью 95% для средней цены акции в конце следующего года,
если в начале года она равна 1000 единиц.
Вариант 3
1. Построить асимптотический доверительный интервал для
параметра X показательного распределения. Точечную оценку
параметра X найти методом моментов.
2. Проведена случайная выборка личных заемных счетов в
банке. Из п = 1000 отобранных счетов 60 оказались с
задолженностью по возврату ссуды сроком до трех месяцев. Найти
доверительный интервал с вероятностью 90% для доли счетов
в генеральной совокупности, которые имеют задолженность до
трех месяцев, если банк насчитывает 30 000 личных заемных
счетов.
3. За последние 10 лет выборочные средние доходности по
активам А и Б составили соответственно 10 и 15% с
исправленными средними квадратическими отклонениями 5 и 7%.
Можно ли утверждать, что вложения в актив Б более выгодны,
чем в А, с уровнем значимости 11%?
Приложения
4. По социологическому опросу среди 100 человек 20%
пользуются стиральным порошком фирмы А. Сколько еще людей
надо опросить, чтобы с вероятностью 99% получить результат
с точностью до 1%?
5. Найти мощность критерия по результатам одной
выборки (хр х2, хп), х. е N(a, а2) с известной дисперсией а2,
построенного для проверки нулевой гипотезы Я0: а = а0 против
альтернативной Нх\ а = ах > а0.
Вариант 4
1. Асимптотический способ построения интервальных
оценок на примере биномиального распределения. Точечную
оценку неизвестной вероятности найти методом моментов.
2. Принцип отношения правдоподобия. Теорема Неймана-
Пирсона.
3. В ходе аудиторской проверки фирмы была проведена
случайная выборка записей по счетам. Из выборки п = 500 записей
10 содержали некоторые ошибки в самой записи или
процедуре. Найти доверительный интервал для доли ошибок во всей
генеральной совокупности с вероятностью 95%. Определить
объем выборки, которую надо произвести аудитору, если он
хочет определить с точностью 0,005 генеральную долю с
доверительной вероятностью 95%.
4. В течение 100 рабочих дней магазин А посещало в
среднем 198 человек в день, магазин Б - 202 человека. Есть ли
основания утверждать (на уровне значимости 5%), что магазин
Б более популярен, чем А, если числа покупателей в день
имеют дисперсии, равные 200?
5. По выборке из 100 изделий нашли, что средний срок
службы равен 1000 часов. Построить доверительный интервал
для среднего срока службы с вероятностью 90%. Время службы
распределено по показательному закону. Для решения задачи
необходимо вывести доверительный интервал для параметра
показательного распределения.
Вариант 5
1. Статистическая гипотеза. Критерий проверки нулевой
гипотезы. Критическое множество. Ошибки первого и второго
рода, размер и мощность критерия.
2. Имея выборки (хр х2, хп) и (yv yv ут) из двух
нормальных генеральных совокупностей, построить доверительный
455
Приложения
456
интервал для разности теоретических средних этих
совокупностей в предположении, что они обладают одинаковыми, хотя и
неизвестными дисперсиями.
3. Среднее время сборки изделия было 90 минут. Инженер
изобрел новый метод сборки этого изделия, и
продолжительность сборки 10 изделий новым методом составила 79, 74, 112,
95, 83, 96, 77, 84, 70, 90 минут. Можно ли утверждать, что
среднее время сборки сократилось (на уровне значимости 5%).
4. В условиях задачи 3 найти наименьший объем выборки,
необходимый для получения значения среднего времени
сборки в пределах 3 минут с доверительной вероятностью 95%.
5. За последние 5 лет выборочная дисперсия доходности
актива А составила 0,04, актива Б — 0,05. Есть ли основания
утверждать на уровне значимости 5%, что вложения в актив А
менее рискованны, чем в Б? Вложения считаются более
рискованными, если дисперсия больше.
Примеры вариантов экзаменационных работ
по математической статистике
Вариант 1
1. Бета-распределение: определение, свойства,
характеристики. Вычисление математического ожидания.
2. Критерий отношения правдоподобия. Теорема Неймана-
Пирсона. Применение к гипотезе о среднем для нормального
распределения.
3. Доказать эффективность оценки методом максимального
правдоподобия для математического ожидания в случае
нормального распределения.
4. В выборке из 400 изделий средний срок службы составил
1500 часов. Известно, что срок службы изделия имеет
показательное распределение. Построить доверительный интервал для
среднего срока службы с надежностью 95%.
5. Средний дневной объем продаж фирмы составлял 860
единиц. После реорганизации за 25 рабочих дней выборочный
средний объем продаж составил 900 единиц с выборочным
средним квадратическим отклонением 35 единиц. Можно ли
утверждать на уровне значимости 5%, что реорганизация
привела к увеличению среднего объема продаж?
Приложения
Вариант 2
1. Гамма-распределение: определение, свойства,
характеристики. Вычисление математического ожидания и дисперсии.
2. Понятие доверительного интервала. Точные
доверительные интервалы для параметров нормального распределения.
3. Доказать эффективность оценки максимального
правдоподобия параметра 9 показательного распределения р(х) = (1 / 0)е~*/е,
х > 0.
4. Проведены испытания новой машины, упаковывающей
товар в пакеты. По выборке из 30 пакетов получено
выборочное среднее квадратическое отклонение веса 0,7 г. Построить
доверительный интервал с надежностью 95% для дисперсии
веса пакета при упаковке машиной.
5. В прошлом году средняя зарплата жителей города Булкино
составляла 7300 руб. В этом году выборка из 400 человек
показала, что средняя зарплата составляет 7320 руб. при
выборочном среднем квадратическом отклонении 150 руб. Можно
ли на уровне значимости 5% утверждать, что зарплата жителей
города увеличилась?
Вариант 3
1. Распределение Стьюдента: определение, свойства,
характеристики. Доказать сходимость при п -*оо к нормальному
распределению N(0, 1).
2. Понятие асимптотического доверительного интервала.
Методы построения асимптотических доверительных
интервалов. Примеры построения интервалов для вероятности «успеха»
в испытаниях Бернулли (двумя методами).
3. Доказать несмещенность, состоятельность и
эффективность эмпирической функции распределения как оценки
теоретической функции распределения.
4. Импортер упаковывает чай в пакеты. Известно, что
наполняющая машина работает со средним квадратическим
отклонением, равным 0,8 г. Выборка 100 пакетов показала
средний вес 99,9 г. Найти доверительный интервал для среднего
веса пакета с надежностью 90%.
5. Проведено исследование батареек фирм «Винтик» и
«Шпунтик». По выборке из 10 батареек фирмы «Винтик»
получен средний срок службы 207 часов с выборочным средним
квадратическим отклонением 11 часов, по выборке из 16 ба-
457
^ Приложения
458
тареек фирмы «Шпунтик» - средний срок службы 194 часа
с выборочным средним квадратическим отклонением 8 часов.
Можно ли утверждать на уровне значимости 10%, что в
среднем срок службы батареек этих двух фирм одинаков?
Вариант 4
1. Распределение Фишера: определение, свойства,
характеристики. Проверить, к какому распределению оно сходится при
т -»оо.
2. Основные понятия в проверке гипотез: основная и
альтернативная гипотезы, статистика критерия и критическая
область, ошибки первого и второго рода, уровень значимости и
мощность критерия.
3. Доказать эффективность оценки максимального
правдоподобия для вероятности «успеха» р распределения Бернулли с
числом испытаний т.
4. За 100 рабочих дней в магазин в среднем обращалось
289 человек в день. Известно, что число покупателей в день
описывается распределением Пуассона. Построить
доверительный интервал для среднего числа покупателей в день с
надежностью 90%.
5. Старая наполняющая машина работала со средним
квадратическим отклонением веса упаковки 1 г. Были проведены
испытания новой машины. По выборке из 30 упаковок товара
получено выборочное среднее квадратическое отклонение 0,7 г.
Можно ли утверждать на уровне значимости 5%, что для новой
машины среднее квадратическое отклонение меньше?
Вариант 5
1. Распределение хи-квадрат: определение, свойства,
характеристики. Доказать, что %2„ = у(п1% 1/2).
2. Метод наименьших квадратов. Система нормальных
уравнений. Теорема Гаусса-Маркова.
3. Доказать эффективность оценки методом моментов для
параметра X распределения Пуассона.
4. В деревне Ложкино проведено выборочное исследование
доходов. По выборке из 25 человек получен выборочный
средний доход 4750 руб. с выборочным средним квадратическим
отклонением 150 руб. Построить доверительный интервал для
среднего дохода с надежностью 95%.
Приложения
5. Фирма разослала 1000 рекламных каталогов и получила
140 заказов. Можно ли утверждать на уровне значимости 5%,
что эффективность рекламы повысилась, если в прошлом году
фирма получила 100 заказов (при том же объеме рассылки)?
Вариант 6
1. Бета- и гамма-функции: определения и свойства. Найти
Г(11/2) и В(9/2,5/2).
2. Критерии согласия Пирсона—Фишера (хи-квадрат) и
Колмогорова.
3. Построить оценку математического ожидания,
эффективную в классе линейных несмещенных оценок, в случае
неравноточных наблюдений. Вычислить ее дисперсию.
4. Фирма разослала 1000 рекламных каталогов и получила
140 заказов. Построить доверительный интервал для
эффективности рекламы (вероятности заказа по каталогу) с надежностью
90%.
5. В городах Глашино и Дашино проведены выборочные
обследования доходов жителей. По выборкам из 100 человек
получено, что в Глашино средний доход 8020 рублей с
выборочным средним квадратическим отклонением 190 рублей,
в Машино средний доход 7960 рублей с выборочным средним
квадратическим отклонением 160 рублей. Можно ли утверждать
на уровне значимости 5%, что в Глашино живут в среднем
богаче, чем в Дашино?
Примеры вариантов экзамена по теории вероятностей
и математической статистики
для менеджеров
Вариант L Теоретическая часть.
1. Формула полной вероятности имеет вид
А. Р(АВ) = Р(А\В)Р(В).
Б. P(A) = ^llP(Hk\A)P(Hk).
В- Р(А) = ^1хР(А\Нк)Р(Нк).
Г. Р(Нк\А) = Р(А\Нк)Р(Нк)/Р(А).
459
Приложения
2. Свойством испытаний Бернулли является следующее:
A) все исходы испытаний равновероятны;
Б) испытания заканчиваются одним из двух исходов;
B) вероятность успеха определяется результатом одного
произвольного испытания;
Г) все приведенные выше ответы верны.
3. Размещением т элементов из п называется:
A) упорядоченный набор п элементов из множества,
содержащего т элементов;
Б) упорядоченный набор т элементов из множества,
содержащего п элементов;
B) неупорядоченный набор т элементов из множества,
содержащего п элементов;
Г) операция перемены мест т элементов во множестве,
содержащем п элементов.
4. Случайная величина называется дискретной, если она:
A) зависит от случая;
Б) принимает конечное или счетное число значений;
B) равна числу успехов в схеме Бернулли;
Г) задается своей функцией распределения.
5. Какое свойство НЕ является свойством функции
распределения:
A) F(x) не убывает;
Бч HmF(x) = l;
B) P{a<Z,<b) = F(b)-F(a)\
Г) F(x) непрерывна.
6. Случайная величина распределена по показательному
закону, если:
A) ее закон распределения имеет вид Р(?, = к) = Хке~х /к ;
Б) ее плотность p(x) = (l/yf2n)e~*2/2;
B) ее плотность р(х) = Хе'**, х > 0;
Г) ее функция распределения F(x) = ekx при х:>0.
460
Приложения
7. Дисперсию дискретной случайной величины можно
найти по формуле:
Г) ни один из ответов не верен.
8. Метод моментов для нахождения оценок заключается в:
A) поиске распределения случайной величины;
Б) приравнивании выборочных моментов к теоретическим;
B) максимизации функции моментов;
Г) вычислении s2.
9. Доверительный интервал для параметра - это интервал:
A) в который параметр попадает с максимальной
вероятностью;
Б) в котором параметр лежит с заданной вероятностью;
B) в котором лежат все возможные значения параметра;
Г) в котором выборочное среднее лежит с заданной
вероятностью.
10. Распределение Фишера имеет:
A) один параметр — число степеней свободы;
Б) один параметр - уровень значимости;
B) два параметра - два числа степеней свободы;
Г) два параметра - уровень значимости и число степеней
свободы.
1. В очередь в булочную случайным образом встали 5
женщин и 2 подростка. Какова вероятность того, что два подростка
стоят в очереди рядом?
2. Фирма нарушает закон с вероятностью 0,25. Аудитор
обнаруживает нарушение с вероятностью 0,85. Проведенная им
проверка не выявила нарушений. Найти вероятность того, что
на самом деле они есть.
A) ве.
Б) D$
B) D\
cov(^);
Задачи
461
ф Приложения
4. Совместное распределение двух дискретных случайных
величин 4 и г| задано таблицей.
Л
-1
0
2
1
0,1
0,1
0,2
2
0,2
0,3
0,1
Зависимы ли эти величины? Вычислить Р(?,+г\<2) и
cov(S,ti).
5. По выборке из 25 упаковок товара средний вес составил
105 г при выборочном среднем квадратическом отклонении
(исправленном) 5 г. На уровне значимости 10% проверьте
гипотезу о том, что средний вес упаковок товара в генеральной
совокупности равен 100 г.
Вариант 2. Теоретическая часть
1. Теорема умножения вероятностей имеет вид:
A) Р(АВ) = Р(А\В)Р(В);
Б) Р(АВ) = Р(А)Р(В),
B) Р(АВ) = Р(В\А)Р(В);
Г) Р(А)Р(В) = Р(А\В)Р(В\А).
2. События А и В независимы, если:
A) Р(АВ) = 0;
Б) Р(А\В) = Р(В);
B) Р(АВ) = Р(А)Р(В);
Г) А и В не пересекаются.
3. Каково классическое определение вероятности:
A) P(A) = N(A)/N;
3. Плотность распределения случайной величины § имеет вид
r<U*[l,4],
PW jc(x-l),xe[l,4].
Вычислить константу С и вероятность Р(?>>3).
Приложения
Б) Р(А) равна 1, если А произошло, и 0, если А не
произошло;
В) P(i, = m) = cymqn-m;
Г) P($ = m) = pqm-1.
4. Случайная величина распределена по Пуассону, если:
A) ее закон распределения имеет вид Р(?> = к) = Хке~х;
Б) ее плотность р(х) = Хе~**, х>С;
B) ее закон распределения имеет вид = к) = ркцп~к\
Г) ее закон распределения имеет вид Р($ = к) = Хке~х /к\
5. Приближенная формула Пуассона используется в случае,
когда:
A) п велико, пр < 10;
Б) п велико, пр > 10;
B) п любое, пр > 10;
Г) недостаточно данных для точного подсчета.
6. Математическое ожидание произвольной дискретной
случайной величины определяется по формуле:
+оо
A) \xf(x)dx;
-оо
Б) ?а ;
' к
B) Т,хкРк;
Г) -^(Xj+... + х,,).
7. Какое из перечисленных ниже свойств НЕ является
свойством функции плотности Дх):
A) Р(?<х)= Г p(x)dx;
J-co
Б) lim^^ /(х) = 1;
B) Дх)>0;
463 I
Приложения
464
+00
Г) 1= jf(x)dx.
-00
8. Распределение Стьюдента имеет случайная величина:
A) ?2+... + ?;;, где ...9%neN(09 1) и независимы;
Б) + где eJV(0, 1) и независимы;
B) 5о/>/(5о+-+^)/Л r^e ?о>-ЛеЛЧ°> 1) и независимы;
Г) §о/>/(^+- + ^)/я г^е §о,...,§яеЛГ(0, 1) и независимы.
9. Ошибкой 1-го рода при проверке статистических гипотез
называется ошибка, при которой:
A) отвергается неверная гипотеза Я0;
Б) отвергается правильная гипотеза Я0;
B) отвергается правильная альтернативная гипотеза Я,;
Г) вероятность отклонения Я0 становится меньше уровня
значимости.
10. Несмещенной оценкой для неизвестной дисперсии
является:
A) -?(хк-х)29
пк=\
Б) -(х,+... + х„);
п
B) -Ц2>.-*)2;
1. Пять рукописей случайным образом раскладывают в 4
папки. Какова вероятность того, что ровно одна папка
останется пустой?
2. Два аудитора проверяют 4 фирмы (по 2 каждый), у двух
из которых имеются нарушения. Вероятность обнаружения на-
Приложения ф
рушений первым аудитором равна 0,7, вторым - 0,9. Найти
вероятность, что все фирмы-нарушители будут выявлены.
3. Совместное распределение двух дискретных случайных
величин § и г| задано таблицей.
л
0
1
2
-1
1/9
2/9
1/18
1
1/9
1/3
1/6
Зависимы ли эти величины? Вычислить Р(^-^г\>2) и
cov(?,ri).
4. Плотность распределения случайной величины xi имеет вид
р(х) =
|0, хе[-1, 1],
1С(1 + х),хе[-1,1].
Вычислить константу С и математическое ожидание Л^.
5. Средний вес таблеток сильного действия должен быть
0,50 мг. Выборочная проверка 121 таблетки показала, что
средний вес таблетки равен 0,53 мг. На уровне значимости
0,01 проверьте гипотезу о том, что выборочные данные
согласуются с нормативом. Считать, что вес таблеток распределен
по нормальному закону со средним квадратическим
отклонением 0,11 мг.
Вариант 3. Теоретическая часть
1. Формула Байеса имеет вид:
А) Р(АВ) = Р(А\В)Р(В);
Ъ) P(A)^P(A\Hk)P(Hk).
' k=\ '
В) P(Hk\A) = P(A\Hk)P(Hk)/P(A)
п P(Hk I А) = Р(А | Hk )P{Hk) i JTPWj I A)P(Hj)
2. Сочетанием m элементов из n называется:
А) упорядоченный набор n элементов из множества,
содержащего т элементов;
16 Теория вероятностей
465
Приложения
I 466
Б) неупорядоченный набор п элементов из множества,
содержащего т элементов;
В) упорядоченный набор т элементов из множества,
содержащего п элементов;
Г) неупорядоченный набор т элементов из множества,
содержащего п элементов.
3. Вероятность того, что в п испытаниях Бернулли
произойдет т успехов, равна:
A) pqm-\
Б) pnqm.
B) ^1ртд"-т,
п\
Г) я! ..А"
т\(п-т)\
4. Случайная величина называется непрерывной, если:
A) она непрерывно изменяется;
Б) она принимает бесконечно много значений;
B) ее плотность равна интегралу от вероятности;
Г) ее функция распределения равна интегралу от
плотности.
5. Какое свойство НЕ всегда справедливо для дисперсии:
A) Dc = 0.
Б) Щ + Л) = Д + Ль
B) D$ = Щ2- (Щ)\
Г) Д = cov($, Q.
6. Случайная величина распределена равномерно, если:
A) ее закон распределения имеет вид Р(% = к) = p<f~x\
Б) ее значения равномерно распределены по прямой;
B) ее плотность p(x) = l/(b-a), хе[а,Ь];
Г) ее закон распределения имеет вид Щ = х) = \/(Ь - а)9
х Е [а, Ь].
Приложения 0
7. Какое из перечисленных ниже свойств справедливо для
дискретной случайной величины принимающей значения
A) D$ = ±xlP($=xk).
Б) = **) < Р(4 =
B) |^ = ^) = 1;
Г) Все ответы верны.
8. Метод максимального правдоподобия заключается в
A) приравнивании функции правдоподобия к 0;
Б) нахождении оценки, ближайшей к параметру;
B) максимизации функции правдоподобия;
Г) поиске наивероятнейшего значения функции
правдоподобия.
9. Распределение Фишера имеет случайная величина
A) ?2+... + ?*,, где еЛГ(0, 1) и независимы;
Б) %2т/х1> гДе xi> х2 независимы и имеют х2-распре-
деление;
_. Y / ТП i i о
B) —, где х*,> кп независимы и имеют х -распре-
деление;
Г) -f=xl> гДе Хя2 имеет х2-распределение.
л/л
10. Доверительный интервал для параметра а нормального
распределения при известной дисперсии имеет вид:
A) X-GUty IIп\
Б) х-аикр/4п<а<х + сикр/4п\
B) X-St^/yfnKClKX+St^/y/n-,
Г) (x-stkj4n<a<{x^stkp)/yfn .
16* 467 !
^ Приложения
4. Совместное распределение двух дискретных случайных
величин ? и г| задано таблицей.
-1
1
2
0
1/8
1/6
1/12
1
1/12
1/6
3/8
Зависимы ли они? Вычислить Р^+цкТ) и cov(^,r|).
5. Взвесив 50 пакетиков товара, нашли выборочное среднее
502 г и выборочное среднее квадратическое отклонение 10 г.
На уровне значимости 5% проверьте гипотезу о том, что вес
пакета равен 500 г.
Вариант 4. Теоретическая часть
1. Формула для числа сочетаний (без повторений) т
элементов из п имеет вид:
ml
Б) —;
ml(n-m)l
468
Задачи
1. Шесть пассажиров садятся в поезд, случайно выбирая
один из шести вагонов. Какова вероятность того, что ровно в
один вагон никто не сядет?
2. Изделие имеет скрытые дефекты с вероятностью 0,15.
В течение года выходит из строя 70% изделий со скрытыми
дефектами и 10% изделий без дефектов. Найти вероятность того,
что изделие имело скрытые дефекты, если оно вышло из строя
в течение года.
3. Плотность распределения случайной величины х. имеет
вид (x)J°9X€l"2Ah
PW 1С(1-х),хе[-2,1].
Вычислить константу С и вероятность Р(0 < % <3)
Приложения ф
В)
Г) ни один из приведенных выше ответов не верен.
2. Теорема сложения вероятностей имеет вид:
A) Р(А + В) = Р(А) + Р(В);
Б) Р(А + В) = Р(А)+Р(В) + Р(АВ);
B) Р(А + В) = Р(А)+Р(В)-Р(АВ);
Г) Р(А + В) = Р(А\В)Р(В).
3. События А и В называются несовместными, если:
A) Р(АВ) = Р(А)Р(В).
Б) Р(АВ) = 1.
B) АиВ = ф.
Г) ЛпЯ = 0.
4. Наиболее вероятное число успехов т в схеме Бернулли
определяется по формуле:
A) пр-р<т <пр+р\
Б) np-q<m <пр + р\
B) np-q<rn <np + q\
Г) пр-р<т <np + q.
5. Математическое ожидание непрерывной случайной
величины находится по формуле:
A) J/(x)dx
-00
+00
469 I
^ Приложения
| 470
6. Какое из свойств НЕ является свойством ковариации:
A) cov(c?, л) = cov(cn, §);
Б) + = cov($, л) + cov(^, 4);
B) cov(?, г|) = 0 для независимых л;
Г) cov(c^, ^) = c2cov(4, §).
7. Случайная величина распределена по Бернулли, если:
A) ее закон распределения имеет вид P(?> = m) = C"pmqn~m;
Б) ее закон распределения имеет вид Р(?> = т) = /?да«7л~т;
B) ее закон распределения имеет вид Р(^ = т) = pqm'\
Г) ее плотность p(m) = C^pmqn'm.
8. Оценка параметра называется несмещенной, если:
A) ее отклонение от оцениваемого параметра равно 0;
Б) ее математическое ожидание равно оцениваемому
параметру;
B) она равна выборочному среднему;
Г) ее дисперсия минимальна.
9. Ошибкой 2-го рода при проверке статистических гипотез
называется ошибка, при которой:
A) отвергается неверная гипотеза Я0;
Б) отвергается правильная гипотеза Я0;
B) отвергается неверная альтернативная гипотеза Я,;
Г) отвергается правильная альтернативная гипотеза Я,.
10. Распределение х2 имеет случайная величина:
A) равная квадрату нормальной случайной величины N(a, о2);
Б) равная квадрату суммы независимых нормальных
случайных величин N(0, 1);
B) равная сумме квадратов независимых нормальных
случайных величин N(0, 1);
Г) ни один из приведенных ответов не верен.
Приложения ф
Задачи
1. Группа из 20 человек пишет контрольную работу из 4
вариантов (по пять человек в каждом). Найти вероятность того,
что среди 5 случайно отобранных работ есть каждый вариант.
2. Фирма участвует в трех проектах, каждый из которых
может закончится неудачей с вероятностью 0,2. В случае
неудачи одного проекта вероятность разорения фирмы равна 20%,
двух - 50%, трех - 90%. Определить вероятность разорения
фирмы.
3. Совместное распределение двух дискретных случайных
величин ^ и г| задано таблицей.
Л
-1
0
2
1
0,2
0,3
0
2
0
0,1
С
вид р(х) =
Определить константу С. Исследовать вопрос о
независимости § и г|. Вычислить cov(?,t|).
4. Плотность распределения случайной величины х. имеет
[0, х г [0,5],
|Сх,хе[0,5].
Вычислить константу С и математическое ожидание Щ.
5. Средний доход фирмы в день составлял 1020 у.е. После
реорганизации фирмы выборочный средний доход в день за
30 рабочих дней составил 1070 у.е. с выборочным стандартным
отклонением 90 у.е. Можно ли утверждать (на уровне
значимости 5%), что реорганизация фирмы привела к увеличению
среднего дохода?
Вариант 5. Теоретическая часть
1. В определение классического вероятностного
пространства входит условие:
A) исходы равновероятны;
Б) исходы независимы;
B) испытания заканчиваются одним из двух исходов;
Г) все приведенные выше ответы верны.
471
^ Приложения
! 472
2. Условная вероятность Р(А \ В) события А при условии В
равна
A) Р(А)/Р(В);
Б) Р(В)/Р(А);
B) Р(АВ)/Р04);
Г) Р(АВ)/Р(В).
3. Локальная теорема Муавра-Лапласа используется в
случае, когда
A) п велико, пр<\0;
Б) п велико, пр>№ ;
B) п любое, пр <10;
Г) недостаточно данных для точного подсчета.
4. Случайная величина - это:
A) набор вероятностей, зависящих от случая;
Б) числовая функция, заданная на вероятностном
пространстве;
B) случайный исход эксперимента;
Г) набор случайных событий, отвечающих заданному
условию.
5. Какое свойство НЕ выполняется для независимых
случайных величин г):
A) cov(?,ri) = 0;
Б) + Л) = I* + Dt\;
B) M(fy\) = ЩМц;
Г) D(fy\) = JXJk\.
6. Пусть случайная величина % распределена по
показательному закону. Какое из следующих свойств верно:
A) при х>0 Р($ = х) = Хег**;
Б) при х>0 ее функция распределения F(x) = e~Xx;
B) при х>0 ее функция распределения F(x) = eXx;
Г) для любого х Р(% = х) = 0.
Приложения ф
473
7. Дисперсия непрерывной случайной величины равна
-00
Б) Di, = *](x-Mtfp(x)ax;
-00
+оо
В) = j(x-x)2p(x)dx;
-оо
1 +00 __
Г) D^jix-xfdx.
—00
8. Оценкой для неизвестного параметра называется:
A) истинное значение параметра;
Б) угаданное значение параметра;
B) функция от выборки;
Г) число, отличающееся от параметра не более, чем на
заданную величину.
9. Доверительный интервал для параметра а нормального
распределения при неизвестной дисперсии имеет вид:
A) х-сикр/п<а<х + аикр/п;
Б) х-си^/у/пкакх + ои^/л/п;
B) x-st^/y/nKaKx+st^/yfn;
О (х-5^/Л<а<(х+8^)/Л.
10. Критической областью при проверке статистических
гипотез называется:
A) область значений наблюдаемой статистики, в которой
верна основная гипотеза Я0;
Б) область значений наблюдаемой статистики, в которой
верна альтернативная гипотеза Я,;
B) область значений наблюдаемой статистики, в которой
отклоняется основная гипотеза Я0;
Г) область значений наблюдаемой статистики, в которой
отклоняется альтернативная гипотеза Я,.
Приложения
Задачи
1. В лифт семиэтажного дома на первом этаже входят пять
человек. Какова вероятность того, что на первых трех этажах
(начиная со второго) вышли два человека при условии, что все
вышли на разных этажах?
2. Поставки продуктов в город производятся из трех
областей в количествах 20, 45, 35%. Доля продукта высшего
качества в поставках составляет 45, 40, 25%. Покупатель купил
продукт высшего качества. Какова вероятность того, что он
произведен в первой области?
3. Плотность распределения случайной величины § имеет
вид р(х) = < ,
УУ ' [Сх2, хе[0,4].
Вычислить константу С и математическое ожидание Щ.
4. Совместное распределение двух дискретных случайных
величин § и т| задано таблицей.
\
П
-1
0
2
1
1/6
1/6
1/3
2
1/12
1/6
1/12
Исследовать вопрос о независимости \ и г]. Вычислить
Р(Ь + л <2) и cov(?,r|).
5. Яблоки упаковываются в коробки весом по 10 кг.
Случайная выборка 9 коробок с яблоками выявила, что
средний вес коробки равен 9 кг с выборочной дисперсией 4 кг. На
уровне значимости 5% проверить гипотезу о том, что средний
вес коробок с яблоками равен 10 кг.
Вариант 6. Теоретическая часть
1. Число размещений (без повторений) т элементов из п
равно
А) п\/т\\
Б) т/п\
474
Приложения ф
В) й!/(и-/я)!;
Г) —.
т\(п-т)\
2. Какое из свойств условной вероятности НЕ верно:
A) Р(А\В)Р(В) = Р(В\А)Р(А);
Б) Р(А\В) = 1-Р(А\В);
B) Р(А\В) = 09 если ЛпЯ = 0;
Г) Р(А\В) = 1, если ЛсЯ.
3. Приближенная формула Пуассона имеет вид:
А) Рп(т)*—е-х, где X = пр;
4. Пусть событие А может произойти совместно с
некоторыми событиями (гипотезами) Я,.. Какое условие нужно для
применения формулы полной вероятности?
A) события Н, образуют полную группу событий;
Б) события Я,, независимы;
B) события Н, содержат в себе один из двух исходов;
Г) все приведенные ответы верны.
5. Пусть ? — непрерывная случайная величина с
плотностью р(х) и функцией распределения F(x). Какое из
следующих свойств верно:
от!
тр;
в)
от!
Г) />»*
т\(п-т)\
A. Р(а < \ < Ь)
Б. Р(а < 4 < 6)
B. Р(а < % < Ь)
Г. P(a < \ < Ь)
F{b) - F(a);
p(b) - р(а);
Р(а) - р(Ь).
(F(a) + F(b))/2.
^ Приложения
476
6. Случайная величина распределена по геометрическому
закону, если:
A) ее плотность /(х) = р(1 - р)х~] при х > 0;
Б) ее закон распределения имеет вид Щ = т) = (1 - />)/яН/>;
B) ее закон распределения имеет вид Pfc = т) = (1 - р)/я~1;
Г) ее плотность /(х) = при х > 0.
7. Дисперсия дискретной случайной величины равна:
A) Л6 = 1<**-^)2;
Б) Я$ = Е(**-^)2Л;
B) Я$ = -?(х,-х)2;
п ^=-Це<**-*)2.
8. Оценка называется состоятельной, если:
A) среди всех оценок она наиболее точно описывает
параметр;
Б) ее математическое ожидание равно оцениваемому
параметру;
B) с ростом числа наблюдений она сходится по вероятности
к параметру;
Г) с ростом числа наблюдений она сходится к вероятности
успеха.
9. Надежностью доверительного интервала называется:
A) вероятность того, что оцениваемый параметр попадет в
интервал;
Б) вероятность того, что оцениваемый параметр не попадет
в интервал;
B) длина доверительного интервала;
Г) половина длины доверительного интервала.
10. Пусть основная гипотеза HQ: а = а0 отклоняется. В этом
случае:
А) делается вывод, что истинное значение параметра а
отличается от д0;
Приложения 0
Б) нужно дополнительно посчитать выборочное среднее х;
В) мы совершаем ошибку 1-го рода;
Г) мы совершаем ошибку 2-го рода.
Задачи
1. Семь клиентов случайным образом обращаются в 5 фирм.
Найти вероятность того, что хотя бы в одну фирму никто не
обратится.
2. В ящике 20 теннисных мячей, в том числе 12 новых и
8 игранных. Из ящика извлекаются наугад два мяча для игры
и после игры возвращаются в ящик. После этого из ящика
вынимают два мяча для следующей игры. Найти вероятность того,
что эти оба мяча будут новыми (неигранными).
3. Совместное распределение двух дискретных случайных
величин ^ и г| задано таблицей
%
Ч
1
2
3
1
С
0,2
0
2
0,2
0,4
0,2
Определить константу С. Вычислить вероятность cov(?, ц) и
Р($+х\>3). Исследовать вопрос о независимости ? и г\.
4. Плотность распределения случайной величины ? имеет вид
ГО, х^ [0,1],
Р |Сх\хе[0,1].
Вычислить константу С и математическое ожидание Щ.
5. Средний дневной объем продаж в магазине составлял
500 единиц. После реорганизации выборочный средний
дневной объем продаж за 25 рабочих дней составил 520 единиц с
выборочным средним квадратическим отклонением 40 единиц.
Можно ли утверждать (на уровне значимости 5%), что
реорганизация привела к увеличению среднего дохода?
477
ф Приложения
478
Примеры задания по математической статистике
для самостоятельной работы
1. Вычислить дисперсию и моду распределения Стьюдента.
2. Проверить, к какому распределению сходится
распределение Фишера F(n, т) при а) л->оо; б)/и-»оо.
3. Доказать основные свойства бета-распределения.
4. Вычислить математическое ожидание, моду и дисперсию
бета-распределения.
5. Показать, что выборочные средние квадратические
отклонения, полученные по исправленной и неисправленной
дисперсии для нормального распределения, являются
смещенными оценками. Вычислить их математическое ожидание.
6. Показать, что оценка максимального правдоподобия для
параметра X показательного распределения является
смещенной. Построить на её основе несмещенную оценку.
7. Для оценивания параметра а нормального распределения
N(0, а2) используют оценку вида а* =1 - XIх/1* Найти констан-
ту с, при которой оценка окажется несмещенной. Вычислить
эффективность оценки.
8. Для равномерного распределения на отрезке [0, 39] найти
оценку максимального правдоподобия, вычислить ее
математическое ожидание. Построить на основе этой оценки
несмещенную оценку и доказать ее сверхэффективность.
9. Случайная величина принимает значения —1, 0 и 1 с
вероятностями (1 - 9)/3; 1/3; (1 + 0)/3 соответственно, 0 е [—1; 1].
Построить для параметра 0 оценки методом моментов и
методом максимального правдоподобия, а также асимптотический
доверительный интервал (на основе метода моментов).
10. Проверяется нулевая гипотеза о том, что случайная
величина равномерно распределена на отрезке [—1; 1], против
гипотезы, что она имеет распределение Лапласа. Построить
критерий отношения правдоподобия при п = 2 с уровнем
значимости а < 1/2.
Приложения
11. Доказать, что распределение Стьюдента с ростом числа
степеней свободы сходится к стандартному нормальному
распределению.
12. Вычислить математическое ожидание и дисперсию
распределения Фишера.
13. Для распределения Коши с плотностью р(х) = —
я(1+(х-0г)
строится оценка максимального правдоподобия параметра 9 по
двум наблюдения. Определить, при каких х1 и х2 эта оценка
существует и единственна.
14. Для распределения Лапласа с плотностью р(х) = (Х/2)е~х^
построить несмещенную оценку параметра X и проверить её на
эффективность.
Проверяется нулевая гипотеза о том, что случайная
величина равномерно распределена на отрезке [0; 1], против гипотезы,
что она имеет показательное распределение р(х) = Хе~кх, х > 0.
Построить критерий отношения правдоподобия при п = 2 с
уровнем значимости а < 1/2.
Приложение 2
ТАБЛИЦЫ
Таблица 1. Значения функции ф(х) = -=е *2
V2tt
X
Сотые доли х
0
1
2
3
4
5
6
7
8
9
0,0
0,39894
39892
39886
39876
39862
39844
39822
39797
39767
39733
0,1
39695
39654
39608
39559
39505
39448
39387
39322
39253
39181
0,2
39104
39024
38940
38853
38762
38667
38568
38466
38361
38251
479
|j| Приложения
Продолжение табл.
X
Сотые доли х
0
1
2
3
4
5
6
7
8
9
0,3
38139
38023
37903
37780
37654
37524
37391
37255
37115
36973
0,4
36827
36678
36526
36371
36213
36053
35889
35723
35553
35381
0,5
35207
35029
34849
34667
34482
34294
34105
33912
33718
33521
0,6
33322
33121
32918
32713
32506
32297
32086
31874
31659
31443
0,7
31225
31006
30785
30563
30339
30114
29887
29659
29431
29200
0,8
28969
28737
28504
28269
28034
27798
27562
27324
27086
26848
0,9
26609
26369
26129
25888
25647
25406
25164
24923
24681
24439
1,0
24197
23955
23713
23471
23230
22988
22747
22506
22265
22025
1,1
21785
21546
21307
21069
20831
20594
20357
20121
19886
19652
1,2
19419
19186
18954
18724
18494
18265
18037
17810
17585
17360
1,3
17137
16915
16694
16474
16256
16038
15822
15608
15395
15183
1,4
14973
14764
14556
14350
14146
13943
13742
13542
13344
13147
1,5
12952
12758
12566
12376
12188
12001
11816
11632
11450
11270
1,6
11092
10915
10741
10567
10396
10226
10059
09893
09728
09566
1,7
09405
09246
09089
08933
08780
08628
08478
08329
08183
08038
1,8
07895
07754
07614
07477
07341
07206
07074
06943
06814
06687
1,9
06562
06438
06316
06195
06077
05959
05844
05730
05618
05508
2,0
05399
05292
05186
05082
04980
04879
04780
04682
04586
04491
2,1
04398
04307
04217
04128
04041
03955
03871
03788
03706
03626
2,2
03547
03470
03394
03319
03246
03174
03103
03034
02965
02898
480
Приложения щ
Продолжение табл.
X
Сотые доли х
0
1
2
3
4
5
6
7
8
9
2,3
02833
02768
02705
02643
02582
02522
02463
02406
02349
02294
2,4
02239
02186
02134
02083
02033
01984
01936
01888
01842
01797
2,5
01753
01709
01667
01625
01585
01545
01506
01468
01431
01394
2,6
01358
01323
01289
01256
01223
01191
01160
01130
01100
01071
2,7
01042
01014
00987
00961
00935
00909
00885
00861
00837
00814
2,8
00792
00770
00748
00727
00707
00687
00668
00649
00631
00613
2,9
00595
00578
00562
00545
00530
00514
00499
00485
00470
00457
3,0
00443
00430
00417
00405
00393
00381
00370
00358
00348
00337
3,1
00327
00317
00307
00298
00288
00279
00271
00262
00254
00246
3,2
00238
00231
00224
00216
00210
00203
00196
00190
00184
00178
з,з
00172
00167
00161
00156
00151
00146
00141
00136
00132
00127
3,4
00123
00119
00115
00111
00107
00104
00100
00097
00094
00090
3,5
00087
00084
00081
00079
00076
00073
00071
00068
00066
00063
3,6
00061
00059
00057
00055
00053
00051
00049
00047
00046
00044
3,7
00042
00041
00039
00038
00037
00035
00034
00033
00031
00030
3,8
00029
00028
00027
00026
00025
00024
00023
00022
00021
00021
3,9
00020
00019
00018
00018
00017
00016
00016
00015
00014
00014
X
Десятые доли х
0
2
4
6
8
4
0,0001338
0000589
0000249
0000101
0000040
5
0,0000015
481
ф$ Приложения
Таблица 2. Значения функции Лапласа Ф0(х) = —Г=\е f2/2dt
X
Ф0<*)
JC
Ф0<*)
JC
Ф0(*)
JC
Ф0(*)
0,00
0,0000
0,32
0,1255
0,64
0,2389
0,96
0,3315
0,01
0,0040
0,33
0,1293
0,65
0,2422
0,97
0,3340
0,02
0,0080
0,34
0,1331
0,66
0,2454
0,98
0,3365
0,03
0,0120
0,35
0,1368
0,67
0,2486
0,99
0,3389
0,04
0,0160
0,36
0,1406
0,68
0,2517
1,00
0,3413
0,05
0,0199
0,37
0,1443
0,69
0,2549
1,01
0,3438
0,06
0,0239
0,38
0,1480
0,70
0,2580
1,02
0,3461
0,07
0,0279
0,39
0,1517
0,71
0,2611
1,03
0,3485
0,08
0,0319
0,40
0,1554
0,72
0,2642
1,04
0,3508
0,09
0,0359
0,41
0,1591
0,73
0,2673
1,05
0,3531
0,10
0,0398
0,42
0,1628
0,74
0,2703
1,06
0,3554
0,11
0,0438
0,43
0,1664
0,75
0,2734
1,07
0,3577
0,12
0,0478
0,44
0,1700
0,76
0,2764
1,08
0,3599
0,13
0,0517
0,45
0,1736
0,77
0,2794
1,09
0,3621
0,14
0,0557
0,46
0,1772
0,78
0,2823
1,10
0,3643
0,15
0,0596
0,47
0,1808
0,79
0,2852
1,11
0,3665
0,16
0,0636
0,48
0,1844
0,80
0,2881
1,12
0,3686
0,17
0,0675
0,49
0,1879
0,81
0,2910
1,13
0,3708
0,18
0,0714
0,50
0,1915
0,82
0,2939
1,14
0,3729
0,19
0,0753
0,51
0,1950
0,83
0,2967
1,15
0,3749
0,20
0,0793
0,52
0,1985
0,84
0,2995
1,16
0,3770
0,21
0,0832
0,53
0,2019
0,85
0,3023
1,17
0,3790
0,22
0,0871
0,54
0,2054
0,86
0,3051
1,18
0,3810
0,23
0,0910
0,55
0,2088
0,87
0,3078
1,19
0,3830
0,24
0,0948
0,56
0,2123
0,88
0,3106
1,20
0,3849
0,25
0,0987
0,57
0,2157
0,89
0,3133
1,21
0,3869
0,26
0,1026
0,58
0,2190
0,90
0,3159
1,22
0,3883
0,27
0,1064
0,59
0,2224
0,91
0,3186
1,23
0,3907
0,28
0,1103
0,60
0,2257
0,92
0,3212
1,24
0,3925
0,29
0,1141
0,61
0,2291
0,93
0,3238
1,25
0,3944
0,30
0,1179
0,62
0,2324
0,94
0,3264
0,31
0,1217
0,63
0,2357
0,95
0,3289
482
Приложения ф
Продолжение табл.
X
Ф0<*)
X
Ф0(*>
X
Ф0(*)
Ф0(*)
1,26
0,3962
1,59
0,4441
1,92
0,4726
2,50
0,4938
1,27
0,3980
1,60
0,4452
1,93
0,4732
2,52
0,4941
1,28
0,3997
1,61
0,4463
1,94
0,4738
2,54
0,4945
1,29
04015
1,62
0,4474
1,95
0,4744
2,56
0,4948
1,30
0,4032
1,63
0,4484
1,96
0,4750
2,58
0,4951
1,31
0,4049
1,64
0,4495
1,97
0,4756
2,60
0,4953
1,32
0,4066
1,65
0,4505
1,98
0,4761
2,62
0,4956
1,33
0,4082
1,66
0,4515
1,99
0,4767
2,64
0,4959
1,34
0,4099
1,67
0,4525
2,00
0,4772
2,66
0,4961
1.35
0,4115
1,68
0,4535
2,02
0,4783
2,68
0,4963
1,36
0,4131
1,69
0,4545
2,04
0,4793
2,70
0,4965
1,37
0,4147
1,70
0,4554
2,06
0,4803
2,72
0,4967
1,38
0,4162
1,71
0,4564
2,08
0,4812
2,74
0,4969
1,39
0,4177
1,72
0.4573
2,10
0,4821
2,76
0,4971
1,40
0,4192
1,73
0,4582
2,12
0,4830
2,78
0,4973
1,41
0,4207
1,74
0,4591
2,14
0,4838
2,80
0,4974
1,42
0,4222
1,75
0,4599
2,16
0,4846
2,82
0,4976
1,43
0,4236
1,76
0,4608
2,18
0,4854
2,84
0,4977
1,44
0,4251
1,77
0,4616
2,20
0,4861
2,86
0,4979
1,45
0,4265
1,78
0,4625
2,22
0,4868
2,88
0,4980
1,46
0,4279
1,79
0,4633
2,24
0,4875
2,90
0,4981
1,47
0,4292
1,80
0,4641
2,26
0,4881
2,92
0,4982
1,48
0,4306
1,81
0,4649
2,28
0,4887
2,94
0,4984
1,49
0,4319
1,82
0,4656
2,30
0,4893
2,96
0,4985
1,50
0,4332
1,83
0,4664
2,32
0,4898
2,98
0,4986
1,51
0,4345
1,84
0,4671
2,34
0,4904
3,00
0,49865
1,52
0,4357
1,85
0,4678
2,36
0,4909
3,20
0,49931
1,53
0,4370
1,86
0,4686
2,38
0,4913
3,40
0,49966
1,54
0,4382
1,87
0,4693
2,40
0,4918
3,60
0,499841
1,55
0,4394
1,88
0,4699
2,42
0,4922
3,80
0,499928
1,56
0,4406
1,89
0,4706
2,44
0,4927
4,00
0,499968
1,57
0,4418
1,90
0,4713
2,46
0,4931
4,50
0,499997
1,58
0,4429
1,91
0,4719
2,48
0,4934
5,00
0,499997
483
Приложения
оо
«1*1
II
со
X
о
о
о
X
X
*
к
S
X
ф
со
X
СП
X
00
00
г-
ЧО
о
СП
сн
I
о"
on
in
чо
ON
оо
00
-"3-
сн
m
чо
о
чо
ЧО
о4
сч
00
о
о
ON
сн
m
г-
г-
СП
оо
сн
чо
чо
о"
о"
о"
чо
о
о
s
оо
СП
о
оо
О
чо
ON
©^
о"
3
СЧ
О
сГ
г-
о
о
СП
СП
СП
о
ол
о4
о
о
о
о
СП
СП
m
о4
о
о4
г-
ЧО
г-
о
о
ON
о
о
чо
ON
CN
о
о
оо
•о
о
о
CN
г-
о
о
о
о
CN
о
о
о
m
о
о
о
о
о
о
о
о
о
сч
о
о
о
о
о
о
о
о
чо
СП
о
о
о
о
о
о
чо
о
о
о
о
СЧ
о
о
о
о
m
о
о
о
о
СП
о
о
о
о
о
о
оо
о
о"
о
о
о
о
о
о
о
о
о
о
S
о
о
о
сч
о
о
о
о
о"
о
о
о
о
оо
ч^-
СЧ
о
о
ON
о
о
о
г-
ЧО
о
о
о"
СЧ
СП
оо
о4
о
сч
о
СП
о
ON
Г"-
о
о4
оо
о
СЧ
оо
о
СП
СП
СП
СЧ
СЧ
оо
©^
о"
оо
СЧ
СЧ
о
ON
чо
СП
СП
о
ON
ON
1
ЧО
СЧ
о
ON
чо
»п
о
СЧ
m
о
СЧ
8
СЧ
СП
СП
СЧ
ЧО
ЧО
о
00
о
00
СЧ
СП
чо
чо
ON
оо
СЧ
СЧ
СЧ
in
чо
г-
CN
о"
СЧ
о
СЧ
ON
оо
о
сп
о
СЧ
г-
оо
ЧО
СП
«п
ON
ON
г-
in
сч^
о"
СП
о
оо
чо
чо
г—
СП
СЧ
о'
оо
m
m
СЧ
484
Приложения
0,13385
0,16062
0,16062
0,13768
0,10326
0,06884
0,04130
0,02253
0,01126
0,00520
0,00223
0,00089
0,00033
0,00012
0,00004
0,00001
0,15582
0,17140
0,15712
0,12345
0,08487
0,05187
0,02853
0,01426
0,00654
0,00277
0,00109
0,00040
0,00014
0,00004
0,00001
0,17547
0,17547
0,14622
0,10444
0,06528
0,03627
0,01813
0,00824
0, 00343
0,00132
0,00047
0,00016
0,00005
0,00001
0,18981
0,17083
0,12812
0,08236
0,04633
0,02316
0,01042
0,00426
0,00160
0,00055
0,00018
0,00005
0,00002
0,19537
0,15629
0,10420
0,05954
0,02977
0,01323
0,00529
0,00192
0,00064
0,00020
0,00006
0,00002
0,18881
0,13217
0,07710
0,03855
0,01687
0,00656
0,00230
0,00073
0,00021
0,00006
0,00001
0,10082
0,05041
0,02160
0,00810
0,00270
0,00081
0,00022
0,00006
0,00001
0,13360
0,06680
0,02783
0,00994
0,00311
0,00086
0,00022
0,00005
0,00001
0,09022
0,03609
0,01203
0,00344
0,00086
0,00019
0,00004
0,00001
0,04707
0,01412
0,00353
0,00076
0,00014
0,00002
ЧО
г-
оо
ON
о
2
CN
СП
ЧО
г-
оо
ON
485
fj^ Приложения
Таблица ц. Критические точки распределения хи-квадрат
Число
степеней
свободы к
Уровень значимости а
0,01
0,025
0,05
0,95
0,975
0,99
1
6,6
5,0
3,8
0,0039
0,00098
0,00016
2
9,2
7,4
6,0
0,103
0,051
0,020
3
11,3
9,4
7,8
0,352
0,216
0,115
4
13,3
10,1
9,5
0,711
0,484
0,297
5
15,1
12,8
Н,1
1,15
0,831
0,554
6
16,8
14,4
12,6
1,64
1,24
0,872
7
18,5
16,0
14.1
2,17
1,69
1,24
8
20,1
17,5
15,5
2,73
2,18
1,65
9
21,7
19,0
16,9
3,33
2,70
2,09
10
23,2
20,5
18,3
3,94
3,25
2,56
11
24,7
21,9
19,7
4,57
3,82
3,05
12
26,2
23,3
21,0
5,23
4,40
3,57
13
27,7
24,7
22,4
5,89
5,01
4,11
14
29,1
26,1
23,7
6,57
5,63
4,66
15
30,6
27,5
25,0
7,26
6,26
5,23
16
32,0
28,8
26,3
7,96
6,91
5,81
17
33,4
30,2
27,6
8,67
7,56
6,41
18
34,8
31,5
28,9
9,39
8,23
7,01
19
36,2
32,9
30,1
10,1
8,91
7,63
20
37,6
34,2
31,4
10,9
9,59
8,26
21
38,9
35,5
32,7
11,6
10,3
8,90
22
40,3
36,8
33,9
12,3
11,0
9,54
23
41,6
38,1
35,2
13,1
11,7
10,2
24
43,0
39,4
36,4
13,8
12,4
10,9
25
44,3
40,6
37,7
14,6
13,1
11,5
26
45,6
41,9
38,9
15,4
13,8
12,2
27
47,0
43,2
40,1
16,2
14,6
12,9
28
48,3
44,5
41,3
16,9
15,3
13,6
29
49,6
45,7
42,6
17,7
16,0
14,3
30
50,9
47,0
43,8
18,5
16,8
15,0
I 486
Приложения ^
Число степеней
Уровень значимости а (двусторонняя критическая область)
свободы К
0,2
0,1
0,05
0,02
0,01
0,002
0,001
1
3,08
6,31
12,7
31,82
63,7
318,3
637,0
2
1,89
2,92
4,30
6,97
9,92
22,33
31,6
3
1,64
2,35
3,18
4,54
5,84
10,22
12,9
4
1,53
2,13
2,78
3,75
4,60
7,17
8,61
5
1,48
2,01
2,57
3,37
4,03
5,89
6,86
6
1,44
1,94
2,45
3,14
3,71
5,21
5,96
7
1,42
1,89
2,36
3,00
3,50
4,79
5,40
8
1,40
1,86
2,31
2,90
3,36
4,50
5,04
9
1,38
1,83
2,26
2,82
3,25
4,30
4,78
10
1,37
1,81
2,23
2,76
3,17
4,14
4,59
11
1,36
1,80
2,20
2,72
3,11
4,03
4,44
12
1,36
1,78
2,18
2,68
3,05
3,93
4,32
13
1,35
1,77
2,16
2,65
3,01
3,85
4,22
14
1,34
1,76
2,14
2,62
2,98
3,79
4,14
15
1,34
1,75
2,13
2,60
2,95
3,73
4,07
16
1,34
1,75
2,12
2,58
2,92
3,69
4,01
17
1,33
1,74
2,11
2,57
2,90
3,65
3,95
18
1,33
1,73
2,10
2,55
2,88
3,61
3,92
19
1,33
1,73
2,09
2,54
2,86
3,58
3,88
20
1,33
1,73
2,09
2,53
2,85
3,55
3,85
21
1,32
1,72
2,08
2,52
2,83
3,53
3,82
22
1,32
1,72
2,07
2,51
2,82
3,51
3,79
23
1,32
1,71
2,07
2,50
2.81
3,49
3,77
24
1,32
1,71
2,06
2,49
2,80
3,47
3,74
25
1,32
1,71
2,06
2,49
2,79
3,45
3,72
26
1,32
1,71
2,06
2,48
2,78
3,44
3,71
27
1,31
1,71
2,05
2,47
2,77
3,42
3,69
28
1,31
1,70
2,05
2,46
2,76
3,40
3,66
29
1,31
1,70
2,05
2,46
2,76
3,40
3,66
30
1,31
1,70
2,04
2,46
2,75
3,39
3,65
40
1,30
1,68
2,02
2.42
2,70
3,31
3,55
60
1,30
1,67
2,00
2,39
2,66
3,23
3,46
120
1,29
1,66
1,98
2,36
2,62
3,17
3,37
00
1,28
1,65
1,96
2,33
2,58
3,09
3,29
Число степеней
0,1
0,05
0,025
0,01
0,005
0,001
0,0005
487
Таблица 5. Критические точки распределения Стьюдента
^j) Приложения
8.
CN
ON
ON
3
5SI
О
SO
ON
3
I
i
CN
00
о
чо
ЧО
«Л
о
ЧО
СЧ
CN
О
ЧО
ON
ON
ЧО
СП
ON
ON
СП
СЧ^
CN
сп
CN
8
1Л>
ON
ЧО
00
°
00
ЧО^
СП
ON
00
Ф
3
s
e
ж
X
Ф
s
5
u
CO
g
о
5
я
ВТ
5
00
ON
о
i i
ф 5
* CO
о
II
с
e
00
CN
ON
ON
OO
OO
ЧО
CN
чо
ЧО
СП
»1
4"
I СЛJ
ON
ON
СЧ
СЧ
81
8
i5S
ON
8
I сч
ON
ON
ON
Si
8
8
I*.
ON
СЧ
31
ЧО
СЧ
00
oo
s
5
ON
ON
ON
СЧ
NO
.CO
1
к
I
ON
ON ,
81
СЧ
OS
4
OO
ON
чо
сч
чо
81
ON
СП
ON
ЧО
чо
СП
ON
чо"
oo"
488
Приложения
<ч
Уровень значимости а = 0,05
5
СЧ
19,41
8,74
ON
in
4,68
4,00
3,57
3,28
3,07
2,91
2,79
2,69
2,60
2,53
2,48
2,42
2,38
СП
Ties
19,40
8,76
5,93
4,70
4,03
3,60
3,31
3,10
2,94
2,82
2,72
2,63
2,56
2,51
2,45
т?
сч"
О
СЧ
Ti-
сч
19,39
8,78
5,96
4,74
4,06
3,63
3,34
3,13
2,97
2,86
2,76
2,67
2,60
2,55
2,49
2,45
ON
СЧ
19,38
8,81
s
ЧО
4,78
4,10
3,68
3,39
3,18
3,02
2,90
2,80
2,72
2,65
2,59
2,54
2,50
00
ON
СП
СЧ
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,23
3,07
2,95
2,85
2,77
2,70
2,64
2,59
2,55
СП
СЧ
19,36
00
оо^
оо"
6,09
4,88
4,21
3,79
3,50
3,29
3,14
3,01
2,92
2,84
2,77
2,70
2,66
2,62
чо
Tien
СЧ
19,33
8,94
6,16
4.95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,92
2,85
2,79
2,74
2,70
о
СП
СЧ
19,30
9,01
6,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
з,и
3,02
2,96
2,90
2,85
2,81
Т*
V)
СЧ
СЧ
19,25
СЧ
ON
6,39
5,19
4,53
4,12
3,84
3,63
3,48
3,36
3,26
3,18
з,п
3,06
3,01
2,96
си
чо
СЧ
9Г61
9,28
6,59
5,41
4,76
ю
СП
Tf
4,07
3,86
3,71
3,59
3,49
3,41
3,34
3,29
3,24
3,20
СЧ
о
о
СЧ
19,00
9,55
6,94
5,79
5,14
4,74
4,46
4,26
4,10
3,98
3,88
3,80
3,74
3,68
3,63
3,59
-
ЧО
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,84
4,75
4,67
4,60
4,54
4,49
4,45
СЧ
СП
Tf
ir>
чо
оо
ON
о
СЧ
СП
Tf
IT)
чо
489
^ Приложения
Таблица 7. Критические точки для статистики Колмогорова Dn
Объем
выборки п
Уровень значимости а
0,10
0,05
0,02
0,01
1
0,95
0,98
0,99
0,995
2
0,78
0,84
0,90
0,93
3
0,64
0,71
0,78
0,83
4
0,57
0,62
0,69
0,73
5
0,51
0,56
0,62
0,67
6
0,47
0,52
0,58
0,62
7
0,44
0,48
0,54
0,58
8
0,41
0,45
0,51
0,54
9
0,39
0,43
0,48
0,51
10
0,37
0,41
0,46
0,49
11
0,35
0,39
0,44
0,47
12
0,34
0,38
0,42
0,45
13
0,33
0,36
0,40
0,43
14
0,31
0,35
0,39
0,42
15
0,30
0,34
0,38
0,40
16
0,29
0,33
0,37
0,39
17
0,29
0,32
0,36
0,38
18
0,28
0,31
0,34
0,37
19
0,27
0,30
0,34
0,36
20
0,26
0,29
0,33
0,35
Критические точки распределения Колмогорова
ea)=i+2?(-i)V2*2x2
к=\
а
0,10
0,05
0,02
0,01
К
1,23
1,36
1,52
1,63
490
Приложения ф
(к — число степеней свободы, / - количество выборок)
1\Л
1
2
3
4
5
6
7
8
9
10
Уровень значимости а = 0,05
2
0,999
0,975
0,939
0,906
0,877
0,853
0,833
0,816
0,801
0,788
3
0,967
0,871
0,798
0,746
0,707
0,677
0,653
0,633
0,617
0,603
4
0,907
0,768
0,684
0,629
0,590
0,560
0,537
0,518
0,502
0,488
5
0,841
0,634
0,598
0,544
0,506
0,478
0,456
0,439
0,424
0,412
6
0,781
0,616
0,532
0,480
0,445
0,418
0,398
0,382
0,368
0,357
7
0,727
0,561
0,480
0,431
0,397
0,373
0,354
0,338
0,326
0,315
8
0,680
0,516
0,438
0,391
0,360
0,336
0,319
0,304
0,293
0,283
9
0,639
0,478
0,403
0,358
0,329
0,307
0,290
0,277
0,266
0,257
10
0,602
0,445
0,373
0,331
0,303
0,282
0,267
0,254
0,244
0,235
Таблица 8. Критические точки распределения Кокрена
ЛИТЕРАТУРА
1. Айвазян С.А., Мхитарян B.C. Прикладная статистика и
основы эконометрики. — М.: ЮНИТИ, 1998.
2. Айвазян С.А., Мхитарян B.C. Прикладная статистика в
задачах и упражнениях. — М.: ЮНИТИ, 2001.
3. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и
управление. — М.: Мир, 1974.
4. Большее Л.Н., Смирнов Н.В. Таблицы математической
статистики. — М.: Наука, 1983.
5. Боровиков В. STATISTICA. Искусство анализа данных на
компьютере. — СПб.: Питер, 2003.
6. Бочаров П.П., Пенинкин А.В. Теория вероятностей.
Математическая статистика. — М.: Гардарика, 1998.
7. Ван дер Варден Б. Математическая статистика. — М.: Высшая
школа, 1975.
8. Венецкий Г.И., Кильдышев А.Н. Математическая статистика.
Изд. 3-е. — М.: Статистика, 1986.
9. Вентцель Е.С. Теория вероятностей и математическая
статистика. — М., Мир, 1972.
10. Вентцель Е.С. Исследование операций: задачи, принципы,
методология. - М: Наука, 1980.
11. Гмурман В.Е. Руководство к решению задач по теории
вероятностей и математической статистике. — М.: Высшая школа,
1998.
12. Гнеденко Б.В. Курс теории вероятностей. — М.: Наука, 1960.
13. Грачева М.В., Фадеева Л.Н., Черемных Ю.Н. Количественные
методы в экономических исследованиях. — М.: ЮНИТИ, 2004.
14. Доугерти К. Введение в эконометрику. — М.: ИНФРА-М,
2001.
15. КибзунА.И., Горяпнова Е.Р., Наумов А.В., Сиротин АН. Теория
вероятностей и математическая статистика. — М.: Физматлит,
2002.
16. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория
вероятностей и математическая статистика. — М.: Высшая школа,
1991.
17. Крамер Г. Математические методы статистики. — М.: Мир,
1975.
492
Литература ^
18. Кремер Н.Ш. Теория вероятностей и математическая
статистика. - М.: ЮНИТИ, 2002.
19. Кузнецов Ю.А. Оптимальное управление экономическими
системами. — Изд. Нижегородского госуниверситета, 2008.
20. Лукаш Е.Н, Медведев П.А., Пахомов В.Ф. Высшая
математика. - М.: МГУ, 1987.
21. Магнус Я.Р., Картышев П.К., Пересецкий АЛ Эконометрика. —
М.: Дело, 1977.
22. Сборник задач по теории вероятностей, математической
статистике и теории случайных функций / Под ред. А.А. Свешникова. —
М.: Наука, 1970.
23. Соколов Г.А., Чистякова Н.А. Теория вероятностей.
Управляемые цепи Маркова в экономике. — М.: Физматлит, 2005.
24. Сулицкий В.Н. Методы статистического анализа в
управлении. — М.: Дело, 2002.
25. Тюрин Ю.Н., Макаров АЛ. Анализ данных на компьютере /
Под ред. В.Э. Фигурнова. — М.: ИНФРА-М, 2003.
26. Тюрин Ю.Н.9 Макаров А.А., Высоцкий И.Р., Ященко И.В.
Теория вероятностей и статистика. — М.: МЦНМО, 2004.
27. Уотшем ТДж., Паррамоу К. Количественные методы в
финансах. - М.: ЮНИТИ, 1999.
28. Фадеева Л.Н Теория вероятностей и математическая
статистика. — М.: Эксмо, 2006.
29. Фадеева Л.Н., Жуков Ю.В., Лебедев А.В. Сборник задач по
теории вероятностей и математической статистике. — М.: Эксмо,
2006.
30. Феллер В. Введение в теорию вероятностей и ее
приложения. — М.: Мир, 1984.
31. Чистяков В.П. Курс теории вероятностей. — М.: Наука,
1982.
32. Ширяев АН Вероятность. — М.: МЦНМО, 2007.
33. Эддоус М., Стэнсфилд Р. Методы принятия решения. — М.:
ЮНИТИ, 1997.
30. Экономико-математические методы и прикладные модели /
Под ред. В.В. Федосеева. — М.: ЮНИТИ, 1999.
Учебное издание
новое экономическое образование
Фадеева Людмила Николаевна
Лебедев Алексей Викторович
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Учебное пособие
Директор редакции И. Федосова
Ответственный редактор В. Щербакова
Редактор В. Космин
Художественный редактор Н. Биржаков
Технический редактор Л. Зотова
Компьютерная верстка С. Терентьева
Корректор Я Перовская
ооо «Издательство «Эксмо»
127299, Москва, ул. Клары Цеткин, д. 18/5. Тел. 411-68-86, 956-39-21.
Home page: www.eksmo.ru E-mail: info@eksmo.ru
Подписано в печать 03.08.2009.
Формат 60х90У16. Гарнитура «Тайме». Печать офсетная.
Бумага писчая. Усл. печ. л. 31,0.
Тираж 2000 экз. Заказ № 5674
Отпечатано с готовых файлов заказчика в ОАО "ИПК
"Ульяновский Дом печати". 432980, г. Ульяновск, ул. Гончарова, 14
Оптовая торговля книгами «Эксмо»:
ООО «ТД «Эксмо». 142700, Московская обл., Ленинский р-н, г. Видное,
Белокаменное ш., д. 1, многоканальный тел. 411-50-74.
E-mail: reception@eksmo-sale.ru
По вопросам приобретения книг «Эксмо» зарубежными оптовыми
покупателями обращаться в отдел зарубежных продаж ТД «Эксмо»
E-mail: international®eksmo-sale.ru
International Salea: International wholesale customers should contact
Foreign Sales Department of Trading House «Eksmo» for their orders.
international@eksmo-sale.ru
По вопросам заказа книг корпоративным клиентам,
в том числе в специальном оформлении,
обращаться по тел. 411-68-59доб. 2115, 2117, 2118.
E-mail: vipzakaz@eksmo.ru
Оптовая торговля бумажно-беловыми
и канцелярскими товарами для школы и офиса «Канц-Эксмо»:
Компания «Канц-Эксмо»: 142702, Московская обл., Ленинский р-н, г. Видное-2,
Белокаменное ш., д. 1, а/я 5. Тел./факс +7 (495) 745-28-87 (многоканальный),
e-mail: kanc@eksmo-sale.ru, сайт: www.kanc-eksmo.ru
Полный ассортимент книг издательства «Эксмо» для оптовых покупателей:
В Санкт-Петербурге: 000 СЗКО, пр-т Обуховской Обороны, д. 84Е.
Тел. (812) 365-46-03/04.
В Нижнем Новгороде: 000 ТД «Эксмо НН», ул. Маршала Воронова, д. 3.
Тел. (8312) 72-36-70.
В Казани: Филиал 000 «РДЦ-Самара», ул. Фрезерная, д. 5.
Тел. (843) 570-40-45/46.
В Ростове-на-Дону: 000 «РДЦ-Ростов», пр. Стачки, 243А.
Тел. (863) 220-19-34.
В Самаре: 000 «РДЦ-Самара», пр-т Кирова, д. 75/1, литера «Е».
Тел. (846) 269-66-70.
В Екатеринбурге: ООО «РДЦ-Екатеринбург», ул. Прибалтийская, д. 24а.
Тел. (343) 378-49-45.
В Киеве: ООО «РДЦ Эксмо-Украина», Московский пр-т, д. 9.
Тел./факс: (044) 495-79-80/81.
Во Львове: ТП ООО «Эксмо-Запад», ул. Бузкова, д. 2.
Тел./факс (032) 245-00-19.
В Симферополе: ООО «Эксмо-Крым», ул. Киевская, д. 153.
Тел./факс (0652) 22-90-03, 54-32-99.
В Казахстане: ТОО «РДЦ-Алматы», ул. Домбровского, д. За.
Тел./факс (727) 251-59-90/91. rdc-almaty@mail.ru
Полный ассортимент продукции издательства «Эксмо»:
В Москве в сети магазинов «Новый книжный»:
Центральный магазин — Москва, Сухаревская пл., 12. Тел. 937-85-81.
Волгоградский пр-т, д. 78, тел. 177-22-11; ул. Братиславская, д. 12. Тел. 346-99-95.
Информация о магазинах «Новый книжный» по тел. 780-58-81.
В Санкт-Петербурге в сети магазинов «Буквоед»:
«Магазин на Невском», д. 13. Тел. (812) 310-22-44.
По вопросам размещения рекламы в книгах издательства «Эксмо»
обращаться в рекламный отдел. Тел. 411-68-74.