Прикладная
статистика
Основы
ЭКОНОМЕТРИКИ
В двух томах
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ

S. A. Aivazian
V. S. Mkhitarian
PROBABILITY THEORY
AND
APPLIED STATISTICS
Volume!
Textbook
ЮНИТИ
UNITY
Moscow
2001

С. А. Айвазян
В. С. Мхитарян
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
и ПРИКЛАДНАЯ
СТАТИСТИКА
Том
1
Рекомендовано Министерством общего
и профессионального образования Российской
Федерации в качестве учебника для студенюв
экономических специальностей высших
учебных заведений
юнмти
UNITY
Москва
2001

УДК 311+330.43@75.8)
ББК 60.6+65в6я73
П85
Первое издание данного учебника подготовлено в рамках Проекта Tads "Преподавание экономических и бизнес-д
средних школах, технических и классических университетах**, реализованного Фо1
ситета "Эразмус", Роттердам (SEOR/EUR) и Государственным университетом — Высшей школой:
Рецензенты:
кафедра статистики С.-Петербургского государственного университета
экономики и финансов; проф. Э.Б. Ершов (ГУ ВШЭ) и проф. Я. Магнус (Университет Тилбурга)
Главный редактор издательства Н.Д. Эриашвили
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т.
П85 2-е изд., испр. — Т. 1: Айвазян С. А., Мхитарян B.C. Теория вероятностей
и прикладная статистика. — М: ЮНИТИ-ДАНА, 2001. — 656 с.
ISBN 5-238-00304-8
Содержание и стиль изложения в учебнике соответствуют принятым Министерством
образования РФ стандартам и учебным программам высших учебных заведений экономического
профиля по дисциплинам 'Теория вероятностей", "Математическая статистика" и
"Многомерные статистические методы" (или "Многомерный статистический анализ"). При этом первые две
дисциплины входят в учебные планы 1-й ступени образования (бакалавриата), а третья может
присутствовать (в зависимости от конкретного вуза) в учебных планах бакалавриата или
магистратуры. Усвоение включенного в этот том материала предусматривает для каждой из
упомянутых дисциплин общий объем аудиторных занятий, равный приблизительно 64 часам C2 часа
лекций и 32 часа практических занятий). Изложение построено таким образом, чтобы добиться
цельного (системного) восприятия всего блока эконометрических дисциплин, представленных
в двух томах второго издания: упомянутые три дисциплины первого тома дополнены во втором
томе широким набором моделей регрессионного анализа, методами и моделями анализа
временных рядов и методами построения и анализа систем одновременных уравнений.
Для студентов, аспирантов, преподавателей, а также специалистов по прикладной
статистике и эконометрике.
ББК 60.6+65в6я73
Учебник
Айвазян Сергей Артемьевич, Мхитарян Владимир Сергеевич
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ПРИКЛАДНАЯ СТАТИСТИКА
Оформление художника Л. В. Лебедева
Лицензия серия ИД № 03562 от 19.12.2000 г. Подписано в печать 10.08.2001. Формат 70x100 1/16
Усл. печ. л. 53,3. Уч.-изд. л. 43. Тираж 20 000 экз. A-й завод - 5000). Заказ 1639
ООО «ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА». Генеральный директор В.Н. Закаидзе
123298, Москва, ул. Ирины Левченко, 1-9. Тел. @95) 194-00-15. Тел/факс @95) 194-00-14
www.unity-dana.ru E-mail: unity@msm.ru
Отпечатано во ФГУП ИПК «Ульяновский Дом печати». 432980, г. Ульяновск, ул. Гончарова, 14
Качество печати соответствует предоставленным оригиналам
ISBN 5-238-00304-8 © С.А. Айвазян, B.C. Мхитарян, 1998, 2001
© «ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА^, 1998,2001
Воспроизведение всей книги или любой ее
части запрещается без письменного
разрешения издательства

ОГЛАВЛЕНИЕ
К читателю 15
Предисловие к первому изданию 16
Предисловие ко второму изданию 20
Введение. Вероятностно-статистические методы в
моделировании социально-экономических процессов и анализе данных . 23
8.1. Математико-статистический инструментарий экономических
исследований 24
В. 1.1. Назначение и составные части учебника 24
В. 1.2. Прикладная статистика 26
В.1.3. Теория вероятностей и математическая статистика . . 28
8.2. Теоретико-вероятностный способ рассуждения в прикладной
статистике и эконометрике 29
8.2.1. Границы применимости теоретико-вероятностного
способа рассуждения 29
8.2.2. Что дает объединение теоретико-вероятностного и
статистического способов рассуждения? 35
8.3. Вероятностно-статистическая (эконометрическая) модель как
частный случай математической модели 40
8.3.1. Математическая модель 40
8.3.2. Основные этапы вероятностно-статистического
моделирования 43
8.3.3. Моделирование механизма явления вместо формальной
статистической фотографии 45
Выводы 48

6 ОГЛАВЛЕНИЕ
Раздел I: Основы теории вероятностей si
Глава 1. Правила действий со случайными событиями и
вероятностями их осуществления 52
1.1. Дискретное вероятностное пространство 52
1.1.1. Процесс регистрации наблюдения на объекте исследуемой
совокупности (случайный эксперимент) ...... . 52
1.1.2. Случайные события и правила действий с ними .... 53
1.1.3. Вероятностное пространство. Вероятности и правила
действий с ними 58
1.2. Непрерывное вероятностное пространство (аксиоматика
А.Н.Колмогорова) 69
1.2.1. Специфика общего (непрерывного) случая
вероятностного пространства 69
1.2.2. Случайные события, их вероятности и правила действий
с ними (аксиоматический подход А.Н.Колмогорова) . . 71
Выводы 75
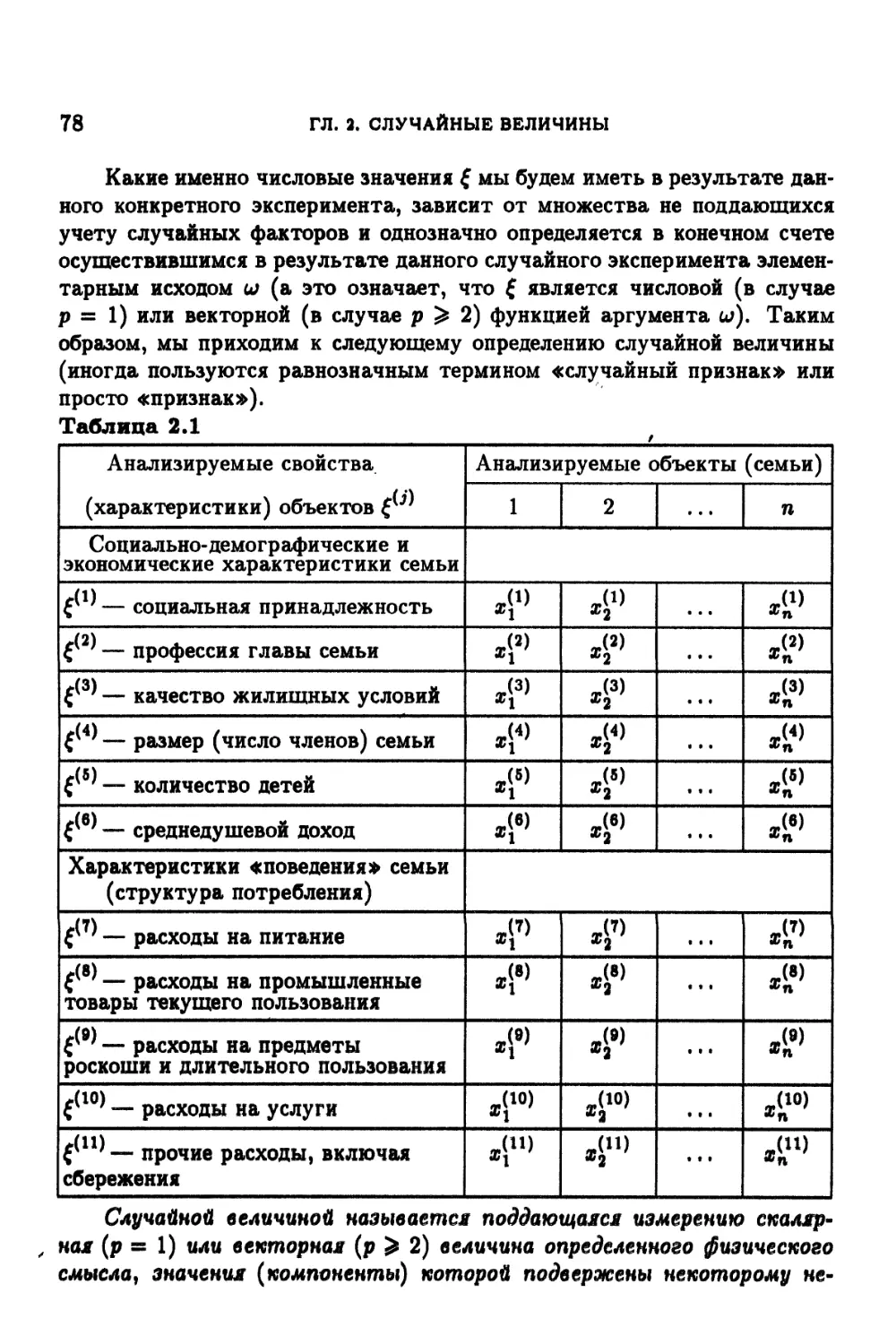
Глава 2. Случайные величины (исследуемые признаки) ... 77
2.1. Определение и примеры случайных величин 77
2.2. Возможные и наблюденные значения случайной величины . . 79
2.3. Типы случайных величин 80
2.4. Одномерные и многомерные (совместные) законы
распределения вероятностей случайных величин 83
2.5. Способы задания закона распределения: функция
распределения, функция плотности 89
2.5.1. Функция распределения вероятностей одномерной
случайной величины 89
2.5.2. Функция плотности вероятности одномерной случайной
величины 92
2.5.3. Многомерные функции распределения и плотности.
Статистическая независимость случайных величин .... 94
2.6. Основные числовые характеристики случайных величин ... 98
2.6.1. Понятие о математических ожиданиях и моментах ... 99
2.6.2. Характеристики центра группирования значений
случайной величины 102
2.6.3. Характеристики степени рассеяния значений случайной
величины 104
2.6.4. Квантили и процентные точки распределения 106
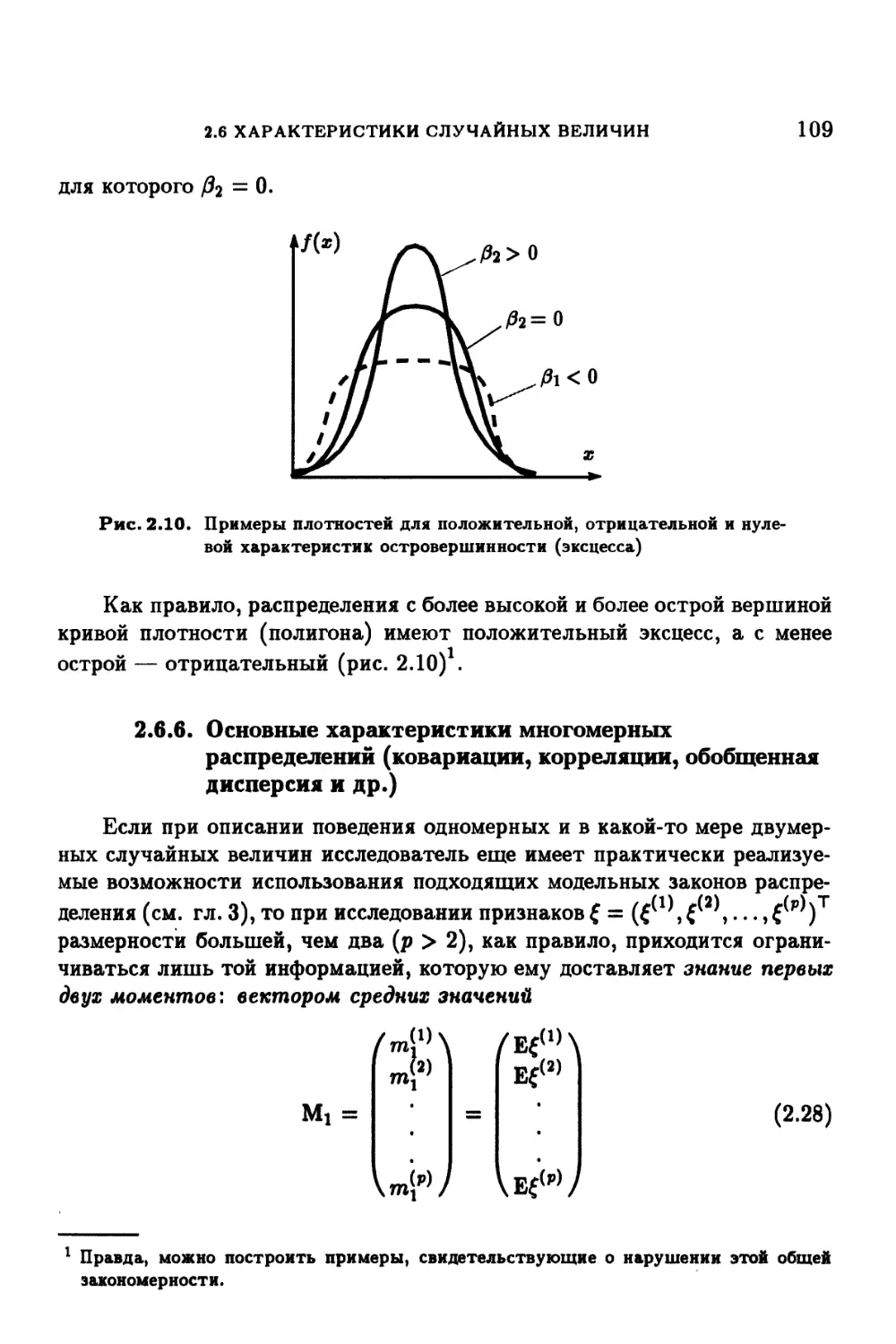
2.6.5. Асимметрия и эксцесс 108

ОГЛАВЛЕНИЕ 7
2.6.6. Основные характеристики многомерных распределений
(ковариации, корреляции, обобщенная дисперсия и др.) . 109
Выводы 112
Глава 3. Модели законов распределения вероятностей,
наиболее распространенные в практике статистических
исследований 114
3.1. Законы распределения, используемые для описания механизмов
генерации реальных социально-экономических данных . ... 115
3.1.1. Распределения, возникающие при анализе
последовательности испытаний Бернулли: биномиальное и
отрицательное биномиальное 115
3.1.2. Гипергеометрическое распределение 119
3.1.3. Распределение Пуассона 121
3.1.4. Полиномиальное (мультиномиальное) распределение . . 123
3.1.5. Нормальное (гауссовское) распределение 125
3.1.6. Логарифмически-нормальное распределение 129
3.1.7. Равномерное (прямоугольное) распределение 132
3.1.8. Распределения Вейбулла и экспоненциальное
(показательное) 134
3.1.9. Распределение Парето 139
3.1.10. Распределение Коши 140
3.2. Законы распределения вероятностей, используемые при
реализации техники статистических вычислений 141
3.2.1. «Хи-квадрат»-распределение с m степенями свободы
(Х2(ет»)-распределение) 142
3.2.2. Распределение Стьюдента с m степенями свободы (t(m)-
распределение) 143
3.2.3. Распределение дисперсионного отношения с числом
степеней свободы числителя mi и числом степеней свободы
знаменателя тг (F(mi,п»2^распределение) 145
3.2.4. Гамма-распределение (Г-распределение) 147
3.2.5. Бета-распределение (^-распределение) *. . . 148
Выводы 151
Глава 4. Основные результаты теории вероятностей 153
4.1. Неравенство Чебышева 153
4.2. Закон больших чисел и его следствия 155
4.2.1. Закон больших чисел 155
4.2.2. Теорема Бернулли 156

8 ОГЛАВЛЕНИЕ
4.3. Особая роль нормального распределения: центральная
предельная теорема 157
4.3.1. Центральная предельная теорема 158
4.3.2. Многомерная центральная предельная теорема 159
4.3.3. Комментарии к центральной предельной теореме . . . 159
4.4. Законы распределения вероятностей случайных признаков,
являющихся функциями от известных случайных величин . . 161
Выводы 166
Глава 5. Цепи Маркова 168
5.1. Последовательности случайных экспериментов и случайных
величин в дискретном вероятностном пространстве 168
5.2. Последовательности, образующие цепь Маркова (определения,
примеры, прикладные задачи) 170
5.3. Основные характеристики и свойства цепей Маркова .... 177
5.3.1. Основные характеристики 177
5.3.2. Классификация состояний и цепей 179
5.3.3. Свойства цепей Маркова 182
5.4. Анализ некоторых задач и примеров 185
Выводы 190
Раздел II: Основы математической статистики . ш
Глава 6. Основы статистического описания и статистика
нормального закона 194
6.1. Генеральная совокупность, выборка из нее и основные способы
организации выборки 194
6.2. Основные выборочные характеристики и их свойства .... 200
6.2.1. Выборочные (эмпирические) функции распределения,
относительные частоты и функции плотности 201
6.2.2. Выборочные аналоги начальных и центральных моментов
случайной величины 207
6.2.3. Эмпирические аналоги центра группирования
генеральной совокупности 208
6.2.4. Эмпирические аналоги показателей вариации
рассеивания случайной величины 209
6.2.5. Выборочные коэффициенты асимметрии и эксцесса . . . 210
6.2.6. Статистическая устойчивость выборочных
характеристик 214
6.2.7. Асимптотически-нормальный характер случайного
варьирования основных выборочных характеристик . . . 216

ОГЛАВЛЕНИЕ 9
6.2.8. Поведение выборочных характеристик в нормальной
генеральной совокупности (статистика нормального закона). 219
6.3. Вариационный ряд и порядковые статистики 224
6.3.1. Закон распределения вероятностей i-ro члена
вариационного ряда V . 225
6.3.2. Совместные (многомерные) распределения членов
вариационного ряда 227
6.3.3. Порядковые статистики как эмпирические (выборочные)
аналоги квантилей и процентных точек распределения . 229
Выводы 229
Глава 7. Статистическое оценивание параметров 231
7.1. Начальные сведения о задаче статистического оценивания
параметров 232
7.1.1. Постановка задачи 232
7.1.2. Статистики, статистические оценки, их основные
свойства 233
7.1.3. Состоятельность 234
7.1.4. Несмещенность 236
7.1.5. Эффективность 238
7.2. Функция правдоподобия. Количество информации,
содержащееся в п независимых наблюдениях относительно неизвестного
значения параметра 241
7.3. Неравенство Рао-Крамера-Фреше и измерение эффективности
оценок ° 244
7.4. Понятие об интервальном оценивании и доверительных
областях (постановка задач) 248
7°.5. Методы статистического оценивания неизвестных параметров. 249
7.5.1. Метод максимального (наибольшего) правдоподобия . . 249
7.5.2. Метод моментов 258
7.5.3. Оценивание с помощью «взвешенных» статистик;
цензурирование, урезание выборок и порядковые статистики
как частный случай взвешивания 261
7.5.4. Построение интервальных оценок (доверительных
областей) 263
7.6. Байесовский подход к статистическому оцениванию 269
7.6.1. «Философия» байесовского подхода 269
7.6.2. Общая логическая схема и базовые формулы байесовского
метода оценивания параметров . . . 270
7.6.3. Примеры байесовского оценивания 273
Выводы 279
Приложение к гл. 7 (доказательство неравенства информации) . . 281

10 ОГЛАВЛЕНИЕ
Глава 8. Статистическая проверка гипотез (статистические
критерии) 283
8.1. Основные типы гипотез, проверяемых в ходе статистического
анализа и моделирования 284
8.1.1. Гипотезы о типе закона распределения исследуемой
случайной величины 284
8.1.2. Гипотезы об однородности двух или нескольких
обрабатываемых выборок или некоторых характеристик
анализируемых совокупностей 285
8.1.3. Гипотезы о числовых значениях параметров исследуемой
генеральной совокупности 285
8.1.4. Гипотезы об общем виде модели описывающей,
статистическую зависимость между признаками 286
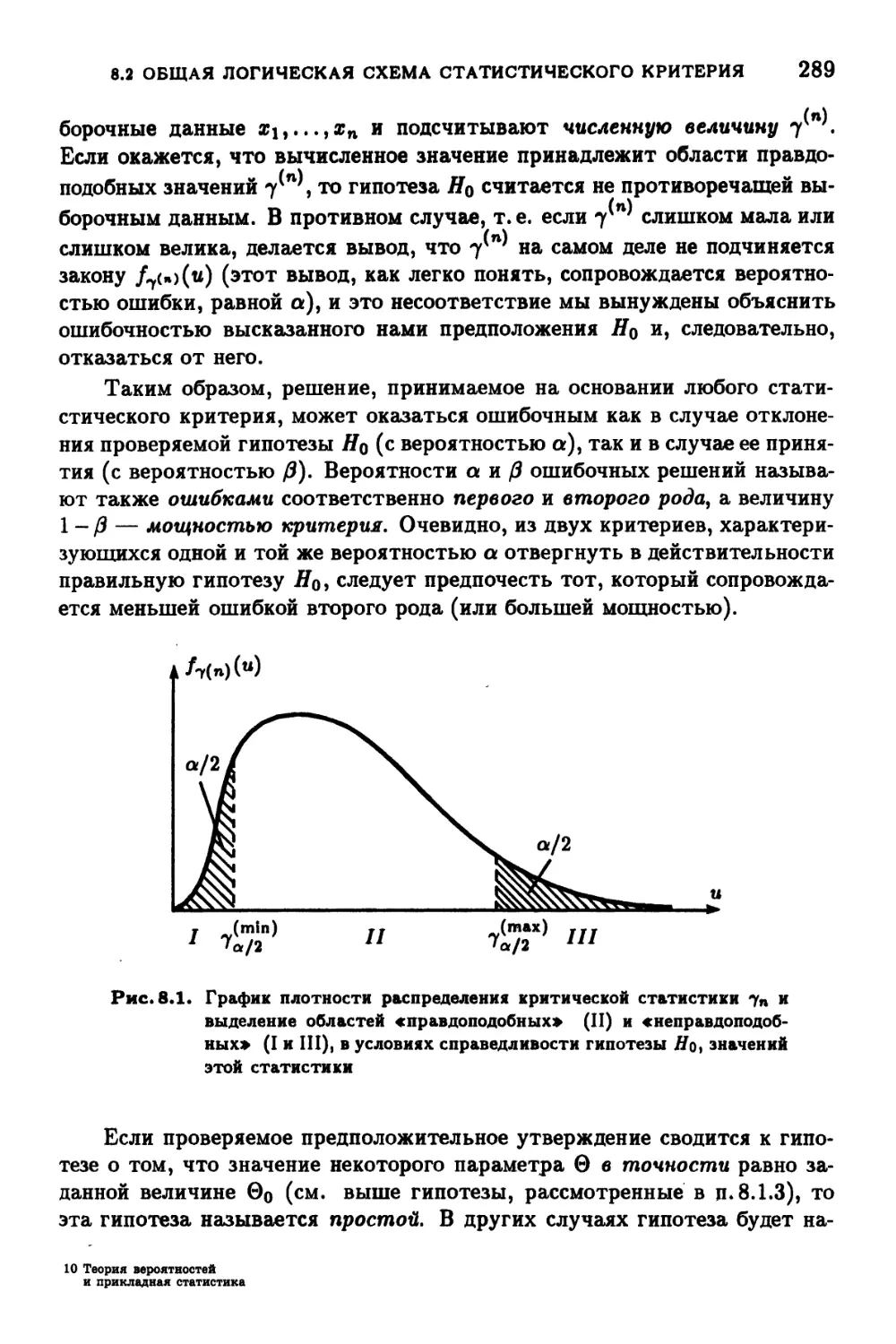
8.2. Общая логическая схема статистического критерия 287
8.3. Построение статистического критерия; принцип отношения
правдоподобия 290
8.3.1. Сущность принципа отношения правдоподобия .... 290
8.3.2. Критерий логарифма отношения правдоподобия для
проверки простой гипотезы 292
8.3.3. Критерий отношения правдоподобия для проверки
сложной гипотезы 293
8.4. Характеристики качества статистического критерия .... 294
8.5. Последовательная схема принятия решения (последовательные
критерии) 297
8.5.1. Последовательная схема наблюдений 297
8.5.2. Последовательный критерий отношения правдоподобия
(критерий Вальда) и его свойства 299
8.6. Методы проверки статистических гипотез: примеры
статистических критериев 300
8.6.1. Критерии согласия #. 300
8.6.2. Критерии однородности 309
8.6.3. Проверка гипотез о числовых значениях параметров . . 317
Выводы 325
Раздел III: Методы прикладной статистики ... 327
Глава 9. Введение в прикладной статистический анализ ... 328
9.1. Назначение и содержание прикладной статистики 328
9.1.1. Два подхода к интерпретации и анализу исходных
статистических данных 328

ОГЛАВЛЕНИЕ 11
9.1.2. Три центральные проблемы прикладной статистики . . 331
9.1.3. Новые постановки задач и ослабление ограничительных
условий в канонических математико-статистических и
эконометрических моделях 338
9.2. Основные этапы прикладного статистического анализа . . . 339
Выводы 346
Глава 10. Статистическое исследование зависимостей
(основные понятия и постановки задач) 349
10.1. Общая формулировка проблемы, пример 349
10.2. Какова конечная прикладная цель статистического
исследования зависимостей 359
10.3. Математический инструментарий 362
10.4. Некоторые типовые задачи практики эконометрического
моделирования 364
10.5. Основные типы зависимостей между количественными
переменными 370
10.6. Основные этапы статистического исследования зависимостей. 375
10.7. Выбор общего вида функции регрессии 382
10.7.1. Использование априорной информации о
содержательной сущности анализируемой зависимости 383
10.7.2. Предварительный анализ геометрической структуры
исходных данных 385
10.7.3. Статистические критерии проверки гипотез об общем
виде функции регрессии 386
10.7.4. Некоторые общие рекомендации 390
Выводы 392
Глава 11. Корреляционный анализ многомерной генеральной
совокупности 396
11.1. Назначение и место корреляционного анализа в
статистическом исследовании 396
11.2. Корреляционный анализ количественных признаков .... 398
11.2.1. Коэффициент детерминации как универсальная
характеристика степени тесноты статистической связи . . . 399
11.2.2. Исследование линейной зависимости у от единственной
объясняющей переменной х: парный коэффициент
корреляции 404
11.2.3. Исследование парных нелинейных связей:
корреляционное отношение 412

12 ОГЛАВЛЕНИЕ
11.2.4. Исследование линейной зависимости у от нескольких
объясняющих переменных х^г\х^2\... }х^:
множественный и частные коэффициенты корреляции .... 417
11.3. Корреляционный анализ порядковых (ординальных)
переменных: ранговая корреляция 428
11.3.1. Исходные статистические данные (таблица или
матрица рангов типа «объект-свойство») 429
11.3.2. Понятие ранговой корреляции 430
11.3.3. Основные задачи статистического анализа связей
между ранжировками 431
11.3.4. Ранговый коэффициент корреляции Спирмэна .... 432
11.3.5. Ранговый коэффициент корреляции Кендалла .... 434
11.3.6. Обобщенная формула для парного коэффициента
корреляции и связь между коэффициентами Спирмэна и
Кендалла 438
11.3.7. Статистические свойства выборочных характеристик
парной ранговой связи 439
11.3.8. Коэффициент конкордации (согласованности) как
измеритель статистической связи между несколькими
порядковыми переменными 442
11.3.9. Проверка статистической значимости выборочного
значения коэффициента конкордации 444
11.4. Корреляционный анализ категоризованных переменных:
таблицы сопряженности 447
11.4.1. Исходные статистические данные (таблицы
сопряженности) 447
11.4.2. Основные измерители степени тесноты статистической
связи между двумя категоризованными переменными . 448
Выводы 453
Глава 12. Распознавание образов и типологизация объектов в
социально-экономических исследованиях (методы
классификации) 457
12.1. Сущность, типологизация и прикладная направленность задач
классификации объектов 457
12.2. Классификация при наличии обучающих выборок (дискрими-
нантный анализ) 471
12.2.1. Класс как генеральная совокупность и базовая идея
вероятностно-статистических методов классификации . 471
12.2.2. Функции потерь и вероятности неправильной
классификации 472

ОГЛАВЛЕНИЕ 13
12.2.3. Принципиальное решение общей задачи построения
оптимальных (байесовских) процедур классификации . 473
12.2.4. Параметрический дискриминантный анализ в случае
нормальных классов 476
12.3. Классификация без обучения (параметрический случай):
расщепление смесей вероятностных распределений 479
12.3.1. Понятие смеси вероятностных распределений .... 480
12.3.2. Задача расщепления смесей распределений 486
12.3.3. Общая схема решения задачи автоматической
классификации в рамках модели смеси распределений
(сведение к схеме дискриминантного анализа) 487
12.4. Классификация без обучения (непараметрический случай):
методы кластер-анализа 488
12.4.1. Общая постановка задачи автоматической
классификации 488
12.4.2. Расстояния между отдельными объектами и меры
близости объектов друг к другу 491
12.4.3. Расстояния между классами объектов 495
12.4.4. Функционалы качества разбиения на классы и
экстремальная постановка задачи кластер-анализа 498
12.4.5. Формулировка экстремальных задач разбиения
исходного множества объектов на классы при неизвестном
числе классов 503
12.4.6. Основные типы задач кластер-анализа и основные типы
кластер-процедур 503
12.4.7. Иерархические процедуры 505
12.4.8. Параллельные кластер-процедуры 507
12.4.9. Последовательные кластер-процедуры 512
Выводы 516
Глава 13. Снижение размерности исследуемого многомерного
признака и отбор наиболее информативных показателей . . . 520
13.1. Сущность, типологизация и прикладная направленность задач
снижения размерности 520
13.2. Метод главных компонент 526
13.2.1. Основные понятия и определения 526
13.2.2. Вычисление главных компонент 529
13.2.3. Основные числовые характеристики главных
компонент 531
13.2.4. Геометрическая интерпретация главных компонент . . 538
13.2.5. Оптимальные свойства главных компонент 541

14 ОГЛАВЛЕНИЕ
13.2.6. Статистические свойства выборочных главных
компонент, статистическая проверка некоторых гипотез . . 544
13.2.7. Применение свойств выборочных характеристик
главных компонент 547
13.3. Факторный анализ . . . . 551
13.3.1. Сущность модели факторного анализа 551
13.3.2. Общий вид линейной модели, ее связь с главными
компонентами 552
13.3.3. Основные задачи факторного анализа 556
13.3.4. Вопросы идентификации модели факторного анализа . 558
13.3.5. Статистическое исследование модели факторного
анализа 559
13.4. Некоторые эвристические методы снижения размерности . . 570
13.4.1. Природа эвристических методов 570
13.4.2. Метод экспериментальной группировки признаков . . 571
13.4.3. Метод корреляционных плеяд 577
13.5. Построение сводного (интегрального) латентного показателя
качества (или эффективности функционирования) сложной
системы 580
13.5.1. Общая постановка задачи 580
13.5.2. Сводный показатель («выходное качество») и его
целевая функция 581
13.5.3. Исходные данные 583
13.5.4. Алгоритмические и вычислительные вопросы
построения неизвестной целевой функции 585
13.5.5. Примеры построения интегрального показателя с
помощью экспертно-статистического метода 589
13.6. Многомерное шкалирование 592
13.6.1. Постановка задачи метрического многомерного
шкалирования 592
13.6.2. Решение задачи метрического многомерного
шкалирования 593
13.6.3. Понятие о неметрическом многомерном шкалировании
(МШ) 595
Выводы 595
Приложение 1. Таблицы математической статистики 601
Приложение 2. Необходимые сведения из матричной алгебры .... 619
Литература 642
Алфавитно-предметный указатель . 644

К ЧИТАТЕЛЮ
Рекомендую студентам и преподавателям, специализирующимся в
области прикладной статистики и эконометрики, 2-е издание учебника
«Прикладная статистика и основы эконометрики», том 1: «Теория вероятностей и
прикладная статистика». Книга подготовлена выдающимися специалистами,
имеющими богатый опыт преподавания излагаемого предмета и ведущими,
наряду с этим, серьезную исследовательскую работу в области эконометрического
анализа социально-экономических процессов. «Предисловия» авторов
данного издания содержат точную, с моей точки зрения, характеристику основного
замысла книги и ее места в ряду аналогичных изданий. Книгу выгодно
выделяют, по меньшей мере, два ее свойства. Во-первых, отбор материала
первого тома, стиль изложения, расставленные в ней акценты подчинены общей
идее востребованности излагаемых методов и моделей именно теорией и
практикой эконометрики. Во-вторых, содержание и структура учебника
отражают более широкий (по сравнению с традиционным) взгляд авторов на
состав вероятностно-статистического инструментария эконометрики. В
частности, авторы включили в состав этого инструментария и цепи Маркова (гл. 5),
зарекомендовавшие себя полезным инструментом в исследовании динамики
различного рода структурных социально-экономических изменений, и различные
многомерные статистические методы (дискриминантный и кластер анализы,
гл.12, методы снижения размерности, гл.13), органично дополняющие
«законно прописанные» в эконометрике методы и модели регрессионного анализа,
и, наконец, байесовский подход к идентификации моделей (п. 7.6), повышенная
востребованность которого обусловлена именно экономической спецификой
статистических исследований, при которой объем исходных данных (число
имеющихся наблюдений), как правило, не слишком превышает размерности
анализируемых моделей.
Много лет я поддерживал самые тесные научные контакты с одним из
авторов книги — Сергеем Артемьевичем Айвазяном, в первые пятнадцать лет, —-
в качестве его научного руководителя (вначале — на механико-математическом
факультете МГУ им. М.В. Ломоносова, затем — в Математическом
институте им. В.А. Стеклова Российской академии наук). Уже в самом начале своего
творческого пути он умел удачно соединять глубокие математические
исследования с живым интересом к различным областям приложений вероятностно-
статистической науки, в том числе и к экономике. Я твердо уверен, что 2-е
издание книги будет встречено читателями с таким же энтузиазмом, как и
первое.
Академик Юрий Васильевич ПРОХОРОВ,
заведующий отделом теории вероятностей Математического института
им. В.А. Стеклова РАН, заведующий кафедрой математической статистики
факультета вычислительной математики и кибернетики МГУ им. М.В. Ломоносова.
25 июля 2001 г.

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Эконометрика — одна из базовых (наряду с микро- и
макроэкономикой) дисциплин экономического образования во всем мире. К
сожалению, до начала 90-х годов эконометрика по существу не была признана в
СССР и России, не включалась в учебные планы подготовки специалистов
(студентов, аспирантов) экономического профиля. Объяснение этому
найти нетрудно: из трех основных составляющих эконометрики —
экономической теории, экономической статистики и математико-статистического
инструментария две первые были представлены в нашей стране явно
неудовлетворительно. Не было доброкачественной экономической теории,
не было системы национальных счетов и необходимого информационного
обеспечения эконометрического моделирования.
Теперь ситуация изменилась. Авторам предлагаемого вниманию
читателя учебника довелось принять непосредственное участие в процессе
«восстановления в своих законных правах» эконометрики: в
формировании базовых положений концепции современного экономического
образования в российской высшей школе, в составлении первых программ и
чтении первых курсов лекций по этой дисциплине на экономическом
факультете Московского государственного университета им. М.В.
Ломоносова (МГУ), начиная с 1992 г., и в Московском государственном
университете экономики, статистики и информатики (МЭСИ), — с 1993 г. В
формировании своей позиции по данной проблеме авторы опирались на
многолетний опыт исследовательской и педагогической работы в
области разработки и практического использования методов
эконометрического моделирования: один из них (С. А. Айвазян), работая с 1969 года в
Центральном экономико-математическом институте Российской академии
наук, занимается эконометрическим моделированием распределительных
отношений в обществе, одновременно являясь автором учебных программ
и постоянным лектором по всему спектру дисциплин эконометрического
профиля — теории вероятностей, математической статистике,
многомерному статистическому анализу (МГУ им. М. В. Ломоносова,
МЭСИ, Российская экономическая школа — РЭШ), методам
прогнозирования в бизнесе (Московское отделение Калифорнийского государственного
университета, г. Хэйвард); другой (В. С. Мхитарян) использует эконо-

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 17
метрические методы в социально-экономических исследованиях и задачах
статистического контроля качества изделий, а также много лет читает
курсы лекций вероятностно-статистического профиля в МЭСИ.
Что побудило авторов написать этот учебник! Ведь богатые
традиции европейских и северо-американских университетов в области эконо-
метрической науки и ее преподавания в системе экономического
образования всех уровней (undergraduate, graduate, post-graduate) отражены в
разнообразной и интересной монографической и учебно-методической
литературе по данному предмету. Достаточно назвать широко
распространенные учебники Дж. Джонстона, Э. Маленво, A. Goldberger, R. S. Pindyck-
D. L. Rubinfeld, W. Greene, C. Dougherty, E. R. Berndt (см. список
литературы в конце книги). Почему бы не повторить переводы двадцатилетней
давности первых двух учебников и не перевести с английского языка
некоторые из других, здесь упомянутых? Мы полагаем, что в условиях острого
дефицита на отечественном рынке эконометрической учебной литературы
эта деятельность была бы крайне желательной, более того —
необходимой. Однако издание нашей книги имеет свой замысел, свою специфику,
и вот в чем они заключаются.
Во-первых, в предлагаемом учебнике отражено понимание
содержания математико-статистического инструментария эконометрики,
несколько отличающееся от общепринятого. По нашему мнению, современные
достижения математико-статистической науки (особенно в многомерном
статистическом анализе), с одной стороны, и существенное расширение
круга экономических задач, требующих эконометрических методов
решения, — с другой, обусловили необходимость более широкого взгляда
на математико-статистический инструментарий эконометрики и, т
частности, включения в него, помимо традиционных разделов по
регрессионным моделям, анализу временных рядов и системам одновременных
уравнений, таких разделов многомерного статистического анализа, как
марковские цепи, классификация многомерных/наблюдений и снижение
размерности анализируемого факторного пространства. Говоря о
широком спектре экономических задач, требующих выходящих за
традиционные рамки эконометрических/методов решения, мы имели в виду,
в частности, статистическое исследование динамики структурных
изменений (в демографии, в стратификационной структуре общества и т.п.),
выявление скрытых (латентных) факторов, определяющих течение того
или иного социально-экономического процесса, построение интегральных
индикаторов качества или эффективности функционирования социально-
экономической системы, типологизацию социально-экономических
объектов и др.

18 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Во-вторых, в ходе многолетнего опыта преподавания различных
дисциплин вероятностно-статистического профиля в экономических вузах и
на экономических факультетах университетов мы пришли к убеждению,
что необходимо строить учебный процесс таким образом, чтобы
добиваться цельного, системного восприятия всего блока этих дисциплин.
Речь идет, в частности, о курсах по элементарным методам
статистической обработки данных (или дескриптивной статистике), теории
вероятностей, математической статистике, многомерному статистическому
анализу (или многомерным статистическим методам), анализу временных
рядов и, наконец, эконометрике. Очевидно, реализации этой цели должен
способствовать и учебник, одновременно содержащий взаимосвязанное
изложение всех этих курсов.
Другими словами, мы попытались написать такую книгу, которую
нам бы хотелось иметь под рукой в процессе нашей преподавательской
деятельности. К сожалению, среди многих прекрасных зарубежных книг по
эконометрике книги, обладающей двумя вышеуказанными особенностями,
не оказалось.
Заметим, что несмотря на наличие ряда иллюстративных примеров
и упражнений, предлагаемый учебник не решает проблемы задачника по
эконометрике. Поэтому для проведения полноценного учебного процесса
он должен быть дополнен набором эконометрических задач и упражнений
(например, в духе книги [Berndt, Б. R.]).
Материал учебника и ответственность распределены между
авторами следующим образом. В. С. Мхитарян принимал участие в написании
глав 6, 7, 8 и 13, а также предложил большую часть задач, которыми
снабжены главы учебника. Остальной материал (включая упомянутые
главы) написаны С.А.Айвазяном. Им же выполнено общее научное
редактирование учебника.
В заключение мы хотим выразить свою признательность. Мы
благодарны, во-первых, руководителям образовательного проекта EU-TACIS
«Преподавание экономических и бизнес дисциплин в средних школах,
технических и классических университетах» профессору Соломону Кохену
(S.Cohen, SEOR и Эразмус Университет, Роттердам, Голландия) и
ректору Государственного университета-Высшей школы экономики —
профессору Ярославу Ивановичу Кузьминову: финансовая поддержка этого
проекта сыграла решающую роль в том, чтобы авторы смогли определить
для себя приоритетной задачей написание данного учебника. Мы
выражаем также свою признательность нашим коллегам: профессору
эконометрики Тилбургского университета и Высшей экономической школы
Лондона Яну Магнусу и профессору Государственного университета-Высшей

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 19
школы экономики — Эмилю Борисовичу Ершову. Их внимание к
учебнику было постоянным (в процессе его написания), взыскательным и
одновременно доброжелательным. Высказанные ими замечания и советы,
бесспорно, способствовали улучшению качества рукописи. Существенное
влияние на замысел и содержание книги оказал опыт исследовательской
и педагогической работы авторов, их постоянные контакты с коллегами
по ЦЭМИ РАН, по научному семинару «Многомерный статистический
анализ и вероятностное моделирование реальных процессов». Без них и
без наших главных критиков и генераторов вопросов — многих поколений
студентов МГУ им. М. В.Ломоносова, МЭСИ, РЭШ, — эта книга вряд ли
появилась бы на свет. Мы благодарны Алле Павловне и Галине
Юрьевне Грохотовым за самоотверженный труд по подготовке оригинал-макета
рукописи книги, а также Николаю Владимировичу Третьякову и Елене
Владимировне Герасимовой за очень полезную и профессиональную
консультационную поддержку Грохотовых в этом объемном и непростом
производственном процессе. Что касается слабых мест и недостатков
учебника, то за них всю ответственность несут, естественно, только авторы.
Мы будем признательны читателям за их отзывы о книге и критические
замечания, направленные в издательство или непосредственно нам.
Москва-Роттердам-
деревня «Плужково» С. А. Айвазян
Московской области. В. С. Мхитарян
1996-1998 гг.

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Что побудило нас подготовить второе издание учебника? Во-первых,
весь пятитысячный тираж первого издания разошелся за неполные два
года несмотря на внушительный объем книги и относительно
специфическую область знаний, к которой она относится. Во-вторых, — это
наш опыт общения со студентами и коллегами-преподавателями. В
том, что учебник пользуется спросом у студентов, убеждает не
только статистика продаж, но и специальные анкетные обследования,
и информация, размещаемая на студенческих интернетовских сайтах
(см. www.sachok.ru). Что касается вузовских преподавателей
эконометрики, то прекрасную возможность общения с ними
предоставила одному из авторов серия специально организованных для них
семинаров в разных регионах России и бывших республик СССР, на которых
отечественные и зарубежные специалисты (в их числе — С.А. Айвазян)
представляли свои циклы лекций в рамках общей программы повышения
квалификации преподавателей по эконометрике. С 1997-го по 2001 год
такие семинары прошли в Москве (дважды), Санкт-Петербурге (дважды),
Екатеринбурге, Нижнем Новгороде, Сочи, Владивостоке, Воронеже,
Перми, Вильнюсе и других городах.
Второе издание выходит стереотипным, без серьезных
доделок или изменений. Устранены лишь обнаруженные (к сожалению, в
весьма большом количестве) опечатки и явные погрешности. Кроме
того, мы предложили издательству выпустить учебник в двух томах:
том 1 — «Теория вероятностей и прикладная статистика» (введение и
главы 1-13 первого издания); том 2 — «Основы эконометрики» (главы
14-17 первого издания). Поскольку материал второго тома подготовлен
полностью С.А. Айвазяном, этот том выходит только под его авторством.
Практика использования студентами и преподавателями первого издания
учебника подсказала нам, что двухтомный вариант книги может
оказаться более технологичным и удобным в использовании.
Отметим, что со временем несколько трансформируются
представления специалистов о самом предмете эконометрики, пополняется багаж его
методов, смещаются акценты. Не со всеми такими представлениями,
принятыми, скажем, в научных кругах США, согласны авторы этого учебни-

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 21
ка. Там, например, принято включать в продвинутые курсы (и учебники)
по эконометрике «Теорию больших выборок» (или «Асимптотическую
теорию»), «Непараметрические и полупараметрические методы принятия
статистических решений», развернутое изложение ме!ода
максимального правдоподобия. С нашей точки зрения, вся эта тематика
традиционно представлена в качестве разделов в других самостоятельных научных
дисциплинах — теории вероятностей и математической статистике. В то
же время важнейшие для эконометрического анализа прикладные методы
многомерной статистики (дискриминантный и кластер анализы,
главные компоненты и др.) по непонятным для нас причинам отсутствуют
в эконометрических курсах и учебниках Северной Америки и Западной
Европы.
Следует, однако, признать, что во втором томе предлагаемого
издания представлены, конечно, далеко не все важнейшие разделы
современной эконометрики (поэтому этот том и называется «О с н о в ы
эконометрики»). В нем нет, например, обобщенного метода моментов, методов
анализа панельных данных, раздела, посвященного моделям с
урезанными и цензу pup ов анными выборками, недостаточно внимания уделено
проблемам исследования стационарности временного ряда и, в связи с этим,
приемам коинтеграции и анализу единичных корней
характеристического уравнения временного ряда. Подобным образом расширенный вариант
нашего второго тома составит, по существу, новый учебник, создание
которого входит в ближайшие планы одного из авторов.
Наконец, о задачах и упраженениях, которыми
необходимо оснастить аудиторные занятия со студентами по прикладной
статистике и эконометрике. Одновременно с выходом данного двухтомного
издания издательство «Юнити-Дана» публикует нашу книгу
«Прикладная статистика в задачах и упражнениях», которая является
естественным дополнением (задачником) к первому тому. Аналогичное дополнение
ко второму тому (задачник по эконометрике) один из авторов планирует
представить в течение ближайшего года.
В заключение хотим поблагодарить профессора Гарвардского
университета Дэйла Джоргенсона (Dale Jorgenson) за внимание, к книге и
очень полезные обсуждения, которые состоялись во время пребывания
С.А. Айвазяна в Гарвардском университете в апреле 2001г. Мы
благодарны также д-ру Джону Киммелу (John Kimmel) из
Североамериканского отделения издательства «Шпрингер-Верлаг» за организацию
рецензий западных специалистов на наш учебник. Мы искренне благодарны
преподавателям статистики и эконометрики различных вузов России и
Литвы — участникам упомянутых выше региональных семинаров по пре-

22 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
подаванию эконометрики за полезные обсуждения отдельных фрагментов
учебника. Наконец, мы благодарны коллективам и руководству
Центрального экономико-математического института Российской академии наук и
Московского государственного университета экономики, статистики и
информатики, плодотворная профессиональная среда существенно помогла
нам в работе над учебником.
Москва, июнь 2001 г.

Введение
THO-
ие

ВВЕДЕНИЕ. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ
МЕТОДЫ В МОДЕЛИРОВАНИИ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ПРОЦЕССОВ И АНАЛИЗЕ ДАННЫХ
В.1. Математико-статистический
инструментарий экономических
исследовании
В.1.1, Назначение и составные части учебника
Бели экономист строит рассуждения и выводы, опираясь в своих
модельных построениях на результаты конкретных измерений
интересующих его экономических, социально-экономических и (или) демографиче:
ских показателей, то тем самым определяется эконометрический
подход к проблеме, а ирструментарий, которым он при этом пользуется,
обязательно содержит те или иные методы и модели прикладной
математической статистики. Ведь назначение эконометрики —
придавать конкретное количественное выражение общим (качественным)
закономерностям экономической теории на базе экономической статистики и
с использованием средств математической статистики (подробнее
определение эконометрики см. в п. 1.1 в томе 2).
Так вот, предлагаемый вниманию читателя учебник как раз и
посвящен описанию математико-статистического инструментария
экономических исследований. Почему же тогда не назвать этот учебник
просто «Методы эконометрики»? По-существу можно было бы считать такое
название этой книги вполне оправданным. Однако от такого решения
авторов удержали два обстоятельства.
Первое обстоятельство связано с установившимся традиционным
пониманием методов эконометрики, при котором они ограничивались

B.I ИНСТРУМЕНТАРИЙ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ 25
линейным регрессионным анализом (включающим классический и
обобщенный методы наименьших квадратов, случаи гетероскедастичных
и автокоррелированных регрессионных остатков, стохастических
объясняющих переменных, а также использование фиктивных и
инструментальных переменных), методами и моделями анализа временных
рядов (так называемые AR-, МА-, ARMA- и ARIMA-модели, а в
последние годы и модели коинтеграции, ARCH- и GARCH-модели) и, наконец,
системами одновременных уравнений. Этот набор традиционных
эконометрических методов описан во втором томе учебника.
Второе обстоятельство связано с первым и заключается в том, что
по своему назначению, по своим инструментальным возможностям
прикладная статистика — самостоятельная научная дисциплина,
обслуживающая значительно более широкий класс реальных задач статистического
анализа данных, чем тот, который традиционно непосредственно
связывается с эконометрикой. К таким задачам в сфере социально-экономической
теории и практики относятся, в частности:
• исследование динамики структуры состояний объектов
(демографической или социальной структуры общества, структуры типологии
потребительского поведения домашних хозяйств и т. п.);
• типологизация социально-экономических объектов (семей, фирм,
предприятий, регионов, стран и т. п.);
• построение интегральных индикаторов качества или
эффективности функционирования социально-экономической системы (уровня или
качества жизни, качества населения, эффективности функционирования
предприятия и т. п.);
• выявление скрытых (латентных) факторов, определяющих течение
того или иного социально-экономического процесса;
• исследование и моделирование генезиса анализируемых
статистических данных.
К традиционным экономическим задачам применения
эконометрических методов принято относить (эта точка зрения представлена,
например, в [Джонстон Дж., с. 16]) макромоделирование функционирования
национальной экономики (агрегированное, не агрегированное,
детализированное) или ее секторов. Традиционные приложения эконометрических
методов на лшкро-уровне сводятся обычно к моделированию поведения
потребителя, производителя и продавца, а также к моделированию
некоторых процессов, происходящих на финансовых рынках.
Современные университетские учебные планы подготовки
экономистов и экономистов-статистиков построены таким образом, чтобы
обеспечивать непрерывность и преемственность обучения по блокам дисци-

26 В. ВВЕДЕНИЕ
плин:
• гуманитарному;
• экономическому;
• предметной статистики;
• математико-статистического инструментария;
• информационных технологий.
В качестве обязательных компонентов в блоке
математико-статистического инструментария представлены курсы по элементарным
методам статистического анализа данных (или дескриптивной
статистике), теории вероятностей^ математической статистике,
прикладной статистике (или многомерным статистическим методам),
эконометрике. Данный учебник посвящен взаимосвязному изложению всех
упомянутых дисциплин блока математико-статистического инструментария.
В.1.2. Прикладная статистика
Нужно ли использовать этот термин или можно ограничиться более
привычным понятием «математическая статистика»? Как соотносится
прикладная статистика с другими статистическими дисциплинами,
такими, как «математическая статистика», «анализ данных», «методы
эконометрики»? Для обоснования правомерности и целесообразности
рассмотрения прикладной статистики как самостоятельной научной дисциплины
следует упомянуть, как минимум, о двух моментах.
Во-первых, до сих пор развитие теории, методологии и практики
статистической обработки анализируемых данных шло по существу в двух
параллельных направлениях. Одно из них представлено методами,
предусматривающими возможность вероятностной интерпретации
обрабатываемых данных и полученных в результате обработки
статистических выводов. Именно эти методы и составляют содержание
подавляющего большинства монографий и руководств по математической
статистике. Другими словами, под методами математической статистики принято
понимать лишь те методы статистической обработки исходных данных,
разработка и использование которых апеллируют к вероятностной
природе этих данных,1 При этом развиваемый в рамках второго направления
1 Такова ситуация, сложившаяся лишь de facto. Формально же, de jure, если исходить
из определения Большого энциклопедического словаря (М., Большая Российская
энциклопедия, 1997, с. 701), математическая статистика понимается более широко, а
именно как «наука о математических методах систематизации и использования
статистических данных для научных и практических выводов. Во многих своих
разделах математическая статистика опирается на теорию вероятностей, позволяющую

B.I ИНСТРУМЕНТАРИЙ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ 27
весьма широкий и актуальный класс методов статистической
переработки исходной информации, а именно вся совокупность тех методов, которые
априори не опираются на вероятностную природу обрабатываемых
данных (представителями методов такого типа являются, например,
разнообразные методы кластер-анализа, многомерного шкалирования, теории
измерений и др.)) остается за общепринятыми рамками научной
дисциплины «математическая статистика».
Во-вторых, специалисты, занимающиеся разработкой и конкретными
применениями методов статистической обработки исходной информации,
не могут игнорировать ту внушительную дистанцию, которая разделяет
момент успешного завершения разработки собственно математического
метода и момент получения результата от использования этого метода в
решении конкретной практической задачи. В процессе прохождения этой
трудной дистанции математику-прикладнику приходится, в частности:
• глубоко вникать в содержательную сущность задачи, адекватно
«прилаживать» исходные модельные допущения (на которых строится
любой математический метод) к выяснению сущности реальной задачи;
• решать задачу преобразования имеющейся исходной информации к
стандартной (унифицированной) форме записи обрабатываемых
статистических данных;
• разрабатывать практически реализуемые вычислительные
алгоритмы и программное обеспечение с учетом специфики обрабатываемой
статистической информации и возможностей имеющейся
вычислительной техники.
Понятийный аппарат, методы и результаты, позволяющие проходить
эту дистанцию, вместе с этапом «прилаживания» и доработки
необходимого математического инструментария и составляют главное
содержание прикладной статистики.
Таким образом, мы приходим к определению прикладной
статистики как самостоятельной научной дисциплины, разрабатывающей и
систематизирующей понятия, приемы, математические методы и
модели, предназначенные для организации сбора , стандартной записи, си-
оценить надежность и точность выводов, делаемых на основании ограниченного
статистического материала».
1 Говоря об «организации сбора» статистических данных, мы имеем в виду лишь
определение способа отбора подлежащих статистическому обследованию единиц (семей,
предприятий, стран, пациентов и т.п.) из всей исследуемой совокупности (см. п.6.1,
а также в п. 9.1 описание типа 2). Мы не включаем сюда разработку методологии
измерителей анализируемых свойств отображаемого объекта: эта работа
предполагает профессиональное (экономическое, техническое, медицинское и т.п.) изуче-

28 В. ВВЕДЕНИЕ
стематизации и обработки статистических данных с целью их
удобного представления, интерпретации и получения научных и практических
выводов.
Для определения той же самой системы понятий, приемов,
математических методов и моделей некоторые специалисты используют термин
«анализ данных», понимаемый в расширительном толковании. Описанию
методов прикладной статистики, выходящих за традиционные рамки
методов эконометрики и одновременно наиболее актуальных для
экономических и социально-экономических приложений, посвящен раздел III данного
учебника.
В.1.3. Теория вероятностей и математическая статистика
Эти две дисциплины основные «доставщики» математического
инструментария для прикладной статистики и эконометрики.
«Теория вероятностей — наука, позволяющая по вероятностям
одних случайных событий находить вероятности других случайных
событий, связанных каким-либо образом с первыми ... Можно также
сказать, что теория вероятностей есть математическая наука,
выясняющая закономерности, которые возникают при взаимодействии
большого числа случайных факторов» (Математическая энциклопедия, М.,
Советская энциклопедия, 1976, т. 1, с. 655-656). Подчеркнем, что
упомянутые в определении закономерности формулируются в терминах модельных
соотношений.
Идеальной средой применимости теоретико-вероятностного способа
рассуждения (и соответствующего математического аппарата) является
ситуация, когда мы находимся в условиях стационарного (т. е. не
изменяющегося во времени) действия некоторого реального комплекса условий,
включающего в себя неизбежность «мешающего» влияния большого
числа случайных (не поддающихся строгому учету и контролю) факторов,
которые в свою очередь не позволяют делать полностью достоверные
выводы о том, произойдет или не произойдет интересующее нас событие.
При этом предполагается, что мы имеем принципиальную возможность
(хотя бы мысленно реально осуществимую) многократного повторения
нашего эксперимента или наблюдения в рамках того же самого реального
комплекса условий. Именно такую ситуацию принято называть
условиями действия статистического ансамбля или условиями соблюдения ста-
ние сущности задач, для решения которых требуется статистическая информация,
а потому она относится к компетенции предметной статистики соответствующей
области.

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 29
тистической однородности исследуемой совокупности (подробнее об этом
см. п. В.2).
Необходимый для нормального понимания методов прикладной
статистики и эконометрики минимум сведений из теории вероятностей
приводится в разделе I данного учебника.
Одно из возможных определений математической статистики
приведено в п. В.1.2 (см. сноску на с. 26). Добавим к этому, что
математическая статистика, являясь по отношению к прикладной статистике и
эконометрике разработчиком и поставщиком существенной части
используемого в них математического аппарата, полностью отстранена от таких
функций этих прикладных дисциплин, как:
• «прилаживание» и доработка необходимого математического
инструментария в соответствии со спецификой анализируемого класса
реальных социально-экономических задач;
• разработка невероятностных (логико-алгебраических,
оптимизационных и др.) методов анализа и моделирования реальных исходных
данных, т.е. методов, не опирающихся на модельные допущения о
вероятностной природе этих данных;
• преобразование разнообразных форм исходных
социально-экономических данных с целью их удобного представления для дальнейшего
анализа и моделирования;
• разработка практически реализуемых вычислительных алгоритмов и
удобного программного обеспечения для используемых в ходе эконо-
метрического анализа методов и моделей.
Раздел II учебника посвящен изложению основных результатов
математической статистики, включая элементарные методы статистического
анализа данных (методы дескриптивной статистики).
В.2. Теоретико-вероятностный способ
рассуждения в прикладной статистике
и эконометрике
В.2.1. Границы применимости теоретико-вероятностного
способа рассуждения
В п. В. 1.2 упоминалось о двух подходах к статистическому анализу
данных: математико-статистическом, основанном на вероятностном
способе рассуждения, и логико-алгебраическом. Ко второму подходу
исследователь вынужден обращаться лишь тогда, когда условия сбора (регистра-

30 В. ВВЕДЕНИЕ
ции) исходных данных не укладываются в рамки так называемого
статистического ансамбля, т.е. в ситуациях, когда не имеется
практической или хотя бы принципиально мысленно представимой возможности
многократного тождественного воспроизведения основного комплекса
условий, при которых производились измерения анализируемых данных.
В условиях же статистического ансамбля исследователь имеет
возможность воспользоваться классическими математико-статистическими
методами обработки данных, когда для обоснования наилучшего выбора
методов статистической переработки, итогового представления и
интерпретации анализируемых данных он использует те или иные априорные
сведения об их случайной (стохастической) природе. При этом мы
исходим из того, что даже постулируемая нами тождественность
воспроизведения основного комплекса условий эксперимента или наблюдения в
большинстве реальных ситуаций (с учетом их сложности,
множественности и частичной неизученности формирующих их факторов) не избавляет
нас от неконтролируемого (случайного) разброса в самих результатах
наблюдения. Так, даже практически идеально отлаженный станок
автоматической линии не в состоянии производить абсолютно идентичные
между собой (и заданному номиналу) изделия. В аналогичных условиях
статистического ансамбля и соответствующего неконтролируемого
разброса изучаемых показателей или событий мы окажемся, например, при
изучении числа дефектных изделий в партиях заданного объема,
отбираемых от массовой продукции и производимых в стационарном режиме
производства, или при регистрации среднедушевого дохода семей,
случайно отбираемых из некоторой однородной (в социальном, географическом и
экономическом смысле) совокупности, и т. д.
Именно разнообразные математические модели таких скрытых
закономерностей вместе с теоретическим и эмпирическим анализом их свойств
и взаимоотношений и предоставляют исследователю теория
вероятностей и математическая статистика.
Наиболее простые и убедительные примеры реальных ситуаций,
подчиняющихся требованию статистической устойчивости (или
укладывающихся в рамки статистического ансамбля), предоставляет нам область
азартных игр. Действительно, подбрасывая монету, бросая игральную
1 Исторически именно эта область существенно стимулировала зарождение и развитие
элементов теоретико-вероятностной научной дисциплины. Первые достаточно
интересные результаты теории вероятностей принято связывать с работами Л. Пачоли
(«Сумма арифметики, геометрии, учения .о пропорциях и отношениях», 1494 г.),
Д. Кардано («Книга об игре в кости», 1526 г.) и Н.Тартальи («Общий трактат
о числе и мере» 1556-1560 гг.). См. [МайстровЛ. Б., с. 6, 25-37].

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 31
кость или вытягивая наугад карту из колоды и интересуясь при этом
вероятностью осуществления события, заключающегося соответственно в
появлении «герба», «шестерки» или «дамы пик», мы имеем все
основания полагать, что
а) можно многократно повторить тот же самый эксперимент в тех же
самых условиях;
б) наличие большого числа случайных факторов, характеризующих
условия проведения каждого такого эксперимента, не позволяет делать
полностью определенного (детерминированного) заключения о том,
произойдет в результате данного эксперимента интересующее нас событие
или не произойдет;
в) чем большее число однотипных экспериментов мы произведем, тем
ближе будут подсчитанные по результатам экспериментов относительные
частоты появления интересующих нас событий к некоторым постоянным
величинам, называемым вероятностными для этих событий, а именно:
относительная частота появления «герба» будет приближаться к 1/2,
выпадения «шестерки» — к 1/6, а извлечения «дамы пик» (из колоды,
содержащей 52 карты) — к 1/52.
Очевидно, требования статистического ансамбля применительно к
указанным выше трем типам экспериментов означают необходимость
использования одной и той же (или совершенно идентичных)
симметричной монеты, Симметричной кости, а в последнем случае — необходимость
возвращения извлеченной в предыдущем эксперименте карты в колоду и
тщательного случайного перемешивания последней.
Соблюдение условий статистического ансамбля в более серьезных и
сложных сферах человеческой деятельности — в экономике, в
социальных процессах, в технике и промышленности, в медицине, в различных
отраслях науки — это вопрос, требующий специального рассмотрения в
каждом конкретном случае.
Оценивая специфику задач в различных областях человеческого
знания с позиции соблюдения в них свойств а)-в) статистической
устойчивости и принимая во внимание накопившийся опыт вероятностно-
статистических приложений, можно условно разбить все возможные
приложения на три категории.
К первой категории возможных областей применения — категории
высокой работоспособности вероятностно-статистических
методов — отнесем те ситуации, в которых свойства а)-в) статистической
устойчивости исследуемой совокупности бесспорно имеют место либо
нарушаются столь незначительно, что это практически не влияет на
точность статистических выводов, полученных с использованием теоретико-

ог в. введение
вероятностных моделей. Сюда (помимо упоминавшейся «игровой»
области) могут быть отнесены отдельные разделы экономики и социологии и
в первую очередь задачи, связанные с исследованием поведения объекта
(индивидуума, семьи или другой социально-экономической или
производственной единицы) как представителя большой однородной совокупности
подобных же объектов. Традиционной областью эффективного
использования вероятностно-статистического аппарата давно стала демография.
Теоретико-вероятностные понятия являются основным языком в таких
инженерных областях, как теория надежности систем, состоящих из очень
большого числа элементов, и теория выборочного контроля качества
продукции. В медицине вероятностно-статистический подход позволил
ввести понятие факторов риска развития основных хронических
заболеваний и провести количественное изучение их влияния, способствуя тем
самым большей индивидуализации, а значит, и эффективности
профилактики и лечения. Результаты специальных вероятностно-статистических
исследований выявили, что вероятность дожить до определенного
возраста подвержена не слишком значительным колебаниям (в зависимости от
условий жизни). Эти результаты и послужили основой составления так
называемых таблиц выживаемости^ в определенной мере и в
определенном смысле (а именно, в среднестатистическом, но не в индивидуальном,
конечно!) поколебавшим известное древнее изречение «никто не знает
часа своей смерти». Вероятностно-статистический способ рассуждения
играет видную роль в исследованиях, проводимых в современной физике
(в первую очередь в статистической физике) и в классической механике
(в статистической теории газов).
Отметим одну важную общую черту, характеризующую
подавляющее большинство задач перечисленных выше областей человеческой
деятельности, в которых оказывается правомерным и эффективным
применение вероятностно-статистических методов. Речь идет о существенной
многомерности обрабатываемой информации, характеризующей
исследуемые явления или объекты, т.е. о ситуациях, когда состояние или
поведение каждого из этих объектов в любой фиксированный момент времени
описывается набором соответствующих показателей. Среди этих
показателей могут быть как количественные (среднедушевой доход в семье,
размер семьи, объем валовой продукции предприятия и т. д.), так и не
количественные, т.е. ранговые (классификация специалиста, сравнительная
характеристика жилищных условий) и классификационные, или
номинальные (профессия, национальность,- нол, причины миграции и т. п.). Все эти
показатели находятся в сложной взаимосвязи друг с другом. Именно в
таких ситуациях принято говорить о многомерности исследуемой схемы, а

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 33
исследователю приходится обращаться к методам многомерного
статистического анализа.
Ко второй категории возможных областей применения — категории
допустимых вероятностно-статистических приложений —
отнесем ситуации, характеризующиеся весьма значительными нарушениями
требования сохранения неизменными условий эксперимента (вторая
половина требования а)) и вытекающими отсюда отклонениями от требования
в). Характерной формой такого рода отклонений от условий
статистического ансамбля является объединение в одном ряду наблюдений
(подлежащих обработке) различных порций исходных данных,
зарегистрированных в разных условиях (в разное время или в разных совокупностях). К
этой же категории приложений можно отнести определенный класс
задач, связанных с анализом коротких временных рядов,
зарегистрированных в условиях, практически исключающих возможность статистической
фиксации сразу нескольких эмпирических реализаций исследуемого
временного ряда на одном и том же временном интервале. Использование
вероятностно-статистических методов обработки в этом случае
допустимо, но должно сопровождаться пояснениями о несовершенстве и
приближенном характере получаемых при этом выводов (например, не следует
слишком доверять в подобных ситуациях различным числовым
характеристикам Степени достоверности этих выводов, т.е. доверительным
вероятностям, уровням значимости критерия и т.п.) и по возможности
должно дополняться другими методами научного анализа.
И наконец, к третьей категории задач статистической
обработки исходных данных — категории недопустимых вероятностно-
статистических приложений — следует отнести ситуации,
характеризующиеся либо принципиальным неприятием главной идеи понятия
статистического ансамбля — массовости исследуемой совокупности (т. е.
конкретной бессодержательностью идеи многократного повторения одного и
того же эксперимента в неизменных условиях, сформулированной в
требовании а)), либо полной детерминированностью изучаемого явления,
т.е. — отсутствием «мешающего» влияния множества случайных
факторов (нарушение требования б)). В подобных ситуациях исследователь
должен пользоваться методами анализа данных (см. [ДидеЭ. и др.]) и не
должен претендовать на вероятностную интерпретацию обрабатываемых
данных и получаемых в результате их обработки выводов.
Строгих математических методов, позволяющих точно определять,
находимся ли мы в условиях статистического ансамбля, не существует:
любая вероятностная модель, так же как и любая математическая модель
вообще, есть лишь некоторая аппроксимация исследуемой реальной дей-
2 Теория вероятностей
и прикладная статистика

34 В. ВВЕДЕНИЕ
ствительности. Можно говорить лишь о ситуациях, очевидно
укладывающихся в рамки статистического ансамбля (бросание монеты, игральной
кости; контроль продукции массового производства, работающего в
отлаженном стационарном режиме, и т. п.), укладывающихся в эти рамки
лишь приблизительно, с оговорками, и явно не соответствующих условиям
статистического ансамбля. Однако даже с последней категорией ситуаций
(названных у нас категорией недопустимых вероятностно-статистических
приложений) нет полной ясности. Так, например, с позиций
статистического ансамбля события типа «в 2050 г. начнется война между странами
А н В» явно не относятся к сфере возможных применений вероятностно-
статистических методов — налицо нарушение требования а)!
Однако существует концепция так называемых субъективных
вероятностей, в рамках которой оказывается правомерным говорить и о
вероятности таких событий. Для этого следует прибегнуть к помощи
экспертов и вместо действительной многократной реализации интересующего
нас эксперимента в одних и тех же условиях ограничиться
воображаемой прогонкой исследуемой ситуации «через сознание» многих экспертов.
При этом, очевидно, эксперт интерпретируется как некий
измерительный прибор, работающий со случайной ошибкой. Точность работы этого
«измерительного прибора», т.е. точность «прочтения» (в сознании
эксперта) исхода интересующего нас события в будущем, очевидно, зависит
как от степени объективного влияния «мешающих» случайных/
факторов (т. е. от степени временной отдаленности интересующего нас момента
времени, общей сложности ситуации и т. п.), так и от степени
осведомленности, компетентности и других субъективных качеств самого эксперта.
Мы не собираемся здесь вмешиваться в спор между субъективистской и
классической вероятностными концепциями. Останемся на той точке
зрения, что единственным объективным судьей в подобных вопросах может
быть лишь критерий практики. В этой связи уместно напомнить
читателю следующие слова Ф. Энгельса из «Анти-Дюринга»: «... Математика,
вообще столь строго нравственная, совершила грехопадение: она
вкусила от яблока познания, и это открыло ей путь к гигантским успехам, но
вместе с тем и к заблуждениям. Девственное состояние абсолютной
значимости, неопровержимой доказанности всего математического навсегда
ушло в прошлое; наступила эра разногласий, и мы дошли до того, что
большинство людей дифференцирует и интегрирует не потому, что люди
понимают, что они делают, а просто потому, что верят в это, так как до
сих пор результат всегда получался правильным»
1 М а р к с К., Энгельс Ф. Соч., т. 20, с. 89.

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 35
Резюмируя содержащееся в данном пункте обсуждение сущности,
назначения и границ применимости теории вероятностей, мы можем через
полтора века после замечательного французского ученого Лапласа
повторить, более обоснованно и убедительно, что «замечательно, что наука,
которая начала с изучения игр, возвысилась до наиболее важных
предметов человеческого знания» .
В.2.2. Что дает объединение теоретико-вероятностного и
статистического способов рассуждения?
Теперь попытаемся на простом примере показать преимущества
вероятностно-статистического (или математико-статистического)
способа принятия решения, его отличие как от чисто статистического, так и
от чисто теоретико-вероятностного.
Статистический способ принятия решения. Пусть читатель
представит себя наблюдающим за игрой двух лиц в кости,
происходящей по следующим правилам. Производится 4 последовательных бросания
игральной кости. Игрок А получает одну денежную единицу от игрока 2?,
если в результате этих четырех бросаний хотя бы один раз выпало шесть
очков (назовем этот исход «шесть»), и платит одну денежную единицу
игроку В в противном случае (назовем этот исход «не шесть»). После
ста туров читатель должен сменить одного из игроков, причем он имеет
право выбрать ситуацию, на которую он будет ставить свою денежную
единицу в следующей серии туров: за появление хотя бы одной
«шестерки» или против. Как правильно осуществить этот выбор?
Статистический способ решения этой задачи диктуется обычным
здравым смыслом и заключается в следующем. Пронаблюдав сто туров
игры предыдущих партнеров и подсчитав относительные частоты их
выигрыша, казалось бы, естественно поставить на ту ситуацию, которая
чаще возникала в процессе игры. Например, было зафиксировано, что в 52
партиях из 100 выиграл игрок В, т. е. в 52 турах из 100 «шестерка» не
выпадала ни разу при четырехкратном выбрасывании кости (соответственно
в остальных 48 партиях из ста осуществлялся исход «шесть»).
Следовательно, делает вывод читатель, применивший статистический способ
рассуждения, выгоднее ставить на исход «не шесть», т. е. на тот исход,
относительная частота появления которого (р) равна 0,52 (больше
половины).
2 См.: Oeuvres completes de Laplace. T. 7: «Theorie analytique des probabilites». Paris,
Gauthier-Villars, 1886, p/CLII.
2*

36 В. ВВЕДЕНИЕ
Теоретико-вероятностный способ решения. Этот способ
основан на определенной математической модели изучаемого явления:
полагая кость правильной (т.е. симметричной), а следовательно, принимая
шансы выпадения любой грани кости при одном бросании равными между
собой (другими словами, относительная частота, или вероятность,
выпадения «единицы» равна относительной частоте выпадения «двойки» и
т.д... равна относительной частоте выпадения «шестерки» и равна 1/6),
можно подсчитать вероятность Р {«не шесть»} осуществления ситуации
«не шесть», т.е. вероятность события, заключающегося в том, что при
четырех последовательных бросаниях игральной кости ни разу не
появится «шестерка». Этот расчет основан на следующих фактах, вытекающих
из принятой нами математической модели. Вероятность не выбросить
шестерку при одном бросании кости складывается из шансов появиться в
результате одного бросания «единице», «двойке», «тройке», «четверке»
и «пятерке» и, следовательно, составляет (в соответствии с определением
вероятности любого события, см. п. 1.1) 5/6. Затем используем теорему
умножения вероятностей (см. п. 1.1.3), в соответствии с которой
вероятность наступления нескольких независимых событий равна произведению
вероятностей этих событий. В нашем случае мы рассматриваем факт
наступления четырех независимых событий, каждое из которых
заключается в невыпадении «шестерки» при одном бросании и имеет вероятность
осуществления, равную 5/6. Поэтому
5 5 5 5
р = Р {<не шесть>} = -.-.-•-
625
1296
Как видно, вероятность ситуации «не шесть» оказалась меньше
половины, следовательно, шансы ситуации «Шесть» предпочтительнее
(соответствующая вероятность равна: 1 - 0,482 = 0,518). А значит,
читатель, использовавший теоретико-вероятностный способ рассуждения,
придет к диаметрально противоположному по сравнению с читателем со
статистическим образом мышления решению и будет ставить в игре на
ситуацию «шесть».
Вероятностно-статистический (или математико-статисти-
ческий) способ принятия решения. Этот способ как бы синтезирует
инструментарий двух предыдущих, так как при выработке с его
помощью окончательного вывода используются и накопленные в результате
наблюдения за игрой исходные статистические данные (в виде
относительных частот появления ситуаций «шесть» и «не шесть», которые,

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 37
как мы помним, были равны соответственно 0,48 и 0,52), и теоретико-
вероятностные модельные соображения. Однако модель, принимаемая в
данном случае, менее жестка, менее ограниченна, она как бы
настраивается на реальную действительность, используя для этого накопленную
статистическую информацию. В частности, эта модель уже не
постулирует правильность используемых костей, допуская, что центр тяжести
игральной кости может быть и смещен некоторым специальным образом.
Характер этого смещения (если оно есть) должен как-то проявиться в тех
исходных статистических данных, которыми мы располагаем. Однако
читатель, владеющий вероятностно-статистическим образом мышления,
должен отдавать себе отчет в том, что полученные из этих данных
величины относительных частот исходов «шесть» и «не шесть» дают лишь
некоторые приближенные оценки истинных (теоретических) шансов той и
другой ситуации: ведь подбрасывая, скажем, 10 раз даже идеально
симметричную монету, мы можем случайно получить семь выпадений «гербов»;
соответственно относительная частота выпадения «герба», подсчитанная
по этим результатам испытаний, будет равна 0,7; но это еще не значит,
что истинные (теоретические) шансы (вероятности) появления «герба»
и другой стороны монеты оцениваются величинами соответственно 0,7 и
0,3 — эти вероятности, как мы знаем, равны 0,5. Точно так же
наблюденная нами в серии из ста игровых туров относительная частота исхода
«не шесть» (равная 0,52) может отличаться от истинной (теоретической)
вероятности того же события и, значит, может не быть достаточным
основанием для выбора этой ситуации в игре! Весь вопрос в том, насколько
сильно может отличаться наблюденная (в результате осуществления п
испытаний) относительная частота рп интересующего нас события от
истинной вероятности р появления этого события и как это отличие, т.е.
погрешность рп - р, зависит от числа п имеющихся в нашем
распоряжении наблюдений? (интуитивно ясно, что чем дольше мы наблюдали за
игрой, т. е. чем больше общее число п использованных нами наблюдений,
тем больше доверия заслуживают вычисленные нами эмпирические
относительные частоты рп, т.е. тем меньше их отличие от неизвестных нам
истинных значений вероятностей р.) Ответ на этот вопрос можно
получить в нашем случае, если воспользоваться рядом модельных
соображений: а) интерпретировать реализацию любого числа игровых партий как
последовательность так называемых испытаний Бернулли, что означает,
что результат каждого тура никак не зависит от результатов
предыдущих туров, а неизвестная нам вероятность р осуществления ситуации «не
шесть» остается одной и той же на протяжении всех туров игры; б)
использовать тот факт, что поведение случайно меняющейся (при повторе-

38 В. ВВЕДЕНИЕ
ниях эксперимента) погрешности Ап = рп — р приближенно описывается
законом нормального распределения вероятностей со средним значением,
равным нулю, и дисперсией, равной рA ~р)/п (см. п. 3.1.5).
Эти соображения, в частности, позволяют оценить абсолютную
величину погрешности |ДЛ|, которую мы можем допустить, заменяя
неизвестную величину р вероятности интересующего нас события (в нашем
случае — исхода «не шесть») относительной частотой рп этого события,
зафиксированной в серии из п испытаний (в нашем случае п = 100, а
р100 = 0,25). Бели же мы смогли численно оценить абсолютную величину
возможной погрешности Ап, то естественно применить следующее
правило принятия решения: если относительная частота рп появления исхода
«не шесть» больше половины и продолжает превосходить 0,5 после
вычитания из нее возможной погрешности |АП|, то выгоднее ставить на «не
шесть»; если относительная частота рп меньше половины и продолжает
быть меньше 0,5 после прибавления к ней возможной погрешности |АП|,
то выгоднее ставить на «шесть»; в других случаях у наблюдателя нет
оснований для статистического вывода о преимуществах того или
иного выбора ставки в игре (т. е. надо либо продолжить наблюдения, либо
участвовать в игре с произвольным выбором ставки, ожидая, что это не
может привести к сколь-нибудь ощутимому выигрышу или проигрышу).
Приближенный подсчет максимально возможной величины этой
погрешности, опирающийся на модельное соображение б) (т.е. теорему
Муавра-Лапласа, см. п. 4.3), дает в рассматриваемом примере, что с
практической достоверностью, а именно с вероятностью 0,95, справедливо
неравенство
/^S. (B.I)
Возведение (B.I) в квадрат и решение получившегося квадратного
неравенства относительно неизвестного параметра р дает
1+t
Рп+*
1+i '
или, с точностью до величин порядка малости выше, чем 1/у/п:
Рп-2
и V п

В.2 ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ 39
В данном случае (при рп = 0,52 и п = 100) получаем
IДп| « 2у/РпA-Рп)/>/й = 2v/0,52.(l-0,52)A/l06« 0,10.
Следовательно,
0,52-0,10<р<0,52 + 0,10.
Таким образом, имеющиеся в нашем распоряжении наблюдения за
исходами ста партий дают нам основания лишь заключить, что
интересующая нас неизвестная величина вероятности исхода «не шесть» на самом
деле может быть любым числом из отрезка [0,42;0,62], т.е. может быть
как величиной, меньшей 0,5 (и тогда надо ставить в игре на ситуацию
«шесть»), так и величиной, большей 0,5 (и тогда надо ставить в игре на
ситуацию «не шесть» ).
Иначе говоря, читатель, воспользовавшийся
вероятностно-статистическим способом решения задачи, вынужден будет прийти в данном
случае к более осторожному выводу: ста партий в качестве исходного
статистического материала оказалось недостаточно для вынесения надежного
заключения о том, какой из исходов игры является более вероятным.
Отсюда решение: либо продолжить роль «зрителя» до тех пор, пока область
возможных значений для вероятности р, полученная из оценок вида (В.2),
не окажется целиком лежащей левее или правее 0,5, либо вступить в игру,
оценивая ее как близкую к «безобидной», т. е. к такой, в которой в длинной
серии туров практически останешься «при своих».
Приведенный пример иллюстрирует роль и назначение теоретико-
вероятностных и математико-статистических методов, их
взаимоотношения. Бели творил вероятностей предоставляет исследователю набор
математических моделей, предназначенных для описания
закономерностей в поведении реальных явлений или систем, функционирование
которых происходит под влиянием большого числа взаимодействующих
случайных факторов, то средства математической статистики
позволяют подбирать среди множества возможных теоретико-вероятностных
моделей ту, которая в определенном смысле наилучшим образом
соответствует имеющимся в распоряжении исследователя
статистическим данным, характеризующим реальное поведение конкретной
исследуемой системы.

40 В. ВВЕДЕНИЕ
В.З. Вероятностно-статистическая
(эконометрическая) модель как частный
случай математической модели
В.3.1. Математическая модель
Математическая модель — это абстракция реального мира, в
которой интересующие исследователя отношения между реальными
элементами заменены подходящими отношениями между математическими
категориями. Эти отношения, как правило, представлены в форме уравнений
и (или) неравенств между показателями (переменными),
характеризующими функционирование моделируемой реальной системы. Искусство
построения математической модели состоит в том, чтобы совместить как
можно большую лаконичность в ее математическом описании с
достаточной точностью модельного воспроизводства именно тех сторон
анализируемой реальности, которые интересуют исследователя.
Выше, анализируя в п.В.2.2 взаимоотношения чисто
статистического, чисто теоретико-вероятностного и смешанного — вероятностно-
статистического способа рассуждения, мы уже пользовались
простейшими моделями, а именно:
• статистической частотной моделью интересующего нас
случайного события, заключающегося в том, что в результате четырех
последовательных бросаний игральной кости ни разу не выпадет «шестерка»;
оценив по предыстории относительную частоту р = 0,52 этого события
и приняв ее за вероятность появления этого события в будущем
ряду испытаний, мы, тем самым, используем модель случайного
эксперимента с известной вероятностью его исхода;
• теоретико-вероятностной моделью последовательности
испытаний Бернулли (см. п. 3.1.1), которая никак не связана с использованием
результатов наблюдений (т.е. со статистикой); для подсчета вероятности
интересующего нас события достаточно принятия гипотетического
допущения о том, что используемая игральная кость идеально симметрична;
тогда в соответствии с моделью серии независимых испытаний и
справедливой, в рамках этой модели, теоремой умножения вероятностей подсчи-
тывается интересующая нас вероятность по формуле (ВЛ);
• вероятностно-статистической моделью, интерпретирующей
оцененную в чисто статистическом подходе относительную частоту р как
некую случайную величину (см. п. 2.1), поведение которой подчиняется
правилам, определяемым так называемой теоремой Муавра-Лапласа; при
построении этой модели были использованы как теоретико-вероятностные

В.З ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ 41
понятия и правила, так и статистические приемы, основанные на
результатах наблюдений.
Обобщая этот пример, можно сказать, что:
• вероятностная модель — это математическая модель,
имитирующая механизм функционирования гипотетического (не конкретного)
реального явления (или системы) стохастической природы; в нашем
примере гипотетичность относилась к свойствам игральной кости:
она должна была быть идеально симметричной;
• вероятностно-статистическая модель — это вероятностная
модель, значения отдельных характеристик (параметров) которой
оцениваются по результатам наблюдений (исходным статистическим
данным), характеризующим функционирование моделируемого
конкретного (а не гипотетического) явления (или системы).
Вероятностно-статистическая модель, описывающая механизм
функционирования экономической или социально-экономической системы,
называется эконометрической. Бели же речь идет о любой
математической модели, описывающей механизм функционирования некой
гипотетической экономической или социально-экономической системы, то такую
модель принято называть экономико-математической или просто
экономической.
В качестве примера экономической модели рассмотрим простейший
(идеализированный) вариант так называемой «паутинной модели»,
которая описывает процесс формирования спроса и предложения
определенного товара или вида услуг на конкурентном рынке. Речь идет о
формализации экономического закона спроса и предложения, гласящего:
количество товара, которое можно продать на рынке (т.е. спрос)
изменяется в направлении, противоположном изменению его цены; количество
товара, которое продавцы доставляют на рынок (т.е. предложение)
изменяется в том же направлении, что и цена; при этом реальная
рыночная цена складывается на уровне, при котором спрос и предложение
равны друг другу (т.е. находятся в равновесии).
Займемся математической формализацией этих положений. Пусть xt
(ден. ед.) — цена товара в «момент времени» t. И пусть у\П' ъ у\ —
количество товара, соответственно предложенного и купленного
(«спрошенного») на рынке в тот же момент времени t. Тогда, с учетом одного такта
времени, необходимого производителям-продавцам на то, чтобы
«среагировать» на цену х, можно математически сформулировать приведенные
1 Первым, кто попытался математически сформулировать этот закон, был А. Курно
(Cournot A., Recherches sur les principes mathematiques de la theorie des richesses, Paris,
1838).

42
В. ВВЕДЕНИЕ
выше общие закономерности в виде:
lim X\ = Xg}
где f(x) — некоторая монотонно возрастающая, а д(х) — монотонно
убывающая функции от аргумента х (т.е. от цены).
Математические соотношения, отражающие закон
спроса-предложения, могут быть проиллюстрированы рисунком В.1
Спрос/предложение
/ А
= ff(*t) - спрос
у\ = /(»t-i) - предложение
Х\
Рис. В.1. График процесса формирования спроса-предложения
(«паутинная» модель)
Из рисунка видно, что процесс формирования равновесной цены
начался с назначения в 1-й (начальный) момент времени цены на уровне
Х\. Производитель-продавец отреагировал на это в следующий B-й)
момент времени величиной предложения, равной 2/2 = f(xi)i в то время
как спрос на этот товар сформировался всего на уровне у\с' = flf(a?i).
Заметное превышение предложения над спросом привело к понижению цены
в следующий B-й) момент времени до уровня х2. Это сразу отразилось
на предложении в следующий C-й) момент времени: оно снизилось до

В.З ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ 43
у^ = /(ж2). Зато спрос резко подскочил и составил во 2-й момент
времени величину з4 = д(х2), и т.д., и т.п. Продолжение этого процесса
обозначено траекторией ( она индексирована стрелками), которая
сходится паутинообразно к точке равновесия — к точке пересечения кривых
д(х) и /(ж).
Реалистическая модель закона спроса-предложения, конечно, сложнее.
В частности, jr' и у*с' зависят не только от цены ж, поскольку связь
между у'п* и у'0', с одной стороны, и ценой х — с другой, носит не
детерминированный, а стохастический характер (о подобных
зависимостях см. гл. 10, 11, а также гл. 2 во втором томе учебника).
Наконец, для того, чтобы эта модель превратилась из
экономической в эконометрическую, следует говорить не вообре о законе спроса-
предложения, а о конкретном его действии в данном месте, данное
время и применительно к данному конкретному товару (или
виду услуг). Соответственно конкретизация вида функций f(x) и д(х)
должна производиться на базе исходных статистических данных о
значениях xty у\ и у\с' за ряд тактов времени (т. е. для t = 1,2,..., п).
В.3.2. Основные этапы вероятностно-статистического
моделирования
Построение и экспериментальная проверка (верификация) вероятностно-
статистической модели обычно основаны на одновременном использовании
информации двух типов:
(а) априорной информации о природе и содержательной сущности
анализируемого явления, представленной, как правило, в виде тех или иных
теоретических закономерностей, ограничений, гипотез;
(б) исходных статистических данных, характеризующих процесс и
результаты функционирования анализируемого явления или системы.
Можно выделить следующие основные этапы
вероятностно-статистического моделирования.
1-й этап (постановочный) включает в себя определение: конечных
прикладных целей моделирования; набора факторов и показателей
(переменных), описание взаимосвязей между которыми нас интересует;
наконец, роли этих факторов и показателей — какие из них, в рамках
поставленной конкретной задачи, можно считать входными (т. е. полностью или
частично регулируемыми или хотя бы легко поддающимися регистрации
и прогнозу; подобные факторы несут смысловую нагрузку объясняющих
в модели), а какие —выходными (эти факторы обычно трудно поддаются
непосредственному прогнозу; их значения формируются как бы в процессе

44 В. ВВЕДЕНИЕ
функционирования моделируемой системы, а сами факторы несут
смысловую нагрузку объясняемых).
2-й этап (априорный, предмодельный) состоит в предмодельном
анализе содержательной сущности моделируемого явления, формировании и
формализации имеющейся априорной информации об этом явлении в виде
ряда гипотез и исходных допущений (последние должны быть
подкреплены теоретическими рассуждениями о механизме изучаемого явления или,
если возможно, экспериментальной проверкой).
3-й этап (информационно-статистический) посвящен сбору
необходимой статистической информации, т.е. регистрации значений
участвующих в описании модели факторов и показателей на различных временных
и (или) пространственных тактах функционирования моделируемой
системы.
4-й этап (спецификация модели) включает в себя непосредственный
вывод (опирающийся на принятые на 2-м этапе гипотезы и исходные
допущения) общего вида модельных соотношений, связывающих между собой
интересующие нас входные и выходные переменные. Говоря об общем
виде модельных соотношений, мы имеем в виду то обстоятельство, что
на данном этапе будет определена лишь структура модели, ее
символическая аналитическая запись, в которой наряду с известными числовыми
значениями (представленными в основном исходными статистическими
данными) будут присутствовать величины, содержательный смысл
которых определен, а числовые значения — нет (их обычно называют
параметрами модели, неизвестные значения которых подлежат статистическому
оцениванию).
5-й этап (идентифицируемость и идентификация модели)
предназначен для проведения статистического анализа модели с целью
«настройки» значений ее неизвестных параметров на те исходные статистические
данные, которыми мы располагаем. При реализации этого этапа
«модельер» должен сначала ответить на вопрос, возможно ли в принципе
однозначно восстановить значения неизвестных параметров модели по
имеющимся исходным статистическим данным при принятой на 4-м этапе
структуре (способе спецификации) модели. Это составляет так
называемую проблему идентифицируемости модели. А затем, после
положительного ответа на этот вопрос, необходимо решить уже проблему
идентификации модели, т. е. предложить и реализовать математически корректную
процедуру оценивания неизвестных значений параметров модели по
имеющимся исходным статистическим данным. Если проблема
идентифицируемости решается отрицательно, то возвращаются к 4-му этапу и вносят
необходимые коррективы в решение задачи спецификации модели.

В.З ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ 45
6-й этап (верификация модели) заключается в использовании
различных процедур сопоставления модельных заключений, оценок, следствий и
выводов с реально наблюдаемой действительностью. Этот этап
называют также этапом статистического анализа точности и адекватности
модели. При пессимистическом характере результатов этого этапа необходимо
возвратиться к этапу 4, а иногда и к этапу 1.
Построение и анализ модели могут быть основаны только на
априорной информации (а) и не предусматривать проведения этапов 3 и 5. Тогда
модель не является вероятностно-статистической (эконометрической
при моделировании экономических закономерностей). Более подробно о
сущности и специфике именно эконометрического моделирования речь
будет идти в гл. 1-3 второго тома учебника.
В.3.3. Моделирование механизма явления вместо
формальной статистической фотографии
Обращаем внимание читателя на ключевую роль успешного
проведения 2-го этапа в общей оценке степени реалистичности и
работоспособности построенной модели.
Другими словами, адекватность и соответственно эффективность
модели будут решающим образом зависеть от того, насколько глубоко и
профессионально был проведен анализ реальной сущности изучаемого
явления при формировании априорной информации (т. е. в рамках второго
этапа). Поясним этот тезис. При вероятностно-статистическом
моделировании и, в частности, на этапе формирования априорной информации о
физической природе реального механизма преобразования входных
показателей в выходные (результирующие) какая-то часть этого механизма
остается скрытой от исследователя (именно об этой части принято в
соответствии с обиходной кибернетической терминологией говорить как
о «черном ящике»). Чем большее профессиональное знание механизма
исследуемого явления продемонстрирует исследователь, тем меньше
будет доля «черного ящика» в общей логической схеме моделирования и
тем работоспособнее и точнее будет построенная модель. Вероятностно-
статистическое моделирование, полностью основанное на логике
«черного ящика», позволяет получить исследователю лишь как бы мгновенную
статистическую фотографию анализируемого явления, в общем случае
непригодную, например, для целей прогнозирования. Напротив,
моделирование, опирающееся на глубокий профессиональный анализ природы
изучаемого явления, позволяет в значительной мере теоретически
обосновать общий вид конструируемой модели, что дает основание к ее широко-

46 В. ВВЕДЕНИЕ
му и правомерному использованию в прогнозных расчетах. Поясним это
на примере из п. 8.6.1.
Пусть целью нашего исследования является лаконичное
(параметризованное с помощью модели) описание функции плотности анализируемой
случайной величины (заработной платы наугад выбранного из общей
генеральной совокупности работника) по исходным данным, представленным
случайной выборкой работников жьж2,.. .,2:750 объема п = 750.
Игнорируя экономические закономерности формирования искомого закона
распределения, т. е. руководствуясь формальным подходом наилучшей
мгновенной статистической фотографии, мы должны были бы запастись
достаточно богатым классом модельных плотностей (например, классом кривых
Пирсона [КендаллМ. Лж., СтьюартА., 1966]) и, перебирая эти модели (с
одновременной статистической оценкой участвующих в их записи
параметров методами, описанными в гл. 7), найти такую функцию плотности,
которая наилучшим в определенном смысле образом (например, в смысле
критерия «хи-квадрат» Пирсона, см. п. 8.6.1) аппроксимирует поведение
имеющейся у нас эмпирической плотности (см. изображение
соответствующей гистограммы на рис. 8.2). На этом пути в результате расширения
запаса гипотетичных модельных плотностей можно добиться очень
высокой точности аппроксимации, вплоть до повторения модельной функцией
неожиданных провалов гистограммы, подобных тем, которые мы имеем
на 14-м и 15-м интервалах группирования на рис. 8.2. Однако, поступая
таким образом, мы добиваемся лишь кажущегося хорошего результата, в
чем легко можно убедиться, попробовав применить выявленный
модельный закон к описанию эмпирической плотности, построенной по другой
выборке, извлеченной из той же самой совокупности. В подавляющем
большинстве случаев выявленная ранее модельная плотность оказывается
непригодной для описания распределительных закономерностей,
наблюдаемых в другой выборке. Следовательно, для этой выборки нужно
строить другую модель, а значит, и само моделирование практически теряет
смысл, так как главное назначение модели — распространение
закономерностей, подмеченных в выборке, на всю генеральную совокупность (что и
является основой решения задач планирования, прогноза, диагностики).
В качестве альтернативного рассмотрим подход,
предусматривающий тщательный предмодельный профессиональный анализ локальных
закономерностей, в соответствии с которыми формируется закон
распределения заработной платы. Эти закономерности (мультипликативный
характер редукции труда, принцип оплаты по труду, постоянство
относительного варьирования заработной платы при переходе от работников
одной категории сложности труда к другой и т.п., см. [Айвазян С. А., 1980]

В.З ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ 47
позволяют уже на следующем, третьем этапе моделирования
теоретически (т. е. без апелляции к имеющейся у нас эмпирической функции
плотности) обосновать выбор класса моделей, в пределах которого мы должны
оставаться при подборе искомой модельной плотности. В рассмотренном
примере таким классом был класс логарифмически-нормальных
распределений (см. п. 3.1.6). После этого мы переходим к статистическому
оцениванию параметров, участвующих в записи законов этого класса, т.е.
переходим к четвертому этапу.
Модель, полученная таким образом, как правило, несколько хуже (по
формальным критериям), чем предыдущая, аппроксимирует
эмпирическую плотность, построенную по данной конкретной выборке. Однако в
отличие от модели, полученной в результате формальной статистической
подгонки экспериментальных данных под одну из теоретических кривых,
она останется устойчивой, инвариантной по отношению к смене
выборок, т.е. она одинаково хорошо может описывать характер
распределения, наблюдаемого в различных выборках из одной и той же генеральной
совокупности. А если все-таки моделирование, идущее от более или
менее бесспорных (быть может, частично подтвержденных экспериментом)
исходных предпосылок о физической природе изучаемого явления, дает
результаты, плохо согласующиеся с реальной действительностью?
Причина этого (при условии аккуратного проведения третьего и четвертого
этапов) одна: плохое соблюдение на практике всех (или части) принятых
при моделировании в качестве априорных допущений исходных
предпосылок. Оценка же этого явления может быть двоякой: если заложенные в
основание модели исходные допущения признаются специалистами
объективными закономерностями, в соответствии с которыми должен
функционировать механизм исследуемого явления, то следует искать и устранять
причины, приведшие к нарушению этих закономерностей, в самой
моделируемой реальности; если же принятые допущения были результатом
вынужденного упрощения на самом деле плохо различимого механизма,
то следует усовершенствовать эти допущения, что приведет, естественно,
и к изменению модели.
В рассмотренном примере интерпретация временного
рассогласования модели и действительности относилась как раз к первому типу.
Проведенные сопоставления модельных и экспериментальных данных по
распределению заработной платы работников за ряд лет A956-1972 гг., см.
[Айвазян С. А., 1980]) четко обозначили период их резкого рассогласования
A960-1966 гг.). Однако по мере удаления этого периода в прошлое
прослеживается явная тенденция к сближению модельных и реальных данных.
Более внимательный анализ показал, что момент резкого рассогласования

48 В. ВВЕДЕНИЕ
следовал непосредственно за весьма существенным директивным
вмешательством в существующие тарифные условия, вмешательством, которое,
как показал дальнейший ход развития, плохо согласовывалось с целым
рядом объективных экономических закономерностей. И факт, что в
дальнейшем мы наблюдаем сближение модельных и реальных данных, говорит
лишь о том, что эти объективные экономические закономерности
постепенно все более сказывались на характере распределения, все более
«выступали на поверхность», отвоевывая себе те или иные правовые формы.
ВЫВОДЫ
1. Предлагаемый учебник посвящен описанию математико-статисти-
ческого инструментария экономических исследований, который
охватывает как традиционные методы эконометрики (регрессионный анализ,
анализ временных рядов и системы одновременных уравнений), так и ряд
наиболее актуальных, в смысле социально-экономических приложений,
разделов прикладной статистики (кластер-анализ и расщепление смесей
распределений, дискриминантный анализ, методы снижения размерности,
построение интегральных индикаторов и др.).
2. Изложение в учебнике строится в соответствии с
современными университетскими учебными планами подготовки экономистов и
экономистов-статистиков и охватывает весь блок математико-статисти-
ческого инструментария, в который входят следующие дисциплины:
дескриптивная статистика, теория вероятностей, математическая
статистика, многомерный статистический анализ, эконометрика.
3. Теория вероятностей — математическая наука, предназначенная
для разработки (и исследования свойств) математических моделей,
имитирующих механизмы функционирования реальных явлений или систем,
условия «жизни» которых включают в себя неизбежность «мешающего»
влияния большого числа случайных (т. е. не поддающихся строгому учету
и контролю) факторов.
4. Математическая статистика — система основанных на
теоретико-вероятностных моделях понятий, приемов и математических методов,
предназначенных для сбора, систематизации, интерпретации и
обработки статистических данных с целью получения научных и практических
выводов. Одно из главных назначений методов математической
статистики — обоснованный выбор среди множества возможных теоретико-
вероятностных моделей той модели, которая наилучшим образом
соответствует имеющимся в распоряжении исследователя статистическим
данным, характеризующим реальное поведение конкретной исследуемой си-

выводы 49
стемы.
5. Прикладная статистика — научная дисциплина,
разрабатывающая и систематизирующая понятия, приемы, математические методы и
модели, предназначенные для организации сбора, стандартной записи,
систематизации и обработки статистических данных с целью их удобного
представления, интерпретации и получения научных и практических
выводов.
6. Эконометрика — экономико-математическая научная
дисциплина, разрабатывающая и использующая методы, модели, приемы,
позволяющие придавать конкретное количественное выражение общим
(качественным) закономерностям экономической теории на базе экономической
статистики и с использованием математико-статистического
инструментария.
7. Теория вероятностей и математическая статистика являются по
отношению к прикладной статистике и эконометрике разработчиками и
поставщиками существенной части используемого в них математического
аппарата. Однако доводка и развитие этого аппарата, подчиненные
требованиям и запросам различного типа приложений, производятся уже в
рамках дисциплин «прикладная статистика» и «эконометрика».
8. Границы применимости вероятностно-статистических методов
определяются, строго говоря, требованием соблюдения (хотя бы
приблизительно) в исследуемой реальной действительности условий
статистического ансамбля, а именно: а) возможностью (хотя бы мысленно реально
представимой) многократного повторения наших экспериментов или
наблюдений в одних и тех же условиях; б) наличием большого числа
случайных факторов, характеризующих условия проведения наших
экспериментов (наблюдений) и не позволяющих делать полностью предопределенного
(детерминированного) заключения о том, произойдет или не произойдет в
результате этих экспериментов интересующее нас событие.
9. Строгих математических методов, позволяющих точно
определять, находимся ли мы в условиях статистического ансамбля, не
существует: любая вероятностная модель, так же как и любая
математическая модель вообще, есть лишь некоторое приближение к
исследуемой реальной действительности. Можно лишь условно разделять
исследуемые реальные ситуации на: 1) относящиеся к области высокой
работоспособности вероятностно-статистических методов; 2) лишь с
натяжкой укладывающиеся в рамки статистического ансамбля (категория
допустимых вероятностно-статистических приложений); 3) недопустимые
для вероятностно-статистических приложений. Однако и применительно
к последней категории ситуаций в ряде случаев помимо методов анали-

50 В. ВВЕДЕНИЕ
за данных используют статистические методы, основанные на концепции
субъективных вероятностей.
10. Всякая математическая модель является упрощенным
представлением действительности, и искусство ее построения состоит в том, чтобы
совместить как можно большую лаконичность параметризации модели с
достаточной адекватностью описания изучаемой действительности или,
другими словами, чтобы достигнуть максимальной концентрации
реальности в простой математической форме.
11. Вероятностная модель — это математическая модель,
имитирующая механизм функционирования гипотетического (не конкретного)
реального явления или системы стохастической природы; вероятностно-
статистическая модель — это вероятностная модель, значения
отдельных характеристик (параметров) которой оцениваются по результатам
наблюдений, характеризующим функционирование моделируемого
конкретного (а не гипотетического) явления или системы; вероятностно-
статистическая модель, описывающая механизм функционирования
экономической или социально-экономической системы, называется экономе-
трической.
12. Важнейшим условием достижения высокой «работоспособности»
модели является успешная реализация второго этапа моделирования, т. е.
проведение тщательного предмодельного анализа физической сущности
изучаемого явления с целью формирования добротной априорной
информации и ее использования при выводе (или выборе) общего вида искомой
модели. Вынужденная (но нежелательная) альтернатива к такому
подходу это логика «черного ящика», т.е. чисто формальная аппроксимация
реальных данных.

Раздел I
еш
[веро^
)cyi
:нос
ствл
ми
ия
;:лучЩны#вели1|н]
?след?емые
[и закон<
•"И
>poi
)aci
[ибо!
сные
[ческих и(
ше
:и1
tarn
?ЯТ1
жова
^"

ГЛАВА 1. ПРАВИЛА ДЕЙСТВИЙ
СО СЛУЧАЙНЫМИ СОБЫТИЯМИ
И ВЕРОЯТНОСТЯМИ ИХ
ОСУЩЕСТВЛЕНИЯ
1.1. Дискретное вероятностное
пространство
1.1.1. Процесс регистрации наблюдения на объекте
исследуемой совокупности (случайный эксперимент)
При построении любой математической теории прежде всего следует
договориться об определениях некоторых понятий и о принятии в
качестве исходных фактов, не требующих доказательства, некоторых допущений
(аксиом). Отправным понятием теории вероятностей является понятие
случайного эксперимента, который определяется как процесс
регистрации наблюдения на единице обследуемой совокупности, произведенный
в условиях статистического ансамбля. В зависимости от конкретного
содержания этого понятия и применяется соответствующий
математический аппарат к решению той или иной конкретной задачи. Одна и та же
реальная задача допускает в зависимости от конечных целей
исследования несколько вариантов конкретизации понятия «случайный
эксперимент». Так, при контроле изделия по альтернативному признаку (т. е.
когда в результате контроля одного изделия оно признается либо годным,
либо дефектным) пользуются в зависимости от конечных целей
исследования по меньшей мере тремя вариантами интерпретации этого понятия:
а) контроль одного изделия; б) контроль партии (выборки), состоящей из
N изделий; в) контроль двух партий (выборок), состоящих соответственно
из Ni и iV2 изделий (схема повторной выборки). Очевидно, в первом
варианте могут быть только два различных исхода («годное - дефектное»),
во втором, если нас интересует только общее количество обнаруженных в

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 53
партии дефектных изделий и не интересует порядок, в котором они были
обнаружены, — (N + 1) возможных исходов (в партии обнаружено нуль,
или одно, или два, ..., или N дефектных изделий), а в третьем — при
том же подходе — (Ni + 1)(-/Уг + 1) возможных исходов (резуль? ат каждого
случайного эксперимента задается в этом случае парой чисел (^,г/), где ?
и т/ — числа дефектных изделий, обнаруженных соответственно в первой
и во второй партиях).
Точно так же при анализе результатов выбрасывания игральных
костей можно понимать под случайным экспериментом одно бросание
(соответственно будем иметь шесть возможных исходов), а можно —
последовательность из заданного числа бросаний, как мы и должны были бы
поступить при строгой формализации примера игры с четырехкратным
бросанием игральной кости, рассмотренного в п. В.2 (нетрудно
подсчитать, что общее число возможных исходов в этом примере выразится
числом б4 = 1296).
Число возможных исходов случайного эксперимента не всегда можно
пересчитать. Всякий случайный эксперимент, связанный с
необходимостью фиксации величины какого-либо параметра обследуемого объекта,
измеряемого в физических единицах непрерывной природы (температура,
давление, время, вес, размеры и т.п.), имеет, как принято говорить,
континуальное множество возможных исходов . Однако о том, как был
осуществлен перенос построения строгой вероятностной теории на этот
общий случай, речь будет идти в следующем пункте.
1.1.2. Случайные события к правила действий с ними
Как уже упоминалось, с каждым случайным экспериментом
связано понятие совокупности всех возможных его исходов. Каждый из этих
возможных исходов будем называть элементарным (неразложимым)
событием (или элементарным исходом), а совокупность всех таких
возможных исходов — пространством элементарных событий (исходов). Таким
образом, в результате анализируемого случайного эксперимента
обязательно происходит одно из элементарных событий, причем одновременно
с ним не может произойти ни одно из остальных элементарных событий (о
событиях, обладающих последним свойством, говорят, что они являются
1 Как известно, множество элементов, составляющих какую-либо совокупность, может
быть конечным (если число элементов в нем конечно), счетным (если его элементы
можно занумеровать числами 1,2,...,п,...: множество целых чисел, множество
рациональных чисел и т. п.) и континуальным (множество всех точек числовой
прямой, плоскости и т. п.).

54 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
несовместными, см. ниже).
Рассмотрим пока лишь дискретный случай, т. е. только те ситуации,
когда все элементарные события можно занумеровать числами 1,2,..., п,
... Иначе говоря, рассматриваемое пространство элементарных событий
состоит лишь из конечного или счетного множества элементарных
событий (обозначим их и\, и2,..., иП}...), а сам факт «пространство П состоит
из элементарных событий ш\ ,и2,... ,u>n,...» кратко обозначим
или
A.1)
П = {(*}, i=l,2f...
Рассмотрим несколько примеров случайных экспериментов и
соответствующих им пространств элементарных событий.
Пример 1.1. Подбрасывание монеты:
П = {ui = аверс (лицевая сторона монеты);
ц>2 = реверс (обратная сторона монеты)} .
Пример 1.2. Выбрасывание одной игральной кости:
П = {иг = 1; и2 = 2; и3 = 3; и4 = 4; иъ = 5; и;6 = 6}.
Пример 1.3. Четырехкратное бросание игральной кости:
П = {(^=A,1,1,1);^ = A,1,1,2); ...; w1296 = F,6,6,6)}.
Пример 1.4. Проверка (по альтернативному признаку) одного
изделия, случайно отобранного из продукции массового производства:
Л = {о7х = годно; с^2 = дефектно}.
Пример 1.5. Проверка (по альтернативному признаку) N
изделий, случайно отобранных из продукции массового производства:
П = {иг = 0; и2 = 1; ...; cj^+1 = ЛГ},
где и — число обнаруженных дефектных изделий.
Пример L6. Проверка (по альтернативному признаку) двух
выборок, состоящих соответственно из N\ и N2 изделий, случайно отобранных
из продукции массового производства:
п = {иг = @,0); и;2 =

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 55
Пример 1.7. Определение и — числа сбоев станков
автоматической линии за наугад выбранную смену:
ft = {иг = 0; щ = 1; ...; ип = п - 1; ип+г = п;...}.
Кроме элементарных событий исследователю приходится иметь дело
с так называемыми составными (или разложимыми) событиями.
Событие С называется составным (разложимым), если можно
указать по меньшей мере два таких элементарных события Ш(г и и><3, что из
осуществления каждого из них в отдельности следует факт
осуществления события С. Этот факт коротко формулируют — «событие С состоит
из элементарных событий и>,-г иц3» — и записывают символически в
виде С = {0^,0^}.
Пользуясь такой терминологией, случайным событием А называют
любое подмножество {и^,w<af... ,u^fc,...} пространства элементарных
событий A.1), т.е.
что следует понимать так: осуществление любого из элементарных
событий и^,.. .уо;,'д,..., «входящих в Л», влечет за собой осуществление
события А.
Поясним эту терминологию на некоторых из примеров 1.1-1.7.
В примере 1.2 события А\ = {выпадет четное число очков} и А^ =
{выпавшее число очков не превзойдет 3} запишутся соответственно А\ =
{о;2,и;4,^б} и А2 = {^ь^,^}.
В примере 1.3 интересовавшее нас в п. В.2 событие А = {хотя бы
один раз при четырехкратном бросании кости появится шестерка} будет
состоять из всех тех четырехмерных векторов о^, в которых хотя бы одна
из компонент равна шести (можно подсчитать, что число таких векторов
равно 671).
В примере 1.5 событие А = {число обнаруженных дефектных изделий
не более 4}, очевидно, может быть записано А = {ui,^,^,^,^}-
В примере 1.7 событие А = {число зафиксированных за смену сбоев
станков автоматической линии меньше 3} можно представить в виде А =
Из определения теории вероятностей (см. п. В.2) следует, что в
первую очередь надо запастись определенной структурой всех возможных
связей между случайными событиями или, другими словами, определенными
правилами действий с событиями и соответствующей терминологией.
Сумма (объединение) событий Ai,A2>* • ->^fc — это такое
событие А (А = А1 + А2 + b>U)> которое заключается в наступлении хотя
бы одного из событий Ai,^2...,i4fe. На языке элементарных событий,

56 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
следовательно, сумма событий А\, А2..., Л* определяется как событие А,
состоящее из всех различных элементарных событий, составляющих
события i4i,A2>-« -,Ak- Таким образом, если нас интересует, например,
сумма А событий А\ = {число обнаруженных дефектных изделий не более
4}={о;1,о;2}... ,^5} (см- пример 1.5) и А2 = {число обнаруженных
дефектных изделий заключено между 2 и 6 включительно}={c^3, иА, о;5 ,<*>6, и7}>
то, очевидно, А = А\ + А2 = {u^,^,. ..,cj5,w6,a;7}) так как о том, что
событие А произошло, будет сигнализировать реализация любого из
элементарных событий и\,..., uj.
Произведение (пересечение) событий Ai, А2,. . .,А* — это такое
событие А (А = А\ - А2 • ... • А*), которое заключается в обязательном
наступлении всех событий Аь Л2? •• -М*- На языке элементарных
событий, следовательно, произведение событий Ai,A2y...,Ak определяется
как событие Л, состоящее лишь из тех элементарных событий, которые
одновременно входят во все рассматриваемые события Л^Лг,. ..9Лд. .
Так что произведением упомянутых выше событий А\ = {cji,^,...,^}
и ^2 = {о;з,о;4,. •• 5^7} (см- пример 1.5) будет, очевидно, событие А =
А\ • Л2 = {чь^^б}* так как реализация каждого из элементарных
событий cj3?k>4 и <*>5 B отдельности означает, как легко видеть, одновременное
наступление событий А] и Л2.
Разность событий А\ и Л2 — это такое событие Л, которое
заключается в одновременном осуществлении двух фактов: событие А\
произошло, а событие А2 не произошло. На языке элементарных событий,
следовательно, разность А = А\ — А2 определяется как событие,
состоящее из всех тех элементарных событий, которые входят в А\, но не входят
в А2, Так что разностью рассмотренных выше в схеме примера 1.5
событий А\ = {u>i,u>2> ...,^5}иЛ2 = {о;з>^4? • • • >^7} будет, очевидно, событие
А = Ai - А2 = {k>i,u>2}> T- е- событие, заключающееся в том, что число
обнаруженных в партии дефектных изделий окажется не превосходящим
единицы.
Противоположное (дополнительное) событие (к событию А) —
это такое событие Л, которое состоит в ненаступлении события А. На
языке элементарных событий, следовательно, А определяется как
событие, состоящее из всех возможных элементарных событий, не входящих
в А. Поэтому, используя понятие разности событий, можно записать
Л = ft — А. Так, например, событием, противоположным событию
А\ = {u7i,u;2,.. .,^5} из примера 1.5, очевидно, будет событие,
заключающееся в том, что число обнаруженных в партии объема N дефектных
изделий окажется большим 4, т. е. А\ = {ljq^ljj^ ... ,cj^ 1}.

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 57
Достоверное событие определяется как событие, состоящее из всех
возможных элементарных событий, т.е. это событие п = {cj,}, i =
1,2,... (см. A.1)). Название этого события оправдано тем
обстоятельством, что пространство элементарных событий состоит из всех
возможных исходов, т. е. в результате анализируемого случайного эксперимента
обязательно произойдет одно из элементарных событий о;,-, а
следовательно, тот факт, что событие п произойдет, достоверен.
Невозможное (пустое) событие 0 — это событие,
противоположное достоверному, т. е. 0 = п - Л = П. Из определения непосредственно
следует объяснение названия этого события: оно не содержит ни одного
элементарного события и{ и, следовательно, при реализации
исследуемого случайного эксперимента его осуществление невозможно.
Несовместными называются события Аг, Л2,..., Л*, если в
результате исследуемого случайного эксперимента никакие два из них не могут
произойти одновременно. На языке элементарных событий это означает,
что среди событий Ai,A2,...,Ak нельзя найти такую пару событий А{ и
Aj, в которой обнаружилось бы хотя бы по одному общему
элементарному событию. Используя понятия произведения событий и невозможного
события, можно определить несовместные события как такую
последовательность событий А\, Л2,..., Ак, для любой пары которой А{ и Aj
справедливо соотношение Л,- • Aj = 0. Очевидно, любые пары (Л, Л)
противоположных событий являются несовместными. Таковыми же являются (по
определению) и все элементарные события.
Полная система событий — это такой набор несовместных
событий А\, Л2,.. ¦, Л^, который в сумме исчерпывает все пространство
элементарных событий, т. е.
( Ах + Л2 + • • • + Ак = П;
для всех i,j = 1,2,...,Л и г ф j.
Очевидно, набор всех элементарных событий можно рассматривать
как частный случай полной системы событий. И вообще любое разбиение
множества элементарных событий п на непересекающиеся классы дает
полную систему событий, в которой каждое из событий задается
соответствующим классом разбиения. Так, обратившись вновь к примеру 1.5,
положив в нем для определенности N = 100 и обозначив буквой d число
дефектных изделий, обнаруженных в партии, состоящей из 100 наугад
извлеченных изделий, отобранных от стационарно действующего массового

58 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
производства, определим систему событий следующим образом:
— партия отличного качества;
А2 = {1 < d < 5} =
— брак в пределах допустимой нормы (партия принимается);
А3 = {6 < d < 10} = {u>7,us,...yuu}
— брак выше допустимой нормы (партия принимается по сниженным
расценкам);
партия целиком возвращается.
Очевидно, события А\у ^2> А^А^ образуют полную систему событий.
1.1.3. Вероятностное пространство. Вероятности и правила
действий с ними
Для полного описания механизма исследуемого случайного
эксперимента недостаточно задать лишь пространство элементарных событий.
Очевидно, наряду с перечислением всех возможных исходов исследуемого
случайного эксперимента мы должны также знать, как часто в длинной
серии таких экспериментов могут происходить те или другие элементарные
события. Действительно, возвращаясь, скажем, к примерам 1.1-1.7, легко
представить себе, что в рамках каждого из описанных в них пространств
элементарных событий можно рассмотреть бесчисленное множество
случайных экспериментов, существенно различающихся по своему
механизму. Так, в примерах 1.1-1.3 мы будем иметь существенно различающиеся
относительные частоты появления одних и тех же элементарных исходов,
если будем пользоваться различными монетами и игральными костями
(симметричными, со слегка смещенным центром тяжести, с сильно
смещенным центром тяжести и т. п.). В примерах 1.4-1.7 частота
появления дефектных изделий, характер засоренности дефектными изделиями
проконтролированных партий и частоты появления определенного числа
сбоев станков автоматической линии будут зависеть от уровня
технологической оснащенности изучаемого производства: при одном и том же
пространстве элементарных событий частота появления «хороших»
элементарных исходов будет выше в производстве с более высоким уровнем
технологии.

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 59
Для построения (в дискретном случае) полной и законченной
математической теории случайного эксперимента — теории
вероятностей — помимо уже введенных исходных понятий случайного
эксперимента, элементарного исхода и случайного события необходимо запастись
еще одним исходным допущением (аксиомой), постулирующим
существование вероятностей элементарных событий (удовлетворяющих
определенной нормировке), и определением вероятности любого случайного
события.
Аксиома. Каждому элементу и{ пространства элементарных
событий Я соответствует некоторая неотрицательная числовая
характеристика pi шансов его появления, называемая вероятностью события о;,-, причем
(отсюда, в частности, следует, что 0 ^ pt ^ 1 для всех i).
Определение вероятности события. Вероятность любого
события А определяется как сумма вероятностей всех элементарных событий,
составляющих событие Л, т.е. если использовать символику Р{А} для
обозначения «вероятности события Л», то
= Е
с1-3)
Отсюда и из A.2) непосредственно следует, что всегда 0 ^
причем вероятность достоверного события равна единице, а вероятность
невозможного события равна нулю. Все остальные понятия и правила
действий с вероятностями и событиями будут уже производными от
введенных выше четырех исходных определений (случайного эксперимента,
элементарного исхода, случайного события н его вероятности) и одной
аксиомы.
Таким образом, для исчерпывающего описания механизма
исследуемого случайного эксперимента (в дискретном случае) необходимо задать
конечное или счетное множество всех возможных элементарных исходов
ft и каждому элементарному исходу щ поставить в соответствие
некоторую неотрицательную (не превосходящую единицы) числовую
характеристику ^, интерпретируемую как вероятность появления исхода щ (будем
обозначать эту вероятность символами JP{cjJ), причем установленное
соответствие типа Ui <-> pi должно удовлетворять требованию нормировки
A.2).
Вероятностное пространство как раз и является понятием,
формализующим такое описание механизма случайного эксперимента. Задать

60 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
вероятностное пространство — это значит задать пространство
элементарных событий П и определить в нем вышеуказанное соответствие типа
Ui~Pi = P{u>i}. A.4)
Очевидно, соответствие типа A.4) может быть задано различными
способами: с помощью таблиц, графиков, аналитических формул, наконец,
алгоритмически.
Как же построить вероятностное пространство, соответствующее
исследуемому реальному комплексу условий? С наполнением конкретным
содержанием понятий случайного эксперимента, элементарного события,
пространства элементарных событий, а в дискретном случае — и любого
разложимого случайного события, затруднений, как правило, не бывает.
А вот определить из конкретных условий решаемой задачи вероятности
Р{и){} отдельных элементарных событий не так-то просто! С этой целью
используется один из следующих трех подходов.
Априорный подход к вычислению вероятностей P{ui} заключается в
теоретическом, умозрительном анализе специфических условий данного
конкретного случайного эксперимента (до проведения самого
эксперимента). В ряде ситуаций этот предопытный анализ позволяет теоретически
обосновать способ определения искомых вероятностей. Например,
возможен случай, когда пространство всех возможных элементарных исходов
состоит из конечного числа N элементов, причем условия производства
исследуемого случайного эксперимента таковы, что вероятности
осуществления каждого из этих N элементарных исходов нам
представляются равными (именно в такой ситуации мы находимся при подбрасывании
симметричной монеты, бросании правильной игральной кости, случайном
извлечении игральной карты из хорошо перемешанной колоды и т.п.). В
силу аксиомы A.2) вероятность каждого элементарного события равна в
этом случае 1/JV. Это позволяет получить простой рецепт и для подсчета
вероятности любого события: если событие А содержит ЛГд элементарных
событий, то в соответствии с определением A.3)
Р{А) = ?±. A.3')
Смысл формулы A.3) состоит в том, что вероятность события в данном
классе ситуаций может быть определена как отношение числа
благоприятных исходов (т. е. элементарных исходов, входящих в это событие) к
числу всех возможных исходов (так называемое классическое определение
вероятности). В современной трактовке формула A.3 ) не является
определением вероятности: она применима лишь в том частном случае, когда
все элементарные исходы равновероятны.

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 61
Апостериорно-частотный подход к вычислению вероятностей P{ui]
отталкивается, по существу, от определения вероятности, принятого так
называемой частотной концепцией вероятности. В соответствии с этой
концепцией вероятность Р{щ} определяется как предел относительной
частоты появления исхода а^ в процессе неограниченного увеличения
общего числа случайных экспериментов п, т. е.
ft^W^^, A.5)
где тп(ш{) — число случайных экспериментов (из общего числа п
произведенных случайных экспериментов), в которых зарегистрировано
появление элементарного события о;,-. Соответственно для практического
(приближенного) определения вероятностей Pi предлагается брать
относительные частоты появления события Ui в достаточно длинном ряду
случайных экспериментов . Подобный способ вычисления вероятностей р^
не противоречит современной (аксиоматической) концепции теории
вероятностей, поскольку последняя построена таким образом, что
эмпирическим (или выборочным) аналогом объективно существующей вероятности
Р{А} любого события А является относительная частота осуществления
этого события в ряду из п независимых испытаний. Разными в этих двух
концепциях оказываются определения вероятностей: в соответствии с
частотной концепцией вероятность не является объективным,
существующим до опыта, свойством изучаемого явления, а появляется только в
связи с проведением опыта или наблюдения; это приводит к смешению
теоретических (истинных, обусловленных реальным комплексом условий
«существования» исследуемого явления) вероятностных характеристик и
их эмпирических (выборочных) аналогов.
Как пишет Г. Крамер, «указанное определение вероятности можно
сравнить, например, с определением геометрической точки как предела
пятен мела неограниченно убывающих размеров, но подобного определения
современная аксиоматическая геометрия не вводит» ([Крамер Г., с. 172]).
Немецкий математик Р. Мизес, с именем которого связывают развитие частотной
концепции вероятности, считал, что каждой вероятностной задаче обязательно
соответствует некоторый реальный процесс (удовлетворяющий введенным им
условиям «статистического коллектива»), а потому полагал теорию вероятностей
дисциплиной естественно-научной («наукой о явлениях реального мира»), но не
математической. Сущность понятия мизесского «коллектива» — в требовании реальной
массовости изучаемого явления (и соответствующего эксперимента), существования
пределов вида A.5) и независимости этих пределов от того, по какой
подпоследовательности произведенных случайных экспериментов, отобранной из всей такой
последовательности, мы этот предел будем вычислять.

62 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Мы не будем здесь останавливаться на математических изъянах
частотной концепции вероятности. Отметим лишь принципиальные сложности
реализации вычислительного приема получения приближенных значений
Pi с помощью относительных частот тп(и{)/п. Во-первых, сохранение
неизменными условий случайного эксперимента (т. е. сохранение условий
статистического ансамбля), при котором оказывается справедливым
допущение о тенденции относительных частот группироваться вокруг
постоянного значения, не может поддерживаться неограниченно долго и с
высокой точностью. Поэтому для оценки вероятностей pi с помощью
относительных частот mn(ui)/n не имеет смысла брать слишком длинные
ряды (т. е. слишком большие п) и потому же, кстати, точный переход к
пределу A.5) не может иметь реального смысла. Во-вторых, в
ситуациях, когда мы имеем достаточно большое число возможных элементарных
исходов (а они могут образовывать и бесконечное, и даже, как это было
уже отмечено в п. 1.1.1, континуальное множество), даже в сколь угодно
длинном ряду случайных экспериментов, мы будем иметь возможные
исходы Uiy ни разу не осуществившиеся в ходе нашего эксперимента; да и
по другим редко реализующимся возможным исходам полученные с
помощью относительных частот приближенные значения вероятностей будут
в этих условиях крайне мало надежными.
Апостериорно-модельный подход к заданию вероятностей Р{о>,},
отвечающему конкретно исследуемому реальному комплексу условий,
является в настоящее время, пожалуй, наиболее распространенным и наиболее
практически удобным. Логика этого подхода следующая. С одной
стороны, в рамках априорного подхода, т.е. в рамках теоретического,
умозрительного анализа возможных вариантов специфики гипотетичных
реальных комплексов условий разработан и исследован набор модельных
вероятностных пространств (биномиальное, пуассоновское, нормальное,
показательное и т.п., см.гл.З). С другой стороны, исследователь располагает
результатами ограниченного ряда случайных экспериментов. Далее с
помощью специальных математико-статистических приемов (основанных
на методах статистического оценивания неизвестных параметров и
статистической проверки гипотез, см. гл. 6-8) исследователь как бы
прилаживает гипотетичные модели вероятностных пространств к имеющимся у
него результатам наблюдения (отражающим специфику изучаемой
реальной действительности) и оставляет для дальнейшего использования лишь
ту модель или те модели, которые не противоречат этим результатам и в
некотором смысле наилучшим образом им соответствуют.
Опишем теперь основные правила действий с вероятностями событий,
являющиеся следствиями принятых выше определений и аксиомы.

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 63
Вероятность суммы событий (теорема сложения
вероятностей). Сформулируем и докажем правило вычисления вероятности
суммы двух событий Аг и А2. Для этого разобьем каждое из множеств
элементарных событий, составляющих события А\ и Л2, на две части:
где A°k объединяет все элементарные события cjj, входящие в Ад., но не
входящие в Ат(к,т =1,2; к ф т), а А\2 состоит из всех тех
элементарных событий, которые одновременно входят и в Ль и в Л2. Пользуясь
определением A.3) и определением произведения событий А\ и А2, имеем:
Pi= 52 Pi+ ? Рг = Р{А°г} + Р{Аг-А2}; A.6)
Р'= Е л+ Е
В то же время в соответствии с определением суммы событий А = Лх + А2
и с A.3) имеем
Р{Аг+А2}=
Из A.6), A.7) и A.8) получаем формулу сложения вероятностей (для
двух событий):
Р{Аг + Л2} = Р{Лг} + Р{А2} - />{ЛгЛ2}. A.9)
Формула A.9) сложения вероятностей может быть обобщена на
случай произвольного числа слагаемых:
к
~Д1 + Д2~... + (-1)""А^1, A.9')
где «добавки» Am(m = 1,2,...,А- 1) вычисляются в форме суммы
вероятностей вида
к к к
«1 = 1 «2=1 »m + l = l
причем суммирование в правой части производится, очевидно, при
условии, что все »i,*2,...,im+i различны и ц < i2 < ••• < *m+i. В частном

64 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
случае, когда интересующая нас система А\, А2>..., А^ состоит лишь из
несовместных событий, все произведения вида А^ • Ai2* ... *А,-т+1 (m ^ 1)
будут пустыми (или невозможными) событиями и соответственно
формула A.9') дает
Р{Аг + А2 + -- + Ак} = Р{Аг} + Р{А2} + -.. + Р{Ак}. A.9ю)
Вероятность произведения событий (теорема умножения
вероятностей). Условная вероятность. Рассмотрим ситуации, когда
заранее поставленное условие или фиксация некоторого уже
осуществившегося события исключают из числа возможных часть элементарных
событий анализируемого вероятностного пространства. Так, анализируя
совокупность из N изделий массового производства, содержащую iVj
изделий первого, N2 — второго, jfV3 — третьего и N4 — четвертого сорта
(Ni + N2 + N3 + N4 = N), мы рассматриваем вероятностное
пространство с элементарными исходами и\,ш2,и3 и щ и их вероятностями —
соответственно рг = N^/N, р2 = N2/N, р3 = ^з/Л" и р4 = N4/N (здесь
Ui означает событие, заключающееся в том, что наугад извлеченное из
совокупности изделие оказалось г-го сорта). Предположим, условия
сортировки изделий таковы, что на каком-то этапе изделия первого сорта
отделяются от общей совокупности и все вероятностные выводы (и, в
частности, подсчет вероятностей различных событий) нам предстоит строить
применительно к урезанной совокупности, состоящей только из изделий
второго, третьего и четвертого сорта. В таких случаях принято
говорить об условных вероятностях, т.е. о вероятностях, вычисленных при
условии уже осуществленного некоторого события. В данном случае
таким осуществленным событием является событие В = {с^ь^а^}, т*е-
событие, заключающееся в том, что любое наугад извлеченное изделие
является либо второго, либо третьего, либо четвертого сорта. Поэтому,
если нас интересует подсчет условной вероятности события А (при
условии, что событие В уже имеет место), заключающегося, например, в том,
что наугад извлеченное изделие окажется второго или третьего сорта, то,
очевидно, эта условная вероятность (обозначим ее Р{А \ В}) может быть
определена следующим соотношением:
Pi А I т - ^ + JV3 _ ^2 + ^3 /N2 + N3 + N4 _ Р{АВ}
1 ' ' " N2 + N3 + N4 " N I N " P{B} '
Как легко понять из этого примера, подсчет условных
вероятностей — это, по существу, переход в другое, урезанно^ заданным условием
В пространство элементарных событий, когда соотношение
вероятностей элементарных событий в урезанном пространстве остается тем же,

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 65
что и в исходном (более широком), но все они нормируются (делятся на
Р{В}) для того, чтобы и в новом вероятностном пространстве
выполнялось требование нормировки A.2). Конечно, можно было бы не
вводить терминологии с условными вероятностями, а просто использовать
аппарат обычных («безусловных») вероятностей в новом пространстве.
Запись в терминах вероятностей «старого» пространства бывает
полезной в тех случаях, когда по условиям конкретной задачи мы должны все
время помнить о существовании исходного, более широкого пространства
элементарных событий.
Получим формулу условной вероятности в общем случае. Пусть В —
событие (непустое), считающееся уже состоявшимся («условие»), а Л —
событие, условную вероятность которого Р{А \ В} требует вычислить.
Новое (урезанное) пространство элементарных событий п состоит только
из элементарных событий, входящих в 2?, и, следовательно, их
вероятности (с условием нормировки A.2)) определяются соотношениями1:
По определению вероятность Р{А \ В} — это вероятность события
А в «урезанном» вероятностном пространстве {П,р}, и> следовательно, в
соответствии с A.3) и A.10)
Рп{А | В} = РЙ{Л} =
Е Pi
= V^
Pi
Рп{В} '
т.е.
/Ъ{4 I В} =
или, что то же,
Ра{АВ} = Рп{А | В} • Ра{В). A.11')
1 Нижний индекс у буквы Р, означающей «вероятность» (Р — первая буква латинской
транскрипции этого слова), поясняет, в каком именно вероятностном пространстве
или пространстве элементарных событий производится вычисление вероятности
соответствующего события.
3 Теория вероятностей
и прикладная статистика

66 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Эквивалентные формулы A.11) и A.11') принято называть
соответственно формулой условной вероятности и правилом умножения
вероятностей.
Еще раз подчеркнем, что рассмотрение условных вероятностей
различных событий при одном и том же условии В равносильно
рассмотрению обычных вероятностей в другом (урезанном) пространстве
элементарных событий п = В с пересчетом соответствующих вероятностей
элементарных событий по формуле A.10). Поэтому все общие теоремы и
правила действий с вероятностями остаются в силе*и для условных
вероятностей, если эти условные вероятности берутся при одном и том
же условии.
Независимость событий. Два события А и В называют
независимыми, если
Р{АВ) = Р{А) ¦ Р{В}. A.12)
Для пояснения естественности такого определения вернемся к теореме
умножения вероятностей A.11;) и посмотрим, в каких ситуациях из нее
следует A.12). Очевидно, это может быть тогда, когда условная
вероятность Р{А | В} равна соответствующей безусловной вероятности Р{А},
т.е., грубо говоря, тогда, когда знание того, что произошло событие В,
никак не влияет на оценку шансов появления события А.
Распространение определения независимости на систему более чем
двух событий выглядит следующим образом. События А\, А%> • • • i Ak
называются взаимно (или совместно) независимыми, если для любых пар,
троек, четверок и т. д. событий, отобранных от этого набора событий,
справедливы следующие правила умножения:
P{AhAhAh) = P{Ah}P{AJ3}P{Aiah
Очевидно, в первой строке подразумевается
(число сочетаний из к по два) уравнений, во второй — С\ уравнений и
т.д. Всего, следовательно, A.13) объединяет С* + С к + V С к = 2 —
к — \ условий. В то же время Сь условий первой строки достаточно для
обеспечения попарной независимости этих событий. И хотя попарная и

1.1 ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 67
взаимная независимость системы событий, строго говоря, не одно и то
же, их различие представляет скорее теоретический, чем практический
интерес.
Свойство независимости событий сильно облегчает анализ различных
вероятностей, связанных с исследуемой системой событий. Достаточно
сказать, что если в общем случае для описания вероятностей
всевозможных комбинаций событий системы ЛЬЛ2,...,Л^ нужно задать 2*
вероятностей, то в случае взаимной независимости этих событий достаточно
лишь к вероятностей P{Ai},Р{А2}}• • • >P{Ak}*
Независимые события весьма часто встречаются в изучаемой
реальной действительности: они осуществляются в экспериментах
(наблюдениях), проводимых независимо друг от друга в обычном физическом смысле.
Именно свойство независимости исходов четырех последовательных
бросаний игральной кости позволило (с помощью A.13)) легко подсчитать
вероятность невыпадения (ни при одном из этих бросаний) шестерки в
задаче из п. В.2. Действительно, обозначив А{ событие, заключающееся
в невыпадении шестерки в t-м бросании (г = 1,2,3,4), и учитывая, что
P{Ai} = 5/6 для всех г = 1,2,3,4, получаем
Р{АгА2А3А4) = Р{Аг}Р{А2}Р{А3}Р{А4}
= E/бL = 625/1296.
Формула полной вероятности. При решении многих практических
задач зачастую сталкиваются с ситуацией, когда прямое вычисление
вероятности интересующего нас события А трудно или невозможно, в то
время как вполне доступно вычисление (или задание) условных
вероятностей того же события (при различных условиях). В случае, когда условия
?ь#2)•••>?&> при которых известны (или легко вычисляемы) условные
вероятности события Л, образуют полную систему событий (см. п. 1.1.2),
для подсчета вероятности Р{А} можно использовать соотношение
+ Р{А | В2}Р{В2} + • • • + Р{А | Вк)Р{Вк), A.14)
которое принято называть формулой полной вероятности.
Для доказательства формулы A.14) заметим, что элементарные
события, составляющие событие Л, можно разбить на к непересекающихся
групп, каждая из которых является общей частью (пересечением) события
А с одним из событий В( (эта возможность непосредственно вытекает из
того, что события В\, В2,..., В к исчерпывают в сумме все пространство
3*

68 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
элементарных событий и попарно не пересекаются), т.е.
А = АВг + АВ2 + • • • + АВк.
Н\
Далее, воспользовавшись теоремой сложения вероятностей A.9 )
(применительно к несовместным событиям, каковыми являются события
ABi, ЛЛ2,...,АВк) и вычислив вероятность каждого из произведений
АВ{ по формуле произведения вероятностей A.11), мы и получаем A.14).
Формула Байеса. Обратимся вначале к следующей задаче. На
складе имеются приборы, изготовленные тремя заводами: 20% приборов на
складе изготовлены заводом JV* 1, 50% — заводом № 2 и 30% — заводом
№ 3. Вероятности того, что в течение гарантийного срока прибору
потребуется ремонт, для продукции каждого из заводов равны соответственно
0,2; 0,1; 0,3. Взятый со склада прибор не имел заводской маркировки и
потребовал ремонта (в течение гарантийного срока). Каким заводом
вероятнее всего был изготовлен прибор? Какова эта вероятность? Бели
обозначить Ai событие, заключающееся в том, что случайно взятый со
склада прибор оказался изготовленным на t-м заводе {% = 1,2,3), а В —
событие, заключающееся в том, что наугад отобранный от продукции всех
трех заводов прибор оказался дефектным (потребовал ремонта), то
сформулированная выше задача, очевидно, сводится к вычислению условных
вероятностей P{Ai | В} по заданным вероятностям Р{Ах} = 0,2; Р{А2} =
0,5; Р{А3} = 0,3; Р{В \ Аг} = 0,2; Р{В \ А2} = 0,1 и Р{В \ А3} = 0,3.
Поскольку события Л15Л2,Лз образуют полную систему, воспользуемся
для выражения искомых вероятностей Р{А{ \ В} известными нам
основными правилами действий с вероятностями. По формуле условной
вероятности A.11)
i I В] = Щ^-. A.15)
Числитель этой дроби по теореме умножения вероятностей A.11')
может быть представлен в виде
Р{МВ} = Р{ВА{} = Р{В | Ai}P{Ai}t A.16)
а знаменатель Р{В} выражается с помощью формулы полной вероятности
A.14):
Р{В} = Р{В | Аг}Р{Аг} + Р{В | А2}Р{А2} + Р{В \ А3}Р{А3). A.17)
Подставляя A.16) и A.17) в A.15), получаем

1.2 НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 69
Р{М\В)ш /frW<*l*> . A.18)
? Р{В | А3}Р{А3)
i=i
Воспользовавшись этой формулой, нетрудно подсчитать искомые
вероятности:
piA ,m_0,2 0,2P°i
0,2 • 0,2 + 0,1 • 0,5 + 0,3 • 0,3 " 0,18
Р{А3 | В) = °-^М = 0,500.
Следовательно, вероятнее всего некондиционный прибор был
изготовлен на заводе № 3.
Доказательство формулы A.18) в случае полной системы событий,
состоящей из произвольного числа к событий, в точности повторяет
доказательство формулы A.18). В таком общем виде формулу
P{Ai|в).
Е Р{В | Aj}P{Aj}
принято называть формулой Байеса.
1.2. Непрерывное вероятностное
пространство (аксиоматика
А. Н. Колмогорова)
1.2.1. Специфика общего (непрерывного) случая
вероятностного пространства
Ранее упоминалось о ситуациях, в которых множество всех
возможных элементарных исходов (пространство элементарных событий п)
может оказаться более чем счетным. Так, например, именно с
континуальным пространством элементарных событий придется иметь дело, если

70 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
каждому элементарному исходу U{ исследуемого случайного
эксперимента (наблюдения) может быть поставлена в соответствие регистрация
одной или нескольких числовых характеристик обследуемого объекта
анализируемой совокупности, измеренных в физических единицах
непрерывной природы (в единицах времени, длины, веса, температуры, давления и
т. п.). Можно, правда, возразить, что, поскольку все измерения делаются с
ограниченной точностью, реальное множество элементарных исходов все
равно окажется не более чем счетным. Однако, с одной стороны,
возможности точности измерений со временем совершенствуются и вместе с этим
должна соответственно трансформироваться и структура
рассматриваемого дискретного вероятностного пространства. С другой стороны,
рассмотрение непрерывных моделей, отвечая физической сущности
анализируемого явления, одновременно расширяет аналитические возможности
теории, предоставляет исследователю более мощный математический
аппарат: достаточно сопоставить возможности простого суммирования и
интегрирования, аппарата разностных и дифференциальных уравнений и
т.д.
Как же осуществляется переход от дискретного к непрерывному
случаю в построении строгой математической теории вероятностей?
Автоматический перенос всей схемы.построения дискретного вероятностного
пространства (см. п. 1.1) на непрерывный случай невозможен. Одно из
принципиальных отличий непрерывного случая от дискретного
заключается в том, что в общем случае мы не можем объявить, подобно тому
как это делалось в дискретном вероятностном пространстве, любое
подмножество множества элементарных исходов п случайным событием,
т.е. событием, характеризующимся принципиальной возможностью его
наблюдения в результате исследуемого случайного эксперимента.
Другими словами, в общем вероятностном пространстве среди всех возможных
подмножеств пространства элементарных событий п часть подмножеств
характеризуется такой возможностью (и их принято называть
случайными событиями или измеримыми подмножествами П), а другая часть —
нет (подмножества U этого типа принято называть неизмеримыми).
Отмеченная особенность общего (непрерывного) случая, по-видимому,
требует введения дополнительных определений и аксиом, относящихся
к определению случайных событий и к правилам действий с ними и
их вероятностями. Это и делается при аксиоматическом (теоретико-
множественном) построении современной теории вероятностей, первое

1.2 НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 71
строгое и полное изложение которой принадлежит А.Н.Колмогорову
[Колмогоров] .
1.2.2. Случайные события, их вероятности и правила
действий с ними (аксиоматический подход
А. Н. Колмогорова)
Определим ту часть подмножеств пространства элементарных
событий П, которая содержит подмножества-события. Схема определения
случайного события А в общем случае подобна той, которая была
принята в дискретном случае. Но если в той ситуации нам достаточно
было определить в качестве исходных понятий элементарные события и\,
о;2,... ,а;дг,... (и любое подмножество пространства элементарных
событий объявлялось событием), то в общем случае мы в каждой конкретной
реальной ситуации должны (из физических, содержательных
соображений) определить дополнительно к П категорию подмножеств П, которые,
очевидно, являются событиями. А затем любое случайное событие А
определяется как некоторое производное от «очевидно событийных»
подмножеств введенной категории.
Определение случайного события. Рассмотрим систему
(конечную или счетную) подмножеств Ai,^?--- пространства элементарных
событий П, каждое из которых является событием. Определим, что
множество ft, состоящее из всех элементарных событий, все
дополнения А{ = П - А*, пустое множество 0 = п — to и всевозможные суммы
А = А{г + АB + • • • + А{п + • • • также являются событиями. Отсюда
непосредственно следует, что и произведения П = А^ А^ • • • А{п • • •
также являются событиями, так как их дополнения П = Л1х + А{2 + • • • в
соответствии с данным определением являются событиями.
Будем обозначать в дальнейшем систему тех подмножеств
пространства элементарных исходов П, которые являются событиями, буквой С.
Аксиома. Каждому подмножеству-событию А из системы С
соответствует неотрицательное и не превосходящее единицы число р(А) = Р{А}У
называемое вероятностью события Л, причем задающая это соответствие
числовая функция множеств р(А) обладает следующими свойствами:
1 Впервые интерпретация случайного события как множества с одновременной
трактовкой его вероятности как меры этого множества была дана, по-видимому, в
работе польского математика А. Ломницкого (Lomnicki A. Nouveau fondements du
calcul des probabilites — Fun dam. Math., 1923, 4). Однако теория вероятностей как
точная математическая теория в надлежащем объеме впервые была построена
А. Н. Колмогоровым.

72 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
а)
б) если события А\, А2,..., Ап,... несовместны, то
Р{Аг + А2 + • • - + Лп + •••} = P{Ai} + Р{Л2} + • • • + Р{Ап} + • • •.
Из этой аксиомы непосредственно следует, в частности, связь между
вероятностями прямого (А) и противоположного (А) событий:
Р{А} = 1 - Р{А}.
Аксиоматическое свойство б) вероятностей формулировалось и
доказывалось в дискретном случае в виде теоремы сложения вероятностей.
Точно так же то, что называлось теоремой умножения
вероятностей (и выводилось из определения и аксиомы в дискретном случае), в
общем случае принимается по определению.
Определение условной вероятности. Условная вероятность
Р{А | В} события А при условии, что уже имеет место событие J9,
определяется с помощью формулы
Р{АВ} = Р{А | В}Р{В}.
Правила действий с событиями и их вероятностями и, в
частности, формула полной вероятности A.14), формула Байеса A.19),
определение независимости для системы событий A.12), A.13) и другие,
доказанные в дискретном случае, имеют место (и могут быть доказаны) и в
случае общего вероятностного пространства.
Итак, для исчерпывающего описания механизма исследуемого
случайного эксперимента в общем случае, т.е. для задания в этом случае
вероятностного пространства, необходимо: 1) описать пространство
элементарных событий П; 2) описать систему С измеримых подмножеств
этого пространства или таких подмножеств, которые должны быть
принципиально наблюдаемыми (т.е. являются событиями); 3) каждому такому
событию А из системы С поставить в соответствие неотрицательное
число Р{А}, называемое вероятностью события Л, причем это соответствие
должно удовлетворять требованиям а) и б) аксиомы (очевидно, такое
соответствие Р есть числовая функция множества, определенная на
подмножествах системы С; функции такого типа принято называть
вероятностными мерами, определенными на системе подмножеств С). Поэтому
если в дискретном случае для краткого символического описания
вероятностного пространства достаточно было пары символов {1),р}, то в общем
случае для этой же цели требуется уже «тройка» {11,0,/*}.
Следует, однако, помнить, что всякая модель, всякая теория, и в том
числе современная аксиоматическая концепция теории вероятностей, есть

1.2 НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 73
лишь форма приближенного представления реальной действительности,
форма, не свободная от недостатков. Чтобы предостеречь читателя от
переоценки возможностей аксиоматической теоретико-вероятностной
модели, рассмотрим несложный пример.
Практика долгосрочного социально-экономического и
научно-технического прогнозирования широко использует различные формы
экспертных опросов. Одной из таких форм является подход, при котором
каждого из опрашиваемых экспертов просят субъективно оценить вероятность
осуществления интересующего нас события в будущем . Подходя к
моделированию этого процесса с позиций субъективистской школы
вероятностей и соответственно интерпретируя каждого из опрашиваемых
экспертов в качестве своеобразного «измерительного прибора», мы можем
определить понятие случайного эксперимента как результат ответа
эксперта на поставленный ему вопрос. В этом случае пространство
элементарных исходов П, очевидно, должно состоять из всех точек отрезка [0,1].
При конструировании системы С «наблюдаемых» подмножеств
пространства U естественно было бы априори потребовать, чтобы любой отрезок
Д = [ci,C2], лежащий внутри отрезка [0, 1] (т.е. О < С\ < сг < 1),
принадлежал бы к категории событий (т.е. для любого отрезка Д = [сьс2]
должна быть определена вероятность Р{Д} = ^{[сь сг]} того, что
численный ответ наугад выбранного эксперта будет принадлежать этому
отрезку). Но тогда в соответствии с определением случайного события в общем
случае событиями будут не только отрезки, но и все, что можно получить
из них применением к ним (взятым в счетном числе) суммирования и
перемножения, а также взятием дополнения (т.е. противоположного события).
Поэтому, выбирая произвольную точку с на отрезке [0, 1] и рассматривая
последовательность отрезков Дп вида Дп = [с — 1/п, с + 1/п], мы
обнаруживаем, что точка должна быть событием, так как она является, как
легко видеть, счетным произведением отрезков Дп. Итак, любая точка
отрезка [0, 1] — событие. Множество рациональных точек, как известно,
складывается из счетного числа точек. Следовательно, это множество —
тоже событие. Но множество иррациональных точек есть дополнение к
множеству рациональных точек. Значит, и множество иррациональных
точек — событие. Но вряд ли естественно, с физической точки зрения^
считать наблюдаемыми (и, следовательно, физически различимыми)
событиями факты принадлежности точки к множеству рациональных и к
множеству иррациональных чисел.
1 Подобная форма экспертиз используется, например, при построении сценариев
будущего социально-экономического и промышленного развития стран.

74 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Как видно из этого примера, и использование общепринятой сейчас
аксиоматической концепции теории вероятностей может приводить к
плохо физически интерпретируемым выводам. В данном примере мы не
провели до конца построение вероятностного пространства, так как не
определили (аксиоматически) способ вычисления вероятностей на
отрезках, т.е. величин Р{А} = P{[ci,C2]}. Физически естественное
аксиоматическое задание этих вероятностей также обусловлено спецификой
реального комплекса условий, характеризующих наш случайный эксперимент.
Так, если представить, что мы находимся в самой
«неблагоприятной» для прогноза ситуации (интересующее нас событие настолько
удалено во времени и неопределенно или опрашиваемые эксперты настолько
некомпетентны, что ответы экспертов оказываются приблизительно
равномерно «разбросанными» по всей длине отрезка [0, 1]), то естественно
предположить, что вероятности Р{Д} будут зависеть только от длины
отрезка Д и не будут зависеть от того, в каком именно месте отрезок
располагается, и определить их соответственно с помощью соотношений
Р{[сьс2]} = с2-сг. A.20)
Легко проверить, что заданные этим соотношением вероятности
удовлетворяют свойствам а) и б) аксиомы.
Подчеркнем, кстати, на этом примере одно из существенных отличий
широкого класса непрерывных вероятностных пространств от
дискретных: вероятность осуществления любого элементарного события (т. е.
любого возможного исхода) и в данном примере равна нулю; однако для
сколь угодно малого отрезка Д вероятность Р{Д} всегда будет
положительной (это непосредственно следует из A.20)). Таким образом, в этом
примере мы впервые встретились с казалось бы парадоксальной
ситуацией, когда события и хотя и являются возможными, но обладают
нулевой вероятностью. Соответственно события и = п — и, являющиеся
дополнением к событиям нулевой вероятности и, хотя и не могут быть
названы достоверными, но имеют вероятность осуществления, равную
единице. О событиях типа и часто говорят как о событиях, происходящих
«почти всегда». При более глубоком рассмотрении можно понять, что
подобные ситуации в непрерывном вероятностном пространстве на самом
деле не являются парадоксальными. Для пояснения этой мысли можно
привести аналогию с физическим телом, имеющим определенную массу,
1 О трех возможных подходах (априорном, апостериорно-частотном и апостериорно-
модельном) к выработке и обоснованию подобных предположений о природе
аксиоматически определяемых вероятностей см. п. 1.1.3.

выводы 75
в то время как ни одна из точек, составляющих это тело, сама массой не
обладает. Очевидно, тело в этой аналогии играет роль события, точка —
роль элементарного исхода, а масса — роль вероятности.
ВЫВОДЫ
1. Основаниями теоретико-вероятностного математического
аппарата являются: понятия случайного эксперимента, его возможного исхода и
пространства элементарных событий: аксиома о существовании и
нормировке вероятностей элементарных событий; определение случайного
события и способа вычисления его вероятности.
2. Способ построения современной строгой вероятностной теории
аксиоматический, причем для построения дискретного вероятностного
пространства, т. е. для модельного математического описания механизма
случайного эксперимента, имеющего лишь конечное или счетное множество
возможных элементарных исходов, достаточно постулировать одну
аксиому (о существовании и нормировке вероятностей элементарных исходов)
и одно определение (о способе вычисления вероятности любого события).
3. Термины «механизм случайного эксперимента», «реальный
комплекс условий, индуцирующий исследуемый статистический ансамбль»
и «вероятностное пространство» являются синонимами и могут быть
математически заданы в дискретном случае с помощью описания всех
возможных элементарных исходов и сопоставления с каждым из них
вероятности своего появления (с помощью аналитического задания, таблично,
графически, алгоритмически).
4. Главная сложность построения вероятностного пространства,
соответствующего исследуемому реальному комплексу условий, — в
конкретном задании вероятностей элементарных событий в дискретном
случае или вероятностной меры — в непрерывном. Из трех возможных
подходов к решению этой задачи — априорного, апостериорно-частотного
и апостериорно-модельного — последний является наиболее легко
практически реализуемым и наиболее эффективным.
5. Основные правила действий в дискретном вероятностном
пространстве задаются теоремами сложения и умножения вероятностей,
формулами полной вероятности и Байеса.
6. В общем (непрерывном) вероятностном пространстве в отличие от
дискретного среди подмножеств пространства элементарных событий п
могут быть такие, для которых не существует принципиальной
возможности их наблюдения в результате исследуемого случайного эксперимента
(«ненаблюдаемые» или «неизмеримые» подмножества). Такие подмноже-

76 ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
ства не могут быть названы событиями, так как если А — событие, то
мы должны иметь возможность сказать, наступило оно или не
наступило в результате эксперимента (в этом смысле оно «наблюдаемо»); только
тогда можно говорить об относительной частоте его наступления в серии
экспериментов, а следовательно, и о вероятности Р{А}.
7. Отмеченная в предыдущем пункте особенность общего
вероятностного пространства требует введения дополнительных определений
и аксиом, относящихся к определению случайных событий и к
правилам действий с их вероятностями. Современная аксиоматическая
концепция теории вероятностей (впервые полно и строго изложенная
А. Н. Колмогоровым в 1933 г.) строит общее вероятностное
пространство, отправляясь от определения случайного события (с помощью
перечисления допустимых теоретико-множественных комбинаций над
подмножествами, априори являющимися событиями) и аксиомы о вероятностях
как о неотрицательных и ограниченных единицей числовых функциях,
аргументами которых являются подмножества-события. Эта концепция
не противоречит рассмотренному ранее способу построения дискретного
вероятностного пространства (она включает в себя этот способ в
качестве частного случая и соответственно сохраняет все правила действий
с вероятностями и событиями) и обусловливает возможность физической
интерпретации вероятности события как относительной частоты его
появления в достаточно длинной серии экспериментов.
8. Использование аксиоматической концепции теории вероятностей
может в некоторых случаях, как и всякая другая модель, приводить к
плохо физически интерпретируемым выводам.
9. В общем (непрерывном) вероятностном пространстве в отличие от
дискретного могут существовать возможные события, обладающие
нулевой вероятностью появления. Соответственно противоположные к ним
события (их дополнения) хотя и не могут быть названы достоверными, но
имеют вероятность осуществления, равную единице.

ГЛАВА 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1. Определение и примеры случайных
величин
Рассматривая приведенные выше примеры случайных экспериментов
(см. п. 1.1.2, примеры 1.1-1.7), мы видим, что в большинстве случаев
результат случайного эксперимента может быть описан одним или
несколькими числами. Так, в примерах 1.2, 1.5 и 1.7 эти результаты означают
соответственно число очков, выпавших при бросании игральной кости;
число дефектных изделий, обнаруженных при качественном контроле N
случайно отобранных из массовой продукции изделий; число сбоев
автоматической линии за наугад выбранную рабочую смену. В примере 1.3
(четырехкратное бросание игральной кости) результат каждого случайного
эксперимента может быть записан четверкой чисел, или четырехмерным
вектором, а в примере 1.6 (проверка основной и дополнительной выборок
изделий объема соответственно N\ и N2, случайно отобранных из
продукции массового производства) — парой чисел, или двумерным вектором.
Лаже в примерах 1.1 и 1.4, на первый взгляд не связанных с регистрацией
числовых характеристик, можно для удобства закодировать
соответствующие случайные исходы, приписывая, например, исходам «аверс»
(пример 1.1) и «изделие годно» (пример 1.4) числовую метку «нуль», а исходам
«реверс» и «изделие дефектно» — числовую метку «единица».
Продолжая наши примеры и рассматривая в рамках теоретико-вероятностной
схемы регистрацию одного или одновременно нескольких интересующих
нас свойств (выраженных реальными или условно закодированными
числами) у каждого из анализируемых объектов, мы приходим к общей
схеме, в которой понятие случайного эксперимента реализуется в
регистрации на каждом из таких случайно отобранных объектов набора числовых
характеристик
(A)B)..,*w), p>i. B.1)

78
гл. а. случайные величины
Какие именно числовые значения ? мы будем иметь в результате
данного конкретного эксперимента, зависит от множества не поддающихся
учету случайных факторов и однозначно определяется в конечном счете
осуществившимся в результате данного случайного эксперимента
элементарным исходом и (а это означает, что ? является числовой (в случае
р = 1) или векторной (в случае р > 2) функцией аргумента и). Таким
образом, мы приходим к следующему определению случайной величины
(иногда пользуются равнозначным термином «случайный признак» или
просто «признак»).
Таблица 2 Л
Анализируемые свойства
(характеристики) объектов г
Социально-демографические и
экономические характеристики семьи
^l1) — социальная принадлежность
?B) — профессия главы семьи
^ ' — качество жилищных условий
^ — размер (число членов) семьи
^5* — количество детей
?*' — среднедушевой доход
Характеристики «поведения» семьи
(структура потребления)
?'7' — расходы на питание
{(*' — расходы на промышленные
товары текущего пользования
f'9' — расходы на предметы
роскоши и длительного пользования
?10' — расходы на услуги
f'11'— прочие расходы, включая
сбережения
Анализируемые объекты (семьи)
1
2
n
xS"
x?»
• • t
xA)
xn
.if}
xi"
xS"
,<"
4"
4">
...
...
...
xn
.?'
4"
x»'>
Случайной величиной называется поддающаяся измерению
скалярная (р = 1) или векторнаж (р > 2) величина определенного физического
смысла, значения (компоненты) которой подвержены некоторому не-

2.2 ВОЗМОЖНЫЕ И НАБЛЮДЕННЫЕ ЗНАЧЕНИЯ 79
контролируемому разбросу при повторенимх исследуемого эксперимента
(наблюдения, процесса). Можно сказать, что случайная величина { —
это функция, определенная на множестве элементарных событий, т. е.
* = ««).
Пример 2.1. В табл. 2.1 приведен еще один пример векторной
(или многомерной) случайной величины вместе с соответствующей ей
общей формой регистрации серии наблюдений (результатов случайных
экспериментов).
Обозначения случайной величины (которая по существу определяет
лишь перечень анализируемых характеристик и по сложившейся в
специальной литературе традиции чаще всего обозначается с помощью одной из
букв греческого алфавита — ?,rj,(,i/ n т.д.) отличаются от обозначений
ее наблюденных значений.
В табл. 2.1 и в дальнейшем эти наблюденные значения в целях
общности обозначаются с помощью строчных букв латинского алфавита (в
таблице — с помощью буквы х) с верхним индексом, указывающим номер
зафиксированной характеристики, и с нижним индексом, определяющим
номер эксперимента или объекта, в котором эта характеристика
зарегистрирована; но в любом случае нужно помнить, что за этими символами
«скрываются» реальные числовые значения соответствующих
характеристик или их условные числовые метки. Так, очевидно, в табл. 2.1 первые
три строки будут состоять из условных числовых меток, а последующие
восемь — из числовых значений, измеренных в определенной шкале и
имеющих четкий физический смысл.
2.2. Возможные и наблюденные значения
случайной величины
Поскольку в соответствии с одним из определений случайная
величина — это функция, определенная на множестве элементарных исходов,
то ее возможные значения и их общее число определяются структурой
соответствующего пространства п элементарных событий: каждому
элементарному событию и соответствует свое возможное значение (. При
этом, правда, может быть, что нескольким элементарным исходам
соответствует одно и то же возможное значение анализируемой случайной
величины, так что, вообще говоря, в конечном дискретном
вероятностном пространстве число возможных значений случайной величины
всегда меньше или равно числу различных элементарных исходов. Так, в
приведенных выше примерах из п. 1.1.2 мы имеем: в примерах 1.1 и 1.4
всего по два возможных «значения», соответствующих элементарным ис-

80 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ходам, — «аверс» и «реверс» (в примере 1.1) и «изделие годно» и
«изделие дефектно» (в примере 1.4); в примере 1.2 — шесть первых
положительных натуральных чисел задают одновременно и все элементарные
исходы, и все возможные значения анализируемой случайной величины;
в примере 1.7 возможными значениями числа сбоев автоматической
линии за смену являются все неотрицательные целые числа. Что касается
примеров 1.3, 1.5 и 1.6, то в них мы как раз оказываемся в ситуации,
при которой число возможных значений анализируемой случайной
величины будет меньше общего числа элементарных событий. Поясним это
на примере 1.3 (примеры 1.5 и 1.6 могут быть проанализированы по
аналогичной схеме). Пусть в примере 1.3 нас интересует число появившихся
«шестерок» в серии из четырех бросаний игральной кости (независимо от
порядка, в котором они будут появляться). Элементарный исход в этом
примере может быть описан последовательностью из четырех символов,
в которой на i-м месте записывают 1, если в результате i-го бросания
игральной кости выпала «шестерка», и 0 — в противном случае. Тогда с
точки зрения классификации элементарных событий последовательности
@, 1, 0, 0) и @, 0, 0, 1) дают разные элементарные исходы, в то время как
с точки зрения анализируемой случайной величины оба эти
элементарных события дают неразличимый результат: и в том, и в другом случае
наблюденное значение анализируемой случайной величины равно единице
(«шестерка» появилась ровно один раз). Конечно, нам не удастся
«пересчитать» все возможные значения случайной величины, определенной на
множестве элементарных исходов непрерывного пространства
элементарных событий п: их общее число образует континуум. Именно такого рода
величины представлены компонентами ? ' ~ ? многомерной
(векторной) случайной величины ?, рассмотренной в примере 2.1.
Следует отличать теоретически возможные значения случайной
величины (обозначим их х\, ж°,..., ж?,... в дискретном случае и просто х —
в непрерывном) от практически осуществившихся в экспериментах, т. е.
от наблюденных ее значений (последние обозначим ?ЬЯ2,.. .,zn)\
2.3* Типы случайных величин
Общая классификация возможных типов случайных величин может
быть представлена с помощью схемы рис. 2.1.
1 Бели интересующая нас случайная величина многомерная (или векторная, см. B.1)),
то обозначения сохраняются с заменой строчных латинских букв х^, я, Х{
соответствующими прописными Х9,Х}Х{.

2.3 ТИПЫ СЛУЧАЙНЫХ ВЕЛИЧИН
81
Бели мы в качестве результата эксперимента (наблюдения)
регистрируем одно число (примеры 1.1, 1.2, 1.4, 1.5 и 1.7 из п. 1.1.2; см. также
случай р = 1 в записи B.1)), то соответствующую случайную
величину принято называть одномерной или скалярной. Если же результатом
каждого эксперимента (наблюдения) является регистрация целого набора
интересующих нас характеристик (примеры 1.3,1.6 и 2.1, а также случай
р ^ 2 в общей записи B.1)), то соответствующую случайную величину
называют многомерной или векторной.
Случайная
величина
?
I
Многомерная
Одномерная
Номинальная

(классификационная)
I
г
Дискретная
г
Ординальная
(порядковая)
Г
Непрерывная
Количественная
Категоризованная
Некатегоризованная
Рис. 2.1. Общая схема классификации основных типов случайных величин
Одномерную случайную величину называют дискретной или
непрерывной в зависимости от того, в каком пространстве элементарных
событий она определена — в дискретном или в непрерывном. Очевидно, во
всех рассмотренных выше примерах 1.1-1.7, так же как и в первых пяти
компонентах из примера 2.1 (табл. 2.1), мы имеем дело с дискретными
случайными величинами. Как уже сказано выше, некоторые
исследователи, отправляясь от ограниченности наших практических возможностей
точности измерений, предлагают вообще обходиться только
дискретными вероятностными пространствами и соответственно только
дискретными случайными величинами. Действительно, даже при измерении непре-

82 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
рывных по своей природе величин (длины, веса, температуры, давления
и т. д.) всегда существует обусловленная разрешающей способностью
используемого «измерительного прибора» максимально различимая
единица измерения, своеобразный неразложимый квант, в целом числе которых
и будет представлено в конечном счете наше измерение. Однако
аналитические возможности непрерывных математических моделей, практика их
непосредственного использования говорят за то, что они являются
эффективным прикладным аппаратом применительно не только к
непрерывным по своей физической природе случайным величинам, но и к таким
дискретным, множество возможных значений которых достаточно велико
(несколько десятков и более).
В зависимости от своей природы, своего назначения одномерные
дискретные случайные величины подразделяются на количественные,
ординальные (или порядковые) и номинальные (или классификационные).
Количественная случайная величина позволяет измерять
степень проявления анализируемого свойства обследуемого объекта в
определенной шкале (см. примеры 1.2, 1.3, 1.5, 1.6, 1.7, а также компоненты
?D)-К(И) в примере 2.1).
Ординальная (порядковая) случайная величина позволяет
упорядочивать обследуемые в ходе случайных экспериментов (наблюдений)
объекты по степени проявления в них анализируемого свойства.
Исследователь обращается к ординальным случайным величинам в ситуациях,
когда шкала, в которой можно было бы количественно измерить степень
проявления анализируемого свойства, объективно не существует или ему
не известна. В табл. 2.1 случайная величина (' — качество жилищных
условий — предусматривает четыре возможные градации (категории
качества): «плохое», «удовлетворительное», «хорошее» и «очень хорошее».
Приписав каждой из обследованных семей (в соответствии с принятыми
нормативными правилами) одну из градаций, мы тем самым получаем
возможность упорядочить обследованные семьи по этому свойству.
Общее число градаций ординального признака может быть меньше, равно и
даже больше числа обследованных объектов (случайных экспериментов).
Номинальная (классификационная) случайная величина
позволяет разбивать обследуемые в ходе случайных экспериментов
(наблюдений) объекты на не поддающиеся упорядочению однородные по
анализируемому свойству классы. Если исследователю наряду с анализируемым
свойством известны все возможные его градации (не поддающиеся
упорядочению), вместе с правилом отнесения обследованного в ходе случайного
эксперимента (наблюдения) объекта к одной из этих градаций, то
соответствующую номинальную величину принято называть категориэованной.

2.4 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 83
Именно к таким признакам относятся случайные величины ?A) —
социальная принадлежность семьи и ?B) — профессия главы семьи из табл. 2.1.
Бели условия эксперимента таковы, что его элементарным исходом
является так называемое парное сравнение ?у, задающее меру сходства (или
различия) по анализируемому свойству объектов с номерами г и j из
обследуемой совокупности, то такую номинальную случайную величину будем
называть некатегоризованной} а ее наблюденные значения
представляются соответственно так называемой матрицей смежности :
Примером некатегоризованного номинального признака может
служить случайная величина, индуцированная случайным экспериментом на
различных парах семей, результатом которого является отнесение или
неотнесение каждой пары к общему классу с точки зрения однородности
(сходства) их потребительского поведения.
2.4. Одномерные и многомерные
(совместные^ законы распределения
вероятностен случайных величин
Мы уже знаем (см. п. 1.1.3), что для полного описания вероятностного
пространства или, что то же, для исчерпывающего задания интересую-
щей нас случайной величины недостаточно задать лишь пространство
элементарных событий п (и тем самым описать множество
теоретически возможных значений анализируемой случайной величины). К этому
необходимо добавить также: в дискретном случае — правило
сопоставления с каждым возможным значением Х< случайной величины ?
вероятности его появления р, = Р{( = Х? }; в непрерывном случае — правило
сопоставления с каждой измеримой2 областью АХ возможных значений
случайной величины ? вероятности р(АХ) = Р{? 6 АХ} события,
заключающегося в том, что в случайном эксперименте реализуется одно из
1 В наиболее распространенном частном случае элементы Ьц могут принимать лишь
два значения: 1, если объекты i и j отнесены в результате случайного эксперимента
(наблюдения) к одной градации (или к одному классу), и 0 — в противном случае.
8 Область возможных значений АХ называется измеримой, если элементарные
исходы и», соответствующие значениям, вошедшим в эту область, образуют измеримое
подмножество или событие, т. е. подмножество, принадлежащее системе С всех
возможных событий (см. п. 1.2.1 и 1.2.2).

84
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
возможных значений, принадлежащих заданной области АХ. Это
правило, позволяющее устанавливать соответствия вида
АХ -> р(АХ) = Р{? € АХ},
B.2)
принято называть законом распределения вероятностей исследуемой
случайной величины ?. Прозрачное пояснение такой терминологии мы
получаем в рамках дискретного вероятностного пространства, поскольку
в этом случае речь идет о правиле распределения суммарной единичной
вероятности (т. е. вероятности достоверного события) между
отдельными возможными значениями X,- (г = 1,2,...).
Очевидно, задание закона распределения вероятностей, т. е.
соответствий типа B.2), может осуществляться с помощью таблиц (только в
дискретном случае), графиков, а также с помощью функций и
алгоритмически (об основных формах задания законов распределения и примерах их
модельной, т.е. аналитической, записи см. гл. 3).
Приведем примеры табличного и графического задания законов
распределения вероятностей.
Тщательный статистический анализ засоренности партий
дефектными изделиями (пример 1.5) позволил построить следующее распределение
вероятностей для случайной величины ?, выражающей число дефектных
изделий, обнаруженных при контроле партии, состоящей из N = 30
изделий, случайно отобранных из продукции массового производства
(табл. 2.2):
Таблица
г
.?
1000 • Pi
2.2
1
0
42
2
1
141
3
2
228
4
3
236
5
4
177
6
5
102
7
6
47
8
7
18
9
8
6
10
9
1
11
10
0
12
11
0
...
...
31
30
0
Значения вероятностей, приведенные в табл. 2.2, даны с точностью до
третьего десятичного знака, поэтому то, что суммирование
представленных в таблице вероятностей дает 0,998 (вместо единицы), легко
объяснимо: недостающие 0,002 как-то «размазаны» между возможными
значениями 10,11,..., 30, но на каждое отдельное возможное значение приходится
вероятность, меньшая 0,0005.
Тот же закон распределения может быть представлен графически
(рис. 2.2).

2.4 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
85
Pi =
0,25
0,20
0,15
0,10
0,05
I
I I
0 1 2 3 4 5 (S 7 8 9 10 11 ...
X? «2 *3 X4
5 X6
8 X9 ^10 XU XU
Рис. 2.2. Графическое задание закона распределения вероятностей для
числа дефектных изделий, обнаруженных в наугад извлеченной
партии, состоящей из 30 изделий массового производства
Геометрическое изображение закона распределения вероятностей
дискретной случайной величины часто называют полигоном распределения
или полигоном вероятностей.
В качестве другого примера рассмотрим фрагмент табл. 2.1, выбрав
из одиннадцати представленных в ней компонент только две: качество
жилищных условий ?* ' и среднедушевой доход { . Еще более упростим
рассматриваемую схему, перейдя от по существу непрерывной случайной
величины С6' к ее дискретному аналогу ?*6', т. е. отказываясь от точного
знания среднедушевого дохода каждой семьи и ограничиваясь лишь
тремя возможными градациями: семья имеет низкий доход (градация ?i ),
средний доход (градация зг2 ') и высокий доход (градация ?3 )• С учетом
качество низкое;
(з)
качество хорошее и х\ —
четырех градаций качества жилищных условий: х\
(з) (з)
^2 — качество удовлетворительное; х$ '
качество очень хорошее — и проведенного вероятностно-статистического
анализа получаем следующий закон распределения вероятностей двумер-
/7F) ЛзК
ной случайной величины (fv ,f '):
Соответствующий двумерный полигон распределения представлен на
рис. 2.3.

86
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Рис. 2.3. Полигон двумерного распределения семей по качеству жилищных
условий (?C)) и уровню дохода (?<6>): рц = Р{?F) = ?$6)°, ?C) =
в
распределения вероятностей многомерной случайной
величины называют многомерным или совместным. Бели каждая из
компонент f' '(/? = 1,2,..., р; см. B.1)) анализируемого многомерного признака
? дискретна и имеет конечное число тк всех возможных значений, то,
очевидно, общее число возможных «значений» случайного вектора ?
будет т = т\ • ТП2 ... тр. В этом случае вместо общей индексации всех
возможных многомерных значений Xt (/ = l,2,...,m) удобнее
пользоваться р-мерной индексацией вида у... qy где первый индекс г
определяет номер возможного значения по первой компоненте, второй индекс
3 — по второй компоненте и т.д. Тогда Ху.,^ будет означать
возможfполученное сочетанием г-го возможного значения
компо2
ное значение
С2'
, j-ro возможного значения компоненты С2' и т.д. до g-го
возp , а вероятности Р{? = Jfy..^} удобно
ненты
можного значения компоненты
обозначать ру д. Таким образом, в табл. 2.3 представлены вероятности

2.4 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
87
Таблица 2.3
*
1
2
3
У-
1
2
3
4
zf
46H
46H
х3
P.J
Х1
0,06
0,05
0,01
0,12
43H
0,03
0,25
0,02
0,30
,«'
0,01
0,35
0,07
0,43
Х4
0,00
0,05
0,10
0,15
Pi.
0,10
0,70
0,20
1,00
При анализе многомерных (совместных) распределений часто
бывает достаточно знать закон распределения лишь для какой-то
части компонент анализируемого векторного признака. Так,
многомерная случайная величина ?, рассмотренная в табл. 2.1,
естественно разбивается на два подвектора: & = (f ,...,?* '), описывающий
социально-демографические и экономическую характеристики семьи, и
6 = (?>•••»?)» описывающий структуру семейного потребления.
Поэтому, если нас интересует лишь социально-демографо-экономическая
структура исследуемой совокупности семей, то предметом нашего
анализа будет закон распределения вероятностей только по компонентам
fAUB\...,fF) подвектора ft.
Частный (маржинальный) закон распределения подвектора ft
анализируемой многомерной случайной величины ? = (ft,ft) описывает
распределение вероятностей признака ft в ситуации, когда на значений
другой части компонент ft не накладывается никаких условий. В
дискретном случае соответствующие вероятности определяются по формулам:
V,. =
р, = Р{Ь = Xf) =
6 =
B.3)
B.3')
/|\0 f2^
где Х\ } и Xj — i-е и j-e возможные значения векторных признаков
соответственно ft и ft, а суммирование производится по всем возможным
значениям Xj в формуле B.3) и по всем возможным значениям X* в
формуле B.3').
Формулы B.3) и B.3') получаются как непосредственные следствия

88 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
теоремы сложения вероятностей A.9"), если принять во внимание
следующие очевидные связи между интересующими нас событиями:
В рассматриваемом примере (см. табл. 2.3) частные распределения
Pi. = Р{|<6) = ж56)О} и p.j = Р{?C) = xfH} подсчитаны по формулам B.3)
и B.3') и задают соответственно распределение семей отдельно по уровню
дохода и по качеству жилищных условий (они приведены соответственно
в последнем столбце и в последней строке табл. 2.3).
Условный закон распределения подвектора ?i анализируемой
многомерной случайной величины f = (?ь&) ПРИ условии, что
значение другого подвектора & зафиксировано на уровне Xj ' , вычисляется
по формуле
Аналогично
Хр} _ ^ B-4')
"ft/
Формулы B.4) и B.4 ) получаются как простые следствия теоремы
умножения вероятностей A.11).
Так, например, если нас интересует условное распределение группы
семей с высоким доходом по качеству жилищных условий, т.е.
распределение р.;D6)°) = Р{?{*] - *?H I ?6) = 46)°}i то вычисления по B.4) на

2.5 СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ 89
основе данных табл. 2.3 дают:
что означает, в частности, что из всей совокупности высокодоходных
семей в плохих жилищных условиях проживает 5%, в
удовлетворительных — 10%, в хороших — 35% и в очень хороших — 50% (то, что речь идет
только о высокодоходных семьях, определяется условием {? = 2з }).
2.5. Способы задания закона распределения:
функция распределения и функция
плотности вероятности
2.5.1. Функция распределения вероятностей одномерной
случайной величины
Как установлено выше (см. п. 2.4), всякая генеральная совокупность
(случайная величина) определяется своим законом распределения
вероятностей р(АХ). Поскольку интересующие нас области АХ могут быть в
общем случае подмножествами общей природы, то возникает вопрос:
каковы те способы задания числовых функций р, определенных на
подмножествах ДХ, которые были бы достаточно удобны в плане конструктивном,
практическом?
Оказывается, для описания распределений одномерных случайных
величин ? достаточно задать способ вычисления вероятностей р(АХ) =
Р{? € АХ} лишь для подмножеств АХ некоторого специального
вида, а именно лишь для полузамкнутых слева интервалов вида
АХ = [a?min,x),
где хт\п — минимально возможное значение исследуемой случайной
величины f (оно может быть равно и — оо), а ж — любое «текущее» (т. е.
задаваемое нами) возможное значение ?. Вероятность же р([хт\п,х)) =

90 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
< х} однозначно определяется заданием правого конца интервала,
т.е. числа ж, а потому может интерпретироваться как обычная функция
от одного числового аргумента ж.
Функцией распределения вероятностей (накопленной частотой)
F{(x) случайной величины ? называют функцию, ставящую в
соответствие любому заданному значению ж величину вероятности события
{?<&}, т.е.
Fe(x) = Р{* < ж}. B.5)
В дальнейшем, если это не будет вызывать недоразумений, будем
опускать нижний индекс f у функции F и называть ее просто «функцией
распределения».
Рассмотрим поведение функции распределения. Во-первых, отметим,
что в дискретном случае событие А(х) = {? < х} состоит из всех
элементарных событий щ = {? = #i}, таких, что Х{ < х. Поэтому в
соответствии с определением вероятности составного события (см. п. 1.1.3)
имеем
\ t: х?<х »: х?<х
(суммирование в правых частях B.5;) проводится по всем тем г, для
которых Xi < X).
Из B.5;) видно, что значения функции F(x) изменяются при
увеличении аргумента х скачкамщ а именно при «переползании» величины х
через очередное возможное значение ж,- функция F(x) скачком
увеличивает свое значение на величину pi = Р{? = Х{}.
Несколько иную картину мы будем наблюдать, анализируя поведение
функции распределения F$(x) в случае непрерывного исследуемого
признака ?. Большинство представляющих практический интерес
непрерывных случайных величин обладает тем свойством, что для любого отрезка
Ах вероятности Р{? G Дж} стремятся к нулю по мере стремления к нулю
длины этого отрезка, и, следовательно, вероятности отдельных
возможных значений х равны нулю (конкретный пример такого рода приведен
в п. 1.2.2 в задаче с экспертным оцениванием вероятности
интересующего нас события). Нетрудно понять, что для таких случайных величин
их функции распределения оказываются непрерывными. На рис. 2.4, а-г
представлены графики функций распределения случайных величин,
рассмотренных соответственно в примерах 1.1, 1.2, 1.5 (с учетом табл. 2.2)
и в примере с экспертным оцениванием вероятности интересующего нас
события (п. 1.2.2).

2.5 СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
91
1,0
0,5
1
а
1,0
5/6
4/6
3/6
2/6
1/6
F(x)
0 12 3 4 5 6
б
1,0
0,5
F(x)
012345678910
Рис. 2.4. Графики функций распределения для: а — оцифрованного
результата подбрасывания монеты (нуль соответствует аверсу,
единица — реверсу); б— числа очков, выпадающих при бросании
правильной игральной кости; в — числа дефектных изделий,
обнаруженных в наугад выбранной партии, состоящей из 30 изделий
(см. табл. 2.2); г — экспертной оценки вероятности
интересующего нас события (при полной некомпетентности экспертов), см.
пример из п. 1.2.2. Стрелки на графиках означают, что точки, в
которые они направлены, не включаются в состав обозначенных
ими интервалов группирования
Из определения функции распределения непосредственно вытекают
следующие ее основные свойства:
а) F{(x) — неубывающая функция аргумента х;
б) F((x) = 0 для всех х < жт-|п;
в) F{(x) = 1 для всех х > хтйХ (хт\п и жтах — соответственно
минимальное и максимальное возможные значения исследуемой случайной
величины ?);

92 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
г) Р{а < f < 6} = F{(b) - /^(а) для любых заданных значений а и b
(для доказательства последнего свойства следует воспользоваться
теоремой сложения вероятностей (см. п. 1.1.3), а также тем обстоятельством,
что события А = {? < а}, В = {? < Ь} и С = {а < ? < 6} связаны между
фбой соотношением В = А + С).
2.5.2. Функция плотности вероятности одномерной
случайной величины
В классе таких непрерывных случайных величин, функции
распределений которых всюду непрерывны и дифференцируемы (а, как уже
отмечалось, этот класс охватывает большинство представляющих
практический интерес непрерывных случайных величин), другой удобной формой
задания генеральной совокупности (исследуемой случайной величины ?)
является функция плотности вероятности Д(ж), определяемая как
предел
или, что то же,
Д(«) = /{(«), B.6')
т.е. Д(ж) — это производная функции распределения F((x) в точке х. Из
эквивалентных соотношений B.6) и B.6 ), определяющих функцию
плотности Д(ж), вытекают непосредственно следующие ее свойства:
а) Д(з?) ^ 0, так как функция F^(x) неубывающая;
б) Р{? 6 [хух + Д)} « Д(ж) • Д для малых отрезков Д (следует из
сравнения первых двух членов тождества B.6));
х
ъ)Р{( е [хт[п,х)} = Fe(a?)= / Д(и) dw для любых ж;
х0 и Д;
Я70 + А
[жо,жо + Д)} = ^(жо + Д)-/>(жо) = / Д(и) dw для любых
гшп
Прокомментируем некоторые из этих свойств функции плотности.
Свойство б) позволяет пояснить вероятностный смысл функции
плотности. Так, предположив для определенности область возможных
значений [жгшщЖтах] исследуемой случайной величины ? конечной и разбив ее

2.5 СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
93
на одинаковые и достаточно мелкие интервалы группирования Д с
центрами
о .До о|Ао о.д
Sl = Smin + —, Х2 = Хг + Д, Х3 = Х2 + Д
и т.д., мы можем поставить в соответствие каждому г-му интервалу
вероятность осуществления события
приближенно равную в соответствии со свойством б) величине Д(ж^) • Д.
Таким образом, по своему смыслу значения функции fe(x)
пропорциональны вероятности того, что исследуемая случайная величина примет
значение в непосредственной близости от точки х. Этот факт, в
частности, может служить основанием к тому, что дискретным аналогом
функции плотности в случае дискретной случайной величины является
полигон частот^ т. е. последовательность точек с координатами (^t',Pt)*
Отсюда же следует, что наиболее вероятным (модальным) значением
исследуемой непрерывной случайной величины является такое ее возможное
значение a?mod, в котором функция плотности достигает своего максимума,
т.е.
= max.
X
а-Зсг а-2<г а-ег а а+<г
Рис. 2.5. Функции: (а) распределения ^норм(х;а;<га) и (б) плотности
а;а2) нормального закона

94 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Геометрическая интерпретация свойства г) состоит в том, что
вероятность события {( 6 [а?о,жо + Д)} оказывается (при любых заданных
х0 и А) равной площади «столбика» под кривой плотности у = Д(ж) с
основанием [х0}х0 + А).
На рис. 2.5 показаны функции распределения jFgHopM(x; а; а2) и
плотности Д Норм(я»а; ^2) одного из распространенных законов распределения —
нормального (подробнее см. п. 3.1 и 4.3). Заштрихованная площадь на
рис. 2.5, б дает геометрически наглядное представление о величине
вероятности Р{{ € [яо,а?о +
2.5.3. Многомерные функции распределения и плотности.
Статистическая независимость случайных величин
Из вышеизложенного ясно, что вопрос об удобных способах задания
закона распределения случайной величины особенно актуален в
непрерывном случае: для описания «поведения» дискретной случайной величины
? универсальной и одновременно конструктивной формой (при «не
слишком большом» числе возможных значений исследуемой случайной
величины) является полигон вероятностей, т.е. форма, при которой каждому
возможному значению я? ставится в соответствие вероятность его
осуществления Pi = Р{( = Х{}. Поэтому сосредоточим теперь свое внимание
на непрерывном случае. Специфика многомерных схем в этом случае
заключается в том, что в отличие от одномерного случая многомерная
функция распределения
V> €(р))(х<1> *<») = Р{^ < .<»>,...,*<» < *<">} B.7)
перестает быть исчерпывающей (по информативности) формой задания
изучаемого закона распределения.
Многомерными аналогами конечных и полубесконечных отрезков
(которые можно получить суммированием и пересечением полубесконечных
отрезков вида [-оо,х)) являются конечные и полубесконечные
гиперпараллелепипеды. Именно для многомерных областей такого типа и
определяет функция распределения B.7) правило вычисления вероятностей.
Однако, если в одномерном случае этого было достаточно для «работы»
в соответствующем вероятностном пространстве, то в многомерном
случае нас это уже не удовлетворяет. В частности, знание одной лишь
формы B.7) оказывается недостаточным для конструктивного решения такой
важной для статистических приложений задачи, какой является задача
описания закона распределения интересующих нас преобразований от
исходных случайных величин ?,?,...,?*р' (общий подход к решению

2.5 СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ 95
этой проблемы описан в п. 4.4).
Поэтому для описания закона распределения многомерной величины
? = (?*,?,...,?) в непрерывном случае используют функцию
плотности вероятности /{(аг1',^2',. ..,агр'), которую определим как такую
функцию /(аг , ...,агр') от р переменных, что для любого (измеримого)
подмножества А возможных значений ( вероятность события {? 6 А}
может быть вычислена с помощью соотношения
W ^\ B.8)
где интегрирование ведется по данной области А в соответствующем
р-мер ном пространстве возможных значений { (т. е. знак интеграла в B.8)
определяет операцию р-кратного интегрирования).
Из данного определения функции плотности вероятности (фпв)
непосредственно следует, что фпв и функция распределения B.7) связаны
между собой соотношениями1:
B.7')
Вероятностный смысл функции плотности тот же, что и в
одномерном случае: вероятность осуществления значения случайной
величины ?, лежащего в некоторой малой окрестности АХ = {аг '*
*A) + Д*<», «« < fB) < «« + Дх<2\...,а<р> < еЫ < «(Р) }
точки X = (аг , я ,..., а?^р^), пропорциональна значению Д(Х) функции
плотности в этой точке и приблизительно равна, в частности, «элементу
1 Так же, как и в одномерном случае, наше описание относится лишь к таким
непрерывным случайным величинам, функция распределения B.7) которых непрерывна
по всем переменным внутри области возможных значений и имеет в этой области по
всем своим переменным непрерывную частную производную. Как отмечалось, такие
случайные величины составляют большинство в классе ситуаций, представляющих
практический интерес.

96 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
вероятности» Д(Х)ДХ, т.е.
Функции, определяемые соотношениями B.7), или B.7;), а также
B.9), называют соответственно совместной функцией распределения и
совместной плотностью вероятности многомерного случайного признака
Для описания частного закона распределения вероятностей
некоторой части компонент ?г = (?* ',?* ,...,f^), s < р, вектора ? (см.
п. 2.4.1) используются частная (маржинальная) функция
распределения F^fV ,..., аг ') и частная (маржинальная) плотность
вероятности, задаваемые соотношениями:
оо}
B.11)
B.12)
где под j^(,) понимается интегрирование по всему множеству возможных
значений случайной величины ? (ср. с B.3) и B.3;)).
Условная плотность вероятности Д(аг ,ж ,...,аг ' | ^2 = С)
случайного вектора ?i = (^ ,f' *•••>?) ПРИ условии, что значения
другого подвектора ^2 = (f >? »---if ) зафиксированы на уров-
не С = (с(в+1),с(а+2),...,с(р)) (т.е. при условии ?(в+1) = с(в+1),.. .,?<"> =
с^р^), определяется аналогично условным вероятностям р*. и p.j (см. B.4) и
B.4')) с помощью теоремы умножения вероятностей (см. п. 1.1.3, формулу
A.11')):
B.13)

2.5 СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ 97
Аналогично
B.13')
В знаменателях правых частей BЛЗ) и B.13') стоят частные
(маржинальные) плотности подвекторов — соответственно & = (( >•••>?)
и ?х =: (?>••• ,? ), вычисленные в соответствии с B.12).
Обратим внимание на существенное отличие частной
(маржинальной) плотности Дх(ж >•••>я ) от условной /^(я ,...,аг ' | ?*в+ ' =
tr+1 ,..., ?*р' = <гр'), хотя обе они описывают распределение одного и
того же набора признаков ^ \...<>^: первая плотность не зависит от того,
какие значения имеют остальные компоненты анализируемой
многомерной случайной величины, в то время как условная плотность существенно
зависит от того, на каких именно уровнях <r + ,...,с'р* зафиксированы
значения остальных компонент ?**+ ,...,? .
Рис. 2.6. Поверхность двумерной плотности вероятности (нормальный
закон с «отсеченными» краями)
На рис. 2.6 изображен график функции плотности двумерного закона
распределения вероятностей — двумерного нормального закона (его
описание см. в п. 3.1). Там же изображены сечения поверхности двумерной
плотности плоскостями or ' = с, т.е. плоскостями, перпендикулярными
4 Теория вероятностей
и прикладная статистика

98 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
оси 0* . В сечении получаются с точностью до нормирующего
множителя одномерные законы (один из них указан стрелкой), характеризующие
условное распределение компоненты (*3' при условии f*1' = с. Прямая ОЛ
прослеживает характер изменения наиболее вероятного значения
случайной величины ?*3' в условном распределении этого признака (при условии
?A) = с) в зависимости от зафиксированного значения с.
Статистическая независимость случайных величин fb&i
...,(* (где признаки ?j могут быть дискретными и непрерывными,
скалярными и векторными) вводится на базе понятия независимости системы
событий (см. A.12) и A.13)). Случайные величины&,&>•- •»& называют
статистически независимыми, если для любых (измеримых) областей их
возможных значений, соответственно А%} А%,..., Л*, имеют место
соотношения
6 Alv{, € Л2,...,& 6 Ак} = Р{& 6 4}...Р{& 6 Ак}. B.14)
В терминах вероятностей Ры2..лк (для дискретных случайных
величин) и плотностей /($, ^)(Л^1\...,Л^) (для непрерывных случайных
величин) условие B.14) может быть записано в виде:
! B.14')
. B.14")
2.6. Основные числовые характеристики
случайных величин
Итак, исчерпывающие сведения об интересующем нас законе
распределения вероятностей можно задать и в виде полигона вероятностей (в
дискретном случае), и в виде функции плотности вероятностей (в общем
случае). Однако при практическом (статистическом) изучении поведения
случайных величин зачастую оказываетсм достаточной гораздо более
скромная информация в виде нескольких числовых характеристик
распределения, позволяющих оценить такие его свойства, как центр
группирования значений исследуемой случайной величины, мера их случайного
рассеивания, степень взаимозависимости различных компонент изучаемого
многомерного признака. Так, например, при изучении закона
распределения заработной платы работников интересуются в первую очередь средней

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 99
заработной платой и одной из мер ее случайного рассеивания —
коэффициентом дифференциации или дисперсией. К тому же подавляющее
большинство используемых в статистических приложениях модельных
законов распределения (биномиальный, пуассоновский, Парето, нормальный,
логарифмически-нормальный, экспоненциальный и др., см. гл. 3) может
быть однозначно восстановлено по одной-двум своим числовым
характеристикам, например по среднему значению и дисперсии.
2.6Л. Понятие о математических ожиданиях и моментах
Будем рассматривать различные функции д(() от исследуемой
случайной величины ( = ?(и>) (в эту схему, очевидно, может быть включен и
частный случай д($) г ?)• Очевидно, и функция д(((ш)) будет случайной
величиной, так как она является в конечном счете функцией, определенной
на множестве элементарных событий и. Результат операции
«осреднения» случайной величины д(()> произведенной с учетом «взвешивания»,
отвечающего заданному распределению вероятностей случайной
величины f, носит название математического ожидания д(() и обозначается
EjfdI. Итак: если ( — непрерывная (может быть, и многомерная)
случайная величина с плотностью (совместной) вероятности /((Л*), то
= f 9(X)f((X) dX B.15)
(интегрирование производится по области всех возможных значений
признака ?); если ? — дискретная случайная величина с возможными
значениями Xi и вероятностями их осуществления р< (г = 1,2,...), то
•*¦ B.15')
Важную роль в теории и практике статистических исследований
играют функции д(() некоторого специального вида: ?*(?) = ?* и #2@ =
1 Если 0@ -- векторнам функция, т.е. д(() = @A)(*)>0C)(О»---»0(р)(О)» то речь
идет о покомпонентном взвешенном осреднении. Общепринятая символика с
использованием буквы Б объясняется тем, что с этой буквы начинается латинское
написание слова «ожидание».
4*

100 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(? - Е?)к (к = 1,2,.. О-1 Математические ожидания функции </*@ и
носят названия соответственно начальных и центральных моментов к-го
порядка случайной величины ?.
Рассмотрим вначале начальные и центральные моменты одномерной
случайной величины ?.
Итак, если для некоторого целого положительного числа к функция
хк интегрируема с весами Д(ж) (суммируема с весами pt) на области
возможных значений ?, то величина
= Г
\
если f непрерывна;
если f дискретна
называется начальным моментом &-го порядка или просто &-м моментом
этого распределения или соответствующей ему случайной величины f, и
мы говорим, что момент конечен или существует.
Очевидно, что если существует момент га*., то существует и цен-
тральный момент
(
— <
(о) _ Р/, \fe _ j J(x ~mi) ft(x) dx, если f непрерывна;
к -»v«-"»i; - ^ ^ / о _ x*
0 l.
i\xi r mi) P*> если С дискретна.
)
Раскрывая (ж - т\) под знаком интеграла (или суммы), легко
установить связи, существующие между центральными и начальными
моментами:
т<°> = 0;
1 Если случайная величина ( многомерна, т.е. ? = (&х\&*\ >•>,&*)), то под 0*(О
?* и gl(() = (( - Е()* мы будем понимать векторные случайные величины,
компоненты которых имеют вид соответственно
где I/ = 1,2,..., р и *i + А?2 + ... + kN = к. Так, например, при А; = 2 в качестве
компонент функции 92@ = €2 могут рассматриваться всевозможные произведения
f@ . ?0), ij = 1,2,... ,р, в том числе, конечно, квадраты (е*1)J, (?<2>J,..., (?<*>J,
а в качестве компонент функции д% (() — всевозможные попарные произведения вида
2 Ниже (см. пп. 3.1.9, 3.1.10, 3.2.2, 3.2.3) будут приведены примеры ситуаций, когда
моменты определенных порядков анализируемой случайной величины не существуют,
т.е. операции интегрирования (суммирования) вида B.16) приводят к «бесконечно
большим» величинам.

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 101
mS0) = m2 - т\\ B.18)
Шд = тз — Зет^тг + 2т?;
(ограничиваемся здесь первыми четырьмя моментами).
Наконец, при исследовании поведения многомерных случайных
величин ? = (С \С г-)Г) важную роль играют р -мерные векторные
функции </(?) = E (?)>••->5 @)> компонентами которых являются
всевозможные попарные произведения центрированных компонент
вектора f, т. е. элементы матрицы
где
Математические ожидания элементов qij принято называть смешан-
ными вторыми центральными моментами или ковариациями
многомерного признака ?, а матрицу
)и=Т?» B-19)
составленную из ковариаций
cov (?«>,?<'>) = Езд = E{tf«> - mi'))(e(i) - !»,«>)} = ay, B.20)
ковариационной матрицей признака ?. По определению, все
ковариационные матрицы являются силсметричньши (т.е. всегда ^;сг;,); нетрудно
показать, что они являются и неотрицательно-определенными.
Действительно, по определению (см. приложение, 2) квадратная (р X р)-матрица
А называется неотрицательно-определенной, если для любого вектора с
действительными компонентами А = (А* , А* ,..., А*р*)т произведение
Ат • А • А будет неотрицательным. Беря последовательность любых
действительных чисел А* ,А*2%...,А и используя тождества
Б
t=i
Е • А, B.21)
t=l
получаем доказательство неотрицательной определенности
ковариационной матрицы S = (tfjj), т.к. левая часть соотношения B.21), очевидно, не
может выражаться отрицательным числом.

102 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.2. Характеристики центра группирования значений
случайной величины
В качестве характеристик центра группирования значений
исследуемого признака в статистической практике используют несколько видов
средних значений, моду и медиану. Опишем эти числовые
характеристики.
Теоретическое среднее Е( исследуемой случайной величины ?
определяется как ее первый начальный момент, или, что то же, как ее
математическое ожидание (см. B.15) и B.16)):
/
х • fz(x) eta, если f непрерывна;
о е B-22)
»>i «Pi, если 4 дискретна.
Среднее значение Е? является, пожалуй, основной и наиболее
употребительной характеристикой центра группирования значений
случайной величины.
Непосредственно из определения среднего значения легко получить
следующие его основные свойства:
а) Ее = с, где с — любая неслучайная величина;
б)
в) * ^
г) Е(? • rj) = Е? • Ет/, если случайные величины ( и г) статистически
взаимно независимы (см. п. 2.5.3).
Среднее геометрическое {теоретическое) значение ??(() случайной
величины ? определяется (для.признаков с положительными возможными
значениями) с помощью формулы
где е « 2,71828... — основание, a In — обозначение натурального
логарифма.
Можно показать, что геометрическое среднее значение G(?) всегда
меньше теоретического среднего Е?.
Геометрическое среднее находит применение цри расчетах темпов
изменения величин и, в частности, в тех случаях, когда имеют дело с
величиной, изменения которой происходят приблизительно в прямо
пропорциональной зависимости с достигнутым к этому моменту уровнем самой
величины (например, численность населения), или же когда имеют дело
со средней из отношений, например, при расчетах «индексов цен».

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 103
Среднее гармоническое значение Я(() случайной величины ?
задается (лишь для признаков с положительными возможными значениями)
соотношением
Гармоническое среднее значение ряда чисел всегда меньше
геометрического среднего значения тех же чисел, а тем более — их среднего
арифметического. Область его применения весьма ограничена. В экономике, в
частности, пользуются иногда гармоническим средним при анализе
средних норм времени, а также в некоторых видах индексных расчетов.
Модальное значение (или просто мода) xmod случайной величины
определяется как такое возможное значение исследуемого признака, при
котором значение плотности Д(ж) (в непрерывном случае) или
вероятности р{? = х} (в дискретном случае) достигает своего максимума. Таким
образом, мода представляет собой как бы наиболее часто
осуществляющееся (в экспериментах или наблюдениях), наиболее типичное
значение случайной величины, т. е. значение, которое действительно является
«модным» .
Медиана хтед исследуемого признака определяется как его средневе-
роятное значение, т. е. такое значение, которое обладает следующим
свойством: вероятность того, что анализируемая случайная величина
окажется больше zmed) равна вероятности того, что она окажется меньше xmed.
Для обладающих непрерывной плотностью непрерывных случайных
величин, очевидно,
и медиану можно определить как такое значение gme<j на оси возможных
значений (оси абсцисс), при котором прямая, параллельная оси ординат
и проходящая через точку жте<ь Делит площадь под кривой плотности на
две равные части (рис. 2.7). В некоторых случаях дискретных
распределений может не существовать величины, точно удовлетворяющей
сформулированному требованию. Поэтому для дискретных случайных величин
1 Мода является естественной характеристикой центра группирования значений
случайной величины лишь в случаях так называемых одновершинных (одномодальных)
распределений. Многовершинные (многомодальные) распределения
свидетельствуют о существенной неоднородности исследуемой совокупности. Их изучение
представляет интерес в первую очередь с точки зрения задач классификации объектов и
наблюдений (см. гл. 12).

104
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
медиану можно определить как любое число xmed, лежащее между двумя
соседними возможными значениями x°io и ж?0+ь такими, что
«mod^med
Рис. 2.7. Характер расположения моды xmod > медианы xmed и среднего
значения Е( для некоторой асимметричной плотности распределения
В случае симметричной плотности (или полигона распределения)
среднее Е?, мода xmod и медиана xmed совпадают между собой. Для
асимметричных распределений это не так (см. рис. 2.7).
2.6.3. Характеристики степени рассеяния значений
случайной величины
Каждая из описанных ниже характеристик степени рассеяния —
дисперсия, среднеквадратическое отклонение и коэффициент вариации —
дает представление о том, как сильно могут отклоняться от своего центра
группирования значения исследуемой случайной величины. Бели говорить
о форме кривой плотности, то эти характеристики описывают степень ее
«размазанности» по всему диапазону изменения ?: чем больше
величина каждой из этих характеристик, тем более «размазанным» выглядит
соответствующее распределение (рис. 2.8).
Дисперсия D? случайной величины ? определяется как ее второй
центральный момент, т.е.
/ (х - Ef J/е(х) dx, если ? непрерывна;
2 . B.23)
а:^ - EfJpi,
если
дискретна.

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
105
1,0 ^
-6-5-4-3-2-1 0 12 3 4 5 6
Рис. 2.8. График плотностей (нормальных законов распределения) с
различными значениями дисперсии и с одинаковым (нулевым)
средним значением
Из определения дисперсии (и из свойств математического ожидания)
можно вывести следующие ее свойства:
а) Dc = 0 (с — некоторая неслучайная величина);
б) D(cO = c2?>f;
в) D(a + 6f) = b • Df (a и b — некоторые неслучайные величины);
г) D(? + rjj) = Df + Dty — в случае, когда ? и г/ являются взаимно
независимыми.
Часто для обозначения дисперсии используют греческую букву
«сигма» (в квадрате), т.е. записывают а^ = Df.
Среднеквадратическое отклонение сг^ получается из дисперсии
извлечением квадратного корня а^ = \/Щ- Оно используется наряду с
дисперсией для характеристики степени рассеивания случайной
величины и оказывается в ряде случаев более удобным и естественным, в первую
очередь, из-за своей однородности (в смысле единиц измерения) с
различными характеристиками центра группирования.
Коэффициент вариации V^ используется в тех случаях, когда
степень рассеивания естественнее описывать некоторой относительной
характеристикой в сопоставлении со средним. В частности,
100% =
100%,
т. е. коэффициент вариации — это отношение (в процентах) среднеквадра-
тического отклонения к соответствующему математическому ожиданию.
Из определения ясно, что V^ — величина безразмерная.

106 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.4. Квантили и процентные точки распределения
При использовании различных методов математической статистики,
особенно разнообразных статистических критериев (см. гл. 8) и методов
построения интервальных оценок неизвестных параметров (см. гл. 7),
широко используются понятия ^-квантилей uq(F) и ЮОф-процентных точек
ug(F) распределения F(x).
Квантилем уровня q (или q-квантилем) непрерывной случайной
величины {, обладающей непрерывной функцией распределения F(x),
называется такое возможное значение uq(F) этой случайной величины, для
которого вероятность события ? < uq(F) равна заданной величине q, т.е.
П*щ) = Pit < «t > = «• B.24)
Очевидно, чем больше заданное значение q @ < q < 1), тем больше
будет и соответствующая величина квантиля ия. Частным случаем
квантиля — 0,5-квантилем является характеристика центра группирования —
медиана.
Для всякой дискретной случайной величины функция распределения
F$(x) с увеличением аргумента х меняется, как мы видели, скачками,
и, следовательно, существуют такие значения уровней д, для каждого из
которых не найдется возможного значения uq, точно удовлетворяющего
уравнению B.24). Поэтому в дискретном случае д-квантиль определяется
как любое число uq(F)> лежащее между двумя возможными соседними
значениями x\q) и я?(*)+ъ такое, что F(x\q)) < q> но F(x\q)^) > q.
Часто вместо понятия квантиля используют тесно связанное с ним
понятие процентной точки. Под 100?%-ной точкой случайной величины
f понимается такое ее возможное значение uq, для которого вероятность
события ? > ия равна q, т. е.
Для дискретных случайных величин это определение корректируется
аналогично тому, как это делалось при определении квантилей.
Из определения квантилей и процентных точек вытекает простое
соотношение, их связывающее:
«f =wd-f). B.25)
Для ряда наиболее часто встречающихся в статистической практике
законов распределения (см. гл. 3) составлены специальные таблицы квантилей
и процентных точек. Очевидно, достаточно иметь только одну из таких

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
107
таблиц, так как если, например, по таблицам процентных точек
требуется найти 0,9-квантиль нормального распределения, то следует искать, в
соответствии с B.25), 10-процентную точку того же распределения.
Наглядное геометрическое представление о смысле введенных
понятий дает рис. 2.9: на этом рисунке q\ = /^ Д(з) dx\ q% = /J° f((x) dx, a
по оси Оу откладываются значения функции плотности f((x).
-3 -2 -1
Рис. 2.9. Геометрическое пояснение смысла gi-квантиля иЯ1 и
процентной точки шЯ2\ случай стандартного нормального
распределения, q\ зз 0,25 (соответственно «о,25 = —0,675) и q% = 0,05
(соответственно и/о,о5 = 1,65)
Квантильные характеристики помимо своей основной роли
вспомогательного теоретического статистического инструментария порой играют
самостоятельную роль основных характеристик изучаемого закона
распределения или содержательно интерпретируемых параметров модели.
Так, широко распространенной характеристикой степени случайного
рассеяния при изучении законов распределения заработной платы и доходов
являются так называемые квантильные {уровня q) коэффициенты
дифференциации K^q), которые определяются соотношением
K*{q) =
Ua
0,25)
(наиболее распространенными среди них являются децильные
коэффициенты дифференциации, когда полагают q = 0,1). При анализе модельных
законов распределения квантили и процентные точки используют также
для обозначения практических границ диапазона изменения исследуемого
признака: так, например, квантилями уровня 0,005 и 0,995 иногда
определяют соответственно минимальный и максимальный уровни заработной
платы работников в соответствующей системе показателей.

108 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.5. Асимметрия и эксцесс
Обращаясь к формуле B.17), определяющей центральные моменты
распределения, легко понять, что если плотность /$(ж) (или
последовательность вероятностей Р{? = ж?}) симметрична относительно среднего
значения тп\ = Е? (т. е. f{rn\ — х) = /(mi + ж)), то все нечетные
центральные моменты (если они существуют) w4j/+1 равны нулю. Поэтому любой
нечетный, не равный нулю, момент можно рассматривать как
характеристику асимметрии соответствующего распределения. Простейшая из
этих характеристик т$ и взята за основу вычисления так
называемого коэффициента асимметрии Р\ — количественной характеристики
степени скошенности распределения
( '
Нормировка с помощью деления Шд на {гщ )* введена для того,
чтобы эта характеристика не зависела от выбора физических единиц
измерения исследуемой случайной величины: формула B.26) определяет
безразмерную характеристику степени скошенности распределения,
инвариантную относительно физических единиц измерения f.
Таким образом, все симметричные распределения будут иметь
нулевой коэффициент асимметрии (см. рис. 2.5, 2.8, 2.9), в то время как
распределения вероятностей с «длинной частью» кривой плотности,
расположенной справа от ее вершины, характеризуются положительной
асимметрией (см. рис. 2.7), а распределения с «длинной частью» кривой
плотности, расположенной слева от ее вершины, обладают отрицательной
асимметрией.
Поведение плотности (полигона) распределения в районе его
модального значения обуславливает геометрическую форму соответствующей
кривой в окрестности точки ее максимума, ее островершинность.
Количественная характеристика островершинности — эксцесс (или
коэффициент эксцесса) /32 оказывается полезной характеристикой при решении
ряда задач, например при определении общего вида исследуемого
распределения или при его аппроксимации с помощью некоторых специальных
разложений. Эта характеристика задается с помощью соотношения
Ниже мы увидим, что своеобразным началом отсчета в измерении
степени островершинности служит нормальное (гауссовское) распределение,

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
для которого 02 = 0.
f/M
109
Рис. 2.10. Примеры плотностей для положительной, отрицательной и
нулевой характеристик островершинности (эксцесса)
Как правило, распределения с более высокой и более острой вершиной
кривой плотности (полигона) имеют положительный эксцесс, а с менее
острой — отрицательный (рис. 2.10I.
2.6.6. Основные характеристики многомерных
распределений (ковариации, корреляции, обобщенная
дисперсия и др.)
Бели при описании поведения одномерных и в какой-то мере
двумерных случайных величин исследователь еще имеет практически
реализуемые возможности использования подходящих модельных законов
распределения (см. гл. 3), то при исследовании признаков ? = (?* \? ',..., ?*р')
размерности большей, чем два (р > 2), как правило, приходится
ограничиваться лишь той информацией, которую ему доставляет знание первых
двух моментов: вектором средних значений
B.28)
1 Правда, можно построить примеры, свидетельствующие о нарушении этой общей
закономерности.

ПО ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
и матрицей ковариаций
*П *П у °2р 1 B29)
где средние значения т[^ компонент ^(|) определяются в соответствии с
формулой B.22) с использованием одномерных частных плотностей
(полигонов) распределения случайных величин (' , а ковариаций а^ =
Е{(?^ - и4^)(|^ - т^)} подсчитываются с использованием
соответствующих двумерных частных плотностей (полигонов) распределения
пары случайных величин (?,?).
Как и в одномерном случае, вектор средних значений является
основной характеристикой центра группирования наблюдений исследуемого
многомерного признака | (в соответствующем р-мерном пространстве ее
возможных значений).
Матрица ковариаций ? характеризует следующие свойства
исследуемого многомерного признака.
1. Степень случайного разброса отдельно по каждой компоненте и
в целом по многомерному признаку. Легко видеть, что диагональные
элементы <гц матрицы ? определяют частные дисперсии компонент ? , т.е.
степень случайного разброса значений одномерной случайной величины
@. Итак,
Многомерным аналогом дисперсии является величина определителя
ковариационной матрицы, называемая обобщенной дисперсией
многомерного случайного признака ( :
Do6{ = det (X2). B.30)
Часто используется и другая характеристика степени случайного
рассеяния значений многомерной случайной величины — так называемый
след ковариационной матрицы ?, т.е. сумма ее диагональных элементов:
tr (S) = (Гц + (Таз + ... + <7рР. B.31)
1 Мы придерживаемся распространенных матричных обозначений: det (А) или \Л\ —
определитель или детерминант (determinant, англ.) матрицы A; tr(A) — след (trace,
англ.) матрицы А.

2.6 ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 111
Из неотрицательной определенности матрицы ? (см. п. 2.6.1) и
смысла диагональных элементов <тц следует, что величины, определенные
соотношениями B.30) и B.31), всегда неотрицательны.
Поясним геометрический смысл обобщенной дисперсии. Можно
сказать, что если, например, исследуемый многомерный признак подчинен
нормальному закону распределения (см. гл. 3), то для любого заданного
уровня вероятности Ро объем области (окружающей центр группирования
Мг), вероятность попадания в которую значений анализируемой
случайной величины ( равна Ро, пропорционален y/D0^ (этот объем
пропорционален также некоторому множителю, зависящему от размерности р, и
пропорционален, кроме того, некоторому числу, определяемому в
зависимости от заданного уровня вероятности Pq).
Характер и структура статистических взаимосвязей,
существующих между компонентами анализируемого многомерного признака,,
также могут быть описаны с помощью ковариационной матрицы. Однако
в этом случае удобнее перейти к определенным образом нормированной
ковариационной матрице, называемой корреляционной, а именно к
матрице
(Гц fj2 ¦¦• Г1р
Г!1 Г22 ... Г2р
х Гр2 ... Грр
где элементы rjk получаются из элементов crjk с помощью нормировки
Характеристики г;> называются коэффициентами корреляции
между случайными величинами ("' и ? , являются измерителями степени
тесноты линейной статистической связи между этими признаками и
обладают следующими свойствами:
а) -1 < rjk < 1, что следует непосредственно из неравенств
б) максимальная степень тесноты связи соответствует значениям
коэффициента корреляции, равным +1 или -1, и достигается либо при
измерении связи признака с самим собой (тогда, очевидно, rjj si), либо при
наличии линейной функциональной связи между ?"' н ( у т.е. в случае

112 ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
^ = &о + Ьг^к\ где &о и Ъ\ — некоторые постоянные величины (при этом
если Ь\ > О, то связь называется положительной, а если Ь\ < О, то связь
называется отрицательно^
в) если случайные компоненты f'J' и {* ' статистически независимы,
то rjk = 0 (следует непосредственно из того факта, что для независимых
случайных величин ?(i) и ?{к) E(f(i) • ?(к)) = (E?(j))(Ef(fc))). Обратное
утверждение (из г^ = 0 следует независимость ?'" и ?* ') верно лишь для
некоторых частных случаев (например, для нормально распределенных
пар (С ,? )) и неверно в общем случае.
ВЫВОДЫ
1. Случайная величина (случайный признак) определяет перечень
показателей — количественных, ординальных (порядковых) или
номинальных (классификационных), которые подлежат статистическому
исследованию в ходе проводимых случайных экспериментов (наблюдений).
2. «Возможные значения» случайной величины определяются
природой и составом пространства элементарных событий п: каждому
элементарному исходу и соответствует «возможное значение» х(и)
исследуемой случайной величиной величины ?, поэтому последнюю можно
определить как функцию ? = €(<*>)) заданную на множестве элементарных
событий.
3. Закон распределения вероятностей исследуемой случайной
величины позволяет сопоставлять с любой измеримой областью АХ
возможных значений вероятность р(АХ) события, заключающегося в том, что
реализовавшееся в результате случайного эксперимента (наблюдения)
значение данной случайной величины окажется принадлежащим этой
области, т. е.
4. Для описания закона распределения вероятностей многомерного
признака ? = (f* ',.. .,?1 ') могут, как и в одномерном случае,
использоваться функция распределения />(жA\.. .,&(р)) = Р{?(г) < жA),.. .,?(р) <
х{р)} и функция плотности Д(жA)...а:(р)) = dpF((x{l\...,x(p))/dx{1\
1 Помимо числовой (скалярной) формы эти «возможные значения» могут быть
представлены и в векторной, и в матричной форме и, более того, могут быть определены
в пространстве самой общей природы (в зависимости от сущности и целей
исследуемого случайного эксперимента).

выводы 113
...,е?ж . Однако в отличие от одномерного случая исчерпывающей
формой задания многомерного закона распределения является только
совместная функция плотности вероятности.
5. Зная совместный закон распределения многомерной случайной
величины ? = (?,?,...,?)» можно получить частный (маржиналь-
ный) закон распределения любого подвектора ft = (?,f ,...,?), 1 <
iq ^ р, 1 ^ к < р, а также условный закон распределения, описывающий -
распределение любого подвектора ft, когда все или какая-то часть
остальных компонент исходного векторного признака фиксируются на заданных
уровнях (см. B.12) и B.13)).
в. Если компоненты ?* , f ,..., ?^р' анализируемого случайного
признака f = (?,...,?) статистически независимы, то многомерный
закон распределения Д(ж ,.. .,гр') может быть описан р частными
одномерными законами, так как в этом случае по определению
7. При практическом изучении поведения исследуемого случайного
признака ? зачастую оказывается достаточным знания ограниченного
набора его числовых характеристик: среднего значения Eft дисперсии D?,
коэффициентов асимметрии и эксцесса (ft и А), а в многомерном
случае — еще элементов а$ь ковариационной матрицы Е.

ГЛАВА 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ
РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ
СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
Говоря о распространенности той или иной модели распределения в
практике статистических исследований, следует иметь в виду две
возможные роли, которые эта модель может играть. Первая из них заключается
в адекватном описании механизма исследуемого реального процесса^
генерирующего подлежащие статистическому анализу исходные
статистические данные. В этом случае выбранная по тем или иным соображениям
(или выведенная теоретически) модель описывает закон распределения
вероятностей непосредственно анализируемой и имеющей четкую
физическую интерпретацию случайной величины (заработной платы
работника, дохода семьи, числа сбоев автоматической линии в единицу времени,
числа дефектных изделий, обнаруженных в проконтролированной партии
заданного объема, и т.д.). Подходы к построению таких моделей, методы
их анализа и обоснования относятся к области «реалистического» (или
содержательного) моделирования.
Другая роль широко распространенных в статистических
исследованиях моделей — использование их в качестве вспомогательного
технического средства при реализации методов статистической обработки
данных. С помощью моделей этого типа описываются распределения
вероятностей некоторых вспомогательных функций от исследуемых
случайных величин. Эти функции используются при построении разного рода
статистических оценок и статистических критериев (о способах
построения оценок и критериев см. главы 6-8). К распределениям этого типа
относятся в первую очередь распределения «хи-квадрат», Стьюдента (t-
распределение) и F-распределение.
Этой условной классификации распределений мы и будем
придерживаться при изложении содержания данной главы.

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГБНБЗИСА ДАННЫХ 115
3.1. Законы распределения, используемые
для описания механизмов генерации
реальных социально-экономических
данных
3.1.1. Распределения, возникающие при анализе
последовательности испытаний Бернулли:
биномиальное и отрицательное биномиальное
Широкий класс случайных величин, которые приходится изучать в
практике статистических исследований, индуцируется
последовательностью независимых случайных экспериментов следующего типа: в
результате реализации каждого случайного эксперимента (наблюдения)
некоторое интересующее нас событие А может произойти (с некоторой
вероятностью р) или не произойти (соответственно с вероятностью q = 1 - р); при
многократном (m-кратном) повторении этого эксперимента верожтность
р осуществления события А остается одной и той асе, а наблюдения,
составляющие эту последовательность экспериментов, являются
взаимно независимыми. Серию экспериментов подобного типа принято
называть последовательностью испытаний Бернулли, Можно описать эту
последовательность в терминах случайных величин, сопоставляя с г-м по
счету экспериментом данной последовательности случайную величину
_ f 1, если событие А произошло;
, если событие А не произошло.
Тогда «бернуллиевость» последовательности fi,{2,...,fm означает, что
Р{& = 1} = Р{$2 = 1} = • • • = Р{?т = 1} = Р> причем случайные величи-
ны ?ь?ь'">?т статистически независимы (определение статистической
независимости случайных величин дано в п.2.5.3).
При определенных (как правило, приблизительно соблюдающихся на
практике) условиях в схему испытаний Бернулли хорошо
укладываются такие случайные эксперименты, как бросание монеты или игральной
кости, проверка (по альтернативному признаку) изделий массовой
продукции, обращение к «обслуживающему устройству» (с исходами
«свободен — занят»), попытка выполнения некоторого задания (с исходами
«выполнено — не выполнено»), стрельба по цели (с исходами
«попадание — промах») и т. п.
«Единичное» испытание Бернулли можно интерпретировать и как
извлечение объекта из воображаемой бесконечной совокупности, в которой
доля р объектов обладает некоторым интересующим нас свойством. Тогда

116 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
интересующее нас событие А заключается в том, что при этом извлечении
мы «вытащим» один из объектов, обладающих упомянутым свойством.
Биномиальный закон описывает распределение случайной
величины Ур{т) = & + & + V fm) T-e- числа появления интересующего нас
события в последовательности из га независимых испытаний, когда
вероятность появления этого события в одном испытании равна р.
Из определения биномиальной случайной величины следует, что ее
возможными значениями являются все целые неотрицательные числа от
нуля до га. Для вывода вероятностей P{vp(m) = х} (х = 0,1,2,..., га)
рассмотрим внимательнее пространство элементарных событий,
порожденное последовательностью испытаний Бернулли. Очевидно, каждому
элементарному событию и соответствует последовательность из нулей и
единиц длины га
S (ш\ S (ш} 8 (ш\ (*\ 2^
Разобьем эти последовательности на классы, включая в один (х-й) класс
все последовательности типа C.2), содержащие одинаковое число х
единиц:
х =
= k:
Имея в виду, что число N(x) элементарных событий в классе с
номером х равно числу сочетаний из т элементов по х (поскольку х единиц
можно разместить на m местах именно таким числом различных
способов), а также тот факт, что вероятность осуществления любого
элементарного исхода, входящего в класс с номером х, равна, как нетрудно под-

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
считать, величине рх{\ — р)т~х, получаем
117
Это и есть формула (аналитическая запись, модель) биномиального
0
0
0
0
i
,4
,3
,2
,1
(m)
= *}
p = 0,2
1 . .
p{vv{m) = х)
а)
0,4
0,3
0,2
0,1
0123456789 10'
0123456789 10'
Рис. 3.1. Полигон вероятностей биномиального распределения для
различных значений р и т = 10: а) р = 0,2; т = 10; р = 0,5; т = 10
закона распределения (см. рис. 3.1). Подсчет его основных числовых
характеристик (который в данном случае легче реализовать, не используя
прямые формулы типа B.17)—B.18), а опираясь на соотношение ир(т) =
fi + h fm> взаимную независимость & и простоту вычисления их
моментов) дает:
М0Д:
среднее:
мода х
дисперсия:
асимметрия:
эксцесс:
Ej/p(m) = mp;
p(m + 1) - 1 < хМОп < p(m + 1);
1 Далее используется одно из широко используемых обозначений для числа сочетаний
из т элементов по я, а именно С?.
2 «Биномиальным» этот закон называется потому, что правая часть C.3)
представляет собой х-й член биномиального разложения (р + A — р))т. Этот же факт позволяет
легко проверить соблюдение аксиомы о нормировке вероятностей, т.е. справедли-
m
вость тождества J2 CmPx(l —p)™'* s 1.
?=0

118 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Биномиальное распределение широко используется в теории и
практике статистического контроля качества продукции, при описании
функционирования систем массового обслуживания, в теории стрельбы и в других
областях практической деятельности.
Отрицательный биномиальный закон описывает распределение
случайной величины Vp{k)> определяемой испытаниями Бернулли ?ь 6,...
(см. C.1)) следующим образом:
Другими словами Vp(k) — это число испытаний в схеме Бернулли (с
вероятностью р появления интересующего нас события в результате
проведения одного испытания) до k-го появления интересующего нас события
(включая последнее испытание). Нетрудно вывести аналитический вид
распределения случайной величины Vp(k). Зафиксируем любое ее
возможное значение х. Из того, что при числе испытаний fp(k) = x впервые
осуществилось заданное число к появлений интересующего нас события,
следует, что на предыдущем шаге, т. е. при числе испытаний, равном ж — 1,
мы имели к — 1 появлений того же события. Следовательно, опираясь
на теорему умножения вероятностей, мы можем выразить вероятность
Р{у~(к) = х} в терминах вероятностей, связанных с поведением
биномиальных случайных величин ир{х — 1) и i/p(l), а именно:
р{р;(к) = х} = р{ир(х -1) = * -1}
= 1}
C.4)
кх-k
0,2
0,1
0
= 0,б
I...
2 4 6 8 10 12
0,2
0,1
7 о
5 7 9 И 13 15 17 19
Рис. 3.2. Полигон вероятностей отрицательного биномиального закона
распределения для различных значений А; при р = 0,5

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 119
Название данного закона объясняется тем, что правые части C.4)
являются последовательными членами разложения некоторого бинома с
отрицательным показателем. Соответствующий C.4) полигон
вероятностей изображен на рис. 3.2.
Основные числовые характеристики закона:
среднее: Ej/p(k) = —;
дисперсия: Di/p {k) ~
2 »
Р
2-р
асимметрия: /3\ =
л 1
эксцесс: 02 =
Модель отрицательного биномиального распределения применяется в
статистике несчастных случаев и заболеваний, в задачах, связанных с
анализом количеств индивидуумов данного вида в выборках из
биологических совокупностей, в задачах оптимального резервирования элементов,
в теории стрельбы.
3.1.2. Гипергеометрическое распределение
В одном из вариантов интерпретации биномиальной случайной
величины ир{т) мы рассматривали некоторую воображаемую бесконечную
совокупность, доля р объектов которой обладает интересующим нас
свойством. Тогда ур{т) означает число объектов, обладающих этим
свойством среди т объектов, случайно извлеченных из данной совокупности.
Гипергеометрическую случайную величину vM N{m) можно считать
модификацией биномиальной случайной величины vp(m), приспособленной
к случаю конечной совокупности, состоящей из N объектов, среди
которых имеются М объектов с интересующим нас свойством. Иначе говоря,
им /v(m) — это число объектов, обладающих заданным свойством среди
т объектов, случайно извлеченных (без возвращения) из совокупности N
объектов, М из которых обладают этим свойством. Очевидно,
возможными значениями случайной величины vM N(m) будут все целые
неотрицательные числа от max{0,m - (N - М)} до min{m,M}. Для вывода
аналитического вида ее закона распределения подсчитаем вероятность
события \ум N(m) — х] как отношение числа всевозможных выборок объема
т, приводящих к осуществлению этого события (числа «благоприятных»

120 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
исходов), к общему числу способов, которыми можно выбрать т объектов
из N (к числу всех возможных исходов). Очевидно, каждому набору из
х объектов с заданным свойством соответствует С^м спос°бов,
которыми можно отобрать остальные т — х объектов из числа объектов, не
обладающих этим свойством. А поскольку такие наборы из х объектов
с заданным свойством можно сформировать С*м различными способами,
то общее число «благоприятных» (для события \ум N(m) = x}) исходов
будет C]vfC/y-Af* Учитывая> что число всех возможных исходов, т.е. всех
возможных способов, которыми можно извлечь га объектов из N
предложенных, равно Cj?, получаем
C.5)
Этот закон широко используется в практике статистического
приемочного контроля качества промышленной продукции, а также в различных
задачах, связанных с организацией выборочных обследований.
Его основные числовые характеристики:
М
среднее: шм N{m) = я*—;
. _ , ч М Л М\ / га\
дисперсия: Di/^^(га) = га^—^ ^1 - —) [I - -) ;
(N-
асимметрия: р
эксцесс: /
где
ci(N) =
(N-2)(N-3)(N-m)}
(N-
(N-2)(N-Z)(N-m)'
«W^L-W-W-m)-^

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 121
- 2)(N - 3) (N - 2)(ЛГ -
- l)iVm
При N -+ ос правая часть C.5) стремится, как и следовало ожидать, к
выражению для биномиального закона распределения C.3), и соответственно
среднее значение, дисперсия, асимметрия и эксцесс гипергеометрического
распределения сходятся к аналогичным числовым характеристикам
биномиально распределенной случайной величины (что легко устанавливается
с помощью соответствующего предельного перехода).
3.1.3. Распределение Пуассона
Если нас интересует число наступлений определенного случайного
события за единицу времени, когда факт наступления этого события в
данном эксперименте не зависит от того, сколько раз и в какие моменты
времени оно осуществлялось в прошлом, и не влияет на будущее, а
испытания производятся в стационарных условиях, то для описания
распределения такой случайной величины обычно используют закон Пуассона
(данное распределение впервые предложено и опубликовано этим ученым в
1837 г.). Этот закон можно также описывать как предельный случай
биномиального распределения, когда вероятность р осуществления
интересующего нас события в единичном эксперименте очень мала, но число
экспериментов ш, производимых в единицу времени, достаточно велико,
а именно такое, что в процессе р —> 0 и т —> оо произведение тр
стремится к некоторой положительной постоянной величине Л (т.е. тр —> Л).
Поэтому закон Пуассона часто называют также законом редких событий.
Обозначим пуассоновскую случайную величину ^о(оо) или просто i/0 (имея
в виду предельный переход от биномиальной случайной величины vv{m)
по р —> О и т —> оо) и выведем ее закон распределения:
Р{уо = ж} = lim P\Vp{m) = я?} = limCmp A — р)
„ т(т- 1)...(т-ж + 1) А* / XV
= Ьт —i '-—р L— 1 1
xl т \ т)
m

122 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
х!
(я = 0,1,2,...).
C.6)
Как видим, закон распределения Пуассона зависит от единственного
параметра Л, содержательно интерпретируемого как среднее число
осуществления интересующего нас события в единицу времени (см. рис. 3.3).
0,4
0,3
0,2
0,1
p{vo = х}
А=1
0
0,4.
0,3
0,2
0,1
2 3
tf
р{щ = х)
А = 4
i
11111... ,,
0123456789 10
Рис. 3.3. Полигон вероятностей пуассоновского закона распределения для
различных значений Л
С помощью «прямого счета» по формулам B.17)-B.18) могут быть
подсчитаны основные числовые характеристики пуассоновской случайной
величины:
среднее: Ещ = Л;
дисперсия: Ъщ = А;
асимметрия: /Зг =
эксцесс: р2 = -г-
Пуассоновская случайная величина используется для описания числа
сбоев автоматической линии или числа отказов сложной системы
(работающих в «нормальном» режиме) в единицу времени; числа «требований
на обслуживание», поступивших в единицу времени в систему
массового обслуживания; статистических закономерностей несчастных случаев и
редких заболеваний.
Привлекательные прикладные свойства этого закона не
исчерпываются вычислительными удобствами и лаконичностью формулы C.6)
(модель зависит всего от одного числового параметра А!). Оказывается, эта

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 123
модель остается работоспособной и в ситуациях, отклоняющихся от
вышеописанной схемы ее формирования. Например, можно допустить, что
разные бернуллиевские испытания имеют разные вероятности осуществления
интересующего нас события РъРг* •••>?*»• В этом случае биномиальный
закон применительно к такой серии испытаний уже не может быть
применен, в то время как выражение C.6) остается приблизительно
справедливым и дает достаточно точное описание распределения интересующей
нас случайной величины, если только в него вместо Л = тр доставить
величину А = тр, где р= (р\-\ \-Рт)/т- Сказанное означает, что можно
предположить, что анализируемая совокупность состоит из смеси
множества разнородных подсовокупностей, таких, что при переходе из одной
подсовокупности в другую меняется доля р содержащихся в них объектов
с заданным свойством, а следовательно, меняется и среднее число А
осуществления интересующего нас события в единицу времени. Можно далее
показать, что если вместо использования среднего значения этих р (или А)
(при котором мы остаемся в рамках модели C.6)) ввести в рассмотрение
закон распределения меняющегося параметра А, интерпретируемого как
случайная величина, то мы придем к другому, но в определенном смысле
близкому к пуассоновскому закону распределения. Так, например, если
предположить, что функция плотности распределения случайного
параметра А имеет вид
где Г(Л) = J х ~ е xdx — гамма-функция Эйлера, положительные числа
о
к и р — параметры закона, а х > 0 — возможные значения А, число
осуществления (в единицу времени) интересующего нас события будет
подчинено известному нам отрицательному биномиальному закону C.4)
(подробнее о распределении f\(x) см. в п. 3.2.5).
3.1.4. Полиномиальное (мультиномиальное) распределение
Полезным обобщением биномиального распределения на случай
более чем двух возможных исходов является подиномиальный
(мультиномиальный) закон распределения. Можно интерпретировать анализируемую
в этом случае ситуацию таким образом, что мы имеем дело с
некоторой бесконечной совокупностью, содержащей объекты / различных типов
(/ ^ 2), представленных соответственно в долях РъРг> •••>?/ (в
биномиальной генеральной совокупности мы имели / = 2, рг = р и р2 = 1 - р).
Таким образом, в результате одного случайного эксперимента (случай-

124 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
ного извлечения объекта из этой бесконечной совокупности) объект
типа j появляется с вероятностью pj. Нас будет интересовать
распределение многомерной случайной величины (i/? (m),j/p (rft),l ..,i/p (иг)),
порожденной m-кратным случайным экспериментом (т.е. извлечением m
объектов), где i/p(m) — число объектов j-ro типа, оказавшихся в этой
выборке, а р = (jpi,p2j • • • ,Pi) (очевидно ? рj = 1 и ?) и?}(т) = ш).
ii ii
Соответствующее многомерное дискретное распределение
описывается выражением (доказывается прямым вероятностным рассуждением)
т!
4() }
! „(I) *«> C.7)
где ar1 •, or ,..., ar ' — любые (заданные) целые неотрицательные числа,
подчиненные условию ]Г) х = т, а выражение C.7) определяет вероят-
ность того, что среди m извлеченных объектов оказалось ровно аг ' объ-
B)
ектов 1-го типа, хк } объектов 2-го типа и т. д. Можно также связывать
полиномиальную случайную величину с т-кратным случайным
экспериментом, каждый из которых может закончиться одним из / возможных
исходов А\, Л2,..., Aiy причем вероятность исхода Aj в единичном
эксперименте равна pj.
Название распределения объясняется тем, что выражение C.7)
является общим членом разложения многочлена (полинома) (pi+РгН l"P/)m*
Вектор средних значений (Е^р (т),..., Ei/р (т)) и ковариации (Г,* =
Е{(г/р^(т) - Ei/^(m))(i/^(m) - Е^(т))} компонент исследуемой
многомерной случайной величины определяются соотношениями:
средние: Ei/p (m) = mpj\ j = 1,2,...,/;
дисперсии: bvp(m) = ог^ = mp^l -Pj), i = 1,2,...,/;
ковариации: ajk = -тр5рк\ j,k = 1,2,...,/, jV Л.
Полиномиальное распределение применяется главным образом при
статистической обработке выборок из больших совокупностей, элементы
которых разделяются более чем на две категории (например, в
различных социологических, эрономико-социологических, медицинских и других
выборочных обследованиях).

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 125
3.1.5. Нормальное (гауссовское) распределение
Это распределение занимает центральное место в теории и практике
вероятностно-статистических исследований. В качестве непрерывной
аппроксимации к биномиальному распределению оно впервые
рассматривалось А. Муавром еще в 1733 г. (см. ниже теорему Муавра-Лапласа, п. 4.3).
Некоторое время спустя нормальное распределение было снова открыто и
изучено независимо друг от друга К.Гауссом A809 г.) и П.Лапласом
A812 г.). Оба ученых пришли к нормальному закону в связи со своей
работой по теории ошибок наблюдений. Идея их объяснения механизма
формирования нормально распределенных случайных величин
заключается в следующем. Постулируется, что значения исследуемой непрерывной
случайной величины формируются под воздействием очень большого
числа независимых случайных факторов, причем сила воздействия каждого
отдельного фактора мала и не может превалировать среди остальных,
а характер воздействия — аддитивный (т.е. при воздействиии
случайного фактора F на величину а получается величина a + A(F), где
случайная «добавка» A(F) мала и равновероятна по знаку . Можно показать,
что функция плотности распределения случайных величин подобного типа
имеет вид
2
где а и а — параметры закона, интерпретируемые соответственно как
среднее значение и дисперсия данной случайной величины (в виду
особой роли нормального распределения мы будем использовать специальную
символику для обозначения его функции плотности и функции
распределения).
Соответствующая функция распределения нормальной случайной
величины ?(а,<т ) обозначается Ф(х; ауа ) и задается соотношением
Ф(х;
Условимся называть нормальный закон с параметрами а = 0 и
а2 = 1 стандартным, а его функции плотности и распределения
обозначать соответственно (р(х) = (р(х\ 0,1) и Ф(х) = Ф(ж; 0,1). Соответственно
1 Строгая теоретическая формализация этих условий содержится, например, в
центральной предельной теореме, см. п. 4.3.

126 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
нормальный э.р.в. с произвольными значениями параметров а и а3 будем
называть (а, а ) нормальным.
Во многих случайных величинах, изучаемых в экономике, технике,
медицине, биологии и в других областях, естественно видеть суммарный
аддитивный эффект большого числа независимых причин. Но
центральное место нормального закона не следует объяснять его универсальной
приложимостью, как это было принято долгое время (по-видимому, под
влиянием выдающихся работ К. Гаусса и П.Лапласса).
В этом смысле нормальный закон — это один из многих типов
распределения, имеющихся в природе, правда, с относительно большим
удельным весом практической приложимости. И потому нам понятна ирония,
звучащая в известном высказывании Липмана (цитируемом А. Пуанкаре в
своем труде «Исчисление вероятностей», Париж, 1912 г.): «Каждый
уверен в справедливости нормального закона; экспериментаторы — потому,
что они думают, что это математическая теорема; математики — потому,
что они думают, что это экспериментальный факт».
Однако не следует упускать из виду, что полнота теоретических
исследований, относящихся к нормальному закону, а также сравнительно
простые математические свойства делают его наиболее привлекательным
и удобным в применении. Лаже в случае отклонения исследуемых
экспериментальных данных от нормального закона существуют по крайней
мере два пути его целесообразной эксплуатации: а) использовать его в
качестве первого приближения; при этом нередко оказывается, что подобное
допущение дает достаточно точные с точки зрения конкретных целей
исследования результаты; б) подобрать такое преобразование исследуемой
случайной величины ?, которое видоизменяет исходный «ненормальный»
закон распределения, превращая его в нормальный. Удобным для
статистических приложений является и свойство «самовоспроизводимости»
нормального закона, заключающееся в том, что сумма любого числа
нормально распределенных случайных величин тоже подчиняется
нормальному закону распределения. Кроме того, закон нормального
распределения имеет большое теоретическое значение: с его помощью выведен целый
ряд других важных распределений, построены различные статистические
критерии и т.п. (х3~9 t- и F-распределения и опирающиеся на них
критерии, см. п. 3.2.1-3.2.3, а также гл. 8).
Графики нормальных плотностей приведены на рис. 2.5, 2.6, 2.8 и 2.9.
Основные числовые характеристики нормального закона:
среднее, мода, медиана: Е? = хто& = ?med = я;
дисперсия: Щ = а2;

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 127
асимметрия:
эксцесс:
центральные
моменты
порядка к > з:
А
А
(°
т*0) = | 1
= 0;
= 0;
•3-...B;
т-1)<г3т
при Л =
при к =
т =
2т-1,
2т
Двумерный нормальный закон описывает совместное
распределение двумерной случайной величины ( = (? >? ) с непрерывными
компонентами ?*1' и ?* , механизм формирования значений которых тот же,
что и в одномерном случае, причем множества случайных факторов, под
воздействием которых формируются значения {'*' и f'3', вообще говоря,
пересекаются (отсюда возможная зависимость ?*1' и f*2').
Введем в рассмотрение основные числовые характеристики
двумерной случайной величины ? =
вектор средних: М = I (з) ) > где
ковариационная матрица: S = I I,
коэффициент корреляции: г=^
Совместная двумерная плотность у>(я , ж ; М, Е) нормального
закона может быть записана в виде
rt<V«ME)
2*[(Гц<гааA - г2)]1'2
2г-^—^Г" C'9)
или в виде
М) J3"" (Х~М) /л л/\
, («5.9;

128 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
где А = (^B)) j верхний индекс Т означает транспонирование матрицы или
вектора, |Е| = det (?) — определитель ковариационной матрицы, ?~ —
матрица, обратная к ковариационной, а ехр{с} = ес. Изображение
поверхности плотности двумерного нормального закона приведено на рис. 2.6.
Частные плотности ^(i)(ar*;nr ,<гц) и ^(а>(ж ,т ,0-ц) могут
быть получены из совместной по формуле B.12):
<»<а»—(а)J
Эти формулы означают, что частные законы распределения
компонент двумерного нормального закона сами являются одномерными
нормальными законами с параметрами соответственно (тг ,<Гц) и
(тB),сг22).
Условные плотности (p(W(x{1) \ ?{2) = х{2)) и <р^2)(х{2) \ ({1) = х{1))
получаются с использованием общих формул B.13) и B.13'):
хе
- г2)
Отсюда следует, в частности, что условное распределение
компоненты (**' при фиксированном значении другой компоненты (?*' = ж^') снова
описывается нормальным законом, параметр среднего значения которого,
как и следовало ожидать, зависит от фиксированного значения яг1*':
1/2
и дисперсия которого не зависит от ат" и равна

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 129
Многомерный нормальный закон описывает совместное
распределение р-мерной случайной величины ? = (?,?, . ..,?*р') с
непрерывными компонентами ? , механизм формирования значений каждой из
которых тот же, что и в одномерном случае, причем множества
случайных факторов, под воздействием которых формируются значения ?* ,? ,
...,?, вообще говоря, пересекаются (отсюда их возможная
взаимозависимость). Задавшись р-мерным вектор-столбцом М средних значений
компонент и (р х р)-матрицей ковариаций ? (см. п. 2.6.6), можно выписать
р-мерную совместную плотность многомерного нормального закона:
-i(A--M)TE-1(A"-M). (ЗЛО)
е
Здесь, как и прежде, X = (аг ,х , . ..,агр') — вектор-столбец
текущих переменных, а |Е| = det(E) — определитель ковариационной
матрицы.
Вырожденность матрицы ? (т.е. равенство нулю определителя |Е|)
делает соответствующее многомерное распределение вырожденным (или
несобственным); это означает, в частности, что разброс значений
исследуемого многомерного признака сосредоточен в подпространстве меньшей,
чем р, размерности. За исключением некоторых специальных случаев мы
всегда будем полагать, что нами уже осуществлен переход в это
подпространство меньшей размерности, так что в наших рассуждениях
предполагается |Е| > 0.
3.1.6. Логарифмически-нормальное распределение
Случайная величина г\ называется логарифмически-нормально
распределенной, если ее логарифм (In г;) подчинен нормальному закону
распределения. Это означает, в частности, что значения логарифмически-
нормальной случайной величины формируются под воздействием очень
большого числа взаимно независимых факторов, причем воздействие
каждого отдельного фактора «равномерно незначительно» и равновероятно
по знаку. При этом в отличие от схемы формирования механизма
нормального закона последовательный характер воздействия случайных факторов
таков, что случайный прирост, вызываемый действием каждого
следующего фактора, пропорционален уже достигнутому к этому моменту
значению исследуемой величины (в этом случае говорят о мультипликативном
характере воздействия фактора). Математически сказанное может быть
5 Теория вероятностей
и прикладная статистика

130 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
формализовано следующим образом. Бели щ = а — неслучайная
компонента исследуемого признака rj (т. е. как бы «истинное» значение г/ в
идеализированной схеме, когда устранено влияние всех случайных факторов),
а &*&* •••>?# — численное выражение эффектов воздействия
упомянутых выше случайных факторов, то последовательно трансформированные
действием этих факторов значения исследуемого признака будут:
V2 =
Отсюда легко получить
t=0
где Arji = ?/j+1 ~ %. Но правая часть C.11) есть результат
аддитивного действия множества случайных факторов, что при сделанных выше
предположениях должно приводить, как мы знаем, к нормальному
распределению этой суммы. В то же время, учитывая достаточную
многочисленность числа случайных слагаемых (т.е. полагая N -* оо) и
относительную незначительность воздействия каждого из них (т.е. полагая
-» 0), можно от суммы в левой части C.11) перейти к интегралу
I
— = In 7f — In щ = In rj - In a.
*>0
Это и означает в конечном счете, что логарифм интересующей нас
величины (уменьшенный на постоянную величину In а) подчиняется
нормальному закону с нулевым средним значением, т.е.
0
откуда дифференцированием по х левой и правой частей этого
соотношения получаем
1 -е"^12 C.12)

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
131
(правомерность использованного при вычислении fv(x) тождества
Р{т/ < х) = Р{\пт1 < In ж} вытекает из строгой монотонности
преобразования In 7/).
Описанная схема формирования значений
логарифмически-нормальной случайной величины оказывается характерной для многих
конкретных физических и социально-экономических ситуаций (размеры и вес
частиц, образующихся при дроблении; заработная плата работника; доход
семьи; размеры космических образований; долговечность изделия,
работающего в режиме износа и старения, и др). Примеры графиков плотности
логарифмически-нормального распределения представлены на рис. 3.4
3
Рис. 3.4. График функции плотности логарифмически-нормального
распределения для различных а при а = 1
Ниже приводятся результаты вычисления основных числовых
характеристик логарифмически-нормального распределения (в терминах
параметров закона а и а ):
среднее: Ет/=ае*а ;
мода: Zmod —ае >
медиана: #med — a\
дисперсия: Dr/ = (Е?/J(е<7 — 1) = а2ес {еа — 1);
асимметрия: fa = (е" — 1)^F^ +2);
2 о 2 о о
эксцесс: j32 = (е* — 1)(е + Зе а + бе" + 6).
Из этих выражений видно, что асимметрия и эксцесс логарифми-

132 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
чески-нормального распределения всегда положительны (и тем ближе к
нулю, чем ближе к нулю а ), а мода, медиана и среднее выстраиваются как
раз в том порядке, который мы видим на рис. 2.7, причем они будут
стремиться к слиянию (а кривая плотности — к симметрии) по мере
стремления к нулю величины а . Принтом, хотя значения логарифмически-
нормальной случайной величины образуются как «случайные искажения»
некоторого «истинного значения» а, последнее в конечном счете
выступает не в роли среднего значения, а в роли медианы.
3.1.7. Равномерное (прямоугольное) распределение
Случайная величина ? называется равномерно распределенной на
отрезке [а, Ь}, если ее плотность вероятности Д(ж) постоянна на этом отрезке
и равна нулю вне его, т. е.
¦{
Ь-а
о
при а < х < 6;
при а < а и х > Ь.
C.13)
Так как график' функции Д(х) изображается в виде прямоугольника
(см. рис. 3.5), то такое распределение также называют прямоугольным.
Рис.3.5. Функция плотности равномерной случайной величины (f((x)) и
суммы двух (/Ч2(ж)) и трех (fn3(x)) независимых равномерно
распределенных на [0,1] случайных величин
Соответственно функция распределения F^(x) равномерного закона
задается соотношениями:

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ 133
0 при х < а;
г ( \ _ ) х~а ™„ „ ^ „ ^ a. /q iq'\
1 6 — а
1 при х > 6.
Примерами реальных ситуаций, связанных с необходимостью
рассмотрения равномерно распределенных случайных величин, могут
служить: анализ ошибок округления при проведении числовых
расчетов (такая ошибка, как правило, оказывается равномерно
распределенной на интервале от -5 до +5 единиц округляемого десятичного
знака); время ожидания «обслуживания» при точно периодическом,
через каждые Т единиц времени, включении (прибытии)
«обслуживающего устройства» и при случайном поступлении (прибытии) заявки на
обслуживание в этом интервале (например, время ожидания
пассажиром прибытия поезда метро при условии точных двухминутных
интервалов движения и случайного момента появления пассажира на
платформе будет распределено приблизительно равномерно на интервале
[О мин, 2 мин]).
Отметим еще две важные ситуации, в которых используется
равномерный закон. Во-первых, в теории и практике статистического анализа
данных широко используется вспомогательный переход от исследуемой
случайной величины f с функцией распределения F(x) к случайной
величине rj = <F(?), которая оказывается равномерно распределенной на
отрезке [0,1] (см. п. 4.4). Этот прием является полезным при статистическом
моделировании наблюдений, подчиненных заданному закону
распределения вероятностей* при построении доверительных границ для
исследуемой функции распределения и в ряде других задач математической
статистики. Во-вторых, равномерное распределение иногда используется в
качестве «нулевого приближения» в описании априорного распределения
анализируемых параметров в так называемом байесовском подходе в
условиях полного отсутствия априорной информации об этом распределении
(см. п. 7.6.).
Числовые характеристики равномерного закона:
среднее, медиана: Е? = xmed =
дисперсия:
асимметрия:
эксцесс:

134 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Отметим в заключение одно важное свойство суммы п независимых
равномерно распределенных случайных величин: распределение этой
суммы очень быстро (по мере роста числа слагаемых) приближается к
нормальному закону. В частности, если & — равномерно распределенные на
отрезке [0,1] и независимые случайные величины, то можно показать, что
плотность fnH(x) случайной величины т/п = ft + • • • + ?л имеет вид
jlgj [хп~г - Ci(. - l)-1] при К х < 2;
/*.(*) = 1 +с*(ж - г)*'1] при 2 < х < 3;
^ ?_jjn- ?»- ^ _ ^п _ 1))П~ ] ПрИ П — 1 < X < П.
(область возможных значений случайной величины rjny очевидно, задает*
ся отрезком [0,п]). Геометрическое изображение последовательного
изменения вида плотности Дж(ж) по мере роста числа слагаемых п (для
п = 1,2,3) дано на рис. 3.5. Это свойство используется, в частности, при
статистическом моделировании нормально распределенных наблюдений.
3.L8. Распределения Вейбулла и экспоненциальное
(показательное)
Рассмотрим один общий механизм формирования распределений,
относящийся, в частности, к случайным величинам, характеризующим
длительность жизни элемента, сложной системы или индивидуума (задачи
теории надежности, анализ коэффициентов смертности в демографии и
т. п.). Пусть ? — время жизни анализируемого объекта (системы,
индивидуума) и F(t) = Р{( < t} — его функция распределения, которую мы
полагаем непрерывной и дифференцируемой. В задачах данного профиля
важной характеристикой является интенсивность отказов (коэффициент
смертности) X(t) исследуемых элементов возраста t, определяемая
соотношением
\/4\ J( \ / /О 1 Л\
A(t) = гГТТч • \6Л4)
Статистически (экспериментально) интенсивность отказов
определяется как отношение удельного числа (т. е. приходящегося на единицу
времени) выбывших в возрасте t элементов к общему числу доживших до

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
этого возраста элементов n(t), т.е.:
135
где п — общее число наблюдаемых во времени (начиная с t = 0) элементов
одинакового возраста, а Д(?) и F^(t), соответственно, эмпирическая
плотность и эмпирическая функция распределения анализируемой случайной
величины ?.
Разрешая уравнение C.14) относительно функции распределения
получаем
C.15)
Таким образом, конкретизация вида функции распределения ^
полностью определяется видом функции интенсивности отказов
(временной зависимостью коэффициентов смертности) A(f).
Многочисленные экспериментальные данные (и в области
демографии, и в области анализа надежности технических элементов и систем)
показывают, что в широком классе случаев функция X(t) имеет
характерный вид кривой, изображенной на рис. 3.6. Из этого графика видно, что
весь интервал времени можно разбить на три периода.
i A(tI000
JL.I4 19 24 29 34 3. 49 54 59 64
! Прира-! Нормальная
^ботка v эксплуатация
Старение и износ
Рис. З.в. Типичное поведение кривой смертности (интенсивности отказов):
кривая описывает изменение коэффициента смертности мужского
населения Франции по данным 1955 г.1

136 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
На первом из них функция X(t) имеет высокие значения и явную
тенденцию к убыванию. На техническом языке это можно объяснить
наличием в исследуемой совокупности элементов с явными и скрытыми
дефектами (сборки, некондиционности отдельных свойств и т.п.), которые
приводят к относительно быстрому выходу из строя этих элементов. Этот
период принято называть периодом «приработки» (или «обкатки»).
Затем наступает период нормальной эксплуатации, характеризующийся
приблизительно постоянным и сравнительно низким уровнем
«смертности» элементов. Природа смертей (или «отказов») в этот период носит
внезапный характер (аварии, несчастные случаи и т. п.) и не зависит от
возраста объекта. И наконец, последний период жизни (или
эксплуатации) элемента — период старения и износа. Природа «отказов» в этот
период — в необратимых физиологических или физико-химических
явлениях, приводящих к ухудшению качества элемента, к его «старению». В
соответствии с этой кривой смертности периоду «приработки»
соответствует возраст от 0 до 9 лет, периоду «нормальной эксплуатации» — от
9 до 39 лет, а периоду «старения» — возраст после 39 лет.
Каждому периоду соответствует свой вид функции A(f), а
следовательно, и свой закон распределения времени жизни ?.
Рассмотрим класс степенных зависимостей, описывающих поведение
А(?), а именно
А(О = Аоа*а-\ C.16)
где Ао>0иа>0 — некоторые числовые параметры. Очевидно,
значения а<1,а=1иа>1 отвечают поведению функции интенсивности
отказов соответственно в период приработки, нормальной эксплуатации
и старения.
Подставляя C.16) в C.15), получаем вид функции распределения F^(t)
времени жизни ? элемента:
F((t) = 1 - e~Xot\ t>0. C.17)
Соответственно плотность вероятности
Д@ = Ао a t°rl е~Ао<в, t> 0. C.17;)
Это и есть распределение Вейбулла. Поведение графиков функции
плотности распределения Вейбулла представлено на рис. 3.7. К тому
же самому типу распределения можно прийти, отправляясь от широкого
класса различных вероятностных законов и интересуясь распределением
крайних членов их вариационных рядов.

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
137
Рис. 3.7. Графики функций плотности распределения Вейбулла для
различных значений а
Основные числовые характеристики распределения Вейбулла:
среднее: Е? = А<^° Г A + -] ;
мода:
дисперсия:
, если а < 1;
Ао а A - ?) а , если а ^ 1;
момент к—го порядка: т*. = Е^ = Ао а • Г ( 1 Н— )
V а/
(здесь Г(г) — так называемая гамма-функция Эйлера, т.е.
о
Экспоненциальное (показательное) распределение хотя и является
частным случаем распределения Вейбулла (когда а = 1, см.
соответствующую кривую плотности на рис. 3.7), но представляет большой
самостоятельный интерес. Из вышесказанного следует, что оно адекватно
описывает распределение длительности жизни элемента, работающего в
режиме нормальной эксплуатации. Экспоненциальный закон (и только
он) обладает, в частности, тем важным свойством, что вероятность
безотказной работы элемента на данном временном интервале (t, t + Д) не
зависит от времени предшествующей работы t, а зависит только от
длины интервала Д. Экспоненциально распределенную случайную величину
можно интерпретировать так же, как промежуток времени между двумя
последовательными наступлениями «пуассоновского» события.
Прикладная популярность экспоненциального закона объясняется не только разно-

138 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
образными возможностями его естественной физической интерпретации,
но и исключительной простотой и удобством его модельных свойств.
Ниже приводятся его функция распределения и плотность вероятности, а
также его основные числовые характеристики:
= 1 - e~Aor, x > 0;
среднее:
мода:
медиана:
дисперсия:
асимметрия:
эксцесс:
«med = у • Ь 2;
/?!=2;
/?2 =6.
Двустороннее экспоненциальное распределение
(распределение Лапласа). Симметричная унимодальная функция плотности этого
закона с «острым» максимумом в точке х = 0 часто используется для
описания распределения остаточных случайных компонент («ошибок») е
в моделях регрессионного типа (см. гл. П.). График этой функции
плотности представляет собой как бы результат «склеивания» графика
показательного распределения со своим зеркальным — относительно
вертикальной оси — отражением (с учетом необходимой нормировки), так что
уравнение функции плотности имеет вид
(-осхжоо).

3.1 МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
139
Рис. 3.8. График функции плотности распределения Лапласса
Нетрудно подсчитать основные числовые характеристики этого
закона распределения:
среднее:
мода:
медиана:
дисперсия:
асимметрия:
эксцесс:
= 0;
= 0;
= 0;
А=0;
3.1.9. Распределение Парето
В различных задачах прикладной статистики довольно часто
встречаются так называемые «усеченные» распределения. Такие
распределения описывают вероятностные закономерности в неполных («усеченных»)
генеральных совокупностях, т. е. в таких совокупностях, из которых
заранее изъяты все элементы с количественным признаком, превышающим
некоторый заданный уровень с0 (или, наоборот, меньшим, чем с0). Скажем,
налоговые органы обычно интересуются распределением годовых доходов
тех лиц, годовой доход которых превосходит некоторый порог cq,
установленный законами о налогообложении. Эти и некоторые аналогичные
распределения иногда оказываются приближенно совпадающими с
распределением Парето, задаваемым функциями:
F((x) = Р{( < *} = 1 - (|)",

140 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
В этих формулах а > 0, а х > с0, т. е. область мыслимых значений данной
случайной величины f есть полупрямая (с0. + оо). Функция плотности
имеет вид монотонно убывающей кривой, выходящей из точки (со,а/со).
2,0
1,0
0,2
0 со 2 3 4
Рис. 3.9. График функции плотности распределения Парето для различных
значений а
Основные числовые характеристики этого распределения существуют
не всегда, а лишь при соблюдении определенных требований к величине
параметра а:
среднее:
мода:
медиана:
дисперсия:
а-1
с© (существует при а > 1);
«med =2e -Со;
(существует при а > 2);
(а-1)'(а-2)
момент k-го порядка: Efk = cq (существует при а > к).
Ot "~~ л»
3.1.10. Распределение Коши
Этот закон весьма специфичен, поскольку ни один из его моментов
положительного порядка (в том числе даже среднее значение) не суще-

3.2 З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
141
ствует. Распределение Коши унимодально, симметрично относительно
своего модального значения (которое, следовательно, одновременно
является медианой) и задается функцией плотности вероятности
с+(х-аL
¦,-оо < х < оо,
где с > О — параметр масштаба и а — параметр центра группирования,
определяющий одновременно значение моды и медианы.
-3
-2
-1
Рис. 3.10. График функции плотности распределения Коши
Соответственно функция распределения задается соотношением
г,/ \ 1 1 л х — а
F(x) = - + - arcth .
4 7 2 7Г с
Отметим два важных свойства («самовоспроизводимости»)
распределения Коши.
1. Если случайная величина ? имеет распределение Коши с
параметрами с и а, то любая линейная функция 60 + bif имеет распределение того
же типа с параметрами с = |&i| • с и а = Ьг • а + Ьо\
2. Если случайные величины fi, ?2> • • • > fn независимы и имеют одно и
то же распределение Коши, то среднее арифметическое ? = (^Н Y?n)ln
имеет то же самое распределение, что и каждое &.
3.2. Законы распределения вероятностей,
используемые при реализации техники
статистических вычислений
Ниже описываются пять законов, основное назначение которых —
предоставление исследователю необходимого аппарата для построения

142 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
разного рода статистических критериев и интервальных оценок
параметров: х -распределение («хи-квадрат»-распределение); «-распределение
(Стьюдента); F-распределение (распределение дисперсионного
отношения); ^-распределение (бета-распределение) и Г-распределение (гамма-
распределение). Объяснение механизма их действия можно связывать со
«статистикой нормального закона», т. е. с изучением распределений
некоторых функций от набора независимых и одинаково стандартно
нормально распределенных случайных величин.
3.2.1. «Хи-квадрат»-распределение с т степенями свободы
(х2 (т ^распределение)
В связи с гауссовской теорией ошибок астроном Ф. Хельмерт
исследовал суммы квадратов т независимых стандартно нормально
распределенных случайных величин, придя таким образом к функции
распределения Fx2(m)(z), которую позднее К. Пирсон назвал функцией распределения
«хи-квадрат»1. Для отрицательных х функция Fx2(m)(ar) = 0, а для
неотрицательных х
Fx4m){x) = Р{Х\т) < х}
U (ЗЛ8)
где параметр закона m — целое положительное число, которое принято
называть числом степеней свободы, а Г(у) — значение гамма-функции
Эйлера в точке у.2
Соответствующая плотность вероятности задается функцией
f{) x*~*e~*' #>Oi C>18/)
1 Helmert F. R. Uber die Wahrscheinlichkeit von Potenzsummen der Beobachtungs-
fehler etc. Z. F. Math, und Phys., 21 A876); Pearson K. On the criterion that
a given system of deviation from the probable in the case of correlated system of
variables..., € Phil Mag.», V. 50 A900), 157.
3 Значение гамма-функции Эйлера в точке у определяется интегралом: Г(у) =
00
/ е"*'**" dt. Из определения непосредственно следует, например, что при целых по-
о
ложительных значениях у: Г(у) = (у-1)! и Г(у+1) = 2-Vy/vlZ-B.By-l) (более
подробные сведения о гамма-функции см. в книге [Большев Л. Н., Смирнов Н. В.]).

3.2 З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
143
Рис. 3.11. График функции плотности х?,-распределения для различных
значений т
,-
Распределение х появилось впервые при исследовании распределения
последовательности независимых и одинаково стандартно нормально
распределенных случайных величин ?ь?2>« ••>??»• Выяснилось, что
случайная величина х (^0 == fi Н + fm подчиняется закону \ -распределения
с т степенями свободы.
Основные числовые характеристики х (т)-распределения:
среднее:
мода:
дисперсия:
асимметрия:
эксцесс:
Бха(т) = т;
mmod = т - 2 (т ? 2);
Dx2(m) = 2т;
3.2.2. Распределение Стьюдента с т степенями свободы
(г(т)-распределение)
Английский статистик В. Госсет (писавший под псевдонимом «Стью-

144 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
дент») получил в 1908 г.1 следующий результат. Пусть fо>?ъ • • •&* —
независимые @,ег2)-нормально распределенные случайные величины. Тогда
плотность распределения случайной величины
описывается функцией
/«(«) =
1
r(f)
m + 1
C.19)
(-00 < Ж < +00).
Распределение C.19) получило название распределения Стьюдента
с т степенями свободы (или *(т)-распределения). Из выражения C.19)
следует, что функция плотности ft(x) не зависит от дисперсии а2
случайных величин & и, кроме того, является унимодальной и симметричной
относительно точки х = 0, (см. рис. 3.12).
-4
-3
-2
-1
О
Рис. 3.12. Графики функции плотности «(т)-распределения при т = 4 и
стандартного нормального распределения е(х;0,1)
Основные числовые характеристики *(т)-распределения:
среднее, мода, медиана: Щт) = xmod = xmed = 0;
Student. The probable error of a mean. — Biometrika, B, 6 A908), 1.

3.2 З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ 145
т
дисперсия: Ш(га) =
т-2
(существует только при т > 2);
асимметрия: /3\ = 0;
эксцесс: /?2 = г
т — 4
(существует только при т > 4).
3.2.3. Распределение дисперсионного отношения с числом
степеней свободы числителя mi и числом степеней
свободы знаменателя га2 (F(mb/n2)-распре деление)
с*
Рассмотрим mi + га2 независимых и @, а )-нормально
распределенных величин f 1,..., f mi; щ, ..., r/m2 и положим
т2
i
Очевидно (см. п. 3.2.1), та же самая случайная величина может .быть,
определена и как отношение двух независимых и соответствующим
образом нормированных х -распределенных величин х (mi) и X (тг)? Т-е-
Английский статистик Р. Фишер в 1924 году показал1, что плотность
вероятности случайной величины F{mi^rh%) задается функцией
я4
* ^77^7 @ < x < oo),
\7Yl\X ) ^
1 Fisher R. On a distribution yielding the error functions of several well-known
statistics. — Proc. Intern. Math. Congr. Toronto, 1924, 805.

146 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
где, как обычно, Т(у) — значение гамма-функции Эйлера в точке у, а сам
закон называется F-распределением с числами степеней свободы
числителя и знаменателя, равными соответственно mi и Ш2,
Основные числовые характеристики jF(mi,ra2 ^распределения:
среднее:
мода:
дисперсия:
эксцесс:
EF(mi,m2) =
(существует при тп2 > 2);
- 2) - ш2
mi(m2 + 2)
2)
7
——57 7Т
-2) (m2 -4)
(при m2 > 4);
Bтг + m2 -
- 4)
(т2 - 6) у (mi + т2 - 2)mi
(при т2 > 6);
— 8
- 3 (при т2 > 8).
Рис. 3.13. График функции плотности F(mi ,т2)-распределения для
различных значений та при mi *= 10
Отсюда непосредственно следует, что при mi,m2 > 2 F-распреде-
ление всегда имеет модальное значение, меньшее единицы, и среднее
значение, большее единицы. Это означает, в частности, что данное
распределение имеет асимметрию, подобную той, что изображена на рис. 2.6 (в

3.2 З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ 147
этих случаях говорят, что распределение имеет положительную
асимметрию независимо от того, существует ли коэффициент асимметрии
Р.Фишером данный тип распределений выводился не для случайной
величины ^(г7г!,т2), а для ее натурального логарифма (поделенного
пополам), т.е. для случайной величины ( = \ lnF(mi,ra2). Распределение
этой случайной величины часто называют z- распределением Фишера.
Однако в современной статистической практике предпочитают использовать
F-распределение, обладающее более простыми свойствами.
3.2.4. Гамма-распределение (Г-распределение)
Описанные ниже два типа распределения представляют весьма
широкие и гибкие двухпараметрические семейства законов, которые
включают в себя в качестве частных случаев различные комбинации уже
известных нам случайных величин. Основное прикладное значение Г- и В-
распределений — в их богатых вычислительных возможностях: функции
распределения х ,t,F к ряд других могут быть вычислены (после
подходящего преобразования переменных) в терминах Г- или 5-распределений.
Кроме того, Г-распределение иногда используется и при реалистическом
моделировании: с его помощью описывается, например, распределение
доходов и сбережений населения в определенных специальных ситуациях.
Рис. 3.14. График функции плотности гамма-распределения для различных
значений а и 6
Дэухпараметрический закон Г-распределения случайной величины

148 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
7(а,Ь) описывается функцией плотности:
ьа
ха-1е-Ьх при Q<x<00.
Г(а)
О при х < О
где Г(а) — Г-функция Эйлера, а > О — параметр «формы» и Ь > 0 —
параметр масштаба. Легко понять, что Г-распределенная случайная
величина с параметрами а и Ь (будем обозначать ее *у(а,Ь)) связана со случайной
величиной 7(а? 1) простым соотношением:
Отметим несколько полезных свойств Г-распределения.
1. Из вида функции плотности х (т)-распределения (см. C.18))
непосредственно следует, что оно является частным случаем Г-распределения:
достаточно положить в C.21) а = т/2 и 6 = 1/2.
2. Сумма любого числа независимых Г-распределенных случайных
величин (с одинаковым параметром масштаба 6) 7i(ai>^) + 7г(а2> Ь) +
Ь 7п(ап>&) также подчиняется Г-распределению, но с параметрами а\
+а2 + • • • +ап и Ь.
Основные числовые характеристики случайной величины *у(а,Ь):
среднее: Ej(a,b) = -;
мода: xmod = —^— (при а ^ 1);
<?ucnepcw^: D7(a, 6) = -j-;
6
2
асимметрия: f}\ = -7=;
/a
эксцесс: fi2 = -.
a
3.2.5. Бета-распределение (^-распределение)
Как отмечалось выше, двухпараметрический закон JS-распределения
обладает весьма высокой гибкостью и общностью: в частности, через
функцию 5-распределения могут быть вычислены такие часто
используемые распределения, как t2, F> биномиальное, отрицательное биномиальное
и др. ^-распределение используется и для описания некоторых реальных

3.2 З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ 149
распределений, сосредоточенных на отрезке [0,1] (например, для описания
распределения величин субъективных вероятностей, полученных в ходе
экспертного опроса, см. п. 2.1.3). Случайная величина /?(аьа2),
подчиняющаяся закону 5-распределения с параметрами а\ и а2 @ < аг < оо,
0 < п2 < оо), имеет плотность вероятности
^х*1] C-22)
для остальных значений ж.
Отметим несколько полезных свойств 5-распределения.
1. Если 7(аъ&) и 7(а2>Ь) — Две независимые Г-распределенные
случайные величины, то отношение /3(ai, a2) = т(аъ &)/(т(аъ &) + 7(а2>&))
подчиняется закону /^-распределения с параметрами а\ и а2.
2. Случайная величина /3A,1) распределена равномерно на отрезке
[0,1] (см. п. 3.1.7).
3. Функция распределения квадрата стьюдентовской величины t (m)
(см. п. 3.2.2) связана с функцией распределения случайной величины /3
соотношением
()
4. Функция распределения случайной величины F(m!,m2) (см.
п. 3.2.3) связана с функцией распределения случайной величины /3
соотношением
5. Между функцией распределения случайной величины /3 и
распределениями биномиального типа (см. п. 3.1.1) существуют соотношения:
F0(m>n-m+i)(x) =
к=п
6. Непосредственный анализ плотности C.22) обнаруживает
симметричность ПЛОТНОСТеЙ f^(aua2)(x) и fj3(a2,ai)(x) ОТНОСИТвЛЬНО ПрЯМОЙ X =
0,5 (рис. 3.15), что в терминах соответствующих функций распределения

150 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
! 2
Рис. 3.15. Графики функций плотности ^-распределения при различных
значениях параметров а\ и aj: 1) а\ =2, аа = 4; 2) «и =4, аз =
2; 3) ах ж 1/2, а3 ж 1/2
может быть записано в виде
(поэтому, в частности, при составлении таблиц ^-распределения обычно
ограничиваются случаем 0 < а\ ^ а2).
Основные числовые характеристики 5-распределенной (с параметра*
ми at и а2) случайной величины
среднее:
мода:
дисперсия:
Е/3(аиа2) =
xmod =
J
г
— 2
(при аг > 1 и а2 > 1);
D/J(o,,o2) =
я 2(fl2 ~
+a2r(ai+fl2 + 1)
_ 3(ax + a2 + 1)[2(аг + o2J + 0102@1 + o2 - 6)]

выводы 151
ВЫВОДЫ
1. Модельный (т.е. аналитический) способ задания закона
распределения вероятностей (з.р.в.) является наиболее удобной формой его
описания. При этом способ вычисления вероятности того, что исследуемая
дискретная случайная величина ? примет заданное значение х (т. е. способ
вычисления значения Р{? = х}), так же как и способ вычисления значения
функции плотности распределения вероятностей х(х) в заданной точке х
для непрерывной случайной величины, определяется явным
аналитическим заданием подходящей функции (см. формулы (З.З)-(ЗЛО), C.12),
C.13), C.17')). Иногда этот способ называют параметрической формой
задания з.р.в.
2. Следует выделить два направления использования моделей з.р.в.
в теории и практике вероятностно-статистических и эконометрических
исследований. Первое направление связано с так называемым
реалистическим моделированием поведения конкретных анализируемых
признаков — среднедушевого семейного дохода, тех или иных поведенческих
или производственных характеристик хозяйственных субъектов,
параметров финансового рынка или демографической ситуации и т.п. В этом
случае модель з.р.в. призвана описать и объяснить механизм
генерирования (генезис) анализируемых исходных данных. Другая роль широко
распространенных моделей з.р.в. — их использование в качестве
вспомогательного технического средства при реализации различных методов
статистического анализа данных — при построении разного рода
статистических оценок и статистических критериев (см. гл. 6-8).
3. К наиболее распространенным в практике
вероятностно-статистических исследований моделям з.р.в., описывающим поведение
дискретных случайных величин, следует отнести биномиальный,
гипергеометрический, пуассоновский, полиномиальный и отрицательный биномиальный
законы.
4. При описании поведения непрерывных случайных величин в
области социально-экономических исследований наиболее
распространенными являются модели нормального (гауссовского), логарифмически-
нормального, паретовского, вейбулловского, экспоненциального, лапласов-
ского, равномерного, Коши, гамма- и бета-распределений.
5. При подборе модели «под анализируемые реальные данные»
следует представлять себе общую схему (или механизм)
формирования значений той или иной «модельной» случайной величины.
Так, например, условия генерирования и специфика пуассоновской
случайной величины определяют ее как число наступления интересующего
нас события за единицу времени, когда факт наступления такого собы-

152 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
тия в случайном эксперименте (испытании, наблюдении) не зависит от
того, сколько раз и в какие моменты времени оно наступило в прошлом,
и не влияет на будущее, а испытания проводятся в стационарном
режиме. Аналогично могут быть описаны и условия генерирования других
модельных случайных величин.
в. Грамотная реализация основных процедур математико-статисти-
ческого анализа данных, в частности, построение точечных и
интервальных оценок для неизвестных значений параметров анализируемой модели
(см. гл. 7), статистическая проверка гипотез, связанных со структурой и
параметрами рассматриваемой модели (см. гл. 8), невозможна без знания
моделей «хи-квадрат», стьюдентовского и фишеровского F-распределений
и умения пользоваться их таблицами.
7. Прикладные возможности моделей многомерных з.р.в.
значительно скромнее. Наибольшее распространение здесь получили многомерный
нормальный закон (для непрерывной многомерной случайной величины,
см. C.10)) и полиномиальный з.р.в. (для дискретной многомерной
случайной величины, см. C.7)).

ГЛАВА 4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
В гл. 2 и 3 изложены основные понятия теории вероятностей, включая
набор моделей законов распределения, наиболее распространенных в
теории и практике статистической обработки данных. Настоящая глава
посвящена описанию некоторых связей, существующих между этими
понятиями и моделями, а также отдельных их свойств, полезных для
понимания сущности излагаемых далее методов экономического моделирования и
статистического анализа данных.
4.1. Неравенство Чебышева
В п. 2.6.3 мы познакомились с основной характеристикой степени
случайного разброса значений случайной величины — с ее дисперсией
а2 = Df. Из смысла этой характеристики следует, что вероятность
зафиксировать при наблюдении случайной величины ? значение, отклоняющее
от ее среднего а = Е? не менее чем на заданную величину А, должна
расти с ростом а . Чем больше величина дисперсии а , тем более
вероятны значительные отклонения значений исследуемой случайной величины
от своего центра группирования а = Е?. Конечно, зная плотность (или
полигон) распределения вероятностей Д(я), можно точно вычислить
вероятность событий вида {|? - а\ ^ Д}, а именно
/ ft(x)dx, если ? непрерывна;
{
т |.-.|>Д ( j
22 Р%, если f дискретна. v ;
Так, например, если f подчиняется (а,а2)-нормалъному закону
распределения, то вероятность событий вида |? — а\ ^ Д зависит только от
того, сколько раз в заданной величине отклонения Д «уложится» средне-
квадратическое отклонение а = /Щ

154 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Однако хотелось бы уметь оценивать вероятности таких событий,
опираясь только на знание величины дисперсии cr2 = D?, не обращаясь к
точному знанию закона распределения анализируемого признака f.
Именно эта задача и решается с помощью неравенства, выведенного русским
1
математиком П. Л. Чебышевым1
D.2)
где а = Е? и ег2 = D{ = Е(? - аJ.
Доказательство этого неравенства несложно:
xi |*-а|>Д х\ |г-а|^Д
00
-00
(в случае дискретного признака доказательство проводится аналогично с
заменой «элементов вероятностей» Д(ж) dx вероятностями р{ = Р{? =
ж?}, а интегралов — соответствующими суммами).
Из хода доказательства видно, что если распределение
исследуемого признака ? симметрично (относительно а = Е?), то имеют место и
односторонние аналоги неравенства:
2
1 - а > Д} = Р{а - ? > Д} < -—%. D.2')
Как и всякий общий результат, не использующий сведения о
конкретном виде распределения случайной величины ?, неравенство
Чебышева дает лишь грубые оценки сверху для вероятностей событий вида
{|? - e| ^ Д}« Так, например, если оценивать вероятность события
{|? - а| > Зет} для нормального признака ?, не зная, что он подчиняется
гауссовскому закону (т. е. используя неравенство Чебышева), то получим
1
1 См.: Чебышев П. Л. О средних величинах. — Математический сборник, 1867,
II. В том же 1867 г. во французском журнале «Journ. math, pures et appl», XII, была
опубликована работа Бьенэмэ, также содержащая как идею доказательства этого
неравенства, так и само неравенство. Поэтому неравенство D.2) часто называют
также неравенством Бьенэме-Чебышева.

4.2 ЗАКОН БОЛЬШИХ ЧИСЕЛ И ЕГО СЛЕДСТВИЯ 155
Интересно сравнить эту величину с точным значением этой же
вероятности, которое получается с помощью таблиц нормального
распределения и равно 0,0027: мы видим, что точное значение вероятности в
40 (!) раз меньше ее грубой оценки, полученной на основании неравенства
Чебышева.
4.2. Закон больших чисел и его следствия
Давно было замечено, что результаты отдельных наблюдений (будь
то экономические, демографические, физические, метеорологические или
иные наблюдения), хотя и произведенных в относительно однородных
условиях, колеблются сильно, в то время как средние из большого числа
наблюдений обнаруживают замечательную устойчивость.
Математическим основанием этого факта служат различные формы
так называемого закона больших чисел. Формулировку первого
частного варианта этого закона связывают с именем французского
математика С.Л.Пуассона (Poisson S.D. Recherches sur la probability de jugements
en matiere criminelle et en matiere civile..., Paris, Gauthier-Villars, 1837).
В формулировке, приведенной ниже, этот закон был впервые доказан
А.Я.Хинчиным (см. Hintchin A. Sur la loi des grands nombres. Comptes
rendus de V Academie des Sciences, 189 A929), 477-479).
4.2.1. Закон больших чисел
Пусть ?b&>-««>?n — последовательность независимых и одинаково
распределенных случайных величин. Бели среднее значение а = Е&
существует, то среднее арифметическое случайных величин ?г,..., ?п по мере
неограниченного роста числа слагаемых (т. е. при п -+ оо) сходится по
вероятности к этому теоретическому среднему значению а, т. е. для
любых сколь угодно малых положительных величин е к 6 наступает такой
«момент» п0, начиная с которого (т. е. при всех п^ п0) будет справедливо
неравенство
> 1 - 6. D.3)
Доказательство этого утверждения не вызывает затруднений, если
дополнительно потребовать существования конечной дисперсии
случайных слагаемых &, т.е. существования D& = а2 < оо.
Действительно, в этом случае для доказательства D.3) достаточно
воспользоваться неравенством Чебышева D.2) применительно к случайной величине

156 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
f (п) = (? 1 + • • • + ?п)/и. Легко подсчитыв
и, следовательно, в соответствии с D.2)
f (п) = (? 1 + • • • + ?п)/и. Легко подсчитываются Е?(п) = а и D|(n) = <т2/п,
()
пе
Выбрав п0 ^ ^т, мы обеспечим выполнение D.3) при любых сколь
угодно малых заданных значениях е и 6.
В качестве следствия закона больших чисел рассмотрим следующий
важный результат, объясняющий эффект устойчивости относительных
частот1.
4.2.2. Теорема Бернулли
Пусть производится п независимых случайных экспериментов (или
наблюдений случайной величины ?), в результате каждого из которых
может осуществиться или не осуществиться некоторое интересующее нас
событие А (например, событие, заключающееся в том, что f € ДХ, где
АХ — заданная измеримая область возможных значений случайной
величины f). Тогда при неограниченном увеличении числа экспериментов п
относительная частота ргп'(А) появления события А сходится по
вероятности к вероятности этого события р(Л), т.е. для любых наперед
заданных и сколь угодно малых положительных величин е и S наступит такой
«момент» (в проведении эксперимента) п0, что для всех п ^ п0 будет
справедливо неравенство
Р{$п)(А)-р(А)\<е}>\-6. D.3')
Доказательство этого утверждения получается из D.3), если в
качестве участвующих там случайных величин & рассмотреть признаки
{1, если в результате i-ro эксперимента
осуществилось событие Л; D.4)
О — в противном случае.
Из определения следует, что все эти случайные величины ?i,...,?n
1 Теорема Бернулли исторически появилась как первая самостоятельная версия закона
больших чисел намного раньше более сильной теоремы D.3) — в 1713 г. Однако в
современном изложении ее, естественно, удобнее подавать как простое следствие
результата D.3).

4.3 НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЦПТ 157
независимы и имеют один и тот же закон распределения, в частности:
г = A-р(А)J-р(А)+@-р(А)JA-р(А)) D.5)
Очевидно, в этом случае |(п) = (& + ... + ?п)/п есть не что иное, как
относительная частота frn'(A) появления события А в п произведенных
случайных экспериментах, причем
Щп) = Djt»\A) = Р(Л)A;Р(Л)). D.6)
Применяя к случайным величинам D.4) закон больших чисел D.3),
мы и получаем, с учетом D.5) и D.6), доказательство теоремы Бернулли
D.3').
4.3. Особая роль нормального
распределения: центральная предельная
теорема (ЦПТ)
Смысл результатов п. 4.2 заключается, грубо говоря, в том, что при
осреднении большого числа (п) случайных слагаемых все менее
ощущается характерный для случайных величин неконтролируемый разброс в
их значениях, так что в пределе по п —> оо этот разброс исчезает вовсе
или, как принято говорить, случайная величина вырождается в
неслучайную. Однако при любом конечном числе слагаемых п случайный разброс у
среднего арифметического этих слагаемых остается. Поэтому возникает
вопрос исследования (опять-таки асимптотического по п -> оо) характера
этого разброса. Фундаментальный результат в этом направлении
(известный как «центральная предельная теорема») был впервые сформулирован
в упомянутом выше труде Лапласа A812 г.) и заключается он в том, что
для широкого класса независимых случайных величин ?i,..., f n
предельный (по п -+ оо) закон распределения их нормированной суммы вне
зависимости от типа распределения слагаемых стремится к нормальному
закону распределения. Однако эта формулировка нуждается в
уточнениях: что значит «нормированная» сумма случайных величин и в каком
именно смысле закон распределения одной случайной величины стремится
к закону распределения другой? Существует несколько вариантов точных

158 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
формулировок центральной предельной теоремы, отличающихся друг от
друга степенью общности и видом постулируемых ограничительных
условий. Мы приведем здесь формулировку Линдеберга и Леви .
4.3.1. Центральная предельная теорема
Если ?ъ &,..., fn — независимые случайные величины, имеющие
один и тот же закон распределения со средним значением Е& = а и с
дисперсией D& = а2, то по мере неограниченного увеличения п функция
распределения случайной величины
f (П)
стремится к функции распределения стандартного нормального закона
при любом заданном значении их аргументов, т. е.
FTln)(x)-+*(x) ПРИ п->°°
для любого значения я, где Ф(аг) = -4« f*^ е~ *~ dt.
Таким образом, центральная предельная теорема дает математически
строгое описание условий, индуцирующих механизм нормального закона
распределения (см. неформальное обсуждение этих условий в п. 3.1.5).
Она оправдывает, в частности, закономерность той центральной роли,
которую играет нормальное распределение в теории и практике
статистических исследований. Содержание центральной предельной теоремы
можно считать дальнейшим (после закона больших чисел) уточнением
стохастического поведения среднего арифметического из ряда случайных
величин.
Центральная предельная теорема может быть распространена в
различных направлениях: когда случайные слагаемые не являются одинаково
распределенными (формулировка А. М.Ляпунова); когда компоненты & не
являются независимыми; наконец, когда случайные величины & являются
многомерными.
1 Levy P. Calcul des probabilites. Paris, 1925; Lindeberg J. W. Eine neue Herleitung des
Exponentialgesetzes in der Wahrscheinlichkeitsrechung. — Math. Zeitschr., 15 A922),
211.

4.3 НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЦПТ 159
4.3.2. Многомерная центральная предельная теорема
Пусть f 1, ?2 j • • • ? fn — независимые и одинаково распределенные
р-мерные случайные величины с вектором средних значений М = Е& =
(Е^г), Е^2),..., Щ\р))Т и ковариационной матрицей S = Е{(&-М) х (& -
М) }. Тогда при п —> оо совместная функция распределения случайного
вектора ?*(п) = GCjL^u - М)]/д/п сходится (для любого значения
векторного аргумента X) к совместной функции распределения р~ мер ной
нормальной случайной величины, имеющей вектор средних 0 = @,0,..., 0) и
ковариационную матрицу 33.
4.3.3. Комментарии к центральной предельной теореме
Замечание 1. Необходима известная осторожность при
использовании центральной предельной теоремы в практике статистических
исследований.
Во-первых, если предельный вид распределения суммы случайных
слагаемых при определенных условиях всегда нормален и не зависит от
вида распределения самих слагаемых, то скорость сходимости
распределения суммы к нормальному закону существенно зависит от типа
распределения исходных компонент. Так, например, при суммировании
равномерно распределенных случайных величин уже при 6-10 слагаемых можно
добиться достаточной близости к нормальному закону, в то время как для
достижения той же близости при суммировании % -распределенных
слагаемых понадобится более 100 слагаемых.
Во-вторых, центральной предельной теоремой вообще не
рекомендуется пользоваться для аппроксимации вероятностей на «хвостах»
распределения, т.е. при оценке вероятностей событий вида {с (n) < xmjn} и
{Т(п) ^ ^тах}> где хт\п и жтах — возможные значения, близкие
соответственно к левой и правой границам диапазона изменения исследуемого
признака f (n). Поскольку в этом случае числовые значения вероятностей
Р{Г(п) < ?min} = *Г(п)(*т1о) И Р{Г(») > ^тах} = 1-^(п)(*т«) МЭЛЫ,
то из малости разностей Fr{n)(xm{n) - Ф(хт{п) и Fr(n)Bmax) - Ф(жтах)
(которая вытекает из центральной предельной теоремы) вовсе не следует
малость относительных ошибок аппроксимации
которые, как правило, оказываются чрезмерно большими. Так,
например, пусть ?*(п) — нормированный среднедушевой доход в семье (соответ-

160 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ственно &,&,... — заработная плата работающих членов семьи и другие
составляющие семейного дохода) и пусть нас интересует доля q семей с
очень высоким доходом, а именно с доходом, не меньшим некоторого
достаточно высокого уровня жтах (руб.) Исследования показали, что точное
значение этой доли q = l-F^^(xmAX) = 0,03, в то время как
соответствующая нормальная аппроксимация дала результат q = 1 — Ф(жтах) = 0,003.
Разность q-q сама по себе мала (как и следует из центральной предельной
теоремы), однако относительная погрешность нормальной аппроксимации
в данном случае составляет десятикратную величину, т. е. 1000%!
Особенно важным это предостережение оказывается при попытках использования
нормальных аппроксимаций в задачах расчета зависимостей типа
«предельная прочность (или пропускная способность) системы — вероятность
разрушения (отказа в обслуживании)».
Замечание 2. Центральная предельная теорема позволяет
проследить асимптотические связи, существующие между различными
модельными законами распределения (см. гл. 3), с одной стороны, и
нормальным законом — с другой. Опираясь на центральную предельную теорему,
можно объяснить, в частности, следующие полезные для статистической
практики факты:
1. Распределение (те,р)-биномиальной случайной величины ?(р,те)
асимптотически (по те —> оо) нормально с параметрами Е?(р, те) = тер
и Df(p, те) = терA -р). Данный результат известен как теорема Муавра-
Лапласа (доказана впервые Муавром в 1733 г., когда еще не была
известна центральная предельная теорема) и является прямым следствием
центральной предельной теоремы, примененной к случайным величинам
D.4) с учетом D.5).
2. Распределение А пуассоновской случайной величины f(А)
асимптотически (по А —> оо) нормально с параметрами Ef(А) = А и D?(A) = A.
3. Распределение (те, iV, М)-гипергеометрической случайной величины
?(#, М, те) асимптотически (по JV —> оо,М —> оо,^-»р>0ите —> оо)
нормально с параметрами E?(JV, М,те) = тер и D?GV, А/, те) = терA — р).
4. Функция распределения нормированной fc-мерной (pi,ft»•'•>?*; п)
1 Случайная величина ?(п), зависящая от параметра п, называется асимптотически
(по п) нормальной, если существуют такие нормирующие не случайные переменные
А(п) и В(п), что функция распределения случайной величины п(п) = А(п) - ?(п) +
В(п) стремится при п —> оо к функции распределения стандартного нормального
закона при любом заданном значении их аргумента х.

4.4 ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН 161
полиномиальной случайной величины
при п -» оо стремится к функции распределения несобственного
(вырожденного) ^-мерного нормального закона с вектором нулевых средних
значений и с ковариационной матрицей
имеющей ранг, равный к — 1 .
5. Распределение случайной величины \ (т) асимптотически (по
т -+ оо) нормально с параметрами Ех2(т) = т и Dx2(m) = 2т.
6. Распределение случайной величины t(m) асимптотически (по т —>
с») нормально с параметрами Ш{т) = 0и Ш(тп) = 1.
4.4. Законы распределения вероятностей
случайных признаков, являющихся
функциями от известных случайных
величин
В теории и практике статистических исследований очень важно уметь
вычислять закон распределения вероятностей для функций от случайных
величин, распределение которых известно. Именно на этом, главным
образом, основана теория статистического, оценивания и проверки
статистических гипотез (см. гл. 7 и 8), так как и статистическая оценка,
и критическая статистика, используемые соответственно при
оценивании неизвестных значений параметров и при построении критериев
статистической проверки гипотез, суть не что иное, как функции от
результатов наблюдения исследуемой случайной величины ?. Для того чтобы
ими осмысленно пользоваться и знать их статистические свойства, мы
должны уметь восстанавливать их закон распределения по
распределению изучаемой случайной величины f (а значит, и ее наблюдений). Ниже
Здесь и далее символ I* означает единичную матрицу размерности к.
6 Теория вероятностей
и прикладная статистика

162 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
описываются основные правила, руководствуясь которыми можно решать
эту задачу.
1. Пусть случайная величина у является монотонно возрастающей
непрерывной функцией от заданной непрерывной случайной величины ?,
имеющей всюду дифференцируемую функцию распределения F^(x)y т.е.
V = #(?)¦ Каждому возможному значению х случайной величины ? будет
соответствовать возможное значение у = д(х) случайной величины 17.
В силу монотонности и непрерывности преобразования д по
заданному значению г) можно однозначно восстановить соответствующее ? с
помощью преобразования, обратного к д (обозначим его д~ ), т.е. f = д~ (?/).
Аналогичное соотношение связывает и возможные значения этих
случайных величин, т. е. х = д~ (у). Заметим, что функция д~ (у), так же как и
функция д(х), является монотонно возрастающей непрерывной функцией.
Попробуем выразить функцию распределения Fv(y) в терминах
заданных нам функций /^B), g и д~ .
У) =
9-\
Дифференцирование обеих частей D.7) по у дает
D.8)
Точно такие же рассуждения в случае монотонно убывающей
функции д(х) приведут нас к некоторому видоизменению формулы D.8):
/А»)- Л(,-<,».(-*2й). D.8')
Можно объединить формулы D.8) и D.8') в одной, справедливой для
любого взаимно-однозначного преобразования д:
fM =
dy
D.8")
Пример 4.1. Вычислить функцию плотности случайной величины
г\ = е€, если известно, что ( подчиняется (а, а*) — нормальному закону.
В данном примере д(х) = ea,g~l(y) = In у, следовательно,

4.4 ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН 163
Подставляя это в D.8/;), получаем
т.е. плотность логарифмически-нормального закона (см. п.3.1.6).
Пример 4.2. Вычислить функцию плотности случайной
величины 71 = а + 6?, если известна плотность /f(z) случайной величины ?. В
данном случае ^(ж) = а + Ья, jT^y) = (у - а)/Ь и (dg~l(y)/dy) = 1/6. В
соответствии с D.7) и D.8") имеем:
ДМ = (—)
I D9)
Ь
Это правило пересчета функций распределения и плотности
позволяет, в частности, использовать таблицы стандартного, т.е. @; 1)-
нормального закона для определения значений функции распределения и
функции плотности нормальной случайной величины ((а,<?2) с
произвольными параметрами а = Е{(а,<г2) и а2 = D?(a,cr2). При этом, как легко
видеть, роль ? играет стандартная нормальная величина ( @,1), а роль
г] — произвольная нормальная величина ?(а,<г2), т.е.
). D.10)
Соответственно имеем:
* ' '
2. Если интересующее нас преобразование г\ = д({) не является
взаимно-однозначными, то сколько-нибудь общие формулы получать не
удается. Вместо этого приходится каждый раз решать определенный
тип задач, прилаживаясь к их специфике. Рассмотрим, например,
случай q = {2:
в*

164 ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Следовательно, после дифференцирования левой и правой частей по
у имеем:
Применение данной формулы к случаю, когда ? является стандартной
нормальной величиной, дает
что является функцией плотности х -распределения с одной степенью
свободы и одновременно — частным случаем гамма-распределения с
параметрами а = Ь = 1/2 (см. п. 3.2.5).
3. Обобщим формулу D.8;/) на многомерный случай. Пусть f =
(? » ?>•••>?) — Р-мерная случайная величина с известной
функцией распределения F((X) и плотностью вероятности /$(Х) и пусть другая
р-мерная случайная величина tj = (*7 ,... ,*/ ) определяется как
заданная непрерывная векторная функция д(?) от компонент ?, т.е.
Предполагается, что соответствие ?/ = д(() является
взаимнооднозначным, т. е. существует обратное преобразование д~1, позволяющее
по заданному «значению» 7/ однозначно восстанавливать
соответствующее «значение» ?:
Соответственно между многомерными возможными «значениями»
X = (хA),...,ж(р)) и У = (•!/,..., 2/') случайных величин ? и т\
имеют место векторные соотношения
Y = g(X) и Х = д-

4.4 ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
165
Тогда совместная плотность вероятности случайных величин г/ =
>,...fi/rt) равна
• • •,УМ) = /«(ft ЧПл ЧП...t8;l(Y))
D.11)
где определитель преобразования {якобиан)
J(Y)
Qy
дую
так же, как и в формуле D.8"), берется по абсолютной величине.
4. Выведем распределение суммы двух независимых случайных
слагаемых (формулу композиции). Пусть независимые случайные величины ?i
и & имеют плотности вероятности соответственно f(t(x) и /$а(у).
Требуется произвести композицию этих плотностей, т.е. найти плотность
распределения случайной величины ц = & + &• По существу, мы должны
рассмотреть совместное двумерное распределение /((!,&)(я* у) и для
определения функции распределения случайной величины г\ найти в
плоскости хОу область возможных значений (fb&J» соответствующих событию
{q<z). На рис. 4.1 эта область заштрихована и обозначена Az. Получаем
ЗД = Р{Ч <*} = Р{Ь +6
= / J%ь*ы(х'у) dxdy
Az
OO 2Г — X
6 Аг)
ьМ dxdy
. D.12)
Здесь мы воспользовались тождеством /(&,&)(«» у) = /ft(^) ' Д3(у)
(справедливым в силу независимости ?х и {2), а при интегрировании по
области Аг пределы интегрирования по оси Ох брали от —оо до +оо, а по
оси Оу — от — оо до прямой у = z — х.

166
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Рис. 4.1. Попадание в область Ая на плоскости хОу соответствует событию
Дифференцирование по z левой и правой частей соотношения D.12)
дает
00
D.13)
-00
Формулу D.13) называют формулой композиции двух распределений
или формулой свертки. Для обозначения композиции (свертки) законов
распределения часто применяют символическую запись
Воспользовавшись формулой D.13), можно вывести упомянутое в
п. 3.1.5 и 3.1.10 свойство «самовоспроизводимости» законов Гаусса и Коши
(сумма нормальных случайных величин сама распределена по
нормальному закону; сумма одинаково по Коши распределенных случайных величин
сама подчиняется закону распределения Коши), а также получить
формулы для плотности распределения сумм равномерно распределенных
величин, приведенные в п. 3.1.7.
ВЫВОДЫ
1. Следует выделить три типа основных результатов теории
вероятностей:
доасимптотические> позволяющие анализировать основные
закономерности в поведении случайной величины по ее главным числовым
характеристикам — среднему значению, дисперсии и т. п. — без апелляции
к знанию общего вида закона ее распределения;

выводы 167
асимптотические, позволяющие анализировать основные
закономерности в поведении сумм большого числа случайных слагаемых (а именно
устанавливать их асимптотическую устойчивость, т.е. их сходимость к
некоторым постоянным значениям по мере роста числа слагаемых, или
описывать асимптотический вид закона распределения этих сумм) без
точного знания законов распределения отдельных слагаемых;
относящиеся к теории преобразований случайных величин,
позволяющие находить закон распределения интересующих нас функций от набора
случайных величин, совместное распределение которых нам известно.
2. Первый тип результатов представлен в данном учебнике
неравенством Чебышева, позволяющим оценивать вероятность зафиксировать
при наблюдении случайной величины ? значение, отклоняющееся от ее
среднего значения а = Е? не менее чем на заданную величину А, без
знания закона распределения исследуемой случайной величины f (см. D.2)).
3. Закон больших чисел и его следствия относятся к первому (менее
глубокому) уровню асимптотических результатов и позволяют
устанавливать сходимость (по вероятности) нормированных сумм большого числа
случайных слагаемых к некоторым постоянным значениям — по мере
роста числа слагаемых — практически независимо от вида распределения
самих слагаемых.
4. Центральная предельная теорема относится к следующему
(более глубокому) уровню асимптотических результатов. Она утверждает,
в частности, что закон распределения нормированной суммы большого
числа случайных слагаемых практически вне зависимости от типа
распределения самих слагаемых стремится (по мере роста числа слагаемых)
к нормальному (гауссовскому) закону распределения (см. п. 4.3.1).
Однако необходима известная осторожность при практическом
использовании центральной предельной теоремы: во-первых, часто можно
подобрать весьма простые (и более точные, чем нормальные!)
аппроксимации для распределения суммы небольшого конечного числа случайных
слагаемых; во-вторых, центральная предельная теорема плохо
работает на «хвостах» распределений, т.е. при оценке вероятностей больших
уклонений анализируемой суммы случайных величин от своего среднего
значения.
5. Основным результатом теории преобразования случайных величин
является правило D.8 ) (или D.11) в многомерном случае), позволяющее
вычислять закон распределения (функцию плотности или полигон частот)
случайной величины, являющейся заданной функцией от набора исходных
случайных величин, совместный закон распределения которых нам
известен.

ГЛАВА 5. ЦЕПИ МАРКОВА
5.1. Последовательности случайных
экспериментов и случайных величин
в дискретном вероятностном
пространстве
Рассмотрим дискретное вероятностное пространство с конечным
числом элементарных исходов u>i,u>2>« «ч^/у и вероятностями их
появления (в результате реализации случайного эксперимента), соответственно
Pi = P{u>i}, P2 = P{v2}>*--fPisf = P{vN}> Пусть нас интересует
вероятность появления заданной последовательности элементарных исходов
(jji1,Ui2)...<iUin в результате реализации п последовательных случайных
экспериментов. Бели случайные эксперименты производятся в рамках
одного и того же вероятностного пространства и независимы друг от друга,
то мы имеем дело с последовательностью независимых случайных
экспериментов, и интересующая нас вероятность определится по
формуле вероятности независимых событий A.13), что в нашем случае дает
. P{uhui2 • • -uin} = P{uh} ¦ P{ui9} ..... P{uin} = pilPi3 •....Pi,. E.1)
Из независимости рассматриваемых событий следует также, что если
бы нас интересовал только результат, полученный на одном каком-то
«шаге» этой последовательности (например, на шаге J), то вероятность
P{uit} определяется единственно величиной pit и никак не зависит от
предыстории, т. е. от того, какие именно результаты мы имели на
предыдущих шагах этой последовательности. Очевидно, в рамки подобной
схемы укладываются ранее рассмотренные примеры 1.1 (последовательность
подбрасываний одной и той же монеты), 1.3 (четырехкратное бросание
игральной кости), 1.5 (проверка по альтернативному признаку п изделий,
случайно отобранных из продукции стационарно функционирующего
производства).

5.1 ПОСЛЕДОВАТЕЛЬНОСТИ СЛУЧАЙНЫХ ЭКСПЕРИМЕНТОВ 169
Однако нетрудно представить себе реальные ситуации, в которых
результат случайного эксперимента на определенном шаге
последовательности в определенном смысле зависит от того, какие именно результаты
наблюдались на предыдущих шагах этой последовательности. Очевидно,
в подобных ситуациях речь следует вести о последовательности
зависимых случайных экспериментов.
В дальнейшем несколько видоизменим терминологию с целью ее
более естественного приспособления к реальным задачам. А именно будем
интерпретировать каждый из элементарных исходов ljj как «возможное
состояние» анализируемого объекта (индивидуума, работника, семьи,
домашнего хозяйства и т. п.). Введем в рассмотрение дискретное время t и
случайную величину &(<*;), значения которой A,2, ...,iV) определяют, в
каком именно состоянии находился анализируемый объект в момент
времени t (t = 1,2, ...,n), т.е. (t(u)i) = i. В каждый следующий момент
времени t + 1 объект из состояния о;,-, в котором он находился, может
перейти в любое другое состояние Uj или остаться в том же самом
состоянии U{. Таким образом, от рассмотрения последовательностей
случайных экспериментов мы переходим к рассмотрению
последовательности случайных величин €i(u),€2(u),...,fn(u), вообще говоря, взаимно-
зависимых. А чтобы «задать поведение» многомерной случайной
величины f = (f,(w),f2(w),...,fn(b>))> необходимо, как мы знаем (см. выше,
п. 2.5.3), задать соответствующий совместный n-мерный закон
распределения вероятностей, который в данном случае (с учетом того, что каждая
из компонент ? может принимать одно из N возможных значений)
описывается с помощью Nn конкретных чисел (вероятностей).
Правда, в случае последовательности независимых случайных
экспериментов мы имеем соответствующую последовательность
независимых одинаково распределенных случайных величин, так что в
соответствии с B.14 ) и E.1)
P{Zl = *1,6 = *2,--.,?n = in} = Pta Рг2 ' ••¦ Pin E.2)
и распределение п-мерной случайной величины ? = (&, ?2> • • • > ?п) задается
всего лишь N числами: р\ ,/>2> • • • >Рдг
Можно ожидать, что и при некоторых специальных типах
зависимостей, существующих между элементами последовательности ?ь &»•••> (т
способ задания ее поведения окажется более простым и экономичным, чем
в самом общем случае. Именно к рассмотрению одного из таких
специальных типов зависимостей мы и переходим.

170 ГЛ. 5. ЦЕПИ МАРКОВА
5.2. Последовательности, образующие
цепь Маркова (определения, примеры,
прикладные задачи)
Продолжая рассмотрение системы «объект — его состояние в
заданный момент времени *», предположим, что эта система
характеризуется «ограниченной памятью», а именно вероятность того, что объект
в момент времени t окажется в заданном состоянии «j», зависит не от
всей предыстории, а только от того, в каком состоянии он находился в
предыдущий момент времени t - 1, т.е.
Р{6 = j | (г = iu B = i2,...,&-! = 1} = Р{Ь = j | ft-i = О- E.3)
О таких зависимостях последовательности случайных величин &, &» • • • > tt
говорят как о зависимостях марковского типа, а соответствующие
последовательности называют цепями Маркова. Бели дополнительно
предположить, что вероятности p\j = Pitt = 3 I &-1 = *} остаются одними
и теми же при всех t (т. е. не зависят от ?), то соответствующая
марковская цепь называется однородной. Именно однородным цепям Маркова и
посвящена данная глава.
Чтобы дать строгое определение однородной цепи Маркова,
необходимо задать способ вычисления совместного распределения вероятностей для
многомерных случайных величин (&, ?2> • • • > &) при любых t = 1,2,... .
Определение. Последовательность случайных величин ?
..., каждая из которых может принимать конечное число значений
Х2> •••>ЯдП называется однородной цепью Маркова, если вероятности
событий вида
{6=*°, 6 = *?„...,& = 4> E-*)
определяются формулой
= Я|,э 6 = &ta> •••»€« = xit] =Pii Piii2 '•••*Pt|_1i|
через начальное распределение вероятностей
Рг = P{tt = 4}, pi = Р{6 = х°2}, ..., pN = Р{6 = Ж^} E.5)
1 Требование конечности числа возможных состояний не обязательно при
определении цепи Маркова. На самом деле допускается и счетное число состояний. Однако
в рамках наших целей можно обойтись и конечным числом состояний.

5.2 ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ 171
и матрицу переходных вероятностей1
Р\\ Р\2 • • •
Р= I Рп Ри '" ^N I E.6)
где
Pij = P{tt = 3 I 6-1 = 0 A** «се* (=1,2,.... E.7)
Выше в качестве возможных значений ж?,^,...,^ случайных
величин & (t = 1,2,...) мы рассматривали лишь номера «состояний»
анализируемых объектов (т.е. полагали х) = j). Однако иногда возможным
значениям анализируемых случайных величин удобнее придавать более
общий смысл.
Проверим корректность приведенного определения и его
непротиворечивость с «марковским свойством» E.3). Для этого, во-первых, требуется
убедиться, что определенные с помощью соотношений E.4)-E.6)
вероятности действительно образуют закон распределения вероятностей, т. е.
«1 «2 U
(суммирование в каждой сумме ведется по всем возможным значениям
жЪж2,...,Жуу).
А во-вторых, показать, что из этого определения следует соотношение
E.3).
Справедливость E.8) вытекает из следующих фактов:
а) очевидно, для любого Jb = 1,2,... 9 < — 1
Piki + Pik2 + • • • + PihN = 1, E.9)
т. к. левая часть E.9) определяет вероятность достоверного события,
каковым является событие, заключающееся в том, что анализируемый
объект на следующем «шаге» перейдет из состояния ik в одно из всех
возможных состояний;
б) учитывая E.9) и последовательно проводя суммирование в правой
части E.8), начиная от суммы ?, переходя к сумме ? и т.д., имеем:
1 Матрицы переходных вероятностей, по определению, обладают следующим
свойством: все их элементы рц неотрицательны, и суммы элементов любой
строки равны единице. Матрицы, обладающие этим свойством, принято называть
стохастическими.

172 " ГЛ. 5. ЦЕПИ МАРКОВА
= Pii ' Ptxi3 " • • • ' Ptt-.2ti.-i " (P«t-il + i
ti ' Ptita # • • ' Pt«.8ii-a '
(последнее тождество следует из определения вероятностей
Соотношение E.3) непосредственно следует из теоремы умножения
вероятностей A.11), если принять обозначения
а для подсчета вероятностей Р{АВ} и Р{В} воспользоваться формулой
E.4).
Заметим, что последовательность независимых случайных величин
. .,fn, определенных в одном и том же дискретном вероятностном
пространстве с конечным числом возможных значений хг, ж25 • • • 5 xN и
соответствующими вероятностями pi = P{?t = ж,} (i = l,2,...,iV; J =
1,2,...,п), можно рассматривать как частный случай цепи Маркова, в
которой начальное распределение вероятностей E.5) задается вектором
Р = (РъР2> • • • »Рдг)> а матрица переходных вероятностей E.6) имеет вид
(Pi P2 ••• Ру/
Pi Р2 • •• PN
Pi P2 •'• Р^
Впервые понятие зависимости типа E.4)-E.6) было введено в 1911 году
замечательным русским математиком Андреем Андреевичем Марковым. Он предложил
простейшее обобщение серии испытаний Бернулли (см. п. 3.1.1), в котором
вероятности двух возможных исходов P{(t = 1} и P{?i = 0}, в отличие от схемы независимых
испытаний, уже зависели от того, каков был предыдущий исход, т.е. от того, какое
именно значение приняла случайная величина &-ь Итак, в предложенной схеме

5.2 ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ 173
(очевидно, при этом роо = 1 - Р01 и рю = 1 - ри). А.А.Марков показал, как,
располагая, помимо значений вероятностей poi и рц, еще величиной вероятности появления
события {( = 1} в первом испытании, можно вычислить вероятность любого события
вида E.*). Он назвал эту схему простейшей цепью. В дальнейшем он обобщил
эту схему на случай произвольного конечного или даже счетного числа возможных
значений случайной величины. Это обобщение и получило название цепи Маркова.
Пример 5.1. Динамика типологии семейного потребления.
В данном примере исследуемыми объектами являются семьи, точнее,
домашние хозяйства. Возможные «состояния» объекта — типы
потребительского поведения. Единица измерения (такт) времени — один год.
Соответственно, элемент pi начального распределения вероятностей
интерпретируется как доля домашних хозяйств, относящихся к t-му типу
потребительского поведения в начальный (первый) «момент времени», а
переходная вероятность рц — как доля семей t-ro типа потребительского
поведения, переходящих за 1 год в «состояние» j.
Пример 5.2. Игра двух лиц до разорения. Исследуемый
объект — один из двух участников игры, которая происходит по
следующим правилам. Суммарный капитал двух игроков фиксирован и равен
iV денежным единицам. Выигрыш одного кона составляет одну
денежную единицу. Анализируемый игрок начинает игру, имея п единиц, и
выигрывает кон с вероятностью р. После проигрыша последней единицы
г'-м игроком (г = 1,2) игра заканчивается его разорением. Очевидно,
«состояние» объекта в этой схеме следует понимать в буквальном смысле:
оно определяется имеющейся у него в наличии суммой денежных единиц
в соответствующий «момент времени», а последний интерпретируется
как очередной кон игры. Итак, мы имеем N + 1 возможных состояний, а
именно: 0; 1; 2;...;АГ.
Начальное распределение вероятностей в данном случае
определяется формулой
р< = />{?(l) = i}=/J при,- = п;
1>ч ' } I 0 для всех % ф п.
В соответствии с правилами игры переходные вероятности р^
определяются соотношениями
{р при j - t = 1 и ji ^ 1;
1-р npHt-j = l и г^ 1;
1 при г = j = 0 и при i = j = N.
Пример 5.3. Демографическая модель передвижки
возрастов. В качестве объекта рассматривается элемент населения страны
или региона (индивидуум), а его «состояние» определяется его
возрастом. Смежные «состояния-возрасты» отличаются друг от друга на один

174
ГЛ. 5. ЦЕПИ МАРКОВА
год. Исключение составляет состояние, определяемое как «предельный
возраст»: к нему будем относить все индивидуумы в возрасте,
превышающим 85 лет. Кроме того, вводятся еще три особых состояния:
«иммиграционное*, «эмиграционное» и «поглощающее». Иммиграционное и
эмиграционное состояния связаны с возможным соответственно прибытием и
выбытием индивидуумов из анализируемого региона в связи с
миграцией населения; а поглощающее — только с выбытием по причине смерти.
Таким образом, мы имеем 89 возможных состояний: первое — возраст до
1 года, второе — до 2 лет, ... , 85-е — до 85 лет, 86-е — свыше 85 лет,
87-е — иммиграционное, 88-е — эмиграционное и 89-е — поглощающее.
Начальное распределение вероятностей pi = Р{^A) = •}, • =
1,2,..., 86,87,88,89 определяется демографической структурой общества,
зафиксированной на конец первого года исследуемого периода. При этом
под Р87 понимается доля иммигрантов этого года во всем населении
региона, а рае — доля эмигрантов. Матрица Р переходных вероятностей ру
может быть определена в терминах возрастных характеристик
смертности (/!{), иммиграционной (ft) и эмиграционной (/?,) активности населения
в виде таблицы 5.1.
Таблица 5,1

Номер


тояния
@
1
2
3
1
85
86
87
88
89
Номер состояния (j)
1
0
0
0
:
0
0
2
1 - и 1 - А
0
0
0
0
92
0
0
3
0
1-М2-02
0
•
0
0
9з
0
0
4
0
0
:
0
0
94
0
0
5
0
0
0
•
•
•
0
0
95
0
0
• • •
• t t
...
...
...
• • •
• • ¦
...
...
85
0
0
0
:
0
0
985
0
0
86
0
0
0
j
1-/*85-&5
1-/*86-А»6
986
0
0
87
0
0
0
:
0
0
0
0
0
88
A
A
A
As
Ae
0
l
0
89
Pi
to
А*з
:
P85
/*86
0
0
1
Участвующие в вычислении вероятностей Pij возрастные
демографические характеристики интерпретируются следующим образом.
Величина /ii оценивается как доля тех людей возраста *', которые умерли в этом
возрасте; значение Д определяет долю тех людей возраста i, которые эми-

5.2 ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ 175
грировали из анализируемого региона (страны) в данном возрасте;
наконец, qi выражает удельный вес людей i-ro возраста среди всех
иммигрантов данного региона, т. е. среди всех людей, прибывающих в
анализируемый регион на постоянное поселение.
Пример 5.4. Модель пребывания студента в вузе. В
качестве объекта рассматривается студент вуза с пятилетним сроком
обучения. Его t-e состояние соответствует его обучению на t-м
курсе (г = 1,2,...,5); 6-е состояние — специалист, окончивший
данный вуз; 7-е — лицо, обучавшееся в данном вузе, но по каким-
то причинам не окончившее его. Чтобы не увеличивать числа
возможных состояний примем допущение, что по правилам данного
вуза зачисление в него переводом студентов из других вузов
невозможно. Из смысла состояний следует, что ненулевыми
элементами матрицы Р переходных вероятностей могут быть только
величины Р1ЪР12,Р17>Р22>Р23>Р27>РЗЗ>Р34>Р37>Р44>Р45>Р47>Р55>Р5в>Рб7> & Также
Рвв = Р77 = Ь
Пример 5.5. Игровые возможности двух шахматистов.
Объектом в данном примере является соревнующийся шахматист, а
состоянием — результат сыгранной им партии A-е состояние — выигрыш,
2-е состояние — ничья, 3-е состояние — поражение). Анализируется
турнирное поведение двух шахматистов А к В. Игрок А каждую партию
турнира независимо от исходов предыдущих партий выигрывает с
вероятностью «в», делает ничью с вероятностью «н» и проигрывает с
вероятностью «сп» = 1 - в - н. Игрок В менее уравновешен: он выигрывает
партию с вероятностями в+е> в и в-е @ < е < тш(в, 1-в,н, 1-н)
соответственно, если предыдущая партия была им выиграна, сыграна вничью
или проиграна. Аналогично ведет себя вероятность его проигрыша: она
равна в этих трех случаях соответственно п - е, п и п + е. Очевидно,
закономерности появления того или иного результата в зависимости от
результата предыдущей партии у каждого из игроков могут быть
описаны с помощью соответствующим образом подобранной однородной цепи
Маркова с тремя возможными состояниями и с матрицами переходных
вероятностей Р(А) (у игрока А) и Р(#) (у игрока В):
(в н п\
в н п I ;
в н п/
Р(В) =
Заметим, что матрица Р(Л) в действительности описывает
последовательность независимых испытаний (которая, как мы видели, является
частным случаем цепи Маркова), а матрица РB?) иллюстрирует реаль-

176 ГЛ. 5. ЦЕПИ МАРКОВА
ную ситуацию, подтверждающую базовую идею А. А. Маркова в
построенной им простейшей цепи, в соответствии с которой вероятность
определенного исхода случайного эксперимента в серии таких испытаний может
зависеть от результата предыдущего исхода.
Очевидно, аналогично могут быть построены примеры марковских
цепей, описывающих динамику межотраслевой структуры трудовых
ресурсов («объект» — работник, «состояние» — отрасль экономики, в
которой он занят в данный «момент времени»), динамику социальной
стратификационной структуры общества («объект» — индивидуум,
«состояние» — социальная страта, к которой он принадлежит в данный «момент
времени») и т. д.
Как и всякое другое моделирование, построение моделей цепей
Маркова не является самоцелью, а лишь инструментом для решения
определенного класса прикладных задач. Сформулируем кратко те основные
прикладные задачи, которые решает исследователь при анализе цепей
Маркова.
Задача 1. Прогноз распределения объектов по возможным
состояниям через Т тактов времени. Другими словами, это означает, что
исследователь хотел бы подсчитать по исходным данным р и Р вероятности
того, что анализируемый объект через заданное число тактов времени Т
будет находиться в заданном «состоянии» j (jf = 1,2,..., N). В примере 1 —
это прогноз распределения домашних хозяйств по различным типам
потребительского поведения, в примере 2 — это прогноз платежеспособности
игроков через заданное число сыгранных конов, в примере 3 — это прогноз
демографической структуры общества.
Задача 2. Расчет среднего времени перехода объекта из состояния
г в заданное состояние j.
Задача 3. Расчет вероятностей перехода из состояния % в
состояние j за заданное число тактов времени т.
Задача 4. Расчет среднего времени пребывания объекта в
заданном состоянии г.
Задача 5. Решение проблемы существования и вычисления
стационарного распределения объектов по возможным состояниям. Речь идет
о ситуациях, когда меняющееся во времени распределение объектов по
состояниям со временем стабилизируется и, начиная с некоторого «момента
времени», остается практически неизменным.

5.3 ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА 177
5.3. Основные характеристики и свойства
цепей Маркова
5.3.1. Основные характеристики
Исходными характеристиками однородной марковской цепи, как это
следует из определения E.4)-E.6), являются:
• вектор вероятностей начального распределения р = (ръР2>- --^Рдт)
и
• матрица Р переходных вероятностей p±j (i>j= 1,2,..., N).
Однако в процессе анализа цепи Маркова приходится сталкиваться с
рядом ее производных характеристик, которые тем или иным способом
вычисляются по исходным.
Вероятность перехода из состояния г в состояние j за t тактов
времени р\у может быть подсчитана по формуле
которая является непосредственным следствием формулы полной
вероятности A.14), если в качестве участвующих в ней событий А и Bq
рассмотреть
Л = {6 = Л6=0 и Bq = {&_, = q Ui = «}.
Бели по аналогии с матрицей Р вероятностей перехода за один шаг
ввести в рассмотрение матрицы Р вероятностей перехода за q шагов
(q = 2,3,...), то, как легко убедиться, формула E.10) может быть
представлена в следующем матричном виде:
Последовательно применяя эту формулу к случаям t = 2, t = 3 и т. д.,
получаем:
рB) ==p(l).p=:p,p = p2j
рC) рB) р р2 р рЗ
f -р р-рр-р, ^511)
p(t) = р«,
т.е. для того, чтобы получить матрицу вероятностей перехода Р^ за t
шагов, надо просто возвести в степень t исходную матрицу вероятностей
перехода Р.

178 ГЛ. 5. ЦЕПИ МАРКОВА
Безусловная вероятность Pj того, что объект в момент t
находится в состоянии j, подсчитывается также с использованием
формулы полной вероятности:
N
В формуле E.12) вероятности pjj- , i = 1,2,..., JV, образуют j-й столбец
матрицы Р"~ \ вычисляемой по формуле E.11).
Вероятности первого возвращения объекта в заданное
состояние. Введем в рассмотрение вероятность Щ первого возвращения в
состояние j через t шагов, т. е.
Опираясь на формулу сложения вероятностей, можно получить
следующие рекуррентные соотношения для вычисления вероятностей щ\
Умение вычислять вероятности fjj позволяет определять и значения
некоторых других характеристик, которые могут оказаться полезными
при анализе марковской цепи. К таким характеристикам можно отнести,
например:
• вероятность fjj того, что, выйдя из состояния j в момент времени
t = 1, объект когда-нибудь вернется в это же состояние:
• среднее время /jljj первого возвращения в состояние j (при условии
fil = О:
Вероятности /ty первого достижения состояния j при
выходе из состояния г ровно через t тактов времени являются естественным

5.3 ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА 179
обобщением вероятностей первого возвращения щ. Соотношения,
позволяющие их рассчитать, также являются следствием формулы сложения
вероятностей. Они имеют вид:
-Pij-JijPji hj Pjj Jij Piv
По этим вероятностям, в частности, могут быть подсчитаны:
• вероятность /у того, что выйдя из состояния i в момент времени
t = 1, объект когда-нибудь попадет в состояние j:
• среднее время \кц первого достижения состояния j при выходе из
состояния i:
5.3.2. Классификация состояний и цепей
Свойства цепи Маркова и соответственно способы решения
связанных с ее анализом задач (см., например, формулировку задач 1-5 в п. 5.2)
существенно зависят от того, из каких именно состояний она состоит.
Поэтому приведем здесь принятую классификацию состояний конечной
цепи Маркова и обусловленную ею классификацию самих марковских цепей.
Состояние j называется достижимым из состояния «, если
существует такое <о ^ 1> что p\j > 0, т.е. если имеется положительная
вероятность попасть из состояния г в состояние j (включая случай г = j).
В терминах вероятностей первого достижения достижимость j из г
может быть определена условиями fjj > 0 и /у > 0 (для г\ф j). Возвращаясь
к нашим примерам, можно без труда убедиться в том, что в примере 5.2
все состояния достижимы из состояний 1,2,...,7V - 1, а в примере 5.3
состояние j является достижимым из любого состояния г, кроме г = 87,
только при условии j > t; состояние 87 — особое: из него достижимы все
состояния цепи, кроме 88-го и 89-го.
Состояние г называется поглощающим, если никакое другое
состояние цепи не может быть из него достигнуто, т. е. если pik = 0 для всех

180 ГЛ. 5. ЦЕПИ МАРКОВА
к ф г (отсюда следует, что рц = 1). Мы уже имели дело с поглощающими
состояниями в примерах 5.2 (состояния t = 0 и t = TV), 5.3 (состояния 88
и 89) и 5.4 (состояния 6 и 7).
Свойство поглощения может быть «коллективным», а именно:
множество С состояний называется поглощающим (или замкнутым),
если никакое состояние вне С не может быть достигнуто ни из какого
состояния, входящего в С. В терминах переходных вероятностей это
означает, что pjk = 0 для всех j и к таких, что j входит в С, а А: не
входит. Отсюда, в частности, следует, что всякое входящее в цепь
замкнутое множество состояний может быть изучено как самостоятельная
(автономная) цепь Маркова независимо от прочих состояний исходной
цепи. Так, если в нашем примере 5.1 допустить существование некого
«элитного» подмножества типов потребительского поведения, за пределы
которого принадлежащие этому подмножеству семьи в процессе своих
переходов из одного состояния в другое никогда не выходят, то мы и будем
иметь пример замкнутого (поглощающего) множества состояний,
которое одновременно можно рассматривать как самостоятельную «подцепь»
Маркова.
Возвратные состояния. Состояние г называется возвратным, если,
отправляясь от него, объект с вероятностью единица когда-нибудь в него
вернется, т.е. fa = I1. Соответственно состояние j называется
невозвратным, если fjj < 1; можно показать, что для этого необходимо и
00 it)
достаточно, чтобы J^Pa < °°-
Периодические состояния. Состояние i называется
периодическим с периодом т > 1, если р\1 = 0 для любого ?, не кратного т, и
г — наименьшее целое число, обладающее этим свойством (т. е. объект не
может вернуться в состояние г за время, отличное от г, 2т, Зт,...).
Состояние принято называть эргодическим, если оно
возвратное и непериодическое.
Определив различные типы состояний марковской цепи, мы
переходим к классификации самих цепей Маркова.
Цепь называется неприводимой тогда, когда в ней нет никаких
замкнутых множеств, кроме множества всех состояний.
Применительно к конечной марковской цепи (которая и является предметом нашего
1 В марковских цепях со счетным числом возможных состояний допускаются
ситуации, когда, несмотря на возвратность состояния (и соответственно выполнение
соотношения /,-,- = 1), среднее время возвращения рц оказывается бесконечно большим.
В этом случае состояние г называется возвратным нулевым. Однако в конечных
цепях Маркова все возвратные состояния ненулевые.

5.3 ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА 181
анализа в данной главе) это означает, что неприводимая цепь Маркова
должна состоять только из возвратных состояний, каждое из
которых достижимо из любого другого состояния цепи. В терминах
матрицы переходных вероятностей Р это означает, что существует такое <о> что
все элементы матрицы Р<0 являются положительными. Таким образом,
из определения замкнутого (поглощающего) множества состояний
следует, что любое такое множество может рассматриваться как неприводимая
конечная цепь Маркова.
Следует отличать определенное выше поглощающее (замкнутое)
множество состояний от множества поглощающих состояний.
Действительно, цепь Маркова может содержать одно или несколько (целое множество)
поглощающих состояний. Очевидно, в этом случае она уже не может быть
неприводимой хотя бы потому, что не все состояния взаимодостижимы (из
поглощающего состояния ни одно другое состояние не является
достижимым по определению). Ясно также, что такая цепь должна содержать
невозвратные состояния, поскольку если поглощающее состояние
является достижимым для какого-либо состояния j, то объект уже не может
вернуться в состояние j с вероятностью единица (а значит, состояние j
невозвратное). Правда, в состав сложной цепи могут входить и замкнутые
множества состояний, но их, как было отмечено, можно отдельно
анализировать каждое как неприводимую цепь Маркова. Поэтому представляет
интерес рассмотреть класс марковских цепей, которые состоят только из
поглощающих и невозвратных состояний.
Конечные марковские цепи с поглощением (или
поглощающие цепи Маркова) и определяются как цепи, состоящие только из
поглощающих и невозвратных состояний. Объекты, описываемые такой
цепью Маркова, постепенно переходят из невозвратных состояний в
поглощающие, находясь в невозвратных состояниях некоторое случайное
время. Очевидно, если такая цепь содержит всего N состояний, из которых
m-поглощающих, то при соответствующей нумерации состояний ее
матрица переходных вероятностей Р может быть представлена в виде
E.20)
где Im — единичная матрица порядка т х га; О — матрица порядка
m х (N - га), состоящая из нулей; Рнп — матрица порядка (N - га) X га,
задающая вероятности перехода из невозвратных состояний в
поглощающие; Рнн — матрица порядка (iV-ra)x(JV —га), состоящая из вероятностей
перехода между невозвратными состояниями.

182 ГЛ. 5. ЦЕПИ МАРКОВА
Очевидно, модели зависимостей, описанные в наших примерах 5.2-
5.4, относятся как раз к этому типу цепей Маркова.
Определим, наконец, для полноты картины еще один тип цепей
Маркова, который, однако, в дальнейшем нам не понадобится.
Периодическая цепь — это неприводимая цепь Маркова, все
возвратные состояния которой имеют один и тот же период т. Строго говоря,
в определении периодической цепи достаточно было бы потребовать
периодичности любого из возвратных неприводимой цепи, т.к. по известной
«теореме солидарности» (см., например, [Боровков А. А., стр.199]) в
неприводимой цепи Маркова все состояния принадлежат одному типу, и,
в частности, если хоть одно из них периодично с периодом г, то и все
остальные состояния этой цепи будут иметь тот же самый период.
5.3.3. Свойства цепей Маркова
Опишем теперь ряд свойств марковских цепей, знание которых
составит необходимую базу при решении прикладных задач, связанных
с их анализом. Доказательства сформулированных ниже утверждений
опускаются (их можно найти, например, в [КемениДж., СнеллДж.] и
в [ФеллерВ.]).
Эргодическое свойство. Пусть N — общее число состояний цепи
Маркова. Для того, чтобы при любом j существовал не зависящий от
г предел
Hm pg> = рИ > 0, ij = 1,2,..., N,
необходимо и достаточно, чтобы цепь была неприводимой и
непериодической, т. е. представляла бы собой одно замкнутое множество
возвратных и взаимодостижимых состояний. При этом числа ру°*
являются единственным решением системы уравнений
N
у, j = lt2,...,N;
E-21)
Кроме того, существует такое h (О < h < 1), что
Напомним, что pj' — это безусловные вероятности того, что объект

5.3 ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА 183
в момент t находится в состоянии j (см. выше E.12)). Так что ру°' есть,
по-существу, вероятности попадания объекта в состояние j через
большой интервал времени. При этом оказывается, что объект «забывает»,
откуда он начал движение, т.к. эти вероятности не зависят от
начального состояния объекта. Распределение (р\ ,рз »• ">Pn ) называют
стационарным, или финальным. Устойчивый режим, в который
входит конечная неприводимая непериодическая цепь Маркова при / -* оо,
характеризуется к тому же следующими свойствами:
(а) среднее время возвращения в состояние j
(б) при больших t среднее время пребывания в состоянии j
приблизительно равно t • pj.
Заметим, что перенесение эргодических свойств цепи на
периодический случай не представляет принципиальных трудностей, хотя и
приводит к заметному усложнению формулировок.
Свойства поглощающих цепей Маркова. Эти цепи были
определены в п. 5.3.2 как состоящие только из невозвратных и поглощающих
состояний конечные цепи Маркова, матрица переходных вероятностей
которых представима в виде E.20). Итак, пусть из общего числа N
состояний такой цепи первые т состояний отнесены к поглощающим. И пусть
нас интересуют величины:
• ctij = Etij — среднее значение времени ty пребывания в
невозвратном состоянии j объекта, вышедшего из невозвратного состояния г
(*,j = m+l, т + 2,...,ЛГ);
N
• а*. = Е( ]? tij) — общее время, включая время пребывания в ис-
j=m+l
ходном невозвратном состоянии t, которое объект проводит во всех
невозвратных состояниях до попадания в какое-либо поглощающее состояние;
• 7у — вероятность попадания в поглощающее состояние j (j =
1,2,...,m) объекта, вышедшего из невозвратного состояния г (i = т +
1, т + 2,...,ЛГ).
Для поглощающих цепей Маркова, задаваемых матрицами
переходных вероятностей вида E.20), имеют место следующие утверждения:
Утверждение 1. Значения а^ определяются как (i)j)-e элементы
матрицы
А = (!„-.«-Р«.Г\ E.22)

184 ГЛ. 5. ЦЕПИ МАРКОВА
где IN_m — единичная матрица порядка (N -~m)x(N - т), а Рнн —
матрица вероятностей перехода между невозвратными состояниями
порядка (N -m)x(N - т) (см. E.20));
Утверждение 2. Значения а*, определяются как компоненты
вектора
( -' ^
а= : =А1, E.23)
\aN-mJ
где 1 — вектор-столбец порядка (N — т) X 1 с компонентами, равными
единице, а А — матрица, определенная соотношением E.22);
Утверждение 3. Значения вероятностей 7tj определяются как
(i>j)-e элементы матрицы
Г = А.РНП, E.24)
где А — матрица, определенная соотношением E.22), а Рнп — матрица
порядка (N — т) х т, задающая вероятности перехода из невозвратных
состояний в поглощающие (см. E.20)).
Свойства цепи, содержащей множество невозвратных
состояний J и замкнутое (поглощающее) множество возвратных
состояний С. При анализе подобных цепей нас могут интересовать ответы
на следующие вопросы:
- какова вероятность того, что объект, отправляясь из невозвратного
состояния, все время будет находиться в множестве невозвратных
состояний J?
- как подсчитать вероятность /j.c того, что объект, выходя из
невозвратного состояния j, когда-нибудь достигнет поглощающего множества
возвратных состояний С?
Ответы на эти вопросы дает, например, следствие теоремы 1 из
[ФеллерВ., с. 393]:
1) В конечной цепи Маркова вероятность того, что объект все
время будет находиться в множестве невозвратных состояний, равна
нулю.
2) Вероятности /j.c того, что исходя из невозвратного состояния
j объект достигнет когда-нибудь поглощающего множества С,
определяются как единственное решение системы линейных уравнений
/й, J6J. E.25)

5.4 АНАЛИЗ ЗАДАЧ И ПРИМЕРОВ 185
В этой системе суммирование производится по всем невозвратным
состояниям цепи, a /..q — это вероятность перейти из j в любое из состояний
множества С за один шаг.
5.4. Анализ некоторых задач и примеров
Теперь, когда мы проанализировали возможные типы состояний и
основные свойства марковской цепи, мы можем приступить к
прикладному анализу некоторых описанных в п. 5.2 примеров. Прикладной анализ
предусматривает решение ряда конкретных задач, в том числе тех,
которые были сформулированы в п. 5.2 (см. задачи 1-5).
Пример 5.1. Динамика типологии семейного потребления.
Здесь нас в первую очередь будет интересовать тип и структура цепи
(классификация состояний, наличие среди них замкнутых множеств
возвратных состояний, невозвратные и поглощающие состояния и т.п.), а
также прогноз распределения домашних хозяйств по типам
потребительского поведения на заданное число тактов времени вперед (задача 1) и на
отдаленное будущее (задача 5). Подавляющее большинство состояний
цепи представлено реально существующими типами потребительского
поведения (методика их статистического выявления описана в п. 12.4). Однако
среди состояний может быть небольшое число гипотетических
(перспективных) типов, которые в начальный (наблюдаемый) момент времени
имеют «нулевое реальное представительство» (очевидно,
соответствующие элементы начального распределения {Pi}i:=YW будут равны нулю).
Что касается типов состояний, то из смысла задачи следует, что данная
цепь, скорее всего, будет состоять из невозвратных состояний и какого-то
числа поглощающих множеств и состояний. Все определится
конкретными значениями переходных вероятностей pij (методика статистической
оценки последних описана, например, в [Мнтоян А. А.]). Что касается
решений задач 1 и 5, то они получаются с помощью формул —
соответственно E.11)—E.12) и, в случае существования стационарного распределения,
E.21). Может представить практический интерес и вопрос о среднем
времени пребывания домашнего хозяйства г-го типа в заданном или даже
во всех невозвратных состояниях до момента его поглощения замкнутым
множеством или поглощающим состоянием. Ответ на этот вопрос может
быть получен с помощью соотношений E.22) и E.23).
Пример 5.2. Игра двух лиц до разорения. Очевидно, перед
тем, как соглашаться на тот или иной регламент игры, наш участник
хотел бы подсчитать вероятность своего разорения (при игре до
разорения), а также свои наиболее вероятные состояния на 2-м, 3-м, 4-м и

186 ГЛ. 5. ЦЕПИ МАРКОВА
последующих конах.
Займемся решением первой задачи. На языке цепи Маркова разорение
нашего участника означает его «поглощение» состоянием j = 0 (оно
соответствует его нулевому наличному капиталу, т. е. разорению). Несложный
анализ состояний цепи показывает, что она состоит из N — 1
невозвратных состояний (состояния 1,2, ..., АГ — 1)и двух поглощающих состояний
(состояния 0 и N). Поглощающий тип состояний 0 и N очевиден, а
невозвратность остальных состояний следует из того, что из каждого из них
с положительной вероятностью достигается одно из поглощающих
состояний (в этом легко убедиться, подсчитав для любого начального
капитала п вероятность п-кратных последовательных проигрышей или (JV — п)-
кратных последовательных выигрышей). Итак, наша схема относится к
категории марковских цепей, содержащих множество невозвратных
состояний и замкнутое (поглощающее) множество возвратных
состояний С. В нашем случае мы имеем два таких вырожденных замкнутых
множества, каждое из которых состоит из единственного поглощающего
состояния. Нас интересует состояние 0. Для определения вероятности
разорения нашего участника /п.о составим и решим систему уравнений
E.25). Очевидно, в нашем случае
f} A = 1 — »• f • J — О ПЛЯ KCPX 4 Ъ
«/1.0 l "> Jj>0 "~ u длх ь^ел J *
так что система E.25) имеет вид:
/i.o -p/2.0 = 1 ~Р
= 0 для j = 2,3,...,JV-2
Решение этой системы (с учетом очевидных граничных условий
/о.о = 1 и fNQ = 0) дает:
. 1
при р ф -;
п 1
- — при р = -
(подробное решение можно найти в [Феллер В., с. 338-339]).
Пример 5.3. Демографическая модель передвижки
возрастов. Рассуждения, аналогичные тем, которые мы использовали при
анализе предыдущего примера, приводят нас к выводу, что данная цепь
Маркова (ее матрица переходных вероятностей приведена в п. 5.2) содержит

5.4 АНАЛИЗ ЗАДАЧ И ПРИМЕРОВ 187
невозвратные состояния 1-87 и два поглощающих (88-е и 89-е).
Следовательно, при анализе данной модели мы можем воспользоваться
описанными в п. 5.3.3 свойствами поглощающих цепей Маркова E.22)-E.24). Это
позволит нам, в частности, при подходящей интерпретации состояния
«предельный возраст» вычислить ряд важных демографических
характеристик. Так, если удалить «предельный возраст» достаточно далеко
(например, понимать под ним возраст свыше 150 лет; при этом,
конечно, возрастет общее число возможных состояний), то соответствующая
этому состоянию компонента вектора а, определяемого с помощью
соотношения E.23), есть не что иное, как средняя (ожидаемая)
продолжительность жизни населения данной страны или региона. Бели же понимать
под «предельным возрастом» возраст выхода на пенсию, то аналогично
можно определить среднее число лет, которое человекшребывает в
пенсионном возрасте (т.е. получает пенсию), и т.д.
Пример 5.4. Модель пребывания студента в вузе. По типу
цепь Маркова, описывающая эту модель, не отличается от предыдущей.
Разница состоит только в том, что из каждого невозвратного состояния
можно не только перейти в соседнее или в одно из двух поглощающих,
но и остаться в том же самом состоянии. Рассмотрим данный пример
подробнее.
Во-первых, приведем анализируемую матрицу Р переходных
вероятностей к виду E.20). Для этого перенумеруем возможные состояния
объекта следующим образом:
1-е состояние: «отчислен из института»;
2-е состояние: «окончил институт»;
3-е состояние: «обучение на 5-м курсе»;
4-е состояние: «обучение на 4-м курсе»;
5-е состояние: «обучение на 3-м курсе»;
6-е состояние: «обучение на 2-м курсе»;
7-е состояние: «обучение на 1-м курсе».
Зададимся для определенности численными значениями переходных
вероятностей p{j (данные заимствованы из [Кемени Дж., Снелл Дж.]) и

188 ГЛ. 5. ЦЕПИ МАРКОВА
выпишем приведенную форму матрицы Р:
р —.
1
0
0,2
0,2
0,2
0,2
0,2
0
1
0,7
0
0
0
0
. 0
: 0
! 0,1
! 0,7
: 0
: 0
' 0
0
0
0
0,1
0,7
0
0
0
0
0
0
0,1
0,7
0
0
0
0
0
0
0,1
0,7
0
0
0
0
0
0
0,1 J
Нас будут интересовать вероятности окончить институт для
студента 1-го, 2-го и т. А курсов (на языке модели марковской цепи — это
вероятности поглощения 7tj> см. п. 5.3.3, формулу E.24)), а также средние
времена пребывания студента г-го курса в институте (на языке модели
марковской цепи — это компоненты вектора а, см. п. 5.3.3, соотношения
E.22)-E.23)).
Вычисления по формулам E.22)-E.24) дают:
-1
)
/ 0,9
-0,7
0
0
V 0
f 1,11
0,86
0,67
0,52
^0,41
0
0,9
-0,7
0
0
0
1,11
0,86
0,67
0,52
0
0
0,9
-0,7
0
0
0
1,11
0,86
0,67
0
0
0
0,9
-0,7
0
0
0
1,111
0,86
0
0
0
0,9^
0 \
0
0
0
1,11/
Соответственно:
= А1 =
1,98
2,65
3,17
V3,58/

5.4 АНАЛИЗ ЗАДАЧ И ПРИМЕРОВ
189
Наконец, матрица Г попадания в поглощающие состояния
Г — А • Р
fl,ll
0,86
0,67
0,52
^0,41
0
1,11
0,86
0,67
0,52
0
0
1,11
0,86
0,67
0
0
0
1,11
0,86
0 \
0
0
0
1,11/
•
/0,2
0,2
0,2
0,2
\0,2
0,7 \
0
0
0
0 /
=
/0,22
0,40
0,53
0,63
\0,72
0,78^
0,60
0,47
0,37
0,28 J
Проанализируем полученные результаты. Компоненты вектора а
свидетельствуют о том, что студенты, достигшие 5-го курса, в среднем
проводят в институте еще 1,11 года (сказывается возможность остаться
на 5-м курсе для повторного прохождения курса). Студенты, достигшие
4-го курса, в среднем проводят в институте еще 1,98 года (помимо
упомянутого выше фактора повторного обучения в данном случае дает себя
знать и перспектива досрочного отчисления). Воздействием этих двух
противоположных факторов (возможность остаться «на второй год» и
быть отчисленным досрочно) объясняются и средние времена пребывания
в институте студентов, начинающих третий год обучения B,65 вместо
трех лет), второкурсников C,17 вместо четырех лет) и поступивших на
1-й курс C,58 года вместо пяти лет).
Второй столбец матрицы Г представляет нам следующую
информацию. При тех конкретных значениях переходных вероятностей, которые
мы использовали в своих расчетах, лишь 28% от поступивших в вуз его
успешно заканчивают. Аналогичный показатель для студентов,
доучившихся до 2-го, 3-го, 4-го и 5-го курса, имеет значения соответственно
37%,47%,60%и78%.
Пример 5.5. Модель игровых возможностей двух
шахматистов. В этом примере главный вопрос, который нас будет
интересовать, это — кто из игроков (А или В) в длительном турнире (или в серии
турниров) выступит успешнее, т. е, наберет большее число очков? Для
ответа на этот вопрос необходимо, по-видимому, подсчитать стационарное
распределение по «состояниям» (выигрыш-ничья-проигрыш) для каждого
из игроков. Поскольку матрица Р(Л) переходных вероятностей,
описывающая поведение игрока А, определяет последовательность независимых
испытаний (как частный случай цепи Маркова), то и стационарное
распределение по состояниям для этого игрока останется тем же самым, т. е.
E.26)
где первое состояние соответствует выигрышу, второе — ничьей, а
третье — поражению.

190 ГЛ. б. ЦЕПИ МАРКОВА
Система уравнений E.21) для стационарных вероятностей игрока В
будет иметь вид:
А~\в) • (в + е) + Р{2°°ЧВ) • в + pt\B) • (в - ?) = А~\
р[°°\в) ¦ н + р<Г\в) • н + р<~>(Я). н = Р
Решение этой системы дает:
) = щ ,<~>(Я) = 1-Р<~>(Я)
Сравнение соответствующих стационарных вероятностей для
игроков Л и 5, задаваемых соотношениями E.26) и E.27), позволяет сделать
следующий вывод: для игроков выше среднего уровня (т. е. при в > п) и
при «не слишком большой» эмоциональности игрока В (т.е. при е < п)
эффективность игры шахматиста В в длительном турнире окажется
выше, чем А.
* * *
Обратим внимание читателя на то, что во всех рассмотренных выше
примерах переходные вероятности ру считались априори заданными. На
практике они в большинстве случаев оцениваются статистически. В
некоторых случаях это делается достаточно просто с помощью
соответствующих относительных частот. В общем случае проблема оценки
переходных вероятностей может оказаться весьма сложной (см., например,
книгу Ли Ц.,Джадж Д., Зельнер А. Оценивание параметров марковских
моделей по агрегированным данным. М.: Статистика, 1977).
ВЫВОДЫ
1. Цепь Маркова с конечным числом состояний является
простейшим обобщением последовательности независимых испытаний. В
частности, она моделирует динамику (в дискретном времени) поведения
объекта, который может находиться в одном из N состояний, в
ситуациях, когда вероятность оказаться объекту в заданном состоянии j в данный
момент времени t зависит только от того, в каком состоянии он находился
в предыдущий момент времени t - 1. Бели в момент времени t - 1
объект находился в состоянии i, то вероятность оказаться в момент времени
t в состоянии j определяется так называемой переходной вероятностью

выводы 191
Pij(t). Цепь называется однородной, если эти переходные вероятности
(для каждой фиксированной пары состояний г и j,i,j = 1,2,..., N)
остаются постоянными во времени, т. е. не зависят от t.
2. Для вероятностного описания временной последовательности
состояний любой длины t достаточно задать (кроме матрицы Р = (pij)
переходных вероятностей) распределение объектов по состояниям в
первый (начальный) момент времени {рьРг> • • • >?#}> где Pi есть вероятность
того, что в начальный момент времени объект находился в состоянии «.
3. Последовательность независимых испытаний, результатом
каждого из которых может быть одно из N возможных событий,
является частным случаем однородной цепи Маркова с N возможными
состояниями, в которой матрица переходных вероятностей Р определяется
всего N различными числами, а именно, состоит из N одинаковых строк
4. Модель марковской цепи может оказаться полезной при решении
ряда важных прикладных задач, среди которых:
t прогноз распределения объектов по возможным состояниям через
заданное число тактов времени и в отдаленном будущем;
• расчет среднего времени и вероятности пребывания объекта в
заданном состоянии или в заданном множестве состояний;
• вычисление вероятности перехода объекта из определенного
состояния г в заданное множество состояний за фиксированное число тактов
времени (в том числе, и за бесконечное время).
5. Способ решения этих и других задач, связанных с анализом цепей
Маркова, зависит от типа анализируемой цепи, который, в свою
очередь, определяется типологией составляющих ее состояний. К основным
типам состояний марковской цепи относятся возвратные (вероятность
когда-нибудь вернуться в возвратное состояние равна единице),
невозвратные (вероятность когда-нибудь вернуться в невозвратное состояние
меньше единицы), поглощающие (попав в поглощающее состояние объект
с вероятностью единица остается в нем навсегда), периодические
(объект не может вернуться в периодическое состояние за время, отличное от
времени, кратного заданному периоду г), зргодические (все возвратные
непериодические состояния).
в. При анализе конкретной конечной цепи Маркова необходимо
предварительно ее классифицировать, определив, является ли она
неприводимой (т. е. состоящей только из возвратных взаимодостижимых
состояний), и если «да», то являются ли эти состояния периодическими. В
условиях неприводимой непериодической марковской цепи справедливы
утверждения зргодической теоремы, в соответствии с которыми суще-

192 ГЛ. 5. ЦЕПИ МАРКОВА
ствует единственное стационарное (финальное) распределение объектов
по состояниям и предлагается способ его расчета.
7. Бели цепь не является неприводимой, то она может в общем случае
состоять из множества невозвратных состояний и какого-то числа
поглощающих (замкнутых) множеств состояний (в частном случае
поглощающее множество состояний может состоять из единственного
состояния). При решении задач, связанных с анализом подобных цепей, следует
воспользоваться соотношениями E.20), E.22)-E.25).

>пи<
IPPM
¦ВЫ CTJ
|ния \
HHbHQJ
|ГИС1
¦ста'
"о за
истическое

ГЛАВА 6- ОСНОВЫ СТАТИСТИЧЕСКОГО
ОПИСАНИЯ И СТАТИСТИКА
НОРМАЛЬНОГО ЗАКОНА
6.1. Генеральная совокупность, выборка из
нее и основные способы организации
выборки
Закономерности, которым подчиняется исследуемая случайная
величина, физически полностью обусловливаются реальным комплексом
условий ее наблюдения (или эксперимента), а математически задаются
соответствующим вероятностным пространством {П,С, Р}, или, что то же,
соответствующим законом распределения вероятностей. Однако при
проведении статистических исследований несколько более удобной
оказывается другая терминология, связанная с понятием генеральной совокупности.
Генеральной совокупностью называют совокупность всех
мыслимых наблюдений (или всех мысленно возможных объектов
интересующего нас типа, с которых «снимаются» наблюдения), которые могли бы
быть произведены при данном реальном комплексе условий. Поскольку
в определении речь идет о всех мысленно возможных наблюдениях (или
объектах), то понятие генеральной совокупности есть понятие условно-
математическое, абстрактное и его не следует смешивать с реальными
совокупностями, подлежащими статистическому исследованию» Так,
обследовав даже все предприятия подотрасли с точки зрения регистрации
значений характеризующих их технико-экономических показателей, мы
можем рассматривать обследованную совокупность лишь как
представителя гипотетически возможной более широкой совокупности предприятий,
которые могли бы функционировать в рамках того же самого реального
комплекса условий.
В практической работе элементы генеральной совокупности удобнее
связывать с объектами наблюдения, чем с характеристиками этих объ-

6.1 ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ 195
ектов. Мы отбираем для изучения индивидуумов, семьи, предприятия,
регионы, страны, но не значения их характеристик. В математической
теории объекты и совокупность их характеристик не различаются и
двойственность введенного определения исчезает.
Как видим, математические понятия «генеральная совокупность»,
«вероятностное пространство», «случайная величина» и «закон
распределения вероятностей» физически полностью обусловливаются
соответствующим реальным комплексом условий, а поэтому их можно считать в
определенном смысле синонимами. Генеральная совокупность называется
конечной или бесконечной в зависимости от того, конечна или бесконечна
совокупность всех мыслимых наблюдений.
Из определения следует, что непрерывные генеральные совокупности
(состоящие из наблюдений признаков непрерывной природы) всегда
бесконечны. Дискретные же генеральные совокупности могут быть как
бесконечными, так и конечными. Скажем, если анализируется партия из N
изделий, когда каждое изделие может быть отнесено к одному из четырех
сортов, исследуемой случайной величиной ? является номер сорта
случайно извлеченного из партии изделия, а множество возможных значений
случайной величины состоит соответственно из четырех точек A,2,3 и 4).
В этом примере, очевидно, генеральная совокупность будет конечной
(всего N мыслимых наблюдений). Как видим из примера, следует отличать
также совокупность всех мыслимых наблюдений от множества всех
мыслимых (или теоретически возможных) значений исследуемой случайной
величины ?. Наблюдений, вообще говоря, «больше», поскольку каждому
фиксированному возможному значению х может соответствовать
несколько или даже бесчисленное множество мыслимых наблюдений.
Понятие бесконечной генеральной совокупности есть математическая
абстракция, как и представление о том, что измерение случайной
величины можно повторить бесконечное число раз. Приближенно бесконечную
генеральную совокупность можно истолковать как предельный случай
конечной, когда число объектов, порождаемых данным реальным
комплексом условий, неограниченно возрастает. Так, если в только что
приведенном примере вместо партии изделий рассматривать непрерывное массовое
производство тех же изделий, то мы придем к понятию бесконечной
генеральной совокупности. Практически же такое видоизменение равносильно
требованию N -+ оо.
Выборка из данной генеральной совокупности — это результаты
ограниченного ряда наблюдений a?i,z2,..,,хп случайной величины ?.
Выборку можно рассматривать как некий эмпирический аналог генеральной
совокупности, то, с чем мы чаще всего на практике имеем дело, поскольку
7*

196 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
обследование всей генеральной совокупности бывает либо слишком
трудоемко (в случае больших ЛГ), либо принципиально невозможно (в случае
бесконечных генеральных совокупностей).
В статистике интерпретация выборки и ее отдельных элементов
допускает в зависимости от контекста два различных варианта,
причем при изложении, как правило, специально не уточняется, о каком
именно варианте идет речь. В целях упрощения не делается различий и в
обозначениях. При первом (практическом) варианте интерпретации
выборки под хьх2,...,хЛ понимаются фактически наблюденные в
данном конкретном эксперименте значения исследуемой случайной
величины, т.е. конкретные числа.
В соответствии со вторым (гипотетическим) вариантом
интерпретации под выборкой ?i,X2,. ..,жл понимается последовательность
случайных величин^ г-й член которой (я,*) лишь обозначает результат
наблюдения, который мы могли бы получить на t-м шаге п-кратного
эксперимента , связанного с наблюдением исследуемой случайной
величины ?. Если условия эксперимента не меняются от наблюдения к
наблюдению и если n-кратный эксперимент организован таким образом, что
результаты наблюдения на каждом (t-м) шаге никак не зависят от
предыдущих и не влияют на будущие результаты наблюдений, то, очевидно,
вероятностные закономерности поведения t-ro наблюдения гипотетической
выборки остаются одними и теми же для всех i = 1,2,.• .,п и полностью
определяются законом распределения вероятностей наблюдаемой
случайной величины, т. е.
P{Xi <х} = Р{? <х} = *•«(»). F.1)
При этом из взаимной независимости наблюдений выборки следует, что
последовательность случайных величин
*1»*2,-»->*я F.2)
состоит из независимых компонент, т. е. их совместная функция
распределения F(a?1 ».)(*!,...,*») = Р{хг < zb...,яп < zn} может быть пред-
1 Говоря о ишаге п-кратного эксперимента», мы не имеем в виду жесткую связь
этих «шагов» с временнымк*характеркстихами проведения эксперимента. Переход
от t-ro наблюдения выборки к i-f 1-му не обязательно выполняется в хронологической
последовательности: выбранные для наблюдения объекты могут образовывать так
называемую «пространственную выборку» и наблюдаться, например, одновременно.

6.1 ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ 197
ставлена в виде
= П *«(«>•
i=l t=l
Если в рамках гипотетического варианта интерпретации выборки
ряд наблюдений F.2) образует последовательность независимых и
одинаково распределенных случайных величин (т. е. выполняются
соотношения F.1) и F.3)), то выборка называется случайной.
Число п наблюдений, образующих выборку, называют объемом
выборки.
Переход к группированным выборочным данным. Бели
объем выборки п велик (п > 50) и при этом мы имеем дело с одномерной
непрерывной величиной (или с одномерной дискретной величиной, число
возможных значений которой достаточно велико, скажем больше 10), то
часто удобнее, с точки зрения упрощения дальнейшей статистической
обработки результатов наблюдений, перейти к так называемым
«группированным» выборочным данным. Этот переход осуществляется обычно
следующим образом:
а) отмечаются наименьшее хгп\п(п) и наибольшее хтлх(п) значения в
выборке ;
б) весь обследованный диапазон [хт\п(п)>хтлх(п)] разбивается на
определенное число s равных интервалов группирования; при этом
количество интервалов а должно быть в пределах 7-20. Выбор количества
интервалов существенно зависит от объема выборки п ; для примерной
ориентации в выборе s можно пользоваться приближенной формулой s » log2 n+1,
которую следует воспринимать, скорее, как оценку снизу для в (особенно
при больших п);
в) отмечаются крайние точки каждого из интервалов cq, ci, С2,..., ca
в порядке возрастания, а также их середины х\, х\,..., х°8\
г) подсчитываются числа выборочных данных, попавших в каждый из
интервалов: щ, i/2,..., vs (очевидно, и\ +1/2+.. .+^« = п); выборочные
данные, попавшие на границы интервалов, либо равномерно распределяются
по двум соседним интервалам, либо уславливаются относить их только к
какому-либо одному из них, например, левому.
1 Запись xmjn(n) и Xmax(tt) подчеркивает тот факт, что наименьшее и наибольшее
значения в выборке, как и все другие характеристики, построенные по выборке
объема п, конечно, зависят от п. Там, где этот факт не требует напоминания, мы будем
опускать п в записи выборочных характеристик.

198 гл. в. основы статистического описания
В зависимости от конкретного содержания задачи в данную схему
группирования могут быть внесены некоторые видоизменения (например,
в некоторых случаях целесообразно отказаться от требования равной
длины интервалов группирования; иногда крайние интервалы целесообразно
делать полубесконечными слева или справа).
Репрезентативность выборки. Сущность статистических
методов состоит в том) чтобы по некоторой части генеральной
совокупности (т. е. по выборке) выносить суждения о ее свойствах в
целом. Поэтому один из важнейших вопросов, от успешного решения
которого зависит достоверность получаемых в результате статистического
анализа выборочных данных выводов, является вопрос
репрезентативности выборки, то есть вопрос полноты и адекватности представления
ею интересующих нас свойств всей анализируемой генеральной
совокупности. В практической работе одна и та же группа объектов, взятых для
изучения, может рассматриваться как выборка из разных генеральных
совокупностей. Так, группу семей, наудачу отобранных из панельных
домов жилищно-эксплуатационной конторы (ЖЭК) одного из районов
города для подробного социологического обследования, можно рассматривать
и как выборку из генеральной совокупности семей (в панельных домах)
данной ЖЭК, и как выборку из генеральной совокупности всех семей
данного района, и как выборку из генеральной совокупности всех семей
данного города, и, наконец, как выборку из генеральной совокупности всех
семей города, проживающих в панельных домах. Оценка степени
репрезентативности имеющихся выборочных данных существенно зависит от
того, представителем какой генеральной совокупности мы рассматриваем
отобранную группу семей. Ответ на этот вопрос зависит от многих
факторов. В приведенном выше примере, в частности, — от наличия или
отсутствия специального (быть может, скрытого) фактора, определяющего
принадлежность семьи к данной ЖЭК или району в целом (таким
фактором может быть, например, среднедушевой доход семьи, географическое
расположение района в городе, «возраст» района и т.п.).
Основные способы организации выборки. При оценке
репрезентативности выборки учитывается и то, насколько распределение в
выборке существенных для изучаемого вопроса показателей характерно для
анализируемой генеральной совокупности в целом. Первый путь
повышения степени репрезентативности — достижение полностью случайного
отбора объектов из генеральной совокупности — часто бывает труден в
организационном плане. Кроме того, сочетание регулярного и случайного
выбора иногда оказывается более эффективным. В любом случае способ
сбора исходных данных должен тщательно планироваться и его необхо-

ел генеральная совокупность 199
димо полностью описывать в отчетах о выполненной работе.
Использование для оценки репрезентативности сравнения
распределений основных показателей в выборке и в генеральной совокупности
также имеет свои трудности, одни из которых носят чисто статистический
характер — недостаточный объем'(число отобранных для обследования
объектов) выборки, неразработанность методов сравнения многомерных
распределений и т.п., а другие — содержательный, ведь часто заранее
неизвестно, распределение каких показателей следует сравнивать при
доказательстве репрезентативности.
Опишем кратко основные способы организации выборки.
Простой случайный отбор — способ извлечения п объектов из
конечной генеральной совокупности N объектов, при котором каждая из
возможных выборок (а всего существует, как известно, Сдг способов
отобрать п элементов из множества N элементов) имеет равную вероятность
быть отобранной. На практике часто нумеруют объекты в генеральной
совокупности числами от 1 до N и затем, используя таблицы случайных
чисел или какой-либо другой метод, обеспечивающий равную вероятность
выбора объекта (например, урну с N шарами, занумерованными цифрами
от 1 до JV), отбирают один за другим п объектов. Полученная таким
способом выборка называется случайной, так как при этом обеспечивается
выполнение условий случайности F.1) и F.3).
Простой отбор с помощью регулярнойу но несущественной для
изучаемого вопроса процедуры часто применяется вместо случайного
отбора. На производстве изделия для контроля их качества часто
отбирают в определенный период времени, что удобно с организационной точки
зрения; в социологических обследованиях — по букве, с которой
начинается фамилия индивидуума, проживающего в домах данной жилищно-
эксплуатационной конторы, и т.п. Получаемые таким образом выборки
часто называют механическими.
Стратифицированный (расслоенный) отбор заключается в том, что
исходная генеральная совокупность объема N подразделяется на
подсовокупности объема N-i, JV2, • • • > ^R* При этом подсовокупности не содержат
общих объектов и вместе исчерпывают всю генеральную совокупность,
так что N1 + N2 + ... + Nr = N. Подсовокупности называют стратами
или слоями. Когда слои определены, из каждого слоя извлекается
простая случайная выборка объема соответственно гсьп2,...,п#. Для того
чтобы можно было полностью воспользоваться выгодами от расслоения,
значения Ni/N должны быть известны. Стратифицированный отбор
применяется, когда слои однородны в том смысле, что входящие в них
объекты имеют близкие характеристики (средние значения которых могут

200 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
быть оценены по малым выборкам); либо когда целесообразно изучать
генеральную совокупность с равной тщательностью во всех слоях; либо
по организационным причинам, когда методы проведения отбора в слоях
должны быть разными. Выборки, полученные таким способом, называют
стратифицированными или расслоенными (иногда — районированными).
Частным случаем стратифицированного отбора является способ
организации выборки, при котором страты (слои) генеральной совокупности
выделены по косвенному признаку, как-то связанному с изучаемым. Так,
изучая средний душевой доход семей, для получения
стратифицированных выборок можно предварительно разбить исследуемую совокупность
семей на группы, однородные по какой-либо из социально-экономических
характеристик главы семьи (например, по заработку). В подобных
случаях говорят о типическом способе отбора и соответственно о типических
выборках.
Методы серийного отбора (и соответственно серийные выборки)
используются тогда, когда удобнее назначать к обследованию не отдельные
элементы генеральной совокупности, а целые «блоки» или серии таких
элементов. Так, при проведении выборочных обследований населения
способ территориально-административного деления страны и характер
ведения соответствующей документации обусловливают большее удобство
сплошного способа обследования целых территориальных единиц (домов,
кварталов), а не отдельных семей. Подобный способ отбора часто
называют также гнездовым.
Комбинированный (ступенчатый) отбор сочетает в себе сразу
несколько из описанных выше способов отбора, образующих различные
ступени (или фазы) выборочного обследования. Так, при выборочном
обследовании условий жизни и структуры семей какого-либо города на первой
ступени можно с помощью случайного отбора назначить городские
районы, в которых будет производиться это обследование, затем способом
механического отбора определить подлежащие обследованию жилищно-
эксплуатационные конторы (ЖЭКи), а внутри ЖЭКов сделать серийную
(гнездовую) выборку домов.
6.2. Основные выборочные характеристики
и их свойства
В практике статистического анализа и моделирования, к сожалению,
точный вид закона распределения анализируемой генеральной
совокупности, как правило, бывает неизвестен. Исследователь располагает лишь
выборкой из интересующей его генеральной совокупности и вынужден

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 201
строить все свои выводы на основании расчета ограниченного ряда
выборочных характеристик. Какие же выборочные характеристики несут
наибольшую информацию о генеральной совокупности, являются в этом
смысле основными? К основным выборочным характеристикам
относятся:
• выборочном {эмпирическом) функция распределения F^n'(x);
• выборочном (эмпирическом) функцим плотности / (х);
• выборочная (эмпирическом) относительном частота р\ появления
t-ro возможного значения х® дискретной случайной величины;
• выборочные начальные и центральные моменты анализируемой
случайной величины (rhk(n)umk(n)) и, в первую очередь, выборочное
среднее значение х(п) = rh\(n)u выборочном дисперсим s2(n) =
т°2(п);
• порядковые статистики а?(,)(п) (г = 1,2,...,п), т.е. члены ряда
наблюдений выборки, расположенных в этом ряду в порядке их
возрастания.
Нас будут интересовать в данном пункте определения и свойства этих
выборочных характеристик. Говоря о свойствах выборочных
характеристик, мы постараемся ответить в числе прочих на следующие два вопроса:
• стремится ли анализируемая выборочная характеристика к
определенному пределу при неограниченном увеличении объема выборки п (т. е.
при п -* оо)?
• как «ведут себя» выборочные характеристики в роли случайных
величин (каковыми все они являются), т.е. что можно сказать о законе
распределения вероятностей каждой из них при достаточно больших (т. е.
при п -» оо) и ограниченных объемах выборок?
6.2.1. Выборочные (эмпирические) функции распределения,
относительные частоты и функции плотности
Итак, объектом нашего анализа является генеральная совокупность,
отражающая поведение случайной величины ? с теоретической функцией
распределения (вообще говоря, нам не известной) F(x) = Р{( < х}. Мы
располагаем лишь случайной выборкой F.2) из этой генеральной
совокупности.
Эмпирическим (или выборочным, т. е. построенным по выборке
объема п) аналогом теоретической функции распределения F(x) является

202 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
функция F^n\x)} определяемая соотношением:
/*">(*) =4^ F.4)
или, в случае группированных данных (см. п. 6.1),
*">(«), |*+* + " + |\ F.5)
п
где v(x) — число наблюденных значений исследуемой случайной
величины в выборке х\, а?2» • • •»хП} меньших х; щ — число наблюденных значений
в выборке, попавших в t'-й интервал группирования, а гх — номер самого
правого из интервалов группирования, правый конец которых не
превосходит х.
Из определения эмпирической функции распределения
непосредственно следует объяснение часто используемого ее другого названия —
«накопленная относительная частота».
Бели анализируемая случайная величина ? дискретна и имеет
возможные значения z°(t = 1,2,...), принимаемые соответственно с
вероятностями Pi = Р{? = X;}, то имеет смысл ввести понятие выборочной
(эмпирической) относительной частоты р\п\ которая определяется как
отношение числа vxo наблюдений в выборке, в точности равных я,, к
общему объему выборки, т. е.
Бели ? — непрерывная случайная величина (генеральная
совокупность) с функцией плотности вероятности f(x) и функцией
распределения F(x)y которая всюду непрерывна и дифференцируема, то,
располагая выборочными данными (выборкой) a?i, а?2> • • • > яп, мы можем построить
выборочный аналог функции плотности — эмпирическую (выборочную)
функцию плотности г'(х).
Для построения эмпирической (или выборочной) функции плотности
/п)(я) на всей области ее определения (т.е. для всех возможных
значений исследуемой величины) используют предварительно
сгруппированные данные (см. п. 6.1) и полагают
где к(х) — порядковый номер интервала группирования, который
накрывает точку х; i/k(sc) — число наблюдений, попавших в этот интервал,
А — длина интервала.

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА
203
Геометрическое изображение эмпирической функции плотности носит
название гистограммы.
Пример 6.1. Анализируется выборка из ста малых предприятий
региона. Цель обследования — фиксация коэффициента соотношения
заемных и собственных средств (а?,) на каждом t'-м предприятии. Таким
образом, п = 100, a t = 1,2,...,п. Результаты обследования п = 100
малых предприятий представлены в табл.6.11.
Таблица 6.1. Коэффициенты соотношения заемных и собственных средств
предприятий
5,56
5,46
5,34
5,36
5,58
5,33
5,79
5,67
5,54
5,27
5,45
5,61
5,53
5,40
5,47
5,49
5,65
5,71
5,39
5,64
5,48
5,11
5,46
5,45
5,46
5,50
5,70
5,73
5,32
5,20
5,45
5,41
5,41
5,49
5,19
5,54
5,71
4,97
5,21
5,23
5,39
5,31
5,48
5,68
5,60
5,40
5,85
5,35
5,73
5,33
5,37
5,57
5,39
5,51
5,63
5,58
5,44
5,72
5,59
5,37
5,46
5,33
5,11
5,50
5,48
5,42
5,47
5,49
5,38
5,24
5,59
5,11
5,42
5,68
5,27
5,29
5,48
5,61
5,25
5,55
5,61
5,54
5,48
5,21
5,22
5,05
5,47
5,57
5,26
5,60
5,31
5,43
5,49
5,38
5,37
5,79
5,55
5,69
5,81
5,51
Требуется построить эмпирические функции распределения F^n\x) и
плотности .Г (ж), а также представить их геометрическое изображение
(графики).
Решение. Построим группированный ряд наблюдений:
а) определим среди наблюдений (в выборке) минимальное хт\п = 5,03
и максимальное хтлх = 5,85 значения;
б) разобьем весь диапазон [жт,п,хтах] на s равных интервалов
группирования, где з » log2 n + 1 = 3,32Inn + 1 = 7,62 » 8, отсюда ширина
интервала Д = Хтлх ~ Хт{п = 5>85 " 5>03 - 0,101. Примем Д = 0,11;
S о
в) определим крайние точки каждого интервала co,ci,c2,...,ce в
порядке возрастания, а также их середины Х\>а?5,...,х°в.
За нижнюю границу первого интервала предлагается принять
величину Со =Smin- f =4,97.
1 Результаты обследования выстроены в таблице размером 10 х 10 в порядке
регистрации по строкам, так что 2-я строка начинается с 11-го наблюдения, 3-я — с 21-го и
т.д.

204
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Тогда ci = со + Д = 5,08; с3 = сх + Д = 5,19;...; с8 = со + 8Д = 5,85.
4,97 + 5,08
Определим середины интервалов: х\ = -^-т
О
х2 =
= 5,1
..., ха =
= 5,80.
= 5,03;
Таблица 6.2. «Группированный»
к
1
2
3
4
5
6
7
8
Интервалы
c*-i - с*
4,97-5,08
5,08-5,19
5,19-5,30
5,30-5,41
5,41-5,52
5,52-5,63
5,63-5,74
5,74-5,85
4
5,03
5,14
5,25
5,36
5,47
5,58
5,69
5,80
ряд наблюдений
2
3
12
19
29
18
13
4
2
5
17
36
65
83
96
100
F(n)(x)
0,02
0,05
0,17
0,36
0,65
0,83
0,96
1,00
0,18
0,27
1,09
1,73
2,64
1,64
1,18
0,36
Границы последовательных интервалов и их середины представлены
в табл. 6.2.;
г) подсчитаем числа выборочных данных, попавших в каждый из
интервалов: i/i,i/2,..., J>e, где и\ + •.. + v9 = п.
Последовательно просматривая данные наблюдений, разносим
значения признака по соответствующим интервалам. Так как значения могут
совпадать с границами интервалов, то условимся в каждый к-и интервал
включать наблюдения, большие или равные, чем нижняя граница
интервала, и меньшие верхней границы, т.е. наблюдения, удовлетворяющие
неравенствам c*_i < х < ск. Общее число наблюдений, отнесенных к к-му
интервалу, равно частоте vk.
В табл. 6.2 приводятся также накопленные частоты и%*> равные сумме
частот Аг-го и всех предшествующих интервалов.
Для построения гистограммы на оси абсцисс откладываются крайние
точки каждого из интервалов со,сг,с2,...,св, а по оси ординат
эмпирический аналог функций плотности рп\х). Тогда А?-му интервалу будет
соответствовать прямоугольник, основанием которого является
замкнутый слева интервал [c*_i,c*), а высота равна f^n\x) = ^3^- Графики,
соответствующие эмпирической (/(п)(ж)) и модельной (f(x)) плотностям,
приведены на рис. 6.1. Для построения модельной кривой плотности
использовалась нормальная модель закона распределения, в которую подста-

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 205
влялись вместо неизвестных параметров — среднего а и дисперсии а2 —
значения соответствующих выборочных характеристик хпз2
(подсчитанные в примере 6.2, см. ниже).
(«) _ "*(*)
() " Ж-Ц
2,7
2,6
2,3
2,1
1,9
1,7
1,5
1,3
1,1
0,9
0,7
0,5
0,3
0,1
\
*¦ 2
гн СО
Рис. 6.1. Гистограмма
Если значения у\х) соотнести к серединам соответствующих
интервалов &1,Х2>**м2» и соединить полученные точки, то получим
ломаную линию (рис. 6.2), которую называют полигоном.
Геометрическое представление эмпирической функции распределения
Яп)(х) называют кумулжнтой или кумулятивной кривой (рис. 6.3). Для
этого на оси абсцисс откладывают границы интервалов с0,сьс2,..., с5, а
по оси ординат значения F(n)(s), взятые из табл. 6.2, причем значения
F(n)(z) относят к верхней с* границе k-то интервала (А: = 1,2,..., а).

206
ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
2,7
2,5
2,3
2,1
1,9
1,7
1,5
1,3
1,1
0,9
0,7
0,5
0,3
0,1
д
/\
/ \
/ \
/ \
/ \
У \
/ \
/ \
/ \
1
—1—1—1—1 ,f, 1 „, 1—1—1—1—1 to.
ю
2
us
Рис. 6.2. Полигон
1,00
0,82
0,72
0,62
0,52
0,42
0,32
0,22
0,12
0,02
Рис. 6.3. Кумулятивная кривая

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 207
6,2.2. Выборочные аналоги начальных и центральных
моментов случайной величины
В основе объяснения перехода от теоретических характеристик,
которые вычисляют на базе точного знания исследуемого закона
распределения, к эмпирическим (или выборочным) лежит интерпретация выборки
F.2) как модели генеральной совокупности, в которой возможными
значениями являются наблюденные (т. е. практически реализованные)
значения a?i, а?2, • • • > Яти ft * качестве вероятностей их осуществления берутся
соответствующие относительные частоты их появления в выборке, т.е.
величины, равные 1/п. Таким образом, выборку можно представить в
табличном виде:
1
п
хг
1
п
...
1
п
Условно рассматривая ее как табличную форму задания дискретной
случайной величины, возможные значения которой zbz2,...,zn
появляются с одними и теми же вероятностями р\ » р% s ... s pn = 1,
легко представить эмпирические аналоги рассмотренных выше начальных и
центральных моментов в виде:
F.7)
F.8)
где средняя арифметическая х есть эмпирический аналог начального
момента первого порядка:
2
Аналогичные формулы для группированных выборочных данных (см.
п. 6.1) выглядят следующим образом:
F.8')

208 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
6.2.3. Эмпирические аналоги центра группирования
генеральной совокупности
В статистической практике в качестве характеристик центра
группирования значений исследуемого признака используют несколько видов
средних значений, моду и медиану (см, п. 2.6.2). Рассмотрим
эмпирические аналоги этих числовых характеристик, которые вычисляются по
выборочным данным х\, а?2, • • • > хп*
Средняя арифметическая х (выборочная средняя) является, пожалуй,
основной и наиболее употребительной характеристикой центра
группирования:
1
Геометрическое среднее определяется по формуле:
•!•...••». F.Ю)
Оно находит применение при расчетах темпов изменения величин и, в
частности, в тех случаях, когда имеют дело с величиной, изменения
которой происходят приблизительно в прямо пропорциональной зависимости
с достигнутым к этому моменту уровнем самой величины (например,
численность населения), или же когда имеют дело со средней из отношений,
например, при расчетах «индексов цен».
Среднее гармоническое вычисляется по формуле:
F.11)
Гармоническими средними иногда пользуются в экономике при
анализе средних норм времени, а также в некоторых видах индексных расчетов.
Следует отметить, что выборочное гармоническое среднее значение
Нп ряда чисел хих^,,...хп всегда меньше выборочного геометрического
среднего значения Gn, которое в свою очередь меньше выборочного
среднего арифметического х.
Выборочная мода imod представляет собой наиболее часто
встречающееся в выборочных наблюдениях значение переменной, т.е. значение,
которое действительно является модным. Практическое отыскание
эмпирического аналога моды по выборочным данным требует построения
группированного ряда наблюдений и будет подробно рассмотрено ниже, в
примере 6.2.

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 209
Медиана, точнее, ее эмпирический аналог xmecb определяется как
среднее (по местоположению) значение ранжированного, т.е.
расположенного в порядке возрастания, ряда наблюдений X(i) < х^) ^ . • • < х(п)
(подробнее о таких рядах см. в п. 6.3). Если п нечетно, то ?me<j =
а если п четно, то xmed = \(х^) +
6.2.4. Эмпирические аналоги показателей вариации
рассеивания случайной величины
Каждая из описанных ниже характеристик степени рассеивания —
выборочные дисперсия, среднеквадратическое отклонение и коэффициент
вариации — дает представление о том, как могут отклоняться от своего
центра группирования элементы выборки.
Эмпирическую (выборочную) дисперсию з можно рассматривать как
приближенное значение теоретической дисперсии (см. B.23) в п. 2.6.3):
±(if F.12)
Выборочное (эмпирическое) среднеквадратическое отклонение
имеет вид:
\
F.13)
Оно используется наряду с выборочной дисперсией з для
характеристики степени отклонения наблюдаемых величин хг, х2,..., хп от среднего
значения х и оказывается в ряде случаев более удобным и естественным,
так как з имеет ту же размерность, что и сама анализируемая случайная
величина, и соответственно характеристики центра группирования.
Несколько более точными приближениями к теоретическим
значениям дисперсии и среднеквадратического отклонения а и а при небольших
объемах выборки являются подправленные выражения з2 из вида
(подробнее о точности в определении теоретических характеристик распределения
см. в п. 7.1.5):
^ FЛ4)
Выборочный коэффициент вариации V используется в тех случаях,
когда степень рассеивания естественно описывать некоторой относительной

210 ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
характеристикой в соответствии со средним (см. п. 2.6.3). В частности,
V = ~ • 100%. F.15)
X
Как видим из F.15), выборочный коэффициент вариации есть
безразмерная величина, измеряемая в процентах.
6.2.5. Выборочные коэффициенты асимметрии и эксцесса
Выборочный коэффициент асимметрии является характеристикой
степени скошенности (см. п. 2.6.5) и подсчитывается с помощью
второго и третьего центральных выборочных моментов по формуле:
(еле)
Из формулы F.16) следует, что для симметричных (относительно
среднего значения Е?) функций плотности распределений Дг должен быть
близок к нулю, в то время как для распределения, гистограмма которого
имеет «длинную часть», расположенную справа от ее вершины, C\ > 0, а
если слева — то & < 0. Выборочный эксцесс Д2 является, как и
соответствующая теоретическая характеристика /?2 (см. п. 2.6.5),
характеристикой поведения плотности (полигона) распределения в районе ее модального
значения. Он подсчитывается по формуле:
Напомним, что своеобразным аналогом отсчета в измерении степени
островершинности служит нормальное распределение, для которого C2 =
0. Для островершинного (по сравнению с нормальным) распределения —
02 > 0, а для плосковершинного — /32 < 0.
Пример 6.2. По данным табл. 6.2 примера 6.1 рассчитать
выборочные характеристики центра группирования, рассеивания, асимметрии
и эксцесса.
Решение. Для удобства вычислений целесообразно составить
вспомогательную таблицу (табл. 6.3). В ней сохранены обозначения табл. 6.2
и введено одно новое: 6ь = x°k - 2 (к = 1,2,..., 8).

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 211
Таблица в.З. Вспомогательная таблица для вычисления выборочных
характеристик по группированным данным
к
1
2
3
4
5
б
7
8
*°*
5,03
5,14
5,25
5,36
5,47
5,58
5,69
5,80
Итого
Vk
2
3
12
19
29
18
13
4
100
4"*
10,06
15,42
63,00
101,84
158,63
100,44
73,97
23,20
546,56
hvk
-0,8712
-0,9768
-2,5872
-2,0064
0,1276
2,0592
2,9172
1,3376
0
6>к
0,37949
0,31805
0,55780
0,21188
0,00056
0,23557
0,65462
0,44729
2,80526
tin.
-0,1653
•0,10356
- 0,12026
- 0,02237
0,00000
0,02695
0,14690
0,14957
•0,08808
&к
0,07201
0,03372
0,025928
0,00236
0,00000
0,00308
0,032996
0,05002
0,22008
2
5
17
36
65
83
96
100
Пользуясь данными табл. 6.3, вычислим среднее арифметическое
значение
546,56
100
= 5,4656.
Для проверки правильности вычисления х полезно убедиться в
выполнении условия ?fc 6kvk = ?*D - х)ик = 0.
На основании данных табл. 6.3 найдем выборочные:
• дисперсию
к
2>805
юо
0,02805;
• среднеквадратическое отклонение s = 0,167;
• коэффициент вариации

212 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
• центральные моменты третьего и четвертого порядков:
>о ?_ 0.Я008 _опо==.
m4 = -^- _ —jpg— - 0,0022,
к
коэффициент асимметрии:
• коэффициент эксцесса:
а „™° 3^ Q.0022 3^ Q
2 а4 @,028J '
Близость значений выборочных коэффициентов асимметрии /3\ и
эксцесса 02 к нулю свидетельствует в пользу выбора нормального закона
распределения для анализируемой генеральной совокупности.
Как уже отмечалось, медиана imed есть значение признака,
приходящееся на середину ранжированного ряда наблюдений. В нашем примере
п = 100 и imed = Х{Щ^*Ф)% Анализ таблицы исходных данных,
представленных в табл. 6.1, показывает, что наблюдения, расположенные в
упорядоченном ряду на 50-м, 51-м и 52-м местах принимают одно и то
же значение, равное 5,47. Другими словами, х^щ = &E1) = хE2) = 5,47,
следовательно, ?med = 5,47.
Мода, как отмечалось выше, равна значению признака xmod >
которому соответствует наибольшая частота. Как следует из табл. 6.3
наибольшая частота и = 29 соответствует значению хто^ = 5,47.
Так как ?,?med и imod практически не отличаются друг от друга,
то есть основание предполагать, что теоретическое распределение
симметрично относительно своего среднего значения, что является еще одним
доводом в пользу выбора модели нормального закона.
Построение модельной кривой плотности нормального закона
распределения. При расчете модельных частот Vk нормального закона
распределения за оценку математического ожидания а и среднеквадратиче-
ского отклонения а принимают значения соответствующих выборочных
характеристик гиа,т.е. а = х = 5,466; а = a = 0,167.

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 213
Модельные частоты находят по формуле:
vl = пРк,
где п — объем выборки; рк — вероятность попадания значения
нормальной случайной величины в к-й интервал.
Вероятности рк в соответствии со свойством г) функции
распределения (см. п. 2.5.1) определяются формулой
Рк = Р{ск-г < ? < ск} = Ф(с*;а,*2) - Ф(ск-цх,з2), F.18)
где Ф(ж;а,<т ) — функция нормального распределения, имеющего среднее
значение а и дисперсию а (см. C.81) в п. 3.1.5). Чтобы вычислять
значения функции Ф(ск',х,з ) для различных значений ск и при заданных
величинах х « s с помощью таблиц стандартной нормальной функции
распределения Ф(х) = Ф(я; 0,1) (таблицы приведены в приложении 1),
воспользуемся результатом D.9) из п. 4.4, в соответствии с которым
Ф(а;а,О = #(=^=;0,1) = Ф^)- F.19)
Соответственно, возвращаясь к F.18), в нашем случае имеем:
Рк =
где х и s — подсчитанные ранее значения выборочного среднего и вы-
борочной дисперсии, а Ф(<) = -4- /-00 e~^rdx — значение функции
стандартного нормального распределения, вычисленное в точке t.
Составим табл. 6.4 для вычисления вероятностей р*, модельных
частот ук и модельной (нормальной) плотности распределения fH(x).
График плотности модельного (нормального) закона распределения
fH(x) представлен на рис. 6.1. Этот график достаточно хорошо
согласуется с гистограммой — графиком эмпирического аналога плотности у (х).

214
ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Таблица 6.4 Расчет модельных частот i/J и модельной плотности
Cfc-l - С*
4,97-5,08
5,08-5,19
5,19-5,30
5,30-5,41
5,41-5,52
5,52- 5,63
5,63- 5,74
5,74- 5,85
2
3
12
19
29
18
13
4
100
— 00
-2,39
¦1,71
¦1,03
-0,35
0,33
1,02
1,70
-
tk
-2,39
¦1,71
- 1,03
-0,35
0,33
1,02
1,70
+оо
-
•(«*-! )
0
0,0082
0,0446
0,1587
0,3632
0,6368
0,8413
0,9554
-
t(«»)
0,0082
0,0446
0,1587
0,3632
0,6368
0,8413
0,9554
1,0000
-
Рк
0,0082
0,0364
0,1141
0,2045
0,2736
0,2045
0,1141
0,0446
1,000
пРк
0,8
3,6
11,4
20,5
27,4
20,5
11,4
4,4
-
т
"*
1
4
11
21
27
21
11
4
100
/«(¦)
0,09
0,36
1,00
1,91
3,45
1,91
1,00
0,36
-
6,2.6. Статистическая устойчивость выборочных
характеристик
Давно было замечено, что результаты отдельных наблюдений (будь
то экономические, демографические, физические, метеорологические или
иные наблюдения), хотя и произведенных в относительно однородных
условиях, колеблются, в то время как средние из большого числа
наблюдений обнаруживают замечательную устойчивость. К такого рода
выборочным средним относятся и все введенные нами выше эмпирические
(т. е. построенные по выборке) характеристики: как выборочные
моменты (начальные и центральные) тк и т^\ так и эмпирические функция
распределения Щп\х), функция плотности Цп\х) и относительные
частоты pi (при интерпретации р^п\рп' и р± в качестве выборочных средних
нужно лишь помнить о возможности их выражения в терминах сумм
случайных величин &,..., ?п, где ?,* равно 1 и 0 в зависимости от того, попало
или нет наблюдение zt в заранее определенную нами область возможных
значений (см. D.4)-D.6) в п. 4.2.2)).
Математическим основанием этого факта служат различные формы
закона больших чисел, который позволяет теоретически обосновывать
устойчивость основных эмпирических характеристик распределения —
среднего значения, дисперсии, асимметрии; эксцесса, функции
распределения и плотности, построенных по выборке жьж2,...,хп. При этом как
всегда, когда речь идет об исследовании выборочных характеристик, мы,
во-первых, подразумеваем, что имеем дело с выборкой, состоящей из
независимых наблюдений, и, во-вторых, интерпретируем выборку во вто-

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 215
ром, гипотетическом, смысле как совокупность независимых
наблюдений, которые могли бы быть произведены над анализируемой случайной
величиной (см. п. 6.1, F.1)-F.3)). При такой интерпретации наблюдения
zbz2,...,zn суть независимые и одинаково распределенные случайные
величины и к ним применимы результаты п. 4.2. Покажем, как из закона
больших чисел и теоремы Я. Берну л ли можно получить статистическую
устойчивость основных выборочных характеристик.
а. Устойчивость выборочных начальных моментов Л*(п) и
любых рациональных функций от них. Пусть существуют моменты тк =
Щк(к = 1,2,...,2&о) всех порядков (вплоть до заданного 2fc0)
исследуемой случайной величины ?. Тогда, применяя закон больших чисел к
случайным величинам & = х*, & = з*,...,^ = хп> где ж, — результат
t-ro наблюдения исследуемого признака, мы немедленно получаем
доказательство сходимости по вероятности всех выборочных начальных
моментов rhk(n) = (Х)Г=1 х* )/n K соответствующим теоретическим моментам
тк = Щ (к = 1,2,..., к0).
Непосредственно применить закон больших чисел к центрированным
наблюдениям хг - х(п),..., хп - х(п) нельзя, так как после центрирования
наблюдения становятся зависимыми.
Однако, воспользовавшись теоремой Е. Е. Слуцкого1 о том, что из
сходимости (при п -+ оо) по вероятности случайных величин &(п) к
некоторым постоянным числам а< (г = 1,2,...,&0) следует сходимость по
вероятности любой рациональной функции ^(?i(n),€2(n),...,ffc0(n)) к ее
значению в точке (ai,a2,. ..,а^0), т.е. к величине <^(аьа2,.. .,afc0) (если
последняя существует), мы немедленно получаем доказательство
сходимости по вероятности всех интересующих нас выборочных центральных
моментов, асимметрии и эксцесса к соответствующим теоретическим
значениям (если таковые существуют). При этом, конечно, мы учитываем,
что центральные моменты, асимметрия и эксцесс являются
рациональными функциями от начальных моментов (см. соотношения B.18) в п. 2.6.1).
б. Устойчивость эмпирических функций распределений и
плотности, а также относительных частот, т. е. их сходимость (при
неограниченном увеличении объема выборки, по которой они построены) к
соответствующим теоретическим функциям и вероятностям, следует
непосредственно из D.3')-D*6). Продемонстрируем это на примере
эмпирической функции распределения F(n)(s). Введем в рассмотрение случайные
1 S 1 u t s k у Б. Uber stochastische Asymptoten und Grenzwerte — Metron, б, К» З
A925), 3.

216 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
величины
с — ?( \ — / 1» если Х{ < х\
Si - s>\*\) ~ | о, если Xi ^ х.
Очевидно, ?ъ€2,...,€п — независимые, одинаково распределенные
случайные величины, причем Е& = F(x) и D& = F(x)(l - Да?))* где
F(x) = P{f < ж} — функция распределения исследуемой случайной
величины ?. Легко видеть, что F^n\x) = [(]C?-i&)/nl = ?(п), и,
следовательно, в соответствии с законом больших чисел F^n\x) -¦ F(x) (no
вероятности), когда n ^ оо.
Таким образом, мы получили ответ на первый из вопросов,
сформулированных в начале пункта и относящихся к «поведению» основных
выбранных характеристик. Тот факт, что при неограниченном увеличении
объема выборки (т. е. при п —> оо) все они стремятся по вероятности к
соответствующим теоретическим характеристикам, дает нам
основание использовать выборочные характеристики для приблизительного
описания свойств всей генеральной совокупности в целом.
6.2.7. Асимптотически-нормальный характер случайного
варьирования основных выборочных характеристик
Смысл результатов предыдущего пункта заключается, в конечном
счете, в том, что при осреднении большого числа (п) случайных
слагаемых все менее ощущается характерный для случайных величин
неконтролируемый разброс в их значениях, так что в пределе по п —> оо этот
разброс как бы исчезает вовсе или, как принято говорить, случайная
величина вырождается в неслучайную. Однако при любом конечном (хотя
и большом) числе слагаемых п случайный разброс у среднего
арифметического этих слагаемых остается. Поэтому и был поставлен второй
вопрос в начале этого пункта относительно «поведения» основных
выборочных характеристик: что можно сказать о характере их
случайного варьирования? Ведь этот характер должен существенно зависеть
от свойств той генеральной совокупности, по выборке из которой мы
построили наши выборочные характеристики. Хотя последнее утверждение
и верно (и, следовательно, характер случайного варьирования
выборочных характеристик надо изучать отдельно для каждого типа генеральных
совокупностей), однако, оказывается, что по мере увеличения объема
выборки (т. е. при п -» оо) они начинают вести себя одинаковым образом
независимо от специфики генеральных совокупностей, по выборкам из
которых они были вычислены.
Поэтому ответ на вопрос о характере случайного варьирования основ-

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 217
ных выборочных характеристик следует формулировать в двух вариантах
в зависимости от размера объема выборки, по которой они строились:
(а) асимптотически, т.е. для больших объемов выборок, что
математически позволяет проводить соответствующее исследование в
условиях п —> оо;
(б) доасимптотически, т.е. для ограниченных объемов выборок,
что требует проведения соответствующего исследования отдельно для
каждого типа генеральной совокупности (для нормальной,
экспоненциальной, равномерной, пуассоновской и т.д.).
Ответ в условиях асимптотики (т.е. при п -> оо) имеет общий
характер, практически не зависит от типа анализируемой генеральной
совокупности и основан на центральной предельной теореме (см. п. 4.3.1).
Опираясь на различные варианты формулировки этой теоремы, можно
показать, что при больших объемах выборок все основные
выборочные характеристики ведут себя как нормально распределенные
случайные величины. Конкретизация закона распределения
вероятностей для каждой конкретной выборочной характеристики производится
с помощью подсчета ее среднего значения и дисперсии. Ниже приводятся
результаты для трех основных выборочных характеристик — среднего ж,
дисперсии з2 и функции распределения F^n'(x):
F20)
В соотношениях F.20) N(m\ А ), как обычно, означает нормальный закон
со средним значением т и дисперсией А , а символика «?n € N(m; A )»
означает, что случайная величина fn асимптотически (по п -» оо)
распределена нормально с указанными величинами среднего значения (т) и
дисперсии (А ). Параметрами а^а ,/32н F(x) обозначены соответственно
среднее значение, дисперсия, коэффициент эксцесса и функция
распределения анализируемой генеральной совокупности.
Вычислим приведенные в F.20) средние значения и дисперсии
выборочного среднего х(п) и эмпирической функции распределения F^n'(x), а
также среднее значение выборочной дисперсии s2(n) (вид ее дисперсии

218 ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
приводится в F.20) без доказательства):
Ег
A Л \ 1 л 1 ft 1
n
п
F.21)
< - аJ
.1=1
= - • nF(x) =
F.23)
F.24)
F.25)
При выводе формул для EF*n'(x) и DPW'(«) использовалось
представление F{n)(x) в виде F{n\x) = (^Г=1 6)/»i ™e
, если Xi < х\
, если Xi ^ х,
и учитывалось, что ?i,6>- -м?п — независимые, одинаково
распределенные случайные величины, причем Е& = 1 • F(x) + 0 • A — F(x)) = F(x) и
b = A - F(x)J
@
- F(x)) =
( ()) () ( ^))( ()) ()( ())
При выводе формулы для Ед было использовано тождество:
Е | 2(в - *) J^(xi - а) \ = 2Е (о - х) I^ xi - па) = -2пЕ(х - оJ.

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 219
Что касаетсся доасимптотического поведения основных выборочных
характеристик, то мы исследуем этот вопрос в следующем пункте
этого п., но только для случая, когда выборка извлекается из нормальной
генеральной совокупности.
6.2.8. Поведение выборочных характеристик в нормальной
генеральной совокупности (статистика нормального
закона)
Как и раньше, речь идет о свойствах выборочных характеристик,
проявляющихся при повторениях выборок того же объема из одной и той
же генеральной совокупности, в нашем случае — из (а, а У нормальной
генеральной совокупности. Соответственно наблюдения хьх2,...,жп,
образующие выборку, интерпретируются как независимые, одинаково
(а, сг2)-нормально распределенные случайные величины (см. п. 6.1,
соотношения F.1)-F.3)). Сформулируем основной результат,
касающийся распределения пары основных выборочных характеристик ($(п),д3(п))
(а, (Т2)-нормальной генеральной совокупности.
Теорема Фишера. Пусть х(п) и з (n) — соответственно
выборочная средняя и выборочная дисперсия, построенные по случайной
выборке (a?!,a?2,...,«n) из (а,<г2)-нормальной генеральной совокупности. Тогда
при любом фиксированном объеме выборки п (а не только при п —> ос)
их совместный закон распределения описывается следующим образом:
распределение х(п) подчинено
0.2
(а, —) - нормальному закону\ F.26)
71
П32(п) . 2
статистика *~ распределена по закону х
а
с п- 1 ст. свободы; F.27)
х(п) и з2(п) статистически независимы. F.28)
Мы не будем приводить здесь подробного доказательства этого
важного результата. Отметим лишь, что нормальность х(п) вытекает из
факта нормальности любой линейной комбинации нормально распределенных
случайных величин, который в свою очередь получается, например, с
помощью индуктивного применения формулы композиции (см. D.13) в п. 4.4)
сначала к сумме двух нормальных случайных слагаемых, затем трех и т.д.
Что касается вывода закона распределения статистики пз /а2 и статисти-

220 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
ческой независимости выборочного среднего х(п) и выборочной дисперсии
52(п), то в основе доказательства этих утверждений лежит
последовательный переход сначала от наблюдений Х{ к центрированным наблюдениям
Х{ = Х{ - а, а затем к у{ с помощью ортогонального преобразования:
при i = l,2,...,n- 1;
при i = п.
Несложно проверить, что полученные таким образом случайные
величины yi/(J являются независимыми, одинаково @,1)-нормально
распределенными и что интересующие нас характеристики х(п) и s (n) выразятся в
терминах j/i, j/2> • • • > Уп следующим образом:
*() +
«•'(»)=:
Отсюда и будет непосредственно следовать справедливость утверждений
F.27) и F.28).
Утверждения F.26)^F.28) теоремы Фишера позволяют
сформулировать ряд следствий, которые окажутся весьма полезными в дальнейших
наших обсуждениях, в том числе при решении задач интервального
статистического оценивания (см. п. 7.5.4) и статистической проверки гипотез
(гл. 8).
Следствие 1. Среднее значение и дисперсия эмпирической
дисперсии s (п), построенной по случайной выборке объема п из
(а, а ^-нормальной генеральной совокупности, определяются формулами:
F29)
Выражение для Es2(n) справедливо и в общем случае (не только для
нормальных выборок), см. выше вывод соотношения F.23). Покажем, как
результаты следствия 1 получаются из F.27). Известно (см. п. 3.2.1), что

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 221
среднее значение и дисперсия X (п - ^-распределенной случайной
величины равны соответственно п-1и 2(п - 1). Поэтому
Следовательно,
2
-^•Es2(n) = п - 1 и -jDs2{n) = 2(n- 1),
откуда непосредственно вытекают соотношения F.29).
Следствие 2. 2?слн ж(п) и 5 (п) соответственно среднее значение
и дисперсия, построенные по случайной выборке из
(а,сг2)-нормальной генеральной совокупности, то статистика
(х — а)у/п — 1 . .
^ = ^ ^ распределена по закону Стьюдента
s
с п - 1 cm.ce. F.30)
Для доказательства этого результата представим статистику t в виде
\ } ^J F.31)
Легко устанавливается, что:
• числитель дроби (в квадратных скобках) распределен по
стандартному нормальному закону (с учетом F.26));
• подкоренное выражение в знаменателе дроби ведет себя как х(п -
^-распределенная случайная величина, поделенная на число степеней
свободы п — 1 (в соответствии с F.27));
• числитель и знаменатель дроби F.31) статистически независимы (в
соответствии с F.28)).
Но тогда правая часть F.31) в точности удовлетворяет определению
«стыодентовской» случайной величины сп-1 степенью свободы (см.
п. 3.2.2), что и завершает доказательство следствия 2.
Три следующих результата (следствия 3, 4 и 5) относятся к
статистике нормального закона, связанной с анализом двух независимых
выборок из нормальных генеральных совокупностей. А именно, пусть мы
располагаем случайной выборкой
*ш«la»-.Maim из ген. сов. N{aucr\) F.32)

222 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
и случайной выборкой
#21» ^22* • • ¦»Ж2пз ИЗ ГОН. СОВ. ЛГ(в2>**2л F.33)
статистически независимой от выборки F.32).
Нас будет интересовать поведение различных комбинаций основных
выборочных характеристик х1(п1),з?(п1),ж2(п2) и sl(n2)> построенных по
этим двум выборкам, где
Л = 1,2, F.34)
4Ы=—Е(^-*лЫJ, к = 1,2. F.35)
дисперсий сг\ и а% имеет место следующий факт;
Следствие 3. В условиях F.32)-F.34) при известных значениях
F.36)
Ыщ) - х2(п2)) € N ((аг - «,); ^ + ^ j.
В частности, при а\ = аз, cri = 0*2 = ст и nj = п2 = п
») ~ *а(п)) 6 Лг(о; ^. F.36#)
Утверждение F.36) следует из F.26) с учетом очевидных вычислений
теоретических среднего значения и дисперсии разности {&\{п\\ — $2(П2))*
Следствие 4. В условиях F.32)-F.35) и при неизвестных, но
одинаковых дисперсиях а\ = а\ = а2 имеет место следующий факт:
[(хг(пг) - 1,(п,)) - (аг - а2)]/J^+X
Y € з.р.в. Стыодента с
пх + па - 2 ст.св. F.37)
Для того чтобы убедиться в справедливости F.37), следует проверить
правильность следующих утверждений:
а) Случайная величина
71 =

6.2 ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 223
распределена по стандартному нормальному закону (следует
непосредственно из F.36) с учетом о\ = а\ = а2 и независимости xi(ni) и х2(п2)).
б) Случайная величина
72 "
п2а\{п2)\
+ ~7~)
п
подчиняется з.р.в. х с пг + п2 - 2 степенями свободы. Этот факт
основан на X2(wi - 1)-распределенности ni32/<r2} Х2(п2 - 1)-распределенности
п2з2/а2 (и то, и другое — в силу F.27)) и независимости з2(щ) и з2(п2) (с
учетом того, что из определения х2-распределения следует, что если две
X2-распределенные случайные величины х (mi) и х (тг) статистически
независимы, то их сумма х (mi) + X (шг) распределена снова по закону
X2, но уже с гп\ + Ш2 степенями свободы).
в) Случайная величина 7i/y ni+n2-2 72? c одной стороны,
тождественно равна левой части соотношения F.37), а с другой стороны,
распределена по закону распределения вероятностей Стьюдента с щ + п2 - 2
степенями свободы. Тождество проверяется непосредственно, а «стьюден-
товская» распределенность этого отношения следует из статистической
независимости 7i и 72 (в силу независимости выборок й F.28)) и
определения случайной величины, подчиняющейся распределению Стьюдента с
т степенями свободы (см. п. 3.2.2).
Представляет самостоятельный интерес частный случай следствия 4,
когда аг = а2:
n"
— € з.р.в. Стьюдента с
з
+ п2 - 2 ст.св., F.37/)
где величина
является по существу оценкой неизвестной дисперсии <т2 по объединенным
наблюдениям двух выборок F.32) и F.33).
Результат F.37) используют, в частности, для построения
статистического критерия проверки гипотезы о равенстве средних в двух
наблюдаемых нормальных генеральных совокупностях (см. гл. 8).

224 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Следствие 5. В условиях F.32)-F.35) и при неизвестных, но
одинаковых дисперсиях <г\ = а\ = а2 имеет место следующий факт:
I) з.р.в. Р(щ-1,п2-1). F.38)
1)
В правой части F.38) обозначен закон распределения вероятностей
Фишера с числом степеней свободы числителя, равным п\ — 1, и числом
степеней свободы знаменателя, равным щ — 1 (см. п. 3.2.3).
Справедливость F.38) следует непосредственно из х (n>k - 1)-распре-
деленности случайных величин n^s^n^/cr , к = 1,2 (в соответствии с
F.27)) и из статистической независимости $i(ni) и s2(n2) (как следствие
независимости выборок F.32) и F.33)).
6.3. Вариационный ряд и порядковые
статистики
Выше отмечалось, что выборка, т. е. совокупность имеющихся у нас
наблюденных значений Ж1,а?2>..->жп исследуемой случайной величины ?,
является той исходной информацией, на основании которой исследователь
строит свои выводы о свойствах изучаемой генеральной совокупности в
целом и, в частности, составляет представление о функции
распределения или плотности анализируемого закона распределения вероятностей.
Оказывается, что и каждый член выборки в отдельности может
доставлять важную информацию о характере анализируемого закона
распределения, если наблюдения предварительно расположить в порядке
возрастания. Так, например: наименьшее и наибольшее выборочные значения
(соответственно хт\п(п) и smax(n)) дают приближенное представление о
диапазоне изменения возможных значений исследуемого признака, а их
разность (xmax(n) - хт\п(п)) — о степени случайного разброса его
наблюдаемых значений; средний член упорядоченного ряда наблюдений —
медиана xmed(tt) — характеризует центр группирования наблюдений
изучаемой случайной величины и так далее. Все это говорит о целесообразности
специального рассмотрения ряда наблюдений, расположенных в порядке
возрастания.
Итак, пусть Ж1,а?2>•• -*хп — выборка, состоящая из п независимых
наблюдений исследуемой случайной величины ? с непрерывной функцией
распределения F^(x) и плотностью вероятности f((x). Построим новый
ряд из элементов имеющейся выборки, расположив x^i = 1,2,...,п) в
порядке возрастания (неубывания) их значений. Обозначим член нового

6.3 ВАРИАЦИОННЫЙ РЯД И ПОРЯДКОВЫЕ СТАТИСТИКИ 225
ряда, стоящий на г-м месте, через хщ, чтобы отличать его от ж,-. Тогда
новый ряд будет представлен неубывающей последовательностью
--»*(п)- F.39)
Каждый член этой последовательности (a?(t)) называется порядковой
статистикой, а сама последовательность F.39) — вариационным рядом
случайной величины f.
Аппарат порядковых статистик широко используется как в теории и
практике статистического оценивания неизвестных параметров и
статистических критериев (особенно при построении устойчивых и «свободных
от распределения» оценок и критериев), так и непосредственно при
моделировании реальных систем и процессов. При исследовании качества
оценок, критериев и моделей, полученных с использованием порядковых
статистик, необходимо уметь описывать законы их распределения
вероятностей в схеме гипотетического варианта интерпретации выборки,
когда члены вариационного ряда хщ интерпретируются не как конкретные
числа, а как случайные величины, значения которых реализуются при
повторениях выборок того же объема из той же самой генеральной
совокупности. И хотя члены вариационного ряда F.39) в отличие от членов
исходной выборки уже не являются взаимно независимыми (по причине
своей предварительной упорядоченности) и соответственно их частные
распределения уже не являются одинаковыми, описываемыми, в
частности, одной и той же плотностью f((x) (см. F.1)), однако, они могут
быть описаны в терминах этой плотности и соответствующей функции
распределения
6.3.1. Закон распределения вероятностей г-го члена
вариационного ряда
Пусть FX{i)(x) = P{a?(f) < х} и /Х@(я), соответственно —
непрерывные дифференцируемые функция распределения и функция плотности
вероятности 1-й порядковой статистики, построенной на основании
случайной выборки Xi,x2,.-.,xn из генеральной совокупности с функцией
распределения F{(x) и функцией плотности вероятности Д(ж). Мы хотим
выразить FX{i)(x) и /Х@(ж) (для любого г = 1,2,. ..,п) в терминах
функций F^(x) и Д(ж).
Реализуем следующую схему вывода требуемых соотношений. Для
любого заданного значения х и некоторого достаточно малого положи-
8 Теория вероятностей
и прикладная статистика

226 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
тельного числа А введем в рассмотрение событие
А . .А'
А далее мы попытаемся выразить вероятность события А(х) одновременно
и в терминах вероятностных характеристик случайной величины хщ (что
тривиально, так как Р{А(х)} = FX(iy(x + у) - FX(i)(x - ^)), и в терминах
схемы п независимых наблюдений хих2^^,хп анализируемой случайной
величины (. Для этого введем в рассмотрение наряду с событием А(х)
еще три события:
Аг(х) =
х + |
В терминах схемы п независимых наблюдений случайной величины
f событие А(х) эквивалентно следующему событию: г — 1 наблюдений (из
общего числа п) оказались меньше х — у (т. е. г — 1 раз состоялось
событие А\(х))) одно наблюдение попало в окрестность [х — у,х + у) точки
ж (т. с. один раз произошло событие А2(х)) и остальные n—i наблюдений
оказались не меньшими, чем х + у (т. е. n — i раз произошло событие
А3(ж)). Чтобы подсчитать вероятность этого события (эквивалентного
событию А(х)) в терминах F^(x) и Д(х), воспользуемся моделью
полиномиального распределения (см. п. 3.1.4). Действительно по существу речь
идет о производстве п независимых испытаний, в результате каждого из
которых может произойти одно из событий Ai(x)y ^(ж) или Аз(ж), причем
вероятности этих событий по построению равны:
й = Р{Аг(х)} = P{xt
х -
Нас интересует вероятность того, что в результате этих п независимых
испытаний г — 1 раз произойдет событие А\{х\ (т.е. щ(п) = г — 1) один

6.3 ВАРИАЦИОННЫЙ РЯД И ПОРЯДКОВЫЕ СТАТИСТИКИ 227
раз — событие А2(х) (т.е. t/2(n) = 1) и п - % раз — событие А3(х) (т.е.
j/3(n) = n - i).
Воспользовавшись формулой C.7) полиномиального з.р.в., имеем:
Р{А(х)} = P{fi(n) = i - 1,1/з(п) = 1,1>з(п) = п - »}
п!
(|-1)!1!(Я-0!1ГЧ" 2, _
F.40)
С другой стороны, Р{Л(ж)} в терминах FX@(a?) определяется в виде
Р{А(х)} = F,(j) (*
Приравнивая правые части F.40) и F.41), деля обе части полученного
таким образом выражения на Д и устремляя Д к нулю, получаем в пределе
))n'V^), •' = 1,2,...,»•
F.42)
Формула F.42) позволяет описать з.р.в. в любой порядковой
статистике, зная з.р.в. анализируемой генеральной совокупности.
6.3.2. Совместные (многомерные) распределения членов
вариационного ряда
Если в статистическом анализе или моделировании используются
функции от нескольких членов вариационного ряда (например, для
оценки среднего значения симметрично распределенной случайной величины
может использоваться полусумма (хщ + Я(п))/2, а для оценки
дисперсии — статистика, пропорциональная разности Ж(п) - Ж(х)), то для
изучения свойств таких функций необходимо уметь описывать совместные
(многомерные) з.р.в. для набора соответствующих порядковых статистик.
Вычисление плотностей вероятности для таких совместных з.р.в. в
терминах Д(ж) и F^(x) не вызывает принципиальных трудностей, хотя и
реализуется в виде весьма громоздких выражений. Мы приведем здесь

228 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
без доказательства выражение функции плотности вероятности для
любой пары порядковых статистик (?(t)>?(j))? где г < j:
X [1 - ед]п"'/*(*)Ш, F.43)
где нормирующий множитель K(i,j,n) определяется формулой
n!
Продемонстрируем способ получения этой формулы на одном важном
частном случае: выведем вид з.р.в. для пары крайних членов
вариационного ряда, т.е. для (жA),Ж(п)). Для этого воспользуемся следующими
очевидными соотношениями между событиями:
{я(п) < у} = {х{1) < х;х{п) <у} + {жA) ^ s;s(n) < у}
< х{ < у}.
Соответственно имеем (учитывая независимость событий {х < Xi < у}
для г = 1,2,...,п):
<) (D х>Чп) < у)
откуда
^A)^(w))(x,y) = Р{х{п) < у} - [F€(y) - F€(x)]n. F.45)
Но событие {ж(п) < г/} эквивалентно произведению независимых
событий {хг < у}, {х2 < у},..., {хп < у}.
Поэтому из F.45) получаем
F-46)
или, после дифференцирования обеих частей по х и по у
2 F.46')
Читатель может убедиться в том, что, подставляя в общую формулу
F.43W6.44) значения i = 1 и j = n, мы получим то л1е соотношение
F.4б').

выводы 229
6.3.3. Порядковые статистики как эмпирические
(выборочные) аналоги квантилей и процентных точек
распределения
Из определения г-й порядковой статистики хщ следует, что
относительная частота (эмпирический аналог вероятности!) наблюдений
выборки, меньше a?(i), равна (i — 1I п. А это означает, что порядковая
статистика X(i) является одновременно выборочным квантилем уровня (• — 1)/п
и выборочной 100A - *~~)%-ной точкой анализируемого распределения.
ВЫВОДЫ
1. Понятие генеральной совокупности является удобным (для
статистических приложений) синонимом понятий «вероятностное
пространство», «случайная величина», «закон распределения вероятностей» и
определяется как совокупность всех мыслимых наблюдений, которые
могли бы быть сделаны в данном реальном комплексе условий.
2. Выборка — это статистически обследованная часть генеральной
совокупности, по которой мы хотим судить об интересующих нас
свойствах генеральной совокупности в целом. Вопрос представительности
(репрезентативности) выборки с учетом обычной ограниченности времени и
средств на ее получение требует от исследователя знания и использования
различных специальных форм организации выборочных обследований.
3. Следует иметь в виду, что, говоря о выборке (или о вариационном
ряде), в зависимости от контекста подразумевают один из двух
различных вариантов интерпретации этого понятия. В первом (практическом)
варианте под хг,х2,. • .,хп понимают фактически наблюденные в данном
конкретном эксперименте значения исследуемой случайной величины, т.е.
конкретные числа или векторы. Во втором (гипотетическом) варианте
под xi,Z2,... ,зп понимают лишь обозначение тех п значений (чисел или
векторов), которые могли бы быть получены при реализации п-кратного
эксперимента (наблюдения) в реальном комплексе условий,
индуцирующем исследуемую генеральную совокупность. В последнем случае сами
Xi и любые функции от них выступают уже не в качестве конкретных
чисел или векторов, а в качестве случайных величин, поскольку их
значения варьируют неконтролируемым образом при каждом новом извлечении
выборки того же объема п из той же самой генеральной совокупности.
4. В практике статистического анализа и моделирования точный вид
з.р.в. анализируемой случайной величины, а соответственно и точные
значения ее основных теоретических числовых характеристик (среднего,
дисперсии и т.п.) бывают неизвестны. Исследователь располагает лишь

230 ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
выборкой из интересующей его генеральной совокупности, а потому
вынужден строить все свои выводы на основании ограниченного ряда
выборочных характеристик. К основным выборочным характеристикам
одномерной случайной величины относятся: эмпирические функции
распределения и плотности (F (я),/*Л'(х)), выборочная относительная
частота р\п^ появления 1-го возможного значения, выборочное среднее значение
(х(п)), выборочная дисперсия (а2(п)), члены вариационного ряда (#(<)).
5. Осмысленное и обоснованное использование в статистическом
анализе основных выборочных характеристик требует знания их свойств, в
том числе ответов на вопросы: 1) стремятся ли они к значениям своих
теоретических аналогов при неограниченном увеличении объема выборки
(т.е. при п -+ оо)? 2) что можно сказать о з.р.в. каждой из
выборочных характеристик? Оказывается, в асимптотическом смысле (т.е. при
п —> оо) ответы на эти вопросы практически не зависят от специфики
генеральной совокупности, из которой извлекалась выборка, и являются
следующими: основные выборочные характеристики с ростом объема
выборки стремятся к своим теоретическим аналогам и ведут себя при
этом как нормально распределенные случайные величины.
6. Исследование поведения основных выборочных характеристик при
конечных (ограниченных) объемах выборок требует учета специфики
генеральной совокупности, из которой извлечена выборка. Пример
результатов такого исследования дает теорема Фишера, описывающая
поведение пары основных выборочных характеристик (x(n),s2(n)) для случая
нормальной генеральной совокупности. Ряд полезных следствий этой
теоремы (статистика нормального закона) используется в дальнейшем при
построении интервальных оценок и статистических критериев проверки
гипотез.
7. Полезным приемом в исследовании свойств анализируемой
случайной величины является расположение имеющихся наблюдений хих2,
..., хп в порядке их возрастания: жA), хB),...,ж(п), так что {хщ}ыТ^ —
это те же самые наблюдения {Я|}^=у^, только упорядоченные (т.е. х\ц <
Ж(Н-1) для всех i = 1,2,...,п- 1). Ряд {«(t)}^^ называют
вариационным рядом, а его члены — порядковыми статистиками. Они также
относятся к основным выборочным характеристикам и, в частности,
широко используются при построении так называемых непараметрических
оценок и непараметрических критериев.

ГЛАВА 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
ПАРАМЕТРОВ
Одна из главных целей, которые ставит перед собой исследователь,
приступая к статистической обработке исходных данных, заключается в
том, чтобы добиться удобной лаконичности в описании интересующих
его свойств исследуемой совокупности (или исследуемого явления), т.е.
представления множества обрабатываемых данных в виде сравнительно
небольшого числа сводных характеристик, построенных на основании
этих исходных данных. При этом желательно, чтобы потеря информации,
существенной для принятия решения, была минимальной. Упомянутые
сводные характеристики являются функциями от исходных результатов
наблюдения х\, x<i, ¦.., хп и называются статистиками (таким образом,
мы уже имеем, как минимум, три различных обиходных варианта
термина «статистика»: научная дисциплина, исходная информация и любая
функция от результатов наблюдения). В предыдущей главе мы уже
имели дело с примерами таких сводных характеристик (статистик): к ним
относятся все выборочные (эмпирические) характеристики генеральной
совокупности — средние значения, дисперсии, коэффициенты эксцесса и
асимметрии, наконец, эмпирическая функция распределения и
эмпирическая плотность.
Добиться лаконичности в описании информации, содержащейся в
массиве обрабатываемых данных, помогает целый набор прикладных
методов математической статистики: выбор и обоснование математической
модели механизма изучаемого явления; изучение свойств анализируемой
системы или механизма функционирования с помощью небольшого числа
сводных выборочных характеристик (среднего, дисперсии и т.п.);
наглядное представление (визуализация) исходных данных с целью
формирования рабочих гипотез о механизме изучаемого явления; анализ
относительных частот, выборочных функций распределения и плотности и другие
методы описательной (или дескриптивной) статистики; анализ
природы обрабатываемых данных; описание интересующих исследователя ста-

232 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
тистических связей между анализируемыми признаками и т.д. Все эти
методы в той или иной степени опираются на две основные составные
части математического аппарата статистики: 1) теорию
статистического оценивания неизвестных значений параметров, участвующих в
описании анализируемой модели; 2) теорию проверки статистических
гипотез о параметрах или природе анализируемой модели.
Изложению основных элементов первой из этих двух составных
частей аппарата математической статистики и посвящена настоящая глава.
7.1. Начальные сведения о задаче
статистического оценивания
параметров
7.1.1. Постановка задачи
Пусть мы располагаем исходными статистическими данными —
выборкой
ЖЬ«2>--м*п G.1)
из исследуемой генеральной совокупности и пусть интересующие нас
свойства этой генеральной совокупности могут быть описаны с помощью
уравнения (математической модели)
М(ж,0) = О, G.2)
где Xi — i-e наблюдение в выборке G.1), х — текущее (т.е. подставляемое
по нашему усмотрению) значение исследуемого случайного признака, 0 =
@* ,..., 0* ') — Ar-мерный параметр, участвующий в записи модели G.2),
значения которого нам были не известны до получения выборки G.1).
Задача статистического оценивания неизвестных параметров 0 по
выборке заключается, грубо говоря, в построении такой Л-мерной
векторной функции &(хи...,хп) = ($1\хи...9хп)9...,Фк)(хи...9хп))Т от
имеющихся у нас наблюдений G.1), которая давала бы в определенном
смысле наиболее точные приближенные значения для истинных (не
известных нам) значений параметров 0 = @^,...,0^)т. Здесь не
уточняется пока, в каком именно смысле приближенные значения $г\..., $к^
соответственно параметров 0*1 ,... ,0**' являются наилучшими.
В качестве моделей G.2) могут, например, рассматриваться модели
законов распределения вероятностей.

7.1 НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 233
Пример 7.1. Пусть нашей целью является исследование закона
распределения наблюдаемой непрерывной одномерной случайной
величины f с неизвестной плотностью вероятности Д(ж) и пусть
предварительный анализ природы исходных данных G.1) привел нас к выводу, что этот
закон может быть описан нормальной моделью. В этом случае
в™ = а2 =
где
и можно показать, что вся информация о параметрах Ф* и #' ' (а
следовательно, и о всей модели) содержится всего в двух статистиках — ж и
s2, где
1 п
х = ±Ух{ G.3)
i n
2 •¦¦ v "^ 2
П t=l
Выше показано, что есть основания использовать статистики G.3) и G.4)
в качестве приближенных значений (оценок) параметров а и а2,
поскольку по мере роста объема выборки, т.е. при п —> оо, эти оценки сходятся
по вероятности к соответствующим истинным значениям а и а2. Однако
вопрос о том, являются ли эти оценки наилучшими, пока остается
открытым. Чтобы иметь возможность обсуждать этот вопрос, нам придется
ввести и обсудить ряд понятий.
7.1.2. Статистики, статистические оценки, их основные
свойства
Любая функция j(xi, • • • 5 хп) от результатов наблюдения Х\, ж2,...,
хп исследуемой случайной величины ? называется статистикой. Мы
уже познакомились с целым рядом статистик: выборочное среднее;
выборочная ковариационная матрица; выборочные коэффициенты асимметрии
/3i и эксцесса fa\ эмпирические функции распределения FK }{х) и плотно-
сти / (ж).
Статистика О, используемая в качестве приближенного значения
неизвестного параметра 0, называется статистической оценкой. Так,
например, статистики ж, s ,/?i и fa можно рассматривать как
статистические оценки соответственно параметров а = Ef, D?, fa и fa, поскольку,

234 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
как это следует из п. 7.2 все эти статистики при п -* оо сходятся по
вероятности к истинным значениям соответствующих параметров.
Обращаем внимание читателя на тот факт, что, говоря о статистиках
и статистических оценках, мы используем всегда гипотетический
вариант интерпретации выборки,т.е. вариант, при котором под хи...ухп под*
разумеваются лишь обозначения тех п значений исследуемого признака ?,
которые мы могли бы получить^ проводя n-кратный случайный
эксперимент (или производя п независимых наблюдений) в данном реальном
комплексе условий. Следовательно, все статистики и статистические
оценки являются случайными величинами: при переходе от одной выбор-
ки к другой (даже в рамках одной и той же генеральной совокупности)
конкретные значения статистической оценки, подсчитанные по одной и
той же формуле G.3) (т.е. значения, полученные с помощью подстановки
в эту формулу соответственно различных конкретных значений
аргумента), будут подвержены некоторому неконтролируемому разбросу.
Правда, значения статистической оценки, подсчитанные по разным выборкам,
хотя и подвержены случайному разбросу, но должны (если наша оценка
«хороша»!) концентрироваться около истинного значения оцениваемого
параметра.
Возникает вопрос о требованиях, которые следует предъявить к
статистическим оценкам, чтобы эти оценки были в каком-то определенном
смысле надежными. Эти требования формулируются обычно с помощью
следующих трех свойств оценок: состоятельности, несмещенности и
эффективности.
7.1.3. Состоятельность
Оценка 0 = в(хи..,,хп) неизвестного параметра в называется
состоятельной, если по мере роста числа наблюдений п (т. е. при п —> оо)
она стремится по вероятности к оцениваемому значению 0, т.е. если
для любого сколь угодно малого е > О Р{\0- 0\ > е} -> 0 при п -+ оо (если
оцениваемый параметр Э векторный, то для состоятельности
соответствующей векторной оценки 0 требуется состоятельность отдельно всех
ее компонент). Заметим, что достаточными условиями состоятельности
оценки 0п параметра 0 являются следующие ее свойства:
1) смещение Вп = Е0п - 0 оценки 0п равно нулю (Вп = 0) или
стремится к нулю при п —* оо, т.е. lim Bn = 0;
п—>оо
2) дисперсия оценки D0n удовлетворяет условию lim D0n = 0.
п—юо
Докажем, что эти условия являются достаточными. Согласно нера-

7.1 НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 235
венству Чебышева, можно записать
€
Подставляя выражение Е0Л = Вп - 0, получим
Переходя к пределу при п «-» оо с учетом того, что по условию Вп = О или
lim Bn = 0, получим
lim
что и требовалось доказать.
Все упомянутые выше оценки Cf,a ,FV '(&)>/ Л35) и Т»Д*)
являются, как это показано в п. 6.2, состоятельными оценками соответствующих
параметров.
С одной стороны, требование состоятельности представляется
необходимым для того, чтобы оценка имела практический смысл (так как
в противном случае увеличение объема исходной информации не будет
«приближать нас к истине»), а потому это свойство должно проверяться
в первую очередь.
С другой стороны, свойство состоятельности — это
асимптотическое (по числу наблюдений п) свойство, т. е. оно может проявляться лишь
при столь больших объемах выборок, до которых мы в нашей практике не
«добираемся». Кроме того, в большинстве ситуаций можно предложить
несколько состоятельных оценок одного и того же параметра. Например,
оценки 0j = ж и 02 = (хт\п + хтлх)/2 являются состоятельными оценками
неизвестного истинного среднего значения в = Е? симметрично
распределенной случайной величины, если это среднее в существует (здесь ж —
выборочное среднее, определенное по формуле G.3), а хт1П и хтах —
соответственно минимальное и максимальное значения среди п наблюдений
исследуемого признака).
Более того, можно привести примеры состоятельных оценок,
уводящих сколь угодно далеко от истины. Представим себе, что произведена
достаточно большая случайная выборка работников некоторой отрасли
экономики с регистрацией величины их заработной платы, т.е. мы
располагаем выборкой вида G.1). Заказчик поручает статистику построить
оценку теоретического значения средней заработной платы а = Е?
анализируемой совокупности с единственным требованием, чтобы эта оценка

236 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
была состоятельной. И представим себе, что статистик по тем или иным
причинам заинтересован в завышении реального результата (или в этом
заинтересован заказчик, о чем он проинформировал статистика). Тогда
статистик может предложить в качестве состоятельной следующую
оценку:
¦{
а0 при п < N - 1;
х при п ^ N - 1,
где а0 — любое угодное статистику (или заказчику) значение, х —
выборочное среднее значение, построенное по выборке G.1), а N — общее
число работников в анализируемой отрасли. Как легко видеть,
состоятельность оценки ап следует из состоятельности ж (так как в процессе
п —> оо мы перейдем рубеж п = N — 1 и, следовательно, асимптотические
свойства ап будут определяться асимптотическими свойствами ж). В то
же время при всех реальных значениях объема выборки п оценка ап будет
давать заданное (угодное заказчику или статистику) значение ао, которое
никак не связано со свойствами анализируемой генеральной
совокупности. И чтобы разоблачить недобросовестность статистика (заказчика),
потребуется в данном случае произвести сплошное обследование платы
работников анализируемой области.
Все это говорит о том, что свойства состоятельности недостаточно
для полной характеристики надежности оценки. Поэтому его надо
дополнить рассмотрением двух других свойств.
7Л .4. Несмещенность
Оценка в = 0(#i,.. . ,жп) неизвестного параметра в называется
несмещенной, если при любом объеме выборки п результат ее осреднения
по всем возможным выборкам данного объема приводит к точному
истинному значению оцениваемого параметра, т. е. Ев = в (если
оцениваемый параметр 0 векторный, то для несмещенности соответствующей
векторной оценки 0 требуется несмещенность отдельно всех ее
компонент).
Проверим, например, являются ли оценки G.3) и G.4) несмещенными
оценками параметров а = Ef и а2 = D?:
A n \ 1 n
1=1

7.1 НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 237
П
n
п
п
. t=l
. a? - 2(aF - a) J>, - a) + ?(* - aJ
Li=i t=i t=i
n
^. _ aJ - 2(x - a)(n3F - na) + n(x - aJ
L 1=1
n
п
п
п
В ходе вычисления Ез мы воспользовались тем фактом, что в случае
независимых и одинаково распределенных, с дисперсией а , наблюдений
,, zn имеем
) n2
4
п2
Мы видим, что х F.21) является несмещенной оценкой параметра а, в то
время как оценка s F.23) параметра а имеет отрицательное смещение,
равное а /п.
В отличие от состоятельности несмещенность характеризует «до-
асимптотические» свойства оценки, т.е. является характеристикой ее
хороших свойств при каждом конечном объеме выборки. Удовлетворение
требованию несмещенности устраняет систематическую погрешность
оценивания, которая, вообще говоря, зависит от объема выборки пив случае
состоятельности оценки стремится к нулю при п —> оо. Если смещение
оценки удалось определить, то оно легко устраняется. Так, в нашем
примере для устранения смещения достаточно перейти к оценке
которая, как легко понять, уже будет несмещенной. Из сказанного
следует также, что требование несмещенности (при соблюдении требования

238
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
состоятельности) особенно существенно при малом количестве
наблюдений.
7.1.5. Эффективность
Представим себе, что мы имеем две состоятельные и несмещенные
векторные оценки @i(&i,..., хп) и 02(a?i,..., хп) неизвестного векторного
параметра 0. Для возможности геометрической интерпретации примера
будем полагать размерность к векторного параметра равной двум (к = 2).
Для анализа свойств двух конкурирующих оценок будем производить
многократное (в данном примере двадцатикратное) оценивание неизвестного
параметра 0 = (в^1\в^)т каждым из двух рассматриваемых способов.
С этой целью подсчитываем значения 0lf- и 02t(i = 1,2,..., 20),
являющиеся результатом подстановки в функции 0i и 02 г-й по порядку выборки
объема п, т. е. извлекаем первую выборку объема п - хц ,jc12> - • > sin>
вставляем эти наблюдения в качестве аргументов функций ©i и 02, получаем
первую пару оценок 0ц и 02i; затем извлекаем вторую выборку объема
п — #2b#22>• • • >ж?т вставляем эти наблюдения в качестве^аргументов
тех же функций 0j и 02 — получаем вторую пару оценок 0i2 и 022, и
т.д. На рис. 7.1. по горизонтальной оси отложены первая компонента
неизвестного (оцениваемого) параметра (#' ') и первые компоненты ее двух
оценок (§$ на рис. 7.1. а и $$ на рис. 7.1. б), а по вертикальной оси —
вторая компонента неизвестного (оцениваемого) параметра @ ) и вторые
компоненты ее двух оценок ($$ на рис. 7.1. а и $$ на рис. 7.1. б).
* •
• 1
•I •
• 1
!*<¦>
б
•
If*
Рис. 7.1. Два способа состоятельного несмещенного оценивания
многомерного параметра 0 = (бК1),^2)), характеризующегося разной
эффективностью: а) более эффективная оценка; б) менее
эффективная оценка

7.1 НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 239
Таким образом, взаимное расположение точки (д[\ ,8^ ) и крестика
),0B*) на рис. 7.1. а дает наглядное представление о близости оценки
, полученной первым способом с использованием t-й выборки, к
истинному значению оцениваемого параметра 0 (аналогичная картина для
второго способа оценивания представлена на рис. 7.1. б). Более тесная
концентрация оценок, полученных первым способом, около истинного
значения, очевидно, склонит нас к мысли о большей эффективности оценки
0! по сравнению с оценкой 02-
Именно этот критерий как мера разброса оцененных значений 02
около истинного значения 0 в соответствующем fc-мерном пространстве и
положен в основу определения эффективности оценки. Оценка 0
параметра 0 называется эффективной> если она среди всех прочих оценок того
же самого параметра обладает наименьшей мерой случайного разброса
относительно истинного значения оцениваемого параметра.
Эффективность является решающим свойством, определяющим качество оценки, и
оно, вообще говоря, не предполагает обязательного соблюдения свойства
несмещенности.
Остается уточнить^ как именно измеряется степень случайного
разброса значений оценки 0 относительно истинной величины параметра 0.
В случае, когда 0 — скаляр (т.е. размерность оценки к = 1), в
качестве такой естественной меры берется средний квадрат отклонения, т. е.
величина Е@ - 0J, что для несмещенных оценок совпадает с их
дисперсией, так как в этом случае D0 = Е@ - Е0J = Е@ - 0J.
В случае, когда оценка 0 — вектор (т.е. размерность оценки k ^ 2),
в качестве меры отклонения от истинного значения векторного
параметра 0 обычно рассматривается ковариационная матрица оценки 0, т.е.
симметричная и неотрицательно-определенная матрица размера Ж х Ж,
которую мы будем обозначать 33@). Соответственно оценка 0j параметра
0 считается более эффективной, чем оценка 02, если существуют их
ковариационные матрицы E@i) и Е@2) и матрица ДЕ = E@!)-E@2)
является неотрицательно- определенной.
Для векторных оценок возможны случаи, когда, несмотря на
существование матриц ?@i) и Е(©2), нельзя ответить на вопрос, какая из
двух оценок эффективнее в указанном выше смысле. Эта
неопределенность устраняется, если в качестве меры отклонения векторной
несмещенной оценки 0 от истинного значения оцениваемого параметра 0
рассматривать не саму ковариационную матрицу оценки Е@), а ее определитель
det 33@) (обобщенная дисперсия) или след tr Е@).
Подчеркнем тот факт, что именно эффективность оценки,
измеряемая средним квадратом ее отклонения от истинного значения пара-

240 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
метра, является решающим свойством, определяющим ее качество, ее
надежность. Бывают ситуации, когда требования несмещенности и
эффективности оценки оказываются несовместимыми. И тогда, как правило,
следует руководствоваться критерием эффективности.
Приведем такой пример. Речь идет о ситуации, в которой
смещенная оценка оказывается лучше несмещенной в смысле среднего квадрата
ошибки.
Пусть мы располагаем выборкой G.1) из (а; а )-нормальной
генеральной совокупности (см. пример 7.1) и нас интересует наилучшая (в смысле
среднего квадрата ошибки) оценка параметра а = Df. Мы уже знаем
(см. п. 7.1.4), что оценка
л Я-
-\2
является несмещенной оценкой теоретической дисперсии а2.
Воспользовавшись соотношением F.29), получаем:
rw n 2ч п2 _о п 2(п-1) 4
- f}( g 1 — -___-—___ . /Jo "— _____ . х ' -—
-*(»-1°-(»-!)¦ °3 -(п-1J п2
2а4
п-1т
Рассмотрим в качестве альтернативы к оценке з2 класс оценок {аЗ2}, где
а — любое положительное число, и попробуем подобрать а0 так, чтобы
Е(ао52 - <т2J = min.
ot
Рассмотрим выражение среднего квадрата ошибки для оценок этого
класса:
E(a-S* - а2J = E[a(tf - а2) - <т2A - а)]2
Легко устанавливается, что правая часть этого выражения,
рассматриваемая (с точностью до умножения на положительное число а4) как
квадратный трехчлен относительно а:
имеет минимум в точке а = Ц=|. Подставляя это значение а, мы имеем

7.2 ФУНКЦИЯ ПРАВДОПОДОБИЯ 241
оценку
П- 1_2 1 V^/ -\2
и ее средний квадрат ошибки
Легко видеть, что величина т^цо* будет всегда меньше величины
ЕA2 — G2J = ~~f, а это и означает, что смещенная оценка s* параметра
а2 оказалась точнее несмещенной оценки s .
7.2. Функция правдоподобия. Количество
информации, содержащейся в
п независимых наблюдениях
относительно неизвестного значения
параметра
Пусть G.1) — выборка, состоящая из п независимых одномерных
наблюдений, извлеченная из исследуемой генеральной совокупности. Закон
распределения вероятностей наблюдаемой случайной величины ?
описывается функцией/(ж,0), зависящей от неизвестного параметра 0, причем
мы будем понимать под /(я, 0) вероятность Р{? = ж}, если f дискретная,
и значение плотности вероятности в точке ж, если ? непрерывна. Если
рассматривать выборку G.1) в гипотетическом смысле, то каждая
конкретная выборка (я1,Ж2,. -*)хп) представляется определенной точкой в
п- мер ном пространстве выборок переменных х\, х^..., хп и имеет смысл
говорить о совместном распределении вектора X = (х\,..., хп). Поскольку
при гипотетическом варианте понимания случайной выборки Х\, Х2,..., хп
суть независимые и одинаково распределенные случайные величины, то
для любого заданного набора значений х\, a?J> • • • > ^п их совместная
плотность (вероятность) будет
L(xl zl ...,*;;«) = /(*?; в). /(*5; в) •... • f(x*ni в). G.5)
Таким образом, функция Z(X*,0), определенная равенством G.5), задает
вероятность получения, при извлечении выборки объема п именно
наблюдений ?!,...,?„ (или величину, пропорциональную вероятности
получения выборочных значений в непосредственной близости от точки X* в

242 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
непрерывном случае). Поэтому, чем больше значение L(X*,0), тем прав-
доподобнее (или более вероятна) система наблюдений X* = (&!,..,,&„)
при заданном значении параметра 0. Отсюда и название функции L —
функция правдоподобия.
Функция правдоподобия в зависимости от постановки задач и целей
исследования может рассматриваться либо как функция параметра 0 (при
заданных фиксированных наблюдениях Х\,..., х»), либо как функция
текущих значений наблюдений хи...,хп (при заданном фиксированном
значении параметра 0), либо как функция обеих переменных X и 0.
Интересно попытаться проследить характер изменения вероятности
G.5) в зависимости от изменения значения параметра 0. Очевидно, чем
резче проявляется эта зависимость, тем больше информации заключено в
конкретных значениях величин X и 0 друг о друге. При этом под
информацией о неизвестном параметре 0, содержащейся в случайной величине
X, понимают степень уменьшения неопределенности, касающейся
неизвестного значения 0, после наблюдения над данной случайной величиной.
Если по наблюденному значению X* случайной величины X можно с
вероятностью единица точно восстановить значение параметра 0, то это
значит, что случайная величина (или ее наблюдение) содержит максимально
возможную информацию о параметре. И наоборот, если распределение
G.5) случайной величины X одно и то же при всех значениях параметра 0,
то нет никаких оснований делать какие-либо заключения о 0 по
результатам наблюдений этой случайной величины (ситуация нулевой информации
относительно значения неизвестного параметра, содержащейся в
наблюдении). Чувствительность случайной величины к параметру может быть
измерена величиной изменения распределения этой случайной величины
при изменении значения параметра. Наиболее часто используемой
характеристикой, на основании которой измеряют изменение в распределении
G.5) при небольшом изменении значения параметра 0, является так
называемое количество информации Фишера (содержащееся в наблюдениях
X = (аьж2,...,яп)), которое определяется для скалярного параметра 0
(т.е. при размерности параметра 0, равной единице) следующим
образом:
[(^J1 / (iI L(X;9)dX. G.6)
Интеграл в правой части G.6) означает на самом деле п-кратное
интегрирование подинтегрального выражения по всем возможным значениям
&i,&2» • • •»&ni соответственно, под dX понимается п-мерный «элемент
интегрирования», т.е. dX = dx\dx2.. .dxn.

7.2 ФУНКЦИЯ ПРАВДОПОДОБИЯ 243
Учитывая независимость и одинаковую распределенность
наблюдений a?i,&2» - • •»*п> получаем
= nj (
dx = n K*5.). G.6')
Если параметр 0 = @* ,...,0* ') А-мерный, причем к ^ 2, то вместо
количества информации G.6) рассматривается информационная матрица
Фишера 1@, X) размерности кх к с элементами
G.7)
Эти понятия были введены Фишером в 20-х годах Hauiero столетия.
Воспользовавшись формулой G.6), нетрудно подсчитать количество
информации 1@; х), содержащееся в одном наблюдении о параметре 0, в
ряде конкретных примеров.
1. Одномерная величина X = х подчинена (а, а2)-нормальному закону
с плотностью <р(х; а,<72), в котором среднее значение а = 0 — неизвестный
параметр, а дисперсия известна. Тогда
7 (dln<p(x;a,(?2)\2 2
J \ da )
G.8)
<р(х;а,а2) dx = -j.
Результат, естественно, интерпретируется следующим образом: чем
больше дисперсия сг2, тем больше разброс в наблюденных значениях
исследуемой случайной величины, тем меньше информации о величине ее среднего
значения заключено в одном наблюдении.
2. Одномерная случайная величина X = х подчинена (а,
^-нормальному закону с плотностью (р(х; а, сг2), в котором среднее значение а
известно, а дисперсия а является неизвестным параметром. Тогда
оо о о
fdh(T )\
г/ 2 ч / /din<р(х;а,<т )\ 2ч .
1{а ;ж)= / I *—s 1 <p{x;a,a)dx
J \ da /
-ОО
ОО
-п-
G.9)
—

244 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
3. Одномерная случайная величина X = х подчинена гамма-распределению
с параметрами (а, ft), причем параметр а известен, а ft является
неизвестным параметром. Тогда
()
7.3. Неравенство Рао-Крамера-Фреше и
измерение эффективности оценок
В п. 7.1.5 введено понятие эффективности оценки неизвестного
параметра 0, которое определяется средним квадратом отклонения оценки от
истинного значения параметра, т.е. величиной Е@ - 0) . В связи с
этим возникает вопрос: нельзя ли описать ту границу эффективности,
т.е. тот минимум (по всем возможным оценкам 0) среднего квадрата
Е@ — 0) , улучшить которую невозможно? Этот минимум и явился бы
тогда той точкой начала отсчета эффективности оценки, отправляясь от
которой можно было бы ввести абсолютную шкалу измерения
эффективности оценок. На этот вопрос дает ответ неравенство Рао-Крамера-Фреше,
известное также как неравенство информации.
Рассмотрим класс всевозможных оценок в скалярного параметра 0,
от которого зависит плотность вероятности f(x;6) исследуемой
генеральной совокупности. Пусть
т.е. величина &g@) дает смещение оценки 0 (очевидно, если оценка 0
несмещенная, то ft$@) s 0).
Если плотность /(ж; 0) удовлетворяет некоторым условиям
регулярности (в смысле характера ее зависимости от параметра 0), а именно:
а) область возможных значений исследуемой случайной величины, в
которой /(ж;0) ф 0, не зависит от 0;
б) в формуле G.11) и в тождестве J L(xi,.. . ,жп; 0) dx\---dxn = 1
допустимо дифференцирование по 0 под знаком интеграла;
в) величина /@; ж), определенная соотношением G.б')} не равна нулю;
тогда для любой оценки 0 неизвестного параметра 0 имеет место еле-

7.3 НЕРАВЕНСТВО РАО-КРАМЕРА-ФРЕШЕ 245
дующее неравенство:
¦ (?-»>¦> Ч***»*? (T.12,
E[(d\f(e)/deJ\
или, что то же,
G
(доказательство этого факта см. в Приложении к гл.7 на стр.281).
Имеется обобщение неравенства G.12) на случай fc-мерного
параметра 0 = @ ,... ,0 ), к ^ 2. В этом случае при тех же условиях
регулярности а)-в) для любой векторной несмещенной оценки 0 неизвестного
параметра 0 матрица
п
G.13)
является неотрицательно-определенной. Здесь Е@) — ковариационная
матрица векторной оценки 0 = ((г , ...,<г '), а I" @,ж) — матрица,
обратная к информационной матрице, определенной соотношениями G.7)
при X = х (т. е. при единственном наблюдении ж).
Неравенства информации G.12)—G.13) дают возможность ввести
количественную меру эффективности оценок в классе регулярных (в
смысле соблюдения условий а)-в)) генеральных совокупностей. Естественно,
в частности, измерять степень эффективности скалярной несмещенной
оценки в неизвестного значения параметра в отношением е(в)
минимально возможной величины дисперсии оценки, определяемой правой частью
неравенства G.12), к дисперсии данной конкретной оценки 0, т.е.
GД4)
Подсчитаем эффективность некоторых оценок параметров а и а в
условиях примера 7.1.
1. Рассмотрим в качестве оценки среднего значения а нормальной
случайной величины среднюю арифметическую (выборочное среднее), т.е.
положим

246 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМБТРО'
Так как наблюдения Х{ независи < ' одинаково распределены, имеем:
П _
п ыг п ыг п
Поскольку (см. G.8)) /(а,х) s 1/а2, то в соответствии с G.14) получаем,
что е(х) = 1, т.е. оценка х в данном случае является неулучшаемой.
2. Рассмотрим в качестве оценки дисперсии о нормальной случайной
величины «подправленную» на несмещенность выборочную дисперсию
2 2 2
Выше получено, что Е 5 = а , т. е. Ъ является несмещенной оценкой
2
дисперсии а2. В п. 7.1.5 было показано, что
Поскольку (см. G.9)) 7(ег2,ж) = 1/2(т4, то в соответствии с G.14)
получаем e(s ) = (п— 1)/п, т.е. оценка 5 не является эффективной, хотя
и близка к ней при больших объемах выборок. В то же время можно
показать, что если в качестве оценки а взять статистику
что в данных условиях допустимо, так как среднее значение а считается
известным, то она окажется точно эффективной.
Подчеркнем в заключение, что информационное неравенство
справедливо лишь в классе регулярных (в смысле соблюдения условий а)-в)
§ 7.3) генеральных совокупностей. В частности, если область возможных
значений исследуемой случайной величины, для которых плотность /(х; в)
положительна, зависит от оцениваемого параметра, то неравенство
информации «не работает». Именно такими нерегулярными плотностями
являются, например, равномерное распределение (в котором
параметрами служат концы диапазона изменения соответствующей случайной
величины, см. п.3.1.7) и экспоненциальное распределение <ю сдвигом 9, т.е.

7.3 НЕРАВЕНСТВО РАО-КРАМЕР А-ФРЕШЕ 247
распределение, задаваемое плотностью
Л**> ¦« при »<
Бели, не обращая внимания на то, что эта плотность не удовлетворяет
условиям а)=-в), вычислить по формуле G.6) количество информации,
содержащейся в п независимых наблюдениях, то получим 1(9;х%}...,хп) =
п. Следовательно, в соответствии с информационным неравенством G.12)
мы должны были бы прийти к выводу, что дисперсия любой оценки 9
параметра 9 не может быть меньше 1/п. В то же время нетрудно вычислить
(см. ниже, (пример 7.6)), что для оценки
9 = хт\п(п) - —, GЛ5)
где, как обычно,гт|„(п) — это минимальное значение в выборке xj,..., а?п,
мы имеем:
п
Так что если для измерения эффективности оценки G.15)
воспользоваться формулой G.14), то получим, что эффективность оценки 9 не
просто больше единицы, но и стремится к бесконечности по мере роста
объема выборки п (так как е(в) = i: Jy = п). В подобных ситуациях
оценки называют иногда «сверхэффективными».
Замечание о дискретных случайных величинах. Все изложенные
выше результаты (понятие количества информации, неравенство
информации, измерение эффективности оценки) распространяются на случай
дискретных признаков при соблюдении тех же ограничений а)-в) с помощью
внесения очевидных видоизменений: плотности f(x;9) заменяются
вероятностями pi(9) = Р{? = Zi | 9}> а интегрирование — суммированием
по всем возможным значениям анализируемой дискретной случайной
величины. Таким образом, в качестве дискретных аналогов количества
информации G.6) и информационного неравенства G.12) будем иметь:
G.16)

248 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
В качестве примера рассмотрим случайную величину f, подчиненную
распределению Пуассона, т. е.
1 = 0,1,2,3,...
2
т. е. дисперсия любой несмещенной оценки А параметра А не может быть
меньше, чем 1/п/(А,ж) = Х/п. Если рассмотреть в качестве оценки А
выборочное среднее ж, то будем иметь:
" ' : . ('-'в)
n J п п
Таким образом, оценка А = х параметра А в распределении Пуассона
является эффективной.
7.4. Понятие об интервальном оценивании
и доверительных областях (постановка
задач)
Вычисляя на основании имеющихся у нас выборочных данных оценку
0(xi,..., хп) параметра 0, мы отдаем себе отчет в том, что на самом деле
величина в является лишь приближенным значением неизвестного
параметра в даже в том случае, когда эта оценка состоятельна (т. е. стремится
кбс ростом п), несмещенна (т. е. совпадает с в в среднем) и эффективна
(т.е. обладает наименьшей степенью случайных отклонений от в).
Возникает вопрос: как сильно может отклоняться это приближенное значение
(оценка) от истинного! В частности, нельзя ли указать такую
величину Д, которая с «практической достоверностью» (т.е. с заранее заданной
вероятностью, близкой к единице) гарантировала бы выполнение
неравенства \в — в\ < Д? Или, что то же, нельзя ли указать интервал вида
@ъ^2)> который с заранее заданной вероятностью (близкой к единице)
накрывал бы неизвестное нам истинное значение в искомого параметра?
При этом заранее выбираемая исследователем вероятность, близкая к
единице, обычно называется доверительной вероятностью, а сам интервал

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 249
{0ив2) — доверительным интервалом (или интервальной оценкой, в
отличие от точечных оценок 0). Доверительный интервал по своей природе
случаен (потому и идет речь о вероятности накрыть некоторую не
известную нам, но не случайную точку в) как по своему расположению, так
и по своей длине. Величины вг^в2 и Д, как правило, тоже строятся как
функция выборочных данных &i,...,xn. Ширина доверительного
интервала существенно зависит от объема выборки п (уменьшается с ростом п)
и от величины доверительной вероятности (увеличивается с
приближением доверительной вероятности к единице).
Все данные здесь определения и понятия без труда переносятся на
случай векторного параметра 0 = (fl'1',...,^ ') с заменой
доверительного интервала доверительной областью в соответствующем fc-мерном
пространстве.
7.5. Методы статистического оценивания
неизвестных параметров
В предыдущем пункте рассмотрены различные варианты
использования функций от исходных наблюдений яЬ?2,... ,жп в качестве оценок
неизвестных параметров, анализировались их свойства. Однако пока не
ясно, каким способом устанавливаются именно те комбинации
результатов наблюдений (статистики), с помощью которых производится (да еще
наилучшим в определенном смысле образом!) оценивание того или
иного параметра. Каким образом, например, было установлено, что именно
комбинации ж, s лучше всего использовать в качестве оценок
неизвестных параметров соответственно среднего значения а = Е? и дисперсии
а = D? нормальной генеральной совокупности? И как конкретно строить
описанные выше доверительные интервалы и области для неизвестных
значений параметров?
Описанию основных приемов, позволяющих получать ответы на
данные вопросы, и посвящен настоящий пункт.
7.5.1. Метод максимального (наибольшего) правдоподобия
В соответствии с этим методом оценка 0МП неизвестного параметра
0 по наблюдениям х\,..., хп случайной величины f (подчиненной закону
распределения Д(я, 0), где / — плотность или вероятность Р{( = х})
определяется из условия
1(жь...,жп;0мп) = тах Z,(ab...,sn;0), G.19)
$

250 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
где L — функция правдоподобия, определенная соотношением G.5).
Таким образом, в формальной записи оценка максимального
правдоподобия 0МП параметра 0 по независимым наблюдениям х\, ¦.., хп может
быть представлена в виде
0МП= arg max П/(*,;©). G.19;)
Естественность подобного подхода к определению статистических
оценок вытекает из смысла функции правдоподобия. Действительно, по
определению (см. п.7.2), функция L(xi,...,a?n;0) при каждом
фиксированном значении параметра 0 является мерой правдоподобности
получения системы наблюдений, равных жьх2,...,хп. Поэтому, изменяя
значения параметра 0 при данных конкретных (имеющихся у нас) величинах
Z!,Z2,...,?n, мы можем проследить, при каких значениях 0 эти
наблюдения являются более правдоподобными, а при каких — менее и выбрать
в конечном счете такое значение параметра 0МП, при котором имеющаяся
у нас система наблюдений х\х..., хп выглядит наиболее правдоподобной
(очевидно, что это значение 0МП определяется конкретными величинами
наблюдений хг, ж2> • • • > жп> т. е. является некоторой функцией от них).
Так, например, пусть ? — заработная плата работников,
подчиненная логарифмически нормальному распределению (см. п. 3.1.6). И пусть
с целью приближенной оценки средней величины логарифма заработной
платы работников а = ЕAп ?) мы зафиксировали значения заработной
платы х\ = 190 ден.ед., Хъ = 175 ден.ед. и х$ = 205 ден.ед. у трех
случайно отобранных из интересующей нас совокупности работников. Тогда,
расположив у{ = ln?<(t = 1,2,3) на оси возможных значений нормально
распределенной случайной величины г\ = 1п?. мы будем стараться
подобрать такое значение амп параметра а в (а, а )-нормальном
распределении, при котором наши наблюдения уь #ь З/з выглядели бы наиболее
правдоподобными, а именно, при котором произведение трех ординат
плотности (р(у;а]ст2), вычисленных в точках соответственно у\ = In 190 = 5,25,
2/2 = In 175 = 5,16 и уз = In 205 = 5,32, достигало бы своего максимального
значения.
На рис. 7.2 изображены графики функции плотности <р(у; а; а2) при
значении параметра амп = у = 5,243, соответствующем наибольшей
правдоподобности наблюдений уг = 5,25, у2 = 5,16 и у3 = 5,32 (сплошная
кривая), и при значении параметра а = 5,443, при котором наши
наблюдения выглядят явно неправдоподобными, — пунктирная кривая (значение
дисперсии о определено в обоих случаях с помощью подправленной на
несмещенность оценки максимального правдоподобия и равно 0,0064).

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
251
; 5,243; 0,08) <р(у; 5,443; 0,08)
Рис. 7.2. Графики нормальной функции плотности при двух значениях
параметра а
Отмеченная естественность подхода, исходящего из максимальной
правдоподобности имеющихся наблюдений, подкрепляется хорошими
свойствами оценок, получаемых с его помощью. Можно показать, в частности,
что при достаточно широких условиях регулярности, накладываемых на
изучаемый закон распределения /(ж;0), оценки максимального
правдоподобия 0МП параметра 0 являются состоятельными, асимптотически
несмещенными (т. е. их смещения стремятся к нулю при неограниченном
увеличении объема выборки), асимптотически нормальными и
асимптотически эффективными (т.е. их ковариационная матрица Е@МП)
асимптотически имеет вид ?@Мп) = w~ х Г" @;ж), где 1@; А") —
информационная матрица Фишера, определенная соотношениями G.7)
применительно к единственному наблюдению, т. е. при X = ж).
Однако из этого не следует, что оценки максимального
правдоподобия будут наилучшими во всех ситуациях. Во-первых, их хорошие
свойства проявляются часто лишь при очень больших объемах выборок (т. е.
являются асимптотическими), так что при малых п с ними могут
конкурировать (и даже превосходить их) другие оценки, например, оценки
метода моментов, метода наименьших квадратов и т.д. Во-вторых, и это,
пожалуй, главное «узкое место» данного подхода, для построения оценок
максимального правдоподобия и обеспечения их хороших свойств
необходимо точное знание типа анализируемого закона распределения /(ж; 0),
что в большинстве случаев оказывается практически нереальным. В
подобных ситуациях бывает выгоднее искать не оценку, являющуюся
наилучшей в рамках данного конкретного общего вида /(ж; 0) (но, как часто
бывает, резко теряющую свои хорошие свойства при отклонениях реаль-

252 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ного распределения от типа /(ж;0)), а оценку, хотя и не наилучшую в
рамках совокупности /(ж;©), но обладающую достаточно устойчивыми
свойствами в более широком классе распределений, включающем в себя
/(ж;0) в качестве частного случая (см. ниже, п. 7.5.4). Подобные
оценки принято называть устойчивыми или робастными (английский термин
robust estimation означает грубое, или устойчивое оценивание). И
наконец, оценки максимального правдоподобия могут не быть даже
состоятельными, если число к оцениваемых по выборке параметров в\,..., 0*
велико (имеет тот же порядок, что и объем выборки п) и растет вместе с
увеличением числа наблюдений. Ниже приведен пример подобной
ситуации (см. пример 7.6).
Попытаемся ответить на вопрос, как конкретно находятся оценки
максимального правдоподобия, т.е. как проводится решение
оптимизационной задачи типа G.19 ).
Если функция /(я;0) удовлетворяет определенным условиям
регулярности (дифференцируемость по 0 и т.п., см. условия а)-в) п. 7.3) и
экстремум в G.19) достигается во внутренней точке области допустимых
значений неизвестного параметра 6, то в точке 0МП должны обращаться
в нуль частные производные функции Ь(хг,..., жя; 0), а следовательно, и
логарифмической функции правдоподобия
п
f(Xi,Q) G.20)
в силу монотонного характера этой зависимости: последняя удобнее для
вычислений. Значит, в данном случае оценка максимального правдоподо-
бия 0МП = @KMn;,..., 0J,,/) должна удовлетворять уравнениям:
и может определяться в качестве решения этой системы уравнений.
Однако могут быть ситуации (случай нерегулярных по 0 законов
распределения), когда система G.21) не определена или не имеет решений, в
то время как решение G.19#) существует. В подобных ситуациях оценку
0мп следует искать другими способами, в том числе с помощью
непосредственного подбора решения G.19).
Пример 7.2. Исследуемая случайная величина ? имеет
нормальную плотность вероятности
, 2ч 1 <«~*>а
(р(х;а\а ) = ~7=-е *^

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 253
с неизвестным средним значением а = Е? и неизвестной дисперсией а2 =
В соответствии с G.5) функция правдоподобия в этом случае будет
Соответствующая логарифмическая функция правдоподобия
1(хъ ...,хп;а, а2) = -- 1пBтг) - - In а1 - —у УЧж,- - aJ.
Дифференцируя I по а и а и последовательно приравнивая
соответствующие частные производные к нулю, получаем конкретный вид системы
G.21):
dl(xli...,xn;a,ai) _ n ]_ 1 А _ ,2 _
да2 ~ 2 S + 2(а2J ??(*' О) ~ °-
П)
Решение этой системы относительно а и а дает оценки максимального
правдоподобия этих параметров:
1 п 1 Л
пмп = ^ 2-/ ж*; а|111 = ^ 2-/^ж* ~" х' '
t=i 1=1
Выше (см. п. 7.3) установлено, что оценка 0МП = ж является эффективной
оценкой параметра а (так как ее эффективность е(амп) = 1), а оценка
<тмп = 5 — асимптотически эффективной оценкой параметра сг (так как
ее эффективность е(Эмп) = {п — 1)/п).
Пример 7.3. Исследуемая случайная величина f подчинена закону
распределения Пуассона, т. е.
/(*; А) = Р{? = х} = ^е"А (х = 0,1,2,...),
с неизвестным значением параметра А.

254 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
В соответствии с G.20) логарифмическая функция правдоподобия,
построенная по выборке a?i, х%>..., жп, имеет вид
п
1(хг,..., хп; А) = V (хг In A - ln(xj!) - A)
Отсюда после дифференцирования по А получаем уравнение метода
максимального правдоподобия
1 п
t - !
Аип —
откуда
Легко видеть, что эта оценка несмещенная, так как
ЕАМП = е( ?>]/» = ( ЕЕж')/п = пА/п = А-
Вычислим эффективность оценки Амп. Нижняя граница дисперсии по всем
возможным оценкам параметра А может быть вычислена в соответствии
с неравенством информации G.12):
(DA)min =
1 1 Л2
пЕ(х -
Дисперсию оценки Амп вычислим, опираясь на следующий известный
факт: дисперсия суммы независимых случайных величин х1ух2>...}хп
равна сумме их дисперсий, т.е.:
Сравнивая (DA)min с DAMn, убеждаемся, что оценка максимального
правдоподобия среднего значения пуассоновской случайной величины является
эффективной.

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 255
Пример 7.4. Исследуемая случайная величина f распределена по
равномерному закону (см. п.3.1.7), т.е.
[ 6 — в противном случае,
где параметры а и 6 неизвестны (подлежат оцениванию).
Легко проверить, что это — случай нерегулярный (в первую очередь
потому, что область возможных значений исследуемого признака, в
которой плотность положительна, зависит от оцениваемых по выборке
параметров а и 6). Поэтому обычная техника, использующая уравнения G.21)
метода максимального правдоподобия, здесь неприменима. Однако в этом
случае экстремальная задача G.19) может быть решена непосредственно.
Действительно,
1(хь...,жп;а,6)= 77 Zn>
(Ь -а)
причем область допустимых значений параметров а и 6, где производится
поиск тех значений амп и 6МП, при которых 1/F — а)п = max, описывается
а,Ь
соотношениями:
6 ^ max {xi} = armax(n),
где а?!,а?2,. •.,xn — имеющиеся в нашем распоряжении наблюдения
исследуемой случайной величины. Очевидно, решение экстремальной задачи
тах Та У*' а < х«А*(п)> Ь > х^х{п)
\° ~" а)
дается соотношениями:
«мп = Smin(rc); 6МП = Хтлх(п).
Опираясь на результаты п. 6.3.1 (см. формулу F.42)), можно
подсчитать:
Еамп = Earmin(n) = а + ^^;
Ь — а *
Е6МП = Ежтах(п) = 6 -
;

256 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Использовать неравенство информации для вычисления нижней
границы дисперсии этих оценок мы не можем, так как случай нерегулярный.
Из G.22) видно, что величины DaMn и D6Mn характеризуют одновременно
средний квадрат отклонения «подправленных на несмещенность» оценок
jj
' n- 1
от истинных значений параметров а и Ь.
Пример 7.5. Снова рассмотрим задачу оценивания параметра
сдвига в в экпоненциальном распределении, задаваемом плотностью
f(x;0)=i
4 ' 1
e {Х в)
0 при х < в.
Как и в предыдущем примере, имеем дело с нерегулярным случаем.
Поэтому приходится непосредственно решать экстремальную задачу вида
(ьп;) xe;
9 &
в < min {zj = armin(n). G.23)
Легко видеть, что 0МП = хт\п(п) является решением этой задачи: при
любом другом 0, удовлетворяющем условию G.23), очевидно
t=i
t=l
и, следовательно,
,..., хп; вмп) > L(xx,..., хп; в).
Опираясь на результаты п. 6.3.1 (см. формулу F.42)), можно
подсчитать:
1
;
п
Шмп = E(smin(n) - Ежт!п(п)J = \; G.24)
п
п
— 9) = D0Mn H—j" = -j.
и и

7.6 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 257
Однако оценка $ип = вмп - ?, получающаяся из оценки 0М„ «подправле-
нием на несмещенность», будет иметь средний квадрат отклонения
Е(&„ - вJ = \. G.25)
71
Пример 7.6 (заимствован из [Ван дер Варден Б. Л., с. 187]).
Рассмотрим ситуацию, когда метод максимального правдоподобия не
приводит к состоятельной оценке.
С целью оценки п концентраций некоторого элемента ai,a2,...,an
в лаборатории производились двукратные измерения (x,,ft) каждой из
концентраций а,. Предполагается, что все 2п результатов измерений
Зъ Уи Ж2> №» • • • > хы Уп имеют одинаковую точность и являются
независимыми нормальными случайными величинами (см. п. 3.1.5), так что в
качестве функции правдоподобия получаем
Неизвестными параметрами являются п средних значений
..., ап и дисперсия а . Нетрудно получить оценки максимального
правдоподобия параметров ас.
«turn = 2^ + »•')•
Решая теперь уравнение максимального правдоподобия G.21), в
которое вместо п{ подставлены значения atMn, получаем
1=1
Нетрудно подсчитать, что Е?^п = а2/2, т.е. метод
максимального правдоподобия дает в этом случае оценку параметра а2 с
постоянным (асимптотически неустранимым) отрицательным смещением,
равным -о-2/2. В качестве наилучшей несмещенной оценки следовало бы
выбрать в данном случае статистику
>s2 1
9 Теория мроятяоотвй
и прикладная отатистикд

258 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
7.5.2. Метод моментов
Пусть { — исследуемая одномерная случайная величина,
подчиняющаяся закону распределения /(я;0), где функция /(х;0) — плотность
вероятности, если ? непрерывна, и вероятность Р{{ = х | 0}, если ?
дискретна, зависит от некоторого, вообще говоря, многомерного параметра
0 = @,..., 0^). И пусть мы хотим оценить неизвестное значение этого
параметра, т. е. построить оценку 0 по имеющейся в нашем распоряжении
выборке, состоящей из независимых наблюдений жь..., хп.
Метод моментов заключается в приравнивании определенного
количества выборочных моментов к соответствующим теоретическим (т. е.
вычисленным с использованием функции /(ж; 0)) моментам исследуемой
случайной величины, причем последние, очевидно, являются функциями от
неизвестных параметров #' ,...,0 . Рассматривая количество
моментов, равное числу к подлежащих оценке параметров, и решая полученные
уравнения относительно этих параметров, мы получаем искомые оценки.
Таким образом, оценки 0^2,...,^2 по методу моментов неизвестных
параметров 0( ,...,0^ являются решениями системы уравнений:
/
a:!, / = 1,2,...,А; G.26)
(очевидно, если анализируемая случайная величина ( дискретна,
интегралы в левых частях G.26) следует заменить соответствующими суммами).
Число уравнений в системах G.26) должно быть равным числу к
оцениваемых параметров. Вопрос о том, какие именно моменты включать в
систему G.26) (начальные, центральные или их некоторые модификации
типа коэффициентов асимметрии или эксцесса), следует решать,
руководствуясь конкретными целями исследования и сравнительной
простотой формы зависимости альтернативных теоретических характеристик
от оцениваемых параметров 0A\...,0 . В статистической практике
дело редко доходит даже до моментов четвертого порядка.
К достоинствам метода моментов следует отнести его сравнительно
простую вычислительную реализацию, а также то, что оценки,
полученные в качестве решений системы G.26), являются функциями от
выборочных моментов. Это упрощает исследование статистических свойств
оценок метода моментов: можно показать (см. [Крамер Г., гл. 27 и 28]),
что при довольно общих условиях распределение оценки такого рода при
больших п асимптотически нормально, среднее значение такой оценки
отличается от истинного значения параметра на величину порядка n, a
стандартное отклонение (т(вмьл) асимптотически имеет вид сп~1^2, где с —

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 259
некоторая постоянная величина.
В то же время, как показал Р. Фишер (Крамер Г.), асимптотическая
эффективность оценок, полученных методом моментов, оказывается, как
правило, меньше единицы, и в этом отношении они уступают оценкам,
полученным методом максимального правдоподобия. Тем не менее метод
моментов часто очень удобен на практике.
Иногда оценки, получаемые с помощью метода моментов,
принимаются в качестве первого приближения, по которому можно определять
другими методами оценки более высокой эффективности.
Вернемся к нашим примерам.
В примере 7.2 в качестве системы G.26) имеем:
1 Л
п м
что дает уже знакомые нам по методу максимального правдоподобия
оценки для параметров:
1 п
п i
Нормальное распределение, так же как и распределение Пуассона (в
чем легко убедиться, обратившись к примеру 7.3), относится к тем
редким случаям, когда оценки по методу моментов совпадают с оценками по
методу максимального правдоподобия.
Построение системы G.26) в примере 7.4 дает:
^ = *(»);
Откуда легко получаем оценки:
2мм =
9*

260 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Можно сравнить асимптотическую эффективность оценок,
полученных методом максимального правдоподобия и методом моментов:
учитывая, что дисперсия оценок G.27) как дисперсия функций выборочных
моментов х(п) и s2(n) имеет порядок п"*\ и принимая во внимание
соотношение G.22), в соответствии с которым дисперсии оценок максимального
правдоподобия тех j*ce параметров имеют порядок п~2, получаем, что
эффективность амм и 6ММ в сравнении с эффективностью ам„ и Ьмп стремится
к нулю при п —> оо.
Реализация метода моментов в примере 7.5 дает
1 + 0 = х(п).
Следовательно, 0ММ = 5F(n) — 1.
Для подсчета среднего значения и дисперсии оценки 0ММ
воспользуемся следующими фактами:
а) случайную величину а?,*, распределенную экспоненциально с
параметром сдвига 0, можно интерпретировать как частный случай гамма-
распределенной случайной величины с параметрами а= 1, 6= 1 и с
параметром сдвига в (см. п. 3.2.5);
б) сумма п независимых случайных величин хь х2,..., хп, каждая из
которых распределена по закону гамма с параметрами а=1и6=1ис
параметром сдвига 0, подчиняется гамма-распределению с параметрами
а = п, 6 = 1 и с тем же самым параметром сдвига в (см. п. 3.2.5).
Поэтому
) - 1) = 4 = -•
п п
Учитывая выражение G.25) для среднего квадрата ошибки
«подправленной» оценки по методу максимального правдоподобия 9мп того же
параметра 9, получаем
Е(УМ„- вK & 1
т.елв этом случае асимптотическая эффективность оценки по методу
моментов стремится к нулю.

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 261
7.5.3. Оценивание с помощью «взвешенных» статистик;
цензурирование, урезание выборок и порядковые
статистики как частный случаи взвешивания
Выборочные моменты т^ всегда являются состоятельными
оценками соответствующих теоретических моментов т*, если последние
существуют (см. п. 6.2). Однако не во всякой генеральной совокупности они
являются наиболее эффективными оценками. Так, например, мы видели
(см. п. 7.5.1 и 7.5.2), что эффективность оценки среднего значения
исследуемой случайной величины с помощью выборочного среднего х = fhi
существенно зависит от типа анализируемой генеральной совокупности:
для нормальной генеральной совокупности она равна единице (см.
пример 7.2 в п. 7.5.1), а для совокупности, «подчиненной равномерному
закону распределения, существенно меньше единицы и сильно проигрывает в
сравнении, например, с эффективностью оценки
2 = gfamin + aw). G.28)
Для построения оценки G.28) нами использованы только два наблюдения
из п имеющихся — наименьшее и наибольшее, т. е. оценка G.28)
относится к классу «взвешенных» порядковых статистик ]?*=1 w*x(i)> где х@ —
t'-e по величине (в порядке возрастания) наблюдение, а ш,- — его «вес»
(очевидно, в статистике G.28) принято w\ ~wn = 0,5, а все остальные W{
равны нулю).
Выборочная медиана xmed демонстрирует удивительную
устойчивость своих хороших свойств в качестве оценки теоретического среднего
значения. Выборочная медиана xmed также относится к классу
«взвешенных» порядковых статистик, т.е. статистик вида ?Г=1 W{X^); для ее
получения в качестве частного случая статистик этого класса достаточно
положить нулю все веса w,-, кроме одного (w»±i = 1, если п нечетно) или
кроме двух (w? = w%+i = j, если п четно).
Остановимся далее на описании основных подходов, связанных с
использованием взвешенных статистик, и на классификации их типов.
Взвешивание выборочных данных жь...,хп. В общем случае
наблюдению х{ приписывается вес wt* = w(xi) ^ 0, который определяется
как некоторая функция от его текущего значения. Обычно веса подчиняют
условию нормировки ]C?=i w(xi) = 1. В частности, можно рассматривать
w-взвешенные моменты случайной величины ? с плотностью Д(ж), как

262 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
выборочные fhk{n>W)> так и теоретические mk(W)\
t=i
= f vkw(x)ft(x)dx.
Под W понимается вектор весов (w(xi),..:9w(xn)) в выражении для
выборочных моментов и функция со значениями w(x) в выражении для
теоретических моментов.
Бели имеют дело с результатами наблюдения одномерной
случайной величины xi,...,хп, то часто вес наблюдения Х( определяют в
зависимости от его порядкового номера в упорядоченном (по
возрастанию) ряду наблюдений, т. е. располагают наблюдения в вариационный ряд
X(i), ЖB),..., Ж(п) и каждому члену вариационного ряда хщ ставят в
соответствие некоторый вес W{.
Примеры такого рода взвешивания (которое приводит к так
называемым порядковым статистикам) приведены выше.
Цензурирование выборки. Этот прием заключается в
приписывании ряду «хвостовых» членов вариационного ряда нулевых весов, а
остальным — одинаковых положительных. Если приписывание нулевых
весов производится по признаку выхода текущих значений наблюдений за
пределы заданного диапазона [а, 6], т. е.
г \ _ / wo > °> если а < x(i) < *;
w\x(i)) — | о, если X(i) < а или хщ > 6,
то говорят о цензурировании 1-го типа. Очевидно, в этом случае число v
оставшихся в рассмотрении наблюдений есть величина случайная {и < п).
Бели же нулевые веса приписываются фиксированной доле а крайних
малых значений и фиксированной доле 0 крайних больших значений, то
говорят, что производится цензурирование 2-го типа уровня (а, /9). В
этом случае число v оставшихся в рассмотрении наблюдений является
величиной, заранее заданной и равной, в частности, пA - а - /?).
Исследователь может прибегнуть к цензурированию вынужденно или
добровольно. Вынужденное цензурирование обусловлено
соответствующими условиями эксперимента: например, мы ставим на разрушающие
испытания п изделий, но можем производить эксперимент в течение
ограниченного времени Т. Очевидно, мы будем вынуждены произвести в
данном случае одностороннее цензурирование 1-го типа, при котором из
рассмотрения исключаются точные значения долговечностей

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 263
(времени до разрушения) всех тех изделий, которые не разрушились за
время Т. С другой стороны, в классе оценок, построенных по цензури-
рованным выборкам, часто можно найти оценки, хотя и не являющиеся
наилучшими в жестких рамках генеральной совокупности определенного
типа, но обладающие выгодными свойствами устойчивости своих
хороших качеств по отношению к тем или иным отклонениям от априорных
допущений.
Урезание распределения. Это понятие связано с ситуациями,
когда исследуемый признак ? просто не может быть наблюдаем в какой-либо
части области его возможных значений. Так, например, если мы
исследуем распределение семей по доходу, но по условиям выборочного
обследования лишены возможности наблюдать семьи со среднедушевым доходом,
меньшим некоторого заданного уровня а (тыс. руб.), то в подобных
случаях говорят, что распределение урезано слева в точке а. В отличие от
цензурированных выборок в выборках из урезанных распределений мы не
имеем возможности оценить даже доли наблюдений, располагающихся за
пределами порога урезания.
Весьма подробные сведения об использовании в задачах
статистического оценивания параметров взвешенных и, в частности, порядковых
статистик и статистик, построенных по цензурированным выборкам, с
обсуждением различных вопросов устойчивости получаемых при этом оценок
читатель найдет, например, в [Кендалл М. Лж., Стьюарт А., 1973, гл. 32]
и [Дейвид Г.].
7.5.4. Построение интервальных оценок (доверительных
областей)
В п. 7.4 введено понятие интервальной оценки неизвестного
параметра 0 = @* ,..., Ф ) , которую называют также доверительным
интервалом, а при многомерном параметре, т. е. при к ^ 2, — доверительной
областью. Как же конкретно построить по выборочным данным хи...,хп
такую случайную область Д0р(а?1,...,а:п), которая с наперед заданной
доверительной вероятностью Р накрывала бы неизвестное нам значение
параметра О? Очевидно, эта область должна конструироваться вокруг
точечной оценки 0 параметра 0, а ее точный вид и объем
определяются характером закона распределения случайной величины 0, в частности,
ее функцией распределения, которая, к сожалению, тоже зависит от
неизвестного истинного значения параметра 0.
Существуют два подхода к преодолению этой трудности. Первый
подход, если его удается реализовать, приводит к построению точ-

264 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ных (при каждом конечном объеме выборки п) доверительных областей
Д0р(жь...,жЛ). А реализовать его удается в тех случаях, когда
существует принципиальная возможность подбора такой функции от
результатов наблюдения жья2,...,яп (т.е. такой статистики), закон
распределения вероятностей которой обладал бы одновременно следующими
свойствами:
(а) не зависит от оцениваемого параметра 0;
(б) описывается одним из стандартных затабулированных
распределений (стандартным нормальным, х -> F-> Стьюдента);
(в) из того факта, что значения данной статистики заключены в
определенных пределах с заданной вероятностью, можно сделать вывод, что
оцениваемый параметр тоже должен лежать между некоторыми
границами с той же самой вероятностью.
При этом в выражении самой этой статистики анализируемый
параметр О и его состоятельная точечная оценка О (полученная одним из
известных методов — максимального правдоподобия, моментов и т.д.)
обычно участвуют в комбинациях разности (в — 0) или отношения @/0).
В качестве примера рассмотрим задачу интервального оценивания
параметров а и а нормальной генеральной совокупности (см. пример 7.2
в п. 7.5.1).
Как известно (см. п. 6.30), статистика
подчинена закону распределения Стьюдента сп-1 степенями свободы.
Поэтому, определив из таблиц по заданной вероятности Р процентные
точки уровня q = A - Р)/2 h1-j = A- Р)/2 /-распределения сп-1
степенями свободы, т.е. 100д%-ную точку tq(n - 1) и 100A - д)%-ную
точку *i-.g(n-1) (причем в силу симметрии t-распределения ti_9(n-1) =
-tq(n - 1)), мы можем утверждать, что неравенство
выполняется с вероятностью Р = 1 - 2д. А это означает, что случайный
доверительный интервал
ДаР(жь...,а:п)= g-tf(n-l)- J—rr\ x + tq(n-l)- /-i—¦
L y/n — 1 y/n — 1J
G.29)
накрывает неизвестное среднее значение а с заданной вероятностью Р.

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 265
Для построения интервальной оценки параметра а1
воспользуемся тем фактом, что статистика *?- подчинена х -распределению (хи-
квадрат) с п-1 степенями свободы (см. п.6.27). Поэтому, определив
из таблиц процентные точки \ -распределения с п - 1 степенями свободы
Xi-g(n - 1) и х*(п ~ !)> гДе> как и прежде, q = A - Р)/2, а Р — заданная
доверительная вероятность, имееь! неравенство
2
которое выполняется с вероятностью Р = 1 — 2q. Разрешая это
неравенство относительно а , получаем, что случайный доверительный интервал
^—; -т-^ 1 G.30)
-1)' *?-,(»-1)J • }
накрывает неизвестное значение дисперсии а1 с заданной вероятностью Р.
Пример 7.7. Из многочисленного коллектива работников фирмы
случайным образом отобрано п = 25 работников. Средняя заработная
плата этих работников составила х = 700 ден. ед. при среднеквадрати-
ческом отклонении s = 100 ден. ед. Предполагается, что распределение
работников фирмы по размерам заработной платы подчиняется (а; а )-
нормальному распределению. Требуется с доверительной вероятностью
Р = 0,95 определить интервальную оценку для:
а) средней месячной заработной платы на фирме;
б) суммы затрат фирмы на заработную плату отдела, состоящего из
520 сотрудников.
Решение.
а) Среднемесячная заработная плата на фирме характеризуется
генеральной средней а. От нас требуется определить интервальную оценку а
с доверительной вероятностью Р = 0,95.
Согласно G.29) имеем
где ^о,о25B4) - 2,5%-ная точка {-распределения.
По таблице процентных точек распределения Стьюдента
приложения 1 находим для q = -^^ = 0,025 и числа степеней свободы и = п-1 = 24
процентную точку <о,О25B4) = 2,064. Тогда
|700±2,064-^Ll .
L %/24J

266 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Таким образом, с вероятностью Р = 0,95 можно гарантировать, что
средняя заработная плата на фирме находится в пределах: 657,88 ден. ед. <
а < 742,12 ден. ед.
б) Сумма затрат фирмы на заработную плату отдела составит
Na ден. ед. Поэтому с вероятностью Р = 0,95 можно гарантировать,
что затраты фирмы на заработную плату не выйдут из интервала:
520 • 657,88 <:Na*Z 742,12 ¦ 520,
т.е.
342098 ден. ед. < Na < 385902 ден. ед.
Пример 7.8. При анализе точности фасовочного автомата было
проведено п = 24 контрольных взвешиваний пятисотграммовых пачек
кофе. Известно, что ошибки в расфасовке автомата подчиняются @;<т2)-
нормальному распределению (величина а1 — неизвестна). По
результатам измерений рассчитано выборочное среднеквадратическое отклонение
з = 0,8 г. Требуется с доверительной вероятностью Р = 0,95 оценить
точность фасовочного автомата, т. е. определить интервальную оценку <т.
Решение: Согласно G.30) имеем интервальную оценку дисперсии
<г'е -j-; -1— »
Lx, xi-,J
где q = ^^ к 0,025. По таблице процентных точек х'-рьспределения
(см. приложение 1) найдем:
= 38,0757;
X(i-,)(n - 1) = Хо,97бB3) = 11,6885.
Тогда с вероятностью 0,95:
2 [24 - 0,64 24 - 0,64]
1 6 L 38,07575 11,6885J"
Отсюда с доверительной вероятностью Р = 0,95 можно утверждать, что
среднеквадратическое отклонение а будет находиться в интервале
0,632 г. < а < 1,146 г.
Предположив, что ошибка фасовочного автомата есть нормальная
случайная величина с нулевой средней и среднеквадратическим отклонением <т,

7.5 МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 267
можно с вероятностью 0,954 утверждать, что вес пачек кофе будет в
пределах [500-2<г; 500 + 2G] = [500-2,292; 500 + 2,292] * [497,71г., 502,29 г.].
Второй подход к построению доверительных областей более прост и
универсален, однако он основан на асимптотических свойствах оценок,
а поэтому дает приближенные результаты и пригоден лишь при
достаточно больших объемах выборок п. Этот подход использует тот факт,
что как оценки максимального правдоподобия, так и оценки по методу
моментов имеют асимптотически нормальное совместное распределение,
т.е. распределение Ar-мерного вектора ?(п) = у/п(® - 0) стремится к
многомерному нормальному закону с нулевым вектором средних значений и с
ковариационной матрицей ?@), зависящей от неизвестного параметра 0.
При этом приближенном подходе допускаются две «натяжки»: во-первых,
асимптотический вид распределений случайной величины ?(п)
используется при конечных объемах выборки п и, во-вторых, вместо неизвестного
значения параметра 0 в матрицу ?@) вставляется его оценочное
значение 0.
Теперь, для того чтобы построить доверительную область для
неизвестного параметра 0 = @* ,...,0^)Т, мы должны воспользоваться
следующим известным фактом (см. [Андерсон, с. 77]): если А-мерный
вектор ?(п) = у/п(& - О) распределен нормально с параметрами 0 и ?@), то
случайная величина
п@-0)т.?-х(в)@-0)
имеет х2-Распре деление с к степенями свободы.
Определив из таблиц по заданной величине доверительной
вероятности Р процентные точки х*-распределения с к степенями свободы Xi-g(ib)
и хя{к), где q = A - Р)/2, и заменив в известной матрице ?@)
неизвестное значение параметра 0 его приближенным значением 0, мы можем
утверждать, что неравенство
*?_,(*) < п@ - 0)т • Л~\®) • @ - в)< х5(*) G.31)
выполняется с вероятностью, приблизительно равной Р.
Замечание 1. В случае единственного оцениваемого
параметра в (т.е. при к = 1) можно воспользоваться непосредственно @, <т|@))-
нормальностью разности в - в и записать вместо G.31)
<д-в< uq(T^9), G.31')
-u
q
где uq — 100?%-ная точка стандартного нормального распределения, а
<г$@) — дисперсия оценки в. Из G.3l') следует запись соответствующего

268 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
доверительного интервала:
Авр(хъ...,хп)= [0-<uq.a?0), 0 + иячтз@)]- G.31w)
Замечание 2. Если в качестве в используются точечные оценки
максимального правдоподобия, то ковариационная матрица Е@) вектора
у/п(ё - О) однозначно определяется информационной матрицей Фишера
(см. п. 7.2) 33@) = I" @), где элементы матрицы 1@) определяются
соотношениями G.7).
Замечание 3. Положительная определенность и
симметричность матрицы ?F) обусловливают эллипсоидальный характер
доверительного множества, задаваемого соотношением G.31).
Пример 7.9. Рассмотрим задачу интервальной оценки по
наблюдениям zb...,zn параметра р биномиального закона (см. п.3.1.1), т.е.
закона распределения дискретной случайной величины ?, определяемого
вероятностями ,
/(»; PfN) = Р{{ = х} = C*Np*{\ -p)N~\ x = 0,l,...,iV,
где N — известное целое положительное число, ар — параметр,
подлежащий оценке @ < р < 1).
Сначала в соответствии с техникой, описанной в п. 7.5.1, подсчитаем
точечную оценку р максимального правдоподобия параметра р.
Логарифмическая функция правдоподобия в данном случае
t=l
Соответствующее уравнение максимального правдоподобия
dl
Решая его относительно р, получаем оценку максимального
правдоподобия:
2
р nN " N '
Пользуясь независимостью ж,- и тем фактом, что Ез< = Np и Вж< = Np(l-p)
(см. п. 3.1.1), имеем:

7.6 БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 269
Задавшись доверительной вероятностью Р = 0,95, используя факт
асимптотической нормальности разности р - р и подставляя в
выражение для дисперсии Dp вместо р его приближенное значение р, получим
в соответствии с G.31") интервальную оценку для р (с уровнем доверия
0,95):
7.6. Байесовский подход к статистическому
оцениванию
7.6.L «Философия» байесовского подхода
Байесовский подход является одним из возможных способов
формализации и операционализации тезиса, в справедливости которого нет
видимых причин сомневаться: степень нашей разумной уверенности в
некотором утверждении {касающемся, например, оценки неизвестного
численного значения интересующего нас параметра) возрастает и
корректируется по мере пополнения имеющейся у нас информации
относительно исследуемого явления. Могут быть различные формы подтверждения
этого тезиса, в том числе не имеющие отношения к байесовскому подходу.
Одна из них выражена, например, в свойстве состоятельности оценки 0П
неизвестного параметра О: чем больше объем выборки п, на основании
которой мы строим свою оценку 0П, тем большей информацией об этом
параметре мы располагаем и тем ближе (в смысле сходимости 0П к 0 по
вероятности, см. выше, п. 7.1.3) к истине наше заключение.
Специфика именно байесовского способа операционализации этого
тезиса основана па двух положениях.
1) Во-первых, «степень нашей разумной уверенности» в
справедливости некоторого утверждения численно выражается в виде
вероятности. Это означает, что вероятность в байесовском подходе выходит ва
рамки ее интерпретации в терминах условий статистического ансамбля
(см. п. В.2.1 введения), но относится к одной из категорий
субъективной школы теории вероятностей.
2) Во-вторых, статистик при принятии решения использует в
качестве исходной информации одновременно информацию двух типов:
априорную и содержащуюся в исходных статистических данных (см. п. В.З
введения). При этом априорная информация предоставлена ему в виде

270
ГЛ. Т. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
некоторого априорного распределения вероятностей анализируемого
неизвестного параметра, которое описывает степень его уверенности в том,
что этот параметр примет то или иное значение, еще до начала сбора
исходных статистических данных. По мере же поступления исходных
статистических данных статистик уточняет (пересчитывает) это
распределение, переходя от априорного распределения к апостериорному,
используя для этого известную формулу Байеса (см. п. 1.1.3; отсюда и
название подхода).
7.6*2. Общая логическая схема и базовые формулы
байесовского метода оценивания параметров
Общая логическая схема байесовского метода оценивания
неизвестных значений параметров представлена на рис. 7.3.
U
Априорные
сведения о
параметре в:
априорное
распределение
р(в)
Исходные

статистические данные
Вычисление
функции
правдоподобия
L(xu...}xn\e)
Вычисление
апостериорного
распределения
параметра в
Заключение
о значении
параметра в:
точечная или
интервальная
оценка
Рис. 7.8. Общая логическая схема байесовского подхода в статистическом
оценивании
Рассмотрим реализацию схемы байесовского оценивания неизвестного
параметра.

7.6 БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 271
Априорные сведения о параметре в основаны на предыстории
функционирования анализируемого процесса (если таковая имеется) и на
профессиональных теоретических соображениях о его сущности,
специфике, особенностях и т.п. В конечном итоге эти априорные сведения должны
быть представлены в виде функции р@), задающей априорное
распределение параметра и интерпретируемой как вероятность того, что пара*
метр примет значение, равное 0, если параметр дискретен, и как функция
плотности распределения в точке 0, если параметр непрерывен по своей
природе.
Примеры вероятностных законов, используемых в качестве
априорных распределений параметров, будут приведены ниже (см. п. 7.6.3).
Заметим лишь, что в ситуациях, когда априорные сведения об
анализируемом параметре слишком скудны, в качестве априорного распределения
р@) используют, например, равномерное на отрезке [©min>@max]
распределение, где [0min, ©max] — априорный диапазон варьирования возможных
значений оцениваемого параметра, т.е.:
Исходные статистические данные хьж2,...,хп — это не что
иное, как выборка объема п из анализируемой генеральной совокупности.
Получая исходные статистические данные, мы к имевшейся ранее
априорной информации о параметре присоединяем выборочную (эмпирическую)
информацию.
Вычисление функции правдоподобия 1(хьж2,...,жп | 0)
производится в соответствии с G.5) по формуле
L(xux2,...,xn I 0) = /(*! | 0) • /(*2 | в). ... •/(*,» | 0), G.33)
где f(x | 0) — функция плотности (или вероятность Р{{ = х | 0}),
описывающая закон распределения вероятностей анализируемой генеральной
совокупности в предположении (или при условии), что значение
оцениваемого параметра равно 0.
Вычисление апостериорного распределения у?@ | хь...,яп)
осуществляется с помощью формулы Байеса (см. п. 1.1.3, формула A.19)),
в которой роль события А{ играет событие, заключающиеся в том, что
значение оцениваемого параметра равно 0, а роль условия В —
события, заключающееся в том, что значения п наблюдений, произведенных
в анализируемой генеральной совокупности, зафиксированы на уровнях

272 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
х\, а?2»... ,#п- Соответственно имеем:
G-34)
Построение байесовских точечных и интервальных оценок
основано на использовании знания апостериорного распределения <p(Q |
хь...,хп), задаваемого соотношением G.34). В частности, в качестве
байесовских точечных оценок 0V ; используют среднее или модальное
значение этого распределения, т.е.:
= Е@ | хи...,хп) = J0у?(в | яь...,*п) <*0, G.35)
©мод =
мод
Отметим, что для вычисления этих оценок нам достаточно знать
только числитель правой части G.34), так как знаменатель этого
выражения играет роль нормирующего множителя и от 0 не зависит (это
существенно упрощает процесс практического построения оценок 0^ и
Отметим также одно важное оптимальное свойство оценки 0^.
Пусть 0(а?1,...,жп) — любая оценка параметра 0. Оказывается, если
качество любой оценки &(хи.. ,,хп) измерять так называемым
апостериорным байесовским риском
или его средним (усреднение — по всем возможным выборкам хь..., хп)
значением д?\ то байесовская оценка G.35) является наилучшей и в том
и в другом смысле.
Для построения байесовского доверительного интервала для
параметра 0 необходимо вычислить по формуле G.34) функцию <р(® \ «ь..., хп)
апостериорного закона распределения параметра 0, а затем по заданной
доверительной вероятности Р определить 1004^- и 1001:5?%-ные
точки этого закона, которые и дают соответственно левый и правый концы
искомой интервальной оценки.
Заметим, что байесовский способ оценивания может давать весьма
ощутимый выигрыш в точности при ограниченных объемах выборок. В

7.6 БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 273
процессе же неограниченного роста объема выборки п оба подхода будут
давать, в силу их состоятельности, все более похожие результаты.
7.6.3. Примеры байесовского оценивания
Рассмотрим теперь на примерах, как практически реализуется
описанная в предыдущем пункте схема байесовского оценивания неизвестного
параметра.
Пример 7.10. Анализируется закон распределения вероятностей
(з.р.в.) семей определенной социально-экономической страты по величине
среднедушевого дохода ?. Проведенные ранее исследования говорят о том,
что з.р.в. среднедушевого дохода внутри однородной страты описывается
логарифмически нормальной моделью (см. п. 3.1.6), а это значит, что
случайная величина 7/ = 1п? подчинена нормальному закону. Требуется по
результатам обследования среднедушевого дохода десяти семей, случайно
отобранных из всей совокупности семей анализируемой страты, а также
по некоторой априорной информации о величине теоретического среднего
9 = ЕAп () построить байесовскую оценку для в.
Математическая постановка задачи. Мы располагаем
следующей информацией об анализируемой генеральной совокупности.
1) Логарифм (натуральный) от величины среднедушевого дохода
(tj = ln?) распределен нормально с неизвестным средним значением в
и известной дисперсией а , т. е.
2) Из предыстории и опыта обследований семей той же самой
страты в других регионах известно, что величина в ведет себя как (во\ст1)-
нормальная случайная величина, где значения в0 и <т1 известны, т. е.
3) Имеются результаты обследования п (п = 10) случайно отобранных
от анализируемой страты .семей по среднедушевому доходу, т. е. случайная
выборка значений Х\, а?2,..., ял, где ж* = In од, а од — среднедушевой доход
t-й обследованной семьи. Ниже приводятся конкретные значения х{\
хх = 0,54; х2 = 1,20; ж3 = 0,36; х4 = 0,80; хь = 0,42; ж6 = 2,10;
х7
ледованной семьи. Ниже приводятся конкре
l = 0,54; х2 = 1,20; ж3 = 0,36; а?4 = 0,80; хь
г = 0,70; я?8 = 0,25; х9 = 0,90; хго = 0,48.

274 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Требуется на основании исходной информации 1) - 3) построить
байесовскую оценку для параметра в и сравнить эту оценку с оценкой^
полученной классическим методом максимального правдоподобия.
Решение. Поскольку мы уже располагаем априорным
распределением р(в) и исходными статистическими данными х\,,..,хП) первые два
этапа схемы, представленной на рис. 7.3, можно считать реализованными.
На 3-лс этапе вычисляем функцию правдоподобия. В нашем случае
имеем:
В этом выражении, как всегда, х = ?Hsi ж»/п> *2 = (]СГ=1(Ж» ~ *J)/п и
при его выводе использовано тождественное преобразование:
I)]1 = ^(Ж хK + п@ х)\
, - вJ = ? [(«| - S) - @ - I)]1 = ^(Ж< - хK + п@ - х)\
t=l t=l 1=1
Следующий D-й) этап, на котором вычисляется апостериорное
распределение <р(в | х\9...,яп), является, как правило, самым трудным в
техническом отношении. Мы будем вычислять функцию <р(в | &i,...,gn) с
точностью до общего нормирующего множителя. Поэтому в тех местах
наших выкладок, в которых мы будем опускать отдельные сомножители-
компоненты этого общего нормирующего множителя, знаки равенства,
связывающие наши преобразования, будут заменяться знаком
эквивалентности
= exp
1 /V 200о , *о , па2 вгп 2вп2 nS2\\
' \<г0 со сто <г а а' ^ / J
G.36)

7.6 БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 275
где
Д2= *° | и а=Х+ °7?. G.37)
1 + 2^ 1 + ^т
Из G.36) следует, что апостериорное распределение <р(в \ Х\}...,яп),
аккумулирующее в себе как априорную, так и выборочную информацию
о параметре 0, снова является нормальным со средним значением а и
дисперсией А , определяемыми соотношениями G.37).
Соответственно байесовская оценка параметра в в данном случае
определяется формулой
ер
Как мы знаем (см. выше, п. 7.5.1), оценка параметра $ по методу
максимального правдоподобия есть
0МП = х.
Мы видим, что байесовская оценка получается как взвешенное
среднее оценки 0МП и среднего значения #о априорного распределения
параметра 0, причем вес 0q тем больше, чем меньше дисперсия <tq априорного
распределения и чем больше дисперсия анализируемой генеральной
совокупности (т. е. чем менее точно производимые наблюдения я,*
характеризуют среднее значение своей генеральной совокупности).
Возвращаясь к конкретным числовым данным нашего примера,
имеем: 0МП = х = 0,775; #° = 0,687.
Пример 7.11. Рассмотрим задачу оценивания неизвестной
вероятности 9 в схеме испытаний Бернулли (см. п. 3.1.1) на основе п
независимых испытаний. Таким образом, можно сказать, что мы исследуем
биномиальную генеральную совокупность (см. формулу C.3)) с
неизвестным значением вероятности «успеха» в в одном испытании, имея
единственное наблюдение х\ — число «успехов» в серии из п независимых
испытаний. Распределение вероятностей f(x | в) для числа успехов щ{п)
задается формулой
\п-ав
Анализ предыстории функционирования систем, аналогичных
исследуемой, позволил определить в качестве априорново распределений р@)

276 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
параметра в бета-распределение с параметрами а и Ь (см. п. 3.2.6,
формулу C.22)):
при
при
В нашем случае при единственном имеющемся наблюдении х\
функция правдоподобия L(xt | в) = f{xx \ в) = С11в*1{\ - в)п'х\ так что
апостериорная плотность <р@ | х\) определится в соответствии с G,34)
соотношением:
/о1
Произведя очевидные сокращения в числителе и знаменателе правой
части этого выражения и учитывая тот факт, что в соответствии с
определениями гамма- и бета-функций
Jo
имеем:
Но отсюда следует, что апостериорное распределение оцениваемого
параметра в снова является бета-распределением. Его среднее значение
известным образом выражается через его два параметра (см. п. 3.2.6),
так что
-X!) п + а + Ь 1 ^
Как мы знаем (см. п. 7.5.1), оценкой максимального правдоподобия
параметра в в данном примере будет отношение
Сравнение всР' и вМП показывает, что эти оценки могут достаточно
сильно различаться (в зависимости от значений а и 6) при небольших

7.6 БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 277
объемах выборок. Однако по мере роста п они, как и следует ожидать
при состоятельных способах оценивания, будут давать все более схожие
результаты.
Пример 7.12. Как известно (см. п. 3.1.8), длительность жизни
элемента (устройства, системы, живого организма), работающего в
режиме нормальной эксплуатации, характеризуется
экспоненциальным з.р.в., т.е. функцией плотности f(x | в) вида
0е~вх при х ^ 0;
0 при х < 0.
Функция правдоподобия L(xux2,... ,жп | в) имеющихся в нашем
распоряжении п независимых наблюдений zb z2> • • • > яп, соответственно,
имеет вид
Максимизация по в логарифмической функции правдоподобия
N
/(а?ь...,жп|0) = 1п? =
приводит нас к оценке максимального правдоподобия 0мп параметра в
вида
*(*) П f-f
* 1=1
Построим байесовские точечную и интервальную
оценки параметра 0 в предположении, что априорное распределение параметра
0 подчиняется гамма-закону с параметрами а и Ь (см. п.3.2.5), т.е.
р-ге-м при 0>О;
при 0 < 0.
В соответствии с формулой G.34) апостериорное распределение
параметра 0 (с точностью до нормирующих множителей, не зависящих от
0) будет характеризоваться функцией плотности
<р@\хи...,хп)~р(О).Ь(х1у...,хп\0) =
G.38)
е <asl при 0 ^ 0
0 при 0 < 0.

' 278 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Правая часть G.38) задает (с точностью до нормирующих
множителей) снова гамма-распределение, но с параметрами а = а + п и b' =
&+?*,.
t=i
Среднее значение гамма-распределений (с параметрами а и &')
случайной величины равно, как известно (см. п. 3.2.5), отношению первого
параметра ко второму, так что точечная байесовская оценка (г '
параметра в будет иметь вид:
а + п
Интервальная байесовская оценка (при уровне доверия Ро = 1 - 2q)
определится 100A-9)" и ЮОд -процентными точками апостериорного
распределения G.38), соответственно, 7i-^(e\ Ь9) и уя(а} Ь;), так что, с учетом
известной связи между процентными точками гамма- и х -распределений
х'), см. (Абрамовиц М., 1979)), имеем (с вероятностью
(UqBa + 2п) < 0 < - *5Bа + 2п).
2(*+?»0
Пример 7.13. В данном примере речь идет об оценке параметра в
пуассоновского закона (см. п. 3.1.3, формулу C.6)), т. е. анализируемая
генеральная совокупность описывается законом распределения вероятностей
вида
Априорное распределение вероятностей параметра 0 подчиняется
гамма-закону с параметрами аи 6 (см. п. 3.2.5, формулу C.21)), т.е.
0 при 0<О.
правдоподобия

выводы 279
Как известно (см. п. 7.5.1), оценка максимального правдоподобия
параметра в имеет вид
в --
мп "" п
Апостериорная плотность (с точностью до нормирующего
множителя) в соответствии с формулой G.34) имеет вид
который соответствует гамма-распределению с параметрами а =
]СГ=1 х% и Ь1 = п + 6, Следовательно, байесовская оценка
Применение байесовского подхода в эконометрике и,*в частности, в
статистическом оценивании неизвестных значений параметров
оказывается в определенных ситуациях крайне актуальным и достаточно
эффективным [А. Зельнер]. Конечно, «узким» местом в его прикладной
распространенности является обоснованный выбор априорного распределения.
Бывают ситуации, когда информация о виде априорного распределения
имеется с точностью до небольшого числа неизвестных параметров,
которые можно оценить по выборке одновременно с оцениванием параметра 0.
В этом случае говорят, что применен эмпирический байесовский подход.
ВЫВОДЫ
1. Одна из центральных задач статистического анализа реальной
системы заключается в вычислении (на основании имеющихся
статистических данных) как можно более точных приближенных значений
(статистических оценок) для одного или нескольких числовых параметров,
характеризующих функционирование этой системы. Принципиальная
возможность получения работоспособных приближений такого рода на
основании статистического обследования лишь части анализируемой
генеральной совокупности (т. е. на основании ограниченного ряда наблюдений,
или выборки) обеспечивается замечательным свойством статистической
устойчивости выборочных характеристик (см. п. 6.2).
2. Статистическая оценка строится в виде функции от результатов
наблюдений, а потому сама по природе является случайной величиной.

280 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
При повторении выборки из той же самой генеральной совокупности и
при подстановке новых выборочных значений в ту же самую «функцию-
оценку» мы, вообще говоря, получаем другое число в качестве
приближенного значения интересующего нас параметра, т. е. имеется
неконтролируемый разброс в значениях оценки при повторениях эксперимента (в
данном случае — выборки)!
3. В качестве основной меры точности статистической оценки 0
неизвестного параметра 0 используется средний квадрат ее отклонения от
оцениваемого значения, т.е. величина Е@ - 0) , а в многомерном
случае — ковариационная матрица компонент векторной оценки 0. Оче^
видно, чем меньше эта величина (или обобщенная дисперсия оценки 0
в многомерном случае), тем точнее (эффективнее) оценка. Для широкого
класса генеральных совокупностей существует неравенство (неравенство
Рао-Крамера-Фреше G.12), G.13)), задающее тот минимум Дт|„ (по всем
возможным оценкам) среднего квадрата Е@ — в) , улучшить который
невозможно. Естественно использовать этот минимум Дт|п в качестве
начальной точки отсчета мерьг^эффективности оценки, определив
эффективность е(в) любой оценки в параметра в в виде отношения
2 *
Е(в - в)
4. Свойство состоятельности оценки в (см. п. 7.1.3) обеспечивает
ее статистическую устойчивость, т.е. ее сходимость (по вероятности) к
истинному значению оцениваемого параметра в по мере роста объема
выборки, на основании которой эта оценка строится. Свойство
несмещенности оценки в (см. п. 7.1.4) заключается в том, что результат усреднения
всевозможных значений этой оценки, полученных по различным выборкам
заданного объема (из одной и той же генеральной совокупности), дает в
точности истинное значение оцениваемого параметра, т. е. Ев = в.
Далеко не всегда следует настаивать на необходимом соблюдении свойства
несмещенности оценки: несущественное само по себе уже при умеренно
больших объемах выборки, оно может чрезмерно обеднить класс оценок,
в рамках которого решается задача построения наилучшей оценки.
5.JC учетом случайной природы каждого конкретного оценочного
значения в неизвестного параметра в представляет интерес построение целых
интервалов оценочных значений Д0, а в многомерном случае — целых
областей, которые с наперед заданной (и близкой к единице),
вероятностью Р накрывали бы истинное значение оцениваемого параметра 0, т. е.
Р{в 6 Др@)} = Рш Эти интервалы (области) принято называть довери-

выводы 281
тельными (или интервальными оценками). Существуют два подхода к
построению интервальных оценок: точный (конструктивно реализуемый
лишь в сравнительно узком классе ситуаций) и асимптотически
приближенный (наиболее распространенный в практике статистических
приложений), см. п. 7.5.4.
6. Основными методами построения статистических оценок
являются:
метод максимального правдоподобия (см. п. 7.5.1);
метод моментов (см. п. 7.5.2);
метод, использующий «взвешивание» наблюдений, —
цензурирование, урезание, порядковые статистики (см. п. 7.5.4).
Различные варианты метода, использующего «взвешивание»
наблюдений, находят все большее распространение в связи с устойчивостью
получаемых при этом статистических выводов по отношению к возможным
отклонениям реального распределения исследуемой генеральной
совокупности от постулируемого модельного.
7. Наличие априорной информации об оцениваемом параметре,
позволяющей сопоставить с каждым возможным значением неизвестного
параметра некую вероятностную меру его достоверности, т.е. сведений об
априорном вероятностном законе распределения оцениваемого
параметра, позволяет существенно уточнить оценки, полученные
традиционными методами (методом максимального правдоподобия, методом моментов и
т.п.) в условиях отсутствия такой информации. Построение таких оценок
осуществляется с помощью так называемого байесовского подхода (см.
п. 7.6), а сами оценки называются байесовскими.
Приложение к гл.7 {доказательство неравенства информации)
Рассмотрим тождества
J 0(хи...,хп)Ь(хи...,хп; B)dzu...dxn
.dzn = l.
Их почленное дифференцирование по в (с учетом условий а) и б), см. с. 244, и
обозначения I яв In L as EJ>=1 In /(«,-; $)) дает
f dl r*(dl\ a
/ — L dx\ ... dxn = Б ( — I =0, откуда следует :

282 ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Применяя к левой части (*) неравенство Коши-Буняковсжого ([E((i?)]a < E{aEf?a)
и принимая во внимание тождества E(dl/dO) а 0, E(dl/d$)* = nE(d\nf{x;$)/dOJ> a
также — равенство левой и правой частей (*), получаем
откуда и следует непосредственно неравенство информации G.12).

ГЛАВА 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА
ГИПОТЕЗ (СТАТИСТИЧЕСКИЕ
КРИТЕРИИ)
На разных стадиях статистического исследования и моделирования
возникает необходимость в формулировке и экспериментальной
проверке некоторых предположительных утверждений (гипотез) относительно
природы или величины неизвестных параметров анализируемой
стохастической системы. Например, исследователь высказывает предположение:
«исследуемые наблюдения извлечены из нормальной генеральной
совокупности» или «среднее значение анализируемой генеральной совокупности
равно нулю». Будем обозначать в дальнейшем высказанное'нами
предположение (гипотезу) с помощью буквы И. Наша цель — проверить, не
противоречит ли высказанная нами гипотеза Н имеющимся выборочным
данным.
Процедура обоснованного сопоставления высказанной гипотезы с
имеющимися в нашем распоряжении выборочными данными хг, х2> • • • > яя,
сопровождаемая количественной оценкой степени достоверности
получаемого вывода, осуществляется с помощью того или иного статистического
критерия и называется статистической проверкой гипотез.
Результат подобного сопоставления может быть либо
отрицательным (лшпые наблюдения противоречат высказанной гипотезе, а потому
от этой гипотезы следует отказаться), либо неотрицательным (данные
наблюдения не противоречат высказанной гипотезе, а потому ее
можно принять в качестве одного из естественных и допустимых решений).
При этом неотрицательный результат статистической проверки
гипотезы не означает, что высказанное нами предположительное
утверждение является наилучшим, единственно подходящим: просто она не
противоречит имеющимся у нас выборочным данным, однако таким же
свойством могут наряду с Н обладать и другие гипотезы. Так что
даже статистически проверенное предположение Н следует расценивать не
как раз и навсегда установленный, абсолютно верный факт, а лишь как

284 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
достаточно правдоподобное, не противоречащее опыту утверждение.
По своему прикладному содержанию высказываемые в ходе
статистической обработки данных гипотезы можно подразделить на несколько
основных типов.
8.1. Основные типы гипотез, проверяемых
в ходе статистического анализа и
моделирования
8,1.1. Гипотезы о типе закона распределения исследуемой
случайной величины
При обработке ряда наблюдений
xi,x2,...,xn (8.1)
исследуемой случайной величины ( очень важно понять механизм
формирования выборочных значений ж,-, т.е. подобрать и обосновать некоторую
модельную функцию распределения FM0Jl(x) (например, из числа
описанных в гл.З), с помощью которой можно адекватно описать исследуемую
функцию распределения F^(x). На определенной стадии исследования это
приводит к необходимости проверки гипотез типа
Я: ВД = FMoa(x),- (8.2)
где гипотетичная модельная функция может быть как заданной
однозначно (тогда F((x) = Fq(x), где Fo(x) — полностью известная функция), так
и заданной с точностью до принадлежности к некоторому
параметрическому семейству (тогда FM0Jl(x) = F(x\ 0), где 0 — некоторый, вообще
говоря, Л-мерный параметр, значения которого неизвестны, но могут быть
оценены по выборке (8.1) с помощью методов, изложенных в п. 7.5 и 7.6).
Проверка гипотез типа (8.2) осуществляется с помощью так
называемых критериев согласия и опирается на ту или иную меру различия
между анализируемой эмпирической функцией распределения Щп\х) и
гипотетическим модельным законом FMOU(x) (примеры реализации
подобных критериев см. в п. 8.6.1).

8.1 ОСНОВНЫЕ ТИПЫ ГИПОТЕЗ 285
8.1.2. Гипотезы об однородности двух или нескольких
обрабатываемых выборок или некоторых
характеристик анализируемых совокупностей
Наиболее типичные задачи такого рода характеризуются следующей
общей ситуацией. Пусть мы имеем несколько «порций» выборочных
данных типа (8.1):
(8.3)
t
Эти порции могли образоваться, например, естественным образом —
в ходе проведения выборочного обследования (скажем, за счет разделен-
ности условий их регистрации во времени или пространстве). Обозначая
функцию распределения, описывающую вероятностный закон, которому
подчиняются наблюдения j-й выборки, с помощью Fj(x) и снабжая тем
же индексом все интересующие нас эмпирические и теоретические
характеристики этого закона (средние значения uj и ау, дисперсии о) и а) и
т.д.), основные гипотезы однородности можно записать в виде:
HF: Fi(x) = F2(x) в • • • & F,(x); (8.4a)
а. а\ = a<i = • • • = а\\ ^o.4.oj
тт . 2 _^ 2 ^ 2 /л л \
В случае неотрицательного результата проверки этих гипотез
говорят, что соответствующие выборочные характеристики (например,
&i,иг,...,й/) различаются статистически незначимо.
Отметим частный случай гипотез типа (8.4а), когда число выборок
/ = 2, а одна из выборок содержит малое количество наблюдений (в
частном случае — одно). В таком виде проверка гипотез типа (8.4а)
означает проверку аномальности одного или нескольких резко выделяющихся
наблюдений. Реализация конкретных критериев однородности описана в
п. 8.6.2.
8.1.3. Гипотезы о числовых значениях параметров
исследуемой генеральной совокупности
Пусть, например, ряд наблюдений (8.1) дает нам значения некоторого
параметра изделий, измеренные на п изделиях, случайно отобранных из
массовой продукции определенного станка автоматической линии, и пусть

286 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
а0 — заданное номинальное значение этого параметра. Каждое отдельное
значение Х{ может, естественно, как-то отклоняться от заданного
номинала. Очевидно, для того чтобы проверить правильность настройки этого
станка, надо убедиться в том, что среднее значение параметра у
производимых на нем изделий будет соответствовать номиналу, т. е. проверить
гипотезу типа
Н: Е( = а0. (8.5)
В общем случае гипотезы подобного типа имеют вид:
Яо: 0 € До, (8.6)
где в — некоторый параметр (вообще говоря, многомерный), от
которого зависит исследуемое распределение, а До — область его конкретных
гипотетических значений, которая может состоять всего из одной точки.
Статистическая проверка гипотез о числовых значениях параметров
играет важную роль в эконометрическом моделировании, регрессионном
анализе, в широком спектре задач статистического исследования
зависимостей, существующих между анализируемыми показателями (этому
кругу вопросов посвящены гл. 10,11 и второй том данного учебника). В
частности, принятие решения о включении или исключении той или иной
переменной в анализируемую регрессионную (эконометрическую) модель, о
наличии-отсутствии статистической связи между наблюдаемыми
признаками существенно опирается обычно на проверку гипотез типа (8.6) при
До = 0. Такого же типа гипотезы приходится проверять при
установлении факта независимости и стационарности имеющегося ряда наблюдений
(см. п. 3.1 тома 2).
Реализация некоторых конкретных критериев статистической
проверки гипотез о числовых значениях параметров анализируемой
стохастической системы описывается в п. 8.6.3.
8,1.4. Гипотезы об общем виде модели, описывающей
статистическую зависимость между признаками
В п. 8.1.1 речь шла, по существу о подборе подходящей модели для
описания закона распределения вероятностей исследуемой случайной
величины. Не менее важное место в общем статистическом и
эконометрическом анализе занимает проблема подбора подходящей модели, с помощью
которой мы можем адекватно описать исследуемую статистическую
зависимость между анализируемыми признаками. В качестве гипотетических
могут проверяться утверждения о линейном, квадратическом,
экспоненциальном, степенном, логарифмическом, полиномиальном и т. п. типе ис-

8.2 ОБЩАЯ ЛОГИЧЕСКАЯ СХЕМА СТАТИСТИЧЕСКОГО КРИТЕРИЯ 287
комой зависимости. Подробнее эта проблематика обсуждается в гл. 10
данного учебника.
8.2. Общая логическая схема
статистического критерия
По своему назначению и характеру решаемых задач статистические
критерии чрезвычайно разнообразны. Однако их объединяет общность
логической схемы, по которой они строятся. Коротко эту логическую
схему можно описать так.
1. Выдвигается гипотеза Яо.
2. Задаются величиной так называемого уровня значимости критерия
а. Дело в том, что всякое статистическое решение, т.е. решение,
принимаемое на основании ограниченного ряда наблюдений, неизбежно
сопровождается некоторой, хотя,.возможно, может и очень малой, вероятностью
ошибочного заключения как в ту, так и в другую сторону. Скажем, в
какой-то небольшой доле случаев а гипотеза Я<> может оказаться
отвергнутой, в то время как на самом деле она является справедливой, или,
наоборот, в какой-то небольшой доле случаев /? мы можем принять нашу
гипотезу, в то время как на самом деле она ошибочна, а справедливым
оказывается некоторое конкурирующее с ней предположение —
альтернативная гипотеза И\. При фиксированном объеме выборочных данных
величину вероятности одной из этих ошибок мы можем выбирать по
своему усмотрению. Бели же объем выборки можно как угодно увеличивать,
то имеется принципиальная возможность добиваться как угодно малых
вероятностей обеих ошибок аи/? при любом фиксированном
конкурирующем предположительном утверждении Я}. В частности, при
фиксированном объеме выборки обычно задаются величиной а вероятности
ошибочного отвержения проверяемой гипотезы Яо, которую часто называют
«основной» или «нулевой». Эту вероятность ошибочного отклонения
«нулевой» гипотезы принято называть уровнем значимости или
размером критерия. Выбор величины уровня значимости а зависит от
сопоставления потерь, которые мы понесем в случае ошибочных заключений
в ту или иную сторону: чем весомее для нас потери от ошибочного
отвержения высказанной гипотезы Яо, тем меньшей выбирается величина
а. Однако поскольку такое сопоставление в большинстве практических
задач оказывается весьма затруднительным (часто трудно даже вообще
сказать, в какую сторону ошибка является для нас более опасной), то, как
правило, пользуются некоторыми стандартными значениями уровня
значимости. К таким стандартным значениям можно причислить величины

288 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
а = 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является
величина уровня значимости а, равная 0,05. Она означает, что в среднем в
пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу
при многократном использовании данного статистического критерия.
3. Задаются некоторой функцией от результатов наблюдения
(критической статистикой) 7*Л* = 7(жъж2?--->жп)- Эта критическая
статистика 7*п\ как и всякая функция от результатов наблюдения, сама
является случайной величиной (см. 7.1.2) и в предположении справедливости
гипотезы #о подчинена некоторому хорошо изученному (затабулирован-
ному) закону распределения с плотностью /7<«o(u).
Один из основных принципов построения критической статистики
(принцип отношения правдоподобия) описан в п. 8.3.1. Поясним здесь
лишь общий содержательный смысл этой статистики: как правило, ею
определяется мера расхождения имеющихся в нашем распоряжении
выборочных данных (8.1) с высказанной (и проверяемой) гипотезой Яо. Так,
в гипотезах типа рассмотренных в п. 8.1.1 критическая статистика 7
определяет меру различия между анализируемой эмпирической функцией
распределения F^n\x) и гипотетической (модельной) функцией FMOJl(x). В
гипотезах типа рассмотренных в п. 8.1.2 величина 7 измеряет степень
расхождения соответствующих выборочных характеристик в различных
выборках; в гипотезах типа рассмотренных в п. 8.1.3 — отклонения
выборочных характеристик от соответствующих гипотетических значений и
т.д.
4. Из таблиц распределения /7(«)(м) находятся 100A - f )%-ная точка
7^/2 и 100f %-ная точка 7а/2 ' разделяющие всю область мыслимых
значений случайной величины 7 на три части: область неправдоподобно
малых (I), неправдоподобно больших (III) и естественных или
правдоподобных (в условиях справедливости гипотезы Но) значений (II) (рис. 8.1).
В тех случаях, когда основную опасность для нашего утверждения
представляют только односторонние отклонения, т.е. только «слишком
маленькие» или только «слишком большие» значения критической
статистики 7 i находят лишь одну процентную точку: либо 100A - а)%-ную
точку 7а * которая будет разделять весь диапазон значений 7*п* на две
части: область неправдоподобно малых и область правдоподобных
значений; либо 100а%-ную точку 7«тах); °на будет разделять весь диапазон
значений 7 на область неправдоподобно больших и область
правдоподобных значений.
5. Наконец, в функцию 7 подставляют имеющиеся конкретные вы-

8.2 ОБЩАЯ ЛОГИЧЕСКАЯ СХЕМА СТАТИСТИЧЕСКОГО КРИТЕРИЯ
289
борочные данные Xi,.,.,xn и подсчитывают численную величину у .
Если окажется, что вычисленное значение принадлежит области
правдоподобных значений 7 i то гипотеза Но считается не противоречащей
выборочным данным. В противном случае, т. е. если 7 слишком мала или
слишком велика, делается вывод, что 7 на самом деле не подчиняется
закону /7(»)(и) (этот вывод, как легко понять, сопровождается
вероятностью ошибки, равной а), и это несоответствие мы вынуждены объяснить
ошибочностью высказанного нами предположения Но и, следовательно,
отказаться от него.
Таким образом, решение, принимаемое на основании любого
статистического критерия, может оказаться ошибочным как в случае
отклонения проверяемой гипотезы #о (с вероятностью а), так и в случае ее
принятия (с вероятностью /?). Вероятности аи/? ошибочных решений
называют также ошибками соответственно первого и второго рода, а величину
1-/9 — мощностью критерия. Очевидно, из двух критериев,
характеризующихся одной и той же вероятностью а отвергнуть в действительности
правильную гипотезу #о, следует предпочесть тот, который
сопровождается меньшей ошибкой второго рода (или большей мощностью).
а/2
(max) nj
7<*/2 Ul
Рис. 8.1 • График плотности распределения критической статистики уп и
выделение областей «правдоподобных» (II) и
«неправдоподобных» (I и III), в условиях справедливости гипотезы #о, значений
этой статистики
Если проверяемое предположительное утверждение сводится к
гипотезе о том, что значение некоторого параметра 0 в точности равно
заданной величине ©о (см. выше гипотезы, рассмотренные в п. 8.1.3), то
эта гипотеза называется простой. В других случаях гипотеза будет на-
10 Теория вероятностей
и прикладная статистика

290 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
зываться сложной.
8.3. Построение статистического критерия;
принцип отношения правдоподобия
Попытаемся выяснить, как конкретно получаются те функции от
результатов наблюдения (критические статистики 7^)> по значениям
которых принимается окончательное решение о том, соответствует ли
проверяемая гипотеза имеющимся у нас данным (8.1) или противоречит им.
8.3.1. Сущность принципа отношения правдоподобия
Для пояснения общего принципа, приводящего к построению
наилучших (наиболее мощных при заданной величине уровня значимости)
критериев, вернемся к условиям примера с заработной платой (см. п. 7.5.1)
и соответственно к рис. 7.2. В этом примере исследовалась
логарифмически нормально распределенная заработная плата ? работников
определенной совокупности, а в качестве исходных данных мы располагали тремя
наблюдениями (тремя обследованными работниками): хх = 19.0 ден.ед.;
а?2 = 175 ден.ед.; х3 = 205 ден.ед. Пусть мы хотим проверить
основную гипотезу (простую) о среднем значении нормально распределенной
случайной величины In ?:
Яо: ЕAп?) = 5,240 = а0
против простой альтернативы
Нг: E(lnf) = 5,443 = аг.
Из рис. 7.2 видно, что гипотеза #о не противоречит имеющимся
наблюдениям (более того, в данном случае наши наблюдения выглядят
наиболее правдоподобными именно при гипотезе Яо), в то время как те же
наблюдения оказываются малоправдоподобными в условиях
справедливости гипотезы Н\.
В общем случае представление о сравнительной правдоподобности
имеющихся наблюдений х\,..., хп (в отношении проверяемой и
альтернативной гипотез) дает нам сопоставление соответствующих функций
правдоподобия (см. формулу G.5)) и, в частности, их отношение
г») LHi(xu...,xn; 0) L(xu...,xnj 0Q f .
7 LHo(xu...9xn; 0) Цхи...9хп; ©о)' К }

8.3 ПРИНЦИП ОТНОШЕНИЯ ПРАВДОПОДОБИЯ 291
где LHi и ХЯо — значения функций правдоподобия наблюдений х%,..., жЛ,
вычисленные в предположении справедливости соответственно гипотез
Н%: 0 = 01 и Яо: 0 = ©0. Очевидно, чем правдоподобнее наблюдения
в условиях гипотезы Яо, тем больше функция правдоподобия 1Но н тем
меньше величина 7 • Бели /у(п)(и) — плотность распределения
статистики 7^ при условии справедливости гипотезы Яо, то построение
критерия проверки гипотезы Яо с заданным уровнем значимости а сводится
к определению 100а%-ной точки 7а распределения Д(»>(и) и к реализации
следующего правила:
если 7 > 7а > то гипотеза Яо отвергается
с вероятностью ошибиться, равной а, так как
в соответствии с законом До (и) и при
справедливости гипотезы #о возможно осуществление
события {7 > 7а} с вероятностью а, т.е.
оо
До(«) А* = а;
7а
оо
если 7 < 7а> т° гипотеза Яо не отвергается.
Критерии, основанные на статистиках 7 вида (8.7) и процедурах
(8.8), носят название критериев отношения правдоподобия, а их
практическая реализуемость и предпочтительность по отношению к другим
возможным критериям подкреплены следующими фактами (справедливыми
в достаточно широком классе ситуаций).
1. Критерии отношения правдоподобия являются наиболее мощными
среди всех других возможных критериев (этот факт для случая сравнения
двух простых гипотез сформулирован и доказан в виде леммы Неймана-
Пирсона, см., например [Крамер Г.]).
2. Плотность До (и) распределения критической статистики 7*п\ как
правило, без труда восстанавливается по функции правдоподобия L
наблюдаемой случайной величины.
Так, в рассмотренном выше примере с проверкой гипотезы о
среднем значении нормальной случайной величины ? (при известном значении
10*

292 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
дисперсии <т2), имеем:
так что
Jn) „
р 9 2
где с = y/n(ai — ао) • —.
Поскольку в нашем примере п = 3; а2 = 0,16; ai = 5,443 и a0 = 5,240,
то с > 0, и если мы положим
где Qa = 100 • 2a% и w^ - ф%-ная точка стандартного нормального
распределения, то неравенство
будет выполняться на множестве всех таких выборок {х\у...,хп)> для
которых у/п{х - ао) ? > Ug, или, что то же,
Получившееся правило проверки гипотезы не зависит от
альтернативного значения параметра аи а потому является (принимая во
внимание лемму Неймана-Пирсона) наиболее мощным при всех возможных
альтернативных значениях параметра а\ > ао, или, как принято в таких
случаях говорить, равномерно наиболее мощным.
8.3.2* Критерий логарифма отношения правдоподобия
для проверки простой гипотезы
Пусть известно, что ряд наблюдений х\,..., хп можно рассматривать
как независимую выборку из распределения, принадлежащего семейству
распределений F(x; 0), где 0 — Л-мерный параметр. Требуется
проверить гипотезу о том, что 0 = 0О (гипотеза (8.6), п. 8.1.3).

8.3 ПРИНЦИП ОТНОШЕНИЯ ПРАВДОПОДОБИЯ 293
Рассмотрим критерий
() ь...^п; в)}. (8.9)
где 0 — оценка (введенная в п. 7.5.1) максимального правдоподобия (ОМП)
параметра 0 по выборке а?1,...,жЛ. Доказано, что при наложении на
семейство F(x; 0) и на значение ©о дополнительных требований,
гарантирующих оптимальные свойства оценок максимального правдоподобия
(см. п. 7.5.1), величина 7 имеет асимптотически (при п -» оо) х ¦
распределение с к степенями свободы (см. [РаоС.Р.]).
В качестве примера применения критерия 7 рассмотрим еще раз
задачу проверки гипотезы о среднем значении нормальной совокупности,
приведенную в п. 8.3.1. В введенных там обозначениях с учетом того,
п
что оценка максимального правдоподобия параметра а0 есть х = * ? х^
имеем:
Поскольку в предположении справедливости гипотезы Но статистика х
нормально распределена со средним а0 и дисперсией <т2/п, 7 имеет
X -распределение с одной степенью свободы (в данном случае это
результат точный, а не асимптотический !).
8.3.3. Критерий отношения правдоподобия для проверки
сложной гипотезы
Рассмотрим модификацию критерия (8.9) для случая, когда в
гипотезе конкретизируются значения не всех параметров, как в предыдущем
пункте, а лишь части из них. Пусть 0 = \fii,..., Ok) — вектор
неизвестных параметров распределения и гипотеза состоит в том, что
Box: *j = 0oj, j = l,...,r<*. (8.10)
Удобно разбить вектор 0 на две части: ©i = @Ь...,0Г) и 02 =
@r+i,...,0fc). Обозначим 02 оценку максимального правдоподобия 02 по
выборке a?i,..., хп при известном значении 0i = 0Ох и @Ь 02) — оценку
максимального правдоподобия (ОЬ02). Критерий для проверки гипотезы
#oi имеет вид:
() м«п; ©Ь02)}. (8.11)

294 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Можно доказать, что при выполнении ряда дополнительных требований,
гарантирующих оптимальные свойства оценок максимального
правдоподобия (см. п. 7.5.1), величина 7*п) имеет асимптотически (при п -> оо)
X2-распределение с г степенями свободы.
8.4. Характеристики качества
статистического критерия
Характеристиками точности статистического критерия проверки
простых или сложных гипотез типа (8.6) служат:
а@) — вероятность отвергнуть основную гипотезу Яо, подсчитанная
в предположении, что истинное значение «проверяемого» параметра
равно ©; величину 1 -а@) называют оперативной характеристикой
критерия, а значение а(©0) в задаче проверки простой гипотезы «Яо: © = ©о»
есть не что иное, как уровень значимости (размер) критерия (вероятность
ошибки первого рода);
/?(©) — вероятность отвергнуть конкурирующую (с основной)
гипотезу, подсчитанная в предположении, что истинное значение
«проверяемого» параметра равно ©; величину 1 -/?(©) называют мощностью (или
функцией мощности) критерия, а значение /9(©i) в задаче проверки
простой гипотезы «Яо: 0 = ©о» против альтернативы «Я^ 0 = 0!» есть
не что иное, как вероятность ошибки второго рода.
Обсудим эти характеристики и зависящие от них свойства критерия.
Пусть ГЛ — область возможных значений критической статистики
7 , а Гп° и Тп1 — описанные в п. 8,2 соответственно области
«правдоподобных» и «неправдоподобных» (в условиях справедливости гипотезы
Яо) значений у . Тогда очевидно:
«.(в) = Pe{f(n) € if1} = J /7(lO(u,0)du;'
(8.12)
= J /y<«>(«; в) А*
где Рв{А) и /7(.)(и; 0) — соответственно вероятность события А и
плотность распределения критической статистики 7*"*, подсчитанные в
предположении, что истинное значение проверяемого параметра равно 6.

8.4 ХАРАКТЕРИСТИКИ КАЧЕСТВА КРИТЕРИЯ 295
В условиях проверки параметрических гипотез вида (8.6) с заданным
уровнем значимости а0 критерий {7(п)>Г^0} называется несмещенным^
если
ап@) < а0 при всех G € Ао;
() > «о при всех 0 $ До.
Г
I
И, наконец, критерий {т(п\г^0} называется состоятельным, если
lim an@) = 1 при всех 0 ? До.
Последнее соотношение означает, в частности, что функция
мощности состоятельного критерия 1 - /?п@) стремится (при п -+ оо) к единице
при любом значении 0, не входящем в область До гипотетичных (в
соответствии с гипотезой Но) значений параметра.
Из (8.12) очевидно, что при любом фиксированном объеме выборки п
перестройка критерия в направлении уменьшения уровня значимости а
(т. е. сужения области Гп') связана с одновременным увеличением
ошибки второго рода, а в общем случае — с уменьшением значений функции
мощности 1 - /7@) (так как при этом расширяется область Гп°
отклонения альтернативы Hi). И наоборот, перестройка критерия (в любом
фиксированном классе критериев, в том числе и в классе наиболее мощных
критериев) в направлении увеличения его мощности связана (при
фиксированном объеме выборки п) с неизбежным одновременным увеличением
его уровня значимости. В то же время неограниченным увеличением
объема выборки (т.е. при п -> оо) можно добиваться сколь угодно малых
значений для вероятностей ошибок вида
„ (аЛ@*)> где 0* G До С До, или
где 0**?ДО, или
Для больших объемов выборок (т.е. асимптотически по п -> оо)
существуют соотношения, связывающие между собой характеристики a* ,/3*
и п (см., например [Кендалл М. Дж., Стьюарт А., 1973. С. 310-311]).
Остановимся здесь на одном полезном соотношении такого типа, позволяющем,
в частности, определять объем выборки n(a>(i\ p), необходимый в
критерии отношения правдоподобия (Неймана-Пирсона) для различения двух
простых гипотез

296 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Яо: выборка извлечена из генеральной совокупности
/(Ж; 0о); (8.13)
#!: выборка извлечена из генеральной совокупности
с ошибками первого и второго рода, не превосходящими заданных
значений соответственно а и C\ величина р = p(HOyHi)} от которой также
зависит объем выборки п, характеризует «расстояние» между
гипотезами Но и Нг и определяется по формуле р(Но,Нг) = /In ffije') [f(x\®i)
-f(x; ©о)] dx, где интегрирование ведется по всей области возможных
значений наблюдаемой случайной величины я, а /(ж; 0) — ее плотность
распределения. В [Айвазян С. А., 1959] показано, что в достаточно широком
классе случаев при различении близких простых гипотез (т. е. при малых
значениях р) справедлива приближенная (асимптотическая) формула
в которой м9, как и прежде, квантиль уровня q (или g-квантиль)
стандартного нормального закона распределения.
Замечание. Обратим внимание читателя на практическую
неизбежность проявления двух «невыгодных» для всей теории проверки
статистических гипотез эффектов: эффекта «слишком малого объема
выборки» и эффекта «слишком большого объема выборки».
Эффект «слишком малого объема выборки» состоит в том, что при
заданной величине уровня значимости критерия а и малом числе
наблюдений п, на основании которых принимается решение, мощность критерия,
т. е. вероятность отклонить проверяемую «нулевую» гипотезу Яо в
ситуации, когда она в действительности не имеет места, оказывается слишком
маленькой (приближенное представление о взаимосвязи величин а,/? и п
дает формула (8.14)). Есть два выхода из этой ситуации: либо
увеличить объем выборки п, либо несколько увеличить уровень значимости а,
что повлечет соответствующее уменьшение fi (т. е. увеличение мощности
критерия 1 - /?).
Для пояснения эффекта «слишком большого объема выборки»
подчеркнем следующее: никто в действительности не считает, что какая-либо
гипотеза выполняется точно: мы просто строим абстрактную модель
реальных событий, которая в какой-то мере обязательно отклоняется от
истины; однако, как мы видим, огромная выборка почти наверняка (т. е. с

8.5 ПОСЛЕДОВАТЕЛЬНЫЕ КРИТЕРИИ 297
вероятностью, стремящейся к единице при неограниченном возрастании
п) отвергает в этом случае нашу гипотезу при любом заданном уровне
значимости а.
Казалось бы, налицо «тупиковая» ситуация: при малых выборках
вывод статистически ненадежен, а при слишком больших — однозначно
предопределен. Так, например, авторы неоднократно наблюдали
обескураживающее действие эффекта больших п на прикладника-исследователя,
пытающегося с помощью критериев согласия подобрать подходящий
модельный закон FM0Jl(x) для описания распределения исследуемой
генеральной совокупности и неизменно приходящего при этом к отрицательному
результату (т.е. к отвержению проверяемой гипотезы).
Чтобы избежать эффекта большой выборки, априорное задание
характеристик точности критерия (уровня значимости а и ошибки второго
рода /3) необходимо увязывать с объемом имеющихся данных п: выигрыш
в «чувствительности» критерия, получающийся в результате
увеличения п, целесообразно использовать для уменьшения как а, так и /3. В
частности, если определить уменьшение а при возрастании п, то очень
малые отклонения от Яо уже не приведут к обязательному отвержению
этой гипотезы: вероятность этого факта будет зависеть от того, с какой
«скоростью» (с ростом п) убывает а.
8.5. Последовательная схема принятия
решения (последовательные критерии)
8.5.1. Последовательная схема наблюдений
Если число наблюдений, на основании которых статистик принимает
решение, не фиксируется заранее, но ставится в зависимость от
результатов зарегистрированных на каждой данной стадии эксперимента
наблюдений, то говорят об использовании последовательной схемы
наблюдений. Поскольку результаты наблюдений на каждой фиксированной
стадии эксперимента представляют собой случайную выборку из генеральной
совокупности и, следовательно, случайны по своей природе, то и момент
прекращения наблюдений (определение которого зависит от этих
результатов) также является величиной случайной.
Впервые идея об использовании последовательной схемы наблюдений
возникла в ходе конструирования экономных планов выборочного стати-
1 Это следует из свойства состоятельности критерия (см. выше).

298 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
стического контроля качества продукции1. Речь шла о выборочной
проверке того факта, что неизвестная нам истинная доля р дефектных
изделий во всем производстве не превосходит некоторого порогового значения
(предельно допустимой доли брака) р0- Авторы упомянутой работы
предложили для этой цели методику проверки с двукратной выборкой. На
первом этапе предложенной ими последовательной схемы извлекается
одна выборка изделий объема щ и оценивается доля брака р% в этой
выборке. Решение о необходимости контроля второй выборки принимается на
основании результатов наблюдений в первой выборке: грубо говоря, если
доля брака в первой выборке р\ оказалась существенно меньше (или
существенно больше) заданного порогового значения ро, то необходимости
в повторной выборке нет и принимается гипотеза р < ро (или
соответственно альтернатива р > р0); если же доля брака р\ в первой выборке
несущественно отличается от заданного порогового значения ро (или, как
говорят, находится в «зоне неопределенности», или в «зоне безразличия»),
то принимается решение о продолжении наблюдений и, в частности, об
извлечении второй выборки объема п2.
При такой методике достигается заметный выигрыш (в среднем) в
числе наблюдений, необходимом для различения интересующих нас
гипотез с заданными характеристиками точности (уровнем значимости а и
мощностью 1 — /3) по сравнению с критерием Неймана-Пирсона,
являющимся наилучшим (наиболее мощным, см. п. 8.3.1) среди всех критериев,
основанных на классической схеме наблюдений (т. е. построенных на
базе выборок заранее заданного объема п). Поэтому к последовательной
схеме наблюдений целесообразно обращаться в ситуациях, когда каждое
наблюдение является дорогостоящим или труднодоступным и по
условиям эксперимента исследователь имеет практическую возможность
реализовать эту схему (далеко не всегда исследователь находится в подобных
условиях).
К величинам а@) и /3@), характеризующим «качество» всякого
критерия (см. п. 8.4), при рассмотрении последовательных критериев
добавляется еще средний объем выборки Еег/(а,/9), необходимый для
проверки гипотез вида (8.6) с заданными характеристиками точности (а,/?)
(нижний индекс 0 при знаке математического ожидания Б означает, что
усреднение проводится при истинном значении параметра, равном 0).
1 Dodge H.F., Romig H. G. A method of sampling inspection — The Bell System
Techn. Journ., 8 A929), pp. 613-631.

8.5 ПОСЛЕДОВАТЕЛЬНЫЕ КРИТЕРИИ 299
8.5.2. Последовательный критерий отношения
правдоподобия (критерий Вальда) и его свойства
Построение статистического критерия при фиксированном объеме
выборки п (см. п. 8.3.1) сводится в конечном счете к разбиению области
возможных значений критической статистики 7 = l(x\><- чхп) на две
части: область правдоподобных и область неправдоподобных (в условиях
справедливости проверяемой гипотезы Яо) значений 7 • При попадании
конкретного значения 7(жъ • • • > #п) в область неправдоподобных значений
принимается решение об отклонении проверяемой гипотезы.
Последовательный критерий, т.е. критерий, основанный на
последовательной схеме наблюдений, построен по той же логической схеме с
одним отличием: последовательно для каждого фиксированного объема
выборки и = 1,2,...,п, п + 1,... область Г„ возможных значений
критической статистики j(xi,...,х„) разбивается на три непересекающих-
WW Ж*
ся части: область Г„ ° правдоподобных, область Г„ неправдоподобных и
область Г„ сомнительных (в условиях справедливости проверяемой
гипотезы Яр) значений, т.е.
На каждом v-ы шаге последовательной схемы наблюдений, т.е. при
наличии наблюдений %\,..., х„, v — 1,2,..., решение принимается по
следующему правилу:
если 7(жъ • • • >ху) € Г„°, то проверяемая гипотеза Яо принимается;
если 7(жь--->а?„) € Г^1, то проверяемая гипотеза Яо отвергается
(или принимается некоторая альтернатива Н\)\
если y(xi,...,хи) 6 Гу, то окончательный вывод откладывается и
производится следующее (i/+ l)-e наблюдение (поэтому область Г* иногда
называют областью неопределенности или областью продолжения
наблюдений).
Таким образом, для того чтобы иметь какой-то конкретный
статистический критерий, надо конкретизировать: а) тип проверяемой
гипотезы; б) способ построения критической статистики 7(жь•••)«!/); в) способ
построения областей Г,/, IV1 и Г? по заданным (требуемым) значениям
характеристик точности критерия.
В качестве конкретного примера последовательного критерия
рассмотрим известный критерий отношения правдоподобия Вальда,
предназначенный для различения двух простых гипотез вида (8.13).
Критическая статистика этого критерия для последовательности не-

300 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
зависимых наблюдений х\,..., х„ определяется соотношением
7 -l
Области правдоподобных (Г^0), неправдоподобных (Г,,1) и
сомнительных (Г^), в условиях справедливости гипотезы #0, значений
критической статистики 7 приближенно задаются соотношениями:
(8.16)
Была доказана оптимальность этого критерия среди всех других
возможных последовательных критериев, а именно: среди всех критериев,
различающих гипотезы (8.13) с ошибками первого и второго рода, не
превосходящими заданных величин, соответственно аи/З, критерий (8.15)—
(8.16) требует наименьшего среднего числа наблюдений Е@ z/(a,/?) как в
условиях справедливости гипотезы #o(t = 0), так и в условиях
справедливости гипотезы Н\{% = 1) [Вальд].
* Исследования показали, что этот критерий примерно в два-четыре
раза выгоднее (по затратам на наблюдения), чем наилучший из
классических критериев — критерий Неймана-Пирсона [Айвазян С. А., 1959].
8.6. Методы проверки статистических
гипотез: примеры статистических
критериев
8.6Л. Критерии согласия
Критерии согласия предназначены для статистической проверки
гипотез о модельном виде закона распределения вероятностей (з.р.в.)
исследуемой случайной величины. Пусть FWOTk(x\0\,. ..,0/ь) — гипотетичный
модельный вид функции распределения анализируемого з.р.в. Функция
^мод(я;0ъ-**90*) может однозначно задавать исследуемый з.р.в. (тогда
все значения параметров в\,...,вк известны априори), а может обозначать

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 301
лишь гипотетичный тип искомого з.р.в., определяемый целым
параметрическим семейством {FMOfl(a:;0i,...,0fc)} (например, мы хотим проверить
гипотезу о том, что з.р.в. анализируемой случайной величины
описывается нормальной моделью, см. п. 3.1.5).
Таким образом, описываемые в данном пункте критерии согласия
предназначены для проверки гипотезы
Яо: Fc(x)e {W*;*lf...A)}> (8-17)
на основании п независимых наблюдений (8.1) анализируемой случайной
величины ?, функция распределения которой, как обычно, обозначена с
помощью F((x). Критические статистики этих критериев основаны на
различных мерах расстояний между анализируемой эмпирической
функцией распределения F^n\x) (см. п. 6.2.1) и гипотетическим семейством
Там, где речь идет о группированных выборочных данных, мы будем
придерживаться терминологии и обозначений п. 6.1.
Критерий согласия х Пирсона. Этот критерий позволяет
проверять гипотезы вида (8.17) как для дискретных, так и для непрерывных
случайных величин в ситуациях, когда параметры ви...вк априори
известны или являются неизвестными. Метод проверки (критерий) основан
на теореме Пирсона-Фишера, которые доказали, что если гипотеза (8.17)
истинна, то при некоторых достаточно общих условиях распределение
критической статистики
W ?("J§))' (8.18)
сходится (при п —> оо) к х (з - А - 1 ^распределению.
Для объяснения обозначений в соотношении (8.18) разберем отдельно
случаи непрерывной и дискретной случайных величин.
В непрерывном случае статистика (8.18) строится по группированным
данным. Группировка данных (8.1) производится в соответствии с
рекомендациями и обозначениями п. 6.1, т. е.: з — это общее число интервалов
группирования; Uj — число выборочных данных, попавших в j-й интервал
группирования; 0 = @ъ...,0*) — векторный параметр, который
участвует в выражении модельной функции распределения ^Мод(я;0ь. ..,#*)?
а 0 — его состоятельная оценка (более корректным способом оценивания
считается тот, при котором в качестве 0 используется оценка
максимального правдоподобия, построенная по группированным данным); при этом

302 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
к в теореме Пирсона-Фишера обозначает число неизвестных параметров,
оцениваемых по выборке, так что в случае априори известных значений
параметров к = 0; наконец, Pj(Q) — это результат модельного расчета
вероятности попасть в j-й интервал группирования, т. е.
Р;(в) = WCi;0) ~ We*-i;§), (8-19)
где Cj_i, Cj — соответственно левый и правый концы j-ro интервала
группирования (j = 1,2,..., s).
Случай анализа дискретной случайной величины отличается от
предыдущего лишь тем, что мы работаем с исходной (а не группированной)
выборкой (8.1), i/j — это число выборочных данных, равных j-му
возможному значению ж$, a — число всех возможных значений случайной
величины, а
S). (8.19')
Итак, теорема Пирсона-Фишера дает нам основание следующим
образом построить процедуру проверки гипотезы (8.17).
1) По выборочным данным (8.1) (сгруппированным при анализе
непрерывной случайной величины) строим состоятельные оценки §
параметров 0 = @1>...*0*)'
2) В соответствии с формулами (8.18)-(8.19)~(8.19') подсчитываем
значение критической статистики 7*Л^
3) По заданному уровню значимости критерия а из таблиц
процентных точек х2-распределения находим 100A - а/2)- и 100а/2%-ные точки
Xi-o/a(^ - Л - 1) и Ха/2(* - А - 1) «хи-квадрат» распределения с a - к - 1
степенями свободы.
4) Если Xi-at/2(* - к - 1) < 7(п) < Ха/2(* - к - 1), то гипотеза (8.17)
не отклоняется; если же 7 ^ Xi-a/2(* - А -1) или 7 ^ Х«/2(* - А? - 1),
то гипотеза (8.17) отклоняется .
1 Отвержение выдвинутой гипотезы в случае «слишком маленьких» значений
статистики критерия 7^") на первый взгляд противоречит здравому смыслу.
Действительно, статистика 7^ характеризует степень отклонения эмпирического
распределения случайной величины ? от гипотетического F: чем меньше 7*п\ тем меньше
это отклонение. Казалось бы, идеальный случай достигается при 7^ г 0. Однако
надо отметить, что хотя 7^ и является мерой отклонения гипотетического закона
F от истинного, но мерой случайной, т. е. величиной, подверженной обязательному
неконтролируемому разбросу. И в этом отношении одинаково неправдоподобными
(маловероятными) следует считать как слишком большие значения 7^п\ так и слиш-

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 303
Так, например, при проверке гипотезы нормальности гипотетический
закон Fmoa будет иметь вид:
а в качестве оценок а и а2 двух неизвестных параметров а и <т2 будут
фигурировать величины
(через x°j обозначается, как и прежде, средняя точка интервала
Значения F(cj\&>&2) = Ф(е^;й,?2), необходимые для подсчета
вероятностей Pi, можно найти, например, из таблицы значений функции
стандартного нормального распределения с учетом соотношения Ф(а?;а,<72) =
Ф(?=А;0,1). Число степеней свободы закона распределения х,
процентные точки которого нам понадобятся, будет равно в данном случае з - 3,
где а — число интервалов группирования.
Пример 8.1. В качестве анализируемой случайной величины у
рассматривается среднедушевой месячный доход (в условных денежных
единицах) домашнего хозяйства некоторого региона. Обследовано 750
домашних хозяйств этого региона (п = 750). В таблицах 8.1а и 8.16
приведены результаты группировки выборочных данных (у,) и их
логарифмов (я, = ln!/i) соответственно (ширина интервала группирования
исходных данных равна 25 усл. ден. ед.).
ком малые. О чем же свидетельствуют слишком малые значения 7^? Одной из
причин подобной «ненормальности» может служить неудачный выбор закона F —
искусственное завышение числа параметров, от которых этот закон зависит.
Другими причинами могут служить нарушения корректности или объективности техники
выборочного обследования, стремление «подогнать» экспериментальные данные под
желаемый результат и т. п.

304
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Таблица 8.1а
Номер
интервала
со
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
Число выборочных
данных, попавших
в этот интервал
(";)
2
15
44
83
108
НО
83
75
49
34
27
21
24
13
13
19
8
3
2
2
Номер
интервала
U)
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Число выборочных
данных, попавших
в этот интервал
to)
1
3
1
2
0
1
0
1
1
2
0
1
0
0
0
0
1
0
0
1

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
305
Таблица 8.16
Номер
интервала
(i)
i
2
3
4
5
6
7
8
9
Число выборочных
данных, попавших
в этот интервал
1
1
0
7
8
15
39
73
109
Номер
интервала
U)
10
и
12
13
14
15
16
17
18
Число выборочных
данных, попавших
в этот интервал
141
123
86
65
52
14
8
5
3
А
Воспользуемся критерием согласия \ Пирсона для проверки
нормальности случайной величины ? = Ьт/ по данным, представленным в
табл. 8.16 (одновременно, соответственно, проверяется логарифмическая
нормальность данных, представленных в табл. 8.1а).
Оценим вначале неизвестные значения параметров а = Е? к а2 = D?
гипотетического нормального распределения по группированным данным,
представленным в табл. 8.16:
18
750
18
1 18
*2 = 749 S "i ' (*5 - йJ = 0,366; Ь = 0,605.
В данном случае
= Ф
- Ф
гле Cj — правый конец j-то интервала группирования (j = 1,..., 18), с0 =
2,5, а Ф(г) — значение функции распределения стандартного нормального
закона в точке z (определяется из табл. П1.2, см. Приложение 1).
Результаты остальных расчетов приведены в табл. 8.2.

306
Таблица 8.2
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Номер

интервала (j)
0
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
2,50
2,75
3,00
3,25
3,50
3,75
4,00
4,25
4,50
4,75
5,00
5,25
5,50
5,75
6,00
6,25
6,50
6,75
7,00
-4,13
-3,72
-3,30
-2,89
-2,48
-2,07
-1,65
-1,24
-0,83
-0,41
0,00
0,41
0,83
1,24
1,65
2,07
2,48
2,89
3,30
*(^)
10"в•18
10"в• 100
10"в-484
10"в • 1926
10"в-6569
10"в • 19226
10"в-49472
0,107488
0,203269
0,340903
0,500
0,659
0,797
0,893
0,951
0,981
0,993
0,998
0,999
р,-@) -
82•10"в
3,84-10
1,44-10~3
4,64-10
12,66-10
30,25-10
0,058016
0,095781
0,137634
0,159097 '
0,159
0,138
0,096
0,058
0,030
0,012
0,005
0,001
nPj(@)
0,062
0,288
1,082
3,484
9,493
22,684
43,512
71,836
103,226
119,323
119,250
103,500
72,000
43,500
22,500
9,000
3,750
0,750
D-п„л6))а
nPi(S)
14,19
1,76
1,08
3,55
0,23
2,60
0,47
0,02
0,32
3,94
0,18
2,96
0,68
1,66
3,21
0,11
0,42
6,75
44,13
Проверка гипотезы о нормальности анализируемых наблюдений
основана на сравнении значения критической статистики (8.18) с табличными
значениями процентных точек х*(*- * -1 ^распределения (см. табл. П1.4).
В нашем случае число интервалов группирования в = 18, число оцененных
по выборке параметров к = 2. Задавшись уровнем значимости критерия
а = 0,05, имеем:
Х1-9(* - к - 1) = хо,975A5) = 6,26; Х\(* -*-!) = Хо,О2вA5) = 27,49,
так что, поскольку 7*п) = 44,13 > 27,49, мы вынуждены отклонить
гипотезу о нормальности анализируемой случайной величины.
Заметим, правда, что решающий вклад в завышенное значение кри-

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
307
тичесхой статистики 7 внесли слишком тяжелые «хвосты»
эмпирического распределения (см. слагаемые этой статистики, соответствующие
первому и последнему интервалам группирования). Поэтому изображен*
ные на рис. 8.2а и 8.26 гистограммы и модельные (соответственно, логнор-
мальная и нормальная) плотности анализируемого распределения
демонстрируют вполне приличное соответствие между выборочными и
гипотетическими модельными законами.
150 300 450 600 750 900
28/15
24/15
20/15
16/15
12/15
8/15
4/15
0
\
\
х = lny
2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 7,0
Рис. 8.2. Гистограмма и теоретическая (модельная) плотность,
характеризующие распределение семей по среднедушевому месячному
доходу (а) и по логарифму среднедушевого месячного дохода (б)

308
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Критерий Колмогорова-Смирнова. Этот критерий позволяет
осуществлять проверку гипотезы (8.17) в условиях, когда модельная
функция FMOU(x) = Fq(x) известна полностью, т.е. не зависит от неизвестных
параметров.
Цусть F^n'(x) — эмпирическая функция распределения. Введем
следующие меры уклонения (расстояния) между функциями F^n\x) и Fo(x):
Статистики y/nDt и y/nDZ являются статистиками критериев
Колмогорова и Смирнова соответственно. При этом
Для практического использования критерия Колмогорова-Смирнова
статистики Dn,Dn>Dn представляются в виде:
Dt = max ( ^ - tt) ;
D~ = max
= max
где t{ = Fo(a?(i)), т.е. это значение гипотетической функции
распределения, взятой в г-й точке вариационного ряда.
рц
Для статистик Z?n, Dn , D~ известны точные распределения [Большее Л. Н.,
СмирновН. В.]. Здесь приведем лишь распределение для D%
О, d < 0;
P{Dt < d} = <
х h _ L _ dj
1, Ol,
о < d < 1;

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 309
где [п- nd\ — целая часть числа п - nd.
Для практических целей обычно достаточно предельных
распределений статистик
где
К(Х) =
lim P(V
n—юо
lim P(y/
n—*oo
Jfc—
0
nDn <
nDt<
A) =
A) =
ЛГ(А);
5(A),
*
A
A
>
<
0;
0;
(О А < 0.
Предельное распределение для статистики y/nDn в точности совпадает
с 5(А).
8.6.2. Критерии однородности
Переходим к описанию некоторых наиболее распространенных
статистических критериев, предназначенных для проверки гипотез об
однородности двух или нескольких анализируемых генеральных
совокупностей, где однородность понимается в том или другом смысле (см. выше,
п. 8.1.2).
Критерий однородности Смирнова. Этот критерий
предназначен для проверки гипотезы совпадения з.р.в. в двух или нескольких
генеральных совокупностях по группированным выборкам, извлеченным из
этих совокупностей, т.е. речь идет о проверке гипотез типа (8.4а). Пусть
имеется / выборок (8.3) объемов соответственно гц, щ,..., щ и пусть
данные каждой из этих выборок сгруппированы так, как это описано в п. 6.1,
причем разбиение диапазонов исследуемых случайных величин на
интервалы группирования во всех выборах произведено одинаковым способом
(при этом выбор общего диапазона варьирования анализируемого
признака во всех выборках определяется наименьшим, по всем выборкам, из
минимальных выборочных значений и наибольшим из максимальных
выборочных значений). Итак, мы имеем s одних и тех же для всех выборок
интервалов группирования и пусть i/y — количество элементов i-й
выборки, попавших в j'-й интервал (г = 1,2,...,/; j = 1,2,...,б). В качестве

310 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
критической статистики критерия используется величина
5 I
где щ% = ? v%i == nt — общее число элементов t-й выборки, i/j = J? i/y —
jssl 1=1
общее (по всем выборкам) число выборочных данных, попавших в j-й ин-
тервал группирования и п = X} Z) v%j ~ суммарный (по всем выборкам)
t=i j=i
объем выборочных данных.
Н. В. Смирновым было доказано, что при неограниченном росте
объемов всех выборок и в условиях справедливости проверяемой гипотезы
(8.4а) з.р.в. статистики (8.20) стремится к закону х с числом степеней
свободы, равным (/ - 1)(* - 1). Поэтому, в соответствии с общей логикой
статистического критерия (см. выше, п. 8.2) гипотеза (8.4а) отвергается,
если 7(П) < Xi-f(C - 1)(* - 1)) или 7(п) > х\(A - 1)(* - 1)), и
принимается при всех остальных значениях критической статистики 7 (здесь,
как обычно, Xq{™) — табличное значение 100^%-ной точки «хи-квадрат»
распределения с т степенями свободы).
В частном случае двух выборок (т. е. при / = 2) статистика (8.20)
может быть записана в виде
и при условии справедливости гипотезы однородности она будет
приблизительно распределена (при больших объемах щ и щ) по закону х с s — 1
степенью свободы.
Пример 8.2. В табл. 8.2 приведены условные данные о заработной
плате работников двух отраслей. В данном примере число сравниваемых
генеральных совокупностей / = 2 и объемы выборок щ = п2 = 100.
Проверим (при уровне значимости критерия а = 0,05) гипотезу о том, что
распределения работников по заработной плате не отличаются друг от
друга в двух анализируемых отраслях.
Вычисление критической статистики (8.20') в данном случае дает:
8 (aiL- Z
7(П) = пщ2 Т V^ , %ту = > J N.;J Г" = 14,58.

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
311
Из таблиц процентных точек % -распределения (см. приложение 1)
определяем пятипроцентную точку «хи-квадрат»-распределения с семью
степенями свободы Хо,обG) = 14,07. Следовательно, гипотезу о
совпадении вероятностных распределений работников по заработной плате в двух
анализируемых отраслях мы должны отвергнуть G > Хо,овG))«
Вероятность ошибиться при этом равна 0,05.
Таблица
Номер
интерв.
группы
U)
1
2
3
4
5
6
7
8
. 8.3
Интервал
заработной
платы
(уел, ден. ед.)
130-150
150-170
170-200
200-250
250-300
300-350
350-400
400-500
Кол-во работников,
попавших в данный интервал
К)
из выборки
1-й отрасли
4
4
15
51
22
3
1
-
К)
из выборки
2-й отрасли
1
1
8
43
34
7
3
3
5
5
23
94
56
10
4
3
"i, - Hi
3
3
7
8
-12
-4
-2
-3
Описанный метод проверки однородности относится к
непараметрическим критериям, так как используемая в нем критическая статистика
никак не зависит от наших предположений относительно
параметрического общего вида анализируемых распределений (или, как иногда
говорят, «свободна от распределения». В этом его преимущество перед
параметрическими критериями. Однако его реализация требует достаточно
больших объемов анализируемых выборок (по меньшей мере они
должны содержать по несколько десятков наблюдений). Следующий критерий
также относится к непараметрическим, однако требования к объемам
выборок здесь существенно мягче.
Критерий Вилкоксона-Манна-Уитни. Этот критерий
предназначен для проверки однородности двух генеральных совокупностей,
понимаемой в смысле отсутствия различий в значениях параметров
местоположений (средних значений, медиан) соответствующих распределений
(но не тождественного совпадения распределений, как это было в
предыдущем критерии). Т.е. речь идет о проверке гипотез типа (8.46).
Итак, мы располагаем выборками (8.3), извлеченными из двух
генеральных совокупностей (/ = 2). Пронумеруем эти выборки так, чтобы
обеспечить выполнение неравенства щ < щ> Объединим выборки и по

312 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
объединенной выборке объема щ + п2 построим общий вариационный ряд.
Обозначим ЯI' — порядковый номер (ранг), который получает при этом
1-й член вариационного ряда, построенного только по первой выборке,
в общем вариационном ряду (т.е. щ ' — это ранг элемента хцц в
общем вариационном ряду, где хц\)ухц2),. ..,хцП1) — вариационный ряд,
построенный только по первой выборке).
Критическая статистика описываемого критерия имеет вид
<> X> (8.21)
и носит название «суммы рангов».
Удалось показать, что в условиях справедливости проверяемой
гипотезы (8.46) статистика (8.21) ведет себя (асимптотически по щ —> оо
так, что Ит^пх/пг) = с > 0) как нормально распределенная случайная
величина с параметрами
Ь «2 + 1),
(8.22)
2 тк (n) ! / , \
<т = D7 = 777nin2(ni + пг)-
При этом сходимость к нормальному распределению очень быстрая:
оно уже эффективно работает при щ > 8.
Это позволяет построить следующее правило проверки гипотезы
(8.46).
1) По заданному уровню значимости критерия а с помощью таблиц
квантилей (процентных точек) стандартного нормального распределения
определяем квантиль Щ-а/2 уровня 1-а/2 (или 100а/2%-ную точку)
стандартного нормального распределения.
2) Вычисляем стандартизованное значение критической статистики
()
/(г +п2)
где значение 7 вычислено по формуле (8.21).
3) Бели окажется, что
то проверяемую гипотезу следует отвергнуть (и соответственно принять
при всех других значениях стандартизованной критической статистики
7ст /•

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 313
Отметим в заключение, что существуют таблицы процентных точек
критической статистики (8.21) (подсчитанные при условии
справедливости гипотезы однородности) и для доасимптотического случая, т. е. для
п < 8 (см. [Большее Л. Н., Смирнов Н. В.]).
Строго говоря, описанные ниже критерии однородности (критерий
Стьюдента, или ?-критерий; критерий дисперсионного отношения,
критерий Бартлетта и др.) применимы только к выборкам (8.3), извлеченным
из нормальной генеральной совокупности: в этом случае, как легко понять,
неотрицательный результат одновременной проверки однородности
средних значений (т.е. гипотезы (8.46)) и дисперсий (т.е. гипотезы (8.4в))
достаточен для неотрицательного вывода по поводу гипотезы об
однородности самих законов распределения {т.е. гипотезы (8.4а)). Специальные
исследования показали, однако, что ^-критерий является (особенно при
больших объемах выборок п) весьма устойчивым по отношению к
отклонениям исследуемых генеральных совокупностей от нормальных. А это
значит, что он может применяться и к выборкам из негауссовских
генеральных совокупностей с той лишь оговоркой, что истинные значения
уровня значимости и мощности критерия в этом случае будут несколько
отличаться от заданных.
Критерий Стьюдента (t-критерий). Этот критерий
предназначен для проверки гипотезы однородности средних значений (8.46) в двух
нормальных генеральных совокупностях, имеющих одинаковую (хотя и
неизвестную) дисперсию а . В качестве критической статистики в данном
критерии используется величина
У
где Xj(nj) и Sj(nj) — соответственно выборочные средние и выборочные
дисперсии, построенные по j'-й выборке (j = 1,2), а з2 вычисляется по
выборочным дисперсиям з\(п\) и s\{п2) по формуле
П\ "т* 71-2 """ **
При анализе статистики нормального закона (см. п. 6.2.8, формулу
F.377)) нами было показано, что в условиях справедливости гипотезы
(8.46) (и при дополнительном условии равенства дисперсий в двух
анализируемых генеральных совокупностях) статистика (8.24) должна
подчиняться распределению Стьюдента с щ + п2 - 2 степенями свободы.
Поэтому, определив из таблиц (при заданном уровне значимости критерия а)

314 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
100а/2%-ную точку ia/2(ni +п2-2) «-распределения с п\ +п2 -2 степенями
свободы, мы принимаем решение об отклонении гипотезы однородности
(8.46), если окажется, что 7 , вычисленная по формулам (8.24)-(8.25),
по абсолютной величине превзойдет значение ta/2 (пг + п3 - 2).
Замечание. Слишком большое значение статистики (8.24), т. е.
такое, при котором отвергается проверяемая гипотеза однородности,
может быть следствием как статистически значимого расхождениж
выборочных средних (т.е. невыполнения гипотезы (8.46)), так и
статистически значимого расхождениж дисперсий (т.е. невыполнения гипотезы
(8.4в)). Поэтому если мы хотим понять, за счет чего обнаружилась
неоднородность анализируемых выборок, то необходимо произвести
дополнительно проверку однородности дисперсий, т.е. гипотезы (8.4в). Эта же
задача может являться и самостоятельной (автономной) целью
исследования.
Критерий дисперсионного анализа является обобщением
?-критерия на случай более чем двух сравниваемых совокупностей (т.е.
/ > 2). В этом случае критерий принадлежности нескольких выборок
(8.3) из нормальных генеральных совокупностей с одинаковой (но
неизвестной) дисперсией к одной общей совокупности основан на критической
статистике
!_, , (8>2б)
3
I
* = ? nj*j(nj)/(ni Н Н щ) — общее выборочное среднее значение, а
(8.27)
Доказано, что если в рамках сформулированных выше условий
справедлива гипотеза однородности (8.46) (а это будет означать, в силу
нормальности сравнимаемых совокупностей и одинаковости их дисперсий, и
справедливость более сильной гипотезы (8.4а)), то статистика (8.26)
подчиняется F-распределению с числом степеней свободы числителя, равным
/ -1, и числом степеней свободы знаменателя, равным щ + п% + • • • + щ - /.
Поэтому, если окажется, что вычисленная по формуле (8.26) статистика
(8.28)

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 315
то гипотезу (8.4а) об однородности выборок (8.3) следует отвергнуть
(в правой части (8.28) Fa(l - 1; ? nt - /) — 100а%-ная точка F-
распределения с указанными выше числами степеней свободы числителя
и знаменателя).
F-критерий однородности дисперсий. Этот критерий
предназначен для проверки гипотезы однородности дисперсий (8.4в) в двух
нормальных генеральных совокупностях. Он основан на использовании
критической статистики
^Ф\ (8.29)
где все обозначения соответствуют ранее введенным.
При анализе статистики нормального закона (см. п. 6.2.8, Следствие 5,
формула F.38)) нами было показано, что в условиях справедливости
гипотезы (8.4в) статистика (8.29) должна подчиняться /^-распределению с
числами степеней свободы числителя и знаменателя, равными
соответственно п\ -1 и па -1. Поэтому при заданном уровне значимости критерия
аопределяем 100A-а/2)%-нуюи 100а/2%-нуюточки Л-а/2(я1~1|Я2~1)
и <Fa/2(fti - 1>П2 - 1) (см. таблицы в приложении 1). Бели окажется, что
- 1,п2 - 1) < 7(л) < F«l%{nx - l.iia - 1),
то гипотеза однородности дисперсий не отвергается (и отвергается при
всех других значениях статистики (8.29)).
Пример 8.3. Реклама утверждала, что из двух типов
пластиковых карт «American Exspress» и «Visa» богатые люди предпочитают
первый. Другими словами, среднемесячные платежи одного
среднестатистического обладателя «American Express» существенно
(статистически значимо) превышают среднемесячные платежи одного
среднестатистического обладателя карты «Visa» . С целью статистической проверки
этого утверждения были обследованы среднемесячное платежи 32
обладателей «American» (щ = 32) и 30 обладателей «Visa» (n2 = 30). В
результате первичной статистической обработки этих двух выборок были
получены следующие значения выборочных характеристик:
^i(^i) = $563 ^2(^2) = $485
?i(fti) = 31684 ?2G*2) = 38416.
Требуется проверить гипотезу (8.46) с уровнем значимости
а = 0,05.

316 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Предварительный анализ законов распределения месячных расходов
как среди обладателей «American» , так и среди обладателей «Visa»
показал, что и тот и другой з.р.в. достаточно хорошо описываются нор-
мальной моделью. Но перед тем, как использовать в решении
поставленной задачи J-критерий (критерий Стьюдента), необходимо убедиться в
однородности дисперсий в анализируемых совокупностях, т. е. проверить
гипотезу (8.4в) при / = 2. С этой целью воспользуемся F-критерием.
Для экономии места таблицы процентных точек составлены только для
случая, когда числитель больше знаменателя, поэтому, если в статистике
(8.31) числитель оказывается меньше знаменателя, то следует изменить
нумерацию выборок. Поэтому в нашем случае выборкой Х« 1 будем
считать выборку из совокупности пользователей «Visa» (т.е. щ = 30).
Итак, в нашем примере отношение (8.29) оказывается равным
1,22. Из таблиц процентных точек находим пятипроцентную точку
^о,О5B9; 31) « 1,84, а поскольку 1,22 < 1,84, то мы имеем основание
принять допущение о равенстве дисперсий в анализируемых совокупностях
в качестве статистически проверенной рабочей гипотезы.
Теперь мы имеем основания воспользоваться критерием Стьюдента
для проверки гипотезы.о равенстве средних значений.
Вычисление критической статистики 7 по формуле (8.24) дает:
1781) (& + &)
Из таблиц процентных точек находим *о,02бC0 + 32 — 2) = 2,00. И
поскольку |7 | = 1,61 < 2,00, то мы делаем вывод о непротиворечивости
гипотезы однородности средних значений имеющимся в нашем
распоряжении статистическим данным. Следовательно, утверждения рекламы о
более высокой состоятельности обладателей «American Express» не имели
объективных оснований.
Критерий Бартлетта позволяет проверять гипотезу об
однородности дисперсий в нескольких (в том числе более чем в двух) нормальных
генеральных совокупностях. Критическая статистика критерия
предложена Бартлеттом и имеет вид
Ш (8-зо)
В формуле (8.30) величина S2 определяется соотношением (8.27),

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 317
- 1), а
(8.31)
При min(ni,..., щ) > 3 в условиях справедливости проверяемой
гипотезы статистика (8.30) распределена приблизительно по закону % с / — 1
степенями свободы. Поэтому (при уровне значимости критерия а) если
оказалось, что вычисленная по формуле (8.30) величина 7п > ХаA — 1)? то
гипотезу об однородности дисперсий в анализируемых нормальных
генеральных совокупностях следует отвергнуть (х«(* - 1) — 100а%-ная точка
«хи-квадрат» -распределения с / — 1 степенями свободы).
8.6.3. Проверка гипотез о числовых значениях параметров
Остановимся теперь на примерах статистических критериев,
позволяющих проверять гипотезы вида (8.6). При этом важные статистические
критерии такого типа, относящиеся к корреляционному анализу, моделям
регрессии, анализу временных рядов, системам одновременных
уравнений, будут обсуждаться в контексте изложения этих тем соответственно
в гл. 10, 11 и в гл. 2, 3 и 4 второго тома. В данном пункте мы опишем
несколько примеров статистических критериев, предназначенных для
проверки простых основных гипотез (чаще всего — при простых же
альтернативах) относительно числовых значений параметров анализируемых
законов распределения вероятностей, т. е. речь идет о проверке основной
(«нулевой» ) гипотезы
-ПО- ЧУ — ysQ
против альтернативы (8.32)
Н\\ 0 = 01 (или 0 ф 0О),
где 0о и ©1 — заданные числовые значения параметра, который
участвует в модельном описании функции распределения вероятностей
анализируемой случайной величины ? (т.е. Р{? < х} = F^(x;Q)).
Критерии проверки гипотез о числовом значении параметра
р биномиального распределения. Рассматриваемая задача
относится к анализу результатов серии п независимых испытаний Бернулли (см.
п. 3.1.1). При этом в имеющейся у нас выборке объема п интересующее нас
событие произошло х раз. Можно интерпретировать эту серию (выборку)
как единственное наблюдение (п,р)-биномиальной случайной величины в

318 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
ситуации, когда параметр п известен, а параметр р нет. Далее речь
пойдет о проверке гипотез типа (8.32), где роль параметра 0 играет параметр
р, т. е. о проверке (по имеющимся у нас результатам наблюдения)
гипотез о численном значении параметра р биномиального распределения при
различных альтернативах.
Принимая во внимание утверждение леммы Неймана-Пирсона о том,
что критерии отношений правдоподобий являются наиболее мощными
среди всех других возможных критериев (см. п. 8.3.1), попробуем вывести
критическую статистику критерия, руководствуясь именно этим
принципом. При этом нам удобнее будет, как это часто бывает при работе с
функциями правдоподобия, не само отношение правдоподобия, а его логарифм
(монотонность этого преобразования обеспечивает нужный результат).
Функция правдоподобия биномиального закона с параметрами п и
р при единственном наблюдении ж, как известно (см. п. 3.1.1), имеет вид:
\П-Х
Так что критическая статистика критерия у , определяемая
логарифмом отношения правдоподобия при произвольном значении параметра
р по отношению к основному гипотетическому р0, будет иметь вид:
(n) _
L(x\po;n) \l-p Po ) 1-Po
Из смысла статистики jn ясно, что «достаточно большие» ее
значения сигнализируют о большей правдоподобности конкурирующей
гипотезы «Я: р ф р0» 5 т.е. о необходимости отвергнуть основную гипотезу
Для того чтобы построить критерий при заданном значении уровня
значимости а, нужно уметь назначить такое пороговое значение са, при
котором
РЬ(П) > са | Яо} = а. (8.34)
А для того, чтобы вычислить ошибку второго рода /3 или мощность
критерия 1-/9, нужно уметь вычислять вероятность
1-Р = РЬЫ>са\Иг}. (8.35)
Из (8.33) следует, что обе эти задачи решаются, если мы будем знать
распределение случайной величины х как при условии справедливости
«нулевой» гипотезы Но (т.е. при значении параметра, равном
заданной величине р0), так и при условии справедливости любой альтернативы

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 319
(т.е. при любом другом значении р анализируемого параметра). Но
признак г, по построению, есть (п>р)-биномиально распределенном
случайном величина со значением параметра р, определяемым в зависимости от
того, в условиях справедливости какой из гипотез мы ее рассматриваем.
Поэтому в дальнейшем мы в качестве критической статистики 7
будем рассматривать (п,р)-биномиально распределенную случайную
величину или любую удобную для нас ее линейную,комбинацию. Правда,
при переходе от непосредственно вычисленной критической статистики
7 1 задаваемой соотношением (8.33), к ее линейным комбинациям смысл
неравенств в фигурных скобках (8.34) и (8.35) может меняться на
противоположный. Рассмотрим подробнее три возможных варианта
анализируемой задачи.
Вариант 1. Проверяется простая гипотеза Яо: р = р© при простой
альтернативе И\\ р = Рь причем р\ > р0. Тогда смысл неравенств в
(8.34) и (8.35) сохраняется и при замене 7 на ж, а именно по заданному
уровню значимости а требуется найти такое са, что
Р{х > са | ро} = а. (8.34')
Но
n
\п—к
Р{х > са | ро} = ? С*р$A - ро)п-* = а. (8.34;/)
Следовательно, требуется решить уравнение (8.3411) относительно са.
Обычно для этого пользуются либо нормальным, либо пуассоновским
приближением, а именно:
• если гипотетичная величина ро «не слишком близка» к нулю или
единице (скажем, 0,10 < р0 < 0,90), а число наблюдений п составляет
хотя бы несколько десятков, то используют теорему Муавра-Лапласа (см.
п. 4.3.1) о приближенной (асимптотической) стандартной нормальности
случайной величины

320
Тогда при
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
= ро
(8.34'")
Следовательно, аргумент функции стандартного нормального
распределения является ничем иным, как квантилем уровня 1—а этого распределения
(ui_a). Так что определив из таблиц величину «i_a, имеем
Po(l-Po) „
n = ttl-°"
(8.36)
Из (8.36) определяем величину са, на которой основано правило проверки
гипотезы Но', если окажется, что х > са, то гипотеза #о отвергается
(с вероятностью ошибки, приблизительно равной а).
Ошибка второго рода этого критерия подсчитывается также с
использованием нормальной аппроксимации биномиального закона, но при
значении параметра р = р\, а именно:
Pl(l-Pl)
п
¦
(8.37)
• если гипотетическая величина р0 близка к 0 или единице (т.е.
Ро < 0,10 или ро > 0,9), а число наблюдений, как и в предыдущем случае,
составляет хотя бы несколько десятков, то для вычисления вероятностей
событий вида {х = А}, где х — (п,р)-биномиально распределенная
случайная величина, лучше пользоваться пуассоновской аппроксимацией, т. е.
e"np. (8.38)
Использование таблиц пуассоновского распределения с параметром
А = пр позволит по схеме, аналогичной предыдущему случаю, определить
сначала са из условия
(8.39)

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 321
а затем вычислить вероятность ошибки второго рода
0 = Р{х < са | Pl} = F(ca | А = пРг) (8.40)
(в соотношениях (8.39) и (8.40) функция F(x | А) обозначает функцию
распределения пуассоновского закона с параметром А).
Вариант 2. Проверяется простая гипотеза #о: р = Ро при простой
альтернативе Н\\ р = рь причем р\ < ро- Схема решения в точности
повторяет предыдущую с заменой смысла неравенства в соотношении (8.34;)
на противоположный. А именно критическая константа са по заданному
уровню значимости а определяется из условия
Р{х < са | ро} = <*• (8.36;а)
Соответственно меняется на противоположный и смысл неравенств в
фигурных скобках соотношений (8.34"), (8.34'"), (8.37), (8.39) и (8.40) с
соответствующими изменениями в последующих выкладках.
Вариант 3. Проверяется простая гипотеза Яо: р = Ро против
сложной альтернативы Н\\ рф ро- В этом случае одинаково
«неестественными» (с точки зрения справедливости гипотезы Яо) будут большие
отклонения х от про как в одну, так и в другую сторону. Это отразится на
схеме построения критерия следующим образом:
• при использовании нормальной аппроксимации следует находить
константу са/2» заменив в правой части (8.34;//) величину а на а/2, тогда
решение об отклонении гипотезы, Яо будет приниматься в случае
где uqy как и прежде, квантиль уровня q стандартного нормального
распределения;
• при использовании пуассоновской аппроксимации потребуется
вычислить две критические константы: 100A — а/2)%-ную и 100а/2%-ную
точки (соответственно Ci_a/2 и са/г) пуассоновского распределения с
параметром А = про; решение об отклонении гипотезы. Но будет
приниматься в случаях х < С!_а/2 иж> са/2-
Пример 8.4. Из массового стационарно функционирующего
производства извлекается контрольная выборка изделий объемом 100 единиц
(п = 100) с целью проверки гипотезы Яо о том, что доля брака
производства составляет ро = 0,05, против гипотезы Н\ о том, что эта доля равна
Р\ = 0,10. Достроить наиболее мощный критерий проверки гипотезы Яо с
уровнем значимости а, не превышающим 0,05, и вычислить его мощность.
11 Теория вероятностей
и прикладная статистика

322 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Решение. Условие задачи соответствует вышеописанному
варианту 1, а соотношение величин ро и п говорит за то, что следует
воспользоваться пуассоновской аппроксимацией при определении критической
константы со,о5- В соответствии с (8.34") и (8.39) с помощью таблиц пуассо-
новского распределения с параметром А = про = 100*0,05 = 5 определяем:
Р{х < 8} « F(9 | А = 5) = 0,932;
P{z<9}«FA0| A = 5) = 0,968.
Так что выбрав са = 10, имеем величину уровня значимости
критерия, равную а = 1 - FA0 | А = 5) = 0,032 < 0,05. Таким образом,
критерий задается критической статистикой — х-числом дефектных
изделий, обнаруженных в выборке объема п = 100, и критической
константой са = 9: если в выборке объема п = 100 окажется более 9
дефектных изделий, то гипотезу о доле брака производства, равной 0,10, следует
предпочесть гипотезе о доле брака производства, равной 0,05.
Подсчет мощности критерия (с учетом формулы (8.40)) дает:
9 10*
1 - & = 1 - Р{х < са | р = 0,10} » 1 - ? -?|- е0 = 0,542.
А?=0
Таким образом, ошибка второго рода, равная /3 = 0,458, оказывается
весьма большой.
Пример 8.5. Независимому статистику поручено проверить
информацию маркетинговой службы некоторого туристического бюро о том,
что 70% клиентов выбирают в качестве формы обслуживания
полупансион. Статистик провел опрос 150 случайно выбранных туристов, из них
полупансион предпочли 84 человека. К какому выводу пришел статистик
при проверке гипотезы Hq: р = 0,70 при альтернативе И\Х р ф 0,70 при
уровне значимости критерия а = 0,05?
Решение. Условия задачи соответствуют вышеописанному
варианту 3, а соотношение величин р0 = 0,70 ип= 150 говорит за то, что можно
воспользоваться нормальной аппроксимацией. Расчет величин,
участвующих в соотношении ?8.41), приводит к следующим результатам:
роA-ро) /84
=l
п
А поскольку щ„а/2 = ^0,975 = 1,96, то неравенство (8.41) имеет
место и, следовательно, есть основания подвергнуть сомнению данные
маркетинговой службы, т.е. отвергнуть гипотезу #q.

8.6 ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ 323
Критерии проверки гипотез о среднем значении нормальной
генеральной совокупности. Все критические статистики, которые
используются ниже для построения критериев проверки гипотез о среднем
значении нормально распределенной случайной величины, получаются с
помощью реализации принципа отношениж правдоподобия (8.7),
описанного в п. 8.3.1. А потому и основанные на них критерии, в соответствии
с леммой Неймана Пирсона, являются в определенном смысле
наилучшими (наиболее мощными). Мы не будем здесь подробно расписывать
логарифмы отношения правдоподобия для конкурирующих гипотетичных
нормальных законов: думаем, у читателя, овладевшего предыдущим
материалом учебника, не возникнет принципиальных трудностей при
самостоятельном выводе критических статистик в данном случае. Поэтому
ограничимся лишь сводкой результатов.
Итак, мы имеем случайную выборку (яьх2,.. .,жп) из
(а,а2^нормальной генеральной совокупности. Рассмотрим различные варианты
постановок задач по статистической проверке гипотез о числовом значении
параметра а = Е?.
1) Яо: а = по при альтернативе Н\\ а> ао\а2 известна.
Критическая статистика 7 = (х — ао)у/п/&.
Правило принятия решения: если 7 > Щ-а> то гипотеза Яо
отвергается с вероятностью ошибки, равной а (здесь и далее г^-квантиль
уровня q стандартного нормального распределения).
Обоснование: статистика 7 в соответствии с теоремой Фишера (см.
п. 6.2) подчиняется стандартному нормальному закону в условиях
справедливости гипотезы Яо.
2) Яо: а — а0 при альтернативе Н\\ а < а^\ а известна.
Критическая статистика: 7 = (ж — ао)у/п/а.
Правило принятия решения: если 7 < —Щ-а> то гипотеза Яо
отвергается с вероятностью ошибки, равной а.
Обоснование: то же, что в предыдущем пункте.
3) Яо: а = по при альтернативе H\i аф а$\ а2 известна.
Критическая статистика: 7 = (ж — а^)у/п/а.
Правило принятия решения: если |7 I > ^1-«/2> то гипотеза Яо
отвергается с вероятностью ошибки, равной а.
Обоснование: то же, что в предыдущих пунктах.
4) Яо: а = а0 при альтернативах Нг: а > а0; или Нг: а < а0; или
Н\: аф ао; о неизвестна. Схемы критериев для каждой из альтернатив
повторяют соответствующие схемы для известной дисперсии а2 со
следующими изменениями, касающимися критической статистики и правила
и*

324 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
принятия решения.
Критическая статистика: 7 = (ж — ао)у/п - 1/s.
Правило принятия решения: гипотеза Яо отвергается, если
7*П* > *а(п - 1) ПРИ альтернативе И\\ а> а0;
7 < —ta(n - 1) при альтернативе Н\: а < а0;
|7 I > 1<*1г{п ~) ПРИ альтернативе Н\: аф а0
(здесь J9(n - 1) — 100д%-ная точка распределения Стьюдента сп-1
степенью свободы).
Обоснование: в соответствии со Следствием 2 теоремы Фишера (см.
п. 6.2, F.30)) статистика 7 распределена по закону Стьюдента сп-1
степенью свободы.
Критерий проверки гипотезы о значении дисперсии
нормальной генеральной совокупности. По случайной выборке (хь х2,...
. ..,жп) из (а,а )-нормальнои генеральной совокупности получена
выборочная дисперсия s (га). Требуется проверить гипотезу (при уровне
значимости критерия а) Яо: сг2 = <7q, где о% — некоторое конкретное
числовое значение. При проверке этой гипотезы используют критическую
статистику
7(П) = ^Р; (8.42)
которая в соответствии с теоремой Фишера (см. F.27) в п. 6.2.8) в
условиях справедливости гипотезы Яо распределена по закону х с п~1 степенью
свободы.
Далее, как и в случаях проверки гипотез о параметре биномиального
закона р или о значении среднего нормальной генеральной совокупности
а, в зависимости от конкурирующей гипотезы Н\ выбирают
правостороннюю, левостороннюю или двустороннюю критическую область:
1) если Н\: а = аг > а0, то гипотезу Яо отвергают (с вероятностью
ill
ошибки а) в случае ns /cq > ха(п — 1);
1 О О
2) если Н\: о = а\ < do, то гипотезу Hq отвергают (с вероятностью
0 0 0
ошибки а) в случае ns /<т0 < Х\~а{п ~~ 1);
3) если Hi', а ф а0, то гипотеза Яо отвергается (с вероятностью
ошибки а) при ns2/al < Xi-a/2(^ - 1)> а также при пз2/а1 > х«/г(^ - 1)-
Здесь, как обычно, Xq(m) обозначает 100д%-ную точку х -распределения
с т степенями свободы.

выводы 325
ВЫВОДЫ
1. Процедура обоснованного сопоставления высказанного
исследователем предположительного утверждения (гипотезы) относительно природы
или величины неизвестных параметров рассматриваемой стохастической
системы с имеющимися в его распоряжении результатами наблюдения,
сопровождаемая количественной оценкой степени достоверности
получаемого вывода, осуществляется с помощью того или иного статистического
критерия и называется статистической проверкой гипотез.
2. По своему прикладному содержанию гипотезы, высказываемые в
ходе статистического анализа и моделирования, подразделяют на
следующие типы:
об общем виде закона распределения исследуемой случайной
величины;
об однородности двух или нескольких обрабатываемых выборок;
о числовых значениях параметров исследуемой генеральной
совокупности;
об общем виде зависимости, существующей между компонентами
исследуемого многомерного признака;
о независимости и стационарности ряда наблюдений.
3. Все статистические критерии строятся по общей логической
схеме. Построить статистический критерий — это значит: а) определить
тип проверяемой гипотезы; б) предложить и обосновать конкретный вид
функции от результатов наблюдения (критической статистики 7 )> на
основании значений которой принимается окончательное решение; в)
указать такой способ выделения из области возможных значений критической
статистики 7* области Г^ отклонения проверяемой гипотезы Яо, чтобы
было соблюдено требование к величине вероятности ошибочного
отклонения гипотезы Яо (т.е. к уровню значимости критерия а).
4. «Качество» статистического критерия характеризуется уровнем
значимости а, мощностью 1 — /?, свойствами несмещенности и
состоятельности. В состоятельных критериях можно добиваться сколько угодно
малых величин ошибок первого и второго рода (а и /3) лишь за счет
увеличения объема выборки п, на основании которой принимается решение.
При фиксированном объеме выборки можно делать сколь угодно малой
лишь одну из ошибок (а или /3), что сопряжено с неизбежным
увеличением другой.
5. Наряду с классической схемой наблюдения, когда объем выборки п
заранее зафиксирован, в практике статистических исследований
используется и последовательная схема наблюдения, при которой на каждом из
последовательно во времени проводимых этапов наблюдения принимает-

326 ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
ся одно из трех решений: «принять гипотезу #о», «отклонить гипотезу
#о», «не принимать окончательного решения и продолжить наблюдения».
При этом выбор решения ставится в зависимость от результатов всех
предыдущих наблюдений, а число наблюдений */, произведенных до момента
принятия окончательного решения, оказывается величиной случайной.
6. Оптимальные последовательные критерии отношения
правдоподобия (критерий Вальда, обобщенный последовательный критерий и др.)
оказываются более экономными по затратам на наблюдения, на основании
которых можно различить проверяемые гипотезы с заданной точностью
(а,/?). Исследования показали, что, применяя последовательные
критерии, можно добиваться двух-, трех- и д&же четырехкратного снижения
необходимого числа наблюдений по сравнению с классическими
оптимальными критериями.

ние
стати
Статис
юкупности
знаван
ально-эконо
аниях
ование
npi
)НОСТ1
немого много]щфмого

ГЛАВА 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ
СТАТИСТИЧЕСКИЙ АНАЛИЗ
9.1. Назначение и содержание прикладной
статистики
Во «Введении» к учебнику (см. п. В.1.2) мы кратко обсудили
вопросы, вынесенные в заголовок этого пункта, дали определение прикладной
статистики как самостоятельной научной дисциплины, попытались
понять «взаимоотношения» прикладной статистики с теорией вероятностей
и математической статистикой, с одной стороны, и с эконометрикой — с
другой. В частности, было установлено, что теория вероятностей и
математическая статистика являются по отношению к прикладной
статистике и эконометрике разработчиками и поставщиками существенной части
используемого в них математического аппарата. Однако доводка и
развитие этого аппарата, подчиненные требованиям и специфике
различного рода приложений, производятся уже в рамках дисциплин
«прикладная статистика» и «эконометрика». Причем эконометрика (наряду
с другими сферами человеческой деятельности, в которых
используются математико-статистические методы) является активным поставщиком
специального класса постановок задач для прикладной статистики.
Далее развиваются и комментируются некоторые из тезисно намеченных во
«Введении» к учебнику положений, относящихся к назначению и
содержанию прикладной статистики.
9.1.1. Два подхода к интерпретации и анализу исходных
статистических данных
Первый подход (вероятностно-статистический) развивается в
рамках классической математической статистики (т. е. в условиях хотя
бы приблизительного выполнения требований статистического ансамбля,

9.1 НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 329
см. п.В.2.1) и предусматривает возможность вероятностной
интерпретации анализируемых данных и получаемых в результате этого анализа
статистических выводов. При подобной (вероятностной) интерпретации
исходных статистических данных в поле зрения исследователя одновременно
попадают две совокупности объектов: реально наблюдаемая,
статистически представленная рядом наблюдений (т.е. выборка), и теоретически
домысливаемая (так называемая генеральная совокупность). Основные
свойства и характеристики выборки, называемые эмпирическими (или
выборочными), могут быть проанализированы и вычислены по имеющимся
статистическим данным. Основные свойства и характеристики
генеральной совокупности, называемые теоретическими, не известны
исследователю, но назначение математико-статистических методов как раз в том и
состоит, чтобы с их помощью получить как можно более точное
представление об этих теоретических свойствах и характеристиках по
соответствующим свойствам и характеристикам выборок (см. гл.6).
Важнейшим моментом в успехе статистического анализа и
моделирования таких данных является удачное решение проблемы их
генезиса, т.е. правильный выбор вероятностной модели механизма генерации
этих данных (набор наиболее распространенных моделей подобного рода
описан в гл.З). Именно отправляясь от решения проблемы генезиса
анализируемых статистических данных, мы можем обоснованно ответить на
вопросы:
• как наилучшим образом выбрать метод статистической обработки
этих данных, например, построить наиболее точную оценку неизвестного
среднего значения анализируемой генеральной совокупности?
• каким должен быть общий вид модели, описывающий ту или иную
зависимость между анализируемыми признаками?
В обоих случаях критерий качества (оценки, степени
адекватности модели) определится на основе принципа максимального
правдоподобия имеющихся у нас наблюдений, который в свою очередь базируется на
знании модели з.р.в. этих наблюдений (см. пп. 7.5.1, 8.3.1).
В принципиально иной ситуации оказывается исследователь, если он
не располагает никакими априорными сведениями о вероятностной
природе анализируемых данных, или если эти данные вообще не могут быть
интерпретированы как выборка из генеральной совокупности. Тогда
при выборе критерия качества (метода оценивания или степени
адекватности конструируемой модели) исследователь вынужден опираться на
соображения конкретно-содержательного плана: как именно получены
анализируемые данные и какова конечная прикладная цель их анализа.
Поскольку эти соображения основаны на обычной логике и реализуются, как

330 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
правило, в виде критерия некоторого алгебраического вида, то и
соответствующий подход принято называть логико-алгебраическим.
Очевидно, в рамках логико-алгебраического подхода (в отличие от вероятностно-
статистического) исследователь не может претендовать на:
• интерпретацию исходных статистических данных в качестве
выборки из некоторой (теоретически домысливаемой) генеральной
совокупности;
• использование вероятностных моделей для построения и выбора
наилучших методов статистической обработки или наилучшего вида
конструируемой модели;
• вероятностную интерпретацию выводов, основанную на
статистическом анализе исходных данных.
В этом заключается главное различие двух возможных подходов к
статистическому анализу исходных данных. Однако и в том и в другом
подходе выбор наилучшего из всех возможных методов анализа и
моделирования данных производится в соответствии с некоторым критерием
качества метода или степени адекватности модели. Различие
описываемых подходов проявляется здесь в способе обоснования выбора этого
критерия качества, а также в интерпретации самого критерия и
получаемых статистических выводов. Но после того, как выбор конкретного вида
оптимизируемого критерия качества осуществлен, математические
средства решения задачи статистического анализа и моделирования данных
оказываются общими для обоих подходов: и в том и в другом случае с
целью оптимизации выбранного критерия качества исследователь
использует методы решения экстремальных задач. Правда, на заключительном
этапе — на этапе осмысления и интерпретации полученных
статистических выводов — каждый из подходов снова имеет свою специфику.
Таким образом, общим для обоих описываемых подходов является
наличие исходной статистической информации на «входе» задачи и
необходимость наилучшего (в смысле оптимизации некоторого критерия
качества) способа статистического анализа или моделирования этой
информации с целью получения научных или практических выводов «на выходе».
' Именно эта общая логическая схема и положена в основу
методологического принципа разработки инструментария прикладной статистики.
Это позволило синтезировать два описанных выше подхода к
статистическому анализу и моделированию. В результате прикладная статистика
объединила в себе как прикладные вероятностно-статистические
методы многомерного статистического анализа, включая модели регрессии
(существенно опираясь при этом на результаты математической
статистики, касающиеся методов статистического оценивания и статистиче-

9Д НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 331
ской проверки гипотез, см. гл. 7 и 8), так и логико-алгебраические
методы анализа данных, понимаемого в узком смысле, т. е. исключающего
использование в своих построениях вероятностных рассуждений и
моделей (достаточно полное представление об этих методах можно получить,
например, по книге [ДидеЭ. и др.]).
9.1.2. Три центральные проблемы прикладной статистики
Перед тем как сформулировать три центральные проблемы
прикладной статистики, следует остановиться на двух основных формах записи
исходных статистических данных (и.с.д.). Первую, наиболее
распространенную, форму представления и.с.д. обычно называют матрицей (или
таблицей) «объект-свойство». В своей наиболее общей записи эта
матрица имеет вид
*<р)(*) \
(9.1)
t = t\, ?2» • • • * ?jV4
где x\ \tk) — значение j-го анализируемого признака, характеризующего
состояние г-го объекта в момент времени tk. Данные (9.1) образуют так
называемую пространственно-временную выборку} при формировании
которой статистическому обследованию подвергаются п объектов (как-то
размещенных в пространстве), причем на каждом из объектов
регистрируются значения р характеризующих его признаков в N последовательные
моменты времени t\, f2» • • • > tN, Очевидно, что запись (9.1) в
действительности определяет целую последовательность (а именно N штук) матриц
«объект-свойство» . Можно также сказать, что данные вида (9.1)
содержат п реализаций р-мерного временного ряда (ar'(J),ar2'(f),.. .,x^p\t)).
Бели мы располагаем так называемыми одномоментными
наблюдениями, то это соответствует случаю N = 1 в общей записи (9.1); при этом
для сокращения обозначений индекс времени t в записи (9.1) мы можем
опускать, а получающаяся выборка
(и.с.д.^ =
Л*) J2) ... »
х2 • • • х2
'ay *' ЗУ' у;;' ''(У)
(9.1')

332 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
называется пространственной статической.
Другой частный случай их.д. мы получаем, если в (9.1) положить
п = 1 (т.е. обследуется во времени единственный объект). Тогда речь
идет об анализе единственной траектории р-мерного временного ряда, а
при дополнительном условии р = 1, — об анализе одного временного ряда.
Заметим, что для экономических приложений наиболее типична
ситуация, когда моменты времени fi, t2>•••»'//) в которые производится
регистрация значений анализируемых признаков, являются
равноотстоящими, т. е. *2 - h = 'з - '2 — ''# = *дг - 'дг-1 = Д'« В этом случае время
удобнее считать и обозначать в числе «тактов» At. Соответственно
тогда вместо *i, t2) • • •) tN мы будем иметь t = 1,2,...,N.
В ряде ситуаций и в первую очередь в ситуациях, когда исходные
статистические данные получают с помощью специальных опросов,
анкет, экспертных оценок, возможны случаи, когда элементом первичного
наблюдения является не состояние г-го объекта в момент t, а
характеристика 7и @ попарного сравнения двух объектов (или признаков)
соответственно с номерами % и j, отнесенная к моменту времени t.
Характеристика 7у определяет результат сопоставления объектов 0{
и Oj в смысле некоторого анализируемого отношения: 7tj может
выражать меру сходства или различия объектов О{ и Oj, меру их связи или
взаимодействия в каком-либо процессе (например, поток продукции
отрасли «t» в отрасль «J»), геометрическое расстояние между объектами,
отношение предпочтения (тогда, например, полагают 7ij = 1, если объект
0( не хуже объекта Oj} и 7tj = 0 в противном случае), наконец,
статистическую меру взаимной коррелированности (если речь идет о
признаках, то в качестве 7»; могут рассматриваться, например, коэффициенты
корреляции или ковариации признаков аг' и зг"). Из данного выше
пояснения смысла характеристик 70* следует, что в большинстве случаев
(но не всегда\) они оказываются симметричными, т.е. 7ij = 7ji
(пример с взаимными потоками продукции из одной отрасли в другую как раз
относится к исключениям из этого правила).
Таким образом, в описываемой ситуации исследователь располагает
в качестве массива исходных статистических данных временной
последовательностью матриц парных сравнений размера пх п (если
рассматриваются характеристики парных сравнений объектов) или рхр (если

9.1 НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 333
рассматриваются характеристики парных сравнений признаков):
7и@. 7и@. •••> 7im@\ .
»*(*>» 722@» •••. 7зт@ \(т = п или р\\
7ml(*), 7ma(t). .-., 7mm(t)/
(9.2)
В статическом варианте, т.е. при N = 1, исследователь
располагает лишь одной матрицей парных сравнений Gij), описывающей
ситуацию в один какой-то фиксированный момент времени.
Очевидно, что от формы записи (9.1) можно непосредственно перейти
к (9.2) (при наличии заданной метрики в пространстве объектов и в
пространстве признаков). Однозначный обратный переход от (9.2) к (9.1) без
дополнительных предположений и специальных методов (скажем,
многомерного шкалирования, см. п. 13.6), в общем, невозможен. Возможны и
другие формы представления и.с.д., однако они встречаются значительно
реже описанных двух, поэтому здесь не рассматриваются.
Теперь можно сформулировать три центральные проблемы
прикладной статистики. Не следует думать, что эти проблемы исчерпывают все
содержание прикладной статистики. Более того, то, что именно эти
проблемы выделены в качестве центральных, имеет условный смысл и
объясняется в первую очередь «эконометрическими интересами» данного
издания.
Проблема I. Статистическое исследование структуры и
характера взаимосвязей, существующих между
анализируемыми количественными переменными. При этом под «переменными»
понимаются как регистрируемые на объектах признаки я' , аг ,..., х^р\
так и время t. Методам и моделям, предназначенным для решения
различных постановок задач в рамках этой проблемы, посвящен целиком том 2
данного учебника, который, в частности, охватывает регрессионный
анализ (гл. 2), анализ временных рядов (гл. 3) и системы одновременных
уравнений (гл.4).
Более подробное обсуждение общей постановки и особенностей этой
проблемы мы откладываем до главы 10, специально этому посвященной.
Это объясняется тем, что по своему значению и в прикладной
статистике, и в эконометрике проблема статистического исследования
зависимостей заметно превосходит две другие.
Проблема П. Разработка статистических методов
классификации объектов и признаков. Говоря о классификации
совокупности объектов, подразумеваем, что каждый из них задан
соответствующей строкой матрицы (9.1;) либо геометрическая структура их попарных

334 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
расстояний (близостей) задана матрицей Gу)> ij = 1,2,...,п.
Аналогично интерпретируется исходная информация в задаче классификации
признаков с той лишь разницей, что каждый из признаков я"' задается
соответствующим (j-м) столбцом матрицы (9.1') или, в случае задания
и.с.д. в форме (9.2), — j-ми строками и столбцами матрицы (9.2).
В дальнейшем, если это специально не оговорено, не будем разделять
изложение этой проблемы на «объекты» и «признаки», поскольку все
постановки задач и основная методологическая схема исследования здесь
общие.
В общей (нестрогой) постановке проблема классификации объектов
заключается в том} чтобы всю анализируемую совокупность объектов
О = {Oi} (i = l,...,n), статистически представленную в виде матриц
(9.1') или (уц)} разбить на сравнительно небольшое число (заранее
известное или нет) однородных, в определенном смысле, групп или классов.
Для формализации этой проблемы удобно интерпретировать
анализируемые объекты в качестве точек в соответствующем признаковом
пространстве. Бели исходные данные представлены в форме матрицы
(9Л'), то эти точки являются непосредственным геометрическим
изображением многомерных наблюдений Х\, Aj,..., Хп в р-мерном пространстве
ОжA),...,0я(р) (т.е. Х{ = (х\1\...,х\р))Т). Если же исходные данные
представлены в форме матрицы парных сравнений 7tj> T0
исследователю не известны непосредственно координаты этих точек, но зато задана
структура парных расстояний (близостей) между объектами.
Естественно предположить, что геометрическая близость двух или нескольких точек
в этом пространстве означает близость «физических» состояний
соответствующих объектов, их однородность. Тогда проблема классификации
состоит в разбиении анализируемой совокупности точек-наблюдений на
сравнительно небольшое число (заранее известное или нет) классов
таким образом, чтобы объекты, принадлежащие одному классу, находились
бы на сравнительно небольших расстояниях друг от друга. Полученные
в результате разбиения классы часто называют кластерами (таксонами,
образамиI, а методы их нахождения соответственно кластер-анализом,
численной таксономией, распознаванием образов.
Статистическим методам классификации посвящена гл. 12 учебника.
1 Cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых
каким-либо общим свойством. Тахоп (англ.) — систематизированная группа
любой категории (термин биологического происхождения). Название «кластер-анализ»
для совокупности методов решения задач такого типа было впервые введено, по-
видимому, Трайоном в 1939 г. (см. : Tryon R. С. Cluster Analysis. II Ann. Arb.j
Edw. Brothers. — 1939).

9.1 НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 335
В зависимости от наличия и характера априорных сведений о природе
искомых классов и от конечных прикладных целей исследования приходится
обращаться либо к методам дискриминантного анализа (они описаны в
п. 12.3), либо к методам расщепления смесей вероятностных
распределений или процедурам кластер-анализа (и те и другие описаны в п. 12.4).
Проблема III. Снижение размерности исследуемого
признакового пространства с целью лаконичного объяснения
природы анализируемых многомерных данных. Возможность
лаконичного описания анализируемых многомерных данных основана на априорном
допущении, в соответствии с которым существует небольшое (в сравнении
с числом р исходных анализируемых признаков х^\х^2\..., х^) число р
признаков-детерминапт (главных компонент, общих факторов, наиболее
информативных объясняющих переменных), с помощью которых могут
быть достаточно точно описаны как сами наблюдаемые переменные
анализируемых объектов, т.е. все элементы матриц (9.1) и (9.2), так и
определяемые этими переменными свойства (характеристики)
анализируемой совокупности. При этом упомянутые признаки-детерминанты могут
находиться среди исходных признаков, а могут быть латентными^ т. е.
непосредственно статистически не наблюдаемыми, но
восстанавливаемыми по исходным данным вида (9.1), (9.1;) или (9.2). Гениальный пример
практической реализации этой идеи дает нам периодическая система
элементов Менделеева: в этом случае роль идеально информативного
единственного признака-детерминанта играет, как известно, заряд атомного
ядра.
Необходимость снижения размерности исследуемого признакового
пространства с целью лаконичного объяснения природы анализируемых
многомерных данных может быть продиктована различными
прикладными задачами статистического анализа и моделирования. Ниже кратко
формулируются несколько типовых задач такого рода.
Отбор наиболее информативных показателей (включая
выявление латентных факторов). Речь идет об отборе из исходного
(априорного) множества признаков X = (ж^,...,ж^)т или о
построении в качестве некоторых комбинаций исходных признаков относительно
небольшого числа р переменных Z(Jf) = (^1'(Jf),...,^p^(A'))T, которые
обладали бы свойством наибольшей информативности в смысле,
определенном, как правило, некоторым специально подобранным для каждого
конкретного типа задач критерием информативности IP'(Z). Так,
например, если критерий IP*(Z) «настроен» на достижение максимальной
точности регрессионного прогноза некоторого результирующего
количественного показателя у по известным значениям предикторных перемен-

336 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
ных х^1\ х^2\..., х^р\ то речь идет о наилучшем подборе наиболее
существенных предикторов в модели регрессии (см. п. 2.6 тома 2). Бели же
критерий Ipi(Z) устроен таким образом, что его оптимизация
обеспечивает наивысшую точность решения задачи отнесения объекта к одному из
классов по значениям X его описательных признаков, то речь идет о
построении системы типообразующих признаков в задачах классификации
(см. п. 12.3 и 12.4) или о выявлении и интерпретации некоторой сводной
(латентной) характеристики изучаемого свойства (см. п. 13.5).
Наконец, критерий Ipt(Z) может быть нацелен на максимальную
автоинформативность новой системы показателей Z, т. е. на максимально точное
воспроизведение всех исходных признаков аг , от ,..., агр) по
сравнительно небольшому числу вспомогательных переменных ж ,..., я* ' (р < р).
В этом случае говорят о наилучшем автопрогнозе и обращаются к
моделям и методам факторного анализа и его разновидностей (см. п. 13.2 и
13.3).
Сжатие массивов обрабатываемой и хранимой информации.
Этот тип задач тесно связан с предыдущим и, в частности, требует в
качестве одного из основных приемов решения построения экономной
системы вспомогательных признаков, обладающих наивысшей
автоинформативностью, т.е. свойством наилучшего автопрогноза (см. выше). В
действительности при решении достаточно серьезных задач сжатия
больших массивов информации (подобные задачи весьма актуальны и в плане
необходимости минимизации емкостей носителей, на которых хранится
архивная информация, и в плане экономии памяти ЭВМ при обработке
текущей информации) используется сочетание методов классификации и
снижения размерности. Методы классификации позволяют подчас
перейти от массива, содержащего информацию по всем п статистически
обследованным объектам, к соответствующей информации только по к
эталонным образцам (к < п), где в качестве эталонных образцов
берутся специальным образом отобранные наиболее типичные представители
классов, полученных в результате операции разбиения исходного
множества объектов на однородные группы. Методы же снижения размерности
позволяют заменить исходную систему показателей X = (аг ,...,а^р*)т
набором вспомогательных (наиболее автоинформативных) переменных
Z(X) = (z^1'(X),...iz^p'(X))T. Таким образом, размерность
информационного массива понижается от р • п до р • fc, т. е. во многие десятки раз,
если учесть, что р и к обычно на порядки меньше соответственно р и п.
Визуализация (наглядное представление) данных. При
формировании рабочих гипотез, исходных допущений о геометрической и
вероятностной природе совокупности анализируемых данных Х\, АГ2,..., Хп

9.1 НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 337
важно было бы суметь «подсмотреть», как эти данные-точки
располагаются в анализируемом пространстве. В частности, уже на
предварительной стадии исследования хотелось бы знать, например, распадается
ли исследуемая совокупность точек на четко выраженные сгустки в этом
пространстве, каково примерное число этих сгустков и т. д.? Но
максимальная размерность «фактически осязаемого* пространства, как
известно, равна трем. Поэтому, естественно, возникает проблема: нельзя
ли спроецировать анализируемые многомерные данные из исходного
пространства на прямую, на плоскость, в крайнем случае — в трехмерное
пространство, но так, чтобы интересующие нас специфические
особенности исследуемой совокупности (например, ее расслоенность на кластеры),
если они присутствуют в исходном пространстве, сохранились бы и после
проецирования. Следовательно, и здесь речь идет о снижении
размерности анализируемого признакового пространства, но снижении, во-первых,
подчиненном некоторым специальным критериям и, во-вторых,
оговоренном условием, что размерность редуцированного пространства не должна
превышать трех. Аппарат для решения подобных задач представлен в
учебнике методом главных компонент и факторным анализом1.
Построение условных координатных осей (многомерное
шкалирование, латентно-структурный анализ). В данном типе задач
снижение размерности понимается иначе, чем прежде. До сих пор речь
шла о подчиненном некоторым специальным целям переходе от заданной
координатной системы X (т. е. от исходных переменных х^х\х^%\..., х^)
к новой координатной системе Z(X)> размерность которой р
существенно меньше размерности р и оси которой 0*' ,...,0*'р' конструируются
с помощью соответствующих преобразований исходных признаков.
Однако в данной постановке задачи исходной координатной системы не
существует вовсе, а подлежащие статистическому анализу и
моделированию данные представлены в статическом варианте (9.2), т.е. в виде
матрицы Gу)» hj = 1,2,..., n — парных сравнений объектов. Ставится
задача: для заданной, сравнительно невысокой, размерности р
определить вспомогательные условные координатные оси 0**1\...,0*^ и
способ сопоставления каждому объекту О* его координат (z\l\...,z\p^) в
этой системе таким образом, чтобы попарные отношения *fij(Z)
(например, попарные взаимные расстояния) между объектами, вычисленные на
1 Наиболее эффективные современные методы для решения задач подобного типа
объединяются в подходе, называемом «целенаправленным проецированием
многомерных наблюдений». Однако описание этого подхода выходит за рамки целей данного
учебника (см. [Айвазян С.А., Бухштабер В.М. и др., 1989]).

338 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
базе этих условных координат, в определенном смысле минимально бы
отличались от заданных величин 7ij (*»i = 1,2,...,п). В определенных
условиях (в первую очередь в задачах педагогики, психологии,
построения различных рейтингов3 и т. п.) построенные таким образом условные
переменные поддаются содержательной интерпретации и могут тогда
рассматриваться в качестве латентных характеристик определенных свойств
анализируемых объектов (такого типа задачи называют часто задачами
латентно-структурного анализа). Снижение размерности происходит
здесь в том смысле, что от исходного массива информации размерности
п • п переходим к матрице типа «объект — свойство» размерности р • п,
где р < п. Аппарат для решения подобных задач состоит из методов так
называемого многомерного шкалирования и представлен в п. 13.6.
9.1.3. Новые постановки задач и ослабление
ограничительных условий в канонических
математико-статистических и эконометрических
моделях
Формализация (математическая постановка) реальных задач
статистического анализа и моделирования экономических данных и на базе
этого опыта выработка типовых математических постановок задач,
выходящих за стеснительные рамки жестких канонических моделей,
составляют, пожалуй, самый важный и самый трудный этап прикладного
статистического исследования. Одновременно это направление деятельности в
прикладной статистике является и самым неблагодарным, поскольку de
facto оказался как бы «незаконнорожденным дитем» теории и практики
статистического анализа данных. Искусство реалистического
моделирования формально не предусмотрено ни в одном из разделов математик©-
статистической науки, а его развитие никак и ничем не стимулируется в
рамках этой дисциплины.
Тем не менее за последние десятилетия прикладная статистика
предложила и проанализировала ряд новых интересных типовых постановок
математико-статистических задач, непосредственно стимулированных
запросами практики (в том числе в социально-экономической сфере). В этой
связи можно упомянуть об уже успевших стать каноническими
постановках задач обобщенного метода наименьших квадратов (см. том 2, гл. 2),
3 В подобных ситуациях элементы чц матрицы (9.2) отражают обычно результаты
попарных сравнений объектов О< и Oj по анализируемому качеству. Например,
численное значение 7rfj может отражать степень уверенности эксперта (или каким-
то способом вычисленную вероятность) того, что объект О\ лучше объекта Oj.

9.2 ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 339
о различных подходах к построению устойчивых статистических
выводов, о развитии методов целенаправленного проецирования и
томографии в связи с исследованием геометрической и вероятностной природы
анализируемых многомерных данных @.1) (см., например, [Айвазян С. А.,
ЕнюковИ.С, МешалкинЛ.Д., Бухштабер В. М., 1989]), а в последние
годы — о формулировке и исследовании таких моделей анализа временных
рядов, как модель коинтеграции, ARCH- и G ARCH-модели (см. гл.З
тома 2), модель многомерной развертки временного ряда [Бухштабер В. М.]
и др.
9.2. Основные этапы прикладного
статистического анализа
Для пояснения роли и места основных приемов статистического
моделирования и методов первичной статистической обработки исходных
данных удобно разложить общую логическую схему статистического анализа
на основные этапы исследования. Подобное разложение носит, конечно,
условный характер. В частности, оно не означает, что этапы
осуществляются в строгой хронологической последовательности один за другим.
Более того, многие из этапов (например, этапы 4, 5 и 6) находятся в плане
хронологическом в соотношении итерационного взаимодействия:
результаты реализации более поздних этапов могут содержать выводы о
необходимости повторной «прогонки» (с учетом новой информации)
предыдущих этапов.
Этап 1: исходный (предварительный) анализ исследуемой реальной
системы. В результате этого анализа определяются: а) основные
цели исследования на неформализованном, содержательном уровне; б)
совокупность единиц, представляющая предмет статистического
исследования; в) перечень (аг ,аг,... ,агр') отобранных из представленного
специалистами априорного набора показателей, характеризующих состояние
(поведение) каждого из обследуемых объектов, который предполагается
использовать в данном исследовании; г) степень формализации
соответствующих записей при сборе данных; д) общее время и трудозатраты,
отведенные на планируемые работы, и коррелированные с ними
временная протяженность и объем необходимого статистического обследования;
е) моменты, требующие предварительной проверки перед составлением
детального плана исследования (например, не всегда априори ясна
возможность идентификации единиц наблюдения); ж) формализованная
постановка задачи, по возможности включающая вероятностную модель
изучаемого явления и природу статистических выводов, к которым должен

340 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
(или может) прийти исследователь в результате переработки массива
исходных данных; з) формы, используемые для сбора первичной
информации и для- введения ее в вычислительное устройство.
По затратам сил наиболее квалифицированного персонала,
участвующего в работе, трудоемкость первого этапа работы весьма значительна
и бывает даже сравнима с суммарной трудоемкостью всех остальных
этапов при условии, что обработка проводится с помощью подходящего
пакета программ1. Поэтому максимального развития заслуживают методы
машинного ассистирования в проведении этой части работы. Оно может
заключаться в подсказке (с одновременной оценкой) форм документации
для сбора первичной информации, медицинских приложений), в
автоматизированном режиме выбора подходящих моделей, в ведении тезауруса
исследования и т. п.
Этап 2\ составление детального плана сбора исходной
статистической информации. При составлении этого плана необходимо по
возможности учитывать полную схему дальнейшего статистического анализа, о
чем часто забывают. Априорное представление о том, как и для чего
данные будут анализироваться, может оказать существенное влияние на их
сбор. При планировании особого внимания заслуживают случаи, когда:
а) используется аппарат теории выборочных обследований, т. е.
определяется, какой должна быть выборка — случайной, пропорциональной,
расслоенной и т.п.; б) хотя бы для части входных переменных эксперимент
носит активный характер, т.е. переменные допускают фиксацию в
каждом конкретном наблюдении на определенном уровне, и выбор плана
обследования осуществляется с привлечением методов планирования
экспериментов. В некоторых руководствах по статистике этот этап называют
этапом «организационно-методической подготовки». Как уже было
упомянуто в п. 6.1, вопросы разработки методологии определения априорной
системы показателей, характеризующих исследуемый объект или процесс,
вынесены за рамки описываемых здесь этапов и должны быть отнесены к
области предметной (в нашем случае — экономической) статистики.
Этап 8: сбор исходных статистических данных и их ввод в
вычислительное устройство. Одновременно в вычислительное устройство
вносятся полные и краткие (для автоматизированного воспроизводства в
таблицах) определения используемых терминов. В программном обеспече-
1 В некоторых специальных статистических исследованиях социально-экономического
и других профилей, характеризующихся большими затратами времени и средств
на сбор исходных статистических данных, сформулированный тезис остается
справедливым лишь при условии исключения этапа 3 из суммарной трудоемкости всех
остальных этапов.

9.2 ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 341
нии должны быть предусмотрены специальные меры, исключающие или
резко уменьшающие возможность появления расчетов не с тем
подмножеством данных или не для той подгруппы объектов.
Таким образом, независимо от того, производится ли исследователем
выбор метода и плана статистического обследования или он уже
располагал результатами так называемого пассивного эксперимента, к моменту
определения основного инструментария статистического исследования
исследователь в общем случае располагает в качестве массива исходных
статистических данных матрицами наблюдений вида (9.1), (9.1 ) или (9.2).
Этап 4- первичная статистическая обработка данных, В ходе
первичной статистической обработки данных обычно решаются следующие
задачи: а) отображение переменных, описанных текстом, в номинальную
(с предписанным числом градаций) или ординальную (порядковую)
шкалу; б) статистическое описание исходных совокупностей с определением
пределов варьирования переменных; в) анализ резко выделяющихся
наблюдений; г) восстановление пропущенных наблюдений; д) проверка
статистической независимости последовательности наблюдений,
составляющих массив исходных данных; е) унификация типов переменных, когда с
помощью различных приемов добиваются унифицированной записи всех
переменных; ж) экспериментальный анализ закона распределения
исследуемой генеральной совокупности и параметризация сведений о природе
изучаемых распределений (иногда этот этап называют процессом
составления сводки и группировки). Кроме того, этап 4 включает в себя
вычислительную реализацию решения следующих вопросов: учет размерности
и алгоритмической сложности задачи и одновременно возможностей
используемого вычислительного средства; формулировку задачи на входном
языке используемого программного обеспечения и т. п. (см. подробнее об
этом в описании этапа 6).
Остановимся на некоторых из затронутых вопросов подробнее.
Анализ резко выделяющихся наблюдений. Часто даже беглый
предварительный просмотр (визуальный или автоматизированный) исходных
данных (9.1) или (9.2) может вызвать у исследователя сомнения в
истинности (или правомерности) отдельных наблюдений, слишком резко
выделяющихся на общем фоне. В этих случаях возникает вопрос: вправе
ли мы объяснить обнаруженные резкие отклонения в исходных данных
(аномальные выбросы) лишь обычными случайными колебаниями
выборки (которые обусловлены природой анализируемой генеральной
совокупности) или здесь дело в существенных искажениях стандартных условий
сбора статистических данных, а возможно, и в прямых ошибках
регистрации (записи)? В последних двух случаях «подозрительные» наблюдения,

342 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
очевидно, следует исключить из дальнейшего рассмотрения.
Единственным абсолютно надежным способом решения вопроса об
исключении резко выделяющихся результатов наблюдений является
тщательное рассмотрение условий, при которых эти наблюдения
регистрировались. Однако во многих случаях проведение такого
содержательного анализа объективно затруднительно или принципиально невозможно.
Тогда необходимо обратиться к соответствующим формальным
(статистическим) методам. Общая логическая схема этих методов следующая:
отправляясь от исходных допущений о природе анализируемой
совокупности данных, исследователь задается функцией
р(Хт;Хг,Х2,...,Хп) (9.3)
от всех имеющихся наблюдений, характеризующей степень аномальности
(меру удаленности от основной массы наблюдений) «подозрительного»
наблюдения ЛГ*, а затем подставляет в (9.3) реальные значения
наблюдений и сравнивает величину с некоторым пороговым значением рог; если
р > /0О, то подозрительное наблюдение X* или полностью исключается из
дальнейшего рассмотрения, или его вклад уменьшается с помощью
весовой функции, убывающей по мере роста степени аномальности
наблюдений (см. п. 7.5.3).
С одним из вариантов методов анализа резко выделяющихся
наблюдений читатель познакомился в п. 8.6.
Восстановление пропущенных (стертых) наблюдений. В
матрицах исходных статистических данных (9.1) или (9.2) по разным
причинам (в том числе и в результате исключения резко выделяющихся
наблюдений) могут быть пропуски отдельных элементов или каких-то частей
строк или столбцов. Исключать по этой причине из дальнейшего
рассмотрения весь объект (строку, в которой обнаружены пропуски) или
признак (столбец, в котором обнаружены пропуски) слишком расточительно
с точки зрения потери полезной информации. Поэтому возникает задача
наилучшего в некотором смысле восстановления пропущенных (стертых)
данных. Конкретизация критерия качества восстановления стертых дан-
пых производится в зависимости от характера последующей обработки
исходных данных, т. е. в зависимости от окончательных целей
исследования (смм например, [Айвазян С. А., ЕнкжовИ.С, Мешалкин Л. Д., 1983]).
1 В вероятностной постановке задачи пороговое значение до определяется из
стандартных статистических таблиц с учетом знания закона распределения статистики р в
предположении необоснованности «подозрений» относительно наблюдения X*. В
других случаях до определяется из содержательных соображений.

9.2 ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 343
Проверка однородности нескольких порций исходных
Данных. Объективные условия сбора исходных статистических данных,
особенно в ситуациях пассивного эксперимента, могут быть такими, что
общая (р X п)-матрица наблюдений (см. (9*1)) получается составлением
нескольких (р х ni)-, (р х п2)-,..., (р х п*)-матриц (частных) наблюдений
(щ + щ + h щ = п), где каждая из частных матриц задает порцию
исходных данных, относящихся к некоторой подсовокупности, состоящей
из Uj объектов. При этом процессы (моменты) обследования этих
совокупностей могут быть разделены в пространстве (во времени).
Очевидно, перед тем как подвергнуть исходные данные основной
статистической обработке (т. е. применять к ним те или иные методы
прикладного статистического анализа, выбор которых обусловлен конечными
целями исследования), исследователь должен ответить на вопрос:
правомерно ли объединение имеющихся в его распоряжении порций (выборок) в
один общий массив или же каждая из порций имеет свою специфику,
следовательно, и обрабатывать их надо по отдельности? В рамках математико-
статистических моделей этот вопрос сводится к выяснению (с помощью
соответствующих статистических критериев), можно ли считать эти
порции данных различными выборками из одной и той же генеральной со-
вокупности (см., например, пп. 8.1.2, 8.6.3, 8.6.4).
Проверка статистической независимости
последовательности наблюдений, составляющих массив исходных данных.
Применение многих статистических методов является правомерным лишь в
ситуациях, когда справедливо допущение о статистической
независимости обрабатываемого ряда наблюдений Xi,-Y2,..МХП. Этот же вопрос
возникает и применительно к рядам {Jft(ti),...,Л^Г^}. Поэтому, перед
тем как подвергнуть имеющиеся результаты наблюдения основной
статистической обработке, необходимо выяснить (с помощью соответствующих
статистических критериев (см. п. 3.1 тома 2)), являются ли они
статистически независимыми или их следует рассматривать как
последовательности взаимозависимых величин.
Унификация типа переменных. Одна из сложностей
автоматизированного анализа информации заключается в том, что среди компонент
яг1 , ar ',..., агр' анализируемого многомерного признака могут быть
показатели трех разных типов: количественные, качественные
(порядковые, ординальные) и классификационные (номинальные). Их определение
и сущность приведены в п. 2.3.
В связи с этим возникает вопрос унификации записи единичного
наблюдения, снятого с объекта г. В соответствии с одним из вариантов
решения этого вопроса г-е многомерное наблюдение в унифицированной записи

344 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
представляется вектор-столбцом размерности гаг+тгН hwp, где га* —
число градаций (интервалов группирования, уровней качества или
однородных групп) признака аг , причем компонентами этого вектор-столбца
могут быть только нули или единицы. При таком подходе к достижению
единообразия записи наблюдений многомерного признака смешанной
природы мы вынуждены мириться, во-первых, с элементами субъективизма в
выборе способов разбиения диапазонов изменения анализируемых
количественных признаков на интервалы группирования и, во-вторых, с
определенной потерей информативности исходных данных, связанной с
переходом от индивидуальных к группированным значениям по количественным
переменным.
В качестве альтернативного подхода к способу унификации записи
исходных данных может быть использована идея, прямо
противоположная той, на основании которой построен только что описанный прием. В
частности, руководствуясь некоторыми дополнительными соображениями
(и допущениями), исследователь пытается преобразовать качественные
и классификационные переменные в количественные, используя процесс
так называемой «оцифровки», или шкалирования, неколичественных
переменных, а также некоторые специальные модели (см. [Айвазян С. А.,
БнюковИ.С, МешалкинЛ. Д., 1983, п. 10.2]).
Экспериментальный анализ закона распределения
исследуемой генеральной совокупности и вопрос ее подходящей
параметризации. Эта часть предварительной статистической обработки
исходного массива данных, представленных в виде (9.1), включает в себя
вычисление основных числовых характеристик распределения:4 среднего
значения, дисперсии, коэффициентов асимметрии и эксцесса, а в
многомерном случае — и элементов выборочной ковариационной матрицы. Кроме
того, исследователь проводит численный и графический анализ
одномерных законов распределения рассматриваемых показателей,
заключающийся в построении соответствующих полигонов частот, гистограмм,
эмпирических функций распределения. Результаты этого
экспериментального анализа, дополненные априорными сведениями о природе
анализируемой генеральной совокупности, зачастую оказываются достаточными для
формулировки одной или нескольких конкурирующих гипотез об общем
(параметрическом) виде закона распределения вероятностей, задающего
эту генеральную совокупность. Не следует пренебрегать такой
возможностью, поскольку знание общего вида вероятностного распределения в
исследуемой генеральной совокупности позволяет сделать наилучший
выбор метода статистического оценивания параметров этого распределения,
а также метода последующей основной статистической обработки масси-

9.2 ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 345
ва исходных данных (из набора конкурирующих методов). Как известно,
выяснение непротиворечивости высказанной исследователем гипотезы об
общем виде распределения анализируемых наблюдений с природой и
спецификой имеющихся в распоряжении исследователя конкретных исходных
данных осуществляется с помощью тех или иных статистических
критериев согласия (си. пп. 8.1.1 и 8.6.1).
Этап 5: составление детального плана вычислительного анализа
материала. Этап начинается с составления справки по собранному
материалу и результатам предварительного анализа. Определяются основные
группы, для которых будет проводиться дальнейший анализ.
Пополняется и уточняется тезаурус содержательных понятий. Четко описывается
блок-схема анализа с указанием привлекаемых методов. Формулируется
оптимизационный критерий, на основании которого выбирается один из
альтернативных методов (или одно из альтернативных семейств методов)
основной статистической обработки исходных данных.
Этап 6: вычислительная реализация основной части
статистической обработки данных. Основная забота исследователя на этом этапе —
эффективное управление вычислительным процессом путем
формулировки задачи обработки и описания данных на входном языке
используемого программного обеспечения. Учитываются размерность задачи,
алгоритмическая сложность вычислительного процесса, возможности
используемого вычислительного средства (длина слова, быстродействие, объем
оперативной памяти, организация базы данных и т.п.) и, наконец,
особенности данных (степень обусловленности используемых при реализации
линейных процедур матриц, надежность априорных оценок параметров и
т.п.).
Этап 7: подведение итогов исследования. Этап начинается с
построения формального статистического отчета о проведенном
исследовании. При интерпретации результатов применения статистических
процедур (оценка параметров, проверка гипотез, отображения в пространство
меньшей размерности, классификация и т. п.) учитывается как место этих
процедур в блок-схеме анализа, так и соотношение объемов используемых
выборок, размерности пространства наблюдений, числа и значений
параметров. Теоретически эти вопросы, несмотря на их крайнюю
актуальность, разработаны довольно мало.
Затем результаты исследования, его основные выводы
формулируются в содержательных терминах. Если исследование проводилось в рамках
математико-статистических методов и моделей, то его выводы
формулируются в терминах оценок неизвестных параметров анализируемой
системы или в виде ответа на вопрос о справедливости проверяемой гипотезы и

346 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
сопровождаются гарантируемыми количественными оценками степени их
достоверности. Если же исследование осуществлялось средствами
анализа данных (т. е. в рамках логико-алгебраического подхода), то его выводы
не претендуют на вероятностную интерпретацию.
В заключение проверяется, в какой мере достигнуты намеченные на
этапе 1 содержательные цели работы, и если достигнуты не все из них, то
объясняется, почему. Работа завершается содержательной
формулировкой новых задач, вытекающих из проведенного исследования.
В некоторых руководствах по статистике этапы 5, б и 7 объединены
в одном этапе, названном «Обработка и анализ» .
Резюмируя описание общей логической схемы статистического
анализа исходных данных, отметим, что основные приемы статистического
моделирования и методы первичной статистической обработки являются
главными в ходе реализации важнейших этапов 1, 4 и 7, а также по мере
необходимости могут привлекаться при реализации этапов 3, 5 и 6.
ВЫВОДЫ
1. Прикладная статистика заимствует часть методов
статистического анализа и моделирования у математической статистики и имеет
пересечения в задачах и целях с эконометрикой. Однако основными
характерными чертами, отличающими прикладную статистику от этих двух
дисциплин, являются следующие:
• основу методологии разработки инструментария прикладной
статистики составляет подход, позволяющий в рамках единой
унифицированной логической схемы синтезировать две автономно
возникших и какое-то время взаимонезависимо развивавшихся
концепции анализа данных и моделирования — вероятностную и логико-
алгебраическую; в результате прикладная статистика объединила в
себе как прикладные вероятностно-статистические методы
многомерного статистического анализа, так и логико-алгебраические методы
анализа данных, не использующие в своих построениях
вероятностных рассуждений;
• главный исследовательский интерес прикладной статистики
сосредоточен на трех проблемах: (а) статистическом исследовании
зависимостей между анализируемыми показателями; (б) статистических
методах классификации объектов и признаков; (в) методах
снижения размерности исследуемого признакового пространства с целью
лаконичного объяснения природы анализируемых многомерных
данных;

выводы 347
• прикладная статистика, в отличие от математической статистики
и в какой-то мере эконометрики относится к весьма динамичным
по своему содержанию и постановкам задач научным дисциплинам:
она постоянно нацелена на выработку новых (стимулированных
запросами практики) постановок задач и на достижение
результатов, позволяющих ослабить ограничительные условия в
канонических математико-статистических и зконометрических моделях.
2. Двумя наиболее распространенными формами представления
исходных статистических данных, поступающих «на вход» прикладного
статистического анализа и моделирования, являются матрицы «объект-
свойство» вида (9.1) и матрицы парных сравнений (объектов или
признаков) вида (9.2). Первая из них содержит результаты измерений
анализируемого набора признаков X = (аг , яг , ...,агр') на статистически
обследуемом множестве объектов О и 02> • • • > ^n> a вторая (чаще всего
получаемая с помощью специальных анкет и экспертных опросов) состоит из
характеристик попарных сравнений статистически обследуемых объектов
по некоторому анализируемому свойству.
3. Проблема статистического исследования зависимостей состоит,
в самой общей формулировке, в выявлении и описании парных и
множественных статистических связей (их смысла, степени тесноты, формы и
т.п.), существующих между компонентами анализируемого многомерного
признака X = (аг1',аг2\.. . ,агр')т. Причем анализ этих связей
производится на основании исходных статистических данных вида (9.1) или
(9.2). Описанию задач и инструментария, относящихся к этой проблеме,
посвящены гл. 10, 11, а также гл. 2, 3 и 4 в томе 2.
4. Проблема классификации объектов (в общей, нестрогой,
постановке) заключается в том, чтобы всю анализируемую совокупность объектов
Oi,O2)-*-90n> статистически представленную в виде матриц (9.1) или
(9.2), разбить на сравнительно небольшое число (заранее известное или
нет) однородных, в определенном смысле, трупп или классов. Описанию
задач и инструментария, относящихся к этой проблеме, посвящена гл. 12.
5. Проблема снижения размерности анализируемого признакового
пространства состоит в таком переходе от исходного набора р признаков
(аг ', аг ,..., ж ) к вспомогательному набору гораздо меньшего числа р
признаков-детерминант z" , г \..., г'р , при котором либо наблюденные
значения самих исходных признаков (т.е. данные матрицы (9.1)), либо
некоторые интересующие нас свойства или характеристики,
определяемые исходными признаками, могут быть наиболее точно (в определенном
смысле) оценены по совокупности значений вспомогательных признаков
z ,г'2\.'«>* • При этом упомянутые признаки-детерминанты могут

348 ГЛ. 0. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
выбираться из числа исходных, а могут конструироваться в качестве
некоторых функций от исходных признаков. К методам снижения
размерности обращаются при решении ряда конкретных типовых прикладных
задач статистического анализа и моделирования, среди которых:
• отбор наиболее информативных показателей в задачах
классификации (п. 12.3 и 12.4), в моделях регрессии (п. 2.6 в томе 2) и при построении
интегральной латентной характеристики («агрегатного скалярного
индикатора») изучаемого свойства (п. 13.4);
• сжатие больших массивов обрабатываемой и хранимой информации;
• визуализация (наглядное представление) многомерных
статистических данных;
• построение условных координатных осей для описания «состояний»
объектов, статистически заданных матрицей парных сравнений (9.2).
в. Общая логическая схема статистического анализа какого-либо
процесса или явления может быть условно разложена на следующие семь
этапов:
1) предварительный анализ исследуемой реальной системы;
2) составление детального плана сбора исходной статистической
информации;
3) сбор исходных статистических данных;
4) преданализ или первичная статистическая обработка данных;
5) составление плана моделирования и вычислительного анализа
материала;
6) вычислительная реализация методов статистического анализа и
моделирования;
7) интерпретация результатов и подведение итогов исследования.
В рамках этой схемы удобно комментировать роль и место основных
разделов и методов прикладной статистики.

ГЛАВА 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ
ЗАВИСИМОСТЕЙ (ОСНОВНЫЕ
ПОНЯТИЯ И ПОСТАНОВКИ ЗАДАЧ)
10.1. Общая формулировка проблемы,
пример
Любой закон природы или общественного развития может быть
выражен в конечном счете в виде описания характера или структуры
взаимосвязей (зависимостей), существующих между изучаемыми явлениями
или показателями (переменными величинами или просто переменными).
Если эти зависимости: а) стохастичны по своей природе, т.е.
позволяют устанавливать лишь вероятностные логические соотношения между
изучаемыми событиями А и 2?, а именно соотношения типа «из факта
осуществления события А следует, что событие В должно произойти, но
не обязательно, а лишь с некоторой (как правило, близкой к единице)
вероятностью Р»; б) выявляются на основании статистического
наблюдения за анализируемыми событиями или переменными, осуществляемого
по выборке из интересующей нас генеральной совокупности (см. гл. 6),
то мы оказываемся в рамках проблемы статистического исследования
зависимостей. Соответствующий математический аппарат, будучи
таким образом нацеленным в первую очередь на решение основной проблемы
естествознания: как по отдельным, частным наблюдениям выявить и
описать интересующую нас общую закономерность, — занимает, бесспорно,
центральное место во всем прикладном математическом анализе.
Перед тем как перейти к формулировке общей и частных задач
статистического исследования зависимостей, условимся описывать
функционирование изучаемого реального объекта (системы, процесса, явления)
набором переменных (рис. 10.1), среди которых:
х^\х^2\...ух^ — так называемые «входные» переменные, опи-

350
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
сывающие условия функционирования (часть из них, как правило,
поддается регулированию или частичному управлению); в
соответствующих математических моделях их называют независимыми, факторами-
аргументами, предикторными (или просто предикторами, т. е.
предсказателями), экзогенными, объясняющими (в книге мы будем использовать в
основном два последних термина);
l/l\ !^2\ • • • 10^ — выходные переменные, характеризующие
поведение или результат (эффективность) функционирования; в
математических моделях их называют зависимыми, откликами, эндогенными,
результирующими или объясняемыми (в книге используются в основном три
последних термина);
Случайные
факторы,
не
поддающиеся
учету
Анализируемая реальная система
(объект)
Механизм преобразования
входных переменных в
результирующие показатели
О)


тирующие

ременные

Объясняющие
переменные
(предик-
торные)
Рис. 10.1. Общая схема взаимодействия переменных при статистическом
исследовании зависимостей
?* \е ',..., ?*т' — латентные (т.е. скрытые, не поддающиеся
непосредственному измерению) случайные «остаточные» компоненты, отра-
(л\ /о\ (т.\
жающие влияние (соответственно на ук \ук ,...,у ) не учтенных «на
входе» факторов, а также случайные ошибки в измерении анализируемых
показателей (в математических моделях мы их, как правило, будем
именовать просто «остатками»).
Тогда общая задача статистического исследования зависимостей (в
терминах изучаемых показателей) может быть сформулирована
следующим образом:

ЮЛ ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР 351
по результатам п измерений
Ux{l) хB) я(.р)' Л1) Л2) 1/!т)П A0 1)
исследуемых переменных на объектах (системах, процессах)
анализируемой совокупности построить такую (векторнозначную) функцию
A0.2)
которая позволила бы наилучшим (в определенном смысле) образом
восстанавливать значения результирующих (прогнозируемых) переменных
У = (у , у ,..., У ) по заданным значениям объясняющих
(экзогенных) переменных X = (хA\хB\...,х{р))Т.
Данная формулировка задачи нуждается в уточнениях. В частности,
прежде всего мы должны ответить на следующие вопросы:
а) каково математическое выражение (или структура модели)
искомой зависимости между У и X, записанное в терминах Y,X,i{X) и
е - (e(l) ?B) e(m))Tt>
б) в соответствии с каким критерием качества апроксимации
значений У с помощью функции f(X) мы будем определять наилучший способ
восстановления значений результирующих показателей по заданным
значениям объясняющих переменных?
в) с какой именно прикладной целью мы проводим все наше
исследование, т. е. для решения каких конкретных задач мы собираемся
использовать построенную в результате исследования функцию f(X)?
Прежде чем обсуждать эти вопросы, рассмотрим пример.
Пример 10.1. Анализируется «поведение» двумерной случайной
величины (?, т/), где ? (ден.ед.) — среднедушевой доход и т/ (ден.ед) —
среднедушевые денежные сбережения в семье, случайно извлеченной из
рассматриваемой совокупности семей, однородной по своему
потребительскому поведению. В табл. 10.1 и на рис. 10.2 представлены исходные
статистические данные вида (ЮЛ), характеризующие среднедушевые
величины дохода (х() и денежных сбережений (yi) за определенный отрезок
времени, а именно за месяц, в каждой (i-й, i = l,2,...,n) обследованной
семье рассматриваемой совокупности семей (в данном условном примере
объем п статистически обследованной совокупности семей равнялся 40). В
этом примере имелась возможность при отборе исходных данных
(выборки) контролировать значения экзогенной переменной ?, что позволило, в

352
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
частности, разбить статистически обследованные семьи на четыре равные
по объему группы по доходам.
j L у, ден.ед.
120
100
80
60
40
20
у
уСр(а?) = go+ 01 а?
0О=?
01=?
A ¦¦
0 40 80 120 160 200 ж, ден.ед.
Рис. 10.2. Графическое представление результатов обследования 40 семей
по их среднедушевому доходу (г,-) и среднедушевым денежным
сбережениям (у,)
Мы видим, что даже в пределах каждой из этих групп величины
среднедушевых сбережений семей подвержены некоторому неконтролируемому
разбросу, обусловленному влиянием множества не поддающихся строгому
учету и контролю факторов (т.е. налицо упомянутый выше
стохастический характер зависимости между х и у). Однако это еще не значит,
что расположение точек (япУ*)* являющихся геометрическим
изображением результатов обследования семей по доходу и сбережениям, должно
быть совершенно хаотичным и не должно обнаруживать некоторой вполне
определенной тенденции, характеризующей зависимость денежных
сбережений в семье (rj) от ее среднедушевого дохода (?). При исследовании
подобных зависимостей встают следующие основные вопросы (в скобках
после вопроса указываются главы и пункты настоящей книги, ему посвя-

10.1 ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР 353
щенные).
1. Как исходя из конкретных прикладных целей исследования
определить смысл, в котором понимается исследуемая зависимость? (п. 10.2 и
10.5).
2. Имеется ли вообще какая-либо связь между исследуемыми
переменными (а в случае многих переменных какова структура этих связей?) и
как измерить тесноту этой связи? (гл. 11).
3. Каков общий математический вид искомой связи между г/ и ?,
т.е. как определяется общая структура соответствующей
математической модели? (п. 10.7).
4. Как, отправляясь от принятой общей структуры модели, провести
необходимую вычислительную обработку исходных данных A0.1) с целью
получения конкретного вида зависимости rj от ?, что позволит в данном
случае производить количественную оценку неизвестных денежных
сбережений семьи по заданной величине ее среднедушевого дохода? (гл. 2, 3, 4
в томе 2).
5. Поскольку наши выводы основаны на обработке ограниченного
ряда наблюдений, то их количественные характеристики, естественно,
подвержены (при повторениях соответствующих выборочных обследований)
некоторому случайному разбросу. Как оценить степень точности наших
выводов! (гл. 2, 3, 4 в томе 2).
6. Как решать сформулированные выше вопросы в ситуациях, когда
среди объясняющих (предикторных) переменных могут быть и
неколичественные? (ответы на 2-й вопрос — в гл. 11).
Вернемся к нашему примеру и попробуем ответить на некоторые из
поставленных здесь вопросов, в том числе на принципиальные вопросы
а), б) и в), ответы на которые позволяют уточнить общую формулировку
задачи статистического исследования зависимостей, данную выше.
Начнем «с конца», т.е. с уточнения конечных прикладных
исследований (см. вопросы 1, а также а) и в)). Известно, что из двух
анализируемых характеристик материальной состоятельности семьи характеристика
денежных сбережений (г/) относится к категории статистически
труднодоступных: содержащиеся в ежегодных и единовременных выборочных
семейных бюджетных обследованиях Госкомстата РФ сведения о
сбережениях, как правило, ненадежны и непредставительны. Поэтому главной
конечной целью нашего исследования (опирающегося, как мы будем
всегда предполагать, на достоверную и репрезентативную выборку исходных
данных) является возможность восстановления (прогноза):
• удельной (т.е. в расчете на одного члена семьи за определенный
отрезок времени) величины денежных сбережений в конкретной семье (у(х))
12 Теория вероятностей
и прикладная статистика

354 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
по заданному значению ее среднедушевого дохода х;
• удельной величины средних денежных сбережений (уср(х)) в семьях
данной группы х по доходам.
Этой цели мы сможем достигнуть, если сумеем математически
описать закономерность изменения условных теоретических средних
значений Уср(х) = Е(т/ | f = x) в зависимости от ж, а также изучить характер
случайного разброса денежных сбережений у(х) отдельных семей данной
группы х по доходам относительно своего среднего значения уСр(я) (при
любом интересующем нас значении среднедушевого дохода х). Это
естественным образом приводит нас к необходимости рассмотрения
математической модели вида
т? = /(*) + *, A0.3)
в которой остаточная компонента е отражает случайное отклонение
денежных сбережений наугад выбранной отдельной семьи с доходом f = х
от среднего значения уср(х) = Е(т/1 ? = х) этих сбережений,
подсчитанного по всем семьям данной группы по доходам, а функция f(x) описывает
характер изменения условного среднего уср(х) (при ? = х) в зависимости
от изменения я, если дополнительно прийти к соглашению, что
характер случайного разброса величин у(х) = (т/ | ? = х) относительно своих
средних Уср(х) таков, что Е(г | ? = х) = 0 при всех ж.
Таким образом, из A0.3) мы непосредственно получаем
УсР = Е(т/1 { = х) = /(*). A0.4)
Чтобы покончить с вопросами 1, а) и в), остается уточнить общую
структуру модели, т.е. определить, в каком классе F функций f(x) мы будем
производить аппроксимацию искомой зависимости уср(х).
В нашем случае, учитывая однородный (по характеру
потребительского поведения) состав исследуемой совокупности семей, естественно
исходить из гипотезы об одинаковой (в среднем) склонности семей к
сбережениям, выражающейся, в частности, в том, что все семьи начиная с
некоторого «порогового» уровня дохода склонны отделять в сбережения в
среднем одинаковую долю дохода. Математически, как легко понять, это
выразится в виде
З/срИ = *о + М, (Ю.5)
где 0О и в\ — некоторые константы {неизвестные параметры модели).
Так что
где под {/(ж;0)} понимается семейство всех тех функций /(ж;0),
которые могут быть получены при подстановке вместо 0 ее различных

10.1 ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР 355
конкретных значений @ — векторный параметр; в нашем случае 0 =
Таблица 10.

Среднедушевой
доход
(ден.ед.)
1
Х\ = х2 ==
... = Хщ =
= х°г = 80
«11 = *12 =
. . . = Х2о =
= х°2 = 120
1

Среднедушевые

сбережения
(ден.ед.)
2
У\ = 15,2
у2 = 10,7
j/з = 18,5
У* = 14,9
Ув = 24,1
»6 = 10,3
У7 = 14,2
У» = 31,0
у9 = 20,4
010 = 20,0
2/п = 70,1
J/12 = 35,0
У13 = 43,0
Уи = 29,0
3/15 = 17,0
1/16 = 48,2
у17 = 18,9
У18 = 53,0
У19 = 39,4
020 = 46,2
Средние сбережения
для семей данной
группы (ден.ед.)
3
»(*?) =
, 10
= Ш Е У< = 17,9
«=1
у(ж») =
20
4Ей = 4о,о
Оценка среднеквадра-
тического отклонения s
и коэффициента
вариации V сбережений для
семей данной
доходной группы
4
*>!)=[*?(*
-у(з?)) = 6,4
J
V(x\) = 36%
«(»•) = Г* Е (»)
L »=и
1 ^
-у(ж5)) = i6,o
J
V{x\) = 40%
12*

356 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Продолжение таблицы 10.1
1
Х2\ = «22 =
. . . = Х30 =
= ж° = 160
«31 = Ж32 =
. . . = «40 =
= х\ = 200
2
3/21 = 49,6
3/22 = 69,4
3/23 = 77,8
3/24 = 43,0
3/25 = 31,8
3/26 = 62,6
г/27 = 100,2
3/28 = 68,8
3/29 = 78,0
З/зо = 29,6
3/31 = 125,5
3/32 = 88,3
З/зз = 62,0
3/34 = 58,8
3/35 = 84,0
З/зб = 79,0
г/37 = 95,5
Узе = 120,8
3/39 = 98,1
3/40 = 29,7
3
У(*з) =
30
4Ей = 6i,i
t=21
у(х°4) =
40
= Ш Е Уг = 84,2
г=31
4
*(*з)=|Уе (и
-*(*з))8] =22,6
V[x%) = 37%
п 1
«Ю = \\ Е (г/i
L «=3i
-у(ж5)) = 28,9
J
V(x°4) = 34%
Такой выбор «класса допустимых решений» F = {/(#)}
подтверждается и характером расположения совокупности точек, являющихся
геометрическим изображением исходных данных в нашем примере (см. на
рис. 10.2 расположение «крестиков», ординаты которых определяются
экспериментально подсчитанными, т.е. вычисленными на основании
имеющихся выборочных данных, условными средними y(z?),t = 1,2,3,4)г.
1 Обращаем внимание читателя на разницу в смысле и обозначениях
экспериментальных (выборочных) и теоретических условных средних соответственно у(х) и уСр(я)-
Строго говоря, на практике теоретических средних мы никогда знать не можем,
однако мы опираемся в своем исследовании на тот факт, что в соответствии с законом

10.1 ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР 357
И наконец, следует уточнить, в соответствии с каким именно
критерием качества аппроксимации неизвестных величин среднедушевых
семейных денежных сбережений у(х) и уср(х) с помощью функции во + О^х
мы будем определять наилучший способ прогноза yQp(x) по х. Наиболее
обоснованное и точное решение этого вопроса опирается на знание
вероятностной природы (а именно типа закона распределения вероятностей)
остатков е в модели A0.3). Так, например, известно (см. гл. 2 тома 2), что
если предположить, что при любых значениях х распределение
вероятностей остатков е описывается @, а )-нормальным законом и что остатки
e(xi),i = 1,2,...,п, характеризующие различные наблюдения,
статистически независимы, то наименьшая ошибка прогноза уср(х) с помощью
модели f(x) € F (т. е. функция f(x) подбирается из класса F) обеспечивается
требованием^метода наименьших квадратов, в соответствии с которым
оценки 0О и 01 параметров в0 и в\ определяются из условия минимизации
по 0q и #i выражения
1=1
В нашем примере явно нарушено условие постоянства дисперсии
остатков (см. табл. 10.1), т.е. условная дисперсия D(s | ? = х) =
D(r/ - в0 - 0i? | f = x) = а (х) существенно зависит от значения х.
Можно устранить это нарушение, поделив все анализируемые величины,
откладываемые по оси г/, а следовательно и остатки ?(ж), на значения s(x)
(являющиеся несмещенными статистическими оценками для 0"(ж)), т.е.
перейдя к анализу остатков е(х) = e(x)/s(x). Тогда можно показать (с
помощью методов, описанных в п. 8.6.1), что гипотеза о @; <т )-нормальном
характере распределения остатков ё(х) не противоречит имеющимся в
нашем распоряжении данным (представленным в табл. ЮЛ) и,
следовательно, требование A0.7) приводит к необходимости решения экстремальной
задачи вида
AоУ)
т. е. к системе из двух линейных уравнений с двумя неизвестными @О и
больших чисел (см. п. 6.2) у(х) —> уСр(х) (по вероятности), когда число наблюдений,
по которым подсчитано у (я), стремится к бесконечности.

358 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
(юУ)
Решение системы A0.7") дйьет нам в качестве оценок во и в\ для
неизвестных параметров соответственно во и в\ выражения:
( Е а*) ( Е А^л) - (Е Ал) (Е а<
U=i / \i=i
n n
ЕЛ 7/ V Л Г-
л t=l л t=l
О n In '
Е а. Е \
t=l i=l
где А,- = s" (xi).
Расчет по этим формулам с использованием данных табл. 10.1 дает
нам ответ на сформулированный выше вопрос 4:
в\ = 0,685;
во = -40,360,
так что статистическая оценка искомой зависимости средней величины
среднедушевых семейных сбережений уСр(х) от значения среднедушевого
дохода семей доходной группы х имеет в этом случае вид
?ср(ж) = -40,36+ 0,685-ж.
При другой статистической природе остатков е или при отсутствии
достаточной информации о типе их вероятностного распределения
возможен иной, чем по A0.7), выбор критерия качества аппроксимации Дп.
Отметим, однако, что наиболее широкое распространение в статистической
практике получили именно различные варианты критерия наименьших
квадратов A0.7) (см. гл.2 в томе 2).
Заканчивая обсуждение примера 10.1 и возвращаясь к общему
описанию задач статистического исследования зависимостей, отметим, что

10.2 КАКОВА КОНЕЧНАЯ ПРИКЛАДНАЯ ЦЕЛЬ? 359
функции t(X) = Е(т/1 ? = X), описывающие поведение условных средних
результирующего показателя г/ (вычисленных при значениях
объясняющих переменных ?, зафиксированных на уровне ? = X) в зависимости от
изменения X, принято называть функциями регрессии.
10.2. Какова конечная прикладная цель
статистического исследования
зависимостей?
С этого вопроса должно начинаться любое статистическое
исследование зависимостей. Ведь от ответа на этот вопрос существенно зависят
план исследования, выбор общей структуры математической модели,
интерпретация получаемых статистических характеристик и выводов и т. д.
Итак, для чего же строятся математические модели типа A0.3),
описывающие статистические зависимости между исследуемыми
переменными: результирующими показателями У = (у* , у ,..., у ), с одной
стороны, и соответствующими объясняющими (экзогенными) переменными
X = (ж*1 ,аг ',. . .,агр'), с другой стороны?
Выделим три основных типа конечных прикладных целей подобных
исследований, расположив их как бы по нарастанию глубины
проникновения в содержательную сущность анализируемой конкретной задачи.
Тип1: Установление самого факта наличия (или отсутствия)
статистически значимой связи между Y и X. При такой постановке
задачи статистический вывод имеет двоичную (альтернативную)
природу — «связь есть» или «связи нет» — и сопровождается обычно лишь
численной характеристикой (измерителем) степени тесноты исследуемой
зависимости. Выбор формы связи (т.е. класса допустимых решений F
и конкретного вида функции f(X) в модели A0.3)) и состава
объясняющих переменных X играет подчиненную роль и нацелен исключительно
на максимизацию величины этого измерителя степени тесноты связи:
исследователю часто не приходится даже «добираться» до конкретного вида
функции f(X) и тем более он не претендует на анализ причинных влияний
переменных X на результирующие показатели. Этой проблеме посвящена
гл.11.
Тип 2: прогноз (восстановление) неизвестных значений
интересующих нас индивидуальных (Y(X) = (rj | ? = X)) или средних (Ycp(X) =
E(rj | ? = X)) значений исследуемых результирующих показателей по
заданным значениям X соответствующих объясняющих переменных. При
такой постановке задачи статистический вывод включает в себя
описание интервала (области) вероятных значений прогнозируемого показа-

360 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
теля Ycp(X) или Y(X) и сопровождается величиной доверительной
вероятности Р, с которой гарантируется справедливость нашего
прогноза, формализуемого с помощью утверждения вида {Y(X) € Д[У(Х)]р}
или [Ycp(X) ? A[Ycp(X)]p} (см. определение доверительного интервала
в п. 7.4 и п. 7.5.4). Как и в предыдущем случае, выбор формы связи (т.е.
класса допустимых решений F и конкретного вида функции {(X) в
модели A0.3)) и состава предикторов объясняющих переменных X играет
подчиненную роль и нацелен исключительно на минимизацию ошибки
получаемого прогноза. Однако в данном случае (в отличие от предыдущего)
исследователь существенно использует значения функции f(X), которые
являются отправной точкой при построении прогнозных доверительных
интервалов. Последние обычно определяются в форме множества всех тех
значений У, которые удовлетворяют неравенствам
{(X) - еР(Х,п) < У < {(X) + еР(Х,п), A0.8)
где ер(Х,п) — гарантируемая (с вероятностью, не меньшей заданного
значения Р) максимальная величина ошибки прогноза . Таким образом,
исследователя интересуют в данном случае лишь значения функции f(X),
но не ее структура, определяющая, в частности, соотношение удельных
весов влияния объясняющих переменных аг ',ar , ...,:гр' на каждый из
результирующих показателей у* '(k = l,2,...,m). Так, например, если
при статистическом оценивании неизвестной истинной зависимости
f(X) = ycp(x{l\xW) = 1 + ЗаA) + 5х{2) A0.9)
исследователю удалось получить оценку функции f(X) в виде
-х
{2)
A0.9')
и при этом было установлено, что объясняющие переменные ж'1' и аг '
5ункционал1
сA)«2жB), A0.10)
п
связаны между собой «почти функциональной» линейной зависимостью
1 Напоминаем читателю, что f, e и Y являются m-мерными векторами (см. A0.2)),
так что запись A0.8) означает справедливость m соответствующих покомпонентных
неравенств.
2 Говоря о «почти функциональной» линейной зависимости между х^ и х&\ мы
имеем в виду близость к единице (по абсолютной величине) коэффициента корреляции
между этими переменными (см. п. 2.6.6, соотношение B.33)).

10.2 КАКОВА КОНЕЧНАЯ ПРИКЛАДНАЯ ЦЕЛЬ? 361
то функция f(X) будет обладать хорошими прогностическими
свойствами, несмотря на существенное отличие ее коэффициентов при г ' и г '
от соответствующих коэффициентов истинной функции f(X). (Обращаем
внимание читателя на тот факт, что коэффициенты при аг ' в
функциях f(X) и f(X) отличаются даже по знаку!) При подстановке заданных
значений объясняющих переменных аг ' и аг ' в правые части A0.9) и
A0.9;), при условии, что эти значения связаны приближенным
соотношением A0.10), мы будем получать совпадающие (или приближенно
совпадающие) результаты f(X) и /(X), характеризующие усредненную величину
Уср(Х) исследуемого результирующего показателя.
Тип 3: выявление причинных связей между объясняющими перемен-
ными X и результирующими показателями У, частичное управление
значениями У путем регулирования величин объясняющих переменных
X. Такая постановка задачи .претендует на проникновение в «физический
механизм» изучаемых статистических связей, т. е. в тот самый механизм
преобразования «входных» переменных X и е в результирующие
показатели У (см. рис. 10.1), который в большинстве случаев исследователь,
не будучи в состоянии его конструктивно описать, вынужден именовать
(следуя сложившейся кибернетической терминологии) «черным ящиком».
И при выявлении причинных связей, и при намерении исследователя
использовать модели типа A0.3) или A0.4) для управления значениями
результирующих показателей Ycp(X) или Y(X) путем регулирования
величин объясняющих переменных X на первый план выходит задача
правильного определения структуры модели (т.е. выбора общего вида
функции f(X)), решение которой обеспечивает возможность количественного
измерения эффекта воздействия на Y(X) каждой из объясняющих
переменных аг , аг ,..., ж в отдельности. Однако как раз это место
(правильный выбор общего вида функции $(Х)) и является самым слабым во
всей технике статистического исследования зависимостей: к сожалению,
не существует стандартных приемов и методов, которые образовывали бы
строгую теоретическую базу для решения этой важнейшей задачи
(некоторые рекомендации по проведению этого этапа исследования содержатся
в п. 10.7).
Заметим, что исследователи, пожалуй, чаще других ставят перед
собой именно цели типа 3. И в таких прикладных задачах, как
управление качеством продукции с помощью регулирования хода
технологических процессов, прогноз и анализ объемов произведенной продукции по
затратам на трудовые ресурсы и капитальные вложения, построение
интегральных целевых функций, описывающих эффективность
функционирования экономических единиц (предприятий, семей) по набору частных

362 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
характеристик и др., это вполне оправдано. Однако, к сожалению, далеко
не всегда целевые установки исследователей подкреплены объективными
возможностями их реализации.
10.3. Математический инструментарий
Методы статистического исследования зависимостей составляют
содержание специального раздела многомерного статистического
анализа, который в свою очередь можно определить как важнейшую составную
часть прикладной статистики, содержащую инструментарий для
построения оптимальных планов сбора, систематизации и анализа многомерных
статистических данных типа (ЮЛ), нацеленный в первую очередь на
выявление характера и структуры взаимосвязей между компонентами
исследуемого многомерного признака (X,Y) и предназначенный для получения
научных и практических выводов. При этом среди р + т компонент
исследуемого многомерного признака (X,Y) могут быть: количественные,
т. е. скалярно измеряющие в определенной шкале степень проявления
изучаемого свойства объекта (денежный доход и сбережения семьи, объем
валовой продукции, численность работников на предприятии и т. п.);
порядковые (или ординальные), т. е. позволяющие упорядочивать
анализируемые объекты по степени проявления в них изучаемого свойства (уровень
жилищных условий семьи, квалификационный разряд рабочего, уровень
образования работника и т.п.); классификационные (или номинальные),
т. е. позволяющие разбивать обследованную совокупность объектов на не
поддающиеся упорядочиванию однородные (по анализируемому свойству)
классы (профессия работника, мотив миграции семьи, отрасль
промышленности и т. п.). Подразделы многомерного статистического анализа,
составляющие математический аппарат статистического исследования
зависимостей, формировались и развивались с учетом специфики
анализируемых моделей, обусловленной природой изучаемых переменных.
Соответствующая специализация этих разделов отражена в табл. 10.2. В ней
же указаны главы данной книги, посвященные описанию указанных
подразделов.
Из табл. 10.2 видно, что данная книга не охватывает методов
исследования зависимостей неколичественного или смешанного (разнотипного)
результирующего показателя от количественных или смешанных
объясняющих переменных: объемность и специфичность указанной темы
обусловливают целесообразность посвящения ей специального издания.

10.3 МАТЕМАТИЧЕСКИЙ ИНСТРУМЕНТАРИЙ
363
Таблица 10.2
п/п
1
1
2
3
4
5
6
7
Природа
результирующих
показателей
(эндогенных переменных)
2
Количественная
Количественная
Количественная
Количественная
Неколичественная
(порядковые, или
ординальные,
переменные)
Неколичественная

(классификационные, или
номинальные,
переменные)
Смешанная
(количественные и
неколичественные
переменные)
Природа
объясняющих
(экзогенных)
переменных
3
Количественная
Единственная
количественная
переменная,
интерпретируемая
как «время»
Неколичественная
(ординальные или
номинальные
переменные)
Смешанная
(количественные и

неколичественные переменные)
Неколичественная
(ординальные и
номинальные
переменные)
Количествен ная
Смешанная
(количественные и
неколичественные
переменные)
Название
обслуживающих
подразделов
многомерного
статистического анализа
4
Регрессионный и
корреляционный
анализ
Анализ
временных рядов
Дисперсионный
анализ
Ковариационный
анализ, модели
типологической
регрессии
Анализ ранговых
корреляций и
таблиц
сопряженности
Дискриминантный
анализ, кластер-
анализ,
таксономия, расщепление
смесей
распределений
Аппарат
логических
решающих функций
Главы
книги,

посвященные
данным
разделам
5
10,11 (том1);
1,2,4 (том 2)
3(том 2)
—
—
11 (том 1)
12 (том 1)
—

364 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Кроме того, принцип систематизации различных схем, принятый в
табл. 10.2, не приспособлен для выделения одного важного (особенно в
области социально-экономических приложений) случая, когда связи
между количественными переменными X и У описываются системой
одновременных уравнений, в которых одни и те же переменные могут играть
одновременно (в различных уравнениях системы) и роль
результирующих, и роль объясняющих. Этому посвящена теория одновременных эко
нометрических уравнений, основные результаты которой представлены в
гл. 1 и 4 тома 2.
10.4. Некоторые типовые задачи практики
эконометрического моделирования
Накопленный опыт практического использования аппарата
статистического исследования зависимостей позволяет выделить те типы основных
прикладных направлений исследований, в которых этот аппарат работает
особенно часто и плодотворно. Если попытаться расщепить общую
проблему оптимального управления сложной системой (т. е. центральную
проблему кибернетики) на основные составляющие (рис. 10.3), то в качестве
этих составляющих как раз и фигурируют именно те направления
прикладных исследований, в разработке которых существенную роль играет
математический аппарат статистического исследования зависимостей.
Остановимся кратко на роли методов статистического исследования
зависимостей в разработке каждого из упомянутых направлений.
I. Нормирование
Общая схема формирования нормативов с использованием методов
статистического исследования зависимостей может быть представлена
следующим образом. Нормативный показатель играет в моделях типа
A0.3)-A0.4) роль результирующей (объясняемой) переменной у, а
факторы, участвующие в расчете нормативного показателя, — роль
объясняющих переменных аг , аг ,..., ж . Предполагается, что привлечение для
расчета норматива у полной системы определяющих его факторов, т.е.
такой системы, с помощью которой возможно детерминированное
(однозначное) определение величины у, либо принципиально невозможно, либо
нецелесообразно из-за чрезмерного усложнения расчетных формул.
Поэтому анализируется связь между у и (ж , ж ,..., ж*р') вида
y = /(*(V2),...,*(p);0) + ?, : • A0.11)

10.4 НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ
365
где е — остаточная случайная компонента, обусловливающая возможную
погрешность в определении норматива у по известным значениям
факторов X = (ж'1', аг2 ,..., ж'р') , a f(X; 0) — функция из некоторого
известного параметрического семейства F = {f(X; 0)}, 0 6 А, однако численное
I
/
Проблема оптимального управления
Нормирование
г
II
Прогноз,

планирование,
диагностика
г
III
Оценка
труднодоступных
для

средственного
наблюдения и
измерения
параметров
системы
i i
к
Исходные статистические
[ сложной системой
г
IV
Оценка
эффективности

функционирования (или
качества)
системы
>
\ данные
(информационная база)
ч
\
V
Оптимальное

регулирование
параметров
функционирования
системы,
ситуационный
анализ
/
Рис. 10.3. Основные направления практического использования аппарата
статистического исследования зависимостей и центральная
проблема кибернетики
значение входящего в ее уравнение параметра 0 (вообще говоря,
векторного) неизвестно. С целью подбора «подходящего» значения 0 проводится
контрольный эксперимент (наблюдение), в результате которого
исследователь получает исходные статистические данные вида A0.1). Далее на
основании этих данных проводится необходимый статистический анализ
модели A0.11) с целью получения оценки 0 неизвестного параметра 0
и анализа точности полученной расчетной формулы Ycp(X) = /(X;0), в
которой величина условной (экспериментальной) средней YC?(X) интепре-
тируется как средний нормативный показатель при значениях
определяющих факторов, равных X,

366 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Данный подход использовался, в частности, при разработке методик
численности служащих (по различным их функциям) на промышленном
предприятии отрасли по набору технико-экономических показателей,
характеризующих предприятие, при построении автоматизированных
систем нормирования ремонтных работ и в других областях.
П. Прогноз, планирование, диагностика
Отправляясь от общей формулировки задачи статистического
исследования зависимостей (см. п. 10.1) и от ее модельной записи A0.11),
определим в качестве результирующей переменной у интересующий нас
прогнозируемый (планируемый, диагностируемый) показатель, а в
качестве объясняющих переменных аг , ж' ,..., агр' — сопутствующие
факторы, значения которых содержат основную информацию о величине
этого показателя . Наличие остаточной случайной компоненты е, как и
прежде, отражает тот факт, что переменные аг ', аг \... агр' содержат не всю
информацию об у, и обусловливает неизбежность погрешности в
определении прогнозируемого (планируемого, диагностируемого) показателя по
известным значениям объясняющих факторов аг ,аг ,...аг . Исходные
статистические данные вида A0.1) исследователь получает, регистрируя
одновременно значения у и (аг , ...,агр') на анализируемых объектах в
прошлом (в базовом периоде) или на других объектах, но однородных с
анализируемыми.
III. Оценка труднодоступных для непосредственного
наблюдения и измерения параметров системы
Восстановление возраста археологической находки по ряду
косвенных признаков; прочности бетона с помощью косвенных (неразрушаю-
щих) методов контроля (например, по отношению диаметров отпечатков
на поверхности испытуемого образца бетона и на воздействующем на него
эталонном молотке); денежных сбережений семьи по ее доходу (в
среднедушевом исчислении) — во всех этих ситуациях исследователь вынужден
иметь дело с показателями, труднодоступными для непосредственного
измерения (они выделены в тексте курсивом). Очевидно, для того чтобы
иметь принципиальную возможность статистически выявить связь, су-
1 В моделях прогноза и планирования в качестве одного из объясняющих факторов
х(*) вводится в явном виде «длина прогноза», или «горизонт планирования», t (в
единицах времени).

10.4 НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ 367
шествующую между труднодоступным показателем у и косвенно
связанными с ним, но легко поддающимися наблюдению и измерению
признаками аг1',»* \...,аг , исследователю необходимо располагать
исходными статистическими данными вида A0.1), которые получают с помощью
специально организованного контрольного эксперимента или наблюдения.
После того как эта связь выявлена (и оценена степень ее точности), она
используется для косвенного определения значений труднодоступных
показателей лишь по значениям объясняющих переменных аг \ аг ,..., ж .
IV. Оценка эффективности функционирования (или
качества) анализируемой системы
Пытаясь оценить (в целом) эффективность деятельности отдельного
специалиста, подразделения или предприятия, проранжировать страны по
некоторому интегральному качеству (например, по качеству жизни
населения или по так называемому общему индексу человеческого развития),
наконец, проставить балльные оценки спортсмену — участнику
командных соревнований в игровых видах спорта за качество его игры в
определенном цикле, мы каждый раз по существу решаем (на интуитивном
уровне) одну и ту же задачу: отправляясь в своем анализе от набора частных
показателей аг ', аг ,..., агр , каждый из которых может быть измерен и
характеризует какую-нибудь одну частную сторону понятия
«эффективность», мы их как бы взвешиваем (т. е. внутренне оцениваем удельный вес
их влияния на общее, агрегированное, понятие эффективности) и
выходим на некоторый скалярный агрегированный показатель эффективности
2/. Этот показатель — латентный (скрытый), так как он принципиально
не поддается непосредственному измерению (не существует или нам
неизвестна объективная шкала, в которой он мог бы быть измерен). Но он с
некоторой точностью восстанавливается по значениям частных
показателей эффективности аг ,аг',. ..,ж' . Это значит, что между латентным
агрегированным показателем у и набором частных критериев
эффективности аг \ж* ,...,агр' существует статистическая связь типа A0.11).
Главная особенность (и трудность) описываемой ситуации
заключается в том, что при получении (сборе) исходной статистической
информации вида A0.1) значения результирующего показателя у могут быть
получены только с помощью специально организованного экспертного опроса
(значения частных критериев эффективности х*1\х^2\..., а? , как
правило, поддаются непосредственному измерению). Форма экпертной
информации о значениях у может быть различной (балльные оценки,
упорядочения, парные сравнения). Но только располагая наряду со статистической

368 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
информацией об X = (аг1 , аг \...,ж ) одной из форм
соответствующей экспертной информации об у, мы можем статистически построить
некоторую аппроксимацию уср(Х) = f(X;Q) для агрегированного
критерия эффективности функционирования системы и использовать ее затем
в качестве формализованного метода оценки интегрального понятия
эффективности (т.е. уже без привлечения экспертов, а лишь по частным
критериям аг1 , ж* ,.. . ,агр'). Такая модифицированная форма
использования аппарата статистического исследования зависимостей предложена
в [Айвазян С. А., 1974] и носит название экспертно-статистического
метода построения неизвестной целевой функции (см. п. 13.5).
В описанную схему вкладывается широкий класс задач теории и
практики измерения комплексного понятия «качество» сложной системы: в
этих задачах у интерпретируется как агрегированный (комплексный)
показатель качества системы, а аг , я ,..., агр' — как отдельные частные
характеристики его качества (надежность, экономичность, удобство
пользования, эстетический вид и т. п.). В качестве параметрических семейств
F = {/(Х;0)}, привлекаемых при статистическом анализе задач данного
типа, чаще других используются функции линейные
f(X; 0) = во + в\х + • • • + evx (Ю-12)
м степенные
f(X; 0) = floO^V1^2*)'2 • • .(х{р))$р. A0.13)
V. Оптимальное регулирование параметров
функционирования анализируемой системы,
ситуационный анализ
Рассмотрим пример (заимствован из [Айвазян С. А., 1968]). При
анализе производительности мартеновских печей на одном из заводов
исследовалась, в частности, зависимость между производительностью в тон-
но/часах (для исключения влияния задержек и простоев часовая
производительность мартеновской печи определялась как частное от деления
массы плавки на продолжительность периода от начала завалки до
выпуска) и процентным содержанием углерода в металле по расплавлении
ванны (пробу брали через час после первого скачивания шлака).
Результаты замеров по 130 плавкам (т. е. объем п обрабатываемой статистической
выборки вида A0.1) равен 130) приведены на рис. 10.4. Очевидно,
величины производительности (у<) и процентного содержания углерода (ж,-)
подвержены некоторому неконтролируемому разбросу, обусловленному
влиянием множества не поддающихся строгому учету и контролю факторов.

10.4 НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ
369
Другими словами, последовательность пар чисел (&j,yj),t = 1,2,..., 130,
представляет в данном случае результаты 130 независимых наблюдений
двумерной случайной величины (?,//). Однако сквозь кажущуюся
хаотичность расположения точек (а^,у*) на рис Л 0.4 просматривается
вполне определенная закономерность зависимости условного среднего
значения производительности уСр(ж) = Е(*7 | ? = з) от величины процентного
содержания углерода х. Поэтому, располагая статистической
зависимостью Уср(х)) мы можем дать рекомендации технологу по оптимальному
(с точки зрения максимизации производительности) управлению
процессом выплавки: поддерживать процентное содержание углерода в пределах
0,6-1,0%.
У, Т/Ч
18-
17-
16-
_
15
• .:*
•
V* *Ч* А*
0,2 0,4 0,6 0,8 1,0 1,2 1,4 a?,%
Рис. 10.4. Зависимость производительности (у, т/ч) от процентного
содержания углерода (х, %) в металле до расплавления
Мы не случайно начали с этого примера. Использование методов
статистического исследования зависимостей в задачах оптимального
регулирования хода технологического процесса и построения
соответствующих автоматизированных систем управления технологическими
процессами можно отнести к примерам грамотных и относительно
распространенных актуальных приложений этого аппарата. Общая схема таких
приложений предусматривает (в дополнение к приведенному выше частному
примеру): а) одновременное рассмотрение нескольких результирующих
показателей у, у,..., у*р' (производительность, качество продукции,
расход сырья и энергии и т. п.) и многих регулируемых параметров тех-

370 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
нологического процесса аг ,аг %...,агр'; б) возможность сбора исходной
статистической информации вида A0.1).
Менее освоенным (но не менее правомерным и актуальным) является
этот подход в задачах оптимального регулирования:
• характеристик социально-экономического поведения людей и целых
коллективов в ситуациях, когда существует принципиальная возможность
выявления статистических связей между этими характеристиками и
набором объясняющих (и хотя бы частично регулируемых) факторов;
• структуры и объемов нагрузок и видов заданий в процессе
профессиональной подготовки специалистов.
Особо выделим макро-уровень подобного моделирования с целью
оптимального регулирования параметров функционирования
анализируемой системы. В этом случае речь идет об оптимальном регулировании
тех макро-параметров национальной экономики, которые поддаются
хотя бы частичному управлению и планированию (институциональные и
структурные преобразования, налоговая и социальная политика,
инвестиционная активность государства и т.п.). Построив и оценив
статистические связи, существующие между этими параметрами (так называемыми
экзогенными переменными), с одной стороны, и результирующими
(эндогенными, т.е. формирующимися внутри и в ходе функционирования
национальной экономики) переменными — с другой, исследователь может,
придавая различные значения управляемым параметрам, отслеживать
соответствующие реакции на это эндогенных переменных. Т.е.
происходит как бы многократная модельная «прогонка» различных сценариев
социально-экономического развития (такой способ исследования
называют также ситуационным анализом). Реализуется этот подход, как
правило, с помощью систем регрессионных уравнений типа A0.3)—A0.4),
которые принято называть в эконометрике системами одновременных
уравнений (см. гл. 1 и 4 тома 2).
10.5. Основные типы зависимостей между
количественными переменными
При изучении взаимосвязей между анализируемыми
количественными показателями следует установить, к какому именно типу зависимостей
относится исследуемая схема. Под типом зависимости мы подразумеваем
в дайном случае не аналитический вид функции Ycp(X) = f(X\ 0) в
моделях вида A0.11) (о выборе общего аналитического вида функции f(X;Q)
см. п. 10.7), а природу анализируемых переменных (X, у) и
соответственно интерпретацию функции f(X;Q) в каждом конкретном случае.

10.5 ОСНОВНЫЕ ТИПЫ ЗАВИСИМОСТЕЙ 371
Зависимость между неслучайными переменными (схема
А). В этом случае результирующий показатель у детерминированно (т. е.
вполне определенно, однозначно) восстанавливается по значениям
неслучайных объясняющих переменных X = (аг ,аг ',. . .,агр') , т.е.
значения у зависят только от соответствующих значений X и полностью ими
определяются. Это — обычная схема чисто функциональной зависимости
между неслучайными переменными, когда у является некоторой функцией
от р переменных X (т.е. у = f(X)), что является вырожденным
случаем зависимостей вида A0.11), когда остаточная случайная компонента е
равна нулю (с вероятностью единица).
Известно, например, что возраст дерева у (в годах) можно
однозначно восстановить по числу колец х на срезе его ствола, а именно у = х.
Примеры адекватного описания реальных зависимостей с помощью чисто
функциональных (нестохастических) связей, к сожалению, крайне редки
в практике исследований. Кроме того, при проведении их анализа нет
необходимости использовать методы вероятностно-статистической теории.
Поэтому в дальнейшем изложении мы не будем больше возвращаться к
этому типу зависимостей.
Регрессионная зависимость случайного результирующего
показателя г] от неслучайных объясняющих переменных X
(схема В). Природа такой связи может носить двойственный характер: а)
регистрация результирующего показателя 7] неизбежно связана с
некоторыми случайными ошибками измерения ?, в то время как предикторные
(объясняющие) переменные X = (аг ,аг , ...,агр') измеряются без ошибок
(или величины этих ошибок пренебрежимо малы по сравнению с
соответствующими ошибками измерения результирующего показателя); б)
значения результирующего показателя ц зависят не только от
соответствующих значений Л*, но и еще от ряда неконтролируемых факторов, поэтому
при каждом фиксированном значении X* соответствующие значения
результирующего показателя ri(X*) = {rf \ X = Л"*) неизбежно подвержены
некоторому случайному разбросу.
В этом случае объясняющие переменные X играют роль неслучайного
(векторного при р > 1) параметра, от которого зависит закон
распределения вероятностей (в частности, среднее значение и дисперсия)
исследуемого результирующего показателя г/. Удобной математической моделью
такого рода зависимостей является разложение вида
r,(X) = f(X) + e(X). A0.14)
Модель A0.14) строится таким образом, что математическое ожидание
случайного остатка е(Х) равно нулю (Ее(Х) = 0) тождественно по X; по-

372 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
этому функция f(X) описывает поведение условного среднего уср(Х) =
Е(г/ | X) = f(X) в зависимости от X. Предполагается обычно, что
при всех X существует конечная дисперсия е(Х) (т.е. De(X) < оо),
причем величина этой дисперсии, вообще говоря, может зависеть от X (т. е.
De(X) = а (X)). Подчеркнем то обстоятельство, что в описанной модели
A0.14) ни природа случайной компоненты е(Х), ни соответственно
характеристики ее вероятностного распределения никак не связаны со
структурой функции f(X) и, в частности, не зависят от значений ее параметра 0 в
параметрической записи модели (т. е. когда вместо всех возможных
функций f(X) рассматривают какое-либо параметрическое семейство /(Х;0),
см., например, A0.12), A0.13)).
Если вернуться к примеру 10.1, то можно убедиться, что он
хорошо укладывается в рамки модели A0.14). Для этого следует лишь
заметить, что имевшаяся в этом примере возможность контролировать
значения объясняющей (предикторной) переменной f по существу переводит
эту переменную из категории случайных величин в категорию
неслучайных (контролируемых) параметров модели. Дальнейший анализ примера
10.1 (см. табл. 10.1, формулу A0.5) и рис. 10.2) подсказал нам следующую
конкретизацию допущений о природе составных частей модели A0.14):
fcp(x) = Е(т, | X) = /(х) = в0 + в1Х;
,\2 A0.15)
где бг0 — константа, не зависящая от х.
Подчеркнем тот факт, что именно зависимость по схеме В, т.е.
регрессионная зависимость результирующего показателя от неслучайных
величин объясняющих переменных, лежит в основе большинства экономе-
трических моделей и, в частности, используется при построении и
анализе классической и обобщенной линейной модели регрессии (см. гл. 2 тома
2).
Корреляционно-регрессионная зависимость между
случайными векторами rj — результирующим показателем и ? —
объясняющей переменной (схема С). В данном типе моделей и компоненты
вектора результирующего показателя 7/, и компоненты вектора
объясняющих переменных f зависят от множества неконтролируемых факторов,
так что являются случайными по своей физической сущности. Мы уже
сталкивались с такой ситуацией в примере, в котором исследовалась связь
между производительностью мартеновских печей и процентным
содержанием углерода в металле (см. рис. 10.4). Зависимости такого типа вообще
характерны для описания хода технологических процессов, реальные зна-

10.5 ОСНОВНЫЕ ТИПЫ ЗАВИСИМОСТЕЙ 373
чения параметров которых ? = (f*X\f*2\... ,?* )Т, равно как и
характеризующие их результирующие показатели т/ = (ц ,*/,...,*/) , как
правило, флюктуируют случайным (но взаимосвязанным) образом около
установленных номиналов.
В подобных ситуациях оказывается полезным рассмотреть
разложение исследуемого результирующего показателя г\ на две случайные
составляющие по формуле типа A0.3). Первая из них определяется некоторой
(векторнозначной) функцией f от объясняющей переменной ?, а вторая
отражает остаточные влияния неучтенных случайных факторов на
анализируемый результирующий показатель ?/. Итак, §
*/ = f(O + e. A0.16)
В частном случае единственного результирующего показателя (ш =
1) и линейного вида функции /(?) имеем:
} + е. A0.17)
/c=l
Подразумевая, как и прежде, под уср(Х) = Е(ту \ ( — X) условное
математическое ожидание результирующего показателя rj (при условии, что
объясняющая переменная ? приняла значение, равное X), мы от A0.17)
приходим к линейному уравнению регрессии
'. A0.18)
А:=1
Возможны случаи, когда вторая (остаточная) компонента в
разложении A0.16) с полной мерой достоверности (т.е. с вероятностью единица)
равна нулю. При этом исследуемые случайные величины г/и(
оказываются связанными чисто функциональной зависимостью т\ = /(?)> но ее
следует отличать от функциональной зависимости неслучайных
переменных (см. выше, схема А).
Пример 10.2. Рис. 10.5 иллюстрирует связь между вакуумом в
печи для обжига стекла f и процентом брака г\ в стекольном производстве
[Айвазян С. А., 1968].
Случайные изменения свойств сырья, а также ряда,
неконтролируемых факторов приводят к случайным колебаниям обеих исследуемых
переменных. Однако расположение точек на рис. 10.5 свидетельствует о том,
что эти колебания взаимосвязаны, подчинены вполне определенной
закономерности: «облако» рассеяния вытянуто вдоль некоторой прямой, не

374
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
параллельной ни одной из координатных осей. Все это подтверждает
целесообразность разложения случайной величины г\ по формуле A0.16) и
исследования связи между г\ и ?, которая в этом случае носит название
корреляционной. К перечисленным вопросам регрессионного анализа
(построение конкретного вида зависимости между переменными, различные
оценки ее точности) в этом случае присоединяется круг вопросов,
связанных с исследованием степени тесноты связи между этими переменными.
Совокупность методов, позволяющих решать эти вопросы, принято
называть корреляционным анализом (см. гл. 11).
Рис. 10.5, Графическое представление данных по связи вакуума в печи для
обжига стекла (() и процента брака в стекольном производстве
М
Зависимости структурного типа, или зависимости по схеме
конфлюэнтного анализа (схема D). В описываемой ниже схеме речь
идет о восстановлении искомых зависимостей по искаженным
наблюдениям анализируемых переменных, причем в отличие от регрессионной схемы
В искаженными оказываются при наблюдении не только значения
результирующего показателя, но и значения объясняющих (предикторных)
near. Этот тип связей упоминается в специальной
ременных аг ,аг ',
литературе как структурные зависимости [Кендалл М. Дж., Стьюарт А.,
1973, с. 500-557] или как зависимости по схеме конфлюэнтного анализа
[Айвазян С. А., 1979].
Таким образом, конфлюэнтный анализ предоставляет совокупность
методов математико-статистической обработки данных, относящихся к
анализу априори постулируемых функциональных связей между
количественными (случайными или неслучайными) переменными Y =

10.6 ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ 375
(уA);...,У(т))Т и X = (жA),жB),...,а?(р))Т в условиях, когда
наблюдаются не сами переменные, а случайные величины
*<*> - ж<*> 4- s(fc) k - 1 2 о-
A0.19)
U) _ f/(i) i P(i) .• — 1 о m- t — 1 2 n
где е)а и Еу) — случайные ошибки измерений соответственно переменных
аг ' и {/') в 1-м наблюдении, an — общее число наблюдений. При этом
общий вид исследуемых функциональных (структурных) связей
'A)\ //A)(*A) *(р); б)\
: = A0.20)
м) \/»\ят х(р); в)/
между ненаблюдаемыми, а точнее, наблюдаемыми с ошибками
переменными считается заданным (неизвестным является лишь значение векторного
параметра 0 = @Ь..., 0дг), участвующего в уравнениях искомых
зависимостей A0.20)).
10.6. Основные этапы статистического
исследования зависимостей
Весь процесс статистического исследования интересующих нас
зависимостей удобно разложить на основные этапы. Эти этапы ниже описаны
в соответствии с хронологией их реализации, однако некоторые из них
находятся, в плане хронологическом, в соотношении итерационного
взаимодействия: результаты реализации более поздних этапов могут
содержать выводы о необходимости повторной «прогонки» (с учетом добытой
на предыдущих этапах новой информации) уже пройденных этапов (см.,
например, схему взаимодействия этапов 3, 4, 5 и 6 на рис. 10.6).
Излагаемая ниже схема приспособлена в основном для исследования
зависимостей между количественными переменными, однако с
минимальными (и очевидными) модификациями она «работает» и при
статистическом анализе связей между неколичественными и разнотипными
переменными.

376 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Этап 1 1 Н Этап 2 { Н Этап 3
j] Этап g | Н Этап 7
J Этап 5
Рис. 10.6. Схема хронологически-итерационных взаимосвязей основных
этапов статистического исследования зависимостей
Этап 1 (постановочный). Прежде всего исследователь должен
определить:
1) элементарную единицу статистического обследования, или
элементарный объект исследования О (это может быть страна, город,
отрасль, предприятие, семья, индивидуум, пациент, технологический
процесс, сложное техническое изделие и т. д.);
2) набор показателей (аг ',аг ',...,агр'; у ,...,у ),
регистрируемых на каждом из статистически обследованных объектов, с
подразделением их на «входные» (объясняющие) и «выходные» (результирующие)
и, если это необходимо, с четким определением способа их измерения;
таким образом, на этом этапе каждому элементарному объекту исследования
ставится в соответствие перечень анализируемых показателей, т. е.
О ^ /x(i) XW х(р). М) vB) (m)v
3) конечные прикладные цели исследования (см. п. 10.2), тип
исследуемых зависимостей (см. п. 10.5) и желательную форму статистических
выводов (а иногда и степень их точности);
4) совокупность элементарных объектов исследования, на которую мы
хотим распространить справедливость действия выявленных в результате
анализа статистических зависимостей (если, например, элементарная
единица ^- семья, то анализируемой совокупностью могут быть семьи
определенной социальной группы населения или семьи определенной страны и
т.д.);
5) общее время и трудозатраты, отведенные на планируемое
исследование и коррелированные с ними временная протяженность и объем
необходимого статистического обследования (какую часть анализируемой
совокупности подвергнуть статистическому обследованию, производить
статистическое обследование в статистическом или динамическом режиме и

10.6 ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ 377
т.д.). Заметим, что именно на этом этапе решаются задачи в) и 1,
описанные в п.10.1.
В решении всех перечисленных вопросов первого этапа исследования
главную роль, бесспорно, должен играть «заказчик», т.е. специалист той
предметной области, для которой планируется проведение этого
исследования.
Этап 2 {информационный). Он состоит в проведении сбора
необходимой статистической информации вида A0.1). При этом возможны две
принципиально различные ситуации: 1) исследователь имеет возможность
заранее спланировать выборочное обследование части анализируемой
совокупности — выбрать способ отбора элементарных единиц
статистического обследования (случайный, пропорциональный, расслоенный и т. д.,
см. п.6.1), хотя бы по части объясняющих переменных аг ,аг ,.. . ,агр'
назначить уровни их значений, при которых желательно произвести
эксперимент или наблюдения (условия активного эксперимента); 2)
исследователь получает исходные данные такими, какими они были собраны без его
участия (условия пассивного эксперимента). В любом случае «на
выходе» этого этапа исследователь располагает исходными статистическими
данными вида (ЮЛ), т. е. каждому (г-му) из статистически обследованных
элементарных объектов О{ поставлен в соответствие конкретный вектор
характеризующих его «входных» и «выходных» показателей:
0. ^ /JD жB) Jp). A) (а) (ш)ч , 1 о п
(здесь n — общее число статистически обследованных элементарных
объектов, т!"е. объем выборки).
Говоря о проведении сбора статистических данных, мы не
включаем сюда разработку методологии и системы показателей отображаемого
объекта: эта работа предполагает профессионально-предметное
(экономическое, техническое, медицинское и т. д.) изучение сущности решаемых
задач статистического исследования зависимостей, поэтому относится к
компетенции соответствующей предметной статистики (экономической и
т.д.) и входит в задачи 1-го этапа исследований.
Этап 3 {корреляционный анализ). Этот этап нацелен на решение
задачи 2 (см. п. 10.1), он позволяет ответить на вопросы, имеется ли
вообще какая-либо связь между исследуемыми переменными, какова
структура этих связей и как измерить их тесноту? Описанию методов, с
помощью которых проводится такой статистический анализ, посвящена гл. 11.
Поскольку перечисленные выше вопросы решаются с помощью
вычисления и анализа соответствующих корреляционных характеристик,
содержание этапа можно определить как проведение корреляционного анализа.

378 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Этап достаточно полно оснащен необходимым математическим
аппаратом и программным обеспечением, поэтому может быть почти полностью
автоматизирован.
Этап 4 (определение класса допустимых решений). Главной целью
исследователя на этом этапе является определение общего вида,
структуры искомой связи между У и X, или, другими словами, описание класса
функций F, в рамках которого он будет производить дальнейший поиск
конкретного вида интересующей его зависимости (см. задачи а) и 3 в
п. ЮЛ). Чаще всего это описание дается в форме некоторого
параметрического семейства функций f(X\ О), поэтому и этап этот называют также
этапом параметризации модели. Так, определив в примере 10.1, что
поиск зависимости среднедушевых семейных сбережений уср от величины их
среднедушевого дохода х мы будем производить в классе F = {0q + 0i&}
линейных функций, мы тем самым завершили четвертый этап
исследования (но конкретных числовых значений параметров #о и в\ мы к этому
моменту еще не знаем).
Следует отметить, что, являясь узловым, в определенной мере
решающим звеном во всем процессе статистического исследования зависимостей,
этот этап в то же время находится в наименее выгодном положении по
сравнению с другими этапами (с позиций наличия строгих и законченных
математических рекомендаций по его реализации). Поэтому его
реализация требует работы специалиста соответствующей предметной области
(экономики, техники, медицины и т. д.) и математика-статистика,
направленной на как можно более глубокое проникновение в «физический
механизм» исследуемой связи. Подходам и методам проведения этого этапа
исследований посвящен следующий пункте этой главы.
Существует подход к исследованию моделей регрессии, не
требующий предварительного выбора параметрического семейства функций F,
в рамках которого проводится дальнейший анализ. Речь идет о так
называемых непараметрических (или частично-параметрических) методах
исследования регрессионных зависимостей. Однако возникающие при их
реализации проблемы (необходимость иметь очень большие объемы
исходных статистических данных, выбор сглаживающих функций — «окон» и
параметров, масштаба, выбор порядка сплайна, числа и положения
«узлов» и т. п.) сопоставимы по своей сложности с проблемами,
возникающими при реализации этапа 4.
Следующие два этапа — 5-й и 6-й — связаны с проведением
определенного объема вычислений и реализуются по существу параллельно.
Этап 5 (анализ мультиколлинеарности предсказывающих
переменных и отбор наиболее информативных из них). Под явлением мультикол-

10.6 ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ 379
линеарности в регрессионном анализе понимается наличие тесных
статистических связей между объясняющими переменными аг1',^ ,. ..,« ,
что, в частности, проявляется в близости к нулю (слабой
обусловленности) определителя их корреляционной матрицы, т.е. матрицы размера
рхр, составленной из парных коэффициентов корреляции г^- = г(ж ,arJ')
(см. п. 2.6.6, соотношение B.32)). Поскольку этот определитель входит
в знаменатель для важных характеристик анализируемых моделей (см.
гл. 2 тома 2), то мультиколлинеарность создает трудности и неудобства
при статистическом исследовании по меньшей мере в двух направлениях:
а) в реализации необходимых вычислительных процедур и, в
частности, в крайней неустойчивости получаемых при этом числовых
характеристик анализируемых моделей (так, коэффициенты при объясняющих
переменных в моделях типа A0.12), A0.13) и др. могут изменяться в
несколько раз и даже менять знак при добавлении (или исключении) к
массиву исходных статистических данных одного-двух объектов или одной-двух
объясняющих переменных);
б) в содержательной интерпретации параметров анализируемой
модели, что играет решающую роль в ситуациях, когда конечной целью
исследования является цель типа 3 («выявление причинных связей» и т.д.,
см. п. 10.2, соотношения A0.9) и A0.9')).
Поэтому исследователь старается перейти к такой новой системе
объясняющих переменных (отобранных из числа исходных переменных
яг ,аг ',..., агр' или представленных в виде некоторых их комбинаций),
в которой эффект мультиколлинеарности уже не имел бы места. Этап
проводится в основном силами математиков-статистиков с подключением
(в самом его конце) специалистов соответствующей предметной области
для выбора из нескольких предложенных вариантов наборов объясняющих
переменных одного, наиболее легко и естественно интерпретируемого.
Рекомендации по проведению этого этапа даны в гл. 2 тома 2.
Этап 6 {вычисление оценок неизвестных параметров, входящих в
исследуемое уравнение статистической связи). Итак, в результате
проведения предыдущих этапов были решены, в частности, следующие
задачи:
а) определены результирующие и объясняющие переменные и тип
исследуемой зависимости (В,С или /), см. п. 10.5);
б) собрана и подготовлена к счету исходная статистическая
информация вида A0.1);
в) изучены характер и теснота статистических (корреляционных)
связей между исследуемыми переменными;
г) выбран класс допустимых решений F, т. е. класс (или параметри-

380 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
ческое семейство) функций f(X), в рамках которого будет подбираться
наилучшая (в определенном смысле) аппроксимация f(X) искомой
зависимости типа A0-14), A0.16) или A0.20).
Теперь можно приступить к определению этой наилучшей
аппроксимации f(JQ, которая является решением оптимизационной задачи вида
f(X) = argefXtprAn(f), A0.21)
где функционал An(f) задает критерий качества аппроксимации
результирующего показателя г\ (или Y) с помощью функции ((X) из класса F.
Выбор конкретного вида этого функционала опирается на знание
вероятностной природы остатков е в моделях типа A0.14) и A0.16),
причем он строится, как правило, в виде некоторой функции от невязок
?к)Ак\..->ё?Чк = 1,2,...,т), где ef > = у[к) - f{k)(Xi) (один из ркс-
пространенных вариантов такого функционала, а именно функционал
метода наименьших квадратов, упоминается в примере 10.1, см.
соотношение A0.7')). Бели в качестве класса F задаются некоторым
параметрическим семейством функций {f(X;0)}, то задача A0.1) сводится к подбору
(статистическому оцениванию) значений параметров О, на которых
достигается экстремум по 0 функционала Дп(Г(Х;0)), а соответствующие
модели называют параметрическими. Эта часть исследования хорошо
оснащена необходимым математическим аппаратом и соответствующим
программным обеспечением (см. гл. 2 и 4 тома 2).
Этап 7 (анализ точности полученных уравнений связи).
Исследователь должен отдавать себе отчет в том, что найденная им в соответствии
с A0.1) аппроксимация t(X) неизвестной теоретической функции fj(X) из
соотношений типа A0.14) или A0.16) (называемая эмпирической
функцией регрессии, см. гл. 2 тома 2) является лишь некоторым приближением
истинной зависимости fj(X) . При этом погрешность 6 в описании
неизвестной истинной функции $т{Х) с помощью i(X) в общем случае состоит
из двух составляющих: а) ошибки аппроксимации SF и б) ошибки
выборки 6(п). Величина первой зависит от успеха в реализации этапа 4, т. е.
от правильности выбора класса допустимых решений F. В частности,
если класс F выбран таким образом, что включает в себя и
неизвестную истинную функцию f (т.е. $т(Х) € F), то ошибка аппроксимации
rfp = 0. Но даже в этом случае остается случайная составляющая (ошиб-
1 В дальнейшем, говоря о вектор-функции Тт(Х)> вектор-погрешности 6 и векторе
результирующих показателей Y(X), мы будем иметь в виду каждую из их компонент
в отдельности.

10.6 ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ 381
ка выборки) 6(п), обусловленная ограниченностью выборочных данных
вида A0.1), на основании которых мы подбираем функцию f(X)
(оцениваем ее параметры). Очевидно, уменьшить ошибку выборки мы можем
за счет увеличения объема п обрабатываемых выборочных данных, так
как при fj(X) ? F (т.е. при йр = 0) и правильно выбранных методах
статистического оценивания (т. е. при правильном выборе оптимизируемого
функционала качества модели Дп(/)) ошибка выборки 6(п) —> 0 (по
вероятности) при п —> оо (свойство состоятельности используемой процедуры
статистического оценивания неизвестной функции fj(X)).
Соответственно на данном этапе приходится решать следующие
основные задачи анализа точности полученной регрессионной
зависимости:
1) в случае F = {f(X;Q)} и fr(^) € F, т.е. когда класс допустимых
решений задается параметрическим семейством функций и включает в
себя неизвестную теоретическую функцию регрессии fj(^M при заданных
доверительной вероятности Р и объеме выборки п указать такую
предельную (гарантированную) величину погрешности 6руП(в^) для любой
компоненты неизвестного векторного параметра Э, что
с вероятностью, не меньшей, чем Р (здесь в^ — истинное значение &-й
компоненты неизвестного параметра 0, а 0^ — его статистическая
оценка);
2) при заданных доверительной вероятности Р, объеме выборки п и
значениях объясняющих переменных X указать такую предельную
(гарантированную) величину погрешности 6p^n(Ycp(X)), что
\Ycp(X)-i(X)\<6P,n(Ycp(X))
с вероятностью, не меньшей, чем Р (здесь Ycp(X) = Е(ту | X) —
неизвестное условное среднее значение исследуемого результирующего показателя
при значениях объясняющих переменных, равных X, a f(J\T) —
построенная в соответствии с A0.21) эмпирическая функция регрессии);
3) при заданных доверительной вероятности Р, объеме выборки п и
значениях объясняющих переменных X указать такую предельную
(гарантированную) величину погрешности 6ptn(Y(X)), что
\Y(X) - t(X)\ < 6P,n(Y(X))
с вероятностью, не меньшей, чем Р (здесь Y(X) — прогнозируемое
индивидуальное значение исследуемого результирующего показателя при
значениях объясняющих переменных, равных X).

382 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Описание методов анализа точности исследуемых регрессионных
моделей содержится в гл. 2 тома 2.
Заметим в заключение, что часть исследования, объединяющая этапы
4, 5, 6 и 7, принято называть регрессионным анализом.
10.7. Выбор общего вида функции регрессии
Итак, как мы видим (см. предыдущий пункт), собственно
регрессионный анализ, т.е. конструирование по исходным данным вида A0.1)
неизвестной функции регрессии f(X) = E(tj \ ? = X), начинается с этапа
4, т. е. с выбора семейства допустимых решений F — класса функций, в
рамках которого предполагается вести поиск наилучшей аппроксимации
f(X) для f(X)\
Наиболее распространенными в статистической практике являются
параметрические регрессионные схемы, когда в качестве класса
допустимых решений выбирается некоторое параметрическое семейство функций
F ={/(*; 0)}в6Г. A0.22)
В этом случае дальнейший поиск аппроксимации f(X) сводится к
наилучшему (в смысле заданного критерия адекватности, см. выше, этап 6,
соотношение A0.21)) подбору неизвестного значения параметра 0, что в
свою очередь осуществляется с помощью полностью формализованного
алгоритма решения соответствующей оптимизационной задачи,
составляющей математическую основу процедуры, называемой статистическим
оцениванием параметра (см. гл.7).
Но до перехода к процедуре статистического оценивания
неизвестного значения параметра мы должны сделать и обосновать выбор типа
параметрического семейства A0.22). Так, например, в качестве класса
допустимых решений можно использовать
линейные функции : /(Х;0) = в0 + ^0* -х{к); A0.22')
степенные функции: /(ЛГ;6) = во(х{1))в1(х{2) H2 . ..(хр)в>; A0.22")
1 Начиная с этого момента мы будем рассматривать случай m = 1 общей
постановки задачи статистического исследования зависимостей, т.е. случай единственного
результирующего показателя у.

10.7 ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 383
алгебраические полиномы степени т ^ 2:
v р v
A0.22'")
и т.д.
Следует подчеркнуть, что этап 4 (см. п. 10.6), т.е. этап
исследования, посвященный выбору общего вида функции регрессии
(параметризация модели), бесспорно, является ключевым: от того, насколько удачно
он будет реализован, решающим образом зависит точность
восстановления неизвестной функции регрессии f(X). В то же время приходится
признать, что этот этап находится, пожалуй, в самом невыгодном
положении: к сожалению, не существует системы стандартных рекомендаций
и методов, которые образовывали бы строгую теоретическую базу для его
наиболее эффективной реализации.
Остановимся на некоторых рекомендациях, связанных с реализацией
трех основных моментов, учет которых необходим при решении проблемы
выбора общего вида функции регрессии: 1) максимальное использование
априорной информации о содержательной (физической, экономической,
социологической и т. п.) сущности анализируемой зависимости; 2)
предварительный анализ геометрической структуры исходных данных вида
A0.1), на основании которых конструируется искомая зависимость; 3)
различные статистические приемы обработки исходных данных,
позволяющие сделать наилучший выбор из нескольких сравниваемых вариантов.
10.7.1. Использование априорной информации о
содержательной сущности анализируемой
зависимости
Анализируя содержательную сущность изучаемой зависимости,
исследователь еще до обращения к исходным статистическим данным может
(и должен!) попытаться ответить на ряд вопросов по поводу характера
искомой регрессионной связи:
а) будет ли искомая функция f(X) монотонной или она должна иметь
один экстремум (может быть, несколько)?
б) следует ли ожидать стремления (в процессе аг ' -* оо) f(X) к асим-
птомам (по одной или нескольким предикторным переменным) и какова
их содержательная интерпретация? Так, например, если f(X) — сред-

384
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
ний объем благ определенного вида, потребляемых семьями группы X по
доходам, то, очевидно, при X —> оо следует ожидать «насыщения», т. е.
f(X) будет стремиться (снизу) к горизонтальной асимптоте (см. п. 4 в
табл. 10.3);
в) какова принципиальная природа воздействия объясняющих
переменных а? ,я ,. . .,ж на формирование результирующего показателя
у — аддитивная или мультипликативная? Так, например, многие схемы
зависимостей в экономике характеризуются мультипликативной природой
воздействия предикторов на у (см. п. 1-3 в табл. 10.3);
г) не диктует ли содержательный смысл анализируемой зависимости
обязательное прохождение графика искомой функции f(X) через одну или
несколько априори заданных точек в исследуемом факторном
пространстве (X, у)?
Поясним необходимость и возможность максимального извлечения
информации об общем виде анализируемой функции регрессии f(X) из
соображений профессионально-теоретического характера на примере.
Пример 10.3. На рис. 10.7 представлены 63 результата
специального эксперимента [Езекиэл М., Фокс К., с. 57]. Расположение точек на
рис. 10.7 не дает ответа на вопрос, описывать ли зависимость между
скоростью автомобиля (х миль/ч) и расстоянием (у футов), пройденным им
после поданного сигнала об остановке, линейной или параболической
зависимостью.
у, футов
0 5 10 15 20 25 30 35 ж, миль/ч
Рис. 10.7. График зависимости тормозного пути автомобиля (у) от скорости
его движения (х)
Этот вопрос остается без ответа и после построения
соответствующих кривых и применения известных статистических критериев,
предназначенных решать, насколько хорошо согласуются кривые с
экспериментальными данными. Однако несложные рассуждения профессионально-

10.7 ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 385
теоретического характера все-таки позволяют сделать этот выбор.
Действительно, для каждого отдельного автомобиля и водителя расстояние,
пройденное до остановки, определяется в основном тремя факторами:
скоростью автомобиля (х) в момент подачи сигнала об остановке, временем
реакции на этот сигнал водителя @Ь ч) и тормозами автомобиля.
Автомобиль успеет пройти путь в\Х до момента включения водителем тормозов
и еще 01 • х после этого момента, поскольку согласно элементарным
физическим законам теоретическое расстояние, пройденное до остановки с
момента торможения, пропорционально квадрату скорости.
Итак, f(x) = вгх + в2х2} что после оценивания 9\ и в2 с помощью
МНК (см. гл. 7) дает f(x) = 0,76а? + 0,056ж2.
10-7.2. Предварительный анализ геометрической структуры
исходных данных
При выяснении вопроса о параметрическом виде исследуемой
зависимости, как правило, идут от простого к сложному. Простейшей же
аппроксимацией неизвестной функции регрессии f(X) — Е(т/ | ? = X)
является, естественно, линейная модель, т. е. функция вида
Л(-ЯГ) = *о + МA) + • • • + 0р*(р). (Ю.23)
Поэтому при предварительном анализе характера исследуемых
зависимостей (т. е. проведения вычислительных процедур по оценке
неизвестных значений параметров, входящих в гипотетичные уравнения связей)
ограничиваются некоторыми приближенными эвристическими приемами,
связанными в основном с изучением «геометрии» парных корреляционных
полей и визуальной проверкой их линейности.
Содержание геометрического анализа парных
корреляционных полей. Под корреляционным полем переменных (и, г;)
понимается графическое представление имеющихся измерений (ui,vi),(u2,v2),
...,(un,vn) этих переменных в плоскости (u,v). Мы уже неоднократно
имели дело с корреляционными полями (см. рис. 10.2, 10.4, 10.5, 10.7).
Анализ парных корреляционных полей состоит обычно в следующем:
а) построение на основании имеющихся исходных данных вида A0.1)
корреляционных полей для всевозможных пар переменных вида (х^\х^)
и (з >У)> отобранных из набора всех р + 1 исследуемых признаков
(х , х ,..., х , у); всего таких пар будет, очевидно, р(р + 1)/2, однако
процесс этот легко автоматизируется с помощью современных
вычислительных средств;
13 Теория вероятностей
и прикладная статистика

386 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
б) визуальное прослеживание характера вытянутости каждого
корреляционного поля: эллипсоидально-линейное (см. рис. 10.6), нелинейно-
монотонное (см. рис. 10.7), с наличием одного или нескольких экстремумов
(см. рис. 10.4) и т.п.;
в) изучение поведения условных средних значений результирующего
показателя при изменении величины переменной, откладываемой по оси
абсцисс и играющей роль предикторной (см. рис. 10.2); для этого (если
значения предикторной переменной неконтролируемы в ходе наблюдения
или эксперимента) предварительно разбивают диапазон значений
объясняющей переменной на интервалы группирования (см. п. 6.1) и
подсчитывают средние значения ординат тех точек-наблюдений, которые попали в
общий интервал группирования.
В результате такого анализа обычно получают формулировку
нескольких рабочих гипотез об общем виде искомой зависимости,
окончательная проверка которых и выбор наиболее адекватной из них
осуществляются (при отсутствии априорных сведений содержательного
характера) с помощью соответствующих математико-статистических
методов. Описание наиболее эффективных, с нашей точки зрения, приемов
такого типа приводятся в п. 10.7.3.
10.7.3. Статистические критерии проверки гипотез об общем
виде функции регрессии
Подчеркнем сразу, что описанные ниже критерии проверки
справедливости сделанного выбора общего вида искомой функции регрессии не
могут ответить на вопрос: является ли проверяемый гипотетичный вид
зависимости наилучшим, единственно верным? Они лишь подтверждают
факт непротиворечивости проверяемого вида функции регрессии
имеющимся у исследователя исходным данным A0.1) либо отвергают
обсуждаемую гипотетичную форму зависимости как не соответствующую этим
данным.
1. Общий приближенный критерий, основанный на группированных
данных (или при наличии нескольких наблюдений при каждом
фиксированном значении аргумента). Пусть высказана гипотеза об общем виде
функции регрессии Яо: Е(т/ | ? = X) = fa{X\0u02,..^0k) (fa(X;Q) -
известная функция, @i,02>-- •>#*) = в — неизвестные числовые
параметры) и пусть вычислены (например, с помощью метода наименьших
квадратов, см. гл. 2 тома 2) оценки 0i,02j • • • >#* неизвестных параметров,
входящих в описание уравнения регрессии. При группировке данных (или
при проведении эксперимента) мы должны соблюдать требование, в соот-

10.7 ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 387
ветствии с которым число интервалов группирования (или число
различных значений аргумента, в которых производились наблюдения) а должно
обязательно превосходить число неизвестных параметров Л, т.е. j-ft > 1.
Бели высказанная гипотеза об общем виде зависимости является
правильной, то статистика
/«(*?; 0Iа
— (Ю.24)
1
должна приближенно подчиняться F(mi, m2^распределению с числом
степеней свободы числителя т\ = & - к и знаменателя т2 = п - s. Все
величины в формуле A0.24) соответствуют ранее введенным обозначениям.
В частности, Х{ — середина i-го гиперпараллелепипеда группирования
(или i-e значение аргумента, в котором было проведено щ наблюдений);
fa(Xi; 0) — значение гипотетической функции регрессии, вычисленное в
точке X = Xi; у. — условное среднее из ординат, попавших в i-й
гиперпараллелепипед группирования (или из ординат, измеренных при t'-м
фиксированном значении аргумента Xi); jfy — j-e по счету значение ординаты
из числа попавших в г-й интервал группирования (или из числа
измеренных при 1-м фиксированном значении аргумента Х{). Легко понять, что
числитель в правой части A0.24) характеризует меру рассеивания
экспериментальных данных вокруг аппроксимирующей выборочной
регрессионной поверхности, а знаменатель — меру рассеивания
экспериментальных данных около своих условных выборочных средних у{ (т. е. меру,
независимую от выбранного вида линии регрессии). Причем и числитель, и
знаменатель являются практически независимыми (в некоторых частных
случаях — точно независимыми) статистическими оценками одной и той
же теоретической дисперсии a = D(i71 ? = X).
Соответственно получаем следующее правило проверки гипотезы об
общем виде функции регрессии. Задаемся, как обычно, достаточно
малым уровнем значимости критерия а (например, a = 0,05). С
помощью таблицы находим 100A — у)%-ную точку V\^.^ и 100у%-ную
точку v% F(k - m, га — ^-распределения. Если окажется, что величина v2,
подсчитанная по формуле A0.24), удовлетворяет неравенствам
v?_t <v2 <v|>
то высказанная нами гипотеза об общем виде функции регрессии
признается не противоречащей экспериментальным данным A0.1). Бели же эти
13*

388 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
неравенства оказались нарушенными, то гипотеза об общем виде
функции регрессии отвергается с уровнем значимости а. При этом если v
«слишком мало» (т.е. v < t>i_^), то, очевидно, при- выборе общего вида
регрессии мы неправомерно реагировали на случайные отклонения точек
(Xi.yi) от истинной функции регрессии и тем самым необоснованно
завысили число параметров &, от которых зависит уравнение регрессии.
Напротив, если v «слишком велико» (т.е. v > Va), то «гибкость»
аппроксимирующей функции регрессии fa(X;Q) следует признать
недостаточной, поэтому целесообразно увеличить число неизвестных параметров
регрессии (например, повысить порядок аппроксимирующего полинома).
Для случая, когда условная дисперсия зависимой переменной
пропорциональна некоторой известной функции аргумента, т.е. Drj(X) =
a2h2(X)> формула A0.24) преобразуется:
vn = —f-a Vi —, (Ю.24')
ri^a Z-f wi Z-f \Vij ~~ Vi)
t=l i=l
где
«, = 1/л2(х,°).
Так, в примере 10.1: п = 4Q; 5 = 4; а = 0,05; Л = 2; дисперсионное
отношение v , подсчитанное по формуле A0.24;), равно 1,04, в то время как
5%-ная точка .РB,36)-распределения vq,05 = 3,26. Это свидетельствует о
том, что гипотеза о линейном виде регрессионной зависимости в данном
случае не противоречит имеющимся в нашем распоряжении
экспериментальным данным.
При проверке линейности регрессии (так же, впрочем, как и при
проверке гипотезы о полиномиальном характере регрессии заданного
порядка) в нормальных схемах зависимостей типа В и С\ (см. п. 10.5)
описанный общий критерий является точным. При этом в линейном случае
статистика v , определенная соотношением A0.24), может быть выражена
в более удобной форме, не требующей предварительного вычисления
выборочной аппроксимирующей функции регрессии. Так, например, в случае
парной линейной регрессии (т.е. при к = 2) имеем:
-А (ю.25)
Й.«)
Здесь рп.? иг — соответственно выборочные корреляционные отношения
(г) по ?) и коэффициент корреляции (см. гл. 11). Логическая схема исполь-

10.7 ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 389
зования статистики A0.25) аналогична ранее изложенным критериям:
задаются достаточно малым @,05 ~ 0,15) уровнем значимости а; находят
по таблице 100а%-ную точку vl распределения F(s-2>n-s); сравнивают
величину v , определенную с помощью A0.25), с процентной точкой va;
если оказывается, что v2 > t?, то гипотезу о линейном виде регрессии
считают статистически необоснованной.
Воспользуемся данным критерием для статистической проверки
линейности регрессии в примере 10.2. Вычисления дают: f = 0,429,
Рп-( = 0,459, так что v2 = 0,513. Принимая во внимание, что
величина 5%-ной точки FD,37)-pacпpeдeлeния равна v^os = 2,63, делаем вывод о
непротиворечивости гипотезы линейной регрессии и данных нашего
эксперимента в данном примере @,513 < 2,63).
2. Общий приближенный критерий, основанный на негруппирован-
ных данных (при известной величине дисперсии остаточной случайной
компоненты).
Встречаются ситуации, когда в результате предварительных
исследований или из других каких-либо соображений нам удается заранее
определить величину дисперсии о остаточной случайной компоненты е в
разложениях вида A0.14) и A0.16) (например, когда е — ошибка измерения
и нам известны характеристики точности используемого измерительного
прибора). В этом случае можно отказаться от стеснительного
требования группированности данных и для проверки гипотезы об общем виде
функции регрессии воспользоваться фактом х (п ™ &)-распределенности
статистики
7 = Л ¦ Г-
(который имеет место при условии справедливости нашей гипотезы).
Задавшись уровнем значимости критерия а и найдя с помощью табл.
величины 100A - у)%-ных и 100§%-ных точек х2-распределения с п - к
степенями свободы соответственно Xi-f (n — Л) и Х%(п - к), проверяем
выполнение неравенства
где 7 подсчитано по формуле A0.26). Если эти неравенства оказались
нарушенными, то от гипотезы Яо об общем виде функции регрессии следует
отказаться. При этом если у «слишком мало» (т.е. 7 ^ Xi-f (л - т)),
то, очевидно, при выборе общего вида мы неправильно реагировали на
случайные отклонения экспериментальных точек (X^yi) и тем самым
необоснованно завысили число параметров А, от которых зависит уравнение

390 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
регрессии.
Напротив, если у «слишком велико» (т.е. 7 ^ х\(п - *))> т°
«гибкость» аппроксимирующей кривой регрессии fa(X;Q) следует признать
недостаточной, поэтому целесообразно увеличить число неизвестных
параметров регрессии (например, повысить порядок аппроксимирующего
полинома).
Для случая, когда дисперсия зависимой переменной (или, что то же,
дисперсия остаточной случайной компоненты) не остается постоянной при
изменении X, а пропорциональна некоторой известной функции
аргумента, т.е. Drf(X) = ah2 (X), формула подсчета статистики 7 несколько
изменится:
п
где Wi = \jh (Xi). В остальном схема проверки гипотезы об общем виде
функц
const.
функции регрессии остается той же самой, что и в случае D?/(X) == а =
10.7.4. Некоторые общие рекомендации
При выборе общего вида искомой функции регрессии /(X), помимо
соображений и приемов, описанных выше, полезно учитывать следующие
общие рекомендации.
1) Не следует гнаться за чрезмерной сложностью функции,
описывающей поведение искомой функции регрессии, руководствуясь
исключительно соображениями оптимизации критерия качества аппроксимизации
Дп(/) (см. A0.21)). Дело в том, что если и оценки 0 неизвестных
параметров модели G, и значение критерия Ап(/) вычисляются на основании
одной и той же выборки, то за счет увеличения размерности к
оцениваемого векторного параметра в = @Ь02> • ¦ • >0*)Т можно добиться, на первый
взгляд, идеального результата. Возможность эта основана на известном в
математическом анализе результате, в соответствии с которым для любой
заданной системы точек (a?i,3h),(ff2,ifo)*•••м(я?п>Уп) (с
неповторяющимися абсциссами) можно подобрать алгебраический полином степени п - 1,
проходящий в точности через все точки этой системы. А это значит, что
все «невязки» у{ - /(а?<), на основании которых строится критерий Ап(/)
(а следовательно, и сам критерий, см. п. 10.6, этап 6), равны нулю, т. е.
«лучше» модели для описания поведения функции регрессии подобрать
невозможно. На самом деле при таком подходе мы как бы заставляем
функцию f(x) реагировать на случайные флюктуации, объясняемые
наличием в представлениях типа A0.14) остаточной случайной компоненты

10.7 ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ 391
е(Х). Поэтому, если мы попробуем применить полученный таким образом
результат к другой выборке из той же самой генеральной совокупности,
то увидим явное рассогласование модельных (f(Xi)) и наблюденных (у,)
значений результирующего показателя. Поэтому при подборе общего вида
функции регрессии, как правило, идут от простого к сложному} т.е.
начиная с анализа возможности использовать простейшую линейную модель
вида A0.23).
2) Следует добиваться компромисса между сложностью
регрессионной модели и точностью ее оценивания. Из общих результатов
математической статистики, относящихся к анализу точности оценивания
исследуемой модели при ограниченных объемах выборки, следует, что с
увеличением сложности модели (выраженной, например, размерностью к
векторного параметра 0, участвующего в ее уравнении) точность
оценивания падает. Например, ширина доверительного интервала А[у(Х)]Р
для неизвестного значения у(Х), при прочих равных характеристиках
анализируемой схемы, увеличивается с ростом размерности параметра 0,
участвующего в вычислении функции регрессии /(Х;0) (см. гл.2 тома
2). Именно поэтому в ситуациях, когда исследователь располагает
ограниченной исходной выборочной информацией вида A0.1), он вынужден
искать компромисс между степенью общности привлекаемого класса
допустимых решений F и точностью оценивания, которой возможно при этом
добиться (пример подобного рода действий по поиску компромисса будет
приведен в гл. 2 тома 2 в связи с задачей определения оптимального числа
объясняющих переменных в линейной модели множественной регрессии).
3) При обнаружении нелинейности в парных статистических связях
анализируемых переменных х^' и y(j = 1,2,...,р) следует
попытаться применить к этим переменным линеаризующие преобразования.
Простейший пример такого приема мы имеем, когда вместо анализа степенной
зависимости вида
У = 0о(*)$1 A0.27)
исследователь рассматривает линейную зависимость между логарифмами
исходных переменных, а именно:
у = 0о + егх, A0.28)
где у = In у, х = In я? и §о = 1п0о« В зависимости от типа
нелинейной связи, существующей между исходными переменными, подбираются
и другие линеаризующие преобразования (см., например, [Айвазян С. А.,
Бнюков И.О., Мешалкин Л.Д., 1985, п.6.2.3]). Один из наиболее общих
подходов к линеаризации анализируемых зависимостей реализуется с по-

392 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
мощью так называемого преобразования Бокса-Кокса (см. гл. 2 в томе 2
учебника).
4) Анализ регрессионных остатков. Ряд статистических
критериев проверки адекватности используемой аппроксимирующей модели
регрессии основан на анализе регрессионных остатков (невязок) ё(Х{) =
У% - fa(Xi))i = 1,2, ...,п. В основе их конструирования — положение,
в соответствии с которым правильный выбор модели fa(X)
предопределяет асимптотическую (по п -* оо) независимость остатков е(А^). Поэтому
статистическая проверка правильности выбора общего вида функции
регрессии сводится к проверке статистической независимости остатков, для
чего могут быть использованы, например, критерии, описанные в гл.З
тома 2 (п. 3.2). В выражении для невязок ё(Х{) под fa(Xi) понимается
значение оцененной аппроксимирующей функции регрессии в точке
5) Поиск модели, наиболее устойчивой к варьированию состава
выборочных данных, на основании которых она оценивается. Идея этого
подхода к выбору общего вида исследуемой регрессионной зависимости
основана на следующем простом соображении. Если общий
параметрический вид зависимости /(ж , аг ,...агр ,0) «угадан» правильно, то
результаты оценивания вь 02,.. .параметра 0 по различным подвыборкам
выборки {х;. , ж| ,..., ж* ; &}|=г^ будут мало отличаться друг от друга
(а следовательно, не сильно будут различаться между собой и
соответствующие значения /(хA),хB),.. .,ж(р);01), /(жA),жB),.. .ж(р);02),...).
И наоборот, при неудачном выборе общего вида искомой зависимости
результаты ее восстановления по различным выборкам, как правило, будут
сильно отличаться один от другого. Описание реализации этого подхода
читатель может найти в [Айвазян С. А., Енюков И. С, Мешалкин Л. Д.,
1985, п. 6.2.3].
ВЫВОДЫ
1. Аппарат статистического исследования зависимостей —
составная часть многомерного статистического анализа — нацелен на решение
основной проблемы естествознания: как на основании частных
результатов статистического наблюдения за анализируемыми событиями или
показателями выявить и описать существующие между ними
стохастические взаимосвязи.
2. Анализируемые переменные величины по своей роли в
исследовании подразделяются на результирующие (прогнозируемые) У и объясня-

выводы 393
ющие (экзогенные, предикторные) X. Среди компонент векторов У и X
могут быть и количественные, и порядковые (ординальные), и
классификационные (номинальные).
3. Центральным математическим объектом в процессе
статистического исследования зависимостей является функция f(A"), называемая
функцией регрессии У по X и описывающая изменение условного
среднего значения Ycp(X) результирующего показателя У (вычисленного при
фиксированных на уровне X значениях объясняющих переменных) в
зависимости от изменения значений объясняющих переменных X.
4. Конечные прикладные цели статистического исследования
зависимостей могут быть в основном трех типов: 1) установление самого факта
наличия (или отсутствия) статистически значимой связи между У и X,
исследование структуры этих связей; 2) прогноз (восстановление)
неизвестных значений индивидуальных или средних значений
результирующего показателя по заданным значениям соответствующих объясняющих
(экзогенных) переменных; 3) выявление причинных связей между
объясняющими переменными X и результирующими показателями У, частичное
управление значениями У путем регулирования величин объясняющих
переменных X.
5. Разделы многомерного статистического анализа, составляющие
математический аппарат статистического исследования зависимостей,
формировались и развивались с учетом специфики анализируемых
моделей, обусловленной в первую очередь природой исследуемых
переменных. Так, изучение зависимостей между количественными переменными
обслуживается регрессионным и корреляционным анализами и анализом
временных рядов (гл.11, а также 2, 3 и 4 тома 2); изучение
зависимостей количественного результирующего показателя от неколичественных
или разнотипных объясняющих переменных — дисперсионным и
ковариационным анализами, моделями типологической регрессии; наконец, для
исследования системы зависимостей, в которых одни и те же переменные в
разных уравнениях этой системы могут одновременно выполнять и роль
результирующих, и роль объясняющих, служит теория одновременных
эконометрических уравнений (гл. 1 и 4 тома 2). Аппарат исследования
зависимостей неколичественных или разнотипных результирующих
показателей от количественных или разнотипных объясняющих переменных в
книге не рассматривается.
в. К основным типовым задачам практики, в которых использование
аппарата статистического исследования зависимостей оказывается
наиболее уместным и эффективным, следует отнести задачи: 1) нормирования;
2) прогноза, планирования и диагностики; 3) оценки труднодоступных

394 ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
(для непосредственного наблюдения и измерения) характеристик
исследуемой системы; 4) оценки эффективности функционирования (или
качества) анализируемой системы; 5) регулирования параметров
функционирования анализируемой системы. Все эти задачи являются
основными составными частями центральной проблемы кибернетики — проблемы
«управления, связи и разработки информации» (см.: Математическая
энциклопедия. Т. 2 — М.: Советская энциклопедия, 1979, с. 850).
7. По своей природе исследуемые зависимости могут быть разделены
на: 1) детерминированные (тип А), когда исследуется функциональная
зависимость между неслучайными переменными; 2) регрессионные (тип В),
когда исследуется зависимость случайного результирующего показателя
от неслучайных объясняющих переменных — параметров системы; 3)
корреляционные (тип С), когда исследуется зависимость между случайными
переменными, причем объясняющие переменные могут быть измерены без
искажений; 4) конфлюэнтные (тип D), когда исследуется функциональная
зависимость между случайными или неслучайными переменными в
ситуации, когда те и другие могут быть измерены только с некоторой случайной
ошибкой.
8. Весь процесс статистического исследования зависимостей может
быть разбит на семь последовательно реализуемых основных этапов,
хронологический характер связей которых дополняется связями
итерационного взаимодействия (см. рис. 10.6): этап 1 (постановочный); этап 2
(информационный); этап 3 (корреляционный анализ); этап 4 (определение класса
допустимых решений); этап 5 (анализ мультиколлинеарности
предсказывающих переменных и отбор наиболее информативных из них); этап 6
(вычисление оценок неизвестных параметров, входящих в исследуемое
уравнение статистической связи); этап 7 (анализ точности полученных
уравнений связи).
9. Этап параметризации регрессионной модели, т. е. выбора
параметрического семейства функций (класса допустимых решений), в рамках
которого производится дальнейший поиск неизвестной функции регрес-*
сии, является одновременно наиболее важным и наименее теоретически
обоснованным этапом регрессионного анализа.
10. Прежде всего исследователь должен сосредоточить свои усилия на
анализе содержательной сущности искомой статистической зависимости,
чтобы максимально использовать имеющиеся априорные сведения о
«физическом» механизме изучаемой связи при выборе общего вида функции
регрессии.
11. Важную роль в правильном выборе параметрического класса
допустимых решений играет предварительный андлиз геометрической

выводы 395
структуры совокупности исходных данных и в первую очередь анализ
геометрии парных корреляционных полей, включающий в себя, в
частности, учет и формализацию «гладких» свойств искомой функции
регрессии, использование вспомогательных линеаризующих преобразований.
12. Сформулированные с помощью содержательного и
геометрического анализа рабочие гипотезы об общем виде искомой функции регрессии
могут быть проверены с привлечением соответствующих математико-
статистических критериев. Среди фундаментальных идей, на которых
базируются эти статистические критерии, следует выделить: а) идею
компромисса между сложностью регрессионной модели («емкостью» класса
допустимых решений) и точностью ее оценивания; б) идею поиска
модели, наиболее устойчивой к варьированию состава выборочных данных, на
основании которых она оценивается; в) идею проверки гипотез об общем
виде функции регрессии на базе сравнения выборочных критериев
адекватности и исследования статистических свойств получаемых при этом
оценок размерности модели.

ГЛАВА 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
МНОГОМЕРНОЙ ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ
11 Л. Назначение и место корреляционного
анализа в статистическом
исследовании
При исследовании реальных социально-экономических явлений и
систем статистику, экономисту приходится сталкиваться, как правило, с
необходимостью статистического анализа многомерной генеральной
совокупности, т.е. с ситуациями, когда на каждом из статистически
обследуемых объектов этой совокупности регистрируются значения целого
набора признаков аг ,ж' ',..., ж . В дальнейшем мы будем обозначать,
как и прежде, этот набор признаков с помощью X == (аг ', аг ,..., агр') ,
а результат регистрации значений этих признаков на t'-м
статистически обследованном объекте — г-е многомерное наблюдение — с помощью
Х{ = (х\ \х\ ,..., х\р') . Таким образом, «стартовая позиция» при
статистическом анализе многомерной генеральной совокупности аналогична
одномерному случаю: исследователь по имеющейся у него случайной
выборке
X\iX2>.-,Xn A1-1)
значений анализируемой многомерной случайной величины ? = (? ,? ,
•••>?) должен сделать те или иные статистические выводы о ее
«поведении».
Мы уже знаем (см. п. 2.6), что исчерпывающие сведения о
поведении анализируемой случайной величины f содержатся в ее законе
распределения вероятностей (з.р.в.) Д(А'), где под f((X) понимается
значение функции плотности вероятности в точке Ху если случайная величина
? непрерывна, и вероятность Р{? = X} того, что случайная величина

11.1 НАЗНАЧЕНИЕ И МЕСТО КОРРЕЛЯЦИОННОГО АНАЛИЗА 397
примет значение, равное X, если ? дискретна. Однако з.р.в.
анализируемой случайной величины исследователю, как правило, неизвестен.
И если при описании поведения одномерных случайных величин
исследователь еще имеет практически реализуемые возможности подбора и
использования подходящих модельных законов распределения (см. гл. 3) с
последующей статистической оценкой участвующих в их записи
параметров (см. гл. 7), то при исследовании признаков размерности р ^ 2 ему
чаще всего приходится ограничиваться информацией, которую
доставляют оценки моментов первых двух порядков, а именно оценками вектора
средних значений Mi = (т\ ,щ ,..., Щр') и ковариационной матрицы
? = (&ij)y — t, j = 1,2,..., j> (см. п. 6.2). Другими словами, можно сказать,
что за редчайшим исключением1, все выводы многомерного
статистического анализа строятся на базе оценок М\ и ?.
Оценка М\ вектора средних значений дает представление о центре
группирования наблюдений анализируемого многомерного признака.
Отличие от одномерного случая, когда мы располагаем оценкой rh\ = х
среднего значения анализируемой случайной величины, заключается лишь в
том, что М\ определяет точку б р-мерном пространстве, в то время как
выборочное среднее rh\ = x определяет точку на числовой прямой. По
существу вся специфика многомерного случая сосредоточена в
ковариационной матрице Е, а при статистическом анализе — в ее оценке ?.
Именно знание ковариационной матрицы позволяет исследователю
строить и анализировать характеристики случайного рассеивания и
статистической взаимосвязи (коррелированности) компонент анализируемого
многомерного признака. Данная глава как раз и посвящена так
называемому корреляционному анализу многомерной генеральной совокупности,
назначение которого — получить (на основе имеющейся выборки (ИЛ))
ответы на следующие основные вопросы:
• как выбрать (с учетом специфики и природы анализируемых пере-
менных) подходящий измеритель статистической связи
(коэффициент корреляции, корреляционное отношение, какую-либо
информационную характеристику связи, ранговый коэффициент корреляции и т. п.)?
• как оценить (с помощью точечной и интервальной оценок) его
числовое значение по имеющимся выборочным данным1!
• как проверить гипотезу о том, что полученное числовое
значение анализируемого измерителя связи действительно свидетельствует
1 Исключения относятся в основном к генеральным совокупностям, описываемым либо
многомерным нормальным, либо полиномиальным з.р.в. (см. соответственно C.9')
и C.7)).

398 ГЛ. П. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
о наличии статистической связи (или, как говорят, проверить
исследуемую корреляционную характеристику на статистически значимое
ее отличие от нуля?
• как определить структуру связей между компонентами
исследуемого многомерного признака, сопоставив каждой паре компонент
двоичный ответ («связь есть» или «связи нет»)!
Какое место занимает корреляционный анализ в общем прикладном
статистическом исследовании? В гл. 9 обозначены три центральные
проблемы прикладной статистики. Начнем с первой и наиболее значимой
из них — с проблемы статистического исследования зависимостей. В
соответствии с предложенным в предыдущей A0-й) главе разбиением
процесса решения этой проблемы на этапы (см. п. 10.6) корреляционный
анализ составляет содержание, по существу, первого (после постановки
задачи и сбора необходимых статистических данных) этапа
статистического исследования зависимостей. Действительно, при исследовании
зависимостей между анализируемыми переменными мы должны дать в
первую очередь ответ на вопрос: а существует ли такая зависимость
или анализируемые признаки статистически независимы? И только
после утвердительного ответа на этот вопрос заняться выявлением вида и
математической формы этой зависимости. Корреляционный анализ как
раз и предоставляет средства, позволяющие ответить на первый вопрос.
Выявление же вида и математической формы искомой зависимости
производится с помощью разнообразных методов и моделей регрессионного
анализа и анализа временных рядов, которым посвящен том 2
учебника. В то же время рассматриваемые в рамках корреляционного анализа
характеристики статистической связи (ковариации, различные
коэффициенты корреляции и т.п.) используются в качестве «входной» (базовой)
информации при решении задач других двух центральных проблем
прикладной статистики — классификации объектов и признаков и снижения
размерности анализируемого признакового пространства (методы и
модели, предназначенные для решения этих двух проблем, описываются в
гл. 12 и 13). Поэтому именно с главы, посвященной корреляционному
анализу, по существу, начинается изложение методов и моделей прикладной
статистики и эконометрики.
11.2. Корреляционный анализ
количественных признаков
Здесь речь идет об измерителях степени тесноты статистической
связи между количественными компонентами вектора X = (яг1 ,аг ,

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 399
..., х^)т. Напомним (см. п. 2.3), что значение количественной случайной
величины есть результат измерения степени проявления анализируемого
свойства статистически обследованного объекта в числовой шкале
определенного физического смысла (в штуках, метрах, денежных единицах,
килограммах, единицах времени и т. д.).
В соответствии с изложенной в п. 10.1 обшей логической схемой
статистического исследования зависимостей анализируемые переменные по
своей роли делятся на результирующие и объясняющие. Поэтому,
оставив за компонентами вектора X роль объясняющих переменных,
введем в рассмотрение результирующую переменную у. Тогда исходные
статистические данные AЫ) пополнятся еще одним вектором-столбцом
Y = (Уъ2/2>• •->Уп) у так что в дальнейшем предметом нашего анализа
будут исходные статистические данные вида
где Х^ = (х[*\х[*\...}х№)Т — вектор-столбец наблюденных значений
j-й объясняющей переменной (j = 1,2,... ,р).
В п. 10.5 описаны основные типы статистических зависимостей (ВУС
и D), которые могут наблюдаться между исследуемыми переменными.
Умение правильно классифицировать каждую конкретную многомерную
систему наблюдений играет решающую роль при правильном выборе
подходящих математико-статистических методов анализа изучаемой
зависимости на стадии регрессионного анализа и при неформальной
содержательной интерпретации выявленной связи.
Однако при решении задач корреляционного анализа удобнее
использовать единый (унифицированный) подход, при котором исследуемая
объясняющая переменная (случайная при типах зависимостей С и D и
неслучайная при зависимостях типа В) интерпретируется как
параметр, от которого зависит закон распределения
результирующего показателя. Его мы и будем придерживаться в данной главе.
11.2.1. Коэффициент детерминации как универсальная
характеристика степени тесноты статистической
связи
Основная идея, лежащая в основе определения коэффициента
детерминации, состоит в следующем. Пусть нас интересует степень тесноты
статистической связи (с.т.с.с), существующей между результирующим
показателем у и объясняющей переменной (вообще говоря, векторной) X.
Очевидно, степень тесноты этой связи может считаться максимальной,

400 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
если по заданному значению объясняющей переменной X можно
однозначно (без всякой случайной ошибки) восстановить соответствующее
значение результирующего показателя у(Х). И обратно: если значение величин
X не несет никакой информации о значении результирующего
показателя j/, то связь отсутствует вовсе, и соответствующий измеритель степени
ее тесноты должен принимать минимальное (на выбранной шкале)
возможное значение.
Для того чтобы математически формализовать эту естественную посылку в виде
подходящего измерителя с.т.с.с, посмотрим, как она интерпретируется в терминах
регрессионной модели типа A0.14).
Итак, мы рассматриваем статистическую зависимость вида
у(Х) = /(Х) + е(Х), A1.2)
где /(X) = Е(у | X) — условное среднее значение результирующего показателя (при
условии, указанном за прямой чертой, здесь и далее означает, что объясняющая
переменная приняла заданное фиксированное значение X), т. е. функция регрессии у по
X, — а е(Х) остаточная случайная компонента, э.р.в. которой, вообще говоря, может
зависеть от X, но при этом предполагается:
A1.2')
и е(Х) не коррелировала с /(X) в схемах зависимости типов С и D (в схемах типа В
величина /(X) не является случайной).
Отметим два важных соотношения, связывающих характеристики варьирования
(условные и безусловные) составных частей модели A1.2)-A1.2'):
A1.3)
D(y | X) ш D(« | X) ж **(Х) A1.4)
В соотношении A1.3), связывающем между собой безусловные характеристики
варьирования, уо = Еу, /о = Е/, а символ Е означает усреднение следующих за ним
величин по всем возможным значениям как у, так и X. Нуждается в пояснении
случай зависимости по схеме В (см. п. 10.5), в которой объясняющая переменная X не
является случайной. В этом случае усреднение по X производится по всем
наблюденным значениям Х\, Хз,..., Хп, так что, например:
/si
/о = Е*. I?f(Xt)
П i=l
- лK - i J2 (nx{) -/ofnjb (W) - лJ;
1 Знак тождества «г» означает, что среднее значение е равно нулю при всех
возможных значениях объясняющей переменной X.

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ* 401
(вариант формул для группированных данных дается в обозначениях п. 6.1). Что
касается условных характеристик, участвующих в A1.4), то они были определены выше
(здесь усреднение производится по всем возможным значениям у при заданном
фиксированном значении X),
Вернемся непосредственно к обсуждению возможного способа
измерения с.т.с.с. Из A1.2) видно, что однозначное восстановление у по X
возможно только в ситуации «вырождения» (отсутствия) случайной
остаточной компоненты е(Х) при всех возможных значениях X, что равносильно
(при нулевом среднем значении е(Х)) отсутствию какого-либо разброса
значений е(Х) относительно нуля. А это означает на языке
вероятностных характеристик тождественное равенство нулю условных дисперсий
D(e | X) = D(y | X) = <rl(X) s 0. A1.5)
Другой крайний (с точки зрения с.т.с.с.) случай — это ситуация, в
которой знание величины объясняющей переменной X не имеет никакой
информации о значении результирующего показателя у. Эта ситуация
возможна, в рамках модели A1.2), лишь тогда (и только тогда), когда
f(X) = с = const. A1.6)
В этом случае поведение результирующего показателя у (определенного
соотношением A1.2) с учетом A1.6)) как бы повторяет, с точностью до
сдвига на постоянную величину с, поведение остаточной случайной
компоненты е и, в частности, в силу A1.3) и с учетом тождества Е(/-/оJ = 0
имеет в точности ту же самую меру случайного рассеивания, т. е.
или
Dj/ = De. A1.7)
Теперь мы подготовлены к тому, чтобы ввести и
проинтерпретировать достаточно универсальный измеритель с.т.с.с. между у и X —
коэффициент детерминации у по X. Обозначим его с помощью Kd{y\X) и
определим соотношением
)=l-^, A1.8)

402 ГЛ. П. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
где De = Ее2 — безусловная дисперсия остаточной случайной
компоненты, которая может быть подсчитана как усредненная по всем возможным
значениям X условная дисперсия D(e | X), т.е.
De = E,(D(« | X)) A1.9)
(нижний индекс х у символа математического ожидания Б означает, что
усреднение проводится по всем возможным значениям X), a Dy — без-
условная дисперсия результирующего показателя у, определенная
соотношением A1.3).
Легко видеть, что введенный соотношением A1.8) коэффициент
детерминации определяет в качестве шкалы измерения показателя
ст.с.с. отрезок [0; 1], причем минимальное (нулевое) значение К.^(у\Х)
соответствует полному отсутствию какой бы то ни было связи
между у и X (поскольку в этом случае, как мы видели, см. A1.7), De = Dy),
а максимальное значение К^(у\Х) = 1 соответствует случаю чисто
функциональной зависимости между у и X, когда значение у может
быть в точности восстановлено по значению X с помощью формулы
у = f(X) (так как De, определенное формулой A1.9) с учетом
тождества A1.5), равно нулю). При этом из определения коэффициента
детерминации A1.8) с учетом соотношения A1-3) следует, что
численное значение К&(у\х) отражает долю общей вариации
результирующего признака у, объясненную изменением функции
регрессии f(x).
До сих пор мы оперировали теоретическими характеристиками
анализируемых переменных. Однако в статистическом анализе их заменяют
соответствующими выборочными характеристиками. Вычисление
выборочного (эмпирического) значения коэффициента детерминации у по X
должно производиться по формуле
2
#<*(y;*) = i--f> A1.8')
где
4
1 Г 1
а выборочное значение дисперсии «невязок» е вычисляется по одной из
двух формул:
!--[Г (*-/<*>)'.
t=i

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 403
если предварительный анализ показал, что условная дисперсия D(e | X)
не зависит от X (т. е. D(e | X) = а\ = const);
s
если условная дисперсия D(e | X) зависит от значения объясняющей
переменной ЛГ, или во всех случаях, когда вычисления ведутся по
группированной выборке.
В соотношении A1.9') /(Я\) есть статистически оцененное значение
неизвестной функции регрессии f(X) в точке X = Xi (методы
оценивания функции регрессии описаны в гл.2 тома 2). В соотношении A1.9')
использованы группированные выборочные данные и обозначения п. 6.1.
В частности, з — это общее число интервалов группирования, i/j —
число выборочных данных, попавших в j-й интервал группирования, j/j, —
значение результирующего признака в г'-м по счету наблюдении,
принадлежащем j-uy интервалу группирования (нумерация наблюдений своя для
каждого интервала группирования), а у^ — среднее значение
результирующего признака, подсчитанное по наблюдениям, попавшим в jf-й интервал
группирования, т.е. jfy. = Biii Vji)/vj>
Пример 11.1. Подсчитаем коэффициент детерминации К^(ууХ)
по данным примера 10.1 (см. табл. 10.1 и рис. 10.2). Вычисления по
формулам A1.8'), A1.9') и A1.9") дают:
1 40
у = 50,8; 4 = 40 _
= ^D0,96 + 256,00 + 510,76 + 835,21) = 369,96;
= 1 - 0,377 = 0,623.
Такое значение коэффициента детерминации свидетельствует о наличии
статистической связи между среднедушевыми денежными сбережениями
семей у (tf — в обозначениях примера 10.1) и их среднедушевым доходом
х (? — в обозначениях примера 10.1), причем степень тесноты этой
связи несколько выше среднего уровня. Более подробное обсуждение шкалы
значений Кд, так же как и вопросы проверки этих значений на стати-

404 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
стически значимое отличие от нуля, отложим до описания некоторых
частных версий этого важного индикатора.
11,2.2. Исследование линейной зависимости у от
единственной объясняющей переменной х: парный
коэффициент корреляции
Рассмотрение этой схемы зависимости между у и х разобьем на два
случая: 1) переменные (ж, у) «ведут себя» как двумерная нормальная
случайная величина; 2) переменные х и у связаны линейной регрессионной
зависимостью типа A1.2)-A1.2/), т.е. у(х) = 0Q + Oix + e(x), где во и 0\ —
некоторые неизвестные параметры, е(х) и х взаимно некоррелированы, а
з.р.в. случайных величин у,е и переменной х не обязан быть нормальным.
1. Случай двумерной нормальности случайных величин
(ж, у). Эта схема зависимости относится к типу С по классификации,
описанной в п. 10.5. Займемся анализом двумерного нормального
распределения (см. п. 3.1.5, формулу C.9)) с целью конкретизации вида
функции регрессии f(x) и других вероятностных характеристик модели A1.2).
Донимая под ^ ' и ?* ' из формулы C.9) соответственно объясняющую
переменную х и результирующий показатель у и воспользовавшись
результатами п. 3.1.5, имеем:
а)
/(я) = Е(у | я) = Е(?B) | fA) = я) = *о + М, (НЛО)
где
1/2
% ^f*, A1.11)
}1* = Еж, (У„ = «г* = Е(х - т}1*I;
так называемый парный коэффициент корреляции между
переменными а: и у;
б)
^) () г2)
х) = 2?(^») | еA) = •) = а}A - г2). A1.14)
Из A1.10) следует, что если анализируемые переменные подчинены
двумерному нормальному закону, то функция регрессии одной из них по

И.2.КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 405
другой имеет линейный вид. Кроме того, из определения коэффициента
детерминации A1.8) с учетом соотношений A1.9), A1.4) и A1.14)
следует, что парный коэффициент корреляции г и коэффициент детерминации
Kd{y, x) связаны простым соотношением
Kd(y;x) = r2(x,y). A1.15)
При этом в отличие от коэффициента детерминации (который по
определению может быть только неотрицательным числом) коэффициент
корреляции может быть как положительным, так и отрицательным. А
поскольку он имеет одинаковый знак с угловым коэффициентом наклона
01 прямой f(x) = 0о + в\Х (см. соотношение A1.11)), то положительное
значение г свидетельствует о положительном (монотонно
возрастающем) характере парной связи у и ж, а отрицательное значение г — об
отрицательном (монотонно убывающем) характере этой связи.
Сформулируем и докажем основные свойства парного
коэффициента корреляции (справедливые в рамках рассматриваемой двумерной
нормальной генеральной совокупности).
Свойство 1. Шкала возможных значений парного коэффициента
корреляции г ограничена отрезком от —1 до +1, т.е. -1 < г < 1, или
и < 1.
Для доказательства этого свойства воспользуемся очевидными
неравенствами
Б
mi
A1.16)
Возводя в квадрат сумму в круглых скобках, имеем
2Е
(х - mY')(y - mj2))
+ Е
>0. A1.17)
Поскольку
(
B)
, к,
„1,

406 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
а
= г (по определению),
то из A1.17) непосредственно следует, что г > -1. Аналогично
рассуждая при анализе выражения, получающегося от возведения в квадрат
разности в круглых скобках левой части выражения A1.16), получаем,
что г < 1. Объединение полученных двух неравенств дает нам
доказательство свойства 1.
Свойство 2. Бели случайные величины х к у статистически
независимы, то г(х,у) = 0.
Доказательство этого свойства следует из определения A1.13) с
учетом того, что для статистически независимых случайных величин их ко-
вариация равна нулю, т. е.
= [Е(х - тр>)] [Е(у - «
Свойство 3. Из факта \г\ = 1 следует наличие чисто
функциональной линейной связи между х и у и наоборот: если х и у связаны чисто
функциональной линейной связью, то \г\ = 1.
Для доказательства этого свойства следует обратить внимание на то,
что неравенства г< 1иг^-1 обращаются в точные равенства тогда и
только тогда, когда обращаются в точные равенства неравенства A1.16)
(по построению). А неравенства A1.16) обращаются в точные равенства
тогда и только тогда, когда выражение в круглых скобках левой части
этого соотношения тождественно равно нулю. Но из равенства
следует, что х и у связаны линейной зависимостью.
Свойство 4. Коэффициент корреляции является симметричной
характеристикой с.т.с.с. между х и у, т.е. г(х>у) = г(у,ж).
Доказательство этого свойства следует непосредственно из
определения A1.13).
Свойство 5. Из равенства нулю коэффициента корреляции (т. е.
из того, что г(х,у) = 0) следует статистическая независимость
переменных х и у.
Чтобы доказать это свойство, надо показать, что из г (ж, у) = 0
следует представление двумерной совместной плотности f(x,y)(u>v) в виде

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 407
произведения частных плотностей fx{u)fy(v). Для этого воспользуемся
обшей формулой двумерного нормального распределения C.9), подставив
в нее значение г = 0. Получаем (с учетом введенных выше
преобразований):
A1.18)
Но правая часть A1.18) представляет собой как раз произведение частной
плотности распределения вероятностей случайной величины х на
частную плотность распределения вероятностей случайной величины у, что и
завершает доказательство.
Дав определение и познакомившись с основными свойствами парного
коэффициента корреляции г, мы должны привести формулу, по которой
вычисляется эмпирический (выборочный) аналог этой характеристики —
г{х,у):
t(xi-x)(Vi~y)
1 A1.13')
Однако для проведения полноценного статистического анализа
свойств исследуемой генеральной совокупности, основанных на этой
характеристике, нам необходимо знать ее статистические свойства. Это
позволит судить о точности приближения A1ЛЗ;) к неизвестному
истинному значению A1.13), строить статистические критерии для проверки
различных гипотез о численных значениях анализируемого коэффициента
корреляции.
В частности, какую величину выборочного коэффициента
корреляции следует считать достаточной для статистически обоснованного
вывода о наличии корреляционной связи между исследуемыми
переменными! Ведь надежность статистических характеристик, в том числе и г,
ослабевает с уменьшением объема соответствующей выборки, а потому
принципиально возможны случаи, когда отклонение от нуля полученной
величины выборочного коэффициента корреляции г оказывается
статистически незначимым, т. е. целиком обусловленным неизбежным
случайным колебанием выборки, на основании которой он вычислен. Ответить
на этот вопрос помогает знание закона вероятностного распределения г.

408 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
В случае совместной нормальной распределенности исследуемых
переменных и при достаточно большом объеме выборки п (а именно при п > 200)
распределение г можно считать приближенно нормальным со средним,
2 A— г2}2
равным своему теоретическому значению г, и дисперсией аг = \ ~п ' .
Однако следует учитывать, что при малых значениях п и г, близких к
±1, это приближение оказывается очень грубым. Кроме того, при малых
п следует принимать во внимание, что величина г является смещенной
оценкой своего теоретического значения г, в частности Ег = г — [гA -
г2)]/2п.
Относительно хорошая степень приближения нормального
распределения при малых значениях |г] позволяет получить простой критерий
проверки гипотезы
Яо: г = 0, A1.19)
т. е. гипотезы об отсутствии корреляционной связи между исследуемыми
переменными х и у. При этом используется тот факт, что статистика
при условии справедливости гипотезы Яо приблизительно распределена
по з.р.в. Стьюдента сп-2 степенями свободы.
Поэтому если окажется, что
A1.20)
то гипотеза Яо об отсутствии корреляционной связи между х и у
отвергается с вероятностью ошибиться, равной а (здесь, как и ранее, tq(m) —
100д%-ная точка ^-распределения с т степенями свободы).
Доверительные интервалы для истинного значения коэффициента
корреляции г можно построить, используя следующее преобразование,
предложенное Р.Фишером:
Он показал, что величина г, определенная соотношением A1.21), уже
при небольших п с хорошим приближением следует нормальному закону
со средним Ez и ?ln |±*f + 2(n-i) и Дисперсией Dz = ^. Это позволяет

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 409
построить доверительный интервал [z\, z^\ для Ex по формуле
г
= arcth f
откуда следует, что истинное значение коэффициента корреляции г с той
же доверительной вероятностью 1 - а заключено в пределах
th zi < r < thz2. A1.22)
Здесь th -гг — это тангенс гиперболический от аргумента z
(определяется с помощью соотношения th z = (е* — е~г)/(ег+е~*)). Соответственно
функция, определяющая величину z с помощью соотношения A1.21), —
это функция, обратная к тангенсу гиперболическому; так что часто
вместо z = jlnj^r пишут z = arcth f (или z = th"" r). Нахождение z no
данному значению г и, наоборот, определение f по заданной величине г
производятся с помощью специальной табл. (см. приложение 1), в
которой в крайних столбцах (левом и правом) приведены значения |г|, а между
ними — соответствующие значения \z\ = arcth \f\ (знаки у аргумента и
функции совпадают, так что если, например, f отрицателен, то и
соответствующее значение z = argth r также отрицательно).
Пример 11.2. По данным п = 39 предприятий получен
коэффициент корреляции г = —0,654, характеризующий тесноту связи между
себестоимостью продукции (у) и производительностью труда (ж). Построим
интервальную оценку для г, задавшись 95%-й доверительной
вероятностью.
По табл. из приложения 1 для г = -0,654 найдем z = -0,7823. Тогда
1 96
*i = -0,7823 - -¦= = -1,1090;
v36
1 96
z2 = -0,7823 + -?= = -0,4556.
v36
Теперь по табл. по найденным z\ и х% найдем соответствующие значения
гх = -0,804 и z2 = -0,426.
Таким образом, можно утверждать, что с доверительной
вероятностью Р = 0,95 истинное значение коэффициента корреляции г между
себестоимостью продукции у и производительностью труда х будет лежать
в интервале от -0,804 до -0,426, т. е. -0,804 < г < -0,426.

410 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Влияние ошибок измерения анализируемых переменных на величину
коэффициента корреляции г. Пусть мы хотим оценить степень
тесноты корреляционной связи между компонентами двумерной нормальной
случайной величины (я?, у), однако наблюдать мы их можем лишь с
некоторыми случайными «ошибками измерения» соответственно ех и еу
(см. схему зависимости D в п. 10.5). Поэтому экспериментальные данные
(ль j/i), • = 1,2,..., п, — это практически выборочные значения
искаженной двумерной случайной величины (я',1/'), где х = х + еж и у = у + еу.
Если предположить, что ех и еу взаимно независимы, не зависят от х и у,
нормальны, имеют нулевые математические ожидания и конечные
дисперсии, соответственно а\ и а\, то двумерная случайная величина (х\ у)
будет также подчиняться двумерному нормальному распределению. Однако,
как легко подсчитать, параметры этого распределения и, в частности,
коэффициент корреляции г' между х и д будут соответственно отличаться
от параметров исходной двумерной схемы (ж, у). Действительно, в
соответствии с основными правилами вычисления первых и вторых моментов
(см. п. 2.6) получаем
axi = Ех = Еж = ах\
ау» = Еу 5= Еу = ау;
2 2 2
<v = 0* + 0*1;
4-^+* AL23)
r' =
Из A1.23), в частности, следует, что коэффициент корреляции
признаков, на которые наложены ошибки измерения, всегда меньше по
абсолютной величине, чем коэффициент корреляции исходных признаков.
Другими словами, ошибки измерения всегда ослабляют исследуемую
корреляционную связь между исходными переменными, и это искажение тем
меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих
исходных переменных. Формула A1.23) позволяет скорректировать
искаженное значение коэффициента корреляции: для этого нужно либо знать
«разрешающие» характеристики погрешностей измерений (и,
следовательно, величины дисперсий ошибок а\ и а\\ либо провести
дополнительное исследование по их выявлению.
2. Общий случай пйрной линейной зависимости. Рассмотрим
регрессионную модель вида A1.2) в случае р = 1 и линейной функции

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ ,411
регрессии /(X), т.е.
у(х) = в0 + М + ф), A1.24)
где $о и 0i — неизвестные параметры модели, единственная объясняющая
переменная ж может быть случайной величиной или неслучайной, е(х) и
х взаимно некоррелированы, а Ее(х) = 0 и De(s) = <т2(я). В отличие
от предыдущей схемы в данном случае не требуется двумерной
нормальности анализируемой пары переменных (ж, у). Очевидно,
рассматриваемая модель может относиться к любому из типов зависимостей В, С и Dy
описанных в п. 10.5 (все зависит от конкретизации природы исследуемых
переменных).
Определенные соотношения A1.13) и A1.13#) — соответственно
теоретический и выборочный коэффициенты корреляции — могут быть
формально вычислены для любой двумерной системы линейной
статистической связи между анализируемыми признаками.
Практически все свойства и рекомендации, касающиеся вычисления,
использования статистических свойств и интерпретации парного
коэффициента корреляции, определенного соотношениями A1.13) и A1.13),
остаются приблизительно справедливыми и в рамках более общей
схемы A1.24) линейной зависимости между хну. Так, например, из пяти
сформулированных выше свойств коэффициента корреляции первые
четыре остаются в силе и в рамках модели A1.24) («не работает» лишь
свойство 5: в общем случае из некоррелированности х и у не следует их
статистическая независимость).
Однако только в случае совместной нормальной распределенности
исследуемых случайных величин х и у коэффициент корреляции г имеет
четкий смысл как характеристика степени тесноты связи между ними. В
частности, в этом случае соотношение \г\ = 1 подтверждает чисто
функциональную линейную зависимость между исследуемыми величинами, а
уравнение г = 0 свидетельствует об их полной взаимной независимости.
Кроме того,, коэффициент корреляции вместе со средними и дисперсиями
случайных величин хну составляет те пять параметров, которые дают
исчерпывающие сведения о стохастической зависимости исследуемых
величин, так как однозначно определяют их двумерный закон распределения
(см. формулу C.9)). Во всех же остальных случаях (распределения х и у
отклоняются от нормального, одна из исследуемых величин не является
случайной и т. п.) коэффициент корреляции можно использовать лишь в
качестве одной из возможных характеристик степени тесноты связи. При
этом, несмотря на то, что в общем случае пока не предложено
характеристики линейной связи, которая обладала бы очевидными преимуществами
по сравнению с г, его интерпретация часто оказывается весьма ненадеж-

412 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
ной. Если же априори допускается возможность отклонения от
линейного вида зависимости^ то можно построить примеры, когда,
несмотря на г = 0, исследуемые переменные оказываются связанными чисто
функциональным соотношением (следовательно, Kd(x,y) = 1). Поэтому
о величинах, для которых г = О, обычно говорят, что они некоррелирова-
«ы, и только после дополнительного статистического и профессионального
анализа (исследование степени отклонения распределения
рассматриваемых величин от нормального и т.п.) можно сказать, следует ли отсюда
их независимость.
Замечания о необходимости известной осторожности при толковании
корреляционной связи никоим образом не обесценивают желательность
проверки значимости любого кажущегося соотношения. При этом
следует использовать характеристики степени тесноты связи: коэффициента
корреляции г и корреляционного отношения р (см. ниже). Но не
всегда знание этих характеристик оказывается достаточным для получения
информации о степени тесноты физической связи между исследуемыми
переменными и тем более об их причинной взаимообусловленности.
11.2.3. Исследование парных нелинейных связей:
корреляционное отношение
При отклонениях исследуемой зависимости от линейного вида, как
уже отмечалось, коэффициент корреляции г теряет свой смысл как
характеристика степени тесноты связи. В этих случаях исследователь должен
воспользоваться имеющимися у него двумерными выборочными данными
(х1)У1)Лх2)У2))-'>(хП)Уп) с целью построения оценок для определенной
выше в некотором смысле универсальной теоретической
характеристики степени тесноты связи — коэффициента детерминации К^(у\х) (см.
A1.8)). Способ построения таких оценок выбирается в зависимости от
природы имеющихся у нас выборочных данных и от характера некоторых
дополнительных допущений.
Корреляционное отношение. Наиболее привлекательной в этом
смысле является ситуация, в которой характер выборочных данных (их
количество, «плотность» расположения на плоскости) допускает их
группировку по оси объясняющей переменной и возможность подсчета так
называемых «частных» средних ординат jfy. внутри каждого (jf-ro)
интервала группирования. Пусть такое группирование данных произведено. При
этом, как обычно, a — число интервалов группирования по оси абсцисс;
Vj{j = 1,2,...,з) — число выборочных точек, попавших в t-ft интервал
группирования; yjt = (X^ii Vj\)lui — среднее значение ординат точек,

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 413
попавших в jf-й интервал группирования. Тогда, как легко понять,
выборочным аналогом (оценкой) введенной ранее (см. п. 11.2.1) дисперсии <т/
будет величина
где общее среднее у — ? ?j=1 Vji/j.- Соответственно получаем оценку для
Kd(y,«) в виде
р\х = 4(х)/4» (И-26)
где выборочная дисперсия sy индивидуальных результатов наблюдения
yji около общего среднего у вычисляется по формуле
i=i t=i
Величину рух принято называть корреляционным отношением
зависимой переменной у по независимой переменной х. Его вычисление не
обременено никакими дополнительными допущениями относительно
общего вида регрессионной зависимости A1.2). Однако в отличие от
коэффициента корреляции корреляционное отношение несимметрично по
отношению к исследуемым переменным, т.е., вообще говоря, рух ф рху.
Кроме того, корреляционное отношение, по определению, является
величиной неотрицательной , так как под ним подразумевается результат
извлечения арифметического значения корня квадратного из р .
В остальном свойства корреляционного отношения во многом похожи
на свойства коэффициента корреляции. Из A1.3) и A1.8), в частности,
немедленно следует, что подобно коэффициенту корреляции корреляционное
отношение не может быть больше единицы.
Из \р\ = 1 следует наличие однозначной функциональной связи между
у и ж, и, наоборот, однозначная функциональная связь между у и х
свидетельствует о том, что \р\ = 1. Далее, отсутствие корреляционной связи
между у к х означает, что условные средние у$% сохраняют постоянное
значение, равное общему среднему у, а потому рух = 0. Наоборот, если
Рух = 0, то yjt = j/, и, следовательно, частные средние jjjt не зависят от ж,
т.е. соответствующая линия регрессии параллельна горизонтальной оси.
1 Иногда, в частности при монотонном характере функции регрессии /(&),
корреляционному отношению приписывают знак, совпадающий со знаком первой производной
этой функции.

414 гл. п. корреляционный анализ
Отметим, что между руш и рту нет какой-либо простой зависимости.
Некоррелированность у с х (т. е. равенство нулю величины руш) не влечет
за собой непосредственно некоррелированности х с у. Возможны
ситуации, в которых один из этих показателей принимает нулевое значение, в
то время как другой равен единице. Допустим, например, что у = х2 и
х принимает значения: -1,0 и +1 с вероятностями 1/3 каждое. В этом
случае рух = 1, рху = 0 (в силу симметрии параболы относительно оси у
и симметричности распределения х).
Можно показать, что корреляционное отношение р не может быть
меньше абсолютной величины коэффициента корреляции г,
характеризующего зависимость между теми же переменными. В случае линейной
зависимости эти две характеристики связи совпадают. Это позволяет
использовать величину разности рух — г в качестве меры отклонения
регрессионной зависимости от линейного вида (см. соотношение A0.25) в
п. 10.7).
И наконец, все замечания относительно смысловой интерпретации
коэффициента корреляции г (в частности, о логическом соотношении
понятий «корреляционная зависимость, связь между переменными, их
причинная взаимообусловленность») остаются в силе и для корреляционного
отношения.
Проверка гипотезы об отсутствии корреляционной
связи. Какую величину корреляционного отношения можно признать
статистически значимо отличающейся от нуля, т. е. достаточной для
статистически обоснованного вывода о наличии корреляционной связи между
исследуемыми переменными? Ведь так же, как и в случае прямолинейного
типа зависимости, принципиально возможны ситуации, когда отклонение
от нуля полученной величины корреляционного отношения р является
статистически незначимым, т. е. обусловленным лишь неизбежными
случайными колебаниями выборки. Для построения соответствующего критерия
воспользуемся фактом приближенной F(s—19 п-з)-распределенности
случайной величины
A1.27)
справедливым в предположении, что Kd(y; х) = 0 (или, что то же, рух = 0)
и что условные распределения результирующей переменной у(х) при
любом фиксированном х описываются нормальным законом с постоянной
дисперсией а .

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 415
Поэтому если окажется, что
1-Й. «-i
то гипотеза Я: pytB = 0 об отсутствии корреляционной связи между у и х
отвергается с вероятностью ошибки а (здесь, как и ранее, г?а(д-1, п-з) —
100а%-ная точка F-распределения с числом степеней свободы числителя
з - 1 и знаменателя п-з находится из табл. приложения 1). При
выполнении обратного неравенства значение корреляционного отношения рух
признается статистически незначимым, т.е. делается вывод, что
гипотеза об отсутствии корреляционной связи между у и х не противоречит
наблюдениям.
Доверительные интервалы для истинного значения
корреляционного отношения рух можно построить, опираясь на тот факт, что
статистика
7(п) _ (гс - *)Рух *- *
приближенно описывается F-распределением с числом степеней свободы
числителя
* _ (д - 1 + пр2ухJ
V\ = к— A1.28)
з-1 + Ъпрух
и числом степеней свободы знаменателя Vi = п — з (см. [Айвазян С. А.,
ЕнюковИ.С, МешалкинЛ.Д., 1985, п.1.1.4]).
Таким образом, получаем следующее правило построения
приближенных доверительных интервалов для истинного значения корреляционного
отношения рух:
1) пользуясь формулой A1.26), вычисляем точечную оценку р2ух для
истинного значения корреляционного отношения рух;
2) по формуле A1.28) подсчитываем вспомогательное число степеней
свободы и{ числителя для аппроксимирующего F-распределения;
3) задавшись уровнем доверия Р = 1 -2а, с помощью табл.
приложения 1 находим 100A - а)%-ную точку и?_а(|/Г, п-з) и 100а%*ную точку
v а(и{,п- з) F-распределения с числом степеней свободы числителя v\ и
знаменателя п — з\
4) утверждаем, что приблизительно с вероятностью Р = 1-2а
истинное значение корреляционного отношения рух удовлетворяет неравенствам
(П - З)р\х 3- 1 2 (П-З)р2ух
<P<

416 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Проиллюстрируем работоспособность описанного метода на
следующем примере. Пусть в результате обработки 132 экспериментальных
точек (xuyi)(i = 1,2,..., 132) получено выборочное значение
корреляционного отношения р = 0,60. При этом мы воспользовались разбиением
диапазона изменения независимой переменной на з = 12 равных интервалов
группирования. Соответственно получаем в качестве вспомогательного
числа степеней свободы числителя величину и{ = i2~i+2-i32*'o,36 w ^7
(частное округляем до целого числа). Задавшись доверительной
вероятностью Р = 0,90, из табл. приложения 1 находим (полагая а = 0,05):
г;0%5B7,120)=1,58;
И наконец, в соответствии с формулой A1.29) находим левый (p^in) и
правый (/5^ах) концы доверительного интервала для истинного значения
Рух-
л 120-0,36 _ _1J_
Рт[п 132-0,64.1,58 132 ' '
2 = 120-0,36 11
Итлх 132-0,64-1,58 132 ' '
Таким образом, при точечной оценке рух = 0,6 истинное значение
заключено в пределах от ^0,24 до ^/0,87 с вероятностью, приблизительно
равной 0,9, т. е. 0,49 < рух < 0,93.
В этом примере хорошо видна существенная несимметричность
концов интервальной оценки относительно точечной оценки (правый конец
интервальной оценки отстоит от точечной оценки на 0,33, в то время как
левый конец — всего лишь на 0,11).
Для значений точечных оценок /52, близких к нулю или к единице,
левый или правый конец интервальной оценки может терять
содержательный смысл, выходя за пределы отрезка [0, 1]. В этом случае в
качестве левого или правого конца интервальной оценки следует брать
соответствующее граничное значение — нуль или единицу (причина
подобных нежелательных ситуаций — в аппроксимационном подходе к
решению данной задачи). Однако описанный прием все-таки следует признать
гораздо более точным, чем применяемый иногда метод построения
интервальных оценок для /9^, необоснованно использующий приблизительную
^?-)-нормальность статистики

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 417
11.2.4. Исследование линейной зависимости у от нескольких
объясняющих переменных жA\ жB),..., ж(р):
множественный и частные коэффициенты корреляции
Аналогично той схеме, по которой излагался п. 11.2.2, разобьем
рассмотрение данной проблемы на два случая: 1) «поведение» вектора
переменных (х^г\х^2\...,х^\у) описывается (р + 1)-мерным нормальным
законом (см. формулу (ЗЛО) в п. 3.1.1); 2) результирующий показатель у
(I) B) (р)
связан с объясняющими переменными хк ',дг ,.••>* линейной
регрессионной зависимостью типа A1.2).
1) Случай многомерной нормальности векторного признака
(я , аг ,..., ж ; у). Свойства многомерного нормального закона
достаточно хорошо исследованы (см., например, [Андерсон Т.]). В частности,
имеют место результаты, аналогичные A1.10)—A1.14), которые были
рассмотрены в рамках двумерной схемы в п. 11.2.2. А именно доказано, что
функция регрессии у по X имеет линейный вид:
f(X) = Е{у | X) = в0 + МA) + • • • + 0Px{v\ (П.30)
где коэффициенты 0j (j = 0,1,... ,р) явным образом выражаются в
терминах компонент вектора средних значений М\ и элементов ковариационной
матрицы ? анализируемого многомерного нормального распределения, а
условная дисперсия у (при условии, что объясняющие переменные
зафиксированы на уровне X) не зависит от X и тоже выражается в явном виде
через элементы ковариационной матрицы S.
Однако в анализе множественных корреляционных связей (так
называют статистические связи между более чем двумя переменными в
отличие от парных связей, рассмотренных выше) есть своя специфика и
возникают принципиально новые проблемы. Эта специфика связана в первую
очередь с необходимостью уметь измерять степень тесноты связи между
результирующей переменной у и множеством объясняющих переменных
жA% аг2),..., агр), а также с возникающими трудностями в интерпретации
парных коэффициентов корреляции между у и х , обусловленными
возможным опосредованным влиянием на эту парную связь других (явно не
учтенных в вычислении г(у\х**')) объясняющих переменных x^l\i ф j).
Последнее обстоятельство, в частности, делает необходимым введение
таких измерителей статистической связи, которые были бы «очищены» от
опосредованного влияния других переменных, давали бы оценку степени
тесноты интересующей нас связи между переменными у и х™' (или х^
и х^') при условии, что значения остальных переменных зафиксированы
14 Теория вероятностей
и прикладная статистика

418 гл. п. корреляционный анализ
на некотором постоянном уровне. В этом случае говорят о
статистическом анализе частных (или «очищенных») связей и используют
соответственно частные («очищенные* ) коэффициенты корреляции или другие
корреляционные характеристики.
Частные коэффициенты корреляции и их выборочные
значения. Поставим в соответствие каждой из ранее введенных парных
характеристик статистической связи между переменными аг ' и x"\ij =
0,1,...,р; х^ = у) частную («очищенную» ) характеристику,
определяемую по той же формуле, но только для условного распределения (см.
п.2.5, B.13)) <р(х^\х^ | Х^'^ = х). Здесь <р — это функция плотности
вероятности переменных х^ и аг"; ЛГ'1'*7' — множество переменных,
дополняющих пару (ar ,arJ') до полного набора рассматриваемых
(наблюдаемых) переменных X = (аг , аг ,..., ж ), а х - (р - 1)-мерный вектор,
определяющий заданные уровни, на которых фиксируются значения
«мешающих» переменных X*1 . Есть два взаимосвязанных обстоятельства,
которые препятствуют широкому практическому использованию частных
характеристик статистической связи в общем (т. е. негауссовском) случае:
• частные характеристики статистической связи, вообще говоря,
зависят от заданных уровней х мешающих переменных (как их выбирать
в каждом конкретном случае?);
• для подсчета выборочных значений частных характеристик
статистической связи необходимо иметь выборку специальной
структуры^ обеспечивающей наличие хотя бы нескольких наблюдений при
каждом из заданного ряда фиксированных значений х мешающих
переменных.
Однако можно показать, что если исследуемые случайные
переменные (аг°',аг ,...,агр') подчиняются многомерному нормальному закону,
то указанные неудобства автоматически исчезают, так как в этом
случае частные коэффициенты корреляции не зависят от уровней мешающих
переменных аг, определяющих условие в соответствующем условном
распределении. В частности, имеет место следующая формула (при условии
невырожденности (р+ 1)-мерного нормального закона):
гДе гу.*о'.л — частный коэффициент корреляции между переменными х^
и х"' при фиксированных значениях всех остальных переменных Х^'*\
a Rki — алгебраическое дополнение (см. Приложение 2) для элемента

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 419
г и в определителе корреляционной матрицы R анализируемых признаков
0) г у, х^1\х^2\..., х^р\ т. е. в определителе
det R =
Го1 Г02 • • • г0р
1 ^12 ••• Г1р
где
Формула A1.31), примененная к трехмерному признаку (аг0) = у,
() iiJ) B)
), при t = 0, j = 1 и XiiJ) = аB) дает:
Последовательно присоединяя к мешающим переменным все новые
признаки из рассматриваемого набора, можно получить рекуррентные
соотношения для подсчета частных коэффициентов корреляции roiB...fc+i)
порядка к (т. е. при исключении опосредованного влияния к мешающих
переменных) по частным коэффициентам корреляции порядка к - \{к =
1,2,...fii-l):
_ 01B»3 к+1)рк+Ц2 к) -Г1к+Ц2 к)
Г01B,3 Аг+1) -
Выборочные (эмпирические) значения частных коэффициентов
корреляции вычисляются по тем же формулам A1.31) - A1.32;) с заменой
теоретических значений парных коэффициентов корреляции г^ их
выборочными аналогами fy (см. формулу A1.13')).
Бели исследователь имеет дело лишь с тремя-четырьмя переменными
(р = 2,3), то удобно пользоваться рекуррентными соотношениями A1.32;).
При больших размерностях анализируемого многомерного признака
удобнее опираться на формулу A1.31), использующую расчет
соответствующих определителей.
Статистические свойства выборочных частных коэффициентов
корреляции {проверка на статистическую значимость их отличия от
нуля, доверительные интервалы). При исследовании статистических
свойств выборочного частного коэффициента корреляции порядка к (т. е.
при исключении опосредованного влияния к мешающих переменных)
следует воспользоваться тем, что он распределен точно так же, как и
обычный (парный) выборочный коэффициент корреляции между теми же
переменными с единственной поправкой: объем выборки надо уменьшить на
14*

420 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
к единиц, т.е. полагать его равным п — fc, а не п. Поэтому при проверке
статистически значимого отличия от нуля выборочного частного
коэффициента корреляции и при построении для него доверительных интервалов
следует пользоваться рекомендациями п. 11.2.2 для парного коэффициента
корреляции с заменой п на п — к.
Рассмотрим некоторые конкретные числовые примеры,
демонстрирующие возможный характер искажающего опосредованного влияния
«третьих факторов» на корреляцию между двумя анализируемыми
переменными.
Пример 11.3. По итогам года 37 однородных предприятий
легкой промышленности были зарегистрированы следующие показатели их
работы: ж*0* = у — среднемесячная характеристика качества ткани (в
баллах); аг1' — среднемесячное количество профилактических наладок
автоматической линии; аг ' — среднемесячное число обрывов нити.
По матрице исходных данных (х\ \х\ \х\ )^=у^7 были
подсчитаны (с помощью A1.13')) выборочные парные коэффициенты корреляции
fy(i,j = 0,1,2): fOi = 0,105; f02 = 0,024; f12 = 0,996.
Проверка «на статистическую значимость», проведенная в
соответствии с рекомендациями п. 11.2.2, свидетельствует об отсутствии
статистически значимой парной корреляционной связи между качеством ткани,
с одной стороны, и числом профилактических наладок и обрывов нити —
с другой, что не согласуется с профессиональными представлениями
технолога.
Однако расчет частных коэффициентов корреляции по формуле
A1.32) дает значения гоц2) = 0,907; rO2(i) = -0,906, которые вполне
соответствуют нашим представлениям о естественном характере связей между
изучаемыми показателями.
Доверительные интервалы для истинных значений гоц2) и rO2(i)
(в соответствии с рекомендациями п. 11.2.2) найдем с использованием
г-преобразования Фишера для доверительной вероятности Р = 1 — а.
Тогда
-I] 1 + ^ Ца/2 г
где uq — g-квантиль стандартного нормального распределения (см.
табл. Приложения 1).
В нашем примере п = 37, а = 0,05. Подставляя поочередно в эту
формулу значения fOiB) = 0,907 и fO2(i) = -0,906 и пользуясь табл. П1.7
значений z = arcth f = \ In ^?, найдем для
г = #01B) = 0,907 :

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 421
Ж! = 1,16
И
z2 = 1,83,
а для
г = гО2A) = -0,906: *i = -1,83
z2 = -1,16,
откуда, вновь воспользовавшись табл., окончательно получим:
0,820 < гМB) < 0,950;
-0,950 < гО2A) < -0,820.
Пример 11.4. С целью исследования влияния погодных условий
на урожайность кормовых трав Хукер (Journ. Roy. Stat. Soc, 1907, v.65,
p. 1) рассмотрел данные Министерства земледелия Англии за 20 лет,
характеризующие урожайность аг0' (в ц/акр), весеннее количество осадков
яг1' (в дюймах) и накопленную за весну сумму «активных» (т.е. выше
+5,5°С) температур аг ' (в градусах по хФаренгейту) однородной в
метеорологическом отношении области Англии, включающей в себя группу
восточных графств. По выборке (х\ \х\ \х\ )i=j^o были подсчитаны
основные статистические характеристики изучаемой трехмерной
случайной величины:
т(!0) = 28,02; т}1* = 4,91; т^ = 594,0;
*о = 19,54; л? = 1,21; 4=7225;
#01 = 0,80; г02 = -0,40; #12 = -0,56.
Действительно ли высокая температура в период созревания трав
отрицательно влияет на их урожайность (ведь г02 = -0,40) или здесь
сказывается опосредованное влияние «мешающего» фактора — количества
осадков аг '?
Вычисление частных коэффициентов корреляции по рекуррентной
формуле A1.32) дает:
roiB) = 0,759; гО2A) = -0,097; г12{0) = -0,436.
Как видим, если исключить одновременное влияние количества
осадков жA) на урожайность (с ростом ж'1' она повышается) и на сумму
активных температур (с ростом аг ' она понижается), то мы уже не
обнаружим отрицательной корреляции между температурой и урожайностью
(^02A) = 0,097, в то время как г02 = —0,40).

422 гл. ii. корреляционный анализ
Построение доверительных интервалов для гоц2) и rO2(i) (с уровнем
доверия Р = 0,95) с использованием ^-преобразования Фишера дает в
данном случае:
0,448 < го1B) < 0,890; -0,419 < rO2(i) < 0,525.
Последнее неравенство свидетельствует о том, что у нас нет
оснований считать положительную очищенную корреляционную связь между
урожайностью и температурой (rO2(i) = 0,097) статистически значимой,
т. к. нуль находится внутри доверительного интервала.
Обратимся теперь к задаче измерения с.т.с.с. между
результирующим показателем у и множеством объясняющих переменных X =
(х^г\х^2\...9х^р')Т в условиях многомерной нормальной совокупности.
В общем случае эта задача решается с помощью коэффициента
детерминации Kd(y,X) (см. A1.8) и A1.8')), который по построению обладает
следующими свойствами:
аH<ад;Х)<1;
б) минимальное значение коэффициента детерминации (К^(у\ X) = 0)
соответствует случаю полного отсутствия корреляционной связи между у
и (я ,..., ж ), так как это может быть только при aj = D/(?) = 0, т. е.
при независимости значений функции регрессии / от величины ее
аргументов X(f(X) = const); это соответствует ситуации, когда усредненная
дисперсия «регрессионных остатков» в точности равна общей вариации
результирующего показателя;
в) максимальное значение коэффициента детерминации {Kd(y\X)
= 1) соответствует полному отсутствию варьирования «регрессионных
остатков» (Ее = 0), что означает наличие чисто функциональной связи
между у и (аг\..., агр'): у = /(аг,... агр'). Следовательно, в этом
случае мы имеем возможность точно (детерминированно) восстанавливать
условные значения у(Х) = {у \ X) по значениям предикторных
переменных X, и соответственно общая вариация результирующего показателя у
полностью объясняется контролируемой вариацией функции регрессии.
Из A1.8 ) следует, что вычисление выборочного значения
коэффициента детерминации предусматривает проведение предварительных
расчетов по статистическому оцениванию неизвестной функции регрессии
/(X), что противоречит хронологии исследований, описанной в п. 10.6.
Сейчас мы увидим, что свойства многомерных нормальных совокупностей
автоматически устраняют это неудобство, позволяя вычислять значение
Kd(y; X) до проведения регрессионного анализа.
Множественный коэффициент корреляции Ry.x используется
в качестве измерителя с.т.с.с. между результирующим показателем у и

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 423
набором объясняющих переменных аг , аг ,..., агр' в моделях линейной
регрессии. Он определяется как обычный парный коэффициент
корреляции между у и линейной функцией регрессии у по X, т.е.
A1.33)
где
f(X) = Е(у | X) = в0
(можно показать, что следующее определение Ry,x является
эквивалентным определению A1.33): Ry.x — это парный коэффициент
корреляции между у и такой линейной комбинацией я \ аг ',..., а? , для
которой значение этого парного коэффициента корреляции достигает своего
максимума).
Можно показать, что при статистической обработке выборок,
извлеченных из нормальных генеральных совокупностей, множественный
коэффициент корреляции Ry.x и его выборочное значение Ry.x обладают
рядом удобных свойств (приведенные ниже формулы и свойства
теоретического множественного коэффициента корреляции Ry,x автоматически
переносятся на выборочный Ry.x заменой участвующих в них
теоретических характеристик соответствующими выборочными значениями).
1. Вычисление Ry.x no матрице парных коэффициентов
корреляции. Обозначая, как и прежде, (р + 1)(р+ 1)-корреляционную матрицу
(гу)у=од,...,р через R, а алгебраическое дополнение элемента г^ в ее
определителе через Л/с/, имеем
2. Вычисление Ry.x no частным коэффициентам корреляции
Rl.X = 1 - A - foi)(l " Г02A))A - ГОЗA2)) . . -(I - Г0РA3...р-1)). A1.35)
3. Множественный коэффициент корреляции мажорирует любой
парный или частный коэффициент корреляции, характеризующий
статистическую связь результирующего показателя, т. е.
Ry.x ^ lroj(/,)|>
где j = 1,2,.. .,р, а /;- — любое подмножество множества индексов /q =
{1,2,..., р}, не содержащее индекса j (это соотношение следует из A1.35)).
Напоминаем, что ж" = у.

424 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
4. Присоединение каждой новой предсказывающей переменной не
может уменьшить величины R (независимо от порядка присоединения), т. е.
Ry.x{\) < Ду.(*О>,*(з>) < #y.(*<i),*<a>,*<3)) < ••• < Лу.(агA)^(а) *<р>)- (П.37)
5. Условная дисперсия результирующего показателя D(j/ \ X) не
зависит от условия (т. е. от значения X) и связана со значением
множественного коэффициента корреляции Ry,x соотношением
D(y\X) = (l-Rlx)Dy. A1.36)
Последний результат позволяет связать между собой две
характеристики степени тесноты статистической связи — коэффициент
детерминации Kd(y\X) и множественный коэффициент корреляции Ry.x*
Действительно, учитывая тот факт, что D(j/1 X) = D(e | X) (см. A1.5)), а значит,
и условная дисперсия остатков не зависит от X, получаем, что
безусловная дисперсия Be (как результат усреднения по X значений условных
дисперсий D(e | X), см. A1.9)) равна D(e \ X). Но тогда мы можем
подставить в A1.36) De вместо D(y \ X) и получим
De = A - Я{а*)Оу, A1.36')
откуда, учитывая формулу A1.8),
Kd(y;X)=R2y.x. A1.37)
Это означает, что в рамках статистического анализа
многомерной нормальной совокупности понятие введенного соотношением A1.8)
коэффициента детерминации К^(у]Х) совпадает с квадратом
определенного в A1.33) множественного коэффициента корреляции Ry,x u что
коэффициент детерминации Кд{у\Х) моэюет быть вычислен в данном
случае до проведения регрессионного анализа {т.е. до оценки функции
регрессии f(X)) с помощью формул A1.34), A1.35).
Для проверки гипотезы Н$: Ry.x = 0> т»е- Для выяснения
вопроса, можно ли считать выборочное значение множественного
коэффициента корреляции Ry,x статистически значимо отличающимся от нуля,
пользуются фактом F(p,n — p— 1)-распределенности случайной величины
справедливым в рамках рассматриваемой многомерной нормальной
совокупности при условии, что истинное значение множественного
коэффициента корреляции Ryx равно нулю. Если окажется, что F(R) >

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 425
vQ (р, п—р— 1), то гипотеза об отсутствии множественной корреляционной
связи между у и (х^г\х^ ',..., ж*р') отвергается при уровне значимости
критерия, равном а (здесь, как и ранее, va(p, п — р- 1) — 100а%-ная
точка F-распределения с числом степеней свободы числителя р и знаменателя
п - р - 1 находится из табл. Приложения 1).
Знание следующих статистических свойств оценок Ry,x>
определяемых по формулам A1.34), A1.35) с заменой участвующих в нврс парных
и частных коэффициентов корреляции их выборочными аналогами,
может оказаться полезным при проведении корреляционного и
регрессионного анализов:
• ERlx » R2y.x + -?-A - Я}.*), A1.38)
что означает наличие положительного смещения (асимптотически
устранимого) у оценки Ry.x коэффициента детерминации Ry.x\
:V1i(i-4f (n.39)
)(n 1)
(дисперсия DRy.x характеризует точность оценивания коэффициента де-
2 ^2
терминации Ду.х с помощью Лу.х и будет использована в регрессионном
анализе при определении числа объясняющих переменных, которые
следует включить в линейную регрессионную модель);
• подправленная на несмещенность оценка R^x коэффициента де-
терминации Ry.x имеет вид
R*v.x и 1 - A - Щ.х) пП_~р]_х- A1-40)
Из последней формулы видно, что «подправленная» оценка Ry.x все-
г да меньше смещенной оценки Ry.x-
Отметим, что при малых истинных значениях Ry.x и при «не
слишком малых» величинах отношения р/п подправленные оценки,
подсчитанные по формуле A1.40), могут принимать отрицательные значения.
, Можно устранить абсурдность отрицательных значений оценки,
используя в качестве «еще раз подправленной» оценки величину
(правда, R*y*x уже не будет несмещенной оценкой).
Вернемся к ранее рассмотренным примерам и оценим в них степень
тесноты множественной связи между результирующим показателем, с
одной стороны, и набором объясняющих переменных — с другой. Будем

426 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
пользоваться рекомендациями (а именно формулами A1.34), A1.35)),
правомерность которых, напомним, строго обоснована лишь в рамках
многомерной нормальной генеральной совокупности.
Пример 11.3 (продолжение). Оценка Ry.(x x ) коэффициента
множественной корреляции между характеристикой качества ткани у и
совокупностью двух факторов: количеством профилактических наладок аг1'
и числом обрывов нити я \ подсчитанная с помощью формулы A1.35),
дает:
= 1 - а,989 • 0,179 = 1 - 0,177 = 0,823.
Отсюда JRy.(j.(i)c(9)) = \Л^553 = 0,9072.
Пример 11.4 (продолжение). Оценка Ry.(x(i)xB)) коэффициента
множественной корреляции между урожайностью кормовых трав (у =
аг ') и природными факторами — весенним количеством осадков (аг ')
и накопленной суммой «активных» температур (ж*2*), подсчитанная по
формуле A1.35), дает:
= 1 - 0,36 • 0,99 = 0,6436.
Отсюда #y.(*<i)a.<2)) = ^0,6436 = 0,802.
2) Исследование линейных множественных связей (общий
случай). Речь идет о корреляционном анализе линейной модели вида
у = в0 + в1ХA) + ... + врх{р) +€(*), A1.41)
где 0 = @0,0ъ • • • >^р)Т — неизвестные параметры модели, объясняющие
переменные, могут быть как случайными (схемы зависимостей типов С и
D), так и неслучайными (схема зависимости типа 2?, см. п. 10.5), е(Х) и
X = (ж , ж ,..., агр'), взаимно некоррелированы, а Ее{Х) = 0, De(X) =
а (X). В отличие от предыдущего случая в модели A1.41) не требуется
совместной многомерной нормальности переменных (у,аг ,аг \...,агр').
В статистической практике свойства и рекомендации, справедливые в
условиях многомерной нормальной совокупности (относящиеся к частным
и множественным коэффициентам корреляции), обычно распространяют

11.2 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 427
и на общий случай A1.41). И, как правило, частные коэффициенты
корреляции, определенные соотношениями A1.31)^A1.32 ), являются
удовлетворительными измерителями очищенной линейной связи между аг1' и х'
при фиксированных значениях остальных переменных X***3' и в случае,
когда распределение анализируемых показателей (аг , аг ,..., агр')
отличается от нормального. При этом их можно интерпретировать как
показатели тесноты очищенной связи, усредненные по всевозможным значениям
фиксируемых на определенных уровнях «мешающих» переменных.
Точно так же множественный коэффициент корреляции Ry.x>
определенный формулами A1.34)-( 11.35), может быть формально вычислен для
любой многомерной системы наблюдений. И в случае линейной
зависимости A1.41) результаты вычисления коэффициента детерминации,
полученные по этим формулам, относительно слабо отличаются от результата
«прямого счета» по формуле A1.81). Однако даже при незначительных
отклонениях типа функции регрессии f(X) от линейной доверять
значению Ry.x как аппроксимации для величины коэффициента детерминации
Kd(y; X) не рекомендуется. В этом случае следует пользоваться
непосредственно формулой A1.8), требующей предварительной оценки функции
регрессии f(X) в точках Xi>X2>-.-,Xn. Возникающие при этом
неудобства (особенно в условиях отсутствия априорной информации об общем
виде функции регрессии f(X)) преодолевают, в частности, следующим
образом:
а) разбивают область возможных значений объясняющих переменных
на многомерные аналоги интервалов группирования —
гиперпараллелепипеды группирования Ai, Д2,..., Дя;
б) подсчитывают условные средние yjt результирующего
показателя по наблюдениям, попавшим в j-й гиперпараллелепипед группирования
(j ,,,);
в) по наблюдениям, попавшим в Aj, оценивают условную дисперсию
результирующего показателя sj по отклонениям этих наблюдений от
своего условного среднего j/^ (j = 1,2,..., s);
г) с помощью взвешенного усреднения условных дисперсий s* (j =
1,2,..., s) оценивают безусловную дисперсию остатков De, участвующую
в формуле A1.8);
д) оценив общую дисперсию $J = (?(& - уJ)/п результирующего
показателя, подставляют оценку De и sy в формулу A1.8) и вычисляют
По существу эта процедура является многомерным аналогом
процедуры вычисления парного корреляционного отношения.

428 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11.3. Корреляционный анализ порядковых
(ординарных) переменных: ранговая
корреляция
Напомним (см. п. 2.3), что порядковая (ординальная) переменная
позволяет упорядочивать статистически обследованные объекты по степени
проявления в них анализируемого свойства. Исследователь обращается
к порядковым переменным в ситуациях, когда шкала
непосредственного количественного измерения степени проявления этого свойства в
объекте ему неизвестна (в том числе по причине объективного отсутствия
таковой) или имеет условный смысл и интересует его только как
вспомогательное средство для последующего ранжирования рассматриваемых
объектов. К подобным ситуациям относится рассмотрение таких
переменных, как «интегральный (сводный) показатель эффективности
функционирования социально-экономической системы» (специалиста,
предприятия, научно-производственного объединения и т.п.), «качество
(мера оптимальности) структуры потребительского бюджета семьи»,
«качество жилищных условий семьи», «степень прогрессивности
предлагаемого проекта решения социально-экономической, технической или другой
проблемы» и т. п.
Таким образом, в отличие от статистического анализа fc-го (к =
0,1,2,... ,р) количественного признака ж' , когда в результате его
измерения (наблюдения) на объектах мы могли каждому статистически
обследованному объекту Oi поставить в соответствие некоторую измеренную в
физически интерпретируемой шкале числовую характеристику х\к\
результатом измерения порядковой переменной является приписывание
каждому из обследованных объектов некоторой условной числовой метки,
обозначающей место этого объекта в ряду из всех п анализируемых
объектов, упорядоченном по убыванию степени проявления в них А:-го
изучаемого свойства. В этом случае х\ ' называют рангом г-го объекта по Аг-му
признаку.
Процесс упорядочения объектов 0i,02»---*0n производится либо с
использованием экспертной информации, т.е. с привлечением
экспертов, либо формализованно — путем перехода от исходного ряда
наблюдений некоторого вспомогательного (косвенного, частного) количественного
признака к соответствующему вариационному ряду (см. п. 6.3).

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 429
11.3.1. Исходные статистические данные (таблица или
матрица рангов типа «объект-свойство»)
Итак, в результате измерения р + 1 порядковых переменных аг ' =
у,аг ,...,агр' на каждом из п анализируемых объектов 01,02,.. . ,ОП
мы получаем таблицу (матрицу) исходных данных следующего вида
(табл. 11.1).
В этой таблице элемент х\ задает порядковое место (ранг),
которое занимает объект Oj в ряду всех статистически обследованных
объектов, упорядоченном по убыванию степени проявления fc-ro анализируемого
свойства (т.е. по переменной аг ').
Очевидно, если рассмотреть столбец с номером А: этой таблицы
(к = 0,1,...,р), то он будет представлять перестановку из п элементов,
а именно перестановку из п натуральных чисел 1,2,..., п, определяющую
порядковые места объектов О\, 02> • • • > Оп в ряду, упорядоченном по
свойству х^к).
Замечание о случаях неразличимости рангов («объединенные
ранги»). При упорядочении объектов по какому-либо свойству аг '(А; =
0,1,..., р) могут встретиться ситуации, когда два объекта или целая
группа их оказываются неразличимыми с точки зрения степени проявления в
них этого свойства. Тогда каждому из объектов этой однородной
группы приписывается ранг, равный среднему арифметическому значению тех
мест, которые они делят, а полученные таким образом ранги принято
называть «объединенными» (или «связными»). Так, например,
упорядочивая семь альтернативных проектов А,5,С,D,E,F,G перспективного
развития некоторой подотрасли с точки зрения их народнохозяйственной
эффективности, эксперт поставил на 1-е место проект С, на 2-е — проект
А, далее располагал проекты В, D и Е, которые считал неразличимыми
(равноценными) по эффективности, а последнее место отвел проектам F
и G. Тогда соответствующий столбец таблицы «объект-свойство» будет
состоять из следующих компонент:
3+4+5 . . 3+4+5 А
хА = 2; хв = = 4; хс = 1; xD = хЕ = = 4;
6 + 7 _
XF = XG = ~2~ = '
Мы видим, что появление объединенных рангов может привести к
дробным значениям рангов, составляющих массив исходных
статистических данных (значения рангов, соответствующие 6-му и 7-му проектам).
При отсутствии объединенных рангов область возможных значений пере-

430
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
менных аг \ очевидно, ограничивается множеством первых п чисел
натурального ряда, где п — число сравниваемых объектов.
Таблица 11.1

Порядковый номер
объекта
(«объект»)
1
2
•
п
Порядковый номер исследуемой переменной («свойство»)
0
*!0)
п
1
4"
4"
4"
3
4"
4"
4?
...
...
:::
к
4Ч
4"
4"
...
...
:::
р
4"
4"
4"
4*
Мы увидим далее, что наличие объединенных рангов несколько
усложняет вычислительные процедуры, связанные со статистическим
анализом соответствующих корреляционных характеристик.
11.3.2. Понятие ранговой корреляции
Под ранговой корреляцией понимается статистическая связь между
порядковыми переменными. В статистической практике эта связь
анализируется на основании исходных статистических данных,
представленных упорядочениями (ранжировками) п рассматриваемых объектов по
разным свойствам (см. столбцы табл. 11.1). Есть ли хоть какая-то
согласованность (или связь) между упорядочением анализируемых объектов
по свойству х^ и упорядочением тех же объектов по другому свойству
я(;)? Можно ли измерить и проанализировать совокупную
статистическую связь, существующую между ранжировками одних и тех же
объектов Oi,02,...>0n, полученными в соответствии со степенью проявления
в них сначала свойства ж'*1' A-й способ упорядочения), затем —
свойства аг*а' B-й способ упорядочения)? Таким образом, речь идет о системе
понятий и методов, позволяющих измерять и анализировать
статистическую связь, существующую между двумя или несколькими ранжировками
одного и того же конечного множества объектов 0г, О2,..., Оп.
Система этих понятий и методов и составляет раздел
математической статистики, который принято называть анализом ранговых корре-

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 431
ляций. Методы ранговой корреляции широко используются, в частности,
при организации и статистической обработке различного рода систем
экспертных обследований.
11.3.3, Основные задачи статистического анализа связей
между ранжировками
Предположим, мы ввели измерители парной и множественной
ранговой статистической связи (см. ниже, пп. 11.3.4, 11.3.5 и 11.3.8), Тогда,
опираясь на эти характеристики, исследователь чаще всего пытается
решить следующие три основные задачи статистического анализа
структуры и характера связей, существующих между изучаемыми порядковыми
переменными.
Задача А: анализ структуры имеющейся совокупности
упорядочений Х{к) = (*J*\4*)»"M*n*))T, к = 0,1,.,.,р. Интерпретируя
каждое упорядочение jf' как точку в n-мерном пространстве, можно
представить, например, три наиболее характерных типа такой
структуры: 1) анализируемые точки равномерно разбросаны по всей области
своих возможных значений (определяемой неравенствами 1 < х\к' < п, г =
1,2,...,п), что означает отсутствие какой-либо связи или
согласованности в представляемых ими ранжировках; 2) расположение р + 1 точек
таково, что часть из них образует ядро из близко лежащих друг от
друга точек («сгусток»), а остальные произвольно разбросаны относительно
этого ядра. В этом случае существование ядра обеспечивает наличие
подмножества согласованных переменных; 3) анализируемые точки —
ранжировки располагаются в пространстве несколькими относительно далеко
отстоящими друг от друга ядрами («сгустками»), что означает наличие
нескольких подмножеств переменных таких, что переменные внутри
одного подмножества обнаруживают высокую статистическую взаимосвязь,
тогда как согласованности между переменными, взятыми из разных таких
подсовокупностей, практически не существует.-
Задача В: анализ интегральной (совокупной) согласованности
рассматриваемых переменных и их условная ранжировка по критерию
степени тесноты связи каждой из них с остальными переменными.
Подобные задали возникают, например, при исследовании степени
согласованности мнений группы экспертов и при попытках условного
упорядочения последних по их компетентности. В основе этого анализа лежит
расчет коэффициента совокупной согласованности — коэффициента конкор-
дации для различных комбинаций исследуемых переменных (см. п. 11.3.8).
Задача С: построение единого группового упорядочения объек-

432 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
тов на основе совокупности согласованных упорядочений «ядра» (или
нескольких групповых упорядочений — при наличии нескольких «ядер»).
Решение этой задачи сводится к построению такого упорядочения, которое
было бы, в определенном смысле, наиболее близким к каждому из
упорядочений заданной совокупности — «ядра». Именно с такой задачей
сталкивается, например, исследователь, желающий установить неизвестное
истинное упорядочение заданной совокупности объектов по
имеющемуся в его распоряжении набору экспертных ранжировок тех же объектов.
Для построения единого (группового) варианта упорядочения Х^еп* часто
используют в качестве ранга х объекта О{ среднее арифметическое
или медиану имеющихся базовых рангов х\ \х\ , ...,а^р' этого объекта.
Обоснование способа построения единого варианта упорядочения может
быть получено, например, в рамках подхода, который опирается на меру
близости между ранжировками (определяется ранжировка я'ед ,
наименее удаленная, в смысле введенной меры близости, от всех ранжировок
Я" , Я" ,..., Я*р' базовой совокупности). Задача С может быть
сформулирована и как задача наилучшего (в определенном смысле)
восстановления ранжировки Х^ , связанной с результирующей переменной у = ж ,
по ранжировкам Х^ ,Х* ,...,Я , индуцируемым соответственно
объясняющими переменными х^ ,аг ',..., ж . В такой формулировке ее
называют также задачей регрессии на порядковых (ординальных)
переменных.
11.3.4. Ранговый коэффициент корреляции Спирмэна
Для измерения степени тесноты связи между ранжировками Х^к' =
(х[к\ х[к\ ...,*(ЛТ и XU) = (х?\*?\...,х\Р)Т К.Спирмэн еще в
1904 г. предложил показатель
п -п
названный впоследствии ранговым коэффициентом корреляции
Спирмэна. Прямым подсчетом нетрудно убедиться, что для совпадающих
ранжировок (т.е. при х\ ' = x\J* для всех i = l,2,...,n) т]^ = 1 а для
противоположных (т.е. при ж' ' = п — х\*' + 1, г = 1,2,...,п) — fjy = —1.
Можно показать, что во всех остальных случаях |г^| < 1.
Формула A1.42) пригодна лишь в случае отсутствия объединенных
рангов в обеих исследуемых ранжировках. Для ее распространения на об-

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 433
щий случай определим для каждой (А?-й) ранжировки Х^к' (к = 0,1,... ,р)
величину
^[(п\к)K-п[% A1.43)
где пг ' — число групп неразличимых рангов у переменной аг \ а щ ' —
число элементов (рангов), входящих в t-ю группу неразличимых рангов (в
частном случае отсутствия объединенных рангов имеем m' = п, п\ ' =
п[ ' = ... = Пп = 1 и соответственно Т* ' = 0; кроме того, группы
неразличимых рангов, состоящие из единственного элемента, по существу,
не участвуют в расчете величины Т1' ').
Тогда ранговый коэффициент корреляции Спирмэна между
ранжировками Х^ ' и Х^*' следует вычислять по формуле
Если Г* ' и Тг3' являются небольшими относительно \{п — п)
величинами, то можно воспользоваться приближенным соотношением (а при
Т(к) _ TU) оно точное)
, . Vn (x{k) -x{i)J
J(n3-»)-(T(*) + T<«)- U1>44j
Правда, при этом же условии (относительная малость Т* + Т^' по
сравнению с |(п — п)) и приближенная формула A1.42) дает хорошую
точность.
Пример 11.5. Два эксперта проранжировали 10 предложенных им
проектов реорганизации научно-производственного объединения (НПО) с
точки зрения их эффективности (при заданных ресурсных
ограничениях). Пронумеровав проекты в порядке ранжировки 1-го эксперта,
получаем в качестве исходных данных: Х^1' = A; 2; 3; 4; 5; 6; 7; 8; 9; 10) ;
Х{2) = B; 3; 1; 4; 6; 5; 9; 7; 8; 10)Т.
Вычисления по формуле A1.42) дают:
что свидетельствует о существенной положительной ранговой связи
между исследуемыми переменными.

434 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Пример 11.6. Десять однородных предприятий подотрасли
были проранжированы вначале по степени прогрессивности их
оргструктур (признак х^)} а затем — по эффективности их
функционирования в отчетном году (признак аг '). В результате были получены
следующие две ранжировки: X*1' = A; 2,5; 2,5; 4,5; 4,5; 6,5; 6,5; 8; 9,5; 9,5) ;
ХC) = A;2;4,5;4,5;4,5;4,5;8;8;8;10)Т.
В первой ранжировке имеем четыре группы неразличимых рангов,
число элементов в которых больше единицы, а во второй ранжировке —
две такие группы. В соответствии с формулой A1.43) получаем:
ТA) = ^ [B3 - 2) + Bа - 2) + B3 - 2) + B3 - 2)] = jj = 2,00;
Т = 12
Точная формула A1.44) дает fjj = 0,917. Вычисление этого же
коэффициента корреляции по приближенным формулам A1.42) и A1.44 ) дает,
соответственно, значения 0,921 и 0,917. Все эти результаты оказываются
совпадающими при округлении до второго десятичного знака.
11.3.5. Ранговый коэффициент корреляции Кендалла
Другой широко используемой характеристикой тесноты
статистической связи между двумя упорядочениями является ранговый коэффициент
корреляции Кендалла, определяемый соотношением
где и{Х^к\Х"') — минимальное число обменов соседних элементов
последовательности X* , необходимое для приведения ее к упорядочению Х*кК
Очевидно, величина и{Х^к\ X"') симметрична относительно своих
аргументов, так что с равным правом можно говорить о минимальном числе
«соседских обменов» элементов последовательности Х^к\ необходимом
для приведения к виду ЛГ .
Из A1.45) сразу следует, что при совпадающих ранжировках Х^к* и
U) ?[V = 1 (так как и(Х^к\х^) = 0), а при противоположных (т.е.
при х\к) = n-x\j) + 1, i = l,2,...,n, так что v(X{h\xU)) = \n(n-l)) —
rjk ' = -1. Нетрудно показать, что во всех остальных случаях \т[у\ < 1.

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 435
(К)
Вычисление ц^ ' связано с необходимостью подсчета величины
i/(X*k\x^') и, следовательно, является более трудоемким, чем
вычисление r^j. Однако, во-первых, коэффициент Кендалла обладает
некоторыми преимуществами по сравнению с коэффициентом Спирмэна,
главные из них: а) относительно большая продвинутость в исследовании его
статистических свойств и, в частности, его выборочного распределения
(см. ниже); б) возможность его использования и в частной («очищенной»)
корреляции рангов; в) большие удобства его пересчета при добавлении
к п статистически обследованным объектам новых, т.е. при удлинении
анализируемых ранжировок: для вычисления нового значения
рангового коэффициента корреляции приходится переранжировать значительную
(S)
часть объектов, что в случае т?.' означает необходимость пересчета
разностей х\к^ - х\^; при вычислении же Ту значения рангов не играют
никакой роли, важно лишь число необходимых «соседских обменов», которое
при добавлении новых объектов подсчитывается рекуррентным способом
(к старому значению i/(Jt' \X^') может быть лишь дополнен некоторый
«добавок»).
Во-вторых, можно воспользоваться рекомендациями, упрощающими
подсчет числа и(Х^к\х^') как при ручном, так и при машинном счете.
Так, при ручном счете полезным оказывается известный факт
тождественного совпадения величин v(X*k\x^') и 1(Х^к\Х^')9 где число
инверсий 1(Х*к\х^') — это просто число расположенных в неодинаковом
порядке пар элементов последовательностей JP и Я" , являющееся
естественной мерой нарушения порядка объектов в одной последовательности
относительно другой. Для удобства подсчета 1(Х^к\Х^')
перенумеруем объекты в порядке, определяемом рангами последовательности X .
Тогда анализируемые ранжировки Х^к\х^ соответствующим образом
видоизменяются, т.е. преобразуются к виду соответственно Х^к\х^\
гда Х{к) = A,2,...,п)т; X™ = («AЛ,*(аЛ,...,х(»Л)т, а число инверсий
I(X{k\x(s)) s I(X{k\xU)), а следовательно, и величина u{X(k\x{i))
определяется по формуле
g ?
= /(*<*>,*<'>) = g ? ,#*>, A1.46)

436
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
где
1, если iq > ii (т. е. нарушен порядок
последовательности JT ');
О — в противоположном случае.
Легко подсчитать, что число инверсий
^ \
может меняться от О
( )
(что соответствует случаю совпадающих ранжировок) до \п{п — 1) (что
соответствует случаю противоположных ранжировок).
Формулы A1.45)—A1 -46) пригодны для подсчета т\- лишь в случае
отсутствия объединенных рангов в обеих исследуемых ранжировках.
Соответствующее «подправленное» значение f?j ' при наличии
объединенных рангов в анализируемых упорядочениях будет определяться
соотношением
~{К) _ 2(^*>+С/0))
" "yo-#%)(«-#%)'
A1.45')
в котором коэффициент fjy вычисляется по формуле A1.45)—A1.46), а
«поправочные» величины U* определяются соотношением
A1.47)
t=l
(смысл величин т"ип}' определен выше, см. A1.43)).
Для пояснения работоспособности формул A1.45)—A1.47) вернемся к
примерам 11.5 и 11.6.
Анализ степени согласованности ранжировок двумя экспертами
десяти проектов реорганизации НПО (пример 11.5), осуществленный с
использованием формул A1,45)—A1.46), дает:

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 437
2 = 0; «/is = 1,1*14 = "is = 6 = 7 = "is = 9 = "l.io = 0;
3 = 1; 4 = 5 = 6 = 7 = 8 = 9 = .10 = 0;
4 = 5 = 6 = 7 = 8 = 9 = "ЗЛО = 0;
5 = 6 = 7 = 8 = 9 = .10 = 0?
6 = I? 7 = 8 = 9 = .10 = 0;
7 = 8 = 9 = "ело = 0;
1/78 = 1; 9 = 1; .10 = 0;
"89 = "ело = 0;
"9.10 = 0.
Таким образом, v{X{1\ХB)) =1 + 1 + 0 + 0+1 + 0 + 2 + 0 + 0 = 5.
Соответственно
= 1" °'222=QJ78
(напомним, что коэффициент Спирмэна в этом примере был равным
0,915).
При вычислении рангового коэффициента корреляции Кендалла в
примере 11.6 следует воспользоваться формулой A1.45'),-так как
исследуемые ранжировки содержат объединенные ранги. Используя результаты
расчета величин rrv ' = 4, тг ' = 2, пг' = п2 = п3 = п4* = 2, щ' =
4, щ = 3, получаем (в соответствии с B.8)):
U{1) = 1B + 2 + 2 + 2) = 4; U{2) = \D • 3 + 3 • 2) = 9.
Обращаясь теперь к формуле B.б'), имеем:
гДл' = w = = 0,833
'' __ IWi __ 18\
90/ V1 90/
(напомним, что соответствующий коэффициент Спирмэна был равен
0,917).

438 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11.3.6. Обобщенная формула для парного коэффициента
корреляции и связь между коэффициентами
Спирмэна и Кендалла
Для удобства стандартной вычислительной реализации системы
алгоритмов корреляционного анализа полезно ввести некоторый обобщенный
прием вычисления парных корреляционных характеристик, определенный
для любой двумерной системы п наблюдений
{к)\
/11 АО\
( '
С этой целью определим некоторое правило, в соответствии с
которым каждой паре (я^ >ж[-2) компонент вектора Х^' (I = &,j) ставится
в соответствие число («метка») аЦ2, причем это правило должно
обладать свойством отрицательной симметричности (т.е. а^2 = — яЦ-j) и
центрированности (т.е. ajj* = 0 при всех / = Л,j и всех г = 1,2,...,п).
Тогда обобщенный коэффициент корреляции г'° ' переменных аг ' и ж^'
определяется формулой
En Vn ЛС*) Л0#)
Г .¦' = t^lZ-yiazzl^taQMia A1.49)
*У /11 ^п (*) 2 ^n ^n (i) 2 "
Легко видеть, что практически все введенные нами характеристики
парной корреляционной связи могут быть получены как частные случаи
формулы A1.49) при соответствующем выборе правила приписывания
числовых «меток» ajlf-2. Действительно:
а) положив аЦ2 = х\^ — x\J> I = &,j, получаем формулу для
обычного парного коэффициента корреляции г^-, если х\ — значение
/-количественной переменной в г-м наблюдении (см. п. 11.2.2, формулу
A1ЛЗ;)), и формулу для рангового коэффициента корреляции Спирмэна
t[j\ если х\' — ранг г-го объекта в ряду, упорядоченном по порядковой
переменной аг ' (см. формулу A1.42));
б) положив
•
ю,-
+1, если zS? <:#;
О, если *i?=*i,°;
i?
— 1, если

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 439
получаем формулы A1.45) и A1.45') для рангового коэффициента
корреляции Кендалла fL , если под х\' понимать ранг г-го объекта в /-м
упорядочении.
Заметим, что значения ранговых корреляционных характеристик
т?. и Ту довольно тесно связаны одно с другим. Это следовало
ожидать, так как обе характеристики являются линейными функциями от
числа инверсий, имеющихся в сравнении последовательностей Х^ ' и X •
различие этих функций состоит в том, что при подсчете
коэффициента Спирмэна инверсиям более отдаленных (по величине) друг от друга
элементов приписываются большие веса. Между масштабами шкал, в
которых измеряют корреляцию коэффициенты т* ' и г* , нет простого
соотношения. Однако уже при умеренно больших значениях п (n ^ 10) и
при условии, что абсолютные величины значений этих коэффициентов не
слишком близки к единице, их связывает следующее простое приближен-
(S) (К)
ное соотношение fK ' « l,5fl ;.
11.3.7. Статистические свойства выборочных характеристик
парной ранговой связи
До сих пор речь шла о выборочных характеристиках ранговой связи.
Попробуем ответить на вопрос: как точно эти выборочные
характеристики (определенные, в частности, формулами A1.42)—A1.47)) оценивают
соответствующие истинные {теоретические) значения?
Для этого в первую очередь следует пояснить, что в данном случае
понимается под теоретическими характеристиками.
Представим себе сначала конечную генеральную совокупность,
состоящую из N объектов Oi,O2,.. .,0дг, каждый из которых снабжен двумя
порядковыми номерами: О. <-+ (x\h\х\*'), % - 1,2,...,АГ, где х\1' означает
место объекта О{ в общем ряду всех N объектов, упорядоченном по
степени выраженности свойства х '(/ = A,jf). Будем полагать, что
статистически обследованное множество объектов 0^, 0*2,..., Oin образуется как
случайная выборка объема п, взятая из совокупности Oi, С?2> • • • ? ON (n <
N).
Определим теоретические (истинные) значения коэффициентов rL'
и rf. ' соответственно теми же соотношениями A1.42) (или A1.44)) и
A1.45) (или A1.45 )), что и выборочные с заменой объема выборки п
объемом генеральной совокупности N. При работе с выборкой производится
естественная перенумерация объектов и их рангов, не меняющая их
упорядоченности в генеральной совокупности ни по одной из переменных.

440 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
В дальнейшем нас будет интересовать, как сильно могут
отличаться выборочные значения г ' и г от соответствующих теоретических,
в том числе в так называемых асимптотических ситуациях, т.е. при
N —> оо и n(N) -* оо.
Проверка статистически значимого отличия от нуля ранговых
корреляционных характеристик осуществляется при «не слишком малых» п
(п > 10) и заданном уровне значимости критерия а с помощью
неравенства
в которых tq(i/) и Wg, как и прежде, соответственно 100д%-ная точка f(i/)-
и g-квантиль стандартного нормального распределения (см. табл. в
Приложении 1). Выполнение неравенств A1.50) и A1.51) сигнализирует о
необходимости отвергнуть гипотезу об отсутствии статистически значимой
ранговой корреляционной связи. В случае небольших объемов выборок
D ^ п < 10) статистическая проверка гипотезы об отсутствии ранговой
корреляционной связи производится с помощью специальных таблиц (см.
Приложение 1).
Таблица значений вспомогательной величины Sc позволяет при
малых п(п = 4,5,..., 10) построить то пороговое значение Гта'х, при
превышении которого (по абсолютной величине) коэффициентом Спирмэна
т* ' следует признать наличие статистически значимой связи между
анализируемыми переменными. Задавшись уровнем значимости критерия
а и числом сравниваемых объектов п, определяем из таблицы величину
Sc = Sc(n,Q), соответствующую нашему п и значению Q = а/2 (или
приблизительно равному а/2). Тогда
(s) 2SJn,Q)
где Кп = j(n — n) (значения этой вспомогательной константы приведены
в последней строке таблицы).
Так, в примере 11.5 для уровня значимости а = 0,06 имеем: п =
10; Q = 0,03; Sc = 5сA0;0,3) = 268; Кго = 330, так что в соответствии с
A1.52)

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 441
Поскольку выборочное значение рангового коэффициента корреляции
Спирмэна г' в этом примере значительно превосходит пороговое
значение (г*5* = 0,915 > 0,624), то гипотеза об отсутствии корреляционной
связи отвергается.
И наконец, в таблице значений вспомогательной величины SK
приведены значения величин 5^, позволяющих вычислить (при малых п =
4,5,...,10) то пороговое значение т$?1, при превышении которого (по
абсолютной величине) коэффициентом Кендалла следует признать
наличие статистически значимой связи между анализируемыми переменными.
Для этого поступают следующим образом: задавшись объемом выборки п
и уровнем значимости критерия а, находят в столбце, соответствующем
данному п, величину, равную (или приблизительно равную) а/2; затем
находят значение SK = SK(n,a) в левом столбце той же самой строки и
(К)
ВЫЧИСЛЯЮТ Гтах по формуле
(к\ 25~(п,а)
(К) (К)
Если окажется, что fK } > т^ах? то гипотеза об отсутствии ранговой
корреляционной связи отвергается (связь статистически значима).
Так, в примере 11.5 при уровне значимости а = 0,06 имеем: п = 10;
0,23 < f < 0,36; следовательно, 5^ = 22 (оно лежит между 21 и 23), так
что
W ~ 10 • 9 " 90 " '
Поскольку rv ; = 0,733 > 0,489, делается вывод о наличии
статистически значимой корреляционной связи между исследуемыми переменными
в данном примере.
Построение доверительных интервалов для неизвестных истинных
значений ранговых коэффициентов корреляции возможно лишь
приближенно и только при измерении ранговой корреляции с помощью
коэффициента Кендалла. При этом используют (при п > 10 и значениях
т{ , не слишком близких по абсолютной величине к единице)
приближенный факт нормальности распределения величины f * со средним
значением Ег* ' « г' 'ис дисперсией Df* ', не превышающей величины
?[1 - (т' ') ]. Можно утверждать, что с доверительной вероятностью, не
меньшей заданного уровня Р, истинное значение коэффициента Кендалла

442 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
т^ заключено в пределах
"
A1.54)
где ия — д-квантиль стандартного нормального распределения.
11*3.8. Коэффициент конкордации (согласованности) как
измеритель статистической связи между несколькими
порядковыми переменными
До сих пор мы рассматривали корреляцию между двумя
порядковыми переменными. Однако при решении основных задач А — С
статистического анализа ранговых связей (см. п. 11.3.3) возникает необходимость
уметь измерить статистическую связь между несколькими (более чем
двумя) переменными. С этой целью Кендаллом был предложен показатель
W{m), названный коэффициентом конкордации (или согласованности),
вычисляемый по формуле
W(m) - 12 V (тГ*™ - m(n+1)\ Ml 55^
где т — число анализируемых порядковых переменных (сравниваемых
упорядочений); п — число статистически обследованных объектов или
длина ранжировки (объем выборки); &ьА:2>• •-Дт — номера
отобранных для анализа порядковых переменных (из исходной совокупности
ж ,ж ,а? ,...,аг , так что, очевидно, m <p+ 1).
Нетрудно устанавливаются следующие свойства коэффициента
конкордации:
а) 0 < W < 1;
б) W = 1 тогда и только тогда, когда все т анализируемых
упорядочений совпадают;
1 Мы приводим здесь формулу для подсчета выборочного значения W коэффициента
конкордации W. Интерпретация и вычисление теоретического значения W
непосредственно следуют из рассуждений, приведенных в п. 11.3.7 в связи с анализом
статистических свойств выборочных парных ранговых коэффициентов корреляции.

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 443
в) если m ) Зи анализируемые ранжировки генерируются подобно
случайному независимому m-кратному извлечению из множества всех п
возможных упорядочений п объектов, то связи между ними нет и W = 0;
г) пусть т* \т) — среднее значение коэффициента Спирмэна,
подсчитанное по значениям m(m -1)/2 коэффициентов f[fl (ij = 1,2,..., га; i ф
j), характеризующих ранговую связь между всеми возможными парами
переменных (xki\x^k*') из анализируемого набора (х^к1\х^к2\...,х^кт^)\
тогда
в частности, из A1.56) следует для случая т = 2, что
?(*й, + 1), A1-56')
т.е. коэффициент конкордации, исчисленный для двух переменных,
пропорционален введенному ранее парному ранговому коэффициенту
корреляции Спирмэна.
То, что шкала измерения W(m) не включает в себя отрицательных
значений, объясняется следующим обстоятельством. В отличие от случая
парных связей при анализе т(т ^ 3) порядковых переменных
противоположные понятия согласованности и несогласованности утрачивают
прежнюю симметричность (относительно нуля); упорядочения, произведенные
в соответствии с переменными аг ,аг ,...,аг , могут полностью
совпадать, но не могут полностью не совпадать в том смысле, который
мы вкладывали в это понятие при т = 2.
Формула A1.55) получена (и справедлива) в предположении
отсутствия объединенных рангов в каждом из анализируемых упорядочений.
Если же таковые имеются, то формула должна быть модифицирована:
\2
^ Y?- (Yj j m(n+l)
где поправочный коэффициент 7* J (соответствующий переменной х^ *')
подсчитывается по формуле A1.43).

444 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11,3.9. Проверка статистической значимости выборочного
значения коэффициента конкордации
Как ведут себя выборочные значения W(m) коэффициента
конкордации при повторении выборок заданного объема п (из одной и той же
генеральной совокупности) при отсутствии какой-либо связи между
анализируемыми га переменными? Другими словами, нас интересует ответ
на следующий вопрос. Предположим, что каждому объекту конечной
генеральной совокупности (состоящей из N элементов) приписан какой-то
определенный ранг по каждой из т рассматриваемых переменных. Так,
например, если т = 3и объекту О,- приписана тройка (х\* = N\ х\' =
1; Xt = 2), то это означает,*что по переменной аг ' он стоит на последнем
(JV-м) месте в упорядоченном ряду всех объектов генеральной
совокупности, по переменной х' ' — на первом и по переменной аг ' — на втором.
Тогда по исходным данным {(х\ \х\ >•••>&! )}*--Т7й7 с помощью
формулы A1.55) может быть вычислен теоретический (генеральный)
коэффициент конкордации W(m)> характеризующий степень тесноты
ранговой связи между переменными аг ,аг ,...,аг . Однако исследователю
известны значения (яг ',аг ',..., агт') лишь для части объектов
генеральной совокупности, а именно для случайной выборки объектов объема
п(п < N). После естественной перенумерации рангов, сохраняющей
правило упорядочения объектов, но переводящей масштаб измерения рангов
в шкалу A,2,...,п) (для этого минимальный из оказавшихся в выборке
рангов по каждой переменной объявляется рангом, равным 1, следующий
по величине — рангом, равным 2, и т.д.), может быть вычислен (по той
же формуле A1.55)) выборочный коэффициент конкордации W(m).
Извлекая другую выборку объема п из той же самой генеральной совокупности,
мы получим, вообще говоря, другое значение выборочного коэффициента
W(m) и т. д.
Спрашивается, как сильно могут^тклоняться от нуля выборочные
значения коэффициента конкордации W(m) в ситуации, когда значение
теоретического коэффициента конкордации W(m) свидетельствует о
полном отсутствии ранговой связи между анализируемыми переменными
х" ',аг ,...,аг*? Для малых значений т и гаB < m ^ 20, 3 < п < 7)
ответ на этот вопрос может быть получен с помощью таблицы значений
величины 5. Обозначенная в ней величина 5 есть не что иное, как
<п-57>

11.3 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 445
«Входами» в эту таблицу является тройка чисел (m,n,S),
«выходом» — вероятность того, что величина S может быть такой, какой она
является в нашей выборке, или большей в условиях отсутствия связи
переменных в генеральной совокупности. Если окажется, что эта вероятность
меньше принятой нами величины уровня значимости критерия а
(например, а = 0,05), то гипотезу об отсутствии связи следует отвергнуть, т.е.
признать статистическую значимость анализируемой связи. Таблица
критических значений W(m) построена несколько иначе. В ней при уровне
значимости а = 0,05 и в соответствии с «входами» (m,n) даны
«критические» значения величины 5, т. е. такие значения, при превышении
которых следует отвергать гипотезу об отсутствии связей (признавать их
статистическую значимость).
При п > 7 для проверки статистической значимости
анализируемой связи следует воспользоваться фактом приближенной х (п ~~ 1
^распределенное™ величины т(п — 1) х W(m), справедливым в условиях
отсутствия связи в генеральной совокупности (значение W{m)^ как и прежде,
подсчитывается по формуле B.16) или B.16;)). Поэтому, если окажется,
что
т(п-1)Щт) > х2а(п- 1), A1.58)
то гипотеза об отсутствии ранговой связи между переменными ж г ,
аг ,...,ar т' должна быть отвергнута (с уровнем значимости
критерия, равным а); в A1.58) величина Ха(п ~ 1) — это Ю0а%-ная точка
Х2-распределения с (п — 1)-й степенью свободы.
Можно использовать и другой способ проверки статистической
значимости исследуемой ранговой связи между несколькими переменными,
основанный на том, что в условиях отсутствия таковой в генеральной
совокупности распределение случайной величины у In \m~J-- W
приближенно описывается Z-распределением Фишера с числом степеней свободы
числителя х/1=п— 1 — ^и знаменателя v2 = (т — 1)и\.
Строгих рекомендаций по построению доверительных интервалов для
истинного значения W в условиях наличия ранговых связей в исследуемой
генеральной совокупности к настоящему времени не имеется.
Рассмотрим примеры, в которых реализуются приведенные выше
рекомендации по статистическому анализу множественных ранговых связей.
Пример 11.7. Рассмотрим три порядковые переменные (аг ,ж ,
ж ) и соответствующие им упорядочения десяти объектов:

446
ГЛ. И. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
xw
Сумма
1
2,5
2
5,5
4,5
1
1
6,5
2
2,5
4,5
9
4,5
4,5
4,5
13,5
3
4,5
4,5
12
7,5
8
4,5
20
6
9
8
23
9
6,5
8
23,5
7,5
10
8
23,5
10
6,5
10
26,5
В соответствии с формулами A1.57), A1.43) имеем:
10/3 о цХ
(-10L (-7
<=i \j=i
J + (-4,5J + C,5J + F,5J + 72 + 92 + 102 = 591;
-2J=1;
12v
/о\ 1 з 3
1 == T77v """" • "" / ==
Следовательно, в соответствии с A1.55')
591
591
^32A02 - 10) - 3A + 1,5 + 7) 742,5 - 28,5
= 0,828.
Пример 11.8. Требуется проверить статистическую значимость
множественной ранговой связи 28 переменных (т — 28), характеризуемой
величиной выборочного коэффициента конкордации 1^B8) = 0,08,
подсчитанного по 13 объектам (га = 13).
Воспользуемся фактом х A2)-распределенности случайной величины
т(п — l)W(m), который имеет место (приближенно) в случае, если в
исследуемой генеральной совокупности множественная ранговая связь
отсутствует. Тогда критерий сводится к проверке неравенства A1.57).
Задавшись уровнем значимости критерия а = 0,05, находим из таблиц значение
5%-ной точки х2-распределения с 12 степенями свободы Xo,osA2) = 21,026.
В то же время т(га - l)W(m) = 28 • 12 • 0,08 = 27.
Поскольку т(га- l)W(m) > Xo,osA2), то оказалось, что даже такого
маленького числа, как 0,08, «хватило» для того, чтобы объявить связь
между 28 исследуемыми переменными статистически значимой.

11.4 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТЕГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 447
11.4. Корреляционный
анализ категоризованных переменных:
таблицы сопряженности
Признак называют категоризованным, если его возможные
«значения» описываются конечным числом состояний или градаций. Слово
«значения» взято в кавычки, так как речь идет, как правило, не о
числовых значениях, а лишь об определенных условных метках возможных
состояний. Так, категоризованный признак «пол индивидуума» имеет две
градации, категоризованный признак «социальное положение
респондента» — столько градаций, сколько установлено социальных страт
(слоев) в данном обществе, категоризованный признак «уровень жилищных
условий семьи» — столько градаций, сколько их определено в данном
обследовании (например, при возможных ответах: «низкий»,
«удовлетворительный», «хороший» и «очень хороший» мы будем иметь четыре
градации). Как мы видим, в класс категоризованных признаков
попадают те номинальные и порядковые (ординальные) переменные, возможные
значения которых описаны заданным (известным) набором градаций.
11.4.1. Исходные статистические данные (таблицы
сопряженности)
Мы ограничимся здесь задачей измерения парных статистических
связей между категоризованными переменными. Формально исходные
данные для пары категоризованных переменных будут иметь уже
знакомый нам вид (9.1У) таблицы «объект-свойство», в которой, правда, в
качестве элементов x\J\j = 1,2; t = 1,2,. ..,п) будут обозначены
условные метки (градации) состояния объекта г по переменной j. Однако мы
не можем работать с этими данными аналогично случаю количественных
переменных: скажем, среднее значение или дисперсия «пола» или
«социальной принадлежности» респондента лишены всякого смысла. Поэтому
при статистическом анализе двух категоризованных переменных
исходные данные преобразуют к виду таблицы перекрестных частот,
называемой двухвходовой таблицей сопряженности признаков ж" и ж" (см.
табл. 11.2) или просто таблицей сопряженности.
1 Напомним, что случайная величина называется номинальной, если знание ее
значений на статистически обследованных объектах позволяет разбить это множество на
не поддающиеся упорядочению однородные по анализируемому свойству классы (см.
п. 2.3)

448
Таблица 11.2
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Градация
признака
1
2
:
i
;
mi
ni
Градация признака аг ;
1
пи
П21
:
Пц
:
^mil
пл
2
п12
П22
:
ni2
*:
^та2
гг.2
i
U2j
:
...
...
Ш2
nlm2
n2m2
\
nim2
:
^mirn,2
ra.m2
nb
n2.
Щ.
:
лТО1.
n
В табл. 11.2 представлены результаты статистического обследования
п объектов по признакам аг1' и ж . В ней пу означает число объектов (из
общего числа п обследованных), у которых «значение» признака аг1'
оказалось зафиксированным на уровне г-й градации, а «значение» признака
аг ' — на уровне j-й градации; n,-. = J^j^i ntj — число объектов,
значение признака аг ' у которых оказалось зарегистрированным на уровне
г-й градации (при отсутствии каких бы то ни было условий на «значе-
B) v-^rrii -
ния» признака аг , a n.j = 2^t=i nij — число объектов, значение призна-
B)
ка хк ' у которых оказалось зарегистрированным на уровне jf-й градации
Переход к задаче измерения степени тесноты связи нескольких (более
двух) категоризованных переменных связан с необходимостью введения
многовходовых таблиц сопряженности и более громоздких обозначений
(количество нижних индексов у анализируемых часто приходится
увеличивать до числа анализируемых переменных).
11,4.2. Основные
измерители степени тесноты статистической связи
между двумя категоризованными переменными
В статистической теории и практике в рамках данной проблемы
существует целый спектр характеристик с.т.с.с. Разные меры связи
акцентируют внимание на разных аспектах взаимоотношений между
переменными, давая в целом многоаспектную информацию о природе изучаемой

11.4 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТЕГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 449
зависимости. Поэтому вряд ли целесообразно давать универсальные
рекомендации по поводу выбора наиболее предпочтительной
характеристики «на все случаи жизни». Выбор описанных ниже измерителей с.т.с.с.
был основан на сочетании двух критериев: 1) наибольшей
распространенности в практике статистических исследований; 2) умении описать
необходимые статистические свойства этих измерителей.
Построение подавляющего большинства используемых в данной
проблеме характеристик с.т.с.с. основано на одной общей идее:
характеристика должна принимать тем большее числовое значение, чем
больше анализируемая ситуация отклоняется от гипотезы взаимной
статистической независимости исследуемых переменных аг ,аг2'. Как мы
знаем (см. п. 2.5.3), формализуется понятие статистической
независимости условием представления двумерного закона распределения векторной
случайной величины X = (ж ,аг ') в виде произведения частных
законов распределения компонент этого вектора, т. е.
где х\ ' и Xj — обозначения принятых в данном исследовании меток
соответственно для г-й градации признака аг1' и j-й градации признака
««.
Выборочный (эмпирический) эквивалент этого условия
предусматривает замену участвующих в нем вероятностей соответствующими
относительными частотами (с заменой, конечно, точного знака равенства на
приближенный), т.е.
^« —-^- A1.59')
п п п v '
или
Dij = ^L _ VIl . !Ll ~ о. A1.59")
nun
Поэтому чем больше от нуля будет отличаться просуммированная по
г и j левая часть соотношения A1.59"), вычисленная по данным таблицы
сопряженности 11.2, тем более высокую с.т.с.с. между анализируемыми
переменными должны обозначать используемые измерители.
Характеристика X квадратичной сопряженности признаков
х и х определяется соотношением
тг т2
15 Теория вероятностей
и прикладная статистика

450 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Его значение может меняться от нуля (при строгой статистической
независимости переменных хA) и х^) до +оо. Являясь, как и всякая функция
от выборочных данных, величиной случайной, X2 ведет себя (в
предположении статистической независимости я иж") приблизительно, —
асимптотически по п —> ос, — как х -распределенная случайная величина
с числом степеней свободы, равным (mi — l)(m2 — 1). Это дает нам право
в случае
21{) A1.61)
заявить о том, что связь между анализируемыми переменными ж" и ж"
является статистически значимой и она тем теснее, чем больше значение
2 " 2
X . Неудобство использования характеристики X связано с тем, что
ее верхняя граница стремится к бесконечности при возрастании объема
выборки п. Поэтому вместо X часто используют характеристику
X2
nmin(mi — 1, Ш2 — 1)
1/2
A1.62)
которая называется коэффициентом Крамера и которая обладает
более привычным для измерителей с.т.с.с. диапазоном изменения, а именно
О < С < 1. При этом нулевое значение С свидетельствует о строгой
статистической независимости анализируемых признаков, а значение С,
равное единице, — о возможности однозначного восстановления значения
одной переменной по известному значению другой.
Информационная характеристика с.т.с.с. Y признаков я и
яB) также основана на мере отклонения от выполнения соотношения
независимости A1.59 ), только вместо разности левых и правых частей этого
соотношения в ней используется их отношение. А именно измеритель У2
определяется соотношением
Правую часть A1.63) можно преобразовать к виду, более удобному для
вычислений
= 2 UC?nO-lnn<i -?»<>»<• ~ Snilnni + nlnn
Эта характеристика обладает теми же свойствами, что и X : ее
значения варьируют от 0 (в случае статистической независимости аг1' и ж'2')

11.4 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТБГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 451
до +оо, и в условиях справедливости гипотезы о статистической
независимости анализируемых признаков она приблизительно (асимптотически по
п -* с») подчиняется з.р.в. х* с (mi - l)(m2 - 1) степенями свободы (для
достижения удовлетворительной точности последнего утверждения
требуется заполненность всех клеток таблицы сопряженности 11.2 ненулевыми
элементами, удовлетворяющими условию min^n^ > 3).
Таким образом, если мы хотим проверить гипотезу о статистически
значимом отличии от нуля характеристики с.т.с.с. У (т. е. гипотезу о
наличии связи между аг ' и ж ), то необходимо убедиться в выполнении
неравенства
2A)), (П.64)
где Хо(т)> как всегда, — 100а%-ная точка х*-распределения с m
степенями свободы (см. соответствующую таблицу в Приложении 1), а о —
заданный уровень значимости критерия, т.е. вероятность принять
решение о наличии статистической связи между анализируемыми
переменными в то время, как в действительности они являются статистически
независимыми.
Бели с помощью той или иной характеристики (X или У ) мы
убедились в том, что статистически значимая связь между аг1' и аг2'
действительно существует, то возникает вопрос интервальной оценки
характеристики этой связи. Для приближенного построения такой оценки мы
должны уметь вычислить дисперсию соответствующей точечной
оценки (см. п.7.5.4), т.е. в нашем случае — дисперсии статистик X2 и У2
в условиях, когда оцениваемый с их помощью теоретический показатель
связи отличен от нуля.
Для характеристики X2 и основанном на ней коэффициенте Крамера
С существуют приближенные формулы :
а\2 = DX2 « 4
'х
1=1 j
A1.65)
a2 = DC » —, —. гг. A1.66)
c nmin(mi — l9m2 - 1)
Заметим, что в формуле A1.65) первое слагаемое в квадратных
скобках (т.е. X2) является главным членом, так что два других слагаемых
1 Точные формулы (они получены Холдуйном в 1939 г.) очень сложны, поэтому здесь
приводится только приближенный вариант, полученный К.Пирсоном в 1915г.
16*

452
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
играют роль остаточного члена. Поэтому другой, более грубый (менее
точный) вариант этой формулы имеет вид
<Т2Х2 = ?Х2«4Х2. A1.65')
Соответственно в качестве приближенных доверительных
интервалов для истинных значений коэффициента квадратичной сопряженности
и коэффициента Крамера используются (при доверительной вероятности
Р = 1 - 2а):
[X2 - «1-в<
A1.67)
[С-Щ-at
С + иг_а
A1.68)
где uq, как обычно, g-квантиль стандартного нормального распределения
(см. соответствующую таблицу в приложении 1), а вместо охъ и ас
подставляются их приближенные значения, вычисленные соответственно по
формулам A1.65) (или A1.65')) и A.66).
Пример 11.9. В табл. 11.3 (из [G i I b у W. H., Biometrika, 8, 94])
дано распределение 1725 школьников (т.е. п = 1725) по значениям двух
анализируемых категоризованных признаков: по качеству одежды (аг ')
и по их умственным способностям (аг '). Были определены 4 градации
(т.е. mi = 4) по первому признаку A: «очень хорошо»; 2: «хорошо»;
3: «удовлетворительно»; 4: «плохо») и 6 градаций (т.е. га2 = 6) по
второму признаку A: «плохие»; 2: «ниже средних»; 3: «средние»; 4: «выше
средних»; 5: «высокие»; 6: «превосходные»).
Таблица 11.3
Градации
признака
х<а)
1
2
3
4
Е
B)
Градации признака ar ;
1
33
41
39
17
130
2
48
100
58
13
219
3
113
202
70
22
407
4
209
255
61
10
535
5
194
138
33
10
375
6
39
15
4
1
59
Е
636
751
265
73
1725
Нас интересует, существует ли связь между манерой одеваться и
способностями, и если «да», то какова степень тесноты этой связи.

выводы 453
Вычисление величины X по формуле A1.60) дает X = 174,92 и
соответственно значение коэффициента Крамера (см. формулу A1.62))
С = 0,184.
Поскольку даже при уровне значимости а = 0,001 соответствующее
пороговое значение Xo,ooiA5) = 37,697 оказывается намного меньшим
статистики X , то связь есть и, по-видимому, характеризуется достаточно
высокой степенью тесноты. Бели сопоставить этот вывод с выборочным
значением коэффициента Крамера (С = 0,184), то мы получаем основание
относиться к этой шкале иначе, чем, например, к шкале абсолютных
значений парного коэффициента корреляции |г|: если для \г\ величина 0,184
означает отсутствие или крайне слабую связь между аг ' и ж , то для
С это значение, как мы видим, свидетельствует о наличии достаточно
тесной связи.
Величина <тс, вычисленная по приближенной формуле A1.66),
оказывается равной у/Т/Зп = 0,014, так что в соответствии с A1.68)
можем сделать вывод, что истинное (теоретическое) значение
коэффициента Крамера заключено в пределах от 0,184 - 1,96-0,014 = 0,157 до
0,184+1,96-0,014 = 0,211.
ВЫВОДЫ
1. Трудности, стоящие на пути практического использования в
статистическом исследовании моделей многомерных з.р.в., обусловили тот факт,
что в подавляющем большинстве случаев все выводы многомерного
статистического анализа строятся лишь на базе оценок вектора средних
значений и ковариационной матрицы исследуемого векторного признака.
2. Корреляционный анализ составляет содержание начальных этапов
исследования всех трех центральных проблем многомерного
статистического анализа. В проблеме статистического исследования зависимостей
корреляционный анализ позволяет выявлять сам факт существования
статистических связей между компонентами анализируемого векторного
признака и оценивать степень тесноты этих связей. Для проблем
классификации объектов и признаков и снижения размерности анализируемого
признакового пространства он предлагает и оценивает подходящие
характеристики парных отношений (ковариации, корреляции, разные виды
парных сравнений), которые используются в дальнейшем в качестве
базовой исходной информации.
3. Универсальной характеристикой степени тесноты статистической
связи (с.т.с.с.) между результирующим количественным показателем у и

454 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
объясняющими количественными переменными X = (ar ,ar\...,arp')
является коэффициент детерминации у по X-Kd{y\X). Другие
распространенные характеристики с.т.сс. (парные, частные и множественные
коэффициенты корреляции, корреляционное отношение) представляют
собой те или иные частные версии коэффициента детерминации,
реализованные в рамках различных конкретных схем зависимостей.
4. Парные корреляционные характеристики позволяют измерять
степень тесноты статистической связи между парой переменных без учета
опосредованного или совместного влияния других показателей,
вычисляются (оцениваются) они по результатам наблюдений только
анализируемой пары показателей.
Б. Факт установления тесной статистической связи между
переменными не является, вообще говоря, достаточным основанием для
доказательства существования причинно-следственной связи между этими
переменными.
в. Парные и частные коэффициенты корреляции являются
измерителями степени тесноты линейной связи между переменными. В этом
случае корреляционные характеристики могут оказаться как
положительными, так и отрицательными в зависимости от одинаковой или
противоположной тенденции взаимосвязанного изменения анализируемых
переменных. При положительных значениях коэффициента корреляции говорят о
наличии положительной линейной статистической связи, при
отрицательных — об отрицательной.
7. При наложении случайных ошибок на значения исследуемой пары
переменных (например, ошибок измерения) оценка статистической связи
между исходными переменными, построенная по наблюдениям,
оказывается искаженной. В частности, получаемые при этом оценки
коэффициентов корреляции будут заниженными. Существуют методы, позволяющие
учесть это искажение.
8. Измерителем степени тесноты связи любой формы является
корреляционное отношение, для вычисления которого необходимо разбить
область значений предсказывающей переменной X на интервалы
(гиперпараллелепипеды) группирования. Возможна параметрическая
модификация корреляционного отношения, при которой вычисление
соответствующих выборочных значений не требует предварительного разбиения на
интервалы группирования.
9. Частный коэффициент корреляции позволяет оценить степень
тесноты линейной связи между двумя переменными, очищенной от
опосредованного влияния других факторов. Для его расчета необходима исходная
информация как по анализируемой паре переменных, так и по всем тем

выводы 455
переменным, опосредованное («мешающее») влияние которых мы хотим
элиминировать.
10. Анализ статистических связей между порядковыми переменными
сводится к статистическому анализу различных упорядочений
(ранжировок) одного и того же конечного множества объектов и осуществляется с
помощью методов ранговой корреляции. В зависимости от типа изучаемой
ситуации (шкала измерения анализируемого свойства не известна
исследователю или отсутствует вовсе; существуют косвенные или частные
количественные показатели, в соответствии со значениями которых можно
определить место каждого объекта в общем ряду всех объектов,
упорядоченных по анализируемому основному свойству) процесс упорядочения
объектов производится либо с привлечением экспертов, либо
формализованно — с помощью перехода от исходного ряда наблюдений косвенного
количественного признака к соответствующему вариационному ряду.
11. Исходные статистические данные для проведения рангового
корреляционного анализа представлены таблицей (матрицей) рангов
статистически обследованных объектов размера п X (р + 1) (число объектов на
число анализируемых переменных). При формировании матрицы рангов
допускаются случаи неразличимости двух или нескольких объектов по
изучаемому свойству («объединенные» ранги).
12. К основным задачам теории и практики ранговой корреляции
относятся: анализ структуры исследуемой совокупности упорядочений
(задача Л); анализ интегральной (совокупной) согласованности
рассматриваемых переменных и их условная ранжировка по критерию степени тесноты
связи каждой из них со всеми остальными переменными (задача В);
построение единого группового упорядочения объектов на основе имеющейся
совокупности согласованных упорядочений (задача С).
13. В качестве основных характеристик парной статистической связи
между упорядочениями используются ранговые коэффициенты
корреляции Спирмэна т* и Кендалла т( \ Значения этих коэффициентов
меняются в диапазоне от -1 до +1, причем экстремальные значения
характеризуют связь соответственно пары прямо противоположных и пары
совпадающих упорядочений, а нулевое значение рангового
коэффициента корреляции получается при полном отсутствии статистической связи
между анализируемыми порядковыми переменными.
14. В качестве основной характеристики статистической связи
между несколькими (т) порядковыми переменными используется так
называемый коэффициент конкордации (согласованности) Кендалла W(m).
Между значением этого коэффициента и значениями парных ранговых
коэффициентов Спирмэна, построенных для каждой пары анализируемых

456 ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
переменных, существуют простые соотношения.
15. Если представить себе, что каждому объекту некоторой
достаточно большой гипотетической совокупности (будем называть ее генеральной
совокупностью) приписан какой-то ранг по каждой из рассматриваемых
переменных и что статистическому обследованию подлежит лишь часть
этих объектов (выборка объема п), то достоверность и практическая
ценность выводов, основанных на анализе ранговой корреляции, существенно
зависят от ответа на вопрос: как ведут себя выборочные значения
интересующих нас ранговых корреляционных характеристик при повторениях
выборок заданного объема, извлеченных из этой генеральной
совокупности. Это и составляет предмет исследования статистических свойств
выборочных ранговых характеристик связи. Результаты этого
исследования относятся прежде всего к построению правил проверки
статистической значимости анализируемой связи и к построению доверительных
интервалов для неизвестных значений коэффициентов связи,
характеризующих всю генеральную совокупность.
18. Основными измерителями степени тесноты парной
статистической связи между категоризованными переменными являются
коэффициент квадратичной сопряженности X и информационная
характеристика связи Y . Эти характеристики используют в ситуациях, когда
анализируемыми переменными' являются ординальные или номинальные
признаки, шкала возможных «значений» которых определена заданным
набором их состояний (градаций).

ГЛАВА 12. РАСПОЗНАВАНИЕ ОБРАЗОВ
И ТИПОЛОГИЯ ОБЪЕКТОВ
В СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ИССЛЕДОВАНИЯХ
(МЕТОДЫ КЛАССИФИКАЦИИ)
12.1. Сущность, типологизация и
прикладная направленность задач
классификации объектов
Необходимость анализа и формализации задач, связанных со
сравнением и классификацией объектов, сознавали ученые далекого прошлого.
«Его (Аристотеля) величайшим и в то же время чреватым наиболее
опасными последствиями вкладом в науку была идея классификации, которая
проходит через все его работы ... Аристотель ввел или, по крайней мере,
кодифицировал способ классификации предметов, основанный на сходстве
и различии ...», — писал Дж. Берналл в «Науке истории общества» (М.:
Изд-во иностр. лит., 1956, с. 117). После Аристотеля с его «деревом вещей
жизни» имеется еще в докомпьютерной эре ряд интереснейших примеров
прекрасно построенных классификаций как в естественных, так и в
общественных науках. Упомянем здесь (в хронологическом порядке) две из
них: а) иерархическая классификация (основанная на понятии сходства)
растений и видов М. Адансона A757 г.); б) знаменитая периодическая
система элементов Д. И. Менделеева A869 г.), представляющая собой по
существу классификацию многомерных наблюдений (каждый химический
элемент может быть представлен в виде вектора характеризующих его
разнотипных признаков, включая характеристики конфигурации внешних
электронных оболочек атомов) с выявленным единым классифицирующим
фактором (зарядом атомного ядра) и с упорядочением элементов внутри
каждого класса.
Однако до разработки аппарата многомерного статистического
анализа и, главное, до появления и развития достаточно мощной электронно-

458 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
вычислительной базы проблемы теории и практики классификации
относились не к разработке методов и алгоритмов, а к полноте и тщательности
отбора и теоретического анализа изучаемых объектов, характеризующих
их признаков, смысла и числа градаций по каждому из этих признаков.
Все методы классификации сводились по существу к методу так
называемой комбинационной группировки, когда все характеризующие объект
признаки носят дискретный характер или сводятся к таковым (пол или
мотив миграции индивидуума, уровень жилищных условий или число
детей в семье и т.п.), а два объекта относятся к одной группе только
при точном совпадении зарегистрированных на них градаций
одновременно по всем характеризующим их признакам (одинаковый пол, мотив
миграции и т. д.).
Однако по мере роста объемов перерабатываемой информации и, в
частности, числа классифицируемых объектов и характеризующих их
признаков возможность эффективной реализации подобной логики
исследования становилась все менее реальной (так, например, число к групп
или классов, подсчитываемое при комбинационной группировке по
формуле к я т\ • т% ...тр, где mj — число градаций по признаку х"', ар —
общее число анализируемых признаков, уже при m;- = 3 и р = 5
оказывается равным 243). Именно электронно-вычислительная техника стала
тем главным инструментом, который позволил по-новому подойти к
решению этой важной проблемы и, в частности, конструктивно
воспользоваться разработанным к этому времени мощным аппаратом многомерного
статистического анализа: методами распознавания образов «с учителем»
(дискриминантный анализ) и «без учителя» (автоматическая
классификация, или кластер-анализ).
Развитие электронно-вычислительной техники как средства
обработки больших массивов данных стимулировало проведение в последние годы
широких комплексных исследований сложных социально-экономических,
технических, медицинских и других процессов и систем, таких, как образ
и уровень жизни населения, совершенствование организационных систем,
региональная дифференциация социально-экономического развития,
планирование и прогнозирование отраслевых систем, закономерности
возникновения сбоев (в технике) или заболеваний (в медицине) и т. п. В связи
с многоплановостью и сложностью этих объектов и процессов данные о
них по необходимости носят многомерный и разнотипный характер, так
как до их анализа обычно бывает неясно, насколько существенно то или
иное свойство для конкретной цели. В этих условиях выходят на первый
план проблемы построения группировок и классификаций по
многомерным данным (т.е. проблемы классификации многомерных наблюдений),

12.1 СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ 459
причем появляется возможность оптимизации этого построения с точки
зрения наибольшего соответствия получаемого результата поставленной
конечной цели классификации.
Цели классификации существенно расширяются, и одновременно
содержание самого процесса классификации становится неизмеримо богаче
и сложнее. Оно, в частности, дополняется проблемой построения самой
процедуры классификации, ранее носившей чисто технический характер.
Прежде чем переходить к примерам и типологизации (в прикладном
и математическом аспектах) задач классификации, определим сам термин
классификация.
В самой общей формулировке под классификацией мы будем
понимать разделение рассматриваемой совокупности объектов или явлений
на однородные, в определенном смысле, группы либо отнесение каждого
из заданного множества объектов к одному из заранее известных
классов (при этом классифицируемое «заданное множество» может состоять
из единственного объекта). Заметим, что термин «классификация»
используется, в зависимости от контекста, для обозначения как самого
процесса «разделения-отнесения», так и его результата.
Сделаем шаг в сторону формализации общей задачи классификации
и сформулируем ее теперь в терминах статичного варианта
различных форм задания исходных статистических данных (см. (9.1) и (9.2)
при N = 1) по схеме «на входе-на выходе задачи».
На «входе» задачи исследователь имеет:
(а) п классифицируемых объектов, представленных данными вида
(9.1) (тогда каждая t-я строка матрицы (9.1) отражает значения р
характеризующих t-й объект признаков х\ ,х\ ,...,ж;- ) или данными вида
(9.2) (тогда каждая г-я строка матрицы (9.2) задает попарные
отношения 7п > 7t2> • • • > 7tn *-ro объекта со всеми остальными классифицируемыми
объектами);
(б) обучающие выборки
XjiiXj2)- --iXjnji j = 1,2, ...,&, A2.1)
каждая (j-я) из которых определяет значения анализируемых признаков
Xji = (XjiyXji ,.• -ixji) на nj объектах (т.е. i = 1,2,.. .,п;), о
которых априори известно, что все они принадлежат j-му классу, причем
число к различных выборок A2.1) равно общему числу всех возможных
классов (так что каждый класс представлен своей порцией выборочных
данных); если классифицируемые данные представлены в форме (9.2), то
каждая (j-я) из обучающих выборок также представляется матрицей вида

460 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
(9.2) размерности rtj X 7ij, однако этот вариант задачи «классификации с
обучением» в книге не рассматривается.
На «выходе» задачи мы должны иметь результат в одной из двух
форм:
(г) если число классов к и их смысл известны заранее, то каждое
из п классифицируемых многомерных наблюдений должно быть снабжено
«адресом» (номером) класса, к которому оно принадлежит;
(п) если число классов и (или) их смысл выявляются в процессе
классификации^ то результатом классификации является разделение
множества классифицируемых объектов на определенное число однородных (в
определенном смысле) групп, каждая из которых объявляется «классом».
Если исследователь располагает на «входе» задачи не только
классифицируемыми данными (а), но и обучающими выборками (б) (см. A2.1)),
то говорят, что решается задача классификации при наличии обучающих
выборок («классификация с обучением»)] в противном случае речь идет
о задаче «классификации без обучения».
Для пояснения сущности основных прикладных типов задач
классификации и конечных прикладных целей, которые ставит при этом перед
собой исследователь, рассмотрим примеры.
Пример 12.1. Выявление типологии потребительского
поведения населения, анализ сущности дифференциации этого
поведения, прогноз структуры потребления.
В качестве исходной информационной базы используются данные
бюджетных обследований семей. Поясним логическую схему
исследования. Многомерная статистика рассматривает совокупность изучаемых
многомерных объектов как совокупность точек или векторов в
пространстве описывающих их признаков. Применительно к схеме потребления
совокупностью объектов, подлежащих изучению, является множество
элементарных потребительских ячеек — семей. Каждая семья
характеризуется, с одной стороны, некоторым набором X факторов-детерминантов
(социально-демографические и другие признаки, описывающие условия
жизнедеятельности семьи), а с другой — набором Y параметров
поведения («переменных поведения»), в которых отражаются ее фактические
потребности.
В качестве социально-демографических факторов, имеющих
существенное значение для изучения потребительских аспектов социальной
жизни, целесообразно использовать, например, общественную и
национальную принадлежность, уровень образования и квалификацию,
характер труда, демографический тип и возраст семьи, тип населенного пункта
и характер жилища, размер и структуру имущества, уровень доходов.

12.1 СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ 461
Различия в потребностях, складывающиеся под влиянием социально-
демографических и природно-климатических условий, являются
объективно существующими; они формируют весь строй поведения
потребителя в конкретно-исторических условиях, а в конечном счете порождают
своеобразные типы потребителей, ориентированные на существенно
разное потребление.
Весь комплекс социально-демографических и других факторов,
существенно воздействующих на структуру потребления, будем называть ти-
пообразующим. Они имеют определяющее значение, в то время как все
другие дают лишь случайную вариацию в пределах одной группы (типа)
потребительского поведения.
В качестве признаков поведения У можно рассматривать три группы
параметров: а) уровень и структуру потребления; б) характер (объем и
содержание) использования свободного времени; в) интенсивность
изменения социального, трудового, демографического статуса.
Итак, рассматриваются числовые характеристики и градации типо-
образующих и одновременно поведенческих признаков каждой семьи из
анализируемой совокупности.
Решение общей проблемы, связанной с выявлением и прогнозом
структуры и дифференциации потребностей населения, распадается на
следующие этапы.
1. Сбор и первичная статистическая обработка исходных данных.
Исследуемые объекты (семьи) выступают в качестве многомерных
наблюдений или точек в двух многомерных пространствах признаков. Фиксируя
в качестве координат этих точек значения (или градации) типообразую-
щих переменных X (т.е. факторов-детерминантов), рассматриваем их в
«пространстве состояния» ЩХ) — пространстве, координатами
которого служат основные показатели жизнедеятельности семей. Фиксируя
же в качестве координат тех же самых объектов значения показателей У
их потребительского поведения, рассматриваем их в «пространстве
поведения» П(У). Очевидно, при надлежащем выборе метрики в
пространствах Т1(Х) и П(У) геометрическая близость двух точек в П(Х)
будет означать сходство условий жизнедеятельности
соответствующих двух семей, так же как и геометрическая близость точек в П(У)
будет означать сходство их потребительского поведения. Среди
методов первичной статистической обработки анализируемых данных, обычно
используемых на этой стадии исследования, широко распространенными
и весьма полезными являются методы изучения различных одно-, дву- и
трехмерных эмпирических расйределений, которые сводятся к построению
и различным представлениям (графическим, табличным) упомянутых вы-

462
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ше комбинационных группировок. Пример табличного представления
одной из таких двумерных комбинационных группировок приведен в табл.
12.1.
Эта комбинационная группировка построена на основе
статистического обследования 400 семей по двум признакам из пространства П(Х): по
х^ (руб.) — величине среднедушевого семейного дохода (с тремя
градациями: «низкий», «средний» и «высокий»), и по х*2' — качеству
жилищных условий (с четырьмя градациями: «низкое», «удовлетворительное»,
«хорошее» и «очень хорошее»). Каждая клетка таблицы соответствует
классу, полученному в результате проведенной комбинационной
группировки; внутри клетки обозначено число семей, имеющих данное сочетание
градаций анализируемых признаков (подобные таблицы называют также
«таблицами сопряженности», см. п. 11.4).
Таблица 12.1
Градация
признака я*
(доход)
«Низкий»
«Средний»
«Высокий»
Сумма
Градация признака аг ' (жилищных условий)
«Низкое»
24
20
4
48

«Удовлетворительное»
12
100
8
120
«Хорошее»
4
140
28
172
«Очень
хорошее»
0
20
40
60
Сумма
40
280
80
400
Для более полного представления результатов подобной
классификации можно было бы ввести в программу компьютера требование выпеча-
тывать номера семей, попавших в каждую из двадцати клеточек таблицы.
Заметим, что непрерывным аналогом комбинационной группировки
является обычный переход от исходных наблюдений непрерывной
случайной величины к «группированным» выборочным (см. п. 6.1). Результат
такого перехода представляется либо в виде таблицы, подобной табл. 12.1,
либо в виде графика (гистограммы).
2. Выявление основных типов потребления с помощью разбиения
исследуемого множества точек-семей на классы в «пространстве
поведения* П(У). Гипотеза существования «естественных», объективно
обусловленных типов поведения, т. е. какого-то небольшого количества
классов семей, таких, что семьи одного класса характеризуются сравнительно
сходным, однотипным потребительским поведением, геометрически
означает распадение исследуемой в «пространстве поведения» совокупности
точек-семей на соответствующее число «сгустков» или «скоплений» то-

12Л СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ 463
чек. Выявив с помощью подходящих методов многомерного
статистического анализа (кластер-анализа, таксономии) эти классы-сгустки, тем
самым определим основные типы потребительского поведения.
3. Отбор наиболее информативных типообразующих признаков
{факторов-детерминантов) и выбор метрики в пространстве
типообразующих признаков. Очевидно, неправомерно рассчитывать на то, что
диапазоны возможных значений каждого из кандидатов в типообразую-
щие признаки окажутся непересекающимися для семей с разным типом
потребительского поведения. Другими словами, значения каждого из
признаков х^3' в отдельности и их набора в совокупности подвержены
некоторому неконтролируемому разбросу при анализе семей внутри каждого
из типов потребления. Естественно считать наиболее информативными
те факторы-детерминанты или те их наборы, разница в законах
распределения которых оказывается наибольшей при переходе от одного класса
потребительского поведения к другому. Эта идея и положена в основу
метода отбора наиболее информативных (типообразующих) признаков-
детерминантов.
4. Анализ динамики структуры исследуемой совокупности семей
в пространстве наиболее информативных типообразующих признаков.
Конечной целью этого этапа является прогноз тех постепенных
преобразований классификационной структуры совокупности потребителей (семей,
рассматриваемых в пространстве типообразующих признаков), которые
должны произойти с течением времени.
5. Прогноз структуры потребления. На этом этапе исследования
опираемся на результаты, полученные в итоге проведения предыдущего
этапа, т. е. исходим из заданной классификационной структуры
потребителей в интересующий нас период времени в будущем. Восстанавливая
классификационную структуру потребления (классификационную
структуру совокупности семей в пространстве признаков П(У),
характеризующих потребительское поведение семьи) по классификационной
структуре потребителей (по классификационной структуре той же совокупности,
но в пространстве типообразующих признаков), будем относить каждую
конкретную семью к тому типу потребления, для которого значения
характеризующих ее типообразующих признаков являются, грубо говоря,
наиболее типичными.
Пример 12.2. Классификация как необходимый
предварительный этап статистической обработки многомерных
данных. Пусть исследуется зависимость интенсивности миграции
населения ж'р' (профессиональной или территориальной) от ряда социально-
экономических и географических факторов аг , аг ,..., агр~ , таких, как

464 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
средний заработок, обеспеченность жилой площадью, детскими
учреждениями, уровень образования, возможности профессионального роста,
климатические условия и т.п. Естественно предположить (и результаты
исследования это подтверждают), что для различных однородных групп
индивидуумов одни и те же факторы влияют на ж'р' в разной степени, а
иногда и в противоположных направлениях. Поэтому до применения
аппарата регрессионно-корреляционного анализа следует разбить все имеющиеся
в нашем распоряжении данные Х{ = (х\ \х\ ',..., ж*. ) (г = 1,2, ...,п)
на однородные классы и решать далее поставленную задачу отдельно
для каждого такого класса. Только в этом случае можно ожидать, что
полученные коэффициенты регрессии агр' по аг , аг ,..., ж ' будут
допускать содержательную интерпретацию, а мера тесноты связи между
агр' и аг1 , аг ,... ,агр~ ' окажется достаточно высокой.
Другой вариант такого рода примера получим, если в качестве
объектов исследования рассмотрим предприятия определенной отрасли, а в
качестве вектора наблюдений Х{ — совокупность объективных
(нерегулируемых) условий работы г-го обследованного предприятия (сырье, энергия,
оснащенность техникой и рабочей силой и т.п.). Классификация
предприятий по X производится как необходимый предварительный этап для
возможности последующей объективной оценки работы коллективов и
разработки обоснованных дифференцированных нормативов: очевидно, лишь к
предприятиям, попавшим в один класс по X, может быть применена
одинаковая система нормативов и стимулирующих показателей. Далее можно
рассматривать задачу, аналогичную сформулированной выше, а именно:
У = (у* ',..., у*9') — вектор показателей качества работы предприятия
(объем и качество выпускаемой продукции, ее себестоимость,
рентабельность и т.п.), a U = (tr , ...,irm') — вектор регулируемых факторов,
от которых зависят условия производства (число основных
подразделений, уровень автоматизации и т.д.), то задачу описания интересующей
нас зависимости вида У = f(U) естественно решать отдельно для
каждого однородного по X класса.
Пример 12.3. Классификация в задачах планирования
выборочных обследований. Здесь речь пойдет о планировании
выборочных экономико-социологических обследований городов. Предположим, что
необходимо достаточно детально проанализировать подробные
статистические данные о городах с целью выявления наиболее характерных черт
в экономико-социологическом облике типичного среднерусского города.
Производить подробный, кропотливый анализ по каждому из городов
Российской Федерации, очевидно, слишком трудоемко, да и нецелесообразно.
По-видимому, разумнее попытаться предварительно выявить число и со-

12.1 СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
465
став различных типов в совокупности обследованных городов по набору
достаточно агрегированных признаков яг ',аг ',...,агр~ ,
характеризующих каждый город (например, понимать под х"' число жителей
города, приходящееся на каждую тысячу жителей, обладающих заданным j-м
признаком, скажем, высшим образованием, специальностью металлурга
и т.п.). А затем, отметив наиболее типичные города в каждом классе
(наблюдения-точки X,-, наиболее близко располагающиеся к «центрам
тяжести» своих классов), отобрать их для дальнейшего (более
детализированного) социально-экономического анализа. При этом, очевидно, мера
представительности отобранных «типичных городов» определится
удельным весом количественного состава точек данного класса среди всех
рассматриваемых точек (городов).
Анализ рассмотренных примеров с учетом, конечно, и другого
накопившегося к настоящему времени опыта решения практических
задач классификации в экономике, социологии, психологии и других
сферах практической и научной деятельности человека позволяет произвести
определенную систематизацию этих задач в соответствии с конечными
прикладными целями исследования (табл. 12.2).
Таблица 12.2
п/п
1
1
2
Тип задачи классификации
\ 2
Комбинационные
группировки и их непрерывные
обобщения
Простая типологизация:
выявление
«стратификационной структуры»
множества статистически
обследованных объектов,
«нащупывание» и описание
четко выраженных
скоплений («сгустков», «клас-
Варианты (примеры) конечных
прикладных целей исследования
для данного типа задачи
классификации
3
1.1. Составление частотных таблиц
и графиков, характеризующих
распределение статистически
обследованных объектов по градациям
или интервалам группирования
характеризующих их признаков
(см. п. 1 в примере 12.1)
2.1. Классификация как
необходимый предварительный этап
исследования, когда до проведения
основной статистической
обработки множества анализируемых
данных (построения регрессионных
моделей, оценки параметров
генеральной совокупности и т.д.) до-

466
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Продолжение таблицы 12.2
1
3
2
теров», «образов», классов)
этих объектов в
анализируемом многомерном
пространстве и построение
правила отнесения каждого
нового объекта к одному из
выявленных классов
Связная неупорядоченная
типологизация:
исследование зависимостей между не
поддающимися
упорядочению классификациям^
одного и того же множества
объектов в разных
признаковых пространствах, одно
из которых построено на
результирующих
(поведенческих) признаках
(отражающих специфику
функционирования объекта,
его
социально-экономическое поведение, состояние
здоровья и т. п.), а другое —
на описательных
(отражающих условия
функционирования и другие
характеристики, от которых могут
зависеть значения
результирующих признаков)
3
биваются расслоения этого
множества на однородные (в смысле
проводимого затем
статистического анализа) группы данных
(см. примеры 12.1 и 12.2).
2.2. Выявление и описание
расслоенной природы анализируемой
совокупности статистически
обследованных объектов с целью
формирования плана выборочных
(например,
экономико-социологических) обследований этой
совокупности (см. пример 12.3).
2.3 Первый шаг в построении
связных типологий (см. п.З
таблицы и пример 12.1)
3.1. Прогноз
экономико-социологических ситуаций или отдельных
социально-экономических
показателей, включая задачу выявления
так называемых типообразующих
признаков, в том числе латентных,
т. е. непосрественно не
наблюдаемых (см. пример 12.1).
3.2. Диагностика в
промышленности, технике, георазведке,
медицине
3.3. Кластер-анализ,
автоматическое (машинное) распознавание
образов — зрительных, слуховых

12.1 СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
467
Продолжение таблицы 12.2
1
4
5
2
Связная упорядоченная ти-
пологизация: модицикация
связной неупорядоченной
типологизации (см. п. 3
таблицы), обусловленная
дополнительным
допущением, что классы,
получаемые в пространстве
результирующих (поведенческих)
признаков, поддаются
экспертному упорядочению по
некоторому сводному (как
правило, латентному,
непосредственно не
наблюдаемому) свойству:
эффективности
функционирования, качеству, степени
прогрессивности
(оптимальности) поведения и т. п.
Структурная типологиза-
ция\ дополнение и развитие
простой типологизации
(см. п. 2 таблицы) в
направлении изучения и
описания структуры
взаимосвязей полученных
классов, включая построение
соответствующих
иерархических систем (на
классифицируемых элементах и
на классах элементов),
анализ роли и места
каждого элемента и класса в
общей структурной
классификационной схеме. При
этом структурная
классификационная схема
определяется составляющими ее
3
4.1. Построение и интерпретация
единого (свободного) латентного
признака-классификатора в виде
функции от исходных
описательных .признаков: классификация
химических элементов по заряду
их атомного ядра (периодическая
система Д. И. Менделеева);
построение фактора общей
одаренности в педагогике и психологии;
построение сводного показателя
эффективности
функционирования предприятия (см. п. 13.5);
построение интегральной
характеристики уровня мастерства
спортсменов в игровых видах спорта
(см. п. 13.5)
5.1. Классификация задач
многоцелевого комплекса (крупной
программы, научного направления
производственного комплекса и
т.п.)
5.2. Классификация элементов и
подсистем по их
функциональному назначению (производств — в
территориально-производственном
комплексе, территориальных
единиц — в народнохозяйственном
разделении труда и потребления,
элементов организационных
структур и т. п.).
5.3. Классификация лиц,
принимающих решение, по их роли и
близости позиций в понимании
ситуации и способе решения
задачи.

468
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Продолжение таблицы 12.2
1
6
2
классами (подсистемами) и
характеристиками
(правилами) их кзаимодей-
ствия
Классификация динамичес-
ских траекторий развития
систем: типологизация
траекторий многомерных
временных рядов
д:(«) = (*A)@.--,*(р)@)т.
среди компонент x^J\t)
которых могут быть как
количественные, так и
качественные переменные
3
5.4. Классификация исследуемых
признаков и анализ структуры
связей между ними
6.1. Задачи анализа типов
динамики семейной структуры,
потребительского поведения семей и др.
В качестве комментария к табл. 12.2 поясним методологическую
общность задач 3.1-3.3: прогноза экономико-социологических ситуаций,
диагностики и автоматического распознавания зрительных и слуховых
образов. Для этого лежащую в основе их решения методологическую схему
связной неупорядоченной типологизации представим следующим образом.
Пусть в качестве исходных данных об объекте О* (г = 1,2, ...,п)
имеем вектор описательных (объясняющих) признаков Х{ = (ж^1 ,.. .,х\р')Т
(это, в частности, характеристики условий жизнедеятельности t-й
обследованной семьи в примере 12.1, значения параметров исследуемого
технологического процесса или результаты обследований i-го пациента в
задачах диагностики, геометрические или частотные характеристики
распознаваемого образа в п. 3.3) и некоторую информацию Yi о том
результирующем свойстве^ по которому производится классификация объектов
(специфика социально-экономического поведения t-й семьи в примере 12.1).
Разница между задачами типа 3.1 и задачами 3.2 и 3.3 заключается
в том, что в задачах прогноза экономико-социологических ситуаций
информация Y{ об исследуемом результирующем свойстве объекта не
является окончательной, т.е. не задает однозначно, как это делается в
задачах 3.2 и 3.3, образа (класса, типа), к которому относится этот
объект. Эта информация в задачах типа 3.1 носит лишь промежуточный
характер и представляется, как правило, в виде вектора
результирующих показателей Yi = (у}1',..., yj )T. Поэтому в отличие от задач 3.2 и
3.3 (в которых уже «на входе» задачи имеем распределение анализируе-

12.1 СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ 469
мых объектов-векторов Х{ по классам, что и составляет так называемую
«обучающую выборку») в задачах типа 3.1 нужно предварительно
осуществить простую типологизацию множества объектов {0,}(i = 1,..., п)
в пространстве результирующих показателей и лишь затем использовать
полученные в результате этой типологизации классы в качестве
обучающих выборок для построения классифицирующего правила в пространстве
описательных признаков П(Х).
«На выходе» же всех задач типа 3.1-3.3 должны быть 1)
набор наиболее информативных объясняющих переменных (так
называемых типообразующих признаков) it \X)>z^ '(Х),...,2гр'(Х), которые
либо отбираются по определенному правилу из числа исходных
описательных признаков х ,ar , ...,х^р~ , либо строятся в качестве
некоторых их комбинаций; 2) правило отнесения {дискриминантная функция,
классификатор) каждого нового объекта О*, заданного значениями
своих описательных признаков X*, к одному из заданных (или
выявленных в процессе предварительной простой типологизации) в
пространстве П(У) классов или образов. При этом типообразующие признаки
Z = (z* (X),. ..,^р (X)) и искомое правило классификации должны
быть подобраны таким образом, чтобы обеснечивать наивысшую (в
определенном смысле) точность решения задачи отнесения объекта к одному
из анализируемых классов по заданным значениям его описательных
признаков X.
Типологизация математических постановок задач
классификации. Целесообразность и эффективность применения тех или иных
методов классификации так же, как их предметная осмысленность,
обусловлены конкретизацией базовой математической модели, т. е.
математической постановкой задачи. Определяющим моментом в выборе
математической постановки задачи является ответ на вопрос, на какой априорной
информации строится модель. При этом априорная информация
складывается из двух частей:
1) из априорных сведений об исследуемых классах; 2) из априорной
статистической (выборочной) информации, т.е. так называемых
обучающих выборок (их определения даны выше).
Априорные сведения об исследуемых генеральных совокупностях
относятся обычно к виду или некоторым общим свойствам закона
распределения исследуемого случайного вектора X в соответствующем
пространстве и получаются либо из теоретических, предметно-профессиональных
соображений о природе исследуемого объекта, либо как результат
предварительных исследований. Получение априорной выборочной информации
в экономике и социологии, как правило, связано с организацией систе-

470
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
мы экспертных оценок или с проведением специального предварительного
этапа, посвященного решению задачи простой типологизации
анализируемых объектов в пространстве результирующих показателей (см. пример
12.1).
Классификация задач разбиения объектов на однородные группы (в
зависимости от наличия априорной и предварительной выборочной
информации) и соответствующее распределение описания аппарата решения
этих задач по пунктам данной главы представлены в табл. 12.3.
Таблица 12.3
Априорные сведения
о классах
(генеральных совокупностях)
Некоторые самые
общие
предположения о законе
распределения
исследуемого
вектора: гладкость,
сосредоточенность
внутри
ограниченной области и т. п.
Различаемые
генеральные
совокупности заданы
в виде
параметрического семейства
законов
распределения
вероятностей
(параметры неизвестны)
Различаемые
генеральные
совокупности заданы
однозначным
описанием
соответствующих законов
Предварительная выборочная информация
Нет информации
Классификация
без обучения:
кластер-анализ,
таксономия,
распознавание образов
«без учителя»,
иерархические
классиффикации
(см. п. 12.4)
Интерпретация
исследуемой
генеральной
совокупности как смеси
нескольких
генеральных

ностей.«Расщепление» этой смеси
с помощью
методов оценивания
неизвестных
параметров (см. п. 12.3)
Классификация
при полностью
описанных
классах: различение
статистических
гипотез (см. гл. 8)
Есть обучающие
выборки
Непараметрические
методы дискриминант-
ного анализа
(см. п. 12.2.3)
Параметрические
методы дискриминант-
ного анализа
(см. пп. 12.2.3, 12.2.4)
Обучающие выборки
не нужны

12.2 КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ 471
12.2. Классификация
при наличии обучающих выборок
(дискриминантный анализ)
12.2.1. Класс как генеральная совокупность и базовая идея
вероятностно-статистических методов классификации
Ставя задачу отнесения каждого из классифицируемых наблюдений
Х{ = (# ,аг , ,,,,г ') , % = 1,2,. ..,п, к одному из классов,
необходимо четко определить понятие класса. Во всех постановках задач
этого и следующего (п. 12.3) параграфов мы будем понимать под «классом»
генеральную совокупность, описываемую одномодальной функцией
плотности f(X) (или одномодальным полигоном вероятностей в случае
дискретных признаков X).
Для пояснения общей идеи, заложенной в основу построения всех
вероятностно-статистических методов классификации, вернемся к
примеру п. 7.5.1 и рис. 7.2. По существу уже в этом примере мы имеем дело с
задачей отнесения трех наблюдений у\ = 5,16, у% = 6,25 и j/3 = 5,32 к
одной из двух гипотетичных нормальных генеральных совокупностей (т. е.
к одному из двух классов), различающихся между собой средними
значениями. И решение мы приняли в пользу класса со средним значением
п\ = 5,243 потому, что в рамках этого класса наши наблюдения выглядят
более естественными, более правдоподобными (что определяется
произведением соответствующих им ординат плотности этого закона). Именно
этот принцип и положен в основу вероятностных методов классификации:
наблюдение будет относиться к тому классу (т. е. к той генеральной
совокупности), в рамках которого (которой) оно выглядит более
правдоподобным. Правда, во-первых, этот принцип может корректироваться с учетом
удельных весов классов и специфики так называемой «функции потерь»
c(j | i), которая определяет стоимость потерь от отнесения объекта i-ro
класса к классу с номером j. И во-вторых, для того чтобы этот принцип
практически реализовать, мы должны располагать полным описанием
гипотетических классов, т.е. знанием функций Л(А'),/2(Х),..., Д(Х),
задающих з.р.в. соответственно для 1-го, 2-го, ..., Л-го классов. Последнее
затруднение обходят с помощью обучающих выборок в случае
классификации с обучением, — и этому посвящен данный параграф, — и с помощью
модели смеси распределений в случае классификации без обучения (этому
посвящен п. 12.3).

472 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
12.2.2. Функции потерь и вероятности неправильной
классификации
Очевидно, желательно строить такие методы классификации,
которые минимизируют потери (или вероятность) неправильной
классификации объектов. Посмотрим, как эти две характеристики качества метода
классификации связаны между собой.
Мы уже ввели величину c(j \ г) потерь, которые мы несем при
отнесении одного объекта г-го класса к классу j (при г = j, очевидно, c,j = 0).
Следовательно, если в процессе классификации мы поступили таким
образом rn(j | г) раз, то потери, связанные с отнесением объектов г-ro класса
к классу j составят m(j \ i)c(j | г). Для того чтобы подсчитать общие
потери Сп при такой процедуре классификации, надо просуммировать
величину произведения m(j \ i)c(j \ i) по всем г = 1,2,..., к и j = 1,2,..., Л,
т.е.
Для того чтобы потери не зависели от числа п классифицируемых
объектов (а величина Сп, очевидно, будет расти с ростом п), перейдем к
удельной характеристике потерь, разделив обе части A2.2) на п, а затем
перейдем к пределу по п —> оо:
С= lim (l-Cn) = lim
П
A2-3)
Предел в A2.3) понимается в смысле сходимости по вероятности
частот m(j \ ()/щ(п) и щ(п)/п соответственно к вероятностям P(j |
г), — отнести объект класса t к классу j, и 7Г^, — извлечения объекта
класса г из общей совокупности анализируемых объектов; величину тг,
называют также априорной вероятностью (или удельным весом) класса г
(о сходимости по вероятности относительных частот см. п. 6.2).
Величина
0 A2.4)
определяет, как легко видеть, средние потери от неправильной
классификации объектов i-го класса, так что средние удельные потери от непра-

12.2 КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ 473
вильной классификации всех анализируемых объектов будут:
к
t=i
В достаточно широком классе ситуаций полагают, что потери c(j \ г)
одинаковы для любой пары г и jf, т.е.
c(j | г1) = с0 = const при j ф г; ij = 1,2,..., к.
В этом случае стремление к минимизации средних удельных потерь С
будет эквивалентно стремлению максимизации вероятности правиль-
k
ной классификации объектов, равной ? тг,Р(г | г). Действительно,
i
с = Е ** Е <i i *')p^ i •) = c° Ё w4 Ё pv i •)
)
t=i \ t=i /
(при выводе этого соотношения мы воспользовались тем, что с(г | i) = 0 и
(з I 0 = 1 для любого г).
Поэтому часто при построении процедур классификации говорят не о
к
потерях, а о вероятностях неправильной классификации 1 - ? тг^Р(г | <)•
t=i
12.2.3. Принципиальное решение общей задачи построения
оптимальных (байесовских) процедур классификации
Сформулируем постановку задачи построения оптимальной
процедуры классификации р-мерных наблюдений
ХиХъ...,Хп A2.5)
при наличии обучающих выборок A2.1).
Классифицируемые наблюдения A2.5) интерпретируются в данной
задаче как выборка из генеральной совокупности, описываемой так
называемой смесью А: классов (одномодальных генеральных совокупностей)

474 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
с плотностью вероятности
где Kj — априорная вероятность появления в этой выборке элемента из
класса (генеральной совокупности) j с плотностью fj(x) или, другими
словами, 7Tj — это удельный вес элементов j-vo класса в обшей генеральной
совокупности A2.6).
Введем понятие процедуры классификации (решающего правила, дис-
криминантной функции) 6(Х). Функция 6(Х) может принимать только
целые положительные значения 1,2,...,/?, причем те X, при которых она
принимает значение, равное j) мы будем относить к классу j) т.е.
Очевидно, Sj — это р-мерные области в пространстве П(Х)
возможных значений анализируемого многомерного признака А", причем функция
6(Х) строится таким образом, чтобы их сумма (теоретико -
множественная, см. п. 1.2) Si + 5г + • • * + Sk заполняла все пространство П(Х) и
чтобы они попарно не пересекались. Таким образом, решающее правило
6(Х) может быть задано разбиением
S = (SuS2,...,Sk) A2.7)
всего пространства П(Х) на к непересекающихся областей.
Процедура классификации (дискриминантная функция) 6(Х) (или S)
называется оптимальной (байесовской), если она сопровождается
минимальными потерями A2.3) среди всех других процедур классификации.
Оказывается (см., например, [Андерсон Т.]), процедура
классификации 5(опт) = (S{onT),...,sionT)), при которой потери A2.3) будут
оптимальными, определяется следующим образом:
к к
ж. .у • «г • \ / \^ | / f , X ^ UI \ / \ I /
A2.8)
Другими словами, наблюдение Ху (v = l,2,...,n) будет отнесено к
классу j тогда, когда средние удельные потери от его отнесения именно в
этот класс окажутся минимальными по сравнению с аналогичными
потерями, связанными с отнесением этого наблюдения в любой другой класс.

12.2 КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ 475
Относительно простой вид приобретает правило классификации
A2.8) в случае равных потерь c(j \ г) (т.е. при выполнении
соотношения c(j | i) = со = const). В этом случае наблюдение^ будет отнесено к
классу j тогда, когда
(т.е. максимизируется «взвешенная правдоподобность* этого
наблюдения в рамках класса, где в качестве весов выступают априорные
вероятности TTj).
Однако соотношения A2.8) и A2.8') задают нам лишь
теоретическое оптимальное правило классификации: для того чтобы его реально
построить, необходимо знание априорных вероятностей 7гЬ7г2,.. .,я> и
з.р.в. fi(X),/2(Х)>..., fk(X). В статистическом варианте решения
этой задачи данные величины заменяются соответствующими
оценками, построенными на базе обучающих выборок A2.1).
Априорные вероятности icj(j = 1,2,..., к) оцениваются просто, если
ряд наблюдений, составленный из всех обучающих выборок A2.1), может
быть классифицирован как случайная выборка объема по6 = щ + щ + • • •+
Пк из генеральной совокупности A2.6). Тогда оценки
*J = ?-> A2-9)
"б
где nj — объем j-й обучающей выборки.
Впрочем, величины тг;- часто определяются априори самой
содержательной сущностью задачи.
Что касается задачи оценки з.р.в. f\(X)}..., fk(X), то ее удобно
разбить на два случая:
1-й случай (параметрический дискриминантный анализ)
характеризуется известным общим видом функций 'fj(X), т.е. все классы
описываются з.р.в. одного и того же параметрического семейства {f(X;Q)}:
класс г отличается от класса j только значением параметра 0, т.е.
/,(*) =/(*;0Д J-1.2,...,*. A2.10)
Тогда в качестве оценок fj(X) неизвестных функций fj(X)
используются функции fj(Xi\ 0j), где Qj — статистическая оценка
неизвестного значения параметра 0j, полученная по наблюдениям j-й обучающей
выборки A2.1). Пример реализации этой схемы приведен в следующем
пункте.

476 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
2-й случай (непараметрический дискриминантный анализ) не
предусматривает знания общего вида функций fj{X) (j = 1,2,...,А). В этом
случае приходится строить так называемые непараметрические оценки
fj(X) для функций fj(X), например, гистограммного или ядерного типа,
либо пользоваться некоторыми специальными приемами (см., например,
[Айвазян С. А., Бежаева 3. И., Староверов О. В., с. 44-50]).
12.2.4. Параметрический дискриминантный анализ в случае
нормальных классов
Предположим, что класс j идентифицируется р-мерной нормальной
генеральной совокупностью с вектором средних значений а,* и
ковариационной матрицей ? (общей для всех классов), j = 1,2,...,&. Тогда при
реализации общих оптимальных правил классификации A2.8) и A2.8') в
качестве функций fj(X) следует использоватьр-мерные нормальные
плотности <p(X\kj>Ii) (см. C.9')), где оценки для векторов средних значений
&j = (ay\aj ,...,&*• )Т и для ковариационной матрицы S = (?^), /,
q = 1,2,... ,р, получены с помощью метода максимального правдоподобия
(см. п. 7.5.1) по обучающим выборкам A2.1); они имеют вид
i* j-i'J¦¦"*¦
hi t D«5? - «i'x^ - 4").
= 1,2,...,
Правило классификации A2.8') наблюдений A2.5) имеет весьма
простой вид в случае к = 2. Действительно, правило A2.8;) эквивалентно
следующему: наблюдение Х„ относится к классу с номером j0 тогда и
только тогда, когда
foffi? > — длявсех i=l,2,...,fc, A2.13)
или, что то же,

12.2 КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ 477
В случае нормальных плотностей fj{X), т.е. функций fj(X),
определяемых по формуле C.9;) с заменой М и S соответственно векторами а,
и матрицей Е, определяемыми по формулам A2.11)—A2.12), соотношение
A2.13 ) эквивалентно соотношению
для всех j = 1,2,..., к. .
Соотношение A2.13 ), таким образом, задает вид дискриминантной
функции в задаче различения нормальных классов при постоянных
значениях потерь от неправильной классификации. Особенно простым
становится это правило классификации в случае двух классов (к = 2) и
одинаковых априорных вероятностей (tti = тг2 = 0,5). В этом случае наблюдение
Хи следует относить к 1-му классу тогда и только тогда, когда
S-1(a1-a2)^0, A2.13w)
и ко 2-му классу во всех остальных случаях. Легко понять, что при
классификации на два класса одномерных (р=1) нормальных наблюдений
решение об отношении наблюдения xv к одному из двух классов будет
определяться знаком произведения [х„ - (аг + a2)/2](ui - a2).
Пример 12.4. Специальное исследование показало, что
склонность фирм к утаиванию части своих доходов (и, соответственно, — к
уклонению от уплаты части налогов) в существенной мере определяется
двумя показателями:
аг1' — соотношением «быстрых активов» и текущих пассивов;
аг2' — соотношением прибыли и просроченных платежей (оба
показателя оцениваются по определенной методике в шкале от 300 до 900 баллов).
В табл. 12.4 представлены значения этих показателей (данные
налоговой инспекции) по 10 фирмам, уличенным в тех или иных формах
уклонения от уплаты налогов (щ = 10), и по 13 фирмам, не имеющим
замечаний по уплате налогов (п2 = 13). Кроме того, имеющаяся статистика
и специальные обследования свидетельствуют о том, что доля фирм, в
той или иной форме уклоняющихся от уплаты налогов, достигает 50%
(т.е. 7Ti = тг2 = 0,5). Наконец, статистическая проверка гипотез о
нормальном характере распределения двумерного признака X = (х^1 ,ж )
внутри каждой из анализируемых совокупностей фирм — уклоняющихся
от уплаты налогов (совокупности 1) и платящих налоги (совокупности 2),

478
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
и о равенстве их ковариационных матриц ЕA) и ?B) дала
неотрицательный результат, т.е. можно считать, что имеющиеся у нас обучающие
выборки A) и B) извлечены из нормальных генеральных совокупностей с
одинаковыми ковариационными матрицами.
Таблица 12.4
пп
@
1
2
3
4
5
6
7
8
9
10
11
12
13
среднее
Обучающая выборка A)
(фирмы, уклоняющиеся
от налогов)
740
670
560
540
590
590
470
560
540
500
-
-
-
а^ = 576,0
-(»)
хи
680
600
550
520
540
700
600
540
630
600
-
-
-
ai2) = 596,0
Обучающая выборка B)
(фирмы, не
уклоняющиеся от налогов)
,0)
X2i
750
360
720
540
570
520
590
670
620
690
610
550
590
a^ = 598,5
хB)
590
600
750
710
700
670
790
700
730
840
680
730
750
оB2) = 710,8
На фирме, не прошедшей проверку налоговой инспекции,
зарегистрированы значения переменных X = (аг \аг ') :xq = 740, Xq = 590.
Определить, к какой совокупности A или 2) будет отнесена эта
фирма (т. е. наблюдение Xq = (х^ \х$ ') ), если воспользоваться методом
параметрического дискриминантного анализа (с учетом нормальности
анализируемых наблюдений).
Из условия задачи следует, что мы должны воспользоваться правилом
классификации, представленным соотношением A2.13W).
Необходимые вычисления дают:
1) оценки средних значений по каждой обучающей выборке A2.1),
подсчитанные по формуле A2.11):
&! = E76,0; 596,0)Т; а2 = E98,46; 710,77)Т;

12.3 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 479
соответственно:
кг -а3 = (-22,46; -114,77)Т; (кг + а2)/2 = E87,23; 653,39)Т;
2) оценка общей ковариационной матрицы ? производится по формуле
A2.12) или, что то же:
1 Г /56240 17240\ /121569 25615\1
10+13-2 [\ 17240 33240,/ + V 25615 56492;J
¦(
8467 2041 \
2041 4273/ '
в результате обращения этой матрицы получаем
а-1 _ / 0,0001335 -0,0000637\
~ V -0,0000637 0,0002645; )
. -_1Г _- ч ( 0,0043 V
_ I r j. - \ _ f740 ~ 587,23\ _ / 152,77 \
2 l«i + *2; - ^ 590 _ б53K9 } -{ _63,39;;
4) поскольку численное значение выражения, определяемого
соотношением A2.13'"), в нашем случае равно
152,77 \Т /" 0,0043 \
-63,39; v-о,о289;-2>489>0'
то наблюдение АГ0 должно быть отнесено к классу 1, а это значит, что
есть основания к тому, чтобы диагностировать анализируемую фирму как
фирму, в той или иной форме уклоняющуюся от уплаты налогов.
12.3. Классификация без обучения
(параметрический случай):
расщепление смесей вероятностных
распределений
В пп. 12.3 и 12.4 описаны методы классификации объектов
(индивидуумов, семей, предприятий, городов, стран, технических систем, признаков

480 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
и т.д.) 0i,O2?-«->0n в ситуации, когда отсутствуют так
называемые обучающие выборки A2.1), а исходная информация о
классифицируемых объектах представлена либо в форме матрицы X «объект-свойство»
(см. (9.1;)), либо в форме матрицы парных сравнений объектов (см. (9.2),
статический вариант), где величина 7ij = Pij характеризует взаимную
отдаленность (или близость) объектов О,- и Oj.
Переход от формы исходных данных типа «объект-свойство» к
форме матрицы попарных расстояний осуществляется посредством задания
способа вычисления расстояния (близости) между парой объектов, когда
известны координаты (значения признаков) каждого из них.
В зависимости от наличия и характера априорных сведений о
природе искомых классов и от конечных прикладных целей исследования
следует обратиться либо к данному пункту 12.3, где описаны методы
расщепления смесей вероятностных распределений, которые оказываются
полезными в том случае, когда каждый (j-й) класс интерпретируется
как параметрически заданная одномодальная генеральная совокупность
fj(X;Qj) (j = 1,2,...,&) при неизвестном значении определяющего ее
векторного значения параметра Qj и соответственно каждое из
классифицируемых наблюдений Xi считается извлеченным из одной из этих (но не
известно, из какой именно) генеральных совокупностей; либо п. 12.4, где
описаны методы автоматической классификации (кластер-анализа)
многомерных наблюдений, которыми исследователь вынужден пользоваться,
когда не имеет оснований для интерпретации классифицируемых
наблюдений в качестве выборки из какой-либо вероятностной генеральной
совокупности или не располагает априорными сведениями, достаточными
для параметрического представления искомых классов. В том же пункте
кратко излагаются основные классификационные процедуры
иерархического типа, используемые в ситуациях, когда «на выходе» исследователь
хочет иметь не столько окончательный вариант разбиения анализируемой
совокупности объектов на классы, сколько общее наглядное
представление о стратификационной структуре этой совокупности (например, в виде
специально устроенного графа — дендрограммы).
12-3.1. Понятие смеси вероятностных распределений
Начнем пояснение понятия смеси распределений с рассмотрения ряда
конкретных примеров.
Пример 12.5. В отдел технического контроля (ОТК) поступают
партии изделий, составленные с помощью случайного извлечения из
объединенной продукции двух станков (станка А и станка В). Изделия кон-

12.3 КЛАССИФИКАЦИЯ ВЕЗ ОБУЧЕНИЯ 481
тролируются по некоторому количественному параметру (линейному
размеру) (мм, так что результатом контроля i-ro изделия партии является
число Х{Ми. Изделия на станках не маркируются, так что в ОТК не
известно, на каком именно станке произведено каждое из них.
Производительность станка Л в 1,5 раза выше производительность станка В.
Задано номинальное значение контролируемого параметра а = 65 мм и
известно, что точность работы станков характеризуется одинаковой
величиной среднеквадратических отклонений o& = y/D^A и &в = \/Щв> равной
1,0 мм1. Позже выяснилось, что станок А был настроен правильно
(производил изделие со средним значением Е(д = 65 мм, равным номиналу), в
то время как настройка станка В была сбита в направлении завышения
номинала (а именно Е?# = 67 мм).
Известно также, что распределение размеров изделий, произведенных
на каком-то определенном станке, описывается нормальным законом с
параметрами а7 = Е?7 и а7 = D?7 G = А или 7 = 5).
Очевидно, анализируемая в ОТК по наблюдениям х\, ж2,..., хп...
генеральная совокупность будет состоять из смеси двух нормальных
генеральных совокупностей, одна из которых представляет продукцию станка
А и описывается в соответствии с вышесказанным плотностью
а другая — продукцию станка В и описывается плотностью
fB(x) = <р(х;
п
Обозначая 07 = (а7,<т7), а удельный вес изделий станка 7 через 7г7
G = Л, 2?), можем записать уравнение функции плотности /(ж),
описывающей закон распределения анализируемого признака ? во всей
(объединенной) генеральной совокупности, в виде:
f(x) = icA<p(x; 0Л) + кв<р(х; 0В). A2.14)
Учитывая, что в объединенной генеральной совокупности продукции
станка А в 1,5 раза больше, чем продукции станка В (поскольку
производительность станка Л в 1,5 раза выше), а также то, что ад = 65 мм,
1 Случайная величина ? и ее числовые характеристики будут снабжаться нижним
индексом (А или В) в тех случаях, когда речь идет о продукции какого-то
определенного станка (соответственно станка А или станка В).
16 Теория вероятностей
и прикладная статистика

482 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ав = 67 мм, а\ — о\ = 1 мм , имеем:
A2.14')
N_
L_
Правыми частями уравнений A2.14) и A2.14') и представлен частный
случай того, что принято называть смесью вероятностных распределений1.
На рис. 12.1 представлены графики функций плотности /д(х), /в(х)
и f(x).
0,32
0,24
0,16
0,08
65
67
X) ММ
Рис. 12.1. Графики функций плотности отдельных компонентов и самой
смеси из примера 12.5
В соотношениях A2.14) и A2Л4;) величины тгд = 0,6 и пв = 0,4
представляют удельные веса соответствующих компонентов смеси (их еще
называют априорными вероятностями появления наблюдений из данного
компонента смеси), а 0д = (ад,<7д) и ©в = (^Ву^в) — векторные
параметры, от значений которых зависят законы распределения компонентов
смеси.
Бели сотрудники ОТК или потребители изделий-полуфабрикатов
захотят по наблюдениям хих2^^ определить, на каком именно станке
произведено каждое из них, то как раз и возникает одна из типичных
задач классификации наблюдений в условиях отсутствия обучающих
выборок (конечно, в данном примере можно представить себе специально
1 Речь идет о частном случае, поскольку в общей модели смеси распределений, во-
первых, могут участвовать более чем два (и даже континуум) составляющих смесь
распределений, а во-вторых, анализируемые распределения могут быть
многомерными и не обязаны быть однотипными (в данном примере оба компонента нормальные).

12.3 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 483
организованное производство этих изделий, в результате которого
можно получить отдельно изделия от станка А и отдельно — от станка В и
использовать их в дальнейшем в качестве обучающих выборок).
Пример 12.6. Речь идет о выявлении и анализе типов
потребительского поведения по данным обследований семейных бюджетов (см.
выше, пример 12.1). Здесь представлен один из фрагментов
исследования, проведенного с целью изучения (на базе семейных бюджетов)
дифференциации потребностей, выявления основных типов потребительского
поведения и определения главных типообразующих признаков (социально-
демографической, региональной, экономической природы). Исследуемым
многомерным признаком является вектор У показателей у,у,..., У
потребительского поведения семьи, т. е. каждой (i-й) обследованной семье
ставится в соответствие многомерное наблюдение
где у\т* — удельное (т.е. рассчитанное в среднем на одного члена семьи)
количество m-го вида благ (товаров или услуг, включая сбережения),
потребляемое i-й обследованной семьей за «единицу времени» (например,
за год) и выраженное в натуральных или денежных единицах.
В соответствии с одним из принятых в исследовании базовых
исходных допущений постулируется существование в анализируемом
пространстве ПР(У) (У 6 ПР(У)) сравнительно небольшого (и неизвестного) числа
к типов потребительского поведения, таких, что различия в структуре
потребления У семей одного типа носят случайный характер (т.е.
обусловлены влиянием множества случайных, не поддающихся управлению
и учету факторов) и незначительны по сравнению с различиями в
потребительском поведении семей, представляющих разные типы. При этом
предполагается, что случайный разброс структур потребительских
поведений У (j) внутри любого (j-ro) типа описывается многомерным (в
нашем случае р-мерным) нормальным законом распределения с некоторым
вектором средних (и в то же время — наиболее характерных, наиболее
часто наблюдаемых) значений
16*

484 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
и с ковариационной матрицей
(см. сведения о многомерном нормальном законе в п. 3.1.5, формула (ЗЛО)).
Однако в начале исследования нет сведений об упомянутых
гипотетических типах потребительского поведения: неизвестно ни их
число fc, ни значения определяющих эти типы многомерных параметров
Qj = (a(j),S(j)). Поэтому мы вынуждены рассматривать имеющиеся
в нашем распоряжении результаты бюджетных обследований семей
YuY29...,Yn A2.15)
как выборку из генеральной совокупности, являющейся смесью
многомерных нормальных законов распределения. Другими словами, функция
плотности /(У), описывающая распределение вектора Y в этой
объединенной генеральной совокупности, имеет вид
A2.16)
где 7Tj (j = 1,2,.. . ,&) — не известный нам удельный вес (априорная
вероятность) семей j-ro типа потребительского поведения в общей
совокупности семей;
многомерная нормальная плотность, описывающая закон распределения
исследуемого признака Y(j) внутри совокупности семей j-ro типа
потребительского поведения (j = 1,2, ...,&).
Далее необходимо по выборке A2.15) оценить неизвестные значения
параметров к, я-1,тг2,. ..,тг*_ь a(j) и E(j) (j = 1,...,А) модели A2.16),
чтобы в конечном счете суметь расклассифицировать (в определенном
смысле наилучшим образом) семьи 12.15 по искомым типам
потребительского поведения. Общая схема действий, увязывающая задачу
статистического оценивания параметров смеси типа A2.16) с задачей автоматической
классификации, изложена в п. 12.3.2.

12.3 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 485
Общая математическая модель смеси распределений.
Рассмотренные в примерах смеси A2.14) и A2.16) представляют собой
частные случаи общей модели смеси. Обобщение рассмотренных в примерах
смесей может быть произведено в направлении: 1) отказа от
конечности и даже дискретности компонентов, составляющих смесь,
распространения понятия смеси на непрерывную смешивающую функцию; 2)
отказа однотипности участвующих в смеси компонентов (под однотипностью
компонентов-распределений понимается их принадлежность к общему
параметрическому семейству распределений, например к нормальному).
Итак, пусть имеется двухпараметрическое семейство р-мерных
плотностей (полигонов вероятностей) распределения
F ={/„(*; 6(w))}, A2.17)
где одномерный (целочисленный или непрерывный) параметр и в качестве
нижнего индекса функции / определяет специфику общего вида каждого
компонента-распределения в смеси, а в качестве аргумента при
многомерном, вообще говоря, параметре 0 определяет зависимость значений хотя
бы части компонентов этого параметра от того, в каком именно
составляющем распределении fu он присутствует. И пусть
Ф = {ф(и)} A2.18)
— семейство смешивающих функций распределения.
Будем, как и ранее, понимать под f(X) функцию плотности, если
исследуется непрерывная случайная величина, и полигон вероятностей
Р{? = ЛГ}, если анализируемая случайная величина дискретна.
Аналогично значение функции ф(и) = жш (и = 1,2,..., к) интерпретируется как
априорная вероятность появления элементов класса о;, если смесь
состоит из конечного числа (к) компонентов /w(X;0(a;)), и ф(и>) — функция
плотности, если смесь состоит из континуального множества компонентов.
Функция f(X) называется смесью вероятностных распределений
(дискретной или непрерывной), если она представима в виде
соответственно
/W = Х>д(х;еш) A2Л9)
или
f(X) = У /w (X; в(и))ф{и) du. A2/19)
В данном пункте нас интересует использование моделей смесей в
теории и практике автоматической классификации, поэтому сузим
данное выше определение смеси и будем рассматривать в дальнейшем

486 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
лишь случай конечного числа к возможных значений параметра и,
что соответствует ситуации, в которой величины ф(и) будут играть
роль удельных весов (априорных вероятностей) тг;- компонентов смеси
(j = 1,2,..., А:) . Бели же дополнительно постулировать
однотипность компонентов-распределений fj(X\Q(j))9 т.е. принадлежность всех
fj(X\ Q(j)) к одному общему семейству {f(X; 0)}, то модель смеси может
быть представлена в виде
Интерпретация в задачах автоматической классификации j-ro
компонента смеси (j-й генеральной совокупности) в качестве j-ro
искомого класса (сгустка, скопления) обусловливает естественность
дополнительного условия, накладываемого на плотности (полигоны вероятностей)
fj(X;Q(j)) и заключающегося в их о дном о дальности.
12.3.2. Задача расщепления смеси распределений
Решить задачу расщепления смеси распределений — это значит по
выборке классифицируемых наблюдений
ХиХ2,...,Хп, A2.20)
извлеченной из генеральной совокупности, являющейся смесью A2.19")
генеральных совокупностей типа A2.17) (при заданном общем виде
составляющих смесь функций fw(X] 0(cj))), построить статистические оценки
для числа компонентов смеси fc, их удельных весов (априорных
вероятностей) тг!, 7Г2,..., я** и, главное, для каждого из компонентов fw(X; 0(o;))
анализируемой смеси A2.19;/). В некоторых частных случаях имеющиеся
Модель смеси вида A2.19') с непрерывной смешивающей функцией ip(w) также
является полезным инструментом социально-экономического анализа и
моделирования. Так, например, при моделировании распределения населения по величине
среднедушевого дохода каждый компонент смеси интерпретируется как население
однородной (по источникам формирования доходов, территориальным и социально-
профессиональным признакам) страты, а все население — как континуальная
смесь таких страт. Подобный подход лежит в основе обоснования логарифмически-
нормальной модели распределения населения по доходу (см. Айвазян С. А. Модель
формирования распределения населения России по величине среднедушевого
дохода// Экономика и математические методы, том 33 A997), X» 4, с. 74-86).

12.3 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 487
априорные сведения дают исследователю точное знание числа
компонентов смеси &, а иногда и априорных вероятностей тгх э я^,..., тг*. Тогда
задача расщепления смеси сводится лишь к оцениванию функций /и(Х; ®(и)).
Отметим, что задача расщепления сохраняет смысл и
применительно к генеральным совокупностям, т. е. в теоретическом варианте. В этом
случае она заключается в восстановлении компонентов /ш(Х;в(и)) и
смешивающей функции ф(и) по заданной левой части f(X) в соотношениях
A2.19) или A2.19') и называется задачей идентификации компонентов
смеси.
12.3.3. Общая схема решения задачи автоматической
классификации в рамках модели смеси распределений
(сведение к схеме
дискриминантного анализа)
Базовая идея, лежащая в основе принятия решения, к какой из к
анализируемых генеральных совокупностей отнести данное
классифицируемое наблюдение Xi} состоит в том, что наблюдение следует
отнести к той генеральной совокупности, в рамках которой оно выглядит
наиболее правдоподобным. Другими словами, если дано точное
описание (например, в виде функций /i(X),..., fk(X) плотности в
непрерывном случае или полигонов вероятностей в дискретном) конкурирующих
генеральных совокупностей, то следует поочередно вычислить значения
функций правдоподобия для данного наблюдения Xi в рамках каждой из
рассматриваемых генеральных совокупностей (т.е. вычислить значения
fi(Xi), /г(^),..., fk{Xi)) и отнести Xi к тому классу, функция
правдоподобия которого максимальна . Если же известен лишь общий вид функций
/i(X;0i), /г(^;02)>-- ->fk{X\®k)> описывающих анализируемые
классы, но не известны значения, вообще говоря, многомерных параметров
01,02,...,0Аг, и если при этом располагают так называемыми
обучающими выборками, то данный случай лежит в рамках параметрической
схемы дискриминантного анализа (ДА) и порядок действий будет
следующим (п. 12.2): сначала по j-й обучающей выборке оцениваем параметр
0j]{j = 1,2,..., fc), а затем производим классификацию наблюдений,
руководствуясь тем же самым принципом максимального правдоподобия, что
и в случае полностью известных функций fj(X).
В схеме автоматической классификации, опирающейся на модель
1 Для большей ясности здесь подразумевается простой случай равных априорных
вероятностей и равных потерь от неправильного отнесения наблюдения X,- к любому
из классов. Более общая схема и более подробно представлена в п. 12.2.

488 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
смеси распределений, как и в схеме параметрического ДА, задающие
искомые классы функции fi(X;&i), /г(-Х';02M--- также известны лишь с
точностью до значений параметров. Но в схеме автоматической
классификации неизвестные значения параметров ©i,02,..., так же, впрочем,
как и параметров А?,7Г1,7Г2,. . .,тгь оцениваются не по обучающим
выборкам (их нет в распоряжении исследователя), а по классифицируемым
наблюдениям Х\, Х2,..., Хп с помощью одного из известных методов
статистического оценивания параметров (метода максимального
правдоподобия, метода моментов или какого-либо другого). Начиная с момента,
когда по выборке A2.20) сумели получить оценки k, it\, 7г2,..., ?*> 0i,..., 0*
неизвестных параметров А:, И"ь7г2,...,тг^, 0ъ©2> •••>©*? модели A2.19 ),
снова имеем схему дискриминантного анализа и собственно процесс
классификации наблюдений A2.20) производим точно так же, как и в схеме
параметрического ДА (т.е. относим наблюдение Xi к классу с номером
jo, если 7tjofjo(Xi; Qjo) = тгх^ЫХц 0,)}).
Итак, главное отличие схемы параметрического ДА от схемы
автоматической классификации, производимой в рамках модели смеси
распределений, — в способе оценивания неизвестных параметров, от
которых зависят функции, описывающие классы. Но оценивание
параметров в модели смеси — процесс неизмеримо более сложный, чем
оценивание параметров по обучающим выборкам. Весьма подробное описание
процедур оценивания параметров смеси вероятностных распределений
читатель найдет в книге [Айвазян С. А. и др., 1989].
12.4. Классификация без обучения
(непараметрический случай):
методы кластер-анализа
12.4.1. Общая постановка задачи автоматической
классификации
Итак, как и в п. 12.3, мы не располагаем обучающими выборками и
имеем лишь п подлежащих классификации наблюдений, заданных либо
матрицей X (9.1 ), либо матрицей 7 (9»2) (в статичном варианте),
содержащей все попарные расстояния (меры близости) между
классифицируемыми наблюдениями. Однако в отличие от п. 12.3 в данном случае
отсутствует и априорная информация о характере распределения
наблюдений Х{ внутри каждого из классов (в предыдущем пункте нам был

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 489
известен общий параметрический вид этих распределений). Теперь же
мы можем располагать лишь самыми общими сведениями об этих
распределениях. Эти сведения могут относиться, например, к
компактности или ограниченности диапазонов изменения компонент
классифицируемых многомерных наблюдений, к свойствам непрерывности (гладкости)
соответствующих законов распределения вероятностей. Заметим, что
параллельно можно обсуждать задачу классификации признаков Х^3' (а не
объектов Х(), с той лишь разницей, что каждый из признаков задается
соответствующей строкой матрицы X. В дальнейшем, если это специально
не оговорено, не будем разделять изложение этой проблемы на «объекты»
и «признаки», поскольку все постановки задач и основная
методологическая схема исследования здесь общие.
В общей (нестрогой) постановке проблема автоматической
классификации объектов заключается в том, чтобы всю анализируемую
совокупность объектов О = {0$} (г = 1,п), статистически представленную
в виде матриц X или 7, разбить на сравнительно небольшое число
(заранее известное или нет) однородных, в определенном смысле, групп или
классов.
Для формализации этой проблемы удобно интерпретировать
анализируемые объекты в качестве точек в соответствующем признаковом
пространстве. Если исходные данные представлены в форме матрицы (X),
то эти точки являются непосредственным геометрическим изображением
многомерных наблюдений Л\,Х2,... ,Хп в р-мерном пространстве ПР(Х)
с координатными осями Оаг , Оаг ,...,0ж . Если же исходные
данные представлены в форме матрицы попарных взаимных расстояний 7?
то исследователю не известны непосредственно координаты этих точек,
но зато задана структура попарных расстояний (близостей) между
объектами. Естественно предположить, что геометрическая близость двух или
нескольких точек в этом пространстве означает близость «физических»
состояний соответствующих объектов, их однородность. Тогда проблема
классификации состоит в разбиении анализируемой совокупности точек —
наблюдений на сравнительно небольшое число (заранее известное или нет)
классов таким образом, чтобы объекты, принадлежащие одному классу,
находились бы на сравнительно небольших расстояниях друг от друга.
Полученные в результате разбиения классы часто называют кластерами
(таксонами, образами) , а методы их нахождения соответственно кластер-
1 Cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых
каким-либо общим свойством. Тахоп (англ.) — систематизированная группа
любой категории (термин биологического происхождения). Название «кластер-анализ»

490 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
анализом, численной таксономией распознаванием образов с
самообучением.
Однако, берясь за решение задачи классификации, исследователь с
самого начала должен четко представлять, какую именно из двух задач он
решает. Рассматривает ли он обычную задачу разбиения статистически
обследованного (р-мерного) диапазона изменения значений анализируемых
признаков на интервалы (гиперобласти) группирования, в результате
решения которой исследуемая совокупность объектов разбивается на
некоторое число групп так, что объекты такой одной группы находятся друг
от друга на сравнительно небольшом расстоянии (многомерный аналог
задачи построения интервала группирования при обработке одномерных
наблюдений см. «Переход к группированным данным» в п. 6.1). Либо он
пытается определить естественное расслоение исходных наблюдений на
четко выраженные кластеры, сгустки, лежащие друг от друга на
некотором расстоянии, но не разбивающиеся на столь же удаленные части. В
вероятностной интерпретации (т.е. если интерпретировать
классифицируемые наблюдения Х\, Х2,..., Хп как выборку из некоторой многомерной
генеральной совокупности, описываемой функцией плотности или
полигоном распределения /(X), как правило, не известными исследователю)
вторая задача может быть сформулирована как задача выявления
областей повышенной плотности наблюдений, т. е. таких областей возможных
значений анализируемого многомерного признака X, которые
соответствуют локальным максимумам функции f(X).
Бели первая задача — построения областей группирования — всегда
имеет решение, то при второй постановке результат может быть и
отрицательным: может оказаться, что множество исходных наблюдений не
обнаруживает естественного расслоения на кластеры (например, образует
один общий кластер).
Из методологических соображений (в частности, для упрощения
понимания читателем некоторых основных идей теории автоматической
классификации и для создания удобной схемы исследования свойств
различных классификационных процедур) будем иногда вводить в рассмотрение
теоретические вероятностные характеристики анализируемой
совокупности: генеральную совокупность, плотность (полигон) распределения,
теоретические средние значения, дисперсии, ковариации и т.п.
Очевидно, если мысленно «продолжить» множество классифицируемых
наблюдений до всей генеральной совокупности, задача классификации заключа-
для совокупности методов решения задач такого типа было впервые введено, по-
видимому, Трайоном в 1939 г. (Tryon R.C. Cluster Analyses//Ann. Arb., Edw.
Brothers. 1939).

12.4 КЛАССИФИКАЦИЯ ББЗ ОБУЧЕНИЯ 491
ется в разбиении анализируемого признакового пространства П (X) на
некоторое число непересекающихся областей. Условимся в дальнейшем
называть такую схему теоретико-вероятностной модификацией задачи
кластер-анализа.
12.4.2. Расстояния между отдельными объектами и меры
близости объектов друг к другу
Наиболее труден и наименее формализован в задаче автоматической
классификации момент, связанный с определением понятия однородности
объектов.
В общем случае понятие однородности объектов определяется
заданием правила вычисления величины Pij, характеризующей либо
расстояние d(O{yOj) между объектами О, и Oj из исследуемой совокупности
O(i,j = 1,2, ...,п), либо степень близости (сходства) t{O^Oj) тех же
объектов. Бели задана функция d@,*,0j), то близкие в смысле этой
метрики объекты считаются однородными, принадлежащими к одному
классу. Естественно, при этом необходимо сопоставление d(O^Oj) с
некоторым пороговым значением, определяемым в каждом конкретном случае
по-своему.
При задании расстояний и мер близости нужно помнить о
необходимости соблюдения следующих естественных требований: требования
симметрии (d(Oi,Oj) = d(Oj,Oi) и r(Oi)Oj) = r(Oj,Oi)); требования
максимального сходства объекта с самим собой (г(О1?О,) = max t(O^Oj))
и требования при заданной метрике монотонного убывания r(O^Oj) no
d(Oi, Oj), т. е. из d(Ok, О\) ^ d(O^ Oj) должно с необходимостью следовать
выполнение неравенства т{О^О{) < r(O;,Oj).
Конечно, выбор метрики (или меры близости) является узловым
моментом исследования, от которого решающим образом зависит
окончательный вариант разбиения объектов на классы при заданном алгоритме
разбиения. В каждой конкретной задаче этот выбор должен
производиться по-своему. При этом решение данного вопроса зависит в основном от
главных целей исследования, физической и статистической природы
вектора наблюдений X, полноты априорных сведений о характере
вероятностного распределения X. Так, например, если из конечных целей
исследования и из природы вектора X следует, что понятие однородной группы
естественно интерпретировать как генеральную совокупность с
одновершинной плотностью (полигоном частот) распределения, и если к тому же
известен общий вид этой плотности, то следует воспользоваться общим
подходом, описанным в п. 12.3. Если, кроме того, известно, что наблюде-

492 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ния Х{ извлекаются из нормальных генеральных совокупностей с одной и
той же матрицей ковариаций, то естественной мерой отдаленности двух
объектов друг от друга является расстояние махаланобисского типа (см.
ниже).
В качестве примеров расстояний и мер близости, сравнительно
широко используемых в задачах кластер-анализа, приведем здесь следующие.
Общий вид метрики махаланобисского типа. В общем случае
зависимых компонент аг ,аг ',..., агр' вектора наблюдений X и их
различной значимости в решении вопроса об отнесении объекта
(наблюдения) к тому или иному классу обычно пользуются обобщенным
(«взвешенным») расстоянием махаланобисского типа, задаваемым формулой
Здесь ? — ковариационная матрица генеральной совокупности, из
которой извлекаются наблюдения Х^, а А — некоторая симметричная
неотрицательно-определенная матрица «весовых» коэффициентов Ат9,
которая чаще всего выбирается диагональной.
Следующие три вида расстояний, хотя и являются частными
случаями метрики do? все же заслуживают специального описания.
Обычное евклидово расстояние
A:=l
К ситуациям, в которых использование этого расстояния можно признать
оправданным, прежде всего относят следующие:
• наблюдения X извлекаются из генеральных совокупностей,
описываемых многомерным нормальным законом с ковариационной матрицей
вида а • I, т. е. компоненты X взаимно независимы и имеют одну и ту же
дисперсию;
• компоненты аг1 ,аг ,...,агр' вектора наблюдений X однородны по
своему физическому смыслу, причем установлено, например с помощью
опроса экспертов, что все они одинаково важны с точки зрения решения
вопроса об отнесении объекта к тому или иному классу;
1 В случаях, когда каждый объект О,- представлен вектором признаков Х{ (т.е. в
случае исходных данных, представленных в форме X), часто удобнее в формулах и
различных соотношениях вместо О,- писать сразу Х{. Например, d(Xi}Xj) вместо

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 493
• признаковое пространство совпадает с геометрическим
пространством нашего бытия, что может быть лишь в случаях р = 1,2,3, и понятие
близости объектов соответственно совпадает с понятием геометрической
близости в этом пространстве, например классификация попаданий при
стрельбе по цели.
Взвешенное евклидово расстояние
\
/е=1
Обычно применяется в ситуациях, в которых так или иначе удается
приписать каждой из компонент аг ' вектора наблюдений X некоторый
неотрицательный «вес» o>fc, пропорциональный степени его важности с точки
зрения решения вопроса об отнесении заданного объекта к тому или иному
классу. Удобно полагать при этом 0<о;д^1,Л;=1,р.
Определение весов и^ связано, как правило, с дополнительным
исследованием, например получением и использованием обучающих выборок,
организацией опроса экспертов и обработкой их мнений, использованием
некоторых специальных моделей. Попытки определения весов и* только
по информации, содержащейся в исходных данных, как правило, не дают
желаемого эффекта, а иногда могут лишь отдалить от истинного
решения. Достаточно заметить, что в зависимости от весьма тонких и
незначительных вариаций физической и статистической природы исходных
данных можно привести одинаково убедительные доводы в пользу двух
диаметрально противоположных решений этого вопроса: выбирать и^
пропорционально величине среднеквадратической ошибки признака аг '
либо пропорционально обратной величине среднеквадратической ошибки
этого же признака.
Хеммингово расстояние. Используется как мера различия
объектов, задаваемых дихотомическими признаками. Оно задается с помощью
формулы
s=l
и, следовательно, равно числу Vij несовпадений значений
соответствующих признаков в рассматриваемых г-м и j-m объектах.
Другие меры близости для дихотомических признаков. Меры
близости объектов, описываемых набором дихотомических признаков,
обычно основаны на характеристиках v\j9 v\j и vy = v\j + vjj', где

494 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
vij \vi) ) — число нулевых (единичных) компонент, совпавших в объектах
Х{ и Ху Так, например, если из каких-либо профессиональных
соображений или априорных сведений следует, что все р признаков исследуемых
объектов можно считать равноправными, а эффект от совпадения или
несовпадения нулей такой же, как и от совпадения или несовпадения
единиц, то в качестве меры близости объектов Х{ и Xj используют величину
Весьма полный обзор различных мер близости объектов
читатель найдет, например, в статье Г. В. Раушенбаха «Проблемы
измерения близости в задачах анализа данных» (сборник «Программно-
алгоритмическое обеспечение, анализа данных в медико-биологических
исследованиях». — М.: Наука, 1987, с. 41-54).
О физически содержательных мерах близости объектов. В
некоторых задачах классификации объектов, не обязательно описываемых
количественно, естественнее использовать в качестве меры близости
объектов (или расстояния между ними) некоторые физически содержательные
числовые параметры, так или иначе характеризующие взаимоотношения
между объектами. Примером может служить задача классификации с
целью агрегирования отраслей экономики, решаемая на основе матрицы
межотраслевого баланса. Классифицируемым объектом в данном примере
является отрасль экономики, а матрица межотраслевого баланса
представлена элементами 4tJ*, где под ац подразумевается сумма годовых поставок
в денежном выражении t'-й отрасли в j-ю. В качестве матрицы близости
(rij) в этом случае естественно взять, например, симметризованную
нормированную матрицу межотраслевого баланса. При этом под
нормировкой понимается преобразование, при котором денежное выражение
поставок из f-й отрасли в j-ю заменяется долей этих поставок по отношению
ко всем поставкам i-й отрасли. Симметризацию же нормированной
матрицы межотраслевого баланса можно проводить различными способами.
Так, например, близость между 1-й и j-й отраслями можно выразить через
среднее значение их взаимных нормированных поставок.
О мерах близости числовых признаков (отдельных
факторов). Решение задач классификации многомерных данных, как правило,
предусматривает в качестве предварительного этапа исследования
реализацию методов, позволяющих существенно сократить размерность
исходного факторного пространства, выбрать из компонент аг \..., х^
наблюдаемых векторов X сравнительно небольшое число наиболее
существенных, наиболее информативных. Для этих целей бывает полезно
рассмотреть каждую из компонент аг ,...,агр' в качестве объекта, подлежа-

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 495
щего классификации. Дело в том, что разбиение признаков аг ,...,агр'
на небольшое число однородных в некотором смысле групп позволит
исследователю сделать вывод, что компоненты, входящие в одну группу, в
определенном смысле сильно связаны друг с другом и несут информацию о
каком-то одном свойстве исследуемого объекта. Следовательно, можно
надеяться, что не будет большого ущерба в информации, если для
дальнейшего исследования оставим лишь по одному представителю от каждой
такой группы (процедура, реализующая эту идею, описана в п. 13.4.2).
Чаще всего в подобных ситуациях в качестве мер близости между
отдельными признаками аг ' и ж , так же как и между наборами таких
признаков, используются различные характеристики степени их корре-
лированности и в первую очередь коэффициенты корреляции. Проблеме
сокращения размерности анализируемого признакового пространства
специально посвящена гл. 13 данного учебника.
12.4*3. Расстояния между классами объектов
При конструировании различных процедур классификации (кластер-
процедур) в ряде ситуаций оказывается целесообразным введение
понятия расстояния между целыми группами объектов. Приведем примеры
наиболее распространенных расстояний, характеризующих взаимное
расположение отдельных групп объектов. Пусть Si — i-я группа (класс,
кластер) объектов, щ — число объектов, образующих группу 5,, вектор
Х{%) — среднее арифметическое векторных наблюдений, входящих в Si
(другими словами, X(i) — «центр тяжести» i-й группы), a p{Si,Sm) —
расстояние между группами 5/ и 5т.
Ниже приводятся наиболее употребительные и наиболее общие
расстояния между классами объектов.
Расстояние, измеряемое по принципу «ближнего соседа»
(«nearest neighbour»)
Pmin(ShSm) = min
Расстояние, измеряемое по принципу «дальнего соседа»
(«furthest neighbour»)
Pm*x(ShSm) = max d(XhXj).
Расстояние, измеряемое по «центрам тяжести» групп

496 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Расстояние, измеряемое по принципу «средней связи»
определяется как арифметическое среднее всевозможных попарных расстояний
между представителями рассматриваемых групп, т. е.
Е Е
ЩПт
Естественно задать вопрос: нельзя ли получить достаточно
общую формулу, определяющую расстояние между классами по
заданному расстоянию между отдельными элементами (наблюдениями), которая
включила бы в себя в качестве частных случаев все рассмотренные выше
виды расстояний?
Изящное обобщение такого рода, основанное на понятии так
называемого «обобщенного среднего», а точнее, степенного среднего,
было предложено А. Н. Колмогоровым. Под обобщенным средним
величин с\, с2,..., cN понимается выражение вида М (сг, с2,..., cN) =
)> в котором F(u) — некоторая функция и соответствен-
разование, обратное к F. Частным случ
среднего является степенное среднее, определяемое как
»i
но F — преобразование, обратное к F. Частным случаем обобщенного
Нетрудно показать, что (при с^ > 0, i = 1,2,..., N)
Mo(ci,с2,..., cN) == ( П ci ) — геометрическое среднее;
N
Mi(ci, с2,..., Сдг) = jj ^2 ci — арифметическое среднее.
Обобщенное (по Колмогорову) расстояние между классами,
или обобщенное /^-расстояние, вычисляется по формуле
В частности, при г —» оо при г —> — оо имеем
A2.21)

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 497
Очевидно также
Из A2.21) следует, что если S(m,q) = Sm U Sq — группа
элементов, полученная путем объединения кластеров Sm и 59, то обобщенное
jff-расстояние между кластерами 5/ и 5(га, q) определяется формулой
Wta С, * I "m[piK)Eb 5m)]T
Понятие расстояния между группами элементов особенно важно в так
называемых агломеративных иерархических кластер-процедурах (см.
ниже п. 12.4.7), поскольку принцип работы таких алгоритмов состоит в
последовательном объединении элементов, а затем и целых групп, сначала
самых близких, а потом все более и более отдаленных друг от друга.
Учитывая специфику подобных процедур, для задания расстояния между
классами оказывается достаточным определить порядок пересчета
расстояния между классом S/ и классом S(m, q) = Sm U 59, являющимся
объединением двух других классов Sm и 59, по расстояниям р\ш = рE/,5т),
piq = p(Si,Sq) и pmq = p(SmySq) между этими классами. С этой целью
часто используется также следующая общая формула1 для вычисления
расстояния между некоторым классом 5/ и классом (m, q):
Р1(туЯ) = p{ShS(m9q)) = aplm + /3plg + <ypmq + 6\plm - piq\, A2.22)
где а,/?, 7 и 6 — числовые коэффициенты, значения которых и определяют
специфику процедуры, ее нацеленность на решение той или иной
экстремальной задачи.
Так, например, полагая а = /? = -# = j и 7 = 0, приходим к
расстоянию, измеряемому по принципу «ближайшего соседа». Если же положить
а = р = 6 = j и 7 = 0, то расстояние между двумя классами определится
как расстояние между двумя самыми далекими элементами этих классов,
по принципу «дальнего соседа». И наконец, выбор коэффициентов
соотношения A2.22) по формулам
1 См.: Keller W. У. Statistical vio Personal Computers. «Compstat-86», Proceedings in
Computational Statistics. — Wien, Physica-Verlag, 1986, pp. 332-337.

498 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
приводит к расстоянию рср между классами, вычисленному как среднее
из расстояний между всеми парами элементов, один из которых берется
из одного класса, а другой — из другого.
Расстояния между классами в теоретико-вероятностной
схеме кластер-анализа. В данной схеме анализируемая генеральная
совокупность интерпретируется как смесь унимодальных генеральных
совокупностей, каждая из которых и представляет один из искомых классов.
Если дополнительно ограничить себя рассмотрением только нормальных
классов, то каждый (/-й) такой класс, как известно (см. п. 3.1.5,
соотношение C.10)), определяется вектором средних значений а(/) и
ковариационной матрицей ?(/). Для измерения расстояния между нормальными
классами с номерами I ит используют так называемое «информационное
расстояние Каллбэка» (S. Kullback)
p2(St,Sm) = i (a(/) - <m))T(S-l@ + S-1(m))(a<0 - a(m))
It i ii A2>23)
i tr {(S(l) - S(m)) (E-V) - S-^m))} .
Бели анализируемые классы (генеральные совокупности)
различаются только средними значениями а(/) и а(ш) (т.е. ковариационные
матрицы у них одинаковы), то расстояние между ними измеряется так
называемым «расстоянием Махаланобисаъ, которое вычисляется по формуле,
получаемой из A2.23) при Е(/) = Е(т) = Е:
p\Sh Sm) = (а(/) - а(т))Т Е (а(/) - а(ш)). A2.24)
В статистической практике формулы A2.23) и A2.24) используются
для вычисления расстояний между классами и при отклонении
распределения наблюдений внутри классов от нормального с^заменой
теоретических характеристик a(j) и E(j') их оценками a(j') и Е(У), построенными
по наблюдениям, составляющим класс с номером j (j = /,m), см. выше
формулы A2.11) и A2.12).
12.4.4. Функционалы качества разбиения на классы и
экстремальная постановка задачи кластер-анализа
Естественно попытаться определить сравнительное качество
различных способов разбиения заданной совокупности элементов на классы, т. е.
определить тот количественный критерий, следуя которому можно
было бы предпочесть одно разбиение другому. С этой целью в постановку

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 499
задачи кластер-анализа часто вводится понятие так называемого
функционала качества разбиения Q(S), определенного на множестве всех
возможных разбиений. Функционалом он называется потому, что чаше всего
разбиение 5 задается, вообще говоря, набором дискриминантных
функций 6х(Х), ?гРО> • • • Тогда под наилучшим разбиением 5* понимается то
разбиение, на котором достигается экстремум выбранного функционала
качества. Выбор того или иного функционала качества, как правило,
осуществляется весьма произвольно и опирается скорее на эмпирические и
профессионально-интуитивные соображения, чем на какую-либо строгую
формализованную систему.
Приведем примеры наиболее распространенных функционалов
качества разбиения.
Функционалы качества разбиения при заданном числе
классов. Пусть исследователем уже выбрана метрика d в пространстве ПР(Х)
и пусть 5 = Eь 5j,..., Sk) — некоторое фиксированное разбиение
наблюдений Х\, Хз,..., Хп на заданное число к классов 5i, 52,.. м S/c
За функционалы качества часто берутся следующие характеристики:
сумма («взвешенная*) внутриклассовых дисперсий
<12-25)
весьма широко используется в задачах кластер-анализа в качестве крите-
рийной оценки разбиения;
сумма попарных внутриклассовых расстояний между элементами
либо
* 1
в большинстве ситуаций приводит к тем же наилучшим разбиениям, что
и QiE), и тоже используется для сравнения кластер-процедур;
обобщенная внутриклассовая дисперсия Qz(S) является, как известно
(см. п. 2.6.6, формула B.30)), одной из характеристик степени
рассеивания многомерных наблюдений одного класса (генеральной совокупности)
около своего «центра тяжести». Следуя обычным правилам вычисления

500 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГЙЗАЦИЯ ОБЪЕКТОВ
выборочной ковариационной матрицы Ef, отдельно по наблюдениям,
попавшим в какой-то один класс 5/, получаем
A2.26)
где под det А понимается «определитель матрицы А», а элементы 0qt{l)
выборочной ковариационной матрицы ?{ класса 5/ подсчитываются по
формуле
=4 ?
1
A2.27)
где х\ — v-я компонента многомерного наблюдения Х{^ а х (/) —
среднее значение v-й компоненты, подсчитанное по наблюдениям /-го класса.
Встречается и другой вариант использования понятия обобщенной
дисперсии как характеристики качества разбиения, в котором операция
суммирования S* по классам заменена операцией умножения
Как видно из формул A2.26) и A2.27), функционал Qz(S) является
средней арифметической (по всем классам) характеристикой обобщенной
внутриклассовой дисперсии, в то время как функционал Qa(S)
пропорционален средней геометрической характеристике тех же величин.
Использование функционалов Qz(S) и Q*(S) особенно уместно в
ситуациях, в которых исследователь в первую очередь задается вопросом: не
сосредоточены ли наблюдения, разбитые на классы 52,5*2,... ,5^, в
пространстве размерности, меньшей, чем р?
Функционалы качества разбиения при неизвестном числе
классов. В ситуациях, когда исследователю заранее не известно, на
какое число классов подразделяются исходные многомерные наблюдения
ХЬХ2,. ..,ХП, функционалы качества разбиения Q(S) выбирают чаще
всего в виде простой алгебраической комбинации (суммы, разности,
произведения, отношения) двух функционалов h(S) и h(S), один из
которых 1\ является убывающей (невозрастающей) функцией числа классов
к и характеризует, как правило, внутриклассовый разброс наблюдений,
а второй 1ч — возрастающей (неубывающей) функцией числа классов к.
При этом интерпретация функционала 1% может быть различной. Под

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 501
1*1 понимается иногда и некоторая мера взаимной удаленности (близости)
классов, и мера тех потерь, которые приходится нести исследователю при
излишней детализации рассматриваемого массива исходных наблюдений,
и величина, обратная так называемой «мере концентрации» всей
структуры точек, полученной при разбиении исследуемого множества наблюдений
на к классов.
Весьма гибким и достаточно общим подходом, реализующим идею
одновременного учета двух функционалов, является подход, основанный на
схеме, предложенной А.Н.Колмогоровым. Эта схема опирается на
понятия меры концентрации ZT(S) точек, соответствующей разбиению 5, и
средней меры внутриклассового рассеяния /f E), характеризующей то
же разбиение S.
Под мерой концентрации Zr(S) предлагается понимать степенное
среднее вида
"^ A2.28)
% a. i
1=1
где v(Xi) — число элементов в кластере, содержащем точку Xj, а выбор
числового параметра г находится в распоряжении исследователя и
зависит от конкретных целей разбиения. При выборе г полезно иметь в виду
следующие частные случаи Zr(S):
к
где к — число различных кластеров в разбиении 5; log Zq(S) = ? ^f" 1°8 ^
— естественная информационная мера концентрации (здесь т^, как и
ранее, число элементов в кластере Si);
«-<*>-.9S G)'
Заметим, что при любом г предложенная мера концентрации имеет
минимальное значение, равное 1/п, при разбиении исследуемого множества
\

502
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
на п одноточечных кластеров, и максимальное значение, равное 1, при
объединении всех исходных наблюдений в один общий кластер.
При конструировании и сравнении различных кластер-процедур
полезно иметь в виду, что объединение двух кластеров 5/ и 5т в один дает
прирост меры концентрации Zi(S), равный
1 Г/ . \2 2 2 ] 2П/Пт
= — Un/ + пт) ~Щ - Пт\ = з—.
П П
Определение средней меры внутриклассового рассеяния /? (S)
также опирается на понятие степенного среднего. В частности, полагают
A2.29)
где под
Ql/°{St) =
ее
понимается обобщенная средняя мера рассеяния, характеризующая класс
Si. Числовой параметр т здесь, как и прежде, выбирается по усмотрению
исследователя. Полагая
где 5(Х) — кластер, в который входит наблюдение AT, a v(X) — число
элементов в кластере 5(Х), формулу A2.29) можно переписать в виде
A2.30)
Е '
При конструировании и сравнении различных кластер-процедур
полезно иметь в виду, что объединение двух кластеров 5/ и 5т в один дает
прирост величины n[ll (S)]T, непосредственно характеризующей
среднюю меру внутриклассового рассеяния, равный
- [QiK\sm)]T}.

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 503
Очевидно, если ориентироваться на сокращение числа кластеров при
наименьших потерях в отношении внутриклассового рассеивания, не
обращая внимания на меру концентрации, то естественно объединять два
кластера, для которых минимальна величина А(п[/| ']т). Бели же
одновременно ориентироваться и на рост взвешенной концентрации ZiE), то
объединение кластеров следует подчинить требованию минимизации
величины
A[nDK))T] =
12.4.5. Формулировка экстремальных задач разбиения
исходного множества объектов на классы при
неизвестном числе классов
Возможно множество вариантов таких формулировок* Рассмотрим
два из них, относящихся к наиболее естественным и часто используемым.
Вариант 1: комбинирование функционалов качества. Требуется
найти такое разбиение 5*, для которого некоторая алгебраическая
комбинация функционала, характеризующего среднее внутриклассовое
рассеяние A2.30), и функционала, характеризующего меру концентрации
полученной структуры A2.28), достигала бы своего экстремума. В качестве
примеров можно привести комбинации, задаваемые формулами вида
aIt(S) + 0h(S) и [h(S)]a[h(S)]P, A2.31)
где /iE) = /т (?); h(S) = zJs) > а и & — некоторые положительные
константы, например, а = /? = 1.
Вариант 2: двойственная формулировка. Требуется найти
разбиение <$*, которое, обладая концентрацией ZT(S*), не меньшей
заданного порогового значения Zo> давало бы наименьшее внутриклассовое
рассеяние /| (S*), или, в двойственной подстановке: при заданном
пороговом значении /0 найти разбиение S* с внутриклассовым рассеянием
ц '(?*) < /о и наибольшей концентрацией ZT(S*).
12.4.6. Основные типы задач кластер-анализа и основные
типы кластер-процедур
Прежде всего целесообразно подразделение всех задач кластер-анализа
на два основных типа: Б] и Б2 в зависимости от объема п совокупности
классифицируемых наблюдений Х\, А^,..., Хп.

504 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
К типу Bi отнесем задачи классификации сравнительно небольших по
объему совокупностей наблюдений, состоящих, как правило, не более чем
из нескольких десятков наблюдений. Сюда, по-видимому, могут быть
отнесены задачи классификации некоторых макрообъектов, таких, как
страны, города, фирмы, предприятия, типы технологических процессов и т. п.
К типу Бг будем относить задачи классификации достаточно
больших массивов многомерных наблюдений (п — порядка нескольких сотен
и тысяч; классификация индивидуумов, семей, изделий, некоторых
промышленных и технических микрообъектов). Подобное разделение задач
классификации на два типа хотя и условно,, но весьма необходимо, и в
первую очередь с точки зрения принципиального различия идей и
методов, на основании которых конструируются кластер-процедуры в том и в
другом случае. Например, для задач типа Бг целесообразно построение
процедур последовательного типа, обладающих достаточно хорошими,
хотя бы асимптотическими по п, свойствами.
С точки зрения априорной информации об окончательном числе
классов, на которое требуется разбить исследуемую совокупность объектов,
задачи кластер-анализа можно подразделить на три основных типа:
(а) число классов априори задано;
(б) число классов неизвестно и подлежит определению (оценке);
(в) число классов неизвестно, но его определение и не входит в
условие задачи; требуется построить так называемое иерархическое дерево
исследуемой совокупности, или дендрограмму.
В соответствии с подразделением задач кластер-анализа на типы
можно выделить следующие три основных типа обслуживающих их
кластер-процедур:
• процедуры иерархические (агломеративные и дивизимные).
Предназначены в основном для решения задач типа (в). Что касается объема
классифицируемой совокупности, то формально иерархические процедуры
применимы и для задач Bj, и для задач Бг. Однако поскольку эти
процедуры основаны на переборе элементов матрицй расстояний p(Xi,Xj) (или
матрицы соответствующих мер близости), то конструктивно
реализуемыми их можно признать лишь в пределах задач типа Bi. Следует отметить,
что иерархические процедуры применяются иногда и для решения задач
типов Б1?(а) и Бь(б);
• процедуры параллельные. Предназначены для решения задач типов
Бь(а) и Бь(б). Они реализуются с помощью итерационных алгоритмов,
на каждом шаге которых одновременно (параллельно) используются все
имеющиеся у нас наблюдения;
• процедуры последовательные. Предназначены в основном для реше-

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 505
ния задач типов Б2, (а) и Бг, (б). Они реализуются с помощью
итерационных алгоритмов, на каждом шаге которых используется лишь небольшая
часть, например одно из исходных наблюдений, а также результат
разбиения на предыдущем шаге.
12.4.7. Иерархические процедуры
Как отмечалось выше, принцип работы иерархических агломератив-
ных (дивизимных) процедур состоит в последовательном объединении
(разделении) групп элементов сначала самых близких (далеких), а затем
все более отдаленных друг от друга (приближенных друг к другу). При
этом агломеративные процедуры начинают обычно с объединения
отдельных элементов, а дивизимные — с разъединения всей исходной
совокупности наблюдений.
С некоторой точки зрения иерархические процедуры, по сравнению
с другими кластер-процедурами, дают более полный и тонкий анализ
структуры исследуемого множества наблюдений. Привлекательной
стороной подобных алгоритмов является и возможность наглядной
интерпретации проведенного анализа. Легко себе представить также использование
иерархических процедур и для решения задач кластер-анализа типов (а)
и (б), т.е. для разбиения наблюдений на какое-то объективно
обусловленное число классов, заданное или неизвестное. При решении задач типа
(а) для этого, очевидно, следует продолжать реализацию иерархического
алгоритма до тех пор, пока число различных классов не станет равным
априори заданному числу к. При решении задач типа (б) естественно
было бы подчинить правило остановки иерархической процедуры одному из
критериев качества разбиения.
К недостаткам иерархических процедур следует отнести
громоздкость их вычислительной реализации. Соответствующие алгоритмы на
каждом шаге требуют вычисления всей матрицы расстояний, а
следовательно, емкой машинной памяти и большого времени. Поэтому
реализация таких алгоритмов при числе наблюдений, большем нескольких сотен,
оказывается либо невозможной, либо нецелесообразной.
Кроме того, имеется широкий класс достаточно естественных
примеров, в которых иерархические процедуры, даже подчиненные на каждом
шаге некоторому критерию качества разбиения, приводят для любого
наперед заданного числа кластеров к к разбиению, весьма далекому от
оптимального в смысле того же самого критерия качества. Если прибавить к
этому широкое экспериментальное подтверждение того же эффекта, то
можно прийти к выводу, что «конечная неоптимальность» оптималь-

506 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ного иерархического алгоритма является скорее правилом, чем
исключением. Специфический характер метода образования групп, свойственный
иерархическим процедурам, оказывается, по-видимому, слишком жестким
ограничением с точки зрения экстремального подхода к решению задач
классификации наблюдений при определенном числе классов.
Приведем некоторые примеры иерархических алгоритмов:
• агломеративный иерархический алгоритм «ближайшего соседа»
(или «одной связи»). Этот алгоритм исходит из матрицы расстояний
между наблюдениями, в которой расстояние между кластерами
определено по правилу «ближайшего соседа» (см. выше). На первом шаге
алгоритма каждое наблюдение Х{ (% = 1,2,...,п) рассматривается как
отдельный кластер. Далее на каждом шаге работы алгоритма происходит
объединение двух самых близких кластеров и соответственно пересчиты-
вается матрица расстояний, размерность которой, естественно, снижается
на единицу. Работа алгоритма заканчивается, когда все исходные
наблюдения объединены в один класс. Поскольку расстояние между любыми
двумя кластерами в этом алгоритме равно расстоянию между двумя
самыми близкими элементами, представляющими свои классы, то получаемые
в итоге кластеры могут иметь достаточно сложную форму, в частности,
они не обязаны быть выпуклыми; ведь два элемента (наблюдения)
попадают в один кластер, если существует соединяющая их цепочка близких
между собой элементов (так называемый «цепочечный эффект»). Это
обстоятельство можно отнести как к достоинствам алгоритма, так и к его
недостаткам.
Существуют различные способы устранения цепочечного эффекта
при образовании классов с помощью алгоритма ближайшего соседа.
Наиболее простым и естественным из них можно признать, например,
введение ограничения сверху на максимальное расстояние между элементами
одного класса: если при формировании классов для некоторых элементов
получаемого кластера взаимное расстояние превысит некоторый
заданный порог, то эти элементы следует разнести по какому-то
дополнительному правилу в разные классы.
• агломеративные иерархические алгоритмы «средней связи» и
«полной связи» (или «дальнего соседа»). Эти алгоритмы отличаются
от описанного выше алгоритма «ближайшего соседа» лишь способом
вычисления расстояния между классами. В алгоритме средней связи под
расстоянием между кластерами понимается среднее из расстояний
между всевозможными парами представителей этих кластеров. В алгоритме
полной связи (или дальнего соседа) расстояние между двумя кластерами
определяется как расстояние между двумя самыми отдаленными друг от

Х2.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 507
друга представителями своих кластеров.
• К-обобщенная иерархическая процедура, т.е. обобщенная по
Колмогорову. Поскольку все вышеперечисленные виды расстояний между
кластерами могут быть получены в качестве частных случаев
обобщенного расстояния Колмогорова A2.21), то представляется естественным
ввести понятие /^-обобщенной иерархической процедуры. Очевидно, в класс
tf-обобщенных иерархических процедур следует включить все обычные
иерархические алгоритмы, использующие в качестве расстояний между
кластерами обобщенное расстояние Колмогорова A2.21) при том или
другом конкретном выборе числового параметра г;
• процедуры иерархические, использующие понятие порога. Общая
схема подобных процедур отличается от обычной логической схемы ранее
описанных иерархических процедур лишь дополнительным заданием
последовательности, как правило, монотонной, порогов с\, с2,..., си которые
используются следующим образом. Для определенности дадим пояснения
для агломеративных процедур. На первом шаге алгоритма попарно
объединяются элементы, расстояние между которыми не превосходит
величины с\, либо мера близости которых не менее сг. На втором шаге алгоритма
объединяются элементы, или группы элементов, расстояние между
которыми не превосходит С2, либо мера близости которых не менее с2, и т.д.
Очевидно, при ct = оо или, при сравнении мер близости, при ct = 0, на
последнем t-м шаге все элементы исходной совокупности окажутся
объединенными в один общий класс. Заметим, однако, что объединение в
кластеры, подчиненные подобным пороговым иерархическим алгоритмам,
приводит к образованию, вообще говоря, пересекающихся промежуточных
классов, которые могут не расцепиться вплоть до последнего шага.
Поэтому эффективность подобных процедур, возможность выбора подходящих
пороговых значений с\,..., ct существенно зависят от внутренней
геометрической структуры исходного множества наблюдений. В частности,
пороговые иерархические процедуры оказываются уместными и достаточно
эффективными в ситуациях, когда отсутствует (или слабо выражен)
цепочечный эффект в структуре исходной совокупности наблюдений и когда
последние, естественно, распадаются на какое-то количество достаточно
отдаленных друг от друга отдельных скоплений точек в исследуемом
факторном пространстве.
12.4.8. Параллельные кластер-процедуры
В алгоритмах кластер-анализа реализуется обычно одна из двух
основных родственных идей, которой исследователь хочет подчинить свое

508 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
разбиение на классы. Это либо идея оптимизации разбиения в смысле
заранее выбранного функционала качества разбиения, либо идея
образования кластеров по принципу определения мест наибольшей сгущенности
(плотности, концентрации) точек наблюдений в рассматриваемом
факторном пространстве. Коль скоро характер параллельных процедур
предусматривает одновременный обсчет всех исходных наблюдений на каждом
шаге алгоритма, то естественно попытаться решать поставленную задачу
с помощью обычного перебора различных вариантов разбиения.
Однако нетрудно подсчитать, что уже при сравнительно небольшом
общем числе классифицируемых точек п (порядка нескольких десятков)
полный перебор всех вариантов разбиения на заданное, а тем более на
неизвестное число классов практически неосуществим. Следовательно,
основной смысл конструирования различных параллельных алгоритмов
классификации — в указании способа сокращения числа перебора
вариантов, в описании пути, приводящего, быть может, лишь к приближенному
решению поставленной задачи, но пути, конструктивно реализуемого и не
слишком дорогого.
а) Алгоритмы, связанные с функционалами качества разбиения. К
таким алгоритмам следует в первую очередь отнести алгоритмы
«последовательного переноса точек из класса в класс». Эти алгоритмы
отправляются от некоторого начального разбиения 5 = {S[ ,..., S^ },
полученного произвольно или с помощью какого-либо из методов
предварительной обработки исходных наблюдений. Вычисляется значение
принятого критерия качества разбиения Q(S), например, вида A2.25) при
заданном числе классов к или вида A2.31) при неизвестном числе классов.
Затем каждое из наблюдений Х{ поочередно перемещается во все кластеры
(при этом оно рассматривается как самостоятельный кластер, если число
кластеров неизвестно) и оставляется в том положении, которое
соответствует наилучшему значению функционала качества Q. Работа
алгоритма заканчивается, когда перемещения наблюдений перестанут приводить
к улучшению (в смысле Q) качества разбиения. Часто описанный
алгоритм применяют несколько раз к одной и той же исходной совокупности
наблюдений, начиная с разных начальных разбиений S , и выбирают в
итоге наилучший (в смысле Q) вариант разбиения.
б) Алгоритмы^ использующие понятие эталонных точек
(множеств). Опишем общую формальную схему одного достаточного
широкого класса алгоритмов, реализация которой может приводить как к
параллельным, так и к последовательным кластер-процедурам.
Под эталонными множествами Е\, Еч,..., Е^ будем понимать каким-
то образом, в частности случайным, сформированные непересекающиеся

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 509
подмножества исходной совокупности наблюдений {Xi,X2,...,Хп}
заранее определенных объемов соответственно mi,т2,...,тп*.. Как правило,
mi + т2 Н \-rrik составляет лишь незначительную долю от общего числа
исходных наблюдений п. В частном случае т\ = т2 = ... = т*. = 1 будем
иметь набор А? эталонных точек. Пусть для любого набора эталонных
множеств Е = {Ei, Е2,..., I?*}, для любого наблюдения Х^ для любой группы
исходных наблюдений А и для произвольного I = 1,2,..., к заданы
некоторые специальные функции (р(Х^ А) и ^ф(Х^ 5/, Е), характеризующие меру
типичности точки Xi как представителя группы точек А (меру
однородности наблюдений Xi и группы наблюдений А) и меру типичности точки Xi
как представителя класса ?/, построенного с использованием эталонного
множества Е\ из Е.
Будем для определенности считать, что чем меньше значения
функций <р и ф9 тем типичнее соответствующая точка в указанном выше
смысле. Тогда общая схема эталонных алгоритмов может быть
представлена следующим образом. При заранее заданном числе классов к каким-
то образом (случайным, с помощью обучающих выборок, из экспертно-
профессиональных соображений или с помощью методов предварительной
обработки исходных данных) выбираются числа т^, т2,..., га*, и
начальная система эталонных множеств Е* ' = {Е\ \е\ ,...#?'}. Класс 5,
формируется из наблюдений, наиболее типичных с точки зрения
представительства эталона Е\ , т. е.
5@) = {Хо <p(Xh ?f>) < <р{Хи Ef\ j = 1,2,..., к, зф1).
Если оказывается, что у?(А^,2?}- ) = (р{Х^Е- '), то можно условиться
относить наблюдение Xi к тому из классов S\ ' и Sj\ который
обладает меньшим порядковым номером. Затем строится новая система
эталонных множеств Е = {Е\г ,Е2 ,. ¦.,Е^ }, в которой эталон fjj1'
формируется из ш/ точек, дающих mi наименьших значений функции
ф(Х>S\ \Yj '). После этого по тому же правилу строят новое
разбиение 5'1' = {Si , 5*2,..., Si }, но уже относительно эталонов Е*1* и т. д.
Итерации продолжают до тех пор, пока не получат устойчивых классов,
т.е. до такого номера г;, при котором S^v* = 5^v" '.
Если число классов, на которое требуется разбить исходную
совокупность наблюдений, заранее не известно, то в описанную схему
необходимо ввести некоторые дополнения. В частности, на начальном этапе
. (о)
устанавливаются: числа Аг ', mi, m2,.. ^ra^o), система эталонных
мноу ,^,
жеств Е* * = {J?i , Е\ \...,2j?(o)}, а также величина </?0 — минимально

510
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
возможная типичность точки, представляющей свой класс, и Vo —
минимально возможная нетипичность двух разных классов1. Как и прежде,
вначале подсчитываются <р(Х^ Е\ ') для всех наблюдений (i = 1,2,..., п)
и для всех эталонов (/ = 1,2,...,Аг0'). Последовательно для каждого г
определяются эталоны Е\^у для которых данное 1-е наблюдение является
наиболее типичным, т. е.
Бели (р(Хг> Ej,\) < ^0, то наблюдение Х\ включается в состав класса
S|/°A; если же <p(Xi,E\?^) > <р0, то наблюдение Х\ принимается
одновременно за новый эталон я?(о)+1 и за новый класс ^о>+1- Затем та же
процедура сравнения производится с (р(Х2у Е^) и т- Д* Д° <P(Xni Щ(п))ш Пусть
в результате у нас образовалось на этом этапе алгоритма Аг°'(О) классов
и столько же эталонов Е = {Е\о*,...,Е$0),0Л (очевидно Ar°*(O) ^ №0').
После этого полученные классы S\ ,5^ ,..., ^(о>/0) проверяются на
значимое попарное различие с помощью порога Vo> a именно, если
то классы Sq и 5}0' объединяются в один класс S(q%i) с номером г(д,/),
равным min(g,/), и с эталоном Е^*, состоящим из max(m9,m/)
наблюдений, дающих соответствующее число наименьших значений функции
V>(X,S2(9i/),E*0*). Последовательное вычисление величин tl>(Sl°\s\0^) и
их сравнение с фо производится до тех пор, пока не окажется, что
Это означает окончание первой итерации алгоритма и образование новой
системы эталонов Е*1* = {J?}1',...,JSJ^Jj} и соответствующих значимо

эле1 В наиболее общих процедурах «пороги» ^о и ^о, так же как и общее число
ментов (п(") < п), составляющих классы S\v\..., s? , задаются переменными, т. е.
изменяющимися по определенному правилу при переходе от одного этапа алгоритма
к другому.

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 511
различимых классов S^ = {5j ,?3 ,. ••?^i(i)}- Затем процедура
повторяется применительно к эталонам Е* ' и т. д. до получения устойчивого
разбиения S^v' всех исходных элементов на некоторое число классов Аг \
При конструировании функций <р(Х,А) и rl>(XySi,E) можно
использовать заданную метрику (расстояние между точками) р(Х, Y) или меру
близости r(X>Y), а также подходящим образом выбранный вариант
обобщенного расстояния типа A2.21).
Используются, в частности, следующие способы задания <р и ф:
ip(X,A) =
где Х(А) — одна из разновидностей среднего_значения всех наблюдений
Х{, принадлежащих группе А. Например, Х(А) может быть обычным
арифметическим средним, т.е. «центром тяжести» группы А;
В качестве примера параллельных кластер-процедур,
укладывающихся в описанную общую схему, рассмотрим теперь серию алгоритмов,
объединенных названием «Форель». Общую для этих алгоритмов
идею проиллюстрируем на примере алгоритма «Форель-1».
Пусть совокупность {Xi,X2i*..9Xn} нужно разбить каким-то обра-
_ п
зом на некоторое число классов (заранее не известное). Пусть X = ~ ? Х{
i=i
и До — радиус минимальной гиперсферы с центром в Х> содержащей все
точки исследуемой совокупности. Зададим произвольный радиус R < Rq
и рассмотрим процедуру выделения классов для заданного R. Из любой
точки Х{ = Xi, принятой за центр, радиусом R описывается гиперсфера
С\. Находится центр тяжести Хч точек совокупности, попавших ъС\. Из
Х2 радиусом R описывается гиперсфера С2 и определяется Х3 — центр
тяжести точек исследуемой совокупности, попавших в C<i> Процедура
построения гиперсфер и точек Х^ повторяется до тех пор, пока точки Х^ не
перестанут меняться. Точки совокупности, попавшие в
«остановившуюся» гиперсферу, принимаются за первый класс S\. Для всех оставшихся
точек, т.е. не попавших в класс Si, вновь применяется описанная выше

512 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
процедура, выделяющая еще один класс 5г, и т.д. до тех пор, пока все
точки совокупности не будут распределены по классам.
Применение описанного алгоритма для ряда последовательных
значений R^ = Ro - *>Д> (А = Tv">v = 1,2,...,ЛГ - 1) позволяет
ориентировочно оценить наиболее предпочтительное число классов для данной
совокупности объектов. При этом основанием для выбора числа классов
может служить многократное повторение одного и того же числа классов
для нескольких последовательных значений Rrv* и его резкое возрастание
на следующем шаге.
Если ставится задача разбить совокупность на заданное число
классов, то одна из моделей модификации алгоритма «Форель-1» — «Форель-
2» методом последовательных приближений позволяет находить
минимальный радиус /Jmin, дающий разбиение на заданное число классов.
Покажем теперь, как процедура выделения одного класса точек из
совокупности, являющаяся основой алгоритмов типа «Форель», может быть
изложена в рамках описанной выше общей схемы «эталонных
алгоритмов». Выделение класса точек из совокупности эквивалентно
разделению совокупности на два класса. В качестве набора эталонных множеств
Е = (EiyE2) будем брать две точки Е = (ei,e2). Функцию у>(Х,е^)
опре(
делим следующим образом: <р(Х,е\) = рЕ(Х,ei); tp(Xi,e2) = #, где R —
выбранная величина радиуса. Функция ф(Х, 5/, Е) может быть определена
многими способами, например так:
12.4.9. Последовательные кластер-процедуры
Если число п классифицируемых наблюдений Xi,X2,. ..,Xn
достаточно велико (от нескольких сотен и более), то, как мы уже отмечали,
реализация кластер-процедур иерархического и параллельного типов крайне
трудоемка, а иногда и практически невозможна. В этих случаях
пользуются итерационными алгоритмами, на каждом шаге которых
последовательно обсчитывается лишь небольшая часть исходных наблюдений,
например одно из них. В том, что п велико, имеются не только неудобства,
но и свои преимущества. В частности, это позволяет исследовать
асимптотические (по п) свойства соответствующих процедур, аналогичные,
например, свойствам состоятельности, асимптотической несмещенности
и т.п., анализируемым в теории статистического оценивания и
статистической проверки гипотез.

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 513
Как и в параллельных алгоритмах, основными средствами и идеями,
при конструировании последовательных кластер-процедур являются:
мера близости или расстояние между группами; порог; эталонные множества
или точки; функционал качества разбиения.
Так же, как и прежде, более простой, а, главное, всегда имеющей
решение, является обычная задача типизации, при которой исходное
множество многомерных наблюдений разбивается на определенное число
«областей группирования» по принципу наперед заданной взаимной близости
элементов, отнесенных к одной области группирования. Простейшим
примером такого рода является разбиение на интервалы группирования
исходной выборки одномерных наблюдений, особенно необходимое как раз
при достаточно больших объемах выборки п.
Именно такую задачу решает, например, простой последовательный
алгоритм, использующий понятие порога с. В этом алгоритме случайным
образом выбирается точка Х\, которая объявляется центром в\ первой
группы. Затем точка Х2 относится к первой группе, если р(Х2,е\) < с.
В противном случае Х2 принимается за центр второй группы Х2 = е2 и
т. д. На 1-й шаге, когда уже имеется г групп, точка Х\ либо становится
центром (г - 1)-й группы, либо относится к той из групп, для которой
p(X^ej) < с. Если таких групп несколько, то выбирается та, к центру
которой точка Х\ ближе всего; если и таких групп несколько, то
устанавливаются некоторые соглашения о том, куда относить Х\ в этом случае.
Остановимся далее на описании двух наиболее общих и наиболее
исследованных последовательных кластер-процедурах.
а) Метод /^-средних. Пусть наблюдения Х\%Х2,...,Хп требуется
разбить на заданное число к (к ^ п) однородных (в смысле некоторой
метрики р) классов.
Смысл описываемого алгоритма — в последовательном уточнении
эталонных точек Е^ = {q' ,е2 ,. ..,4. } (v — номер итерации, v =
0,1,2,...) с соответствующим пересчетом приписываемых им «весов»
irv' = {u[v\u2\ ... ,и>ь}. При этом нулевое приближение е'0' строится
с помощью случайно выбранных первых к точек исследуемой
совокупности, т. е.
eW . х
ei — AD
wjo) = l, г = 1,2,...,*.
Затем на 1-м шаге «извлекается» точка Xk+i и выясняется, к какому из
эталонов е\ ' она оказалась ближе всего. Именно этот, самый близкий
к Xfc+i? эталон заменяется эталоном, определяемым как центр тяжести
старого эталона и присоединенной к нему точки Х^+г (с увеличением на
17 Теория вероятностей
и прикладная статистика

514 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
единицу соответствующего ему веса), а все другие эталоны остаются
неизменными (с прежними весами) и т. д. Таким образом, пересчет эталонов и
весов на v-м шаге, т.е. при извлечении очередной точки Xfc+V, происходит
по следующему правилу:
в противном случае,
/ v (v-l)\ • /v (v-l)\
если p\Ak+v>ti ) = шп р(Ль+ы^ h
и± ', в противном случае,
При этом если обнаруживается несколько (по i) одинаковых
минимальных значений р(Л*+«>с< '), то можно условиться относить точку
Xk+V к эталону с минимальным порядковым номером.
При достаточно большом числе итераций или при достаточно
больших объемах классифицируемых совокупностей п и при весьма широких
ограничениях на природу исследуемых наблюдений дальнейший пересчет
эталонных точек практически не приводит к их изменению, т.е. имеет
место сходимость (в определенном смысле) E'v' к некоторому пределу при
v —> оо.
Если же в какой-то конкретной задаче исследователь не успел
добраться до стадии практически устойчивых (по v) значений эталонных
точек, то пользуются одним из двух вспомогательных приемов. Либо
«зацикливают» алгоритм, «прогоняя» его после рассмотрения последней
точки Хп = Xk+(n-k) снова через точку Х\% затем Хг, и т.д., либо
производят многократное повторение алгоритма, используя в качестве начального
эталона Е( ' различные комбинации из к точек исследуемой совокупности
и выбирая для дальнейшего наиболее повторяющийся (в некотором
смысле) финальный эталон E*n~ \
Окончательное разбиение S исследуемой совокупности многомерных
наблюдений на к классов производится в соответствии с правилом
описанного выше минимального дистанционного разбиения 5(Е) относительно
центров тяжести (эталонов) Е = Е*п~ , которое, кстати, является
частным случаем разбиений ранее описанной общей схемы эталонных
алгоритмов, получающихся при

12.4 КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ 515
т.е.
5|(В) = {X: р{Х,Е{) < р(Х,Е^ j = 1,2,...,*; j ф /}.
Если оказывается, что р(Х} Е() = р(Х% Ej), то точку X относят к тому из
классов 5/ и Sj, который обладает меньшим порядковым номером.
Проведенные исследования свойств метода А-средних (см., например,
[Айвазян С. А. и др., 1989] говорят о том, что в достаточно общих
ситуациях при больших объемах выборочных совокупностей этот алгоритм
строит разбиение, близкое к наилучшему в смысле функционала A2.25).
б) Метод fc-средних при неизвестном числе классов. Для
обобщения описанного метода на случай неизвестного числа классов следует
задаться двумя константами Фо и Фо, названными соответственно мерой
грубости и мерой точности. Работа алгоритма также состоит в
последовательном построении эталонных точек E*v' = (Щь\...9Е$ух) и весов
u[v ,.. *)Wuv\y но число классов k(v) может меняться при этом от
итерации к итерации.
На нулевом шаге итерации берется любое начальное Аг(О) и полагается
Затем производится процедура «огрубления» эталонных точек. А именно,
подсчитывается расстояние между двумя ближайшими эталонными
точками и сравнивается это расстояние с заданной мерой грубости Фо. Если
это минимальное расстояние меньше Фо, то соответствующая пара
эталонных точек заменяется их взвешенным средним с весом, равным сумме
соответствующих двух весов. Процедура огрубления заканчивается
тогда, когда расстояние между любыми двумя эталонными точками не
меньше чем Фо. Пусть в результате процедуры огрубления мы имеем число
эталонных точек к(О)(к(О) < &@)), эталонные точки Ej(j = 1,...Д@))
^0)
На первом шаге итерации извлекается точка A*(o)+i и
вычисляется расстояние от X^o)+i до ближайшей к ней эталонной точки Ej(j =
1,...Д@)). При этом если это расстояние больше Фо, то Xfc(o)+i
объявляется НОВОЙ ЭТаЛОННОЙ ТОЧКОЙ i?A;@)+l = A*jfe(o)+1 С ВеСОМ Ш{(о)+1 = 1?
а все остальные эталонные точки и соответствующие им веса остаются
неизменными.
Бели это минимальное расстояние меньше чем Фо> то самый
близкий к Хд.(о)+1 эталон заменяется эталоном, определяемым как центр
тяжести старого эталона и присоединенной к нему точки Xk(o)+i. Вес точки
17*

516 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Xfc@)+i считается равным 1. Вес этого нового эталона равен сумме весов
объединяемых точек (старого эталона и точки Xk(o)+i)-
Все остальные эталоны и соответствующие веса остаются
неизменными. Таким образом, пересчет эталонов и весов в этом случае происходит
точно так же, как и в обычном методе fc-средних.
После процедуры огрубления эталонных точек переходят ко 2-му
шагу итерации и так далее.
Выбирая различные константы Фо, Ф<ь мы будем с помощью этого
алгоритма получать различные разбиения. Выбор величин Фо и Фо
можно считать удачным, если разбиение, соответствующее этим величинам,
признается оптимальным или с точки зрения экспертов, или в смысле
принятых функционалов качества разбиения.
ВЫВОДЫ
1. Разделение рассматриваемой совокупности объектов или явлений
на однородные (в определенном смысле) группы называется
классификацией. При этом термин «классификация» используют, в зависимости
от контекста, для обозначения как самого процесса разделения, так и его
результата. Это понятие тесно связано с такими терминами, как
группировка, типологизация, систематизация, дискриминация, кластеризация, и
является одним из основополагающих в практической и научной
деятельности человека.
2. Среди типов прикладных задач классификации следует выделить:
1) комбинационные группировки и их непрерывные обобщения —
разбиение совокупности на интервалы (области) группирования; 2) простая
типологизация: выявление естественного расслоения анализируемых
данных (объектов) на четко выраженные «сгустки» (кластеры), лежащие
друг от друга на некотором расстоянии, но не разбивающиеся на столь
же удаленные друг от друга части; 3) связная неупорядоченная
типологизация: использование реализованной в пространстве результирующих
показателей простой типологизации в качестве обучающих выборок при
классификации той же совокупности объектов в пространстве
описательных признаков; 4) связная упорядоченная типологизация, которая
отличается от связной неупорядоченной возможностью экспертного
упорядочения классов, полученных в пространстве результирующих показателей, и
использованием этого упорядочения для построения сводного латентного
результирующего показателя как функции от описательных переменных;
5) структурная типологизация дает на «выходе» задачи
дополнительно к описанию классов еще и описание существующих между ними и их
элементами структурных (в том числе иерархических) связей; 6) типоло-

выводы 517
гизация динамических траекторий системы: в качестве
классифицируемых объектов выступают характеристики динамики исследуемых систем,
например, дискретные или непрерывные временные ряды или траектории
систем, которые в каждый момент времени могут находиться в одном из
заданных состояний.
3. Определяющим моментом в выборе подходящей математической
постановки для конкретной задачи классификации является ответ на
вопрос, на какой исходной информации будут основаны наши выводы.
Исходную информацию целесообразно подразделять на: а) априорные
сведения об искомых классах; б) предварительную выборочную информацию
(так называемые обучающие выборки); в) наблюдения, подлежащие
классификации. Определение необходимого для решения анализируемой
задачи классификации математического инструментария (моделей, методов)
в зависимости от характера и состава исходной информации может быть
осуществлено с помощью табл. 12.3.
3, Если исследователь (статистик, эконометрист) располагает,
наряду с классифицируемыми данными, так называемыми обучающими
выборками A2.1), то для решения задачи классификации он должен
обратиться к методам дискриминантного анализа (см. п. 12.2). При этом
каждый класс интерпретируется как одномодальная генеральная
совокупность, закон распределения вероятностей (з.р.в.) которой оценивается по
соответствующей обучающей выборке. Если априорные сведения
позволяют сделать вывод об общем параметрическом виде з.р.в. каждого
класса, то используют методы параметрического дискриминантного анализа
(ДА). Если общий вид закона распределения внутри классов неизвестен,
то обучающие выборки используются для получения непараметрических
оценок внутриклассовых з.р.в., а сами процедуры классификации
называют непараметрическим ДА.
5. Общая постановка задачи классификации объектов в условиях
отсутствия обучающих выборок (т.е. задачи автоматической
классификации) состоит в требовании разбиения этой совокупности на некоторое
число (заранее известное или нет) однородных в определенном смысле
классов. При этом априорные сведения об искомых классах могут давать
основания для того, чтобы интерпретировать каждый искомый класс как
параметрически заданную одномодальную генеральную совокупность, и
тогда для построения правила классификации может быть использована
модель смеси распределений. При более скудных априорных сведениях
о классах используются методы и модели кластер-анализа^ включая
иерархические методы классификации. В обоих случаях исходная
статистическая информация (наблюдения, подлежащие классификации) пред-

518 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ставлены матрицами вида (9.1) «объект-свойство». В задачах кластер-
анализа исходная статистическая информация может быть представлена
также матрицей попарных расстояний (или близостей) вида (9.2).
Понятие «однородности» основано на предположении, что геометрическая
близость двух или нескольких объектов означает близость их
«физических» состояний, их сходство.
в. Решить задачу расщепления смеси распределений (в выборочном
варианте) — это значит по имеющейся выборке классифицируемых
наблюдений, извлеченной из генеральной совокупности, являющейся смесью
генеральных одномодальных совокупностей известного параметрического
вида, построить статистические оценки для числа компонентов смеси, их
удельных весов и параметров, их определяющих. После этого отнесение
классифицируемых наблюдений к тому или иному классу производится по
тем же правилам, что и в схеме дискриминантного анализа. В
теоретическом варианте задача расщепления смеси заключается в восстановлении
компонентов смеси и смешивающей функции (удельных весов) по
заданному распределению всей (т.е. смешанной) генеральной совокупности и
называется задачей идентификации компонентов смеси (эта задача не
всегда имеет решение).
7. Базовая идея, лежащая в основе принятия решения, к какой из к
анализируемых генеральных совокупностей следует отнести
классифицируемое наблюдение, является одной и той же как для модели
дискриминантного анализа (классификация при наличии обучения; см. п. 12.2), так
и для модели смеси: и в том и в другом случае наблюдение приписывают
к той генеральной совокупности (к тому компоненту смеси), в рамках
которой (которого) оно выглядит наиболее правдоподобным. Однако
главное отличие схемы параметрического ДА от схемы автоматической
классификации, построенной на модели смеси распределений, — в способе
оценивания неизвестных параметров, от которых зависят функции,
описывающие классы (в первом случае — по обучающим выборкам, а во втором
неизмеримо сложнее — в рамках одного из методов оценки параметров
смеси распределений).
8. Основными «узкими местами» подхода, основанного на
методе максимального правдоподобия статистического оценивания
параметров смеси распределений, являются (помимо необходимости «угадать»
общий параметрический вид распределения, задающего каждый из
классов) требование ограниченности анализируемой функции правдоподобия,
высокая сложность и трудоемкость процесса вычислительной реализации
соответствующих процедур и медленная сходимость порождаемых ими
итерационных алгоритмов.

выводы 519
9. Математическая постановка задачи автоматической
классификации в рамках неиерархических схем кластер-анализа требует
формализации понятия «качество разбиения». С этой целью в рассмотрение
вводится понятие критерия (функционала) качества разбиения Q(S),
который задает способ сопоставления с каждым возможным разбиением S
заданного множества объектов на классы некоторого числа Q(S)}
оценивающего (в определенной шкале) степень оптимальности данного разбиения.
Тогда задача поиска наилучшего разбиения 5* сводится к решению
оптимизационной задачи вида
Q(S) -> extr,
^v ' sea'
где А — множество всех допустимых разбиений.
В статистической практике выбор функционала качества разбиения
Q(S) обычно осуществляется весьма произвольно и опирается скорее
на эмпирические и профессионально-интуитивные соображения, чем на
какую-либо точную формализованную схему.
10. В статистических классификационных процедурах
иерархического типа главной целью анализа является получение наглядного
представления о стратификационной структуре всей классифицируемой
совокупности в виде дендрограммы.
11. Выбор метрики (или меры близости) между объектами, каждый
из которых представлен значениями характеризующего его многомерного
признака, является узловым моментом исследования, от которого
решающим образом зависит окончательный вариант разбиения объектов на
классы при любом используемом для этого алгоритме разбиения. В каждой
конкретной задаче этот выбор должен производиться по-своему, в
зависимости от главных целей исследования, физической и статистической
природы анализируемого многомерного признака, априорных сведений о его
вероятностной природе и т. д. В этом смысле схемы, основанные на
анализе смесей распределений, а также классификация по исходным данным,
уже представленным в виде матрицы попарных расстояний (близостей),
находятся в выгодном положении, поскольку не требуют решения вопроса
о выборе метрики.
12. Важное место в построении классификационных процедур, в
первую очередь иерархических, занимает проблема выбора способа
вычисления расстояния между подмножествами объектов. Полезное обобщение
большинства используемых в статистической практике вариантов
вычисления расстояний между двумя группами объектов дает расстояние,
подсчитываемое как обобщенное степенное среднее всевозможных попарных
расстояний между представителями рассматриваемых двух групп (см.
A2.21)).

ГЛАВА 13. СНИЖЕНИЕ РАЗМЕРНОСТИ
ИССЛЕДУЕМОГО МНОГОМЕРНОГО
ПРИЗНАКА И ОТБОР НАИБОЛЕЕ
ИНФОРМАТИВНЫХ ПОКАЗАТЕЛЕЙ
13.1. Сущность, типологизация и
прикладная направленность задач
снижения размерности
В исследовательской и практической статистической работе
приходится сталкиваться с ситуациями, когда общее число р признаков
аг ,аг ',... , z , регистрируемых на каждом из множества обследуемых
объектов (стран, городов, предприятий, семей, пациентов, технических
или экологических систем), очень велико — порядка ста и более. Тем не
менее имеющиеся многомерные наблюдения
Л2)
\Х
(р) )
г = 1,2,...,п,
A3.1)
следует подвергнуть статистической обработке, осмыслить либо ввести в
базу данных для того, чтобы иметь возможность их использовать в
нужный момент.
Желание статистика представить каждое из наблюдений A3.1) в
виде вектора Z некоторых вспомогательных показателей z , z' ... ,z ' с
существенно меньшим (чем р) числом компонент р бывает обусловлено в
первую очередь следующими причинами:
• необходимостью наглядного представления (визуализации)
исходных данных A3.1), что достигается их проецированием на специально

13.1 СУЩНОСТЬ ЗАДАЧ СНИЖЕНИЯ РАЗМЕРНОСТИ 521
подобранное трехмерное пространство (р = 3), плоскость (р = 2) или
числовую прямую;
• стремлением к лаконизму исследуемых моделей, обусловленному
необходимостью упрощения счета и интерпретации полученных
статистических выводов;
• необходимостью существенного сжатия объемов хранимой
статистической информации (без видимых потерь в ее информативности), если
речь идет о записи и хранении массивов типа A3.1) в специальной базе
данных.
При этом новые (вспомогательные) признаки z'1 , г" ,..., z ' могут
выбираться из числа исходных или определяться по какому-либо правилу
по совокупности исходных признаков, например как их линейные
комбинации. При формировании новой системы признаков к последним
предъявляются разного рода требования, такие, как наибольшая
информативность (в определенном смысле), взаимная некоррелированность,
наименьшее искажение геометрической структуры множества исходных данных
и т. п. В зависимости от варианта формальной конкретизации этих
требований приходим к тому или иному алгоритму снижения размерности.
Имеется, по крайней мере, три основных типа принципиальных
предпосылок, обусловливающих возможность перехода от большого числа р
исходных показателей состояния (поведения, эффективности
функционирования) анализируемой системы к существенно меньшему числу р
наиболее информативных переменных. Это, во-первых, дублирование
информации^ доставляемой сильно взаимосвязанными признаками; во-вторых,
неинформативность признаков, мало меняющихся при переходе от
одного объекта к другому (малая «вариабельность» признаков); в-третьих,
возможность агрегирования, т.е. простого или «взвешенного»
суммирования, по некоторым признакам.
Формально задача перехода (с наименьшими потерями в
информативности) к новому набору признаков 2т1',Зг \...,2гр ' может быть описана
следующим образом. Пусть Z = Z(X) = (z ,*г ,..., 2гр') —
некоторая р'-мерная вектор-функция от исходных переменных аг ,аг ',...,агр'
(р < р) и пусть Ipt(Z(X)) — определенным образом заданная мера
информативности р'-мерной системы признаков Z(X) = (z' (X),..., z"v (X)) .
Конкретный выбор функционала Ip'(Z) зависит от специфики решаемой
реальной задачи и опирается на один из возможных критериев: критерий
автоинформативности, нацеленный на максимальное сохранение
информации, содержащейся в исходном массиве {^}1==^-^ относительно самих
исходных признаков; и критерий внешней информативности, нацеленный

522 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
на максимальное «выжимание» из {Xi}i=y$ информации, содержащейся
в этом массиве относительно некоторых других (внешних) показателей.
Задача заключается в определении такого набора признаков Z,
найденного в классе F(A') допустимых преобразований исходных показателей
()()
A3.2)
Тот или иной вариант конкретизации этой постановки
(определяющий конкретный выбор меры информативности IP»(Z) и класса
допустимых преобразований) приводит к конкретному методу снижения
размерности: к методу главных компонент, факторному анализу, экстремальной
группировке параметров и т. д.
Математическая модель, лежащая в основе построения того или
иного метода снижения размерности, включает в себя обычно три
основных компонента.
1. Форма задания исходной информации. Речь идет об
ответе на следующие вопросы: а) в каком виде (т.е. в виде (9.1), (9.2) или
еще каком-либо) задана описательная информация об объектах? б)
имеется ли среди исходных статистических данных обучающая информация,
т.е. какие-либо сведения об анализируемом результирующем свойстве?
в) если обучающая информация присутствует в исходных статистических
данных, то в какой именно форме она представлена? Это могут быть, в
частности, в привязке к объекту О* (i = 1,2,..., п): значения «зависимой»
количественной переменной («отклика») yi в моделях регрессии; номер
однородного по анализируемому свойству класса, к которому относится
объект Oi в задаче классификации; порядковый номер (ранг) объекта О,-
в ряду всех объектов, упорядоченных по степени проявления
рассматриваемого свойства, в задачах анализа предпочтений и построения
упорядоченных типологизаций; наконец, значения У* = (у\ ,...,у{ ) набора
результирующих признаков, характеризующих анализируемое в
классификационной задаче свойство .
1 Речь идет о нахождении (в виде функции от X) такого вектора Z(X) =
(z(l\X),...,z(p )(X))T, который обращает в максимум или минимум (в
зависимости от конкретного содержательного смысла оптимизируемого критерия
информативности) значение Ipi(Z). Поэтому справа в данном соотношении записано extr
(«экстремум»).
2 Перечисленные варианты не исчерпывают всех возможных форм представления
обучающей информации. Так, например, при надлежащей интерпретации элементов

13.1 СУЩНОСТЬ ЗАДАЧ СНИЖЕНИЯ РАЗМЕРНОСТИ 523
2. Тип оптимизируемого критерия IP*(Z) информативности
искомого набора признаков Z = (яг ,,..,ягр') . Как уже
отмечалось, критерий информативности может быть ориентирован на
достижение разных целей.
Следует выделить целый класс критериев автоинформативности,
т. е. критериев, оптимизация которых приводит к набору
вспомогательных переменных Z = (яг1 ,. ..,ягр) , позволяющих максимально точно
воспроизводить (в том или ином смысле, в зависимости от конкретного
вида критерия) информацию, содержащуюся в описательном массиве
данных типа (9.1) или (9.2). Если описательная информация представлена в
виде матрицы «объект - свойство» (9.1), то речь идет о максимально
точном восстановлении р х п значений исходных переменных а^1 , ж| ,..., х\р'
по значениям существенно меньшего числа (р х п) вспомогательных
переменных z\ ,...,?;. Бели же описательная информация
представлена в виде матрицы попарных сравнений объектов (9.2), то речь идет о
максимально точном воспроизведении п элементов этой матрицы
(i,j = 1,...,п) по значениям существенно меньшего числа {р1 х п)
вспомогательных переменных z\ ,..., z\p ' (i = 1,..., n).
Будем называть критериями внешней информативности (имеется
в виду информативность, внешняя по отношению к информации,
содержащейся в описательном массиве (9.1) или (9.2)) такие критерии Ip*(Z),
которые нацелены на поиск экономных наборов вспомогательных
переменных Z(X) = (z* (X),...,2гр (X)) , обеспечивающих максимально
точное воспроизведение (по значениям Z, а значит в конечном счете по
значениям X) информации, относящейся к результирующему признаку
(варианты ее задания перечислены выше, в п. 1).
3. Класс F(X) допустимых преобразований исходных
признаков X. Вспомогательные признаки Z = (z* ,. ..,2гр ') в случае
представления исходной описательной информации в форме матрицы
«объект - свойство» (т.е. в виде (9.1)) конструируются в виде функций от
X, т.е. Z = Z(X). Как обычно в таких ситуациях, чтобы обеспечить
содержательность и конструктивную реализуемость решения
оптимизационной задачи A3.2), следует предварительно договориться об
ограниченном классе допустимых решений F(Jf), в рамках которого эта
оптимизационная задача будет решаться. Очевидно, от выбора F(X) будет су-
7ij матрицы (9.2) она может быть также отнесена к разновидностям обучающей
информации (если, скажем, 7ij понимать как результат сравнения по анализируемому
результирующему свойству объектов О,- и О;-).

524
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
щественно зависеть и получаемое решение Z{X) = (jt (X),..., it '
упомянутой оптимизационной задачи.
Итак, следуя предложенной выше логике, мы должны были бы
произвести типологизацию задач снижения размерности по трем «входам»
(или «срезам»): форме задания исходной информации, типу (смыслу)
оптимизируемого критерия информативности и классу допустимых
преобразований исходных переменных. Однако в предлагаемой ниже форме
представления результатов типологизации задач снижения размерности
(табл. 13.1) эти принципы реализованы в упрощенном виде за счет
следующих двух практических соображений: 1) подавляющее большинство
методов снижения размерности базируется на линейных моделях, т. е. класс
Таблица 13.1
(АИ — автоинформативность, ВИ
внешняя информативность)
п/п
1
1
2
3
Класс и смысловая нацеленность критерия
информативности; форма задания
исходной информации
2
АИ: максимизация содержащейся ъ z ,..., zx '
доли суммарной вариабельности исходных
признаков аг ,..., ж .
Описательная информация: в форме (9.1).
Обучающая информация: нет
АИ: Максимизация точности воспроизведения
корреляционных связей между исходными
признаками по их аппроксимациям с помощью
вспомогательных переменных z" ,..., г9 К
Описательная информация: в форме (9.1).
Обучающая информация: нет
АИ: разбиение исходных признаков на группы
высококоррелированных (внутри группы)
переменных и отбор от каждой группы фактора,
имеющего максимальную интегральную
характеристику корреляционных связей со всеми
признаками данной группы.
Описательная информация: в форме (9.1).
Обучающая информация: нет
Название
соответствующих
моделей и методов.
Главы и пункты
книги
3
Метод главных
компонент, п. 13.2
Модели и методы
факторного
анализа и главных
компонент,
п. 13.2 и 13.3
Метод
экстремальной
группировки
параметров, п. 13.4

13.1 СУЩНОСТЬ ЗАДАЧ СНИЖЕНИЯ РАЗМЕРНОСТИ
525
Продолжение таблицы 13Л
1
4
5
6
7
2
АИ: приписывание каждому объекту 0» значений
условных координат (z\ ,..., zf ') таким
образом, чтобы по ним максимально точно
восстанавливалась заданная структура попарных
описательных отношений между объектами.
Описательная информация: в форме (9.2).
Обучающая информация: нет
АИ: максимальное сохранение заданных
описательным массивом (9.1) анализируемых
структурно-геометрических и вероятностных
свойств после его проецирования в пространство
меньшей размерности (в пространство,
натянутое на г'1',..., тг , р < р).
Описательная информация: в форме (9.1).
Обучающая информация: нет
ВИ: минимизация ошибки прогноза
(восстановления) значения результирующей
количественной переменной по значениям
описательных переменных (предикторов).
Описательная информация: в форме (9.1).
Обучающая информация: в форме
зарегистрированных на объектах 0\,..., 0п
значений соответственно у\,..., уп
результирующего количественного
показателя у
ВИ: минимизация вероятностей ошибочного
отнесения объекта к одному из заданных
классов по значениям его описательных
переменных.
Описательная информация: в форме (9.1).
Обучающая информация: для каждого
описанного с помощью (9.1) объекта
указан номер класса, к которому
он относится
3
Многомерное
шкалирование,
п. 13.6
Методы
целенаправленного
проецирования
и отбор типо-
образующих
признаков в
кластер-анализе,
метод главных
компонент, п. 13.2
и гл.12
Отбор
существенных
предикторов в
регрессионном
анализе,
гл. 2 в томе 2
Отбор типо-
образующих
признаков в
дискриминантном
анализе, гл. 12

526
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Продолжение таблицы 13.1
1
8
9
2
ВИ: максимизация точности воспроизведения
(по значениям вспомогательных признаков)
заданных в «обучении» отношений объектов
по анализируемому результирующему свойству.
Описательная информация: в форме (9.1).
Обучающая информация: в форме попарных
сравнений или упорядочений объектов по
анализируемому результирующему свойству
(см. сноску к п. 1 о возможности
использования формы (9.2) для представления
обучающей информации)
ВИ: максимизация точности воспроизведения
(по значениям условных вспомогательных
переменных) заданных в «обучающей
информации» попарных отношений объектов
по анализируемому результирующему свойству.
Описательная информация: нет.
Обучающая информация: в форме (9.2)
(см. сноску к п. 1)
3
Методы

латентно-структурного анализа,
в том числе
построение
некоторой
сводной латентной
характеристики
изучаемого

результирующего свойства,
п. 13.5
Многомерное
шкалирование
как средство

латентно-структурного анализа,
п. 13.6
допустимых преобразований F(X) — это класс линейных (как правило,
подходящим образом нормированных) преобразований исходных
признаков аг ',...,ж , 2) спецификация формы задания исходной информации
связана со спецификацией смысловой нацеленности критерия
информативности, а поэтому их удобнее давать в общей графе.
Данная в табл. 13.1 типологизация, как и всякая иная
классификация, не претендует на исчерпывающую полноту. Заметим, что пункт 9
этой таблицы повторяет по существу пункт 4, они отличаются только
интерпретацией исходных данных вида (9.2) и соответственно конечными
прикладными целями исследования.
13.2. Метод главных компонент
13.2.1. Основные понятия и определения
Во многих задачах обработки многомерных наблюдений и, в
частности, в задачах классификации исследователя интересуют в первую оче-

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 527
редь лишь те признаки, которые обнаруживают наибольшую
изменчивость (наибольший разброс) при переходе от одного объекта к другому.
С другой стороны, не обязательно для описания состояния
объекта использовать какие-то из исходных, непосредственно замеренных на
нем признаков. Так, например, для определения специфики фигуры
человека при покупке одежды достаточно назвать значения двух признаков
(размер-рост), являющихся производными от измерений ряда параметров
фигуры. При этом, конечно, теряется какая-то доля информации (портной
измеряет до одиннадцати параметров на клиенте), как бы огрубляются
(при агрегировании) получающиеся при этом классы. Однако, как
показали исследования, к вполне удовлетворительной классификации людей с
точки зрения специфики их фигуры приводит система, использующая три
признака, каждый из которых является некоторой комбинацией от
большого числа непосредственно замеряемых на объекте параметров.
Именно эти принципиальные установки заложены в сущность того
линейного преобразования исходной системы признаков, которое приводит
к главным компонентам. Формализуются же эти установки следующим
образом.
Следуя общей оптимизационной постановке задачи снижения
размерности A3.2) и полагая анализируемый признак X р-мерной случайной
величиной с вектором средних значений а = (аг , ...,сг') и
ковариационной матрицей ? = (<7^) (i,j = 1,2, ...,р), вообще говоря, неизвестными,
определим в качестве класса F(X) допустимых преобразований
исследуемых признаков аг ,аг , ...,агр' их всевозможные линейные
ортогональные нормированные комбинации, т. е.
-«<*>
), , = 1,2,...,Л,
где
для j = 1,2,...,р и к = 1,2,...,р, но j ф /с, а в качестве
критерия (меры) информативности р'-мерной системы показателей Z(X) =
A)B).м*(р1)(Л1)) выражение

528 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Тогда при любом фиксированном р = 1,2,... ,р вектор искомых
вспомогательных переменных Z(X) = (^г\х),.. . ,?р (Х))Т определяется
как такая линейная комбинация
A3.5)
(где
матрица, строки которой удовлетворяют условию ортогональности), что
Полученные таким образом переменные 2* \Х),...,Игр\Х) и
называют главными компонентами вектора X. Отсюда вытекает следующее
определение главных компонент.
Первой главной компонентой Тг (X) исследуемой системы
показателей X = (ж^ ,...,ж ) называется такая нормированное
центрированная линейная комбинация этих показателей, которая среди
всех прочих нормированно-центрированных линейных комбинаций пере-
менных ж*1 ,..., агр' обладает наибольшей дисперсией.
k-й главной компонентой zr (X) (к = 2,3, ...,р)
исследуемой системы показателей X = (ж , ...,аг ) называется такая
нормированно-центрированная линейная комбинация этих показателей,
которая не коррелирована с k-l предыдущими главными компонентами
и среди всех прочих нормированно-центрированных и некоррелированных
с предыдущими к — 1 главными компонентами линейных комбинаций
переменных аг ,...,агр* обладает наибольшей дисперсией.
Замечание 1 (переход к центрированным переменным).
Поскольку, как увидим ниже, решение задачи (а именно вид матрицы
линейного преобразования L) зависит только от элементов ковариационной
матрицы Е, которые в свою очередь не изменяются при замене исходных
переменных ж'" переменными х^*' - с' (г3' — произвольные постоянные
числа), то в дальнейшем будем считать, что исходная система показателей
уже центрирована, т.е. что Еж*" = 0, j = 1,2,...,р. В статистической
практике этого добиваются, переходя к наблюдениям х\3' = ж^ -Зг , где
= ]?Г=1 ж| /п (для упрощения обозначений волнистую черту над цен-

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 529
трированной переменной и над главной компонентой в дальнейшем
ставить не будем).
Замечание 2 (переход к выборочному варианту). Поскольку в
реальных статистических задачах располагаем лишь оценками а и ?
соответственно вектора средних а и ковариационной матрицы ?, то во всех
дальнейших рассуждениях под а'" понимается зг , а под d^j —
выборочная ковариация vkj = ElUO*!** - x{k))(x\j) - xU))/n (j,* = 1,2,...,р).
Замечание 3. Использование главных компонент оказывается
наиболее естественным и плодотворным в ситуациях, в которых все
компоненты аг1 , аг ', ..., х^р* исследуемого вектора X имеют общую
физическую природу и соответственно измерены в одних и тех же единицах. К
таким примерам можно отнести исследование структуры бюджета
времени индивидуумов (все аг' измеряются в единицах времени), исследование
структуры потребления семей (все аг ' измеряются в денежных единицах),
исследование общего развития и умственных способностей индивидуумов
с помощью специальных тестов (все аг ' измеряются в баллах), разного
рода антропологические исследования (все аг' измеряются в единицах меры
длины) и т.д. Если же признаки аг ,аг %...,# измеряются в
различных единицах, то результаты исследования с помощью главных компонент
будут существенно зависеть от выбора масштаба и природы единиц
измерения. Поэтому в подобных ситуациях исследователь предварительно
переходит к вспомогательным безразмерным признакам ж** , например,
с помощью нормирующего преобразования
xy> = jV. Г« = 1.2 л
где ац соответствует ранее введенным обозначениям, а затем строит
главные компоненты относительно этих вспомогательных признаков X* и их
ковариационной матрицы ?^*, которая, как легко^ видеть, является
одновременно выборочной корреляционной матрицей R исходных наблюдений
13.2.2. Вычисление главных компонент
Из определения главных компонент следует, что для вычисления
первой главной компоненты необходимо решить оптимизационную задачу ви-

530 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
да A3.2), т.е. в данном случае:
Г D (/!*)-> max;
где li — первая строка матрицы L (см, A3.5)). Учитывая
центрированность переменной X (т.е. ЕХ = 0) и то, что Е(ХХ ) = 33, имеем
DAXX) = ЕAгХJ = Е^ЛГХ7/!7) = 7
Следовательно, задача A3.6) может быть записана
-»max; .
,,,т . " A3-в>
V ПП = 1)
Вводя функцию Лагранжа <р(/г, А) = ^ЗД - А(/1/1 - 1) и дифференцируя
ее по компонентам вектор-столбца /j , имеем (см. Приложение 2):
т
что дает систему уравнений для определения 1\:
(S-AI)/aT = 0 A3.7)
(здесь 0 = @,0,..., 0) — р-мерный вектор-столбец из нулей).
Для того чтобы существовало ненулевое решение системы A3.7) (а
оно должно быть ненулевым, так как 1\1\ =*1), матрица Е - AI должна
быть вырожденной, т. е.
|Е-А1| = 0. A3.8)
Этого добиваются подбором соответствующего значения А.
Уравнение A3.8) (относительно А) называется характеристическим для
матрицы Е. Известно (см. Приложение 2), что при симметричности и
неотрицательной определенности матрицы ? (каковой она и является как всякая
ковариационная матрица) это уравнение имеет р вещественных
неотрицательных корней Ai ^ Аз > • • • > Ар ^ 0, называемых
характеристическими (или собственными) значениями матрицы ?.
Учитывая, что D^1* = D(hX) = ^Е/^ и hJllT = А (последнее
соотношение следует из соотношения A3.7) после его умножения слева
на /ь с учетом l\lj = 1), получаем DHrl'(X) = А.

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 531
Поэтому для обеспечения максимальной величины дисперсии
переменной г' нужно выбрать из р собственных значений матрицы Е
наибольшее^ т. е.
Подставляем Ах в систему уравнений A3.7) и, решая ее относительно
hi> • • • >hpy определяем компоненты вектора 1^.
Таким образом, первая главная компонента получается как
линейная комбинация lrl\x) = 1\Х} где /j — собственный вектор матрицы
?, соответствующий наибольшему собственному числу этой матрицы.
Далее аналогично можно показать, что & (X) = 1^Х} где /*. —
собственный вектор матрицы 33, соответствующий А-му по величине
собственному значению А^ этой матрицы.
Таким образом, соотношения для определения всех р главных
компонент вектора X могут быть представлены в виде A3.5), где Z =
(i*,..., */Tf X = (аг',..,,агр')т, а матрица L состоит из строк
h = Сл > • • • *'jp)i 3 = l7p> являющихся собственными векторами матрицы
Е, соответствующими собственным числам А;*. При этом сама матрица L
в соответствии с условиями A3.3) является ортогональной, т.е.
LLT = LTL = I. A3.9)
В дальнейшем в целях упрощения обозначений мы будем опускать
«тильду» над переменными главных компонент, т.е. обозначать главные
компоненты просто Z = (jzt , 2' \ ..., z"v ').
13.2.3. Основные числовые характеристики главных
компонент
Определим основные числовые характеристики (средние значения,
дисперсии, ковариации) главных компонент в терминах основных
числовых характеристик исходных переменных и собственных значений
матрицы S:
) ()
б) ковариационная матрица вектора главных компонент:
Лг = E(ZZT) = Е
Умножая слева соотношения
(S - АДОГ = 0,

532 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
на lj (j = 1,р), получаем, что
L?LT = Ez =
V О АР /
A3.10)
Из A3.10), в частности, следует подтверждение взаимной
некоррелированности главных компонент, а также Л z ' = А*, (к = 1,р);
в) сумма дисперсий исходных признаков равна сумме дисперсий всех
главных компонент. Действительно,
к) = trEz = tr(LELT) = tr ((LE)LT)
p
= tr (LT(LE)) = tr ((LTL)S) = trE гГб/1;
Ar=l
A:=l
г) обобщенная дисперсия исходных признаков X (det E^) равна
обобщенной дисперсии главных компонент. Действительно, обобщенная
дисперсия вектора Z равна
det Vz = det(LELT) = det((LE)LT) = det (LT(LE))
= det ((LLT)S) =det(E).
Следствие 1. Из 6) и в), в частности, следует, что критерий
информативности метода главных компонент A3.4) может быть
представлен в виде
где Al5A2,...,Ap — собственные числа ковариационной матрицы S
вектора X, расположенные в порядке убывания.
Кстати, представление Ip>(Z(X)) в виде A3.4;) дает исследователю
некоторую основу, опорную точку зрения, при вынесении решения о том,
сколько последних главных компонент можно без особого ущерба
изъять из рассмотрения, сократив тем самым размерность исследуемого
пространства.
Действительно, анализируя с помощью A3.4 ) изменение
относительно доли дисперсии, вносимой первыми р главными компонентами, в
зависимости от числа этих компонент, можно разумно определить число

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ
533
компонент, которое целесообразно оставить в рассмотрении. Так, при
изменении Ipi, изображенном на рис. 13.1, очевидно, целесообразно было бы
сократить размерность пространства с р = 10 до р =3, так как
добавление всех остальных семи главных компонент может повысить суммарную
характеристику рассеяния не более чем на 10%.
X—X
1 23456789 10
Рис. 13.1. Изменение относительной доли суммарной дисперсии
исследуемых признаков, обусловленной первыми р1 главными
компонентами, в зависимости от р1 (случай р = 10)
Следствие 2. Если X* — вектор нормированных признаков
ж** ',...,ж* , т.е. Еж**' = 0 « Da;*'^ = 1 для j = 1,р, то
согласно замечанию 3 ковариационная и корреляционные матрицы совпадают
(т. е. Ex* = R) « «з б) « в) следует
или
Тогда критерий информативности A3.4) может быть представлен в
виде
Xl + "p+Xr ' A3.4")

534 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Проиллюстрируем вычисление и анализ главных компонент на
примере.
Пример 13.1. При формировании типообразующих признаков
предприятий отрасли были обследованы 24 предприятия (п = 24) по
трем технико-экономическим показателям: объему выпускаемой
продукции ж* , основным фондам аг2' и фонду оплаты труда аг' (все переменные
измерялись в денежных единицах). По полученным в результате
обследования исходным статистическим данным (х\ \х\ \х\ '), г = 1,2,...,24,
была определена выборочная ковариационная матрица
D51,39 271,17 168,70'
271,17 171,73 103,29
168,70 103,29 66,65 4
Решая, в соответствии с A3.8), кубическое уравнение (относительно
А) вида
451,39-А 271,17 168,70
271,17 171,73-А 103,29
= 0,
168,70 101,29 66,65-А
находим Ах = 680,40, А2 = 6,50, А3 = 2,86.
Подставляя последовательно численные значения Ai, А2 и А3 в систему
A3.7) и решая эти системы относительно неизвестных /t- = (^ъ^2>^з)
{% = 1,2,3), получаем
1г = @,8126 0,4955 0,3068),
12 = (-0,5454 0,8321 0,1006),
h = ( -0,2054 -0,2491 0,9465).
В качестве главных компонент получаем
zA)=0,81xA)+0,50a:B)+0,31a;C),
*<3)= -0,21хA)-0,25*B) +
Здесь под ж , аг ' и аг' подразумеваются отклонения объема
выпускаемой продукции (аг '), основных фондов (аг ') и фонда оплаты труда (аг3')
предприятия от соответствующих средних значений.
Вычисление относительной доли суммарной дисперсии,
обусловленной одной, двумя и тремя главными компонентами, в соответствии с фор-

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 535
мулой A3.4') дает
9A) = 1 .I1 , * = 0,9864;
9B) = *'**' = 0,9958;
9C) =1-
Отсюда можно сделать вывод, что почти вся информация о специфике
предприятия данного типа содержится в одной лишь первой главной
компоненте, которую и естественно использовать при соответствующей ти-
пологизации предприятий.
Матрица «нагрузок» А = (ay), i,j = 1,2,...,р, главных
компонент на исходные признаки также является важной
характеристикой главных компонент. Бели анализируемые переменные X =
(аг1 ,аг ,. . .,ж'р') предварительно процентрированы и
пронормированы (см. выше замечания 1 и 3), т.е. если главные компоненты
строятся для признаков X* = (х*{1\х*{2\. ..,s*(p))T, Es*(i) = 0, Dx*@ = 1,
i = 1,2,...,р, то элементы матрицы нагрузок ау определяют
одновременно степень тесноты парной линейной связи (т. е. парный коэффициент
корреляции) между а; и it3' и удельный вес влияния пронормированной
j-й главной компоненты на признак х*^% .
Матрица нагрузок А определяется соотношением
A = LTA*, A3.11)
где
о \
A3.12)
0 х/К I
Докажем, что элементы ау действительно обладают
сформулированными выше свойствами. Введем в рассмотрение нормированные главные
компоненты ZH = B5 ,*? »•••!*?) > получающиеся из обычных
главных компонент домножением на А"*, т.е.
ZH = A~*Z. A3.13)
Очевидно, что г„ ' = z /у/Х] и соответственно
В4Л = 1- A3.14)

536 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Выразим из соотношения A3.5) X* через Z:
X* = l~lZ = LTZ A3.15)
(при этом учтено, что мы, во-первых, упростили обозначения и вместо
Z теперь используем Z, а во-вторых, что матрица L — ортогональна по
условию (см. A3.3)) и, следовательно, L~ = L (см. Приложение 2)).
Принимая во внимание A3.11) и A3.13), из A3.15) получаем:
т.е.
X* = LTA*A~*Z = AZH, A3.16)
aipzip\ A3.16')
т. е. коэффициент atJ- действительно определяет удельный вес влияния j-й
ирован
Далее,
Е [(**<*>-Е**>
р
нормированной главной компоненты г„ на г-й исходный признак.
@ щ _
_ ( {i
= Е (х«*&) = Е [(anzil) + ... + aip4p)LJ)]
ati, A3.17)
т. е. коэффициент ay действительно определяет величину парного
коэффициента корреляции между ж***' и z' (при выводе соотношения A3.17)
использовались нормированность и центрированность переменных ж***' и
Zh , а также тот факт, что а%' = z /^/Aj).
Отметим еще два свойства элементов матрицы нагрузок А.
Из определения матрицы А A3.11) следует:
АТА = (аН)AтА*) = А*(ААТ)А* = А*А^ = А,
а это означает, что сумма квадратов элементов любого j-го столбца
матрицы А равна дисперсии (j-й) главной компоненты Aj, т. е.
a2xj + a22j + • • • + a2pj = \j. A3.18)

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ
537
Возводя в квадрат обе части соотношения A3.16 ) и беря
математическое ожидание от результата, непосредственно имеем:
D x*(i) = Е (antf + ¦ • • + aipziP)J = ?4 В DйJ =
т.е. с учетом Da; = 1 получаем, что сумма квадратов элементов
любой (i-й) строки матрицы нагрузок А равна единице.
Приведенные здесь свойства используются, в частности, при
содержательной интерпретации главных компонент. Так, соотношение A3.16 ) да-
U)
ет основание придавать главной компоненте zK ' содержательный смысл,
соответствующий исходному признаку ж***0 , для которого коэффициент
aioj достигает максимального значения (при условии, что \a(oj\ > 0N).
Пример 13.2. Компонентный анализ проведен по данным
двадцати сельскохозяйственных районов (п = 20) области, которые содержат
A)
результаты измерении следующих показателей: аг ' — число колесных
тракторов на 100 га; аг ' — число зерноуборочных комбайнов на 100 га;
аг' — число орудий поверхностной обработки почвы на 100 га; аг ' —
количество удобрений, расходуемых на гектар; аг ' — количество средств
защиты растений, расходуемых на гектар.
Требовалось выделить р < 5 первых главных компонент для анализа
и дать им содержательную интерпретацию.
Расчеты проводились по нормированным данным и представлены в
табл. 13.2.
Таблица 13.2
Главные компоненты jzt1'
Собственные значения А^
Вклад i-й главной компоненты (%)
в суммарную дисперсию
Суммарный вклад первых
главных компонент (%)
г**
3,04
60,8
60,8
1,41
28,2
89,0
0,43
8,6
97,6
zD)
0,10
2,0
99,6
0,02
0,4
100,0
При расчете относительного вклада главных компонент учитывалось,
что SjLa Aj = р = 5. Для анализа были оставлены две первые главные
компоненты (р = 2), на которые приходится 89% суммарной вариации.
Для интерпретации главных компонент построена матрица
факторных нагрузок
._@,95* 0,97* 0,94* 0,24
1-0,19 -0,17 -0,28 0,88*
),56\Т
,67*; •

538 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Звездочкой (*) отмечены элементы \а^\ > 0,6, которые следует учитывать
при интерпретации главных компонент яг1' и я .
Из вида матрицы нагрузок А следует, что первая главная компонента
наиболее тесно связана с показателями: аг ' — число колесных тракторов
(ап = r(ar \z^ ) = 0,95); ar ' — число зерноуборочных комбайнов (п2\ =
г(ж ,2т1') = 0,97); ж ' — число орудий поверхностной обработки почвы
на 100 га (a3i = г(аг ,-г ') = 0,94). Поэтому первая главная компонента
-г1' интерпретирована как уровень механизации работ.
B)
Вторая главная компонента zK ' тесно связана с количествами
удобрения (ж ) и средств защиты растений {яг '), расходуемых на гектар.
Соответственно ту ' интерпретируется как уровень химизации
растениеводства.
13.2.4. Геометрическая интерпретация главных компонент
Всякий переход к меньшему числу (р) переменных лг ,..., 2гр ',
осуществляемый с помощью ортогонального линейного преобразования
(матрицы) С = (с^), г = 1,2,... ,р;, j = 1,2,... ,р, можно рассматривать как
проекцию исследуемых р-мерных наблюдений Х\7Хз,.. *,Хп в
пространство размерности р\ натянутое на оси Oz^l\Oz" ,.. .,0лг , где
(i) jxU\ г=1,2,...,р;. A3.20)
При этом проекциями р-мерных исходных наблюдений Xi (г = 1,2,.. .,п)
будут р -мерные точки
Zi = CXi, г= 1,2,..., п. A3.21)
Для пояснения сущности того линейного преобразования исходной
системы признаков, которое приводит к главным компонентам, рассмотрим
его геометрическую интерпретацию на примере двумерной системы
наблюдений (х\ ,ж[^), г = 1,2,. ..,п, извлеченной из нормальной генераль-
нои совокупности со средним значением a = (a ,a ') и ковариационной
матрицей
Здесь Gi и 02 — дисперсии компонент соответственно г ' и г , а г —
коэффициент корреляции между ними. Геометрически это означает, что

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 539
точки (ж[ , ж[ ) будут располагаться примерно в очертаниях эллипсоидов
рассеивания вида (см. рис. 13.2а)
В этом случае для изучения (аг ,аг ') удобно перейти к новым координа-
там (zK \zK ) с помощью преобразования:
= _ (,<»> _ aA)) sin a + (*B) - aB)) cos a,
где
tg2a=
После этого преобразования точки (z\ \z\ ') также будут
распределены нормально, но компонента z ' уже не будет зависеть от z" . Кроме
того, если выбрать направления так, что D*r ' ^ Dz , то
геометрически это будет означать следующее: сначала производится перенос начала
координат в точку (ar , a '), а затем оси поворачиваются на угол а так,
чтобы ось 2г ' шла вдоль главной оси эллипсоида рассеивания (рис. 13.2а).
Чем ближе \г\ к единице, тем теснее группируются наблюдения около
главной оси эллипсоида рассеивания (т.е. около новой оси -г1') и тем менее
значащим для исследователя является разброс точек в направлении оси
zy , а следовательно, и сама эта координата. В предельном случае \г\ = 1,
исследуемые наблюдения в координатах (jt ,лг ') вообще не отличаются
по координате ,гг2' (см. рис. 13.26).

ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
.B).
Рис. 13.2. Эллипс рассеяния исследуемых наблюдений и направление
координатных осей главных компонент z^ и z^: а) умеренный
разброс точек; б) отсутствие разброса точек в направлении второй
главной компоненты (вырожденный случай)

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 541
13.2.5. Оптимальные свойства главных компонент
Описываемые ниже свойства первых р главных компонент во многом
объясняют их широкую распространенность в практике статистических,
в том числе эконометрических, исследований. Оказывается, к главным
компонентам можно прийти, решая оптимизационные задачи, на первый
взгляд не имеющие ничего общего с оптимизационной задачей типа A3.2).
Свойство наименьшей ошибки «автопрогноза» или
наилучшей самовоспроизводимости. Можно показать, что с помощью пер-
/ A) B) (р') / / ^ ч
вых р главных компонент zK , zK ,..., zKH } (p < р) исходных признаков
аг ,аг ',..., яг р' достигается наилучший прогноз этих признаков среди
всех прогнозов, которые можно построить с помощью р линейных
комбинаций набора из р произвольных признаков.
Поясним и уточним сказанное. Пусть требуется заменить
исходный исследуемый р-мерный вектор наблюдений X на вектор Z —
(jzt ,z ,... ,2гр ') меньшей размерности р, в котором каждая из
компонент являлась бы линейной комбинацией р исходных (или каких-либо
других, вспомогательных) признаков, теряя при этом не слишком
много информации. Информативность нового вектора Z зависит от того, в
какой степени р введенных вспомогательных переменных дают
возможность «реконструировать» р исходных (измеряемых на объектах)
признаков с помощью подходящих линейных комбинаций 2т1', г ,..., z^v К
Естественно полагать, что ошибка прогноза X по Z (обозначим ее а) будет
определяться так называемой остаточной дисперсионной матрицей
вектора X при вычитании из него наилучшего прогноза по Z, т.е. матрицей
А = (Ду), где
Здесь Х^Г=1 buz — наилучший, в смысле метода наименьших квадратов,
прогноз аг ' по компонентам яг , 2г ,..., агр ' (см. гл. 2 тома 2). Ошибка
прогноза X по Z задается как некоторая определенная функция от
элементов матрицы Д, т.е. а = /(Д), где /(Д) определяет некоторый критерий
качества предсказания.
Рассмотрим следующие естественные меры ошибки прогноза:
/(А) = tr (Д) = Дп + Да2 + • • • + АРР; A3.22)

542 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
/(А) =
Здесь tr(A) и ||А|| — соответственно след и евклидова норма матрицы
А. Доказано, что функции A3.22) и A3.23) одновременно достигают
минимума тогда и только тогда, когда в качестве г' , 2г ,..., аг ' выбраны
первые р главных компонент вектора Х} причем величина ошибки
прогноза а явным образом выражается через последние р-р собственных
чисел исходной ковариационной матрицы Е или приближенно — через
последние р-р собственных чисел Ap*+i,..., Ар выборочной ковариационной
матрицы S, построенной по наблюдениям A*i,X2,...,Хп. В частности,
при /(А) = tr(A): а » Ap/+i + АрЧ2 + • • • + Ар;
при /(А) = ||Д||: а а ^Aj41 + Aj42 + • • • + Aj.
Поясним идею описания (прогноза) исходных признаков аг ,ж' ,...,
x"v' с помощью меньшего, чем р, числа их линейных комбинаций на
примере 13 Л.
В этом примере р = 3. Зададимся целью снизить размерность
исходного факторного пространства до единицы (р = 1), т. е. описать все
три признака с помощью линейных комбинаций только от одной
вспомогательной переменной.
В соответствии с описанным выше экстремальным свойством
«автопрогноза» главных компонент возьмем в качестве этой единственной
вспомогательной переменной первую главную компоненту, т. е.
переменную
Метод наименьших квадратов приводит к следующему правилу
вычисления неизвестных коэффициентов Ьц (см. гл. 2 тома 2):
0,81cov(a;A),a;(')) + 0,50соу(хB),ж@) + 0>31cov(a;C)>a;(<))
Подставляя в эту формулу значения cov(ar ,аг""), взятые из ковари-

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 543
ационной матрицы Е примера 13.1, получаем
где е^ — случайные (остаточные) ошибки прогноза исходных
центрированных компонент по первой главной компоненте 2г.
Бели в качестве относительной ошибки прогноза исходного
признака аг1' по первой главной компоненте г' ' рассмотреть величину Si =
(De^/Dx^) • 100%, то несложные подсчеты дают 6г = 2%, 62 = 1,2%
и 63 = 0,8%.
Суммарная характеристика относительной ошибки прогноза
признаков а: , аг и ж по яг ' (в соответствии с вышеописанным) может быть
подсчитана по формуле
«сум.отн = 100% . A)tr(m (зк = 100% - Х**Х*Х = 1,36%.
Свойства наименьшего искажения геометрической
структуры множества исходных р-мерных наблюдений при их
проектировании в пространство р первых главных компонент. Речь идет
о следующих трех оптимальных свойствах главных компонент
(формулируются без доказательства).
Свойство 1. Сумма квадратов расстояний от исходных точек-
наблюдений Х\,Х2,... ,Хп до пространства, натянутого на первые
р главных компонент, наименьшая относительно всех других
подпространств размерности р , полученных с помощью произвольного
линейного преобразования исходных координат.
Наглядным пояснением этого свойства может служить рис. 13.2а, на
котором ось 2г соответствует подпространству, натянутому на первую
главную компоненту (т.е. р = 2 и р = 1), а сумма квадратов
расстояний до этого подпространства есть сумма перпендикуляров, опущенных
из точек, изображающих наблюдения Х( = (а^ , ж;- '), на эту ось.
Свойство 2. Среди всех подпространств заданной размерности
р (р < р), полученных из исследуемого признакового пространства с
помощью произвольного линейного преобразования исходных координат
аг ',аг ',...,а? , в подпространстве, натянутом на первые р главных
компонент, наименее искажается сумма квадратов расстояний между
всевозможными парами рассматриваемых точек-наблюдений.

544 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
В данном свойстве за критерий наименьшего искажения
геометрической структуры совокупности исходных наблюдений ХьЛ^,... ,ХП
принимается величина
т. е. сумма квадратов евклидовых расстояний между всевозможными
парами имеющихся наблюдений.
После проектирования точек Х{ в р -мерное пространство,
определяемое матрицей преобразования С, мы получим точки-проекции Zt = CXi
(t = 1,2,..., п) и соответствующую им сумму квадратов евклидовых
расстояний
мр,
t=l i=l
Можно показать, что при р <р Мр(Х) ^ Mp*(Z(C)).
Так вот, на преобразовании L, с помощью которого получают первые
р главных компонент, достигается минимум разности Mp(X)-Mp/(Z(C)),
т.е.
МР(Х) - Мр, (Z(L)) = nun [МР(Х) - Мр, (Z(C))].
Свойство 3. Среди всех подпространств заданной размерности
р (р < р), полученных из исследуемого факторного пространства с
помощью произвольного линейного преобразования исходных координат
A) (Р) i
аг , ...,аг , в пространстве, натянутом на первые р главных
компонент, наименее искажаются расстояния от рассматриваемых точек-
наблюдений до их общего «центра тяжести», а также углы между
прямыми, соединяющими всевозможные пары точек-наблюдений с их общим
«центром тяжести».
13.2.6. Статистические свойства выборочных главных
компонент; статистическая проверка некоторых
гипотез
Смысл математике-статистических методов, как известно, состоит
в том, чтобы по некоторой части исследуемой генеральной
совокупности (по выборке или, что то же, по ограниченному ряду наблюдений
Х\, X<i,..., Хп) выносить обоснованные суждения о ее свойствах в целом.
Применительно к рассматриваемой задаче нас в первую очередь
интересует, как сильно свойства и характеристики выборочных главных

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 545
компонент могут отличаться от соответствующих свойств и
характеристик главных компонент всей генеральной совокупности и, в частности,
как эта мера отличия зависит от объема выборочной совокупности (п),
по которой эти выборочные главные компоненты были построены. Так,
например, для изучения природы внутренних связей между
характеристиками различных статей семейного бюджета потребления и для
выявления небольшого числа наиболее существенных в этом смысле
показателей исследователь может обследовать какое-то количество (п) семей и
по полученным результатам наблюдения Xi,X2,...,Хп построить
главные компоненты z" , z* ,...,rp'. Однако, увеличивая объем выборки п,
т. е. добавляя к имеющимся наблюдениям результаты наблюдения по
дополнительно обследованным семьям, естественно ожидать, что пересчет
главных компонент с учетом добавленных наблюдений^ вообще говоря,
изменит (хотя, быть может, и незначительно) ранее полученные
значения интересующих нас характеристик: A;, /t- (г = 1,2,... ,р) и т.п. В то
же время существует, по-видимому, такое (столь большое) п, дальнейшее
увеличение которого уже не будет практически приводить к изменению
основных характеристик главных компонент (другими словами, мы
вправе ожидать, что в соответствии со свойством статистической
устойчивости (см. п. 6.2) главные компоненты выборок достаточно большого объема
практически совпадают с главными компонентами всей генеральной
совокупности).
Выяснению некоторых вопросов, связанных с оценкой близости
различных выборочных (^* , /j, А,) и теоретических (z , /^, А,) характеристик
главных компонент, и посвящен настоящий пункт. Приведенные ниже
результаты исследований неизменно опираются на допущение нормальности
исследуемой генеральной совокупности и взаимной независимости
извлеченных из нее наблюдений. Как и прежде, под Х\,Х2,. ..уХп будем
понимать центрированные наблюдения, которые, строго говоря, даже при
независимых исходных наблюдениях уже не будут независимыми. Однако
при достаточно больших п можно пренебречь этим эффектом нарушения
независимости. Таким образом, Х{ ? </V@,E), г = 1,2,...,п (как
следует из предыдущего, вектор средних значений о = ЕХ определяет лишь
точку в р-мерном пространстве, в которую переносится начало координат
при переходе к главным компонентам, и с самого начала будем считать
этот перенос уже осуществленным).
Вспомогательные факты, относящиеся к свойствам
выборочных характеристик главных компонент (см., например,
[Андерсон]). Если все характеристические корни Ai,A2,...,Ap ковариационной
матрицы S различны, что и имеет место в большинстве приложений ана-
18 Теория вероятностей
и прикладная статистика

546 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
лиза главных компонент, то справедливо следующее:
1) характеристические корни Ai,A2,...,Ap и соответствующие им
собственные векторы l\,h^-'Jp выборочной ковариационной матрицы
? являются оценками максимального правдоподобия для
соответствующих теоретических характеристик (соответственно Ai, А2,..., Ар
и /i9 /а9 - --Jp) u обладают всеми хорошими свойствами этих оценок
(состоятельность, асимптотическая эффективность). Следовательно,
выборочные главные компоненты Иг1' = liX (о = 1,р) можно
интерпре(
тировать как оценки главных компонент z всей генеральной
совокупности. Если среди характеристических корней Ai,A2,...,Ap встречаются
равные между собой, то оценки максимального правдоподобия для А; и /;
определяются иначе. Аналогичные результаты имеют место и при оценке
характеристических корней и соответствующих им собственных векторов
корреляционной матрицы]
2) величины у/п - 1(А^ - А,) (г = Т7р) асимптотически (по п —> оо)
(
нормальны со средним значением 0 и с дисперсией, равной 2А<, и
независимы от других выборочных характеристических корней;
3) выборочный характеристический корень А; распределен
асимптотически (по п —> оо) независимо от компонент соответствующего ему
собственного вектора U (i = 1,р);
4) ковариация между r-й компонентой выборочного собственного
вектора /,- и q-й компонентой выборочного собственного вектора lj
равна величине
В заключение приведем два факта, относящихся к ситуациям, в
которых компоненты нормального вектора наблюдений X взаимно
независимы:
5) пусть X 6 7V(a,E), где ковариационная матрица имеет
диагональный вид, т. е. cov(a? ,аг") = 0 при i ф j, iyj = 1,2,.. .,р. И пусть
|R| = det (?ij) — определитель выборочной корреляционной матрицы,
построенной по наблюдениям (Х\,..., Хп). Тогда при достаточно больших
п (п -* оо) статистика критерия отношения правдоподобия для
проверки гипотезы о диагональном виде ? может быть определена в виде
^ = -(n - 2p^11)ln |R|, а для ее функции распределения справедливо
приближенное соотношение

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 547
при относительной ошибке, не превосходящей сотых долей процента;
6) пусть наблюдения Xj извлечены из так называемой сферической
р-мерной нормальной совокупности N(a;cr J), т.е. компоненты
каждого из векторов Xj взаимно независимы и имеют одинаковые дисперсии
&Xj, равные а . Тогда ковариационная матрица ? = а I имеет
единственный корень (кратности р), оценкой максимального правдоподобия
которого является величина
причел* величина А/<т2 распределена по закону x*(p(n - !))•
Статистика критерия отношения правдоподобия для проверки
гипотезы о сферичности распределения исследуемого вектора наблюдений
имеет вид
и =
и при достаточно больших п (п -» оо)
при относительной ошибке данного приближенного соотношения, не
превосходящей сотых долей процента.
13.2.7. Применение свойств выборочных характеристик
главных компонент
Опишем некоторые методы построения разного рода интервальных
оценок для интересующих нас неизвестных характеристик главных
компонент и критерии статистической проверки гипотез, относящихся к этим
характеристикам:
1) интервальная оценка (доверительный интервал) для i-го
характеристического корня At получается (при больших п) с учетом
асимптотической нормальности статистики yjn - 1(А; - А;):
(!3.24)
18*

548 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
где данное неравенство справедливо с вероятностью 1 — а (величиной а
заранее задаемся), a uq — g-квантиль стандартного нормального
распределения (находится из таблиц Приложения 1).
Возвращаясь к примеру 13.1, по формуле A3.24) находим 95%-ный
(а = 0,05) доверительный интервал для наименьшего
характеристического корня А3 по его выборочному значению Аз = 2,86. В этом случае п = 24,
1*0,975 = 1,96, так что 1,81 < А3 < 6,78.
Возможно обобщение асимптотического (по п —> оо) доверительного
интервала на случай кратных, т.е. повторяющихся корней. Если г —
кратность корня А„ то 100A - а)%-ный доверительный интервал для
неизвестного значения Aj задается неравенством
^ A3.25)
где
\i= -(A< + Aj+1 + -.. + AH.r_1).
Вопрос о том, что неизвестный характеристический корень Aj
имеет кратность и, в частности, кратность, равную г, может быть решен с
помощью следующего критерия:
2) проверка гипотезы о равенстве нескольких (а именно г)
характеристических корней: Xi = At+i = ••• = Aj+r-i* Очевидно,
альтернативой этой гипотезе является утверждение, что не все корни среди
An А;+ъ • • •> А^+г_1 равны между собой. Оказывается, в предположении
справедливости проверяемой гипотезы статистика
( А
Л
распределена (асимптотически по п -> оо) по закону «хи-квадрат» с г(г +
1)/2 - 1 степенью свободы. Поэтому гипотеза А,- = Al+i = • • • = A^+r—i
отвергается (с вероятностью ошибиться, равной а), если
1г
о о
гДе Ха(т) — 100а%-ная точка х -распределения с т степенями свободы.
Особый интерес может представить специальный случай г = р — г +1,
т.е. проверка гипотезы о равенстве последних г собственных значений А,

13.2 МЕТОД ГЛАВНЫХ КОМПОНЕНТ 549
что будет означать независимость и сферичность г последних признаков
исследуемого вектора наблюдений.
Возвратимся к примеру 13.1. Тот факт, что оценка второго
собственного значения (А2 = 6,50) попадает в доверительный интервал для Аз (см.
выше), приводит к мысли, что, возможно, А2 = А3. Проверим эту
гипотезу. В данном случае п = 24, р = 3, г = 2, г = 2, так что
72 = -23Aп 6,50 + In 2,86) + 46 In 6>50 + 2'86 = 3jo.
А поскольку Хо,обB) == 5,99 и, следовательно, 72 < Xo,osB), то
гипотезу Х2 = Аз следует принять. Но тогда следует пересчитать доверительный
интервал для А2 = А3 с учетом его кратности (в соответствии с A3.25)).
Несложные подсчеты (при а = 0,05 и соответственно Щ-% = мо,975 = 1,96)
дают: 2,62 < Аг < 6,21, последнее неравенство будет справедливо в
среднем в 95 случаях из 100;
3) проверка гипотезы о независимости признаков аг1',^ , ...,ж ,
являющихся компонентами вектора наблюдений X. Такая проверка
нужна для установления целесообразности применения метода главных
компонент: если признаки являются взаимно независимыми, то переход к
главным компонентам сведется, по существу, лишь к упорядочению
исходных признаков по принципу убывания их дисперсий. Воспользуемся
статистикой критерия отношения правдоподобия для проверки гипотезы
о диагональном виде ковариационной матрицы с целью проверки
независимости компонент вектора наблюдений в следующем примере.
Пример 13.3. Исследовалось время, затрачиваемое работниками
швейной фабрики на выполнение различных элементов операции глаженья
одежды. Эту операцию можно разделить на следующие шесть элементов:
1) одежда размещается на гладильной доске (я );
2) разглаживаются короткие швы (ж );
3) одежда перекладывается на гладильной доске (аг ');
%) разглаживаются длинные швы на три четверти (ж );
5) разглаживаются остатки длинных швов (ar ');
6) одежду вешают на вешалку (аг *).
В этом случае Х„ представляет собой вектор измерений элементов
1/-й выполненной операции. Компонента аг ' — это время, затраченное на
выполнение i-го элемента операции, п = 76. Данные (время в секундах)
обработаны, получены выборочные вектор среднего значения а и корре-

550
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ляционная матрица R:
а =
/ 9,47 \
25,56
13,25
31,44
27,29
V 8,70 /
/1,000
0,088
0,334
0,191
0,173
U,123
0,088
1,000
0,186
0,384
0,262
0,040
0,334
0,186
1,000
0,343
0,144
0,080
0,191
0,383
0,343
1,000
0,375
0,142
0,173
0,262
0,144
0,375
1,000
0,334
0,123 >
0,040
0,080
0,142
0,334
1,000 У
Для исследователей представляет интерес проверка гипотезы о
взаимной независимости шести случайных величин. Часто при изучении затрат
времени предлагается новая операция, в которой элементы комбинируются
иным способом. В новой операции некоторые элементы могут повторяться
по нескольку раз, а некоторые могут быть выброшены. Если оказываются
независимыми величины, обозначающие время, затрачиваемое на
различные элементы операции, то естественно считать, что и в новой операции
они останутся независимыми. Тогда распределение затрат времени на
новую операцию можно будет оценить, пользуясь средними значениями
и дисперсиями, вычисленными для остальных элементов. Кроме того,
нас интересует возможность выделения небольшого количества
вспомогательных признаков (двух-трех), с помощью которых можно производить
некоторую содержательную классификацию исследуемых работников (в
том или ином смысле).
В этой задаче статистика критерия отношения правдоподобия,
определенная в соответствии с п. 5, имеет вид: j = —\п — 2p^*n)ln|R| =
-^¦ln 0,472 = 54,1, а р(р - 1)/2 = 15. Задавшись уровнем значимости
критерия а = 0,01 (вероятность ошибочно отвергнуть проверяемую
гипотезу), находим (из таблиц) величину 1%-ной точки х -распределения с 15
степенями свободы: Xo,oiA5) = 30,6. Поскольку 7 > Xo,oiA5), то
гипотезу следует отвергнуть, т.е. приходим к выводу, что значения затрат
времени на различные элементы операции нельзя считать независимыми.
Прикладная направленность компонентного анализа отчасти
продемонстрирована приведенными в данном пункте примерами, но в основном

13.3 ФАКТОРНЫЙ АНАЛИЗ 551
отражена в табл. 13.1. В частности, из оптимальных свойств главных
компонент следует, что они оказываются полезным статистическим
инструментарием в задачах «автопрогноза» большого числа анализируемых
показателей по сравнительно малому числу вспомогательных (латентных)
переменных, визуализации многомерных данных, построения типообразу-
ющих признаков; при типологизации многомерных объектов, при
предварительном анализе геометрической и вероятностной природы массива
исходных данных (это отражено в п. 1, 2, 5 упомянутой таблицы). Мы
увидим в гл. 2 и 4 тома 2, что к методу главных компонент обращаются
и при построении различного рода регрессионных моделей.
13.3. Факторный анализ
13.3.1. Сущность модели факторного анализа
Развиваемые в рамках модели факторного анализа методы исходят
из общей базовой идеи, в соответствии с которой структура связей
между р анализируемыми признаками аг ,аг \.. . ,агр' может быть
объяснена тем, что все эти переменные зависят (линейно или как-то иначе)
от меньшего числа других, непосредственно не измеряемых («скрытых»,
«латентных») факторов р \р ',...,/*р' (р < р), которые принято
называть общими и которые в большинстве моделей конструируются так,
чтобы они оказались взаимно некоррелированными. При этом в общем
случае, естественно, не постулируется возможность однозначного
(детерминированного) восстановления значений каждого из наблюдаемых
признаков аг' по соответствующим значениям общих факторов /' ,..., /
(в предположении, что мы их умеем вычислять): допускается, что каждый
из исходных признаков orJ' зависит также и от некоторой своей
(«специфической» только для него) остаточной случайной компоненты и ,
которая и обусловливает статистический характер связи между аг , с одной
стороны, и / ,..., / — с другой.
Конечная цель статистического исследования, проводимого с
привлечением аппарата факторного анализа, как правило, состоит в выявлении
и интерпретации латентных общих факторов с одновременным
противоречивым стремлением минимизировать как их число, так и степень
зависимости аг' от своих специфических остаточных случайных компонент
гг . Как и в любой модельной схеме, эта цель может быть достигнута
лишь приближенно.

552 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
В некотором смысле искомые общие факторы у ,...,/*р' можно
считать причинами, а наблюдаемые признаки ж* ,..., агр' —
следствиями. Принято считать статистический анализ такого рода успешным, если
большое число следствий удалось объяснить малым числом причин.
Таким образом, методы и модели факторного анализа нацелены, так
же как и метод главных компонент, на сжатие информации или, что то
же, на снижение размерности исходного признакового пространства. При
этом из трех упомянутых в п. 13.1 предпосылок возможности снижения
размерности (взаимная коррелированность исходных признаков, малая
«вариабельность» некоторых из них, агрегирование) методы
факторного анализа базируются в основном на первой.
Возникновение схемы и моделей факторного анализа обязано
задачам психологии, относится к началу двадцатого века и связано с именами
Ч. Спирмэна, Л.Тэрстоуна, Г. Томсона . Однако в силу ряда
исторических причин и, в частности, из-за субъективных пристрастий и
специфических научных интересов первых исследователей, работавших в
данной области, вероятностно-статистические аспекты этого раздела
многомерного статистического анализа долгое время оставались практически
неразработанными, а интерпретации и анализу различных моделей
факторного анализа была присуща некоторая неопределенность. Лишь с
середины 50-х годов начинают появляться интересные результаты именно
вероятностно-статистических исследований этого аппарата, среди
которых работа [Anderson Т. W, Rubin H.] признается основополагающей.
Параграф посвящен описанию канонической линейной модели
факторного анализа. Весьма обширный (и достаточно сложный) материал,
касающийся подробностей вычислительной реализации разнообразных
версий модели факторного анализа, обусловленных различными вариантами
априорных допущений о ее структуре (см. ниже п. 13.3.5), остается при
этом вне рамок нашего описания. Читателю, интересующемуся этими
аспектами проблемы, можно порекомендовать обратиться, например, к
[Харман Г.].
13.3.2. Общий вид линейной модели, ее связь с главными
компонентами
Как и прежде, будем для удобства полагать исследуемые
наблюдения Хх,^,...,Хп центрированными. Переход от исходных наблюдений
1 В качестве первой опубликованной по этой теме работы называют обычно
статью Spearman С. General intelligence objectively determined and measured /Amer. J.
Psychol, 1904, vol. 15, pp. 201-293.

13.3 ФАКТОРНЫЙ АНАЛИЗ 553
Х\, Хг,..., Х^ к центрированным осуществляется с помощью простого
переноса начала координат в «центр тяжести» исходного множества
наблюдений. Тогда линейная версия модели факторного анализа представляется
в виде соотношений
или в покомпонентной записи -
@ _ ? /,, /,ч ? • A3.26)
Здесь Q = (qij) — прямоугольная матрица размера р х р
коэффициентов линейного преобразования (нагрузок общих факторов на
исследуемые признаки), связывающего исследуемые признаки аг ' с
ненаблюдаемыми (скрытыми) общими факторами у ,..., ур , а вектор-столбец
U = (гг ,..., vrp ') определяет ту часть каждого из исследуемых
признаков, которая не может быть объяснена общими факторами, в том числе vr1'
включает в себя, как правило, ошибки измерения признака аг' (сравнить
с A3.16)).
Применительно к каждому конкретному наблюдению Ху {у =
1,2,..., п) соотношение A3.26) дает ^
или в покомпонентной записи
*1° = Е Q
A3.26')
Будем предполагать, что вектор остаточных специфических факторов
U подчиняется р-мерному нормальному распределению JV(O, V), не зависит
от F и состоит из взаимно независимых компонент, т. е. его
ковариационная матрица V = Е([/{/ ) имеет диагональный вид, где по диагонали
стоят элементы Уц = Dvrl\
Вектор общих факторов F = (/,---,/) , в зависимости от
содержания конкретной задачи, может интерпретироваться либо как р -мерная
нормальная случайная величина со средним Е F = 0 (в силу
центрированности исходных наблюдений) и с ковариационной матрицей специального
вида E(FF ) = Ip/, либо как вектор неизвестных неслучайных
параметров, вспомогательных переменных, значения которых меняются от
наблюдения к наблюдению. При последней интерпретации вектора общих
факторов более правильной является запись модели в виде A3.26'), причем
условия центрированности, независимости и нормированности дисперсий

554 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
компонент вектора F в этом случае имеют вид:
Однако при обоих вариантах интерпретации вектора общих факторов
F исследуемый вектор наблюдений X оказывается нормально
распределенной р-мерной случайной величиной: при первом варианте как линейная
комбинация двух нормальных случайных векторов (F и (/), а при втором
варианте за счет нормальности специфических факторов гг. При этом
из A3.26) и из сделанных выше допущений немедленно следует, что
1 аЦ =
или в матричной записи
Примером достаточно прозрачной интерпретации модели факторного
анализа может служить ее формулировка в терминах так называемых
интеллектуальных тестов. При этом наблюдение по признаку Xj
выражает отклонение оценки, например, в баллах, данной j-му индивидууму на
экзамене по г-му тесту, от некоторого среднего уровня. Естественно
предположить, что в качестве ненаблюдаемых общих факторов / ,..., / ,
от которых будут зависеть оценки индивидуумов по всем р тестам,
выступят такие факторы, как характеристика общей одаренности
индивидуума р ', характеристики его математических у\ технических у*
или гуманитарных у ' способностей.
Отметим, что соотношения A3.26) формально воспроизводят
запись модели множественной регрессии (см. гл. 10), в которой под /'*'
(г = 1,2,...,р) понимаются так называемые объясняющие переменные
(факторы-аргументы). Однако принципиальное отличие модели
факторного анализа от регрессионных схем состоит в том, что переменные / ,
выступающие в роли аргументов в моделях регрессии, не являются
непосредственно наблюдаемыми в моделях факторного анализа, в то время
как в регрессионном анализе значения р ' измеряются на статистически
обследованных объектах.
Замечание о связи метода главных компонент
и метода факторного анализа. Рассмотрим следующую
общую схему, включающую в себя в качестве частных случаев обе сравни-

13.3 ФАКТОРНЫЙ АНАЛИЗ 555
ваемые модели. Примем гипотезу, что существуют такие взаимно
некоррелированные факторы /' , у ,..., что
A3.28)
или в матричной записи
Х = AF,
где по поводу случайных переменных у \у ',... без ограничения
общности можно предположить, что D/ = 1.
Очевидно, представление A3.28), если оно существует, не
единственно, так как переходя от F с помощью произвольного ортогонального
преобразования С к новым переменным Z = CF, будем иметь вместо A3.28)
следующее соотношение:
X = BZ, где В = АС~\
Исследователю не известны коэффициенты а|<7-, но он хочет
научиться наилучшим (в некотором смысле) образом аппроксимировать признаки
ж ,..., ж с помощью линейных функций от небольшого (заранее
определенного) числа т факторов у (го), • • • > / (m)> которые поэтому
естественно назвать главными или общими. Аппроксимация признаков X с
помощью f (m),...9ym\m) означает представление X в виде A3.28),
но с «урезанной» суммой, стоящей в правой части, т.е.
Х(т) = AmF(m),
где Ат — матрица порядка р х т, составленная из первых т столбцов
матрицы A, a F(m) = (/A)(m),..., /(m)(m))T.
Оказывается, что, по-разному формулируя критерий оптимальности
аппроксимации X с помощью F(m), придем либо к главным компонентам,
либо к общим факторам. Так, например, если определение элементов
матрицы Ат подчинить идее минимизации отличия ковариационной
матрицы S исследуемого вектора X от ковариационной матрицы Еg = Am • Am
аппроксимирующего вектора Х(т) (в смысле минимизации евклидовой
нормы ||? — Sjf ||), то у (т) определяется пропорционально г-й главной
компоненте вектора X, в частности / (ш) = А^ *z , где А* — г-й по
величине характеристический корень ковариационной матрицы ?, a z ' — г-я

556 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
главная компонента X; при этом г-й столбец матрицы Ат (г = 1,...,га)
есть y/y^iU , где /,- — собственный вектор матрицы Е, соответствующий
характеристическому корню А,-.
Если же определение аппроксимирующего вектора Х(т) = AmF(m)
подчинить идее максимального объяснения корреляции между
исходными признаками ж*1' и аг" с помощью вспомогательных (ненаблюдаемых)
факторов / (га),/*2'(га),.. .,/*т'(га) и, в частности, идее минимизации
величины
TOy(s(V'Vcoy(a-(i)(,,v,., ч...„, A329)
при условии неотрицательности величин &ц — Drr , то можно показать,
что г-я строка оптимальной в этом смысле матрицы преобразования Ат
состоит из т факторных нагрузок общих факторов /' (га),.. .,/*m'(m)
на г-й исходный признак аг' в модели факторного анализа вида A3.26).
Другими словами, сущность задачи минимизации (по Ат и F(m))
величины A3.29) состоит в следующем. Первый из т общих факторов / (га)
находится из условия, чтобы попарные корреляции между исходными
признаками были как можно меньше, если влияние на них этого фактора
/ (т) учтено. Следующий общий фактор /• '(га) находится из
условия максимального ослабления попарных корреляционных связей между
исходными признаками, оставшихся после учета влияния первого общего
фактора / (га), и т.д.
Из сказанного, в частности, следует, что методы главных компонент
и факторного анализа должны давать близкие результаты в тех случаях,
когда главные компоненты строятся по корреляционным матрицам
исходных признаков, а остаточные дисперсии Уц сравнительно невелики.
13.3.3. Основные задачи факторного анализа
При разработке моделей факторного анализа приходится
последовательно анализировать и решать следующие вопросы.
Существование модели. Далеко не для всякой заданной структуры
связей между исходными признаками X = (х ,..., ж ) можно (при
заданном р < р) построить модель факторного анализа, т. е. указать такие
общие факторы /' ,...,/ (или доказать их существование), которые
объясняли бы имеющуюся корреляцию между различными парами аг ' и
arJ' в рамках модели A3.26). При каком характере связей между исход-

13.3 ФАКТОРНЫЙ АНАЛИЗ 557
ными признаками ж*1 ,..., ж , т. е. при каких корреляционных
(ковариационных) матрицах R = (r^y) (E = (<7»j))> а также при каком соотношении
между числом наблюдаемых признаков р и числом скрытых общих
факторов р (р < р) сделанное допущение о наличии определенных связей
между я*1' (г = 1,2, ...,р), с одной стороны, и у*' (j = 1,2, ...,р') — с
другой, является обоснованным и содержательным — в этом и
заключается вопрос существования модели. В терминах модели A3.26) это
означает, что не всякая ковариационная матрица ? допускает представление
вида A3.27), а следовательно, не всякий вектор наблюдений X допускает
интерпретацию в рамках модели факторного анализа типа A3.26).
Очевидно, условия представимости вектора наблюдений X в рамках модели
факторного анализа должны формулироваться в терминах свойств
ковариационной матрицы Е, а также в виде некоторых соотношений между
размерностью исходного пространства р и числом общих факторов р\
Единственность {идентификация) модели. Оказывается, что если
р, ? и р таковы, что допускают построение модели факторного анализа,
то определение соответствующих факторов F = (/ ,...,/) и
коэффициентов линейного преобразования Q = (ftj), связывающего X и F, не
единственно. Спрашивается, при каких дополнительных ограничениях на
матрицу преобразования Q и на ковариационную матрицу V = (tty)
остаточных специфических факторов гг ,..., и определение параметров
искомой модели факторного анализа будет единственным?
Алгоритмическое определение структурных параметров модели.
При заданной ковариационной матрице S исходных признаков и
известном числе общих факторов р (и в предположении, что решение задачи
определения структурных параметров Q и V существует) как конкретно
вычислить неизвестные параметры модели?
Статистическое оценивание (по наблюдениям Хь Х2,., .>Хп и при
заданном р ) неизвестных структурных параметров модели.
Статистическая проверка ряда гипотез, связанных с природой
модели и значениями ее структурных параметров, таких, как гипотеза об
истинном числе р общих факторов, гипотеза адекватности принятой
модели по отношению к имеющимся результатам наблюдения, гипотеза о
значимом отличии от нуля интересующих нас коэффициентов q^
линейного преобразования Q и т. п.
Построение статистических оценок для значений ненаблюдаемых
общих факторов ft\ff\...,f\p<) (t = l,2,...,n).
Далее мы кратко остановимся на решении некоторых из этих задач.

558 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
13.3.4. Вопросы идентификации модели факторного анализа
Будем в дальнейшем предполагать, что имеется по меньшей мере
одно решение (Q,V) уравнений A3.27). При исследовании вопроса
единственности решения системы A3.27) относительно (Q,V) (при заданных
следует различать два аспекта проблемы. Во-первых, надо понять,
при каких дополнительных условиях на искомую матрицу нагрузок Q и
на соотношение между р и р не может существовать двух различных
решений Q^1' и Q , таких, чтобы одно из них нельзя было бы получить из
другого с помощью соответствующим образом подобранного
ортогонального преобразования С (единственность с точностью до ортогонального
преобразования или с точностью до вращения факторов). Оказывается,
достаточным условием единственности такого рода является требование
к матрице Q, чтобы при вычеркивании из нее любой строки оставшуюся
матрицу можно было бы разделить на две подматрицы ранга р\ откуда
автоматически следует требование р <(р- 1)/2.
Можно показать, что для р = 1 и р = 2 это условие является
одновременно и необходимым, откуда, в частности, следует, что случаи р = 2,
р = 1 и р = 4, р = 2 не допускают идентификации модели факторного
анализа в указанном выше смысле.
Будем предполагать далее, что имеется по меньшей мере одно
решение (Q, V) системы A3.27) и что оно единственно с точностью до
ортогонального преобразования.
Вставляя в уравнения A3.27) вместо найденного решения (Q, V)
другую пару матриц (QC,V), где С — матрица (размера р х р) любого
ортогонального преобразования, легко убедиться, что и она (эта пара
матриц) удовлетворяет данной системе уравнений. Следовательно,
возвращаясь к модели A3.26), получаем, что наряду с общими факторами
F = (/ ,..., / ) можно рассмотреть (при тех же нагрузках qij) общие
факторы Z = С F. Поскольку, как известно (см. Приложение 2),
ортогональное преобразование координат F геометрически означает вращение
осей у ',...,/*р' около начала координат на некоторый угол, то
получается, что при отсутствии дополнительных условий на природу искомой
матрицы нагрузок Q общие факторы ух\..., рр' могут быть определены
лишь с точностью до вращения системы координат в соответствующем
р -мерном пространстве. Существует несколько вариантов
дополнительных условий на класс матриц Q, в котором следует искать решение
системы A3.27), обеспечивающих уже окончательную однозначность решения
(Q,V). От конкретного содержания этих условий зависит и способ
численного выявления структуры искомой модели и соответственно способ

13.3 ФАКТОРНЫЙ АНАЛИЗ 559
статистического оценивания неизвестных параметров од, уц и факторов
/*\ Поэтому остановимся на них параллельно с описанием методов
статистического исследования модели факторного анализа.
13.3.5. Статистическое исследование модели факторного
анализа
Итак, в распоряжении исследователя — последовательность
многомерных наблюдений ХиХ2,...,Хп, и с помощью модели A3.26) нужно
перейти от исходных коррелированных признаков я'1',яг2',.. . ,ж ,
являющихся компонентами каждого из наблюдений, к меньшему числу
некоррелированных вспомогательных признаков (общих факторов) у ,...,/'.
Для этого надо суметь определить оценки неизвестных нагрузок q^
остаточных дисперсий г;^ и, наконец, самих общих факторов /* .
Как упоминалось, в основной модели A3.26) при р > 1 оказывается
слишком много неизвестных параметров для однозначного определения.
Поэтому вначале исследователь должен выбрать какую-то систему
дополнительных априорных соотношений, связывающих неизвестные
параметры модели, которые делают решение задачи однозначным и позволяют
получить относительно простое частное решение системы A3.27).
Затем он может отказаться от этих дополнительных соотношений, подбирая
с помощью подходящего ортогонального преобразования (вращения осей)
тот вариант оценок нагрузок q^ и остаточных дисперсий г>ц, который ему
кажется предпочтительнее в основном в отношении возможности
содержательной интерпретации получаемых при этом общих факторов и их
нагрузок. Остановимся подробнее на основных этапах статистического
исследования модели факторного анализа.
Варианты дополнительных априорных соотношений между
q^ и уц} постулируемых исследователем с целью однозначной
идентификации анализируемой модели:
1) решение (Q, V) системы A3.27) лежит лишь в классе таких матриц
Q и V, для которых матрица QTVQ имеет диагональный вид, причем
диагональные элементы ее различны и упорядочены в порядке убывания;
2) из всех решений системы A3.27) выбирается лишь то, для которого
матрица Q Q диагональна, причем все диагональные элементы различны
и упорядочены (в порядке убывания);
3) решение системы A3.27) ищут лишь среди таких матриц Q,
которые для заранее заданной матрицы (размера р х р) В = F^), г = 1,... ,р,

560 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
j = 1,... ,р', ранга р удовлетворяют требованию
(
d2l
dn 0
d2l d22
В частности, выбор
\оо..л о...о/
приводит к ограничению на Q типа
9п О О
921 922 О
о \
о
Чр\ 9р2 9рЗ • • • Чрр1 '
что означает: первый исходный признак х" ' должен выражаться только
через один первый общий фактор у , второй признак аг * — через два
общих фактора у1' и/'ит.д.
Содержательную интерпретацию условий 3) следует искать в
ситуациях, когда исследователь располагает некоторой априорной
информацией, из которой можно, во-первых, извлечь реальный гипотетический
смысл общих факторов и, во-вторых, постулировать наличие
определенного числа нулевых элементов в матрице нагрузок Q (с более или менее
точным указателем их «адреса»), что означает априорное отрицание
зависимости исходных признаков аг ' от некоторых их общих факторов у*'
(j = 1,2,... ,р ). Эта же идея реализуется и в других, менее
формализованных вариантах дополнительных условий («простые структуры»,
«нулевые элементы в специфических позициях»), на которых здесь не будем
останавливаться.
Описание общего итерационного подхода к выявлению
структуры модели факторного анализа. Конкретная реализация этого
подхода зависит от выбора варианта идентифицирующих условий типа 1)-3).

13.3 ФАКТОРНЫЙ АНАЛИЗ 561
Как правило, исследователю известна лишь оценка Е ковариационной
матрицы 33. Поэтому в дальнейшем мы будем писать Е, подразумевая, что
это в действительности ее выборочное значение.
Логическая схема итераций следующая:
• задаемся некоторым нулевым приближением V( ' матрицы V;
• используя A3.27), получаем нулевое приближение Ф*0' = ? - V*0*
матрицы Ф = QQT = Е - V;
• по Ф с помощью некоторого специального приема (см. ниже)
последовательно определяем нулевые приближения щ эщ\...,ву для
столбцов qi, q2,.. ¦, qp' матрицы Q.
Затем определяем следующее (первое) приближение V" и т, д.
Специальный прием определения столбцов ft (i = 1,2,... ,р;) матрицы
Q при известной матрице Ф = QQ опирается на то, что матрица Ф
может быть представлена в виде Ф = 9i?i + 02 92 Н Н Яр1 Яр1* Используя
специфику выбранных идентифицирующих условий, определяют вначале
столбец </i. Затем переходят к матрице Фа = Ф — 9i?i = 9202 Н 1" Яр* Яр1
и определяют столбец <ft и т- Д-
Статистическое оценивание факторных нагрузок од и
остаточных дисперсий уц. Оценивание производится либо методом
максимального правдоподобия (см. гл. 7), либо так называемым центроидным
методом. Первый метод используется обычно при идентифицирующих
условиях типа 1) и 2). Он хотя и дает эффективные оценки для од и va,
но требует постулирования закона распределения исследуемых величин
(разработан лишь в нормальном случае), а также весьма
обременительных вычислений. Центроидный метод используется при
идентифицирующих условиях типа 3). Давая оценки, близкие к оценкам максимального
правдоподобия, он, как и всякий непараметрический метод, является
более «устойчивым» по отношению к отклонениям от нормальности
исследуемых признаков и требует меньшего объема вычислений. Однако из-за
определенного произвола в его процедуре, которая приведена ниже,
статистическая оценка метода, исследование его выборочных свойств (в общем
случае) практически невозможны.
Общая схема реализации метода максимального правдоподобия
следующая. Составляется логарифмическая функция правдоподобия как
функция неизвестных параметров од и Уц, отвечающая исследуемой модели,
т.е. с учетом нормальности Xi9...9Xn модели A3.26) и соответственно
A3.27); в качестве дополнительных идентифицирующих условий берутся
условия 1) или 2). С помощью дифференцирования этой функции
правдоподобия по каждому из неизвестных параметров и приравнивания по-

562 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
лученных частных производных к нулю получается система уравнений, в
которой известными величинами являются выборочные ковариации (Ту, а
также числа р и р\ а неизвестными — искомые параметры g,j и г;,,-. И
наконец, предлагается вычислительная (как правило, итерационная)
процедура решения этой системы. Реализация описанной выше (для случаев 1
и 2) общей итерационной вычислительной схемы с заменой неизвестной
ковариационной матрицы исходных признаков ? ее выборочным аналогом
? приведет как раз к оценкам максимального правдоподобия параметров
Qij и t/ij (i = 1,2,... ,р; j = 1,2,... ,р ). Отметим также, что при
достаточно общих ограничениях доказана асимптотическая нормальность оценок
максимального правдоподобия Q и V, что дает основу для построения
соответствующих интервальных оценок.
Как выше отмечено, центроидный метод является одним из
способов реализации вычислительной схемы, приспособленной для выявления
структуры модели факторного анализа и оценки неизвестных параметров
в случае идентифицирующих условий типа 3). Этот метод поддается
весьма простой геометрической интерпретации. Отождествим исследуемые
признаки аг ,..., ж с векторами, выходящими из начала координат
некоторого вспомогательного р-мерного пространства, построенными таким
образом, чтобы косинусы углов между аг1' и arJ' равнялись бы их парным
корреляциям (гу), а длины векторов аг ' — стандартным отклонениям
соответствующих переменных (aj ). Далее изменим, если необходимо,
направления, т. е. знаки отдельных векторов так, чтобы как можно
больше корреляций стало положительными. Тогда векторы будут иметь
тенденцию к группировке в одном направлении в пучок. После этого первый
общий фактор у ' определяется как нормированная (т. е. как вектор
единичной длины) сумма всех исходных векторов пучка, и, следовательно, он
будет проходить каким-то образом через середину (центр) этого пучка;
отсюда название «центроид» для общего фактора в этом случае.
Переходя затем к остаточным переменным х„ = х™ - qnfl\
подсчитывая ковариационную матрицу е'1' = ? - qiqj для этих остаточных
переменных и проделывая относительно аг1 ' и 1г ' ту же самую
процедуру построения пучка и т.п., выделяем второй общий фактор («второй
центроид») jT2' и т. д.
Формализация этих соображений приводит к следующей
итерационной схеме вычислений по определению факторных нагрузок </у и
остаточных дисперсий Уц. Задаемся некоторым начальным приближением

13.3 ФАКТОРНЫЙ АНАЛИЗ 563
для дисперсий остатков V. Обычно полагают
L 0*0 J
Подсчитываем Ф* ' = ? - V* '. Выбираем в качестве нулевого
приближения 6^ первого столбца Ь\ вспомогательной матрицы В столбец,
состоящий из одних единиц
Далее определяем нулевое приближение q[ ' первого столбца матрицы
нагрузок
т _
Затем вычисляется матрица Ф\' = Ф^ ~Я\ я[ и определяется нулевое
приближение gjj второго столбца матрицы нагрузок
*
( '
где вектор Ь^ состоит только из +1 или — 1, а знаки подбираются из
условия максимизации знаменателя правой части A3.30) и т.д. Получив,
таким образом, нулевое приближение Q^ = (q\ , ...,gy ) для матрицы
нагрузок Q, вычисляем V*1^ = Е - Q Q и переходим к следующей
итерации. При этом матрица В^ ' не обязана совпадать с В .
Кстати, как нетрудно усмотреть из вышесказанного, г-й столбец матрицы В
задает веса, с которыми суммируются векторы одного пучка для
образования г-го общего фактора («центроида»). Поскольку смысл центроидной
процедуры в простом суммировании векторов пучка, она иногда так и
называется — «процедура простого суммирования», то исследователю
остается определить лишь нужное направление каждого из векторов
пучка, т.е. знаки единиц, образующих столбцы 6j. Непосредственная
ориентация (при подборе знаков у компонент вектора 6^) на максимизацию
выражений Ь^ Ф^1&| хотя и несколько сложнее реализуема, чем
некоторые эвристические приемы, опирающиеся на анализ знаков элементов
остаточных матриц Ф*_ь но быстрее и надежнее приводит к выделению
именно таких центроидов, которые при заданном р будут обусловливать

564 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
возможно большую часть общей дисперсии исходных признаков, т. е.
минимизировать дисперсию остаточных компонент г^.
Недостатком цен трои дного метода является зависимость центроид-
ных нагрузок qij от шкалы, в которой измерены исходные признаки.
Поэтому исходные признаки аг ' обычно нормируют с помощью среднеква-
1/2
дратических отклонений а{[ , так что выборочная ковариационная
матрица Е заменяется во всех рассуждениях выборочной корреляционной
матрицей R.
Анализируя описанную выше процедуру центроидного метода,
нетрудно понять, что построенные таким способом общие факторы могут
интерпретироваться как первые р «условных» главных компонент
матрицы ? - V, найденные при дополнительном условии, что компоненты
соответствующих собственных векторов могут принимать лишь два
значения: плюс или минус 1.
Оценка значений общих факторов. Это одна их основных
задач исследования. Действительно, мало установить лишь сам факт
существования небольшого числа скрыто действующих общих факторов
у ,..., yv , объясняющих природу взаимной коррелированности
исходных признаков и основную часть их дисперсии. Желательно
непосредственно определить эти общие факторы, описать их в терминах исходных
признаков и постараться дать им удобную содержательную
интерпретацию.
Приведем здесь идеи и результаты двух распространенных
методов решения этой задачи, предложенных в разное время М. Бартлеттом
A938 г.) и Г.Томсоном A951 г.). В обоих случаях предполагаем задачу
статистического оценивания неизвестных нагрузок Q = (?у) и
остаточных дисперсий V = (уц) уже решенной.
Метод Бартлетта рассматривает отдельно для каждого
фиксированного номера наблюдения v {у = 1,2, ...,п) модель A3.25) как
регрессию признака х„ по аргументам <f.i>9-2>.. . ,?.р'; при этом верхний индекс
г = 1,2,...,р у признака (и соответствующий первый нижний индекс у
нагрузок) играет в данном случае роль номера наблюдений в этой
регрессионной схеме, так что
Таким образом, величины /?,/?,...,/* интерпретируются как
неизвестные коэффициенты регрессии ху по 9.ъ9.2»--ч?.р'- В соответ-

13.3 ФАКТОРНЫЙ АНАЛИЗ 565
ствии с известной техникой метода наименьших квадратов (с учетом «не-
равноточности» измерений, т.е. того, что, вообще говоря, Dаг *' ф Dar2'
при i\ ф г2), определяющей неизвестные коэффициенты регрессии Fv =
(fllK...,flpl))T из условия
получаем
F^i^y^qy'^Y^X, (*/=1,...,п). A3.31)
Очевидно, если исследуемый вектор наблюдений X нормален, то эти
оценки являются одновременно и оценками максимального правдоподобия.
Нестрогость данного метода — в замене истинных (неизвестных нам)
величин qij и va их приближенными (оценочными) значениями q^ и дц.
Модель Томсона рассматривает модель A3.26) как бы «вывернутой
наизнанку», а именно как регрессию зависимых переменных / ,..., /
по аргументам х* ,..., аг . Тогда коэффициенты с^ в соотношениях
или в матричной записи
где С — матрица коэффициентов Cij размера р'хр, находят в соответствии
с методом наименьших квадратов из условия
?
ГГ f«. Гс xU) 1 - min W I f<f) - Vc -x
()(
Поскольку решение экстремальной задачи A3.32) выписывается в
терминах ковариаций аг' и /^ , то отсутствие наблюдений по
зависимым переменным / можно компенсировать знанием этих ковариаций,

566
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
так как легко подсчитать, что
.0)
Б
(*<*>,..., *<»,/<*>,...,/<>'>)
/QQT+V Q\
Отсюда, используя известные формулы метода наименьших
квадратов (см. гл. 2 тома 2), получаем (с заменой матриц Q и V их выборочными
аналогами)
F^CI+rr^V^ (*/=1,2,...,п),
где матрица Г (размера р х р) определяется соотношением
A3.33)
Сравнение выражений A3.31) и A3.33) позволяет получить явное
соотношение между решениями по методу Бартлетта F' ' и методу Томсона
Если элементы матрицы Q V Q достаточно велики, то эти два
метода будут давать близкие решения.
Статистическая проверка гипотез. Проверка гипотез,
связанных с природой и параметрами используемой модели факторного
анализа, составляет один из необходимых моментов исследования. Теория
статистических критериев применительно к моделям факторного анализа
разработана весьма слабо. Пока удалось построить лишь так
называемые критерии адекватности модели, т.е. критерии, предназначенные для
проверки гипотезы #о, заключающейся в том, что исследуемый вектор
наблюдений X допускает представление с помощью модели факторного
анализа A3.26) с данным (заранее выбранным) числом общих факторов
р. При этом критическая статистика 7(^1 >• -^Хп), т.е. функция от
результатов наблюдения, по значению которой принимается решение об
отклонении или непротиворечивости высказанной гипотезы Hq, зависит
от вида дополнительных (идентифицирующих) условий модели. Так если
рассматривается модель с дополнительными идентифицирующими
условиями вида 1), т. е. дополнительно постулируются диагональность матри-
>«Ч *|" ^ь. -ш ^ч
цы Г = Q V Q, то гипотеза #о отвергается (с вероятностью ошибиться,

13.3 ФАКТОРНЫЙ АНАЛИЗ
приблизительно равной а) в случае
567
где число степеней свободы щ = \[{р — рJ -(р+р')]; его положительность
обеспечивается условием р <{р— 1)/2, а Ха{и\) — как и ранее, величина
100а%-ной точки \ -распределения с v\ степенями свободы (находится из
таблиц).
На языке ковариационных матриц гипотеза Hq означает в данном
случае, что элементы матрицы Е — (QQ + V) должны лишь
статистически незначимо отличаться от нуля, или, что эквивалентно, матрица
Е — V должна иметь ранг, равный р . А это в свою очередь означает,
что последние р — р характеристических корней Ар»+ь • ••»Ар уравнения
|?-V —AV| = 0 должны лишь незначимо отличаться от нуля. Статистика
7i(Xi,...,Хп) может быть записана в терминах этих характеристических
корней:
7i(Xb...,Xn) = n ]Г 1пA + А€).
Если же в качестве идентифицирующих условий дополнительно к
A3.26), или, что то же, к A3.27), постулируется наличие какого-то
заранее заданного числа т нулевых нагрузок q^ из общего числа р • р на
определенных («специфических») позициях, то гипотеза Яо отвергается
(с вероятностью ошибиться, приблизительно равной а) в случае, когда
где число степеней свободы v^ = \р{р - 1) - (рр - ш).
Иногда удобнее вычислять критическую статистику
в терминах характеристических корней 2i f z2,..., 2р (нумерованных в
порядке убывания их величин) выборочной корреляционной матрицы R
исследуемого вектора наблюдений X:
2Р+П
t=p'+l ~« \ v^ i ~
(p-p)ln
Статистики ii(Xi,. ..,Xn) и 7з(^1»'">^п) получены в результате
реализации известной схемы критерия отношения правдоподобия.

568
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
До сих пор не удалось построить многомерной решающей процедуры
типа ^(Е), т.е. оценки для неизвестного числа общих факторов р. В
настоящее время приходится ограничиваться последовательной
эксплуатацией критериев адекватности Но: р = р<> (ро заранее задано) при
альтернативе Нг: р > ро. Если гипотеза Н$ отвергается, то переходят к
проверке гипотезы Н^: р = р0 + 1 при альтернативе Н[: р > р0 + 1 и
т. д. Однако по уровням значимости а каждой отдельной стадии такой
процедуры трудно сколько-нибудь точно судить о свойствах всей
последовательной процедуры в целом. ^ ^
Пользуясь асимптотической нормальностью оценок Q и V, можно
было бы попытаться строить критерии для проверки гипотез, касающихся
значений факторных нагрузок, например, гипотез о том, что некоторые
признаки не зависят от заранее определенных факторов, т. е. что на
определенных местах матрицы Q стоят элементы, статистически незначимо
отличающиеся от нуля. Однако построение этих критериев затруднено
из-за сложности процедуры вычисления ковариационных матриц оценок
Qh V.
Продемонстрируем реализацию некоторых этапов факторного
анализа на примере.
Пример 13.4. В табл. 13.3 приведены коэффициенты корреляции
между отметками по шести школьным предметам, подсчитанные по
выборке из 220 учащихся.
Таблица 13.3
Содержательный
смысл признака
Отметка по
гэльскому
языку аг '
английскому
языку ж' '
истории ж' '
арифметике аг '
алгебре аг '
геометрии аг '
Номер признака
1
1
0,439
0,410
0,288
0,329
0,248
2
0,439
1
0,351
0,354
0,320
0,329
3
0,410
0,351
1
0,161
0,190
0,181
4
0,288
0,354
0,164
1
0,595
0,470
5
0,329
0,320
0,190
0,595
1
0,464
6
0,248
0,329
0,181
0,570
0,464
1
Нагрузка
факторов
на признаки
0,606
0,611
0,458
0,683
0,686
0,575
0,337
0,197
0,384
-0,365
-0,335
-0,212
В последних двух столбцах таблицы даны факторные нагрузки gtl, gt-2
на исследуемые признаки в бифакторной модели (р = 2), подсчитанные

13.3 ФАКТОРНЫЙ АНАЛИЗ
569
по приведенной здесь корреляционной матрице с помощью центроидного
метода. Простой анализ величин и знаков этих нагрузок склоняет нас к
тому, чтобы интерпретировать первый фактор /**' как фактор общей
одаренности, а второй фактор /* ' — как фактор гуманитарной одаренности.
Метод Г. Томсона A3.33) дает в качестве оценки общих факторов
выражения:
= 0,245хA) + 0,208жB) + 0,158яC) + 0,278жD) + 0,271жE) + 0,157жF);
= 0,352хA) + 0,201жB) + 0,309z
C)
0,351жD) - 0,303яE) - 0,126яF).
0,5
-0,5-
,B)
0,5
.(в)
\
X»)
Рис. 13.3. Изображение исходных признаков
общих факторов f^l\ f^
&F) в плоскости двух
В целях геометрической интерпретации центроидного метода
рассмотрим рис. 13.3, на котором осями координат являются общие факторы г
и р \ а координаты точек (д ,/.\ ) = (ftb?i2) определяются нагрузка-

570 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ми i-то исходного признака на общие факторы (г = 1,2,...,6).
Соответственно точку (gn,<7t2) УД°бно интерпретировать как изображение г-го
исходного признака х . Расположение точек на рис. 13.3
свидетельствует о естественном распадении совокупности исходных признаков на две
группы: группу гуманитарных признаков (аг \х* ,ж ') и группу мате-
/ D) E) FК
матических признаков (аг , аг ',аг ').
Подобная геометрическая интерпретация помогает выбрать вращение
системы общих факторов, наиболее подходящее в отношении
возможности их содержательной интерпретации. Дело в том, что, как уже
отмечали, параметры модели факторного анализа, в том числе и сами общие
факторы / , / ,...,/, определяются не однозначно, а лишь с
точностью до некоторого ортогонального преобразования, т. е. с точностью до
вращения осей /' ,/* ',...,/*р' в пространстве. При этом выбор
окончательного решения, т.е. закрепление системы у \у >•••>/ в
определенном положении, находится в распоряжении исследователя. Другими
словами, исследователь должен решить вопрос: как, располагая
некоторым частным решением /,/,...,/, полученным, например, с
помощью центроидного метода, выбрать такое ортогональное преобразова-
« r(i) гB) Ар')
ние, такой поворот осей у ,/v ,...,/, при котором получаемые при
этом новые общие факторы у \у \...,ур' допускают наиболее
естественную и убедительную интерпретацию. Рассматривая расположение
исходных признаков в плоскости у '0у ' или в пространстве, натянутом
на первые три общих фактора, естественно повернуть координатную
систему таким образом, чтобы координатные оси прошли через наиболее
четко выраженные сгущения точек-признаков (см. поворот, намеченный
пунктирными осями у ' и у ' на рис. 13.3). При этом иногда бывает
полезно отказаться от ортогональности общих факторов, переходя к
косоугольной системе координат.
13.4. Некоторые эвристические методы
снижения размерности
13.4.1. Природа эвристических методов
Описанные выше сокращения размерности исследуемого
признакового пространства (метод главных компонент и модели факторного анализа)
допускали интерпретацию в терминах той или иной строгой вероятност-

13.4 НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 571
ной модели и, следовательно, подразумевали возможность исследования
свойств рассматриваемых процедур в рамках теории математической
статистики. В данном пункте речь пойдет о методах, подчиненных
некоторым частным целевым установкам (наименьшее искажение
геометрической структуры исходных «выборочных точек», наименьшее искажение
их эталонного разбиения на классы и т. д.), но не формулируемых в тер^
минах вероятностно-статистической теории . Процедура выбора целевой
установки, подходящей именно для данной конкретной задачи,
практически не формализована, носит эвристический характер, т.е., как правило,
обусловливается лишь опытом и интуицией исследователя. Поэтому
будем называть такие методы эвристическими.
При отсутствии априорной или выборочной предварительной
информации о природе исследуемого вектора наблюдений и о генеральных
совокупностях, из которых эти наблюдения извлекаются, точно в таком же
невыгодном положении находятся и методы факторного анализа и
главных компонент. Однако для них все-таки существует принципиальная
возможность теоретического обоснования (при наличии соответствующей
дополнительной информации), в то время как лишь некоторые из
эвристических методов удается впоследствии теоретически обосновать в рамках
строгой математической модели.
Подчеркнем, что факт описания здесь методов снижения размерности,
не использующих предварительной информации, например, обучающих и
квазиобучающих выборок, целесообразно расценивать лишь как следствие
признания неизбежности ситуаций, в которых такой информации не
имеется, но не как стремление рекламировать эти методы в качестве наиболее
эффективных. В действительности же обоснование и эффективное
решение задач снижения размерности без слепой надежды на удачу можно, по
нашему мнению, получить лишь на пути глубокого профессионального
анализа, дополненного статистическими методами, использующими
предварительную выборочную (обучающую) информацию.
13.4.2. Метод экстремальной группировки признаков
При изучении сложных объектов, заданных многими параметрами,
возникает задача разбиения параметров на группы, каждая из которых
1 Отсутствие строгой вероятностно-статистической модели, лежащей в основе тех или
иных методов, не исключает возможности использования отдельных вероятностно-
статистических понятий и соответствующей терминологии, как это имеет место,
например, в методе экстремальной группировки признаков, в методе
корреляционных плеяд и некоторых других.

572 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
характеризует объект с какой-либо одной стороны. Но получение легко
интерпретируемых результатов осложняется тем, что во многих
приложениях измеряемые параметры (признаки) лишь косвенно отражают
существенные свойства, которыми характеризуется данный объект.
Так, в психологии измеряемые параметры — это реакции людей на
различные тесты, а выражением существенных свойств, общими
факторами являются такие характеристики, как тип нервной системы,
работоспособность и т.п. Подобная природа формирования набора частных
характеристик объекта или системы присуща широкому классу явлений
и процессов в экономике, социологии, медицине, педагогике и т. д.
Оказывается, что во многих случаях изменение какого-либо общего
фактора сказывается неодинаково на измеряемых признаках, в частности,
исходная совокупность из р признаков обнаруживает такое естественное
«расщепление» на сравнительно (с р) небольшое количество групп, при
котором изменение признаков, относящихся к какой-либо одной группе,
обусловливается в основном каким-то одним общим фактором, своим для
каждой такой группы. После принятия этой гипотезы разбиение на
группы естественно строить так, чтобы параметры, принадлежащие к одной
группе, были коррелированы сравнительно сильно, а параметры,
принадлежащие к разным группам, — слабо. После такого разбиения для
каждой группы признаков строится случайная величина, которая в
некотором смысле наиболее сильно коррелирована с параметрами данной
группы; эта случайная величина интерпретируется как искомый фактор, от
которого существенно зависят все параметры данной группы.
Очевидно, подобная схема является одним из частных случаев
общей логической схемы факторного анализа. В отличие от ранее
описанных классических моделей факторного анализа при эвристически-
оптимизационном подходе группировка признаков и выделение общих
факторов делаются на основе экстремизации некоторых эвристически
введенных функционалов. Разбиения, оптимизирующие функционал J\ или </2
(см. ниже), называются экстремальной группировкой параметров.
Вообще под задачей экстремальной группировки набора случайных величин
ar1 ',ar2',...,arp' на заранее заданное число классов р понимают
отыскание такого набора подмножеств 5Ь52>• • • >?Р' натурального ряда
чисел 1,2,...,р, что \Jl=isi =: О»2*•••>?}> а Si П Sq = 0 при / ф q, и
таких р нормированных (т.е. с единичной дисперсией D у' = 1)
факторов /' \у ,...,/', которые максимизируют какой-либо критерий
оптимальности.
Остановимся здесь на алгоритмах для двух различных критериев
оптимальности.

13.4 НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 573
Первый алгоритм экстремальной группировки признаков в качестве
критерия оптимальности использует функционал
* = ? [corr(*«\/<»)]V"+ ? [с«гг(.« /'>)]',
в котором под согг(ж, /) понимается обычный парный коэффициент
корреляции между признаком х и фактором /. Обозначим А\ = {аг , г е 5/}, / =
1,2,...,р. Максимизация функционала Jj (как по разбиению признаков
на группы А\,..., Лр/, так и по выбору факторов у \у \ ..., ур ')
отвечает требованию такого разбиения параметров, когда в одной группе
оказываются наиболее «близкие» между собой, в смысле степени коррелиро-
ванности, признаки: в самом деле, при максимизации функционала «/i, для
каждого фиксированного набора случайных величин у ,/' ,...,/', в
одну /-ю группу будут попадать такие признаки, которые наиболее сильно
коррелированы с величиной /';втоже время среди всех возможных
наборов случайных величин у \у ,..., / будет выбираться такой набор,
что каждая из величин у в среднем наиболее «близка» ко всем
признакам своей группы.
Очевидно, что при заданных классах S\, S2, • • • > Spf оптимальный
набор факторов у \у ,..., ур ' получается в результате независимой
максимизации каждого слагаемого
v
max Ji = У^ А/,
откуда
где А/ — максимальное собственное значение матрицы R/, составленной из
коэффициентов корреляции переменных, входящих в А\. При этом
оптимальный набор факторов у , / = 1,2,... ,р;, задается формулами:
Е
@ (О
х
(
х
где rij = corr(x(t),x^'), a or1' = (a^,a^,.. .,a^f) — собственный вектор
матрицы R/, отвечающий максимальному собственному значению А/, т.е.

574 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
С другой стороны, считая известными факторы у , /* ,..., рр ,
нетрудно построить разбиение S\, 5г,..., 5Р», максимизирующее Ji при
фиксированных /*\ /*2\ ..., /р \ а именно:
/^) для всех 9 = 1,2,...,р'}.
A3.35)
Соотношения A3.34) и A3.35) являются необходимыми условиями
максимума J\.
Для одновременного нахождения оптимального разбиения Sb52,...,
Spi и оптимального набора факторов / , / ,..., / предлагается
итерационный алгоритм, последовательно осуществляющий выбор
оптимальных (по отношению к разбиению, полученному на предыдущем шаге)
факторов, а затем выбор разбиения, оптимального к факторам, полученным
на предыдущем шаге.
Пусть на и-и шаге итерации построено разбиение параметров на
группы А\,..., Api. Для каждой такой группы параметров строят факторы /?'
по формуле A3.34) и новое (v+1) разбиение параметров А\ \..., А^+ '
в соответствии с правилом: параметр аг1' относится к группе А\ , если
) (д= 1,2,...,р;). A3.36)
Если для некоторого параметра аг1' найдутся два или более факторов
таких, что для аг^ и этих факторов в A3.36) имеет место равенство, то
(О
параметр ж ' относится к одной из соответствующих групп произвольно.
Очевидно, что на каждом шаге итераций функционал J\ не
убывает, поэтому данный алгоритм будет сходиться к максимуму. Максимум
может быть локальным.
Для описания второго алгоритма экстремальной группировки
признаков введем функционал
J2 =
corr
corr
(*<<>,/<"'>)|.
В содержательном смысле функционал J2 похож на функционал J\ и
его максимизация также соответствует основному требованию к
характеру разбиения признаков на группы. Доказано, что необходимыми и
достаточными условиями максимума функционала Ji являются следующие:

13.4 НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 575
• разбиение параметров на группы А\,..., Api таково, что
функционал
р
D
165,
(где gi — некоторые числовые коэффициенты, равные либо +1, либо -1)
достигает максимума как по разбиению на группы, так и по значениям
коэффициентов д^ Здесь под Hz понимается, как обычно, дисперсия
случайной величины z\
• факторы у ' определяются соотношениями
A3.37)
Логическая схема доказательства этого следующая. Сначала,
варьируя функционал «72 и используя метод множителей Лагранжа для учета
условия D/*' = 1, показывают, что в точке максимума функционала J2
фактор /*' имеет вид A3.37). Затем доказывается, что если /*' имеет
вид A3.37), то при любом наборе коэффициентов ^ = ±1 и любом
разбиении параметров на группы имеет место соотношение J2 ^ «/з* а если
же J$ достигает максимума, то J2 = «/3. Из этого утверждения следует, в
частности, что для нахождения групп 5/ и факторов /'' достаточно
максимизировать функционал J3- При фиксированном разбиении на группы
функционал J3 достигает максимума тогда, когда для каждого /
соответствующие коэффициенты д^ максимизируют величину
A3.38)
Поэтому естественно воспользоваться рекуррентной процедурой
максимизации J%. В процедуре циклически перебираются переменные
аг , х^ ,..., х^р , на каждом шаге принимается решение об отнесении
очередного параметра аг' к одной из групп A\,...,Apt и определяется знак
Пусть к 1/-му шагу алгоритма построены разбиения параметров на
группы А[и',..., Лр, , вычислены коэффициенты д\ ',д^ > • • •»fly > равные
+ 1 или -1, и пусть на этом шаге рассматривается признак аг' € А\"'.
Тогда строятся р вспомогательных коэффициентов fl^1/ (' =: 1,..., р')

576 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
по формуле
где
{1 при х > О,
О при х = О,
— 1 при х < О
и для всех / = 1,2,... ,р вычисляются разности
\
d( Е ^
Затем выбирается такой номер I = /*, что
Д^1* = max A
1
и признак о:'1' исключается из группы Л/ и присоединяется к группе Л;*;
остальные группы признаков на этом шаге не меняются. В результате
получаем новое разбиение признаков — Л| jAJj \---Mp»' • Новые
значения коэффициентов <7^* ' определяются по формулам: д^ == flfj
На следующем (i/ + 1)-м шаге алгоритма рассматривается параметр
, если г ф р, и ж^1 , если i = р.
• Процедура заканчивается, если при рассмотрении всех признаков
очередного цикла сохранились как разбиения признаков на группы, так и
значения всех коэффициентов; полученное разбиение и значения
коэффициентов рассматриваются как оптимальные (доказано, что на каждом шаге
алгоритма значение J$ не убывает).
Нетрудно проследить идейную близость метода экстремальной
группировки факторов с методами, опирающимися на логическую схему
факторного анализа. Так, например, отправляясь от общей модели вида
A3.26)
9=1

13.4 НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 577
первую компоненту р1' и «нагрузки» 1ц в методе главных компонент
можно определять из условия минимума выражения ?*=1 D (я - 1ц f )
при нормирующем ограничении D у ' = 1. Решение этой условно
экстремальной задачи очевидным образом сводится к нахождению максимума
выражения Sf-Jcorr^1*,/1*)]2 ПРИ условии D/A) = 1.
Для построения следующего фактора /*2' (второй главной
компоненты) рассматриваются случайные величины аг2' = аг|'-согг(« , y')pl\
Для этих случайных величин аналогичным образом находится свой
фактор, который и является фактором /' , и т. д.
Очевидно, что при реализации первого алгоритма метода
экстремальной группировки признаков для каждой группы признаков А/ строится
фактор, имеющий смысл первой главной компоненты для признаков этой
группы.
В центроидном методе общий фактор ищут в виде
A3-39)
1=1
где Qi = ±1 и gi выбирается так, чтобы максимизировать величину
. A3.40)
1 = 1
Сравнение выражений A3.39) и A3.40) с выражениями A3.37) и A3.38)
показывает, что максимизация функционала Зг приводит к построению для
каждой группы признаков фактора, отличающегося на некоторый
множитель от первого общего фактора, который был бы построен для этой
группы центроидным методом.
13.4.3. Метод корреляционных плеяд
Задача разбиения признаков на группы часто имеет и
самостоятельное значение. Например, в ботанике для систематизации вновь открытых
растений делают разбиение набора признаков на группы так, чтобы 1-я
группа характеризовала форму листа, 2-я группа — форму плода и т. д.
В связи с этим и возник эвристический метод корреляционных плеяд.
Метод корреляционных плеяд, так же как и метод экстремальной
группировки, предназначен для нахождения таких групп признаков —
«плеяд», когда корреляционная связь, т.е. сумма модулей
коэффициентов корреляции между параметрами одной группы (внутриплеядная связь)
19 Теория вероятностей
и прикладная статистика

578 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
достаточно велика, а связь между параметрами из разных групп (межпле-
ядная) — мала. По определенному правилу по корреляционной матрице
признаков образуют чертеж — граф, который затем с помощью различных
приемов разбивают на подграфы. Элементы, соответствующие каждому
из подграфов, и образуют плеяду.
Рассмотрим корреляционную матрицу R ~ (r^), t,j = l,2,...,p,
исходных признаков. Нарисуем р кружков; внутри каждого кружка
напишем номер одного из признаков. Каждый кружок соединяется линиями со
всеми остальными кружками; над линией, соединяющей г-й и j-й
элементы (ребром графа), ставится значение модуля коэффициента корреляции
\rij\. Полученный таким образом чертеж рассматриваем как исходный
граф.
Задавшись (произвольным образом или на основании
предварительного изучения корреляционной матрицы) некоторыми пороговыми
значениями коэффициента корреляции г0, исключаем из графа все ребра,
которые соответствуют коэффициентам корреляции, по модулю меньшим г0.
Затем задаем некоторое т\ > Го и относительно него повторяем
описанную процедуру. При некотором достаточно большом г граф распадается
на несколько подграфов, т. е. таких групп кружков, что связи (ребра
графа) между кружками различных групп отсутствуют. Очевидно, что для
полученных таким образом плеяд виутриплеядные коэффициенты
корреляции будут больше г, а межплеядные — меньше г.
В другом варианте корреляционных плеяд предлагается
упорядочивать признаки и рассматривать только те коэффициенты корреляции,
которые соответствуют связям между элементами в упорядоченной системе.
Упорядочение производится на основании принципа максимального
корреляционного пути: все р признаков связываются при помощи (р — 1)
линий (ребер) так, чтобы сумма модулей коэффициентов корреляции была
максимальной. Это достигается следующим образом: в корреляционной
матрице исходят наибольший по абсолютной величине коэффициент
корреляции, например, \r^m\ = г* ' (коэффициенты на главной диагонали
матрицы, равные единице, не рассматриваются).
Рисуем кружки, соответствующие параметрам аг ' и аг , и над
«связью» между ними пишем значение г . Затем, исключив г1', находим
наибольший коэффициент в rn-м столбце матрицы (это соответствует
нахождению признака, который наиболее сильно после аг ' «связан» с аг ')
и наибольший коэффициент в 1-й строке матрицы (это соответствует
нахождению признака, наиболее сильно после агт' «связанного» саг"), Из
найденных таким образом двух коэффициентов корреляции выбирается
наибольший — пусть это будет |гу| = г. Рисуем кружок ж , соединяем

13.4 НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 579
его с кружком аг' и проставляем значение г2\ Затем находим признаки,
наиболее связанные с я , х*т* и я , и выбираем из найденных
коэффициентов корреляции наибольший. Пусть это будет \riq\ = г*3*. Требуем,
чтобы на каждом шаге получался новый признак, поэтому признаки, уже
изображенные на чертеже, исключаются, следовательно, q ф /, q ф ш,
9 Ф 3-
Далее рисуем кружок, соответствующий я , и соединяем его с х^'
и т. д. На каждом шаге находятся параметры, наиболее сильно связанные
с двумя последними рассмотренными параметрами, а затем выбирается
один из них, соответствующий ббльшему коэффициенту корреляции.
Процедура заканчивается после (р- 1)-го шага; граф оказывается состоящим
из р кружков, соединенных (р- 1) ребром. Затем задается пороговое
значение г, а все ребра, соответствующие меньшим, чем г, коэффициентам
корреляции, исключаются из графа.
Назовем незамкнутым графом такой граф, для которого для любых
двух кружков существует единственная траектория, составленная из
линий связи, соединяющая эти два кружка. Очевидно, что во втором
варианте метода корреляционных плеяд допускается построение только
незамкнутых графов, а в первом варианте такое ограничение отсутствует.
Поэтому разбиения на плеяды, полученные разными способами, могут не
совпадать.
В работе [Лумельский В. Я.] приводятся результаты
экспериментальной проверки алгоритмов экстремальной группировки параметров, а
также сравнение полученных результатов с результатами, даваемыми
методом корреляционных плеяд.
Эксперимент проводился на физиологическом материале:
исследовались влияния шумов и вибрации на работоспособность и самочувствие.
Регистрировались 33 признака (р = 33), из них 7 параметров,
характеризующих температуру тела; 4 — кровяное давление; 14 — аудиометрию
(порог слышимости на заданной частоте); 2 — дыхание; 4 — силу и
выносливость рук и 2 (обособленных параметра) — пульс и скорость реакции.
С точки зрения физиолога «идеальным» было бы разбиение, при
котором все характеристики температур образовали бы отдельную
группу; параметры, характеризующие давление, — свою отдельную группу и
т.д., обособленные параметры образовали бы группы, состоящие из
одного элемента. Наиболее близким к «идеальному» оказалось разбиение,
полученное вторым алгоритмом экстремальной группировки, хотя
алгоритм и присоединяет обособленные параметры к другим группам.
Наименее точные (среди трех сравниваемых алгоритмов) результаты дал метод
корреляционных плеяд.
19*

580 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Исторически раньше возникшие различные варианты метода
корреляционных плеяд являются в действительности несколько упрошенными
эвристическими версиями более совершенных в математическом плане
алгоритмов исследования структуры связей между компонентами
многомерного признака, использующими графы-деревья и стохастические сети.
13.5. Построение сводного (интегрального)
латентного показателя качества (или
эффективности функционирования)
сложной системы
13.5.1» Общая постановка задачи
И в профессиональной деятельности, и в своей повседневной жизни
человек постоянно сталкивается с ситуациями, когда ему приходится
сравнивать между собой и упорядочивать по некоторому не поддающемуся
непосредственному измерению свойству ряд сложных систем. Речь
может идти, в частности, о сравнении стран по уровню или качеству
жизни, предприятий отрасли по эффективности их деятельности, сложных
изделий (например, определенного программного или технического
средства) — по обобщенной характеристике качества, специалистов — по
эффективности их участия в выполнении поставленной задачи, участников
игровых видов спорта — по уровню проявленного ими (в определенном
состязании) мастерства и т.д. При этом общее представление о
степени проявления анализируемого латентного (т. е. не поддающегося
непосредственному измерению) свойства складывается как результат
определенного суммирования целого ряда частных (и поддающихся измерению)
характеристик, от которых зависит в конечном счете это свойство. Так,
различные интегральные характеристики уровня благосостояния
общества («уровень жизни», «качество жизни», «индекс человеческого
развития») определяются набором показателей структуры и объемов
потребления, качества населения и социальной сферы, экологического состояния
окружающей среды. Точно так же эффективность работы предприятия
определяется в основном совокупностью таких параметров, как
себестоимость и реализуемость продукции, фондоотдача, текучесть кадров,
количество рекламаций и т. п. В том же плане можно рассмотреть задачу
измерения степени оптимальности социально-экономического поведения семьи
в зависимости от значений параметров, определяющих структуру и объем
семейного бюджета, времени и денег. Наконец, к типичным задачам тако-

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 581
го рода относится проблема измерения мастерства спортсмена в игровых
видах спорта по значениям частных числовых характеристик его игровой
деятельности (см. ниже пример с хоккеем).
Математико-статистической формализации подобных задач и
вытекающим из нее рекомендациям по построению некоторого условного
числового измерителя анализируемого латентного свойства сложной системы и
посвящен данный пункт.
13*5.2. Сводный показатель («выходное качество») и его
целевая функция
Пусть обобщенная сводная характеристика / анализируемого
свойства объекта определяется набором частных критериев, задаваемых
поддающимися учету и измерению переменными аг ,аг ',...,агр' (в
дальнейшем будем называть их «входными»), однако сама эта
характеристика является латентной, т. е. не поддается непосредственному
количественному измерению (для нее не существует объективно обусловленной
шкалы). Естественно предположить, что интуитивное экспертное
(профессиональное) восприятие этой характеристики (обозначим его у) можно
представить как несколько искаженное значение /(аг , ...,агр'), причем
это искажение 6 носит случайный характер и обусловленно как
разрешающей способностью такого «измерительного прибора», каковым в данной
схеме является эксперт, так и существованием ряда слабо влияющих на у,
но не входящих в состав X = (аг ,... ,агр') «входных переменных».
Тогда модель, связывающая между собой интуитивное представление о
сводном показателе качества (у), сам сводный показатель (f(X)) как функцию
от X и случайную погрешность 6(Х), может быть определена в виде
y = f{X) + 6(X). A3.41)
Практически, не ограничивая общности данной схемы, можно
принять естественные допущения относительно первых двух моментов
остаточной случайной компоненты 6(Х):
Е6(Х) = О, DS(X) =? а\Х) < оо. A3.41')
Тогда, очевидно, обобщенная (сводная) характеристика f(X) может
интерпретироваться как регрессия у по X, и если бы в качестве
исходной статистической информации располагали бы наряду со значениями
Х{ = (ж;- ,..., х\р') и результатами регистрации соответствующих
значений зависимой переменной од (i — номер наблюдения), то данная схема

582 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
непосредственно сводилась бы к обычной модели регрессии (см. гл. 10).
Специфика модели A3.41), A3.41') состоит в том, что вместо прямых из-
мерений у можно получить (с помощью экспертов) лишь некоторые
специального вида сведения о его значениях, чаще всего — сравнительного
плана (типа ранжировок или парных сравнений обследованных объектов
по свойству у). Это обусловливает и более скромные претензии в
отношении целей статистического анализа этой модели: вместо требуемого в
регрессионном анализе восстановления (оценивания) функции f(X)
ставится задача оценивания f(X) с точностью до произвольного
монотонного преобразования.
Определение. Целевой функцией исследуемого обобщенного
свойства («выходного качества») называется любое преобразование
вида ^(?^,...,?^) = <р(Х), сохраняющее заданное соотношение порядка
между анализируемыми объектами Oi,O2)...,#n по усредненным
значениям выходного качества, т.е. обладающее тем свойством, что из
/(Хн) ^ fWh) > •" > fWi*) c необходимостью следует выполнение
неравенств <р(Х^) > vi^ii) ^ ••• ^ <fi(XiH) и, наоборот, из последней
серии неравенств вытекает выполнение соответствующих неравенств для
f(Xik), k = 1,2,..., п. Очевидно, данное здесь определение целевой
функции неоднозначно. Действительно, если <р{Х) есть целевая функция и
U(tp) — любая взаимно-однозначная монотонно возрастающая функция,
то всякая функция вида ф(Х) = U[<p(X)] также будет целевой
функцией. Это означает, что допущение о наличии определенной шкалы в
измерении единого сводного показателя играет во многих случаях чисто
вспомогательную роль и нацеливает на поиск, связанный с выявлением
этой шкалы лишь с точностью до произвольного допустимого
преобразования шкал. Ведь в соответствии с данным определением само значение
целевой функции не отражает никакой реальной, физически
содержательной количественной закономерности. Реальные закономерности
отражаются только соотношениями «больше» или «меньше» между
значениями этой функции для различных наборов величин входных параметров
X = (аг ,...,я )т. Тем самым эти соотношения отражают
предпочтение с точки зрения анализируемого выходного качества одних значений X
перед другими. Поэтому в задачах, в которых возможно регулирование
значений X (в некоторой допустимой области), наиболее рациональным
управлением естественно признать то, которое максимизирует, при
заданных ограничениях на X, значения целевой функции.
Данное определение целевой функции предполагает ее
содержательную (экономическую, социально-экономическую, квалиметрическую,
психологическую и т. д.) интерпретацию в зависимости от контекста иссле-

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 583
дования.
Итак, функция /(X), с помощью которой можно было бы производить
сравнительную оценку анализируемого «выходного качества» на
рассматриваемых объектах, определена лишь с точностью до произвольного
монотонного преобразования. Тем не менее для построения алгоритма ее
восстановления было бы удобно параметризовать модель A3.41), т.е.
определить параметрическое семейство F = {/(ЛТ;0)}, в рамках которого будет
производиться поиск целевой функции f(X). Выбор этого
параметрического семейства, как правило, не удается подкрепить исчерпывающим
теоретическим обоснованием, а потому с этого момента исследователь имеет
дело не с целевой функцией f(X)} а с некоторой ее аппроксимацией f(X),
Имея в виду достаточную однородность обследуемых объектов по
всем неучтенным переменным, т. е. по переменным, не вошедшим* в
состав ж ,,.., я(р\ и ограниченность интервала времени, в течение
которого будем использовать искомую аппроксимацию целевой функции, а также
реализуя идею разложения любой функции в ряд Тейлора, ограничимся в
дальнейшем изложении аппроксимацией линейного вида, т. е.
а(О. A3'42)
Коэффициенты G = @{ь0ь«**Hр) оцениваются статистически по
исходным данным, структура и происхождение которых описываются
ниже.
13.5.3» Исходные данные
Итак, пусть речь идет о построении непосредственно не
поддающегося измерению единого сводного показателя эффективности
функционирования (качества) объекта и пусть с этой целью были собраны
исходные данные по п таким объектам: Oi,O2,...,ОП* На основании этих
исходных данных как раз и оцениваются параметры 0 искомой
целевой функции f(X;Q). Эти исходные данные состоят их двух частей:
экспертной и статистической (отсюда название метода — экспертно-
статистический).
Экспертная часть исходных данных. Эта часть исходных
данных относится к сведениям о значениях случайной величины yi (г —
номер обследованного объекта) в модели A3.41) и получается с
помощью специально организованного опроса экспертов и соответствующей
статистической обработки экспертных оценок. При этом сведения об у^
(• = 1,2,..., п) получают от экспертов в одной из следующих форм.

584 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Форма (а) — наиболее информативный (а потому наиболее трудный
для экспертов) вариант. Предусматривает получение экспертных
балльных оценок выходного качества
Via.»№.•...•№. f A3.43a)
где yij9 — оценка выходного качества объекта О*, полученная от jf-ro
эксперта (здесь п — число оцениваемых объектов, т — число участвующих
в оценке экспертов).
Форма (б) — средний по информативности (и по степени трудности
для экспертов) вариант.
Предусматривает получение лишь экспертных упорядочений
обследованных объектов по степени проявления в них анализируемого свойства,
т. е. ранжировок вида
Д12э,Д22э,...,Яп2э ^ A3.436)
где Rij9 — ранг (место), присвоенный объекту Oi j-u экспертом в ряду
из п обследованных объектов, упорядоченном этим экспертом по степени
проявления анализируемого свойства.
Форма (в) — наименее информативный (и наименее трудный для
экспертов) вариант. Информация от каждого (j-ro) эксперта поступает в
форме булевой матрицы парных сравнений
7j, = (lik.jj, i,k = T7n, j = 1,2,...,m, A3.43b)
где 7tfc.j, — результат парного сравнения j-м экспертом объектов Oi и
может выражаться либо единицей, либо нулем по одному из следующих
правил:
если эксперт производит сравнение объектов Oi и Од. типа их
упорядочения по анализируемому свойству, то
{1, если по мнению j-ro эксперта О,- не хуже О*, , к
О в противном случае; \ • ¦ )
если эксперт производит сравнение объектов О,- и Ok лишь с точки
зрения принадлежности этих объектов к однородному (по анализируемому

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 585
свойству) классу, то
/ 1, если объекты 0{ и 0к однородны, /1О/|О /к
i*k.j9 ^ q в ПрОТИВНОМ случае. v '
Вычислительные трудности, связанные с реализацией алгоритма
оценивания параметров 0 искомой целевой функции /(Х;0), естественно,
возрастают по мере перехода от более информативных вариантов
экспертной информации об у{ к менее информативным.
Статистическая часть исходных данных. Как выше уже
отмечено, входные переменные (частные критерии) ar ,ar2',...,arp', на
основании которых формируется представление об исследуемом
выходном качестве, поддаются непосредственному измерению (регистрации) на
каждом из обследуемых объектов. Поэтому, статистически обследовав
анализируемые объекты 0i,O2,...,ОП по переменным лг ',аг ,...,агр ,
будем иметь статистическую часть исходных данных в виде матрицы
(таблицы) типа «объект-свойство»:
41* х? ... х[р)\
,(D .B) Jp)
х2 х2 ... х2
'M)'"ji)""'""'(p)
A3.44)
.(О
где х\' — значение /-й входной переменной, зарегистрированное на t-м
объекте.
Таким образом, приступая к оценке параметров 0 искомой целевой
функции f(X;Q) в модели A3.41), исследователь располагает исходной
информацией об объектах 0ь02»-*-»0п, состоящей из данных таблицы
A3.44) и одного из вариантов A3.43а)-A3.43в) сведений об од.
13.5.4. Алгоритмические и вычислительные вопросы
построения неизвестной целевой функции
Опишем вначале общую логическую схему оценивания параметров О
целевой функции A3.42). Располагая конкретными значениями ©о
параметров 0, для каждого объекта О{ можем вычислить величину среднего
единого сводного показателя /(Xt;0o) и далее, ориентируясь на
сравнение значений f{X\\ 0о),/(-^25 ©о)> —A^n5 ©о)? получить основанную на
целевой функции ранжировку объектов по искомому качеству
Д1(во),Я2@о),...,Яп@о)

586 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
либо их разбиение на однородные (по /) классы, которое так же, как и
уже имеющиеся экспертные разбиения A3.43в), может быть представлено
в виде булевой матрицы 7(®о; A).
Оценку 0 неизвестных параметров 0 предлагается подбирать таким
образом, чтобы: 1) минимизировать расхождения в экспертных (ууэ) и
полученных с помощью целевой функции (/(Х<; 0)) балльных оценках
выходного качества (в варианте (а) экспертной информации); 2)
максимизировать согласованность экспертных и полученной с помощью целевой
функции ранжировок объектов по анализируемому выходному качеству
(в варианте (б) экспертной информации); 3) минимизировать
расхождения в экспертных и полученном с помощью целевой функции разбиениях
объектов на классы (в варианте (в) экспертной информации).
Из сказанного следует, что экспертностатистический метод
построения единого сводного показателя нацелен на формализацию (в виде
соответствующим образом подобранной целевой функции /(Х;0)) тех
критерий ных установок, которыми руководствовались привлеченные к
контрольному эксперименту эксперты при формировании своих оценок.
Поэтому состоятельность и эффективность этого метода целиком
зависит от компетентности и согласованности используемых в нем
экспертных оценок.
Оценивание неизвестных параметров целевой функции при
балльных экспертных оценках выходного качества. В этом случае
задача сводится к обычной схеме регрессионного анализа и
соответственно к использованию метода наименьших квадратов. Действительно,
располагая данными вида A3.43а)-( 13.44), можем записать модель A3.41) в
виде
\вад)о вад)& A3-46)
\вад)«о,
где величина (как правило, неизвестная) Оу характеризует погрешность в
оценке j-м экспертом выходного качества i-ro объекта. Критерий метода
наименьших квадратов дает нам оценку 0 векторного параметра 0 как
решение оптимизационной задачи вида (см. гл. 2 тома 2)
ЕЕ T-fafc - /№9))' - mm. A3.47)
Бели не располагают никакими сведениями относительно величин о^,
то принимают упрощающее предположение 0у = const, и задача A3.47)
соответственно упрощается. В некоторых случаях удается априори
задаться «весами» Uj, оценивающими сравнительную компетентность j-vo

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 587
эксперта (J = 1,2,..., га). Тогда эти веса вставляются в A3.47) в качестве
сомножителей слагаемых вместо величин l/cr*j.
Конкретные рекомендации по вычислительной реализации решения
задач типа A3.47) приведены в гл. 2 тома 2.
Оценивание неизвестных параметров целевой функции при
экспертных ранжировках и парных сравнениях объектов.
Каждая экспертная ранжировка R,jt = (Aij,, Дад,»...» A*jB) (i-я строка в
A3.43в)) может быть представлена в виде булевой матрицы 7j, в
соответствии с правилом A3.43в). Поэтому в дальнейшем (в данном пункте)
будем считать, что экспертная информация о выходном качестве объектов
представлена в виде матриц парных сравнений вида A3.43в).
В общем случае задача состоит в том, чтобы на основе известных
сравнений N пар объектов (не обязательно всех возможных пар из п
объектов т.е. N может быть меньше С*) определить скалярную функцию
/(Х;0), такую, что парные сравнения, установленные по этой функции
относительно тех же пар объектов, минимально (в смысле заданного
критерия) отличались бы от экспертно установленных.
В случае парных сравнений в виде отношений предпочтения (см.
правило A3.43в') формирования элементов 7tfJb.j»)» поставив на первое
место в каждой из N экспертно оцененных пар лучший (не худший) объект,
будем иметь пары (tb&i), значения целевых функций элементов которых
должны были бы удовлетворять системе неравенств
Однако в общем случае эта система оказывается несовместной.
Поэтому в каждое неравенство (г9, kq) вводится невязка
0, если f(Xiq; 0) - f(Xkq; 0) > 0;
~(f(Xiq; 0) - f(Xkq; 0)) в противном случая
и вектор оценок 0 определяется из условия минимума суммы невязок
??Li&*,A!,@) пРи некоторых ограничениях (типа нормировки) на
компоненты искомого параметра 01.
1 Алгоритм основан на результатах, изложенных в работе: Киселев Н. И, Экспертно-
статистический метод определения функции предпочтения по результатам парных
сравнений объектов //Алгоритмическое и программное обеспечение прикладного
статистического анализа: Ученые записки по статистике. — М.: Наука, 1980. Т. 36.
С. 111-122.

588 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
В случае парных сравнений, задающих разбиение объектов на
однородные классы (см. правило A3.43в) формирования элементов
7t/c.;,)> матрицы 7U'--->7m, задают m различных разбиений множества
{0г,02,...,0п} на классы, элементы каждого из которых близки по
анализируемому выходному качеству. Для любых двух разбиений у8 и jr
может быть введена мера близости этих разбиений
Пусть f(X\Q) = ]Cfs=i ^\Щ — некоторая линейная аппроксимация /.
Задавшись некоторым е > О, можно с помощью f(X\ 0) построить
разбиение п объектов^на классы. В один класс при этом попадут те объекты,
у которых 0 < f(X; 0) < е, в другой — те, у которых е < f(X; 0) < 2е и
т.д. Полученное разбиение *у(е,О) зависит, очевидно, от значений ? и 0.
Подбираются такие значения ? и 0, чтобы величина Y??=i ^Gь>7(?;©))
была минимальна.
Для наилучшего выбора вектора коэффициентов 0 можно
использовать также так называемый «метод голосования». При любом е > 0 с
помощью линейной функции f(X\Q) = ]?f=1 0/a^ строится разбиение п
объектов следующим образом. Пусть в разбиениях классы
пронумерованы и 7j, — ^-й класс в j-u экспертном разбиении. Для любого объекта
Xi подсчитывается величина
Г)88 Е
где
если | ?2,1 вк(х\к) -
Объект Х{ относится к тому классу, для которого величина Г(Х», 7J, )
максимальна. Полученное разбиение обозначим через 1j(e;Q)<
Параметры е и 0 подбираются из условия минимизации величины
YfjLi ^Gj,>7j(?;@)) (ПРИ наличии априорных «весов компетентности»
vb..., vm минимизируется взвешенная сумма 52]Li vj'd(jj9,7i(?; 0)))-
Используется алгоритм эвристического типа.
Замечание. Выше отмечалось, что успех описываемого
подхода целиком зависит от качества экспертной части исходной информации.
Поэтому прежде чем непосредственно приступить к процедурам
оценивания параметров 0 целевой функции, необходимо тщательно исследовать

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 589
структуру и степень согласованности экспертных мнений. В варианте
балльных оценок это сводится в основном к анализу резко выделяющихся
наблюдений. В варианте ранжировок используется аппарат ранговой
корреляции (см. гл. 11) в первую очередь для того, чтобы проверить гипотезу
об отсутствии какой бы то ни было согласованности в упорядочениях
различных экспертов. В варианте парных сравнений исследуется структура
попарных расстояний между экспертными разбиениями на классы.
13.5.5. Примеры построения интегрального показателя с
помощью экспертно-статистического метода
В п. 13.5.1 упоминались примеры реальных задач, в которых
главной целью исследования было построение интегрального индикатора для
некоторого сводного латентного «выходного качества» системы.
Вернемся к некоторым из этих задач, чтобы дать краткое описание их решения
или ссылку на литературный источник, в котором это решение подробно
приводится.
1) Построение интегрального показателя уровня мастерства
хоккеиста, проявленного им в данном матче. В рамках создания
автоматизированной информационной системы для чемпионата мира по
хоккею 1973 г. (системы «АИС-хоккей-73») рабочей группой
Центрального экономико-математического института АН СССР была решена
задача построения интегрального показателя уровня мастерства хоккеиста
(отдельно для защитников и для нападающих) по одиннадцати частным
показателям его игровой деятельности:
х( ) — количество очков за результативность (по системе «гол+пас»);
аг ' — число бросков в створ ворот противника;
дЛ ) _ число выигранных силовых единоборств;
х\ ) — число отборов шайбы у противника;
х^ — разность шайб («забито-пропущено») в микро матче данного
игрока;
дД6) — общее число точных передач;
аг7* — число точных длинных первых передач;
х\ ) — число парированных бросков противника;
дЛ9) — суммарное время участия хоккеиста в игре в период, когда его
команда играла в большинстве или меньшинстве;
— число удачно выполненных обводок;
— сумма штрафного времени.
Экспертная часть исходной информации была получена в результате

590 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
заполнения экспертами специальных анкет, в которых уровень мастерства
хоккеиста в данном матче оценивался по стобалльной системе (т. е.
имелся вариант A3.43а) экспертной информации). «Съем» статистической
части информации A3.44) по каждому из участников хоккейного матча
производился специальными членами судейской комиссии.
В результате использования экспертно-статистического метода были
получены следующие два варианта аппроксимаций для линейных целевых
функций — отдельно для оценки мастерства защитников (
нападающих (/Нап(-*0):
- Ю + 4*A) + а<2) + 4а<3> + *<6) + 0,2а(в) + Зх<8> + «<
= 8аA) + *<а) + х<3> + 0,5а<4> + 0,2*<в> + 4*<8> + 2*<9>
/на„
Знание целевой функции позволяет в данном случае: 1) производить
формализованную оценку мастерства хоккеиста, проявленного им в
данном матче или в серии матчей, основанную только на знании отдельных
числовых показателей, характеризующих его игру; 2) наиболее
целесообразно строить индивидуальные планы тренировок, особое внимание
уделяя совершенствованию тех компонентов игры, которые вошли в целевую
функцию с относительно большими весами и за счет которых,
следовательно, можно добиться наиболее существенного прироста в оценках
мастерства.
Как и в любой работе такого профиля, в данной были последовательно
реализованы следующие семь основных этапов:
этап 1: постановка задачи;
этап 2: предварительный отбор входных параметров;
этап 3: организация экспертных обследований;
этап 4: организация службы наблюдений, т.е. съема значений
входных признаков;
этап 5: вывод целевой функции (определение ее общего вида и
вычисление весовых коэффициентов);
этап 6: экспериментальная проверка адекватности целевой функции;
этап 7: рабочая эксплуатация целевой функции.
Ход и результаты данной работы подробно описаны в [Айвазян С. А.,
Бежаева 3. И., Староверов О. В., с. 218-223].
2) Построение сводного показателя эффективности
деятельности промышленного предприятия* Объектами исследования
являются 17 промышленных предприятий, специализирующихся на выпуске
асинхронных двигателей переменного тока различного назначения. Цель
исследования — построение единого сводного показателя экономической

13.5 ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ 591
эффективности работы предприятия в форме линейной функции от ряда
частных показателей экономической эффективности. С помощью
сочетания экспертного анализа и статистических методов снижения размерности
(метода экстремальной группировки признаков п. 13.4.2, метода главных
компонент, — п. 13.2) из априорного набора, состоящего из 22 частных
показателей эффективности, было оставлено в качестве входных
переменных экспертно-статистического метода восемь:
я*1' — удельный вес продукции высшей категории качества в общем
объеме товарной продукции (ТП) предприятия;
аг' — динамика1 выпуска ТП на 1 рубль затрат;
яг' — выработка нормативно-чистой продукции (НЧП) на единицу про-
мышленно-производственного персонала (ППП);
х^ — выполнение плана выпуска НЧП на единицу ППП;
аг' — динамика фондоотдачи;
аг ' — выполнение плана выпуска ТП;
аг ' — выполнение плана по оборачиваемости нормируемых оборотных
средств (отношение фактического числа оборотов к
нормативному);
аг ' — выполнение плана по балансовой прибыли.
Из двенадцати привлеченных к задаче экспертов пять дали оценку
интегральной эффективности деятельности анализируемых предприятий
(по результатам их работы в 1982 и 1983 гг.) в десятибалльной системе,
остальные семь проранжировали предприятия, причем четверо из них
дополнительно представили результаты своих парных сравнений. Поэтому
реализовывались все три версии оценивания неизвестных коэффициентов
линейной целевой функции. Приведем здесь для примера один из
полученных с помощью ЭСМ вариантов решения, а именно вариант,
ориентированный на экспертные балльные оценки только одного из экспертов:
{lhl2hl3)i4)i5){6)
Д)
0,07жG)-0,02л(8).
Мера согласованности балльного оценивания предприятий,
произведенного с помощью этого эксперта и данной целевой функции,
характеризуется величиной коэффициента корреляции, равной 0,77. Обращает
на себя внимание тот факт, что формализация критерийных установок
эксперта показала практическое игнорирование им при формировании
интегральной оценки эффективности функционирования предприятия всех
1 Показатель динамики исчисляется как отношение прироста анализируемого
показателя в данном периоде к его величине в предшествующем.

592 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
частных показателей выполнения плана (т.е. входных переменных аг ,
х^е\ аг*). В то же время если бы этому специалисту предложили
непосредственно (экспертно) оценить значимость коэффициентов при этих
переменных, то результат, можно не сомневаться, был бы совсем иным!
13.6. Многомерное шкалирование
13.6Л. Постановка задачи метрического многомерного
шкалирования
Пусть исходная информация об объектах задана в форме матрицы
их попарных сравнений (9.2), где элемент 7у этой матрицы
интерпретируется как евклидово расстояние между объектом О, и объектом Oj
(i,j = 1,2,. ..,n), т.е.
Gп 7i2 ... 7in'
72i 722 ... 72n
7m 7n2 ... 7*
где
7« =
?(*!*>-afJ. A3.50)
Однако ни координаты объектов Xi = (х\,...,х\р') , ни даже
размерность их признакового пространства р нам не известны. Требуется
на основании известных данных A3.49) восстановить неизвестную
размерность р анализируемого признакового пространства и приписать
каждому объекту О, координаты Х{ = (х^,ху\..,х\р') таким образом,
чтобы вычисленные по формуле A3.50) попарные евклидовы расстояния
по возможности совпали бы с заданными матрицей у. При этом речь
идет о восстановлении координат Х\,Х2^^}Хп с точностью до
ортогонального преобразования, т.к. при ортогональном преобразовании
системы координат попарные расстояния между объектами не меняются.
Таким образом, цель методов метрического многомерного шкалированил
состоит в том, чтобы отобразить информацию о конфигурации
исходных многомерных данных, заданную матрицей расстояний у, в виде
геометрической конфигурации п точек в соответствующем многомерном
пространстве.

13.6 МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ 593
13.6.2. Решение задачи метрического многомерного
шкалирования
Введем в рассмотрение центрированную матрицу искомых
наблюдений
лц ""
A3.51)
X —- "X; J
а также матрицу В = (ftij), *\i = 1,2,..., n, скалярных произведений
p
h.. — (Y. Y\*(Y. Y\ — \ ^(*W ч?^\(*№ — ч?Ь)\ AЧ*\0\
A:=l
Метод определения искомых координат Xi,A2,...,Хп
анализируемых объектов (с точностью до ортогонального преобразования), а
заодно и размерности р пространства, в которое они отображаются, основан
не на непосредственном использовании матрицы исходных данных 7 (см.
A3.49)), а на преобразовании ее в матрицу В. Можно показать, что
элементы матриц 7 и В связаны между собой соотношением
Далее используются следующие свойства матрицы В:
(i) матрица В неотрицательно определена;
(ii) ранг матрицы В равен размерности р искомого пространства
отображения;
(ш) ненулевые собственные числа Ai,A2,...,Ap матрицы В,
упорядоченные в порядке убывания, совпадают с соответствующими соб-
ственными числами матрицы S = Хц Хц, где матрица Хц
определена соотношением A3.51); отметим, что матрица Е* = S2/n есть
выборочная матрица ковариаций искомого вектора признаков X;
(iv) пусть 1Г = (/гь'г2> * • - Jrp) есть r-й собственный вектор матрицы
S2, соответствующий т-му по величине собственному значению Лг
(г = 1,2,...,р); тогда вектор Z*r' = (*{,*? ,...>*п )Т значений
r-й главной компоненты вектора X будет
Z(r) = Хц/Г; A3.54)
20 Теория вероятностей
и прикладная статистика

594 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
при этом, если 1Г = (lri,lr2> • • • > 'гп) — **-* собственный вектор
матрицы В, соответствующий тому же собственному числу Аг (т. е.
В if = Xrlf), то
, г =1,2,...,р. A3.55)
В конечном счете из приведенных свойств следует, что, решая
проблему собственных чисел и собственных векторов для матрицы В и
ограничиваясь ненулевыми собственными числами Ai > А2 > ••• ^ Лр > О,
получим координатное представление A3.55) анализируемых объектов в
пространстве главных компонент искомого многомерного признака X. А
поскольку мы можем решить задачу только с точностью до
ортогонального преобразования, то представление объектов в виде A3.55) и будет
решением проблемы метрического многомерного шкалирования. Заметим,
что из построения следует возможность следующего выражения элементов
bij через z\r) и zjr) (г = 1,2,...,р):
!Ч)- A3-56)
Г=:1
Если же мы хотим представить имеющиеся данные в пространстве
заданной (но меньшей у чем р) размерности р\ то можно показать, что, беря
только первые р координат в выражении A3.55), мы обеспечим
максимальное (среди прочих представлений исходных статистических данных
в пространстве размерности р < р) приближение их геометрической
структуры, заданной элементами 6tJ* матрицы В в смысле критерия
t=i j=i
В соотношении A3.57) величины b\j (X) означают значения
геометрических характеристик, вычисленных по формулам A3.53), в которых
стоящие в правых частях попарные расстояния 7tj вычислены в
координатах предлагаемого р -мерного пространства (как следует из A3.56), в
случае р = р этот критерий принимает нулевое значение при
использовании представления A3.55)).

выводы 595
13.6.3. Понятие о неметрическом многомерном
шкалировании (МШ)
В неметрическом МШ предполагается, что различия (близости) 7ij
измерены в ординальной шкале, так что важен только ранговый порядок
различий, а не сами их численные значения. Процедуры неметрического
МШ стремятся построить такую геометрическую конфигурацию точек в
пространстве заданной размерности р, чтобы ранговый порядок
попарных расстояний между ними, по возможности, минимально отличался от
того порядка, который задан матрицей 7* Одна процедура
неметрического МШ отличается от другой выбором вида критерия различия двух
разных упорядочений.
ВЫВОДЫ
1. В исследовательской и практической статистической
деятельности часто приходится иметь дело с исходными данными высокой
размерности, т.е. с ситуациями, когда число регистрируемых на каждом из
статистически обследованных объектов показателей составляет несколько
десятков, а иногда — сотни и даже тысячи. В подобных ситуациях
легко объяснимо желание исследователя существенно снизить размерность
анализируемого признакового пространства, т.е. перейти от
исходного набора показателей к небольшому числу вспомогательных переменных
(которые либо отбираются из числа исходных, либо строятся по
определенному правилу по совокупности исходных показателей), по которым
впоследствии он мог бы достаточно точно воспроизвести интересующие
его свойства анализируемого массива данных. Одним из наиболее
распространенных методов снижения размерности исследуемого
признакового пространства является метод главных компонент.
2. Имеется по меньшей мере три основных типа принципиальных
предпосылок, обусловливающих возможность практически
«безболезненного» перехода от большого числа исходных показателей состояния
(поведения, качества, эффективности функционирования) анализируемого
объекта к существенно меньшему числу наиболее информативных
переменных. Это, во-первых, дублирование информации, доставляемой сильно
взаимосвязанными показателями; во-вторых, неинформативность
показателей, мало меняющихся при переходе от одного объекта к другому
{малая вариабельность показателя); в-третьих, возможность
агрегирования, т. е. простого или взвешенного суммирования некоторых физически
однотипных показателей.
3. В оптимизационной постановке задачи снижения размерности
20*

596 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
решение, получаемое с помощью метода главных компонент,
максимизирует критерий информативности, определяемый суммарной
дисперсией заданного (небольшого) числа искомых вспомогательных переменных
(при соответствующих условиях их нормировки). Для вычисления к-й
главной компоненты г (X) (к = 1,...,р) следует найти собственный
вектор Ik — (//сь • • • >'/ср) ковариационной матрицы ? исходного
набора показателей X = (аг ,...,агр')Т, т.е. решить систему уравнений
(? - А*1)/д. = 0, где А* — А-й по величине корень (при их
расположении в порядке убывания) характеристического уравнения |Е — А1| = 0.
Компоненты Ikj (j = 1,р) собственного вектора /*. являются искомыми
весовыми коэффициентами, с помощью которых осуществляется переход
от исходных показателей аг1 ,. . .,агр' к главной компоненте z" (X), т.е.
4. Основные числовые характеристики вектора Z = (z* , ...,2гр')
главных компонент могут быть выражены через основные числовые
характеристики исходных показателей и собственные числа их
ковариационной матрицы ? (см. п. 13.2.3).
5. Вектор р (р < р) первых главных компонент Z*p \x) =
(z^(X)y. ..,jtp (X)) обладает рядом оптимальных свойств, среди
которых отметим следующие:
а) свойство наименьшей ошибки автопрогноза или наилучшей
самовоспроизводимости: с помощью р первых главных компонент z ',,.., тг '
исходных показателей х^ ,..., агр' (р' < р) достигается наилучший (в
определенном смысле) прогноз этих показателей среди всех прогнозов,
которые можно построить с помощью р линейных комбинаций набора из р
произвольных признаков;
б) свойство наименьшего искажения некоторых геометрических
характеристик совокупности исходных многомерных наблюдений Ai,...,
Хп при их проецировании в пространство меньшей размерности,
натянутое на р первых главных компонент *' ,..., z"v К
6. Главные компоненты, построенные не по истинной
ковариационной матрице ? вектора исходных показателей X = (аг\...,ж^)Т, а по
ее выборочному аналогу (оценке) S, называются выборочными главными
компонентами и в определенных (достаточно широких) условиях
обладают (вместе с собственными числами и векторами матрицы S) всеми
традиционными свойствами «хороших» оценок: состоятельностью,
асимптотической эффективностью, асимптотической нормальностью.
7. Геометрически определение первой главной компоненты равносиль-

выводы 597
но построению новой координатной оси О г ' таким образом, чтобы она
шла в направлении наибольшего разброса исходных данных, т.е. в
направлении вытянутости анализируемого «облака» многомерных
наблюдений. Затем среди направлений, перпендикулярных к О г" ',
отыскивается направление «наибольшей вытянутости» Or и т. д. Бели
характер вытянутости анализируемого «облака» данных в исходном
признаковом пространстве существенно отличен от линейного, то линейная модель
главных компонент может оказаться неэффективной.
8. Главные компоненты используются при решении следующих
основных типов задач анализа данных:
1) упрощение, сокращение размерностей анализируемых моделей
статистического исследования зависимостей или классификации с целью
облегчения счета и интерпретации получаемых статистических выводов;
2) наглядное представление (визуализация) исходных многомерных
данных, получаемое с помощью их проецирования в пространство,
натянутое на первую, первые две или первые три главные компоненты;
3) предварительная ортогонализация объясняющих переменных в
задачах построения регрессионных зависимостей как средство «борьбы» с
мультиколлинеарностью (см. гл. 2 в томе 2);
4) сжатие объемов хранимой статистической информации.
9. Различные версии моделей и методов факторного анализа (центро-
идный, максимального правдоподобия, экстремальной группировки
параметров, корреляционных плеяд и др.) основаны на общей базовой идее,
в соответствии с которой значения всех признаков аг ,...,аг '
анализируемого набора формируются под воздействием сравнительно небольшого
числа одних и тех же (общих) факторов /,...,/, не поддающихся,
правда, непосредственному измерению (и потому называющихся
латентными). В определенном смысле эти общие факторы выступают в роли
причин, а наблюдаемые (анализируемые) признаки — в роли следствий.
10. Поскольку число общих (латентных) факторов существенно
меньше числа анализируемых признаков, то методы факторного анализа в
конечном счете нацелены (так же как и метод главных компонент) на
снижение размерности анализируемого признакового пространства.
11. Статистическая реализация модели факторного анализа
предусматривает последовательное решение вопросов существования такой
модели, ее идентификации (т.е. возможности ее однозначного
восстановления по исходным статистическим данным), алгоритмического
определения ее структурных параметров (т. е. определения способа
вычисления неизвестных параметров модели при точно известной ковариационной
матрице анализируемого многомерного признака) и их статистической

598 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
оценки по имеющимся наблюдениям, включая статистические оценки для
самих общих (латентных) факторов.
12. Наиболее распространенной в практике статистических
исследований и наиболее теоретически разработанной является каноническая
модель факторного анализа, в которой признаки линейно зависят от
факторов, факторы взаимно некоррелированы между собой и со случайными
остатками модели, а случайные остатки в свою очередь взаимно
некоррелированы и нормально распределены. .
13. Между методом главных компонент и линейной моделью
факторного анализа имеется идейная общность: и тот и другой метод можно
рассматривать как метод аппроксимации набора анализируемых
перемещенных переменных с помощью линейных функций от сравнительно
небольшого числа одних и тех же вспомогательных переменных (главных
компонент — в одном методе и общих факторов — в другом). Их
различие — лишь в конкретизации критерия точности аппроксимации.
14. Наиболее «узкие места» в практической дееспособности модели
факторного анализа связаны с решением задачи оценки числа р общих
факторов модели и с содержательной интерпретацией найденных общих
факторов. Для успешного решения последней задачи широко пользуются
неоднозначностью (с точностью до ортогонального преобразования)
определения общих факторов и соответственно возможностью их
разнообразных «вращений» в факторном пространстве.
15. Наряду с математико-статистическими методами снижения
размерности, т.е. с методами, допускающими описание и интерпретацию в
терминах строгой вероятностной модели, существуют и широко использу-
.ются в статистической практике так называемые эвристические методы.
Свое название они оправдывают тем, что порождаются обычно
некоторыми частными целевыми установками, выраженными в виде
установленных на содержательно-субъективном уровне оптимизируемых
критериев качества решения задачи. К таким методам, в частности, относятся
методы экстремальной группировки, метод корреляционных плеяд.
16. Задача построения не поддающегося непосредственному
измерению интегрального (агрегатного) сводного показателя у эффективности
функционирования (качества) объекта по заданным значениям частных
критериальных характеристик аг ', аг ,..., агр' анализируемого свойства
может рассматриваться как задача снижения размерности
исследуемого признакового пространства до единицы. Эта же задача может быть
сформулирована в терминах построения целевой функции
анализируемого обобщенного свойства исследуемых объектов.
17. Базовая идея экспертно-статистического метода построения

выводы 599
единого сводного показателя эффективности функционирования
(качества) объекта заключается в «настройке» искомых коэффициентов 0,
целевой функции <р(Х) на заданную (в различной форме) экспертную
информацию, относящуюся к сравнению статистически обследованных объектов
по анализируемому интегральному свойству. Название метода
объясняется тем, что его реализация основана как на статистической информации
об объектах, так и на экспертной (это представленные в той или иной
форме экспертные оценки анализируемого интегрального свойства у).
18. Вычислительная реализация экспертно-статистического метода
(т.е. алгоритм определения искомых «весов» 0j) сводится к известному
методу наименьших квадратов лишь в тех сравнительно редких
случаях, когда от экспертов удается получить балльные оценки У\%>*.*%уп>
анализируемого интегрального свойства по каждому из исследуемых
объектов. Бели же в распоряжении исследователя лишь сравнительные оценки
объектов по анализируемому свойству (упорядочения, парные сравнения,
классификации), то вычислительная процедура по определению
коэффициентов $j существенно усложняется (ее описание и обоснование требуют
специальной разработки).
19. Экспертно-статистический метод имеет широкий диапазон
возможных применений, однако необходимым условием его достоверности и
эффективности является четкое определение анализируемого
интегрального свойства и компетентность используемых экспертных мнений.
20. Многомерное шкалирование,— совокупность методов,
позволяющих по заданной информации о мерах различия (близости) между
объектами рассматриваемой совокупности приписывать'каждому из этих
объектов вектор характеризующих его количественных показателей; при этом
размерность искомого координатного пространства задается заранее, а
«погружение» в него анализируемых объектов производится таким
образом, чтобы структура взаимных различий (близостей) между ними,
измеренных с помощью приписываемых им вспомогательных координат, в
среднем наименее отличалась бы от заданной в смысле того или иного
функционала качества. Процедуры многомерного шкалирования
применяются, когда данные заданы в виде матрицы попарных расстояний
между объектами или удаленностей или их порядковых отношений. В первом
случае используются методы так называемого метрического
шкалирования, а во втором — неметрического шкалирования.

Приложения
Прилоршие 1. Таблйцц ^тематической
Прил
ие z. ш еооходимы
свщдения
алг#ры

ПРИЛОЖЕНИЕ 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Таблица П1.1. Значения функции плотности ф(х) = ф(х\0;1) стандартного
нормального закона распределения. ф(х) = -4-ге"" V.
X
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
Ф(х)
0,3989
0,3984
0,3970
0,3945
0,3910
0,3867
0,3814
0,3752
0,3683
0,3605
X
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
#*)
0,3521
0,3429
0,3332
0,3230
0,3123
0,3011
0,2897
0,2780
0,2661
0,2541
X
1,06
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
Ф(х)
0,2420
0,2299
0,2179
0,2059
0,1942
0,1826
0,1714
0,1604
0,1497
0,1394
X
1,66
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
ф(х)
0,1295
0,1200
0,1109
0,1023
0,0940
0,0863
0,0790
0,0721
0,0656
0,0596
X
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
Ф(х)
0,0540
0,0488
0,0440
0,0396
0,0355
0,0317
0,0283
0,0252
0,0224
0,0198
X
2,56
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
ф(х)
0,0175
0,0154
0,0136
0,0119
0,0104
0,0091
0,0079
0,0069
0,0060
0,0051
0,0044
Замечание 1. Значения функции плотности ф(хо;а; <т2) нормального
закона со средним а и дисперсией а2 подсчитывается по формуле
(если величина аргумента (а?о — а)/<г попадает между табличными значениями
ж, то для определения Ф(х^а) пользуются линейной интерполяцией функции
ф(х)).
Замечание 2. При определении значений функции ф(х) для
отрицательных величин аргумента х следует использовать тождество (выражающее
свойство четности функции Ф(х))
ф(-х) = ф(х).
(П1.2)
Пример П1.1. Требуется определить значение ф(хо;а;<т2) при xq =
3,36, а = 1 и <т2 = 4.
Решение: х = ^^ = Зу3д = 1,18. Два окаймляющих х соседних
табличных значения аргумента — это a?i = 1,15 и х% = 1,20, поэтому, используя
линейную интерполяцию, получаем:
= 0A,15) - \
М5) - 0A,20)] = 0,199.
Значение 0C,36; 1; 4) получаем по формуле (П1.1):
ф(х0 = 3,36; 1; 4) = 10A,18) = 10,199 = 0,0995.

602
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.2. Значения функции Ф(х) = Ф(ж;0;1) стандартного нормального
распределения. Ф(х) = -i- / e"* /2dt.
-00
X
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
ад
0,500000
0,519939
0,539828
0,559618
0,579260
0,589706
0,617911
0,636831
0,655422
0,673645
0,691463
0,708840
0,725747
0,742154
0,758036
0,773373
0,788145
0,802338
0,815940
0,828944
X
1,00
,05
1,10
,15
,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
«(»)
0,841345
0,853141
0,864334
0,874928
0,884930
0,894350
0,903200
0,911492
0,919243
0,926471
0,933193
0,939429
0,945201
0,950528
0,955434
0,959941
0,964070
0,967843
0,971283
0,974412
X
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
3,00
•Ш
0,977250
0,979818
0,982136
0,984222
0,986097
0,987776
0,989276
0,990613
0,991802
0,992857
0,993790
0,994614
0,995339
0,995975
0,996533
0,997020
0,997445
0,997814
0,998134
0,998411
0,998650
Замечание 1. Значение функции распределения Ф(а?о; а; а2)
нормального закона при среднем значении а и дисперсии а2 в заданной точке xq подсчи-
тывается по значениям функции Ф(х) = Ф(х;0; 1) с помощью формулы
(П1.3)
(если величина аргумента (хо—а)/(г попадает между табличными значениями х}
то для определения Ф((яо — о)/<т) пользуются линейной интерполяцией функции
¦(»))•
Замечание 2. При определении значений функции Ф(х) для
отрицательных величин аргумента х следует использовать тождество
(П1.4)
Пример П1.2. В условиях примера П1.1 имеем:
Ф(*о = 3,36; о = 1;<г2 = 4) = ФA,18)
= ФA.15) + };** I \f5 [ФA,2О) - ФA,15)] = 0,881.

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
603
Таблица П1.3. Значения ф-квантилей ич стандартного нормального
распределения.
35ТВ
120072
52
53
0%
56
57
58
59
0,60
61
62
0.65
66
67
68
69
0.000000
025069
050154
075270
.mm,
150969
176374
201893
227545
0,253347
279319
305481
331853
U«OoOO 2nj
412463
439913
467699
495850
0,70
Я
73
0%
76
77
78
79
0.80
81
82
83
0JB5
$6
87
88
89
0,524401
553385
582842
612813
0,90
91
92
93
0)V# I -T-X«7V
706303
738847
772193
806421
0,841621
877896
915365
954165
97
971
972
973
974
0,975
1Ж
080319
126391
174987
226528
979
0,980
981
982
1,281552
340755
405072
475791
ДО&
750686
880794
895698
911036
926837
943134
1,959964
977368
fl.
033520
2,053749
074855
096927
0,983
9
984
0,985
8
989
0,990
991
992
993
994
0,995
}72
144411
2,170090
197286
ma
290368
2,326348
999
408916
457263
512144
2,575829
652070
mm
3,090232
Пример П1.3. Найти 0,9-квантиль uo,g. Величину uo,9 находим из
таблицы в графе, расположенной справа от соответствующего значения q = 0,9,
т.е. иО|9 = 1,281552.
Замечание 1. Бели заданная величина q попадает между двумя
соседними табличными значениями q\ и q% {q\ < q<i\ это может случиться при
графической проверке нормальности распределения), то следует
воспользоваться линейной интерполяцией, а именно формулой
ggi (uqi -ii^).
42 ~ Ч\
Замечание 2. При нахождении g-квантилей для значений q < 0,5
следует воспользоваться соотношением uq = — u\~q. Например, uo,4 = ~^i-ot4 =
= -0,25335.
Замечание 3. При отыскании 100Q%-Hbix точек wQ следует
восполь= u^^q. Например, wo,os = uo,95 = 1,64485.
зоваться соотношением

Таблица П1.4. Значения 1QOQ%-Hbix точек
нями свободы.
х2-РаспР€Леления с. " стспе"
о
"9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0.4SS
392704 -КГ»
0,0100251
0,0717212
0,206990
0,411740
0.675727
0,989265
1,344419
1,734926
2,15585
2,60321
3,07382
3.56503
4,07468
4,60094
5.14224
5.69724
6.26481
6.84398
0.990
157088.10-»
0,0201007
0,114832
0,297110
0,554300
0.872085
1,239043
1,646482
2,087912
2,55821
3.05347
3,57056
4,10691
4,66043
5.22935
5,81221
6,40776
7,01491
7.63273
0.97S
982069-10"»
0,0506356"
0,215795
0,484419
0,831211
1,237347
1.68987
2,17973
2.70039
3,24697
3,81575
4,40379
5,00874
5,62872
6,26214
6,90766
7,56418
8,23075
8.90655
0.9S0
393214.10-»
0,102587
0.351846
0.710721
1.145476
1,63539
2,16735
2,73264
3.32511
3.94030
4,57481
5.22603
5,89186
6,57063
7.26094
7.96164
8,67176
9,39046
10,1170
Q
0.900
0.0157908
0.210720
0.584375
1.063623
1.61031
2.20413
2.83311
3,48954
4.16816
4,86518
5,57779
6,30380
7,04150
7,78953
8.546Т5.
9,31223
10,0852
10,8649
11,6509
0.100
2.70554
4.60517
6,25139
7.77944
9.23635
10,6446
12,0170
13,3616
14,6837
15,9871
17,2750
18,5494
19,8119
21,0642
22.3072
23,5418
24,7690
25.9894
27.2036
0.0S0
3.84146
5,99147
7,81473
9,48773
11,0705
12.5916
14.0671
15,5073
16,9190
18.3070
19.6751
21.0261
22.3621
23.6848
24.9958
26,2962
27,5871
28.8693
30. Н35
0.02S
5.02389
7,37776
9.34840
11,1433
12.8325
14.4494
16,0128
17,5346
19,0228
20,4831
21.9200
23,3367
24.7356
26.1190
27.4884
28.8454
30,1910
31,5264
32,8523
0.010
6.63490
9.21034
11,3449
13.2767
15,0863
16,8119
18,4753
20,0902
21,6660
23,2093
24.7250
26.2170
27.6883
29,1413
30.5779
31.9999
33.4087
34,8053
36,1908
O.00S
7,87944
10,5986
12,8381
14,8602
16,7496
18,5476
20,2777
21,9550
23,5893
25.1882
26,7569
28,2995
29,8194
31,3193
32,8013
34.2672
35.7185
37.1564
38,5822

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
605
9968
S3
5662
со
1
34.1696
4104
«о
4120
8
4426
8508
о
,59083
о»
26040
СО
43386
п
о
о
•5
9321
38.
35,4789
6705
6151
Я
,2396
СО
.5913
—
,28293
о
89720
СО
,03366
«о
,7956
2894
о
36.7807
9244
3
8133
,0415
S
I
СЧ
,9823
О
54249
О)
64272 1
со
,1813
6384
38.0757
1725
Я
0069
8
.8479
,0905
со
,6885
,19567
о
26042
о»
,5585
9798
39.3641
4151
$
1963
8
6587
ю
,8484
СО
4011
еч
8564
о
88623
о»
3
1
3141
40.6465
6525
3816
$
,4734
<о
6114
Z
,1197
СО
5240
2
Я
о
а
,2899
со
6417
41.9232
8852
3
,5631
3
,2919
3791
,8439
с»
1981
еч
1
=
8
I
,9630
43.1944
1133
9
7412
,1138
со
1513
В
8786
еч
8076
,9933
г
2782
44.4607
3372
,9159
Jo
,9392
со
9279
(О
,3079
5648
со
4613
еч
3
,3356
s
,5879
О)
45.7222
5569
еч
1
7677
о>
7083
0471
<о
.2565
2
1211
52
,6720
|
s
46.9792
7729
S3
2560
о
,5992
,4926
ео
7908
<о
9535
7867
2
S
,7659
8
6907
S
59.3417
7585
Й
8050
1л
S0S0
5093
4331
Я
1643
7065
<3
о
,4900
1539
71.4202
,5048
&
1671
г
,6886
СО
7642
3
3574
3
7067
а
9907
,9517
о>
3794
§
83.2976
0819
о
4589
$
1879
,4817
4848
со
5346
3
S
1.215
«ь
).425
<=>
95.0231
5312
8
5271
3290
Й
,7393
Со
7576
4418
$
2752
S
5,321
!.329
106.629
.879
о
5782
,2778
S
3915
S
1532
&
5400
3
1720
S3
S
3.299
2
I.U6
118.136
1.145
'.565
S
2912
1260
г
6466
3
7541
1963
г
8
3.169
i.807
со
129.561
1.342
СЧ
1.498
3581
9295
&
2219
0648
3276
&
100

606
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
89.9Д 2Й582 8>Д&Д &B.8SQ SSfe83
8.9.2Д аД9Д2 8.888.8 ? »ДS.fc 338Sfc
?5 S?. ЗДгДЯ =8.8.8.8 аДВВД8858в
5 28 SSS8Д 288? S?& SSSSR S8.&&3
*й a -.8.S.S.!R. 2.8.s.*.s. БД55.*5.^ s.ff ^ s is
9S8 2SS5S SSS8S 8S5SS ?????
те* «еч« «ечец — -» -•*—-.*«-.* -Г——"-."—"
S*S2S Я5S.9.R Я2.8.S.» SS8SS.RB.J8RВ
S.SS*с5 Яй28S R3I.5S8 S.85S.ff
g о»«л «о €о*еч**<*е«*©»* w*e<*e«fw*<N* —*-.*—*—»«* »'«'.'.Т_*
S 5 Я» Й8.В 65 Я Я Я 522 8 S 88 8 К 86 8Х S
...йЯ2Z2 S388S Я888.8.
g со* сч*сч* csTcsT w* es*cJ csT €ч" сч* сч* csT —" —•* *-Г -«" «-JГ —* -Г
о- вДЯ.а».8«В585 «ЙЯ.2.S- 8.8.8.8.8 ««8.8 5?
56Я.» Я8.В85. ЯSS852 SS8SS 8.8.65.»»
ОгГ О* 1О СО* СО С^*СЧ*ѻà CS* СЧ* €М* СЧ* СЧ С** СЧ €Ч" СМ* СЧ CS* <N —* -^" —" —*
SЙЙ8. йS.B.8S З.Я.8.Я.2. 2Ц28.8.5.SS88
eooTio'co* coco*C4*C4*<N* сч*сч*с* счсч* сч*е»"счс^сч* q*c!c+~mS
%ЩЦЗ 9836й 9Я8Я.Я.5222= 8.8.88.S
соаГш*4*!* с^Гсосч*сч*сч* сч*сч"с«1*с<Гсч* сч"сГсч*сч*сч* сч*еГсч*е«Гсч*
Я Я. 55.S !» = 8 В S S «в Й Я й Я а 8.2. -.2.2 Г 2
t^*or«rt*-** «*« с**ечеч* еч**?сч*еч*еч* с«*м"е«©Гем* еч*с<*еч*е^еч*
a ais = a s» ss. es 99 я яд я.я.й я.я я.я.2.
s 2.« s ад в as в.« г »а 9.93.98.
co*oTio*V со*со*со*€чеч* сч сч*е*сч*сч сч*ея*еч*сч*сч*
as*» в * »=о а 8 г »в ses s s з s в »й »
о>о%*>*+*сосъ€0€осо с*с*ci*<N*€4* сч"сч*см*с«е^ ****
88 S as 8В#8 * 8 Я Я 2 2 2 Вл8 S S 85
o>ao\r>** Vco*eo*co*c9* со*со*со*со*со* «"со'со'со*^ см*е>Гсмеч*оГ

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
607
CD CO Г*- tO CO
Ю lO Ю Ю iO
33SS55S
SSSSS
ffprgSS
SsSSS
S5SSSS3
sssss&s
CD CD CD CD 00
CD CD CD CD CD
S08SS
cs cs cs cs —•
SSoocS
cs cs cs cs os
CN CS CS CS CS
cocoScsS
<N CS CSCSCS
SSsSS
CS CS CS CS СЧ
CD CD CD 00 00
cs cs cs cs cs
83S8b
c^* •¦* ^^f* r*» C5
ю ю ^e* со со
153333
RS8S?5
S3SK188
CD CD GO 00 K*
S8c58o3
CSj CS — -4 —•
SScSSS
CN CSCSj -«—•
Scs22S
CS CSCS CSC4
??coco8
cscscs cscs
CS CSCS CSCN
JO CD QQ I/)
JfJ CD 00 Ю
""-^SP:
jj 2оо"ю"
°.$!SS
cs —°°
ggoOiO
•чг crToo to*
^cooSS
g2 00 <o
^cSSc?
gj CD 00* Ю
gcDOOO
ЙСЛОЮ
jScncn.«>
8 CD* CD tO
gtogjs?;*:
^cococscs
SSE5cdp2
^ CO CO CSCS
9ScoSR
^ CO CO CO CS
"Г CO CO COCS
Soo&SS
^•co со cocs
^r со со со cs
S 00 5 25
^•co cocoes
ЗЗГосЗо
ч<|" со со со со
чг чг СО COCO
rt8S<?*S
•^^г со со со
ji2Sco2
м» ^* со со со
оо?гЗЗсЗ
^ ^«со со со
Swages
•nf ч0« СО СО СО
cftcSQObScO
^* ^<* со со со
Scocn@3
Ю ч|* СО СО СО
хп^г *# со со
CSg>Sco-
iOiO^OiOiO
SSco?32
cs cs cs cs cs
CN CS CS CS CS
cs cs cs cs cs
О vO 'd* CO CS
cs cs cs cs cs
p?Jo5i Sfo
CSCS CSCSCS
SSSS'co3
cs cs cs cs cs
KiSw?$c^
cs cs cs cs cs
cs cs cs cs cs
???§?
es cs cscs cs
es cs cscs cs
CO CS CS CS CS
сЭсЯсЗг^г?
CO CS CS CS CS
-Sc^SiS
со со cs cs cs
S3 88$>o3
со со со cs cs
CO CO CO CO CS
ScScSSi:
со со со со со
г?$о9"*со
со со со со со
SggScort
чс со во со со
*S^So?

о08
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
>
з
о
о»
о
о
о
to
чг
сч
о
\Л
сч
О
*"*
О»
00
to
-
oo$SS
2.11
2,06
2.01
1.97
1.93
CM CM CM CM ~
CM CM CM CM CM
2.25
2.19
2,15
2.11
2.07
§53212 =
см см см см см
CM CM CM CM CM
CM CM CM CM CM
g?$! ?§coco
CS CM CM CM CM
S?i??co
CM CM CM CM CM
см см см см см
CM CM CM CM CM
*-+ VO •— OO ^Ч*
t*4* VO VO tO 1O
сч см см см см
en *«• о vo со
|n» (v. (>» ^Q ^0
см см см см см
O> oo oo г*- г*»
CM CM CM CM CM
О о en en en
CO CO CM CM CM
см см S5SS2
со со со со со
3 3 wo to to
CO CO CO CO CO
55-555
sasss
en en en en oo
§83oS
CM CM CM CM *—
SSScSS
см см см cs см
о oo wo со —
CM CM СЧ CM CM
cmcmc3S2
CM CM CM CM CM
CO CO CO CM CM
CM CM CM CM CM
CM CM CM CM CM
CM CM CM CM CM
«— en vp «ч* см
CM CM CM CM CM
QNIQ CO**-«
vo to to wo to
см см см см см
CS CM CM CM CM
SoooooS?2
CM CM CS CM CM
2S33S
со со со со со
9*^^99
Vo со со со со
S2-555
55555
assets
te8S.8S.
SSSSo^
•en en en en o>
о en en en en
см см см см см
CM CM CM CM CM
CM CM CM CM CM
см см см сч см
CS CM CM CM CM
CS CM CM CM CM
en t** vo ю со
CM CM CM CM CM
о en r* to to
VO tO CO wO to
CS CM CM CM CM
(O^CO—O
CMCMCM CSCS
cncnScncn
см см смечем
со со со со со
со со со со со
55555
см — en wo о
vo ю со см о
1,68
1.58
1.47
1,35
1.22
a.pgsa
as.s.s.fc.
CS — — — —
см cs — — —
^ScncKoo
CM CM •-• —• —•
CS CM CM •— —•
CM CM CS CS —
CO CM -^ О О
CS CM CSCS CS
5JScs-2
CS CS CS CS CS
со to г** en •**
to *# со см см
CS CMCS CM CS
en —• со to r*»
tia to to ^* cO
CS CS CM CS CS
cnStSSS
CM CSCS CMCS
COCN-08
CO CO CO CO CO
55SS--
i О CO О
с> см о
чг см vo
со оо см
°
vo en vo ro
en cn -^
со ^r vo en
<N - - -
vo en vo со
en cs —
S wo en см
^r vo о
CM
to en tjp *4f»
en cn -—
vo en г*, "чг
СП Г^ чо«
o> см —*
) СП Г-. ^«
art см —*
I O>
I CO
vO VO
CO VO
i СП Г- «чГ
O> CM —«
1 r*» en о
> со ^ ooe
! en* c^T чг*
en cs «-»
CO VO Г*- OO
CM CO VO СП
en со — —
со со en c-i
^» О -«г см
vo со см wo
55 8?* 8*2'
1Л10-00
см cn r- en
8 8?" 8* 2'
t*^ VO
СП
cO
.888
ел со см
^см со

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 609
Л 58.838
О> «О 1Л V V СО СО СО СО CO СЧСЧСЧСЧСЧ* СЧ*С*СЧ*СЧСЧ СЧСЧСЧСЧСЧ* CS~Г —Г —Г —Г
о-Г о *л «*•«*• •*• со со со со c*Te*e*eie" сч*сч*сч"еч ся счсч'сч счсм" cs—*—"—* —
8SS85 8SXSS2 8 8.8 ? Б 35383.5 88.88.8 5
**чг Vсо"со со со* сосцсчсчсч cs сч'счсчсч* eleiсч сч сч счсч—"—
Vcocococo еососчо»сч счсчсч€ч*сч с4оГсясч*еч c/cs-T—*-^
sssss sstssa
J9 яS8.88 SS'*2gS SSJ2S5 Ч
^rcococo" со*со*сосо€Ч c^cics*C4C4 см* cs сч* сч сч сч'
^ Wcococo со сосососо счсясчсчсч ечсчечсчеч
a?«a* ssqss a^sas sssas es.B.sec.
* V COCOCOCOCO COCOC4C4<N СЧСЧСЧСЧСЧ
^ ssa.s
co*co* со"со*со*со со* со со*со со*со* cic4C4C4*cs
cococococo cococococo cococococo счсчсчсчсч
^^^чг^* fococococo cococococo cococococo сосчсч'счсч
^ ^O •"• ^O *¦¦* l
^^> C^* %JP 1^9 W7 ^^F 4^ W"^ »'^ w^ w^ ^^ w^ ^ ' ч^* ^^^ ^^ ~» м
*л ^« *r чг чг ^t* со со со со cococococo cococococo соечсчечеч
$S8?2S
'ЧГ'Фча*4*' 4tf*4tf*COCO CO CO CO CO CO CO CO CO CO СО СО СО СО СЧ (
^*^CO COCOCO CO CO COCOCOCOCO COCOCOCMCN
йJS«
о со" t***o «о toto'in *d*V V^r^^V чг^со*со*со сососососо cococococo
V ^^r^r^r^r ^ *• ^r ^ *r «чгсосососо
. sjssbs sssas sssss p:.ssss. sss.ss
-*о ooTo*o>ep ooooooooeo coeor^*r^r*- t*-t*r^t*r** r^« r*-1»* *o о

610
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.6. Значения 100$%-ных точек tQ(v) распределения Стьюдента с
v степенями свободы.
V
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
*9
30
40
60
120
оо
0-0.4
?<?-0.8
0,325
289
277
271
0,207
205
263
2С2
201
0.260
260
259
259
258
0.258
258
257
257
257
0.257
257
256
256
256
0.256
256
256
256
256
0,256
255
254
254
253
0,36
0.6
1,000
0,816
765
741
0,727
718
711
700
703
0.700
697
695
694
692
0,691
690
689
688
688
0,687
686
С86
685
685
0,684
684
684
683
683
0,683
681
679
677
674
0,1
0.2
3.078
1,886
1,638
,533
1,476
1,440
1.415
1,397
1,383
,372
1,363
,356
,350
,345
1,341
1,337
1,333
1,330
1,328
1.325
1,323
1,321
1,319
1,318
1,316
1,315
1,314
1,313
1,311
1,310
1,303
1,296
1,289
1,282
0.0S
0.1
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,812
1,796
1,782
1,771
1,761
1,753
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1.703
1,701
1,699
1,697
1,684
1,671
1,658
1,645
0,035
0,05
12,700
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,056
2,052
2,048
2,.045
2,042
2,021
2,000
1,980
1,960
0.01
0,03
31,821
0,905
4,541
3,747
3,365
3,143
2,998
2,896
2,821
2,764
2,718
2,681
2,650
2,624
2,602
2,583
2,567
2,552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2,479
2,473
2,467
2,462
2,457
2,423
2.390
2,358
2,326
0,00»
0,01
63,657
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,106
3,055
3,012
2,977
2,947
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2.807
2,797
2.787
2,779
2.771
2.763
2.756
2,750
2,704
2,660
2,617
2,570
0,ОО85
о.оог
127,32
14,089
7,453
5,598
4,773
4,317
4,029
3,833
3,690
3,581
3,497
3,428
3,372
3,326
3,286
3.252
3 ,222
3,197
3,174
, 3.153
3, 135
3, 119
3,104
3,091
3,078
3,067
3,057
3,047
3,038
3,030
2,971
2,915
2,860
2,807

П I. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.7. Преобразование Фишера (^-преобразование) выборочного
коэффициента корреляции f (г = arcthf).
611
7
1,00
1
2
3
4
1.05
6
7
8
9
.10
1
2
3
4
,15
6
7
8
9
1,20
1
2
3
4
).25
6
" 7
8
9
).30
1
2
3
4
),35
6
7
8
9
,000
0000
0100
0200
0300
0400
0500
0601
0701
0802
0902
1003
1104
1206
1307
1409
1511
1614
1717
1820
1923
2027
2132
2237
2342
2448
2554
2661
2769
2877
2986
3095
3205
3316
3428
3541
3654
3769
3884
4001
4118
,002
0020
0120
0220
0320
0420
0520
0621
0721
0822
0923
1024
1125
1226
1328
1430
1532
1634
1737
1841
4944
2048
2153
2258
2363
2469
2575
2683
2790
2899
3008
3117
3228
3339
3451
3564
3677
3792
3907
4024
4142
,004
0040
0140
0240
0340
0440
0541
0641
0741
0842
0943
1044
1145
1246
1348
1450
1552
1655
1758
1861
1965
2069
2174
2279
2384
2490
2597
2704
2812
2920
3029
3139
3250
3361
3473
3586
3700
3815
3931
4047
4165
оое
0060
0160
0260-
0360
0460
0561
0661
0761
0862
0963
1064
1165
1267
1368
1471
1573
1676
1779
1882
1986
2090
2195
2300
2405
2512
2618
2726
2833
2942
3051
3161
3272
3383
3496
3609
3723
3838
3954
4071
4189
,008
0080
0180
0280
0380
0480
0581
0681
0782
0882
0983
1084
1186
1287
1389
1491
1593
1696
1799
1903
2007
2111
2216
2321
2427
2533
2640
2747
2855
2964
3073
3183
3294
3406
3518
3632
3746
3861
3977
4094
4213
г
0,50
1
2
3
4
0,55
6
7
8
9
0,60
1
2
3
4
0,65
6
7
8
9
0,70
2
3
4
0,75
6
7
8
9
0,80
1
2
3
4
0,85
6
7
8
9
,000
5493
5627
5763
6901
6042
6184
6328
6475
6625
6777
6931
7089
7250
7414
7582
7753
7928
8107
8291
8480
8673
8872
9076
9287
9505
0,973
0,996
1,020
1,045
1,071
1,099
1,127
1,157
1,188
1.221
1,256
1,293
1,333
1,376
1,422
,002
5520
5654
5791
5929
6070
6213
6358
6505
6655
6807
6963
7121
7283
7447
7616
7788
7964
8144
8328
8518
8712
8912
9118
9330
9549
0,978
1,001
1,025
1,050
1,077
1,104
1,133
1,163
1,195
1,228
1,263
1,301
1,341
1,385
1,432
,004
5547 г
5682
5818
5957
6098
6241
6387
6535
6685
6838
6994
7153
7315
7481
7650
7823
7999
8180
8366
8556
8752
8953
9160
9373
9594
0,982
1,006
1,030
1.056
1,082
1,110
1,139
1,169
1,201
1,235
1,271
1.309
1,350
1,394
1,442
.006
5573
5709
5846
5985
6127
6270
6416
6565
6716
6869
7026
7185
7348
7514
7684
7858
8035
8217
8404
8595
8792
8994
9202
9417
9639
0,987
1,011
1,035
1,061
1,088
1.116
1,145
1.175
1.208
1,242
1,278
1,317
1,358
1,403
1,452
,008
5600
5736
5874
6013
6155
6299
6446
6595
6746
6900
7057
7218
7381
7548
7718
7893
8071
8254
8441
8634
8832
9035
9245
9461
9684
0,991
1,015
1,040
1,066
1,093
1,121
1.151
1,182
1.214
1.249
1,286
1,325
1,367
1,412
1,462

612
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Г
0,40
1
2
3
4
0,45
6
7
8
9
г
,000
4236
4356
4477
4599
4722
4847
4973
5101
5230
5361
,000
,002
4260
4380
4501
4624
4747
4872
4999
5126
5256
5387
,002
,004
4284
4404
4526
4648
4772
4897
5024
5152
5282
5413
,004
,006
4308
4428
4550
4673
4797
4922
5049
5178
5308
5440
,006
,008
4332
4453
4574
4698
4822
4948
5075
5204
5334
5466
,008
г
0,90
1
2
3
4
0,95
6
7
8
9
г
Продолжение
,000
1,472
1,528
1,589
1,658
1,738
1,832
1,946
2,092
2,298
2,647
,000 .
,002
1,483
1,539
1,602
1,673
1,756
1,853
1,972
2,127
2,351
2,759
,002
,004
1,494
1,551
1,616
1,689
1,774
1,874
2,000
2,165
2,410
2,903
,004
s табл.
,006
1,505
1,564
1,630
1,705
1,792
1,897
2,029
2,205
2,477
3,106
,006
П1.7.
,008
1,516
1,576
1,644
1,721
1,812
1,921
2,060
2,249
2,555
3,453
,008
Указание. При работе с отрицательными значениями гиг
используйте свойство нечетности функций th z и arcth f, т.е. arcth (-r) =
-arcth f,
Примеры.
1. Дано f = 0,206. Определить z = arcth 0,206.
Находим (в левом столбце таблицы) строку, соответствующую f =
0,20. Чтобы получить заданное значение г, к 0,20 надо прибавить 0,006, а
потому искомое число находится (в этой строке) в столбце, расположенном
под 0,006. Итак, z = arcth 0,2090.
2. Дано г = -0,515. Определить z = arcth (-0,515).
Находим (в левом столбце таблицы) строку, соответствующую f =
0,51. Чтобы получить значение г = 0,515, к 0,51 надо прибавить 0,005,
а потому arcth 0,515 находится как среднее арифметическое двух чисел
данной строки, расположенных в столбцах, соответствующих верхним
индексам 0,006 и 0,004, т.е.
arch 0,515 .
. 0,56955.
Соответственно, *•= arcth (-0,515) = -arcth 0,515 = -0,56955.
3. Дано z = 0,8752. Определить г = th z.
Находим в таблице число, равное 0,8752, и определяем, какому
значению г оно соответствует. В нашем случае f = 0,704.
Примечание. В тех случаях, когда в таблице не найдется в
точности заданного, берут два приближенных (ближайших к нему)
значения — с недостатком и с избытком. Искомое значение г будет лежать
между двумя значениями f\ и г% > соответствующими этим приближенным
величинам z.

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.8. Верхняя граница доверительного интервала для истинного
значения коэффициента корреляции при условии отсутствия
линейной корреляционной связи (при доверительной вероятности
Р = 1 - 2Q).
613
п -2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25.
30
35
40
45
50
60
70
80
90
100
Q
0,05
0,9877
9000
805
729
669
0,621
582
549
521
497
0,476
457
441
426
412
0.400
389
378
369
360
0.323
296
275
257
243
0,231
211
195
183
173
164
0.096
0,9*692
9500
878
811
754
0,707
666
632
602
576
0.553
532
514
497
482
0.468
456
444
433
423
0.381
349
325
304
288
0,273
250
232
217
205
195
0.01
0,9*507
9800
9343
882
833
0,789
750
715
685
658
0.634
612
592
574
558
0.543
529
516
503
492
0,445
409
381
358
338,
0,322
295
274
257
242
230
0,005
0.9»877
9*000
9587
9172
875
0.834
798
765
735
708
0,684
661
641
623
606
0.590
575
561
549
537
0,487
449
418
393
372
0,354
325
302
283
267
254
0,002»
0.9*692
9*500
9740
9417
9056
0,870
836
805
776
750
0.726
703
683
664
647
, 0,631
616
602
589
576
0,524
484
452
425
403
0,384
352
327
307
290
276
0,0005
0.9*877
9»000
9414
9741
9509
0,9249
898
872
847
823
0,801
780
760
742
725
0,708
693
679
665
652
0.597
554
519
490
465
0,443
408
380
357
338
321
Примечание. Верхний индекс B,3 в т. д.) над цифрой 9
означает, что эта цифра занимает первые 2,3 я т. д. разряда десятичной
дроби. Например, 0,9*692 — 0,9999692.
Пример. Если мы оцениваем корреляционную связь по п « 20
наблюдениям, то при доверительной вероятности Р « 0,95 (т. е. при
2Q = 0,05) значение коэффициента корреляции, не превосходящее по
абсолютной величине 0,444, еще не говорит о статистической значимости
этой корреляционной связи (т. е. о том, что истинное значение
коэффициента корреляции г отлично от нуля).

614 П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.0.
Проверка статистической значимости корреляционной связи
с помощью рангового коэффициента корреляции Спирмэна тE)
sc
12
14
16
18
20
Q
0,458
375
208
167
042
20
Пш
*С
22
24
26
28
30
32
34
36
38
40
-5
Q
0,475
392
342
258
225
0,175
117
067
042
0083
40
л
se
50
52
54
56
58
60
62
64
66
68
70
-в
Q
0,210
178
149
121
088
0,068
051
029
017
0083
0,0014
70
л
*С
74
78
82
86
90
94
98
102
106
НО
Q
0,249
198
151
118
083
0,055
033
017
0062
0014
112
л
108
114
120
126
132
138
144
150
156
162
1-8
Q
0,250
195
150
108
076
0,048
029
014
0054
ООН
168
л
SC
156
164
172
180
188
196
204
212
220
228
t-9
Q
0,218
168
125
089
060
0,038
022
011
0041
0010
240
п
sc
208
218
228
238
248
258
268
278
288
298
308
-10
0
0.235
184
139
102
072
0,048
030
017
0087
0036
0.001
330
Таблица ШЛО.
Проверка статистической значимости корреляционной
связи
с помощью рангового коэффициента корреляции Кендал л а т<*>
SK
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
л
4
0,625
375
167
042
5
0,592
408
242
-ИГ
042
0,0083
8
0,548
452
360
274
199
0,138
089
054
031
016
0,0071
0028
0009
0002
9
0,540
460
381
306
238
0,179
130
090
060
038
0,022
012
0063
0029
0012
0,0004
SK
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
а
в
0,500
360
235
136
068
0,028
0083
0014
7
0,500
386
281
191
119
0,068
035
015
0054
0014
0.0002
10
0.500
431
364
300
242
0J90
146
108
078
054
0.036
023
014
0083
0046
0.0023
ООП

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.11*. Вероятности того, что критическая статистика проверки
статистической значимости выборочной величины
коэффициента хонкордации W(m) достигнет или превзойдет
табличное эначевие 5 (при п = 3 сравниваемых объектах).
615
0
2
6
8
14
18
24
26
32
38
42
50
54
56
62
72
74
78
86
96
98
104
114
122
126
1 ftQ
128
134
146
150
152
158
162
168
182
200
/и-а
,000
0,833
0,500
0,167
1,000
0,944
0,528
0,361
0,194
0,028
,000
931
,653
.431
,273
,125
.069
.042
,0046
,000
.054
691
.522
367
,182
.124
,093
,039
,024
,0085
0,0»77
.000
.966
740
,670
430
,252
.184
!l42
,072
,052
,029
,012
,0081
0,0055
0.0017
0,0*13
,000
0.964
0,768
0.620
0,486
0,305
0,237
0.192
0,112
0,085
0.051
0.027
0,021
0,016
0,0084
0.0036
0,0027
0,0012
0,0*32
0,0*32
0,0*21
1.000
0.967
0,794
0,654
0,531
0.355
0.285
0,236
0,149
0,120
0,079
0,047
0,038
0,030
0,018
0,0099
0,0080
0,0048
0.0024
0,0011
0,0*86
0,0*26
0,0*61
0,0*61
0,0*61
0,0*36
1,000
0.971
0.814
0,686
0,569
0,398
0,328
0,278
0.187
0,154
0,107
0,069
0,057
0,048
0.031
0,019
0,016
0,010
0,0060
0,0035
0.0029
0,0013
0,0*66
0,0*35
0,0*20
0,0*97
0,0*54
0,0*11
0,0*11
0,0*11
0,0*11
^,0*60
т-10
1,000
0,974
0,830
0,710
0,601
0,436
0,368
0>,316
0,222
0,187
0,135
0.092
0,078
0,066
0,046
0,030
0.026
0.018
0,012
0,0075
0,0063
0,0034
0,0020
0.0013
0,0*83
0,0*51
0,0*37
0,0*18
0,0*11
0,0*85
0,0*44
0,0*20
0,0*11
0,0*21
0,0*99

616
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение
Вероятность того, что данное значение S будет достигнуто
иди превзойдено, для n—4,m—Знт—5
1
3
5
9
11
13
17
19
21
25
27
29
33
35
37
41
43
45
49
51
53
57
59
/71 "
1.000
0.958
0.910
0,727
0,608
0,524
0,446
0,342
0.300
0.207
0.175
0.148
0.075
0.054
0.033
0.017
0,0017
0,0017
1.000
0,975
0,944
0.857
0,771
0,709
0,652
0.561
0.521
0,445
0,408
0,372
0.298
0.260
0.226
0,210
0.162
0,141
0,123
0,107
0.093
0,075
0.067
61
65
67
69
73
75
77
81
83
85
89
91
93
97
99
101
105
107
109
из
117
125
0.055
0,044
0,034
0.031
0.023
0.020
0.017
0.012
0,0087
0.0067
0.0055
0.0031
0.0023
0.0О18
0,0016
0,0014
0.^64
О.СЯЗЗ
0.0*21
0.0*14
0.0*48
0.0*30
Продолжение
Вероятность того, что данное значение 5 будет достигнуто
иди преазойдено, для л—4 н т—2, т—4 н т—б
0
2
4
6
8
10
12
14
16
18
20
22
24
т-2
1,000
0,958
0^33
0.792
0,625
0.542
0.458
0.375
0.208
0.167
0.042
т—4
1,000
0.992
0,928
0.900
0.800
0,754
0,677
0.649
0.524
0.508
0,432
0,389
O.3S5
т-в
1,000
0,996
0,957
0,940
0,874
0,844
0,789
0,772
0,679
0,668
0,609
0,574
0,541
s
82
84
86
88
90
94
96
98
100
102
104
106
108
Шайб
0.035
0,032
0.029
0,023
0.022
0,017
0.014
0.013
0.010
0.0096
0.0О85
0.0073
0.0061

П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение Таблицы П1.11*
617
S
26
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
E2
64
66
68
70
72
74
76
78
80
m-2
тц«4
0.324
0.242
0.200
0.190
0.158
0,141
0.105
0,094
0,077
0.068
0.054
0.052
0.036
0.033
0,019
0,014
0,012
0,0069
0,0062
0.0027
0.0027
0.0016
0.0*94
0.0*94
0,0*94
0.0*72
0,512
0,431
0,386
0,375
0.338
0,317
0,270
0.256
0.230
0.218
0,197
0.194
0.163
0.155
0,127
0,114
0.108
0.089
0,088
0.073
0.066
0.060
0.056
0.043
0,041
0.037
S
ПО
114
116
118
120
122
126
128
130
132
134
136
138
140
144
146
148
150
152
154
158
160
162
164
170
180
т — в
0,0057
0,0040
0,0033
0,0028
0,0023
0,0020
0,0015
0.0*90
0,0*87
0,0*73
0,0*65
0,0*40
0,0*36
0,0*28
0.0*24
0,0*22
0,0*12
0,0^95
0,0*62
0.046
0.0*24
0.046
0,042
0,0*80
0,0*24
0,0*13
Продолжение
Вероятность того, что данное значение S будет достигнуто
илн превзойдено! для л««5 и т»3
0
2
4
Ь
8
10
12
14
16
18
20
т — 3
1.000
1.000
0.988
0.972
0.941
0.914
0,845
0.831
0.768
0,720
0.682
22
24
26
28
30
32
34
36
38
40
42
/п-»3
0,649
0.595
0,559
0,493
0,475
0.432
0,406
0.347
0.326
0,291
0,253
44
46
48
50
52
54
56
58
60
62
64
т«3
0,236
0.213
0,172
0.163
0.127
0,117
0,096
0,080
0,063
0.056
0.045
5
66
68
70
72
74
76
78
80
82
86
90
т»3
0.038
0.028
0.026
0.017
0,015
0.0078
0,0053
0,0040
0.0028
0.0»90
0.0*69

618
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.116. Критические значения статистики S при уровне значимости
а = 0,05 для проверки статистической значимости
выборочного значения коэффициента конкордации W(m).
т
3
4
5
6
8
10
15
20
3
48,1
60,0
89,8
119,7
4
49,5
62,6
75,7
101,7
127,8
192,9
258,0
п
5
64,4
88,4
112,3
136,1
183,7
231,2
349,8
468,5
6
103,9
143,3
182,4
- 221,4
299,0
376,7
570,5
764,4
7
157,3
217,0
276,2
335,2
453,1
571,0
864,9
1158,7
Дополнительные значения
m
9
12
14
16
18
для п = 3
S
54,0
71,9
83,8
95,8
107,7

ПРИЛОЖЕНИЕ 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ
МАТРИЧНОЙ АЛГЕБРЫ
Все модели и методы эконометрики, эксплуатирующие понятия и
приемы многомерного статистического анализа, — а это и классификация
многомерных данных, и всевозможные конструкции факторного анализа,
включая метод главных компонент, и множественная регрессия, и,
конечно, системы одновременных уравнений, и все, что связано с решением
систем алгебраических уравнений (а сюда относятся и корреляционный
анализ, и анализ временных рядов), — требуют, для своего компактного
и эффективного описания и анализа, использования аппарата
матричной алгебры. И если при описании этих моделей мы еще, как правило,
можем обойтись без такого аппарата (правда, за счет утомительных и
чрезвычайно громоздких выкладок и выражений, приводящих к
покомпонентной записи требуемых соотношений), то при анализе их свойств
и выводе связанных с этим математических результатов без
использования методов линейной алгебры мы вынуждены были бы в ряде
ситуаций просто отступить, не добившись желаемого.
Поэтому специалисту (или студенту, готовящемуся стать таковым),
предполагающему всерьез работать с эконометрическими методами и
моделями, необходимо внутренне настроиться на неизбежность расходования
некоторого времени и интеллектуальных усилий на овладение
определенным минимумом сведений из матричной алгебры.
При описании этих сведений мы будем следовать обозначениям,
принятым в данном учебнике, а именно: буквы, набранные жирным шрифтом,
будут обозначать матрицы, а буквы прописные будут использоваться для
обозначения векторов (представляющих собой, правда, важный частный
случай тех же матриц). Доказательства приводимых здесь фактов из
линейной алгебры будут, как правило, опускаться.
П2.1. Виды матриц и действия с ними
Матрицей называется прямоугольная таблица чисел (элементов)
вида
(
a2i а22 ... а2т \ ,по -v
I • (П2.1)

620 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
В общем обозначении элемента а^ матрицы А первый нижний индекс (г)
указывает номер той строки, а второй нижний индекс (j) — номер того
столбца, на пересечении которых находится этот элемент. Бели матрица
А содержит пт элементов, расположенных на п строках и т столбцах, то
говорят, что мы имеем п х т-матрицу А или матрицу А размерности
п х т.
Квадратной матрицей называется матрица, у которой число
строк равно числу столбцов, т.е. п х п — матрица (при любом целом
п > 1). Элементы аи, «22> • • • > апп квадратной матрицы образуют ее
главную диагональ.
Среди квадратных матриц выделим:
• диагональную матрицу D, у которой все элементы, кроме элементов,
стоящих на главной диагонали, равны нулю, т. е.
du 0 0 ... 0 0
0 d%2 0 ... 0 0
(
0 0 ... 0 dnn
to
заметим, что ковариационная матрица Е = (<7у) любой
последовательности ?,?,...,? взаимно не коррелированных
случайных величин является диагональной, т.к. cry = E[(^f' — Е^')^^' -
E?(i))] = 0 при любых %ф].
• единичную матрицу 1П, которая является частным случаем пхп
диагональной матрицы, поскольку все ее диагональные элементы равны
единице:
10 0 ... 0 0>
0 1 0 ... 0 0
,0 0 0 ... 0 L
нижний индекс п определяет размерность матрицы, и в тех случаях,
когда эта размерность очевидна из контекста, он может опускаться.
симметрическую (симметричную) матрицу, а именно такую
матрицу, у которой элементы, симметрично расположенные относительно
главной диагонали, равны между собой, т.е. а^ = а^ для всех г,
j = 1,2,...,п; заметим, что всякая ковариационная матрица ? =
((Tij) является симметрической по определению, т.к. ^*
Равенство матриц. Две матрицы А = (ajj) и В = (Ьу) называются
равными, если они имеют одну и ту же размерность и если ay = by для

П 2.1 ВИДЫ МАТРИЦ И ДЕЙСТВИЯ С НИМИ 621
всех г и j. Это означает, что равные матрицы совпадают поэлементно.
Вектор-строка — это матрица размерности 1 х т (т > 1),
т.е. матрица, состоящая из единственной строки длины га.
Например, результаты наблюдения значений р анализируемых переменных
аг ,ж ,... ,ж на одном объекте, зарегистрированные в определенный
момент времени t, образуют вектор-столбец
Xt = (x?\x?\...,x[p))- (П2.2)
Вектор-столбец — это матрица размерности п х 1 (п > 1), т.е.
матрица, состоящая из единственного столбца длины п. Например,
результаты наблюдения одной какой-либо переменной а; на п
статистически обследованных объектах (или на одном объекте, но
зарегистрированные в п последовательных моментов времени) можно представить в виде
вектора-столбца
X
U) _
х
Ь)
2
(П2.3)
Чтобы выделить эти специальные частные случаи матриц, мы
будем обозначать векторы-строки и векторы-столбцы прописными буквами
алфавита, а их компоненты — теми же самыми, но строчными буквами.
Условимся обозначать в дальнейшем вектор-строку длины га,
состоящую из одних нулей, с помощью 0j,m (или просто 0т, если из контекста
ясно, что речь идет о строках). Аналогично вектор-столбец из нулей
длины п будем обозначать 0n.i (или просто 0Л).
Перейдем к описанию действий над матрицами.
Транспонирование матрицы А определяется как действие, в
результате которого из А получается новая матрица АТ, строками которой
служат столбцы матрицы А, а столбцами — строки матрицы А при
сохранении их порядка. Таким образом, первая строка матрицы А
становится первым столбцом матрицы А , вторая строка матрицы А —
вторым столбцом матрицы А и т. д., так что (г,./')-й элемент atJ- матрицы А
становится (j, г)-м элементом матрицы А . Так, при построении
регрессионных моделей мы оперировали как с п х (р+ 1)-матрицей наблюдений

622 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
объясняющих переменных
««•...
*2 •••*»'!, (П2.4)
"'B)' '(V)
так и с транспонированной (р+ 1) X п-матрицей
(П2.5)
Заметим, что из определений операции транспонирования и свойства
симметричности матрицы следует непосредственно, что
транспонирование не меняет симметрическую матрицу, т. е. если А — симметрична, то
А =Аи обратно: если А = А, то матрица А квадратна и симметрична.
Очевидно также, что последовательное двукратное применение к
матрице А операции транспонирования приводит к исходной матрице А, т. е.
(АТ)Т = А.
Сложение двух матриц. Бели А и В-матрицы одной размерности,
то можно определить новую матрицу С = А + В, которая будет иметь ту
же размерность, что и А и В, а ее элементы с^ определяются для всех t
и j соотношениями с^ = а^ + 6tJ*. Заметим, что из определений операций
транспонирования и сложения непосредственно следует, что
(А + В)Т = ЛТ + ВТ. (П2.6)
Умножение матрицы на число. Произведение матрицы А на
число Л определяется как
т. е. каждый элемент матрицы А умножается на это число.
Произведение матриц. Бели число столбцов nxm-матрицы А
равно числу строк га х ^-матрицы В, то может быть определена операция
умножения АВ матрицы А на матрицу В (при этом говорят, что
«матрица В умножается на матрицу А слева»). Элементы с^ такого
произведения С = АВ определяются для всех % = 1,2,...,п и j = 1,2,...,&

П 2.1 ВИДЫ МАТРИЦ И ДЕЙСТВИЯ С НИМИ 623
соотношениями
* m
ы
Таким образом, (i,jf)-fi элемент произведения С вычисляется как
скалярное произведение г-й строки матрицы А и j-ro столбца матрицы В, т.е.
как сумма попарных произведений элементов г-й строки первой матрицы
на соответствующие (т. е. стоящие на тех же по порядку местах)
элементы j-ro столбца второй матрицы. При этом автоматически определяется
размерность матрицы-произведения С: она будет иметь столько же строк
(п), сколько имел первый сомножитель, и столько же столбцов (А), сколько
их имел второй сомножитель.
Заметим, 4to при перестановке сомножителей произведение В А
может просто не существовать, но даже если оно существует (как это и
бывает в случае, если матрицы А я В — квадратные и одной
размерности или если сомножители имеют размерности п х т и т х п), то, вообще
говоря, коммутативный закон для умножения матриц не имеет места,
т. с.
АВ ф ВА. (П2.8)
Отметим еще несколько полезных для эконометрических приложений
свойств произведения матриц.
Ассоциативный закон:
ABC = (АВ)С = А(ВС). (П2.9)
Дистрибутивный закон:
А(В + С) = АВ + АС, (В + С)А = ВА + СА. (П2.10)
Умножение на единичную матрицу: для любой пхп-матрицы А
имеют место тождества
А1Л = 1ЛА = А. (П2.11)
Транспонирование произведения матриц:
(А1А2...А,)Т = Л1Л^1...Л2ТЛ1Т (П2.12)
(доказывается индукцией: непосредственным сравнением элементов
матриц (AjA2) и А2 Ai доказывается справедливость (П2.12) для случая
к = 2 и т.д.).
Произведения вида АА и А А играют заметную роль в
эконометрических построениях. Так, произведение X X, в котором матрица X
определена соотношением (П2.4), является непременным «участником» всех

624 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
основных формул классического метода наименьших квадратов.
Заметим, что если А — матрица размерности nxm, то произведение АА
будет иметь размерность п х я, в то время как произведение АТА — это
матрица размерности тхт. Но в любом случае произведения вида АА
и к к всегда являются квадратными симметрическими матрицами.
Обратим внимание на специальный случай, когда X = (х
хп) — это вектор-столбец, состоящий из п элементов (или вектор-
столбец длины п). Тогда
п
Т (П2.13)
это 1 х 1-матрица, т. е.
ХХТ
хтх
число, а
( х2
X2Xi
ж "л
^^^^
i=l
хгх2
х2
ХпХ2
... хгхп
... х2хп
... 4
(П2.14)
это матрица размерности п х п.
Матрицы типа (П2.13) и (П2.14) играют заметную роль в
регрессионном анализе и в системах одновременных уравнений (см. гл. 14, 15, 17).
Действительно, если в качестве компонент х» вектора X рассмотреть ре-
грессионные «невязки» од - во — 0\х\ • • • *" ^рх\ (• = 1 j2,...,п), то
произведение (П2.13) даст нам сумму квадратов «невязок», которая
играет важную роль в анализе точности регрессионной модели. Если же в
качестве компонент х< вектора X рассмотреть отклонения г-й
объясняющей переменной аг1' от своего среднего значения а'1' (• = 1,2,...,р),
то произведение (П2.14) после применения к нему операции усреднения
(математического ожидания) Б даст р х р-ковариационную матрицу
объясняющих переменных Е*.
Прямое (или кронекерово) произведение п х т-матрицы А и
к х /-матрицы В обозначается А ® В, имеет размерность пк х ml и под-
считывается по формуле
А ®В = а21.В .а"В .'У. .а2Ш.В •
\aniB ап2В ... аптЪ/
где правая часть представляет собой матрицу, составленную из блоков
вида а^В. Каждый такой блок сам является матрицей и, как легко видеть,

П 2.1 ВИДЫ МАТРИЦ И ДЕЙСТВИЯ С НИМИ 625
имеет размерность к х L Повторенные п раз по строкам, они дают общее
количество строк, равное пк, а повторенные т раз по столбцам, они дают
общее количество столбцов, равное ml (подробнее о матрицах блочного
типа, или о составленных матрицах, так же, как и свойствах прямого
произведения, см. ниже в п. П2.8).
Отметим, что некоторые эконометрические построения (в первую
очередь, связанные с вычислительными проблемами систем регрессионных
уравнений, см. гл. 4 в томе 2) значительно упрощаются, если использовать
понятие прямого (кронекерова) произведения.
Матричное дифференцирование. Достаточно полное изложение
аппарата векторного и матричного дифференциального исчисления
читатель найдет в книге [Magnus J.R., Neudecker H.] . Мы же остановимся
лишь на тех определениях и результатах, которые непосредственно
использованы в нашем учебнике.
Пусть 0 = @i,02>--->0m) — т X 1-матрица (т.е. вектор-столбец
длины т), компоненты которой играют роль неизвестных параметров
эконометрической модели, а Л@) = (ai@),a2(©)>«-Man@)) — nxl-
матрица (т.е. вектор-столбец длины п), компоненты который
интерпретируются как некоторые характеристики этой модели, зависящие от 0.
Производной п х l-векторной функции А(&) по т х 1-векторному
аргументу 0 называется т х п-матрицй
(П2.16)
Матрицы вида (П2.16) используются, в частности, в качестве матриц
преобразований («якобианов») в теории преобразований случайных
величин (см., например, п. 4.4).
Рассмотрим важные для эконометрических приложений частные
случаи функции А(@):
1 . Л@) = Х0, где X — симметрическая матрица размерности п х т.
Логда flfe ' = ^е ' = А.
2°. Д@) = 0 В0, где В — симметрическая квадратная матрица
размерности тх т.
Тогда Mel = S&gSL = 20ТВ.
1 Готовится русский перевод этой книги.
21 Теория вероятностей
и прикладная статистика

626 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
3°. A(Q) ss ХТ0, где X — вектор-столбец длины т.
Тогда ^ \
П2.2. Основные числовые
характеристики квадратной
матрицы: определитель, след
Любой квадратной матрице А можно сопоставить некоторый набор ее
числовых характеристик. В данном пункте остановимся на двух из них.
Одна из таких характеристик называется определителем
{детерминантом) матрицы А и обозначается det А или |А|, а другая определяется как
след матрицы А и обозначается tr(A).
Определитель (детерминант) п X n-матрицы А вычисляется по
формуле
det А - ? Е • • • ? (-
где суммирование ведется по всем возможным комбинациям различных
столбцов (т.е. по всем возможным перестановкам вторых индексов), а
v{ju3%* • • • >in) — это минимальное число инверсий (т. е. парных обменов
местами), которое надо совершить с элементами исходной перестановки
A,2,...,п), чтобы получить перестановку (ibiai-.-fim)- Очевидно,
общее число слагаемых в правой части (П2.17) составит при таком
определении n-факториал (п!).
Для малых размерностей матриц это определение приводит, в
частности, к следующим результатам:
а) п = 2 : det А = det [ вп °12 ] =
\ а21 а22 /
( а12 а\$ \
a2i а22 агз I
«31 «32 «33 /
«12а23«31 - «13«22«31 - «11«23«32 —
Приведем здесь важнейшие свойства определителя:
1) det( А В) = det(B A) = det A • det В;
2) det(AA) = An det A (A - число , п — размерность матрицы А);
3) det[diag(alba22,...>апп)] = ana22 •... • апп\
4) detln = l;
5) det AT = det A;

П2.2 ОСНОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ КВАДРАТНОЙ МАТРИЦЫ 627
6) det А = 0, если в матрице А есть две одинаковые строки {два
одинаковых столбца);
7) инверсия {обмен местами) двух строк {столбцов) матрицы А
приводит к изменению знака ее определителя;
8) значение определителя матрицы А не изменится, если к любой
его строке {столбцу) добавить линейную комбинацию других строк
{столбцов).
Последнее свойство нуждается в пояснении. Обозначим Ait =
(ац,а*2>...,dim) — г"Ую строку пхт матрицы А. Линейной комбинацией
строк с номерами и, *2» • • •» Ч называется строка, определяемая в
соответствии с правилами действий с матрицами по формуле
b\Aix. + A2 Ai2. + • • • + \kAik,
где Aj, А2,..., А/с — некоторые числа. Точно так же определяется линейная
комбинация столбцов Atj = {atj} o2j,...,anj)T, j = j,, j2,... Jti
9) разложение определителя по элементам строки {или столбца).
где Ay — (n - 1) х (n - 1)-матрица, получающаяся из матрицы А
вычеркиванием из нее г-й строки и j-ro столбца. Величина detA^
называется минором матрицы А, а величина (—l)l+Jdet Ay —
алгебраическим дополнением элемента ay в матрице А. Кстати, понятие
алгебраического дополнения используется в учебнике, например, при
вычислении коэффициента детерминации R и частных
коэффициентов корреляции по корреляционной матрице R исследуемого
многомерного признака (см. п. 11.2).
Отметим, что если квадратная матрица имеет отличный от нуля
определитель, то она называется невырожденной.
След квадратной п х n-матрицы А (обозначается tr А, от
английского слова «trace» ) определяется как сумма ее диагональных элементов,
т.е.
tr А = аи + а22 + • • • + апп. (П2.18)
Основные свойства следа матрицы:
(i) tr(AB) = tr(BA);
(ii) trln = n;
(iii) tr(AA) = AtrA, где А — число;
(iv) trAT = trA;
21*

628 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
(v) tr(A + В) = trA + trB;
(vi) в качестве частного случая свойства («) особо отметим ситуации, в
которых роль А играет вектор-столбец X = (х\, ж2> • • • > &п) > а роль
В — X ; и хотя ни для X, ни для X след не определен, их
произведения ХХТ vl X X являются квадратными, соответственно, п х п-
и 1 х 1-матрицами и для них действует правило (г), т.е.
tx(XXT) = tr{XTX),
Т 2 2 2
где, обращаем внимание читателя, матрица X X = Zi+X2+.. .+хп —
это число.
Заметим, что и определитель, и след матрицы имеют четкую
вероятностную интерпретацию, например, когда в качестве А
рассматривается ковариационная матрица Е^ многомерной случайной величины
f = (f ,?,...?) ¦ В этом случае и trE^ и detE^ характеризуют
степень многомерного рассеяния значений этой случайной величины, а
det Е^ называется обобщенной дисперсией ? (см. п. 2.6.6).
П2.3. Обратная матрица и ее свойства
В операциях с числами для любого отличного от нуля числа а
существует число а~ = 1/а, которое мы называем обратным и которое
обладает тем характеристическим свойством, что аа~ = а" а = 1. В
матричной алгебре роль единицы, как мы видели, выполняет единичная
матрица 1П, поскольку при умножении на 1п любой квадратной матрицы
размерности п х п справа и слева эта матрица не меняется (см П2.11).
Поэтому по аналогии с алгеброй чисел определим:
• пусть А — квадратная невырожденная (т.е. det А ф 0) матрица;
тогда матрица А" называется обратной, если АА"~ = А~ А = I.
Можно показать, что такое определение обратной матрицы А =
(aJjP) приводит к следующей формуле для вычисления ее элементов о^р:
бр _ (-1)*J det А,,
a
где Aji — как и прежде, матрица, получающаяся из матрицы А
вычеркиванием из нее jf-й строки и г-го столбца (т. е. числитель правой части
(П2.19) является алгебраическим дополнением элемента aJt в исходной
матрице А, или, что то же, — алгебраическим дополнением (г, j)-ro элемента
в транспонированной матрице А ).

П2.3 ОБРАТНАЯ МАТРИЦА И ЕЕ СВОЙСТВА 629
Пример П2.1. Двухпродуктовая версия статической модели
«затраты-выпуск» Леонтьева. Пусть ац — затраты продукта % на
выпуск единицы продукта j (•', j =1,2). И пусть Х( — общий выпуск
продукта i и Cj — конечный спрос на этот продукт. Тогда уравнения,
связывающие между собой введенные выше величины, будут иметь вид (в
предположении, что нет ни потерь, ни излишков продуктов):
+ «12^2 + С\ = ЯЪ
+ + С2 = Х2)
или, после приведения подобных членов,
— 021*1 + A ~ °22 )Х2 = С2«
Запишем эту систему, используя матричные обозначения:
АХ = С, (П2.20)
где X = (хьх2)т, С - (сис2)Т, а
Мы хотим разрешить систему (П2.20) относительно х\ и х2, т. е.
определить, какое общее количество первого и второго продукта должно быть
произведено, чтобы обеспечить производственное потребление и конечный
спрос. Чтобы уединить X в уравнении (П2.20), домножим обе части этого
уравнения на матрицу А слева:
X = А С,
где в соответствии с (П2.19)
Л-1 _ 1 f 1 - <»22 <*12 "\
det А V «21 1 ~ «и ) '
С учетом того, что det А = A — ац)A - а2г) - fli2a2i> имеем:
- а22)-а12а21
——т———- [a2ici+(l-an)c2].
- а22)-а12а21

630 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Основные свойства обратной матрицы:
1) матрица А" для любой невырожденной матрицы А —
единственна;
2)det A =(det A);
V11"
5НАВ)" sB^A,
(ABC) = C"BA и т. д.
(напомним, что все матрицы, участвовавшие в формулировке свойств
обратной матрицы, — квадратные и невырожденные).
Теперь мы можем дополнить перечень основных типов матриц,
приведенный в п. П2.1. Введем в рассмотрение класс ортогональных матриц,
определив:
• квадратная невырожденная матрица А называется
ортогональной, если А = А" .
Из определения ортогональной матрицы непосредственно следует, в
частности, что А А = АА = I. Нетрудно также вывести, что
определитель ортогональной матрицы всегда равен по абсолютной величине
единице^ т.е. |det А| = 1. Действительно, поскольку det A = det А
(свойство 5) из п. П2.2), a det (АВ) = det A-det В (свойство 1) из п. П2.2), то для
ортогональной матрицы det(AA ) = det A det A = (det A) = det 1=1.
Отсюда получаем, что | det А| = 1, если А ортогональна.
Мы еще будем обращаться к ортогональным матрицам в пп. П2.5 и
П2.6.
П2.4. Ранг матрицы и линейная
зависимость ее строк (столбцов)
Наряду с рассмотренными в п. П2.2 двумя основными числовыми
характеристиками квадратной матрицы — ее определителем и ее следом,
в общем случае, включающем и прямоугольные матрицы, существует еще
одна очень важная числовая характеристика матрицы — ее ранг.
Перед тем, как сформулировать строгое определение этого понятия,
рассмотрим понятие линейной зависимости строк (столбцов)
анализируемой п х m-матрицы А.
Строки А{. = (ан,а<29**-?а*т)) * = 1,2,...,п, матрицы А
называются линейно зависимыми, если существуют числа Ai, А2,..., Ап, не
все равные нулю, и такие, что
+ А2Л2. + ... + \пАп. = 0i.m (П2.21)

П2.4 РАНГ МАТРИЦЫ И ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ЕЕ СТРОК 631
(здесь 0х.т, в соответствии с принятыми выше обозначениями, — это
строка длины т, состоящая из нулей).
Аналогично: столбцы A.j = (aij,O2j,•••>anj) > 3 = 1,2, ...,m,
матрицы А называются линейно зависимыми, если существуют числа
А*ьА*29--*)А*т) не все равные нулю, и такие, что
^Ал + ц2А.2 + ... + цтА.т = 0пЛ. (П2.21')
В противном случае строки (столбцы) называются линейно
независимыми.
Можно доказать, что максимальное число линейно независимых
строк п х т-матрицы А совпадает с максимальным числом ее линейно
независимых столбцов и, одновременно, — с максимальным порядком
ее не равного нулю минора (напомним, что минором порядка к матрицы
А называется определитель к х &-матрицы, получающейся из матрицы А
вычеркиванием из нее п — к строк и то - к столбцов).
• Ранг п х m-матрицы А (будем обозначать его ранг А) определяется
как максимальное число ее линейно независимых столбцов.
Очевидно, что в силу приведенного выше свойства, ранг матрицы А
может быть определен и как максимальное число ее линейно независимых
строк, и как максимальный порядок ее отличного от нуля минора.
Кстати, последнее определение часто бывает наиболее удобным с точки зрения
возможности практического вычисления ранга конкретной матрицы. При
этом, определяя ранг матрицы как максимальный порядок ее отличного от
нуля минора, подразумевается, что достаточно того, чтобы нашелся хотя
бы один ненулевой минор порядка А;, в то время как все миноры порядка
к + 1 уже будут равны нулю. Так, например, в 4 X 3-матрице
А =
все четыре минора 3-го порядка равны нулю. Следовательно ранг А < 3.
И хотя большинство миноров 2-го порядка тоже равно нулю, все-таки
существуют миноры этого порядка, отличные от нуля. А это значит, что
ранг А = 2.
Заметим, что применительно к матрице X наблюденных значений
объясняющих переменных (см. (П2.4)) в регрессионном анализе
линейная зависимость столбцов означает линейную зависимость
объясняющих переменных.

632 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Из определения ранга матрицы более или менее непосредственно
вытекают следующие его основные свойства:
1) ранг А ^ min(n, m); если ранг А = min(n, m), то говорят, что матрица
А — это матрица полного ранга;
2) ранг 1п = п;
3) ранг (diag(on 5 ^22* • • • ? апп)) = &? гДе & — число ненулевых элементов
в ряду ац,а22)---5лпп;
4) ранг (А В) < ппп{ранг А, ранг В};
5) ранг В = п, если В — квадратная невырожденная матрица
размерности пхщ
6) ранг (А В) = ранг А, если А — произвольная матрица размерности
п х ш, а В — невырожденная т х т-матрица;
7) ранг (В А) = ранг А, если А — произвольная матрица размерности
п х т, а В — невырожденная п X п-матрица;
8) ранг (Bi А В2) = ранг А, где А — произвольная матрица порядка п х
ш, а Bi и Вг — невырожденные квадратные матрицы размерностей,
соответственно, (n x п) и (m x т);
9) ранг А = ранг АТ.
Отметим также один важный для эконометрических приложений
(особенно для проблемы идентифицируемости модели) факт, связанный
с понятием ранга матрицы. Пусть X = (аг ,аг ,...,аг')т — набор
переменных (среди которых, в целях большей общности, мы допускаем
присутствие и переменной, тождественно равной единице), а А —
матрица размерности п х р. Система уравнений относительно X может быть
записана в виде
АЛ- = ОлЛ. (П2.22)
При решении системы (П2.22) важным моментом является соотношение
между числом неизвестных и числом линейно независимых уравнений,
содержащихся в системе. Так вот, оказывается, что число линейно
независимых уравнений в системе (П2.22) равно рангу матрицы А.
П2.5. Характеристические
(собственные) числа квадратной
матрицы и соответствующие им
собственные векторы
Широкий круг задач многомерного статистического анализа и
эконометрики сводится (в вычислительном плане) к необходимости анализа и

П2.5 ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА КВАДРАТНОЙ МАТРИЦЫ 633
решения параметрического семейства систем уравнений типа
(А-А1п)* = 0п.ь (П2.23)
где А — некоторая п х п-матрица, X = (хь &2> - • •» хп) — вектор-столбец
неизвестных, а А — некоторый числовой параметр. Для того, чтобы
существовало нетривиальное (отличное от нулевого) решение, необходимо,
чтобы матрица А - А1Л была вырожденной, т. е. необходимо потребовать,
чтобы
det(A-AIn) = 0. (П2.24)
Из правил вычисления определителя матрицы (см. (П2.17)) следует,
что левая часть (П2.24) представляет собой алгебраический полином от А
степени п, так что соотношение (П2.24) — это алгебраическое уравнение
степени п относительно А. Само это уравнение, а следовательно, и его
корни Ai, A2,..., АЛ по построению полностью определяются элементами
матрицы А. Приходим к определению:
• Характеристическими (собственными) числами пхп-матрицы
А называются корни характеристического уравнения (П2.24)-
Беря любое из собственных чисел А; и подставляя его в исходное
соотношение (П2.23), мы получаем уже конкретную систему уравнений
(относительно X) вида
= 0пЛ. (П2.24')
Существование нетривиального решения X(i) этого уравнения
обеспечивается равенством нулю определителя det(A-AjIn). Соответственно,
приходим к еще одному определению:
• Вектор-столбец X(i) = (x\l\х% ,. . .,ж„, ) , являющийся решением
уравнения (П2.24'), называется характеристическим
(собственным) вектором матрицы А, соответствующим
характеристическому {собственному) числу А,-.
А поскольку алгебраическое уравнение степени п имеет п корней
(среди которых, вообще говоря, могут быть совпадающие и комплексные), то
всякая квадратная п X n-матрица А имеет п собственных чисел (не
обязательно различных) и п соответствующих им собственных векторов.
В дальнейшем, отправляясь от интересов прикладной статистики и
эконометрики, мы сосредоточим свое внимание на свойствах
характеристических чисел и характеристических векторов только действительных
симметрических положительно (или неотрицательно) определенных
матриц А (будем для краткости их называть далее, соответственно, спо- и

634 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
сно-матрицамиI.
1) Всякая спо- (сно) п х n-матрица имеет п положительных
(неотрицательных) действительных характеристических чисел; и наоборот,
матрица, все характеристические числа которой положительны
(неотрицательны) является спо- (сно-) матрицей.
2) Собственные векторы X(i) и X(j), соответствующие разным
собственным числам, всегда взаимно ортогональны, т. е.
XT(i)X(j) = Q при А^А,-.
Поскольку собственный вектор определяется с точностью до
коэффициента пропорциональности, то можно пронормировать собственные векторы
ХA), ХB)>..., Х(п) так, что все они будут образовывать ортонормиро-
ванную систему, т.е.
J "!^"' длявсех U=l,2,...,n.
Заметим, что п X п-матрица А, составленная из столбцов X(i) (t =
1,2,..., п), т. е. матрица
Х=^ХA) : ХB)
будет ортогональной^ т.е. X X = 1П.
3) Всякая спо- и сно- матрица А может быть приведена с помощью
ортогонального преобразования X к диагональному виду, в котором на
диагонали будут стоять характеристические числа, т. е.
ХТАX = diag (Хг, А2,..., Ап).
П2.6. Некоторые свойства
симметричных положительно
(неотрицательно) определенных
матриц
На протяжении всего данного пункта мы будем полагать (если
специально не оговорено другое), что А — симметрическая положительно
1 Симметрическая п х п-матрица А называется положительно (неотрицательно)
определенной у если для любого ненулевого вектора X = (х\> хг,..., хп)Т
выполняется неравенство ХТАХ > О (ХТАХ > 0). Более подробно о симметрических
положительно и неотрицательно определенных матрицах см. в п. П 2.6.

П2.6 СВОЙСТВА МАТРИЦ 635
определенная матрица размерности п, т. е. для любого ненулевого
вектора X = (a?i,a?2> • • • >#п)Т выполняется неравенство
ЛГТАХ>0. (П2.25)
1) При любой т х n-матрице В матрица ВТВ будет всегда
симметрична и неотрицательно определена. Действительно, для любой (n x 1)~
матрицы X (т.е. для вектора-столбца длины п)
п
ХТ(ВТВ)X = (ВХ)ТВX = YTY =
т.к. произведение вектора-строки У = (ВХ) на вектор-столбец Y =
В X приводит, очевидно, к неотрицательному числу.
2) Если п^типх т-матрица В — матрица полного ранга (т. е. ранг
В = т), то матрица В А В — положительно определенная; в частном
случае п = тп В является невырожденной квадратной матрицей размерности
пх п.
3) Матрица А" , обратная к А, также является симметрической и
положительно определенной.
4) Единичная матрица 1П является симметрической положительно
определенной (т.к. для любого вектора-столбца X длины п X 1пХ =
ХТХ = ? х] > 0).
t=i
5) detA > 0, т.е. определитель любой спо- матрицы положителен;
отсюда, в частности, следует, что и все главные миноры матрицы А
положительны (минор матрицы называется главным, если он является
определителем подматрицы, образованной из исходной матрицы вычеркиванием
из нее строк и столбцов, имеющих одинаковые номера).
6) След матрицы А может быть вычислен как сумма ее собственных
значений, т.е.
trA = A! + A2 + ---+An.
где, напомним, А — спо- матрица размерности п х n, a Ai, А2,..., Ап — ее
собственные числа.
7) Всякая спо (га х го)-матрица А может быть представлена в виде
А = ССТ, (П2.25а)
где С некоторая невырожденная (тп х т)-матрица.

636
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Действительно, из доказанного в п. 13.2.3 соотношения A3.10)
следует, что любая спо матрица А может быть приведена к диагональному виду
при помощи некоторого ортогонального преобразования L, т. е.
LALT = A,
(П2.256)
где,
А =
\ 0
а Аь А2,..., Ат — собственные значения (действительные и
положительные) матрицы А. Домножая обе части соотношения (П2.256) слева на LT
и справа на L, получаем
А = LTAL. (П2.25В)
1 /2 1 /2
Представляя матрицу А в виде А = А ' А ' , где
0 \
и обозначая С = L А ' , получаем из (П2.25В) доказательство
возможности представления матрицы А в виде (П2.25*).
Пример П2.2. Продемонстрируем использование свойств
симметрических положительно определенных матриц при анализе многомерных
распределений и их статистик. Пусть X = (х\>х^...,хп) —
последовательность одинаково @, сг2)-нормально распределенных случайных
величин, т.е.
Е^ = 0, t= 1,2,...,п;
Dxi = Еж? = (т2, t = 1,2,...,п;
cov (xi,Xj) = E(xiXj) = 0 при г ф j>
или, в компактной записи, X € iVrt@n#i; о 1п). И пусть в процессе анализа
модели нам пришлось заниматься исследованием квадратичной формы от
анализируемых случайных величин вида X АХ, где А, как и ранее, спо-
матрица.
В соответствии со свойством 3) спо- и сно- матриц (см. п. П2.5)
существует такая ортогональная матрица С, с помощью которой матрица

П2.7 ИДЕМПОТЕНТНЫЕ МАТРИЦЫ 637
А может быть приведена к диагональному виду, а именно:
CTAC = diag(AbA2,...,An),
где Ai, А2,..., Ап — собственные числа матрицы А, а элементы матрицы
С полностью определяются собственными векторами той же матрицы А.
Введем вспомогательные переменные
У = СТХ (соответственно, X = CY) (П2.26)
и посмотрим, как будет выражаться анализируемая квадратичная форма
X АХ в терминах этих новых переменных:
ХТАХ = (СУ)ТАСУ = УТ(СТАС)У
п
= yTdiag(AbA2,...,An)y = Y, А^?- (П2-27)
t=i
Следовательно, для того чтобы понять, как «ведет себя»
квадратичная форма X АХ, необходимо выяснить, какому закону распределения
вероятностей подчиняются переменные уг, у2, • • • 5 2/п-
Из (П2.26) следует, что У, будучи линейной функцией от X, также
подчиняется нормальному закону со средним значением
ЕУ = Е(СТХ) = СТЕХ = 0пЛ
и с ковариационной матрицей
Ъу = Е(УУТ) = Е(СТХХТС) = СТЕ(ХХТ)С
= СТ(<721П)С = (Т2СТС = а\
(в этой выкладке мы воспользовались тем, что ковариационная
матрица Лх вектора X равна по условию а 1П, а также — ортогональностью
х р р у
матрицы С, из чего следует С С = 1П).
Таким образом, мы убедились в том, что вспомогательные
переменные 2/ь 2/2Г-^2/п так же, как и исходные случайные величины
a?i,a?2,.. .,a:n, (О,сг )-нормальны и взаимно независимы. А это позволяет
описать распределение интересующей нас квадратичной формы (П2.27)
законом суммы масштабированных х(У) — распределенных случайных
величин.

638 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
П2.7. Идемпотентные матрицы
Особенно важны в прикладной статистике и эконометрике
соотношения типа (П2.27), в которых матрица А относится к классу так
называемых идемпотентных матриц.
• Идемпотентной называется симметрическая1 матрица А,
обладающая тем свойством 1 что она совпадает со своим квадратом} т. е.
А» А3. (П2.28)
Перечислим основные свойства идемпотентных матриц.
1) Любая целая положительная степень к идемпотентной матрицы А
дает снова исходную матрицу А, т.е. А* = А (следует непосредственно из
определения).
2) Собственные числа идемпотентной матрицы могут принимать
только одно из двух значений: 0 или 1; а следовательно, в соответствии
со свойством 1) из П.П2.5 все идемпотенткые матрицы неотрицательно
определены.
Докажем справедливость этого утверждения. В соответствии с
характеристическим уравнением (П2.23)
После домножения обеих частей этого характеристического уравнения
слева на матрицу А имеем:
А2X = А (АХ) = А (XX) = Х2Х. (П2.29)
Но одновременно с этим, используя идемпотентность матрицы А, мы
можем записать:
А2Х = АХ = \Х. (П2.29')
Сравнивая правые части (П2.29) и (П2.29'), получаем
а т. к. X/0я.ьто
А2 - А ж О,
т.е. либо А = 0, либо А = 1, что и доказывает свойство 2).
1 Иногда требование симметричности не включают в определение идемпотентной
матрицы.

П2.8 МАТРИЦЫ БЛОЧНОЙ СТРУКТУРЫ 639
3) Ранг идемпотентной матрицы равен числу ее ненулевых
собственных чисел, что совпадает со следом исходной матрицы.
4) Бели ранг п х n-идемпотентной матрицы А равен п - Л, то
использование ее собственных векторов для преобразований типа (П2.26)
будет приводить квадратичную форму ХТАХ относительно п
независимых @, (т2)-нормально распределенных случайных величин к виду
ХТАХ ж у\ + у\ + ... + fnwak% (П2.30)
где элементы УьМ^мУп-* также взаимно независимы и (О,?2) —
нормально распределены. А это значит, что квадратичная форма ХТАХ
подчиняется <г)?{п - ^-распределению.
П2.8. Матрицы блочной структуры
Содержание анализируемой задачи зачастую обусловливает
целесообразность разбиения матриц, которыми мы оперируем, на отдельные
блоки. Так, например, при анализе модели многомерной регрессии или систем
одновременных уравнений в рамки нашего анализа попадают m
зависимых (эндогенных) переменных Y = (у^\у^2\...,l/m*)T и Робъясняющих
(экзогенных, предопределенных) переменных X = (а^1\а^2\...,я^)т.
Важным объектом анализа является при этом ковариационная матрица
Ъ2 всего вектора переменных Z = (?), которая будет состоять,
соответственно, из четырех блоков Syr, ?yx, ?хк и Ехх> а именно:
(П2.31)
Очевидно, матрица Ъ2 будет иметь размерность (m+p)x(m+p), в то
время как блок Ъуу (матрица ковариаций между компонентами вектора Y)
имеет размерность тх т> блок Ъух (матрица «перекрестных»
ковариаций эндогенных переменных с предопределенными) имеет размерность
m х р, блок Иху (матрица «перекрестных» ковариаций
предопределенных переменных с эндогенными) имеет размерность р х т, и, наконец,
блок Лхх (матрица ковариаций между компонентами вектора X) имеет
размерность р х р.
Заметим, что для того, чтобы пользоваться некоторыми общими
правилами оперирования с блочными матрицами, следует соблюдать
необходимые требования при их разбиении, а именно:

640 П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
• блоки, стоящие друг над (или под) другом по вертикали, должны
иметь одинаковое количество столбцов; а блоки, стоящие рядом
(слева или справа друг от друга) по горизонтали, должны иметь
одинаковое количество строк.
Сложение блочных матриц. Бели две матрицы А и В
одинаковой размерности разбиты на блоки, соответственно, A;j и В^ (г =
1,2,...,k\\ j = 1,2,...,fc2) одинаковым образом (т.е. размерности
блоков Aij и Bij совпадают), то их сложение производится по правилу
\
А21 "Г -D21 • А22 "Г <D22 • • • • • A2IC2 Т* **2/р2
Умножение блочных матриц формально также производится по
правилам умножения обычных матриц, однако разбиение А и В на
блоки А^ и В^ должно быть произведено таким образом, чтобы количество
столбцов в первом сомножителе совпадало бы с количеством строк во
втором сомножителе. Например:
ц + А22В21 ' А21В12+А22В
Определитель блочной матрицы. Пусть матрица А разбита на 4
блока
/п 12
А= (П2.32)
21 : А22
таким образом, что блоки Ац и А22 являются квадратными матрицами
(как это было в нашем примере (П2.31)). Тогда можно воспользоваться
следующей общей формулой подсчета определителя матрицы А, во многих

П2.8 МАТРИЦЫ БЛОЧНОЙ СТРУКТУРЫ 641
случаях существенно упрощающей вычисления:
det I ..V .; I =detA11-det(A22-A21A111A12)
= det A22 • det (Ац — А12А22 A21).
В частном случае блочно-диагоналъной матрицы А (т. е. когда
матрицы А12 и A2i состоят из одних нулей) данная формула принимает вид
det A22-
0 : A22
Обращение блочной матрицы (П2.32) производится по формуле
a i" / а п
11 • А12
/ \ А22 А А* • А22
22/ \—A A2iAn . A
где
А = (А22 — A2iAu A12) и А = (Ац — А12А22 A21) .
Прямое (кронекерово) произведение п х m-матрицы А и
к х /-матрицы В было введено в п. П2.1 (см. соотношение (П2.15)).
Поскольку результат такого перемножения матриц А и В представляется
матрицей блочной структуры, рассмотрим несколько полезных свойств
прямого произведения:
1) если матрицы А и В квадратны и обратимы, то
2) если А — п х n-матрица, а В — k x ft-матрица, то
det (A ® В) = (det A)n(det В)*;
3)(А®В)Т = (АТ®ВТ);
4) tr(A<8>B) = trA-trB.

ЛИТЕРАТУРА
АбрамовичМ. Справочник по специальным функциям. /Пер. с англ./ — М.:
Наука, 1979.
Айвазян С. А, A968). Статистическое исследование зависимостей. М.:
Металлургия.
АйвазянС.А. A974). Об опыте применения экспортно-статистического метода
построения неизвесткой целевой функции. — В кн.: Многомерный статистический
анализ в социально-экономических исследованиях. M.s Наука, С. 56-86.
АйвазянС.А. A979). Конфлюэнтный анализ. — В кн.: Математическая
энциклопедия. М. Т. 2. С. 1083.
АйвазмнС.А. A980). Вероятностно-статистическое моделирование
распределительных отношений в обществе. — В кн.: Статистическое моделирование
экономических процессов. Ученые записки по статистике. М., Статистика, Т.37.
Айвазян С, А,, ЕнюковИ, С, МешалкинЛ.Д. Прикладная статистика.
Исследование, зависимостей. — М.\ Финансы и статистика, 1985.
Айвазян С, Ач БухштаберВ, M.t ВнюковИ, С, МешалкинЛ.Д, Прикладная
статистика. Классификация и снижение размерности. — М,: Финансы и
статистика, 1989.
Андерсон Т. Введение в многомерный статистический анализ. М., Фиэматгиэ,
1963.
БоксДж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. /Пер.
с англ./ — М.: Мир, 1974, вып. 1 и 2.
Большее Л. #., Смирнов Н. В. Таблицы математической статистики. М.: Наука,
1965.
Боровков А. А. Курс теории вероятностей. М.: Наука, 1972.
Бухштабер В. М. Метод многомерной развертки в анализе временных рядов.
Обозрение прикладной и промышленной математики. Т. 4 A997): № 4.
ВалъдА. Последовательный анализ. /Пер. с англ./ — М.: Физматгиз, 1960.
ДжонстонДж. Эконометрические методы. /Пер. с англ./ — М.: Статистика,
1980.
Дидэ Э., и др. Методы анализа данных: подход, основанный на методе
динамических сгущений. /Пер. с франц./ — М.: Финансы и статистика, 1985.
ЕзекиэлМ., Фокс К. Методы анализа корреляций и регрессий. /Пер. с англ./ —
М.: Статистика, 1966.
КемениДж., СнеллДж. Конечные цепи Маркова. /Пер. с англ./ — М.: Наука,
1970.
КендэлМ. Временные ряды. /Пер. с англ./ — М.: Финансы и статистика, 1981.
КендаллМ.Дж., СтъюартА. A966). Теория распределений. /Пер. с англ./ —
М.: Наука.
КендаллМ.Дж., СтъюартА. A973). Статистические выводы и связи. /Пер. с
англ./ — М.: Наука.
КендаллМ.Дж., СтъюартА. A976). Многомерный статистический анализ и
временные ряды. /Пер. с англ./ — М.: Наука.
Колмогоров А. Н. Основные понятия теории вероятностей. М. — Л., ОНТИ, 1936.

ЛИТЕРАТУРА 643
Крамер Г. Математические методы статистики. — 2-е изд. Пер. с англ. — М.:
Мир, 1975.
Лумелъский В. Я. Агрегирование объектов на основе квадратичной матрицы.
Автоматика и телемеханика, 1970. № 1. С.133-143.
Магнус Я. Р., Катышев П. К., ПересецкийА.А. Эконометрика. Начальный
курс. C-е изд.) — М.: Дело, 2000
МайстроеЛ, Е. Развитие понятия вероятности. — М.: Наука, 1980.
МаленьоЭ. Статистические методы в эконометрии: Пер. с франц. — М.:
Статистика, 1975, вып.1; 1976, вып.2.
МитомнА.Л, Потребительское поведение семей: дифференциация, динамика,
классификация. -— М.: Экономика, 1990.
Феллер Я. Введение в теорию вероятностей и ее приложения: Пер. с англ. — 2-е
издание. М,: Мир, 1964.
Харман Г. Современный факторный анализ: Пер. с англ. — М.; Статистика,
1972. Мир, 1983.
Эфрон В. Нетрадиционные методы многомерного статистического анализа: Пер.
с англ. — М.: Финансы и статистика, 1988.
Anderson Т. W.f Rubin H. Statistical inferences in factor analysis. Proc. 3 Berkeley
Symp. Math. Statist, and Probab. — Univ. Calif. Press, 1956. Pp. 11-50.
BerndtE,R. The practice of econometrics. Classic and contemporary. Addison-
Wesley Publishing Company. Reading-Massachusetts-Menlo Fare-California, 1990.
Dougherty C. Introduction to econometrics. Oxford University Press. New York-
Oxford, 1992.
GoldbergerA. A course in Econometrics. Cambridge-Mass.: Harvard University
Press, 1990.
Green W. #. Econometric analysis. Macmillan Publishing Company, New York, 1993.
Hayashi F. Econometrics. — Princeton University Press, Princeton and Oxford, 2000.
Horowitz J. Semiparametric Methods in Econometrics. — Springer-Verlag New York,
Inc, 1998.
Johnston J. and Di NardoJ. Econometric Methods, 4th edition. — Me Graw-Hiil,
1997.
JorgensonD, Welfare. Vol. 1: Aggregate Consumer Behavior. Vol.2: Measuring
Social Welfare. — MIT Press, Cambridge, Massachusetts, 1997.
Kennedy P. A Guide to Econometrics, 4th edition. — Blackwell Publishers, 1998.
Magnus J.R4 NeudeckerH. Matrix Differential Calculus with Applications in
Statistics and Econometrics. New York, John Wiley, 1988.
PindyckR., RubinfeldD. L. Econometric models and economic forecasts. MeGraw-
Hill Kogakusha Ltd, Tokio, 1976.
RuudP. An Introduction to Classical Econometric Theory. — Oxford University Press.
New York-Oxford, 2000.

644
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Асимптотическое распределение 216
Автоинформативность 336, 524-525
Автоматическая классификация 480,
487
Автопрогноз 541
Аксиоматика Колмогорова 69-70
Алгебраическое дополнение 413, 627
Алгебраический полином 383
Апостериорное распределение 271
Апостериорно-модельный подход 62
Апостериорно-частотный подход 61
Апостериорный байесовский риск
272
Априорная статистическая
(выборочная) информация 469
Априорное распределение 270
Априорный подход к вычислению
вероятностей 60
Асимметрия 108, 210
Асимптотическая несмещенность 251
— эффективность 251
Асимптотические свойства оценок
234, 251
Б
Байеса теорема (формула) 69, 271-
272
Байесовские оценки параметров 271-
272
Байесовский подход 269
Байесовский риск 272
Байесовское правило классификации
473, 474
Безусловная вероятность 177
Бернулли последовательность
испытаний 115
— теорема 155
Бета-распределение 148, 276
Бинарные (булевые,
дихотомические) переменные 493
Блочно-диагональная матрица 641
Блочная структура матриц 639-641
Булева матрица парных сравнений

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
645
584
Бюджетные обследования семей 353
Вариационный ряд 225
Вероятностная модель 41, 50
Вероятностное пространство 59,195
— — дискретное 52
— — непрерывное 69
Вероятностно-статистическая модель
40-41, 50
Вероятность ошибочной
классификации 473
Вероятность события 59-60
— — условная 64
Взвешенное евклидово расстояние
493
Взвешивание выборочных данных
261
Визуализация данных 336
Возможные значения случайной
величины 79
Восстановление пропущенных
наблюдений 342
Выбор общего вида модели
382-385
Выборка 195, 329
— механическая 199
— случайная 199
— ступенчатая 200
Выборочные характеристики 209-
210
Гамма-распределение 146
Гамма-функция Эйлера 142, 145, 147
Генеральная совокупность 194, 329
Геометрическая природа
совокупности исходных данных 339, 383, 394
Гипергеометрическое распределение
119-121
Гипотеза статистическая 283-287
простая 289, 292
сложная 290, 293
— — нулевая (основная) 287
— — альтернативная 287
Гистограмма 203, 462
Главные компоненты 526-551
Группированные выборочные
данные 207
д
Двумерный нормальный закон
распределения 97, 127
Детерминант (определитель) 626
Дендограмма 480, 504
Дескриптивная статистика 231
Дискриминантная функция 469, 474
Дискриминантный анализ 335
— — параметрический 475, 476
— — непараметрический 476
Дисперсионный анализ 314, 363, 393
Дисперсия 104

646
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— обобщенная ПО
— эмпирическая 209
Дихотомические (бинарные)
переменные 493
Доверительная вероятность 33, 248
— область 249, 264
Доверительный интервал 248, 280
Достоверное событие 57
Зависимость детерминированная 371
— марковского типа 169
— статистическая 359
— структурного типа 374
Закон больших чисел 154-155
Закон распределения вероятностей
84, 150
— — — многомерный 86
Зона (область) неопределенности 299
и
Иерархические процедуры
классификации 497, 504-507
Интервал группирования 386
Интервальное оценивание 248
Информационная матрица Фишера
243
— характеристика связи 460
— расстояние Каллбэка 498
Информационный этап исследования
340
Испытания Бернулли 171
Исходные статистические данные 43,
329-333, 447
Итоговый этап исследования 345
к
Категоризованные переменные 448
Квантиль 106
Клаюс 471
Классификация 459
— без обучения 460
— с обучением 460
Классификационные переменные 362
Кластер 334, 489
Кластер-анализ 334, 480, 491
Ковариационная матрица 101, ПО,
397
Ковариационный анализ 363
Количественные переменные 362
Количество информации (Фишера)
242
Комбинационная группировка 458,
462
Комбинированный (ступенчатый)
отбор 200
Конфлюентный анализ 374
Корреляционная матрица 111, 533
Корреляционное отношение 412
— поле 385
Корреляционный анализ 377

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
647
— асимметрии 108
— вариации 105
— детерминации 399, 401, 403, 424,
425, 454
— дифференциации 107
— квадратической сопряженности
449
— конкордации (согласованности)
442-446
— корреляции 111, 397, 404, 405
выборочный 388, 407
— — множественный 422-425
парный 111, 404, 405
— — ранговый (см. «Ранговый
коэффициент корреляции»)
частный 418, 419
— эксцесса 108
Критерии статистические 283, 290-
294
— — наиболее мощные 291, 293
Критерий автоинформативности 524-
525
— Барлетта 316
— Вальда 299-300
— Вилкоксона-Манна-Уитни 311
— внешней информативности 524
— дисперсионного анализа 314, 315
— информативности 335, 523, 532
— качества аппроксимации
(адекватности модели) 351
— Колмогорова-Смирнова 308
— логарифма отношения
правдоподобия 292
— наиболее мощный 291-292
— несмещенный 295
— однородности дисперсий 315
— отношения правдоподобия 291,
318
— последовательный 299-300, 325
— равномерно наиболее мощный 292
— Смирнова 309
— согласия 284, 300-309
— состоятельный 295
— Стьюдента (^-критерий) 313
Критическая статистика 288
Кумулянта (кумулятивная кривая)
205
л
Латентно-структурный анализ 337
Латентный показатель 335, 580, 581
Линейные комбинации нормально
распределенных величин 219
Логарифмическая функция
правдоподобия 252
Логарифмически-нормальный закон
распределения 129
Логико-алгебраический подход 330
м
Марковская цепь 169
Массив исходных статистических
данных 331, 447-448

648
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Математико-статистические методы
39
Математическая модель 40
Математическая статистика 29, 48
Математическое ожидание 99
Матрица 619
— квадратная 620
— ковариационная 101, ПО, 397, 533
— корреляционная 111, 533
— идемпотентная 637
— нагрузок 537
— невырожденная 627
— неотрицательно определенная 634
— обратная 628
— «объект-свойство» 331
— парных сравнений 332
— переходных вероятностей 170
— полного ранга 635
— положительно определенная 634
— симметрическая 620
— транспонированная 621
Мера близости 491
Медиана 103
— главных компонент, см. Главные
компоненты
— корреляционных плеяд 577
— ^-средних 513
— максимального правдоподобия
249-258
— моментов 258
Методы машинного ассистирования
340
Многомерная случайная величина
80-81
— функция плотности 95
— — распределения 94
Многомерное наблюдение 348
— шкалирование 337, 592
— — метрическое 592-594
— — неметрическое 595
Многомерный статистический
анализ 362
Множественная линейная регрессия
371
Множественный коэффициент
корреляции 422-425
Мода 103
— вероятностная 40-41, 50
— вероятностно-статистическая 40-
41,50
— закона распределения 114
— многомерной развертки
временного ряда 339
— регрессионная 359, 371
— смеси распределений 473, 485
— факторного анализа 551-553
— эконометрическая 41
— экономическая 41
Мощность статистического
критерия 289, 294
Мультиколлинеарность 378
н
Накопленная частота 90
Начальное распределение вероятно-

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
649
стей 169
Начальные моменты случайной
величины 100
— — выборочные 207
Невозможные события 57
Независимость наблюдений 196-197
— случайных величин 98
— событий 66
Незамкнутый граф 574
Неидентифицируемость 558
Неймана-Пирсона лемма 291
Непараметрические (или частично-
параметрические) методы 378
Непараметрический дискриминант-
ный анализ 476
Непрерывное вероятностное
пространство 69
Неравенство информации (Рао-Кра-
мера-Фреше) 249
— Чебышева 153
Неразличимые («связные»,
«объединенные») ранги 429, 436
Несмещенность оценки 236
Несовместные события 57
Нормальный (гауссовский) закон
распределения 125
о
Обобщенная дисперсия ПО
Обобщенный коэффициент
корреляции 438
Обращение матрицы 479, 628
— — блочной 640
Обучающая выборка 459, 469, 480
Общие факторы (в факторном
анализе) 553
Объем выборки 197
Объясняющая переменная 351
Обычное евклидово расстояние 493
Однородная цепь Маркова 169
Однородность объектов 491
Оперативная характеристика
критерия 294
Описательная (дескриптивная)
статистика 231
Определитель (детерминант)
блочной матрицы 640
— — матрицы 626
Оптимальная (байесовская)
процедура классификации 474
Оптимизационные (тремальные)
формулировки статистических задач 330
Основные выборочные
характеристики 201
— типы зависимостей 373
Отбор информативных типообраэу-
ющих признаков 335, 463
Отклонение среднеквадратическое 105,
209
Отношение правдоподобия 290-291
— предпочтения 587
Отрицательный биномиальный
закон 118
Оценка значений общих факторов
559
— — — — метод Бартлетта 564

650
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— — — — модель Томсона 565
— максимального правдоподобия
250, 227
— параметров уравнения
статистической связи 379
— статистическая 233
— — несмещенная 236
— — состоятельная 234
— — эффективная 239
Ошибка аппроксимации 400
— второго рода 289
— выборки 198
— классификации 471
— первого рода 289
Оцифровка 344
п
Параллельные кластер-процедуры 507-
508
Параметризация генеральной
совокупности 344
— многомерного распределения 109-
111
— регрессионной модели 394
Параметрические регрессионные
схемы 382
Параметрический дискриминантный
анализ 475-477, 487
Парные сравнения 587, 592
Пассивный эксперимент 341
Первичная статистическая
обработка данных 341, 461
Переходные вероятности 172
План вычислительного анализа
данных 345
План сбора исходной статистической
информации 340
Плотность вероятности 92
Подведение итогов исследования 345
Показатели качественные
(порядковые, ординальные) 343
— классификационные
(номинальные) 343
— количественные 343
Полигон 205
— распределения (вероятностей) 85
Полиномиальная регрессия 383
Полиномиальное (мультиномиальное)
распределение 123, 226
Полная система событий 57
Последовательная схема наблюдений
297
Последовательные кластер-процедуры
5049-505
Последовательный критерий Вальда
299
Предикторы в модели регрессии 336
Преобразование Бокса-Кокса 392
Прикладная статистика 27, 49, 346
Принцип отношения правдоподобия
288, 290
Проблема группового выбора
(упорядочения) 432
Проверка однородности исходных
данных 342
— статистической независимости

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
651
последовательности наблюдений 343
— значений результирующего
показателя 365-366
Произведение (пересечение) событий
56
Пропущенные (стертые) наблюдения
342
Простая типологизация 465
Простой случайный отбор 199
Пространственная выборка 331
Пространственно-временная
выборка 331
Пространство элементарных
событий 53
Противоположное (дополнительное)
событие 56
Процедуры классификации 469, 474
— — иерархические 504, 505-507
— — параллельные 504, 507-509
— — последовательные 504
Процентная точка распределения 106
Прямое (кронекерово) произведение
матриц 640
Равномерно наиболее мощный
критерий 292
Разность событий 56
Ранг матрицы 630-632
— объекта 428-429
Ранговая корреляция 379, 381
Ранговый коэффициент корреляции
349, 430
Кендалла 384, 434
— — — — случай связных рангов
436
Спирмэна 383, 432
— — — — случай связных рангов
433
Распределения вероятностей закон
84, 150
бета @) 148
— — — биномиальный 116
Вейбулла 136
гамма G) 141, 146
— — — гипергеометрический 119
— — — двусторонний
экспоненциальный (Лапласа) 138
Коши 140

логарифмически-нормальный 129
— нормальный (гауссовский)
125
— — — — двумерный 127
— — — — многомерный 129
— — — отрицательный
биномиальный 118
Парето 139
полиномиальный
(мультиномиальный) 123
— — — Пуассона 121
равномерный
(прямоугольный) 132
совместный (многомерный)
86, 94-95
Стьюдента (t) 143
— — — условный 88, 96

652
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
F (Фишера) 144
— — — «хи-квадрат» (х2) 141
— — — частный (маргинальный)
87,96
— — — экспоненциальный
(показательный) 134, 137
Рассеяние внутриклассовое 496-497
Расслоенная выборка 200
Расстояние между классами
объектов 495
«ближнего соседа» 495
— — — — «дальнего соседа» 495
информационное (Кал-
лбэка) 498
— — — — Махаланобиса 498
— — — — обобщенное (по
Колмогорову) 496-497
_ — — — «средний связи» 496
«центров тяжести» 495
— — объектами 491
— — — взвешенное евклидово 493
— — — евклидово 492
— — — хеммингово 493
Расщепление смеси распределений
335, 486
Реализация временного ряда 331
Реальный комплекс условий
(случайного эксперимента) 30
Регрессионная зависимость 371
Регрессионный анализ 352
Регрессия 359
Результирующая переменная 351
Репрезентативность выборки 198
Решающее правило 474
Риск байесовский апостериорный 272
Робастные (устойчивые) оценки 252
Ряд вариационный, см.
Вариационный ряд
Сбор статистических данных 340
Сводка и группировка данных 341
Серийная выборка 200
Симметрическая матрица 620
Сжатие массивов информации 336
Система одновременных уравнений
364, 370
Систематизация прикладных задач
классификации 465-468
Ситуационный анализ 370
Случайная величина 78, 112
— — дискретная 80
— — многомерная (векторная) 81
— — некатегоризованная 83
— — непрерывная 80
— — номинальная
(классификационная) 82
— — одномерная (скалярная) 81
— — ординальная (порядковая) 82
След матрицы 627
Слуцкого теорема 215
Случайное событие 53, 55, 71
— — достоверное 57
— — невозможное 57

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
653
— — противоположное 56
— — элементарное 53
Смесь распределений вероятностей
480, 482
— двух нормальных законов
распределения 481
— многомерных нормальных
законов распределения 484
Снижение размерности исследуемого
пространства 520
Сно-матрицы 634-637
Собственное (характеристическое)
значение (число) матрицы 531, 633
Собственный (характеристический)
вектор матрицы 531, 533, 633
Совместное (многомерное)
распределение см. Распределения
вероятностей закон совместный
Состояние поглощающее
(замкнутое) 178, 179
— возвратное 179
— достижимое 178
— периодическое 179
— эргодическое 179
Состоятельность оценки 234
Сплайн 378
Спо-матрицы 634-637
Способы организации выборки 198-
200
Среднее значение выборочное 208
— — геометрическое 102,208
— — гармоническое 103, 208
— — теоретическое 99
Среднеквадратическое отклонение 105
Средние удельные потери 472
Средний объем выборки 297
Средняя мера внутриклассового
рассеяния 501-502
Стандартная нормальная функция
распределения 213
Статистика 233
Статистика
предметно-содержательная (социально-экономическая и др.)
27-28
Статистическая гипотеза 283
— — об однородности нескольких
выборок 285
о виде модели статистической
зависимости 286
— — о типе закона распределения
284
о числовых значениях
параметров 285-286
Статистическая независимость
случайных величин 98
Статистическая проверка гипотез
283
Статистическая оценка 233
Статистически значимая связь 450
Статистические методы
классификации 333
Статистическое исследование
зависимостей 333, 349, 351
— моделирование 133
— оценивание параметров 232
Степень согласованности мнений
группы экспертов 436
— тесноты статистической связи
352
Стратифицированный (расслоенный)
отбор 199

654
АЛФАВНТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Структура модели 353, 361
Сумма (объединение) событий 55
Сходимость по вероятности 154
произведения матриц 623
т
Таблица (матрица)
«объект-свойство» 331
Таблица сопряженности 396, 448
Теорема (формула) Байеса 69, 271-
272
— Бернулли 155
— Вейерштрасса (см. Вейерштрас-
са теорема)
— Муавра-Лапласа 159
— сложения вероятностей 63
— Слуцкого 215
— умножения вероятностей 64
Теоретико-вероятностная модель 40
Теория вероятностей 28, 39, 48
Типологизация задач снижения
размерности 524
— математических постановок
задач классификации 469
— простая 465
— связная неупорядочная 466
— — упорядоченная 467
— структурная 467
Типообразующие факторы
(признаки) 335, 461
Томография 339
Точечная оценка 248
Транспонирование матрицы 621
Унификация типа переменных 343
— характеристическое матрицы 633
Урезание выборки 261-262
— распределения 263
Уровень значимости критерия 33,
286
Условная вероятность 64
— плотность вероятности 96, 128
Условный закон распределения
вероятностей 88, 96-97
Устойчивость статистическая
(выборочных характеристик) 214-215
Устойчивые статистические выводы
339
Факторные нагрузки 553, 559
Факторный анализ 551-553
Формула Байеса 68, 271-272
— композиции (свертки) 164
— полной вероятности 67
Функционал (критерий) качества
метода или модели 329, 351, 357, 498-
503, 519, 521-523, 527, 555-556, 573
Функциональная зависимость 373,
402
Функция мощности критерия 294

АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
655
Функция плотности вероятности 92,
112, 125, 127, 132, 136, 138-140, 142,
143, 145, 147-149.
— потерь 472-473
— правдоподобия 241-242, 250
— — логарифмическая 252
— распределения вероятностей 90
— регрессии 352, 354
207
— — случайной величины 100
Центрированное наблюдение 215, 541
Центроидный метод 561
Цепи Маркова 169
— — неприводимые 179
— — периодические 181
— — поглощающие 180
Цепочечный эффект 506
Характеристики выборочные 355
— качества классификации 472
— — оценивания 234-240
— — статистического критерия
294-295
Характеристические (собственные)
векторы 531, 532, 663
— — числа (значения) 530, 546, 663
Характеристические уравнения 530,
663
ц
Целевая функция 368, 582
Целенаправленное проецирование 337,
Цензурирование выборки 262
Центральная предельная теорема 157,
166
— — — многомерная 158
Центральные моменты выборочные
Частная (маржинальная) плотность
вероятности 96
— — функция распределения 96
Частный коэффициент корреляции
418-420
— (маржинальный) закон
распределения вероятностей 87
Частота (случаев) 202
— относительная 35, 37, 202
Число степеней свободы 142, 143, 144
ш
Шкала измерений 362
— — количественная 362
— — номинальная
(классификационная) 362
ординальная (порядковая) 362

656
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Шкалирование многомерное — см.
Многомерное шкалирование
Эвристические методы снижения
размерности 570
Экзогенные переменные 350
Эконометрика 49
Эконометрическая модель 41
Экономико-математическая модель 41
Экспертно-статистический метод 368,
583
Экспертное упорядочение объектов
584
Экспоненциальное (показательное)
распределение 137
Экстремальная группировка
параметров 572
— постановка задач классификации
503
Экстремальные (оптимальные)
свойства главных компонент 541
Эксцесс (распределения) 108, 210
Элементарное событие 53
Эмпирическая (выборочная)
дисперсия 209
— — функция плотности 202
— — — распределения 201
Эмпирические аналоги начальных
моментов 207
— — центральных моментов 207
— — центра группирования 208
Эндогенные переменные 350
Эргодическое свойство 181
Этапы вероятностно-статистического
моделирования 43-45
— статистического исследования
зависимостей 375-380
Эффективность оценки 238