1

П. С. АЛЕКСАНДРОВ
Профессор Московского Университета,
почётный член Московского математического общества
КОМБИНАТОРНАЯ
ТОПОЛОГИЯ
/с ///"
. ч'.а" ((*?ц
О Г И 3
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 194 7 ЛЕНИНГРАД

Редактор С. В Фомин. Техн редакторы: Я. А. Тумаркана и С. Н. Ахламов.
Подписано к печати 30/V 1947 г. Печ. л. 41,25. Авт. л-47,1. Уч.-авт. л. 49,5.
"1ип.зн. в печ. л. 48Еаэ. Тир. 5000 экз. А 02249. Шна книги 2£ р.70 к. Переплёт 2 р.Зак. № 1558'
4-я типография им. Евт. Соколовой треста «Полгаграфкнига» ОГИЗа
ррга Совете Министров ССОР. Ленинград, Измайловский пр., 09.

ОГЛАВЛЕНИЕ.
Предисловие • . ♦ • 17
ЧАСТЬ ПЕРВАЯ-
ВВЕДЕНИЕ.
ГЛАВА ПЕРВАЯ. ОБЗОР ЭЛЕМЕНТАРНЫХ СВОЙСТВ ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВ.
§ 1. Обозначения из теории множеств, постоянно употребляемые
в этой книге 24
1:1. Операции над множествами 24
1:2. Отображения , 24
1:3. Обозначенные элементы; системы множеств и их кратность;
покрытия 25
§ 2. Топологические пространства -» 26
2:1. Определение топологических пространств и основных,
связанных с ними понятий 26
2:2. Задание топологии при помощи окрестностей 28
2 :3. Метрические и метризуемые пространства 29
2:4. Непрерывные отображения 32
2:5. Равномерная сходимость отображений 33
2:6. Топологическое произведение пространств 33
§ 3. Связность 36
3:1. Определение и основные теоремы 36
3:2. Компоненты 38
§ 4. Аксиомы отделимости. Бикомпактность 39
4:1. Аксиомы отделимости 39
4:2. Теоремы о непрерывных функциях в нормальных
пространствах 40
4:3. Бикомпактность 41
4 :4. Дальнейшие теоремы о бикомпактах. Метризационные
теоремы и теоремы включения • . . . . 41
4:5. Непрерывные отображения бикомпактов 42
§ 5. Непрерывные разложения компактов и их связь с
непрерывными отображениями («склеивания»).
Локально-бикомпактные пространства. Топологические многообразия.
Примеры 42
5:1. Непрерывные разложения. Пространство данного
разложения 42
5:2. Примеры непрерывных разложений и склеиваний.
Проективное пространство п измерений , 44
1*

4
ОГЛАВЛЕНИЕ
5 :3. Локально-бикомпактные пространства. Топологические
многообразия. Примеры 48
§ 6. Частично упорядоченные множества и дискретные
пространства 50
6:1. Определения 50
6:2. Примеры частично упорядоченных множеств 50
6:3. Множества А@(р) и 0®(р) 51
6:4. Двойственность частично упорядоченных множеств .... 52
6:5. Дискретные пространства 53
§ 7. Полные метрические пространства и компакты 54
7:1. Определение и простейшие свойства полных метрических
пространств 54
7:2. е-сети в компактах 55
7 :3. Пространства непрерывных отображений 56
7:4. Деформации. Гомотопические классы отображений
компакта X в компакт У 57
§ 8. Покрытия нормальных пространств, в частности, компактов. 57
8:1. Замкнутые и открытые покрытия топологических
пространств. Предмет комбинаторной топологии 57
8:2. Подобные покрытия 58
8:3. е-покрытия компактов. Лебеговы числа покрытия 60
8:4. Определение размерности 62
ГЛАВА ВТОРАЯ. ТЕОРЕМА ЖОРДАНА.
§ 1. Формулировка теоремы Жордана. Совместные границы
областей 65
1 :1. Формулировка теоремы Жордана 65
1 :2. Области в Rn и их границы 66
1 :3. План доказательства теоремы Жордана 70
1 :4. Обозначения. Ориентация простых дуг и простых
замкнутых линий • 71
§ 2. Угловая функция непрерывного отображения отрезка в
плоскость. Порядок точки относительно замкнутого пути в
плоскости 72
2:1. Функции Fa(p, С, х) и f(p, С, хъ х2) 72
2:2. Порядок точки относительно замкнутого пути 73
2:3. Формула сложения 75
2:4. Порядок точки относительно жордановой кривой 76
2:5. Порядок точки p€R2 относительно непрерывного
отображения окружности в R2\p; степень непрерывного
отображения окружности в окружность 78
§ 3. Теорема: простая дуга не разбивает плоскость 82
§ 4. Доказательство теоремы Жордана 86
4:1. Основное вспомогательное построение 86
4:2. Случай <о (s, Ф) = 0; множество Г = /?2\Ф состоит, по
крайней мере, из двух компонент 88
4:3. Окончание доказательства теоремы Жордана 91

ОГЛАВЛЕНИЕ
5
ГЛАВА ТРЕТЬЯ. ПОВЕРХНОСТИ.
1. Элементарные кривые и одномерные комплексы 94
1 :1. Элементарные кривые и их разбиения на дуги 94
1 :2. Порядок связности кривой (одномерное число Бетти) ... 96
§ 2. Поверхности и их триангуляции 99
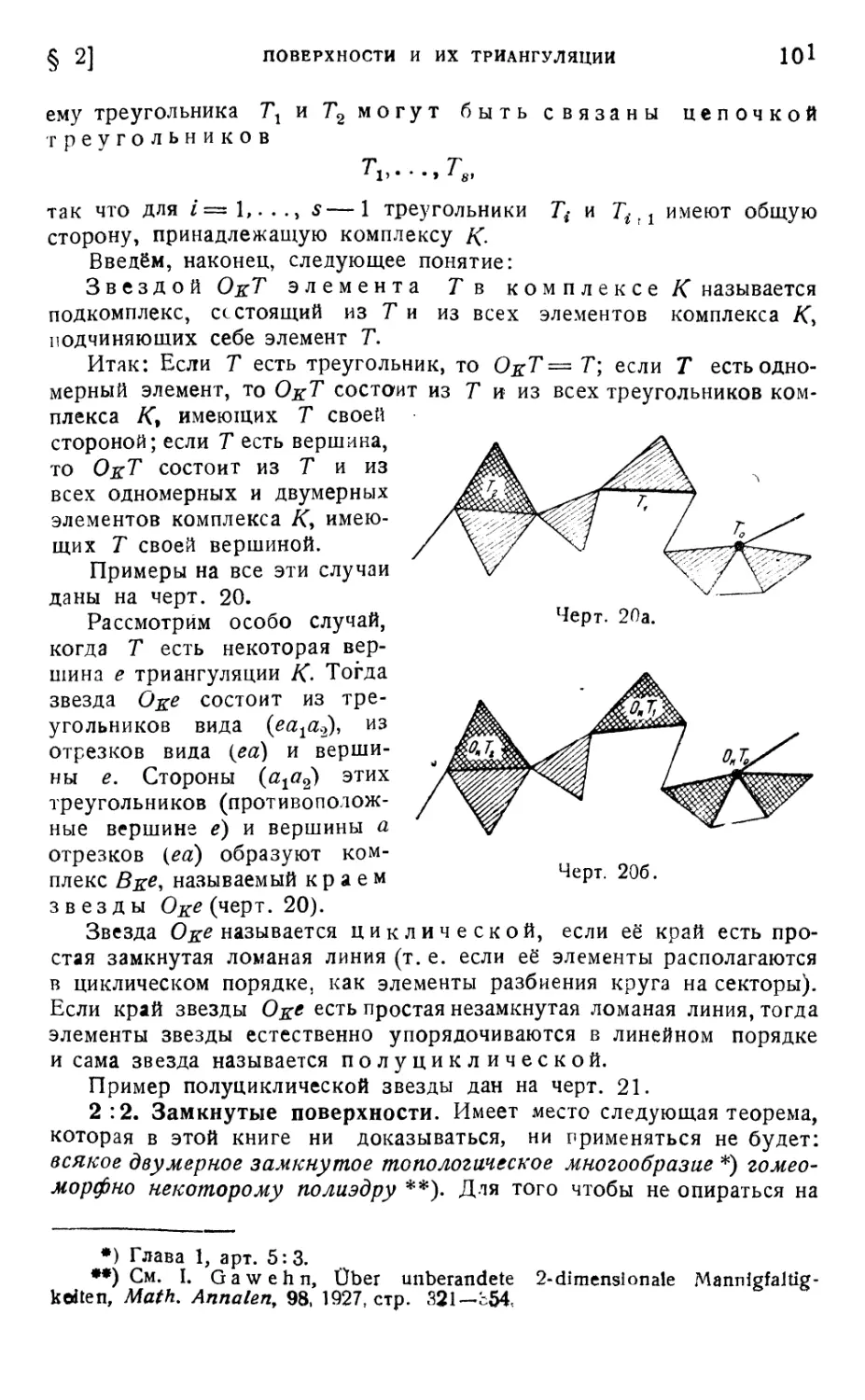
2:1. Комплексы и полиэдры двух измерений 99
2:2. Замкнутые поверхности 101
2:3. Поверхности с краем 104
2:4. Подразделения триангуляции 106
2:5. Комплексы остовов 107
§ 3. Разрезы и склеивания 107
3:1. Идентификация элементов в комплексах остовов 107
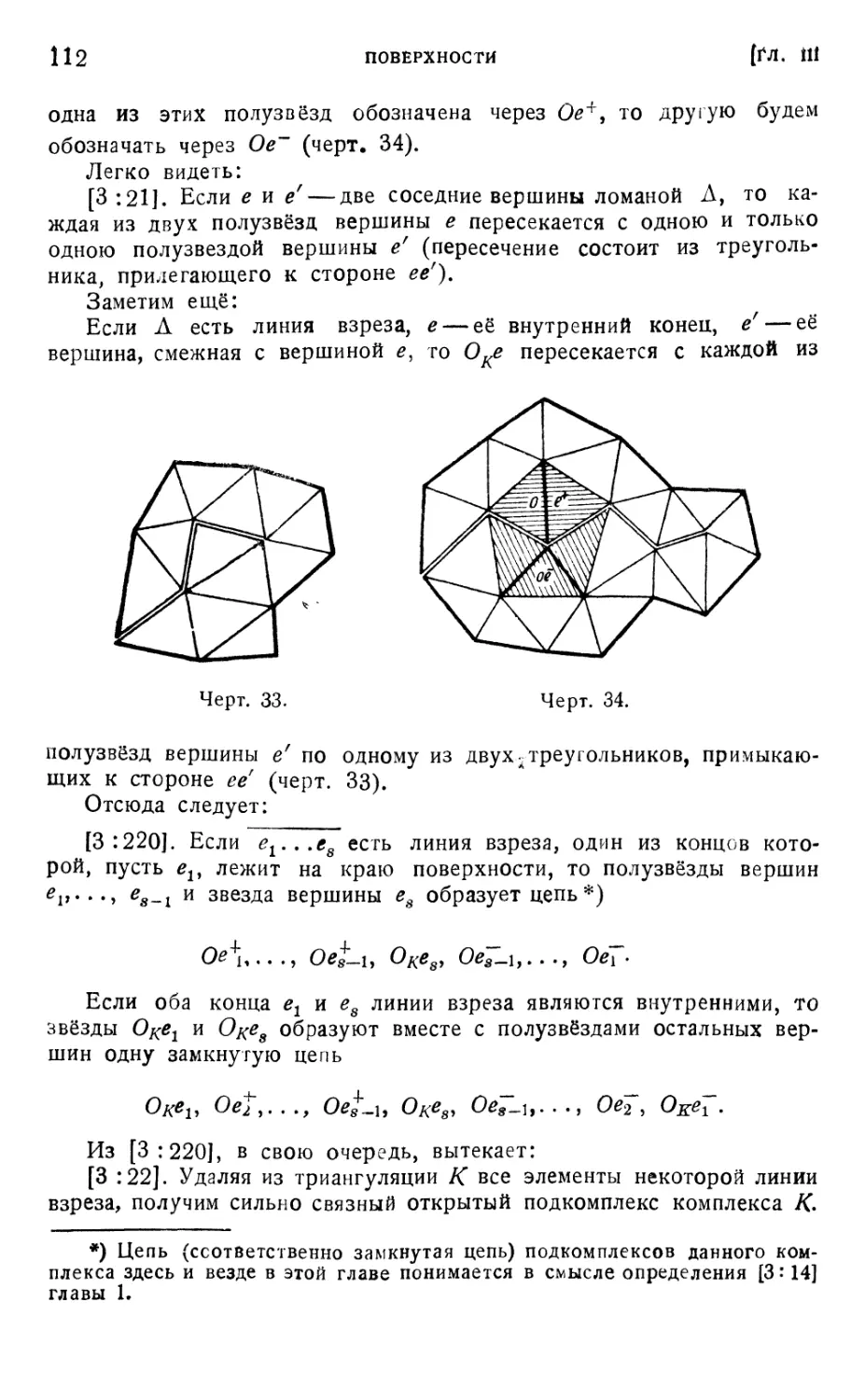
3:2. Линии разрезов и полузвёзды их вершин Ill
3:3. Операция разреза 115
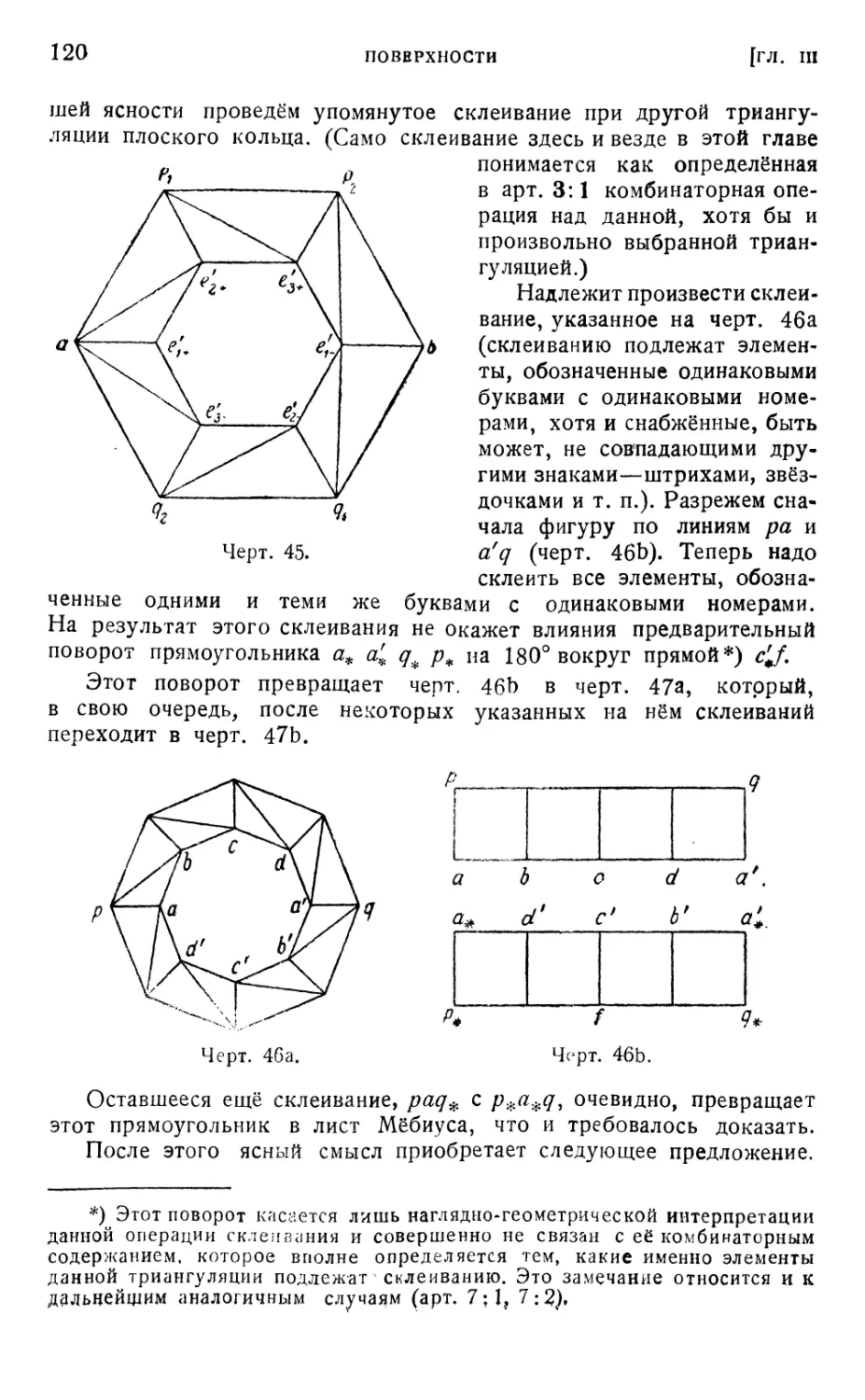
3:4. Заклеивание дыр 119
§ 4. Ориентируемость поверхнфстей 122
4:1. Определения 122
§ 5. Порядок связности поверхности. Теорема Эйлера 127
5:1... 127
§ 6. Простые поверхности 129
6:1. Замкнутые разрезы 129
б: 2. Определение простых триангуляции. Инвариантность при
правильных подразделениях ................ 131
6:3. Элементарные леммы " 133
6:4. Классификация простых поверхностей 133
§ 7. Классификация замкнутых поверхностей 137
7:1. Род поверхности. Нормальные поверхности данного рода * 137
7:2. Основная теорема топологии поверхностей 139
ЧАСТЬ ВТОРАЯ-
КОМПЛЕКСЫ. ПОКРЫТИЯ. РАЗМЕРНОСТЬ.
ГЛАВА ЧЕТВЕРТАЯ. КОМПЛЕКСЫ.
Вводный параграф: предварительные замечания о симплексах . . 144
0:1. Симплексы и их остовы .... • 144
0:2. Грани . . 145
0:3. Комбинаторная сумма . 146
0:4. Замыкание симплекса 146
§ 1. Основные определения 146
1:1. Триангуляции. Примеры: [Тп] и Тп 146
1:2. Полиэдпальные комплексы . . . • 148
1 :3. Комплексы остовов • • 148
1 :4. Общее определение симплициального комплекса 150
1 :5. Примеры симплнциальных комплексов 151
1:6. Сл\ плициал» ные отображения и изоморфизмы комплексов
остовов и вообще симплициальных комплексов 152
1 :7. Общее определение комплекса 15*
1 :8. Замкнутые и открытые подкомплексы. Комбинаторные
замыкания и звёзды 155
1 ;9. Теорема о включении в R2nirX ....,,,,.,»,.. 157

6
ОГЛАВЛЕНИЕ
§ 2. Некоторые замечательные комплексы остовов 158
2:1. Нерв конечной системы множеств 158
2:2. Барицентрические производные и барицентрические
подразделения • 160
2:3. Пирамида над комплексом 163
2:4. Призмы над комплексом остовов • 164
2:5. Призма, натянутая на комплекс остовов и его симплициаль-
ный образ 165
§ 3. Тело комплекса. Полиэдры 166
3 :1. Определения 166
3:2. Звёздные окрестности. Открытые звёзды 167
3:3. Симплициальные отображения триангулированных
полиэдров 168
§ 4. Подразделения полиэдральных комплексов 169
4:1. Определение подразделения 169
4:2. Последовательные барицентрические подразделения. . . . 170
4:3. Центральные и элементарные полразделения комплексов. 171
4:4- Подразделения незамкнутых подкомплексов и
полиэдральных комплексов 173
§ 5. Барицентрические звёзды 174
5:1. Барицентрические звёзды 174
5:2. Барицентричесьий комплекс триангуляции 175
5:3. Замкнутые барицентрические звёзды 177
5:4. Подкомплексы комплекса К""\ их тела и барицентрические
подразделения 177
§ 6. Кривые комплексы и кривые полиэдры 180
6:1. Определения 180
6:2. л-мерные многообразия 181
§ 7. Связность комплексов 183
7 :1. Связные комплексы. Компоненты 183
7:2. Случай полных симплициальных комплексов 184
7 :3. Компоненты К и К 185
ГЛАВА ПЯТАЯ. ЛЕММА ШПЕРНЕРА И ЕЁ СЛЕДСТВИЯ.
§ 1. Предварительные замечания 188
1 :1. Триангуляции и барицентрическое подразделение замкнутого
симплекса • 1?8
§ 2. Лемма Шпернера 191
2:1. Лемма Шпернера 191
2:2. Следствие из леммы Шпернера. Окончание доказательства
теоремы о мостовых 193
2:3. Инвариантность числа измерений для Rn 195
§ 3. Теорема об инвариантности внутренних точек 196
3:1 196
3:2. Теорема об инвариантности внутренних точек для
топологических многообразий 201
§ 4. Теорема о неподвижных точках при непрерывных
отображениях элемента .,,,,.,,,.,<. , . . . . 2С1

ОГЛАВЛЕНИЕ 7
ГЛАВА ШЕСТАЯ. ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ.
§ 1. Теоремы об £-сдвигах и о включении в /?tt 203
1:1. Определение s-отображений и s-сдвигов. План параграфа . 203
1:2. Операция выметания 207
1 :3. Барицентрическое отображение пространства в нерв
открытого по) рытия 208
1 :4. Теорема об s-отображениях . 209
1 :5. Барицентрические приближения данного непрерывного
отображения £ омпакта Ф в Rn. Теорема об е-сдвигах 210
1 :6. Теорема о включении r-мгрных компактов в R*r+i .... 214
§ 2. Теорема о существенных отображениях 215
2:1. Определение и формулировка теоремы 215
2:2. Доказательство теоремы [2:1] 216
§ 3. Теорема сложения. Индуктивная размерность . 219
3:1 Формулировка и доказательство теоремы сложения .... 219
8:2. Индуктивная размерность 221
§ 4. Последовательности подразделений 224
4 :1. Неприводимые s-покрытия 224
4:2. Подразделения • . . 226
§ 5. Некоторые приложения к топологическим многообразиям и
полиэдрам 234
5:1. Случай топологических многообразий (в частности, R)l и Sn) 234
5:2. Сильная связность , , , . . 236
HAl/ГЬ ТРЕТЬЯ.
ГРУППЫ БЕТТИ.
ГЛАВА СЕДЬМАЯ. ЦЕПИ. ОПЕРАТОР Д.
§ 1. Ориентация 239
1 :1. Ориентация пространства R" 239
1 :2. Ориентация симплекса и остова . . . • • . . 241
1:3. Тело ориентированного симплекса 243
1 :4. Продолжение ориентации /" в ориентацию Rn.
Произведение ориентации t"Rn и f[1^ . 243
1:5. Ориентация (^о^-1) 245
1 :-б. Аффинные образы ориентации • • 246
§ 2. Индекс пересечения плоскостей и симплексов 247
2 :1. Индекс пересечения плоскостей 247
2:2 Индекс пересечения симплексов 249
2:3. Пересечения и симплициальные отображения 249
§ 3. Коэффициенты инцидентности 250
3:1. Определение коэффициентов инцидентности 250
3:2. Свойства коэффициентов инцидентности 251
§ 4. Клеточные комплексы; ^-комплексы 253
4:1. Определение ^-комплекса и клеточного комплекса .... 253
4:2. Матрицы инцидентности клеточного комплекса 256
§ 5. Цепи 258
5:1. Определение цепи 258
5:2. Некоторые замечания о цепях , 260

8
ОГЛАВЛЕНИЕ
5:3. Одночленные цепи. Запись ц^пей в виде линейных форм . 261
5:4. Цепл симплициальчого комплекса 262
5:5. Скалярчог произведение цепей 263
5:6. Распространение цепей; куски цепей 264
§ 6. Нижний граничный оператор (оператор А) .... 265
6:1. Очределение А-границы 265
6:2. Примеры цепей и их границ 267
6:3. Циклы; цепи, гомологичные нулю; группы Zr($() и НГ{Щ . 270
6:4. Гомология. Знак ~. Гомологическая независимость цепей . 270
6:5. Куски цепей и циклов 272
6:6. Продолжение цепей и циклов 273
§ 7. Основной случай: $ есть ^-комплекс 275
7:1. Основная формула ДДхг = 0 275
7:2. Замкнутые и открытые подкомплексы «-комплекса 276
7:3. Слабые гомологии целочисленных циклов; двойная область
коэффициентов 276
§ 8. Симплициальные образы цепей 277
8:1. Симплициальные образы ориентированных симплексов . . 277
8:2. Гомоморфизм S\ группы Lr(K$) в //(АТ«), порождённый сим-
плициальным отображением S^ комплекса Ка в Ка .... 278
8:3. Переместительность операторов А и S% 279
Я:4. Случай открытых подкомплексов 281
§ 9. Некоторые вспомогательные построения 282
9:1. Пирамида над цепью 282
9:2. Приложение построений арт. 9:1 283
9:3. Призма над цепью '285
9:4. Прилсжение к симплициальным отображениям 287
Приложение к главе VII .. 289
ГЛАВА ВОСЬ МАЯ. Д-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ).
§ 1. Определения. Примеры. Простейшие общие свойства 292
1: 1. Определение групп Дг(£, Щ 292
1 :2. Группа Д"($», <&) 293
1:3. Группы Д0(Я, Ж) 293
1 :4. Простейшие примеры групп Аг 295
1 :5. Некоторые элементарные я-мерные комплексы и их группы
Бетти 304
1 :6. Группа A°°(tf,90 307
1 :7. Разложение группы Дг($, 91) в прямую сумму по компонентам
комплекса $ . 309
1 :8. Гомоморфизм группы ДГ(Л^, 2() в Ar(/Ctt, Щ, порождённый
симплициальным отображением S^a симплициального
комплекса К§ в симплициальный комплекс К* 310
5 2. Группы АГ0(К) 311
2 : 1. Группы кручения ...... 311
2:2. Группы д£0(£) 312
2:3. Случай конечного «-комплекса. Гомологические базы .... 312
2:4. Формула Эйлера-Пуанкаре для л-мерного конечного
«-комплекса ,.,.,,,...,.,,,. ..,.,,,,., ЗН

ОГЛАВЛЕНИЕ
9
§ 3. Псевдомногообразия 315
3:1. Псевдомногообразия 315
3:2. Ориентируемые псевдомногообразия 317
3:3. Группы А^(/С^) для л-мерного неориентируемого
псевдомногообразия. Дезориентирующие последовательности . . . 321
§ 4. Некоторые дополнения и примеры 323
4:1. Группы Бетти комплексов [Тп] и Тп = [Т^]\Тп ..... 323
4:2. Поверхности , 324
4:3. Простые псевдомногообразия. Элементарные триангуляции . 325
4:4. Приложения к проективным пространствам 328
§ б. Симплициальные отображения псевдомногообразий 330
5:1. Степень отображения 330
5:2. Первоначальное определение степени симплициального
отображения 331
ГЛАВА ДЕВЯТАЯ. ОПЕРАТОР V И ГРУППЫ у' (tf, У). КАНОНИЧЕСКИЕ БАЗЫ.
ВЫЧИСЛЕНИЕ ГРУПП ДГ(#, Л) И уГ (Я, И) ПО ГРУППАМ Д£ С<П.
§ 1. Оператор V 334
1 :1. Определение цепи Vxr • 334
1:2. За шсь цепи Vxr в виде линейной формы 336
1:3. Операторы А и V суть сопряжённые гомоморфизмы
соответственно решётки //(&) в решётку//"1 ($) ц решётки Z/~J(&)
в Ьг(й) 337
1 :4. Группы Z* (Я, 2Г), Щ(®Л), Ar(^,2t) 337
1 :5. Куски цепей 338
1 :6. Группы V^(^t5t) = ZO(^,5T) 339
1 :7. Группы Vn(unt J) для л-мерных псевдомногообразий . . . 339
§ 2. Базы решёток /^(Я) ... 342
2:1. Предварительные замечания 342
2:2. Сопряжённые базы решёток LrQ{$) . . . • 342
2:3. Выражение элементов групп //($, Ж) через базы решётки
Lr0(R) 343
§ 3. Канонические системы баз. Группы V|J ($) 344
3:1. Предварительные замечания • 344
3: 2. Канонические базы групп Z£ 345
3:3. Канонические гомологические базы 346
3:4. Система канонических баз групп V 347
3:5. Система V-баз комплекса й; Группы Vq (Я) 348
§ 4. Вычисление групп Д'(Я, 9Г) и V(£, Ж) по группам Д*(Я) ... 354
4:1. Вычисление групп &Г($,Ж) 354
4:2. Вычисление групп V(tf, Ж) . . . 356
4:3. Области коэффициентов У, 9^, Sfti • . . . 357
4:4. Группы Д^Я) и Vrm (Я) '. . 358
\: 5, Целочисленные цепи п гомологии пр модулю m « , ? 9 , . 360

10
ОГЛАВЛЕНИЕ
§ 5. Вычисления групп Д'Ч£, ЗГ) и V(tf, Ж) по группам Д*"(Я. 9tt) и
^W 362
5:1. Теорема [5:1] • 362
5:2. Теорема [5j2] . . . 363
§ 6. Гомоморфизм S$ группы Lr(Ka,%) в Lr (К,%), порождённый
симплициальным отображением S\ комплекса ^ в ^а . . 364
6:1. Определение гомоморфизма St 364
6 : 2. Переместительность операторов V и 53х 365
6:3. Теорема [6:3] '. 365
ГЛАВА ДЕСЯТАЯ. ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ.
§ 1.
1 :1. Определение чисел Ьг (Ф) 370
1:2. Определение групп Ъг (Ф) 371
1:3. Формулировка теорем об инвариантности чисел и групп
Бетти 371
§ 2. Подразделения цепей. Фундаментальные системы
подкомплексов и цепей. Инвариантность Д- и V-групп при
элементарных и барицентрических подразделениях 372
2:1. Изоморфизм <?" . 372
2:2. фундаментальные системы подкомплексов комплекса К . . 374
2:3. Фундаментальные системы цепей 377
2:4. я-комплекс, определённый данной фундаментальной
системой цепей 382
2:5. Изоморфное отображение 8 группы V (Я) в группу Lr ($3) 384
2:6. Изоморфизм гр\пп Бетти при "элементарных и
барицентрических подразделениях комплекса К 385
§ 3. Нормальные и канонические сдвиги в полиэдрах 386
3:1. Нормальные сдвиги подразделений триангуляции 386
3:2. Примеры на нормальн »ie гомоморфизмы 5^ и Й 390
§ 4. Канонические системы баз для подразделений
^триангуляции Ка- Гомоморфизм S*, сопряжённый нормальному
гомоморфизму^ 391
4:1. Канонические системы баз для Ко 391
4:2. Нормальные гомоморфизмы в канонических базах 394
4:3. Гомоморфизм, сопряжённый к нормальному 394
§ 5. Комплексы К&г> Малые сдвиги в полиэдрах и компактах.
Теорема о мостовых и инвариантность чисел Бетти 396
5:1. Комплекс Ajz-ei е-цепи метрического пространства /?.... 396
5:2. е-сдвиги 396
5:3. Канонические сдвиги 397
5:4. Числа yj (AT). Канонические сдвиги в полиэдрах 398
5:5. Теорема о мостовых. Инвариантность чисел Бетти .... 399
§ 6. Инвариантность групп Бетти 402
6:1 402
0:2. Инвариантность групп Бетти для полиэдральных
комплексов ....... . ♦...,..,• 403

ОГЛАВЛЕНИЕ 11
§ 7. Инвариантность псевдомногообразий 404
7 :1. Формулировки теорем . • 404
7:2. Доказательство теоремы [7:14] 405
ГЛАВА ОДИННАДЦАТАЯ. Д-ГРУППЫ КОМПАКТОВ.
§ 1. Определение групп А**(Ф, Щ 407
1 :1. Истинные циклы 407
§ 2. Леммы об е-сдвигах и s-гомологиях ■ . . 409
2:1. Призмы и е-сдвиги 409
2:2. Случай полиэдра Ф = Д'« 411
§ 3. Гомоморфизм групп А** (Ф), порождённый непрерывным
отображением компакта 413
3:1. Непрерывный образ истинного цикла 413
3:2 414
3:3. Гомологическая классификация отображений 415
3:4. Деформация непрерывного отображения истинного цикла.
Деформация истинного цикла 416
§ 4. Основная теорема оА^группах полиэдров 417
4:1. Основная теорема [4:1] 417
4:2. Построение гомоморфизма Sf группы Дф в А£ 417
4:3. Отображение S® есть отображение на всю группу А£ . . . 418
4:4. Отображение 3* группы Аф на А£ есть изоморфизм .... 418
4:5. Правила для нахождения образов при изоморфизмах S® и
(St)'1 419
4 :6. Циклы zr £ Z£ и гомологии в Ф = К« 420
4:7. Образ цикла гл £ Z£ при непрерывном отображении С поли-
эдра Ф = Кл в компакт Ф'. Непрерывные циклы, их
параметрические представления и деформации 421
4:8. Ориентируемость и ориентации замкнутых
псевдомногообразий 422
4 :9. Гомоморфизм С*, группы Д£ = А** (Д^, Щ в группу А£, =
= А^(Лга/, %), порождённый непрерывным отображением
Сф, полиэдра Ф = Ка в полиэдр Ф' = К'^ • 423
§ 5. Симплициальные приближения непрерывных отображений
полиэдра в полиэдр 424
5:1. Определение симплициального приближения непрерывного
отображения Сф, полиэдра Ф = АГа в полиэдр Ф' = Клг . • 424
5:2. Основное свойство отображения S£? 425
§ 6. Степень непрерывного отображения замкнутых
псевдомногообразий 426
6:1. Определение степени 426
6:2. Определение степени непрерывного отображения л-мерного
цикла в л-мерное ориентируемое псевдомногообразие . . . 427
6:3. Вычисление степени отображений 427
6 :4. Основные свойства степени отображения 429

12
ОГЛАВЛЕНИЕ
ГЛАВА ДВЕНАДЦАТАЯ. ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ.
§ 1. Комплекс Ктt8 431
1:1. Определение Kv t и основные обозначения 431
1:2. Циклы и гомологии в Кт е 432
1 :3. (е, ^-сдвиги ' 433
1 :4. Канонические сдвиги 434
§ 2. Г-циклы (относительные циклы) и Г-гомологии компакта Ф.
Группы Zj(I\E), #£(Г,2Г), Д£(Г,И) 435
2:1. Определения 435
2:2. Группы Z% (Г, 21), //*(Г, И), Д£(Г, 9Г) 438
2:3. Канонические и бесконечно малые сдвиги. Изоморфизм
групп Д£о(Г, ЗД) и Д£>(Г,90 приГСФ0Сф 438
2:4. Группы Дф(Г, 51) и размерность Ф 440
2:5. Замечание 440
§ 3. Гомоморфизм группы ДГ(Г, Щ в группу Д*\г, 2Г), порождённый
(¥, ^-отображением С%, • . . 441
3 :1. Гомоморфизм Сф, 441
3:2. (Ф, ч7')-гомологиччые и ("Ф\ 1Р")-гомотопные между собою
отображения; (ч7, ч7')-деформации 442
3:3, Деформация относительного цикла компакта Ф 444
§ 4. Группы ДГ(Г) в случае, когда Ф и W — полиэдры 444
4:1. Предварительные замечания 444
4:2. Основная теорема 445
4:3. Гомоморфизм С£ группы Д£г = Дг (К*\Кхра, Я) в Д£,г, =
= &г(Клг\Кхргаг, 2t), порождённый (W, ^-отображением Cj- 446
4:4. Гомологическое определение размерности полиэдра. Новое
доказательство инвариантности числа измерений 447
4:5. Определение гомологической размерности компакта. . . . 447
§ 5. Псевдомногообразия с краем 448
5:1. Ориентация псевдомногообразия с краем 418
5:2. Предварительные замечания и определение степени
непрерывного отображения псевдомногообразия с краем . . • . 449
5:3. Некоторые свойства степени отображения 450
5 : 4. Примеры 451
§ 6. Группы Д£ (Ф) (Локальные Д^-группы компакта Ф) 453
6:1. Определение групп Д^(Ф) 453
6:2. Локальный характер групп Д£ 455
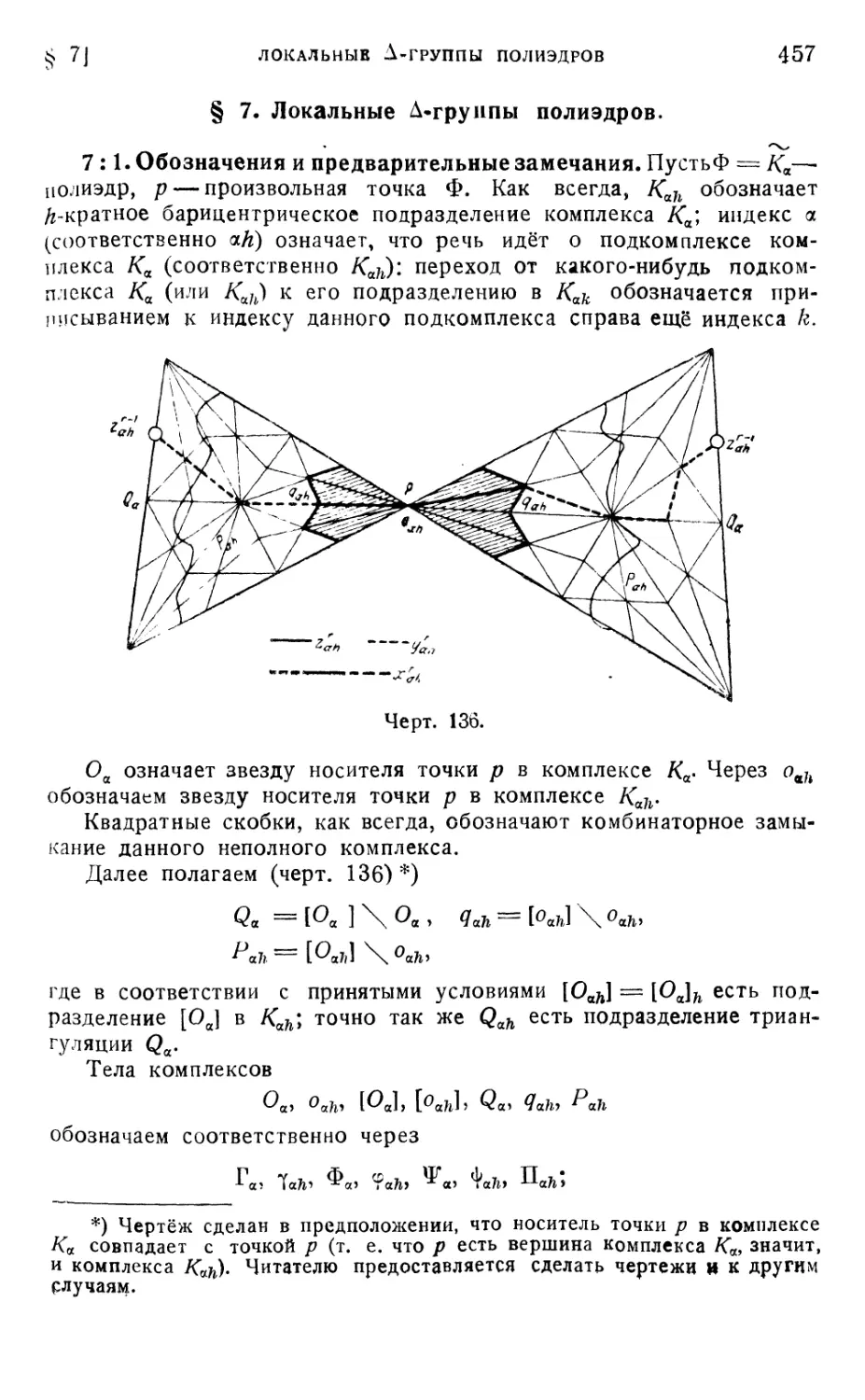
§ 7. Локальные Д-группы полиэдров 457
7 :1. Обозначения и предварительные замечания 457
7:2. Основная теорема * 458
7:3» Приложение к инвариантности псевдомногообразий , . - . 464

ОГЛАВЛЕНИЕ
13
ЧАСТЬ ЧЕТВЁРТАЯ.
ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ. ЗАКОНЫ
ДВОЙСТВЕННОСТИ. Д-ГРУППЫ КОМПАКТОВ.
ГЛАВА ТРИНАДЦАТАЯ. ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ
(^МНОГООБРАЗИЯ).
§ 1. Определение и простейшие свойства 467
1 :1. Определение /г-многообразий 467
1:2. Элементарные свойства /г-многообразий 468
1:3. Случай п <3 470
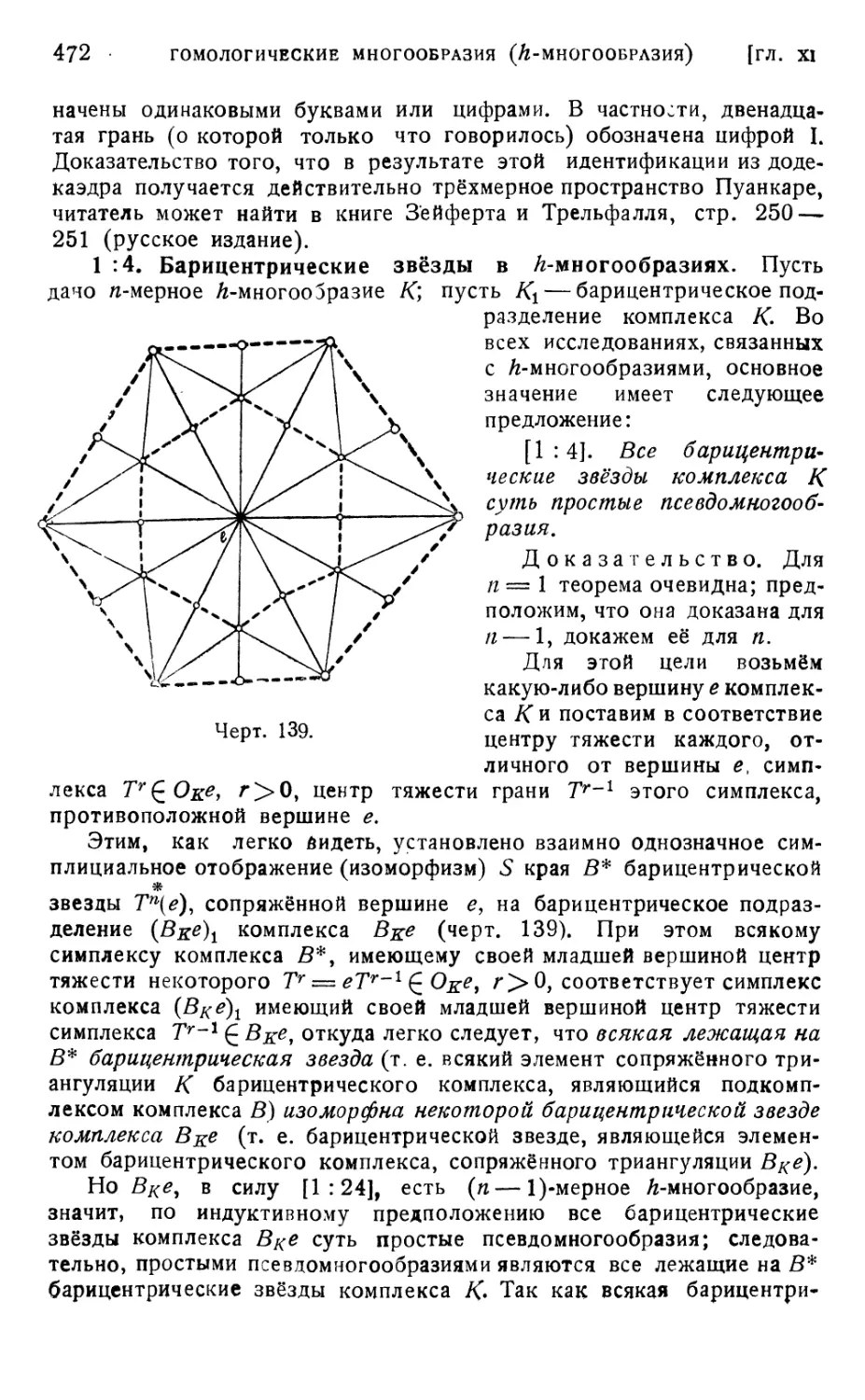
1 : 4. Барицентрические звёзды в /г-многообразиях 470
§ 2. Барицентрический комплекс /г-многообразия 473
2 :1. Обозначения; основные предварительные факты 473
2:2. Комплекс $* 474
§ 3. Индекс пересечения, изоморфизм Dq и закон
двойственности Пуанкаре........ 475
*
3:1. Индекс пересечения (^ X ^?) ' 475
3:2. Индекс пересечения и коэффициенты инцидентности . . . 478
3:3. Изоморфизм Dq и закон двойственности Пуанкаре .... 481
3 : 4. Индекс пересечения (хр X *q), где хр € Lp (К, Ж)>
xq£Lq(K*. Ж) и 51 есть кольцо 485
3:5. Теорема Веблена [3:5] , 487
§ 4. Комбинаторный случай закона двойственности Александера. 489
4:1. Формулировка теоремы 489
4:2. Обобщение теоремы [4:10] 491
4:3. Случаи/? = 0 и р = п—^предварительные замечания к
доказательству теоремы [4:2] 494
4 : 4. Изоморфное отображение Д£>? группы Z^(Kq)/C^ (Ко) на
группу zqK;1w\K;)iHq-1(K*\K*) 495
4:5. Определенней простейшие свойства коэффициента
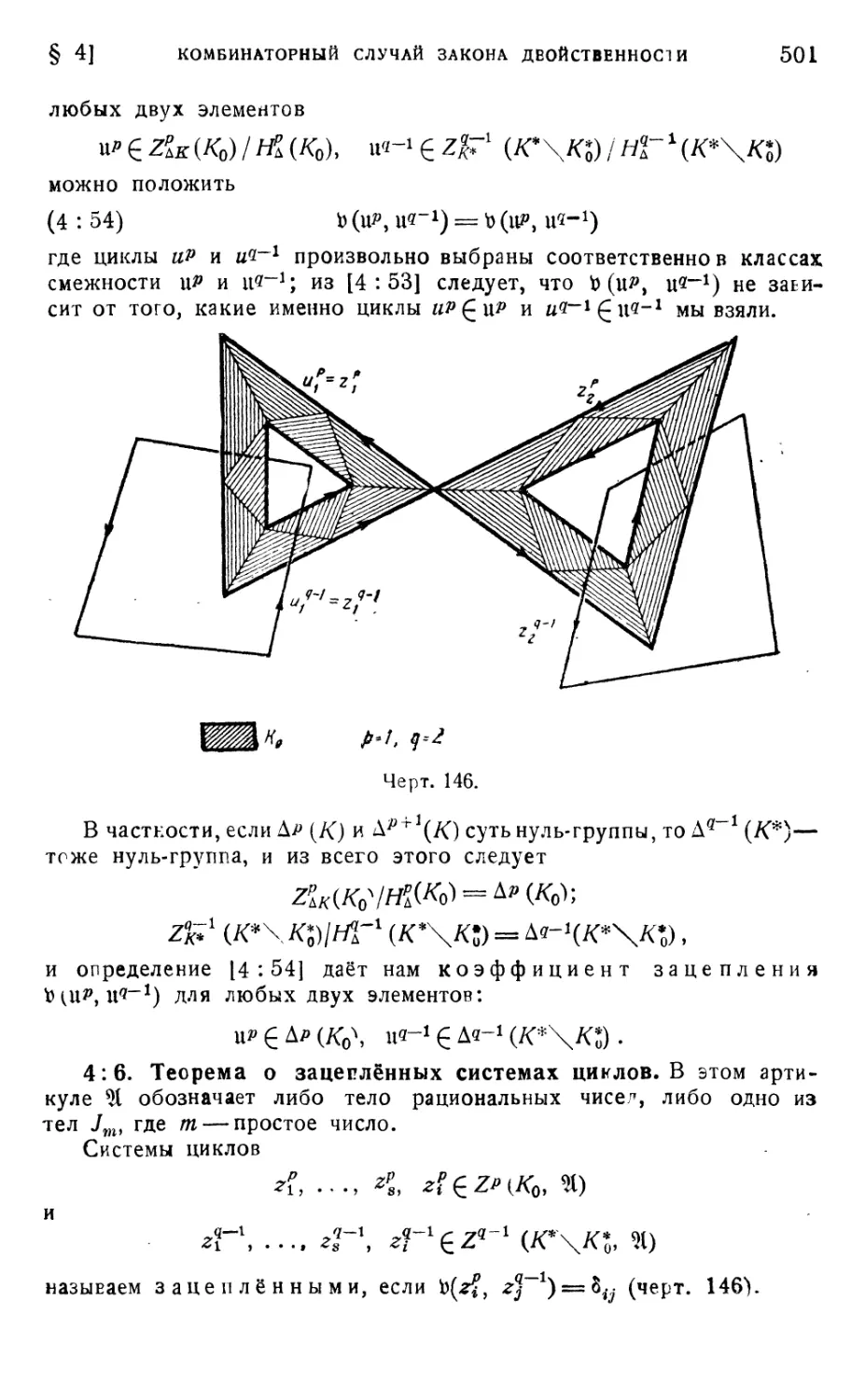
зацепления Ь[иР, uq"x) двух А-циклов иР £ Н* (К) и uq~x 6 И^1 (/С*) 499
4 ; 6. Теоремы о зацепленных системах циклов 501
ГЛАВА ЧЕТЫРНАДЦАТАЯ. Д-ГРУППЫ КОМПАКТОВ И ЗАКОН
ДВОЙСТВЕННОСТИ АЛЕКСАНДЕРА-ПОНТРЯГИНА.
§ 1. Д-группы бикомпактов 505
1 :1. Спектры и их Д-группы .... 505
1 :2. Гомоморфизмы S* 508
1 :3. Д-группы бикомпактов ... 509
1 : 1 Группы Доо 510
§ 2. Конфинальные части спектров. Случай компактов 511
2:1. Конфинальные части спектров 511
2:2. Случай, когда Ф — компакт 512
2:3. Случай, когда Ф — полиэдр 513

14
ОГЛАВЛЕНИЕ
§ 3. Д-группЫ открытых множеств S*. Фэрмулировка законе
двойственности Александера-Понтрягина и основные
следствия его. Случай конечного Ф 515
3:1. Группы Дг (Г), где Г открыто в 5" 515
3:2. Барицентрическое подразделение цепе% xr£Lr(F) .... 515
3:3. Топологическая инвариантность групп Дг (1) 617
3:4. Закон двойственности Александера-Понтрягина и основные
следствия его 518
3:5. Случай конечного Ф • 520
§4. Комплексы ДГа, К0а, К\, К\%, Qal; множества (/„ и Гв 523
4:1. Определения и обозначения 523
4:2. Непрерывное отображение С множества Оа на полиэдр Q 525
4:3. Некоторые свойства ipynn Zr (i ) 526
§ 5. Комбинаторная лемма 527
5:1. Предварительные замечания и формулировка леммы .... 527
5:2. Основное тождество 528
5:3. Окончание доказательства леммы [5 :1] 532
§ 6. Спектр К0 множества Ф 534
6 :1. Покрытия Qcr и (о« 534
6:2. Спектр К0 компакта Ф 535
6:3. Проекции Si 536
§ 7. Дальнейшие вспомогательные предложения 536
7:1. Переместительность операторов 5р и у£ 536
7:2. Следствие из формул (5:1) и (7:1) 537
§ 8. Доказательство закона двойственности
Александера-Понтрягина 538
8:1. Гомоморфизм Д£Югр)ппы Д#(Ф) в группу Д7"1 (i) 538
8:2. Отображение kD't есть изомирфизл. 539
8:3. Изоморфизм \Dri отображает группу V^(K0) на всю
группу Д^""1 (1) 540
ГЛАВА ПЯТНАДЦАТАЯ. ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН
ДВОЙСТВЕННОСТИ АЛЕКСАНДЕРА.
0:1. Предварительные замечания 541
§ 1. Индекс пересечения и коэффициент зацепления 541
1 :1. Индекс пересечения двух цепей хр и yq пространства Rn. 541
1:2. Формулы для вычислений с индексами пересечения . . . 542
1:3. Следствия из теоремы [1:2]. Обобщение условий, в которых
определён индекс пересечения .... • 545
1:4. Коэффициент зацепления • 548
1:5. Формулы для вычислений с коэффициентами зацепления . 550
1:6. Случай г*> <Е Z*(/C0). -г3"1 € Zq'1 (К*) 552
§ 2. Зацепление истинных циклов • 553
2:1. Определение коэффициентов зацепления для истинных
циклов • 553
2 :2. Деформационная теорема для истинных циклов 555

ОГЛАВЛЕНИЕ 15
§ 3. Малый закон двойственности Александера .♦,,.**.. 556
3:1. Пре варигельнь:е замечания и формулировка теоремы . . 556
3:'Л Доказательство теоремы [3:1] 557
3:3. Малый закон двоис венности Понтрягина 560
3:4. Зшкнутые (п~ 1)-мерные псевдомноюобразия в Sn при л>2.
Теорема Жордана-Ьрауэра 562
3:5. Некоторые замечания о зацеплении псевдомногообразий . . 564
ЧАСТЬ ПЯТАЯ.
ВВЕДЕНИЕ В ТЕОРИЮ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ
ПОЛИЭДРОВ.
ГЛАВА ШЕСТНАДЦАТАЯ. БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ
ОТОБРАЖЕНИЙ В Rn И Sn.
§ 1. Иорядэк точки относительно (п—1)-мернэго цикла в Rn . . 568
1 :1. Комбинаторный случай 568
1:2. Порядок точьи о £ Rn относительно истинного цикла zn~l 570
1:3. Теоремы Пуанкгре-Боля и Р)ше 571
1:4. Гомологии BRn\o 571
1:5. Порядок точки относительно ци*ла как степень центральной
проекции цикла на сферу 572
§ 2. Теорема существования корней 573
2:1. Теорема существования корней - 573
§ 3. Локальная степень отображения лмерной цепи в Rn ... 574
3:1. Определение и основные свойства локальное степени . . . 574
3:2. Симплициальные приближения 575
3:3. Случай отображения в сферу Sn 577
§ 4. Топологические отображения 577
4:1. Теорема [4:1] 577
4:2. Теоремы инвариантности . . . . • 579
§ 5. Векторные поля и непрерывные отображения 580
"»: 1. Связь между векторными полями и отображения\ и .... 580
5 : 2. Индекс изолированного нуля р векторного поля §8 . . . . 581
5: 3. Векторные поля на шаре . . . • 583
5 : 4. Теорема Ьрауэра о неподвижных точках отображений л-мер-
ного элемента 5£3
5:5. Векторнь.е поля на сферах чётной размерности 584
5:6. Симметрия сфер; ещё одна теорема о неподвижных точках 585
5 : 7. Упражнения 586
§ 6- Классификация непрерывных отображений л-мерной сферы
в л-мерную сферу 588
6:1. Теорема Хопфа; вводные и вспомогательные замечания к ней 588
6-2. Случай, когда степень отображения равна нулю 591
6 :3. Редукция теоремы Хопфа к «теореме о продолжении» . . 594
6:4. Доказательство «теоремы о продолжении» 595

16
ОГЛАВЛЕНИЕ
ГЛАВА СЕМНАДЦАТАЯ. НЕПОДВИЖНЫЕ ТОЧКИ. НЕПРЕРЫВНЫХ
ОТОБРАЖЕНИЙ ПОЛИЭДРОВ.
§ 1. Теорема существования для неподвижных точек 598
1:1. Неподвижные симплексы 598
1:2. Формула Хопфа 599
1:3. Число Лефшеца для непрерывного отображения полиэдра
в себя • 602
1 :4. Примеры 603
1 :5. Некоторые замечания о числе Лефшеца 604
§ 2. Индекс неподвижной точки • 605
2:1. Определение индекса 605
2:2. Некоторые свойства индекса 606
2:3. Нормальные неподвижные точки. Топологическая
инвариантность индекса неподвижной точки 607
2:4. Неподвижные точки аффинных отображений 610
§ 3. Алгебраическое число неподвижных точек непрерывного
отображения полиэдра в себя 610
3:1. Определение регулярных неподвижных точек. Формулировка
основной теоремы 610
3:2. Обобщение 6U
3:3. Регулярные неподвижные точки симплициальных
отображений 612
3:4. Сведение теоремы [3:1] к аппроксимационной теореме. . 613
3 :5. Доказательство аппроксимационной теоремы 614
3:6. Некоторые замечания об алгебраическом числе
неподвижных точек • 618
Прибавление I 620
Прибавление II 645
Указатель 657

k
ПРЕДИСЛОВИЕ.
Настоящая книга является введением в современную
гомологическую топологию, доступным всякому читателю, имеющему
некоторую общую теоретико-множественную и алгебраическую культуру
и стремящемуся получить некоторые познания в области топологии
путём систематического изучения основных глав этой дисциплины.
Таким образом, некоторое знакомство с идеями современной
топологии можно в настоящем сочинении почерпнуть лишь из
кропотливого изучения основных топологических фактов,- которые, вместе
со всем необходимым для их получения техническим аппаратом,
часто громоздким и нисколько не увлекательным, я стремился
изложить со всей логической строгостью, не боясь быть порою
скучным и утомительным. Книга может служить учебником топологии для
аощрантов и университетских студентов старших курсов,
специализирующихся в топологии, или в любой другой области математики,
так или иначе связанной с топологией.
При написании этой книги я широко пользовался сочинением
Topologie I, являющимся совместным трудом известного
швейцарского математика Н. Hopfa и моим. В частности, глава 17
настоящей книги является переводом, а глава 16 — переработкой
соответственно глав 14 и 12 упомянутого совместного произведения. Я считаю
[Нужным особенно подчеркнуть это заимствование, так как две
названные главы книги Александрова-Hopf а принадлежат всецело перу
Н. Hopfa. Оба прибавления к настоящей книге (об абелевых группах
|и об аналитической геометрии /г-мерного пространства) также в ОС-
ровном заимствованы из книги Александрова-Hopf а, правда, с зна-
1 ^ Александров П. С.

18
ПРЕДИСЛОВИЕ
чительными сокращениями. Кроме этих фундаментальных
заимствований имеется много мелких, разбросанных в разных местах текста,
которые едва ли необходимо перечислять в отдельности.
*
\
Центральное место во всей книге занимают главы 8 и 9, в которых
и излагается то, что называется комбинаторной теорией гомологии.
Необходимый технический аппарат — комплексы и цепи — излагается
в главах 4 и 7, причём глава 4 имеет
комбинаторно-геометрическое, а глава 7 — алгебраическое содержание. В гл. 8 и 9
изучаются не только обычные («нижние» или Д-) гомологии, но и так
называемые верхние или V-гомологии, которые в современных
топологических исследованиях приобретают с каждым днём всё большее
значение. Я старался всю теорию изложить возможно проще и
понятнее, пояснив её большим числом элементарных примеров,
усвоение которых важно для понимания существа дела.
Топологически-инвариантное содержание теория гомологии
получает в главах 10 и 11, где несколькими различными способами
доказывается инвариантность групп Бетти. При этом я совершенно
изгоняю так называемые «непрерывные циклы», так как мне кажется,
что не на непрерывные, а на «истинные» циклы наао смотреть как
на основной путь приложения гомологических понятий, применимый
к любым компактам, но практически удобный и при изучении
полиэдров во всех случаях, где разумно пользоваться понятиями, сама
формулировка которых топологически инвариантна (например, при
применениях топологии к вариационному исчислению). В
принципиальных вопросах построения общей гомологической теории
компактов (особенно, если иметь в виду обобщение этой теории на
неметризуемый случай — прежде всего, произвольных бикомпактов),
конечно, предпочтительно пользоваться «спектральной теорией» (как
она изложена в 14-ой главе), основанной на непосредственном Ис1
следовании частично упорядоченного множества всех конечных от-«
крытых или замкнутых покрытий данного пространства; однако,]
когда надо изучить гомологические свойства конкретно-заданного
индивидуального компакта, то истинные циклы с лежащей в основе
их определения метрикой скорее всего ведут к цели.
Дальнейшим развитием гомологического аппарата современной!
топологии является локализация его, приводящая (посредством по-

ПРЕДИСЛОВИЙ
1Й
нятия относительного цикла и относительной гомологии) к
определению групп Бетти в данной точке. Этим путём становится
возможным изучать, например, многообразия с краем, а также
осуществить построение так называемой гомологической теории размерности.
Из последней мы даём в настоящей книге лишь само определение
гомологической размерности и доказательство того, что для
полиэдров она совпадает с числом измерений в элементарном
смысле слова. Относительным циклам и их применениям посвящена
гл. 12.
Мы рассматриваем в настоящее время метод гомологии как
основной стержень топологии потому, что чрезвычайно значительная
часть новых геометрических фактов, открытых в топологии,
формулируется в гомологических терминах. К числу наиболее важных
из этих фактов относятся законы двойственности Пуанкаре и Але-
ксандера-Понтрягина. Им в основном посвящены главы 13—15. Здесь
же находят своё естественное место понятие гомологического
многообразия, а также элементы теории пересечений, равно как и теория
зацеплений. Эта последняя теория в её простых построениях
оказывается также удобным методом исследования простейших
классических вопросов теории непрерывных отображений, которым
посвящена 1б-ая глава. Наконец, в 17-ой главе (целиком заимствованной,
как уже было сказано, из моей совместной книги с Hopf ом)
доказывается знаменитая формула Лефшеца-Hopf'a об
алгебраическом числе неподвижных точек непрерывного отображения полиэдр
в себя.
Из всего богатства конкретного фактического материала, к
которому приводит теория гомологии, читатель может выбрать то, что
ему интереснее или доступнее. Например, он может, изучив главу 8
и взяв из глав 10—11 то или иное доказательство инвариантности
групп Бетти, перейти сразу к теории зацеплений (глава 15) и
далее к теории непрерывных отображений (главы 16 и 17),
ограничившись, если пожелает, классическими вопросами, изложенными
в главе 16. Или он может после глав 8, 9, 10 перейти к 13-ой и
14-ой главам, т. е. в основном — к законам двойственности.
Наконец, читатель, желающий приобрести самые первые топологические
понятия, может, более или менее в любом порядке, читать главы 2,
3, 5, или — при преобладающем интересе к вопросам теоретико-
множественного характера—главы 5 и 6, обращаясь к предыдущим
главам (в основном, к главе 4) лишь по мере ссылок. Аннотации
2*

20
ПРЕДИСЛОВИЕ
к отдельным частям и главам книги вообще помогут читателю
выбрать ту или иную последовательность изучения различных её
отделов.
* *
Излишне говорить, что предлагаемая вниманию читателя книга
далеко не исчерпывает даже основных отделов современной
комбинаторной топологии. Будучи ориентирована в направлении задач
достаточно общих и в то же время достаточно элементарных, эта
книга, как явствует из предыдущего, ищет эти задачи в основном
среди задач гомологической топологии. Всё огромное направление
гомотопических методов — начиная с классического понятия
фундаментальной группы Пуанкаре *) и кончая группами, введёнными Гуре-
вичем, и исследованиями последних лет, принадлежащими в области
гомотопических проблем Н. НорГу, Понтрягину, Эйленбергу и
многим другим, — осталось целиком за пределами нашего изложения.
Однако, я не коснулся также многих глубоких вопросов
гомологической топологии: теория пересечений и произведений представлена
в этой книге лишь совсем элементарным случаем p-\~q=zn (т. е.
случаем, когда в пересечении получается нульмерный образ). Поэтому
выпали, конечно, все результаты в теории непрерывных
отображений, получающиеся помощью метода «произведения» и «пересечения»
(Product-Method Лефшеца), с развитием, данным ему НорГом. По
некоторым из перечисленных вопросов можно в качестве литературы
указать серию статей, которые должны появиться в ближайших
топологических выпусках «Успехов математических наук». Там же можно
найти и мои статьи по гомологической теории размерности.
Дальнейшее развитие вопросов, связанных с законами двойственности,
составляет предмет моей работы «Гомологические свойства
расположения комплексов и замкнутых множеств», опубликованной в
«Известиях Академии Наук СССР», серия математическая за 1943 год**).
К сожалению, эта статья, написанная уже после того, как работа
над настоящей книгой была вполне закончена, не смогла получить
отражение в книге; иначе в главах 13 и 14 могли бы быть сделаны
*) С которым можно познакомиться из Курса топологии Зейферта^
Трелт фалля.
**) Вопросам теории двойственности и гомологической теории
размерности я предполагаю посвятить специальную монографию, в которой эти
вопросы, возможно, получат более полное и в то же время более доступное
изложение, чем в имеющихся журнальных статьях.

ПРЕДИСЛОВИЕ
21
различные усовершенствования. Тем более я рекомендую
названную статью в качестве дополнительной литературы. В таком же
порядке может быть рекомендована и книга Hurewicz-Wallman, Dimension
Theory.
Рукопись этой книги была совершенно закончена летом 1941 года.
Естественно, что разразившиеся события надолго отсрочили издание,
а истекшие пять лет, в течение которых продолжалось дальнейшее
движение и советской и зарубежной научной мысли, уже сейчас, в
момент выхода книги в свет, заставляют считать желательными многие
изменения в её тексте, начиная даже с вопросов обозначений и
терминологии (см., например, мою цитированную статью из Известий
Академии Наук). Однако, каждое даже небольшое изменение в столь
громоздком сочинении повлекло бы за собою другие, и в конце
концов пришлось бы предпринять переработку всей книги, что
отсрочило бы её издание снова на далёкий срок. Вот почему мне
приходится пойти на издание этой пять лет пролежавшей рукописи
в её теперешнем виде, отложив всевозможные усовершенствования
её (необходимость которых мне более очевидна, чем кому-нибудь)
до второго издания.
В заключение, мне хочется поблагодарить различных лиц,
оказавших мне при написании этой книги ту или иную помощь.
Прежде всего, я очень благодарен Л. С. Понтрягину, который
подробно ознакомился со многими и притом существенными частями
моей рукописи и сделал по их поводу ряд ценных замечаний и
предложений. Они часто давали мне возможность существенно улучшить
моё изложение. В случаях, когда Л. С. Понтрягин сообщал мне
новые и более простые доказательства отдельных предложений
(так, например, в четвёртой и тринадцатой главах) я это отмечаю
в тексте. В целом же постоянное дружественное общение с Л. С. Пон-
трягиным на протяжении всего длительного срока моей работы над
этой книгой служило мне большой поддержкой и, конечно, пошло
этому сочинению очень на пользу. М. Р, Шура-Бура внимательно

22
ПРЕДИСЛОВИЕ
прочитал всю книгу в корректурах и ему я обязан многими
отдельными усовершенствованиями изложения (особенно в третьей главе).
Отдельными ценными замечаниями я обязан А. Н. Колмогорову,
А. С. Пархоменко и А. М. Роднянскому. А. Н. Колмогорову я,
кроме того, благодарен за исполнение многих чертежей.
При изготовлении окончательного текста этой книги и части
чертежей большую помощь оказал мне мой лаборант, студент
Московского университета Ю. Смирнов, которому я здесь выражаю
искреннюю благодарность.
За участие в чтении корректур и составление указателя я
благодарю С. В. Фомина.
Наконец, я очень признателен Издательству в лице его
директора Г. Ф. Рыбкина и главного редактора математической
литературы А. И. Маркушевича за в высшей степени внимательное
отношение ко всем моим пожеланиям, связанным с изданием этой книги.
Болшево, дер. Комаровка,
22 июня 1946 г.
П. Александров

ЧАСТЬ ПЕРВАЯ.
ВВЕДЕНИЕ.
Эга часть состоит из трех глав, из которых первая имеет
вспомогательный характер, а две другие, независимые между собою,
посвящены наиболее элементарным вопросам «геометрической»
топологии— теореме Жордана и элементарной теории замкнутых
поверхностей. Эти две главы (вторая и третья) вместе с пятой главой
образуют своего рода первый концентр, содержащий ряд интересных и
важных топологических фактов и не пользующийся общими понятиями
комбинаторной топологии, важность которых, однако, в этих главах
уже достаточно выясняется.
ГЛАВА ПЕРВАЯ.
ОБЗОР ЭЛЕМЕНТАРНЫХ СВОЙСТВ ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВ.
Эта глава представляет собою очерк элементарней теории
топологических пространств и не предназначена для обязательного изучения;
целесообразны следующие формы пользования настоящей главой:
1. Читатель просматривает обозначения, приведённые в § 1, а затем
обращается к этой главе, лишь встречая в дальнейших главах ссылки на
неё.
2. Если глава прочитывается, то недостающие доказательства
проводятся читателем самостоятельно или же берутся им, например, из книги
Хаусдорфа, Теория множеств, гл. 6 и 7.
Применение результатов этой главы будет в дальнейшем встречаться
не часто. Однако, некоторыми понятиями и предложениями, установленными
здесь, мы, конечно, будем систематически пользоваться. К ним относятся
(кроуе таких элементарных понятий, как понятие непрерывно;о
отображения, замкнутого и открытого множеств и т. п.): понятия деформации,
лебегова числа покрытия, частично упорядоченного множества, а также
применяемая в гл. 6 теорема о полноте метрического пространства непрерывных
отображений одного компакта в другой.
Поняием биксмпакта мы пользуемся в этой книге лишь один раз — при
определении так называемых шерхних групп Бетти бикомпактов, в гл. 14;
вполне возможно было бы и там ограничиться случаем компактов (чита-
тель может так и сделать). Таким образом, все
элементарно-топологические понятия, вводимые в этой главе, могли бы быть введены для одних
ишь метрических пространств; это также можно иметь в виду при
пользовании этой главой.
тий жение в этой главе подробно в тех случаях, когда касается поня-
ког' суц*ественно применяемых в дальнейшем, а также во всех случаях,
н да приводятся теоремы, которых нет в книге Хаусдорфа. В осталь-
опое°Л^Чаях изложени- конспективно. Само собою разумеется, что все
Ноет СЛСНИЯ и Ф°РмУлИровки всех теорем даны с йодной
обстоятельностью,

24 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I 1
§ 1. Обозначения из теории множеств, постоянно употребляемые 1
в этой книге. 1
1:1. Операции надмножествами. Соединение множеств 4, 1
В, С,..., т. е. множество всех элементов, принадлежащих хотя бы
одному из множеств Л, В, С,. . ., обозначается через A U В U С . ..
В соответствии с этим соединение множеств Ла, где а — индекс,
пробегающий конечное или бесконечное число значений, обозначается |
через 1Ыа. j
Пересечение множеств Л, В, С,. . ., т. е. множество всех эле- j
ментов, принадлежащих всем множествам Л, В> С,..., обозначается j
через А П В П С . . ., соответственно через П Аа.
a j
Разность множеств А и В, т. е. множество тех элементов мно- j
жества Л, которые не являются элементами множества В, обозна- |
чается через А\В. При этом не предполагается, что В есть подмно- ]
жество Л, так что
А\В = А\(А()В).
Запись ,4с5 или равносильная ей запись В^А означает, что
множество Л есть подмножество множества В, т. е. что каждый
элемент множества А есть элемент множества В.
Запись АаВ или BzdA означает, что Л есть собственное
подмножество множества В} т. е. что каждый элемент множества А
есть элемент множества В, но при этом имеется хотя бы один
элемент множества В, не являющийся элементом множества Л.
Отношение «а есть элемент множества Л» записывается так:
а£А
или иногда
АЭа.
Отрицание отношений, выражаемых знаками с, с, £ и т. п.,
обозначается перечеркиванием этих знаков. Так например, а (£ Л
означает, что я не есть элемент множества Л.
1:2. Отображения. Если каждому элементу х множества X
поставлен в соответствие однозначно определённый элемент y=f{x)
множества Y, то говорят, что дано отображение /множества
X в множество Y. При этом элемент f (х) называется образом
элемента х при отображении /. Множество всех элементов f{x)£ F,
получающихся, когда х пробегает некоторое подмножество Л
множества X, называется образом множества Л при отображении /
и обозначается через /(Л). Множество всех х£Ху для которых
f(x)£B, где В есть некоторое данное подмножество множества F,
называется прообразом множества Bc^Y при отображении / и
обозначается через /-1 (В). В частности, если В состоит из одного
элемента y^^Y, то f~l (В) обозначается через f'1 (у$) и называется
прообразом элемента у0 при отображении /„

§ 1| ОБОЗНАЧЕНИЯ, УПОТРЕБЛЯЕМЫЕ В ЭТОЙ КНИГЕ 25
Если образом X при отображении / является всё множество Г,
т0 отображение / называется отображением на Y.
Если дано отображение Д множества Хг в Х2 и отображение
ft множества Х2 в Л"3, то, ставя в соответствие каждому элементу
хг £ -Afj элемент f\{fl (хг)) £ Х3, получим отображение
JB J3J2,
множества Хг в Х3. При этом для всякого Л3^Х3 имеем
Замечание. Часто вместо f(x), /(Л), /_1(у), f"1 (В) мы будем
писать fx, /A, f~ly, f~lB.
1:3. Обозначенные элементы; системы множеств и их
кратность; покрытия. Предположим, что каждому элементу а
множества А поставлен в соответствие некоторый элемент множества
/И, причём различным элементам множества А может оказаться
поставленным в соответствие один и тот же элемент множества М.
Через та обозначим пару, состоящую из данного элемента а
множества А и соответствующего ему элемента т множества М. Такие
пары в некоторых случаях удобно называть «элементами
множества М, обозначенными при помощи индексов а».
Например, пусть f(x, 0) есть функция двух переменных х и 0,
определённая для всех пар значений л:, в, 0<Сл;<;1, 0 <^ 6.^1.
Тогда для каждого данного постоянного значения G имеем функцию
одного переменного х, причём для различных значений Ьг и 62
функции /ц{х) и /в2(х) могут оказаться совпадающими. Можно сказать,
что дано множество обозначенных при помощи индексов 6, 0 <^ G <^ 1
функций /о (х).
Обычно для краткости вместо: «множества обозначенных при
посредстве индексов а£А элементов та множества Ж» говорят о
семействе или системе элементов, зависящих от
данного индекса (или данного параметра) а; например, говорят
о семействе функций fy (x), зависящих от параметра 0.
Другой важный пример — пример систем подмножеств данного
множества R. Пусть каждому элементу i некоторого множества
индексов поставлено в соответствие подмножество Аг множества /?,
причём различным индексам могут соответствовать совпадающие
(т. е. состоящие из тех же элементов) множества А,г Полученное
множество обозначенных подмножеств Аг множества R для
краткости называется просто системой подмножеств
множества /?.
Система подмножеств данного множества /? называется
покрытием множества /?, если соединение множеств| входящих в эту
систему, есть всё множество /?.

26 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
В этой книге будут почти исключительно рассматриваться
конечные системы множеств, в частности, конечные покрытия. При
этом основным будет являться понятие о кратности покрытия.
Кратностью данной конечной системы множеств называется
наибольшее из таких целых чисел п, что в данной системе множеств
имеется п элементов с непустым пересечением.
Замечание. Система множеств называется простой, если в ней
нет совпадающих элементов (т. е. если всяким двум различным индексам
i и j соответствуют различные множества Л> и Aj). Конечно, всегда можно
ограничиться рассмотрением одних лишь простых систем; однако, иногда
удобно не стеснять себя требованием прост01Ы тех или иных систем
множеств. Примеры этому мы увидим в гл. 14.
§ 2. Топологические пространства*).
2:1. Определение топологических пространств и основных
связанных с ними понятий.
Определение (2:11). Топологическим
пространством называется множество /?, состоящее из элементов произвольной
природы, в котором определены некоторые подмножества A cz/?,
называемые замкнутыми множествами топологического
пространства /?; при этом предполагаются выполненными следующие
условия, называемые аксиомами топологического п р о -
с 1 ранства:
1д. Пересечение любого числа и соединение любого конечного
числа замкнутых множеств есть замкнутое множество,
2д. Всё множество R и пустое множество суть замкнутые
множества.
Замечание 1. Элементы множества R называются точками
данного топологического пространства.
Множества, дополнительные к замкнутым в /?, т. е. множества
вида R\A, где А замкнуто, называются открытыми
множествами топологического пространства R. Они, очевидно, удовлетво-
яюрт следующим условиям:
1г. Соединение любого числа и пересечение любого конечного
числа открытых множеств открыто.
2г. Всё множество R и пустое множество открыты.
Замечание 2. Можно было бы определить топологическое
пространство как множество R, в котором выделены некоторые
подмножества, называемые открытыми множествами, так что
удовлетворяются условия 1Г—2г. Тогда множества, дополнительные к
открытым, удовлетворяют условиям \А — 2а и называются
замкнутыми.
Определение [2:12]. Пересечение всех замкнутых множеств,
содержащих данное множество М, называется замыканием
множества М в топологическом пространстве R и обозна-
*) Хаусдорф, Теория множеств, §§ 21 -~ 24*

§ 2]
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
27
тся через М. Точки множества М называются точками
прикосновения множества М.
го-13]. Операция замыкания, т. е. перехода от любого
жества дд к ег0 замыканию М, удовлетворяет следующим
условиям:
Т. мТш = лГим
37 \jvf) = AT для любого М.
4~ Замыкание пустого множества пусто.
Замечание 3. Можно было бы определить топологическое
пространство как множество, в котором для каждого подмножества М
определено замыкание М, так что эта операция замыкания
удовлетворяет условиям 1 — 4. Тогда замкнутые множества определяются
как множества, совпадающие со своими замыканиями. Этим путём
мы получаем в точности те топологические пространства, которые
были определены в начале этого параграфа.
Определение [2:14]. Окрестностью данной точки р в
топологическом пространстве R называется всякое открытое множество,
содержащее точку р.
Точка р^М называется внутренней точ-кой множества М
относительно топологического пространства /?, если существует
содержащаяся в М окрестность точки р. Множество всех внутренних
точек множества М есть открытое множество ГсМ. Множество ЛГ\Г
называется границей множества М в пространстве /?. Точка
пространства R называется изолированной в /?, если множество,
состоящее из одной этой точки, открыто.
[2:141]. Тогда и только тогда р £ М, когда каждая окрестность
точки р содержит хотя бы одну точку множества М.
Точка р называется точкой накопления или
предельной точкой множества УИ, если каждая окрестность точки р
содержит бесконечное множество точек множества М.
Определение [2:15]. Множество М называется плотным
в /?, если JW=R.
Замечание 4. Понятие топологического пространства есть
совокупность двух понятий: понятия множества точек данного
топологического пространства и понятия определённой в этом
множестве топологии, т. е. системы множеств, являющихся
замкнутыми (открытыми) множествами данного топологического
пространства (или определённой в данном пространстве операции замыкания, —
см. замечание 3).
[2:16]. Пусть дано топологическое пространство R и лежащее
в нём множество М. Топология пространства R следующим образом
Определяет топологию множества М\ замкнутые множества в М суть

28 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I jj
1
по определению пересечения с М замкнутых множеств простран~ \
ства R. !
Когда говорят о каком-либо множестве М, лежащем в тополо- |
гическом пространстве /?, как о топологическом пространстве, то i
всегда имеют в виду именно эту топологию — топологию,
определённую объемлющим топологическим пространством R.
Условия 1д и 2д при этом, очевидно, выполняются.
Легко доказывается:
[2:17]. Открытые множества в М суть пересечения с Ж открытых
множеств пространства R.
2:2. Задание топологии при помощи окрестностей.
Теорема [2 :21J. Пусть дано некоторое множество R,
элементы которого мы условно называем точками. Пусть каждой
точке p^R отнесены некоторые, содержащие точку /?,
подмножества О (р) множества R, называемые окрестностями точки р
в данной системе окрестностей £). Предположим, что при этом
выполнены следующие условия:
\q. Пересечение любых двух окрестностей каждой данной
точки p£R содержит окрестность точки р.
2с>. Если q есть точка, содержащаяся в окрестности О (р)
точки р £ /?, то существует окрестность О (q) точки q,
содержащаяся в О (р).
Назовём точку р точкой прикосновения множества М, если
каждая окрестность точки р содержит по крайней мере одну
точку множества М. Множество всех точек прикосновения
множества М назовём замыканием М множества М. Определённая
таким образом операция замыкания удовлетворяет условиям
1 — 4 арт. 2 :1 и, следовательно, превращает множество R в
топологическое пространство] при этом все окрестности О (р)
оказываются открытыми множествами пространства R
(условие 20).
Назовём для удобства множество всех окрестностей точек
топологического пространства R (определённое в [2:14]) абсолютной
системой окрестностей топологического пространства /?; эта
система удовлетворяет условиям \q—2^; топология данного
топологического пространства может быть определена, следовательно,
применением теоремы [2:21] к абсолютной системе окрестностей
пространства.
[2:22]. Множество 2? открытых множеств Г топологического
пространства R называется базой пространства/?, если кажцое
открытое множество пространства R есть соединение некоторых множеств,
являющихся элементами множества 23.
Очевидно,
[2:23]. Для того, чтобы множество 23 открытых множеств
топологического пространства было базой этого пространства,
необходимо и достаточно, чтобы для каждой окрестности О произвольной

§ 2]
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
29
точки р (т. е. для каждого открытого множества, содержащего
точку р) можно было найти элемент Г базы 23, удовлетворяющий
условию
р£ГсО.
Отсюда и из теоремы [2:141 ] следует:
[2:24]. Пусть SB — база пространства R. Тогда и только тогда
точка р является точкой прикосновения множества М, когда каждая
окрестность точки р, являющаяся элементом базы 23,
содержит по крайней мере одну точку множества М.
Определение [2: 25]. Пусть R—топологическое пространство.
Системой окрестностей топологического
пространства/? называется всякая, удовлетворяющая условиям теоремы [2 : 21]
система окрестностей, приводящая по правилам теоремы [2 :21]
именно к той топологии, которая задана в топологическом
пространстве R»
Из [2:24] следует, что элементы всякой системы окрестностей
топологического пространства R; образуют базу в R; обратно, считая каждый
элемент Г базы L окрестностью всякой точки х £ Г, получим систему
окрестностей пространства R.
Пример. Числовая прямая с её обычной известной из анализа
топологией имеет наряду с другими следующие системы
окрестностей: 1. Окрестность точки р есть произвольный, содержащий эту
точку интервал. 2. Окрестность точки р есть произвольный,
содержащий эту точку интервал с рациональными концами. 3.
Окрестность точки р есть произвольный интервал вида (р—г, р-\-г\ где
г—рациональное число.
Определение [2:251]. Топологическое пространство
называется пространством со счётной базой, если оно имеет
базу, состоящую из счётього или конечного множества элементов.
Такие пространства называют также пространствами «счётного
веса>. Вообще наименьшее кардинальное число т, такое, что
данное топологическое пространство имеет базу мощности т, называется
весом пространства.
Пример. Множество всех интервалов с рациональными концами
есть счётная база числовой прямой.
[2:26]. Пусть L есть база пространства R и MczR. Для
получения базы М достаточно взять множества, являющиеся
пересечениями М с элементами L. Поэтому вес М не превосходит веса R.
2 :3. Метрические и метризуемые пространства.
Определение [2:3]. Метрическим пространством
называется множество элементов произвольной природы {«точек» про-
транства), в котором каждым двум элементам х и у поста-
лено в соответствие неотрицательное число р (х, у), называемое
" асс пю ян ие м между х и у, так что выполняются следующие
Условия:
!• Тогда и только тогда р (х, у) = 0, когда точки
вственны между собой (аксиома тождества).
х и у то*

30 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ (ГЛ. 1
2. р (х>у) — р0>, я) {аксиома симметрии).
3. Для любых трёх точек х, уу z метрическою пространства
имеет место неравенство
р(*э ^О + рСу. *)>р(*> *)
аксиома треугольника).
Неотрицательная фун кция р (х, j/) двух переменных точек х, у
пространства /?, удовлетворяющая указанным условиям, называется
метрикой данного метрического пространства.
Замечание. Всякое множество, лежащее в метрическом
пространстве R, рассматриваемое с той метрикой, которую оно получает
из Ry является метрическим пространством.
Метрика данного метрического пространства определяет в нём
топологию следующим образом. Назовём расстоянием между
точкой р и множеством Ж, лежащим в данном метрическом
пространстве R, нижнюю грань неотрицательных чисел р(/?, х) при х,
пробегающем все точки множества М. Назовём замыканием
множества Ж в метрическом пространстве R множество всех
точек р, для которых р (/?, М) = 0. Назовём, наконец (в соответствии
с замечанием 3 арт. 2 :1), множество М замкнутым, если оно
совпадает со своим замыканием*). Легко проверить, что эта топология
удовлетворяет аксиомам топологического пространства. Только что
определённую в данном метрическом пространстве топологию называем
топологией, определяемой данной метрикой или
просто естественной топологией данного метрического
п ростр ан с т ва.
[2 : 31]. Верхняя грань й^оз чисел р(х, у), где х к у пробегают
множество точек метрического пространства /?, называется
диаметром пространства R.
[2:32]. Пусть е >0. Назовём е-окрестностью множества
(или точки) Р метрического пространства R множество 0(Р, е) всех
точек x£R, удовлетворяющих неравенству р(Р, #)<е.
Замечание, г-окрестности называют также сфери ческими
окрестностями (радиуса в). Легко видеть, что они суть
открытые множества.
[2 : 33]. Пусть М — множество, лежащее в метрическом
пространстве /?; тогда и только тогда р £ М, когда всякая сферическая
окрестность 0(р, е) точки р содержит хотя бы одну точку множества М.
[2:331]. Сферические окрестности точек метрического
пространства R образуют систему окрестностей пространства R (в
смысле [2 : 25].
[2 : 34]. Последовательность
(2 :34) xl9 *a,..M *„,...
*) Можно было бы с самого начала сказать: множество М замкнуто»
если всякая точка/?, находящаяся от М на нулевом расстоянии (р(р, М) = 0)
содержится в At

§ 2]
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
31
точек метрического пространства R по определению сходится
к точкел:^/?, если расстояние р (л;, хп) стремится к нулю при п-> оо,
т. е. если каждая (сферическая) окрестность точки х содержит все
точки этой последовательности, кроме, быть может, конечного числа.
[2 :35]. Точка р метрического пространства R тогда и только
тогда является точкой прикосновения множества Ж, когда к ней
сходится последовательность точек множества М. Точка р тогда и
только тогда является точкой накопления множества М, если к р
сходится последовательность попарно различных точек множества М.
[2 :36]. Метрическое пространство R тогда и только тогда имеет
счётн/ю базу, если оно содержит счётное (или конечное) плотное
в R множество.
В самом деле, если Uv ..., Un, ... — база метрического
пространства R и xn£Un, то множество всех хп плотно в R. Обратно,
если D—{xn] плотно в /?, то множества О (xnj г), где хп
пробегает всё Д а г пробегает множество всех положительных
рациональных чисел, образуют базу в R.
Из [2 :3б] и [2:26] следует:
[2:37]. Если в метрическом пространстве R плотно некоторое
счётное множество и A d R — бесконечно, то и в А плотно
некоторое счётное множество.
Примеры метрических пространств. 1. Эвклидово
п-м е р н о е пространство Rn: его точки х суть
последовательности п действительных чисел х = (х19..., хп), расстояние между
двумя точками х = (х},.. ., хп) и у = (уи...9 yj) даётся формулой:
р (*, у) = Y(b—yJrF~~+ (Хп—уУ'
2. Все множества, лежащие в эвклидовых пространствах,
являются также метрическими пространствами. Среди них отметим особо:
/2-мерный замкнутый шар Еп с центром а и радиусом р
состоит из всех точек х £ Rnf отстоящих от точки а на
расстоянии ^р;
я-м ерный открытый шар Еп с центром а и радиусом р
состоит из всех точек x£Rr\ отстоящих от точки а на расстоянии <р;
(п— 1)-ме рн а я сфера 5П_1 = Еп\Еп с центром а и
радиусом р состоит из всех точек х £ Rn, расстояние которых от точки а
равно р.
3. Гильбертово пространство /?°°: его точки суть
бесконечные последовательности действительных чисел
X = (ЛГр . . ., Хп,. . .),
со
удовлетворяющие условию V,vJ < оо ; расстояние между точками
х =^= (лг1э . . ., хт . ..) и у = (уи ..., уп, . ..) даётся формулой

32 обзор свойств топологических пространств [гл. t
р (х> У) = "| / у (-^п—Уп)2 9 являющейся непосредственным обоб-
f 71 = 1
щением формулы расстояния в эвклидовом пространстве *).
4. Множество всех точек х = (х1,. . ., хп,. . .) гильбертова
пространства, удовлетворяющих условию хп^-^п для всех /г = 1,2,. . .,
называется гильбертовым кирпичом (по аналогии с
обыкновенным кирпичом, ширина которого бывает, как известно, вдвое
меньше длины, а толщина — вдвое меньше ширины).
Замечание. Всякое метрическое пространство, содержащее
счётное и плотное в нём множество, гомеоморфно некоторому
множеству, лежащему в гильбертовом кирпиче (теорема Урысона,
см. Хаусдорф «Теория множеств», § 26, теорема X).
2:4. Непрерывные отображения топологического пространства
X в топологическое пространство У могут быть определены каждым
из следующих эквивалентных между собою способов:
[2:4lj]. Отображение С непрерывно, если прообраз С"1(В)
каждого замкнутого в У множества В замкнут в X.
[2:412]. Отображение С непрерывно, если прообраз каждого
открытого в У множества В открыт в X.
[2:413]. Отображение С непрерывно, если для любого множества
Л^Х имеем С(1)сС(Л).
[2:42]. (Определение непрерывности Коши.) Отображение С
топологического пространства X в топологическое пространство У
называется непрерывным в точке а£Х, если для всякой
окрестности О (Ь) точки Ь = С(а) £ У можно найти такую окрестность 0(a)
точки а, что С (0(a)) с: 0(b),
[2:43]. Отображение С тогда и только тогда непрерывно в
смысле определения [2:412]— [2:41Б], если оно непрерывно в каждой
точке а пространства X в смысле определения [2:42].
В случае метрических пространств имеем, кроме того:
[2:44]. Отображение С метрического пространства X в
метрическое пространство У тогда и только тогда непрерывно, если
из сходимости какой-либо последовательности
•* 11 ^2» * * •» Хт • • . В А
к точке х £ X всегда следует сходимость последовательности
С(хг\ С(ха),...,С(*я),...в У
к точке С(лг).
[2:45]. Пусть непрерывное отображение С топологического
пространства X на топологическое пространство У взаимно
однозначно. Если отображение С~г пространства К на X, обратное к вза-
*) См. Хаусдорф, Теория множеств, стр. 107—108, где в частности
доказывается, что из сходимости £ х2п и Яу^ следует сходимость Yi(xn—УИ)2-
п п~ п

§ 2j ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА 33
имно однозначному отображению С непрерывно, то отображение С
называется взаимно непрерывным, или, короче,
топологическим отображением X на У; топологические отображения
называются также гомеоморфизмами. Два топологических
пространства на ?ываются гомеоморфными между собою,
если одно из них может быть топологически отображено на другое.
Топологическое пространство, гомеоморфное метрическому,
называется метризуемы м про с гранством.
2:5. Равномерная сходимость отображений.
Определение [2:51]. Последовательность
С С С
отображений какого-либо множества X в метрическое пространство Y
называется равномерно сходящейся к отображению С
множества X в У, если ко всякому е > 0 можно найти такое
натуральное число ле, что для любого я>яе и всех х£Х имеем
о(С(х\ Сп(х))<г.
Так же, как в учебниках анализа, доказывается теорема:
[2:52]. Предел равномерно сходящейся последовательности
непрерывных отображений топологического пространства X в
метрическое пространство У е^ть непрерывное отображение X в У.
2:6. Топологическое произведение пространств. Приложим
введённые в 2: 2 понятия к определению топологического
произведения топологических пространств.
Произведением двух множеств X и У со времён Кантора назы-
«'-:п.'|'ся множество всех пар (.v, у), где х£_Х, у£Х. Произведением
:--..-j:eci3 Л"в некоторая системы Х={Ха\ называется множество
>-.. s: систем вида
содержащих по одному элементу ха каждого множества Хл. Точками
аналогического произведения топологических пространств Ха по
определению являются элементы произведения множеств Ха. Точки
-v*€^a называются «координатами» точки £={ха}. Топологию
определяем сначала для случая двух пространств X и У: окрестности
точки ; = (#, у)опре \еляам как произведения произвольных
окрестностей точек х и -у, взятых соответственно в X и Y. Без труда
Доказывается, что условия \0—20 теоремы [2:21] при этом оказы-
B;iK>-iC/i выполненными.
Обобщение этой топологии на случай любого кардинального
числа пространств Ха впервые найдено А. Н. Тихоновым: для
получения окрестности точки £° = \х°} надо по произволу выбрать
конечное число «координат» х° этой точки,—-пусть это будут
° Л.1екс« "дров Ю С.

34 Оёзор свойств топологических пространств [гл. 1
и выбрать по окрестности 0(х°а.)^Хч каждой из этих координат.
Окрестность точки £0, определённая этим выбором, состоит из всех
таких £ — {ха}, что
Хч€0(х11)9...,хжа£0(х18)
(остальные координаты принимают всевозможные значения).
Снова доказывается, что условия теоремы [2:21] выполнены.
Примеры. 1. Плоскость есть топологическое произведение
двух прямых, тор*) — произведение двух окружностей, трёхмерное
пространство —произведение трёх прямых.
Вообще я-мерное эвклидово пространство (с топологией,
определённой его обычной метрикой) есть топологическое произведение
п прямых.
Топологическое произведение п окружностей называется я-мерным
тором.
2. В трёхмерном пространстве дана система координат oxyz.
Возьмём в плоскости г = 0 единичную окружность S1 = x2-\-y2=z 1
и рассмотрим механизм Мг, состоящий
из двух стержней оа и ас, каждый
из которых имеет длину 1 и которые
скреплены в точке а шаровым
шарниром так, что стержень оа может
свободно вращаться в плоскости г = О
вокруг неподвижной точки о, тогда как
стержень ас может свободно вращаться
Черт. 1. в трёхмерном пространстве вокруг
точки а.
Пусть дано определённое положение {ра, ас) системы наших
двух стержней. За окрестность этого положения естественно
принять множество всех положений {оа, ас), при которых
расстояния р(а,а'), р(с,с') меньше данного s>0. Таким образом,
множество всех положений нашего механизма превращается в
топологическое пространство, которое обозначим через Р.
Докажем, что пространство Р гомеоморфно топологическому
произведению окружности 6м на двумерную сферу S2. В самом деле,
если нам дано определённое положение системы двух стержней оа
и ас, то дана точка а окружности S] ==z х2-{-у2 — 1 и точка сферы
£2 = л;2 4-]/24-г2= 1, в которой эту сферу пересекает луч, исхо-
дящий из точки о в направлении векюра ас. Обратно, каждая пара
точек p(zSx, p'(zS2 определяет положение ор первого стержня и то
положение второго стержня, которое получим, отложив от точки р
*) Тором называется поверхность, полученная от вращения
окружности вокруг оси, лежащей в плоскости этой окружности и не
пересекающей её (черт. 1).

§ 2]
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
35
вектор, равный вектору орг. Таким образом, установлено взаимно
однозначное и, как легко видеть, взаимно непрерывное соответствие
между пространством Р и топологическим произведением окружности
на двумерную сферу. Можно коротко сказать: Многообразие всех
положений механизма М1 есть топологическое произведение
окружности S1 на двумерную сферу S2.
3. Пусть теперь дан механизм Af2, состоящий из стержня
оадлиной 1, свободно вращающегося в пространстве вокруг точки о (на-
—*
чала координат), тогда как стержень ас скреплён в точке а со
стержнем ос так, что может свободно вращаться в плоскости,
проходящей через точку а перпендикулярно к прямой оа, т. е. в плоскости,
касательной к сфере S1 в точке а этой сферы.
Множество положений этого механизма снова естественно
превращается в топологическое пространство Q: чтобы получить
окрестность положения (оа, ас), надо взять все положения оа\ а'с\ при
которых точки а' и ог отстоят соответственно от а и с меньше, чем
на данное е>0. Рассуждения, при помощи которых мы установили
гомеоморфизм пространства Р (пример 2) с топологическим
произведением окружности на сферу, в наших условиях уже неприменимы
(читателю предоставляется убедиться в этом непосредственно).
Пространство Q не гомеоморфно произведению окружности на сферу.
Не доказывая эгого утверждения во всём его объёме, мы докажем, что
Q во всяком случае не разлагается в топологическое произведение
окружности и сферы тем естественным способом, которым мы разлагали на
множители пространство Р. Под этим мы имеем в виду следующее. Каждой
точке пространства Q, т. е. каждому положению (оа, ас) нашего механизма
соответствует вполне определённая точка а сферы S2. Докажем, что не су"
шествует никакого гомеоморфизма между пространством Q и
топологическим произведением [S1 X S2] окружности S1 на сферу S2 = х* + У2 + z~ = Ь
удовлетворяющего следующему условию: каждой точке q = (oat ас)
пространства Q соответствует точка (p,a)£[Sl X S2], где р — какая-нибудь
точка окружноста S1, а точка а определена условием q = (оа, ас).
Предполагая, что такой гомеоморфизм имеет место, рассмотрим множество Ф
всел точек (р0, р')£ [^Х^2]. гДе Ро — Раз навсегда выбранная точка
окружности Slf а р' пробегает всю сферу S2. Из наших предположений следует,
что каждой точке (р0, /?') 6 Ф^П^Х^2] соответствует некоторый вполне
определённый вектор V(p') длиной 1, исходящий из точки р' сферы S2
и лежащий в плоскости, касающейся этой сферы в точке р'. При этом век-
торы 55 (р') непрерывно зависят от точки р'. Мы, таким образом, получаем
на сфере S2 так называемое непрерывное поле касательных
векторов, нигде не обращающихся в нуль. Между тем, в главе 16 будет
Доказано, что таких непрерывных векторных полей на двумерной сфере не
существует (глава 16, теорема [5:510]).
4. Данная механическая система есть точка, способная двигаться
по данной окружности с произвольной скоростью. Каждое
состояние этой системы определяется двумя данными: положением данной
точки на окружности и скоростью её. Топологизируя множество

26 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. !
этих состояний естественным образом (близость положений и
близость скоростей), получим в качестве многообразия состояний
(«фазового пространства») произведение окружности на прямую, т. е.
бесконечный цилиндр.
5. Назовём двоеточием пространство, состоящее из двух
изолированных точек.
Произведение счётного числа двоеточий гомеоморфно канторову
совершенному множеству. Если т какое-нибудь кардинальное число,
то через DT обозначается весьма замечательное пространство —
произведение т двоеточий.
Произведение т пространств, каждое из которых гомеоморфно
замкнутому отрезку числовой прямой, также очень важно; оно
обозначается через i?T. Пространство /?^0) т. е. топологическое
произведение счётного числа замкнутых отрезков, гомеоморфно
гильбертову кирпичу*). (Читателю рекомендуется доказать последнее
утверждение.)
6. Назовём связным двоеточием пространство /?, состоящее из
двух точек а, Ь, со следующей топологией: в R имеется три и только три
замкнутых множества, а именно: пустое множество; множество, состоящее
из точки а; множество, состоящее из обеих точек а и Ъ.
Пусть т — произвольное кардинальное число. Произведение z
связных двоеточий называется пространством 1\.
Свойства пространств Fx интересны даже для конечных т.
§ 3. Связность.
3:1. Определение и основные теоремы.
Определение [3:1]. Топологическое пространство
называется связным, если его нельзя представить в виде соединения двух
непересекающихся, непустых замкнутых множеств.
Так как всякое множество, лежащее в данном топологическом
пространстве, само является топологическим пространством, то в
силу [2:16] понятие связности определено и для множеств, лежащих
в топологических пространствах.
Пример 1. Числовая прямая, а также открытый и замкнутый
отрезки связны**).
Докажем несколько теорем о связности.
Основная лемма [3:11]. Если А и В —- два
непересекающихся замкнутых множества топологического пространства R
и множество М^А U В связно, то оно содержится в одном из
множеств А или В.
В самом деле, в противном случае имели бы М — {М{\А)\}{М{\В),
где МПА и М(]В — непересекающиеся, непустые замкнутые в М
множества.
*) Арт. 2:3, пример 4.
**) См., например, Александро в-К о л м о г о р о в, Введение в
теорию функций действительного переменного, изд. 3-е (1938), стр. 97,
теорема XXII.

§ з]
связность
* 37
[3:12]. Если всякие две точки пространства R принадлежат
некоторому связному множеству М с: /?, то R связно.
Б самом деле, пусть
R=-AtUA2J
где Аг и Л2— непересекающиеся непустые замкнутые множества.
Берём точки рх £ А1У р2£ А2 и находим содержащее их связное
множество MczR.
В силу [3: 11] множество М содержится в одном из
множеств Аи Л2. Но тогда и обе точки pv p2 принадлежат к одному
из множеств Л15 Л2, что противоречит выбору этих точек.
Замечание 1. Из связности отрезка и из [3:12] следует, что всякое
выпуклое множество, в частности, пространство Rn связно.
[3 : 13]. Соединение двух связных множеств А и В, лежащих
в некотором топологическом пространстве R и имеющих
непустое пересечение, связно.
В самом деле, пусть A U В = С, А П В —D =}•0.
Если
с = с1ис2,
где С,,С2 — непересекающиеся замкнутые в С множества, -jo в силу
[3 :11], каждое из множеств Л, В содержится водном из двух
множеств Cj,C2. Пусть, например. ЛсзС( гдрповательно, А(]В^_Сп
а потому и B^CV т. е. С2 пусто, что и требовалось доказать.
Определение [3:14]. Конечная последовательность множеств
[3: 14] Л„ ..., Ая
называется цепью множеств (подробнее: цепью, связывающей
4j с Д.), если для любого/, 1 <'/<£— ], имеем Л ПЛ.н-i —:^-
Замечание 2. Если, кроме того, Ая f\ А\~£0, го цепь (3:14)
называйся з а м к н у той.
Система (любой мощности) множеств называется сцеплён-
к о й, если любые дра множества, являющиеся элементами этой
системы, могут быть связаны цепью, состоящей из некоторых
элементов той же системы.
Из [3: 13] следует:
|3 :14]. Соединение связных множеств, лежащих в некотором
типологическом пространстве R и образующих цепь, связно.
Из [3:14] и [3:12] вытекает далее:
[3:15]. Пусть в топологическом пространстве R дана сцеплен-
пая система связных множеств Аа; соединение всех множеств Аа
связно.
В частности:
[3:16]. Соединение любого числа связных множеств данного
т°пологического пространства R, имеющих попарно не пустое
пересечение, связно,

38
ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ
[гл.
I
Определение [3:17]. Связное открытое множество
топологического пространства R называется областью
пространства /?.
[3: 18]. Пусть в топологическом пространстве R дана
система ® непустых областей Га. Соединение Г всех областей Га £ ®
только тогда связно, когда ® есть сцепленная система.
Доказательство. В самом деле, пусть система ® не
сцеплена. Тогда существует две области Тг £ © и Г2£®, которые не
могут быть связаны никакой цепью элементов системы Ф>. Обозначим
через Г" соединение всех элементов системы О, могущих быть
связанными с Гг цепями элементов ®; через Г" обозначим соединение всех
остальных элементов системы ®. Множества Г"
и Г" являются непересекающимися непустыми
открытыми множествами, а их соединение есть Г;
отсюда следует, что Г не связно, что и
требовалось доказать.
[3 :19]. Если множество А, лежащее в
топологическом пространстве /?, связно и Л^В^Ау
то и В связно.
Доказательство. Пусть
h
Я.
£
в^вгив2,
где Вх и В9 не пересекаются и замкнуты в В.
Докажем, что одно из множеств Ви В% пусто.
Так как А связно, то А содержится в одном из
множеств BvB2f пусть в Вх. Но Вг замкнуто в В,
поэтому все принадлежащие к В точки
прикосновения множества Л, т. е. всё множество В,
содержится в В±\ значит, В2 пусто, что и требовалось
доказать.
Пример 2. Множество А состоит из всех
точек кривой у = sin— для 0<я<1. Так как
эта кривая гомеоморфна прямой, то А связно.
Присоединяя к А любое множество точек, лежа-
—-l^j/^l оси ординат (например, две точки
, получим связное множество В.
3:2. Компоненты. Пусть р — точка топологического
пространства /?. Так как множество, состоящее из одной точки р, связно,
то во всяком случае имеются связные множества, лежащие в R и
содержащие данную точку р. Соединение всех связных множеств,
содержащих данную точку р, связно в силу [3:16] и является
наибольшим связным множеством, лежащим в /? и содержащим точку/?;
оно называется компонентой точки р в /?. Из [3 :19] следует,
что компонента каждой точки р топологического пространства /?есть
Черт. 2.
щее
на отрезке
1 1
— О". ^ = "9

§ 4J АКСИОМЫ ОТДЕЛИМОСТИ. БИКОМПАКГНОСГЬ 39
замкнутое множество. Из [3 :13] следует, что компоненты двух точек р
и рг или тождественны или не пересекаются.
Итак,
[3:2]. Всякое топологическое пространство распадается
на компоненты своих точек.
Пример 3. Пусть Р — канторово совершенное множество,
лежащее на отрезке 0^x<;i оси абсцисс. Множество Q состоит
из всех точек (х, у) плоскости, удовлетворяющих условиям х£Р,
O^y^Cl. Множества Qx, каждое из которых состоит из точек
(х, y)(zQ> гДе х фиксировано, и 0<;^<С1 суть компоненты
множества Q. Множество этих компонент имеет мощность континуума.
Упражнение. Доказать, что непрерывный образ связного
топологического пространства есть связное топологическое пространство.
§ 4. Аксиомы отделимости. Бикомпактность *).
4 :1. Аксиомы отделимости. Множество MczR называется
одноточечным, если оно состоит лишь из одной точки.
[4:1]. Окрестностью множества Ж называется всякое
открытое множество, содержащее М.
[4:11]. Топологическое пространство называется
Го-пространством, если два различных одноточечных множества всегда имеют
в нём различные замыкания**).
Легко видеть, что это определение эквивалентно такому:
[4:11']. Пространство R называется ^-пространством, если при
произвольном выборе двух его точек хотя бы одна из этих
точек имеет окрестность, не содержащую другую точку.
[4:12]. Топологическое пространство называется
^-пространством, если все одноточечные его множества замкнуты.
Пли:
[4:12']. Пространство R есть ^-пространство, если при любом
выборе двух его точек, каждая из этих точек имеет окрест-
ность, не содержащую другую точку.
[4:13]. Топологическое пространство R называется Г2-п р о -
странствомилихаусдорфовым пространством, если для
любых двух различных его точек можно найти две непересекающиеся
их окрестности.
Теорема [4:131]. Пусть R есть Г0-, соответственно, Тг- или
^-пространство. Пусть ?(— система окрестностей топологического
пространства R. Тогда окрестности, упоминаемые в [4:11х],
соответственно в [4:12'] и [4:13], могут быть выбраны из окрестностей,
°бразующих систему 91.
*) См. Хаусдорф, Теория множеств, § 25—27. Дальнейшие
сведения по теории топологических пространств можно получить из моей
статьи <0 понятии пространства в топологии», «Успехи математических:
На)к», том II, вып. 1(17). В дальнейшем, эта статья цитируется как «Про-
( транство в топологии».
**) См. примеры, приведённые в конце этого артикула.

40 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
[4:14]. Хаусдорфово пространство называется нормальным,
если для любых двух его непересекающихся замкнутых множеств
можно найти непересекающиеся окрестности.
Этому определению можно дать и такую форму:
[4:141]. Хаусдорфово пространство R нормально, если при любом
выборе замкнутого множества Ac:R и окрестности О(А) множества А
можно найти окрестность 02(Л) множества Л, удовлетворяющую
условию 0,(^0 (А).
[4: 15]. Все метризуемые пространства нормальны.
[4:16]. Пространство со счётной базой тогда а только тогда
метризуемо, когда оно нормально (П. С. Урысон).
Доказательство теоремы [4:16] опирается на теорему [4:21]
(см. ниже)*).
Примеры. 1. Пространство R состоит из двух точек;
замкнуты в R только: всё R и пустое множество. R не есть
7"0-пространство.
2. Связное двоеточие (арт. 2:6, пример 6) есть
^-пространство, не являющееся ^-пространством. Пространство F~ (арт. 2 :6)
при любом т также есть Г0-пространство, но не ^-пространство;
пространство /\. облагает следующим свойством универсальности:
оно содержит топологический образ всякого Т0-
пространства веса ^ т (см. опред. [2: 251]) **). Обратно, всякое
подмножество пространства ^т ее ib Г0-пространство веса ^т.
Конечные Г0-пространства являются важнейшим частным случаем так
называемых дискретных пространств (см. § 6); среди них
интересны лишь те, которые не являются ^-пространствами (так как все
конечные ^-пространства состоят из изолированных точек).
3. Возьмём отрезок 0<^х<4 с его обычной топологией и
присоединим к нему некоторую новую точку £. В качестве
окрестностей к точке £ возьмём любое мно.-кс. гво, состоящее из точки ; и
из всех, кроме произвольного конечного числа, точек отрезка Q^v^l.
Полученное топологическое пространство есть ^-пространство, но
не Г2-пространство.
4. Пространства Dz и R. при т>К0 могут служить примерами
неметризуемых нормальных пространств; всякое нормальное
пространство веса <^Ч гомеоморфно некоторому подмножеству
пространства/?„ (теорема А. Н. Тихонова) ***), все подмножества пространства
/?_ суть Г2-пространства веса ^т, но не все они нормальны.
4:2****). Теоремы о непрерывных функциях в нормальных
пространствах.
[4:21] (Урысон). Для того чтобы хаусдорфово пространство R
было нормальным, необходимо и достаточно, чтобы ко всяким
*) Хаусдорф, Теория множеств, § 25, арт. 3.
**) См. «Пространство в топологии», § 5, теор. 2.
* *) См. «Пространство в топологии», § 3.
:- :*i:) См. «Пространство в топологии». § 3.

С 4] АКСИОМЫ ОТДЕЛИМОСТИ. БИКОМПАКТ'НОСТЬ 41
двум непересекающимся непустым замкнутым множествам А0 и
/L пространства R можно было бы найти непрерывную во всём
пространстве R действительную функцию f(x), удовлетворяющую
Оля всех x£R неравенству 0^f(x)^l и принимающую во всех
мочках множества А0 значение 0, а во всех точках множества Ах
значение 1.
[4:22] (Брауэр-Урысон). Всякую непрерывную функцию /(*),
определённую на некотором замкнутом мноон естве А нормального
пространства R, можно продолжить на всё пространство R (т. е.
можно построить непрерывную во всём пространстве R
действительную функцию Fix), совпадающую ка А с функцией f(x).
Следствие. Так как задать непрерывное отображение
пространства R в «-мерное эвклидово пространство Rn, значит задать
систему п действительных функций #* ==/г-(я), x£R (где xv...,xn—
координаты в Rn), то из [4:22] следует:
[4 : 23]. Всякое непрерывное отображение / замкнутого множества А
нормального пространства R в я-мерное эвклидово пространство Rn
можно распространить на всё пространство R.
4:3. Бикомпактность.
Определение [4:31]. Топологическое пространство R
называется бикомпактным, если из всякого покрытия пространстваR
открытыми множествами можно выделить конечное число элементов,
также образующих покрытие пространства R.
Хаусдорфово бикомпактное пространство называется
бикомпактом. Метризуемое бикомпактное пространство назыгается
компактом. Очевидно, компакты являются частным случаем
бикомпактов.
[4:32]. Метризуемое пространство тогда и только тогда
п-\:чптся компактом, когда во всякой последовательности его
v »7r:v содержится сходящаяся подпоследовательность.
И • 33]. Среди множеств, лежащих в эвклидовом пространстве,
компактами являются все замкнутые и ограниченные множестваt
■v только эти множества.
[4:34]. Всякое замкнутее множество бикомпакта (соответст-
ппчнп, компакта) само есть бикомпакт (соответственно компакт).
[4:35]. Если бикомпакт Ф является множеством, лежащим
в хаусдорфовом пространстве /?, то Ф есть замкнутое множество
пространства R.
4 : 4. Дальнейшие теоремы о бикомпактах. Метризационные теоремы
и "еоремы включения.
[к 41]. Все бикомпакты суть нормальные пространства.
\А -.42]. Для того, чтобы бикомпакт был компактом, т. е. был мет-
Ри^-'ем, необходимо и достаточно, чтобы он обладал счётной базой
Прыгай).
14:43]. Топологическое произведение любого конечного или бесконеч-
fl(>zo чипа бикомпактом есть бикомпакт (Тихонов).
[4:431]. Топологическое произведение конечного или счетного числа
компактов есть компакт-

42 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
[4:44]. (Александров). Среди хлусдорфовых пространств шее
компакты и только они являются непрерывными образами канторова
совершенного множества *).
[4:45] (Александров**). Среди хаусдорфовых пространств все
бикомпакты веса </с и только они являются непрерывными образами замкну-
тых множеств пространства Z)T.
Замечание. Этот результат не может быть-улучшен: имеются при
всяком несчётном т бикомпакты веса т, не являющиеся непрерывным
образом всего пространства Dx (примером такого бикомпакта может служить
множество всех порядковых чисел <>т, где окрестностью данного числа
является всякий содержащий его порядковый интервал; а)т есть наименьшее
порядковое число мощности т).
4:5. Непрерывные отображения бикомпактов.
[4:5]. Всякое хаусдорфово пространство, являющееся
непрерывным образом бикомпакта, есть бикомпакт***).
[4:511]. Всякое метрическое пространство, являющееся
непрерывным образом бикомпакта (в частности, компакта), есть
компакт.
Замечание. Несколько труднее доказать, что всякое хаусдорфово
пространство, являющееся непрерывным образом компакта, есть компакт ****).
Следовательно:
[4:52]. Взаимно однозначное ив одну сторону непрерывное
отображение бикомпакта X на хаусдорфово пространство Уесть
топологическое отображение.
[4: 53]. Всякое непрерывное отображение компакта X на ком»
пакт У равномерно непрерывно*****) (т. е. ко всякому г>0 можно
подобрать такое 8>0, что из х£Х, х'£Х, р(х,х')<Ъ следует
Р(од,а*')<в).
§ 5. Непрерывные разложения компактов и их связь
с непрерывными отображениями («склеивания»).
Локально-бикомпактные пространства. Топологические
многообразия. Примеры.
5:1. Непрерывные разложения. Пространство данного
разложения******). Каждое непрерывное отображение С компакта X
на компакт У порождает разложение & компакта X на попарно
непересекающиеся замкнутые множества — на прообразы С"1 (у) точек у£У.
Это разложение обладает следующим свойством:
[5 :11]. Если A0£QL есть элемент разложения © и Г есть
произвольно выбранная окрестность множества Л0в пространстве X,
*) Хаусдорф, Теория множеств, стр. 175, теорема XI.
**) См. «Пространство в топологии», § 5.
***) Хаусдорф, Теория множеств, стр. 147, теорема XVI.
****) См. Ал е кс ан д ро в-Hopf, Topologie, I, стр. 98, теорема IX.
#****) Хаус до рф, Теория множеств, стр. 149, теорема XIX.
******) Александров, Stetige Abbildungen kompakter Raume, Math.
Annalen, 96(1926), стр. 555—573; Александров-Нор f, Topologie, I,
гл. 1, § 5 и гл. 2, § 2 (теория построена для любых бикомпактов).

§ 5] НЕПРЕРЫВНЫЕ РАЗЛОЖЕНИЯ КОМПАКТОВ 43
то существует такая окрестность Тха Г множества А0 в X,
что всякое множество Л£&, пересекающееся с Гх, лежит в Г.
В самом деле, пусть Л0 = С-1(у0) и условие [5:11] не выполнено
(считаем компакт X определённым образом метризованным). Тогда
имеем последовательность множеств
обладающих следующими свойствами:
1. Существует точка х'п£Ап, находящаяся от А0 на расстоя-
. 1
НИИ < — .
п
2. Существует точка х"п£Ат находящаяся от А0 на расстоянии
большем, чем некоторое постоянное s > 0. Без ограничения общности
можем предположить, что обе последовательности 1х'\ и [х"\
сходятся: lim х'п = хг £ А0, lim х"п = х" £ Х\А0% причём из х"£Х\А0
следует, что С(х!')фу0. Так как отображение С непрерывно, то
уп=С(х'п) сходится к С(хг) — С(А0)—у0; но так как x"n£Aw то
С(х'п) = уп, и в силу непрерывности С
limyn = lim С (х'п) = С(х") фу0.
Этим противоречием наше предложение доказано.
Определение [5:12]. Разложение компакта X на попарно
непересекающиеся замкнутые множества А называется непрерыв-
ным, если оно обладает свойством [5:11].
[5:13]. Всякое разложение S компакта X на попарно
непересекающиеся замкнутые множества А порождает следующим образом
некоторое топологическое пространство F, называемое
пространством данного разложения: множества А суть по
определению точки пространства К; окрестности точки А0 £ Y определяются
так: берётся какая-нибудь окрестность Г множества А0 в пространстве Х\
соответствующая окрестность £/г (A0) точки А0 в пространстве Y
по определению состоит из всех А £ F, удовлетворяющих в X
условию ЛсГ.
Легко проверить, что определённые таким образом окрестности
в Y удовлетворяют условиям теоремы [2:21], так что Y есть
топологическое пространство. Более того, из нормальности компакта X
следует, что Y есть хаусдорфово пространство.
Далее:
[5 :14]. Если разложение S непрерывно, то ставя в соответствие
каждой точке х£Х содержащее эту точку множество А £ Г,
получим непрерывное отображение С пространства X на
пространство Y.
В самом деле, пусть х£А0£Х, значит, С(х) = А0) пусть дана
окрестность (L (А0) точки А0 £ Y; для порождающей окрестность
Ur(A0) окрестности Г множества А0 в X определяем окрестность Тг
множества А0 в смысле [5:11]. Тогда Гг есть окрестность точки #

44 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
в X, и образ окрестности Тг при отображении С лежит в заданной
окрестности Ur(A0) точки Л0= С(х)£ У. Непрерывность отображения
этим доказана (критерий Коши [2:42]!).
Так как хаусдорфово пространство, являющееся непрерывным
образом компакта, само есть компакт *), то
[5:15]. Пространство, порождённое непрерывным разложением
данного компакта X, есть компакт, являющийся непрерывным
образом компакта X.
Замечание. Если компакт У является пространством
непрерывного разложения & компакта X или гомеоморфен этому
пространству, то говорят, что компакт У
возник путём идентификации
(отождествления) некоторых точек
ф*0 компакта X: именно, все точки
какого-либо из множеств А £ &
отождествляются между собою
и порождают таким
образом точку пространства У.
Это отождествление в случае, когда
все А суть конечные множества, часто называют
склеиванием.
5:2. Примеры непрерывных разложений и склеиваний.
Проективное пространство п измерений.
1. Пусть X есть двумерная сфера с определённой на ней
системой географических координат. Элементами непрерывного разложения
являются: а) пара полюсов данной системы
координат; б) «параллельные круги»
(окружности) этой системы. Пространство этого
разложения, очевидно, гомеоморфио
окружности.
2. Пусть X—тор; рассмотрим
непрерывное разложение тора на его меридианы & ~ с (см.
черт. 3, на котором вычерчен меридиан Ь = 0>.
Пространство этого разложения также
гомеоморфио окружности.
3. Вообще, если Z есть топологическое про- Черт. 4.
изведение компактов X и К, то множества Аю
состоящие из всех точек (хщ y)£Z, где у £ У фиксировано, а л:
пробегает всё пространство X, являются элементами непрерывного
разложения пространства Z; пространство этого разложения гомеоморфио У.
4. Изображённое на черт. 4 непрерывное разложение круга
(окружность вместе с обоими взаимно перпендикулярными диаметрами
образует один элемент разложения) обозначим через (L Пространство
эгого разложения гомеоморфио компакту, состоящему из четырёх
замкнутых прямолинейных отрезков с одним общим концом,
*) См. замечание в арт, 4:5,

§ 5j
НЕПРЕРЫВНЫЕ РАЗЛОЖЕНИЯ КОМПАКТОВ
45
5. Пусть X есть квадрат 0<[#^1, О^^^С1 плоскости (х, у).
Непрерывное разложение 6 квадрата X имеет своими элементами:
а) отдельные внутренние точки квадрата; б) пары точек {(*, 0),
(х, 1)} при 0<*<1; в) пары точек {(0, у\ (1, з01 при 0<.у<1;
г) четвёрку точек {(0, 0), (0, 1), (1, 0), (1, 1)}. Пространство этого
разложения гомеоморфно тору. Короче говорят: тор получается
склеиванием соответствующих друг другу точен:
противоположных сторон квадрата (черт. 5).
6. В аналогичном смысле говорят: склеивая между собой
соответствующие точки каждой пары противоположных граней куба,
получаем трёхмерный тор
(топологическое произведение трёх окружностей).
7. Пусть Q3 — замыкание области
трёхмерного пространства, лежащей между двумя
концентрическими сферами £2 и s2. Склеивая
между собою соответствующие (т. е.
расположенные на одном и том же луче,
выходящем из центра) точки обеих сфер,
получим топологическое
произведение двумерной сферы на
окружность.
Это склеивание можно представить себе
зом (черт. б).
Разрежем экваториальной плоскостью тело Q3 на два конгруент-
ных тела Ql и Q%. При этом каждая из сфер S2 и s2 разрезается
на две полусферы: северную С2, с2 и
южную /О'2, ю'К Экваториальные
окружности обеих сфер S2 и $2 обозначим
через S' и sr.
Тело Qc можно рассматривать как
деформированный цилиндр с
основаниями С2 и с1 и боковой поверхностью
П'2~Пс в виде плоского кольца,
заштрихованного на чертеже.
Тело Qw также есть цилиндр с
боковой поверхностью П2 = П£> и с
основаниями /О2 и /о2.
В каждом из тел Qc и QJW надлежит произвести склеивание
соответствующих точек верхнего и нижнего оснований; это склеивание
"ревращает оба тела в два трёхмерных кольца *). После этого
остаётся только упразднить сделанный экваториальный разрез, т. е.
отождествить между собою соответствующие точки обоих торов
и IlL
Черт. 5.
ещё и следующим обра-
д*
гором.
) Под трёхмернмм кольцом понимаем (замкнутое) тело, ограниченное

46 ОЁЗОР СВОЛСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [гл. I
Итак, топологическое произведение сферы на окружность
получается «удвоением» трёхмерного кольца, т. е. склеиванием
соответствующих точек границ двух конгруентных трёхмерных колец.
Замечание. Легко и непосредственно убедиться в том, что
пространство, получающееся в результате «удвоения» трёхмерного
кольца, есть топологическое произведение двумерной сферы на
окружность.
Упражнение. Доказать, что трёхмерный тор получается из
области, заключённой между двумя соосными торами (черт. 7)
склеиванием соответствующих точек обоих ограничивающих торов.
8. Проективные пространства, я-мерное проективное
пространство Рп определяется следующим образом. Точками я-мерного
проективного пространства являются
отношения *) всевозможных
последовательностей из (п -)-1)
действительных чисел
х = (х0 : Х1 : • • • : хп)>
среди которых, по крайней мере, одно
отлично от нуля.
Окрестности точки а=(а0 :аг:... :ап)
определяем так. Берём в отношении
(а0 : а1: . .. : ап) числа а0, . . ., ап так, чтобы al -|- . . . -J- #n = 1 >
и берём все такие последовательности х = (х0: хг: . .. : хп\ что
Соответствующие таким последовательностям точки проективного
пространства и образуют по определению окрестность Ов(а) точки а.
Это определение позволяет построить несколько моделей про-
*) Пусть даны две последовательности из л+1 действительных чисел
причём в каждой из них имеются числа, отличные от нуля. Эти
последовательности называются пропорциональными между собою или
определяющими одно и то же отношение, если для любых
двух нумеров /, k = О, 1,.,., п имеем
х<Ук = хкУи
Легко видеть, что пропорциональность числовых последовательностей
(состоящих из одного и того же числа элементов) удовлетворяет условиям
рефлексивности, симметрии и транзитивности. Поэтому множество всех
последовательностей вида х09...,хп (п фиксировано, среди х± имеются
отличные от нуля) распадается на классы пропорциональных между собою
последовательностей. Эти классы называются отношениями (а именно,
отношением каждой входящей в класс последовательности чисел).
Отношение последовательности х0,..., хп обозначается через (х0: х±\...: хп).
Последовательность, состоящая из одних нулей, отношения не имеет. Если
дано отношение (х0: aj :...: хп), то всегда в нём можно выбрать числа
л-и,..., хп так, чтобы х\+ ... +х\= 1.

§ 5)
НЕПРЕРЫВНЫЕ РАЗЛОЖЕНИЯ КОМПАКТОВ
47
ективного пространства. Так, например, можно каждой точке
(x0'-Xi: ---:xn)£Pn поставить в соответствие прямую (#-|-1)-мер-
н0го эвклидова пространства /?w + 1 (£0 ;.. .; Ьп), проходящую через
начало координат и определяемую уравнениями
-i^- = — = -~- ^п
Xq Xi Хп
/^.— текущие координаты).
Читателю предоставляется доказать, что если за расстояние между
двумя прямыми принять угол ср между ними, 0^ср<--, то
множество этих прямых превращается в метрическое пространство и
установленное нами соответствие между этим метрическим пространством
и пространством Рп будет топологическим.
Таким образом, мы построили геометрическую модель
проективного пространства, в которой точками являются прямые, проходящие
через начало координат. Возьмём теперь в /?n+1 произвольную, не
проходящую через начало координат ^-мерную плоскость Rn, и в
качестве представителя каждой прямой (проходящей через
начало) рассмотрим точку её пересечения с плоскостью Rn. Это даёт
обычную интерпретацию проективного пространства как
эвклидова пространства, пополненного бесконечно, удалёнными
элементами.
Другую модель получим, если в качестве представителя каждой
прямой будем рассматривать пару точек её пересечения с единичной
сферой в Rni{:
g-f *;+...+£=!
«это соответствует выбору в каждом отношении (х0: xt: . . . : хп)
последовательности дг0,. . . ,хп, удовлетворяющей условию л*о-(- . . .-\-x\i = 1).
Отсюда видно, что «-мерное проективное пространство возникает
ил и-мерюй сферы У при склеивании между собой диаметрально-
противоположных точек этой сферы.
Разобьём нашу сферу EJ -|~ • • • + 4i = 1 экваториальной
плоскостью £Л = 0 на две полусферы ;„>0 и Еп<0. К ^северной»
полусфере ^>0 присоединим экватор £и = О, Й + • . • г Ея = 1;
полученный компакт g + • • • Н~ *п == * > 5/г < 0 обозначим
через Q\
Каждая пара диаметрально противоположных точек 5й, не
лежащих на экваторе 5й"1, имеет своего (и притом единственного)
представителя в Qn, так что склеивать между собой надо будет только
Диаметрально противоположные точки экватора. Итак, для
получения n-мерного проективного пространства достаточно взять одну
п°лусферу n-мерной сферы У\ присоединить к ней экватор Sn~1
11 произвести склеивание диаметрально противоположных точек

48 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [-71. I
экватора. Так как компакт Qn гомеоморфен n-мерному шару, то
n-мерное проективное пространство получается из n-мерного
замкнутого шара склеиванием диаметрально противоположных
точек его границы,
5:3. Локально-бикомпактные пространства. Топологические
многообразия. Примеры. Топологическое пространство называется
локально-бикомпактным, если каждая точка этого
пространства имеет окрестность, замыкание которой представляет собою
бикомпакт.
Например, я-мерное эвклидово пространство локально-бикомпяктно
(не будучи, очевидно, бикомпактным).
Связное локально-бикомпактное пространство со счётной базой,
каждая точка которого имеет окрестность, гомеоморфную п-мерному
эвклидову пространству, называется я-мерным
топологическим многообразием. Многообразие называется замкнутым,
если оно бикомпактно; небикомпактные топологические
многообразия называются открытыми.
Примеры замкнутых топологических
многообразий.
1. л-мерная сфера (см. арт. 2:3, пример 2).
2. я-мерный тор, т. е. топологическое произведение п
окружностей; вообще,
топологическое произведение любого конечного числа
замкнутых топологических многообразий есть замкнутое
топологическое многообразие (в частности, топологическое произведение
сфер любых размерностей есть замкнутое топологическое
многообразие).
3*). Рассмотрим шестёрки действительных чисел
/?12,Pl3, PlU P<U, P±li Pj>3,
которые не все равны нулю и связаны между собою соотношением
(5 131) /?12P3i + Pl3J042+PuP23 = O.
Каждая тамая шестёрка определяет некоторую прямую в трёхмерном
проективном пространстве **), плюккеровыми координатами ***)
*) См. Б о х е р, Введение в высш)ю алгебру, гл. 7, § 35.
**) Если, например, р12ф0, то прямою, проходящую через точки
Ф'• Р12-Pis''Pit) И (— /?12:0:/723^24).
***) Если прямая проходит через точки (л^: х*: хь :х4) и (У\'.Уч'.уз'.у^),
то её плюккеровы координаты (определённые с точностью до
пропорциональности) суть Pij = yfy?" » отсюда и обозначение р^. Тогда детерминант,
имеющий первой и третьей строками хъхъхъх^Л а второй и четвёртой
строками уь у*, .Уз» Уь очевидно, равен нулю; это равенство и выражается
соотношением (5:31;.

§ 5] НЕПРЕРЫВНЫЕ РАЗЛОЖЕНИЯ КОМПАКТОВ 49
которой являются шесть чисел р^\ при этом две шестёрки
определяют одну и ту же прямую тогда и только тогда, когда они
пропорциональны между собою.
Обратно, каждая прямая определяет однозначно класс
пропорциональных между собою шестёрок. Таким образом, прямые трёхмерного
проективного пространства взаимно однозначно соответствуют
отношениям шестёрок действительных чисел, удовлетворяющих
условию (5 :31).
Окрестности в пространстве прямых определяются аналогично
тому, как мы определяли окрестности в проективном пространстве:
пусть прямая определена отношением (Р°12*-Р°1Ъ: р°и :Р1±:Р%:Р1з)-
Выбираем среди пропорциональных между собою шестёрок, определяющих
данное отношение (р\2"-р\ъ :Ри:Р°и :Р% :^2з) некотоРУю «нормальную
шестёрку» р\%у p\v p°w p°3V p%, р%,
удовлетворяющую условию (pj2)2+ • •. + (Р23)2 = 1- После
этого рассматриваем все шестёрки р12, /?i3, Pu, /?34,
/>42. рж> удовлетворяющие условиям: р\г-)-...-}-
+ /4=1 и \Р\г~Рм1<в» — »lPSs—^23 К s-
Соответствующие прямые (р12 :pis:pu.pu-p*i'-p2s)
и образуют s-окрестность данной прямой
(P°i2 :Р% : Ри :Ри :Р°42: PlJ- Эта топология
превращает множество всех прямых в четырёхмерное
замкнутое многообразие.
Рассмотрим теперь пятимерное проективное
пространство Р5. Точки его суть отношения
{X} :лг2 \ х§\х±\х^\Хь).
Гиперповерхность второго порядка, определяемая в Ръ уравнением
Х\х1 "Т" Х2^6 I -^З-^б === ^>
очевидно, гомеоморфна четырёхмерному многообразию всех прямых
трёхмерного проективного пространства.
Замечание. Всякая область (связное открытое множество)
донного я-мерного замкнутого многообразия может служить
примером открытого я-мерного многообразия. Однако, далеко не всякое
открытое многообразие гомеоморфно области замкнутого: открытое
двумерное многообразие, изображённое на черт. 8, не гомеоморфно
никакому подмножеству какого бы то ни было замкнутого
двумерного многообразия.
Общее замечание по поводу понятия
многообразия. Лишь в главе 5 будет доказана следующая основная
теорема:
Одно а то же топологическое пространство не может быть
при различных пит одновременно n-мерным и т-мерным многооб*
разием.
4 Ачександров П. С.

50 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. 1
§ 6. Частично упорядоченные множества и дискретные
пространства *).
6:1. Определения.
Определение [6:11]. Множество 9, состоящее из элементов
какой угодно природы, называется частично упорядоченным,
если в нём установлено отношение порядка, т. е. дано
правило, позволяющее для некоторых пар его элементов сказать, что
один из двух данных элементов следует за другим (или подчиняет
себе другой). При этом указанное отношение порядка должно
удовлетворять следующим условиям (аксиомам порядка): .
1. Если Ъ следует за а, то а не следует за Ь.
2. Если Ъ следует за. а и с следует за 6, то с следует за а.
Определение [6:12]. Если для любых двух различных
элементов а и Ь частично упорядоченного множества в либо а следует
за Ь, либо b следует за а> то частично упорядоченное множество 6
называется упорядоченным.
Замечание 1. Если b следует за а, то говорят также, что а
предшествует b (или а подчинено Ь) и пишут Ь^>а или а<6.
Замечание 2. Первая аксиома порядка утверждает, что
отношения а<СЬ и а>6 исключают друг друга. Отсюда, в частности,
следует, что никогда не может быть а>а, так как тогда мы имели
бы одновременно а># и я<а.
Определение [6:13]. Взаимно однозначное отображение /
частично упорядоченного множества Qt на частично упорядоченное
множество 62 называется отображением (или соответствием)
подобия, если при отображении / сохраняется отношение порядка,
т. е. если условие
№>f(p') в е2
выполняется тогда и только тогда, когда выполняется условие /?>р'
в 6Г Два частично упорядоченных множества Oj и в2 называются
подобными между собою, если между ними возможно установить
соответствие подобия.
6:2. Примеры частично упорядоченных множеств.
1. Любое множество симплексов или вообще
выпуклых многогранников **) является частично
упорядоченным, если считать, что многогранник Т2 следует за многогранником
7\, Т2>7\, коль скоро Т1 есть собственная грань многогранника 72.
Это отношение порядка в множестве выпуклых многогранников
называется геометрическим.
2. Множество, состоящее из точек, прямых и плоскостей данного
эвклидова пространства, частично упорядочено, если считать, что точка
подчинена прямой, если она лежит на этой прямой, а прямая подчинена плоскости^
если она лежит в этой плоскости. |
*) Александров, Diskrete Raume, Математический сборник, 2 (1937>|
«Пространство в топологии», § 6. 1
**) См. прибавление 2, § 3. ]

§ 6]
ЧАСТИЧНО УПОРЯДОЧЕННЫЕ МНОЖЕСТВА
51
3. Множество в, состоящее из действительных функций, определённых
на некотором точечном множестве X, частично упорядочено, если положить
/1>Л» коль СК0Р° Л(Х)>МХ) Д^я любого х£Хн /i(a)>/2(*) хотя бы для
одного х£Х.
Следующий пример частично упорядоченных множеств является
в известном смысле основным:
4. Частично упорядоченное множество
подмножеств каког о-л ибо множества М. Пусть дано множество в,
элементами которого являются некоторые подмножества А% данного
множества М:
Для двух каких-нибудь элементов Ла и А$ множества 0 полагаем
Ла>Ло, если А$ есть собственное подмножество множества Ла, т. е.
если ЛазЛр. Введённое таким образом отношение порядка называется
естественным отношением порядка в данном множестве
множеств в; это отношение порядка превращает, очевидно, множество
в в частично упорядоченное множество.
5. Если М состоит из п -f-1 элементов, то множество всех
непустых подмножеств множества М, с естественным отношением
порядка в нём, подобно множеству всех граней /2-мерного
симплекса с геометрическим отношением порядка в нём.
6:3. Множества А&р и 0®р. Пусть В есть частично
упорядоченное множество и /; £ 0 — элемент этого множества.
Через А&Р обозначим множество всех элементов х £ 0,
удовлетворяющих условию х^р.
Множество А@р называется комбинаторным замыканием
элемента р в частично упорядоченном множестве 0. Из этого
определения следует, что всегда р £ Л@р.
Через 0&р обозначим множество всех элементов #£0,
удовлетворяющих условию х^р. Множество 0%р называется звездой
элемента р в частично упорядоченном множестве 0. Из этого
определения следует, что всегда р £ 0%р.
Примеры L Пусть 0 — частично упорядоченное множество всех
точек, прямых и плоскостей трёхмерного пространства. Если р есть точка в,
То А<$Р состоит из одной только точки р; если р есть прямая, то Аер есть
множество, элементами которого являются прямая р и все точки, лежащие
на эюй прямой; если р есть плоскость, то AQp есть множество, элементами
которого являются: плоскость р% все прямые и все точки, лежащие в
плоскости Р- Аналогичным образом, множество 0$р имеет своими элементами:
если р есть точка — точку р и все проходящие через эту точку прямые
и плоскости;
если р есть прямая —прямую р и все плоскости, проходящие через
ЭтУ прямую;
если р есть плоскость — одну только плоскость р.
2. Пусть 0 есть частично упорядоченное множество
треугольников, их сторон и вершин, изображённое на черт. 9* Если р £ 0, то
%Р состоит из всех симплексов, имеющих р своей собственной
4*

52 обзор свойств топологических пространств [гл. i
или несобственной гранью. Например, в случае, изображённом на
черт. 9, имеем:
если р есть треугольник, то 0%р состоит из единственного
элемента р, А&р состоит из треугольника р, его сторон и вершин;
если р есть отрезок, то 0®р состоит из этого отрезка и из
треугольников, имеющих р своей стороной (таких треугольников на
нашем чертеже имеется один, два или четыре), А@р состоит из
отрезка р и его концов;
если р есть вершина, то 0©р состоит из треугольников,
имеющих р своей вершиной, и сторон, имеющих р своим концом; А%р
состоит из одной этой вершины.
Теорема [6:3]. Всякие частично упорядоченное множество
0 подобно множеству 51 подмножеств А@р с естественным
отношением порядка в нём.
Доказательство предоставляется читателю в качестве лёгкого
упражнения.
6:4. Двойственность частично упорядоченных множеств. Пусть
дано частично упорядоченное множество в. Можно составить
частично упорядоченное множество 0' из тех же
элементов, из которых состоит 0, но с обратным
отношением порядка: именно, будем в 0' считать
а < Ь, если в 0 имеем а > Ь. Частично
упорядоченное множество 0/ называется
двойственным к частично упорядоченному
множеству 0. Отношение двойственности, очевидно,
Черт. 9. взаимно: если 0' двойственно к 0, то 0
двойственно к 0''.
Замыкания элементов в 0' совпадают со звёздами элементов
в 0 и обратно: А^р = 0@р, 0^р = А@р.
Мы видели, что всякое частично упорядоченное множество подобно
множеству замыканий своих элементов с естественным отношением
порядка. Поэтому частично упорядоченное множество 0', двойственное
к 0, подобно множеству звёзд элементов 0, также с естественным
отношением порядка.
Примеры 1. Пусть 0 состоит из граней, рёбер и вершин куба
с геометрическим отношением порядка. Двойственное частично
упорядоченное множество 0' подобно множеству граней, рёбер и
вершин октаэдра, также с геометрическим отношением порядка.
2. Частично упорядоченное множество, состоящее из всех
собственных граней я-мерного симплекса с геометрическим отношением
порядка, подобно своему двойственному частично упорядоченному
множеству. Для осуществления соответствия надо каждой грани
симплекса отнести противолежащую ей в этом симплексе грань.
3. Пусть трёхмерное пространство разбито на конгруентные
кубы со стороной 1 и с целочисленными координатами вершин. 0
состоит из всех этих кубов, их граней, рёбер и вершин с геометри-.
ческим отношением порядка. Двойственное к 0 частично упорядочен-

§ 6]
ЧАСТИЧНО УПОРЯДОЧЕННЫЕ МНОЖЕСТВА
53
ное множество подобно самому в. Для осуществления соответствия
подобия надо сдвинуть всю систему кубов на вектор с компонентами
(~~> "9"' Т/ и отнести каждому элементу р' сдвинутой системы
элемент р старой системы, имеющий с р' общий центр.
6:5. Дискретные пространства.
Определение [6:51]. Г0-пространство называется
дискретным пространством, если в нём сумма любого числа
замкнутых множеств есть замкнутое множество (или, что то же самое, если
в нём пересечение любого числа открытых множеств есть
открытое множество).
Теорема [6:52]. Назовём подмножество А частично
упорядоченного множества 0 замкнутым, если из р£А, р'<.р
следует р'£А.
Эта топология превращает 0 в дискретное пространство R =
=/(0). Обратно, всякое дискретное пространство R может быть
превращено в частично упорядоченное множество 0 = ?(/?), если
положить для двух элементов, p£R и р/£/?, рфр\
Р'<Р,
коль скоро J
р'£р,
при этом
Я?(Д)) = Я,
?(Дв)) = е.
Доказательство состоит в автоматической проверке аксиом
дискретного пространства и, соответственно, частично упорядоченного
множества и может быть предоставлено читателю.
В силу теоремы [6 :52] частично упорядоченные множества
могут быть отождествляемы с дискретными пространствами. При этом
комбинаторное замыкание элемента р£0 совпадает с замыканием
в пространстве /(0) множества, состоящего из единственной точки р,
а звезда элемента /?£ 0 есть минимальная окрестность точки р в/(0),
т. е. пересечение всех открытых множеств пространства /(0),
содержащих точку р.
Переход от данного частично упорядоченного множества 0 к
двойственному 0' соответствует переходу от данного дискретного
пространства R к двойственному дискретному пространству R\
замкнутые множества которого суть открытые множества пространства R
(и наоборот).
Подобное отображение одного частично упорядоченного
множества на другое есть не что иное, как топологическое
отображение соответствующих дискретных пространств.
Удобство, происходящее от этого отождествления частично
упорядоченного множества с дискретным пространством, заключается
г,режде всего в возможности перенесения на частично
упорядочение множества различных теорем, доказанных о топологических
пространствах, например, шс«х теорем о связности.

54 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
§ 7. Полные метрические пространства и компакты*).
7:1. Определение и простейшие свойства полных
метрических пространств.
[7:11]. Последоввательностъ точек
метрического пространства R называется фундаментальной по*
следовательностью, если ко всякому s>0 можно подобрать
такое натуральное число п„ что для любых р^п„ q^*n6 имеем
Р(хр> xq)<s.
Очевидно, всякая сходящаяся последовательность является
фундаментальной.
[7:12]. Метрическое пространство называется полным, если
всякая его фундаментальная последовательность является
сходящейся.
Из свойств полных метрических пространств отметим следующие
два:
[7:13]. В полном метрическом пространстве R всякая
последовательность убывающих замкнутых множеств
диаметры которых стремятся к нулю, имеет пересечение,
состоящее из одной точки.
В самом деле, так как диаметры множеств Ап стремятся к нулю,
то П Ап не может содержать двух точек; беря йп£Ап, получаем
фундаментальную последовательность {ап}, предельная точка которой
содержится в ПАп.
[7: 14]. Если каждое из открытых множеств Гь Г2,.. . Гп,. ..
полного метрического пространства R плотно в /?, то их
пересечение Е = П Гп также плотно в R.
Доказательство теоремы [7:14] опирается на лемму:
Лемма. Если открытое множество Г метрического
пространства R плотно в R, то в любом открытом множестве Г0<=/?
содержится открытое множество Г/ (произвольно малого диаметра),
замыкание которого лежит в Г0ПГ.
В самом деле, так как Г плотно в /?, то в Г0 содержится точка
р множества Г; так как А = (Я\Г0) U (R\V)) = #\(Г П Г0)
замкнуто, то р(р, Л)>0.
Пусть положительное число е произвольно мало и во всяком
случае меньше р (/?, А). Положим Г/ = 0(р, а). Все точки множества Г'
отстоят от р не более, чем на е, и поэтому лежат в ГПГ0. Этим
лемма доказана.
i Докажем теперь теорему [7:14]. Для этого достаточно в любом
открытом множестве Г cz R найти точку множества Е.
*) Хаусдорф, Теория множеств, § 27, 28.

§7]
ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА И КОМПАКТЫ
55
Берём открытое множество т[, диаметра < 1, удовлетворяющее
условию TiS^i ПГ.
Предположим, что построены открытые множества
Г^з . .. эГ„, 8(Г;)<~. (при /= 1, 2,.. ., л),
удовлетворяющие условиям
11 с Гп . . . ,1 п<^Л. п.
Строим на основании леммы открытое множество lw-j-i Диа"
метра < 2£+1» удовлетворяющее условию T^i cz Yn П Гп + 1.
Пересечение Г1 Гл не пусто (состоит из одной точки) и
содержится в Г П Е, что и требовалось доказать.
Общеизвестными примерами полных метрических пространств
являются: числовая прямая, я-мерное эвклидово пространство,
гильбертово пространство и др.
7:2. s-сети в компактах, а-сетью в метрическом пространстве
R называется конечное множество Nc^R, обладающее тем
свойством, что ко всякой точке х пространства R можно найти точку
множества N, отстоящую от х меньше, чем на а.
Из отсутствия в пространстве R (при некотором данном е) г-сетк
следует существование в R последовательности точек, попарные
расстояния между которыми ^> а.
В самом деле, возьмём какую-нибудь точку а\ пространства R;
множество, состоящее из одной точки а\, не является s-сетью (так как мы
предположили, что в пространстве R при данном фиксированном е вообще нет
ни одной s-сети). Поэтому существует точка а*, стстоящая or а\ на
расстоянии ;>s.
Но множество, состоящее из двух точек а± и аъ также не является
s-сетью, поэтому в R существует точка as, отстоящая от обеих точек а\ и
а2 на расстоянии >е.
Продолжая это рассуждение, получим последовательность
(7:21) аь аъ..., ап,...
точек /?, попарные расстояния между которыми ;> е.
Замечание 1. Так как последовательность (7 :21), очевидно, не
имеет ни одной предельной точки, то доказано предложение:
[7*.21]. Во всяком компакте при любом а>0 имеется г-сеть.
Определение [7:22]. Метрическое пространство назы*
вается вполне ограниченным, если в нём при каждом а>0 имеется
е-сеть.
Замечание 2. Только что построенная нами
последовательность (7 *. 21) обладает, очевидно, тем свойством, что никакая её
подпоследовательность не является фундаментальной. Итак: если
метрическое пространство R не вполне ограничено, то в нём имеется
последовательность, не содержащая никакой фундаментальной под-
последовательности.

56 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
С другой стороны, если R вполне ограничено, и
К ={<*!,..., as]
есть у сеть пространства/?, то всё R покрыто множествами 0(ар —);
число этих множеств конечно, а диаметры их -^ а, поэтому
всякая бесконечная последовательность точек R
(7 :22) ^,^2,...,^,...
содержит бесконечную подпоследовательность, диаметр которой
меньше любого наперёд заданного числа е>0.
Дадим е значения ая -> 0 и построим подпоследовательность
(7:22!) a^...%aiKt...
данной последовательности (7:22), имеющую диаметр <ар затем
подпоследовательность (7 :222) последовательности (7 :22Д имеющую
диаметр<е2, и т.д. Переходя затем к диагональной
последовательности, получим подпоследовательность последовательности (7:22),
являющуюся фундаментальной.
Итак:
[7:23]. Метрическое пространство тогда и только тогда
вполне ограничено, когда во всякой последовательности его точек
можно найти фундаментальную подпоследовательность.
Так как всякий компакт представляет собою, очевидно, полное
метрическое пространство, то из [7:21] и [7:23] следует:
[7:24]. Для того, чтобы метрическое пространство было
компактом, необходимо и достаточно, чтобы оно одновременно было
полным и вполне ограниченным.
[7 : 25]. Всякое вполне ограниченное метрическое пространство R
содержит счётное плотное в пространстве R множество {имеет
счётную базу).
В самом деле, если А/^есть ел-сеть и s^-^О при k->со, то счётное
множество N= UNk плотно в R.
7: 3. Пространства непрерывных отображений. Пусть X —
топологическое пространство, а У—ограниченное (т. е. имеющее конечный
диаметр) метрическое пространство. Обозначим через (5, (X, У)
метрическое пространство, построенное следующим образом. Точками
б, (Х9 У) являются все непрерывные отображения X в У. Расстояние
между двумя точками Cl £ d (X, У) и С2£&(Х, У) определяется как
верхняя грань всех чисел р(С1(лг), С2(х)) при х, пробегающем всё
пространство X.
[7:31]. Если У—компакт, а X—любое топологическое
пространство, то пространство QL(X,Y) есть полное метрическое
пространство.
Доказательство. Пусть
(7 131) £-1, С%,. . ., С п,..,

§8]
ПОКРЫТИЯ НОРМАЛЬНЫХ ПРОСТРАНСТВ
57
фундаментальная последовательность точек пространства 6 (Х9 Y). Это
значит, что для каждого е можно найти такое #в, что одновременно
для всех х£Х п любых р>пе, q>nz имеем
(7:32) Р(^(ЗД)<в.
Для каждой точки х£Х последовательность точек
(7 :33) Сг(х), С2(х),.,., Сп(х\...
в этих условиях является фундаментальной, т. е., в силу
компактности Y, — сходящейся последовательностью точек в Y. Из (7:32)
тогда следует, что сходимость последовательности отображений Сп
равномерна, значит, предельная функция С непрерывна и С£&(Х,У).
Очевидно, в метрическом пространстве & (X, Y) последовательность
(7:31) сходится к С£ QL(X, Y), что и требовалось доказать.
7 : 4. Деформации. Гомотопические классы отображений
компакта X в компакт Y. Пусть даны два непрерывных отображения С0
и Сг компакта X в компакт Y. Обозначим через П пространство,
являющееся топологическим произведением компакта X на отрезок
/ = [я <! 6 ^ 6] числовой прямой; точки пространства П суть пары (х, 6),
где х£Х, 6£/. Непрерывное отображение С(х, 6) пространства П
в У называется деформацией, переводящей друг в друга
отображения С0 и Си если для всех х£X имеем
С(х, а) = С0(х), С(х, Ь) = Ct(x).
Два непрерывных отображения С0 и Сх компакта X в компакт Y
называются гомотопными между собою, если существует
деформация С (х9 6), переводящая их друг в друга.
Так как отношение гомотопии двух непрерывных отображений
компакта X в компакт Y обладает свойствами рефлексивности,
симметрии и транзитивности, то множество всех непрерывных
отображений компакта X в компакт Y распадается на классы гомотопных
между собою отображений, или, короче, на гомотопические
классы.
Замечание. Обычно полагают а = 0, #=1, пишут Сц(х)
вместо С(х, 6) и говорят о семействе непрерывных
отображений С9 (х) компакта X в компакт Y, непрерывно
зависящем от параметра 6, 0 <; 6 <; 1.
§ 8. Покрытия нормальных пространств, в частности,
компактов.
8:1. Замкнутые и открытые покрытия топологических
пространств. Предмет комбинаторной топологии. Мы уже знаем, что
(конечным) покрытием какого-либо множества М называется
(конечная) система подмножеств множества М, соединение которых есть
всё множество Ж; в дальнейшем мы будем рассматривать покрытия
данного топологического пространства, а именно, открытые по^

58 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. ij
крытия, состоящие из открытых множеств, и замкнутые покры*!
тия, состоящие из замкнутых множеств; во всех случаях, не!
оговаривая этого особо, будем рассматривать лишь!
конечные покрытия. Кратностью покрытия а назы-1
вается наибольшее из таких целых чисел я, что существует п\
элементов покрытия а, имеющих непустое пересечение. 1
Определение [8:11]. Система множеств (J называется]
вписанной в систему множеств а, если каждый элемент системы $\
содержится хотя бы в одном элементе системы а.
Покрытие р какого-либо множества Ж называется следующим
за покрытием а того же множества Ж, если {3 вписано в а и в то
же время а не вписано в [3.
Только что введённое понятие следования вводит в любое
множество покрытий какого-либо множества М порядок,
удовлетворяющий, как легко видеть, всем аксиомам частично упорядоченного
множества и превращает, таким образом, любое множество
покрытий данного множества М в частично упорядоченное множество.
Когда мы будем говорить о частично упорядоченном множестве ка-j
ких-либо покрытий данного множества М, то всегда будем иметь
в виду только что определённый порядок в этом множестве покрытий.
Комбинаторная топология, в широком смысле слова, изучает
свойства топологических пространств путём исследования свойств]
частично упорядоченного множества их открытых (или замкну-\
тых) покрытий.
8:2. Подобные покрытия. Определение [8:21]. Две конеч-|
ные системы занумерованных множеств \
<х={Л1э 4а,...,Лв},
Р={Я„ В2,...,Дв}
называются подобными между собою, если какие-нибудь;
множества одной системы имеют тогда и только тогда непустое пе-|
ресечение, когда непустое пересечение имеют соответствующие (т. е.1
снабжённые теми же номерами) множества второй системы. j
Равноправие, существующее в общей комбинаторной топологии между|
употреблением частично упорядоч-енных множеств открытых и замкнуты^
покрытий основано на следующих двух теоремах:
[8 :22]. Ко всякой системе замкнутых множеств \
а = {Ль...Л} |
нормального пространства R можно найти такую систему соответ%
ственно содержащих множества Л1,...,Л^ открытых множеств \
Oi,...,Oe,
что системы множеств я _
a = {Alt...,Aa} \
и _ <* = {Оь...,Оа}.
а даже а и со = {0ъ...,б8} подобны между собою *).
*) Для случая, когда /? — компакт, очень простое доказательство этой
теоремы дано в арт. 8:3. |

§ 8J
ПОКРЫТИЯ НОРМАЛЬНЫХ ПРОСТРАНСТВ 59
[8:23]. Ко всякому открытому покрытию
a> = {0lf....Oe}
нормального пространства R можно найти такое замкнутое покрытие
а = {Аь... ,AS}
пространства, что
Ai^Oit / = 1, 2,...,s.
Замечание. При этом, как будет видно из доказательств, в теореме
[8:23] можно даже предположить, что А4 суть замыкания открытых
множеств, образующих покрытие пространства R.
Доказательство [8:22]. Обозначим через Л соединение
всевозможных множеств вида Ai% П---П Ал> гДе А-^-'-И^ таковы, что
Ах П Ah П.-- ПЛ^ = 0.
Так как замкнутое множество А не пересекается с Аь то R\A есть
окрестность множества AL. Следовательно (в силу [4 :141]), существует такое
открытое множество 01? что A±^0lt Oi^R\A.
Системы множеств
a^{Ah...,As}
и __
ai = {Oi, Ab--'As}
подобны между собою. В самом деле, если А± f) А$г П • • • П А%к Ф 0> то
тем более Ох f| Ah f| ... П Aik ф 0. Обратно, из Ах f) Ah f) ... f| Aijc =» 0
следует, что Aiy f) ... f| Л^,^Л и, значит,
Oxfl Ai П-..П Aik^Ot fl Л=*0.
Предположим, что открытые множества О^Э^г» *=lj 2,...,/*<s
построены таким образом, что а и
ar={oh...,Ort Ar+b...,As}
подобны. Рассуждая о системе множеств аг и о множестве Аг+\ так же,
как мы только что рассуждали о системе а и множестве Аь получим такое
открытое множество Огц24-+1» чт0 система аг и
ан-1 = {01,..., Or+1, Ar+2,- --'As},
а значит, и система а и аг+1 подобны между собою. Рассуждение
заканчивается на системе ae = {0lf..., Os], удовлетворяющей поставленным
требованиям.
Доказательство [8:23]. К системе
a' = {R\Ob...,R\Os}
строим по только что доказанному такую систему открытых множеств
Что /?\0|COj, и система {о(,..., 0's] подобна системе а'. Из этого
подобия, в частности, следует, что
{O[[\...[\O't\ = 0.
Полагая 0'\ = /?\0• , получим (так как Я\СК замкнуто)

60 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [ГЛ. I
значит (так как R\Oi cz О')
0"4£.li\(R\0d = 0i.
Наконец, так как
О] U • • • U 0"8 = R\{0[ П ... П 0'8) = R,
то, полагая /^ = Oj, имеем искомое покрытие
a = {A1)...,As}.
8:3* е-покрытия компактов. Лебеговы числа покрытия.
Определение [8:31]. Покрытие метрического
пространства называется г-покрытием% если все элементы этого
покрытия по диаметру меньше г.
Лемма Лебега [8:32]. Ко всякому замкнутому покрытию
а = {Аг,...,Аа]
компакта Ф можно найти положительное число 8, обладающее
следующим свойством: если имеется множество МаФ диаметра
<[8, пересекающееся с какими-нибудь элементами
(8:321) Aiv...,Aik
покрытия а, то пересечение этих элементов не пусто.
Доказательство ведём от противного: предположим, что
такого числа Ь нет. Тогда для положительного числа — (где п —
натуральное число) можно найти такую комбинацию элементов
(8:321) Ail9...,Atk
покрытия а, что некоторое множество МпаФ диаметра ^ —
пересекается со всеми множествами Ai9...,Aik и что в то же время
пересечение самих этих множеств Ai....,Ail пусто:
1 к
М П Л^0г..,ЖП А€кФ°> Atl(\... ()\ = 0.
Так как число всех комбинаций (8:321) из различных элементов
покрытия а конечно, то найдётся, по крайней мере, одна комбинация
Л^,.. ., А$к,
которая в только что указанном смысле соответствует бесконечному
множеству различных п. Это значит, что для бесконечного числа
различных п имеем множества Мп диаметра ^ —, пересекающиеся
со всеми данными А{ , ...,Л^ , но в то же время
Ан П,..П^ = 0.

§ 8]
покрытия нормальных пространств
61
Выберем из каждого Мп по точке рп. Перейдя, если нужно, к
подпоследовательности, можем предположить, что последовательность
Pi» Р2» • • • »Рп> • • •
сходится в некоторой точке р £ Ф. Очевидно, в любой близости от
точки р найдутся точки каждого из множеств Л^,..., Л^; поэтому
(так как множества Ai9,**,А€ замкнуты), р принадлежит к
каждому из них и, вопреки нашему предположению,
Определение [8:33]. Всякое положительное число 8,
удовлетворяющее условиям леммы Лебега для данного замкнутого
е-покрытия а компакта Ф, называется лебеговым числом
покрытия а; таким образом, лебеговым числом замкнутого покрытия
является всякое достаточно малое положительное число. При этом,
считая s данным, мы будем подчинять наши лебеговы числа ещё
одному дополнительному условию, а именно, будем требовать, чтобы
они были меньше, чем половина разности между s и наибольшим
из чисел, являющимся диаметром какого-либо из множеств А(. Из
этого определения лебегова числа непосредственно следует:
[8:331]. Если 2а есть лебегово число замкнутого г-покрытия
а = {Л1,.. .,Л8}
компакта Ф и если Oi = 0 (Aif а) есть о-окрестность множества
Aiy то ш = [Ои..., Os} и ш = {01э.. ., Os] являются г-покры-
тиями компакта Ф, подобными покрытию а {из них а>, очевидно,
открыто, а о> замкнуто).
Лемма [8:34]. Ко всякому открытому покрытию
»*=[Ou...t Os}
компакта Ф можно найти положительное число y} = yj(od),
обладающее следующим свойством: всякое множество ЖсФ, имеющее
диаметр < % целиком содержится, по крайней мере, в одном
элементе покрытия оо.
Доказательство. Назовём «чересчур большим» всякое
множество МаФ, не содержащееся ни в каком элементе покрытия оо.
Обозначим через ч\ нижнюю грань диаметров всех чересчур больших
множеств МаФ и докажем, что она положительна. Этим лемма
[8:34] и будет доказана.
Пусть
Ми М2,...,ЛГШ...
-—какая-либо последовательность чересчур больших множеств, диа«

62 обзор свойств топологических пространств [гл. i
метры которых стремятся к т). В каждом Мп выбираем по точке рп;
переходя, если нужно, к подпоследовательности, можем
предположить, что точки рп сходятся в некоторой точке р£Ф. Точка р
лежит в некотором элементе 0{ покрытия со и имеет, следовательно, от
замкнутого множества R\0% положительное расстояние 2е, так что
(8:341) 0(р, 2е)сО,;
по самому своему определению никакое Мп не содержится в Oi и
тем более в О (/?, 2е). Между тем, для всех достаточно больших п
имеем рп£0(р, г), поэтому для всех таких п диаметр Мп
непременно должен быть > е [так как иначе имели бы Мп^О(р, 2е)].
Но так как ч\ есть предел диаметров Мп, то г\ ^> г, что и
требовалось доказать.
Закончим это предварительное исследование покрытий
следующим весьма общим и совершенно элементарным предложением,
которое будет удобно в дальнейшем.
[8:35]. Пусть дано какое-нибудь свойство 6 замкнутых
покрытий (например, свойство иметь данную кратность). Для того,
чтобы в каждое открытое покрытие оо компакта Ф можно было
вписать замкнутое покрытие, обладающее свойством S,
необходимо и достаточно, чтобы при каждом г>0 существовало
замкнутое ^покрытие компакта Ф, обладающее свойством @.
В самом деле:
Условие необходимо: взявши для любого данного е>0
какое-нибудь открытое е-покрытие и затем вписанное в него
замкнутое покрытие, обладающее свойством 6, получим замкнутое
е-покрытие, обладающее свойством (£.
Условие достаточно: если при всяком е>0 существуют
£*покрытия, обладающие свойством @, то для получения
обладающего свойством (5 замкнутого покрытия, вписанного в данное открытое
покрытие со, достаточно определить по лемме [8:34] число т| = 7](ш)
для покрытия ш и взять произвольное, обладающее свойством @,
замкнутое ^-покрытие а; по самому определению числа г\ покрытие
а оказывается вписанным в со.
8:4. Определение размерности.
Определение [8:41]. Размерностью бикомпакта Ф
называется наименьшее из таких целых чисел п, что во всякое
открытое покрытие пространства Ф можно вписать замкнутое
покрытие кратности <; п -j- 1; размерность Ф обозначается через
dim Ф*
Если таких чисел п нет, то размерность полагается равной
бесконечности: dim Ф —ос.
Замечание 1. Если dim Ф — оо, то к любому целому
числу п можно подобрать такое открытое покрытие а>
пространства Ф, что всякое вписанное в а> замкнутое покрытие имеет
кратность >я-{- 1.

&j ПОКРЫТИЯ НОРМАЛЬНЫХ ПРОСТРАНСТВ 63
Упражнение. Доказать, что определение размерности Может
быть сформулировано ещё и так:
[8:41']. Размерностью бикомпакта Ф называется наименьшее из
таких целых чисел п, что во всякое открытое покрытие Ф можно
вписать простое замкнутое покрытие кратности, равной n-j-1.
Замечание 2. Размерность пустого множества по определению
принимается равной —1.
На основании [8 :35] можно сказать:
[8:42]*). Размерность компакта Ф есть наименьшее из тех
целых чисел п, для которых при каждом е>0 найдётся
замкнутое е-покрытие компакта Ф кратности ^л-j-l.
Если таких п нет, то размерность Ф по определению бесконечна.
Тогда для любого п можно найти такое е > 0, что всякое
замкнутое s-покрытие имеет кратность >/i-f-l-
Так как при топологическом отображении бикомпакта Ф на
бикомпакт Ф' открытые и замкнутые множества бикомпакта Ф
переходят, соответственно, в открытые и замкнутые множества бикомпакта Ф
и покрытие данной кратности одного пространства переходит в
покрытие той же кратности другого пространства, то гомеоморфные
между собою бикомпакты имеют одну и ту же размерность. Этот же
самый факт выражают, говоря, что размерность есть топологически
инвариантное свойство того или иного пространства, или
топологический инвариант.
Понятию размерности посвящена значительная часть главы 5
и вся глава б этой книги. При этом мы ограничиваемся случаем,
когда Ф — компакт. В настоящей же главе мы установим лишь одно
свойство размерности, непосредственно следующее из определения;
мы его докажем только для компактов, предоставляя читателю
доказать его для любых бикомпактов:
[3:43]. Если компакт Ф0 содержится в компакте Ф, то
dim Ф0 ^ dim Ф.
*) Наглядный смысл этого определения очень прост: при п = 2 оно
утверждает, чго всякая двумерная «площадь» (компакт) может быть «вымо-
щена> сколь угодно мелкими «камнями» (замкнутыми множествами) так,
что «камни» примыкают лруг к другу не более чем по три, и не может быть
вымощена сколь угодно мелкими камнями так, чтобы были только
примыкания по два, поэтому утверждение (доказанное в гл. 5), что, например,
квадрат имеет размерность 2 и называется «теоремой о мостовых» — при
замощении площадей и улиц брусчаткой всегда бывают примыкания по три,
а примыкания по четыре могут быть избегнуты.
При заполнении некоторого трёхмерного объёма достаточно мелкими
камнями (например, при заполнении большой полости кирпичной кладкой)
необходимо возникают уже примыкания по четыре.
Большим достижением математической мысли было усмотрение того
факта, что в этом числе^примыканий (в кратности покрытий) и заключается
содержание* понятия размерности. Это достижение принадлежит Лебегу,
впервые сформулировавшему «Теорему о мостовых» (в 1911 году), и
доказавшему её (впрочем, не вполне безупречно). Первое полное доказательство
теоремы о мостовых было дано Брауэром в 1913 году.

64 ОБЗОР СВОЙСТВ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ [гл. t
В самом деле, взявши при данном s>0 некоторое замкнутое
е-покрытие <*={Аи. .., А8} компакта Ф, получим г-покрытие
ао = {Ф0ПЛ1,...,Ф0ПЛ8}
компакта Ф0, причём кратность покрытия а0, очевидно, не
превосходит кратности покрытия а. Отсюда и следует утверждение [8 :43].
Замечание 3. Из теорем [8:22] и [8:23] следует:
[8:44]. Размерность бикомпакта Ф может быть определена
как наименьшее целое число п, удовлетворяющее условию:
Во всякое открытое покрытие бикомпакта Ф можно вписать
открытое покрытие того же бикомпакта, имеющее кратность
В частности, размерность компакта Ф может быть
определена как наименьшее целое число /г, обладающее тем свойством,
что при всяком е>0 существует открытое ^покрытие
кратности ^ п -j- 1 компакта Ф.

ГЛАВА ВТОРАЯ.
ТЕОРЕМА ЖОРДАНА.
Данное в этой главе доказательство теоремы Жордана принадлежит"
Э. Шмидту *).
Это доказательство совершенно элементарно и не требует никаких
предварительных топологических знаний кроме простейших сведений
о связности (гл. 1, § 3), необходимых для понимания самого содержания
теоремы. Вторым достоинством доказательства Э. Шмидта является то, что
вспомогательные построения, на которые опирается это доказательство
(угловая функция, порядок точки относительно непрерывного отображения
и т. д.), имеют широкую область применения далеко за пределами самой
теоремы Жордана, и принадлежат к числу тех элементарных топологических
понятий, знакомство с которыми необходимо всякому, изучающему
например, теорию дифференциальных уравнений или теорию функций
комплексного переменного.
§ 1. Формулировка теоремы Жордана. Совместные границы
областей.
1:1. Формулировка теоремы Жордана. Компакт Ф, гсмеоморф-
ный окружности, называется простой замкнутой линией (или
замкнутой жордановой кривой); компакт, гомеоморфный
прямолинейному сегменту, называется простой (или жордановой)
дугой. Предмет этой главы заключается в доказательстве
следующей важной и знаменитой теоремы:
Теорема Жордана. Пусть Ф— простая замкнутая линия,
лежащая в плоскости /?9. Дополнительное открытое множество
/?'2\Ф распадается на две области**) Г0 и Yv границей каждой
из которых является кривая Ф.
Другими словами:
1. /?2\ф===г0иг1, Г0 ПГ^О;
2. Г0 и Tj суть области;
з. Ф^ГоХГ^Глг,.
Замечание 1. Мы говорим, что замкнутое множество Л тополо-
гического пространства R разбивает пространство /?, если
*) Erhard Schmidt, Ueber den Jordanschen Kurvensatz, Sltzungs-
berichte d. preussischen Akadem'ie d. Wiss., 28, 1923, стр. 318 — Ь29.
**) Напоминаем, что областью называется связное
открытое множество.
5 Александров П. С.

66
ТЕОРЕМА ЖОРДАНА
[гл. ц
открытое множество R\A несвязно; если же R\A связно, то А по
определению не разбивает пространства/?.
Замечание 10. Несвязные пространства и только они
разбиваются пустым множеством.
Обыкновенно теореме Жордана дают следующую, более
компактную формулировку:
Всякая плоская замкнутая жорданова кривая Ф разбивает
плоскость R2 на две области и является их совместной границей.
Всех утверждений, содержащихся в теореме Жордана — три:
1. Открытое множество R2\Ф состоит из двух компонент Г0 и Г\;
2. Каждая из этих компонент есть открытое множество *);
3. Ф является общей границей областей Г0 и Гг
Как мы увидим ниже, с теоремой Жордана тесно связана
следующая, также весьма важная теорема:
Никакая лежащая в плоскости R2 простая дуга Ф не
разбивает этой плоскости.
Другими словами: если простая дуга Ф лежит в плоскости R2,
то открытое множество /?2\Ф связно.
Обе теоремы, доказываемые в этой главе, являются частным
случаем теорем, которые будут доказаны как в главе 14, так
и в главе 15.
1:2. Области в Rn и их границы.
Сделаем прежде всего следующее замечание:
[1:21]. Всякое выпуклое открытое множество в Rn
(например, открытый я-мерный шар) связно в силу теоремы [3: 12] |
главы 1. Связно поэтому и всякое множество, гомеоморфное вы- ]
пуклой области пространства Rn.
[1:22]. Для того, чтобы открытое множество Гс/J» было связ- j
ным, необходимо и достаточно, чтобы всякие две точки Г можно j
было соединить простой ломаной (т. е. ломаной без кратных точек), j
лежащей в Г. ;
Доказательство. Условие достаточно: если всякие две!
точки Г можно соединить лежащей в Г ломаной (хотя бы и имею- j
щей кратные точки), то Г связно в силу теоремы [3:12] главы 1.
Необходимость условия означает:
Если в открытом множестве Г имеются две точки а и £, ко-1
торые нельзя соединить лежащей в Г простой ломаной, то Г не свя-1
зно. 1
Докажем последнее утверждение. Обозначим через Та множество!
всех точек Г, которые можно соединить с а ломаными, лежащими!
в Г. Через Г& обозначим множество всех остальных точек Г. 1
*) Компоненты открытого множества пространства R могут не быть!
открытыми множествами в R\ например, если взять в качестве R канторово!
совершенное множество (с его обычной топологией), то каждая точка!
х £ R является сво^й компонентой в R; другими словами, компонентами R%
являются содноточечные» множества, и ни одно из них не открыто в /?.|
Это замечание позволит читателю оценить интерес теорем [1:25] и [1:27].|

§1]
ФОРМУЛИРОВКА ТЕОРЕМЫ ЖОРДАНА
б?
Если р — произвольная точка Г, то все точки, Rn, отстоящие от р
меньше чем на некоторое положительное в = р (рМп\Г)> принадле*
жат Г и поэтому могут быть соединены с р отрезком, лежащим в Г.
Отсюда легко следует, что Та и Гь открыты в Г; так как Га ЛГ& = О
иа£Га, ££ГЬ, то несвязность Г, значит, и вся теорема [1:22]
доказаны.
[1:23]. Пусть Г есть область пространства/?п, /г>-2, а£сГ-
конечное множество. Тогда множество Г\£ связно ( и значит, пред*
ставляет собою область).
В самом деле, пусть а и Ъ — две точки открытого множества
Т\Е; соединим их ломаной в Г; сколь угодно малым сдвигом
вершин этой ломаной её можно привести в общее положение*)
относительно конечного множества Е, после чего она не будет содержать
ни одной точки Е и, следовательно, будет соединять а и д в Т\Е.
[1:24]. Пусть Еп есть я-мерный замкнутый шар, лежащий в Rn.
Открытое множество Rn\En связно.
В самом деле, преобразование взаимными радиусами-векторами
переводит /?п\£п в £w\o, где Еп есть соответствующий открытый
шар, а о-—центр этого шара. Так как Еп\р по доказанному связно,
то свяьно и Rn\En.
[1 :25]. Компоненты всякого открытого в R*1 множества открыты
(т. е. являются областями).
Прежде чем доказывать теорему [1 :25], сделаем следующее
замечание:
Определение [1: 26]. Метрическое пространство R называется
связным в точке р, если р имеет сколь угодно малые
(посвоему диаметру) связные окрестности; R называется локально связ-
н ы м; если оно связно во всякой своей точке.
Так как сферические окрестности в Rn связны, то не только /?и,
но и всякое открытое множество в Rn локально связно **). Примером
не локально связного компакта может служить изображённая на черг. 2
(стр. 38) кривая, состоящая из отрезка —l<j><;i осиу и из линии
y--=^sln - дляО<х^—. Во всех точках этой кривой, лежащих на
оси ординат, наша кривая не связна.
После этих замечаний ясно, что [1 :25] является частным случаем
следующей важной теоремы:
[l : 27]. Компоненты всякого локально связного пространства
суть открытые множества (и следовательно, области) этого про*
странства.
Доказательство теоремы [1:27]. Пусть R — локально
Связное пространство, Q — одна из его компонент и р —точка Q.
*) Определение общего положения см. в Прибавлении II.
**) Из определения [1 :26] следует, что открытое множество всякого
локально связного пространства само локально связно.

68
ТЕОРЕМА ЖОРДАНА
[гл. п
Обозначим через U какую-либо связную окрестность точки р. По
теореме [3:13] главы 1 множество QUU связно, значит (так как
Q—компонента), совпадает с Q; итак, р — внутренняя точка Q, что
и требовалось доказать.
[1 :28]. Среди компонент открытого множества Rn\<&, где Ф —
компакт, лежащий в Rn, имеется одна и только одна неограниченная
компонента. _
! В самом деле, пусть Еп — какой-нибудь шар, содержащий Ф внутри
себя (такой шар существует, так как Ф — ограниченное множество).
Множестве Rn\En связно, следовательно, оно содержится в одной
из компонент множества /?П\Ф, которая, таким образом, оказывается
неограниченной. Все
остальные компоненты лежат в Еп
и потому ограничены.
Определение [1:29].
Компакт Ф называется
абсолютной границей
в Rn, если Ф разбивает про-
странство Rn и является
границей каждой из
компонент открытого множества
#"\Ф.
Определение [1:291].
Абсолютная граница в Rn
называется регулярной
границей, если она
разбивает Rn ровно на две
области.
Такие кривые, как
окружность, эллипс и т. п., явля-
Черт. 10. ются регулярными
границами областей в R2; сфера
и тор могут служить примерами регулярных границ областей в /?3.
Теорема Жордана утверждает, что всякая замкнутая жорда-
нова кривая, лежащий на плоскости R% является регулярной
границ»й в R2.
На первый взгляд кажется, что всякая абсолютная граница
является регулярной: трудно представить себе, например, плоское
замкнутое множество, разбивающее плоскость более чел ра две области
и являюр'^ея общей границей всех этих областей. Тем не менее,
такие замкнутые множества существуют; они впервые былчпостроены
Брауэром в 1909 г. Н'лжеследующий пример представляет собою
незначительное видзи.мнение первоначального примера Брауэра
(впервые опубликованное японским математиком Yoneyama).
Вообразим себе остров Ф0, расположенный r море Г. Остров
представляем себе хотя бы в виде круга (вместе с его окружноеюю),

J] ФОРМУЛИРОВКА ТЕОРЕМЫ ЖОРДАНА 69
так что море Г = /?2\Ф0 является открытым множеством. Пусть на
острове Ф0 имеются два круглых озера — холодное и тёплое (каждое
из озёр есть внутренность круга).
Вообразим себе следующую программу работ. В первый час от
моря и от обоих озёр должно быть проложено внутрь острова по
одному слепому каналу; каждый из этих каналов извивается так, что
расстояние от каждой точки суши острова как до морской воды, так
и до воды каждого из двух озёр сделается меньше чем 1 км (черт. 10).
В следующие полчаса каждый из каналов должен быть
продолжен так, чтобы в конце этого^получаса расстояние от каждой точки
суши (оставшейся от острова) до моря и каждого из двух озёр
сделалось меньше чем г/2 км.
В следующие 1/1 часа каналы
продолжаются так, что
расстояние от каждой точки
суши до морской, тёплой
пресной и холодной пресной
воды делается меньше lji км
и т. д.; после I+V2 +
+XU • •• +(1/2)п час°в
работы все три канала должны
быть продолжены так, что
расстояние от каждой точки
суши до моря и каждого
озера меньше чем (у) км.
При этом каналы никогда
не соприкасаются ни друг
с другом, ни с самими собою,
т. е. остаются слепыми.
Через два часа таких работ от
острова остаётся лишь
некоторое нигде не плотное на плоскости замкнутое множество Ф0, и в
любой близости любой его точки имеется как морская вода, так и вода
каждого из двух озёр: замкнутое множество Ф0 является совместной
границей трёх плоских областей — моря и обоих озёр*).
Замечание. Компакт Фс/?2, являющийся совместной границей
двух плоских областей (двух компонент открытого множества /?2\Ф),
может не быть абсолютной границей: множество Ф (черт. 11),
состоящее из окружности и спиралевидно навивающейся пя неё кривой,
разбивает плоскость на три области, но шляется границей только
Двух из этих областей (одна из этих областей на черт. II
оставлен белой, другая покрыта пунктиром; третья область есть
внешняя область к кругу; она покрыта двойной штриховкой).
*) Тем же методом можно построить абсолютную грзнчцу в ило:кости R'l4
разбивающую плоскость на любое конечное или лаже на счётное число об-
частей,

70
ТЕОРЕМА ЖОРДАНА
[ГЛ. II
Теорема [1:2]. Для того, чтобы компакт Ф был абсолютной
границей в Rn, необходимо и достаточно, чтобы он разбивал
пространство Rn, no крайней мере, на две области и чтобы в то же
время при любом выборе замкнутого множества Ф0сФ множе*
ство /?П\Ф0 было связным-
Доказательство. Пусть Ф разбивает Rn на области 1\, Г2,. . .,
Т\,.. . (в конечном или счётном числе*)) и является границей
каждой из них.
Пусть Ф0сФ. Так как Ф = Х\\1\, то, в силу теоремы [3:19]
главы 1, каждое из множеств
Г,и(Ф\Ф0)
связно, а в силу теоремы [3:16] главы 1, связно и множество
и(Г,и(Ф\Фо)) = Я»\Ф0-
i
Этим доказана одна половина теоремы [1:2] (необходимость
изложенного в ней условия).
Пусть теперь Ф разбивает Rn на облясти Г^Г^,..., ГА.,...,
а никакое замкнутое множество Ф0 с: Ф не разбивает пространства Rn.
Докажем, что тогда при любом k
ф = г*\г*-
Прежде в^его ясно, что точка р£^к\Уи не может принадлежать
ни к какому 1\, следовательно, принадлежит к Ф. Итак,
Пусть 1фк\ так как TiczRn\Tki то Rn\Vk не пусто и
/?пччфд = Г, и(/?»\Г*)
есть соединение двух непустых непересекающихся открытых
множеств Vk и АП\ГЛ- Поэтому Rn\$k не связно, т. е. Фк разбивает Rn.
Так как Ф^^Ф, ю, r силу наших предположений, должно быть
Фл. = Ф; так как это верно для любого k> то теорема доказяна.
1:3. План доказательства теоремы Жордана. Сделаем прежде
всего следующее простое замечание:
Лежащая в плоскости простая дуга или простая замкнутая
линия Ф нигде не плотна в плоскости.
В самом деле, всякое лежащее на Ф связное множество
разбивается некоторой парой своих точек; внутренность круга есть связное
множество, не разбивающееся никаким своим конечным
подмножеством. Значит, множество Ф не содержит внутренности никакого
круг*, т. е., будучи замкнутым, нигде не плотно в плоскости.
После того, как в § 2 будет дан основной аппарат всего
доказательства—понятие порядка точки относительно замкнутой кривой,
мы сначала доказываем в § 3, что простая дуга не разбивает плос-
*) В пространстве со счётной базой всякая совокупность попарно
непересекающихся открытых множеств конечна иди счётнд.

§ 1]
ФОРМУЛИРОВКА ТЕОРЕМЫ ЖОРДАНА
71
кость; затем в § 4 доказывается, что замкнутая жорданова кривая
разбивает плоскость на две области.
Выведем отсюда и последнее утверждение теоремы Жордана:
жорданова кривая Ф является границей каждой из двух компонент
открытого множества /?П\Ф. Для этого, в силу теоремы [1:2],
достаточно показать, что никакое замкнутое множество Ф0 с Ф не
разбивает плоскости Ф. Пусть дано Ф0сФ. Возьмём на кривой Ф какую-
либо точку S, не принадлежащую множеству Ф0. Так как Ф0 замкнуто,
т0 существует открытая дуга <а6>, содержащая точку £, и
свободная от точек множества Ф0. Множество Ф1 = Ф\<а£>
является простой дугой, лежащей на Ф и содержащей Ф0.
Требуется доказать, что /?2\Фо связно; но так как все точки ФХ\Ф0
являются предельными для /?2\Ф1э то, в силу теоремы [3:19] главы 1,
связность R2 — Ф0 следует из связности %2\Ф1.
Итак, для доказательства всех утверждений теоремы Жордана
достаточно доказать, что жорданова кривая разбивает плоскость на
две области и что простая дуга плоскости не разбивает.
1: 4. Обозначения. Ориентация простых дуг и простых
замкнутых линий. Простую дугу с концами а и b обозначаем через ab,
соответствующую открытую дугу (т. е. множество ab\(a U Ь))
обозначаем через <я&>. Если простая дуга обозначена через Лит. п.,
то Л обозначает соответствующую открытую дугу.
Так как простая дуга есть топологический образ отрезка, то можно
говорить об ориентированной простой дуге, т. е. -о дуге с заданным
на ней направлением *) от а к Ъ или от b к а. Ориентированная про-
*) Направление от а к Ъ на простой дуге аЬ устанавливается так.
Берём какое-нибудь топологическое отображение С отрезка 0<!х<!1 на
простую лугу ~ab, при котором точка 0 переходит в а, точка 1 переходит
в Ь. Это отображение определяет на дуге ab порядок точек: для двух точек
У = С(х),у' = С(х') дуги ab полагаем у <У, если на отрезке ul имеем х<х'.
Остаётся доказать, что установленный таким образом порядок не
зависит от выбора отображения С.
Пусть С^ и С2 — топологические отображения отрезка 01 на дугу ab,
удовлетворяющие условию d (0) = С2 (0) = я, Q (1) = С2(1) = &. Если бы
эти отображения устанавливали на ab два разных отношения порядка, то
Для некоторых двух точек
у = Сг fa) = С2 fa) € ab^
* У = С* (х') = Сч (Хо) € ab
было бы, например, J l v 2 v
0*41) *l<-*i. Х<ь>Х2.
При топологическом отображении С = С^1 Q отрезка (ТГна себя имеем
(1:42) | С(0> = 0' СУ = \
I С(хх) = хъ С(х1) = х2.
Но С как топологическое отображение 01 на себя, оставляющее
неподвижными концы отрезка, есть строго монотснная функция, так что
равенства (1 :42) не совместимы с неравенствами (1:41).
Полученное противоречие доказывает наше утверждение.

72
ТЕОРЕМА ЖОРДАНА
[гл. п
стая дуга обозначается через (ab), соответственно, (Ьа),
ориентированная открытая дуга обозначается через (ab)f соответственно, (да).
При топологическом отображении окружности на данную жор-
данову кривую направление обхода на окружности порождает
определённое направление обхода и на данной жордановой кривой.
Точное определение направления обхода или ориентации
жордановой кривой таково. Задать ориентацию жордановой кривой Ф —
значит задать на всякой простой дуге Ф0 cz Ф определённое
направление таким образом, чтобы на всяких двух дугах Ф0 с; Ф, Фх cz Ф, из
которых олна является частью другой, выбранные направления были
бы одинаковы.
Жорданова кривая Ф с определённой на ней ориентацией назьь
вается ориентированной кривой и обозначается через Ф.
§ 2. Угловая функция непрерывного отображения отрезка
в плоскость. Порядок точки относительно замкнутого пути
в плоскости.
2:1. Функции Fa(p,C, x) и /(/?, С, xv x^\. Пусть дано непрерывное
отображение С отрезка е0е1=^(е0^х^.е1) числовой прямой в плоскость
/?3. Пусть p£R2 — точка, не принадлежащая множеству Ф = С(е0е1).
Пусть, наконец, а — точка отрезка е0ег- Предположим, что
в плоскости R2 определённое направление отсчёта углов (например,
направление против часовой стрелки) выбрано в качестве
положительного.
Угол 1ятС{а)рС(х) определён лишь с точностью до целочисленных
кратных 2^. Однако, его можно определить однозначно для всех
х, ео4^х^е1У если выбрать определённое значение этого угла для
данною х = х0 и потребовать, чтоЗы его значение для любого х
непрерывно зависело от х. В самом деле, разделим отрезок е0ег точками
на столь малые отрезки a^avaxa^ ... ,а8_ха8> чтобы образ каждого
из них при отображении С находился внутри некоторого острого
угла с вершиной в р. Тогда, если значение угла С{а)рС(х)
определено для некоторого фиксированного х0, <fy<^o<C#i+i> т0 оно
однозначно определяется по непрерывности для всех значений х,
лежащих на отрезке a%af+l; значит, в частности, для x — ctt и x = ai+l.
Но если значение угла С(а)рС(х) задано для х = а$+г, то оно
однозначно определяется на всём отрезке ai + 1ai+2i затем на ai+%ai+3
и т. д. Точно так же, если ^С(а) рС(х) определён для х — аь то
значение этого угла однозначно определяется по непрерывности на
отрезке a!ai_1 и т.д. Таким образом, угол С (а) р С (х) оказывается
определённым для всех точек х отрезка £0£j.

УГЛОВАЯ ФУНКЦИЯ ОТОБРАЖЕНИЯ ОТРЕЗКА В ПЛОСКОСТЬ 73
Определение [2: 11]. Значение угла С(а)рС(х), однозначно
определённое для всех х, е0^х^е^ требованием, чтобы при х = а
9то значение равнялось нулю, обозначается через Fa(p, С, х).
Замечание 1. Функция Fa(p, С, х), очевидно, непрерывно
зависит от х, а и р. Более того, легко видеть, что она непрерывна
по отношению к совокупности всех своих аргументов р, С, х, а: при
фиксированных х,а,р,С для каждого е>0 можно подобрать такое
S>0, что для х\ а\ //, С', удовлетворяющих условиям
\х'— х\<Ъ, |а'_а|<8, р(р',р)<8, р(С,С)<8,
значение Fa'(p'\ С\ хг) определено и отличается от Fa(p, С, х) меньше,
чем на е. (При этом, в соответствии с главой 1, арт. 7:3, условие
о (С, С)<8 означает, что р(С' (S),C(S))<S для всех S, g0<6<g1.)
Замечание 2. Для любых точек а, а/ отрезка бо^ имеем
(2:11) Fa.{p, С, х) = /=>(/>> С, fl)-f Fe(p, С, *).
Отсюда следует, что разность Fa(p, С, х2) — Fa(p, С, хг) не зависит
от а.
О пр е дел е ние [2 : 12].
(2:12) /(р, С, х1э ха) - Fa(p, С, х2) — Fa{p, С, *х)
(при каком-нибудь a£e0ety, функция /(р, С, аГц дг2) также
непрерывно зависит от своих аргументов.
2:2. Порядок точки относительно замкнутого пути.
Предположим теперь, что отображение С удовлетворяет условию
С(е0) = С(ег).
В этом случае говорят, что отображение С «определяет в плоскости
некоторый замкнутый путь» *). Тогда функция /(/;, С)=/(рэ С, e0i et)
равна некоторому целочисленному кратному 2тг.
Таким образом, для любой точки р, не принадлежащей
множеству C\e0e1)i определено целое число а>о(р) = =- /(р, С), зависящее
только ог данного непрерывного отображения С и от точки р.
Число ©с(р) называется порядком точки р
относительно отображения С (обычно говорят: порядок точки
относительно замкнутого пути, определённого данным непрерывным
отображением).
Очевидно: если порядок &с{р) определён для данной точки р, то
он определён и для всех точек, достаточно близких к р, причём,
в силу непрерывности и целочисленности функции <*>c(p)i Для всех р'>
достаточно близких к р, имеем
<»с(р') = <»(&р)-
*) Наглядный геометрический смысл этого термина ясен; однако, мы
не будем им пользоваться: лля строгого определения понятия замкнутого
пути следовало бы ещё указать, при каких условиях два различных
непрерывных отображения определяют один и тот же «замкнутый путь».

74
ТЕОРЕМА ЖОРДАНА
[гл. и
Отсюда следует
[2: 21]. Для всех точек р, принадлежащих одной и той же
компоненте открытого множества R2\C(e0e1)i функция &с(р)
принимает одно и то же значение.
В самом деле, если pt и р2 принадлежат к одной и той же компоненте
Г открытого множества R2\C(e0e1), то их можно соединить ломаной
линией, лежащей в Г; для всех точек р этой ломаной функция о>с(р)
определена и, следовательно (вследствие своей непрерывности
и целочисленности), сохраняет постоянное значение. Поэтому
^о(Р1) = ^с(р2)^
что и требовалось доказать.
Очевидно: если всё множество С(е0е1) лежит внутри угла а, 0<а
<2тг, с вершиной в р, то |Др, С, xv х2)|<а для любых, лежащих
на отрезке е0е1 точек xv x2.
Поэтому
[2 :22]. Если непрерывное отображение С отрезка e(f1 в
плоскости /?2 таково, что С (е^ = С^), и всё множество С(е0е^ лежит
в одной из двух полуплоскостей, на которые плоскость R2
разбивается некоторой прямой, то для любой точки /?, принадлежащей
второй из этих полуплоскостей, имеем ^с(р) = 0-
Сделаем ещё два важных замечания.
[2:23]. Пусть С есть непрерывное отображение отрезка e0et на
окружность К, взаимно однозначное на открытом интервале {е0е^)
и удовлетворяющее условию С(е0) = С(е^. Пусть р есть центр
окружности К; тогда шс(р) = -|- 1 или а)6(р)= —1 в зависимости от
того, будет ли при движении точки х по отрезку е0ех от е0 к ех
точка С(х) обходить окружность в положительном или в
отрицательном направлении.
В силу [2:21] то же утверждение справедливо и для любой
точки /?, лежащей внутри К-
Очевидно, в предложении [2 :23] окружность К можно заменить,
например, контуром треугольника.
[2 :241]. Назовём допустимой такую деформацию Q, 0<6^1,
отображения С=С0, при которой данная фиксированная точка р
никогда не попадает на множество С9 (е0ег) и для всех 0 <^6<С1, имеем
Тогда для всех данных значений 6, 0<^^<;1, число ®сь(р)
определено; в силу непрерывности функции Fa (p, С, х) относительно С
и целочисленности о>с6(/>), все <*>се(р), 0 <1 Ь <Л, равны между собою.
Итак:
[2:24]. Порядок ^с(р) не меняется при допустимых
деформациях отображения С.

§ 21 УГЛОВАЯ ФУНКЦИЯ ОТОБРАЖЕНИЯ ОТРЕЗКА В ПЛОСКОСТЬ 75
2:3. Формула сложения. Пусть даны два отрезка числовой
прямой etfl и е^ е0<ег<е2; пусть Cjji С2_суть непрерывные
отображения, соответственно, отрезков е0ег и еге2 в плоскость/?2,
удовлетворяющие условию
(2 :31) Cj (О = О, (*,).
Обозначим через С отображение отрезка е0е2, совпадающее с Сг на е0ег
и с С2 на ^^2- Пусть, наконец, р— точка плоскости R2, не
принадлежащая множеству
Сг {etf>> U С2 ^^2) = С(е0е2).
Тогда (арт. [2 : 1], замечание 2)
(2 : 32) Feo (р, С, е2) = Feo (р, С, *2) + Fei (р, С, *а).
Пусть теперь
(2 :33) С(е0) = С(ег) = С{е2)
[т. е. С, (е0) = С, (ег) = С2 (*^ = С2 (*а)].
Тогда определены co^ip), <°Св(р), ®с(р\ и из определения этих
чисел и из формулы (2 : 32) легко следует
(2 : 34) «с (Р) = <°Cl(p) + <»Ъ(р)'-
Нам понадобится в дальнейшем одно приложение формулы (2: 34)
c7 = Ci(0) = C1(2) = C1(4),
ft = C1(l) = C1(3),
C^^QiOl),
I (5^7=^(23"
(Й5) = C!*(34). 4epT. 12.
Рассмотрим отрезок 04 числовой прямой и непрерывное
отображение Cj этого отрезка в /?2, удовлетворяющее следующим условиям:
(2:35) ( С1(4) = С1(2) = С1(0),
\ С1(2^Гх) = С1{2—х) для 0<*<1Э
откуда следует
^(3)^(1).
Пусть р£/?2— точка,_не принадлежащая множеству Сг (04),
Отображения отрезков 02 и 24, порождаемые отображением С}, обозна*

76
ТЕОРЕМа ЖОРДАНА
[гл. и
чим соответственно через С02 и С24, Обозначим, наконец, через С0
отображение отрезка 04, определённое так:
Г С0(х) = С1(х) для 0<л:<1 и для 3<*<4,
1 С0(х) = С1(1) = С1(3) для 1 <*<3.
Тогда определены числа <»>#,(/?), <^с^(р)У ®с**(р), ^сй(р), и имеет
место равенство
(2 : 36) шСо (/?) = ш^о» (р) -f и>с» (р).
В самом деле, из (2 : 34) следует
<»с, (р) = «с» (р) + «с* (р).
Остаётся, таким образом, доказать, что о)Со(/?) = а)е1 (р).
Но отображение С0 получается из С1 допустимой деформацией
Сь(х)^С1(х), |
С6(1 + х)=С1(1+6х), 0<*< 1,
^(2 + ^ = ^(1+6(1—^)), 1>6>0,
С8(3 + *) = С1(3 + *); j
откуда, в силу неизменности ш^(р) при допустимых деформациях
отображения С, сразу вытекает равенство ®с0(р) = <°Ci(P) и>
следовательно, равенство (2 : 36).
2:4. Порядок точки относительно жордановой кривой. На
протяжении всего этого параграфа Ф означает жорданову кривую,
лежащую в плоскости R2. Простым отображением отрезка
01 числовой прямой на жорданову кривую Ф назовём всякое
непрерывное отображение С отрезка 01 на Ф, при котором открытый
интервал (01) отображается топологически, и
С(о) = с(1) = *'€Ф.
Всякое простое отображение отрезка 01 определяет некоторое
направление обхода кривой Ф: если 0<я<£< 1, то мы считаем, что
простое отображение С порождает на жордановой кривой Ф
направление обхода ег С (а) С (b)ef.
Докажем следующее предложение:
[2:41]. Пусть р£/?2\Ф, С и Сг — два простых отображения
отрезка 01 на жорданову кривую Ф, порождающих на Ф одно и то же
направление обхода. Тогда
®0 (Р) = ш<?' (Р)'
Для доказательства достаточно, на основании [2:24], показать,
что простые отображения С и С', порождающие на Ф одно и то же

С 2] УГЛОВАЯ ФУНКЦИЯ ОТОБРАЖЕНИЯ ОТРЕЗКА В ПЛОСКОСТЬ 77
направление обхода, могут быть переведены друг в друга
деформацией С9, 0<;6<;i, при которой для всех значений 6, 0 ^ 6 ^ 1
имеем
(2:41) С9(01) = Ф, Св(0) = Св(1) = *'.
Это утверждение достаточно доказать для случая, когда Ф есть
окружность длины 1. Но в этом случае оно следует из предложения:
[2 : 42]. Пусть С0 —какое-нибудь простое отображение отрезка 01
на окружность Ф длины 1; отображение Сх определяется так:
Ci(0) = C0(0) = e';
для 0-<х-<1 определяем Ci{x) как конец дуги длины х,
отложенной по окружности Ф от точки е! в направлении, порождённом
отображением С0.
Тогда отображения С0 и С1 переводятся друг в друга
деформацией CQ, удовлетворяющей условию (2 :41).
В самом деле, положим для каждого 6, 0 <6^1,
Q(0)-C6(1) = C0(0).
Рассмотрим при0<д:<1 ту дугу Lx = С0 (л:) Сх (х) окружности Ф,
которая имеет своими концами точки С0(х) и Cf(-x) и не содержит
точки е'\ определим Сь(х) как точку, делящую дугу Lx в
отношении 6 : (1 — 0). Определённое таким образом CG есть непрерывная
деформация.
Упражнение. Доказать, что два простых отображения С0 и Cv
порождающих на Ф противоположные направления обхода, не могут
быть деформируемы друг в друга.
Определение [2:4]. Пусть даны ориентированная жорда-
нова кривая Ф и точка р£/?2\Ф; число а>с(р)> где С— какое-нибудь
простое отображение отрезка 01 на Ф, порождающее на Ф данное
направление обхода, называется порядком точки р относительно
ориентированной жордановой кривой Ф и обозначается через ш(р,Ф),
Нам понадобится, наконец, следующее предложение:
[2 : 43]. Пусть на плоскости R^ ламы три простые дуги с общими
концами а, Ь> не имеющие попарно никаких общих точек кроме
концов. Обозначая эти дуги соответственно через abv ab2> ab&
а ориентированные дуги соответственно через (ab)v (ра)х; {ob)2,
{Ьа)2; (аЬ\у (£а)3, имеем ср" ^т?:г^з^»;нт:г жорд-псиы кривые
Jab)1 U \Ьа)ъ ТаЬ)г U Jba)27 Jah).z U (Ьа)ъ.
Тогда для любой точки р, не лежащей ни на одной из данных трёх
дуг, имеем
(2:43) <о (р, &Ь)г U (*5)9 ) -f © (a Jab\ U (te)8) = а>(р, Щг U (^)8).

78
теорема жордана
[гл. и
Эта формула вытекает из (2 : 36) и из следующего почти
очевидного предложения:
[2 : 431]. Пусть дано непрерывное отображение С0 отрезка 01
на жорданову кривую Ф, определённое следующим образом: С0
отображает топологически отрезок 0 -^ на некоторую дугу кг = е'е'г с: Ф,
далее,
и, наконец, отрезок -~-1 отображается топологически на дугу Л2 =
= е[е' £ Ф, отличную от Х1# Отображение С0 переходит при помощи
деформации Q, удовлетворяющей условию (2 : 41), в простое
отображение.
Это предложение достаточно доказать в предположении, что Ф
есть окружность длины 1. В этом случае и Си и С9 определяются
совершенно так же, как и при доказательстве [2 :42].
2:5. Порядок точки p£R2 относительно непрерывного
отображения окружности в R2\p; степень непрерывного
отображения окружности в окружность*). Пусть Sp — ориентированная
окружность; длину её для простоты принимаем за 1. На S$ выбираем
произвольную точку do. Направление обхода на S^ называем
положительным, если оно совпадает с выбранной на S^ ориентацией.
Пусть (У— непрерывное отображение окружности S$ в
плоскость R2; пусть p£R2 не принадлежит множеству С$ (5^).
Обозначим через С91 непрерывное отображение отрезка 0<><Л
на окружность S^ ставящее в соответствие каждой точке х, 00^1,
конец дуги длины х, отложенной на S$ в положительном
направлении от точки а*.
ТогдаС=СРС?1 есть отображение отрезка 01 в R2\p,
удовлетворяющее условию С(0) = С(1).
Порядок точки относительно отображения С, как легко видеть,
не зависит от выбора промежуточного отображения С^1 (т. е. от
выбора точки Яр, вполне определяющей это отображение С^1).
Таким образом, порядок точки р относительно отображения
С=*ОС£ зависит только от отображения (У (а также от выбран-
ной ориентации окружности S$ и направления положительного
отсчёта углов в R2). Поэтому естественно назвать этот порядок
порядком точки относительно отображения (У окружности S^ в /?2\р»
т. е. положить по определению
v<fl(p) = <»c(p)-
*) Этот артикул при доказательстве теоремы Жордана применяться не
будет.

& 2] УГЛОВАЯ ФУНКЦИЯ ОТОБРАЖЕНИЙ ОТРЕЗКА В ПЛОСКОСТЬ 79
Пусть теперь Sa — лежащая в R2 окружность с центром р,
ориентированная в направлении положительного отсчёта углов в /?2.
Пусть С? есть непрерывное отображение S^ в Sa. Тогда только
что определённый нами порядок центра р окружности Sa
относительно непрерывного отображения С£ окружности S$ в Sa
называется степенью отображения С®.
Задача этого артикула показать, что степень отображения СЩ
вполне характеризует гомотопический класс *) этого отображения.
Для этого определим прежде всего так называемое нормальное
отображение С$ степени ш (где со — произвольное целое число).
Для простоты предполагаем, что обе окружности Sa и S$ имеют
длину 1.
Выберем раз навсегда определённые точки а^ £ S^ и аа £ Sa.
Нормальным отображением степени оо окружности S^ в 5в называется
отображение v£? ставящее в соответствие каждой точке ££*Sp точку
v£(£) £ Sa, определённую следующим образом. Берём дугу а£ на So
в положительном направлении. Откладываем на Sa от точки аа в по_
ложительном направлении, если (о > 0, и в отрицательном направле.
нии, если о><0, дугу аач\, длина которой равна умноженной на | со |
длине дуги а£. Конец г\ дуги aaf\c:Sa и есть по определению
точка v£(£). Отображение v£, очевидно, имеет степень со;
нормальное отображение степени нуль есть отображение окружности S^
на точку ал.
Поставленная цель будет достигнута, если мы докажем
следующие два предложения:
[2:51]. Всякое непрерывное отображение С\ окружности S*
в Sa гомотопно нормальному отображению степени, равной
степени отображения О.
[2:52]. Два гомотопных между собою непрерывных отобра»
женин ориентированной окружности S* в ориентированную
окружность Sa имеют одинаковую степень.
Доказательство [2:51]. Заметим прежде всего: всякое
непрерывное отображение окружности S^ в Sa гомотопно такому
отображению, при котором С^(ао) = аа. (Гомотопия осуществляется
простым поворотом на соответствующий угол.) Поэтому
достаточно доказать теорему [2:51] лишь для отображений С£,
удовлетворяющих условию Cjj(<Zp) = aa. Переходим к этому
доказательству.
Пусть степень отображения (Уа есть со. Рассмотрим непрерывную
функцию F(fi(x)9 определённую на всей числовой прямой следующим
образом.
*) См. главу 1, арт. [7:4].

80 ТЕОРЕМА ЖОРДАЙА [ГЛ. Й
Для 0<ХЛ полагаем
Fcs (x) = F0(p, С, х\
где C=ClC2l и р—центр окружности Sa (отображение С?1
определено, как выше; точка a^^S^ всё время фиксирована). Для всех
остальных значений х определяем F$ (х) при помощи функциональ-
ного уравнения
F(fi (x -f 1) = F(fi (x) -+- 2тгш;
ос а
ПОМНИМ, ЧТО О) =г= <ас (/?) = — FQ (/7, С, 1).
Функция Fc$(x) (при фиксированной точке а3) однозначно опреде-
ос ^
лена отображением С$ и называется угловой функцией,
соответствующей отображению С|.
Назовём вообще угловой функцией всякую действительную
непрерывную функцию F(x), определённую на всей числовой прямой
и удовлетворяющую условиям
/40) = О,
F(x-\-l) = F(x) + 2vt,
где у — некоторое постоянное целое число.
[2 :511]. Всякая угловая функция F{x) есть угловая функция,
соответствующая некоторому непрерывному отображению С\
окружности S^ в Say при котором С\(а^) = аа.
В самом деле, отнесём каждой точке Ь=С%1х окружности S$
точку 7] окружности Sa, имеющую полярный угол F(x)
(отсчитываемый от точки аа). Эту точку ч\ назовём С£ (£). Из свойства угловой
функции легко следует, что С| есть однозначное непрерывное
отображение окружности Sp в Sa.
Очевидно, F (х) есть угловая функция, соответствующая
отображению С\. Так как, с другой стороны, образ точки S = C^jc g 5p
при отображении L? однозначно определён своим полярным углом
FcHx)> то существует лишь одно непрерывное отображение С|
^удовлетворяющее условию С1(аэ) — яа), которому соответств}"ет данная
угловая функция
F(x)=*F(fl(x).
Итак, установлено взаимно однозначное соответствие между
удовлетворяющими условию С?(ар) = я0 непрерывными отображениями
О окружности Sp в окружность Sa и угловыми функциями.

§ (2) УГЛОВАЯ ФУЙКЦИЯ ОТОБРАЖЕНИЯ ОТРЕЗКА В ПЛОСКОСТЬ 81
Отметим, наконец, ещё следующее предложение, доказательство
которого может быть предоставлено! читателю:
[2 :512]. Если Fq(x\ 0<!6^;i, есть семейство угловых функций,
непрерывно зависящих от параметра 6, то соответствующие им
непрерывные отображения С£ также непрерывно зависят от параметра 6.
После этого доказательство теоремы [2:51] доводится до конца
без всяких затруднений.
Возьмём угловую функцию F (х) = F0(x), соответствующую
данному отображению С£ степени ш, и положим 0<;6<Л
Гь (Х) = (! _ в) F (х) + 2*8а>*.
Докажем, что F$ (х) есть угловая функция. Так как
/>,(0) = (1 — 6)F(0) = 0,
то достаточно доказать равенство
FB(x+l) — Fb(x)*=2™.
Но
Fo(x+l) — Fb(x) = (l — b)lF(x+l) — F(x)] + 2Tzto.
Так как F (х) есть угловая функция, соответствующая
отображению С? степени ш, то
ее *
F(x + l) — F(x) = 2™,
так что
Fb (X -}-1) — /'в (*) = (1 — Q) 2тго) 4- 2тг6ш = 2™
и т. д.
Итак, все FB (x) суть угловые функции, непрерывно зависящие от
О и переводящие F0 (x) в угловую функцию
F^x) = 2тто)Х,
которой, очевидно, соответствует нормальное отображение степени со;
этим, в силу предложения [2:512], доказана вся теорема [2:51].
Доказательство [2:52]. Пусть даны два гомотопных
отображения 0(У и хС^. Требуется доказать, что они имеют одну и ту
же степень
Пусть 0С£, ХС\ переходят друг в друга при помощи деформации
«ер, о<е<ь
Берём отображение С?1 отрезка 01 на окружность S^
определённое в начале этого артикула (стр. 78). Тогда еС^С0.1 представляет
собою допустимую деформацию отображения ъС^СР} в отображение
l^jjC^1, так что на основании [2:24] порядок центра р окружности
S* относительно отображений оС%С°* и хСНУ* один и тот же. А это
О Александров Л. С»

82
ТЕОРЕМА ЖОРДАНА
[гл. п
и значит, что отображения 0С$ и г(Уа (окружности S$ в окружность
Sa) имеют ту же степень. Теорема [2:52] этим доказана.
Доказанные нами в этом артикуле факты — теоремы [2:51],
[2 :52] и факт существования для любого целого числа ш нормального
отображения степени ш — могут быть объединены в одно предложение.
[2:5]. Существуют непрерывные отображения
ориентированной окружности So в ориентированную окружность Sa любой
заданной степени о; два непрерывных отображения S* в Sa тогда
и только тогда гомотопны между собою, когда они имеют одну
и ту же степень.
Замечание 1. Пусть'С—какое-нибудь непрерывное отображение
окружности So, в R2\p; пусть SaczR2— окружность с центром в р; пусть
Са—центральная проекция (из точки/?) множества R2\p в Sa.
Порядок точки р относительно отображения С равен степени
отображения СаС окружности Sq в Sa. (Это утверждение следует из [2:24].)
Замечание 2. Методы этого параграфа допускают очень
разнообразные приложения — в анализе, в теории функций комплексного
переменного и т. д. Так, например, можно доказать основную теорему
высшей алгебры буквально в двух словах при помощи понятия порядка
точки относительно непрерывного отображения.
§ 3. Теорема: простая дуга не разбивает плоскость.
Определение [3:1]. Пусть Ф — замкнутое множество, лежа»
щее в плоскости /?2; мы скажем, что Ф не разделяет друг от друга
точек р и q открытого множества R2\Фf если р и q принадлежат
к одной компоненте множества /?2\Ф, т. е. могут быть связаны
простой ломаной линией, лежащей в Я2\Ф.
Для доказательства заглавной теоремы этого параграфа заметим,
прежде всего:
[3:2]. Даны: простая дуга Ф = аЬ, лежащая на плоскости /?2, и
точка с этой дуги, отличная от Ь\ кроме того, даны точки р, q в
Г = /?2\Ф. Предположим, что дуга ас сФ не разделяет точки р и
q (в случае с = а дуга ас обращается в точку а). Тогда можно
найти такую точку с' на дуге <с^>сф, что дуга асг также не
разделяет точки р и q.
В самом деле, пусть pq ломаная, соединяющая точки р и #ине
имеющая общих точек с ас. Тогда
p(ac,pq) = e>0.
Возьмём точку с' на дуге cb так близко к точке с, что
8(cc')<s-
Очевидно, се', а следовательно и ас', не имеет общих точек с pq,
что и требовалось доказать.

к 3| теорема: простая дуга не разбивает плоскость 83
[3 :3], Пусть тонки р a q не разделены никакой простой дут
гой ас, лежащей на ab и отличной от всей дуги ab. Тогда дуга
^Ь также не разделяет точек р и q.
Прежде чем доказывать эго предложение, выведем из [3:2] и
[3 :3] заглавную теорему этого параграфа.
Пусть простая дуга Ф = ab разбивает плоскость. Тогда имеются
две точки р и q, разделённые дугой ab.
Множество, состоящее из единственной точки а, очевидно, не
разделяет точек р и q. Поэтому на основании [3:2] можно найти
дугу аа\ лежащую на ab и не разделяющую точек р и q.
Обозначим через с верхнюю грань [на ориентированной дуге (ab)] множества
тех точек ar £ ab, для которых дуга
aal^ab не разделяет точек р и q.
В силу [3 :3], дуга ас не разделяет
точек р и q. В силу [3:2], точка с
совпадает с by т. е. ab не разделяет
точек/7 wq. Итак, остаётся доказать [3:3].
Обозначим через К! такой круг
с центром Ьу что точки а, р, q лежат
вне К'. Пусть с' — последняя на (ab)
точка пересечения дуги ab с
окружностью /Со круга К!. Дуга асг с ab
находится от точки b на положительном
расстоянии. Пусть К— круг с центром b
и радиусом, меньшим чем р (р, асг)\
окружность этого круга обозначим че- Черт. 13.
рез К0. Таким образом, первая [на (ab)]
точка ^множества К0 ftab лежит на (ab) за последней точкой множеств
Ко U ab, так что все точки, следующие на (ab) за какой-
нибудь точкой множества K0fl ab, лежат внутри К!.
Докажем теперь [3 : 3] сначала в том частном случае, когда
множество ab П Kq состоит из единственной точки с.
Так как ас по предположению не разделяет точки/? и q, тосущест-
вует ломаная pq, не пересекающаяся с ас (черт. 13). На
ориентированной ломаной (pq) обозначим через рх первую и через qL —
последнюю точку пересечения её с К0. Обе точки рг и qt отличны от
точки с, а поэтому могут быть соединены дугою pxqx окружности /С0,
не содержащей точки с. Линия 'рр1 U ptqx U qxq (где pp1czpq, ргдх а
^i(0,^c/?^) соединяет точки р, q и не имеет общих точек с ab.
Переходим к случаю, когда ab П К0 состоит более чем из одной
точки (черт. 14).

84
ТЕОРЕМА ЖОРДАНА
[гл. и
Обозначим через А = (^д?2) какой-нибудь смежный интервал к
множеству ab П К0 на окружности К0, ориентированный в
положительном направлении (т. е. в направлении, соответствующем обходу К0
против часовой стрелки).
Через kt = (d2dt) обозначим ориентированную дугу окужности
/С0, дополнительную к дуге к (таким образом, направления, взятые
на к и Я1} суть направления, соответствующие обходу К0 против
часовой стрелки).
Рассмотрим какое-нибудь топологическое отображение С°х
отрезка 01 числовой прямой на_ простую дугу Я; далее, топологическое
отображение С1^ отрезка (Г2) на ориентированную дугу (a\dj cTaF,
затем топологическое
отображение C^t отрезка (23) на дугу
{dxd^)CLab\ определённое
равенством
^(2+аг) = С^(2-^
0<х<1,
и, наконец, топологическое
отображение С\ отрезка (34) на кх.
Отображения Ck, Cd%dl, Cdldt,
С\х вместе составляют
отображение С отрезка 04, причём мы
находимся в условиях (2 :35);
соответствующее отображение
С0 есть, очевидно, отобра-
Черт. 14. жение отрезка (04) на
окружность /С0, ориентированную против
часовой стрелки. Отображение С02 есть отображение 02 на
«замкнутый путь», состоящий из дуги к и дуги (d2d1)cz(ab), а отображение
Си есть отображение 24 на «замкнутый путь», состоящий из дуги
(dtd2) с ab и дуги кг. При этом по формуле (2 :36) для любой точки х,
не лежащей в KQ U d2dt (где d.2dxczab)> имеем
(3 :31) соСо (лг) = coco, (x) -f co^ (*),
т. е.
(3 :ЗГ) »oiW = ffl(iW-fflc»(4
Вся дуга d2d1czab состоит из точек, следующих на (я£) за одной
из точек d2i dx этой дуги, т. е. за некоторой точкой множества К0 П ab;
поэтому дуга d^d^aab лежит внутри круга К\ значит, и всё
множество С02 (02) = kU d2dx лежит внутри К'. С другой стороны, точки р

§ з]
теорема: простая дуга не развивает плоскость
85
и д лежат вне круга К'% поэтому, на основании [2 :22],
(3: 32) <»с« (р) = 0, ©с«(?) = 0.
Обозначим через с последнюю, считая по дуге {ab), точку
пересечения этой дуги с окружностью К0.
Среди ломаных рд, соединяющих точку р с точкой д,
назовём допустимыми те, которые удовлетворяют следующим
условиям:
1. рд не имеет ни одной общей точки с дугой ас.
2. Ни одна вершина ломаной рд не лежит на окружности К0.
3. Ни одно звено ломаной рд не касается окружности К0.
Допустимые ломаные рд существуют. В самом деле, по
предположению, точки р,д можно соединить ломаной, не имеющей ни одной
общей точки с дугой ас. Взявши
такую ломаную, можно сколь
угодно малым видоизменением её,
ясным из черт. 15, достигнуть
того, чтобы условия 2 и 3 также
были выполнены.
Если допустимая ломаная рд
имеет общие точки с ab, то все
эти точки лежат на дуге (cb)cab,
т. е. внутри круга К, поэтому,
если допустимая ломаная рд Черт. 15.
имеет общие точки с ab, то
она непременно пересекает окружность К0, причём ни одна из
точек пересечения рд с К0 не принадлежит дуге ab.
[3:31]. Если допустимая ломаная рд пересекает К0, то её
всегда можно заменить допустимой ломаной (рд)', число
точек пересечения которой с К0 меньше, чем у первоначальной
ломаной рд-
Доказательство [3:31]. На ориентированной ломаной (рд)
различаем среднее точек пересечения с Ко «точки входа», в
которых (рд) входит внутрь круга К, и «точки выхода», в
которых (рд) выходит из круга К.
Пусть /?! есть первая на (рд) точка входа. Она лежит на
некотором смежном интервале К (черт. 14). Так как концы dt и d2
интервала А суть точки пересечения К0 с ab, а точка с есть
последняя на (ab) точка множества К0 П ab, то все точки дуги (dxd2) cz ab
предшествуют на (ab) точке с; поэтому ломаная рд не имеет ни
одной общей точки с дугой d^d^ cz ab. Обозначим через х перемен-

86
ТЕОРЕМА ЖОРДАНА
[гл. н
ную точку ломаной (pq). Так как точка рх не принадлежит к
множеству C2i(24) = d1d2 U Х1э то <йс*(х) при переходе через точку рх
не меняется. Что же касается функции (oqq (лг), то она при переходе
через точку р{ и вообще через любую точку входа, лежащую на Я,
очевидно, испытывает скачок-}- 1. Вследствие равенства (3 : 310
функция (Q(/*(x) при переходе через лежащую на I точку входа также
испытывает скачок -f-1.
Так как <»#<» (q) = 0, то при движении по ломаной (рд) от рх
к д непременно должны встретиться точки пересечения рд с С02(02)==
= d%dx U А, т. е. точки пересечения рд с А; среди них, в силу
только что доказанного, должны быть точки выхода. Пусть
д1—последняя на (рд) точка выхода, принадлежащая интервалу X.
Возьмём две точки рх и qf лежащие на (рд) весьма близко,
соответственно, к рх и qu причём р1 предшествует на (рд) точке ръ а
q'± следует на (рд) за qv Очевидно, если р'± и qx взяты достаточно
близко к рх и qu то обе они будут лежать вне круга К- Так как
дуга р1<71 сг X находится на положительном расстоянии от ab, то —
всё в том же предположении, что р[ и qx взяты достаточно близко
к р1 и qx— существует ломаная prq'v лежащая целиком вне К,
проходящая весьма близко к дуге pxqx cr I, и не имеющая общих точек с ah.
Возьмём теперь ломаную
состоящую из куска ррх ломаной pq^ из только что построенной
ломаной pxqx и из куска q'±q ломаной pq. Полученная лома-
ная pprx U p[q[ U q[q есть, очевидно, допустимая ломаная; число
её точек пересечения с /С0, по крайней мере, на два меньше, чем число
пересечений с К0 первоначально данной ломаной pq.
Предложение [3 : 31] этим доказано. Доказана и вся теорема [3 : 3],
так как, применяя конечное число раз предложение [3 : 31] к какой-
нибудь допустимой ломаной pq, получим в конце концов допустимую
ломаную, соединяющую точки р и q, не имеющую ни одной точки
пересечения с К01 но такая допустимая ломаная, соединяя точки р и q,
не имеет, как мы знаем, общих точек с ab, что и требовалось доказать.
§ 4. Доказательство теоремы Жордана.
4:1. Основное вспомогательное построение. Обозначим через s
произвольную точку плоскости, не лежащую на кривой Ф. В течение
всего этого артикула точка s будет одна и та же.
Проведём из точки ^ два различных луча saf и sb\ где а\ bf —
какие-нибудь точки кривой Ф. На каждом из этих лучей устзноэим

§ 4]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЖОРДАНА
87
направление движения от s к а!, соответственно от s к У. После
этого обозначим через а первую точку пересечения луча sa' с Ф,
а через b— первую точку пересечения луча sbr с Ф.
Возьмём на кривой Ф определённое направление обхода; его будем
условно называть положительным. Из двух дуг, на которые кривая Ф
разбивается точками а и Ь, обозначим через Аг ту, по которой
движение от точки а к точке b идёт по положительному направлению,
а вторую из поименованных дуг обозначим через Л2.
Обозначим теперь через Фх ориентированную жорданову кривую,
-> —>
состоящую из дуги Ai = (ab) и из ломаной (bsa). Обозначим через Ф2
—>•
ориентированную жорданову кривую, состоящую из дуги А2 — (Ьа)
и из ломаной (asb). Мы находимся в условиях [2 : 43], так что для
любой точки /?, не лежащей ни на Ф, ни на ломаной (asb), имеем
(4:11) со (р, Фг) -f о) (р, Ф2) = о) (р, Ф).
Пусть точка х пробегает дугу Л2. Тогда функция ш(х, Фг) всё
время определена и остаётся постоянной. Постоянное значение её
->
для всех х£ А2 обозначаем через <av Точно так же, функция ш(х, Ф2)
постоянна на А1; её значение для всех x£At обозначаем через о>2.
Докажем следующую основную лемму:
[4 : 11]. Пусть для какой-нибудь точка /?£/?2\Ф имеет место,
по крайней мере, одно из неравенств
(4 : 12) ш (р, Фг) ф a)lf со (р, Ф2) ф ш2.
Тогда точки pus могут быть соединены ломаной,
лежащей в /?2\Ф.
Доказательство. Пусть, например,
(4 : 121) ^{р^г)Ф^\
вследствие основной теоремы § 3 существует ломаная ps,
лежащая в /?2\АГ Пусть pj — первая [на (ps)] точка, принадлежащая
ломаной asb. Тогда на куске (ррх) ломаной ps нет ни одной точки
кривой Фр так что со(лг, Ф^ определено и постоянно для всех
точек х^ррх\ при этом, в силу (4 : 121), значение функции о>(х, Фх)
для всех х£ррг отлично от <ог, т. е. от значения той же функции на А2,
откуда следует, что ни одна точка ppt не является точкой А2.
Другими словами, ломаная ppv не 'пересекаясь с дугой Аи не
пересекается^ с А2. Значит, она не пересекается и с Ф. Точка рг лежит
на asb и отлична от точек а, Ь; следовательно, она может быть

88
ТЕОРЕМА ЖОРДАНА
[ГЛ. II
связана с s отрезком pj$, лежащим на (asb). Ломаная ррх (J pxs
связывает р с s в /?2\Ф, чем лемма доказана.
4:2. Случай o>(s,Ф) = 0; множество Г = /?2\ф состоит, по
крайней мере, из двух компонент. Проведём прямую D, не
пересекающую Ф, так что Ф лежит в одной из двух полуплоскостей,
на которые плоскость /?2 разбивается прямой D; в той
полуплоскости, которая не содержит точек кривой Ф, выбираем произвольную
Черт. 16.
точку s. Точка 5 остаётся одной и той же на протяжении всего
этого артикула (черт. 16).
На основании [2 :22] имеем
(4 :21) со(^,Ф) = 0.
Докажем, что в наших предположениях относительно точки 5 и
в обозначениях предыдущего артикула:
[4 :21]. Одно из двух чисел <о1? ш2 равно нулю, а другое ±1.
Доказательство. Обозначим через а0 и Ь0 точки пересече,
иия прямой Л, соответственно, с лучами sa и sb. Проводим из 5
ЛУЧ sq0t пересекающий прямую D в некоторой точке #0, лежащей
между а0 и bQ. Пусть q— точка, лежащая на sqQ между s и q0.
Обозначим через Ф.3 ориентированную жорданову кривую, состоящую
~> -> '
из дуги Аг = (аЬ)аФ и ломаной bb0a0a. Наконец, обозначим через А
>
ориентированный в направлении a0b0s контур треугольника a0bQs.
Тогда по теореме [2 : 43J имеем

с 4] ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЖОРДАНА 89
Но
o)(qr,A) = ztl, <о(?,Ф3) = 0,
так что
—>•
(4 : 211) <а(д,Фг) = ±:1.
Подобным же образом получаем
—>
(4 : 212) ©(?^2) = ±1.
Если точка дг скользит по лучу sq в бесконечность, то рано или
поздно делается, и потом навсегда остаётся
о (х,Фг) = 0, со (*, Ф2) = 0.
->
Поэтому луч sq пересекает как дугу Аи так и дугу Л2.
Пусть At есть первая дуга из двух дуг Aj и А2, с которою
мы встречаемся, идя по лучу sq в бесконечность. Покажем, что
в этом случае .*)
(4:213) ш2==.±1, о)1==:0.
Пусть #j есть первая точка луча sq, принадлежащая дуге Л^
отрезок qqx не имеет общих точек с Ф2, так что (о (х, Ф2) постоянно
—> —►
для точек этого отрезка; так как со (q, Ф2) = ± 1, то и (о (д^, Ф2) = ±1.
Так как ^ £Л1? то
(4:214) ш2 = ±:1.
В частности, если q' есть последняя точка луча sq, лежащая
на Ар то
(4:215) ш(^, Ф2) = ±1.
Отсюда и из того, что со (л:, Ф2) = 0 для всех достаточно далё-
■—>
ких от кривой Ф точек луча sq, следует, что, идя по этому лучу
от точки q'x в бесконечность, мы непременно встретим кривую Ф2 и,
следовательно, дугу А2. Пусть #2 есть первая точка луча sq, лежащая
за точкой q' и принадлежащая дуге А2. Так как q^ — последняя
на луче sq точка А1э то со (л:, Фх) постоянно на всём протяжении
*) Этим и будет доказано [4:21]. Если бы первой дугой, с которой
зстречается луч sq, была бы дуга Л2, то было бы

90
ТЕОРЕМА ЖОРДАНА
[гл. и
луча sq от точки q[ до бесконечности, и это постоянное значение
функции ш (л:, Фх) равно нулю. Таким образом,
Так как q2 £ Л2, то из последнего равенства следует
(4:216) coj = 0.
В (4:214) и (4:216) содержится утверждение (4:213), так что
[4:21] доказано.
■—> —>
Замечание. Так как ш(х,Ф1) = 0 для всех точек х луча sq,
лежащих за точкой q то, в частности, имеем для произвольной,
лежащей между д'± и q% точки q12 этого луча,
(4:217) в)(?12,Ф1) = 0.
Докажем топерь, что кривая Ф разбивает плоскость /?2, по
крайней мере, на две компоненты. Так как во всех достаточно далёких
от кривой Ф точках р £ /?2\Ф имеем ш (р, Ф) = 0, то, на основании
теоремы [2:21], достаточно найти какую-нибудь точку р £ /?2\Ф,
для которой со (/?, Ф)^0. Покажем, чго такой точкой является,
например, точка q12. В самом деле, так как отрезок q[q12 не
имеет общих точек с Л2, значит, и с Ф2, то
<»(?i2>$2) ==<»(?i> С)-
Следовательно, на основании (4:215),
(4:218) ш(?12,Ф2) = ±1.
Из (4:218), (4:217) и (4:11) следует
(4:219) а)(?12|'ф) = ±Ь
что и требовалось доказать.
Выведем из [4:11] и [4:21] следующее предложение:
[4:22]. Всякая точка /?£/?2\Ф, удовлетворяющая условию
(4:220) а>(р,Ф) = 0,
может быть соединена с точкой s ломаной, лежащей в /?2\Ф.
Доказательство. На основании (4:11) из (4:220) следует

§ 4]
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ЖОРДАНА
91
Отсюда и из [4:21] заключаем, что, по крайней мере, одно из
неравенств
должно иметь место, так что [4:22] вытекает из [4: 11].
— —>■
Так как для всех точек х ломаной sp с /?2\Ф функция со (л;, Ф)
сохраняет постоянное значение, то множество всех точек,
удовлетворяющих условию (4:220), связно; оно, кроме того, очевидно, открыто,
значит, представляет собою область Г0с/?2\Ф. Из [2:21] следует,
далее, что область Г0 является одной из компонент множества /?2\Ф.
4:3. Окончание доказательства теоремы Жордана. Итак, мы
доказали:
[4:31]. Число компонент множества /?2\Ф не менее двух,
причём множество точек р £ /?2\Ф, для которых
(4:31) о>(р, Ф) = 0,
образует одну из компонент множества R2 \Ф.
Остаётся доказать:
[4:32]. Множество точек р^/?2\Ф, для которых
(4:32) со(/7, Ф)#°,
образует вторую компоненту множества /?2\Ф.
Для этого, в свою очередь, достаточно доказать:
[4: 320]. Пусть точки sup множества /?2\Ф
удовлетворяют условиям
(4:320) а)(5, Ф)^0, ш(/?, Ф)^°>
тогда существует ломаная sp с /?2\Ф, соединяющая точки pus.
Доказательство [4:320]. Точка s, упомянутая в [4:320],
остаётся во всём этом артикуле одной и той же. Для неё мы делаем
построение арт. 4:1. Докажем теперь, в наших теперешних
условиях, в обозначениях артикула 4: 1, равенство
(4:321) ш1=ш2 = 0.
Возьмём какой-нибудь круг Q, содержащий внутри себя кривые
Ф, Ф1? Ф2. Пусть s0 есть точка, лежащая вне круга Q. Тогда
(4:322) о)(50>Ф) = 0,
(4:323) ш(*0Д) = 0,
(4:324) а>(501Фа) = 0.
Пусть s0s — ломаная, соединяющая точки sQ и s в /?2\Aj (такая
ломаная существует в силу § 3). Так как функция ш(х, Ф)
принимает для х — $0 и x = s различные значения, то ломаная SqS пере-

92 ТЕОРЕМА ЖОРДАНА [ГЛ. II
секает Ф и, следовательно (так как она не пересекает AJ, имеет
общие точки с Л2. Пусть с2 есть первая лежащая на (s0$) точка
дуги А2. Тогда функция оо (х, Ф) сохраняет на куске s0c2 ломаной
s0s постоянное значение, равное а>($0, Ф), т. е. нулю. С другой
стороны, на отрезках (sa) и (sb) функция со (х, Ф) также постоянна и
принимает значение oo(s, Ф)фО. Отсюда следует, что ломаная (s0c2) не
имеет ни одной общей точки с ломаной asb, а значит, и с кривой Ф^
Поэтому функция (о (х, Фг) сохраняет на s0c2 постоянное значение,
равное, в силу (4:323), нулю. Так как с2£А2, то (о1==0.
Совершенно таким же образом доказывается, что и а>.3 = 0.
Из равенства (4:321) утверждение [4:320] следует без всякого
труда: в самом деле, вследствие (4:32), (4:321) и (4:11), по
крайней мере, одно из неравенств
® (А фг) Ф<*и* (рЛ*) Ф®2
должно иметь место, а тогда [4:320] вытекает из основной леммы
[4:11]. Этим всё доказано.
Из [4:31], [4:32] и (4:218) следует:
[4:3]. Если Ф есть жорданова кривая и Г0, Г — две области,
на которые она разбивает плоскость, то для всех точек р
каждой из этих областей оо(/?, Ф) принимает одно и то же
значение, равное нулю для внешней (т. е. неограниченной) области
и равное ± 1 для внутренней (т. е. ограниченной) области.

ГЛАВА ТРЕТЬЯ.
ПОВЕРХНОСТИ.
В этой главе устанавливаются топологические типы простейших
двумерных фигур — замкнутых поверхностей.
Изложению их основных свойств предпосылаются краткие сведения
по топологии элементарных кривых (§ 1).
Далее, в § 2, даются определение замкнутой поверхности, а также
определения двумерных полиэдров и двумерных комплексов—триангуляции
и их подкомплексов. Здесь же излагается и комбинаторная характеристика
триангуляции замкнутых поверхностей, а также вводится понятие
двумерного комплекса остовов, при помощи которого со всей строгостью
определяется понятие идентификации (склеивания) данных элементов комплекса.
§ 3 посвящен строгому изложению всех определений, связанных с
разрезами и склеиваниями, и доказательству относящихся сюда элементарных
теорем, на которых в значительной степени основывается дальнейшее
изложение (§ 5—7).
В § 4 и 5 изложены ориентируемость и порядок связности
поверхностей, а в § 6 и 7 устанавливаются нормальные формы так называемых
простых (schlichtartige) поверхностей (§ 6) и замкнутых поверхностей (§ 7).
Применённый здесь метод установления нормальных форм замкнутых
поверхностей в основном принадлежит Александеру *).
В этой главе, долженствующей познакомить читателя с элементарным и
геометрически наглядным материалом, допущены некоторые вольности
изложения. Здесь в отличие от всех других глав этой книги изложение в ряде
случаев опирается hi некоторые теоремы (относящиеся к категории так
называемых теорем инвариантности), которые доказываются лишь в
дальнейших (в пятой и десятой) главах, а в настоящей главе только
формулируются.
Так как приводимые в этих главах доказательства упомянутых теорем,
само собою разумеется, независимы от результатов главы 3, то такой приём
кажется мне законным. Без его применения пришлось бы или отложить
изложение топологии поверхностей очень далеко или перегрузить его
доказательствами инвариантности специально для двумерного случая.
Ещё большие вольности допущены в доказательстве самой основной
теоремы теории поверхностей и в непосредственно предшествующих ей
построениях: после того как все основные понятия, связанные с разрезами
и склеиваниями, изложены с аккуратностью, как я надеюсь, безупречной,
я считал возможным ограничиться в применениях этих понятий
«той разумной строгостью, которая, избавляя от ошибок, сообщает
непреложность выводам»**), и предоставить проведение всех подробностей
доказательств в виде упражнения читателю: при упомянутой уже полноте
определений проведение отдельных логических этапов рассуждения совершается
автоматически (как вычисления в классическом анализе); помещение их
в книге загромоздило бы изложение и только уменьшило бы его ясность.
*) Annals of math., 16, 1915, стр. 158—161.
**) А. Н. Крыло в, Предисловие к «Теории вероятностей» П. Л. Че*
бышева.

94
ПОВЕРХНОСТИ
[ГЛ. Itt
§ 1. Элементарные кривые и одномерные комплексы.
1 :1. Элементарные кривые и их разбиения на дуги.
Определение [1:11]. Элементарной кривой
называется компакт, являющийся соединением конечного числа простых
дуг, имеющих попарно не более конечного числа общих точек.
Точка р элементарной кривой Ф называется обыкновенной,
если у неё есть окрестность относительно Ф, являющаяся открытой
дугой (т. е. гомеоморфная прямой линии)*). В противном случае
точка р называется особой. Особые точки в свою очередь
разделяются на точки ветвления и концевые точки. Точки
ветвления являются общим концом трёх или более простых дуг, лежащих
на Ф и не имеющих кроме общего конца р никаких общих точек.
Точка р £ Ф называется концевой, если у неё имеется окрестность
относительно Ф, замыкание которой есть простая дуга, одним из
концов которой является точка р. Число особых точек
элементарной кривой конечно.
Пусть элементарная кривая Ф есть соединение простых дуг LV...,LS.
Подразделивши, если нужно, эти простые дуги на конечное число
меньших простых дуг, можем без ограничения общности
предположить, что каждая точка, принадлежащая более чем одной из дуг
LV...,L8, является общим концом всех дуг, к которым она
принадлежит и что две дуги имеют не более одной общей точки. Пусть
а1У...9ап все точки, являющиеся концевыми точками хотя бы одной из
дуг LV...,L8. Все особые точки кривой Ф находятся в числе точек
^!,...,ап, но не все точки alitt.,anнепременно особые. Возьмём в
трёхмерном пространстве точки Ь1У..., Ьп так, чтобы никакие четыре из
них не лежали в одной плоскости; тогда, в частности, никакие три
не будут лежать на одной прямой. Если точки ai и а- являются
концами дуги Lh1 то соединяем точки bi и bj отрезком L'h. Два таких
отрезка L'h и L'k либо не имеют ни одной общей точки, либо имеют
общий конец, соответствующий общему концу дуг Lh и Lk.
Отсюда следует, что кривая Ф гомеоморфна полигональной
линии, т. е. линии, являющейся соединением конечного числа отрезков,
не имеющих попарно общих точек, кроме, быть может, общих
концов (черт. 17).
Итак:
[1 :12]. Всякая элементарная кривая гомеоморфна полигона ль*
ной линии, лежащей в Rs.
*) Открытой дугой называется простая дуга без двух её концов;
открытая дуга гомеоморфна прямой, но не всякое множество, гомеоморфное
прямой, является открытой дугой: например, график функции у = sin — ,
0<л:< —, гомеоморфен прямой, но открытой дугой не является. Однако,
всякое множество, лежащее на элементарной кривой и гомеоморфное пря*
мой, является открытой дугой или простой замкнутой линией без одной точки.

£ 1] ЭЛЕМЕНТАРНЫЕ КРИВЫЕ И ОДНОМЕРНЫЕ КОМПЛЕКСЫ 95
Поэтому при изучении элементарных кривых можно ограничиться
полигональными линиями, лежащими в трёхмерном пространстве.
Пусть р — какая-нибудь обыкновенная точка полигональной
линии Ф. Она является либо внутренней точкой одного и только
одного отрезка, либо общим концом двух и только двух отрезков,
т. е. во всяком случае внутренней точкой некоторой лежащей на Ф
простой дуги, состоящей из одних лишь обыкновенных точек. Эту
простую дугу можно продолжить в обе стороны до тех пор, пока
мы или упрёмся в особую точку или
опишем замкнутый простой полигон.
Отсюда легко следует:
[1 :13]. Всякая обыкновенная точка d
элементарной кривой Ф есть внутренняя
точка однозначно определённой кривой
Ф сФ, которая представляет собою:
либо простую замкнутую линию,
являющуюся компонентой*) точки р в Ф;
либо простую замкнутую линию, одна
единственная точка которой является
особой точкой линии Ф;
либо простую дугу, оба конца
которой являются особыми точками Ф.
Кривая Фр называется
компонентой регулярности точки р.
Среди компонент регулярности только
особой точки Ф, которые суть простые
Черт. 17.
те не содержат ни одной
замкнутые линии,
являющиеся компонентами кривой Ф. Каждая другая компонента
регулярности содержит одну особую точку, если она замкнута, и две, если
она есть простая дуга.
Определение [1 :14]. Разность между числом особых точек
элементарной кривой и числом тех из её компонент регулярности,
которые содержат особые точки, называется (эйлеровой)
характеристикой кривой.
Так как при всяком топологическом отображении элементарной
кривой особые точки и компоненты регулярности сохраняются, то
Две гомеоморфные кривые имеют одну и ту же характеристику.
Ясно также, что характеристика простой дуги равна 1, а простой
замкнутой линии равна нулю. Характеристика лемнискаты равна—1.
[1 • 15]. Пусть элементарная кривая Ф разбита на попарно
непересекающиеся открытые дуги и их концы; полученные открытые дуги
и точки, являющиеся их концами, называем соответственно
одномерными и нульмерными элементами данного разбиения кривой Ф.
•^то разбиение называется одномерным комплексом, если никакие
Две открытые дуги не имеют двух общих концов.
*) Глава 1, арт. 3:2.

96
ПОВЕРХНОСТИ
(гл. Ю
Число нульмерных элементов обозначаем через р0, число
одномерных через р1# Тогда число р0 — рг (называемое эйлеровой
характеристикой разбиения К) равно эйлеровой
характеристике кривой Ф.
В самом деле, заменяя две дуги (ab) и (be), общая вершина
которых b есть обыкновенная точка кривой Ф, одной дугой (ас),
мы и р0 и pj уменьшаем на 1, так что р0 — рг при этом не меняется.
Но повторяя несколько раз этот процесс «стирания» нульмерных
элементов разбиения, мы придём в конце концов к компонентам
регулярности, откуда без труда следует [1 :15].
Очевидно:
[1 :16]. Эйлерова характеристика кривой Ф равна сумме
эйлеровых характеристик её компонент.
1 :2. Порядок связности кривой (одномерное число Бетти).
Сделаем сначала следующее предварительное замечание. Пусть
дано конечное число каких-нибудь множеств М19...,М8,
состоящих из совершенно произвольных элементов. Суммой этих
множеств по модулю два называется множество М«a/k^-f- ... -\-Ms>
состоящее из тех и только тех элементов, каждый из которых
является элементом нечётного числа множеств Mt,..., М8. Если таких
элементов нет, то сумма множеств Мг ,. . ,М8 по модулю два равна
нулю (т. е, пустому множеству):
Пусть теперь Ф — элементарная кривая. Рассмотрим следующие
множества, элементами которых являются компоненты регулярности
кривой Ф:
1. Множества, состоящие из одного элемента, а именно, из
некоторой компоненты регулярности, являющейся простой замкнутой
линией.
2. Множества, элементами которых являются компоненты
регулярности, соединение которых есть простая замкнутая линия.
3. Пустое множество.
Эти множества компонент регулярности называются простыми
циклам и.
Сумма по модулю два нескольких простых циклов называется
циклом.
Множество всех циклов кривой Ф образует группу, если за
групповую операцию принять сложение по модулю два *).
Циклы
(1:211) *,..♦.,*.
линейно зависимы между собой, если некоторые из них, пусть
*) При этом —z~z для любого цикла z, так как z~}-z = 0,

§ 1] ЭЛЕМЕНТАРНЫЕ КРИВЫЕ И ОДНОМЕРНЫЕ КОМПЛЕКСЫ 9f
Zi**-">zfn (все *'# Различны между собою) имеют по модулю два
сумму, равную нулю *).
В противном случае циклы (1 :211) называются линейно
независимыми.
Определение [1:21]. Порядком связности или
«одномерным числом Бетти» ти1 (Ф) элементарной кривой Ф
называется наибольшее из таких чисел /г, что в Ф имеется система,
состоящая из п линейно независимых циклов.
Очевидно, число it1 (Ф) можно было бы определить так же, как
наибольшее число линейно независимых простых циклов,
имеющихся в Ф.
Замечание. Пусть К— какое-нибудь разбиение элементарной
кривой Ф на открытые дуги и их концы («вершины»).
Назовём простым циклом разбиения К всякое множество
одномерных элементов /С, которые вместе со своими вершинами
образуют содержащуюся в Ф простую замкнутую линию; циклом назовём,
как и прежде, сумму по модулю два нескольких простых циклов.
Тогда ясно, что циклы разбиения К находятся в однозначном
соответствии с циклзми кривой Ф так, что группы тех и других циклов
изоморфны между собою; отсюда следует, что порядок связности Ф
совпадает с порядком связности одномерного
комплекса /С, т.е. с максимальным числом линейно независимых
циклов разбиения К.
Очевидно:
[1 :22]. Порядок связности кривой Ф равен сумме порядков
связности компонент кривой Ф.
[1 :23]. Если элементарная кривая Ф0 есть подмножество
элементарной кривой Ф, то
Я>(Ф0)^7С»(Ф1).
Докажем следующее основное предложение, известное под назка-
нием теоремы Эйлера (для кривых).
[1 :24]. Эйлерова характеристика элементарной кривой равна
разности между числом компонент кривой и порядком её
связности.
Или, обозначая через р0 и рг число нульмерных и одномерных
элементов какого-либо рлзэиения К кривой Ф на дуги, через тс°
число компонент этой кривой, а через rJ её одномерное число Бетти,
имеем
(1 :24) Ро —Pl = «° —it*.
Для связной кривой формула (1 :24) переходит в
(1:241) Ро — Pi = 1—**-
*) Можно было бы вместо этг го сказать: если некоторая линейная
комбинация их, не все коэффициенты которой = 0 (mod 2,) равна нулю.
• Александров П. С.

98
ПОВЕРХНОСТИ
[гл. Щ
Достаточно доказать формулу (1 :241) дли Связной кривой, тогда
формула (1 :24) для любой кривой следует из [1 :1б] и [1 : 22]. \
Итак, пусть Ф—-связная кривая. Без ограничения общности
можно предположить, что Ф — полигональная кривая с данным
разбиением К на прямолинейные отрезки.
Строим данную кривую Ф следующим образом: начинаем
построение с какого-либо отрезка и потом присоединяем один за другим
новые отрезки так, чтобы в любой момент построения иметь
связную кривую. Очевидно, это всегда возможно. Одновременно с при-
соединением каждого отрезка присоединяем и ту вершину этого
отрезка, которая ещё не была
присоединена ранее, если такая вершина имеется.
Присоединения новых отрезков могут
быть двух родов:
1. Присоединение первого рода
происходит тогда, когда до присоединения
в уже построенной фигуре имелась лишь
одна из двух вершин присоединяемого
отрезка,
■cjtpr. 18. 2. Присоединение второго рода —
когда уже до этого присоединения были
присоединены об^ вершины присоединяемого отрезка (черт. 18).
При присоединении первого рода число р0— ог и число т:1, как
легко видеть, остаются неизменными.
При присоединении второго рода число р0—р1? очевидно,
уменьшается на 1. Докажем, что при этом число тг1 увеличивается на 1,
значит, 1—тг1 уменьшается на единицу; этим будет доказана и вся
формула (1 :241): в начале построения, т. е. для кривой, состоящей
из одного отрезка, и правая и левая части формулы (1:241)
равнялись 1 и, следовательно, формула была верна; при присоединении
нового отрезка правая и левая части формулы (1 :241) изменяются
одинаково, так что формула (1 :241) остаётся верной. Итак, остаётся
доказать, что при присоединении второго рода число т:1
увеличивается на 1.
Пусть данное присоединение заключается в том, что к связной
кривой Ф0 присоединяется отрезок | ab |, вершины которого а и b
уже содержатся в Ф0. Так как кривая Ф0 связна, то точки а и b
можно в Ф0 соединить ломаной. Ломаная эта вместе с отрезком \ab\
образует цикл г0. Пусть теперь порядок связности Ф0 равен т*.
Возьмём в Ф0 систему из ~J линейно независимых циклов
Так как г0 содержит отрезок \ab\, не входящий ни в один из цик-.|
лов^,. . ., гге1, то циклы г0, г1,...,гк^ также линейно независимы, j
Остаётся доказать, что циклы !

§ 21
ПОВЕРХНОСТИ И ИХ 1РИАНГУЛЯЦИИ
99
где z есть произвольный цикл разбиения К, линейно зависимы. Это
следует из наших предположений, если цикл z лежит на Ф0. Если
же цикл z не лежит на Фс, то он содержит отрезок | ab | и тогда
цикл z-\-z0 лежит на Ф0 и, следовательно, является суммой
некоторых среди циклов zx ,. . ., zri\ пусть, например, z-f- z0 = z{ -j-
j- . .. -f zh; тогда z ~\~ z0 -j- zx -j- . . . -f- zh = 0, что и требовалось
доказать.
Замечание. Какое бы разбиение К элементарной связной
кривой Ф мы ни взяли и в каком бы порядке мы ни строили кривую
Ф из отрезков, являющихся элементами К, если в процессе этого
построения мы имеем всё время связную кривую, то число
присоединений второго рода оказывается всегда одним и тем же, а именно,
равным порядку связности данной кривой.
В самом деле, наше утверждение, очевидно, верно для кривой,
состоящей из одного отрезка; так как при каждом присоединении
второго рода число ъ1 увеличивается на единицу, а при
присоединении первого рода не изменяется, то утверждение верно вообще.
§ 2. Поверхности и их триангуляции.
2:1. Комплексы и полиэдры двух измерений. Под
треугольником понимаем внутренность треугольника, под отрезком или
ребром— открытый отрезок (отрезок без концов).
Определение [2:11]. Всякое конечное 'множество К,
элементами которого являются треугольники, отрезки и отдельные точки,
лежащие в данном R}\ называется триангуляцией, если
выполнены условия:
1. Никакие два элемента множества К не имеют общих точек.
2. Все стороны и все вершины какого-либо треугольника,
являющегося элементом множества /С, и обе вершины всякого отрезка,
являющегося элементом множества К> сугь элементы множества К.
Комплексами в этой главе будут называться
триангуляции и всевозможные их подмножества. Числом
измерений комплекса называем наибольшее число (в нашем случае
0,1 или 2), являющееся числом измерений некоторого элемента
данного комплекса. ^
Телом комплекса/С называется точечное множество К данного
Rn, являющееся соединением всех элементов комплекса К. Тела
триангуляции называются полиэдрами. Если полиэдр
Ф есть тело триангуляции К, Ф =/С, то говорят, что
К—триангуляция полиэдра Ф.
Легко видеть, что полиэдры суть замкнутые ограниченные
множества данного /?п, т.е. суть компакты.
Элементами комплекса /С, подчинёнными данному элементу
Т£К> будем называть: вершины и стороны Г, если
Т—треугольник, вершины Г, если Т—отрезок. Если Т подчинено элементу Г,
то Т подчиняет себе элемент Тг.
7*

iou
ПОВЕРХНОСТИ
[гл. m
Подкомплекс К0 данного комплекса К называется замкну-
т и м (соответственно открытым), если каждый элемент комплекса К,
подчинённый некоторому элементу комплекса К0 (соответственно
подчиняющий себе некоторый элемент комплекса Я0), сам
принадлежит комплексу К0.
Очевидно:
[2: 11]. Замкнутый подкомплекс триангуляции есть
триангуляция.
Определение [2:12]. Комплекс называется с в я з н ым, если
его нельзя представить в виде соединения двух непустых не
пересекающихся замкнутых подкомплексов.
Теорема [2:13]. Для связности триангуляции необходимо
и достаточно, чтобы две любые вершины её могли быть связаны
ломаной линией, состоящей из элементов этой
триангуляции.
Условие необходимо: пусть а и b — две
вершины триангуляции /С, которые нельзя связать
в К никакой ломаной. Обозначим через Ка
множество всех тех элементов Л", у которых хоть одна
(и следовательно, всякая) вершина может быть
связана ломаной с а; обозначим через Къ
множество остальных элементов К. Легко видеть, что Ка
и Къ — замкнутые подкомплексы комплекса К; они
непусты, так как а£Ка, Ь£ Кь. Мы получаем
противоречие с предположенной связностью /С
Условие достаточно: если К несвязно и
Черт. 19.
где Кх и К% — замкнутые подкомплексы К, то ни одна вершина Кх
не может быть связана ломаной р.и с одной вершиной К%, что и
требовалось доказать.
Если полиэдр связен, то всякая его триангуляция связна
(разбиению триангуляции на два непустых не пересекающихся замкнутых
подкомплекса соответствует разбиение её тела на два непустых не
пересекающихся замкнутых хМножества). Наоборот, если триангуляция
связна, то её тело также связно: из [2: 13] легко следует, что
всякие две точки множества К могут быть соединены ломаной в К
(черт. 19). Итак:
[2:14]. Если хоть одна триангуляция данного полиэдра
связна, то полиэдр связен) если полиэдр связен, то все его
триангуляции связны.
Двумерный комплекс называется размерно-однородным,
если всякий его одномерный и всякий нульмерный элемент подчинён
некоторому двумерному. Двумерный размерно однородный комплекс
называется сильно связным, если всякие два принадлежащих

§ 2] ПОВЕРХНОСТИ И ИХ ТРИАНГУЛЯЦИИ 1()1
Черт. 20а.
ему треугольника 7\ и Т2 могут быть связаны цепочкой
треугольников
так что для /==1,..., s—1 треугольники Га- и Titl имеют общую
сторону, принадлежащую комплексу К.
Введём, наконец, следующее понятие:
Звездой ОкТ элемента Гв комплексе К называется
подкомплекс, ее стоящий из Т и из всех элементов комплекса К>
подчиняющих себе элемент Т.
Итак: Если Т есть треугольник, то ОкТ=Т; если Т есть
одномерный элемент, то ОкТ состоит из Т и из всех треугольников
комплекса К, имеющих Т своей
стороной; если Т есть вершина,
то ОкТ состоит из Г и из
всех одномерных и двумерных
элементов комплекса К>
имеющих Т своей вершиной.
Примеры на все эти случаи
даны на черт. 20.
Рассмотрим особо случай,
когда Т есть некоторая
вершина е триангуляции К. Тогда
звезда Оке состоит из
треугольников вида (£#!%), из
отрезков вида {еа) и
вершины е. Стороны (ata2) этих
треугольников
(противоположные вершине е) и вершины а
отрезков (еа) образуют
комплекс Вке, называемый краем
звезды Оке (черт. 20).
Звезда Оке называется циклической, если её край есть
простая замкнутая ломаная линия (т. е. если её элементы располагаются
в циклическом порядке, как элементы разбиения круга на секторы).
Если край звезды Ок* есть простая незамкнутая ломаная линия, тогда
элементы звезды естественно упорядочиваются в линейном порядке
и сама звезда называется полуциклической.
Пример полуциклической звезды дан на черт. 21.
2:2. Замкнутые поверхности. Имеет место следующая теорема,
которая в этой книге ни доказываться, ни применяться не будет:
всякое двумерное замкнутое топологическое многообразие *) гомео-
морфно некоторому полиэдру **). Для того чтобы не опираться на
Черт. 206.
*) Глава 1, арт. 5:3.
*•) См. I. Gawehn, Ober unberandete 2-dimensionale MannigfaJtig-
kdten, Math. Annalen, 98, 1927, стр. 321—Ь54,

102
ПОВЕРХНОСТИ
[гл. ш
эту теорему, мы с самого начала ограничиваемся рассмотрением
лишь тех двумерных замкнутых многообразий, которые гомеоморфны
полиэдрам, и именно их называем замкнутыми поверхностями.
Фактическое положение вещей таково, что класс таким образом
опр де ённых замкнутых поверхностей совпадает с классом всех
двумерных замкнутых многообразий.
Если выбрать какую-нибудь триангуляцио К некоторого
полиэдра Ф0, гомеоморфного данной замкнутое поверхности Ф, и
некоторое опреде. ённое топологическое отображение С полиэдра Ф0 на
поверхность Ф, то в силу этого о ображения триангуляции К будет
со пветствопать некоторая «кривая триангуляция»
поверхности Ф, состоящая из криволинейных треугольник )в, их сторон и
еершин. На ример, если взять октаэтр или икосаэдр, вписанные в
Черт. 21. Черт. 12.
сф?ру, и спрс е стиро°ать их на эту с4 еру из её ц°нтра, го сфера
разобьётся, ч первом с 1учае га 8, во втором —на 20, сферических
треугольник >в; эти треугольники, их стороны и в° )шины и oyiyi
элементами соотьег *1»?ующей кривой триангуляции сферы, Точн ) так
же изображённая на ч°рт. 22 тр !анг}мяция полиэдра, гомеоморфного
тору, перехолит при тоюлоги веском отображении в кривую
триангуляцию тора.
Замечание. Так как все поверхности гомеоморфны полиэдрам,
то теологическое и учение поверхностей мьжег быть ограничено
теми поверхно:тями, которые сами являются полиэдрами. Поэтому
мы ниже бучем без дальнейших оговорок предполагать, что все
ряссматриваемые «-'ами поверхности суть полиэдры. Это. в частности,
позволит совершенно избежать пользования кривыми
триангуляция ми.
Примем без доказательства следующую теорему, которая будет
доказана в главе 5 (теооема [3 : 140]).
\2 :20] Пусть А и В — два множества, лежащих в некотором
топологическом пространстве R, и каждое из них гомеоморфно
плоскости. Если при этом АаВ, то А открыто в В.
Теперь мы можем доказать следующую основную теорему:
[2 :21]. Для того, чтобы триангуляция К была
триангуляцией замкнутой поверхности^ необходимо и достаточно, чтобы

& 2] ПОВЕРХНОСТИ И ИХ ТРИАНГУЛЯЦИИ 103
она была связной и чтобы звезда всякой вершины её была
циклической*
Доказательство. 1. Условие необходимо. Пусть К —
триангуляция замкнутой поверхности Ф — /(. Связность К следует на
основании [2:14] из связности Ф. Прежде чем доказывать
цикличность всякой звезды 0#е, где е — вершина К, докпжем, что ко
всякому отрезку Т1 £К примыкает более одного треугольника. Это
утверждение, очевидно, следует из:
[2:210]. Пусть Т—треугольник (лежащий в плоскости /?2);пусть
^—замыкание треугольника Т в R2 и р^Т\Т. Не существует
никакого множества Г, гомеоморфного
плоскости и удовлетворяющего условию 11_^—~—~~~—т\£г
Р£ТЕТ-
В самом деле, пусть такое множество
1' существует. Тогда Г и R2 находятся
соответственно в условиях множеств Л
и В теоремы [2 :20], поэтому Г открыто
в R2 и р — внутренняя точка Г, значит,
и подавно, внутренняя точка Т2
относительно /?2, что, очевидно, не так.
Полученное противоречие доказывает
утверждение [2:210].
Из того, что к каждому одномерному Черт. 23.
элементу триангуляции К примыкает не
менее двух треугольников, легко следует, что в звезде О^е можно
найти циклически упорядоченную последовательность треугольников,
каждые два соседних элемента которой имеют общую сторону вида
i eet\. Эти треугольники и только что упомянутые стороны их образуют
подкомплекс О' комплекса Oj?e, и надо только доказать, что О' = Оке.
Для этого возьмём гомеоморфную плоскости R2 окрестность Г
точки е относительно Ф.
Положим , ^ч „ч
* = р(*,Ф\Г)>0
и обозначим через d наибольшее число, являющееся диаметром
какого-либо элемента комплекса О'. Возьмём положительное число
I1 ^ ~ . Подобное преобразование с центром е и коэффициентом \i
переводит комплекс О' в комплекс О", удовлетворяющий условию
г£0"с:Г (см> черт. 23, на котором изображены комплекс О',
пересечение его элементов с Г и комплекс О").
Тела обоих комплексов О' и О", как легко видеть, гомеоморфны
внутренности круга и, значит, гомеоморфны плоскости. Поэтому
множества О" и Г находятся в условиях множеств Д и В теоремы [2:20].

104
ПОВЕРХНОСТИ
[гл. ш
О" должно быть открыто в Г. Но если в О^е имеется не при-
надлежащий к О' элемент Т, то этот элемент не пересекается с О'
и тем более с О"\ с другой стороны, е есть предельная точка Т и,
следовательно, не может быть внутренней относительно Г точкой О".
Полученное противоречие доказывает тождество О' = 0# £.
2. Условие достаточно. Из связности триангуляции К
следует связность её тела; д жажем, что из цикличности всех звёзд
Оке следует, что каждая точк! р £ Ф принадлежит открытому
подмножеству полиэдра Ф, гомеоморфному плоскости, или, что то же,
внутренности круга.
Прежде всего, О^е по самому своему определению — открытый
подкомплекс комплекса /С, а дополнительный подкомплекс К\Оке —
замкнутый подкомплекс комплекса К- Поэтому тело комплекса К\Оке,
будучи полиэдром, замкнуто в Ф = /(, а Оке открыто в Ф. Но
множество Оке, очевидно, гомеоморфно внутренности круга. Пусть
теперь р — какая-нибудь точка Ф и Т—единственный содержащий
точку р элемент триангуляции /С. Обозначим через е какую-нибудь
вершину Т. Тогда р £ Оке* чем всё доказано.
[2:22]. Ко всякому одномерному элементу Т1 триангуляции
К замкнутой поверхности Ф прилегают два и только два
треугольника этой триангуляции,
В самом деле, если е есть какая-либо вершина отрезка Г1, то
все прилегающие к Т1 треугольники триангуляции К являются
элементами циклической звезды Оке\ так как в О^г имеются ровно два
треугольника со ст >роною Г1, то [2:22] доказано.
2:3. Поверхности с краем. Под поверхностью во всей этой
главе понимается связный компакт Ф, гомеоморфный полиэдру и
обладающий следующим свойством. Все точки Ф распадаются на два
класса: внутренние точки, имеющие окрестности, гомеоморфные
плоскости, и краевые точки; при эюм точка р £ Ф называется
краевой, если некоторая её окрестность может быть
топологически отображена на соединение треугольника Г2 и одной из его
сторон Т1 так, что при этом отображении точка р переходит в точку
открытого отрезка Г1.
Множество всех краевых точек поверхности называется краем
поверхности. Если оно не пусто, поверхность называется
поверхностью с краем; в противном случае поверхность замкнута
в смысле предыдущего артикула. В соответствии с замечанием в
предыдущем артикуле мы в дальнейшем всегда будем предполагать, что
рассматриваемые нами поверхности сами суть полиэдры.
Из [2 :2 * 0] следует:
[2:31]. Разделение точек поверхности на внутренние и краевые
действительно есть разбиение на два не пересекающихся класса:
краевые тонки поверхности характеризуются среди всех точек

§ 2] ПОВЕРХНОСТИ И ИХ ТРИАНГУЛЯЦИИ 105
поверхности тем, что она не имеют окрестностей, гомеоморфны%
плоскости; при топологическом отображении одной поверхности
на другую внутренние точки переходят во внутренние, а краевые —
в краевые.
Из самого определения краевых точек следует, что каждая краевая
точка поверхности является относительно края поверхности
внутренней точкой некоторой простой дуги, состоящей из одних лишь краевых
точек. С другой стороны, при любом выборе триангуляции К
поверхности Ф все краевые точки Ф располагаются на одномерных и
нульмерных элементах этой триангуляции; из этих двух обстоятельств
вытекает, что край поверхности есть элементарная кривая, лишённая
особых точек и, следовательно, представляющая собою соединение
нескольких простых замкнутых линий, не имеющих попарно общих
точек. Эти простые замкнутые линии, являющиеся компонентами
края поверхности, называются контурами данной поверхности.
Пусть р — краевая точка поверхности Ф; возьмём какую-нибудь
триангуляцию К этой поверхности. Точ<а р либо лежит на
некотором отрезке Г1 этой триангуляции, либо является её вершиной. В
первом случае, в силу [2:210], к Г1 примыкает лишь один
треугольник триангуляции /С, и все точки Г1 являются краевыми. Во втором
случае р есть вершина триангуляции /С, являющаяся общим концом
двух и только двух лежащих на краю поверхности Ф отрезков рег
и ре8 триангуляции К, к каждому из которых примыкает по одному
треугольнику. Так как все остальные элементы звезды Охр, кроме
точки р и отрезков рех и pes, состоят из внутренних точек
поверхности, то ко всякому отрезку вида peh \z£.i^=s, примыкают два
треуготьника триангуляции К- Отсюда легко следует, что вся звезда
Окр есть полуциклическая звезда. Обратно, если звезда какой-либо
вершины е триангуляции К есть полуциклическая звезда, то точка е
есть краевая точка. Итак:
[2:32]. Пусть К—какая-либо триангуляция поверхности Ф.
Для того, чтобы точка р была краевой, необходимо и достаточно,
чтобы она удовлетворяла одному из следующих двух условий:
а) р лежит на отрезке триангуляции К, являющемся
стороною только одного треугольника этой триангуляции;
б) р есть вершина полуциклической звезды триангуляции К-
Те элементы (рёбра и вершины) триангуляции /С, которые лежат
на краю поверхности Ф, называются краевыми элементами этой
триангуляции, остальные элементы триангуляции называются внутренними.
Край поверхности Ф является соединением краевых элементов любой
данной триангуляции этой поверхности.
[2 :33]. Триангуляция всякой поверхности есть сильно связный
комплекс.
В самом деле, пусть Т[ и Т28 — два треугольника триангуляции К]
пусть их нельзя связать цепочкой треугольников
(2:33)
Т1 . Т2

106
ПОВЕРХНОСТИ
[гл. ш
так что Т* и Гг?+1 имеют общую сторону. Обозначим через Кг
подкомплекс комплекса /С, состоящий из треугольников, могущих быть
связанными с 7\[ такими цепочками, и из сторон и вершин эгих
треугольников; через К2 обозначим подкомплекс комплекса /С, состоящий
из всех не вошедших в Кх треугольников, рёбер и вершин.
По самому своему определению К1 и К2 имеют пустое пересечение.
С другой стороны, вследствие сильной связности циклической
и полуциклической звёзд, звезда каждой вершины комплекса /Q
(относительно К) принадлежит целиком к Kv а звезда каждой
вершины комплекса К2 (относительно К) целиком принадлежит к К2,
так что Kt и К2 — взяимно дополнительные открытые, а значит, и
замкну-ые непустые подкомплексы комплекса К] но это
противоречит связности комплекса К*
Черт. 24. Черт. 25.
2:4. Подразделения триангуляции. Иногда бывает нужно
перейти от данной триангуляции поверхности к более мелкой
триангуляции," являющейся подразделением первоначальной. Мы рассмотрим
лишь следующие случаи подразделений:
1. Элементарное подразделение триангуляции
поверхности относительно данного одномерного элемента Т1 этой
триангуляции: оно заключается в том, что Г1 делится на два отрезка, а каждый
из прилежащих к нему треугольников разбивается на два
треугольника, как на черт. 24; все остальные элементы триангуляции
остаются без изменений.
2. Произведя элементарное подразделение относительно всех
одномерных элементов дчнн )$ триангуляции, получим так называемое
барицентрическое подразделение триангуляции,
строение которой ясно из черт. 25 (барицентрическое подразделение
треугольника состоит из шести треугольников, на которые данный
треугольник разбивается своими тремя медианами).
[2 :41]. Всякое подразделение данной триангуляции,
получающееся в результате конечного числа элементарных подразделений,
называется правильным.
Никаких подразделений, кроме правильных, нам в этой главе
рассматривать не придётся. Барицентрическое подразделение, как легко
показать, правильно.

§ з]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
107
2 : б. Комплексы остовов. Остовом треугольника называется
множество, состоящее из трёх его вершин; остовом отрезка
называется множество, состоящее из двух его вершин; остовом вершины
называется сама эта вершина. Всем элементам данной триангуляции
взаимно однозначно соответствуют их остовы, причём один элемент
триангуляции К тогда и только тогда подчинён другому, когда остов
одно» о из этих элементов является собственным подмножеством
осгоча другого.
Поэтом изучение данной триангуляции с успехом может быть
заменено изучением множества остовов всех элементов этой триангуляции
или, как говорят, комплекса остовов тр и ангу л я ции Я*.
В связи с этим вводит я следующее.
Определение [2:51]. Пусть дано некоторое конечное
множество Еу элементы коюрого условно называются вершинами. Пусть
в Е выделены некоторые подмножества, называемые остовами,
состоящие из одного, двух или трёх элементов (вершин) Уменьшенное
на 1 чисо вершин, образующих лангый остов, называется числом
его измерений. Множество остовов будет в этой главе
называться комплексом остовов, если оно удовлетворяет
следующим условиям:
а) Вся сое непустое подмножество остова есть остов.
б) Всякое множество, состоящее из одной вершины, есть остов.
Наибольшее число (0,1 или 2), являющееся числом измерений
некоторого элемента данного комплекса остовив, называется числом
измерений этого комплекса.
Замечание. Понятие комплекса остовов будет обобщено
к главе 4 на случай любого числа измерений.
Определение [2:52|. Два комплекса остовов К и К'
называю 1ся изоморфными меж <у собью, если существует взаимно
однозначное отображение множества всех вершин одного комплекса
на множество всех вениин другого комплекса, при котором остовы
обоих комплексов соответствуют друг другу.
Комплекс остовов К и триангуляция К' н 1зываются изоморфными,
*сли К и комплекс остовов триангуляции К изоморфны между со-
бою. Две триангуляции называкнся изоморфными между собою, если
изоморфны их комплексы остовов.
Имеет место следующая важная теорема, доказательство которой
^удет дано в главе 4, арт. 1 :9.
[2 :53]. Всякий двумерный комплекс остовов изоморфен
некоторой триангуляции, лежащей в /?б.
§ 3. Разрезы и склеивания.
3:1» Идентификация элементов в комплексах остовов. Пусть
дан комплекс осювсв /С Множество Е всех вершин комплекса К
разобьём на попарно не пересекающиеся подмножества—«классы»
Ev,.t>E's; каждому классу Е'. поставим в соответствие некоторую

108
ПОВЕРХНОСТИ
[гл. ш
новую «вершину» е.; условимся, что пара или тройка вершин eg
образует остов тогда и только тогда, когда в соответствующих
классах Е'. можно выбрать по вершине ei так, что выбранные таким
образом вершины et образуют остов комплекса К.
Определённые этим путём остовы образуют комплекс остовов К!\
говорят, что комплекс К' получился из комплекса К
идентификацией (отождествлением) некоторых вершин
комплекса К; каждая вершина е. комплекса К! получилась
отождествлением между собою всех вершин комплекса К, входящих
в класс £у
Пусть теперь К—какая-нибудь триангуляция; пусть
К^—комплекс остовов, получившийся в результате идентификации некоторых
вершин комплекса остовов триангуляции К. Возьмём какую-нибудь
триангуляцию К', изоморфную комплексу /^ (такие триангуляции
существуют в силу теоремы [2 :53]).
Говорят, что триангуляция К! произошла из
триангуляции К путём идентификации некоторых элементов
триангуляции К.
Идентификация элементов комплекса остовов (или триангуляции)/(
порождает, очевидно, некоторое отображение множества всех
вершин комплекса К на множество всех вершин комплекса К'\ если
еп£Е'п то вершина </. соответствует вершиче еп. При этом
отображении вершин каждый остов комплекса К отображается на
некоторый остов комплекса К\ и происходит отображение всего
комплекса /Сна комплекс К?* Отображения этого рода называются
с и м п л и ц и а л ь н ы м и отображениями*) триангуляции К на
триангуляцию К'. Мы будем в этой гла^е рассматривать лишь такие
идентификации, при которых выполнены следующие условия:
1. Нлкакие лве вершины, образующие остов комплекса К, не
отображаются нч одну вершину комплекса К!\
2. Каждый треугольник триангуляции К' является при данной
идентификщии образом лишь одного треугольника триангуляции К*
3. Каждьй отрезок триангуляции Кг является образом не более
чем двух отрезков триангуляции К. Идентификации,
удовлетворяющие этим трём условиям, мы будем в этой главе называть
склеиваниями.
Примеры. 1. Возьмём триангуляцию прямоугольника,
изображённую на черт. 26. Разобьём множество всех восьми вершин этой
триангуляции на следующие классы: каждый из классов £', / =
= 1, 2, 3, 4, состоит из одной вершины е4; вершины еь и еп
образуют £'5, а вершины е6, е8 образуют класс E'Q. Эта идентификация
превращает данную триангуляцию К прямоугольника в некоторую
триангуляцию К' боковой поверхности треугольной призмы (черт. 27):
*) Подробнее с v. об эюм в главе 4, арт. 1 :&

§з]
разрезы и склеивания
1С9
обоим отрезкам \е6е9\ H.j|e7e8| триангуляции К соответствует один
и тот же отрезок | еУ6 | триангуляции К'.
Так как боковая поверхность призмы гомеоморфна боковой
поверхности цилиндра и плоскому круговому кольцу, можно сказать
также, что только что описанная идентификация превращает триангуля-
Черт. 26.
цию К прямоугольника в триангуляцию К' цилиндра или плоского
кольца. u
2. Следующая идентификация отличается от предыдущей только
тем, что теперь класс Е'ь состоит из вершин е-и и е8, а класс Е'
состоит из вершин *6 и в,. Эта идентификация" превращает триан-
Черт. 2Я.
гуляцию К прямоугольника в триангуляцию К поверхности, известной
ноГГаТрГ 2П8ОВерХН°СТИ ИЛИ ЛИСТа Мёб«Уса и изобрТГн
Замечание. Для краткости будем идентификацию! называть
ойеГ0"И:"йНаПГГНОЙ СТ0Р°НЫ Ы "Р-оУ-льника^'направлГн-
2-скл?Г (' e) ° Ж6 пРям°Угольника, а идентификацию
ронойТГГТ направленной СТ°Р°НЫ (Ve) с направленной сто-
гих полЖ; АналогичнУю терминологию будем применять и в дру-
скобка™ УЧаЯХ> Направленные 0ТРезки обозначаем круглыми
Угол3;нГкГТаТ^"ИЗОбраЖёННуЮ НЗпЧерТ- 29 тРиангУляцию прямо-
У ольника. Разобьем, множество её 19 вершин на классы Е\ следую-

no
ПОВЕРХНОСТИ
(гл. ill
щим образом: при /=1, 2, 3, 4, 17, 18, 19 полагаем E. — eh далее:
# = {*,.
^а» *п? еи\-> Е(> 'е
Е'={е
*12i>
:6' ^13 J»
^9> *16J» ^9~i^l0> e15J-
Эта идентификация — склеивание направленной стороны (еГ), еи)
прямоугольника с направленной стороной (е8> еп) и (е5, е8)
с (еи, еп) — превращает данную триангуляцию прямоугольника в
триангуляцию тора.
4. Следующая идентификация отличается от предыдущей только
тем, что теперь
т. е. (<?5, еи) попрежнему склеивается с (е8, еи), но (£б, е8)
склеивается теперь с (еп, ен). В результате впервые в нашем изложении
получается триангуляция, не
умещающаяся в трёхмерном пространстве,
а именно, триангуляция так
называемой поверхности (или
«бутылки») Клейна, изображённой
на черт. 30, Ь.
щ
У&7
г* /
«в /
\ /
*з У
е? А
ег )
Ух
е<г
Черт. 29.
5. Положим теперь (черт. 29)
£; = {*,} для/=1, 2,3, 4, 1Л 18, 19; Е'ъ = {е5, еп}; Е',} = (ев, е12);
Е7 —■ {^7» eis\
• Е' ■
\^8> еШ> ^9 :
I £in={*:
10' с1в1
(так что сторона (е5, £6) склеивается со стороной (£и, £12), (г6, £7)
склеивается с (е12, <?13),. . ., (г10, £п) с (г16, £5)). Эта идентификация
переводит данную триангуляцию прямоугольника в некоторую
триангуляцию проективной плоскости. Чтобы убедиться в этом,
отобразим топологически наш прямоугольник на верхнюю полусферу
сферы х2-{-у2-\-22=1 таким образом, чтобы образы точек <?5,
£6,..., e1Q разбивали экватор на 12 равных дуг. Тогда наша
идентификация может быть истолкована как склеивание каждых двух
диаметрально противоположных точек экватора. Но этим путём, как мы
знаем из главы 1, арт. 5 :2, пункт 8, полусфера превращается в
топологическое пространство, гомеоморфное проективной плоскости.

§ 3]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
111
гЗамечание. Звёзды всех вершин только что полученной нами
триангуляции проективной плоскости суть, очевидно, циклические
звёзды. Отсюда следует, что проективная плоскость является
замкнутой поверхностью.
3:2. Линии разрезов и полузвёзды их вершин*). Пусть
Ф == К—поверхность, данная в определённой триангуляции К. В
качестве линии разреза мы будем рассматривать в этом параграфе
простые ломаные линии А, составленные из элементов триангуляции
К и удовлетворяющие одному из следующих условий:
1. А есть замкнутая ломаная, все элементы которой являются
внутренними элементами триангуляции К (т. е. не лежат на краю
поверхности Ф). Это — случай внутренних
замкнутых разрезов (черт. 31). - rg*^
2. А есть простая незамкнутая ломаная, все А ^г\^\
элементы которой суть внутренние элементы X^W----74/\
К, кроме обоих концов этой ломаной, кото- \/\ /\к^\
рые лежат на краю поверхности (случай W \А^^\1
поперечного разреза, черт. 32). Х-—/~^lL^
3. А есть простая незамкнутая ломаная, / ^J^^J
содержащая не менее двух звеньев, один из \/\^ /
концов которой, быть может, лежит на краю \J^****
поверхности; ни один из остальных элементов \U**^
на краю не лежит (случай взреза, черт. 33).
Рассмотрим какую-нибудь звезду Оке, центр Черт. 32.
которсй е есть одна из вершин линии
разреза А; в случае взреза предполагается, кроме того, что вершина в
отлична от внутреннего конца линии взреза (черт. 34). В этих
предположениях множество всех не принадлежащих к А
элементов звезды Оке является соединением двух не пересекающихся
связных комплексов, двух «полузвёзд вершины е*\ если
*) В этом артикуле речь идёт только о линиях разреза; самих
разрезов еще не произведено; операция разреза будет определена лишь
в арт. 3:3. Поэтому удвоение отрезков на чертежах в арт. 3:2 должно
игнорироваться читателем: это удвоение приобретает смысл лишь в арт. 3:3.

112
ПОВЕРХНОСТИ
[ГЛ. Ill
одна из этих полузвёзд обозначена через 0+, то другую будем
обозначать через Ое" (черт. 34).
Легко видеть:
[3 :21]. Если е и е'— две соседние вершины ломаной А, то
каждая из двух полузвёзд вершины е пересекается с одною и только
одною полузвездой вершины е' (пересечение состоит из
треугольника, прилегающего к стороне ее').
Заметим ещё:
Если А есть линия взреза, е — её внутренний конец, ег — её
вершина, смежная с вершиной е, то Оке пересекается с каждой из
Черт. 33. Черт. 34.
полузвёзд вершины е' по одному из двух-треугольников,
примыкающих к стороне ее (черт. 33).
Отсюда следует:
[3:220]. Если ег. . .es есть линия взреза, один из концов
которой, пусть еи лежит на краю поверхности, то полузвёзды вершин
£р-.., es_x и звезда вершины е8 образует цепь *)
0"ь..., Oef-u 0Kes, 0*7Li,..., OeT-
Если оба конца ег и es линии взреза являются внутренними, то
звёзды 0^ег и 0^е8 образуют вместе с полузвёздами остальных
вершин одну замкнутую цепь
Океи Oet,..., Oef„u 0Kes, Oe^LU---> Oef, Оке^.
Из [3:220], в свою очередь, вытекает:
[3 :22]. Удаляя из триангуляции К все элементы некоторой линии
взреза, получим сильно связный открытый подкомплекс комплекса /С.
*) Цепь (соответственно замкнутая цепь) подкомплексов данного
комплекса здесь и везде в этой главе понимается в смысле определения [3:14]
главы 1.

§3]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
113
В самом деле, всякую цепочку треугольников, связывающую два
каких-нибудь треугольника *) Тх и 7V триангуляции А*, всегда можно
заменить цепочкой треугольников, связывающих Тх и 71, в обход
линии взреза (черт. 35).
Пусть теперь А = ег...е8
есть линия поперечного разреза. Из двух полузвёзд вершины ех
возьмём одну какую-нибудь, которую обозначим через Ое'Г. Она
пересекается с вполне определённой полузвездой вершины е2, которую
обозначим через Ое+; в свою очередь, Ое* пересекается с вполне
определённой полузвездой вершины *8, которую обозначим через
0^ и т. д. Таким образом, по-
лучим цепь полузвёзд
(3:23+) 0.+ ..., Ое+.
Подобным же образом, отправляясь
от полузвезды Oev получим цепь
полузвёзд
(3:23-) О*",..., Ое~.
Итак,
[3:230]. Полузвёзды вершин
поперечного разреза образуют две
цепи (3:23+) и (3:23-). ЧеРт- 35-
Из [3:230] выводим:
[3:23]. Удаляя из триангуляции К все элементы некоторой
линии поперечного разреза, получаем открытый подкомплекс
комплекса /С, который либо сам сильно связен, либо является
соединением двух непересекающихся сильно связных комплексов.
При этом, если концы данного поперечного разреза Л лежат на
двух разных контурах, то после удаления Л всегда остаётся
сильно связный комплекс.
Для доказательства первого утверждения достаточно обнаружить,
что любой треугольник Тх£ К можно связать с треугольником,
входящим в одну из полузвёзд (3:23+) или (3:23-) цепочкой
треугольников, последовательно примыкающих друг к другу по сторонам,
не входящим в А.
Для доказательства возьмём треугольник Тп, входящий,
например, в одну из полузвёзд (3:23+). Свяжем в триангуляции К
треугольники Тг и Th цепочкой треугольников. Если каждые два по-
*) Под цепочкой треугольников данного комплекса К, связывающей два
треугольника 1\ £ К и 7^ £ ЛГ, всегда понимается такая последовательность
треугольников Ть..„ Г, комплекса К что Т{ и Ti+X, /= 1 v — 1, имеют
оощую сторону, принадлежащую К-
8 Александров П. С.

114
ПОВЕРХНОСТИ
[гл. ш
следовательных треугольника этой цепочки примыкают др/г к другу
по стороне, не принадлежащей к А, то наша цель достигнута;
в противном случае, пусть Т{, TiJrl—первая пара треугольников
нашей цепочки, примыкающих по стороне, принадлежащей к А.
Тогда Т{ принадлежит к одной из полузвёзд (3:23+) или (3:23_),
и цепочка Ти..., Тг есть искомая.
Переходим теперь ко второму утверждению теоремы [3:23].
Если из триангуляции К удалить все элемьнты поперечного разреза
А, концы которого принадлежат различным контурам т:1 и тг2
поверхности /С, то получится сильно связный комплекс.
Доказательство этого утверждения получается так же легко и
теми же методами, как получались и предыдущие теоремы
этого рода; надо только сделать следующее самоочевидное
замечание. В данных условиях все полузвёзды вершин поперечного
разреза A = £?1,...J es вместе со звёздами Оке всех отличных от
ei и es вершин полигонов тсх и тс2 образуют одну замкнутую цепь
(черт. 40).
Пусть, наконец,
A = el...ese1
есть линия замкнутого внутреннего разреза. Возьмём какую-нибудь
из двух полузвёзд вершины ег и обозначим её через Oef ;
единственную пересекающуюся с ней полузвезду вершины е% обозначим через
Oef; единственную пересекающуюся с Oef полузвезду вершины е.д
обозначим через Oef и т. д. Таким образом, дойдём до вершины es
и получим цепь полузвёзд
(3:241) Oef.. ., Oef.
Так как вершины е8 и ех—соседние, то полузвезда Ое+
пересекается с вполне определённой и единственной полузвездой вершины
еи так что возможны два случая:
1. Полузвезда Oef пересекается с полузвездой Oef.
2. Полузвезда Oef пересекается с отличной от Oef полузвездой
Oef-
В случае 1 цепь (3:241) является замкнутом цепью; в этом
случае, начиная с полузвезды Oef и рассуждая так же, как только что,
получим вторую замкнутую цепь полузвёзд
0еГ,. . ., Oef, Oef
и назовём ломаную А линией замкнутого двубережного
разреза (см. черт. 31, а или черт. 41).
В случае 2 мы получили незамкнутую цепь
Oef,..., Oef, Oef;

31
разрезы и склеивания
11S
полузвезда Ое{ пересекается с вполне определённой и единственной
полузвездой вершины £2, которая отлична от Oef (так как Oef
пересекается с Oef) и, следовательно, есть ОеТ] точно так же полузвезда
Ое^ пересекается с Ое^ и не пересекается с Oef- Продолжая это
рассуждение, продолжим нашу цепь полузвёзд до цепи
Oef, Oef,. .., Oef, Oe
i >•
0е8
Полузвезда OeJ пересекается с одной из двух полузвёзд вершины ех
и при этом не пересекается с полузвездой OeJ~ (так как ОГ
пересекается с Oef), значит, пересекается с Oef. Итак, в случае 2 все
полузвёзды располагаются в одну замкнутую цепь
(3:242)
Oef,
Oef, Oe,,..., Oe~, Oef.
В случае 2 ломаная называется линией замкнутого одно-
бережного разреза (см. черт. 31£, 42а; речь идёт о
«средней линии» листа Мёбиуса, которую можно видеть на
черт. 31#; это — линия сссссс,
вычерченная двойными штрихами). Незначительно
изменяя доказательство [3:22] и [3:23],
получим:
[3:24]. Удаляя из триангуляции К линию
замкнутого однобережного разреза, получим
сильно связный открытый подкомплекс
комплекса К.
[3:25]. Удаляя из триангуляции К линию
замкнутого двубережного разреза, получим
либо сильно связный открьпый подкомплекс
комплекса К, либо соединение двух не
пересекающихся сильно связных открытых
подкомплексов К.
На изображённой на черт. 36 триангуляции
плоскости (одноимённые отрезки и
Черт. 36.
проективной
вершины склеены) замкнутая
ломаная e1e2e^eie6eQe1 является линией однобережного разреза. Две
полузвезды вершины ех обозначены соответственно знаками -f- и —.
3:3. Операция разреза. После этих определений, рассуждений
и примеров можем, наконец, перейти от линии разреза к
описанию самой операции разреза. Эта операция заключается
в переходе о г данной триангуляции К к некоторой новой
триангуляции /<", зависящей от линии разреза Л и определённой лишь с
точностью до изоморфизма. Очевидно, достаточно определить комплекс
остовов триангуляции К'-
Определим сначала вершины триангуляции К'. В случае взреза
это будут:
Во-первых, все не принадлежащие ломаной Л вершины
триангуляции /С, а также внутренний конец или оба внутренних конца этой

116
ПОВЕРХНОСТИ
[гл. m
Черт. 37.
ломаной; во-вторых, «новые вершины» ер взаимно, однозначно
соответствующие всем полузвёздам вершин ломаной Л.
В случае поперечного разреза, а также в случае замкнутого
внутреннего разреза вершинами триангуляции Кг являются:
во-первых, все, не принадлежащие ломаной Л, вершины триангуляции АГ;
во-вторых, новые вершины e'v взаимно однозначно соответствующие
полузвёздам вершин Л. Из этого определения вершин комплекса К!
следует: каждой новой вершине е'€ комплекса К' однозначно
соответствует некоторая вершина ei ломаной Л: именно та вершина е4,
одной из двух полузвёзд которой соответствует е^\ при этом,
очевидно, каждая вершина ломаной ei
(за исключением конца, если Л — линия
взреза) ставится в соответствие двум
и только двум новым вершинам е\ (по
числу полузвёзд вершины еД Эти две
новые вершины еь которым
соответствует одна и та же вершина ei
ломаной Л, будем в случае надобности
обозначать через (>')+ и (^)-или
просто через e'i+ е^.
Остовы комплекса К! определяются
так: во-первых, каждый остов
триангуляции К, все вершины которого входят в К\ является в то же
время остовом К'\ остовы вида \е\е$\ и \е^ек\ тогда и только тогда
входят в К\ когда полузвезда, отвечающая вершине eri} содержит
| £«•£/!, соответственно \eiejek\; в случае взреза к остовам комплекса
К' присоединяются остовы вида \екег], где ег — внутренняя концевая
точка взреза, а ек —- смежная с ней вершина линии Л; остовы вида | е{ ег. |,
\eie)ek\ и \eiejek\ ВХ°ДЯТ в К' тогда и только тогда, когда
полузвёзды отвечающие вершинам ер е. и (в последнем случае) е'ь,
пересекаются, причем во втором случае это пересечение содержит |^^е^|.
Непосредственной проверкой убеждаемся в том, что звёзды
всех вершин триангуляции К суть циклические или полуциклические
звёзды, откуда следует, что К' есть триангуляция поверхности или
нескольких (в силу [3 : 22] — [3: 25] не более двух) непересекающихся
поверхностей.
Из определения остовов триангуляции К! и из доказанных в этом
артикуле предложений без труда следует:
[3:31]. При взрезе, один из концов которого ех лежит на краю
поверхности, ломаная Л== et.. .es+t заменяется простой
незамкнутой ломаной
*'i+K+---e'8+e8+ie8-e'(8-i) *i- *!-»
являющейся частью одного из контуров поверхности Kf (черт. 37).

§ 3]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
117
Число контуров у К и К' одно и то же.
При взрезе А = е1, . . es+u оба конца которого — внутренние,
незамкнутая ломаная Л заменяется замкнутой ломаной линией
еге2+.
s • s
являющейся новым контуром К'*
Число контуров у К' на единицу
больше, чем у К (черт. 38).
[3 : 32]. При поперечном разрезе
Л = ех... es незамкнутая ломаная
линия Л заменяется двумя
незамкнутыми ломаными линиями
е[м . . . е'+ и е\~ . . . е'ч
Черт. 38.
при этом, если оба конца ломаной принадлежат к одному контуру
поверхности /С, то число контуров у К' может оказаться на единицу
больше, чем у К (черт. 39), если
контур е1а1. . . a^esb{. .. Ьчег
заменяется двумя контурами
а е е. ...
JJ. S— (8—1)
•W
в р
1+ C2-f '
Если же один конец ломаной А
лежит на одном контуре, а дру-
Черт. 39. Черт. 40.
гой на другом, то число контуров у Кг на единицу меньше, чем
У К так как два контура
e1a1...av.e1 и еьЬ1...Ьнев
заменились одним контуром (черт. 40)
[3:33]. При замкнутом внутреннем двубережном разрезе
замкнутая ломаная заменяется двумя замкнутыми ломаными (черт. 41)
е\ + . . . е л и е\- . . . £г_,

118
ПОВЕРХНОСТИ
[гл ш
являющимися двумя новыми контурами; число контуров, таким
образом, увеличивается на 2. При замкнутом однобережном разрезе
замкнутая ломаная А = е1... ese1
заменяется замкнутой ломаной
•ез+ *!-'
в1+.
являющейся новым контуром поверхности
К'\ таким образом, число контуров у Кг
на 1 больше, чем у К (черт. 42).
На каждой из фигур К и К!9
изображённых на черт. 42, одинаково обозначенные
элементы подлежат склеиванию. После этого
комплекс К есть триангуляция листа
Мёбиуса, на котором eie<2ie^e1 есть линия
замкнутого однобережного разреза. Этот разрез
Черт. 41. превращает комплекс К в комплекс К\
изоморфный триангуляции плоского кольца.
Комплекс К имеет один контур ap^bq^a; комплекс /С имеет два
контура: apipibqiqtfi и
*i+*2-fe3-f
Н-
Читателю рекомендуется изготовить модель коуплекса /('(лист Мёбиуса) из
бумаги и разрезать её по линии е^еъех ножницами.
Замечание. Оба комплекса: открытый подкомплекс К\А
комплекса К и триангуляция /(", в которую после разреза
переходит К, состоят, как легко
видеть, из одного и того же числа ( и Pi Al
попарно непересекающихся сильно
ez+
е'г-
е3*
el
b
9, Чг
Черт. 42Ь.
связных комплексов; если это число равно 1, мы говорим, что
данный разрез не разбивает поверхность; если оно больше единицы,
мы говорим, что происходит разбиение, и прилгом (вследствие
[3:22]—[3:25]) на две компоненты.
Итак:
[3:34]. Взрезы, поперечные разрезы с концами, лежащими на
двух pQMHX коцтурах, и афцобереоюные замкнутые разрезы не

§ 3]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
119
разбивают поверхности-, замкнутые двубережные разрезы и
поперечные разрезы с концами, лежащими на одном контуре, или
не разбивают поверхность или разбивают её на две поверхности,
3:4. Заклеивание дыр. Под этим мы будем подразумевать
несколько различных операций, уменьшающих число контуров
поверхности «а 1 или на 2. Речь будет итти о двух типах
заклеивания одной дыры и о заклеиваниях пары дыр.
1. Первый тип заклеивания одной дыры. Пусть дан
контур, представляющий собою замкнутую ломаную с чётным числом
сторон, последовательные вершины которой занумерованы так
(черт. 43):
#1» с1> ^2» * * *» ^s» ^i» Cs* * * ' ' ^2? ^1' ^1*
Склеиванию подлежат при любом i вершины ci и c'v После
этого склеивания наша замкнутая ломаная переходит в простую лома-
Чеьт. 43. Черт. И.
ную с концами ах и а'у Склеивание этого типа представляет собою
операцию, обратную взрезу.
2. Второй тип заклеивания одной дыры. Пусть дан
контур
ах а2 аъ...а8 а[ а'2 а'&. . .a's
(см. черт. 42Ь, где at=e[^ я2-<+, а3 =*£+, а[ = е[_, а'2 = е'^
^з^^з- или чеРт- 44). Склеиванию снова подлежат вершины ai иа'г
Склеиванием этого типа на поверхности уничтожается однобереж-
ный разрез.
Применяя склеивание второго типа к одному из двух контуров
плоского кругового кольца или (что то же самое) к одному из двух
оснований боковой поверхности цилиндра, получим лист Мёбиуса
(черт. 45).
Доказательство заключается, по существу, в проведении в
обратном порядке рассуждений, сделанных по поводу черт, 42. Для боль-

120
ПОВЕРХНОСТИ
[ГЛ. Ill
шей ясности проведём упомянутое склеивание при другой
триангуляции плоского кольца. (Само склеивание здесь и везде в этой главе
понимается как определённая
в арт. 3:1 комбинаторная
операция над данной, хотя бы и
произвольно выбранной
триангуляцией.)
Надлежит произвести
склеивание, указанное на черт. 46а
(склеиванию подлежат
элементы, обозначенные одинаковыми
буквами с одинаковыми
номерами, хотя и снабжённые, быть
может, не совпадающими
другими знаками—штрихами,
звёздочками и т. п.). Разрежем
сначала фигуру по линиям ра и
a'q (черт. 46b). Теперь надо
склеить все элементы,
обозначенные одними и теми же буквами с одинаковыми номерами.
На результат этого склеивания не окажет влияния предварительный
поворот прямоугольника я* < ^ рт на 180° вокруг прямой*) c'J.
Этот поворот превращает черт. 4бЬ в черт. 47а, который,
в свою очередь, после некоторых указанных на нём склеиваний
переходит в черт. 47Ь.
Черт. 45.
Черт. 46а.
а
а*
Р*
b
d'
о
с'
d
bf
Черт. 46b.
а \
а*.
9*
Оставшееся ещё склеивание, рад* с p-^a^q, очевидно, превращает
этот прямоугольник в лист Мёбиуса, что и требовалось доказать.
После этого ясный смысл приобретает следующее предложение,
*) Этот поворот касается лишь наглядно-геометрической интерпретации
данной операции склеивания и совершенно не связан с её комбинаторным
содержанием, которое вполне определяется тем, какие именно элементы
данной триангуляции подлежат склеиванию. Это замечание относится и к
дальнейшим аналогичным случаям (арт. 7;19 7:2),

§ 3]
РАЗРЕЗЫ И СКЛЕИВАНИЯ
121
[3 : 41]. Заклеивание по второму типу дыры с краем Г, прорезанной
в сферической поверхности (черт. 48*)), даёт тот же результат, что
и заклеивание несколько большей дыры с краем Г" листом Мёбиуса:
заштрихованная кольцевидная полоса превращается после склеивания
по второму типу её внутренней границы Г в лист Мёбиуса с краем Г'.
Поэтому заклеивание дыры по второму типу мы будем называть
заклеиванием дыры листом Мёбиуса.
i ^3. Заклеивание двух дыр
одной «ручкой» заключается в
том, что края этих дыр склеиваются.
а
а'
b
V
с
с'
d
d'
f
Черт. 47а.
а \Ь \с ш
Р*
Черт. 47Ь.
Рассмотрим подробнее эту операцию в случае, когда имеются две
круглые дыры, прорезанные в сфере. Пусть края этих дыр суть
замкнутые ломаные
Г = ах. . . а8а1, Г' — а\. . . da'v
При описываемом склеивании возможны два случая.
Первый случай: ручка первого рода. Пусть точка
я'описывает контур Г в одном каком-нибудь направлении, например против
часовой стрелки, если глядеть на сферу снаружи. Пусть при этом
подлежащая склеиванию с точкой а точка аг контура Г" описывает Г'
Черт. 48.
Черт. 49.
Черт. 50.
н противоположном направлении (т. е. но часовой стрелке, если
глядеть на сферу снаружи). В эгом случае мы говорим, что склеива-
*) Вместо сферической поверхности на чертежах для удобства всюду
Дана полусфера с диаметральной плоскостью, что топологически, очевидно,
одно и то же; буквы ка чертеже относятся к самой внутренней из трёх
окружностей.

122
ПОВЕРХНОСТИ
[гл. ш
ние контура Г с контуром Г" есть склеивание первого рода,
или что мы приклеиваем к Г и Г" ручку первого рода
(черт. 49). Пусть теперь при движении точки а по контуру Г
в одном направлении (против часовой стрелки, если смотреть на
сферу снаружи) соответствующая точке а точка а! описывает Г"
в том же направлении (т. е. тоже против часовой стрелки).
В этом случае мы говорим, что имеет место склеивание второго
рода или что к Г и Г' приклеена ручка второго рода
(черт. 50).
§ 4. Ориентируемость поверхностей.
4:1. Определения.
Определение [4 : 10]. Треугольник вместе с некоторым
направлением обхода его границы называется ориентированным
треугольником: каждое из двух возможных направлений обхода треугольника
называется ориентацией треугольника. Таким образом, у
треугольника ABC существует две ориентации ABC и ВАС, Если одна из
ориентации треугольника Г2 обозначена через t2, то другая обозначается
через — t2. Каждая ориентация данного треугольника порождает
определённое направление на сторонах этого
треугольника или, как говорят, определённую ориентацию этих
сторон: ориентация ABC порождает на сторонах АВ, АС, ВС
ориентации 45, ВС, СА (черт. 51).
Пусть в триангуляции К какой-нибудь поверхности даны два
прилежащих друг к Другу треугольника, т. е. два треугольника
с общей стороной. Пусть выбраны определённые ориентации этих
треугольников. Мы говорим, что эти ориентации одинаковы
или противоположны, в зависимости от того, порождают ли
они на общей стороне обоих треугольников противоположные
или одинаковые направления.
Так, например, на черт. 52 ориентации ABC и ABD
противоположны (так как они порождают на общей стороне АВ одно и то же
направление АВ), а ориентации ABC и BAD одинаковы (так как
они порождают на АВ противоположные направления).
Замечание 1. В этом определении существенно предполагается,
что данные треугольники являются элементами одной и той же
триангуляции: к случаю, изображённому на черт. 53 (чертёж плоский),
определение одинаковой ориентации двух треугольников не
применяется.
Определение [4 : 11]. Триангуляция К поверхности Ф назы-
вяется ориентируемой, если можно ориентации всех
треугольников, входящих в /С, выбрать так, чтобы ориентации всяких двух
прилежащих друг к другу треугольников оказались одинаковыми. В
противном случае триангуляция К называется неориентируемой.

§ 4]
ОРИЕНТИРУЕМОСТЬ ПОВЕРХНОСТЕЙ
123
Определение [4 :111]. Пусть К—ориентируемая
триангуляция. Тогда для всех треугольников 7"'\..., Т могут быть выбраны
такие ориентации t\,. .., *Р, что ориентации всяких двух прилежащих
треугольников одинаковы. Удовлетворяющее этому условию
множество ориентации t\9..., t) всех треугольников т\ £ К называется
ориентацией триангуляции /С.
Если дана ориентация t\ какого-нибудь треугольника, Г? из К,
то требование одинаковости ориентации всяких двух прилежащих
друг к другу треугольников однозначно определяет сначала
ориентации всех треугольников, прилежащих к Т\, а затем шаг за шагом,
в силу сильной связности триангуляции /С, определяет и ориентации
С
D "
Черт. 51. Черт, -52. Черт. 53.
всех вообще треугольников К. Итак, каков бы ни был треугольник
Г|, входящий в ориентируемую триангуляцию /С, и какова бы ни
была ориентация t2. треугольника Т2^ существует единственная
ориентация всей триангуляции /С, содержащая данную ориентацию
треугольника Т2.
Поэтому:
[4:112]. Каждая ориентируемая триангуляция имеет две
и только две ориентации.
Замечание 2. Определения [4 : 11] и [4 : 111], как и теорема
[4 : 112], применимы не только к триангуляциям поверхностей, но
и ко всем открытым сильно связным подкомплексам этих
триангуляции, например, к циклическим и полуциклическим звёздам.
Пусть Q — циклическая или полуциклическая звезда. Комплекс Q,
очевидно, изоморфен комплексу Q', лежащему в плоскости.
Ориентируя все треугольники Q\ например, против часовой стрелки,
получим ориентацию Q', а следовательно, и ориентацию Q.
Итак:
[4:12]. Циклические и полу циклические звёзды ориентируемы.
При этом имеет место следующее предложение (черт. 54).
[4 :121]. Пусть Q — полуциклическая звезда вершины е; пусть (еге)
и (ее8) — граничные отрезки этой звезды (т. е. отрезки, к каждому
из которых примыкает лишь по одному треугольнику, соответ-

124
ПОВЕРХНОСТИ
[гл. ш
ственно (е1ее2) и (е8_гее8) звезды Q). Каждая ориентация Q
порождает на отрезках {exe) и (ees) направления, являющиеся продолжением
друг друга (т. е. направления (еге) и (ees) или направления (еег) и (е8е).
Это предложение без труда доказывается, например, полной
индукцией по числу треугольников, входящих в Q.
В этой главе мы принимаем без доказательства следующий факт,
который будет доказан в главе 10 (естественно, независимо от
результатов настоящей главы).
[4:13]. Пусть К и Кг—произвольные триангуляции одной и
той же поверхности или двух гомеоморфных между собою
поверхностей'^ если одна из этих триангуляции
ориентируема, то ориентируема и другая.
Эта теорема называется теоремой об
инвариантности ориентируемости;
она делает естественным следующее
определение.
[4: 14]. Поверхность Ф называется
Черт. 54. ориентируемой, если какая-нибудь (и,
следовательно, любая) её триангуляция
ориентируема. В противном случае понерхность называется не-
ориен тируемой.
Из [4:13] следует:
[4:15]. Если данная поверхность ориентируема (неориентиру-
ема), то тем же свойством обладает и всякая поверхность
гомеоморфная данной. \
Определение [4 :16]. Пусть К—триангуляция поверхности Ф.
Последовательность ориентированных треугольников этой
триангуляции Г2, ...,Т2 с ориентациями Г..,., Г называется дезориен-
тирующей последовательностью, если выполнены
следующие условия:
При /=1,..., s—1 треугольники Т~ и 7\+1 прилегают друг
к другу и ориентированы одинаковым образом; треугольники Г" и
Т"г также прилегают друг к другу, но ориентированы взаимно
противоположно.
Если К— ориентируемая триангуляция, то из ориентированных
треугольников ее нельзя составить никакой дезориентирующей
последовательности. В самом деле, если z есть та ориентация К, которая
содержит t"u то, как легко видеть, ориентации ^2,..., f также
содержатся в г; но тогда в ориентации z содержались бы два
противоположно ориентированных прилежащих треугольника Г и t. Обратно,
если триангуляция К неориентиру ема, то из ориентированных
треугольников её мелено выделить дезориентирующую
последовательность, В самом деле, выберем какой-либо треугольник Т2 триан-
гз>

Ml
ОРИЕНТИРУЕМОСТЬ ПОВЕРХНОСТЕЙ
125
Черт. 55.
гуляции К и дадим ему какую-либо ориентацию tv Дадим всем
треугольникам, прилегающим к треугольнику Tv ориентации, одина-
ковые с ориентацией tv Вообще будем ориентировать всё новые и
новые треугольники нашей триангуляции так, чтобы треугольник,
прилегающий к уже ориентированному треугольнику, получал
ориентацию, одинаковую с уже выбранной ориентацией его соседа. Так как
триангуляция К по предположению
неориентируема, то, продолжая
описанный процесс достаточно далеко,
мы неизбежно придём к такому
треугольнику Г", который получит
две противоположные ориентации
в зависимости от того, каким
из уже ориентированных соседей
треугольника Т мы воспользуемся для определения ориентации
2 2
самого 7j. Другими словами, от Т± и Т§ можно притти, переходя
последовательно от одного треугольника к смежному с ним, двумя
путями, приводящими к противоположным ориентациям Т§.
2 *> 2 ^
Идя от Тх к Т"8 по первому пути и затем от Т8 к Т[ по второму,
мы получим дезориентирующую последовательность треугольников.
Итак, мы доказали:
[4: 17]. Для того, чтобы данная триангуляция была
неориентируема, необходимо и достаточно, чтобы на ней существовала хотя
бы одна дезориентирующая последовательность треугольников.
Пример. Рассмотрим изображённую на черт. 55 триангуляцию
листа Мёбиуса. Давая треугольникам этой триангуляции ориентации,
обозначенные на черт. 55 стрелками, получим дезориентирующую
последовательность. Итак, лист Мёбиуса есть неориентируемая
поверхность.
Из теоремы [4:17] следует: если подкомплекс К0 триангуляции
К представляет собою неориентируемую триангуляцию, то
триангуляция К неориентируема. Отсюда, в свою очередь, вытекает: если
триангуляция К содержит в качестве подкомплекса некоторую
триангуляцию листа Мёбиуса, то К есть неориентируемая триангуляция.
Легко усмотреть, что приведённые выше триангуляции поверхности
Клейна и проективной плоскости содержат триангуляции листов
Мёбиуса. Следовательно, и поверхность Клейна и проективная плоскость
суть неориентируемые поверхности. В этом легко убедиться и
непосредственно.
Пусть К— триангуляция какой-либо неориентируемой
поверхности.
На части поверхности /С, покрытой треугольниками некоторой
дезориентирующей последовательности, всегда лежит лист Мёбиуса,

126 поверхности [гл. hi
протриангулированный треугольниками некоторого правильного
подразделения *) триангуляции К. На черт. 56 изображена дезориентирующая
последовательность; на черт. 57 — некоторое правильное
подразделение треугольников этой последовательности; заштрихованные
треугольники образуют лист Мёбиуса.
Итак:
[4:18]. Для того, чтобы поверхность Ф была неориентиру-
ема, необходимо и достаточно, чтобы некоторая триангуляция
Kt поверхности Ф содержала в качестве подкомплекса
триангуляцию листа Мёбиуса. За триангуляцию Kt можно при этом взять
правильное подразделение любой данной триангуляции К
поверхности Ф.
Замечание. Можно было бы доказать, что всякая поверхность,
содержащая подмножество, гомеоморфное листу Мёбиуса, неориенти-
руема. Обратное утверждение содержится в только что доказанном.
Докажем следующее основное^ предложение:
[4:19]. Для того, чтобы поверхность Ф была неориентируема,
необходимо и достаточно, чтобы некоторая её триангуляция К
содержала линию однобережного разреза.
Доказательство. Пусть К содержит линию однобережного
разреза
А — eie% • • • esei •
Рассмотрим замкну']ую цепь полузвёзд
Oet,..., Ое+, ОеГ,..., Ое'8'9 Oef
[см. (3:242)]. Из треугольников полузвёзд Oef, . . . , (Jet, 0*f
образуем замкнутую цепь (черт. 58)
Т1 = \еае1а\,...} Гл = К-А N ■••» Tr^\desex\.
*) Достаточно сзять двукратное барицентрическое подразделение.

§ 5] ПОРЯДОК СВЯЗНОСТИ ПОВЕРХНОСТИ. ТЕОРЕМА ЭЙЛЕРА 127
Ориентируем как-нибудь полузвезду Oet; пусть эта ориентация
порождает на \ete2\9 например, направление (е^). Ориентацией
полузвезды Oei определена, в частности, ориентация треугольника,
входящего в обе полузвезды Ое+ и Ое+, следовательно, и
ориентация всей полузвезды Oet. Таким образом, шаг за шагом
определятся ориентации всех полузвёзд Oet, .. ., Oet, OeZ,
причём, в силу [4:121], все эти ориентации порождают на ломаной А
одно и то же направление обхода, которое при нашем выборе
ориентации Oet есть направление
>
е\Ч • • • *8ev
Каждые два треугольника Ti и Гж, /=1, 2,..., s—\ при этом
оказываются ориентированными одинаково, тогда как T1 = \ese1a\ и
Тг = | de8e11 ориентированы так, что
эти ориентации порождают на общей а с d ь
стороне eset этих треугольников
>
одно и то же направление {е8ег)\
значит, треугольники 7\ и Тг ориен- е,
тированы противоположным
образом. Цепочка треугольников _
ъ г д -*
Т Т
*' " ' ' г ЧерТв 58.
с установленными выше ориента-
циями образует дезориентирующую последовательность, так что
К— неориентируемая триангуляция.
Обратно, если К—данная неориентируемая триангуляция, то
некоторое правильное подразделение триангуляции К содержит
триангуляцию листа Мёбиуса и на нём линию однобережного разреза,
что и требовалось доказать.
§ 5. Порядок связности поверхности. Теорема Эйлера.
5:1. Во всём этом параграфе К обозначает триангуляцию
некоторой поверхности Ф.
[5:11]. Обозначим через р0, р1? р2 соответственно число вершин,
рёбер и треугольников, являющихся элементами данной триангуляции
К поверхности Ф; число
Х(Я) = Ро — Pi + Pa
называется эйлеровой характеристикой триангуляции.
В этой главе мы принимаем без доказательства следующую
теорему, которая будет доказана в главе 10.
к
1 N
£____ N.
4 X
\. <■;
//_..-\.
ч. <г

128
ПОВЕРХНОСТИ
[гл. lit
Теорема об инвариантности эйлеровой
характеристики [5:12]. Если К и Кг — триангуляции одной и той же
или двух гомеоморфных между собою поверхностей, то эйлеровы
характеристики этих триангуляции равны.
В силу теоремы [5:12] естественно назвать эйлеровой
характеристикой данной поверхности эйлерову характеристику какой-нибудь
триангуляции этой поверхности.
Упражнение. Показать (рассматривая какие-нибудь
триангуляции соответствующих поверхностей), что эйлерова характеристика
сфе^ы и проективной плоскости равна соответственно 2 и 1, а
эйлерова характеристика плоского кольца (цилиндра), листа Мёбиуса,
тора и поверхности Клейна равна нулю.
Замечание 1. В этой главе мы будем говорить, что одномерный
замкнутый подкомплекс L триангуляции К не разбивает эту
триангуляцию, если открытый подкомплекс tC\L^-K является сильно
связным комплексом.
Определение [5:13]. Порядком связности
триангуляции К называется наибольшее из таких целых чисел k, что
существует не разбивающий триангуляцию К замкнутый одномерный
подкомплекс, порядок связности которого равен k. Порядок связности
триангуляции К обозначается через q(K)-
Замечание 2. Из теоремы Жордана легко следует, что всякая
элементарная кривая, порядок связности которой больше нуля,
разбивает сферу.
Отсюда без применения каких-либо теорем инвариантности
вытекает, что порядок связности любой кривой триангуляции сферы и,
следовательно, всякой поверхности, гомеоморфной сфере, равен нулю.
Читателю рекомендуется провести доказательство этого утверждения.
Теорема Эйлера [5:14!:
(5:14) yXK) = 2-q(K).
Доказательство. Пусть L—не разбивающий Л" замкнутый
одномерный подкомплекс 7риангуляции К, порядок связности
которого равен q = q (К). Перенумеруем треугольники, входящие
в К, в таком порядке: 7^,..., Т* чтобы треугольник Т\
1 = 1, 2,..., о2—1, примыкал к одному из треугольников Tf,..., Т\
по некоторой своей стороне Tf, не принадлежащей L (это можно
сделать, так как L по предположению не разбивает К).
Удалим из К = К0 треугольник Г*; оставшийся подкомплекс
триангуляции К обозначим через Кх\ затем удалим одновременно
треугольник T:t и отрезок Г*; оставшийся комплекс обозначим
через К2 и т. д., лека не исчерпаем все р2 треугольников. Мы полу-
чим комплексы Кх, /С2, • . . , /С»-и причём Тн есть единственный
двумерный элемент подкомплекса ЛГр9_1; наконец, K9t = ^pi-iX^pt
есть одномерный комплекс.

§ 61
ПРОСТЫЕ ПОВЕРХНОСТИ
129
Докажем, что все комплексы /Q связны. Для К0 = К это по
предположению верно. Принимая, что /Q связно, докажем, что связным является и
комплекс Кц.х = Ki\T?+l\ Т\. Достаточно доказать, что всякие
две вершины a, b этого комплекса можно в нём связать ломаной.
Возьмём ломаную ab, связывающую вершины а и b в К{. Если эта
ломаная не содержится в /Q+1, то это значит, что одним из её
звеньев является сторона Т\ треугольника Tf Если мы докажем,
-что две другие стороны Т* и Г* треугольника Т%_г содержатся
в /Q+n то можно будет в ломаной ab звено 7i_i заменить двух-
звенной ломаной, состоящей из Т\ и Т\, и всё будет готово. Но
сторона Т\ (или Г*) лишь тогда может не входить в Ki+ц если она
-является стороной Т£_х некоторого треугольника Т\ с h<i-\-\.
Однако этого не может быть, так как если отрезок Т\, являясь
стороной Tf_v является ещё стороной Г£_1Э A</-f-1
треугольника Т\л то он должен был быть ещё стороной некоторого третьего
треугольника Т\ с k < /г, что невозможно. Связность /Q+1 этим доказана.
Комплекс К не разбивает /С, так как все треугольники
триангуляции К были занумерованы в виде цепочки, не пересекающей ЛГра;
так как /(р,=>Л, то по теореме [1:23] имеем ^(К^)^^1^) = #,
и следовательно, по определению L и q ^(К^) = ^(Х) = #.
Одномерный комплекс К?% имеет р0 вершин и pj—(р2—1) рёбер
(так как из К удалено р2—1 рёбер); таким образом, по формуле
(1 :24)
Ро — [Pi — (Ра — 1)1 = ^W — «ЧАр.) = 1 — ?>
или р0 — р1^|-р2 = 2—#, что и требовалось доказать.
Из [5:12] и [5 :14] следует:
[5:15]. Теорема об инвариантности порядка
связности. Любые две триангуляции двух гомеоморфных
поверхностей имеют один и тот же порядок связности.
Поэтому естественно назвать порядок связности какой-либо
триангуляции данной поверхности порядком связности самой
этой поверхности,
§ 6. Простые поверхности.
6:1. Замкнутые разрезы. В этом и следующем параграфах
мы под триангуляцией всегда понимаем триангуляцию некоторой
поверхности, а под линией замкнутого разреза
триангуляции К всякую состоящую из элементов триангуляции К простую
замкнутую ломаную линию Л, по крайней мере, один из
отрезков которой является внутренним элементом триангуля*
Ции К (т. е. не лежит на её краю).
" Александров П. С.

130
ПОВЕРХНОСТИ
£гл. и®
Если линия замкнутого разреза А содержит более одной вершины,,
лежащей на краю АГ, то А, как легко видеть, состоит из одной или*
нескольких линий поперечного разреза и из вершин, а может быть
и дуг, лежащих на краю К (этих дуг может и не быть —
см. черт. 59—60).
Сама операция разреза заключается в этом случае в осуществлении,
поперечных разрезов по содержащимся в А линиям этих разрезов.
Если же А имеет на краю единственный элемент, вершину е^
(черт. 61), то операция разреза nj линии А определяется так:
берётся какая-нибудь вторая вершина е ломаной А и сначала произво-
Черт. 59. Черт. 60. Черт. 61.
дится взрез по одной из двух дуг е0еаА, например, по дуге е^ехет
а затем поперечный разрез по второй дуге е0е, содержащейся в А.
Замечание. В случаях, исключающих недоразумения, мы
вместо «линия разреза» будем кратко говорить «разрез».
Нам понадобится в дальнейшем следующее предложение:
[6:11]. Если триангуляция К содержит неразбивающий её за*
мкнутый разрез А, некоторые элементы которого лежат на краю,,
то в некотором правильном подразделении К! триангуляции К можно
найти не разбивающий К! замкнутый разрез А/, все элементы
которого являются внутренними.
Переходя к доказательству утверждения [6 :11], заметим прежде
всего следующее.
Для того чтобы замкнутый разрез А не разбивал триангуляции Kt
достаточно, чтобы два треугольника Тг и Г2, имеющие общую»
сторону, входящую в А, можно было соединить цепочкой
треугольников, в которой два последовательных треугольника имеют общую
сторону, не принадлежащую А. Мы говорим в этом случае, что Tt
и Т2 соединяются цепочкой треугольников, минуя разрез А.
Докажем, что, переходя, если нужно, к барицентрическому^
подразделению, всегда можно предположить, что «звёзды» вершин ег
и вр принадлежащие контуру Г, могут пересекаться лишь, когда в Г
имеется ребро l^fyl- В самом деле, пусть дана триангуляция К
и её барицентрическое подразделение К'. Легко видеть, что в К1
не существует внутреннего ребра, оба конца которого лежат на

§ 6]
ПРОСТЫЕ ПОВЕРХНОСТИ
131
границе поверхности. Отсюда следует, что триангуляция К' обладает
следующим свойством: «звёзды» лежащих на краю поверхности
вершин ег и е" пересекаются только в том случае, когда обе
вершины е' и е" принадлежат одному контуру Г и являются соседними
вершинами на этом контуре. Это свойство мы с самого начала
предполагаем выполненным в триангуляции К.
Для получения линии Л' надо каждый лежащий на краю
поверхности кусок Л0 линии разреза Л «согнать» с края (чертЛ62). Это
Черт. 62.
достигается следующим образом: берём барицентрическое
подразделение К' триангуляции К\ затем рассмотрим часть е[ ег... е8___г е'9^х
линии разреза, состоящую из куска Л0 = в1. . .e8_v лежащего на
краю поверхности, дополненного двумя внутренними рёбрами \е\ ех \
и | *s_i е'8-\ \> ЭТУ часть линии разреза заменяем ломаной А1 = е'1.. *е'8_и
вершинами которой являются внутренние вершины триангуляции К',
лежащие на краю «звёзд» вершин куска Л0 (в триангуляции К')-
Докажем, что после такой замены мы получим простую замкнутую
ломаную Л', не разбивающую триангуляцию К'. В самом деле,
ломаная А1э как легко видеть» является простой незамкнутой ломаной,
лежащей внутри триангуляции К'; кроме того, все вершины, лежащие
на Л1? за исключением е\ и е8_ь не лежат на Л. Так что ломаная Л'
является соединением двух простых незамкнутых ломаных, имеющих
лишь общие концы, и потому оказывается простой замкнутой ломаной.
Остаётся доказать, что ломаная А' не разбивает триангуляцию К'-
Это утверждение в свою очередь легко вытекает из следующего.
В триангуляции К' существуют два треугольника, примыкающие
друг к другу по общему лежащему на At ребру, которые можна
соединить цепочкой треугольников, минуя Л'.
Для доказательства этого последнего утверждения рассмотрим
цепочку треугольников Г/, ..., Т8 триангуляции К\ связывающую
треугольники Г/ и Т8\ примыкающие к ребру \et' ег |, минуя Л. В эту
цепочку войдёт по крайней мере один треугольник со стороной,
лежащей на А1э и вершиной на А0; в самом деле, таким
треугольником является один — и только один — из треугольников Г/ и Т8';
предположим, что Г/. Пусть Tkf — последний треугольник в
цепочке, обладающий указанным свойством (очевидно k=f=s); тогда, как
легко видеть, Ти и Т^х имеют общее ребро, лежащее на Аи и
могут быть связаны между собой цепочкой треугольников, минуя А'.
9*

132
ПОВЕРХНОСТИ
[гл. ш
6:2. Определение простых триангуляции. Инвариантность
при правильных подразделениях.
Определение [6:21]. Триангуляция поверхности Ф
называется простой, если любой замкнутый разрез её разбивает.
Примером непростой триангуляции являются триангуляции поверхности
Мёбиуса или тора. Можно показать: Если триангуляция данной
поверхности Ф проста, то всякая триангуляция всякой поверх-
ности, гомеоморфной поверхности Ф, также проста.
Однако нам понадобится лишь следующий факт:
[6:22]. Триангуляция, являющаяся правильным подразделением
простой триангуляции, проста.
Доказательство. Достаточно вывести из существования не-
разбивающего разреза в элементарном подразделении К' триангуля-
b ции К существование неразбивающего разреза
в Я*. Пусть К' есть элементарное
подразделение по отношению к внутренней стороне*)
| ас | с примыкающими к ней
треугольниками \abc\ и |#afc|; новую вершину на \ас\
обозначим через е. Если в К1 существует
неразбивающий разрез Л, не являющийся
таковым в К, то он содержит по крайней
мере один из отрезков | be |, | ed\. Если Л
содержит лишь один из этих отрезков и идёт,
например, по bee, то, заменяя в Л ломаную bee отрезком | be \,
получим неразбивающий разрез в /С
Пусть Л содержит и \Ье\ и \ed\. Рассмотрим два случая:
1°. Пусть одна из точек а и с, скажем с, принадлежит либо Л,
либо контуру Г поверхности, содержащему хотя бы одну вершину
разреза Г. Треугольник \ade\ можно связать, минуя разрез Л, с одним
из треугольников \bec\, \dec\ цепочкой, не содержащей второго
из них. Если соединёнными оказываются | ade | и | bee |, то отрезок | be |,
часть контура Г до первой вершины Л и далее часть Л, не
содержащая deb, образуют неразбивающий разрез**) старой триангуляции.
2°. Пусть ни а ни с не принадлежат Л и: либо одна из точек а, с,
напримзр с, является внутренней, либо на контуре Г, содержащем
эту точку, нет точек, принадлежащих Л; тогда, заменяя в Л
отрезок bed ломаной bed, снова получим неразбивающий разрез на К*
[6:23]. Всякая триангуляция К0, являющаяся подкомплексом
простой триангуляции /С, проста.
В самом деле, всякая линия замкнутого разреза Л на Ко является
линией замкнутого разреза на К. Пусть Т± и 7£ — два треугольника
К0 с общей стороной, входящей в Л. Так как их нельзя соеди-
*) В случае краевой стороны bd нижеследующие рассуждения только
упрощаются.
** В нашем предположении сторона \Ьс\ оказывается непременно
внутренней.

§ 61
ПРОСТЫЕ ПОВЕРХНОСТИ
133
нить в К цепочкой треугольников, не пересекающих А, то тем более
их нельзя соединить такой цепочкой в /Со, что и требовалось доказать.
6:3. Элементарные леммы. В дальнейшем нам понадобятся
следующие предложения, доказательство которых предоставляется
читателю.
Лемма [6:31]. Если имеется топологическое отображение
окружности S круга Q на окружность S' круга Q\ то это отображение
можно распространить на весь круг (т. е. найти такое
топологическое отображение круга Q на круг Q', при котором соответствие
точек окружности остаётся прежним).
Указание. Применить полярную систему координат.
Лемма [6:32]. Если задано топологическое отображение
некоторой дуги ab окружности S круга Q на диаметр cd полукруга Ql9
то его можно продолжить так, что весь круг Q будет
топологически отображаться на весь полукруг Qu причём окружность круга
отображается на край полукруга.
Замечание. Назовём топологическим кругом всякий
компакт Q, являющийся топологическим образом обыкновенного
круга Q0. В главе 5 будет доказано, что при всяком
топологическом отображении круга Q0 на Q окружность круга Q0 отображается
на одну и ту же простую замкнутую линию £<= Q, называемую т.опо-г
логической окружностью топологического круга Q.
Если принять это утверждение, то леммы [6:31] и [6:32]
остаются, очевидно, верными, если в них под Q и S понимать
топологический круг и его топологическую окружность.
6:4. Классификация простых поверхностей. Поверхность
называется простой, если она имеет хотя бы одну простую
триангуляцию.
Теорема [6:41]. Всякая простая поверхность, край которой со-
стоит из одного контура, топологически отображается на круг.
Доказательство. Как всегда, обозначим через р2 число
треугольников (простой) триангуляции К поверхности Ф. Теорема,
очевидно, верна для р2=1. Предполагая теорему [6:41] верной для
р2^я, докажем её для р2 ===== лг —|— 1. Среди треугольников
триангуляции К имеются прилегающие к краю поверхности Ф. Пусть
Т2 = \е0еге2\ — такой треугольник.
Возможны три случая:
а) Все три вершины, но только две стороны е0е2 и е2ег
треугольника Т2 лежат на краю поверхности Ф.
б) Все три вершины, но только одна сторона е0ег треугольника
Т2 лежит на краю поверхности Ф.
в) Две вершины е0 и ег и одна сторона е0ех треугольника Т2
лежат на краю поверхности Ф.
В случаях а) и в) замкнутый разрез е0е1е2, т. е. в случае а)
поперечный разрез А = e0ev а в случае в) поперечный разрез
A=e0e2ie1 (черт. 63 — 65) превращает К в две непересекающиеся триан-

134
ПОВЕРХНОСТИ
[гл. ш
гуляции. Одной из них является треугольник Т2 с его стор онами и
вершинами, а другой — некоторая триангуляция Kv Край Кг есть
простая замкнутая ломаная, состоящая из Л и из куска e0cet края К.
Триангуляция Кг проста в силу теоремы [6:23] и содержит п
треугольников. Следовательно, поверхность Кг можно топологически
отобразить на полукруг Qx круга Q так, чтобы Л отобразилась на
диаметр этого полукруга. Отображая Т на второй полукруг Q2
круга Q так, чтобы на А это отображение совпало с предыдущим,
получим отображение всей поверхности Ф на круг Q.
В случае б) точки g0, ег и e% разбивают край поверхности Ф на
три куска Аг = е0се29 Л2 = e2deu Л3 = е^. Замкнутый разрез по
линии, состоящей из At и стороны е2е0
треугольника Г2, т. е. поперечный разрез по е0е2,
Черт. 63 (ел. а).
4VX
*
Черт. 64 (ел. б).
А
"
Черт. 65 (ел. в).
превращ ает триангуляцию К в две непересекающиеся простые
триангуляции Кг и /С2, каждая из которых содержит не более чем п
треугольников. Поэтому поверхности Kt и /С2 гомеоморфны кругу.
Отображая каждую из них на два полукруга одного и того же круга
так, чтобы оба отображения совпадали между собою на е0е2, получим
отображение поверхности К на круг, что и требовалось доказать.
Теорема [6:42]. Простая замкнутая поверхность
гомеоморф на сфере.
Доказательство. Удаляя из простой триангуляции К
замкнутой поверхности Ф один треугольник Г2, получим простую
триангуляцию Ki с одним контуром. Отображая топологически Кг и Г2
на две полусферы так, чтобы оба отображения совпадали на границе
треугольника Т2 и переводили её в экватор сферы, получим иско-
мое отображение всей поверхности К на сферу.
Упражне ни е. Рассуждениями, анологичными применённым при
доказательстве теоремы [6:41], доказать, не пользуясь теоремой
инвариантности, что эйлерова характеристика любой триангуляции поверхности, гомео-
морфной кругу, равна единице. Вывести отсюда (также не пользуясь
теоремой инвариантности) классическую теорему Эйлера:
Любая триангуляция поверхности, гомеоморфной сфере, имеет эйлерову
характеристику, равную двум.
Замечание 1. Из теоремы Жордана следует, что всякая
триангуляция сферы проста. Итак:

§ 6]
ПРОСТЫВ ПОВЕРХНОСТИ
135
Если одна какая-нибудь триангуляция замкнутой поверхности Ф
проста, то Ф гомеоморфна сфере и тогда все триангуляции Ф
тросты.
Определение [6:43]. Нормальной простой
поверхностью Qr с г контурами называется сфера с прорезанными
<в ней г круглыми дырками, края которых не имеют попарно общих
точек. Края дырок причисляются к поверхности.
Замечание 2. Так как при топологическом отображении
одной поверхности Ф на другую Ф' края поверхностей Ф иФ'
соответствуют друг другу *), а гомеоморфные множества (в частности,
элементарные кривые") состоят из одного и того же числа
компонент, то гомеоморфные поверхности имеют одно и то же число
контуров.
Замечание 3. Прорезать в сфере круглую дыру всё равно,
•что отсечь от неё шаровой сегмент.
Замечание 4. Определённые в [6:43] поверхности Qr,
очевидно, гомеоморфны поверхностям, получающимся, если из круга Q
удалить внутренность г—1 попарно не пересекающихся кругов,
лежащих внутри круга Q. Именно так поверхности Qr будут
изображаться на чертежах.
Теорема [6:44}. Всякая простая поверхность Ф с г
контурами гомеоморфна нормальной простой поверхности Qr.
Теорема эта, очевидно, содержится в
[6:45]. Пусть дана поверхность Ф с г контурами, имеющая
простую триангуляцию К. Пусть дано топологическое
отображение С одного из контуров поверхности Ф на один из контуров
нормальной поверхности Qr. Отображение С можно продолжить
& топологическое отображение всей поверхности Ф на
поверхность Qr (переводящее, в силу иншариантности края, край
поверхности Ф в край поверхности Qr).
Доказательство теоремы [6:45]. Из [6:41] и леммы
[6:31] следует, что теорема [6:45] верна для г=1.
Предположим, что теорема 16:45] в-ерна для г^я, и докажем её для
г = п -4- 1.
Итак, пусть К—простая триангуляция поверхности Ф с п-\-\
контурами, среди которых отметим два каких-нибудь контура Ft и Г2.
Поверхность Q„+i представляем себе в определённой триангуляции
(для того, чтобы иметь возможность говорить о разрезах на этой
поверхности). Среди контуров поверхности Qn+\ выделим два
произвольных контура Г/ и Гу. Возьмём на К простую ломаную А,
соединяющую Г\ и Г2; точно так же возьмём ломаную Л' на Qn+\,
соединяющую Г/ и Г2'. После разреза (черт. 66) по ломаным А
<и А' поверхности Ф и Qn+\ перейдут соответственно в Фх = Кх и
*) Это предложение будет доказано (независимо от результатов
настоящей главы) в главе пятой.

136
ПОВЕРХНОСТИ
[гл. и»
Qn+i, и причём каждая пара контуров: Гр Г2 и Г[, Г^ заменяется одним*
контуром
r = I1UA+UI2UA->
соответственно
r' — LlUA'+UIa'UA'"",
где 11э L2 и т. д. — простые дуги, возникшие иэ Тг и Г^ и т. д,.
после разреза (например, Lx есть простая дуга е^е%е+, —см. черт. 67),
Поверхности Фг и Qn+i,i имеют лишь по п контуров. Поверхность
Qn+\,i можно, очевидно, отождествить с поверхностью Qn.
Докажем, что Фг — простая поверхность. В самом деле, если бы
триангуляция Ки в которую перешла триангуляция К после нашего»
Черт. Ьб. Черт. 67.
разреза, содержала неразбивающий замкнутый разрез, то некоторое
правильное подразделение К\ триангуляции Кх содержало бы
неразбивающий замкнутый разрез D\y без элементов, лежащих на
краю. При склеивании, возвращающем Кх в К> подразделение к[
триангуляции Кх перейдёт в некоторое правильное подразделение Кг
триангуляции /С, а неразбивающий разрез D\ триангуляции К—в>
неразбивающий разрез триангуляции К'. Но это невозможно, так как
триангуляция К\ будучи правильным подразделением простой
триангуляции К, по теореме [6:22] проста.
Пусть теперь дано топологическое отображение CW линии 1\ н&
Гь Оно определяет топологическое отображение С^ простой дуги
Lx на простую дугу Lu отображающее оба конца е+, е^ дуги Ьг
соответственно на концы простой дуги L\. Отображение Ст£\
можно продолжить в отображение С\, замкнутой линии Г на Г', пр№
котором A+,Ij, A", L2 отображаются соответственно на A' + ,Z,J, А'"",/,'
и две лежащие друг против друга точки дуг А+ и А" переходят
в две лежащие друг против друга точки А'+ и А'-.
По индуктивному предположению топологическое отображение q^
м°жно продолжить в топологическое отображение С%ъ поверх-

§ 7]
КЛАССИФИКАЦИЯ ЗАМКНУТЫХ ПОВЕРХНОСТЕЙ
137
ности Фх на 0п+1,ь т- е- на Qn- Если теперь произвести склеивание^
упраздняющее только что сделанные разрезы, то гомеоморфизм Cq^
между Фг и Q/24-i,i перейдёт в гомеоморфизм Cq^i между Ф и Qn+if
совпадающий на Г^ с заданным первоначально гомеоморфизмом Сг/.
Теорема [6:45], а значит, и [6:44] этим доказаны.
Из [6:44] и замечания 2 следует:
[6:440]. Две простые поверхности гомеоморфны между собок>
тогда и только тогда, если они имеют одно и то же число
контуров.
Докажем теперь, что простая поверхность с г контурами имеет
эйлерову характеристику 2'—/\ В силу инвариантности эйлеровой*
характеристики, достаточно доказать
(6:46) Х«М = 2 —г.
Так как эйлерова характеристика сферы равна 2, то, в силу той!
же инвариантности эйлеровой характеристики, равенство х = X(Qr) =
= 2 — г вытекает из следующего очевидного предложения:
Удаляя из триангуляции К произвольный треугольник и сохраняя*
его вершины и стороны, мы уменьшаем эйлерову характеристику
этой триангуляции на единицу.
Упражнение. Доказать при помощи теоремы Жордана, 'что*
всякая триангуляция простой поверхности проста. При
доказательстве достаточно рассматривать произвольные криволинейные
триангуляции нормальных простых поверхностей.
§ 7. Классификация замкнутых поверхностей.
7:1. Род поверхности. Нормальные поверхности данного рода.
Определение [7:11]. Пусть Ф — замкнутая поверхность.
Родом поверхности Ф называется половина её порядка связности,
если Ф ориентируема, и уменьшенный на 1 порядок её связности,
если Ф не ориентируема. Род замкнутой поверхности Ф обозначается?
через р (Ф).
Выясним геометрический смысл понятия рода.
Заметим прежде всего: заклеивая ручкой пару дырок
простой нормальной поверхности Qn мы неизменяем
её эйлеровой характеристики. В самом деле, при
склеивании двух контуров (разбитых на одно и то же число дуг) число
треугольников не изменяется, тогда как число отрезков и
вершин уменьшается на одно и то же число (если край каждой дырки
имел k сторон и k вершин, то общее число одномерных и общее-
число нульмерных элементов триангуляции после заклеивания
уменьшается на k).
Точно так же, заклеивая в поверхности Qr одну из дыр листом
Мёбиуса, мы не изменяем эйлерову характеристику поверхности.
Возьмём произвольное целое число р ]> 0. Рассмотрим теперь
нормальную простую поверхность Qip, т. е. сферу с р парами дырок,.

138
ПОВЕРХНОСТИ
[гл. ш
Обозначим через Фр замкнутую и, как легко видеть, ориентируемую
поверхность, которая получится, если все эти р пар дыр заклеить
ручками первого рода. На основании только что сказанного
эйлерова характеристика поверхности Фр равна эйлеровой характеристике
^поверхности Q2py т. е. 2— 2р. Итак,
Х(Ф,) = 2 — 2р.
Так как, с другой стороны ([5:14])
Я(Фр)*=2 — q,
то # = 2р, т. е. р = -к есть род поверхности Фр.
Итак:
[7:12]. Пусть р — произвольное неотрицательное целое число; за-
жлеивая ручками первого рода все р пар дырок нормальной простой
поверхности Q2p, получим замкнутую ориентируемую поверхность
«Фр рода р.
Поверхность Ф^ называется нормальной замкнутой
ориентируемой поверхностью родар или просто «сферой
с р ручками».
Заклеим теперь в поверхности Qp+t все её р -}-1 дыр листами
'Мёбиуса. Получим замкнутую неориентируемую поверхность Wpi
эйлерова характеристика которой равна эйлеровой характеристике
поверхности Q^-f-i» т. е. 1 —р.
Из формулы Эйлера следует, что p — q—1, т. е. что р есть род
«еориентируемой поверхности Wp.
Итак:
г[7:13]. Заклеивая листами Мёбиуса все p-f-1 дыр поверхности
Qp%v получим замкнутую неориентируемую поверхность Ч?р рода р.
Она называется нормальной замкнутой неориентиру е-
мой поверхностью рода р.
* В связи с только что сделанными построениями естественно
спросить себя, что получится, если пару дыр поверхности Qr заклеить
ручкой второго рода. Ответ на этот вопрос даётся следующим
предложением, которое сейчас же понадобится нам.
[7:14]. Заклеивание на поверхности Qr пары дыр ручкой
второго рода равносильно заклеиванию каждой из этих дыр листом
Мёбиуса (и потому приводит к неориентируемой поверхности).
Доказательство. На черт. 68 изображена пара дыр,
подлежащая заклеиванию ручкой второго рода; точки 1, 2, 3, 4, 5, 6, 7, 8
склеиваются соответственно с точками 1', 2', 3', 4', 5', 6', 7', 8'.
Произведём поперечные разрезы по линиям 33' и 77' (черт. 69) и
«четырёхугольник» (черт. 69, 70) 33' 77' повернём на 180° вокруг
оси АА' (черт. 71).
Склеивая подлежащие склеиванию элементы (обозначенные
одинаковыми цифрами), получим черт. 72.

.§ 7] КЛАССИФИКАЦИЯ ЗАМКНУТЫХ ПОВЕРХНОСТЕЙ 139
Теперь остаётся только каждую из двух дыр ЗаЬЗ'а'Ь' и 7d'c'7cd
заклеить так, как указано (т. е. склеить 3 с 3\ а с a', b с Ь' и т. д.),
что представляет собою заклеивание второго типа, т. е. заклеивание
каждой из этих дыр листом Мёбиуса.
7:2. Основная теорема топологии поверхностей. Задача
всего этого артикула заключается в доказательстве следующих двух
«предложений, образующих вместе так называемую основную теорему
топологии поверхностей.
[7:2]. Всякая замкнутая поверхность
<[> гомеоморфна нормальной замкнутой
ориентируемой поверхности Фр некоторого
^целочисленного) рода р (если Ф
ориентируема) или нормальной замкнутой неориен-
тируемой поверхности Фр рода р (если Ф
не ориентируема).
Отсюда непосредственно вытекает, что
для всякой замкнутой ориентируемой
поверхности Ф род р(Ф) есть целое, значит
порядок связности — чётное число.
Из [7:2] и из инвариантности эйлеровой
•характеристики и ориентируемости следует:
[7:21]. Две замкнутые поверхности Ф и Ф' гомеоморфны
тогда и только тогда, когда они обе ориентируемы или обе
Черт. 69. Черт. 70. Черт. 71.
не ориентируемы и когда, кроме того, для них выполнено ка-
кое-нибудь и, значит, любое из следующих равенств:
1. Равенство эйлеровых характеристик.
2. Равенство порядков связности.
3. Равенство родов.
Переходя к доказательству теоремы [7 :2], заметим прежде
всего:
[7:211]. Пусть Ф — замкнутая поверхность, ^==^(ф). Всякий
подкомплекс любой триангуляции К поверхности Ф, состоящий
Черт. 68.

140
ПОВЕРХНОСТИ
[гл. ш
из <7+1 попарно непересекающихся згмкнутых линий
разбивает эту триангуляцию.
В самом деле, Lx U ... U L^+i есть одномерный комплекс
порядка связности #+1, откуда утверждение [7:211] и следует.
Обозначим через д' = д'(Ф) наибольшее такое число, что на
некоторой триангуляции К поверхности Ф существует qr попарно
непересекающихся замкнутых линий Lj,.. ,,Z,3/, образующих
подкомплекс L — Lx U ... U Lafy не разбивающий /С
[Из 7:2 11] следует, что
Произведём разрез по всем линиям*
L1}..., Lq/. В результате этого разреза
триангуляция К0 превратится в триангуляцию*
Кх некоторой поверхности /С1 = Ф1.
Докажем, что /Q есть простая
триангуляция. В самом деле, если бы на триангуля-
Черт. 72. Ции Кг существовал не разбивающий её-
разрез, то на некотором подразделении К\
этой триангуляции существовал бы не разбивающий её разрез,
состоящий из одних внутренних элементов; следовательно, на
соответствующей триангуляции К! поверххности Ф можно было бы провести
#'+1 попарно непересекающихся разрезов, не
разбивающих триангуляцию К\ что противоречит определению числа q'.
Итак, Ф-t есть простая поверхность, гомеоморфная, в силу [6:44]*
некоторой нормальной простой поверхности Qr.
Чтобы вернуться от Фх к Ф, надо произвести склеивание,
упраздняющее сделанные разрезы поверхности Ф по линиям Z,1?. . .,Zy.
Одновременно будем производить соответствующие склеивания на Qr.
В результате Фг превратится в Ф, a Qr превратится в некоторую*
замкнутую поверхность S, гомеоморфную Ф.
Что будет представлять собой S? Для ответа на этот вопрос
рассмотрим подробнее разрез Ф вдоль фиксированной линии Ь==Ь4
и обратную операцию — склеивание. Возможны следующие случаи::
1. Разрез L однобережный.
Его уничтожение есть заклеивание второго типа, которому
соответствует на Qr заклеивание дыры листом Мёбиуса. Если Ф —
ориентируемая поверхность, то этот случай представиться не может.
2. Разрез L двубережный; он порождает два контура Z,+, Z,-,
которым соответствуют две дыры: Z,[, Z,2, поверхности Qr; отсюда следует,,
что если все разрезы L — двубережные, то г есть чётное число 2р.
Упразднению разреза L поверхности Ф соответствует на Qr
заклеивание пары дыр L\, Z,2, которое осуществляется либо ручкой

§ 7| КЛАССИФИК\ЦИЯ ЗАМКНУТЫХ ПОВЕРХНОСТЕЙ 141
первого рода, либо ручкой второго рода, в зависимости от
чего мы самый разрез L называем двубережным
разрезом первого или второго рода.
В силу [7 :14], двубережный разрез второго рода на
ориентируемой поверхности невозможен.
Итак, если Ф — ориентируемая замкнутая поверхность, то г еСть
чётное число 2р, и гомеоморфная поверхности Ф поверхность S
получается из Qr Заклеиванием всех дыр (распределённых на пары)
ручками первого рода.
Другими словами:
Для каждой ориентируемой замкнутой поверхности Ф
определяется целое число р^=0 таге, что поверхность Ф гомеоморфна
нормальной ориентируемой поверхности рода р («сфере с р ручками»),
и, следовательно, сама является поверхностью рода р: две
ориентируемые замкнутые поверхности тогда и только тогда гомео-
морфны между собой, когда они имеют один и тот же род
или, что то же самое, одну и ту же эйлерову
характеристику.
Перейдём теперь к случаю замкнутой неориентируемой
поверхности. Превращая замкнутую неориентируемую поверхность Ф
в простую поверхность Qr, мы можем встретиться с разрезами
всех трёх типов, причём среди них найдётся либо, по
крайней мере, один однобережный разрез, либо» по крайней мере, один
двубережный разрез второго рода (либо и то и другое).
Таким образом, каждая замкнутая неориентйруемая поверхность
гомеоморфна замкнутой поверхности S, получающейся из некоторой
простой поверхности Qr следующими операциями:
а) заклеивание некоторых дыр поверхности Qr листами Мёбиуса;
б) заклеивание некоторых пар дыр поверхности Qr ручками
второго рода;
в) заклеивание некоторых пар дыр поверхности Qr ручками
первого рода.
Покажем, что всегда можно ограничиться лишь операциями
типа а).
Прежде всего, в силу [7:14], каждую операцию типа б) можно
заменить двумя операциями типа а).
Докажем теперь:
[7:22]. Совокупность двух операций:
1) заклеивание дыры листом Мёбиуса,
2) заклеивание пары дыр ручкой первого рода равносильно
совокупности двух операций:
1) заклеивание дыры листом Мёбиуса,
2) заклеивание пары дыр ручкой второго рода.
В самом деле, пусть (черт. 73) дыры I w II склеиваются ручкой
первого рода, а дыра /// заклеивается листом Мёбиуса, т. е. в ней
склеиваются диаметрально противоположные точки (а и а', Ъ и Ъг и т. д.).

142
ПОВЕРХНОСТИ
[ГЛ. И»
Произведём разрез по линии aABCDEFa' (черт. 73). Повернём
фигуру A'B'C'D'E'F'dcb (черт. 74) вокруг горизонтальной оси cf на 180е"
(черт. 75) (на черт. 74 и 75-
* . 4 . В _. ось cj дана пунктиром).
Заклеим дыру ///, склей»
подлежащие склеиванию
элементы (черт. 76).
Придадим к'онту р у
ABCDEFA'B'C'D'E'F'A фор-
му окружности (черт. 77).
Полученная круглая дыра,
очевидно, подлежит
заклеиванию листом Мёбиуса, а дыры /
и // — ручкой второго рода, что
и требовалось доказать.
Пусть неориентируемая
поверхность Ф получается из
простой поверхности Qr несколькими операциями типов а), б), в).
Так как всякая операция типа б) может быть заменена операциями
типа а), то мы можем предположить, что операции типа а) наличе-
1> А В
Черт. 73.
Черт. 74.
Черт. 11.
ствуют. Но в этом случае каждая операция типа в) может быть
заменена операцией типа б), так что всё сведётся к операциям а) и б).
Заменяя все операции типа б) операциями типа а), сведём всё
построение неориентируемой замкнутой поверхности Ф из простой
поверхности Qr к одним лишь операциям типа а).
Итак:
Всякая замкнутая неориентируемая поверхность гомеоморф-
на поверхности, полученной из нормальной простой
поверхности Qr {сферы с прорезанными в ней дырами) заклеиванием дыр
поверхности Qr листами Мёбиуса.
Теорема [7*. 2] этим доказана во всех своих частях.
Примеры.

§7]
КЛАССИФИКАЦИЯ ЗАМКНУТЫХ ПОВЕРХНОСТЕЙ
14&
1. Для проективной плоскости Ф имеем
Х(Ф)=1> ?(ф)=Ь р(Ф) = 0.
Проективная плоскость получается заклеиванием в сфере одной*
дыры листом Мёбиуса или (что то же самое) склеиванием по их~
краям листа Мёбиуса с кругом.
2. Для поверхности Клейна имеем
Х(Ф) = 0, ?(Ф) = 2, р(Ф)=1.
Поверхность Клейна получается, если две дыры, прорезанные в сфере,..
{ г
/71
? с
J >'
Л
4'v
л
/ J
Ч^ ^Л'
У
Черт. 76.
Черт. 77.
заклеить листами Мёбиуса или . (что, очевидно, то же самое), еслю
два листа Мёбиуса склеить их краями.
Замечание 1. Из всего сказанного следует:
Порядок связности замкнутой ориентируемой поверхности Ф
есть чётное число, равное числу дыр в сфере, которые нужно
(попарно) заклеивать ручками первого рода, чтобы получить
поверхность, гомеоморфную данной поверхности Ф.
Порядок связности замкнутой неориентируемой поверхности Ф
равен числу дыр в сфере, которые нужно заклеить листами Мёбиуса*,
чтобы получилась поверхность, гомеоморфная данной поверхности.
Замечание 2. Если порядок связности данной замкнутой
неориентируемой поверхности Ф есть чётное число #=2/?, то
поверхность, гомеоморфную Ф, можно получить, взяв простую поверх*
ность Q2p (сфера с 2р дырами) и заклеив р пар дыр этой поверхности:*
ручками второго рода (при р = 1 получаем поверхность Клейна).

ЧАСТЬ ВТОРАЯ.
КОМПЛЕКСЫ. ПОКРЫТИЯ. РАЗМЕРНОСТЬ.
В этой части так же, как и в предыдущей, — три главы. В первой из
«их (глава 4) подробно изучается понятие комплекса; таким образом, в этой
главе (и в главе 7) строится комбинаторный (и алгебраический) аппарат
топологии; обе названные главы имеют, по существу, вспомогательный
характер. Главу 7 можно читать непосредственно после главы 4.
В главе 5 элементарными средствами (при помощи так называемой
леммы Шпернера) доказывается несколько важных топологических
фактов — инвариантность числа измерений для полиэдров, инвариантность
^внутренних точек, а также теорема о неподвижных точках при
непрерывных отображениях симплекса. Главу 5 можно читать и до прочтения
главы 4.
Глава б, посвященная введению в теорию размерности, опирается на § 1,
арт. 2:1, 2:2; § 3, арт. 4:1—4:3 и 5:1—5:3 главы 4 (и на указанные
е ссылках места из главы 1). Главу б естественно читать после прочтения
главы 5.
ГЛАВА ЧЕТВЁРТАЯ.
КОМПЛЕКСЫ.
Вводный параграф: предварительные замечания о симплексах.
В этом параграфе напоминается определение n-мерного сим-
шлекса (см. Прибавление 2) и вводятся основные понятия, связанные
с этим определением.
Мелкий шрифт этого параграфа при первом чтении
рекомендуется пропустить, — он понадобится лишь в главе 14.
0:1. Симплексы и их остовы. Пусть в /я-мерном эвклидовом
пространстве /?w даны л-f-l линейно независимых точек е0, elt..., en,
О^п^гп; в силу линейной независимости, эти точки определяют
я-мерную плоскость Rn (e0, еи.. ., en)czRm и в ней систему
барицентрических координат *). Те точки плоскости ^(е^ £1?..., еп), все
барицентрические координаты которых jx0, ^j,.. ., jaw в системе
<(е0, £1э..., еп) положительны, по определению образуют ^мерный
симплекс Г=ф0. .. еп\ с вершинами еф.. ., еп.
Уменьшенное на 1 число вершин симплекса называется его
числом измерений, или размерностью. Число измерений симплекса
обычно обозначается верхним индексом. Так Тп обозначает /г-мер-
«ый симплекс.
*) См. Прибавление И, арт. 1 :2.

ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ О СИМПЛЕКСАХ 145
Нульмерный симплекс представляет собою точку. Одномерный
симплекс с вершинами е0 и ех представляет собою открытый
отрезок \е0 ех\ (концы к отрезку не причисляются). Двумерный симплекс
есть треугольник, а трёхмерный — тетраэдр (тоже открытые, т. е.
без граничных точек).
Определение [0:11]. Множество всех п-\-1 вершин данного
n-мерного симплекса называется остовом этого симплекса.
Симплексы в Rm взаимно однозначно соответствуют своим
остовам.
Замечание. Иногда оказывается целесообразным рассматривать
системы я+1 различных, но линейно зависимых между собой точек в Rm, как
остовы «вырождающихся» /г-мерных симплексов. При этом удобнее
всего вырождающийся /2-мерный симплекс считать тождественным с его
остовом.
Таким образом, приходим к такому определению:
Всякое множество из п-\- I точек пространства Rm, лежащее в
плоскости Rk^Rm, число измерений k которой меньше, чем п, называется
вырождающимся n-мерным симплексом пространства Rm. Под остовом
вырождающегося симплекса понимается сам этот вырождающийся
симплекс *).
0:2. Грани. Если остов симплекса Тг есть подмножество
остова симплекса Т2, то симплекс Тх называется гранью
симплекса Г2. Если симплекс Тг=\е0.. *ег\ есть грань симплекса
T2 — \e0...erer+l...en\t то 7\ состоит из всех точек пространства
Rn(e0i. . ., еп), у которых барицентрические координаты \i4 в системе
еф. . ., еп положительны для / ^ г и равны нулю для / > г.
Число r-мерных граней /г-мерного симплекса равно числу
сочетаний С^ из п -J- 1 элемента nor-j-1. Нульмерные грани
симплекса суть его вершины. Сам симплекс называется своею
несобственной гранью, остальные грани называются собственными.
Замечание 1. Важно заметить, что во всей этой книге под
гранью (без дальнейших оговорок) данного симплекса всегда
разумеется собственная или несобственная грань этого
симплекса.
Вместо того, чтобы говорить, что симплекс Тг есть собственная
грань симплекса Т2;говорят, что симплекс Тг подчинён
симплексу Т2 и пишут Тг<СТ2 или 72>Т1. Если симплекс 7\ есть
собственная или несобственная грань симплекса Т21 то пишут Т1^Т2
или Г2>7\.
Для того, чтобы выразить, что симплексы Тх и Т2 находятся
в одном из соотношений 7\<Г2 или Г2<Г1, говорят, что эти
симплексы инцидентны.
Грани Т£ и Ts2 симплекса Тп называются противоположными^
если каждая вершина симплекса Тп есть вершина одной из граней
*) В тех местах этой книги, в которых мы будем пользоваться
вырождающимися симплексами, это будет всегда оговорено. Во всех остальных
случаях под симплексом будет всегда пониматься симплекс, как мы его
определили в крупном шрифте (т. е. невырождающийся симплекс).
Ю Александров П. С.

146
КОМПЛЕКСЫ
(гл. iv
Тг или Ts и если грани эти не имеют общих вершин (черт. 78).
1 2
В этом случае
r^-s = n— 1.
Иногда удобно обозначать грань Тг симплекса \е0. .. еп\,
противоположную грани Ts этого симплекса, ставя над вершинами грани
Ts знак л; так, \е0... е^..еп\ обо-
УК значает грань \е0. . ,ei~1ei+1... еп\.
у// N. Замечание 2. Если Тп = \eQ... еп\
л-3 <£-—г ^^ есть вырождающийся симплекс (или, что
^ч/^^ по нашей терминологии одно и то же,—
г*0л$*2 r*J s~J вырождающийся остов), то собственной
' гранью Р* называется всякий симплекс
(вырождающийся или нет), остовом кото-
Черт. 78 Рого является какое-либо собственное
подмножество остова {е0. • • £п\* Из этого
определения следует, что у вырождающегося
симплекса могут быть невырождающиеся грани: например, три точки
А В, Су лежащие на одной прямой, образуют вырождающийся треугольник,
имеющий, однако, три невырождающиеся стороны АВ, ВС, С А.
0:3. Комбинаторная сумма. Пусть Ти Т^,..., Тк—
какие-нибудь грани симплекса Т. Соединение остовов симплексов 7^, Т^,. ..,
Тк есть подмножество остова симплекса Т и потому остов некоторой
его грани Т0<^ Т. Симплекс Т0 называется комбинаторной
суммой симплексов Ти 72,..., Тк и обозначается \Тг Т2- - .Тк\.
Комбинаторная сумма определена, таким образом, для симплексов,
являющихся гранями одного и того же симплекса.
Очевидно:
1. Всякий симплекс есть комбинаторная сумма любых двух своих
противоположных граней.
2. Всякий симплекс есть комбинаторная сумма своих граней
данного числа измерений (в частности, всех своих вершин).
0:4. Замыкание симплекса Тп = \е0ех.. ,еп\ в пространстве Rm
обозначается через Тп = е0... еп и называется замкнутым
симплексом. Замкнутый симплекс Тп = е0 .. . еп состоит из всех тех
точек пространства Rn(e0, ег,...,еп)у барицентрические координаты
которых в системе eQy eu...,en не отрицательны.
Граница fn\Tn симплекса Т1 является соединением всех
собственных граней симплекса 7п и иногда обозначается через Тп (по
основаниям, которые выяснятся впоследствии).
§ 1. Основные определения.
1 :1. Триангуляции. Примеры: [Тп] и Тп.
Определение [1:11]. Конечное множество /("попарно не
пересекающихся симплексов, лежащих в некотором Rn,
называется тр и ан гул яци ей, если всякая грань всякого симплекса,
являющегося элементом множества /С, также является элементом мно-

§ 1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
147
жества К. Множество К при этом частично упорядочено:
симплекс 7\ £ К считается подчинённым симплексу Г2 £ К, если Тг есть
собственная грань симплекса Г2.
Наибольшее число, являющееся числом измерений какого-либо
элемента триангуляции К, называется числом измерений, или
размерностью триангуляции /С.
Замечание. Естественность этого определения вытекает,
например, из рассуждений и результатов главы 3: значительную часть
топологии составляет изучение так называемых полиэдров, т. е.
множеств Фс/?и, которые могут быть «триангулированы» (разбиты
на симплексы, образующие некоторую триангуляцию), другими
словами, которые являются соединением симплексов
некоторой триангуляции. Одновременно с полиэдрами изучаются,
конечно, и их топологические образы—так называемые кривые
полиэдры, являющиеся далеко идущим многомерным обобщением
замкнутых поверхностей, изученных в главе 3. Так как кривые по*
лиэдры, будучи топологическими образами полиэдров в собственном
смысле этого слова, имеют те же топологические свойства, что
и эти последние, то топология полиэдров исчерпывает собою и
исследование топологических свойств всех кривых полиэдров.
Триангуляции являются основным вспомогательным средством, основным
аппаратом топологии полиэдров, которая представляет собою не
только одну из важнейших частей топологии, но-и содержит в себе
методы исследования и более общих топологических пространств,
прежде всего компактов. Отсюда понятно огромное значение
триангуляции в современной топологии: не являясь конечной целью,
окончательным предметом изучения топологии, имея в топологии лишь
служебное положение, триангуляции и их ближайшие обобщения
занимают тем не менее место основного средства, основной
вспомогательной конструкции современного топологического
исследования. Это своеобразное служебное и в то же время основное
положение триангуляции в топологии достаточно убедительно показано
в третьей (и пятой) главе этой книги.
Примеры триангуляции строятся легко. Несколько примеров
одномерных, двумерных и трёхмерных триангуляции изображено
на черт. 79, а также на чертежах гл. 3. Множество всех
собственных граней тетраэдра, октаэдра или икосаэдра также может служить
примером двумер ной триангуляции.
Особо выделим два элементарных примера, которые будут
постоянно нужны в дальнейшем.
1. Триангуляция, состоящая из /z-мерного симплекса Тп и всех
его граней, обозначается через [Тп] и называется
комбинаторным замыканием симплекса V1.
2. (п—1)-мерная триангуляция, состоящая из всех собственных
граней n-мерного симплекса, Тп обозначается через Тп и назы-
вается краем симплекса Тп (в отличие от границы Тп симплекса Тп,
10*

148
КОМПЛЕКСЫ
[гл. иг]
которая есть множество точек, являющееся соединением
всех собственных граней симплекса Тп).
1 :2. Полиэдральные комплексы. Если в определении
триангуляции заменить слово «симплекс» словом «выпуклый многогранник»*),
оставив всё остальное без изменения, то получится определение п о-
лиэдрального комплекса. Это понятие хоть и значительно
Черт. 79.
менее важно, чем понятие триангуляции, но
является настолько естественным обобщением
последнего понятия, что отказаться от него
невозможно. Кроме того, иногда замена
триангуляции данного полиэдра более общим
полиэдральным комплексом позволяет упростить
некоторые построения. Примерами полиэдральных комплексов могут
служить: комплекс, состоящий из всех граней куба или додекаэдра;
изображённое на черт. 80 разбиение на
четырёхугольники, их стороны и вершины
некоторой поверхности, гомеоморфной
тору, и многие другие.
Если Тп есть выпуклый многогранник,
то его комбинаторное замыкание [Тп] и
его край Тп определяются совершенно так
же, как и в случае симплекса (см.
предыдущий артикул).
1 :3 Комплексы остовов. Это понятие в высшей степени
важно, особенно для геометрической трактовки вопросов теоретико-
множественной топологии; но и в вопросах топологии полиэдров
комплексы остовов получат в этой книге существенные применения.
Определению комплексов остовов предпошлём следующее замечание.
Симплексы, в частности, симплексы некоторой данной
триангуляции /С, взаимно однозначно соответствуют своим остовам, причём
*) При этом, выпуклые многогранники (так же, как симплексы) берутся
открытые (т. е. без граничных точек): под квадратом понимается
внутренность квадрата, под кубом — внутренность куба и т. п.
Черг, 80.

§ 1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
149
симплекс Тг £ К тогда и только тогда подчинён симплексу Т2 (т. е.
является собственной гранью симплекса Т2), когда остов 7\ есть
собственное подмножество остова Т2.
Во многих вопросах, касающихся триангуляции, природа
симплексов как точечных множеств несущественна, а имеют значение,
во-первых, порядок, господствующий в триангуляции, как частично
упорядоченном множестве, и, во-вторых, то обстоятельство, что
для каждого симплекса определено число его измерений. Во всех
таких, как говорят, чисто комбинаторных вопросах
естественно и удобно заменять данную триангуляцию множеством
её остовов, т. е. множеством остовов симплексов данной
триангуляции, причём каждому остову в качестве его числа измерений
относится уменьшенное на единицу число составляющих этот остов
вершин. Таким образом, мы приходим к так называемым комплексам
остовов, определение которых сразу в самом общем виде и будет
сейчас дано.
Определение [1:31]. Пусть дано некоторое множество
М элементов, условно называемых вершинами. Пусть среди
непустых конечных подмножеств множества М выделены
некоторые, называемые остовами. Числом измерений остова называется
уменьшенное на 1 число составляющих его вершины. Данное
множество остовов частично упорядочено естественным
образом *) {остов Тг подчинён остову 72, если Т1 cz Т2); оно
называется комплексом остовов.
Итак, мы можем сказать:
комплекс остовов есть любое множество некоторых конечных
подмножеств какого-либо множества М.
Комплекс остовов К называется полным, если всякое непустое
подмножество какого-либо остова, входящего в /С, также есть остов
(т. е. элемент комплекса К).
Замечание. Комплекс остовов данной триангуляции (т. е.
комплекс остовов всех элементов этой триангуляции) есть конечный
полный комплекс остовов. Среди всех комплексов остовов
конечные и притом полные комплексы являются самыми
важными. Однако, часто приходится пользоваться и неполными
комплексами остовов.
Определение [1 :32]. Пусть К—комплекс остовов.
Определим комплекс остовов [К] следующим образом: Каждое непустое
подмножество каждого остова комплекса К по определению
является остовом комплекса [К]. Определённый таким образом комплекс
остовов [К] является полным. Он называется комбинаторным
замыканием комплекса К.
Очевидно, К есть подкомплекс комплекса [К]. Итак:
[1 :33]. Всякий комплекс остовов есть подкомплекс некоторого
полного комплекса остовов.
*> Глава 1, арт. 6:2, пример 4°.

150
КОМПЛЕКСЫ
[гл. iv
If:4. Общее определение симплициального комплекса. Начнём
со следующего примера. Рассмотрим тетраэдр Г, вписанный в шар.
Его вершины лежат на поверхности шара и определяют, с одной
стороны, грани и рёбра тетраэдра, а с другой стороны, —
получающиеся из этих граней и рёбер центральной проекцией сферические
треугольники и их стороны. Таким образом, одному и тому же
комплексу остовов соответствует, с одной стороны, обыкновенная
триангуляция Г, а с другой стороны, «криволинейная триангуляция
сферы», элементы которой имеют те же остовы, что и
триангуляция Т. И те и другие элементы являются «симплексами» одни —
настоящими, другие — сферическими, определёнными данными остовами;
множество этих «симплексов» в обоих случаях естественно считать
«симплициальным комплексом». Так приходим к следующему весьма
общему и окончательному определению.
Определение [1:41]. Пусть дан полный комплекс остовов К\
пусть каждому остову {е0,...,ег} комплекса К однозначно
поставлен в соответствие некоторый элемент |е0...£г|, называемый
абстрактным симплексом с вершинами е0, ..., ег; при этом требуем,
чтобы соответствие это было взаимно однозначным (различным
остовам соответствуют различные симплексы) и чтобы каждому
нульмерному остову, т. е. каждой вершине е, соответствовала в качестве
симплекса \е\ сама эта вершина е. Остов {е0,...,ег} называется при
этом остовом симплекса \е0.. ,ег\; число измерений г остова {е0,...,ег}
называется числом измерений симплекса |£0...£г|.
Симплекс \e'Q ... е'\ подчинён симплексу \е0.. . ег\ или является
собственной гранью симплекса \е0...ег\, если остов {^,...,^} есть
собственное подмножество остова {е0,...,ег}.
Множество всех построенных таким образом абстрактных
симплексов называется полным симплициальным комплексом,
а первоначально данный комплекс остовов К называете я
комплексом остовов данного полного симплициального
комплекса.
На основании сказанного всякий полный симплициальный
комплекс является частично упорядоченным множеством.
Из этого определения следует, что все полные комплексы
остовов, а также и все триангуляции образуют частные случаи полных
симплициальных комплексов*). Полными симплициальными комплексами
являются и так называемые кривые триангуляции (см. о них в § 6
этой главы), двумерный случай которых знаком нам из главы 3.
Определение [1 :42]. Всякое подмножество («подкомплекс»)АГ0
какого-либо полного симплициального комплекса К называется
просто симплициальным комплексом. При этом эле-
*) В первом случае абстрактным симплексом |*0>.. .,ег\ с остовом {е0,. ..,ег}
ярляется сам этот остов, во втором — обыкновенный симплекс с вершинами
е0 ,..., ег.

§ 1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
151
менты комплекса К0 имеют те же остовы, с тем же числом
измерений и между ними сохраняется тот же порядок, что и в комплексе К.
Комбинаторное замыкание [Ко] комплекса К (в К) есть по
определению полный подкомплекс комплекса /С, комплексом остовов
которого является комбинаторное замыкание комплекса остовов
комплекса К0.
Определение [1:43]. Если имеется наибольшее число,
являющееся числом измерений некоторого элемента симплициального
комплекса /С, то это число называется числом измерений
симплициального комплекса /С; если такого наибольшего числа нет,
то комплекс К называется бесконечномерным.
1 :5. Примеры симплициальных комплексов. 1. Пусть
К—триангуляция, К0 — какой-нибудь подкомплекс К; К0 есть симплициальный
комплекс.
2. Пусть Г — открытое множество пространства Rn или я-мер-
ной сферы Sn. Конечное множество {е0,...,ег}, лежащее в Г,
называется остовом, если его выпуклое замыкание лежит в Г (в случае
Г с Sn требуется, кроме того, чтобы всё множество {e0i..., er) лежало
в некоторой полусфере сферы Sn, а выпуклое замыкание понимается
в смысле господствующей в Sn сферической метрики). Полученный
полный комплекс остовов обозначается через Кг- Рассматривая в Агг
подкомплекс, состоящий из всех остовов, диаметр которых меньше
некоторого определённого положительного числа г, получим полный
комплекс остовов, обозначаемый через Ат,е.
Рассмотрим симплициальный комплекс, имеющий Кг,
соответственно /Сг,е, своим комплексом остовов со следующим определением
симплексов: если точки е0,... ,ег, образующие данный остов, линейно
независимы в Rn (в Sn), то симплексом \е0...ег\ называется
обыкновенный (или сферический) симплекс с вершинами е0,... ,ег.
Если же точки е0, ...,ег линейно зависимы между собою (что, в
частности, всегда имеет место, если г>я), то полагаем
|*0-"*г1— {*0i-f*rb
т. е. отождествляем симплекс \е0 ... ег\ с его остовом. Полученные таким
образом симплициальные комплексы иногда также обозначают через
Кг и Ктч9.
3. Пусть R— метрическое пространство. Через Kr обозначаем
полный комплекс остовов, получающийся, если всякое конечное
подмножество пространства R считать остовом; в Kr содержится
подкомплекс Kr,s9 состоящий из всех остовов комплекса Kr, имеющих
диаметр <г.
Замечание. Особенно важен случай, когда R есть компакт.
Если R есть множество, лежащее в Rn, то можно заменить
комплексы Kr и Krs* симплициальными комплексами с теми же остовами,
но с симплексами^ определёнными, как в конце предыдущего
пункта.

152
КОМПЛЕКСЫ
[гл. iv
4. Пусть Г—открытое множество компакта Ф. Называем остовом
всякое конечное подмножество компакта Ф, имеющее непустое
пересечение с Г. Полученный неполный комплекс остовов называется Кф,т\
если потребовать, чтобы все остовы имели диаметр <s, получим
неполный комплекс остовов /Сф,г,в^/Сф,г.
В § 2 мы познакомимся с дальнейшими важными примерами
комплексов остовов.
1:6. Симплициальные отображения и изоморфизмы комплексов
остовов и вообще симплициальных комплексов.
Определение [1 :61]. Пусть каждой вершинее^полного
комплекса остовов Ко поставлена в соответствие вершина ea = Sae^
комплекса остовов Ка так, чтобы при этом образом всякого остова {^0»"#>^г}
комплекса К$ являлся некоторый остов комплекса Ка (различным
вершинам комплекса К$ может при этом соответствовать одна и та же
вершина комплекса Ка)- В силу поставленного условия, отображение ^
множества вершин комплекса К$ во множество вершин комплекса Ка
порождает отображение комплекса Ко в комплекс Ка, называемое
симплициальным отображением полного комплекса
остовов /Ср в комплекс остовов 7Са и обозначаемое также
через SjJ.
Если Ко и Ка являются комплексами остовов соответственно
полных симплициальных комплексов Ко и Ка > то> ставя в соответствие
каждому симплексу \е^0 ... е^г\ £К* симплекс комплекса К'а, вершинами
которого являются 5^р0,..., «S^pr, получим по определению симплици-
альное отображение S^ симплициального комплекса 1С в симплици-
альный комплекс К'л (порождённое одноимённым симплициальным
отображением комплекса остовов комплекса Ki в комплекс остовов
комплекса Ка).
Определение [1 :62]. Симплициальным отображением
неполного симплициального комплекса К$ называется всякое
рассматриваемое лишь на К$ симплициальное отображение
комбинаторного замыкания [К$] комплекса К$.
Определение [1:63]. Взаимно однозначное симплициальное
отображение полного симплициального комплекса Ко, на*} полный
симплициальный комплекс Ка называется изоморфным
отображением или изоморфизмом. Два полных симплициальных комплекса
называются изоморфными или имеющими один и тот же
комбинаторный тип, если один из них может быть изоморфно
отображён на другой.
*) В соответствии с общими определениями главы 1 отображение s\
называется отображением симплициального комплекса Ко, на
симплициальный комплекс Ка, если каждый остов комплекса АГа есть образ хотя бы
одного остова комплекса Ко.

§ 1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
153
Два полных симплициальных комплекса тогда и только тогда
изоморфны, когда изоморфны комплексы их остовов (в частности,
всякий полный симплициальный комплекс изоморфен комплексу своих
остовов). Таким образом, можно сказать, что комбинаторный тип
полного симплициального комплекса однозначно определён
комплексом его остовов.
Замечание об изоморфизме. Симплициальное отображение
6^ полного симплициального комплекса К§ на полный
симплициальный комплекс Ка тогда и только тогда является изоморфизмом, когда
на каждую вершину комплекса Ка отображается одна и только одна
вершина комплекса /Ср.
Примеры изоморфных симплициальных
комплексов.
1. Триангуляция, состоящая из всех собственных граней какого-
либо выпуклого многогранника с треугольными гранями (например,
тетраэдра, октаэдра, икосаэдра и т. п.), изоморфна «кривой
триангуляции» сферы, которая получается, если взять сферу, лежащую
внутри данного многогранника, и спроектировать его на эту сферу
из её центра.
2. Возьмём триангуляцию К. Построим симплициальный комплекс/С'
с тем же комплексом остовов, что и К, но симплексами которого
по определению являются замыкания симплексов комплекса К.
Комплекс К! изоморфен комплексу К-
Замечание о склеиваниях. Пусть К$ и Ка — два
симплициальных комплекса и S$ — симплициальное отображение К§ на-/Са:
Каждой вершине еа1£ Ка соответствует в комплексе /С класс tt
вершин *р., таких, что
Sle^j—eai-
Таким образом, симплициальное отображение S^ порождает
разбиение множества всех вершин е^ комплекса К$ на классы. Отметим,
что вершины еао, ...,£«*• G^C* образуют в Ка остов тогда и только
тогда, когда из соответствующих классов с0, ...,ег можно выбрать
вершины e^^tj, j = Q, 1, ... ,г так, что они образуют остов в К$.
Мы можем сказать, что симплициальное отображение S& заклю
чается в отождествлении*) между собою всех вершин /^,
образующих один и тот же класс е^.
Пусть, наоборот, задан конечный полный симплициальный
комплекс К§, и его вершины разделены на классы ег-. Мы можем
определить новый симплициальный комплекс Ка следующим образом:
^определяется как комплекс остовов; его вершинами являются классы
*) Ср. главу 1, арт. 5:1, и главу 3, арт. 3: 1.

154
КОМПЛЕКСЫ
[гл. iv
с^ вершин комплекса К$. Классы е0,... , сг образуют остов, если из
них можно выбрать вершины е^£г{, / = 0,1,..., г, так, чтобы они
образовывали остов в К^ Очевидно, что при этом получится полный
комплекс остовов.
Естественно определяется симплициальное отображение S$
комплекса К$ на /Са: каждой вершине е^^К^ относится содержащий её
класс е^.
Предположим, что данное симплициальное отображение К$ на К%
удовлетворяет следующему условию: при отображении S^ никакие
две вершины, принадлежащие к одному и тому же остову комплекса /Сй,
не отображаются на одну и ту же вершину комплекса ЛГа. Такие
отображения называются склеиваниями; при склеивании
всякий элемент комплекса Ко отображается на элемент того же числа
измерений комплекса Кл и, следовательно, два элемента разных
размерностей комплекса К§ не могут отобразиться на один и тот
же элемент Ка) но два элемента той же размерности комплекса К$
могут «склеиться» между собою, т. е. отобразиться на один и тот
же элемент комплекса Ка.
Склеивания, рассмотренные нами в главе 3, образуют частный
случай только что введённого общего понятия склеивания.
1:7. Общее определение комплекса. Рассматривая различные
определённые в этом параграфе типы комплексов, можно заметить,
что все они являются частными случаями обшего понятия
частично упорядоченного множества В, каждому элементу 6 которого
отнесено некоторое неотрицательное целое число db — число
измерений элемента 6 — так, что из ^<62 следует d^t<Cdb9.
Это общее понятие и можно считать понятием комплекса в
широком смысле слова.
Изоморфным отображением одного комплекса на другой
называется такое подобное отображение, при котором число измерений
сохраняется.
Можно было бы доказать, что это определение изоморфизма в
случае полных симплициальных комплексов совпадает с тем, которое
мы дали в 1 : б.
Только что сформулированные общие понятия комплекса и
изоморфизма позволяют дать определению полного симплициального
комплекса следующую безукоризненно простую и прозрачную форму:
Полный симплициальный комплекс — это всякий комплекс в
общем смысле слова, изоморфный некоторому полному комплексу
остовов. Симплициальные (не непременно полные) комплексы — это
любые подкомплексы *) полных симплициальных комплексов.
Замечание. Понятие изоморфизма в применении к неполным
симплициальным комплексам нас интересовать не будет: в нашем
*) Подкомплексом комплекса К называется всякое подмножество Ко^К
с теми же размерностями элементов и тем же отношением порядка между
ними, что и в К

§ 1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
155
изложении всякий неполный симплициальный комплекс всегда будет
появляться в качестве подкомплекса некоторого вполне
определённого полного комплекса /С, и мы будем рассматривать лишь такие
изоморфные отображения комплекса /С0, которые порождаются
изоморфизмами полного комплекса /С
1 :8. Замкнутые и открытые подкомплексы комплекса /С.
Комбинаторные замыкания и звёзды *).
Подкомплекс К0 комплекса К называется замкнутым (откры-
т ы м) подкомплексом комплекса /С, если всякий элемент комплекса К,
подчинённый какому-нибудь элементу комплекса К0 (подчиняющий
себе какой-нибудь элемент комплекса /С0\ сам является элементом
комплекса /С0.
Доказательство следующих предложений может быть
предоставлено читателю:
[1 :81]. Если К0 замкнуто (открыто) в /С, то К\К0 открыто
(замкнуто) в К.
[1:82]. Если К0 произвольный, a Kt — замкнутый (открытый)
подкомплекс комплекса /С, то К0 П Кх есть замкнутый (открытый)
подкомплекс комплекса /С0.
[1 :83]. Всякий замкнутый подкомплекс полного симплициального
комплекса есть полный симплициальный комплекс.
Определение [1:84]. Если К0 — какой-нибудь подкомплекс
комплекса К, то комплекс, состоящий из всех, элементов комплекса К0
и из всех элементов /С подчинённых хотя бы одному элементу К0
(подчиняющих себе хотя бы один элемент комплекса /Г0), называется
комбинаторным замыканием [К0] (звездой OrK0) подкомплекса К0 в
комплексе К.
[1 :85]. При любом К0^К комплекс [К0], замкнут, а комплекс
OrK0 открыт в К.
Замечание. Во всём дальнейшем будут рассматриваться лишь
звёзды OrT отдельных элементов комплекса /С, т. е. комплексы OrK0
для случая, когда К0 состоит из одного элемента Т£К. Элемент Т
при этом называется центром звезды OrT. Некоторые примеры зве'зд
даны на черт. 20—25 главы 3.
Определение [1:86]. Комплекс
(1:86) ВкТ=[ОкТ\\ОкТ,
состоящий из всех не принадлежащих звезде OrT элементов,
подчинённых хотя бы одному элементу ОкТ, называется краем звезды OrT.
Так как OrT открыто в Я* и тем более в [OrT], to BrT по своему
определению (1:86) и в силу [1:81] замкнуто в [OrT] и,
следовательно, в К. Итак:
*) Содержание этого артикула относится ко всем комплексам в том
общем смысле, который был дан этому понятию ц предыдущем артикуле.

156
КОМПЛЕКСЫ
[гл. iv
[1: 87]. ВКТ есть замкнутый подкомплекс комплекса К; если К—
полный симплициальный комплекс, то и В%Т есть полный симплици-
альный комплекс.
Определение [1: 88]*). Пусть К—конечный симплициальный
комплекс и 7>£/С Рассмотрим комплекс FrTpczK, состоящий из
всех симплексов Т^£_К, удовлетворяющих условию: существует
симплекс 7?+r+1 £ ОкТр, для которого Т\ является гранью,
противоположной грани 7^<Г*+Г+1. Этот комплекс FkTp называется поясом
звезды ОкТр (в комплексе К).
Звёзды в симплициальных комплексах. Пусть в сим-
плициальном комплексе /Сданы звёзды ОкТ1У OjgTg,..., 0%ТГ. По
самому определению звезды, пересечение ОкТг П ... П ОкТг всех
q.„ q_-.^ этих звёзд состоит из всех симплексов Т£К,
/ ^ Ш/> / ^ одновременно удовлетворяющих условиям
** V*—S----V Пример. Комплекс К состоит из десяти
изображённых на черт. 81 треугольников и из двух
Черт. 81. вершин р1 и р2. Пересечение звёзд Окрг и 0Rp2
состоит из двух заштрихованных треугольников.
Теорема [1 /89]. Пересечение звёзд ОкТг,..., ОкТг полного
симплацаального комплекса К не пусто тогда и только тогда,
когда в К существует симплекс, имеющий все симплексы 7\,.. .,ТГ
в числе своих граней. В этом случае, обозначая через Т0
комбинаторную сумму симплексов Т1,...,ТГУ имеем
ОкТг П 0КТ2 П .. . П 0КТГ = 0КТ0.
Доказательство. Из полноты комплекса К следует: если
симплексы Tv...,Tr из К являются гранями одного и того же
симплекса Т из К, то комбинаторная сумма
т0 = \т1тя...т\
всех этих симплексов сама есть симплекс комплекса К. Очевидно,
всякий симплекс из К, имеющий симплексы 7\,.. ., Тг своими гранями,
имеет и грань Т0.
Пусть симплекс Т входит в пересечение звёзд 0KTV. . ,У0КТГ
комплекса К.
Тогда симплексы Ти...,Тг являются гранями симплекса Г,
который, следовательно, имеет и грань Т0= [ТХТ2. .. Тг] и поэтому
является элементом звезды 0#7*0.
Обратно, всякий симплекс Т£ОкТ0 имеет грань Т0 и,
следовательно, грани Tlt...9Tr, т.е. входит в пересечение всех звёзд
OrTv. . .,ОкТг. Теорема, таким образом, доказана.
*) Это определение понадобится лишь в гл. 13.

§11
ОСНОВНЫЕ ОПРЕДЕЛЕНИЙ
157
Следствие. В частности, звёзды Ок^о, •.., Окег данных вершин
е0У..., ег комплекса К тогда и только тогда имеют непустое
пересечение, когда в К имеется симплекс Г0 = |£0.. .£г|.
1 :9. Теорема о включении в /?2»+i.
Теорема [1 :9]. Всякий конечный полный n-мерный комплекс
остовов К (значит, и всякий n-мерный конечный полный симпли-
циальный комплекс) изоморфен некоторой триангуляции К',
лежащей в (2п -f- 1)-мерном эвклидовом пространстве *).
Построение триангуляции /('. Пусть вершины
комплекса К суть ev..., es. Возьмём в R2n+1 точки e'^...fe' в общем
положении **). Каждому остову Т= \eiQ. . ,eif\ £ К поставим в
соответствие симплекс Т' — \е. . . .е'£ | c/?2w+1; этот симплекс существует, так
как, в силу общего положения точек e'v ..., е в Т?2^1 и
неравенства г^Сп, точки ef. , .. ., е'. линейно независимы. Симплексы Г'., оче-
го 1г 1
видно, образуют комплекс К\ изоморфный комплексу К. Докажем,
что К' есть триангуляция. Для этого достаточно доказать, что
никакие два симплекса Т\^К\ Т'.£К' не пересекаются. Пусть вершины
симплекса Т! суть е'. ,.. ., ef. , а вершины симплекса Г/ пусть е'.. .,£,',
причём некоторые из вершин могут быть общими для Т'. и Т' Пусть
е'к ,. ,., e'j. —все точки, являющиеся вершинами хотя бы одного из
симплексов Т. и Т.. Число r-j- 1 этих точек удовлетворяет
неравенству
»"+l<fp+ l) + (7+ !)<("+ 1) + («-И) = 2я + 2,
так как размерности симплексов Т'г и Т\ не больше, чем п. В силу
общего положения точек e^...te's в пространстве /^-И, точки
е'к ,...,е'к являются вершинами некоторого невырождающегося
симплекса Т0 размерности не выше 2п-\-1. Симплексы Т'. и Т\ являются
гранями симплекса Т0 и, следовательно, не пересекаются, если они
различны.
Из [1:9] следует:
[1:91]. Всякий n-мерный конечный комплекс остовов К
изоморфен подкомплексу некоторой n-мерной триангуляции, симплексы
которой лежат в /У*»*1.
В самом деле, комбинаторное замыкание [К] есть полный
n-мерный комплекс остовов, изоморфный на основании [1 :9]
триангуляции Q, симплексы которой лежат в /?2w+1. При изоморфизме между
[К] и Q комплексу /fc: [К] соответствует некоторый подкомплекс
комплекса Q, что и требовалось доказать.
*) Приводимое ниже чрезвычайно простое доказательство теоремы [1:9]
сообщено мне Л. С. Понтрягиным. , ,
**) То-есть так, что при k <2я + 2 всякие k из числа точек е1 , - • •, е8
линейно независимы (см. Прибавление II).

158
КОМПЛЕКСЫ
[гл. iv
§ 2. Некоторые замечательные комплексы остовов.
2:1. Нерв конечной системы множеств. Это понятие будет
иметь многочисленные и весьма существенные применения в этой
книге.
Пусть дана конечная система множеств
(2:1) а = {Лд ,..., А8}.
Каждому из множеств А^ поставим в соответствие вершину ait
Эти вершины *)
alt..., а8
и будут вершинами комплекса остовов Ка, который мы сейчас
определим и назовём нервом системы а. Именно, мы говорим, что
данная совокупность вершин
V-' \
тогда и только тогда является остовом комплекса/^,
когда множества
Л,о,..., Aif>
имеют непустое пересечение.
Замечание 1. В этом определении не исключается случай,
когда несколько различных между собою элементов системы а
являются совпадающими между собою множествами (т. е. отличаются
между собою лишь своими номерами в (2:1)**)»
Замечание 2. Из определения нерва непосредственно следует,
что всякое непустое подмножество какого-нибудь остова нерва
также есть остов нерва. Итак:
[2: 11]. Нерв всякой конечной системы множеств есть полный
симплициалъный комплекс.
Из определения кратности конечной системы множеств (глава 1,
арт. 1 :3) и определения нерва непосредственно следует:
[2: 12J. Число измерений нерва системы множеств на единицу
меньше кратности этой системы.
Замечание 3. Природа вершин ai нам совершенно безразлична:
за вершины ai можно брать любые элементы, находящиеся во
взаимно однозначном соответствии с элементами системы а; с
логической точки зрения проще всего брать за вершины аг сами элементы
Af системы а, тогда и нерв данной системы множеств был бы
определён с полной однозначностью, а не только с точностью до выбора
вершин.
*) Являющиеся элементами совершенно произвольного множества; ср.
определение [1 :31].
**) См. главу 1, арт. 1:3.

§ 2]
НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КОМПЛЕКСЫ ОСТОВОВ
159
Однако, как покажет будущее, произвол в выборе вершин и
проистекающая из него некоторая, впрочем несущественная,
неопределённость только удобны на практике.
Мы будем поэтому считать, что нерв системы множеств
определён лишь с точностью до изоморфизма, т. е. будем называть
всякий комплекс, изоморфный нерву данной системы
множеств, также нервом этой системы множеств.
Переходя к примерам нервов, заметим, прежде всего, что
следствие теоремы [1 :89], очевидно, можно сформулировать так:
[2:13]. Звёзды вершин конечного полного симплициального
комплекса К образуют систему подкомплексов комплекса К,
имеющую комплекс К своим нервом.
V~
»-:—I
^°Ч
t4
1
■ "1
•с
1 >v
1
1
к
»
' 1
ж
. 1
I
^ъг'
i
1
V*^
у*^
^^
г
j\*^
"* >в-^
-Л -
4;i
^*
i "
Черт. 82.
Черт. 83.
Черт. 84.
Из [2:11] и [2:13] следует: все конечные полные симплициальные
комплексы, и только они, являются нервами конечных систем
множеств. Поэтому конечные полные симплициальные комплексы для
краткости называются иногда просто «нервами».
Примеры нервов: 1. Рассмотрим систему девяти замкнутых
квадратов, изображённую на черт. 82. Нерв этой системы есть
трёхмерный комплекс, изображённый на том же чертеже пунктиром.
2. Второй пример получим, взяв за систему а двадцать
изображённых на черт. 83 замкнутых квадратов. Нерв этой системы также
изображён на том же чертеже пунктиром.
3. Система а состоит из шести замкнутых граней куба; её нерв
есть комплекс, состоящий из всех двухмерных граней, рёбер и
вершин октаэдра.
4. Система а состоит из семи замкнутых множеств: из
замкнутого треугольника, его замкнутых сторон и вершин. Нерв этой
системы есть трёхмерный комплекс, изображённый на черт. 84.
Замечание 4. Нерв, построенный вблизи данной
системы точечных множеств. Пусть элементы Л1}.
ной системы множеств
а = {А19...9 А8]
суть точечные множества данного Rn; пусть е>0. За вершины
аи...,а8 нерва Ка системы а возьмём какие-нибудь точки простран-
А8 дан-

160
КОМПЛЕКСЫ
[гл. iv
ства Rn, в котором лежат множества Л1э...,Лв, причём все точки
a1%...9a8 должны быть различны между собой и
удовлетворять дополнительному условию
р(я,, Л,)<е /= 1, 2 ,..., s.
Нерв Ка системы а с выбранными под этим условием вершинами
а\ >• • • > as называется нервом, лежащим в е-близости или
в е-окрестности системы ос.
Если п не меньше числа измерений т нерва /Са, то, выбирая точки
av...,as в общем положении, видим, что все остовы нерва
оказываются множествами линейно независимых точек, так что за
симплексы нерва Ка можно брать лежащие в Rn симплексы,
определённые соответствующими остовами нерва. Если же п>2т-{- 1, то
полученный нерв Ка не только будет лежать в
е-окрестности системы а: он будет, кроме того,
триангуляцией.
Итак:
[2:14]. Пусть а — конечная система множеств, лежащих
в Rn, и е>0. Во всяком пространстве /?m=>£m достаточно
большого числа измерений можно построить триангуляцию КЛ,
являющуюся нервом системы а, лежащим в ^-близости системы а.
. Изображённый на черт. 83 нерв системы замкнутых квадратов
является нервом, лежащим при любом е в е-близости этой системы.
2 :2. Барицентрические производные и барицентрические
подразделения. Пусть в — конечное частично упорядоченное множество.
Его элементы р называем вершинами; те подмножества множества в,
которые, если их рассматривать вместе с господствующим в в
порядком, являются упорядоченными, назовём остовами.
Полученный (очевидно, полный) комплекс остовов обозначается
через £(в) и называется барицентрической производной
частично упорядоченного множества в.
Перейдём теперь к случаю, когда частично упорядоченное
множество в есть полиэдральный комплекс К или подкомплекс К
полиэдрального комплекса *). В этом случае триангуляцию Ки
изоморфную комплексу В (К), можно построить особенно наглядным
образом. Для этого поступим так.
Пусть многогранники, являющиеся элементами комплекса /(, суть
* 1> • • • 1* 8'
Все эти многогранники лежат в некотором Rn> В каждом из
многогранников Тг берём точку еь которую называем центром
многогранника: обычно за точку ei берут в самом деле центр тяжести
многогранника Tt. Эти точки £г- объявляем вершинами (комплекса Кц
который сейчас построим). Несколько вершин ei образуют остов,
*) См. арт. 1:2; читатель может ограничиться случаем, когда К есть
триангуляция или подкомплекс триангуляции.

§ 2]
НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КОМПЛЕКСЫ ОСТОВОВ
161
если множество соответствующих им многогранников Ti является
(при геометрическом отношении*) порядка между ними)
упорядоченным. Это значит, что данные несколько вершин могут
быть записаны в такой последовательности:
ЧТО
02:20) T,0>Th>...>ril.
(т. е. каждый из многогранников 7^- , . . ., Tir. кроме 7^, есть
собственная грань предыдущего).
Из (2 : 20) и ei £ Т{ следует, что точки е,- . .. , eir линейно
независимы в Rn и, значит, существует симплекс \ei ... eir\aRn.
Итак, все наши остовы [ei . .. eif) суть остовы некоторых
симплексов \е{ ... eir\ czRn. Эти самплексы\е,1 . ..^.| и являются
по определению элементами комплекса Кх.
По самому своему построению комплекс Кх изоморфен
барицентрической производной комплекса /С: изоморфное соответствие
получаем, заставляя симплекс \ei ...eir\ комплекса ^соответствовать остову
[Т. > . . . > Tir) комплекса В{К). Поэтому комплекс Кх называется
геометрической реализацией барицентрической
производной В {К)>
Замечание 1. Если \^iQ...eir\ есть симплекс комплекса Кх и
\>...>т,„
ю иершина ei называется старшей, а вершина е4 младшей
вершиной симплекса \eiQ. . .ei}].
Теорема [2:21]. Комплекс Кх есть триангуляция.
Доказательство. По своему определению Кг есть
конечный комплекс. Так как Кх и В (К) изоморфны между собою,
и В (К) — полный комплекс, то и Кг — полный комплекс.
Остаётся доказать, что никакие два различных симплекса
комплекса Кх не пересекаются.
Утверждение очевидно для нульмерных симплексов комплекса Kv
Прежде чем переходить к общему случаю, сделаем следующее
замечание:
Так как два различных элемента Ть и Tj комплекса К не
пересекаются, то два симплекса \е . . .ei \ £ Кх и \eJQ. . -е^\^Кг заведомо
не пересекаются, если их старшие вершины ei и ej различны.
Предположим теперь доказанным, что два симплекса комплекса Кг
не пересекаются, если их размерности меньше или равны г. Это
верно для г = 0. Рассмотрим два симплекса \eiQ.. . ег- | £ Кх и \eJQ. . . ej £ Кг
*) То-есть 7}<Тг-, если Tj есть собственная грань многогранника Т^
П Александров П. С.

162
КОМПЛЕКСЫ
[ГЛ. IV
размерностей не более, чем г-\-\. Если они пересекаются, то
старшая вершина у них одна и та же, е$ = е.. Но тогда симплексы
\ei eit- »-ег \ и \ejoej\ - • • ез\ являются проекциями из точек ei0 — ej0
симплекса \eix. . .еА и |^---^J и, следовательно, пересекаются
лишь, если пересекаются l^.-.^J и \е^.. ,е^\. Но размерности
симплексов l^.-.^J и l^.-.^-J не превосходят г, поэтому, если эти
симплексы пересекаются, то непременно совпадают:
Но тогда совпадают и симплексы \е{е{1. . .ei | и fye^. .. еЛ, что
и требовалось доказать.
[2:210]. Каждый симплекс Тг комплекса К целиком лежит
на некотором элементе Т комплекса К (т. е. является
подмножеством многогранника Т).
В самом деле, среди вершин ег,..., eir симплекса Г[ старшая
вершина ег лежит на элементе Т{ £/С, а все остальные — на его
гранях; поэтому весь симплекс T[ = \ei .-.eir\ лежит в Тг .
Пусть теперь К—полиэдральный комплекс *). В этом случае
триангуляция Кг, называется барицентрическим
подразделением комплекса К, и теорема [2:210] существенно дополняется
предложением
[2 : 22]. Каждый элемент Тк комплекса К есть соединение
лежащих на нём симплексов барицентрического подразделения Кг**).
Доказательство. Теорема очевидна, если k = 0, т. е. если
Тк есть вершина комплекса К, так как всякая вершина комплекса К
есть в то же время вершина комплекса Кх.
Предположим, что теорема [2:22] доказана для k^r, и
докажем её для £ = г-|- 1. Рассмотрим все симплексы Tlh комплекса Ки
старшая вершина которых есть центр тяжести одной из
собственных граней данного (г-\- 1)-мерного элемента Тг+1 £ К Все эти
симплексы т[ъ образуют барицентрическое подразделение комплекса
ТН-1- = [7Y+1]\7V+1, причём, согласно нашему предположению,
всякая точка границы тг+1\Тг+1 многогранника Т^1 принадлежит
некоторому симплексу Т'}1.
Пусть теперь дана какая-нибудь точка р^Т^1; если точка р
есть центр тяжести многогранника 7У+1, то она есть вершина
комплекс комплекса /Q. Пусть/? не есть центр тяжести Г^1; обозначим
через // проекцию точки р на ТГ+1\ТГ+1 из центра тяжести о
многогранника Тг+Х и пусть Т'1П = \ег. . .е€\ есть содержащий точку р' сим-
*) До сих пор комплекс /Смог быть любым подкомплексом
полиэдрального комплекса.
**) Без большого ущерба читатель может ограничиться случаем, когда К
есть триангуляция, и в соответствии с этим понимать под многогранниками,
элементами комплекса К, всегда симплексы.

§ 21
НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КОМПЛЕКСЫ ОСТОВОВ
163
илекс комлпекса Kv Тогда р есть точка лежащего на Тг+Х
симплекса |о£х...^| комплекса /С1? что и требовалось доказать.
Объединим предложения [2 :21], [2 :210] и [2 :22] в одну теорему:
[2:2]. Барицентрическое подразделение полиэдрального
комплекса К есть триангуляция Kv причём всякий симплекс комплекса Кх
лежит на некотором симплексе комплекса К и всякая точка,
принадлежащая какому-нибудь симплексу комплекса К, принадлежит
и некоторому симплексу комплекса Kv
С
а
^ Черт. 85.
Примеры. 1. На черг. 85 изображены: а)] барицентрическ о
подразделение двумерной триангуляции, состоящей из двух
треугольников ABC и BCD (со всеми их сторонами и вершинами);
Ь) реализация*барицентрической производной подкомплекса
(незамкнутого) этой триангуляции,
состоящего из треугольников ABC
и BCD, их сторон АВ, АС и BD
и из вершин А и D.
„/ 2. На черт. 86 изображено
барицентрическое подразделение
Черт. 86. Черт. 87.
полиэдрального комплекса, состоящего из всех граней, рёбер и
вершин куба (изображены лишь обращенные к зрителю элементы).
3. На черт. 87 изображён один из 24 трёхмерных симплексов
барицентрического подразделения комплекса [Г3].
2:3. Пирамида над комплексом. Пусть К—симплициальный
комплекс, который мы отождествляем с комплексом его остовоп.
11*

164
КОМПЛЕКСЫ
[гл. iv
Пусть о — вершина, не принадлежащая комплексу /С.
Строим комплекс остовов <oi<">, причём по определению
остовами комплекса <о/С> являются: вершина о, все остовы ком-
множества вида [о еи...у ег}} где \е1У.. ., ег) —
какой-нибудь остов комплекса К. Комплекс
<о/С>, а также всякий комплекс, полученный
из < о/С>изоморфным отображением,
оставляющим неподвижными все элементы комплекса
К (рассматриваемого как подкомплекс
комплекса < о/С>), называется пирамидою с
основанием К или просто пирамидой
н а д /С.
Пирамида над полным симплициальным
комплексом есть полный симплициальный комплекс.
Комплекс
оК= <оК>\К
Черт.
т. е. звезда вершины о в комплексе < о/С> , называется
открытой пирамидой с вершиной о над комплексом К.
Следующее, принадлежащее Л. С. Понтрягину, замечание
существенно понадобится нам в главе 13.
[2:31]. Пусть К—полный симплициальный комплекс, е —
вершина К, В—край звезды Оке> Т—произвольный элемент
комплекса В. Тогда звезда симплекса еТ в К есть открытая
пирамида с вершиной е над звездой симплекса Т в комплексе В:
(2:31)
ОкеТ=еОвТ.
Доказательство заключается в непосредственной проверке того,
что обе части равенства (2:31) состоят из одних и тех же
симплексов. Осуществление этой проверки может быть предоставлено
читателю; на черт. 88 комплекс состоит из
тетраэдров
Т=\ел<
|.
\ееъеъеА и всех их гРаней;
о3*2|> комплекс В состоит из
треугольников \еъе^\\ и \e.se2eL\ со всеми их
сторонами, ОвТ состоит из отрезка \е%е2\ и
треугольников \в2е2е1\ и \бве2еА\) обе части
равенства (2 :31) состоят из треугольника \ее3е2\
и из двух тетраэдров | ееге2е^) и \ееье2е±\.
2:4. Призмы над комплексом остовов.
Каждое разбиение параллелограмма на два
треугольника диагональю этого
параллелограмма, а также известное из учебников
элементарной геометрии, изображённое на черт. 89
разбиение трёхгранной призмы на тетраэдры
являются частными случаями следующего общего построения. Пусть
К—непустой конечный полный комплекс остовов. Занумеруем
Черт. 89.

§ 2] НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КОМПЛЕКСЫ ОСТОВОВ 165
в определённом порядке все вершины К'. av...,a8. Рассмотрим ещё
новые «вершины» bv..., bs, взаимно однозначно соответствующие
вершинам а[,..., а8. Вершины ai и Ьг являются по определению
вершинами комплекса остовов /С[01], который мы сейчас построим.
Остовами комплекса К[01] являются по определению все
непустые собственные и несобственные подмножества множеств вида
(2:4) я*0,..., <*i» *<*, ..., bir,
где /0 < .. . < 4 < . . . < ir
и \aio...,ai]r..air\£K
(в частности, все остовы \ а,- ... а* 1 комплекса К и все соответ-
N ' I 'О Г
ствующие этим остовам \at ... air\ остовы \bf . . .bir\).
Комплекс К[01] называется призмой надкомплексом
остовов /С. Если Е есть r-мерный комплекс, то К[01] есть (г-\~ 1)-мерный
полный комплекс остовов.
Комплекс К называется нижним основанием призмы К[01]
(и обозначается иногда через /С0). Верхним основанием
призмы K[0i] называется комплекс /CjC/C^i], изоморфный
комплексу /Си состоящий из всех остовов | Ьг . .. bir\, соответствующих
остовам \аг .... aif\ комплекса /С
2:5. Призма, натянутая на комплекс остовов и его сим-
плициальный образ. Пусть в конечном полном-комплексе остовов К
даны замкнутый подкомплекс К0 и его симплициальное отображение
S° в комплекс К, удовлетворяющее условию: для каждого Т0£К0
можно найти Т(^К так, что Т0 и $°Т0 являются гранями симплекса Т.
Занумеровав все вершины К0 в определённом порядке at,...,as,
построим над К0 призму К\0]]', соответственно занумерованные
вершины верхнего основания К1 призмы К\01] суть -bv...,bs. Положим
теперь для 1= 1,2 ,. . ., s
501а{ = а{, 501*< = 6°д<.
Тогда каждому остову
T=\aiQ... af]piir.. bir\£K[0l\, /0 < • • • <Л
соответствует остов*)
S!*T=\ai(>...alkb«atl...SPatr\£K,
так что определено симплициальное отображение S01 призмы К\01] в К\
её образ S01 К\01] при этом отображении называется призмой,
натянутой в К на К0 и S°K0.
*) Ведь aiQi,..., а^. ,..., а-1у образуют остов в К:ь поэтому (в силу наших
предположений) вершины я,-,. .., а {к , air, S°aiQ,..., 5°я^,..., S°airt
значит, и подавно ai(),..., aik% S°aik, ..., S°air образуют остов в К.

166
КОМПЛЕКСЫ
[гл. iv
§ 3. Тело комплекса. Полиэдры.
3:1. Определения.
Определение [3 : И]. Пусть К—комплекс, являющийся
триангуляцией или подкомплексом триангуляции. Соединение элементов
комплекса К (рассматриваемых как точечные множества данного Rn)
называется телом комплекса /Си "обозначается через К.
Замечание 1. Это же определение применимо и к более
широкому классу комплексов, а именно, ко всем комплексам (в
широком смысле слова), элементами которых являются симплексы, или
вообще многогранники данного Rn.
О п р е деление [3 :12]. Множество, являющееся телом
некоторой триангуляции, называется полиэдром.
Замечание 2. Из [2:2] следует, что тело всякого
полиэдрального комплекса является вместе с тем и телом некоторой
триангуляции (например, телом барицентрического подразделения комплекса К)
и, следовательно, полиэдром. Итак, полиэдры могут быть
определены как тела полиэдральных комплексов.
Имеет место следующая теорема:
[3:13]. Пусть К есть конечное множество выпуклых многогранников
данного Rn, подчинённое лишь одному условию: всякая грань любого
элемента множества К сама есть элемент множества К. Соединение К
всех элементов (рассматриваемых как точечные множества
данного Rn) есть полиэдр.
Проведение доказательства этой теоремы предоставляется читателю;
наметим путь этого доказательства. Предположим, что теорема доказана
для случая, когда все элементы К лежат в соединении конечного числа
w-мерных плоскостей (для т»0 предложение очевидно), и докажем его
для случая, когда все элементы К лежат в соединении конечного числа
(т | 1)-мерных плоскостей /?7+],..., R™+1 данного Rn. Пусть Rb...tRu
суть все плоскости, определённые как пересечение двух каких-нибудь
плоскостей R™'^1 и Rj1^'1, а также как плоскости, несущие какой-нибудь
ш-мерный элемент комплекса К» Если какая-нибудь из этих плоскостей,
положим /?;, имеет число измерений т, то пишем R™ вместо /?,-, если же
число измерений плоскости R$ меньше т, то обозначаем через R™ какую-
нибудь Ая-мерную плоскость, проходящую через R^ Таким образом,
получаем m-мерные плоскости /?{",...,/?™. Эти m-мерные плоскости разбивают
// = Я™"*"1 U • • • и#Г+1 на конечное число выпуклых множеств, открытых
в И; те из этих областей, которые содержат точки множества /С, являются
выпуклыми многогранниками, лежащими в К- Эти выпуклые
многогранники обозначаем через Т\, ..., Гг. По индукционному предположению
множество К ГН^Ги • • • U R™) есть полиэдр; триангуляция этого
полиэдра порождает и триангуляцию границы каждого из выпуклых
многогранников IY Проекция каждой из этих триангуляции из какой-либо
внутренней точки соответствующего Г^ приводит к триангуляции всего
множества (Г, U ... U IV U (КП (/?Ги • • • U К)) = X которое и оказывается,
таким образом, полиэдром*).
*) Подробное доказательство — см, Александров —Hopf, Topologie I,
стр. 141 —143.

§ 3] ТЕЛО КОМПЛЕКСА. ПОЛИЭДРЫ 167
Из теоремы [3:13] сразу следует:
[3:14]. Соединение конечного числа полиэдров, лежащих в данном R17,
есть полиэдр.
В качестве дальнейшего упражнения укажем на доказательство
следующей теоремы:
[3:15]. Пересечение двух полиэдров есть полиэдр; замыкание
разности дзух полиэдров есть полиэдр.
Всякая триангуляция, телом которой является данный полиэдр,
называется триангуляцией данного полиэдра.
Пример. Тп есть симплекс. Тело комплекса [Тп] есть,
очевидно, множество [Тп] = 7Х
Если К есть триангуляция и Г£ /С, то [Т] Q К, и поэтому Тс К.
Поэтому всякий полиэдр есть сумма замыканий конечного числа
симплексов, т. е. замкнутое ограниченное множество эвклидова
пространства. Следовательно, все полиэдры суть компакты.
Теорема [3:1]. Если К' есть подкомплекс полиэдрального
комплекса /С, то К' замкнуто {открыто) в К тогда и только
тогда, когда К' есть замкнутый (открытый) подкомплекс
комплекса К.
Доказательство. Так как открытые множества в К суть
дополнения до замкнутых (относительно К), а открытые
подкомплексы комплекса К суть дополнения до замкнутых (относительно
К), то достаточно доказать утверждение, Касающееся замкнутых
множеств и подкомплексов.
Пусть К! — замкнутый подкомплекс комплекса К. Тогда ком-
плекс К' полиэдрален, а потому множество К! есть полиэдр,
значит, компакт, и потому замкнуто во всяком объемлющем множе-
сгве, в частности, и в К.
Пусть К! — незамкнутый подкомплекс комплекса К и Т£К-~
не принадлежащая комплексу К' грань какого-либо элемента
комплекса К'\ все точки симплекса Т Q К суть не принадлежащие К'
предельные точки множества К\ которое, таким образом, не замкнуто.
3:2. Звёздные окрестности. Открытые звёзды.
Определение [3:2]. Пусть К—триангуляция. Пусть р £ К.
Единственный элемент Т(р) комплекса /С, содержащий точку р,
называется носителем точки р в комплексе К. Открытое в К
множество Окр = ОкТ(р) называется звёздной окрестностью
точки р относительно комплекса К.
Определение [3:20]. Звёздные окрестности вершин
триангуляции К (относительно этой триангуляции) называются
открытыми звёздами триангуляции К.
Итак, открытые звёзды триангуляции суть открытые
подмножества ее: тела.

168
КОМПЛРЖСЫ
[гл. iv
Теорема [3:21]. Открытые звёзды Оце триангуляции К
покрывают весь полиэдр К.
В самом деле, пусть р — произвольная точка полиэдра К9 пусть
Т—носитель точки /?, пусть е — вершина симплекса Т.
Очевидно,
р£Т£Оке,
Р € т^Оке>
что и требовалось доказать.
Теорема [3:22]. Пересечение тел нескольких подкомплексов
полиэдрального комплекса К есть тело пересечения этих
подкомплексов.
Достаточно доказать эту теорему для двух подкомплексов
^(Е^И К^^К т. е. доказать, что
кх и\ к2 = к1п к2.
Из p^TQK, П К2 следует р£ Кг П ЛГ2, т. е. Д'^ТГа^Е Кх П К2.
Пусть, наоборот, р £ Кг U К2. Так как единственный элемент
комплекса К, содержащий точку р, есть носитель Т(р) этой точки,
то T(p)£Kv Шб^т.е. Г(р) £ /ft П К2, значит, р^)^П ^,
чем включение Кх П /С2 £Е ^i Л ^2 также доказано.
[3:23]. Открытые звёзды О^0,. .., 0^г триангуляции А'
пересекаются тсгда и только тогда, когда в /С имеется симплекс
Это утверждение вытекает из [3:22] и из следствия теоремы
[1:89].
Другими словами:
[3:24]. Всякая триангуляция является нервом системы своих
открытых звёзд.
3:3. Симплициальные отображения триангулированных
полиэдров. Симплициальное отображение S$ триангуляции /Ср в
триангуляцию КЛ следующим образом порождает непрерывное
отображение S? полиэдра К^ в полиэдр Ка. Пусть Т$ = \е0. . .ег\ —
какой-нибудь симплекс комплекса Ко. В вершинах симплекса Тн отображение
5^ = 5^ определено и этим задано афинное отображение S$
симплекса Гр на симплекс S^ Та £ КЛ с вершинами S^e^ 5^х,..., S\er.
Искомое отображение б£ полиэдра Ко в Ка определено, таким обра-

§ 4] ПОДРАЗДЕЛЕНИЯ ПОЛИЭДРАЛЬНЫХ КОМПЛЕКСОВ 169
зом, в каждом симплексе Т^£Кр Непрерывность отображения S$
доказывается легко: пусть р £ К$, пусть Гр есть носитель точки р и
р = \\трп. Без нарушения общности можно предположить, что все
рп лежат в одном и том же Т'^Т^. Барицентрические координаты
точек рп относительно остова симплекса Т'ъ сходятся к
барицентрическим координатам точки р, поэтому массы, которыми заряжаются
образы вершин симплекса Т' для получения точек Slpnl сходятся
к массам, определяющим точку S^p, откуда lim S^pn = <S^p. Ото-
бражение S& называется симплициальным отображением
полиэдра /Ср в полиэдр Ка, порождённым симплициальным
отображением S^ комплекса /С3 в Ка.
Рхли симплициальное отображение S% комплекса К$ на комплекс
/ч7 взаимно однозначно, то взаимно однозначным и, следовательно,
топологическим является и отображение полиэдра К§ на полиэдр Ка,
откуда следует:
Теорема [3:31]. Если К$ и Ка — изоморфные между собою
триангуляции, то полиэдры К^ и Ка гомеоморфны.
Так как всякая я-мерная триангуляция изоморфна триангуляции,
лежащей в /?2*m-i, то имеет место такое предложение:
Теорема [3:32]. Всякий n-мерный полиэдр гомеоморфен
полиэдру, лежащему в R2"*-1.
§ 4. Подразделения полиэдральных комплексов.
4:1. Определение подразделения.
Определение [4:11]. Пусть К произвольный
полиэдральный1) комплекс. Подразделением комплекса К называется
всякий полиэдральный комплекс /Са, удовлетворяющий следующим
условиям:
1. Тело комплекса /С«- совпадает с телом комплекса К.
2. Каждый элемент комплекса К* как точечное множество
содержится в некотором элементе комплекса К
Элементы комплекса К попарно не пересекаются. Поэтому, если
К?, есть подразделение комплекса К, то каждый элемент Т
комплекса /Са содержится только в одном элементе комплекса К.
Единственный элемент Tj комплекса К, содержащий данный элемент
Tai комплекса Ка, называется носителем элемента Tai в
комплексе К.
*) Читатель может предполагать, что все упоминаемые в этом параграфе
полиэдральные комплексы суть триангуляции.

170
КОМПЛЕКСЫ
[гл. iv
Если Tat£K* имеет своим носителем T^/f и Th есть элемент
комплекса К, отличный от 7}, то Тч Г) 7\ = 0. В самом деле, если бы
Та1 и Тп имели общую точку, то тем более имели бы общую
точку Tj и Тп, что невозможно, так как Tj и Тп суть различные
элементы комплекса К.
Итак:
Теорема [4:12]. Если Ка есть подразделение комплекса /С,
то клждый элемент Tai комплекса Ка содержится в одном и
только одном элементе комплекса К ~- в носителе элемента Tai—■
и не пересекается ни с каким другим элементом комплекса К»
Из [4:11] и [2:2] следует, что определённое з артикуле 2:2
барицентрическое подразделение полиэдрального комплекса К
действительно есть подразделение в только что установленном
смысле.
Так как барицентрическое подразделение любого
полиэдрального комплекса состоит из симплексов, то
[4 : 13]. Всякий полиэдральный комплекс имеет в числе своих
подразделений триангуляции.
Определение [4:14]. Подразделением симплекса Тп
называется комплекс, состоящий из всех лежащих на Тп элементов какого-
либо подразделения комплекса [Тп].
4:2. Последовательные барицентрические подразделения.
Пусть Кг есть барицентрическое подразделение комплекса К, К2 —
барицентрическое подразделение комплекса Kv вообще /Cv —
барицентрическое подразделение комплекса K,_v Комплекс Кч называется
v-кратным барицентрическим подразделением комплекса К.
Если /г-мерный симплекс Тп имеет диаметр rf, то симплексы
барицентрического подразделения комплекса [Тп] имеют диаметр
<^тгуя? (см- Прибавление 2, теорема [4:2].)
Отсюда следует: если все симплексы триангуляции К имеют
диаметр <;^,то все симплексы комплекса К^ имеют диаметр ^ ( , ■ i У d.
Так как lim (—— j =0, то имеем следующий результат:
Теорема [4:21]. Всякий полиэдральный комплекс имеет сколь
угодно мелкие симплициальные подразделения, т. е. подразделения,
состоящие из симплексов, диаметры которых меньше любого
наперёд заданного положительного числа.
Следствие. Всякий полиэдр имеет сколь угодно мелкие три»
ангуляции.
Из [4 :21] следует *):
*) См. главу 1, арт. 8:4. В следующем параграфе (теорема [5:34])
теорема [4:22] доказывается вновь; это второе доказательство более просто
потому, что опирается непосредственно на определение размерности [8:42]
(глава 1), а не на сравнительно сложную теорему [8:44] той же главы.

§ 4] ПОДРАЗДЕЛЕНИЯ ПОЛИЭДРАЛЬНЫХ КОМПЛЕКСОВ 171
[4:22]. Если полиэдр Ф есть тело n-мерной триангуляции К,
то dim Ф < п.
В самом деле, пусть Кх есть подразделение триангуляции К, все
симплексы которого имеют диаметры < е. Тогда открытые звёзды
триангуляции Кх образуют открытое 2г-покрытие полиэдра Ф, нерв
которого есть Kv Утверждение [4:22] следует отсюда на
основании теоремы [8: 44] главы I.
4: 3. Центральные и элементарные подразделения комплексов.
Мы подробно рассмотрели барицентрические подразделения
комплексов, так как это важнейший тип подразделений. Однако,
барицентрические подразделения не являются самыми простыми.
а) Пусть Кп есть полиэдральный комплекс. Обозначим через Кп~1
комплекс, составленный из всех элементов комплекса Кп, имеющих
размерность ^ п—1, и предположим, что нам дано какое-нибудь
подразделение К^"1 комплекса К71"1- Подразделение Кпш~1 комплекса
Кп"х следующим образом индуцирует некоторое подразделение К"
комплекса Кп, называемое центральным подразделением
комплекса /("относительно данного подразделения
д'л-i комплекса К71"1: в каждом /г-мерном элементе Tf комплекса
Кп берём центр тяжести oi и рассматриваем многогранники,
являющиеся проекциями из oi лежащих на Тп^\Тп. элементов комплекса
Кп~1. Эти многогранники, а также точки ot и элементы комплекса
А7^-1 и являются по определению элементами комплекса К",
Доказательство того, что Кп% действительно есть подразделение
комплекса Кп, не представляет трудностей.
Барицентрическое подразделение любого полиэдрального
комплекса Кп следующим образом сводится к ряду центральных
подразделений. Барицентрическое подразделение К\ нульмерного
комплекса К°, состоящего из вершин комплекса Кп, есть сам комплекс К0-
Предположим, что уже построено барицентрическое подразделение
К[ комплекса Кг, состоящего из всех симплексов комплекса Кп,
размерность которых ^г. Тогда получаем барицентрическое
подразделение Щ+1 комплекса /Cr+1 как центральное подразделение
комплекса К\ * относительно барицентрического подразделения К\
комплекса Кг.
б) Элементарное подразделение. Центральное
подразделение комплекса [Г*] относительно [Тп]\Тп называется просто
центральным подразделением [7^]; лежащие на Тп симплексы этого
подразделения образуют центральное подразделение симплекса Тп.
Центральное подразделение Тп, соответственно [Гп], называется также
элементарным подразделением относительно Тп.
Элементарное подразделение Тп относительно 7> < Тп по определению
состоит из всех симплексов \ТКТп-р^\, где Тг. есть какой-либо
элемент центрального подразделения Р7, а Тп~р~^ есть грань сим^

172
КОМПЛЕКСЫ
[гл. iv
плекса Т1\ противоположная симплексу 7>; при этом [Тг.Тп~р~х],
как всегда, обозначает симплекс, остов которого является
соединением остовов симплексов 7/ и тп-р-х%
Элементарное подразделение триангуляции К относительно
симплекса Тр £ К по определению получим, заменив каждый симплекс
Т£ ОкТр его элементарным подразделением относительно Тр и оставив
все остальные симплексы (т. е. все симплексы комплекса K\OgTP)
без изменения.
На черт. 90 и 91 изображены различные случаи элементарного
подразделения двух- и трёхмерного симплекса.
Из определения элементарного
подразделения непосредственно
вытекают следующие замечания,
которые понадобятся в главах 7 и 10.
Замечание 1. Пусть
fn-p-i __ | е?fl.. ,en, | есть грань
симплекса
* === \е0 ' • • ерер 4 1 • • • enU
противоположная грани Тр = \е0. . .ер\. Пусть е есть центр
симплекса Тр. Тогда симплексами элементарного подразделения
симплекса Тп относительно симплекса Тр являются все симплексы вида
Черт. 90.
1 ее,-
<ir^P
и только они.
Замечание 2. Пусть V11 есть элементарное подразделение
симплекса Тп относительно его грани Тр. Для того чтобы подмножество
Е множества всех вершин комплекса [Vn] было остовом этого
комплекса, необходимо и достаточно, чтобы оно не содержало остов
Черт. 91.
симплекса Тр; среди остовов комплекса [V"] остовы комплекса Vn
характеризуются тем, что они содержат вершину е и все вершины
грани Тп-р-*<СТ1\ противоположной грани Тр.
Замечание 3. Сохраняем обозначения предыдущего замечания.
Если г^п— 1, то r-мерный симплекс Тг комплекса Vn не может
иметь в числе своих вершин более р — 1 вершин симплекса Тр.
В самом деле, в противном случае симплекс Тг, имея среди своих
вершин п—р} вершин ephl,. . .,еп, симплекса Тп~р~1у а также вер-

§ 4] ПОДРАЗДЕЛЕНИЯ ПОЛИЭДРАЛЬНЫХ КОМПЛЕКСОВ 173
шину е, имел бы всего, по меньшей мере, р -)- п—р -\- 1 = п -\- 1
вершин, чего не может быть, так как г=^я—1.
Покажем, что барицентрическое подразделение триангуляции К
сводится к ряду элементарных подразделений. Для этого прежде
всего подразделяем все старшие симплексы комплекса К элементарно
по отношению к ним самим. При этом из симплексов вида Тп=- \е0. . .еп\
возникают симплексы *) Тп. = \ое0. . .ei . . ,еп\. Затем каждый из этих
симплексов подразделяем элементарно по отношению к грани
е0 . . . ei ... еп\. Получающиеся симплексы имеют вид
ТЬг = \° °he0 ёП • • • ёгг • • • еп\-
После элементарного подразделения этих симплексов по отношению
к грани \е0.. .ё{ .. ,ei . . ,еп\ получаются симплексы ТУ i { , первые
три вершины которых суть **) о, ог , oilit, а остальные являются
вершинами 7Х
Продолжая описанный процесс (симплекс Tf . , определяем
как Г? .... = \о Ол .. .о, • • • 7 е, ... е4 I), получаем в конце концов
ч h ' 1 *i гл Ч- + 1 л
симплексы вида |оог1. . . о^ ••• ^ |, которые вместе со своими гранями
и образуют барицентрическое подразделение симплекса 74
4:4. Подразделения незамкнутых подкомплексов
полиэдральных комплексов. Пусть К—подкомплекс полиэдрального
комплекса /С'. Тогда комплекс [К] есть полиэдральный комплекс.
Подразделением комплекса К называется всякий комплекс, состоящий из всех
тех симплексов какого-либо подразделения /Са комплекса [/С],
которое лежит на элементах комплекса К (т. е. имеет эти элементы
своими носителями).
В частности, если Ка есть барицентрическое (соответственно
элементарное) подразделение комплекса [К], то подкомплекс комплекса
Ка, состоящий из всех симплексов комплекса /Са, имеющих
симплексы К своими носителями, называется барицентрическим
(соответственно элементарным) подразделением комплекса К.
Замечание 1. Из этого определения следует, что можно
говорить об элементарном подразделении комплекса К относительно не
принадлежащего этому комплексу симплекса (а именно, относительно
любого симплекса Г(= [ЛТ]\#).
Замечание 2. Если К—незамкнутый подкомплекс симпли-
Циального комплекса, то барицентрическое подразделение комплекса К
не будет полным комплексом и потому не может быть изоморфным
барицентрической производной комплекса К.
О По поводу обозначений см. конец замечания 1 в арт. 0:2.
**) Если Тг есть грань симплекса Тп = \е0 ... еп\ и eiy ,... ,eih. —
вершины Tnt не являющиеся вершинами Тг9 то oil%%min есть центр тяжести
симплекса Тг.

174
КОМПЛЕКСЫ
[гл. iv
§ 5. Барицентрические звёзды.
5:1. Барицентрические звёзды. Пусть /Сесть /г-мерная
триангуляция, Кг — её барицентрическое подразделение. Обозначим через
все симплексы комплекса К) среди них пусть будут
нульмерные симплексы, т. е. вершины комплекса К Вершины
комплекса Кг суть центры тяжести
симплексов
^11» ^12? "
>^ (eU = ei ^ЛЯ '^Ро)>
причём мы пишем еи>ег^ если 7^>7},
так что симплексы комплекса /Q имеют
вид
Черт. 92.
ki/n>*n>-••>*!*.
Определение [5:1]. Обозначаем через 7*, /=1, 2,...,5, и
называем барицентрической звездой, сопряжённойэле-
менту Т$£К, подкомплекс комплекса К1У состоящий из всех
симплексов комплекса Ки младшая вершина которых есть центр тяжести
еи симплекса Г*. В свою очередь, симплекс Т4 называется
сопряжённым барицентрической звезде 7^. Краем барицентриче-
с к о й звезды Ti называем комплекс 7\- , состоящий из всех не
принадлежащих к Т\ граней симплексов комплекса 7*.
Барицентрические звёзды, сопряжённые вершинам ei комплекса
/С, называются главными звёздами. Это— барицентрические
звёзды 7i, . .., Г* (черт. 92).
[5:11]. Если 7\-< 7}, то размерность комплекса Г* больше
размерности комплекса 7}.
В самом деле, пусть размерность 7) есть г и пусть
\*Чх>е13%> - ' ->eUr>eu\
есть r-мерный симплекс комплекса Tj. Тогда симплекс
\е1.и>еи> • • • >eUr>eij>eu\
есть (г-|- 1)-мерный симплекс комплекса Ti (черт. 92).

§тг>]
БАРИЦЕНТРИЧЕСКИЕ ЗВЕЗДЫ
175
5:2. Барицентрический комплекс триангуляции.
Определение [5:2]. Барицентрическим комплексом
триангуляции К называется множество /С*, элементами которого
являются все комплексы Г4- и только они; множество /С* при этом частично
упорядочено по правилу:
Tj<7?, если Т4>Т^
Этот порядок и естественные числа измерений комплексов 7\-
делают множество К* комплексом в общем смысле этого слова,
установленным в арт. 1:7, так что самый термин барицентрический
комплекс, так же как и термины «открытый» и «замкнутый»
подкомплекс комплекса /£* вполне оправданы.
Докажем ряд простых, но важных свойств комплекса К*.
(5:2П 7\U ... Uf8 = Kv
В самом деле, если Tlh^K{ и еи есть младшая вершина Tlh, то
Из [5:21] следует:
(5:210). Г;и...и? = ^=1(. -
[5:22]. Если 1ф], то Т*4ПТ* = 0.
В самом деле, если бы Tlb£T'i[\Tj, то симплекс Т^^Кх имел
бы две младшие вершины еи и etj, что невозможно.
[5:220]. Если 1ф], то Г*П7*==0.
Следует из [5 :22] и теоремы [3:22].
[5:23]. Каждая неглавная барицентрическая звезда 7\- подчинена,
по крайней мере, одной главной звезде.
В самом деле, если ек<^еи, то 7\>7^.
[5:24]. Край барицентрической звезды Ti есть соединение
барицентрических звёзд, подчинённых звезде 7^.
Доказательство. Из самого определения комплекса Т^аКх
следует:
[5:240]. Комплекс т] состоит из всех симплексов вида
'Г1Ь==|^0>^1> ••' >*ljr|> ГДе eljr>el*> И Т0ЛЬК0 и3 них*
Поэтому, если
Tih=*\eij0>-->eijr\ €?*п
го
eljr>eU И Т1н€Ъг< Т^

176
КОМПЛЕКС dI
[гл. w
Обратно, если Tlh £ Г*< Т?, то
Tih = \eij0>--->*ijr>eij\> eij>eu и Tlh£T].
[5:25]. Комбинаторное замыкание [Ti] барицентрической
звезды Ti в комплексе К1ч т. е. подкомплекс комплекса Kv
состоящий из всех собственных и несобственных граней симплексов,
*
входящих в Ti> может быть записан в виде
(5:25) [Т*} = Т*иГ^.
Из [5:240] следует:
[5:250]. Комплекс [Ti] состоит из всех симплексов Tlh £ K± вида
Т,ь = \elj0>eiji > • • • >eijr | > гле eijr>eii-
Отсюда следует:
[5:26]. Если т]< Т], то [fi]cz[T*].
Из [5:21], [5:23], [5:24] и [5:25] вытекает:
[5:27]. Соединение комбинаторных замыканий главных
барицентрических звёзд комплекса К есть комплекс Kv
Теорема [5:28]. Тогда и только тогда
1Т-0)() ... П[Г1Г]^0,
когда симплексы Т{ ,... , Tif суть грани одного и того же
симплекса комплекса К) в этом случае
[Т\] П ... П[Г;г] = [7У,
где Ti есть комбинаторная сумма симплексов Ti ,..., Т{ .
Доказательство, а) Пусть
|^0>--->^р|€17*01П...[ПГ;г1;
тогда на основании [5:250]
т. е. все симплексы Тг- ,. . . , Tif суть грани симплекса 7}; значит,
комбинаторная сумма Гг- симплексов 7\- ,.. . , Tif, существует и есть
грань симплекса Tj :
Т- ~>Т-
Поэтому fjp<CT*i9 | e1Jo >.. . >eljp | £ ^ <z_[Ti]. Итак,
[7^]П ...П[фс [rj].

s 5|
6АРИЦЕНТРИЧЕСКИЕ ЗВЕЗДЫ
177
б) Для доказательства обратного включения заметим, что по
определению комбинаторной суммы имеем
T{>Tib,k = 0,l,..., r,
значит,
T*t<T*ik, [Т*,]с[7*„],
[7,*,]с[Г%,]П...П[Г''<г],
что и требовалось доказать.
В частности, комбинаторные замыкания главных звёзд
*■ г0» * • * » ' irt to у • • • j Iу "<> Po'
пересекаются тогда и только тогда, когда в К существует
симплекс
Другими словами:
Теорема [5: 29]. Нерв системы комбинаторных замыканий
главных барицентрических звёзд комплекса К есть сам комплекс К
(черт. 92).
5:3. Замкнутые барицентрические звёзды.
Определение [5:31]. Тело комбинаторного замыкания [Т%],
-*^ро, главной барицентрической звезды Г% сопряжённой вершине е{
комплекса /С, называется замкнутой барицентрической
звездой, сопряжённой вершине eit\ вершина ei называется центром
замкнутой барицентрической звезды.
Таким образом, замкнутые барицентрические звёзды
суть полиэдры.
Из [5 :27] следует:
[5: 32]. [7*] U ... U [Т9*] = К1 = К.
Из [5 :29] и [3:21] следует:
[5:33]. Замкнутые барицентрические звёзды комплекса Коб-
разуют замкнутое покрытие полиэдра К, называемое
барицентрическим покрытием полиэдра К, сопряжённым его
триангуляции К. Нерв этого покрытия есть комплекс К-
Так как симплексы, а следовательно, и замкнутые
барицентрические звёзды комплекса К могут быть предположены сколь угодно
малыми по своему диаметру, то из [5:33] следует:
Теорема [5:34]. Тело всякой n-мерной триангуляции имеет
при любом е замкнутые г-покрытия кратности я-f-l.
5:4. Подкомплексы комплекса К*', их тела и
барицентрические подразделения. Пусть К—какая-либо триангуляция,
Kt — её барицентрическое подразделение, /С*—её барицентрический
комплекс. Пусть Ко — какой-либо подкомплекс комплекса /С
Обозначим, через /С*о подкомплекс комплекса /С*, состоящий из всех бари-
12 Александров II. С.

m
кОмплЕкСы
[гл. iv
центрических звёзд комплекса /С, сопряжённых элементам
комплекса Ко-
Обратно: всякому подкомплексу /С* комплекса /С* соответствует
подкомплекс Ко^ЦК, состоящий из всех элементов комплекса /С,
сопряжённых элементам /С*. Комплексы /С0 и/(^называются
сопряжёнными подкомплексами соответственно
комплексов /Си /С*.
Из определения комплексов /С* и К*0 следует, что комплексы К0
и /С* двойственны друг другу*), поэтому, если К0—замкнутый
(соответственно открытый) подкомплекс комплекса /С, то К*0—открытый
(соответственно замкнутый) подкомплекс комплекса /С*. Элементы
комплекса /С* суть барицентрические звёзды, т. е. некоторые
подкомплексы комплекса Ki\ соединение всех барицентрических звёзд,
являющихся элементами комплекса /С*, есть подкомплекс Kq±
комплекса /Q, называемый барицентрическим подразделением
комплекса /С*.
Телом /С* комплекса /С* называется тело комплекса К*ох (оче-
видно, /С* есть соединение тел барицентрических звёзд, являющихся
элементами комплекса К*).
[5 :41]. Если /С* есть замкнутый подкомплекс комплекса /С*,
то /С^ есть замкнутый подкомплекс комплекса Kv
В самом деле, если Т*£К*0, то вследствие замкнутости /С* в /С*
комбинаторное замыкание элемента Г*£/С* в комплексе /С*
содержится в /С*, и, следовательно, на основании [5:25], [5:24]
чем утверждение [5:41] доказано.
Следствие. Тело всякого замкнутого подкомплекса /С*
комплекса /С* есть полиэдр.
Замечание. Если К0— замкнутый подкомплекс комплекса К
и К*0 — сопряжённый комплексу Ко подкомплекс комплекса /С*, то
/С*\/С* есть замкнутый подкомплекс комплекса К* и, следовательно,
К*\К1 есть полиэдр.
Докажем, наконец, следующее предложение, которое существенно
понадобится в главе 10:
[5:42]. Замыкание симплекса Т триангуляции К содержится
в соединении замкнутых барицентрических звёзд, сопряжённых
вершинами симплекса Т, и не пересекается ни с одной замкнутой
барицентрической звездой, центр которой не является вершиной
симплекса Г.
Доказательство. В течение всего этого доказательства
через р обозначается точка замкнутого симплекса Т, а через
Ти = \ещ> • • • > elir\
*) Как частично упорядоченные множества (глава 1, арт. 6:4).

§5]
БАРИЦЕНТРИЧЕСКИЕ ЗВЕЗДЫ
179
носитель точки р в комплексе Кх. Отсюда следует, что TiQ есть
носитель точки р в К; поэтому 7, есть собственная или
несобственная грань симплекса Г. Тем более,
7^ Г,
так что все вершины симплекса Tir суть в то же время
вершины симплекса Т.
Пусть eh = elh — какая-нибудь вершина симплекса Г.г; симплекс
Ти=\е140>--->*1<г\
есть грань симплекса
l*i<o>--->*i<r>-••>*!*!'
входящего в барицентрическую звезду, сопряжённую вершине еп
и р содержится в замкнутой барицентрической звезде с центром eh.
Но еп как вершина Tir есть и подавно вершина симплекса Т, так
что первая половина теоремы [5:42] доказана.
Для доказательства второй половины теоремы заметим: если р
содержится в замкнутой барицентрической звезде, сопряжённой
вершине ej£K, то Ти есть грань некоторого симплекса комплекса К1У
имеющего е$ в числе своих вершин; так как
Тц = \е14о>--->ецг\
и ej есть вершина /С, то е$ есть вершина 7\-, значит, и подавно
вершина Г, что и требовалось доказать.
Замечание. Так как и замкнутые симплексы и замкнутые
барицентрические звёзды суть компакты, то замкнутый симплекс Г,
пересекаясь лишь с замкнутыми барицентрическими звёздами,
сопряжёнными его вершинам, находится от остальных замкнутых
барицентрических звёзд на положительном расстоянии. Так как, с другой
стороны, замкнутые барицентрические звёзды покрывают весь
полиэдр К, то некоторая окрестность замкнутого симплекса Т
содержится в соединении замкнутых барицентрических звёзд,
сопряжённых вершинам симплекса Г, и не пересекается ни с какими другими
замкнутыми барицентрическими звёздами. Так как К есть конечный
комплекс, то:
[5: 43]. Для каждой триангуляции К полиэдра К можно найти
такое
e = s(/O>0,
что е-окрестность любого замкнутого симплекса Т комплекса К
содержится в соединении замкнутых барицентрических звёзд, сопряжённых
вершинам симплекса Г, и не пересекается ни с какой другой
замкнутой барицентрической звездой.
12*

180
КОМПЛЕКСЫ
[гл. iv;
§ 6. Кривые комплексы и кривые полиэдры. '
6 :1. Определения. Определение полиэдра (определение [3 :12])'
не является топологически инвариантным: топологический образ
полиэдра, вообще говоря, не есть полиэдр.
Наряцу с комплексами и полиэдрами естественно рассматривать
их топологические образы. Мы вводим следующие определения:
Определение [6:11J. Кривым полиэдром называется
всякий компакт, гомеоморфный полиэдру.
При топологическом отображении полиэдра Р на кривой полиэдр
§ симплексы Ti данной триангуляции К полиэдра Р отображаются
на некоторые подмножества кривого полиэдра §. Совокупность
этих множеств образует так называемый кривой комплекс. Мы
приходим к следующему определению:
[6:12]. Конечная система с^ подмножеств §г, /==1, 2,..., s,
топологического пространства Jti называется кривым
комплексом, если их соединение
Зс = §х и ... и ss
может быть, таким образом, топологически отображено на некото-
рый полиэдр Р = К, что при этом отображении множества §'i
взаимно однозначно соответствуют симплексам §t некоторой
триангуляции К полиэдра Р (т. е. образ каждого из множеств §г есть
симплекс T,h и обратно, прообраз каждого из симплексов §i есть
множество
отсоединение элементов («кривых симплексов») §t кривого
комплекса Q/if есть кривой полиэдр e/f, называемый телом кривого
комплекса ^\ кривой комплекс ^/С называется кривой триангу-
ляцией кривого полиэдра &%*.
Примеры кривых комплексов приведены на черт. 93 и 94.
Замечание 1. Одному и тому же кривому комплексу q%*
соответствуют различные, но непременно изоморфные между собою
триангуляции К. Числом измерений &%* называется число измерений
триангуляции К, изоморфной кривому комплексу &%*. В главе 5 будет
доказано, что размерность *) полиэдра равна числу измерений
любой его триангуляции, поэтому число измерений К (равное числу
измерений q^T) совпадает с размерностью обоих гомеоморфных
между собою компактов К и <££. Итак, в предположении, что основная
теорема главы 5 доказана, можно сформулировать следующее
предложение:
Теорема [6:1]. Все кривые триангуляции данного кривого
полиэдра имеют одно и то же число измерений, равное
размерности этого кривого полиэдра.
*) Глава 1, арт. 8: 4.

§ 6]
КРИВЫЕ КОМПЛЕКСЫ И КРИВЫЕ ПОЛИЭДРЫ
181
Замечание 2. Каждая кривая триангуляция кривого полиэдра §
изоморфна некоторой (вообще говоря, кривой) триангуляции данного
полиэдра Ру гомеоморфного §. Но, с другой стороны, каждая
кривая триангуляция § изоморфна триангуляции некоторого
(соответственно выбранного) полиэдра Р, гомеоморфного §. Таким образом,
совокупность всех комбинаторных типов кривых триангуляции
кривого полиэдра может быть определена двояко:
а) как совокупность кривых триангуляции одного
и того же произвольно выбранного полиэдра Р, гомеоморфного
кривому полиэдру §\
Черт. 93. Черт. 94.
б) как совокупность триангуляции различных полиэдров,
гомеоморфных кривому полиэдру с?.
Замечание 3. Чисто комбинаторные (т. е. независящие от
понятия непрерывности) условия для того, чтобы две данные
триангуляции имели гомеоморфные тела, до сих пор не известны. В
частности, не доказанной остаётся до сих пор w так называемая
основная гипотеза («Hauptvermutung») комбинаторной
топологии, утверждающая, что любые две триангуляции гомеоморфных
полиэдров имеют изоморфные подразделения.
6:2. /г-мерные многообразия. Полиэдр, являющийся в то же
время я-мерным топологическим многообразием *), называется
замкнутым полиэдральным многообразием; кривые
полиэдры, являющиеся топологическими многообразиями, обычно
называются просто замкнутыми многообразиями. До сих пор
неизвестно, совпадает ли таким образом определённый класс замкнутых
многообразий с классом всех топологических замкнутых
многообразий: неизвестно, существует ли замкнутое топологическое
многообразие, не являющееся кривым полиэдром.
Одномерные замкнутые многообразия гомеоморфны окружности.
Двумерные замкнутые многообразия суть не что иное, как уже
рассмотренные нами в главе 3 замкнутые поверхности.
*) Глава 1, арт. 5:3.

182
КОМПЛЕКСЫ
[гл. IV
Простейшим примером л-мерного замкнутого многообразия
является п мерная сфера Sn. Её триангуляция может быть
получена, если внутри сферы SnczRn+1 взять (п-\- 1)-мерный симплекс
и спроектировать его границу из некоторой его внутренней точки
на сферу.
Трёхмерный тор (т. е. топологическое произведение трёх
окружностей, см. главу 1, арт. 2:6) также является многообразием: для
получения триангуляции трёхмерного тора достатэчно взягь
двукратное барицентрическое подразделение трёхмерного куба, склеиванием
противоположных граней которого был получен трёхмерный тор
(глава 1, арт. 5:2, пример б).
Так же легко построить и триангуляцию топологического
произведения сферы на окружность: нужно только воспользоваться
моделью этого произведения, данной в главе 1, арт. 5:2, пример 7.
Для построения триангуляции /2-мерного проективного
пространства определим сначала правильный (я+ 1)-мерный октаэдр в /?w+1
как выпуклый многогранник с 2 (п -f-1) вершинами еъ е^ k =
= 1, 2, ...,/2+1, причём ек, соответственно e'k, имеет все
координаты, равные нулю, кроме £-й, равной 1, соответственно —1.
Граница (/2-[- 1)-мерного октаэдра как граница всякого (п -f-
^-мерного выпуклого многогранника гомеоморфна я-мерной сфере *) Sn
и дана в триангуляции Кп, обладающей свойством центральной
симметрии относительно начала координат (это значит, что каждый
элемент триангуляции Кп переходит при помощи симметрического
преобразования
x'k= —xk, £ = 1, 2, ..., /г-f 1
пространства Rn+1 в некоторый другой элемент той же
триангуляции Кп).
Двукратное барицентрическое подразделение**) /С* триангуляции
Кп, очевидно, также обладает свойством центральной симметрии.
Склеивая между собою симметричные элементы триангуляции /Й, мы
и получим искомую триангуляцию Кп проективного пространства Р".
Наряду с только что построенной триангуляцией /CJ нам придётся
(в главе 8, арт. 4:4) рассматривать и другую триангуляцию
проективного пространства Р}\ которую будем обозначать через К".. Она
получается, если взять двукратное барицентрическое подразделение
*) В данном частном случае это легко доказать непосредственно,
например, при помощи полной индукции по числу измерений: правильный
(п +1)-мерный октаэдр явлмется соединением двух пирамид с
вершинами (0, 0,...,1) и (0, 0,...,—1), построенных на /г-мерном правильном
октаэдре.
**) Можно было бы обойтись и простым, т. е. однократным
барицентрическим подразделением; двукратное бармцентрическое подразделение
удобно для некоторых специальны^ целей (см. ниже описание
триангуляции /ф,

§ 7] связность комплексов 183
/z-мерного октаэдра и его границы и склеить между собою
симметричные относительно начала косрдинаг элементы триангуляции
границы (т. е. триангуляции К^т1).
Простейшая триангуляция проективной плоскости Р2 получается
склеиванием симметричных между собою элементов (граней, рёбер
и вершин) правильного икосаэдра (двадцатигранника).
§ 7. Связность комплексов *).
7:1. Связные комплексы. Компоненты. Комплекс К
называется связным, если его нельзя представить в виде соединения
двух непустых непересекающихся замкнутых подкомплексов.
Замечание. Если /С= К' U /С", К! П К" = 0 и К', К"
замкнуты, то К1 = К\К", К" — К\К' и, следовательно, К! и /С" открыты.
Поэтому определение связности может быть сформулировано и так:
К—связный комплекс, если его нельзя представить в виде
суммы двух непустых непересекающихся открытых подкомплексов.
Или:
К—связный комплекс, если никакой собственный подкомплекс
комплекса К не является одновременно замкнутым и открытым в /С
[7:11]. Если связный подкомплекс К0 комплекса К содержится
в соединении двух замкнутых (открытых) непересекающихся
подкомплексов Кх и К2 комплекса К> то он содержится либо в /Q либо в К%.
В самом деле, если бы было
то К0 П Кх и /С0 П К2 были бы непустыми замкнутыми (открытыми)
подкомплексами комплекса /С0, и так как
К0=(К0П К,) U (КоП /Q,
то комплекс К0 не был бы связным.
[7:12]. Присоединяя к связному подкомплексу К0 комплекса К
какой-либо элемент Т£К, подчинённый некоторому элементу
(подчиняющий некоторый элемент) Т0£К0, получим связный
комплекс К0 U Т.
В самом деле, если
к0и т=к, и./еа,
где Кг и К2 замкнуты (открыты) в К0 U Т, то, в силу [7:11],
можем предположить, что K0czK1% но тогда вследствие замкнутости
(открытости) Кг i K0U Т имеем T£KV так что К2 пусто, что и
требовалось доказать.
*) Все результаты этого параграф! (кроме результатов арт. 7:3) верны
для комплексов в самом общем смысле слова, даже для всех частично
упорядоченных множеств (дискретных пространств) и являются частными
случаями соответствующих теорем для Г0-пространств (глава 1, § 3).

184
КОМПЛЕКСЫ
[гл. iv
[7:13]. Соединение Q любого числа связных подкомплексов К%
комплекса К, содержащих данный фиксированный элемент Г£ Ку
связно.
В самом деле, пусть
Q=Qi U Q2
есть разбиение Q на два замкнутых в Q подкомплекса; пусть Г£ Qt;
тогда вследствие [7:11] любой комплекс Ка содержится в Qv т.е.
Q = Q1 и Q2 = oy что и требовалось доказать.
Из [7 :13] следует:
[7 :14]. Соединение всех связных подкомплексов комплекса /С,
содержащих данный элемент Г£ ЛГ, есть связный подкомплекс Qk (Г),
называемый компонентой элемента Г в комплексе К.
Компонента Qk(7) обладает, очевидно, следующим
свойством максимальности: не существует никакого отличного
от Qk(T) связного подкомплекса Q'cz К, содержащего Qk(T).
Из [7:13] далее следует, что не может существовать двух не
тождественных пересекающихся связных подкомплексов Qt и Q2
комплекса Ку удовлетворяющих условию максимальности (так как Qt U Q2
было бы связным и Qj (J Q2:D Qv Qi^Qz^Q*)-
Поэтому:
[7 :15]. Компонента Qx(T) может быть определена как
единственный максимальный связный подкомплекс К, содержащий Т.
И далее:
[7:16]. Две компоненты Qk(T) и Qk (Г'), имеющие непустое
пересечение, совпадают между собой.
Наконец, из [7 : 12] следует:
[7:17]. Всякая компонента Qk (T) одновременно замкнута и
открыта в К.
Итак:
[7 :1]. Всякий комплекс однозначно распадается на
непересекающиеся, одновременно замкнутые и открытые, максимальные
связные подкомплексы — компоненты. Связный комплекс состоит из
одной компоненты.
Заметим в заключение, что из [7:12] вытекает:
[7:18]. Если Т< Г, то QK (Г) = QK(Г).
7:2. Случай полных симплициальных комплексов. Пусть К—
полный симплициатьный комплекс. Из [7:18] следует, что для
любого Т£К и любой вершины £< Т компоненты Qr(T) и Qk(?)
совпадают, так что можно ограничиться рассмотрением лишь
компонент вершин комплекса К. Далее, определение связности в нашем
случае может быть сформулировано так:
[7:20]. Полный симплициальный комплекс ЛГ связен, если при
всяком представлении его в виде соединения двух непустых
замкнутых подкомплексов Kt и К2 У комплексов Кх и К2 имеется, по
крайней мере одна, общая вершина,

§ 7]
СВЯЗНОСТЬ КОМПЛЕКСОВ
185
Назовём, наконец, ломаной, соединяющей вершины^
и es в комплексе /С, всякую конечную последовательность рёбер
(одномерных симплексов) комплекса К вида
1*1*2 1> 1*2*3 I ,'■•> K-l*s|.
[7:21]. Компонента вершины е в полном симплициальном
комплексе К состоит из всех симплексов комплекса К> вершины
которых могут быть соединены ломаными с вершиной е.
Предложение [7:21] легко следует из:
[7:22]. Полный симплициалъный комплекс связен тогда и
только тогда, когда любые две его вершины могут быть
соединены в нём ломаной.
Доказательство. Если комплекс может быть представлен
в виде суммы двух замкнутых подкомплексов К' и К", не имеющих
общих вершин, то никакая вершина комплекса Кг не может быть
соединена ломаной ни с какой вершиной К" (так как в этой
ломаной непременно было бы звено | eiei+11, где ei £ К\ ei+1 £ К!' и,
следовательно, само это звено не могло бы принадлежать ни к К\
ни к /Г'),
Таким образом, первая часть теоремы [7:22] доказана.
Чтобы доказать вторую часть теоремы, предположим, чго
имеются две вершины ег и е" комплекса К, которые не могут быть
соединены ломаной; рассмотрим комплекс Ке', состоящий из всех
элементов комплекса /С, вершины которых могут быть соединены с е'
ломаной. Дополнительный к KQr подкомплекс К" = К\Ке' не пуст,
так как содержит вершину е". Оба комплекса Ке' и К" замкнуты
и не имеют общих вершин. В то же время К= Ке' U К". Теорема
доказана.
7 :3. Компоненты К и К- Пусть дана триангуляция К полиэдра /С
[7:31]. Если К—связный комплекс, то К—связный полиэдр.
8 самом деле, пусть р и р' — две точки полиэдра /С, Г и Тг —
их носители в /С, е и е'—какие-либо вершины соответственно
симплексов Т и Т'. Берём ломаную, соединяющую в К вершины ей/:
1**1 Ь |*i*2l»« • -\es-les I/ К*'1>
и прямолинейные отрезки ре и е'р' соответственно в Г и V'.
Имеем в К ломаную линию (в элементарно геометрическом смысле)
реехе2...е8-1е8е'р\
соединяющую р и //, чем связность К доказана.

186 комплексы [гл. iv
Из [7:1], [3:1] и [3:22] следует далее:
Если Qp...,Qs суть компоненты комплекса /С, то Qi суть
попарно непересекающиеся полиэдры, одновременно замкнутые и
открытые в /С
Отсюда непосредственно вытекает, что каждая компонента
полиэдра К содержится в некотором полиэдре Qit а так как Q^ связно,
то совпадает с этим Q4.
Итак:
[7:3]. Компоненты полиэдра К совпадают с телами
компонент его триангуляции К.
[7 :30]. Следствие. Все триангуляции данного полиэдра состоят
из одного и того же числа компонент, равного числу компонент
самого этого полиэдра.

ГЛАВА ПЯТАЯ.
ЛЕММА ШПЕРНЕРА И ЕЁ СЛЕДСТВИЯ *).
В этой главе доказывается несколько фундаментальных
топологических теорем, впервые установленных Брауэром. Среди них на
первом месте:
Теорема I. Размерность **) замкнутого симплекса равна
числу его измерений (т.е. числу его вершин без единицы).
Другими словами (гтава 1, § 8):
Теорема Г (теорема о мостовых для симплекса).
При всяком s > 0 замкнутый n-мерный симплекс имеет
замкнутые покрытия кратности я-j-l; если е достаточно мало, то
всякое замкнутое г-покрытие замкнутого n-мерного симплекса
имеет кратность ^ п -\~ 1.
Первое утверждение этой теоремы содержится в теоремах [5 :34]
и [4:22] главы 4. По существу, это утверждение совершенно
элементарно, и читатель может, не обращаясь к четвёртой главе,
доказать его в виде упражнения (см. по этому поводу указания,
сделанные в § 1).
Второе утверждение теоремы V выражает собой глубокий
геометрический факт: он-то и составляет основное содержание этой главы.
Непосредственным следствием второго утверждения теоремы I'
является ***):
Теорема И'. Пусть Ф есть n-мерный полиэдр (т.е. полиэдр,
некоторая триангуляция которого имеет число измерений п). При
всяком достаточно маломs>0 всякое замкнутое г-покрытие
полиэдра Ф имеет кратность/^>п-\- 1.
Отсюда и из уже цитированной теоремы [5:34] главы 4
вытекает :
Теорема П. Размерность любого n-мерного {т. е. имеющего
n-мерную триангуляцию) полиэдра Ф равна я.
Далее, из теоремы I в этой главе выводится:
*) Все результаты этой главы заново доказываются, с одной стороны,
в главах 10 и 14, а с другой, — в главах 10 и 15, однако менее
элементарным образом, чем здесь. Эту niaiy можно читать, не читая предыдущих, а
лишь обращаясь при ссылках к главе 1 и прочтя предварительно вводный
параграф главы 4 о симплексах.
**) Глава 1, определение [8:42].
***) Читатели, пропустившие главу 4, переходят сразу к теореме Щ.

188
ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ
[Л. V
Теорема III (инвариантность числа измерений Rn).
Два эвклидовых пространства Rn и Rm разных чисел измерений
п и т не гомеоморфны между собою.
Важным усилением этой теоремы является следующее
предложение, которое доказывается в § 3.
Теорема IV (инвариантность внутренних точек
множеств, лежащих в Rn, при топологических
отображениях в Rn). При топологическом отображении С
множества Ac^Rn на множество BczRn всякая внутренняя точка
множества А {относительно Rn) переходит во внутреннюю
(относительно Rn) точку множества В (и следовательно,
невнутренняя точка множества А переходит в невнутреннюю точку
множества В).
Замечание. Теорема IV доказывается не только для
пространства Rn, но и для всех так называемых топологических
многообразий Мп (см. определение их в главе 1, арт. 5:3).
Доказательства всех перечисленных теорем, даваемые в этой
главе, отличаются от первоначальных доказательств Брауэра; они
основываются на одном, по существу, элементарном
предложении комбинаторного характера, известном под названием
леммы Шпернера (формулируется и доказывается в § 2). Лемма Шпер-
нера не только позволяет доказать теоремы I—IV неожиданно
просто, но и сама по себе является замечательным
геометрическим фактом.
Та же лемма Шпернера позволяет дать очень простое
доказательство ещё одной классической теоремы Брауэра, а именно,
теоремы о существовании неподвижных точек при
произвольном непрерывном отображении в себя
замкнутого симплекса (конечно, и любого компакта, гомеоморф-
ного замкнутому симплексу). Это доказательство теоремы Брауэра
принадлежит Кнастеру, Куратовскому и Мазуркевичу и является в
настоящее время классическим. Оно излагается в § 4.
§ 1. Предварительные замечания*).
1:1. Триангуляции и барицентрическое подразделение
замкнутого симплекса. Перечислим все предложения главы 4, которые
понадобятся в настоящей главе.
а) Из триангуляции понадобится только триангуляция
замкнутого симплекса 7",— этим термином обозначается конечное множество
Кп попарно не пересекающихся симплексов (различного числа измерений),
удовлетворяющее следующим условиям:
1. Всякая грань какого-либо симплекса, являющегося элементом
множества Кп% сама есть элемент множества К11.
*) Этот параграф предназначается лишь для читателей, не читавших
главу 4.

§ 1]
предварительные замечания
189
2. Каждый элемент- Тг множества Кп содержится («лежит») в одной и,
очевидно, только в одной грани *) симплекса Р\ называемой носителем
симплекса Тг.
3. Соединение всех множеств, являющихся элементами множеств Кп,
есть замкнутый симплекс 74
Из этого определения следует:
Всякая грань 1Г симплекса Тп есть соединение лежащих на ней
симплексов подразделения К11-
В самом деле, если ;; £ Тг и Tbt^Kn содержат точку р, то носитель
симплекса Т\ есть непременно Тг, так как в противном случае две грани
симплекса Тп (а именно, Тг и носитель симплекса 7^) имели бы общую
точку р. Итак, каждая точка р £ Тг содержится
в лежащем на 1Г симплексе триангуляции Кп, что
и требовалось доказать.
Далее:
Если Tj<C.Tj£Kn и Тг есть носитель
симплекса Гг-, то носитель симплекса Tj есть грань
симплекса 7У. ___
В самом деле, Тг есть замкнутое множество,
являющееся соединением всех граней симплекса
Тг. Поэтому всякая точка прикосновения Тг
лежит на некоторой грани симплекса Тг. Так как
7^-состоит из точек прикосновения симплекса Гг-,
следовательно, и симплекса Тг, то носитель сим- Черт. 95.
плекса Tj есть грань симплекса Тг, что и
требовалось доказать. __
б) Среди всех триангуляции замкнутого симплекса Тп наиболее важно
его барицентрическое подразделение: элементами
барицентрического подразделения замкнутого симплекса Ith являются все
собственные и несобственные 1рани (/z + 1)! симплексов вида
00*0° ...0,< , ',
где о есть центр тяжести сих плекса Тп, о,- —центр тяжести какой-либо его
{п — 1)-мерной грани V\~\ о( .—центр тяжести какой-либо (п — 2)-мер-
ной грани Tf72 симплекса 7?""1 и т.д. вплоть до вершины о* .... сим-
Ч1 2 ' 1 1 П
плекса Тп.
Барицентрическое подразделение замкнутого отрезка получается
посредством деления его пополам. Барицентрическое подразделение
треугольника изображено на черт. ^5. Один из симплексов барицентрического
подразделения тетоаэдра изображён на черт. 87 главы 4.
Из арт. 4:2 Прибавления II следует:
Если диаметр замкнутого симплекса Тп равен dt то диаметр любого
симплекса барицентрического подоазделения Тп не превосходит —1— d.
п + 1
Отсюда, в свою очередь, вытекаег, что, произведя /г-кратное
барицентрическое подразделение симплекса Тп, получим при достаточно большом
h произвольно мелкую триангуляцию этого симплекса, т. е. триангуляцию,
все симплексы которой имеют диаметры, меньшие чем произвольно
заданное е>0.
*) Ещё раз напоминаем, что под гранью данного симплекса всегда
разумеется собственная или несобственная грань этого симплекса.
ж

190
ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ
[гл. v
в) Нам понадобится следующий факт: Замкнутый симплекс Т» можно
представить как соединение п+\ замкнутых множеств А*, Аи... А,
взаимно однозначно соответствующих вершинам е0, еь..., еп симплекса
1™ так, чтоА}. содержит вершину ег и не имеет ни одной общей точки
с замкнутой гранью симплекса Т>\ противоположной вершине ег.
Этот факт содержится в результатах главы 4: достаточно определить
Аг как замкнутую барицентрическую звезду с центром ег, т. е. как
соединение всех симплексов барицентрического
подразделения Тп, имеющих в числе своих
вершин данную вершину ег симплекса 74
Можно построить нужные нам множества
Аг и несколько иначе: проведём через центр
тяжести симплекса Тп плоскость Rn—i,
параллельную плоскости грани \е(\..шег^1
er±i.. .еп\. Эта плоскость отсечёт от Тп
замкнутый симплекс, содержащий вершину ег,
который и обозначим через Аг (черт. 96).
г) При любом е>0 можно всё простран-
Черт. 96. ство Rn покрыть счётным числом замкну-
тых множеств Аг диаметра <Ч так, что
никакая точка пространства не принадлежит более чем п-\-\ из этих
множеств и что любой шар
1 1 2 * ' п
пересекается лишь с конечным числом множеств Аг.
Для доказательства построим сначала симплнциальное, е-р аз-
биение («бесконечную триангуляцию») /^пространства #™, т. е. множество
К попарно не пересекающихся симплексов (разного числа измерений),
обладающее следующими свойствами:
1. Каждая грань любого симплекса множества К сама является
элементом множества К.
2. Соединение всех симплексов, входящих в К, есть Rn.
3. Каждый шар пространства Rn пересекается лишь с конечным числом
симплексов множества К.
4. Диаметры всех симплексов К меньше е. Построить такое множество
симплексов (такой бесконечный ком п л е к с) К можно следующим
образом: разбиваем Rn на кубы:
"*г£'Ог<('Иг + 1К (/ = 1,..., п),
и их грани. Каждый из этих кубов подразделяем барицентрически. Это
значит: все их рёбра делим пополам, потом делмм каждый квадрат на 8 равных
треугольников, спроектировав из центра квадрата уже произведённое
подразделение его границы. Аналогично подразделяем все трёхмерные кубы,
спроектировав из центра каждого куба уже произведённое подразделение
его границы, и т. д.
Полученные таким образом симплексы различного числа измерений и
образуют искомый комплекс К,
Каждая точка р £ Rn содержится в одном и только одном симплексе
комплекса К, называемом носителем точки р.
После того как построено симплициальное е-разбиение К пространства
Rn, представим каждый из замкнутых «-мерных симплексов этого разбиения
в виде суммы я-f-l замкнутых множеств А^ удовлетворяющих условиям в).
Если ет есть какая-нибудь вершина разбиения К, то обозначаем через Ф^
соединение всех только что построенных А„ содержащих вершину ет. Так

§ 2)
Лемма Шпернера
191
как симплексы нашего разбиения имели диаметры <е, to множества Фп
имеют диаметры <^2е. Ясно, что любая ограниченная область пространства
Rn пересекается лишь с конечным числом множеств Фт. Докажем, наконец,
что никакая точка p£Rn не содержится более чем вп + 1 множествах Фт.
В самом деле, из самого построения множеств Фт следует такое
предложение:
Если носитель точки p£RnecTb симплекс Tr = \eh .. ,eh \ £/С то точка
р содержится лишь в множествах Фл ,..., Ф^ .
Из только что доказанного следует (независимо от результатов главы 4):
Всякий компакт (значит, i частности, и всякий замкнутый симплекс,
лежащий в пространстве Rn) имеет при всяком е>0 замкнутое г-покры-
тие кратности <;« + !.
Этим первое утверждение теоремы Г
доказано.
д) В § 3 нам понадобится теорема,
утверждающая, что граница л-мерного симплекса
Тп при всяком е> 0 имеет замкнутые е-покры-
тия кратности <; п. Это предложение также
является частным случаем теоремы [5:34]
главы 4. Однако, его легко доказать и
непосредственно.
Для этого достаточно представить каждую
из (п—1)-мериыхзамкнутых граней симплекса
Черт. 97.
множеств Aif содержащих
Тп как соединение множеств А$,
удовлетворяющих условиям в), и для каждой вершины
ет симплекса Тп определить Фт как соединение
вершину ет.
е) Заметим, наконец, что из барицентрических подразделений всех
(п — 1)-мерных (замкнутых) граней данного я-герного симплекса Тп
получается по определению барицентрическое подразделение
границы Тп\Тп симплекса Тп. На черт. 97 изображён случай п = 3
(изображены лишь грани, обращенные к зрителю).
§ 2. Лемма Шпернера.
2:1. Лемма Шпернера. [2 :1]. Пусть Тп = \е0.. ,еп\ есть п-мер.
ный симплекс, а Кп — триангуляция его замыкания 7Х Пусть
каждой вершине е'к £ Кп поставлена в соответствие $ершина Se'k =
== eik симплекса Тп с соблюдением следующего условия:
[2 :10]. Se'k есть всегда одна из вершин носителя точки ек
(т. е. одна из вершин той грани симплекса Тп, на которой лежит
точка е'к).
Тогда непременно существует такой n-мерный симплекс.
Г<=К0--ЧЯ1
триангуляции К, что все вершины Se'k,...,Sek различны между
собою.
Доказательство. Пусть Г*,..., 7^ —все я-мерные симплексы
триангуляции Кп. Назовём симплекс Г? нормальным, если всем его

192
ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ
[ГЛ. V
вершинам поставлены в соответствие различные вершины симплекса Тп.
Мы докажем следующее предложение, более сильное, чем лемма
Шпернера:
[2:11]. Число нормальных симплексов нечётно.
Для я==0 теорема [2:11] очевидна. Предположим, что она
доказана для всех (я—1)-мерных симплексов и докажем её для я-мерного
симплекса Тп.
Назовём «отмеченной» гранью какого-либо симплекса TV1 всякую
(п—1)-мерную грань симплекса Т?, вершинам которой поставлены в
соответствие вершины е19е2,. .., еп симплекса Тп.
Заметим прежде всего:
[2:12]. Число отмеченных граней симплекса Г? есть либо 1,
либо 2, либо О, причём у всех нормальных симплексов, и только
у них, число отмеченных граней равно 1.
В самом деле, если симплекс Т1} = I е. ... е. I нормален и
i i г0 in\
Se'.Q = e0, Se'ti =e, 5^ = ew
то \е. . . . е'. |, очевидно, единственная отмеченная грань симплекса Tf.
Пусть симплекс Т1} ненормален, но имеет всё же отмеченную грань
\е. ... ег. \, так что, например, Se'. =eu Se'. =а е9,. . ,,Se/ =£„.
Тогда Se{' есть одна из вершин eiy. . ., ел, пусть Se/ =^; симплекс
Т? имеет две и только две отмеченные грани, а именно,
\е. . .. е'. \ к -\е. е'. . . . е'.\.
Предложение [2:12] этим доказано.
Обозначим через at число отмеченных граней симплекса V) и положим
а = £ а{.
/=i
Из только что доказанного следует, что число нормальных
симплексов имеет ту же чётность, что и число а. Поэтому достаточно
доказать, что число а — нечётно.
Рассмотрим какой-нибудь (п—1)-мерный симплекс
Tn-l£Knt
Возможны три случая:
1. Т"-1 лежит внутри симплекса V1. Тогда либо Г""1
не является отмеченной гранью никакого симплекса Г", либо
симплекс Т^1 является отмеченной гранью в точности двух
(прилегающих к Т"-1) симплексов Т? и Т% и, следовательно, при подсчёте
суммы а = ^ аг будет сосчитан два раза.
2. Симплекс Тп~г лежит на какой-либо грани
симплекса Т\ отличной от грани Р1-1 = | ei... еп \.

§ 2|
ЛЕММА ШПЁРНЁРА
193
В этом случае в силу условия [2:10] симплекс Г""1 не может
быть отмененной гранью никакого симплекса Тпг
3. Симплекс Г?-1 лежит на грани Тп~х =\е1. .. еп\.
Этот случай мы разобьём снова на два случая:
За. По крайней мере, двум вершинам симплекса Т"—1 поставлена
в соответствие одна и та же вершина симплекса Тп~1 = \ех.. > еп\.
В этом случае Tf—1 не может быть отмеченной гранью никакого
симплекса Tf.
36. Всем вершинам симплекса Тп~х поставлены в соответствие
различные вершины симплекса Тп~х = \е1.. . еп|. В этом случае
симплекс Г!*"1 является отмеченной гранью одного единственного
(прилегающего к нему) симплекса Г?.
Из этой классификации различных случаев следует: чётность
числа а та же, что и чётность числа тех (п—1)-мерных
симплексов Г^"1, которые находятся в условиях 36.
Рассмотрим ближе этот случай Зб. Симплексы Кп, лежащие на
симплексе Г""1 и на его гранях, образуют триангуляцию Кп~1
замкнутого симплекса Тп~\ причём, в силу отображения с>, каждой
вершине Кп~1 поставлена в соответствие одна из вершин
симплекса Тп~х с соблюдением условия [2:10]. Таким образом,
симплекс Тп~1 и комплекс К11'1 находятся в условиях теоремы [2:11] для
числа измерений (п—1), которую мы предположили доказанной.
Следовательно, число тех, лежащих на Tn~1i {n — 1)-мерных симплексов
Г^"-1, всем вершинам которых поставлены в соответствие различные
вершины симплекса Гп-1, нечётно. Другими словами, нечётно число
тех Тп~\ которые находятся в условиях 36, а это значит, что число а
также нечётно, что и требовалось доказать.
2:2. Следствие из леммы Шпернера. Окончание
доказательства теоремы о мостовых. Из леммы Шпернера выведем такое
следствие:
[2 :21]. Пусть Тп есть n-мерный симплекс с вершинами е0, el,...ien.
Пусть
а = {Л0, . . .^Ап)
есть покрытие замкнутого симплекса Т;\ состоящее изп~\-\
замкнутых множеств Л0,. . ., Лп, удовлетворяющих условию: всякая
замкнутая грань \е£ . . . eir\ симплекса Тп содержится в А4 \} . . . U Aif
(в частности е^А{ для любого / = 0, 1,...эя).
Тогда пересечение всех множеств Аг не пусто.
Доказательство. Очевидно [хотя бы на основании леммы
Лебега*], что предложение [2:21] будет доказано, если мы докажем:
[2 :22]. Какова бы ни была произвольно мелкая триангуляция Кп
замкнутого симплекса Тп, найдётся хотя бы один замкнутый сим-
*) Глава 1, [8:32].
I'J Александров П. С.

194 ЛЕММАШП ЕРНЕРА И ЕЕ СЛЕДСТВИЙ [гЛ. V
плекс Т£ этой триангуляции, пересекающийся со всеми множествами
Л0,. . ., Ап.
Для доказательства теоремы [2 :22] поставим в соответствие
каждой вершине е'£ Кп такую вершину Se = ei носителя точки е' чтобы
было
(2:22) e'^At.
Очевидно, отображение S удовлетворяет условию [2 :10] леммы
Шпернера.
Применяя лемму Шпернера к отображению 5, находим симплекс
Т!££Кп, всем вершинам которого поставлены в соответствие
различные вершины симплекса Тп. А это значит, что остов симплекса
Т? пересекается со всеми множествами Л0,. .., Ап, что и требовалось
доказать.
Из теоремы [2:21] легко выводим:
[2 :23]. Пусть
а = [А0,. . ., Ап)
—такое замкнутое покрытие замкнутого симплексаТп = \е0...\. епчто
1. е<£А4,
2. Аг не имеет общих точек с замкнутой гранью Т?~~\
противоположной вершине ei%
Тогда
А0П...ПАпфО.
Для доказательства [2:23] достаточно показать, что из условий
теоремы [2:23] следуют условия теоремы [2:21]. Рассмотрим
замкнутую грань \е{.. .eir\, и пусть I отлично от всех /0,.-.,V Тогда
\%- • -eiriS. 77""S значит> А{ не пересекается с | е{ . . . eif\. Так как это
справедливо для любого 1ф /0,. . ., ir, то необходимо | ei0• • • eir\ cz
с=_Л U . . . U Air, что и требовалось доказать.
Переходим теперь к доказательству второго утверждения
теоремы о мостовых:
[2 :24]. При достаточно малом е > 0 всякое замкнутое г-по-
крытие п-мерного замкнутого симплекса имеет кратность^ п -\- 1.
Доказательство. Пусть е настолько мало, что никакое
множество диаметра меньше г не пересекается со всеми
(п—^-мерными замкнутыми гранями симплекса Тп (так как пересечение всех
замкнутых (п—1)-мерных граней симплекса Тп пусто, то такое е
можно найти хотя бы по лемме Лебега (глава 1, [8:32]).
Выбрав таким образом е, возьмём каксе-нибудь г-покрытие
а = {А0,...,А8}.
В силу нашего выбора числа е, никакое Aj, содержащее данную
вершину ei симплекса Тп, не пересекается с замкнутой гранью 7?"Л

§2]
ЛЙММА ШПЕРНЁРА
19§
противоположной вершине е{. Отсюда, в частности, следует, что ни
одно Аг не содержит более одной вершины симплекса Тп .
Предположим теперь, что нумерация элементов покрытия выбрана
так, что
ео € ^о» • • •» еп 6 ^п*
Если s > я, то возьмём какое-либо множество Aj с номером J > n и
поступим следующим образом: отыщем замкнутую грань Г?""1, не
пересекающуюся с Aj9 вычеркнем из покрытия а эл^ент Aj и
заменим Ai через Л< U Л^, обозначив в заключение это
множество опять-таки через At. Пос/е этой замены покрытие а перейдёт
в покрытие а(1), число элементов которого на единицу меньше числа
элементов покрытия а, а кратность, как легко видеть, во всяком
случае не больше кратности покрытия а. Легко убедиться также
в том, что никакой элемент покрытия ос(1), содержащий какую-либо
вершину симплекса Тп, не пересекается с замкнутой гранью,
противоположной этой вершине.
Повторив, если нужно, эту операцию несколько раз, получим,
наконец, покрытие
а = |л0,. . ., Лп},
удовлетворяющее всем услориям теоремы [2:23]. Следовательно,
существует точка, принадлежащая всем множествам Л0,..., Лп, т.е.
кратность покрытия а^ не меньше, чем п-\- 1, а так как при
нашей 3iMene одного покрытия другим кратность покрытия во всяком
случае не повышалась, то первоначальное покрытие а имело
кратность ^ п -\- 1> что и требовалось доказать.
2 :3. Инвариантность числа измерений для /?".
[2:31]. Всякий компакт, лежащий в Rn, имееп
размерность О.
В самом деле, всякий компакт Фс/?и, будучи ограниченным
множеством, лежит в некотором я-мерном замкнутом симплексе Тп;
гак как Тп имеет при всяком е > 0 замкнутые е-покрытия
кратности п-\- 1, то и Ф имеет при всяком е замкнутые е-покрытия
кратности гг —j— 1, что и требовалось доказать.
Отсюда вытекает:
[2 :32]. Никакое множество A^Rn, содержащее внутренние
точки (относительно Rn), не может быть топологически
отображено в Rm, где т < п.
В самом деле, при таком отображении всякий л-мерный
симплекс, содержащийся, в силу наших предположений, в Л, перешёл
бы в некоторый компакт размерности <#, что невозможно, так как
размерность компактов при топологических отображениях ке
меняется.
В частности, само пространство Rn не может быть отображено
в Rm при /я<л. Отсюда следует:
13*

196 ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЙ [гл. it
[2:33.] Теорема об инвариантности числа
измерений R . При пфт пространства Rn и Rm не гомеоморфны
между собою.
Из [2 :33] и определения топологического многообразия (глава 1,
арт. 5 :3) следует:
[2:34]. Если тфпу то n-мерное и т-мерное топологические
многообразия не могут быть гомеоморфны между собою.
§ 3. Теорема об инвариантности внутренних точек
3: 1.
[3:1]. При всяком топологическом отображении какого-нибудь
множества AczRn на какое-нибудь множество BczjRn всякая
внутренняя точка множества А переходит во внутреннюю точку
множества В> всякая невнутренняя точка А переходит в
невнутреннюю точку Л.
При этом «внутренняя точка» (соответственно «невнутренняя
точка») значит: «внутренняя точка» (соответственно «невнутренняя»)
относительно Rn.
Доказательство основывается на следующей лемме:
Лемма [3:11]. Пусть
*={AV...,A8]
— замкнутое покрытие кратности п -J- 1 замкнутого ограниченного
множества Фс/J», обладающее тем свойством, что существует
лишь одна точка р^Ф, принадлежащая п-\-\ элементам
покрытия а. Тогда, если р есть невнутренняя точка Ф, то, изменив,
покрытие а лишь в произвольно малой окрестности точки *) р
можно преобразовать покрытие а в покрытие af кратности ^ п.
Доказательство леммы. Возьмём произвольно малый
«-мерный симплекс V\ содержащий внутри себя точку р. Всякая
точка границы Тп симплекса Тп принадлежит не более чем к п
элементам покрытия а. Поэтому существует такое s>0, что
s-окрестность каждой точки из Тп пересекается не более чем с п
элементами покрытия а.
Возьмём теперь какое-нибудь замкнутое s-noKj ытие
? = {#!>• • •> Вт)
кратности п множества Тп.
Для каждого множества Bj£$ определяем некоторое множество
Ai(j) £ a следующим образом:
*) Под изменением покрытия а в данной окрестности Ор точки р мы
понимаем переход от покрытия а = {Аъ..., А8} к такому замкнутому
покрытию а' = {А'ь .... A's}, что Ai\Ov = A'j\Ovt / = 1,..., s.

§ 3] ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ВНУТРЕННИХ ТОЧЕК 197
1. Если Bj не пересекается с Ф, то берём в качестве А{ф
произвольное множество At, пересекающееся с Тп.
2. Если множество Bj пересекается с Ф, то, в силу выбора е,
оно пересекается не более чем с п элементами покрытия а; один
какой'Нибудь из элементов а, пересекающихся с Вр мы и
обозначаем через Ai(j). В обоих случаях, конечно, одно и то же
множество Ai может оказаться множеством Ац3~) для различных By
Построим теперь систему а" замкнутых множеств А/' следующим
образом:
Всякое А{ £а, не являющееся множеством Аг^ ни для какого В^
есть, по определению, элемент А" системы а"; если же Аг есть
множество Ац^ для одного или нескольких В^ то определяем Л/' как
соединение всех этих Bj и множества А^ Очевидно,
Фир^иЛ/',Л/'£а''.
Системы а" и а находятся во взаимно однозначном соответствии,
причём для каждого данного / либо Л/ = Лг-, либо А" есть
соединение множества Аг и некоторого подмножества множества Тп.
Поэтому, если какая-нибудь точка q принадлежит некоторым
множествам Aiv..., Air, то q или принадлежит множествам А{р.. ., Air,
или лежит на t (оба случая, конечно, не исключают друг друга).
Значит, если мы докажем, что никакая точка Тп не принадлежит
более чем п элементам системы а", то этим будет доказано, что р
есть единственная точка, принадлежащая л —[— 1 элементам системы а".
Докажем, что никакая точка Тп не принадлежит более чем п
элементам системы а".
Пусть q — какая-либо точка Тп. Если q не принадлежит Ф, то
q принадлежит не более чем к п множествам Вр пусть к
BJv-> Bjm> соответствующие Ai{j) пусть будут Aiv Ai2,. . ., Л,.да,
числом не более п; точка q принадлежит лишь к элементам
Лг-,. Ai системы а" т. е. не более чем к п элементам.
1 ' т '
Пусть теперь q есть точка Тп П Ф и Av. . ., Ah, Bu. .., Вк суть
все элементы покрытий а и (3, содержащие точку q. Все множества
£>i,..., Вк лежат в s-окрестности 0(q, s) точки # и среди всех, не
более чем п элементов покрытия а, пересекающихся с 0(q, s),
несомненно, имеются и множества Л1?...,ЛЛ. Итак, пусть все
элементы а, пересекающиеся с 0(qy s), суть
Среди них находятся и все Ai(j) для ;' = 1, 2,. . ., &, поэтому среди
всех элементов системы а" содержать точку q могут лишь
^i >..., Л^", числом не более п, чем наше утверждение и доказано,

198 ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ , [гЛ. V*
Возьмём теперь внутри симплекса Тп какую-либо точку о, не
принадлежащую множеству Ф (так как р — невнутренняя точка Ф,
то найти нужную нам точку о всегда можно).
Рассмотрим те элементы системы а", которые пересекаются
с Т*1; пусть это будут
Л " А "
Обозначая через (оА/') соединение всех замкнутых отрезков
вида oq, где q£ Tn П А/\ положим
л';' = (л;'\(л;' п г»)) и {оа\) для ;=i,..., v
и
A'l' ^=A':\Tn для i>v.
Множество А".' может отличаться от множества А", лишь на точки,
принадлежащие к Тп, поэтому точка, не принадлежащая к Тп, не
может содержаться более чем в п множествах А'!'. Что же
касается точек Тп, то из них лишь точка о может принадлежать
к п-\- 1 множествам А/" (так как в противном случае проекция
точки q на Тп принадлежала бы к п-\-\ множествам А" вопреки
доказанному выше). Так как о(£ф, то, полагая для всех /
а'.==а";пф,
получаем покрытие
«' = М/,..., а;\
множества Ф кратности ^п.
Очевидно, каждое А/ может отличаться от соответствующего
Ai лишь на точки, принадлежащие к Тп, а так как симплекс Тп
можно было взять произвольно малым, то мы вправе сказать, что
покрытие а' произошло из покрытия а видоизменением этого
последнего в произвольно малой окрестности точки р. Лемма, таким
образом, доказана.
Из леммы выведем:
[3:12]. При топологическом отображении С замкнутого
n-мерного симплекса Т71 в n-мерное эвклидово пространство R"
всякая внутренняя точка р симплекса Тп переходит во
внутреннюю точку множества Ф — С(Тп).
Доказательство. Пусть Тп== \е0. . ,еп\. Возьмём
барицентрическое подразделение границы симплекса Тп и спроектируем его
из точки р. Получим триангуляцию К замкнутого симплекса Тп,
отличающуюся от барицентрического подразделения только тем, что
«центром тяжести» симплекса Тп является точка р. Обозначим
через Ai соединение замыканий всех симплексов комплекса К%
имеющих е^ своей вершиной*

§ 3] ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ЬНУТРЕННИХ ТОЧЕК 199
Точка р является единственной общей точкой множеств
Л0,.--> Ап\ при этом как само покрытие
а={Аэ,..., Ап]
замкнутого симплекса 7W, так и всякое покрытие, которое
получится из а видоизменением множеств At в достаточно малой
окрестности точки р, удовлетворяет условиям [2:23].
Отсюда следует:
При достаточно малом s > 0 всякое покрытие а', полученное
из а видоизменением множеств Аг в s-окрестности точки р, есть
покрытие кратности ^п-\-1.
Пусть теперь точка q = C(p) есть невнутренняя точка множества
Ф = С(Тп). Возьмём 8 > 0 столь малым, чтобы образ 8-окрестности
точки q (относительно Ф) при отображении С'1 лежал в
s-окрестности точки р. Пользуясь леммой [3 :11], видоизменим множества
C(Ai) в 8-окрестности точки q так, чтобы получилось покрытие
3' кратности -О множества Ф. При отображении С-1 покрытие (3'
переходит в покрытие а/ той же кратности ^ я, являющееся
видоизменением покрытия ос в s-окрестности точки р, что невозможно.
Утверждение [3:12] этим доказано.
Теорема [3:1] доказывается теперь в нескольких словах. Пусть
р внутренняя точка множества А<=/?и; точка р является
внутренней точкой некоторого я-мерного симплекса Тп <= А и поэтому при
данном топологическом отображении С множества А в Rn
переходят в точку q, являющуюся внутренней точкой множества С (Тп)
и тем более внутренней точкой множества С(А\
Всякая невнутренняя точка р множества А переходит при
топологическом отображении С в невнутреннюю точку С(р) множества
С (А), так как в противном случае внутренняя точка С(р) множе-
С!ва С (А) перешла бы при топологическом отображении С-1 в
невнутреннюю точку р множества Л, чего не может быть.
Теорема [3 :1] этим полностью доказана.
Из теоремы [3:1] непосредственно вытекает следующее лишь
формально более общее утверждение, которое, однако, нам
понадобится в следующем артикуле:
[3 : 13]. Пусть Un и Vn — топологические пространства, гомео-
морфные R71; пусть дано топологическое отображение С множества
Acz{Jn на множество Bc^Vn; тогда всякая внутренняя точка
множества А относительно Vй переходит при отображении С
во внутренюю точку множества В относительно V7K
В [3:13] содержится предложение:
[3:14]. Пусть Un и Vn гомеоморфны Rn; пусть
С—топологическое отображение открытого в Un множества А в
пространство Уп. Тогда множество С (А) открыто в Vn. В частности,
всякий топологический образ всего пространства Un в Vй есть
открытое множество пространства Vй.

200
ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ
[гл. v
Так как при т </2 мы можем рассматривать Rm как нигде не
плотное множество пространства Rn^ то топологическое
отображение Rn на Rm невозможно. Мы получили, таким образом, новое
доказательство теоремы [2:33].
Замечание. Отметим отдельно частный случай теоремы [3 :Н],
которым (при я = 2) мы пользовались в главе 3.
[3:140]. Пусть Un и Vn—два (лежащих в каком-нибудь
топологическом пространстве) множества, гомеоморфных R4. Если при
этом VnS. Vй, то Vй открыто в Vn.
Определение [3:15]. Компакт, гомеоморфный /2-мерному
замкнутому симплексу, называется /2-мерным элементом.
Так как размерность топологически инвариантна и размерность
симплекса гавна числу его измерений, то число п в определении
[3 :15] действительно есть размерность я-мерного элемента и потому
определено однозначно (т. е. никакое топологическое пространство
не может быть при пфт одновременно /2-мерным и /тг-мерным
элементом).
Докажем следующее важное предложение:
[3:16]. При всех топологических отображениях замкнутого
n-мерного симплекса Тп на n-мерный элемент Еп граница Тп\ Тп
симплекса переходит в одно и то же множество S71-1,
называемое границей n-мерного элемента Еп\ открытое
множество En\Sn~1 плотно в Еп и обозначается через Еп\ оно
называется внутренностью элемента Еп.
Доказательство. Пусть С1 и С2 — два топологических
отображения Тп на Еп. Если бы, например, для точки х £ Тп\Тп было
С2(х)£С{(Т»\Т>%
то было бы Cj-1 C2(x)^fn\Tv; между тем, С^С2 есть
топологическое отображение Тп на себя, при котором, в силу [3:1],
множество ТИ\ТИ отображается на себя. Полученное противоречие
доказывает, что
с2 (Тп\т") Е ci(Тп\тп)-
Таким же образом доказывается, что
т. е. что
Ci (Т"\Тп) = С2(Р'\Г").
Так как Т11 открыто и плотно в Тп, то множество Еп, будучи
образом множества Тп при топологическом отображении Тп на Еп9
открыто и плэтно в Ёп.
Теорема [3:16] этим доказана,

§ 4]
ТЕОРЕМА О НЕПОДВИЖНЫХ ТОЧКАХ
201
3:2. Теорема об инвариантности внутренних точек для
топологических многообразий. Из [3:1] без труда выводится
очень важный факт, а именно, следующая теорема, представляющая
собою обобщение теоремы [3:1]:
[3 :2]. При всяком топологическом отображении какого-нибудь
множества Л, лежащего в п-мерчом топологическом
многообразии Mnv на какое-нибудь множество В, лежащее в п-ме-рном
топологическом многообразии М*, всякая внутренняя точка
множества А {относительно Мпл переходит во внутреннюю точку
множества В {относительно М™), всякая невнутренняя точка А
(относительно М") переходит в невнутреннюю точку В
(относительно Мп^.
Доказательство. Можно ограничиться доказательством
утверждения, касающегося внутренних точек, — случай
невнутренних точек получается после этого дословно так же, как в
последних строчках доказательства теоремы [3:1].
Итак, пусть дано топологическое отображение С множества
ДсМ}п на множество Лс=М2м.
Пусть р—внутренняя точка множества А относительно Мхп.
Пусть Vй есть окрестность точки С(р) в Мап, гомеоморфная
пространству Rn.
Возьмём такую лежащую в А и гомеоморфную пространству Rn
окрестность Un точки /?, чтобы её образ при отображении С лежал
R Vй.
Так как Un и Vй гомеоморфны R7\ то С (Un) открыто в 1/п,
по Vй открыто в Af2", значит, C(Un) открыто в М2п. Так как
/)£№с=Л, то C(p)^C(Un)^B; этим всё доказано.
§ 4. Теорема о неподвижных точках при непрерывных
отображениях элемента.
В этом параграфе доказывается следующее предложение.
Теорема о существовании неподвижной точки
при непрерывном отображении «-мерного элемента.
При всяком непрерывном отображении С n-мерного элемента Ёп
в себя имеется, по крайней мере, одна неподвижная точка (т. е.
такая точка р£Ёп, что С(р) = р).
При доказательстве, очевидно, можно без ограничения общности
предположить, что Еп есть я-мерный замкнутый симплекс
Т»=\е0...еп\.
Пусть С — данное непрерывное отображение Тп в себя и пусть
при отображении С точка р ^■ Тп с барицентрическими координатами

202 ЛЕММА ШПЕРНЕРА И ЕЕ СЛЕДСТВИЯ [ГЛ. V
т0,...} тп переходит в точку // = С(р) с барицентрическими
координатами m'Qi..., т'п (барицентрические координаты берутся
в системе {е0>.. ., еп}).
Обозначим через Л4- множество всех тех точек р £ Гл, для которых
mf^mi. Ясно, что все At суть замкнутые множества. Докажем,
что они образуют покрытие Тп, удовлетворяющее условиям теоремы
[2:21], т. е. что произвольная замкнутая (собственная или
несобственная) грань | е{ ... eir\ симплекса Тп покрыта множествами Аг ..., Air
Пусть р — произвольная точка замкнутой грани \е. .. ,eir\. Тогда
miQ -f ... + mir = 1 > miQ' + ... -f- mir', откуда следует, что, по
крайней мере, для одного ik имеем tnk'^.mik и, значит, p£Aik.
Итак, ко множествам Лг- может быть применена теорема [2:21];
значит, имеется точка /?, принадлежащая всем А^
Для этой точки выполнены неравенства
которые в силу условий
т0 + • • • + Шп = ш0 + • • • + тп = 1, ° < Щ\
переходят в равенства
Другими словами, С(р)=р, что и требовалось доказать.

ГЛАВА ШЕСТАЯ.
ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ*).
Определение размерности дано в главе 1, арт. 8:4. В главе 5 доказана
основная теорема, без которой само понятие размерности не имело бы
права на существование, а именно, теорема Брауэра о том, что размерность
замкнутого симплекса равна числу его измерений. Из этой теоремы (см.
главу 5, вводные замечания) без труда выводится, что размерность любого
полиэдра равна числу измерений любой триангуляции этого полиэдра. Этим
л о некоторой степени оправдано общее понятие размерности. Однако,
только до некоторой степени: действительное право на введение в
математику нового основного, а не только чисто служебного понятия мы получим
лишь тогда, когда оказывается, что это понятие существенно выясняет тот
Или иной, достаточно важный, круг математических явлений, а не служит
лишь для доказательства одной или двух теорем. Понятие размерности
в этом смысле вполне оправдало себя: теория размерности, построенная
за последнюю четверть века, представляет собою полную геометрического
содержания главу общей топологии, существенно и в различных
направлениях углубившую наши знания о геометрических свойствах компактов,
а до некоторой степени и произвольных их подмножеств.
Своего полного развития теория размерности достигает лишь в так
называемой гомологической теории размерности, которая в этой книге не
излагается: она опирается на некоторые теоремы комбинаторной топологии
полиэдров, которые здесь не приведены. Поэтому мы вынуждены
ограничиться лишь первыми основными предложениями теории размерности, т. е.
дать введение в эту теорию и отослать читателя для более глубокого
изучения современного состояния вопроса к журнальной литературе**).
§ 1. Теоремы об е-сдвигах и о включении в Rn.
1:1. Определение е-отображений и s-сдвигов. План параграфа.
Определение [1:11]. Непрерывное отображение С компакта
X в компакт У называется s-o т о б р ажен и ем, если прообраз
С-г(у)с:Х каждой точки у компакта У имеет диаметр <е.
*) Все понятия, введённые в § 8 главы 1, в настоящей главе
предполагаются известными.
**) См. кроме классических работ Брауэра (Crelle, 142) и Урысона (Fund.
Math., томы VII—VIII) и книги Менгера, Dimensionstheorie (1928): Александров,
Dimensionstheorie, Math. Ann. 106 (1932), стр. 161—238; Александров, Hopf,
Понтрягин, Ober den Brouwerschen Dimensicnsbt griff, Compositio Math.,
4 (1937), стр. 239—255, изложение этих работ дано в «Успехах
математических наук т. 2, вып. 1 (17) (1947)». Систематическое изложение теории
размерности с введением в геометрическую теорию дано в книге Hurewicz —
Wallman, Dimension Theory (Princeton, 1942).

204
ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ
[ГЛ. VI
Определение [1:12]. Пусть компакт X есть множество,
лежащее в метрическом пространстве /?; пусть С—непрерывное
отображение X и /?. Это отображение называется е-сдвигом
компакта X в пространстве R, если для каждой точки х£Х
имеем р(х, Cx)<£.
Если при е-сдвиге С две точки х и х1 компакта X отображаются
на одну и ту же точку у, то
Р (*, х') < р (л:, у) + Р (у, хг) < е -f е = 2s,
откуда следует, что диаметр C~1(y)t равный (ввиду компактности X)
максимуму р (х, х') при х£С-г(у)у хг^С'1(у) меньше 2£. Итак:
[1:13]. Всякий е-сдвиг С компакта X есть ^-отображение
компакта X на С(Х).
Пример. Пусть X есть гильбертов кирпич (глава 1, арт. 2:3).
Поставим в соответствие каждой точке
х = (хи. . ., хп, *. .) £ X
точку
C(x) = (xv...,xn9 0, 0, 0,...) £Х.
Полученное отображение С гильбертова кирпича на я-мерный
прямоугольный параллелепипед представляет собою ^-^-сдвиг.
Итак:
[1:140]. Гильбертов кирпич при всяком е>0 может быть при
посредстве £-сдвига отображён на полиэдр, а именно, на
обыкновенный конечномерный параллелепипед.
Отсюда следует:
[1:141]. Каждое замкнутое множество гильбертова кирпича может
быть при любом s>0 посредством s-сдвига отображено в полиэдр.
Так как все компакты гомеоморфны множествам, лежащим в
гильбертовом кирпиче, то из [1:141] легко следует:
[1:142]. Всякий компакт при всяком е>0 может быть s-omo-
бражён в полиэдр.
Упражнение. Доказать, что среди всех замкнутых множеств
гильбертова пространства только компакты при всяком £>0
могут быть £-сдвигом отображены в полиэдры (и вообще в замкнутые
ограниченные множества, лежащие в конечномерных эвклидовых
подпространствах данного гильбертова пространства). Доказать
аналогичное предложение, касающееся £-отображений (вместо £-сдвигов).
План первого параграфа. Первая основная задача этого
параграфа заключается в доказательстве следующего предложения:
Теорема [1:4] (теорема об ^отображениях). Пусть
Ф—компакт. При всяком £ компакт Ф может быть г-отображён
на полиэдр\ при этом, если dim Ф = п} то компакт Ф при
всяком £ может быть ^отображён на n-мерный полиэдр, а при
достаточно малом £>0 не может быть ^-отображён ни в какой
полиэдр размерности < п. Если компакт Ф лежит в гилъберто-

§ ij теоремы ok s-сдвигах и о включений в Rn 205
вом или эвклидовом пространстве, то при всяком е упомянутые
s-отображения могут быть осуществлены посредством г-сдвигов.
Доказательство этой теоремы проводится в такой
последовательности.
Прежде всего доказывается, что для каждого данного я-мерного
компакта Ф существует такое е==е(Ф)1 что всякий компакт,
являющийся образом компакта Ф при каком-нибудь г-отображении, имеет
размерность ~^>п (теорема [1:16]). Доказательство этой теоремы
основано на лемме [1:15].
После этого доказывается, что из возможности s-отобразить
данный компакт Ф в полиэдр П следует возможность s-отобразить
компакт Ф на некоторый полиэдр П0сЦ,
Этот переход от отображений в полиэдр к отображениям на
полиэдр делается очень просто, при помощи так называемой
операции выметания (арт. 1:2). По пути доказывается важная
теорема [1:25], характеризующая n-мерные компакты, лежащие в Rn.
Центральное место всего доказательства заключается в том,
чтобы для всякого е>0 построить s-отображение данного я-мерного
компакта Ф в некоторый я-мерный полиэдр. Это делается в арт.
1:3 и 1:4 при помощи так называемых* барицентрических
отображений.
После этого остаётся доказать, что для Ф, лежащего в
гильбертовом или эвклидовом пространстве Rm, наши s-отображения
осуществляются посредством е-сдвига. Эта цель легко достигается в арт.
1:5*). Метод, доказательства заключается в том, что к каждому
непрерывному отображению С компакта Ф в данное пространство Rm
строится сколь угодно мало отличающееся от него
«барицентрическое (см. выше) отображение Сш» в полиэдр той же размерности,
что и Ф.
Если С есть тождественное отображение, то С& оказывается
з-сдвигом.
Эти барицентрические приближения непрерывных отображений
приводят к решению и второй основной задачи этого параграфа,
именно к доказательству теоремы [1:6], утверждающей, что всякий
^-мерный компакт гомеоморфен некоторому (замкнутому и
ограниченному) множеству, лежащему в R2n+l: оказывается, что барицентрические
отображения, достаточно хорошо приближающие данное непрерывное
отображение я-мерного компакта Ф в Rm, где т^2п-\-1, являются
^-отображениями, откуда выводится, что при всяком s множество
всех г-отображений я-мерного компакта Ф в w-мерный замкнутый
шар Ет при т^2п-\-\ плотно в пространстве (ЦФ, Ет) всех
непрерывных отображений Ф в Ет.
*) Так как доказательство опирается на замечание 2 главы 4, арт. 3:1
и, следовательно, пользуется свойствами выпуклых многогранников, не
доказанными в этой книге, то параллельно даются несколько ослабленные
формулировки, не опирающиеся на не доказанные в этой книге предложения.

206
ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ
(гл. vi
Так как &(Ф, Ет)— полное метрическое пространство, а е-отобра-
жения образуют в (£(Ф, Е) открытое множество, то из доказанного
легко следует, что и топологические отображения Ф в Ет не только
существуют, но даже образуют множество, плотное в (ЦФ,£"). Этим
будет доказана теорема [1:6] и усиливающая её теорема [1:63].
Лемма [1:15]. Пусть С есть г-отображение компакта X
в компакт Y. Существует такое положительное число г\у что
всякое множество ВcF диаметра ^ч\ имеет прообраз С~1(В)
диаметра меньше е.
Доказательство от противного. Пусть такого if] нет. Тогда
ко всякому натуральному числу п можно в Y найти множество Вп
диаметра < —, прообраз которого Ап = С~1(Вп) имеет диаметр >-s.
Пусть хп и хп— точки Ап, для которых
р (хп, х'п) = 8 (Ап) > е.
Переходя, если нужно, к подпоследовательностям, можем
предположить, что последовательности хп и хп сходятся соответственно
к точкам х£Х и х'£Х. Так как р (СхП9 Слг„)<—, то Сх = Сх' =
==у; с другой стороны, р(х9х')^>г, что противоречит тому, что
С есть г-отображение.
Приложим только что установленный факт к доказательству
следующего важного предложения:
[1:16]. Пусть размерность компакта Ф равна п. Существует
такое е = е (Ф) > 0, что всякий компакт Ф', являющийся образом
компакта Ф при каком-нибудь г-отображении, имеет
размерность ^> п.
Доказательство. Выберем г так, чтобы компакт Ф не имел
никакого замкнутого s-покрытия кратности <] п. Пусть
Ф' = С(Ф),
где С—некоторое s-отображение. Определим для этого s-ото-
бражения число т), как в [1:15], и возьмём какое-либо замкнуто
^-покрытие
«' = W ^)
компакта Ф'. Тогда множества Ai = C~1{Ai) образуют е-покрытие
а компакта Ф, имеющее кратность, равную кратности покрытия а'.
По определению числа s, кратность покрытия а во всяком
случае не меньше чем «—{— 1; такова же, значит, и кратность
покрытия а'. Итак, всякое т]-покрытие компакта Ф' имеет кратность
^A2-f-l, откуда следует, что
dim Ф'^п.

§ 1] ТЕОРЕМЫ ОБ 8-СДВИГАХ И О ВКЛЮЧЕНИИ В Rn 207
1:2. Операция выметания.
[1:21]. Теорема о выметании. Пусть Ф— замкнутое
множество, лежащее в полиэдре П; пусть К—триангуляция
полиэдра П. Существует подкомплекс К' триангуляции К и не-
прерывное отображение С компакта Ф на полиэдр К', обладающее
следующим свойством: какова бы ни была точка х £ Ф, имеется
симплекс Г£/С, замыкание которого содержит обе точки: х и С(х).
Доказательство. Пусть Т1У...УТ8 — все симплексы
комплекса /С, содержащие точки Ф и занумерованные в таком порядке,
что число измерений 7*+1 не превосходит числа измерений 7^.
Положим Ф0 == Ф, обозначим через С0 тождественное отображение
множества Ф0 и предположим, что множество Фг- и отображение Ci
уже определены. Если Г^+1сф{) то полагаем Фг+1 = Фг- и
обозначаем через Q+1 тождественное отображение Фг-. Если 7\-+10 Фг-, то
берём точку oivl £ 7*+1\Ф^ и обозначаем через Q+1 «выметание
множества Ф^ из 7*+1», т. е. отображение множества Ф^
определённое на Ф/\7^+1 как тождественное, а в ФгП7^+1 как
центральная проекция множества Ф^ П Г<+1 из точки oi+1 в границу 7*+1\7\+1
симплекса Г<+1. Полагаем Ф<+1 = Ci+1 (Ф^). Идя таким образом
шаг за шагом, приходим, наконец, к компакту Ф8, являющемуся
телом некоторого подкомплекса К' триангуляции К, и к
отображению
С = CgCg-j. . .С0,
являющемуся, как легко видеть, искомым отображением компакта Ф
на полиэдр К' = Ф8.
[1:22.] Пусть Ф — замкнутое подмножество полиэдра II;
каково бы ни было е>0, существует г-сдвиг С компакта Ф
в полиэдре П, при котором Ф отображается на полиэдр IT,
являющийся телом некоторого подкомплекса Кг некоторой
триангуляции К полиэдра Ф.
Для доказательства достаточно взять столь мелкую триангуляцию
К полиэдра II, чтобы все симплексы этой триангуляции имели диаметр
<г, и применить теорему [1:21].
Из [1:141] и [1:22] следует:
[1:23]. Всякий компакт, лежащий в гильбертовом кирпиче
при любом s > 0, может быть посредством ^сдвига отображён
на некоторый полиэдр.
Из [1:142] и [1:23] легко следует:
[1:24]. Всякий компакт при всяком s>0 может быть
ь-отображён на полиэдр.
[1:25]. Для того чтобы компакт Ф, лежащий в Rn,
содержал внутренние точки (относительно Rn), необходимо и
достаточно, чтобы было
dim Ф = #.

208 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. VI
В самом деле, так как Фс/?п, то во всяк м случае
сИтФ.^; п;
если Ф содержит внутренние точки относительно Rn и, следовательно,
некоторый я-мерный симплекс Тп, то dim Ф ^ dim Тп = п и,
значит, diir^ = п.
Пусть теперь компакт Ф с Rn не содержит внутренних точек.
Так как Ф — ограниченное замкнутое множество в нашем Rny то
существует симплекс Тп =э Ф.
Возьмём триангуляцию К замкнутого симплекса Т'\ все элементы
которой имеют диаметры, меньшие чем данное г. Так как Ф не
содержит никакого ^-мерного симплекса, в частности, никакого
я-мерного симплекса триангуляции К, то в каждом из я-мерных
симплексов Tnt £К можно найти точку ог-, не принадлежащую Фп.
Произведём теперь операцию «выметания», т. е. отобразим множество
ФПГ/ в Т"\ТП1 посредством центральной проекции из точки ot.
Так как все точки Ф, лежащие на Г/\ Г?, при этом остаются на
месте, то эти выметания, определённые в различных я-мерных
симплексах триангуляции /С> дают в своей совокупности одно
непрерывное отображение Ф в (п—1)-мерный полиэдр, являющийся
i\i i всех я-мерных симплексов
комплекса К- Отсюда следует, что при всяком s>o существует s-oto-
бражение компакта Ф в некоторый {п—1)-мерный полиэдр, так
что в силу теоремы (1:16)
dim Ф<#— 1,
что и требовалось доказать.
1:3. Барицентрическое отображение пространства в нерв
открытого покрытия. Пусть дано открытое покрытие
метрического пространства X и пусть в некотором R11 дан
изоморфный нерву покрытия ш симплициальный комплекс /Сш, элементами
которого являются симплексы (быть может вырождающиеся)
данного Rn.
Телом комплекса Кф будем называть соединение Кю всех
входящих в Кш невырождающихся симплексов и выпуклых замыканий
вырождаюшихся симплексов. Так как комплекс /С^ —полный, то тело
его в только что объяснённом смысле, можно определить также и
как соединение выпуклых замыканий всех вырождающихся и
невырождающихся симплексов этого комплекса.
Определяем в X непрерывные функции ^, /=1, 2, . .., я,
полагая для каждой точки х£Х
Mx) = Hx>X\Oi),

§ 1] ТЕОРЕМЫ ОБ е-£ДВИГАХ И О ВКЛЮЧЕНИИ В R1' 201)
•
и строим непрерывное отображение Сш пространства X в Rn
следующим образом: пусть х — произвольная точка пространства X; в
вершины аи . . ., as комплекса /Сш, соответствующие элементам Ov . .. ,Os
покрытия со, помещаются соответственно массы jjl, (х),. . ., |^(л:);
центр тяжести этих масс и есть, по определению, точка С^(х). Так
как функции \ii (x) непрерывны, то С^ есть непрерывное отображение
пространства X в Rn. Докажем, что С0) е с т ь отображение
пространства X в тело комплекса Кш. Для этого
заметим, что функция \^i{x) принимает отличные от нуля значения
в точках множества Ot и только в них. Поэтому, если х —
произвольная точкам, принадлежащая Oio , . . ., Oir и только этим элементам
покрытия со, то все функции \iio , . . ., pir принимают в точке х
значения, отличные от нуля, а все остальные функции \ь{ принимают
в точке х значение нуль. Так как x£Oio П ... П Oif.L то в Кш
есть симплекс с вершинами ai() ,. . . , ai}. и точка Сш (х% очевидно,
принадлежит выпуклому замыканию остова aiQ ,. . ., air , чем
утверждение наше и доказано.
Определение [1:31]. Построенное только что не ферывное
отображение С0) пространства X в тело К^ комплекса /Сш называется
барицентрическим отображением X, соответствующим
покрытию со и данному выбору вершин нерва ДГС1) этого покрытия.
Мы сейчас дадим несколько приложений только что
введённого понятия.
1 :4. Теорема об а отображениях. Пусть, в обозначениях
предыдущего артикула^ кратность покрытия со равна г-\-1. Тогда, если п
достаточно велико, а именно n^2r^\-li то, выбирая в Rn
вершины av. . . ,а8 в общем положении, получим триангуляцию /С10,
изоморфную нерву покрытия со. В этих предположениях имеют место
георемы [1:41] и [1 : 42]:
[1 :41]. При барицентрическом отображении. Сы пространства
X п К^ прообраз симплекса Т*' — \ai{). . .af \ £ l\v, есть:
^К-'-^-^со/оП ... n oh)\ и о,.
И самом деле, так как /Са) триангуляция, то различные
симплексы Т{(^КФ попарно не пересекаются; поэтому, если точка
v==C(x) принадлежит симплексу \aiQ . . .oir\, то она не
принадлежит никакому другому симплексу триангуляции Дга); другими
словами, среди масс \уч {х) положительны массы уЛх\. . . ,У/Г (*)> а
остальные массы \±i{x) равны нулю. А это значит, что точка а: принадлежит
к ^0, • • • ,0^ и ни к какому другому элементу покрытия со:
х£ ()€}П...П01г\ИО,
14 Александров П. С.

210 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гЛ. vl
[1 :42]. Если шесть s-покрытие, s>0, то барицентрическое otqJ
бражение Сф есть s-отображение пространства X в полиэдр /Сш, чи|
ело измерений которого на 1 меньше кратности покрытия со.
Отсюда и из теоремы [1:16] в свою очередь вытекает:
[1 :43]. Всякий r-мерный компакт при всяком в>0 может быт|
s-отображён в некоторый r-мерный полиэдр и при достаточно ма]
лом s не может быть s-отображён ни в какой полиэдр меныиепЦ
числа измерений.
Мы сейчас усилим этот результат.
Пусть о) — {Oj,. . . ,Og} есть открытое е-покрытие крлтнос ги r-f-1.
компакта X размерности г. Пусть лежащая в некотором Rn триан*|
гуляция Км изоморфна нерву покрытия со. Рассмотрим барицентри«|
ческое отображение Сш компакта X р К&, по теореме [1 :42] ото-1
бражение С^ есть s-отображение в К^. Подвергнем теперь мко-1
жество Сш {X) с Кш операции выметания С' (арт. 1 :2). В результате!
получим замкнутый подкомплекс К'ф триангуляции Д"ш и непрерыв»!
ное отображение С'СЮ компакта X на полиэдр KL Вспомнив опре*|
деление выметания С, без труда видим, что при отображении С'СШ!
на какую-либо точку у симплекса Т' = \а} ...air\ комплекса К' }
может отобразиться лип.ь такая точка х£Х, которая при отобрав
жении CL0 отображается в некоторый симптекс Г, имеющий сим*|
пле.сс Т' своей собственной или несэбствеиной гранью и, следован
тельно, имеющий точки aiy...,air в числе своих вершин. Отсюда!
следует, что прообраз точки у^Тг при отображении С'СШ является!
подмножеством множества О, П . . . П Oir и, значит, имеет диа-1
метр < г. , I
Итак: I
Всякий компакт размерности г при всяком s > 0 может бытш
г-отображё'н на некоторый r-мерный полиэдр и при достаточно маА
ломг^>0 не может быть г-отображё'н ни в какой полиэдр раз А
мерности <г.
Другими словами: |
[1:44]. Размерность компакта Ф может быть определена!
как наименьшее из чисел г, обладающих тем свойством, что!
при всяком г > 0 компакт Ф может быть г-отображё'н на неА
который полиэдр числа измерений г. Если таких чисел г нет, т<А
размерность Ф равна бесконечности. |
1:5. Барицентрические приближения данного непрерывного!
отображения компакта Ф в Ru. Теорема об s-сдвигах. Пусть!
дано непрерывное отображение С гомпакта Ф в Rn и число s>0.|
Возьмём столь малое а>0, чтобы из р(^,/)<о (в Ф) следовало!
р(Сх, Сх) <~ (в Rn); в остальном о совершенно произвольно..]
ПУ^гь Л-{Ои...,0,} \

§ 1] ТЕОРЕМЫ ОБ £-СДВИГАХ И О ВКЛЮЧЕНИИ В RH 211
— открытое о-по:фытие компакта Ф. В каждом из множеств Ог
выбираем по точке ог; попарно различные точки aifRn выбираем
под условием
(1:50) р(Со<,а<)<!
и делаем их вершинами нерва К& покрытия со. Под симплексами
комплекса /Сш понимаем снова симплексы (вырождающиеся или нет),
определённые соответствующими остовами комплекса К^- Тело К^
комплекса /Сш и барицентрическое отображение Сш компакта Ф в /Сш
определяем как в 1 :3. Называем это отображение
барицентрическим а-приближением отображения С
(соответствующим покрытию (о и сделанному выбору вершин яг-). Название это
оправдано тем, что дтя каждой точки х £ Ф имеем
(1:51) 9(Сх,С„х)<е.
В самом деле, пусть х— произвольная точка Ф. Пусть О. ,.. .fOir
суть все элемента покрытия оо, содержащие точку х. Тогда
расстояние точки х от каждой из точек ог ,.. . ,ог-г меньше, чем о, так что
расстояние точки Сх от каждой из точек Coi()i.. . ,Coiy меньше, чем-j.
В силу (1:50) имеем, для / = /0,...,гг неравенство р(Сл*,а^)<у.
Другими словами, все точки а{ ,..., air лежат внутри
шара радиуса ~ с центром Сх. Внутри этого же шара лежит
выпуклое замыкание множества {ai ...а2- ], зна шт, и точка С^х,
откуда неравенство (1 :51) следует.
Пусть dim Ф = г. Тогда покрытие со можно взять кратности /* —|— 1
так, что комплекс Кф есть r-мерный комплекс, а его тело К& —
соединение конечного числа замкнутых симплексов размерностей <J>*).
Итак:
[1:51]. Ко всякому непрерывному отображению С г-мерного
компакта Ф в Rn можно найти сколь угодно мало отличающееся
от С непрерывное отображение Си> компакта Ф в некоторое
лежащее в данном Rn множество /Сс0, являющееся соединением ко-
печного числа замкнутых симплексов размерности ^ г; за
отображение Сш можно взять барицентрическое приближение Сш
отображения С, построенное при помощи любого достаточно
мелкого открытого покрытия ш компакта Ф, имеющего
кратность г-\- 1.
*) В силу главы 4, арт. 3:1, замечание 2, множество К& есты-мерный
(лиэдр, но мы ,не хотим здесь этим пользоваться.
14*

212 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гЛ. VtJ
Замечание. Если С отображает Ф в шар Еп9 то можно предИ
положить, чго и К^^Ёп. В самом деле, если р(С,С^) меньше|
некоторого заданного г, то Кф лежит в концентрическом к Еп\
шаре Е% радиуса р —|— г, где р — радиусе. Обозначим через С подоб-|
нте сжатие Z™ в Еп\ при этом сжатии каждый из симплексов соста-j
вляющих /Сш, переходит в некоторый симплекс, лежащий в Еп, и сумма i
этих симплексов есть KJ — С\K(i))czEn. Отображение ССШ
отличается от С меньше чем на е ~\- е = 2е и переводит Ф в К J а Еп.
Заметим при этом, что если Сш было о-отображением (при
некотором а>0), то, в силу взаимной однозначности С\ отображение
С'Сц, также есть о-отображение. \
Пусть попрежнему dim Ф = г и, кроме того, я^> 2r-J- 1.
Положительное число s произвольно, о достаточно мало: именно, из р(х,лг')<<з
в Ф должно следовать р {Сх^Сх'Х — в Rn. Пусть о-покрытие со
компакта Ф имеет кратность г-f- 1. Выбирая вершины av...,a8 в Rn
в общем положении, получим r-мерную триангуляцию /Сш.
Отображение С(0, удовлетворяя условию (1 :51), удовлетворяет, кроме того,'
и предпосылкам теоремы [1 :41]*) и поэтому является о-отображением.
Итак, пользуясь только что сделанным замечанием, имеем:
[1 :52]. Пусть С—произвольное непрерывное отображение
г-мерного компакта Ф в шар Еп, где п^> 2r-j- 1. Каковы бы ни были
полоэюителъные числа г и о, можно найти о-отображение Сф
компакта Ф в некоторый r-мерный полиэдр К^Еп,
удовлетворяющее неравенству р(Сх,С^х)<^в. для всех х£Ф.
Нам существенно понадобится в дальнейшем следующее
предложение, сразу вытекающее из [1 :52]:
[1 :520]. Пусть п>-2г+1. При всяком а>0 множество всех
^-отображений r-мерного компакта Ф в n-мерный замкнутый
шар Еп плотно в пространстве © (Ф, Еп) всех непрерывных
отображений компакта Ф в Еп.
Отметим ещё одно следствие теоремы [1:52]. Пусть С есть
тождественное отображение; тогда отображение Сш есть г-сдвиг, и
мы получаем следующий результат:
[1:521]. Всякий r-мерный компакт Ф <£ Rn при всяком е>0
может быть отображён посредством е-сдвига на некоторый г-мерный
полиэдр Кф, лежащий в пространстве R2^+1y содержащем данное
пространство Rn.
Замечание. 1. Пусть Вт — произвольное эвклидово пространство,
содержащее r-мерный компакт Ф. Если /и>2/--г-1, полагаем п = т\ если
/w<2r+l. полагаем /г = 2/-+1 и берём пространство Rnt содержащее дан-
*) Сформулированным в начале арт. 1 :4.

§ 1] ТЕОРЕМЫ ОБ S-СДВИГАХ И О ВКЛЮЧЕНИИ В Rn 213
ное пространство Вт. Вершины ai^Bn комплекса Кф берём в произвольно
заданной близости к Вт cz Bn. ^
Применением теоремы [1:521] производим е-сдвиг компакта Ф в /С^.
Возвращая малым сдвигом Q вершины Кф в пространство Вп\ получим ото-
бражение С1 полиэдра Кш на множество С\ (KJ) являющееся соединением
конечного числа замкнутых симплексов (вида Сг (Г), где Г £ К&).
Так как эти симплексы имеют размерность -<г и среди них есть
/--мерные, то С\ (/Сш) есть г-мсрный полиэдр *). Итак:
[1:522]. Всякий r-мерный компакт, лежащий в Вп при всяком £>0,
может быть посредством г-сдвига отображён на r-мерный полиэдр,
лежащий в том же Вп.
Пусть, наконец, Ф есть r-мерный компакт, лежащий в
гильбертовом кирпиче. Пусть дано произвольное s>0 и открытое е-покры-
тие кратности г -\-1:
* = {Ov...,Os)
компакта Ф.
Возьмём г-сдвиг С компакта Ф в некоторое Rn, n^2r-\~\.
Барицентрическое приближение Сф отображения С можно выбрать так,
чтобы оно было отображением компакта Ф в полиэдр K^czR71,
триангуляция /Сш которого изоморфна нерву покрытия ш и состоит из
симплексов диаметра <2s. -—
Отображение Сш, отличаясь от s-сдвига С меньше, чем на s,
является 2в-сдвигом.
Наконец, подвергая Сш (Ф)^КШ ещё операции выметания С,
являющейся в наших условиях 2г-сдвигом, получаем 4г-сдвиг С'С^ компакта Ф,
отображающий этот компакт на полиэдр К'ШУ K'j^K^ числа
измерений ^ г. При достаточно малом е число измерений полиэдра KJ,
в силу [1:16], не может быть меньше г и, следовательно, равно г.
Итак:
[1:530]. Всякий r-мерный компакт, лежащий в гильбертовом
кирпиче, при всяком s>0 может быть посредством г-сдвига отображён
на некоторый r-мерный полиэдр.
Из доказанного следует:
[1:53]. Размерность компакта Ф? лежащего в гильбертовом
кирпиче, может быть определена как наименьшее из чисел г,
удовлетворяющих следующему условию: при всяком г>0 существует
е-сдвиг компакта Ф в гильбертовом кирпиче, отображающий Ф на
некоторый r-мерный полиэдр.
Замечание 2. Из доказательств теорем этого артикула
следует, что за полиэдр, на который Ф отображается посредством
г-сдвига, всегда может быть принято тело некоторого подкомплекса
нерва всякого достаточно мелкого открытого (а в силу теоремы
[8:331] главы 1 и всякого достаточно мелкого замкнутого покрытия
*) Глава*А4, арт. 3:1, замечание 2.

214 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. VI
компакта Ф), причём сам эгот нерв должен быть построен в
достаточной близости к данному покрытию а> (см. главу 4, арт. 2:1,
замечание 4).
1:6. Теорема о включении r-мерных компактов в /??н J.
В этом артикуле доказывается следующая основная теорема:
Теорема [1:6]. Всякий г-мерный компакт гомеоморфен
некоторому множеству, лежащему в /?2r+1.
Доказательство опирается на теорему [1:520] и ia
следующую лемму:
Лемма [1:61]. Пусть X и Y — произволънь е компакты a s>0;
пусть ©(.Y, Y) — пространство непрерывных отображений ком-
пакта X в Y. Множество всех г-отображений компакта X в
компакт Y открыто в пространстве &(Х, Y).
Достаточно доказать, что всякое отображение С'£Qi(X, К),
достаточно мало отстоящее (в смысле метрики (5, (X, Y)) от е-отобра-
жения С, само является s-отображением. Определим к числу е и
данному е-отображению С число г\ согласно леммз [1:15] и
предположим, что Сг удовлетворяет неравенству р (С, С)< ^. Пусть
теперь хг и х2 — две точки компакта X, отображающиеся посредством
С на одну h ту же точку у £ Y. Тогда
р (С*„ Cx9)^?(CxvCfx{) + p(CfxvCfx2) + p(C\x2iCx2)<^ |
+ о + -| = ^
откуда по определ нию числа ч\ следует, что p(^pa:2)<s, т. е. что
С' есть е-отоб[ ажение. Лемма [1:61] этим доказана.
Переходим теперь к доказательству теоремы [1:6]. Обоз а-
чаем (для любого натурального т) через ]\п множество в.ех
-отображений r-мерного компакта Ф в (2г-| - 1)-черный
замкнутый шар Еп. По только что оказанному Гт есть открытое множество
прос ранства (£(Ф,£''); по теореме [1:520] множество Гт плотно
в (£^Ф,£П). По теореме [7:31] главы 1 пространстро £(Ф,Е") есть
полное метрическое пространство, следовательно, по теореме [7:14]
павы 1 пересечение всех Тт есть не пустое множество Е (это
множество даже плотно в (£(Ф,£И). Элементы множества Е суть
непрерывные отображе ия Ф в Ёп, каждое из которых при любом s>0
есть s-отображение. Отсюда следует, что все лементы множества
Е су;ь взаимно однозгачные ( тображения Ф в Е7\ а так как Ф и
Еп — компакты, то все эти отображения суть топологические
отображения, что и требовалось доказать.
Замечай е 1. В только что проделанных рассуждениях со»
держится доказательство следующей теоремы.

§ 2] ТЕОРЕМА О СУЩЕСТВЕННЫХ ОТОБРАЖЕНИЯХ 215
Т е о р ем а [ 1 : 62]. Ко всякому непрерывному отображению С
компакта Ф размерности г в эвклидово пространство Rn, где
//>-2r-j-l> и для всякого s>0 можно найти топологическое
отображение С0, удовлетворяющее для всех х£Ф условию
р(Сх,С0х)<г.
Замечание 2. Из теоремы [1:6] следует, что среди всех
топологических пространств конечномерные компакты и только они
гомеоморфны замкнутым ограниченным множествам, лежащим в
эвклидовых пространствах.
§ 2. Теорема о существенных отображениях.
2:1. Определение и формулировка теоремы. Пусть
С—непрерывное отображение компакта Ф на /г-мерный элемент Еп с границей
S»-1 = Еп\Еп (см. главу 5, теорема [3:16]*). Обозначим через Ф0
прообраз Sn~l при отображении С, т. е. множество всех точек Ф,
отображающихся посредством С в S11"1. Отображение С называется
существенным, если всякое непрерывное отображение Сг
компакта Ф в Еп, совпадающее с С во всех точках множества Ф0, есть
отображение на Ёп.
Из этого определения следует, что если С есть не существенное
отображение, то можно найти такое совпадающее- на Ф0 с <?_непре-
рывное отображение Сх компакта Ф в Я", при котором некоторая
внутренняя точка о элемента Еп оказывается не принадлежащей
множеству С1(Ф) **).
Приведённое определение существенных отображений — самое
простое, но не самое наглядное: наглядный смысл понятия
существенности отображений наилучшим образом выясняется из следующего
замечания:
12:11]. Назовём допустимой деформацией такую
деформацию С0 отображения С = С0, О-^О .<^ 1, при которой на Ф0 все
отображения С{) совпадают с отображением С. Отображение С0
несущественно то еда и только тогда, когда допустимой
деформацией его можно перевести в отображение Cv при котором
СДФ)^^"1.
Доказательство [2:11]. Без ограничения общности можно вести
доказательство в предположении, что Еп есть шар, ограниченный
сферой S71-1.
о *) В наших дальнейших рассуждениях Еп будет либо я-мерный
замкнутый симплекс, либо «-мерный шар.
**) В самом деле, если бы вся внутренность Еп элемента Еп
содержалась в С\(Ф), то, в силу замкнутости, множества Сх (Ф) имели бы СХ(Ф) = Еп%
т. е. d было бы отображением на ~Efl.

216 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. V11
Если допустимая деформация Q существует, то отображение С0,
очевидно, несущественно в смысле определения, данного в начале ;
этого артикула.
Пусть теперь С несущественно в первоначальном смысле. Тогда ■
существует отображение, которое мы обозначим через С,,,
совпадающее с С0 на Ф0, и при котором некоторая точка о£Е11 не
принадлежит к множеству C1/g (Ф). Заметим прежде всего, что допустимой
деформацией можно С0 перевести в С;: для этого достаточно для
любой точки х £ Ф и любого 6, 0 <; 6 ^ — , обозначить через Сьх
точку, которая делит направленный отрезок (CQx,Cх) в отношении
•=(т-«)-
Обозначим теперь при -^ <! 9 <; 1 через С9 деформацию
отображения G/2, естественно возникающую при центральной проекции
множества Сг1 (Ф) из точки о в 5й-1, а именно: для каждого х£Ф
j '" >
и 6, -о*<;0<;1, строим луч oCi/2x, обозначаем через Схх точку
пересечения этого луча со сферой^"*1 и через Сьх— точку,
которая делит отрезок 0>.)хС1х в отношении^— ~о)'(^—*Ч-
Полученная деформация Q, 0 ^8^1, есть искомая допустимая деформация.
В этом параграфе доказывается следующее предложение,
являющееся, как и теорема об s-отображениях (об s-сдвигах), доказанная
в предыдущем параграфе, одной из основных теорем теории
размерности:
Теорема [2:1]. Всякий r-мерный компакт может быть
существенно отображён на r-мерный замкнутый симплекс; всякое
непрерывное отображение r-мерного компакта на n-мерный
элемент при я > г всегда есущественнно.
Замечание 1. В частности, всякое непрерывное отображение
отрезка на квадрат («кривая Пеано») несущественно.
Замечание 2. Из теоремы [2:1] следует, что
размерность компакта Ф может быть определена как наибольшее из тех
целых чисел г, для которых возможно данный компакт существенно
отобразить на r-мерный замкнутый симплекс, или, что то же самое,
на r-мерный шар.
2:2. Доказательство теоремы [2:1]. Докажем сначала второе
утверждение теоремы [2:1]: при п^>г всякое непрерывное
отображение r-мерного компакта Ф на n-мерный элемент Еп
несущественно. Очевидно, без ограничения общности результата можно
предположить, что Еп есть замкнутый я-мерный шар.
Пусть С — данное отображение Ф в Еп\ по теореме [1:51] (и
замечанию к этой теореме) можно найтисколь угодно мало отличающееся от С

§ 2] TFOPEMA О СУЩЕСТВЕННЫХ ОТОБРАЖЕНИЯХ 217
отображение С^ компакта Ф на некоторое множество К^аЕ71,
являющееся соединением конечного числа замкнутых симплексов
размерности <>; вследствие неравенства г<я множество К^ нигде не
плотно в Еп. Поэтому несущественность отображения С будет
доказана, если мы докажем следующее предложение:
[2:21]. Пусть С—существенное отображение какого-либо
компакта Ф в п-мерный шар Еп\ существует такое е>0, что
при всяком непрерывном отображении Сх компакта Ф в Еп,
отличающемся от С меньше чем на з (т. е. удовлетворяющем
неравенству р (Сх, Схх)<г для всех х^Ф), некоторый n-мерный шар
£п, концентричный шару £rt, содержится в С1 (Ф).
Мы докажем более сильное предложение:
[2:22]. Пусть С—существенное отображение компакта Ф
на шар Еп радиуса 1 с центром о. Пусть Е^ — шар оадиуса ?р,
концентричный шару Еп.
Пусть Sn"1 — сфера, ограничивающая шар Еп и Ф0 = C_1(Sn_1X
Если £<у, то при всяком непрерывном отображении Сх
компакта Ф- в Еп, удовлетворяющем условию
р(Сх, С^)<8 для всех х£Ф0,
имеем £jcci№*
Доказательство [2:22]. Пусть s <-«-; через Еп _1 обозначим
шар радиуса г с центром в о. Во всех точках х £ Ф0 отображение
Сх \ю предположению отличается от С—С0 меньше, чем на г. Пусть
х— произвольная точка компакта Ф и 0-^0^1; обозначим через С$х
— >
точку, делящую отрезок С0(х) С^х) в отношении 0:(1 — 0).
Построим теперь шар Епг радиуса г<1, столь мало отличающегося
о г 1, что для всякой точки лг£Ф, для которой
р(о, Сх)^г,
отрезок С (л:) С1 (х) лежит вне шара £*. Границу шара Епг
обозначаем через S™~~\ Определяем отображение Се, 0 <[0 ^ 1, следующим
образом:
1. Если [){ру Сх) ^ г, то проводим луч оС (х) и рассматриваем
заключённый между 5я-1 и S?"1 отрезок А этого луча, взятый
с направлением к центру о наших шаров. Тогда С$х есть
точка отрезка С(х)С\{х), делящая этот отрезок в том же отнэш^

218 В°ЕгТЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. VI
нии, в каком точка Сх делит на 1равлснный отрезок А. В частности,
если Cx^Sn~l, то для всех 6 имеем С^х—Сх.
С другой стороны, если Сх £ S?~ , то Сцх = Сцх.
2. Если Сх лежит внутри шара Епг, то Сцх—С^х. Так как
С0, очевидно, совпадает с С0=С, то семейство отображений
С0 образует деформацию отображения С, при которой для всех х £ Ф0
при любом 6 имеем Cqx = Cx. Другими словами, Q образуют
допустимую деформацию существенного отображения С. Поэтому все
отображения Cq суть отображения компакта Ф на шар Еп. Тем
более весь шф Е" содержится при любом 0 в Се(Ф).
При отображениях Сгц лишь те точки компакта Ф могут
отобразиться в Е*и, которые при отображении С отображаются в Щ\ но
в этих точках отображения Q и С$ совпадают между собою,
следовательно, СВ(Ф)^Е^, в частности, С/Ф^^'Ь чем 1!РеДложение
[2:22] и, следовательно, второе утверждение теоремы [2:1] доказаны.
Переходим к доказательству первого утверждения теоремы [2:1].
Всякий п-мерный компакт Ф может быть существенно
отображён на n-мерный замкнутый симплекс.
Доказательство. Возьмём столь малое s>0, что компакт
Ф не может бьпь 2г-огсбражён ни в какой полиэдр размерности < п.
Пусть С0 есть е-отсбражение компакта Ф на некоторый я-мрр-
ный полиэдр П. Определим число 7) в соответствии с леммой
[1:15] и рассмотрим триангуляцию К" полиэдра II, все симплексы
которой по диаметру меньше ^. Пусть Т7],. . ., Т" — все я-мерные
симплексы триангуляции. Положим
и определим отобгаженге С0/; компакта Ф^ па Т\1 как отображение,
совпадающее на Фг- с С0.
Докаи ем, что, по крайней мере, для одного / отображение Coi
существенно. Предположим противное; тогда для каждого i
существует допустимая деформация Q/, O^O^l, переводящая
отображение Coi в отображение Сн того же компакта Фг- во множество
Ti\Tll. На всех mi ожествах Фог-, следовательно, во всех точках,
принадлежащих более чем к одному Фг-, для любого 0 и для любого
i имеем Сы = С0: поэтому, т олагая для любого 6, 0 < 6 ^ 1,
СГ1(х) = С0(х), если х£ ц Ф0<
г
И
С{) (х) = Сн (х\ если х £ Ф,-,

§ 3] ТЕОРЕМА СЛОЖЕНИЯ. ИНДУКТИВНАЯ РАЗМЕРНОСТЬ 219
получим деформацию Q отображения С=С0 компакта Ф, п] ичем Сг
отображает Ф в (п — 1)-мерный полиэдр /С»-1 = 1<п\(Т? U .. . U Г*).
Деформация Сн обладает следующим свойством: если Т£Кп есть
носитель точки С0(х), то при любом 6, в частности, и при 6=1,
точка C(j (х) принадлежит к Т. Отсюда следует, что в данную точку
y(z ^G К11'1 могут при отображении Сг отобразиться лишь такие
точки компакта Ф, которые при отображении С0 переходят в точки
симплексов, имеющих симплекс Т сроею собственной или
несобственной гранью; другими словами, обозначая через Г тело звезды 0^7,
имеем
СГ\х)с:С-\Г).
Так как диаметр Г меньше, чем т], то множество С^~ (Г), значит, и
подавно, множество СГ1 (Г) имеет диаметр < г, т. е. отобран ение Сх
является а-отображением компакта Ф в (п—1)-мерный полиэдр /Cw_1,
что противоречит рыбору числа е.
Итак, отображение Cci = C0 сущее гренно, по крайней мере, на
одном из множеств Ф(; пусть, например, на Фг Поставим теперь
в соответствие каждой вершине симплекса Т™ саму эту вершину;
каждой, ! е принадлежащей симплексу 7\п? вершине комплекса К11
поставим в соответствие какую-нибудь вершину симплекса Т™. Таким
образом, получаем симпличиальное отображение С полиэдра II на
замкнутый симглехс Т^ причём на Г^сП отображение С есть
тождественное отображение. Отсюда легко следует, что
отображение С'С есть существенное отображение компакта Ф на я-мерн'/й
замкнутый симплекс 7^', что и требовалось доказать.
§ 3. Теорема сложения. Индуктивная размерность.
[3:1]. Формулировка и доказательство теоремы сложения.
Теорема [3: 1]. Пусть в комитете Ф дано конечное число
замкнутых множеств; если размерность каждого из этих
множеств не превосходит п, то размерность их соединения также
не превосхедит п.
Доказательство теорзмы [3:1] достаточно провести для
случая двух множеств. Итак, пусть в компакте Ф даны два
замкнутых множества Ах и Л2, размерность каждого из которых
не превосходит п. Докажем, что Л = Лt U Л2 имеет размерность<п.
Для этого надо доказать, что при любом е > 0 существует
замкнутое г-покрытие компакта Л кратности, не превосходя.ней лг -J— 1.
Возьмём s-покрытие
а0={л;,...,<}

220 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. VI
кратности ^я-г-1 множества А0 = А1 П Л2 и обозначим через 2о
лебегово число покрытия а0. Рассмотрим для А =1,2 какое-нибудь
замкнутое а-покрытие кратности ^ п -]- 1 множества Ах
Пусть
А) Ах
все элементы покрытия ах, не пересекающиеся с А0. Обозначим
далее, через А\9\9. . .,A\,mi все элементы ах, пересекающиеся с Л?'
и через Л/д, ..., Ai%mxi все элементы сиъ пересекающиеся с Аг (О^),
но не пересекающиеся ни с одним из множеств А°19.. .,Л?_1. Положим
В) = А) для i=l, 2,...,ах
и
B^A^U ...UAl^.UA^U ...А1т2. Ляя i=l,2,...,s0;
некоторые В/ могут при этом оказаться пустыми.
Множества/В/, в), В\ образуют, очевидно, замкнутое е-покрытие
(3 множества А. Остаётся доказать, что кратность покрытия (3
не превосходит п-\-1. Для этого заметим, прежде всего, что
никакое В) не пересекается ни с каким В|, так как точка,
принадлежащая к В) и к В%, принадлежала бы к А0 и поэтому не
существует, так как ни В/, ни В& по самому своему определению не
пересекаются с Л0.
Далее, а0, а1? а2 суть системы множеств, каждая из которых
имеет кратность ^ л —|- 1; кроме того, 2а есть лебегово число
системы а0 и В® cz О (Л/, а). Отсюда следует, что может
существовать не более п-\-\ множеств каждого из типов В/, В/» В\ с непустым
пересечением. Поэтому, если кратность системы (3 превосходит
число лг —J— 1, то это означает, что в [3 существует az-J-2 множеств
вида
(3:11)
или вида
(3:12)
Bix,. • ■
Biv-
R° • R1
P° • Я2
Д1
* * ' В\+1
с непустым пересечением. Докажем, что это невозможно. При этом,
конечно, достаточно ограничиться одним каким-нибудь случаем,
например, случаем (3 :11). Итак, пусть существует точка р,
принадлежащая к множествам
В л,. . . ,В/ г В/ ..,..., В/ , „.

§ 3] ТЕОРЕМА СЛОЖЕНИЯ. ИНДУКТИВНАЯ РАЗМЕРНОСТЬ 221
Принадлежа множеству B°ir точка р принадлежит к некоторому
множеству AjkS9 пересекающемуся с A°ik] при этом, если бы Х = 2,
то точка р принадлежала бы к A)kt^ , значит, к А2 и к В] +1, т.е.
В\ ^ пересекалось бы с Л2, значит, и с Л0, что невозможно. Итак:
Р£А\ЛП ... ПА1^ПВ1+1П ... Пв1 + 2,
т. е.
р е A)v4 П . .. П А}^ П 4+1П .. . П А}п+Ъ
При этом все А\. ^ различны между собой, так как А\к ч.
пересекается с A°ik и не пересекается ни с каким Л/, j < ik. Так
как и все At ,r различны между собой и отличны от всех А^^то
точка р принадлежит к п-\-2 элементам покрытия аи что
невозможно.
Теорема [3:1] этим доказана.
3 :2. Индуктивная размерность.
Теорема [3:21]. Если каждая точка компакта Ф обладает
сколь угодно малой (по диаметру) окрестностью, граница*) которой
имеет размерность О—1, то dim Ф^/z.
Доказательство. Дано, что каждая точка /?£Ф имеет при
данном сколь угодно малом з>0 окрестность О/?,
удовлетворяющую условиям:
1. 8(Ор)<е,
2. dim(Op\O/0</i —1.
Требуется построить замкнутое в-покрытие компакта Ф кратности
О-И-
Построим для каждой точки р £ Ф окрестность Ор,
удовлетворяющую условиям 1 и 2, и выберем из них конечное число
окрестностей
О^Ор,,..., Оя = Ор„
покрывающих всё пространство Ф.
По теореме [3:1] множество
А'= (0,40,) U ... U (бя\Ов)
имеет размерность ^п~— 1, так что существует замкнутое е-иокрм-
тие
a' = {Al',..., AJ]
кратности .</г множества А'.
*) Границей открытого множества Г в топологическом пространстве R
называется замкнутое множество Т\Г.

222 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [\Л. Vt
Пусть 2<5—лебегово число системы а' (в компакте Ф). Через О',
обозначим о-окрестность множества А. в Ф.
Соединение всех Осесть некоторая окрестность О1 множества Л'.;
Полагаем теперь
^ = 0<VOiU ...UO^UO'), / = 2,...,s,
и рассмотрим систему множеств
* = [av..., as, о;,..., о'и].
Так 1ч а к
Лх U . . . U As U О' = Ф,
то и подавно система а является (замкнутым) покрытием
пространства Ф и покрытие это, очевидно, есть s-покрытие. Далее, так как
дг = о, и (6i\di)coi и л'с о, и о',
то при I < k
Ai П Ak£Ot Л (Ок\(0, U 0'))c&t П (0^\Д) = О,
поэтому кратность покрытия а самое большее на единицу
превосходит кратность системы О',. . . ,0^, которая в свою очередь не
превосходит п. Итак, кратность покрытая а меньше или равна n-j-l,
что и требовалось доказать.
Теорема [3 :21] даёт повод определить для топологических
пространств R некоторый новый топологический инвариант, называемый
индуктивной размерностью и обозначаемый через ind R.
По определению, единственным топологическим пространством,
индуктивная размерность которого равна—1, является
пространство, не содержащее ни одной точки (пустое множество).
Предположим, что мы уже определили все пространств.!,
индуктивная размерность которых <^я—1, где п—некоторое
неотрицатель ,ое целое число. Тогда мы скажем, что топологическое
пространство R имеет индуктивную размерность <^ п, если ко
всякой окрестности Ох произвольной точки х £ R можно подобрать
окрестность О^х^Ох той же точки х, граница которой имеет
индуктивную размерность ^ п — 1.
Если пространство R, будучи пространством индуктивной
размерности <С п, в то же время не является пространством
индуктивной размерности <^п~-1, то говорят, что индуктивная размерность
пространства R равняется п.
Замечание 1. Для метрических пространств в это
определение, очевидно, можно внести стедующее изменение:

§ 3] ТЕОРЕМА СЛОЖЕНИЯ. ИНДУКТИВНАЯ РАЗМЕРНОСТЬ 223
Предполагая, что пространства, имеющие индуктивную
размерность ^п—1, уже определены, говорим, что метрическое
пространство R имеет индуктивную размерность ^ я, если для каждой
точки x£R и произвольного е > 0 можно найти окрестность Ох
диаметра < г, граница которой имеет размерность ^ п — 1.
Замечание 2. Mj говорим, что пространство имеет
индуктивную размерность ^п в данной точке х:
incL/? О,
если ко всякой окрестности Ох этой точки х можно найти
окрестность Охх той же точки х, содержащуюся в Ох и имеющую
границу индуктивной размерности <^п—1.
Если пространство R в точке х имеет индуктивную р°зме^-
ность <^я, но не О—1, то говорим, что ind^ R — п.
Пример 1. Если R есть канто-
рово совершенное множество или
множество всех иррациональных чисел, то
ind^/ч? = 0 в каждой точке x£R.
2. Компакт, состоящий из точки о
и из сходящихся к о кругов, попарно
не имеющих общих точек (черт. 98, а),
имеет в тичке о размерность 0.
Если же каждый круг касается
внешним образом следующего (ка*<:
показано на черг. 98, Ь) и R снова состоит из всех этих кругов и
из точки о, к которой они сходятся, то ind0 R—1.
Одним из основных предложений теории размерности является
следующее:
Теорема [3:22] (Урысон). Длч всякого компакта Ф
размерность совпадает с индуктивной размерностью:
Чсот. 98.
(3:22)
dim Ф = ind Ф.
В этом параграфе мы до :ажем лишь часть это"! теоремы,
именно, неравенство *)
(3:221)
dim Ф < ind<l\
Обратное неравенство dim Ф >> ind Ф будет доказано в следующем
параграфе.
Неравенство (3:221) легко следует из [3:21].
*) Это неравенство легко переносится и на сличай, когда Ф —
произвольный бикомпакт (см. П. С. Александров, Теорема слежения в
теории размерности бикомпактных пространств, Сообщения Ак. наук Груз.
ССР, 2, 1941, стр. 1-5).
Имеет ли место равенство (3:22) для любых бикомпактов Ф, — до сих
пор неизвестно.

224 введение в теорию размерности [гл. vi
В самом деле, для пустого множества (и только для него)
имеем
indO = dimO = — 1.
Таким об;азом, можем сказать, из ind Ф <; —1 следует dim Ф <;—1.
Предположим доказанным, что из ind Ф ^ п — \ следует
dim Ф ^ п—1, и докажем, что из *пйФ^я следует dirr^^n.
Этим неравенство (3:221) и будет установлено.
Но если ^Ф<;#, то каждая точка х£Ф имеет сколь угодно
малую окрестность Ох, граница которой имеет индуктивную
размерность ^п—1, значит, и подавно, размерность ^п—1, из
чего по теореме [3:21] следует, что dim Ф <; я, что и требовалось
доказать.
Следствие из теоремы [3:22]. Каждый компакт
размерности п содержит при всяком г<^п компакт размерности г.
Замечание. До сих пор неизвестно, всякий ли компакт
бесконечной размерности содержит компакт любой наперёд заданной
конечной размерности ^проблема Л. А. Тумаркина).
§ 4. Последовательности подразделений.
4:1. Неприводимые s-покрытия. В этом артикуле иод
покрытием понимается покрытие данного компакта Ф.
Определение [4:11]. Замкнутое е-покрытие
(4:11) а={Л1)...,Л
S)
называется неприводимым г-покрытием, если не существует
никакого замкнутого s-покрытия с нервом, изоморфным
собственному подкомплексу нерва Ка покрытия а.
Неприводимые s-покрытия обладают некоторыми замечательными
свойствами, которые мы сейчас и установим.
Определение [4:12]. Замкнутое е-покрытие а называется
специальным покрытием, если его элементы являются
замыканиями попарно непересекающихся открытых множеств компакта Ф.
[4:13]. Всякое неприводимое г-покрытие (4:1) n-мерного ком-
пакта Ф имеет кратность <^ п ~\ 1.
Доказательство. Обозначим через 2с? лебегово число
неприводимого покрытия (4:11), через Ot обозначим ^-окрестность
множества Л1 в Ф. Покрытие
(4:131) *={Ov ..., G,}
есть открытое е-покрытие компакта Ф, подобное покрытию (4:ll)
(см. главу 1, [8:21], [8:331]).
Обозначим теперь через
«' = К,..., л.;,}
какое-либо замкнутое а-покрытне компакта Ф кратности п-\-\*

§ 4j ПОСЛЕДОВАТЕЛЬНОСТИ ПОДРАЗДЕЛЕНИЙ 22f)
После этого обозначаем через Л'^ соединение всех А'
пересекающихся с Ах\ через А\ обозначим соединение всех Л^
пересекающихся с Ар но не пересекающихся ни с одним из множеств
Лр ..., Ai-V Тогда А".^-0$. Поэтому покрытие а", состоящее из
всех непустых множеств A"v является е-нокрытием, нерв которого
есть собственный или несобственный подкомплекс нерва покрытия со
или, что то же самое, нерва покрытия а (ведь покрытия а и со
подобны, между собою). Из неприводимости s-покрытия а заключаем,
чю нерв покрытия а" совпадает с нервом покрытия а. Поэтому
теорема [4:13] будет доказана, если мы покажем, что кратность
покрытия а" не превосходит (я-|-1).
Пусть
х £ /Ц П . .. П Л^; ix < /о < . . . < lr
Гак как ни одно слагаемое A'h не является слагаемым двух
различных сумм Л", то существуют такие попарно различные между
собою элементы
^Е^ A\SA\
покрытия а', что
х€Аъх П ...П А!к
откуда следует, что v не превосходит порядок покрытия а\ т, е.
не превосходит п~\-1, что и требовалось доказать.
Так как нерв всякого замкнутого s-покрытия, очевидно,
содержит подкомплекс, являющийся нервом некоторого неприводимого
■покрытия, то из [4:13] следует:
[4:131]. Нерв любого г-покрытия «-мерного компакта Ф
содержит подкомплекс, являющийся нервом некоторого г-покрытия
компакта Ф кратности <^я-{-1.
[4:14]. Всякое неприводимое г-покрытие а. компакта Ф подобна
некоторому специальному в-покрытию а .
Доказательство. Пусть
(4:1) «=Mi, ..., А„}
неприводимое е-покрытие компакта Ф. Пусть 2а есть лебегово
число покрытия а; через Oi обозначим о-окрестноегь множества Лг-.
Тогда ^
<* = [0и....08}
"сть замкнутое з-покрытие, подобное покрытию а. Итак, при л ю-
бом е компакт Ф имеет неприводимые г-покрытия, элементами
которых являются замыкания открытых множеств.
Предположим, что исходное покрытие а уже обладает этим
свойством, т. е., что Лг- = Гг-, для / = 1, 2,..., $, где 1\- — открыто.
^ Александров II. С.

226 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гЛ. Vf
Введём следующие обозначения:
А[ = Av А'а =Щ,...,А'к^Ак\{А[\}Т7Г\ГА1^).
Очевидно,
1. A'kSAu>
2. A'k^Ab\(Al\}...\}Alt-1).
ъ. л;=г,\(л;и...и^_1>.
Поэтому множества А'к образуют замкнутое s-покрытие а', нерв
которого есть подкомплекс нерва Кл покрытия а и, следовательно,
ввиду неприводимости а совпадает с Ка- Далее, обозначая через Г/
множество всех внутренних точек множества Д[, имеем, на основании
свойства 3,
г;=г*\о<и...ил;.1)) л;=г;
и при /<&
v гк с ф \ At = ф \Т; с ф \ г;.,
чем теорема [4:14] доказана.
4:2. Подразделения. Снова рассматриваем покрытия одного и
того же компакта Ф.
[4:21]. Замкнутое покрытие (3 называется подразделением
замкнутого покрытия а, если каждый элемент покрытия а есть
соединение некоторых элементов покрытия (3 и при этом каждый
элемент покрытия р содержится в одном и только одном элементе
покрытия а.
[4:22]. Последовательность замкнутых покрытий av <x2) ..., ат
называется цепью подразделений компакта Ф, если ат есть
зш-покрытие компакта Ф, limsw = 0, и при любом т покрытие
aw+1 есть подразделение покрытия аш.
[4:23]. Две последовательности покрытий компакта Ф
а1> • • •> ат>' • •
и
Pl> • • •> Pw)- • •
называются подобными между собою, если покрытия ат и $т
подобны.
В основе всех результатов этого параграфа лежит следующая
теорема:
[4:24]. Всякая последовательность
(4:24) av ..., «„,...,
где ат есть неприводимое гт-покрытие компакта Ф и lim ew = 0*
содержит подпоследовательность, подобную некоторой цепи под*
разделений компакта Ф.

§ 4J ПОСЛЕДОВАТЕЛЬНОСТИ ПОДРАЗДЕЛЕНИЙ 227
Доказательство. Положим мх = 1 и предположим, что тк
уже определено. Обозначим через тк^1 первое такое натуральное
число, что 2sm есть лебегово число покрытия атг Полученную
таким образом подпоследовательность последовательности (4 :24)
обозначаем вновь через
(4:24) «1,.-.,«,*,...,
а соответствующие s—через sw.
Итак, (4:24) есть последовательность неприводимых зт*покры-
гий компакта Ф, причём 2sw+1 есть лебегово число покрытия aw,
откуда, в частности, следует, что 2sw+x < гт. Более того,
обозначая через Ьт наибольшее число, являющееся диаметром какого-либо
элемента покрытия ат> имеем (ср. главу 1, определение [8:33])
оо
(4:241) 28* + 8»<2в»+х + 8«<в»-
Пусть
ах=*{А19...9А4
Предположим, что все элементы покрытия ат занумерованы
в виде
•^#ji • • «1 А%
т
где *!>•••»%„, обозначают различные комбинации из т индексов
Пусть
суть все пересекающиеся с Л#1 элементы покрытия aw+1. Вообще,
пусть
Суть все элементы покрытия aw+1# пересекающиеся с Л#л, но не
пересекающиеся ни с одним из множеств Л#1,..., Л^л_г;
соединение только что отобранных элементов покрытия aw+1 обозначаем
через Л*л. Докажем, что А*кфО, т. е., что всегда имеются такие
элементы покрытия aw+1, которые пересекаются с Л#л, но не
пересекаются ни с одним A*h, /г<&. В самом деле, множества А*к
содержатся в еш+1-окрестности соответственно множеств А#к и,
следовательно, образуют еш-покрытие компакта Ф, нерв которого
есть подкомплекс нерва Ка покрытия aw, совпадающий ввиду
неприводимости покрытия ат со всем комплексом Kain'> отсюда и следует, что
ни одно из множеств Л*л не может быть пустым.
Рассмотрим теперь последовательность множеств вида
(4:242) AisAiii#Atlt2iS> .. • , Aili2t im,.. •
15*

228
.ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ
[гл. vt
Так как 8(4^...^) <JL и Л-Ь.лмп Л'1...,-т,ш+1 / 0, то
последовательность множеств (4 :242) сходится к одной точке, которую
обозначим через xili3ammimmau
Множество всех точек xi±.. .<m*m+1*w+a. • •> где
индексы /1}..., /„фиксированы, а все остальные
индексы Aw+j, Aw+2f . • свободно принимают все доступные
для них значения, обозначается через В4л * .
Докажем несколько свойств множеств В4л * •
1. Из самого определения этих множеств следует, что
2. Множества Biittti замкнуты. В самом деле, пусть дана
последовательность точек
(4:243) *и..лт^+1?4+^
множества В4л..ш4 .
Так как каждый из индексов А^+1,А^ ,2,. . . может принимать
лишь конечное число значений, то в (4:243) существует
подпоследовательность (4 :2431), в которой A* t принимает одно и то же
значение hm+1, в (4 :2431) существует подпоследовательность (4:2432),
в которой А^,2 принимает постоянное значение Ада,2, и т.д.
Диагональная подпоследовательность последовательностей
(4:2431), (4:2432) и т.д. сходится к точке
чем доказано что В^..ч есть компакт и, следовательно, замкнутое
множество пакта Ф.
3. При вся/сом данном фиксированном т множества Bix... 4i
образуют замкнутое покрытие $т компакта Ф.
В самом деле, пусть х— произвольная точка компакта Ф.
Выберем множества
(4:244) Л/*, Ал .ъ,...,А.т м м
v ' 1 ' Н l2 'i H —1т
под условием, чтобы точка х содержалась в каждом из них и
рассуждаем как при доказательстве предыдущего пункта. Получаем
подпоследовательность (4 :2441) последовательности (4 :244), в
которой первый индекс /™ принимает одно и то же значение iu затем
подпоследовательность (4 : 2442) последовательности (4 :2441), в
которой второй индекс принимает одно и то же значение /2 и т- А- В
результате получаем последовательность натуральных чисел
1>и *2>"*> lmt ••*

§ 4] ПОСЛЕДОВАТЕЛЬНОСТИ ПОДРАЗДЕЛЕНИЙ 229
и последовательности (4:244), (4:2441), (4 : 2442),... (4 : 244/я)...,
из которых каждая (кроме первой) есть подпоследовательность
предыдущей, и которые таковы, что все элементы в (4 : 244w) имеют
в качестве первых индексов /^--Лл- Диагональная
подпоследовательность, как легко видеть, схотится к точке х4 * ...* ..., а так как все
элементы этой диагональной подпоследовательности (будучи
элементами последовательности (4:244)) содержат точку х, TQx — xii(2... t ...
и, значит,
х£Ви...€ .
(з «л,-
4. Так как В4 ...* лежит в ( И гк ]-, т. е. в 2зш+1-окрестно-
сти множества Лг-Г..г- £ aw, причём 2sw+1 есть лебегово число
покрытия атУ то pw есть еш-покрытие компакта Ф, имеющее
(вследствие неприводимости ат) тот же нерв К$т— Кат9 что и покрытие
осш. Итак:
Покрытие $т есть неприводимое ет-покрытие, подобное
покрытию <хт.
Обозначим через Г^...^ множество тех точек Biv..i , которые
не принадлежат никакому отличному от В^... < элементу покрытия
3i;i. Из неприводимости покрытия [3W следует, что множество Г. ...{
непусто (так как если бы Г^...^ было пусто, то, выкидывая из
покрытия (3W элемент Bii...i , получили бы гт-покрытие [3^, нерв
которого есть собственный подкомплекс комплекса Къ ). Так как
Т\-г.. t есть разность между Ф и соединением всех отличных от
Biv„{ элементов покрытия (3W, то Г^... ^ —открытое множество,
состоящее из всех точек лг^Ф, обладающих следующим свойством:
при всяком представлении точки х в виде
Х~ХМ •'•ътът+1--
имеем А1 = /1,...э km = im. Отсюда сразу следует
(4 :245) Г<1...^лт+1...лт4яЕг*г-*ш-
Пусть теперь х — произвольная точка множества Biv.4 и s —
произвольное положительное число. Возьмём столь большое л, чтобы
было *т+п<*- т°чка х принадлежит некоторому #а..лдалт+1...лт+п
и, следовательно, отстоит от ?i1...im%m+v..%m+n на Расстоянии
<£m+n<s- В силу (4:245) отсюда следует, что [>(х,\\\..ч )<е. Так
как s произвольно, тол:£1\-ь..ит- Итак> ва...<п ^н^С Так как
два различных множества 1\ ....• (при одном и том же /л) по са-
*1 'm v r '
мому своему определению не пересекаются, то:
5. Бег покрытия |3W су/щ> специальные покрытия.

230 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [гл. VI
Из только что доказанного свойства 4 следует, что никакой элемент
покрытия j3w+i не может содержаться более чем в одном элементе
покрытия (Зм. Так как, с другой стороны, всегда #*i.../wfw + iЕВп...гт
и каждое В4 ... f есть соединение содержащихся в нём ^1-«/wfm+1>
то:
6. Покрытие (5ШЧ г есть подразделение покрытия j3w.
Установлением всех этих свойств покрытий §т теорема [4:24]
доказана.
Предположим теперь, что dim Ф—r; тогда все покрытия §т
имеют кратность ^г-]-1« Предполагая, что ех достаточно мало,
можем считать, что кратность всех $т равна r-f-Ь Элементы
покрытия $т будем теперь обозначать через Bf,
7. Каждое из покрытий (3W обладает следующим свойством:
пересечение любых р -f-1 элементов В™,. .., В™ покрытия (5m, 0 <!/?<>
имеет размерность О— р.
Доказательство. Дано s>0. Требуется найти замкнутое
s-покрытие кратности г—р -f- 1 компакта В — В™ П ... П В™. Берём
столь большое натуральное число я, чтобы sw<s. Обозначим через
Bfk, k=l,..., siy все элементы покрытия р„, содержащиеся в дан*
ном В™£$т. Полагаем
£fc = J5Jfcns«n...n^, А=1 ^о
и докажем, что множества Ек образуют искомое е-покрытие
множества В. Из самого определения множеств Ек следует, что эти
множества замкнуты и что диаметр их меньше е. Докажем, что
каждая точка х£В содержится, по крайней мере, в одном Еи. Так как
х £ В0т, то х содержится, по крайней мере, в одном из В™г Кроме
того, х содержится во всех Bfy i = 1,. .., /?, следовательно, х
содержится в некотором Ек. Итак, множества Ек образуют замкнутое
s-покрытие множества В. Остаётся показать, что это покрытие имеет
кратность <>—р + 1. Пусть точка х£В содержится в Е11...,ЕН.
Надо доказать, чтоу^г — /?-f- 1. Так как х^В^лля всех /= 1,.. .,/?,
то для каждого из этих / имеется содержащее точку х множество
fijj* . Кроме того, х £ Вп01 П . . . П Вп0^ Так как все перечисленные
множества В^, /=!,..., р, и B™k, k — 1,. . .,v суть попарно
различные элементы покрытия |3W, имеющего кратность /"-J-l, to/?-|""v
<[r-f-l, т.е. v<>— /J+b что и требовалось доказать.
Подведём итог всему доказанному.
Теорема [4: 25]. Для каждого r-мерного компакта Ф можно
построить цепь подразделений
(4:25) Pi.Pa.-•-.?*,...
состоящую из покрытий (Зда, обладающих следующими свойствами;

§ 4]
ПОСЛЕДОВАТЕЛЬНОСТИ ПОДРАЗДЕЛЕНИЙ
231
а) Каждое (5W есть специальное неприводимое ет-покрытие
кратности г+ 1.
б) Пересечение любых рЦ-1, О^р^. г, элементов покрытия
$т имеет размерность <1и — р.
Выведем отсюда следующее важное предложение:
[4 :26]. Каждая точка г-мерного компакта Ф обладает сколь
угодно малой окрестностью, граница которой имеет размерность
О —1.
Доказательство. Пусть е > 0 дано. Возьмём такое /я, чтобы
было 2sw<e. Для данной точки х£Ф определим окрестность Отх
как разность между Ф и соединением всех элементов покрытия рш,
не содержащих точку х:
Отх = Ф\[}В<* х£в».
Замыкание окрестности Отх лежит в соединении всех В^^^т,
содержащих точку дг, и имеет поэтому диаметр ^2sw<s. Граница
окрестности Отх, с одной стороны, лежит в соединении всех S*J£ (3W,
содержащих точку х, а с другой стороны — в соединении всех
#™£(3Ш, не содержащих точку х. Другими словами, граница Отх
лежит в соединении всех множеств вида В™ П Б™, где В™ £ (3W
содержит точку х, а В™£$т точку х не содержит. Так как каждое
из множеств BfOB™ имеет (в силу [4:25]) размерность ^я—1,
по по теореме [3:1] размерность их соединения, а следовательно,
и размерность границы окрестности Отх также ^п—1, что и
требовалось доказать.
Из теоремы [4:26] легко выводится:
[4 :260]. Пусть А— замкнутое множество п-мерного
компакта Ф. Какова бы ни была окрестность О А множества А с Ф,
можно найти лежащую в ОА окрестность ОхА множества А,
граница которой имеет размерность ^п—1 (и также
содержится в ОА).
Доказательство. Для каждой точки х £ А берём окрестность
Ох, удовлетворяющую условиям
'Ох<£ОА, dim (Ох\Ох)< я—1.
Так как А — компакт, то можно выбрать конечное число этих
окрестностей 01 — Oxv...,08 = Ox8, покрывающих всё
множество А. Соединение этих окрестностей образует окрестность
ОхА множества Л, причём граница множества ОгА содержится, как
легко видеть, в соединении границ окрестностей Ои...,Оа и,
следовательно, имеет размерность <^я—1. Так как OtAczOA} то
всё доказано.

232 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ ['Л. VI
Выведем из теоремы [4:26] неравенство
(4:261) ш(1Ф<(НтФ;
этим будет закончено доказательство теоремы [3:22].
Из dim Ф = —1 (г. е. dim Ф-^—1) следует, что Ф — 0 и, значит,
^Ф<;—1. Предположим доказанным, что из dim Ф <^ п—1
следует ^Ф<;я—1; докажем, что из ёшФ^Ся следует шс1Ф<;л;
этим и будет доказано неравенство (4:261).
Если diir^^ft, то по теореме [4:26] у каждой точки лг£Ф
существует сколь угодно малая окрестность, граница которой имеет
размерность ^п—1, и следовательно, в силу наших предположений,
и индуктивную размерность ^ п — 1. Но тогда по определению
индуктивной размерности ^Ф<1я, что и требовалось доказать.
Выведем из теоремы [4 :25] ещё одно важное предложение.
Отображение С множества X на множество Y назовём л-крат-
ным, если прообраз каждого элемента множества Y при
отображении С состоит не более чем из п элементов множества X, причём
имеется хотя бы один элемент множества F, прообраз которого
состоит из п элементов множества X; число п называется в этом
случае кратностью отображения С.
Теорема [4:27]. Всякий компакт Ф размерности п, не
содержащий изолированных точек, может быть представлен как
образ канторова совершенного множества при некотором (п-\~1)~
кратном непрерывном отображении-, с другой стороны, всякий
компакт, являющийся образом канторова совершенного
множества при некотором (п-\- \)-кратном непрерывном отображении,
имеет размерность ^.п и не содержит изолированных точек.
Докажем сначала вторую часть теоремы. Пусть
компакт Ф является образом канторова совершенного множества Р
при {п -4-1)-кратном непрерывном отображении С. Разобьём Р на
два куска *) Р1 и Р% диаметра ^, каждый из них на два куска Рп
и Р12 диаметра § и т. д. **). Образы Bh.. .im= CPir ..im кусков
Pi{.. ч (при данном т) образуют гт-покрытие (Зт компакта Ф,
причём limsm = 0. При этом, если при данном т точка х£Ф
принадлежит v различным элементам Bix...im покрытия (3W, то в v
различных кусках Pi .. ч имеется по точке, принадлежащей к
прообразу С~\х). Так как С есть («~f- 1)-кратное отображение, то
v<^-f-l, т. е. кратность каждого из покрытий $п не превосходит
п -\- 1 и, следовательно,
dim Ф < п.
*) Под куском канторова совершенного множества понимаем
пересечение его с любым сегментом числовой прямой, концы которого не
принадлежат Р, мы будем рассматривать лишь непустые куски.
**) См., например, Александров и Колмогоров, Введение в
теорию функций действительного переменного, изд. 3, гл. 4.

§ 4]
ПОСЛЕДОВАТЕЛЬНОСТИ ПОДРАЗДЕЛЕНИЙ
233
Вели бы Ф содержало изолированную точку х, то С^1х было бы
открытым множеством в Р, и так как в Р нет конечных (даже
счётных) открытых множеств, то С не могло быть конечно-кратным.
Вторая половина теоремы [4:27] этим доказана.
Доказываем первую половику теоремы [4:27].
Пусть Ф есть м-мерный компакт без изолированных точек.
Строим для него цепь подразделений
(4:27) pls p2,...,p?w,...,
удовлетворяющую всем условиям теоремы [4:25] и, кроме того,
следующему дополнительному условию: покрытие $г содержит не
менее двух элементов, и при любом т диаметр каждого элемента
покрытия pw+i меньше половины наименьшего из чисел, являющихся
диаметрами какого-либо из элементов покрытия $т. Так как все
покрытия j3w — специальные и Ф не содержит изолированных точек,
то среди элементов покрытия $т нет элементов, состоящих лишь
из одной точки, так что диаметры всех В7?. . . i £ (3W отличны от
пуля и наше дополнительное условие выполнимо.
Из этого условия следует, что каждое Bf...{ , (~ Р содержит
не менее двух множеств В^К . .*м*ш+1 £ (Wi-
Возьмём теперь кантороно совершенное множество Р и разобьём
его на столько попарно не пересекающихся кусков Pi диаметра <.-~- ,
как велико число элементов В{ покрытия $v Так как диаметр Р
равен 1, а число потребных нам кусков 5>2, то требование
^Л^)^С-гг выполнимо.
Пусть при данном т камторово множество Р разбито на попарно
не пересекающиеся куски Р^...^ диаметра <С?у^Г> взаимно
однозначно соответствующие элементам покрытия $т. Каждый кусок
1\'\-• чт разбиваем на столько кусков диаметра <1 ^гр' к^к
велико число элементов покрытия [Зш+1, содержащихся в Bit...{ •
Таким образом, строятся куски Р{1..ч для любого т. Ставя
и соответствие каждой точке
i^ph n pili2 п ...п /v3.../J№n...
множества Р точку
* = С® = Bh П Р,ч,2 П . . . П Bhil. . Чт П . . .
компакта Ф, получим, как легко видеть, непрерывное отображение
С канторова множества Р на компакт Ф. Если v различных точек
4»---,Ev множества Р отображаются, в силу С, на одну и ту же
точку компакта Ф, то? взяв такое ту что никакие две из точек

234 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [ГЛ. VI
£1э...,?у не принадлежат к одному и тому же множеству Pit...{ ,
видим, что точка х = С(^) = ... = C(£v) принадлежит к v элемен-.
там покрытия $т. Так как все покрытия (Зш имеют кратность
0~|-1, то v^n-j-1, т. е. кратность отображения С не
превосходит п-\-1, что и требовалось доказать. %
Упражнение. Доказать следующую теорему:
Всякий компакт Ф размерности <С п является образом
некоторого замкнутого подмножества канторова совершенного
множества при некотором непрерывном отображении кратности
-< п -}-1; обратно, все компакты, являющиеся образами
замкнутых подмножеств канторова совершенного множества при
непрерывных отображениях кратности <^я-[- 1, имеют размерность
<я.
Другими словами, размерность компакта Ф может быть
определена как наименьшее из чисел пу удовлетворяющих следующему
условию: существует непрерывное отображение кратности п-\-1
некоторого замкнутого подмножества канторова совершенного
множества на компакт Ф.
§ 5. Некоторые приложения к топологическим
многообразиям и полиэдрам.
5:1. Случай топологических многообразий (в частности, Rn
и Sn)> Пусть Мп — замкнутое /г-мерное топологическое многообразие.
Мы знаем, что dim Mn = nt значит, ind Mn = n, поэтому существуют
точки х£Мп, для которых lndxMn = n. А так как все точки х£Мп
имеют гомеоморфные окрестности, то в любой точке х^Мп имеем
ind^ Мп = п. В частности,
indJ?SM = П
и
indxRn = n
в любой точке, соответственно, x£Sn и x£Rv. Итак:
[5:11]. Всякое n-мерное топологическое многообразие имеет
в каждой из своих точек индуктивную размерность п.
Выведем отсюда следующую теорему:
[5:120]. Никакой компакт размерности <^п — 2 не разбивает
пространство Rn.
Доказательство. Предположим, что компакт Ф размерности
<; п — 2 разбивает Rn.
Пусть Г — ограниченная компонента открытого множества Rn \ Ф
и р — какая-нибудь точка области Г. Возьмём вокруг точки р шар
Еп столь большого радиуса, чтобы множество Ф лежало внутри
этого шара. Возьмём, с другой стороны, произвольное е > 0 и шар
Jn с радиусом е и центром в начале координат о пространства Rn,

§ 5] ПРИЛОЖЕНИЯ К ТОПОЛОГИЧЕСКИМ МНОГООБРАЗИЯМ 235
Отобразим подобным преобразованием шар Еп на шар еп. Тогда
область Г перейдёт в область f, содержащую точку о, а компакт
Ф перейдёт в компакт ср размерности <Ся — 2, при этом и f и ср
лежат внутри шара епу а граница области f содержится в ср и,
следовательно, имеет размерность <С п — 2. Так как f есть окрестность
точки о, имеющая диаметр < 2г, иг произвольно, то ind0 Rn ^n — 1,
что противоречит теореме [5:11]. Это противоречие доказывает
теорему 15:120].
Из теоремы [5:120] в свою очередь вытекает:
[5:12]. Замкнутый п-мерный шар Еп не разбивается никаким
компактом размерности <> — 2. ^
В самом деле, пусть замкнутый n-мерный шар Еп разбивается
компактом Ф размерности <С я — 2. Без ограничения общности можно
предположить, что Ф не содержит центр шара, который обозначим
через о.
Из наших предположений следует, что
Ёп = Л U Ф U D,
причём Л, Ф, Г) попарно не пересекаются и Л и D суть непустые
открытые в Еп множества. Пусть для определённости о£А.
Преобразование взаимными радиусами-векторами переводит сферу
Sn — Еп\Еп в себя, открытые множества А\о и D,
соответственно, в Л1 и Dj, замкнутое множество Ф в замкнутое множество
Ф^, при этом
Я» = (Л U At) U (Ф U Фг) U (D U Dj).
Легко видеть, что
Л U Alf Ф U Ф1Э DU D,
попарно не имеют общих точек, при этом Л U Аг и D U Z)j открыты
и не пусты, так что компакт Ф U Фг разбивает пространство Rn, чего
не может быть, так как dim Фг — dim Ф <; п — 2, значит, по теореме
[3:1] и сПт(Ф U Ф^^л— 2. Теорема [5:12] этим доказана.
[5:13]. Никакое n-мерное топологическое многообразие Мп не
разбивается никаким компактом размерности ^п — 2.
Доказательство. Для каждой точки р£Мп возьмём
окрестность U(p), гомеоморфную Rn. Пусть, в силу некоторого
гомеоморфизма С между Rn и U(p) некоторый замкнутый шар EnaRn
отображается на V(p) cz £/(p), где V(p) = C{En). Таким образом,
получаем для каждой точки р £ Мп определённую окрестность V (р),
гомеоморфную /?п, причём V(p) гомеоморфно замкнутому шару.
Можно выбрать счётное, а в случае замкнутого многообразия Мп
даже конечное, множество этих окрестностей V(p), т§к чдо их
соединение есть всё Мп-

236 ВВЕДЕНИЕ В ТЕОРИЮ РАЗМЕРНОСТИ [['Л. VI
Пусть эти V(p) суть
(5:13) Vu V2, ..., Vs, ...
Так как Мп связно, то система множеств (5:13) по теореме
[3:18] главы 1 является сцепленной.
Пусть теперь Ф с= Мп есть компакт размерности <; п — 2. Каждое
из множеств ФП V{ нигде не плотно в V{ по теореме [1:25].
Следовательно, сцепленной является и система множеств
У,\Ф, У2\Ф, -.., Т,\Ф, ...
Каждое из множеств 1А\Ф связно, в силу [5:12], значит, по
теореме [3:15] главы 1 соединение множеств 1^\Ф, т. е.
множество Мп \ Ф, ^связно, что и требовалось доказать.
В частности:
[5:131]. Никакая, область пространства Rn не разбивается
никаким компактом размерности <; л—2.
5 : 2. Сильная связность.
О пред е л е ни ej5 : 21]. Компакт Ф размерности п называется
сильно связным, если никакое замкнутое множество размерности
<; п — 2 его не разбивает*).
Из этого определения и теоремы [3:22] непосредственно следует:
[5:22]. Если Ф — сильно связный n-мерный компакт, то
\пйхФ = п во всякой точке х£Ф.
В силу результатов предыдущего артикула, примерами сильно
связных компактов могу г служить все замкнутые топологические
многообразия, а также я-мерный замкнутый шар и гомеоморфные
ему компакты. Читателю предоставляется доказать, что замыкание
всякой области данного замкнутого топологического многообразия
есть сильно связный компакт.
Замечание. Имеет место следующая теорема, которая в этой
книге доказываться не будет:
Теорема Гуревич а-Т у м а р к и н а. Всякий n-мерный компакт
содержит сильно связный n-мерный компакт.
Переходим к рассмотрению сильно связных полиэдров.
Определение [5:23]. Конечная последовательность л-мерных
симплексов
у1> * * *' J s
данного симплициального комплекса К называется цепочкой
симплексов этого комплекса (подробнее: цепочкой, связывающей в К
симплексы Т™ и Т™), если при любом /= 1, 2, . . ., s—1 симплексы
?7 и ^7+1 имеют общую (п—1)-мерную грань, являющуюся
элементом комплекса /<.
*) Сильно связные л-мерные компакты были введены Урысоном под
названием /z-мерных канторовых многообразий.

§ 5j ПРИЛОЖЕНИЯ К ТОПОЛОГИЧЕСКИМ МНОГООБРАЗИЯМ 237
Определение [5:24]. Симплициальный я-мерный комплекс К
называется размерно однородным, если каждый его элемент
является собственной или несобственной гранью некоторого
/1-мерного элемента комплекса К. Размерно однородный я-мерный
комплекс К называется сильно связным, если каждые два я-мер-
пых симплекса комплекса Л' MOiyr быть в нём связаны цепочкой
«-мерных симплексов.
[5:251]. Если триангуляция К есть сильно связный п-мер-
ный комплекс, то тело её К есть сильно связный n-мерный по-
лиэдр.
Доказательство. Пусть 'Р*, .. ., Т£ суть все я-мерные
симплексы комплекса К. Тогда, в силу размерной однородности
комплекса К, имеем
(5:251) £=7?и ... U Т?.
Пусть Ф с К—-произвольное замкнутое множество размерности л — 2.
Пели Тп~1 — произвольный (п — 1)-мерный симплекс комплекса А", то
Г"-1Ч\Ф:£0;
01 сюда и из сильной связности комплекса д легко следует, что
система множеств
7»\Ф, ..., 7»\Ф
является сцепленной. Значит (по теореме [3: 15] главы 1),
К\Ф = (Т»\Ф) U ... U (7вп\Ф)
связно, что и требовалось доказать.
[5 :252]. Всякая триангуляция К сильно связного п-мерноги
полиэдра Ф есть сильно связный комплекс.
В самом деле, из [5:22] прежде всего следует, что К есть
размерно однородный комплекс. Пусть комплекс К не является сильно
связным. Тогда существуют два я-мерных симплекса 7^г£/Си Тп} £ К,
которые не могут быть связаны в К никакой цепочкой. Обозначим
через Q: множество всех n-мерных симплексов комплекса К,
которые могут быть связаны цепочками с Т£; через Q2 обозначим
множество всех остальных я-мерных симплексов комплекса К; оба
множества Qr и Q2 непусты (так как T»£Qti Tg£Q2). Комбинаторные
замыкания
суть замкнутые подкомплексы триангуляции К> пересечение Ко кото-

238 ВВНДЁНИЁ й ТЕОРИЮ РАЗМЕРНОСТИ |ГЛ. vj
рых имеет размерность <>—2. Так как К= Кг U К2, то значит,
К= К, U К2
и
К\К^= (К^Ко) U (К2\Ко).
Так как Kt\K0 и /C2\^o СУТЬ непересекающиеся непустые откры-
тые множества полиэдра К, то этот полиэдр разбивается
полиэдром К0 размерности ^.п — 2, что противоречит сильной связности
полиэдра К.
Итак:
[5:25]. Сильно связные полиэдры могут быть определены как
тела сильно связных триангуляции] если одна триангуляция
полиэдра Ф сильно связна, то тем же свойством обладает всякая
триангуляция всякого полиэдра, гомеоморфного полиэдру Ф.
>

ЧАСТЬ ТРЕТЬЯ.
ГРУППЫ БЕТТИ.
Группы Бетти (определение которых даётся в главе 8) являются
центральным понятием комбинаторной топологии. Их изучению посвящена не
только вся эта часть книги, но и многое в нашем дальнейшем изложении.
В главе 7 строится основной алгебраический аппарат комбинаторной
топологии, при помощи которого, в частности, определяются и
исследуются сами группы Бетти. Этот аппарат состоит из понятий цепи и
граничного оператора А. Эти понятия и являются основными в
этой главе. Они, в свою очередь, опираются на понятие ориентации, с
которого начинается глава 7, и на понятие ^-комплекса, к которому
естественно приводит рассмотрение множества всех ориентированных симплексов
какой-нибудь триангуляции.
После того как в главе 7 введены все вспомогательные алгебраические
понятия, в главе 8 даются определение и элементарная теория
классических («нижних») групп Бетти, или, как мы их здесь называем, А-групп
триангуляции (и вообще ^-комплексов). Кроме отдельных примеров иллюстрацией
этой теории служит исследование ориентируемых и неориентируемых
псевдомногообразий, которым и заканчивается глава 8.
В главе 9 исследуются более сложные вопросы теории групп Бетти.
Прежде всего вводятся так называемые верхние группы Бетти, или у-груп-
пы. Далее, группы Бетти исследуются при помощи так называемых
канонических баз, которые, в частности, позволяют установить связи между
группами Бетти по различным областям коэффициентов.
В главе 10 доказывается инвариантность групп Бетти, т. е.
изоморфизм групп Бетти различных (кривых) триангуляции одного и того же
полиэдра (или гомеоморфных между собою полиэдров).
В главах 11 и 12 понятие Д-групиы переносится с полиэдров на
произвольные компакты. Следует, однако, заметить, что вполне адэкватным
образом это перенесение возможно лишь при помощи средств, выходящих
за пределы этой книги, а именно, при помощи теории топологических групп.
Обойти эту трудность удаётся, но лишь путём определения для любых
компактов уже не А-, а у-групп, что мы и делаем в этой книге, но
значительно позже, в главе 14.
В главе 12, в частности, вводятся локальные А-группы, при помощи
которых затем, в главе 13» арт. 1:1, даётся простое инвариантное
определение так называемых /г-многообразий.
ГЛАВА СЕДЬМАЯ.
ЦЕПИ. ОПЕРАТОР А.
§ !♦ Ориентация»
1:1. Ориентации пространства Rn. Понятие ориентированного,
т. е. направленного, отрезка знакомо читателю ещё из курса
элементарной алгебры. Настоящий параграф посвящен я-мерным
обобщениям этого понятия.
Назовём упорядоченным остовом /i-мерного эвклидова
пространства Rn совокупность записанных в определённом порядке

240
ЦЕПИ. ОПЕРАТОР А
[гл. vii
п-\~\ линейно Независимых точек этого пространства. Таким
образом, два различных упорядоченных остова могу г состоять из одних
и тех же точек, отличаясь друг от друга только порядком этих
точек. Как известно*), существует одно и только одно аффинное
отображение я-мерного пространства Ril на себя, переводящее данный
упорядоченный остов (eQl ev...,en) в некоторый другой
упорядоченный остов (e'Q1 e'v ...,/), т. е. перевидящее точки е0, еи • •:,еп
соответственно в точки e'Q, e'v . . ., ег.
Назовём на время упорядоченные остовы (<?0, е1У ..., еп) и
(e'Q, e'v . . ., е^) э к в и в а л еитн ы м и, если это отображение
положительно **). Из свойств аффинных отображений следует, что только
что введённое отношение эквивалентности приводит к разбиению
множества всех упорядоченных остовов данного «-мерного эвклидова
пространства на два класса.
Ориентировать пространство- значит остовы одного из этих
классов назвать положительными, а другого-- отрицательными. То же
понятие можно сформулировать iai<:
Определение [1:1]. Ориентировать п-мерное эвклидово
пространство — значит определить на всех его упорядоченных
остовах (eQ, eLi. ..,еп) функцию
принимающую на всех остовах одного класса значение -f-1, а
на всех остовах другого класса — значение —1. Такая функции
R,L(e0, ev . . . ,еп) называется ориентацией пространства*
Пространство с определённой в нём ориентацией R,il(c0, ev . . . ,еп) называется
ориентированным пространством.
Замечание I. В этом параграфе мы через R11 будем обозначать
я-мерное ориентированное пространство, обозначая пространство без
определённой ориентации через \R]i[ В дальнейшем, когда
элементарные теоремы об ориентации уже будут установлены, мы будем
обозначать через Rn как ориентированное, так и неориентированное
пространство: едва ли это приведёт к недоразумениям.
Замечание 2, Очевидно, каждое эвклидово пространство \R\
имеет две взаимно ир ггивоположные ориентации. Если одна из этих
ориентации обозначена через Rn, то другая есть — R11.
Замечание 20. Если п — 0, т. е. пространство представляет
собой точку о, то во» всём пространстве существует один
единственный упорядоченный остов. Тем не менее, определение [1:1] сохраняет
свою силу и для этого случая: ориентация R° по определению
принимает в точке о значение -;-1, а ориентация --R0 по определению
принимает в точке о значение —1.
*) См. Прибавление И, арт. 1 :5.
**) Прибавление II.

§ и
Ориентации
241
Нульмерное^ Пространство о с ориентацией /?°(oj= -f- l,
соответственно R°(o) =—1, называется обычно «точкой о с
коэффициентом + 1, соответственно —1».
Замечание 2V Ориентация/?1 прямой \^\ принимает на
упорядоченных остовах (^0,^) и (е'0,е[) одно и то же значение, если векторы
е0е1 и е'0е'х имеют одинаковое направление.
Замечание 22. Ориентация плоскости принимает на
упорядоченных остовах (e0ieve2) и (e'Q, e'v e'2) одно и то же значение, если
оба обхода: (е^е^е^ и (e'Q9e'v ^треугольников \е0, eve2\ и \e'0,e've!2\
совершаются в одном и том же направлении (т. е. оба против
часовой стрелки или оба по часовой стрелке).
Следующее замечание очень важно:
Замечание 3. Пусть в пространстве \R^\ дан (я—1)-мерный
симплекс |£|...£п| и две точки e'Q и е"0У не лежащие в плоскости
\Rn-L\ этого симплекса. Тогда (произвольная) ориентация Rn
пространства \Rn\ принимает на упорядоченных остовах (е'0, е19...,еп
и (^, еи.. .,еп) одно и то же значение, если e'Q и е"0 лежат по
одну сторону плоскости \Rn~% и противоположные
значения, если точки e'Q и e"Q лежат по разные стороны
плоскости \Rn~l\.
В самом деле, на основании теоремы [1 -.52] Прибавления II,
аффинное отображение, переводящее (e'Q, ev...,en) в (е'^еи.. .,еп),
положительно, если е'0 и е"0 лежат по одну сторону от плоскости
|/?w-1|, и отрицательно — в противоположном случае.
1:2. Ориентация симплекса и остова. Рассмотрим (я-|- 1)!
различных упорядоченных остовов, которые могут быть получены из данного
я-мерного остова, в частности, из остова данного «-мерного
симплекса *). Эти упорядоченные остовы называются различными
упорядоченными остовами данного остова или симплекса.
Множество всех этих упорядоченных остовов разбивается на два
класса: два упорядоченных остова принадлежат по определению к
одному классу, если они переходят друг в друга посредством чётной
перестановки.
Замечание 1. Если данный я-мерный остов есть остов
некоторого симплекса Tncz\Rn\, то два его упорядоченных остова тогда и
только тогда принадлежат в только что установленном смысле к
одному и тому же классу, когда они эквивалентны в смысле арт. 1:1,
т. е. переводятся друг в друга положительным аффинным
отображением (см. Прибавление II, теорема [1:53]).
Ориентировать остов или симплекс — значит отнести всем его
упорядоченным остовам, принадлежащим к одному какому-нибудь
*) Под л-мерным остовом здесь можно разуметь любое множество,
состоящее из п -f-1 элементов, значит, в частности, остов симплекса, а
также остов вырождающегося симплекса эвклидова пространства.
16 Александров П. С.

242
цепи, оператор А
[гл. vtt
классу знак -j- , а всем упорядоченным остовам, принадлежащим
другому классу, знак — . Другими словами:
Определение [1:2]. Ориентацией данного остова или
симплекса Тп — | eQl. . . ,еп\ называется определённая на всех
упорядоченных остовах (eiQy. . . ,ein) данного остова (симплекса) \е0.. .еп\
нечётная функция*) tn(e{ ,.. .>е^, принимающая значения dzl.
Замечание 2. Для определения некоторой ориентации данного
симплекса достаточно её задать на одном каком-нибудь
упорядоченном остове этого симплекса, например, на упорядоченном остове
(eQ9.. . ,£w); тогда на всех упорядоченных остовах того же класса наша
ориентация будет принимать то же самое, а на Fcex упорядоченных
остовах другого класса — противоположное значение. Ориентация,
принимающая на упорядоченном остове (е0,...<еп) значение -)-1,
обозначается через
ориентация, принимающая на упорядоченном остове (#0,.. . ,еп)
значение — 1, обозначается через —
— (е0...еп).
[1 :20]. Симплекс (остов) с определённой его ориентацией
называется ориентированным симплексом (остовом).
Итак:
[1:21]. При любом п = 0,1,2,... каждый n-мерный симплекс
(остов)
Т»=\е0...е»\
имеет две ориентации или порождает два ориентированных
симплекса (остова):
(е0...еп) и — (е0...еп).
Один из этих ориентированных симплексов обозначается обычно через
Р\ другой через —tn. Если V1 есть ориентация симплекса Тп, то
пишут \t»\=Tn. Тогда и \ — t"\ = Tn.
Замечание 3. Мы будем постоянно отождествлять между
собой оба эти понятия: ориентация данного симплекса и
ориентированный симплекс, так как каждое из них однозначно определяет
другое.
Замечание 40. В случае я = 0 симплекс 7,0=|е0| имеет
только одну вершину и, следовательно, только один упорядоченный остов
*) Нечётной функцией от данных п-\-\ аргументов называется функция,
меняющая знак (и сохраняющая свою абсолютную величину) при всякой
нечётной перестановке своих аргументов. Из этого определения следует,
что при чётной перестановке своих аргументов нечётная функция сохраняет
своё значение.

§ i]
ОРИЕНТАЦИЯ
'243
(e0). Тем не менее, определение [1:2] сохраняет силу и в этом
случае: если (е0) есть ориентация, принимающая в точке е0 значение -f-1,
то —(е0) есть ориентация, принимающая в точке е0 значение —1.
Эти ориентации нульмерного симплекса называются кратко: точка е0
с коэффициентом +1, соответственно —1.
Замечание 4. Если я>-1, то обе ориентации данного я-мерного
симплекса взаимно однозначно соответствуют классам его
упорядоченных остовов: данной ориентации соответствует тот класс, на
котором эта ориентация принимает значение ~\~1.
Поэтому в случае п^> 1 можно (и в большинстве случаев принято)
отождествлять оба понятия: ориентация симплекса и класс
упорядоченных остовов этого симплекса, причём под ориентированным
симплексом (е0. . .еп) понимается класс, содержащий упорядоченный остов
(е0,...,еп). Однако, надо помнить, что при п = Оэго отождествление
понятий невозможно, так как классов упорядоченных остовов в этом
случае имеется только один, а ориентации, как всегда, две.
Замечание 5. Все определения этого артикула дословно
сохраняются и для вырождающихся симплексов.
1:3. Тело ориентированного симплекса. Пусть trl —
ориентированный симплекс данного \Rn\. Соответствующий замкнутый симплекс,
т. е. выпуклое замыкание остова симплекса \tn\, называется телом
ориентированного симплекса tn.
Замечание. Это же определение применимо-и к
ориентированным вырождающимся симплексам: телом ориентированного
вырождающегося симплекса называется выпуклое замыкание его остова
(как мы знаем, вырождающиеся симплексы совпадают со своими
остовами).
Тело ориентированного симплекса V1 обозначается через iu.
1 :4. Продолжение ориентации tn в ориентацию кп.
Произведение ориентации tnRn и t\t\. Пусть в Rn дан симплекс Тп•— \е°0. . ,е°п |;
пусть tn — какая-либо ориентация симплекса Тп. Функция tn
определена на всех упорядоченных остовах симплекса Тп\ в силу
замечания 1, арт. 1 :2 функцию tn можно продолжить на множество всех
упорядоченных n-мерных остовов (е0,...,еп) пространства |/^'|,
полагая
''Ч'о>---.«п)=^'(*2>- ' ->^)>
<^ли аффинное отображение, переводящее (^о>---»^л) в (eo>--'Ai)>
положительно, и полагая *)
если это аффинное отображение отрицательно.
*) Читатель помнит, что V1 есть функция, а V1 (р0>...,еп) значение этой
Функции на данном остове.
16*
ш

244
Цйпй. Оператор А
[гл. vtt
Таким образом, продолжая ориентацию tn на все \Rn\ *), получаем
ориентацию Rn данного \Rn\\ эта ориентация Rn называется
одинаковой с ориентацией tn или равной ей: считая функцию t*
продолженной на \Rn\, можем просто написать
Л* (*о>--мО = <*('<>. ■••>*«)
для любого упорядоченного остова (е0,...}еп) пространства |/?Л|;>
если ориентации Rn и tn одинаковы, то ориентации—Rn и /*,
естественно, называются противоположными.
Пусть теперь дана какая-нибудь ориентация tn симплекса
Тп = \tn\<z.\Rn\ и какая-нибудь ориентация Rn пространства \Rn\l
функцию tn считаем продолженной на всё пространство \Rn\. Тогда
для любого упорядоченного остова (г0,.. . ,еп) пространства | /?п|
определено произведение
^о>--->0-#п(*о>-••><>,
равное 1, если ориентации Р1 и Rn одинаковы, и равное —1, если
эги ориентации противоположны.
Итак:
[1:41]. Произведение .двух ориентации tn и Rn (т. е. двух
функций tn{е0,...,еп) и Rn(eQ,... ,£п), определённых на всех
упорядоченных остовах пространства |i?w|) постоянно и равно 1, если
ориентации tn и Rn одинаковы, и равно — 1, если эти ориентации
прот ивопо ложны.
Пусть, наконец, в | Rn | даны два симплекса
7J = \е10.. .е1п\ = и у ^ ==а Г20 ••• е2п I
и какие-нибудь их ориентации t* и t%. Считая эти ориентации
продолженными на все |/?w|, можно без дальнейших объяснений говорить
о равенстве или противоположности их, а также об их произведении.
При этом снова произведение двух ориентации <* и t™ есть
постоянная, равная 1? если эти ориентации одинаковы, и — 1, если они
противоположны.
Замечание. Ориентация областей пространства
| Rn\. Так как между ориентациями симплекса Тп и несущего его
пространства \Rn\ установлено взаимнооднозначное соответствие, то
можно ещё по новому определить понятие ориентированного
симплекса: ориентированный симплекс tn есть совокупность двух
понятий: симплекса \tn\ и ориентации несущего этот симплекс
пространства | Rn |. Удобство этого понятия заключается в том, что оно
непосредственно переносится на случай любой области я-мерного
*) Для краткости будем говорить: «продолжить ориентацию tn на всё
пространство | Rn |> вместо «продолжить ориентацию tn на множество всех
л-мерных упорядоченных остовов пространства \Rn\*.

§ 1]
ОРИЕНТАЦИЯ
245
пространства, в частности, любого выпуклого многогранника, шара,
полупространства и т. п.
Определение [1:42]. Ориентированной областью
пространства \Rn\ называется совокупность двух понятий: 1)
данной области и 2) некоторой ориентации Rn несущего её
пространства \Rn\.
Очевидно, в частности, что всякая область Tnc:Rn имеет две
ориентации; если одна из них обозначена через tny то другую
обозначим через —tn.
1:5. Ориентация {erf11"1).. Пусть симплекс Тп~х — \ег. . .еп есть
грань симплекса Тп— \е0е1.. .еп\; пусть дана ориентация t71-1
симплекса Т4"1. Определим ориентацию (е^71*1) симплекса ^следующим
образом: пусть (е0, е^ . .., ei ) — произвольный упорядоченный остов
симплекса Тп> начинающийся с вершины е0. Положим
Оо^ОК, eiv • • • Ая) = <я-1 (eiv . . . ,ein\
т. е. дадим ориентации (е0№-г) на (*?0, ег , ..., ei\ по определению,
то значение, которое ориентация tn~l принимает на (eiv ..., ei у
Этим ориентация (e^t71-1) в силу замечания 2 арт. 1:2 определена
на всех упорядоченных остовах симплекса Тп.
Если
(*0, eiv . . . >ein) и (*0, eh, . . . , eQ
два упорядоченных остова, начинающихся с вершины е0, то чёткость
перестановки
та же, что и чётность перестановки
поэтому ориентация, принимающая на (е0, е^ ,. . ., е1п) значение
tn~l (eiv. . . ,*<я), принимает на (*0, е^. . . ,ejf) значение Р^ (е^. . . ,ejn\
Другими словами: ориентация (е^п"г) не зависит оттого,
какой именно упорядоченный остов (eQi eijf . .. , ejn)
послужил для её определения, а зависит
единственно от данной ориентации t71"1; поэтому и
обозначение (e0tn~x) является правомерным.
Замечание. При п > 1, определение ориентации (e^t71'1)
можно упростить: если t71"1 = {е1.. .еп), то (e0tn~~l) no
определению есть 0?о£<. . .£п)-
Из теоремы [1 :521] Прибавления II вытекает следующее важное
предложение:
[1 :б]. Пусть в \Rn\ дана плоскость \Rn~l\ и вне её две точки
е' и ё'\ пусть в \Rn~x\ даны два одинаковым образом ориенти-

246
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
рованных симплекса tf1 и йГх. Тогда ориентации (e'tt^1) и (е''^"1)
одинаковы или противоположны в зависимости от того,
расположены ли точки ег и е" по одну сторону или по разные стороны
от плоскости \Rn~1\.
Особенно важен частный случай предложения [1 :5]:
[1 :51]. Если в плоскости \Rn~x\ дан ориентированный
симплекс tn~x и даны две точки ег и е", лежащие в пространстве \ Rn\
вне плоскости \ Rn~l |, то ориентации (e'tn~]) и (Лп_1) одинаковы,
если точки ег и е" лежат по одну сторону плоскости | Z?™-11, и
противоположны, если эти точки лежат по разные стороны этой
плоскости.
1 :6. Аффинные образы ориентации. Пусть дано аффинное
отображение Sa пространства \R™\ на пространство |/?«,'. Если
Щ — какая-нибудь ориентация пространства |/?р|, то определяем
ориентацию б1Щ пространства | /?«| требованием, чтобы она
принимала на упорядоченном остове (Sael, ..., Sle^) то значение, которое
ориентация Щ принимает на (eL ..., е^)\
(1:6) Si I$( Slel ..., Si el) = Rn? (el, ..., 4),
или, что то же самое,
(1: б-3) SiЩ (el ...,<£) = /?р (ОЙ)"1*?, • • ., ($1У1е«ь)
для любого упорядоченного остова (el, ..., е*г) пространства |/?«г
Так как всякая ориентация симплекса однозначно связана с
некоторой ориентацией несущего это г симплекс пространства, то
в (1 :б-1) содержится и определение образа дезориентации f§
любого симплекса или вообще выпуклого многогранника Т$ при
аффинном отображении si-
В соответствии с этим можно сказать:
[1 :61]. Образом ориентированного симплекса
# = (*§... 4)
при (невыротдающемся) аффинном отображении Si является
ориентированный симплекс
Slt^(Slel..Slel).
Из этих определений непосредственно следует:
$2# -52/?? = <? •/?;-'>
W" • 6g /Ъ = 'а 1 **?

§ 2] ИНДЕКС ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ И СИМПЛЕКСОВ 247
где 4ь 4*1» *?з — какие-нибудь ориентации каких-нибудь л-мерных
симплексов пространства |/?р|.
Пусть теперь [ R™ | = | /?" | = | /?n | и S есть аффинное отображение
|/?п| на себя. Тогда Rn(Se0, ..., Sew) равно Rn(e0, .. ., еп) или
равно—Rn(e0,. . ,,еп) в зависимости от того, положительно ли
или отрицательно отображение S; а так как SRn(Se0, ...3Sen) no
определению равно Rn{e0, . ..,<?w) и (Se0, ...,Sen) есть любой
упорядоченный остов пространства \Rn\, то всегда
(1:62)
SRn = sign 5 • Rn,
где sign 5 обозначает знак аффинного отображения.
Точно так же, для любой ориентации tn симплекса Г",
продолженной на всё пространство \Rn\y имеем:.
(1:63)
Stn = sign 5 • tn.
Замечание. Само собою разумеется, что пользоваться
формулой (1:63) имеет смысл, только предполагая ориентацию tn (и,
следовательно, ориентацию Stn), продолженной на всё пространство | Rn |.
§ 2. Индекс пересечения плоскостей и симплексов *).
2:1. Индекс пересечения плоскостей. Пусть ХР и Yv — две
ориентированные плоскости ориентированного пространства Rrb, p-\~ q = п,
находящиеся в общем положении, то-есть пересекающиеся в
единственной точке о. Определим
индекс пересечения (Х*>Х Уа^ ^Rn
ориентированных плоскостей Хр
и Y<i в ориентированном Rn. Для
этого выберем в плоскостях | Хр \
и \Yv\ по симплексу Тхр =
— \оа1...ар\ и Т^ = \obx. . .bq
с общей вершиной о. Тогда точки
о, «!,...,Op, bv...,bq линейно
независимы в \Rn\, и Тп =
— \oa1...a:pb1...bq\ есть д-мер-
ный симплекс пространства | Rn \
(черт. 99).
Выберем произвольные ориентации t\ и Щ симплексов Тр и
Предположим, что наши обозначения выбраны так, что t^ = (oax . ,
и /| = (о^ ... bq), тогда дана ориентация tn = (о^. . ,арЬг
плекса Тп и определены произведения tfXP, t\Y^, tnRn,
Полагаем
(2 :1)
та
1 2 '
.ар)
.bq) сим-
(Хр X *^W = *РХР -tlYq. t"Rn
*) Чтение этого параграфа может быть отложено до гл. 15.

248 ЦЕПИ. ОПЕРАТОР Д [ГЛ. VII
и докажем', что (2:1) зависит только от данных ориентации Хр, К«, Rn
и не зависит от того или иного выбора симплексов ТРу Tg и их
ориентации t?9 t2.
Пусть Tf, = \oa[.. .а'\ и Т*, = \ob[. . .Ъ' | — два других сим-
плекса, выбранных так же, как Tf и Т*\ пусть ^, = (оя£. .. <А
и ^2/==(°^i" • "Ю — произвольные ориентации этих симплексов;
пусть *» = (од/. . .a' b'v . .Ь'Х Требуется доказать, что
(2:10) ^,Л> . /|, уя. • *7#л = *f ** - /f K« • W».
Обозначим через St и 59 аффинные отображения \Хр\ на себя
и \Y%\ на себя, переводящие, соответственно, упорядоченный остов
(0,«lf...,flfp) В (О, <,...,^) И (О, *1э...,*д) В (0^,...,^).
Эги аффинные отображения порождают аффинное отображение 5
пространства \Rn\ на себя, причём 5 переводит (о, av. . .ар,Ь19. . . 6д)
в (о,^,. .., <^,. ..,</) и sign S = sign 5t • sign 52.
Имеем по формуле (1 : 63)
*?, = sign<V*f; *J, = signS2.<f; <? = signS.*»,
значит, >
^,да = sign 5j • %Хр; Щ, Y* = sign S2 • ^ K?; t»R» = sign 5 • tnRn,
так что
^,да - q,Y* • /?/?» = sign 5j • sign S2 - sign 5 • t%XP - ЦУ* - №,
так как
sign 5 = sign 5, • sign S2, то-есть sign Sx • sign S2 • sign 5=1,
то равенство (2:10) доказано.
Очевидно:
(2:11) (-XP X Y*)eRn = {Xp X — K*)*iz» = (-» X К*),(-в«) =
= _(^X ^).22W.
Теорема [2:1]. (*p X K«) = (—1)**(K« X *)*)•
В самом деле, полагая tP-1 = (аг. . . ар), t%—1 = (b1.. bq),
имеем
(да X Г*) = (o*f ~а)ХР ' (о'?"1) ^ ■ (о*?"1 ^Г1) #п>
(К^Х^?) = (^Г1) VQ-iotP-^XP-ioq-UP-^Rn.
где
iotP-H*-1) = (рах ...apbx... bq)t
{oq-l%-l)*={pbl...b1pl.. .ар).
*) Там, где это не может вызвать недоразумения, мы будем писать
(Х*> У«) вместо (дах ^)*д»

§ 2] ИНДЕКС ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ И СИМПЛЕКСОВ 249
Перестановка, переводящая (о, аи.. ., ар,Ь1 ,.. ., bq) в (о, bv.. ,,bq> aly
...,а^), — состоит из pq транспозиций, так что
(0<2-i/P-i) = {-\уч (oq-iq-i),
откуда и следует теорема.
2 :2. Индекс пересечения симплексов. Пусть t& и Щ два
ориентированных (быть может, вырождающихся) симплекса в
пространстве Rny p-\-q — n, относительно которых мы предполагаем
выполненным по крайней мере одно из следующих двух условий:
1°. Тела*) tp и ^| этих симплексов не пересекаются: tpx[\t\ = О
или
2°. Вершины симплексов t? и Щ находятся в Rn в общем
положении **); отсюда, в частности, следует, что симплексы не
вырождаются и что tP П t\ либо пусто, либо состоит из единственной
точки о, являющейся внутренней точкой обоих симплексов |^| и \Ц\
Мы определяем индекс пересечения (tP X Ц) симплексов t\ и t
следующим образом:
1°. Если i{ П#* = 0, то(^Х^)=0.
2°. Если tP П t\ ф 0, то симплексы tp и Щ не вырождаются,
их плоскости \Хр\ и |Кя| пересекаются в единственной точке, а
именно в точке о. Обозначаем через Хр и Y% ориентации этих
плоскостей, равные ориентациям iPx и Ц, и полагаем
Замечание. Совершенно аналогично определяется и индекс
пересечения двух ориентированных выпуклых многогранников t\ и
t\ в ориентированном пространстве Rn.
Требование общего положения tf и t% может быть
сформулировано таким образом: выполнено, по крайней мере, одно из условий
1) 7?п7* = о,
2) плоскости этих многогранников и их граней находятся в Rn в
общем положении.
2:3. Пересечения и симплициальные отображения.
Теорема [2:3]. Пусть дани ориентированные n-мерные
пространства Щ и R% ив них пары пересекающихся
ориентированных плоскостей'.
ХР и Yf в #», \Х%\ П|^| = оР,
ХР и Y* в RI \ХРа\ П | Y*\ = о*.
*) Арт. 1: 3.
**) Прибавление II, арт. 1:4,

250 ЦЕПИ. ОПЕРАТОР А [ГЛ. VII
Пусть дано аффинное отображение S^ пространства \R^\
на | R" | , при котором \Xg | отображается на | Х% |, a j F21
на | Y* |. Пусть, наконец,
5Р/Й = в/?«, s = ±l.
ар а
Тогда
(2: 3) (6J Л? X SJ Грвй» = .(^ X фвл,.
Предложение это, в сущности, не нуждается в доказательстве;
легко, в самом деле, понять, что
<&Ц X S\Yf) в81щ = (ХР X Г$)в1$,
откуда (2 :3) следует на основании (2 :11).
§ 3. Коэффициенты инцидентности.
3:1. Определение коэффициентов инцидентности. Пусть tr и
/r-i — два ориентированных симплекса (данного Rn или данного
симплициального комплекса). Определим следующим обршом число
{tr\tr~1}, называемое коэффициентом инцидентности
ориентированных симплексов tr и tr-1.
1°. Если \tr~x\ не есть грань симплекса \tr\, то {tr :tr~1) = 0.
2°. Пусть tr-1 — грань симплекса tr, we есть вершина
^^противоположная грани l^-1!- Тогда однозначно определена
ориентация (е^-1) симплекса \tr\.
В случае, если (etr~1) = tr, полагаем {tr:tr~1)=l, если же
(etr-1) = —tr, полагаем (tr:tr~1) = — 1.
Игак, (tr:tr-1) есть s = ±: 1, определённое из уравнения
{ер-г) = г1Г.
Обозначение. Знак А» поставленный над вершиной ei в
выражениях вида \е0...ег\, (е0...ег)у означает, что эта вершина
выпускается. Так, О0. . .ёк. ..ег) = {е0.. .ек^1е1{Л1.. .ег).
Положим на время tr = {eQ. . .er), t7^1 = {е0. . .ёк. . .ег) и
заметим важную формулу
(3:11) {Г\Гк-1) = {—\)\
непосредственно вытекающую из определения коэффициента
инцидентности и из тождества
Р' = {е0. ..ег) = (-1)*(***о- • А-- • -О-
В частности,
(3:110) ((Wa • ■ • ег) : (*i*2 • • • ег)) = 1,
(3 : 111) ((*o*i*a- • -*г) :<>oV • -er))= — L

§ 3]
КОЭФФИЦИЕНТЫ ИНЦИДЕНТНОСТИ
251
Примеры коэффициентов инцидентности.
1°. Пусть fi=(e0e1).
Имеем*)
K*o*i) :(^о)1 =—1> К*оО '• (ei)\ = 1-
2°. Пусть
'a = (¥i^ ^ = («oe2)-
Имеем
(*а:*1) = _1.
3°. Для *3 = (e0*i*2^ и t* = {e0ele^ имеем (£3: t2) = —1;
наоборот, для Р = {ехе0е^ имеем (f3: t2) = 1.
3 :2. Свойства коэффициентов инцидентности. Первое
свойство:
[3:2,]
(—F: tr-i) = (tr: — F-1) = — (tr: F-1).
Первое равенство следует из того, что, если
tv = s (еГ-1), то — tr = —s i^-1), второе же
из того, что {е(—tr~1)) =— (ер-1).
Второе свойство коэффициентов Черт. 100.
инцидентности заключается в следующем:
Пусть дан симплекс Тг = \е0еге2. . .ег\ и две его (г—1)-мерные,
определённым образом ориентированные грани, а именно:
(3 : 20) t'Q-! =- (^2. . .*,) и /pi = (^2. . .ег).
Тогда, какова бы ни была ориентация tr симплекса Тг, имеем
(3:21) (^:*;--i) = — (^:^~1)
(см. черт. 100 для г = 2).
Доказательство. В силу первого основного свойства
(-*r:*r i) = _(^:^-i), (_^:<r-i):
(^:^1),
поэтому достаточно доказать равенство (3:21) для одной
какой-нибудь ориентации симплекса Гг, например, для
Р = (е0еге.2 . . .ег\
Но на основании (3:11) для этой ориентации имеем
Дадим второму основному свойству коэффициентов инцидентности
другую формулировку, важную потому, что именно она понадобится
нам для дальнейших обобщений. Вот эта формулировка.
*) Обозначая через (е0) вершину е0, взятую с коэффициентом -f-1 (ск\
арт. 1; 2, замечание 40).

252
ЦЕПИ. ОПЕРАТОР Д
[ГЛ. VII
Пусть дан симплекс | tr\ = \e0ele^.. .ег\ и какая-нибудь (г—2)-мер-
пая, произвольно ориентированная грань tr~2 = (е2... ег) симплекса | tr |.
Двум (г—1)-мерным граням i^"1!^^^- • -*г| и I'i"1! — I^0^2• • -ег\>
инцидентным с !/г~2|, дадим такие ориентации Р^1 и /[-1, чтобы
(3:22) (r-i:^-2) = 1> (^r-i:fr-2^=le
Тогда
(3:23) (^:^i) + (^:^-i) = o.
В самом деле, так как((е0е2. . ,ег):(е2* .\*г))—(О^а- • -*г):(*2- • ^г))3
= 1, то ориентации /g-1, ^-1, удовлетвбряющие условию (3 :22), суть
А при этом условии формула (3 :23) переходит в уже доказанную
нами формулу (3: 21).
Формулу (3:23) можно обобщить далее, если отказаться от
требования (3 :22). Получаем следующую общую формулировку:
[3:2И]. Пусть l^""1! и \t\-l\— Две грани симплекса |^|,
инцидентные с гранью |^r_2j. При любом выборе ориентации tr, ^J-1,
l^-1 и tr~2 этих симплексов имеем
(3 : 24) (tr : <g-i) (*j-i : t'-*) + (tr: /J-1) (if-1 : ^-*) - 0.
Эта формула справедлива, если ориентации t*-\ и t^"1
удовлетворяют условию (3 :22), так как тогда она переходит в уже
доказанную форму (3 :23). Справедливость формулы (3 :24) в общем случае
следует из того, что при замене какой-либо из ориентации tfj"-1»
t\-1 на противоположную, обе части равенства (3 : 24) сохраняют
своё значение.
Пусть теперь ТС—полный симплициальный комплекс. Пусть tr и tr~2
произвольные ориентации какого-либо r-мерного и какого-либо
(г — 2)-мерного симплексов комплекса/С. Для каждого (г—1)-мерного
симплекса комплекса К выберем определённую ориентацию и
обозначим её через ^J"1. В этих условиях формула (3 :24) может быть
переписана в виде
(3 : 25) 2 (*г : еГг) W'1 : *~*) ^ °>
где суммирование распространено по всем fr1.
Для доказательства формулы (3 :25) достаточно заметить, что
при фиксированных trw tr~2 существует только два t\'\ пусть t^~x и
tr-1, для которых выполнены условия (tr : /J-1) =f= О и (Ц-1: tr~2) ф 0.
После этого, формула (3 : 25) совпадает с формулой (3 :24), уже
доказанной нами.

§ 4] клеточные комплексы; л-комшшксы 253
§ 4. Клеточные комплексы; а-комплексы *).
4:1. Определение а-комплекса и клеточного комплекса.
Изложенные выше свойства коэффициентов инцидентности делают
естественным следующее определение клеточных
комплекс о в и а-к омплексов, являющихся непосредственным обобщением
множеств ориентированных симплексов симплициальных комплексов
(соответственно полных симплициальных комплексов).
Определение [4:11]. Пусть дано множество $, состоящее
из элементов, называемых клетками. ^ называется клеточным
комплексом, если выполнены следующие условия.
[4:111]. Каждой клетке поставлено в соответствие некоторое
неотрицательное целое число, называемое размерностью этой клетки.
[4:112]. Каждой r-мерной клетке 1Г£$ однозначно
соответствует r-мерная клетка —tr£$, причём
Клетки tr и — tr называются взаимно противоположными.
[4:113]. Каждой паре клеток соседних размерностей г и г—1,
то-есть каждой паре, первый элемент которой есть какая-нибудь
r-мерная клетка tr, а второй элемент (г—1)-мерная клетка tr-1,
отнесено целое число {tr:tr~1), называемое коэффициентом
инцидентности клеток tr и tr-1.
[4:114]. Для каждой клетки tr множество тех р-1, для
которых (р-.р-^фО, конечно.
[4:115]. Коэффициенты инцидентности удовлетворяют условию
(— tr: tr-1) = {tr: — Г-1) = — (tr : tr-x).
Клеточный комплекс называется с-комп ле к с ом,
если он удовлетворяет следующему условию.
[4:116]. Пусть даны: произвольная r-мерная клетка tr и
произвольная (г—2)-мерная клетка tr~*\ в каждой паре взаимно проти-
*) Читатель может при первом чтении выпустить весь этот параграф,
понимая в дальнейшем под клеточным комплексом Ш и под я-комплексом
множество всех ориентированных симплексов некоторой триангуляции /С,
а под замкнутым (открытым) подкомплексом клеточного комплекса $
множество всех ориентированных симплексов некоторого замкнутого
(открытого) подкомплекса комплекса К. В этих условиях or означает число г-мер-
ных симплексов триангуляции К\ число ориентированных r-мерных
симплексов/^ или r-мерных клеток комплекса К есть тогда, очевидно, 2 or. Однако,
в гл. 10 понадобится и общее понятие клеточного комплекса.
В моей работе «Гомологические свойства расположения комплексов
и замкнутых множеств» (Известия Академии наук СССР, серия
математическая, 6 (1942), вып. 5), написанной после окончания настоящей книги
и являющейся естественным дополнением к ней, вместо термина «я-ком-
плекс» употребляется термин «клеточный комплекс»; клеточные же
комплексы (в смысле, вводимом в настоящем параграфе), названы «клеточными
пространствами».

254
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VI!
воположных {г—1)-мерных клеток одну какую-нибудь обозначим
через /[-1. Тогда
где суммирование распространено по всем tfj-1.
Определение [4:117]. Взаимно однозначное отображение F
клеточного комплекса $г на клеточный комплекс St2 называется
изоморфным отображением или изоморфизмом, если выполнены
следующие условия:
a) Образ F (t) £ $t2 любого элементу / £ 5?i имеет ту же
размерность, что и элемент /.
b) Если элементы t и —t клеточного комплекса St\ взаимно
противоположны, то взаимно противоположными являются и элементы
F(t) и F{—t) клеточного комплекса 512«
c) (F{t4:F(t'-1)) = (tr:tr-1).
Два клеточных комплекса называются изоморфными между собою,
если один из них может быть изоморфно отображён на другой.
Очевидно, что клеточный комплекс, изоморфный ^-комплексу,
есть а-комплекс.
Определение [4:118]. Если среди чисел, являющихся
размерностями элементов клеточного комплекса Я), имеется наибольшее
число я, то п называется размерностью клеточного
комплекса 51.
Замечание 1. Из свойств коэффициентов инцидентности
в полном симплициальном комплексе с очевидностью следует, что
множество всех ориентированных симплексов полного симплици-
ального комплекса К есть а-комплекс. Следующий пример
показывает, что множество ориентированных симплексов неполного
симплициального комплекса К, являясь, очевидно, клеточным
комплексом, может и не быть а-комплексом. Комплекс К состоит из
треугольника \е0ехе2\, его стороны \е0ег\ и вершины ev Полагая
/2 = (е0е1е2\, t1 = (е0е^), t° = (еД имеем
2 itr : /J-1) \ft-1: tr~2) = (^ : t1)(t1 : t°) = 1 ф 0.
Мы, однако, докажем (арт. 7:2), что множество всех
ориентированных симплексов всякого открытого подкомплекса полного
симплициального комплекса есть ^-комплекс. Аналогичное
утверждение для замкнутых подкомплексов следует из того, что всякий
замкнутый подкомплекс полного симплициального комплекса есть
полный симплициальный комплекс.
Определение [4:12]. Если (Р'\Р'-Л) /: 0, то клетки Р' и trl
называются инцидентными между собою (говорят, что Р'
инцидентна с trl и tr~l инцидентна с Р').
Определение [4:13]. Клетка Р'-р подчинена клетке tr:
p'^fr-P (р>1)

§ 4]
клеточные комплексы; д-комплёксы
255
в клеточном комплексе й, если в ^ можно найти такие клетки
о > i ' » р '
что
Замечание 2. Только что введённое определение подчинения
и данное в Я) определение размерности позволяют рассматривать
клеточный комплекс как комплекс ^ в смысле общего
определения 1:7 гл. 4.
Замечание 3. Из определения [4:13] следует, что если
t>t\
то и
— t>t\ *> — *', —t> — tr.
Определение [4:14]. Клеточный комплекс й)' называется
клеточным подкомплексом клеточного комплекса ^, если
каждый элемент комплекса St' является элементом той же
размерности комплекса St и при этом:
1°. Два взаимно противоположных элемента $$' являются
взаимно противоположными и в S?.
2°. Любые два элемента соседних размерностей tr и t7""1 комплекса
St' имеют в S' и в t тот же коэффициент инцидентности.
Замечание 4. Из определения [4:14] сл'едует: если элемент
t клеточного комплекса St является вместе с тем элементом клеточ-
! ого подкомплекса St' комплекса SI, то — t также есть элемент W.
Определение [4:15]. Клеточный подкомплекс ®0 клеточного
комплекса $1 называется замкнутым (открыты м)
подкомплексом клеточного комплекса St, если всякий элемент $?, подчинённый
некоторому элементу комплекса St0 (подчиняющий себе некоторый
элемент комплекса Й0), есть элемент $0.
Замечание 5. Никаких других подкомплексов клеточного
комплекса, кроме клеточных подкомплексов, мы никогда
рассматривать не будем, поэтому клеточные подкомплексы данного
клеточного комплекса St будут в дальнейшем все-
гда называться просто подкомплексами клеточного
комплекса Ш.
Замечание 6. Имея в виду замечания 2 и 3, мы можем
дословно перенести всю изложенную в гл. 4, § 7 теорию связности
комплексов (включая понятие и свойства компонент) на клеточные
комплексы.
Замечание 7. В огромном большинстве клеточных
комплексов, которые приходится рассматривать в топологии, коэффициенты
инцидентности принимают значения только -{-1, —1 и 0. В конце
следующего артикула будут даны примеры клеточных комплексов,
в которых коэффициенты инцидентности принимают и другие
значения.

[гл. vii
256 ЦЕПИ. ОПЕРАТОР А
4:2. Матрицы \ инцидентности * клеточного комплекса. Пусть
R есть конечный n-мерный клеточный комплекс. Обозначим через
2рг число его r-мерных клеток (г=0, 1, ..., п). Предположим,
что клетки комплекса 5? каждой данной размерности определённым
образом занумерованы. Тогда для г = 0, 1, 2,..., п—1 естественно
рассмотреть матрицу, состоящую из 2рг4 * строк и 2рг столбцов,
в которых на пересечении /-й строки
и у-го столбца стоит коэффициент тС-
цидентности /-й (r -f- 1>мерной и j-й
r-мерной клетки. Из этих матриц можно
вывести все свойства комплекса SL
Однако, можно поступить и более
I I 4.0 I
t
t\>
t;
<i.
0 >
3 l6
*—"N
'0 J
4
*;
<
l) )''
*;
*'0
^
i)
Черт. 101.
t1 t°
Черт. 102.
*S
экономно, а именно, можно, обозначая в каждой паре взаимно
противоположных клеток одну через trp ъ другую через —/J, /=1,
2,..., рг, рассматривать матрицы £% в которых на пересечении
/-й строки и /-го
стоит число
столбца (/=1, 2,.
•,Р
,г+Ь
; = 1, 2,...,р')
Зная эти матрицы и пользуясь первым основным свойством
коэффициентов инцидентности, можно, очевидно, получить коэффициент
инцидентности любых двух клеток соседних размерностей и,
следовательно, знать всё о комплексе.
Определение [4:21]. Матрица
Е<
1 Рг »г
811 •••%• *
,^г+\1. ■ .^r+ly
Pr I
•■V
Рг
• V+V1
*&=(<1+1:<р.
г=0, 1,..., л—1,
называется r-й матрицей инцидентности клеточного
комплекса &.
Замечание 1. Если $ есть комплекс ориентированных
симплексов симплициального комплекса К, то матрицы инцидентности
клеточного комплекса R называются матрицами
инцидентности симплициального комплекса К.

§ 4] клеточные комплексы; ^-комплексы 257
Дадим несколько примеров клеточных комплексов и их матриц
инцидентности.
1. На черт. 101 и 102 изображено разбиение тора на четыре
криволинейных четырёхугольника. Ориентации этих
четырёхугольников, их сторон и вершин являются элементами клеточного комплекса $.
Обозначая через t2v t\, t\ указанные на черт. 102 ориентированные
элементы, получаем матрицы инцидентности:
t\
*3
п
t\
1
-1
0
0
t\
-i
i
0
о -
'i
0
0
1
-1
t\
0
0
"1 -
1
*l
*\
t\
tl
Vfi =
'I
n
1
о
-l
0
0
1
0
—1
*.:
i
0
-1
0
<s
-1 0
0 1
1 0
0 —1
<2
-10 0
0 1 -1
1 0 0
0 -1
1 0
0 —1
-1 0
0 1
2. Клеточный комплекс $ состоит из элементов
t° с матрицами инцидентности
:/};
t\
:*°,
:/°,
{t*:t\) = (t*:tl) = (t[:t?) = Vl:t<>) = 0.
3. Клеточный комплекс 5? состоит из элементов z±
причём (Pit1) = 2, (Р:Р) = 0.
4. Клеточный комплекс 51 состоит из элементов г+
связанных между собою коэффициентами инцидентности
Замечание 2. К последнему примеру приходим геометрически,
рассматривая шестиугольник со склеиваниями и ориентациями,
указанными на черт. 103. Точно так же геометрической основой
примера 3 является модель проективной плоскости как круга со
склеенными диаметрально противоположными точками; в примере 2 имеем
тор, представленный как квадрат со склеенными противоположными
сторонами. Точный смысл этим утверждениям будет придан лишь
в гл. 10, арт. 2:4.
17 Александров II. С.

258
ЦЕПИ. ОПЕРАТОР А
[гл. vii
Замечание 3. Читатель без труда проверит, что все только
что построенные клеточные комплексы являются а-комплексами.
Пример клеточного комплекса, не являющегося ^-комплексом, дан
в арт. 4:1, замечание 1; другие подобные примеры читатель
построит в качестве лёгкого упражнения. При этом следует иметь
в виду, что в известном смысле окончательным понятием является
понятие а-комплекса, тогда как понятие
клеточного комплекса имеет лишь
вспомогательное значение; сколько-нибудь
ц'ь интересных и важных свойств
клеточных комплексов, не
являющихся а-комплексами,
неизвестно.
§ 5. Цепи.
5:1. Определение цепи.
Предположим,что на плоскости
Черт. 103. Черт. 104. или в пространстве дана
ломаная линия без самопересечений.
Выбор направления движения на ней задаёт на каждом из
отрезков (одномерных симплексов), являющихся звеньями этой ломаной,
определённую ориентацию. Таким образом, рассмотрение полиюналь-
ных путей естественно приводит к рассмотрению множеств,
элементами которых являются ориентированные одномерные симплексы.
Это множество одномерных симплексов было бы естественно
упорядочить, но мы этого делать не будем, так как это привело бы нас
к другим понятиям, чем те, которые мы собираемся изучать.
Рассмотрим теперь такие пути, в которых некоторые звенья
проходятся по нескольку раз. Такой путь уже не является просто
множеством направленных отрезков, его приходится рассматривать
как множество направленных отрезков, каждому из которых отнесено
некоторое целое число, показывающее, сколько раз этот отрезок
пробегается, с какой кратностью или с каким коэффициентом этот
отрезок входит в данный путь. Пусть, например, дан полигональный
путь ехе^егехе^к (см. черт. 104). Его можно рассматривать как
совокупность направленных отрезков (е^), (£2^з)> (*s*i)> (e2e*)> взятых
соответственно с кратностями 2, 1, 1, 1. Если говорить о
направленном отрезке (егег) вместо (^i)» то ег0 в нашем пути придётся
снабдить коэффициентом—1.
Подобным же образом путь ехе^еьехеье%е^ снабжает отрезки (е^),
(е2ез)> (ezei)> ietez) соответственно коэффициентами
1,0,0,-1
(нули получаются, так как каждый из отрезков (е2е3) и (е&ех)
проходятся два раза и притом в противоположных направлениях).

§5]
ЦЕПИ
259
Логическое содержание только что намеченного понятия состоит
в том, что каждому ориентированному симплексу (в нашем случае
одномерному) данного симплициального комплекса (в нашем случае
комплекса, состоящего из 4 отрезков: |^2|i l^sl» \eaei\* I^J) ста"
вится в соответствие некоторое целое число — «коэффициент», с
которым данный ориентированный одномерный симплекс входит в наш
путь, причём определённая таким образом на данном множестве
ориентированных симплексов целочисленная функция оказывается
нечётной: x(tl) = — х{ — tl)„ Этот последний факт выражает
эквивалентность двух суждений: направленный отрезок (е^) входит в наш
путь с коэффициентОхМ а, и направленный отрезок (е^4) входит в наш
путь с коэффициентом — а. Такие целочисленные функции
называются целочисленными цепями, в данном случае
одномерными целочисленными цепями.
Понятие одномерной целочисленной цепи подлежит обобщению
в нескольких направлениях. Во-первых, можно определить не
непременно одномерную, а вообще /--мерную целочисленную цепь и притом
на любом клеточном комплексе 51 как целочисленную нечётную
функцию xr(tr)% значение которой определено для каждой клетки
tr комплекса 51, причём нечётность понимается в очевидном смысле:
xr( — t>') = — xr(tr),
а целочисленность означает, что значения функции хг суть целые
числа. Во-вторых, можно отказаться от целочисленности и вместо
этого потребовать, чтобы значения функции были элементами неко-
торой данной абелевой группы 31, называемой в этом случае обычно
областью коэффициентов. Таким образом, приходим к следующему
основному определению:
Определение [5:1]. Пусть даны: клеточный комплекс й
и абелева группа 21 ф О, которую называем областью ковффици*
ентов\ пусть каждому r-мерному элементу комплекса 51
поставлен в соответствие элемент xr(tr) группы 21, так что
выполняется условие
хг (— £*•)== — xr (tr) (условие нечётности).
Полученная функция xr(tr), определённая на % называется г-мер*
ной цепью комплекса St no области коэффициентов 21.
Замечание 1. Во всей этой книге будут рассматриваться
только конечные цепи, т. е. цепи, принимающие отличные от
нуля значения лишь на конечном числе элементов комплекса 51*
Поэтому под цепью мы всегда понимаем конечную цепь.
Определение [5:11]. Совокупность U (5?, 21) всех/--мерных
Цепей комплекса 51 по области коэффициентов 21 образует группу
относительно операции сложения: суммой двух цепей
х\ 6АГ(®, 21) и x££Z/(5l, 21) называется цепь, принимающая на каждом
элементе комплекса 5? значение, равное сумме значений, принимаем
17*

260
ЦЕПИ. ОПЕРАТОР А
[гл. vii
мых на этом элементе цепями х[ и хгг Нулевым элементом группы
Lr(% %) является цепь, принимающая на всех tr£$t значение нуль *Vt
Замечание 2. Для удобства отождествим между собою нуле*1
вые элементы всех абелевых групп 51, которые мы будем рассматрй^
вать в качестве областей коэффициентов. Это даёт возможным счи*1
тать тождественными и нулевые элементы всех групп //($, %) и
называть их просто «нулевой r-мерной цепью комплекса 5Ъ> (неза*'
висимо от области коэффициентов). \
Замечание 3. Если 51 есть я-мерный клеточный комплекс, то
вводим и для г>я группу Lr(R, 51), которая по определению состоит
из одного лишь нулевого элемента. Кроме того, для всех клеточных
комплексов 5? определяем группу Z,-1 (^, 51), состоящую, по
определению, также лишь из нулевого элемента.
5:2. Некоторые замечания о цепях. Наиболее важные
области коэффициентов суть следующие аддитивны$.
группы: I
1) группа J всех целых чисел;
2) группа ]т целых чисел, приведённых по модулю т (т — целой
число); i
3) группа 4R всех рациональных чисел;
4) группа Зт-! всех рациональных чисел, приведённых по модулю 1,
т. е. фактор-группа группы SR по подгруппе У;
5) группа П всех действительных чисел, приведённых по модулю 1,
т. е. фактор-группа группы всех действительных чисел по
подгруппе J.
Группа //(К, J) обозначается просто через ££(51); её элементы
называются r-мерными целочисленными цепями
комплекса St.
Группа Lr(R,Jm) обозначается через L^ffi); её элементы
называются r-мерными цепями по модулю т. Среди этих
областей коэффициентов все, за исключением 9^х и П, являются кольцами
с единичным элементом **).
Группы Jm (при простом т) и 9t суть даже алгебраические тела
(поля).
*) При первом чтении можно ограничиться единственной областью
коэффициентов — аддитивной группой целых чисел, опуская всё, относящееся
к другим областям коэффициентов. Аргумент 31 мы будем обыкновенно
опускать и писать Lr(R) вместо Lr (Ш, Ж).
**) Кольцом в этой книге называется группа % в которой определено
ассоциативное и коммутативное умножение, дистрибутивное относительно
сложения.
Кольцо с единичным элементом — это такое кольцо 2t, один из
элементов которого, называемый единицей и обозначаемый 1, удовлетворяет
условию 1 • а = а для любого а £ 2L Нам удобно считать тождественными между
собою единичные элементы всех колец, которые мы будем рассматривать
в качестве областей коэффициентов.

§ 5]
ЦЕПИ
261
Замечание 1. Особого внимания заслуживает случай т = 2.
Так как группа J2 состоит из двух элементов 0 и 1, причём 1 -{- 1 = о,
то для xr£Lr2($) и любой клетки Р£$ имеем
& ( — tr) = — лг (Г) = хг (f),
т. е. любая цепь по модулю 2 принимает на двух взаимно
противоположных клетках одно и то же значение. Поэтому, если клеточный
комплекс 51 состоит из ориентированных симплексов симплициаль-
ного комплекса /С, то цепь jer£L£(5?) относиг каждому симплексу
ТГ£К определённое значение xr{Tr) = xr (tr) = xr (— ir). Это
позволяет рассматривать цепи по модулю 2 симплициальных комплексов
как функции со значениями 0 и 1, заданные на множестве
симплексов Т[, Т\,... комплекса /С.
Такие функции взаимно однозначно соответствуют подмножествам
множества всех г-мерных элементов этого комплекса: это
соответствие получится, если отнести к каждой цепи xr£L^,(&) множество
г-мерных симплексов 74 £/С, на которых цепь хг принимает
значение 1.
Замечание 2. В теории множеств называют
характеристичен ой функцией подмножества В множества А функцию,
определённую на Л и принимающую во всех элементах множества В
значение 1, а во* всех элементах множества А\В значение нуль.
Таким образом, r-мерные цепи по модулю 2 симплициального
комплекса К могут быть определены как характеристические
функции различных подмножеств множества всех
г-мерных симплексов комплекса К.
Замечание 3. (Оно понадобится нам в дальнейших главах этой
книги, начиная с одиннадцатой.) Пусть К—полный комплекс
остовов или вообще полный симплициальный комплекс. Пусть хг —
какая-нибудь цепь комплекса К. Через | хТ \ обозначается комбинаторное
замыкание подкомплекса комплекса К, состоящего из всех
симплексов, на которых цепь хг принимает значения, отличные от нуля.
Элементы (в частности, вершины) комплекса \хг\ называются
элемент а м и (в частности, вершинами) цепи хг.
Пусть, наконец, элементами комплекса К являются симплексы,
а также, быть может, вырождающиеся симплексы некоторого Rn.
Пусть хг — цепь комплекса К. Телом цепи хг называется
соединение тел всех ориентированных симплексов *) комплекса К, на
которых цепь хг отлична от нуля. Тело цепи хг обозначается через
хг и представляет собою компакт (даже полиэдр).
5 :3. Одночленные цепи. Запись цепей в виде линейных форм.
Пусть tr — элемент клеточного комплекса ^, пусть а — элемент
области коэффициентов 5L Через atr обозначается r-мерная цепь
*) Тело ориентированного симплекса (также и вырождающегося) есть
выпуклое замыкание его остова (см. арт. 1:3).

262
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
комплекса $, принимающая на tr значение а, а на всех г-мерных
элементах комплекса ^, отличных от±/г, значение нуль.
Из определения [5:1] следует, что значение цепи at? на элементе
— V есть —а. Цепи вида atr называются одночленными
цепями, при этом цепь atr условно называется клеткой V, взятой
с коэффициентом а. В частности, если % есть кольцо с единичным
элементом, то цепь \tr (т. е. цепь, принимающая значения 1 на f
и значения 0 на всех клетках, отличных OT±.tr) обозначается через
tr и отождествляется с клеткой Р.
[5:31]. Всякая цепь есть сумма одночленных цепей.
Доказательство. В каждой паре взаимно противоположных
клеток комплекса S? обозначим один определённый элемент через t\.
Пусть значение цепи хг на клетке tl есть аг\ тогда имеет место
тождестщо
(5:31) хГ = Ъ*£>
по существу совершенно очевидное.
В самом деле, на любом t\ значение цепи а$ есть aiy а значения
всех цепей а$ , ] ф /, равны нулю, поэтому значение цепи^а/l на
ti есть а^ т. е. равно значению цепи хг на той же клетке.
На клетке — % и хг и 2а/[ принимают значения—а{. Так как t\
и—t\ (при различных значениях /) исчерпывают собою множество
всех элементов комплекса $, то утверждение [5:31] доказано.
Итак шсякая r-мерная цепь комплекса $ может быть записана
в виде линейной формы (5:31), где t% обозначает (при различных /)
по одному представителю из каждой пары взаимно противоположных
элементов клеточного комплекса $, а аг есть элемент области
коэффициентов 21. Различным цепям соответствуют при этом различные
линейные формы (5:31), и обратно.
При этом сложению цепей, определённых как функции, очевидно,
соответствует обычное сложение линейных форм, так что группа
//($, 91) может быть рассматриваема как группа линейных форм
(5:31). Отсюда следует, что группа Z/($, 91) есть прямая сумма
ог групп, изоморфных группе 9(, где 2рг есть число /--мерных
элементов клеточного комплекса $.
5:4. Цепи симплициального комплекса. Если 51 есть клеточный
комплекс, состоящий из всех ориентированных симплексов
некоторого симплициального комплекса К, то цепи комплекса R называются
цепями симплициального комплекса АГ, в соответствии с чем группа
//($, Ж) обозначается через IS (К, 91) и называется группой г-мерных
цепей симплициального комплекса /С Число рг есть в этом случае
просто число r-мерных симплексов комплекса К.
Из общего определения цепи и определения ориентированного
симплекса следует, что цепи симплициального комплекса К могут
быть определены непосредственно следующим образом: г-мерной

§ 5]
ЦЕПИ
26 3
цепью симплициального комплекса К по области коэф-
фициентов % называется функция л:г, определённая на множество
всех r-мерных упорядоченных остовов (e0i. . ,,ег) комплекса К и
удовлетворяющая следующим условиям:
1°. Значения функции хг принадлежат группе 51.
2°. Если( °" "" r J есть нечётная подстановка вершин
упорядоченного остова (£0,. . ,,ег), то
х? \ei0i • • • Ay) == хГ \еоч • • • А)-
Замечание. Так как каждая чётная подстановка разлагается
на чётное число нечётных подстановок (транспозиций), то из 2°
следует:
3°. Если( °'' ' г \ есть чётная подстановка, то хг(е{л,. . *,еЛ =
vv--v
= Хг (#0, . . . ,£г).
В терминах артикула 5:3 можно сказать: r-мерная цепь
симплициального комплекса К по области коэффициентов % есть линейная
форма относительно ориентированных симплексов t\ комплекса К
с коэффициентами аг£%.
5:5. Скалярное произведение цепей. Пусть область
коэффициентов % есть кольцо с единичным элементом.
Пусть
две цепи клеточного комплекса $ по кольцу коэффициентов 51.
Полагаем
(5:51) (^-yO = 2*A6*-
Элемент (л:г • у) £ ЭД называется скалярным произведением
цепей хг и уг.
Мы определили скалярное произведение двух цепей по одному
и тому же кольцу коэффициентов 31. Пусть теперь 91—
произвольная область коэффициентов, т. е. произвольная абелева группа.
Любой элемент а группы 51 можно перемножить с любым целым
числом zt я (где я^>0) по правилу:
п раз
а-п = па~а-\-а-{-...-{-а.
Поэтому, если
есть цепь клеточного комплекса 5? по произвольной области
коэффициентов 91, а

264
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
есть целочисленная цепь, то определено скалярное произведение
в частности, если yr=str{, то хг>уг = а4. \
Итак, значение цепа хг на элементе t/ клеточного комплекса 5?
равно скалярному произведению этой цепи и элемента t/
(рассматриваемого как целочисленная одночленная цепь). Поэтому мы
будем обозначать значение цепи хг на элементе tr клеточного
комплекса Ш через (хг • tr) (сохраняя там, где это удобно, и
обозначение xr(tr)). В соответствии с этим линейную форму (5:31) можно
переписать в виде
^=2(^. tf)tf.
5 : 6. Распространение цепей; куски цепей. Операторы ^0 и Е®.
Пусть ^0 есть подкомплекс *) клеточного комплекса Ш. Пусть
хг — 2 aihr— какая-нибудь цепь комплекса £?. Рассматривая
функцию хг лишь на клетках, принадлежащих комплексу й0, или сохраняя в
линейной форме /=Va^ лишь те члены, для которых t* £S£0,
получим цепь комплекса ®0, называемую куском цепи jcr, лежащим
на 5?0, и обозначаемую через**) ^хг. В частности, если xr(ty = 0
для всякого /[G^\^o> т0 говорим, что цепь jcr лежит на Ш0.
Пусть теперь х* есть цепь комплекса й0; определяя функцию
xr£Lr(^) равенствами
xr{tr) = x0{tf), если Р£®0,
хг({г)=;0, если tr£®0,
получим цепь хг комплекса ^, называемую продолжением
цепи хг £ IX (й0) на комплекс ^ и обозначаемую через Е^ хг
(подробнее, через Е®?хг0).
Замечание. Если рассматривать цепи как линейные формы,
то всякую цепь комплекса $0 надо считать тождественной с её
продолжением на $ (так как две линейные формы тождественны, если одна из них
получается из другой приписыванием членов, коэффициенты у которых
равны нулю); другими словами, надо считать, что Lr ($0) есть подгруппа
группы Lr (Щ. Если же стоять на функциональной точке зрения,
*) Читатели, читавшие §4, помнят, что рассматриваются лишь
клеточные подкомплексы (арт. 4:1, замечание 5) ^данного клеточного
комплекса к. Читатели, пропустившие §4, понимают под $ множество всех
ориентированных симплексов некоторой триангуляции К, а под $0 —
множество всех ориентированных симплексов некоторого подкомплекса
**) В моей цитированной выше (стр. 253, сноска) работе «О
гомологических свойствах расположений комплексов и замкнутых множеств» цепь ^хг
обозначена через J$xr, Это на первый взгляд более громоздкое обозначе*
ние во многих случаях оказывается заслуживающим предпочтения»

§ 6] нижний граничный оператор (оператор А) 265
то цепь xrQ(-Lr(®0) отлична от цепи Е$х^£Ьг(Ё\ так как хг0 есть
функция, определённая на $0, а Е$х* есть функция, определённая на $; две
функции тождественны тогда и только тогда, когда они определены
на одном и том же множестве и принимают на каждом элементе его одни
и те же значения. Чтобы оттенить это различие, иногда называют цепи,
определённые, как функции, у-Депями» а цепи, определённые как линейные
формы, А-цепями.
Ставя в соответствие каждой цепи xr£Lr{§) цепь $0 xr £Z/(5t0),
получим гомоморфное отображение группы Z/(S) на группу Lr(Sl0);
это отображение есть отображение на группу Lr ($q), так как,
очевидно, для всякого -V£Z/($-0) имеем
*£ = $>£**£.
Ставя в соответствие каждой цепи x0r£Lr(§(0) цепь E®x0r £ Lr(St),
получим гомоморфное и даже изоморфное отображение группы Z/($0)
в Lr($), но приЙ)0:£^ не на //($). Эти гомоморфизмы называются
соответственно гомоморфизмами (или операторами) $0 и Е$.
§ 6. Нижний граничный оператор (оператор А).
6 :1. Определение А-границы.
Определение [6:10]. Пусть Е — клеточный комплекс, /r£5t
Через А^г обозначаем (г—1)-мерную цепь, принимающую на
каждой клетке tr~1^R значение (tr it^1).
Цепь k$tr называется границей клетки tr (часто:
нижней границей или А-границей) в комплексе St
Если из каждых двух взаимно противоположных (г—1)-мерных
клеток комплекса 3S одну обозначать через /J-1, другую через — tf—1,
то цепь k®tr в виде линейной формы записывается так:
(6:10) Aft<r=S('r^-1)'/-1-
Замечание 1. Если /Сесть полный симплициальный комплекс,
а St—клеточный комплекс его ориентированных симплексов, то
при tr = (е0. . .er), tf-1 = (е0. . ,ej.. .ег) имеем по формуле (3:Ц)
A^=2(-iy^.-1.
Это выражение для всех полных симплициальных комплексов К,
содержащих данный симплекс tr, одно и то же; поэтому можно
в нём опустить указатель й и переписать его в виде
(6 :100) Д(*0. . .er) = S (- 1У (*<>• • -Ъ- • -er), .
называя цепь (6 :100) просто границей ориентированного
симплекса (е0. .. ег) (предполагается: в любом полном симплици-
альном комплексе).

266 ЦЕПИ. ОПЕРАТОР А [ГЛ. VII
Определение [6:11]. Пусть
произвольная r-мерная цепь клеточного комплекса $.
Определяем (г — 1)-мерную цепь к#хг равенством
(6 : 11) А* *г = ]£****#•
i
Подставляя сюда значение &$tr. из (6:10), получаем
* з
т. е.
(6:111) А* хг = 2 (t{ : */-*) a, tf~K
Фиксируя произвольно tf-1, заключаем из (6:111), что значение
цепи L$xr на t/-1 равно S(V :^r"1)fl<-
Этому результату можно дать несколько иную форму. Пусть tr~1 —
произвольная (г—1)-мерная клетка. В каждой паре r-мерных
клеток, имеющих с tr~l коэффициент инцидентности, отличный от нуля,
обозначим через tf ту, для которой этот коэф {зициент
инцидентности положителен. Тогда, так как а4 — (хг • £/), имеем
(6 : 12) (ДЛ хг • tr-i) = 2 С/ : Р"1) (*г • V),
где суммирование распространено по всем £/*, инцидентным с t9"—1.
Формула (6:12) может служить определением цепи &®хг.
Замечание 2. Если ^ есгь клеточный комплекс всех
ориентированных симплексов симплициального комплекса К, то все отличные
от нуля коэффициенты инцидентности равны it: 1 и (6 : 12) переходит в
(6 :121) (А**" • F-1) = 2(*г ■ кг\
где сумма берётся по всем клеткам t/, для которых (t/ \tr-l)= -J- 1.
Если tr~1 — (e1...er), то
(6 :122) А* хг (ег... ег) = 2 *г (е{ег. . . ег\
где сумма берётся по всем вершинам ег £ [/С], для которых
существует в К симплекс \eie1.. .ег\.
Замечание 3. Для нульмерных цепей x°£L°(&) полагаем
А,$л;0 = 0, в соответствии с тем, что L~l (5t) есть по определению
нуль-группа.
[6 : 13]. Из определения цепи A,<?vr непосредственно следует, что
A*(V + V) = A**T+A**J;

§ б] НИЖНИЙ ГРАНИЧНЫЙ ОПЕРАТОР (ОПЕРАТОР А) 267
\o\o\o\o\o\v\o\o\o\o\o\
ВКШИЮМИКЗёэв
ошанямияаян
другими словами: ставя в соответствие каждой цепи хг£Ьг($,%)
её Д-границу &®хг, получаем гомоморфное отображение группы
£'(Л, 91) в группу Zr-i(St).
Это гомоморфное отображение называется гомоморфизмом
или оператором А.
Замечание 4. Если 5? есть клеточный комплекс
ориентированных симплексов полного симплициального комплекса К, то вместо А$ во
всех случаях пчшут А#, а часто и вовсе
опускают индекс К.
6:2. Примеры цепей и их границ.
1°. Комплекс 51 представляет собой
разбиение плоскости на конгруэнтные
квадраты со стороной 1, с вершинами в
точках с целочисленными координатами.
Ориентированные квадраты этого
комплекса образуют ^-комплекс. Цепь л:2
принимает значения, указанные на черт. 105
(даны значения, принимаемые этой цепью
на квадратах, ориентированных против
часовой стрелки). Цепь Ах2 принимает значение 1 (соответственно 2)
на отрезках, отмеченных одной, соответственно двумя, стрелками и
ориентированных по этим стрелкам. На остальных отрезках Ал;2
принимает значение нуль.
2°. На черт. 106 изображена триангуляция куска плоскости.
Двумерная цепь х2 принимает на треугольниках, ориентированных про-
штшткшняшв
о\о\о\о\о\о\о\о\о\о\о\
Черт. 105.
Черт. 106.
тив часовой стретки, значения, которые на них показаны; на
треугольниках, на которых никакое значение не указано, цепь х2
принимает значение 0. Граница Ах2 этой цепи принимает значения 1 ц

268
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
2 на отрезках, снабжённых стрелками и ориентированных по этим
стрелкам, на остальных отрезках Ах2 принимает значение 0.
3°. На черт. 107 изображён квадрат, разбитый на 24
треугольника. Эти треугольники, ориентированные против часовой стрелки,
обозначаются через ^,..., t\^ Обозначим
через txv.. . Л\, отрезки, лежащие на
границе квадрата, ориентированные, как показы-
\ц вают стрелки.
Склеим теперь t\ с t\, t\ с t\, t\ с t\y
I I c *io> ^5 c *u> *e c ^i2» так чт0 вместо
'5 двенадцати отрезков £},...,^2 будем иметь
только шесть, которые обозначим попреж-
U\ нему через t^...ft\ (с теми же ориентация-
ми, которые эти отрезки имели раньше).
Это склеивание превратит комплекс,
состоявший из наших 24 треугольников, их
вершин и сторон, в триангуляцию К
проективной плоскости, число двумерных,
одномерных и нульмерных элементов которой равно соответственно
с
t'n
('г
Ч
У
ч
*\
n m 1 1
t;
<J
Черт. 107.
Положим
Тогда
р2 = 24, Pi = 33, г0= 13-
24
= Ztj.
Итак, цепь 2г* есть граница некоторой целочисленной цепи х
комплекса К- Докажем, что никакая целочисленная цепь комплекса К
не имеет г1 своей границей. Пусть, в самом деле, существует
целочисленная цепь у2, удовлетворяющая условию ky2 = z1. Прежде
всего убеждаемся в том, что на всех t2. цепь у2 принимает одно и
то же значение. В самом деле, в противном случае можно было бы
найти два треугольника А и t2., на которых цепь у2 принимала бы
1 j
разные значения, и которые бы имели общую сторону, лежащую
внутри квадрата. Но в этом случае цепь ку2 непременно
принимала бы на общей стороне этих двух треугольников значение,
отличное от нуля, что находится в противоречии с предположением
&у2 = г1.
Итак, цепь у2 принимает на всех t} одно и то же значение а:
У*
•• ах*
Так как x2=2z1, то ky2 = 2az1) что при
находится в противоречии с предположением]^2 =
целочисленном а

§ 6] НИЖНИЙ ГРАНИЧНЫЙ ОПЕРАТОР (ОПЕРАТОР Д) 2б9
Упражнение. На черт. 108 изображена триангуляция К10
проективной плоскости, состоящая из 10 треугольников, их
сторон и вершин. Цепь zl = t\-\-t\-\-t\ (ориентированные отрезки t\
указаны на чертеже) предстарляет собою цикл. Докажите, что
2гх есть граница некоторой целочисленной цепи и что цепь г1
не является границей никакой целочисленной цепи комплекса /С10.
4°. Черт. 109 после склеивания
противоположных сторон квадрата
представляет собою триангуляцию тора.
0 />
V '
*7'
/ и
^ /
/ J
Черт. 1С8.
Черт. 109.
Цепь х1 принимает на треугольниках, обозначенных круглыми
стрелками и ориентированных nG этим стрелкам, значение 1; на осталь-
t\
\А
ч
ч/
у.
о/
п
ч
Черт. ПО.
ti
ных треугольниках цепь х2 принимает значение 0. Ориентированные
отрезки t\, z=l, 2,...,12 указаны на чертеже. Положим
г = 12
■2
г = 7
2*, *i-2U *
^=6
■ 2 /J.
Тогда Дл:2 = г1 — (2*} + zp.
5°. Черт. ПО после склеивания сторон t\ прямоугольника
переходит в триангуляцию листа Мёбиуса. Ориентации t\ треугольников

270
ЦЕПИ. ОПЕРАТОР А
[гл. VII
этой триангуляции указаны на чертеже так же как и ориентирован-
6
ные отрезки t\. Полагая л;2= 2 ^> zl — 2 &> имеем Ал;2 = <г1 -f-
6°. Комплекс Л" представляет соэой пространство между двумя
концентрическими сферами, разбитое на призмы радиальными
разрезами. Цепь Xs принимает значение -f- 1 на всех этих призмах,
одинаково ориентированных. Цепь Ах3 принимает на всех основаниях
этих призм, лежащих на внутренней сфере, значения +1, а на
внешней —1, на остальных же 0.
6:3. Циклы; цепи, гомологичные нулю; группы Zr($) и Нг(&).
Рассмотрим ближе гомоморфное отображение А группы Z/(5l, 31)
в Z/-1 ($, 31). Ядро этого гомоморфизма обозначаем через Z£ ($Д).
Группа Z£($, 21) <=//($, 31) состоит из всех цепей хг,
удовлетворяющих условию А# хг = 0. Эти! цепи называются /--мерными
циклами (подробнее: r-мерными А-циклами) клеточного
комплекса 51 по области коэффициентов 51.
Так как для любой нульмерной цепи х° имеем Ах° = 0, то все
нульмерные цепи суть циклы, т. е.
Z°(5l, 51) = ЩШ, 51).
Образом группы Z/(5l, 51) при гомоморфизме А является
некоторая подгруппа группы Z/-1 ($, 51), которую мы обозначаем через
/^/д""1 (^, 51). Очевидно, для того чтобы цепь хг являлась элементом
группы Я£ (51, 51), необходимо и достаточно, чтобы существовала
цепь xr+1^Lr+\R, 21), удовлетворяющая условию &&хг+г = хг.
Теорема [6:3]. Если St есть n-мерный клеточный комплекс,
то Н™ (51, %) есть нуль-группа.
В самом деле, группа Lw+1(5l) есть в этом случае нуль-группа,
так что образ её при любом гомоморфизме, значит, и при
гомоморфизме А, есть нуль-группа, что и требовалось доказать.
Замечание. Как и в случае групп Z/(5t, 51), мы часто будем
опускать аргумент 51, а также, когда это возможно, и значок А.
Таким образом, вместо ZrL (51, 20 и И\ (51, 51) мы будем обычно писать
просто Zr(5l) и Яг(51). Особо важные частные случаи 51 = 7 и
21 —7Ш будем выделять, употребляя сокращённые обозначения
*№)> tfj(ft) вместо ZJ(^f Д Я£(Й\7) и Z;(St), Я^(й) вместо
-ВД Ли), «ДО, JJ.
Если клеточный комплекс 51 состоит из всех ориентированных
симплексов симплициального комплекса К, то вместо Zr(5l), ЯГ(Я)
и т. п. пишем Zr(K), Hr(K) и т. д.
6:4. Гомология. Знак —. Гомологическая независимость
цепей. Цепи, являющиеся элементами группы Яг(51, 51), называются
/--мерными цепями, гомологичными нулю в 51 по области

§ б] НИЖНИЙ ГРАНИЧНЫЙ ОПЕРАТОР (ОПЕРАТОР Д) 2?1
коэффициентов 21. Для обозначения того, что цепь хг
гомологична нулю, пишут
(6:41) JC — 0 в Ж (по 91).
Из того, что ИГ(Щ есгь группа, сразу следует, что знак —
обладает следующими свойствами:
1°) 0 — 0;
2°) из хг—0 следует — хг—0;
3°) из х[~0, ^~0 следует x[±xl~(\
Мы говорим, что цепи хгх и х^ гомологичны между
собою в $ (по области коэффициентов 21) и пишем
х\~х\ в Л (по 2(),
если
х[ — хг2~0 в 51 (по 21).
Из только что установленных свойств знака — 0 следует:
1°) X — X)
2°) если хх~х2, то х2~хг;
3°) если хг~ х2 и х2—лг8, то хх-^х^
Кроме того, если хг—уг и х2~у2, то хх ±х2~уг rtу2.
Пусть
(6:42) ^...,^
-цепи клеточного комплекса & по области коэффициентов 91
(наиболее важен тот частный случай, когда цепи (6:42) суть
целочисленные цепи). Пусть cl9...,cs — целые числа. Линейная комбинация
V^jtf цепей (6:42) называется тривиальной, если все
коэффициенты ci равны нулю; в противном случае она называется
нетривиальной.
Если все цепи хг{ суть цепи по области коэффициентов Jm, где
т — простое число, то линейная комбинация V с{хг{ (все ci—целые
числа) называется тривиальной, если все с{ делятся на т.
Определение [6:42]. Пусть 21 одна из областей
коэффициентов У, SR или Jm. Цепи (6:42) по области коэффициентов 21
называются гомологически независимыми в К, если никакая
нетривиальная линейная комбинация этих цепей не гомологична
нулю в SL по 21.
Замечание 1. Особенно важен случай систем гомологически
независимых целочисленных цепей.
Замечание 2. Так как все упомянутые в [6:42] области
коэффициентов 21 суть кольца, а цепи xr £ U ($, 21) суть линейные
формы с коэффициентами из 21, то можно говорить и о линейных
комбинациях 2fli^ цепей (6:42) с коэффициентами а4£31 и
сформулировать то же определение [6:42] также и следующим образом:

272
ЦЕПИ. ОПЕРАТОР А
[гл. vn
[6:420]. Цепи (6:42) клеточного комплекса 51 по области
коэффициентов *[ (где 51 есть одно из колец У, 9t или Jm) называются
гомологически независимыми в $, если цепь вида V a^JJ, гдеа4£51,
лишь тогда гомологична нулю в $ по 31,_кд>гда каждый из
коэффициентов ai есть нулевой элемент группы 51.
Доказательство эквивалентности определений [6:42] и [6:420]
предоставляется читателю.
6:5. Куски цепей и циклов. Пусть Я — клеточный комплекс,
5?0— клеточный подкомплекс комплекса 5t Пусть xr£Lr{&).
Вообще говоря, k$$0xr ф К0А^л:г, как показывает следующий
элементарный пример. Пусть клеточный комплекс В состоит из всех
ориентированных сторон и вершин треугольника \е0 е1 е2\; пусть $0 есть
замкнутый подкомплекс комплекса $, состоящий из ±(е0 ег)у
Определяем х1 £ L1 (Ж) как линейную форму
л;1 = (ео е\) + (*i ez) ■+ 0-2 *<>)•
Очевидно, $0 х1 = (е0ех)у А^л:1 = 0, KqA^a:1 = 0,
^0^х1 = е1 — е0ф0.
Тем более важно следующее предложение:
Теорема [6:51]. Если 5?0 есть открытый подкомплекс
комплекса & и xr£Lr(&), то
Д*0Я0*г = Яод**г.
Доказательство. Пусть tr~l — произвольная (г—1)-мерная
клетка комплекса Е0. Так как $0— открытый подкомплекс
комплекса $, то всякая клетка trv для которой (/J : tr~r) ф 0,
принадлежа к О®?-1, принадлежит к $0, причём значение (Р: р-1) не
зависит от того, рассматриваем ли мы клетки t\ и tr~l как
элементы комплекса & или как элементы комплекса 510.
В частности, множество клеток trp инцидентных *) с клеткой
Р'-1 в $, совпадает с множеством клеток, инцидентных с клеткой
tr~l в комплексе $0, и соответствующие коэффициенты
инцидентности (t^'.P-1) равны в обоих комплексах.
Поэтому V (ir.'.tr-1)xr{tri) имеет одно и то же значение, берём
ли мы сумму по всем ^£5?, инцидентным с Р'-1, или по всем
trj£8>0* инцидентным с tr~x. Но первая сумма равна значению
510А^д:г, а вторая — значению А^Д0хг на tr~x.
Следствие. Если xr£ZrL(5?) и &0 есть открытый клеточный
подкомплекс клеточного комплекса Ж, то й0гг £ Z£($0).
*) См. определение |4 :12|.

§ б] НИЖНИЙ ГРАНИЧНЫЙ ОПЕРАТОР (ОПЕРАТОР Д) 273
В самом деле,
6 :6. Продолжение цепей и циклов. Пусть снова 510 есть
подкомплекс *) клеточного комплекса & и пусть *£ £ Z/($0). Рассмотрим
продолжение E$xrQ цепи хг0 па комплекс $, т. е. цепь E^xr0^Lr (S),
определённую так:
Е$хЪ(П = х1(П если t'ZSto.
Е$хг0(У) = 0, если *'$5?0-
Вообще говоря,
Для того чтобы убедиться в этом, достаточно определить St как
клеточки комплекс, состоящий из двух ориентации (е0ег) и (еге0)
одномерного симплекса (е0ех) и его вершин ±(>0), ±: (е^.
Открытый подкомплекс К0 комплекса К состоит по определению лишь из
двух ориентированных одномерных симплексов (eQet) и (еге0).
Полагаем
*о ^ (*o*i)-
Очевидно, A^0.\:J = 0, следовательно, и E#Aa0#J = &•
Но
ДяЬ^= ^i — ^o^-O. .
Тем более важно следующее предложение, в некотором смысле
двойственное теореме [6:51]:
Теорема [6:61]. Если 51 есть клеточный комплекс, а 510—
замкнутый подкомплекс комплекса 5?, шо для всякой цепи
xr^Lr(%) имеем
^Ейх1= E^Qxr0.
Для доказательства рассмотрим произвольную (г—1)-мерную
клетку ^-i£$.
Тогда
A*£**S (*- 0 = 2 (<«: ^') £« «5 (Ф
(суммирование по всем tfj£St, инцидентным с ^~1). Слагаемые в этой
сумме, соответствующие клеткам ^, не входящим в $0, равны нулю,
так как для таких tr. имеем Z^xjj (гр = 0. Слагаемые,
соответствующие клеткам ^£5?0, суть (*p^-i) £**;(# = (^:^"1)^(^).
В частности, если ^-1 не входит в St0, то, в силу замкнутости
подкомплекса 510 комплекса 51, ни одна клетка tf, инцидентная
с £г-1, не может принадлежать к $0.
*^ См. подстрочное примечание в начале арт. 5:6.
18 Александров П. С.

274
ЦЕПИ. ОПЕРАТОР Д
[гл. vii
Итак:
j если ^-'^Ro, то b*E»xrQ (?-*) = О,
(1) j если ^_i £ ^0, то A^jcj (/r-i) = ^ (^: *•-») *J(ty,
где суммирование производится по всем t%£R0, инцидентным с ^_1.
С другой стороны, по определению операторов Es и At:
J если F-1 £ %, то Eg A K xr0 (f-1) = О,
I если /'-^gSo, то £*A*0^(f-1) = Aif0Jc;(?-1)=s
где суммирование производится по всем £££$0, инцидентньф с р-1.
Сравнивая (1) с (2), видим, что
что и требовалось доказать.
Рассматривая цепи как линейные формы *), т. е. считая, что
Lr (510) с Lr(5l) и что, следовательно, оператор Е$ есть
тождественное отображение группы /,Г(Д0), соответственно Lr-1(^Q)9 на себя,
можем теорему [6:61] сформулировать и так:
[6:610]. Если $0 есть замкнутый подкомплекс клеточного
комплекса 51 и *5£Lr(St0), то
В частности, если $0 есть полный симплициальный комплекс К0,
то он замкнут во всяком объемлющем его симплициальном
комплексе К- Поэтому:
[6 :6100]. Каков бы ни был симплициальный комплекс /С,
содержащий полный симплициальный комплекс К0 в качестве
подкомплекса, для любой цепи xr0^Lr (К0) имеем
Д**; = Д*04.
В частности, если Д^ол;£ = 0, то и Дгх^==0, т. е.:
[6:62]. Д-цикл замкнутого подкомплекса К0с К есть в то же
время и Д-цикл комплекса К.
[6: 63]. Д-цикл полного симплициального комплекса К0 есть
Д-цикл всякого симплициального комплекса /С, содержащего К0 в
качестве подкомплекса.
*) См. замечание в арт. 5:6.

§ 7] основной Случай: $ есть d-комплекс 275
§ 7. Основной случай: $ есть а-комплекс
7:1. Основная формула ААлгг = 0. Пусть tr — элемент
клеточного комплекса Ж. Вместо Д# пишем просто А. Вычислим значение
цепи ДД*Г на каком-либо элементе 1Г~2£$. По формуле (6:12)
имеем
(ДА*' . f-2) = ^ (/J-1 :^-а)(Д^ • ^-1)>
где суммирование взято по всем ^J""1, инцидентным с /г-а. Но, по
определению цепи Д^г,
так что
(7 :110) (АД*' • *"-*) = 2 (^ : *J ~1) (? ~* : <г-а) *)•
J
Отсюда и из определения а-комплекса (§ 4) непосредственно
следует:
[7:11]. Для того, чтобы клеточный комплекс $ был а-ком-
плексом, необходимо и достаточно, чтобы для любого элемента
tr£& выполнялось условие
(7:11) ДД^ = 0.
Из (7:11), в свою очередь, вытекает, что для любой цепи
хг=^а$ будет ДДл;г= ^а4ЬМ* = 09 т. е.
[7 : 1]. Если й есть а-комплекс, то для любой цепи х
комплекса & имеем
(7:1) ДДх = 0,
или
[7 :1']. Во всяком а-комплексе граница всякой цепи есть цикл.
Или, наконец:
[7:1//]. Если & есть а-комплекс, то
(7:10 Я£(ЯД)ЕЗ[(& эд)-
*) Читатели, пропустившие § 4, заканчивают настоящий артикул так:
из [7:110] и [3.25] следует ДД^ = 0
и, значит, для любой цепи xr€Lr(K)
(7:1) ДДх»- = С.
Другими словами:
[7 :1']. Граница всякой цепа есть цикл
Или
(7: F) Hr(K)C.Zr(K).
18*

276
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
Замечание. Условие [7 :1] = [7 : Г] = [7 :1"], очевидно, не-
обходимо и достаточно для того, чтобы клеточный комплекс ft
был а-комплексом.
7 :2*). Замкнутые и открытые подкомплексы а-комплекса.
Теорема [7:2]. Всякий замкнутый и всякий открытый
подкомплекс а-комплекса есть а-комплекс.
Доказательство. Пусть ft0— открытый подкомплекс
а-комплекса ft; пусть tr и tr-~ — какие-нибудь элементы соответственно
размерностей г и г — 2 комплекса ft0- Все элементы К"1
комплекса ft, инцидентные с tr~2 в ft, принадлежат ft0, и
коэффициенты инцидентности {tr:t^~1) и (tr.~1 \tr-2) в ft и в fto одни и
те же. Поэтому и сумма
(7 :21) ^(tr •tj-1)Vj'~i :tr~2)
не зависит от того, берём ли мы её в 51 или ft0. Так как ft есть
^-комплекс, то сумма (7:21), взятая в ft, значит, и взятая в ft0,
равна нулю, так что ft0 есть ^-комплекс.
Пусть теперь ft0— замкнутый подкомплекс а-комплекса St и tfr £ft0.
По теореме [6 :610] имеем
так что ^0 есть я-комплекс.
Так как комплекс ориентированных элементов полного симпли-
циального**) комплекса есть ^-комплекс, то из [7:2] вытекает:
[7 :20]. Комплекс ориентированных элементов любого
замкнутого, а таг же любого открытого подкомплекса полного симпли-
циального**) комплекса есть а-комплекс.
7 :3. Слабые гомологии целочисленных циклов; двойная
область коэффициентов. Вернёмся к примеру 3° артикула 6:2. Там
был рассмотрен целочисленный цикл г*, который сам не
гомологичен нулю в ft, тогда как цикл 2г* гомологичен нулю в ft. Другими
словами, цикл г^ не будучи элементом группы Я* (ft, J), является
элементом её дивизионного замыкания ***) в группе Z|(S, J).
Определение [7:31]. Пусть Ш — какой-нибудь а-комплекс.
Дивизионное замыкание группы #£(ft) в группе ZJ (ft), совпадающее,
очевидно, с дивизионным замыканием той же группы в Z£(ft),
обозначается через Я[Д£); циклы, являющиеся элементами группы Я£($),
называются циклами, слабо гомологичными нулю в ft.
*) Читатели, пропустившие § 4, пропускают и этот артикул.
**) Или полиэдрального.
***) Определение дивизионного замыкания подгруппы см. Прибавление I,
арт. 1 :2.

§8]
СИМПЛИЦИАЛЬНЫЕ ОБРАЗЫ ЦЕПЕЙ
277
Если гг^Я^(Е), то существует цепь xrfl £££+ *($),
удовлетворяющая условию
где а—натуральное число. Тогда — xr+1 £ Z/ (Я, 91) и, очевидно,
Итак, циклы, слабо гомологичные нулю в Л, могут быть
определены как целочисленные циклы, являющиеся границами цепей
с рациональными коэффициентами, т. е, цепей
х'*1 £[*($, 81).
Другими словами:
(7 :31) Щ($) = ZJ(R)n .^(Я, 31).
§ 8. Симплициальные образы цепей.
8:1. Симплициальные образы ориентированных симплексов.
Пусть t\ — ориентированный симплекс комплекса Ко.
<5 = (^о--«
доопределим целочисленную цепь
SH^L/iK,,},
задавая её значения на всех ориентированных симплексах Г
комплекса /Са следующим образом:
Г. Если Ь^\ГА Ф\Р\, то полагаем
(5^-0 = 0-
2°. Пусть Гл = {ел...е„) и S\\t§ = |Л|. Тогда
***<* ^?0 == ^аг'о> • • ' » ^* *V ~ ^очг>
(где * ,.. ., eai суть те же еа0>. . ., £аг, но, может быть, в другом по-
рядке); тогда, очевидно,
где s = ztl есть знак перестановки:
\h h • • • V

278 ЦЕПИ. ОПЕРАТОР Д [ГЛ. VII
В этом случае полагаем
Согласно этому определению цепь ££/£ = (), если в/Са нет симплекса
try удовлетворяющего условию
$1Щ\ = \К\>
т. е. если образ симплекса \РЛ при отображении S\ есть симплекс
меньшего, чем г, числа измерений.
Другими словами имеем: ^ Р = 0 тогда и только тогда, когда среди
вершин
по крайней мере, две совпадают.
Если же все вершины S§ е ро,. . . ,S$ e$r различны между собой, то
\Sle,0...S\e,r\
есть симплекс комплекса Ка и S^tC есть ориентированный симплекс
8:2. Гомоморфизм 5J группы Lr(/Cp) в Lr(Ka), порождённый
симплициальным отображением S$ комплекса К§ в /fe.
Пусть
х\ === i аУ itf
У
—какая-нибудь цепь комплекса /^ по области коэффициентов %.
Полагаем
(8:21) ^.^S^fy-
У
Цепь Slx££Lr(Ka) называем образом цепи x^£Lr(K$) при симпли-
циальном отображении 5£.
Очевидно, для двух цепей х£± £ 1Г (/Ср), л;£2 £ Z/ (/^)
имеем
так что определённое равенством (8:21) отображение группы ЬГ(К$)
в Lr(Ka) представляет собою гомоморфизм,
Вычислим значение цепи

§ 8]
СИМПЛИЦИАЛЬНЫЕ ОБРАЗЫ ЦЕПЕЙ
279
на каком-либо ориентированном симплексе F = tr комплекса /С«.
Для этого, обозначая через tr. произвольную, но определённую
ориентацию каждого симплекса Trai комплекса К„ поступаем так:
или, так как а$ = (*£ • #.),
(8 = 22) (Si х; ■ rj = £ (5S ^ ' ^ Ц ' <&)■
/
Эта формула может быть несколько упрощена, если выбрать
ориентации #. симплексов Tjf.£/Cp так, чтобы при
ар/ J аг '
всегда было
а р/ аг
При этом выборе ориентации Е формула (8:22) переходит в
(8:23) (^-^)=2(^-'p,
/
где суммирование распространено" на все #.,
удовлетворяющие условию
Задавая ориентации симплексов соответствующими упорядоченными
остовами, можем, наконец, переписать равенство (8:23) в виде
(8: 24) S\ xl (*а0. . . О - 2 х\ Ы' ' ' W'
где (еа0,. . . ,£аг) есть какой-либо упорядоченный остов комплекса /Са,
и сумма справа берётся по всем упорядоченным остовам (%/,.. .,0я/г)
комплекса /fp, для которых
8:3. Переместительность операторов А и 5^. Докажем для
любой цепи xZ£Lr(K$) тождество
(8:3) AS|^ = 5JA^.
Вследствие линейности операторов 5J и А достаточно доказать
тождество (8:3) для случая х1^ = t\,, | ^ | £ К$.

280
ЦЕПИ. ОПЕРАТОР А
[ГЛ. VII
Пусть t\ = (е°0. . .е^.). Рассмотрим два случая:
1°. 5^=0;"
2°. ЩфО.
Первый случай. SP#=0. Это значит, что, по крайней мере,
для одной пары вершин е^, е$к симплекса |/Г|
(8:30) 5^ = 5^.
В этом случае A Si ti = 0, и надо только доказать, что и S\ A # = 0.
Подразделим исследуемый случай снова на два случая:
1а) Имеется только одна пара вершин е^ь е^. симплекса #,
удовлетворяющих условию (8:30).
16) Имеются, по крайней мере, две такие пары вершин.
В случае 1а) без ограничения общности можно предположить,
что единственная пара вершин, о которой идёт речь, есть пара е^0,
e^v т. е. что
тогда как для всякой пары вершин e^h e$k, отличной от пары е$0,
*р„ имеем Sle^Sle^.
Тогда
(8:301) Д/£ = 2(—D* (*р0. • ■ V • -*эЛ
причём для &^£0, &^1 имеем
так как среди вершин ^0,. . .,e^ki. . ,,^г имеются вершины £ро> *pi»
а для них £Р *ро = 5^ *р1.
Следовательно, из (8:301) получаем
52 А % = ^ ('pi '<ю • • • V) — Sl ('eo ^2 • • • V> =
= (52 *Р1 5Р *р2. . . 5Р ^ - (5Р *р0 5Р ^. .. фрг) ■
Но ^о^зо == 5£ вр1, поэтому
и значит
5Р А Й = 0,
а р
В случае 16) среди вершин 5^еро,.. .,5аЦь_„ S£e3fc+i>- • -»^ерг
при любом А: имеются, по крайней мере, две тождественные, поэтому
Sl(e0...ek...er) = 0

§ 8] * СИМПЛИЦИАЛЬНЫЕ ОБРАЗЫ ЦЕПЕЙ 281
Итак, в случае 1° тождество SjA^p = 0, и следовательно,
тождество (8 :3) доказано.
Во втором случае, т. е. когда s£ %ф0,
SJ р = (<Sa^so • " • $*е$г)>
и
Д*р = 2(—1)*(*ро. . .£3fc...epr),
= S ( — 1 )fc 0&po • - - i1*pft. - ■ s£*pr)>
т. e.
as£*S = s£a*p,
что и требовалось доказать.
Из (8 :3) следует, если х$ есть цикл, то и slx$ есть цикл; если
х$~ 0 в /fp, то 5^АГр—О в /fe, т. е.:
[8 :31]. При гомоморфизме si группы Lr(К$) в Lr(Ka) группа
Zr{K$) отображается в Zr (/Q, а НГ(К$) в Нг(Ка).
8:4. Случай открытых подкомплексов. Пусть даны два
полных симплицнальных комплекса Ка и К§ и в них-замкнутые
подкомплексы Ка0аКа и /fp0cz/fp- Положим для краткости:
G* = ^Сх \^оо» ^р— ^ \ ^W
Пусть дано симплициальное отображение si комплекса /Ср в Ка>
удовлетворяющее условию
(8:40) sS(ffpo)£K«o.
Каждой цепи xl £ Z/ (Gg) ставим в соответствие цепь GJS\x\ £ Ir(Ga).
Этим установлено гомоморфное отображение GaS% группы Lr(Gp)
в Lr(Ga). Докажем, что
[8:4]. Гомоморфизм Ga5^ коммутирует с граничным
оператором А в смысле следующей формулы:
(8 : 4) 0Л^х\ = &GaGaSl4-
В самом деле, так как Gp— открытый подкомплекс комплекса
/Ср, то на основании теоремы [6 : 51]
Дб^ = GpA^ = (/Ср\/Ср0) А^ = А^— КВ0Ал-
так что
(8 : 41) Sl^xl« S£A4— 55/fpoA4

282 ЦЕПИ. ОПЕРАТОР А [ГЛ. VII
Из (8:40) следует, что siK^xl£Lr (К«0),
так что GeSa/(po*p = 0 и
(8:42) GaS[^xl=GaSlb4-
С другой стороны,
(8 : 43) ^GaGasUl = G^sUl = 0aS^4-
В формулах (8 : 42) и (8 : 43) содержится (8 : 4).
Непосредственным следствием теоремы [8 : 4] является:
[8:40]. При гомоморфизме GaS£ группы Lr(G$) в Lr(Ga)
группы Zr{G§) и Hr{G§) отображаются соответственно в Zr(G<x)
и /F(Ge).
§ 9. Некоторые вспомогательные построения.
9:1. Пирамида над цепью. Пусть К—комплекс остовов. Пусть
<о/С>—пирамида над К (глава 4, арт. 2:3). Пусть tr —
ориентированный симплекс комплекса К. Ориентированный
симплекс *) (off) комплекса < о/С> называется пирамидой над
ориентированным симплексом ^.
Если
хг= ^а/г
есть цепь комплекса К, то цепь
(9: И) (o*0=Ik(<4)
комплекса < оК > называется пирамидой над цепью хг.
Для г>0 легко получаем
(9:12) А<оЯ> (оР) = Р — (рЬкР),
откуда
(9 : 13) Д<оЯ> (охг) = хг — (оДдаГ).
В частности, если zr есть цикл, то
(9: 14) Л<о#>(<0 = ^.
Для г = 0 имеем
(9: 120) Д(о/°) = *° —(о),
и если лг°= 2^,
(9: 130) Д(о*°) = л:0 —(2<*,)(о).
*) См. 3:1,

§ 9] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ 283
Замечание. Для открытой пирамиды оК (глава 4, арт. 2:3)
имеем аналогичные формулы:
(9: 120 boK(otr) = — obKF,
(9 : 130 ДоИ°*г) = — о&кхг,
(9: 14') До* (0*0=-О,
(9:1200 Кк(оР) = -(о\
(9:1300 Де*(о*°) = -(2«,)(«>).
i
[9:2]. Приложение построений арт. 9:1. Пусть г —
натуральное число и К— полный комплекс остовоп, обладающий следующим
свойством:
[9:210]. Любые r-f-2 вершины комплекса К образуют остов
этого комплекса.
Докажем, что в этих предположениях
(9:21) Z£(K) = /"№),
т. е. всякий r-мерный цикл комплекса К гомологичен в К нулю.
Для доказательства (9 : 21) обозначим через Кг замкнутый
подкомплекс комплекса К, состоящий из всех r-мерных остовов
комплекса К и из всех их граней.
Построим пирамиду <о/Сг>, и каждой вершине в комплекса
< оКг> поставим в соответствие вершину Se комплекса К по
следующему правилу:
1. Если е £ Кг, то полагаем Se = e.
2. В качестве So определяем некоторую произвольно
фиксированную вершину е0 комплекса /С
Из условия (9 : 210) следует, что S есть симплициальное
отображение комплекса <о/Сг> в К.
Пусть теперь гг — произвольный ~ r-мерный цикл комплекса К-
Цикл 2? есть в то же время цикл комплексов Кг и <оКг> и на
основании (9:14) гомологичен нулю в <о/Сг>; поэтому на основании
[8:31] цикл Szr — 2r гомологичен нулю в К, что и требовалось
доказать.
Частные случаи. Г. Если К=[Тп], то для любого г
справедлива формула (9 : 21).
В самом деле, при г <! п—1 комплекс [Тп] удовлетворяет
условию (9:2), так что формула (9:21) верна; при г>м формула
(9:21) следует из того, что группа Zrh{[Tn\) при г>м есть нуль-
группа.
2°. Пусть К= Ат", где Тп есть выпуклое открытое множество *)
пространства Rn. Условие (9:210), очевидно, выполнено для
любого г, и поэтому формула (9 : 21) верна также для любого г.
*) Определение комплекса К^п см. в главе 4, арт. 1 :5, пример 2.

284
ЦЕПИ. ОПЕРАТОР А
[гл. vii
3°. Пусть К— Тп= [Тп]\Тп есть комплекс, состоящий из всех
собственных граней л-мерного симплекса Тп\ условие (9 : 210) выпол*
нено для г<п—1; поэтому для 0<г<п—1 имеем
Zl(r) = rtl(r).
4°. Приложение к элементарным подразделен и ям*)
симплексов. Приложим понятие пирамиды над цепью к
доказательству следующего предложения, которое существенно
понадобится нам в главе 10.
[9 : 22]. Пусть Vй есть элементарное подразделение п-мерного
симплекса Tn=\eQa..en\ относительно его грани Т& = \е0.. ,ер\.
Тогда при 0<>О—1 всякий г-мерный цикл комплекса Vя
гомологичен нулю-в Vn:
1г(Уп) = Нг{\Г).
Доказательство. Пусть zr — какой-либо цикл комплекса V"
(0 < г ^ я — 1) **). Обозначим через Qr комбинаторное замыкание
комплекса, состоящего из всех симплексов, на которых цепь zr отлична
от нуля.
Построим теперь пирамиду
/Ср= <oQr>\
в ней в качестве замкнутого подкомплекса содержится пирамида К$0
над Qr П [Vn]\lA Дополнительный открытый подкомплекс К$\К$0
обозначим через Gg.
Имеем, обозначая через А границу в К§.
k(ozr) = zr— окгг,
причём okzr лежит на К$0 так что
(9:221) Що*) =*.
Положим теперь Ка=[Уп],
S\e = e, s[el = ei, slo = e0.
Так как, в силу замечания 3 арт. 4 : 3 главы 4, ни один из
симплексов комплекса Qr не имеет в числе своих вершин более р
вершин симплекса 7^, то S$ определяет одноимённое симплициальное
отображение комплекса К$ в К^ при котором К$0 отображается в***)
Ka0 = [Vn]\Vn- Отсюда, заменяя в формуле (8:4) цепь хг через
oz7" и полагая Ga = Vй, имеем
Vя SP Д <?р (аг*> = А ^ Vnsl (огП,
*) См. гл. 4, арт. 4:3, откуда заимствованы, в частности, и обозначения.
**) В комплексе Vn нет нульмерных элементов.
***) Проверка этого утверждения производится автоматически на
основании определения комплекса АГ8 и замечаний 1 и 2 главы 4, арт. 4:3.

§ 9] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ 285
т. е., в силу (9 : 221),
или, так как, очевидно,
S?zr = zr, Vnzr = zr,
о. 1 '
zr= &ynVnSl{ozr),
что и требовалось доказать.
9 : 3. Призма над цепью. Пусть К0—конечный полный комплекс
остовов; вершины /С0 занумерованы раз навсегда:
(9 : 30) а19... ,а8.
Построим при помощи этой нумерации вершин призму /С01 над
комплексом К0 (глава 4, арт. 2 : 4).
Пусть вершины верхнего основания
призмы /С01, соответствующие вершинам
(9 : 30), суть
(9 : 31) Ь
Если
то полагаем
^ = K0...a;,r), tlh^{bh0...bhr). .
Ориентированный симплекс/^ называется
проекцией ориентированного
симплекса trh комплекса К0 в верхнее основание
призмы Kov Если дана цепь хг0 =
— ^chtoh£Lr(K0), то полагаем х[ = 2 ciAh и называем цепь л:*
проекцией цепи хг0 в верхнее основание призмы АГ01.
Положим теперь для / = 0, . . ., г (черт. 111)
Черт. 111.
(9:32)
далее,
ил
■ой:
■{ь>
ho •
• hflbi
• чУ,
п4=2(—№&
и, наконец, для
(9:33)
хо = i ст/о/г
Цепь Пл:г называется призмой над цепью xr £Lr (/С) (в
призме /С01). Докажем основное тождество:
(9 : 34) АП4 = 4 — *i — ПД;с£-

286
ЦЕПИ. ОПЕРАТОР Д
[ГЛ. VII
Ввиду линейности обоих операторов А и П достаточно доказать
(9 : 34) для частного случая хг0 = % .
Пусть для краткости
*о = («о • • • агУ>
тогда
t[ = {b0...br).
Положим
&""1 = (а0 ... Л< ... яг), /*+1 = (b0 ... tyfy . .. аг\
(9:35) / = (*„.•• bfy . . . <*< . .. дг) (/>Л
^г,/ = (£0 .. . ^ . .. £Л ... ar) (i<;).
Так как в ^r+1 вершина ^ стоит на (j-\- 1)-м, а вершина aj на
(У4"2)-м месте, то
(9:36) Ay" = 2 (- 1)У'* — 2 (— 1У,4 =
=(- iyyr.j-/j) + 2(- 1)у-* — 2(- i)yf.
Так как *)
п£=2(-1)У+1,
то, пользуясь равенством (9:36), получаем
3 33
+ 2(- iy (2 (- i)VM- 2 (- Dy*>
Ho
/J = W,Jfl> o^° = 4 £ = fu
поэтому
2/^-2/;=^-'i
и, значит, •> •?'
Amo^^-^+2(-iy(2(-i)Vr'1-2(-i)V0 =
J *" < 3 i > 3
Требуется доказать, что
ДПЙ—й—£ —ПАЙ-
j=r
•) 2 означает 2 .

§ 9] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПОСТРОЕНИЯ 287
Значит, остаётся доказать
пай = 2(2 (- i)'+v,—2 (—1)<+^).
Но так как А^=2(—^-У&Г1 и оператор П—-линейный, то доста-
i
точно доказать, что
mS"1 =*2(-D^- S(-Vf*.
Имеем, в силу (9:32) и (9:35)
П/оГ1 = /i Для ; = 0, ...,i— 1,
П/оГ1 = j +1^* для У = '*> • • •» г — * •
Но, по определению,
п4~1=2(—iyn/оГ1
и, значит,
-*S(-i)^~S(-i^
j = о j = * -f i
что и требовалось доказать.
Если ^o^Zr(/C0) есть цикл, то ПА^о = 0, формула (9:34)
переходит в
(9:37) АП4 = 4 — гЬ
и мы имеем:
[9:37]. Каждый цикл комплекса К0 гомологичен в призме К01
своей проекции в верхнее основание этой призмы.
9:4. Приложение к симплициальным отображениям. В
качестве приложения только что проведённых построений докажем
следующую теорему, которая понадобится впоследствии (глава 14):
Теорема [9:4]. Пусть даны двасимплициальныхотображения
Si и Sa комплекса К§ в комплекс Кк, удовлетворяющих следую-
щему условию: каков бы ни был симплекс Т§ £ К$> существует
симплекс Та£Ка, имеющий в числе своих граней оба симплекса
sIt$ и S/Гр. Тогда при любом выборе цикла г$£21(К$) циклы
Si z\ и Slz\ гомологичны между собою в Ка.
Доказательство. Занумеруем в некотором определённом
порядке вершины e$v ...,e$s комплекса К$ и построим, опираясь

288
ЦЕПИ. ОПЕРАТОР А
[гл. vii
на этот порядок вершин, призму /С301 над- комплексом К§ (см. главу 4,
арт. 2:4).
Каждой вершине е^ — е^ нижнего основания К$0=К$ призмы
/Cboi ставим в соответствие вершину sle${ комплекса ЛГа, вершине
е$н верхнего основания К^ (являющейся проекцией в верхнее
основание вершины е^) ставим в соответствие вершину Sae^ комплекса Ка.
Покажем, что этим установлено симплициальное отображение «S
призмы /<poi B комплекс АГа. В самом деле, рассмотрим
произвольный остов
Т = J ^00 • • • е$0к е&1к • • • е$\п I
призмы ЛГзо1-
По определению призмы,
Кро • • • еЪп I
есть остов комплекса А^.
В силу отображения 6", остову
Т— |<?р00 .. . ер0ке$1к .. . <?з1п |
соответствует множество вершин
S(T) = \ S%0 . . . Sle^ S?eok . . . s'\n \
комплекса /Са. Но это множество есть подмножество множества
являющегося, по условию теоремы, остовом комплекса Ки> поэтому
и 5(Г) есть остов комплекса Кл.
При симплициальном отображении S, очевидно,
о г 03 г Р г <-/3 г
О-гро —Oa-S'p, 0£pi=Oe2p.
Так как (на основании [9:37])
г$о ~ £pi в #poi»
то
5гр0—-Szli в ЛГа,
т. е.
что и требовалось доказать.

Приложение к главе VII
а-КОМПЛЕКС ОРИЕНТИРОВАННЫХ ЭЛЕМЕНТОВ ПОЛИЭДРАЛЬНОГО
КОМПЛЕКСА.
1. Коэффициенты инцидентности полупространства и
плоскости, выпуклого многогранника и его грани. Пусть \Еп\—
полупространство я-мерного эвклидова пространства \Rn\, отсечённое
плоскостью \Еп~1\, или выпуклый многогранник с гранью \Еп~1 |.
Возьмём для \Еп\ и | Еп~х | какие либо ориентации Еп и
соответственно Еп~х. Определим коэффициент инцидентности (Еп : Z:n_1). Для
этого возьмём в \Еп\ симплекс Тп, имеющий грань Г"-1, лежащую
в | Еп~х [. Дадим симплексам Тп и Т11'1 ориентации*77 и tn~ly
соответственно, одинаковые с ориентациями Еп и Еп~~1.
По определению
(1: 11) (£»: E»-1) = (t» г/»-1).
Легко видеть, что (1 : 11) зависит только от ориентации IIй а П>! 1
и не зависит от выбора симплекса Г".
Пусть tn~l какой-либо симплекс, лежащий в Е"-1 и
ориентированный одинаковым образом с Е1'-1. Пусть е — точка, лежащая
внутри Е'К Тогда {Еп\ Еп~х) = -j-1 или —1, в зависимости оттого,
одинаковы ли или противоположны друг другу орпепгации (etn l)
и Еп) другими слонами,
(1: 12) (П* :£"-1) = (^""1)^"-
Если же ориентация t"-1 противоположна ориентации /i'1-1, то
(1 :13) (/?': Е"-1) = —(el"-*)H\
поэтому:
[1 : 1J. Если t"*1 — какая-нибудь ориентация симплекса
Г,ь~1с:\Еп'Л\ и е- - точка, лежащая внутри \Еп\у то
(1 :1) (/:« :Е» "^ ^ (^''-3)/;» • Р1~*Е»-1.
Если E>1~выпуклый ориентированный многогранник, а /:" ~1 его
произвольно ориентированная грань, то, как мы сейчас докажем,
коэффициенты инцидентности {ЕИ\Еп'1) обладают теми же
основными свойствами^ что и коэффициенты инцидентности ориен-
ш ированных симплексов.
* У Александр >в II. О.

290
ПРИЛОЖЕНИЕ К ГЛАВЕ VII
Первое свойство:
(—Еп : Еп-г) = (Еп : ~En~i) = —(Еп : Е» -*)
не требует доказательства.
Второе свойство:
(1:14) 2 (£" : ^Г1) (£Гг : £""8) = 0,
i
где £™ и £л-2 — произвольные ориентации многогранника \Еп\ и его
(п — 2)-мерной грани \En~2\, а суммирование берётся по всем (п—1)-
мерным граням J jE"T* 1|> причём Ef ~l — одна какая-нибудь
ориентация грани jjEj*~l|.
Докажем это свойство.
Так как среди всех (п—-1)-мерных граней многогранника \Еп\
только две грани, пусть | Е™~1 | и \Е™~1\, прилегают к |£w_2|, то
подлежащее доказательству равенство (1 :14) может быть
переписано в виде
(1 :15) (En:E^1)(E^-l:E}i~<2)^(En:E^-r)(E^l:E^2) = 0.
Так как левая часть равенства (1 :15) не меняется при замене
£п-1 на —е<п-1 или £w-i на —Е^-1, то достаточно доказать
равенство (1 :15) для одного какого-нибудь выбора ориентации Е%—\
Е^ л. Выберем же ориентации Е™ 1 и Е™ ~1 гак, чюбы было
(fi»-1 :£»-*) = +1, (f»-1:^-2)^^!,
тогда (1 :15) переходит просто в
(1 :150) (£»:£J-1)-f(£n:£?-1) = 0.
Для доказательства равенства (1 :150) возьмём в > Е"~2\ симплекс
Т"- 2 и ориентацию
этого симплекса, равную ориентации Еп-2.
Возьмём внутри l^""1! и [Е*-1] точки п0 и ех и обозначим
через t™-1, t™-1 ориентации симплексов 7'{J ~] ~- \е0е2ег. . ,еп | и
7^-1 = \ехе^е^. . ,сн |, равные соответственно ориентациям Е"-1 и
£J-J. Так как
(t»~* :tl 2)- (Zfj;-1 :/*"2)^ 1
и
(/»-2 : t" 2) — (Е>± -] : £"-2J — I
и

ПРИЛОЖЕНИЕ К ГЛАВЕ VII
291
Возьмём, наконец, точку е внутри \Еп\ и обозначим через tn, tn
ориентации симплексов Т0п = \ ее0е2.. ,еп\ и 7^ = \еехе2. . ,еп\,
равные ориентации Еп. Тогда
Так как точки е0 и ^ а значит, и симплексы Т™ и Г", лежат по
разные стороны плоскости |£7^~2|, то ориентации (е0ее2е%. . ,еп) и
(е^^з • . . еп) этих симплексов противоположны между собою; но
ориентации /^ и ^ одинаковы, поэтому если
t^ = s(e0ee2eB...en)y
то
f = — e(W3"-*n)
и
(£» :£?-1) = (^ :^-х)= —«((We- • •*»):(¥»«.• ••«»)) =
= ( —е)(-1) = в,
т, е.
(£": ££->) — - (^ •^Г"1),
что и требовалось доказать.
2. Так как для ориентированных выпуклых многогранников
определены коэффициенты инцидентности и при этом как первое,
так и второе свойство коэффициентов инцидентности остаётся в
силе, то ориентированные элементы полиэдрального комплекса К
образуют а~комплекс: цепи, циклы и т. д. этого а-комплекса
называются соответственно цепями, циклами и т. д. полиэдрального
комплекса К.
19*

ГЛАВА ВОСЬМАЯ.
Д-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ).
§ 1. Определения. Примеры. Простейшие общие свойства.
1 :1. Определение группы Д»'(Я)Д). Пусть St есть а-комплекс *)
Определение [1:1]. Группа
(1 : 1) А- (Я, «) = Z'A 1&Я)///£(ЯД)
называется r-мерной (нижней) группой Бетти или
r-мерной Д-группой или просто Дг-группой а-комплекса $ по
области коэффициентов %. Элементы группы ДГ(51Д) называются
/--мерными гомологическими классами комплекса 51 по
области коэффициентов 91. В частности, группа ДГ<Д,/)
обозначается просто через Д£(51); её ранг обозначается через тгг(51)
и называется r-мерным числом Бетти комплекса 51; её
элементы называются целочисленными гомологическими классами.
Вообще же вместо ДГ($Д) обычно пишем просто Дг(51). Пусть К есть
симплициальный комплекс. Предположим, что комплекс
ориентированных симплексов комплекса К есть а-комплекс St. Тогда вместо ДГ(51Д),
tJ(S() и т. д. пишем кг(К,%), кг(К) и т. д. и говорим о Дг-группах
и числах Бетти комплекса К. Это определение позволяет, в
частности, говорить о Д-группах полных симплициальных комплексов,
а также открытых и замкнутых подкомплексов полных
симплициальных комплексов.
Замечание. Группы Ar(St,Jm) называются группами Бетти
по модулю т и для краткости обозначаются через Д^(51). Если
т — простое число, то ранг группы Д^(5?) по модулю **) т
называется г-мерным числом Бетти комплекса Я по модулю
т и обозначается через ъг (R).
*) Глава 7, арт. 4:1; при чтении настоящей главы читатель может пони-
матьпод д-комплексом ® просто множество всех ориентированных симплексов
некоторой триангуляции К, под % — группу У и во всех выражениях вида
Ьг(%Щ, Z**(M), //г(#Д), Ы($%щ и т. д. заменять ft через К и
вычёркивать Ж.
**) См. Прибавление 1} арт. 3:3.

§ 1] ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 293
1 :2. Группа ДП(Л*Д\ Если Лм есть «-мерный комплекс, то
группа Ln+1(Rn,%) есть нуль-группа; поэтому группа №*(ЛПД) есть
нуль-группа и
(1 :2) АЛ(ЯЯД) = 2»»(ЯЯД).
1 :3. Группы А0 (АД). Во всём этом артикуле К означает
полный симплициальный комплекс.
« р°
Определение [1 :31]. Нульмерный цикл z°=y\aiei полного
/=i
симплициального комплекса К называется нормальным, если он
удовлетворяет условию V#f=0.
Очевидно, сумма двух нормальных циклов есть нормальный
цикл; если z°— нормальный цикл, то и — z°— нормальный цикл;
нульмерный цикл, тождественно равный нулю, есть нормальный
цикл. Поэтому нормальные нульмерные циклы образуют подгруппу
z00(K№) группы z°(/c,«).
Далее: если х1 есть одночленная одномерная цепь
xl = at\, t) = (ei0 ец)9
то Ал:1 = аМ1. = а (еп — ei0) = aei\ — aei0 s
т. е. граница одночленной одномерной цепи есть нормальный цикл.
Так как всякая цепь есть сумма одночленных, то мы доказали
следующее предложение:
[1 :32]. Граница всякой одномерной цепи есть нормальный
нульмерный цикл.
Следствие. Нульмерный цикл г^, гомологичный в К
нормальному циклу z°, нормален.
В самом деле, из [1 :32] следует, что г° — z\ нормальный цикл,
значит, сумма значений циклов z° и z\ одна и та же, а так как эта
сумма для г° равна нулю, то она равна нулю и для z°v
Докажем теперь обращение теоремы [1 :32] для случая связного К.
[1:33]. Всякий нормальный нульмерный цикл связного ком-
п 1скса гомологичен нулю.
Пусть
Р°
г = 1
есть нормальный цикл. Так как Vtf^O, г. е.а^* -а2— ад - ...—ярп,
то

294 Д-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
и достаточно доказать, что нульмерный цикл et — ег гомологичен
нулю.
Так как К—связный комплекс, то существует ломаная,
связывающая вершины ех и ei в комплексе К.
Пусть exeh . . . eikei
— эта ломаная. Положим
Очевидно, Ах1 = A (exeh) -f b(e4±ei2) -f . . . + A (eik_x eik) +
+ K*<kei) = (eh — ei) + (*<a — e4l) -f • • • -f (eik — eik_x) -f
-\-{ei — eik)=^=et — еъ чем теорема [1 :33] доказана.
[1 :34]. Пусть ех — какая-нибудь вершина связного комплекса К\
всякий нульмерный цикл z° комплекса К гомологичен некоторому
одночленному циклу вида аеХ1 где а есть некоторый элемент
области коэффициентов 51.
В самом деле, пусть z°-=^^aiei\ положим У\а1 = а} тОгда
г0— аех есть нормальный цикл, следовательно:
г°—ае1^0,
что и требовалось доказать.
Итак, нульмерные гомологические классы комплекса К взаимно
однозначно соответствуют циклам аех, значит, элементам группы 51.
Мы доказали предложение:
[1 :35]. Если К есть связный комплекс, то группа А°(/СД)
изоморфна группе %.
Следствие. Нульмерное число Бетти и нульмерное число
Бетти по простому модулю т связного комплекса равно единице
Обобщением этого предложения является следующая теорема:
[1 :36]. Нульмерное число Бетти, а также нульмерное число
Бетти по простому модулю т любого полного симплициалъного
комплекса равно числу компонент этого комплекса.
Доказательство. Пусть /Cv — компоненты комплекса К]
в каждом /С, берём вершину еч\ тогда для любого нульмер юго
цикла
имеем
К}г° ~ анен в /("„ а^ £ 91,
где только конечное число слагаемых может быть отлично от нуля;
Остаётся доказать^ что все нульмерные цикльд е^ гомологически

§ 1] ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 295
независимы между собой. Пусть линейная комбинация ^а^е^ яв"
ляется границей некоторой одномерной цепи х1:
V
Так как каждая компонента /С, представляет собой одновременно
замкнутый и открытый подкомплекс комплекса К, то по теореме
[6: 51] главы 7 имеем
&£\уХ — ^v^v» • * » ■ * •' *■'■" *■ ••'
et ег е3 *4 es е$ ?,
значит, в силу [1 :32], имеем av = 0,
что и требовалось доказать.
Из доказанного легко вытекает ерт*
следующее важное предложение:
[1:37]. Если 91 = 7 и при некотором целом с ф О цикл cz°
гомологичен нулю в К, то цикл z° также гомологичен нулю в К.
Другими словами *): группа Н%(К) дивизионно замкнута в Z°(/Q,
Щ(К) = Н°(К), или: группа к°0(К) не содержит отличных от
нуля элементов конечного порядка.
Для доказательства предположим, что сг°—<0 в К
сг° = Ах1.
Тогда, обозначая через /Q компоненты комплекса /С, имеем
KiC3fl = bKtx\
откуда на основании [1:32] следует, что Idcz0 = cKiZ° есть
нсрмальный цикл. Но тогда KiZ° также нормальный цикл, и потому,
в силу [1:33],
/Сг°-0 в К{
и
^=2^г0~0 в К
г
что и требовалось доказать.
1:4. Простейшие примеры групп Дг.
1°. Пусть К—комплекс, состоящий из всех отрезков \е1е2\,
l^2esl>--4 \es-jes\ и вершин еи £2>---> ев простой незамкнутой
ломаной линии e1...esm На черт. 112 взято s = 7.
Докажем, что группа А1 (К) == Z1 (К) есть нуль-группа. Положим
V = (%+i) * = 1, 2,.. ., s—U
*) См. Прибавление Т арт. 1:2,

296 Д-ГРУППЫ К0МП1ЕКСЭВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
S-1
Пусть z1==^^ait^— цикл. Тогда все ал равны между
1
собой. В самом деле, в противном случае можно было бы найти
два прилегающих друг к другу отрезка t\ и tfj, на
которых цикл принимал бы различные значения af-t и а{. Но в этом
случае цепь А г1 принимала бы в общей вершине е£ этих отрезков
значение а^х — а{фО и г1 не было бы циклом.
Итак, все а{ равны одному и тому же а £51:
г1 = а^]9 я £ Я.
1
s-1
Но AV^ = £S—ev значит, kz = a(es — e^; так как z1— цикл, то
1
а = 0, что и требовалось доказать.
2°. Комплекс К состоит из всех отрезков и Bef шин простой
замкнутой ломаной линии (черт. 113). Ориентируем все её отрезки
в одном направлении, например (считая ломаную К плоской)—против
часовой стрелки. Полученные одномерные ориентированные симплексы
обозначим через t/. Пусть
г1 =
2М
есть цикл. Совершенно так же, как в предыдущем примере,
доказываем, что все ai должны быть равны между собой, так что
р всякий одномерный цикл
комплекса К имеет вид
С другой стороны, легко
^
/7 \ /\ / видеть, что У]^, следова-
е5 е6 гсльно, и (c1 = aV/J. при лю-
Черт. 113. Черт. 114. бом а есть цикл, поэтому
группа /} (К) состоит из всех
пеней вида а V t\> где а произвольный элемент группы ?(. Значит *),
\1(К)^ /J(K)^%; в частности, при 41 = J группа Д1 (К) = Z1 (К)
есть бесконечная циклическая группа.
3°. Комплекс К состоит из всех отрезков и вершин двух
замкнутых ломаных линий, имеющих общую вершину и не имеющих
никаких других общих элементов (черт. 114).
Ориентируем каждую ломаную в определённом направлении
(например, считая их расположенными в одной плоскости, — против
часовой стрелки). Соответственно ориентированные отрезки первой
ломаной обозначим через ^., а второй ломаной- через t\.t
*) Знак '^ есть .знак изоморфизма двух групп.

§ 1] ОПРЕДЕЛЕНИИ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 297
Тогда всякие цикл z1(^Zl(K) принимает на всех отрезках одной
какой-нибудь из наших ломаных линий одно и то же значение,
например, значение ах на всех t\. и значение а2 — па всех t\m<t и
поэтому имеет вид
!*.2'И
или, полагай
D
Г
С другой стороны, так как z\ и z}2— циклы, то и все щпи вида
а1гЦ~aiz\ являются циклами; легко, далее, видеть, что
ахг\ -j- сцг\ = О
тогда и только тогда, когда a1 = atJ~~0. Другими словами, группа
A1(/C) = Z1(/0
изоморфна прямой сумме Й-р-\Ч; при % = ./'группа A1 (I\) ~- Z1 (К)
есть свободная абелева группа ранга 2.
4°. Следующее замечание понадобится нам при исследовании
дальнейших примеров (начиная с 5°) и по характеру своему
непосредственно примыкает к только что сделанным
рассуждениям.
Пусть К—одномерный комплекс, состоящий
из всех изображённых на черт. 115 отрезков и
их вершин.
Всякий одномерный цикл, zl этого
комплекса равен тождественно нулю, если он равен
нулю на, всех горизонтальных отрезках
комплекса К, не лежащих на стороне АВ
квадрата ABC П. Д
В самом деле, рассматривая отдельно
каждую из вертикалей AD, EF, PQ и ВС,
v >еждаемся повторением рассуждения 1°, что с1 равно нулю
на всех отрезках комплекса К, лежащих на каждой из этих вер-
■икалей. После этого применение рассуждения 1° доказывает, что z1
равно нулю и на всех отрезках комплекса К, лежащих на стороне АВ.
Вопрос. Пусть дан какой-нибудь одномерный цикл -г1 комплекса К-
Почему нельзя, применяя рассуждение 1° и рассматривая цикл-г1 на каждой
и? вертикалей и горизонталей черт. 115, доказать, что z*= 0? Найти
несколько отличных от нуля одномерных циклов комплекса К и выяснить,
почему вышеприведенное рассуждение для них теряет силу»
£ Р
Черт. 115.
В

298 А-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
5°. Пусть К0 — изображённый на черт. 116 двумерный комплекс,
состоящий из 18 треугольников, их сторон и вершин. Обозначим
через К0 подкомплекс комплекса К0, состоящий из всех
элементов KQi лежащих на границе квадрата ABCD.
Ориентируем границу квадрата A BCD
против часовой стрелки; соответственно
ориентированные 12 отрезков
комплекса Ко обозначим через /J,.
12
<L.
Цикл V/J обозначим через г1.
Ориентированные против часовой
стрелки 18 треугольников комплекса
К0 обозначим через ^-,/=1,2, ..., 18.
Докажем прежде всего лемму.
Лемма. В К0 каждый
одномерный цикл гомологичен нулю.
Доказательство. Для ка-
Черт. 116. ждого ориентированного отрезка /
комплекса К0> который на черт. 116
имеет горизонтальное или диагональное направление, мы
определяем одномерный цикл z(t) как цепь, принимающую значение 1
на следующих ориентированных отрезках:
1°) отрезок t\
2°) вертикальные отрезки от конечной точки t до АВ\
3°) проекция отрезка —/на АВ\
4°) вертикальный отрезок вверх до начальной точки t.
На остальных отрезках комплекса К0 цикл z (f) по определению
равен нулю *).
зз
Пусть теперь г1 = 2а^1 данный одномерный цикл комплекса К0
ориентации t\ уже выбраны нами для /=1,2,..., 12
(21 отрезков выбираем их произвольно, например,
и снизу вверх).
Построим цикл
для остальных
слева направо
где сумма
2'"<*(<!>
взята по всем горизонтальным и диагональным отрезкам; так как,
очевидно, всякий цикл г(ф является границей некоторого четырёх-
*) В отступление о г наших обычных обозначений в данном случае z(t)
означает цикл, построенный для каждого из рассматриваемых нами
отрезков /, а не значение некоторого цикла z на отрезке Л

§ 1] ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 299
угольника, составленного из треугольников *) комплекса К0, то
легко доказать, что zl ~ z', что касается цикла г\ то
элементы, на которых он отличен от нуля, суть либо
вертикальные отрезки, либо лежащие на АВ горизонтальные отрезки; отсюда
на основании 4° вытекает, что zf =0, следовательно, z1 ~ 0.
Теперь мы хорошо известным способом склеиваем из квадрата
ABCD тор: мы склеиваем АВ с DC и AD с ВС. Это склеивание
переводит комплекс К0 (черт. 116) в триангуляцию К тора,
состоящую из 18 треугольников, 27 отрезков и 9 вершин, а комплексно
в комплекс Д", состоящий из 6 отрезков и 5 вершин, образующих
вместе две замкнутые ломаные с одной общей вершиной. При этом АВ
и DC переходят в цикл г\ = t\ +1\ -\-1\ = — t\—t\ —1\, AD и ВС
переходят в цикл z\ = t\ -\-1\ +1\ = — t\0— t\x —1\2.
Оба цикла z\ и z\ суть, очевидно, циклы комплекса К, причём
(см. 3°) всякий одномерный цикл комплекса К имеет вид
агг\ + а2г\.
Вычислим группу AJ(/0- Пусть г1 — произвольный одномерный
цикл комплекса К. Положим Q = K0\K0 и
Ту же самую цепь х10, но рассматриваемую как цепь комплекса /v,
обозначим через х1.
Из kz1=0 легко следует, что Ах* есть нульмерный цикл
комплекса Kq. Так как Aa*J— нормальный цикл, а К0 — связный
комплекс, то AxJ-'O на К0, так что существует одномерная цепь yxQ
комплекса /С0, ограниченная циклом Ал;^; тогда х^—у10 еегь цикл,
и из леммы следует, что существует цепь х2 комплекса К0>
ограниченная циклом xl0— ylQ:
*хо = хо — Уг
причём
На черт. 117 zl принимает на жирно вычерченных отрезках,
ориентированных, как показывают стрелки, значение 1, на всех остальных
одномерных симплексах значение нуль; х\ = Qz1 принимает значение 1 на тех
из только что упомянутых отрезков, которые лежат внутри квадрата;
AxJ состоит из двух вершин е и е', взятых соответственно с
коэффициентами 1 и — 1.
*) То-есть границей цели, принимающей на составляющих этот
четырёхугольник треугольниках (ориентированных против часовой стрелки) одно
и то же значение 1 или — 1 и равной нулю на остальных треугольниках.
На чертеже один такой четырёхугольник заштрихован.

300 А-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ VIII
Цепь j/J принимает на вычерченных жирным пунктиром отрезках До и на
отрезке (е0е) значение 1, на всех остальных одномерных симплексах
значение нуль. Цепь jCq принимает на заштрихованных
треугольниках, ориентированных против часовой
стрелки значение —1, на остальных
треугольниках— значение нуль.
Обозначим через х2 ту же цепь х^ но
рассматриваемую как цепь комплекса К- Цепи
х1
Длг2
z'= z1 — Ах2 лежат на К.
Черт. 117.
В случае, разобранном на черт. 117, цепь
л1 — Ал*2 (на К) имеет вид, изображённый на
черт. 118; отрезки, на которых эта цепь принимает
значения, отличные от нуля, а именно, значение 1,
вычерчены жирно; ориентации указаны стрелками'.
Цикл zr = z1— Ах2 на К изображается, как
указано на черт. 119 и 120.
Так как z' = г1—Ах2, по самому своему определению
гомологичный ци:<лу г1 лежит на К, то он имеет вид axz\-\-a2zx2.
В случае, изображённом на наших чертежах очевидно, tft = tf2=l.
Пусть читатель сам построит несколько различных циклов г\
гомологичных на К циклу z\ -J- 2 z\.
Итак мы доказали: каждый одномерный цикл zl комплекса К
удовлетворяет гомологии
(1 :40) zi^aiz\ + a2zl
Докажем теперь, что каждый цикл*?1 комплекса К
удовлетворяет лишь одной гомологии этого вида, т. е. что коэффициенты
!/'
/
/
/ \
ц
А
/ 1
! ! т
4
Черт. 1J 8.
Черт. 119.
Черт. 120.
ах и й2 в (1:40) однозначно определены, если дан цикл z1. Этим
будет доказано, что группа А1 (К) изоморфна группам всех
целочисленных линейных форм с двумя переменными, т. е. есть свободная
абелева группа ранга 2.
Достаточно доказать, что из
(1:41)
№
a,,z:,
о
к

§ 1| ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 301
следует
(1:42) «1 = 0, а2 = 0.
Из предположения (1: 41) следует существование двумерной цепи*2
комплекса К, ограниченной циклом агх\-\-a2z}^ Легко видеть, что
значения цепи х2 на всех {\ равны одному и тому же числу а, но
тогда, обозначая- через х20 соответствующую цепи х2 цепь
комплекса /С0» имеем &х^ = azxQ%
Переход от комплекса К0 к комплексу АГ, происходящий
вследствие склеивания, есть симплициальное отображение /С0 на /С, при
котором К0 переходит в К, а цикл zl0 переходит, как легко
видеть, в нуль; так как, с другой стороны, при этом симилициальном
отображении цепь х'^ переходит в х2 и граница образа всегда есть
образ границы, то
Д х2 = atz\ -\~ a.2z\ = 0,
что по самому определению циклов z\ и z\ возможно лишь при
а1 = 0* а2 = 0, что и требовалось доказать.
6°. Склеиваем сторону АВ нашего квадрата (черт. 116) со
стороной DC, а сторону AD со стороною СВ (следить за
направлениями!). В результате этого склеивания из комплекса /С0 получается
триангуляция К' поверхности Клейна (глава 3, арт. 3 : 1).
Вычислим группу Д1 (К'). Прежде всего, совершенно так же, как и в
случае тора, доказываем, что каждый одномерный цикл zl удовлетворяет
гомологии (1 :40); однако, теперь числа ах и а9 уже не определены
однозначно гомологией (1 :40). Вместо этого имеем следующий
результат:
Для того, чтобы осуществлялась гомология
а^ + ^ОвГ,
необходимо и достаточно, чтобы было al = 0, а2 = 0 (mod 2).
Эго следует из тех же рассуждений, какие мы делали в случае
тора, причём наш новый результат получается вследствие того, что
теперь при симплициальном отображении, переводящем Kq в Л/
цикл z* перейдёт не в нуль, а в цикл 2z\\ таким образом, вместо
тождества a^-l-a^ej —0 получим теперь тождество
a\z\ ~\~ а221=== %аг1>
откуда следует
ах = 0, я2=2я.
Так как а — целое число, то наше предложение доказано. Из него
следует:

302 Д-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) Ггл. VII*
Одномерные гомологические классы комплекса К взаимно
однозначно соответствуют линейным формам аг{-|-л2г5, где ах — целое
число, а а2 — вычет по модулю 2.
Отсюда, в свою очередь, вытекает, что группа А1 (ЛГО есть прямая
сумма бесконечной циклической группы и группы порядка 2; одномерное
число Бетти триангуляции К' поверхности Клейна равно единице.
7°. Вернёмся кчерт. 116 и произведём подразделение изображённой
на нём триангуляции посредством проведения второй диагонали
квадрата. Эту триангуляцию (состоящую уже из 24 треугольников, их сторон и
вершин) будем снова обозначать через /С0. Склеим теперь направленные
отрезки t\ с /}, t\ с t\, t\ с t\, t\ с t\^ t\ c tln и t\ с t[r При этом
склеивании комплекс К0 переходит в триангуляцию К" проективной
плоскости*), а комплекс К0 в некоторый замкнутый пзлигон К"\ при
этом произведённая операция склеивания переводит выбранную нами
ориентацию полигона ABCD (против часовой стрелки) в некоторую
определённую ориентацию полигона /С". Замкнутый полигон К"
с установленной таким образом ориентацией может быть
рассматриваем как одномерный цикл г1 комплекса К". При симплициальном
отображении комплекса К0 на /£", возникающем вследствие
склеивания, цикл г\ комплекса К0 переходит в цикл 2г\\ с другой
стороны, рассуждениями, аналогичными предыдущим, мы доказываем,
что всякий одномерный цикл г1 комплекса К" гомологичен циклу
вида ахг\, но теперь уже а^ -0 в К" тогда и только тогда, когда
a1^0(mod2). Отсюда легко выводим:
Группа ЬХ{К") есть группа порядка 2; одномерное число Бетти
триангуляции К" проективной плоскости равно нулю.
Замечание 1. Можно легко доказать, что всякий
целочисленный двумерный цикл каждого из комплексов К, К', К" принимает
одно и то же значение на всех ориентированных треугольниках f^}
/ == 1, 2,. . . , 18 **), т. е. имеет вид
18
где а — некоторое целое число. Легко также видеть, что цепи этого
вида на комплексе К суть действительно циклы, тогда как на
комплексе Kf
Аг2 = 2аг],
а на комплексе К"
№ == 2аг].
*) Если бы не было произведено подразделение первоначальной
триангуляции /Со» то в результате склеивания не получилась бы триангуляция
(в полученном комплексе можно было бы найти два треугольника с одними
и теми же вершинами).
**) В случае К" число треугольников равно 24,

§ 1] ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 303
Отсюда следует, что группа A2(/C) = Zj*(/0 есть бесконечная
циклическая группа, а группы А2 (А") = Z\ {К') и А8 (/(") = Zf (/О суть
нуль-группы; двумерное число Бетти триангуляции К тора равно 1,
тогда как двумерное число Бетти триангуляции К' и К" поверхности
Клейна и проективной плоскости равно нулю.
Замечание 2. В главе 10 мы увидим, что все триангуляции
одного и того же полиэдра, а также гомеоморфных между собою
полиэдров имеют изоморфные группы Аг и, следовательно, равные
числа Бетти. Поэтому при рассмотрении предыдущих примеров можно
говорить о группах и числах Бетти тора, поверхности Клейна и
проективной плоскости.
Упражнение 1. Если склеить направленные стороны AD и ВС
квадрата ABCD, а стороны АВ и DC оставить свободными (черт. 116),
то получим триангуляцию плоского кругового кольца. Если же
склеить AD с СВ, оставив вновь АВ и DC свободными, то получим
триангуляцию листа Мёбиуса. Доказать, что в обоих случаях группа
А1 есть бесконечная циклическая группа.
Упражнение 2. Доказать, что группы А*(К), кЦК') и &\(К")
(где АГ, К\ К"—-рассмотренные выше триангуляции тора,
поверхности Клейна и проективной плоскости) суть группы порядка 2 и
что двумерное число Бетти по модулю 2 для тора, поверхности
Клейна и проективной плоскости равно 1.
Упражнение 3. Исходя из триангуляции К куба аналогичной
триангуляции квадрата ABCD, изображённого на черт. 116,
доказать, что двумерное число Бетти трёхмерного тора М^ (глава 1,
арт. 5:2, пример 6) равно 3. Образующие элементы группы А2(Лф
суть гомологические классы трёх двумерных циклов, возникающих
в результате склеивания противоположных граней куба.
Группа (А2(/Иф есть свободная абелева группа ранга 3. Группа
Л!(Л^) есть также свободная абелева группа ранга 3. За её
образующие могут быть приняты гомологические классы трёх циклов,
получающихся в результате идентификации рёбер куба.
Аналогичными рассмотрениями можно доказать, что для
многообразия Ж3, определённого как топологическое произведение окруж-
носги на двумерную сферу *), группы А1 (Мп) и A2(Af3) являются
бесконечными циклическими группами, и следовательно, одномерное
и двумерное числа Бетти равны ].
Если воспользоваться первой моделью этого многообразия (тело,
ограниченное двумя концентрическими сферами S2 и s2 с индифика-
цией этих сфер), то за образующую группы А2 (Ж3) можно взять
юмологический класс цикла г* получающегося так: берём
триангуляцию какой-либо сферы 6^, концентрической со сферами S2> s2,
*) Глава 1, арт. 5:2, пример 7.

304 Д-ГРУНПЫ КОМПЛЕКГОВ (НИЖНИК ГРУППЫ ЬЕТТи) [ГЛ. VIII
ориентируем все треугольники этой триангуляции, например, против
часовой стрелки, и даём цепи z^ на всех этих ориентированных
треугольниках значение 1.
За образующую группы Д^/И3) можно принять гомологический
класс одномерного цикла г\^ возникающего после склеивания S2 и s2
■—>■
из направленного отрезка pq (см. черт. 5 главы 1, арт. 5:2).
Найти циклы г20 и zxQ на второй модели многообразия М*
(удвоенный тор.).
Упражнение 4. Доказать, что а-комплексы, определённые
в главе 7, арт. 4:2, примеры 1, 2, имеют те же группы Бетти, чго
и триангуляция тора, рассмотренная в настоящем артикуле, пример 5.
Доказать, что я-комплекс, определённый в главе 7, арт. 4:2,
пример 3, имеет те же группы Бетти, что и триангуляция проективной
плоскости, рассмотренная в настоящем артикуле, пример 7. Наконец,
я-комилекс $, определённый в главе 7, арт. 4:2, пример 4, имеет
такие группы Бетти:
AJJ(^) есть бесконечная циклическая группа,
AJ(^) » циклическая группа порядка б,
Дд(й) » нуль-группа,
Д£(й) » циклическая группа порядка 6.
1:6. Некоторые элементарные я-мерные комплексы и их
группы Бетти.
[1:51]. Пусть комплекс К состоит из единственного элемента —
о шого /z-мерного симплекса. Группа \п(/(,%) = Z'1 (К,Щ изоморфна
группе 91. Группы Дг (А\ 51) при гфп суть нуль-группы.
[1:52]. Пусть /С=[Р']. Группа А" (/С, 51) = Z» (/СД) есть нуль-
группа. Группы ДГ(А", 51) (0 < г < п) суть нуль-группы (на основании
главы 7, арт. 9:2, 1°).
[1:53]. Пусть К=Тп^1Т"\\Тп. На основании главы 7, арт.
9:2, 2°, группы Дг(7,'/, 51) при 0 < г </z — 1 суть нуль-группы. Мы
увидим в артикуле 4:1, что группа Д^-^А') есть бесконечная
циклическая группа (это легко доказать и сейчас, непосредственно). Легко
показать также, что при любом 51 группа A" j (А", 51) изоморфна
группе 51 (арт. 4:1).
[1:54]. Пусть Оа — звезда /7-мерного симплекса Тр в какой-либо
//-мерной триангуляции IQ. Предположим, что в ()а имеется хоть один
отличный от Тр элемент, следовательно, хоть один (/>-+- lj-мерный элемент Тр~*~1*
[1 :Ь4,Г^Р]. Если г</7, то Д'*(07, 21) есть нуль-группа.
В самом деле, при г < р комплекс Оа не содержит ни одного
/--мерного элемента, поэтому LX (Оа, 20, Zr (Оа, 20, д-'(Оу, 2Г) СУТЬ нуль-группы.
При г = р единственный /--мерный элемент комплекса Оа есть Тр.
Давая симплексу Тр произвольную ориентацию ip и выбирая ориента-
цию tp+1 так, чтобы было (tpi l:tp) ™ 1, видим, что ^Qatp ' 1 — /р, откуда
следует, что Zp (Оя, VI) = //7>(Оа, ?() и А/> (Оа7 20 ( сть нуль-группа. Из
доказана го следует:

§ 1) ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 305
[1:54,о]. Звезда 0,к любого элемента триангуляции К* имеет отличную
от нуля группу До(0,у, Ж) лишь в случае, когда вся звезда Оа состоит из
одной («изолированной») вершины комплекса АГа.
[1 :54,w,M-i]. Пусть АГа есть я-мерный комплекс; пусть число л-мерных
симплексов комплекса Ка> имеющих данный (п — 1)-мерный симплекс Т™"1 £ Д^
своей гранью, равно k. В этом случае группа кп0(Оа) есть свободная абелева
группа ранга k — 1.
Доказательство. Пусть 7™, ..., 1™. с^ть все примыкающие к 'р'-1
/2-мерные симплексы комплекса Д^. Пусть /«-1 — какая-нибудь ориентация
симплекса V1"1. Дадим симплексам ГД /—1, 2,...,& такие ориентации /V,
чтобы (^:/п-1)=1. Цепи
^ = /J»~-4* / = 2,3,..-Л
суть целочисленные циклы я-мериого комплекса Оа. Так как симплексы
Т^,..., '/£ все различны между собой, то цепи 4*>- ••>zu суть линейно нез!
висимые элементы группы 2™(0а) и, следовательно, группы А о (07).
Остаётся доказать, что они являются системой образующих группы 2™ (Оа).
Рассмотрим сначала случай Лг = 1. Тогда циклов ^ вовсе нет, и требуется
доказать, что группа Z™ (Оа) есть нуль-группа. Это утверждение вытеьаетиз
того, что в наших предположениях все /z-мерные цепи комплекса Оа имеют
вид atv где а есть целое число, и при azfzO ни одна из этих цепей не есть
цикл, так как A 0%at* = at4-1. Предположим теперь, что наше утверждение
доказано для k = //г, и докажем его для k = m -f- 1. Из нашего
предположения следует." что всякий цикл zn£Zr0l(Oa)t в который симплекс /™ + не
входит (входит с коэффициентом нуль), есть линейная комбинация циклов
Пусть теперь
тогда
Положим
тогда
m |-1
г—1
«i-j-l
д*» = (2"0'п"~1==0
z'n= (гп — ат + 1^+1) + ат^\\
т.е. z/n есть цикл комплекса Оа, и притом, очевидно, такой, что симплекс
*т-и B этот иикл не входит. Значит, г'п есть целочисленная линейная
комбинация циклов z",...,*^, а цикл
*n = Z'n + aw+1(/^+1 — **) = ^ + *w+i*w + i
есть целочисленная линейная комбинация циклов z™,•.., Zm+v что и тре"
бовалось доказать.
20
Александров П. С.

306 Д-груПпы огплчксОв (нижние группы ёегти) [гл. Viii
[1:55]. Пусть К—симплициальный комплекс. 7 '" £ К и /•> р.
Положим Q = Ок{Тр) и В = Ек{Тр) (см. главу 4, определение [1:87]).
Предположим, что комплекс К обладает следующим свойством: если
Vй £ Q, то грань симплекса 1т, противоположная грани Тр содержится
в К. Тогда группы Ar+L(Q, %) и &Г~Р(В,%) изоморфны между собою.
Доказательство. Каждому симплексу Тт = \тртт~р~1\ £ Q
размерности m^P~\-l соответствует симплекс 7,ж~^~1^^, а именно, грань
симплекса Тт, противоположная грани Тр; при этом каждый симплекс
Р\ /г>-0 комплекса В оказывается поставленным в соответствие одному
единственному симплексу Tm = Tpn' +1 = \TpThl^Qi так что установлено
взаимно однозначное отображение комплекса Q\Tp на В. Выберем
определённую ориентацию tp симплекса Тр; тогда каждой ориентации tm
симплекса Тш соответствует единственная ориентация ^-Р-1 = ftm симплекса
Тт~Р~19 удовлетворяющая условию
tm= (tPtw-P-1);
если
tP = (e0...ep), tm -= е(<?0. . .epepi.1. . .ет\ е = =!=1,
ftm=*tm-p-l = e(ep + 1...em).
Таким образом, установлено взаимно однозначное отображение /
множества всех ориентированных симплексов комплекса Q\TP на множество
всех ориентированных симплексов комплекса В. Докажем что
1 : 551) (//'» -./I" *) = ( — \)Р \f- : №~К
Пусть
и
и, значит,
ft™ = e(ep+u..em^1evl),
Из главы 7, формула (3: 11), имеем
(№:№-*) = (— 1)W; {ftM:f№-i) =z(— \y-p-Uc'.
откуда и следует (1:551).
Замечание. Обратное оюбражению / отображение множества всех
ориентированных симплексов В на множество всех ориентированных
симплексов комплекса Q\TP обозначаем через /-1.
Пусть теперь /*>/?-(-!• Каждой цепи
соответствует цепь
/*r+i €/>-*(£, 81),
принимающая на каждом ориентированном симплексе tr~P комплекса В то
значение, которое цепь хг^г принимает на f~1tr+1.
Другими словами: если xr^1 = Y.aitir+1, то
fxr + l =&№ + !.
Этим установлено изоморфное отображение / группы Ir+1(Q, 51) На
Lr~p(B,%).

§ 1] ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 30?
Докажем, что для любой цепи xr+1£Lr+1(Q, А) имеем
(1:552) Д/с*ч-1 = (— 1) ^-и/Д^г-н.
Для этого достаточно показать, что
(1 :5520) Д/^+i = (—\)р\- i/Д/;- f 1
для любого ориентированного симплекса tr^1 комплекса Q.
Для доказательства формулы (1:5520) рассмотрим какой-нибудь
ориентированный симплекс р-Р-1 комплекса В и симплекс tr = /~г (f-P-1).
Вычислим значения обеих цепей AJtr+L и /Afr^1 на tr-P~l.
Пусть
fU^ = t>-P.
Тогда
(Д/fH-i. tr-p-i) = (tr-P:tr-p-i) = (//r+i ://r) = (— l)^+i (/r-t-i :/r)f
(/Д/r+i. ^-^-i) == (№Ы . /r) = (*г-к: /rjf
чем (1 :5520) доказано.
Из (1:552) следует, что при изоморфизме / группы Lr+* (Q, 51) на
Lr~P(B, 9t) группы Zr+L(Q, 9С)и Hr-rl(Q, Ж) отображаются соответственно
на Zr~P(B, 91) и на Jir~P(Bt Ж), так что / порождает одноимённый
изоморфизм группы Ar-1(Q, 91) на группу Ьг-Р (В, Ж), что и требовалось
доказать.
Следствие. Пусть К—триангуляция, е — её вершина. Для любого
г>1 группа Аг+1(Оке,Ж) изоморфна группе ^фке,Ж).
В главе 13 нам существенно понадобится следующее предложение,
являющееся частным случаем предыдущей тес ремы:
[1 :550]. Пусть К' = еК—открытая пирамида над силтлициальным
комплексом AT (см. главу 4, арт. 2 :3). При г > 0 группы Lr (К) и АТ^1(еК)
изоморфны между собою.
В cav.ovt деле, в пирамиде <>Л'> открытая ьирамида еК есть звезда,
а К—край звезды вершины е, причём грань любого симплекса \еТ\^еК
противоположная вершине еу есть симплекс Т£ К. Таким образом, все ус'
ловия теоремы [1:55] (при р = 0, Тр = е) выполнены, откуда и следует
[1 :550].
1 : 6 *). Группа Д00(АГ, 91). Во всём этом артикуле К есть полный сим-
плициальный комплекс.
Группа Д°° (К, Ж], определяется так:
(1:61) Доо {К, Ж) = Zi° {К, 9t)/#° (К, 91),
где Z00 (К3 Ж) есть группа всех нормальных нульмерных циклов комплекса
К по области коэффициентов 91. В силу [1:32],
И о (/С, 91) £ДОо (/£ 5f),
поэтому фактор-группа (1 :61) имеет смысл.
[1:62]. Группа Д°и(/С, Ж) есть прямая сумма групп, изоморфных
группе 91, взятых в таком числе, как велико уменьшенное на 1 число
компонент комплекса К.
Доказательство (для случая конечного числа компонент). Группа
Д° (К, Ж) есть прямая сумма 5 групп, изоморфных группе 91, где s есть
число компонент комплекса К; другими словами, группа Д° (/С, 91) может
8
быть рассматриваема как группа линейных форм z = 2 а%х% от s
переменам»!
ных х€ с коэффициентами из Ж.
*) Ср. Александров — Нор!, гл. V, § 1, пункт 5 (стр. 209). Этот артикул
существенно применяется в главах 14 и J5. Чтение его можно отложи ib до
этих глав.
20*

308 Л-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
Из определения группы к00(К, 91) следует, что эта ipynna изоморфна
S S
группе тех линейных форм ^#Л-, для которых ^а€ = 0. Поэтому тео-
рема [1 :62] содержится как частный случай в следующем общем
предложении теории групп:
Лемма [1 :63]. Пусть %п есть группа всех линейных форм
п
(1:63) г=2*<*<
от п переменных х,\ с коэффициентами из абелевой группы %. Пусть 93
есть подгруппа группы %п, состоящая из всех линейных форм (1:63)
с суммой коэффициентов, равной нулю; тогда 23 изоморфна группе %n~L
п
линейных форм у = 2^Л от п—\ переменных хъ ..., хп с коэффици-
i—'l
ентами из Ж.
Для доказательства рассмотрим следующее отображение группы 33
в группу 5ln~l: каждому элементу
п
z= ^а^.
ставим в соответствие элемент
п
У = /(*) = ^ам
группы 3CW_1. Отображение / есть отображение на всю группу W1"1.
В самом деле, если
п
У= ^bixi
есть произвольный элемент %п~1, то элемент
п
отображается, в силу /, на у.
Чтобы доказать, что / есть изоморфизм, достаточно показать, что, в силу
/, лишь нулевой элемент группы 23 отображается на нуль группы 21те-1.
В самом деле, если
п
У = 2 Ь*Х*> = °'
т. е. Ь2 = Ьъ = ... = Ьп = 0, и f(z) =y. Но хъ хг, ..., хп имеют в z те же
коэффициенты, что и в у, т. е. коэффициенты, равные 0, и так как сумма
всех коэффициентов в z равна нулю, то коэффициент при хх в г также
равен нулю и, следовательно, z равно нулю, чго и требовалось доказать.
[1:641. Ранг %№(К) группы А00 (К), а также ранг %0^(К) по модулю
т (при простом т) группы Д^(АГ), равен уменьшенному на единицу
числу компонент комплекса К.
Доказательство. Теорема следует из [1 :62], если [1 :62] доказано
без предположения конечности числа компонент комплекса К. Так как
в такой общности мы теорему [1:62] не доказывали, то доьажем [1 :64]
непосредственно.

§ 1] ОПРЕДЕЛЕНИЯ. ПРИМЕРЫ. ПРОСТЕЙШИЕ ОБЩИЕ СВОЙСТВА 309
Пусть /Cv — компоненты комплекса К Одну определённую среди них
обозначим через Ко- В каждой компоненте Afv возьмём по вершине е^
рассмотрим нульмерные циклы
А = е, — е0 v ф 0.
Для доказательства [1:64] достаточно убедиться в том, что:
1°. Каждый нульмерный нормальный цикл z° гомологичен в К некоторой
линейной комбинации циклов z°t
2°. Циклы г^ гомологически независимы между собой*).
Доказательство пункта 1° таково: прежде всего, z° = 2^ г°. Далее, в
силу (1 :34), имеем К^°^а^е^ в К^ значит,
(1:64) zo^ 2X^°~2*-A= 2*v(*v-*o) +(2*,)*и-
МММ V
Так как цикл z® нормален, а цикл, гомологичный нормальному цикл v
также нормален (следствие из [1:32]), то цикл 2 ач еч нормален и, следо-
• м
вательно, 2av = 0' Внося это в (1:64), получаем нужную нам гомологию
"V
*°~2*v(0v —*о)-
м
Для доказательства п. 2° предположим, что ^а^~0,т. е.
м
м
тогда для любой ксмпоненты К^г м- ф 0,
АГи 2 а^ — ed = av-pv- ~ °»
v
значит, я^ = 0, что и требуется доказать.
1 : 7. Разложение группы &г ($Д) в прямую сумму по компонентам
комплекса Й. Пусть й — произвольный «-комплекс. Для случая, когда Й
состоит из конечного числа компонент, проведём доказательство следующей
теоремы (верной и для комплекса с бесконечным числом компонент).
[1 :71]. Группа Дг (®Д) есть прямая сумма групп Дг(Я\, Щ, где йч—
компоненты комплекса Я.
Эта теорема легко следует из:
[1 :72]. Если а-комплекс й есть соединение двух непересекающихся
замкнутых подкомплексов W и W % то имеют место следующие
разложения в прямые суммы:
(1:721) Ьг(8,Ы) = 1г(&',Щ +//(£", 30,
(1 : 722) Zr (Я, Щ = Zr (Г, Ж) + Zr (8", %),
(1: 723) Иг (£, Щ = Нг (Г Д) -f #г(Я", Щ,
(1:724) Д»-(^,9Х) = Д',(й/,91) + Дг(&">^)-
Для доказательства (1:721) достаточно заметить, что для любого
xr£Lr($,%) имеем
хг == &'хг -\- &"хг.
*) Глава 7, определение [6 :42].

310 Д-группы комплексов (нижние группы бетти) [гл. viii
Таким образом, Lr(U,%) есть сумма своих подгрупп //(£',50 и Lr(U",<$t),
Так как Lr(U', Ж) иLr ($", 21), рассматриваемые как подгруппы группы Lr(®, 91),
вследствие $' f] &" = 0 имеют единственный общий элемент 0, то //($, Ж)
есть прямая сумма подгрупп Lx (£', Ж) и //($", 21).
Если**" £ ^"(/0 (соответственное £ Hr (К),гг = Д*г+1), то имеем в силу
открытости подкомплексов AT', А!7' (гл. 7, теорема [6:51]):
К'г* £ Z' (AT') A/Cx'+i = АГ'*Г, A''*** £ Яг (AT')
соответственно
так что гг однозначно представим в виде
zr — z'r + z"rf
где z"r e Z* (K'h z"r $ Zr(K") соответственно г'* £ Hr (К'), z"r £ H? (К").
А так как в силу замкнутости подкомплексов К* и К,г в К имеем
Zr{K')<^Zr{K), Zr(K")^zr(K), Hr (Кг) с: H? (К), Нг (К") Я Нг (К),
то формулы (1 :722), (1 :723) доказаны. Но из этих формул следует и (1 :724).
1:8. Гомоморфизм группы Дг (К$, 51) в Дг(/Са, 51), порождённый
симплициальным отображением S£ симплициального комплекса
К$ в симплициальный комплекс Afa, Пусть дано симплициальное
отображение S$ симплициального комплекса /Сз в симплициальный
комплекс Ка- Мы видели в главе 7, арт. 8:2, что отображение SJJ
порождает одноимённый гомоморфизм группы Z/(/e8, 51) в группу Lr(Ka, 51),
при котором Z^ (/C3,51) отображается в ZrA (Afa, 50 и Я£ (А^ 51)
отображается в ИГА (/Са, 51). Поэтому (см. Прибавление I, арт.
^^гомоморфизм Si группы Lr (АГз, 51) вЬг(К^ 51) порождает гомоморфизм группы
Аг(/Сз,51) в группу д*Ч#а, 50, который обозначается также через 5?
и называется гомоморфизмом группы Аг (/Си, 50 в Ar (/fa, 51),
порождённым симплициальным отображением S$
комплекса К$ в Ки.
Замечание 1. Симплициальные отображения S$ и 6'Ркомплекса
a a
/Сз в комплекс Ка называются (г, 51)-г омологичными между собою,
если они порождают один и тот же гомоморфизм группы Ar(AC8,5t) B
группу A^(/^a,5i).
Отображения (г, 51), гомологичные при любом г (при любом 51),
называю гея 51-г омологичными (г-г омологичными) между собою.
Наконец, два симплициальных отображения комплекса К$ в К**
которые (г, 50-гомологичны между собою при любых г и 51,
называются вполне гомологичными между собою.
Замечание 2. Из теоремы [8:40] главы 7 следует: если /Са,
Купонные симплициальные комплексы, Као*--К* и А'зо^^з— их замкнутые
подкомплексы, S?— симплициальное отображение К$ и Ка1 при котором
$1(Кро)<^Као и Grj = Kz\Kvo, Gp = Kp\K$o, io гомоморфизм GaSl группы
Lr(Go, Щ в U'(Ga,%) порождаех^одноим^нный) гомоморфизм груцпы Дг((/а» ЭД

§ 2]
группы Ar(/C)
311
§ 2. Группы Д'0(/0*).
2:1. Группы кручения. Пусть снова К-—произвольный а-ком-
плекс. Элементы конечного порядка группы AjJ(SJ) образуют
подгруппу группы Д£(й); эта подгруппа называется r-меркой группой
кручения комплекса S? и обозначается через 6r(S); если группа
вг(Д) отлична от нуля, то мы говорим, что комплекс ^обладает
r-мерным кручением; если группа 6Г(^) есть нуль-группа, то мы
говорим, что комплекс й не имеет /--мерного кручения. Из [1:37]
следует, что для любого полного симплициального комплекса К
группа 9° (К) есть нуль-группа.
Если !й есть я-мерный комплекс, то группа А™ (Я)) совпадает
с группой Z% (й) и поэтому также свободна. Итак:
[2 :11]. Никакой полный симплициальный комплекс не обладает
нуль-мерным кручением**).
[2 :12]. Никакой п-мерный комплекс не обладает n-мерным
кручением.
Следствие [2:13]. Одномерные комплексы не имеют кручения.
Примеры (см. арт. 1 : 4,7°). Проективная плоскость, как и
поверхность Клейна, имеет одномерное кручение: для той и другой
поверхности одномерная группа кручения есть группа второго
порядка.
Возьмём какую-нибудь триангуляцию К листа Мёбиуса
(например, триангуляцию, рассмотренную в арт. 1 :4, упражнение 1, или
более простую триангуляцию, из главы 3, арт. 3 : 1). Удалим из этой
триангуляции все элементы, лежащие на краю поверхности (т. е.
в случае триангуляции арт. 1 : 4 все элементы, лежащие на
сторонах АВ и DC). Полученный открытый подкомплекс триангуляции К
имеет одномерную группу кручения порядка 2.
Определение [2:14]. Пусть zr — целочисленный цикл
комплекса S; порядком цикла zr называется порядок содержащего
этот цикл гомологического класса, рассматриваемого как элемент
группы Д£(^).
Очевидно, циклы, слабо гомологичные нулю, и только они имеют
Конечный порядок; среди них порядок 1 имеют циклы,
гомологичные нулю. Другими словами, гомологические классы циклов, слабо
гомологичных нулю, суть элементы группы вг(^) (в частности,
гомологический класс циклов, гомологичных нулю, есть нулевой
элемент группы 6r(ST)). Ставя в соответствие каждому циклу, слабо
гомологичному нулю, т. е. каждому элементу иг группы НГ(Ш) го-
*) См. Прибавление I, §4.
**) Теорема верна и для неполных симплициальных комплексов.
Читателю предоставляется доказать это. С другой стороны, я-комплекс,
состоящий из клеток ±t\ ±t° с коэффициентом инцидентности (t1:l°) = c2.
Имеет нульмерное кручение.

312 А-группы комплексов (нижние группы бегти) [гл. viii
мологический класс этого цикла, получаем, очевидно, гомоморфное
отображение группы //r(SD) на группу 6Г(£); ядром этого
гомоморфизма является группа ЯГ(Ш.
Поэтому:
[2: I]. Для любого а-комплекса группы 8Г (££) и ГГ (Ш)/НГ{Щ
изоморфны между собой.
2:2. Группы Д£0(й). Фактор-группа
Ло(^)/вг(^)
не содержит никакого отличного от нуля элемента конечного
порядка; это следует из того, что группа 6Г(51), по самому своему
определению, есть дивизионно замкнутая подгруппа группы Aj(^).
[2:21]. Группы Д£ (®)/вг (£) и Д£0 (®)=ZJ(S)//£(S) изоморфны.
Доказательство. Рассмотрим гомоморфное отображение
группы Z£($?) на группу Д£($), состоящее в том, что каждому
циклу ^^ZJ(^) ставится в соответствие его гомологический класс.
При этом гомоморфизме прообразом группы 6Г(51) является группа
НГ(Щ, поэтому на основании теоремы [1 : 10] Прибавления I имеем
изоморфизм между
Z04S?)/#4^)h А;(Я)/в^(Я),
что и требовалось доказать.
Группа 6Г(Й), как группа, состоящая из элементов конечного
порядка, имеет ранг нуль, поэтому, в силу формулы (3 :2)
Прибавления 1 (формула сложения рангов), группы Д^(®) = Д£($)/вг (й)
и Д£($) имеют один и тот же ранг кг(Щ.
Подведём итог всему сказанному:
[2:2]. Пусть й — произвольный а-комплекс.
Группы
AS (Я)/** (Я) и AJ(ft) = Z|;(R)//£(ft)
изоморфны между собой) они не содержат никакого отличного от
нуля элемента пснечного порядка) их ранг есть r-мерное чисао
Бетти комплекса $?.
2:3. Случай конечного а-комплекса. Гомологические базы.
Теперь мы предполагаем до конца этого параграфа, что Ш есть
конечный а-комплекс; пусть 2рг есть число r-мерных элементов
комплекса 5?; в частности, если Я) есть комплекс всех ориентированных
элементов некоторого симплициального комплекса (или комплекса
выпуклых многогранников) К, то рг есть число r-мерных элементов
комплекса К; группы i;(ft), Z0r($), tfg(ft), Д;(Ж) и т. д. будем
обозначать просто через Z.J, ZJ, #J, Д£.

§ 2]
группы А^ (/С)
31
Ранг группы LrQ, очевидно, равен рг, поэтому подгруппы ZJ и
Щ группа LrQ и фактор-группа Д£ группы ZrQ имеют также
конечные ранги (см. Прибавление I, арт. 3:2). Итак:
[2:31]. Числа Бетти конечного комплекса конечны.
Группа IJ, а потому и группы ZJS Щ, Д£ суть группы с
конечным числом образующих: цепи trp i=l, 2,...,рг являются
образующими группы Lrr Так как группа Д£э по теореме [2 :2] не
содержит отличных от нуля элементов конечного порядка и имеет
ранг ттг, то:
[2:32]. В'случае конечного комплекса ^ группа Д£0 есть
свободная абелева группа с тгг независимыми образующими.
Так как все элементы группы вг имеют конечные порядки и 0Г
имеет конечное число образующих, то:
[2: 33]. Группы кручения конечного а-комплекса конечны. Далее,
из теоремы [4: 35] Прибавления I следует:
[2:34]. Группа Д£ конечного а-комплекса есть прямая сумма
конечной группы кручения &г и свободной, изоморфной с Д£0 группы
ранга ъг.
В случае конечного а-комплекса 51 группа Д£, как всякая абелева
группа с конечным числом образующих, однозначно определяется
своим рангом rJ и своими коэффициентами кручения (Прибавление I,
теорема [4:351]). Коэффициенты кручения группы Д£(51) называются
коэффициентами кручения комплекса Я).
Введём, наконец, следующее определение, которое часто
применяется:
[2:35]. Система гомологически независимых *) r-мерных
целочисленных циклов
(2:35) г;,..., £s
комплекса % называется г-ж ерной гомологической базой
или (.(Д)-базой комплекса % если гомологические классы циклов
zrL. образуют базу свободной группы Д£0 (®) = Zr ($) /НГ(Щ.
Это же самое определение можно, очевидно, сформулировать
и так:
[2 : 350]. Гомологически независимые между собою целочисленные
циклы (2 :35) образуют (УД)-базу комплекса $?, если каждый
/--мерный целочисленный цикл zr £ Zr0 (&) может быть записан в виде
где vr£Hr(K) и с{ суть целые числа (определённые, как легко
видеть, однозначно).
*) Глава 7, определение [6:42].

314 Л-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
Замечание. Пусть %— какое-либо из алгебраических тел 9?
или JW9 где т — простое число. Всякая максимальная
система гомологически независимых между собою
г-м ерных циклов (2:3 5) комплекса 51 по телу
коэффициентов 21 называется r-мерной гомологической базой
комплекса ® по телу коэффициентов % (в случае % = Jm говорят
о гомологических базах по модулю т). Легко видеть,
что эти базы могут быть также определены как системы
гомологически незаяисимьх циклов (2:35) (по телу коэффициентов %),
обладающих тем свойством, что каждый цикл zr£Zr{$,%)
гомологичен некоторой линейной комбинации V а^ц at £ % циклов системы
(2:35), т. е. может быть записан в вид° ^r=wr-f-V а{ггг где
Упражнение. Построить примеры одномерных и двумерных
и (УД)-блз, рассмотренных в 1:4 триангуляции тора, поверхности
Клейна и проективной плоскости. Построить для последних двух
поверхностей также гомологические базы по модулю 2 (тех же
размерностей: 1 и 2).
2:4. Формула Эйлера-Пуанкаре для «-мерного конечного
а»комплекса. В этом артикуле % — J. n
Определение [3:41]. Число V(—l)rpr называется эйле-
ровой характеристикой *) комплекса St.
Формула Эйлера-Пуанкаре:
п п
(2:4) 2(~-l)>y-=2(_iy;:r.
Г = 1 Г=0
Для доказательства формулы (2:4) вспомним:
[ Г) рг есть ранг группы LrQ = Lr0(§t):
(2:41) р- = р
2°> А есть гомоморфное отображение группы Lr0 на группу
Я£-1, поэтому группы L^/Zq и Я^"1 изоморфны, в частности, имеют
тот же ранг:
(2:42) K^/^ = P(«r1V'
3°) если для трёх групп А, В, С выполнено соотношение А/В = С,
то рА = рВ-\-{;С (Прибавление 1, формула (3:2)). Отсюда, на
основании (2:41) и ^2:42) имеем для г = 0, 1, 2, . .., п.
р^р^ + .чяг1)- ■
*) Как всегда, 2рг есть число r-мерных элементов «-комплекса £;
значит, в основн м случае, когда К есть комплекс ориентированных
элементов триангуляции Д", через рг обозначается число /--мерных симплексов,
Триангуляции К

§ 31
ПСЕВДОМНОГОСБРАЗИЯ
315
т. е.
(2:43) p(Z$) = p»--p(H>;->).
При этом, согласно нашим определениям, Ь~л = Z^i = Я~ есть
нуль-группа, так что
(2:44) Р(/^) = 0.
С другой стороны, tJ есть рлнг группы Aj = Z£//#J, поэтому для
г=0, 1, 2, . .., /г
(2:45) ^ = P(ZJ) —P(«S).
Внося (2:43) в (2:45), получаем формулу, представляющую и
самостоятельный интерес, именно:
(2:46) *Г = РГ —РСТ1) —рЮ (для г^°> *> 2> •••> *)•
Так как Щ есть нуль-группа, то
(2 : 47) р (Н*) = 0, те* == р» — р («J-1).
Умножая обе части равенства (2:46) на (—\)г и складывая
(при г=0, 1, 2, ...,«), получим, имея в виду (2:44) и (2:47),
как раз (2 :4).
Примеры на применение формулы Эйлера-Пуанкаре будут даны
в следующем параграфе.
§ 3. Псевдомногообразия.
Во всём этом параграфе мы понимаем под комплексом К
конечный симплициальный комплекс, ориентированные симплексы которого
образуют ^-комплекс; в частности, за К можно принять любую
триангуляцию, а также любой открытый подкомплекс триангуляции
(единственные два случая, которые в дальнейшем будут
рассматриваться).
3:1. Псевдомногообразия.
Определение [3:11]. Комплекс Кп размерности п называется
размерно однородным, если каждый элемент его является
собственной или несобственной гранью какого-нибудь я-мерного
элемента комплекса Кп.
Определение [3:12]. Конечная последовательность я-мерных
симплексов комплекса К
(3:12) 7*,..., Г»
называется цепочкой симплексов, связывающей
симплексы Т" и 7^ в комплексе /С, если всякие два соседних
элемента Т\ и Т» 1= 1, 2, • . •* £ — 1, последовательности (3:1^

316 Д-группы комплексов (нижние группы бетти) [гл. viii
прилегают друг к другу, т. е. имеют общую (л—1)-мерную
грань, принадлежащую комплексу К-
Определение [3:13]. Комплекс Кп называется сильно
связным, если он размерно однороден и если каждые два л-мер-
ных симплекса комплекса Кп могут быть связаны в Кп некоторой
последовательностью л-мерных симплексов этого комплекса.
Определение [3:14]. Сильно связный n-мерный комплекс Кп
называется n-мерным (комбинаторным)*) псевдомногообразием,
если каждый (л—\)-мерный элемент этого комплекса
является гранью двух и только двух n-мерных симплексов
комплекса Кп.
Замечание. Полные псевдомногообразия обычно называются
замкнутыми псевдомногообразиями.
Наряду с псевдомногообразиями в только что определённом
смысле рассматриваются ещё так называемые псевдомногообразия
с краем, которые определяются так:
Определение [3:15]. Конечный полный л-мерный сильно
связный симплициальный комплекс ^называется л-мерным
комбинаторным *) псевдомногообразием с краем, если
каждый (л—1)-мерный симплекс, комплекса Кп подчинён двум или
одному л-мерным симплексам этого комплекса. Подкомплекс
комплекса /£w, состоящий из всех собственных и несобственных граней
тех (л—1)-мерных симплексов /("> которые подчинены лишь одному
л-мерному симплексу /^ называется кр ае м комплекса Кп*
Всякое полное псевдомногообразие есть частный случай
псевдомногообразия с краем: край в этом случае есть пустое множество.
Примеры псевдомногообразий. 1°. Простая замкнутая
ломаная линия еЛе%. . .е8^1е8е1 даёт пример одномерного полного
псевдомногообразия К, состоящего из вершин еи £2> • • •> es и
одномерных симплексов l^^l» |в.2вз|> • ••> ks-il> \esei\-
Легко видеть, что этими примерами (при различных s)
исчерпываются, с точностью до изоморфизма, все одномерные полные
псевдомногообразия.
2°. Любая триангуляция замкнутой поверхности (см. главу 3)
является примером замкнутого двумерного псевдомногообразия. Точно
так же триангуляции поверхностей с краем могут служить примером
двумерных псевдомногообразий с краем.
3°. Если склеим две противоположные вершины октаэдра (черт.
121), то получим двумерный кривой полиэдр, триангуляции которого
могут служить примером двумерных замкнутых псевдомногообразий,
не являющихся триангуляциями поверхностей. Соответствующее
трёхмерное тело (рассматриваемое в некоторой триангуляции) есть
трёхмерное псевдомногообразие с краем.
4°. Напротив, если склеим две пирамиды их вершинами (черт.
122\ то не получим даже псевдомногообразия с краем (почему?).
*) Прилагательное «комбинаторный» в этой главе опускаем.

§ 31
ПСЕВДОМНОГООБРАЗИЯ
317
5°. Любое подразделение комплекса [Гп], где Vх есть я-мерный
симплекс или вообще я-мерный выпуклый многогранник, есть я-мер-
иое псевдомногообразие с краем*). При этом край является (я—1)-
мерным полным псевдомногообразием.
Комплекс, состоящий из одного я-мерного симплекса, является
я-мерным псевдомногообразием (при я>0, очевидно, неполным).
3 : 2. Ориентируемые псевдомногообразия.
Определение [3:21]. Пусть TV и 7\ — два я-мерных
симплекса с общей (я—1)-мерной гранью TV~X. Пусть tV~x— какая-
Черт. 121. Черт. 122.
нибудь ориентация симплекса TV-1; ориентации tV и t™ симплексов
TV и TV называются когерентными, если
г fl
Очевидно, определение это не зависит от выбора ориентации tV^1
симплекса TV"1
J
Пусть теперь
(3:21) Г?, ...,TJ
я-мерные симплексы я-мерного псевдомногообразия /С.
Ориентации
(3 : 22) '?,..., ^
*) Сильная связность полученного комплекса вытекает из гл. 6.

318 Д-групНы Комплексов (нижние группы бетти) [гл. viii
этих симплексов называются когерентными между собою, если для
любых двух симплексов 7> и Г™ из (3 : 21), имеющих общую (п— 1)-
мерную грань, ориентации t*} и t% когерентны.
Определение [3:22]. Пусть Кп есть я-мерное
псевдомногообразие или псевдомногообразие с краем. Кп называется
ориентируемым, если существует множество когерентных ориентации
всех л-мерных симплексов комплекса Кп\ в противном случае Кп
называется неориентируемым.
Итак, если Кп — неориентируемое псевдОхМиогообразие (или не-
ориентируемое псевдомногообразие с краем), то, как бы ни были
выбраны ориентации t7} всех я-мерных симплексов Т%£Кп, всегда
найдётся, по крайней мере, одна пара некогерентных ориентации/™
t\ двух прилегающих симплексов Тп и Т\.
Замечание 1. Пусть Кп — псевюмногообразие с краем и
Кп~~1 — его край. Легко видеть, что Кп тогда и только тогда
ориентируемо, когда ориентируемо неполное псевдомногообразие
Кп\Кп~1. Поэтому все вопросы, связанные с ориентируемостью
псевдомногообразий с краем, непосредственно сводятся к анатогич-
ным вопросам для неполных псевдомногообразий (без края).
Примеры. 1°. Край л-мерного симплекса (т. е. комплекс
/С*-1 = [Тп]\Тп есть ориентируемое (п—1)-мерное
псевдомногообразие. Для того чтобы убедиться в этом, достаточно выбрать
какую-нибудь ориентацию tn симплекса Тп и такие ориентации V\~^
его (п—1)-мерных граней, чтобы (Г:^~1) = 1.
2°. Триангуляции неориентируемых замкнутых поверхностей
(например, проектиЕной плоскости или поверхности Клейна) являются
неориентируемыми полными псевдомногообразиями.
3°. Возьмём какую-либо триангуляцию неориентируемой
поверхности с краем (например, листа Мёбиуса) и удалим из этой
триангуляции все лежащие на краю элементы её. Получим
неориентируемое неполное псевдомногообразие.
Утверждения 2° и 3° должны быть доказаны читателем (см. главу 3, § 4).
Если
(3:21) ^V"'7?
есть совокупность всех л-мерных симплексов ориентируемого исев-
домногообразия Кп и ориентации
(3:22) *?,...,'?
когерентны, то ориентации
/п tn
очевидно, также когерентны.
С другой стороны, если ориентации t* и *» двух прилежащих
по некоторой (п — lj-мерной грани TJ—1 симплексов Т% и TJJ коге-

§ 3]
ПСЁВДОМНОГООВРАЗИЯ
319
рентны, то ориентации t™ и — /™ некогеренгны. Поэтому задание
определённой ориентации t? одного кякого-нибудь симплекса T'f
однозначно определяет когерентные с V.1 ориентации всех
симплексов TJJ, прилежащих к Т7} по (п— 1)-мерным граням, а следовательно
(ввиду сильной связности комплекса Д'Л), и когерентные ориентации
всех вообще симплексов (3:21).
Итак:
[3:23]. Существуют только два множества когерентных
ориентации всех n-мерных симплексов
(3:21) У'»,..., Т»
л-мерного ориентируемого псевдомногообразия Ки: если
(3:22) 'Г,--.,'?
есть одно множество когерентных ориентации симплексов (3:21),
то второе множество есть
1 1 » * * * * V
[3:24]. Пусть (3:21) есть совокупность всех n-мерных
симплексов n-мерного псевдомногообразия Кп. Ориентации (3 :22) тогдл
и только тогда когерентны, если цепь
(3 :24) *?=>]'?
есть цикл.
Это непосредственно вытекает из того, что значение цепи А^
па любом tn~x есть
где |^7| и |^| суть прилежащие к l^"1! симплексы Кп.
Определение [3:25]. Пусть Кн — ориентируемое
псевдомногообразие (или ориентируемое псевдомногообразие с краем Кп~1)«
Пусть
(3 :22) t», ...,£
суть когерентные ориентации всех я-мерных симплексов комплекса Кп.
Тогда цикл 2^= УГ? называется ориентацией Кп.
Из этого определения и из [3:23] следует:
[3 :2б]. Пусть Кп—ориентируемое псевдомногообразие или
псевдомногообразие с краем; пусть (3:22) — множество когерентных
ориентации n-мерных симплексов кохмплекса Кп'. Тогда Кп имеет
Две и только две ориентации: Z^ = ^ti и—^f — 2 — *?•
г i
Основными теоремами об ориентируемости являются теоремы
[3:27] и [3:28].

320 Д-группы комплексов (нижние группы бетти) [гл. viil
Теорема [3:27]. Группа Д£ (Кп) = Z» (Кп) ориентируемого
n-мерного псевдомногообразия Кп есть бесконечная циклическая
группа, имеющая каждую из двух ориентации Кп своим
образующим элементом.
Это предложение, очевидно, следует из:
[3:270]. Всякий л-мерный цикл zn£Zn(Kn, 91)
псевдомногообразия Кп имеет вид гп = аг™, где г™ — какая-либо ориентация Кп
и а£%.
Для доказательства достаточно убедиться в том, что всякий цикл
zn принимает на всех когерентных ориентациях
одно и то же значение. Это утверждение вследствие сильной
связности К'\ в свою очередь, достаточно доказать лишь для двух
симплексов \t*}\ и |^|, имеющих общую (п — 1)-мерную грань \tn ~Л \.
Но, так как zn = V ахЩ есть цикл, то
о = (ДЛ;-1) = a^.-.t^) -\-ah(t>> г/»-1),
а так как в силу когерентности
(;»:*;-1) = -(/«:/;-1)^о,
то ah — a,h что и требовалось доказать.
Замечание 2. Так как, с другой стороны, в обозначениях
[3:270] цепь вида аг™ есть цикл, то доказаны следующие
предложения:
[3:271]. Если Кп—ориентируемое я-мерное псевдомногообразие,
то группа Дя(/Ся, %) = Zn(Kn, 91) изоморфна группе 31.
Замечание 3. На основании теоремы [3:27] мы можем теперь
дать такое определение ориентации псевдомногообразия:
[3 : 250]. Ориентацией я-м ерного ориентируемого
псевдомногообразия Кп называется какой-либо
образующий элемент группы AJ (Кп) = Z™ (Кп).
Теорема [3:28]. Если Кп есть неориентируемое псевдомно-
гообразие или псевдомногообразие с краем, то группа ZnQ (Kn) есть
нуль-группа.
Докажем, в самом деле, что из существования на Кп отличного
от нуля целочисл иного цикла
(3:28) ^=2^
следует отсутствие края и ориентируемость псевдомногообразия Кп*
Докажем, прежде всего, что для цикла (3:28) имеем
\а{\ = \ah\ для любых /, h.

§ 3]
ПСЕВДОМНОГООБРАЗИЯ
321
Это равенство снова достаточно доказать в предположении, что
симплексы Т"1 и Т% имеют общую грань Г™"1. Но в этом случае,
для любой ориентации /?г-1 этой общей грани имеем
О = Д*« (/«-I) = a, (*»: /y-i) + яй (*»: /»-i),
откуда af = :±:flft. Так как zn^0, то, обозначая через а общее
значение всех |^|, имеем на /Cw целочисленный цикл
zn = 1гп = у е<*« где е, = ^ = ±1.
Пусть край псевдомногообразия Кп непуст и, следовательно,
содержит (п—1)-мерный симплекс \tn~l\. Обозначим через \f}\
единственный я-мерный симплекс, прилегающий к \Р1-Ц. Тогда
что противоречит тому, что г7^ есть цикл.
Итак, Кп не имеет края.Чтобы доказать, что Кп есть
ориентируемое псевдомногообразие, достаточно положить t'" = г$\\ тогда
сразу видно, что цикл
представляет собой ориентацию псевдомногообразия К11. Теорема
[3: 28] доказана.
3:3. Группы А™ (/С2) для л-мерного неориентируемого
псевдомногообразия. Дезориентирующие последовательности.
Теорема [3:31]. Для всякого псевдомногообразия Кп группа
±" (Кп) = Z% (Кп) есть группа порядка 2.
Доказательство. Если zn = ^^^ ^Z^(Kn), то либо для
всех t* имеем я^ = 0, либо для всех tn{ имеем аг—\. В самом деле,
если бы для двух симплексов t™ и t% с общей гранью Щ—х имели
fl. = 0 и %=1, то было бы
(bzn-tf*-1)=l.
Из равенства аг — аь для прилежащих симплексов Р1 и ^
следует то же равенство для любых Щ и ^ вследствие сильной связности
комплекса /<Ч
С другой стороны, на любом псевдомногообразии Кп цепь
zn=z 2^J есть цикл по модулю два, так как всякий симплекс К?_1| ^Кп
есть грань двух и только двух симплексов \Р*\ £ Кп, следовательно,
(А*» • ^-!) =1 + 1 = 0 (mod 2).
Следствие, n-мерное число Бетти по модулю 2 для всякого
л-мерного псевдомногообразия равно 1.
21 Александров П. С.

322 Д-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
Приведём ещё одну формулировку определения ориентируемости
псевдомногообразия, которая в некоторых случаях оказывается
удобной.
Определение [3:32]. Последовательность n-мерных
ориентированных симплексов
(3:32) q, q,q,..., t«
называется дезориентирующей последовательностью,
если:
1. Для любого *=1, 2, ...,s — 1 симплексы \t™\ и |^ | имеют
общую (п— 1)-мерную грань \Р}~~1\\ симплексы \t™\ и |^| также имеют
общую грань Щ"г\.
2. При /=1, 2,...,£•—1 ориентации Р* и t™ когерентны;
ориентации tns и t% некогерентны, так что (^г^-1) = (^:^~1).
[3: 33]. Для того, чтобы n-мерное псевдомногообразие Кп было
неориентируемым, необходимо и достаточно, чтобы во множестве
его ориентированных n-мерных симплексов можно было найти
хотя бы одну дезориентирующую последовательность.
В самом деле, пусть дезориентирующая последовательность (3:32)
существует; если zn £ Zn (Kn), то, как легко видеть,
(гп • q) = (гп • tn) = . .. = (гп • t*) = a.
Но тогда
А-ги • V*-1 = 2а
и, следовательно, а = 0. Итак, всякий цикл zn(^Zn{Kn) принимает
на симплексах ^, t\,...,^ значение 0. Если бы Кп было
ориентируемо, то за гп можно было бы принять одну из ориентации Кп
и zn не могло бы принимать ни на одном из n-мерных симплексов
значения 0. Итак, из существования дезориентирующих
последовательностей следует неориентируемость Кп.
Пусть теперь Кп неориентируемо. Построим дезориентирующую
последовательность следующим образом:
Возьмём какую-либо ориентацию ^ симплекса Т* £ Кп и
предположим, что уже построены когерентно-ориентированные симплексы
£*, tnn..., t% так, что симплексы \t™\,. . .,[^| и их грани образуют
сильно связный комплекс и прилегают друг к другу.
Вследствие неориентируемости Кп построенные нами симплексы
|^|,..., |^| не исчерпывают множества всех n-мерных симплексов
комплекса Кп- Вследствие сильной связности Кп среди п-мерных
симплексов комплекса Кп, отличных от |^|,..., |^|, имеется
симплекс \t%. J, прилегающий, по крайней мере, к одному из
симплексов |^|, |^|,. . ., |^|, так что симплексы I ** |,. . . ,| tfj* | образуют
сильно связный комплекс.

§ 4] НЕКОТОРЫЕ ДОПОЛНЕНИЯ И ПРИМЕРЫ 3^3
Возможны два случая:
1°. Существует ориентация t%,x симплекса |^+1|, когерентная
с ориентациями t%, t™y..., t\.
2°. Такая ориентация ^+1 не существует.
В силу неориентируемости К71, рано или поздно наступит
случай 2°. В этом случае \t* J прилегает, по крайней мере, к двум
ранее построенным симплексам, положим к \t*\ и |tf*|, /</?, таким
образом, что одна из ориентации |^+1|, пусть *£+1, когерентна
с t£ и с — *».
Тогда, связывая ^ и tfj* цепочкой когерентно-ориентированных
симплексов t£, ff, fjf.. .,** ^ (где все л, A,-,/s меньше &~{~1), получим
дезориентирующую последовательность
/я /л /л /л fn m
Li> Л' Vt' '"• 7 3» Л' * + 1
и предложение [3:33] доказано.
[3:34]. £слгг /Сте—неориентируемое n-мерное псевдомногообра-
зае и т—нечётное число, то группа
есть нуль-группа.
В самом деле, пусть zn^Zn(Kn)- Пусть (3 : 32) дезориентирующая
последовательность. Тогда, как легко видеть (ср. доказательство
теоремы [3 :270]),
(гп . t«) = (z» - q)= . .. =i*» ■ t«)=*a£Jm
и, следовательно,
О^Д**-^-1 —2 а.
Но так как т нечётно, то элемент 2-a£Jm равен нулю, только
если а = о, что и требовалось доказать.
Замечание. В главе 9, теорема [4:43] будет доказано, что
в случае неориентируемости я-мерного псевдомногообразия Кп и
чётного т группа Д^(/Сп) есть группа второго порядка. В той же
главе 9 (теорема [1:7]) будет доказано, что псевдомногообразие
Кп тогда и только тогда ориентируемо, когда группа &п~х(Кп)
есть нуль-группа, и что для неориентируемого Кп группа б^-1 (Кп)
есть группа второго порядка.
§ 4. Некоторые дополнения и примеры
4 :1. Группы Бетти комплексов [Тп] и тп=[Тп]\Тп. Результаты
§ 2 и 3 позволяют прежде всего докончить исследование групп А*'
комплексов [Тп] и fn = [Tn]\Tn. В самом деле, так как 7П —
ориентируемое псевдомногообразие (арт. 3:2, пример 1) и, значит,
связный комплекс, то на основании [1: 35], [1 :53] и [3 :271] имеем:
21*

$24 А-группы комплексов (нижние группы бетти) [гл. vm
[4:11]. Группы Д°(Г\51) и \п~1(Тп,Щ изоморфны группе 51;
группы Ar(fn,%) при 0<г<п—1 суть нуль-группы.
Если tn — какая-нибудь ориентация симплекса Тп, то Мп есть
образующий элемент группы Z1*—1 (Тп) и вся группа Z^l(tn, 51)
состоит из циклов вида аМ7\ где а £51. Так как все эти циклы
гомологичны нулю в [Тп] (будучи границами цепей atn), то:
[4:12]. Группы Д°([ГП],5() изоморфны группе 51, группы
кг([Тп]> 51) при г>0 суть нуль-группы.
Следствие. Нульмерное и (п—1)-мерные числа Бетти
комплекса Тп равны 1, все остальные числа Бетти Тп равны 0. Все
числа Бетти комплекса [Тп] (кроме нульмерного, очевидно, равного 1)
равны нулю.
4.2. Поверхности. Триангуляция /С2 замкнутой (ориентируемой)
поверхности есть двумерное замкнутое (ориентируемое)
псевдомногообразие. Поэтому всегда
г,0(/С2)=1,
тогда как
ъ2(К2)=1, если К2 ориентируемо,
и
тг2(/С2) = 0,
если /С2 неориентируемо.
Обозначим через р род поверхности (т. е. число её ручек, если
поверхность ориентируема, и уменьшенное на 1 число дыр,
заклеенных листами Мёбиуса, если поверхность неориентируема). Тогда,
как мы знаем из главы 3, арт. 7 :1,
Х(/Са) = 2 — 2/7
для ориентируемых поверхностей и
-/(^) = i_ p
для неориентируемых.
Так как, с другой стороны, всегда
х (К2) = *° (К2)—к1 (к2) 4- *2 (к2),
то имеем для ориентируемых поверхностей
l_7ri(Af2)-fl=2 — 2p,
а для неориентируемых
1 — ти1(К2) + °=1— р,
т. е.

§ 4] НЕКОТОРЫЕ ДОПОЛНЕНИЯ И ПРИМЕРЫ 325
Итак:
[4 :21]. Если К2 есть триангуляция ориентируемой замкнутой
поверхности рода р, то
*0(tf9) = l, *1(K*) = 2p, тг2(/Г2)=1.
Если К есть триангуляция неориентируемой поверхности рода /?,
то
ttO^^I, TCi(K2)=/l> 1С9(^а)==0в
Отсюда и из выражения рода поверхности через её порядок
связности (глава 3, арт. 7 :1) следует, далее:
[4:22]. Порядок связности ориентируемой поверхности равен
её одномерному числу Бетти; порядок связности
неориентируемой поверхности на единицу больше её одномерного числа Бетти.
Из теоремы [7 :21] главы 3 и из [4 : 21] следует, наконец, такая
форма основной теоремы топологии поверхностей:
[4:23]. Две замкнутые поверхности тогда и только тогда
гомеоморфны между собою, когда их числа Бетти
соответственно равны между собою.
4 : 3. Простые псевдомногообразия. Элементарные
триангуляции.
Определение [4:31]. Комбинаторное л-мерное
псевдомногообразие Qn называется простым, если оно-ориентируемо, и при
0<г<п группа A£(Qw) есть нуль-группа.
Триангуляция К называется элементарной, если она может
быть представлена в виде
K=QUK0, Qn/C0 = 0,
где Q есть простое n-мерное псевдомногообразие, а
К0—триангуляция, каждый элемент которой подчинён хотя бы одному элементу
комплекса Q (и, следовательно, имеет размерность ^ п — 1).
Замечание. При этих условиях псевдомногообразие Q,
очевидно, представляет собою открытый подкомплекс триангуляции А\
Обозначим через хп какую-либо ориентацию
псевдомногообразия Q, через Jx — подгруппу группы ZJ~1(/C0), состоящую из всех
циклов вида сАхте, где с — целое число.
Тогда имеет место предложение:
[4:32]. При г <; лг— 2 груяпы Л£(/С) и Aj(/C0) изоморфны
между собою; группа А™— 1(К) изоморфна фактор-группе
^%~\К0) / Jx; что же касается группы А» (/С), то возможны
дв г случая:
а) &хп = 0, тогда группа k™(K) = Z™{K) состоит из всех
цепей вида схп, при целом с, значит, представляет собою
бесконечную циклическую группу.
б) ^xnфOy тогда A™(/Q есть нуль-группа.

326 Д-группы комплексов (нижние группы бегги) [гл. viii
Доказательство. Пусть г^п—1. Каждый гомологический
класс gJ£Aj(/fo) содержится б некотором гомологическом классе
lr=f (5q) G^o(^)j и этим установлено гомоморфное отображение/
группы Д£(К0) в Д£(#). Гомоморфизм / отображает Д£(К0)
на Aj(/C). Для того, чтобы убедиться в этом, достаточно доказать,
что всякий цикл zr£ZrQ(K) гомологичен в К
некоторому циклу zrQ£Zr0(K0).
Докажем это последнее утверждение.
Из наших условий следует существование такой цепи
4+1€^+1(Q), что
Qz<- = AQxr+\
откуда, в свою очередь, вытекает *)
(4:321) A*£H = Q^-Ky£,
где
Уг0 = К0Ах^еЦ(К0).
Из (4:321) получаем
Д*£+! = Q* + у0=-. (Qzr + К0гг) — (К0г" —yr0) = *—*0,
где
j < = K0zr-yl^Ll(K0),
j z"0^zr-Ax^eZl(K),
и, значит, zrQ£ZrQ(K0), чем наше утверждение доказано.
Итак, / есть гомоморфное отображение группы
AJ(^) на Д; СЮ-
Ядро гомоморфизма / есть совокупность тех
гомологических классов -г£ £ А£(K0), которые
содержатся в нулевом элементе группы A£(/f), т. е. которые
состоят из циклов
(4:322) г1егг0(К0)ПНг(К).
Пусть сначала г^п — 2. Если
то Qxr+1 £Z*+1(Q) и, следовательно,
откуда вытекает
Д х^ = Qxr" +X+1. ЛГ+1 € ^+1 W
*) Пишем Д^'д+1 вместо %лг£+\

§ Ц
НЕКОТОРЫЕ ДОПОЛНЕНИЯ И ПРИМЕРЫ
327
и, значит (так как A Qxr+1 -f- A^-H = АД jt£+2 == 0),
г* = A **•+* = A Qat+1 + А /^лг^ = А (/C0jc'+i —^+х) £ «5
Спитак, из *5 6 ZJ (/С0) П #£(Ю следует г£(= Я£(#0), так что при го-
моморфизме / на нулевой элемент группы Ajf(/C) отображается лишь
нулевой элемент группы Д£(/С0). Другими словами: в случае
г^п — 2 гомоморфизм / есть изоморфизм.
Переходим к случаю г = п — \. Если г™-1 £ Z™-1 (К0) П Н^'1(Ю,
т. е. <г^~1 = А^п, у* £ Z.JJ (Дп). то (так как в /С0 нет n-мерных
симплексов) yn£Z%(Q\ значит, уп = схп, и z™-1 = с L xn (^J х. Итак,
ядро гомоморфного отображения / группы Д^-1^) на А™-1 (/С) есть
группа Jx, так что изоморфизм групп &q~~1(K0)/Jx иДу-^/С)
доказан.
Остаётся рассмотреть случай г — п.
Пусть zn(zz™(K)', так как в /С0 нет л-мерных симплексов, то
zn£L%(Q) и, следовательно, ^n^Z^(Q), т. е. г = схп, при целом с.
Но цепь вида слги тогда и только тогда есть цикл комплекса Кп,
когда Дд:л = 0, что и требовалось доказать.
Рассмотрим теперь симплициальное отображение S^ элементарной
триангуляции К§ = Q3 U #po на триангуляцию /Са, причём
предполагаем, что отображение S£, рассматриваемое на Q$, в
следующем смысле является изоморфным:
1°. Каждый симплекс T^Q^ отображается на симплекс ^Г££/(а
той же размерности г.
2°. Если
то 7Т является единственным симплексом комплекса К^
отображающимся при посредстве S\ на Т£.
Замечание. Так как Si есть симплициальное отображение, то
отношение подчинения между симплексами при отображении SjJ,
конечно, сохраняется.
Симплициальные отображения Sjjj, удовлетворяющие этому
условию, будем называть допустимыми.
[4:33]. Пусть S$ есть допустимое симплициальное
отображение элементарной триангуляции К§ = Qp U К$0 на триангуляцию
Кь- Тогда Ка есть элементарная триангуляция, причём, полагая
Q« = SPQp, #«о = ЭДо. ttMeeM /Ca = QaUtfa0, где Qa и К«0
удовлетворяют условиям [4:31].
Предложение [4:33] следует из того, что Qa П Ка0 = О и чт0
отображение £Р, очевидно, порождает изоморфное отображение

328 Д-ГРУЛНЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
клеточного комплекса всех ориентированных симплексов комплекса
Qp на клеточный комплекс всех ориентированных симплексов
комплекса Qa.
4:4. Приложения к проективным пространствам. Введём
следующие обозначения. Через К?0 обозначаем двукратное
барицентрическое подразделение границы Sn правильного (п-\- 1)-мерного
октаэдра Еп+1, вершины которого отсекают на осях координат
пространства Rn+i векторы ±1 (см. главу 4, арт. 6:2). Триангуляция
Kq0 симметрична относительно начала координат о. Триангуляцию
проективного пространства Рп, возникающую при склеивании
симметричных относительно о элементов триангуляции /С?0, обозначаем
через К*0.
Через /Й обозначаем двукратное барицентрическое
подразделение замкнутого л-мерного октаэдра Еп; К& симметрично
относительно начала координат о (в Rn); соответствующая триангуляция
его границы S71-1 есть тогда KV'~1czKa,v Склеивая симметричные
относительно начала координат о (в Rn) элементы триангуляции
/Cq0~\ преобразуем триангуляцию /Q* в триангуляцию К™г проектиЕ-
ного пространства Рп. Очевидно, К"х и А^ являются
элементарными триангуляциями, а склеивание, переводящее А^ в k™v есть
допустимое симплициальное отображение триангуляции KZ на А™,.
При этом
есть двукратное барицентрическое подразделение открытого октаэдра.
Замечание. В этом артикуле мы опираемся на теорему
инвариантности групп Бетти (доказанную в главе 10),
которая гласит:
все триангуляции одного и того же или двух гомеоморфных
между собою полиэдров имеют изоморфные группы Бетти.
Теорема [4:41]. Пусть п^>\. Группы Бетти любой
триангуляции Кп n-мерного проективного пространства таковы.
Д£ (Aw) = 0, если г четно и 0 < г < п.
A£(An)^i2> если г нечётно и 0<г<я.
дп (дп) _ о, если п четно.
A" (Aw)~7, если п нечётно.
Следствие. Проективное пространство нечётного числа
измерений ориентируемо) проективное пространство чётного
числа измерений неориентируемо.
Лемма [4:411]. Пусть х% — ориентация псевдомногообразия
Qn = А?1\А'й)~1. Обозначим через тг симметрическое относительно о

§ 4] НЕКОТОРЫЕ ДОПОЛНЕНИЯ И ПРИМЕРЫ 329
отображение комплекса Д" на себя. Пусть Tgf1 = \е0. . .en-t\ —
какой-нибудь симплекс триангуляции А?^1; положим
ejfc = TC** Л = 0, 1,..., п— 1,
так что симплекс T'l£—1 = \e'...e J есть антипод симплекса Т^г1.
Пусть Щ—1 = (е0. . .^-J — такая ориентация симплекса Г™-1, что
(Дх». ;»-!)=+1.
Тогда
(Д^-х^-1) = (-1)»
В самом деле, симметрическое преобразование
(4:411) хп= — хпу &=»1, 2,...,w
пространства /?w относительно начала координат о, которое будем
обозначать также через тг, имеет детерминант (—1)п, откуда (помня,
что триангуляция /Q\ симметрична относительно о) легко выводим,
что кх™ = ( — 1)пх" (здесь тгд:" обозначает образ цепи х" при сим-
плициальном отображении тг триангуляции K?t на себя).
Так как те есть изоморфное отображение клеточного комплекса
ориентированных симплексов комплекса /Й на себя, то
(Д^.^-1) = (Дл:».^-1),
откуда
(А^ • */»-*) = (Д(_ 1}^п . ^п-i) = (__ 1)Я (Д^п . ^п-1) =
= ( —1)»(А^.^Г1) = (-1)»
что и требовалось доказать.
[4 :412]. Пусть ffr"1, ^~Х — такие ориентации симплексов 7^-*
и Т'£-\ что
/А П Ж—1\ /a W v/W—1Ч ^
(Ахр • % ) = (Дл:р-/р/ ) = 1-
Тогда
В самом деле, если $-1 = (б?0 .. . ^п-1) и /'pf1 = О*0 * • • **n-i)»
то на основании леммы
Но
•Set/p/ = (Sa во . . . Sa en_1),
^а* Рг (Оае^0. . . Оа ^.j),
откуда утверждение и следует.

330 А-ГРУППЫ КОМПЛЕКСОВ (НИЖНИЕ ГРУППЫ БЕТТИ) [ГЛ. VIII
По формуле [8:22] главы 7 из [4:412] вытекает:
[4 :413]. Если /«Г1 = $2'рГ1 == (— х)п ^рГ"1 —ориентированный
симплекс комплекса Као"1 := Si К^о~ и х™ = х"—ориентация
псевдомногообразия Qb = Q%, то
(Д*.х2 • СГ1) = (А^х? • ^Г1) + (V? •(-!)" «'рГ1) = 1 +(-1)«,
т. е. при л нечётном: &ках« = 0, при /г чётном: Ал:ах" = 2^~"1,
где -г?~~1=2Сг~1 — ориентация псевдомногообразия /(Sf"1 (оьазываю-
г
щегося при я чётном ориентируемым).
Доказательство теоремы [4:41] проводится теперь легко
при помощи полной индукции относительно п. При п = 1 теорема
верна: Р1 = К1 гомеоморфно окружности, следовательно (см. арт.
1 :4, 2°) AJ(/C!) есть бесконечная циклическая группа.
Предположим теорему доказанной для Рп~19 в частности, для триангуляции*)
^п—1 полиэдра Рп~1 и докажем её для Pni а именно, докажем, что
утверждения теоремы [4:41] верны, если в них положить/Cw = /Ce?.
Для г-^п — 2 это непосредственно следует из [4:32] и из
индукционного предположения, для г = п — 1 и г=п — из [4:32],
[4:413] и индукционного предположения (при применении теоремы
[4:32] в случае чётного п надо иметь в виду, что группа Jx
состоит из циклов вида 2сг£~~1, где с — целое, так что группа Ao—1(/Coi),
изоморфная в силу [4:32] группе Z*—\K<l^)/Jx, есть группа порядка 2.
§ 5. Симплициальные отображения псевдомногообразий.
5:1. Степень отображения. Пусть К$ и К а — ориентируемые
w-мерные псевдомногообразия. Мы знаем, что группы
Д?(/Ср) =23 (/ф
А? (К.) =Z?(/C«)
являются в этом случае бесконечными циклическими группами с
образующими элементами
где 2'?У и 2*«* СУТЬ ориентации псевдомногообразий К§ и /Са.
У *
В силу теоремы [8 :31] главы 7
т е> ^а^р £^o(/Coj,
(5:11) ^4-т4,
*) См. замечание перед формулировкой теоремы [4:41].

§ 5] СИМПЛИЦИАЛЬНЫЕ ОТОБРАЖЕНИЯ ПСЕВДОМНОГООБРАЗИЙ 331
или, так как (#" ./^) = 1,
(5:12) ($5*ря.&) = т.
где 7 есть некоторое целое число (положительное, нуль или
отрицательное). Это число f, вполне определённое симплициальным
отображением Si и выбранными ориентациями 2 $/ и 2 Ci наших псев-
домногообразий К$ и /С*, называется степенью симплициаль-
ного отображения S« псевдомногообразия К$ в
псевдомногообразие /С«.
5:2. Первоначальное определение степени симплициаль-
ного отображения. Формула (8:22) главы 7 даёт (если положить
в ней х$ — г™, хга = г^ и иметь в виду, что С?j? •$/)== 1):
У
откуда, сравнивая с (5 :12), получаем
(5:21) Т = 2(^аф-4").
Обозначая через щ число тех | ty |, для которых 5« $/ = С/»
и через vf число тех |tf£/|, для которых ^£3/ =— ^/> выводим из
(5:21)
(5:22) т = *< —v<.
Итак:
[5:21]. Пусть ^«=2^ и #" = 2$/ су/ль ориентации ориен-
J з
тируемых псевдомногообразий К* и К$ и Sol есть симплициальное
отображение К$ в Ка- Разность между числом тсг- тех | £*у-|, для
которых при данном г имеем Sa %•=%{, и числом vf /Л£лг |ф|.
для которых Slt^j = — С', #£ зависит от I и равна степени симп-
лициального отображения Sa.
Эта формулировка и представляет собою первоначальное, бра-
уэровское определение степени симплициального отображения.
[5 : 22]. Если образ s\K§ =f= Ка (т. е. slK$ cz /Q, то степень
отображения 6« равна 0.
В самом деле, если | d | не входит в $%К$, то для любого j
имеем (Slty . tat) = 0 и -у = 0 по формуле (5 : 21).
Замечание 1. Степень симплициального отображения 5«
ориентируемого псевдомногообразия АГз в ориентируемое
псевдомногообразие Ка зависит от выбора ориентации К§ и Ка. При этом, как
легко видеть, при замене данной ориентации какого-либо из
псевдомногообразий /Сз и Ка на противоположную, степень отображения
сохраняет свою абсолютную величину, но меняет свой знак,

332 Д-грулпы комплексов (нижние группы бетти) [гл. viii
Замечание 2. Пусть теперь К^ и Аа снова я-мерные
псевдомногообразия, однако, не непременно ориентируемые. Группы
Д" (tfp) = Zl (К?) и Д? (IQ = Z\ (Ka)
состоят каждая из двух элементов: нуля и zl = 2^/»
соответственно 2р=2^Р/- Поэтому, либо slz$ = 0 либо б£гр = г«.
Мы говорим, что чётность отображения 5а в первом случае
равна нулю, а во втором равна единице. В первом случае для
каждого данного Т%£КЛ число 7$£Ар, отображающихся на Т%
четно, а во втором нечётно.
Чётность симплициального
отображения иногда
называется «степенью по модулю
два» этого отображения.
Замечание 3
(примеры). Пусть Ка —
замкнутый m-угольник, вершины
Черт. 123. которого, занумерованные
подряд, например, против
часовой стрелки, обозначим через at,..., am. Возьмём натуральное
число 7 и занумеруем вершины замкнутого (-[^О-угольника К$ также
против часовой стрелки следующим образом:
Считая оба одномерных псевдомногообразия Аа и Ар
ориентированными против часовой стрелки и полагая для любых /=1,...,y
;=1, 2, 3,..., ш:
получим симплициальное отображение 5а псевдомногообразия Ар
на Аа, причём степень этого отображения равна ^. Меняя
ориентацию одного из этих псевдомногообразий, получим отображение
степени— y- Па черт. 123 /я = 3, ^ = 2.
Полученное симплициальное отображение si обладает при/г=1
следующим свойством: для всех я-мерных симплексов 7Й£ А« имеем
tcz- = y, v/ = 0 (т. е*. каждый я-мерный ориентированный симплекс
комплекса А<Г покрывается при отображении Si образами од и
н а к о в о ориентированных симплексов комплекса К? в числе,
равном степени отображения).
Пусть теперь п — какое-нибудь натуральное число; предположим,
что /г-мерные ориентируемые псевдомногообразия К™ и Ар суть
триангуляции лежащих в Rn+X полиэдров, гомеоморфных л-мерной
сфере Sn, и что нам дано удовлетворяющее только что
сформулированному условию симплициальное отображение 6; комплекса AjT
на комплекс А? степени у. Поместим пространство ft*1*1 в простран-

§ 5] СИМПЛИЦИАЛЬНЫЕ ОТОБРАЖЕНИЯ ПСЕВДОМНОГООБРАЗИЙ 333
ство /?w+2 и возьмём в /j?42\/^w+i две точки о и ог по разные
стороны от плоскости R11^1. Построим пирамиды <о/С">, Ко'Ка^''
<о/С^>, <о'К">. Каждая из двойных пирамид
/C"+1 = <o/Cj> U <o'/CS>, Kp-\= <oKni>[)<o'K">
представляет собою ориентируемое замкнутое (п -\- 1)-мерное
псевдомногообразие с телом, гомеоморфным Sn+1
Продолжим теперь на весь комплекс К$^1 симплициальное
отображение 5« комплекса К™, полагая sl(o) = o, Sl(o') = o'.
Получим симплициальное отображение комплекса К^ на /С+\
обладающее свойством тгг. = y> vi = 0 для всех 7^ £/C+1 и имеющее,
следовательно, степень ^. Таким образом, для любого натурального
числа п и для любого целого у фО получаем триангуляции К*> К$
полиэдров, гомеоморфных «-мерной сфере, и симплициальные
отображения степени у триангуляции К% в Кпл. Заметим, наконец, что для
получения отображения степени нуль достаточно весь комплекс К?
отобразить на одну какую-нибудь вершину комплекса К*- Итак:
[5:24]. Для любого натурального п и для любого целого у
существует симплициальное отображение степени у одной
триангуляции n-мерной сферы в другую.
Замечание 4: случай п = 0. Пара точек е0, ех называется
нульмерной сферой. Нульмерные нормальные циклы ех—е0
и е0—ег называются ориентациями нульмерной сферы.
Итак, нульмерная сфера имеет, так же как и я-мерная при я>Л, две
и только две ориентации. Однако, псевдомногообразием нульмерная
сфера не является, так как она не обладает свойством связности.
Пусть даны две нульмерные сферы S^= {еа0, еа1) и S®= {^0, е^}.
Возможны следующие четыре отображения сферы S9 в S®:
!) С1 (е^) = Сг (ер1) = еа0; 2) С2 (*ро) = С2 (*р1) = еа1;
3) С,(*ро) = еа0, C8(*pi) = eel; 4) С4(*ро) = *в1, С(*р1) = еа0.
Выберем теперь какие-нибудь ориентации га и z§ сфер 5« и 5Р,
например, ориентации ги = е\ — е% и г$ = е\ — е|> Тогда
Q (4) = С2 (4) = 0, С3 (4) = 4 С, Оф = — г\.
Естественно сказать, что степень первых двух отображений
равна нулю; степень третьего отображения равна 1, а степень
четвёртого равна ( — 1).

ГЛАВА ДЕВЯТАЯ.
ОПЕРАТОР V И ГРУППЫ V (#, Я). КАНОНИЧЕСКИЕ БАЗЫ.
ВЫЧИСЛЕНИЕ ГРУПП Дг (®, 91) И V'(®,91) ПО ГРУППАМ
Лг0 (Я)
§ 1. Оператор V.
1:1. Определение цепи Vxr. Пусть ^ есть а-комплекс. Для
любой r-мерной цепи xr£Lr (й, W) следующим образом определяем
(r-f-1)-мерную цепь V$xr, называемую V-границей (или верхней
границей) цепи хг. В каждой паре взаимно противоположных клеток
комплекса Ш обозначаем одну какую-нибудь клетку через ti и
определяем значение цепи у$хг на (r-f- 1)-мерной клетке tr^x
посредством формулы:
(l:l)v V^r (4+1) = 2X+1: Ф *Г«Ъ
г
(суммирование по всем ti).
Для сравнения напоминаем определение
(1:1)д Д^(4"1) = 2 tf :trrl) xrtf).
г
Замечание. Если а-комплекс ^ определён как комплекс
ориентированных элементов некоторого симплициального или
полиэдрального комплекса К, то вместо V^
пишем V#. Если невозможны
недоразумения, то вместо V&
(соответственно V#) пишем просто V.
Примеры. 1°. Комплекс К
состоит из всех рёбер и вершин тетраэдра
\ое\е2ев\- Нульмерная цепь л:0
принимает значение 1 в вершине о, значение О
во всех остальных вершинах
комплекса К. На ориентированных отрез-
Черт. 124. ках (его), 1=1, 2, 3 (черт. 124) цепь
Vjc° принимает значение 1, на
остальных одномерных элементах комплекса К цепь V®x° принимает
значение нуль. Если обозначим через х1 цепь Vx°, то V^aaO.

§ 11
ОПЕРАТОР V
335
2°. Комплекс К состоит из двух треугольников \ехе2е±\ и \e2ese4\
(черт. 125), их сторон и вершин. На ориентированных симплексах
(^^2), (e2es)t (г3£4), {еАех) цепь х1, по определению, принимает
значение 1, на симплексе (е2е±) — значение нуль. Цепь Vx1 принимает
на ориентированных треугольниках (е.е^) и (eQe»e±) значение 2
(черт. 125). 4/
3°. Черт. 126 (а также и черт. 127) изображает тор, разбитый
на криволинейные четырёхугольники (противоположные стороны
квадрата ABCD идентифицированы
попарно). Комплекс К состоит из Вг~ » \ »—i - i » \С
Till
(Til
» 1 •*■■ I a» 1 »■ 1
T 1 I \
» [ в*-—[ m J m> I
I ; T I
*»■ ' » 1 — ■ i-. ^ , 1
0
Черт. 125.
Черт. 126.
упомянутых четырёхугольников, их сторон и- вершин. На
ориентированных, как указано на черт. 126, одномерных элементах
комплекса К («горизонтальных» и «вертикальных») цепь х1, по
определению, принимает значение 1; тогда
Ух1 = 0. Тот же результат полу- D c
чится, если Xх положить равной 1
(Г)
ГГ) ^
ГГ\
о
ГГ)
ГГ)
гл
Черт. 127,
Черт. 128.
лишь на горизонтальных отрезках и на вертикальных положить х1
равной 0, или наоборот.
Если положить *i (ete2) = *i (е2*3) = *i (*3е4) - *i (v ) = i (черт.
i-йо;, а на остальных отрезках положить х1 рапной 0, то Vx1 есть
двумерная цепь, принимающая на заштрихованных квадратах (черт. 128)

336 ОПЕРАТОР V И ГРУППЫ V**($?, Щ. КАНОНИЧЕССИЕ БАЗЫ [ГЛ. IX
значение нуль, а на незашгрихованных квадратах, ориентированных,
как указано стрелками, значение 1.
4°. Черт. 129 изображает плоскость, разбитую на конгруентные
квадраты. Комплекс К состоит из этих квадратов, их сторон и
вершин. Цепь х1 принимает значение 1 на
отмеченных стрелками отрезках
ориентированных так, как показывают эти стрелки. На всех
остальных одномерных элементах комплекса К
цепь равна нулю: Vx1 = 0.
1 :2. Запись цепи Чхг в виде линейной
формы. Если цепь хг записана в виде
линейной формы
хг = 2а&$1<>
Черт 129
то бывает удобно цепь Vxr записать также
в виде линейной формы. Так как по
определению (1:1) цепь Vxr принимает на tl+1 значение 2(4+1^?)я*то, Vxr
г
записывается в виде линейной формы так:
Т Y f ? I
*i—I—I—г"*1—I
*>•] J | [ «4 J
I 1 1 Г*7 1
* 4 А А I
(1:21),
Vx' = 22(4+1:^)a,.4+1.
Для сравнения перепись?RaeM аналогичную формулу для &хг:
(1:21)д
A^^SSCtf:^-1)^"1.
В частности, еслихг = ^ т.е. если д^ = 8л, to(1:21)v переходите
h
Сопоставим эту формулу с формулой для А^+1:
и рассмотрим матрицу инцидентности Ег = \\ е£к\\ = ||(4 : t\
*Щ-
,г + П
)г+1
> + 1
*рг+1
\t\..
■ •
.fn..
•
' Bhk
■ •
Получаем следующее правило: Каждый столбец матрацы Ег
выражает собою V'-границу симплекса ^возглавляющегоэтот
столбец; каждая строка матрицы Ег выражает ^-границу симплекса

§ 1] ОПЕРАТОР V 337
^л , возглавляющего эту строку. Или: число гм- = (/л+1 .'*£)
равно значению цепи Vtl на симплексе fn~1u значению цепи А/^+1
на симплексе /£.
1:3. Операторы А «V суть сопряжённые гомоморфизмы *)
соответственно решётки Lr($) в решётку Lr~1(R) и решётки Z/"1^)
в IS (St).
В самом деле, для любых
и
имеем
(Ддс- • y-i) = 2 Ц (/? : /J"1) а<*, = 2 tf: tf-1) аА'
3 i ij
(*' • Vy-1) = 2 a, 2 (£ :О ^ = £ (tf :/J"1) a<fy
i j ij «
т. e.
(1 :31) (A^-y-1) = (^r-Vy*1),
что и требовалось доказать.
Заменяя в формуле (1 :31) цепь уг"1 через хг, а цепь хг через
У+1, можем придать это1 формуле вид (А/ + 1 • xr) = (yr+1 • ухг),
или
(1 :310) (Vxr • y+1) = (** * ЛУ+1)-
Отсюда выведем основное тождество
(1 :32) VV^ = 0
для любой цепи хг произвольного д-комплекса 51.
Тождество это доказываем, вычисляя значение цепи VVxr на
произвольном элементе tr+2£$t:
(VV^ • Г+2) = (Vxr • АГ+2) = (xr • ДАГ+2) = 0
Г
следует
1:4. Группы Z^(ffi,9l\ Я^(Я,Я), V'(ffi,9l). Из определения (1:1)
V(x[±:xrt) = Vx[±V xrr
Поэтому, ставя в соответствие каждой цепи хг её V-границу Vxr,
получаем гомоморфное отображение V группы 1Г(Ш, 21) в группу IS+1 (^,30.
Ядром этого гомоморфизма является группа Z£(®, 51),
состоящая из всех г-мерных V-Ци к лов, т. е. из всех лмерных цепей,
*) См. Прибавление 1, арт. 5:4.
22 Александров П. С

33В ОПЕРАТОР V И ГРУППЫ Vr($,5i)- кАНОНИЧЕбКЙЕ БАЗЫ [гл. it
V-граница которых равна нулю. Образом группы Lr($,9J)
при гомоморфизме V является подгруппа №+х (^ 31) группы Z/+1 (S?, 31),
состоящая из всех (r-f- 1)-мерных цепей, являющихся V-границами
некоторых r-мерных цепей хг £ V (S?, 31).
Из основного тождества (1:32) следует:
^•граница всякой цепа есть V-цикл. Поэтому для любого г
группа Hr^ (S?, 31) есть подгруппа группы Zr(^, 31).
Элементы zr группы Нг(^,31) называются V-гомологичными
нулю (в 5? по 31):
^-0 (в йпо 31).
Если г[ е Z; (ft, 3D, < £ Z; (ft, 31) и г£ — г\ £ #£ (ft, 31), то V-цик-
лы г[ и хгъ называются V-гомологичными между собою (в ft по 31):
г[~г' (в ft по 31).
Замечание 1. Знак V-гомологии ^ обладает всеми
перечисленными в Лаве 7, арт. 6:4 свойствами знака гомологии ~.
Определение [1:4]. Группа
V (ft, 31) = Z; (St, 31)///; (ft, 31)
Называется г-мерной V-группой, верхней группой Бетти
или просто группой Vr комплекса ft.
Замечание 2. V-граница всякой я-мерной цепи я-мерного
комплекса ftn равна нулю; другими словами, на n-мерном комплексе
все n-мерные цепи суть V-циклы:
Zn (<^« щ = Ln (®n9 «ft).
С другой стороны, V-граница единственного (нулевого) элемента
группы Z._1(ft,9l) есть нульмерная цепь, тождественно равная нулю.
Поэтому tf°(ft, 31) есть нульгруппа, так что V° (ft, 3t) = Z°v (Я, 31).
Замечание 3. Группа Vr(ft,J) обозначается также через Vj (ft),
группа Vr(ft, Jm) через V^(ft); вместо Vr(S?, 31) будем часто писать
V(ft) и т. д.
1:5. Куски цепей. Пусть xr£Z/(ft) и ft0 есть замкнутый
подкомплекс комплекса *ft. Из замкнутости подкомплекса ft0 вытекает,
что для любого ^r+1£ft0 имеем
(V*0 ft0 *r ' ^r+1) = (v*o *r * 'r+1), (^o v^ *r ' tr+1) = (V^r • *r+1)-
Итак:
[1:51]. Для xr£Lr(§t) и любого замкнутого подкомплекса ft0
комплекса ft имеем
(1:51). Ч^=-ВД^Г.
В частности^ если xr£ZrA(U)t то ft0xr £ Z'_(ft0)<

§ 11
ОПЕРАТОР V
339
Г: 6. Группы V°(ft,9()==Z0(®,9l). Так как Я» (Я, Я) есть нуль-
группа, то:
V°(S?,9l) = Z°(S?,3t),
и для вычисления группы V°(S?, %) надо выяснить, какие нульмерные
цепи являются V-циклами. Ограничимся случаем, когда Я есть комплекс
ориентированных симплексов полного симплициального комплекса К-
Пусть сначала К—связный комплекс, г° — нульмерный V-цикл
комплекса йГ. Докажем, что во всех вершинах ei комплекса К цикл
г° принимает одно и то же значение.
Вследствие связности К достаточно доказать, что цикл г°
принимает одно и то же значение в любых двух вершинах е0, ev яшляю-
щихся концами отрезка | е0 et | £ К. Но это утверждение следует из
того, что Vг° принимает на (е0ег) значение г°(ех) — z°(eQ). Обратно,
если цепь х° принимает во всех вершинах одно и то же значение,
то V х° принимает на всяком отрезке (e4ei+1) значение
*°('<+i) —*°('<) = 0,
так что
V х° = 0.
Итак,
[1:611]. Нульмерные V-циклы связного полного симплициалЬ*
ного комплекса К могут быть определены как нульмерные цепи,
постоянные на К, т. е. принимающие во всех вершинах К одно
и то же значение.
Отсюда сразу следует:
[1:621]. В случае связного полного симплициального комплекса
К группа V0 (К, 91) изоморфна группе %.
С другой стороны, из [1:611] следует:
[1:61]. Нульмерные V'-циклы любого полного симплициального
комплекса суть нульмерные цепи, постоянные на каждой
компоненте К.
[1:62]. Для любого полного симплициального комплекса К
группа V°(/C, 5t) есть прямая сумма групп % взятых в числе,
равном числу компонент комплекса К. Следовательно: группа V°(/C, %)
изоморфна группе Д° (К, 51).
Замечание. Этот результат содержится в общей теореме [4:2].
1:7. Группы Vn(Kn,J) для я-мерных псевдомногообразий. В
этом артикуле Кп есть л-мерное замкнутое псевдомногообразие. Мы
рассматриваем лишь целочисленные цепи.
Пусть tn — какой-либо ориентирошанный ^-мерный симплекс
комплекса Кп- Тогда целочисленная цепь tn, как всякая я-мерная цепь
n-мерного комплекса Кп, есть V-цикл.
[1:71]. V-цикл tn не гомологичен нулю на Кп, т. е. не
существует никакой (п — 1)-мерной целочисленной цепи хПь~1
комплекса Кп, удовлетворяющей условию
Vat -1 == tn.
22*

340 ОПЕРАТОР V И ГРУППЫ УГ(ЯД). КАНОНИЧЕСКИЕ БАЗЫ [гЛ. IX
Для доказательства достаточно заметить:
[1:710]. Сумма коэффициентов всякого я-мерного V-цикла г7\
гомологичного нулю на Кп, есть чётное число.
Доказательство. Так как всякий я-мерный V-цикл,
гомологичный нулю на Кп, имеет вид Vx4-1 = Va^ V fj*-1, где xn~l £ Ln~l (Kn),
то утверждение [1:710] достаточно доказать для V-циклов вида
V^—1. Но, если \tn. | и|^*_ | суть два примыкающих к |^_1|
симплекса, а^г tn —их произвольные ориентации, то
где Sj, e2=i±:l, так что гх-\-г^ = § или =t2, что и требовалось
доказать.
Если Кп ориентируемо, то [1:710] может быть усилено:
[1:720]. Если V^? есть какая-либо ориентация ориентируемого
я-мерного псевдомногообразия Кп и,гте—"Va^ есть V-цикл,
гомологичный на Кп нулю, то V#£=0.
В самом деле, для любого ^—1 имеем
v^-1 =tn —tn
(где \t* \ и \tf | суть примыкающие к |/j*| симплексы), другими
словами, утверждение [1:720] верно для всякого V-цикла вида
V^—1, значит, и для всякого V-цикла вида V хп-г.
Из [1:720] следует:
[1:72]. Если \tn\£Kn и Кп ориентируемо, то atn^0 на/Сптоль-
v
ко, если а = 0.
Пусть снова 1(п — любое я-мерное псевдомногообразие.
[1 :73]. Если t% и t™ — два ориентированных я-мерных симплекса
комплекса Кп, то
Вследствие сильной связности Кп достаточно доказать [1 :73] для
двух симплексов \t*\ и \t4H имеющих общую (я—1)-мерную грань
|^ — 1|. Но в этом случае
(1:73) V^"i = (^:^-1)^ + (^:^-1)<J>
и так как
то ?*±Р*~0, что и требовалось доказать.
Замечание. Если f} и t%— когерентные ориентации, то
(^ :^~1)= ~(^ :^-1) и (1 :73) переходит в V^l.-1 = =t(^ — /JJ)#
т. е. в №~^'у отсюда следует:

§ 1]
ОПЕРАТОР V
341
[1:74]. Если Кп не ориентируемо, то для любого
ориентированного симплекса № имеем
2#~0.
* v
В самом деле, если ^, t™,...ytns— любая дезориентирующая
последовательность на Кп, то
т т т т
1 v v vsv х
т. е.
t* ft, 2#~0.
1 v г г v
Так как для любого \t"\ £ Кп имеем Р*~±^у то 2/^0, что и
требовалось доказать.
Из [1 : 73] далее следует:
[1 :75]. Любой целочисленный л-мерный V-цикл zn удовлетворяет
на Кп гомологии
zn ~ atn,
где \tn\ — любой я-мерный симплекс Кп и а—целое число.
Из [1 :75], [1 :72], [1 :74] вытекает:
Основная теорема [1:7]. Пусть Кп есть n-мерное
псевдомногообразие] если Кп ориентируемо, то V™(Kn) есть
бесконечная циклическая группа] если Кп не ориентируемо, то V™(Kn)
есть группа порядка 2.
Выведем из доказанных в этом артикуле предложений ещё одно
важное свойство замкнутых псевдомногообразий:
[1 :76]. Пусть К0 есть собственный замкнутый подкомплекс
n-мерного замкнутого псевдомногообразия Кп. Тогда V™(/Q есть
ну ль группа.
Доказательство. Пусть tn — ориентированный я-мерный
симплекс комплекса /С0. Достаточно доказать, что я-мерный V-цикл tn
гомологичен нулю в К0-
Пусть \t*\ £ Кп\К0]берём какую-нибудь его ориентацию^. В силу
[] :73], имеем
tn ~ г№ в Кпу е = ± 1,
v 1
так что существует цепь хп~1 ^L^™1 (Kn), удовлетворяющая условию
Так как К0 — замкнутый подкомплекс комплекса Кп, то, в силу
теоремы [1 :51], имеем
V* KqX™-1 = Ко^к" х™-1 = K0tn — /С0е/? = Р\
о

342 ОПЕРАТОР V И ГРУППЫ Vr(®, ЭД. КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
т. е.
**~0 в /С0>
V
что и требовалось доказать.
§ 2. Базы решёток LJ($).
2:1. Предварительные замечания. Начиная с этого параграфа
и до конца главы, мы предполагаем, что ^ есть n-мерный
конечный а-комплекс.
Матрицами гомоморфизмов Л при начальных базах
Pv ...,^г, г = 0, 1,...,д
решёток LJ(S5) (см. Прибавление I, арт. 2:7 и арт. 5:2) являются
матрицы инцидентности
E-i = ||t£-4|, где е'-1 =^:Г_-1у
Пусть *»•={*;,...,*£.},
(2:11) *» = 2вм'«. A-l, 2,...,p',
есть какая-либо база решётки LJ(S) и пусть
(2:12) Д^-^^Г1^-1' А = 1. 2,...,РГ,
А:
тогда всякое равенство вида
(2:13) Ьхг = W-1, хг = 2ал^
является линейной комбинацией с коэффициентами аь равенств (2 :12).
При этом, обозначая через А матрицу ||«£4||, имеем для матрицы
Hr_1 = IKft_1|! Формулу
Нг-1=ЛгЕг-1(Дг-1)-1.
2:2. Сопряжённые базы решёток Ь^(Щ. Пусть
Г if-= {«;,...,«£■},
(2:21) . _ _ ,
( w»*=k wJ");
(2:22) 1 w*-* = K-v--,«7ii}
суть две пары сопряжённых между собою баз*) решёток LJ(^), соот-
*) Прибавление I, арт. 5:3.

§ 2]
БАЗЫ РЕШЕТОК £q (£?)
343
ветственно Ljj-1^). Пусть Hr""x = Ihjy""1!] есгь матрица
гомоморфного отображения Д-группы LrQ($) в группу L£~х(51) в базах Wrf
Wr~l:
(2 :23) Aw
f)r-.llWr-~i
i ==3 2j^ij "J
Так как гомоморфизмы А и V являются сопряжёнными, то на
основании теоремы [5:4] Прибавления I имеем
(2:24)
Votf
г—1
2л щ
Wi.
Итак, если строки матрицы Hr_1 выражают А-границы элементов
базы Wry возглавляющих эти строки в таблице
г
Wx
г
W
?г
г — 1
wx
.Wi
.w
?r—1
г—1
Чу
то столбцы матрицы Н.^-1 выражают V-границу элементов базы
IF*"-1, возглавляющих эти столбцы в таблице
W\
Wi
W{
— г— 1
Wx
.W4
— r — \
■ чу-i
r—l
Число riif1 есть, таким образом, коэффициент, с которым w] 'г
входит в А*<у£, и коэффициент, с которым w£ входит в Vwj~~l.
В соответствии с замечанием к теореме [5:4] Прибавления I
можно также сказать, что r^f есть /-я контравариантная
компонента элемента kw^Lo^iK) в базе Wr и /-я к®вариантная
компонента элемента V^J-1 в базе \Fr.
2:3. Выражение элементов групп Lr(&, Щ через базы
решётки Lo ($).
Теорема [2:3]. Пусть
есть база группы Цу(Щ\ пусть % — произвольная, абелева группа.

344 оператор V и группы Vr(5l, 21). канонические базы [гл. ix
Тогда каждая цепь xr £ Lr (5?, 51) однозначно представляется
в виде
i
где a^ty.
В самом деле, пусть
хх = ^ciijtj, tj = ^bjkxk-f
j k
матрицы \\ау\\ и К ^|| унимодулярны и взаимно обратны, так что
, "<A* = ^e\i (/ = *).
Каждая цепь д:г = 2<VJ(: £r(^i 91), */€Я представима в виде
J
2 bfifrxl = %akxrk, аА = 2 *Лл-
Для доказательства единственности этого представления достаточно
показать, что из ^а£Х{ = 0 следует ai=^0. Это^сделать легко:
*'
2 a-i** = О
i
означает
2 ял/5=о,
значит, 2aA'j = 0 (Для любого у). Умножением на #-л и суммиро-
i
ванием по j получаем отсюда
2аАЛл = 2аЛл = «л = 0 (для любого £),
что и требовалось доказать.
§ 3. Канонические системы баз. Группы Vj(ft).
3:1. Предварительные замечания. В этом параграфе мы для
краткости пишем Lr вместо Lr($,J); вместо Z\ ($, Д Н\ (51,7),
#*(Я, Д £д(®, Д ... пишем соответственно Zl, #1, №", Z£, ...
[3:11]. Группа Z\ есть дивизионно-замкнутая подгруппа группы Lr.
В самом деле, при а £7, а ^ О, из
лг' £ Z/, я*г £ Zl
следует
Дахг = akxr = 0,
значит,
Д;С = О,
т. е.

§ 3] КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ. ГРУППЫ Vq (Я) 345
Так как группа LrjZ\ изоморфна группе Яд-1, то из теоремы
[2:61] Прибавления I следует:
[3:12]. Группа Lr разлагается в прямую сумму:
(3:12) Lr=Y*±2?L,
где подгруппа Yr группы Lr изоморфна группе Нг~г.
3:2. Канонические базы групп Zl. Полагая в теореме [2:52]
Прибавления 1
получаем:
[3:21]. Группа Z\ имеет базу
(3:21) гги . . ., г/\ иги . . ., и/; vru ..., v/,
удовлетворяющую следующим условиям:
a) v[, . .., tv* суть элементы подгруппы Hi; порядок элемента
/=1,2, ..
6[>1, причём
и\, /=1,2, ..., тг относительно Н\ есть натуральное число
вГ=зО(тос1вГ+1).
б) Циклы Ь\и[% . . ., 6^мГг к <яь .. ., i£r образуют базу группы Hi.
в) Циклы и[, .. ., и^; t;i, , .. ., т£г образуют базу группы Иг.
Определение [3: 22]. База (3:21) группы Zi", удовлетворяющая
условиям а), б), в), называется канонической базой группы Z£.
[3:23]. Числа б£ гу/яь r-мерные коэффициенты кручения комплекса й
и, следовательно, определены однозначно; число я*" есть /--мерное число
Бетти комплекса АГ.
В самом деле, обозначая через Z£, £/[, Vj бесконечные циклические
группы, порождённые, соответственно, элементами zrh> и7-, vrp имеем
разложения в прямые суммы:
Л = 1 «'=1 J' = l
(3 : 22) {
и, следовательно (см. теорему (1:52) Прибавления I),
(3 : 23)*) Д£ (Я) « S Z£ + 2 <"№<>•
*) Знак я^ есть знак изоморфизма между двумя группами.

346 ОПЕРАТОР V И ГРУППЫ Vr(Sf, 3t). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
Группы U%fiiU% суть конечные циклические группы порядков 6Г, группы
Z£ суть бесконечные циклические группы; их число тсг есть ранг группы
Д£($), т. е. г-мерное число Бетти комплекса $. Прямая сумма 2 (^i/®2MP
состоит из всех элементов конечных порядков группы Aj($) и совпадает
(с точностью до изоморфизма) поэтому с r-мерной группой кручения 6**($)
комплекса $:
г*
(3:24) вг(Я)=2Мда)-
4=1
Так как конечная группа 9г($) есть прямая сумма чГ циклических
подгрупп порядков б£ и 6r^O(mod8£ , t), то числа б£ и тг определены
однозначно группой 9**($): числа 8J* суть коэффициенты кручения группы 9**($)
(см. Прибавление I, арт. 4:3), значит, и группы Aq($), что и требовалось
доказать.
3:3. Канонические гомологические базы. Пусть хг —
произвольный целочисленный цикл. Тогда, так как Zj = 2^ + 2^+2 Кя
то хг однозначно представляется в виде линейной комбинации
2 атА+2 ь/i + 2 ъ$.
Так как г
есть база группы Н*, то хг = 2^г£"~Ь 2*<аЛ~ 2^5 тогда
и только тогда содержится в Яд, когда
2 «*** + 2 W+2С;*1=2rfAr«f+2бл>
что, в силу линейной независимости цепей ^, arv vrp имеет место
лишь при условии
Итак:
[3:31]. Каждый целочисленный цикл xr^Z^ однозначно
представляется в виде
(3:3i) хг=2ал4+2**"* + 2^5-
Z/и/ел л:г тогда и только тогда гомологичен нулю, когда в (3:31)
ял = 0, *,— 0 (mod вр.
Отсюда следует:
[3:32]. Всякий целочисленный цикл гомологичен циклу вида
2а*г»+2*«в*'
гд* коэффициенты ah определены однозначно, а Ь4 — с точностью
др целочисленных кратных соответствующих Ъгг

§ 3] КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ. ГРУППЫ Vo (й) 347
С л едет в и е. Элементы ггр...уг^г канонической базы группы Z£
образуют r-мерную (УД)-базу комплекса 55.
Из теоремы [2: 63] Прибавления 1 следует и обратное утверждение:
[3:33]. Всякую r-мерную (]${)-базу комплекса & можно до-
полнить до канонической базы группы Z£.
3:4, Система канонических баз групп!/. Пусть для каждого г1
г=0,...,л, выбрана определённая каноническая база (3:21)
группы Zr (®). В силу изоморфизма А между группами Lr/ZrL и #£-!;
базе
группы Я^-1 соответствует база
Si» • • • э 5xr—ь tyi > • • • у ty9r—i
группы Lr/Z\% причём для любых хг. £j£, .Vj G ^j
имеем
Выберем раз навсегда цепи jtj£r/\, yj^tyj.
В силу теоремы [2:64] Прибавления I, цепи
образуют базу группы Z/.
Получаем следующий основной результат:
Теорема и определение [3:4]. Пусть й — конечный
а-комплекс размерности п. Для всех г = 0,1, 2,... ,п можно
построить базы
(3 :4) х\,... ,д£_1; X» • • • Ofr-i; ^ • • • ,<г'> ^ • • • ><г; *£ • • • Кг
групп Lr, причём имеют место соотношения'.
а) цепи z[,... ,г£г; urv... ,^г; т^,... ,г£г суть циклы и образуют
базу группы ZrL\
б) циклы игх,...,и*г; vrv...,^r образуют базу группы И\\
в) для яс£л: /=1,...,тг порядок элемента и* относительно
HrL есть натуральное число 6^>1, причём 6Г= 0 (mod 6^+ ) и циклы
6i#i,. . .,б£г; и^,; ifv...yVr9r образуют базу группы HrL\
г) имеют место соотношения
(так что цепи л^,.. .,л^г-1 и j/J,.. .,yrar-i Циклами не являются).
Базы (3:4), построенные для всех г=0, 1,...,л и удочлетво-

348 ОПЕРАТОР А И ГРУППЫ ДГ(Я), %). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
ряющие для всех г условиям а) — г), образуют, по определению,
систему канонических баз групп V.
Замечание. Как мы видели, тгг есть r-мерное число Бетти,
a 6J суть r-мерные коэффициенты кручения комплекса ^.
Из условий а) — г) следует, что гомоморфизм А группы Z/
в группу Z/-1 имеет при канонических базах (3 : 4) следующую матрицу:
Г1
V
Ik'-*
к
п
Г1
r-1 r-l
Хх ...Xzr-.2
0
1 °
0
0
0
r-l r-1
Ух -У,г-2
0
0
0
0
0
1 r-1 r-1
0
1
0
0
0
0
r— 1 r-1
е-
0
0
0
0
r-1 r—1
\vi -V-ij
0
1
' 1 ;
0
0
0
(каждая строчка выражает А-границу цепи, возглавляющей эту строчку).
Выпишем ещё матрицу гомоморфизма А группы Lr+1 в группу Lr
(см. таблицу (3 : 42) на стр. 349).
Пример 1*). Пусть К—комплекс, состоящий из трёх сторон
и трёх вершин треугольника |^^з1- Построим систему
канонических баз комплекса К следующим образом:
г>1 = *з — *2> *>!j = *i —«в» z{l = e&
y\ = t{ = (*Л), У\ = t\ = (Vi)» *! = '1 + *\ + & где 4 = ('i**)-
•) См. главу 7, арт. 4: 2, примеры 1—3, и главу 8, арт. 1: 4, упражнение 4.

§ 3] КАНОНИЧЕСКИЕ CHCfEMbI БАЗ. ГРУППЫ Vq (£) 349
Lr+i
1
Г
k+1
•
г
*.
к%
к1
•
<k
ч+1
оН-1
0
0
0
0
0
x'.-O^-i
0
0
0
0
0
<.../,
0
0
0
0
0
u\...U r
1 X
°!
Ч'
о
0
0
0
<•••<'
0
1
*1
0
0
0
Пример 2 *). В есть я-комплекс, состоящий из элементов
-4- /2 . -Ь- /1 • -Н- /1. -4-/0
-—«-р *-!> «-2» "— V
причём (fr: /J) = (t\: ф = 0, (t\: ф = {t\: *°) = 0.
Имеем систему канонических баз:
~0 /0. у\ /1. оЛ /1. ^2 /2
^1 — ^, ^ — «.j, ^2 — *2, ^х ^.
Пример 3*). 51 есть я-комплекс, состоящий из элементов
с коэффициентами инцидентности
(*»:*{) = 2, (*}:*°) = 0.
Имеем канонические базы:
2о — /о «1 — tl х2 = /2
*1 —fi> wi — М> л1 — V
*) См. главу 7, арт. 4 ; 2, примеры 1 —3, и главу 8, арт. 1 : 4, упражнение 4.

Й50 оператор V и группы Vr (Stt 21). клноническйЕ вазУ [гл. it
3:5. Система V-баз комплекса 5?; группы VJ(^). Пусть
(3:51) ^={^,...,<r_i; x>->Xr-i; ^-..,<r; «&-,«&; *[,...,*£}
(г = 0,1,.. .,я) есть каноническая система баз комплекса $.
Система баз решёток Lr> г = 0,1,.. .,я, сопряжённых базам (3: 51),
называется с и с тем ой V-баз комплекса $. Элементы этих
баз, сопряжённые соответственно элементам:
обозначаем через
(3:52) ej, ..., ^r_i; ^, . .., ^_i; Jj, ..., Jjr; *',.. .,^Г;Я» -o£.
Самую базу (3:52) обозначаем через Wr. Помня, что
гомоморфизмы Д группы Lr в группу Lr~x и группы Z/+1 в группу I/
выражаются, соответственно, таблицами (3 :41) и (3 : 42), и применяя
правило артикула 2:2, видим, что гомоморфизмы V групп Lr"1 в Lr
и Lr в Lr+1 выражаются, соответственно, таблицами:
Rr-i
Г1
U^r—1
Г
г1'
г
0
о
0
0
0
-Г-viJ
0
0
0
0
0
-r—l -r—l
0
0
0
о
о
-r-1 —r—l
er1 ;
0
0
0
0
УГ'-уЫ
0
1
' 1
0
0
0

§ 3] кАЙОНИЧЕСКИЕ СИСТЕМЫ БАЗ. ГРУППЫ VQ ($) Зб1
53»-+1)
\
74+1
7+1
k+l
г-1
"i^1
"<t+1
ten
—r+1
K^
^+1
Hj...tt^+i
0
0
0
0
0
v\...vrr-i
1 Q
0
0
0
0
0
-r -r
1 к
о
0
0
0
0
У ХГГ
e*.
">
0
0
0
0
0
1
1
0
i °
0
где каждый столбец выражает V-границу возглавляющего его
элемента.
Отсюда видно, что цепи щ, v) и г£ суть V-циклы, а цепи
xl и у\ не являются V-циклами:
(3:54)
:0.
Примеры V-б а з. Рассмотрим примеры канонических баз, построен*
ных в apt. 3:4, и построим соответствующие V-базы. Получим (в случае
примера 1)
У г = —%> y°2 = ev z\ = et-\-e2 -f %} fyi = *ь
V\—tl ^з, Vz = t2 h, Zx = U
n-o —i
В случае примера 2 (арт. 3:4) построенная там система канонических
баз является самосопряжённой, т. е. совпадающей с соответствующей
системой V-баз.
В случае примера 3 имеем систему V-баз:
*-р ,о ~1 л ""2 >2
Zi = tU Xt = tU lli = t%
причём, как и должно быть, имеем

352 ОПЕРАТОР V И ГРУППЫ Vr ($, ?D. КАНОНИЧЕСКИЕ БАЗЫ ^Л. 1Х
Так как (3:52) есть база группы Z/, то каждая цепь xr£Lr
однозначно представима в виде
хг = 2<V? + 2 V i + 2*л** + 2^Д + 2^У1,
причём
(3 : 55) vjc = 2a,V«r + 2^ + Ц^ + l&V^ + S«,VJT =
=24v^-+2«,v J?=Ълйгк+1 + 2«ДГ '■
1 1
Поэтому цепь хг тогда и только тогда является V-циклом, если
в представлении (3 : 55) имеем
, £ = 1,2,.
. /=1,2, ...,а'.
Другими словами, элементы
i/ ___ 1 о t^-1
* — а, ^,• • •,с ,
у = 1,2,. . .,ог"1,
А= 1,2,. . .,тсг
баз (3:52) образуют базу группы ^г
Далее, так как W и Wr_1 являются соответственно базами
групп Z/ и Z/-1, то всякое равенство вида
есть линейная комбинация равенств вида
А это значит, что цикл
(3 :56) A:r = 2¥l'+2^i+Ilv^
тогда и только тогда содержится в /Уг,если в (3:56) имеем
ch = 0, а{ = 0 (mod ОГ"1) для всех h = 1, 2,. .., rJ,
* -— i, z.,. . ., с
Другими словами, V-циклы
ъ'гЪи • • • > e7-iv-i> *Г. • • • .^^
образуют базу группы Hrv. Таким образом, обозначая бесконечные
циклические подгруппы группы Z/, порождённые элементами
—г г г ~~г г

§ 3] КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ. ГРУППЫ Vy(.Sf) ЙоЗ
соответственно через ^
Хъ, Yii Z/i, Ui, Vj
имеем разложения в прямую сумму:
zr а? кг хг-1 аг-1
" = 2*2 + 2 *?+23J+ 2й + Ж
^=22Г+2й + 2"»?.
откуда (см. теорему [1: 52] Прибавления I)
П = Z, /я; = 2 z\ + 2^/ 6Г 1й!)-
Здесь группа Tfi/^Ul есть конечная циклическая группа поряд-
ка 6J"1, так что, в силу (3:23), группа 2(^Г//^~1^0ИЗОМОРФ"
на (г—1)-мерной группе кручения в^-1^).
Группы Z£ суть бесконечные циклические группы, так что груп-
пг
па V z£, очевидно, изоморфна группе A£0(5t).
h=l
Итак:
Теорема [3:51]. Группа Vg(S?) изоморфна прямой сумме
(г—1)-мерной группы кручения вг_1(£) и свободной абелевой
группы ранга ?rr(St).
Пусть Кп — ориентируемое псевдомногообразие; по теореме
[1 :7] группа У™(Кп) есть в этом случае бесконечная циклическая
группа и, значит, ъп (Кп) = 1, а ®п-\Кп) есть нуль-группа.
Если же Кп — неориентируемое псевдомногообразие, то по тео«
реме [1 :7] группа V%(Kn) есгь группа второго порядка, и,
следовательно, т:п (Кп) = О, а б™-1 (Кп) — второго порядка.
Итак:
Теорема [3: 52]. Ориентируемое n-мерное псевдомногообразие
не имеет (п—1)-мерного кручения] (п—1)-мерная группа
кручения n-мерного неориентируемого псевдомногообразия есть группа
второго порядка.
Из теорем [3:51] и [1 :7б] следует далее:
[3:53]. Пусть Ко — собственный замкнутый подкомплекс п-мер-
ного замкнутого псевдомногообразия К- Тогда К0 не имеет (п — 1)-
мерного кручения.
23 Александров П. С.

354 ОПЕРАТОР V И ГРУППЫ Vr(S?, 51). КАНОНИЧЕСКИЕ БАЗЫ (гл- IX
В самом деле, по теореме [3:51] группа Чо(К0) изоморфна
прямой сумме групп ^п~1 (К0) и доо(Х0). Но по теореме [1 :76]
группа V[J(Xo) есть нуль-группа, поэтому и в"-1 (Х0)> как и ^оо(К0)
есть нуль-группа.
Примеры групп V(S). Вернёмся к примерам, рассмотренным
в конце арт. 3:4. В первых двух примерах V-группы изоморфны
А-группам тех же размерностей. В третьем примере группа Vq
есть нуль-группа, а группа Vo есть группа порядка 2.
Упражнение. Читателю рекомендуется определить А-группы
различных комплексов, рассмотренных в главе 8, арт. 1 :4, как
непосредственно вычисляя эти гру ты, так и применяя теорему [3 : 51].
§ 4. Вычисление групп Д'(®,21) и V (S, 21) по группам AJ(Sf).
4:1. Вычисление групп Дг($, Ж). Возьмём каноническую систему баз
групп Lr:
(4:11) *[,..., *!>-i; X»---»Xr-1; <«...,<r; «[,...,<r; <,...,<r,
Пусть дана цепь xr £ Lr(8,Ж). На основании теоремы [2:3] цепь лгг
однозначно представляется в виде
(4:12) хг = ^ акх\ + 2 ^ + 2 'л *л + 2М + 2М
aA62C, &гб2Г, '*€% diZW.ejZW,
и её граница
тогда и только тогда равна нулю, когда
<4ЛЗ> 1 ^ = 0, /-1,2,..., аг-1.
Итак, для того, чтобы цепь xr£Lr(u, Ж) была циклом, необходимо и до-
стаючно, чтобы в представлении (4: 12) были выполнены условия (4: 13).
Другими словами:
Все циклы zr£Zl($, Ж) и только они (однозначно) представимы
в виде
(4:130) гг = 2*л*й + 2***л + 2d<u* + 2^/>
где Cfodfrej—произвольные элементы группы Ж, а каждое ак —
произвольный элемент группы ftr-i^ (как мы знаем, через тЖ обозначается под-
группа группы % состоящая из всех элементов а £ Ж, удовлетворяющих
условию та = 0).
Замечание. Цикл zr называется циклом первого рода, если в
(4:130) все ак == 0. В противном случае z? называются циклом второго
рода.

и цепь
§ 4] вычисление групп Аг (И, 9() и У(®,?0 355
Рассмотрим теперь прямую сумму
~jr-\ ъ'г %r Qr
(4:14) @= 2вл-19Г+ 2^+2^+2%
где каждое из прямых слагаемых %h, %iy Щ есть группа 21. Каждому
элементу
(4:15) (аъ ...,aTr_i; гь ...,скГ\ dh ...,dxr; еь ...,<v)
группы © однозначно соответствует цикл
Обратно, мы только что видели, что каждому циклу (4:12) в силу условия
(\: 13) однозначно соответствует элемент (4:15) группы @. Итак: Группа
Z[($M) изоморфна группе (4:14).
Пусть теперь дан цикл
(4:12) xr = ^akxrk + ^cnzrh + Jjltf + ^etf
?пь
Найдём условия, необходимые и достаточные для того, чтобы было кхг + 1 = ***.
Имеем
д*г. 1 = 2«;д<+1 + 2*>.v+l + 24<4+1 + 24К+1 + 2ИК+1=
Очевидно, для равенства Lxr^1 = xr необходимо и достаточно, чтобы было
( ^ = 6^4 / = 1,2,..., ^
*/-&}, ; = 1,2,..., а'',
^ = 0, £=1,2,..., т^-1,
ch = 0, /г = 1, 2,..., тс»\
Поэтому циклы, гомологичные нулю, т. е.цепихг £Нг(й,%) и только
они однозначно представимы в виде
*гв2*<и< + 2*^
га* <*г. e ejsr, ^ ^ ад.
Рассмотрим прямую сумму
х*" а*"
(4 :140 <§' = 26<^ + 2^*' % = 9Ь
Каждому элементу
(4:16) (rft <Lr; *1э ... , евг), Ь = Ь\а\
23*
(4:130

356 ОПЕРАТОР V И ГРУППЫ Vr($, %). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
(где а{ £ К произвольно) группы &' соответствует цепь
являющая с i границей цепи
^«-s^+4s*;->';+i+sex+l+s4«j;+i+s*,4+i.
где ait b- даны в (4: Ь>'), а сл, dk, ег совершенно произвольны.
Итак, каждому элементу (4:16) группы (§>' однозначно соответствует
некоторый элемент хг группы #д ($, Vt)- Обратно, если **"£//£($, VI).
^ = Дл'г+1, то в представлении (4:12) выполнены условия (4:13') и циклу
хг соответствует элемент
(db ... , dx*\ еъ...9 е/)
группы (2'. Итак:
Группа Н\(Ш, VI) изоморфна группе (1:14').
Отсюда легко выводим следующее предложение:
Теорема [4:1]. Группа &г($, Щ изоморфна прямой сумме
тГ—1 jr ТГ
J--1 ? 2 = 1 «я-1
В самом деле, теорема [4:1] следует из определения Дг($, VI) =
= Z£ ($, 2()/Яд(^, 31) теоремы [ 1 :52] Прибавления 1 и из того, что группы
Z^(.H, VI), Яд (К, VI) изоморфны соответственно группам (4:14) и (4:14').
4:2. Вычисление групп Vr(&, VI) производится при помощи
рассуждений, аналогичных только что произведённым. Однако, вместо канонических
±-блз надо отправляться от V-баз.
Пусть лг£//($, Vf) произвольно. Имеем представление
у т Y Y—1 Т~~Л.
(4:2!) кг^ 2 "Л I" £ bj[+ 2 ^Л+ S di"i+ 2 ^
/.=1 г=1 7i=i *=i j=i
через элементы V-базы. При этом [в силу (3:54)]
_г gr jr г
/.—1 /=-1 A- = l Z«l
Итак: Y\vr — О тогда и только тогда, когда в представлении (4:21)
0J>* = O Л=1, 2, ...,тг
(4 :22)
Ь = 0 / = 1, 2, ...,ог.
Отсюда так же, как и в 4:1, выводим:
[4:21]. Группа Zr (Й, VC) изоморфна прямой сумме
„г Гг тг-1 вг-1
2 ГГД+ 2 21/,+ 2 %+ S И;,
где VI/t, VQ, Vfj с разными индексами все означают ту же группу VC.

§ 4] вычисление групп Д»* ($, %) и V** ($, «JI) 357
Если даны V-цикл (4:21) и цепь
*"* = 2'^Г1+2 ^Г1+2 'н ^4 2 «-11- S '#-',
v^-i=^ * и-1+2 ад-1=2 «г 1й«ч+2 *;»; •
Поэтому #** = Vxr~1 тогда и только тогда, когда
[ ^ = 6^4'
(4:220) ej==b'jt
I лй = &г = ^ = 0.
Отсюда, так же, как и в 4:1, выводим:
[4:22]. Группа tf ($, $С) изоморфна прямой сумме
xr-i 9r-i
Из определения V(£, 51) = Zry(<MI) /И^ (Я, ?Г), из [4:21], [4:2l>] и
теоремы [1 :52] Прибавления I следует:
Теорема [4:2]. Группа Vr(®, Щ изоморфна прямой сумме
Se^+ 2^+" 2 (я/е^зд,
где 2 ^С ^с/яь прямая сумма ъг слагаемых, каждое из которых равно X
4:3. Области коэффициентов У, Эт, ^.Рассмотрим некоторые частные
случаи теорем [4:1J и [4:2]:
а) Ж = У. Так как 6У при любом б >1 есть нуль-группа, а группа У/6У
есть циклическая группа порядка 0, то теорема [4:11 даёт при 5Х = У уже
известный результат:
д'<, (я)=S-7+2 Ц = 2У+0'' <А>.
Теорема [4:2] даёт при 51 = У
9* t* —1 У
результат, также известный нам (теорема [3:3]).
б) Ж = fft. Так' как при любом натуральном 6 имеем ^ = (0), f)<K =. №, то
к'
V,(tf, Or) = 2 Я-

358 ОПЕРАТОР V И ГРУППЫ Чг($£, %). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
Итак:
Группы Дг($, Ш) и V(&, Ш) изоморфны между собою и вполне
определяются r-мерным числом Бетти комплекса Ш.
Замечание. Из [4: И и [4:2] следует: если комплекс $ не имеет
ни г-мерного ни (г—1)-мерного кручения, то при любой данной области
коэффициентов Ж группы Дг($, Ж) и Vr (®, Ж) являются прямыми суммами тсг
групп, изоморфных группе Ж и, следовательно, вполне определены
единственным числовым инвариантом: /--мерным числом Бетти комплекса Ш.
в) Ж = ffii. Имеем при любом натуральном 6
поэтому ЬЖХ » JBt тх = 3*1,
*г(я. ад = 2 ^-1 + 2^ = вг_1^ + 29^
| ъ — * k
(4:31) { *-1
v4«. s»i)= 2 v + 2^ = erw + 2^-
4:4*). Группы А^ (Я) и V^(K). Пусть 2C = Jm. Имеем при любом 0>1
(Г т == \J()hn == ^ (пи 9)»
Jm/vJm == WmJii == ■*(«г» о)'
поэтому (пишем у^ (Л) вместо уг ($, /w)
д; <*) = 2 \т вг_к + 2-/» + 2 ^(Н.,в;).
(1:41)
Vm(^)-2J(^Je,:) + S^ + 2 J(mbr.-u
Значит, в частности,
(4:410) A^W=V*(«).
Формулы (4:41) запишем ещё в виде теоремы.
Теорема [4:41]. Группы Д^($) и VmW изоморфчы прямой
сумме:
кг циклических групп порядка т,
т** —* циклических групп порядка (т, 6J""1), / — 1, 2,...,xr~l,
ir циклических групп порядков (т, О!-), / = 1, 2,...,тГ-
Дополним этот результат ещё следующими замечаниями:
Так как Jrwi в) = Щт и 2^ = в'(Я), то
i = i
тг _г тг т**~1
*) См. Прибавление I, арт. 4:5, замечание g.

§ 4] вычисление групп А>( , %) и. V (8t, 21) 359
Итак:
(4:411) Дгт(Я) = ^(Я) = V J(mt eH}+2V, вЛ + 2^i =
Наконец, 'замечая, что
(> (л>)«+2 ^ = (*г w+2 О™ = (Лг w)»»
можем ещё записать
(4:412) Д^(й)= ^т(Я)=(йг-1(й))я1+(дг(я))я1.
Замечание 1. Вернёмся к формулам (4:41) и предположим, чю т
делится на все 8^~ , 6^(для этого достаточно, в частности, чтобы т
делилось на порядки групп в*—1 (&) и в*"(£). Тсгда
(«.ej-^^ej-1, (m. 8J)-0J
и
2 v. о =2/бГ1=5вг"1(Я)>
= 1 г = 1
Имеем:
T e о р е м a [4 :42]. Если т делится на все 6J и 6J""1 (в частности, если т
делится на порядки групп &г (Ш) и B^-i ($), т0
*т W = V^W = в'-'(Я) + вг(Я) + 2 Ли-
Нз [3:52] и [4:42] вытекает:
[4 :43]. Если Кп — псевдомногообразие ит — четно, то Д^(/Сп) = V^w(/Cn)
^с/иь группа второго порядка.
Замечание 2. Пусть w — простое число. Тогда для любого
натурального 6 имеем
(/я,8) = w, если 6=0 (mod m),
(/и, 6) = 1, если 0 ф 0 (mod zw).
Пусть (при любом г) число коэффициентов кручения 8J, делящихся на /я, есть
Из [4: 41] следует:
[4:44]. При простом т группы Агт (&) и \гт ($) с_у/яь прямые суммы
пГ + °m + ^m_1 циклических групп порядка т, так что r-мерное число
Бетти по модулю т есть
(4:42) «;=«' + С +
Г—1

3G0 ОПЕРАТОР V И ГРУППЫ V**(Sl\ 91). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
Умножением обеих частей тождества (4:42) на (—1)г и суммированием
по г от г = О до /- = п получаем (замечая, что Ь^ — о^ = 0)
11 П П
2(-i)4,= 2(-»Гп''= 2 (-1>грг.
Г=0 Г=0 Г = 0
Доказанная таким образом формула
п п
(4:43) 2 (-D-«i" 2 (-!)»'(>'•
называется формулой Эйлер а-П уанкаре по (простому) модулю т.
4:5. Целочисленные цепи и гомологии по модулю т.
Определение [4:51]. Пусть xr = S^ а^\ £ Lr — целочисленная цепь.
Полагаем
<j<m л — ^j ui li >
где а™ есть вычет щ по модулю т. Если $w лг**£2Гд(^, Уш) говорят, что
целочисленная цепь хг есть цикл по модулю т.
Определение [4:52]. Мы говорим, что цело численный цикл xr £ ZrL
гомологичен нулю по модулю т, хг -^0 (mod w), если
Теорема [4.53]. Для того чтобы целочисленный цикл хг был
^0(mod т), необходимо и достаточно, чтобы при некотором yr £ Z[ было
хг — туг ^ Яд .
Условие необходимо: пусть
значит, с) ществует такая цепь xr(fy £ Zr (Й, Jm\ что
STC хг == Ахг+1.
~Отл — ад, ^
Обозначим через xr+i какую-нибудь целочисленную цепь,
удовлетворяющую условию
SR r^+i = хг^~Ь
-Отл — ■* (т) '
Тогда
Ът хг = А^1 = AS^'+i = ^A^r+i,
^m(^~^r+1) = 0;
Так как Длг+i и хг суть целочисленные циклы, то ту1\ а
следовательно, и уг есть целочисленный цикл и
чем необходимость условия доказана.

§ 4] ВЫЧИСЛЕНИЕ ГРУПП №($,%) и yr (^ <}() 361
Условие достаточно:
Если
хг— myr = Ajfr+1,
то
®шхг = »mA*r+i = А8тл^+1,
чго и требовалось доказать.
Теорема [4:54]. Пусть хг целочисленный цикл,
(4 :541) *' = 2^л + 2в<и< + SM"
Для /«ого чтобы имело место соотношение
xr~0 (mod w),
необходимо и достаточно, чтобы в представлении (4:541) было
(4:542) <Ъ = 0 (mod т)\ а{==0 (то& (m> qj ^
(для всех ft и /).
В самом деле, пусть лг^^О (mod /я); по предыдущей теореме имеем
в этом случае
хг = kxr+i -f "О7**» .Vr £ £j.
Пусть
г=2<Й+2«Х+2&К.
*•« = 24 4+1+2 ^Г1+24 <+1+2 4 4+1+2 «/ "Г1 '■
значит,
д^+1=2 ^<+i+2 b?yj+1=s ei e« < +- s *; »;.
следовательно,
, 2^4+Ъч<+2VJ = 2я"**»+2 (*«?+е« <•)«?+
т. е.
(4 :543) ch = юс*, а* = ma) -f- Q J fl£ fy = /h*J + fc)
Первые два равенства (4:543) уже содержат в себе условия (4:542),
необходимость которых, таким образом, доказана.
Пусть теперь условия (4:542) выполнены. Тогда
ch = Щ%> Ч = W,ri) а\ = 4m + М*
при целочисленных fh, ait $it так что (4:541) переходит в
^=«2 ъА + * 2«ч«Г+2 WW+2 VJ =
=m (2 тл4+2«tf)+А &xi+1+2М+1)-
т. е.
xr^0 (mod /я).
Теорема [4:55]. Если целочисленный цикл хг не гомологичен нулю
(целочисленно), то он не может быть при всяком т гомологичен нулю
по модулю т.

362 ОПЕРАТОР V И ГРУППЫ Vr (®, 31). КАНОНИЧЕСКИЕ БАЗЫ [гл. IX
Мы докажем более сильное предложение, а именно:
[4:551]. Если х* (£ Н\, но х* £/*'"
то для любого натурального числа т, делящегося на порядок группы в** (Я),
имеем
лГ'+'О (mcd m).
Если же не только х>' (£ И^ но и .vr(£tf£, то при любом достаточно
большом т
дггН~0 (mod m).
В самом деле, пусть сначала х? ^7/д и пусть ш делится на порядок
группы вг (.И), значит, и на все ft?.
Тогда
Поэтому, если ;с>^0 (mod /и), то, в силу условия (4: 542),
fl< = 0(mod GJ), т. е. at- = 0ja;:
при целом #1, так что (4:541) превращается в
(4 : 543) хг = ^ cft*J + 2 a>^+1 + 2 &Mf * =
Но излгг£#д следует, что все ^ равны нулю, так что
Пусть теперь хг(^Нд. Тогда в (4:541) не все q суть нули. Если,
например, Схф0, то, беря ш>|с1|, видим, что первое из условий (4:542) для с±
не может быть выполнено и, значит, не может быть xr~0 (mod m).
§ 5. Вычисление групп Дг(®, 91) и Vr(,t, 21) по группам A'(®, SRJ
5:1. В предыдущем параграфе даны формулы, позволяющие для любой
области коэффициентов % вычислить группы Д**($, %) и Vr($t, 31), коль
скоро известны группы AJJ($) и Дд_1($). Однако, иногда бывает целесообразно
сводить группы Дг (®Д) и V ($Д) не к группам Aq($), а к группамД^Д^
[или Vr(^,9^i)] и в особенности к группам Д^ ($). Для этого достаточно
свести к этим группам группы Д£ ($).
Теорема [5:1]*). Если для всех г = 0, 1,... известны группы
А*" ($, 9ВД,/но для вс^л: г известны и группы Д^(Я), следовательно^ группы
Д**($,5£) и Vrf$, 21) л/ш любом заданном ?Г. ffo/ш для данного г известна
группа Vr ($, 9?,), то для этого г известна и группа Д£ ($).
Оба утверждения теоремы [5:11 вытекают из формул (4:31) на
основании следующей леммы:
#) Приведённое здесь доказательство теоремы [5:1] принадлежит Hopf'y.

§ 5] вычисление групп А' (®, 91) и v;($, 51) 363
Лемма [5:11]. Если группа ® есть прямая сумма некоторой конечной
группы 5ГС@ и конечного числа подгрупп ®i,..., Qbp группы ®, каждая
из которых изоморфна группе Шъ то и число р и группа % (с точностью
до изоморфизма) однозначно определены.
Доказательство леммы. Пусть
(5:11) ® = % + ®1+...+®р.
Докажем прежде всего, что подгруппа
© = ©!+...+©,
состоит из тех и только тех элементов х группы ($, которые удовлетворяют
следующему условию:
Ко всякому натуральному числу т можно найти такое у 6 ©, что ту = х.
В самом деле, если лг£@ и /я;>1, то
л: = Xl + ... + хр1 х% € Щ.
Но в ©^ можно найти ух так, чтобы /wyt- = xim
Полагая у ==у±-\- ... -\-ур, получим ту = х.
Пусть, обратно, для данного х £ ($ и любого т > 1 можно найти такое
(зависящее от т) у £ ©, что /тгу == х. Возьмём в качестве т порядок группы X.
Если
х = /тгу, .у = * -f- s, / £ S£, s£&,
то
х =» ту = w/ + ms £ <3,
чем наше утверждение доказано.
Итак, при всяком разбиении вида (5:11) элементы группы ©
характеризуются независимым от данного разбиения образом: Это значит, что при
всех разбиениях вида (5:11) группа (§> состоит из одних и тех же элементов,
т. е. есть одна и та же подгруппа группы. Поэтому и группы 5£,
соответствующие разным разбиениям (5:11), с точностью до изоморфизма
однозначно определены: все они изоморфны группе ®/@. Остаётся показать,
что при
© = (^ + ... + ©р,
где все jSi изоморфны Шъ число р определено однозначно. Для этого в свою
очередь достаточно показать, что р определяется равенством 2р = N, где
.V есть число элементов х группы (§>, удовлетворяющих условию 2дг = 0.
Если х = х1 -\- ... + хр (xi £ @>г) удовлетворяет этому условию, то для
каждого / должно быть 2xi = 0. Но в Ш\ имеется ровно два элемента х^
для которых 2хг = 0, именно, xi = 0nxi= ; поэтому число элементов х £ ©,
для которых 2х = 0, действительно равно 2^.
Лемма [5:11] и теорема |5: II этим вполне доказаны.
5: 2. Т е о р е м а [5:2]. Для данного комплекса $ существует
натуральное число т > 1, удовлетворяющее следующему условию: если
известны группы Д^($) для всех г = 0,1, 2,..., то известны и все группы Aj($),
а следовательно, и все группы &г(®, 2С), Vr ($, Ж) для всякого данного %.
Доказательство. Пусть т0—натуральное число, делящееся на
порядки всех групп 6^($) (если некоторое 9**($) есть нуль-группа, то её
порядок равен 1).
Докажем, что при любом натуральном т вида т = km0, где k !> 2 целое,
утверждение теоремы [5:2] верно.
В самом деле, имеем на основании теоремы [4:42]
(5 : 21) Агт (ft) = № №) + вг-1(Я) + | Jm

364 ОПЕРАТОР V И ГРУППЫ Vr(St, 91). КАНОНИЧЕСКИЕ БАЗЫ [ГЛ. IX
откуда для подгруппы т0^т(й)^ А^($) получаем (помня, что т0$г (й) и
/т?0вг-1($) суть нуль-группы)
Но
так что
к*"
Итак, число тс'', т. е. r-мерное число Бетти комплекса Ё, может быть опре-
т
делено как число прямых циклических слагаемых порядка k = —, на которые
распадается группа т0^(Щ; следовательно, числа тг** нам известны.
Остаётся определить группы в**($).
Группа во ($) есть нуль-группа. Пусть группа ^г~1(й) с точностью до
изоморфизма уже определена. Тогда, так как кг нам известно, то и группа
*г
вг-Цй) + SЛ?гопРеДелена с точностью до изоморфизма. Но тс гда из (5:21)
определена с точностью до изоморфизма и группа
вг (Л) = А|Г(Л)/(0г-1(Л)+ J Jm).
Таким образом, шаг за шагом определяются все группы 0^(Я).
§ 6. Гомоморфизм 5р группы Lr(Ka,%) в Lr(K$, 91),
порождённый симплициальным отображением 5£ комплекса /Ср в Ка-
6:1. Определение гомоморфизма 5р. Пусть /Са и А'з— полные
симплициальные комплексы, 5£ — симплициальное отображение
комплекса /Ср в комплекс /Са.
Определим гомоморфизм 5ргруппы Lr (АГа, 91) в группу Z/(/Cp, 91)
следующим образом: для любой цепи л££ Z/ (ЛГа, 91) и любого
ориентированного симплек са # комплекса АГр полагаем
(6:1) (5?^-^) =*(^-6%)
(это значит, что цепь 5рлг« по определению принимает на ty
значение, равное значению цепи хга на симплексе 5^р/, если Sl%- ф О, и
значение 0, если 5«^/ = 0).
Если 91 = J или 9t = Jm и кроме л£ £//(/(«, 91) дана ещё цепь
4 = 2^^6^г(^р, 91), то из (6:1) следует:
{Spcl • хрг) = (5?^ • 1>/еу) = 2^ (5р*« • t\j) =
= 2^ • S%) = 2(л£ • 5^,4) = (хги • 2*/W = (*Г • skg).
Итак,
(6:11) (5р*£ •*?)«(*£ •$£*&).

§ 6] гомоморфизм 5р группы Lr(K„ %) в Lr(K$y 91) 365
[6: ПЬ Гомоморфизмы Si и S« являются сопряжёнными.
6 :2. Переместительность операторов V и ££. Докажем для
любой цепи Xa(zLr(Ka,%) тождество
(6 :2) V5^a = ^v4,
аналогичное тождеству (8:3) главы 7.
В силу (6:1) и формулы (Vxr • уг+г) = (хг • kyr --1) —
[формула (1 :310)], имеем
(s;vx:. ф1)=(v^. sg^1)=(*« • A^«4+1)>
Так как AS^/"1 = зЦа^1, то всё доказано.
Примеры на гомоморфизм читатель найдёт в арт. 3 :2 главы 10,
который может быть прочитан сейчас же.
6:3. Теорема [6:3]. Пусть Кл и К« — конечные полные симплициаль-
ные комплексы^ a S% и S$ —два симплициальных отображения
комплекса АТр в Ка. Если SV и $'| порождают для любой размерности г и
для любого т = 0, 2, 3, ... один и тот же гомоморфизм группы &гт(К$)
в группу &гт(Ка), то при любой области коэффициентов % и любой
размерности г гомоморфизмы SI и s'q группы Vr (A"a, Ж) в группу уг(Кр,Ш
также совпадают между собою, - {
Доказательство. Построим для Ка и К* канонические системы баз:
Щ= [х*. У& *?*. "е* VU' K = {<* уг*н< <h. <»> <н)
и сопряжённую систему
-Г^ТГ___\-Г —Г —Г -Г -Г \ -гг^.Л \—Г~Г Г -Г -г\
Щ ~~ Щ1 v$? z$? x$i' Уф)4 ^a= 1"«Л' VbJ? Serft» X*h> y«h).
Рассмотрим матрицы гомоморфизмов s\ и S'\ группы Lq(Kq) в Lr0(K«)
при базах WZhW1^ каждая строчка матрицы состоит из коэффициентов той
линейной комбинации элементов WT9% в которую при гомоморфизме s\
переходит возглавляющий данную строку элемент базы Wp
Так как при гомоморфизме Sf циклы переходят в циклы и циклы,
гомологичные нулю, переходят в циклы, гомологичные нулю, то S^z^ есть
линейная комбинация элементов г* w vr , тогда как S$ur. есть линейная
а/г» а/г' а/г а аг
комбинация элементов uruh% vrah и, наконец, S^v^ есть линейная комбинация
элементов 6^<„ <Л.
Аналогичное замечание касается, конечно, и гомоморфизма £'£. Итак,
матрица гомоморфизма S^ имеет вид, показанный на табл. (3:6) (выписываем
явно лишь те элементы матрицы S^» которые нас сейчас будут интересовать).
Матрица гомоморфизма S'^ имеет такое же устройство; мы её не выписываем,
ограничиваясь замечанием, что элементы её будут обозначаться теми же
буквами, что и соответствующие элементы матрицы S^ но со штрихами.

Збб оператор V и группы Vr(M\ s)t). Канонические ёазы [ri. \t
хг.
y\i
*v
u\i
*
aih
0
0
0
0
0
0
<*ih
Cih
0
0
*h
eih
fih
Pih
bin
KhSm
<n
Так как гомоморфизмы S\ и S'£ группы l.r0(K$) в /-^(Ка) порождают
один и тот же гомоморфизм группы Д^(АГ^) в Д^Л^), то для любого
/=1,2,..., «J
т. е.
^zr — V$?r
еСТЬ линейная комбинация одних лишь циклов ftrahurah и vrah% так что
(6:31) cih = c'ih
для любых / = 1, 2,..., те^, Л = 1, 2, ..., я£#
Далее,
так что xL есть цикл по модулю отг- = б^г1. Так как гомоморфизмы S^ и
Sr\ порождают при любом п\ значит, в частности, и при т = miy один
и тот же гомоморфизм группы Д^(АГр) в ^гт (Ка), то, придавая оператору
$w смысл, установленный в определении [4:51], имеем
24 <Ф5, - 5?*Р е "Г (к, jmi).
Отсюда на основании последних двух равенств (4:130 выводим
т. е.
(6:32) ^-^«©(mode;^1),
(6:33) dih -d'ih~0 (mod O^"1),

§ б] Гомоморфизм Ц группы //(/С$1) в Z/ (Л*3, 91) 367
или при целочисленных Рм^Иг
aih — aih — ^ift G p7 • * = 1. • • • . ^3~ » Л = 1, . . . , -У~ ,
*м = ^й 6 ?7 > i = 1,..., х*?"
*<л-4 = ^Л71. ^i.-.-^Г1. л = 1.....<.
Рассмотрим теперь матрицу гомоморфизма S^ в базах Р/£, IF£. Так как
гомоморфизмы So и S£—сопряжённые, то, применяя теорему |5 :4]
Прибавления I, имеем *)
^1 и\ь = 2 aihu\i + линейная комбинация "z/L
г
Щ г1ъ == 2 ^л «5< 4- 2 **'Л *£г + линейная комбинация t7j[f,
г г
и аналогично
Sq иглП — ^ fl*7i ll\i + линейная комбинация ©Г.,
t*
5рв"г«Л = 2di*""P< + 2 с)л^5< + линейная комбинация l)\i;
г г
Па основании (6:31)^(6:32), (6 :_33)
имеем (помня, что Vx^T1 = б^г1 ц^ и V^"1 = ^.)
(6 : 34) Щ Hrah — s'f Hrah = 2 fx^e^r1 й£. + линейная комбинация ~Ъ\г =
= 2*х*л^дср7"1 4" линейная комбинация VjoT1-
(6 : 35) Sp i"^ Spa г^ == 2 ^^^Г1 + линейная комбинация ^з» =
~ 2 ^м^х^Г1 + линейная комбинация Vj>L »
или
( ^з <fo153a Kh в ^3 Для любого h = 1,..., < г,
(6:36) { _ __ _, _
( 5? <и5ра <л в ^з Для любого Л = 1 те« -
Так как всякий целочисленный V-цикл комплекса Ка гомологичен некоторой
линейной комбинации циклов urah, гглП и V-гомологии между V-циклами
сохраняются как при отображении So, так и при отображении So*, то
для любого z*€Z* (ATp, J)
имеем
*) Рекомендуется переписать матрицу (6:3), заменив в её левом
(вертикальном) указателе xr^i% У^г^%1 и^, vf^ соответственно через и^,^, ^,
•*£*» .Ур» и заменив в её верхнем (горизонтальном) указателе xrah, y^h,z *h f
<fc><7» соответственно через ^~v\ *'й, <Л, 34.

368 оператор V и группы Vr(®9 ЭД). Канонические ёазы [гл. IX
что означает, что гомоморфизмы S^ и S£ групп Lг0 (Ка) в L\ (K$) порождают
один и тот же гомоморфизм группы Vq (/Ca) B Vq (АГр).
Для того чтобы доказать, что при любой области
коэффициентов Ж симплициальные отображения S% и S'£ порождают одинаковые
гомоморфизмы групп Vr(Ka, 5T)j_ B Vr(ATB, 5t), заметим, что, в силу
рассуждений арт. 4:2, всякий V-цикл ,г£б^ (Ка,Ю однозначно представим в виде
< = 2 а А + 2 сл *«л + 2 Ь А + 2 еА'
где ал, Cft, Ьл, ел суть элементы группы 2t, причём ah удовлетворяет условию
(6:37) в^ад = 0.
В силу (6:36), остаётся, очевидно, лишь доказать, что для любого V-цикла
вида uhx^h имеем
(6:38) ^ Щ ahxrah~~S'« анхглН в *р по %.
Для этого, вернувшись к основной таблице (6:3), выпишем равенства
Щ ~*«h = 2 **л "Р< + 2Лл*р< + 2 ^**р< + 2 bib*M + 2 ^^йЗ'р,.
г i 4 i i
Так как
то
Так как
slu$i~S'luli (в *« п0 У^
то
(б:39)ь ^-^(mod6^).
Полагая ^л — еш~ Аш и принимая во внимание (6:37), выводим из (6: 39)^,
(6:39)&
Sl ah xlh ~~ S$ ah Kh = 2 Л^ ah Uli + 2 №h —Aft) ah vli-
i i
Так как z£ ~ 0 (в /Cp no J), то всё сводится к доказательству гомологии
(6:39) 2 АшЧ^~ 0 (в tfp по ЭД.
Для этого доказательства вспомним, что xL есть А-цикл по модулю ^•=В^1
и что
5H""^4r2^aIft + линейная комбинация цепей <л, углП% zrahJvrah.
На основании первой из формул (4:13^) имеем при некотором ^m^Jmi
или при некотором целом mih
Aih = mihQrtth (mod т&

§ 6] гомоморфизм £р группы &(КЛЛ) в ЬГ(К^Щ 369
или, наконец, при целых mih, nih
Значит, _
2 АШ Ч. *Ji = 2 mihKhah~u\i + 2 ПМЬ р?***"*? •
Принимая во внимание (6:37), получаем
i i V
что и требовалось доказать.
Из [6:3] и теоремы [9:4] главы 7 вытекает следующий факт, который
существенно понадобится нам в гла«е 14.
Следствие из теоремы [6:3]. Пусть даны два симплициальных
отображения s\ и S'\ конечного полного симплициального комплекса К$
в конечный полный симплициальный комплекс Ка- Предположим, что для
любого симплекса Та £ К§ существует симплекс Га£АГа, имеющий в числе
своих (собственных или несобственных) граней как S^Ta, так и 5^7р.
Тогда S\ и S'\ порождают один и тот же гомоморфизм 5о = S'jJ
группы У(#«Д) в Vr(K$M).
24 Александров П. С.

ГЛАВА ДЕСЯТАЯ.
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ.
В этой главе доказывается, что группы Бетти различных триангуляции
гомеоморфных между собой полиэдров изоморфны между собой.
В § 1 намечается тот подступ к этому доказательству, который в § б
приведёт нас к цели.
В § 2 доказывается вспомогательная теорема об инвариантности групп
Бетти при барицентрических подразделениях триангуляции.
В §§ 3 и 5 излагаются так называемые нормальные и канонические
сдвиги, а также е-сдвиги в компактах и полиэдрах, которые являются
основой значительной части рассуждений и этой и следующей глав. 4
В § 4 делаются некоторые вспомогательные построения, которые
примыкают к построениям § 3, но понадобятся нам лишь в главе 14; чтение
этого параграфа можно отложить до чтения главы 14.
В § 6 даётся доказательство основной теоремы, опирающееся на §§ 2, 3 и 5.
В § 7 доказывается так называемая теорема об инвариантности
псевдомногообразия: если какая-либо триангуляция данного полиэдра есть
комбинаторное псевдомногообразие, то тем же свойством обладает и всякая
триангуляция этого (и всякого, гомеоморфного ему) полиэдра.
§ 1.
1:1. Определение чисел br (Ф). Пусть Ф есть компакт, а г-— целое
число ^>0.
Определение [1:1]. Через дг(Ф) обозначается наименьшее
целое число &, удовлетворяющее следующему условию.
Во всякое открытое покрытие а> пространства Ф можно вписать
замкнутое покрытие а, для нерва Ка которого имеем тг**(/Q) = £.
Если такого числа k нет, то полагаем br (Ф) = оо.
Если br (Ф) = со, то ко всякому числу k можно подобрать такое открытое
покрытие пространства Ф, что для всякого вписанного в ш замкнутого
покрытия а имеем nr (Ka)*>k.
Ha основании теоремы [8:35] главы 1 можем сказать:
[1 :П]. Число дг(Ф) есть наименьшее из целых чисел k,
удовлетворяющих условию: для всякого s>0 существует замкнутое
t-покрытие компакта Ф, нерв которого имеет k своим г-мерным
кислом Бетти.
Замечание. Пусть т — простое число. Рассматривая вместо
чисел Бетти нервов К% замкнутых покрытий а компакта Ф числа
Бетти по модулю т, получим определение чисел #^(Ф),
совершенно аналогичное определению чисел ЬГ(Ф).

§ 1]
ОПРЕДЕЛЕНИЕ ЧИСЕЛ ЬГ(Ф)
371
Очевидно, если компакты Фи Ф' гомгоморфны между собой, то
*г(ф)=*г(Ф'), *i($) = *«(Ф0-
Другими словами, и числа 6Г(Ф), и числа Ъгт (Ф) являются
топологическими инвариантами.
1 :2. Определение групп 83г (Ф).
Алгебраическая лемма. Пусть А и В — абелевы группы
с конечным числом образующих. Если А изоморфно некоторой
подгруппе группы В, а группа В изоморфна некоторой подгруппе
группы Л, то группы А и В изоморфны между собой.
Доказательство — см. Прибавление I, теорема [4:41].
Пусть теперь Ф — компакт, г — целое число ^ 0. Определим
следующим образом некоторое (быть может, пустое) множество
33Г(Ф) абелевых групп.
Множество 83 (Ф) по определению состоит из всех определённых
с точностью до изоморфизма групп 23, удовлетворяющих
следующему условию:
Каково бы ни было открытое покрытие со пространства Ф,
существует такое вписанное в со замкнутое покрытие а пространства Ф,
что группа 23 изоморфна группе До (АГа), где Ка есть нерв покрытия ос.
Из теоремы [8:35] главы 1 следует:
£8Г (Ф) может быть определено как множество всех групп 23,
удовлетворяющих условию:
Каково бы ни было s>0, существует такое замкнутое е-ло*
крытие а компакта Ф,что &о{Ка) изоморфно 23.
Группу 230££ВГ(Ф) называем наименьшей группой в
системе £3Г(Ф), если всякая группа 23£33Г(Ф) содержит
собственную или несобственную подгруппу, изоморфную группе 230.
Система 33Г(Ф) может Ее содержать ни одной наименьшей группы
в только что указанном смысле; но если 93Г(Ф) содержит
наименьшую группу, то (в силу алгебраической леммы) только одну.
Определение [1:2]. Наименьшая группа (если она
существует) в системе 83Г(Ф) обозначается через 23Г(Ф).
Замечание. Очевидно, если 23Г(Ф) существует, то существует
и 23Г(Ф') для всякого Ф', гомеоморфного компакту Ф, причём
группы 23Г(Ф') и 23Г(Ф) изоморфны между собою. Другими словами,
группы 23Г(Ф) топологически инвариантны.
1 :3. Формулировка теорем об инвариантности чисел и групп
Бетти, Основная задача этой главы заключается в доказательстве
следующих теорем *):
Теорема [1:31]. Для любой триангуляции К полиэдра Ф
имеем
*) Попутно будет заново доказана и теорема о мостовых.
24*

(
3?2 ИНВАРИАНТНОСТЬ ГРУПП вЕТГЙ [гЛ. %
Теорема [1 :32]. Если Ф— полиэдр, а К—какая-нибудь его
триангуляция, то группа 23>'(Ф) существует и изоморфна
группе AS(/C).
Из эгих теорем в силу топологической инвариантности ЬГ(Ф)
и 93 (Ф) следует:
Теорема [1 :33]. Если К и К' сутр, соответственно,
триангуляции двух гомеоморфных полиэдров Ф иФг, то группы &о(К)
и AJ(/C') изоморфны, а числа кг(К) и ъг(К') равны между собою.
(Равенство чисел ^rQ(K) и кг(К') при этом, очевидно, следует
из изоморфизма групп Д£(/С) и Д£ (/()'.)
Теорема [1 :33] называется теоремой об инвариантности
групп Бетти и доказана впервые в 1916 г. Александером. В
названии теоремы слово инЕариантность надо понимать в смысле
инвариантности (неизменности) групп Бетти при переходе от
триангуляции К данного полиэдра Ф к любой триангуляции Кг какого-либо
гомеоморфного с Ф полиэдра Фг. Эту инвариантность можно, конечно,
понимать и в смысле инвариантности при переходе от одной какой-
либо триангуляции данного полиэдра Ф к произвольной другой,
вообще говоря, кривой триангуляции того же полиэдра Ф. В самом
деле, в соответствии со сказанным в арт. 6 :1 главы 4, замечание
2, мы можем сформулировать теоремы [1 :31] — [1 :33] также
и следующим обргзсм:
[1 :34]. Для всех кривых триангуляции К одного и того же
кривого полиэдра Ф группы AJ(/C) изоморфны между собой, так
как все они изоморфны группе ЯЗГ(Ф), а числа rJ(K) принимают
одно и то же значение, равное ЬГ(Ф).
Так как при любой данной области коэффициентов 51 группы
Дг(У(Д)и Sr {К,%\ вполне определены, коль скоро определены (для
всех г) группы Д£(/С) (см. главу 9, арт. 4:1 и 4:2), то из [1 :33]
следует:
Общая теорема об инвариантности групп Бетти
[1:35]. Если К и К' суть, соответственно, триангуляции двух
гомеоморфных между собою полиэдров Ф и Фг, то группы ДГ(/СД),
Vr(K,%) изоморфны, соответственно, группам ДГ(/С'Д) иУг(/С'Д)
для любого г)>0 м любой области коэффициентов 21.
§ 2. Подразделение цепей. Фундаментальные системы
подкомплексов и цепей. Инвариантность А- и у-групп
при элементарных и барицентрических подразделениях.
2:1. Изоморфизм si. Во всём этом параграфе комплексы Ка, К$
суть триангуляции, или открытые подкомплексы триангуляции.
Пусть К$ — подразделение комплекса Ка. Для каждого элемента
Тги £ Ка выбираем определённую ориентацию f^ Элемент ТС £ /Ср на-
зыааем главным, если 7Т лежит на некотором Т^£Ка той же

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 373
размерности г. Из двух ориентации данного главного элемента
ГГ^/Ср обозначаем через К ту, которая одинакова с ориентацией ^
носителя Т* элемента 7Т. Если Т£ — не главный элемент, то обо-
« р р '
зчачаем через ^ какую-нибудь его ориентацию. Вместо Lr(Ka, 51),
Z/(Kp,»> ZJ (#«,«), Z;(/Cp,«), АЧ/С.Д), Дг(/Ср, 51) и т. д. пи-
щем соответственно Z£, L£, Z£, Z£, A^, A£ и т. д. Элементы групп
L£, L£ обозначаем соответственно через л£, л£, если нужно, с
дополнительными индексами.
Определение [2:11]. Пусть дана цепь хга.
Определим цепь х\ следующим образом:
а) если Т£—главный элемент, лежащий на TJ, то
б) если Г£— не главный элемент, то
Цепь je£ обозначаем через О^ и называем подразделением
цепи л;£ в комплексе К$>
Замечание. Для одночленной цепи хг = tfr имеем. очевидно,
Для любой цепи -^"S^^i
(2:П2) *p*I = 2N№
г
Ставя в соответствие каждой цепи xra£Lra цепь SgJe£, получим
гомоморфное отображение группы Z£ в L£; в самом деле, легко
видеть, что
Далее, если хга ф 0, то и s^x* ф 0. Таким образом, отображение
s* есть изоморфное отображение группы Z/ в группу L*
Теорема [2:12].
(2:12) Д^ = *рЛ*а-
Вследствие (2:112) достаточно доказать, что
Д5;Г = ^АГ.
8 « Р «

374
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[гл. х
Пусть 7£-1 произвольно. Если 7Т-1 лежит в Т*9 то существуют
два и только два элемента ТТп и Т£к комплекса /Ср, имеющие Т^"1
своей гранью. При этом, так как ориентации tL и Кк одинаковы,
то при любом выборе ориентации Я-1
<Vr1)--(fc:<r1>
и на основании формулы (2:111) и определения оператора А
(д фи. {$-*) - (Д2 % • Т1)=(А ^ • Г1)+<А % ■ Г1) ~
=<V-<rl>+(fc:'Tl>ee<)-
Так как Г'—1 с Гг не есть главный элемент, то значение цепи
р а '
£рД^ на ft—1 равно нулю. Итак, если Г'-"1 с 7£, то и А$*Г и
SpAtfJ принимают на Р~х значение нуль.
Пусть теперь Т'-1 лежит на грани Р^1^/^ элемента Т^£Ка-
Тогда к 7|-1 примыкает только один симплекс TZczT£. Обозначим
через Rr и Rr-1 пространства, несущие соответственно симплексы
Тга и Т^"1- через С обозначим аффинное отображение пространства
Rr на себя, переводящее ориентированный симплекс tr в
ориентированный симплекс tt. Отображение С, рассматриваемое лишь на /?r_1,
обозначаем через С. Так как симплексы Г£ и Г£=СГ£ лежат по
одну сторону плоскости /?r_1 =з C/?r_1, то в теореме [1:521]
Прибавления II надо положить © ===== —f—1 и, в силу этой теоремы,
sgnC- sgnC/ = +l-
Но ориентации *£ и # одинаковы, поэтому sgnC=-f-l, значит, и
sgn С' <= -J- 1> поэтому
ос ар
И
(2:121) Щ:/j-i) = («r: C^-i) = ft:£-*).
Но (tr:tr~1) есть значение АГ на ^_1, совпадающее со значением
цепи sa Atra на #-1. С другой стороны, цепь А$«^ принимает на ^_1
то же значение, чго и А#, т. е. значение (/р/Г-1), чем ввиду
равенства (2:121) теорема [2:12] доказана.
2:2, Фундаментальные системы подкомплексов комплекса /О
Как уже было указано в начале этого параграфа, /С, ЛГа, ЛГр
обозначают в течение всего параграфа триангуляции или открытые под»
комплексы триангуляции.
Определение [2:21]. Фундаментальной системой
подкомплексов комплекса К называется всякая система под-

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 375
комплексов U*czK различных размерностей (от нуля до
размерности п всего комплекса /С), удовлетворяющая следующим условиям:
1°. Все U% суть простые попарно не пересекающиеся
псевдомногообразия *); их соединение есть весь комплекс К-
2°. Для всякого Щ комплекс В*~\ состоящий из всех не
принадлежащих U* симплексов Т£КУ подчинённых хотя бы одному из
симплексов Щ, есть (г—1)-мерный комплекс, являющийся
соединением некоторых из псевдомногообразий £Л, 0 s^s^ г—1.
Замечание. Полагая Us. < Urv если U\ с Вг{~\ видим, что
множество всех i/J есть частично упорядоченное множество К)
считая естественную размерность комплекса Щ числом измерений
элемента Щ^К, можем считать множество К комплексом в смысле
общего определения главы 4, арт. 1:7. Этим замечанием мы будем
в дальнейшем пользоваться.
Множество всех £/*.<£/£ обозначаем через ЯГ"1. Очевидно, Щ~1
есть замкнутый подкомплекс комплекса К\ соединение всех комплексов
U% являющихся элементами ВТ—1, есть Вг~1.
о II
Из 2 легко вытекает:
[2:22]. Соединение подкомплексов №, являющихся элементами
некоторого подкомплекса К0 комплекса К, тогда и только тогда
является замкнутым подкомплексом К0 комплекса К, когда
/С0—замкнутый подкомплекс комплекса К.
Из [2:22] следует аналогичное утверждение для открытых под-
комплексов.
[2:23]. Множество всех Щ, где s не превосходит некоторого
данного г, является замкнутым подкомплексом комплекса К, обозна*
чаемым через Кг. Таким образом, К^Кп* Соединение всех
элементов комплекса **) Кг есть замкнутый подкомплекс комплекса /С
обозначаемый через Кг.
Нам понадобятся в дальнейшем следующие просто доказываемые
предложения:
[2:24]. Если L/J"1<L^, то J/J-1 есть открытый подкомплекс
комплекса Brfx.
В самом деле, так как и^~г не подчинён (в силу своей
размерности) никакому элементу комплекса Щ~~г, то множество всех
отличных от U%~1 элементов, входящих в В[~_1,есть замкнутый
подкомплекс К0 комплекса iBf"*1, а соединение всех элементов /С0 есть
замкнутый подкомплекс К0 комплекса BJ"-1. Поэтому, {У£-1 = J3J—1\/С0
*) r-мерное псевдомногообразие Ur называется простым, если оно
ориентируемо и если при 0<р<> все его д#-группы суть нуль-группы.
**) То-есть соединение всех комплексов Щ, являющихся элементами
комплекса Кг.

376 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [ГЛ. X
есть открытый подкомплекс комплекса В?—1, что и требовалось
доказать.
Аналогично:
[2:25]. Всякий Щ есть открытый подкомплекс комплекса Кг.
Примеры фундаментальных систем
подкомплексов. 1. Пусть К есть тгиангуляция тора, рассмотренная в главе 8,
арт. 1 :4, пример 5 (черт. 117). Обозначим через U^ подкомплекс
комплекса К, состоящий из всех элементов Л, лежащих внутри
квадрата ABCD (черт. 117). Через L/J, соответственно Щ, обозначим
подкомплекс комплекса /С, состоящий из всех элементов комплекса К,
лежащих на (открытом) отрезке AB — DC, соответственно на AD —
= ВС. Наконец, обозначим через Щ вершину A — B—C=D.
Комплексы Ц2, U\> U\, U\ образуют фундаментальную систему
подкомплексов комплекса К (читателю рекомендуется доказать это при
помощи рассуждений, аналогичных рассуждениям главы 8, арт. 1 :4,
пример 5).
2. Пусть К есть триангуляция проективной плоскости,
рассмотренная в]главе 8, арт. 1 :4, пример 7 (черт. 117). Через £/*
обозначим подкомплекс комплекса К, состоящий из всех элементов /С,
лежащих внутри квадрата ABCD; через 1/J обозначим комплекс,
состоящий из отрезков |*}| = |Й|, |*J| = |3b I'JHI'JI» l'2l = Kol«
*б1 ===r!^iil» 1*б1 = UL| и из веРшин этих отрезков; через Щ
обозначим вершину А = С. Комплексы U2V U\y Щ образуют
фундаментальную систему подкомплексов комплекса К.
3. Имеет место следующая общая теорема (нам понадобится лишь её
частный случай [2:26], — см. ниже):
[2:261]. Пусть К\ есть подразделение комплекса К; обозначим через
7J элементы комплекса К, г = 1,2,..., т, i = 1, 2,..., рг; через U\
обозначим комплекс, состоящий из всех элементов комплекса Къ лежащих на
Т[ (т. е. имеющих симплекс Т\ своим носителем). Комплексы Urt образуют
фундаментальную систему подкомплексов комплекса К±.
Проще всего теорема [2:261] доказывается методами арт. 6:2 после
того, как доказана теорема об инвариантности групп Бетти (которая
опирается лишь на теорему [2:26]). Теорему [2:261] для случая, когда Ki есть
барицентрическое подразделение комплекса К, читатель может в
виде упражнения доказать и сейчас. Прямое доказательство теоремы [2:261]
в общем виде дано, например, в книге Александров-Hopf, Topologie, I, глава 6.
Теорема [2:261] в значительной степени выясняет значение
фундаментальных систем подкомплексов. Как уже сказано, мы не будем пользоваться
этой теоремой во всей её общности, но её частный случай, касающийся
элементарных подразделений, существенно нужен для доказательства
инвариантности групп Бетти. Этот частный случай мы сейчас и докажем.
[2: 26]. Пусть Кх — элементарное подразделение *) комплекса К
относительно какого-нибудь симплекса Т£К. Обозначим через К
множество всех подкомплексов Щ комплекса Кг, являющихся под-
*) Глава 4, арт, 4:3.

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 377
разделениями симплексов TJ комплекса К- (Каждый из комплексов
Ur. либо состоит лишь из одного неподразделённого симплекса
комплекса К, переходящего в неизменном виде в комплекс Кц либо
является элементарным подразделением некоторого симплекса
комплекса К>) Множество К есть фундаментальная система
подкомплексов комплекса К-
Доказательство. В силу теоремы [9:22] главы 7,
достаточно убедиться в том, что элементарное подразделение К§ какого-
либо симплекса Т™ есть ориентируемое псевдомногообразие.
Индукцией по числу измерений симплекса Т™ без труда доказывается
прежде всего, что К$ есть сильно связный комплекс, к каждому
(п—1)-мерному элементу которого примыкает ровно два л-мерных,
т. е. что К§ есть псевдомногообразие. Ориентация К§ получается,
если взять ориентацию tP симплекса Т£ и построить цепь sit™, как
в арт. 2:1: цепь эта есть, очевидно, я-мерный цикл комплекса К§.
2:3. Фундаментальные системы цепей.
Определение [2:31]. Система целочисленных цепей и%
(различных размерностей) комплекса Кя называется
фундаментальной системой цепей этого комплекса, если выполнены
следующие условия:
1°. А#дИГ. есть линейная комбинация (с целыми коэффициентами)
цепей ИрГ1.
2°. Цепи игч линейно независимы между собою.
3°. В каждом гомоло?ическом классе $р€д£(/(р) имеются
цикли, являющиеся линейными комбинациями цепей и*
4°. Если х* £ ИГА (АГр, 7) и хго есть линейная комбинация цепей
х\=2м5*>
то существует такая линейная комбинация
h
что
Д*|;+1= яр-
Важность понятия фундаментальной системы цепей основывается на
следующих теоремах [2:32] и [2:43]:
Теорема [2:32]. Пусть дана фундаментальная система
подкомплексов UL некоторого n-мерного комплекса К^ Обозначим
через u^i определённую ориентацию псевдомногообразия Щ^ Тогда
система всех цепей и* есть фундаментальная система цепей
комплекса К$,

378 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [ГЛ. X
Доказательство. Сохраняем обозначения предыдущего
артикула, снабжая их индексом р: Щр В^р Щ и т. д.
Покажем, что цепи #' удовлетворяют всем условиям 1° — 4°
определения [2:31].
Условие 1°. Так как и* есть цикл на ориентируемом
псевдомногообразии 1К{, то Д&Г. может отличаться от нуля лишь на (г—1)-
мерных симплексах комплекса Ж~1= [УуХ^зг ^° ЩГ1 слагается
из USj размерностей s<j; г—1, поэтому, если Аи* отлично от нуля
на некоторых симплексах ^г1, то
I /** — 1 I г г/г—1 г- Rr—l
Так как Utr1 (в силу [2:24]) — открытый подкомплекс комплекса
В^1 (на котором лежит цикл A«L), то {/'т^Ди^ есть цикл
псевдомногообразия U^"1, т. е. имеет вид с1Ж'г1 при целочисленном с^.
Так как Ди^ есть сумма своих кусков, лежащих на различных
УГ^сЯр-1, то Дм' = 2^м8/"1' чем и Д°казано> что условие 1°
выполнено.
Условие 2° непосредственно вытекает из того, что цепь и*
лежит на Upi и что два различных псевдомногообразия ^ н^
имеют общих элементов.
Для того чтобы обнаружить, что условия 3° и 4° также
выполнены, докажем две леммы.
Лемма [2:33]. Пусть Щ — соединение всех £/* s<;r. Если
цепь л££1£(/?"р) лежит на К\ и имеет границу, лежащую на К^~х,
то х* есть линейная комбинация цепей и'
В самом деле UL есть, в силу [2:25], открытый подкомплекс,
комплекса Кг*\ поэтому, имея в виду, что &КрХ* лежит на Л^-1,
можем написать
Итак, Щ{х% есть цикл на ориентированном псевдомногообразии UZ.
и, значит, Ц{хг = с{иг{,
Следствие. Всякий r-мерный цикл на Кг имеет вид ^с4ит^{.
i
В частности, всякий n-мерный цикл комплекса К$ имеет вид
i
Лемма [2 : 34]. Пусть
Ax'tzz-чк;-1).

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 379
Обозначим через q = q(xr§) наибольшее такое целое число, что для
некоторого и$(£К имеем Щ.хЪфО. Тогда, если q>ry то
существует цепь уга £ 1Г0 (/Ср), удовлетворяющая условиям:
а) хЪ—У^ЩЩ* Д*5 = а^;
б) ?0>р<?(*р.
Доказательство. По определению числа # > г, цепь х\
лежит на комплексе /Ср и не лежит на /CjF""1. Псевдомногообразия 1/р/
суть открытые подкомплексы комплекса К$\ поэтому
Итак, UliX^ есть цикл на Ufa. Так как г <Cq и Щ( — простое
псевдомногообразие, то U$ixl~0 на Щг
Пусть *р/+1 £ Lr+1 (1$) удовлетворяет условию
Тогда
A^JCp/+1=^*|i на Ufa,
Ajrp^+1 = 0 на /Ср\(1/|,и-ЯГ1)-
Полагая
y\t =о на £# и на tfp\(£/& U В&Г1),
имеем
и
4—КГ1 *? = St/p4/ 4- = А^ S аг^1 - S /е»>
ИЛИ
(2 : 341) х1-{КГЧ-Ъу*1) = AjCpS^ •
Так как Sj"p« лежит на Л$~\ то вся цепь
КГЧ-З-У^/е
лежит на АГГ\ причём из (2:341) следует
Так как л$—j£e Ло(*р) <=2о(*р).
то
Д*? (*р —^р = Д*р*5 — А Vp=°-

380 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [ГЛ. X
т. е.
(2:342) Д*р*5==Дф£.
Лемма [2 : 34] полностью доказана.
Докажем теперь, что условие 3° выполнено. Пусть
Последовательно применяя лемму [2 : 34] при х\ = z\, Д#3 х\ = 0 ,
получим цикл z\Hy v*=zq(xr)—г, лежащий на К$ и гомологичный
циклу z\ на /Q. В силу леммы [2 : 33], цикл z$H имеет вид 2^ЙР*»
как и требовалось.
Условие 4°. Пусть
4=2 ^ щ{,
4 = д^4+1>
Пусть
^Гб^о+1(^).
?(*£+1)>г+1.
Цепь Хр имеет границу, лежащую на Л'£; поэтому лемма [2 :34]
применима к л;|з , и мы получаем цепь у£+1, удовлетворяющую
условиям
?сО<?(4+1)>
Продолжая в случае надобности применять лемму [2 : 34], получим
в конце концов такую цепь v$+1, что
значит, на основании леммы [2 : 33] цепь v^1 есть линейная
комбинация цепей ii^f1, что и требовалось доказать.
Из [2 : 26] и [2 : 32] следует:
[2 :350]. Пусть К$ есть элементарное подразделение
комплекса Ка',, цепи sp/£/, где trai суть ориентированные
симплексы комплекса Ка, образуют фундаментальную систему цепей
комплекса К$.
Назовём (как в главе 3, арт. 2: 4) правильным
подразделением данного комплекса Ка всякое подразделение Л^,
получающееся в результате конечного числа последовательных элементарных
подразделений.

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМУ 381
[2 : 35] *). Пусть К§ есть правильное подразделение комплекса /Са.
Если trai суть ориентированные симплексы комплекса Ка> мо цепи
s\trai образуют фундаментальную систему цепей комплекса К§.
В частности, это утверждение справедливо, если К$ —
барицентрическое подразделение комплекса Ка.
Доказательство. Мы скажем, что правильное
подразделение К$ комплекса КЛ имеет ранг р, если К§ может быть получено
из /Са посредством р элементарных подразделений и не может быть
получено из Ка посредством меньшего числа элементарных
подразделений. Предположим, что теорема [2 : 35] верна для всех
правильных подразделений ранга ^р—1; докажем её для правильного
подразделения К$ = К„р ранга р. Пусть даны комплексы
Аа = /Сво» Ав1, • • • , Aajo»
каждый из которых является элементарным подразделением
предыдущего.
Надо доказать, что цепи s*aptrai удовлетворяют условиям 1° — 4°
определения [2 : 31]. Это очевидно для условий Г и 2°.
Переходим к условию 3°. Пусть дан гомологический класс $«^£ AJ (Кар).
Требуется найти в £гр цикл вида 2а*5«//«г'- Так как К^р есть
*
элементарное подразделение комплекса Кар„{, то в £р содержится
цикл вида
г V4 а{р— 1) /г— 1
Z%p — ^j Сi $ар 1Л(р—i)f.
Так как Ка(р-г) есть подразделение ранга р — 1 комплекса Ка, то
цикл
i
гомологичен в Kap-i некоторому циклу вида 2a*5*(p~i)^'* откУДа
i
J _ Ap—\)r у a fr K ,
следовательно, цикл ^a^pfai содержится в &р.
i
Займёмся, наконец, условием 4°.
Пусть дан цикл ггар^Но(Кар) вида
z*p ==г 2j ais*p ^cu •
i
Требуется^ доказать, что он является границей цепи вида slpX^ ,
где лГ^б^Ч^а)- Так как К*р есть элементарное подразделение
*) Теорема верна длялюбого подразделения 2Гр комплекса Е"а и следует
из теоремы [2:261].

382 ИНВАРИАНТНОСТЬ ГРУИП БЕТТИ [гл. X
комплекса /fe(p_D , то цикл zrap — slp~ 2^5"(/?-i)^ является гра-
ницей некоторой цепи вида
* — о«СР-1)у - Q« . /Г. _ д а(р-1) г+1 ___ «(^ —1)д г+1
*
И
Так как Ka(p-i) есть подразделение ранга р—1, то из последнего
равенства следует
*
значит,
<Сгхр ЬЛр j/J Ui*"xi Ь%р da(p—l) j^l uiboii &ар 1ЛЪ<х(р — 1)Лх
= Asa xr+1
что и требовалось доказать.
2:4. a-комплекс, определённый данной фундаментальной
системой цепей. Пусть дана фундаментальная система цепей комплекса /fp,
состоящая из цепей u\i /=1,2,..., рг, г=0,1,...
Построим клеточный комплекс & следующим образом:
а) Элементы комплекса 5? суть некоторые
г г , г г
Uly . . . , U^r у "if . . . , U^y ,
взаимно однозначно соответствующие .цепям ±иг^, причём
элементу щ соответствует цепь u\i, а элементу — щ соответствует
цепь — и\и Полученное взаимно однозначное отображение множества
всех iii на множество всех цепей ±u\i обозначим через [3:
$и* = u\t, Р( — щ) = — u$i.
б) Коэффициенты инцидентности (±«J:±rw[el) определяем так.
На основании условия 1°, арт. 2:3 имеем
(2:41) A^-S^™1^1,
где ifjj1 суть целые числа.
Полагаем
г г—1Ч г—1
(Ui'.Uj ) — Vlij ,
и далее,
(«Г : - «Г1) = - Ч&-*; (- uf : «г""1) = - ifo-1 I

§ 2] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ, ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ S#3
Таким образом, за матрицы инцидентности клеточного
комплекса $ можем принять матрицу
г
V
Ui
г
Upr
г—1 г—1 г—1
«1 - - - Я/ ■ ■ ■ Црг~1
г — 1 г—1 г — 1
•Чи ■■■'Чу ■••'tyr-i
V—1 г—1 .J*—1
г—1 г—1 V —1
в соответствии с чем имеем
(2:42) A^S^T1"/-1;
г
(2:43) ДиГ^З^'иГ2.
[2 : 4]. Основное уело
##£
AAaJ = О
выполнено, так что ^ ££/яь а-комплекс.
В самом деле, в силу (2:42), (2.43), (2:41), имеем
У У У . ft
= 2j 12j 1'У Ч/fc J "ft ,
ft У
fc у
Так как ДДир/ = 0, то 2(2'Ч?у—1^Г2) M?ft~2== 0, ч го вследствие ли-
ft У __ __
нейной независимости цепей u\k означает ^jr\ij \jk = 0 для любых
У
/, h и ДДи£=0.
Итак, клеточный комплекс й есть а-комплекс. Мы
называем этот комплекс а-комплексом, определённым данное
фундаментальной системой цепей.
Замечание 1. Пусть К$ есть элементарное*) подразделение
комплекса Ка. Рассмотрим фундаментальную систему, состоящую из
цепей Sptli, где trai — ориентированные симплексы комплекса КЛ, и
обозначим через Ш определённый этой фундаментальной системой
а-комплекс. Этот а-комплекс изоморфен а-комплексу 51а, состоящему
из ориентированных симплексов комплекса КЛ*
Это утверждение непосредственно следует из теоремы [2:12] и
определения а-комплекса й.
*) Нижеследующее утверждение верно для любого подразделения К
(см. теоремы [2: 35] и [2:261).

384 инвариантность nWn бёттй [т. Щ
щ
Замечание 2. Вернёмся к примерам 1 и 2 арт. 2 :2 и к поЦ
строенным там фундаментальным системам подкомплексов комплекса /С1
являющегося в примере 1 триангуляцией тора, а в примере 2 триЗ
ангуляцией проекшвной плоскости. Ориентации элементов этий
фундаментальных систем подкомплексов образуют, в силу теоремы!
[2 :32], фундаментальную систему цепей:
2 110
Щи Щ\, Щ%у Щи
соответственно
2 10
Щи Щи Щи
Соответствующие а-комплексы
{ ±al±alu±^±u\) и { ±ul±ui±ii\ )
суть не что иное, как а-комплексы, рассмотренные нами в главе 7,]
арт. 4 :2, примеры 2 и 3. \
2 :5. Изоморфное отображение р группы Z/ ($) в группу 1Г(/Срм
Поставим в соответствие каждоЛ цепи \
|
цепь ij
Полученное отображение Р группы Z/($) в группу Lr(K§) есть,
очевидно, гомоморфизм. Но гомоморфизм р есть изоморфизм, так как]
из рд;г = 0 следует, в силу линейной независимости цепей и\и что|
все аг- = 0, т. е. хг = 0.
Далее,
ДР4-Д^ = 2^ГЧГ = ^ I
и для любой цепи xr£Lr(&)
(2 :51) ДрАГ = рД^,
откуда следует, что при посредстве р группа Zl($) отображается)
в Zl(K$), группа Hi(St) в Hl(K$). Отсюда, в свою очередь,
вытекает, что Р порождает одноимённый гомоморфизм группы Дг($) в
группу Д'(Яр).
Из условия 3° артикула 2 :3 следует далее, что гомоморфизм р
группы Дг($) в группу Дг(/Ср) является отображением на всю
группу кг(К$), а из условия 4° следует, что р есть изоморфное
отображение группы Д(51).
Итак:
[2 :51д]. Изоморфное отображение р группы ЬГ(Ж) в группу
Lr(K$) порождает одноимённый изоморфизм группы Дг(&) н$
группу Дг(/Ср). J

§ 3] ПОДРАЗДЕЛЕНИЕ ЦЕПЕЙ. ФУНДАМЕНТАЛЬНЫЕ СИСТЕМЫ 385
Из доказанного таким образом изоморфизма групп Дг(5?) и Дг(/(р)
и результатов главы 9, §§ 3, 4, следует, что:
Группы Vr($) и Vr(/fp) также изоморфны.
Итак:
[2 :5]. При всякой области коэффициентов % группы Дг ($, %) и
Vr(&, 21) соответственно изоморфны группам Аг(/Ср, 51) и Vr(/(g,%).
Замечание 1. Вернёмся к триангуляциям тора и проективной
плоскости, рассмотренным в примерах 1 и 2 арт. 2:2, и к
фундаментальным системам цепей этих триангуляции, рассмотренным
в арт. 2:4, замечание 2. В замечании 2 арт. 2 :4 мы видели, что
^-комплексы, определённые этими фундаментальными системами, суть
не что иное, как а-комплексы, с которыми мы имели дело в главе 7,
арг. 4:2, примеры 2 и 3, и в главе 8, арт. 1 :4, упражнение 4;
группы Бетти этих а-комплексов. (указанные в главе 8, арт. 1 :4,
упражнение 4) изоморфны на основании теоремы [2 :5] одноимённым
группам Бетти триангуляции К тора, соответственно проективной
плоскости.
Замечание 2.Изоморфное отображение р группы V($) в группу IX(Кр),
вообще говоря, не переместительно с оператором V, Другими словами, V$xr
сможет не равняться $Vxr>
Чтобы убедиться в этом, достаточно рассмотреть комплекс К^
состоящий из отрезков
\t^\ = \AB\, \t^\ = \BC\
а их концов
Л == t^v В = /^3, С = /р2.
Полагая
t\x={AB), ^^(BC), ^ = 4i+^2H ^i = 4i' ^2 = 42испРеделяя^'
//о. и1 по правилам предыдущего артикула, имеем
pvaj = p«i== «1 = ^ + ^2,
г. е.
Ч$и\ф$Чи\.
2:6. Изоморфизм групп Бетти при элементарных и
барицентрических подразделениях комплекса К- Пусть К$ есть
элементарное подразделение комплекса К% относительно некоторого
симплекса Т£1К*\. В силу теоремы [2:350], имеем, обозначая через t\i
ориентированные симплексы комплекса /Са, фундаментальную систему
цепей о£ = 5§*«* комплекса /С3.
Но я-комплекс $«, состоящий из всех ориентированных
симплексов комплекса Кю изоморфен «-комплексу к, определённому
фундаментальной системой цепей u\i (арт. 2:4, замечание 1). В силу
теоремы (2 :5] группы Бетти комплекса К$ изоморфны группам Бетти
комплекса $, следовательно, группам Бетти Яв, т. е. группам Бетти
комплекса /Ск.
-^5 Алексачлров П.. С.

386 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [ГЛ. Щ
Итак: I
[2:60]. Группы Бетти комплекса К« изоморфны одноимённым]
группам Бетти элементарного подразделения комплекса КЛ отноЛ
сительно любого симплекса Т£ [Кл]. |
Так как барицентрическое подразделение получается в результате^
нескольких последовательных элементарных подразделений, то имеем !
следующую основную теорему:
Теорема [2:61] *).Пусть Ка — триангуляция или открытый
подкомплекс триангуляции, К§ — барицентрическое или вообще
любое правильное подразделение комплекса Ка. При всяком г и
всякой области коэффициентов 51 группа Аг (/Са, 21) изоморфна
группе kr(Kp 21), а группа Vr(Ka, Щ —группе V (АГр, 91).
§ 3. Нормальные и канонические сдвиги в полиэдрах»
3:1. Нормальные сдвиги подразделений триангуляции. Пусть
/Гр есть подразделение триангуляции К^ Каждая точка полиэдра
Р = К$ = Кл содержится в единственном симплексе комплекса Кх—
носителе этой точки в комплексе Д*а. В частности, каждая вершина
e^j комплекса К$ имеет своего носителя в комплексе /Са.
Каждой вершине е^ комплекса Ар поставим в соответствие
определённую вершину е^ = S\e^ комплекса Ка под одним только
условием: eaj есть какая-нибудь вершина симплекса,
являющегося носителем в Ка точки е^.
Докажем, что заданное таким образом отображение вершин
определяет симплициальное отображение комплекса Ко, в Кл- Пусть вер*
шины £р0,..., еВг образуют остов в комплексе Лр. Обозначим через-
Та носитель (в комплексе Аа) симплекса | е$0.. ,е^г | = Т$. Так как
каждая вершина е^ есть предельная точка симплекса \е^.. ,е^г\у
значит, и подавно симплекса Га=> | е$0.'.. е$г |, то все вершины е$ф .. . ,е$г
лежат в Та9 откуда следует, что носитель в А0 каждой из вершин
2ро»-.-»£рг есть некоторая (собственная или несобственная) грань
симплекса Гв. Значит, S^e^,...9S$e$r суть вершины симплекса Та.
Итак:
отображение б£ множества всех вершин комплекса К$ во
множество вершин комплекса Ка определяет симплициальное
отображение, обозначаемое нами также через S$ комплекса /Ср в
комплекс /Са.
Всякое построенное таким образом симплициальное отображение
S^ подразделения К9 комплекса Ка в комплекс Ка называется
нормальным отображением или нормальным сдвигом.
*) Теорема верна и в том случае, если К$ есть любое подразделение
комплекса #а. Для случая, когда Ко есть триангуляция, это утверждение
следует, например, из [2:261] и подстрочного примечания к теореме
[2:35]. '

§ 3] НОРМАЛЬНЫЕ И КАНОНИЧЕСКИЕ СДВИГИ В ПОЛИЭДРАХ 387
Как и всякое симплициальное отображение (см. главу 7, арт. 8:2),
нормальный сдвиг Si порождает гомоморфное отображение 6| группы
L\ = 1/(/СрД) в группу Z/ = Lr(Ka$L\ называемое нормальным
гомоморфизмом группы Ц в Lra.
Из общих результатов главы 7, арт. 8:31, и главы 8, арт. 1:7
следует, что нормальный гомоморфизм S$ порождает называемое
также нормальным—гомоморфное отображение S? группы ДЦ==
= Л'(/СрД)в AJ=A'(/Ce,9t).
[3:11]. Нормальный гомоморфизм S^ группы 1Л в Lra есть
отображение на всю группу 1/%т
Это предложение, очевидно, вытекает из следующего основного
тождества, верного для любой цепи xr £ II и нормального
гомоморфизма S&:
(3:11) а S?$Zxr = xr,
где £"л/ есть подразделение цепи хга в комплексе Л^-
Тождество (3:11) достаточно доказать для одночленной цепи
хя = Кт Д°казательство основывается на следующей лемме:
Лемма Александера: Пусть дано какое-нибудь
симплициальное отображение S комплекса К в комплекс [Тп],
состоящий из симплекса Тп и всех его граней *). Обозначим через tn какую-
нибудь ориентацию симплекса Тп. Если д'ля целочисленной цепи
xn^V\K) имеем
Sbxn = Af\
mo
Sxn = tn.
В самом деле, Sxn есть некоторая целочисленная ^-мерная цепь
комплекса [Тп]. Но так как комплекс [Тп] содержит лишь один
/^-мерный симплекс, именно, симплекс Тп9 то цепь Sxn необходимо
одночленная, т. е. имеет вид ctn, где с — некоторое целое число
и \fl\=Tn.
Нужно доказать, что с=1. Из
Sxn = ctn
следует
SLxn = ^Sxn = c\tn.
Но нам дано, что 5А#П = Д£П, следовательно, с=1, что и
требовалось доказать.
Замечание 1. Лемма Александера и приведённое её
доказательство остаются в силе, если за область коэффициентов взять
колыю Jm.
*) Причём предполагается только, что К— симплициальный комплекс,
сфиентированные симплексы которого образуют а-комплекс.
25*

388
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[ГЛ. X
Применим теперь лемму Александера к доказательству тождества
3:111) Sts«tr=tr,
' а р а а'
из которого, как уже было упомянуто, сразу следует и тождество
(3:11).
Для г = 0 тождество (3:111) верно, так как
и отображение S^ сводится при этом случае к тождественному
отображению вершины 1^| на самоё себя.
Предположим теперь, что (3:111) доказано для г — п—1,и
докажем это тождество для г = п.
Пусть ориентации tfJJ-1, - - . ,^~А всех (п —1)-мерных граней симплекса Г£
выбраны так, что
A tn = Рг1 + . .. + tn~x.
а аО 1 1 а/2
Тогда
р of р аО i ' р ал
В силу наших предположений
Ср\а/л—1— /л—1 С(Зса/л—-1— fn—1
так что
ара ара аО I «ал а
и, значит, по лемме Александера (в которой надо положить tn = tn*
то и требовалось доказать.
Замечание 2. Если за область коэффициентов взять У2, то,
как легко видеть, формула (3:111) переходит в лемму Шпернера
(глава 5).
Из тождества (3:11) непосредственно вытекает ряд важных
следствий :
[3:12]. Нормальное отображение S? есть отображение
комплекса Кр на комплекс Ка-
В самом деле, пусть ТЛ — произвольный симплекс комплекса Ка,
Ki — ег0 ориентация, 7£,.. .,7? —лежащие на 7£. r-мерные
симплексы комплекса Ка. По крайней мере, один из симплексов Tip / =
= 1, 2,.. .,#, отображается при посредстве S$ на !Г\, так как в
противном случае имели бы 5^|^ = 0, а не
Пусть теперь до конца параграфа Ка есть триангуляция.

§ 3] НОРМАЛЬНЫЕ И КАНОНИЧЕСКИЕ СДВИГИ В ПОЛИЭДРАХ 389
[3:13]. При гомоморфизме Si группы L\ нагруппу Z/, группы ZJ
и Щ отображаются соответственно на группы Z£ и Нга.
Предложение [3:13] непосредственно вытекает из [3:111].
Из [3:13] следует, что гомоморфизм S$ группы Д£ == Дг (К$, 91)
в группу Д£ = Дг(/Са, 51), порождаемый гомоморфизмом S[ группы IJL
на Z/, есть гомоморфизм на всю группу Дг.
Докажем, что S£ есть изоморфное отображение группы Д£ на группу
Д£. Нижеследующее доказательство этого предложения читатель может
вести в различных предположениях общности относительно
подразделения К$: можно ограничиться случаем, когда К$ есть
элементарное подразделение триангуляции Ка; можно сделать более широкое
предположение, что К$ есть правильное подразделение триангуляции
Ки (см. [2:350], [2:35]); этот случай охватывает, в частности, случай,
когда К$ есть барицентрическое подразделение Ка (даже
многократное); можно, наконец, предположить, что К$ есть любое
подразделение триангуляции АГа. В соответствии с выбранной степенью
общности придётся ссылаться на [2:350], или на [2:35], или, наконец,
на подстрочное примечание к теореме [2:35]. Во всём дальнейшем
изложении применяются лишь правильные (почти исключительно одно-
или многократные барицентрические подразделения); ценой очевидных
редукций в дальнейшем всегда можно будет ограничиться и случаем
элементарных подразделений.
Итак, доказываем теорему:
[3:14]. Нормальное отображение S% подразделения К^пгриангу^
ляции Ка на Ка порождает одноимённый изоморфизм группы Д£
на Д£ (обратный изоморфизму sp.
Достаточно доказать лемму:
[3:15]. Если г^Ц и S\z^H^ то г^Щ.
Для доказательства [3:15] заметим, что, в силу [2:350] (соот-
ветстаенно [2:35] или подстрочного примечания к [2:35]), имеются
такие цепи хр-1 £ Ц+1 и zra£Zra, что
(3:15)" Д*£Н = *5-*;
г'
откуда
т. е. S\z*—ггл£Нга. Отсюда следует: если S^z^H^ то и г££#£,
значит, $|<6#р, т- е-> в силу (3:15),
что и требовалось доказать.
Замечание. Нормальный гомоморфизм Щ группы Z,£ в группу 1р •
определяемый как гомоморфизм, сопряжённый нормальному гомоморфизму
$lt порождает одноимённый гомоморфизм группы ^Г{К^Щ в группу

390
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[гл. х
Vr (К& Ш)- Этот последний гомоморфизм является изоморфным отображением
группы Vr(Ka,Щ на УГ(К$,Щ; доказательство второго предложения мы
дадим в следующем параграфе.
3:2. Примеры на нормальные гомоморфизмы Si и S*
1°. Пусть /Са=[Г2] — комплекс, состоящий из треугольника, его
сторон и вершин, К$ — барицентрическое подразделение Ка.
Рассмотрим симплициальное отображение S$ комплекса К$ в /Са,
получающееся, если отнести каждой вершине комплекса К} одну
из вершин её носителя в /Са. На черт. 130 мы подле каждой
вершины комплекса К$ ставим в
скобках её образ при отображении 5*.
Через tl обозначим треугольник
abc, ориентированный против
часовой стрелки (и цепь, принимающую
на t\ значение 1).
Полагаем для краткости
Черт. 130.
треугольниках*) комплекса К^
обозначаем через х$ цепь,
принимающую значение 1 на всех
ориентированных против часовой стрелки
Заштрихованный треугольник
комплекса К§, ориентированный "против часовой стрелки, обозначаем
через t\. Через х* обозначим цепь комплекса /fp, принимающую
значение 1 на всех ориентированных по стрелкам отрезкам комплекса
/Гр, вычерченных на черт. 130 жирно.
Непосредственным вычислением проверяем, что в соответствии
с общими теоремами
Далее вычисляем:
так что в соответствии с теоремой (6 :2) главы 9
*) Очевидно, можно было бы написать дг| = ^|/^, причём kxi — slkt^
Мы не пользуемся здесь обозначением s^ чтобы не затруднять читателя,
читающего этот артикул непосредственно после арт. 6:2 главы 9.

§ 4]
КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ
391
era
2°. снова ка = [Т';};
К$ есть подразделение комплекса /Са, изображённое на черт. 131.
Подле каждой вершины К$ указан в скобках её^образ при
отображении SK Через t2 обозначен
треугольник 7^, ориентированный против часовой
стрелки; через xj обозначена цепь,
принимающая на всех ориентированных
(против часовой стрелки) треугольниках К§
значение 1; через у\— цепь,
принимающая на треугольниках Кр
ориентированных против часовой стрелки,
указанные на них значения. Через у*
обозначаем цепь, принимающую значение 1 на ориентированных по стрелкам
отрезках К*,, вычерченных жирно, и значение нуль на остальных
одномерных симплексах комплекса Ко.
Непосредственным вычислением проверяем:
S*x* = t\ SHl = t2,
а 3 а' ч-?А а>
й(а)
VAf- =
■■3t\
а/
--y'h
§ 4. Канонические системы баз для подразделения
/Ср триангуляции Ка- Гомоморфизм S%, сопряжённый
нормальному гомоморфизму ^
4:1. Канонические системы баз К^ Во всём этом параграфе
читатель может понимать под Kf либо элементарное подразделение
триангуляции ЛГа, либо любое правильное подразделение триангуляции Ка, либо,
наконец, вообще любое подразделение этой триангуляции. В зависимости от
выбранной степени общности придётся пользоваться либо теоремой [2:350],
либо теоремой [2:35], либо, наконец, подстрочным примечанием к этой
теореме. Уже случай элементарного подразделения достаточен для тех
приложений, которые мы имеем в виду.
Пусть Ж = J. Вместо LJ(/Q, Z£(/Q,.... 20г(/ф,... пишем /.* Z£,. ..,z£,...
В группах /,£, Z£, Щ рассмотрим подгруппы /,^, Z^, ^ доставленные
из цепей вида s^x^ где х^ принадлежит соответственно группам z£» Zr Hr
и s^t как всегда, есть оператор подразделения (арт. 2:1).
Очевидно,
Z/l(4 = L0o П Zp,
-op"
Лоз:
••Ц*[\Щ.
^оз = Lo$ П#£-

392
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[гл. х
Группы ZL, Zop дивизионно замкнуты в /,£ (и подавно Z}^ дивизионно
замкнута в Zo). Поэтому группа Z^/^ есть свободная абелева группа и всякая
база группы Zqo может быть дополнена до базы группы Z^ элементами,,
произвольно взятыми по одному из каждого класса Щ 6 Z^/Zq^.
[4:11]. В каждом классе rjo^Zo/Zjo, имеются элементы h^HL
В самом деле, пусть zj| — произвольный элемент класса fy£ £ Z^/Z^..
В силу теоремы [2:350] (соответственно [2:35] или подстрочного
примечания к теореме [2: 35]), имеется цикл z'* — s*zfa',£ ZL, гомологичный циклу
z\ в Ко\ цикл
г г г г,Г
h? = z? — z^ £ И$
содержится в том же классе Щ, что и zL
Отсюда следует:
[4: 12]. Любая база группы ZL может быть допошена до базы Z£
циклами /z^., взятыми по одному в каждом из классов ^^zy^ и
принадлежащими к Н^.
Мы хотим теперь построить систему канонических баз групп /.£,.
г = 0, 1,...,л, удовлетворающих некоторым дополнительным условиям*
связанным с тем, что АГр есть подразделение К«.
Псстроим, прежде всего, для каждого г = 0, ...,п каноническую базу
группы Zra. Этим построением определена база группы ZL , состоящая из
циклов:
К этой базе присоединяем некоторые циклы Vy £Hr^ так, чтобы
получилась каноническая база
4> • • ->4>; Kv • • •><=* <i> • • •> <,*•» <»• • •><'"**
группы Zo.
В силу изоморфизма А между LZ/Zp и Яр-1 базе
fir —1 г —1 р,г—1 г—1 . r-1 vr — 1 ^г-1 г-1
группы #3_1 соответствует Саза
4» • • • » f0zr-V tfQl, • • •> ^r-1 ^ • • •» ^r-1
группы Ij/Zf; при этом, так как б^1 w^™1 = s° Ч"1 "ГГ1 и «'о/"1 = ^Kj"^
то в ^ и i)Jj можно соответственно выбрать цепих\{ = s^ xrai, yr^ = б"j'^.
Выбираем такие цепи х*{ = sj*^ € lip У% = ^->'Г/£ 9oj и> *Фоме того*
произвольные цепи j>J, € J/ для всех г = 1 х*—*, ;*= 1, .. ,,<jr-i

§ 4]
КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ
39$
Получаем искомую систему канонических баз:
( УГ УГ Vr \9Г • МГ Vr
x0l, .. .,4f^r_lf y01,...,yQQr-v Уг> • • ->Уа,г-1
(4:13a) r = 0,...,/i{ <!,...,</, «Sif-ttt^ vlv-As
I
v\,...,v
групп /.о с соотношениями
f Д „Г Г\Г—1 „Г— 1. i. Г „Г — 1. a.,»' „,Г—1
(4:14д)
А4яА4вЧвЧ = о-
B«; v *v; гой-. 'о*- w J'r
Сопряжённые базы, к канонической системе баз записываются в виде-
(4:13v)
и удовлетворяют условиям
(4 :14v) V?№ = й-U-+1; v^, = ^+1; vJf, = »?'.
В самом деле, в таблице
I
i ~»roi
1 *
"zm
~xr
УГо
Уи
*Ь
yroj
уj'
,r
z0h.
«Oft
<l
<>
~r-\
Ы
x'r1
• о
0
0
0
0
0
0
V0f
0
0
0
0
0
0
0
^
уг1
0
0
0
0
0
0
0
~zr~x
z0h
zr~x
z0h
0
0
0
0
0
0
0
-r-1
X0k
rr-l
Jl\ r-1
6, r-1
0
0
0
0
0
о !
Уо/
0
1
'•1
0
0
0
0
0
У if
0
0
1
'•1
0
0
0
0

394
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[гл. х
каждая строка (читаемая, как линейная форма относительно х^ \ У^Г1,
У*"1, sjjj"1, «олГ1» ^of1» ^г"""1) выражает А-границу возглавляющего эту
строку r-мерного элемента базы (4:13д); следовательно, каждый столбец
той же таблицы (читаемый, как линейная форма относительно «Jf, v^j, t>£
^ofc> *ол> Уог> УI') выражает V-границу возглавляющего эту строку (г — 1>мер-
ного элемента базы (4 :13v), откуда сразу следуют равенства:
переходящие в равенства (4:14v); если заменить (г—1) на /*.
Как в главе 9, арт. 3:5, убеждаемся, что циклы
zoh> иок> vol> VV
образуют базу группы Z^, а циклы
еТ — 1 Т "~Т "~~Y
к U0Jc> V0l> VV
— базу группы Щ1%
4:2. Нормальные гомоморфизмы в канонических базах. Посмотрим
теперь, какой вид в системах канонических баз комплексов АТр и К0
приобретает матрица нормального гомоморфизма s£ групп Z.£ в L^.
Имеем
Пусть, кроме того,
si у], = 2й/-< *:,+2 6.« у*+2 <н <*+2 dfu <n+2 efi<i,
i j h k I
где коэффициенты справа—какие-то целые числа.
Наконец, так как vrv 6 Щ, то Si vrv £ Н[, т. е. s\vrv = ^/tyA-6*a!* +
+ ISffz'z^Iz* где Pz'a* #rz— целые числа. Все" это может быть записано в виде
таблицы, помещённой на стр. 395, где каждая строка (читаемая, как
линейная форма относительно xraiy _у£., zroh, urakt v £z) выражает образ
возглавляющего эту строку элемента базы (4:13д)при гомоморфизме SP-
а
4:3. Гомоморфизм, сопряжённый к нормальному. Переходя к
сопряжённым базам и помня, что гомоморфизмы si и #о—сопряжённые,
замечаем на основании теоремы (5:4) Прибавления I, что каждый столбец нашей
таблицы (читаемый, как линейная форма относительно^, tfj,, ~г%„ ~zron, *£k э
Уо1> y\f) выражает образ возглавляющего этот столбец элемента базы
iuli> vaj* zlb> х1ъ У1г> ПРИ гомоморфизме Щ.

§ 4]
КАНОНИЧЕСКИЕ СИСТЕМЫ БАЗ
395
иы
V0j
1 *;-
z0h
х0к
Yol
Y
4,
У*
уг'
у,
zuh
и0к
«0/
V\r
1
0
aj'i
0
0
0
0
0
1
Щ'з
0
0
0
О
0
0
Cj'h
1
0
О
О
Лак
<к
О
О
di'k
О
1
0
pi>A
О
О ;
ejn
О
О
1
Яп
В частности,
У
Ho ^J/€/^p' поэтому, обозначая через u£it u"^, g£ft, ^*л соответственно
V-классы элементов у*р urQV zrab9 ~~г\# имеем
(4-3) "3§&=&. s^l;ft=lL;
но V-классы it^, ^ образуют базу группы Vr(/Q, а V-классы u^, ~jjt —
базу группы V(/Cp). Из (4:3) следует, что, в силу гомоморфизма "51 эти
две базы оказываются поставленными во взаимно однозначное соответствие,
т. е. что"5о есть изоморфное отображение группы Vr(Ka) на Vr(ATg).
Подведём итог результатам этого параграфа.
[4:3]. Пусть S^ есть нормальное отображение подразделения К*
триангуляции Кл на Ка и соответствующее гомоморфное
отображение группы Ц на Lra% Пусть "Щ есть сопряжённое гомоморфное
отображение группы L^ в LLГомоморфизмS% порождает
(одноимённое) изоморфное отображение группы Vr(ATa) на Vr(/Q.

396
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[гл. х
§ 5. Комплексы /0?„. Малые сдвиги в полиэдрах и компактах.
Теорема о мостовых и инвариантность чисел Бетти.
6:1.Комплекс Kr,г\ e-цепи метрического пространства /?. Пусть
даны метрическое пространство R и число е>0. Назовём е-осто-
вом или е-симплексом пространства/? всякое конечное
множество точек пространства 7?,имеющее диаметр <з. Очевидно, е-остовы
пространства R образуют полный комплекс остовов, который мы
обозначим через /0?,е; цепи комплекса Кр>ъ называются е-цепями
метрического пространства R. Можно сказать:
s-цепью метрического пространства R называется всякая
конечная линейная форма zr = 2С^> г^е ** сУть
ориентированные г-симплексы пространства R и ci суть элементы данной
области коэффициентов 21.
Циклы комплекса Kr,z называются е-циклами метрического
пространства R.
Другими словами:
г-цепь zr = Ъсг ft называется г-циклом пространства R, если
Если s<e/, то всякий е-остов есть и вместе с тем и е/-остов, так
что Kr,9 cz/0?,e/.
Если s-цикл zr гомологичен нулю в Кяу, то он называется
е'-гомологичным нулю в пространстве R.
Другими словами, мы говорим, что
г-цикл zr пространства R гг -гомологичен нулю в R, и пишем
zr~, О в /?,
если существует г''-цепь хг+г пространства /?, имеющая гг своей
г~границей: Ал:г+1 = гг.
Далее, е-цепи пространства R (будучи, по определению, цепями
комплекса Kr*) образуют группу Lr(KR,z, Щ; поэтому сложение
и вычитание е-цепей, в частности, е-циклов не требует дальнейших
пояснений. В связи с этим заметим, что два е-цикла Z* и zr9
называются s'-гомологичными между собой в /?, если разность
этих циклов е'-гомологична нулю в R:
5:2. е-сдвиги. Пусть М — множество, лежащее в метрическом
пространстве R. Предположим, что каждой точке х£М поставлена
в соответствие точка у = 5(лг)£ R под единственным условием, что
расстояние между х и S(x) меньше, чем заданное положительное г.
Удовлетворяющее этому условию отображение 5 множества М в R
называется s-сдвигом множества М в R. Никаких предположений о
непрерывности отображения не делается.

§ 5] комплексы /е#|е. мллые сдвиги в полиэдрах и компактах 397
Пусть, далее, даны е>0, е'>0и е'-сдвиг 5 множества М в R.
Так как для любых двух точек р и рг множества М их образов
q =5(x), q' = S(x') имеем
P (Я, Я') < Р (<7> Р) + Р (р, р') + Р (Я', ?') < Р (р, р') + 2г>
то всякому е-остову подпространства МЯ-R, в силу отображения 5,
соответствует е^~2е'-остов пространства /?. Другими словами,
отображение S множества М порождает симплициальное отображение
комплекса Kr,% в комплекс /(#,•-{-%'• Это отображение называется
з'-сдвигом комплекса Kr,% обозначается также через 5.
В силу симплициального отображения S, каждой е-цепи
соответствует (е-|-2а')-цепь
Sxr = %c4S t\ G L\Kn^)\
эсли f4 s= (eQ.. .er), то S^ = (S£0 -. .S*r). Цепь Sxr называется
з'-сдвигом цепи #r.
5:3. Канонические сдвиги. Пусть Ф — компакт (особенно часто
встречается случай, когда Ф определено, как замкнутое
ограниченное множество, лежащее в некотором эвклидовом пространстве Rn).
Пусть М — какое-либо подмножество компакта Ф: Пусть,
наконец, дано замкнутое е-покрытие
(5:31) a = {AV..., As}> Ax[} ... [}А8 = Ф
пространства Ф и нерв Ка покрытия а, реализованный в Ф или если
Фс^й, в заданной окрестности Ф. Это значит, что вершина е4 нерва,
соответствующая элементу А4 покрытия а, есть точка множества Аь
или точка Rn, отстоящая от Л не дальше, чем на некоторое заданное
о > 0, во всяком случае настолько малое, чтобы оно было лебеговым
числом покрытия а, чтобы, в частности, для любых А4 было 8(Л^) -|- 8 < а
(при этом 8(ЛД как всегда, есть диаметр множества А4) (см. об этом
главу 4, арт. 2:1, замечание 4).
Определим теперь s-сдвиг S® множества Мс:Ф следующим
образом. Пусть р — произвольная точка множества М; возьмём множество
А4£а} содержащее точку р (если таких А4 несколько, выберем
какое-либо определённое среди них). Пусть е4— вершина нерва,
соответствующая множеству А{.
Полагаем
9 = S*(p) = e,.
Так как и р, и e4 = Sf (р) принадлежат одному и тому же
множеству диаметра <е, то отображение Заесть е-сдвиг множества М.
Полученные таким образом s-сдвиги называются каноническими
сдвигами множества Жс=Ф относительно покрытия
а компакта Ф.

398
ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ
[ГЛ. X
Замечай и е 1. Для того, чтобы вполне определить канонический
сдвиг множества ЖсФ, относительно данного покрытия а компакта
Ф, надо, во-первых, выбрать определённую реализацию нерва
покрытия а, во-вторых, выбрать для каждой точки р£М
(принадлежащей более чем к одному множеству А/) определённое содержащее
эту точку множество А$.
Теорема и определение [5:31]. Пусть Sf есть
канонический сдвиг компакта Ф относительно замкнутого покрытия а;
пусть 8 есть лебегово число покрытия а; отображение 5Ф
порождает симплициальное отображение S® комплекса /Сф в нерв
Ка покрытия а.
Симплициальное отображение S®, равно как и производимый
им гомоморфизм группы Ь\КФ ^) в группу Z/(/Ca\ также
называется каноническим сдвигом относительно покрытия а.
Для доказательства теоремы [5:31] достаточно заметить, что если
\Р\ — \р0...рг\естьЪ-остоввФ и pk^Ai ,то, по определению числа
8, имеем Aio П ... П А^фО и, следовательно, вершины eiQ = Sfp0,.. . >
eir=Sfpr определяют симплекс «S^|^r| комплекса Ка-
Замечание. Так как (см. главу 7, теорема [5:31])
S? (Zr (Кф.*) ) Е & (7U 5* (№ (Кф,ь)) Sff (K*\
то при каноническом сдвиге всякий 8-цикл компакта переходит в
цикл комплекса Ка, всякий 8-цикл, 8-гомологичный нулю, переходит
в цикл, гомологичный нулю в комплексе /Са.
6:4. Числа ч\(К)* Канонические сдвиги в полиэдрах. Пусть
Ф — полиэдр, Ка — какая-нибудь триангуляция полиэдра Ф:
ф = £.
Через а обозначаем барицентрическое покрытие, сопряжённое
триангуляции К* (см. главу 4, арт. 5:3).
Канонические сдвиги множества М^КЛ относительно покрытия
называем, когда это оказывается удобным, каноническими
сдвигами относительно комплекса /Са. Точно так же лебеговы
числа покрытия а называются лебеговыми числами комплекса Кл.
Напомним одно свойство барицентрического покрытия а (см.
главу 4, теорема [5:42]): __
Пусть Tai£Ka; замкнутый симплекс Гс/ пересекается только с теми
элементами покрытия а, центры которых суть вершины симплекса Та<.
Обозначим через е(/Са) (как в главе 4, теорема [5:43]) наименьшее
из чисел, являющихся расстоянием между каким-либо си шлекссм
Та£Кл и соединением всех элементов а, центры которых не являются
вершинами Tai.

§ 5] КОМПЛЕКСЫ Крп. МАЛЫЕ СДВИГИ В ПОЛИЭДРАХ И КОМПАКТАХ 39$
Наконец, через ^(/Q обозначим какое-либо лебегово число
покрытия а, меньшее, чем все s(Tai)> Нервом покрытия а является
комплекс Ка', канонический сдвиг полиэдра Ф относительно
покрытия а порождает, поэтому, симплициальное отображение в Кл
комплекса/Co,s,где 8 — лебегово число покрытия а.
В частности, если М — множество всех вершин некоторого
подразделения К§ триангуляции Ка, то канонический сдвиг множества М
относительно Ка ставит в соответствие каждой вершине е*
комплекса /Ср. центр, содержащей эту вершину замкнутой барицентрической
звезды комплекса /Са, т. е. (см. главу 4, теорема [5:42]) некоторую
вершину носителя точки £Q в комплексе /Са. Поэтому всякий
канонический сдвиг множества вершин Ка относительно Ка порождает
нормальный сдвиг комплекса К$ в /Са.
Мы коротко формулируем этот результат так:
[5:41]. Всякий канонический сдвиг подразделения К§
триангуляции Ка относительно Ка является нормальным сдвигом.
Мы дадим сейчас усиление этого предложения, которое будет
постоянно применяться в дальнейшем.
Основная теорема [5:42]. Пусть К* есть подразделение
триангуляции Кч полиэдра Ф = КЛ = К§- Пусть ч\ = ч\ (KJ и d^ есть
какой-нибудь ч\-сдвиг множества М всех вершин комплекса К^
в полиэдре Ф; пусть, наконец, S J есть канонический сдвиг
полиэдра Ф относительно КЛ. Тогда отображение -S% d^ есть
нормальное отображение комплекса Ка на комплекс Ла, так что для
любой цепи xra £ Lr (/Q имеем
(5:42) 3*(Рф*1х1 = *Гл;
в частности, для любого ориентированного симплекса ta комплекса Кт
имеем
(5:420) 5?4 *!'« = '.•
Доказательство. Если е^— какая-либо вершина Ко., то по
самому определению числа ч\ (/Q точки d^ е^ может принадлежать лишь к
таким элементам барицентрического покрытия а, центры которых
суть вершины носителя точки е^ в комплексе Ка] отсюда сразу следует
что S® d^e^ есть вершина носителя точки е^ в комплексе /fa, что
и требовалось доказать.
5:5. Теорема о мостовых. Инвариантность чисел Бетти. Как.
мы сейчас увидим, и теорема о мостовых*), и равенство
(5:51) *'(Ъ = *'(*«)
сразу следуют из теоремы [Г:42].
*) Глава 5, вводные замечания, теорема 1Г и II.

400 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [ГЛ. Щ
Доказательство теоремы о мостовых. Пусть даня
триангуляция Ка л-мерного полиэдра Ф: 1
Ф = £Л. |
'":4
Положим e = 7)(/Q и докажем, что всякое замкнутое s-пскрытие ,,i
9 = {Л1Э...Л} Ч
полиэдра Ф имеет кратность ^ п-\-\. Нерв покрытия ср обозначив!
«через Кг
Пусть 8 есть лебегово число покрытия ср. Рассмотрим подразделе*'
«ие К§ комплекса /Са столь мелкое, что все симплексы К$ имеют
диаметр <8. Обозначим через d? канонический сдвиг комплекса Ка
относительно ср. Этот сдвиг есть s-сдвиг, поэтому, обозначая через 5Ф
канонический сдвиг относительно Ка, мы находимся в условиях
теоремы [5:42J, так что S® cfi есть нормальное симплициальное
отображение комплекса Ка на комплекс Ка-
Значит, Ка есть образ подкомплекса d$ K$ комплекса К® при
симплициальном отображении 5J, откуда следует, что $ К&, и тем
'более Kv имеет число измерений >п, что и требовалось доказать.
Доказательство равенства [5:51]. Существуют сколь
угодно мелкие замкнутые покрытия ^ полиэдра Ф = /Са, для нерва
К^ которых имеем xr(K() — Tir(Ka). В самом деле, достаточно
определить y, как барицентрическое покрытие*), сопряжённое
достаточно мелкому многократному барицентрическому подразделению /Ст
комплекса /Са. Поэтому
ти остаётся только показать, что для всякого достаточно мелкого
замкнутого покрытия ср полиэдра Ф = Ка имеем (обозначая, как всегда
нерв покрытия ср через /Q
<5:511) rJ{K,)>^{K^
Для доказательства этого неравенства положим вновь
и покажем, что неравенство (5:511) верно для любого s-покрытия.
Через К§ обозначаем столь мелкое многократное
барицентрическое подразделение комплекса К"а, что все симплексы Ка по диаметру*
меньше 8, где 8 есть лебегово число данного е-покрытия. Как и при
*) Глава 4, арг. 5:3.

§ 5] КОМПЛЕКСЫ Krz. МАЛЫЕ СДВИГИ В ПОЛИЭДРАХ И КОМПАКТАХ 401
доказательстве теоремы о мостовых, обозначаем через d?
канонический сдвиг комплекса Ко относительное, через S® — канонический
сдвиг относительно ос. Тогда 5Ф^ есть нормальное симплициальное
отображение К*, на /Са. Пусть
Sal' • " " ,8aicr
— линейно независимые элементы группы Ajj(/Ca). Выберем произвольно
циклы £^£j£i - Эти циклы гомологически независимы между собою:
гомология
2^.-0 в Ка
i
(при целочисленных с€ имеет место лишь в том случае, когда все с
равны нулю.
Так как S® ^ есть нормальное симплициальное отображение, то
5Ф d?S'2r. = 2r. .
а ее р at он
Выведем отсюда, что циклы d^ sj*г^. гомологически независимы между
собой в /Сф. В самом деле, если имеется цепь х^1 ^ AJ+1 (/Q,),
ограниченная линейной комбинацией циклов d$s*z[i:
Axr'ri = yCid? ь*гг., .
<f Jmmi * <0 р af '
г
то, полагая хг+1 = 5фхг+1, и
а от с а ее ^J г a (р р « ^4J 4 at
/ I
Но, в силу гомологической независимости циклов г^\, из
соотношения
A*»'+i = у c4zr.
a ^J * <xi
i
следует, что все ci равны нулю.
Итак, в Kip имеется, по крайней мере, тг = тгг(/Са) гомологически
независимых между собою циклов d^slz^, чем неравенство [5:511]
л, значит, равенство (5:51) доказаны.
Из только что доказанной нами инвариантности чисел Бгтти
я из формулы Эйлера-Пуанкаре вытекает топологическая
инвариантность эйлеровой характеристики:
[5:52]. Если полиэдры Ф = К и Ф'—К гомеоморфны между
собой, то их триангуляции К а Кг имеют одну а ту же эйлерову
характеристику.
Или:
[5:520]. Все кривые триангуляции одного и того же или
кривого полиэдра, ала двух гомеоморфных кривых полиэдров, имеют
пдну и ту же эйлерову характеристику.
—*> Ллек-андоов П. С.

)
402 ИНВАРИАНТНОСТЬ ГРУПП ВЕТТИ [ГЛ>. X
Замечание. Доказательство равенства (5:51)
*:» (£«)=*; (я.)
(для простого т) протекает совершенно так же, как только что»
проведённое доказательство равенства (5:51), и может быть
предоставлено читателю.
§ 6. Инвариантность групп Бетти.
в:1. В этом параграфе даётся доказательство теоремы [1:32]„
следовательно, и теорем [1:33] — [1:35], а также обобщение этих
теорем на случай полиэдральных комплексов. Из самой
формулировки теоремы [1:32] и определения групп 23г (Ф) следует, что дляь
доказательства теоремы [1:32] достаточно доказать следующие два
предложения:
[6:11]. Если Ф = КЛ есть полиэдр, то система ?рупп 58Г(Ф)
непуста.
[6:12]. Группа AJJ(/Q изоморфна некоторой подгруппе всякой
группы 23£25Г(Ф).
Для доказательства [6:11] достаточно заметить:
Каково бы ни было в>0 существует замкнутое е-покрытие х
с нервом Kv такое, что группа Ад(/Ст) изоморфна группе Л^(/Св).
Для того, чтобы построить покрытие f, достаточно взять столь,
большое натуральное число /г, чтобы замкнутые барицентрические
звёзды Л-кратного барицентрического подразделения К^ комплекса
Ка были по своему диаметру меньше е. Эти звёзды образуют
замкнутое s-покрытие полиэдра Ф, нерв которого есть K«h; группа
До С^ссл) изоморфна группе Д£(ЛГа). Переходим к доказательству [6:12],.
Пусть 23£2$Г(Ф); пусть т]== у7](/Са). Берём такое замкнутое
т|-покрытие X полиэдра Ф, что 21 изоморфна группе Д£(К\), где К*
есть нерв покрытия X.
Пусть К$—столь мелкое многократное барицентрическое
подразделение /Са, что симплексы Кр по диаметру меньше некоторого*
лебегова числа покрытия X. Рассмотрим канонический сдвиг S&
множества вершин комплекса К$ относительно покрытия X и
последующий канонический сдвиг s* относительно комплекса Ка) получим
нормальное отображение S\Sl комплекса К§ на комплекс /Са.
Ставя в соответствие каждой цепи хга комплекса КЛ цепь
(6:11) 5Р^6^(^х)
(где &, как всегда, есть оператор подразделения), получаем
гомоморфизм группы ££(/Q в Z/J (К\), порождающий одноимённый гомо-

§ 6] ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ 403
морфизм группы AJJ(/Q в Д£(Х0- Докажем, что этот последний
гомоморфизм есть изоморфизм. Для этого достаточно, что из
(6:12) S^~0 в Кх
следует
<~0 в Ка.
Но из (6:12) следует существование цепи у^1 £ LJ (Л\),
ограниченной циклом Sls*zra;
Воздействуем на обе части этого равенства оператором SKa:
Так как 5\SjJ есгь нормальное отображение комплекса А'& на комплекс
А а, то левая часть этого равенства есть г£, так что
где 5^y[+1 £ Lr0+1 (Aa\ что и требовалось доказать.
6:2. Инвариантность групп Бетти для полиэдральных комплексов.
Пусть К—полиэдральный комплекс*). В силу результатов приложения к
главе 7, ориентированные элементы комплекса А образуют я-комплекс;
группы Бетти этого я-комплекса называются группами Бетти полиэдрс1Ль-
ного комплекса А.
Теорема [6:2]. Группы Бетти полиэдрального комплекса А
изоморфны одноимённым группам Бетти произвольной триангуляции К
полиэдра А.
Достаточно доказать, что группы Бетти полиэдрального комплекса А,
изоморфны одноименным группам Бетти барицентрического подразделения
К\ комплекса А. Для этого, обозначая через 1\ элементы комплекса А,
через 1)\—их барицентрические подразделения, в свою очередь,
достаточно доказать, что 1)\ образуют фундаментальную систему подкомплексов
комплекса К\. Наконец, последнее утверждение будет, очевидно, доказано,
если мы убедимся, что U\ суть простые комбинаторные псевдомногообразия.
Доказательство того, что Щ есть псевдомногообразие, проводится очень
просто (например, полной индукцией по числу измерений) и во всяком
случае может быть предоставлено читателю. Ориентируемость
псевдомногообразия U] получается сразу: достаточно выбрать какую-нибудь
ориентацию выпуклого многогранника 7f; соответствующие ориентации всех
/--мерных симплексов псевдомногообразия и\ дадут ориентацию этого псевдо-
*) Глава 4, арт. 1 :2.

404 ИНВАРИАНТНОСТЬ ГРУПП БКГТИ [ГЛ. X
многообразия. Остаётся доказать, что для 0<р<г всякий р-мерный цикл
zp £ Z^(Uri) гомологичен нулю в Urt. Для этого заметим, что А^ zp есть
(р — 1)-мерный цикл комплекса
£r-i — [Ur\\Ur
i /' i
и что полиэдр В\~х гомеоморфен (/*—1)-мерной сфе^е, откуда следует,
что
Выбирая цепь хР (iLp0{Bri~ )» ограниченную циклом zp-1, видим, что
zp — xP^Z^dU^l). Так как Uri есть выпуклый многогранник, a \Urj\ —
его триангуляция, то zp — хР^О в [£/[], так что существует цепь
ограниченная циклом гР—хр. В этих условиях
Аиг хР^1 = zP,
i
что и требовалось доказав,
§ 7. Инвариантность псевдомногообразий.
7:1. Формулировки теорем. В этом параграфе доказывается
теорема:
[7:11]. Если триангуляция К полиэдра Ф есть
комбинаторное псевдомногообразие, то всякая триангуляция всякого
полиэдра, гомеоморфного полиэдру Ф, также есть комбинаторное
псевдомногообразие.
Эта теорема делает естественным следующее определение.
[7 :12]. Полиэдр Ф называется псевдомногообразием, если какая-
нибудь {и следовательно, любая) триангуляция Ф есть
комбинаторное псевдомногообразие.
Для доказательства теоремы [7: 11] введём следующее
определение:
[7: 13]. Точка /2-мерного полиэдра Ф называется
обыкновенной точкой этого полиэдра, если она имеет окрестность, гомеоморф-
ную Rn\ в противном случае данная точка называется особой.
Из этого определения следует, что множество всех
обыкновенных точек полиэдра Ф открыто в Ф и, значит, множество особых
точек замкнуто.
Теорема [7:11], очевидно, содержится в предложении:
[7:14]. Если хотя бы одна триангуляция n-мерного полиэдра
Ф является комбинаторным псевдомногообразием, то
1°) полиэдр Ф есть сильно связный компакт*)]
*) Глава 6, арт. 5:2.

§ 7] ИНВАРИАНТНОСТЬ ПСЕВДОМНОГООБРАЗИЙ 405
2°) размерность множества особых точек полиэдра Ф не
превосходит п — 2.
С другой стороны, если полиэдр Ф удовлетворяет условиям
1° и 2°, то всякая триангуляция этого полиэдра есть
комбинаторное псевдомногообразие.
Теорема [7: 14] позволяет дать определению [7:12] я-мерных
псевдомногообразий следующую, как говорят, инвариантную форму:
[7: 120]. Полиэдр называется n-мерным псевдомногообразиему
если он представляет собою сильно связный компакт
размерности п, особые точки которого образуют множество размерности
Сп — 2-
Заметим, наконец, что из теоремы об инвариантности групп Бетти
(теорема [1:33]) и из определения ориентируемости
комбинаторного псевдомногообразия *) следует:
[7:15]. Если одна какая-нибудь триангуляция полиэдра Ф
является ориентируемым (неориентируемы м) комбинаторным
псевдомногообразием, то тем owe свойством обладает и всякая
триангуляция полиэдра Ф.
Итак, остаётся доказать, лишь теорему [7: 14].
7:2. Доказательство теоремы [7:14]. Пусть триангуляция К
полиэдра Ф есть я-мерное комбинаторное псевдомногообразие. Тогда
комплекс К сильно связен, и следовательно, по теореме [5:251]
ыавы б сильно связным является и его тело . Ф. Кроме того, все
точки Ф, носители которых в К имеют размерность ^п—1,
очевидно, суть обыкновенные точки полиэдра Ф; следовательно,
особые точки этого полиэдра образуют замкнутое множество
размерности <;л— 2. Первая половина теоремы [7:14] этим
доказана.
Пусть теперь «-мерный полиэдр Ф удовлетворяет условиям 1° и 2°
)еоремы [7:14]; надо доказать, что произвольная триангуляция /С.
полиэдра Ф есть «-мерное комбинаторное псевдомногообразие.
Из сильной связности полиэдра Ф следует, в силу теоремы [5 : 252]
главы б, что триангуляция К есть сильно связный комплекс. Остаётся
доказать, что каждый (п-—1)-мерный симплекс Тп~1 этой
триангуляции подчинён двум и только двум /г-мерным. Это следует из
предложения:
[7:21]. Если в n-мерной триангуляции К симплекс Тп"г
подчинён лишь одному или, по крайней мере, трём п-мерным
симплексам, то всякая точка р £Тп~х есть особая точка полиэдра /С
В самом деле, рассмотрим оба случая.
1°. Пусть Тп~1 подчинён лишь одному симплексу Г7г£ К]
возьмём несущую симплекс Тп я-мерную плоскость Vn. Если бы
точка р£Тп~1 имела окрестность UnczVn относительно^, гомеоморф-
ную Rn, то на основании теоремы [4:10] главы 5 множество Оп
::: ) Глава 8, а[Т 3:2

406 ИНВАРИАНТНОСТЬ ГРУПП БЕТТИ [гл. X
было бы открыто в V'1 и, следовательно, точка р была внутренней
относительно V71 точкой замкнутого симплекса Тп, что очевидно
не так.
2°. Пусть симплекс Т*1-1 подчинён симплексам Т^ТЦ, Tg
комплекса К (и, быть может, ещё другим симплексам этого комплекса).
Множество Г*== Г* и Тп~х (j 7J, очевидно, гомеоморфно Rn.
Пусть Vn— окрестность точки р^Т11-1 относительно ЛГ, гомеоморф-
ная Rn\ тогда вследствие положительности числа р(р, Ф\Уп)
существует подобное преобразование с центром подобия р множества Гп
в некоторое множество Un^Tnf]Vn.
В силу теоремы [4:110] главы 5, множество Un открыто в V",
значит, и в /С, чего не может быть, так как р есть предельная точка
не пересекающегося с Un симплекса 7J.

ГЛАВА ОДИННАДЦАТАЯ.
Д-ГРУППЫ КОМПАКТОВ.
§ 1. Определение групп ДГ(Ф,91).
1 :1 Истинные циклы. Пусть Ф — компакт. Последовательность
г г г
2и ^2» • • • i Zh, • • •,
где гТ}Ь есгь r-мерный 6/гцикл *) компакта Ф по области коэффи-
диентов 91, называется г-мерным истинным циклом компакта Ф
ю области коэффициентов 91, если:
1°. lim ол = 0.
h -» оо
2°. Каково бы пи было г>0 существует такое натуральное
число A(s), что для А'>й(г), А">й(г)
Истинные циклы обозначаются так:
'1 :П) гг = (гги 4',..., **,..•)•
Суммой двух истинных циклов
(1 :12) г\ = (гГь г£2,. • •, z\h )
и
г ( г г г .
Z2 = (^215 ^22» • • • , Z2h, • • • j
называется истинный цикл
Это сложение превращает множество всех r-мерных истинных
циклов компакта Ф по области коэффициентов 91 в группу Zr{$> 91).
В самом деле, только что определённое сложение, очевидно,
ассоциативно; с^еди истинных циклов имеется нулевой цикл, получающийся,
У См. главу 10, лрт. 5:1,5:2.

408 А-группы компактов [гл. хв
) г
если в формуле (1 :11) для всех / положить z\ = 0. Наконец, к циклу
(1 :11) имеется противоположный ему цикл
— Хг = ( — гги — г*2, ..., —4,...):
удовлетворяющий условию
z' + i-zr) = o.
Истинный цикл (1 : 11) называется гомологичным н у л ю в Ф„
если для всякого е>0 можно найти такое Л(з), что для всех /г>/г(г)
z!' ~ 0 в Ф.
h e
Два истинных цикла х[ и z\ называются гомологичными между
собою, если их разность гомологична нулю.
Если истинные циклы
Zi = (^n, г^,..., zlh,...) и Za=(^i, 222,..., ^л,--.)
гомологичны нулю в Ф, то их сумма также гомологична нулю в Ф.
В самом деле, для любого е и /г>Л](е), /г>/г.2(е) имеем г-цепи&
х\и и л:j/,! , соответственно ограниченные циклами z[n и г^ь.
Тогда для к, большего, чем кг (е) и /г2 (г), имеем
что и требовалось.
Так как, кроме того, нулевой истинный цикл гомологичен нулю и
из того, что zr ~ 0, следует (—zr)~0, то /--мерные истинные циклы,
гомологичные нулю в Ф, образуют подгруппу Нг (Ф, 91) группы Z r (Ф, 91)-
Определение [1 :1]. Дополнительная группа
\г(ф,щ = гг{$>, 3t) /#г(Ф, %)
называется /--м е р н о й А-г р у п п о й (или просто Аг-группой) к о м-
пакта Ф по области коэффициентов 91; элементами группы Аг (Ф, 91)
являются классы гомологичных между собою истинных циклов
(«гомологические классы компакта Ф»).
Замечание 1. Так как истинный цикл определён, как
последовательность 8Л-циклов z\L, то понятие «подпоследовательности данного
истинного цикла» не требует пояснений. Точно так же естественно,
что циклы z\, составляющие истинный цикл (1 :11), называются
«членами» или элементами истинного цикла (1 :11).
Очевидно, всякая подпоследовательность истинного цикла сама
есть истинный цикл. Из второго условия, определяющего понятие
истинного цикла, сразу следует, что всякая подпоследовательность
истинного цикла zr есть истинный цикл, гомологичный циклу zr-

§ 2] ЛЕММЫ ОБ 3-СДВИГАХ И S-ГОМОЛОГИЯХ 409
Замечание 2. Если Фгсф, то всякий истинный цикл
компакта Фг является вместе с тем и истинным циклом компакта Ф,
однако, истинный цикл (1 :11) компакта Ф может не быть истинным
циклом компакта Ф' даже и тогда, когда Ф' cz Ф содержит вершины
всех циклов z\ *).
Поэтому имеет смысл такое определение:
Пусть дан истинный цикл (1:11) компакта Ф; всякое такое
замкнутое подмножество Ф'сф, что (1:11) есть вместе с тем и
истинный цикл компакта Ф', называется носителем истинного цикла
в компакте Ф. Примеры, иллюстрирующие понятие истинного цикла
и, в частности, содержание этого замечания, будут даны в следующем
параграфе.
§ 2. Леммы об г-сдвигах и г-гомологиях **).
2: 1. Призмы и а-сдвиги. Пусть R — метрическое пространство,
хг— какая-либо е-цепь пространства R. Пусть 5 есть s'-сдвиг
множества вершин цепи хг, переводящий цепь ху в цепь
x'r = Sxr.
Считая вершины цепи хг занумерованными в определённом раз
навсегда порядке, рассмотрим призму K[oi] над комплексом остовов
J\z=\xr\ (см. главу 4, арт. 2:4). Определим следующим образом
отображение S' множества всех вершин призмы K[oi] в пространстве R:
если ei есть вершина нижнего основания призмы /C[oi] (т. е. вершина
цепи jcr), то полагаем Srei^=-ei; если же е$ есть вершина верхнего
основания призмы /C|oi], a ei — соответствующая ей вершина нижнего
основания, то полагаем S'e/ = Set.
Если (е0'. . . ек'ек. . . ег) есть какой-либо остов призмы К\щ, то
его образ при отображении S' есть, очевидно, множество | Se0,. . .,
Se]{, ek,..., er\, диаметр которого равен наибольшему среди чисел
?(ei, ej)i P(Se4, Sej), p(eit Se3), где ei9 ej — какие-нибудь две
вершины, принадлежащие к одному и тому же octobv комплекса К.
Но
(;(eh ^)<s,
г ?(Seh Se})^rj{Sei9 ^) + pfo, ej) -f p (*,, SejX
(2:11) J <£'Ч-£ + 3'-г-]-2з',
I p(*f, Sej) ^ p (ei9 ej) + p (*,., Sej) < s -f- s'.
*) Вершиной о-ц2ии я,*= VV^ называется вершина всякого
симплекса/J, входящего в линейную форму хг = ^с$ с коэффициентом,
отличным от нуля (см. главу 7, арт. 5:2, замечание 3).
**) Глава 10, арт. 5:1 и 5:2.

410 А-ГРУППЫ КОМПАКТОВ [ГЛ. XI
Итак, в силу отображения S', каждому юстову призмы К[щ
соответствует некоторый (s -\- 2г/)"остов пространства R. Другими
словами, S' есть симплициальное отображение комплекса К\щ в
комплекс Кв, е-f 2е'.
При симплициальном отображении 5' комплекса /Qoi] в Квч • -{- 2е'
призма xli~x над цепью *) хг переходит в некоторую (г-}-2в')-цепьэ
которую будем обозначать через Usxr и называть призмой,
натянутой на цепь хг и на её s'-сдвиг x'r = Sxr. Точно так же призма^
над цепью zr~x = Ajtr (в комплексе A^oi]), в силу S', переходит в
призму П8Ал;г, натянутую на Ахг и на Skxr.
При этом симплициальное отображение S' переводит
соотношение (9 :34) главы 7 в
(2 :12) MIsxr = xr — x'r + Uskxr.
В частности, если хг есть s-цикл, то ПвАд;г = 0, так что (2 :12)
переходит в
.(2 :120) АП8лгг = хг — х'г,
и мы получим следующее важное предложение:
12 :12]. Всякий ъ-цикл метрического пространства R всегда
(е-\-2е')'гомологичен в R всякому своему г-сдвигу.
Замечание 1. Пусть Ф — компакт, а — его замкнутое s-покры-
тие; пусть Ка — нерв покрытия а={ Av...y А8 }, реализованный
вблизи Ф, так, чтобы было S (ai U Af) < е, где аг — вершина
нерва, соответствующая Л4-£а; пусть о — лебегово число покрытия а,
удовлетворяющее условию
28-}-8(flrfU Л<)<е
для всякого г. Пусть, наконец, sf — канонический сдвиг Ф
относительно а (см. главу 10, арт. 5:3).
Мы видели, что всякая призма, натянутая на 8-цепь хг и на её
канонический сдвиг 8Фахг, есть (8-|~2г)-цепь. Однако, в нашем случае,
обозначая через е' наибольшее среди чисел b(ai[)Ai)i вместо
формул (2:11) получаем более точные оценки
P<A,^)<8<e,
Р (** 5?^) < р (*,, е0) + р {ер Ste3) < о + в' < в,
Р (S?e4, Stej) ^ p {Steit ег) -^ р (e4, e0) -f p (ej} S*ej) <
<er + 8 + s, = s + e/,
откуда следует, что призма, натянутая на 8-цепь и на её
канонический сдвиг, есть 2з-цепь. Отсюда, в частности, вытекает:
*) Глава 7, арт. 9:3.

*§ 2] ЛЕММЫ ОБ о-СДВИГАХ И в-ГОМОЛОГИЯХ 411
[2 : 13]. Если о есть лебегово число замкнутого ^.-покрытия а.
компакта Ф, то всякий Ь-цикл компакта Ф будет 2г-гомо логичен
всякому своему каноническому сдвигу относительно покрытия а.
2:2. Случай полиэдра Ф —/Са. Пусть Ка есть триангуляция
полиэдра Ф; пусть К$ есть подразделение комплекса Ка] всякое
нормальное отображение *) si комплекса К$ на Ка есть, очевидно,
е-сдвиг, где е есть наибольшее из чисел 8(7af) для любого
симплекса Тл{£Ка.
В нашем случае для любого симплекса Т^ комплекса Ка все
вершины вщ, ..., е^ равно как и их образы ^/0 = ^^0» • • •»
eai = s\e^ лежат в Tah где Tai есть носитель симплекса Т^\
поэтому все симплексы вида \еа1- . . .ел^е^к. . .е^ | суть е-симплексы, и
всякая призма, натянутая на цепь х\ £ Lr (K$) и её нормальный
образ $£л£ £ Lr (/Q, есть е-цепь.
Отсюда следует:
[2:21]. Пусть Ка— триангуляция полиэдра Ф = /Св; пусть
з— максимум диаметров симплексов Ка; пусть К$—подразделение
комплекса Ка\ при нормальном отображении si комплекса К§ на
комплекс Ка всякий цикл г§ комплекса К§ переходит в z-гомоло-
гичный ему в Ф цикл S&l комплекса /Са.
Следствие. Пусть
суть последовательные барицентрические подразделения
триангуляции Ка полиэдра Ф; максимум диаметров симплексов Kah
стремится к нулю при возрастающем h. Пусть z\ — какой-либо цикл
комплекса К^ и пусть ггаЪ ггл1, ..., г^,... суть его
последовательные подразделения в комплексах /Са1, Ка2, ••-, Каы- • • Тогда
(2:21) z£) = (*«, zxU г.2, ..., *£»,...)
есть истинный цикл полиэдра Ф.
В самом деле, обозначая через &h максимум диаметров
симплексов Каъ, имеем, в силу наших предположений Итгп = 0, а в силу
П->со
[2:21] имеем
г
Za(h-{-k)~hZah-
Замечание. Если г^О в ifa, to г«^0 в Ф. В самом деле,
пусть ;ta+1 £//+1(/(л), Ахх+1=г«. Обозначим через х^1 подразде-
*) Глава 10, арт. 3 :1.

412
А-ГРУППЫ КОМПАКТОВ
[ГЛ. XI
ление цепи xl+1 в комплексе Kah- Тогда xlt1 есть гп — цепь, причём»
в силу теоремы [2:12] главы 10, \
^Kt1 = z\h,
что и требовалось доказать.
Следствие из предложения [2:21] даёт нам неограниченный
запас истинных циклов полиэдров; более того, истинными циклами
типа (2:21) можно ограничиться при изучении всех вопросов
гомологической теории полиэдров: мы докажем в § 4, что всякий
истинный цикл полиэдра гомологичен истинному
циклу, возникающему от последовательных
барицентрических подразделений некоторого
цикла произвольной триангуляции Ка данного
полиэдра.
Дадим в заключение настоящего параграфа
несколько примеров истинных циклов,
отличных от только что приведённых.
1°. Занумеруем все рациональные числа
интервала 0 < 0 .< 1 в последовательность ги
г2> • • » rh> • • •
Рассмотрим ориентированную окружность-
г1 и тор М1, происшедший от вращения
Черт. 132. окружности г1 вокруг не пересекающей её
оси /?/?', лежащей в её плоскости. Рассмотрим
теперь ориентированную окружность г]ь,
получившуюся от поворота окружности г1 вокруг оси рр' на угол 2rh~r
считая от начального положения окружности г1; окружность zlh
делится на 2Л+2(А=1, 2, 3,...) равных частей, которые
ориентируются согласно с выбранной ориентацией г1 окружности г1.
Полученный одномерный цикл обозначается через zh.
Тогда z1 = (z\, z\% ..., Zh,...) есть истинный цикл на торе JVPr
не гомологичный нулю на М2.
2°. Рассмотрим замкнутую кривую Ф1, изображённую на черт.
132 и состоящую из отрезка — 1<!У<^1 оси ординат, участка
кривой y = sin— для 0<%<; и какой-либо гладкой дуги,
соединяющей точки (0, —1) и (—, О J и не имеющей, кроме этих
двух точек, общих точек с множеством, состоящим из оси ординат
и кривой у = sin — , 0 < х ^ — .
Рассмотрим упорядоченную в круговом порядке против часовой
стрелки конечную последовательность точек Ф1:

§ 3]
ГОМОМОРФИЗМ ГРУПП Дг (Ф)
413
причём
p(****+i)<V
Эта последовательность определяет й^-цикл компакта Ф1. Строя
такие последовательности (отправляясь всё время от той же точки
^о=г=("^г» О J и идя против часовой стрелки) для 8ft -> О, получим
истинный цикл
Z1 = (г\, . . ., г\,. . .),
не гомологичный нулю в Ф1.
Группы А°(Ф1) и А^Ф1) суть бесконечные циклические группы;
группы АГ(Ф!) при г>1 суть нуль-группы; доказательство
предоставляем в качестве упражнения читателю. (Указание. При любом s
компакт Ф1 переводится s-сдвигом в замкнутый полигон без
кратных точек.)
При вращении чертежа вокруг некоторой не пересекающей Ф1
оси ррг кривая Ф1 образует кольцевидную поверхность Ф2. Истинный
цикл z1, построенный на кривой Ф!с:Ф2, не гомологичен нулю и на
Ф2. На Ф2 можно построить и истинный цикл, аналогичный
построенному в примере 1°. Группа А1(Ф2) есть свободная абелева группа
ранга 2, группы А2(Ф2) иА°(Ф2) суть бесконечные циклические группы;
руппы АГ(Ф2) при г>2 есть нуль-группы. Таким образом, группы
ДГ(Ф2) изоморфны группам Аг тора (той же размерности г).
Упражнение. Доказать, что для связного компакта
(континуума) Ф группа А°(Ф) есть бесконечная циклическая группа. Для
компакта Ф, состоящего из п компонент, группа Д°(Ф, 91) есть
прямая сумма п групп 21.
§ 3. Гомоморфизм групп АГ(Ф), порождённый непрерывным
отображением компакта.
3:1. Непрерывный образ истинного цикла. Пусть дано
непрерывное отображение С компакта X в компакт У; определяем для
каждого положительного числа г число
sc= sup р[С(х), С(х')]
(верхняя грань берётся по множеству всех пар точек х, хг
пространства X, для которых р(ху jc')<e).
При непрерывном отображении С всякий s-ociop пространства X
переходит в £С-остов пространства К, поэтому отображение С
порождает одноимённое симплициальное отображение комплекса Кх, г в
комплекс Ку,гС, которое в свою очередь порождает гомоморфное
отображение групп Lr(Kx,t) в Lr(Kr, ес).

414
А-ГРУППЫ КОМПАКТОВ
[ГЛ. XI
Это гомоморфное отображение щл также обозначаем через С;.
оно ставит в соответствие цепи
цепь
При этом (глава 7, 8 :3) гомоморфизм С, как порождённый симпли-
циальным отображением, коммутирует с граничным оператором А:
(3:1) ДСл^ — СД*',
откуда сразу следует, что при отображении С всякий s-цикл
компакта X переходит в з^-цикл компакта F, всякий s-цикл
компакта X, который s-гомологичен нулю в Х> переходит в вс-го-
мологичный нулю е#-цикл пространства К, всякие два в-гомоло-
гичных между собою е-цикла компакта X переходят в два е<;-
гомологичных между собою е^-цикла компакта Y. Так как
отображение С как непрерывное отображение компакта равномерно
непрерывно, то при s, стремящемся к нулю, стремится к нулю и е^. Из.
только что установленных фактов непосредственно вытекает: Если
(3:11) 2? = (zru 4, ..., **,...)
есть истинный цикл компакта X, то
(3:12) (с/и ей,..., с*;;,...)
есть истинный цикл компакта Y; истинный цикл (3 :12)
компакта Y мы обозначаем через Czr и называем образом
истинного цикла zr при непрерывном отображении С.
Полученное отображение С группы Zr(X) в группу Zr(Y}
является гомоморфным.
Из тех же соображений следует: Если zr~0 в А', то CV—О
в F. Таким образом, при гомоморфизме С группа Hr(X)^Zr(Xy
отображается в группу Hr(Y).
Отсюда следует (Прибавление I, арт. 1 :1), что гомоморфизм С
группы Zr(X) в группу Zr(Y) порождает одноимённый гомоморфизм*
группы Ьх{Х) в группу АГ(У).
Если С есть топологическое отображение компакта X на
компакт К, то гомоморфизм С есть изоморфное отображение
групп Zr(X) и Ьг(Х) соответственно на Zr(Y) и АГ(К).
Итак:
[3:1]. Гомеоморфные компакты имеют изоморфные Ьг-группы*
3:2. Из определения гомоморфизма С непосредственно следует
предложение:
[3 :2]. Пусть С\ есть непрерывное отображение компакта Ф1
на компакт Ф2, a Cl есть непрерывное отображение компакта
Ф2 на компакт Ф3.

§ 3]
гомоморфизм групп ДГ(Ф)
415
Тогда *)
(3:2) С\=С\С\
есть непрерывное отображение компакта Фг на Ф3 и формуле?
(3 :2) остаётся справедливой, если под С*, С|, Cl понимать
неданные непрерывные отображения, а порождённые этими
отображениями гомоморфизмы соответственно Д^Ф^ в АГ(Ф2), Д**(ф ),
в Д'(Фа), Ar(*i) * Д'(Ф3).
3:3. Гомологическая классификация отображений. Два
непрерывных отображения Q и С2 компакта X в компакт Y
называются (г, ЭД)-гомологичными между собою, если они порождают
один и тот же гомоморфизм С=С1 = С2 группы Ar(<Y, 51) в группу
ДГ(У, 51). Если отображения Сх и С2 оказываются (г,
^-гомологичными при данном г и всех 51 или при данном 51 и всех г, то они
называются соответственно r-гомологичными и 51-гомоло-
гичными между собою. Наконец, если отображения С1 и С2
оказываются (г, 51)-гомологичными между собою при всех
размерностях г и всех областях коэффициентов 51, то они называются
вполне гомологичными между собою. Очевидно, каждое из-
этих отношений удовлетворяет основным аксиомам равенства
(рефлексивности, симметрии и транзитивности); поэтому, объединяя в
u,5t)-, /"-, 51-классы все непрерывные отображения компакта X
в компакт К, являющиеся между собою (г, 51)-, г- или 51-гомо-
логичными, получим разбиение множества 2 всех непрерывных
отображений ^ в F соответственно в (г, 51)-, г-, 51-классы. Однако,
ещё более мелким и гораздо более важным подразделением
множества всех непрерывных отображений X в Y является
подразделение просто на гомологические классы, т. е. на классы вполне
гомологичных между собою отображений.
Теорема [3:3]. Гомотопные отображения вполне гомологичны
между собой.
Пусть С0 и С1—два гомотопных между собой непрерывных-
отображения компакта Ф в компакт Ф/. Для доказательства того,
что отображения С0 и Q вполне гомологичны между собой,
достаточно показать, что для любого истинного цикла
zr = (*i, *£,..., 4, ...)
компакта Ф истинные циклы C0zr и Схгг гомологичны между собой
в Ф'. А для этого, в свою очередь, достаточно убедиться в том,.
что для любого е>0 существует такое &е, что для произвольного
Переходим к доказательству этого последнего утверждения.
Пусть С6, 0-^6^1 есть какая-нибудь деформация отображения С&
*\ Глава 1. арт. 1 : 2.

416
Д-ГРУППЫ КОМПАКТОВ
[ГЛ. XI
в Сг Возьмём столь малое положительное число 6, чтобы из
р(р\ рг/)<ь в Ф и 1Ь/ — Ь"\<ъ следовало
(3:31) р(С6//, СиЛх-g-e в Ф'.
Выберем теперь столь большое k?J, чтоэы при &>£s цикл ггк
был о-циклом.
Возьмём &>£?i и занумеруем в каком-либо порядке все вершины
комплекса *) \гЪ\. Пусть это будут а15 ..., as. Обозначим через П7.
призму, построенную над комплексом остовов |<г£| (см. главу 4,
арт. 2:1). После этого разделим отрезок O^fi^l на равные
между собою отрезка
(0,0,), (6„62), ..., (68_х, 1)
длины, меньшей о; полагая 60 = 0, 6g=l, докажем для любого
/ = 0, 1, • • •, S — 1 соотношение
(3 : 33) С6,+1 г[. — Q. zr,~ 0 в /fo,,e .
Рассмотрим отображение S множества всех вершин av и Ь^
соответственно нижнего и верхнего оснований призмы П7. (см. главу
4, арт. 2 : 4), определённое 1ак:
{ 5(av) = Q.(av), v = 1. 2,
| S(b4) = Ci(+1(a4).
Из определения числа 6 (условие 3:31) легко выводим, что при
отображении 5 каждый остов комплекса ПА переходит в s-octob
компакта Ф', т. е. в некоторый остов комплекса Кф', е. Таким
образом, отображение 6" является симплициальным отображением
комплекса Ик в комплекс /£ф',е ; если мы обозначим через Лгк призму
над цепью ггк в комплексе ПА (см. главу 7, арт. 9 : 3), то при
симплициальном отображении S цепь Лг^ переходит в s-цепь
5Ш£, причём
Д5П4 = Се;+14 — Счггк.
Этим формула (3 : 33) доказана. Если написать гомологии (3 : 53)
для i —О, 1, ..., s—1 и сложить, то получится
С\гтк — С0г£~0 в Кф',г,
что и требовалось доказать.
3:4. Деформация непрерывного отображения истинного цикла.
Деформация истинного цикла. Мы только что доказали теорему:
*) См. главу 7, арт. 5:2, замечание 3.

§ 4] ОСНОВНАЯ ТЕОРЕМА О АГ-ГРУППАХ ПОЛИЭДРОВ 41?
[3:4]. Если С0 и Сг — гомотопные между собою отображения
компакта Ф в компакт Ф', а ъТ — истинный цикл компакта Ф,
то истинные циклы C0zr и Схгг гомологичны между собой в Ф\
К этому результату примыкают следующие понятия.
Определение [3:41]. Пусть даны: компакт Ф, замкнутое
множество ЧР^Ф, истинный цикл z компакта \Г, непрерывное
отображение С0 компакта W в некоторый компакт Ф' и деформация
Q, 0<С6 <; 1, этого отображения. Семейство истинных циклов CQ(z)
компакта Ф', упорядоченное по параметру 6, называется
деформацией отображения С0 истинного цикла z. В частности, если
Ч^Ф'и С0 есть тождественное отображение \Г в Ф', то деформация
отображения С0 истинного цикла z называется просто деформацией
истинного цикла z в компакте Ф\ Из теоремы [3:4]
следует
[3 : 42]. Всякий истинный цикл z компакта Ф переходит при
деформации в компакте Ф в цикл, гомологичный в Ф циклу z.
(Короче: никакая деформация истинного цикла z в Ф не выводит
этого цикла из его гомологического класса.)
§ 4. Основная теорема о Аг-группах полиэдров.
(Второе доказательство инвариантности А-и V-rpynn.)
4:1. Основная теорема [4:1]. Пусть К,,-— триангуляция
полиэдра Ф = /Са. Группа ДГ(Ф,ЭД) изоморфна группе &Г(КЮ 51).
Замечание. Из теоремы [4:1] следует теорема [1:35] главы
10 (общая теорема об инвариантности групп Бетти).
Переходим к доказательству теоремы [4 : 1]
Вместо Z* (Ф, 21), Иг (Ф, 21), А- (Ф, 21), Z' (К„ 21), № (К„ 21), A- (/fa, 2t)
пишем соответственно Z$>, ИФ, Аф, Z*, Я«> К] вместо Lr (Кф, 8, 2t)
и т. д. пишем L%,% и т. д.
4:2. Построение гомоморфизма Sf группы Аф в А£. Пусть а,
как всегда, есть барицентрическое покрытие полиэдра Ф,
сопряжённое триангуляции /С, этого полиэдра. Пусть 8 есть лебегово число
покрытия а. Обозначим через $t какой-нибудь канонический сдвиг *)
компакта Ф относительно покрытия а. Отображение st порождает
одноимённое симплициальное отображение комплекса /Сф, § в Ка и,
следовательно, гомоморфное отображение Sa группы Li,8 в L«,
коммутирующее с оператором А. Гомоморфизм vSa заключается
в том, что всякой о-цепи
(4:21) xr^cft
компакта Ф соответствует цепь
(4 : 22) S;V = 2 *<&&
*) Глава 10, арт. 5 : 3.
27 Александров П. С

418
А-ГРУШ1Ы КОМПАКТОВ
(гл. xt
при этом всякий 8-цикл zr переходит в цикл Sfzr£ Zra, всякий
8-гомологичный нулю 8-цикл zr переходит в цикл S azr,
гомологичный нулю в /Са, всякие два 8-гомологичных между собою
8-цикла переходят в гомологичные между собою циклы комплекса Ка.
Пусть дан истинный цикл
(4:23) z' = (4,4..., *», •••)
компакта Ф. Начиная с некоторого h, все z\ суть 8-циклы
8-гомологичные между собой; поэтому для всех достаточно
больших h все Sa Zh гомологичны между собой, т. е. принадлежат к
одному и тому же гомологическому классу j« £ Д£, которые мы
обозначим через Sabzr.
Ставя в соответствие каждому истинному циклу ъг компакта Ф
гомологический класс Sa lr £ Д£, получаем гомоморфное отображение St
группы Z% в группу Д«.
Так как при каноническом сдвиге S\ всякий о-цикл, 8-го-
мологичный нулю в Ф, переходит в цикл комплекса Ка,
гомологичный нулю в Ка, то образом истинного цикла, гомологичного нулю,
является при гомоморфизме sf нулевой элемент группы Д£. Отсюда
следует, что все гомологичные между собою истинные циклы
компакта Ф, в силу гомоморфизма St, переходят в один и тот же
элемент группы Д«.
Другими словами, канонический сдвиг порождает гомоморфное
отображение группы-Дф в группу Д«* Это отображение мы также
будем обозначать через S« •
4:3. Отображение 5«D есть отображение на всю группу Д««
Пусть $£ — произвольный элемент группы Д£ и zra какой-нибудь
цикл гомологического класса fx. Обозначим через К^ь й-кратное
барицентрическое подразделение комплекса /Са, через zrah—
подразделение цикла z\ в Kah. Канонический сдвиг Sa, применённый к
вершинам комплекса Ка]Ь, осуществляет нормальное симплициальное
отображение комплекса К^п на комплекс /Са, поэтому Sa zlh = z^)
другими словами, для истинного цикла zr = (zl,za'1 , ..., zW, .. .) и
его гомологического класса $ф£Дф имеем
сф_г г яф г г
Оа Z Zay Ool 5 Ь <уа >
чем наше утверждение доказано.
Переходим к последнему пункту доказательства.
4:4. Отображение sf группы Дф на Д« есть изоморфизм.
Это утверждение вытекает из следующего предложения:

§ 4J ОСНОВНАЯ ТЕОРЕМА О ДГ-ГРУППАХ ПОЛИЭДРОВ 41 §
[4 : 41]. Пусть дан истинный цикл
полиэдра Ф; если
Stzr~0 в Ка,
то zr~0 в Ф, т. е. для всякого е>0 имеется такое ke, что
при £>&е
40в7Ф.
Доказательство. Пусть 28а<е есть лебегово число
комплекса Ка; берём h так, чтобы Ка}1 было ^-комплексом, а
соответствующее барицентрическое покрытие 8а-покрытием.
Пусть 8а^<^а — лебегово число комплекса КлН; выбираем k% так,
чтобы при k^kz все zrk были 8а?1-циклами.
Пусть &;>&е.
Тогда (по [2:13])
(4:410) zlg^sthzl-
Так как Кап есть правильное подразделение триангуляции Ка, то,
в силу теоремы [2:35] главы 10, существует такой цикл zra
комплекса /Са, что
и, следовательно,
(4:411) z'~s*zr.
х ' к 25 ah <х
При каноническом сдвиге S® левая часть этой гомологии
переходит в S®zrki а правая в г£
Но по предположению Sfzrk ~ 0 в /fa, значит, и £*лг£~0 в /СаЛ. Так
как Kah есть 8а-комплекс, то
Значит, по (4:411)
s\zr~0 в Ф.
ah a e
47° в ф'
что и требовалось доказать.
4:5. Правила для нахождения образов при изоморфизмах S®
и (S^)*"1. Сформулируем ещё раз правила фактического осуществления
изоморфного отображения Sf группы Д^ на Д£ и обратного ему
изоморфизма (S®)-1 группы Д£ на Агф.
Первое правило. Дан элемент %ф группы Д^, требуется
найти соответствующий элемент ^ = ^^ф группы Д£. Для этого
берём произвольный истинный цикл гг из гомологического класса

420 Л-группы компактов [гл. х\
Зф и выбираем столь большое /г, чтобы^щге циклы zrk, k>hy были
о-циклами, 8-гомологичными между собою (8 — лебеговэ число
покрытия а). Канонический сдвиг Sf относительно а любого из циклов
2и> k>h есть цикл комплекса /Q, гомологический класс которого
и есть искомый элемент группы Д£.
Второе правило. Дан элемент f группы А£.
Требуется найти соответствующий элемент ^ф = (5ф)""^г группы
к-
Для этого берём произвольный цикл zr £ jr и его
последовательные барицентрические подразделения
zr zr zr
«Г «2,# ' •» а/г'
они образуют истинный цикл zr, гомологический класс которого
и есть искомый элемент группы Дф.
Замечание. В предыдущих рассуждениях содержится, в
частности, доказательство одного утверждения, сделанного в конце 2:2,
а именно:
Всякий истинный цикл
7r = (zr Zr ZT )
полиэдра Ф = /Ca гомологичен истинному циклу вида
где
Z\ £ ^i, a ZaV Z «2» ' * * ' *<*&' * * *
суть последовательные барицентрические подразделения цикла zr.
В самом деле, пусть, в силу канонического сдвига S®,
относительно а истинному циклу ъТ соответствует цикл zro. Тогда на
основании рассуждения 4:3 истинный цикл гг при том же
каноническом сдвиге переходит также в га.
Поэтому
Sj(z" — zp = 0,
а это, в силу 4:4, обозначает, что zr~zA в Ф, что и требовалось
доказать.
4:6. Циклы ^r6^a и гомология в Ф =/Са. Так как второе
правило артикула 4:5 осуществляет некоторое вполне определённое
изоморфное отображение группы Z£ в группу Z^, то мы вправе,
когда это оказывается удобным, отождествить любой цикл zr £ Z£
с истинным циклом
(4:61) *(в) = «,*.1,...,^,...),
состоящим из цикла zr^ и его последовательных барицентрических
подразделений. В частности, естественно говорить, что цикл zr £Z

§ 4] ОСНОВНАЯ ТЕОРЕМА О ДГ-ГРУППАХ ПОЛИЭДРОВ 421
гомологичен нулю, если z/\ гомологичен нулю в Ф. Точно так же,
можно говорить о том, что циклы z^Z^ и zra£Za гомологичны
между собою в Ф и т. д. ^
[4:6]. Если цикл zr%^2.r гомологичен нулю в полиэдре Ф = Д^,
то zrCHr.
а ^- а
В самом деле, пусть е — лебегово число комплекса Ка- Из наших
предположений следует существование такого натурального числа h
и такой е-цепи хг+1 в Ф, что Ajcr+1 = zr^. Канонический сдвиг от-
OLfl
носительно КЛ переводит jcr+1 в некоторую цепь д;/+1 £ L/+1, a z*h
в г/, причём Длг/+1 = г/, что и требовалось доказать.
Следствие [4:61]. Если два цикла zu£Za и z'a£Z^
гомологичны между собою в полиэдре Ф, то они гомологичны между
собою и в комплексе /Са.
4:7. Образ цикла <za£Z£ при непрерывном отображении С
полиэдра Ф = Ка в компакт Ф\ Непрерывные циклы, их
параметрические представления и деформации. Пусть дана
триангуляция КЛ и непрерывное отображение С полиэдра Ф = ^в компакт Ф'.
Соображения, изложенные в предыдущем артикуле, делают
естественными следующие определения:
[4:71]. О б р а зо м цикла za(^Zra при непрерывном
отображении С полиэдра Ф в компакт Ф' называется истинный цикл
z=C(za) = (Cz0i, CzaV...y СгаЬ...) (см. 3:1), где гв1,..., zaliy...
суть последовательные барицентрические подразделения цикла za.
[4:72]. Истинный цикл z компакта Ф' называется непрерывным
циклом компакта Ф', если его можно представить как
непрерывный образ некоторого цикла za£Zr
(4:7) г = {Сг„Сгл*...,Сг^...\
где Л'а — триангуляция, циклы га1,..., zak — последовательные
барицентрические подразделения za, а С—некоторое непрерывное
отображение полиэдра Кл в компакт Ф'. Само представление (4:7)
называется параметрическим представлением непрерывного
цикла z, (подробнее: представлением относительно Кл и С).
Всякая деформация непрерывного отображения С истинного цикла
(га> га\у • • • > г*к> • • •) полиэдра Ка называется деформацией данного
параметрического представления непрерывного цикла z (для
сокращения вместо этого иногда употребляется выражение
«параметрическая деформация непрерывного цикла z», являющееся, строго го-
воря, неправильным).
Два параметрических представления
^оЮ = (CqZ^ С0^а1,. . ., С0глк>. ..)
называются гомотопными между собою, если одно из них переходит
в другое непрерывной деформацией.

422
А-ГРУППЫ КОМПАКТОВ
[ГЛ. XI
Замечание. Во всех применениях этих определений в главе 16
компакт Ф/ является полиэдром.
4:8. Ориентируемость и ориентация замкнутых
псевдомногообразий. Из изоморфизма между группами Ате(Ф) и Ап(/Са)для всякого
полиэдра Ф и произвольной его триангуляции /Са сразу следует:
[4:81]. Если Ф есть я-мерное замкнутое псевдомногообразие, то
возможны лишь два случая: либо А^(Ф) = АП(Ф,J) есть бесконечная
циклическая группа, тогда все триангуляции Ка
псевдомногообразия Ф суть ориентируемые комбинаторные
псевдомногообразия, и Ф называется ориентируемым
псевдомногообразием, либо А^(Ф) есть нуль-группа, — тогда все /Са суть не-
ориентируемые комбинаторные нсевдомногообразия, и Ф называется
неориентируемым псевдомногообразием.
Если Ф — ориентируемое я-мерноезамкнутое псевдомногообразие,
то каждый из двух образующих элементов ±$ф группы А^(Ф)
называется ориентацией псевдомногообразия Ф.
Если К% есть какая-либо триангуляция ориентируемого
псевдомногообразия Ф, aztj^ суть две ориентации комбинаторного
псевдомногообразия К^ то ориентации %™ соответствует та
ориентация псевдомногообразия Ф= К^ которая содержит истинный цикл
(4:81) (*:,*",!..., *2*,...);
точно так же ориентации $£ псевдомногообразия Ф = К?
соответствует та ориентация $ комбинаторного псевдомногообразия К*>
которая удовлетворяет условию
п , п п п \ £■ п
Ха — \£а, z^•> • • • > ZaLk) • • • / vl о Ф'
Таким образом, ориентации псевдомногообразия Ф и любой его
триангуляции Ка взаимно однозначно соответствуют друг другу.
Всякий истинный цикл zn, содержащийся в данной ориентации j^
псевдомногообразия Ф, называется ориентирующим циклом
этого псевдомногообразия (подробнее: ориентирующим циклом,
определяющим данную ориентацию псевдомногообразия Ф).
Если дана какая-нибудь триангуляция К% псевдомногообразия Ф,
то каждая из двух ориентации ±$ комбинаторного псевдомногс-
образия Кп также часто называется ориентирующим циклом
псевдомногообразия Ф.
Замечание 1. Пусть дано непрерывное отображение С
ориентируемого замкнутого/f-мерного псевдомногообразия Ф; образом Ф
при этом отображении является некоторый компакт Ф'. При
отображении С каждая ориентация г™ псевдомногообразия Ф переходит
в некоторый элемент Ci% группы Ао(Ф'), называемой образом
этой ориентации при отображении С
Замечание 2.Иногда вместо выражений «ориентация* и
«ориентирующий цикл» данного псевдомногообразия говорят просто
«ориентированное псевдомногообразие:», разумея под этим данное псевдомного-

§ 4] ОСНОВНАЯ ТЕОРЕМА О ДГ-ГРУППАХ ПОЛИЭДРОВ 423
образие вместе с некоторой его ориентацией или вместе с
некоторым определённым ориентирующим циклом (чаще всего вместе с
некоторой ориентацией какой-либо триангуляции данного
псевдомногообразия). Особенно часто — в случае, когда данное
псевдомногообразие есть я-мерная сфера— употребляют в этом смысле термин
ориентированная сфера. Некоторая логическая нечёткость этой
терминологии обычно не приводит к недоразумениям.
4:9. Гомоморфизм С*, группы Д£==Дг(ХхДОв группу д£, =
= Аг(/С/Д), порождённый непрерывным отображением С®г
полиэдра Ф = Ка в полиэдр Ф' = Кг,. В силу установленного в
предыдущих артикулах изоморфизма между группами А^ и А^г с одной
стороны, и группами Д^, и Ыг — с другой, гомоморфизм Ср группы
А^ в группу Д^г, порождённый одноимённым непрерывным
отображением полиэдра Ф в полиэдр Ф' переходит в гомоморфизм группы Д£
в Д£/, который будем обозначать через С*/. Из 4:5 легко следуют
правила для построения этого гомоморфизма. Сформулируем их.
Пусть дан элемент %г группы Дг, требуется найти элемент
(4:90) С;,£ = 5:Г,С*;(5*)-Ув
группы Д^. При этом, помня как строятся отображения S®',
и (S^)-*1, и обозначая через КаП, как всегда, /z-кратное
барицентрическое подразделение комплекса /Са, а через s* изоморфное
отображение Дг наДг7р порождаемое подразделением (переходом от /Са
к Кл1ъ, — см. главу 10, арт.2 :1), мы можем пареписать (4:90) в
окончательном виде:
(4:9) C„«V = S*e,C*,^S/,
где h — достаточно большое натуральное числе (см. ниже).
Словесное выражение формулы (4: 9) таково:
[4:9]. Непрерывное отображение CJ, полиэдра Ф = Ка в
полиэдр Ф' = К'г следующим образом определяет гомоморфное
отображение С% группы Д[ в группу Д£,. Положим*) ч\' = у\(Ка,'г).
Выбираем столь малое 8>0, чтобы**) oc<yj/. После этого берём
столь большое h, чтобы симплексы комплекса К^г имели диаметры
меньшие, чем о.
Пусть теперь дан произвольный элемент $£ группы Д£. В
гомологическом классе уберём произвольный цикл zr и рассматриваем
его подразделение zrah===zS«nZr в к^ш Цикл С%, zJb есть ч{-цикл
полиэдра Ф'; канонический сдвиг 5J' цикла C*,zJ относительно
*) См. главу 10, арт. 5:4.
**) Определение числа ос см. в арт. 3:1.

424 А-группы компактов [гл.. ad
К/, есть циклг1^, комплекса Когомологическийклассцикла zra, а еспа^
искомый элемент С\, ъга группы Д£,. A
В случае, когда CJ, есть топологическое отображение полиэдра;
Ф = Ка на гомеоморфный ему полиэдр Ф' = К[п отображение С*/
есть изоморфное отображение группы Д£ на группу Д£,; наконец^,
если Ф = Ф' и С®, есть тождественное отображение, то отображение
С*„ приобретающее в этом случае вид
(4:9) Cafzr—S%sil1 zr ,
превращается в изоморфное отображение группы А£ на группу Д£,,
где Ка и /С' суть две (вообще говоря, кривые) триангуляции
полиэдра Ф.
§ 5. Симплициальные приближения непрерывных
отображений полиэдра в полиэдр.
5:1. Определение симплициального приближения
непрерывного отображения С|, полиэдра Ф==Ка в полиэдр Ф' ===== К[,.
Пусть т)' = 7j(/Са/). Возьмём такое 8>0, чтоб!л *) 8(7<т]/ и столь
мелкое подразделение Kah комплекса Кя, чтобы симплексы
комплекса Kah имели диаметры < 8. Соображение С переводит всякий
8-остов, лежащий в полиэдре Ф, в tj'-остов, лежащий в полиэдре Ф/;
поэтому, если обозначить через Sf/ канонический сдвиг полиэдра Ф'
относительно покрытия а', то отображение Sf/ CJ,, рассматриваемое
на множестве вершин комплекса Ка1п порождает симплициальное
отображение
оф' г^Ф с all
*V ^Ф' °а'
комплекса Kah в комплекс K[f.
Симплициальное отображение S°Jl комплекса К^п в комплекс К'а,,
а также порождаемое им симплициальное отображение S^1 полиэдра
ф = Kah в полиэдр Ф' = К', называется симплициальным
(ah, а')-пр и б л и жен и е м непрерывного отображения CJ,.
Последовательное осуществление гомоморфного отображения s*h
(оператор подразделения) группы Z/ в группу L*h и гомоморфизма
5£? порождённого симплициальным отображением S$l комплекса Kah
в К'лП производит гомоморфизм S°jls*h группы DI в группу //„
записывающийся так:
(5:П) 5?^< = ^/C*/S«ft^
для любого zr£Lr.
Oi ^~ ОС
*) Арт. 3:1.

§ 5] СИМПЛИЦИАЛЬНЫЕ ПРИБЛИЖЕН Я НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ 425
Так как гомоморфизм S^ s«h коммутирует с оператором А, то
он порождает одноимённый гомоморфизм 5"?$£л группы Д£ в Д^:
Сравнивая (5:12) с (4:9), заключаем:
(5' \) С* гг = Sah 9a гг
т. е.:
[5: 1]. Гомоморфизм группы Д£в группу Д£„ порождаемый
непрерывным отображением полиэдра Ф = АГа в полиэдр Ф'= /(£,, #о
лучается, если взять достаточно мелкое подразделение К^
комплекса Ка и воздействовать на элементы группы Д£ сначала
оператором подразделения s*h, а затем каким-либо симплициаль-
ным (cah, af^приближением непрерывного отображения С.
5:2. Основное свойство отображения S^1.
Теорема [5:21]. Непрерывное симплициальное отображение
S*£ полиэдра Ф = Ка = КиП в полиэдр Ф' = К', гомотопно
непрерывному отображению CJ,.
Лемма [5:210]. Пусть даны два непрерывных отображения С0
и Сг компакта Ф в полиэдр Ф' = /С£, обладающих следующим
свойством', какова бы ни была точка х£Ф, обе точки С0х и Сгх
принадлежат замыканию некоторого симплекса триангуляции K'v-
Тогда отображения С0 и Сг гомотопны между собой.
Доказательство леммы. Полиэдр Ф' лежит в некотором
Rv. Всякий замкнутый симплекс есть выпуклое множество, поэтому
из наших условий следует, что, какова бы ни была точка х£Ф,
прямолинейный отрезок С0х Схх, соединяющий точки С0х и Сгх
в f>ny целиком лежит в Ф'. Для каждого значения О, О<0<1, обо_
значим через Сьх точку отрезка С0х Сгх, делящую этот отрезок,
направленный о г С0х к Схх, в отношении 6:(1—0). Полученная
деформация С§х переводит отображение С0 в Cv чем лемма
доказана.
Переходим теперь к доказательству теоремы [5:21]. На основании
леммы для доказательства [5:21] достаточно обнаружить, что для
всякой точки р £ Ф (обозначения теоремы [5:21]) носитель точки
Ъ*£р в комплексе Krf есть собственная или несобственная грань
носителя точки С®,р.
Пусть р€ТаЪ€КлЪ и Tah^\a^...ar\. Пусть С*,р£ 7/, £/С/, ;
так как диаметр множества Cj, Tah меньше ч\' и СJ, Tah заведомо
имеет с Г£, общую точку С £,/7, то всё множество CJ, ТаП лежит

426
А-ГРУППЫ КОМПАКТОВ
[ГЛ. XI
в соединении элементов покрытия *) а', имеющих центрами вершины
Т' п и не пересекается с остальными элементами покрытия а\
Поэтому все S®/ С*, а0 = a'Q, . . .,S*/ CJ, аг = д£ суть вершины
симплекса 7^„ и, следовательно, симплекс
есть собственная или несобственная грань симплекса Т'п что и
требовалось доказать. Итак:
[5:2]. Непрерывное отображение полиэдра Ф в полиэдр Ф'
гомотопно и, следовательно, гомологично всякому своему симпли-
циалъному приближению.
Из того, что носитель точки S^p в Krr есть грань носителя
точки С®,р в том же комплексе, следует:
[5:22]. Если диаметры всех симплексов комплекса Кг, меньше
данного е > 0, то для любой точки р £ Ф
P(Clp,S^p)<e.
Взяв симплициальное разбиение К ', полиэдра Ф' достаточно
мелким, заключаем из [5:22]:
[5:23]. Пусть дано непрерывное отображение С полиэдра Ф = Ка
в полиэдр Ф'. Каково бы ни было е>0, существует такое
симплициальное приближение S^f отображения С (являющееся сим-
плициальным отображением некоторого подразделения Кап) комплекса
Кь в некоторую достаточно мелкую триангуляцию К', полиэдра
Ф', что для всякой точки р £ ф'
P(Cp,S$p)<a.
§ 6. Степень непрерывного отображения
замкнутых псевдомногообразий.
Во всём этом параграфе Ф и Ф' суть замкнутые я-мерные
псевдомногообразия, которые везде предполагаются ориентируемыми. С
обозначает непрерывное отображение псевдомногообразия Ф в
псевдомногообразие Ф'; Ка и Krr суть произвольные триангуляции
соответственно Ф и Ф'.
6:1. Определение степени. Выберем определённые ориентации
%ф и it>/ псевдомногообразий Ф и Ф'. Тогда группа А™ состоит
из элементов т $ф, а группа А™, из элементов т $ф/, где т — про-
*) с/, как всегда барицентрическое покрытие, сопряжённое
триангуляции K'af

§ б] СТЕПЕНЬ НЕПРЕРЫВНОГО ОТОБРАЖЕНИЯ '' 427
извольное целое число. В силу порождённого непрерывным отобра-
жением С гомоморфизма С группы А^ в группу А£,, имеем
где f есть некоторое целое число, называемое степенью
непрерывного отображения С.
Замечание. Число f вполне определено, если даны
отображение С и, кроме того, ориентации псевдомногообразий Ф и Ф';
замена какой-либо из этих ориентации на противоположную влечёт
за собой перемену знака числа -[•
6:2. Определение степени непрерывного отображения я-мер-
ного цикла в я-мерное ориентируемое псевдомногообразие.
Непосредственным обобщением определения [6:1] является следующее
понятие.
Пусть дано непрерывное отображение С компакта Ф в я-мерное
замкнутое ориентируемое псевдомногообразие Ф'. Пусть выбрана
определённая ориентация $ф, псевдомногообразия Ф', т. е.
определённая образующая бесконечной циклической группы AJ,; пусть,
наконец, дан истинный я-мерный цикл ъп в компакте Ф; при
отображении С истинный цикл г4 переходит в истинный цикл Съп
псевдомногообразия Ф', лежащий в некотором гомологическом классе
V 5ф/6^ф/1 целое число f называется степенью отображения
истинного цикла гп в псевдомногообразие Ф'.
В большинстве применений этого определения компакт Ф будет
полиэдром; истинный цикл ъп будет в смысле определения [4:6]
циклом некоторой триангуляции полиэдра Ф и, следовательно, Съп —
непрерывным циклом.
6:3. Вычисление степени отображения. При посредстве
изоморфизма Sf образующая j группы А™ переходит в образующую
ы=г™ циклической группы A™ = Z™, причём всегда можно выбрать
ориентации t\ «-мерных симплексов комплекса Ка так, чтобы
zn = yitn..
a J-J он
Точно так же можно выбрать ориентации t%,. «-мерных
симплексов комплекса К'а' так, чтобы для выбранной ориентации $ф,
псевдомногообразия Ф' было
СФ' -. ! .уП Wn
°«/ 5 ф/ — 5«/ — "V 2u «'Г
i
В этих условиях циклы
Z(a') = \z™/> Z^r\ » • • • » Z'^U1 ' ' !)

428
Д-ГРУППЫ КОМПАКТОВ
гл. XI
принадлежат соответственно к гомологическим классам $ф и $' / ,и
мы имеем
Далее, (б4^)-1^ = £Ф; но £ф есть гомологический класс истин*
ного цикла zy = (г*, гД ,.. .,^,...), переходящий, в силу С*"
гомологический класс истинного цикла
Этот последний гомологический класс, в силу канонического
сдвига Sf,'9 переходит в класс, содержащий ^z f = yz™. Итак,
S%C%f{s\)-lz^==^f, т. е на основании (4:90)
Сагп = чгп.
a a ' a
Итак:
[6:31]. Если Сф/ есть непрерывное отображение ориентиров
ванного псевдомногообразия Ф в ориентированное псевд о
многообразие Ф', то гомоморфизм С*, группы Д£ в группу Д£, и
гомоморфизм (У, группы Д^2 в группу Д£,, порождённый непрерывным
отображением С, определены соответственно формулами
(6:31)2, С*> = Т8ф/,
где
у« V^ /w ^w — "XT' /и
^a = Jj a*> a' Jj V*
г г
суть ориентации КЛ и К',, соответствующие ориентациям $ф а
;$ф/, а т ^/W6 степень непрерывного отображения С^,.
Замечание 1. Мы приняли .равенство (6 :31)J, за определение
числа •[> т. е. степени отображения С; мы теперь видим, что с
таким же успехом за определение числа у можно принять и равенство
(6:31)J.
Можно сказать также:
[6 :32]. Пусть Кг и К[, суть произвольные триангуляции Ф и
Ф', IQh есть достаточно мелкое подразделение триангуляции Ка,
a S*? есть (ah, а')—симплициалъное приближение непрерывного
отображения С|,.
Если ориентации Ка и Ф, а также К', и Фг соответствуют
друг другуу то степень непрерывного отображения CJ,, равна
степени симплициального отображения S*?.
Замечание 2. Теорема [6 :32] является частным случаем
теоремы [5 :2]. Я предпочёл, однако, заново доказать здесь теорему [6 :32]>

§ б] СТЕПЕНЬ НЕПРЕРЫВНОГО ОТОБРАЖЕНИЯ 429
чтобы лишний раз продемонстрировать, как пользуются при изучении
непрерывных отображений их симплициальными приближениями.
6:4. Основные свойства степени отображения. Из самого
определения степени следует:
[6:41]. Два (я, J)-zomoлогичных, значит, и подавно два вполне
гомологичных и, тем более, два гомотопных между собой
отображения одного замкнутого ориентированного
псевдомногообразия в другое имеют ту же степень.
Замечание: случай п— 1. Применяя замечание 3 главы 8,
арт. 5: 2, без труда убеждаемся в том, что определённое в главе 2,
арт. 2 :5, «нормальное отображение степени р одной
ориентированной окружности в другую действительно имеет степень ^. Так
как ни степень, определённая в главе 2, арт. 2 :5, ни степень,
определённая в настоящей главе, не меняются при переходе от
данного отображения к отображению, гомотопному ему, и так как
всякое отображение одной окружности в другую гомотопно некоторому
нормальному отображению, то степень любого непрерывного
отображения одной ориентированной окружности в другую,
определённая в настоящей главе, равна степени того же отображения,
определённой в главе 2, арт. 2:5.
Вернёмся снова к общему случаю двух л-мерных замкнутых
ориентируемых псевдомногообразий Ф и Ф'. Существуют лишь два изоморфных
отображения бесконечной циклической группы -А^ на бесконечную
циклическую группу Д£,: изоморфизм, переводящий j^ в $£„ и
изоморфизм, переводящий jj в — jj, (при этом j£ и g*,, суть
определённые ориентации Ф и Ф').
Поэтому:
[6:42]. Степень топологического отображения
псевдомногообразия Ф на псевдомногообразие Ф' равна 1 или —1.
[6:43]. Пусть дано непрерывное отображение С* замкнутого
ориентированного псевдомногообразия Фх в замкнутое
ориентированное псевдомногообразие Ф2 и непрерывное отображение С\
псевдомногообразия Ф2 в Ф3; тогда отображение С\-=С\С\
псевдомногообразия Фг в Ф3 имеет степень, равную произведению степеней
отображений С\ и С|.
В самом деле, пусть j1? j2 и $3 СУТЬ соответствующие
ориентации псевдомногообразий Фи Ф2, Ф3.
Пусть отображения С* и С| имеют соответственные степени -fi
и y2. Тогда
q (с,1 &)) = с* (Tl8a) = тле; (ы) = ььь
что и требовалось доказать.

430
Д-ГРУППЫ КОМПАКТОВ
[гл. хг
[6: 44]. Если С(Ф) с Ф', т. е. если С(Ф) ф Ф', то степень
отображения С равна нулю.
В самом деле, пусть р' есть точка Ф', не принадлежащая С(Ф);
пусть s = р(/?',С(Ф)). Возьмём столь мелкую триангуляцию К'п
чтобы симплексы комплекса К'Л, были по диаметру меньше е, и пусть
К',0 есть комбинаторное замыкание комплекса, состоящего из всех
симплексов комплекса К*'* содержащих хоть одну точку
множества С(Ф). Очевидно, К[,0 есть собственный подкомплекс
комплекса К^п так что группа Д^(А^,0), а следовательно, и группа
кп(Ка'<) есть нуль-группа. Отображение С
псевдомногообразия ф в ф' отображает Ф в полиэдр К^0\ поэтому для всякого
истинного цикла zw£ZJ цикл С(гп) гомологичен нулю в /£,0,
следовательно, и подавно в Ф'; другими словами, для любого g£A£
оказывается, что С($) есть нулевой элемент группы AJ„ что и
означает 7 —0«
Примеры непрерывных отображений различных степеней
даны в следующей главе, арт. 5:6; этот артикул может быть
прочитан уже сейчас.

ГЛАВА ДВЕНАДЦАТАЯ.
ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ.
Во всей этой главе Ф обозначает компакт, Г — открытое
множество в компакте Ф, W = Ф\Г.
§ 1. Комплекс /Сг,е.
1 :1. Определение Кт,г и основные обозначения. Через АГг.е
или подробнее /Сф,г\е мы обозначаем комплекс Кф,е\К,ч?е.
Другими словами, симплексами (остовами) комплекса Ат\в
являются все те и только те s-симплексы компакта Ф, у которых
хотя бы одна вершина принадлежит множеству Г.
Так как Кт,е = Кф,е \Я>г, е, и /Смг,е есть полный, следовательно,
замкнутый, подкомплекс комплекса /Сф,е, то /Сг,е есть откры-
тый подкомплекс полного симплициального
комплекса Кф, е-
Замечание. Обозначением Кф,г,г мы будем пользоваться
очень .редко, в случаях, когда наряду с компактом Ф имеется ещё
какой-нибудь другой компакт, также содержащий Г в качестве
открытого множества. Важнейший из этих случаев — это тот, когда
из двух данных компактов один является подмножеством другого.
Итак, пусть ГсФ0сФ, где Ф0 замкнуто, а Г открыто в компакте Ф.
Тогда каждый остов комплекса /Сф0д> является, как легко видеть,
остовом комплекса /Сфд>, т. е.
(обратное включение, вообще говоря, не имеет места: в Кф,г,г
могут быть не принадлежащие комплексу /Сф0,г,е остовы, а именно,
все остовы комплекса /Сф,е, которые имеют, по крайней мере, одну
вершину, принадлежащую к Г, и, по крайней мере, одну вершину,
принадлежащую к Ф\Ф0).
Установим далее следующие обозначения. Вместо 1г(Кф, е, 91),
£Г(/СФ,ЕД) и т. д. будем писать L%^ Z£e и т. д.
Вместо Z/(Xr,E, 9t), Zr(ATr,, ,91) и 'т. д. ' будем писать If , ZrVfi
и т. д.
Наконец, вместо Д#ф гхг пишем просто Длг, а вместо Д#г в хг
пишем Дгл:** (первое из этих двух соглашений относится к любой цепи
хГ £ Ш> в» а второе к любой цепи хГ £ L£ f).

432 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [гл. Xlt
1 :2. Циклы и гомологии в /Сг> Так как Ат,е есть открытый
подкомплекс комплекса Лф, Е, то на основании теоремы [6:51]
главы 7 имеем для любой цепи хг £ LJ
(1 :20) Аг /Сг, в *г = Яг, г &хг;
в частности, для любой цепи xr ^Lrv g
(1 :200) Аг^ = АГг,вАл:^.
Отсюда легко следует:
[1 :21]. Если хг£Ьгф е, то Кг,*хг тогда и только тогда есть
цикл комплекса Кг,е, когда Дл;г£ Z^f"1. В частности, если д;г£1£б)
то тогда и только тогда xr £ ZFe, когда &xr£ Z^T-1.
Из той же формулы (1 :20) легко вытекает:
[1:22]. Если jcr£Z,^s, то тогда и только тогда
(1:220) Яг,.*''~0 в /Civ,
когда существует такая цепь л;г+1 £ LJJ+1, что
(1:221) А*"*1—л^^..
В самом деле, если (1:220) выполнено, то существует такая цепь
xr+1^Lpi\ что
кгхг^ = Кг,*хг;
НО JCr + 1 = Ат,е-Х;Н \ ПОЭТОМУ
Аг х^1 = Аг КГл x>'J 1 = /<г,е А *' ' 1,
т.е. Кг,*хг = Кг,г^хг^, или
/Сг..(Да:г11 — *г) = °
и, значит,
(1:221) AJCr+i_^r^Lr _
Если наоборот (1:221) выполнено, то
КгА^х^1 — х') = 0,
т. е.
Кг,ехг = Кг,* А х^1 = Аг /fr,.*'*1 ,
значит,
Кт,е Г-ОВ /Сг,. .
В частном случае, когда xr^Zrvo имеем:
[1:221]. Цикл zr£ZVe тогда и только тогда гомологичен нулю
в Kr,s> когда существует цепь *г+1(:£фе> удовлетворяющая условию

§ 1]
КОМПЛЕКС /Сг,,
433
Пример. Пусть Ф—квадрат, Г — его внутренность, ч7—его
граница, К—указанная на черт. 133 триангуляция квадрата, о которой
мы предполагаем, что все её элементы по диаметру меньше данного
е. Ориентированные против часовой стрелки треугольники этой
триангуляции пусть будут
ч>-
л
32 '
причём мы предполагаем, что 11\ |,.. . ,| t\b | суть треугольники, лежащие
поверх средней линии квадрата. Ориентированные одномерные
симплексы *J,...,*£a указаны на чертеже. Положим
32 16 VL
1=1
тогда
*» = 2tf, ^-'i+'i+'S-Hi. / = 23.
/=l
j=i
Далее, л:1 £ Яг1,в. В самом деле,
где
J1 £ £*,«•
1:3. (е, чТ)-сдвиги.
Определение [1:31]. Назовём (е,?)-сдвигом компакта Ф
всякое его отображение 8Ф в себя, удовлетворяющее следующим двум
условиям:
1°. Для любой точки х£Ф имеем р(х, £фл;)<е.
2°. Для любой точки л;£ч7 = Ф\Г имеем 5флг£\Р.
Пусть 8 и а — произвольные положительные числа. При всяком
(е,ЧГ)-сдвиге происходит симплициальное отображение комплексов Кф,%
и Kw,b соответственно в /Co,s + 2e и Лш,о -Н2« (см. главу 10, арт.
5:2), и поэтому порождаются
гомоморфизмы 5Ф , SXrnSV = /fr,8+2t $Ф ГРУПП
1ф,п (глава 7, арт. 8:2 и 8:4), lis
и Z^5 соответственно в Ьгф>5+2е, Z,^+2e
т 54-2в • ^ас здесь интересует третий
из этих гомоморфизмов Sr. Если хг
«сть произвольная цепь комплекса Кг,ь
то
1 / i /
1 '
/
V,/
/
/
••■■А
. . .... _™,
/
/>
V
Srxr==%"jS%v
Черт. 133.
где в линейной форме 2%^Ф/!/5 сохраняются лишь члены я^5ф/Г5, в
которых 5Ф^8 суть ориентированные r-мерные симплексы комплекса
2-8 Александров Ы. С.

434 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ„ ХЩ
Кг,ь+2е- Гомоморфизм Sv коммутирует с оператором Аг: для любого
хг^Ь[л ь имеем (см. главу 7, арт. 8:4)
Srkrxr = Аг6тд:г.
Теорема [1:32]. Для любого цикла zr комплекса Кт,ъ и ег&
(e,Wycdeuza S® имеем
zr~sr*r в Кгм-^1
Доказательство совершенно аналогично доказательству тео^
ремы [2: 12] главы 11. f
Проведём его. Берём вновь призму Щг, натянутую на zr и на S®zr
(см. главу 11, арт. 2:1); её симплексы (т. е. симплексы, на которых цепь
Uzr принимает значения, отличные от нуля) по диаметру меньше, чем
о + 2з (см. главу 11, арт. 2: 1); значит, Шг££^+1. На основании
формулы (2:12) главы 11 имеем
MLzr = zr — S®zr — ПА**-,
где ПАгг есть призма, натянутая на Агг и 5фАгг = 5*гАгу. Так
как Ukzr лежит на Кф,ъ+?ш, то, в силу [1:22],
zr — S;zr~0 в Кг,ь+2*,
что и требовалось доказать.
1:4. Канонические сдвиги. Пусть а = {Л1У. .. ,Л8} — какое-либо
замкнутое е-покрытие компакта Ф; пусть элементы покрытия, пересе-;
кающиеся с W, суть А19...,Аи; тогда множества W Г1 Аи. . . ,\Г П Аи
образуют покрытие Wa компакта №с=ф. Нерв покрытия а, как всегда,
обозначаем через КаУ его вершины через a1,...,as, причём ai и А^
соответствуют друг другу. При этих обозначениях аи . . .,аи суть вер-^
шины нерва /Gf,« покрытия Wa. Комплекс Kwj3 ^сть подкомплекс ком^
плекса Ка\ вершины ai0,. . ,,airкомплекса /Смгв тогда и только тогда;
определяют симплекс в /<Va, когда
w п л,0 п ... п л^о.
Группы 1'(/ев1ЗП, Z/ (#чг«Д), Lr(Ka\Kwa, 31) и т. д. обозначав!!
соответственно через Z/, L^a, Ipa и т. д.
При каноническом сдвиге S® компакта Ф относительно а каждой
точке р £ Ф соответствует вершина я^ комплекса /Са, каждой точке
р £ \F соответствует при этом вершина aiy. комплекса /С^а.
Пусть теперь 8 настолько мало, что является одновременно
лебеговым числом обоих покрытий а и *Fa. В силу канонического сдвига
5Ф, каждый о-остов компакта Ф переходит, как мы знаем, в
некоторый остов комплекса Ка; при этом всякий 8-остов \е0...ег\, при-*
надлежащий к ХУ\ переходит в остов комплекса АЯга- В самом деле,

§ 2] Г-циклы и Г-гомологии компакта Ф 435
для каждого ер у = 0, ...,г точка S®ej есть некоторое а^.,
выбранное под условием, что е3-£А{.; так как все ej содержатся в W, то
множества W П Aio,. . . Д П Aif все пересекаются с множеством,
состоящим из точек е0,...,ег и имеющим диаметр <8. Так как 8
есть лебегово число покрытия *Fa, то множества W ПЛ<0,...,ЧГ П Aif
имеют непустое пересечение, а это и значит, что aiQ,. . .,air образуют
остов в Кч« •
Из доказанного следует:
[1:41]. Пусть а = {Av. . .,Л8} есть замкнутое е-покрытие
компакта Ф; пусть среди множеств Aj пересекаются с ¥с=Ф множества
4lf...,Att; тогда W П AU...,W П Лад образуют покрытие Wa
множества W, нерв которого Къа есть подкомплекс нерва Ка покрытия ос.
Если 8 есть одновременно лебегово число покрытий а и Wot, то
канонический сдвиг Sf компакта Ф относительно а производит вместе
с тем канонический сдвиг компакта W относительно \Га и порождает,
следовательно, гомоморфизмы SJ, S^a и S£ =(/Са\/Счга) 5* групп
^ф,з» ^чг,8' ^г,« соответственно в Z/, 1^а и LJ, .
Эти гомоморфизмы коммутируют *) с соответствующими
граничными операторами:
если хг £ 1/ф 5, или xr £ Z,^ 5, или xr £ Lr,8, то соответственно
§2. Г-циклы (относительные циклы) и Г-гомологии кокпак^аФ;
группы г^(ГД),/^1Г,Я),А^(ГЯ).
2:1. Определения.
Определение [2:11]. Последовательность
(2:11) Z'= (*;,*£,...,*£,...),
гле ^A-G-^rs и Нт8.==0, называется r-мерным Г-ц и к л о м компак-
та Ф, если для каждого е > 0 найдётся такое ka> что для любых двух
натуральных чисел р>&е и q>k9 имеем
*) О гомоморфизме (K*\KWo) £ф см. главу 7, арт. 8 :4 (там
аналогичный гомоморфизм обозначен через GaSl).
28*
(1:41)

436 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ4 Xlff |
Пример. Пусть Ф — квадрат, Г — его внутренность, W — его
граница. Пусть К—какая-нибудь триангуляция квадрата Ф и /Счесть
л-кратное барицентрическое подразделение комплекса К- Пусть
t*v. . -J2 n — ориентированные одинаковым образом (например, против
часовой стрелки) треугольники комплекса Кп и 2гп = ^2пГ Тогда *;
Zr = 0£,.. . ,<г^,. . .) есть Г-цикл компакта Ф. '
Замечание 1. В этой главе, так же, как и в предыдущей, мы
рассматриваем всегда цепи как линейные формы и помним, что две
хотя бы и различных комплексов К и К\ считаются
тождественными, если они совпадают как линейные формы (т. е. если каждый .
симплекс, входящий с отличным от нуля коэффициентом в одну цепь,
входит с тем же коэффициентом и в другую цепь, из чего следует, ;
что симплексы, входящие с отличными от нуля коэффициентами в {
какую-либ данных цепей, являются симплексами обоих
комплексов /Си \ Только другим выражением этого же соглашения о
равенстве цепей является утверждение, что всякая цепь хг какого-
либо комплекса К является цепью и всякого другого комплекса К\
содержащего все симплексы, входящие в цепь хг с отличными от нуля
коэффициентами.
В соответствии с этим мы говорим, что Г-цикл
z = (z^ z^.. . ,2^,...)
компакта Ф ен Г-циклу
7гг — (z'r z'r z'r \
компакта Ф', если для каждого k
Мы говорим также, что
является оановременно Г-циклом компакта Ф и Г'-циклом компакта
Ф', если ггк есть цепь как комплекса Кг,цу так и комплекса КГьк и
если при любом е>0 для всех достаточно больших р и q
выполнено как условие zr ~ zr в /Сг,е, так и условие zrp—■ zrq в Аг/,е.
Пример. Пусть Ф и Ф'—два конгруентных квадрата,
лежащих в трёхмерном пространстве во взаимно перпендикулярных
плоскостях и имеющих общую диагональ Ф0. Обозначим через Г и Г
внутренность, а через W и W — границу соответственно Ф и
Ф'; через ч70 обозначим множество, состоящее из двух концевых
точек общей диагонали Ф0 обоих квадратов.
Положим, наконец, Г0 = Ф0\^го-
Пусть К—комплекс, элементами которого являются: общая
диагональ обоих квадратов и оба её конца. Пусть Кп есть м-кратное

2] Г-циклы и Г-гомологии компакта Ф 437
барицентрическое подразделение комплекса К (т. е. подразделение
диагонали К на 2п равных отрезков). Возьмём на диагонали Ф0
определённое направление и обозначим через txnV ..., t^n
ориентированные в этом направлении отрезки комплекса /О Положим
4=1
Тогда z1 есть одновременно Г-цикл компакта Ф, Г-цикл компакта-
Ф' и Г0-цикл компакта Ф0.
Отметим особо един частный случай только что сделанного
замечания:
[2:10]. Если компакт Ф0 есть замкнутое подмножество компакта
ф и ?0сф0, Г0 = Ф0\ч70, Г = Ф\ч70, то всякий Г0-цикл компакта
Ф0 является вместе с тем и Г-циклом компакта Ф.
Замечание 2. Если нет необходимости указывать то
множество Г, по которому берётся данный Г-цикл, или если это Г является
переменным (например, когда говорится о существовании некоторого
Г-цикла компакта Ф, обладающего такими-то свойствами), то термин
Г-цикл предпочитают заменять термином «относительный цикл*)»; итак,
7Г = (Zr Zr Zr }
есть относительный цикл компакта Ф, если в Ф существует
такое открытое множество Г, что гг есть Т-Цикл компакта Ф.
Определение [2:110]. Пусть Z** есть относительный цикл
компакта Ф. Всякое замкнутое подмножество Ф0 компакта Ф,
обладающее тем свойством, что гг является относительным циклом
компакта Ф0, называется носителем относительного цикла zr в
компакте Ф.
Итак, если ъг есть Г-цикл компакта Ф, а Ф0с=Ф— какой-нибудь
носитель zr, то существует такое замкнутое множество \Г0сФ0, что
гг есть (Ф0\|Г0)-цикл компакта Ф0.
Определение [2:12]. Г-цикл компакта Ф называется Г-го-
мологичным нулю в Ф:
zr~Q в Ф,
г
если для каждого s>0 существует такое kt, что для всех k>kt:
г^г0 в Кт,*.
**) Понятие относительного цикла во всём разнообразии его конкретных
осуществлений (как комбинаторных, так и теоретико-множественных)
впервые введено Лефшецом (S. Lefschetz). Это понятие оказало большое
влияние на происшедшее в последние два десятилетия развитие комбинаторно-
топологического аппарата и сделало возможным открытие ряда новых
топологических фактов, которые без понятия относительного цикла нельзя было
бы даже сформулировать.

438 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
Пример. Пусть снова Ф — квадрат, Г — его внутренность,
Пусть п — натуральное число и t^v t^v ..., txn2n — отрезки,
полученные от деления ориентированной диагонали квадрата на 2п
равных частей. Положим г1 = V/* Тогда
i
Z = (Z^ Z^ . . . , Z^ . . . )
есть одномерный Г-цикл квадрата Ф, Г-гомологичный нулю в Ф.
Замечание 3. Пусть Ф0 и ^сф0 — замкнутые множества
компакта Ф. Если гг есть (Ф0\ч?)-цикл компакта Ф0, то zr есть
(Ф\\р)-цикл компакта Ф; если при этом zr~0 в Ф0, то ^^0
Фо\гГ ФоХ^
в Ф. Доказательство предоставляем читателю.
2:2. Группы Z% (Г, 51), Яф(Г, 51), A J (Г, 51). Если
zr _ (~r zr 2г \
И
7r — / ~г ?г ?г \
А2 ^ 21' 22' ' ' '» 2fo» ' ' '/
— два Г-цикла компакта Ф, то
ZI I Z2 == (г11 I г21» ^12 » ^22' ' ' * » ^Гй 1 ^аЛ' * * *)
есть также Г-цикл Ф, называемый суммой циклов zrt и г*. Это
определение сложения превращает, как легко видеть, множество
всех r-мерных Г-циклов компакта Ф (по данной области
коэффициентов 51) в группу, которая обозначается через Z0(T, 5t). В группе
ZJ(I\ 51) содержится подгруппа Нф(Т, 51), состоящая из всех
элементов группы ZJ, (Г, 51), Г-гомологичных нулю в Ф. Дополнительная
группа Z^(T, 51)/Яф (Г, 51) обозначается через Аф (Г, 51):
Д'ф (Г, 51) = Z% (Г, Щ/Нф (Г, 51).
2:3. Канонические и бесконечно малые сдвиги. Изоморфизм
групп А^о(Г, 51) и Дф(Г, 51) при Т^Ф0^Ф. Из [1:41] следует, что
при каноническом сдвиге Sf компакта Ф относительно его замкну-
того покрытия а происходит гомоморфное отображение Sr группы
Z%(T, 51) в Zr(Ka\Kv«, 5t), при котором Я'(Г, 51) отображается
в Иг(Кг\Ку¥а, 51). Отсюда следует:
[2:51]. Канонический сдвиг Sf компакта Ф относительно
покрытия <х порождает гомоморфное отображение Sa групп Аф г = Дф (Г, 51)
в A?e=A'(K".V<W«. «)•
[2:32]. Пусть
(2:3) *• = (*;, 4, • •., 4, • • •), **€<#.»*
есть Г-цикл компакта Ф и пусть Skzrk = z"^ есть (еА, \Г)-сдвиг цепи

§ 2] Г-циклы и Г-гомологии компакта Ф 439
гг причём limefe = 0. Так как в этом случае z'£ есть цикл ком-
* к-+оо h
плекса /Сг,$, + 2е., гомологичный в нём циклу zr1<y то
*есть Г-цикл, Г-гомологичный циклу zr.
Переход от zr к z'r, а также самый Г-цикл z/r называются
бесконечно малым сдвигом Г-цикла zr.
Приложим понятие бесконечно малого сдвига к доказательству
упомянутого в заголовке артикула 2:3 изоморфизма.
Положим Ф0\Г == Ф0 П W = W0.
Пусть р — произвольная точка компакта Ф; если р £ Ф0, то
положим Sp=p, если же р(£Фо, то Р^^Х^о» и мы обозначим через
Sp какую-либо вполне определённую среди тех точек q £ W0, для
которых р(р, q) достигает минимума.
Пусть (2:3) — какой-нибудь Г-цикл компакта Ф. Обозначим через
вк наибольшее среди чисел р(р, Sp), где р — какая-нибудь вершина
комплекса |г£|. Докажем, что
lims7{. = 0.
fc->oo
В самом деле, в противном случае можно было бы построить
сходящуюся последовательность
Pi* Р& • • • > Prv> • • •»
где pn6^r\l^o есть вершина некоторого \zrkn\ и р(ри, Spn),
следовательно, и р(рп, 1Г0) больше некоторого, не зависящего от п
положительного г. Но рп есть вершина некоторого симплекса Trn £ \zrk j,
по крайней мере, одна из вершин которого принадлежит Г и,
следовательно, Ф0. Поэтому точка p = lim/?n, принадлежащая к W
(вследствие того, что Рп^Ф), принадлежит и к Ф0, т. е. к WQ, что
противоречит тому, что £<р(рт *Г0) для всех п-
Итак, ставя в соответствие каждой вершине /^£1^1 точку Spk,
получим бесконечно малый сдвиг Г-цикла zr компакта Ф в Г-цикл
Szr компакта Ф0. Таким образом, установлено гомоморфное
отображение S группы Z^r на группу ZJ г («на> потому, что при
гомоморфизме S каждый Г-цикл компакта Ф0 переходит сам в себя).
При отображении 5 группа Нф г отображается на Нгф г, так что
имеет место гомоморфное отображение S группы А^ г на А^ Так
как циклы zr и 5zr, очевидно, Г-гомологичны между собою в Ф>
то из SzryO в Ф0 следует zr ~ 0 в Ф, так что 5 есть
изоморфизм между АгфГ и AJ, г, что и требовалось доказать.

440 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. Щ
2:4. Группы Дф (Г, 31) и размерность компакта Ф. Понятад
бесконечно малого сдвига позволяет легко доказать следующую
важную теорему:
[2:4]. Если компакт Ф имеет размерность п, то для г > я, дли
любой области коэффициентов 51 и для любого открытого множества
Зсф группа Дф(Г, 51) есть нуль-группа.
Другими словами: Всякий r-мерный Г-цикл zr n-мерного компакта
Ф при г>я непременно Г-гомологичен нулю в Ф.
Для доказательства построим для каждого т какое-либо н^ -
покрытие <xw= 1А™9 ..., А™\ компакта Ф кратности п+1, через вт
обозначим лебегово число покрытия aw, через Кт обозначим нерв
покрытия aw, реализованный в Ф, так чтобы вершины а™
комплекса/^, соответствующие пересекающимся с W элементам Л?1
покрытия <aw, были точками множества ч7. Всякая подпоследовательность
какого-либо Г-цикла Zr Г-гомологична всему циклу ъг в Ф; поэтому
для доказательства утверждения
Zr~0 в Ф
достаточно доказать аналогичное утверждение для какой-либо
подпоследовательности цикла zr. Возьмём такую подпоследовательность
цикла zr, чтобы её k-ft элемент был циклом комплекса Кг,гк и
обозначим её снова через
7Г = (zr Zr Zr Л
Пусть теперь z^' — Skzrh есть канонический сдвиг цепи zrk
относительно покрытия ал. Тогда
SzT^iz'S, г'/, ..., г>, ...)
есть бесконечно малый сдвиг Г-цикла zr, и поэтому zr~Szr. Но zryr
есть r-мерная цепь я-мерного комплекса Кк) так как г > /г, то
zr* = 0, и поэтому zr ~ 0 в Ф, что и требовалось доказать.
2 :5. Замечание. Если замкнутое множество W компакта Ф
состоит из одной точки, то для любого г]>1 группы Z£(T), #£(1%
Аф(Г) совпадают соответственно с 2Г(Ф), #Г(Ф), ДГ(Ф).
Доказательство. Пусть г>0 произвольно. Так как К®,
состоит из одной точки, то /7^ при r^l и #°.t суть нуль-группы.
Далее, множества r-мерных симплексов (г^1) комплексов /Сф,*
и Кг,* совпадают между собою, откуда легко следует, что не только
Ьгфъ и ЬгТг , но и Z0e и ZrVz тождественны между собою.
В самом деле, если xr£ZrT^ то Дхг £#£",*; а так как Нг~1 есть
нуль-группа, то Д.г* = 0, т. е' xr£ZrWz.

§ 3] ГОМОМОРФИЗМ, ПОРОЖДЕННЫЙ (ТД^-ОТОБРАЖЕНИЕМ 44 Г
Остаётся доказать, что #ф,е, и НгТъ также совпадают между собою..
Очевидно, из гг^Нгфг следует гг£Н£г. Пусть гг£Ще. Тогда
существует элемент xr+l группы ^г^1==^Й1» удовлетворяющий
условию Arjcr+1=2r. Но разность Axr+1 — Arxr+2 есть элемент
группы L^e и поэтому равно нулю, что означает
Ал:г+1 = Агл:г+1 =гг,
откуда гг£Нгфг.
Из доказанного следует, что /--мерные истинные циклы компакта
Ф совпадают с /--мерными Г-циклами, т. е. что Zr^) = Z£(T) и что
данный истинный цикл тогда и только тогда гомологичен нулю в Фу
когда он Г-гомологичен нулю. Итак, НГ(ФД) = Н£ (ГД), значит, и
АГ(ФД) = А^(ГД), что и требовалось доказать.
Задача. Пусть dimW = p, ч^сгФ. Доказать, что при г>р -{-1
группы А^(Г) и АГ(Ф) изоморфны между собою.
§ 3. Гомоморфизм группы А^(ГД) в группу А^Г', 51),
порождённый (ЧР\ ^-отображением CJ,.
3:1. Гомоморфизм С|,. Пусть Ф и Ф'— компакты, Г
неоткрытые подмножества соответственно компактов Ф и Ф',
¥ = Ф\Г, ЧГ' = Ф'\Г'.
Пусть С^, — непрерывное отображение Ф в Ф', обладающее тем
свойством, что образ множества W при отображении С*, содержится
в ч7':
(3:11) C*,W^W.
Такое непрерывное отображение назовём коротко (ч7,ч7')-о то б-
ражением.
Из условия (3:11) вытекает, что при симплициальном
отображении С^, комплекса Кф,г в комплекс Кф\%с, происходящем,
вследствие непрерывного отображения CJ,, комплекс Kw,z
отображается в Kw,sc (см. главу 11, арт. 3:1). Отсюда, в свою
очередь, вытекает на основании главы 7, арт. 8 :4, чго отображение
CJ, порождает гомоморфное отображение Г'С|, = Krre CJ группы
Lrv% в группу Z,£e , коммутирующее с оператором А в том смысле,
что для любой цепи хг£ЬгГг имеем
(3 :12)
АГГ'С*^' = ГС*/АГ^.

442 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
Так как отображение С®, компакта Ф в компакт Ф' равномерно
непрерывно и, следовательно, гс стремится к нулю при г,
стремящемуся к нулю, то каждому Г-циклу
^компакта Ф соответствует, в силу отображения ТС®п Г'-цикл
L ^фг* —Vх ^ф/^i»1 ^ф/^2» •••> х ^фг*к,л'')
жомпакта Ф\ так что непрерывное отображение С*, порождает
гомоморфизм С$, = Т'С*, группы Z&T) в Z£,(T')-
Из тех же соображений равномерной непрерывности и из (3:11)
следует, что при гомоморфизме С£, группа Н£(Г) отображается
в /Уф/(Г')« Поэтому, гомоморфное отображение С£, группы Z0(£)
в Z^, (Г') порождает одноимённый гомоморфизм группы Аф(Г) в
группу Дф'(Г'), который мы и называем гомоморфизмом, порождён.
н ы м (47 Д')-о тображением С®, компакта Ф в компакт Ф'.
3 : 2. (ч7,ч7')-гомологичные и (ч7,ч7')-гомотопные между собою
отображения; (^Д^-деформации. Пусть снова даны компакты Ф,Ф'
и ТсфД'сф'; как всегда, Г = Ф\Т, Т' = Ф'\Ф'. В полной
аналогии с определениями главы 11 мы считаем, что два
(ч7,ч7^-отображения С0 и Сх компакта Ф в компакт Ф' являются (ЧРД'У-гомо-
логичными между собою, если они для всех г и всех 51
порождают один и тот же гомоморфизм групп Агф (ГД) в Д^,(Г'Д).
Определение [3 :21]. Деформация Q, 0^6.^1 непрерывного
^(ч7,ч7')-отображения С0 в непрерывное (чТД^-отображение Cv
называется (ч7,ч7')-д еф ор м ацией, если при любом Q, O^O^l,
отображение Се есть (чТД^отображение.
Два (Ч^Д^-отображения компакта Ф в компакт Ф' называются
?(ч7,^г/)-гомотопными между собою, если одно из них можно (\F,47')-
деформацией перевести в другое.
Теорема [3 :22]. Два (W,W'yzoMornonHbie между собою (W,W)*
отображения С0 и С1 всегда (W ^^-гомологичны между собою.
Эта теорема вытекает из:
[3:23]. Если С0 и Сх суть (ч?Д^-гомотопные между собою
отображения, а
Ъг = (zv z2, . .., Zy, . ..)
-есть какой-нибудь Г-цикл компакта Ф, то Г'-цикл— Y'C0zr и VrCxZr
компакта Ф' всегда Г'-гомологичны между собою.
Дадим доказательство теоремы [3: 23], развивающееся совершенно
параллельно доказательству теоремы [3:3] главы 11. Надо доказать,
что для каждого г>0 существует такое &е, что и для всех &>&е
Г'С0г*~ Г'С,г* в Kit*.

ГОМОМОРФИЗМ, ПОРОЖДЕННЫЙ (W, ^^-ОТОБРАЖЕНИЕМ 443
Для этого, как в главе 11, рассматриваем какую-нибудь (*Р, W)-
деформацию Се отображения С0 в С1 и определяем 8>0 так, чтобы из
?(Р\ Р")<Ъ в Ф и |6' — 6Л|<8
следовало
Выбираем теперь ke столь большим, чтобы при &>&е симплексы
комплекса |гП были по диаметру меньше, чем 8.
Берём определённое &>&е; нумеруем в определённом порядке
вершины комплекса \г*\:
еь ■ • • > ^и-'
Делим отрезок 0^6<; 1 на отрезки равной длины <8 точками
0 = 4 9,,..., 0, = 1
и доказываем для любого г = 0, 1,...,$—1 соотношение
(3:24) г'Св,+1г* — ГСвД~0 в ЯК.,
из которого следует теорема [3:23].
Для этого строим призму Щ над комплексом остовов |^|.
Комплекс ПЛ отображаем в AV,E при посредстве гимплициального
отображения 5, следующим образом определяемого в вершинах рт и qm
соответственно нижнего и верхнего оснований призмы Лк:
5(рт) = Св|(рт), S(qm)=Cb.+i(pm).
При отображении 6' призма Иг£ над г£ в ITfc перейдёт в
некоторую цепь 5Ш£ £ !£, в, причём
(3:25) А <>Ш£ = 5ДПг£ = Ce,+1*J - Q^ - SUA^,
где ПА.г£ есть призма, построенная в том же комплексе над цепью
При симплициальном отображении 5 все вершины ПА,г£ перейдут
в точки множества ч7, так что
(3:26) 5ШЦ-<Е^.
Из (3:25), (3:26) следует
Г^П4 = Г'С9т4-Г'С6Д,
а так как АГгГ" = Г'А, то
Дг.Г'5П^ = ГС<+1^-Г'Св^,
чем формуда (3:24) и вместе с ней теоремы [3:23] и [3:22] доказаны

444 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
3:3, Деформация относительного цикла компакта Ф. Пусть
дан Г-цикл
компакта Ф; рассмотрим произвольную (ЧГ.ЧР^-деформацию Сь>
0<^6^1 тождественного отображения С0 компакта Ф. Упорядоченное
по параметру 6 семейство Г-циклов C0zr компакта Ф называется
деформацией Г-цикл a zr в Ф.
Из теоремы [3:23] следует, что Г-циклы zr = C0zr и Cxzr
компакта Ф будут Г-гомологичными между собою в Ф:
[3:31]. Всякий Y-цикл zr компакта Ф переходит при
деформации Q в компакте Ф в Т-цикл компакта Ф, который Т-гомоло~
гичен в Ф циклу zr.
Следствие. При наших обычных предположениях о Ф, Г, ЧГ
пусть существует (ч7, ч7')-деформация Q компакта Ф в себя, при
которой Ct№)ciW. Тогда всякий Г-цикл zr компакта Ф непременна
Г-гомологичен нулю в Ф.
В самом деле, Сх (Ф) и, следовательно, W есть носитель Г-цикла
С3гг, поэтому Qz'^O; но zr~Clzr, что и требовалось доказать.
§ 4. Группы АуТ) в случае, когда Ф и 47 — полиэдры.
4:1. Предварительные замечания. Пусть Ф—полиэдр, Ч/сФ —
полиэдр, являющийся телом комплекса Kwa, представляющего
собою подкомплекс некоторой триангуляции Ка полиэдра Ф:
Ф = ЛГв, ¥ = &„ Кчг*сКл.
Как всегда, Г==Ф\1Г.
Барицентрическое подразделение комплекса Ка обозначаем через
/Са1; барицентрическое покрытие полиэдра Ф, соответствующее
триангуляции /Са, как всегда, обозначаем через а.
Пусть е — какая-нибудь вершина комплекса Kwa; она является
в то же время вершиной комплекса Кл. Обозначим через Т*(е)
барицентрическую звезду вершины е относительно комплекса Ка', через
Ту(е)—барицентрическую звезду вершины е относительно Кчта.
Комплекс Т£(е) состоит из всех симплексов комплекса Ка1,
имеющих е своей младшей вершиной и лежащих на симплексах
комплекса KWa: поэтому, обозначая через Т^(е) и Т\ё) соответствующие
замкнутые барицентрические звёзды (глава 4, определение [5:31]),.
имеем
f* (е) = W П Т\е) (где е £ Kva).
С другой стороны, из теоремы [5:42] главы 4 следует: если
^ П Т*(е)^0, то е есть вершина комплекса Kwa, и, значит, по
только что установленному Т^(е) = 47 П Т*(е). Отсюда следует

§ 4] группы Д£(Г) в случае, когда Ф и W — полиэдры 445
[4:11]. Покрытие ч7а, состоящее из (непустых) пересечений
элементов покрытия а с W, есть барицентрическое покрытие,
соответствующее триангуляции /С^а.
4:2. Основная теорема.
[4:2]. Группа Д^(Г) = Д£ изоморфна группе Ы (КЛ\Кч>д = Д£а.
Доказательство. Пусть 8>0 столь мало, что оно является
одновременно лебеговым числом обоих покрытий а и ¥а.
Из теоремы [2:31] следует, что канонический сдвиг S®
осуществляет гомоморфное отображение S^ =(Ka\Kwa)Sf группы Д£ в
группу Д£а.
а) Гомоморфизм Sra является отображением на всю группу
Д£г. В самом деле, если г^ ££ д«гг и z^t 2^,. .., г^. . .суть
последовательные барицентрические подразделения цепи г£, то
zr = (^i> *l2, • • •, z*h, • •.)
есть Г-цикл, причём
поэтому, обозначая через f тот элемент («гомологический класс»)
группы Д£, к которому гг принадлежит, имеем
б) Гомоморфизм Sv^ есть изоморфизм. Чтобы убедиться в этом,
достаточно доказать:
Пусть дан Г-цикл полиэдра Ф
(4:20) Z'= (*;,*',..., 4,.. .);
если (Ka\Kw*) S*zr ~ 0 в Ka\Kw«, то Zr£H}r, т. е. для всякого
а>0 имеется такое &е, что при k>kt <г£~0 в Кг,ъ-
Доказательство этого факта проводится при помощи рассуждений, вполне
аналогичных рассуждениям главы 11, арт. 4:4.
Проведём это доказательство. Через Kah и Куол обозначаем
соответственно /г-кратное барицентрическое подразделение комплексов
Ка и Kva- Дано е>0; пусть 8a<s есть лебегово число комплексов
Ки а К\\>*\ берём h так, чтобы /Са?1 было ^-комплексом. Пусть Зл<8а —
лебегово число комплексов Kah и /Счгай. Выбираем ke так, чтобы
при k^ke все г* были 8л-циклами.
Пусть &>&s. Рассматриваем канонический сдвиг Sfh относительно
Тогда
4 ~ (КЛ \ Kwa) StiA В /Сг,8в,
S*h2rk£Zpay ГДе Zra = Zr (/Ce\ /<V«).

446 относительные циклы и их применение [гл. XI»
На основании теоремы [2:35] главы 10 существует
так что
и, следовательно,
(4:21) 4-vI в /Сг|8в.
Канонический сдвиг Sa относительно Ка, применённый к (4:21),.
даёт:
слева t
(К* \ Kv«) Sfzrk £ Zr (Ka \ Кчч),
справа
(Ка \ Кфа) Sa S ahZa = Za,
поэтому
(Ка\Кш) S*2*k~zrB Ка\Кц.г1.
Но по предположению
(Ка\ Kwa) Sf4 ~ 0 В Ка \ Кча,
значит,
4-0 в Ка\К*а
и W-0 в Kah\Kvah£: Кг,ьа
и, в силу (4:21), zrk~Q в /Сг.^Е^г.в,
что и требовалось доказать.
4 :3. Гомоморфизм С«, группы А«г = А** (/Са \ /fw«, Щ в А«т, =
=Аг(/^\/Сф/а'э 51), порождённый (W, ^^-отображением Cj/. Пусть.
даны полиэдры Ф = /Са, W = /Счг« /Счг« Е ^ и Ф' = Я«', \F' = Kwr
Kwa'^Ka, а также (W,W')-отобршеп№ С%г\ отображение С%г
порождает гомоморфизм Са' группы А«г в группу А«чу, причём
совершенно так же, как в арт. 4 :7 главы 11, мы убеждаемся в
справедливости следующего правила:
[4:31]. Берём столь малое 8'>0, чтобы оно было лебеговым
числом одновременно для а/ и W'a'; берём 8 столь малым, чтобы *)•
«с<8'.
Берём столь мелкое /СаЛ, чтобы его симплексы были меньше 8.
Пусть $д£Д«г произвольно. Для получения C«r ^^Afv берём
произвольное г*£ 3« и *оздейст!уем на него сначала оператором
подразделения Sah, далее берём образ цикла sl^ при отображении Г'Сф», т. е.
цикл Р'Сф^ г^ комплекса /fr'*'» который, наконец, подшергаем
каноническому сдвигу (Ка'\Кчга') 5а'. В результате получаем цикл
*) Глава 11, арт. 3:1 (пишем о вместо о ф ).

§ 4] ГРУППЫ ДГ(Г) В СЛУЧАЕ, КОГДА Ф И W — ПОЛИЭДРЫ 447^
(Xct'\ Kvfaf) S а'Сф ^Л^а КОМПЛеКСа Ка'\Къ''а'у ГОМОЛОГИЧеСКИЙ КЛЭСС
которого и есть искомый элемент
Рассмотрим теперь симплициальное отображение S^ комплекса Клц.
в комплекс Av, построенное по правилу главы И, арт. 5:1, ш
являющееся симплициальным приближением непрерывного
отображения Сф'. Легко видеть, что S$* отображает Kwan в /Cw/v и по
этому порождает гомоморфизм (К*г\Кч'*')$& группы Аг« в
группу A£v.
Так же как в § 5 главы 11, мы видим, что
[4 :32] С£ и (K*'\K4r'«')Sl'hs*h представляют собою один и тот
же гомоморфизм группы Д?а в группу Arv-
4:4. Гомологическое определение размерности полиэдра.
Новое доказательство инвариантности числа измерений. Пусть
Ф—тело я-мерной триангуляции Кп и Тп^Кп> Тогда Тп
представляет собою открытое множество компакта Ф, и по теореме [4 :2]
группа Аф (Тпу 91) изоморфна Ап-группе комплекса, состоящего из-
единственного элемента Тп9 т. е. изоморфна группе 91 и,
следовательно, отлична от нуля.
Итак, во всяком я-мерном полиэдре Ф можно найти такое
открытое множество Г=Г№, что группа Д*ДГД) отлична от нуля по
любому 51. С другой стороны, для г>я при любых Г и 9t группа
А ф (Г, 91) есть нуль-группа (теорема [2:4]). Итак:
[4:4]. Число измерений полиэдрального комплекса К
(размерность полиэдра К) есть наибольшее среди таких чисел я, что в К
существует открытое множество Г, для которого группа Д~ (Г, 91)
отлична от нуля.
При этом за 91 можно взять любую область коэффициентов.
Теорема [4 : 4] даёт новое инвариантное — так называемое
«гомологическое* определение числа измерений триангуляции полиэдров
и, следовательно, новое доказательстю его инвариантности.
4:5 *). Определение гомологической размерности компакта.
Доказанная только что теорема естественно приводит к следующему
определению:
Определение [4: 5]. Гомологической размерностью d (Ф, 91)
компакта Ф по области коэффициентов 91 называется
наибольшее такое целое число п, что для некоторого открытого мно-
*) См. Александров, «Теория размерности», Успехи Математических.
Наук, т. 2, вып. 1 (17) (1947) (изложение работы «Dimensionstheorie»
1932 г.), а также Александров, Hopf, Понтрягин, «О Брауэровском
понятии размерности», там же (где указана и дальнейшая литература)-

448 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. Х1||
жества Г^Ф группа Аф (Г, 21) отлична от нуля. Если такощ(
числа п нет, то по определению ^
*/(Ф, И)=со
•(тогда для любого п имеется такое Г„с:Ф, что Аф(Г, %)ф0).
Из теоремы [2:4] следует:
[4:51]. Для любого компакта Ф и любой области коэффи^
циентов 21 |
д?(Ф, 21)^ dim Ф. I
Из [4 :4] следует:
[4 :52]. Для любого полиэдра Ф и любой области
коэффициентов 21 имеем
^(Ф, 21) = dim Ф.
Имеет место следующий основной результат, доказательство
которого выходит за пределы этой книги:
[4:52]. Для любого компакта Ф
(ШпФ = 1*(Ф, fftt)
(где 9?! есть аддитивная группа рациональных чисел, приведённых
по модулю 1).
Таким образом, dim Ф есть также одна из гомологических
размерностей и притом, в силу [4: 52], — наибольшая среди них.
Л. С. Понтрягин построил примеры компактов Ф, лежащих в /?\
гомологические размерности которых по некоторым областям
коэффициентов отличны от dim Ф. Компакты Ф, удовлетворяющие при
любой области коэффициентов 21 условию
</(Ф, 21) —dim Ф,
естественно назвать размерно полноценными. Таковы все
полиэдры (на основании теоремы [4:52]). Можно было бы доказать,
что все компакты, лежащие в /?3, также являются размерно
полноценными.
§ 5. Псевдомногообразия с краем.
5:1. Ориентация псевдомногообразия с краем. Пусть Ф=Ка есть
я-мерное псевдомногообразие с краем W = /6^; как всегда, Г = Ф \4P".
Какова бы ни была триангуляция Ка псевдомногообразия Ф, группа Дга
(см. [4 :2]) изоморфна группе А™. Отсюда, как в главе 11, арт. 4: 8,
выводим инвариантность ориентируемости псевдомногообразия с краем,
т. е. следующее предложение:
[5:11]. Если Ф есть n-мерное псевдомногообразие с краем *F,
Г = Ф\№, то возможны лишь два случая: либо группа Дф(Г, J)
есть бесконечная циклическая группа, тогда все триангуляции Ф

§ 51
ПСЕВДОМНОГООБРАЗИЯ С КРАЕМ
449
суть ориентируемые комбинаторные псевдомногообразия с крае и
и Ф называется ориентируемым, либо группа Аф(Г, J) есть
нуль-группа, тогда все триангуляции Ф суть неориентируемые
комбинаторные псевдомногообразия с краем, и Ф называется
неориентиру емым.
Каждый из двух элементов ± gj, являющихся образующими
элементами бесконечной циклической группы Лф(Г, У), называется
ориентацией ориентируемого псевдомногообразия Ф. Повторением
рассуждений главы 11, арт. 4 : 6, легко убедиться в том, что ориентации Ф
вполне определённым образом взаимно однозначно соответствует
ориентация ±$£ любой триангуляции Ка псевдомногообразия Ф.
5:2. Предварительные замечания и определение степени не*
прерывного отображения псевдомногообразий с краем. Пусть Ф
и Ф' суть /г-мерные ориентируемые псевдомногообразия с краем или
замкнутые.
Пусть С—непрерывное отображение компакта Ф в Ф', которое
предполагаем удовлетворяющим некоторым условиям,
сформулированным ниже.
Если Ф илиФ' есть псевдомногообразие с краем, то обозначаем
этот край соответственно через ч7 или W.
Если Ф замкнуто, то полагаем ч? = 0.
Если Ф и Ф' замкнуты, то полагаем ч7 — 0, Ч?" = 0.
Этот случай уже разобран нами в главе 11, § 6.
Если Ф — псевдомногообразие с краем, а Ф' замкнуто, то ч?'
будет определено сейчас же ниже.
Относительно непрерывного отображения С предполагаем:
Если Ф' есть псевдомногообразие с краем W\ то
С OF) сф',
если же Ф; замкнуто, а Ф нет, то предполагаем, что C(W) есть
одна точка *), которую и обозначаем в этом случае через W.
Во всех случаях полагаем
Г = Ф\ч7, Г' = Ф'\Ф'.
Пусть теперь выбраны определённые ориентации f1 и ^п псевдо*
многообразий Ф и Ф'. Дальше рассуждаем дословно, как в главе 11,
с той только разницей, что всё время вместо А" (Ф), Д^СФ')
говорим теперь о Д£(Г, J) и Дф^Г", У), а вместо истинных циклов и
гомологии в компактах Ф и Ф' говорим соответственно о Г-циклах
и Г-гомологиях компактов Ф и Ф'. Это приводит нас прежде всего
*) Достаточно потребовать, чтобы dim С OF) •< п—2; проведение
дальнейших рассуждений в этом предположении предоставляется самому читателю
в виде упражнения; при этом следует иметь в виду задачу, поставленную
в конце § 2; она должна быть решена прежде всего.
29 Александров П. С.

450 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
к понятию степени отображения С: отображение С порождает
одноимённый гомоморфизм группы А^(Г)в AJ, (Г7), при котором
где 7 есть целое число, называемое степенью отображения.
Пусть /Са, /<а/ суть триангуляции псевдомногообразий Ф и Ф', а
KwttC^Kt, и Къ'а'С^ Ка' — триангуляции W и-ч77; как всегда, Kah
обозначает /z-кратное барицентрическое подразделение комплекса /Св.
При достаточно большом h имеем симплициальное отображение 5«л
комплекса Ka1l в /Са/, отображающее Kw^n в /С^/ и являющееся
симплициальным приближением отображения С (см. арт. 4 : 3).
Совершенно так же, как в главе 11, арт. 6: 2, доказываем, что
степень отображения С равна степени симплициального
отображения Б'ф комбинаторного псевдомногообразия К^ в комбинаторное
псевдомногообразие /Са/, (глава 8, § 5, особенно [5: 22]).
5:3. Некоторые свойства степени отображения. Сохраняя
обозначения и предположения, введённые в начале этого параграфа,
допустим, что Ка разбито на конечное число л-мерных
комбинаторных псевдомногообразий Каъ X=l,...,s, с краями Kwa\, причём
для любых X', Ъ!г имеем
Пусть 2 *"< е^ть данная ориентация Ка; для каждого /Сах возь-
i
мём ориентацию Д]/*м, где суммирование распространено по всем
1&<1€*"л.
Пусть при отображении С каждое из псевдомногообразий ф = Ки\
л*
отображается в Ф' так, что край 4^=: УС ^отображается в \F';b3hb
только что установленную ориентацию каждого из
псевдомногообразий Ф, можно говорить о степени 7х отображения С
псевдомногообразия Фх в Ф'. Тогда, обозначая через -у степень отображения С
псевдомногообразия Ф в Фг, имеем теорему сложения:
(5:31) T = 2fx-
Для доказательства формулы (5:31) построим по правилам
главы 11, арт. 5:1, симплициальное приближение *S£?
отображения С полиэдра Ф в Ф', при котором Kw* и все Kwa\
отображаются в Куг*/. Алгебраическое число симплексов комплекса К„
покрывающих какой-нибудь ориентированный симплекс fit, комплекса К*'
(см. главу 8, теорему [5 : 22]), равно сумме алгебраических чисел
симплексов комплексов Ка\, А=1, 2,...,$, покрывающих тот же
симплекс fin откуда и следует формула (5:31).

§ 5] ПСЕВДОМНОГООБРАЗИЯ С кРАЕМ 451
Теоремы арт. 6 : 3 главы 11 дословно переносятся на случай
псевдомногообразий с краем, причём в теореме [6 : 33]
предполагается, конечно что отображения С\ и Сз являются соответственно
0^1) ^а)" и (^2i тРз)'отобРажениями-
[5:31]. Если Ф—замкнутое псевдомногообразие, а Ф/ — псе-
^до многообразие с краем, то степень отображения С равна нулю.
В самом деле, в этом случае Г = Ф, всякий /z-мерный Г-цикл
псевдомногообразия Ф есть истинный цикл Ф и отображается он
на я-мерный истинный цикл псевдомногообразия Ф', необходимо
гомологичный нулю (других я-мерных циклов в Ф' нет). Поэтому,
если $ф и $ф' суть ориентации Ф и Ф' и $п£$ф, то элемент ч$ф,
группы Дф/(Г"), содержащий C(zn)> есть нулевой элемент группы
ДФ,(Г), т. е. Т = 0.
5 :4. Примеры.
Пример 1. Полиэдры Ф и Ф' представляют собой две
двумерные сферы, каждую из которых будем представлять себе как гаус-
д, сову сферу, т. е. как плоскость
0* ~^г ^ у ~—
Черт. 134.
w'~/(cos <£>'-{-i sincp')- Отображение С®, ставит в соответствие
каждой точке w = r (cos ср -j-1 sin ср) сферы Ф точку w' = C(w)=
= г (cos n<o -\- i sin яср) сферы Ф'.
Триангулируя сферу Ф как двойную треугольную пирамиду, а
сферу ф/ как двойную пирамиду с основанием в виде Зя-уголь-
ника, легко докажем, что степень отображения Ср равна п.
Пример 2. Фи Ф' суть торы. Введём на торе Ф
«географические» координаты — углы © и ф, отсчёт которых ясен из черт. 134.
На торе ф' таким же образом введём координаты ©' и у.
а) Зададим отображение С^ следующим образом:
О (?,« = ("?> 4»>
т. е.
ср' = пер, <!/ = ф.
29*
комплексного переменного, w—
— г (cos ср -j- / sin ср), соответственно

452
ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ
2kn
ГЛ.
ч
Если тор Ф разбить меридианами <р == —- (А = 0,1,..., л 1) н<
колец, то каждое кольцо при отображении С%* накроет тор $'_
степенью -f 1. Отсюда легко следует (в силу теоремы сложения [5 •*§
или при помощи построе™
надлежащих триангуляции Щ
ров Ф и Ф'), что степень от
бражения С®, равна п. I
Ту же степень имеют ощ
бражения
£*'(?• Ф) = (?» лф),
б) Рассмотрим вообще от
бражения вида -
Сф'(?> Ф) = (Я? + *Ф» С? 4~ ^Й
т. е.
с/ = a© -J- Ь^, ¥ = су + dty."Si
Здесь ^, Л, с, d — целые числа, причём мы предполагаем, что числу
а и b и числа с и d попарно взаимно просты. В противном случ^
отображение CJ, разбивается на два последовательных отображения;
из которых одно имеет вид о' — т9, 'К=Р<Ь а другое
с взаимно простыми а\ br и с\ d'.
Для того, чтобы отображение С%г было отображением на'[вес)
тор Ф', очевидно, необходимо, чтобы детерминант \\ был отлш
чен от нуля. Линии a®-\-bty — 0 и сср4~^ = 0 на торе Ф услов||
называем «спиралями» *). Эти две «спирали» разбивают юр на кр|
волинейные параллелограммы, каждый из которых при отобрази*
нии СФ' покрывает тор Ф'. Число этих параллелограммов равно\аА
(читателю предоставляется это доказать) **). Следовательно, степей
It I
. Черт. 135 изображает разбиение тор
спиралями
3<? — 2^ = 0 и 2ср + ф==0
на 12 1=7 параллелограммов.
*)ср и ф определены с точностью до целочисленных кратных 2тг.
**) Например, при помощи перехода к плоской «развёртке» тора*

§ б] группы Д^,(Ф). (локальные Аг-группы компакта Ф) 453
Пример З..Ф есть тор, Ф'— двумерная сфера. Обе
поверхности помещены в трёхмерное пространство и каждой точке р тора
поставлена в соответствие её проекция С%г(р) из центра сферы Ф'
на эту сферу. Отображение Сф/ будет непрерывным отображением
Ф на Ф', если центр сферы не лежит на поверхности тора.
Степень Сф/ будет равна 1, если центр сферы лежит внутри тора,
и 0, если он лежит снаружи.
Замечание. Ещё в главе 2, арт. 2:5 (см. также главу 11,
арт. 6 :4), было доказано, что существуют отображени я окружности
на окружность, имеющие любую заданную степень. Это
утверждение верно и для л-мерной сферы при любом п\ см. об этом
главу 16, арт. 6:1; соответствующие рассуждения главы 16,
арт. 6:1, рекомендуется прочитать уже сейчас.
§ 6. Группы А^ (Ф).
(Локальные А^группы компакта Ф.)
6:1. Определение групп А^(Ф). Начнём с нескольких
вспомогательных определений.
Пусть даны два открытых множества Г и Tj компакта Ф и
ттепь ^г = 2а/^ комплекса Кть*. Полагаем
IV = Кг Пгх,е*г.
Другими словами, цепь Тхг определена лишь на комплексе Кг П гьв
и совпадает там с цепью хг. Или, наконец, цепь Тхг получается из
цепи *г = 2^? сохранением в линейной форме 2#^£ лишь членов
с симплексами tr. , хотя бы одна вершина которых принадлежит
множеству 1\.
Если
1 = [z^, 22 , . . . , 2^ , . . • )
есть Yt — цикл компакта Ф, то
iv = (r*j, г*£ ,..., г*; ,...)
есть (Г П ГО-цикл Ф.
Переходим теперь к основным определениям этого параграфа.
Определение [6:13]. Пусть р—произвольная, но
фиксированная точка компакта Ф.
Пусть Г—окрестность точки р (т. е. открытое множество,
содержащее р).
Всякий Г-цикл компакта Ф называется циклом в точке р^Ф.
Определение [6 :14]. Пусть z[ = (2*v zr12i > . .., z[h , . . .) и
Z2 :E=S \Z2V Z22 » * ' • ' *1~h ' * * ' '

452
ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ
[гл.
хи
Если тор Ф разбить меридианами ср = (А = 0,1,..., л—1) на п
колец, то каждое кольцо при отображении С%> накроет тор Ф' со
степенью -|~ 1. Отсюда легко следует (в силу теоремы сложения [5 : Щ
или при помощи построения
надлежащих триангуляции
торов Ф и Ф'), что степень
отображения CJ, равна п.
Ту же степень имеют
отображения
<?!'(?• <Ю = (?» л<Ю,
б) Рассмотрим вообще
отображения вида
с*Ф'(?> ф) = (#? ~|- £ф> *? -Ь ^К),
т. е.
е/ = дер _|_ ^ <}/ :
: СО -\~ &Ъ.
Здесь а, Ь, с, d — целые числа, причём мы предполагаем, что числа
а и Ь и числа* cud попарно взаимно просты. В противном случае
отображение CJ, разбивается на два последовательных отображения,
из которых одно имеет вид cp' = m<p, Y—Pty> a Другое
с взаимно простыми a', b' и с', d'.
Для того, чтобы отображение CV было отображением на-весь
аЬ\
cd\
был отли-
тор Ф', очевидно, необходимо, чтобы детерминант
чен от нуля. Линии яср-[-£ф = 0 и c®-\~dty=Q на торе Ф условно
называем «спиралями» *). Эти две «спирали» разбивают тор на
криволинейные параллелограммы, каждый из которых при
отображении Сф' покрывает тор Ф'. Число этих параллелограммов равно J
(читателю предоставляется это доказать) **). Следовательно, степень
отображения С%> равна гЧ . ЧеРт- 135 изображает разбиение тора
спиралями
Зср — 2^ = 0 и 2ср -|- ф ^ °
3 2 I
= 7 параллелограммов.
на
*)ср и ф определены с точностью до целочисленных кратных 2я.
**) Например, при помощи перехода к плоской «развёртке» тора*

к 6] группы Л^,(Ф). (локальные Аг-группы компакта Ф) 453
Пример 3. Ф есть тор, Ф' — двумерная сфера. Обе
поверхности помещены в трёхмерное пространство и каждой точке р тора
^ставлена в соответствие её проекция Сф^(р) из центра сферы Ф'
, эту сферу. Отображение Сфг будет непрерывным отображением
Г на Ф', если центр сферы не лежит на поверхности тора.
Степь Сфг будет равна 1, если центр сферы лежит внутри тора,
О, если он лежит снаружи.
.^Замечание. Ещё в главе 2, арт. 2:5 (см. также главу 11,
6:4), было доказано, что существуют отображени я окружности
^окружность, имеющие любую заданную степень. Это утвержде-
верно и для л-мерной сферы при любом п\ см. об этом
|шу 16, арт. 6:1; соответствующие рассуждения главы 16,
|т. 6:1, рекомендуется прочитать уже сейчас.
|f § 6. Группы Д^(Ф).
t: (Локальные Дг-группы компакта Ф.)
6:1. Определение групп Д^(Ф). Начнём с нескольких вспомо-
Штельных определений.
*щПусть даны два открытых множества Г и Tj компакта Ф и
*r = 2a/f комплекса Krltf Полагаем
&
I» Г^ = /СгПг».«*г-
f Другими словами, цепь IV определена лишь на комплексе Кг П гьв
" срвпадает там с цепью хг. Или, наконец, цепь Тхг получается из
«и хг = У\а^ сохранением в линейной форме ^а$ лишь членов
симплексами F хотя бы одна вершина которых принадлежит
Ьжеству 1\.
Р Если
Mi, L V*i» ^2 > * '
щгь Tj — цикл компакта Ф, то
J' rz' = (IX, Г*;,..
•■ *£
.., г
fctb (Г П 1\)-цикл Ф.
и Переходим теперь к основным определениям этого параграфа.
Определение [6:13]. Пусть р — произвольная, но фиксиро-
Юанная точка компакта Ф.
Пусть Г—окрестность точки р (т. е. открытое множество,
содержащее р).
Всякий Г-цикл компакта Ф называется циклом в точке р^Ф.
^Определение [6 :14]. Пусть z[ = (г\г, г\ъ , . .., z\b , . ..) и
Z2 ^ (г21> ^22 » • ' Ч ^2h ' * * * )

454 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ.
соответственно суть Гх- и Г2-Ииклы в точке р £ Ф. Полагая
г=г1Пг2,
имеем, в частности,
так что Г-цикл
(6: 14) (Г^ + Г^, Г^ + 14, > • •> Щь + Щп >■ ■ •)
есть цикл в точке р. Цикл (6:14) называется суммой ц
лов zJhz^.
Это определение сложения, как нетрудно видеть, преврагшИ
множество всех r-мерных циклов в точке р£Ф (по данной облйД
коэффициентов 21) в группу, которую мы называем группой <2£(Ф,
Определение [6:15]. Г-цикл в точке р£Ф
Z = (2^ 2^ , . . ., 2^ , . . .)
называется гомологичным нулю в точке р:
zr~0,
р т
если существует такое открытое множество TjCzr, содержаи
точку /?, что цикл Г^ есть цикл, Г-гомологичный нулю в Ф.
цикла в точке р называются гомологичными между собою в точ
р, если их разность гомологична нулю в точке р. ^
Замечание 1. Из самого определения гомологии в точ|Ц
следует:
Пусть гг есть цикл в точке р(Ф и Г0 — окрестность точки,
в Ф (т. е. открытое множество, содержащее р). Тогда
zr~rozr в Ф.
р о
Замечание 2. Если zr = (zrv 2* , .. ., zrk , ...) есть Г-циКж
Г-гомологичный нулю в Ф, и если Ф0 замкнуто, а Г0сГ
открыто в Ф, то Г0гг~0 в Ф0. гщ
Доказательство. Пусть цепи х^+1 комплексов Ктщ
lims7t. = 0 выбраны так, что I
Так как Кг0,е при всяком г открыто в Кг,г, то
чем наше утверждение и доказано.
Циклы в точке р£Ф, гомологичные нулю, образуют, как
нетрудно видеть, подгруппу группы Zr (Ф, %), которую обозначаем через
#1(Ф, 51),

§ 6] группы Ар (Ф). (локальные А^-группы компакта Ф) 455
О п р е д е л е н и е [6 :16]. Группа А£ (Ф, 51) = Zrp (Ф, 31)/Я£(Ф, 31)
называется r-мерной группой Бетти (или Аг-группой) компакта Ф
в точке р по области коэффициентов 31. Ранг группы А£(Ф, Jft)
относительно $R называется r-мерным числом Бетти
компакта Ф в точке р. Другими словами, r-мерное число Бетти
компакта Ф в точке р есть наибольшее среди тех чисел k, для
которых можно найти к элементов группы Zr (Ф, 5ft), никакая
нетривиальная линейная комбинация которых с коэффициентами из 5ft не
содержится в #£(Ф, 01).
Замечание 3. Вместо Zrp(®, 31), #£(Ф, 31), Д£(Ф, 31) будем
писать просто Z£, Hrp, AJ.
Замечание 4. Если говорят о группах А£ при переменном
р £ Ф, то их часто называют r-мерными локальными группами
Бетти компакта Ф.
6:2. Локальный характер групп Д£. В этом артикуле мы
докажем, что группы Аг действительно выражают некоторое локальное
свойство компакта Ф, т. е. свойство, зависящее лишь от строения
этого компакта в произвольно малой окрестности данной его точки р.
Это утверждение содержится в следующих предложениях [6:21] и
[6 :22].
[6:21]. Пусть Ф0 — замкнутое подмножество компакта Ф,
содержащее некоторую окрестность точки р (относительно Ф).
Тогда группы А£ (Ф0, 31) и А£ (Ф, 51) изоморфны.
Для доказательства возьмём окрестности Г0 и Г точки р,
удовлетворяющие условию
Г0ЕГ1ЕФ0,
предположим
Ф^Ф0, е = р(Г0, Ф\Ф0).
Тогда
в = р(Г0, Ф\Ф0)>Р (Г0,Ф\Г1)>0.
Пусть
Т0гг = (Г0г^ Г0г£, ..., 10ггк ч •••)•
Лишь конечное число среди |Г0<г*£ | могут содержать симплексы, не
все вершины которых принадлежат к Ф0 (так как такие симплексы
имеют диаметр > е).
Пусть это будут
Полагаем

454 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
соответственно суть 1\- и Г2-циклы в точке р £ Ф. Полагая
г=г1Пг2,
имеем, в частности,
так что Г-цикл
(6: 14) (Г^ + Г^, Гг;а + Г*£, , ..., Щь + Щп >• • О
есть цикл в точке р. Цикл (6:14) называется суммой цик-
лов zj и zr2.
Это определение сложения, как нетрудно видеть, превращает
множество всех r-мерных циклов в точке р£Ф (по данной области
коэффициентов %) в группу, которую мы называем группой -21 (Ф, %),
Определение [6:15]. Г-цикл в точке р £ Ф
называется гомологичным нулю в точке р:
z-0,
если существует такое открытое множество TjCir, содержащее
точку р, что цикл Ttzr есть цикл, Г-гомологичный нулю в Ф. Два
цикла в точке р называются гомологичными между собою в точке
р, если их разность гомологична нулю в точке р.
Замечание 1. Из самого определения гомологии в точке
следует:
Пусть zr есть цикл в точке р£Ф и Г0 — окрестность точки р
в Ф (т. е. открытое множество, содержащее р). Тогда
zr~ TQiT в Ф.
р °
Замечание 2. Если zr*=(zrv z\ , ..., z\ , ...) есть Г-цикл,
Г-гомологичный нулю в Ф, и если Ф0 замкнуто, а Г0^Г^Фо
открыто в Ф, то rozr~0 в Ф0.
Доказательство. Пусть цепи х^+1 комплексов К\\ек
lims7t. = 0 выбраны так, что
Так как ^„t при всяком е открыто в /СГ)в, то
П4 = г0дг^+1 = дГог0^+1)
чем наше утверждение и доказано.
Циклы в точке р£Ф, гомологичные нулю, образуют, как
нетрудно видеть, подгруппу группы Zr (Ф, %), которую обозначаем через
К(Р, И).

§ 6] группы Ар (Ф). (локальные А>'-группы компакта Ф) 455
Определение [6:16]. Группа А^ (Ф, %) = Zrp (Ф, %)/Нгр(Ф,%)
называется r-мерной группой Бетти (или А**-группой) компакта Ф
в точке р по области коэффициентов 5(. Ранг группы А£ (Ф, Щ
относительно SR называется r-мерным числом Бетти
компакта Ф в точке р. Другими словами, r-мерное число Бетти
компакта Ф в точке р есть наибольшее среди тех чисел k, для
которых можно найти k элементов группы Zr (Ф, JR), никакая
нетривиальная линейная комбинация которых с коэффициентами из 5ft не
содержится в Я£(Ф, Ж).
Замечание 3. Вместо 2£(Ф, 51), Я£(Ф, 31), Д^(Ф, 51) будем
писать просто Z*, Нгр, Ыр.
Замечание 4. Если говорят о группах А£ при переменном
р £ Ф, то их часто называют /--мерными локальными группами
Бетти компакта Ф.
6:2. Локальный характер групп Д£. В этом артикуле мы
докажем, что группы Ау действительно выражают некоторое локальное
свойство компакта Ф, т. е. свойство, зависящее лишь от строения
этого компакта в произвольно малой окрестности данной его точки р.
Это утверждение содержится в следующих предложениях [6:21] и
[6:22].
[6:21]. Пусть Ф0 — замкнутое подмножество компакта Ф,
содержащее некоторую окрестность точки р (относительно Ф).
Тогда группы А£ (Ф0, 51) и А£ (Ф, 51) изоморфны.
Для доказательства возьмём окрестности Г0 и Г точки р,
удовлетворяющие условию
ГоЕГ,ЕФо,
(Предположим
м Ф ф Ф0> г = р (Г0, Ф \ Ф0).
аогда
Пусть
s = р (Г0, Ф\Ф0) > р (Г0, Ф\ГХ) > 0.
Лишь конечное число среди |Г0.г£| могут содержать симплексы, не
ice вершины которых принадлежат к Ф0 (так как такие симплексы
Имеют диаметр > г).
„ , Пусть это будут
Долагаещ

456 относительные циклы и их применение [гл. хц
Тогда
Ставя в соответствие каждому циклу zr^Zr((i>) цикл (Г0) zr,
получаем гомоморфное отображение (Г0) группы Zr (Ф) в 7/ (Фо)-)«
При этом, если
гг ~ 0 в Ф,
то (в силу замечания 2 арт. 6 :1)
Go) ^-Ов Фо,
1 о
так что (Г0) порождает одноимённый гомоморфизм группы ^(Ф)
в Д» (Фо)- Так как
то из (Г0)гг~0 в Ф0 следует zr~0 в ф, т, е, (Г0) есть
изоморфизм группы Д£ (Ф) в Д£ (Ф0). Пусть
есть Г0-цикл компакта Ф0, содержащийся в $0.
Ра
имеем
Рассматривая zr как элемент группы Zr (Ф),
откуда следует, что (Г0) отображает Д£ (Ф) на дг (Ф), что и
требовалось доказать.
Из только что доказанного предложения [6:21] следует:
Теорема [6: 22]. Пусть в метрическом пространстве R даны
два компакта Ф2с/? и Ф2?=^> пересечение которых содержит
непустое множество Г, открытое как в Фг, так и в Ф2.
Если р£Г, то группы Д£(Ф1? 21) и Д£(Ф2, 51) изоморфны между
собой.
В самом деле, обе эти группы изоморфны по доказанному группе
а;(г> щ-
Определение [6:2]. (Локальные группы Бетти локально
компактного метрического пространства.) Пусть R — локально
компактное метрическое пространство и р — какая-нибудь точка/?. Под
(определённой с точностью до изоморфизма) группой Д£ (/?, 51)
понимаем группу Дг (Г, 51), где Г — какая-нибудь окрестность точки р
в пространстве R с компактным замыканием Г.
Из доказанного следует, что это определение не зависит от
специального выбора окрестности Г,

§ 7J
ЛОКАЛЬНЫЕ Д-ГРУППЫ ПОЛИЭДРОВ
457
§ 7. Локальные Д-грунпы полиэдров.
7 :1. Обозначения и предварительные замечания. ПустьФ = Кл—■
полиэдр, р — произвольная точка Ф. Как всегда, Kah обозначает
/г-кратное барицентрическое подразделение комплекса Ка\ индекс а
(соответственно а/z) означает, что речь идёт о подкомплексе
комплекса Ка (соответственно Ка}1): переход от какого-нибудь
подкомплекса Ка (или Kuh) к его подразделению в Каи обозначается
приписыванием к индексу данного подкомплекса справа ещё индекса k.
Черт. 136.
Оа означает звезду носителя точки р в комплексе Ка. Через олП
обозначаем звезду носителя точки р в комплексе Ка]Ъ.
Квадратные скобки, как всегда, обозначают комбинаторное
замыкание данного неполного комплекса.
Далее полагаем (черт. 136)*)
Q* = [О. ] \ Оа , qafl = [oah] \ oah,
Pah=[Oah\\Oah>
где в соответствии с принятыми условиями [ОаЛ] = [Оа]ь есть
подразделение [О J в Kah\ точно так же Qah есть подразделение
триангуляции Qa.
Тела комплексов
0«, °*ъ, [OJ, [oah], Q«, qah9 Pah
обозначаем соответственно через
Г«, Т«Л. Ф«> Т«Л, ^«э Ф«Л> ПаЛ;
*) Чертёж сделан в предположении, что носитель точки р в комплексе
Ка совпадает с точкой р (т. е. что р есть вершина комплекса Кл, значит,
и комплекса К^ъ). Читателю предоставляется сделать чертежи и к другим
рлучаям.

458 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. ХЩ
при этом Фа, <раЬ, Ч?а, фаЛ, Uah суть полиэдры и
Фа = Га U W„ ?a/i = 7«7* U ^а7„ НвЛ = (Фв\ <?аЛ) U фаЛ.
Обозначаем, наконец, через С6, 0^:6^1, деформацию поли^
эдра П^, определённую следующим образом. Через каждую точк^У
у £ПаЛ проведём луч pj; и рассмотрим точку Сху этого лучаЛ
в которой он выходит из замыкания носителя точки у в комплексе!
Ка. Очевидно, Сгу £ Wa. По определению, точка Сву лежит н($
отрезке [у, Cty] и делит его в отношении 6 :(1—6). >
В силу деформации С9, весь полиэдр Hah, значит, и tyah пере-!
водится в Ч7а, причём вся деформация происходит в ILah и все точки*
множества Wa остаются неподвижными. Отсюда следует, что каж-<
дый истинный цикл полиэдра фаЛ гомологичен в Па7г некоторому!
истинному циклу полиэдра Ч7а.
Отсюда (на основании [4 :61] главы 11):
[7:11]. Каждый цикл комплекса qah гомологичен в РаЬ
некоторому циклу комплекса Qah.
7:2. Основная теорема.
[7:2]. Группа Д^(Ф, 91) изоморфна группе Дг(Оа, %). ;
Доказательство. Так как группа Д£ (Ф, Щ изоморфна группе 1
А;(Ф«, Я) О силу [6:21]), а группа Д'(Оа, %) —группе Д^а (Га, Щ
(в силу [4:2]), то достаточно доказать изоморфизм Д^(Фа, 51) и)
Дф (Га, 31). 1
ОС ;
Вместо 2^а(Га, %), Яфа(Га) 51), Афв(Г«, 91) будем писать Z'.j
Нг, А', вместо Z^«, 51), /£(Фв> «), Д£(Ф„, 91) будем писать ZpA
н;, д;.
Изоморфное отображение / группы Дг на Д^ строится так.
Каждый элемент zr группы Zr есть в то же время элемент?
группы Zp, так что
(7:21) Zr<=.Zp-
Кроме того, из zr — 0 в Фа следует zr~0 в Ф так что
га *
(7:22) /*ЕЯ£
Из (7:21) и (7:22) вытекает, что тождественное 'отображение
группы Zr в группу z£ порождает гомоморфное отображение /
группы Дг в группу AjJ. Докажем, что этот гомоморфизм / есть
изоморфное отображение группы А** на группу Д£.
Первый шаг. Гомоморфизм I есть отображение группы Дг
на группу А^.

§ 7]
ЛОКАЛЬНЫЕ Д-ГРУППЫ ПОЛИЭДРОВ
459
В самом деле, пусть $£ 6 4р- Берём в гомологическом классе
1гр некоторый цикл ъ\ в точке р; при некотором Г, содержащем
/?, цикл ъ\ есть Г-цикл. Берём столь большое /г, чтобы 7аЛ^Г (см.
черт. 136).
Тогда 7«л"Цикл Теж2' гомологичен циклу Zi в точке р и,
следовательно, содержится в $£.
Будучи -у^-ииклом в полиэдре сраЛ, являющимся телом комплекса
[oe7J, цикл ^ал zj»> несомненно, -у^-гомологичен и, следовательно,
гомологичен в точке р циклу zr вида
(7:23) zr = (z[h sl + 1zrah ,. . .,slzrahi. .-.)»
где г£л £ Zr(oa^) и $£г«л есть подразделение цепи г\ь в /СаЛ.
В силу [7:11], цикл Аг^ гомологичен в Pah некоторому циклу
гг*п комплекса Qah, так что существует цепь (черт. 136)
(7:24) ybZL'iP*),
удовлетворяющая условию
(7:25) Д.4 =гг^г — Дг^-
Пусть & > h; тогда в комплексе РаЛЛ.
(7: 26) As£ j4 = sU'ah г — Д**4.
Положим теперь
(7:27) *«» =*«*+.&.
В силу (7: 27), (7: 26),
(7: 28) As£ xrah = Ast <л + Д*£ yln = 4 *г.л * 6 ^r ~J (Q.*)-
Из (7 :28) следует, что
z'r = (.*4, s* + i *«*,..., 4*«fc>...) £ ^-
Наконец, так как 5а Хл есть ^епь комплекса РаМ, тело которого
не пересекается с ^ah, то
и, следовательно,
так что zr ~ z'r в /7 и, значит, ъ'г £ ZJJ. Итак, в каждом
гомологическом классе $£ ^ А^ содержится хотя бы один элемент группы

460 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
Zr, а это и значит, что гомоморфизм / группы Дг в группу Д^,
порождённый тождественным отображением группы Zr в Z^, есть
отображение на всю группу Д^.
Второй шаг. Гомоморфизм I группы Дг на Д£ есть
изоморфизм. Пусть f £ Дг и пусть 1(f) есть нулевой элемент группы
Д£, т. е. пусть один какой-нибудь и, следовательно, всякий Га-цикл,
Черт. 137.
содержащийся в f, гомологичен нулю в точке р. Надо доказать,
что тогда ir есть нулевой элемент группы Дг. Для этого достаточно
найти в $г-цикл, Га-гомологичный нулю в Фа.
В гомологическом классе f, как и во всяком элементе группы
Дг, содержится цикл zj вида
(7:29) з£ =(*![, 4i,..., *«*,...)>
где г« £ Zr(Oa) и га есть подразделение г£ в Kah.
Докажем, что z\^ 0 в Фа этим и будет доказана теорема.
Так как по предположению z[ гомологичен нулю в р, то
существует такая окрестность Г точки р, что
Г21Т0 в Фа.
Берём столь большое h, чтобы ч*ь ^ Г (черт. 137). Тогда из
Tzi ^0 в Фа следует (на основании замечания 2 арт. б : 1), что
г
Т«лЙ~0 в ср^.

§ 71
ЛОКАЛЬНЫЕ Д-ГрУППЫ ПОЛиЭДРОЁ
461
Наконец, отбросим в (7 :29) первые h членов zra, zral,.. ., г^л-ь
получим Га-гомологичный циклу z[ Га-цикл zr, который можем
записать в виде
(7:291) 1Г = (г1ъ, 5л + 1*Гл ,.. ., s\zrahi..,\
причём
(7:292) W^^O в ?вЬ.
Ja/i
Достаточно доказать, что zr-v.O в Фа.
1 а
Для этого замечаем, прежде всего, что
h г л h г Л г
поэюму
(7 : 293) «ыЬгг = (oa7i *«&, s& +1 оаЬг»л ,.. ., skoahz^h ,...)>
и из
иггл;0 в ?аЛ
Л ah
следует, что
гак что существует такая цепь
что
A^fc-«r«t1=Oe;
Полагая
u<xh
hzoih ^
ylh = АовЬ xJii1"* — A xrat\
имеем
(7:294) ле^ча
(7:295) kx\tг = oahzrah — углН .
При этом из
О = ДДх«л+ * = &ОаП Zah A Vlh
следует
(7:296) Д4 = Aoeh*«*.
Положим теперь для k — h, A-j-1,...
(7: 297л) г & = 4 ((*л — о«л 4л) + у«л )
и докажем последовательно три утверждения (7 :297), (7:298), (7:299),
наглядный смысл которых ясен из черт. 137:
(7:297) z'—«'v *£fc+1 ,..., <;ft , ...)€^>

462 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ* XI
т. е. г'т есть Га-цикл компакта Фа;
(7:298) z^z'r в Фа;
1 а
(7:299) z'^UOUVF.)
(т. е. г'г есть (П^ЧД^-цикл компакта ПаД
Прежде чем доказать эти три утверждения, убедимся, что из
них уже следует нужное нам соотношение
(7:2991) z'~0 в ФвЛ
1 a
и, значит, вся теорема [7:2]. В самом деле, так как гГг есть
(ПаЛ\Чга)-цикл полиэдра ПвЛ, а деформация Q есть (*Fa,
^-деформация полиэдра Hah, причём
^(11^) = ^,
то, в силу следствия теоремы [3:31],
значит, и
z\ ~ 0 в Пвй,
7'г ~ Л В Ф
т. е.
(7:2992) z^~0 в Фа.
Нужное нам соотношение (7 :2991) содержится в (7 :298) и (7 :2992).
Итак, остаётся доказать (7:297), (7:298), (7:299). Для
доказательства (7 :297) имеем [вследствие (7: 297^)]
т. е., в силу (7 :296),
Так как при />&
угг <>к? 'г
то при достаточно больших k и / имеем
поэтому z'r есть Га-цикл компакта Фв.
Для доказательства (7 :298) имеем
т. е. на основании (7 :295)
SJcZah еак — aSkX*h

§ ?] ЛОКАЛЬНЫЕ Д-ГРУППЫ ПОЛИЭДРОВ 463
или
Наконец, для доказательства (7 :299) имеем
(7 :294) yrah £ и (qah) cir (Prt\QeJl),
откуда (давая & значения /г-j— 1, /г —}— 2,...)
И
что и требовалось доказать.
Следствие 1. Если /?'* есть /z-мерное эвклидово пространство
и /7-точка /?№, то A* (/?", 21) изоморфна 21, а А£ (/?», 21) при
0<г<я есть нуль-группа.
В самом деле, пусть Тп есть я-мерный симплекс, содержащий р.
Но определению [6: 2] группа kr (Rn9 21) при любом г>0 изоморфна
группе &гАТп, 21), т. е., по теореме [7:2], группе Ап комплекса,
состоящего из одного я-мерного симплекса Гп, по области
коэффициентов 21.
Следствие 2. Размерность полиэдра Ф равна наибольшему
среди тех чисел г, для которых группа Д£(Ф, 21) для какой-либо
точки р£Ф отлична от нуля. При этом за 21 можно взять любую
область коэффициентов.
Следствие 3. Пусть Ф-полиэдр. В каждой не изолированной
точке р полиэдра Ф группа Д^ (ф) есть нуль-группа.
Это утверждение непосредственно следует из теоремы [7:2] и
из теоремы [1 :54,0] главы 8.
Особо подчеркнём:
Следствие 4. Если Ф-—полиэдр, р£Ф и А£ (Ф, 21) не есть
нуль-группа, то носитель точки р во всякой триангуляции Ка
полиэдра Ф есть собственная или несобственная грань некоторого г-мер-
ного симплекса Тг £ Ка.
Доказательство. Если носитель точки р в /Сесть
/^-мерный симплекс Тт, где m>r, то комплекс 0 = ОкТт не содержит
ни одного r-мерного элемента, а поэтому Дг(0) и, следовательно,
Д£ есть нуль-группа. Если носитель Тт точки р имеет размерность
#г<г, но не является гранью никакого r-мерного симплекса
комплекса К, то тело комплекса [ОкТт] есть полиэдр Ф0 размерности
<г, так что А^(Ф0) есть нуль-группа. Но, в силу [6:21], группа
А^(Ф) и Д^(Ф0) изоморфны между собою, чем наше предложение и
Доказано.

464 ОТНОСИТЕЛЬНЫЕ ЦИКЛЫ И ИХ ПРИМЕНЕНИЕ [ГЛ. XII
Следствие 5. Если носитель точки р в триангуляции /z-мер-
ного полиэдра Ф является (п — 1)-мерной гранью k и только k
симплексов Tf, ..., Г^ комплекса Кп, то группа Д^Ф) есть
свободная абелева группа ранга k—1.
Это предложение непосредственно вытекает из теоремы [7:21
и теоремы [1 :54; /z, п — 1] главы 8.
7 : 3. Приложение к инвариантности псевдомногообразий *).!
Назовём гомологически особой точкой /z-мерного полиэдра
Ф такую точку р£Ф, для которой группа АГ1(Ф, J) не есть беско*>
нечная циклическая группа. Из следствий 1 и 5 вытекает, что точка
замкнутого /z-мерного псевдомногообразия Кп, носитель которой^
в данной триангуляции Кп, имеет размерность ^ п — 1, не является
гомологически особой.
Таким образом, множество гомологически особых точек Кп имее^
размерность <Гя— 2. Обратно, если множество гомологически осо-
бых точек какого-либо полиэдра Кп имеет размерность ^ п — 2щ
то каждый (п—1)-мерный симплекс триангуляции Кп является
общей гранью двух и только двух я-мерных симплексов Кп\ если
Kni кроме того, сильно связный полиэдр, то он является замкнутые
псевдомногообразием. >
Итак, мы доказали следующую теорему (глава 10, § 7): <>
[7:3]. Замкнутые n-мерные псевдомногообразия могут быть
охарактеризованы, как n-мерные сильно связные полиэдры ф>
множество гомологически особых точек которых имеет размера
ность <;# — 2. .,
Если при этом А^(Ф)^=0, то Ф ориентируемо, если А70г(Ф)=^ 0,
то Ф неориентируемо. г
Отсюда следует теорема инвариантности для
псевдомногообразий: I
[7:31]. Если данная триангуляция полиэдра Ф есть п-мерное
замкнутое {ориентируемое) комбинаторное псевдомногообразие9
то всякая триангуляция всякого гомеоморфного с Ф полиэдра ф'
также есть n-мерное замкнутое (ориентируемое) псевдомного*
образие.
Упражнение. Сформулировать и доказать теорему,
аналогичную теореме [7 :3], для псевдомногообразий с краем.
*) См. главу Ю, § 7.

ЧАСТЬ ЧЕТВЁРТАЯ.
ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ- ЗАКОНЫ
ДВОЙСТВЕННОСТИ.
V-ГРУППЫ КОМПАКТОВ.
Полиэдры занимают в топологии в некотором роде промежуточное
положение: с одной стороны, образуемый ими класс фигур слишком широк,
с другой стороны, слишком узок. Слишком широк, если иметь в виду
богатство конкретных геометрических фактов и задач, обнаруживающееся при
переходе от полиэдров вообще к их частному случаю — к
многообразиям, которые с самых различных точек зрения оправдали себя как один из
основных и центральных предметов топологического исследования. С
другой стороны, класс полиэдров и их топологических образов оказывается
слишком узким и случайным, если интересоваться большими общими
концепциями современной топологии и искать тот естественный запас фигур,
в котором эти концепции, не переставая быть геометричными
(т. е. не теряя своей исходной связи с нашим пространственным
воображением), раскрывают всю полноту и всё разнообразие своего
математического содержания: если искать такой запас фигур, то в него необходимо
включить во всяком случае все компакты, а повидимому, даже и все
бикомпакты (бикомпактные хаусдорфовы пространства). И это не для того, чтобы
раздвинуть как можно шире самые пределы доступного нам обобщения, а
для того, чтобы понять глубокие закономерности, управляющие большой,
трудной и разнообразной областью математических явлений.
Поэтому не удивительно, что в наши дни всё" с большей отчётливостью
выделяются два направления в топологии: во-первых, топслогия
многообразий, во-вторых, топология бикомпактных и локально бикомпактных хаус-
дорфовых пространств.
Каждое из этих направлений широко разветвляется, и от каждого мы
можем взять в эту книгу лишь немногое, лишь самые простые, самые основные
факты: мы пересечём оба эти направления в той их части, которая до*
ступнз так называемым гомологическим методам, которыми мы только
и занимаемся, начиная с главы 7, и с которыми не расстанемся да самого
конца этой книги. При этом исследовании мы увидим, как обе ьти ветви
топологии смыкаются в одной из высших точек каждой из них: в так
называемом законе двойственности Александера-Понтрягина, являющемся
кульминационной точкой н нашего изложения (глава 14).
Срастание обеих ветвей, о которых идёт речь, можно было бы
проследить и дальше — в гомологическом кольце локально биком пактных
пространств («кольцо пересечений» многообразий), которое, однако, уже
выходит, к сожалению, из рамок этой книги.
Гомологическая теория компактов, одним из самых замечательных
предложений которой и является закон двойственности Александера-Понтрягина,
может быть построена двумя способами. Первый способ основан на том,
что основные понятия Д-цикла и Д-гомологии переносятся на компакты
и служат к определению, в первую очередь, Д-групп компактов. Этим
путём мы шли в главах 11 и 12; его полное развитие с необходимостью

466 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (//-МНОГООБРАЗИЯ) [гЛ. ХШ
приводит к топологизации Д-групп и к рассмотрению областей
коэффициентов, которые сами являются топологическими и притом бикомпактными
группами *).
Второй путь заключается в перенесении на компакты и бикомпакты
V-теории. Этот путь впервые был предложен А. Н. Колмогоровым; вариант,
которым мы идём в этой книге, наиболее тесно примыкает к V-теории
обыкновенных комплексов.
В случае топологических пространств V-теория имеет перед А-теорией то
решающее преимущество, что в ней не требуется никакой топологизации
групп. Повидимому, именно V-теория наиболее приспособлена к
исследованию фигур, более общих, чем полиэдры. По существу, обе теории
эквивалентны, так как двойственны друг другу в смысле понтрягинской теории
характеров.
Основные понятия V-теории бикомпактов и доказательство закона
двойственности Александера-Понтрягина даны в главе 14. Это доказательство
опирается на комбинаторный случай закона двойственности, являющийся
теоремой о расположении подкомплексов комбинаторного /г-многообразия
и изложенный в главе 13. Само понятие /г-многообразия даётся в самом
же начале главы 13. Даётся сразу инвариантное определение,
основывающееся на понятиях, введённых в главе 12, но эта зависимость лишь
кажущаяся, так как несколькими строками дальше ввсдится понятие
«комбинаторного /^многообразия», которым мы только и пользуемся в главе 13. Таким
образом, и 13-ю и 14-ю главы можно читать, не читая глав 11 и 12 (в этом
случае арт. 3:3 главы 14 следует пропустить).
Понятие /г-многообразия (введённое в 1926 —1927 гг. приблизительно
одиовееменно Александером, Понтрягиным и ван-Кампеном) является тем
обобщнием понятия многообразия, которое естественно для построения
гомологической теории: именно, в определении/г-многообразия выделяются
локальные гомологические свойства обыкновенных многообразий —
их гомологическая однородность и гомологическая простота, более
доступные для изучения, чем полная топологическая однородность. В главе
13 даётся элементарная теория /z-многообразий, основными фактами
которой, кроме уже упомянутого комбинаторного случая закона двойственности
Александера, являются закон двойственности Пуанкаре и данное Вебленом
его усиление.
В главе 15 излагается наиболее элементарная часть закона
двойственности Александера-Понтрягина, именно, та его часть, которая касается
кривых полиэдров (в частности, общая теорема Жордана-Брауэра для /2-мерного
пространства). Изложение опирается лишь на главу 13 и на простейшие
понятия из главы 11; оно совершенно не зависит от главы 14. Этому, так
называемому «малому», закону двойственности предпослана теория
зацепления циклов в /2-мерном эвклидовом пространстве, принадлежащая к
классическим элементарным частям топологии и имеющая право на
самостоятельное внимание читателя.
Из дальнейшей литературы по всему только что затронутому кругу
вопросов укажем, кроме уже упомянутой работы Понтрягина:
П.С.Александров, «О гомологических свойствах расположения
комплексов и замкнутых множеств», Известия АН СССР, 6 № 5, 1942.
П. С. Александров, «Группы Бетти и кольцо гомологии локально
бикомпактных пространств», Доклады АН СССР, 26, 1940, стр. 631.
П. С. Ал е к с а ндр о в, «Общая теория гомологии», Учёные записки
Моск. унив., 45, 1940, стр. 1—60, § 9—10.
А. Н. Колмогоров, четыре заметки в Comptes Rendus Acad. Sci., Paris,
202, 1936, стр. 1144, 1325, 1558, 1641.
*) См. Л. С. Понтрягин, «Общий закон двойственности для замкнутых мно*
жеств», Успехи Математических Наук, т. II, вып. 2 (18) (перевод работы
1934 г.), а также цитированную ниже статью Steenrod'a.

§ 1J ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА 467
J. W. Alexander, On the Connectivity Ring of an Abstract Space,
Annals of math. 37, 1936, pp. 698—708.
N. E. Steenrod, Universal Homology Groups, Amer. Journ. of Math,48,
1936, pp. 661—701.
В этих работах можно найти ссылки на более раннюю литературу.
ГЛАВА ТРИНАДЦАТАЯ.
ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (А-МНОГООБРАЗИЯ).
§ 1. Определение и простейшие свойства.
1 : 1. Определение ^-многообразий.
Определение [1:1]. Связный п-мерный полиэдр,
целочисленные локальные группы Бетти которого в каждой точке
изоморфны локальным группам Бетти n-мерного эвклидова
пространства, называется n-мерным гомологическим многообразием или,
короче, п-мерным /г-многообразием.
Другими словами, л-мерное ^-многообразие — это такой
n-мерный связный полиэдр Ф, что для каждой точки р £ Ф группа Ар (Ф,У)
есть бесконечная циклическая группа, а АГ^(Ф,7) для всех г<л
есть нуль-группа.
Замечание 1. Если Ф есть /г-мегнэе ^-многообразие, то, как
будет доказано в замечлнии 3, для любой области
коэффициентов % группа А^(Ф, 21) при г < п есть нуль-группа, а группа
А^(Ф, %) изоморфна группе 91.
Из теоремы [7:2] предыдущей главы следует:
[1: 11]. Если Ф есть /z-мерное ^-многообразие, то всякая триан-
1уляция Ка полиэдра Ф обладает следующим свойством:
(1:11). Для любой звезды Оа = бКлТЛ, Га£ Ка9 группа А% (Оа)
есть бесконечная циклическая группа, а группы Д£ (Оа) при г < я
суть нуль-группы.
Замечание 2. Отсюда на основании следствия 5 теоремы
(7:2] предыдущей главы, в частности, следует, что ко всякому
(я—1)-мерному симплексу комплекса Ка примыкают два и
только два л-мерных симплекса. Кроме того, Ка, очевидно, размерно
однородный комплекс (см. главу 8, определение [3:11]). Если какая-
нибудь триангуляция полиэдра Ф обладает свойством (1:11), то им
обладает и всякая триангуляция полиэдра Ф, и Ф есть л-мерное
^-многообразие. Таким образом, л-мерные симплициальные
комплексы, удовлетворяющие условию (1:11), и только они, изоморфны
триангулициям ^-многообразий; эти комплексы называются комби-
на торными й-м ногообразиями.
Во всей этой главе 'мы только и будем иметь дело с
комбинаторными ^-многообразиями; поэтому рассуждения этой главы по
существу не зависят от главы 12, но инвариантное содержание
получают именно в силу результатов главы 12.
30*

468 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (А-МНОГООБРАЗИЯ) [ГЛ. Xtili
Замечание 3. Из теоремы [4:1] главы 9 следует: если А0г(Ов)
при г<л есть нуль-группа, а А^(Оа)— бесконечная циклическая 1
группа, то Аг(Оа,21) также есть нуль-группа, а Аи(Оа, %) изоморфна j
группе 31. Отсюда вытекает утверждение замечания 1.
Замечание 4. Из определения [1:1] и следствия 1 теоремы
[6:2] предыдущей главы непосредственно следует, что всякое
п-мерное многообразие есть ^-многообразие. \
1 :2. Элементарные свойства А-многообразий.
[1:21]. Пусть К есть n-мерное комбинаторное к-многообразие%\
е — вершина К\ звезда 0%е есть n-мерное ориентируемое псевдо-}
многообразие.
В самом деле, так как К есть л-мерный размерно однородный
комплекс, то, как легко видеть, Оке также размерно однородный
л-мерный комплекс. *
Если Тп~г — какой-нибудь (п—1)-мерный симплекс 0#е, то оба^
/z-мерных симплекса, примыкающие к Тп~1 в К, принадлежат 0%е. 1
Докажем, что О^е есть сильно связный комплекс. 4
Предположим, что это не так; тогда в 0%e существуют два
л-мерных симплекса Т\ и T*+v которые не могут быть связаны^!
цепочкой л-мерных симплексов. Пусть Г™, . .., Тп все /2-мерные^
симплексы Оке, связанные с Т\ цепочками л-мерных симплексов»-;
a Tn^v ..., T^^+v — остальные n-мерные симплексы комплекса
О^е. Обозначим через К' комплекс, состоящий из всех принадпЗ
лежащих 0%е граней симплексов Г", . . ., Г", а через К" — k°mJ
плекс, состоящий из всех принадлежащих Оке граней симплексов!
7^+ii. ••, ^+v (B обоих случаях берутся как собственные, так!
и несобственные грани. Тогда К' и Кп замкнуты в Оке: i
а пересечение К! и К" не может иметь размерность > п — 2. Эт<н
пересечение непусто, так как е есть общая вершина всех элементов!
Оке и> следовательно, принадлежит всякому непустому замкнутом^]
подкомплексу комплекса 0#£, в том числе К' и Кг/- \ц
Из определения комплексов К' и К" следует далее, что если Тл'тХ%
есть (п—1)-мерный симплекс какого-либо из этих комплексов, то,1
оба прилегающих к Тп~1 л-мерных симплекса принадлежат к тому же!
комплексу К! или К", что и Т7*-1. Поэтому, взяз все л-мерные|
симплексы комплекса К' с коэффициентом 1, получим я-мерныйл
цикл по модулю 2:
А^г1{кг^2)^гЦрке,]2). \
Точно так же, взяв все д-мерные симплексы комплекса К" с
коэффициентом 1, получим цикл по модулю 2: }
zS^ZI{K",J^ZI{Ok£>J.2). ,j

§ 1]
ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА
469
Так как циклы znx и z^ суть отличные от нуля и друг от друга
элементы группы Z2(Oa'£,J2), то порядок группы Zl(0KeyJ2) = А^(0#е,У2)
больше двух. Между тем, группа А^(О^) есть бесконечная
циклическая группа, а группа AJJ-1 (0#е)есть нуль-группа, откуда следует
(глава 9, теорема [4:1]), что группа Ал (0#£, J2) имеет порядок 2.
Полученное противоречие доказывает, что Оке сильно связно и,
значит, представляет собою л-мерное псевдомногообразие.
Так как группа A п0(Оке) отлична от нуля, то псевдомногообразие
Оке ориентируемо, чем предложение [1:21] доказано.
Теорема [1: 22]. Всякое h-многообразие есть замкнутое
псевдомногообразие.
Доказательство. Пусть К—какая-нибудь триангуляция
/г-мерного А-многообразия.
Принимая во внимание замечание 2 в арт. 1:1, надо только
доказать, что К есть сильно связный комплекс. Пусть это не так.
Тогда К можно представить в виде суммы двух непустых размерно
однородных л-мерных замкнутых подкомплексов К' и К",
пересечение которых есть комплекс размерности ^п — 2.
Пусть е — какая-нибудь вершина /С'П/(". Имеем
Оке = (Оке П К') Щрке П К"),
причём, из е £ К' П К" и размерной однородности /г-мерных
комплексов К' и К" следует, что О^е П К' и Оке П К" суть непустые /г-мер-
ные (даже размерно однородные) комплексы; эти комплексы
замкнуты в Оке, так как К! и К" — полные комплексы. Наконец,
(Оке П К') П {Оке П /С") с /С'П/Г,
поэтому размерность пересечения (Оке П /С') П (Оке П /С") не
превосходит п — 2. Отсюда следует, что никакой /г-мерный симплекс
комплекса Оке П /С' нельзя связать цепочкой /г-мерных симплексов ни
с каким я-мерным симплексом О/^П/С", значит комплекс Оке не
может быть сильно связным; тем более, он не может быть
псевдомногообразием— в противоречие с теоремой [1:21]. Этим теорема
[1 :22] доказана.
Теорема [1 : 22] оправдывает следующее определение:
Определение [1:23]. Данное /г-многообразие называется
ориентируемым, если оно представляет собою ориентируемое
псевдомногообразие. В противном случае оно называется
неориентир у е м ы м.
[1:24]. В обозначениях [1:21] край Вке звезды Оке при
я;>2 есть (п—1)-мерное простое*) h-многообразие.
*) Псевдомногообразие (в частности, /г-многообразие) размерности п
называется простым, если оно ориентируемо и его Аг-группы при 0<г<я суть
нуль-группы.

470 гомологические многообразия (/г-многоовразия) [гл.
Доказательство. При 0<г группа А^+1 (Оке) изомо{
группе hr0(BKe) на основании следствия теоремы [1 : 55] главы-!
Отсюда и из [1 : 11] следует, что группы &г0(Вке)
0<г< п — 1 суть нуль-группы, тогда как группа A^"1 (BKe) ее
бесконечная циклическая группа.
Остаётся доказать, что при 0 < г < п— 1 группа Аг звезды любе!
элемента Т £Вке относительно В ке есть нуль-группа и что группа Ai
этой звезды есть бесконечная циклическая группа. И то, и друг|
утверждение следует из того, что, полагая В%е = В, имеем *) О^еТ*
= еОвТ и что поэтому, в силу главы 8, теорема [1 : 550], rpymj
&г(ОвТ) и кг+г(ОкеТ) изоморфны между собой**). 7
1 :3. Случай п <;3. Все одномерные замкнутые псевдомно^
образия гомеоморфны окружности (глава 8, арт. 3:1, пример 1°); т|
как окружность есть многообразие (значит, и подавно ^-многообразие!
то при п = 1 понятия замкнутого псевдомногообразия, А-многооб|
зия и многообразия совпадают между собой.
Переходим к случаю п = 2. Здесь, прежде всего, имеются 34
кнутые ориентируемые псевдомногообразия, не являющиеся Л-мн<Ц
образиями: такое псевдомногообразие, например, получим, идеи
фицируя между собой две какие-нибудь точки двумерной сфер
(черт. 122).
Далее, мы знаем, что существует бесконечное множество попарь
не гомеоморфных между собой замкнутых двумерных многообраз!
(замкнутых поверхностей) и среди них бесконечно много ориентиру
мых и бесконечно много неориентируемых. Докажем, что ими исче|
пываются и все двумерные /г-многообразия.
В самом деле, пусть К—триангуляция двумерного А-многообр<
зия К и е — какая-нибудь вершина К\ из [1 :21] следует, что Kpi
звезды Оке есть замкнутое одномерное комбинаторное псевдомного
образие, т. е. замкнутый полигон без кратных точек; отсюда ера
вытекает, что тело звезды 0%е гомеоморфно внутренности круга. Ита!
всякое двумерное //-многообразие есть многообразие. Докажем, накс
нец, что всякое трёхмерное ^-многообразие также является много-
образием. Для этого достаточно доказать, что тело звезды Оке ДЛщ?
любой вершины е триангуляции К трёхмерного /г-многообразия Шч
гомеоморфно внутренности трёхмерного шара. Это обстоятельства*
в свою очередь, будет доказано, если мы убедимся, что край В%е
упомянутой звезды Оке имеет тело, гомеоморфное двумерной сфере.
Но, в силу [1 :24], комплекс В & является простым двумерным
^-многообразием, т. е. тело комплекса Вке есть замкнутая поверх-
*) Глава 4, теорема [2:31].
**) Приведённое здесь доказательство теоремы [1*24] сообщено мн~е
Л. С. Понтрягиным.

§ 1] ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА 471
ность, одномерная А-группа которой есть нуль-группа; значит, эта
поверхность гомеоморфна сфере, что и требовалось доказать.
Мы доказали следующее предложение:
[1 : 3]. При п^Ъ всякое n-мерное замкнутое h-многообразие
является многообразием.
Заметим, что уже при п — 4, а также при всех л>4 имеются
замкнутые ^-многообразия, не являющиеся многообразиями.
Дело в том, что для любого п^4 имеются замкнутые (п —
^мерные многообразия (так называемые «пространства Пуанкаре»), не
гомеоморфные (п —
^-мерной сфере, но имеющие,
несмотря на это, А-группы,
изоморфные А-группам
соответствующих размерностей
(п — 1)-мерной сферы.
Предположив этот факт
доказанным, возьмём в /^9^+1
полиэдральный комплекс К,
являющийся триангуляцией
некоторого (п — 1)-мерного
пространства Пуанкаре; все
вершины комплекса К
предполагаем в общем
положении. В том же jf^n+i
возьмём ещё две точки е0 и ех
так, чтофы они вместе со
всеми вершинами К были
в общем положении.
Спроектировав К из е0 и еи
получим две пирамиды с
общим основанием /Си вершинами ^0и^. Эти две пирамиды вместе
образуют я-мерный комплекс Кп, являющийся, как легко доказать,
триангуляцией я-мерного /г-многообразия. Однако, Кп не есть
многообразие, так как О^е0 и Ок^1 не гомеоморфны внутренности я-мер-
ного шара.
Итак, построение ^-многообразий, не являющихся многообразиями,
сводится к построению пространств Пуанкаре.
Следующий пример, заимствованный из «Топологии» Зейферта
и Трельфалля, является, повидимому, простейшим примером
трёхмерного пространства Пуанкаре: искомое многообразие получается,
если проидентифицировать противоположные грани додекаэдра,
предварительно повернув в каждой паре противоположных граней одну
тс
из них на угол ^ относительно другой. Точная схема этой
идентификации указана на черт. 138. На нём изображены 11 граней
додекаэдра, двенадцатая изображается внешней областью ко всей фигуре.
Подлежащие идентификации элементы (вершины, рёбра, грани) обоз-
Черт. 138.

470 гомологические многообразия (/г-многоовразия) [гл. хп
Доказательство. При О<г группа Д£+1 (0^) изоморфна
группе &1(Вке) на основании следствия теоремы [1 : 55] главы 8.
Отсюда и из [1 : 11] следует, что группы k0(BKe) при
0<г< п — 1 суть нуль-группы, тогда как группа Д^"1 (В%е) есть
бесконечная циклическая группа.
Остаётся доказать, что при 0 < г < п— 1 группа Дг звезды любого
элемента Т £Вке относительно В %е есть нуль-группа и что группа Ag-^
этой звезды есть бесконечная циклическая группа. И то, и другое
утверждение следует из того, что, полагая В%е = В, имеем*) 0/^7 =
= еОвТ и что поэтому, в силу главы 8, теорема [1 : 550], группы
Аг(0БГ) и ^+1(ОкеТ) изоморфны между собой**).
1 :3. Случай п <^3. Все одномерные замкнутые
псевдомногообразия гомеоморфны окружности (глава 8, арт. 3 : 1, пример 1°); так
как окружность есть многообразие (значит, и подавно ^-многообразие),
то при п = 1 понятия замкнутого псевдомногообразия, /г-многообра«
зия и многообразия совпадают между собой.
Переходим к случаю п == 2. Здесь, прежде всего, имеются
замкнутые ориентируемые псевдомногообразия, не являющиеся Л-много-
образиями: такое псевдомногообразие, например, получим,
идентифицируя между собой две какие-нибудь точки двумерной сферы
(черт. 122).
Далее, мы знаем, что существует бесконечное множество попарно
не гомеоморфных между собой замкнутых двумерных многообразий
(замкнутых поверхностей) и среди них бесконечно много
ориентируемых и бесконечно много неориентируемых. Докажем, что ими
исчерпываются и все двумерные ^-многообразия.
В самом деле, пусть К—триангуляция двумерного /г-многообра»
зия К и е — какая-нибудь вершина К; из [1 :21] следует, что край
звезды Оке есть замкнутое одномерное комбинаторное
псевдомногообразие, т. е. замкнутый полигон без кратных точек; отсюда сразу
вытекает, что тело звезды 0%е гомеоморфно внутренности круга. Итак,
всякое двумерное ^-многообразие есть многообразие. Докажем,
наконец, что всякое трёхмерное ^-многообразие также является
многообразием. Для этого достаточно доказать, что тело звезды Оке для
любой вершины е триангуляции К трёхмерного ^-многообразия К
гомеоморфно внутренности трёхмерного шара. Это обстоятельство,
в свою очередь, будет доказано, если мы убедимся, что край Вке
упомянутой звезды Оке имеет тело, гомеоморфное двумерной сфере.
Но, в силу [1 :24], комплекс B%e является простым двумерным
^-многообразием, т. е. тело комплекса В#е есть замкнутая поверх-
*) Глава 4, теорема [2:31].
**) Приведённое здесь доказательство теоремы [1*24] сообщено мне
Л. С Понтрягиным.

§ 1] ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА 471
ность, одномерная А-группа которой есть нуль-группа; значит, эта
поверхность гомеоморфна сфере, что и требовалось доказать.
Мы доказали следующее предложение:
[1 : 3]. При п^Ъ всякое n-мерное замкнутое h-многообразие
является многообразием.
Заметим, что уже при л ==4, а также при всех я>4 имеются
замкнутые ^-многообразия, не являющиеся многообразиями.
Дело в том, что для любого п^4 имеются замкнутые (п —
^мерные многообразия (так называемые «пространства Пуанкаре»), не
гомеоморфные (п —
^-мерной сфере, но имеющие,
несмотря на это, А-группы,
изоморфные А-группам
соответствующих размерностей
(п — 1 )-мерной сферы.
Предположив этот факт
доказанным, возьмём в /?9^+1
полиэдральный комплекс К,
являющийся триангуляцией
некоторого (п— 1)-мерного
пространства Пуанкаре; все
вершины комплекса К
предполагаем в общем
положении. В том же R2n+i
возьмём ещё две точки е0 и ех
так, чтофы они вместе со
всеми вершинами К были
в общем положении.
Спроектировав К из е0 и еи
получим две пирамиды с
общим основанием /Си вершинами е0не1. Эти две пирамиды вместе
образуют я-мерный комплекс Кп, являющийся, как легко доказать,
триангуляцией /z-мерного /г-многообразия. Однако, Кп не есть
многообразие, так как О#£0 и Ок^1 не гомеоморфны внутренности
/г-мерного шара.
Итак, построение Л-многообразий, не являющихся многообразиями,
сводится к построению пространств Пуанкаре.
Следующий пример, заимствованный из «Топологии» Зейферта
и Трельфалля, является, повидимому, простейшим примером
трёхмерного пространства Пуанкаре: искомое многообразие получается,
если проидентифицировать противоположные грани додекаэдра,
предварительно повернув в каждой паре противоположных граней одну
из них на угол -^ относительно другой. Точная схема этой
идентификации указана на черт. 138. На нём изображены 11 граней
додекаэдра, двенадцатая изображается внешней областью ко всей фигуре.
Подлежащие идентификации элементы (вершины, рёбра, грани) обоз*
Черт. 138.

472 гомологические многообразия (^-многообразия) [гл. XI
начены одинаковыми буквами или цифрами. В частности,
двенадцатая грань (о которой только что говорилось) обозначена цифрой I.
Доказательство того, что в результате этой идентификации из
додекаэдра получается действительно трёхмерное пространство Пуанкаре,
читатель может найти в книге З'ейферта и Трельфалля, стр. 250 —
251 (русское издание).
1 :4. Барицентрические звёзды в ^-многообразиях. Пусть
дано л-мерное /г-многооэразие К) пусть К\ — барицентрическое
подразделение комплекса К. Во
всех исследованиях, связанных
с /г-многообразиями, основное
значение имеет следующее
предложение:
[1:4]. Все
барицентрические звёзды комплекса К
суть простые
псевдомногообразия.
Доказательство. Для
п = 1 теорема очевидна;
предположим, что она доказана для
п — 1, докажем её для п.
Для этой цели возьмём
какую-либо вершину е
комплекса К и поставим в соответствие
центру тяжести каждого,
отличного от вершины et
симплекса Тг£Оке, ^>0, центр тяжести грани Тг~1 этого симплекса,
противоположной вершине е.
Этим, как легко видеть, установлено взаимно однозначное сим-
плициальное отображение (изоморфизм) 5 края £* барицентрической
звезды Тп(е), сопряжённой вершине е, на барицентрическое
подразделение (Вке)1 комплекса В%е (черт. 139). При этом всякому
симплексу комплекса Z?*, имеющему своей младшей вершиной центр
тяжести некоторого Тг = еТг~1 £0%е, г>0, соответствует симплекс
комплекса (Вке\ имеющий своей младшей вершиной центр тяжести
симплекса Тг~г £ Bge, откуда легко следует, что всякая, лежащая на
В* барицентрическая звезда (т. е. всякий элемент сопряжённого
триангуляции К барицентрического комплекса, являющийся
подкомплексом комплекса В) изоморфна некоторой барицентрической звезде
комплекса В%е (т. е. барицентрической звезде, являющейся
элементом барицентрического комплекса, сопряжённого триангуляции Вке).
Но В%е, в силу [1:24], есть (п—1)-мерное ^-многообразие,
значит, по индуктивному предположению все барицентрические
звёзды комплекса Вке суть простые псевдомногообразия;
следовательно, простыми псевдомногообразиями являются все лежащие на £*
барицентрические звёзды комплекса /£ Так как всякая барицентри-

§ 2] БАРИЦЕНТРИЧЕСКИЙ КОМПЛЕКС /f-МНОГООБРАЗИЯ 473
ч^ская звезда комплекса К, имеющая размерность ^ п—1 лежит
на краю В* некоторой /z-мерной барицентрической звезды Т*п(е),
то мы доказали: все барицентрические звёзды комплекса К,
имеющие размерность ^п — 1, являются простыми
псевдомногообразиями.
Остаётся лишь доказать, что всякая «-мерная барицентрическая
звезда Т*п(е), т. е. звезда, сопряжённая некоторой вершине е
комплекса Кп, есть простое псевдомногообразие. Но это непосредственно
вытекает из [1 :24] и из уже цитированного следствия теоремы
[1 : 55] главы 8 (также из [1 • 11] и из того, что Т*п(е) есть звезда
вершины е в комплексе Кг). Доказательство теоремы [1:4] этим
закончено.
Замечание. По пути мы доказали, что комплексы В* [край
барицентрической звезды Т*(е)] и (Вке)х (барицентрическое
подразделение края звезды Bge) изоморфны между собой.
§ 2. Барицентрический комплекс комбинаторного /ммного-
образия.
2:1. Обозначения; основные предварительные факты. Пусть
К—какая-нибудь триангуляция л-мерного /г-многообразия К. Через Кх
обозначаем барицентрическое подразделение триангуляции К; через Tf
обозначаем р-мерные симплексы триангуляции /С, через Tff
сопряжённые им барицентрические звёзды (р -f- q = п). В силу теоремы [1 : 4]
настоящей главы и теоремы [5 :24] главы 4, барицентрические
звёзды комплекса К образуют фундаментальную систему
подкомплексов комплекса Кх (глава 10, определение [2:21]). Из тех же
георем следует и некоторое усиление этого результата, которое мы
сейчас сформулируем.
Обозначим через К* комплекс всех барицентрических звёзд
комплекса К, через К*0 — какой-нибудь замкнутый яг-мерный (т^п)
подкомплекс комплекса /С*, через К01 Е: ^1 — барицентрическое
подразделение комплекса /С*, т. е. соединение всех вообще
барицентрических звёзд, являющихся элементами К*0\ мы знаем*), что К01 есть
триангуляция. В этих условиях из теоремы [5 :24] главы 4 и теоремы
[1 :4] следует, что элементы комплекса К*0 образуют
фундаментальную систему подкомплексов комплекса К01.
Отсюда и из теоремы [2:32] главы 10 получаем далее:
[2:10]. Пусть t^ суть произвольные ориентации
барицентрических звёзд Г*Г£/С*. Тогда t*^ образуют фундаментальную
систему цепей**) комплекса К01.
*) Глава 4, арт. 5 :4.
•*) Глава 10, определение [2:31].

474 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (^-МНОГООБРАЗИЯ) [ГЛ.
При A^s^/C* эта теорема переходит в:
[2:1]. Система всех ориентированных барицентрических зв
t*r комплекса К есть фундаментальная система цепей комплекса \
Сформулируем отдельно предложения, утверждающие, что ус|
вия 3° и 4° главы 10, определения [2 :31], выполнены для фуц
ментальной системы цепей t*£:
[2:11]. В каждом гомологическом классе
Sr€*r(*oi) }
содержится барицентрическое подразделение sxz* некоторого ццщ
вида г* = 2а^1г
[2:12]. Если цикл вида г£ = stz*,zde г* = 2fl^i/" гомологи*^
нулю в Kv то этот цикл является границей некоторой цепи вщ
2:2. Комплекс й*. Построим теперь, по правилам арт. 1 ;;
а-комплекс й*, определённый данной фундаментальной систем*
цепей f{..
Элементы комплекса ^* будем обозначать через + /*г, причём ес1
ственно fr. соответствует t*f., а —t*r соответствует —£*£. Так $
пара цепей £*£ и —^вполне определена ориентируемым псевдомног
образием Т*г (как пара его ориентации), то а-комилекс Ш* впод|
определён Комплексом /С* в том же смысле, в каком симплициай
ный комплекс К0 определяет ^-комплекс своих ориентирован*^
симплексов. Поэтому, продолжая эту аналогию с симплициальи|
комплексом, мы будем называть группы I
. Lr(St*), Z'(ffi*), Д'(Я*), V'\®*) ij
и т. д. соответственно группами '4
LT(K*), Zr(K*), &r(K% V(/C*) и т. д.
На основании теоремы [2:5] главы 10 можем сформулироват
следующий основной результат:
Т е о р е м а [2 :2], Группы
Д'(Я), Wi), W*)
изоморфны между собой; группы
V'(/C), Wi)> V'(tf*)
также изоморфны между собой

§ 3]
ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ D?
475
§ 3. Индекс пересечения, изоморфизм D? и закон
двойственности Пуанкаре.
3:1. Индекс пересечения (/^Х^7)- Пусть К — ориентируемое
я-мерное /г-многообразие; выберем определённую ориентацию
комбинаторного Л-многообразия К\ т. е. такие ориентации tf, . .., t^n
всех его «-мерных симплексов, чтобьГУ № было циклом. Этим
установлены и ориентации № всех л-мерных симплексов комплекса Kv
Рассмотрим какой-нибудь ориентированный симплекс tf
комплекса К и сопряжённую симплексу | tf \ барицентрическую звезду Т\Я
(всегда p-)rq = n)) дадим этой звезде
произвольную ориентацию t*£. Задание
ориентации f£ равносильно заданию
элемента t*g клеточного комплекса /С*.
Рассмотрим какой-нибудь лежащий на
\tf\ симплекс \tf | комплекса Кг
где aUo<aUl < ... <аи (см. главу 4,
арт. 5:1), т. е. aUo, аи±,. . .,axi суть
центры тяжести граней
Т?о<т1<--<тГ\<Т!
симплекса Г^черт. 140).
Черт. 140.
Рассмотрим, с другой стороны, какой-нибудь ^-мерный симплекс
l<fJH«1<*1<,fl---«i<e|€7',V
причём
аи < аир + г < • • • < аип> т- е- aih *i<p+1, • • • > (*ип
суть центры тяжести симплексов Г? < TV+1 < . .. < 7\п . Дадим
* 1р + 1 1п
симплексам \Щ | и \t\^\ ориентации соответственно одинаковые с
выбранными ориентациями tf симплекса Т% и fft звезды Т*%. Пусть
это будут
:1;Ч =
Симплекс | ащ .. . аНр_г аи аи^ ... auJ есть некоторый
симплекс \t™ | комплекса Kv лежащий на Т^, причём мы обозначим

474 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (/^-МНОГООБРАЗИЯ) [ГЛ. ХЩ
При /С* = /е* эта теорема переходит в:
[2 :1]. Система всех ориентированных барицентрических звезд
t*r комплекса К есть фундаментальная система цепей комплекса Д^
Сформулируем отдельно предложения, утверждающие, что уело-
вия 3° и 4° главы 10, определения [2:31], выполнены для
фундаментальной системы цепей t**.\
[2:11]. В каждом гомологическом классе
Г€ДГ№
содержится барицентрическое подразделение sxz* некоторого цикла
вида z* = 2ДОг
[2:12]. Если цикл вида г£ = sxz*,zde z* = У]^/^ гомологичен
нулю в Kv то этот цикл является границей некоторой цепи вида
2:2. Комплекс й*. Построим теперь, по правилам арт. 1 ; 2,
а-комплекс §?*, определённый данной фундаментальной системой
цепей ff..
Элементы комплекса ^* будем обозначать через jf.^r, причём
естественно fr. соответствует tf*J, а—t*r соответствует—1*£ . Так как
пара цепей t*£ и. — t*^ вполне определена ориентируемым
псевдомногообразием ^*С (как пара его ориентации), то я-комнлекс ^* вполне
определён Комплексом К* в том же смысле, в каком симплициаль-
ный комплекс Kq определяет а-комплекс своих ориентированных
симплексов. Поэтому, продолжая эту аналогию с симплициальным
комплексом, мы будем называть группы
. ZT(St*), Z'(St*), Д'(Я*), V\®*)
и т. д. соответственно группами
LT(K*), Z*{K*\ &Г(К% V'(/C*) и т. д.
На основании теоремы [2:5] главы 10 можем сформулировать
следующий основной результат:
Т е о р е м а [2 :2]. Группы
&г(К), Дч/d), Д'(#*)
изоморфны между собой; группы
Ч*(К), ЩКг), V(tf*)
также изоморфны между собоц

§ 3]
ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ D*
475
§ 3. Индекс пересечения, изоморфизм D« и закон
двойственности Пуанкаре.
3:1. Индекс пересечения (/fX^)- Пусть К — ориентируемое
я-мерное ^-многообразие; выберем определённую ориентацию
комбинаторного ^-многообразия К\ т. е. такие ориентации t%9 . .., /"п
всех его «-мерных симплексов, чтобы V tf было циклом. Этим
установлены и ориентации № всех л-мерных симплексов комплекса К v
Рассмотрим какой-нибудь ориентированный симплекс Щ
комплекса К и сопряжённую симплексу \tf\ барицентрическую звезду Т\Я
(всегда р-\-д = п)\ дадим этой звезде
произвольную ориентацию t*g. Задание
ориентации £* равносильно заданию
элемента ff клеточного комплекса К*.
Рассмотрим какой-нибудь лежащий на
\tf\ симплекс \tf | комплекса Кг
где ali0<alil < .. . < аи (см. главу 4,
арт. 5:1), т. е. aUo, aUl,. . .,а11Г суть
центры тяжести граней
T!o<ni<---<Tf^1<Tf
симплекса 7f (черт. 140).
Рассмотрим, с другой стороны, какой-нибудь ^-мерный симплекс
ч.,\
l1f
ИМ
причём
<*и < % + 1 < • • • < лИя, т. е. а1Ь alip+1
суть центры тяжести симплексов Т% < Г? + 1 < ... < 7\п . Дад
* 1р +1 *п
симплексам |tff | и |^J ориентации соответственно одинаковые с
выбранными ориентациями tf симплекса TV и fft звезды Т$. Пусть
это будут
1;т)= ±1.
Симплекс | ащ .. . л1^_1 аи alifi+1 ... axiJ есть некоторый
симплекс [** | комплекса /fj, лежащий на Т^, причём мы обозначим

476 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (А-МНОГООБРАЗИЯ) [ГЛ. ХШ
через tfj1 ту ориентацию симплекса | Р*х |, которая определяет
ориентацию всего /г-многообразия К- Тогда
где if = zt l.
Докажем, что число sTj-y = zt 1 не зависит от выбора
симплексов \tf | и \tft | и, следовательно, зависит только от tf, t*Q. и
выбранной ориентации /г-многообразия /С
Срстоящее из симплексов \t% |, |^,|, ... и их граней
барицентрическое подразделение симплекса \tf\ есть сильно связный
комплекс. Поэтому, если мы докажем, что число г^-у не меняется при
замене симплекса 11^ | симплексом | tP , |, имеющим с ^ общую (р—1)-
мерную грань, то этим будет доказана независимость числа гщ от
выбора симплекса \tP |.
Итак, пусть |^а| и \tP ,\ имеют общую (р—1)-мерную грань
аи0 • • • яцл_, <*щ + 1 . .. а1€|, т. е. пусть
1^ I = I «х*о - - - ах*л •••«к|.
\%Л = \<*ио---аМк' •••flul •
Тогда симплексы
I *ix I = I аио • • • fli<* ' * * fli* аИр+1 * * * fl"» I
l'ix/ I = I ai*o • ■ -aHft auaup+\ •• -anw|
имеют общую (я — 1)-грань
Если
^= *(aUo---auk--- a«)
и
и tfp-1 есть какая-нибудь ориентация симплекса
например,
^"1=(flwo---fli<ft-iflHft + 1 -.-«и),
то
И /
жены по разные стороны своей общей грани.
так как симплексы tf и Ц^п одинаково ориентированы и располо-

§ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ Dt 477
Но
(/ftt :*/'"!) = (-1)* г,
С^:^-1) = (-!)*«'•
Поэтому г = — г.
Аналогично, если ориентации
*и = Т (*ц0 • • • «i/fc • * • «i^+1 * • • «1/я)
и
равны ориентации ^ и, значит, одинаковы, а
то
(*»,:*»-») = (-1)^', "
Итак,
s4r' = (— e)'i (— т) = ^т.
так что г7|-( не зависит от замены |^ | на |^ ,|. Совершенно так же,
пользуясь сильной связностью комплекса T*f, доказываем, что число
щЧ не зависит от выбора симплекса |^|.
Определение [3:1]. Число ет|-( = ±1, зависящее лишь от tf
£*? и выбранной ориентации ^-многообразий К называется индек"
сом пересечения №. и t*Q в ориентированном А-многообразии К*
и обозначается через (я?Х**?)«
Замечание 1. Пусть /?w, /?р , 7?^— плоскости, несущие
соответственно симплексы |/J*J, |/p|, |^v|, ориентированные так же, как и
/*х, /*, /«v. Тогда (tfXt*f) есть не что иное, как определённый
в главе 7, арт. 2:1, индекс пересечения (#f X#2V-
Индекс пересечения (tfXt*l) при А ^ / (т. е. когда
барицентрическая звезда Г*я не является сопряжённой симплексу Тр по
определению полагается равным нулю.

478
ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (А-МНОГООБРАЗИя) [гЛ, XII!
Замечание 2. Так как при замене tp. на — /?, или t*Q на —1*4
г, соответственно т), меняется на —г, соответственно на —т), то
е-1 г1
Qi вместо allt стоит
а,, и md
(( —/f)X<?)«=
= (tfx(- t*f)) = - (*f X**7).
Далее, при замене данной
ориентации А-многообразия /С на
противоположную, 7 меняется на —-у,
поэтому индекс пересечения № и /*«
меняет знак при перемене ориентации
всего А-многообразия.
3:2. Индекс пересечения и
коэффициенты инцидентности.
Черт. 141.
Лемма [3:21]. Если \Щ'~х\<Щ\,'пьо
(3:2) (*f Х<*?) = (<?:*?- х) ('*/ +': '*?) (—W^ ~ ХХ^+ 3).
Доказательство. Так как из \Щ"Х\<Щ следует \t**\<\t**i-1]
и, значит, (^:^-1) = zt1, (t*j + 1:t*?) = ±l9 то и правая и левая
части равенства (3:2) по абсолютной величине равны 1. Остаётся
доказать, что и знаки обеих частей равенства (3:2) одинаковы.
Рассмотрим сначала самый важный частный случай, когда
(3:21) (*j»:^-i)=l; (/*j+ *:**?.)== Ь
Возьмём лежащий на \tf\ симплекс
HVl = Kb •'•aUp-2aijali\>
где, как всегда, ац0,. . -*ац __2, al:Ji а и суть центры тяжести
симплексов Г?<...<7?~2<7?-1<7^'(черт. 141).
Возьмём симплекс
Возьмём, наконец, ориентации t\ и ^ + г симплексов Щ | и |^в+1|,
одинаковые с ориентациями tfnt***1:
% = £ («1/о • • • аи<*и), Ц+1 = т] (а^аи aiip + 1... alif).
Тогда|<Рр-!| = |fli/0.. .aj лежит на l^"-1^!^), причём, беря
ориентацию tP~l =se(a\iQ.. . al3)9 имеем

^ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ Z> 479
Поэтому, обозначая через stt^ цепь, являющуюся барицентрическим
подразделением цепи #>,
имеем
(3:210) AV? = A^+... = (-iy^-i + ....
Но
а по предположению (3:21)
поэтому
т. е.
(3:211) bsfl = ^ -1 + • ■ •
Сравнивая (3:210) и (3:211), получаем
СИсюда следует, что ориентация (—\)ptf~l симплекса одинакова
с ориентацией №-~1 его носителя l^"1}.
Аналогичным образом
й,1=К+1-ч1бПсТ-
причём, беря ориентацию t^t =ч\(ацаир + 1- ■ • auJ> имеем
('?e+,S'?,)=b
По
Д/^=Д*у + 1 + ... = ^ + ...,
и, с другой стороны, по нашим предположениям (3:21)
откуда следует, что
Л = п 4- .. .,
т- е. что ^ ориентировано одинаково с ориентацией
t"\t псевдомногообразия Г*^.

480 гомологические многообразия (^-многообразия) [гл. xftj
•1
Пусть, наконец, данная ориентация псевдомногообразия Ki onpei
деляется ориентированным симплексом
Подведём итоги сделанным рассуждениям: ориентация
одинакова с ориентацией ££; ориентация ,'
одинакова с ориентацией £*?.; ориентация
одинакова с ориентацией Kv Это значит, что при данной ориентации Ktl
(3:221) ЩХ?Я)^гщ-
С другой стороны, ориентация (—iypq~1 — (—l)Pe(aliQ ... al3)
одинакова с ориентацией tfj-1, ориентация №+г = ?1 (я^-ЯцЯц , . . .пи )
одинакова с ориентацией /Т?"*"1 и, как прежде, ориентация
Ч(аио---аир-2а13аЦр+1---аип) одинакова с ориентацией Kv Это
значит, что при данной ориентации Кх
(3:23) (^"1X^+1) = (-1)^stiT,
т. е.
Итак, в предположении
(3:21) (^:^-i)=i, (#/+i :/*v) == i
формулы (3:2) доказаны.
Откажемся теперь от предположения (3:21) и пусть ;
(tf:q-i) = ztJ, (*;«+! :^) = 7у... ;
Тогда
и, следовательно, по доказанному
(V? >< #) = (—^ ((Г1 x v?z+1)-
Ho
(*? x ф) = s|. (*p x О = %• (e^f X fp,

§ 3J ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ /У7 481
так что
(tf X t*f) = Зд (8,/f X П) = *tj (-1)? (*р X V*}41) =
что и требовалось доказать.
3:3. Изоморфизм Dq и закон двойственности Пуанкаре.
Пусть tf— произвольно выбранная ориентация симплекса Т#
ориентируемого (и ориентированного) я-мерного /s-многообразия К* Из
двух возможных ориентации ориентируемого псевдомногообразия
Т**. обозначаем через fv. ту, для которой
(<fX'*?)=».
Посмотрим, каковы при этом выборе обозначений матрицы
инцидентности ||(<7+1^?)ll = lhJJb
Прежде всего, если l^"1) не есть грань симплекса \tf\, то
(М : tP-1) = 0и (t4^ : t*f) = 0.
По лемме предыдущего артикула имеем в случае |^""1|<|/f|J
г. е. в случае, когда (tf :1Р~1)ф0:
Щ X **f) = (~1У Щ • tPj~l)С*У+1 : t*f)(1f~l X /*?+1)
или, помня, что (# X t*f) = 1, (/f1 X '*?+1) = 1,
откуда, умножая обе части на (— l)P(tf: й~1) и помня, что
(tf:t?-l)=z±h
получим
(3:31) (t*^1 : t*f) = (—l¥(tf :
сопоставим теперь в соответствие каждой цепи хр£1р(К, 51) цепь
x*Q- £№ (/С* Д), принимающую на каждом t*f тоже значение, которое
хР принимает на tf:
Эту цепь x*Q обозначаем через Dqxp. Таким образом, очевидно,
определено изоморфное отображение Dq группы Lp (К) на группу
Докажем следующее основное свойство изоморфизма Dq:
( bD*XP = (—iy+1D*-14xP,
\ V£>W = (— \y>Dv+xkxP.
31 Александров П. С.

482 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (/^-МНОГООБРАЗИЯ) [гл. хШ
В самом деле, полагая для крап-сосги I
и помня, чю
■'-^(-IV'V/1,
v*J
значит,
имеем
(ADW • Z*?-1) =» Vy,? fD^ • /;:|) ~ yr<f.{xP . /I7) =
= (—1)*-">^(л*.^ =
c-(_1)p+»(Va? • /P + i) = (— If+1 {D4~l Vxp ■ t*']-1).
Аналогично
J г г J
Замечание 1. Выпишем только что доказанные тождества:
(3:320) j (y^^p.^+i^^^p^.p.^-^
Из первого равенства (3:32) следует:
а) Если Vx^ = 0, то и AD?x^ = 0, т. е. группа Zpv(K) отобр|
жается при посредстве изоморфизма D? в группу Zl(I\*).
б) Если AD'W=^0, то Z)?-1 Vjtf'^O, значит, V.v* — 0; другиш
словами: если образом, некоторой цепи xp£Lp(I() при изоморфизм
DQ является А-цикл, то хр есть V-цикл, или: прообраз группу
%1 (/С*) при изоморфизме D? группы i>(/0 на 1Я(К*) есть групп
^ {К).
Из а) и б) заключаем: . 1
[3:321]v. При изоморфизме D? группы Lp(K) на £«(#*) групщ
Zy(K) и Zl(K*) соответствуют друг другу. .<
Аналогично выводим из второго равенства (3:32): ;
[3 :321]д. При изоморфизме D? группы LP(K) на L<i(K*) группе
ZHK) и &(К*) соответствуют друг другу.
Докажем далее:
[3:322]v. При изоморфизме Di группы LP {К) на группу Ш(К**)
группы Н? (К) и Hi (ЛГ*) соответствуют друг другу.

§ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ D? 48$
Доказательство.
а) Пусть г1>£1Ц (К); тогда существует такая цепь xp-x£D}-x(K)*
что
Тогда на основании первой формулы (3 : 32)
AD2+1 хР-1 = (— i)PD<i V л?'-1 = (— VpDvzP,
т. е.
D^ £ //J (/С*).
б) Пусть DW>£IIl(K*)>
тогда можно найти x*v+1 £ L*+1(/C*) так, чтобы
Обозначая через /)р изоморфное отображение группы 1Я(К*) на
Lp(K), обратное изоморфизму D?, положим
Тогда (читая первое равенство (3 :32) справа налево и заменяя в
нём р на р—1) получаем
(— \у>й* Vx*-1 = AD^+1a^~1= AZX*-1 Z>p_1jc*ff+1 = Дд;*в+1=0«гР,
откуда (действуя на (—l^D^VxP"1 и на D?^ оператором ОД
(—1)p4xp-1=zp,
т.е. гР£НР(К).
Теорема [3:322]V этим доказана.
Аналогично, пользуясь второй формулой (3:32), получаем:
[3:322]д. При изоморфизме D* группы Н^(К) и Н» (/С*)
соответствуют друг другу.
Из [3:321]у и [3:322]у получаем:
[3 :32]v. Изоморфизм Dq группы L? (К) на Lq (К*) порождает
изоморфное отображение группы VP(K) на группу Д« (/(*).
Но группы Д2(/С*) и Д«(/С) изоморфны между собой (по
теореме [2:2]).
Следовательно, имеет место:
Теорема [3:33]. Закон двойственности Пуанкаре
(в формулировке Колмогорова). Пусть К—
ориентируемое n-мерное h-многообразие; р и q — два произвольных
неотрицательных целых числа, дающих в сумме пу тогда для любой
области коэффициентов группы VP(K) и №(К) изоморфны между
собой.
31*

482 гомологические многообразия (^-многообразия) [гл. хш
В самом деле, полагая для краткости
ij V/ j ;i iJ% \ j tj
и помня, что
гГ1=(-1;'Ч/', .
значит,
гР =(—1у>Н-г/?,
ij v 7 О'
имеем
(ADW • ^J-1) =3 У?{%}Р1хр • /""*р = ^г^.(хр • *f) =
i
e(_l)P+i(Vjci'-^ + 1) = ( —lf4"1^"^^./*^-1).
Аналогично
(VDW • <*? + 1) = 2ri7<+ Ч7^7*7' • t*%) = У,г\ я +\xp • tP) =
Замечание 1. Выпишем только что доказанные тождества:
(3:320) j (v^^.^+i^^i^^p.^iy
Из первого равенства (3:32) следует:
а) Если Чхр = 0, то и ADW = 0, т.е. группа Z^(K)
отображается при посредстве изоморфизма D% в группу Zi(K*).
б) Если ADW = 0, то Dv-mlVxP = 0t значит, Vxp = 0; другими
словами: если образом,некоторой цепи xp£Lp(K) при изоморфизме
D2 является А-цикл, то л'# есть V-цикл, или: прообраз группы
^а (/С*) при изоморфизме D% группы LP {К) на //*(/(*) есть группа
Из а) и б) заключаем:
[3:32l]v. При изоморфизме D<i группы LP {К) на №(К*) группы
Z^(K) и Zl(K*) соответствуют друг другу.
Аналогично выводим из второго равенства (3:32):
[3 :321]д. При изоморфизме Di группы LP (К) на L<i(K*) группы
ZP(K) и ZUK*) соответствуют друг другу.
Докажем далее:
[3:322]7. При изоморфизме D% группы LP (К) на группу L<i(K*)
группы Н? (К) и Hi (ЛГ*) соответствуют друг другу.

§ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ Ь<1 48$
Доказательство.
а) Пусть г*> £ № (К); тогда существует такая цепь х?~1 £ U}~1 (/f),
что
Тогда на основании первой формулы (3 : 32)
AD2+1 хР-1 = (— \yD* Vxp-1 = (— \YDQzP,
т. е.
DW (= //« (/С*).
б) Пусть D<izP£Iil(K*),
тогда можно найти я*^-1 £Z/*+1(/C*) так, чтобы
Обозначая через /) изоморфное отображение группы Z/?(A~*) на
Цр(К), обратное изоморфизму />/, положим
Тогда (читая первое равенство (3:32) справа налево и заменяя в
'нём р на р—1) получаем
(— 1)Р£>« У*1*-1 = AD^1xP"1= AD?*1 Dp^x***1 = Lx*^+1=D^zp9
откуда (действуя на (—l^ZKVx?-1 и на D^ оператором О ),
(—lyv^p-1™^,
т. е. гР £ № (/С).
Теорема [3 :322] V этим доказана.
Аналогично, пользуясь второй формулой (3:32), получаем:
[3:322]д. При изоморфизме D* группы #£(/0 и № (К*)
соответствуют друг другу.
Из [3:321]у и [3:322]у получаем:
п [3:32]v. Изоморфизм Dq группы L? (К) на 13 {К*) порождает
изоморфное отображение группы 1V{K) на группу Дв(/С*).
Но группы М(/С*) и Ья{К) изоморфны между собой (по
теореме [2:2]).
Следовательно, имеет место:
Теорема [3:33]. Закон двойственности Пуанкаре
(в формулировке Колмогорова). Пусть К—
ориентируемое n-мерное h-многообразие; р и q — два произвольных
неотрицательных целых числа, дающих в сумме л, тогда для любой обла-
"СгПи коэффициентов группы VP(K) и Аз (К) изоморфны между
собой.
31*

484 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (^-МНОГООБРАЗИЯ) [гл. ХМ
Частные случаи. Пусть 51 = 7. Так как
Д& (К) = в«(Х)-}-Д «,(£),
то имеет место:
[3: 330]. Группы кручения &р~х(К) и Ш(К) изоморфны, а числа
Бетти кЦК) и %^{К) равны между собой.
Теорема [3:330] представляет собой закон
двойственности Пуанкаре в его первоначальной форме.
Полагая %z=Jvl, выводим из теоремы [3:33] изоморфизм групп
Vm<X) и km(K); значит, вследствие изоморфизма групп Vfn(K)
и Ат(К) [глава 9, формула (4:410)] имеет место:
[3:33ш]. Закон двойственности Пуанкаре по м о-
дулю т. При всяком т группы д^СЮ и Дш(ЛГ) изоморфны
между собой.
Все эти результаты верны в применении к ориентируемым
/z-мерным ^-многообразиям: для неориентируемого л-мерного
/^-многообразия /( имеем я° (К) = 1, я" (К) = 0.
Тем более, важно подчеркнуть:
[3:332]. Закон двойственности Пуанкаре по
модулю 2. Для любого {не непременно ориентируемого) п-мерного
h- многообрази я К группы А^ (К) и Af(^) изоморфны между собой.
Для доказательства достаточно все рассуждения, касающиеся
пересечений, вести «по модулю два», т. е. заменяя во всех вычислениях
этого параграфа все целые числа их вычетами по модулю 2 и
считая все симплексы и звёзды неориентированными. Все вычисления от
этого чрезвычайно упростятся, так как отпадут все соображения,
касающиеся знаков, и станут применимы ко всем ^-многообразиям
(а не только к одним ориентируемым).
Из [3 : 332] следует щ (К) = Щ{К), а отсюда — при нечётном п
вытекает равенство
2 (-wo=s (-^лю=°-
Итак:
[3 : 34]. Эйлерова характеристика любого h -многообразия
нечётной размерности равна нулю*).
*) В частности, триангуляции трёхмерных многообразий имеют
характеристику нуль. Частичным обращением этого утверждения является
следующее предложение, доказываемое без большого труда:

§ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ D« 485
Замечание 2. Полагая в [3:330] р = п, значит, ^==0, видим,
что группа On-1(/0 изоморфна группе в°(/С) и, следовательно, есть
нуль-группа. Таким образом, из закона двойственности Пуанкаре
заново следует частный случай уже известного нам факта (глава 9,
теорема [3 :52]), а именно: ориентируемое n-мерное к-многообра-
зие не имеет (п—Х)-мерного кручения.
3 :4. Индекс пересечения (хр X x*q), гДе хр £ LP (КУ 21),
*2£L2(/C*, 91) и 51 есть кольцо. Сохраняя все обозначения,
введённые в начале этого параграфа^ выберем ориентации tf и t% так,
чтобы было(^Х t*%)— 1, значит, для любых / и j
(^х,*р = 8,..
Пусть
хР = ^а^Р£ LP(ДГД),x*Q = ^ Ъ$*\ €^(**,*)•
Определяем:
(3 :4) (хр X **«) = ^ aibo Щ X '/) = 2еА-
[3:41]. Для любых двух цепе й л;** £ L? (АГД), yP£LP(K,%)
имеем
(3:41). (^х^/) = (^«Я
В самом деле, если
ТО
и, значит,
(хр X D^) = 2*А = (** • J*).
Непосредственным следствием определения (3 : 4) являются, далее,
оба соотношения дистрибутивности:
(3 : 42) j (jcp X (**? + **£)) = (** X ***) + (** X х*$,
Пусть триангуляция А^ возникает из триангуляции К$ некоторого
выпуклого многогранника путём склеивания некоторых элементов комплекса Kl
лежащих на границе выпуклого многогранника Ка. Комплекс К% тогда
и только тогда является триангуляцией трёхмерного многообразия, когда
его эйлерова характеристика равна нулю.
Доказательство этой теоремы можно найти в главе 9, § 60 книги «Топо-
догдя» Зейферта и Трельфалдя,

486 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (Л-МНОГООБРАЗИя) [ГЛ. XIII
а также
(3: 43) (ахР X x*Q) =>(лг* X ax*Q) =>й(^Х**q)•
В теории пересечений основное значение имеет формула
(3 : 44) (хр X Ax*ff+1) = (—iy (Ал? X **«+1),
или
(Lxp X ***+1) = (~- \У(хр X Дх**+1).
Формула (3 :44) будет, в силу (3 : 42) и (3 : 43), доказана, если
мы докажем её для частного случая хр — tf, л;*2 :=£*?.
Итак, надо доказать только
(3:440) (<f ХД^+1) =(-l^(A'f Х<*3+1)-
Но, полагая s^ = (^:^-1), имеем на основании [3:31]
^*l+1 = (-l)*Se«'*v
Поэтому (помня, что Щ X t*f) = 1)
(^ X Д/**.+0 = (-1^2%' (<F Х**# = (-1У*№ X **?) = (-1)* e{j
ь
(мр х **j+1) = 2MT1 x **5+1)=ч№г1 x <*jM) = *&
Итак:
0f X A**f *) = (- l)*(A*f X <*J+1),
что и требовалось доказать.
Следствие из(3: 44). Пусть л;*2 есть цикл, т. е. Дл:*« = 0. Тогда
в (3:44) после замены р на р -+-1 и, следовательно, #-|-1 на q
левая часть равна нулю, и следовательно,
(ДЛГР+1 X х*ч) = 0.
Но в виде &ХР+1 может быть представлен любой цикл гР,
гомологичный нулю. И гак:
[3 :451]. Если z*<* £ Z*(/C*), ^ 6 #д(#)> w0
(^ X **«) = 0.
Аналогично:
[3:452]. Если zp ^Z\(K) и **«£//£(#*), mo (*р X **«)=* 0:

§ 3] ИНДЕКС ПЕРЕСЕЧЕНИЯ, ИЗОМОРФИЗМ D« 487
В самом деле, в этом случае Аг^==0, г*# = Дд;*4+1 и
(гР X z*q) — (zp X кх*^J) = (— \у (Дг* X х*^1) = 0.
Только что доказанные утверждения [3:451] и [3:452] можно
объединить в одно:
[3 :45]. Если из двух циклов zp a z*Q хотя бы один гомологичен
нулю, то
{zp X z*q) = 0.
Из [3:45] непосредственно следует:
Если zPx~z$ (в К), г*«~г*| (в /С*), то
(?р X **$ = (** Х**$)-
Это даёт возможность определить индекс пересечения
двух гомологических классов ЪР£№(К) и $*2£Дз(/е*)
следующим образом — по определению:
($*Xf<0==(^X**<0, *
где циклы zp£$p, z*q£%*z выбраны произвольно.
Замечание. В случае целочисленной области коэффициентов
теорема [3:45] может быть усилена. Пусть z*4 £ Z^ (/С*, J),
гГ' £ № (/С, i). Тогда существует такое целое число с, что
czp£Hp(K, J) и, следовательно, (czP X -г*3) = 0. Но целые числа
(сг0 Xг*9) И С2"77 X <г*дг) связаны между собой соотношением
{czP X z*Q) = c(zp X z*q)> из которого следует, что и (г^ X •г*9:) = 0-
Итак:
[3:46]. £сли W3 двух циклов zp и г*я хотя, бы один слабо
гомологичен нулю (в К, соответственно в /С*), //го (г^ X •г*2) = 0.
3 :5. Теорема Веблена [3 :5]. Ко всякой (7, Щ-базе zp , ..., zp
комплекса К можно подобрать такую (J, Щ-базу z*\, . . . ,г*#
комплекса /С*, **/7хо
Эля любых tj = 1, 2, .. ., я. Яри эягол* тс = т& == тгя равно р-мер~
ному и q-мерному числу Бетти многообразия К.
Доказательство основывается на формуле (3:41)»

488 гомологические многообразия (А-многообразия) [гл. хпМ
В самом деле, в силу теоремы [3:33] главы 9 можно включить!
циклы гР, . . ., zp в каноническую базу ]
ХР, ..., хРр-иуР,. . ., yPp_v гРу. . ., *£, и*\. . ., иРр, j
я?,.--, Кр >
решётки LP (К); в сопряжённой базе *•
(3:51) ^,. . ., Ърр-19 V?,. . ., 'vpp_v1p, ..., ^ *?,. . ., 3V/
рассмотрим V-циклы
(3:52) ^,. . ., zp.
Так как при изоморфизме DQ группы Щ (К) и Н\ (УС*) соответ- \
ствуют друг другу, то никакая нетривиальная линейная комбинация <
А-циклов
(3 :53) D*zf,. . ., ОягР
не гомологична нулю в /С*.
Для того чтобы доказать, что эти циклы образуют (J, Щ)-базу^
комплекса К, достаточно показать, что каждый цикл гя£ Zl(K*)f
отличается от некоторой линейной комбинации циклов D^z? лишь
на элемент группы №(/С*).
Докажем это. Прежде всего z^^=sD^zp, где~>*> £ Z*J (/(). В силу^
основных свойств базы (3:51),
следовательно (так как D« есть изоморфизм),
Так как некоторое целочисленное кратное V-цикла
V-гомологично нулю в К, то такое же кратное А-цикла
v*Q =» 2 ^Dff«f + 2 bpivP
А-гомологично нулю в К*9 т. е. z*z — 2 chD*zPf=v*z£ №(/С*), что
и требовалось доказать. _
Наконец, в силу (3 :41), имеем (sf X £ff*f) = (*f • *J) = 8#>
этим всё доказано.
Следствие из теоремы Веблена. Пусть zp £ Zp (AT),
#о zP(fc№(K); тогда существует такой цикл z*<J (^Zq(K*), что
{zp X г**)^0.

§ 4] КОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 489
В самом деле, если {г*,. . .,г^} есть какая-нибудь (У, 91)-база
комплекса /С, то существуют такие с{, не все равные нулю,
что
гР — ^с^Р£МР(К).
Пусть, например, с{фО. Строим согласно теореме Веблена циклы
г*? £ Z\ (К*), / =• 1,. . ., it так, чтобы (г? X г*р = 8^. Тогда,
в силу [3 :46],
(*р X **<0 == 2 СМ X **?) - <i^°-
Задача. Доказать аналог теоремы Веблена и её следствия для
области коэффициентов Jm при простом т.
§ 4. Комбинаторный случай закона двойственности
Александера.
4:1. Формулировка теоремы. Во всём этом параграфе
К обозначает /г-мерное комбинаторное
ориентируемое /г-многообразие, К0 — замкнутый
подкомплекс комплекса К\ комплекс барицентрических
звёзд комплекса К обозначаем через /С*; через К*0
обозначаем подкомплекс комплекса /С*, состоящий
из всех звёзд, сопряжённых симплексам комплек-
с а /С0.
Известно (глава 4, арт. 5 :4), что /^ — открытый, следовательно,
К*\К*0 — замкнутый подкомплекс комплекса /С*.
Комплекс K*\K*Q не имеет нульмерного кручения.
Это следует из того, что комплекс Q*, состоящий из всех одно-
и нульмерных элементов комплекса К*\К*0, изоморфен одномерному
полному симплициальному комплексу и имеет те же нульмерные
группы Бетти, что и комплекс К*\К^.
Наконец, через р и q обозначаем, как прежде, два
неотрицательных целых числа, сумма которых
равна п. Задача настоящего параграфа заключается в
доказательстве следующей теоремы, которая и представляет собой
комбинаторный случай закона двойственности Александера.
Теорема [4:10]. Пусть 91— произвольная область
коэффициентов. Если для некоторого р, 1<!р<1я— 2, группы Vp(K,W)u
V*+1 (К, 91) суть нуль-группы, то группы Vp (АГ0, 91) и Ag_1 (К*\К*о, 90
изоморфны между собой. Если VW_1(^C ЭД естъ нуль-группа, то
группа Vw-1(K'o, 91) изоморфна группе £fl° (К*\Ко) (в частности,
в случае 9t = J, число компонент комплекса К*\Кх> равно
izn~l (ATq^ + 1). Наконец, если V1 (/С, 91) естъ нуль-группа, то группа
дп-Ч#*\Х?э %) есть прямая сумма ^°(К0)—1 групп, изо морф-

490 гомологические многообразия (А-многообразия) [гл. хш
ных группе % (в случае 91 = 7 число компонент комплекса К0 равно
т:"-1 (/С* \ Ко) -Ь 1, группа в7*-1 (К*\К$) есть нуль-группа).
На основании теоремы [3:51] главы 9 из [1 :10] вытекает
следующая, более компактная формулировка:
[4:1]. Комбинаторный случай закона
двойственности Александера.в первоначальной форме. Если
для всех гу 0 < г < /z, группы До (К) суть нуль-группы, то при
1 <;/?<; я — 2 группа вр_1(ЛГ0) изоморфна группе №~1(К*\К0*) и
TzP(Ko) = Kq-1(K*\K$. Группа в^-Ч^Ч^) ее///& нуль-группа, а
те»-1 (/С*\/fS) = it°(/Со) — 1; г/туя/m 0"-2(А'о) ее//гь нмль-группа*)
и «о (/С*\/С?) = -пгп-1 (/f0) + 1.
Прежде чем переходить к доказательству теоремы [4:10],
выведем из неё некоторые следствия и дальнейшие частные случаи.
При /?=1 имеем q—1 =/г — 2, так что из [4:1] заключаем,
что группа вга~2(/С*\/ф изоморфна группе 6°(/С0), т. е. есть
нуль-группа. Далее, по теореме [3:53] главы 9, группа 0П-1 (/С0)
также есть нуль-группа. Сопоставляя эти результаты с результатами,
содержащимися в [4:1], и помня, что никакой я-мерный комплекс
не имеет я-мерного кручения, получаем:
[4:11]. Если для всех г, 0<г<л, группы Aj(/C) суть нуль-
группы, то при г^п — 2 комплексы К0 иК*\К% не имеют г-мер-
ного кручения.
Частным случаем этого предложения является:
[4:12]. Если К—триангуляция трёхмерной сферы, а К0 —
замкнутый подкомплекс комплекса К, то К0 не имеет кручения
никакой размерности.
Положим теперь в [4:10] 3l = 7w, где т — любое целое число
^2. Так как группы А^ и V^ изоморфны, то получаем следующий
результат:
[4:13]. Закон двойственности Александера по
модулю т (комбинаторный случай). Если для всех г, 0<^г<^п}
группы Ao(/Q суть нуль-группы, то при 1 <;/;><>— 2 группы
&т(К0) и А%Г1(К*\Ко) изоморфны между собой] группы Д^~ (К0)
и &т(К*\Ко) также изоморфны; наконец, группа Д^-1 (К*\К%)
изоморфна прямой сумме т,° ^К0) — 1 групп Jm.
В теоремах [4:1] и [4:13] содержится следующий важный факт,
который подчеркнём особо:
*) В самом деле, из [4:10] следует, что группа V"-1 (Ко) = ®п-2(/Со) +
-MoiT1 (Ко) изоморфна Д00(^*\/ф. Но Д00(/С*\/Со) есть свободная абе-
лева группа, поэтому G^-2 (К0) есть нуль-группа. Ранг группы Щ^1 (Ко)
есть я1»"1 (/Со), a paEir группы А00 (К*\К%) на единицу меньше, чем число
компонент комплекса К*\К*0 (см, главу 8, арт. 1 ;5),

§ 4] КОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 491
10\
м
'3
16
А"
1 \^
I 4 X
^^2
к ?^
N^i"
г ^ч
//
р
14
97
\20
s\
\гз
Vs.
\?£
12
0
15
1
13
\£;
6 * N
\г>4
9 ^1
\^7
Vv j
А*
| v
\Ш
13
[4:14]. Комбинаторный случай я-мерной теоремы
Жордана. Если для всех г, 0</-<я, группы Д£(/<) суть нуль-
группы, то число компонент комплекса К*\Ко равно ъ*1"1 (/С0) + 1,
а также равно щп (К0) -f-1 при любом простом т.
Пример на теорему [4:1]. Пусть К есть триангуляция
трёхмерной сферы, а К0 — двумерное замкнутое комбинаторное
псевдомногообразие, являющееся подкомплексом комплекса К
(например, триангуляция замкнутой поверхности). Тогда:
1. Группа В1 (/С0) есгь нуль-группа (т. е. псевдомногообразие К0
ориентируемо и не имеет кручения).
2. Одномерные числа Бетги комплексов К0 и К*\К* равны.
3. К*\К% состоит из двух компонент.
4:2. Обобщение теоремы [4:10]. Назовём V-цикл z% комплекса
К0 продолжаемым (на Еесь комплекс /С), если существует
V-цикл zp комплекса /С, такой, что
К0гР — гР. Продолжаемые р-мерные
V-циклы комплекса АГ0 образуют
подгруппу группы Z^(KG), которую
будем обозначать через Ск(К0).
Примеры продолжаемых
и непродолжаем ых V - ц и к-
лов. Пусть К—триангуляция тора,
изображённая на черт. 142 (стороны
ААГ и Л"А'", а также АА" и А'А'"
склеены между собой).
Обозначим через АГ0 комплекс,
состоящий из трёх отрезков 11\ |,
] t\|, \t\\ и их вершин А = Аг =
= А" = Ат, С=С\ D=^Dr.
Таким образом, К0 есть триангуляция меридиана АА' = АпАт нашего
тора. Обозначим через tu fa, t\ указанные на черт. 142 ориентации
отрезков \t\\, \t\\> \t\\. Так как К0 есть одномерный комплекс, то
всякая его одномерная цепь является V-циклом. Докажем, что все
одномерные V-циклы комплекса К0 продолжаемы на весь комплекс
/С. Достаточно доказать это утверждение для циклов вида t\9 /= 1,
2, 3, например, для tlt Но для этого V-цикла продолжаемость
следует хотя бы из того, что цепь г1 == *} + *1 +*7 + *» + *м + 4б
(черт. 142) является V-циклом комплекса К удовлетворяющим
условию Ко?1 = t\*
Обозначим теперь через Ко комплекс, состоящий из шести
отрезков 11\ |, 141, 11\ |, |*11, \t\ |, 11\ | и их вершин А = А' = А" = Л'",
C=>C\ D — D\ M = M\ P, Q. Докажем, что V-цикл t\ — t\ kqm-
D1 3
Черт. 142,

492
ГОМОЛОГИЧЕСКИЕ
10
М
многообразия (^-многообразия) [гл. хш|
плекса Ко не продолжаем на комплекс К Для этого рассмотрим
какой-нибудь V-цикл г1 комплекса К и обозначим через !
si> Ъ> ^ ^ъ Ча» v чь ^> чз; С,, с2, сз z
значения г1 соответственно на *
i
f1 *) А • z1 z1 А- А А А. А А А
(черт. 142 и 143). Запишем, что значения цепи V-г1 на шести
ориентированных по часовой стрелке треугольниках
А 1 С ? D 3 />' MAP, РАС, PCQ, QCD, QDM\ M'DA'
равны нулю. Получим шесть уравнений: |
-&1—41 + ^ = 0,
— ^2 — ^2 + С2 = 0,
+ &3-Н2 — ^2 = °>
— ^з — % + С3 = 0,
почленное сложение которых даёт ра-
Черт. 143. венство М
(Н) ^1 + 'Ч2+% = ^ + ^2-Ь71з; I
этому равенству удовлетворяет всякий V-цикл zr £ Z\ {К). Но если |
KqZ1 = ^1 ^4, ТО У\х = 1, 7][ = — 1, Т|2 = 7]8 = Y|2 = % = 0, ЧТО ПрОТИ- 1
воречит равенству (Н). Непродолжаемость V-цикла t\ —t\£ Z1 (K0)J)l
этим доказана. 1
Рассмотрим третий пример. Пусть Ко есть комплекс, состоящий!
из трёх сторон |*и|, |*}9|, |*} | и трёх вершин треугольника PACg
(черт. 142). Читателю предоставляется доказать, что V-циклы t\9 di> J
/i9 комплекса Ко непродолжаемы на комплекс К |
После этих примеров, которые, как можно надеяться, достаточно 1
выясняют понятие продолжаемости V-цикла, докажем, что для лю-1
бых К и К0 имеет место включение /f
4
Г 5
VV
V
0 6 ]
(4:211)
Пусть
fl?(/Qc;C£(/g.
Тогда, пользуясь обозначениями главы 7, арт. 5:6, имеем
v^r^^zSc/O,

§ 4] кОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 493
причём на основании формулы (1 :51) главы 9
K0zp = /CoVExg"1 — VKoExp0-1 = V*?"1 = *g,
что и требовалось доказать.
Далее:
[4:21]. Если VP(K) есть нуль-группа, то
СРк(Ко)^Нр(Ко)
и, следовательно,
(4:21) C£(/Q = /^(/Co).
Для доказательства (4:21) достаточно убедиться в том, что при
Vp (ЛГ) == 0 для всякого zp£Zp(K) имеем
К0гРе^(КоУ
В самом деле, в силу наших предположений, существует цепь
х77"1 ^Lp"1(K)i имеющая гр своей ^границей:
следовательно,
что и требовалось доказать.
Заметим, наконец, что из того, что Vp+1 (К) есть нуль-группа,
по закону двойственности Пуанкаре следует, что нуль-группами
являются Да""1 (/С), значит, и Д«"" *(/(*).
Обозначим теперь для любых К и К0а К через 2?к*(К*\К%)
или просто через 2#* пересечение групп Za (/C*\KJ) и #1 (/С*)
т. е. подгруппу группы Z\ (К*\К%), состоящую из
всех циклов, гомологичных нулю в К*; при этом
Zr*(K*\K%) или просто Z\* совпадает с пересечением групп
2°Д°(Г\/С*0) и /#(**)•
В предположении, что Дг (/(*), соответственно А00 (/С*), есть
нуль-группа, Za(/C*\/CS)» очевидно, совпадает с Z#*(/(*\/Q;):
(4:22) zb(iC*\/CS) = ZX(/C*\^). r>°-
Кроме того, группа Hl(K*\K%) всегда содержится в Z#*(/C*\Ko).
Итак, если Vp (К) и Vp+1(/C) суть нуль-группы, то Ск(К0)
совпадает с НР(К0\ a ZK4^\^o) с Zr4^*\^o); естественно
в этих условиях группа 2%(К0)1Ск(К0) совпадает с 2%(K0)lH% (K0) =
s=Vp(/f0), а группа
с группой

494 гомологические Многообразия (А-многообразия) [гл. хщ;
Поэтому, теорема [4:10] (в части р > 0) содержится в следую-1
щем предложении:
Теорема [4:2]. Пусть К — любое n-мерное ориентируемое\
h-многообразие; для 0 < р < п—1 группы Z!^(K0)JCk{Kq) u\
ZrV1 (K*\Ko)IHl~~1 (К*\Ко) изоморфны между собой. \
4:3. Случай /7 = 0 и р = п—1; предварительные замечания
к доказательству теоремы [4:2]. Прежде чем доказывать теорему!
[4 :2], выведем из неё утверждения теоремы [4 :W](a следовательно,!
и [4:1]), касающиеся групп A»"1 (/C*\/Cj) и Доэ(/Г\/С;). 1
Если р — п—1 и Vя-1 (/С, 31) есть нуль-группа, то С£-Х(К0) сов-|
падает с Я^-1 (/С0), так что Z^-^/To)/^-^/C0i совпадает с Vй-4^oVl
В этом случае, в силу связности К*, группа Zk*(K*\Kq) совпа-1
дает cZ00(/C*\/C0*), и утверждение теоремы [4:2] заключается в ут-|
верждевдш изоморфизма между группами ^п"г(К0) и A00(AT*\/Q.j
Переходя к случаю р = 0, вспомним, что те и только те нуль-J
мерные цепи связного комплекса К являются V-циклами, которые!
постоянны, т. е. во всех вершинах комплекса К принимают одно и]
тоже значение (глава 9, арт. 1:6). Поэтому группа Z0 (К0) состоит!
из тех нульмерных цепей комплекса К0, которые постоянны на каж«|
дой компоненте этого комплекса. Отсюда следует, что группа Z0 (К0)
есть прямая сумма слагаемых, каждое из которых изоморфно группе ]
21, а число которых равно числу компонент комплекса /С0, т. е.
1г° (К0).Группа Cj> (АГ0) состоит из тех элементов группы Z° (АГ0), которые <
постоянны на всём К0. Отсюда легко следует, что группа^
Z°(K0)/C%,(K0) изоморфна прямой сумме к°(/С0)—1 групп 21; но,|
в силу теоремы [4:2], группа Z° (Kq)IC°k(Kq) изоморфна группе|
z^1 (№\ty/H2~1 (К*\К!1)> так чт0 эта последняя группа есть]
сумма тг°(/?0) — 1 слагаемых, изоморфных группе 21. 'i
В предположениях теоремы [4 : 10] группа V1 (К) есть нуль-группа;,!
нуль-группой поэтому является и группа А"-1 (К), так что группа]
Zfcl(K*\K$IHZ-1(K*\lQ совпадает с Ь»-1 (К*\К$, которая,!
следовательно, есть прямая сумма к°(К0)—1 групп, изоморфных!
группе 21, что и требовалось доказать. I
Пример на теорему [4:2]. Пусть К—триангуляция тора* j
изображённая на черт. 142. Область коэффициентов 21 = J. Рассмот-;
рим три случая:
1° АГ0 состоит из трёх отрезков |*J|, \t\\, \t\\ и их вершин;
2°/С0 состоит из шести отрезков |*||, |^|, |/*|, \t\\, \t\\, \t\\*
их вершин;
3° К0 состоит из трёх отрезков |/J|, IfJJ, \t\9\ и их вершин.
Во всех трёх случаях вследствие связности К (значит, и К*)
z°(**VO=z** (Ar*\/g, г^(к*\к;)/нц1С\к;)^оо(к*\к0).

§ 4] КОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 495
В первом случае Z^(/C0) = C]K(K0\ значит, Zl(K0)/ClK(K0) есть
нуль-группа. По теореме [4:2] нуль-группой является и группа
AO0(/C*\/С*\ т. е. комплекс К*\К* связен.
Во втором и третьем случаях С]К(К0) есть собственная подгруппа
группы Z*(K0), так что фактор-группа Z1 (К0)1С]К(К0) отлична от
нуля, и по теореме [4: 2] комплекс К*\К*0 несвязен. Легко убедиться
в том, что в обоих случаях группа Z1 (К0)''С1 ^К0) есть бесконечная
циклическая ipynna, в соответствии с чем комплекс /С*\/С* состоит
из двух компонент.
Читателю предлагается исследовать различные примеры
приложения теоремы [4:2] к случаю, когда К есть триангуляция
трёхмерного тора, или же триангуляция топологического произведения
двумерной сферы па окружность.
Основным аппаратом нижеследующего доказательства теоремы
[4 : 2] является определённое в арт. 3 : 3 изоморфное отображение DQ
группы DJ(K) на группу 1Я{К*). Обозначим через Dp обратное
изоморфизму Z)2 изоморфное отображение группы ££(/<*) на LP {К) и
заметим следующее очевидное свойство изоморфизмов Ын Dp:
[4:31]. Пусть Q — какой-либо подкомплекс комплекса К)
обозначим через Q* подкомплекс комплекса /С*, состоящий из всех
барицентрических звёзд, сопряжённых элементам Q. Тогда для любого
xp£Lp(K) имеем
Q*DZxP = DqQxP,
точно так же для любого yz^LQ-iK*)
QDpy* = DpQ*y*.
Элементы комплексов /С, К0> /(*, /С* обозначаем соответственно
через Г, TQy Г*, Г*, если нужно — с дополнительными индексами;
ТР и Т*% или ТР и Т*9 всегда обозначают пару сопряжённых
элементов; раз навсегда выбранные ориентации элементов Ги Г*
обозначаем через / и /*.
4:4. Изоморфное отображение AD? группы Zp(K0)/Cp(K0)h2l
группу Z<fcHK*\KZ)l№-l(K*\lC0). Каждому ^£^(/С0) ставим
в соответствие цепь AD? zp0£ И^1 (К*). В силу основного свойства
изоморфизма D* [формула (3:32) ] имеем для любого | t*f—l \ £ /С*
г±: (ДД7 гР • **;y-i) = (£>«-i Vzpq • t*<j~l) = (v z$ - *f+1) = 0,
т. e.
(4:41) bD*zP£Zl-*(K*\Kl),
а так как, кроме того, AD? zp £ №A~l (К*), то
bD*zP£Z%rKK*\KZ).

49б гомологические Многообразия (А-многообразия) [гл. хШ
[4:41]. Ставя в соответствие каждому V-циклу zp0 комплекса
К0 h-цикл AD^, получаем гомоморфное отображение A DQ груп-
пы гР(Ко) в группу Z^(K*\K*0).
Нам надо доказать:
[4:42]. Гомоморфизм Ш* группы Z?(Kb) в группу Zfc1 (К*\К%)
порождает одноимённый гомоморфизм группы
zr(K0)/c£(K0) в z^(k*\k;)/hi->(k*\k*0).
[4:43]. Гомоморфизм Д£>? группы ZP (К0)1С£(К0) в
группу г%гХК*\К1)1Щ-1(К*\К£) есть изоморфизм.
[4:44]. Изоморфизм A Di есть отображение на группу
Для доказательства [4:42] достаточно показать:
[4:420]. Если гГ£СР(К0), то А Я* «g 6 Т W VO •
Черт. 144.
Для доказательства [4:43] достаточно показать:
[4 :430]. Если z*0 £ Zp (К0) и А £>« *g £ ^Г1 (* *\*Р. т0
Для доказательства [4:44] достаточно показать:
[4#44°]. Для всякого т~х £Z^r* (K*\K*0) существует такое
*Ро€*т что *D*zp~u*-i в К*\К*0.

§ 4] КОМБИНАТОРНЫЙ СЛУЧ\Й ЗАКОНА ДВОЙСТВЕННОСТИ 4§7
Пояснением к предложениям [4:420] и [4:430] может служить
черт. 144, где К0 состоит из отрезка \е0ег\ и его двух вершин.
Далее, ^== (*o*i) ecTbV-цикл комплекса АГ0, продолжаемый на весь
комплекс К (за цикл комплекса /С, совпадающий на К0 с гх0, можно
взять цепь, принимающую на всех отмеченных стрелками отрезках
значение 1 и принимающую значение нуль на остальных отрезках).
Замечание. Если за К0 взять комплекс, состоящий из всех
сторон и вершин треугольника | е0 ех е21, то V-цикл
иг продолжаем на К, в соответствии с чем AD^zp0 не гомологично
нулю в К*\К*0 (точки е\ и е*г разделены друг от друга контуром
треугольника | е0 ех е% | и тем более комплексом Л*).
Доказательство [4:420] (черт. 144). Пусть г\ £ С£ (К0);
это значит, что
где zp£Z%(K). Тогда
D*zP = x(i-\-y(iy
где
jet = K*qD*zp, у* = (K*\K*0) D*zp
и
0 = LDizP = Дл;« + Ay*,
т. е.
А (—.у*) = Дл:« = U<*qD*zp.
Но, в силу [4 : 31],
*P*zp = D* Kq& ,
так что
А (—уч) = Д£>« /<0гР = ДО*г^.
Но — yv£L<i(K*\Kl), так что
AD^G^-4^*\/r0),
что и требовалось доказать.
Доказательство [4:430] (черт. 144). Пусть z*£Zp(K0) и
ADtegefl2-4K*VQ-
Надо найти такое zp£Zp(K), чтобы было гР==АГ0^.
Для этого берём сначала такое yq£LP(K*\K*0)> что
куц = bD*z\
и, значит,
Dvzr—y<t£Zl(K*).
32 Александров П. С.

498 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (А-МНОГООБРАЗИЯ) [ГЛ. X
Полагаем
zi' = Dp(DizP-yi)^ZP{K)
и доказываем, что гР есть нужный нам V-цикл, т. е. что
гРг^К0гР.
В самом деле, прежде всего
zp = D, {D4Zp —у'Г) = Dp ОчгР — Dpy4 = г* — Dpyi.
Далее, так как уч^1Л (АГ*\А*), то
Dpy«£lJ>(K\K0),
значит, K0Dpy« = 0 и /f0«lf== *o(*g—^V«)= M? = *£, что и ТР*
бовалось доказать.
—/г;
Черт. 145.
i/f,a:<
-2J
Тогда
Доказательство [4:440]. Пусть (черт. 145)
*« = А>* + (А"\Ар*в
ив-1 = Д*а = д ф9 4- Д (К*\К$ х%

§ 4] КОМБИНАТОрНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 499
или (так как /фс« = Kp*Dpx* = D<*K0Dpx<i)
или, наконец,
W-1 у AD«*g в Д * \ /С*,
где
гР = К0Орх*еи>(К0)-
Остаётся доказать, что zp£Zp(K0). Для этого вычисляем VzpQ на К0
lzp = V/C0D^ = AT0VD^ = ± ^0Ор+1Дх« = ± K0Dp^u^ = о,
чем [4:440] и вся теорема [4:2] полностью доказаны.
4:5. Определение и простейшие свойства коэффициента
зацепления to(af\ И2-1) двух А-циклов и?^Н\{К\ и*-1^/^-1 (К").
Все рассуждения этого артикула основываются на основных
формулах арт. 3 :3, а именно, на формулах
для любых
х*€1*(К), xV + i£LP+l(K),
у*£1Я(К*)9 ^+1€w+1'(#*)
и на следствии [3:45] из них:
[3:45]. Если из двух циклов zp£Zp(K), zv£Zl(K*) хотя бы
один гомологичен нулю, то (zpXzq) = 0-
Отсюда непосредственно вытекает:
[4:51). Если две цепи хр+х^ LP+\K), xp+l £ LP+1(K) имеют,
общую границу Дхр-Ь1 = кхр+г = ир, то для любого
tte-i£ Не-!"(#*)
имеем
(хР + ^мв-1) = (хр+^й^"1)-
В самом деле, в этом случае
XJ+1 —xg + ^ZJ+Htf).
и следовательно,
((a:p+i — хР+1)Хив~1) = 0,
т. е.
(xP+1X«fl""1) = (^+1X«Q[""1)-
Только что доказанное обстоятельство позволяет сформулировать
следующее определение:
Определение [4:5]. Пусть ир£Нр(К)н и*"1 £ Я*-1^*)-
Коэффициентом зацепления циклов иР и uq~x называется
Ъ(ир, из-1) = (-«р+1Хив"1)»
32*

500 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (^-МНОГООБРАЗИЯ) [ГЛ. ХШ
где!кр +* £ Lp+i (К) — произвольная цепь, удовлетворяющая условию
Из [4 :51] следует, что Ъ(ир, Ш~1) не зависит от выбора той
или иной цепи хр+*, удовлетворяющей условию Axp+I = ир.
Докажем несколько простых свойств коэффициентов зацепления:
[4:52]. Если ир^НЦК\ и*"1 G//*-1 (**).
то
(4:52) ь(ир, й«-1) = (— 1)р+1(и*Х.У«).
В самом | деле, пусть ap+j ^ 1Р + 1 (/С) выбрано под {условием
Из формулы (3\* 44) следует
Ы<У, и^1) = (л^Х Ду<0 = (— 1 )р+1 (Дхр*1 X .У*) =
= (—1)р+*(йрХУ«).
что и требовалось доказать.
Из определения Ъ(иРу и^1) следует далее:
[4:531]. Пусть К0 — замкнутый подкомплекс комплекса /£ а
ЛГ0*£Л*—'Комплекс, состоящий из барицентрических звёзд,
сопряжённых элементам комплекса /Q>; если up£Hp(K0), то при любом
выборе цикла uQ-1 £ Z^Z"1 (K*\K0*)> гомологичного нулю в /С*,
имеем Ъ(иР, М'1) = 0.
В самом деле, в силу наших предположений,
где
и
Ь(«р, а«-1) = (^+1Х«в'1) = 0-
Подобным же образом (при помощи [4 : 52]) доказывается:
[4 :532]. Если uQ-1 £ Hi"1 (К*\К*0), то при любом выборе
цикла up£Zp(K0), гомологичного нулю в К, имеем Ь(Ш\ a£-1) = 0.
Из [4:531] и [4:532] непосредственно следует:
[4 :53]. Пусть и\ и ир суть два цикла комплекса К0у
гомологичных нулю в К и гомологичных между собой в К0Ш, пусть ul~~x
и и\~1 суть два цикла комплекса К*\К^У гомологичных нулю в К*
и гомологичных между собой в К*\К1\ тогда
*К, и?"1) =*(«?, й?"1)
(черт. 146).
Теперь обозначим через Z%k (АГ0> подгруппу группы Z\ (Ко) >
состоящую из icex циклов, гомологичных нулю в К- Тогда для

§ 4] КОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОЕ И 501
любых двух элементов
и" <Е ZlK {K0) I Hi (K0), u«-i £ Z$Tl (K*\K*0) / Щ~х (К*\К$
МОЖНО ПОЛОЖИТЬ
(4 : 54) & (u?, u^-1) = to (и?, и^-1)
где циклы цр и и*?-1 произвольно выбраны соответственно в классах
смежности up и ця-"1; из [4:53] следует, что Ъ (и^э и^""1) не заЕИ-
сит от того, какие именно циклы up(^\\p и u^~~l ^u^-1 мы взяли.
Черт. 146.
В частности, если Л^ (К) и Ар + 1(/() суть нуль-группы, то А9'-1 (/С*)—
тоже нуль-группа, и из всего этого следует
Zfc1 {K*\ KDIHT1 (К*\К:) = А<7-*(/<*\Л*0).
и определение [4:54] даёт нам коэффициент зацепления
Ъ{\хр, и**-1) для любых двух элементов:
4:6. Теорема о зацепленных системах циклов. В этом
артикуле 51 обозначает либо тело рациональных чисе/*, либо одно из
тел Jm, где т — простое число.
Системы циклов
гГ\ .... гГ\ гГ'ег*-1 {К*\К*0, Щ
называем зацепленными, если Ь(г£, г^_1) = 8^. (черт. 146).

502 ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (/г-МНОГООБРАЗИЯ) [ГЛ. ХШ
Теорема [4:61] (Понтрягин). Ко всякой системе
гомологически независимых между собой циклов
(4:611) г?,..., 4, zp£ZP(K0, %)
комплекса К0 можно построить зацепленную с ней систему циклов
(4:612) г\-\....гЧг\ zj'1 ^ ^~\К*\К%У%)
комплекса К*\К§ .
Доказательство. Дополняем систему циклов (4: 611) до
какой-нибудь канонической б!зы
(4:613) *f,jtf, *?,..., zp8fupklvpt
решётки LP(K0, 31) и в базе
а?,"г#, г?, . .., zps, xl, yi,
сопряжённой к базе (4:613), рассматриваем V-циклы Г?,..., i*j;
строим для них Д-циклы
Ш*1Р , . . .,Д£№г?
комплекса К*\К%. В силу (3 : 41) имеем
(4x№?) = (4-?) = 3(i,
значит, на основании формулы (4:52)
Ъ (4, AD«??) = ( - l)P+i (*f X D&j) = (— Yf+%;
циклы
суть искомые.
[4:611]. Ко всякой системе гомологически независимых цело-
числеННых циклов
(4:611) *f ,..-,*?
комплекса К0 можно построить систему целочисленных циклов
(4:612) гГ\ • -., г/"1
комплекса K*\Kq, удовлетворяющую условию
В самом деле, рассматривая циклы (4:611) как циклы с
рациональными коэффициентами, строим по теореме [4:61] к системе
(4:611) зацепленную с ней систему рациональных циклов
я'?""»---» */s"~1; обозначая через ci общий'знаменатель входящих »
^в"1 дробных коэффициентов и полагая
получим искомую систему (4:612).

§ 4] КОМБИНАТОРНЫЙ СЛУЧАЙ ЗАКОНА ДВОЙСТВЕННОСТИ 503
Теорема [4:62] ^Понтрягин). Пусть це,. численные циклы
<4:621) гри ..., г\
образуют (7, Щ-базу комплекса К0. Тогда можно построить
зацепленную с системой (4 : 621) систему целочисленных циклов
(4:622) гГ1,...,^""1
комплекса К*\КЪ> образующих (J, Ш)-базу этого комплекса.
Доказательство. Для построения системы целочисленных
циклов (4 : 622), зацепленной с системой (4 : 621), достаточно
заметить, что эта система, будучи (7, 91)-базой комплекса /С0, может быть
дополнена до канонической базы
<4:613) xlyf,zt,4,vf
группы LP (Kqv Щ (см. главу 9, теорема [3:33]).
После этого рассуждаем, как при доказательстве теоремы [4 : 61]:
в сопряжённой базе
<4:623) и?,^?,^,*^?
рассматриваем циклы
и строим для них А-циклы
(4 :624) AD^,...,AZXi£.
Буквально так же, как при доказательстве теоремы [4: 61],
убеждаемся в том, что циклы (4:624), умноженные на (—1)*+1,
образуют систему, зацепленную с системой (4 : 621).
Система (4 :624) состоит из тг = гл-1 (К*\К1) циклов; поэтому для
того, чтобы доказать, что эти циклы образуют (J, $Я)-базу комплекса
К*\К%, достаточно показать, что каждый цикл г**-1 ^Z^"1(K*\Kq)
отличается от некоторой линейной комбинации циклов AD^zf
лишь на элемент группы №~г (К*\Ко).
Докажем это. Прежде всего, на основании (4 : 440)
(4 : 625) г'/-1 =- A D<izp0 + и*-1,
где
В силу основных свойств базы (4 : 623)
4 = 2а«/+2W + 2<vS,
следовательно, так как &Di есть гомоморфное отображение Zy(/C0)
в ZV1 (K'\Kt),
ДО-*4 = ^a^Diuf + ^bfiDvtf -f 2<;йд£>('4 •
Так как некоторое целочисленное кратное V-цикла

504
ГОМОЛОГИЧЕСКИЕ МНОГООБРАЗИЯ (Л-МНОГООБРАЗИЯ) [ГЛ, XIII
гомологично нулю в К0 и, следовательно, содержится в C#(/Q,.
то, в силу [4 : 420], такое же целочисленное кратное цикла
гомологично нулю в К*\К& т- е-
значит, и zff-1~2£rhAZ)fl5J==«ff-1-f ^-^««-Ч^Ч #о)>
что и требовалось доказать.
В заключение приведём пример, иллюстрирующий основнук>
конструкцию, при помощи которой доказываются теоремы [4:61}
и [4 : 62]. Конструкция эта
заключается в том, что к
некоторой канонической базе
комплекса К^аК строите»
сопряжённая база, и элементы-
*1, • • • t *к
этой последней подвергаются
воздействию оператора Д£)^
Пусть, например, К—
триангуляция сферы 53; при-
этом сферу sS3 представляемг
себе как обыкновенное
трёхмерное пространство,
пополненное единственной
бесконечно удалённой точкой.
Пусть комплекс K0ci К
состоит из трёх сторон и трёх
вершин треугольника | ехе^е^
Берём каноническую базу решётки Ll(K0) (см. главу 9, арт. 3 : 4„
пример 1):
У\ = А = (*2*з), yl = *l = (Vi )> *\ = A -f t\ + t\, где t\ = (еЛ).
В сопряжённой базе (глава 9, арт. 3 : 5, примеры V-баз)
Черт. 147.
й = /Ь
■'S,
берём V-цикл z\ = tl=a {ехе2) и строим Д-цикл &D<iz{ (здесь q = 2, р = 1У
п = 3). Цикл ДЖг{ показан на черт. 147 в виде ориентированного
полигона (границы ориентированной барицентрической звезды t*2=D^t\)^

ГЛАВА ЧЕТЫРНАДЦАТАЯ.
V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ
АЛЕКСАНДЕРА-ПОНТРЯГИНА.
§ 1. V-группы бикомпактов.
1:1. Спектры и их V-группы.
Определение [1:11]. Бесконечное частично упорядоченное^
множество 0 называется неограниченным, если ко всяким двум
элементам х{ £ 0, *2£0 можно найти элемент лг3£0, следующий
за хх и за х2.
Определение [1:12]. Пусть дано неограниченное частично*
упорядоченное множество К конечных полных симплициальных
комплексов /Са. Если АГр следует в К за АГа, то мы пишем просто Р>а.
Предположим, что для всякой пары комплексов АГа, К§
множества К, из которых Ка следует за Ка1 определено одно или
несколько симплициальных отображений £| комплекса /Ср в /Са,
называемых проекциями и удовлетворяющих следующим условиям:
1°. Если sl и S'l — две проекции комплекса К$ в Ка, то для
каждого симплекса То£Ко имеется симплекс Та£Ка, содержащий'
в числе своих граней оба симплекса S^Tp и УаГр.
2° Если 7>Р>а и Sl есть проекция К$ в /Са, a Sj есть
проекция /CY в /Ср, то симплициальнов отображение SlSj комплекса К( в Ка
есть проекция. В этих условиях частично упорядоченное множество К
вместе с определёнными в нём симплициальными отображениями St
называется проекционным спектром или просто спектром.
Из теоремы [9:4] главы 7 и теоремы [6:3] главы 9 следует:
[1 : 13]. Если 5а и S'l— две проекции комплекса К$ в Ка в
спектре К, то для любого za£Zv(K'a) имеем:
SpZ^SpZa В К$*
Отсюда, в свою очередь, следует:
[1:14]. Пусть za£Zr7(Ka\ z^Zrv(K^) и ?><*, 7>р.
Если при некотором выборе проекций Sl и S'J имеем
(1:14) 5>в?57% в К,,

£06 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
то соотношение (1:14) верно и при в:яком другом выборе этих
шроекций.
Определение [1:15]. V-циклы za(zZv(Ka), Zp£Zy(K$)
называются гомологичными между собой в К,
za~z$ в К,
если существует такое -у» Т>а> Т>Р> что
т. е. если
Легко видеть, что это определение гомологии между V-циклами
комплексов спектра К обладает свойствами рефлексивности,
симметрии и транзитивности.
Только последнее из этих свойств нуждается, быть может, в кратком
доказательстве.
Пусть
*«€Z;(*.). z^Zrv (Afp). z.t£Z;{K-()
K>*. *>P, к>& »*>т-
'.Возьмём К-, так, чтобы •/>>., V>jj.. Тогда
~sTsl*<ffsYs{z^ S^-S^z, в Кг
Так как и S^SJJ^ и Sj'S^p суть проекции одного и того же цикла
-2p£Z^(/(p) в комплекс /С,, то
так что
S^«xz„7 Щг, в К„
т. е.
za ~-> z^ в К.
Итак:
Множество всех г-мерных V-циклов всевозможных комплексов К*
спектра К распадается на классы циклов, гомологичных между
собой в К; эти классы называются r-мерными Ч-классами спек-
тра К и обозначаются через С (если нужно, с различными
индексами).
Определим сложение V-классов. Для этого заметим прежде всего,
ято в любых двух V-классах Cii и Сг можно найти элементы zx
щ г"л% принадлежащие к одному и тому же комплексу КЛ £ К:

§ 1] V"rpynnbI бикомпактов 507
В самом деле, выберем произвольно
возьмём /Са^К так, чтобы <х><х1э а>а2, и положим
Для определения суммы двух v-классов Ci и С' возьмём
произвольно принадлежащие к одному и тому же Ка циклы г'л £Ci и
^«£ ^2; по определению V-класс Сз> содержащий цикл г^^-г'^
называется суммой V-классов С± и t£. Легко убедиться в том, что
так определённая сумма двух V-классов £i и ££ действительно
зависит лишь от данных слагаемых V-классов £i и £з> а не от выбора
В самом деле, пусть
Надо доказать, 'что в некотором Kv V>a, Y>|i
Так как z^^z* в К, то существует ATTl, Ti>a, Ti>p, так что
так как z\~z§ в К, то существует ЛГ-(„ т2>а, f2>Pi так что
I» « V ^ Р
Возьмём y>Ti» t>72- Тогда
ЭД,^Ч4 в *т
«ли, складывая почленно,
Беря какие-нибудь проекции 5* и S^ и помня, что
°Y ^Yi « V ^fe' *i *Tl*« V (
получаем
что и требовалось доказать.

508 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
Только что определённое сложение г-мерных V-классов спектра
К коммутативно и, как нетрудно видеть, ассоциативно. Нулевым
элементом по отношению к этому сложению является г-мерный
V-класс Ог, содержащий нулевые элементы всех групп Vr(/Ca);
очевидно, для любого /--мерного V-класса Сг имеем
Г *• -j- 0r _ Yj%
Заметим, что V-класс Ог состоит из всех тех г-мерных V-циклов
2Г всевозможных комплексов /Са^К, для которых можно найти
#36к> Р>«, так что
<>^~0 в К^
Далее, для каждого V-класса Сг существует V-класс —Сг,
удовлетворяющий условию
£r + ( — Cr) = 0'J
чтобы найти —Сг, достаточно взять какой-нибудь zra£'C,r и
определить — Сг как V-класс, содержащий V-цикл —zra (легко Еидеть>
что это построение не зависит от того, какой именно zr£ rJ мы взяли>
и что —rJ состоит из всех V-циктов вида —zr, где гг££г).
Итак:
Определённое выше сложение ^-классов превращает множество
всех r-мерных ^-классов спектра К в группу, которая называется
r-мерной ^-группой или Чг-группой спектра К и обозначается через
V(K).
1:2. Гомоморфизм Ъ«. Два V-циклага £ Z£ (Ka) ъ z'j^Z* (/Q,
гомологичных между собой в /Са, и подавно гомологичны между собой
в К; поэтому каждый V-класс любого комплекса /Са£К целиком
содержится в некотором V-классе спектра К; этим установлено
вполне определённое гомоморфное отображение Sa группы Vr(/Ca)
в группу Vr(K).
В дальнейшем нам понадобится следующая весьма специальная.
теорема:
[1:21]. Пусть К — спектр, обладающий следующим свойством,
каковы бы ни были комплекс АТа £ К и следующий за ним комплекс
Яр£К, р>а, проекции S\ порождают изоморфное отображение
S^ группы Vr(/Ca) на группу Vr(7^). В этом случае при любом*
ЛГа£К гоуппа Vr(/Q изоморфна группе Vr(K).
Доказательство. Достаточно показать, что каждый V-класс
(/ спектра К содержит один и только один V-класс комплекса Kz>
где КЛ произвольно взято в К.
Итак, пусть Cr£Vr(K) и Ка£ К даны.
Пусть z^rJy ?a^zr(Kal); возьм_ём К^К, р>а, p>alf тогд*
2^ = Sfrza £ ^r- Так как гомоморфизм Sj группы 1/ (Ка) в 1/ (К$)
порождает изоморфизм группы Vr (Ка) на Vr (/(g), то существует такой V-цикл:

§ 1]
V-ГРУППЫ БИКОМПАКТОВ
50f
гч £ Zrv (/Ca), что S%za~z$ в /fp. Очевидно, *в£Сг. Итак, V-класс
Cr£Vr(K) содержит V-класс цикла za^Zrv(K(X). Остаётся доказать,
что из y£Z£(/Ca), г'~г% в К следует У ~ га в /Са. Но из /^
в К следует существование такого К$ £ К, j3>a, что Лг^З*^- в /fy;
так как S^ порождает изоморфное отображение группы Vr(/Ca) на
группу Vr(/Cp), то из
следует
чем теорема [1:21] доказана.
1:3. V-группы бикомпактов*). Пусть дан бикомпакт Ф,
состоящий из бесконечного множества точек. Рассмотрим неограниченное
частично упорядоченное множество в всех конечных открытых
покрытий **) бикомпакта Ф; покрытия эти будем обозначать через а,
р, Т и т. д., через Ка обозначаем нерв покрытия а и будем
считать комплекс Кр следующим за Ка, если (3>ос.
Пусть р>а. Ставя в соответствие каждому элементу покрытия
(3 какой-либо из содержащих его элементов покрытия а, получаем
отображения покрытия (3 в покрытие а, называемое проекцией [3 в а.
Каждой проекции покрытия (3 в покрытие а соответствует симпли-
циальное отображение комплекса Щ в комплекс /Са; эти
отображения и называются проекциями /Ср в /Са. Для них выполнено
условие 1° артикула 1:1. В самом деле, пусть даны две проекции S\
и S'f комплекса К$ в Ка, и пусть
какой-либо симплекс комплекса К§. Обозначая одной и той же буквой
вершину нерва и соответствующее ему множество — элемент
покрытия, видим, что £? содержится как в 5^?, так и в S'\e$, так что
SW П S'№ П . . . П SM П S'P*? => ri П . . . П е\ ф 0.
а и a ° a r a P — О т '
Симплекс Та£ Ка, вершинами которого являются S£ej}, 5^g,..., S^,
S'$e^ имеет в числе своих граней как «S^Tp, так и S^Tp.
Условие 2° артикула 1 : 1 для нашей проекции Sjjj также,
очевидно, выполнено.
Итак:
Частично упорядоченное множество К, состоящее из нервов
Ка всевозможных конечных открытых покрытий а бикомпакта Ф
с только что определёнными в нём проекциями, образует
проекционный спектр, называемый полным проекционным спектром
*) Глава 1, арт. 4:3.
**) Глава 1, арт. 8:1.

510 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
этого бикомпакта, ^-группы спектра К называются Ч -группами
бикомпакта Ф и обозначаются через У(Ф).
Замечание 1. Все рассуждения и определения этого артикула
можно было бы повторить, понимая под а, |3, f,... не открытые,
а замкнутые покрытия бикомпакта Ф; можно было бы показать, что
определение V-групп бикомпакта Ф, которое получилось бы таким
образом, даёт с точностью до изоморфизма те же группы, которые
мы определили, исходя из открытых покрытий.
Замечание 2. Вышеприведённое определение V-групп
формально применимо к любым топологическим пространствам; и в
нормальных пространствах при этом имеет место изоморфизм V-rpynn,
определённых на основе открытых и замкнутых покрытий; однако,
лишь для бикомпактов на наше определение можно смотреть, как
на окончательное; уже в случае локально бикомпактных нормальных
пространств целесообразным оказывается другое определение *):
1: 4. Группы V00. Пусть Ка — конечный полный симплициальный
комплекс. Обозначим через Z00(Ka) подгруппу группы Z°(/Ca),
состоящую из всех нульмерных V-циклов, постоянных на всём К±
(см. главу 13, арт. 4:3, случай р = 0).
Замечание 1. Элементы группы Z00(Ка) суть нульмерные
V-циклы, продолжаемые на любой полный симплициальный комплекс
Пусть теперь Ка и К$ суть два комплекса, являющихся
элементами спектра К, и пусть 2°£Z° (Ka), z^Z0 (Кр). Скажем (ср.
определение [1 :15]), что г° и zi принадлежат к одному и тому же
У°°-классу спектра К, если существует такое "f, ^ > а, у > р, что
Доказательство правомерности такого определения проводится в
точности так же, как в арт. 1:1. Определяя сложение У00-классов
совершенно так же, как в случае V-классов, мы превратим множества
всех У00-классов в группу, которую назовём У00-группой спектра К
и обозначим её через V00(K). Если К есть полный спектр
бикомпакта Ф, то называем группу V00(K) группой У00(Ф).
Замечание 2. Предоставляем читателю доказать следующую
теорему:
[1:41]. Если 51 есть данная область коэффициентов и число
компонент бикомпакта Ф конечно и равно тг°, то группа У00(Ф) есть
сумма ^°—1 прямых слагаемых, каждое из которых изоморфно
группе 91.
*) См. П. С. Александров, Группы Бетти и кольцо гомологии
локально бикомпактных пространств. Доклады Академии наук СССР, 26, 1940,
стр.631; см. также «Общая теория гомологии». Учёные записки Московск.
гос. университета, 45, 1940, стр.1—60; «Гомологические свойства
расположения комплексов и замкнутых множеств», Известия АН СССР, серия
математическая, 1942, вып. 5.

§ 2] КОНФИНАЛЬНЫЕ ЧАСТИ СПЕКТРОВ. СЛУЧАЙ КОМПАКТОВ 511
Доказательство основывается на арт. [4:3] главы 13 и на том,,
что все /Са£К состоят в данном случае не более чем из 7и°
компонент, причём за каждым комплексом Ка следует некоторый
комплекс /Ср, состоящий из 7г° компонент.
§ 2. Конфинальные части спектров. Случай компактов.
2:1. Конфинальные части спектров.
Определение [2:11]. Частично упорядоченное множество в'
называется частью частично упорядоченного множества в, еслш
каждый элемент в' есть элемент в, и из условий
*i€e,.*a€ft/. *1>*2 в В',
следует
xt>x2 в В.
Часть В' неограниченного частично упорядоченного множества
В называется конфинальной (со всем В) частью, если В' есть
неограниченное частично упорядоченное множество и для каждого*
х£ В можно найти такое у £ В', что
у>х в В.
Определение [2:12]. Спектр К' называется конфинальной
частью спектра К, если выполнены следующие условия:
1°. Спектр К', рассматриваемый как частично упорядоченное-
множество составляющих его комплексов, является конфинальной.
частью частично упорядоченного множества К.
2°. Пусть К$ следует в К/ за Ки; всякая проекция комплекса К$,
в комплекс Ка в спектре К' является проекцией в К.
Всякая конфинальная часть К' полного проекционного спектра К
бикомпакта Ф называется проекционным спектром бикомпакта Ф.
Теорема [2:13]. Если спектр К' есть конфинальная часть
спектра К, то группы Vr(K) и Vr(K') изоморфны между собой.
Доказательство. Множество всех г-мерных V-циклов К£
всевозможных комплексов, входящих в К', является подмножеством
множества г-мерных V-циклов всевозможных комплексов, входящих
в К; если гга—гГ в К/, то и подавно zra ~ г£ в К, поэтому
каждый V-класс спектра К' содержится в некотором (и, конечно,
единственном) V-классе спектра К. Этим установлено однозначное
отображение группы Vr(K') в группу Vr(K), являющееся, как нетрудна
видеть, гомоморфным отображением Vr (К') в Vr(K).
Докажем, что полученный гомоморфизм представляет собой
изоморфное отображение группы Vr (К/) на группу Vr(K). Для этого
достаточно показать, что в каждом V-классе спектра К
содержится один и только один V-класс спектра К'.
Пусть С—какой-либо V-класс спектра К и пусть га££. Так
как Кг — конфинальная часть К, то существует комплекс tfp£K',
следующий за Ка в К. Тогда V-цикл z§ = 5^га комплекса К§ £ КА

Si2 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
-содержится в некотором V-классе Ц спектра К', и этот V-класс
С', имея с С общий элемент г3, содержится в С. Итак, каждый V-класс
«спектра К содержит, по крайней мере, один V-класс спектра К'.
Остаётся доказать, что никакой V-класс спектра К не может
содержать более одного V-класса спектра Кг. Для этого, в свою очередь,
.достаточно показать, что два V-цикла
гомологичных между собой в К, гомологичны между собой и в К\
.Доказываем это утверждение. Пусть
г*~^г$ в К.
Значит, существует такой комплекс /CTl£K, "h>a, Ti>?> что
Берём в К' комплекс АГТв, следующий в К за Кь\ такой K1%£K.f
существует, так как К/— конфинальная часть частично
упорядоченного множества К.
После этого берём в К' комплекс Кр следующий в К' за Кх,
J($ и Ki%. Такое /СГ£К' существует, так ка< К' есть
неограниченное частично упорядочзнное множество.
В К' определены проекции S«$ и Sp а так как каждая из этих
^проекций есть в то же время проекция в К, и -у > а, -у>{}, f>Ti
т К, то имеем в /С гомологии
т. е.
что и требовалось доказать.
Следствие. Чг-группы бикомпакта Ф изоморфны 1г-группам
любого спектра этого бикомпакта.
2:2. Случай, когда Ф — компакт.
Теорема [2:21]. Пусть В—частично упорядоченное
множество всех открытых покрытий *) компакта Ф, состоящего из
бесконечного числа точек; пусть В'—часть частично упорядоченного
множества В, содержащая сколь угодно мелкие покрытия (т. е.
удовлетворяющая условию: какого бы ни было е>0 в в'имеются
«-покрытия компакта Ф). Тогда В' есть конфинальная часть В.
Замечание 1. Обратное предложение очевидно: если в' есть
зсонфинальная часть В, то при любом е>0 в В' содержатся г-по-
жрытия компакта Ф.
*) Глава 1, арт. 8 : 1.

§ 2] кбНФИнАльныв части Спектров. Случай компактов 513
Доказательство теоремы [2:21]. Пусть а—произвольное
покрытие компакта Ф; возьмём следующее за а в в покрытие <хг
Существует*) такое s>0, что всякое s-покрытие компакта Ф вписано
в <х1 и поэтому следует за а. Взяв какое-либо е-покрытие f£0\
видим, что -у следует за а.
Остаётся доказать, что в' неограниченно. Для этого берём для
любых двух покрытий ос и р из 6' следующее за ними в в покрытие
ах и определяем для него число е>0 и покрытие ^ как только что.
Замечание 2. За упоминающееся в теореме [2:21] частично
упорядоченное множество в' можно взять любую последовательность
покрытий
(2:2) »'={«i ос2, ...,ал, ...],
где ак есть е^-покрыгие и lim ек = 0. При этом, при любом k
покрытие ал+1 вписано в ак) так что 6' может быть предположено счётным,
упорядоченным по типу натуральных чисел, множеством. Беря
соответствующую множеству в' коне] инальную часть К' полного проекционного
спектра К компакта Ф, получим счётный упорядоченный по типу
натуральных чисел спектр К' компакта Ф.
Наконец, выбирая последовательность (2:2) так, чтобы при л'ю-
бом k каждый элемент <xk+i содержался в одном и только одном
элементе <*&**), получим спектр К/ компакта Ф, в котором для любых
двух покрытий <xh и <хъ &>/*, определена одна и только одна
проекция S*l покрытия ак в ап.
Наконец, если dim Ф = я, то весь спектр К' можно составить
из я-мерных комплексов. Отсюда, в частности, вытекает, что:
[2:22]. Если (ПтФ = /г и г>пу то Vr(<£) есть нуль-группа.
2 : 3. Случай, когда Ф—полиэдр. Пусть /Сесть триангуляция
полиэдра Ф. Рассмотрим последовательность комплексов
К %1> ^2>- • -у Кг> • • •>
из которых каждый есть барицентрическое подразделение
предыдущего. Через av обозначим открытое покрытие Ф, элементами
которого являются открытые звёзды триангуляции Av (см. главу 5,
определение [3:20]). Тогда /Cv есть нерв покрытия ccv, так что
обозначение /Cv можно рассматривать как сокращение записи Ка #
*) Глава 1, лемма 8:34.
**) Для получения последовательности (2 :2), удовлетворяющей этому
условию, надо взять какую-нибудь последовательность
подразделений (гл. 6, § 4)
а{9 ос2', ... ,ал',...
(каждое а%—замкнутое покрытие) и поступить так: заменяем элементы
покрытия а/ столь тесными окрестностями их, чтобы получить открытое
покрытие alf подобное покрытию а±\ и чтобы каждый элемент а2' содержался
лишь в одном элементе av После этого заменяем элементы покрытия а/
достаточно тесными их окрестностями и т. д.
33 Александров П. С.

514
^-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ
[гл. xiv
Пусть ^ — какая-либо вершина комплекса ATV+1; обозначим
через 5J+1^+1s=^J какую-либо вершину носителя точки е^М в
комплексе /С/, отображение S^1 есть нормальный сдвиг /fv+1 в Кч
(см. главу 10, арт. 3:1); при этом открытая звезда О^М вершины
ej+l содержится в открытой звезде вершины е* (черт. 148), так что
SI+1 есть проекция av+1 в av.
Таким образом определены проекции в проекционном спектре К,
состоящем из Bcex/fv. Так как диаметры элементов покрытий
устремятся к нулю при возрастающем v, то полученный спектр К есть,
Черт. 148.
в силу теоремы [2:21], спектр полиэдра Ф. Поэтому, группа Vr(<£)
изоморфна группе ЩК). Но, в силу теоремы [4: 3] главы 10, сим-
плициальные отображения S^1 порождают изоморфные отображения
V*4/Cv) в Vr(K+i), поэтому, в силу теоремы [1:21], группа Vr(K)
изомирфна любой из групп Vr(/Q, значит, и группе V^/O- Итак,
мы доказали следующее предложение:
Теорема [2:4]. Если Ф—полиэдр,а К—какая-нибудь его
триангуляция, то группа УГ^Ф) изоморфна группе ЧГ(К).
В этой теореме, очевидно, содержится теорема инвариантности
групп Vr{K), а следовательно, и групп kr(K) для полиэдральных
комплексов /С.
Замечание. Если компакт Ф состоит лишь из конечного числа
точек, то предыдущее определение групп Уг(Ф)не применимо, так
как частично упорядоченное множество всех покрытий Ф конечно.
Но в этом случае Ф оказывается нульмерным комплексом и,
следовательно, можно воспользоваться определением групп V, данным в

§ 3j А-ГРУППЬ1 ОТКРЫТЫХ МНОЖЕСТВ SH 5\U
главе 9. Таким образом, еслиФ состоит из конечного числа, а
именно из тс точек, то:
группа У°(Ф,91) есть прямая сумма те групп, изоморфных группе 91;
группа У00(Ф, Щ (которая только и будет нас интересовать) еегь
прямая сумма тг — 1 групп, изоморфных группе 91;
группа УГ(Ф, %) при г>0 есть нуль-группа.
§ 3. А-группы открытых множеств 5Л.
Формулировка закона двойственности Александера-Понтрягина
и основные следствия его. Случай Ф, состоящего из конечного
числа точек.
3:1. Группа ДГ(Г), где Г открыто в Sn. Мы уже рассматривали
(глава 4, арт. 1:5, пример 2) комплекс остовов Кг: вершинами
комплекса Кг являются всевозможные точки открытого множества Г;
множество вершин
образует остов, если существует открытая полусфера сферы Sn,
содержащая множество {е0, .. .,ег) и если выпуклое замыкание этого
множества*) лежит в Г.
Симплекс комплекса Кг с данным остовом {е0, ..., ег] есть
сферический симплекс, быть может, вырожде ющийся — с вершинами
е0>...,ег. При этом определении симплексов комплекс Кг есть
полный симплициальный комплекс.
Ьг-группы комплекса Кг называются ^'-группами открытого
множества Г и обозначаются через АГ(Г).
Замечание 1. Вместо Z/(/(r), Z\Kr), Hr(Kr) и т. д. будем
писать //(Г), Zr(JT), //(Г) и т. д. Цепи комплекса Кг называются
просто цепями открытого множества Г. В частности,
конечно, можно рассматривать случай Г = Ьп и говорить о цепях
пространства 6п.
Замечание 2. Пусть лгг£//(Г). Симплексами цепи хг
называем симплексы, на которых цепь хг отлична от нуля.
Комплекс, состоящий из всех симплексов цепи хг и из их граней,
обозначается через \хг\; это — конечный полный симплициальный комплекс.
Телом цепи лг называется соединение выпуклых замыканий
всех симплексов комплекса \хг\. Тело цепи хг представляет собой
компакт, лежащий в Г; оно обозначается через хг.
3:2. Барицентрическое подразделение цепей xr£Lr(T). Пусть
дано открытое множество Г в ъпа#п+1. Пусть Л—конечный
замкнутый подкомплекс комплекса Кг размерности г. Для определения
барицентрического подразделения комплекса К поступим так.
Помещаем пространство^/?™-*-1 внекоюрое пространство fim, m^2r-jrl,
*) На всём протяжении этой главы все геометрические понятия (отрезок,
выпуклое N-ноже тви, iим. леке, барицентрические подразделение симплекса
и т. п.; понимаю 1ся в смысле ил.еюи.ейся в Sn сферической карьки.
33*

Sl6 ^-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ (гл« Х*^
и произвольно малым сдвигом вершин комплекса К переводим
этот комплекс в r-мерную триангуляцию К\ лежащую в
пространстве Rm и изоморфную комплексу К. Обозначаем через К[
барицентрическое подразделение триангуляции К'. Сдвигом вершин 5**1,
обратным сдвигу S, все симплексы комплекса К\ а следовательно,
и лежащие на них симплексы комплекса /f/ переводятся в^и
комплекс К[ переходит в некоторый комплекс АГР называемый барицен-»
трическим подразделением комплекса /С. При этом носителем
какой-либо вершины комплекса Кх в К называется симплекс Т^К,
являющийся образом носителя соответствующей яершины комплекса
К[ при сдвиге S-1.
Замечание. Само собой разумеется, что это определение
барицентрического подразделения комплекса /(с: Кг не является
однозначным; однако, всякие барицентрические подразделения комплекса
К изоморфны между собой.
Приведённое определение барицентрического подразделения
позволяет говорить и о многократных барицентрических
подразделениях комплекса К, причём можно всегда достигнуть того, что при
достаточно большом h остовы А-кратного барицентрического
подразделения комплекса К имели диаметры, меньшие любого
заданного з>0.
Из сказанного следует, что всякую цепь xr£Lr(F) можно
подвергнуть (одно- или многократному) барицентрическому
подразделению и таким образом получить цепь shx?y симплексы которой сколь
угодно малы по своим диаметрам. Далее, так как определены
носители в К вершин барицентрического подразделения Кх комплекса К,
то можно, в том же смысле, как в главе 10, арт. 3:1, говорить
о нормальных сдвигах. Сохраняется и основная теорема о
нормальных сдвигах: посредством нормального сдвига /z-кратное
барицентрическое подразделение shxr цепи хг переходит в хг. Отсюда следует,
что (многократное) барицентрическое подразделение всякого цикла
zr£Zr(T) гомологично в Г циклу zr. Пусть теперь zr£Zr(T)n
P = Qw—полиэдр, лежащий в Г и содержащий внутри себя тело
цепи zr. (Такой полиэдр проще всего получить, определяя Q™ как
комплекс, состоящий из всех симплексов достаточно мелкого сим-
плициального разбиения Sn, замыкания которых лежат в Г.)
Подвергая zr одно- или многократному барицентрическому
подразделению и каноническому сдвигу относительно триангуляции Q^,
получаем цикл zr этой триангуляции, гомологичный циклу zr в Г.
Итак:
[3:21]. Всякий гомологический класс §**^ АГ(Г) содержит циклы
триангуляции Q™, где Qn — произвольная триангуляция, тело ко-
торой содержит внутри себя тело какого-либо цикла zr£tf.
Отсюда сразу следует:
[3:22]. Если г^п, то Дг(Г) = 0.

§ 3]
Д-ГРУППЫ ОТКРЫТЫХ МНОЖЕСТВ Sn
517
3:3. Топологическая инвариантность групп ДГ(Г).
Теорема [3:31]. Если Тг и Г2 — гомеоморфные между собой
открытые множества в Sn, то группы Дг(1\) и АГ(Г2) изоморфны
между собой.
Доказательству теоремы [3:31] предпошлём следующие определения:
[3:32]. Истинным циклом открытого множества
Гс5п называется всякий истинный цикл какого-либо компакта ФсГ,
Очевидно, r-мерные истинные циклы открытого множества FcSft
образуют при обычном определении сложения (см. главу 11, арг. 1:1)
группу, которую обозначаем через Zr(T).
[3:33]. Истинный цикл zr£Zr(T) называется гомологичным
нулю в Г, если qh гомологичен нулю в некотором компакте,
лежащем в Г.
Очевидно, r-мерные истинные циклы, гомологичные нулю, в Г
образуют подгруппу НГ(Т) группы Zr(T).
Определение [3:34].
(3:34) Д'(Г)^гЧГ)/Я'(Г).
Теорем а [3:31] следует из:
[3:35]. Группы ДГ(Г) и ДГ(Г) изоморфны между собой.
Доказательство теоремы [3:35].
Пусть дан произвольный истинный цикл
тг = (zr zr zr \
множества Г. Он лежит в некоторой полиэдре Ф = /СмсгГ и
каноническим сдвигом переводится в некоторый цикл ^ra^ZrA(K^). Этим
установлено гомоморфное отображение S группы Zr(r) в Zr(T), при
котором НГ(Т) отображается в ЯГ(Г). Гомоморфизм 5 порождает
одноимённый гомоморфизм АГ(Г) в АГ(Г). Гомоморфизм 6"
отображает ДГ(Г) на ДГ(Г). В самом деле, в каждом гомологическом классе
$Г£ДГ(Г) содержится цикл zra некоторой триангуляции Qa (см. [3:21]).
Очевидно, истинный цикл (z£, zra , . . .,г«Л, . . .), где z\b есть Л-крат-
ное барицентрическое подразделение zr^ при гомоморфизме 5
переходит в z*. Остаётся доказать, что гомоморфное отображение S
группы ДГ(Г) в группу ДГ(Г) есть изоморфизм. Для этого, в свою
очередь, достаточно доказать следующее предложение:
[3:351]. Если zr = Szr£ НГ(Г), mo zr£Hr(T). Обозначая
через Qn комплекс, состоящий из всех симплексов достаточно мелкогр
симплициального подразделения Sn, замыкания которых лежат в Г,
можно рсегда предположить, что
^=sz'=^e«!;(Q?),
что Z? есть истинный цикл полиэдра Q™ и что весь сдвиг S
происходит в этом полиэдре. После этого утверждение [3:351] доказы*
вается слово в слово так же, как [4:41] в главе И,

518 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
3:4. Закон двойственности Александера-Понтрягина и
основные следствия его. Теорема, составляющая основное содержание
этой главы, формулируется так:
Закон двойственности Алекс анд ера-Понтрягин а.
Пусть Ф—компакт, лежащий в Sn. Пусть Г есть дополнительное
открытое множество (Г = 5П\Ф). Пусть р и q — два
неотрицательных целых числа, дающих в сумме п. Тогда группы УР(Ф) и
Ая-^Г) изоморфны между собой, причём при р = 0 под ЧР(Ф)
понимается группа У00(Ф), а при р = п—1 под группой Дя-^Г)
понимается группа Д00(Г) (т. е. группа А00(ЛГг)).
Замечание. В частности, число компонент Г равно ти^-^Ф)-]- 1,
где тг^-^Ф) есть ранг группы УП-1(Ф).
Закон двойственности Александера-Понтрягина является одним из
основных фактов всей современной топологии. Прежде чем
переходить к его доказательству, перечислим некоторые его следствия и
частные случаи, которые могут служить иллюстрацией важности этой
теоремы.
Прежде всего, ввиду того, что гомеоморфные компакты Ф имеют
изоморфные группы УГ(Ф), из закона двойственности Александера-
Понтрягина следует:
[3:41]. Если Ф и Ф' — гомеоморфные замкнутые множества
в Sn, то группы АГ(5П\Ф) и АГ(5П\Ф') изоморфны между собой.
Точно так же из закона двойственности Александера-Понтрягина
в соединении с теоремой [3:31] следует:
[3:42]. Если Г и Г'—гомеоморфные открытые множества
в Rn, то группы Vr(Sn\T) и Vr(Sn\V) изоморфны между собой.
Частным случаем теоремы [3:41] является:
[3:410]. Два гомеоморфных между собой замкнутых
множества Ф и Ф' в Sn разбивают пространство Sn на одинаковое
число компонент.
Отсюда (на основании теоремы [1:29] главы 2):
[3:43]. Если из двух гомеоморфных замкнутых множеств в Rn
одно является абсолютной (регулярной) совместной границей, то
то же утверждение верно и для второго множества.
Перейдём к частному случаю, когда Ф с Sn есть кривой полиэдр.
В этом случае (см. главу 9, теорема [3: 5])
(3:440) у£(Ф) = ®Р~\Ф) + Д8>(Ф)
есть группа с конечным числом образующих. Поэтому А^-^Г) также
есть группа с конечным числом образующих и, следовательно,
(3:441) Д«-ЧГ) = в*-ЧГ) + Д&-ЧГ),
где А^(Г) — свободная, а №~г(Т)— конечная подгруппа группы
Aj-^l1), состоящая из всех элементов конечного порядка группы
Ag-\D. Группа №~г(Г) называется (q—1>мерной группой круче-

§ 3] А-группы открытых множеств Sn 519
ния открытого множества Г. Из изоморфизма У^(Ф)^^А^~1(Г) и из
(3:440) и (3:441) следует
А6>(Ф)«А$Г,(Г).
Итак:
Закон двойственности Александера для кривых
полиэдров в Sn:
Если Ф cz Sn есть кривой полиэдр и р-\- q = п, то р-мерное
число Бетти кривого полиэдра Ф равно (q— \)-мерному числу
Бетти открытого множества Г = 5П\Ф, а (р—Химерная группа
кручения Ф изоморфна (q— 1)-мерной группе кручения Г.
Возьмём теперь область коэффициентов Jm. Как известно [глава 9,
формула (4:4Ю)], для всякого (кривого) полиэдра Ф
Vi(*)«A^).
Поэтому:
Закон двойственности Александера по модулю w
(для кривых полиэдров Ф в Sn). Группы
А*(Ф) и ДГЧГ)
изоморфны между собой.
Пусть, наконец, Ф есть (п — 1)-мерное замкнутое
псевдомногообразие в Sn. Тогда Д^-1(Ф) есть группа второго порядка, значит,
Д£°(Г) также есть группа второго порядка, т. е. Г состоит из двух
компонент. Но в этом случае А^° (Г) есть бесконечная циклическая
группа, следовательно, и Aw_1 (Ф) есть бесконечная циклическая
группа и, значит, Ф ориентируемо.
Так как для любой триангуляции К11"1 псевдомногообразия Ф и
для любого замкнутого собственного подкомплекса К0а Кп~1 группа
^п~1(К0) есть нуль-группа, то никакой полиэдр вида К%~\ и
следовательно, как легко видеть, никакое собственное замкнутое
подмножество Ф0сФ не разбивает Sn. Другими словами, Ф есть
регулярная совместная граница.
Итак:
[3:44]. Теорема Жордана-Бр ауэр а. Всякое (п —
^-мерное замкнутое псевдомногообразие, лежащее в 5П, ориентируемо,
разбивает пространство Sn на две и только две области и
является границей каждой из этих областей.
Так как никакое замкнутое собственное подмножество лежащего
в Sn замкнутого (п—1)-мерчого псевдомногообразия не разбивает
Sn, то, в силу теоремы [3:410], то же утверждение имеет место и
для множеств, гомеоморфных собственным подмножествам таких
псевдомногообразий. Отсюда вытекает, что никакая внутренняя точка
какого-либо компакта Фс£п не имеет сколь угодно малых о рест-
ностей (относительно Ф), граница которых гомеоморфна собственному

520 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
подмножеству (п — 1)-мерной сферы. Так как граничные точки Ф
такими окрестностями, очевидн), обладают, то мы получим следующую
характеристику внутренних и граничных точек компактов Ф с: Sn.
[3:45]. Внутренние точки компакта Ф с S11 (относительно Sn)
характеризуются тем, что при достаточно малом е > 0 они не
имеют г-окрестности с границей, гомеоморфной собственному
подмножеству (п— 1)-мерной сферы; граничные точки Ф
характеризуются тем, что при любом е > 0 они имеют г-окрестности,
границы которых гомеоморфны собственным подмножествам
(п — \умерной сферы.
Так как эга характеристика топологически инвариантна, то из
неё следует:
[3:46]. При топологическом отображении какого-либо
компакта Ф с Sn в Sn всякая внутренняя точка Ф относительно Sn
переходит во внутреннюю, всякая граничная — в граничную.
Замечание. Так как всякая внутренняя точка любого
множества Лс5и является внутренней точкой некоторого компакта Ф^ЛГ,
то мы доказали полную теорему об инвариантности внутренних
точек, т. е. теорему [3:1] главы 5.
3:5. Случай Ф, состоящего из конечного числа точек. Пусть
компакт Ф состоит из конечного числа точек о{, о2, ..., ог.
Для доказательства закона двойственности Александера-Понтрягина
в этом частном случае нужно, в силу замечания, сделанного в конце
арт. 2:3, доказать следующие утвержд°ния:
1°. Группа А^"1 (Г, 31) есть прямая сумма тг—1 групп,
изоморфных группе %.
2°. При г<С,п—1 группа АГ(Г, %) есть нуль-группа.
Доказательство утверждения 1°. Пусть
Kv А2, • • • , Aft, . . .
— последовательность триангуляции пространства Sn, каждая из
которых является подразделением предыдущей и максимальный диаметр
симплексов которых стремится к нулю при возрастании h. Без
ограничения общности можно сделать следующие предположения:
1) При любом h каждая из точек о{ лежит в некотором я-мер-
ном симплексе комплекса А^, причём ни один из этих симплексов
не содержит более одной точки о$.
2) Симплексы Ты комплекса Kh занумерованы так, что при
/ <; тг точка ог лежит в Ты.
Выберем определённую ориентацию пространства Sn и перенесём
её на все Т^. Получим ориентированные симплекса t*r Положим,
наконец, <г^т-1 = Д^., г=1, 2, ..., ти и докажем предложения:
[3:51]. Каждый цикл zn~l ^Zn-1 (Г, 21)гомологичен в Y
некоторой линейной комбинации циклов -г^г1, /— 1, 2, . . ., тг—1.
тг—I
f3 : 52]. Если 2 Wif1 ~ ° в v? т0 cix== • • • = cr.-\ = 0,
М

§ 3] А-группы открытых множеств Sn 521
При доказательстве этих предложений мы будем свободно
пользоваться правом рассматривать циклы множества Г как истинные
циклы, что законно в силу арт. 3:3. Самому доказательству
предпошлём два замечания:
а) Обозначим через Qh комплекс KV\(T^ U . .. U Т£я). Тогда
тс
2г5иг1—® в Фл (и тем более в Г).
В самом деле, так как 2*л* есть цикл» т- е-
ТО
1—1 />ТС
т. е.
f=i
б) При любом /г имеем
В самом деле, проектируя границу симплекса 7^ на границу
симплекса TJI из oh получаем деформацию цикла г%г1 в цикл z™rl,
так что эти циклы гомотопны, следовательно, гомологичны между
собой в Г.
Из замечания б) следует, что вместо [3:51] достаточно доказать:
[3:510]. Каждый цикл г71-1 £ Z11-1 (Г, %) гомологичен в Г циклу
тс—1
вида y^c^f1 при некотором /г, зависящем от г4-1.
Докажем предложение [3:510]. В силу [3:21], цикл zn~l
гомологичен в Кь некоторому циклу г%~1 £ Z11-1 (К^ 31). Цикл г™~1
гомологичен в Къ нулю: г7£~1 = кх™.
Если х\ = 2 <М/"' то
т. е.
к
уП~\ _ , Х^/7 . -уП — 1
^T'-S^^T1 B <&

522 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
тс—1
Так как, в силу замечания а), имеем aKz™~] ~ — ^j^^Sw"1* T0
тс—1
г^-1—2(й* — а^м1 в ^л» тем более, в Г, что и требовалось
доказать.
Доказательство [3:52]. Пусть
тс—1
*w-1 = 2*i*,T1~° в Г.
г=1
Тогда существует такое А, что г™-1 — 0 в Qhy и, следовательно
(глава 11, арт. 4:6), если г^г1 обозначает подразделение цикла г^г1
в Кш то
S^^ZT1-0 в Он-
/sal
ТС—1
Л—1.
Пусть х^ = У\а4^( есть цепь, ограниченная циклом УУ*гл7
/>« /=i
тогда
М2С«&-2М,)==°-
i=l г>тс
тс—1
Так как Kh есть /z-мерное псевдомногообразие, a У]*^/- 2a* ^w
есть /г-мерный цикл, то все t%. должны входить в этот цикл с одним
и тем же коэффициентом. Но t%n входит с коэффициентом нуль, значит,
все ci (и все а{) также равны нулю, что и требовалось доказать.
Обозначим через $~1 элемент группы Д*-1^, 21), содержащий
цикл 2%гг. Из [3:51] и [3:52] слелует, что каждый элемент группы
ДП-1(Г, щ однозначно представим в виде
an-les2<*8?-s *<€« а<«—1),
т. е. что ДП_1(Г, 21) есть прямая сумма it—1 слагаемых, каждое
из которых изоморфно группе 21. Утверждение 1° доказано.
Для доказательства утрерждения 2° предположим, что при
г<я—1 нам дан какой-нибудь цикл zr £ Zr (Г, 21), нормальный
в случае г = 0. Возьмём в Г точку о', расположенную так, что ни
одна из плоскостей, натянутых на точку о' и какой-либо из
симплексов цикла гг, не содержит ни одной из точек оь ..., ок.
Так как все упомянутые плоскости имеют размерность
^г-\-1 ^Сп — 1, то такой выбор точки ог всегда возможен.
Заставим теперь все вершины цикла zr в течение единицы
времени прямолинейно и равномерно скользить в точку о'. От этого
произойдёт деформация во множестве Г цикла zr в цикл, тгжде-
ственно равный нулю. Итак, всякий г-мерный цикл открытого мно-

§ 4] комплексы /Са, KQa9 A£ K*e, Qal\ множества Ga и Гв 523
жества Г в наших условиях гомотопен и, тем более, гомологичен
нулю в Г, что и требовалось доказать.
Этим закончено доказательство закона двойственности Алексан-
дера-Понтрягина в случае компакта Ф, состоящего из конечного
числа точек.
§ 4.*) Комплексы Кв, К0а, /С*, К%а, Qai;% множества Оа и Га.
4:1. Определения и обозначения (черт. 149). На всём
дальнейшем протяжении этой главы Ф обозначает состоящее из
бесконечного числа, точек замкнутое множество, лежащее в Sn;
Г = ^\Ф.
Пусть К—триангуляция Sn,
Обозначим через k натуральное число; через Кк обозначим
^-кратное барицентрическое подразделение комплекса К, через
Kqjc — подкомплекс комплекса Кк, состоящий из всех симплексов
комплекса Кк, содержащих точки множества Ф, и из всех граней
этих симплексов. Очевидно, при любом k
(4:11) ФЕ^о*.
(4:12) #o.ft+iE
Летело комплекса Кк\К^ обозначим через Gk.
Обозначим через /С* комплекс барицентрических звёзд комплекса
Кк9 через К^к — подкомплекс комплекса К*к, состоящий из
барицентрических звёзд комплекса Кк, сопряжённых симплексам
комплекса Кок. Так как Кок — замкнутый подкомплекс комплекса Кк,
то К£к — открытый, а К1\К*1{ — замкнутый подкомплекс комплекса
Кк. Поэтому тело комплекса К$к открыто в 5П, а тело комплекса
К^\К*к есть полиэдр, ошой из триангуляции которого
является барицен триче ско е подразделение Qkl комплекса **)
К1\К*к. Множество всех внутренних относительно Sn точек
полиэдра (2кх = К1\Кцк обозначим через Тк.
На основании теоремы [5:42] главы 4 имеем
(4:13) Фс^с^, r2 0,DOpQ,prft.
Обозначим через ек наибольшее число, являющееся диаметром
некоторого симплекса Тк £ Кк> Тогда
Фс£0**£О(Ф>2гД
(4:14) . Г=>гл=>5»\0(Ф,2з*);
*) См. главу 4, арт. 5:4.
**) См. главу 4, арт. 5:4.

524 V-ГРУЛПЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
/rcsss
otv^N,
Ш
\\7^
ч \
\^

§ 4] комплексы А^> Kfr, /С*, К*0а, Qal; множества 6а и ?а 525
так как lim гк = 0, то
(4:15) Г=иГ,.
СО
и:
Далее, так как KQk^ /С*л и tf^ открыто, то р(Ф, Qftl)>0.
Положим теперь kt = 1 и, предполагая, что для натурального
числа а число &а определено, обозначим через &в+1 первое
натуральное число, удовлетворяющее следующим условиям:
2°. 2е*. „ меньше, чем sfr и чем наибольшее число, явля-
ющееся диаметром некоторого множества Ф П Га, где Тл£Кк .
Замечание. Обозначая через Оа открытые звёзды триангуляции
УС* мы видим, что, в силу второго требования условия 2°, никак не
может случиться, чтобы каждое из множеств Ф П Оа содержалось
в некотором ФПОа+1; так как с другой стороны, каждое ФПОа+1
содержится в некотором Ф П Оа, то второе требование условия 2°
гарантирует, чта покрытие Ф, составленное из всех ФПОа+1, следует
(в смысле арт. 1:3) за покрытием, составленным из всех ФЛОв.
Только для этой цели это требование и введено.
Из условия 1° следует
0(Ф, 2«*e+1)cS»\(bel
и, значит,
Теперь мы раз навсегда вводим следующие обозначения.
Комплексы /(&а, Кока> К% » %1к » Qkui обозначаем соответственно через
Ка, /С0а, К*а, /CJ, Qav открытые множества Г* и Oh^ обозначаем
соответственно через Га и Ga.
Барицентрические подразделения комплексов /Са, KQa обозначаем
соответственно через /Са1, /С0а1.
На основании доказанного в этом артикуле имеем:
СО гь, СО
(4:16) r=UQal=Ura,
(4:17) Овэ(?в1;
(4:18) r,+1DQal3ra.
4:2. Непрерывное отображение С множества Ga на полиэдр Qal.
Докажем следующее предложение:
[4:21]. Существует непрерывное отображение С множества
Ga на полиэдр Qall оставляющее неподвижными все тонки Qal.

526 V-груИпы Компактов и закон двойственности {гл. xiV
Доказательство. Пусть Тгл1 есть симплекс комплекса J(ai,
не принадлежащий комплексу QaU но лежащий на некотором
симплексе
Т?£Ка\КСа.
Тогда
Тгч =|rwo>...>rwr|,
причём Тпло £ К«\ К0„ а 7>6ЛГ0а- ПУСТЬ ТТ'*1 есть первый
принадлежащий комплексу Кс& симплекс из симплексов Г™<>,..., Тпг.
Вследствие замкнутости комплекса К0 имеем
7>i€tfo< ?>««
П1=|г?>...>г»«|б<гв1.
7,:]=|^+,>--->7>1бль.1.
Каждая точка симплекса Тг однозначно определяет содержащий
её отрезок р"р\ соединяющий некоторую точку р"£Т" с
некоторой точкой р' £Т'л .
Положим теперь С(р)=р'.
Этим отображение С определено для всех точек p£Ga\QaX.
Для p£Qal положим С(р)=р. Отображение С непрерывно и
удовлетворяет требованиям [4 : 24].
4:3. Некоторые свойства группы Zr(T). Из (4: 16) и (4:18)
следует, что всякая цепь х открытого множества Г является при
всяком достаточно большом а цепью открытого множества Га и тем
более полиэдра QaV Значит, на основании [3:21] каждый цикл
z£Zr(T) гомологичен в Г некоторому циклу zal£Zr (Qal).
Но Qal есть барицентрическое подразделение комплекса
/С*\/С*а с К*, поэтому, в силу теоремы [2:11] главы 13, цикл
^al£Zr(Qal) гомологичен в Qal, значит, и подавно в Г, некоторому
циклу вида s*aizl где K€z^K\Ka)-
Итак.*
[4:31]. Каждый гомологический класс 8Г£ДГ(Г) содержит при
всяком достаточно большом а цикли вида s^z*, где
Из теоремы [2:12] главы 13 следует далее:
[4:32]. Если ^ £ Н\«?«,), г\£Z\ (K*a \ 1CJ,
то

§5]
КОМБИНАТОРНАЯ ЛЕММА
527
§ 5. Комбинаторная лемма.
5:1. Предварительные замечания и формулировка леммы.
Так как Кл1 есть барице 1Тричвскре подразделение комплекса /Са, то
каждый симплекс 7а1 £ /Са1 содержится в одной и только одной
барицентрической звезде комплекса /Са, называемой носителем
симплекса 7а1 в /Са; симплекс Tal£Kai называется главным, если его
размерность совпадает с размерностью его носителя в /С*.
Легко убедиться в том, что главные симплексы T%i£Kal имеют
вид
(5:11) ^ = |7?>ГГ1>. • •> 7*|,
где Т«£/еа, • • -,Т%£КЛ суть симплексы, центрами тяжести
которых являются вершины симплекса Tai-
В самом деле, пусть Т*%£К% есть носитель главного симплекса 7^-
Барицентрическая звезда Т*\ сопряжена некоторому Т%£КЛ и по самому
определению барицентрической звезды 7*2 ее* ^-мерные симплексы имеют вид
(5:11).
Если т£ £ /Сви 7*« £ Ка сопряжены друг другу, то нам удобно будет
говорить, что симплекс 7? сопряжён каждому из главных симплексов
та с т*а
1 al Vl l a*
Пусть среди комплексов /flf /C2, ..., Ка,. . .[см. арт. 4 :2] выбраны
два комплекса /Са и АГр, (3 > а, и дано нормальное симпли-
циальное отображение*) 5« комплекса К§ в комплекс Кл.
Обозначаем через s$[' оператор подразделения в К$г (т. е. оператор
перехода от ц?пей какого-либо /Са'или Л*„ <*'<;£, к их
подразделениям в К^); через D« обозначаем изоморфизм группы LP(KU) на
группу Lz(K9), определённый в предыдущей главе, арт. 4:3. Тогда
имеем следующее предложение:
Основная лемма [5:1]. Для всякого V-цикла г% £Zy(/Q,
равного нулю на ЛГа, имеет место соотношение:
(5 : 1) s\,DlSlzl ~ s^Dlg в Qpi.
Переходя к доказательству этой леммы, дадим прежде всего
определённую ориентацию пространству Sn; будем обозначать через /£,
t\ ориентации симплексов 7«£/(а, 7р£/Ср одинаковые с выбранной
ориентацией Sn.
Далее, для р < п выберем по произволу определённую
ориентацию t% каждого симплекса 7«^/Са. После этого ориентацию t\
какого-либо симплекса Т$£К$ выберем так, чтобы при 5«7^==7в
*) Глава 10, арт. 3:1.

528 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XlV
было Бщ = /«; если же SlT$ имеет размерность меньше р, то
ориентацию /f выбираем произвольно.
Ориентации /а, tf барицентрических звёзд Та9 £ К* и Тдр£Кр,
сопряжённых соответственно симплексам Т%^Ка и T$£Af3> выбираем
гак, чтобы
(#Х#)=1, (4х^) = ь
Соответствующие ориентации главных симплексов T2i £ 7^ и
7|i £ Tpq обозначаем через /«i, tf$1#
5:2. Основное тождество. Определим следующим образом
вспомогательное симплициальное отображение Sa{ комплекса К$г в /Са1:
вершине комплекса K$v являющейся центром тяжести симплекса
Тр^/Ср, ставится в соответствие вершина комплекса /fal, являющаяся
центром тяжести симплекса S«T$. Таким образом симплексу
т;{ = [ т$* > 7?1 > • • . > т?г | е /с?1
соответствует симплекс
(5:21) 5Si^lS=rel=|^^>. • .>5f7^|6^i.
Мы сейчас исследуем, как действует отображение sl\ на главные
симплексы комплекса K$v
[5:22]. Всякий q-мерыый неглавный симплекс
удовлетворяет условию nq < р.
В самом деле, так как при / = 0,1,..., q^=n—pf nt — ty+1^>l,
п^>п0, то при ftg/^p имели бы п0 = пу пх — п—1,..., nq = p,
т. е. симплекс 7«i был бы главным. Этим [5:22] доказано.
Посмотрим теперь, какие главные симплексы
в силу slu отображаются на данный главный симплекс
7li = |7l?> • • • >Т»\£Ка1.
Если 5в}Г^ = Tlu то необходимо S|,7|l = Г". С другой стороны,
если SlT%= T", то один и только один симплекс вида
(5:23р) Т?1 = |7^>ГР"-1>- • ->7^|

§ 5] КОМБИНАТОРНАЯ ЛЕММА Й29
отобразится, в силу sl\, на данный симплекс
(5:23а) 7!i = m>7?-1>. • • >7*|.
В самом деле, если 6^7^ = Г^, где 7$ь Гр\ даны равенствами
(5:23^) и (5:23а), то каждый из симплексов 7$~\. ..,Гр
однозначно определён как единственная грань симплекса Тр>
отображающаяся, в силу S^ соответственно на Т^-1,..., Г«.
Итак: главные симплексы 7^ £ Л^, отображающиеся при посредстве
sl\ на данный главный симплекс
т%1 = \П>тТ1> ■ ■ •>it\€Klu
взаимно однозначно соответствуют симплексам 7$ £ /ц,
отображающимся при посредстве si на Г«.
Замечание. Обозначим через Sa аффинное (невырождающееся)
отображение замкнутого симплекса Т$ на 7^, порождаемое
отображением Sa вершин Гр на Г«. Так как при невырождающемся
аффинном отображении S$ замкнутого симплекса Т\ на Г« центр тяжести
каждой грани Гр переходит в центр тяжести её образа при
отображении Si, то для каждого главного симплекса ^ £ К$\ имеем
^ai^pi — ^«^ р-
Этим замечанием мы сейчас воспользуемся.
Пусть симплексы 7f £ ЛГа, Т$ £ Ка суть симплексы, сопряжённые
соответственно 7^, Грь Перейдём к ориентированным симплексам
£, С ^> 4 <?ь $• Пусть
Тогда
Докажем, что у\ = С.
Для этого заметим прежде всего, что, в силу теоремы [2:3],
главы 7,
(5:23) (^X^^) = C(^X^),
где яод индексом пересечения симплексов понимаем индекс
пересечения плоскостей, несущих эти симплексы и ориентированных
так же, как они *). В силу сделанного выбора ориентации №, имеем
*) Это соглашение является отступлением от правила главы 7, арт. 2:2,
так как наши симплексы не находятся в общем положении; поэтому со
глашение действует лишь в течение данного доказательства.
34 Александров П. С.

530 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
Кроме того,
Поэтому для левой части равенства (5:23) имеем
(% х %t)=(/; х -пп)=-ч (% х ф =-- %
тогда как правая часть равенства (5 :23) есть
Итак, действительно, т] = С. Поэтому коэффициент, с которым
№х входит в «S^S^ai (суммирование по всем главным Цх)9 равен
коэффициенту, с которым ^входит в Si Yfi (суммирование по всем
Ц). Но этот последний коэффициент равен 1 [см. главу 10,
формулу (3:11)].
Таким образом, мы доказали:
[5 : 24]. Коэффициент, с которым данный главный
ориентированный симплекс t^ комплекса Ка1 входит в БЦ Е^ равен 1; или
(5:24) SPiSft = S*«,
(суммирование по всем главным ^-мерным симплексам соответственно
комплексов К$х и Ка1).
Теперь докажем следующее фундаментальное соотношение, из
которого потом и выведем лемму [5 : 1]:
[5:2]. Для любой цепих? £Ьр(Ка) имеет место тождество
(5:2) ^4iD^ = *;,/«.
Доказательство [5:2]. Для любого главного симплекса
*
Щх комплекса К$х имеем, обозначая через t%b носитель симплекса Щх
в ТС а через Щ — симплекс, сопряжённый звезде Ц*
Цх Dfsi xi ■ ъ)=(°$ Щ к ■ Ъ=Ф xi • ф=(*? • si ф-
Положим для краткости:
У$\ — 5?1 U$ ^^Ха
Мы только что вычислили:
(5:25) 0?1-^> = К-5Р^),
для любого главного T££K$i. Для неглавных Ш£К$1 по самому
определению оператора s^ имеем (уч.Ц{) = 0 (при любом выборе
ориентации Щх симплекса Г£).
Пусть теперь
(5 :26) Т£ = | 7"о > ГН > ... > 7>|
— произвольный ^-мерный симплекс комплекса Ки1) если ТааХ — глав-

§ 5|
комёинаторная Лемма
531
ный симплекс, то ориентация №{ симплекса Т%{ уже выбрана; если
же 7^— неглавный симплекс, то обозначаем через ^
какую-нибудь его ориентацию. Обозначим через
7?u = l7M>rM1>--->7?jl' J^1- 2'---v'
все главные симплексы K$v отображающиеся, в силу 5^[, на 7^ (при
этом, конечно, различные 7^. могут иметь один и тот же
сопряжённый симплекс 77. так что при различных j симплексы ТР. не
непременно различны между собою).
пусгь 55{^ = V2,. где %-==tl-
По определению оператора S^| и на основании (5 : 25)
(5 : 27) {S^l • <*) = 2 Oft • Vft j)=2 П/ (*S • 5g^)-
Рассмотрим два случая:
1°. Симплекс 7^— неглавный. Тогда на основании [5:22]
в (5 :26) имеем па<р; так как Sj| 7£; = 7*<? , то (*р • £Р^ ) = О
для всех У—1, 2,..., v. Подставляя это в (5:27), получаем
ОЗД •'*,) = о.
По самому определению оператора s*x значение цепи s^D^x? на
неглавном симплексе ^ также равно нулю, так что в случае
неглавного Т\ имеем
2.° С и м п л е к с Т£ — главный. Тогда (5 : 26) переписывается
в виде
^, = |7^>Г«-1>...>ГР|
И
= 7?,
а при нашем выборе ориентации t\. даже
Внося это в (5 :27), получаем
Но на основании [5 : 24]
так что
С другой стороны,
34*

532 V-группы компактов и закон двойственности [гл. xtv
т. е.
CSPJУ1 tq ) = (s* Dqxq • t* ).
Итак, на любом ^-мерном симплексе комплекса /Са1 обе части
равенства (5: 2) принимают одно и то же значение, что и требовалось
доказать.
5:3. Окончание доказательства леммы [5:1] основывается на
следующем предложении:
[5:31]. Если V-цикл г^£ Z^(/Q равен нулю на К0(Х и цикл
zt = 531^з5зг£ отличен от нуля на данном Tlx£K$v то оба
замкнутых симплекса Т$г и 5?}Т^ лежат в некотором выпуклом под-
множестве множества Ga=Ara\^o«, а именно, во множестве
О^ТР, где Т?£К\К0а и Т»>ТР.
Замечание. Если Г£< 1п, то 0\т<пл Тр состоит из Тр и из всех
граней (включая и несобственную грань 7J), подчиняющих себе грань 7^;
среди всех точек замкнутого симплексаТ^точки множества Ох плТ?
характеризуются тем, что все соответствующие вершинам7^ барицентрические
координаты этих точек положительны. Из этой характеристики сразу следует, что
множество Огупл Г£ выпукло.
В самом деле, из наших условий следует, что 7Y есть главный
симплекс:
т11 = \тр>--->Ц~*>--->Ц\*
и что 5з^ отлично от нуля на Г£, что, в свою очередь, означает,
что
Симплекс 5Р}Г|, имеет вид
sn=№Ч> ■ • • > slT$I > где ^Л = ТР« •
Обозначим через Тпа носитель симплекса Т? в комплексе Кл и
положим Tr* = S^T4g. Так как S? есть нормальное отображение, то
7*?^ 7^о, значит,
Вершины симплекса 5^7^суть центры тяжести симплексов
и, следовательно, лежат в выпуклом множестве 0[Г™°]1> с: 0[Р*] 7^,

§ 5]
КОМБИНАТОРНАЯ ЛЕММА
533
поэтому и замкнутый симплекс S^\T^ целиком лежит в множестве
(5:311) ВДе'О^Т».
Остаётся доказать, что
(5:312) Ц^О^ГК
Обозначая через 7^л /—1, 2,..., q, носитель симплекса 7р'~г
в Ка (и помня, что Т£ есть носитель симплекса Г"), имеем
(5:313) Т£>Г*1>...>7>
Вследствие нормальности отображения 6"£ симплекс 7^ = S^Tg
есть собственная или несобственная грань симплекса Тп^\ поэтому
и в силу (5:313) имеем
(5:314) Тп^Тп^ ...l^Tnq^TP,
у / a a ft а
откуда и следует, что все симплексы (5:314) лежат в Olp1] Т?\
в частности, в ОгрЧ Т£ лежат и центры тяжести симплексов
т. е. вершины симплекса Tgv Так как 0г*л17^ есть выпуклое
множество, то, содержа все вершины Т&, оно содержит и весь
замкнутый симплекс 7|\ чем предложение [5:31] доказано.
Доказательство леммы [5:1] заканчивается теперь так.
В условиях [5:31] все остовы призмы, натянутой на [П] и 5^}[Т« ]?
лежат в выпуклом множестве
Ввиду выпуклости множества 0\?пл 7* оно содержит и выпуклые
замыкания всех остовов только что упомянутой призмы. Соединение
выпуклых замыканий всех остовов всех призм, построенных для
всех Т£у удовлетворяющих условиям [5:31], представляет собой
компакт (даже полиэдр) П, содержащийся в Ge= Ка\К0ю и на П
лежит призма, натянутая на циклы гЯ{ и 5^|г Поэтому (в смысле
главы 11, арт. 8:6)
т. е.—помня всё время определение z4 данное в [5 : 31] —
(5:32) э^Ор'гР ~ Щ^Цг? на П.
По формуле (5:2) имеем

534 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВ ННОСТИ [ГЛ. XIV
далее, так как sa,DqzP лежит на II, то
s*DW = sl\s*.DQzP ~ s*D*zP на П,
pi a a pi al a e al a a '
так что в (5:32) можно ^[^З1^а^зг? заменить через s*D^e£; получаем
Как мы видели в 4:2, существует непрерывное отображение С мно-
жества G$ на Qpj, оставляющее неподвижными все точки Q$\ и,
следовательно, переводящее лежащий на Qpi цикл sliD^S^—sl\Dlz% в
самого себя. Поэтому
(5:33) ^О^-^да-О в ^n)c<V
Но
поэтому из (5:33) следует (на основании теоремы [8:61] главы 11)
что и требовалось доказать.
§ 6. Спектр К0 множества Ф.
6:1. Покрытия Qa и <оа. Сохраняя все обозначения арт. 4:1,
обозначим через Qa открытое покрытие сферы 5**, состоящее из открытых
звёзд*) комплекса Ка:
Qt = {0',...,0<sJ.
Как известно, комплекс Ка есть нерв покрытия Qa. Пусть среди
всех OJ, ...,0* множества 0\, ...,0£ и только они
пересекаются с Ф. Положим
(6:11) о« = ФПО«, /=1,2,..., 60a.
Открытые множества о°.,...,оа компакта Ф образуют по-
*■ sia
крытие этого компакта, которое обозначаем через соа.
[6:12]. Комплекс К0а есть нерв покрытия а>а.
В самом деле, вершинами комплекса Коа являются те и только
те вершины комплекса Ка, открытые звёзды которых (относительно
Ка) пересекаются с Ф. Другими словами, вершины комплекса Коа
находятся во взаимно однозначном соответствии с элементами
покрытия ша (вершине е комплекса Кол соответствует элемент Ф П Ок*е
покрытия <оа) **).
*) Глава 4, арт. 3 :2.
**) Элементами покрытия Заявляются «обозначенные» множества (гл. 1,
арт, 1:3); некоторые из них могут совпадать гедметрически,

§ 6]
СПЕКТР К0 МНОЖЕСТВА Ф
535
Далее, пересечение открытых звёзд вершин £?,...,£« ком-
плекса Ка тогда и только тогда непусто, когда в ЛГа есть симплекс
Та с вершинами еа. ,..., еа. , причём
*0 гг
оГе^П . .. П 0„ е« = £L 7a.
Поэтому нерв покрытия ша состоит из тех и только из тех
симплексов комплекса /Са, звёзды которых пересекаются с Ф, т. е.
которые являются собственными или несобственными гранями
пересекающихся с Ф симплексов комплекса Ка- А это и значит* что нерв
покрытия ша есть К0а-
Если Р>а, то, очевидно, Qp вписано в Qa и, следовательно, ш3
вписано в ша.
С другой стороны, из условия 1° арт. 4:1 следует, что
существует такой симплекс 70а £ К0а, что диаметр множества Ф Г) Г0а больше
удвоенного диаметра любого Гр £ К$.
Значит, существует элемент покрытия <оа, не содержащийся
ни в каком элементе покрытия Qp и тем более ни в каком
элементе покрытия шб. Таким образом, a>a не вписано в о^.
Мы доказали:
[6:13]. При [3 > а покрытие ш3 следует за покрытием ша.
6:2. Спектр К0 компакта Ф. Поставим в соответствие каждому
элементу Oj + 1 покрытия Qa+1 некоторый вполне определённый
элемент 0* = 5«+1 (0/ + 1) покрытия 2a, содержащий данное
множество 0/+ 1.
Этим определена некоторая проекция покрытия Qa+1 в
покрытие Qa, а также некоторая проекция sl£^~l покрытия a>a+1 в
покрытие ша: элементу о/ + 1 = Ф П 0/ + а покрытия а>а+1 поставлен
в соответствие элемент о" = Sq? + 1oj +1 в Ф П 5£+1 0/+ ! покрытия
ша, причём 0/рОу+1 и, следовательно, о*5°/ + 1-
Для р > a —|- 1 полагаем
Оа ^в ... Ор-2 0{3_ 1, Ооа = <>0а ••• <>0,3—2 Оо,£ —Ь
Таким образом, для любых двух натуральных чисел а и р, р>а,
имеем единственную проекцию si покрытия 2р в 2а и единственную
проекцию Sol покрытия шр в ша, причём для ^>Р>а всегда
(6:21) Sl = sisl 5Й = 5Й5§?.
Проекциям покрытий соответствуют одноимённые симплици-
альные отображения нервов этих покрытий, т. е. проекция SI
комплекса К$ в Ка и проекция 5q« комплекса К0$ в /С0а, причём на К0$
отображения si и 5о« совпадают.
При этом тождества (6 :21) означают, что эти проекции
удовлетворяют условию 2° арт. 1:1; условие 1° арт. 1 :1 также выполнено,

536 V-ГРУППЫ КОМПАКТОВ И ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XIV
потому что симплициальные отображения S«, Sol порождаются
одноименными проекциями покрытий Qs, o>8 в Qa, <oa. Итак,
последовательность комплексов
{К0а}, « = 1, %.-.,
с только что определёнными в ней проекциями Sol образует спектр
компакта Ф. Этот спектр мы обозначим через К0. Так как У^(Ф) =
= VP (К0), то для доказательства закона двойственности Алексан-
дера-Понтрягина нам достаточно показать, что группы W(K0)
и Дз—1 (С) изоморфны между собой. Это будет сделано в § 8.
6 :3. Проекции S«. Докажем, наконец, что проекция S« комплекса
К$ в комплекс Ка есть нормальное симплициальное отображение,
т. е. обладает следующим свойством:
[б :31]. Для любой вершины еа £ К&, (3>«, вершина si e$ есть
вершина носителя в Кл точки е$.
В самом деле, по определению S£ имеем в частности,
0KfficzOKa(Slep);
е^Та^ОКа(Дер\
что и означает, что sle$ есть вершина носителя TaczKa точки е$.
Следствие [6:32]. Для любого Гр£/Сз симплекс si T$ есть
(собственная или несобственная) грань носителя симплекса Гр в
комплексе Ка.
В самом деле, если Т$аТа£Ки, то носитель каждой вершины
Г8 есть грань симплекса Та, поэтому по [6:31] образ каждой
вершины симплекса Г3 есть вершина симплекса 7а, чем [6:32]
доказано.
§ 7. Дальнейшие вспомогательные предложения.
7:1. Переместительность операторов S$u\/E. Рассмотрим
комплексы Ка, /Са и их подкомплексы К0а и /С03. Проекция si
комплекса К§ в Ка порождает гомоморфное отображение Sp группы
Lp(Ka) b'Lp(/Cs), та же проекция, рассматриваемая лишь на
подкомплексе K0aczKa порождает гомоморфное отображение Sop группы
^Ч^оа) в ^(Хор)- При этом им^ет место следующее предложение.
[7:1]. Для всякого Zoa£2%(K0ai) выполнено соотношение
(7 :1) S$ VE*& ; VESllzl в Ка\К0^
Доказательство. Так как операторы Sp и V коммутируют
между собой [см. главу 9, формула|(б :2)], то подлежащая
доказательству формула (7: 1) может*быть|записана в виде
4S^Ezl7VES°ol4,B K\K0,

§ 7] ДАЛЬНЕЙШИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 537
или в виде
(7:11) V (Ъ1 Е& — ES°ol<&)~0 в Ка\К0и.
Но (7:11), очевидно, следует из
(7 :12) ЦЕ4* — ES%4« 6 Lp{K\K0u).
Остаётся доказать эту последнюю формулу.
Имеем для любого симплекса Tf^/Cp и любой его ориентации t\
(Sg&g,.<?) = (fo£,-s5*$);
поэтому если si T% £ К0л, то
С другой стороны, если rf£Af0g, то
(ES°ol4« • Ф = (5$*0* - Ф = (*£, • S? /?).
Но если Г|£ЛГор, то si 1%£ K0ai поэтому для Т%£К0$ имеем
откуда следует (7:12) и, значит, (7:1).
7:2. Следствие из формул (5:1) и (7:1). В доказательстве
закона двойственности Александера-Понтрягина большое значение
будет иметь следующее предложение, являющееся простым следствием
формул (5:1) и (7:1)
[7:2]. Пусть снова ^oaG^v(^oa)- Тогда
(7 : 2) si Щ S°ol zlr six Д£>2 *?« * Qpr
Значение этой формулы заключается в том, что именно при
помощи неё доказывается, что гомоморфизмы AD«, применённые
к группам 7^ (/f0a), порождают отображение группы Vp (Ф) на Ая-1 (Г).
Доказательство формулы (7:2). Подставим в формулу
(5:1)
4 + 1 = VE4>a;
получим
(7:21) s\x D%~1 Si VEzp0a ~ sfr Dl^VEzt в Qpi.
Но, в сипу (7 :1),
Sl4EzvQa?4E~S§zla в Ка\К0а,
значит,
Dt'^Ezt-Dl-^ESllzt в K:\KU
так что в левой части формулы (7:21) можно Dp" SlVEz^
заменить через E>i~~14ES°*zPa, что даёт
(7 :22) ^OJ-1 VES°«zPa7 s^D^V^ в Qpi.

538 V-группы компактов и зако i zlboMctbfhhocth [гл. xiv
Но но формуле (3:32) главы 13 имеем
D'i-iVES§zl = (- 1)р+1Д^Е^ = ( - 1У+»Д0$*г*,
ГУ-^ЕгР^ = ( - Гу+'ДЯ^ = (- 1)'+1А0**£,.
Внося это в (7:22) и деля обе части равенства на (—IV-1,
получим
что и требовалось доказать.
§ 8. Доказательство закона двойственноеги
Александера-Понтрягина.
8: 1. Гомоморфизм Д£И группы V^ (Ф) в группу А^-^Г),
порождённый гомоморфизмами AD^ групп Z^(K0a) в группы
№~1(К1\Кох)- Каждому V-циклу г?л £ Zpv (К0л) поставим в
соответствие цепь ADr^a. Мы знаем [глава 13, формула (4:41)], что
и, следовательно,
(8:11) K^D^tezrl{T).
Лемма [8:1]. Если V-циклы z^ (= ZP (К0а) и г^ £ Z^ (ЛГор)
принадлежат одному и тому же V-классу спектра К0 компакта Ф,
то
ai a Oa Д pi р Ор
Доказательство. Так как г^ и <г& принадлежат к одному
и тому же V-классу спектра К0, то существует такое -у, ^ > а, *у > J3,
что [см. формулу (4:211) главы 13]
Для доказательства леммы достаточно доказать, что
(8:13) ^ДО^-^ДО^вГ.
Это и будет сейчас сделано.
Из (8:12) следует на основании предложения [4:420] главы 13
и, следовательно,
(8 :14) ^D^^7s^D^z^ в Г.

§ 8] ДОКАЗАТЕЛЬСТВО ЗАКОНА ДВОЙСТВЕННОСТИ 53^)
Но из (7 :2) получаем [заменяя р в (7:2) через -[]
Заменяя в (7:2) а через [В, a (3 через ^» получаем
^71 V0u"r^ д VI Р Of3 ^ '
так что (8 :14) переходит в
чем лемма [8:1] доказана.
Пусть теперь LP произвольный V-класс спектра К0. Бе^ём
произвольный элемент zPa£Zp(K0a) в V-классе Q)\ обозначаем через Kd^p
тот А-класс ^-1^Д«-1 (Г), который содержит цикл $£ Д£Кг£а.
Из леммы [8:1] следует, что Д-класс ^_1 не зависит от выбора
того или иного г%а £ £р, так что AD есть гомоморфное отображение
группы V^(K0) (т. е. группы Ур(Ф))в группу Д^*"1 (Г).
8:2. Отображение AD# есть изоморфизм. Пусть
O£Vp(K0), AD<?O = 0
Надо доказать, что
^ = 0.
Так как по предположению
ДО^ = 0,
то для некоторого <г$а££р имеем
sa ДО?г£ -ОвГ,
ai a 0a '
значит, при достаточно большом р ;> a
и, следовательно, — 0 в Q3i (на основании теоремы [4:6] главы 11).
По формуле {7: 2) имеем
значит, _
и потому (на основании [4:32])
^дааТовк;\л0*г

540 V-группы компактов и закон двойственности [гл. xiv
Отсюда, в силу главы 13, [4:430],
(8:2) ^а€%(*ов).
Но^го«^Ср' и при р>1 группы С£(/Сор) и № (АГ03) совпадают
[глава 13, формула (4:21)]. Поэтому (8:2) означает, что 0 = 0,
что и требовалось доказать.
8:3. Изоморфизм AD# отображает группу V^(K0) на всю
группу Аз-1 (Г). Пусть
ив-1 £ А?-1 (Г).
В силу [4:31], мы можем найти в А-классе и^-1 цикл и^~1 вида
где
На основании теоремы [4:440] и формулы (4 :22) главы 13
существует такой V-цикл zp^ £ ZP (К0а), что
и, следовательно,
Обозначая через О (; V(K0) тот V-класс спектра К0, к
которому принадлежит г^х, имеем
AD«0 = u*-1,
что и требовалось доказать.

ГЛАВА ПЯТНАДЦАТАЯ.
ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ
АЛЕКСАНДЕРА.
0:1. Предварительные замечания. Областями коэффициентов
в этой главе всегда являются кольца с единичным элементом.
В основе всех построений этой главы и многих построений
следующей главы лежит неоднократно упоминавшийся по разным
поводам комплекс Крп соответственно Ksn> т. е. комплекс Кг при
Г = /?п (соответственно T — Sn) (см. гляву 4, арт. 1:5, пункт 2,
или главу 14, арт. 3:1).
В течение этой и следующей глав Ф обозначает замкнуто.е
ограниченное множество пространства Rn. При этом мы всегда
будем рассматривать всякую г-цепь компакта Ф как цепь
пространства Rn.
Другими словами, во всякой s-цепи хГ = 2а^£ компакта
Фс/?п мы понимаем под ft ориентированные (быгь может,
вырождающиеся) симплексы комплекса Кеп, определённые соответствующими
остовами компакта Ф с Rn. В частности, это относится к элементам zrk
истинных циклов ъг = (ги z\> -.. ,zrk, ■ • •) компакта Ф cz Rn (глава 11).
Важное для нас понятие тела хг цепи хг определено в главе 7,
арт. 5:2, замечание 3 (определение повторено в главе 14,
арт. 3:1, замечание 2).
0 двух цепях х и у пространства Rn мы говорим, что они
находятся в «относительно общем положении» друг к другу,
если для любого симплекса Тг цепи х и любого симплекса Г2 цепи у
выполнено, по крайней мере, одно из следующих двух условий:
а) выпуклые замыкания остовов Тг и Г2 не пересекаются, б)
симплексы Тг и Г2 не вырождаются, и их вершины образуют систему
точек в общем положении (см. прибавление 2, арт. 1 : 4).
При данном натуральном я обозначаем через р и q
неотрицательные целые числа, дающие в сумме п.
§ 1. Индекс пересечения и коэффициент зацепления.
1 :1. Индекс пересечения двух цепей хр и уч пространства /?п.
Пусть
— две цепи пространства Rn в относительно общем положении. Их

542 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [гл. XV
индекс пересечения (хр ХУО определяем так:
(1:1) (*"X.y*) = 2(tfX#)«^,
h J
где (tf'X.t]) есть определённый в главе 7, арт. 2:2, индекс
пересечения двух ориентированных симплексов tf и t] (равный -j-1,
— 1 или 0). Таким образом, индекс пересечения двух цепей есть
элемент данного кольца коэффициентов 91.
Следующее предложение часто очень полезно:
[1:11]. Пусть хр и уя. — две цепи пространства Rn,
находящиеся в относительно общем положении. Существует такое
е>0, что всякие две цепи х'р и у'о., возникшие соответственно
из хр и уя. путём г-сдвига, находятся также в относительно
общем положении, причём
{х'р Xy'*) = (xPXvq).
В самом деле, достаточно потребовать, чтобы е было меньше,
чем половина наименьшего положительного числа, являющегося
расстоянием выпуклых замыканий двух каких-нибудь симплексов
комплексов \хр\ и \уя\.
1 :2. Формулы для вычислений с индексами пересечения. Из
теоремы [2 :1] главы 7 следует
(1: 21) (хр ХЯ = (—\)ря (уя X хр).
Следующие формулы, (1 :22) и (1:23), вытекают непосредственно
из определения (1 :1):
(1-22) I [ХР Х {У1 +УЬ] = (ХР Х УЬ + {ХР Х У1)у
I Ы + *?) X у«] = (х? X Я) + (4 X у*);
(1: 23) (ахР X yq) — (хр X <У«) = cl(xpX Vq)-
Очень важно следующее предложение:
Теорема [1:2]. Пусть пг -\-п2 = п -f-1 и Цепи х"1, vn*
находятся в Rn в относительно общем положении. Тогда
(1 :24) (хп* X V) = ("О"1I*** ХУ).
Доказательство. На основании формул (1 : 1) и (1:22) и
(1:23) достаточно вместо (1:24) доказать аналогичную формулу
для двух ориентированных симплексов:
(1 : 240) (t? X Д#) = (-1)*1 (Д# X #)•
Если замыкания симплексов Tll = j t*х\ и 7?*=1*2*| не
пересекаются, обе части этого равенства суть нули, и, следовательно,
формула (К* 2402 верна.
Пусть Til П Т"* ф 0. В этом случае пересечение несущих
плоскостей этих симплексов, в силу предположенного общего положе-

§ 1] ИНДЕКС ПЕРЕСЕЧЕНИЯ И КОЭФФИЦИЕНТ ЗАЦЁПЛЙНЙЯ 543
ния, есть прямая, пересечение же самих этих симплексов, в силу
их ограниченности и выпуклости, — отрезок (открытый)
Т?ПТ£ = {охо2).
Каждая из двух точек ох и о2 лежит на границе одного из
симплексов ГГ1 и Тп±г и является внутренней точкой другого. При этом
могут представиться два существенно
различных случая:
1°. Точки Oj и о2 лежат на границе
одного из
симплексов
Черт. 150.
какого-либо
7?1 и 7?\
2°. Oj лежит на границе Т*\ а о2—
на границе Т1Ъ.
Доказательство в случае 1°.
(На черт. 150 изображён случай /г1=/г2=2.)
Пусть ох и о2 лежат на границе Т"1*).
В силу общего положения, точки ог и о2 суть внутренние точки
двух различных граней ГЙ"" и ГЙ"""1 симплекса Г"1. Обозначим
через Г"1""2 общую грань граней ГЙ-1 и ГЙ-1 и через аг и а2 —
не принадлежащие к ней вершины соответствен но граней Tif1 и
7^2-1- Какова бы ни была ориентация /J*1-2 грани Г"1-2, симплексы
входят в А/"1 с противоположными знаками (в силу второго
свойства коэффициентов инцидентности, глава 7, арт. 3:2). Так как
левая часть равенства (1 :240) обращается в нуль, ибо точки оА и
о2> в силу общего положения, должны быть внутренними точками
симплекса 7^% утверждение (1 :240) эквивалентно следующему:
(1:2401)
(^х^-^г'хй8).
Для доказательства (1 :2401) выберем в плоскости симплекса t"*
какой-нибудь (л2—1)-мерный симплекс \t2\ так, чтобы отрезок
(о^з) не пересекал плоскости \t2\ и чтобы вершины 11% | были
в общем положении в Rn с вершинами симплекса 7V (на черт
,ti— 2
*) Это предположение не является ограничительным, так как, несмотря
на кажущуюся асимметрию формулы (1:24) в отношении цепей xnl и уПг ?
легко убедиться, что из (1 :24) на основании (1 :21) следует формула
(1 : 24') (У** X А*"1) = (-1)"» (V* X х"1),

544 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
150 симплекс \t2\ есть одна из граней симплекса Т%*). Будем иметь
(ЯГ1 X t?) = (ЙГЧо,^-*)) • (#(<>А)) ■ (Я» (V?1-^)),
(Й-1 X <?) = (ЯГ>2^~2)). (/? (<va)) • (#•(о2^'-%))-
Но на основании теоремы [1:51] главы 7
пг1 (vr2)=(<мг2) (°^г,_2)=■+1.
так как точки at и 0j лежат в плоскости симплекса t^~x с одной
стороны от плоскости грани t^~2.
Аналогично
'Г>2'Г2) = («stf»-8) (<vr2) = +1.
Следовательно,
(1 * 241) \
Далее,
(1:242) ^(о^) = ф(о^),
так как точки ох и о2 лежат в плоскости симплекса t** по одну
сторону от плоскости симплекса t2 (отрезок (рхо2) не пересекает
эту плоскость), и, наконец,
(1: 243) R» (о^~%) = R» (o2q>-\\
так как точки ог и о2 лежат в Rn по одну сторону от плоскости
симплекса (t^~H2) (пересечение этой плоскости с плоскостью
симплекса tV? есть плоскость симплекса
t2, и отрезок (oto2) не пересекает
последней).
Из (1:241), (1:242) и (1:243) сле-
^г -</ ^ ^г дует (1:2401), значит, (1:240), т. е.
а^ . i >> / (1 :24) в случае 1°.
Доказательство в случае 2°
(на черт. 151 изображён случай пг =
= п2 — 2). Пусть точки о1 и о2 лежат
Черт. 151. на границе соответственно симплексов
rf и ГЦ", а именно на гранях Г^"1 и
Г£«—L (в силу общего положения точки ох и о2 не могут
принадлежать граням меньшего числа измерений). Обозначим через а{
вершину симплекса Тр, не принадлежащую грани ТЪ~~ 1(/= 1,2).
Пусть /JH-1 и ^2*"~1 — такие ориентации, что
Тогда формула (1 :240) принимает вид
(1 :2402) (*»» X ^Ц»-1) = (— l)ni C^-1 X ^')-

§ 1] ийдекс Пересечения и коэффициент зацепления 5-U>
Для доказательства (1:2402) пусть, далее, Ьх и Ь2— какие-нибудь
вершины соответственно |^1—1| и (/J1""1!", пусть |№~2| и \t^~2\ —
грани симплексов j^1"1! и |^а~~*|, противоположные этим вершинам.
Ориентации |^i~2| и |^*~2| выберем так, чтобы было
Так как отрезок (ог-^), /==1, 2, не пересекает плоскость |^г*~2|,
то точки oi и bt лежат в плоскости грани tp~~l с одной стороны
от плоскости грани ^~2, поэтому
(1 :244) *?<-! (о,^-2) = + 1, /-1,2.
Далее, точки о2, ах лежат в плоскости симплекса f^ с одной сто*
роны от плоскости грани Ц^~~1 [она же — плоскость симплекса
(о^-2)], поэтому, в силу теоремы [1 :5] главы 7, ориентации
(°2°i^?1~~2) и ^1 = (а1^Г~1) одинаковы, т. е.
(1 :245) ^(о2о1^-2) = +Ь
Аналогично
(1 :246) t?p {рх о2 рн-*) = К* (о, f^-1) = -f 1.
Теперь вычисляем
(^ X #-') = (^(02 О, ^~2)) • (^-Ч^ ^~2)) * (ЛП (02 °1 ^~2 *?-*)),
или, на основании формул (1 : 244)—(1 :24б),
{ffh X ф-1) = /?" (о2 о, ^н-2 tn,-Th
{t^-1 X *?) = Rn (ог t^-'% tn*--).
Но
(о2 о! f^i-2 ^~2) (рг tp-*o2 q*-2) = ( ~ 1 л,
откуда и следует (1 :2402).
Теорема доказана.
1:3. Следствия из теоремы [1: 2]. Обобщение условий, в
которых определён индекс пересечения.
Теорема [1 :31]. Пусть в Rn даны цикл zp и цепь х%
находящиеся в относительно общем положении. Если*)
*) Множество хг («тело цепи» хг) определено в главе 7, арт, 5:2,
замечание 3.
35 Александров П. С.

54 0 ЗАЦЕПЛЕЙИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [гЛ. XV
то
(гР X xq) = 0.
Доказательство. Пусть г^==Лд:^Н1, где xi'+l лежит
в Rn\kxft. Определим для цепей гР и x(t положительное число
s<2p(x^!1, Д*я) в соответствии с [1:11] и переведём
посредством s-сдвига цепи хрл'1 и х<1 соответственно в х'р^х и x'fi так,
чтобы выполнялось условие:
1°. Множество всех вершин обеих цепей х'рлх и х'ч находится
в общем положении. Тогда, в силу [1:11], будет выполнено и
условие:
2°. Для г'р^кх'Р*1 имеем
(г'р X х'ч) = (гР X *3)-
Достаточно доказать, что
(г'РХх'<1) = 0.
Но цепи х'р*1 и л:'? находятся в условиях теоремы [1 :2], поэтому
{z'p X *'«) = {Ьх'рл 1 X *'*) = ± (*^ + 1 X Д*'<0 = 0,
что и требовалось доказать.
В частности:
[1 :310]. Если гР и г\ — циклы в Rn, находящиеся в
относительно общем положении, то (гр X £?) = 0.
В самом деле, пусть сначала р<я (и при р = 0 цикл г{
нормален). Тогда ?р~0 в RJ\ Дг? = 0, и утверждение [1:310]
содержится в [1 :31].
Пусть теперь р = 0 и г°{ — не нормальный цикл. В этом случае
q — n. На основании формул (1 :22) и (1 :23) можно принять, что
г°х есть некоторая точка с коэффициентом -f-1, выбранная в общем
положении по отношению к цепи г™. Пусть тогда у0 есть вторая
точка с коэффициентом -f- 1, выбранная в Rn\z% (множество г™
ограничено, поэтому такую точку у0 выбрать, конечно, можно).
Тогда
(У)Х^) = 0;
цикл zJ—у0 — нормальный, и для него доказано, что
к*;—/ох <г*|=о.
На основании формул (1 : 22) и (1: 23) отсюда следует, что
(г°х **) = (>.
Оставшийся неразобранным случай р — п не требует особого
доказательства, так как в этом случае # = 0, и, в силу симметрии

§ 1] ИНДЕКС ПЕРЕСЕЧЕНИЯ Й КОЭФФИЦИЕНТ ЗАЦЕПЛЕНИЯ 547
нашего утверждения относительно гР и г?, теорема в этом случае
также верна.
Теорема [1 :2] позволяет значительно обобщить условия, в
которых определён индекс пересечения двух цепей: а именно,
определить при р -f- <7 = п индекс пересечения для любых двух цепей хр
и д-з пространства Rn, удовлетворяющих условию
(1 :32) ~хр[\1х<1 = О, Кхр[\х* = О,
которое мы кратко формулируем так: ни одна из цепей хр,
хя. не пересекается с границей другой.
Для достижения поставленной цели выберем столь малое е>0,
чтобы 3s было меньше, чем р(хР, Длгя), р(&хр, x<t) и чем
наименьшее из расстояний между двумя какими-нибудь различными
вершинами любой из цепей хр, ху.
Подвергнем вершины цепи хр такому s-сдвигу S', чтобы цепь
х'р, возникшая из хр в результате этого сдвига, находилась в
относительно общем положении с цепью х**.
Индекс пересечения (х'р X xQ) определён, и мы полагаем
(1 :33^) {хр X х*) = (х'р X х*).
Покажем, что это определение индекса пересечения (хр X xq) не
зависит от специального выбора цепи х'р, т. е. от того, какому
именно е-сдвигу мы подвергли цепь хр. Пусть при другом
г-сдвиге 5" (удовлетворяющем условиям, наложенным на S') мы
получим цепь х"р. Докажем, что
(1 : 331) (х'р X x<t) = (х"р X **).
Так как при сдвигах S' и S" никакие две различные вершины
цепи хр не слились между собой (т. е. не перешли в одну и ту же
вершину соответственно х'р или х"р), то цепь х"р может быть
получена из цепи х'р посредством 2г-сдвига 5 = 5"5'-1.
Считая все вершины цепи хр занумерованными в определённом
порядке и перенеся этот порядок и на вершины цепей х'* и х"р,
можем говорить о призме Пдс'-Р, натянутой на цепь х'р и на её
образ х"р при отображении 5 (глава 7, арт. 9 : 3). Вся эта призма
лежит в Зе-окрестности множества хр, т. е. во всяком случае в
/?п\Дл;я. По формуле (9: 34) главы 7 имеем
ДЩ> = х'р — х"р — ПЬх'*>,
так что
х'Р — х"* — ЦЬх'Р~0 в /?w\A*i,
и следовательно, по теореме [1 : 31]
((х'р _ Х"Р — ПА*'*) X х#) = 0.

548 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
Но, так как ИЬх'р лежит в Зе-окрестности множества Ахр, значит,
в /?я\#г, то (TLAx'pXxq) = 0, T- е-
{{х'р — х"р) X хя) = О, (х'р X х*) = (х"р X **),
что и требовалось доказать.
Дополним полученный результат следующим естественным
замечанием. Переведём цепь хя посредством некоторого s-сдвига в
цепь х'я9 находящуюся в относительно общем положении с цепью
хр (при этом г сохраняет своё прежнее значение). Докажем, что
(1:33,) (хрХ **) = (** Хх'*)>
где левая часть (хр X хя) определена по формуле (1 :33^), а правая
(^Х^?) имеет смысл, установленный в арт. 1:1. Для
доказательства формулы (1 :33,) выберем е-сдвиг х'р цепи хр так, чтобы цепь
х'р была в относительно общем положении как по отношению
к хя, так и х'я. Тогда непосредственно (т. е. в смысле арт. 1 :1)
определены индексы пересечения {х'р X хя) и {х'р X х'я), и
рассуждениями, совершенно подобными предыдущим, доказывается, что
{х'р X х'я) = {х'р X хя),
{хр X х'я) = {х'р X х'я)
и, значит,
(хр X х'я) = {х'р X хя),
что и требовалось доказать.
Итак:
[1 : 33]. Если ни одна из цепей хр и хя не пересекается с
границей другой, то индекс пересечения {хр X хя) может быть
определён любою из формул
(хр X хя) = (х'р X хя), (хр X хя) = (хр X х'я)9
(1:33)
(хр X хя) = (х'р X х'я),
где х'р и х'я возникают из хр и хя произвольным достаточно
малым сдвигом, подчинённым единственному дополнительному
условию, чтобы цепи, стоящие в каждой скобке формул (1 :33),
находились в относительно общем положении.
Замечание. Формулы [1:21] — [1 :24], очевидно, верны и в
наших теперешних более общих предположениях.
1 :4. Коэффициент зацепления. Пусть ^и^-1-- два
непересекающихся цикла в /?", причём р -\~q = п и г? в случае р = 0
есть нормальный цикл. Выберем цепь хр*1, ограниченную
циклом г?:
Ахр+1 —гР.

§ 1] ИНДЕКС ПЕРЕСЕЧЕНИЯ И КОЭФФИЦИЕНТ ЗАЦЕПЛЕНИЯ 549
Условие (1 : 32) выполнено, следовательно, индекс пересечения
(д:Р+1 Х-2'!"1) определён.
[1:41]. Значение (xP^y^zf^1) не зависит от специального
выбора цепи хР*1: для любых двух цепей х^1 и х[р+1,
удовлетворяющих условию Ах?*1 =zP, Ax^+1=^, имеет место
(1 :41) (хр+1Х^Г1) = (^р+1Х^-1).
В самом деле, ХР+1—х/р+1 есть цикл; следовательно, на
основании [1:310]
[(XP+1 — х'р*1) X г*-1] = 0.
Отсюда на основании формулы (1 : 22) следует наше утверждение.
Определение [1:42]. Пусть г«—1 и Дл;Р+1 ===гР—циклы с
непересекающимися телами. Индекс пересечения (х^1 X ^f"1) (не
зависящий от специального выбора цепи л;Р+1, ограниченной циклом-?^)
называется коэффициентом зацепления цикла zP с циклом
z^-1 (в данном ориентированном Rn) и обозначается через Ъ (^, -г-^""1);
он является элементом области коэффициентов 91.
Докажем следующую замечательную и важную формулу:
(1 :40) *) to iz\, *f-i) = ± to (г*-\ г?),
точнее:
(1 :4)*) Ь(гР, -г|-1) = (—l^+P+ib^-1, z£).
Доказательство. Выберем цепи XP+1 и _у« в относительно
общем положении и такие, что
На основании (1 : 24) и (1 :21) получаем
*>И> zqr1) = (xP+1 ХАЯ = (-1У+1(Л^+1 ХУ0 =
= (—1)^+1(— l)**(>ffXA*p+1)==(—1)^+^+1 to (г!-1, гР),
что и требовалось доказать.
Из только что доказанного следует:
Если to(^P, г^-^^О, то и to(^^-^ гР)фОу в этом случае
циклы z^ и ^l"1 называются зацеп л енны ми между собой. Простейшие
примеры зацеплений изображены на черт. 150 и 151, где z1 = Ы\,
z\=zte\ и to О}, z\) равно нулю на черт. 150 и равно 1 на черт. 151 •
*) Предполагается, конечно, что обе части этих равенств определены,
т. е. что в случае р = 0 цикл z\ нормален, а в случае q = 1 цикл z\
нормален.

550 зацепления, малый закон двойственности [гл. xv
На черт. 152 имеем z\ = М\, 4 = Д/£, Ь(г\, г°)= 1. На черт. 153,
154, 155, 156 под кривыми линиями следует подразумевать
надлежащим образом ориентированные ломаные с достаточно мелкими
звеньями. Коэффициенты зацепления
соответственно равны 1,0, 2, 0. Читателю
рекомендуется во всех случаях убедиться
в справедливости формул (1 : 40) и (1 :4)
путём конструкции соответствующих
цепей х\ и х\, ограниченных циклами г| и z\t
Если кольцо 3l = J2, то на черт. 155
у, (г}, 4) = 0.
1:5. Формулы для вычислений с
коэффициентами зацеплений. В этом
артикуле мы предполагаем, что в случае
р = 0 циклы z°v z°lx и г^2 — нормальны;
Черт. 152. циклы z\~l, z%~1, zgf1 (в случае р = /г—1)
могут быть и не нормальными.
Из определения коэффициентов зацепления и из формул (1 : 22)
и (1:23) следуют формулы:
(1:51)
( * Щх ± гР2), z^\ = Ь (г*и, гр1) ± Ь (г*,, z\~*), .
(1:52) to (a*f ,**-*) = »(г^ , огр1) = cto (г* , гр1) .
<©■
<о
Черт. 153. Черт. 154. Черт. 155.
Далее имеет место следующая важная
Теорема [1:53]. Если г^ ~ 0 я Rn\z%-\ то
Ч*Ь *Г*) = » fcT1, *f) = 0.
В самом деле, если г^ ~ 0 в /?п\^'-1, то существует цепь
xP+iaR^z?-1 такая, что Дл;р+1=^, и (^/»+1 Х^""1) = 0.
Замечание 1. Полагая на плоском черт. 157
гО = (д;0 __ у0) _^ 0,0 _ ^

§ 1] ИНДЕКС ПЕРЕСЕЧЕНИЯ И КОЭФФИЦИЕНТ ЗАЦЕПЛЕНИЯ 551
где и0, v°— взятые с коэффициентом 1 точки, лежащие в области,
внешней к лемнискате г\, имеем Ъ(г\, 2°) — 0. При этом цикл г1г
зацеплен с каждым из нормальных
циклов х°—и°, у0—v° и
г\^0 в R2\z°2, 4+° в R*\*l
Таким образом, теорема [1:53] в
общем случае обращена быть не может.
В трёхмерном пространстве аналогич-
Черт. 15Р.
ный пример получаем, заменив пары точек л:0 — а0, у0-— v°
окружностями. Читателю рекомендуется возвратиться к этим примерам
при чтении последнего артикула этой главы.
Замечание 2. На основании теоремы [1:53] из черт. 158
видно, что кривые черт. 156 не зацеплены при 31 = /. Аналогично
можно убедиться в незацеплённости кривых
черт. 155 при 3t = J2, вписав в гхх лист
Мёбиуса, не пересекающийся с z\ (его
границей по mod 2, как и в наглядно
геометрическом смысле, будет |г^|).
В теореме [1 :53] можно наряду с
основным кольцом коэффициентов 31, по
которому заданы циклы г? и г%—\
рассматривать ещё и некоторое кольцо %'zd%. Тогда
имеет место предложение:
[1:53']. Если цикл г^ гомологичен нулю
в Rn\z%~'1 no кольцу коэффициентов %'
то Ь(г^,^~1) = 0.
Это предложение непосредственно следует из [1:53], если
рассматривать циклы гР и z?—1 как циклы по области коэффициентов
ЗГ и помнить, что нулевой элемент в обоих кольцах % и 31' один
и тот же.
Важнейшим частным случаем является как и всегда, случай
3t= / Г = ЭТ:
Черт. 158.

552 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
[1:54]. Если г{ и z*}-1—-целочисленные циклы uzP£Hp (Rn\zt'1)
или если zi-1 £№-* (Rn\zP), то Ь (^t ^f"1) = 0.
Отсюда вытекает:
[1:55]. Если zpx~ гр1г в Rn\z^~1 no телу рациональных чисел
И, то Ь (zPn , *§-*) = b (*fa, г*-1).
1:6. Случай г*>£ Z?(/Q, г*?-1 ^Zg^C/C*). Вся предыдущая
теория остаётся, конечно, в силе, если в ней Rn заменить через 5**:
достаточно рассматривать Sn как пространство Rn с присоединённой
одной бесконечно удалённой точкой; можно было бы и с самого
начала строить всю теорию для Sn> рассуждая в терминах
сферической геометрии*).
Пусть теперь К—какая-нибудь триангуляция сферы Sn; через
Кг и К* обозначаем соответственно барицентрическое
подразделение и комплекс барицентрических звёзд (барицентрический комплекс-
триангуляции К (глава 4, арт. 5:2). Выбираем раз навсегда
определённую ориентацию комплекса К.
Пусть ^ £ Z£ (/(), ^ff-^ZJ-^/C*). Тогда для циклов zp и г**?"1
определён в главе 13, арт. 4:5, коэффициент зацепления Ь (zp, z**!-1).
С другой стороны, мы только что определили коэффициент
зацепления^^, ^г*^-1) цикла zp и барицентрического подразделения
s1z*^-ml цикла z*^-1 (условия арт. 1:4, очевидно, выполнены). Дока*
жем, что оба этих коэффициента равны:
(1:61) b(zP, s1z**-i) = 'o(zP,z*<i-i)
Вернёмся к обозначениям главы 13. Обозначим через £»
ориентации я-мерных симплексов Тп£К, одинаковые с выбранной
ориентацией К\ пусть tP, p<n,—произвольные ориентации симплексов
7Т£ Кх, пусть t4 — барицентрическая звезда, сопряжённая симплексу
Тр и ориентированная так, что в смысле главы 13, арт. 3:1, имеем
(t?\t4) == 1. Из этого определения, в частности, следует, что**?, есть
центр тяжести симплекса Г? взятый с коэффициентом -j-1.
Цепи Щ и t*% находятся в условиях (1:32), поэтому индекс
пересечения этих цепей определен и в смысле [1:33], индекс
пересечения Щ и t*%, определённый в этом смысле, обозначим до конца
параграфа через (Ц® t*%) и докажем лемму:
(1:62) ^®'*2) = (*fX**2).
*) В этом случае, однако, необходимо ограничиться только нормаль
иыми нульмерными циклами,

§ 2] ЗАЦЕПЛЕНИЕ ИСТИННЫХ ЦИКЛОВ 553
Так как при 1ф1 тела W и /*? не пересекаются и (/£Х**3)—1,
то достаточно доказать
(1:63) (/£®/*|)=1.
Формула (1:63), как легко видеть, верна для # = 0, р = я.
Предположим, что она доказана для данного q и докажем её для
q~\-\. Предположим, другими словами, доказанным равенство
{Ц ® t*j) == 1
и докажем, что
Для этого возьмём |*£ |£ O^l*?""11; тогда Щ:^г)ф0 и по формуле
(3:2) главы 13
0*<z+i. ру _ (_i)p (tP-.tP-1).
Применяя формулу (1:24) настоящей главы, получаем
{tP^®t4^)={tPf: tP.-1) (A tP®**jf+i}=(— 1)р (*? :/J-1) (^® Д <**+*) =
= (-1)* (tf : /f"1) (W: **f) Щ ® **р =
= (-V(-W:fl)(<J:f1)(<f®«?)=l)
что и требовалось доказать.
Теперь обозначим через xp+1 — *S\ch tP+x какую-либо цепь
комплекса К, ограниченную циклом zp.
Пусть
Тогда (по определению [4:5] главы 13)
ЦгР, г*з-1) = (^р+1 х г**-*) = 2'<<*л(<?+1 X ^*Г1),
/л
тогда как коэффициент зацепления тех же циклов в смысле 1 :4
равен 2е* ^bUf^1®^"1)- В силу (1:62), оба выражения равны, что и
требовалось доказать.
§ 2. Зацепление истинных цикло в.
2:1. Определение коэффициентов зацепления для истинных
циклов. Пусть Ф с: Rn. Каждый е-цикл zp компакта Ф является
циклом открытого множества*) 0(Ф,г); поэтому, если дан какой-либо
цикл г^-1 открытого множества /?п\0(Ф,г), то можно говорить о
коэффициенте зацепления Ъ(гр, г**-1) циклов zp и z*-1.
*) См. предварительные замечания в начдде этой главы.

554 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
Ilycib теперь даны: истинный цикл
компакта Ф и цикл г^~1 £ Z^"1 (Г) открытого множества V = /?Л\Ф.
Существует такое е > 0, что цикл z^~l является циклом открытого
множества Г£ = /?и\0(Ф,е). С другой стороны, из определения
истинного цикла следует, что все г£ при достаточно большом k являются
циклами открытого множества О (Ф,з) и гомологичны между собой
в этом открытом множестве. Отсюда нд основании [1:53], в свою
очередь, вытекает, что для всех достаточно больших & коэффициент
зацепления b(£?, z^"1) имеет одно и то же значение, которое и
называется коэффициентом зацепления 1>(zP', г^-1)
истинного цикла ър компакта Ф и цикла г^-1 открытого
множества Г = Я.п\Ф.
(2:10) ъ(гР, -г«-1) = Ь(г^., г*"1)
для достаточно большого k.
Пусть теперь Ф и Ф' — два непересекающихся замкнутых
множества в Rn. Возьмём такое s>0, чтобы окрестности О (Ф,е) и
О (Ф',е) не пересекались. Пусть
2Р = {гР, ^,...,г£,...)
2«-1=(г?-1| гГ1,...^"1,...)
— два истинных цикла соответственно компактов Ф и Ф'. Для всех
достаточно больших k циклы г£ лежат в 0(Ф,е) и гомологичны там
между собой, а циклы z^~x лежат в 0(Ф',г) и также гомологичны
там между собой, поэтому для всех достаточно больших k
коэффициент зацепления Ь (zpk, ^<j~1) принимает одно и то же значение,
которое и называется коэффициентом зацепления^(zp, z^-*1)
истинных циклов гР и z*_1.
Замечание 1. Очевидно,
ъ{ър, г«-1) = Ь(^,г^)
для всех достаточно больших / и у.
Из этих определений без труда следует, что формулы (1:51) и
(1:52) справедливы как для коэффициентов зацепления истинных
циклов компакта Ф с циклами открытого множества Г = /?П\Ф,
так и для коэффициентов зацепления истинных циклов, лежащих
соответственно на непересекающихся компактах Ф и Ф'.
Далее,
[2:11]. Если
Z4-1 ~0 в Г
или
zp ~ 0 в Ф,
то

§ 2] ЗАЦЕПЛЕНИЕ ИСТИННЫХ ЦИКЛОВ 555
Точно так же для двух истинных циклов ър и z^_1,
принадлежащих соответственно непересекающимся компактом Ф и Ф', имеем
)o(zp, z«_1) = 0,
если выполнено хоть одно из условий
гР ~ О в Ф, z^-1 ~ О в Ф'.
Отсюда следует:
[2:111]. Пусть z? и грг — истинные циклы компакта Ф,
гомологичные между собой в Ф, a z^-1 — истинный цикл в Ф'с:/?П\Ф.
Тогда
»(zf, zfl-1) = Кй,е z«-1).
Определение [2:120]. Системы циклов
(2:121) zf, ..., zj в Ф
и
(2:122) ^J-1,...,**-1 в Г
называются зацепленными между собой, если
Ъ(ж$, *J->) = V /, у=1, 2,..., *.
Здесь (2: 121) суть истинные циклы компакта Ф, тогда как под (2:122)
можно понимать как циклы открытого множества Г = 1^*\Ф, так и
истинные циклы какого-либо компакта Ф' с Г.
Теорема [2:12]. Если системы (2:121) и (2:122)
зацеплены между собой, то циклы (2 :121) гомологически независимы
между собой в Ф, а циклы (2 :122) — в Г.
Доказательства обоих утверждений совершенно одинаковы.
Пусть, например, 2C*Z? -0 в Ф. Тогда, в силу [2:11], имеем
для любого h = 1, 2, ..., s.
Но
i
так что для любого h = 1, 2, .. ., s
*л = 0>
что и требовалось доказать.
2:2. Деформационная теорема для непрерывных циклов.
[2 :2]. Пусть г? и zjj--1—дяа непрерывных цикла в Rnf
данных своими параметрическими представлениями*):
zp = (C0zP1, C0zP,...)
z<-> = (C0*r>, C0*f->,...).
*) Глава 11, арт. 4:7 <

556 8АЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
Пусть даны деформации
и 0<6<1
этих параметрических представлений, причём для каждого
значения Ь имеются непересекающиеся компакты Фе и Ф'ь в Rn,
являющиеся соответственно носителями непрерывных циклов ъ\ и
z%~~1, тогда
Доказательство. Для данного 60, 0<60<;i, построим
непересекающиеся окрестности О(Фе0\ 0(Ф'%) множеств Фе0 и Ф'^у
построим, далее, такую окрестность £/е0 точки 6 относительно сегмента
0^6<;1, что для любого G££/g0 имеем ФеЕО(Фе0) и Ф'е^О(Ф^0),
тогда на основании теоремы [3:41] главы 11 zf ~ г\ в О(Фе0) и
ъ\~~х ~ z^""1 в 0(Ф' ). Поэтому на основании результатов
предыдущего артикула Ь (zf, zj*-"1) сохраняет постоянное значение, когда
6 изменяется в пределах Uh0. Так как это верно для любого 0О, то
b(zf, z^""1) сохраняет постоянное значение на всём сегменте
0<;6^1 и, следовательно, b(z£, z^~1) = b(zf, г\—*), что и
требовалось доказать.
Замечание. В основу всех рассуждений этого параграфа
можно вместо эвклидова пространства Rn положить сферическое
пространство Sn.
§ 3. Малый закон двойственности Александера.
3:1. Предварительные замечания и формулировка теоремы.
Во всём этом параграфе приняты такие обозначения: Ф есть
кривой полиэдр, расположенный в Sn\ Г=5П\Ф; через К0 обозначена
кривая триангуляция Ф; через 51 обозначено тело рациональных чисел или
любое тело Jmi где т — простое число; через ^(Ф), тг£ (Г)
обозначается r-мерное число Бетти (в случае 21 = ffi) и r-мерное число
Бетти по модулю т (в случае % — Jm) соответственно полиэдра Ф
и открытого множества Г; при этом т:° определено (при любом из
наших 51) как уменьшенное на 1 число компонент. В этих
обозначениях малый закон двойственности ллександера
выражается формулой
(3:1) ^(Ф) = ^Г1(П,
верной для любого 0<;рО — 1. q = n — р.
В этом параграфе мы дадим элементарное доказательство малого
закона двойственности Александера, опирающееся на главу 13, но
совершенно независимог от результатов главы Н-

§ 3] малый закон двойственности алекСандера 55?
Через Q обозначаем некоторую, остающуюся всё время
неизменной, триангуляцию пространства Sw, через Qf — некоторое
подразделение триангуляции Q, состоящее из симплексов диаметра <е,
через Кг—комплекс, состоящий из тех симплексов комплекса Qe,
замыкания которых пересекаются с Ф, и из всех граней этих
симплексов. Через Фе обозначаем тело триангуляции /Се.
3:2. Доказательство теоремы (3:1).
Лемма [3 :20]. Пусть 3s — лебегово число комплекса /С0.
Всякий цикл zp £ Zp (К0у 91), не гомологичный нулю в К0, не
гомологичен нулю и в Фе.
Доказательство. Пусть цикл z£Zp (K0> 91), рассматриваемый
как истинный цикл*), гомологичен нулю в Фе.
Возьмём столь большое /г, чтобы /г-кратное барицентрическое
подразделение shz цикла z было границей некоторой а-цепи хщ
полиэдра Фе:
kx^snz.
Каждой не принадлежащей Ф вершине ei цепи хъ поставим в
соответствие одну из ближайших к ней точек Ф; определённый таким
образом s-сдвиг переводит цепь дге в Зе-цепь дг3е компакта Ф,
причём
А •% = shz.
При каноническом сдвиге относительно триангуляции К0 (кривого)
полиэдра Ф цепь xZt переходит в некоторую цепь х0 комплекса iC0,
a shz переходит в z = kxQy что и требовалось доказать.
В лемме [3:20] содержится:
Лемма [3 :21]. Если циклы
(3:21) zPv...,z'8, zP£ZP(K0,%)
гомологически независимы в К0 и Зг есть лебегово число комплекса
Kq, то эти циклы гомологически независимы между собой и в Фе.
Лемма [3:22]. Пусть циклы
(3:21) *?,...,*£, *Ч£2:р(КъЛ)
гомологически независимы между собой в К0) тогда в Г можно
найти систему циклов
(3:22) z\~\ ...,г|-ь ^-^«-"ЧГ, «),
зацепленную с системой (3 :21) и, следовательно, состоящую из
циклов, гомологически независимых между собой в Г.
Доказательство леммы [3:22]. В самом деле, в силу
леммы [3 :21], циклы
(3:21) *!,...,*>
*) См. главу 11, арт. 4:6.

558 ЗАЦЕПЛЕНИЯ, МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [ГЛ. XV
(рассматриваемые как истинные циклы компакта Фе) гомологически
независимы в Фе; каноническим сдвигом S|? они переводятся в циклы
(3:210) *&,...,*£,
комплекса /Се, гомологически независимые в /Се. По теореме [4 :61]
главы 13 строим зацепленную с системой (3:2-1) систему циклов
(3:22) г*-*,...,**-1
в Ге. Так как гЯ ~ ?р. в Фе, то
так что системы (3 :21) и (3 :22) зацеплены.
Замечание. Пусть (3:21) — целочисленные циклы комплекса
/С0, образующие (У, 91)-базу в /f0. Повторяя только что сделанные
рассуждения, но ссылаясь в конце их на теорему [4:62] главы 13
(вместо теоремы [5:61]), получаем зацепленную с (3:21) систему
(3:22), состоящую из целочисленных циклов.
Итак:
[3 :220]. Пусть целочисленные циклы (3 ;21) образуют (У, 91)-
базу в комплексе АГ0. Тогда существует зацепленная с (3:21)
система целочисленных циклов (3 :22).
К этому предложению мы вернёмся в ар г. 3:3.
Лемма [3:23]. Пусть циклы
(3 :23) г?~\ . . ., гГ \ 4~' € Z*~* (Г, 91)
гомологически независимы между собой в Г. Существует
зацепленная с системой (3 :23) система циклов
(3:21) *?,...,*?, ^^ZP(K0i 91),
гомологически независимых между собой в /С0.
Доказательство леммы [3:23]. При некотором е>0 все
циклы (3:23) лежат в полиэдре Ге=5п\Фе и там и подавно
гомологически независимы. Поэтому по предыдущей лемме существуют
циклы
'р 'р
Z\ , . . ., Zs
в 5п\Г£сфе, удовлетворяющие условию
Заменяя циклы z* их достаточно мелкими подразделениями,
получаем после канонического сдвига нужные нам циклы
*li • • •» *si
что и требовалось доказать.
Пусть теперь
(3:21) *?,...,*?. *?£ZP(Ko, 91)

§ 3] МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ АЛЕКСАНДЕРА 559
— максимальная система гомологически независимых между собой
циклов комплекса /Cq. Тогда
Строим зацепленную с (3:21) систему циклов
(3:22) гГ\ .. .,4~\ ^Г^-ЧГ, «).
Циклы (3:22) гомологически независимы в Г. Докажем, что они
образуют максимальную систему гомологически независимых
циклов в Г.
В самом деле, если бы существовал цикл zv-1 £ Z*-1^, 91)
такой, что
были гомологически независимы в Г, то по лемме [3:23] в К0
существовали бы s -(- 1 гомологически независимых р-мерных циклов,
в противоречии с тем, что ^{K0) = s. Так как система (3:22)
максимальная, то
4-1(Г) = « = я§(Ф),
что и требовалось доказать.
Замечание. Совершенно так же мы доказали бы, что всякая
система циклов (3 :21), зацепленная с максимальной системой циклов
(3:22) открытого множества Г, также максимальна.
Итак: ^
[3:2]. Пусть в Sn дан кривой полиэдр Ф = К0-
Ко всякой максимальной системе гомологически независимых
р-мерных циклов комплекса К0 (соответственно открытого
множества Г = 5П\Ф) можно построить зацепленную с нею систему
Черт. 159. Черт. 160.
^q — \)-мерных циклов открытого множества Г (соответственно
комплекса К0), и всякая такая система будет максимальной.
Областью коэффициентов при этом является либо поле
рациональных чисел, либо какое-либо из полей Jm, где т — простое число.
Иллюстрацией к теореме [3:2] может служить черт. 159. На нём
pz=zq=:l, д = 3; кривой полиэдр Ф заштрихован.
Замечание. Циклы z\ и zl на черт. 160 образуют (У, ЭТ)-базу
в Ф, а циклы z\~~~l и zf~x образуют (У, $Я)-базу в Г (на черт. 160

560 ЗАЦЕПЛЕНИЯ. МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ [гЛ. XV
продемонстрирована гомология zq~x ~ z\~~ -\-z%~1 в Г). Таким
образом, черт. 159 и 160 иллюстрируют не только теорему [3 :2], но
и так называемый малый закон двойственности Понтрягина, к
которому мы сейчас и переходим.
3:3. Малый закон двойственности Понтрягина. Так как для
определённых в начале этого параграфа областей коэффициентов 51
понятие гомологической базы совпадает с понятием максимальной
системы гомологически независимых между собой циклов данной
размерности, то теорема [3:2] может быть сформулирована так:
[3:30]. Ко всякой р-мерной гомологической базе комплекса К0
(открытого множества Г) по области коэффициентов 91 можно
построить зацепленную с ней (q — 1)-мерную гомологическую базу
открытого множества Г (соответственно комплекса К0). Эту
теорему можно назвать малым законом двойственности Понтрягина
для областей коэффициентов 91 = Jm, 91 = 9t.
Более глубоким фактом является аналогичное предложение,
касающееся (У, 9?)-баз:
[3:3]. Малый закон двойственности Понтрягина. Ко
всякой р-мерной (7, Щ-базе комплекса К0 (открытого
множества Г) можно построить зацепленную с нею (q—1)-мерную
(7, Щ-базу открытого множества Г (комплекса К0).
Доказательство. Мы знаем (теоремы [3:220] и [3:2]), что
ко всякой р-мерной (У, $И)-базе
(3:31) *f,...,*J
комплекса /С0 можно построить зацепленную с ней максимальную
систему целочисленных циклов
(3:32) гГ1""»^-1.
Докажем, что система (3 : 32) является (У, 9?)-базой для Г.
Докажем, другими словами, что ко всякому (д—1)-мерному
целочисленному циклу г^—х можно найти линейную комбинацию ^Cjzj^1
циклов (3 :32) с целыми коэффициентами Cj, так что
i
Прежде всего, в силу максимальности системы (3: 32), имеем
z 7 ^ cjzj »
3
где с3- — рациональные числа.
При этом
Ь(#, гч-1) = ^ с.ь tf, гЧ->) = £ СА' = с*'

§ 3] МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ АЛЕКСАНДЁРА 561
Так как Ь(г?, г^"""1) целое число, то все коэффициенты ci —
целые; поэтому и
i
есть целочисленный цикл; так как он гомологичен нулю по о5ласти
•^
коэффициентов 9?, то он содержится в W~~l (Г), чем и доказано,
что циклы (3 :32) образуют (7, 9?)-базу множества Г.
Замечание. Этим, в частности, доказано, что (7, 91)-базы
открытого множества Г существуют для всякой размерности /\
Пусть теперь система (3:32) есть какая-нибудь (7, 1й)-база
множества Г.
Возьмём какую-нибудь (У, 9?)-базу (3:31) комплекса К0 и
построим зацепленную с ней (7, 9?)-базу.
(3:33) иГ"1,...,^"1
множества Г. Так как (3:32) и (3:33) суть (7, 91)-базы
множества Г, то
TVS"»»*-1.
к
h
причём целочисленные матрицы A = (ah^) и В = (ЬкЬ) взаимно
обратны и, следовательно, унимодулярны.
Ищем теперь целочисленные линейные комбинации
циклов гР. так, чтобы
«?-2ц*Г
Для этого решаем относительно неизвестных 5fh систему уравнений
b(2 ^. 2«-i) = 8Л; i, Л = 1, 2, . .. , ie»»(/Q = я«-1(Г).
Но
Поэтому наши уравнения переписываются в виде
т. е.
или, так как b С^,^"1) = Sj&, в виде
Так как 'det(aw) = ztl, то эта система решается в целых числах
и притом однозначно.

562 зацепления. Малый закон действенности [гл. xV
Полученные целочисленные циклы uf образуют максимальную
систему гомологически независимых между собой целочисленных
циклов комплекса /С0» Рассуждения совершенно подобные тем, с
которых мы начали доказательство настоящей теоремы, показывают,
что циклы uf образуют (УД)-базу комплекса АГ0, что и требовалось
доказать.
3:4. Замкнутые (п— 1)-мерные псевдомногообразия в Sn при
п >-2 .Теорема Жор дана-Брауэра. Так как ^(Г) (при всяком 51) равно
уменьшенному на 1 числу компонент Г, то из (3:11) (полагая
г==п —1 и 91 = 7Ш) выводим:
[3:41]. Для любого кривого полиэдра Ф, лежащего в Sn, имеем
,гп-1(ф) = 1сп-1(ф).
Пусть, в частности, Ф—какое-нибудь (п—1)-мерное
псевдомногообразие. Тогда тг^~1(Ф)=11 значит, по только что доказанному
и ъп—\Ф) = 1. А это значит, что Ф ориентируемо. Так как тс0(Г)=* 1,
то Г состоит из двух компонент.
Итак:
[3:411]. Всякое (п — \)-мерное замкнутое псевдомногообразие,
лежащее в Sn, ориентируемо и разбивает пространство Sn на
две области.
Теперь докажем, что для любого замкнутого множества Ф' с: Ф
открытое множество Г' = Яп\Ф' связно. Для этого достаточно
доказать, что всякие две точки рх и р2 множества Г/ содержатся
в некотором связном подмножестве этого множества. Для
доказательства последнего утверждения возьмём столь мелкую кривую
триангуляцию К псевдомногообразия Ф, что подкомплекс Ко
комплекса /С, состоящий из всех пересекающихся с Ф' симплексов К
и их граней, есгь собственный подкомплекс комплекса /С, тело ко-
торогб Ко не содержит ни одну из данных точек рг и р2.
Тогда тггг-1(/С0) = 0, следовательно, в силу (3*2), открытое мно-
жество Г0 = /?П\/С0£ЕГ/ связно. Так как Г0 содержит обе точки
Pi и Рг» то всё Доказано.
Из доказанного следует (см. главу 2, арт. 1:2):
[3:42]. Теорема Ж ор д ана-Брау эр а. Всякое (п —
Химерное замкнутое псевдомногообразие, лежащее в Sn, ориентируемо,
разбивает пространство Sn на две области и является
совместной границей этих областей.
Этот результат, очевидно, остаётся в силе при замене Sn на Rn:
достаточно спроектировать Sn на Rn стереографически из какой-
либо точки, не принадлежащей данному псевдомногообразию Ф.
Рассмотрим ближе случай замкнутого {п—1)-мерного
псевдомногообразия Ф, лежащего в Rn. Та из двух компонент открытого
множества Г = #п\Ф, которая ограничена, называется внутренней по
отношению к Ф и обозначается через Г0, а неограниченная компо-

§ 3] МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ АЛВКСАНДЕРА 563
нента Г называется внешней по отношению к Ф и обозначается
через Гоо.
Пусть гп~х — какая-нибудь ориентация псевдомногообразия Ф.
Если о'^Гсо, то »(г»-1,о') = 0. В самом деле, так как для лю-
блх двух точек о\ о'7 области Гоо имеем о' ~ о" в Гоо, то Ъ(гп~г9о')
принимает одно и то же значение для всех о' £ Гоо- Чтобы убедиться,
что это значение равно нулю, достаточно взять о' вне какого-либо
куба Q% содержащего Ф внутри себя: тогда zn~1~0 в Qn и,
следовательно, для о' £ Rn\Qn
*)(^п-\о') = 0.
Для того чтобы определить biz*-1,о), где о£Г, заметим, прежде
всего, что на основании теоремы [3 : 220] существует целочисленный
нульмерный цикл
г* = 2<* А + 2«,Ч. ot 6 Г0, о', £ Гоо,
удовлетворяющий условию
Так как Ъ{гп-1> о7)=0, и y^a[oi ~ (^аг)°> где о — какая-нибудь
точка множества Г0, то
Цгп-^ао) = 1, где а = ^а{.
Так как
^)(г^-1,до) = аЬ(г^-1,о)
и а—целое число, то
Ъ(гп-\о) = ±:1.
Итак, для всех точек о £ Г0 коэффициент зацепления Ъ(гп-х,о)
принимает одно и то же значение, равное 1 или —/.
Замечание 1. Докажем последнее утверждение, не пользуясь
теоремой [3: 220], а опираясь лишь на [3 :22]. В силу [3 :22],
существует нульмерный цикл z° по полю коэфициентов 51, для
которого ^(гп-1, z°)=\, существует, значит, целочисленный цикл z°,
для которого Ь(гп-1У г°) ф 0. Повторяя только что произведённое
рассуждение, убеждаемся в том, что \>(zn-1,ao) ф 0, значит, Ъ(гп-19о) ф0.
Эти рассуждения остаются в силе и при замене области
коэффициентов J областью коэффициентов ]т\ т — простое число.
Итак,
ty^-^o^Omodm,
где т — любое простое число. Но отсюда следует, что b{zn-lyo) = rtl.
Итак, можем высказать следующую теорему:
[3:43]. Пусть Фс^п есть (п — 1)-мерное замкнутое
псевдомногообразие', пусть гп~1 какая-нибудь ориентация Ф. Для всех
точек о каждой из двух областей, на которые Ф разбивает
пространство Rn, коэффициент зацепления Ъ (г™-1, о) принимает
одно и то же значение, равное нулю для внешней области и
Равное ± 1 для внутренней.

564 Зацепления* мАлыЙ закон Двойственности (гл- х^
Определение [3:44]. Число \>(zn-1i о), где о£/?п\Ф,
называется порядком ориентированного
псевдомногообразия Ф относительно точки о.
3:5. Некоторые замечания о зацеплении псевдомногообразий.
Все циклы в этом артикуле — целочисленные, все гомологии —
слабые (т. е. по области коэффициентов Jft). Мы видели в арт. 1:5,
замечание 1, что может случиться, что полиэдр Ф является телом
некоторого цикла zp и что цикл zQ-1 открытого множества Г =
= Rn\$ не гомологичен нулю в Г, не будучи в то же время
зацеплен с циклом zp. Пусть теперь Ф есть лежащее в Rn замкнутое
ориентируемое /?-мерное псевдомногообразие, zp — некоторая
ориентация псевдомногообразия Ф и zQ-1— некоторый цикл открытого
множества Г?=з/?П\Ф, не гомологичный нулю в Г. По теореме
[3:3] в Г существует цикл z%-ly образующий (У, 9?)-базу Г, и
такой, что Ь(<гР><г^~|)= 1. Тогда z^-1 — cz%~x в Г, и так как г«-1/^0
в Г, то с ф О, и следовательно,
i>(zp, zv-1) = сЬ(zp% z<(-1) = сфО.
Итак:
[3:51]. Пусть Ф — замкнутое ориентируемое р-мерное
псевдомногообразие в Rn, a zz-1 — какой-нибудь (q— 1)-мерный цикл в
Г = /?П\Ф; цикл zv-1 тогда и только тогда гомологичен нулю в Г,
когда он не зацеплен с псевдомногообразием Ф (т. е. когда для
ориентации zp псевдомногообразия Ф имеем Ь(г^, г«-1) = 0).
В частности, пусть Ф и Ф/—два непересекающихся замкнутых
ориентируемых псевдомногообразия размерностей р и q—1,
расположенных в Rn; если одно из них гомологично нулю *) в области,
дополнительной ко второму, то и второе гомологично нулю в области,
дополнительной к первому, и это явление наступает тогда и только
тогда, когда эти псевдомногообразия *) не зацеплены между собой.
Назовём коэффициентом зацепления двух лежащих
в Rn непересекающихся замкнутых ориентируемых
псевдомногообразий Ф и Ф/ размерностей р и q—1
абсолютную величину коэффициента зацепления каких-либо ориентации
этих псевдомногообразий. Полученное не отрицательное число
выражает некоторое свойство взаимного расположения
псевдомногообразий Ф и Ф/ в Rn\ обращение или необращение этого числа в нуль
соответствует наивному смыслу понятия «незацепленности» или «за-
цепленности» (например, двух замкнутых линий в /?3). Докажем, что
коэффициент зацепления двух псевдомногообразий выражает
действительно топологическое свойство их взаимного расположения,
т. е. свойство, инвариантное по отношению к топологическим
отображениям пространства /?w, содержащего оба эти псевдомногообра-
Зйя. Докажем, другими словами, следующее предложение:
*) Здесь гомологии и зацепления псевдомногообразий относятся, конечно,
не к самим псевдомногообразиям, а к (произвольным) ориентациям их.

§ 3] МАЛЫЙ ЗАКОН ДВОЙСТВЕННОСТИ АЛЕКСАНДЕРА 565
[3:52]. Пусть С—топологическое отображение пространства
Rn на себя или на другое пространство R*. Тогда коэффициент
зацепления двух псевдомногообразий Ф и Ф', ФсRn> Ф'cz/?w,
равен коэффициенту зацепления псевдомногообразий С\Ф) и С(Ф').
Для доказательства возьмём ориентирующий истинный цикл г*
псевдомногообразия Ф и истинный цикл z^""1 в Г = /?Я\Ф,
имеющий с гР коэффициент зацепления 1 и образующий (7, 5Ю-базу
области Г. Ориентирующий цикл z'^-1 псевдомногообразия Ф'
удовлетворяет соотношению z'tf-1*—' azj-1 в Г, b(z^, z's-1)^^, причём
\а\ есть коэффициент зацепления псевдомногообразий Ф и Ф'. Так
как группы Бетти области Г при топологических отображениях
пространства Rn преобразуются изоморфно (см. главу 14, арт. 3:3, где
доказана даже более сильная теорема об инвариантности групп
Бетти области Г при топологических отображениях самой области
Г, то цикл C(z/«-1) удовлетворяет соотношению C(z'*-l)~aC U?""1)
в С(Г), а цикл C(zf~1) образует (J, 5Л)-базу области С(Г). Беря
в С(Ф) цикл, имеющий с C(z^-1) коэффициент зацепления 1, видим,
что этот цикл является ориентацией псевдомногообразия С(Ф) (а не
кратным этой ориентации), откуда следует, что C(z^), также
являющийся ориентирующим циклом псевдомногообразйя С(Ф), имеет
с C(z([~1) коэффициент зацепления dzl. Следовательно,
b(C(z*>), C(z,«-1))=:^b(C(z^), C(zf~1)) = ±a,
т. е. коэффициент зацепления псевдомногообразий С(Ф) и С(Ф')
равен \а\, что и требовалось доказать.

ЧАСТЬ ПЯТАЯ.
ВВЕДЕНИЕ В ТЕОРИЮ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ
ПОЛИЭДРОВ.
Теория непрерывных отображений полиэдров является одной из самых
важных и интересных частей топологии. В особенности теория
непрерывных отображений многообразит", в частности сфер, послужила предметом
многих замечательных топологических исследований последних десятилетий.
Как и во многих других случаях, фундамент теории был заложен в
классических работах Брауэра (1911 —1913 гг., тт. 70—72 «Mathematische
Annalen»). Именно эти работы Брауэра и примыкающие к ним по своим
методам работы Хопфа являются основным предметом последних двух глав
этой книги, в особенности предпоследней, главы 16. Глава 17 пгсвящена
замечательной теореме о неподвижных точках непрерывных отображений
полиэдров, доказанной Лефшецем для многообразий, а Хопфом — впервые для
любых полиэдров.
Выбор материала этих последних глав вызван не только
окончательностью, важностью и, так сказать, «классичностью» излагаемых результатов, но и
обаянием непосредственной геометрической наглядности, которым прсникну-
ты как и сами доказываемые здесь теоэемы, так и методы их доказательства.
Наконец, надо отметить значение всего этого круга вопросов в истории
математики вообще и топологии в частности: именно на теории
непрерывных отображений простейших многообразий топология, в то время ещё
совсем молодая ветвь математической науки, окрепла и, если пбзволено так
выразиться, осознала свои силы; именно эта теория .сала первые
приложения топологии к анализу и этим показала, что топология
многими нитями связана с остальной математикой; именно здесь были
заложены первые основы глубокого и всё возрастающего воздействия топологии
на развитие математической мысли нашего времени.
Из литературы по теории непрерывных отображений многообразий и
вообще полиэдров кроме уже упомянутых работ Брауэра, следует указать
на знаменитый мемуарЛефшеца «Intersections and transformations of complexes
and manifolds», Trans. Amer. Math. Гос., 28, 1926, pp. 1—49, положивший начало
алгебраической теории непрерывных отображений многообразий, т. е.
исследования этих отображений при помощи теории пересечений (мы
познакомились в главе 13 лишь с простейшим понятием этой теории — с
понятием индекса пересечения). Дальнейшим развитием теории Лефшеца
явилась работа Хопфа «Zur Algebra der Abbildungen von Mannigfaltigkeiten»,
Journ. r. u. ang. Math. (Crelle), 163, 1930, pp. 71—88 (см. также его же
статью Beitrage zur Klassifizierung von Flachenabbildunge, Crelle, 165, pp.
225—236. В другом направлении, в направлении так называемых
гомотопических методов, идут работы Хопфа «Zur Topologie der
Abbildungen von Mannigfaltigkelten», Math. Ann., 100, 102, 1929, pp. 562—623, которые
в высшей степени могут быть рекомендованы для изучения *).
*) К этим работам Хопфа примыкает работа Кнеаера. Glattung von Fla-
chenabbiidungen, Math. Ann., 100,1928, стр. 609—617, специально посвященная
случаю п ==2, т. е. непрерывным отображениям поверхностей (этот случай
оказался недоступным общим методам Хопфа).

ВВЕДЕНИЕ В ТЕОРИЮ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ 567
Работа Хопфа «Ober die Abbildungen d. dreidimensionalen Sphere attf die
Kugelfiache», Math. Ann., 104, 1931, pp. 639—665, послужила началом ряда
исследований о непрерывных отображениях сфер разного числа измерений
друг на друга. Проблема классификации этих отображений,
т. е. выяснения числа попарно не гомотопных между собой отображений
/«-мерной сферы на «-мерную, тривиальна при т<^п: в этом случае все
отображения Sm в Sn гомотопны между собой, в частности, гомотопны
отображению Sm на одну какую-нибудь точку сферы Sn. При т = п эта
проблема решена Хонфом; её решение составляет предмет § 6 главы 16 этой
книги *). Наконец, проблема классификации при ту п оказалась
чрезвычайно трудной; она до сих пор решена лишь в частных случаях глубокими и
трудными исследованиями Хопфа **), Л. С. Понтрягина ***) и др* Работа
Хопфа об отображениях трехмерной сферы в двумерную является
превосходным введением в эту интересную и трудную главу топологии.
В тесной связи с работами Хопфа по теории непрерывных отображений
находятся, с одной стороны, работы Freudenthal^ [Compositio Math. v. 4
(1937) pp. (535—238)] и Брушлинского. [Math. Ann., 109 (1934)], с другой
стороны, весьма замечательные исследования Гуревича (Witold Hurewiez)
о группах гомотопии [Proceedings, Academie van Wetenschappen, Amsterdam,
v. 38 (1935) и v. 39 (1936)]. Изучению этих работ должно i редшествовать
знакомство с понятием фундаментальной группы, которое можно почерпнуть,
например, из книги Зейферта-Трельфалля «Топология», главы 7 и 8 (гакже
из главы 8 книги Л. С, Понтрягина «Непрерывные группы» или из уже
цитированного мемуара Хопфа из Math. Ann., 100).
В последнее.время к теории непрерывных отображений с большим
успехом применяется теория V-гомологий; см. об этом, например, последнюю
(восьмую) главу недавно вышедшей книги Hurewiez-Wallman «Dimension
Theory», Princeton, 1941, а также работу Л. С. Понтрягина в т. 9
Математического Сборника «Classification of mappings of theedimensional complex into the
two-d;mensional sphere», в которой он переходит от классификации
отображений трёхмерной сферы в двумерную к аналогичной проблеме для
отображений трёхмерного полиэдра в дв> мерную сферу. В этой работе Л.С.
Понтрягина можно найти и дальнейшую литературу по этому кругу вопросов.
Чрезвычайно важную по своим приложениям к анализу, но ещё едва
народившуюся область топологии составляет исследование непрерывных
отображений бесконечно мерных, в частности, функциональных пространств.
Из относящихся сюда работ отметим Leray-Schauder «Topologie et
equations fonctionnelles» Annales Scientifiques de l'Ecole Normale superieure, и
E. Rothe «Zur Theorie der topologischen Ordnung und der Vektorfelder in
Banachschen Raumen», Compositio Mathematica vol. 5(1937), pp. 177—197.
Наконец, необходимо отметить только что вышедшею очень
интересную монографию J. Leray, Topologie algebrique, Париж, 1946 (по частям
опубликована также в Journal de Math. 24, вып. 2 и 3, 1945), в основном
посвященную законам двойственности и непрерывным отображениям.
*) Решена Хопфом и проблема классификации непрерывных
отображений «-мерного полиэдра в «-мерную сферу; см. Александро в-Х о п ф,
Topologie, глава 13.
В настоящее время решена и гораздо более общая проблема
классификации непрерывных отображений «-мерного компакта на «-мерную
сферу. Хорошее изложение этих вопросов можно найти в книге Hurewiez-
Wallman, Dimension Theory, гл. VIII, которая вообще может быть очень
рекомендована. Наконец, и проблема классификации отображений любого
«-мерного нормального пространства на «-мерную сферу решается в
основном теми же методами (см. об этом мою монографию «Законы
двойственности и теория размерности», которая появится в серии монографий,
издаваемой Матемагич. Институтом Академии Наук).
**) Hopf, Fund. Math. 25, 1935, pp. 427—440.
***) Понтрягин, Матем. Сборник 9 (51): 2, 1941, стр. 331 —3§9t

ГЛАВА ШЕСТНАДЦАТАЯ.
БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ
В Rn И В Sn.
В этой главе *) даются элементарные классические теоремы о
непрерывных отображениях, в основном открытые Брауэром, а также
непосредственно примыкающие к ним более новые результаты; самым важным из
них является принадлежащая Хопфу классификация непрерывных
отображений одной я-мерной сферы на другую. Данные здесь доказательства
принадлежат Хопфу; они возникли на почве методов Бпауэра и представляют
собой их дальнейшее развитие и усиление. Основой изложения является
понятие степени отображения (глава 8, арт. 5:1, и глава 11, § 6),
а также систематическое приложение одного частного и геометрически
особенно наглядного случая зацепления двух циклов zr, z8 пространства
jRn **), а именно случая, когда г==0 и zr есть некоторая точка o£Rn,
взятая с коэффициентом 1, a z8 есть (я — 1)-мерный цикл, носитель которого
не содержит точки о.
Под «отображением» какого-либо точечного множества и в этой и
в следующей главе понимается всегда непрерывное отображение.
§ 1. Порядок точки относительно (п—1)-мерного цикла в Rn.
1:1. Комбинаторный случай. Итак, рассмотрим коэффициент
зацепления Ь(гп-1уо)у где о есть точка (ориентированного) Rn, взятая
с коэффициентом 1, а гп~г такой (п—1)-мерный цикл, что о (£ zn~l
(в случае п = 1 предполагается, кроме того, что цикл zn~x —
нормальный). Этот коэффициент зацепления Ь{гп-г, 6) называется с по
рядком точки о относительно цикла г4-1». При этом, если о'—
какая-нибудь точка, лежащая вне некоторого шара Еп, содержащего
внутри себя всё тело zn-1 цепи ***) zn-1 то, полагая z°= о — о',
имеем, очевидно,
(1:1) ЬСг*-1, о) = Ь(гп-1, z°).
Нам удобно будет в дальнейшем предполагать, что точка о'
выбрана с соблюдением следующего условия: отрезок оо' находится
в общем положении с комплексом (г*1-1! (т. е. пересекается лишь
с (п—1)-мерными и притом невырождающимися симплексами этого
комплекса).
*) Являющейся переработкой гл. 12 книги: Алексанлров-Х^пф, Topologie, I.
**) См. предварительные замечсния в начале главы 15; на них опираются
обозначения, принятые в настоящей главе.
***) Гл. 15 арт. 0:1; параграфы 1, 2 главы 15 предполагаются в
настоящей главе известными.

§ 1] ПОРЯДОК ТОЧКИ ОТНОСИТЕЛЬНО (П 1)-МЕРНОГО ЦИКЛА 569
Порядок точки о относительно цикла z71-1, т.е. to (г*1-1, о),
может быть интерпретирован двояко:
Первая интерпретация:
(1:11) К*""1, о) = (*пХо),
где хп— произвольная цепь, ограниченная циклом zn~l и
находящаяся в общем положении с точкой о (последнее условие в этой
главе означает: n-мерные симплексы комплекса \хп\ не
вырождаются, и только они среди всех симплексов \хп\ могут содержать
точку о).
Если *я = 2'«*? и °€1*?1. то С?Хо) = ^ (см. главу 7, арт.
2:1). Если из всех симплексов |*"|£|л;п| точка о содержится в
!*ll> •■ '» l^sl И Т0ЛЬК0 в НИХ; Т0
(1:12) Ь(гп-1, о) = 2'«С?/?1)
или, если коэффициенты ^ в цепи xw симплексов £™, для которых
?<^ и tfRn~ -\-\, обозначить через с+, а симплексов tV1, для
которых tJRn = —1, обозначить через с~ то
(1:12') Ь(«-а, о) = 2с«+-2сГ-
Правая часть равенств (1:12) и (1:12') называется кратностью,
с которой цепь хп покрывает точку о или, короче, «числом
покрытий» точки о цепью хп. Таким образом, на основании (1 : 12')
порядок b(2fn~1, о) может быть определён как число покрытий
точки о любой цепью хп, ограниченной циклом г"-1
и находящейся сов общем положении.
Вторую интерпретацию порядка точки о относительно
цикла гп~х получаем из сопоставления формулы (1:1) с формулой
(1:4) главы 15, при сохранении сделанных выше оговорок
относительно точки о' и цикла г° = о — о'. Формула (1:4) главы 15 даёт
(при р = 0, q — п — 1)
(1:13) *)(г°, ^-1) = — to (г»-1, г°).
Берём ориентацию (oof) отрезка |оо'|. Так как
Д(оо') = о' — о= — *°,
имеем из (1:13)
(1:14) [(oof) X г»'1] = — Ъ (г°, г"-1) = to (г»-1, г°) = to (г»-1, о).
. >.
Пусть теперь (о, оо) — луч, исходящий из точки о и
проходящий через о*'. Очевидно, для всех точек о' этого лучя, достаточно
далёких от точки о, индекс пересечения [(оо') X г*-1] принимает
одно и то же значение, которое мы поэтому можем обозначить
через [(о, оо)Х^_11-
Поэтому формулу (1:14) можем переписать так:
(1 ; 15) [(О, со) X г*»-1! «К*»-1, о).

570 ВРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XVf
Итак:
Порядок точки о относительно циклагп~1 £ Zn~1(Rn\of 51) есть
индекс пересечения [(о, оо) Укгп"1] с Циклом zn~l любого
исходящего из точки о луча, находящегося в общем положении с
циклом г4"1.
Это и есть вторая интерпретация порядка точки.
1:2*). Порядок точки о £ Rn относительно истинного цикла z71-1.
Пусть дан истинный цикл zn~l на каком-либо компакте ФaRn
и точка о£Г=/?п\Ф; всегда определённый в наших условиях
коэффициент зацепления \>(zn-19 о) называется порядком точкио
относительно истинного цикла zn_1.
На основании теоремы [1:55] (глава 15) имеем:
Если для двух точек о и ог множества Г
(1 :21) о~о' в Г,
то
b(z«-if 6) = \>(гп-\ о').
Но гомология (1 :21) означает, что точки о и о7
можно соединить в Г ломаной, т. е. что они
принадлежат к одной и той же компоненте
множества Г.
Итак:
[1:2]. Если компакт Фа Rn есть носитель
Черт. 161. истинного цикла г?1-1, то для всех точек о£Г
определён порядок )o{zn"1y о) относительно цикла
zn~l. При этом для всех точек о одяой и той же компоненты
множества Г порядок to(zw_1, о) принимает сдно и то же значение.
На черт. 161 кривая Ф есть носитель непрерывного цикла z1
(чертёж — плоский, так что п = 2). На чертеже указаны различные
значения, а именно 0, 2, 1, —1, которые принимает ^(z11""1, о) в
зависимости от того, к какой компоненте множества Г = Rn\Ф
принадлежит точка о.
Замечание 1. На основании сказанного в предыдущем
артикуле можно подробнее определить b(zw_1, о) так:
Первая интерпретация. Пусть
уП~1 (уП — \ уП — 1 ?П~1 \
*) Без всякого ущерба для существа дела читатель может во всей этой
главе ограничиться рассмотрением истинных циклов лишь следующих
типов:
где г£ есть цикл некоторой триангуляциии А"а, a z*h — его /г-кратное
барицентрическое подразделение. 2°) zr = Cz£, т. е. истинный цикл, являющийся
образом истинного цикла типа 1°) при непрерывном отображении С
полиэдра К« в Rn (или в Sn),

§ 1] ПОРЯДОК ТОЧКИ ОТНОСИТЕЛЬНО (П 1)-МЕРНОГО ЦИКЛА 571
и цепи х\, ограниченные соответственно циклами г^""1, выбраны в
общем положении к точке о; тогда для всех достаточно больших k
индекс пересечения [х\ X о) принимает одно и то же значение,
равное b(zn""1, о).
Вторая интерпретация. Если k достаточно велико, то
^(z*-1, о) = [(о,оо ЭХ^""1]» где (о, оо) есть какой-нибудь луч,
исходящий из точки о и находящийся в общем положении с ^-3.
Замечание 2. Если гп~х ~ 0 в Ф, то для всех о£Г имеем
i)(z^_1, o) = 0. Отсюда следует: если zllrrl ~ z'n~l в Ф, то для
всех о£Г имеем to(zn-1, о) = i^z'*-1, о).
Замечание 3. Пусть Г'г есть я-мерный симплекс, содержащий
точку о, и £"- — какая-нибудь ориентация 74 Тогда b (Д/,г, о) =* :±: 1,
откуда следует, что Ып не гомологично нулю в Rn\p.
1:3. Теоремы Пуанкаре-Боля и Руще. Частным случаем замечания
2 является:
[1 :3]. Если непрерывные отображения С0 и Сх компакта Ф во
множество Rn\o гомотопны между собой в Rn\o и z4"1 есть
истинный цикл компакта Ф, то Ь (C0zn-1,o) = b(C1zn-1, о).
В самом деле, если отображения С0 и Сг гомотопны в Rn\o, то они
гомотопны и в некотором компакте Ф0czRn\o (за Ф0 можно,
например, взять достаточно большой замкнутый куб, из которого
удалена достаточно малая окрестность точки о). Поэтому С^г4-1 ~
~Clzn~1 в <£0aRn\o и, значит, Ъ(С0гп-г, о) = ^(C^z»-1,*)).
Предпосылки теоремы [1 :3], в частности, выполнены, если для
любой точки р£Ф отрезок С0{р) Сг(р) лежит в Rn\o (достаточно
определить С$(р) как точку, делящую отрезок С0(р)Сг(р) в
отношении 6:(1—6), чтобы получить деформацию С9, 0^6^1,
переводящую С0 в Cj). Полученный таким образом частный случай
теоремы [1:3] известен под названием теоремы Пуанкаре-
Боля.
Ещё более частный случай теоремы [1 :3] получим, если
потребуем, чтобы отображения С0 и Ct достаточно мало отличались друг
от друга, а именно, чтобы было р(С0(р), ^ (р))<р(С0(/?), о) для
всех р£Ф. Этот частный случай теоремы [1:3] (и теоремы
Пуанкаре-Боля) иногда называется «теоремой Руше».
Заметим, наконец, что условия теоремы [1 :3] (и даже теоремы
Пуанкаре-Боля) выполнены, если и С0 и Сг являются отображениями
компакта Ф в некоторую сферу S11-1 с центром о,
удовлетворяющими требованию: ни при каком р^Ф точки С0(/?) и СДр)
не являются диаметрально противоположными
точками сферы S11"1. Этим замечанием мы, в частности,
воспользуемся в § 5.
1 :4. Гомологии в Rn\o. Пусть tn — произвольный л-мерный
симплекс в /?#, ориентированный одинаково с данной раз на всегда
ориентацией пространства/?^. Обозначим через о какую-нибудь точку
симплекса 7^=|^|. Из (1 :11) следует, что Ъ(№п7 о)=Ь

572 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XVI
Теорема [1 :41]. Всякий истинный цикл г71-1 любого
компакта Ф czRn\o удовлетворяет гомологии
(1:41) z»-1 ~ Ь (zn"\ о) Д Г в Rn\o.
Доказательство. Обозначим через С0 тождественное
отображение компакта Ф, а через Сг — проекцию этого компакта из о
в Тп\Тп, т. е. отображение, ставящее в соответствие каждой точке
р£Ф точку пересечения луча (ор) с Т1г\Тп.
Отображения С0 и Сг находятся в условиях теоремы Пуанкаре-
Боля и поэтому гомотопны между собой, так что
zn-i „ qi zii~i в %п\коФ
Так как истинный цикл С^-1 лежит на границе симплекса Г*, то
там, и тем более в Rn\o, имеет место гомология Схъп~1 ~ ^\Ып%
значит, и гомология г*1"1 ~ ^А^, откуда следует
to (z»-1, о) = to (7Д/Я, о) = -(to (АР, о) = y,
что и требовалось доказать.
Замечание. Так как Мп не гомологично нулю в Rn\o, то.
из гомологии хп~г ~ 0 в Rns\o, в силу [1 :41], следует, что
непременно to(zn-1, о) = 0.
Из [1:41] далее вытекает: Если Ъ{гп-1, о) = 0, то
z^-^O в /?w\o.
Другими словами, равенство r)(zn-!, о) = 0 представляет собой
не только не о бх од им о е, но и достаточное условие для
того, чтобы было zn""1^-0 в Rn\p.
Отсюда, в св"ою очередь, вытекает:
Теорема [1:42]. Два не содержащих точки о истинных
цикла ъ*~1 и гп~х тогда и только тогда гомологичны между
собой в Rn\o, когда fc^»"1, o) = b(z2n"1, о).
1 :б. Порядок точки относительно цикла как степень
центральной проекции цикла на сферу. Пусть снова о£Тп и
tn—ориентация Тпу одинаковая с выбранной ориентацией Rn. Ориентацию
Мп границы симплекса Тп назовём ориентацией,
соответствующей данной ориентации Rn.
Замечание 1. Если S71"1 есть сфера с центром о, то под её
ориентацией, соответствующей данной ориентации Rn9 понимаем ту ориентацию
Sn-1, в которую посредством центральной проекции из о переходит только
что выбранная ориентация tdn псевдомногообразия Тп\Тп,
Обозначим, как прежде, через Сг проекцию компакта Фc:Rn:\o
из о в границу симплекса Тп, а через гп~1 — какой-нибудь лежащий
в Ф истинный цикл. Так как Ып есть ориентация
псевдомногообразия Sn~x, то
(1;5) Схгп-1~ч№ в Sn~\

§2]
fftOPfcMA СУЩЕСТВОВАНИЙ КОРНЕЙ
S73
а в силу замечания, сделанного к теореме [1:41], непременно
Т = fc(zn-1, о). Но по самому определению степени отображения
число Y» стоящее в правой части равенства (1:5), есть степень
отображения Сг истинного цикла гп~г в ориентированное
псевдомногообразие тп\Тп (ориентирующий цикл есть Ltn). Итак:
Теорема [1:5]. Порядок точка о относительно истинного
цикла г*-1, лежащего в Rn\o, равняется степени проекции этого
цикла из о в границу симплекса Тп Э о, ориентированную
соответственно данной ориентации Rn.
Замечание 2. Если гп-г есть непрерывный цикл:
(1 :51) 2^ = Се?-1,
то степень отображения Сг цикла zn~iJ очевидно, равна степени
отображения CtC цикла г^"*1. Поэтому:
[1 : 51]. Порядок точки о относительно лежащего в Rn\o
непрерывного цикла z*1-1, заданного своим параметрическим
представлением (1: 51), равна степени отображения СгС цикла z^-1 в
границу симплекса Тп^оу ориентированную соответственно с данной
ориентацией Rn. В частности, если цикл г71"1 лежит на S™-1 =
*=Тп\Тп, т. е. если С есть отображение в S"-1, то ^(z7*-1, о)
совпадает со степенью отображения С цикла &%~Л в Sn"1.
Упражнение. Пусть С есть непрерывное отображение
ориентированной окружности z1 в R2\o. Доказать, что порядок точки о
относительно Czl совпадает с порядком, определённым в главе 2,
арт. 2 :2.
§ 2. Теорема существования корней.
2: 1. Теорема существования корней. Пусть z есть (п — 1)-
мерный истинный цикл в Rn с носителем Ф:
z = (zly z%, ..., zn, ...)
и о — точка открытого множества T = Rn\^>. Мы знаем из
предыдущей главы: если z~0 в /?н\о, то порядок b(z, о) равен нулю.
Отсюда непосредственно следует:
Теорема [2:1]. (Общая теорема существования корней).
Пусть z*-1 — истинный цикл с носителем W0, гомологичный
нулю в компакте Ф0 з W0.
Пусть С—непрерывное отображение компакта Ф0 в Rn и
o^Rn\C(W0). Если
то существует, по крайней мере, одна точка р0£Ф0, такая, что
Ср0=*о.
В самом деле,
Cz0w~1~ 0 в СФ0,

574 ЁРАУЭРОЙСкАЙ ТЕОРИЙ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ (ГЛ. Xvf
поэтому, если бы было
СФ0 с Rn\o,
то было бы Ci0"-t~0 вЯ»\о,
значит> b(Cio»-So) = Of
вопреки нашим предположениям.
В большинстве применений этой теоремы z0n_1 есть цикл
некоторой триангуляции К0, гомологичный нулю в К0. Особенно важны
следующие частные случаи:
[2:10]. Пусть Е)г есть n-мерный шар, Sn~l — ограничивающая
его (п— \умерная сфера, zn~l — определённая ориентация Sn"1t С—
непрерывное отображение Еп в Rn, о £ Rn\CSn~1. Если b (Схп~1,о)ф0)
то существует, по крайней мере, одна точка р^Е11, такая, что
Ср = о.
Зам е чан и е. Второй частный случай теоремы [2:1] касается
полиэдральных областей пространства Rn.
Под полиэдральной областью пространства Rn мы
понимаем в этой главе область вида Г =Тп\(Т1п[} ... [} TJ1), причём
замкнутые я-мерные симплексы Т\9...,Т* лежат в симплексе
Тп и попарно не пересекаются.
Возьмём некоторую триангуляцию К* полиэдра Г. Всем я-мер-
ным симплексам Г^ триангуляции Kl дадим ориентации #/,
одинаковые с выбранной ориентацией tn симплекса Тп.
Цикл VAtfJ. = ^"1 называем границей
ориентированной области Г (в триангуляции /С«). В этих предположениях
имеет место следующий частный случай теоремы [2:1].
[2 :11]. Пусть Г — полиэдральная область пространства Rn и
С—непрерывное отображение полиэдраТ в пространство R^. Пусть
о—точка пространства Rn, не лежащая на C{z™~ ), где z™~1 —
граница полиэдральной областиТ (см. выше). Если ^(Сг^-1, о)ф0,
то имеется хотя бы одна точка области Г, отображающаяся
посредством С на точку о.
§ 3. Локальная степень отображения я-мерной цепи в Rn.
Вводное замечание. Пусть х есть цепь некоторой
триангуляции. Под непрерывным отображением цепи л:
понимаем непрерывное отображение её тела, полиэдра х.
ЗМ. Определение и основные свойства локальной степени.
Пусть С—непрерывное отображение я-мерной цепи в
ориентированное пространство Rn\ пусть о £ Rn. Предположим, что С не имеет
корней на Дхп, т. е. что ни одна точка полиэдра &хп не
отображается в о. В этих условиях число Ъ (Скхп, о) = т (о, хп, С) называется
степенью отображения С в точке о.

§ 3] ЛОКАЛЬНАЯ СТЕПЕНЬ ОТОЁРАЖЕНИЯ Л-МЁРНОЙ ЦЕПИ В /?" 575
Замечание. В записи -у (о, хп, С) будем иногда пропускать
некоторые аргументы.
Из этого определения и элементарных свойств порядка точки
относительно цикла следует:
[3:11]. Пусть хп = xf-|-х™ и ни одна точка множеств \х™,
Ах? не отображается в о. Тогда
тС*") = тг(*?)-НЮ-
[3:Г2]. Для любого целого коэффициента а имеем
7 (ахп) = аТ (хп).
Отсюда следует:
[3:13]. Пусть хп = 2а<*?' пусть каждая точка множества С-1 (о)
лежит в некотором Щ\ (так что C\tn.ciRn\o при любом /). Тогда
Далее:
13:14]. Пусть даны отображения С0 и Сх цепи хп в Rn; пусть
на Дд:п дана деформация Се отображения С0 (рассматриваемого лишь
на Алг™) в Cv причём для всех 6 0<6<1, имеем Се (Кхп)сиRn\o,
тогда 7 (о, хп, С0) = Т (о. *п, Сх).
В частности (теоремы Пуанкаре-Боля и Руше):
[3:140]. Если для любого р £ кхпотрезок С0(р)С1(р) не
содержит точку о, то
Т(о>ля,С0) = т(о>^, СО.
[3:141]. Если для любогор £ Ахн
р(С0р, С^рХрССор, о),
то
Цо,х»,С0) = ч(р,х»9 Сх).
И, наконец, самое важное следствие:
[3:15]. Если ч(о,хп,С) определено, то для всякого
непрерывного отображения Сх цепи хп в Rn, достаточно мало
отличающегося от С на &хг\ степень *[{0>хП-> С\) определена и равна ч(о,хп, С).
3:2. Симплициальные приближения. Возьмём теперь в
качестве Сх любое достаточно хорошее симплициальное приближение
отображения С (см. главу 11, арт. 5:1), при котором вершины
определяющего отображение Сх подразделения \х%\ комплекса \хп\ выбраны
так, чтобы при г<я точка о не содержалась ни в одном из
множеств С{ТГ), где Тг£\х™\. Обозначая через sx оператор
подразделения, имеем
ks1xn=zsltixn~£ixn на Для,
значит,
Сх Ь$х хп~Сг Ьхп на Дхл czRn\o,

576 брАуэрсжская теория Непрерывны* отображений [гл. tvi
т. е.
^(C^^jc», о) = Ъ (CjAa:w,o),
Т (о, 5,^,^ = 7 (о, ^.Q).
Но, в силу [3:15], имеем •у(о,л;,г, С) =-у (о, л;Л, СД значит,
(3:21) Т (о, *я. О = т (о, slX», С,\
т. е.:
[3:21]. Степень непрерывного отображения С цепи хп в точке
о £ Rn\C(xn) равна степени любого симплициального отображения
{некоторого подразделения sxxn цепи хп), достаточно хорошо
приближающего отображение С.
При этом всегда можно потребовать, чтобы Сг удовлетворяло
следующему условию ре?улярности: Все корни отображения^
(т. е. все точки множества С-1 (о)) лежат в /z-мерных
симплексах комплекса | st xn | (причём каждый из этих симплексов
содержит не более одного корня).
Так как к удовлетворяющему условию регулярности отображению
применима теорема [3:13], то вычисление локальной степени любого
непрерывного отображении сводится к вычислению у(о,<й,С), где С
есть невырождающееся аффинное отображение симплекса tn в Rn,
причём о£С \in\. Но в этом случае имеем, полагая t'n — Ctn,
Т(о,*Л, С) = t'»R\
т. е. f — -j- 1 и ли — 1, в зависимости от того одинаковы между собой или
противоположны ориентации t'n и Rn; в самом деле, в первом из
этих двух случаев индекс пересечения (tf'wX°) равен -f-1, а во
втором —1.
Комбинируя этот результат с теоремой [3 :13], потучаем:
[3:22]. Если С есть симплициальное отображение цепи хп *=
?=V^^ в Rn, удовлетворяющее условию регулярности, то
где ъ = 0, если о£С|*]»|,
•^ =1, если o£C\tr}\ и ориентация симплекса Ctf совпадает
с ориентацией Rn,
■^=з — 1, если о£С|£)М и ориентация симплекса Ctf
противоположна ориентации Rn.
В частности, если xw==V^ есть ориентированное
комбинаторное псевдомногообразие, то
Т(о,хя, С)*=2Т< = * —v»
где тс есть число симплексов £?, «покрывающих при отображении С
точку о положительно», a v есть число симплексов f}t
«покрывающих при отображении С точку о отрицательно».

§ 41
ТОПОЛОГИЧЕСКИЕ ОТОБРАЖЕНИЙ
577
3:3. Случай отображения в сферу Sn.
Теорема [3:3]. Пусть сферы S% и Sn ориентированы и дано
непрерывное отображение С сферы S% в сферу Sn степени ^о
Сферу Sn рассматриваем как эвклидово пространство Rn с
бесконечно удалённой точкой и:
Sn~Rn\iu.
Предположим, что для некоторой точки o£Rn имеем
С-\о)аТ»,
гбе Т™ — некоторый n-мерный симплекс некоторой триангуляции
К0 сферы S™; обозначим через t* ориентацию симплекса Т™,
одинаковую с данной ориентацией S%.
Тогда
(3:3) *(СД#, о) = -ус
Доказательство. И правая и левая части равенства (3:3)
не меняют своих значений, если заменить непрерывное отображение
С достаточно хорошим симплициальным приближением Сг к нему.
Поэтому можно с самого начала преаположить, что С есть сим-
плициальное отображение некоторого подразделения ЛГа
триангуляции К0 сферы SJ в некоторую триангуляцию К сферы Sn, причём о
лежит в некотором я-мерном симплексе Тп £ К. Ориентацию 7П,
одинаковую с данной ориентацией Sn, обозначаем через f.
Сферу Sn рассматриваем как эвклидово пространство Rn с бес*
конечно удалённой точкой и, не принадлежащей Тп.
Обозначим через /*. симплексы комплекса К%9 получившиеся от
подразделения Т% и ориентированные так же, как 5J*. Пусть,
наконец, тс, соответственно v, есть число тех №р для которых
CtP=tny соответственно Ct^.= —tn. Тогда, в силу теоремы
[5:22] главы 8, имеем ^=тг --v. С другой стороны, полагая
*о =]£ *й> имеем
to (СД/» , о) = » (СД*у, о) = (С*» X о) = ти — v,
что и требовалось доказать.
§ 4. Топологические отображения.
4:1. Теорема [4:1]. Пусть Тп есть п-мерный симплекс,
р£Тп и С—такое топологическое отображение Тп в Rn, что
Ср = о. Пусть tn — какая-нибудь ориентация Тп. Тогда
-Г(о, *», С) = =Ы-
37 Александров II. С.

578 брауэровская теория непрерывных отображений [гл. xVl
Доказательство. Пусть S11-1 — граница симплекса Тп. Так
как <& = CSn-1 есть замкнутое {п—1)-мерное псевдомногообразие,
а СМп — одна из ориентации C5n_1, то на основании теоремы [3:43]
главы 15 для всех точек ог одной из двух компонент, на которые
CS71-1 разбивает Rn, имеем b(CAtn, o') = dtl. По теореме [2:1]
должна существовать точка р'£7п, для которой Ср' = о'. В силу
взаимной однозначности С, эта точка будет лежать в tn — A tn, т. е.
будет точкой симплекса Тп. Образ отрезка ррг при отображении Сесть
непрерывный путь в Rn\Ck tn, следовательно, о и о' принадлежат
одной компоненте множества Rn\Ch tn. Отсюда
т (о, *", С) = Ь (СЫп, о) = \> (СД*», о') = ± 1,
что и требовалось доказать.
Следующее предложение усиливает теорему [4 :1].
Теорема [4:11]. Пусть Г — область в n-мерном
ориентированном эвклидовом пространстве Rn; пусть С—топологическое
отображение области Г в ориентированное n-мерное эвклидово
пространство R'n. Пусть t™ и Щ — произвольные симплексы,
удовлетворяющие условию t™czV, t™ сГ, ориентированные так же,
как Rn.
Пусть o^Cl^l, o2£C|^|. Тогда
7(о1,^,С) = 7(оа,^,С) = =!=1.
Доказательство. Рассмотрим сначала случай |^| Л |/™|-=£0,
взяв симплекс Щ, ориентированный так же, как R}\ и лежащий
вместе со своей границей в \t^\ [\ |^|, и точку о£|/"|; заключаем
так же, как при доказательстве [4:1], что
Но
Т (о, q, С) = Т (о, *», С) = Т (о, *» С) = т (оа, *«, С),
так что в этом частном случае теорема доказана.
Так как любые два симплекса |^| и |^|, лежащих в Г, можно
соединить цепочкой последовательно пересекающихся л-мерных
симплексов, лежащих в Г, то теорема верна и в общем случае.
Если при любом выборе /йсГ, o^C\tn\ имеем
Т(о,^, 0 = + 1,
то говорят, что топологическое отображение С области Г в
пространство Rn имеет степень 1; в противном случае (т. е. когда для
всех /псГ, o£C\f% имеем -у(°> tn% с) = —1) говорят, что
топологическое отображение С области Г имеет степень —1.

§4]
Фонологические отображения
679
I ^4:2. Теоремы инвариантности.
^Теорема [4:21]. (Инвариантность порядка п.) Пусть ог есть
точка пространства R™, zt — истинный (п — 1)-мерный цикл
a Rf\ov Пусть i™ есть n-мерный симплекс пространства R11,
содержащий как ои так и zx> С — топологическое отображение
симплекса t* в n-мерное пространство R™ и т *= zt 1 — степень
этого отображения. Тогда
Доказательство. Пусть \Р^\ есть «-мерный симплекс про*
странства /?^, содержащий точку о^^=Сох. Пусть симплексы t% и
t™ ориентированы так же, как несущие их пространства R™ и /?*
Обозначим Сгх через z2.
Согласно теореме [1 :41],
(4:21) *! — »(*!, о,) Д*у bTjVj,
(4 :22) z2 ~ to (z2, о2) Д*у в R!f\o2.
По определению степени х имеем
*(СД*»,оа)=т,
следовательно, по теореме [1 :41]
(4: 23) СД*у~тД*£ в Я»\о2. -
Так как C(t™\ol)czRf\Och то, в силу (4:21), имеем
Сгх = z2 ~ to ^, о,) CA/J в /?»\ол,
т. е., принимая во внимание (4:23),
(4:24) z2~xb(z1, ох)Щ в #f\o2.
Так как to (z2, о2) определяется равенством (4 :22), то из (4 :24)
следует to(z2, o2) = 'cto(z1, ох), что и требовалось доказать.
Из определения локальной степени отображения и теоремы [4 :21]
следует:
Теорема [4:24]. (Инвариантность локальной степени.) Пусть
Сг есть непрерывное отображение цепи хп в пространство R™,
не имеющее (относительно точки ог £ R*) корней на &хп и для
которого, таким образом, определена его степень y в точке ог\
пусть, далее, t™ есть ориентированный так же, как и R™ п-мер-
ный симплекс пространства R%, содержащий внутри себя как
точку ov так и образ Сг хп полиэдра хп. Пусть, наконец, С\
есть топологическое отображение симплекса |^| в
пространство R%.
Тогда локальная степень отображения С\ Сг цепи хп в точке
о2 = CJ ох равна т^» где т = — 1 есть степень отображения С\ •

580 ёраУэровСкая Теория непрерывных отображений [гл* xvi
§ 5. Векторные поля и непрерывные отображения *),
5:1. Связь между векторными полями и отображениями.
Систему действительных непрерывных функций vu . . . , vnt
заданных на точечном множестве М эвклидова пространства Rn, мы
можем геометрически толковать, во-первых, как отображение v9
относящее каждой точке р£М точку v(p) эвклидова пространства **)
R%, имеющую в нём координаты vt (/?), ... , vn (p); во-вторых, как
векторное поле, состоящее из векторов v(p) (пространства *)
/?*), отнесённых, соответственно, к точкам р £ М и имеющим
компоненты
Мр)> •• • > vn(p)-
Таким образом, исследование векторных полей в Rn эквивалентно
исследованию отображений. В частности, многие понятия и
теоремы предыдущих параграфов могут быть интерпретированы как
предложения, касающиеся векторных полей. Мы проведём эту
интерпретацию лишь в некоторых частных случаях.
Под отображением v, соответствующим векторному полю 23 (р),
состоящим из векторов v(p), мы будем постоянно понимать, в
соответствии со сказанным выше, отображение, ставящее в соответствие
каждой точке р£М точку v(p) с координатами vt(p\ т. е. конец
вектора v(p), отложенного от начала координат.
Пусть г4'1 есть (п — 1)-мерный истинный цикл некоторого
компакта Фc:Rfl; пусть на Ф задано непрерывное векторное поле 23,
не имеющее на Ф нулей (т. е. v (р)^0 для всех р £ Ф). Под сх а р а к-
герисгикой» поля 23 на г71-1 понимают порядок начала
координат пространства R™ по отношению к циклу v{zn~l\ где
v обозначает отображение компакта Ф в /?*J, соответствующее
полю 23.
На основании теоремы [1 :5] этому определению можно придать и
такую форму:
Каждой точке р £ Ф поставим в соответствие луч, исходящий из
начала координат пространства /?**, несущий вектор v(p); этот луч
пересекает единичную сферу S™-1 пространства R™ в некоторой точке
С1(р). Этим установлено непрерывное отображение Q компакта Ф
в S™-1. Считая сферу S4'1 ориентированной в соответствии с
данной ориентацией пространства R**, рассматриваем степень
отображения С1 цикла zn~l в ориентированную сферу S11-1. Эта степень и
есть характеристика векторного поля 23 на цикле zn~1.
Из этого определения непосредственно следует, что
характеристика векторного поля зависит только от направления, но не от
*) Этот параграф целиком заимствован из написанной Хопфом гл. XII
книги: Александров-Хопф, Topologie.
**) Пространство /?f может, конечно, и совпадать с пространством Rn.

§ 5] ВЕКТОРНЫЕ ПОЛЯ И НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 581
длины векторов. Из результатов предыдущих параграфов вытекают
далее следующие факты:
[5:11]. Пусть 930 и 93х— два поля на Ф, не обращающиеся там
нигде в нуль и обладающие следующим свойством:
Существует непрерывно зависящее от параметра 6,0 <;б ^ 1
семейство везде на Ф непрерывных и нигде не обращающихся в нуль
векторных полей 93q (при 8 = 0, 6=1 получаем данные поля 930
и 93Д Тогда характеристики полей 930 и Щ равны.
Замечание. Условие теоремы [5:11], в частности, выполнены,
если ни для какой точки р£Ф векторы 930(/>) и 932(р) не
оказываются противоположными по направлению (теорема Пуанкаре-Боля).
[5:12]. Пусть Г — полиэдральная область пространства Rn (см.
арт. 2 :1). Каждое векторное поле, непрерывное и отличное от нуля
во всех точках полиэдра Г, имеет на границе области Г
характеристику 0 (теорема [2:11]).
[5 :13]. Каждое векторное поле, непрерывное и отличное от нуля
во всех точках шара, имеет на ограничивающей этот шар сфере
характеристику 0 (теорема [2 :10]).
[5:14]. Характеристика поля внешних нормалей на
(п—^-мерной сфере равна -f- 1, а поля внутренних нормалей (—1)^.
В самом деле, пусть сфера «Sn_1 задана уравнением Va:|=1 и
нормальные векторы имеют длину 1: тогда соответствующее
отображение v в случае внешних нормалей задаётся формулами vi = xiy a
в случае внутренних — формулами vi= — xi. Отображение v
(рассматриваемое во всём пространстве Rn) аффинно, и его детерминант
равен -\-\ в первом случае и (—1)п — во втором; оно имеет
поэтому всюду степень -f- 1 (соответственно (—1)п), но степень
отображения v в начале координат о (г. е. порядок точки о
относительно образа сферы S71-1 при отображении v) и есть
характеристика векторного поля на этой сфере, чем наше утверждение
доказано.
5:2. Индекс изолированного нуля р векторного поля 95,
заданного на некотором множестве MczRn, содержащем р в качестве
внутренней точки, определяется следующим образом: пусть v —
соответствующее полю 93 отображение множества MaRn в
пространстве R™.
Пусть р£Тп<£М; пусть ъп~х — какой-либо (п — 1)-мерный
истинный цикл с носителем ФаТп, удовлетворяющий условию
(5:21) W1, p)—1.
Тогда по определению 1пс1^93 есть характеристика поля 93 на гп"^
(т. е. порядок начала координат пространства /?** относительно
цикла (ozn~v).
В силу теоремы [1 :42] этот порядок не зависит от того, какой
именно цикл f1"1, удовлетворяющий условию (5:21), был взят.

582
БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ.
Проще всего положить
гп-\ __ Д^п>
где р 6И = Т*аМ и /•» есть ориентация симплекса Тп, одинаковая
с данной ориентацией Rn. v,/,„_i „ч__| тяк или
Пусть цикл z»-1 с носителем Ф с Г», *(*,-,,/>)= '• так или
иначе выбран. Пусть S»-1 есть (я- 1)-мерная сфера пространства
Я« с центром о, и радиусом 1, ориентированная соответственно с
данной ориентацией Я»; сферу эту будем называть сферой
напоавлений. Ставим в соответствие каждой точке р£Ф ту
точку "(J)^^-1, в кот°Р°Й сферУ % пеР*секает ЛУЧ °*<Р).
параллельный вектору v(p). „„»„„„„ rtTnrtna-
По теореме [1:5] тогда indp<8 равен степени отобра
жения С, цикла z»'1 в с^ду S» >.
Замечание. Для определения индекса нуля векторного поля
„лины векторов не имеют никакого значения, а важны только их
н^равл ГяПоэтому понятие индекса может применяться не только
к векторным полям, но и к полям направлен ийи При этом
под направлением понимается луч (0,оо) пространства R*, или, если
угодно, совокупность всех векторов вида av, где ъфО - некоторый
Черт. 162.
фиксированный вектор, а «-произвольное Г^быГт оТкГх
Rmppto нулей векторного поля мы говорим об особых TOiKax
foco6eHHoS поля "направлений, т. е. о точках, в которых поле
НаТрЛиемИеЙр7SS нГраВ=ГизолМированнЫми особенностями
даны на черт. 162- 165."Особой точкой на каждом из этих
чертежей является начало координат. Индекса черт 162 и 163 равен
+ 1, на черт. 164 и 165 соответственно +3 и — I, Рее 1ертежи
плоские,

§ 5] ВЕКТОРНЫЕ ПОЛЯ И НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 583
5:3. Векторные поля на шаре.
Теорема [5:3]. Каждое векторное поле, непрерывное и
отличное от нуля во всех точках n-мерного замкнутого шара Еп,
принимает по крайней мере в одной точке сферы 5п-1=г?г-1.
Черт. 163.
Черт. 164.
ограничивающей шар Еп, направление внешней нормали и, по край-
ней мере, в одной точке Sn-r—направление внутренней нормали.
Доказательство. Согласно [5:13], данное поле 23 имеет на
zn~l характеристику 0. Каково бы ни было поле 2В на zn~ly
имеющее характеристику, отличную от
нуля, существует, согласно
замечанию к [5:11], точка р на S™-1,
в которой векторы v(p) и w(p)
противоположны по направлению.
Согласно [5:14] за поле 2В может
быть принято поле внешних или
внутренних нормалей, следовательно,
поле 93 на S11-1 содержит, по
крайней мере, одну внутреннюю нормаль
и, по крайней мере, одну внешнюю
нормаль.
5:4. Теорема Брауэра о
неподвижных точках отображений
я-мерного элемента. Пусть • С
есть отображение я-мерного шара
EnaRn в то же самое пространство Rn. Каждой точке р^Ё11 ста-
——►
вим в соответствие вектор v(p) = pCp; это непрерывное поле имеет
нули в тех и только в тех точках Еп, для которых Ср=р, т. е.
в «неподвижных точках» отображения С. Если С не имеет
неподвижных точек, то выполнены условия теоремы [5:3] и,
следовательно, на ограничивающей Еп сфере S4-1 существует, по крайней
мере, одна точка р, в которой вектор VkP) совпадает с направле-
Чгрт. 165.

584 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XVI
нием внешней нормали, следовательно, точка Ср лежит вне Еп,
Итак:
Теорема [5:40]. Пусть Еп есть n-мерный шар в Rn и
5й-1-—ограничивающая его сфера. Всякое непрерывное
отображение С шара Еп в пространство Rn, при котором CSn~lSz.En
имеет в Еп, по крайней мере, одну неподвижную точку.
В частности, каждое отображение шара Еп в себя имеет,
неподвижную точку. Это свойство, очевидно, относится не только к шару,
но и к каждому гомеоморфному ему множеству, т. е. к каждому
/z-мерному элементу. Следовательно, справедлива:
[5:4]. Те о рема Брауэра о неподвижных точках
элемента. Каждое отображение n-мерного элемента в себя
имеет, по крайней мере, одну неподвижную точку.
5:5. Векторные поля на сферах чётной размерности.
Теорема о неподвижных точках. Пусть п нечётно и
£n-i есть сфера в Rn. По теореме [5:14] поле Ша внешних и поле
SR{ внутренних нормалей к S11-1 имеют на ней разные
характеристики. Отсюда следует: каково бы ни было поле 23 на S™-1, его
характеристики отличны от характеристики, по крайней мере,
одного из полей %1а и Wif следовательно, по теореме [5:11] должна
существовать на S™-1 точка, в которой вектор v противоположен
по направлению одному из нормальных векторов, т. е. сам является
нормальным вектором. Этим доказана:
Теорема [5:51]. Каждое векторное поле, непрерывное и
отличное от нуля во всех точхах сферы S4"1 чётной размерности,
имеет, по крайней мере, один вектор, нормальный к Sn~l в Rn.
Отсюда как частный случай следует:
Теорема [5:510]. (Теорема Пуанкаре-Брауэра.) На
сфере Sn чётной размерности не существует непрерывного поля
касательных направлений *).
В противоположность этому при нечётном я, например, формулы
V2j-1 — X2j> V2j — X2j-1 (у = 1, 2, . . , ^ J
задают непрерывное поле касательных направлений с компонентами
п + 1
vi на сфере Sn, заданной уравнением V^.= l.
i = l
Из теоремы [5:51] легко выводится:
Теорема [5:52]. При всяком отображении сферы Sn чётной
размерности в себя существует, по крайней мере, одна
неподвижная точка или, по крайней мере, одна точка, отображающаяся
в свою диаметрально противоположную (или и то и другое).
*) Таким образом, у ежа, свернувшегося в клубок, все иглы не могут
лежать гладко, а некоторые непременно будут торчать, Поэтому теорема
[5:510] названа Гильбертом «теоремой о еже»,

§ 5] ВЕКТОРНЫЕ ПОЛЯ И НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 585
Доказательство. Если отображение С сферы Sn в себя
не имеет неподвижных точек, то векторы рСр образуют на Sn
непрерывное и отличное от нуля векторное поле. На основании
теоремы [5:51] в этом случае существует точка р, в которой вектор
рСр совпадает с нормалью к сфере Sn. Но это возможно лишь в том
случае, ести точка Ср диаметрально противоположна к р.
В противоположность этому при п нечётном формулы
X2j~l === ~~ Х2р X2j = XQj-l\J = *» 2, . , . , — J
определяют отображение сферы Sn9 заданной уравнением *У.х2{=1
в себя, при котором не существует ни неподрижных точек, ни
точек, отображающихся в свою диаметрально противоположную.
5:6. Симметрия сфер; ещё одна теорема о неподвижных точках.
Симметрией пространства Rn относительно лежащей в нём
/--мерной плоскости /?г, Ог^гг^я, называется отображение его на себя,
получающееся следующим образом: в Rn выбирается система
прямоугольных координат xiy /=1, 2,...,га таким образом, чтобы
плоскость Rr имела уравнения
Х\ === Х% = . . . = Xn_r :==1 ".
Тогда симметрия С относительно Rr определяется формулами:
{ х'4=—х{ при l^i^n — г,
(5:61) { , , , .
\xi==x1 при п — r~\-\^i^n.
Это отображение переводит каждую (п—1)-мерную сферу с центром
на Rr в самое себя.
Теорема [5:6]. Рассматривая симметрию С пространства Rn
относительно плоскости Rr лишь на сфере Sn"1 с центром
о==(0,.. .,0), получим отображение сферы Sn~l {на себя),
которое гомотопно в Rn\o тождественному отображению тогда
и только тогда, когда r==n (mod 2).
Доказательство. Детерминант отображения С, заданного
формулами (5 :б1), равен (—\)п~г. Поэтому (см. доказательство [5:14]
Ь(Сгя-1,о) = (—1)*-',
где zn~l есть сфера Sn~~l, ориентированная соответственно данной
ориентации Rn. С другой стороны, Ъ(гп~~19о)= +1. Поэтому, если
гфп (mod 2) и, значит, (—\)п~г = —1Э то циклы zn~~x и Czn~~x
не могут быть гомотопны друг другу. Следовательно, в этом случае
отображение С сферы S71-1 в себя не гомотопно в Rn\o тожде»
ственному отображению,

586 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XVI
Если же r==n(tnod 2), то формулы
x2/~i=*2<-icos9ic — x2i sinlk, \ n__r
V = ^-isinb~x2i cos6n, J J =1.2,..., —
я) = xit i — n — r \-1,.. ., n
задают при 0 ^ 6^ 1 семейство отображений Q, осуществляющее
искомую деформацию тождественного отображения в симметрию С
(эта деформация является даже движением сферы Sn~1 в себе).
Особого внимания заслуживает частный случай:
Теорема [5:6]. Симметрия сферы Sn_1 относительно её
центра о тогда и только тогда гомотопна в Rn\o тождественному
отображению, когда п четно.
Из этой теоремы далее следует:
Теорема [5:61]. Если п нечётно, то всякое отображение С
сферы S71-1 в себя, гомотопное в Rn\o тождественному, имеет
неподвижную точку.
В самом деле, если бы С не имело неподвижной точки, то С'
и симметрия С сферы S71-1 относительно её центра о
удовлетворяли бы условиям теоремы Пуанкаре-Боля; поэтому С было бы
в Rn\o гомотопно симметрии С, значит, в силу [5 :60], не могло бы
быть гомотопно тождественному отображению.
5:7. Упражнения.
1°. Пусть дана система п действительных непрерывных функций от п
действительных переменных
Уг = /Ахь х* • • - ,хп) /=1,2 п,
с непрерывными частными производными вблизи данной точки о = (x°f
х% ..., jcJJ) £ Rn. Пусть функциональный детерминант (якобиан) этой системы
функций в точке о отличен от нуля. Тогда, как известно из анализа, эта
система функций осуществляет топологическое отображение С некоторой
окрестности точки о на некоторую окрестность точки
о' = (У\, у1 У1), где у* = ff (x°v .... х°„).
Доказать, что отображение С имеет в точке о' степень 1 или
— 1, в зависимости от знака якобиана.
Замечание. Требование непрерывности частных производных при
этом несущественно, существенно лишь менее сильное требование
существования полного дифференциала: именно это требование позволяет в данном
вопросе заменить отображение С приближающим его вблизи точки о
аффинным отображением, откуда и получается решение поставленной задачи;
полезно заметить, что при её решении мы не пользуемся тем фактом, что
отображение С является топологическим.
2°. Функция
у = ахп
комплексного переменного х осуществляет отображение комплексной сферы
на себя, имеющее степень п. Рассматривая эту сферу как плоскость с
присоединённой бесконечно удалённой точкой, можем утверждать, что
локальная степень нашего отображения в точке о равна п. При помощи этого
результата доказать более общее предложение:

§ 5J ВЕКТОРНЫЕ ПОЛЯ И НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ 587
Пусть степенной ряд
J> = an*n + *»+i*w+1+..M апФО>
сходится в окрестности точки нуль. Тогда он осуществляет
отображение этой окрестности на некоторую вторую
окрестность точки нуль, имеющее в точке нуль степень п.
3°. Аналитическая формулировка теорем [5:3] и [5:51].
п
Теорема [5:3]. Пусть в шаре ^лг? < 1 дана система непре-
рывных функций vi(xif...,xn)t / = 1,2,..., п, которые нигде в этом шаре
не обращаются одновременно в нуль. Тогда существует положительное
число X и отрицательное число v, обладающие тем свойством, что
каждая из систем уравнений
Vi(xbx%...,xn) =zlXi /= 1,2,..., п
Щ(хъ хъ хп) = vxi I = 1, 2,..., л
п
имеет по решению на Сфере 2*j = 1.
/=1 п
Теорема [5:51]. Пусть при нечётном п на сфере ]>►]•*/ ^ * даны
непрерывные функции v{(xb хъ... ,хп), / = 1,2 ,..., «. Существует такое
действительное число X, что система уравнений
vi (XV ХЪ • • •»хп) == ^хг
п
имеет на сфере ^х\ = 1 решение.
г=1
4°. Приложение теоремы [5:4] к доказательству
теоремы Фробениуса о существовании собственных
значений матриц. Собственным значением квадратной матрицы ||#^||
называется корень её характеристического уравнения
det^-—%|==0.
Теорема Фробениуса. Всякая квадратная матрица ||#^||,
состоящая из неотрицательных действительных чисел, имеет, по крайней
мере, одно неотрицательное действительное собственное значение.
В самом деле, рассмотрим отображение (п — 1)-мерного проективного
пространства Pw_1, даваемое равенствами
х\ = 2<ч/ xj г = 1,2,..., я.
Точки пространства Р^"1, все координаты xi которых не отрицательны,
образуют замкнутый (п — 1)-мерный симплекс в Р71"1. Так как все я^-;>0,
то этот симплекс при нашем отображении отображается в себя и,
следовательно, содержит, по крайней мере, одну неподвижную точку. Координаты
этой неподвижной точки удовлетворяют уравнениям
п
^xi = Z^UjjXj
при некотором действительном ХфО. Это \ есть собственное значение
матрицы; при этом, так как и а^ и Xj не отрицательны, то и \ не
отрицательно, что и требовалось доказать.
Приведённые примеры уясняют, каким образом топологические теоремы
о неподвижных точках могут прилагаться к доказательствам теврем суще-

588 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XV
ствования. Легко понять также, что для доказательств теорем существования
для различных функциональных (в частности, для интегральных) уравнений
необходимы соответствующие усиления теорем о неподвижных точках
(например, теорема о существовании неподвижной точки при всяком
непрерывном отображении в себя выпуклого компактного в себе множества,
лежащего в гильбертовом пространстве).
§ 6. Классификация непрерывных отображений я-мерной сферы
в /z-мерную сферу.
6:1. Теорема Хопфа; вводные и вспомогательные замечания к
ней. Мы знаем, что два гомотопных между собой непрерывных
отображения одного ориентируемого (и ориентированного) я-мерного
замкнутого псевдомногообразия в другое имеют одну и ту же степень
(глава 11, теорема [6:31 J). В частности, это, конечно, верно для
случая, когда оба наши псевдомногообразия являются «-мерными
сферами. В этом частном случае имеет, однако, место и обращение
только что сделанного утверждения: два отображения я-мерной
сферы в я-мерную сферу, имеющие одну и ту же степень, гомотопны
между собой. Таким образом, мы приходим к следующему
замечательному результату, доказательству которого и посвящен настоящий
параграф.
Теорема Хопфа [6:1J. Пусть S% и Sn — две n-мерные
сферы с выбранными в них раз навсегда ориентациями; я^>1. Два
непрерывных отображения сферы S™ в сферу Sn тогда и только
тогда гомотопны между собой, когда они имеют одну и ту же
степень *).
Замечание 1. Из главы 8, арт. 5:2, замечание 3, следует,
что при любом п ;> 1 и любом целом ^ существуют отображения
одной /z-мерной сферы в другую, имеющие степень -у.
Доказательству теоремы Хопфа предпошлём несколько
вспомогательных предложений.
Определение [6:11]. Если отображение данного множества X
во множество Y является отображением X на одну какую-нибудь
точку множества Г, то это отображение называется
нуль-отображением.
Замечание 2. Два нуль-отображения я-мерной сферы (вообще
любого компакта) в /г-мерную сферу Sn при я^>1 гомотопны между
собой. Это следует из того, что при п ^ 1 любые две точки Sn
могут быть связаны в Sn простой дугой (дугой окружности).
*) Для п = 2 эта теорема была доказана ещё Брауэром в 1912 г., общий
результат получен Хопфом в 1926 г.
Приводимое здесь доказательство принадлежит Хопфу и взято частью
из книги: А л ек с анд ро в-Хопф, Topologie I (глава 13, § 1), частью из
лекций Хопфа, читанных в Берлинском университете в 1926—1927 гг. Оно
отличается большой геометрической наглядностью.
Другое, также весьма простое доказательство теоремы Хопфа дано
Уитнеем в 1937 г, (Duke, Math. Journal, 3, 1937, стр. 46—50),

§ 6] классификация Непрерывных отображений 589
[6:12]. Пусть Е^— полиэдр, гомеоморфный n-мерному
замкнутому симплексу. В случае, если отображение Сг границы Е\ по-
лиэдра Е\ в какой-либо компакт Ф гомотопно
нуль-отображению, и только в этом случае отображение Cv может быть
продолжено на весь полиэдр Е™.
Очевидно, достаточно доказать это предложение в
предположении, что Е\ есть /z-мерный замкнутый симплекс Т*.
Пусть Се, 1 ;> 6 >> 0, — деформация отображения С1 в
нуль-отображение С0, ставящее в соответствие точкам S^-1 = 77[\7^ одну
и ту же точку е0£Ф. Возьмём внутри 7^ точку р0 и положим
С(р0) = е0. Пусть р — произвольная точка 7^, отличная от точки /?0.
Обозначим через рг точку пересечения луча р0р с SJ1"1,
через 6 — отношение, в котором точка р делит отрезок р0р'.
Положим
Полученное отображение С замкнутого симплекса Г* и есть
искомое. Обратно, если дано продолжение С отображения Сг на весь
замкнутый симплекс Tnv то отображение Сг границы S^-1 этого
симплекса гомотопно нуль-отображению.
В самом деле, пусть р0 — центр тяжести симплекса Т^.
Обозначим через Т£ подобный образ Т™ с центром подобия р0 и
коэффициентом подобия 6, 0<;б<]1. Для каждой точки p^S™"1
обозначим через рь точку пересечения луча р0р с границей симплекса Г™
и положим
Сь(р) = С(рь).
Семейство отображений С9, 1 >- 6 >- 0, осуществляет деформацию
отображения С± сферы S^-1 в нуль-отображение С'0> ставящее в
соответствие всем точкам p^S^-1 одну и ту же точку С(р0)£Ф.
[6:13]. Пусть С0 и Сх — два непрерывных отображения
компакта Ф в сферу Sn\ пусть в Sn имеется не пустое открытое
множество Г, обладающее следующим свойством: для каждой
точки р£Г множества С0_1(Р) и С~1 (р) тождественны между
собой. В этих условиях отображения С0 и Q гомотопны между собой.
Доказательство. Выбираем какую-либо определённую
точку и^Ги рассматриваем Sn как пространство Rn, пополненное
бесконечно удалённой точкой и. Пусть для какой-нибудь точки р £ Ф
один из образов С0(р) или Сг (р) отличен от точки и, тогда образ
точки р и при втором нашем отображении отличен от и (потому
что и £ Г). Для нашей точки р определяем Q (р) при 0 <; 6 <; 1 как
точку, делящую отрезок С0(р) Сх(р) в отношении 6 :(1 — в). Таким

590 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [ГЛ. XVI
образом, отображение Q определено для всех точек р £ Ф, образы
которых при отображениях С0 и Сг отличны от точки и. Если же
С0(р) = и, то мы полагаем Q (р) = С0 (р) = и для всех 6.
Непрерывность каждого отображения С9 очевидна во всякой точке
р $ С-1 (Г) = С-1 (Г). Если же р £ С"1 (Г), то множество С"1 (Г)
есть окрестность точки р, во всех точках которой отображения С0
и Cv значит, при любом 6 и отображения С0 и Cq совпадают между
собой, так что Q непрерывно и в точках р£С~г (Г). Наконец,
семейство отображений Cq непрерывно зависит от параметра 6 и,
значит, осуществляет искомую деформацию отображения С0 в
отображение Cv
[6:14]. Пусть я>-2; пусть С — непрерывное отображение
сферы S™ в сферу Sn) пусть р £ Sn. Существует непрерывное
отображение Cv сферы S™ в Sn, гомотопное отображению С и
удовлетворяющее следующему условию: С~г (р) содержится в
некотором n-мерном симплексе Т™ (некоторой триангуляции S%),
образ которого С^(Т^) является собственным подмножеством
множества Sn.
Доказательство. Так как всякое непрерывное отображение
$п в Sn гомотопно своему симплициальному приближению, то мы с
самого начала можем предположить, что С есть симплициальное
отображение некоторой триангуляции Ко сферы S" в некоторую
триангуляцию Кп сферы Sn. Мы вправе, далее, предположить, что
точка р лежит в некотором я-мерном симплексе триангуляции Кп.
Пусть, наконец, и есть отличная от р точка, также
принадлежащая некоторому я-мерному симплексу триангуляции Кп. Прообраз
каждой из точек р и и состоит из конечного числа
точек /C£ = SJ (только для этого нам и требовалось,
чтобы отображение С было симплициальным).
Мы рассматриваем Sn как эвклидово пространство Rn с
бесконечно удалённой точкой и. Мы рассматриваем также S™ как
эвклидово пространство R™ с бесконечно удалённой точкой и0, не
принадлежащей (конечному) множеству С-1 (р) (j С-1 (и).
Пусть TJJ есть я-мерный замкнутый симплекс пространства R™,
не содержащий ни одной точки множества С-1 (и) (всегда можем
предположить, что Т% есть элемент некоторой триангуляции
сферы S1*). Из наших предположений следует, что
C(T%)czRn.
Пусть точкар0£ С-1(р)не лежит в Тп0; так как й>2, то в Т\
можно найти такую точку р0, что на всём отрезке р'0р0 нет ни
одной точки множества С'-1 (и). Можно поэтому найти я-мерный сим-

§ б] КЛАССИФИКАЦИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ 591
плекс T^aS™, содержащий отрезок р'0р0, находящийся на
положительном расстоянии от конечного множества С-1 (и) и не
имеющий на своей границе ни одной точки множества С~1(р).
Имеем:
C(T'on>)czR» = Sn\u.
Мы теперь определяем отображение Сг так:на5£\7^ полагаем
Сг = С; далее полагаем С1(р'0) = р; наконец, если q0 — произвольная
точка границы симплекса Т'0п, то отображение Сх определено на
отрезке p'0q0 как пропорциональное отображение этого отрезка на
отрезок pCt (q0) пространства Rn. Так как Сг отличается от С лишь
в Т'0п и так как С(Т'0п) и Сг(Топ) замкнуты и ограничены в Rn,
то содержащее точку и множество
Г — 5»\ [С (%«) U Сг (То*)]
удовлетворяет условиям леммы [6:13]; поэтому С и Сг гомотопны
между собой.
Очевидно, С~г(р) U С~1 (и) есть конечное множество. Един -
ственная лежащая в Т'0п точка множества С"1 (р) есть точка р0,
являющаяся точкой симплекса Т™. Число всех точек С—г(р) конечно-
Таким образом, при переходе от С к Сх прообразы точек и и р
остаются конечными, а число точек прообраза /?, не принадлежащих 7™,
уменьшилось. Отображение Cv правда, может не быть симплициаль-
ным, эднако, единственное интересующее нас свойство симплициаль-
ных отображений — конечность прообразов точек р и и, как уже
сказано, имеет место для отображения Cv Наконец, множество
есть собственное подмножество множества Sn.
Повторяя, если нужно, тот же процесс конечное число — пусть
v — раз, приходим к такому отображению Cv, гомотопному С, что
весь прообраз С-1 (р) лежит в Т£ и С/ (7^) czRn ф Sn9 что и
требовалось доказать.
6:2. Случай, когда степень отображения равна нулю. В этом
артикуле мы доказываем следующую теорему:
[6:21п]. Непрерывное отображение n-мерной сферы S^ в п-мер-
ную сферу Sn, имеющее степень нульу гомотопно
нуль-отображению.
Замечание. При доказательстве теоремы [6 :21п] мы будем
под S™ понимать не сферу в собственном смысле слова, а
границу (n-j-1)-мерного симплекса 7^+1, которую и будем
называть /г-мерной «сферой».
Доказательство теоремы [6:21„] будет вестись посредством
индукции совместно с доказательством следующих теорем:

592 БРАУЭРОВСКАЯ ТЕОРИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ [гл. XVI
[6:22n]. Пусть t™+1—одинаковая с данной раз навсегда
ориентацией пространства /?п+1 ориентация (п -J-1)-мерного
симплекса 7^+*, границу которого обозначаем через S™. Пусть о £ /Jn+1
и С—непрерывное отображение S™ в #п+1\о.ЕслиЪ (СА^+1, о) = 0,
то отображение С можно продолжить в отображение
замкнутого симплекса f™+x в /?w+i\o.
[6 :23п]. Сохраняя обозначения, теоремы [6 :22J, предположим,
что С есть отображение «сферы» S™ в сферу SnaRn+l с
центром о и что степень отображения С равна нулю. Тогда С может
быть продолжено в отображение замкнутого симплекса Т™+х в Sn.
Порядок совместного доказательства этих теорем такой:
последовательно доказываются следующие четыре утверждения:
1°. Теоремы [6: 210] и [6:21J верны.
2°. Из [6 :21я] следует [б :23w] для л^О.
3°. И з [б : 23 J следует [б: 22„] для п ^ 0.
4°. Из [б:22п] следует [6 :21п+1] для п^1.
Доказательство 1°. Теорема [6 :210] верна, так как
отображение нульмерной сферы в нульмерную, имеющее степень нуль,
есть нуль-отображение*). Теорема [6:21^ содержится в теореме
[2:5] главы 2 и в замечании о случае п=\ в главе 11, арт. 6:4.
Доказательство 2° содержится в лемме [6 :12].
Доказательство 3°. Нам дано, что всякое отображение С,
степени нуль, «сферы» S™ в сферу Sn может быть продолжено в
отображение симплекса TJl+1 в Sn. Требуется доказать, что всякое
отображение С «сферы» S™ в Rn+1\o, для которого Ь(СД^-И, о) = 0
может быть продолжено в отображение симплекса Т^+х в /?'И1\о.
Эту задачу продолжения разобьём на две задачи: введём в /?w+*
«систему полярных координат», состоящую из полюса о
и единичной сферы Sn с центром о; под полярными координатами
точки p£/?w+1\o понимаем: радиус-вектор г(р) точки р (т. е.
расстояние этой точки от о) и проекцию т о ч к и р в Sn (т. е.
точку пересечения луча (ор) с Sn), которую обозначаем через <?(р).
Наша задача продолжения распадается теперь на две задачи:
а) Продолжить определённую на S™ положительную функцию
гС(р) в функцию, определённую на всём Т*+1.
б) Продолжить отображение ®С сферы 5^ в Sn до
отображения 7£+* в Sn.
3 а дача а) решается без труда применением теоремы Брауэра-Уры-
сона о продолжении непрерывных функций (глава 1, теорема [4 :22]);
при продолжении положительной функции всегда можно потребовать,
чтобы продолженная функция также была положительной;
последнее замечание, верное и вообще [см., напр., Александров-Хопф,
*) Глава 8, арт. 5:2, замечание 4.

§ 6] КЛАССИФИКАЦИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ 593
гл. 1, § 6, Zusatz на стр. 78], в данном случае следует из Хаус-
дор^а, Теория множеств (стр. 134, последние три строки перед
геор. X), т. к. речь идёт о функции, положительной на компакте S™
и, следовательно, имеющей на этом компакте положительную нижнюю
грань.
Переходим к задаче б). Так как степень отображения оС
«сферы» S™ в Sn равна порядку точки о относительно СА/^1
(теорема [1 :51]), т. е. нулю, то решение задачи б) уже содержится
в наших данных (теорема [6:23J).
Доказательство 4°. Дано отображение С, степени нуль,
«сферы» 5J+1b<Sw+1 при п^>\. Требуется деформировать С в
нуль-отображение. Для этого достаточно продеформировать С в такое
отображение С, при котором образ «сферы» S™+] есть собственное
подмножество сферы Sn+1: всякое собственное подмножество сферы
может быть стянуто в точку, и это стягивание даёт нам деформацию
отображения С в нуль-отображение.
Так как л^>1, то мы вправе применить лемму [6:14] и
предположить, что С с самого начала удовлетворяет условию:
Имеется такая точка o£S™+1, что прообраз С-1 (о) лежит
в (п -]- 1)-мерном симплексе TJ+1, образ замыкания которого [т. е.
множество С{Т^+Х)\ является собственным подмножеством сферы Sn+1.
Мы делаем это предположение и обозначаем через и
определённую точку множества Sn+1\C(T%+1).
После этого мы рассматриваем Sn+1 как эвклидово
пространство /?и+1, пополненное бесконечно удалённой точкой и, так что
С(Г?+1)с=5и+1\и = /ги+1.
Так как С-1 (о)с= 7^+*, то можем применить теорему [3:3] (в
которой надо заменить п через п-\-\). Это даёт
Ъ(СМ» + \ о) = ?с —О,
где *2 + 1 обозначает ориентацию TJ+1, одинаковую с ориентацией 5™+*.
Отсюда на основании теоремы [6 :22п] (которая ведь
предположена Еерной) следует, что существует отображение С1
замкнутого симплекса 7?+1 в Rn+ls\oz= Sn+1\(ol) и), совпадающее на
ТУ+1\^о+| с С- Положим С1{р) = С(р) для любой точки
Теперь С2 есть уже отображение SJ+1 в Sn+1\o, т. е. на
собственное подмножество сферы Sn+1. Открытое множество
r = S" + i\[C(7? + 1) U С^Го4"1)]
38 Александров II. С.

594 браУэровСкая теория непрерывных*Отоьражёний [гл. xvt
не пусто (оно содержит точку и), и для каждой его точки q
множества C~1{q) и СГх(я) совпадают, так что на основании леммы
[6:13] отображения С и Ct гомотопны между собой, чем
утверждение 4°, а с ним и все три теоремы [б :21], [б :22], [6 :23]
доказаны.
6:3. Редукция теоремы Хопфа к «теореме о продолжении».
Теорема о продолжении. Пусть Т^—замкнутый симплекс,
лежащий в симплексе Т™ с= Rn. Границы симплексов То и Т?
обозначаем соответственно через So""1 и S™"1. Полиэдральную область
Ti\Tq обозначаем через Г и даём ей ориентацию, одинаковую
с выбранной заранее ориентацией Rn\ границу ориентированной
таким образом области Г {в некоторой триангуляции Ка)
обозначаем через г™~~1. Пусть дано непрерывное отображение С
множества
в (п — \умерную сферу Sn~l, имеющее степень нуль на цикле
zn~x
* ос
Тогда отображение С может быть продолжено на весь
полиэдр Г.
Предположим теорему о продолжении доказанной и выведем из
неё теорему Хопфа.
Возьмём в симплексе Го какую-нибудь определённую точку о.
Нам даны отображения С0 и Cv одной и той же степени, «сферы»
.So в S».
Построим следующим образом отображение С множества
So'1 U Sni~l=f \Г в Sn~K
На So""1 отображение С по определению совпадает с С0.
На Si""1 отображение С определяется так: если р' —
произвольная точка Si"1, а р — точка пересечения луча ор' с So" , то по
определению *)
С(р') = С1{р).
По теореме о продолжении продолжаем отображение С на весь
полиэдр Г.
Пусть теперь б — действительное число, заключённое между 0 и 1:
0^6^ 1. Определим непрерывное отображение С9 «сферы» Sq~~
*) Можно сказать короче, что отображение С на S±n 1 есть
отображение Q, перенесённое с S^-"1 на Sf"""1 при помощи центральной проекции
из о.

§ 6] Классификация непрерывных отображений 595
в сферу 5й"1 следующим образом. Пусть р0—произвольная точка
So ~~ . Обозначим через рг точку пересечения луча ор с Sl*~\ через
рь — точку отрезка р0ри делящую его в отношении 0 (1—6).
Полагаем *)
Сь(Ро)=-с(Р*У
Семейство непрерывных отображений Q, 0-^6^1 «сферы»
So""1 в 51*-1, очевидно, осуществляет деформацию отображения С0
в С1э чем теорема Хопфа доказана. Остаётся доказать теорему о
продолжении.
6:4. Доказательство «теоремы о продолжении».
Сформулируем сначала несколько элементарных фактов.
1°. Пусть в симплексе Т£ дана точка р0; пусть С —
отображение Т%\Т% в сферу S71-1; отображение С может быть продолжено
на всё множество То\р0.
_ В самом деле, пусть р — произвольная, отличная от /?0, точка
Р\ Обозначаем через р1 её проекцию на S^"1 из р0 и полагаем
С(р) = С(р').
Замечание. Доказанное предложение остаётся в силе, если
заменить замкнутый симплекс Т™ любым гомеоморфным ему
множеством Еп.
2°. Пусть То и Г" — непересекающиеся замкнутые симплексы,
лежащие внутри симплекса 74 Пусть дана ориентация tn симплекса 74
Границу ориентированной полиэдральной области
Г=7»\(7?и Г")
(в некоторой триангуляции К*) обозначаем через го""1. Всякое
непрерывное отображение С полиэдра Г в сферу Sn~l имеет на г"~~
степень нуль.
В самом деле, в силу [1 :51], степень отображения С на zl ~г
равна порядку центра сферы S4-1 относительно цикла Сг?~~ ; если
бы этот порядок был отличен от нуля, то центр сферы
принадлежал бы на основании теоремы [2:11] образу полиэдра Г, чего на
самом деле нет, так как С есть отображение в сферу S71-1.
После этих предварительных замечаний переходим к
доказательству теоремы о продолжении. Сохраняем обозначения предыдущего
*) Если, например, 7" возникает из 7J посредством подобного
преобразования с центром подобия о и коэффициентом подобия 2, а 7^—
посредством подобного преобразования с коэффициентом 1 + 6, то С0 возникает
из перенесения путём центральной проекции из о на S"~l отображения С
границы симплекса ТЦл
38*

596 праУэровская теория непрерывных отображений [гл. xvl
артикула. Пусть К есть триангуляция полиэдра Г. В вершинах этой
триангуляции, лежащих на 5" и на So, отображение С определено.
Определяем его произвольно во всех остальных вершинах этой
триангуляции.
Пусть теперь т < п. Предположим, что отображение С
определено на всех элементах триангуляции Кл число измерений которых
не превосходит т — 1. Определим его на всех w-мерных элементах
этой триангуляции, не лежащих на S?-"1 и Sq^1. Для этого
заметим прежде всего, что на границе Тт\Тт любого /гс-мерного
элемента комплекса К отображение С гомотопно нулю. В самом деле,
оно гомотопно своему симплициальному приближению С, которое
отображает Тт\Тт на нигде не плотное подмножество сферы
Зп-г.
Отображение С «сферы» Тт\Тп\ будучи гомотопно нулю, может
быть по лемме [6:12] продолжено на симплекс Тт.
Таким образом, шаг за шагом отображение С продолжается на
все симплексы комплекса К, число измерений которых не
превосходит п— 1.
Выберем теперь в каждом «-мерном симплексе Г? £ К по точке
рг и продолжим отображение С границы симплекса Г" на всё
множество Ti\Pi согласно замечанию 1°. Теперь С продолжено уже
на весь полиэдр Г кроме конечного числа
«исключительных» точек pj,..., ps. Докажем, что при s> 1 число s
может быть уменьшено. Для этого соединим какие-нибудь две
исключительные точки, например, pt и р2, ломаной р^2 без
самопересечений, лежащей в Г, и окружим эту ломаную весьма тесной
замкнутой полиэдральной окрестностью Еп> гомеоморфной я-мерному
замкнутому симплексу («поместим эту ломаную в запаянную с обоих
концов узкую трубку»). Сохраняя отображение С неизменным вне
и на границе окрестности Епу упраздним его в точках Еп и после
этого продолжим заново на множество Еп—р2> Видоизменённое таким
образом отображение С имеет уже меньшее число исключительных
точек.
Применяя несколько раз это построение, приходим к
непрерывному отображению, определённому во всех точках полиэдра Г кроме
единственной точки р% и являющемуся продолжением данного в
начале одноимённого отображения множества S*~~ U Si ~" в S11-1.
Остаётся устранить эту единственную исключительную точку р#.
Пусть р# £ Г" £ К. Без ограничения общности можно
предположить, что Г"сГ. Ориентируем область Т0= Тп\(Тп0[} Г")
одинаковым образом с выбранной ориентацией области Г (и Rn) и
обозначаем через Zq~x границу ориентированной области Г0. Очевидно,

§ б) КЛАССИФИКАЦИЯ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ 597
г^~~1=гп'-1 — ^С'где С есть ориентация Г*, одинаковая с
ориентацией Г. Степень отображения С на г""""1, равная сумме степеней
на zn-1 и Д^, есть, в силу замечания 2°, нуль. Так как по
условию теоремы степень С на zn~x также равна нулю, то равна нулю
и степень С на Д^. Поэтому, сохранив отображение С вне и на
границе симплекса Т™ и упразднив его внутри Г", можем на
основании [6 :23] заново продолжить его на замкнутый симплекс 7?, чем
достигнуто и продолжение отображения Сна весь полиэдр Г •
Теорема о продолжении, а вместе с ней и теорема Хопфа
полностью доказаны.

ГЛАВА СЕМНАДЦАТАЯ.
НЕПОДВИЖНЫЕ ТОЧКИ НЕПРЕРЫВНЫХ ОТОБРАЖЕНИЙ
ПОЛИЭДРОВ.
Эта глава посвящена доказательству знаменитой теоремы Лефше-
ца-Хопфа, выражающей так называемое алгебраическое число
неподвижных точек данного непрерывного отображения полиэдра в себя через
числовые имварианты гомологического типа этого отображения, т. е. через
числа, определённые порождёнными данным отображением эндоморфизмами
гр)пп Бетти отображаемого в себя полиэдра.
Теорем я Лефщеца-Хопфа доказана для случая многообразий и
отображений с конечным числом неподвижных точек Лефшецем в 1926 г. В 1927 г.
Хопф дал совершенно новое и элементарное доказательство сразу в
наиболее общем случае. Таким образом была получена теорема, охватывающая
почти всё известное нам в настоящее время о неподвижных точках
полиэдров (не специально многообразий) и содержащая—даже в случае
многообразий— большинство ранее известных теорем о неподвижных точках (в
частности, теоремы, изложенные в предыдущей главе).
Все доказательства, приведённые в этой главе, принадлежат Хопфу.
Сама глава представляет собой перевод с небольшими редакционными
изменениями и некоторыми пропусками написанной Хопфом главы 14 нашей
совместной книги.
§ 1. Теорема существования для неподвижных точек.
1:1. Неподвижные симплексы. Пусть К$ есть подразделение
я-мерной триангуляции Ка и S^ — симплициальное отображение К$
в Ка. Если Т£ есть r-мерный симплекс комплекса /Ср, то число
измерений симплекса S£7T не превосходит г; если оно равно /% то
может случиться, что симплекс 7? лежит на S^TL т. е. является
одним из симплексов подразделения симплекса
6^ГГ£/Са в комплексе /Ср. В этом случае симплекс Т££ К§
называется неподвижным симплексом симплициального
отображения S®.
Если tr ecib некоторая ориентация неподвижного симплекса Т£
(мы говорим короче: «#J есть ориентированный неподвижный
симплекс»), то ^ = 5^3 также есть ориентированный симплекс, а его
подразделение з*Рл в АГр —цепь, причём Ц входит в эту цепь с
коэффициентом

§ 1] ТЕОРЕМА СУЩЕСТВОВАНИЯ ДЛЯ НЕПОДВИЖНЫХ ТОЧЕК 599
Этот коэффициент не зависит от выбранной нами ориентации К
симплекса 7£, так как при замене tt на —Е оба множителя в скалярном
произведении (1 : Ю) меняют знак. Неподвижный симплекс Т££/Ср
называется положительным неподвижным симплексом, если
и отрицательным, если (s^S^tl • *£) = — 1.
Мы теперь определяем: алгебраическим числом г-мерных
неподвижных симплексов симплициального отображения S\
называется разность между числом положительных и числом
отрицательных r-мерных неподвижных симплексов этого
отображения.
Мы сейчас дадим этому числу новую интерпретацию.
Пусть Lo = Lj(ATp) есть группа всех r-мерных целочисленных
цепей триангуляции К§. Симплициальное отображение S\
триангуляции АТр в Ка порождает одноимённый гомоморфизм*)
группы Ц в группу Ll = Ll(Ka), а подразделение триангуляции Ка
(т. е. переход от Кл к К$) — изоморфизм s? группы Lra в LL
Отображение sZSl является, таким образом, эндоморфизмом / группы
Lg. Мы утверждаем, что след SpfLL или, короче, .Sp L* этого
эндоморфизма**) равен r-мерному алгебраическому числу неподвижных
симплексов.
В самом деле, r-мерные ориентированные симплексы t'
(/=1, ..., рг) триангуляции К§ образуют базу группы LI.
Эндоморфизм / задаётся системой равенств
(1:П) /ft = 2*<./<P/ (/=1, ..., П
где коэффициенты а,ц могут принимать значения 0, -f~ 1 или —1.
Симплэкс |^L| является неподвижным симплексом в том и только в
том случае, если аифО, а именно: он является положительным или
отрицательным неподвижным симплексом, смотря по тому, равняется
ли аи-\-\ или —1. Следовательно, алгебраическое число г-мерных
неподвижных симплексов равно
(1 :1) 2«« = 5рЦ.
1 :2. Формула Хопфа. Мы показали, что для существования
неподвижных симплексов при отображении S^ достаточным условием
*) Глава 7, арт. 8 :2.
**) Прибавление I, арт. 2:7,

600 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [ГЛ. XVII
является неравенство нулю следа SpLZ эндоморфизма f— s*S\ группы
Lrr Существование неподвижных симплексов (так же, как и их число)
является свойством симплициального отображения SjJ. Мы, однако,
покажем, что оно является гомологическим свойством
отображения Si полиэдра Ка в себя, соответствующего симплициальному
отображению 5^, и выясним топологический смысл этого свойства. Для
этого мы выразим число неподвижных симплексов через числа,
характеризующие поведение ггупп Бетти при соответствующих
эндоморфизмах, что и составляет содержание формулы, открытой Хопфом
и называемой его именем. Формула Хопфа доказывается
посредством рассуждений, аналогичных доказательству формулы Эйлера-
Пуанкаре, с той лишь существенной разницей, что встречавшиеся
нам прежде ранги различных групп заменяются теперь следами
эндоморфизмов, испытываемых этими группами.
Вследствие переместительности операторов Д и^ при
эндоморфизме /=s«Sj| группы /,£ подгруппы Z\ = ZrL{K^ </), Щ==НГА(К^^
и //£ = h^(K$f J) также испытывают эндоморфизмы. Отсюда
следует, что эндоморфизм / порождает эндоморфизмы фактор-групп
L\/Zr« = A\ и Z\/Hl = Д£Эд, которые мы также будем обозначать
через /. Эти фактор-группы ЛГ и Д£о3, как и группы ZL Щ и Щ,
являются свободными абелевыми группами. Поэтому определена
следы SpZrp SpH', Spfy и SpA^ Sptsr^ всех этих групп
(г = 0, ..., п) при эндоморфизмах /.
Так как все дальнейшие рассуждения касаются лишь комплекса
К?, то индекс |3 больше не будем писать (таким образом, вместо
Ц, Zrv Щ9 Щ и Л£, Ьгщ и т. д. пишем просто Z/, Zr, Hr, № и
А', Д0'0 и т. д.).
Покажем, что
(i :21) SpAr = SpHr~K
Оператор Д отображает группу Lr гомоморфно на Иг-\ причём для
любой цепи x£Lr kfxr—fkxr. Ядром этого гомоморфизма
является группа Zr. Очевидно, что для изоморфизма Д группы Аг =
= Lr/Zr на группу Яг_1, порождённого гомоморфизмом Д группы
U на Нг~1, будет выполняться то же соотношение
А/- /А,
так что изоморфизм Д группы Аг на Нт~г трансформирует
эндоморфизм / группы Аг в эндоморфизм / группы Нг-\ откуда и следует
ф )рмула (1 :21).

§ 1] ТЕОРЕМА СУЩЕСТВОВАНИЯ ДЛЯ НЕПОДВИЖНЫХ ТОЧЕК 601
В силу аддитивности следов (прибавление 1, теорема [2:8]),
имеем
SpAr == Sp (Lr/Zr) == SpLr — SpZr,
и формула (1 :21) переписывается в виде
(1 :22) SpLT — SpZr = SpHr~!.
Далее, так как A00 = Zr/Hr, где #г есть дивизионное
замыкание группы Нг в Zr, имеем *)
(1 :23) SpZr — SpH>'^Spbr00\
складывая (1 :23) и (1 :22), получим
SpV ~~ SplV = Sp/f-1 4 Sp^w
или
(1:24) SpLr = Sp Д^ -f Sptf' + 5р№ -*.
Умножим полученную формулу на (—1)г и просуммируем по г от
0 до п. Тогда, принимая во внимание, что группы И-1 и Нп суть
нуль-группы и, следовательно, SpH'1 = SpHn = 0, получим
формулу Хопфа:
п п
(1 : 25) ^ (— lyspl' = Е ( - 1)^>Доо.
Формула Хопфа является обобщением формулы Эйлера-Пуанкаре,
так как, если К$ совпадает с Ка w симплициальное отображение
Si является тождественным (как и отображение sty, то все
эндоморфизмы / являются тождественными отображениями соответствующих
групп на себя, и их следы равны рангам соответствующих групп.
В частности, SpLr — pr и Sp^0 = тсг. Непосредственным следствием
формулы (1:25) является следующая:
Теорема существования неподвижных симплексов
[1: 2]. Если
2(-1)г5рДг.^о,
то существует, по крайней мере, один неподвижный симплекс.
В самом деле, в этом случае, по крайней мере, для одного значения г
имеем SpU^O; при этом г существует I, для которого в формулах
(1:1) и (1:11) <%=£(), следовательно, |^.| является неподвижным
симплексом, что и требовалось доказать.
Пусть, например, АГа есть триангуляция замкнутого л-мерного
симплекса. Тогда все группы Д£0 при г>0 суть нуль-группы,
поэтому 5/?Д£0 = 0 при /•>(); но 5>Доо = 1, как при всяком отобра-
*) Так как SpHr — SpHr, см. Прибавление 1, 2:8, замечание.

602 неподвижные точки отображений полиэдров [гл. xvii
п
жении связного комплекса. Следовательно, ^ ^рД£0 = 1 и в АГ? суще-
ствует, по крайней мере, один неподвижный симплекс.
1:3. Число Лефшеца для непрерывного отображения полиэдра
в себя. Пусть С есть непрерывное отображение л-мерного полиэдра
Р в себя. Согласно главе 11, § 3 и 4, это отображение порождает
одноимённый гомоморфизм С группы Д£(Р) в себя; при этом группа
кручения вг(Я)с:Д£(Р) тоже отображается в себя, поэтому
гомоморфизм С группы А£(Р) в себя порождает эндоморфизм группы
&o0ttkl(P)/tyr(P), который мы будем попрежнему обозначать
через С. Так как Д£0 есть свободная абелева группа, то определён
след Sp^0 = Spo^0 эндоморфизма С этой группы. Если Р = Ка =
= /Ср и C=S^ (где Ка, К§ и S$ имеют тот же смысл, что и в
предыдущих артикулах), то только что определённый след Spc^r00
совпадает со следом Spfkr00, определённым в артикуле 1:2 (так как
каждый цикл из Ка находится в одном гомологическом классе
полиэдра Р со своим подразделением в К$).
Определение [1:3]. Числом Лефшеца непрерывного
отображения С полиэдра Р в себя называется
Ас=2(-1)^Д-0.
Замечание. Число А^ выражает некоторое свойство
гомоморфизма С группы Д£0 в себя, т. е. свойство гомологического класса
отображения С. Поэтому всякие два вполне гомологичные и, тем
более, всякие два гомотопные отображения полиэдра Р в себя имеют
одно и то же число Лефшеца.
Теорема существования неподвижных точек
[1:3]. Если число Лефшеца Ад отображения С отлично от нуля,
то существует, по крайней мере, одна неподвижная точка этого
отображения, т. е. такая точка р £Р, для которой Ср = р.
Доказательство. Пусть Ао^Ь0. Определим на Р
действительную функцию ср(р) = р(р, Ср). Мы должны показать, что эта
функция принимает хотя бы в одной точке полиэдра Р
значение 0. В силу компактности Р и непрерывности ср, достаточно
показать, что при всяком s>0 существует точка /?£Я, для которой
<р(р) = р(С/?,/?)<8.
Пусть дано некоторое число е>0. Аппроксимируем отображение
С симплициальным отображением S^ некоторого подразделения К$
некоторой достаточно мелкой триангуляции Ка полиэдра Р так,
чтобы выполнялись следующие условия:
<~»
1°) С гомотопно S$.
2°) Симплексы триангуляции АГв имеют диаметр < тр

§ 1] ТЕОРЕМА СУЩЕСТВОВАНИЯ ДЛЯ НЕПОДВИЖНЫХ ТОЧЕК 603
3°) Для всех точек р£Р
(см. главу 11, § 5).
В силу 1°), имеем Л~а = Л(7 (см. только что сделанное замечание
о числе Лефшеца).
Таким образом, Л^а^О, и на основании теоремы [1:2] при
отображении S£ существуют неподвижные симплексы. Пусть р —
произвольная точка неподвижного симплекса Гр £ /Ср, тогда/? и S$p
принадлежат одному и тому же симплексу S^T^^K^ следовательно^
на основании 2°)
(1:31) Р(р, SgPK-j-
В то же время на основании 3°)
(1:32) Р(СЛ ^р)<~.
Из (1:31) и (1:32) следует
р(Р, Ср)<е,
что и требовалось доказать.
1: 4. Примеры. 1°) Из геометрического смысла нульмерной группы
Бетти следует непосредственно, что при всяком отображении
связного полиэдра Р в себя 5рД°0=1. Если для всех г>0 числа Бетти
кг(Р) равны нулю, т. е. Д£0 = 0 при г>0, то и все следы Spkr00
равны нулю при г>0. В этом случае для всякого отображения С
полиэдра Р в себя Aq=1, так что имеет место теорема:
[1:41]. Всякое непрерывное отображение в себя связного
полиэдра Я, все числа Бетти которого {кроме it0) равны нулю,
имеет, по крайней мере, одну неподвижную точку. К таким
полиэдрам, например, относятся: я-мерные замкнутые симплексы,
проективные пространства чётных размерностей.
2°) В следующих двух теоремах мы будем пользоваться тем, что
гомотопные отображения гомологичны и, следовательно, числа
Лефшеца таких отображений одинаковы.
Если весь полиэдр Р отображается в одну из своих точек, то
для этого отображения 5рД8<>=1 и£рД£0 = 0 при г>0,
следовательно, Л(7= 1. Отсюда вытекает теорема:
[1:42]. Если непрерывное отображение С произвольного
полиэдра Р в себя гомотопно нуль-отображению*), то при
отображении С существует, по крайней мере, одна неподвижная точка.
*) То-есть отображению всего полиэдра Р на одну какую-нибудь точку
этого полиэдра.

604 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [ГЛ. XVII
3°) При тождественном отображении полиэдра Р в себя группы
Бетти также отображаются тождественно. Поэтому Sp^0 = кг щи
п
всяком г, и число Лефшеца равно V(—1)гкг, т. е. эйлеровой харак-
/•=0
теристике полиэдра Р. Отсюда:
[1:43]. Если эйлерова характеристика полиэдра К отлична от
нуля и непрерывное отображение С полиэдра К в себя гомотопно
тождественному, то отображение С имеет неподвижную точку.
К полиэдрам, упомянутым в [1:43], относятся, например, все
поверхности (замкнутые и с краем), кроме тора, бутылки Клейна,
кругового кольца и листа Мёбиуса.
4°) Если Р есть я-мерное замкнутое ориентируемое
псевдомногообразие, у которого числа Бетти размерностей 1,2, ..., п—1
равны нулю*), а С—отображение степени f псевдомногообразия Р в
себя, то Spk°00=\, SpA™0~4 и Sp^Q = 0 при 0 < г < п. Поэтому
Л<у=1+(—1)"Т.
Отсюда следует, в частности:
[1:44]. Если все числа Бетти размерностей 1,..., п—1
замкнутого ориентируемого n-мерного псевдомногообразия Р равны
нулю*), то при всяком отображении этого псевдомногообразия в
себя, имеющем степень ф — (—\)п, существуют неподвижные точки.
1 :5. Некоторые замечания о числе Лефшеца. Мы видели, что
условие Ас ф 0 является достаточным для существования
неподвижных точек при отображении С. Покажем, что это условие не является
необходимым. Имеет место даже следующее весьма элементарное
предложение:
[1 :5]. Можно построить непрерывное отображение С0
лемнискаты на себя, имеющее число Лефшеца, равное нулю и
обладающее тем свойством, что отображение С0 (и всякое гомотопное,
даже всякое ^.-гомологичное ему отображение С) имеет, по
крайней мере, одну неподвижную точку.
Доказательству предпошлём следующую лемму:
[1 :51]. Если С есть отображение окружности в себя, имеющее
степень с, то число неподвижных точек этого отображенияу по
меньшей мере, равно \с —1|.
Отсюда, в частности, следует, что всякое отображение
окружности в себя, не имеющее неподвижных точек, имеет степень + 1 и,
следовательно, гомотопно тождественному отображению.
Доказательство леммы [1:51] чрезвычайно просто:
рассмотрим угловую функцию F(x), соответствующую отображению С (см.
главу 2, доказательство теоремы [2 : 51]). Тогда F(l) — F (0) = 2тгс.
Полагая f(x) = F(x) — x, имеем /(1)—/(0) == 2тг (с—1), откуда
следует, что, по крайней мере, для \с—1| значений переменного*
*) Например, если Р есть л-мерная сфера, иди — при нечётном п — проек
тивное пространство п измерений.

Ml
индекс неподвижной точки
605
функция / (л:) принимает значения, равные целым кратным 2^. Обо-
чзначая через х{ эти значения, имеем F{xi)==xi-\-2^ki при целых ki9
откуда следует, что соответствующие точкам хг точки окружности
суть неподвижные точки отображения С, чем лемма [1 :51] доказана.
Переходим к доказательству [1 :5]. Вместо лемнискаты
рассматриваем соединение двух касающихся друг друга в точке р0 окружностей zx
и z2. Через zt и z.2 обозначаем произвольно выбранные ориентации
этих окружностей. На каждой из этих окружностей установим отсчёт
углов от точки р0 в направлении, соответствующем данной
ориентации этой окружности, и зададим отображение С0 формулами:
co(«i) = — ai на fi>
Q(«2) = 2a2 на z2f
где при i=l,2 обозначаем через ai только что введённую угловую
координату на окружности z{.
При отображении С0 (и при всяком ^-гомологичном ему
отображении С) циклы zt и z2 переходят соответственно в — ^ив 2z2, так
что Sphlo =1 и, следовательно, Л = 0.
С другой стороны, из леммы [1 :51] следует, что отображение С0,
имея на окружности zt степень —1, оставляет на zv по крайней
мере, | — 1 — 11 = 2 точки этой окружности неподвижными.
Докажем, что при всяком отображении С, которое Sft-гомологично
отображению С0, имеется, по крайней мере, одна (лежащая ма z{) неподвижная
точка (и это несмотря на то, что при отображении С окружность z1 вовсе
не непременно отображается в себя). Имея в виду последнее замечание,
построим вспомогательное отображение С окружности z1 в себя
следующим образом. Если для р £ zx имеем С (р) £ zb то полагаем С'(р) = С(р).
Если же С(р) £~z<iy то полагаем С(р)—/V Отображение С/ непрерывно и
обладает следующим свойством: если р есть точка zi9 отличная от р0, а Q
и С± суть достаточно хорошие симплициальные приближения к
отображениям С и С (рассматриваемым лишь на z{), то при этих отображениях
точка р покрывается образом цикла zx с одной и той же кратностью (это
легко следует из того, что во всех точках zb отображающихся посредством С
в г1э отображения С и С совпадают). Но из равенства С fa) =—2^ следует,
что эта кратность для отображения С± равна — 1, такова же она, значит, и
для отображения С\. Последнее обстоятельство, в свою очередь, означает, что
отображение С окружности z\ в себя имеет степень — 1 и, следовательно,
по крайней мере, две неподвижные точки. Пусть р есть неподвижная точка
отображения С, отличная от точки р0. Тогда С(р)—рфр0% значит,
С'(р) = С(р) и, следовательно, С (/?)=/?, что и тр бовалось доказать.
§ 2. Индекс неподвижной точки.
2:1. Определение индекса. Пусть С—непрерывное отображение
области Т c^Rn в пространство Rn. Назовём вектором сдвига
в точке л;, соответствующим отображению С, вектор
vG(x) = xC(x). Векторы v°(x) образуют векторное поле i*a, опреде-

бОб НеноДвижНыё точки Отображений полиэдрой [гл. xvli
ленное во всех точках Г и называемое полем сдвига
отображения С. Нули этого поля совпадают с неподвижными точками
отображения С.
Пусть р — изолированная неподвижная точка отображения С, т. е.
изолированный нуль поля $$с. Индекс этого нуля (см. главу 16, арт.
5:2) называется индексом неподвижной точки р
отображения. На основании рассуждений арт. 5:2 главы 16 этот индекс
можно определить, например, так:
[2: 11]. Предполагаем пространство/?" ориентированным и все его
(п— 1)-мерные сферы ориентированными в соответствии с выбранной
ориентацией пространства Rn. Возьмём лежащий в Г замкнутый шар
Ёп> ограниченный сферой S*1—1 — tn\En, не содержащий ни одной
отличной от р неподвижной точки отображения С. Возьмём «сферу
направлений» *) So-1 пространства Rn и каждой точке x^S'11^1
поставим в соответствие ту точку С0х сферы So~~ , в которой эту
сферу пересекает луч, исходящий из её центра, параллельный
вектору сдвига v°(x). Степень отображения С0 сферы Sn~~l в сферу
5?""1 и называется индексом неподвижной точки р и обозначается
ind ар.
Замечание. Индекс indcp не зависит от выбора сферы Sn~l>
входящей в его определение; более того, сфера S71 — 1 может быть
заменена любым (п—1)-мерным истинным циклом zw — 1, относительно
которого точка р имеет порядок 1 (см. главу 16, арт. 5:1, 5:2);
это следует из того, что ind cp есть порядок Ъ(С0гп'~1, о), и из
элементарных свойств порядка.
Определение [2:12]. Если область Г содержит лишь конечное
число неподвижных точек отображения С, то сумма индексов этих
точек называется алгебраическим числом неподвижных
точек отображения С в области Г.
2:2. Некоторые свойства индекса.
[2:21]. Пусть С есть непрерывное отображение /z-мерного
замкнутого симплекса TnaRn в Rn. Пусть на Тп имеется лишь конечное
число неподвижных точек и все они лежат в Т*1. Ориентацию Тп9
одинаковую с выбранной ориентацией Rn, обозначим через t71. Тогда
характеристика поля сдвигов %$° на Мп равна алгебраическому числу
неподвижных точек внутри Тп.
В самом деле, пусть pv---iPs— все неподвижные точки
отображения С, лежащие в Тп. Заключим их в попарно непересекающиеся
симплексы Ti,..., Tf; их ориентации, одинаковые с выбранной
ориентацией #п обозначим через /?,...,£? и рассмотрим
полиэдральную область Г0= Tn\(f± U ... U Т?). В ней нет ни одной
*) То-есть просто некоторую раз навсегда выбранную сферу, в качестве
которой мы берём единичную сферу S^""1 с центром в начале координат
и радиусом 1.

§ 2] индекс неподвижной точки 607
неподвижной точки отображения С, т. е. ни одного нуля поля slic.
Значит, характеристика этого поля на границе области Г равна нулю
(теорема [5:12] главы 16), откуда следует, что характеристика поля
У$° на At71 равна сумме характеристик того же поля на Д*?, ...,А^,
т.е. сумме индексов неподвижных точек plt...p8.
[2 :22]. Пусть Си С- два непрерывных отображения
замкнутого симплекса TnciRn в пространство Rn, имеющие на Тп лишь
конечное число неподвижных точек, которые все лежат в Тп. Пусть
кроме того, для всех точек р£Тп\Т>1 выполняется неравенство
р(Ср, С'р) <р(С>, р).
Тогда отображения С и С имеют в Тп одно и то же
алгебраическое число неподвижных точек.
В самом деле, в условиях теоремы [2 :22] векторные поля 33е7 и
Ъ°' (рассматриваемые на Тп\Тп) могут быть непрерывно и без
обращения где бы то ни было на Тп\Тп в нуль переведены друг в друга.
Поэтому они имеют на границе симплекса Тп одну и ту же
характеристику, откуда, в силу [2:21], и следует теорема [2 :22] (см.
главу 16, теорема [5: 11]).
Замечание. Если отображение С арт. 2:1 задано системой функций
xi =Л(*1 хп)> *" = 1,... * л,
и эти функции непрерывно дифференцируемы по всем xj, то индекс
неподвижной точки о «вообще говоря» равен =tl, а именно, он может отличаться
от rtl только в тех точках, в которых якобиан
(2.23) det^-J —det(^ — 6, J, J ~ \ о, если izfzj,
равен нулю.
2:3. Нормальные неподвижные точки. Топологическая
инвариантность индекса неподвижной точки. Пусть обозначения Г и С
сохраняют своё значение, установленное в 2:1. Предположим, что
неподвижная точка о£Г отображения С обладает следующим
свойством:
Существует n-мерный элемент *) Еп=Еп U S*—* с: Г с границей
Sn~1y содержащий внутри себя точку о, не содержащий никакой
отличной от о неподвижной точки отображения С и не
пересекающийся с образом CfS71"1) своей границы.
В этом случае неподвижная точка о называется нормальной.
Дадим элементу Еп ориентацию, одинаковую с выбранной
ориентацией Г. Граница ориентированного таким образом элемента Еп
есть истинный (непрерывный) цикл z"-1. Докажем следующее
предложение:
*) /z-мерным элементом называется топологический образ я-мерного
замкнутого симплекса.

608 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [ГЛ. XVII
[2:31]. При только что установленных обозначениях индекс
нормальной неподвижной точки равен степени отображения С
в точке о элемента Еп, или, что то же самое, порядку точки о
относительно цикла Czn"1,
Доказательство. Рассмотрим какое-либо топологическое
отображение я-мерного замкнутого симплекса Тп на элемент Еп и
перенесём при помощи этого отображения аффинную геометрию
симплекса Тп на Еп. В смысле этой геометрии обозначим, при 0 <^ 6 ^ 1
и р £ Sn~x через р6 точку, делящую «отрезок» ро в отношении
Q :(1— 6). Вследствие нормальности неподвижной точки о точка /?9 при
6>0 не может содержаться в C(Sn~l), так что
РъфС(р).
Деформация
**(Р)=Р*С(Р)
непрерывно переводит поле ^8С=^80 в поле 331э состоящее из
векторов
*i О) = о С(р),
причём в процессе деформации векторы поля не обращаются в нуль.
Отсюда следует, что поля 330 и $В1 имеют на ztl~1 одну и ту же
характеристику. Но характеристика поля 332 на zn~{ есть порядок
точки о относительно C(zn"1)i что и требовалось доказать.
Важность понятия нормальной неподвижной точки в
значительной степени основывается на следующих предложениях, которые
вместе с только что доказанной теоремой [2:31] послужат нам к
доказательству инвариантности индекса неподвижной точки.
[2:32]. Изолированная неподвижная точка о£Г отображения С
области T^Rn в пространство Rn называется нормализуемой,
если существует элемент ЕпаТ> содержащий точку о внутри себя,
и деформация С9, 0^6^1, отображения С0 = С, рассматриваемого
лишь на Еп, удовлетворяющая следующим условиям:
1°) Ни одно из отображений Се, 0^6^1, не имеет неподвижных
точек на границе элемента Еп.
2°) Точка о есть нормальная неподвижная точка отображения Cv
[2:33]. Всякая изолированная неподвижная точка о£Г
непрерывного отображения С области Г нормализуема.
Доказательство. Возьмём какой-нибудь л-мерный симплекс
Т*,о£Тп, ТпаГ9 такой, что Тп не содержит отличных от о
неподвижных точек отображения С. Обозначим через о произвольную
неотрицательную непрерывную функцию, определённую на всём
замкнутом симплексе Тп и принимающую в точке о значение 0, а
во всех точках границы симплекса Тп значение 1. Через ^обозначим
диаметр симплекса Тп. После этого определим деформацию Q
отображения С=С0 симплекса Тп следующим образом:

§ 2]
ИНДЕКС НЕПОДВИЖНОЙ ТОЧКИ
609
Для всякой точки х£Тп обозначим через Сьх точку луча
' —>■
хС(х), отстоящую от точки х на расстояние р [С(х),х] -f-в d<o(x).
Ни одно из отображений С6 не имеет на границе симплекса Тп
неподвижных точек; точка о£Тп является единственной в Тп
неподвижной точкой отображения Cv притом нормальной, так как для
*€ fn\Tn
имеем
р [С;(*),х] = р [C(x)tx]+d>d,
так что С (х) (£ 74
Применим только что установленный факт к доказательству
следующей теоремы:
[2:34]. Теорема о топологической инвариантности
индекса изолированной точки непрерывного
отображения. Пусть о есть изолированная неподвижная точка при
отображении С области YaRn в пространство Rn. Пусть F есть
топологическое отображение R4 на себя (или на другое
пространство /?*). Тогда индекс неподвижной точки о' = F(p) при
отображении FCF~l равен индексу неподвижной точки о при
отображении С.
Ту же теорему можно, очевидно, сформулировать и так:
[2:340]. Пусть R — топологическое пространство, гомеоморфное
пространству Rn. Пусть Г — область пространства R и
С—непрерывное отображение Г в R, имеющее изолированную неподвижную
точку о. Возьмём какое-нибудь топологическое отображение F
пространства Rn на R и перенесём при помощи этого отображения эвкли-
дову геометрию пространства /?^в пространство R. Тогда индекс
неподвижной точки о отображения С, определённый, как и выше,
при помощ i перенесённой в R эвклидовой геометрии, не зависит от
этой геометрии (т. е. будет один и тот же для всех топологических
отображений F пространства Rn на R).
Для случая, когда о есть нормальная неподвижная точка, теорема
[2:34] следует из [2:31] и теоремы о топологической
инвариантности локальной степени непрерывного отображения (теорема [4:22]
главы 16).
В общем случае теорема [2:34] следует из [2:33]. Нам при этом
удобнее пользоваться формулировкой [2:340].
Заметим прежде всего, что понятие нормальности неподвижной
точки не зависит от той или иной геометрии, внесённой в R, и что по
доказанному всякая нормальная неподвижная точка данного
непрерывного отображения С имеет во всех геометриях один и тот же
индекс.
Пусть теперь С—какое-нибудь непрерывное отображение области
Г в пространство R> имеющее данную точку о £ Г изолированной
неподвижной точкой. Рассмотрим элемент Еп а Г, содержащий о внутри
39 Александров II. С.

f)30 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [гЛ. XVtt
себя, и непрерывную деформацию Сь отображения С0 = С в
отображение Си имеющее точку о нормальною неподвижною точкой.
Предполагаем, что деформация Q> удовлетворяет условиям 1°) и 2°)
определения [2:32]. Из этих условий следует, что во всякой
геометрии, которую мы можем ввести в пространство R, характеристик
векторных полей 93с° и Жс* на границе элемента Еп — одна и та же,
откуда следует, что во всякой геометрии индексы indco0 и indClo
равны между собой. Но индекс indClo во всех геометриях — один
и тот же, следовательно, индекс indc0o также во всех геометриях
один и тот же, что и требовалось доказать.
2 : 4. Неподвижные точки аффинных отображений. Дадим ещё
одно приложение понятия нормальной неподвижной точки:
определим при помощи этого понятия индекс неподвижной точки
аффинного отображения. _
' Теорема [2:4]. Пусть Ttl есть п-мерный замкнутый
симплекс пространства Rn и S — такое его аффинное отображение в Rn,
что Tn<£ST" и на Т11\Тп нет неподвижных точек
отображения S. Тогда внутри Т'г имеется ровно одна неподвижная точка
с индексом -\-\ или —1, смотря по тому, будет ли аффинное
отображение положительным или отрицательным.
Доказательство. Так как Тп с: 6" V1 = Т[\ то размерность
симплекса Тх равна п и, следовательно, отображение 5 не
вырождается, т. е. существует обратное отображение S-1. Так как Т<= Tj,
то отображение S~l симплекса 1\ в себя имеет, по крайней мере,
одну неподвижную точку. То же утверждение верно и для
отображения 5\
Если бы отображение S имело две неподвижные точки ох и о2
в Гл, то вследствие его аффинности все лежащие в Vх точки прямой
охо2 были бы неподвижными; в частности, вопреки предположениям,
были бы неподвижными точки пересечения этой прямой с границей
симплекса Vх. Таким образом, в Т>1 существует только одна
неподвижная точка; она нормальна, следовательно, на основании арт. 2:3
её индекс равен степени отображения 6" в точке о, т. е. -{- 1 или
— 1 в зависимости от знака 6\ Эта теорема будет применяться в
арт. 3:4.
§ 3. Алгебраическое число неподвижных точек непрерывного
отображения полиэдра в себя.
3:1. Определение регулярных неподвижных точек.
Формулировка основной теоремы. Пусть Р есть размерно однородный
л-мерный полиэдр, С —непрерывное отображение его в себя и о —

§ 3] АЛГЕБРАИЧЕСКОЕ ЧИСЛО НЕПОДВИЖНЫХ ТОЧЕК 611
неподвижна» точка этого отображения. Неподвижная точка о
называется «регулярной» (относительно триангуляции К этого
полиэдра), если она является изолированной неподвижной точкой (т. е.
имеет окрестность, не содержащую других неподвижных точек) и
лежит в некотором л-мерном симплексе Гтриангуляции К.
Вследствие непрерывности отображения С точка о имеет окрестность £/,
образ которой CU тоже лежит внутри 7. Следовательно,
рассматривая Т как часть несущего этот симплекс эвклидова пространства R",
мы можем говорить об индексе неподвижной точки о.
Если отображение С имеет только регулярные (относительно К)
неподвижные точки, то сумма их индексов называется
«алгебраическим числом» неподвижных точек отображения С.
Следующая теорема утверждает, что это число вполне определяется
гомологическим типом отображения С:
Теорема [3:1]. Если непрерывное отображение С тела Р = К
размерно однородного n-мерного комплекса К на себя имеет
только регулярные {относительно К) неподвижные точки, то их
алгебраическое число равно (—1)п Ас.
Эта теорема будет доказана в арт. 3:3,3:4, 3:5. Она
является усилением теоремы [1:3] о существовании неподвижных точек.
Теоремы арт. 1:4 тоже могут быть теперь усилены. Если Р связно
и tJ(P) = 0 при г > 0, то алгебраическое число неподвижных точек
любого отображения (все неподвижные точки которого регулярны)
равно (—\)п\ если С гомотопно нулю, то (при любом Р = К) это число
равно эйлеровой характеристике комплекса К, умноженной на (—)1";
если С есть отображение сферы Sn в себя, имеющее степень d, то
алгебраическое число неподвижных точек равно (— \),l-\-d и т. д.
3:2. Обобщение. Теорема [3:1] может быть распространена и на
любые непрерывные отображения (без ограничительного требования
регулярности неподвижных точек), т. е. и на такие отображения, лля
которых алгебраическое число неподвижных точек покамест ещё не
определено. Это можно сделать на основании следующей теоремы:
Теорема [3:2]. Пусть С—произвольное непрерывное
отображение размерно однородного n-мерного полиэдра Р в себя и
г-—произвольно малое положительное число. Существует непрерывное ото-
бражение Сг полиэдра Р в себя и триангуляция К этого полиэдра,
обладающие следующими свойствами:
1°) Отображения С и Сг отличаются друг от друга меньше,
чем на г,
р [С(х), Сг(х)] < г для всех х £ Р.
2°) Все неподвижные точки отображения Сг регулярны
относительно триангуляции К.
При этом, если г достаточно мало, то все отображения Се,
удовлетворяющие условиям 1°) и 2°), гомотопны отображению С и
имеют одно и то же алгебраическое число неподвижных точек,
равное (-— 1)пАс.
39*

612 неподвижный точки отображений Полиэдров [гл. xvtt ;
Вторая часть теоремы [3 :2] непосредственно следует из тео-1
ремы [3:1]: если е выбрано настолько малым, что аппроксимирую*!
щие отображения все принадлежат одному и тому же гомологиче-1
скому типу, то число Лефшеца каждого из этих отображений равно!
Ас и, следовательно, на основании [3:1] алгебраическое число его!
неподвижных точек равно (—l^A^. 1
3 :3.1 Регулярные неподвижные точки симплициальных отобра-1
жений. Таким образом, мы должны доказать только теорему [3 : 1|1
и первую часть теоремы [3 :2] (существование отображений Се). 1
Мы ещё усилим утверждение теоремы [3 :2], потребовав, чтобы!
аппроксимирующие отображения были симплициальными. Однако, i
перед тем как будет сформулировано это усиление, мы хотим чисто 1
комбинаторно охарактеризовать свойство симплициального отображе-1
ния иметь только регулярные неподвижные точки: |
[3:30]. Пусть К2 есть подразделение размерно однородной!
я-мерной триангуляции Кх. Пусть S есть симплициальное отображе- \
ние комплекса К2 в /Cj. Если существует r-мерный неподвижный
симплекс при г < п, то S имеет, по крайней мере, одну
нерегулярную (относительно /Сх) неподвижную точку. Обратно: если 5 имеет
только я-мерные неподвижные симплексы, то S имеет только
регулярные (относительно /Q неподвижные точки и именно ровно одну
в каждом я-мерном неподвижном симплексе триангуляции /С2.
В самом деле, если Т^К2 есть r-мерный неподвижный симплекс
отображения 5, то существует, по крайней мере одна неподвижная
точка р £ Г£ отображения S. Так как она лежит на симплексе
7^* = 6Т£, то она нерегулярна, если г < п. Обратно, пусть 5 не имеет ;
неподвижных симплексов размерности, меньшей, чем п; пусть
р есть неподвижная точка отображения S и Т2—её носитель;
в триангуляции К2 (т. е. симплекс триангуляции К2, в котором,
лежит точка р). В таком случае Т2 является неподвижным симплексом j
отображения S и, следовательно, имеет размерность п. На его
границе не может быть неподвижных точек, так как она состоит
из симплексов размерностей, меньших чем я. Поэтому на
основании [2:4] р является единственной неподвижной точкой в Г2 и,
значит, регулярной неподвижной точкой.
Обещанное выше усиление первой части теоремы [3:2] может
быть сформулировано следующим образом:
Аппроксимационная теорема [3:3]. Пусть даны г>0
и непрерывное отображение С размерно однородного п-мерного
полиэдра Р в себя. Существуют триангуляции Кг и К2 полиэдра Р,
из которых К2 есть подразделение Кх и симплициальное
отображение S триангуляции К2 в Kv удовлетворяющие следующим условиям:
1°) Для всех точек х£Р выполнено неравенство
9[C(x)fS(x)]<e.

§ 3] АЛГЕБРАИЧЕСКОЕ ЧИСЛО НЕПОДВИЖНЫХ ТОЧЕК 613
2°) Все неподвижные симплексы Т2 £ К2 отображения S имеют
размерность п.
3:4. Сведение теоремы [3:1] к аппроксимационной теореме.
Кроме теоремы [3 :3] мы должны ещё доказать теорему [3 :1]. Мы,
однако, сведём её к теореме [3 :3], которую в этом артикуле
предположим доказанной.
Пусть отображение С удовлетворяет условиям теоремы [3:1] и
пусть oh /==1,..., s, суть его неподвижные точки (их—конечное
число). Пусть, далее, 7J, / = 1,.. ./Js, есть носитель точки oi в К и
Tf. —я-мерный симплекс, лежащий в Т*9 содержащий точку oi и
настолько малый, что CTf.cz TJ. Функция /(лг) = р (аг, Сх) при-
S
нимает на множестве Я\ U Тпи наименьшее значение bi > 0. Далее,
г = 1
согласно теореме [2:22] для каждого / существует такое число
&i > 0 fa именно, минимум функции f(x)] на Т"., что каждое
отображение Cv для которого р (С, Сг) < ai имеет в T*t такое же
алгебраическое число неподвижных точек, что и С.
Примем за е положительное число, меньшее, чем каждое из
чисел bi и аг-(/=1,..., s); пусть S есть отображение, упомянутое
в формулировке теоремы [3 :3].
Так как s < Ьь то отображение *S не имеет неподвижных точек
вне симплексов Т£.; так как s < a^ то в каждом из симплексов
Tf. отображения С и S имеют одинаковое алгебраическое число
неподвижных точек. Из обоих этих фактов следует, что
алгебраические числа Jc и J~ неподвижных точек соответственно отображе-
ний С и S равны между собой:
(3:41) Jc^Jfr
Мы можем далее предположить, что е настолько мало, что ото-
бражения С и S гомотопны, а следовательно, и гомологичны между
собой, так что, в частности,
(3:42) А0 = Аз'.
Формулы (3:41) и (3:42) сводят доказательство утверждения
теоремы [3 :1] к доказательству аналогичного утверждения
/S~ = (-1)»A~
для симплициального отображения 5, обладающего только д-мерными
неподвижными симплексами. Но для, такогр отображения мы имееэд

614 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [ГЛ. XVII
(в обозначениях § 1) SpLr = 0 при г < п, и формула (1 :25)
принимает вид
ИЛИ
Как выяснено в конце арт. 1:1, число SpLn равно
алгебраическому числу я-мерных неподвижных симплексов, т. е. разности
между числом положительных и отрицательных я-мерных
неподвижных симплексов, и, следовательно, на основании теоремы [2:4]
сумме индексов неподвижных точек в я-мерных симплексах; а так
как других неподвижных точек нет, то
ys, = (_1)„A~,
что и требовалось доказать.
Остаётся доказать только аппроксимационную теорему [3 :3].
3:5. Доказательство аппроксимационной теоремы. Во всём
этом артикуле Кх обозначает барицентрическое подразделение
триангуляции /С, а «подразделение триангуляции» означает всегда
(многократное) барицентрическое подразделение.
Так как каждое непрерывное отображение может быть с любой
точностью аппроксимировано симплициальным, то можно с самого
начала предположить, что С=50, где S0 есть симплициальное
отображение некоторого подразделения К0 триангуляции К1 в
триангуляцию К,
Пусть, далее, диаметры симплексов триангуляции К меньше, чем
~ , где s — некоторое заданное положительное число. Мы построим
последовательность симплициальных отображений
полиэдра Р в себя, такую, что
а) отображение Sr (г = 0, ... , п) есть симплициальное
отображение некоторого подразделения /С(г) триангуляции К1 в К, все
неподвижные симплексы которых имеют размерность не ниже г;
б) pOr>Sr+I)<-^.
Если такая последовательность будет построена, то Sn = 6'
удовлетворяет всем условиям теоремы [3 :3]: все неподвижные симплексы
отображения Sn имеют размерность не ниже я, и для всякой точки
х£Р выполнено неравенство
p(Snx,Cx)<in • -^- = 3.
Отображение S0 и подразделение К0 нам даны. Предположим
нтр построены отображения $г и подразделение /((г), и построим

§ 3] АЛГЕБРАИЧЕСКОЕ ЧИСЛО НЕПОДВИЖНЫХ ТОЧЕК 615
6V+1 и К^г^^' Самому индуктивному построению предпошлём
несколько предварительных замечаний. Назовём симплекс Т некоторого
подразделения К' триангуляции К главным (относительно /С),
если размерность его носителя в К не выше (а следовательно,
равна) размерности самого симплекса Т. Если К" есть
подразделение триангуляции К*', то каждый симплекс Т£ К'\ главный
относительно К, будет, очевидно, главным и относительно К\ а его
носитель в К' будет главным относительно К. Наконец, заметим,
что каждый неподвижный симплекс отображения К' в К будет,
конечно, главным относительно К.
Лемма [3:51]. Если К^г) есть одно- или многократное
барицентрическое подразделение триангуляции К, то звёзды Ок(г)Т*
иОк^Т* двух любых главных отно-сителъно К симплексов T8t и
Т| одинаковой размерности s не пересекаются.
Д оказате л ь ст во. Лемма [3:51] может быть
сформулирована так:
[3:510]. Два симплекса комплекса К^ одной и той же
размерности s, главные относительно К, не могут быть гранями одного
и того же симплекса комплекса К^.
Если К^г) есть подразделение К'\ а К' — подразделение JK, то
каждый симплекс подразделения К^г\ главный относительно К,
является и подавно главным относительно К'\ поэтому предложение
[3 :510] достаточно доказать в предположении, что К^г) есть
однократное барицентрическое подразделение комплекса /С.
Но в этом случае предложение [3:510] следует из того, что
срети р-мерных граней симплекса \Tf> . . . > Ту > .. . >7,g° |
барицентрического подразделения комплекса К только симплекс
Т^> ... > Т$°\ может быть главным.
Переходим к индуктивному построению, составляющему
содержание основной части доказательства теоремы [3 :3].
Итак, отображение^ и подразделение /С(г) даны. Требуется
построить отображение 5г+1 и подразделение /С(г+1). Пусть Тг
(/==1,... ?&) суть все r-мерные неподвижные симплексы
отображения Sr. Мы строим подразделение /С(г+1) триангуляции К^г\
подразделяя специальным образом все звёзды Ок{г)Тг{ ; отображение Sr+1
получим, изменяя отображение Sr только на этих (попарно
непересекающихся!) звёздах. Подразделение триангуляции К^г)
производится следующим образом:
Строим прежде всего центральное подразделение каждого
неподвижного симплекса TV относительно его границы (неподразделённой)
(см. главу 4, арт. 4:3); затем строим центральное подразделение
(г-\- 1)-мерного симплекса Tr+1 £Ок(г) Т* относительно его границы
(причём один симплекс этой границы, а именно, ТГ, уже подразде-

616 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [гл. XVII
лён). Далее процесс продолжается точно так же: после того как
подразделены (г-\- &)-мерные симплексы, мы строим центральное
подразделение каждого (г~f-ft + 1)-мерного симплекса звезды Ок^Т'
относительно уже построенного подразделения его границы.
Построение заканчивается подразделением всех /z-мерных симплексов звезды
OkWTJ и делается для всех / = 1,..., &.
Определим теперь си'мплициальное отображение Sr+1 комплекса
/С(г+1) в комплекс К.
1°. Если вершина £(r+1) £ /fCr+i) есть в то же время вершина
комплекса /£(г\ то полагаем
2°. Пусть вершина e(rfl) £ /£(r+i) не есть вершина комплекса К^'
Тогда е есть центр одного из симплексов какой-либо звезды OgWTV
и мы снова разбираем два случая:
2°г Вершина g^+i) есть центр тяжести симплекса Г£ Ок(г)ТТ
отличного от симплекса 7Т . Тогда выбираем произвольную вершину е
симплекса SrT* £ К и полагаем Sr+1£(r+1) = е.
2°2. Вершина g^+i) есть центр симплекса 7Т. Тогда объявляем
вершиной Sr+1e£K произвольно выбранную вершину какого-либо
симплекса звезды 0KSrTr., не являющуюся вершиной симплекса SrTr.
(такую вершину всегда можно выбрать, так как г<я и К есть
размерно однородный комплекс).
Покажем, что при построенном нами отображении SrJrl
множества всех вершин комплекса К^г+1^ во множество всех вершин К
остов всякого симплекса Т£ /С(г+1> переходит в остов некоторого
симплекса триангуляции К. Достаточно, очевидно, показать это для
симплексов Т, входящих в подразделение звёзд Ок(г)Тг.. Рассмотрим
отдельно два случая:
1) Среди вершин симплекса Т подразделения звезды 0^г)Т{
имеется центр симплекса Тг.\ в этом случае остальными
вершинами симплекса Т могут быть только вершины симплекса
Т\ и центры других симплексов звезды Ок(г)ТТ; все эти вершины
отображаются по определению Sr+1 в вершины симплекса 5r7T, a
центр симплекса Тг — в некоторую вершину е£ [OjcS^.T^], таким
образом, все вершины симплекса Т отображаются в
вершины симплекса | eSrTr. | £ 0KSr Tr. £ К.
2) Среди вершин симплекса Т подразделения звезды Ок(г)Т4г
нет центра симплекса 7/; в этом случае вершинами
симплекса Т могут быть центры других симплексов
звезды Ок(г) Т/ и вершины некоторого симплекса Тг края этой звезды;
все эти вершины, посредством Sr{.v отображаются в, некоторые вер-

§ 3] АЛГЕБРАИЧЕСКОЕ ЧИСЛО НЕПОДВИЖНЫХ ТОЧЕК 617
шины симплекса SrTrt и симплекса S^ £ [Ол:5гГГ]; таким образом,
все вершины симплекса Т отображаются в вершины симплекса
\SrT*T'\€lOKSrTl\czK.
Замечание. Из только что проделанных рассуждений следует:
[3:511]. Обозначим через 0{ тело звезды Ozi^Tf, через
Г\: — тело звезды OgSyTf. Если симплекс Т£К(г+1) лежит в О*,
то 5гМ7'сГ<.
Докажем теперь, что симплициальное
отображение Sr+1 обладает свойствами а) и б), упомянутыми выше.
а) Отображение Sr+1 не имеет неподвижных симплексов
размерности ниже г-f-l. В самом деле, пусть Тг есть симплекс
триангуляции /f (г+1> размерности, меньшей или равной г. Если
Т'£К(г^\\}Ок(г)Т{гу
то Т', очевидно, не является неподвижным симплексом
отображения 5г+1, так как на ]F((r+1)\U OrfriTf отображение Sr+1
совпадает с Sry а последнее имеет неподвижные симплексы только
размерности, большей или равной г, причём неподвижные симплексы
размерности г суть Т{£Ов\г)Т{- Пусть Т* ^OtfDTf. Если
V есть неподвижный симплекс отображения Sr+V то он должен быть
главным относительно /С, а следовательно, и относительно К^К
Так как все отличные от Т/ симплексы ззезды OrfrtTf имеют
размерность >г, то носителем симплекса Т' в АГ(г) должен быть
симплекс 77*, а размерность симплекса Т' должна быть г, при этом
одной из вершин симплекса Г' является центр
симплекса 7у.
Так как Г/ — неподвижный симплекс отображения 5Г, то
TfaSJf^K, значит,
(3:52) T'<zT*<zSrT*£K,
т. е. носителем симплекса V в К является симплекс
SrTf; поэтому если бы Т был неподвижным симплексом
отображения Sr\v то было бы
Sr+17v =5rT/,
что невозможно, так как по определению отображения 5rfJ одна
из вершин симплекса Т', а именно, центр симплекса Тгр
отображается в вершину комплекса /С, не являющуюся вершиной
симплекса $ГТ'.
б) Для любой точки р £ К имеем
p(V-W)<j'

618 НЕПОДВИЖНЫЕ ТОЧКИ ОТОБРАЖЕНИЙ ПОЛИЭДРОВ [ГЛ. XVII
В самом делз, Srhl отличается от Sr только на множествах 0{\ но
для любой точки р^Ог имеем по определению множеств 01 и Vi
(см. [3:511])
Srp€Vt
и в сияу предложения [3:511],
Симплексы триангуляции К имеют диаметр <^— поэтому
НГ«)<^ и p(SrP, SrnP)<~,
чем всё доказано.
3:6. Некоторые замечания об алгебраическом числе
неподвижных точек. Алгебраическое число неподвижных точек
отображения С, конечно, нельзя смешивать с числом неподвижных точек
данного отображения в непосредственном смысле этого слова:
обозначая это последнее через ас, имеем равенство ас = |АС| в том и только
в том случае, когда все неподвижные точки имеют индекс -j- 1 или
когда они все имеют индекс —1. Если же все неподвижные точки
суть так называемые простые неподвижные точки, т. е. если индекс
каждой из них равен _+. 1, тогда можно лишь утверждать
неравенство ао>[Ас], так как, обозначая число неподвижных точек индекса
-f-1, соответственно индекса—1, через тг, соответственно через v,
имеем Лс=тс — v, ac = n-{-v. Этот случай в известном смысле слова
может считаться «общим», а случай, когда неподвижная точка имеет
индекс ф±1, «исключительным»: некоторые основания к такому
взгляду на вещи можно почерпнуть, например, в замечании в конце
арт. 2:2. Поэтому с некоторым правом можно утверждать: число
неподвижных точек непрерывного отображения, «вообще говоря»,
не меньше, чем абсолютная величина их алгебраического числа.
Следует, однако, заметить, что число неподвижных точек данного
индивидуального непрерывного отображения выражает
обстоятельство довольно случайного характера: ведь в топологической
теории непрерывных отображений нас в основном интересуют i e те
или иные свойства каждого отдельного отображения, а свойства,
принадлежащие целому классу гомотопных (или
даже всему классу гомологичных) между собой
отображений. Степень отображения, а также алгебраическое число
его неподвижных точек могут служить примерами таких свойств.
Естественно поэтому спросить себя о минимальном числе
неподвижных точек, осуществляющемся в пределах
данного гомотопического (соответственно
гомологического) класса отображений. Это число обозначаем через
\q (соответственно через \^)у где С — какое-нибудь отображение
данного класса. Очевидно, ас^>^с^>К Для люЗого отображения С\

§ 3] АЛГЕБРАИЧЕСКОЕ ЧИСЛО НЕПОДВИЖНЫХ ТОЧЕК 619
К сожалению, о числах Хс и к^ кроме их конечности для
каждого класса, следующей из теоремы [3:3], нам мало что известно.
Правда, из Лсф О во всяком случае следует Хс^Х^>0. С другой
стороны, в арт. 1 :5 мы видели, что возможно неравенство Х^>ЛС==
= 0. При отображении окружности в себя, имеющем степень с,
осуществляются точные "соотношения Лс=1—с, Хс = [1—с\; при
отображении замкнутого симплекса в себя имеем к0 — Аа=1.
Пополнив плоскость бесконечно удалённой точкой, так, чтобы
получилась сфера S2, рассмотрим какое-нибудь параллельное
перенесение этой плоскости (бесконечно удалённая точка при этом
остаётся неподвижной); получим отображение, для которого лс=1,
Лс=2 и, следовательно, Хс< Л с. Задача исследования числа Хс
интересна и трудна; ей посвящены многочисленные работы Нильсена;
при этом употребляются методы, существенно отличные от тех,
которые излагались в этой книге. Но как бы там ни было,
алгебраическое число неподвижных точек даёт первую и до настоящего времени
самую важную оценку во всех вопросах теории неподвижных точек
непрерывных отображений.

ПРИБАВЛЕНИЕ I.
АБЕЛЕВЫ ГРУППЫ.
Предполагается, что читатель знаком лишь с самыми элементарными
понятиями теории групп [см., например, П. С. Александров «Введение
в теорию групп», вторую главу «Современной алгебры» Ван-дер-Вардена
или первую главу книги Л. С. Понтрягина «Непрерывные группы»
(последнее изложение особенно рекомендуется читателю, но содержит больше
материала, чем мы будем предполагать известным)]. Таким образом, следующие
понятия предполагаются известными: понятие группы, подгруппы,
гомоморфного и изоморфного отображения, понятие фактор-группы (или
дополнительной группы) и простейшие предложения об этих* понятиях. Понятие
циклической группы также предполагается известным.
Во всём последующем изложении под группой
понимается всегда коммутативная (а белев а) группа, в
соответствии с чем групповая операция будет называться
сложением.
Изоморфизм двух групп Л и В обозначается так: Ля^В.
§ 1. Общие сведения.
1:1. Гомоморфизм. Ядром гомоморфного отображения С группы Л в
группу В называется подгруппа группы Л, состоящая из всех элементов,
отображающихся при посредстве С в нулевой элемент группы В.
Напомним прежде всего:
Для того чтобы гомоморфное отображение С группы А на группу В
было изоморфным, необходимо и достаточно, чтобы ядро гомоморфизма С
было нуль-группой, т. е. состояло из одного нулевого элемента.
Пусть С — гомоморфное отображение группы А в группу Д аЛоиД>—
соответственно подгруппы групп А и В. Если при гомоморфизме С группа
Ло отображается в Во, то элементы группы А принадлежащие одному и
тому же классу смежности относительно подгруппы Л0, переходят, в силу С,
в элементы, принадлежащие к одному и тому же классу смежности группы
В относительно подгруппы Д> Другими словами, каждый класс смежности
группы Л относительно Ло отображается, в силу С, в некоторый класс
смежности группы В относительно Дэ-
Ставя в соответствие каждому классу смежности а £ Л/Ло тот класс
смежности ft £ £/Д, который содержит образ а при отображении С,
получим гомоморфное отображение (£ фактор-группы Л/Ло в фактор-группу В/Во,
которое называется гомоморфным отображением группы Л/Ло
в группу В/В0, порождённым данным гомоморфизмом С
группы Л в группу В.
Общая теорема о гомоморфизмах [1:1]. Пусть С—
гомоморфное отображение группы А на группу В; пусть при этом отображении
подгруппа Ло группы А является прообразом подгруппы Во группы В.
Тогда порождённое гомоморфизмом С гомоморфное отображение (£
фактор-группы Л/Ло в фактор-группу B/Bq есть изоморфное отображение
Л/Ао на В/Во*

111
ОБЩИЕ СВЕДЕНИЯ
621
Замечание. В частном случае,. когда В0 есть нуль-группа, эта
теорема превращается в:
[1:10]. Если Ао есть ядро гомоморфного отображения С группы А
на группу В, то С порождает изоморфное отображение группы A/Aq на В.
Доказательство теоремы [1:1]. Так как С— отображение на В
то (S есть отображение на В/Во. Если класс смежности а £Л/Ло является
элементом ядра гомоморфизма (5, то, в силу С, все элементы класса а
отображаются на элементы Во, откуда следует, что а = Л<> Итак, ядро
гомоморфизма (£ состоит из одного нулевого элемента а = Ло группы Л/Ло, чем
теорема [1:1] доказана.
Определение [1:11]. Гомоморфное отображение группы в себя
самоё называется эндоморфизмом этой группы.
1:2. Некоторые замечательные подгруппы данной группы Л. Сама
группа А и нуль-группа (состоящая из одного нулевого элемента группы Л)
называются несобственными подгруппами группы Л, все остальные
подгруппы называются собственными.
Если а £ Л, то циклическая подгруппа группы Л, состоящая из всех
элементов вида та, где т — целое число, называется подгруппой группы Л,
порождённой элементом а. При этом по определению
та = а -\- ... + а,
т раз
если т положительно, та = 0 £ Л, если т = 0, и
та = (-а) + ... + (—д),
| w | раз
если т отрицательно.
Если циклическая подгруппа, порождённая элементом а, бесконечна, то
а называется элементом бесконечного пор'ядка группы Л. В
противном случае а называется элементом конечного порядка, причём
порядок элемента а равен по определению порядку (т. е. числу элементов)
циклической группы, порождённой элементом а.
Пусть т — данное целое число. Множество всех элементов та, где
а пробегает всю группу Л, есть подгруппа группы Л, обозначаемая через тА.
Определение [1:21]. Пусть Л0 — подгруппа группы Л. Обозначим
через Л0 множество всех тех элементов а€А, для каждого из которых
имеется хотя бы одно такое натуральное число т, что тя€Л0.
Множество Л0 есть подгруппа группы А, называемая дивизионным
замыканием подгруппы Л0 в группе Л.
Подгруппа Л0 по определению д ив и з и он н о замкнута в Л, если
она совпадает сэ своим дивизионным замыканием в Л.
Множество всех элементов конечного порядка данной группы Л есть,
как легко видеть, дивизионно замкнутая подгруппа группы Л.
Теорема [1:22]. Подгруппа Ао группы А тогда и только тогда
дивизионно замкнута в Л, когда фактор-группа А/А0 не содержит
отличных от нуля элементов конечного порядка.
Доказательство предоставляется читателю.
1:3. Разложение группы Л в прямую сумму её подгрупп.
[1 :3]. Группа Л называется суммой своих подгрупп Л1? ...,Л„,
если каждый элемент а группы Л, по крайней мере, одним
способом может быть представлен в виде
а = аг -(-... + ап% где я$£Л$, i = 1,..., п.
Если такое представление каждого элемента а£А единственно, то
сумма называется прямой.
Подгруппы Аь ..., Ап при этом называются прямыми слагаемым
данной прямой суммы.

622
АБЕЛЕВЫ ГРУППЫ
[1:31]. Пусть А есть сумма своих подгрупп Ах и А2. Эта сумма
тогда и только тогда прямая, когда пересечение Ах и А2 состоит из
одного лишь нулевого элемента.
Доказательство.
1. Пусть ^/€Л1П^2» аф®\ тогда возможны два представления вида
а = а1-\-а2, ах£Аи a2€A2t
именно:
ах = а, а2 = 0 и а1 = 0, а2 = а.
2. Пусть Ах П Л2 есть нуль-группа и
а = аг + а2 = а[ + a'v
причём a^Ait a^Ai, / = 1,2. Тогда элемент ^ — а1 = а.Л — а2 содержится
как в Ait так и в Л2, и, следовательно, равен нулю, откуда получаем ах = ai9
а2 = я2, что и доказывает теорему.
1:4. Прямая сумма данных групп. Пусть даны какие-нибудь группы
Ai, ...,An (в конечном числе). Рассматриваем всевозможные конечные
комбинации вида (alf...,an), где яг- пробегает всю группу Aj (/ = 1 п).
Во множестве всех этих комбинаций определяем сложение
(alf..., ап) + (^ ап) = (а1 + а[ ап + а'п).
Это определение превращает множество А в группу, называемую прямой
суммой заданных групп АЬт..,Ап.
Это определение хотя и отличается от определения разложения
данной группы в прямую сумму её подгрупп (арт. 1:3), но очень тесно
связано с этим последним. В самом деле, обозначим через А° подгруппу
только что построенной группы /4, состоящую из всех комбинаций вида
(О, ...taif .. .,0), где а^А^
Легко видеть, что группа А разлагается в прямую сумму своих подгрупп А°и
Во многих случаях можно отождествлять каждую из групп А^ с
соответствующей ей группой А°р считая элементы яг- и (0, .. .,а^ ..., 0) обеих этих
групп тождественными между собой. Это позволяет отождествить между
собой и оба понятия прямой суммы. Если группа А есть прямая сумма
(подгрупп Аи . ..,ЛП), то пишем
А=Аг+ • . . +А?Р
1:5. Прямые суммы и фактор-группы.
[1 :51]. Если А = А1 + АЪ то фактор-группа А/Аг изоморфна А2.
Доказательство. Пусть а €А/А± и я = ях + я26 а, ах£Аь а2€.А>\
тогда а2 = а—а^ а. Так как разность двух элементов Л2 принадлежит к Л2
и, следовательно, может принадлежать Аь только будучи нулём, то а% есть
единственный, содержащийся в классе смежности а элемент группы Л2.
Поэтому, полагая С(а) = а2, получим взаимно однозначное отображение
группы A\Ai на подгруппу А2. Так как это взаимно однозначное
отображение, кроме того, гомоморфно, то оно представляет собой изоморфизм, чем
теорема и доказана.
[1 :52]. Пусть
А = А±+ ...+Ап)
пусть А\ — подгруппа группы Лг- (/= 1 п)\ элементы вида
а' = а'х + ... + ап(а^А^ образуют подгруппу А' группы А (являющуюся

§ 2]
Свободные абелёвы группы
623
прямой суммой групп Л{). В этих условиях фактор-групп а А/А'
изоморфна прямой сумме фактор-групп Ai\A!i (/ = 1, ..., //):
A/A'^AJA[+... +Ап/А'п,
где прямая сумма взята в смысле определения арт. 1 :4.
Доказательство. Элементы группы 23 = А11Л[ -+-... -\- Ап\Хп имеют
вид b = (ctlf .. .,ап), где а г-пробегает все элементы группы А^А^. Каждому
элементу
а = а1-\- ... -\- ап€А,
гд? й^6Лг-, мы ставим в соответствие элемент
b = C(fl) = (alf ...,an) e SB.
где элементы а^ определены условием д$6аг-. Полученное отображение С
группы А на 23 есть гомоморфизм. Для доказательства того, что
гомоморфизм С порождает изоморфное отображение (£ группы А/А' на 33,
достаточно показать *), что ядром гомоморфизма С является группа А'.
Последнее утверждение доказывается так: нулевыми элементами гр^пп
At/Aj являются Ait поэтому элементу
a = aL-\- ... +ап€А
только тогда ставится в соответствие нулевой элемент группы $3, когда
(liZAj для всех /, т. е. когда а £ Л'.
§ 2. Свободные абелевы группы.
2:1. Определение. Группа X называется свободной (абелевой)
группой «ранга» л, если в ней можно найти также элементы хь..., xiV
что всякий элемент х£Х единственным образом может быть представлен
в виде
(2:1) * = <?!*!+ ... + спхп,
где c,j — целые числа. Всякое множество элементов х^...,хп группы Х>
удовлетворяющей только что высказанному условию, называется базой
свободной группы X. Свободная группа X с базой, состоящей из элементов
хь...,хп, обозначается через X = [xv ..., хп] или просто через Хп; она,
очевидно, является прямой суммой бесконечных циклических групп Х^ по
рождённых соответственно элементами х\.
Свободная группа «ранга» п изоморфна группе всех линейных форм
с\х\ + • • • + сп*п с целочисленными коэффициентами от п «перемен-
Н Ы X» Х\, . . м Хп.
[2:1]. Ни один отличный от нуля элемент свободной группы
X = [хъ ..., хп] не имеет конечного порядка.
В самом деле, если элемент х==а1х1-{- ... +апхп группы X имеет
конечный порядок с, то имели бы са±х± -\- ... + сапхп = 0, значит, сах =
=0, .... сап = 0, т. е. ях = ... = ап = 0.
2:2. Ранг абелевой группы. Выражение вида
^1Х1 "Т~ • * * "I Cfi-Xji,
где хъ...,хп суть элементы данной группы А, а сь ... , сп — целые
числа, называются линейной комбинацией элементов xh ...,xn
группы А. Линейная комбинация называется тривиальной, если в ней
*) В силу теоремы о гомоморфизмах.

624 абёлёвы Группы
все коэффициенты с^ суть нули, в противном случае она называется йетри*
виальной. Элементы лгь ..., хп группы А называются линейно
зависимыми, если некоторая нетривиальная линейная комбинация этих
элементов равна нулю. В противном случае элементы хъ ...>хп называются
линейно независимыми.
Рангом группы Л называется наибольшее из чисел т, обладающих
тем свойством, что в А имеется т линейно независимых элементов. Если
среди таких чисел нет наибольшего числа, т.е. если в группе А можно
найти сколь угодно много линейно независимых между собой элементов,
то ранг группы А по определению равен бесконечности. Ранг группы А
обозначается через рА
Определения этого и предыдущего артикулов находятся между собой
в согласии в силу следующего предложения:
Теорема [2:2]. Ранг свободной группы «ранга» п равняется п.
Доказательство. Элементы хь ...,хп базы свободной группы
линейно независимы. В самом деле, так как элемент 0 может быть
представлен в виде (2:1) единственным образом, то из
сххх -f .. - + спхп = О
следует
*i ■= • • • = сп = 0.
Остаётся доказать, что всякие п -f-1 элементов ylf ...tyn+i свободной
группы Х=[хъ хп] линейно зависимы. Доказательство будем
вести индукцией l-по п. При п = 1 теорема очевидна: i элементы у1 = ахг и
у2 = bxt линейно зависимы. (Если а = 0, то 1 • уг -f- 0 -уъ = 0, если афО, то
— Ь-уг + а-у2 = 0.)
Пусть теорема доказана для n = k — 1; докажем её для п = k.
Пусть даны k + 1 элементов:
к
(2:2) yh = J$ahi*i, h=l, ..., k + l,
группы [хъ ..., хк]. Тогда k элементов
Ук ^Ун — <*hlxl9 h = 1, ..., k,
принадлежат свободной группе [х2, ..., хку «ранга» k — 1 и, следовательно,
по индуктивному предположению линейно зависимы; значит, существуют
такие целые числа cv .... ск, не все равные нулю, что
к _
2 с'нУп = °>
Л=1
следовательно,
к
(2:20 2<£b = Mi.
Л*=1
где
*i = 2 chahl-
Л=1
Совершенно аналогично, рассматривая элементы
~Ун =Ун — auxh h = 1, ..., k; / = 1, ..., А',
при любом фиксированном / получим
к
(2:2,-) 2^=^' /«1, .... Л.
Л=1

«4
СВОБОДНЫЕ АВЕЛЕВЫ ГР>ППЫ
№б
Если хотя бы для одного значения / было bi = 0, то согласно (2: 2$)
элементы j/^ ..., ук и, следовательно, элементы уъ ..., ук±\ были бы линейно
зависимы. Если все bt отличны от нуля, то, как легко видеть из равенства
(2: 2) для h = k -\- 1 и равенств (2: 2г), элемент
bib2 ... Ькук+1
является линейной комбинацией элементов ylt ...,ук, причём коэффициент
ПРИ Ук+х отличен от нуля. Следовательно,' элементы уь ..., j^+1 линейно
зависимы. Теорема доказана.
Из полученной таким образом характеристики «ранга» свободной группы,
как её ранга, следуют теоремы:
[2:21]. Каждая база свободной группы \хъ ..., хп] состоит из п
элементов.
[2:22]. Если две свободные группы [xlf ..., хп\ и [уъ ...,ут]
изоморфны, то т = п.
Обратное предложение о том, что две свободные группы [хъ ..., хп]
и [Уъ •••» Уп\ изоморфны, очевидно.
2:3. Линейные уравнения. Непосредственным следствием теоремы
[2 : 2] является известная
Теорема [2:3]. Система
w-fi
(2:3) j***5***0» '**Ь •••» п>
п линейных уравнений с п-\-\ неизвестными с,к и с целочисленными
коэффициентами aik всегда имеет ненулевые целочисленные решения.
Доказательство. Согласно теореме [2:2] любые п +1 элементов
Ук = 2 aikxh k=\, . . ., П + 1,
свободной группы [хъ ..., хп] линейно зависимы, значит, существуют такие
целые числа Slf ..., 1п\-ъ не все равные нулю, что
п+1
т. е. l^aikik — Q ПРИ всяком /= 1, ..., щ следовательно, числа £л являются
решениями системы (2:3).
Так как числа Ьк можно сократить на общий множитель, если таковой
имеется, мы можем усилить утверждение теоремы, добавив требование,
чтобы числа 5i_ £п+1 были взаимно просты.
2:4. Базы свободной группы. Элементы хь ..., хп образуют не
единственную базу группы [хь ♦.., хп].
Из определения базы следует, что система элементов ylt ..., уп группы
[xlt ..., хп] тогда и только тогда является базой группы [х± хп], если
эта система удовлетворяет следующим условиям:
1) Каждый элемент х £ [х ь .... хп] может быть представлен в виде
п
х=2 а*у*
/—1
2) Коэффициенты а^ однозначно определяются элементом х. Второе
условие следует из первого, а именно, имеет место:
Теорема [2:4]. Если элементы уь ..., уп группы X = [хь ..., хп]
обладают тем свойством, что всякий элемент этой группы является
40 Александров П. С.

626
АвЕЛЁВЫ ГРУППЫ
линейной комбинацией элементов ylf ..,, уп, то эти элементы образуют
базу группы X.
Доказательство. Рассмотрим наряду с группой X свободную группу
п
Z— [zh ..., zn] и поставим в соответствие каждому элементу z = 2 aizi 6 Z
1=1
п
элемент f(z) = y£la,iyi£X. В силу условий теоремы [2:4], отображение
i=i
f есть гомоморфизм группы Z на группу X, причём /(^) =^(/ = 1, ..., п).
Так как элементы z^ образуют базу группы Z, то теорема будет доказана,
если мы покажем, что, отображение / есть изоморфизм; для последнего же
достаточно доказать, что ядром гомоморфизма / является нуль-группа, другими
словами, что из f(z)=?Q следует гя»0.
Итак, пусть z£Znf(z) = 0. Выберем элементы Z'V ..., zn группы Z
так, чтобы было f(z-) = х$ элементы z, zv ..., zn согласно теореме [2:2]
линейно зависимы, т. е. существуют такие числа Ь, Ьъ ..., bhi не все
равные нулю, что
bz + Mi + • • • + bnzn = 0.
Так как / есть гомоморфизм и f(z) = 0, /(^) = xif то
btxx + ... + Ьпхп = 0,
откуда
и, следовательно,
bz = 0; Ь ф 0.
Но единственным элементом конечного порядка свободной группы Z
является нулевой элемент, следовательно, г = 0, что и требовалось доказать.
Из доказанной теоремы следует:
[2:40]. Для того чтобы элементы yh ..-,yn образовывала базу
группы X = [xlf ..., хп], необходимо и достаточно, чтобы элементы х$
могли быть представлены в виде
(2 : 40) Xi = 2 ааУк, / = 1, .... п.
&=i
Действительно, из (2:40) следует, что каждый элемент гр>ппы X,
представляющий собой по определению линейную комбинацию элементов х^ может
быть представлен и как линейная комбинация элементов v-t\ на основании
[2:4] отсюда следует, что у к образуют базу группы X.
Пример. Пусть
У\ = х\ + с2х2 + • • • + спхп,
где Ci — любые целые числа. Тогда элементы
Уь -v2» • • • > хп,
образуют базу группы X. В самом деле,
Х-^ == у'{ -~~-~ С^Хъ —— . . • — ^)iXfi»
2:5. Подгруппы свободных групп. Не только все применения теории
групп в этой книге, но и вся теория абелевых групп с конечным числом
образующих основывается по существу на следующей теореме:
Теорема} [2:51] Пусть Хп—свободная абелева группа ранга п. Всякая
подгруппа U группы Хп, отличная от. 0, сама есть свободная абелева

§2]
СВОБОДНЫЕ АВЕЛЕВЫ ГРУППЫ
627
группа и её ранг k не превосходит п. Более того, молено выбрать базу
Уъ •••• Уп группы Хп и базу Hlf-..., ик, &<я, группы U так, что
Щ = ®4Уь i = l, ..., kt
где Ьь ..., 0А являются натуральными числами и 0т делится на bit
i = 1, .... k— 1.
Доказательство *). Справедливость теоремы для я = 1
непосредственно следует из того, что всякая подгруппа бесконечной циклической
группы с образующим элементом х есть циклическая ipynna с образующим
элементом 6л:, где 0 — натуральное число.
Пусть теорема [2:51] уже доказана для группы X'1-1. Если в группе
X1 дана отличная от 0 подгруппа U, то всякому выбору базы для группы
Хп однозначно соответствует некоторое целое положительное число,
наименьшее из положительных чисел, встречающихся в качестве
коэффициентов в тех линейных формах относительно этой базы, которые являются
элементами подгруппы I]. Этот минимальный положительный коэффициент
меняется, вообще говоря, при изменении базы группы Хп. Ищем теперь
такую базу группы Xnt для которой этот коэффициент достигает
наименьшего из возможных для него значений. Пусть это будет база
(2:511) {хь .... хп}.
Пусть Bj, ^^l, есть наименьший положительный коэффициент,
соответствующий этой базе, и пусть
«1 = Ч-Ч + а2х2 + • • • + аПХП
есть один из тех элементов подгруппы U, запись которых в базе (2:511)
содержит 6Х в качестве одного из коэффициентов **).
Докажем, прежде всего, что каждый из коэффициентов аъ ..., ап
делится без остатка на 6Х. Пусть, в самом деле, a%=\q-{-r, где 0<r<<Oi.
Преобразуем базу (2:511), заменяя в ней элемент х1 через xl-\-qx%.
Относительно новой базы
Ха —■— лj ~~\~ ах%, х% • • •> хт%
элемент и^ записывается следующим образом:
«1 = Чх[ + гхъ + а'бЧ + • • • + апхп-
Мы приходим, следовательно, к такой базе группы Хп относительно
которой запись одного из элементов подгруппы U содержит один
положительный коэффициент, меньший, чем Qj. Это противоречие с выбором числа 0Х
доказывает наше утверждение.
Пусть ai = \qi> / = 2,...,/z. Преобразуем базу (2:511) группы Х>\
заменяя элемент хх элементом
У\ = х1 + #2*2 + • • • + Япхп-
Очевидно, что их = \у± Собираем, далее, все те элементы подгруппы Uy
в записи которых относительно новой базы коэффициент при у1 равен нулю.
Эти элементы составляют подгрупп}' {]' группы с7, пересечение которой
с циклической подгруппой [иД, порождённой элементом иь есть нуль-группа.
Докажем, что сумма подгрупп [иД и [/' совпадает с U.
Пусть
U = ЬХ Уъ -f Ь2Х2 + • • • + ЬпХп
*) Доказательство теоремы [2:51] заимствовано мною из книги А. Г. К у-
р о ш а «Теория групп».
**) Предположение, что 6(. есть коэффициент при элементе щ, является
законным, так как мы не считаем базу группы Xй упорядоченной.
40*

628
ЛВЁЛЕВЫ ГРУППЫ
есть произвольный элемент подгруппы U. Если Ь1 — \q -}- Л 0 < r<fy
то содержащийся в U элемент '
иг = и — qUl = ryL + b2-u -f ... -f bnxn
имеет в качестве коэффициента при у1 число, меньшее, чем blt откуда по
определению числа 0Х следует г = 0. Поэтому элемент «' содержится в
подгруппе U\ а элемент
и = #% -f и7
входит в сумму подгрупп \и{\ и U'.
Из только что доказанного следует, что если V = 0, то £/ = [aj и наша
теорема доказана. Если же Ц'фО, то мы получаем разложение подгруппы
£/ в прямую сумму:
U=\ux\ + U'.
Подгруппа V содержится в подгруппе X' — \хъ.. .,д"п], представляющей
собой свободную группу ранга /г—1; поэтому, в силу индуктивного
предположения, группа U' свободна. Существуют, далее, такие базы у2»• • • %Уп
для X' и #2>- • -,ик для ^'» что ^ — 1 <! я — 1 и z^ = 0?у,-, где 6tf>0 и 6t-+1
делится на 6г-, г=2, 3,...,£.
Мы установили, таким образом, что подгруппа Uесть свободная группа
ранга ky k <; л. Для доказательства того, что базы
(2:512) {У1.Уъ...Уп>
группы Хп и
(2:513) {«!,«*...,я*}
подгруппы US=.Xn удовлетворяют всем требованиям доказываемой теоремы,
нам остаётся лишь показать, что число 62 делится без остатка на число 61#
11усть 02 = \qQ + г0, 0 < г0 < 01# Преобразуем базу (2 :512) группы Хп,
заменяя элемент уг элементом
у[=У1 — ЯоУь
относительно этой новой базы лежащий в U элемент щ—щ записывается
в виде
«2 — tfl=(— ®l)y[ + r0y2,
откуда снова, ввиду выбора числа 6lf следует г0 = 0. Теорема [2 :51] доказана.
Замечание.' Число 6г- является порядком элемента^, *<Ж
группы Хп относительно подгруппы U> т. е. наименьшим из
натуральных чисел 6, для которых Ъу$ £ U. В самом деле, если 6_уг- £ U, то при
некоторых целых с+
откуда вследствие линейной независимости элементов уг- имеем Cj = 0
для / ф i и 6 = cfii.
Из того, что 6/j>4 6 £/, следует, что yi 6 £/, где £/, как всегда,
обозначает дивизионное замыкание подгруппы U (в группе Хп\ С другой
стороны, пусть х 6 U и
л- = С1У1 + - • - + скук + ck+1yki.x + ... + ад^.
При некотором целом сфО имеем cx^U, т. е. при некоторых целых
аь...,ак
cctyi + ... + сскук + ... + сс„уп = агЬ1У1 + ... + а$кУъ
откуда, в силу линейной независимости уь—.упу
ссх = ахЬъ. ..,сск = акЬъ сск+1 = ... = ссп = 0
и, значит, ск+х = ... = сп = 0 и х = Cj^i + ... + <йУл-

§ 2]
СВОБОДНЫЕ АБЕЛЕВЫ ГРУППЫ
62«
Итак:
[2:511]. Элементы уь—у к базы {Уь...,уп} образуют базу группы. U.
Установим теперь новые обозначения, которые будут удобны в
приложениях теорем [2:51] и [2:511]. Элементы yi базы уь.. .,уп, для которых
/>£, обозначим через s1f.. .4z*\ элементы^-, /<>, для которых 0г->1,
перенумеруем, так же как и соответствующие им 0^ в обратном порядке
(так, чтобы получилось 6^=0 (mod 0t-+1) и обозначим их через ub...,ih
(соответствующие 0г- будут 6Х 0Т, 0^^ееО (mod 0г--н)- Наконец, те yiy для
которых 0< = 1, обозначим через vh..., vT Сформулируем теперь
полученные выше результаты так:
[2:52]. Пусть X—свободная абелева группа, U — произвольная
подгруппа группы X. Группа X имеет базу
(2:52) *1,...,*я; «1,...,Ыт; vi,---,va,
удовлетворяющую следующим условиям:
а) %>ь ..., va суть элементы группы U\ порядок элемента щ от-
носительно подгруппы U есть натуральное число 0^>1, причём
0,= 0 (mod 0m):
б) элементы Ьгиь.. .,0л/т и vb...,va образуют базу группы U\
в) элементы ult...,ur; vh va образуют базу группы U.
Всякая база (2:52) группы X, удовлетворяющая условиям теоремы
[2:52], называется канонической базой свободной группы X
(относительно её подгруппы U).
2:6. Некоторые замечания о канонических базах. Пусть U—U есть
дивизионно замкнутая подгруппа свободной абелевой группы X. Берём
каноническую базу
{*!,...,**, vlt...,vr}
группы X относительно подгруппы U (вследствие дивизионной замкнутости
группы U все 0г- = 1). Тогда [vlt.. .,vz] = U.
X=[zb...,zK] + [vb...,vJ
(2:61) A7£/ = [8i,...,5j.
где fa £ X/U есть класс смежности, содержащий элемент Zj. Итак:
[2:61]. Фактор-группа свободной группы X по дивизионно замкнутой
подгруппе U есть свободная группа. Имеет место разложение в прямую
сумму X = U-\- V, где V есть подгруппа группы X, изоморфная группе X/U.
Замечание. Подгруппа V условием Х= U -\- V, вообще говоря,
определена неоднозначно, но все такие V изоморфны между собой (так как
изоморфны группе XIU). В наших обозначениях за V можно принять группу
[Zb...tzK]. ^
О п р е д е л е н и е [2:62] Пусть U= U — дивизионно замкнутая подгруппа
свободной группы Яранга п. Элементы x\t-..,хр группы X по определению
образуют U-6 азу группы X, если их классы смежности & £ X/U
образуют базу свободной группы X/U.
Очевидно:
[2:621]. Элементы хь ...,хр группы^ тогда и только тогда образуют
£/-базу, когда никакая нетривиальная линейная комбинация этих элементов
не содержится в U и, кроме того, каждый элемент х группы X может быть
представлен в виде
(2:621) * = и+2сЛ'
где u£U и Ci суть целые числа.
[2:63]. Если U—дивизионное замыкание подгруппы U свободной
группы X ранга п, то всякая U-база группы X может быть дополнена до
канонической базы группы X относительно подгруппы (/.

630
АБЕЛЕВЫ ГРУППЫ
В самом деле, пусть xh...txp есть £/-база группы Ха
(2 : 630) *lf... ,гге; иь... ,ит; trlf... ,t>ff
(есть некоторая каноническая база группы X относительно подгруппы О.
Докажем, что
(2 : 63) Xi ... ухр\ иь... ,йт; vit... д>5
есть каноническая база группы X (откуда, в частности, следует, что р = п).
Для этого, очевидно, достаточно доказать, что
(2:631) X=[xb...txp] + [uh...tu^ vx v9].
Из определения £/-базы следует, что
[■*!....,*„] П ?/=0
и что каждый элемент х £Х может быть представлен в виде (2:621). Эти
два обстоятельства означают, что (в силу [1 :31]),
_ X=[xb...,xp\ + fj%
откуда, в силу U = [и1? ..., ит; vh..., va]y следует (2:631).
В заключение этого артикула докажем следующее важное, хотя и
совершенно элементарное предложение:
[2:64]. Пусть L — свободная группа ранга п\ пусть 2 — давизаонно
замкнутая подгруппа группы L\ пусть хъ...,хр-
пы LJZ, a 2j,..., zq— база свободной группы Z; л
произвольный элемент класса смежности r^, i = 1,..., р.
Тогда
{лг1э . . ., Хр\ 2|,. . ., Zg)
есть база группы L.
Докажем:
а) каждый элемент х £ L может быть представлен в виде
* h
б) такое представление единственно; утверждение б), очевидно,
равносильно утверждению:
б') элементы х± хр\ z1 zq линейно независимы.
Доказательство а). Обозначим через г класс смежности элемента
х £ L относительно подгруппы Z Так как хь..., хр образуют базу группы L/Z,
то при некоторых я^..., ар
значит, х = S аМ»
а потому при некоторых ch
х ~~ 2 «л = 2 с^»
т. е. * л
*= 2ял + 2^'
*' h
чем а) доказано.
Доказательство б'). Пусть ^ВД+ЦЗД3^ Надо доказать,
что все аг- и все ch равны нулю. Имеем
(2 : 641) 2 aixi = ~ S '*** ^ Z'
или, переходя к классам смежности,
У я,-г,- =г 0.

§ 2] СВОБОДНЫЕ АБЕЛЕВЫ ГРУППЫ 631
Так как ^(как элементы базы свободной группы L/Z) линейно независимы
между собой, то все а^ суть нули и, значит [из (2:641)],
2 chzh = °»
откуда (в силу линейной независимости элементов zn) замечаем, что все ch
суть нули.
2:7. Гомоморфизмы, в частности, эндоморфизмы свободных групп.
Матрица гомоморфизма (при данных базах). След эндоморфизма. Пусть
дано гомоморфное отображение / свободной группы X ранга р в свободную
группу Y ранга q.
Пусть в X и в К даны соотзетственно базы jclf...# xp\ yi,...,yqi
Тогда Х=[хъ...,хр]ш ¥=№...., yq].
я.
/С*л)= 2аадУ* i==1 Р-
/«1
Матрица
(аи *у alq\
ар\>- • •» д^|- ••» ^j»g '
называется матрицей гомоморфизма/ группы Л в группу JB
(при базах xlt..„ xp\ уъ ..., yq).
Гомоморфное отображение группы в себя называется
эндоморфизмом.
Пусть / есть эндоморфизм свободной Группы X ранга п; пусть
хь...,хп — база группы X и
(2:71) /(**)= 2 «л**<- -
it '
Число
2 аМ
h
называется «следом» эндоморфизма/(относительно базы.*i,...,лгте).
Теорема [2:7). След эндоморфизма не зависит от выбора базы.
Доказательство. Пусть уь ..., уп — другая база группы X,
связанная с хъ ..., хп соотношениями
(2:72) .Ур = 2 й№*« •
(2:73) *<z = 2tW*"
г
Пусть эндоморфизм / в базе ylt ..., .уте задаётся равенствами
(2:74) /CVi) = 2*^*-
Мы должны доказать, что
(2:75) 2*^ = 2%-
h j
Если подставить выражения (2:73) для xq в (2:72), получим
Ур = 22 WVJV .
откуда вследствие независимости ,уг
(2 : 76) 2 UPQVqr - >< ,
</

632
АВЁЛЕВЫ ГРУППЫ
где
— ) 0» если Р Ф г'
ьрг | ] f если р =~ г.
Аналогично, подставляя выражения (2:72) для ур с заменой индексов р, q
индексами г, s я равенство (2:73), получим вследствие независимости хя:
(2:77) ^VqrUrv — ha-
г
Далее из (2:72), (2:71) и из (2:74), (2:72) получаем
/(Уз) =/(2а#-*л) в 2 И#/С*л) = 22и^л«*<7
Л h h q
И
/(.У?) = 2 Ь&Ук *= 22 b3kakqXq •
следовательно,
22 Ujhahqxq ~ 22 bjkukqX(p
h q k q
откуда вследствие независимости дг^
2 и#дЛд =» 2 bjknkq •
/г /i
Умножим это равенство на г^г и просуммируем по q. Принимая во вн.ша-
ние (2 ;76), получим
22 Ujhahqvq> ** 2 ^jkhr =* ^> ,
/га к
откуда, принимая во внимание (2:77),
2 ЬИ ** 222 VQJUJhahq = 22 Sg^/ig ^ 2 ahh »
/ 3 h q q h h
что требовалось доказать.
На основании доказанной теоремы можно говорить просто о следе
данного эндоморфизма, не указывая базу, по которой этот след
берётся.
2:8. Теорема сложения следов. Пусть F — подгруппа свободной группы
X, отображающаяся при эндоморфизме / группы X в себя. Так как Y есть
свободная группа (см. арт. 2:5), то определён след SpY эндоморфизма f
группы К. След эндоморфизма / группы X обозначим через SpX.
Из f(Y)czY следует, что дивизионное замыкание Y группы Y в X при
отображении / также отображается в себя. Действительно, если x£Y, то
существует такое число тфО, что тх£ Y; тогда mf(x) — f(mx)£ Y, следо-
вательно, f(x) £ К. Так как Y при отображении / переходит в себя, эндо-
морфизм / порождает (см. арт. 1:1) эндоморфизм / фактор-группы X/Y.
Если XjYzfiO, то X/Y есть свободная группа (по теореме [2:61]) и,
следовательно, определён след Sp (X/Y) эндоморфизма / этой группы. Если
Л/К=*0, полагаем по определению Sp(X/Y) = 0.
Теорема [2:8]. Если при эндоморфизме f свободной группы X под-
группа У этой группы отображается в себя, то
SpX=SpY+Sp(XlY).

§ 3]
НЕКОТОРЫЕ ТЕОРЕМЫ О РАНГЕ ГРУПП
633
Доказательство. Если К = 0, теорема очевидна. Пусть УфО.
Выберем каноническую базу xv .'.., хп группы X относительно Y. Тогда при
некотором г <я имеем
Г = [хь .. .,xr], Y=*[h*i Mrl»
причём некоторые 0г-, а именно, все 9г% начиная с некоторого i = к < г,
могут быть равны 1. Если rr+lf ...,гте суть классы смежности группы X
по подгруппе Y, содержащие соответственно элементы хг+\% ...,.%, то
но формуле (2: 61)
*/? = [Vhi tw].
Пусть
(2:81) /(^) = 2^Л. Л = 1 я.
/«1
Так как группа У отображается в себя, то
(2:82> a«-*w{hiZr+C*.
Так как Y также отображается в себя, то для элементов bhxh базы группы Y
получим
(2:83) /(Мл) = 2а'лА*«. h=*lt...tr.
С другой стороны, из (2:81) и (2:82) следует
г
(2:84) /(O**fc) = 0fc2aw*<;
i = l
из (2:83) и (2; 84) следует а'^ = $hahi, значит, при / = Л, ат = яЛ?1 и
(2:85) SpY=JZahh.
Тем самым, в случае г = п, т. е. ЛУК = 0, теорема доказана. Пусть г<л.
Из соотношений (2:81) для /г = г + 1,.. .,я и из того факта, что хь...,хг
суть элементы группы Y, являющейся нулём группы X/Y, следует
п
/(*Л)= ]£ Л***Л, ^ = /'+1;...,Г7,
откуда
^ 77
(2:86) Sp{XIY)= 2 а^'
Л—г-1-1
Из (2:85) и (2:86) следует утверждение теоремы.
Замечание. Если Х= К, то из [2:8], в частности, следует
§ 3. Некоторые теоремы о ранге групп.
3:1. Ранг группы А тогда и только тогда равен нулю, когда все
элементы А — конечного порядка.
Доказательство. Если все элементы группы А — конечного порядка
то, каковы бы ни были элементы х^..^хп группы Л, имеем, обозначая

634
АБЕЛЕВЫ ГРУППЫ
через С{ порядок элемента xiy
с1х1 + ... -f спхп = О,
так что элементы хь...,хп линейно зависимы. Итак, не существует
непустого множества линейно независимых между собой элементов группы
Л, так что ранг группы А равен нулю.
Обратно, если рЛ = 0, то для каждого элемента х£А найдётся такое
отличное от нуля целее число с, что сх = О, так что все элементы А —
конечного порядка.
3:2. Для любой группы А и любой её подгруппы Ло имеет место
следующая формула сложения рангов *):
(3:2) рЛ = рЛ0 + р(Л/Ло).
Докажем сначала неравенство
(3:21) рЛ>рЛ0 + р(Л/Ло).
Для этого достаточно доказать следующее предложение.
[3 :21]. Пусть элементы хь.. .,хр группы Л0 линейно независимы; пусть
элементы tfo...,^ группы Л/Ло также линейно независимы] пусть,
наконец, j^€t)/. Тогда элементы
xi хр, yi>-',yq
группы А линейно независимы между собой.
Для доказательства этого последнего утверждения предположим, что
при некоторых целых а^ и bj имеем
(3:211) 2***< + 2Vi = °-
Р
Переходя к классам смежности относительно Ло и помня, что 2 aix% € ^о»
i=\
выводим из (3 : 211)
(3:212) 2^; = 0.
/-1
откуда, в силу линейной независимости t)j, получаем bj — О С/= 1,.. .,#),
так что (3:211) переходит в
Р
(3:213) 2fl^ = °-
отсюда вследствие линейной независимости xi получаем #г- = 0 (/ = 1,.'.. ,/0-
Этим линейная независимость xiy yj и, следовательно, неравенство
(3:21) доказаны.
Прежде чем переходить к доказательству неравенства
(3:22) рЛ<рЛ0 + р(Л/Л0),
отметим, что из (3:21) следует:
[3:210]. Для всякой подгруппы Л0 группы А имеем
рЛ0 < рЛ и р (А/А0) < рА.
Докажем теперь неравенство [3:22]. При этом, очевидно, можно
ограничиться случаем, когда ранги групп Ло и Л/Ло конечны (так как если хотя
бы один из этих рангов бесконечен, то неравенство (3:22) делается
очевидным).
*) Предположения о конечности какого-либо из чисел ?А, р(Л/Ло), рЛ0
при этом ие делается.

§ 3]
НЕКОТОРЫЕ ТЕОРЕМЫ О РАНГЕ ГРУПП
635
Пусть рЛ0 = Л р(Л/Ло)=.<?; пусть хь.. .,л:^ — линейно независимые
элементы группы Л0; пусть \)Ъ.. .,^~ линейно независимые элементы
группы Л/Л0 и yj € fy.
Лемма. Для каждого элемента z^A можно найти отличное от
нуля целое число с и целые числа cit dj, такие, что
V Ч
с* = 2 СЛ* + 2 **Л'*
В самом деле, пусть г 6 5 £ Л/Л>
Элементы §, th»---^ группы Л/Лолинейно зависимы между собой, так
ч
что некоторая комбинация Ъ% — 2 bfij этих элементов равна нулю: .
Ч
(3:221) ^-2^ = 0,
0 = 1
при этом из линейной независимости элементов ^ следует, что ЬфО.
Равенство (3:221) означает:
(3:222) *'«=&* —2^6 4,.
Элементы z', jclt...,хр группы Aq линейно зависимы между собой, так
v
что некоторая нетривиальная линейная комбинация az' — 2аЛ их равна
нулю:
Р
(3:223) az' — 2 Wi = 0»
причём из линейной независимости х^ следует, что а ф 0.
Из (3:222) и (3:223) вытекает
ч v q
(3 : 224) abz = «У + 2 flVj в 2 ***»' + 2 ^Л>
y=i »=i j=i
т. е., полагая с = аЬ ф0, Ci = а$, d^ = abj,
р ч
^=2^л-+2^'
чем лемма доказана.
Переименуем теперь элементы уь.. ,fyq в -tf^+i,. ..,*p+g.
Нам нужно доказать, что pA^p-\-q, т. е. что всякие р -\- q + 1
элементов
группы Л линейно зависимы. Для доказательства этого утверждения
заметим сначала, что, в силу леммы, имеются такие целые числа скф0 и с^
что
P+Q
(3: 225) ckzk = 2 '<*■** *«! 0"г^+ 1).
С другой стороны, из теоремы об однородных линейных уравнениях
(арт. 2:3) следует существование таких целых чисел £х,..., S^+^+i, которые не

636
АБЕЛЕВЫ ГРУППЫ
все равны нулю и удовлетворяют равенствам
(3:226) 2 **& = 0, i=l,-'.,(P + g).
Из (3:225) и (3:226) вытекает
2 **'*** =2(2 ^чК ^0;
так как не все £А. равны нулю и все с1г отличны от нуля, то линейная ком-
бннация 2 ^кскгк не тривиальна и, значит, zlf...t zp+q±x линейно зави-
симы между собой, что и требовалось доказать.
3:3. Ранг групп по модулю т. Целочисленная линейная комбинация
2Wi элементов х+ группы А называется нетривиальной по
модулю /и, если не все сг- делятся на т. Элементы х^ называются линейно
зависимыми по модулю т, если некоторая нетривиальная по модулю т
линейная комбинация этих элементов равна нулю. Наибольшее среди таких
целых чисел г, что в группе А имеется г линейно независимых по модулю т
элементов, называется рангом группы А по модулю т и
обозначается через ртА
Почти дословно повторяя рассуждение предыдущего артикула (но
заменяя в соответствующих случаях равенства сравнениями), читатель без труда
докажет теорему:
[3 :3]. Пусть т — простое число и группа А такова, что тА есть нуль-
группа (что при простом т означает, что всё элементы группы А имеют
порядок т). Тогда для любой подгруппы Aq группы А имеем
ртА = ртА0+рт (Л/Л0).
Замечание 1. Неравенство
(3:31) РтА>РтЛо + рт(А/А0)
доказывается и без предположения простоты числа т. Условие тА = О
входит в рассуждения следующим образом. При доказательстве неравенства
(3:31), аналогичном доказательству неравенства (3:21), мы из равенства
(3:212) выводим fy = 0 (mod яг), откуда следует, в силу (3:211),
р q
2 a{Xi = — 2 Vi € тА>
/=1 7 = 1
а это в силу тА = О даёт
р
2 а%4 = О,
г — 1
т. е. a~f) (modw).
При доказательстве неравенства
рЛ<рЛ0 + р (А/Ао)
аналогичным образом приходится воспользоваться условием тА = 0 для
вывода соотношения (3:222). Простотой числа т приходится
воспользоваться для того, чтобы из
a£0(modm), b = £(modm)
вывести ab ф§ (mod m). Заметим, наконец, что относительно целых чисел £г-
приходится ещё потребовать, чтобы они не имели общего делителя (см.
замечание в конце арт. 2:3),

§ 4] ГРУППЫ С КОНЕЧНЫМ ЧИСЛОМ ОБРАЗУЮЩИХ 637
Замечание 2. В соответствующем месте книги Александров а-
Хопфа «Topologie», I, *на стр. 572—573 имеется ошибка,
заключающаяся в том, что требование тА = 0 (в обозначениях названной книги mJ = 0)
пропущено. Восстановление этого требования возвращает рассуждениям
только что указанного места полную строгость.
§ 4. Группы с конечным числом образующих.
4:1. Определение. Система @ элементов группы ^называется
«системой образующих» группы X, а элементы этой системы —
«образующими», если каждый элемент группы А может быть представлен, по
крайней мере, одним способом в виде линейной комбинации ^\щх^
элементов Xi€& (где at — целые числа).
Мы будем сейчас заниматься группами, имеющими систеиы
образующих, состоящие из конечного числа элементов. Такие группы называются
«группами с конечным числом об р азу ю щи х». Простейшими
примерами групп с конечным числом образующих являются свободные
группы конечного ранга; всякая база свободной группы является системой
ее образующих. Далее, все конечные (т. е. состоящие из конечного числа
элементов) группы являются группами с конечным числом образующих, так
как совокупность всех элементов любой группы является системой её
образующих.
Замечание. Мы будем говорить, что группа порождается п
элементами, если она имеет систему образующих, состоящую из п элементов.
Теорема [4:11]. Для того чтобы группа порождалась п
элементами, необходимо и достаточно, чтобы она была гомоморфным
образом свободной группы ранга < п.
Доказательство. Первое утверждение. Пусть хь ... ухп
есть система образующих группы Х\ рассмотрим свободную группу
У = [уь... ,уп] ранга п. Равенство
даёт гомоморфное отображение свободной группы [уь ... ,уп] на X.
Второе утверждение. Если / есть гомоморфное отображение
свободной группы !>!,— ,уп\ на ГРУППУ X, то элементы f(yt),... yf(yn)
являются её образующими.
Из доказанной теоремы и из [3:2] следует
т. е.:
[4:12]. Ранг группы с п образующими не превосходит п.
4:2. Теорема [4:21]. Если группа X порождается п элементами,
то то же верно и для фактор-группы группы X по Любой её подгруппе Z.
Доказательство. Группа X есть гомоморфный образ свободной
группы К ранга О (теорема [4:1]); группа X/Z есть гомоморфный образ
группы X; произведение гомоморфизмов есть гомоморфизм, следовательно,
X/Z есть гомоморфный образ свободной группы К, что и требовалось
доказать.
Теорема 14:22]. Если группа X порождается п элементами, то
то же верно и для любой её подгруппы Z.
Доказательство. Пусть /— гомоморфное отображение свободной
группы Y ранга п на Л" (теорема [4:11]). Легко видеть, 4To/-:t(Z) есть
подгруппа группы Y и, следовательно, свободная группа ранга < п. Её
образ по теореме [4:11] порождается п элементами.
Теорема [4:23]. Пусть Z есть подгруппа группы X. Если группа Z
и фактор-группа X/z суть группы, имеющие конечную систему
образующих, то то же верно и для группы X.

638
АБЕЛЕВЫ ГРУППЫ
Док1зательство. Пусть zb...,zr и rt ts суть соответственно
системы образующих групп Z и XjZ. Пусть, далее, хь.. ,txs суть
произвольные элементы соответственно из классов tb...,rs. Элементы
zb... ,zr, хь... ,х8 порождают всю группу X. Пусть, в самом деле,
х£Х—произвольный элемент группы X и пусть содержащий его класс
смежности есть 2^Л'» тогДа -v = '2: + 2^/*./' где г€^9 следовательно,
z = 2 а*г* и х = 2 ai zi "Ь 2 fy ■*./» чт0 и требовалось доказать.
4:3. Основная теорема о группах с конечной системой образующих.
Определение [4:31]. Циклическим разложением
данной группы Л называется всякое представление её в виде прямой суммы
конечного числа циклических групп
(4:31) A = e1+...+Qr+Z1+...+Z„
при этом через 0г- обозначаются конечные, а через Zj—-бесконечные
циклические группы.
Циклическое разложение (4:31) называется каноническим, если
порядки 0^ групп вг- удовлетворяют дополнительному условию
(4:310) 6=0 (mod6i+1).
Основная теорема [4:32]. Всякая абелева группа с конечным
числом образующих допускает каноническое циклическое разложение.
Доказательство. Согласно теореме [4:11] всякая группа Л с
системой из п образующих является гомоморфным образом свободной
группы X ранга п и потому изоморфна фактор-группе этой группы X по
некоторой её подгруппе U.
Возьмём каноническую базу
zh ...,zn; иь...,щ; vlt...,va
группы X относительно подгруппы U (см. теорему [2:52]). Тогда
^ = [^il+...+M + ["i] + ... + [«x] + [^H-...+Kl
U = [0lHl] + ... + [6тит] + \Vl\ + ... + К],
следовательно, по теореме [1:62]
XIU = М + ... + [*„] + [Н1]/[в1Й1] + ... + [иа]/[втит] + 0 + ... + 0,
.4 = z1+...+z, + e1+... + eT,
гле Zi, . ..^^ — бесконечные циклические группы, а Оь ..., в~ суть
циклические группы соответственно порядков 6lf . ..,0Т
и 6^ = 0 (mod 6<+1),
что и требовалось доказать.
Замечание. Числа 0lf ..., 0Т называются коэффициентами кручения
данного канонического разложения группы Л или просто
коэффициентами кручения группы Л; этот последний термин оправдай
следующей теоремой:
[4:320]. Всякие два канонических разложения группы А изоморфны
между собой в том смысле, что состоят из одного и того оке числа
соответственно изоморфных между собой циклических групп и имеют,
в частности, те же коэффициенты кручения.
Эту теорему мы доказывать не будем (читатель может найти
доказательства, например, в §86—87 книги «Топология» Зейферта-Трел fa-
фалл я. Заметим только, что из формулы (3:2) и теоремы [3 :1]
непосредственно следует одно из утверждений теоремы [4:320|, а именно:
[4:33]. Число бесконечных циклических групп, входящих в любое
циклическое разложение группы X, равно рангу рХэгпой группы.

§ 4] ГРУППЫ С КОНЕЧНЫМ ЧИСЛОМ ОБРАЗУЮЩИХ 639
Далее:
[4:34]. В любом циклическом разложении группы А прямая сумма
входящих в это разложение конечных групп совпадает с подгруппой в
группы А, состоящей из элементов конечного порядка группы А.
Доказательство. Пусть в циклическом разложении группы А
>* = el+...+et-T-z1+...+zlc
группы 6_, ...,0Т конечны, a Zb ,..,ZK бесконечны, при этом может
случиться, что одно из чисел х или тс равно нулю (если t = 7t = 0, то А есть
нуль-группа).
То, что каждый элемент прямой суммы 9t -f- ••• + В^ имеет конечный
порядок, очевидно. Пусть, обратно, дан элемент и конечного порядка
группы А:
и = тщ -+-... + ам~ + \zx + ... + ък2к е е,
где щ, zh суть соответственно образующие групп 0^, Zh. Если ти = 0, т. е.
та^щ + ... + та~их -_- тЪ^ + ... -\- mbKzK = О,
и тфО, то Ъг= ... = Ък = 0, следовательно, и £ в_ + ... -f- й_.
Таким образом, действительно
ei+... + e, = e.
Из теорем [4:33| и [4:34] следует важная
Теорема [4:35]. Каждая группа А с конечным числом образующих
разлагается в прямую сумму
A = ® + Z,
где 9 есть подгруппа всех элементов конечного порядка группы A, a Z—
свободная группа ранга pZ = рА (под свободной группой нулевого ранга
понимается нуль-группа).
Следствие [4:351]. Строение *) группы с конечным числом
образующих вполне определяется её рангом и строением группы её
элементов конечного порядка.
Следствие [4: 352]. Группа с конечным числом образующих, не
содержащая элементов конечного порядка, есть свободная группа,
Замечание. Из [4:32], [4:320], [4:33] следует:
[4:353]. Строение группы с конечной системой образующих вполне
определяется её рангом и коэффициентами кручения.
4 : 4. Дальнейшие следствия.
Теорема [4:4Г]. Пусть X и Y— две группы, из которых одна, пусть,
например, X, имеет конечную систему образующих. Пусть далее Хг
и У суть две подгруппы соответственно групп X и Y, причём
(4:41ш) Х^У
а
(4:41,,) Y^X',
тогда
XzxY.
Доказательство. Прежде всего из (4 :41 у) и теоремы [4 :22]
следует, что К также имеет конечное число образующих. Далее, из (4:41 ^
и (4:41^) на основании (3:21) соответственно следует
рХ<рК и рК<рХ,
откуда
______ ?Х=?У.
*) Мы говорим, что две группы имеют одинаковое «строение», если они
изоморфны между собой.

640
АЬЁЛЕВЫ ГРУППЫ
На основания [4:351] остаётся только доказать, что
(4:42) Qxtt9r
где ва, и ®у означают подгруппы элементов конечного порядка
соответственно групп X и Y. Для аналогично определяемых групн вх/ и 9^' из (4:41л.)
и (4:41у) соответственно получим
(4:43ж) 0а, «ву/
и
(4:43,) ву^ва^'-
Обозначая порядки групп 9Ж, 0^, вж', в^' соответственно через гг, 7), а' и 7/,
получим
(4:44ж) а = ¥
и
(4:44у) Ь = а'.
Так как ©^ СО^.тоЬ7 <;b, откуда на основании (4 :44ж) и (4:44^) следует,
что а <! af. Но 9Ж' с= 6>г, поэтому а'<; а, т. е. а = а7 и, следовательно, 0Ж' = Вт,
откуда на основании (4:43^) вытекает (4:42).
Теорем а [4:42]. £сля А' есть группа с конечным числом
образующих и Z— некоторая её дивизионно замкнутая подгруппа, то в X
существует свободная (или нулевая) подгруппа У, такая, что
X=Y+Z.
Доказательство. Фактор-группа X/Z не содержит элементов
конечного порядка (теорема [1:22]) и имеет конечное число образующих
(теорема [4:21]), поэтому она является свободной группой (или нуль-группой).
Случай X/Z—0, т. е. X—Z, тривиален. Пусть
A/Z=[ th У,
где tyi,...,t)s — некоторые классы смежности по группе Z. Выберем из этих
классов соответственно элементы t)lf...,nsH обозначим через У группу всех
s
линейных комбинаций вида 2^^». Для доказательства теоремы достаточно
/=1
показать: 1) Каждый элемент х £ X может быть представлен в виде х = у + zt
где j/С Г, *£Z, и ?) ГП^={0}.
Доказательство первого утверждения: если л'£2л**?*' то х~~~^аъУг~
г
= z£Z, значит, х ~у + *, где у = 2*<-У*€ ^-
Доказательство второго утверждения: если ZaujУ{ g Z, то ^ я$ ^ = О,
следовательно, а$ = 0 для всех L
4:5. Некоторые замечания.
Замечание 1. Пусть
(4:51) Уь.-->УГ> zb...yzp
—система образующих группы Л, причём элементыуь.. .,уг имеют конечные
порядки 6lf...,eT, а элементы zl9...9zp суть элементы бесконечного порядка.
Система образующих (4:51) называется базой группы А если равенство
i h
только тогда имеет место, когда <з^ = 0 (mod 6^) /=1,...,х, и все С}г суть
нули.

§5]
РЕШЕТКИ
641
Замечание 2. Мы уже знаем, что подгруппа тХ произвольной группы X
по определению состоит из всех элементов тх^Х, где х пробегает всю
группу X, Далее, через тХ обозначается подгруппа всех элементов x£Xt
для которых тх = 0. Через Хт обозначается фактор-группа XjmX. Легко
видеть, если
х^х' + х'+.-.+х^к
то
(4:52) , тХ= тХ' + тХ»+ ... + „*К
(4 :53) тХ= тХ' + тХ"+ ... + тХ^\
а также (на основании теоремы [1:52])
(4 = 54) Л.«=С+^ + »+^.
Легко, далее, убедиться в том, что для групп Jm при /я1>?/тг2>2
где (/Wj,/w2), как всегда, означает общий наибольший делитель чисел /wi'it
m2. Так как то же самое, конечно, верно и для любой группы, изоморфной
Jm , т. е. для всякой конечной циклической группы 9^^Ут то
w0 ^ J(n,m)~(Jn)mtt®m, а всякая конечная группа разлагается в прямую
сумму конечных циклических, поэтому на основании (4:52) и (4:54)
получим следующую теорему:
Теорема [4:5]. Для всякой конечной ?pyrtnu 0 и для всякого т > 2
§ 5. Решётки.
5 :1. Скалярное произведение в группах с заданной базой. Пусть в
свободной абелевой группе ранга л, которую будем обозначать через
Хп, дана база
Каждый элемент х группы Хп однозначно представляется в видел; =* Ijjflffr»
Определение [5:11]. Пусть
—два элемента группы Хп. Целее число
(х-у) = ^а&
называется скалярным произведением элементов х и у
группы Xй относительно базы {*i,...,/n}.
Очевидно,
(Х'У) = (у-х),
((Ч + х2) -У) = (*i • J') + (*2 -УУ
(х • (У 1 + -Уг)) = (■*" • Ji) + (* • У&
Для любого элемента
имеем
частности,
41 Александров П. С.
(л: • /,) = а{.

642
АБЕЛЕВЫ ГРУППЫ
5:2. Решётки. Свободная абелева группа ранга я, состоящая из всех
линейных форм 2а<*< с Целыми коэффициентами и данными «переменны,
ми» /i,...,£n при обычном сложении в качестве групповой
операции называется целочисленной решёткой*) ранга п и
обозначается попрежнему через [ti%.. .,tn]. База группы [ti,...%tn], состоящая
из самих переменных tb...,tn (т. е. из линейных форм 2аг**» все
коэффициенты которых равны нулю, кроме одного, равного единице), называется
начальной базой решётки. Скалярное произведение относительно
этой базы называется просто скалярным произведением в данной решётке.
Естественно, что всякая база группы [th...,tn] называется базой решётки.
Если
{*1 *те>
— какая-либо база решётки [t^ tn]t то каждый элемент х этой решётки
•однозначно представляется в виде
н коэффициенты ai естественно называть контравариантными
компонентами элемента х в базе {хх хп}. Очевидно, каждый элемент
решётки [tb.-»,tn] вполне определяется своими контравариантными
компонентами относительно какой-нибудь базы этой решётки.
Числа
0i = O*-*i).....anas5C*--*fi)
называются ковариантными компонентами элемента х в базе
\хь... ,хп}. Очевидно, в начальной базе {*!,...,*»} ковариантные
компоненты каждого элемента решётки [^,...,/л] совпадают с контравариантными.
[5:21]. Каждый элемент решётки вполне определён своими
ковариантными компонентами относительно какой-либо базы этой решётки.
Доказательство. Пусть Xj = ^a{tjt / = 1,..., п — данная база и
даны (x>Xi) = at. Требуется найти коэффициенты с* в представлении
х = ^с%
Заметим прежде всего: так как xt хп образуют базу, то tv...ttn
шыражаются через Х£
«и det#{- detbj= 1. Так как и det#j и detM суть целые числа, то каждое
из них равно ± 1.
Для определения ci имеем уравнения
<5:21) (x-x1)=((c4t+...+cntn).xi) = ai, i = l ff.
Так как ^ = 2^0' т0 УРавнеНия (5:21) переписываются в виде4,
а)с1+ ••• +а? cn = ah / = 1,...,л,
ж решаются по правилу Крамера (так как det я*'= =£ 1, то решения целые)
5:3» Сопряжённые базы решётки. Две базы
Х={хг хпУ*
*={*! *w>
*) Другими словами, решётка есть свободная группа, одна из баз
«второй раз навсегда выделена.

§ 5]
1»6ШЙТКЙ
643
решётки [tb.. .,tn] называются сопряжёнными, если
для любых /, j = 1,.. .,п; элементы х^ и л:^ называются
соответствующими элементами двух сопряжённых баз.
[5:3]. Для каждой базы X решётки [/i,..,,*wJ существует
единственная сопряжённая ей база X.
В самом деле, если
х{ = a^tx + ... + aintm i = 1,..., n
суть элементы данной базы X и
*ь = h\xi + • • • + ^Л/Л» Л = 1.- • •. п>
то элементы *lf...f *w непосредственно даны условиями
j i
Так как матрица коэффициентов || bhi\\ унимодулярна (как обратная матрица
к матрице || aih\\), то 7Ь..., Тп образует базу группы [tlt...t t^, что и
требовалось доказать.
5:4. Сопряжённые гомоморфизмы. Пусть даны решётки
Л-К...., $ и В-[if /g|.
Гомоморфизм / решётки Л в решётку В и гомоморфизм g решётки В
в решётку Л называются сопряжёнными лгежду собой,если для двух
любых элементов х£А пу£В имеем
(/(■Ф» *=(*•* (У)).
Относительно сопряжённых гомоморфизмов докажем следующую
теорему:
[5: 4]. Пусть
Х= {xi хр}. Х*={х~ъ.. .чх"р}
— пряженные базы решётки Л, a
— сопряжённые базы решётки В\ пусть f и g— сопряжённые
гомоморфизмы (соответственно А в В и В в А); пусть, наконец,
ч
f(*i)= 2<4/J> /=l,...,/7.
Тогда
g(yj)= ^ijXi, У= 1 q.
i=l
Для доказательства достаточно на основании [5:21] убедиться в том, что
— р —
для любого /= 1 q элементы g(yj)£A и Yf^x^^A имеют одни и те же
ковариантные компоненты в базе X. Вычислим эти компоненты:
(g Gj) • xh) =-(xh-g (у})) = (/ (xh) Gj) =
« _ J*
- (2 сЛ^А *^) = Zichk(yk -Уз) = O/i
41*

644
АБВЛЕВЫ ГРУППЫ
И
р р —
( 2 СЧХ* ' ХЪ> = 2 cijixi ' ХЪ) = Chj
что и требовалось доказать.
Замечание. Из только что выведенной формулы
(gGj)'*h) = chj
следует, что су, будучи у-й контравариантнои компонентой элемента Дх^)
в базе К, есть в то же время /-я ковариантная компонента элемента g(yj)
в базе X.
5:5. Решётки по простому модулю т.
Определение [5:5]. Обозначим через m[tb... > tn] группу,
элементами которой являются все линейные формы ^aih* гДе h СУТЬ данные
«переменные», а коэффициентами являются вычеты по простому модулю т\
группа m[tv ..., tn] называется решёткой ранг л л*) по модулю т.'
Сами эти переменные tb...,tn образуют начальную базу решётки (при этом
мы отождествляем t$ с линейной формой 1 • ^, где 1 есть единичный
элемент тела Jm).
Определения скалярного произведения контравариантных и ковариант-
ных компонент, сопряжённых баз и сопряжённых гомоморфизмов, а также
относящиеся к этим понятиям теоремы [5:3], [5:4] остаются в силе
(вместе с их доказательствами, которые даже несколько упрощаются от
того, что вместо кольца J нам теперь дано тело Jm).
*) Ранг группы m[tlt..., tn] по простому модулю т (арт. 3:3)
действительно равен л.

ПРИБАВЛЕНИЕ II.
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЙ.
Предварительные замечания. В этом прибавлении собраны
некоторые применяемые в этой книге определения и теоремы многомерной
аналитической геометрии. Предполагается, что читатель владеет этим
предметом примерно в объёме книги Шрейера и Ш п е р н е р а «Введение
в линейную алгебру в геометрическом изложении». В соответствии с этим
многие доказательства предоставляются читателю.
При вычислениях с точками я-мерного пространства мы будем
пользоваться векторными обозначениями:
Если а и b суть точки пространства Rn с координатами ос1э а2,.. .,ам,
соответственно рх, Рг»-"» Рп т0 а+ b есть т°чка с координатами
«l + Pl» а2+ Р2.-••,<%+Рп-
Далее, Хя есть точка с координатами
XallXoc2,.. .,Xan.
Под \а\ мы понимаем число 1 / Va?« Таким образом, расстояние между
точками а н b есть
р(в, д) = | a _ * | .
При этом аксиома треугольника р(с, a)< p(ct b) + р(£, а) записывается
в виде
|*-а|<|<?-*|+ !*-«!.
или по замене с — ЬнаапЬ~а на b
|a+6| <la| + |*| .
Далее имеем
|Ха| = |Х|.|*|.
Комбинируя это соотношение с неравенством треугольника, получим
12м«|<2М-Ы-
§ 1. Пространство Rn и его плоскости.
1:1. Эвклидово «-мерное пространство обозначается в этой книге всегда
через Rn. Его /--мерные подпространства 0О<!я обозначаются через /?*",
иногда, впрочем, через Хг или Yr и называются r-мерными плокостями
пространства Rn. Само пространство Rn является своей ^единственной
/г-мерной плоскостью («несобственным подпространством»).
Всякая (п—1)-мерная плоскость Rn~l пространства Rn разбивает Rn
на два открытых полупространства Н? и Щ\ если плоскость /?*-i дана
уравнением
aiXt+...+ anxn = 0,

b4t> НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЙ
то открытые полупространства //£* и Н^ определяются неравенствами
а\.х\ + • • • + опхп>0 и #1*1+• • •+Яп-%<0- Говорят, что две точки
пространства Rn лежат по одну сторону от плоскости /?w_1, если они лежат
в одном и том же полупространстве, определённом плоскостью JR^-1; если
же одна из данных точек лежит в одном полупространстве, а другая в
другом, то говорят, что они лежат по разные стороны от плоскости Вп~1.
Замыкание открытого полупространства Щ, /=1,2, т. е.
Щ = Щ\Ь№-\ / = 1,2,
называется замкнутым полупространством.
1:2. Линейная независимость точек. Барицентрические координаты.
Точки а0, 0i,..., аг пространства Rn называются «линейно
независимыми», если они не лежат ни в какой плоскости размерности <г.
В соответствии с этим каждые я+ 2 или более точек пространства Rn
линейно зависимы.
Если точки а^ i = 0, ...,/•, имеют координаты х^\ xf\ ...,л^п), то их
линейная независимость эквивалентна тому, что матрица
из одновременного вы-
имеет ранг г. Этот
полнения равенств
и
следует, что
факт
/*<£)... *<»>1\
U>..4*««iJ
можно выразить ещё так:
Х0д0 -(-...-{- lrar = 0
Х0 + Xi -j- ... + Xr = 0
Х0 = л! = ... = Хг = 0.
Через всякие /•+ 1 линейно независимые точки а0, alf ...,ar проходит одна
и только одна r-мерная плоскость — плоскость R (а0, . ..,яу) «натянутая» на
точки до» аъ •.•!#,•. Она содержится во всякой плоскости R8, заключающей
точки а0, аь • • •> аг-
Барицентрические координаты. Плоскост ь R (д0» • • •, аг) со"
стоит из тех точек пространства Rnt которые могут быть представлены
в виде
(1:2) а = ^о + f^i + -. - + fV*r
при дополнительном условии, что
(1:21) f*o+f*i+...+P'rel;
с другой стороны, числа [а0, ...,^г однозначно определены точкой а и
соотношением (1: 2), (1 :21); их называют «барицентрическими
координатами» точки а в координатной системе (#0> • • • > аг)> Это обозначение,
введённое Ф. А. Мёбиусом, имеет следующее основание: иод «материальной
точкой» пространства Rn понимают точку с отнесённым к кей
действительным числом а — «массой» материальной точки; если даны материальные
точки ai с массами а^ и щ = j -*—: , то точка (1:2) есть по опре-
с0 + • • • + ат
делению центр тяжести этого распределения масс.
При этом числа с^ могут и не быть положительными. Они могут быть
любыми действительными числами, удовлетворяющими условию
%+ .-• +<угФ°-
1:3. Теорема о пересечениях и линейных замыканиях. Под
«пересечением» двух плоскостей R>\ Rs пространства Rn мы, как обычно,

§ 1]
ПРОСТРАНСТВО Rn И ЕГО ПЛОСКОСТИ
647
понимаем множество точек, общих обеим этим плоскостям; плоскостью
«натянутой» на Rr и R8, или, кратко, «линейным замыканием» двух
плоскостей называем плоскость наименьшей размерности, коюрая
содержит как Rrt так и R1; однозначность её определении очевидна.
Легко доказываются следующие теоремы:
[1:31]. Пересечение плоскостей Вг и В8 либо пусто, либо есть
плоскость Rd% где d^r-\-s — п.
[1 :32]. Размерность h линейного ,амыкания плоскостей Вг и Bs
удовлетворяет неравенству: h < г + 5 + 1.
[1 :33]. Если пересечение плоскостей Вг и Bs не пусто, п.о d-\-h~
= г + 5.
Так как всегда п^п, то теорема [1 :31] содержится в [1; 33].
1:4. Общее положение.
Определение. Множество точек Вп по определению
находится «в общем положении», если для каждого числа г<!я + 1
всякие г точек данного множества линейно независимы.
Из теорем предыдущего артикула следует:
[1 :41]. Пусть точки ао, ...,ar, bo, ...,ЬЯ находятся в общем
положении; пусть r</z, s <!/г. Тогда для пересечения и линейного замыкания
плоскостей Вг = В(а0,.. .,аг) и Rs = B(ho, ..., bs) имеют место такие
утверждения:
Если г + s < я, то линейное замыкание имеет размерность г \ s + 1,
а пересечение пусто. $
Если г-\ s^h, wo линейное замыкание имеет размерность п (оно,
таким образом, совпадает с пространством Rn), а пересечение либо пусто,
либо имеет размерность r-\-s — п.
Всякое конечное множество точек можно при помощи произвольно
малого сдвига привести в общее положение, другими словами, ил'еет место
предложение:
[1:42]. Пусть {ao,...,as} — произвольное конечное множество точек
в Вп и г — положительное число. Тогда существует множество точек
{а'0, ...ya's} в общем положении, причём
p(a'i, aiXE> гДе ' = 0, 1, . ...5.
Доказательство. Положим а0 = я0- Пусть для / < т < s ■— 1 точка
ai£0(aif e) уже построена так, что #0, ...,ат находятся в общем
положении. Тогда выбираем точку ат^х £ 0(ат+ь е), не лежащую ни в одной из
плоскостей B/(ai, ...,ai)f где /о,...,/г не превосходят т, и г<^п. При
m==s — 1 наша цель достигнута.
Если данные точки aQt ...,аг линейно независимы, т. е. не лежат ни
в какой плоскости размерности <г, то то же верно и для любых точек
#0'--#»flr' Достаточно мало отстоящих, соответственно от а0,...,аг. Из
этого простого замечания следует
[1 :43]. Если точки a0t ...,ак находятся в общем положении, то
существует такое о>0, что и любые точки aQ, ...,ак, удовлетворяющие
условиям р(аг-, я^)<о, / = 0, 1, ...,&, находятся в общем положении.
1:5. Аффинные отображения. По поводу определения аффинных ото
бражений пространства Rn в себя см., например, Шрейер-Шпернер, § 13.
Из свойств аффинных отображений мы здесь упомянем в первую очередь
инвариантность центра тяжести, легко устанавливаемую
простыми вычислениях и: если дано аффинное отображение С пространства В11
самого в себя и если а — центр тяжести материальных точек а}.,
k = 0, 1, ..., г, с массами тъ то С {а) будет центром тяжести материальны\
точек С(аф с теми же массами т^

648 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Замечание. При этом предполагается: если C(ah) = С(ак) = Ь% то
в точку Ь помещается масса тк-\-тп.
Из инвариантности центра тяжести следует:
[1:51]. Если в Rn даны два конечных множества точек: множество
до ап, состоящее из п + 1 линейно независимых точек, и множество
&о* •••>^те» то существует единственное аффинное отображение С
пространства Rn на собственное или несобственное линейное подпространство
пространства Rn, переводящее точки до, ...,flw, соответственно Ь0,...,Ьп.
Это отображение С мы получим, поставив в со )тветствие произвольной точке
а с барицентрическими координатами {^.••,1% (взятыми по отношению
к координатному «остову» (ао,...,ап)) центр тяжести масс ^0f...,fxw,
помещённых в точках bo,...,bn.
Аффинное отображение называется собственным или
несобственным в зависимости от того, ярляется ли оно взаимно однозначным
или нет. Собственные отображения и только они суть отображения на Rn.
Они могут быть охарактеризованы тем, что отображают всякую линейно
независимую систему п +■1 точек пространства Rn на линейно независимую
систему, состоящую также из п-\-\ точек.
Аналитически это условие выражается так:
Аффинное отображение С, заданное при помощи соотношений
(1:51) х\ = u{\)Xl + . ..+ ufxn + щ isl л
(причём Xi и х/ суть координаты точек прообразов и соответствующих
образов), тогда и только тогда является собственным, когда
детерминант отображения отличен от нуля:
det С-
«<{>.
. и j
в 0>.
п
п
Ф0.
Аффинное отображение называется положительным, если его
детерминант положителен, отрицательным — если его детерминант
отрицателен. Это определение законно, так как знак детерминанта аффинного
отображения не зарисит от выбора той или иной системы координат.
Пусть С^ 0<!6<;i есть непрерывно зависящее от параметра *) 6
семейство собственных аффинных отображений пространства Rn на себя. Так
как детерминант отображения С^ есть непрерывная функция от 6 и,
следовательно, не обратившись в нуль, не может изменить знак, то все
отображения Сд, в частности, С0 и С\% имеют один и тот же знак.
Очевидно, тождественнее отображение С0 пространства Rn во всякой
системе юординат имеет детерминант -f-1; поэтому всякое аффинное
отображение Сь которое может быть преобразовано в тождественное
посредством непрерывной деформации Cq (где все Cq суть собственные аффиьные
отображения Rnua себя), положительно. В качестве примера отрица!ель-
ного аффинного отображения пространства Rn на себя рассмотрим
симметрию относительно (п—1)-мерной плоскости Rn~1dRtl.
Делая плоскость R11-1 координатной плоскостью хп = 0, можем
определить это отображение равенствами
Xf{=sXi ДЛЯ / = 1 («— l)i
откуда сразу видно, что детерминант нашего отображения в выбранной
системе координат равен —1 и, значит, всякое аффицное отображение, кото-
*) Глава 1, арт. 7;4V

§ 1] ПРОСТРАНСТВО Rn И ЕГО ПЛОСКОСТИ 649
рое можно перевести в симметрию относительно (п—1)-мерной плоскости
непрерывной деформацией Cq, при которой все С% являются собственными
аффинными отображениями пространства Rn на себя, отрицательно.
Применим только что рассмотренные примеры к доказательству следующей
теоремы, которая существенно применяется в главе 7:
[1:52]. Пусть в (п-Х)-мерной плоскости Rn~lczRn дана система
из п линейно независимых точек еь ... чеп. Пусть, кроме того, в Rn
дани две точка вп и erf', не лежащие в плоскости Rn~l. Тогда
аффинное отображение С$, переводящее линейно независимые точки е^у eit ..., е„
соответственно в е®", еъ ..., еп, положительно, если точки erf и е^'
лежат по одну сторону плоскости R4'1, и отрицательно—в
противоположном случае.
Теорема [1:52] является члстным случаем следующего предложения
(которое используется в главе 10):
[1:521]. Пусть С есть аффинное отображение пространства Rn на
себя, при котором некоторая (п—\умерная плоскость Rn~1
отображается на себя. Аффинное отображение плоскости R™-1, порождённое
отображением С, обозначим через С.
Обозначаем через е число, равное -\-\, если при отображении С
каждое из двух полупространств, на которые Rn разбивается плоскостью
R*1"1, отображается на себя, и равное — 1, если при отображении С
каждое из этих полупространств отображается на другое
полупространство. Тогда для знаков отображений С и С имеем соотношение
sgn С- sgn С = е
(в частности, при sgn С = +1 имеем sgn С = е, откуда и вытекает теорема
[1:52]).
Доказательство теоремы [1:521]. При п = 1 теорема очевидна;
пусть я;>2. Возьмём sRn систему координат хь ..., хп так, чтобы плоскость
Rn~l была координатной плоскостью ^ = 0. Пусть в выбранных
координатах отображение С записывается в ви.ле
п
х\ = 2Л«Л» / = 1, 2,... ,я.
Так как плоскость #w-i переходит в самое себя, то при х\ = 0 и любых
*ъ --->хп имеем х{ — 0, т. е. а^х^ + ... + ainxn = 0 ПРИ любых х^ • • •, xv
и, значит,
я12 = ... = а1п = 0.
Другими словами, отображение С имеет вид '
х\ — а\\хь
Х2 = <3,21ЛГ1+ • • • + #2п-%»
хп ~ атх\ ■+■•••+■ аппхп*
откуда следует, что det С = atl det С
Но знак коэффициента аи совпадает со знаком е так что sgnC = e sgn С
что и требовалось доказать.
Аффинное отображение, осуществляющее транспозицию двух каких-
нибудь из числа заданных п +1 линейно независимых точек e$,...,en,
т. е. переводящее тот и е^ ...Ле^ ...,г%, ...,еп соответственно в
*?о, . •., еъ ... , ei en, отрицательно. Для того чтобы убедиться в этом,
достаточно взять аффинную систему координат в пространстве Rn,
единичными координатными векторами которой были бы векторы ecelt ..., е§е ,
при начале е0: детерминант нашего отображения, в этой координатной
систему очевидно, равен —1?

650 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕС(ОЙ ГЕОМЕТРИИ
Из этого замечания следует:
[1:53]. Пусть точки *о.---» вп линейно независимы в Rn. Знак
аффинного отображения, осуществляющего данную перестановку
ео ... еп )
е' е • '
го"' V
этих точек, совпадает со знаком этой перестановки.
1:6. Определение аффинного отображения пространства Rn
аффинными отображениями двух плоскостей Хр и Yq,p-{-q = n.
Пусть р + q = п и Хр,уУ — две плоскости в /?п, пересекающиеся в
единственной точке о, так что линейное замыкание этих плоскостей
совпадает со всем Rn.
Пусть даны аффинные отображения Ct и С2 соответственно А^ и F3
на себя, удовлетворяющие условию С\ (о) = С2 (о) = о. В этих условиях
существует единственное аффинное отображение С пространства R>1
на себя, совпадающее на Хр и У^ соответственно с С± и С2. Отображение
С называется отображением, порождённым отображениями С\ и С2 или
просто продолжением этих отображений на Rn.
Доказательство. Если в Rn выбрать систему координат с началом
о так, что первые р её единичных векторов лежат" в ХР, а остальные —
в К#, и задать отображения С\, С* в координатах (хь ..., хр),
соответственно (хр+ъ ...,хп) равенствами
хх = а11х1+.. .-f а1рхр хр^х = ар+1, р+1хр+1-{-. ,.-\-ар+1, пхп
ХР == ap\.Xl\~' • --\гаррХр Л П == аМ)р + 1^+1+' • • +ДП« ПХЮ
то искомое отображение С запишется в координатах (jclt ,.,, лг^, ..., лгп) так:
*i =aii*i+...+<*i/r*/>,
•*р == apixi~b~ • • * + аррхр>
-*"n = #n»p+l-*i?+ГТ« • * "Т" annxrv
Следствие
(1 :61) detC = det£rdetC2.
§ 2. Выпуклые множества.
2:1. Определение выпуклых множеств. Прямая, определённая двумя
точками а, Ь, есть множество всех точек вида \а-\-р.Ь, где X+^=l (см. арт. 1:1).
Подмножество этой прямой, определённое условиями X ;> 0, ja]>0,
соответственно Х>0, [х>0, называется замкнутым отрезком я£, соответственно
открытым отрезком (ab).
Определение [2:11]. Множество М точек пространства называется
выпуклым, если оно вместе со всякими своими двумя точками а и b
содержит и весь отрезок аЬ.
Простейшие примеры выпуклых множеств суть: всё пространство Rn
и его плоскости (любого числа измерений), полупространства, отрезки,
одноточечные множества, пустое множество.
Определение [2: 12]. Замкнутое ограниченное выпуклое
множество, лежащее в Rn и содержащее внутренние точки (относительно Rn),
называется п-мерыым выпуклым телом.

§ 2]
ВЫПУКЛЫЕ МНОЖЕСТВА
651
2:2. Простейшие свойства выпуклых множеств.
2:21. Всякое выпуклое множество связно.
В самом деле, любые две точки р и q выпуклого множества М
принадлежат связному подмножеству множества М (именно отрезку /?#). Значит,
М связно. Непосредственно из определения [2:11] следует:
[2:22]. Пересечение произвольного (конечного или бесконечного)
множества выпуклых множеств выпукло.
Далее:
[2 :23] Если М выпукло и о > О, то О (Му о) выпукло.
Доказател ь с т в о. Пусть Ьь Ь2 — точки окрестности О (М, о) и
b — точка отрезка Ьф2\ нужно показать, что Ь принадлежит к О (М, о).
В М существуют точки аъ я2» такие, что | Ьх— £i|<o, \b2— л2|<С^
То, что b есть точка отрезка b1b2, означает, что
b^lbx + iLb* Х>0, р->0, Х + р. = 1.
Если обозначить через а точку X а^-^- \ха* отрезка а\а2, то
b — а = X {Ьг — ах) + [а (#2— #2),
откуда
| 6 — а |< X | ^ — я г | + р. | Ь2 — а21< (X + р,) о = о;
так как а£М (вследствие выпуклости М), то из последнего неравенства
следует, что Ь^О(М, о), что и требовалось доказать.
Следствие. Открытый шар О(р, о) есть выпуклое множество.
Пересечение всех множеств 0(М, о) с произвольными числами о>0 есть
замыкание множества М. Поэтому из теорем [2:22] и [2:23] следует:
[2:24]. Замыкание выпуклого множества выпукло.
Следствие. Замкнутый шар есть выпуклое тело.
2:3. Внутренние и граничные точки выпуклого множества.
[2:31]. Пусть М — выпуклое множество, а — произвольная точка
множества М, b — внутренняя точка множества М (относительно
Rn^M), с — точка отрезка ab, отличная от а. Тогда с есть внутренняя
точка множества М.
Доказательство. Существует о>0, такое, что 0(b, o)ciAf; далее
имеем: с = X а + ц Ь, где Х-|-р.= 1,Х;>0, и так как с ф а, то \х > 0.
Докажем, что О (с, \хо) cz M.
Если d£0(c, \xb)t т. е. если | d — с | = | d — \а — уЬ |< \хЬ, то
i — d — — а — М<Го;
следовательно, точка
d — —d a
IX [X
содержится в О (bt o)czAf. Так как
d = \а 4- [Ad',
то d лежит на отрезке adr ciM, что и требовалось доказать.
Следствие. Множество внутренних точек выпуклого множества
выпукло.
Если а — граничная точка, b — внутренняя точка множествами, то,
в частности, по теореме [2:31] на отрезке ab не может лежать никакой
отличной от а граничной точки; отсюда имеем:
[2:32]. На каждой полупрямой, выходящей из внутренней точки
ограниченного выпуклого множества М, лежит одна и только одна точка
границы множества М,

652 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМ1ТРИИ
Из [2:32], в свою очередь, вытекает:
[2:320]. Если выпуклое множество MaRn имеет внутренние точки,
то множество внутренних точек этого множества М плотно в М (и
открыто в Rn).
2:4. Число измерений выпуклого множества Q есть по
определению наибольшее число г, обладающее тем свойством, что в Q можно
найти г4-1 линейно независимых точек я0,...,#г. Если в Q выбраны
линейно независимые точки аъ,...,а„ то р Q содержится в плоскости
Rr(ao,...,ar) (так как если бы в Q была точка а, не принадлежащая к
этой плоскости, то в О имелись бы г ~\-2 линейно независимых точек
я, я0, .... аг). Множество всех точек x£Rr (ап. ...,яг), барицентрические
координаты которых в системе ап,...,яг положительны, есть открытое
множество пространства Rr (#0,---.яг), содержащееся в Q. Итак:
[2:41]. Всякое выпуклое множество Q числа измерений г лежит в
однозначно определённой r-мерной плоскости, не су щей плоскости
выпуклого множества Q, и содержит по отношению к этой
плоскости внутренние точки.
Когда мы говорим о внутренних точках выпуклого
множества Q, не упоминая о том пространстве, по отношению к которому
эти точки являются внутренними, то всегда имеем в виду внутренние точки
выпуклого множества Q относительно его несущей
плоскости. Из [2:31] следует, что внутренние точки выпуклого множества Q
образуют r-мерное выпуклое множество, плотное в Q.
[2:42]. Все n-мерные выпуклые тела гомеоморфны между собой.
Доказательство. Докажем, что /г-мерное выпуклое тело Qn cz Rn
гомеоморфно «-мерному замкнутому шару Еп. Возьмём за центр шара
какую-нибудь внутреннюю точку о выпуклого множества Qn. Пусть х —
произвольная, отличная от точки о точка Qn. Обозначим через р (х) лежащую
на луче ох граничную точку Q'1, через q (х) — точку, в которой луч ох
пересекает границу шара Еп; через С (х) — точку, которая делит отрезок
oq(x) в том же отношении, в котором точка х делит отрезок ор (х).
Получаем отображение С выпуклого тела Q4 на шар Еп; предоставляем читателю
провести доказательство того, что это отображение взаимно однозначно и
взаимно непрерывно (см., напр., Александров-Хопф, стр. 601—602).
§ 3. Выпуклое замыкание. Симплексы. Выпуклые многогранники.
3:1. Выпуклое замыкание произвольного множества М a Rn
определяется как пересечение всех выпуклых множеств, содержащих М. По
теореме [2:22] оно является выпуклым множеством. Очевидно, М
совпадает со своим выпуклым замыканием тогда и только тогда, когда М
выпукло.
[3:11]. Диаметр *) выпуклого замыкания М* множества М равен
диаметру М.
Доказательство. Достаточно показать следующее: если число В
обладает тем свойством, что \х—j/|<8 для любой пары точек х, у из
М% то \а — #|<о для любой пары точек a, b из М*.
Пусть а и b— две фиксированные точки из M*t далее, пусть х —
произвольная точка из М. Так как \х—_у|<одля всех точек у£М, то
MczO(xt о) вследствие выпуклости 0(х, о) и по определению выпуклого
замыкания имеем Ж* cz О {х, о), в частности, а £ О (х, о), следовательно,
х£0(а, о). Это верно для любой точки х£М, так чго МаО(а, о), значит,
*) Диаметром множества называется верхняя грань расстояний между
двумя произвольными точками этого множества,

§ 3] ВЫПУКЛОЕ ЗАМЫКАНИЕ. СИМПЛЕКСЫ. ВЫПУКЛЫЕ МНОГОГРАННИКИ 653
и М*аО(а, о) и, в частности, b£0(a, Ь). Это означает, что \а — Ь\<^Ь%
что и требовалось доказать.
3:2. Выпуклые замыкания конечных множеств. Определение
симплекса и замкнутого симплекса. Мы предоставляем читателю доказать
следующую теорему *).
[3:21]. Выпуклое замыкание конечного множества точек д0» •••• **s
пространства R^ состоит из всех точек а £ R}\ которые могут быть
представлены в виде
(3:21) а = [х0д04- ... +р8*а
при произвольных неотрицательных p.0f..,p-s, дающих в сумме 1.
Другими словами, выпуклое замыкание конечного множества a0,...,tftS
состоит из центров тяжести всевозможных неотрицательных масс,
помещённых соответственно в точках ao,...,as. В частности, если точки
ао,...,ая линейно независимы (из чего следует, что s^n)t то выпуклое
замыкание множества {a0,...,as> состоит из всех точек плоскости
R* (яо,.. -,fls), барицентрические координаты которых в системе {а0,.. .,as}
неотрицательны.
[3:22]. Пусть а^...,аг — линейно независимые точки в Rn (значит,
г^п). Множество точек плоскости Rr(a^ ..., аг), барицентрические
координаты которых в системе {ctQt...,ar} 'положительны, есть выпуклое
открытое в Rr (дсь- •«» аг) множество, называемое r-мерным
симплексом с вершинами ао,...,яги обозначаемое через | uq ... аг\. За-
•) Доказательство (подробно изложенное в книге Александров-Hopf,
стр. 602—604) сводится к следующему. Обозначим множество всех точек
(3:21) через [я0.-..> #s]» а выпуклое замыкание множества {а0, ..., а8}
через {д0, ..., as}*.
Требуется доказать, что {aQt ..., as}* = [a0, .. .,* as]. Для этого
сформулируем следующие три леммы:
[3:211]. Множество [я0, ..., as] выпукло;
[3:21?]. Пусть 0O<s. Для любой точки а £ [tf0, ...ta8] можно найти
точки а' £ [л0, ...,дг]иа"^ [#r+i> •••» аь\ такие, что а лежит на отрезке
[3:213]. Если точки aQ% ..., as содержатся в выпуклом множестве Q, то
[я0, ...,а,]с:0.
Лемма [-5:211] выводится из определений автоматическим вычислением.
Лемма [3: 212] доказывается так. Если а = psaQ -}- ... + lV*s« то в
предложении
v = Sn^o, Х" = 2 пФО
о г-и
полагаем
о
*" = 2а "F а*>
тогда tf = XV-f-X'V. Если же, например, X'= 0, то а £ [er+t, ..., До] и
лемма тривиальна. Лемма [3:213] доказывается индукцией по числу s. Если
а £ \с^ ...,#s] и #0 £ <?,..., яя £ Q, то берём по лемме [3:212] точку
&" € [^1» •••• аЛ ток, чтобы л £ а0а". По индукционному предположению
[tflf ..., яч] <= <?; так как #0 £ <?, то в силу выпуклости Q т'меем а £ #0я"с Q,
что и треб» валось доказать. Из лемм [3:211] и [3:213] непосредственно
Следует [3:21J. l * * ■ Г

654 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
мыкание симплекса | ао.. .лг|, совпадающее, очевидно, с выпуклым
замыканием множества дочек а0»---|Яг называется замкнутым
симплексом с вершинами a<v,#r и обозначается через д0 • • • <V
Если aiQ, .... aipt 0 </></% суть некоторые среди вершин a^...,ar
симплекса \а0 ... аг\, то /7-мерный симплекс \а^ ... а$ \ называется /7-
мерной гранью симплекса | ао ••• Qr\- В частности, сам r-мерный симплекс
1^0 ••• аг\ является своей единственной r-мерной гранью. Эта грань
называется несобственной гранью r-мерного симплекса; остальные грани
называются собственными.
Две грани | а^ ... щ | и \а^ ... aj \ симплекса [ д0 ••• <*г\
называются противоположными, если каждая вершина симплекса \ао...аг\
есть вершина одной и только одной из двух граней. Очевидно,
если/7-мерный и ^-мерный симплексы являются противоположными гранями г-мер-
ного симплекса, то р + q = г— 1.
Легко доказывается:
[3:23]. Если Тр = \а^0 ... aip\ и Tq = \aj0 ... aj \ — две
противоположные грани симплекса Тг = | я() ... аг |, то каждая точка симплекса
Тг лежит на одном и только одном открытом прямолинейном отрезке,
соединяющем некоторую точку симплекса Тр с некоторой точкой
симплекса Tq»
Из теоремы [3:11] далее следует:
[3:24]. Диаметр симплекса | а0 ... аг\ равен наибольшему из чисел
Р fa, Д/)«
3:3. Выпуклые многогранники. Так как полупространства данного R11
суть выпуклые множества, то пересечение любого числа полупространств
(открытых или замкнутых) выпукло.
[3:31]. Ограниченное непустое множество данного Rn, являющееся
пересечением конечного числа открытых (соответственно замкнутых)
полупространств этого Rn, называется выпуклым многогранником
(соответственно замкнутым выпуклым многогранником).
Замыкание выпуклого многогранника есть замкнутый многогранник
того же числа измерений; обратно, множество внутренних точек замкнутого
выпуклого многогранника есть выпуклый многогранник.
Пусть в Rn дан л-мерный выпуклый многогранник Qn. Пересечение
всякой (п — 1)-мерной плоскости Rn'"1ciRn с Q* и с Qn выпукло. Плоскость
Rn-i называется опорной плоскостью многогранника Qn9 если она,
пересекаясь с Qnf не содержит ни одной точки Qn. __
Пересечение всякой опорной плоскости Rn~l с границей Qn\Qn
многогранника Qn совпадает с множеством R*1"1 fl Qn и потому есть
замкнутый вмпуклый многогранник Qr, г < п — 1, если при этом г = п—1, то
Qr называется (п — 1)-мерной гранью многогранника Qn.
Итак, (п—\)-мерной гранью выпуклого многогранника Qn называется
всякий (п — \)-мерный многогранник, являющийся множеством
внутренних точек какого-либо замкнутого многогранника, получающегося как
пересечение Q*1 с некоторой опорной плоскостью многогранника Qn.
Далее, (п — 2)-мерные грани (п — 1)-мерных граней Qn называются
(п — 2)-мерными гранями многогранника Qn и т. д. Нульмерные грани
выпуклого многогранника Qn суть точки и называются вершинами
многогранника Qn.
Имеет место следующая теорема:
[3:32|. Никакие две грани выпуклого многогранника не имеют общих
точек, соединение всех г-мерных граней выпуклого многогранника Qn,
0<г</г—1, есть граница Qn\Qn этого многогранника.
Замечание. Сам многогранник Qn также причисляется к числу,
граней в качестве единственной л-мерной или несобственной грани.

§ 41
центр тяжести Симплекса
655
Доказательство теоремы [3:32] предоставляем читателю, предупреждая
о том, что доказательство это, не представляя серьёзных трудностей, все же
довольно длинно и утомительно *). Заметим, наконец, что наименьшее
возможное число вершин «-мерного выпуклого многогранника есть /г + l.
Выпуклые /г-мерные многогранники, число вершин которых равно /г-{-1.суть
не что иное, как /г-мерные симплексы.
§ 4. Центр тяжести симплекса.
4:1. Определение [4:1]. Центром тяжести конечного
множества точек аь...,ак пространства Rn называется точка
Ь = £- (аг + ... + ак\
т. е. центр тяжести системы равных масс, помещённых в эти точки.
Центром тяжести симплекса (и вообще выпуклого
многогранника) мы в этой книге называем центр тяжести множества его
вершин в только что установленном смысле.
4:2. Пусть MaRn — конечное множество диаметра d% состоящее из
k точек; пусть Мг — непустое подмножество множества М\ обозначая
центры тяжести множеств М и М\ соответственно через Ь и Ьъ имеем
(4:20) p(Wl)<^zirf.
В самом деле, если М = {аь- • .,#£}, М^** {#i,.. .,ад. }, (I </гх <&), то по
определению центра тяжести имеем
2 к i h '
значит,
*i-*-£(i**-*i')=-]s-i!<«r-»x
1 J=l L .7 = 1
и
(4:2!) ^-&=^2 2^-^
Среди всех fc&j слагаемых я^ — аг- имеется /гг слагаемых, для которых
./= /<&!, и эти слагаемые равны нулю. Значит, число отличных от нуля
k kx
слагаемых в сумме 2 2 ^ — а^ Равно ^1 — ki = ki(k — 1). Поэтому из
i=i j=i
(4:21) и из предположения \а§—<^|<tf следует
\Н-Ъ\<1ьх k1(k-\)d = ^-dt
что и требовалось доказать.
Следствие [4:2]. Пусть Тп есть /г-мерный симплекс диаметра < d,
пусть Г — грань произвольной размерности (собственная или несобственная)
:) См. Александров-Hopf, стр. 609—614.

656 нЁкотбРЫЕ Сведения из аналитической rECtotefptftf
симплекса Тп\ пусть V — грань симплекса Т. Обозначая центры тяжести
симплексов Т и Т" соответственно через br и Ь'\ имеем
В самом деле, если размерность симплекса V есть г, то по только что
доказанному имеем р(Ь', #")< ■ i d. Но . . < , откуда и следует
наше утверждение.
§ 5. Центральная проекция.
Пусть в Rn дана точка о, которую будем называть центром п р о-
екции. Пусть M^Rn\o. Под открытой (соответственно
замкнутой) проекцией множества М из точки о понимается точечное
множество оМ (соответственно [оМ]) пространства Rn, являющееся соединением
всех открытых отрезков (од;) (соответственно замкнутых ох), где х
пробегает всё множество М.
Пусть N cz Rn\o — какое-либо множество, пересекающееся со всякой
полупрямой, соединяющей точку о с какой-либо точкой х^М в одной
единственной точке тс (х). Ставя в соответствие каждой точке х£М точку
k(x)£N получим отображение тс множества М во множество N.
Отображение тс, а также образ п(М) множества М при этом
отображении называется проекцией множества Af вомножество N аз
точки о. В случаях, когда возможны недоразумения, мы для обозначения
проекции как отображения будем употреблять термин проектирование.
Имеет место следующее предложение, доказательство которого может
быть поедоставлено читателю:
[5:1]. Пусть пересечение множества М с каждой выходящей из о
полупрямой состоит лишь из одной точки. Пусть Мх и уИ2—&ва
подмножества множества М. Тогда проекция пересечения множеств М± и М^
совпадает с пересечением их проекций. При этом под проекцией можно
понимать как открытую, так и замкнутую проекцию.
Казань, 10 декабря 1941 г.

УКАЗАТЕЛЬ
Аксиомы топологического пространства 26
Алгебраическое число неподвижных точек
606, Ы8
Александер 372
Александров 42, 203, 223, 567
База гомологическая 313, 346
— группы 629
— — канонирская 345, 348, 629
свободной 625
— пространства 28
Базы решёток 342
сопряжённые 643
Бикомпакт» бикомпактность 41
Брау*р 41, 68, 187, 203, 566, 568, 588
Бруилимский 567
Бутылка Клейна ПО
Вектор сдвига 605
Вершины симплекса 114
— цепи 261
Вес пространства 29
Взрез 111
Гильберт 584
Гильбертов кирпич 32
1 ипотеза основная комбинаторной
топологии Ш
Гомеоморфизм 33
Гомоморфизм 620
Ф
— CJ, 442
— sl зю
— нормальный 387
Гомоморфизмы ^о и Е$ 265
Граница абсолютная 68
— клетки ^65
— множества 27
— ориен1ированного симплекса 265
— ориеширонанной области 574
— регулярная 68
— симплекса 146
—- йен и 334
у- граница 344
Грани противоположные (симплекса) 145
Грань симплекса 14э
Группа абелева 623
— Бетги 292
— — верхняя 328
__ локальная 455, 456
— — нижняя 292
— круч*ни4 311
— свободная (абелева) 623
— полиэдра 417, 457
А- группа компакта 408
V группа 388
Гуревяч 667
Двоеточие 36
— связное 36
Двойственности закон Александера 490, 518
малый 556
— — — Понтрягина 517, 536
— — Понт 1гина малый 560
Пуанкаре 483, 484
Деформация 67
— Г-цикла 444
— .допустимая 74, 215
— истинного цикла 417
Диаметр множества 652
— пространства 30
Дуга Жорданов-» ,65
— ориентированная 71
— открытая 94
— простая 65
Заклеивание 119, 121
Замывание выпуклое 652
— ко.юинаторное .51
барицентрической звезды 176
комплекса 149
подкомплекса 155
симплекса 1*7
— линейное 647
— множества 26, 30
Звезда 101
— барицентрическая 174, 472
замкнутая 177
— главна^ 175
— открытая 168
— подкомплекса 155
— полуциклическая 101
— циклическая 101
Идентификация (элементов триангуляции
108
Изоморфизм Efl 481
— комплексов остовов 153
Индекс неподвижной точки 606
— пересечения 247, 249, 477, 487
Канонические системы баз 391
Ки> пич гильбертов 32
Классы отображений гомотопические 57
Кнастер 18а
Колмогоров 483
Компакт 41
— сильно связттый 236, 237
Комплекс 9J, 154
— бар щен1рический 473
триангуляции 175
— бесконечный 190
— клеточный 253
— кривой 180
— остовов 107, 149
^ — полный 149
—-— полного симплициального комплекса

658
УКАЗАГЕЛЬ
Комплекс полиэдральный 148
— размерно однородный 100, 315
— саязный 100, 183
— сильно связный 100, 316
— симилициальный 150, 154
бесконечномерный 151
полный 150, 154
д- комплекс 253, 383
Компонента точки 38
— регулярности точки 95
— элемента в комплексе 184
Компоненты ковариантные, контравариант-
ные 6<*2
Контуры поверхности 105
Конфинальная часть (множества, спектра) 511
Координаты 33
— оариценгрические 646
Коэффициент зацепления 500, 501, 549, 554,
564
— инцидентности 250
— кручения 313, 638
Край звезды 101, 155
|барицентрической 174
— поверхности 104
— симпле <са 147
Кратность покрытия 26, 58, 569
Кривая Жордана 65
— элементарная 94
Куратовский 188
Кусок цепи, цикла 172, 264
Леви 567
Лемма Александера 387
— Лебега 60
— Шпернера 188, 191
Лефшец 437, 566
Линия замкнутая 65
— разреза 111
двубережного, однобережного 115
замкнутого 129
Лист Мёбиуса 109, 121
Ломаная 185
Мазуркевич 188
Матрица гомоморфизма 631
Менгер 203
Метрика пространства 30
Многогранник выпуклый 654
— замкнутый 654
Многообразие замкнутое 181
— топологическое 48
h многообразие 467
Множество выпуклое 650
— замкнутое 26
— неограниченное 505
— одноточечное 39
— открытое 26
— плотное 27
— упорядоченное, частично упорядочен.юе
50, 51
Нерв 158, 159
Носитель относительного цикла 437
— симплекса 189
Нуль-отображение 588
Область пространства 38
ориентированная 245
полиэдральная 574
Образ ориентации 422
— цикла 421
— элемента множества 24
Образующие элементы^группы 637
Общее положение точек 647
цепей 541
Окрестность звёздная 167
— множества 39
— сферическая 30
Окрестность точки 27
е-окрестносгь 30
Окружность топологическая Ш
Оператор А 265
— v 334
Операция выметания 205
— разреза 115
Ориентация границы симплекса 572
-— когерентная 317
— остова 242
— пространства 240
— псеадомногообразия 319, 320, 422
— симплекса 242
— сферы 333, 423
— треугольника 122
Ориентируемость поверхности 122—124
Остоа 107
— ориентированный 242
— симплекса 145
— упорядочеьнык 242
е-остов 396
Отображение аффинное собственное,
несобственное 647, 648
— барицентрическое 205, 209, 211
— множества 24
— непрерывное 32
цепи 5
— нормальное 386
— отрезка простое 76
— подобия 50
— .имплициальное 108, 152
допустимое 327
— существенное 215
— топологическое 33, 577
«•отображение 203, 204, 209
Отображения гомологичные 57
— е-гомологичные 415
— симплициальные гомологичные 310
Пересечение множеств 24
— плоскостей 646
Пирамида 164, 282
Плоскость опорная 654
— проективная ни
— г-мерная 643
Поверхность замкнутая 102
— Клейна ПО
— Мёбиуса 109
— неориентируемая, ориентируемая 124
— простая 133
нормальная 135
— рода р 138
— с краем 104
Подгруппа (собственная, несобственная) 621
Подкомплекс замкнутый 100, 155
— клеточный 255
— открытый 100
Подразделение замкнутого покрытия 226
— комплекса 169
барицентрическое 162, 178
— правильное 380
центральное 172
элементарное 171
— симплекса 170
— барицентрическое 189
— триангуляции 106
— цепи 373
: 1одчинение симплексов 145
Покрытие 25
— замкнутое, открытое 58
е-покрытие 60, 224
Покрытия подобные 58
Поле векторное 580
— направлений 582
Полиэдр 99, 147, 166, 180
Полупространство 646
Понтрягин 157, 448, 470, 502, 503, 567

УКАЗАТЕЛЬ
659
Шоследоватеяьность дезориентирующая 124,
322
Порядок связности 97, 128, 129, 311
— точки относительно замкнутого пути 73
ориентированной кривой 77
цикла 668, 570
Пояс звезды 156
Приближение симплиииальное 424, 575
«-прибли кение 211
Призма 165» 166, 285
Проблема Тумаркина 224
Продолжение цепей, циклов 173, 264
Проектирование 656
Проекционный спектр, проекции 504, 505
Проекция ориентированного симплекса, цепи
— точки 592
— центральная 656
^Произведение скалярное цепей 263
элементов группы 641
— топологических пространств 33
Производная барицентрическая 16J
.Прообраз множества 24
Пространство бикомпактное 41
— гильбертово 31
— дискретное 53
— локально-бикомпактное 41
— метризуемое 33
— метрическое 29
вполне ограниченное 55
полное 54
связное в точке, локально связное 67
— нормальное 40
— проективное 46, 323
— Пуанкаре 471
— со счётной базой (счётного веса) 29
— топологическое 26
— Т0, Tt, T, (хауедорфово) 39
— эвклидово 31
ЦсевДомногообразие 316, 404, 434
— замкнутое 316
— ориентируемое, неориентируемоэ 318, 422,
449
— простое 325, 375
— с краем 316
Радиус-вектор 592
Разложение непрерывное компакта 43
— циклическое группы 638
Размерность бикомпакта 62
— гомологическая 447
— индуктивная 221, 222
— — в данной точке 223
— клеточного комплекса 254
— симплекса 144
^Разность множеств 24
Разрез внутренний, внешний 111
— двубережный, однобережиый 114, 115, 138
— замкнутый 129
— поперечный 111
Ранг группы 624, 633, 636
— решётки 642
Расстояние между точками 29
точкой и множеством 30
ЗРешётка целочисленная 642
Род двубережного разреза 141
— поверхности 137
«Ручка I, II рода 121, 122, 138
«Связность 36
Сдвиг бесконечно малый 439
— канонический 337
относительно покрытия 398
— комплекса 399
.— нормальный 386
#-сдвиг 204, 210
/'<•, ЧГ)-сдвиг 433
«-сеть 56
Симметрия пространства 585
— сферы 586
Симплекс 50, 144, 453
— абстрактный 150
— замкнутый 146, 654
— вырождающийся 145
— неподвижный 598, 601
— ориентированный 242
е-симплекс 396
Симплексы инцидентные 145
Система множеств сцепленная 37
простая 26
— образующих 637
— окрестностей абсолютная 28
топологического пространства 2Э
— подкомплексов фундаментальная 374
— подмножеств 25
— цепей фундаментальная 374
— элементов 25
Системы баз канонических 341, 348
— v-баз 348
— зацепленные циклов 502
Склеивание 44, 108, 154
След эндоморфизма 631, 632
Соединение множеств 24
Спектр 505
Степень отображения 79, 331, 427, 450, 574
Сумма прямая (групп) 621, 622
— симплексов комбинаторная 146 •
Сфера 31
— направлений 582
— нульмерная 333
— ориентированная 423
Сходимость последовательности точек 31
Сходимость равномерная отображений 3&
Тело выпуклое 650
— комплекса 99, 166, 180
—- симплекса ориентированного 243
— цепи 261, 515
Теорема Брауэра 188, 683, 584
— Веблена 487
— деформационная
— Жордана 36, 65, 491
— Жордана-Брауэра 519, 562
— Лефшеца Хопфа 598
— о выметании 207
— об еже 584
— о мостовых 187, 193, 401
— о продолжении 594, 595
— о существенных отображениях 215
— Пуанкаре 571
— П у ан кар е-Б pay эр а 584
— Руше 571
— сложения 219
— Тихонова 40
— существования корней 573
— Урысон! 32, 223
— Фробениуса И7
— Хопфа 588
— Эйлера 97. 128
Тихонов 33, 41
Топология естественная 30
—, определяемая метрикой 30
Тор 34, 45
Точка ветвления 94
— внутренняя 27, 104, 196, 201
— изолированная 27
— концевая 94
— краевая 104
— накопления 27
— неподвижная 201, 683. 584, 602, 606v 607,
610, 611, 614, 618.
— нормализуемая 608
— нормальная неподвижная 60
— обыкновенная 94, 404
— особая 94
(гомологически) 464

«60
УКАЗАТЕЛЬ
Точке особая полиэдра 404
— — поля направлений 582
— предельная 27
— прикосновения 26
Точки линейно независимые 646
Триангуляция 99, 147
— замкнутого симплекса 188
— кривая 102, 180
— поверхности простая 132
— полиэдра 167
— элементарная 325
Урысон 40, 203
Фактор-группа* 622
Формула Хопфа 601
— Эйлера-Пуанкаре 314, 363
Фрейденталь 567
Функция угловая 80
— характеристическая 261
Характеристика векторного поля 580
Хопф (Hopf) 566, 567, 568, 588
Центр проекции 656
— тяжести 646, 655
Цепи гомологичные 270, 271
Цепь множеств 37
замкнутая 37
— комплекса 2Ь9
— одночленная 262
— открытого множества 515
— подразделений 226
Цепь симплекса 515
— целочисленная 259
е-цепь 396
Цепочка симплексов 236, 315
— треугольников 113
Циьл 96
— в точке 453
-— зацепленный 549
— истинный 408, 516
— — открытого множества 516
— клеточного комплекса 270
— непрерывный 421
— нульмерный нормальный 29$
— ориентирующий 422
— относительный 437
V-Цикл 491, 506
Циклы «-гомологичные 396
Число &Г(Ф) 370
— Бетти 97, 401, 455
— лебегово 61
Шар 31
Шаудер 567
Шмидт 65
Эйлерова характеристика 95, 127, 314^
Элемент /г-мерный 200
— обозначенный 25
— цепи 261
Эндоморфизм 621
Ядро гомоморфизма 326