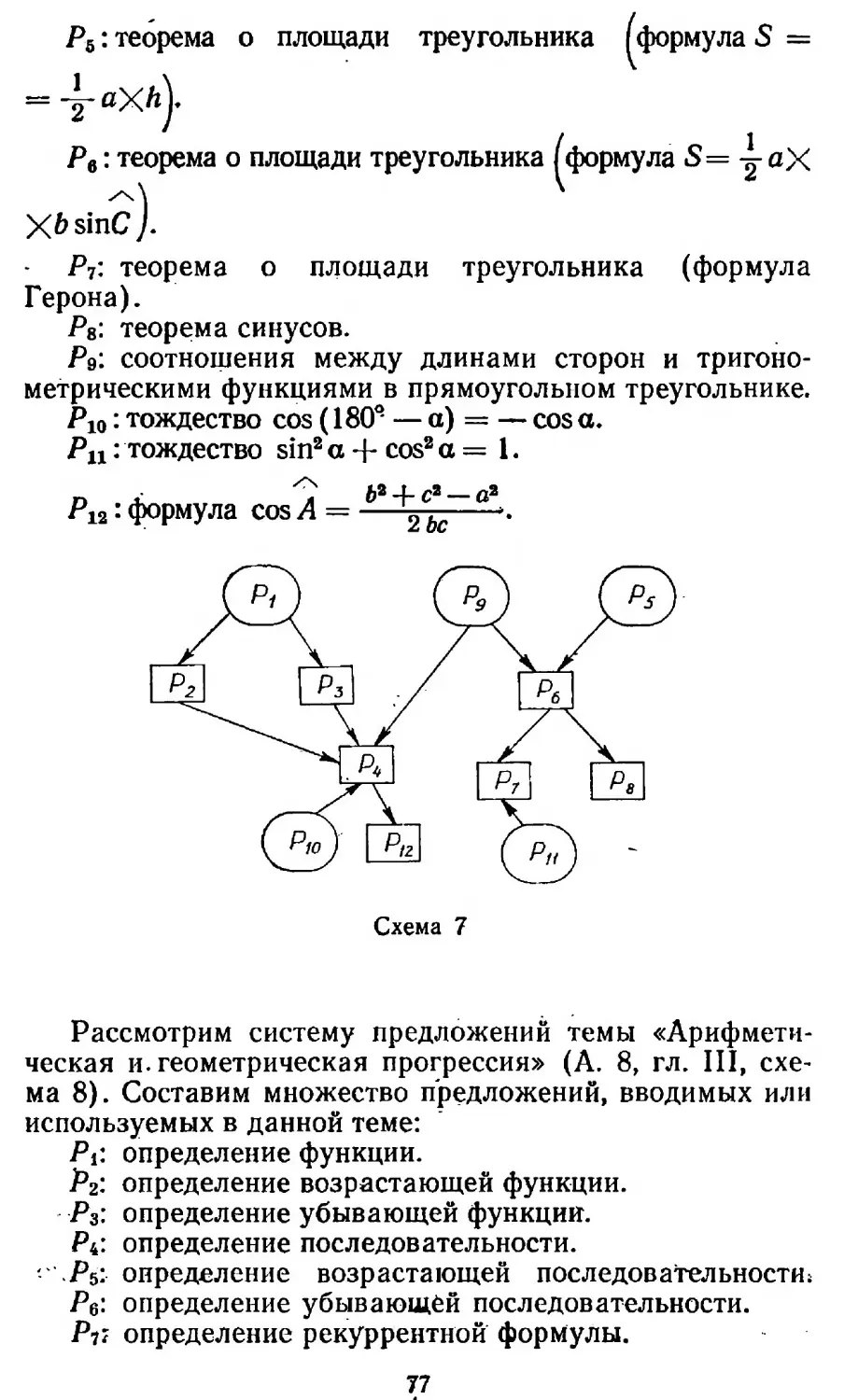
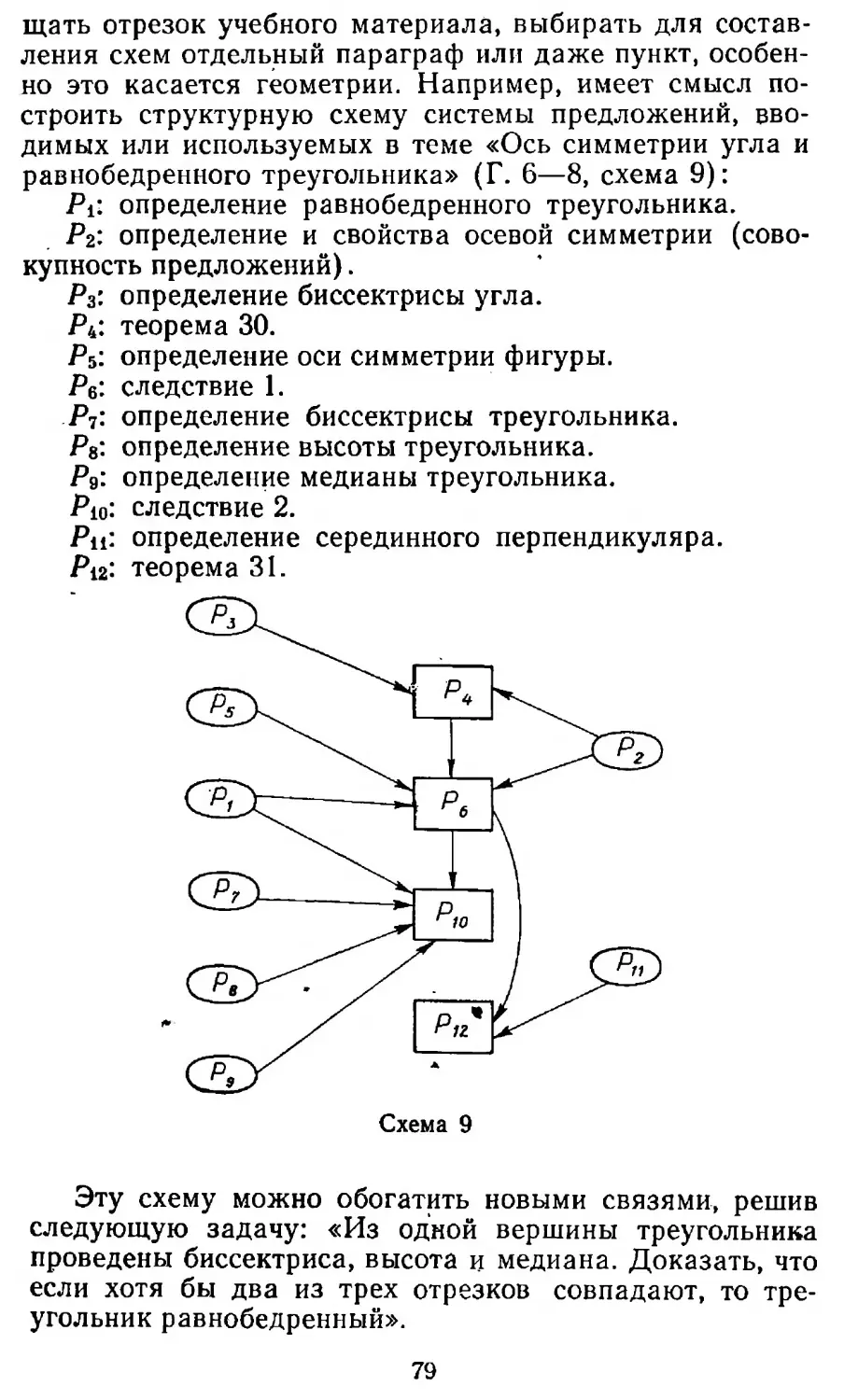
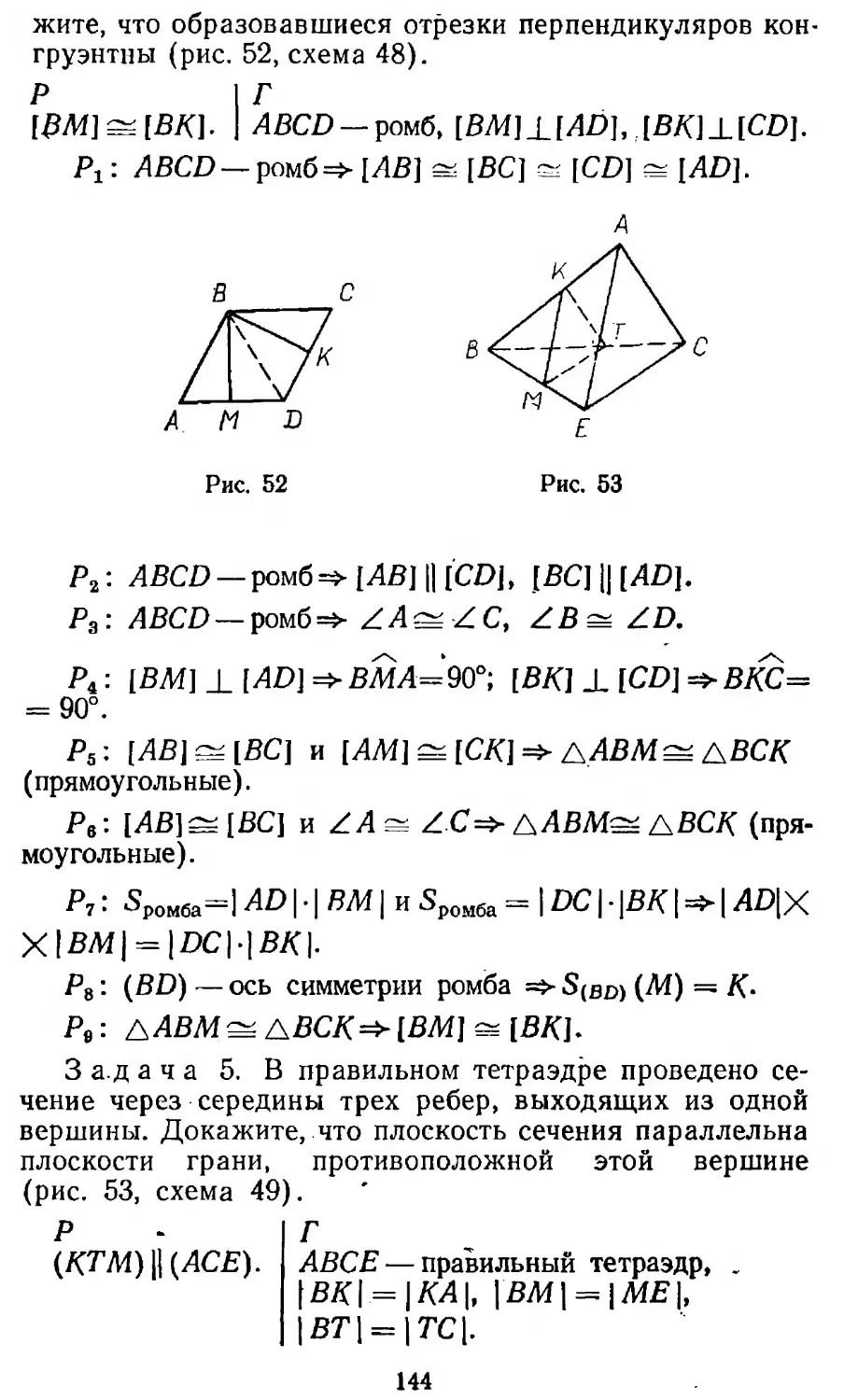
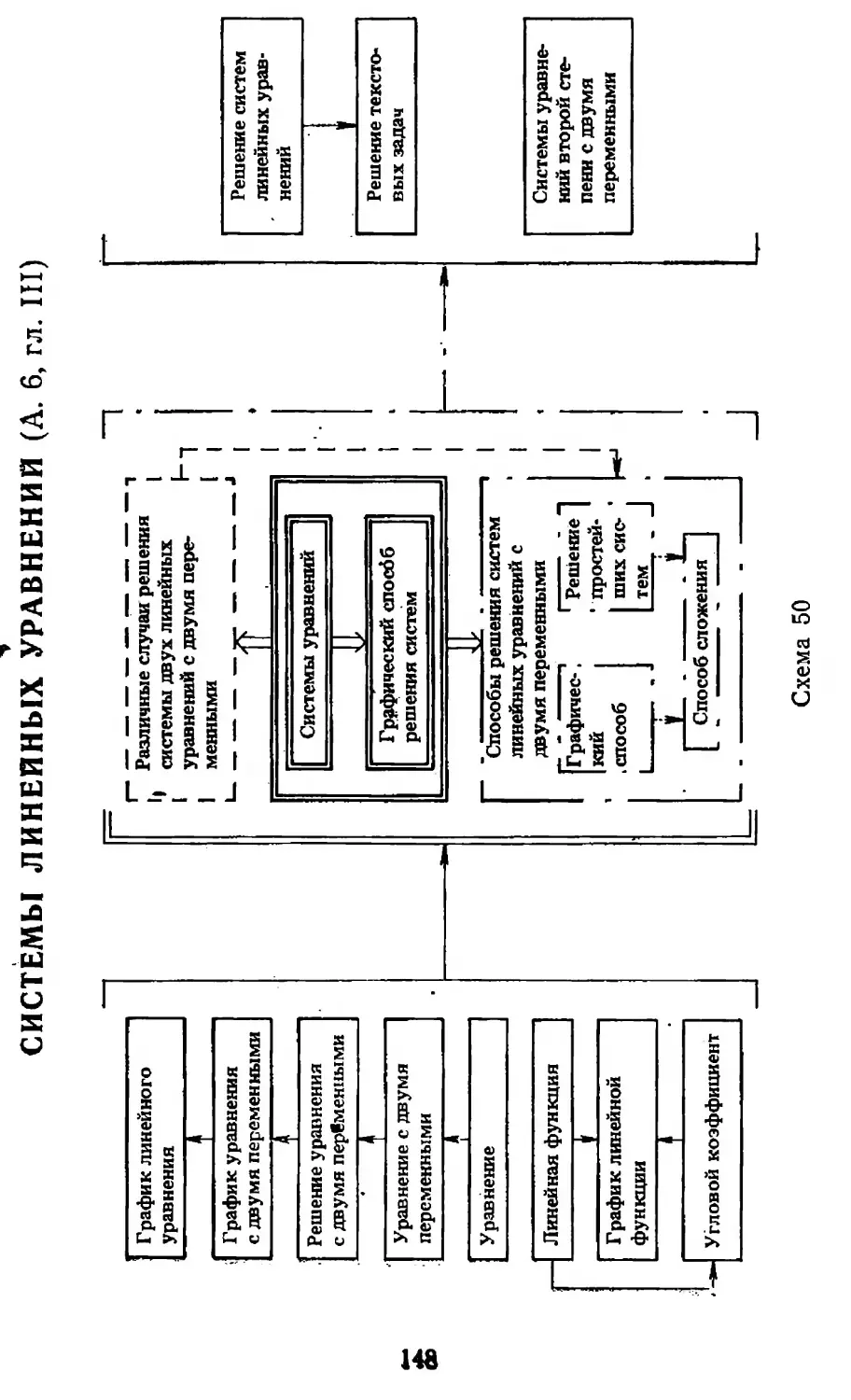
Методы обучения математике. Некоторые вопросы теории и практики - Столяр А.А., Каплан Б.С., Рузин Н.К.

Author: Столяр А.А. Каплан Б.С. Рузин Н.К.

Tags: математика методика преподавания учебных предметов в общеобразовательной школе

Year: 1981

Similar

Некоторые вопросы математики и механики

Методика факультативных занятий в 9-10 классах. Избранные вопросы математики

Математика. Методика обучения учащихся доказательству математических предложений

Методика факультативных занятий в 7-8 классах. Избранные вопросы математики

Text

Б. С. КАПЛАН, Н. К. РУЗИН, А. А. СТОЛЯР
Методы
обучения

МИНСК 1981
Б. С. КАПЛАН, Н. К. РУЗИН, А. А. СТОЛЯР
МЕТОДЫ
ОБУЧЕНИЯ
МАТЕМАТИКЕ
(НЕКОТОРЫЕ ВОПРОСЫ
ТЕОРИИ И ПРАКТИКИ)
Под редакцией
доктора педагогических наук,
проф. А. А. Столяра
МИНСК «НАРОДНАЯ АСВЕТА» 1981
ББК 74.262
К 20
УДК 51(07.07)
Рекомендовано Управлением школ
Министерства просвещения БССР
Пособие разработано на кафедре
методики преподавания математики
Могилевского педагогического института
Введение и главы I, II, IV написал А. А. Столяр,
главу III — Б. С. Каплан,
главу V — Н. К- Рузин, А. А- Столяр
Каплан Б. С. и др.
К 20 Методы обучения математике: Некоторые во-
просы теории и практики. / Б. С. Каплан, Н. К. Ру-
зин, А. А. Столяр; Под ред. А. А. Столяра.— Мн.:
Нар. асвета, 1981.—191 с., ил.
В пер.: 55 к.
Книга содержит краткое теоретическое описание и детальный,
иллюстрированный примерами из школьной практики, показ примене-
ния различных методов обучения математике.
Пособие адресуется учителям математики.
, 20202—004 ББК 74.262
К М303(05)—81 4306010000 51(07)
© Издательство «Народная асвета», 1981.
От авторов
Одна из задач, поставленных Коммунистической пар-
тией Советского Союза в области народного образования,
состоит в приведении методов обучения в соответствие с
требованиями жизни.
Этой задаче применительно к обучению математике
и посвящается предлагаемое пособие для учителей.
Под современными методами обучения математике
понимаются методы, отвечающие требованиям современ-
ной жизни, учитывающие специфику математики как
нйуки и учебного прёдмета.
Решение практических задач обучения математике
возможно лишь На базе системы научных знаний в обла-
сти теории обучения математике, представляющей со-
бой продолжение и конкретизацию общей теории обуче-
ния (дидактики) с учетом специфики учебного предмета
{математики).
Однако одних теоретических знаний здесь недостаточ-
но* Необходимы и практические умения выбирать и при-
менять наиболее целесообразные методы обучения в той
или иной конкретной учебной ситуации, характеризуемой
определенным содержанием обучения и уровнем мысли-
тельной деятельности учащихся.
Содержание обучения определяется школьными про-
граммами и учебниками. Поэтому знание программ и
учебников, наряду со знанием целей обучения математи-
ке, представляет собой важнейшее условие успешного
выбора подходящих методов обучения.
з
Как же должен знать школьный учебник учитель? .
Простое, пусть даже точное, воспроизведение текста
учебника недостаточно для учителя. Чтобы творчески
подходить к преподаванию математики, ему необходимо
глубоко понимать математические и дидактические идеи,
заложенные в школьном учебнике, логическую структу-
ру изложения, внутренние и внешние связи учебного ма-
териала. Это. понимание и позволяет осуществить выбор
методов обучения, соответствующих специфике содержа-
ния обучения и его структуре.
Выбор и целесообразное сочетание различных мето-
дов — один из важнейших элементов творческой деятель-
ности учителя, так как учебник не определяет однознач-
но методы обучения.
Рассмотрим возможности применений некоторых
современных методов обучения математике, отражаю-
щих как общедидактические поиски, так и методы иссле-
дования в самой математике. Это, возможно, сделает
понятным, каким образом процесс обучения математике
может быть построен наподобие процесса исследования
в математике, каким образом такое обучение окажет
более интенсивное влияние (чем традиционное) на раз-
витие творческого мышления учащихся.
Основная цель настоящего пособия оказать учителю
практическую помощь в повышении качества и развива-
ющего эффекта обучения математике. Поэтому, наряду
с некоторыми вопросами теории обучения математике,
пособие содержит большой ^практический материал (ме-
тодические разработки, рекомендации, блок-схемы ал-
горитмов, структурные схемы систем понятий и предло-
жений, доказательств). Эти материалы занимают при-
мерно 2/3 объема пособия. Они не только иллюстрируют
теорию, но пригодны для непосредственного применения
в практике преподавания, а также могут служить образ-
цами для самостоятельной разработки учителями ана-
логичных материалов по другим темам школьного курса.
Структурные схемы доказательств (приложение I) и
блок-схемы общих методов решения некоторых классов
задач (приложение II) составлены для настоящего по-
собия В. В. Николаевой,
Авторы выражают благодарность доктору физико-
математических наук, профессору Левину В. И. и канди-
дату педагогических наук Гуревичу В. Ю. за ценные за-
мечания, способствовавшие улучшению рукописи.
4
Введение
Актуальные проблемы среднего
математического образования

• j.
у Учебно-воспитательные задачи, которые призван ре-
шать в своей педагогической деятельности учитель ма-
тематики, следуют из:
й? а) задач общего политехнического среднего образо-
вания, сформулированных в Программе КПСС;
б) новых социальных целей и задач, поставленных
Партией в области народного образования с учетом по-
згребностей общества развитого социализма в эпоху
Научно-технической революции;
f в) роли математической науки в жизни современного
общества;
"г) развития математики;
д) ее специфики в качестве учебного предмета, раз-
вивакуцих и воспитывающих возможностей.
"Программа КПСС следующим образом определяет
Задачи среднего образования:
v «Среднее образование должно обеспечить прочное
звание основ наук, усвоение принципов коммунистиче-
ского мировоззрения, трудовую и политехническую подго-
товку в соответствии с возрастающим уровнем развития
•науки и техники, с учетом потребностей общества, спо-
собностей и желаний учащихся, а также нравственное,
эстетическое и физическое воспитание здорового подрас-
тающего поколения» *.
1 Программа Коммунистической партии Советского Союза,—
М., 1976, с. 123.'
5
Эти общие задачи уточнены и дополнены последую-
щими съездами КПСС с учетом уровня развития науки
и техники в эпоху величайшей в истории человечества
научно-технической революции и потребностей социали-
стического общества.
В Отчетном докладе ЦК КПСС XXV съезду партии
говорится: «...В современных условиях, когда объем не-
обходимых для человека знаний резко и быстро возрас-
тает, уже невозможно делать главную ставку на усвое-
ние определенной суммы фактов. Важно прививать уме-
ние самостоятельно пополнять свои знания, ориентиро-
ваться в стремительном потоке научной и политической/
информации» 1,
Таким образом, задача овладения учащимися проч-
ными знаниями основ наук дополняется задачей приоб-
ретения ими значительного интеллектуального потенци-
ала, важнейшим элементом которого является умение
творчески мыслить. Ведь им предстоит жить и работать
в динамичном, стремительно обновляющемся мире, уча-
ствовать в великих коммунистических преобразованиях.
И необходимо, чтобы с первых школьных лет подраста-
ющему поколению прививалось трудолюбие, формирова-
лось и постепенно развивалось их творческое мышление.
Из этих основополагающих задач общего образования
вытекают и конкретные задачи математического обра-
зования.
Одна из существенных особенностей современной на-
учно-технической революции состоит в том, что наука ста-
новится непосредственной производительной силой, ве-
дущим звеном в системе наука—техника—производство.
Широкое применение получила математизация и мате-
матическая техника во всех областях науки и практиче-
ской деятельности, в том числе и в таких, где еще срав-
нительно недавно не предполагалась возможность
использования математических методов (например,
управление, биология, языкознание и др.).
В такой ситуации совершенно естественно повышение
требований к математической подготовке выпускников
средней школы. Наше общество нуждается, а в дальней-
шем еще в большей мере будет нуждаться в специали-
стах с хорошей математической подготовкой и развитой
логикой мышления.
1 Материалы XXV съезда КПСС.— М„ 1976, с. 77.
6
; Учитывая перспективы развития ЭВМ и АСУ, акаде-
мик А. Н. Колмогоров отмечал, что «нашей молодежи
йсе больше придется «разговаривать» на искусственных
языках с такими собеседниками, как вычислительная
машина и управляющая система. При записи программы
вычислительной машины или автомата всякая двусмыс-
ленность недопустима: каждый знак должен иметь по-
стоянное единственное значение. Это общая тенденция
культуры новейшего времени — все большее внимание
к «знаковым системам», форме выражения мысли, будь
то запись теоретических утверждений или приказов
управляющим системам». (Диалог о математике.— Учи-
тельская газета, 1974, 12 янв.)
Математическое образование не могло остаться ин-
вариантным и относительно тех глубинных изменений,
которые произошли в самой математике в конце XIX—
начале XX в., когда были разработаны новые базисные
(теоретико-множественные) идеи, на которых строится
вся современная математика.
Пока математика развивалась главным образом «в
вышину», это развитие не затрагивало ее элементарных
основ, изучаемых в школе. Но когда произошел пере-
смотр основ математики и были разработаны общие
объединяющие базисные идеи, возникла потребность в
построении и школьной математики на базе этих же идей.
В этом, по существу, смысл осуществляемой в насто-
ящее время реформы среднего математического образо-
вания. Основная цель этой реформы — приближение
школьной математики к современной математике — нау-
ке по своим базисным идеям, логическому строению и
языку.
Можно ли утверждать, что введением новых школь-
ных программ и учебников по математике завершается
реформа математического образования?
V По-видимому, нет.
Во-первых, необходимы и в настоящее время ведутся
дальнейшие поиски по совершенствованию школьных
программ и учебников; по разгрузке их от второстепен-
ного материала, по совершенствованию трактовки школь-
ной математики.
Во-вторых, до сих пор реформа касалась, в основном,
содержания обучения и недостаточно затрагивала ме-
тоды обучения.
Методы же обучения однозначно не определяются
7
изложением учебника. Одно и то же содержание в за-
данном изложении школьного учебника может изучаться
различными методами. Разумеется, специфика содержа-
ния, основные идеи и структура предмета, так же как к
цели обучения и уровень мыслительной деятельности
учащихся, должны учитываться при выборе наиболее
подходящего метода обучения.
Современному содержанию математического образо-
вания должны соответствовать современные методы
обучения.
Однако необходимо отметить, что современные ме-
тоды обучения математике не противопоставляются
традиционным и проблема состоит не в том, чтобы заме-
нить традиционные методы современными, а в том, чтобы
правильно, психологически и дидактически обоснованно
сочетать их в процессе обучения.
Что же мы будем понимать под «традиционными» и
«современными» методами обучения?
Традиционные методы обучения ориентированы
на усвоение готовых знаний. Внешне эти методы прояв-
ляются в хорошо известной форме, когда учитель излага-
ет материал, привлекая, разумеется, различные дидак-
тические средства, а ученики воспринимают, затем за-
учивают и воспроизводят его. При этом учебная деятель-
ность школьника является, в основном, репродуктивной,
а главный результат такого обучения — усвоение суммы
знаний (и далеко не всегда системы знаний).
Современные методы ориентированы не на
усвоение готовых знаний, а на обучение деятельности по
самостоятельному приобретению новых знаний-
Анализ познавательной деятельности выявляет три
основных компонента: а) набор общих логических прие-
мов мышления; б) набор специфических (в данном слу-
чае для математики) приемов мышления и в) систему
знаний.
Система знаний является и важным компонентом
познавательной деятельности, и ее результатом. Это объ-
ясняется тем, что формирование и развитие системы зна-
ний происходит постепенно в процессе учебной деятель-
ности с помощью общелогических и специфических
приемов мышления на базе уже сформированной части
системы знаний. На «голом месте», без всяких знаний,
невозможна никакая умственная деятельность.
К логическим приемам мышления относятся: индук-
8
Шя и дедукция, анализ и синтез, сопоставление и срав-
нение, классификация, обобщение и конкретизация, аб-
страгирование. Эти приемы могут быть описаны и усво-
ены на любом содержании. Применение их в обучении
Математике таково, что оно, с одной стороны, отражает
'Логику школьной математики, с другой — приемы усвое-
ния, т. е. устанавливает связь между содержанием и ме-
тодами обучения.
у Специфические для математики приемы мышления
могут, быть описаны лишь в рамках научной теории об-
учения математике, построенной на базе психологической
Концепции обучения математической деятельности. Эле-
менты такой теории излагаются в первой главе. Осталь-
ные главы посвящены применению на практике совре-
менных методов обучения.
Правомерность названия «современные методы» вы-
текает из соответствия этих методов современным со-
циальным целям и задачам, которые ставятся КПСС в
области народного образования.
Р Из этих целей и задач мы исходим при разработке
^£ак теоретической модели обучения математике, так и
Це практических применений. Можно, разумеется, строить
^различные теоретические Модели. Мы рассмотрим лишь
дедну из них, практическое применение которой неизбеж-
но включает активную познавательную деятельность
^учащихся, обеспечивающую не только усвоение систе-
: Мы знаний, но и необходимый развивающий эффект
-обучения.
Глава I
Теоретические основы обучения
математике
§ 1. психологическая концепция
В основу теории обучения математике должна быть
положена определенная базисная психологическая кон-
цепция обучения.
Разработанная нашими психологами теория рассмат-
ривает всякое обучение как обучение некоторой деятель-
ности (в конечном итоге мыслительной, так как и всякая
практическая деятельность является внешним отраже-
нием некоторой мыслительной деятельности).
Исходя из этой общей психологической теории об-
учения, в результате ее конкретизации получаем концеп-
цию обучения математике как обучение определенного
рода мыслительной деятельности, присущей математике
и называемой поэтому математической деятельностью.
Естественно возникает вопрос о правомерности та-
кой постановки проблемы обучения. Способен ли ученик,
допустим младших классов школы, к математической
деятельности?
Очевидно, что к математической деятельности, про-
текающей на высоком уровне общности и абстракции,
не способен ни третьеклассник, ни десятиклассник. Но к
какой-то математической деятельности, соответствующей
его уровню мышления (или даже несколько выше этого
уровня), способен и первоклассник. Все зависит от той
модели учебной математической деятельности, которая
будет положена в основу теории обучения. Эта модель
должна быть приспособлена для формирования и раз-
10
вития тех структур умственной деятельности, которые
характерны для математического мышления и способ-
ствуют открытиям в математике.
Известный психолог Дж. Брунер, рассматривая про-
блемы психологии обучения' (роль структуры знаний в
обучении, готовность к обучению и природу интуиции),
утверждает, что решение этих проблем вытекает из од-
ного центрального положения: «Умственная деятель-
ность везде является той же самой, на переднем ли фрон-
те науки или в третьем классе школы» 1. Это положение,
разумеется, не надо понимать буквально. Умственная
деятельность третьеклассника и умственная деятель-
ность ученого математика, конечно, не тождественны.
По крайней мере, факторы, стимулирующие открытия,
различны. Но когда ученик в специально созданной пе-
дагогической ситуации что-то открывает для себя, он
рассуждает как первооткрыватель. Когда первоклассник
(или дошкольник), образуя пары элементов из двух
множеств, открывает, что в одном множестве больше
предметов, чем в другом, он уже осуществляет некото-
рую, хотя и весьма примитивную, математическую дея-
тельность. Когда в дальнейшем ученик переходит от опе-
раций над множествами конкретных предметов к опера-
циям над соответствующими числами (числами элемен-
тов этих множеств), отвлекаясь при этом от природы
предметов, то это уже деятельность более высокого уров-
ня. Открывая законы операций над числами, отвлекаясь
При этом от конкретных чисел, заменяя их переменными
для чисел, ученик осуществляет деятельность еще более
высокого уровня. Далее, когда ученик (с помощью учи-
теля) открывает возможность логического вывода одних
законов операций из других (логической организации
математического материала, полученного в результате
многократного обобщения и абстрагирования при
описании конкретных ситуаций), он осуществляет
деятельность еще более высокого уровня, результатом
которой является построение «маленькой» математиче-
ской теории. Когда ученик применяет построенную тео-
рию к новым конкретным ситуациям и возникающим в
них задачам, он опять осуществляет важный аспект ма-
тематической деятельности.
Точка зрения, утверждающая, что «открывать» новое
1 Брунер Дж. Процесс обучения: Пер. с англ.-*М., 1962, С. 17,
11
в математике для ученика труднее, чем заучивать гото-
вое, ошибочна. Верно лишь, что для педагога труднее
учить открывать, чем учить заучивать. Школьнику же,
при соответствующей постановке обучения, легче дейст-
вовать как математику, открывать самому истину, чем
заучивать готовую систему предложений и доказательств
без понимания их происхождения, значения и взаимных
связей. *
Если преподавание нацелено главным образом не на
заучивание уже построенной системы, а на организацию
рассуждений учащихся с тем, чтобы они были в состоя-
нии открывать для себя те факты, которые составляют
содержание предложений системы, а затем и логически
упорядочить их, то это приводит к более быстрому раз-
витию мышления учащихся и к пониманию изучаемого
материала. -
Ученик достигает понимания математики, если в
процессе обучения он принимает активное участие в раз-
витии математических идей, процедур, в построении
(пусть и маленьких, локальных) математических теорий.
9
§ 2. МОДЕЛЬ УЧЕБНОЙ МАТЕМАТИЧЕСКОЙ
' ДЕЯТЕЛЬНОСТИ
Принятую концепцию обучения можно кратко сфор-
мулировать в виде следующего исходного положения
теории обучения математике: обучение матема-
тике есть дидактически целесообразное
сочетание обучения математическим
знаниям и математической деятельности
(т. е. специфической для математики познавательной
деятельности).
Для построения соответствующей теории обучения
математике необходимо, прежде всего, принять опреде-
ленную модель учебной математической деятельности,
отражающую, с одной стороны, основные стороны реаль-
ной математической деятельности, с другой — хорошие
возможности для приспособления к школьному обуче-
нию.
Обычно говорят, что математика — дедуктивная нау-
ка, а математическое' мышление отождествляют с дедук-
тивным (доказательным) мышлением. Однако это лишь
одна из сторон (один из аспектов) математики и мате-
матического мышления.
12
Математика в процессе формирования напоминает
^1юбые другие области человеческих знаний: мы должны
открывать теоремы прежде, чем их доказывать, догады-
ваться об идее доказательства прежде, чем строить это
доказательство. Поэтому, если хотим обучать не только
Тотовой математике, но и математической деятельности,
мы должны учить не только «доказывать», но и «дога-
дываться», а процесс обучения математике должен в
какой-то мере имитировать процесс математического
творчества.
Математик не разрабатывает абстрактную дедуктив-
ную теорию из ничего. Прежде всего замечают, что не-
которые конкретные системы (механические, электриче-
ские, биологические, экономические и т. д.), какими бы
различными они ни казались по природе объектов и смыс-
лу отношений, обладают определенным сходством в
структуре, в свойствах отношений между объектами. За-
тем начинают абстрагировать и изучать структуру связей
во множестве объектов, лишенном частных характеристик
исходных конкретных систем, разрабатывают математи-
ческое описание, общее для всех этих систем, которое да-
лее подвергается логической организаций (аксиоматиза-
ции). Так рождается* абстрактная теория, систематизи-
рующая множество конкретных систем, которые стано-
вятся ее моделями.
Логически модель появляется после теории, психоло-
гически она предшествует абстрактной теории, являясь
стимулом для ее построения (и это особенно важно в
обучении).
Различные неправильные толкования предмета мате-
матики объясняются, в частности, отрывом дедуктивной
математической теории как от реальной основы, эмпири-
ческого материала, описанием которого она является, так
и от приложений, ради которых она построена.
Г. Мы исходим из модели, выделяющей три основных
аспекта математической деятельности:
1) математическое описание конкретных ситуаций,
или математизация эмпирического материала (МЭМ);
2) логическая организация математического матери-
ала (ЛОММ), полученного в результате первого аспек-
та деятельности, или построение математической теории
(«маленькой, локальной», или «большой, глобальной»);
. 3) применение математической теории (ПМТ), по-
лученной в результате второго аспекта деятельности
13
Эта модель, как и всякая другая, разумеется, отра-
жает лишь упрощенно, схематично моделируемый объ-
ект, т. е. реальную математическую деятельность. Одна-
ко из большого разнообразия аспектов этой деятельно-
сти она выделяет действительно основные, к тому же,
по-видимому, наиболее важные с познавательной точки
зрения.
Эта модель хорошо согласуется с важнейшей зако-
номерностью общей теории познания: «От живого со-
зерцания к абстрактному мышлению и от него к прак-
тике — таков диалектический путь познания истины,
познания объективной реальности»
Три стороны единого процесса познания отражаются
в трех взаимосвязанных аспектах математической дея-
тельности.
Выделенные три основных аспекта математической
деятельности представляют собой специфические для
математики приемы мышления, которые используют в
определенных сочетаниях общелогические приемы.
Наиболее частое применение тех или иных логиче-
ских приемов в различных аспектах математической де-
ятельности может быть представлено в виде следующей
таблицы:
Логичеокие приемы мышления . л Аспекты математической деятельности
МЭМ ломм пят
индукция дедукция анализ синтез сравнение сопоставление классификация обобщение абстрагирование конкретизация X 4-
1 Дэдцн В. И- Поли, собр. сеч., т. 29, с. 152— IS&
14
Эмпирический материал — это окружающие нас ре-
альные системы вещей или же системы объектов и отно-
шений из другой научной области (физики, химии, био-
логии и т. д.), подлежащие математическому описанию,
или специально приготовленные для целей обучения
предметы (дидактический материал), или, наконец, ма-
тематический материал (система математических объ-
ектов), когда он подвергается дальнейшей математиче-
ской организации (обобщению и абстрагированию) с
целью создания более общих понятий, теорий.
Например, для открытия индуктивным путем закона
коммутативности сложения (натуральных чисел) пер-
воначальным эмпирическим материалом служат непере-
секающиеся множества А и В конкретных предметов
(карандашей и ручек или черных и красных палочек).
Простым опытом, присоединением А к В и наоборот, В к
А, обнаруживается, что
ЛиВ=В1М.
Варьируя число элементов этих множеств, получаем
равенства:
24-3=3+2; 2+4=44-2; 4+7 = 7+4; 5+7=7+5;
6+8=8+6; 3+10=10+3 и т. д.
Совокупность этих равенств представляет собой, с
одной стороны, математический материал, полученный
из различного исходного эмпирического материала в
результате его математического описания (абстрагиро-
ванием численности множеств от конкретной природы
их элементов и операции сложения чисел от объедине-
ния множеств), с другой стороны, эти равенства состав-
ляют эмпирический материал, подвергаемый дальней-
шему обобщению и абстрагированию с целью получения
нового математического материала, более высокого
уровня общности и абстракции.
Внимательно присматриваемся к приведенным равен-
ствам для выявления содержащегося в них общего и
отделения его от их частного содержания. Замечаем: в
левой части каждого из этих равенств записана сумма
двух чисел, в правой — сумма этих же чисел, только
записанных в другом порядке. Как же сохранить только
это общее, отвлекаясь от конкретных чисел, входящих
в эти равенства?
Если просто отбросить в записях равенств названия
15
конкретных чисел, мы получим общую форму «с пустыми
местами»
«..

которая не отражает выявленную в частных равенствах
общую закономерность, так как не отмечено, какие пус-
тые места должны заполняться названием одного числа.
Чтобы устранить недостаток полученной формы, можно
изображать пустые места, которые должны заполнять-
ся названием одного числа, в виде пустых «окошек»
одинаковой формы. В результате получаем
«□+о=о+п».
В дальнейшем разъясняется, что для большего удоб-
ства в математике вместо пустых «окошек» различной
формы применяются различные буквы и получается,
например:
a-\b^b-\-a, или х+у=у+х.
Эти буквы, играющие роль пустых мест в записях,
называются переменными, а числа, имена которых
можно поставить вместо этих букв,— их значе-
ниями.
Как видно, дальнейшее обобщение и абстрагирова-
ние привело к открытию закона коммутативности сло-
жения (натуральных чисел) и одновременно к важней-
шему языковому понятию переменной.
В дальнейшем математические предложения
х + у = у + х для всех х, y^N;
х-у = у-х для всех х, yeQ;
х -|- у ==у + х для всех х, j/ G V,
выражающие коммутативность конкретных операций в
конкретных множествах, в свою очередь могут служить
эмпирическим материалом, из которого путем обобще-
ния и абстрагирования можно получить общее понятие
коммутативной операции:
«х * у=у* х для всех х, уеЛ1».
Мы получили общую форму закономерности, выра-
женной в приведенных выше трех (частных) предложе-
ниях, заменив в них имена конкретных операций (+, •»
+) переменной для операций (*) и имена конкретных
множеств (N, Q, V) переменной длй множеств (М).
16
Как правило, математический материал, получаемый
в результате описания конкретной системы объектов
(эмпирического материала), представляет собой конеч-
ное множество M={ph .... , рп] предложений, выра-
жающих свойства отношений между объектами системы,
обнаруженные посредством наблюдения, опыта, ин-
дукции.
Возникает проблема логической организации мате-
матического материала (ЛОММ), выяснения возмож-
ности вывода одних предложений множества М из дру-
гих предложений этого же множества, принимаемых в
качестве исходных, или структуры, порождаемой в этом
множестве отношением следования (М, =>).
Рассмотрим несколько примеров обучения МЭМ и
ЛОММ, сопоставляя их с традиционным обучением.
а) Традиционное изучение параллелограмма строит-
ся по следующей схеме (являющейся стандартной для
традиционного обучения вообще): определение — тео-
ремы, выражающие свойства сторон, углов и диа-
гоналей параллелограмма — задачи на применение
теории.
При таком изучении учебная деятельность ученика,
в основном, сводится к заучиванию формулировок и до-
казательств, т. е. к репродуктивной деятельности, не
способствующей в достаточной мере развитию творче-
ского мышления учащихся.
Описываемая концепция обучения математической
деятельности предполагает применение иной схемы из-
учения, при которой ученик становится участником по-
строения самой теории параллелограмма.
Эмпирический материал, под-
лежащий математическому опи- /'к--------------*
санию — четырехугольник ABCD / /
(на этом этапе геометрическое /
понятие «четырехугольник» слу-
жит эмпирическим материалом, Рис j
подвергаемым дальнейшему ма-
тематическому описанию).
Опытным путем (измерениями, поворотом листа бу-
маги с нарисованным четырехугольником ABCD вокруг
точки О (рис. 1) ит. д.) обнаруживаются следующие
свойства рассматриваемого объекта:
2 Зак. 1239
17
Pi'-[AB] \\[CD];
р2:[ВС] HMD];
р3: \АВ\ = |CD|;
р4:|ВС| = |ДР|;
р5: А = С;
р6: В = D;
р7: А + В = 180°;
р8:В + С = 180°;
p9:C + D = 180°;
p1Q '.D + A= 180°;
Р11: |ЛО| = ]ОС|;
- p12:|B0| = |0D|;
Pi3:Zq(ABCD)=CDAB
(О—центр симметрии);
р14: ЬАВС &ACD\
p^kABD^bBCD.
В результате описания рассматриваемого объекта
(четырехугольника ABCD) мы получили множество
предложений
М={Рь р2, ... г Pis} -
Естественно возникает проблема: нужно ли истин-
ность всех этих предложений устанавливать опытным
путем? Нельзя ли сократить опыт и из некоторых (ми-
нимального числа) предложений, установленных опыт-
ным путем, вывести логически все остальные?
Эта проблема возникает и в самой математике при
построении теории, описывающей какой-нибудь класс
структур. Возникновение и постановка этой проблемы в
процессе обучения математической деятельности (в свя-
зи с построением «маленькой» теории) показывает, что
осуществление описываемой модели обучения прибли-
жает процесс и методы обучения математике к процессу
и методам исследования в самой математике.
Для решения сформулированной выше проблемы не-
обходимо исследовать логические связи между предло-
жениями pi—pis. Возникает потребность в «логическом
эксперименте», состоящем в исследовании различных
возможностей логической организации (упорядочения с
помощью отношения следования) множества предложе-
ний М.
Исследование ведется по такой схеме: сначала ста-
вится задача, нельзя ли найти какое-нибудь одно из
предложений pi—pi5, из которого (и, разумеется, неко-
торых ранее уже известных, истинных предложений гео-
метрии) следуют все остальные.
Например, если взять рь то уже pi=>P2 ложно, т. е.
18
р2 не следует из р±. Действительно, можно построить та-
кой четырехугольник ABCD, в котором ЛВЦС2), но ВС не
параллельно AD. Такой контрпример способствует до-
стижению правильного понимания следования (следова-
ние pi=>P2 ложно, т. е. р2 не следует из р1у если можно
указать случай, когда pi истинно, а р2 ложно).'
В результате поиска устанавливается, что из одного
р13 можно вывести все остальные предложения сово-
купности М. Затем ставится задача, нельзя ли из двух
предложений, принятых в качестве посылок, вывести все
остальные. Исследование выявляет, что такими посылка-
ми могут быть: pi и р2, pi и р3, р2 и р^ р3 и р4, рп и pi2 и др.
Разумеется, не ставится задача отыскания всех таких
возможностей.
После проведения этого исследования выбирают один
из вариантов логической организации (в частности, тот,
который изложен в учебнике) и дают соответствующее
определение параллелограмма (с помощью свойств, при-
нятых в выбранном варианте в качестве посылок).
Как видно, при таком изучении темы определение
завершает, а не начинает его. При этом учащиеся сами
приходят к этому определению как к одному из возмож-
ных, понимая, что выбор определения, по существу, озна-
чает выбор того или иного варианта логической орга-
низации математического материала, того или иного
варианта построения теории параллелограмма (выбора
«локальной» аксиоматики, выступающей здесь в каче-
стве определения). Формируется представление об экви-
валентности различных определений параллелограмма,
а по существу, различных теорий параллелограмма,
представляющих собой лишь различные организации од-
ного и того же множества предложений.
В результате применения описанной схемы обучения
формируется взгляд учащегося на изложенный в учеб-
нике материал, как на изложение результатов проведен-
ного в классе исследования.
Что же остается делать ученику после изучения в
классе темы традиционными методами обучения (ТМО)
и современными методами обучения (СМО) в принятой
концепции?
ТМО
Заучить по учеб-
нику то, что объяс-
* *
СМО
»
Углубить усвоение с помо-
щью учебника одного из вари-
19
нено в классе учи- антов теории, построенной при
телем. его участии (под руководством
учителя) в процессе проведен-
ного в классе исследования.
Естественно возникает вопрос: рекомендуется ли
проводить такое исследование по каждой маленькой те-
ме, подобной рассмотренной выше?
Универсальное применение подобного метода потре-
бовало бы больше времени, чем традиционное обучение.
Однако, во-первых, речь идет о совершенно различных
вещах: в одном случае, об обучении определенному ас-
пекту мыслительной деятельности, результатом которой
является построение «маленькой» теории, в другом
же — о заучивании готовой теории. Во-вторых, если
учесть, что описанное выше исследование включает се-
рию задач на доказательство, объединенных общей иде-
ей, то времени здесь требуется не больше, чем при про-
хождении этого же теоретического материала в обычном
изложении, включая решение такого же числа ‘задач.
В-третьих, описываемый метод, как и всякий другой, не
может считаться универсальным. Однако его применение
к изучению определенных тем, для которых он пред-
ставляется особенно подходящим, подготовит учащихся
к тому, чтобы и на изложение других тем в школьном
учебнике смотреть как на результат подобной деятель-
ности, только осуществленной другими.
б) Рассмотрим еще один пример из геометрии.
Свойства, включенные в определение осевой симмет-
рии, как отображения плоскости на себя (рь все точки
прямой / остаются на месте и р2: каждая из двух полу-
плоскостей с границей I отображается на другую) обна-
руживаются с помощью опыта поворота плоскости вокруг
оси I на 180° или перегибания листа бумаги. Из свойств
Pi и р2 логическим путем выводятся новые свойства осе-
вой симметрии: любые две различные симметричные
относительно I точки:
р3: принадлежат различным полуплоскостям с грани-
цей Z;
р4: лежат на одном перпендикуляре к прямой /;
р5: на равных расстояниях от /;
pG: осевая симметрия — перемещение;
р7: симметричные фигуры конгруэнтны.
Свойства рз—р71 полученные логическим путем, можно
20
проверить в той же конкретной ситуации, созданной опы-
том, с помощью которого обнаружены и свойства pi и р2.
Г Описываемая концепция обучения математической
^деятельности предполагает иную последовательность со-
четания интуитивных и логических элементов в процессе
^бучения. В нашем примере можно сразу с помощью опы-
Ча (поворота плоскости или перегибания листа бумаги)
Обнаружить все свойства pi—р7. Множество предложений
Рг» . • , Pi} составляет математическое описание
Эмпирического материала. Затем ставится проблема со-
вершенствования этого описания, т. е. максимально воз-
можного сокращения опыта, выяснения того, какое ми-
Гнимальное число свойств этого отображения достаточно
Принять за исходные, чтобы все остальные обнаружен-
ные опытным путем свойства уже оказались доказуемы-
ми на базе принятых («локальных аксиом» «маленькой
Теории»). Решение этой проблемы предполагает прове-
дение исследования возможных способов логической ор-
ганизации полученного в результате описания конкрет-
ной ситуации математического материала, состоящего
%нашем примере из 7 предложений.
# Постановка и частичное решение таких проблем при-
влекает учащихся к самому построению, шаг за шагом,
^Геометрической теории.
. Понимание сущности и различных возможностей ло-
кальной логической организации геометрического мате-
риала (в рамках небольших тем) является предпосыл-
кой и необходимым условием' достижения понимания
аксиоматического построение геометрической теории в
тхелом.
в) Рассмотрим возможный вариант привлечения
Щучащихся к построению маленькой теории арифметиче-
ской прогрессии, используя при этом тот же конкретный
^эмпирический) материал, который приводится в учеб-
Цбм пособии ’, но в ином порядке и более эффективно,
g- Вместо того чтобы с самого начала сообщить уча-
щимся характеристическое свойство арифметической
йррогрессии, как это делается в учебном пособии, можно
С помощью подводящих вопросов или подсказок ориен-
тировать их на самостоятельное открытие общих свойств
^Последовательностей:
1 Макарычев Ю. Н., Миндюк Н. Г., Монахов В. М. и др. Алгеб-
ра. 8.- Мп гл. Ш, § 6.
(1) 5; 8; И; 14; 17;...
(2) 1; 2; 3; 4; 5; 6; 7; 8;...
(3) 1; 3; 5; 7; 9; 11;...
(4) 0; —2; -4; -6; -8; ...
Вопрос, по какому закону (правилу) образуются
члены каждой из этих последовательностей, не вызыва-
ет затруднений.
Если обозначить члены последовательности через а^\
а%, ... ; , то обнаруженное общее свойство после-
довательностей (1) — (4) запишется так:
Pi- dn+i = cin-\-d для любого п (для fl) d = 3; для (2)
d=l; для (3) d=2; для (4) d = —2).
Обращая внимание учащихся на любые три последо-
вательных члена каждой из последовательностей (1) —
(4), обнаруживаем, что любой член последовательности,
начиная со второго, • равен среднему арифметическому
двух соседних членов (предшествующего и последующе-
го) , т. е.
I I”" I I ** л
р2: ап =----я—— для любого и > 2.
По-видимому, можно открыть и способ вычисления
любого члена, зная первый член последовательности и
разность. Маленький опыт помогает открыть общую фор-
мулу. Можно задать вопрос: сколько раз надо прибавить
к первому члену последовательности (1) разность 3, что-
бы получить 4-й член (5+3-3=14), 5-й член (5+4-3 =
= 17), 10-й член (5+9-3=32)? Возникает гипотеза
рз* CLn=Д1+ (n— 1) d для любого 2.
Ставится задача вычисления суммы п первых членов
любой из последовательностей (1) — (4). Конечно, если и
невелико, задача может быть решена непосредственным
сложением п членов. Но если, например, предлагается
вычислить сумму первых 100 членов последовательности
(2), т. е. сумму натуральных чисел от 1 до 100, естест-
венным является поиск более простого способа вычисле-
ния этой суммы. Можно напомнить учащимся, что иног-
да мы меняем местами слагаемые, группируем их ка-
ким-то удобным способом, т. е. применяем законы ком-
мутативности и ассоциативности сложения. Но если этих
подсказок недостаточно, то можно предложить сделать
22
то, что сделано в учебном пособии (с. 67—68). Обнару-
живается еще одно важное свойство
PC = #2“]“ Я 71—1 = ЛзН~Лп-2= • • • , ИЛИ =
= a1+b+fln-/i для любого и /г^п—1, а способ вы-
числения суммы п первых членов для частной задачи (2)
приводит к открытию общей формулы
P5-Sn =
а1 + ап
Таким образом, мы получаем общее описание после-
довательностей (1) — (4) в виде множества из пяти
предложений
М = {pi, р2, Рз, Pi, Ръ}.
Естественно возникает необходимость в логической
организации этого множества предложений (превраще-
ния его в маленькую теорию), т. е. необходимость выде-
ления из него минимального подмножества А свойств,
характеризующих последовательности (1) — (4), из ко-
торых следуют все остальные предложения из М,
Первая попытка уже увенчается успехом: из р^ сле-
дуют все остальные предложения из М. Далее выясняем,
что pz равносильно Значит, и из рг следуют все осталь-
ные предложения. Получаем другой вариант логической
организации этого математического материала и, соот-
ветственно, другой вариант определения арифметической
прогрессии. Исследование логических связей между
предложениями из М может быть продолжено.
§ 3. ОБЩЕДИДАКТИЧЕСКИЕ ОСНОВЫ
Теория обучения математике, являясь продолжением
и конкретизацией общей теории обучения (дидактики),
должна опираться на определенную общедидактическую
систему.
В качестве общедидактической основы теории обуче-
ния математике мы принимаем современную дидактиче-
скую систему проблемного обучения.
Эта система строится на базе известных принципов
дидактики (научности, систематичности и последователь-
ности в обучении, сознательности усвоения, активности
учащихся, наглядности обучения, прочности знаний, ин-
дивидуального подхода), дополненных принципом про-
блемности обучения, согласно которому процесс обуче-
23
ния протекает как создание и снятие последовательности
проблемных ситуаций.
Конкретизация общедидактической системы проблем-
ного обучения и ее сочетание с концепцией обучения ма-
тематической деятельности приводит к трем основным
(специфическим для обучения математической деятель-
ности) типам проблемных ситуаций, отличающимся учеб-
ными целями, природой известного и неизвестного, не-
согласованность между которыми порождает проблем-
ную ситуацию, и результатами снятия (разрешения) про-
блемной ситуации.
Основные типы проблемных ситуаций
в обучении математической деятельности
Основные аспекты математи- ческой деятель- ности Основные типы проблемных ситуаций
цель известное неизвестное результаты
МЭМ Введение новых понятий ЭМ, подлежащий математическому описанию Математи- ческий ап- парат, необ- ходимый для описания ЭМ Новые -математи- ческие зна- ния
ломм Система- тизация знаний ММ — совокуп- ность математиче- ских предложений, описывающих ЭМ, почерпнутых из опыта, логи- чески не упоря- доченных Способ ло- гической организации ММ Система математи- ческих зна- ний i !
пмт Раскрытие возможно- сти приме- нения зна- ний в но- вых ситуа- циях ЭМ (конкретная ситуация, зада- ча) и необходи- мая МТ (матема- тическая теория) Способ применения МТ к ново- му ЭМ, в новых си- туациях Перенос математи- ческих знаний
Разумеется, в обучении математике могут встречаться
и другие типы проблемных ситуаций. Однако основными
24
согласно концепции обучения математической деятель-
ности, являются три типа, характеристика которых дана
в приведенной таблице.
Первые два типа проблемных ситуаций, возникающих
в деятельности по МЭМ и ЛОММ, уже встречались в
описанных выше (§ 2) примерах. Третий тип, возникаю-
щий в деятельности по применению теории, будет пред-
метом рассмотрения в следующем параграфе.
Система общедидактических принципов дополняется
двумя собственными принципами теории обучения мате-
матике (дидактики или педагогики математики):
(1) школьный курс математики по своим базисным
идеям и структуре должен отражать фундаментальные
идеи и логику современной математики (разумеется, в
определенной мере, в какой это допускает уровень мыс-
лительной деятельности учащихся);
(2) процесс обучения математике должен строиться
наподобие процесса исследования в математике, он дол-
жен имитировать процесс творческого поиска в матема-
тике (опять-таки, разумеется, в определенной мере, в
какой это допускает уровень мыслительной деятельности
учащихся на различных этапах обучения).
Как видно, принцип (1) относится к построению со-
держания учебного предмета и представляет собой кон-
кретизацию общедидактического принципа научности,
последовательности и систематичности С учетом специ-
фики математики-науки, ее фундаментальных идей, язы-
ка и логики. Принцип (2) относится к построению про-
цесса обучения и конкретизирует общедидактический
принцип проблемности с учетом методов самой мате-
матики.
Принцип (1) служит основой для модернизации
школьной математики, ее приближения к современной
математике по своим базисным идеям, логике и языку,
принцип (2) — для модернизации методов обучения ма-
тематике, их приближения к методам самой математики.
Заключенные в скобки ограничения, которыми окан-
чиваются формулировки двух принципов, отражают об-
условленность их применения психологией обучаемых.
§ 4. ОБУЧЕНИЕ ПРИМЕНЕНИЮ
МАТЕМАТИЧЕСКОЙ ТЕОРИИ
Аспект математической деятельности, который мы
назвали применением математической теории (ПМТ),
25
требует специального рассмотрения ввиду сложности
структуры, большого разнообразия применений матема-
тической теории и особой значимости.
Последнее объясняется тем, что немногие из выпуск-
ников школы станут математиками и будут заниматься
так называемой «чистой математикой». Подавляющее
большинство их будет применять математику в практи-
ческой деятельности, связанной с той или иной областью
науки, техники или производства, так как уже сейчас, а
тем более в будущем трудно будет назвать такую об-
ласть практической деятельности, где не применялась бы
математика.
Всякая теория, в том*‘числе, разумеется, и математи-
ческая, важна своими применениями. Поэтому основная
цель изучения какой-нибудь теории состбит в том, чтобы
научиться ее применять.
Большое разнообразие применений математической
теории можно условно разбить на два класса: примене-
ния к другой теории (математической или нематемати-
ческой) и применения непосредственно к решению прак-
тических задач.
К первому классу относятся встречающиеся в школь-
ном, обучении применения алгебры в геометрии (уравне-
ния геометрических фигур на координатной плоскости и
в координатном пространстве), геометрии в алгебре (гра-
фики функций и уравнений), алгебры и геометрии в на-
чалах анализа, математической теории в физике и др.
Эти применения традиционно называют межпредмет-
ными связями, и проблема межпредметных связей давно
обсуждается в методической литературе, но до сих пор
не получила удовлетворительного решения.
Все еще имеющаяся изолированность отдельных раз-
делов внутри школьного курса математики, так же как
изолированность математики от других школьных учеб-
ных предметов в традиционном преподавании, объясня-
ется, в частности, пренебрежением такого рода приме-
нениями. Вместе с тем и применения одной теории к дру-
гой можно считать применениями к практике, только уже
опосредованными.
В современном развитии математики все большее зна-
чение приобретают именно ее опосредованные связи с
практикой через другие естественные науки, которые не-
посредственно связаны с техникой и производством.
Наиболее существенные связи математики с практикой
26
осуществляются посредством математических моделей,
используемых естественными, а в последнее время и дру-
гими науками.
Всякое применение теории предполагает построение
модели.
В случае, когда одна теория применяется в другой,
строится модель второй в объектах первой (например,
модель геометрии в объектах векторной алгебры). Если
же теория применяется к решению практической задачи,
строится математическая модель задачи, например со-
ставляется система уравнений. Различие здесь в том, что
в первом случае и модель, и моделируемый объект — си-
стемы теоретических понятий, т. е. находятся на одном
уровне абстракции. Во втором случае строим абстракт-
ную модель конкретной задачи. Но и сама задача пред-
ставляет собой конкретную модель абстрактной системы
уравнений (исходя из интуитивного понимания «модели»
можно считать отношение «быть моделью» симмет-
ричным).
С точки зрения обучения математической деятельно-
сти построение математической модели представляет со-
бой аспект деятельности, по своей структуре аналогич-
ный МЭМ.
В применениях математической теории к другой тео-
рии эмпирическим материалом служит система объектов
этой другой- теории (области применения), в примене-
ниях же к практической задаче — конкретная ситуация,
определяемая условиями задачи.
Например, физика снабжает математику конкретны-
ми примерами различных видов функций. Отвлекаясь от
физических объектов, мы исследуем эти функции как
абстрактные математические объекты, затем применяем
полученные знания к изучению различных физических
процессов, моделируемых с помощью этих функций.
Таким образом, связь между математикой и физикой,
согласно описываемой концепции обучения математиче-
ской деятельности, представляется двусторонней. Физи-
ческие ситуации служат исходным эмпирическим мате-
риалом, математическое описание которого мотивирует
введение и изучение новых математических объектов.
Эти новые математические понятия применяются затем
для описания и изучения (на математической модели)
исходных и других физических процессов.
Так, например, равномерное движение мотивирует
27
необходимость изучения функций, выражаемых форму-
лами у=ах и у = ах-\-Ь, с помощью которых выражаются
и скорость в равномерно-переменном движении (как
функция времени), и объем, и давление газа как функ-
ции температуры (при определенных физических усло-
виях). Равномерно-переменное движение, в частности
свободное падение, описывается с помощью квадратич-
ной функции, находящей другие многочисленные физи-
ческие интерпретации.
Математическое описание определяемой условиями
задачи конкретной ситуации с помощью уравнения или
системы уравнений обычно не является полным, и воз-
никает вопрос о достаточности этого описания (модели)
для решения задачи. Именно неполное описание часто
является причиной того, что решение уравнения или си-
стемы уравнений может и не быть решением задачи.
Поэтому проверка этого решения по условиям задачи
обычно считается составной частью процесса решения
задачи. Однако можно уменьшить степень неполноты ма-
тематической модели задачи добавлением к уравнению
(системе уравнений) системы неравенств (возможно, дру-
гих предложений), выражающих ограничения, наклады-
ваемые условиями задачи на различные фигурирующие
в ней величины. По существу здесь «проверка по усло-
виям задачи» включена в математическое описание этих
условий. В таком случае решение полученной смешанной
системы уравнений и неравенств является и решением
задачи.
Проиллюстрируем эти общие положения конкретным
примером.
Рассмотрим задачу: «В трех баках было вместе 50 л
бензина, причем в первом было на 10 л больше, чем во
втором. Когда из первого бака вылили в третий 26 л, во
втором и третьем баках стало бензина поровну. Сколько
бензина было первоначально в первом баке?»
Обычное (по установившейся школьной практике) ре-
шение этой задачи состоит в сведении его к решению
уравнения
х—10 = 50—х— (х—10) +26,
где через х обозначено первоначальное количество лит-
ров бензина в первом баке. Решение этого уравнения,
х=32, считают и решением задачи, так как оно «удо-
влетворяет условиям задачи», согласно которым х>0.
28
Однако более глубокий анализ условий задачи обна-
руживает, что они накладывают на величину х более
сильные ограничения и решение уравнения не является
решением задачи.
Провести такой анализ поможет таблица, составляе-
мая обычно в процессе решения задачи:
К-во бензина в л Первоначально После переливания
.В первом баке X х—26
Во втором баке х—10 х—10
В третьем баке 50—х—(х—10) 50—х—(х—10)4-26
Некоторые из фигурирующих в таблице величин по
смыслу задачи положительны, некоторые — неотрица-
тельны, а две из них равны. Выразив это математически,
получаем систему, состоящую из одного уравнения и пяти
неравенств:
(1)
X — 10 = 50 — X— (х— 10) + 26,
х > 0,
х— 10 > 0,
50 — х — (х — 10) + 0,
х — 26 0,
50 — х— (х— 10) + 26 > 0.
Эту систему можно упростить .(исключением тех не-
равенств, которые являются следствиями других):
х— 10 - 50 — х— (х— Ю) + 26,
(2)
х— 26 >0,
50 — х— (х— 10) >0.
Таким образом, по существу, решение задачи сводит-
ся к решению системы (2), а не к решению одного урав-
нения.
Система (2) легко приводится к системе
(х = 32,
(3) х > 26,
(х < 30,
противоречивость которой очевидна.
29
Отсюда следует, что и условия задачи (приводящие
к противоречивой системе предложений) противоречивы,
и задача не имеет решения.
Проиллюстрированное на этой задаче математическое
описание конкретной ситуации, определяемой условиями,
имеет явные преимущества перед традиционным реше-
нием задачи способом составления уравнения: а) приуча-
ет к более глубокому анализу условий задачи; б) об-
учает построению математических моделей (хотя, разу-
меется, в очень простых случаях); в) предупреждает
ошибки, часто допускаемые при традиционном способе,
когда забывают проверить решение уравнения (или си-
стемы уравнений) по условиям задачи, или проверяют,
как в нашем примере, не все условия.
Как научить учащихся решать задачи?
Очевидно, это одна из наиболее сложных и важных
педагогических проблем. Сложность ее объясняется тем,
что отсутствует общий метод (алгоритм), овладение ко-
торым гарантировало бы умение решить любую задачу.
Важность ее объясняется тем, что, с одной стороны,
теоретические знания нужны для решения разного рода
задач, возникающих в любой области деятельности, с
другой стороны, именно обучение через задачи в наи-
большей мере является развивающим обучением.
В рамках описываемой концепции обучения матема-
тической деятельности обучение решению задач следует
понимать как обучение мыслительной деятельности, осу-
ществляемой в процессе решения задач.
Анализ этой деятельности выявляет два, тесно пере-
плетающихся в процессе решения задач, компонента:
алгоритмический, когда человек решает задачу (под-
задачу) по известному ему общему методу (алгорит-
му), и эвристический (творческий), когда он решает
нестандартную задачу (для которой нет общего метода
решения).
В первом случае человек решает задачу не задумы-
ваясь, «машинально», во втором — он задумывается, ве-
дет «поиск решения». Эти два вида деятельности сущест-
венно отличаются по своей структуре.
Допустим, что четвероклассникам предложена зада-
ча: сложить два числа, 25 036 и 6317. Все решают не за-
думываясь, кто быстрее, кто медленнее, некоторые, воз-
можно, ошибаются, затем исправляют ошибки. При этом
30
отсутствуют признаки напряженности поиска и радости
открытия. Все решают по известному правилу, «тра-
фарету».
Совершенно иным является поведение учащихся, если
предложить им, например, такую задачу: «Собрали
100 кг грибов, влажность которых составляет 99%. Когда
грибы подсушили, влажность снизилась до 98%. Какой
стала масса грибов после подсушивания?»
Как только сообщены условия задачи, учащиеся за-
думываются (здесь, в отличие от первой задачи, «есть
над чем подумать»), идет напряженный поиск, сменяю-
щийся затем радостью открытия.
Значимость нестандартных задач именно в том и со-
стоит, что они предъявляют настоящий вызов интеллекту
и способствуют в наибольшей мере его развитию.
Стратегия обучения зависит от того, идет ли речь о
решении стандартных или нестандартных задач.
* Школьная математика полна разного рода стандарт-
ных задач, начиная от задачи сложения многозначных
чисел («в столбик») и до задач дифференцирования
и интегрирования определенных классов функций.
В школьной математике имеется и большое разнообра-
зие нестандартных задач (на доказательство, преобра-
зование алгебраических выражений, решение некоторых
уравнений, неравенств, систем уравнений и т. д.).
Можно выделить три вида учебных ситуаций, связан-
ных с решением задач, требующих различных страте-
гий обучения:
I — решение стандартных задач, общий метод реше-
ния которых еще неизвестен учащимся;
II — решение стандартных задач, общий метод ре-
шения которых уже известен учащимся;
III — решение нестандартных задач.
В ситуации I речь идет о предварительном решении
однотипных частных задач и стратегия обучения должна
быть ориентирована на открытие учащимися (с помощью
учителя) общего метода решения всех задач данного
класса.
В ситуации II речь идет о применении уже известных
общих правил, формул и здесь требуется лишь умение
конкретизировать, выполнять общее предписание к пред-
ложенной частной задаче. Предварительно необходимо
отнести эту задачу к классу задач, решаемых с помощью
известного общего метода. Таким образом, в этой ситуа-
31
ции стратегия обучения должна быть ориентирована на
обучение распознаванию принадлежности частных задач
к классам задач, решаемых определенными, уже извест-
ными методами.
В ситуации III, наиболее сложной с дидактической
точки зрения, стратегия обучения должна быть ориенти-
рована на обучение методам поиска решений.
Следует считать ошибочной точку зрения, согласно
которой якобы нельзя обучать решению нестандартных
задач. Можно обучать решению нестандартных задач,
если под этим понимать обучение методам поиска реше-
ний подобных задач. Много полезного в этой области со-
держится в известных книгах Дж. Пойа («Как решать
задачу», «Математическое открытие»).
Втгастоящее время, когда разработаны регулярные
методы поиска решений задач, предназначенные для об-
учения ЭВМ (искусственного интеллекта), представляется
возможным заимствование некоторых из этих методов и
их адаптация для обучения школьников (естественного
интеллекта) поиску решения задач.
По существу, эти методы, разработанные в кибернети-
ке, получены в результате глубокого анализа и после-
дующей формализации деятельности человека в процес-
се решения задач. Поэтому оправдано их заимствование
для обучения человека этой деятельности.
Стратегии обучения решению задач (стандартных и
нестандартных) рассматриваются в последних двух (IV
и V) главах настоящего пособия. Там же помещены не-
которые дидактические материалы.
Разумеется, применение описываемой концепции и
разработанных на ее основе дидактических материалов
в обучении школьников решению задач лишь в какой-то
мере способствует решению поставленной педагогиче-
ской проблемы: «Как научить учащихся решать задачи?»
Результаты обучения зависят от большого числа фак-
торов, в частности и не в последнюю очередь от того,
насколько учитель глубоко усвоил различные стратегии
обучения решению задач и творчески их применяет в
практике обучения.
Глава II
Проблемное обучение
(практические материалы)
§ 1. ПОСТРОЕНИЕ МАЛЕНЬКИХ ТЕОРИЙ
В качестве иллюстрации принятой модели обучения
математической деятельности мы приводили выше (гл. I,
§ 2) примеры построения маленьких теорий (параллело-
грамма, осевой симметрии, арифметической прогрессии)
в процессе обучения.
Рассмотрим еще несколько примеров в более деталь-
ной методической обработке.
Пример 1.
Описываемое ниже исследование предшествует введе-
нию понятия касательной к окружности.
Рассмотрим геометрическую г
ситуацию, изображенную на ри- 4_____________X а
сунке 2.
Математическое описание этой (
ситуации начинается с перечисле- к 0 )
ния участвующих в ней объектов. -------'
Первый вопрос, который мо- рис 2
жет быть поставлен перед учащи-
мися: «Что вы видите (что изо-
бражено) на рисунке 2?»
На рисунке изображены: точки О, А, Х\ прямая а;
окружность с центром О и радиусом г — окр(О, г); круг
с центром О и радиусом г — кр (О, г).
Таким образом, на рисунке 2 изображено множество'
объектов М= {О; А; X; а; окр(О, г); кр(О, г)}, состоящее
3 Зак. 1239
33
из трех (выделенных) точек, прямой, окружности и
круга.
Математическое описание рассматриваемой ситуации
предполагает выявление свойств структуры, которую
имеет множество М, наделенное отношениями: принад-
лежности (точки к множеству точек), перпендикулярно-
сти (между прямыми), равно, больше, меньше (между
расстояниями, числами).
Таким образом, речь идет об описании не множества
М, а структуры (М, е=, _1_, =, >, <).
С помощью наблюдений и опыта (некоторых измере-
ний) обнаруживаются следующие свойства, характери-
зующие эту структуру:
Рь Аеа;
р2: А<=окр(О, г);
ръ аПокр(О, г) =А
(А — единственная общая точка прямой и окружности);
р4: |ОА|=г;
р5: [OA]J_a
(это одно из наиболее очевидных свойств структуры, из-
ображенной на рис. 2);
р6: X е а;
Pi: X кр (О, г);
рв: | ОХ | > г;
р9: | О А | = d (О, а)
(d(O, а) — расстояние от точки О до прямой a: d(O, а) =
= min{|OX| |Xea});
Рю • X А;
-рп:|ОА| < |ОХ|;
Р12: А е кр (О, г);
р13: X окр (О, г).
Множество P={plt р2, ... , Р1з} предложений, выра-
жающих свойства структуры (М, е, _1_, =, >, < }, и
составляет математическое описание этой структуры с
помощью того понятийного аппарата, которым уже вла-
деют учащиеся к моменту ее рассмотрения.
34
Однако это описанйе с логико-математической точки
зрения несовершенно. Оно представляет собой логически
еще неупорядоченный (неорганизованный) математиче-
ский материал и еще не представляет собой теории.
Возникает проблема выявления логических связей
между предложениями множества Л1, вычленения из
множества М логически независимых свойств описывае-
мой структуры, т. е. проблема логической организации
математического материала (ЛОММ) .
Наиболее очевидными являются логические связи
между предложениями р4, р2, рз, р4 и pi2. Действительно,
из р3 непосредственно следует рх и р2: А = а П окр (О, г) =>
и 4^окр(О, г).
Тем учащимся, которые затрудняются обнаруживать
эти связи, можно задать такие вопросы:
Что такое пересечение двух множеств?
Если точка принадлежит пересечению двух множеств,
принадлежит ли она одному из этих множеств, другому?
Какие же из перечисленных предложений следуют
Непосредственно из р3?
(Постановка этих вопросов вытекает из анализа и
выявления возможных причин затруднений учащихся.)
Далее, если учесть определение окружности,
окр(О, г)={У||ОУ|=г},
становится очевидной истинность следования р2=^р4:
Ле7У||0Г| = г}=>|0Л| = г.
Из того же, что истинны следования р3=>р2 и р2 =^Р4>
становится очевидной истинность следования р3 => р4 (отно-
шение следования транзитивно).
Учитывая далее, что окружность — граница, а стало
быть часть круга, обнаруживаем также истинность следо-
вания р2=>'Р12-
Ле окр (О, г)_ и окр (О,г) с= кр (О,г) => Л е кр (О,г), а
следовательно и истинность следования Рз^Рп-
По-видимому, некоторые учащиеся обнаружат и дру-
гие достаточно очевидные логические связи, например,
что из р7 следует pi3.
Если же учащиеся будут затрудняться в обнаруже-
нии этой связи, то можно задать им, например, такой
вопрос:
Если бы точка X принадлежала окружности, то ка-
кой еще фигуре она бы определенно принадлежала?
з*
35
Ёсли учащиеся затрудняются ответить на этот во-
прос, можно" задать им следующий вопрос:
Частью какой другой фигуры является окр(О, г)?
Приходим, в конце концов, к заключению об истинно-
сти следования
Хеокр(О, г)=>Хекр(О, г).
Приняв это предложение в качестве одной посылки, а
в качестве другой — ръ т. е. отрицание предложения X ЕЕ,
екр (О, г), заключаем о ложности предложения Х^окр (О, г)
или об истинности его отрицания X окр (О, г) (пред-
ложения р13). Здесь неявно применено правило контрапо-
зиции: «если из Р следует Q, то из не Q следует не Р»
(«если то Q=>P»).
Из определения круга следует истинность следований:
ОХ | <>=>Хе= кр (О, г) и Хее кр (О, г) =>| ОХ К г, т. е.
равносильность | OX |< г X е кр (О, г), а
правилу контрапозиции) следует., что
отсюда (по
X кр (О, г) => | ОХ | > г и | ОХ | > г => X кр (О, г), т. е.
истинны следования р? => р8 и р8 => ръ или равносильность
Pi <=* Ра-
Исходя из определения расстояния от точки до пря-
мой и из свойства перпендикуляра, опущенного из точки
на прямую, получаем: А ge а и [О A] J_ я => | О А | = d (О, а),
т. е. и р5=>р9.
При описанном выше выявлении логических связей
были использованы следующие знания: определения пе-
ресечения двух множеств, окружности, круга, подмно-
жества, отрицания отношения «^», расстояния от точки
до прямой. Кроме того, в рассуждениях неявно исполь-
зовались некоторые широко применяемые в математике
правила следования (силлогизма, контрапозиции), кото-
рые могут быть предметом рассмотрения на факульта-
тивных или внеклассных занятиях и могут разъясняться
на приведенном математическом материале.
Выявленные выше (и некоторые другие явно высту-
пающие) логические связи (например, р4 и р8=>рп) уже
позволяют нам заменить исходное множество Р предло-
жений, полученное в результате наблюдений и опыта, од-
ним из следующих его подмножеств:
36
Pi = {Рз, Рв, Рв, Pl, Pio), ИЛИ
Рг= {Рз, Рз, Рв, Рз, Рю}, или
Рз= {Рз, Рв, Ръ Рз, Рю}, или
Pi={ps, Рв, Рв, Рз, Рю}-
Рассмотрим одно из этих множеств предложений (эк-
вивалентных между собой в том смысле, что имеют одно
и то же множество следствий Р), например Pi.
Относительно этого множества предложений, естест-
венно, возникает та же проблема: являются ли предло-
жения этого множества логически независимыми? Нель-
зя ли вывести какое-нибудь из этих предложений из
остальных (и, разумеется, некоторых ранее уже извест-
ных геометрических предложений) ?
Нетрудно заметить, что из р3, Рв и рю следует р7, или
равносильное ему предложение р8. Таким образом можем
еще упростить множество предложений Ръ заменив его
подмножеством
Р1 — {Рз» Рб» Ре» Рю}* *
Очевидно, что р& и pi0 не следуют ни из р3, ни из р5,
ни из. обоих этих предложений (X — заданная произ-
вольная точка прямой а, отличная от Л), можно их счи-
тать «локальными» аксиомами.
Остается выяснить, нельзя ли вывести р5 из р3, или рз
из р5.
Из р3 следует, что Х^а и Х=/=Д=ф-|ОХ| >Л т. е.
Ре и рю=>р8» или из р3, р6, р10 следует р8 и, так как,
кроме того, из р3 следует р4, то из р3 получаем
.(1)Хеа и ХфЛ=>|ОД| < |ОХ|, т. е. р и Рю=>Р11»
или Рз, р6, Рю^Рп-
Но (1) равносильно |ОД| = d (О, а), а из [ О А | = d(O, а)
следует [ОА\ ± а, т. е.
Рз, Рб» Р10=^ Рб*
Если обратить наши рассуждения, получим
Рб» Рб» Рю^Рз-
(Разумеется, некоторые учащиеся будут затруднять-
ся найти эти доказательства. Поэтому здесь, естественно,
37
возникает проблема организации и управления поиском
доказательства. Как это можно сделать, будет показано
в главе V.)
Предложения и рю входят в состав посылок при
выводе £5 из рз, или рз из р5 (точка X и была включена с
самого начала в рассматриваемую ситуацию для* облег-
чения поиска этих доказательств).
Можно утверждать, что предложения р3 и равно-
сильны (при данном множестве посылок). Если р3 при-
нять за определение касательной к окружности, т. е.
определить касательную к окружности как прямую,
имеющую с окружностью только одну общую точку, то
предложение будет теоремой, выражающей свойство
касательной к окружности (касательная к окружности
перпендикулярна радиусу, проведенному в точку каса-
ния). Если же принять за определение касательной к
окружности предложение (касательной к окружности
называется прямая, перпендикулярная радиусу в конце
его, принадлежащем окружности), то предложение рз
будет теоремой, выражающей свойство касательной (ка-
сательная к окружности имеет с ней только одну общую
точку).
Как видно, определение касательной к окружности
появляется в конце проведенного исследования, связан-
ного с математическим описанием рассматриваемой
структуры. При этом выясняется возможность двух раз-
личных определений и соответствующих построений «ма-
ленькой теории» (касательной к окружности), состоящей
из определения и двух' теорем, устанавливающих равно-
сильность предложений рз и р5.
Обращаясь после такого исследования к учебнику,
учащиеся обнаруживают, что изложенный в нем мате-
риал (Г. 6—8, § 84, п. 29. «Взаимное расположение пря-
мой и окружности» f) получен ими в процессе проведен-
ного исследования (разумеется, под руководством учи-
теля). Две теоремы, приведенные в учебнике (т. 35 и 37),
после принятого определения касательной устанавли-
вают равносильность двух предложений, обозначенных
нами через р3 и р5.
Совершенно очевидно, что усвоение учащимися фраг-
мента математической теории, в построении которого они
1 Здесь и дальше через Г обозначается сокращенно «Геомет-
рия», через А — «Алгебра», через М — «Математика».
38
приняли активное участие, материала, являющегося ре-
зультатом (в какой-то мере) самостоятельного исследо-
вания (организованного и управляемого учителем в про-
цессе обучения), будет более глубоким и осознанным,
чем то, которое
Рис. 3
является результатом заучивания мате-
риала по учебнйку после его изложе-
ния учителем традиционными мето-
дами.
Пример 2.
Рассмотрим задачу математическо-
го описания изображенной на рисунке 3
ситуации (перед введением понятия
ромба в VII классе).
В результате наблюдения и опыта
получаем следующее множество пред-
ложений, выражающих свойства рас-
сматриваемой.ситуации:
рх: (ABCD) — параллелограмм;
р2:|ЛВ| = |ВС|;
р3: |ВС| = |СО|;
Pi:\CD\ = \AD\;
Ps: | ЛЕ>] = \АВ
Рб: (ЛС) J_ (£Ю);
: A'BD = DBC;
Рй: ADB = BDC;
Рй: DAC = С АВ;
Р10: DC А =-- АСВ;
Рп: 5(ло (ABCD) = ADCB;
Р12 • S{bd) {ABCD) = С В AD.
Получили множество Р= {Pi, Рг, , Р12}, и возникает
проблема логической организации этого математическо-
го материала, т. е. выделения из Р подмножества пред-
ложений (возможно минимального), из которого (и, ра-
зумеется, ранее известных геометрических предложений)
следовали бы все остальные предложения из Р. Иными
словами, необходимо преобразовать множество Р пред-
ложений в маленькую теорию.
39
Исследование раскрывает различные возможности
ЛОММ, т. е. различные возможности построения теории.
Замечаем, что каждое из предложений р2 — рь выра-
жает одно и то же свойство (две смежные стороны па-
раллелограмма ABCD конгруэнтны) и любое из этих
предложений совместно с pi образует подмножество
исходных предложений, из которых следуют все осталь-
ные. Не будем различать эти четыре варианта, считая
их одним, например Pi={pi, р2}, т. е. построение теории
на базе множества Pi исходных предложений.
‘ Аналогично выясняется, что каждое из предложений
Рч — Рю выражает одно и то же свойство (одна из диаго-
налей параллелограмма ABCD лежит на биссектрисе
одного из его углов). Проверкой устанавливается, что и
любое из этих предложений вместе с pi образует подмно-
жество исходных предложений с требуемым свойством,
например Р2= {рь р7}.
Исследуя множество Рз={Рь Ре}, обнаруживаем, что
и оно может служить базисом для построения теории.
Предложения ри и рц выражают одно и то же свой-
ство (одна из диагоналей параллелограмма ABCD — его
ось симметрии) и множество Рь={Ръ Ри) (иди {pi, piz})
дает еще один вариант построения теории.
Таким образом получаем четыре различных варианта
построения «теории ромба» и, соответственно, четыре
возможных определения ромба:
Pi — параллелограмм с двумя конгруэнтными смеж-
ными сторонами,
Р2 — параллелограмм, у которого одна диагональ —
биссектриса одного из его углов,
Р3 — параллелограмм со взаимно перпендикулярны-
ми диагоналями,
Р4 — параллелограмм, у которого одна диагональ —
его ось симметрии.
Описанное исследование проводится в виде решения
нескольких серий задач на доказательство, связанных
общей идеей ЛОММ.
Решение этих задач способствует достижению пони-
мания доказательств и предупреждает часто допускае-
мые ошибки, связанные с вопросом «что из чего следует».
Пример 3.
Рассмотрим изучение средней линии трапеции (Г. 6—8,
п. 48).
Учащиеся уже знакомы со средней линией треуголь-
40
ника и ее свойствами. Целесообразно привлечь эти зна-
ния учащихся при изучении средней линии трапеции.
Но делать это можно по-разному. Опишем два варианта
построения процесса исследования. В обоих вариантах
этот процесс включает создание проблемной ситуации,
стимулирующей открытие учащимися свойств средней
линии трапеции, поиск, открытие,и построение доказа-
тельства этих свойств.
Вариант 1.
1. Пусть [Ah— средняя линия треугольника AiBJ\
(рис. 4).
Рис. 4
Вспоминаем свойства средней линии треугольника:
(I) [AWIItAPJ и (2) 1^1 =
2. Пусть в трапеции ABCD (рис. 4) М и N — середи-
ны непараллельных сторон, т. е. |ДЛ4| = |ЛЕВ| и |£W| =
= |NC'|. {Л4ЛЫ — средняя линия трапеции ABCD.
Как можно сформулировать определение средней ли-
нии трапеции?
Этот вопрос не вызовет затруднений у учащихся.
Некорректные формулировки исправляются, и уточня-
ются самими учащимися.
3. Естественно возникает проблема выяснить, какими
свойствами обладает средняя линия трапеции.
Весьма вероятно, что многие учащиеся сразу же
усмотрят из рисунка параллельность средней линии осно-
ваниям трапеции. Если же учащиеся будут затрудняться
в выдвижении гипотезы, то надо обратить их внимание
на свойства средней линии треугольника.
После того как будет выдвинута гипотеза о парал-
лельности средней линии трапеции ее основаниям, мож-
но выяснить, какое предложение достаточно доказать
для подтверждения этой гипотезы. Если некоторые уча-
41
щиеся укажут предложение «[Л4Л7]||(Л/)] и [A12V]lj[Z?6?]», то
можно задать им такой вопрос:
Необходимо ли доказывать параллельность средней
линии обоим основаниям трапеции?
Вероятно, некоторые учащиеся догадаются, что до-
статочно доказать параллельность средней линии одному
из оснований, т. е. для подтверждения выдвинутой гипо-
тезы достаточно доказать предложение «[Л4Л/]||[Л£)]» или
предложение «[Л4ЛГ]||(ВС]».
Второе свойство средней линии трапеции не подска-
зывается рисунком. Можно обратить внимание учащих-
ся на то, что мы выдвинули гипотезу о наличии у средней
линии трапеции свойства, аналогичного (сходного) с
первым свойством среднем линии треугольника. Естест-
венно возникает вопрос, пет ли у средней линии трапеции
свойства, аналогичного второму свойству средней линии
треугольника, т. е. вопрос о связи длины средней линии
с длинами оснований. Маловероятно, что эта связь будет
правильно угадана учащимися.
Мы не должны опасаться ошибочных предположений
учащихся. По существу, во всяком поиске в какой-то ме-
ре применяется так называемый «метод проб и ошибок»,
и мы должны давать учащимся возможность ошибаться,
а затем приводить их к пониманию допущенной ошибки.
Если по неправильной аналогии ученик выскажет ги-
потезу, что средняя линия трапеции (как и средняя ли-
ния треугольника) равна половине нижнего основания,
то нетрудно привести этого ученика к построению опро-
вержения собственной гипотезы (достаточно предложить
ему изменить длину одного верхнего основания трапеции,
и он обнаружит, что меняется и длина средней линии,
хотя длина нижнего основания не изменилась).
Для приближения учащихся к открытию второго
свойства средней линии трапеции можно задать им та-
кой вопрос:
Нельзя ли образовать в трапеции какие-нибудь тре-
угольники, чтобы связать среднюю линию трапеции со
средней линией треугольника?
По-видимому, учащиеся предложат провести какую-
нибудь из диагоналей трапеции. Проведя, допустим, диа-
гональ [BD] (рис. 5) и обозначив через Р точку пере-
сечения ее со средней линией [М/V], некоторые учащиеся
будут утверждать, что [7ИР1 — средняя линия треугольни-
ка ABD, a [ZW] — средняя линия треугольника BCD и
42
сразу же «докажут» параллельность средней линии трапе-
ции ее основаниям, а также откроют и «докажут» второе
свойство средней линии, так как | МР | = |ЛО| и |РЛ[=
=4i5ci> т° i^i=|мр|+i^i=4-(мд|+1 £?с|).
Возможно, некоторые уча-
щиеся сами заметят существен- В ~___________С
ный пробел в этих рассужде-. \
ниях и скажут, что все это ML . \л/
верно, если мы докажем, что /
Р — середина диагонали [ВО]. д1----------------
Если же учащиеся этого не
заметят, то можно поставить Рис. 5
такие вопросы:
На каком основании вы
утверждаете, что [Л4Р] — средняя линия треугольника
ABD, a [PN] — средняя линия треугольника BCD?
Что называется средней линией треугольника?
Что же остается доказать, чтобы обосновать утвер-
ждение «(Л4Р] — средняя линия треугольника ABD и
[PN] — средняя линия треугольника BCD»?
С помощью таких вопросов выясняется, что для под-
тверждения высказанной гипотезы достаточно доказать,
что | ВР | = | PD |.
Каков же дальнейший естественный ход мыслей?
По-видимому, предположение о том, что Р не есть се-
редина отрезка [ВВ].
Мы имеем здесь наглядный пример, когда косвенное
доказательство («от противного») возникает как естест-
венный ход мыслей в процессе исследования.
Возможно, кто-то догадается провести через точку М
прямую, параллельную основанию, и сможет доказать,
что она проходит через середины отрезков BD и CD.
В таком случае получится доказательство, приведенное
в учебнике (п. 48).
Рассмотрим косвенное доказательство.
Из предположения, что | BP | =/= | PD |, следует, что на
[BjD] существует точка Plt отличная от Р (Р^Р) и та-
кая, что | BPi | = | PJJ |, т. е. Pi — середина [BD] (рис. 6).
Из этого допущения учащиеся получат ряд следст-
вий: [МР!] — средняя линия треугольника ABD\ [PiA/J —
средняя линия треугольника BCD\ следовательно,
43
[МЛ] | [AD] и [PiN] || [ВС], и так как [ВС] || [AD], то и
[PiN] | [AD],
Обращаем внимание учащихся на два полученных
следствия: (МЛ) II (АП) и (Р^)[|(АП).
Возможно, некоторые учащиеся заметят, что через
точку Pi проведены две различные прямые MPi и PiN,
обе параллельные одной пря-
В____________С мой AD, что противоречит ак*
\ сиоме параллельных.
Если же не заметят, то
/ р можно поставить следующие
д --------------—^jD вопросы:
Сколько прямых, параллель-
Рис 6 ных (AD), проведено через
точку Л?
Почему вы утверждаете, что
прямые MPi и P\N различны?
Таким образом, предположение, что середина отрезка
BD отлична от точки Л приводит к противоречию (с ак-
сиомой параллельных). Следовательно, это предположе-
ние ложно, а его отрицание (Л = Л истинно.
Теперь учащиеся сами сформулируют теорему, вы-
ражающую свойства средней линии трапеции и построят
ее доказательство, которое, по существу, уже открыто
ими (разумеется, с помощью учителя).
(Если же искать прямое доказательство, изложенное
в учебнике, возможно, придется приблизить учащихся к
первому шагу (обычно наиболее трудному в прямых до-
казательствах) с помощью таких (подсказывающих)
вопросов:
Какую прямую нужно провести через середину М от-
резка АВ, чтобы быть уверенным, что она пройдет и че-
рез середину, отрезка BD? На основании какой теоремы
это можно утверждать?)
Целесообразно продолжить исследование с целью вы-
яснения, не являются ли установленные свойства средней
линии характеристическими свойствами трапеции (выде-
ляющими из множества четырехугольников подмножест-
во трапеций). Можно попробовать выяснить это для каж-
дого из двух свойств в отдельности.
Для первого свойства это очевидно: если отрезок, со-
единяющий середины двух противоположных непарал-
лельных сторон, параллелен двум другим сторонам че-
44
тырехугольника, то этот четырехугольник — трапеция
([ад и [ЛР] и [ад и [ВС] => [лг>] и [вер.
Здесь возможны лишь затруднения в формулировке
обращения первого свойства. В таком случае целесооб-
разно преобразовать формулировку первой части дока-
занной теоремы «средняя линия трапеции параллельна
ее основаниям», представив ее в виде условного выска-
зывания с использованием определения средней линии:
если четырехугольник — трапеция, то отрезок, соединяю-
щий середины двух непараллельных сторон, параллелен
двум другим ее сторонам (основаниям). При такой фор-
мулировке легко получить обратное предложение: если
в четырехугольнике отрезок, соединяющий середины двух
непараллельных сторон, параллелен двум другим его
сторонам, то этот четырехугольник — трапеция.
ь В трапеции средняя линия соединяет середины двух
противоположных непараллельных сторон, в формули-
ровке же обратного предложения слово «противополож-
ных» опущено, поэтому здесь уместен такой вопрос: нуж-
но ли включить это слово в формулировку обратного
предложения?
Если предложить учащимся изобразить на рисунке
случай, когда отрезок соединяет середины двух смежных
сторон четырехугольника, то этот рисунок подскажет им,
что в таком случае не выполняется условие: отрезок, со-
единяющий середины двух смежных сторон четырехуголь-
ника, не может быть параллельным двум другим его
сторонам. Таким образом, обратное предложение сфор-
мулировано правильно.
Истинность обращения второго свойства средней ли-
нии трапеции менее очевидна. Возникает проблема: если
отрезок, соединяющий середины двух противоположных
непараллельных сторон четырехугольника, равен полу-
сумме двух других его сторон, то будет ли этот четырех-
угольник трапецией?
Выдвигается гипотеза, что такой четырехугольник —
трапеция, т. е. что предложение ] АМ | *= | МВ | и ]ОАГ|=
= |АГС| и I УИЛГ I = _!_§£ЦИ£1 => [BCJIIMD] (рис. 6) ис-
тинно (является теоремой). Как же это доказать?
.Проведенноё исследование свойств средней линии
трапеции подсказывает нам и путь доказательства этой
обратной теоремы.
Вероятно, некоторые учащиеся догадаются провести
45
диагональ [В£>], рассмотреть AABD и ABCD и заметят,
что если Р — середина диагонали, то получаем доказа-
тельство параллельности [ВС] и [ЛР].
Таким образом, остается доказать, что |BP[ = |PZ)|,
а для этого опять учащиеся допустят, что это не так и
что существует на [В£>] точка 1\ (Р^Р) такая, что
|BPi| = |PiZ)|. Если же не догадаются, то направить их
поиск можно с помощью тех же вопросов, которые были
поставлены при поиске доказательства первого предло-
жения. Дальнейший же ход доказательства, приведение
к противоречию, уже существенно отличается от преды-
дущего.
В случае затруднений можно обратить внимание уча-
щихся на то, что при доказательстве предложения,, об-
ратного первой части теоремы о свойствах средней линии
трапеции, мы ссылались на первое свойство средней ли-
нии треугольника. Можно предполагать, что при дока-
зательстве предложения, обратного второй части, -надо
использовать второе свойство средней линии тре-
угольника.
Используя это свойство, учащиеся получат: |MPi| +
+ |PrAf | = (|ВС.| +|ЛС|). Но, с другой стороны, так
как то + >|^| =4-(1^1 +
-Ь| ЛО|), т. е. lAlPJ + IP^O-i-dBCl + I^DI).
Получили противоречие:
|/ИР1Ц-|/’1^| = 4'(1ВС1 + 1Л£)1) и \МРг\ + \Р^\>
>4 (]ВС| + ИР|),
доказывающее теорему: если отрезок, соединяющий се-
редины двух противоположных непараллельных сторон
четырехугольника, равен полусумме двух других, его сто-
рон, то этот четырехугольник — трапеция.
Здесь, естественно, возникает и такой вопрос: оста-
нется ли это предложение теоремой, если в его форму-
лировке опустить слово «непараллельных»? Нельзя ли
построить четырехугольник, который не является трапе-
цией, хотя в нем отрезок, соединяющий середины двух
противоположных сторон, параллелен двум другим его
сторонам?
Учащиеся найдут контрпример — параллелограмм.
46
Вариант 2.
Неудача с гипотезой о том, что средняя линия трапе-
ции равна половине нижнего основания, приводит к дру-
гой гипотезе, что длина средней линии трапеции опреде-
ленным образом зависит от длин обоих ее оснований.
Возникает идея образовать треугольник, средняя ли-
ния которого совпала бы со средней линией трапеции
ABCD, а основание было бы связано с обоими основа-
ниями трапеции.
Возможно, некоторые учащиеся догадаются рассмот-
реть центральную симметрию с центром N (рис. 7).
Если же никто не догадается, можно поставить такие
вопросы:
Если рассмотреть центральную симметрию с центром
N, то в какую точку перейдет точка С, точка В?
Что можно сказать о треугольниках BCN и NDE?
Об отрезках ВС и DE?
Откуда следует, что [DEJcz(Л/))?
Чему равно основание треугольника АВЕ?
Чем является средняя линия трапеции в треугольнике
АВЕ?
Откуда следует, что | BN | = | NE | ?
Постепенно, шаг за шагом, конструируется доказа-
тельство:
1) ZN(C) = D; Zn(B) = E\
2) Zn(&NBC) - &NDE=> &NBC^ &NDE;
3) £\NBC^ &NDE^\BC\ = \DE\\
4) 2лг([ВС]) = [Г£}=^[ВС]|[[ОД и (BC)\\(AD)=>
[DE] a: (AD); -
5) \AE\ = \AD\ + \DE\^\AD\ + \BC\;
47
6) ZN ([ВЛ/]) = [Л/Е[ I BN I = INEI и MN — средняя
линия дЛВЕ;
7) [MA/]—средняя линия £\ABE=>[MN]||[АЕ] и |Л1А/|=
=4-м£|’
8) [MN] || [ЯП] и [ЯР] |] [ВС] => [А4А/] ||[ВС];
9) |МА/| = 4-|ЯВ| и |ЯЕ| = | ЯРЦ-[ВС|=>|Л4А/| =
= 4-(|ЛРЦ-|ВС1).
Пример!
Наметим одну из возможных схем привлечения уча-
щихся к построению «маленькой теории» предела после-
довательности.
Под последовательностью будем понимать «беско-
нечную числовую последовательность», т. е. отображе-
ние
Целесообразно исходить из рассмотрения разнооб-
разных примеров последовательностей, составляющих
для нас эмпирический материал, подлежащий дальней-
шей математизации (с помощью новых понятий).
Рассмотрим, например, последовательности:
(1) 1, 2, 3.....п, ...;
(5) —2, 4, —8, .... (—1)п2",
(8)--~г...........(-D"
(9) -1, 1,-1.......(-1У,
И®) То"» ПР “Пр • ’ ( Ч"+1 "пр • • • 5
(io 1,4’2-
2 о 3
3 , О, 4 ,
48
и их изображения с помощью точек координатной
прямой.
Наблюдая эти изображения, можно обнаружить су-
щественные различия в «поведении» последовательно-
стей (рис. 8).
X/ х2
(9\ . У3 *2________________
о II 1. 1. Г
5 4 3 2
(з)-*—----------&--------------&-----
1 ' О / 4 9
(в)
(Ю)
(ll) -г
___1_
10
Х% Xq Х& Xf
1
10
Ч Г1 I
2
2 4 6/

О
_1_
О
1 /
г
Х<
Л
г
О
7_ 15 /
8 16
Рис. 8
1) Для некоторых из них ((2), (4), (6), (7), (8), (9),
(10), (12)) можно указать отрезки прямой, содержащие
все члены последовательности, для других ((1), (3), (5),
(11)) не существует таких отрезков.
4 Зак. 1239
49
Это различие в поведении последовательностей могут
заметить сами учащиеся. Если же они не заметят» мож-
но помочь им, приблизить их к открытию этого различия
с помощью вопросов:
Сравните расположение на координатной прямой то-
чек, изображающих члены последовательностей (1) и
(2), (3) и (4), (5) и (6).
Можно ли указать отрезок координатной прямой, со-
держащий точки, изображающие все члены последова-
тельности (1), (2), (3), (4), (5), (6) и т. д.?
Какой отрезок можно указать для последовательно-
сти (2), (4), (6), (7), (8), (9), (10), (12)?
Как записать эти отрезки как отрезки числовой пря-
мой (т. е. как подмножества /?)?
10 ’ 101 [ 2 ’ | )
С помощью приведенных вопросов образуется интуи-
тивное представление об ограниченности и неограничен-
ности последовательностей и возникает проблема мате-
матического описания этих свойств.
Выписанные отрезки числовой прямой подсказывают
нам способ перевода интуитивного представления об
ограниченности последовательности в точное математи-
ческое понятие (если существует отрезок, содержащий
все члены последовательности, то существует положи-
тельное число такое, что все члены последовательности
по модулю не больше его).
Если же возникают затруднения, можно поставить
вопрос: существует ли положительное число, обладаю-
щее таким свойством: все члены последовательности
((1), (2), (3), (4),...) не больше этого числа по
модулю?
Так приходим к определению: (хп) —ограниченная
последовательность, если существует положительное
число а такое, что для любого п |хп| ^.а.
Свойство ограниченности последовательности можно за-
писать кратко, если ввести два символа: «Н» для обозна-
чения выражения «существует» (квантора существования)
и «V» Для обозначения выражения «для любого» (кван-
тора общности) следующим образом:
Ла > 0 \/п (| хп | а).
50
(Можно предполагать, что эти два символа войдут в
скором будущем в школьные учебники, по крайней мере,
старших классов.)
Если последовательность не обладает свойством огра-
ниченности, то она называется неограниченной и запись
того, что последовательность (хп) неограничена, можно
получить как отрицание свойства ограниченности: не
существует положительное число а такое, что для любо-
го п или для всякого положительного числа а
существует п такое, что \хп | т. е.
За > 0 уп (|хп или у а > 0Ил (|xrt| > а).
2) Замеченное различие, с помощью которого выде-
лились классы ограниченных и неограниченных последо-
вательностей, не единственное в поведении рассматри-
ваемых последовательностей.
Наблюдая геометрические изображения последователь-
ностей, обнаруживаем еще одно наглядно выступающее
различие. У некоторых последовательностей образуются
«скопления» членов вокруг одной или нескольких точек,
у других таких скоплений нет. Так, в последовательностях
(2), (4), (6) подобные скопления наблюдаются вокруг точ-
ки 0, в последовательностях (7), (11), (12) — вокруг точ-
ки 1, в последовательностях (8) и (9) —вокруг точек 1 и
— 1, в последовательности (10) — вокруг точек и —
(рис. 8).
Возникает проблема математического описания явле-
ния, которое мы назвали «скоплением» членов последо-
вательности. Но прежде всего необходимо выяснить, все
ли скопления одинаковы по своей структуре.
Для приближения учащихся к открытию различных
типов ^скоплений членов последовательностей можно
предложить им сравнить скопления членов последова-
тельностей, например (7) и (’11), вокруг точки 1. Чтобы
облегчить им это сравнение, можно выбрать произволь-
ный отрезок с серединой в точке 1, например длиной 1,
т. е. [1—0,5; 1+0,5], и поставить вопрос: какое множест-
во членов последовательностей (7), (11) попадает внутрь
этого отрезка, какое остается вне его? Затем можно
уменьшить длину отрезка, скажем в 10 раз, т. е. взять
отрезок с серединой в точке 1 длиной 0,1 {1—0,05;
•1+0,05] и поставить тот же вопрос.
51
Выявляется существенное различие между скопле-
ниями членов этих двух последовательностей вокруг точ-
ки Г: оказывается, что в любой «окрестности» точки 1
(здесь уместно ввести этот термин) попадает бесконеч-
ное множество членов как последовательности (7), так
и последовательности (11)* Это свойство характеризует
всякое «скопление» членов последовательности. Однако
между рассматриваемыми двумя' скоплениями есть су-
щественное различие: вне всякой окрестности точки 1
остается всегда конечное множество членов последова-
тельности (7), а для последовательности (11) это свой-
ство не выполняется, уже вне тех двух окрестностей, ко-
торые мы рассматривали, находится бесконечное мно-
жество членов этой последовательности. Иными словами,
какую бы окрестность точки 1 мы ни взяли, можно найти
такой номер И, начиная с которого все члены последова-
тельности (7) (т. е. с номерами не меньше п) попадают
в эту окрестность. Для последовательности же (11) та-
кого номера нельзя найти.
(Важно разъяснить это различие всякими возмож-
ными способами, чтобы сделать его интуитивно ясным.
Разумеется, нужно «подталкивать» учащихся к само-
стоятельному открытию этого различия с помощью воп-
росов-подсказок.)
После выявления двух видов скоплений можно пред-
ложить учащимся отнести каждое из ^наблюдаемых на
рисунке 8 скоплений к одному -из этих видов (I—(7),
(2), (4), (6), (8), (12) и И—(11), (9), (10)).
Теперь можно сообщить учащимся, что нас будут
интересовать лишь скопления первого вида (именно они
играют важную роль как в самой математике, так и в ее
приложениях), поэтому возникает проблема их матема-
тического описания.
Анализ интуитивного представления о такого рода
скоплениях приводит к уточнению этой проблемы. Необ-
ходимо, прежде всего, описать математически «попада-
ние» члена хп последовательности в окрестность точки 1
длиной, например, 2е, т. е. внутри отрезка [1—е; 1-4-е].
В таком случае расстояние между точками хп и 1 должно
быть меньше е, т. е. \хп—11 <е.
Таким образом, предложение «хп попадает внутрь
отрезка [1-е; 14-е] (е-окрестности точки 1)» равносиль-
но неравенству
|хп—1|<е. (1)
52
Теперь возникает вопрос: как выяснить, с какого но-
мера п все члены последовательности попадают в 8-окре-
стность точки 1 (речь идет о конкретной последователь-
ности (7))?
Выполняется следующая процедура:
1 I—е
б)“7Г+Г<е^п> “~
Е 1 — S п.= е Начиная с какого п выполняется (1)
0,1 9 10
0,05 19 20
0,01 • • •’ 99 100
Таким образом убеждаемся, что какое бы мы ни взя-
ли е>0 (т. е. окрестность длиной 2е), всегда существует
такое По, что для всех п>п0 выполняется неравенство
(1), т. е. все члены последовательности, начиная с
/io+1-го, попадают в е-окрестность точки 1.
Используя символы для обозначения квантора общ-
ности и существования, это утверждение можно записать
кратко так:
Ve > О3ло Vn (п > п0 => | хп — 11 < в). (2)
В таком случае говорят, что «число 1 является пре-
делом последовательности (хп)», в данном случае пог
следовательности (7), и это обозначается так: lim(xn) = 1;
Таким образом, lim(xn)=l по определению равно-
сильно (2), т. е.
♦
lim(хл) = Г^1 Ve > О3по tfn(n > н0=>|хл— 11 < е).
Df
После повторения учащимися описанной выше про-
цедуры для других последовательностей ((2), (4), (6),
(8), (12)) осуществляется последний шаг в. обобщении
1 <=> — по определению равносильно (означает), Df — от латин-
Df
ского «Definition — определение.
53
результатов проведенного исследования (переход от Г к
числу а) и приходят к общему определению предела по-
следовательности:
1нп(хл) — а <=> ve
Df
0Лио (п > по=^1хл — а| < е).
Как видно, и в этом примере определение нового по-
нятия (предела последовательности) появилось в виде
итога проведенного коллективного исследования ситуа-
ций, описываемой с помощью этого понятия.
3) Возвращаясь к рассмотренному эмпирическому ма-
териалу, замечаем, что в тех случаях, когда наблюдается
скопление членов I вида (последовательность имеет пре-
дел), такое скопление имеется только вокруг одной точ^
ки (последовательность имеет только один предел). Слу-
чайно ли это?
Учащиеся, по-видимому, догадаются, что это не слу-
чайно. Если же возникнут затруднения, можно помочь,
подсказав им рассуждать «от противндгб»? т. е. попы-
таться опровергнуть возникшую гипотезу об единствен-
ности предела. Надо допустить, что какая-то последова-
тельность имеет два различных предела а и &. Геометри-
ческая картина на координатной прямой подсказывает
опровержение такой возможности, т. е. доказательство
теоремы об единственности предела последовательности.'
Описанная схема построения в процессе обучения ма-
ленькой теории обеспечивает активность учащихся не в
усвоении результатов, готовой теории, а в получении их,
в построении теории, и в этом она принципиально отли-
чается от схемы обучения по традиционной методике.
§ 2. ОБУЧЕНИЕ ЭЛЕМЕНТАМ ИССЛЕДОВАНИЯ
В ПРОЦЕССЕ РЕШЕНИЯ ЗАДАЧ
Обучение через задачи предполагает, в частности,
тщательный.отбор задач, их группировку в определен-
ные последовательности, допускающие построение про-
цесса решения наподобие процесса • исследования. При
этом выявляются возможности обобщения задач, форму-
лировки и решения новых, достижения посредством ре-
шения последовательности задач нового, порой неожи-
данного теоретического результата, углубляющего зна-
ния изучаемых объектов.
Приведем в качестве иллюстрации два примера.
54
Пример 1.
Предлагаем учащимся следующие однотипные за-
дачи:
Изобразить на координатной плоскости множества
£i={(x, У) I12};
Е2={(х, У) |2х+^4};
Ез={{х, у) |х>0};
Еь={(х, у)|у>0}.
Сначала эти множества изображаются на различных
рисунках (рис. 9, а, б, в, г), затем они переносятся на
один рисунок (рис. 9, 6).
Нис. 9
Возникает вопрос: что представляет собой множество Е
(четырехугольник, образовавшийся на рисунке 9,6)?
Этот вопрос, по-видимому, не вызовет затруднений.
В противном случае можно сформулировать вопрос так:
как связано множество Е с множествами £i, Е2, Е3, Е^?
Е=Е{ Г) Е2 Л Ез р Ei.
Как же составить «характеристическое свойство» для
55
множества Е из заданных характеристических свойств
множеств Eit Е3, Е3, Et?
Е = {(х, у)|3х+4у^12 и 2х+у^4 и х^О и у^О}
(это следует непосредственно из определения пересече-
ния множеств), т. е. Е — множество решений системы не-
равенств
(1)
Зх + 4у< 12,
2х + у < 4,
х>0,
!/>0.
Теперь может быть поставлена следующая задача:
изобразить подмножество Е, на котором сумма х+у рав-
на 1; 2; 3; 4.
По существу, здесь имеем еще одну серию однотипных
задач: найти пересечение £Q {(х» у) |х+у=а}, где а=
= 1,2, 3, 4.
Проводятся параллельные прямые x-j-y=a, где
а = 1, 2, 3, 4 (рис. 9, е) и обнаруживается, что
£(!{(*. У) ]x-j-y=4) —0 (рис. 9, е).
Теперь, естественно, возникает вопрос: какие значения
может принимать сумма х+у на множестве £?
Геометрическая картина подсказывает нам, что наи-
большее значение эта сумма принимает в вершине четы-
рехугольника, удовлетворяющей системе (Зх-|-4у=12 и
2х+у=4), т. е. здесь х+у=0,8+2,4=3,2.
По рисунку заключаем, что наименьшее значение
х+у принимает в вершине 0. Таким образом, на множе-
стве £ 0^х+у^З,2.
Замечаем, что наибольшее и наименьшее значения
сумма х+у принимает на границе четырехугольника.
Случайно ли это?
Чтобы ответить на этот вопрос, нужно выяснить, чем
отличаются точки границы от внутренних точек много-
угольника (новая проблема, если это раньше не рас-
смотрено).
Можно предложить учащимся в произвольном много-
угольнике F (рис. 10) отметить несколько точек, лежа-
щих на границе (Л, В), и несколько внутренних точек
(М,Р).
Чтобы приблизить учащихся к открытию решения,
можно поставить такие вопросы:
Для каждой точки на границе проведем окружность
56
произвольного радиуса с центром в этой точке. Все ли
точки внутри такой окружности принадлежат много-
угольнику F?
А для внутренней точки всегда ли можно провести та-
кую окружность с центром в этой точке, чтобы внутри ее
лежали только точки многоугольни-
ка? А если эта внутренняя точка
очень близка к границе?
Таким образам постепенно выяс-
няется, в чем состоят характеристи-
ческие свойства граничных и внут-
ренних точек многоугольника.
Теперь можно вернуться к нашей
проблеме: почему наибольшее и
наименьшее значения сумма х+у
принимает на границе четырехугольника, а не в его
внутренних точках?
Начнем с выяснения того,
что описывает класс урав-
нений
a^R. Очевидно, пучок
параллельных прямых,
так как угловые коэф-
фициенты всех этих
прямых равны 1.
Пусть какая-нибудь
из этих прямых, напри-
мер x+y^a[t проходит
через внутреннюю точ-
ку Л41(Х1, у\) четырех-
угольника Е (рис. 11).
Тогда на основа-
нии характеристическо-
го свойства внутренних
точек можно провести
окружность с центром
Mi, внутри которой ле-
Е. Выберем две точки
где
жат только внутренние
внутри окружности:
точки
внутри окружности: М2(х2, у2) так, чтобы х2>хх и
У2>Уъ и Мз(х3, уз) так, чтобы x3Oi и у3<У1 (это всегда
возможно). Тогда х2+у2=^2>^1 и Хз+уз=^з<^1 (через
М2 проходит прямая пучка я+у=а2, а через М3 — пря-
мая пучка xj-y=a3).
Таким образом, если сумма х+у принимает во внут-
ренней точке Е некоторое значение (например, в точке
57
All), то это значение не может быть ни наибольшим, ни
наименьшим.
Если же прямая x+y=Ct имеет общую точку (л0, уо)
с Е, лежащую на границе, то это означает, что либо для^
c>Ci, либо для c<ZCi не будет общих точек прямой
х-\-у=с с многоугольником Е.
Что отсюда следует?
Отсюда следует, что g — наибольшее или наимень-
шее значение суммы х-{-у на множестве Е.
Как видно, приведенный пример охватывает не одну,
а серию задач, подготавливающих учащихся к усвоению
в дальнейшем геометрического метода решения задач ли-
нейного программирования, для простейшего случая двух
переменных. Но, кроме того, сам процесс решения' об-
учает элементам исследовательской деятельности.
Пример 2.
В качестве второго примера рассмотрим серию задач,
связанных с геометрией треугольника.
Прежде всего необходимо обратить внимание учащих-
ся на то, что треугольник (простейший многоугольник)
обладает большим разнообразием свойств (лишь очень
небольшая часть этих свойств изучается в школьной гео-
метрии) .
1. Начнем со следующей задачи:
Пусть АВС — произвольный треугольник (рис, 12).
Существуют ли точки X, принадлежащие АВС и облада-
ющие свойством Saxb — Saxc, т. е. если соединить точку X
с вершинами ДАВС, то два из образовавшихся треуголь-
ников, а именно, с общей вершиной А, имеют равные
площади (равновелики)? А если существуют такие точ-
ки, то сколько их?
Эту задачу можно иначе сформулировать так: «Найти
множество точек X таких, что Хе ДАВС и Saxb =
= Saxc, т. е.
{Х| ХеДАВС и Saxb = Saxc}»-
Поиск^гочек, обладающих указанным свойством, мож-.
но (хотя и необязательно) начать с рассмотрения отве-
тов на следующие вопросы:
Существуют ли такие, точки на стороне АВ, на сто-
роне АС?
Почему не существуют? (Один из треугольников АХВ
или АХС вырождается в отрезок.)
58
Существуют ли такие точки на стороне ВС?
Возникает гипотеза, что середина D стороны ВС об-
ладает требуемым свойством.
Подтверждение этой гипотезы обычно не вызывает
затруднений (рис. 12).
SADB= Злос = 4-|^1-Л и IBD\ = |DC|
^Sadb = Sado
Рис. 12
Рис. 13
Одна точка, удовлетЬоряющая условиям задачи, есть
(точка D). Теперь будем искать такие точки внутри
ДЛВС.
Естественно возникает гипотеза (подкрепляемая уже
найденной точкой D и наглядностью чертежа): всякая
точка медианы AD обладает требуемым свойством (если
Х=А, то оба треугольника АХВ и АХС вырождаются в
отрезки и можно им приписать площадь, равную 0, т. е.
для точки А выполняется равенство Saab=Saac)-
Теперь предстоит доказать эту новую гипотезу.
Берем произвольную точку X медианы AD, т. е.
Хе[А£>], отличную от D и А, для которых условие задачи
выполняется (рис. 13).
Что нужно доказать? (Saxb=Saxc-)
Возможно* кто-то догадается, как это сделать. Если
нет, то поиск можно вести по следующей системе во-
просов:
Нельзя ли треугольники АХВ и АХС связать с други-
ми треугольниками, с помощью которых удалось бы это
доказать? *
59
ДЛХВ и =
ДЛХС и дсхп=длос
Что отсюда следует о площадях треугольников?
Saxb+Sbxd = Sadb, (1)
5axc4“5cxd = 5adc« (2)
Что уже известно о площадях некоторых из этих тре-
угольников?
Sadb — Sadc»
(3)
Что же остается доказать?
Sbxd = Scxd- (4)
Как это. доказывается? (Аналогично (3).)
Что же следует из (1), (2), (3) и (4)?
Saxb^Saxc, что и требовалось доказать.
Итак, мы доказали, что всякая точка медианы AD об-
ладает требуемым свойством. Можем ли мы теперь утвер-
ждать, что искомое множество точек X есть медиана AD
треугольника АВС? (Нет.)
Почему?
Может быть, существуют еще точки, обладающие тре-
буемым свойством, но не лежащие на медиане AD. Ка-
жется, что ^дких точек'нет.
. Но что значит «кажется»?
Это — гипотеза, которую надо
/уЧ или доказать, или опровергнуть.
// \ X. Как же можно сформулиро-
/х1 \ у ч. вать то, что надо доказать?
г X & [AD] => S дхв $АХС-
В D b
Как доказать это предложе-
Рис. 14 ние?
Может быть, попытаться срав-
нить площади треугольников АХВ
и АХС (рис. 14) с площадями треугольников, образован-
ных аналогичным образом с помощью какой-нибудь точ-
ки Хи лежащей на медиане AD?
Какую выбрать точку Xi на медиане AD?
Семиклассник предложил взять Xi = (AZ))f|(XC)
(рис. 14).
60
Как теперь использовать уЖе доказанное свойство
точки
SaxiB^Saxic, ho Saxb<ZSaxib, так как
ДДХВс^ДДХ4В, HSAxc>SAXiC,TaK как ДДЛ^СсДДХС,
следовательно, Saxb^Saxc-
Теперь уже можно считать задачу решенной.
Что представляет собой искомое множество точек?
{Х|Х(=ДДВС} и Sax в — Sax с —[ДР].
2. Обобщим теперь исходную задачу.
Мы искали точки X, принадлежащие ДДВС и обла-
дающие свойством
Saxb — Saxc-
Естественно возникает вопрос: вне треугольника АВС
(но в одной с ним плоскости) существуют ли точки, об-
ладающие этим свойством? Иначе говоря, отличается ли
{Х| Saxb = ‘$axc} от [Д-D]?
Где, естественно, искать такие точки?
По-видимому, на лучах [£>Д) и [Д£)).
Возьмем точку Хе[£>Д), но такую, что Х&ДАВС
(рис. 15).
Рис. 15
Рис. 16
Как доказать, что точка X обладает свойством
Saxb — Saxc^
Это доказательство совершенно аналогично приведен-
ному выше для случая, когда ХеДДВС (это. условие в
нем не использовалось).
Возьмем теперь точку X такую, что Хе[ДР) и
Х^ДДВС (рис. 16).
Доказательство свойства Saxb = SAxc аналогично
предыдущему.
61
Существуют ли еще Точки, йе лежащие йа Прямой
AD, но обладающие тем же свойством?
Проведенное выше доказательство предложения
X £ [ДО] => Saxb¥=Saxc
остается в силе и для предложения
X (£ (AD) => Saxb^Saxc-'
Итак, доказано, что
{X | SAXB = SAXC} = (AD), где ] BD | = [ DC |.
Что представляет собой множество точек X таких, что
Sbxa=SbXc (два треугольника с общей вершиной В рав-
новелики)? *
Здесь уже все доказано.
{X | SBXA = Sbxc} = (BE), где | АЕ [ = [ ЕС |.
3. Поставим теперь новую задачу: существует ли точ-
ка X такая, что
SAXB = SAXc и SBXA — SBXc?
Иначе говоря, требуется найти
{Х| SAXB = SAXc и 5вхА = £вхе}.
Так как это множество, в соответствии с определени-
ем пересечения множеств, можно представить в виде
{X | 5ахв = 5ахс} П {X[Sbxa — Sb.yc}» в {XISaxb —
— Saxc} = (Л7)) и {X | Sbxa = Sbxc} = (5£), то {X SAXB =
— SAxc и Sbxa = Sbxc} = (AD)(](BE) = 0 (рис. 17).
(После. решения задач 1 и 2
задача 3 уже не вызывает затруд-
/ нений у учащихся.)
/ Таким образом, таких точек X,
вК^\ которые удовлетворяют условию
с задачи, только одна — точка О
\ пересечения медиан AD и BE.
4 4. Найденная точка О облада-
Рис’ 17 ет, однако, еще одним свойством.
Действительно,
Вахв — и Sbxa ~ Sbxc => Saxc = $вхс » т. е.
точка О обладает также свойством
SAXc = SBXc,
Но все точки плоскости треугольника АВС, обладаю-
62
щйе этим свойством, по уже доказанному принадлежат
прямой CF, где [CF] — третья медиана треугольника
АВС (рис. 18).
Следовательно, Oe[CF], или
[ВД]Л[ЛЕ]П[СЛ=О,
т. ё. мы этим самым доказали, что три медианы тре-
угольника пересекаются в одной точке.
5. Попытаемся теперь вьГЯснить, в каком отношении
делится медиана AD точкой О.
Выясним прежде всего,,, в каком отношении находятся
площади треугольников ВОС и АВС.
Ввос = -4-5лвс- (Почему?)
о
В ЛОВ = В ДОС = ScOA’
Что отсюда следует об отношении ' высот этих тре-
угольников, |ОЛ| и |ЛМ| (рис. 18)?
|<М 1 = 4- [ЛАП. (Почему?)
О
Проведем через О прямую PQ,
параллельную (ВС).
На рисунке 18 имеем следую-
щую ситуацию: две параллельные
прямые PQ и ВС пересекают сто-
роны угла MAD. Какая теорема
применима к этой ситуации и что
по этой теореме следует?
По теореме Фалеса следует: так как | НМj = -|ЛЛ4|
и (|ЯМ| = |(М|), то и 10DI = 41 AD I, или |ЛО|:|ОР|=
= 2:1.
Таким образом, мы нашли, что медиана AD делится
точкой О в отношении 2 к 1, считая от вершины А (отку-
да- проведена медиана).
Если теперь повторить то же по отношению к стороне
ЛС, т. е. опустить высоты треугольников АОС и АВС на
эту сторону, провести через О прямую, параллельную
(ЛС), и повторить те же рассуждения, к какому выводу
придем?
63
lOfl = 4-1 ВЕ\, или |ВО|:|ОЕ| = 2: 1.
Аналогично получим, что и
|OF| = 4-1CFI, или |CO|:|OF| = 2:1.
О
Чем же можно теперь дополнить доказанное выше (4)
предложение?
Точка пересечения медиан делит каждую ме-
диану в отношении 2:1, считая от соответст-
вующей вершины.
6. Обратимся еще раз к рисунку № и выделим на нем
еще одну ситуацию, к которой применима теорема Фале-
са: две параллельные прямые PQ и ВС пересекают сто-
роны угла^ВАО. Что отсюда следует?
]РВ| = 4-МВ|.
Нельзя ли использовать это для нахождения другого
способа решения задачи 3? Как это сделать?
Некоторые учащиеся догадаются. Если же возникают
затруднения, можно их приблизить к открытию нового
способа, задав такие вопросы:
Мы ищем точки X такие, что если соединить их с вер-
шинами ДАВС, то образуются три равновеликих треуголь-
ника. Чему же должна равняться площадь каждого из этих
( 1 Q \
треугольников? 1-3-^лвсЬ
Где может лежать вершина X треугольника ВХС, если
Sbxc = -у Sabc?
Эта вершина может лежать на прямой, параллельной
(ВС) и отстоящей от нее на расстоянии, равном высо-
ты ДАВС.
Как делит эта прямая сторону АВ?
Она отсекает от нее считая от точки В, значит,
эта прямая — (PQ) (рис. 18).
Получаем новый способ решения задачи 3: делим сто-
рону АВ (или какую-нибудь другую сторону) на три рав-
64
ные части (|ДЛ4[ = |МР| = |РВ[), проводим (PQ)||(ВС)
и (MN)\\(AC) (рис. 19). (PQ)n(W)=O.
А
Рис. 19
Рис. 20
Если исходить из этого способа решения задачи 3, то
можно доказать, что (AD)()(BE) =0 (рис. 20).
Рассмотренные задачи образуют систему, так как
между ними существуют определенные связи: задача
2 — обобщение задачи 1; решение задачи 3 — пересече-
ние решений двух задач типа 2; задача 4 выявляет новое
свойство результата решения задачи 3 (свойство медиан
треугольника); задача 5 открывает еще одно свойство
медиан; задача 6 выявляет новый способ решения за-
дачи 3.
Основной результат решения этой системы задач —
открытие и доказательство двух важных свойств медиан
треугольника.
Обучение через задачи осуществляется с помощью
подобных систем задач, решение которых приводит к но-
вым теоретическим знаниям.
Разумеется, связи, превращающие совокупность за-
дач в систему, могут быть иными, отличными от перечис-
ленных выше. Важно, чтобы сама система задач была
ориентирована на получение новых теоретических
знаний.
5 Зак. 1239
Глава III
Структурирование и систематизация
математических знаний
§ 1. СУЩНОСТЬ СТРУКТУРИРОВАНИЯ
И СИСТЕМАТИЗАЦИИ
Структурирование и систематизация относятся к
аспекту математической деятельности, названному нами
логической организацией математического материала
(ЛОММ).
Структурирование — мыслительная деятельность по
установлению ближайших связей между отдельными по-
нятиями, предложениями.
Структурирование является подготовкой к преобразо-
ванию совокупности знаний в систему (к осуществлению
систематизации).
Систематизация — мыслительная деятельность по
установлению более удаленных связей, в процессе кото-
рой изучаемые объекты организуются в определенную
систему.
Систематизация освобождает память от необходимо-
сти запомнить материал как сумму частных, изолирован-
ных, не связанных между собой сведений и фактов, так
как группирует их в более крупные единицы, которые
легче удержать в памяти и воспроизвести в нужных слу-
чаях. Только тогда мы можем сказать, что учащиеся
имеют знания по предмету, когда они сформированы в
определенную систему. Еще К- Д. Ушинский, Характери-
зуя значение системы знаний, писал: «Только система,
конечно, разумная, выходящая из самой сущности пред-
метов, дает нам полную власть над нашими знаниями.
Голова, наполненная отрывочными, бессвязными знания-
66
ми, похожа на кладовую, в которой все в беспорядке и
где сам хозяин ничего не отыщет...» 1 Систематизация не
может осуществляться без структурирования, без выде-
ления связей между объектами, которые преобразуют
множество изучаемых объектов в систему.
В проблеме систематизации выделим два аспекта:
а) умение учителем систематизировать учебный мате-
риал; б) обучение учащихся структурированию знаний,
включение новых знаний в систему.
В рамках первого аспекта учитель должен овладеть
навыками логико-дидактического анализа учебного ма-
териала, навыками составления различных структурных
схем, позволяющих наглядно представить содержание
учебного материала, логические связи между отдельны-
ми его элементами, понятиями, предложениями. Резуль-
татом овладения перечисленными навыками явится раз-
работка программы обучения не только на один урок, а
на всю тему или даже на весь курс.
Второй аспект предусматривает обучение учащихся
выявлению в изучаемом материале существующих отно-
шений между объектами, фактами, понятиями; обучение
использованию различных структурных схем, а иногда
и их составлению; обучение конкретизации общего по-
ложения и обобщение конкретных фактов; обучение
включению новых знаний в уже имеющуюся систему.
§ 2. СТРУКТУРНАЯ БЛОК-СХЕМА ТЕМЫ
Наглядное представление о системе учебного мате-
риала темы дают специальные структурные блок-схемы.
На этих схемах учебный материал темы представлен в
виде трех блоков: А, В, С (рис. 21). Блок А — ранее из-
ученный или подготовительный материал, используемый
при изучении данной темы, блок В — теоретический ма-
териал, изучаемый в данной теме, блок С — применение
изученной теории. В свою очередь блок В подразделяет-
ся на три: Bi — основные понятия, предложения темы,
Вг — сопутствующий (неосновной) материал, В3 — выра-
батываемый внутри данной темы аппарат, приме-
няющийся на практике. Каждый из блоков представляет
собой систему математических предложений (определе-
ний, теорем и т. д.), сгруппированных также в блоки.
1 Ушинский К. Д. Сочинения: В 11-ти т.— М., 1949, т. 5, с. 355.
5е
67
При изготовлении больших таблиц, используемых на
уроке, лучше вместо различных видов линий использовать
одинаковые линии, но разного цвета: черного, красного, си-
него, зеленого.------— черная, -.—красная,-------
зеленая,--------синяя. Необходимо заметить, что одина-
ковость линий блоков Л и С не случайна, ибо материал,
Рис. 21
являющийся применением теории в одной теме, может стать
необходимым для введения основных понятий и изучения
теоретического материала в другой теме.
Блок-схемы являются как бы систематизированной
программой деятельности на определенный период.
Использование их в обучении чрезвычайно разнообраз-
ное: организация повторения материала, необходимого
для изучения темы; построение определений некоторых
понятий; показ логической организации материала и вы-
яснение возможностей, иной, чем в учебнике, последова-
тельности его изучения, возможно более рациональной;
организация самостоятельного изучения отдельных воп-
росов; выяснение совокупности сведений, получаемых в
результате изучения теории; выяснение связи материала
темы с другими темами, как предшествующими, так и
последующими.
Имея такую схему, учитель видит, на что надо обра-
тить внимание при повторении материала, какой мате-
риал является наиболее важным. Используя схему, мож-
но более продуманно составить календарные или тема-
тические планы, представить себе значение и цель
каждого урока.
Учащиеся, которым схема сообщается в самом нача-
ле изучения темы, по ней могут определять, какие вопро-
сы и в какой последовательности будут рассматриваться
в данной теме, какие вопросы являются наиболее важ-
ными, какова связь с другими темами, какой материал
68
надо повторить, чтобы сознательно и активно усваивать
новый материал. Учащиеся, которые по каким-либо при-
чинам пропустили занятия, могут использовать схему
для самостоятельного изучения материала и ликвидации
существующего пробела в знаниях. Можно организовать
самостоятельное изучение материала отдельных блоков
по учебнику, которое состоит в том, что учащиеся рас-
крывают содержание по плану, предложенному учите-
лем. Например, содержание отдельных блоков схемы
«Векторы и их применение» (см. Приложение, схема 55)
осуществлялось по такому плану:
отношение
1) множество пар,
2) различные отношения, которые можно установить
между двумя множествами,
3) в геометрии отношение — множество .пар точек;
отображение
1) особый вид отношений (не всякое отношение),
2) виды отображений: отображение «в», отображе-
ние «на»,
Я л
3) отображение пространства на себя;
преобразование пространства
’отображение пространства на себя особого вида;
перемещение
1) преобразование пространства особого вида,
2) свойства перемещения: а) тождественное преобра-
зование — перемещение; б) композиция перемещений —
перемещение; в) преобразование, обратное перемеще-
нию,— перемещение;
конгруэнтность
1) отношение, устанавливаемое с помощью переме-
щения:
Ф2 «=> ЯР — перемещение (Ф2 = Р (Ф^),
69
2) свойства конгруэнтности: рефлексивность, симмет-
ричность, транзитивность.
Аналогичную работу можно проводить и по раскры-
тию содержания блоков «направление», «угол между на-
правлениями», «угол между векторами», «коллинеарные
векторы».
Уже по самому названию блока «Векторная алгебра»
учащиеся понимают, что теория темы представляет собой
изучение алгебраических операций и их свойств над век-
торами. Вместе с учителем определяется последователь-
ность изучения теории, результатом которой явится со-
ставление перечня основных сведений о векторах, необ-
ходимых для решения задач.
Для того чтобы учащийся смог воспользоваться схе-
мой при самостоятельном повторении материала даже
по прошествии длительного периода времени после окон-
чания школы, скажем, при подготовке к вступительным
экзаменам, необходимо перечертить эту схему в тетрадь.
Отводить на это время на уроке не следует, так как на
весь период изучения темы схема вывешивается в каби-
нете математики.
После того как учащиеся овладеют достаточными на-
выками в работе со схемами, можно поставить перед
ними^задачу составления таких схем по отдельным те-
мам, но это возможно только после изучения темы. Мож-
но поставить и более узкую задачу — составить часть
схемы (отдельные ее блоки).
§ 3. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ПОНЯТИЙ
Если на первом этапе изучения материала важно
определить общую структуру темы, ее связи с другими
темами, последовательность изучения, то далее неизбеж-
но встает вопрос о связи между отдельными понятиями,
т. е. о выяснении структуры системьГпонятий.
Понятия — основной элемент учебного материала.
Однако нельзя рассматривать понятия изолированно, так
как «каждое понятие находится в известном отношении,
в известной связи со всеми остальными» Ч С одной сто-
роны, связи определяют переходы от одних понятий к
другим в процессе рассуждения. С другой стороны, пони-
1 Ленин В. И. Философские тетради.—Поли. собр. соч.,
т. 29, с. 179.
70
мание взаимоотношений между понятиями служит осно-
вой усвоения системы понятий. В результате же усвое-
ния системы понятий мы получаем систему знаний, что
является целью обучения. ,
Пусть Л4 = {П1, П2, ... , Пп} — множество понятий не-
которого фрагмента учебного материала, Р — бинарное
отношение П<РП,, которое означает, что понятие Пг-
используется в определении понятия П>. Это отношение
порождает во множестве М определенную структуру
(Л1, Р)/которую мы и будем называть системой по-
нятий.
Только тогда можно считать понятие включенным в
систему, если установлены связи (отношения) между
этим и уже известными понятиями.
Наглядно изобразить систему понятий позволяет ори-
ентированная графовая структура, в которой вершины
изображают понятия, а стрелки выделяют пары понятий,
находящихся в отношении Р, т. е. две вершины Пг и П;
соединены стрелкой, исходящей из IL и оканчивающейся
в П/, тогда и только тогда, когда ПгРП^. Такую графо-
вую структуру будем называть структурной схе-
мой системы понятий.
На построенной схеме можно выделить наиболее важ-
ные понятия, представляющие собой своего рода «несу-
щие опоры» системы, иначе говоря, такие понятия, исклю-
чение которых приведет к разрыву логической связи
между понятиями. Одновременно выделяются и побочные
понятия, не имеющие непосредственного отношения к са-
мому строению теории. Все это позволяет критически
оценить роль отдельных понятий в общей системе и про-
извести возможную перестановку, перераспределение по-
нятий по степени их важности в логической структуре
учебного материала.
Для того чтобы составить структурную схему системы
понятий, необходимо предварительно выписать все поня-
тия (как вновь вводимые, так и уже известные) данного
отрезка учебного материала (пункта, параграфа, главы).
Например, составим структурную схему системы поня-
тий пункта 19 «Математика. 4» — «Уравнение». Выпи-
шем множество понятий: предложение, переменная, вы-
сказывание, предложение с переменной, равенство, зна-
чение переменной, уравнение, корень, множество, решить
уравнение. Из списка понятий видно, что в него вошли
и те понятия, которые связывают материал пункта с ра-
71
нее пройденным. Изобразим теперь структурную схему
соответствующей системы понятий.
Схема 1
На схеме прямоугольником изображены понятия, кото-
рые вводятся в данном пункте, овалом — уже известные.
Аналогичной данной схеме является структурная схе-
ма системы понятий пункта 20 — «Неравенство».
72
‘Схемы показывают построение определений новых по-
нятий, последовательность их введения. Сравнивая обе
указанные схемы, можем сказать, что методика введения
понятий уравнения и неравенства должна быть одина-
ковой. -
Структурную схему можно вычертить заранее и после
объяснения материала использовать ее для закрепления,
можно строить вместе с учащимися в процессе объясне-
ния, а можно сделать ее предметом изучения, что пред-
полагает обучение учащихся построению схем, начиная,
естественно, с более простых. Так схему для пункта 23
(^«Математика. 4». «Правильные и неправильные дроби»)
учащиеся могут построить самостоятельно под руковод-
ством учителя, ибо эта схема довольно проста (схема 3).
Если в младших классах мы строим структурные схе-
мы небольшого отрезка учебного материала, то в стар-
ших классах"иногда целесообразно выделить для пост-
роения структурных схем системы понятий больший от-
резок; например несколько пунктов, параграф, главу.
Такая схема позволяет усмотреть связи более удален-
ные» что способствует глубокому пониманию изучаемого
материала.
Любое понятие либо определяется через какие-то
другие, либо является неопределяемым, основным. В свя-
зи с этим полезно строить структурные схемы сведения
некоторого понятия к основным. Особенно это важно в
геометрии, где одной из целей является раскрытие сущ-
ности дедуктивного (аксиоматического) построения кур-
са. Приведем примеры (схемы 5 и 6).
Важно с самого начала изучения геометрии в VI клас-
се уже обучать учащихся построению таких схем для то-
го, чтобы избежать формализма в знаниях.
§ 4. СТРУКТУРНАЯ "СХЕМА СИСТЕМЫ ПРЕДЛОЖЕНИЙ
Достижению глубокого понимания логической орга-
низации учебного материала и выявлению возможностей
другой логической организации, а также выяснению зна-
чимости каждого предложения теории служит структур-
ная схема системы предложений некоторого отрезка
учебного материалам
Пусть М = {Pi, Р2, ..; , Рп} — множество математиче-
ских предложений данного отрезка учебного материала,
a S — бинарное отношение: PiSPj означает «предложе-
73
Схема 4
74
Схема 5
Схема 6
75
ние Pi используется в доказательстве предложения Pj».
Множество Af с отношением S, т. е. структуру (Al, S) бу-
дем называть системой предложений.
Систему предложений можно наглядно изобразить в
виде графовой структуры, при этом вершины изобра-
жают предложения (элементы системы), а стрелка, исхо-
дящая из вершины Pi и оканчивающаяся вершиной Pj,
изображает связь PiSPj.
Для того чтобы построить структурную схему систе-
мы предложений некоторого отрезка учебного материа-
ла, надо прежде всего выписать все предложения дан-
ного отрезка учебного материала как вновь рассматри-
ваемые, так и известные, на которые мы опираемся при
доказательстве новых. К числу таких предложений мо-
гут относиться аксиомы, теоремы, определения, интуи-
тивно ясные и очевидные предложения и т. п.
Структурную схему системы, предложений можно
использовать для выяснения уровня строгости того или
иного доказательства и возможности-его улучшения, для
выяснения возможности другой логической организации
материала, для выделения наиболее важных предложе-
ний темы, организации повторения необходимых для
данного материала вопросов и раскрытия связи с ранее
пройденным материалом, применения аналогичного под-
хода к построению других доказательств. Структурную
схему системы предложений можно сделать предметом
изучения с учащимися.
При построении структурной схемы системы предло-
жений будем пользоваться такими обозначениями:
овалом — известное, ранее изученное предложение,
прямоугольником — новое предложение, предложе-
ние данной темы.
Построим структурную схему системы предложе-
ний темы «Метрические соотношения в треугольнике»
(Г. 6—8, гл. VIII, схема 7). Выпишем все предложения,
вводимые или используемые в данной теме:
Рь теорема Пифагора.
Р2: предложение о квадрате стороны, лежащей против
острого угла в произвольном треугольнике.
Р3: предложение о квадрате стороны, лежащей про-
тив тупого угла в произвольном тупоугольном тре-
угольнике.
Рс теорема косинусов.
76
Р6: теорема о площади треугольника Iформула S =
1 Ч/Л
= -g- aXh j.
Рв: теорема о площади треугольника /формула S= -7 аХ
Xfesinc).
Pi. теорема о площади треугольника (формула
Герона).
Pg. теорема синусов.
Р9; соотношения между длинами сторон и тригоно-
метрическими функциями в прямоугольном треугольнике.
Ры: тождество cos (180“ — а) = — cos а.
Ри: тождество sin2 а + cos2 а = 1.
"и• формула cos Л = —у?-----
Схема 7
Рассмотрим систему предложений темы «Арифмети-
ческая и. геометрическая прогрессия» (А. 8, гл. III, схе-
ма 8). Составим множество предложений, вводимых или
используемых в данной теме:
Pi: определение функции.
Р2- определение возрастающей функции.
Р3: определение убывающей функции.
₽4: определение последовательности.
' .Р5: определение возрастающей последовательности;
Р6: определение убывающей последовательности.
Рц определение рекуррентной формулы.
77
Ps: определение формулы общего члена последова-
тельности.
Pq: определение постоянной последовательности.
Р10: определение арифметической прогрессии.
Ра: определение разности арифметической про-
грессии.
Pi2: признак арифметической прогрессии.
Рю: формула n-го члена арифметической прогрессии.
Pi4: формула суммы первых п членов арифметической
прогрессии.
Pi5: определение геометрической прогрессии.
Рю: определение знаменателя геометрической про-
грессии.
Pi7: признак геометрической прогрессии.
Рю: формула n-го члена геометрической прогрессии.
Pio: формула суммы п первых членов геометрической
прогрессии.
Схема 8
Из приведенных примеров структурных схем системы
предложений видно, какое предложение является глав-
ным, наиболее употребительным, какие предложения на-
до знать, чтобы вводить то или иное определение или до-
казывать то или иное предложение.
Из-за большого числа предложений следует сокра-
78
щать отрезок учебного материала, выбирать для состав-
ления схем отдельный параграф или даже пункт, особен-
но это касается геометрии. Например, имеет смысл по-
строить структурную схему системы предложений, вво-
димых или используемых в теме «Ось симметрии угла и
равнобедренного треугольника» (Г. 6—8, схема 9):
Pi: определение равнобедренного треугольника.
Р2: определение и свойства осевой симметрии (сово-
купность предложений).
Р3: определение биссектрисы угла.
Р4: теорема 30.
Р5: определение оси симметрии фигуры.
Р6: следствие 1.
Р7: определение биссектрисы треугольника.
Р8: определение высоты треугольника.
Р9: определение медианы треугольника.
Рю: следствие 2.
Рн: определение серединного перпендикуляра.
Pi2: теорема 31.
Эту схему можно обогатить новыми связями, решив
следующую задачу: «Из одной вершины треугольника
проведены биссектриса, высота и медиана. Доказать, что
если хотя бы два из трех отрезков совпадают, то тре-
угольник равнобедренный».
79
Используя теорему 31, а также решение приведенной
выше задачи, можно иначе определить равнобедренный
треугольник, например как треугольник, у которого вы-
сота и биссектриса, проведенные из одной вершины, сов-
падают, или как треугольник, у которого два угла кон-
груэнтны. Тем самым появляется возможность обучения
учащихся различным логическим организациям одного
и того же материала.
Наиболее важными системами предложений в мате-
матике являются доказательства. Доказательства также
можно представить наглядно в виде графоподобных
структурных схем. Эти схемы, раскрывая идею и внутрен-
ние связи доказательства, являются одновременно крат-
ким конспектом, составленным на общепонятном языке.
Вершинами графа доказательства служат предложения,
стрелки указывают на то, что из чего следует. Если из
предложений-посылок А и В следует предложение-заклю-
чение С, то это изобразится так:
С
Изображение того, что из A, Bt С следует Р, выглядит
так:
j.
Примеры структурных схем доказательств даны в
приложении I (схемы 61—76).
§ 5. НЕКОТОРЫЕ ПРИЕМЫ СИСТЕМАТИЗАЦИИ
Помимо средств систематизации, описанных в преды-
дущих параграфах, существуют и другие, которые не ме-
нее эффективно можно использовать в обучении мате-
матике. к числу таких приемов можно отнести анало-
гию, составление подводящей системы задач, конкрети-
зацию.
Применение аналогии
1. Аналогия в структурах определений понятий.
Ставя перед учащимися проблему поиска определе-
80
ния понятия многогранника, (перевода интуитивного по-
нятия в точное), мы попытаемся применить аналогию со
структурой определения понятия многоугольника, для
чего строим схему последнего (схема 10).
Многогранник тоже представляет собой объединение
внутренней области и «окаймления» ее. Выяснив по ана-
логии смысл «окаймления», можно построить структур-
ную схему определения понятия многогранника (схе-
ма 11).
Примечательно еще и то, что одна схема служит про-
должением другой.
Структура определения сферы и шара аналогична
структуре определения окружности и круга.
Окружность: окр(О, г) = {Х| |ОХ| =г и г>0}.
Круг: кр(О, г) = {Х| |ОХ| и г>0).
Сфера: сф(О, г) == {Х| | ОХ| =г и г>0}.
Шар: ш(О, г) = {Х|ОХ|^г и г.>0}.
В этих записях опущено указание об универсальных
множествах, из которых выделяются подмножества то-
чек X (в первом случае — плоскость, во втором — про-
странство) . * ‘
Известно, что корень n-й степени и логарифм опре-
деляются через соответствующее уравнение: хп = а и
ах = Ь. Поэтому и структуру определения понятия лога-
рифма можно построить по аналогии со структурой опре-
деления корня n-й степени.
х = У а & хп = а, а > 0 I х = loga b <=> ах = Ь9 а > 0;
Df Df
аф 1, b > 0.
2. Применение аналогии при систематизации знаний и
навыков на примере изучения геометрических преобра-
зований в V классе.
При изучении .каждого вида преобразований учащие-
ся должны прочно усвоить: а) что любая фигура преоб-
разуется в конгруэнтную; б) как (какими элементами)
задается данное преобразование, а также должны овла-
деть навыками построения образов некоторых фигур в
этих преобразованиях. Исходя из одинаковости целей
обучения геометрическим преобразованиям, структура их
изучения аналогична. Рассмотрим эту структуру на при-
мере изучения темы «Параллельный перенос».
Проводим математизацию эмпирического материала,
6 Зак. 1239
81
Схема 10
Схема 11
82
формирующую интуитивное представление об этом по-
нятии и основном его свойстве: любая фигура при парал-
лельном переносе преобразуется в конгруэнтную.
Выяснив, как можно задать параллельный перенос, вы-
рабатываем у учащихся навыки построения образа про-
извольной точки как самой элементарной фигуры. Ста-
вим проблему построения других фигур. В общем случае
эта проблема не может быть решена конструктивно, од-
нако для таких фигур, как отрезок, луч, прямая, угол,
ломаная, многоугольник, "окружность, она разрешима в
силу свойств преобразования. Параллельный перенос пе-
реводит прямую в прямую, луч в луч, отрезок в отрезок,
поэтому для построения их образов достаточно построить
образы двух точек, принадлежащих фигурам, причем
Рис. 23
для отрезка это концы его, для луча одна из точек явля-
ется его началом (рис. 22). В заключение рассматрива-
ется построение образов треугольника и окружности
(рис. 23). Изучая остальные геометрические преобразо-
вания, целесообразно подчеркнуть аналогию в системе
6*
83
изучения данного преобразования и параллельного пе-
реноса.
3. Применение аналогии при построении доказа-
тельства.
Доказательства многих предложений аналогичны по
структуре с уже известными доказательствами, поэтому
учащиеся сами могут осуществлять поиск, предвари-
тельно проанализировав структуру известного доказа-
тельства.
Пусть надо доказать предложение: во всякий тетраэдр
можно вписать шар (1).
Рассмотрим структуру доказательства аналогичного
предложения: во всякий треугольник можно вписать
круг (2).
а) Множество точек, равноудаленных от сторон
угла — биссектриса угла (рис. 24, а).
б) Находим множество точек, равноудаленных от
двух пар сторон треугольника.
в) Доказываем, что точка, являющаяся пересечением
этих двух множеств, равноудалена от трех сторон тре-
угольника, а следовательно, она является центром впи-
санного круга (рис. 24, б).
Рис. 24
Структуру доказательства предложения (1) строим
аналогично структуре доказательства предложе-
ния ’(2).
а) Множество точек, равноудаленных от граней дву-
гранного угла — биссектор (рис. 25, а).
б) Находим множество точек, равноудаленных от
граней двух двугранных углов AD и DC. Это будет пря-
мая DK — пересечение двух биссекторов (рис. 25, б).
в) Доказываем, что прямая DK равноудалена от трех
граней ADC, ADB, BDC.
- г) Доказываем, что точка пересечения прямой D/Cc
84
биссектором двугранного угла АС равноудалена от всех
граней тетраэдра (рис. 25, в).
а
Рис. 25
Применение подводящей системы
задач
Под подводящей системой задач будем понимать по-
следовательность таких задач, которые, во-цервых, могут
быть решены учащимися самостоятельно, во-вторых, на-
целивают их на успешный поиск решения более трудной
целевой задачи.
Подводящая система задач осуществляет доступную
учащимся связь между известными знаниями и новыми,
т. е. позволяет включить новые знания в систему за счет
активной- самостоятельной деятельности учащихся.
Такая система задач не только активизирует само-
стоятельную деятельность учащихся, но и обладает боль-
шой общностью, так как почти нет сложных задач, к ко-
торым невозможно было бы подобрать соответствующую
систему подводящих задач. Систему подводящих задач
можно использовать и при изучении теоретического ма-
териала. Сама система использует ранее изученный ма-
териал, показывает новые возможности его применения,
т. е. осуществляет целенаправленное повторение, что
также немало важно.
Через систему подводящих задач мы управляем мыс-
лительной деятельностью учащихся, неявно обогащаем
их разнообразными методами поиска решения.
Приведем некоторые примеры.
1) Целевая задача: разложить а4+4 на множители
(6 класс). Задача для учащихся VI класса довольно
85
трудная. Для ее решения рассмотрим систему подводя-
щих задач:
а) разложить выражение (х24-2)2—4х2 на множители;
б) разложить на множители выражение
х4+4х2+4—4х2;
в) целевая задача.
2) Целевая задача: пусть М — точка пересечения
медиан ДЛВС, О — произвольная точка пространства.
Доказать, что
дм = 4- (ОА + дв + ОС) (9 класс).
О
Для решения этой задачи рассмотрим систему подво-
дящих задач.
а) Что такое сумма двух векторов? Построить из-
ображение суммы двух векторов по правилу параллело-
грамма (рис. 26).
Рис. 28
—>> —> —>
б) Выразить вектор АО через АВ и AD.
АО = 4г ДС = 4г (ДВ + AD).
в) М— середина отрезка АВ, О — произвольная точка
---------------------------------> ------->- >-
пространства (рис. 27). Выразить ОМ через О А и ОВ.
—> । —> —►
Используя результат б), имеем ОМ = (ОД -f- ОВ).
г) М GE [4В], причем | AM |: | МВ | = т: п, О — произ-
-------------------------> —>- --->
вольнаяточка. Выразить ОМ через О А и О В (рис. 28).
дм = ОА 4- AM = ОД + —4— (дв — ОД)= —7— ОВД-
86
д) Решение целевой задачи (рис. 29).
|ЛуИ|:|Л4Л1| = 2: 1,
=-г^л+4-олх=4-ол+44-
2 —>- —> —>-
= (ОЛ + ОВ + ОС).
(ОВ + ОС) =
Рис. 29
В процессе поиска решения целевой задачи мы полу-
чили ряд важных теоретических положений, которые мо-
гут быть использованы и в других задачах. Подводящая
система задач может быть продолжена, т. е. сама целе-
вая задача становится элементом подводящей системы
для другой целевой задачи. В данном случае продолже-
нием может являться такая задача: треугольник АВС
спроектирован параллельно на плоскость а в треуголь-
. ник Л1В1С1, причем |7L4i| = а, |BBi|=b, |CCi|=r. Най-
ти |ЛШ1|, где М — точка пересечения медиан ДЛВС,
Mt — ее проекция (рис. 30).
ОЛ11=4- (ОЛ2 + OBi + ОС1).
о
—► 2 —> —> —>-
ОМ = -у- (ОА 4 OZL+ ОС), так как М± — точка пере-
сечения медиан треугольника ДВ/4.
Вычитая из первого равенства второе почленно, по-
лучим:
AfMj = 4- МА + ВВ1 + СС1)-
<5
87
| ММг 1 = -4-1 AAt + BBj -f-CC, I = 4- (a+Z>+c), так как
о О
AAl tt BB± f f ccv
3) Общеизвестна значимость конструктивных задач
в курсе стереометрии. Они способствуют развитию про-
странственных представлений, сознательному усвоению
теории, развивают конструктивные навыки. Однако учеб-
ное пособие хотя и содержит такие задачи, не даёт чет-
кой дидактической системы обучения решению конструк-
тивных задач, способствующей активному восприятию
новых знаний. Устранить указанный недостаток можно,
реализовав следующую систему -подводящих задач, где
целевой задачей будем считать задачу на построение се-
чения куба или тетраэдра плоскостью.
а) Используя изображение куба и тетраэдра, рас-
сматриваются задачи на построение точек пересечения
прямой и плоскости (после изучения взаимного распо-
ложения двух прямых, прямой и плоскости в про-
странстве) .
Например (рис. 31). Дано: AtefDDJ,
Построить пересечения (МР) с
плоскостями граней куба. Важ-
но, решая первые конструктив-
ные задачи, провести -анализ.
Предположим, что точка
= (МР)П(41В1С1). Тогда эта точ?
ка лежит на линии пересечения
плоскостей AiBiCi и DDiC, так
как она лежит в обеих этих пло-
скостях. Точкой пересечения пря-
мой МР с плоскостью AiBiCi яв-
ляется точка пересечения прямых
МР й DiCi. После закрепления
навыков в решении аналогичных
задач, где прямая задана двумя точками, лежащими на
непараллельных ребрах одной грани куба, следует ре-
шить такие задачи:
Построить точки пересечения прямой МР с плоско-
стями граней куба, если P^[DDi].
Дан тетраэдр ABCD. MefAD], Р — внутренняя точка
88
грани CDB. Построить точку пересечения (МР) с пло-
скостью грани АВС, если (Л1Р)^(ДВС).
Построить точки пересечения прямой МР с плоскостя-
ми граней тетраэдра ABCD, если М — внутренняя точка
грани ADB, Р — внутренняя точка грани CDB и прямая
МР непараллельна плоскостям АВС и ADC.
б) Задачи на построение линии пересечения двух
плоскостей. При решении этих задач необходимо пока-
зать, что они сводятся к задачам предыдущего типа.
Примерами таких задач могут быть задачи § 9 «Геомет-
рия. 9—10» (одна решена в тексте, другая задача 72).
Решать задачи этого типа следует после изучения взаим-
ного расположения двух плоскостей.
в) Задачи на построение сечений. Перед построением
выясняем, основываясь на концепции «фигура — множе-
ство точек», что может являться результатов пересече-
ния многогранника (куба, тетраэдра) плоскостью: пу-
стое множество, отрезок, многоугольник. В частности, пе-
ресечением может являться одна из граней многогран-
ника. Дав определение сечения, устанавливаем, что для
его построения необходимо построить ломаную, которая
замкнута и концы каждого отрезка ее лежат на ребрах
многогранника. Начать решение задач на по’строение се-
чений, лучше с такой задачи: «Дан куб ABCDA{B\C\D\.
Построить сечение куба плоскостью, заданной тремя точ-
ками Л4, Р, К; Л4е(ЛВ], P^[4BJ, /teJBiCJ, причем
[МВ| = |МЛ|, \PD[=\PA\, \KBi\=]KCi\ (рис. 32)».
Рис. 32
Конструктивная задача на построение сечения может
являться средством создания проблемной ситуации, вы-
зывающей необходимость изучения теории. Например,
89
построить сечение куба ABCDAiBtCiDi плоскостью, про-
ходящей через три точки: М — внутренняя точка грани
ВВ1С1С, Ре[ЛД1], (рис. 33). Проблема реше-
ния этой задачи вызывает необходимость изучения тео-
Рис. 34
ремы о линиях пересечения двух параллельных плоско-
стей третьей. Установив факт, выраженный теоремой, мы
тем самым облегчаем во
многих случаях решение за-
дач на построение сечения в
дальнейшем.
Решение задачи 147
(Г. 9—10, гл. I) требует
пр едв а р ител ьного изучения
свойств параллельного про-
ектирования (рис. 34).
г) Важное значение в
предлагаемой системе имеет
и составление конструктив-
ных задач самими учащими-
ся. Составленные задачи
оформляются в виде карточек, изготовленных на плотной
бумаге размером 10X10 см. На одной стороне карточ-
ки — чертеж фигуры с нанесенным на нее условием, на
другой — решение.
Конкретизация общего положения
Конкретизация представляет собой применение общих
законов, принципов к отдельным частным случаям и по-
лучение на этой основе новых закономерностей и свойств
объектов.
Пусть имеем два множества объектов Р и К, причем
Р<=К, любой элемент из Р подчиняется закономерности
а, любой элемент из К — закономерности р, и р для эле-
ментов множества Р принимает вид а. Тогда конкрети-
зацией будем называть отыскание а, если известны
Р, К, р. Покажем это на ряде примеров.
1) Площадь поверхности многогранника по опре-
делению
п
S — J^Sif где — площадь i-н грани.
4=1
Поставим задачу нахождения более удобного вида фор-
мулы для некоторых многогранников.
90
а) Площадь поверхности призмы можно записать
формулой
п
•S = 2 *^бок» где *5/ площадь £~и бо~
i=i
новой грани.
После введения понятия перпендикулярного сечения
призмы получаем иную формулу для площади боковой
поверхности призмы 5б0К — Р± | ААГ |, где Р±—периметр
перпендикулярного сечения, | ААг | — длина бокового ребра.
В частном случае — для прямой призмы будем иметь
»$бок = Р осн I ААл |, Росн — периметр основания.
б) Площадь поверхности пирамиды записывается
формулой
л
Если пирамида правильная, то
S6oK = -у- Л>сн * Л гДе I— апофема боковой грани.
Для пирамиды, у которой все боковые грани одинаково
наклонены к плоскости основания,
*^бок —
coscp ’

в) Площадь поверхности усеченной пирамиды может
быть вычислена по формуле 3 = Sx -J- S2 -f- SCoK, где Slt
Л
32 — площади оснований, а 3Сок = V S{. Для правильной
z=i
пирамиды
где Ри Р2 —периметры оснований, L — апофема.
г) Площадь поверхности правильного многогранника вы-
числяется по формуле
3 = тп A-ctg
180“
где а — длина ребра, п — число ребер в одной грани,
т — число граней. Конкретизация этой формулы пред-
ставляется в виде таблицы:
91
п т Название многогран- ника Площадь
3 4 правильный тетраэдр а2/3
3 8 октаэдр 2а2 /3
3 20 икосаэдр 5а2/3~
4 6 гексаэдр (куб) 6аа
5 12 додекаэдр 3aactg 36°
Приведенная систематизация обуславливает целесо-
образность изучения материала по площадям в одном
месте курса, после рассмотрения видов многогранников
и их свойств.
2) Одним из понятий, часто используемых при реше-
нии задач по геометрии, является понятие расстояния
между фигурами, которое символически можно запи-
сать так:
|ф, ф^ =min{|ZB| |ЛеФ и ВеФ1).
Поставим задачу: выяснить, что представляет собой рас-
стояние между парами элементарных фигур: точка, пря-
мая, плоскость. Такая систематизация важна, так как
определение расстояния именно между этими объектами
наиболее часто встречается как при решении задач, так
и в практической деятельности.
а) Расстояние между двумя точками
|Д,В| = |ЛВ| (рис. 35).
б) Расстояние между точкой и прямой
|Л, а| = |АВ |, где [ЛВЦ_а и В^а (рис. 36).
Если Леа, то |Л, а| =0.
в) Расстояние между точкой и плоскостью
|Л, а| — |ЛВ|, где [ЛВ]_1_а и Веа (рис; 37).
Если Леа, то |Л, а| =0.
92
г) Расстояние между двумя плоскостями.
- Если af|p = 0, то |а, р| = |ЛВ|, где Леа, Вер,
[ЛВи_а (рис. 38).
Если а П Р=#0> то |а, р| —0.
д) Расстояние между прямой и плоскостью.
Рис. 35 Рис. 36 . Рис. 37
Если а|"|а = 0, то |а, а| = |ДВ|, где Леа, Веа,
[ЛВ]4_а, (рис. 39).
Если а П а#=0, то |а, а| =0.
е) Расстояние между двумя прямыми.
Если а П Ь^?0, то |а, Ь| =0.
Если а||& и а=/=6, то Iа, 4>| = [ДВ|, где Леа, В^Ь,
[ЛВ]_1_а.
Если а — Ь, то |а, 6| = |а, Р|, где аса, b ср, а||р
(рис. 40).
Рис. 38
Результат этой систематизации можно оформить в
виде таблицы и использовать ее в дальнейшем.
3) Рассмотрим один интересный пример из алгебры.
Общее положение: (А2т 4- В2я 4- ... 4- С2Й = 0).
а
(Л = 0иВ = 0и ... и С == 0),
93
где А, В, С — некоторые выражения с переменной
(переменными) т, п, k^N. Различные конкретизации
этого общего положения осуществляются при решении
уравнений и систем уравнений. Например:
а) 5х2 4- 5у2 + 8 ху 4- 2у — 2х 4- 2 = 0;
б) 4х2 + г/2 — 4х 4- 4у Ц- 5 = 0;
в) х2 4- 4х cos (ху) 4-4 = 0;
г) sin2 х + 4- sin2 Зх = sin х sin2 Зх;
д) cos х 4- cos у — cos (х 4- у) =
е) (х + у 4-z = 2,
12 ху — г2 = 4;
ж) х4 4* У1 4*= 3,
з) При каком а система
имеет единственное решение? Найти это решение.
Покажем реализацию общего положения при реше-
нии примеров а), ж), г).
a) 5x24-5z/24-8x«/4-2y4~2—2х=0,
(У2+21/+1) 4- (х2-2х+1) 4- (4x24-4y24-,8xi/) = 0,
({/+1) Ч- (х-1 )24-4 (х4-!/) *=0,
Ответ: {(!; — 1)}.
ж) х4 4- у14- г4 = 3,
94
' X* + yi + 24 = 3,
• — 2X6 — 2/ — 2z® = — 6,
x® 4- f/6 4- z® = 3.
Сложив почленно все уравнения, получим:
х4—2х®4~1/4—2t/®+z4—2z54-x®4-«/e4-2e=0,
(х®—2х54-х4) 4- (t/®-2y54-t/4) 4- (z®-2z54-z4) =0,
(х3—х2)24- (у3—у2)2+ (z3—z2)2=0.
С Xs — х2 = 0,
I Ув~У2 = 0,
[j? — г2 = 0.
х, у и z могут быть равны 0 или 1. Учитывая исходную
систему, констатируем, что решением может быть лишь
тройка (1; 1; 1).
Ответ: {(1; 1; 1)}.
г) sin2 х 4- 4- sin2 Зх = sin х sin2 Зх,
sin2 х— sin х sin2 Зх 4- 4- sin4 Зх 4-
4
----sin4 3x = 0,
4
2
sin2 3x—
sin x —
sin2 3x cos2 3x = 0,
sinx —
y^-sin26x — 0,
sinx= -j-sin23x,
sin 6х = 0,
sinx= -o~sin23x,
при х 4- sin2 Зх = 4- sin2 ~ ]
0, если k — четное,
1, если k—нечетное.
Среди четных подходит только k = 6п и тогда х = лп, пе
ЕЕ Z. Если k нечетно, то sin х — ~ sin2 Зх обращается в ра-
венство
95
sin
kn
7Г
Откуда
kn
"6"
= (-пя1Няп’
fe = (—l)”-|-6n, ax = (—1)~4-л/г, пе2.
Ответ:
r JT
| лп, (—1)у+м,пе2
4) Еще один пример конкретизации общего положения
можно показать,на материале геометрии 10 класса.
Формулы для вычисления объемов различных фигур
вращения, кроме цилиндра, могут быть получены из од-
ной общей формулы
ь
V = л J /2 (х) dx
а
путем конкретизации функции f.
Так, в случае:
а) конуса х
б) усеченного конуса
/ (*) = -^-х + г;
в) шара
f (х) = /R2 —х®.
Приведенные примеры показывают, что такое исполь-
зование общих положений способствует определенной си-
стематизации материала, обеспечивающей прочность знаний.
Глава IV
Общие методы решения задач
§ 1. ИНТУИТИВНОЕ ПОНЯТИЕ АЛГОРИТМА.
СВОЙСТВА. СТРУКТУРА. БЛОК-СХЕМЫ
1. Рассмотрим задачу: «Делится ли натуральное чис-
ло а на натуральное число Ь?»
По существу, мы имеем здесь не одну задачу, а бес-
конечный класс однотипных задач (столько задач, сколь-
ко существует пар натуральных чисел {а\ Ъ)).
Естественно возникает вопрос: существует ли общий
метод, позволяющий для любой частной задачи этого
дласса (получаемой подстановкой вместо а и b конкрет-
ной пары натуральных чисел) в конечное число шагов
дать требуемый ответ (в виде «да» или «нет»)?
Таким общим методом, как известно, является про-
цедура «деления углом»: делим а на b (для любой пары
(а; Ь) это выполнимо в конечное число шагов), если оста-
ток 0 ответ «да», если остаток отличен от 0 — ответ
«нет».
Рассмотрим еще одну задачу: «Имеет ли уравнение
ах2-)-Ьх-1-с=0, где a, b, c^Q,
корни (вещественные) ?»
Здесь опять имеем бесконечный класс однотипных за-
дач (столько задач, сколько троек (а; 6; с) рациональных
чисел), и опять возникает тот же вопрос: существует ли
общий метод, позволяющий для любой задачи этого клас-
са в конечное число шагов дать требуемый ответ в виде
«да» или «нет»?
Как известно, такой общий метод существует и он со-
7 Зак, 1239
97
стоит в следующем: определяется знак дискриминанта
D = b2—4ас (это, очевидно, всегда выполнимо за конеч-
ное число шагов: вычислить Ь2, вычислить 4ас, сравнить
два рациональных числа Ь2 и 4ас)> если то ответ —
«да»гесли же Z)<0, то ответ — «нет».
Мы рассмотрели два класса задач, требующих ответа
вида «да» или «нет». Вопрос, который мы дважды по-
ставили, «существует ли общий метод, позволяющий для
любой задачи данного класса в конечное число шагов
дать ответ «Да» или «нет», называют проблемой разре-
шения для этого класса задач, а общий метод, если он
существует, называется разрешающей процедурой, или
разрешающим алгоритмом.
Слово «алгоритм» происходит от имени среднеазиат-
ского математика Мухаммед ибн Муса «а л - X о р е з м и»
(т. е. «из Хорезма»), через труды которого (IX—X вв.)
в Европу проникли способы действий с числами в деся-
тичной системе счисления.
В течение столетий значение слова «алгоритм» посте^
пенно обобщалось, и сегодня под алгоритмом, как видно
из приведенных примеров, интуитивно понимают общий
метод (предписание, инструкция, свод правил), указы-
вающий, какие действия и в каком порядке необходимо
выполнить для решения (в конечное число шагов) лю-
бой задачи из данного класса однотипных задач.
В математике встречаются, однако, не только классы
задач, требующих ответа вида «да» или «нет». Имеется
большое разнообразие классов задач, которые требуют
в качестве ответа предъявление некоторого объекта (,чис-
ла, функции и т. д.). Формулировка таких задач начина-
ется обычно словом «найти» или словами «чему равно»
И Т. IF.
Рассмотрим задачу: «Чему равен наибольший общий
делитель (НОД) натуральных чисел а и b (а>Ь)Ъ>
Здесь опять имеем бесконечный класс однотипных
задач, требующих в качестве ответа предъявление опре-
деленного натурального числа (наибольшего общего де-
лителя данной пары, чисел). И здесь возникает тот же
вопрос: существует ли общий метод, позволяющий для
любой задачи этого класса в конечное число шагов дать
требуемый ответ?
Таким общим методом является метод последователь-
ного деления (известный под названием «алгоритм
Евклида»): делим а на Ъ\ если остаток п=0, то
98
НОД(а; b)=?b, если п=/=0, то делим b на п; если оста-
ток /2== 0, то НОД (а; Ь) =л, если же Г2=#=0, то делим п
на г2 и так далее до получения остатка гп = 0. Тогда
НОД (а; b)=^rn-i> где rn_i — последний отличный от О
остаток.
Здесь, разумеется, может возникнуть вопрос: всегда
ли описанный процесс закончится, т. е. всегда ли в ко-
нечное число шагов получим нулевой остаток?
Легко доказать, что описанная процедура последо-
вательного деления конечна (любой из остатков неотри-
цателен (fi^O), а последовательность остатков убывает
(b>ri>r2>...), следовательно, она конечна и послед-
ний остаток равен 0).
Рассмотрим следующую задачу: «Решить систему не-
равенств
х> а9
х<Ь> где a, b £ Z,
во множестве R вещественных чисел», или, иными слова-
ми, «найти множество вещественных решений системы не-
равенств т. е. найтй множество Е — {х\х £ R и
(х< Ь9
х> а и х< 6}».
Здесь опять имеем бесконечный класс однотипных за-
дач (столько задач, сколько пар (а; Ь) целых чисел) и
возникает тот же вопрос: существует ли общий метод,
позволяющий для любой задачи этого класса в конечное
число шагов дать ответ в виде некоторого множества
(множества решений системы)?
Общий метод для этого класса задач хорошо изве-
стен: сравнить а и & (из двух целых чисел мы умеем
определить в «конечное число шагов», какое из них
больше);- если a<zb, то Е=]а; &[; если же а^&,
то£ = 0.
. . Рассмотрим еще одну задачу: «Решить уравнение
ах2+Ьх+с=0, где a, b, c^Q, во множестве /?», т. е.
«найти множество вещественных корней этого уравне-
ния», т. е. пайТи Е= {x\x^R и ах2+Ьх-{-с=0}.
Мы имеем здесь бесконечный класс однотипных за-
дач, требующих в качестве ответа предъявление некото-
рого множества (множества корней данного уравнения),
и опять возникает тот же, вопрос: существует ли общий
метод, позволяющий для любой задачи этого класса в
7*
99
конечное число шагов дать ответ в виде некоторого мно-
жества?
Общеизвестен метод решения данного класса задач,
который можно описать так:
1) вычислить дискриминант D = b2—4яс;
2) если D < 0, то Е = 0;
3) если D = 0, то Е = (—^-1;
п f—b + VD —b — VD\
' 2а ’ 2а J
Здесь возникают вопросы: все ли шаги описанного
процесса выполнимы; всегда ли можно в конечное число
шагов определить точные значения корней уравнения
ах2+Ьх+^=0?
Очевидно, когда D > 0 и D не является полным квад-
ратом, то ]/ £) — иррациональное число, а следовательно,
и корни уравнения — иррациональные числа и в конечное
число шагов можем указать лишь приближенные значения
корней с любой степенью точности. Таким образом, на по-
ставленный вопрос о существовании общего метода можно
ответить положительно лишь при условии, что допускает-
ся в качестве ответа и множество приближенных значений
корней уравнения ах2 + Ьх + с = 0 (с любой заданной сте-
пенью точности).
Мы рассмотрели три класса однотипных задач вида
«найти» или «чему £авно». Поставленный для каждого
из этих классов задач вопрос: существует ли общий ме-
тод, позволяющий для каждой задачи данного класса в
конечное число шагов дать адекватный ответ, называ-
ется проблемой вычисления, а искомый общий метод,
если он существует, называется вычислительной процеду-
рой, или вычислительным алгоритмом.
В школьной математике мы имеем дело с большим
разнообразием разрешающих и вычислительных алго-
ритмов (и те и другие называются кратко алгоритмами),
но там же встречаем и много общих методов решения
задач, очень похожих на алгоритмы, но обладающих не
всеми свойствами, характеризующими всякий алгоритм.
2. Мы упомянули выше, что интуитивно под алгорит-
мом понимают общепонятное, точное предписание о том,
какие действия и в каком порядке необходимо выпол-
нить, чтобы решить (в конечное число шагов) любую
100
задачу из данного (обычно бесконечного) класса одно-
типных задач.
Это предложение, разумеется, не является математи-
ческим определением, так как в нем встречается много
терминов, смысл которых хотя и интуитивно, может быть,
ясен, но точно не определен («предписание», «общепо-
нятное», «точное», «действие», «шаги»). Однако оно пред-
ставляет собой разъяснение того, что обычно вкладыва-
ется в интуитивное понятие алгоритма, а для наших це-
лей (разработки методики обучения решению различных
алгоритмически разрешимых классов задач) это понятие
достаточно.
Какие же свойства характеризуют всякий алгоритм?
Анализ*рассмотренных выше (1.1) и других примеров
выявляет следующие общие свойства, присущие каждо-
му алгоритму:
а) массовость, т. е. алгоритм предназначен не для
решения одной частной задачи, а для решения любой за-
дачи из данного класса однотипных задач;
б) детерминированность, т. е. алгоритм, представ-
ляет собой строго определенную последовательность ша-
гов, он однозначно определяет первый шаг и какой шаг
следует за каждым шагом, не оставляя решающему за-
дачу никакой свободы выбора следующего шага в про-
цессе решения;
в') результативность, т. е., решая любую задачу из
данного класса задач по данному алгоритму, в конечное
число шагов получаем результат (разумеется, для раз-
личных задач этого класса число шагов, может оказаться
различным, но оно всегда конечно).
Необходимо отметить, что понятие «шаг», применяе-
мое в разъяснении интуитивного понятия алгоритма и
свойств детерминированности и результативности, явля-
ется относительным. Например, в рассмотренном выше
алгоритме Евклида деление одного числа на другое рас-
сматривалось как шаг, но сама процедура деления одно-
го числа на другое представляет собой алгоритм, т. е.
конечную последовательность шагов.
Один и тот же общий метод решения может быть
представлен в виде последовательности шагов по-разно-
му (это часто' встречается и в процессе решения задач
в школе, разные учащиеся по-разному определяют от-
дельные шаги процесса решения), и не всегда отдельные
шаги соответствуют отдельным «элементарным» дейст-
101
виям (само понятие «элементарное действие» относи-
тельно). Поэтому результативность определяется по эф-
фективной выполнимости (осуществимости в конечное
число шагов, без всяких усилий, машинально) каждого
шага алгоритма.
(Сложность проблемы обучения учащихся решению
задач, в частности, состоит и в том, что далеко не все
учащиеся- бывают одинаково подготовленными к тому,
чтобы определенные «шаги» выполнять машинально, не
задумываясь.)
3. Более детальное исследование различных алго-
ритмов, их структуры, выявляет возможность представ-
ления каждого алгоритма в виде последовательности
двух типов шагов, которые мы назовем соответственно
операторами и логическими условиями.
Оператор обозначает некоторое действие (в. ши-
роком смысле), в результате которого образуется какой-
то новый промежуточный результат из уже имеющихся
к данному моменту промежуточных результатов или
исходных данных. Следующий за данным оператором
шаг предписан алгоритмом однозначно, независимо от
полученного в результате применения этого оператора
промежуточного результата.
Логическое условие включает: а) проверку,
находятся ли некоторые промежуточные результаты или
исходные данные в определенном-отношении или обла-
дают ли они определенным свойством; б) решение вопро-
са о том, какой шаг будет следующим в зависимости от
результатов проверки. Применение логического условия
(в отличие от применения оператора) не приводит к но-
вому промежуточному результату, оно лишь определяет
дальнейший ход процесса решения задачи.
Последовательность из операторов и логических
условий называют. также операторно-логической струк-
турой (ОЛС).
Всякий алгоритм представим в виде оператор но-ло-
гической структуры. Однако, очевидно, не всякая ОЛС
представляет алгоритм.
В школьном курсе математики мы встречаем общие
методы решения многих классов задач, представимые в
виде ОЛС, но не являющиеся алгоритмами, так как не-
которые входящие в них операторы или проверки логи-
ческих условий не являются эффективно выполнимыми.
Например, задача распознавания отношения между
102
двумя прямыми решается следующим общим методом
(применимым к любой задаче этого класса): для любых
двух данных прямых необходимо: 1) проверить, совпа-
дают ли они; 2) если да, то они параллельны; 3)^если
нет, то проверить, лежат ли они в одной плоскости;
4} если нет, то они скрещиваются; 5) если да, то прове-
рить, имеют ли они общую точку; 6) если нет, то они па-
раллельны; 7) если да, то они пересекаются.
Предписанная этим методом проверка логических
условий не является эффективно выполнимой средствами
школьной геометрии. Действительно, у нас нет средств
для проверки выполнимости условия принадлежности
двух прямых одной плоскости, и не во всех конкретных
случаях мы в состоянии ответить на вопрос: имеют ли
две данные прямые общую точку (может быть, имеют,
может быть, нет, проверить это не всегда возможно). Та-
ким образом, описанный общий метод решения данного
класса однотипных задач не обладает результативно-
стью. Однако эта объективная характеристика метода не
снижает его значимости в обучении, она отражает харак-
тер рассматриваемого класса.задач. Поэтому в дидакти-
ке возникла потребность в различных ослаблениях выра-
ботанного в математике понятия алгоритма. Одним из
таких-ослаблений является алгоритм сводимо-
с т и — предписание, которое сводит решение задач
некоторого типа к решению задач, принимаемых за ре-
шенные.
Так, описанный выще общий метод можно рассмат-
ривать как алгоритм сводимости: задача распознавания
отношения между двумя прямыми сводится к задачам
проверки принадлежности прямых одной плоскости и
наличия общей точки, задачи эти мы принимаем за ре-
шенные.
Имея в виду значимость в обучении общих методов
решения задач, не только в тех случаях, когда они пред-
ставляют србой алгоритмы, но и когда они лишь «в ка-
кой-то мере алгоритмичны», мы рассматриваем ОЛС как
описание общих методов решения задач, не выделяя спе-
циально алгоритмов.
Наличие в ОЛС отдельных операторов или проверок
логических условий неалгоритмического характера отра-
жает тесное переплетение в процессе решения задач двух
компонент мышления: алгоритмической и эвристической
(творческой).
ЮЗ
Составление и использование в обучении ОЛС в тех
случаях, когда не все шаги общего метода носят алгорит-
мический характер, является важным дидактическим
средством, способствующим выделению в процессе реше-
ния задач тех шагов, которые требуют творческого
поиска.
4. Всякую ОЛС можно наглядно и в тб же время точ-
но представить в виде блок-схемы, состоящей из
блоков и стрелок следующим образом: каждый шаг пред-
ставляется с помощью блока. Блок, представляющий
оператор, изображается в виде прямоугольника, внутри
которого записано содержание оператора. Блок, пред-
ставляющий логическое условие, изображается в виде
ромба, внутри которого записано Проверяемое логическое
условие. Если за шагом А непосредственно следует шаг
В, то от блока А к блоку В проведена стрелка. От каж-
дого прямоугольника исходит только одна стрелка, от
каждого ромба — две стрелки: одна с пометкой «да», иду-
щая к блоку, следующему за логическим условием, если
это условие выполняется, другая — с пометкой «нет», иду-
щая к блоку, следующему за логическим условием, если
оно не выполняется. «Вход» и «выходы» изображаются
фигурами в виде овала, внутри которого записана исход-,
ная задача либо результат.
По существу, блок-схема представляет собой ориен-
тированный граф с одним входом (вершиной, к которой
не проведена ни одна стрелка) и одним или несколькими
выходами (вершина, из которой не исходит ни одна
стрелка). Вершины этого графа (прямоугольники и ром-
бы) изображают операторы и логические условия ОЛС, а
ребра — стрелки указывают последовательность шагов.
Рассмотренные выше (пп. 1.2) ОЛС можно предста-
вить в виде следующих блок-схем (схемы 12—17).
§ 2. ОБУЧЕНИЕ ОБЩИМ МЕТОДАМ РЕШЕНИЯ ЗАДАЧ
1. В школьном курсе математики в каждой его теме,
начиная от сложения натуральных чисел и до дифферен-
цирования и интегрирования функций, встречаются клас-
сы однотипных задач, решаемых общими методами (для
которых существуют алгоритмы или близкие к алгорит-
мам общие методы решения).
Обучение общим методам не сводится, однако, к со-
общению учащимся этих методов в готовом виде. Оно
104
Делится ли
d на Ь ?
(a,^)e/V)
105
Схема 15
Схема 16
Схема 17
106
предполагает «восхождение» к общему методу от реше-
ния разнообразных частных задач, создание педагогиче-
ских ситуаций, приближающих учащихся к самостоятель-
ному обобщению метода решения частных задач и откры-
тию общего метода решения.
Возникает новый тип учебных задач: описать или на-
глядно представить в виде блок-схемы общий метод ре-
шения класса задач, исходя из анализа процесса реше-
ния некоторых частных задач этого класса.
Задача описания или наглядного представления об-
щего метода решения некоторого класса задач требует:
а) тщательного анализа разнообразия частных задач
этого класса, приводящих к различным результатам;
б) выявления операторов и последовательности их вы-
полнения при решении частных задач данного класса;
в) выявления всех логических условий, влияющих на
дальнейший ход процесса и приводящих, в^конце концов,
к различным результатам; г) определение операторных
последовательностей для всех возможных случаев выпол-
нения -или невыполнения всех выделенных логических
условий.
Решение подобного рода задач, как видно, включает
элементы исследования.
Рассмотрим некоторые примеры.
2. Рассмотрим класс однотипных задач «Решить
уравнение ах=6» (А. 6, п._ 4).
Для подготовки учащихся к описанию общего метода
решения недостаточно решать конкретные уравнения ви-
да Зх=18; 0,5х=7; 2х=9 и т. п., в которых а=#=0.
Именно потому, что в обычной практике ограничива-
ются этими частными задачами, учащиеся, решая и урав-
нение ах—b, получают единственное решение без вся-
ких условий.
Но если перед решением общей задачи рассматрива-
ются и такие уравнения, как 0*х=5 и 0*х=0, составляю-
щие вместе с первыми все разнообразие уравнений клас-
са ах=Ь, приводящих к различным результатам, то в
результате анализа решения этих частных случаев и выяс-
нения соответствующих логических условий, от выполне-
ния или невыполнения которых зависит принадлежность
уравнения к одному из этих подклассов, приходим к опи-
санию общего метода и его представлению ? риде fyiQK'
схеми (схема 18).
№7
Схема 18
Разнообразие результатов и их зависимость от логи-;
ческих условий можно показать с помощью наглядной
таблицы:
Опыт описания общего метода решения уравнения
ах=Ь является основой для решения более сложных за-
дач, например «Решить уравнение а(Ь— 1)х —Ь1 2—1»,
обычно вызывающие затруднения у большинства семи-
классников.
Условие, при котором это уравнение имеет единствен-
ное решение («п(6—1)=#0», или «я=#0 и 6#=1»), уста-
навливается без особых затруднений, по аналогии с урав-
1 В зависимости от того, в каком множестве (Q или R) реша-
ется уравнение.
108
нением ax=b. Затруднения возникают в связи с необхо-
димостью выявления логических условий, определяющих
все разнообразие результатов. По существу, остается вы-'
яснить, как решается уравнение, когда неверно, что
«а=#0 и 6=И= 1», т. е. когда «а = 0 или Ь=1» (здесь неявно
применяется один из законов логики, известный под на-
званием закона де Моргана, «неверно, что Р и Q» равно-
сильно «не Р или не Q», часто вызывающий затруднения
и не только у учащихся).
Из условия «а —0 или Ъ = 1» получаем два случая, при-
водящих к различным результатам: «а = 0 и Ь^=1 и Ь=£
=/= —1» и «6 = 1 или (а = 0 и & = —1)». Так приходим к
следующей блок-схеме (схема 19)
а~0и
и таблице результатов:
6¥=1 Ь^-1 Е
( & +1
И J И —*• 1 а
Л ' и и 0
И л и Q (R)
л и л Q-(R)
109
3. Рассмотрим последнюю тему курса алгебры седь-
мого класса (А. 7, гл. IV, § 12) «Квадратные уравнения».
Прежде всего выясним, какие классы стандартных
задач имеются по этой теме, общие методы решения ко-
торых должны усвоить все учащиеся.
Исходя из содержания программы и учебного посо-
бия (А. 7, гл. IV), можно составить такой перечень клас-
сов стандартных задач по теме «Квадратные уравнения»:
1) решение квадратных уравнений графическим спо-
собом;
2) решение квадратных уравнений выделением квад-
рата двучлена;
3) решение квадратных уравнений (по формуле);
4) определение знаков корней квадратного уравнения
(с применением теоремы Виета);
5) составление квадратного уравнения по заданным
его корням;
6) разложение квадратного трехчлена на множители;
7) ф построение графика функции х-+у=ах2-\-Ьх-\-с.
Для всех перечисленных классов задач в результате
изучения данной темы должны быть сформулированы
или представлены в удобной, наглядной форме общие ме-
тоды решения. Усвоение этих методов будет более глубо-
ким и прочным, если учащиеся будут привлечены- в про-
цессе обучения к поиску и описанию соответствующих ме-
тодов решения.
Рассмотрим первый из перечисленных классов стан-
дартных задач по теме «Квадратные уравнения».
В учебном пособии (А. 7) решается одна частная за-
дача этого класса (х24-2х—8=0) и не все подготовлено
для необходимого обобщения и формулировки общего
метода (алгоритма) решения данного класса задач. Не-
обходимо решить еще две частные задачи (например,
х2—2x4-1 =0 и х2+2х4-2 = 0), составляющие вместе с
рассмотренной там разнообразие задач данного класса,
приводящих ко всем возможным различным результатам.
По существу, в учебном пособии описан и общий ме-
тод, но он не выделен, четко не сформулирован, наглядно
не изображен. Это дело методики обучения. Как же целе-
сообразно строить методику? Как подвести итоги реше-
ния частных задач таким образом, чтобы учащиеся сами
пришли к открытию общего метода (алгоритма)?
Можно это подведение итогов сочетать с обобщением
следующим образом.
110
взгляд назад •
на решение частных задач
Конкретная геометричес-
кая задача привела нас к не-
обходимости решить уравне-
ние
х2 -J- 2х — 8 = 0.
Как мы поступили?
1) Мы представили урав-
нение в виде х2 = 8 — 2х, т.е.
оставили в левой'части урав-
нения один член второй сте-
пени, остальные члены трех-
члена перенесли в правую
часть.
2) В одной системе коор-'
динат построили графики (Гх,
Г2) функций
f х: х -> у = х2 и
f 2: х + у = 8 — 2х
(Г1 = {Л4(х, у}\у = х2} и
Г2 = {М(х, у) 1 у = 8 - 2х)}.
3) Нашли пересечение
двух графиков (параболы и
прямой)
Г i f\Г
а) Для первой задачи
/\Л Г2={Я(—4; 16), В(2;4))в
т.е. йарабола и прямая пере-
секаются в двух точках. При
х = —4 и при х = 2 соответ-
ствующие значения выраже-
ний х2 и 8 — 2х равны, поэ-
тому —4 и 2 являются кор-
нями уравнения х2 = 8 — 2х,
а следовательно, и уравнения
х2 + 8х —2 = 0.
Обобщение
метода решения
Пусть необходимо ре-
шить уравнение вида.
ах2 + Ьх + с = 0(а =/= 0).
Как мы поступим?
1) Мы представим ура-
внение в виде ах2 = —Ьх—
— с, т.. е. оставим в левой
части уравнения один член
второй степени, остальные
члены трехчлена перенесем
в правую часть.
2) В одной системе ко-
ординат построим' графики
(Гь Г,) функций
fi: х у = ах2 и
fs: х у = —Ьх — с
(G = {М(х, у) | у = ах2} и
Г2={Л1(х, f/)|y=—Ьх—с)}.
3) а) Если
У1)>
В(х%, у2)}, то множество £
решений (корней) уравне-
ния ах2 — — Ьх — с, или
уравнения ах2 4- Ьх + с=0,
состоит из двух Чисел—
абсцисс точек А и В, т. е.
Е = {хг; х2} (рис. 41).
Но какие еще могут
быть случаи пересечения
параболы и прямой?
11!
Если через Е обозначим
множество решений этого
уравнения, то Е = {хп х2}
(рис, 41),
б) Если все описанное вы-
полним для уравнения х2—
— 2х + 1 = 0, то получим
ЛПЛ = Л(1; 1) и £-{1}
(рис. 42).
в) Если все выполнить для
уравнения xas+ 2х 4- 2 = 0, то
Л П Г2= 0 и £= 0 (рис. 43),
б) П Г2 — {Д(хп £/1)}>
т. е. прямая касается па-
раболы в одной точке
Д(хх; У1)- В этом случае
хх будет единственным
корнем уравнения ах2 +
+ Ьх + с = 0, т. е. Е — {хх}
(рис. 42).
в) ЛПЛ=0, не-
прямая и парабола не име-
ют общих точек и урав-
нение ах2 + Ьх + с — 0 не
имеет корней, т. ё. Е = 0
(рис. 43).
Каков наиболее ответственный момент в управлений
этим процессом обобщения? Этот вопрос возникает перед
учителем, и правильный ответ на него способствует
Рис. 41 Рис. 42 Рис. 43
успешному управлению процессом. Очевидно, что таким
моментом является выделение трех возможных случаев:
а) ЛПЛ={Л(Х1; У1),В(х2-, у2)};
б) ЛП Г2=Д(хг, *л) и
в) Г2=0.
112
Для того чтобы стимулировать открытие учащимися
этих трех случаев, очевидно, необходимо решить предва-
рительно графическим способом три конкретных квад-
ратных уравнения, приводящих к этим случаям (что мы
и предложили выше).
После такого обобщения, приводящего, по существу,
к открытию общего метода (алгоритма), учитывая также
приведенное в учебном пособии замечание о том, что,
приступая к графическому решению квадратного урав-
нения, удобно предварительно разделить все его члены
на первый коэффициент (если, разумеется, он отличен
от 1), можно составить следующую блок-схему алгорит-
ма решения квадратного уравнения графическим спосо-
бом (схема 20),
Приведенная блок-схема является итогом изучения
вопроса и одновременно- средством наглядности, способ-
ствующим прочному усвоению общего метода решения
задач данного класса.
Составление подобных блок-схем в качестве итога
изучения соответствующего класса задач представляет
собой упражнение с важными дидактическими и разви-
вающими функциями.
Рассмотрим в качестве следующего примера четвер-
тый из перечисленных выше классов стандартных задач:
определение знаков корней квадратного уравнения с по-
мощью теоремы Виета.
Решение любой частной задачи этого класса не вы-
зывает затруднений. Рассмотрение же задачи в общем
виде ах2-^Ьх^с=0 требует проведения исследования и
выделения всех условий, приводящих, к различным ре-
зультатам.
Составление блок-схемы соответствующего алгорит-
ма (схема 21) является полезным упражнением для бо-
лее сильных семиклассников и* может быть предметом
факультативных или внеклассных занятий.
Результаты исследования вопроса о знаке корней
квадратного уравнения х2+рх+^=0 могут быть записа-
ны в виде истинностной таблицы, включающей лишь те
наборы истинностных значений четырех выделенных
8 Зак. 1239
113
Рассмотреть уравнение
Оставить в левой части
один член второй степени:
В одной и той же системе
координат построить
G П 6 = {Л ; В(хг,yj }
Схема 20
114
условий, (9 = 0, 9>0, р=0, р>0), которые возможны в
рамках рассматриваемой задачи:
<7 = 0 q > 0 р «= 0 Р > 0 Знаки корней х, и нения х* 4- рх Н хж у’рав- Н = 0
И — И — Х1 = 0; хг = 0
И —- л И Xi = 0; х2 < 0
И л л Jfi = O; х? > о
л и и <- 0; хг < о
л и — л *1 > 0; х2 > 0
л л — V х± < 0; х2 > 0
Для последнего случая можем найти и соотношение
между модулями корней:
Я = 0 я> о р = 0 Р > о •
л л — хг < 0 ; х2 > 0
л л и 1 *1 1 = 1 *S 1
л л л и 1*11 > l*sl
л л л л 1*11 < l*al
4. Используя приведенный выше пример класса задач
«Решить уравнение (1), рассмотрим теперь в об-
щем виде переход от решения частных задач некоторого
класса К к описанию алгоритма для решения любой за-
дачи этого класса.
Пусть задачи класса К могут иметь несколько типов
результатов Pi, Рг, . -. , Рп. Например, задачи класса (1)
могут иметь три различных типа результатов: Pi — един-
ственное решение; Рг — отсутствие решений; Р3 — беско-
нечное множество решений.
Во множестве К задал установим отношение эквива-
лентности (~) следующим образом: две задачи будем
считать эквивалентными, если типы их результатов сов-
падают. Обозначим через Р(3) —тип результата за-
дачи 3. <
Тогда Зх ~ 32 Р (3i) = Р (За)-
В приведенном выше примере (I) частные задачи
116
Определить знаки корней уравнения
ал2+6л+с=0 (£}&0)
Схема 21
116
«Решить уравнение 4х=12» и «Решить уравнение
—2х = 7» эквивалентны, так как имеют результаты одно-
го типа (хотя корни этих уравнений различны, по каждое
из этих уравнений имеет точно один корень и в обоих
случаях этот корень находится одним и тем же способом,
с помощью одного и того же действия).
Совершенно очевидно, что введенное отношение «~»
является отношением эквивалентности (оно рефлексив-
но, симметрично и транзитивно) и поэтому порождает
разбиение множества К задач на классы эквивалентности
(подклассы /С), причем число этих подклассов К равно
числу различных типов результатов. В примере (1) по-
лучаем разбиение на три класса эквивалентности (Ль
Лг, Лз), определяемых соответственно условиями: а^О;
а = 0 и 6=#0; а = 0 и Ь = 0.
Множество частных задач некоторого класса К на-
зовем полной системой частных задач (ПСЧЗ) этого
класса, если в нем содержится по крайней мере по од-
ной задаче (по одному представителю) из каждого
класса эквивалентности. ПСЧЗ является минимальной,
если она содержит точно по одной частной задаче (по од-
ному представителю) из каждого класса эквивалент-
ности.
Например, множество частных задач «Решить урав-
нение 2х=5»; «Решить уравнение 2x-J-3 = 54-2x>; «Ре-
шить уравнение 3%+7 = 7-|-Зх» представляет собой одну
из возможных минимальных ПСЧЗ класса (1).
Для достижения целей обучения открытию алгорит-
ма минимальная ПСЧЗ, как правило, оказывается недо-
статочной/ Например, для анализа и обобщения способа
решения задач подкласса Ki
«Решить уравнение ах=Ь, где а#=0», (2)
нужно решить несколько частных задач (2х= 7; — Зх=15;
-^-х= 0,5; 2х ’= 8; Зх = 0).
По существу, в классе задач (2) тоже устанавливает-
ся отношение эквивалентности задач по знаку единствен-
ного корня уравнения или по его принадлежности к тому
или иному числовому множеству.
Потому, естественно, возникает понятие дидактиче-
ской системы частных задач (ДСЧЗ), которая обяза-
тельно должна быть полной, но, как правило, не являет-
ся минимальной. В отличие от ПСЧЗ, которая зависит
117
только от рассматриваемого класса задач, ДСЧЗ носит
прагматический характер и зависит от целей обучения и
от того, кого мы обучаем, от уровня математических зна-
ний и развития учащихся. В частности, реализация инди-
видуального подхода требует варьирования ДСЧЗ.
В отличие от ПСЧЗ, представляющей собой множест-
во частных задач, ДСЧЗ — упорядоченное множество
частных задач, указывающее не только, какие частные
задачи необходимо решить, но и в каком порядке. По-
этому две ДСЧЗ, отличающиеся только порядком эле-
ментов, следует считать различными, так как они могут
иметь различный педагогический эффект. ДСЧЗ харак-
теризуется тем, что выбор, число и порядок частных за-
дач, подготавливающих переход к описанию общего ме-
тода решения, подчинен целям обучения и не .может быть
заранее определен для всяких классов задач.
Отметим, что умение, осуществлять" переход от реше-
ния частных задач к описанию алгоритма для решения
класса задач весьма нужное, в частности для людей, ра-
ботающих с ЭВМ, а число таких людей самых различных
профессий все более увеличивается. Нет сомнения в том,
что школа должна прививать учащимся такое умение хо-
тя бы для простейших классов стандартных задач, ре-
шаемых в школьном курсе математики.
5. Различные классы стандартных задач встречаются
и в школьном курсе геометрии (мы рассмотрели выше
(§ 1, п. 2) один такой класс задач).
В приложении приводится набор блок-схем общих
методов решения некоторых классов задач по различным
темам школьных курсов алгебры и геометрии.
Глава V
Методы поиска решения задач
§ 1. СТАНДАРТНЫЕ И НЕСТАНДАРТНЫЕ ЗАДАЧИ
Анализ роли задач в обучении математике, например
с начала XVIII в. («Арифметика» Л. Ф. Магницкого по-
явилась в 1703 г.), приводит нас к следующей схеме:
обучение решению задач — обучение, сопровождающееся
решением задач — обучение через задачи.
Сейчас все большее распространение получает про-
грессивный метод обучения через задачи как реализация
системы проблемного обучения. Основные идеи этого ме-
тода находят в какой-то мере отражение в новых учеб-
никах. Задачи становятся не только и не столько целью,
сколько средством обучения.
На первом этапе решение задач было целью обучения.
Ученик должен был заучить образцы и затем подводить
под эти образцы решения задач. В основном решались
типовые, стандартные задачи, принадлежащие
классам алгоритмически разрешимых задач, т. е. таких,
для которых существует общий метод (алгоритм) реше-
ния. Обучению построения алгоритмов для решения раз-
личных классов стандартных задач была посвящена пре-
дыдущая глава.
Многообразные ситуации, возникающие на математи-
ческом и нематематическом материале, приводят как к
стандартным, так и нестандартным задачам.
Постепенное изменение целей обучения привело к не-
обходимости научить детей решению не только стандарт-
ных, но и нестандартных задач, которые нельзя
119
отнести к классам алгоритмически разрешимых. Именно
по отношению к нестандартной задаче возникает необхо-
димость в поиске решения.
«...задача предполагает необходимость сознательного
поиска соответствующего средства для достижения ясно
видимой, но непосредственно недоступной цели. Решение
задач означает нахождение этого средства»
Отбор новых, нестандартных задач ведется в разных
направлениях. Особый интерес представляют задачи ком-
бинаторного характера. А. Н. Колмогоров указывает не
внедрение в школьное преподавание элементов дискрет-
ной математики как на неизбежную необходимость. Эти
элементы «в самой науке выдвинулись на первый план
в связи с задачами переработки информации и развитием
машинной вычислительной техники» 1 2.
В будущем непосредственное овладение формальны-
ми языками, «позволяющими формулировать задачи для
машин, перерабатывающих информацию, может стать
действительно массовой потребностью. Пока же обще-
образовательной школе важнее создать надлежащие на-
выки мысли, чем тратить большое время на изучение кон-
кретных «машинных языков» 3.
Определенные группы задач, предназначенных для
классных и внеклассных занятий, вполне пригодны для
выработки «надлежащих навыков мысли», навыков, на-
правленных на поиски решения задач, аналогичных про-
граммам, составляемым для счетных машин.
В отличие от классической комбинаторики, которую,
в основном, интересует число различных размещений,
перестановок, сочетаний объектов, в новых задачах более
важен поиск путей получения комбинаций, обладаю-
щих заданными свойствами, анализ структуры комби-
наций. .
Новый смысл придается сейчас традиционным зада-
чам на переливание, взвешивание и т. п. Они дают воз-
можность иллюстрировать методы поиска решения от-
нюдь не только занимательных задач. Не существует
алгоритма решения подобных задач, который позволил
бы в конечное число шагов получить результат. Нужно
найти возможность целенаправленного поиска с учетом
1 Пойа Д. Математическое открытие.— М., 1976, с. 143.
2 Колмогоров А. Н. Современная математика и. математика в
современной школе.— Математика в школе, 1971, № 6.
3 Там же.
120
эвристической информации, свойственной каждой зада-
че данного типа.
Большая ценность решения комбинаторных задач в
том, что они способствуют воспитанию приемов мышле-
ния* связанных с проблемой обучения ЭВМ регулярным
методам поиска решения задачи. Поэтому при их анали-
зе и решении уместно пользоваться соответствующей ма-
шинной терминологией.
В процессе решения задачи 1 можно выделить два су-
щественных составных элемента: а) представление
(описание) задачи и б) поиск решения. Представ-
ление задачи включает ее перевод на язык математики.
Такой перевод может быть различным. От способа пред-
ставления задачи зависит и поиск ее решения. Более
удачное представление способствует сокращению объема
поиска, менее удачное может значительно увеличить
объем поиска, усложнить процесс решения.
Поиск в одном случае может служить нахождению
всех решений, в другом — одного из решений (наиболее
короткого, рационального, достаточно хорошего, любого),
в третьем — установлению возможности или невозмож-
ности решения.
Далее мы рассмотрим два подхода к решению задач,
отличающихся представлением задачи, а следовательно,
и организацией поиска решения. Первый подход харак-
теризуется представлением задачи в. простран-
стве состояний, второй — сведением (ре-
дукцией) задачи к совокупности подзадач.
§ 2. ПРЕДСТАВЛЕНИЕ ЗАДАЧ И МЕТОДЫ ПОИСКА
В ПРОСТРАНСТВЕ СОСТОЯНИИ
Представим себе игру в домино. Первый игрок вы-
ставляет кость 1—2. Сразу возникает система поиска
следующего хода: можно прикладывать кость или к 1,
или к 2, Если второй игрок выставит кость 1—5, то затем
можно будет воспользоваться пятерками, а если он вы-
ставит 1—6, то шестерками и т. д. Возникает так назы-
ваемое пространство состояний (поле деятель-
ности, поле состояний).
Пространство состояний можно также иллюстриро-
1 Здесь и далее под задачей мы будем понимать нестандартную
задачу.
121
вать на примере широко распространенной игры в слова.
Например, записывается слово КОТ (рис. 44). Изменяя
каждый раз лишь одну букву, надо получить другие су-
ществительные, имеющие здравый смысл. Изменяя пер-
вую букву, получим БОТ, ДОТ, ЛОТ, ПОТ, РОТ; изме-
няя вторую — получим КИТ; третью — КОК, КОЛ, КОМ,
КОН. Затем уже в этих словах заменяем каждый раз
одну из букв и т. д. Если бы заранее требовалось подоб-
ным образом из слова КОТ получить слово БЫК, то мы
имели бы типичную задачу, решаемую поиском в
пространстве состояний,
С представлением задачи в пространстве состояний
связаны следующие понятия: а) состояние (начальное
Рис. 44
состояние, целевое со-
стояние), описание со-
стояния; б) оператор,
преобразующий одно
состояние в другое;
в) .пространство состоя-
ний; г) пространство
поиска (перебора).
В нашей задаче на-
чальным состоянием
является слово кот,
целевым — слово бык.
В данном случае в ка-
честве описаний состоя-
ний. можно принять са-
ми эти состояния. Опе-
ратором служит замена
одной буквы другой
так, чтобы получилось
осмысленное слово (но-
вое состояние). Мно-
жество состояний, неяв-
но заданное начальным
состоянием и всевоз-
можными операторами,
называется пространством состояний. Поиск решения
(пути от начального* состояния к целевому) состоит
в явном построении части пространства состояний, назы-
ваемой пространством поиска или перебо-
р а. Чем более рационален метод поиска, тем меньше
пространство поиска.
122
Различают два вида поиска. Например, начинающие
игроки-шахматисты пользуются методом слепого пе-
ребора всех возможных вариантов-ходов. Опытные же
игроки могут предвидеть развертывание партии на не-
сколько ходов вперед; они пользуются методом н а-
правлеиногоперебора.
Метод слепого перебора, проб и ошибок, применяется
в обучении математике, так как это естественный ход
мысли при решении задачи. Когда ученик пытается рас-
смотреть все возможные варианты выбора арифметиче-
ского действия, то он обычно, к сожалению, получает за-
мечание от учителя: «Надо думать, а пе перебирать все
подряд!» Однако, рассматривая обучение математике как
обучение математической деятельности, мы допускаем
право ученика на ошибку, признаем необходимость ана-
лиза ошибочных результатов. Перебор различных вари-
антов и их оценка с точки зрения достижения цели —
это и есть процесс мышления.
Наглядно процесс поиска в пространстве состояний
удобно представить графом. Графовая модель выражает
программу, чаще всего создаваемую учеником в процес-
се анализа и решения задачи. В этой программе четко
указана последовательность выполняемых действий.
Граф служит сохранению информации, которую невоз-
можно удержать в памяти, предупреждает от блужданий,
связанных с повторением уже рассмотренных комбина-
ций. Графовая модель — это особый вид наглядности, по-
зволяющий сосредоточить внимание ученика на содержа-
нии и решении задачи.
Напомним кратко некоторые сведения о графах, не-
обходимые для понимания дальнейшего изложения ма-
териала.
Графом называется совокупность конечного числа
точек, называемых вершинами графа, и попарно соеди-
няющих некоторые из этих вершин линий, называемых
дугами или ребрами графа.
•Если каждую вершину графа можно соединить с лю-
бой другой его вершиной некоторой линией на графе, не
проходящей ни по одному ребру более одного раза, то
граф называется связным.
Связный граф., не содержащий циклов (т. е. замкну-
тых цепей), называется деревом (рис. 45). Первона-
123
чально выбранная вершина А называется корнем дере-
ва; каждая вершина дерева может служить его корнем.
Если вершинам сопоставлять состояния (вершине А —
начальное состояние), а стрелкам — переходы от одного
состояния к другим в результате применения операторов,
получим дерево пространства состояний
/рис. 46).
Рис. 46
В дальнейшем мы не везде на ребрах будем изобра-
жать стрелки. Когда направление поиска очевидно,
стрелки будем опускать.
Каждая ветвь полученного дерева может рассматри-
ваться самостоятельно, как поддерево. Поддерево, полу-
чающееся в процессе перебора, называется деревом пе-
ребора (поиска).
Рассмотрим представление задач и методы поиска на
ряде конкретных примеров.
Задача 1. Имеем три кучки орехов: 11, 7, 6 штук.
Требуется переложить орехи так, чтобы в каждой кучке
их стало поровну. Добавлять можно лишь столько оре-
хов, сколько их там уже есть. Какое минимальное число
перекладываний понадобится?
Сначала составим описание, задачи в пространстве
состояний.
Начальное состояние — представление данных
задачи, определенная конфигурация объектов, изобра-
жаемая начальной вершиной графа. В данной задаче в
качестве описания начального состояния можно принять
тройку чисел (11; 7; 6)1. Тогда результат решения будет
целевым состоянием, описание которого (8; 8; 8).
1 В дальнейшем для простоты скобки опускаем.
124
Одно состояние преобразуется в другое при помощи
определенных разовых приемов, однозначно установлен-
ных правил — операторов. В данной задаче это
всевозможные перекладывания орехов из одной'кучки в
другую по столько штук, сколько в последней уже есть.
Применяя операторы, каждую предыдущую (родитель-
скую) вершину мы преобразуем в последующую (дочер-
нюю) вершину до получения целевой вершины, если
это возможно. Применение к данной вершине всех до-
пустимых операторов, в результате чего получаются
дочерние вершины, назовем раскрытием этой вер-
шины.
Последовательность операторов, ведущая от началь-
ного состояния к целевому, образует решающую по-
следовательность.
Для данной задачи начальная часть графа перебора
выглядит так (схема 22):
(И, 7, 6)
(4,14, 6) (5, 7,12) (11,1,12)
Схема 22
Перебор выполнен в определенной последовательно-
сти: из 11 орехов можно переложить 7 во вторую кучку
или 6 в третью; из 7 орехов можно переложить 6 штук в
третью кучку. Других вариантов net!
Так мы раскрыли начальную вершину графа. Далее
раскрываем последнюю из полученных дочерних
вершин,, затем опять последнюю и т. д. Избегаем повто-
рения комбинаций, так как это не приведет к новым ре-
зультатам. Порядок расположения кучек безразличен,
поэтому вершины 8, 10, 6 и 6, 10, 8 одинаковы. Вершины,
приводящие только , к повторным результатам, являются
неперспективными, и мы их закрываем, т. е. прекращаем
их раскрытие.
Раскрывая каждый раз последнюю из образовавших-
ся вершин, мы применили метод перебора в глубину
(схема 23).
i
125
10,2,12 22,1,1 11, 2,11
I
5,8,11 18,4,2 9,8,7
1,16,7 2,8,14 9,1,14
18,1,5 9,2,13
‘ 7, 4,13
i
6, 5,13 6,8,10 3,16, 5
3, 8,13
3,11,10 6,16,2
♦
4,16,4
♦
8,12,4
8,8,8
Схема 23
Однако нет никакой уверенности в том, что найденное
число перекладываний орехов минимально. Поэтому по-
лезно было бы раскрывать вершины в той последователь-
ности, в какой они получены (схема 24).
Далее перебор можно не продолжать, так как более
короткого решения получить не удастся. В этом случае
поиск выполнен методом полного перебора.
Если бы в задаче требовалось найти все варианты ре-
шения, то пришлось бы продолжать перебор до тех пор,
пока не были бы исчерпаны все перспективные вершины.
126
Перебор в глубину и полный перебор есть методы
слепого перебора. При этом мы применяем операто-
ры, не анализируя дочерние вершины с точки зрения их
близости к цели. В противоположность слепому перебору
Схема 25
существует метод упорядоченного перебо-
р а, когда применяются элементы эвристики: при раскры-
тии начальной вершины мы можем заметить, что дочер-
няя вершина 4х, 14, 6 наиболее перспективна, так как дает
возможность получить кучку из 8 орехов. Затем более
перспективной будет вершина 4, 8, 12, непосредственно
ведущая к цели. Дерево упорядоченного перебора из-
ображено на схеме 2§.
127
^-ilnxtgx
Схема 26
5in2X±C0S2X
sln2x+cos2x --slnxslnx sln2x±coszx ' si.nzx
cosx
sin2x+coszx~l
sln2x
cosx
прибед.
кобщ.зн.
f-sln2x
cosx
1-sln2x-cqs2x
cos2x
cosx
clx
Схема 27
Задача 2. Докажите тождество —---------------sinxtgx =
: COS X °
= COSX.
Начальное состояние: —----------sinxtgx.
COS x to
128
Целевое состояние: cos х.
Раскроем начальную вершину (схема 26).
Получили три дочерние вершины. При этом имеют ме-
сто элементы эвристики, учет целесообразности преобра-
зований: например, мы не фиксируем кажущиеся совер-
шенно неперспективными вершины, которые могут быть
получены,, скажем, применением формул синуса или ко-
синуса половинного аргумента.
Продолжим поиск решения методом перебора в глу-
бину, т. е. раскрывая каждый раз последнюю из образо-
вавшихся дочерних вершин (схема 27).
Мы нашли один из возможных путей решения. Если
же надо найти несколько вариантов для выбора наибо-
лее рационального, то следует вернуться к последней из
оставшихся перспективных вершин и т. д. В данном слу-
чае надо раскрыть вершину
sin2 х 4- cos2 х — sm2x cos2 x
-----—------------->------> cosx.
cos x cos x
Выполняя поиск доказательства данного тождества
методом полного перебора, мы должны были бы каждый
раз раскрывать дочерние вершины в том порядке, в ка-
ком они получены до тех пор, пока будет достигнута цель
• (если требуется найти один вариант решения) или пока
не будут раскрыты все перспективные вершины (если
надо найти-более рациональный вариант). При этом сле-
дует избегать повторения одинаковых вершин.
На глубине, равной 4, найдена целевая вершина.
Наиболее перспективный путь решения выделен жирной
линией (схема 28).
Если бы мы пожелали найти все способы решения, то
одинаковые вершины не следовало бы опускать. Напри-
мер, раскрыв вторую и третью вершины в последнем ря-
ду, мы получили бы еще два равноценных решения, хотя
пути достижения цели не были бы одинаковыми.
Поиск решения'методом упорядоченного перебора ера*
зу привел бы нас к пути, выделенному в
остальные варианты мы сразу же опускали
спективные. Например, из —sinxtgx
лишь —5------sin х si? так как в данном
COS X COS X
вается возможность записи общего знаменателя и исполь-
схеме 28. Все
бы как непер-
следовало бы
случае открьь
9 Зак. 1239
129
зования формулы 1 — sin2 х = cos2 х. Никакие другие вари-
анты не дают таких богатых перспектив.
Дерево упорядоченного перебора (расположим его го-
ризонтально) выглядит так:
1 . , 1 . sin х 1 — sin2 х
sin X tg x -> sin X — > >
cos X---------------------------------------. & COS X-COS X-COS X
COS2X
COSX
-> cos X.
COSX COSX COSX COSX COSX COSX
Sin2X+CDS2X-Sin2X C0S2X cos2x
---- --------- ------—- COSX --------
COSX COSX COSX
Схема 28
Задача 3. Тома Детской энциклопедии стоят на
полке в следующем порядке: 1, 3, 2, 5, 4. Требуется по-
ставить их в натуральном порядке, причем можно брать
любые два соседних тома и переставлять их влево меж-
ду другими томами. Найти все возможные варианты ре-
шения.
(Об аналогичной задаче см.: Савина А. От школьной
задачи к проблеме.— Квант, 1976, № 12.)
Начальное состояние задачи — это последователь-
ность чисел 1, 3, 2, 5, 4. Целевое состояние: 1, 2, 3, 4, 5.
Операторы: различные перестановки пар цифр в соответ-
ствие с условием задачи.
130
Перейдем к решению задачи (для краткости опустим
запятые между цифрами):
Схема 29
Первый том оставили на месте, после него поместили
пары томов 25 и 54; первый и третий тома оставили на
месте, затем поместили тома 54 (схема 29). Других слу-
чаев перемещения пар томов влево нет.
Далее продолжим поиск методом полного перебора
до глубины 3 (схема 30). Если решений не найдется, то
увеличим глубину перебора. При этом не будем фикси-
ровать вершины, одинаковые с уже имеющимися на дан-
ной ветви, так как это возвратило бы нас к повторению
(получился бы замкнутый цикл):
Схема 30
Решая задачу таким образом, мы нашли кратчайшее
решение: 13254—12534—12345. Такого решения можно
было бы достичь методом упорядоченного перебора, рас-
суждая следующим образом: после 1 тома надо поста-
вить том 2. Для этого пару 25 поместим после 1. Полу-
чим 12534. Затем том 3 надо поставить после 2. Для это-
го пару 34 поместим между 2 и 5.
9*
131
Не при всяком первоначальном расположении томов
задача имеет решение. Рассмотрим, например, дерево пе-
ребора при начальной расстановке томов 13245 (схе-
ма 31). Сначала выполним перебор на глубину 2:
Схема 31
Как видим, целевая вершина не найдена. Но если
продолжить перебор, то из вершины 14325 получим 12543
и 14253, а из вершины 12354 получим 15423. Все осталь-
4 1 6
б 2
7 8
Рис. 47
ные вершины будут повторяющимися. Вывод: задача не
имеет решений.
Задача 4. Игра в 8. В квадратной коробочке рас-
ставлены фишки, как показано на рисунке 47. Требуется
переместить фишки, не вынимая их, а лишь занимая по-
очередно свободное место так, чтобы в итоге все фишки
были расположены по порядку номеров, а середина квад-
рата была свободной.
В этой задаче описанием состояния может служить
массив из трех трехзначных чисел.
Описание начального
состояния: /413Y
(625
\708j
Описание целевого
состояния: /123\
I 405 ]
\678/
132
Зададим сначала глубину перебора, равную 4, затем
еще углубимся на 1 и получим ответ (схема 32). Пустое
место будем обозначать через 0.
413
625
708
615 615 465 765 653 658 425
728 728 728 028 728 720 678
643 435 103 413 401 413 103
015 610 465 765 653 658 425
728 728 728 208 728 702 678
403 413 413 401 403 413 413
215 250 275 623 612 682 062
678 678 678 785 785 7Q5 785
123
405
678
Схема 32
Догадка помогла бы нам сразу выбрать среднее под-
дерево, так как здесь 8 уже находится на месте, а 7 и 6
легко переставить на нижний ряд. Кратчайший поиск ре-
шения выделен на чертеже двойной стрелкой.
§ 3. СВЕДЕНИЕ ЗАДАЧ К ПОДЗАДАЧАМ
В педагогике математики широко применяется так
называемая схема анализа решения задачи (чаще всего
арифметической). Если рассматривать анализ задачи с
позиции поиска решения, то путь этого поиска называют
движением назад, т. е. движением от вопроса к исходным
133
данным. Затем можно выполнить решение, продвигаясь
в обратном направлении. Это будет движение вперед,
т. е. синтез задачи.
Рассмотрим два примера.
1) Задача. Тракторная бригада вспахала за 3 дня
250 га. В первый день она вспахала 36%, а во второй —
34% всей площади. Какую площадь бригада вспахала в
третий день?
Анализ задачи. Чтобы ответить на вопрос за-
дачи, надо знать, какую площадь вспахала бригада за
три дня и какую — за два первых дня вместе. Чтобы
узнать, какую площадь вспахала бригада за два первых
дня вместе, надо знать, какую площадь вспахала бригада
за I и II дни отдельно. Чтобы узнать, какую площадь
бригада вспахала за I день, надо знать общую площадь
и сколько процентов общей площади она вспахала за
I день, а чтобы узнать, какую площадь вспахала брига-
да за II день, надо знать общую площадь и сколько про-
центов общей площади бригада вспахала за II день.
Данным многословным рассуждениям большую на-
глядность придает специальная схема анализа (схе-
ма 33):
Схема 33
Эту схему анализа можно представить короче (схе-
ма 34).
Рассмотрим, в чем проявляется зд^сь сведение зада-
чи к подзадачам. Надо определить, какую площадь вспа-
хали за III день. Но мы будем решать другую задачу (ее
134
Схема 34
подзадачу): узнаем, какую площадь вспахали за I и II
дни вместе. (После этого легко можем найти ответ на
вопрос задачи.) Идем дальше: вместо нахождения пло-
щади, вспаханной за I и II дни вместе, решим две другие
подзадачи: найдем, какую площадь вспахали за I день
и за II день отдельно и т. д. В каждом случае заменяем
задачу более простой подзадачей.
Возможна принципиально иная схема анализа, кото-
рой будет соответствовать иной способ решения задачи
(схема 35):
Схема 35
Ограничимся здесь этими двумя способами решения.
Объединим обе схемы анализа в одну схему (схема 36).
Дуги, соединяющие стрелки, обозначают, что для реше-
ния задачи, от которой исходят стрелки, необходимо ре-
шить все указанные стрелками задачу:
135
Схема 36
2) Рассмотрим > решение геометрической задачи:
«Диагонали трапеции взаимно перпендикулярны и рав-
ны 3,6 дм и 6 дм. Вычислите площадь этой трапеции
(рис. 48)».
Рис. 48
Дано: АВСВ — трапеция, [ВС]||[Д£)], [ДС]_ЦВ£)],
|ЛС =6 дм, |ВВ|=3,6дм.
СпреДСЛИТ Ь^ *5тра[1.
Введем дополнительные обозначения: 1401 =х,
|0С|—6—х, |В0| = у, |ОО|=3,6—у.
Выполним дополнительное построение (оно показано
штриховой линией): [ВО] перенесем параллельно себе
на [BCJ.
Поиск решения задачи первым способом (схема 37):
Схема 37
136
5Трал = 4-1 АО I-1 ВО I + 4 |Л01 • I DO 1 + 1 |D0|• |С0| +
+ (6 —х)г/)=4-21>6 = 1°’8 дм2.
Решение задачи вторым способом (схема 38).
5трап = 4’3>6(6^~ х) + 4"'3’бх= 1,8-6 —1,8x4-
4- 1,8х = 10,8 дм2.
Совершенно аналогичный случай с рассмотрением
ДДВС и ДДОС опускаем.
Решение задачи третьим способом (схема 39):
5трап = 4|ЛС1-1В£>1=4",6‘3’6= 10’8
Теперь все три способа можно объединить в одну схе-
му (схема 40):
Схема 40
137
Несмотря на различия в поиске решения арифметиче-
ской и геометрической задач, можно выделить общую
идею: решение задачи (ответ на главный вопрос) сво-
дится к решению более простой задачи, подзадачи,
к ответу на промежуточный вопрос.
Облегчению организации поиска решения и служит
схема.
Последнюю схему рассмотрим подробнее. Ее нельзя
назвать деревом (деревом перебора). Для нахождения
площади трапеции достаточно раскрыть вершину 1,
ИЛИ-вершину 2, ИЛИ-вершину 3, т. е. лишь одну из
них (решить лишь одну из соответствующих этим вер-
шинам задач). Поэтому вершины 1, 2, 3 называют
ИЛ И-вершинами. Далее надо поступить так. Для рас-
крытия вершины 1 необходимо раскрыть вершины 4,
5, 6 и 7 (т. е. непременно решить все соответствующие
этим вершинам задачи). Поэтому вершины 4—7 назы-
вают И-вершинами. Для раскрытия вершины 2 при-
шлось бы раскрыть вершины 8 и 9, а для раскрытия
вершины 3 — вершину 10 и т. д. И-всршины на схеме
объединены дугами.
Вот такая графовая схема поиска решения задачи
(поиска доказательства) и называется И/ИЛ И-графом.
Поиск прекращается, когда все дочерние вершины ста-
новятся элементарными, представляют собой элемен-
тарные задачи, т. е. такие, которые решают-
ся за один шаг поиска иэти решение которых уже
известно.
Цель поиска заключается в том, чтобы показать, что
начальная вершина разрешима, т. е. ее раскрытие при-
водит к элементарным задачам. В противном случае сле-
дует вывод о том, что задача не имеет решения (доказы-
ваемое утверждение ложно).
Применение метода редукции, т. е. сведения за-
дачи к подзадачам, наиболее характерно для поиска до-
казательств при решении геометрических задач. Рас-
смотрим некоторые дополнительные положения теории
поиска доказательства.
Совокупность условий задачи (теорема), принимае-
мых в качестве посылок (гипотез), будем обозначать в
виде множества Г, а предложение, выражающее заклю-
чение, буквой Р. Символом Р/Г обозначим задачу: «до-
138
казать предложение Р при условии Г», «вывести утвер-
ждение Р из множества посылок Г».
Задача 1. Докажите, что любая трапеция, вписан-
ная в окружность, равнобедренная (рис. 49).
ABCD — равнобедренная
трапеция.
Трапеция ABCD вписана в
окружность.
Запишем предложения, связан-
ные с условием задачи, которые
могут оказаться полезными при
решении задачи '(среди них различ-
ные следствия из Г). Доказатель-
ство каждого из этих предложений
можно считать элементарной зада-
чей.
Рис. 49
Рх: [ ЛВ] Si ]CD] => трапеция равнобедренная (рис. 49)
Р2: AB = cb=>[AB]s±[CD].
р3: [ВС]||(ЛР] и (ВС] и [AD]— хорды =>ЛВ=CD (ра-
нее решенная задача).
Р4: Ое/ и /_L[BC]=HBT| = |TC|.
Ps: О<=1 и /_1_ [ВС] =>/_!_ [ЛО].
Рв: 0^1 и /_L [ЛВ]=НЛР[ = |РО|.
Р?: ABCD — трапеция => [ВС] || [ЛВ].
Предложения могли бы быть записаны и в ином по-
рядке, и в ином количестве.
Начальную вершину И/ИЛИ-графа изобразим так: |Р/Г|.
Чтобы доказать, что трапеция ABCD равнобедренная,
надо доказать, что [ЛВ]а?[СВ]. Следовательно, задача
сводится к двум подзадачам: а) доказать, что трапеция
равнобедренная, исходя из данных посылок Г, дополнен-
ных новой посылкой [ЛВ]^[СО], и б) доказать конгруэнт-
ность отрезков [ЛВ] и [СО], исходя из данных посылок Г
(это новая задача, более простая) (схема 41).
Но задача а) элементарна, решается одним шагом —
применением предложения Pt. Следовательно, в поисках
доказательства надо далее раскрывать лишь вершину б).
139
Схема 41
Чтобы доказать конгруэнтность [ЛВ] и [CD], други-
ми словами,-вместо того чтобы доказать конгруэнтность
[ЛВ] и [CD], можно опять же решить две подзадачи: в) до-
казать равенство дуг АВ и CD при условии Гиг) дока-
зать, что конгруэнтность отрезков следует из посылок Г,
дополненных равенством этих дуг (схема 42).
Схема 42
Далее опять следует раскрывать лишь левую вершину.
Первоначальная задача упростилась: надо доказать не то,
что трапеция равнобедренная, а лишь то, что АВ = CD.
Полный И/ИЛИ-граф поиска
доказательства будет таким,
как показано на схеме 43.
/ \ Если теперь проследить по
д'Х)_________пути решения снизу вверх, то
/ получим следующие структур-
/ ные схемы доказательства (схе-
мы 44, 45).
с В следующих примерах поиск
Рис. 50 представлен И/ИЛИ-графом без
предварительных рассуждений^
Задача 2. Докажите, что любая точка биссектрисы
угла равноудалена от его сторон (рис. 50, схема 46).
Р Г
|КЛ| = |КС|. [В К) — биссектриса Z.ABC,
К. — произвольная точка [В К)'.
[ГЛ] X [ВА]; [KCJ ± [ВС].
140
Схема 43
Схема 44
141
Схема 45
Схема 4(>
Чтобы доказать, что |4/С| = |СК|, достаточно решить
другую задачу: ААВК&кВСК.. Но конгруэнтность тре-
угольников можно доказать разными способами. Здесь
представлены два из них. Соответствующие стрелки не
связаны дугой, так как достаточно решить лишь одну из
задач, представленных вершинами, к которым ведут эти
стрелки (ИЛИ вершины графа),
142
Двигаясь теперь от заключительных вершин вверх,
получим доказательство, решение задачи.
Задача 3. Две окружности пересекаются в точках
А и В. Из точки А проведены диаметры окружностей AAi
и ABi. Точки Л1, В, Вх принадлежат одной прямой. Дока-
жите это (рис. 51, схема 47).
Рис. 51
(Лхвх).
Окр. О f| окр. Ох = {Л, В}.
[ЛЛХ];—диаметр окр. О.
[ЛВХ]—диаметр окр. Ov,
РХ:'[ЛЛХ], [ВХЛ]—диаметры иВЕокр. О,
В е окр. Ох =ф- Z ЛВЛХ и Z ЛВВХ — вписанные.
Р2: ZЛBЛxи Z ЛВВХ вписанные =^ЛВЛХ=90° и ЛВВХ—
= 90°.
Ра: ABAi -f- ЛВВХ - 180° => В е (ЛХВХ).
Схема 47
Задача 4. Из вершины тупого угла ромба опуще-
ны перпендикуляры на противоположные стороны. Дока-
143
жите, что образовавшиеся отрезки перпендикуляров кон-
груэнтны (рис. 52, схема 48).
[вм] = [в/а
Pj: ABCD — ромб
ABCD — ромб, [ВМ)_L[AD],, [ВК]± [CD].
[АВ] as [ВС] ~ [CD] as ]/[D].
Рис. 52
Рис. 53
Р2: ДBCD —ромб => [ДВ] || [CD], [ВС] || (AD].
Р3: ABCD — ромб=> ZA^ZC, ZB = ZD.
Pi - [BM]J_ [ДС] =>ВМД= 90°; [BK] A.[CD]=^BKC=
= 90°.
P5: [ДВ]^[ВС] и [ДМ] [СК] =ф-&АВМ^ &ВСК
(прямоугольные).
Рв: [ДВ]^[ВС] и/Д' ZC^/АЛВМ^ /\ВСК (пря-
моугольные).
Р, 5ром6а=] AD | • | ВМ | и 5ромба = | DC | • )ВК | => | AD\X
X|BM| = |DC|-|BK|.
Р8: (BD) — ось симметрии ромба => S(bd> (Л4) = К-
Ре: ЛАВМ^ЛВСК=> [ВМ] [ВК].
3 а д а ч а 5. В правильном тетраэдре проведено се-
чение через середины трех ребер, выходящих из одной
вершины. Докажите, что плоскость сечения параллельна
плоскости грани, противоположной этой вершине
(рис. 53, схема 49).
(КТМ)Ц(ДСВ).
АВСЕ — правильный тетраэдр, .
|ВК| - [КА |, ]ВМ| = |М£|,
IBTI^ITCI.
144
Схема 48
Схема 49
Рх: [А7И]—средн, линия ДЛВ£,=>[ЛМ] || [АВ].
Р2\ 1^1—средн, линия ДАВС=>[/СТ] Ц [АС]»
Р3: ИМ] || [АВ], [/СТ] || [АС] => (/СТЛ4) II {АСЕ).
Целенаправленный поиск решения задачи отвечает
современным психологическим концепциям интеллекту-
ального развития, концепции обучения математической
деятельности; он соответствует наиболее прогрессивным
методам обучения — исследовательским, занимающим
центральное место в системе проблемного обучения.
10 Зак. 1239
145
Подведем некоторые итоги. В пяти рассмотренных
задачах на доказательство использован один и тот же
«алгоритм поиска».
Решая задачу Р/Г, мы поступили- следующим об-
разом:
1) Отобрали совокупность уже известных истинных
предложений Л4={РЬ , Рп}> связанных с доказы-
ваемым.
2) К условиям Г добавили дополнительную посылку"
Pi(Pi^M) так, чтобы задача Р/Г, Pi стала элементар-
ной. Тогда решаемая задача Р/Г сводится к двум подза-
дачам: (1) Р/Г, Pi (элементарная) и (2) Pi/Г.
3) Если задача (2) тоже элементарная (т. е. реша-
ется в один шаг поиска или ее решение уже известно из
имеющегося опыта), то поиск закончен.
Если же задача (2) не является элементарной, то
поиск ее решения продолжается таким же образом (воз-
вращаемся к пункту 2), заменяя в нем Р на Рг-, а Рг^на
подходяще подобранное Pj).
Возможны два исхода поиска: успех и неудача. Успех
зависит от удачного отбора (обычно в уме) совокупно-
сти М, а это требует творчества. Никаких жестких пред-
писаний здесь нет. Этим алгоритм поиска отличается от
алгоритма решения стандартной задачи. Он строго не
детерминирует процесс поиска и обладает результатив-
ностью лишь в том случае, когда одним из его результа-
тов считать неудачу. Роль алгоритма поиска состоит в
организации целенаправленного поиска, а это чрезвы-
чайно важно для обучения.
ПРИЛОЖЕНИЕ I
(к главе III)
СТРУКТУРНЫЕ БЛОК-СХЕМЫ
РАЗЛИЧНЫХ ТЕМ.
СТРУКТУРНЫЕ СХЕМЫ
ДОКАЗАТЕЛЬСТВ.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИИ (А. 6, гл. Ш)
Решение систем
линейных урав-
нений
Решение тексто-
вых задач
Системы уравне-
ний второй сте-
пени с двумя
переменными
Схема 50
АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ (А. 8, гл. Ш)
Схема 51
МНОГОЧЛЕНЫ (А. 6, гл. V)
Тождественные преобразования
целых выражений
I Преобразование произ-।
* ведения одночлена на
| многочлен I
Преобразование произ- I
• ведения двух многочле- •
I нов
I Преобразование произ- I
• ведения суммы и раз-
| Преобразование разно- I
. сти квадратов двух
। выражений ।
I Преобразование квадра- '
". та двучлена i 1
I Преобразование трех- 1
Схема 52
МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ (Г. 6—8, гл. VIII)
Площадь
треугольника
Теорема
Пифагора
Тригонометри-
ческие функции
Соотношения в
прямоугольном
треугольнике
Решение задач
В других областях
знаний
Свойство скалярного
произведения векторов
Схема 53
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ' (А. 9—10, гл. I)
СП
ND
Схема 54
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ (Г. 9—10, гл. II)
Коллинеарные векторы
Компланарные векторы
Угол между векторами j |
Вектор
Сложение
векторов
, изведеине двух
Свойства ска-
лярного умно-
жения векторов
Применение
векторов в
физике
Вывод теорем
сложения в
алгебре
Вектор в системе
координат плоскости
н пространства
Векторная алгебра
' Умножение .
’ вектора
| на число
Разложение
векторов j-
по некол-х
линеарным
,, векторам
• — “1
Свойства
умножения
. вектора
* на число
Решение
задач
Перпендикулярность
в пространстве
тора по трем
не компланарным
векторам
Г Необходимые
и достаточные
I условия кол-
линеарности
векторов
Схема 55
ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ (А. 9—10, гл. II)
Функция
функций
Иэменение
функции
Способы
задания
функции
Вычисление
пределов
Теоремы о
пределах
Числовая
функция
Производная -
сумм функ-
ций
Производная
сложной
функции
рацнональ-
Единствен- ность пре- Непрерьт ность
дела
Предел
функции
Непрерыв-
ность ра-
циональной
функции
Приращение
функции
Г Производная Л Г” Производная
произведевдя । частного 1
Производная
степенной
функции с
рациональ-
ным показа-
телем
Схема 56
функции
Производная
степенной
функции с
целым пока-
зателем
Применение производной к
приближенным вычислениям.
Дифференциал функции
I
Касательная к графику
функции в точке
Применение производной к
исследованию функций
Нахождение
промежут-
ков моно-
тонности
Нахождение
критических
точек
Нахождение
min И max
Наибольшее
и наименьшее
значения
I
Построение
графиков
Исследование квадратичной функции
1 ...
Решение квадратичных неравенств
Решение текстовых задач на максимум и минимум
Применение производной в физике
Нахождение производных некоторых функций
Интеграл
ел
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (ТФ, А. 9—10, гл. III)
Схема 57
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Формулы преобразования
Г w ' -------1
1 Преобразование нроизве-
' дения ТФ в сумму .
* Преобразование суммы
' ТФ в пооизведение
।----- ; ______А--- - •

Формулы
приве-
дения
; SinoC, COSoC
^через
Формулы
кратного- ।
аргумен-
та
1
Формулы понижения i
степени •
।
Дифференцирование ТФ
I---------— ’ ------------ - --------1
Решение простейших
тригонометрических
уравнений
.(0<|л| <£•.)=> [sinx|<|z|<|tgx| •
♦ Непрерывность ТФ • t
[________I_____
I л->0 * I
I— - —I— - —I
,________i_____,
• Производные ТФ •
I--- . _---- . _J
I---------- . -------------
1) sin л = а
2) cosx=a
з) а
4) ctg.<x = a
Продолжение схемы 57
156
ИНТЕГРАЛ (А. 9*—10. гл. IV)
Схема 58
КООРДИНАТНЫЙ МЕТОД В ПРОСТРАНСТВЕ (Г. 9—10, гл. IV)
Схема 59
Рис. 54
е о р е м а 50 (Г. 6—8).
1) Против большей стороны тре-
угольника лежит больший угол.
2) Против большего угла тре-
угольника лежит большая сторона.
159
Теорема 8 (Г. 6—8)<
Для любых точек А, В и С, не принадлежащих од-
ной прямой, расстояние ]ЛС| меньше суммы расстоя-
ний [АВ | и | ВС|.
Схема G2
Теорема 16 (Г. 6—8).
Отображения, сохраняющие расстояния, обратимы.
Схема 63
160
Теорема 12 (Г. 6—8).
Длина простой ломаной больше расстояния между
ее концами.
Схема 64
Теорема 32 (Г. 6—8).
Расстояние от точки до ее проекции ~на прямую
меньше расстояния от этой точки до любой другой точ-
киданной прямой.
Схема 65
11 Зак. 1239
161
Теорема 39 (Г. 6—8).
|Если две прямые симметричны относительно неко-
торого центра, то они параллельны.
Схема 66
Теорема 40 (Г. 6—8).
Если две прямые перпендикулярны одной и той же
прямой, то эти прямые параллельны.
Схема 67
162
Теорема 3 (Г. 9—10),
Если плоскость проходит через прямую, параллель-
ную другой плоскости, и пересекает эту плоскость, то
линия пересечения плоскостей параллельна данной
прямой.
Схема 68
Теорема 14 (Г. 9—10).
Если прямая перпендикулярна каждой из двух пе-
ресекающихся прямых, лежащих в плоскости, то эти
прямая и плоскость взаимно перпендикулярны.
----- I—------г
cb = o i асаu.d=xa+ijb
—---- -------у - -
с а = с(ха + цЬ)
♦ _ , .
са = хса + усб~
Схема 69
163
Теорема 4 (Г. 9—10).
Если через каждую из двух параллельных прямых
проведена плоскость, причем эти плоскости пересека-
ются, то их линия пересечения параллельна каждой
из данных прямых.
Схема 70
Теорема 6 (Г. 9—10).
Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой пло-
скости, то эти плоскости параллельны.
|алд-В o\\ot йпй,
Допущение-.
$ а н/з
Схема 71
164
Теорема 7 (Г. 9—10).
Если две параллельные плоскости пересечены
третьей плоскостью, то линии пересечения парал-
лельны.
Схема 72
Задача 131 (Г.9—10). Задача 14 (Г.9—10).
Схема 73
Схема 74
165
Теорема 21 (Г. 9—10).
Для того чтобы прямая, лежащая в плоскости, бы-
ла перпендикулярна наклонной, необходимо и доста-
точно, чтобы эта прямая была перпендикулярна про-
екции наклонной.
Теорема а):
Схема 75
Теорема б):
Схема 76
166
ПРИЛОЖЕНИЕ II
(к главе IV)
БЛОК-СХЕМЫ ОБЩИХ МЕТОДОВ
РЕШЕНИЯ НЕКОТОРЫХ
КЛАССОВ ЗАДАЧ
РАСПОЗНАВАНИЕ ВИДА ДРОБИ (М. 4, п. 23)
Схема 77
РАСПОЗНАВАНИЕ СМЕЖНЫХ УГЛОВ (М. 4, п. 23)
Схема 78
168
СЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ (М. 5, пп. 19, 20)
I
- Да
Да
Нет
Нет
Схема^ 79
169
ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ
ЦЕЛЫХ ЧИСЕЛ (М. 5, п. 27)
СРАВНЕНИЕ ДРОБЕЙ С РАЗНЫМИ
ЗНАМЕНАТЕЛЯМИ (М. 5, п. 43)
Заменить данные дроби
дробями с равными
знаменателями
П
Нет
Да
m>k
Нет
п ~ п
Схема 81
170
РАСПОЗНАВАНИЕ ПРЯМОЙ И ОБРАТНОЙ
ПРОПОРЦИОНАЛЬНОСТИ (А. 6, пп. 12, 13, 16, 17)
Определить, является ли функция f
прямой или обратной пропорциональ-
ностью
Схема

РАСПОЗНАВАНИЕ ФУНКЦИИ (А. 6, § 4)
С Является ли отаошение
f — функцией?
Выяснить способ задания f
f задано
формулой
Существует ли X.
значение X , которому
формула сопоставляет
более одного зна-
ченхя у ?
Нет
Схема 83
Л
ПОСТРОЕНИЕ ГРАФИКА ЛИНЕИНОЦ ФУНКЦИИ y—kx+l
(А. 6, пп. 20, 21)
k=O
к. <0
k >0
к >0
Нет
Г - прямая, проходящая^
через начало координат
и составляющая с осью ОХ
острый угол
f — прямая,
проходящая
через нача-
ло коорди-
нат и сос-
тавляющая
е ось» ОХ
тупой угол
f — прямая,
пересекающая
ось ОУ п точ-
ке (O,t ) и
образующая
с осмо ОХ
тупой угол
Пересе каюшая
ось ОУ в точ-
ке ( 0,1 ) и
образующая с
осью ОА' ост-
рый угод
Схема 84
прямая, па-
раллельная оси
//.проходящая
через точку (0,1}
ОПРЕДЕЛЕНИЕ ЧИСЛА РЕШЕНИИ СИСТЕМЫ
ДВУХ ЛИНЕЙНЫХ УРАВНЕНИИ
С ДВУМЯ ПЕРЕМЕННЫМИ (А. 6, п. 26)
174
ГРАФИЧЕСКОЕ РЕШЕНИЕ
ЛИНЕЙНЫХ УРАВНЕНИЙ
СИСТЕМЫ
(А.'6, п. 25)
сл
Схема 86
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ДВУМЯ ПЕРЕМЕННЫМИ
СПОСОБОМ СЛОЖЕНИЯ (А. 6, п. 28)
Схема 87
176
ПРИВЕДЕНИЕ МНОГОЧЛЕНА
К СТАНДАРТНОМУ ВИДУ (А. 6, п. 44)
РАСПОЗНАВАНИЕ МНОГОЧЛЕНА (А. 6, п.
12 Зак. 1239
177
РЕШЕНИЕ ЛИНЕЙНОГО НЕРАВЕНСТВА
С ОДНОЙ ПЕРЕМЕННОЙ (А. 7, п. 17)
Схема 90
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ ВИДА:
|х<и,( А. 7, п. 18)
(х < k
Схема 91
178
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ ВИДА:
(х>п, (А. 7, п. 18)
|х>&
И»
Схема 92
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ ВИДА:
Схема 93
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕН-НОЙ ВИДА:
ах+ & > О, (А. 7, п. 18)
_сх + d •> О
Схема 94
180
РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЕХЧЛЕНА
НА МНОЖИТЕЛИ (А. 8, п. 3)
Схема 95
РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ (А. 8, п. 6)
Уравнении не
iiMCCi дсйспш*
тельных корней
РАСПОЗНАВАНИЕ ЧЕТЫРЕХУГОЛЬНИКА (Г. 6—8, гл. И)
Схема 97
РАСПОЗНАВАНИЕ КОЛЛИНЕАРНОСТИ
ВЕКТОРОВ (Г. 6—8, п. 55)
Схема 98
РАСПОЗНАВАНИЕ ОБРАТИМЫХ ФУНКЦИЙ
(А. 8, п. 21)
184
ВЫЧИСЛЕНИЕ СТЕПЕНИ С РАЦИОНАЛЬНЫМ
ПОКАЗАТЕЛЕМ (А. 8, п. 29).
Схема 100
РЕШЕНИЕ ПРОСТЕЙШИХ ПОКАЗАТЕЛЬНЫХ
УРАВНЕНИЙ (А. 8, п. 32)
Схема 101
185
РЕШЕНИЕ ПРОСТЕЙШИХ ПОКАЗАТЕЛЬНЫХ
НЕРАВЕНСТВ (А. 8, п. 32)
Схема 102
186
РЕШЕНИЕ ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ (Г. 6—8, п. 18)
Выяснить, какие элементы
треугольника известны
Схема 103
187
ИССЛЕДОВАНИЕ ФУНКЦИИ
НА МОНОТОННОСТЬ (А. 9—10, гл. II)
Схема 104
188
РАСПОЗНАВАНИЕ ОТНОШЕНИЯ МЕЖДУ ЛУЧАМИ
(А. 9—10, п. 16)
Схема 105
189
ИССЛЕДОВАНИЕ КВАДРАТИЧНОЙ ФУНКЦИИ (А. 9—10, л. 27)
Схема 106
ОГЛАВЛЕНИЕ
От авторов................................................ 3
Введение. Актуальные проблемы среднего математического
образования ........................................... .5
Глава I. Теоретические основы обучения математике
§ 1. Психологическая концепция............................. 10
§ 2. Модель учебной математической деятельности . 12
§ 3. Общедидактические основы.............................. 23
§ 4. Обучение применению математической теории . 25
Глава II. Проблемное обучение (практические материалы)
§ 1. Построение маленьких теорий............................33
§ 2. Обучение элементам исследования в процессе решения
задач . ... . 54
Глава III. Структурирование и систематизация математи-
ческих знаний
*_
§ 1. Сущность структурирования и систематизации 66
§ 2. Структурная блок-схема темы ... 67
§ 3. Структурная схема системы понятий . 70
§ 4. Структурная схема системы предложений , 73
§ 5. Некоторые приемы систематизации . 80
*
Глава IV. Общие методы решения задау
§ 1. Интуитивное понятие алгоритма. Свойства. Структура.
Блок-схемы........................................... ... 97
§ 2. Обучение общим методам решения задач . . . 104
Глава V. Методы поиска решения задач
§ 1. Стандартные и нестандартные задачи....................119
§ 2. Представление задач и методы поиска в пространстве
состояний............................. . .121
§ 3. Сведение задач к подзадачам . 133
Приложение I (к главе III) . 147
Приложение П (к главе IV) 167
Борис Самуилович Каплан
Николай Константинович Рузин
Абрам Аронович Столяр
Методы обучения математике
(Некоторые вопросы теории и практики)
Редактор В. В. Амбражевич. Обложка художника Г. И. Красинско-
г о. Художественный редактор О. И. Романцов. Технический редактор
С. И. Л и ц к е в и ч. Корректор Р. С. А х р е м ч и к.
ИБ № 979
Сдано в набор 14.05.80. Подписано в печать 19.12.80. Формат 84Х108’/з2. Бум.
тип. № 3. Гарнитура литературная. Высокая печать. Усл, печ. л. 10,08.
Уч.-изд. л. 9,16. Тираж 37 000 экз. Зак. 1239. Цена 55 к.
Издательство «Народная асвета» Государственного комитета БССР по де-
лам издательств, полиграфии и книжной торговли. 220600 Минск, Парковая
магистраль, 11.
Ордена Трудового Красного Знамени типография издательства ЦК КП Бе-
лоруссии. 220041 Минск, Ленинский проспект, 79.