Методы решения экстремальных задач и их применение в системах оптимизации - Евтушенко Ю.Г.

Author: Евтушенко Ю.Г.
Tags: вычислительная математика численный анализ
Year: 1982
Similar
Методы решения экстремальных задач
Численные методы решения задач электрофизики
Численные методы в примерах и задачах
Численные методы безусловной оптимизации и решения нелинейных уравнений
Text
                    ОПТИМИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ
Редактор серии
Н. Н. МОИСЕЕВ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1982

Ю. Г. ЕВТУШЕНКО
МЕТОДЫ РЕШЕНИЯ
ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
И ИХ ПРИМЕНЕНИЕ
В СИСТЕМАХ
ОПТИМИЗАЦИИ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1982

22.18
Е 13
УДК 519.6
Евтушенко Ю. Г. Методы решения экстремальных задач
и их применение в системах оптимизации. — М.: Наука, Главная
редакция физико-математической литературы, 1982 (Оптимизация и
исследование операций).—432 с.
Книга посвящена созданию диалоговых человеко-машинных систем
оптимизации. Основное внимание уделяется систематическому описа-
описанию алгоритмов решения задач нелинейного программирования и оп-
оптимального управления. На модельных примерах проводится сравни-
сравнительный анализ алгоритмов. Показано, что наиболее высокую эффек-
эффективность использования методов оптимизации можно получить путем
последовательного применения разных алгоритмов. Обсуждаются воп-
вопросы организации человеко-машинного процесса расчетов, даны при-
примеры реализации диалоговых систем оптимизации.
Книга предназначается для специалистов в области математичес-
математического программирования, теории оптимального управления, инжене-
инженеров, студентов старших курсов, аспирантов, применяющих и разви-
развивающих методы оптимизации.
Илл. 19, библ. 237 назв.
Юрий Гаврилович Евтушенко
МЕТОДЫ РЕШЕНИЯ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
И ИХ ПРИМЕНЕНИЕ В СИСТЕМАХ ОПТИМИЗАЦИИ
(Серия: «Оптимизация и исследование операций»)
Редактор И. Е. Морозова
Техн. редактор Л. В. Лихачева. Корректоры Е. В. Сидоркина, В. Я. Сорокина
ИБ № 12119
Сдано в набор 11.01.82. Подписано к печати 20 05.82. Т-11679. Формат
84X108V32* Бумага тип. № 1. Литературная гарнитура. Высокая печать.
Условн. печ. л. 22,68. Уч.-изд. л. 23,32. Тираж 9000 экз. Заказ № 3671.
Цена 2 р. 10 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова Союзполиграфпрома
при Государственном комитете СССР по делам издательств, полиграфии и
книжной торговли. Москва, М-54, Валовая, 28
Отпечатано во 2-ой типографии изд-ва «Наука».
Москва, Шубинский пер., 10 Зак.1705.
17П0П7ПППП ПЯ1 ® Издательство «Наука».
17UzU/UUUU — Uo 1 -- м Главная редакция
9 физико-математической
2 литературы, 1982

ОГЛАВЛЕНИЕ
Предисловие 7
Основные обозначения 10
Глава I. Введение в теорию оптимизации 13
§ 1. Выпуклые множества и выпуклые функции 13
§ 2. Дифференцируемость выпуклых функций 21
#§ 3. Необходимые и достаточные условия локального экстре-
экстремума функций многих переменных 29
§ 4. Необходимые и достаточные условия минимума функ-
функций на множествах 34
§ 5. Свойства минимаксных задач 38
§ 6. Условия минимума в задачах нелинейного програм-
программирования, не использующие дифференцируемость . . 52
§ 7. Условия минимума в задачах нелинейного программи-
программирования, использующие дифференцируемость .... 64
§ 8. Необходимые условия минимума в задачах оптималь-
оптимального управления 78
Глава П. Теоремы о сходимости и их приложения к иссле-
исследованию численных методов 88
§ 1. Устойчивость по первому приближению 88
§ 2. Метод функций Ляпунова 94
§ 3. Теоремы о сходимости итеративных процессов .... 104
§ 4. Сходимость процессов, порожденных многозначными
отображениями 116
§ 5. Методы решения систем нелинейных уравнений ... 122
§ 6. Численные методы отыскания минимакса 141
Глава III. Метод штрафных функций 159
§ 1. Метод внешних штрафных функций 159
§ 2. Оценки точности метода штрафных функций 173
§ 3. Метод параметризации целевой функции 185
§ 4. Метод внутренних штрафных функций 193
§ 5. Метод линеаризации 199
Глава IV. Численные методы решения задач нелинейного
программирования, основанные на использовании
модифицированных функций Лагранжа .... 206
§ 1. Простейшая модификация функции Лагранжа .... 207
§ 2. Модифицированные функции Лагранжа 218
§ 3. Обоснование сходимости метода простой итерации . . 224

6 ОГЛАВЛЕНИЕ
§ 4. Решение задач выпуклого программирования .... 236
§ 5. Редукция к максиминной задаче 242
§ 6. Редукция к минимаксной задаче 250
Глава V. Релаксационные методы решения задач нелиней-
нелинейного программирования 258
§ 1. Применение метода приведенного градиента для реше-
решения задач с ограничениями типа равенства 258
§ 2. Обобщение метода приведенного градиента 262
§ 3. Дискретный вариант метода приведенного градиента 273
§ 4. Метод условного градиента 277
§ 5. Метод проекции градиента 281
Глава VI. Численные методы решения задач оптимального
управления 284
§ 1. Основные расчетные формулы 287
§ 2. Необходимые и достаточные условия минимума . . . 300
§ 3. Численные методы, основанные на редукции к задачам
нелинейного программирования 304
§ 4. Дискретные принципы минимума 312
§ 5. Численные методы, основанные на использовании дис-
дискретных принципов минимума 329
§ 6. Некоторые обобщения 333
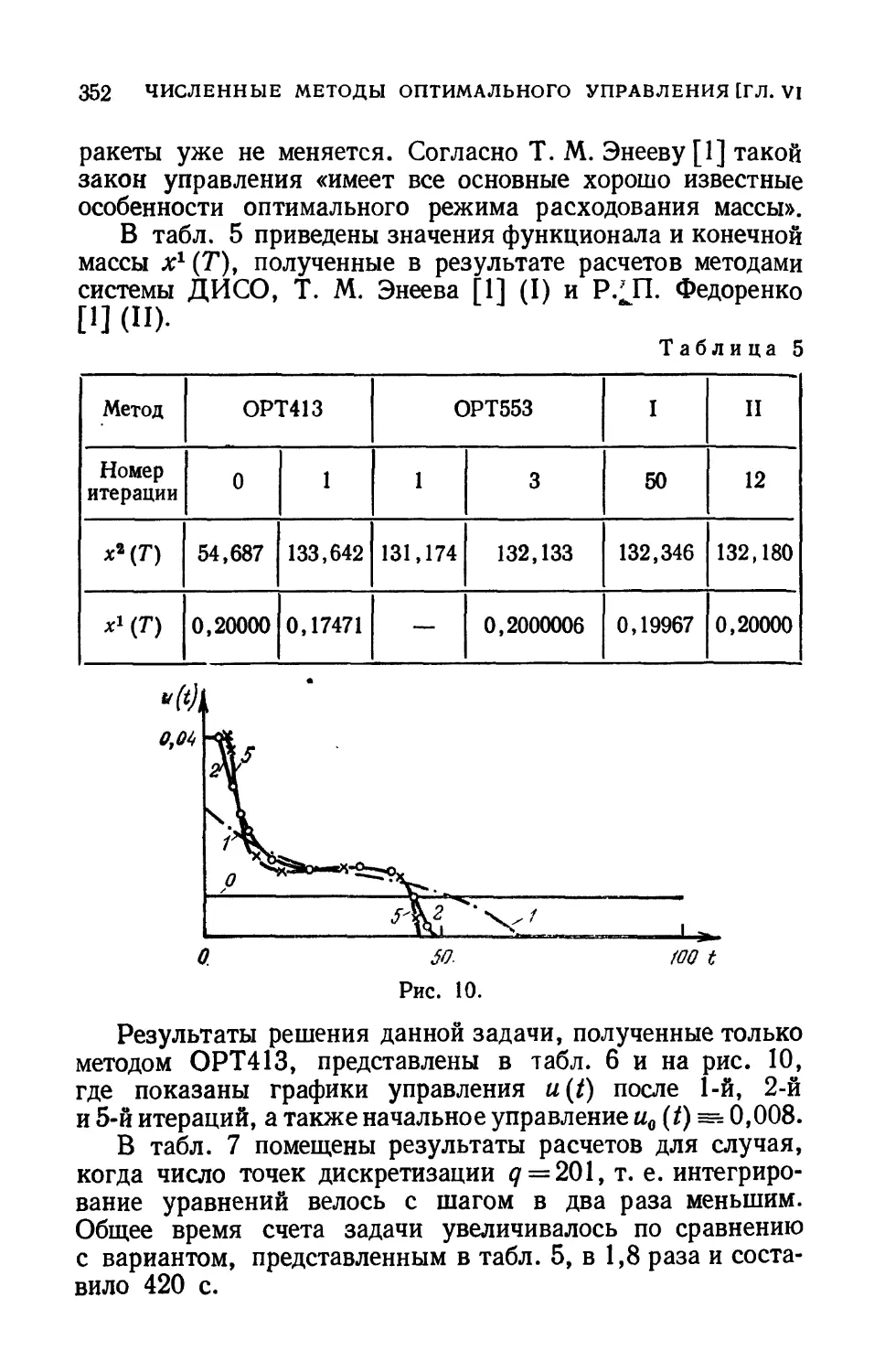
§ 7. Примеры численных расчетов - 341
§ 8. Приложение к дифференциальным играм 363
Глава VII. Диалоговые системы оптимизации 372
§ 1. Общие принципы построения диалоговых систем . . . 372
§ 2. Библиотека программ решения задач безусловной
минимизации 384
§ 3. Примеры численных расчетов задачи безусловной
минимизации 387
§ 4. Библиотека программ для решения задач нелинейного
программирования 391
§ 5. Примеры численных расчетов задачи нелинейного про-
программирования -. 395
Приложение I. Дифференцируемость 404
Приложение II. Некоторые свойства матриц 407
Приложение III. Некоторые свойства отображений ... 412
Комментарии и библиография 414
Литература 419

ПРЕДИСЛОВИЕ
Методы оптимизации находят все более широкое при-
применение в науке и технике. К ним обращаются инженеры-
конструкторы, разработчики систем автоматизированного
проектирования, создатели автоматизированных систем
управления, экономисты, физики-экспериментаторы, зани-
занимающиеся обработкой наблюдений, специалисты в области
исследования операций и многие другие. Обширные при-
приложения способствуют бурному развитию вычислительных
методов оптимизации, созданию новых разнообразных нап-
направлений исследований. Практическая реализация многих
численных методов требует огромного объема вычислений,
поэтому широкое применение эти методы нашли в послед-
последние годы в связи с появлением мощных быстродействую-
быстродействующих электронно-вычислительных машин. Опыт показы-
показывает, что наиболее эффективно решение оптимизационных
задач можно проводить с помощью диалоговых человеко-
машинных систем, дающих возможность в процессе рас-
расчетов каждой конкретной задачи использовать разнообраз-
разнообразные оптимизационные методы.
Данная книга посвящена описанию вычислительных
методов решения задач нелинейного программирования,
задач оптимального управления при наличии смешанных
ограничений и применению этих методов в диалоговых
человеко-машинных системах оптимизации.
Книга состоит из семи глав. В первой главе приве-
приведены основные сведения из выпуклого анализа, изложены
необходимые и достаточные условия экстремума в задачах
нелинейного программирования, оптимального управле-
управления. Во второй главе описаны численные методы решения
систем нелинейных уравнений и отыскания минимакса;
эти методы, имеющие самостоятельный интерес, исполь-
используются в дальнейшем. Третья, четвертая и пятая главы
посвящены численным методам решения задач нелинейного

8 ПРЕДИСЛОВИЕ
программирования. В третьей главе приведены различные
модификации метода штрафных функций. В четвертой
главе излагаются методы, основанные на использовании
различных модификаций функции Лагранжа. В пятой гла-
главе описаны релаксационные методы. Глава шестая посвя-
посвящена численным методам решения задач оптимального
управления. Изложенные методы базируются на примене-
применении методов нелинейного программирования. Такой подход
позволил достичь значительных результатов: он дал воз-
возможность сравнительно просто и эффективно решать задачи
с фазовыми ограничениями, с простейшими недифференци-
руемыми функционалами, проводить оптимизацию не только
по управлению, но и по управляющим параметрам. Для
решения задач оптимального управления появилась возмож-
возможность использовать методы, основанные на применении
модифицированных функций Лагранжа, метод условного
градиента, проекций градиентов, метод Ньютона и многие
другие. Седьмая глава посвящена вопросам создания и
эксплуатации диалоговых человеко-машинных вычислитель-
вычислительных систем оптимизации. Такие системы оснащены обшир-
обширными библиотеками программ оптимизации, предусмотрен-
предусмотренный в них диалоговый сервис дает возможность пользова-
пользователю управлять процессом решения задач на ЭВМ, в зависи-
зависимости от текущих результатов расчетов выбирать наиболее
рациональную последовательность применяемых методов,
корректируя в случае необходимости параметры методов,
вносить изменения в постановку решаемых задач. Диалого-
Диалоговые системы позволяют создать универсальный инстру-
инструмент решения разнообразных практических задач. Дана
краткая информация о некоторых существующих систе-
системах оптимизации, более подробно описана диалоговая
система оптимизации ДИСО, приведены результаты ее ис-
использования для решения двух тестовых задач.
В приложениях приведены некоторые необходимые для
изложения сведения из математического анализа, линей-
линейной алгебры и теории точечно-множественных отображе-
отображений.
По темам, затронутым в книге, существует обширная
библиография (полное количество работ значительно пре-
превосходит тысячу наименований). Приведенный в конце
книги список литературы не претендует на полноту. В него
включены в основном лишь те статьи и монографии, кото-

ПРЕДИСЛОВИЕ 9
рые непосредственно использовались при написании этой
книги. Основное внимание в книге было уделено тем мето-
методам, которые были апробированы и на протяжении послед-
последних лет развивались в Вычислительном центре АН СССР.
Автор выражает глубокую признательность Н. Н. Мои-
Моисееву, который поддержал идею написания этой книги,
проявил внимание к работе. Профессор О. Геллман пре-
предоставил автору возможность работать в библиотеке уни-
университета г. Турку, что позволило широко использовать
в книге результаты зарубежных исследований. Сотруд-
Сотрудники ВЦ АН СССР О. П. Бурдаков, А. И. Голиков,
Н. И. Грачев, В. Г. Жадан, В. А. Пуртов прочитали отдель-
отдельные части рукописи, сделали целый ряд полезных заме-
замечаний, которые были с благодарностью приняты.
В написании § 5 гл. II принимал участие О. П. Бур-
Бурдаков, вместе с Н. И. Грачевым был написан § 7 гл. VI.
/О. Г. Евтушенко

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Теоремы, леммы и определения нумеруются тремя числами: пер-
первое из них — номер главы, второе—номер параграфа, а третье —
порядковый номер самой теоремы, леммы, определения в параграфе.
Формулы нумеруются двумя числами: первое из них — номер параг-
параграфа, второе—номер формулы в параграфе. Если ссылка производится
на формулу из другой главы, то к ней слева добавляется еще один
индекс, указывающий номер главы.
х ? X—х является элементом множества X;
хфХ—х не является элементом множества X;
XczY—множество X составляет часть или совпадает с множе-
множеством Y;
X = Y—множества X и Y совпадают;
X[)Y—объединение множеств X и К;
X[\Y—пересечение (общая часть) множеств X и К;
X\Y—разность множеств X и К, т. е. совокупность всех х ¦? X
таких, что х ф. Y;
XxY—декартово произведение множеств X и К, т. е. совокуп-
совокупность пар х, у, где x?Xt y?Y;
intX—совокупность внутренних точек множества X (см. опре-
определение 1.1.2);
X—замыкание множества X (см. определение 1.1.3);
Х = 0—множество А' пусто;
{х:Т} — множество всех точек х, удовлетворяющих условию Т;
^) — число X удовлетворяет условию а < X < Ь;
[а, Ь]—число X удовлетворяет условию а^Х^Ь;
/: X -> Y—однозначное отображение из X в Y;
W: X -+2Y—многозначное отображение из X в Y (см. Прило-
Приложение III);
Vx —читается «для всех *»;
За: —читается «существует х».
dis (л:, у) —расстояние между двумя точками х и у;
dis (л:, Х)~ infdis(*, у) — расстояние между точкой х и множе-
Х
ством X;
G(q) — открытая окрестность точки q;

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ Ц
G (X)—открытая окрестность множества X;
Ge (X) — е-окрестность множества Х\ G8 (X) = {х: dis (х, X) < е};
Rn—вещественное линейное нормированное л-мерное простран-
пространство;
Еп— евклидово л-мерное пространство;
ЕЧ — положительный ортант из Еп, т. е. совокупность всех век-
векторов из Еп, все координаты которых неотрицательны;
х?Еп—вектор х является элементом пространства Еп\
х1 — i-я координата вектора х\ в некоторых местах для большей
ясности пишется также *(/);
е1—единичный i-ik орт, вектор-столбец, i-я координата которого
равна единице, остальные координаты—лули;
рт—транспонированный вектор;
Вт — транспонированная матрица;
||*||—норма вектора xf в большинстве мест имеется в виду евкли-
евклидова норма (более подробно см.- Приложение II);
|| Л ||—норма матрицы Л, согласованная с нормой векторов;
| Л | —определитель матрицы Л;
р^О—все координаты вектора р неотрицательные;
В > О—симметричная матрица В порядка п положительно опре-
определена, т. е. для любых х?Еп и таких, что ||д:|)^0, величина
хтВх > 0;
В^О—симметричная матрица В порядка п положительно полу-
полуопределена, т. е. для любых х?Еп величина хтВх^0;
?>(z)—диагональная матрица, у которой 1-й диагональный эле-
элемент есть i-я координата вектора г, размер матрицы D определя-
определяется размерностью вектора z;
Is — единичная матрица порядка s;
/+—совокупность неотрицательных действительных чисел;
О»,» — нулевая матрица пХш (во многих местах, где это не при-
приводит к недоразумениям, индексы ппг опускаются);
(а, Ь) Ф 0 — по крайней мере у одного из векторов a?Rc или
Rm норма не равна нулю;
z = fa, b]—вектор 2$Rc+m является объединением векторов а
и Ь;
<а, &> — скалярное произведение векторов а и Ь\
h+ (x)y h_ (x)~вектор-функции, у которых 1-е компоненты опре-
определяются по формулам:
hl+ (*) = тах [0, Ы (*)], hL (*) = min [0, hl (x)],
если A, v?Ec, to (h + v)% =У] [max [0,

12 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
* / ч - • df(x)
/х \х)—-«-мерный вектор, i-я компонента которого равна •¦' у- ;
/ххМ— квадратная матрица порядка п> (i, /)-й элемент которой
д2/ (х)
равен ¦ ;
gx(x) — прямоугольная матрица, (i, /)-й элемент которой равен
vS'(^)—производная функции S по скалярному аргументу^;
Re г—действительная часть комплексного числа z;
Imz — мнимая часть комплексного числа г;
z—число, сопряженное числу z;
\z\ — модуль числа г;
Нтл:^ — верхний предел последовательности {х^}\
Аг-»-оо
Птд:^—нижний предел последовательности {дс^};
i—дифференцирование по независимой переменной t\
df (x) — множество субградиентов функции / в точке х (см. опре-
определения 1.2.1 и 1.2.2);
Qi(x)—оценки скорости сходимости (их определение дано в § 3
гл. II);
о (х) — множество активных ограничений типа неравенства в точ-
точке х (см. формулу A.7.3));
L(x> w, v)—функция Лагранжа в задаче нелинейного програм-
программирования A.6.1) (см. формулу A.6.4));
Argmin/(*)—совокупность всех тех точек х?Х, в которых до-
хех
стигается минимум функции / на X;
sup—точная верхняя грань;
inf—точная нижняя грань;
¦—доказательство окончено.

ГЛАВА1
ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ
В этой главе даны определения и основные теорети-
теоретические результаты, используемые при разработке и обо-
обосновании численных методов решения экстремальных за-
задач. Приводятся также необходимые и достаточные условия
экстремума в разнообразных оптимизационных задачах.
Собранный материал носит вспомогательный характер
и важен для понимания последующих глав.
§ 1. Выпуклые множества и выпуклые функции
1. Основные определения. Пусть х, у?Еп. Отрезком,
соединяющим точки х и у, называется совокупность всех
точек, представимых в видеЯд: + A—Х)у, где O^X^Cl.
Определение 1.1.1. Множество ХаЕп называется
выпуклым, если отрезок, соединяющий любые две точки
из X, принадлежит X.
Определение 1.1.2. Точка х?X называется внут-
внутренней точкой множества X, если для любого конечного
у?Еп найдется такое число % > О, что х-\-Ху€Х для
всехО<Я<Я. Совокупность всех внутренних точек мно-
множества X обозначается intX.
Из выпуклости множества X вытекает выпуклость
intX.
Множество называется открытым, если каждая его
точка внутренняя. Множество X называется замкнутым
в Еп, если его дополнение в Еп, т. е. множество Еп\Х>
является открытым.
Определение 1.1.3. Точка х называется предельной
точкой множества X, если существует последовательность
точек xk ? X, сходящаяся к х. Совокупность всех предель-
предельных точек множества X называется его замыканием и
обозначается X.

14 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Определение 1.1.4. Множество X называется ком-
компактным, если любая последовательность его точек со-
содержит подпоследовательность, сходящуюся к некоторой
точке из X.
В пространстве Еп термин «компактное множество»
является синонимом «ограниченного замкнутого множе-
множества».
Определение 1.1.5. Функция f(x), определенная
на множестве Ху называется выпуклой на X, если для
любых двух точек х, у?Х и любых значений Х^Е1 та-
таких, что O^X^l и^д: + A —Х)у?Х> выполнено условие
f(bx + (l-X)y)^Xf(x) + (l-X)f(y). A.1)
Если дополнительно потребовать, чтобы при Я=^0,
\ и хфу в этом неравенстве знак ^ можно заменить
на <, то функция f(x) будет называться строго выпук-
выпуклой на X.
Если в формуле A.1) знак ^ можно заменить на ^,
то функция f(x) будет называться вогнутой на X. Если
функция f(x) выпуклая, то функция—/ (х) вогнутая.
Благодаря этому все свойства выпуклых функций легко
переносятся на вогнутые функции.
Функция f{x)y определенная на выпуклом множестве X,
будет выпуклой, если для любых х, у?Х п любых зна-
значений К ? Е1 таких, что 0 ^ X <; 1, выполнено условие A.1).
Если f(x)—выпуклая функция х на всем простран-
пространстве Еп, то будем говорить, что функция f(x) выпуклая.
Простейшим примером выпуклой на Еп функции является
евклидова норма вектора Цх|| = !/*<#» *>• Действительно,
воспользовавшись неравенством треугольника
свойством нормы||Я*||-= | К11|а:||, |A — X) у\\ = \ 1 — Я,| |у\\, для
О <! X ^ 1 получим
\\Xx+(l-X)y\\^Xlx\\+(l-X)\\yl
откуда следует выпуклость функции \\x\\.
В качестве примера открытого выпуклого множества
можно указать множество точек, лежащих внутри п-мер-
ной сферы радиуса 8 с центром в точке х:
»: \\х-х\\<г].

|!] ВЫПУКЛЫЕ ФУНКЦИИ И МНОЖЕСТВА 15
Если Ху y?Ge(x)9 то, согласно неравенству треугольника,
откуда следует выпуклость множества Ge(x).
В дальнейшем множество Ge(x) будем называть 8-о/с-
рестностью точки х.
Определение 1.1.6. Определенная на Еп функция
f(x) называется бесконечно большой, если для любого
положительного числа М существует такое число R(M),
что при всех Ху удовлетворяющих условию Jx|> R, имеет
место неравенство f(x) > М.
Расстояние между точкой х и множеством X будем
обозначать dis(x, X):
dis«(A:, Х)
Если множество X выпукло и замкнуто, то в этом вы-
выражении достигается минимум в единственной точке
р(х)&Ху которая называется проекцией точки х на мно-
множество X и определяется из условия
р (х) = Arg min || х—р ||. A.2)
рех
Покажем, что dis(x, X) является выпуклой функцией х.
Пусть хх и хг — произвольные точки из Еп и 0 ^ X ^ 1.
Тогда для любого z 6 X имеет место неравенство
—X)x2—zl A.3)
Используя определение A.2), обозначим рг = р (хг)у р2 =
= р(х2)у причем р1У р2?Х. В силу выпуклости множе-
множества X ему принадлежат все точки отрезка, соединяю-
соединяющего рг и р2у поэтому, положив в неравенстве A.3) г —
Х|AК)р2у получим
2y X).
Отсюда следует выпуклость иа Еп функции dis(x, X)-
Очевидно также, что для компактного множества X эта
функция является бесконечно^ большой.

16 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ ^ГЛ- 1
Определение 1.1.7. Эпиграфом (надграфиком)
выпуклой функции f(x), обозначаемым epi/, называется
множество конечных точек из ?w+1, расположенных на
графике и выше графика /:
Определение 1.1.8. Эффективной областью вы-
выпуклой функции /, обозначаемой dom/, называется мно-
множество точек из Еп, в которых / принимает конечные
значения или значение —оо:
Множество dom/ есть проекция epi/ на ?я, 'т. е.
dom f = {x?En: ЗрёЕ1 такое, что [л:, HjGepi/}.
Определение 1.1.9. Выпуклая функция /назы-
/называется собственной, если множество dom/ не пусто и
/(*)> — оо V*?dom/.
Другими словами, собственная функция не принимает
значения —оо и не равна тождественно +оо. В даль-
дальнейшем, занимаясь выпуклыми функциями, будем считать
их собственными, не оговаривая специально это свойство.
Выпуклая функция непрерывна во всех внутренних
точках множества, на котором она определена.
Определение 1.1.10. Непустое множество КсЕп
называется выпуклым конусом, если выполнены условия:
1) х+У€К при любых х, у?К\
2) кх?К при любом х?К и всяком Я^О.
Оба эти условия эквивалентны требованию, чтобы
ах+$у?К для любых х, у?К и всяких а^О, р^О.
Неотрицательный ортант El является выпуклым ко-
конусом. Если А—матрица тхп и х?Епу либо х?Е1У то
множество всех решений системы Л#<0 представляет
собой многогранный конус.
Гиперплоскостью в Еп называется множество
где с?Еп, ||с 1=7^0, а—-действительное число. Это множе-
множество выпукло и всегда не пусто. Если точка хт ? Г, то
гиперплоскость Г можно представить в виде
х—*«> =

§1] ВЫПУКЛЫЕ ФУНКЦИИ И МНОЖЕСТВА 17
т. е. Г состоит из тех и только тех точек ху для кото-
которых вектор х—х* ортогонален вектору с. Вектор с назы-
называют нормальным вектором гиперплоскости Г.
Будем говорить, что гиперплоскость Г с нормальным
вектором с отделяет два непустых множества ХиУ, если
существует такое число у, что для любых х?Х, y?Y
выполнены неравенства
Определение 1.1.11. Гиперплоскость Г называется
опорной к множеству X, если <с, ху^а при всех х?Х
и <С) у> = а для некоторой точки у?Х. Если у?Х, то
вектор с называется опорным вектором множества X
в точке у у одновременно с есть нормальный вектор опор-
опорной к X гиперплоскости, проходящей через точку у.
Теорема 1.1.1 (об отделимости). Пусть ХаЕп —
непустое, выпуклое множество, не содержащее начала
координат. Тогда существует гиперплоскость, отделяю-
отделяющая мнооюество X и начало координат.
Доказательство теоремы можно найти во многих кни-
книгах по выпуклому анализу (см., например, X. Никайдо
[1], О. Мангасарян [1], Р. Рокафеллар [1]).
2. Свойства выпуклых функций, не использующие
дифференцируемость.
Теорема 1.1.2. Пусть строго выпуклая функция f (x)
достигает наименьшего на Еп значения в некоторой
точке х*. Тогда f(x)—бесконечно большая функция.
Доказательство. Пусть S — поверхность сферы
единичного радиуса с центром в точке х*у хг — произволь-
произвольная точка, лежащая снаружи S. Соединим х* и хг прямой
линией, точку пересечения этой линии с 5 обозначим х.
Можно записать
К)х1у 0 < Л, < 1.
Величину коэффициента Я, зависящую от выбора точки х1у
определим из условия |)? — лг*Ц=1, получим

lg ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ
Из условия выпуклости / (х) по х следует, что / (л:)
Х/() + A^)/() Отсюда находим
~f {х*]'
Если [*i|—*oof то 1—M#i)—*0, и из этих неравенств
заключаем, что / (х±) —*оо, т. е. / (#) — бесконечно большая
функция. Щ
Теорема 1.1.3. Функция /, определенная на выпук-
выпуклом множестве Ху выпукла на X тогда и только тогда,
когда ее эпиграф есть выпуклое множество в Еп+1.
Доказательство. Пусть множество epi/ выпукло,
Ху у?Х, тогда
[х, /(*)]€ epi/, [у, / ДО] € epi Л
Из условия выпуклости эпиграфа следует, что для любого
0<Х1
-^)/ДО] € epi/.
Согласно определению эпиграфа отсюда следует, что
т. е. / выпукла на X.
Докажем необходимость. Пусть / выпукла на Х\
[х, |x]€epi/, [у, v]^epi/. Из свойства выпуклости / для
любых 0<^<1 имеем/(и+A— X)у)<^Щ(х)+A— Х)/ДО<
^ k\i + A — К) v. Следовательно,
при любых O^X^l, т. е. множество epi/ выпукло
в Еп+1. В
Теорема 1.1.4. Функция f(x) выпукла на Еп тогда
и только тогда, когда для любых х, у?Еп функция
выпукла при любых 0 ^ К ^ 1.
Доказательство. Пусть / выпукла, х, у — произ-
произвольные точки из Еп. Покажем, что эпиграф функции ty(k)y
определяемый условием

§ ,] ВЫПУКЛЫЕ ФУНКЦИИ И МНОЖЕСТВА 19
есть выпуклое множество. Пусть [A,lf aj^epiij), [X2, а2]?
€ epi i|>,
Тогда имеем
/(*.) =
Следовательно, [гХ) a,], [г2, a2]?epi/. Множество epi/
выпуклое, поэтому для любого О <I v ^ 1 имеем
— v)a2]€epi/,
откуда следует, что
Учитывая определение функции i]>, получим
Поэтому эпиграф функции г|) есть выпуклое множество и,
следовательно, функция о|? выпукла. Аналогично доказы-
доказывается обратное утверждение. §|
Теорема 1.1.5. Если выпуклая функция f принимает
в точке а?Еп конечное значение, то множество X, опре-
определяемое условием
не пусто и выпукло.
Доказательство. Множество X не пусто, так как
оно заведомо содержит точку а. Для любых точек х9
у?Еп и O^Ji^l выполнено условие A.1). Будем счи-
считать дополнительно, что х, у?Х, тогда
В силу произвольности числа К из интервала [0, 1] при-
приходим к выводу, что замкнутый сегмент прямой линии,
соединяющей две точки х и у из X, принадлежит X.
Поэтому множество X выпуклое.

20
ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Теорема 1.1.6. Пусть ft(x)—семейство выпуклых
функций ig[l:m]. Тогда при любых а?.>0, i?[l:m],
выпуклыми также будут следующие функции:
) = max
Ф.(х)= max [0, ft(x)].
ie[l]
Доказательство. Для любых #, у?Еп,
имеют место неравенства
2
t=l
где/—некоторое число из множества [1:т]. Поэтому
Отсюда следует выпуклость Ф2(л:). Добавляя к набору
функций /,.(*) выпуклую функцию fm+1(x) =0, приходим
к выпуклости ЦK(х). Щ
Теорема 1.1.7. Пусть функция f(x) выпукла и
функция скалярного аргумента ф (г) монотонно возрастаю-
возрастающая выпуклая функция z. Тогда сложная функция ф (/ (х))
выпукла по х.
До к а з а тельство. Воспользуемся неравенством A.1).
Из монотонности ф следует, что
В силу выпуклости ф имеем
V(Xf(x) + (l-k)fm<
что доказывает выпуклость сложной функции.

2] ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛЫХ ФУНКЦИЙ 21
§ 2. Дифференцируемость выпуклых функций
1. Дифференцируемость по направлению.
Теорем]а 1.2.1. Если f{t)—выпуклая функция ска-
скалярного аргумента t, то функция
ф(/)^/(О-/(*о)
t—/0
при t > t0 ограничена снизу и не убывает с возрастанием t.
Доказательство. Пусть to<it1<Ci2t тогда
Из свойства выпуклости /(/) следует
2<я°тж12-ь)т) =
tx—г
t2—i
откуда получаем, что
^=ф(Ц| BЛ)
т. е. ф является монотонной, не убывающей функцией t
при t>t0. Покажем ее ограниченность при t—>+?0.
Пусть tm < t0 < t. Несложно получить неравенство, ана-
аналогичное B.1):
о * о
Таким образом, монотонно убывающая при t—++t0 функ-
функция ф(/) ограничена снизу и, следовательно, существует
предел
@
который можно назвать производной функции / (t) справа
в точке t0. Аналогично доказывается, что выпуклая функ-
функция f(t) имеет производную слева в точке t0. Щ
Теорема 1.2.2. Пусть выпуклая функция f(x) при-
принимает конечное значение в точке х?Еп. Тогда для лю-
любого направления q ? Еп, \\ q \ — 1 существует производная f
по направлению q:
3^3 — mil

22
ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Доказательство. Рассмотрим отрезок, соединяю-
соединяющий точку х и y = x + q. Определим функцию скалярного
аргумента t:
Из теоремы 1.1.4 следует, что функция г|)(/) выпукла
при любых 0 ^ t ^ 1. Согласно предыдущей теореме при
этих же значениях t она имеет производные слева и справа.
Поэтому существует предел
что и требовалось доказать. Щ
В приведенной теореме не существенно, чтобы вектор
направления q был единичный, им может быть любой
м-мерный вектор. В дальнейшем производную функции /
в точке х по направлению вектора q ?Еп будем обозначать
Символ + обозначает, что производная берется право-
правосторонняя. Аналогично можно определить левостороннюю
производную по направлению q:
Несложно убедиться в том, что
Используя предыдущие теоремы, можно показать, что
в каждой точке х> в которой значение выпуклой функции /
конечно, существуют левосторонние и правосторонние
производные по произвольному направлению q, причем
D+f(x,q)>D-f(x,q).
2. Свойства субградиентов.
Определение 1.2.1. Пусть функция f(x) опреде-
определена веюду на Еп, Каждой точке x?dom/ поставим в со-
соответствие множество
»}, B.2)
которое будем называть множеством субградиентов или
обобщенных градиентов функции / в точке х. Конкрет-
Конкретный элемент из df (x) называется субградиентом или обоб-
обобщенным градиентом функции f(x) в точке х.

2] ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛЫХ ФУНКЦИЙ 23
Теорема 1.2.3. Пусть выпуклая функция f(x) при-
принимает конечное значение в точке х. Вектор z?df (x)
тогда и только тогда, когда
/p) B.3)
для любого вектора р?Еп.
Доказательство. Пусть субградиент г удовлетво-
удовлетворяет B.2), положим y = x + tp, где t > 0. При» этом для
любого р
t^f( + t)f(x). B.4)
Разделим это неравенство на /, тогда
Устремляя t к нулю, получим требуемое неравенство B.3).
Обратно, пусть имеет место B.3). Несложно показать,
что для любого вектора р выпуклая функция / (х) удов-
удовлетворяет условию
D+f(x, p) =
Поэтому из этого условия и из B.3) следует; что нера-
неравенство B.4) имеет место при любом р. Обозначив у =
= x + tp, приходим к B.2), откуда следует, что г—суб-
г—субградиент функции / в точке х. Щ
Теорема 1.2.4. Мнооюество субградиентов df(x)
выпуклой, определенной всюду на Еп функции f выпукло
и замкнуто в каждой точке x^&omf.
Доказательство. Пусть г1$ z2?df(x), тогда для
любых у?Еп имеем
<г19 y-x>^f(y)-f(x)9 B.5)
<z2, y-x>^f(y)-f(x). B.6)
Умножим B.5) на X, B.6) на A-Я), где 0<А,<1, и
сложим, получим
Так как это неравенство имеет место для любых у?Епу
приходим к выводу, что
откуда следует выпуклость множества субградиентов.

24
ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Докажем замкнутость df (х) в точке х. Пусть последо-
последовательность zk?df(x), {zk\-+z%, причем z*?df (x). Тогда
существуют такие у?Еп и е > О, что
<г*, y-x> = f(y)-f (*) + *• B.7)
Для любого элемента zk последовательности {zk\ должно
выполняться условие
B.8)
Вычитая из B.8) равенство B.7), получим
e<<z.—z*, # —*><lz* — гЛ-Цу—лг||.
Отсюда следует, что для любого k > О
но это противоречит сходимости последовательности {zk}
к г*. Поэтому заключаем, что z#?df (x) и множество суб-
градиентов, таким образом, замкнуто. Щ
Из этой и предыдущей теорем следует, что если в точке
х не пусто множество субградиентов функции / (л:), то
D+f(x, p)= max <z, p>.
zedf(x)
Понятие субградиента переносится на тот случай, когда
функция / определена только на некотором множестве X.
Определение 1.2.2. Пусть функция f (х) определена
на множестве X, внутренняя часть которого не пуста. Для
точки х?Х определим множество df(x), которое есть
объединение всех векторов z g En, удовлетворяющих для
любых у?Х условию
Множество df (x) называется множеством субградиентов
или обобщенных градиентов функции / в точке х.
Для выпуклой функции множество субградиентов не
пусто, ограничено, выпукло в любой внутренней точке
области определения.

gJj] ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛЫХ ФУНКЦИЙ 25
3. Свойства выпуклых дифференцируемых функций.
Теорема 1.2.5. Пусть выпуклая на открытом мно-
множестве X<= Еп функция.f дифференцируема в точке х?Х.
Тогда для любых х?Х имеет место неравенство
<fx(x),x-x><f(x)-f&). B.9)
Доказательство. Так как х принадлежит откры-
открытому множеству X, существует такая окрестность Ge(x)
точки х, что Ge (л:) целиком принадлежит X. Пусть х ? X
и хф~х. Соединим точки х и х прямой линией, положим
у = х+р(х—х), 0<|i<l. B.10)
Если 0 < \i < г/\\х—*||, то
Из выпуклости / (х) на выпуклом множестве Ge (x) сле-
следует, что
Воспользуемся условием дифференцируемости / в точке
х (см. Приложение I), получим
-Х)). B.11)
Здесь функция а удовлетворяет условию
Нтсф, Х(у—х)) = 0.
Перейдем в B.11) к пределу при Я,—>0, получим
B.12)
Точка у принадлежит выпуклому множеству, поэтому,
используя B.10) и A.1), получим
f (У)Ч (x)^f (x + ii(x~x))-f (x)^ii[f (х) -f (хI
Подставив это выражение вжB.12) и, приняв во внимание
B.10), придем к требуемому результату B.9). Щ

26 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Теорема 1.2.6. Пусть функция f дифференцируема
на открытом выпуклом мнооюестве X. В этом случае f
выпукла на X тогда и только тогда, когда для любых
х1У х2?Х выполнено неравенство
<M*l). *•-*!> </(*¦)-/(*!)¦ B.13)
Доказательство. Необходимость следует из пре-
предыдущей теоремы. Докажем достаточность. Если х19 х2? X,
ОХ^ 1, то из выпуклости X следует, что х^+Х (х2—хг) ?
Из формулы B.13) получим
умножая первое из этих неравенств на A—X), второе —
на К и, складывая, приходим к неравенству
откуда следует выпуклость функции /. Щ
Если в формуле B.13) поменять местами хг и л:2, то
получим следующую формулу:
<M*i). x%—Xi><*f(x*)-f(Xi)«f*(**)* хш-хг>. B.14)
Теорема 1.2.7. Пусть функция f дифференцируема
на открытом выпуклом множестве X. В этом случае f
выпукла на X тогда и только тогда, когда для любых хи
х2?Х выполнено неравенство
0<<М*»)—M*i). *а—*i>. B.15)
Доказательство. Пусть f (x) выпукла на X и xlt
х2?Х. Согласно предыдущей теореме имеют место нера-
неравенства
Складывая эти неравенства приходим к формуле B.15).
Докажем достаточность. Пусть хи х2$Х. Тогда для
любых 0 ^ % ^ 1 имеем хг + ^ (х2—хх) g X. По теореме
о среднем значении (см. Приложение I) существует такое
число 0 < X < 1, что
-*i))t *.-*!>. B.16)

2] ДИФФЕРЕНЦИРУЕМОСТЬ ВЫПУКЛЫХ ФУНКЦИЙ 27
Согласно условию B.15) имеем
откуда следует, что
Учитывая B.16), получим
Согласно предыдущей теореме отсюда следует выпуклость
функции f(x). Щ
Аналогичным образом доказываются следующие две
теоремы.
Теорема 1.2.8. Пусть строго выпуклая на откры-
открытом множестве ХаЕп функция f (x) дифференцируема
в точке х?Х. Тогда для любых х? X, хфх имеет место
неравенство
</*(*). x-x><f{x)—f(x).
Теорема 1.2.9. Если функция f дифференцируема на
открытом выпуклом множестве X, то f строго выпукла
на X тогда и только тогда, когда для любых х19 Х2?Х,
Xi?=x2, выполнено неравенство
<fx (*i)» хш—хг> < f {х%)—1(хг).
Утверждения приведенных теорем переносятся на вогну-
вогнутые функции, при этом в формулировках теорем знаки
^, < заменяются соответственно на ^, >.
4. Свойства дважды дифференцируемых выпуклых
функций.
Теорема 1.2.10. Пусть выпуклая на открытом мно-
множестве ХаЕп функция f дважды дифференцируема в точке
х?Х. Тогда матрица fxx(x) положительно полу опреде-
определена, т. е. для любых у?Еп имеет место неравенство
xx(x)y. B.17)
Доказательство. Для любого у существует такое
число Я^О, что при каждом О^Я^А, точки
и, согласно теореме 1.2.5,

23 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
С другой стороны, учитывая свойство дифференцируе-
мости, получим
где lim р (х, Ц) = 0.
Поэтому 0<^±-yTfxx(x)y + \\yl*$(x, Xy). Устремляя Я
к нулю, приходим к B.17).
Теорема 1.2.11. Если функция f дважды дифферен-
дифференцируема на открытом выпуклом множестве X, то f
выпукла на X тогда и только тогда, когда матрица fxx (x)
положительно полуопределена на X.
Доказательство. Необходимость следует из пре-
предыдущей теоремы. Докажем достаточность. Если хг, х2?X,
то, согласно формуле Тейлора (см. Приложение I), для
некоторого 0 < т < 1 имеет место равенство
^j{x2—x1)Tfxx (х1 + %(х2—х1)) (хг—хг).
Правая часть этого равенства неотрицательная, поэтому
левая часть также неотрицательна и, согласно теоре-
теореме 1.2.6, функция / выпукла на X. Щ
Так же просто доказывается следующая теорема.
Теорема 1.2.12. Пусть функция f дважды диффе-
дифференцируема на открытом выпуклом множесп.ве X. Для
того чтобы функция f была строга выпукла на X, до-
достаточно, чтоды матрица fxx{x) была положительно
определена на X.
5. Псевдовыпуклые функции.
Определение 1.2.3. Пусть функция / определена
на некотором открытом множестве из Еп, содержащем
множество X, функция / называется псевдовыпуклой в точ-
точке х относительно множества X, если / дифференцируема
в точке х и из выполнимости для любых х 6 X условия
0<</*(*)> х-х> B.18)
следует, что f(x)^.f(x) для всех х?Х.

§3] УСЛОВИЯ ЛОКАЛЬНОГО ЭКСТРЕМУМА 29
Если функция^/ определена всюду на Еп, дифферен-
дифференцируема в точке х и из выполнимости неравенства B.18)
для всех х?Еп следует, что /(*)</(*) для любых х, то
функцию / будем называть псевдовыпуклой в точке х.
Предположим, что функция / выпукла на выпуклом
множестве X, дифференцируема в точке х$Ху в которой
функция / принимает наименьшее на X значение. Тогда
функция / псевдовыпукла в точке х относительно множе-
множества X. Действительно, в этом случае имеет место нера-
неравенство B.9), поэтому из выполнения B.18) автоматически
следует, что f{x)^.f(x) для любых х?Х.
§ 3. Необходимые и достаточные условия
локального экстремума функций многих переменных
1. Основные определения. Пусть функция / определена
на некотором множестве ХсЕп. Будем говорить, что х*
является точкой локального минимума функции / на мно-
множестве X, если существует такая окрестность G (х*) точки
х*, что для всех х> принадлежащих пересечению множеств
X и G (х%), имеет место неравенство
/(*•)</(*)¦ C.1)
Если для всех х ? X Г) G (х*), х Ф х* имеет место строгое
неравенство
/(*•)</(*). C-2)
то будем говорить, что х* является точкой локального изо-
изолированного или строгого минимума функции / (х).
Если неравенство C.1) имеет место для любых х?Х,
то х* называется точкой минимума функции / на X.
Задача об отыскании минимума функции / на множестве
X обозначается символом
min/(x). C.3)
х
Совокупность всех точек #«,?Х, удовлетворяющих при
любых х?Х условию C.1), обозначается
Хф = Arg min / (х)
хеХ
и называется множеством решений задачи C.3). Обычно
в задачах минимизации достаточно найти хотя бы одну
точку х* 6 Х%.

30 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
В тех случаях, когда X совпадает со всем простран-
пространством Епу C.3) называется задачей безусловной миними-
минимизации функции /, точка хт, удовлетворяющая C.1) при
любых х 6 Еп, называется глобальным минимумом функции
f (х). Если C.1) имеет место для всех x?G(xJ)y то х,
называется точкой безусловного локального минимума функ-
функции f(x). В случае выполнимости C.2) для всех x?G(x#),
хфх* точка х* называется точкой локального изолирован-
изолированного или строгого минимума функции f(x).
2. Необходимые и достаточные условия локального
минимума.
Определение 1.3.1. Точка хт называется стацио-
стационарной точкой дифференцируемой функции f (x), если имеет
место условие
/*(*.)-= 0. C.4)
Теорема 1.3.1 (необходимые условия минимума).
Пусть локальный минимум функции f на множестве X
достигается в точке *»€intX. Тогда:
1) если функция f дифференцируема в х*, то х* явля-
является стационарной точкой функции /;
2) если функция f дважды дифференцируема в точке
х*, то матрица fxx{x*) положительно полуопределена.
Доказательство. Из определения 1.1.2 следует,
что для произвольного вектора у?Еп существует такое
число X > 0, что при любых 0 ^ X < X точка х* + Ху?
€G(x*)c:X. Используя дифференцируемость /, запишем
условие C.1) в виде
(**Лу), C.5)
где функция а такова, что lima (л:», Ху) =^0. С учетом
этого свойства из C.5) находим
lim f<b+W-fM =<fAx.), y>.
Поэтому из C.5) следует
Для выполнения этого неравенства при произвольном у
необходимо, чтобы выполнялось условие C.4).

§3j УСЛОВИЯ ЛОКАЛЬНОГО ЭКСТРЕМУМА 31
Если функция / дважды дифференцируема в точке хф9
то вместо C.5) воспользуемся следующей формулой:
f(x.) = .
=jyTfxAx.)y+»№mx., ty). C.6)
где HmP(x., Xy)=Q.
Устремляя К к нулю, получим
±yf xx(
В силу произвольности вектора у?Еп отсюда следует
положительная полуопределенность матрицы fxx(x*), что
завершает доказательство. Щ
Теорема 1.3.2 (достаточное условие локального ми-
минимума). Пусть определенная на X функция f дважды
дифференцируема в точке х* ? int X, в ней выполнено уело-
вие стационарности C.4) и матрица fxx (x*) положительно
определена. Тогда х* является точкой безусловного локаль-
локального изолированного минимума функции /.
Доказательство. Из положительной определен-
определенности матрицы fxx (x*) следует существование такого числа
С>0, что yTfxx{x*)y^2C\y\2 при всех У&Еп. Обозна-
Обозначим Ах = х—хт> тогда из определения второй производной
с учетом C.4) и C.6) получим, что
Функция р(л:%, Дл:) такова, что существует окрестность
G(x*)y в которой С+Р(#*> Дл:) > 0 для всех x?G(x*).
Поэтому приходим к неравенству C.2), справедливому для
любых x?G(xm), хфх+i что и требовалось доказать. Щ
3. Необходимые и достаточные условия локального
максимума. Можно рассмотреть задачу об отыскании мак-
максимума дифференцируемой функции / на множестве X:
maxf(x). C.7)
ех
Если максимум в этой задаче достигается во внутрен-
внутренней точке х* множества X, то необходимо, чтобы в этой
точке выполнялось условие C.4) и, если функция / дважды

32 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
дифференцируема в л:*, то матрица fxx(x*) должна быть
отрицательно полуопределена, т. е. для любых у?Еп имеет
место неравенство
Достаточное условие строгого локального максимума функ-
функции / в точке х#, удовлетворяющей C.4), состоит в отри-
отрицательной определенности матрицы fxx(x*).
Таким образом, если во внутренней точке х* множества
X достигается локальный максимум или минимум диффе-
дифференцируемой функции /, то в ней выполнено условие C.4).
Поэтому при решении экстремальных задач полезно бывает
найти стационарные точки. Задача отыскания стационар-
стационарных точек дифференцируемой функции / совпадает с зада-
задачей решения системы уравнений fx(x) = 0. Поэтому для
решения задач C.3) и C.7) могут быть использованы
методы решения систем уравнений, некоторые из них будут
приведены в следующей главе.
4. Критерий Сильвестра. Обозначим Дх (х), Д2 (х), .. ¦
..., Ая(х) последовательные главные миноры матрицы
Теорема 1.3.3 (критерий Сильвестра). Для того чтобы
матрица fxx (x) была положительно определенной, необхо-
необходимо и достаточно, чтобы выполнялись условия
Ах (х) > О, Д2 (х) > 0, ..., Д„ (х) > 0. C.8)
Для того чтобы матрица fxx (x) была отрицательно опре-
определенной, необходимо и достаточно, чтобы выполнялись
условия
Дх (х) < 0, Д2 (х) > 0, ..., (-1)» Д„ (х) > 0. C.9)
Доказательство критерия можно найти в многочислен-
многочисленных книгах по линейной алгебре. С каждой симметричной
матрицей fxx(x) можно связать квадратичную форму
Неравенства C.8) и C.9) дают необходимые и доста-
достаточные условия положительной и отрицательной опреде-
определенности квадратичной формы Ф(х). В курсах математи-
математического анализа (см., например, Г. М. Фихтенгольц [1])
рассматриваются только те случаи, в которых выполнены
условия C.8) и C.9), все другие возможности относятся

§3] УСЛОВИЯ ЛОКАЛЬНОГО ЭКСТРЕМУМА 33
к «неопределенным», так как они не дают достаточных
условий экстремума функций. Ниже, в § 5, будет показано,
что случаи, когда в C.8) и C.9) имеют место противо-
противоположные строгие неравенства, будут соответствовать до-
достаточным условиям локального максимина и минимакса.
5. Случай выпуклых функций.
Теорема 1.3.4. Пусть функция f выпукла на Еп.
Тогда всякий локальный минимум функции f является
одновременно \глобальным на Еп минимумом, множество
точек минимума функции f выпукло. Если функция f
строго выпукла, то X* состоит из единственной точки.
Доказательство. Пусть для всех х ? G (хш) выпол-
выполнено условие C.1). Возьмем произвольную точку у?Еп,
тогда для достаточно малых 0 < А,< 1 имеем х*+Х(у—##) ?
?G(x*). Используя выпуклость /, получим
Отсюда следует, что f (x*)^f(y). В силу произвольности
точки у?Еп заключаем, что х* является точкой глобаль-
глобального минимума функции f. Q
Обозначим c = f(x*), тогда, согласно теореме 1.1.5,
выпуклым будет множество минимумов
Предположим, что минимум строго выпуклой функции
f достигается в двух различных точках х19 х2?Х. Тогда
из выпуклости Х# и строгой выпуклости / следует, что
при любом 0 < X < 1
Из противоречия следует единственность точки минимума.
Теорема 1.3.5. Пусть f—выпуклая на Еп функция.
Условие 0 ?д/ (х*) имеет место тогда и только тогда,
когда f достигает своего глобального на Еп минимума
в точке хш.
Доказательство. Из определения множества суб-
субградиентов следует, что O?df(x*) тогда и только тогда,
когда f(x)^f (хт) для любых х6Еп. Отсюда заключаем,
что х*—глобальный минимум f(x).
Если функция f выпукла на Еп и дифференцируема
в точке X; то fx(xm) = O тогда и только тогда, когда х*
является точкой глобального минимума функции /. Щ
2 Ю. Г. Евтушенко

34 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. Г
§ 4. Необходимые и достаточные условия
минимума функций на множествах
1. Основные определения. Предположим, что функ-
функция / определена на некотором открытом множестве, со-
содержащем множество X, и множество
не пусто. В тех точках х?Х, где функция / дифферен-
дифференцируема, можно определить точечно-множественное ото-
отображение
x), у-х>. D.1)
Отсюда следует, что W{x)aX. Если функция / диф-
дифференцируема всюду на Ху то условие D.1) каждой точке
х?Х ставит в соответствие множество W(x)c:X. Таким
образом, W осуществляет точечно-множественное отобра-
отображение множества X в себя. Говоря о неподвижных точках
отображения W(x), будем считать, что эти точки таковы,
что
х?Х, x?W(x). D.2)
Если x(fcW(x), то существует точка у?Х такая, что
<fx(x), y-xXO.
Если x?W(x), то имеет место неравенство
О<</*(*)> У-*> Vy?X. D.3)
Это условие иногда называют вариационным неравенством]
всякую точку х? X, в которой выполнено D.3), называют
решением вариационного неравенства. Для того чтобы х
была неподвижной точкой отображения W> необходимо и
достаточно, чтобы она была решением вариационного не-
неравенства D.3).
В каждой фиксированной точке х ? Еп% где fx (x) Ф О,
множество
представляет собой гиперплоскость, проходящую через
точку ху с вектором нормали fx(x). Вместе с тем К(х)
является касательной гиперплоскостью к гиперповерхности

§41
УСЛОВИЯ МИНИМУМА ФУНКЦИЙ НА МНОЖЕСТВАХ 35
в точке х. Множество Г (л:) является линией уровня функ-
функции /(*)» градиент fx(x) направлен по нормали к линии
уровня, внутрь множества
«: f(y)>f(x)\.
Гиперплоскость К (х) порождает два полупространства:
О <</*(*)> y—x>, <fx(x), */-*>< 0.
Пусть точка х?К такова, что в ней выполнено усло-
условие D.3). Тогда в первом из приведенных полупространств
содержится множество X. Поэтому D.3) можно интерпре-
интерпретировать как условие того, что множество X целиком
содержится в одном из двух замкнутых полупространств,
определяемых касательной гиперплоскостью К {х). Согласно
определению 1.1.11 в такой ситуации касательная гипер-
гиперплоскость К (х) является опорной к множеству X в точке х,
вектор fx {x) есть опорный вектор множества X в точке х.
2. Условия минимума второго порядка.
Теорема 1.4.1. Пусть функция f определена на от-
открытом множестве в Еп> содержащем выпуклое множе-
множество X, и существует точка х ? X*, в которой функция f
дифференцируема. Тогда необходимо, чтобы х была не-
неподвижной точкой отображения W(x).
Доказательство. Пусть х—произвольная точка
множества X. Согласно определению 1.1.1 из выпуклости
множества X следует, что для любых чисел А,? [0, 1] имеет
место включение х + К(х—х)?Х. Так как / дифферен-
дифференцируема в точке х и х?Х%> имеем
= *.</,(*). х—Х> + Цх—х\а{х, Ь(х—х)),
где
М*—*))=•¦ 0.
Отсюда получим, что для любых 1?[0, 1]
0<</,W, x—x>+\x—xla(xt X(x—x)).
2*

35 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Устремляя К к нулю, приходим к неравенству
О<</*(*), х-х>, D.4)
справедливому при любых х?Ху откуда следует, что
щ) а
щ) а
Приведенная теорема дает необходимое условие гло-
глобального минимума функции / на выпуклом множестве X.
Как будет показано ниже (в § 4 гл. VI), это необходи-
необходимое условие тесно связано с полученным в теории опти-
оптимального управления дискретным вариантом принципа
максимума Л. С. Понтрягина.
Введенное в теореме требование выпуклости множе-
множества X существенно. Легко привести примеры, где нару-
нарушение этого требования делает утверждение теоремы не-
неверным. Тем не менее возможен локальный вариант тео-
теоремы, где не требуется выпуклость X. Неравенство D.3)
при этом будет иметь место лишь для векторов уу при-
принадлежащих пересечению X и некоторой окрестности мно-
множества Х«.
Теорема 1.4.2. Пусть функция f определена на от-
открытом множестве в Еп, содержащем X, множество Х«
не пусто и выпукло, существует точка х?Хф, в которой
функция f дифференцируема. Тогда существует такая
окрестность G(Xj) множества X*, что для всехх? X f| G(X*)
имеет место неравенство D.4).
Из определения 1.2.3 псевдовыпуклости вытекает сле-
следующая теорема, дающая достаточные условия глобаль-
глобального минимума функции / на множестве X.
Теорема 1.4.3. Пусть функция f псевдовыпукла в
точке х относительно множества X и х является непод-
неподвижной точкой отображения Wy тогда х?Х*.
3. Случай выпуклых функций. Предположим вначале,
что функция / (х) определена и выпукла на открытом мно-
множестве, содержащем множество X, существует точка х* ? X»
и функция / дифференцируема в точке х?Х. Тогда из
формулы B.14) следует неравенство
О </(*)-/(*.)<</*(*), *-**>, D.5)
справедливое для всех х, принадлежащих множеству X.

„1 УСЛОВИЯ МИНИМУМА ФУНКЦИЙ НА МНОЖЕСТВАХ 37
§4J
Для *€*, *€
имеем
Поэтому D.5) можно представить в виде
/ (*)—/ (*•) < <fx(х), х—х> Чх. € **, VJe W(x). D.6)
Это неравенство будет неоднократно использовано ниже.
Пусть х?Х, x?W(x)f тогда
О = </*(*), x—x> Vx?W(x)
и для любых у?Х выполнено D.3). Из неравенства D.6)
заключаем, что в этом случае х?Хф. Для любых ?Х
х ?Х, согласно D.5), имеем
<f*(x), х*—х><0.
Неравенство D.3), таким образом, нарушено при у = х*.
Мы приходим к следующему результату:
Для того чтобы выпуклая дифференцируемая в точке
х?Х функция f достигала в х наименьшего значения на
выпуклом мнооюестве X, необходимо и достаточно, чтобы
имело место условие D.3) (т. е. точка х была неподвиж-
неподвижной точкой отображения W(x) или градиент fx{x) был
опорным вектором множества X в точке х).
4. Необходимое условие минимума второго порядка.
Может оказаться, что в точке х?Х выполнено условие
стационарности
/,W = 0. D.7)
Если функция / выпуклая, то отсюда следует, что л;?Х«.
В общем случае свойство D.7) делает малосодержательным
условие D.4). Поэтому приходится вводить необходимые
условия более высоких порядков.
Теорема 1.4.4 (необходимое условие минимума вто-
второго порядка). Пусть функция f определена на откры-
открытом множестве из Еп, содержащем выпуклое множество X,
функция f дважды дифференцируема в точке х ? X», в ко-
шорой выполнено D.7). Тогда необходимо, чтобы для любых
х?Х имело место неравенство
О <(*-*)*7« (*)<*-*)• D-8)

38
ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Доказательство. Пусть я—произвольная точка
множества X. Из выпуклости X следует, что для любых
^[0, 1] имеет место включение
Используя условие, что функция / дважды дифференци-
дифференцируема в точке х?Х, получим
Здесь НтC(л:, X (х—л:)) = 0. Устремляя Я к нулю, прихо-
дим к неравенству D.8). Щ
Подобно тому как это было сделано выше, в стаци-
стационарной точке х можно определить точечно-множественное
отображение Хх (х) = Arg min (x—х)т fxx (х) (х—х).
хеХ
Здесь для отыскания множества Хг(х) приходится ре-
решать задачу минимизации квадратичной формы на мно-
множестве X. Можно поставить задачу об отыскании непод-
вижных точек этого отображения или о решении квадра-
квадратичных вариационных неравенств
определяя тем самым точки, удовлетворяющие условию
минимума второго порядка.
§ 5. Свойства минимаксных задач
1. Постановка минимаксных задач. Пусть F (х, у) —
определенная для всех х g En и у?Ет непрерывная функ-
функция. Ставятся задачи нахождения безусловного максимина
и минимакса
min F(xy у), E.1)
= min max F(x, у). E.2)
?ЕП вЕт
На примере второй задачи разъясним смысл, вкладывае-
вкладываемый в приведенную запись. При каждом фиксированном

3 СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 39
х?Еп находится образ точечно-множественного отображе-
отображения В(х):
B(x)^ArgmaxF(x, у). E.3)
еЕ*
После этого определяется функция максимума
<p(*) = F(*f B(x)). E.4)
Здесь выражение F(x, B(x)) обозначает, что вычисляется
значение F (х, ~у), где ~у?В(х). Из определения E.3) сле-
следует, что F (х, у) принимает одно и то же значение для
любых ~у?В(х), что оправдывает такую форму записи-
Определим далее множество
Множество Х% и точечно-множественное отображение
В(х) назовем синтезом задачи E.2), хотя бы одну пару
точек [**, #«,], где хт$Хт, у*?В(х*), назовем решением
(глобальным) минимаксной задачи E.2). Величину V2 =
=F (jc«, t/«) назовем минимаксной гарантированной оценкой.
Нахождение для каждого х хотя бы одного элемента
из множества В(х) будем называть внутренней задачей.
Определение хотя бы одной точки из X* назовем внешней
задачей.
Чтобы упростить изложение, в этом параграфе будем
считать, что все встречающиеся операции поиска экстре-
экстремумов имеют решения. В E.2) это означает, что много-
многозначное отображение В определено при любых х, множе-
множество X* не пусто.
Теорема 1.5.1. Если задачи E.1) и E.2) имеют ре-
решения, то
V^Vt. E.5)
Доказательство. Для любого фиксированного
У$Ет выполнено неравенство
min F(x9 yXF(x, у).
Еп
Аналогично для всякого фиксированного х
F(x9 y)^maxF(x, у).
SE

40 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Поэтому для любых у?Ет и х € Еп
m\nF(x, y)^maxF(х> у),
Еп Ем
В силу произвольности х и у получим окончательно
max minF(x, у) <!minmax F (х, у). Щ
Ет €Еп ЕпЕт
2. Задачи на условный минимакс. В задачах E.1) и
E.2) никаких условий на х и у не накладывалось, поэтому
их можно назвать задачами о поиске безусловного макси-
мина и минимакса. Рассмотрим случай, когда на х и у
наложены ограничения:
^, у), E.6)
V2 = min max F (x, у). E.7)
Определение решения этих задач дается аналогично тому,
как это делалось выше (см. E.3) и E.4)):
:, у), <p(x)=--F(x, B(x))f
E 8)
Для приложений весьма важен вопрос: какие свойства
функции F(x, у) изменяются и какие сохраняются после
осуществления операции максимизации по у, т. е. при
переходе от F (х, у) к ф (*)? Чтобы ответить на этот вопрос,
рассмотрим вначале свойства непрерывности, выпуклости
и выполнимости условия Липшица.
Для сокращения записи обозначим
Будем говорить, что функция F (г) удовлетворяет условию
Липшица на Z с константой /, функция ф(л:) удовлетво-
удовлетворяет условию Липшица на X с константой /, если для
любых ги z2?Z и х19 х2?Х выполнены соответственно
условия

?5] СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 41
Теорема 1.5.2. Если функция F(xt у) непрерывна
на прямом произведении компактных множеств Z=XxY,
то функция ф (л:) также непрерывна на X. Если функция
p(z) удовлетворяет условию Липшица на Z, то функция
Ф (х) также удовлетворяет условию Липшица на X с той
же константой. Если при каждом у^У функция F(x, у)
выпукла по х на выпуклом множестве X, то и q>(x) вы-
выпукла на X.
Доказательство. Функция F(x, у), будучи непре-
непрерывной на компактном множестве Z, равномерно непре-
непрерывна на этом множестве. Поэтому для любого е > 0 су-
существует такое 6(е), что если Цл^—*2||<6(е), хи х2?Х,
то
1/4*1, y)-F{x%%y)\<*
для любого у ? Y. Рассмотрим выражение
| ф to)—ф (*2)| = | F {xu y!)—F{x2, y2)\.
Здесь обозначено у1^В(х1I у2?В(х2). Рассмотрим два
случая. В первом имеем
Учитывая определение множества В(х), получим
Если функция jF (г) удовлетворяет условию Липшица по г,
то она удовлетворяет и условию Липшица по ху равно-
равномерно по у у поэтому
Во втором случае
0<ф(л;2)—ф(хх).
Аналогичным образом получаем, что
0<Ф(*,)—Ф^Х/Ч*,, yJ—F(xl9 у2)
и если F удовлетворяет условию Липшица, то
Объединяя эти два случая, приходим к выводу, что при
любых хг и х2? X, таких, что \хг—х2\ < б(е), имеет место
неравенство |ф(#!)—ф(аг2)|<6, т.е. функция ц>(х) непре-
непрерывна на компактном множестве X. Если F удовлетворяет
условию Липшица, то имеет место E.9).

42 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Если F выпукла по х, то для любых х1У х2?Х,
О ^ А, ^ 1 имеют место оценки
= maxF(Xx1 + {l — к)х2, #)<
yeY
[XF(xu y) + (l-
что доказывает выпуклость функции ф. Щ
Свойство дифференцируемости функции F не сохра-
сохраняется при переходе к функции ф. Имеет место следующая
Теорема 1.5.3 (Данскина—Демьянова). Пусть X —
открытое множество в Еп, Y—компактное множество
в Ету функция F непрерывна вместе с Fx(x, у) по сово-
совокупности переменных в XxY. Тогда определяемая из
E.8) функция ф(лг) имеет в каждой точке х?Х произ-
производную по любому направлению g?Ent ||g|=l, причем
^= max </>,(*,*),*>.
Доказательство теоремы можно найти в книгах Дж.
Данскина [1], В. Ф. Демьянова и В. Н. Малоземова [1].
В последней книге доказана также и следующая теорема,
являющаяся обобщением теоремы 1.4.1 на случай мини-
минимизации функции максимума.
Теорема 1.5.4. Пусть X—замкнутое выпуклое мно-
множество в Епу Y—компактное множество в Ету функция F
непрерывна вместе с Fx (я, у) по совокупности переменных
в XxY. Тогда, для того чтобы функция <р(х) достигала
минимального на X значения в точке х* ? X, необходимо,
а в случае выпуклости ф(лг) на X—и достаточно, чтобы
inf max <Fx(x*, у), х—#«,>^=0.
х в{)
В заключение приведем теорему о существовании реше-
решений задач E.6) и E.7).
Теорема 1.5.5. Если функция F(x, у) непрерывна
на произведении компактных множеств X и Y, то реше-
решения задач E.6) и E.7) существуют и имеет место нера-
неравенство
= maxminF(A:, у) ^ V2 = min max F (xy у). E.10)
Y xex xex Y

§ 5]
СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 43
Доказательство теоремы почти дословно повторяет до-
доказательство теоремы 1.5.1.
3. Седловые точки. Точка г, = [лг„ у*] называется сед-
ловой точкой функции F (х, у) в задачах E.6) и E.7), если
х*€^> У*?У и Для любых х?Х, y?Y имеют место не-
неравенства
F (*•. У)<Р (*•, У*) < F (*, у*). E.11)
Лемма 1.5.1. Если задачи E.6) и E.7) имеют реше-
решения, то, для того чтобы имело место равенство
V1 = F(x,, y*) = V2, E.12)
необходимо и достаточно, чтобы zm была седловой точкой
функции F(x, у).
Доказательство. Пусть \хш, уш]—седловая точка
функции F(x, у). Тогда
maxF(x«,
Очевидны следующие неравенства:
minmaxF(#, у) ^ max F (#„, у),
ех sY eY
minFfx, Уф)^: max mini7 (x, у),
x v x
Объединяя последние три группы неравенств, получаем,
что
minmaxF(A:, y)^F(x*, #«)<!maxniinF(A;, у),
xsx yeY yeY xex
Сравнивая это неравенство с E.10), приходим к выводу,
что справедливо равенство E.12).
Пусть имеет место E.12). Покажем, что точка \хт, #«] —
седловая. Из E.12) следует
F (*• • у%) = min max F (х, у) = max F (xm, y)>F (*., у),
ex Y yeY
(, y) = minF(x,
xex ex
Объединяя эти неравенства, получаем, что имеет место
E.11), т. е. [хт, у*] есть седловая точка функции F (л:, у). Щ
Определение 1.5.1. Функция F(x9 у) называется
выпукло-вогнутой, если F(x9 у) выпукла по х для всех

44 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
фиксированных у?Y и F(х, у) вогнута по у для всех
фиксированных х?Х. Функция F (х, у) называется строго
выпукло-вогнутой, если при любом фиксированном у она
строго выпукла по л: и при любом фиксированном х строго
вогнута по у.
Теорема 1.5.6 (Неймана). Пусть выпукло-вогнутая
функция F(x, у) непрерывна на прямом произведении
выпуклых компактных множеств X и Y. Тогда функция
F(x, у) имеет седловую точку.
Доказательство теоремы можно найти, например, в
книгах Д. Неймана и О. Моргенштерна [1], Э. Г. Давы-
Давыдова [2].
4. Понятие локальных решений. Если решения внут-
внутренней и внешней задач трактовать как нахождение ло-
локальных экстремумов, то придем к понятию локальных
решений минимаксных и максиминных задач. Такие реше-
решения получаются, например, если мы попытаемся численно
решить задачу E.2), используя лишь методы локальной
безусловной минимизации и максимизации.
Определение 1.5.2. Пусть точки х* и ут обладают
соответственно окрестностями G (х*) и G(y#) такими, что
для любых векторов х ? G (х*) условие
g(x) = Avg max F(x, у)
определяет однозначную вектор-функцию g(x)> причем х*
является точкой строгого минимума функции F(x, g(x))
на G(x*) и y* — g(x*). Тогда г* = [х*> #*] называется точ-
точкой строгого локального минимакса в задаче E.2).
Если гш—точка строгого локального минимакса, то для
любых хбG(л:*), хфх«, y€G(ym), уФё{х), выполнены
строгие неравенства
F(x,, g(x.))<F(x9 g(x))9 E.13)
F(x,y)<F{x, g(x)). E.14)
Последнее неравенство выполнено и при х=хф, y=?g(xm).
Аналогичным образом можно определить локальные
или глобальные по ху локальные или глобальные по у,
строгие или не строгие по х, строгие или не строгие по у
решения задач E.1) и E.2). Приведенные определения

§5j СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 45
локальных решений являются обобщением известных поня-
понятий о локальных экстремумах. Минимаксная задача E.2)
может иметь несколько локальных решений. Однако после
их нахождения нельзя утверждать, что среди этих реше-
решений есть глобальное: необходимо еще рассмотреть все
глобальные по у, локальные по х решения и выбрать из
них то, для которого значение F(x> у) наименьшее. Изу-
Изучение и отыскание локальных решений важно для опре-
определенного ниже класса функций, у которых точки локаль-
локального минимакса являются одновременно и точками глобаль-
глобального минимакса. Для максиминных задач E.1) локальные
решения определяются аналогично.
Определение 1.5.3. Пусть точки х% и у« обладают
соответственно окрестностями G(x#) и G(y*) такими, что
для любых векторов у€О{у*) условие
d(y).= Arg. min F(x, у)
G()
определяет однозначную вектор-функцию d{y)> причем ут
является точкой строгого максимума функции F(d(y)9 у)
на G(y«) и d (#«) = #*. Тогда z* = \x#, t/«] называется точ-
точкой строгого локального максимина в задаче E.1).
Неравенства E.13), E.14) в этом случае заменяются
следующими:
F(d(y), y)<
y)<F(x,y).
Определение 1.5.4. Функция F(xy у) имеет в точ-
точке z* строгое локальное седло, если z« является одновре-
одновременно точкой строгого локального минимакса и макси-
мина.
Объединяя неравенства E.13)—E.15), получаем, что
в седловой точке выполнены неравенства
F fa, y)<F (хФУ уф) < F (х, */,), ,- lfi.
F (d(y), y)<F (х., у,) < F (x; g(x)). 1°ло'
Здесь y?G(yt), у Фу., x^G(x.)f хфх..

46 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. J
5. Необходимые и достаточные условия локального
минимакса. Введем квадратную симметричную матрицу
размера /г2:
Ф(*. У) = рхх(*> y)—Fxy(x, У)Руу(х, y)Fyx(*> У)-
Теорема 1.5.7. Пусть функция F(г) дважды непре-
непрерывно дифференцируема в некоторой окрестности G(zJ
точки zm. Для того чтобы в задаче E.2) вектор г* был
точкой строгого локального минимакса, достаточно, чтобы
выполнялись условия
Fyy(z.)<0, Ф(г,)>0. [ОЛ/)
Если в задаче E.2) вектор г* является точкой строгого
локального минимакса, то необходимо, чтобы было
(*•) - 0л1, Fx (г.) = 0я1э F (z.) < 0, а если F (z<) < О,
Ф()>0
Доказательство достаточных условий основано на
анализе неравенств E.13) и E.14). Из условий Fy(zm)=Omlf
Fyy(z*) <0, следует, что ут является точкой строгого ло-
локального максимума функции ^(л:,, у) по у. Так как мат-
матрица Fyy(zm) отрицательно определена, существует неко-
некоторая окрестность G (z*) = G(xt)xG (ут) точки г«, где
матрица Fyy (z) также отрицательно определена и для всех
# € G (Хщ) неявное уравнение Fy (x, у) = 0 определяет одно-
однозначным образом непрерывно дифференцируемую функцию
У==ё(х)> причем y*=g(x9). Эта функция может быть
получена как решение задачи Коши для следующей системы
квазилинейных уравнений
S
E.18)
с п независимыми переменными [х1, ..., хп] и начальным
условием g(x*) = ym.
Обозначим g(x) решение системы E.18), определенное
на G (хт), принимающее значение из G (у9). Значения век-
вектор-функции y = g(x) являются точками локального мак-
максимума функции F (х, у) по у. Неравенство E.14), таким
образом, имеет место. Подставим y = g(x)bF(x, у), полу-
получим функцию максимума, которую обозначим

§5] СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 47
Дифференцируя ф как сложную функцию х с учетом E.18)
получим
, ч dF (x, g (х)) г, / i w
Vx(*)= dx ~РЛ*> g(x))>
t g(x))Fyx(*t
В частности, при x = x* будет g(x*) = y*, поэтому мат-
матрица ухх (*¦) положительно определена и л:» является точкой
строгого локального минимума функции ер (я) и имеет
место E.13). Из аналогичных рассуждений следуют сфор-
сформулированные в теореме необходимые условия локального
минимакса. В . ¦
Достаточные условия теоремы можно сформулировать
как достаточные условия глобального решения E.2). При
этом следует наложить на ^(л:, у) более жесткие требо-
требования. Считая, что при каждом х?Еп внутренняя задача
в E.2) имеет решение и разрешима внешняя задача, сформу-
сформулируем следующее достаточное условие глобального мини-
минимакса.
Теорема 1.5.8. Пусть функция F(л:, у) при каж-
каждом фиксированном х?Еп строго вогнута по у и функция
F(x, B(x)) строго выпукла по х. Тогда точка локального
минимакса в E.2) является одновременно и глобальным
решением задачи E.2).
Аналогичным образом формулируются необходимые и
достаточные условия максимина в задаче E.1).
Теорема 1.5.9. Пусть функция F(z) дважды непре-
непрерывно дифференцируема в окрестности точки г*. Для того
чтобы в задаче E.1) z, была точкой строгого локального
максимина, достаточно, чтобы выполнялись условия
М**) = 0, F9(z.) = 0, Fxx(z.)>Ot
N (г.) = Fyx (г.) F?x (г.) Fxy (z,)-Fyy (z,) > 0.
6. Критерий минимаксной определенности. Если функ-
функция F (х9 у) всюду дифференцируема по х и у, то усло-
условия теоремы 1.5.8 можно записать в аналитической форме,
для любых хг и х2 из ?", ххфх% и уи у2 из Ет, уг Ф у2:

48 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
должны выполняться неравенства
<Fx(xl9g(x1))9 *¦—*i>< *¦(*!. g(*i))— F(xug(xJ), - 19v
<Fy(x> Уж), У2—У1>>Р(х, y2)—F(x, у±), к *
здесь г(л:1) = Arg max F(xu y)t g(x2) = Arg max F (x2, y).
Если функция F(x, у) дифференцируема и строго вы-
выпукло-вогнута, то условия E.19) заведомо выполняются.
Действительно, для таких функций второе неравенство
имеет место, а первое следует из неравенств
max F (x2, y)—F (xly g(xt))=F (x2,g(x%))—F (xlf g(xx)).
Если функция F (xy у) дважды непрерывно дифферен-
дифференцируема, то достаточное условие записывается так: для
любых х 6 Еп и у?Ет выполнены условия
Fyy(x, y)<Q, Ф(х9 g(x))>0.
Последнее требование будет заведомо выполняться, если
имеет место более сильное условие, проверка которого не
требует знания функции g(x): для любых х?Еп, у?Ет
выполнены условия
FV9(x, y)<0, Ф(х, у)>0.
Придадим этим условиям иной вид. Введем квадратную
симметрическую матрицу
Здесь использовано разбиение матрицы R(z) на четыре
матрицы-клетки. Последовательные главные миноры мат-
матрицы R(z) обозначим Ax(z), A2(z), ..-, &n+m{z). В част-
частности, Ae(«) = |Fw(z)|, A»+e = |/?B)|.
Докажем следующий
Критерий. Для того чтобы матрицыФ(г), —Fyy(z)
были положительно определены, необходимо и достаточно,
чтобы для последовательных главных миноров матрицы
R(z) имели место неравенства
(-l)'A,(z)>Of *€[l:/n], E.20)
г)>0э /€[1:п]. E.21)

§5] СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 49
Эквивалентность неравенств E.20) отрицательной опре-
определенности матрицы Fyy (z) следует из критерия Сильвестра.
Чтобы доказать E.21)v представим главный минор Am+/(z)
матрицы R (z) в виде
WJ^W. F.22)
Здесь FyX/—матрица размером mx/, Т7*.^.—матрица /х/.
На пересечении t-й строки и /г-го столбца этих матриц
d2F d*F лг
находятся и соответственно. Умножим верх-
нюю строку блочной матрицы E.22) слева на матрицу
Fx.yFyy размером jxrn и вычтем ее из нижней строки.
Определитель Ада+у, как известно, при этом не изменится,
получим
А.+/ (г)-1 РуУ(г) |• |FXjXj{z)-FXjy(z)F~yy (z)FyXj (z)\. E.23)
Обозначим 8j (z), /€[1:я], последовательные главные
миноры матрицы Ф(г). Из E.23) следует, что 6/(z) свя-
связаны с последовательными главными минорами матрицы
R(z) формулами
Таким образом, если неравенства E.20) и E.21) имеют
место, то последовательные главные миноры матрицы Ф (z)
положительны и, следовательно, матрица Ф(г) положи-
положительно определена. Верно и обратное —из положительной
определенности Ф(г) и —Fvv(z) следуют условия E.20),
E.21). ¦
Интересен один частный случай, когда у—скаляр (т= 1).
Условия E.20) и E.21) в этом случае будут иметь вид
Согласно результатам § 3, для того чтобы стационарная
точка z функции F (z) была точкой безусловного локаль-
локального минимума, достаточно, чтобы последовательные глав-
главные миноры матрицы R(z) были строго положительны:

50 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Для того чтобы стационарная точка z была точкой
безусловного локального максимума функции F (z), доста-
достаточно выполнение условий
(-1)'А, (*)><>, /€[1:л+1].
Оставшийся четвертый вариант условий
(-1)'А, (*)<<>, *g[l: /i+l]f
соответствует достаточным условиям максимина в задаче
max min F (х> у).
Еп Е1
Рассмотренный случай показывает тесную связь доказан-
доказанного критерия с критерием Сильвестра. Эту связь можно
развить и далее, введя понятия, аналогичные положитель-
положительной и отрицательной определенности. Например, квадра-
квадратичную форму
2*7? (г.) г - xTFxx (г.) х+2y^Fyx (г.) х + yTFyy (г.) у
можно назвать минимаксно определенной в точке z«, если
для любых х ф 0, уфО имеют место неравенства
уУ
< max [xTFxx (z*)x + 2xTFxy (г.) у+ yTFyy (г.) у].
Максимум правой части неравенства по у достигается при
ук= — Fyy(z*)Fyx(z*)x. Поэтому приведенное неравенство
эквивалентно следующему:
Доказанный выше критерий дает необходимые и доста-
достаточные условия минимаксной определенности квадратичной
формы. Функцию F (z) можно назвать строго минимаксной,
если для всех z, z 6 Еп+т квадратичная форма zTR(z)z
минимаксно определена. Для таких функций выполнены
условия теоремы 1.5.8, и их локальное минимаксное реше-
решение одновременно является глобальным.
Введенный таким образом класс функций можно поста-
поставить в один ряд с известными классами выпуклых и вы-
выпукло-вогнутых функций. Действительно, у строго выпук-
выпуклых функций, если существует локальный минимум, то
он единственный и совпадает с глобальным. У строго

?5] СВОЙСТВА МИНИМАКСНЫХ ЗАДАЧ 51
выпукло-вогнутых функций, если существует локальное
седло, то оно единственно и совпадает с глобальным.
У строго минимаксных функций, если существует локаль-
локальный минимакс, то он единственный и является вместе
с тем глобальным. Введенный класс богаче класса строго
выпукло-вогнутых функций (у которых yTFyy(z)y<0,
xTFxx (z) x > 0), так как содержит в себе последний. Важ-
Важность введения такого класса функций связана, с тем, что
для них решение задач E.2) можно проводить, используя
итеративные локальные численные методы.
Рассмотрим два простейших примера, иллюстрирующих получен-
полученные свойства минимаксных задач. Будем считать, что х и у скаляры.
Пример 1. Пусть
F(x, y) = e
В силу периодичности функции по у можно ограничиться интервалом
0<#<1. Стационарными точками будут х = 0, у = 0,25 и х = 09
^ = 0,75. Первая пара является решением задачи E.2), в ней V2 = l.
Уравнение E.18) имеет вид
Интегральной линией, проходящей через первую точку, является
у = х + 0,2Ь. E.24)
Несложно показать, что найденная точка будет глобальным решением
минимаксной задачи, а точка ^ = 0и функция E.24) дают в данной
задаче синтез (глобальный). Вторая точка х = 0, у=0,75 является
локальным и одновременно глобальным решением максиминной зада-
задачи E.1), в которой Vi~—1. Ни одна из найденных точек не является
седловой.
Пример 2. В качестве F (х, у) возьмем квадратичную форму:
—x*+2kxy-y2,
В задаче отыскания минимакса глобальным решением являются х =
= #=0, К2=0. Уравнение E.18) решением имеет линейную функцию
y = kx. Максимин в данной задаче не достигается на ограниченном
множестве.
7. Один частный случай. Рассмотрим простейший ва-
вариант минимаксной задачи, в которой отыскивается
(х), ф(х)= max /'(*), E.25)
где f*(x)—некоторый набор функций. Теорема 1.5.3 Дан-
скина—Демьянова здесь формулируется следующим обра-
образом:

52 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Теорема 1.5.10. Пусть функции /'(я), *€[1:с],
непрерывно дифференцируемы в некоторой окрестности
точки х. Тогда функция максимума ф (л;) дифференцируема
в точке х по любому направлению q, |<jfjj=l, причем
^f= max </<(*),?>,
B(x) = {i?[Uc\: Ф (*) = /'(*)}¦
Если все функции f{ непрерывно дифференцируемы, то
необходимое условие минимума в задаче E.25) формули-
формулируется следующим образом:
Теорема 1.5.11. Для того чтобы х* была точкой
минимума функции <р(х) на Еп, необходимо, а в случае
выпуклости ф (х) и достаточно, чтобы выполнялось нера-
неравенство
inf max <#(*•). <I»0> E-26)
|| G11=1 1ЪВ{ХШ)
или, что то же самое
inf ^)>0. E.27)
Точки хф, удовлетворяющие E.26), E.27), называют
стационарными точками функции максимума ц>(х). Обо-
Обозначим L0(x) выпуклую оболочку, натянутую на векторы
fx{x), где i?B(x):
i*B{x) ieB(x)
Теорема 1.5.12. Для того чтобы функция <р(х)
достигала минимума в точке #*, необходимо, а в случае
выпуклости <р(х) и достаточно, чтобы
Это условие является обобщением условия C.4) на
функции максимума.
§ 6. Условия минимума
в задачах нелинейного программирования,
не использующие дифференцируемость
I. Основные понятия. Общая задача нелинейного про-
программирования состоит в отыскании
min/(*)f F.1)
хеХ

§6J УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 53
где множество X определяется следующим условием:
X = {х е Еп: g (х) = О, h (х) < 0}. F.2)
Здесь введены две вектор-функции, осуществляющие ото-
отображения
g(x): ?« — ?*, h(x): En-+Ec.
функцию f(x), вектор-функции g n h в дальнейшем
будем называть функциями, определяющими задачу F.1).
Вектор-функция g задает ограничения типа равенства,
h—ограничения типа неравенства. Множество решений за-
задачи F.1) будем обозначать X*. Определим множество
Хо - {х € Еп: g (х) = 0, h (х) < 0}. F.3)
Введем так называемую функцию Лагранжа:
L(x, и, v) = f(x) + <u, g(x)> + <v, h(x)>. F.4)
Векторы и?Ее и *»€ 5е'будем называть множителями
Лагранжа или двойственными векторами.
Определение 1.6.1. Точка х называется допусти-
допустимой, если х?Х.
Определение 1.6.2. В точке [#*, uj? Еп+С выпол-
выполнено условие дополняющей нежесткости, если
*'>'(**) = 0 V/€[l:c]. F.5)
Определение 1.6.3. В точке [л;*, yj ^ ?1/г+с выпол-
выполнено условие строгой дополняющей нежесткости, если
в ней имеет место условие дополняющей нежесткости и для
любого /€[1:с] из условия А'(*,) = 0 следует, что rf > 0.
Определение 1.6.4. Задача F.1) называется задачей
выпуклого программирования, если функции, определяющие
задачу, выпуклые, а вектор-функция g(x) линейно зави-
зависит от х.
Определение 1.6.5. Задача F.1) называется зада-
задачей линейного программирования, если функции, опреде-
определяющие задачу, линейны по х.
Определение 1.6.6. В задаче F.1) выполнено усло-
условие Слейтера> если множество Хо не пусто.
Определение 1.6.7. В задаче F.1) выполнено усло-
условие Карлина, если не существует векторов и ? Ее, v g E%,
1^1=7^0, для которых при любых х?Еп выполнено нера-
неравенство
0 «и, g(x)> + <v, h(x)>. F.6)

54 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Если выполнено условие Слейтера, то имеет место усло-
условие Карлина. Действительно, тогда по меньшей мере для
1с € Хо имеем: g {х) = 0, h (х) < 0, и при любых и ? Ее,
v?Ec+y || v || ФО выполнено неравенство
v, h(x)><0,
противоположное требуемому F.6).
Ниже, в п. 5, будет показано, что в случае задач
выпуклого программирования условия Карлина и Слей-
Слейтера эквивалентны.
2. Достаточные условия минимума. Сформулируем
и докажем ряд теорем, дающих достаточные условия мини-
минимума в задаче F.1). Рассмотрим две вспомогательные
задачи отыскания максимина и минимакса функции Лаг-
ранжа:
Vx = sup sup inf L (x, u, v)9 F.7)
ueEe v€.?c xeEn
V2= inf sup sup L(x, uy v). F.8)
?« Ee
Точку [х*9 и„ t>j€?n+l«, где v*>0, m = e + c, будем
называть седловой точкой функции L, если для любых
х?Еп, и?Ее, v?Ec+ выполнены неравенства
(x, u.,v.). F.9)
Теорема 1.6.1. Пусть [л:*, &*, v*\—седловая точка
функции Лагранжа L. Тогда точка х* является решением
задачи F.1), в точке [л;,, и„] имеет место условие допол-
дополняющей нежесткости.
Доказательство. Из левой части F.9) следует,
что для всех и?Ее, v?Ec+ выполнено условие
Shf(xm)[v/-vi]^o. F.Ю)
1
Положим v = t»«, а'== «^ для всех i € [1 :е], за исключением
только одной компоненты а* = а{ +1. Подставив эти век-
векторы в F.10), получим g*(x*)^0. Можно положить uk=
=и$—1, и тогда придем к условию gk(x*)^Q. Остается
одна возможность g*(x*) = 0. В силу произвольности k
приходим к выводу, что g(x») = 0. Взяв в F.10) и = «„
t^ = t^ для всех i6[l*c]t-3a исключением v* = ui4*l П(>-

« 6] УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 55
лучим, что Л* (#*) ^ 0. В силу произвольности s из [1:с]
приходим к выводу, что к(х*)^0. Таким образом, точка
хФ?Х> т. е. является допустимой.
Положим в F.10) и = и*у v = 0, тогда получим
0<<А(*,)> »•>. F.11)
Вместе с тем А (#*) ^ 0 и 0 ^ v*, поэтому для все?с / ? [1 :с]
выполнено неравенство h* (х*) vi ^ 0.
Сравнивая это неравенство с F.11), приходим к вы-
выводу, что имеет место F.5). Из правого неравенства F.9)
с учетом F.5) получим, что для всех х?Еп выполнено
условие
В частности, для любых х?Х имеем/(х*)</(л:). Отсюда
заключаем, что х*?Хф. Щ .
Если считать, что в F.7) внутренняя задача разре-
разрешима, то можно ввести в рассмотрение функцию двойст-
двойственных векторов, положив
Y(a, v)= inf L(x, u, v).
Тогда внешняя задача для F.7) будет состоять в нахож-
нахождении
Vt= sup sup у (и, v).
и*Ее vtE%
Теорема 1.6.2. Пусть X*Ф 0, тогда справедливы
оценки
Vt </(*•) = У*. хт?Х.. F.12)
Доказательство. Рассмотрим вначале задачу F.8).
В ней внутренняя задача решается просто:
ft/ \ т / ч if№*
р (а:) = sup sup L (х, иу v) = < ,
еСЛИ
если
Решая внешнюю задачу, приходим к выводу, что минимум
функции р (*) достигается на допустимом множестве и со-
совпадает с минимумом функции f(x) на X, поэтому
хеХ

56 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Для любых х G Xf u?Ee, v?Ec+ имеет место неравен-
неравенство
f(x)>L(x9 и, v).
Проведем минимизацию левой и правой частей этого не-
неравенства по х ?Х, получим
/W^/W = niin/(#)^min L(x, и, v)*^ inf L(xtut v).
6 силу произвольности и?Ееу v?Ec+, приходим к левой
части F.12). §|
Теорема 1.6.3. Пусть решением задачи F.7) является
точка [л;*, и*, v*\ € Еп+ту у которой х*? X, v#^0, выпол-
выполнено условие дополняющей нежесткости. Тогда х*?Хщ.
Доказательство. При и = и*, v = vm точка Л'*
должна быть решением внутренней задачи в F.7), т. е.
при любом х?Еп выполняется неравенство
Если х?Х, то из этого неравенства следует, что
/(*¦)<!(*, и» vm)^f(x)9
откуда заключаем, что х* € X*. Щ
3. Вычислительный аспект. Приведенные теоремы ука-
указывают возможные пути построения численных методов
решения задачи F.1). Из теоремы 1.6.1 следует, что в том
случае, когда существует седловая точка функции Лаг-
ранжа L, можно вместо решения задачи F.1) отыскивать
седловые точки I. Такие методы будут рассмотрены ниже
(в § 1 гл. IV).
Из теоремы 1.6.2 приходим к выводу, что, решив мини-
минимаксную задачу F.8), мы получим решение задачи F.1).
Практическая реализация такого подхода возможна, если
есть уверенность в том, что существует ограниченное реше-
решение \х> Ну Щ] минимаксной задачи. Действительно, пусть
все I^'I^t, О^и'^т, тогда минимаксную задачу F.8)
заменим следующей:
Р1 = т\п max max L(x, и, v). F.13)
En U'| ^ <т

§6J УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 57
разрешив внутреннюю задачу, получим
2 \g*{x)\+ S hf+ (x)]\. F.14)
1 / 1 JJ
Таким образом, введя только одну гипотезу о существо-
существовании ограниченных решений F.8), мы свели исходную
задачу F.1) к нахождению безусловного минимума неко-
некоторой вспомогательной функции от х. В дальнейшем,
в гл. III, мы придем к этому же результату, изучая метод
штрафных функций.
Теорема 1.6.3 дает возможность отыскивать решения
максиминной задачи F.7). Если ее решением оказывается
допустимая точка (х*?Х), выполнено условие дополняю-
дополняющей нежесткости, то хт является решением исходной задачи.
Это свойство также будет использовано в гл. IV.
4. Модифицированные функции Лагранжа. Все при-
приведенные в этом параграфе достаточные условия базирова-
базировались на рассмотрении вспомогательных задач, связанных
с введением функции Лагранжа L. Возникают следующие
вопросы:
Можно ли для получения достаточных условий мини-
минимума и, что более важно, для построения численных мето-
методов решения задачи F.1) использовать вспомогательные
функции более общего вида, чем функция Лагранжа L?
Не позволит ли такой прием гарантировать для более
широкого класса задач нелинейного программирования раз-
разрешимость вспомогательных задач? К каким другим вспо-
вспомогательным задачам, удобным для численной реализации,
можно редуцировать задачу F.1)?
В настоящее время ведутся интенсивные работы, кото-
которые, по-видимому, позволят в будущем ответить на постав-
поставленные вопросы. Теоретические исследования и численные
эксперименты указывают на целесообразность рассмотре-
рассмотрения новых вспомогательных функций, называемых обычно
модифицированными или обобщенными функциями Лаг-
Лагранжа, и на введение с их помощью новых вспомогатель-
вспомогательных задач, отличных от отыскания седловых точек, мак-
симина или минимакса. Приведем одно нетрадиционное
достаточное условие минимума в задаче F.1), основанное
на использовании специальной вспомогательной функции,
имеющей следующий вид:
y). F.15)

58 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ 1.ГЛ. 1
Здесь у—некоторый вектор, его размерность пока не суще-
существенна (в частности, у может быть скаляр), ?—непре-
?—непрерывная функция своих аргументов. Обозначим
= kxg minH(x, у). F.16)
Предполагая, что при некотором векторе у множество
х(у) не пусто, перейдем к задаче отыскания действитель-
действительных решений следующей системы:
= 0, А (*)<<>, где х?х(у). F.17)
Связь этой вспомогательной задачи с исходной F.1) разъяс-
разъясняет
Теорема 1.6.4 (Ю. Г. Евтушенко [12]). Пусть суще-
существуют векторы у* и х%, удовлетворяющие F.17): функ-
функция g, входящая в F.15), такова, что для любых х?Х
имеет место неравенство
1(х, у.ХЪ(х.9 у.), F.18)
тогда: 1) множество решений X* задачи F.1) не пусто
и х«?Х*\ 2) множество решений X* можно представить
в виде
Х* = ХПх(у*). F.19)
Доказательство. Покажем вначале, что
F.20)
Пусть х* ? X П х {у*), тогда из условия хт ? х (ут) следует,
что для любых х?Еп имеет место неравенство
Здесь в качестве х возьмем вектор, принадлежащий до-
допустимому множеству Ху учтем F.18), тогда получим, что
f(Xm)^f(x) при любых х?Х\ но это возможно, только
если х*?Х*, что доказывает включение F.20).
Для доказательства F.19), надо показать, что
Хт\(Х()хШ) = 0. _ F.21)
Предположим противное, что существует вектор х, удовле-
удовлетворяющий одновременно двум условиям:
х^Х.% х$ХПх(у.). F.22)

§6] УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 59
Так как lc?XmczX9 второе условие F.22) означает, что
х?*Ы- Поэтому
Н(х.9 у<) = /(*•)+?(*•¦ у.Х/(*)+Е(*. у.).
Снова воспользуемся неравенством F.18), получим, что
/(*•)</(*)• Это неравенство противоречит исходному
предположению о том, что х$Х*. Поэтому оба условия
F.22) удовлетворить одновременно нельзя, следовательно,
имеет место F.21). Учитывая F.20), приходим к утверж-
утверждению F.19). Щ
Теорема 1.6.4 позволяет редуцировать исходную задачу
нелинейного программирования к решению системы нели-
нелинейных равенств и неравенств; вытекающие из этого ре-
результата разнообразные численные методы будут описаны
в § 2 гл. IV.
5. Некоторые вспомогательные результаты.
Лемма 1.6.1. Пусть F.1)—задача выпуклого прог-
программирования и множество Хо, определяемое условием
F.3), пусто. Тогда существуют такие векторы и?Ее,
v?Ec+, (иу v)=?0, что для любых х?Еп имеет место не-
неравенство F.6).
Доказательство. Определим два множества
А(*) = {*. У- z$Ee
хеЕп
Если точки \г19 уг], [г2, у2] принадлежит Л, то для
; X ^ 1 имеем
Поэтому множество Л выпукло. Из условия леммы Хо= 0
следует, что начало Координат г = 0, у = 0 не принадле-
принадлежит множеству Л. Согласно теореме об отделимости 1.1.1,
существуют такие и?Ее, v?Ec, (и, Ь)ФО, что из усло-
условия [a, b] g Л следует
0<<м, a> + <vy by. F.23)
Компоненты вектора b можно сделать сколь угодно боль-
большими, поэтому вектор v^O. В F.23) положим a = g(x),

60 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
() + c+i |И=1, 8 > 0, тогда [а9 b]czA(x)c:A;
для любого х?Еп имеем
В силу того, что 8—произвольное положительное число,
отсюда заключаем, что выполнено неравенство F.6). Ц
Лемма 1.6.2. В случае задач выпуклого программи-
программирования условия Слейтера и Карлина эквивалентны.
Доказательство. Дав определение 1.6.7, мы ука-
указали, что из выполнимости условия Слейтера следует
справедливость условия Карлина. Покажем, что если усло-
условие Слейтера не выполнено, то не имеет места и условие
Карлина. Согласно предыдущей лемме из условия Хо = 0
следует, что существуют такие и?Ее9 v?E+9 (и9 v)=fcQ,
что выполнено неравенство F.6). Если ЦаЦ^О, то усло-
условие Карлина нарушено. Предположим противное, пусть
v = 0. Линейная вектор-функция g(x) представима в виде
g(x) = Ax-\-b9 где А—матрица ехп. Не нарушая общ-
общности, можно считать, что строки матрицы А линейно
независимы, так как в противном случае можно было бы
понизить число ограничений, не изменив допустимое мно-
множество. Запишем F.6) в виде
u> Vx?En9 \\и\\фО. F.24)
Покажем, что отсюда следует: АТи = 0. В противном слу-
случае F.24) в качестве* возьмем
(—Ати, если <6, ы><0,
Х=< o<w, by Ати
[2
еСЛИ
Подставив эти выражения в правую часть F.24), полу-
получим, что если <Jby иу^.0, то
Если <6, w>>0, то хтАти + <Ь> и>=— <6, и>< 0.
Эти соотношения противоречат левому неравенству F.24).
Поэтому Ати = 0, что противоречит линейной независи-
независимости строк матрицы А. Следовательно, ||а||=5^0, и усло-
условие Карлина не выполнено. Щ
6. Необходимые и достаточные условия минимума.
Приведенные в п. 2 три теоремы позволяют решение ис-

§б] УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 61
ходной задачи F.1) заменить отысканием седловых точек
функции Лагранжа либо решением минимаксной или
максиминной задач. К сожалению, такая редукция FЛ)
к более простым задачам не является универсальным прие-
приемом, далеко не во всякой задаче функция Лагранжа обла-
обладает конечными седловыми точками, не всегда выполня-
выполняются условия теоремы 1.6.3. Изложим некоторые резуль-
результаты, дающие достаточные условия существования ограни-
ограниченных двойственных векторов. В одной из первых работ
по нелинейному программированию Ф. Джоном [1J для
анализа задачи F.1) было предложено использовать
функцию
L°{x9 и, v, q) = qf(x) + <u, g(x)> + <v, h(x)>. F.25)
Точку [**, и„ и., ?.]€?я+ш+1, у которой q*?E\y
ит?Ев9 i>«6 2s+, («*, b«, я*)фЪ, будем называть седловой
точкой функции L0, если для любых х?Еп, и?Ее,ь?Е%
имеют место неравенства
L°(x*f и, v, <7*)<L°(x*, н„и„ <7*)<L°(*, и„ v.9 q.). F.26)
Сравнивая эти неравенства с F.9), приходим к выводу,
что если [л:#, и*, vm9 q*\—седловая точка функции L0 и
9* > О» то совокупность [х*> ujq0, vjq*] является седло-
вой точкой функции L. Обратно, если [л:«, и*у ty]—сед-
ty]—седловая точка функции L, то [л:*, м», vm, 1]—седловая точка
функции L0.
Аналогом теоремы 1.6.1 для функции L0 является
Теорема 1.6.5. Пусть [х%, ищ> v*> q*\—седловая тон-
тонка функции L0, (G*, v*)Ф0. Тогда х*?Л9 имеет место
F.5) и либо qm> 0, Хъ^Х*, либо q* = Q и в задаче F.1)
не имеют места условия Карлина и Слейтера.
Доказательство. Так же, как это было сделано
при обосновании теоремы 1.6.1, можно показать, что
х*$Х и имеет место F.5). Если 0 < ^*, то х*$Х%. Если
<7% = 0, то Jv*||=^=0, из правого неравенства F.26) получим
Это неравенство показывает, что условия Карлина и Слей-
Слейтера нарушены. Щ
Теорема 1.6.6 (Удзавы — Карлина о седловой точке).
Пусть в задаче выпуклого программирования F.1) мно-

62 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
жество решений не пусто. Тогда для каждого лс*€^* су-
ществует седловая точка \хт, иф9 и», q9] функции L0, в
точке [хт, v0] выполнено условие дополняющей нежест-
нежесткости.
Доказательство. Из того, что #»?Х*, следует,
что система
/(*)-/(*.)< О, *(*)-0, *W<0 F.27)
не имеет решения. Воспользуемся леммой 1.6.1. Поскольку
из высказывания «h (х) ^ О не имеет решения» следует
высказывание «h (x) < 0 не имеет решения», утверждение
леммы 1.6.1 можно сформулировать следующим образом.
Если система F.27) не имеет решения, то существуют
такие и*?Ее, v*?E%, q*?E\.y не равные нулю одновре-
одновременно, что для всех х?Еп выполнено неравенство
<><?.(/(*)—/(*•)) + <*•• g(x)> + <v» Л(*)¦>. F.28)
Положив здесь х = х*> получим, что <и#, А(л:*)>^0, но
так как t;t>0 и А(х*)<!0, приходим к выводу, что имеет
место F.5). Из F.28) следует, что для всех х?Ен
что доказывает правое неравенство в F.26).
Из условия Л (#*)<; 0 следует: <у, Л(л:*)>^0 при
O Учитывая F.5), получаем, что для любых и?Ее и
т. е. справедливо левое неравенство в F.26). Щ
Теорема 1.6.7 (Куна—Таккера о седловой точке).
Пусть в задаче выпуклого программирования F.1) мно-
окестзо решений Хт не пусто, выполнено либо условие
Слейтера, либо Карлина. Тогда для каждого х,?Х9 су-
существуют такие векторы и?Ее, v € ?+> что совокупность
[х*9 и, v] является седловой точкой функции Лагранжа L.
Доказательство. Согласно предыдущей теореме
существует седловая точка [**, а*, и», #*] функции L0,
в точке [х*> v*] выполнено условие F.5). Если <7*>0, то
[**, ujq*, vjq*\—седловая точка функции L.

§ 6] УСЛОВИЯ МИНИМУМА БЕЗ ДИФФЕРЕНЦИРУЕМОСТИ 63
Докажем, что qm > 0. Предположим противное, что
<7« = 0. Тогда (иф, а*)#0, из правой части F.26) следует,
что для любых х выполнено неравенство
что невозможно при ||г>*||=^0, vm^Q9 так как противоре-
противоречит условиям Карлина и Слейтера. Рассуждая точно так
же, как при доказательстве леммы 1.6.2, можно показать,
что||i^| #0. Поэтому <?,#0, ~u = ujq*, v = vjq*. Щ
7. Некоторые обобщения. Приведенные здесь резуль-
результаты обобщаются на тот случай, когда вместо F.1) рас-
рассматривается задача поиска
min /(*), F.29)
XU
где ?/ — множество из Еп9 внутренняя часть которого не
пуста, множество X определяется условием F,2). Множест-
Множество решений задачи F.29) по-прежнему обозначается X*,
функция Лагранжа определяется по формуле F.4). В за-
задачах F.7), F.8) и F.16/ вместо условия х?Еп вводится
х? U. Условия F.9), F.26), определяющие седловые точки,
и неравенство F.6) должны быть справедливы при любых
x?U. В случае задач выпуклого программирования тре-
требуется, чтобы множество U было выпуклым.
Легко убедиться, что приведенные в этом параграфе
теоремы и леммы с учетом сделанных добавлений оста-
остаются в силе и в случае задачи F.29). В теоремах 1.6.6,
1.6.7, и обеих леммах требуется, чтобы множество U
было выпуклым. Запись задачи нелинейного программи-
программирования в виде F.29) будет в дальнейшем часто встре-
встречаться, она бывает полезной, когда по каким-либо при-
причинам операция минимизации функций на множестве U
оказывается легко реализуемой. Например, U имеет про-
простую структуру, или нахождение минимума на U можно
проводить, используя аналитические формулы. Задача
F.29) может оказаться удобнее и для теоретических ис-
исследований, так как, наложив специальные ограничения
на U (например, потребовав компактность множества (/),
мы существенно упрощаем задачу и анализ методов ее
решения.

64 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
§ 7. Условия минимума
в задачах нелинейного программирования,
использующие дифференцируемое™
1. Основные определения и предварительные резуль-
результаты. Рассмотрим задачу F.1), используя функцию Лаг-
ранжа F,4).
Определение 1.7.1. Пусть функции, определяющие
задачу FЛ), дифференцируемы в точке хф, тогда точка
[#*, «*, *>*] € Еп+т называется точкой Куна— Таккера, если
дс*€Х, в [лг,, v^^E**0 выполнено условие дополняющей
нежесткости F.5), ^>0и
Lx(x%, и*, v,)=*fx(x*)+gx(xm)um + hx(x.)v* = O. G.1)
Определение 1.7.2. Пусть функции, определяющие
задачу F.1), дифференцируемы в точке л:*, тогда [х*, м*,
0*, Я*]€En+m+1 называется точкой Ф. Джона, если хт?Ху
в [**, iy| ? Еп+С выполнено условие дополняющей нежест-
нежесткости F.5), <7#^0, v*^0 не все и*, v*, q* равны нулю и
L*x{x*, u*y с ^) = 0. G.2)
Если [#», «*, о», <7*]—точка Ф. Джона и <7*=1, то
[^*, «*, tyj — точка Куна-—Таккера.
Введем два индексных множества:
= 0}f G.3)
Те функции gi(x)9 У (х)у у которых gi(x) ()
называются активными ограничениями в точке х. Индекс-
Индексное множество а (л:), таким образом, определяет совокуп-
совокупность активных ограничений типа неравенства в точке х.
Определение 1.7.3. Ограничения g(x) = 0, /*(*)<0
удовлетворяют условию регулярности в точке х?Х, если
вектор-функции g(x)9 h(x) дифференцируемы в лг, векто-
векторы gx(x)9 hl(x), t[l: в],/€<*(*)» линейно не зависимы.
Определение 1.7.4. Ограниченияg(х) = 0 и Л(*)<0
удовлетворяют условию Эрроу—Гурвица—Удзавыв точке
х?Х, если вектор-функция h(x) дифференцируема в х,
g(x) непрерывно дифференцируема в х, векторы gx(x) для
всех i ^ [1 :е] линейно независимы, существует вектор z g ?"",
удовлетворяющий соотношениям
gl (х) z = 0, <г, hj(x)> < О V / 6 о (*). G.4)

$7] СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 65
В ряде случаев следует накладывать специальные ог-
ограничения на g(x), h(x) и в точках, не принадлежащих
допустимому множеству. Это имеет место в следующем
определении:
Определение 1.7.5. Ограничения g(х) = 0 и h(х) ^0
удовлетворяют условию усиленной регулярности, если век-
вектор-функции g(x) и h(x) всюду диффенцируемы; в точках
х ? X выполнено условие регулярности ограничений, в каж-
каждой точке х(^Х существует вектор г?Еп, удовлетворяю-
удовлетворяющий соотношениям
{x)z = Qf h(x)+hTx(x)z^0.
При рассмотрении задач выпуклого программирования
можно, не нарушая общности, считать, что условие
g(x) = 0 определяет (я—е)-мерное линейное многообразие,
так как, если бы это условие не имело места, то можно
было бы уменьшить количество ограничений типа равен-
равенства, убирая зависимые условия; при этом допустимое
множество X не изменится. Поэтому в дальнейшем будем
считать, что в случае задач выпуклого программирования
ранг матрицы gx (x) максимальный, равен е.
В случае задач выпуклого программирования условие
Эрроу,—Гурвица—Удзавы будет выполнено, если вектор-
функция к(х) дифференцируема и имеет место условие
Слейтера. Действительно, пусть g(x) =0, h(x)< 0, тогда,
используя линейность g(x) и выпуклость h(x)$ получим
x) = 09
t(x)<0 V/?a(*) ( ' }
Обозначив z = x—x, приходим к соотношениям G.4).
Иемма 1.7.1 (Моцкина о транспонировании). Пусть
матрицы А и В имеют соответственно размеры aXd,
bxd, причем Ь > 0. Тогда имеет решение либо система
Лг=^0, Bz<0, z?Ed>
либо система
Обе системы неразрешимы одновременно.
Доказательство можно найти в книге Г. Куна и
А. Таккера [2].
3 Ю-

66 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. \
Лемма 1,7.2. Пусть функции g, h дифференцируемы
в точке х?Х, в которой выполнено условие Эрроу—Гур-
вица—Удзавы, а в случае задач выпуклого программиро-
программирования—условие Слейтера или Карлина. Тогда для любых
и?Ее> v € Е%> таких, что все ul\ v'\ i ? [1 :е], j ? а (х), не
равны нулю одновременно, имеет место условие
G.6)
Доказательство. Если о(х) = 0, то требуемое
неравенство следует из линейной независимости векторов
g*(*)> i€[be]. Если множество о(х) не пусто, то вос-
воспользуемся предыдущей леммой, взяв в качестве А мат-
РВДУ ёх{х)> в качестве строк матрицы В градиенты Ц(х),
/€<*(#)• Система G.4) разрешима, поэтому имеет место
неравенство G.6) при любых и, v, удовлетворяющих ус-
условию леммы. В случае задач выпуклого программирова-
программирования используются условия G.5), вытекающие из условия
Слейтера. Щ
2. Необходимые и достаточные условия минимума в
выпуклом программировании. Для задач выпуклого прог-
программирования в определениях 1.7.1 и 1.7.2 условие диф-
ференцируемости можно опустить, а вместо требований
G.1) и G.2) ввести следующие: существуют векторы
такие, что соответственно
wi=o.
G.7)
G.8)
Теорема 1.7.1. Пусть в задаче выпуклого програм-
программирования F.1) множество решений X* не пусто. Тогда:
1) всякая точка Куна — Таккера [х*, и*, v*\ является
седловой точкой функции Лагранжа L(xy а, и), ;с*€Х*;
2) всякая точка Ф. Джона [#*, «*, v*, q*] является
седловой точкой функции Ь°(х, и, v, q)\ при q* > 0 имеем:

7-j СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 67
3) если выполнено условие Слейтера или Карлина, то
существуют точки Куна—Таккера и Ф. Джона [х«, и*,
v*, q*\ причем q*>0.
Доказательство. Из выпуклости f(x), h (#), ли-
линейности g (x) следует, что для произвольных х?Еп имеют
место условия
x—x.>, . G.9)
А/(*)>А'(*») + <*', х-хт>, G.10)
Умножим G.10) на vfm и просуммируем по /, умножим
G.11) скалярно на и* и сложим полученные неравенства
с G.9). Учитывая, что vm^Q, принимая во внимание оп-
определение функции L .и условие G.7), получим
L(x, и*,
(х*) и*
Таким образом, мы доказали правое неравенство в усло-
условиях F.9). Левое неравенство имеет в данном случае вид
В силу условий дополняющей нежесткости правая часть
этого неравенства равна нулю, и, так как х% ? X, получаем,
что <i>, А(х»))<0 для любых и>0. Поэтому неравенства
F.9) выполнены, и, используя теорему 1.6.1, заключаем,
что Хщ?Хф. Аналогично с использованием G.8) доказы-
доказывается утверждение 2).
Согласно теореме 1.6.7, при выполнении условия Слей-
Слейтера или Карлина существует седловая точка [л:*, и9, v%]
функции L. Из теоремы 1.6.1 следует, что хт ^ X* и имеет
место F.5). Согласно теореме 1.3.5 из правого неравен-
неравенства F.9) следует G.7). Поэтому [#*, и*, v*\ является
точкой Куна—Таккера. Из теоремы 1.6.6 следует сущест-
существование у функции L0 седловой точки [#«, и«, t>*, q*\, ко-
которая является точкой Ф. Джона, причем, согласно тео-
теореме 1.6.5, (?*>0. ¦
з*

68 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
3. Достаточные условия минимума в общей задаче
нелинейного программирования. Для допустимой точки х«
и двойственного вектора v* определим два выпуклых ко-
конуса:
G.12)
, ^/,W<0}; G.13)
здесь индексы /, s, i принимают всевозможные значения
из множеств 8(х«, i>*), o(x%)\Q(x^ v*)y o(x*) соответст-
соответственно (см. G.3)).
Лемма 1.7.3. Пусть [х*, и*, v*\ —точка Куна—
Таккера в задаче F.1). Тогда конусы Кг(х*, v*) и /С2(х«)
совпадают.
Доказательство. Покажем вначале, что /С2(х*)с
czKi(x*, Vt). Пусть х^К2{х*)у тогда следует показать,
что
У/€в(^, v.). G.14)
Используя G.1), получим
(x.) vm =
Так как каждое слагаемое в этом равенстве неположи-
неположительно и все а{>0 для /€0(^*>__^*)» приходим к выводу,
что имеет место G.14), поэтому х^Кх(х^ v*).
Докажем, что Кг{х*у Vt)cK2(x*). Пусть x€Ki(xmt у»),
тогда из G.1) следует, что
Поэтому х€К2(х*), что завершает доказательство. Щ
Определение 1.7.6. Матрица вторых производных
LXx(x*f um, v*) положительно определена на конусеКг(хф9 ^),
если квадратичная форма xTLxx(хф9 и*, v«)x>Q для
любых ненулевых векторов х, принадлежащих конусу
Кг(х%, Vm).

§7j СЛУЧАЙ ДИФФЁРЕНЦИРУЕМОСТИ 69
Определение 1.7.7. Матрица вторых производных
L (#¦> и*> v*) равномерно положительно определена на
конусе Кг (**, v*) с константой С1У если xTLxx (*», и*, vjx^z
C\xf для любых векторов х, принадлежащих конусу
)
Переформулируем лемму Р. Финслера (см. Приложе-
Приложение II) применительно к рассматриваемой задаче.
Лемма 1.7.4 (Р. Финслера). Пусть матрица вторых
производных Lxx(x*, u%y v*) функции Лагранжа положи-
положительно определена на конусе /Ci(#*, у*), в точке [х*9 и«]
выполнено условие строгой дополняющей неоюесткости.
Тогда существует такое число т«, что при любом т > т«
положительно определена матрица
2
/есг(**)
Теорема 1.7.2 (Мак-Кормика). Пусть [х*, и%у vJ б
^ ?п+т—точка Куна—Таккера в задаче F.1); функции,
определяющие задачу, дважды дифференцируемы, матрица
вторых производных Lxx(xm, и*, и«) положительно опре-
определена на конусе Ki(xm, v*). Тогда х* является изолиро-
изолированным локальным минимумом в задаче F.1).
Сформулированная теорема является одним из основных
результатов теории нелинейного программирования. После
публикации этой теоремы были получены разнообразные
модификации, и некоторые обобщения. Следуя работе
С. Хана и О. Мангасаряна [1], сформулируем и докажем
теорему, обобщающую результат Г. Мак-Кормика.
Теорема 1.7.3. Пусть [х*, и*, v*, q*]?En+m+1—
точка Ф. Джона в задаче F.1); функции, определяющие
задачу, дважды дифференцируемы в точке х%, матрица
вторых производных Ь*хх(х*, и%, и», ^*) положительно
определена на конусе Кг (х*, v*) или К2 (*•). Тогда точка хт
является изолированным локальным минимумом в за-
задаче F.1).
Доказательство. Предположим противное, т. е.
что лс« не является локальным изолированным минимумом.
Тогда существует последовательность допустимых точек {хк\
такая, что все хкфхт, \\тхк = х% и, кроме того, для
k -> 00
каждой точки хк выполнено неравенство

70 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Обозначим ук = (хк—х*)/\\хк —хт\. Из построения то-
точек xk следует, что выполнены условия
о=
Здесь О (г) означает, что 1ш О(г)~0. Поэтому существу-
ет такая предельная точка у последовательности] {ук}>
что
откуда получаем, что у()
Воспользуемся условием существования вторых произ-
производных функций, определяющих задачу, тогда
Умножая полученные соотношения соответственно на
и», i>{, 1?о(хф) и суммируя их, получим
Устремляя хк к х^ получим, что ук~+У> при этом
^^L( )/, что противоречит положительной
^L( ^) рр
определенности матрицы Цх(х*у и*, v*9 qt) на ()
Если выполнены условия теоремы 1.7.2, то при q*= 1
будут выполнены условия теоремы 1.7.3, что доказывает
справедливость теоремы Г. Мак-Кормика 1.7.2. Тео-
Теорема 1.7.3 дает более сильные достаточные условия, чем
теорема 1.7.2; существуют задачи, для которых обеспечены

§7] СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 71
условия теоремы 1.7.3, но не удается выполнить условия
теоремы 1.7.2.
В дальнейшем потребуется следующая
Лемма 1.7.5. Пусть в точке Куна — Таккера
[хш, и*у vm] выполнены условия теоремы 1.7.2. Тогда для лю-
любого вектора [и, v] € Ет такого, что и1 > | и\ |, * € [1 :е],
v > v*, точка х* является строгим локальным минимумом
функции
М*. «. ») = /(*) + 23 tt'l^WH" S ^W- G.15)
i ss 1 / = 1
Доказательство. Если утверждение леммы не-
неверно, то существует последовательность точек xki схо-
сходящаяся к хт> такая, что хкфхт и
Ьг{хк> и, 1>).<М*«, «> *>)•
Отсюда следует, что
^ = 1 /=i
Пусть
Функцию ty(x) можно представить как функцию макси-
максимума, положив
| & {х) | = max \g* (*), — g* (*)], tt+ (х) = max [О, W (х)\
Тогда, согласно теореме 1.5.10, производная функции яр (л:)
по направлению у в точке х* удовлетворяет условию
Из G.1) выразим градиент /*(*«) и подставим в найден-
найденное неравенство, получим
/6 о (*.)

72 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Так как и1 > |и[| и^> v{, каждое слагаемое, стоящее
в квадратных скобках, неотрицательно и, следовательно,
равно нулю. Поэтому
) = 0,
для всех i?[l:e], j?B(X; v*), s^a(xi,)\Q(x$t9 v*). Таким
образом, у€Кг(х^ v*) и yTLxx(x*, «*, v«)y>0, откуда
получаем, что для всех xk, начиная с некоторого, выпол-
выполнено неравенство L(xk> а», а %) > L (я%, и», а*).
Далее имеем неравенства
Полученное противоречие доказывает лемму. Щ
4. Модификации теоремы Г. Мак-Кормика. В даль-
дальнейшем при изучении численных методов потребуются дру-
другие формулировки теоремы 1.7.2. Приведем их.
Если в точке [#*, iy) выполнено условие строгой до-
дополняющей нежесткости, то а (#«) = 8 (#*, »,), задаваемые
условиями G.12), G.13) конусы Кг(х^ vm) и К2(хт) в точке
Куна—Таккера совпадают с конусом
xTgx(x.) = 0,
) = 09 jeo(x.)}. G.16)
Теорему 1.7.3 можно сформулировать следующим обра-
образом.
Теорема 1.7.4. Пусть [л:«, и*, v*] есть точка Куна—
Таккера в задаче F.1), в [#*, v*] выполнено условие стро-
строгой дополняющей нежесткости; функции, определяющие
задачу, дважды дифференцируемы в точке л;*, матрица
Ьхх(хф9 и*, v*) положительно определена на конусе К3{х*).
Тогда хч является изолированным локальным минимумом
р задаче F.1).
С помощью введения дополнительных переменных за-
задачу F.1) сведем к отысканию минимума при наличии
только ограничений типа равенства и для редуцированной
задачи сформулируем достаточные условия минимума. Вве-
Введем вектор р?Ес. Допустимое множество в задаче F.1)
представим в виде
+

§7] СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 73
Исходная задача F.1) теперь будет состоять в минимиза-
минимизации функции / по двум векторам х и р:
minmin/.
х Ес
Поэтому целесообразно расширить вектор х, обозначив
z = [x, р]?Еп+с, и объединить функции, определяющие
ограничения:
Задачу F.1) представим в виде
min/, Z = {z?En+c: R(z) = 0}. G.17)
Z
Введем для этой задачи двойственный вектор у?Ет, т
= е + с, функцию Лагранжа запишем в виде
1=1
с
«г—_ Г IT
G.18)
Матрицу Rz размером (п+с)хт представим в виде
о t*\-[8x(x)\hx(x)_I
%е
Если в задаче F.1) точка хт?Хф и в ней выполнены
условия регулярности ограничений g(x) = 0, A(x)^0, то
точка ** = [*;, Р*]?Еп+с, где
pi = 2V-hf(x.) , /6[1:«]. GЛ9)
является допустимой, оптимальной в задаче G.17), в ней
выполнены условия регулярности ограничений /?(г) = 0.
Верно и обратное утверждение: если точка г, == [*«, /?J
допустимая,^оптимальная в задаче G.17), в нейлвыпол-
нено условие регулярности ограничений R (г) = 0, то точка хт
допустимая,|оптимальная в задаче F.1) и в точке хт вы-
выполнено условие регулярности ограничений g(x) = 0,
А()<0

74 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Пусть [#¦, и*, v*\—точка Куна—Таккера в задаче F.1),
тогда, положив у* = [и9, v*\ и используя F.5), G.18),
G.19) и условие *«?X*, получим
. ^) = 0, 1*(гт, f/#)=0. G.20)
В более подробной записи эти условия имеют вид
& = 0,
G.21)
Таким образом, всякой точке Куна —Таккера [л;*, и*, и»1
для задачи F.1) соответствует стационарная точка [z«, у*]
функции Лагранжа Lx(z, у) для задачи G.17). Обратно,
если [г„ у*]—стационарная точка функции Лагранжа L1
и и{ = t/?+' ^ 0 для / ^ а (я*), то [х», а», ^„] является точкой
Куна —Таккера в задаче F.1). Обозначим
L1 (г и \-[h*!&' uv.vJ i ....?.^ .1 G
J
Теорема 1.7.5. Пусть функции, определяющие за-
задачу F.1), дважды дифференцируемы в точке хт?Х.
Существует такой вектор ут?Ет, что условия G.20)
выполнены в точке [г*, ут] ? Еп+т+с, где z« = [**, рт] 6 Еп+С
и координаты рт определяются из G.19). Матрица
L\{zv У*) положительно определена на подпространстве
К, (х.) = {ze E»+<: z*Rz (г.) = 0ы}. G.23)
Тогда точка хф является изолированным локальным ми-
минимумом в задаче F.1).
Доказать теорему можно, проводя те же рассуждения,
что и при доказательстве теоремы 1.7.3, но проще пока-
показать, что из условий теоремы следуют условия теоремы 1.7.4.
Пусть z=[x, v]eK*M- Тогда
) + у5>/* = 0 J€[l:c].

§7] СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 75
Если /€0(*«)t то> согласно G.19), р{ = 0 и в качестве
вектора z 6 К4 (**) можно взять вектор, у которого от-
отлична от нуля только одна координата zn+f = vJ\ Из поло-
положительной определенности L^(z*, У*) на К* fa) тогда
следует, что (zn+JJ v{ > 0 и, следовательно, и{>0для
всех j?ofa)- Поэтому в точке [хт, vm] выполнено усло-
условие строгой дополняющей нежесткости. Из того, что
р/=0 для всех / €(*(#¦), заключаем, что всякий вектор
\х, v], принадлежащий K4fa), таков, что вектор х? К3 fa)-
Все условия теоремы 1.7.4, таким образом, выполнены.
Описанный прием сведения общей задачи F.1) к за-
задаче G.17) с ограничениями только типа равенства будет
использован в дальнейшем при описании численных мето-
методов. Введенный вспомогательный вектор р будем назы-
называть искусственным вектором.
5. Необходимые условия минимума. Для задач выпук-
выпуклого программирования необходимые и достаточные усло-
условия минимума даны в теореме 1.7.1. Сформулируем необ-
необходимые условия минимума для общей задачи нелинейного
программирования F.29).
Теорема 1.7.6. Пусть U—выпуклое множество,внут-
множество,внутренняя часть которого не пуста; функции, определяющие
задачу F.29), заданы на некотором открытом множестве^
содержащем Uf и дифференцируемы в точке х9, принад-
принадлежащей мнооюеству решений Хш задачи F.29), вектор-
функция g имеет непрерывные частные производные
в точке хт. Тогда:
1) необходимо, чтобы существовали qm?E\, um$Ee,
v*?E%, не равные нулю одновременно и такие, что
в точке [*„, t;,] выполняется условие дополняющей не-
нежесткости F.5), для любых x?U имеет ,место нера-
неравенство
О <<*-*., L°xfa, um, iv, ?.)>; G.24)
2) если функция L°{xf и«, i>«, qm) псевдовыпукла по х
относительно множества ?/, то необходимо, чтобы
хеи
3) если множество U открытое, в точке хщ выполнено
условие Эрроу — Гурвща—Удзавы, то в задаче F.29) су-
существует точка Куна — Таккера [*«,, w«, tyj.

76 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Доказательство теоремы можно найти, например, в книге
О. Мангасаряна [1], первое утверждение^доказано также
в книгах Ф. П. Васильева [1], Н. Н. Моисеева и др. [1].
6. Параметрическое программирование. Функции, опре-
определяющие задачу F.1), могут зависеть от некоторого пара-
параметра. Исследование зависимости решений от параметра
составляет предмет параметрического программирования.
Коротко остановимся на этом вопросе. Рассмотрим задачу
отыскания
min max F(x, у), G.25)
eXeY()
*i B(x9
где Н: En-+Ek9 B(x, y): EnxEm-+Es. Здесь внутрен-
внутренняя задача является задачей нелинейного программирова-
программирования и состоит в нахождении
y(x)=Arg max F(x, у). G.26)
yeY(x)
Составим функцию Лагранжа
L*(y9 К x) = F(x, S
у)S
Предполагаем, что для любых х множество Y (х) не пусто
и существуют такие векторы у(х), X (х), что они образуют
точку Куна—Таккера:
0, G.27)
Х'(х)В*(х, у(х)) = 09 Я>0, В(х, у(*))<0. G.28)
Внешняя задача заключается в отыскании
хех
Считая, что функции F(x, у), у(х) непрерывно диф-
дифференцируемы, получим
Второе слагаемое, ворбще говоря, не равно нулю и
это существенно усложняет решение внешней задачи,

§7J СЛУЧАЙ ДИФФЕРЕНЦИРУЕМОСТИ 77
требуя вычисления матрицы -?--. К счастью, ситуация су-
существенно упрощается благодаря тому, что имеет место
следующая формула:
A S
& G.29)
1=1
Действительно, предполагая, что функции F, Б, у(х) не-
непрерывно дифференцируемы по х, продифференцируем пер-
первое соотношение G.28), получим
'х(х, у(х)) +
Умножая это равенство на %*(х), учитывая первое из
соотношений G.28), находим
Учитывая G.27), получим
Откуда следует формула G.29).
Для внешней задачи функция Лагранжа имеет вид
Необходимое условие минимума состоит в выполнении
условий
t
Рх (** У*)~.t В*я(«•, у.)XJ + S ц{Я4 (^) = О,
,1$/У'(х.)=0р |1. > О, Я(^)<0,
здесь у* =^у (д;,), X. = Я (^).
Предполагая, что функции Х(х), у(х) известны, мы
приходим к обычной задаче нелинейного программирова-
программирования, в которой ищется минимум функции F (х, у(х)).

78 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. 1
Приведем теорему, дающую достаточные условия диф-
ференцируемости функций у (х), Х(х). Обозначим а (х, у(х))=
= {/€[l:s]: В'(х, */(*)) = 0}.
Теорема 1.7.7. Пусть функции F, В, Н дважды
непрерывно дифференцируемы по всем аргументам, в точке
Куна—Таккера [у(х), Х(х)] для задачи G.26) выполнены
достаточные условия максимума, вытекающие из тео-
теоремы 1.7.2 Мак-Кормика, в точке [у{х), Х{х)] выпол-
выполнено условие строгой дополняющей нежесткости, гра-
градиенты В1Х (х, у (х)) линейно независимы для / ? а (х, у (х)).
Тогда функции у(х), Х(х) дифференцируемы, их произ-
производные определяются из следующей системы:
Г Lly(x,y(x)) | —ву(*> У(ХЩ Чх
,у(х))\ D(B(x, y(x)))\ *±
\_dx_
Llx(x,y(x))
Р(Ь)Вх(х,У(х))
производная функции у(х) определяется формулой G.29).
Данная теорема представляет незначительную модифи-
модификацию теоремы 6, приведенной во второй главе книги
А. Фиакко и Г. Мак-Кормика [1], где дано ее доказа-
доказательство, основанное на использовании теоремы о неяв-
неявных функциях.
§ 8. Необходимые условия минимума
в задачах оптимального управления
1. Основная задача оптимального управления. Предпо-
Предположим, что поведение управляемого процесса описывается
системой обыкновенных дифференциальных уравнений
/(*(<), u(t)9 t), 0<*;<7\ x@) = x.. (8.1)
Здесь вектор x(t)?En, его обычно называют фазовым век-
вектором; вектор и (t) ? Ег называется вектором управлений
Все компоненты вектор-функции f (х, и, t) дифференци-
дифференцируемы по совокупности переменных х и и. Рассмотрим
вначале случай, когда задан интервал Т изменения неза-
независимой переменной t и фиксирован начальный фазовый

§ 8] УСЛОВИЯ МИНИМУМА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ 79
вектор х0. Во многих прикладных задачах роль независи-
независимой переменной t играет время, система (8.1) описывает
некоторый процесс движения, поэтому часто говорят, что
рассматриваемая задача есть задача с фиксированным вре-
временем (движения). Тот случай, когда никаких ограничений
на вектор х(Т) не наложено, называется задачей со сво-
свободным правым концом.
Кусочно-непрерывную функцию и = и (t), принимаю-
принимающую на интервале O^it^T произвольные значения из
некоторого заданного множества U r-мерного простран-
пространства Ег, будем называть допустимым управлением.
Задав допустимое управление «(/), из решения задачи
Коши (8.1) однозначным образом определим непрерывное
кусочно-дифференцируемое решение x = x(t) на интервале
О ^ / ^ 7\ Критерием качества управления является тер-
терминальный функционал
R=b(x(T)), (8.2)
определенный на паре {x(t), u(t)}. Функция Ь (х) предпо-
предполагается всюду дифференцируемой.
Задача состоит в отыскании допустимого управления
u(t) и соответствующего ему решения x(t) системы (8.1)
таких, чтобы функционал R принимал наименьшее воз-
возможное значение.
Поставленная задача оптимального управления отли-
отличается от рассматриваемых в классическом вариационном
исчислении задач только тем, что здесь введено требова-
требование u(t)?U. Необходимое условие минимума для таких
задач впервые сформулировано и доказано Л. С. Понтря-
гиным и его учениками и носит название принципа мак-
максимума. Ниже мы дадим его формулировку в форме, не-
несколько отличной от приведенной в первоисточнике.
Введем в рассмотрение вектор-функцию p(t), удовлет-
удовлетворяющую следующей системе обыкновенных дифферен-
дифференциальных уравнений:
Используя принятые сокращенные обозначения, эту си-
систему можно переписать в компактном виде
-М*@. "('), t)P(t). (8.3)

80 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
Потребуем, чтобы в конце движения выполнялось условие
(8.4)
Таким образом определенную вектор-функцию p(t) будем
называть импульсом. Введем вспомогательную .функцию
Н(х, и, U Р) ==</(*. и, t), р>,
называемую обычно гамильтонианом.
Допустимое управление u(t), определенное на интервале
0 ^ t ^ T и доставляющее наименьшее значение функцио-
функционалу R, будем называть оптимальным управлением и
обозначать ««(/), соответствующее управлению и* (t) реше-
решение системы (8.1) оптимальной траекторией и обозначать
x*(t). Если в (8.3) и (8.4) в качестве u(t) и x(t) взять
соответственно a*@HJC*@' To полученный импульс будем
обозначать р*(/). Необходимое условие минимума в постав-
поставленной задаче оптимального управления состоит в сле-
следующем.
Теорема 1.8.1. Пусть и*(t)—оптимальное управле-
управление, х* (t)—оптимальная траектория системы (8.1). Тогда
существует импульс p*(t) такой, что при O^t^iT вы-
выполнены условия:
1) в точке и = и« (t) достигается минимальное значение
функции H(x*(t), и, t, pm(t)) no и на множестве U, т. е.
(*), и, /, p.(t))\ (8.5)
ueU
2) если правые части системы (8.1) не зави-
зависят явно от t (система автономная), то функция
Н(x*(t), u*(t), p*(t)) принимает постоянное значение.
Приведенное необходимое условие минимума будем назы-
называть принципом минимума для задач оптимального управ-
управления. Л. С. Понтрягиным был сформулирован принцип
максимума, причем использовался импульс, удовлетворяю-
удовлетворяющий системе (8.3), но, в отличие от (8.4), краевое усло-
условие имело вид
поэтому условие (8.5) записывалось по-иному:
ы. (f) €Arg max #(**(/), и, t, p*(t)).
«б U

§8] УСЛОВИЯ МИНИМУМА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ 81
Таким образом, отличие не является существенным, однако
избранная нами формулировка несколько удобней, осо-
особенно при рассмотрении игровых задач и при установлении
связи принципа минимума с аналогичными необходимыми
условиями минимума для задач нелинейного программи-
программирования.
Воспользуемся результатами § 4. Согласно теоре-
теореме 1.4.1, если при фиксированном значении f функция
#(#*(/), и, t, /?¦(/)) дифференцируема по и в точке
и = иф(г) и множество U выпуклое, то из (8.5) следует,
что имеет место условие
и.@€Argmin<#.(*•(<). МО. t,P.№u-u.(f)>. (8.6)
не U
Это необходимое условие обычно называют линеаризо-
линеаризованным принципом минимума.
В настоящее время существует целый ряд различных
доказательств теоремы 1.8.1. Они опубликованы во многих
книгах, поэтому здесь доказательство приводить не будем,
сошлемся лишь на книги Л. С. Понтрягина, В. Г. Болтян-
Болтянского, Р. В. Гамкрелидзе, Е. Ф. Мищенко [1], Н. Н. Мои-
Моисеева [1], Р. Габасова и Ф. М. Кирилловой [2].
Можно попытаться на основе принципа минимума по-
построить численный метод решения задач оптимального
управления. При всяком фиксированном наборе x%(t), t,
p*(t) из условия (8.5) найдем точечно-множественное отоб-
отображение
/>•), (8.7)
на котором гамильтониан Н (хф9 и, t> p*) достигает мини-
минимума по u?U. После подстановки (8.7) в уравнения (8.1)
и (8.3) получим систему из 2/г обыкновенных дифферен-
дифференциальных уравнений для я-мерных вектор-функций х* (t),
P.{t):
x* = f(x*> P(x», U P*), t),
P* = -fA**> P(*. t,P.h t)p.. (Ь'Ь)
Для этой системы п условий задано в начальный мо-
момент (на левом конце) и п условий в конечный момент
(на правом конце):
(8.9)

82 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. 1
Таким образом, решение исходной задачи формально све-
сведено к решению краевой задачи для системы из 2/г диффе-
дифференциальных уравнений. Если решить эту задачу, т. е.
определить функции xm{t)f /?*(/), удовлетворяющие си-
системе (8.8) и условиям (8.9), то оптимальное управление
ut (/) для исходной задачи должно находиться среди функ-
функций, представимых в виде (8.7). Описанный прием весьма
удобен при аналитическом решении исходной задачи. Для
численных расчетов он оказался, к сожалению, малоприем-
малоприемлемым. Дело в том, что полученная краевая задача обычно
оказывается существенно нелинейной. Отображения р часто
бывают разрывными, что приводит к тому, что правые
части системы (8.8) становятся негладкими либо даже неод-
неоднозначными. Краевая задача не всегда обладает единствен-
единственным решением, процедуры ее решения часто оказываются
расходящимися. В лучшем случае для такой задачи можно
определить хорошее начальное приближение, и только
после этого появляется реальная возможность решения
краевой задачи. Эти обстоятельства заставляют для задач
оптимального управления искать иные вычислительные
методы, их описанию посвящена гл. VI.
2. Оптимизация по вектору управляющих параметров.
Среди задач оптимального управления часто встречается
случай, когда оптимизация состоит не только в выборе
управления u(t), но и в определении оптимального значе-
значения вектора управляющих параметров ? ? Es. Система (8.1)
в этом случае имеет вид
¦ЗГ«/(*. и. '. 6)- (8.10)
Минимизируемый функционал также зависит от g: R =
r=b(x(T)y |). Требуется найти допустимый вектор управ-
управлений u(t), вектор управляющих параметров g и соответ-
соответствующее им решение x(t) системы (8.10) такие, что функ-
функционал R принимает возможно меньшее значение.
Необходимое условие минимума дается теоремой 1.8.1,
в которой в качестве / (х, и, t), b(x) берутся соответственно
/ (х, и, t, ?) и Ь(х, \) и вводится одно дополнительное усло-
условие минимума функционала R по ?, имеющее вид
6)+ $/$,(*(*). "@. '. 6)Р(/)Л-О. (8.11)

§8J УСЛОВИЯ МИНИМУМА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ 83
Оно должно выполняться вдоль оптимальной траектории,
т.е. при u(t) = u%(t)9 x(t) = xm(t), p(') = />• @.6=*Б», где
|# — оптимальный вектор управляющих параметров. Усло-
Условие (8.11) добавляет к (8.8), (8.9) s скалярных ооотноше-
ний, необходимых для определения компонент вектора ?.
Теорема 1.8.1 и приведенные здесь утверждения явля-
являются основополагающими результатами в теории рптималь-
ного управления. Ниже будет показано, как с их помощью
можно исследовать разнообразные частные задачи.
3. Задача с фиксированным временем и подвижным
правым концом. В сформулированной выше основной за-
задаче дополнительно потребуем, чтобы фазовый вектор x(t)
в заданный конечный момент Т принадлежал терминаль-
терминальному множеству
где дифференцируемые вектор-функции g и h осуществляют
отображения
g: Еп-*Ее, h: En~*Ec.
Как и в случае задач нелинейного программирования,
в качестве функционала возьмем функцию, аналогичную
F.25):
R(х, й, v, q) = qb(х) + 2 ufgf (д) + 2 vW(x), (8.12)
i = 1 / as 1
здесь q?Ei, u?Ee, v?E%.
Утверждение теоремы 1.8.1 остается в силе, следует
внести лишь некоторые изменения: вместо (8.4) надо ис-
использовать следующее условие:
p(T)^Rx(x(n й9 v, q). (8.13)
Кроме того, должны быть выполнены условия дополняю-
дополняющей нежесткости
Если условия на правом конце удовлетворяют условию
регулярности ограничений, то можно положить q = 1; вве-
введение новых неизвестных двойственных переменных и, v
«компенсируется» условием х (Т) 6 X. С помощью принципа
минимума задачу можно свести к краевой.

84 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. I
4. Задачи Лагранжа, Майера и Больца. В случае за-
задачи Лагранжа минимизируемый функционал записывается
в виде интеграла
т
/?=$Д (*(*), «(*), t)dt,
О
где В—дифференцируемая функция х и и.
Введем дополнительную фазовую переменную хп+1 при
помощи уравнения
*gi = B(x, и, t)9 х»+Ц0) = 0.
Теперь задачу можно сформулировать как задачу об отыс-
отыскании управления u(t), доставляющего на фиксированном
интервале движения [О, Т] минимум терминального функ-
функционала
при наличии связей
?-/<*,«. 0. *г=В(х, и, t).
Таким образом, в расширенном фазовом пространстве Еп+1
задача свелась к основной, рассмотренной выше. В каче-
качестве гамильтониана берется функция
#(*, *»+1, и, U Р> Pn+1) = <f(x, и, t), р> + В(х9 и, *)РЯ+*.
Уравнение (8.3) и условие (8.4) заменяются следующими:
-§.=—fxP-Bx, р(Т)=о, р-+1@«1.
Если требуется, чтобы в конце движения х?Х, то из
(8.13) следует, что должно выполняться условие
p(T)=t й*&(х (Л)
1
где о(х(Т))—множество активных ограничений типа не-
неравенства. Это условие в вариационном исчислении обычно
называют условием трансверсальности, оно имеет простой
геометрический смысл: вектор р (Т) € Еп должен быть орто-
ортогонален касательному подпространству к терминальному
множеству X.

§ 8] УСЛОВИЯ МИНИМУМА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ 85
Задача Майера с фиксированным временем состоит в ми-
минимизации функционала вида
R=b(x(T), Т). (8.14)
С помощью введения дополнительной фазовой переменной
x*+1 = t систему (8.1) сведем к автономной
— — f Га: и х»+1) dx"+1 - 1
Л-Пх,и,х ), л -1,
R = b(x(T), x»+i(T))
Расширенный импульс состоит из вектора р (t), удовлетво-
удовлетворяющего системе (8,3), и скаляра рп+1, для которого
p±t{x, и, t)pHt). (8.16)
Условия в конце движения следующие:
p»+1(T)=bT(x(T)fT).< (8.17)
Гамильтониан расширенной системы постоянен вдоль опти-
оптимальной траектории:
<f(x9 и, t), p(t)>+p»+1(t) = const.
Задача сведена, таким образом, к основной.
В задаче Больца функционалом является выражение
5а(д:, и, tfdt.
о
Введем две дополнительные фазовые переменные
dt ~"" ' dt "" °\л* и> л /»
тогда минимизируемый функционал будет иметь вид
В расширенном фазовом пространстве Еп+2 задача снова
сведена к основной, к ней применима теорема 1.8.1.
5. Задача с нефиксированным временем. Требуется
найти вектор управлений u(t), интервал [О, Г] изменения
независимой переменной t и соответствующее решение x(t)
системы (8.1) так, чтобы терминальный функционал (8.14)

86 ВВЕДЕНИЕ В ТЕОРИЮ ОПТИМИЗАЦИИ [ГЛ. 1
принимал наименьшее возможное значение. Предполагаем,
что такой интервал существует и отличен от нуля.
Сделаем в системе (8.15) замену независимой перемен-
переменной, положив t = %\. Тогда система (8.15) примет вид
e. (8.18)
Считаем, что новая независимая переменная т изменяется
на фиксированном отрезке [О, Го]. Для системы (8.18)
будем отыскивать вектор управлений и (т) и управляющий
параметр | так, чтобы при т = То функционал R = b(x (То),
хп+1(Т0)) принимал возможно меньшее значение.
Мы пришли к задаче с фиксированным временем, сво-
свободным правым концом и одним управляющим параметром.
Из условия (8.11) следует, что вдоль оптимальной траек-
траектории выполняется условие
Го
S ~0. (8.19)
Учтем, что подынтегральное выражение постоянно, перей-
перейдем к первоначальным переменным и, воспользовавшись
условием на правом конце (8.17), получим
Ьт(х(Т)9 Т) + Н(х(П и(Т)9 Т, р(Г)) = 0,
Ьх(х(П Т). (8.20)
После решения оптимизационной задачи (т. е. нахождения
u(t) и |) оптимальное время движения определяется по
формуле Т**Т&, где То—заданное перед началом расче-
расчетов произвольное положительное число (можно всегда счи-
считать, например, что То— 1). Утверждение теоремы 1.8.1
о выполнении свойства (8.5) остается в силе, первое соот-
соотношение в (8.20) формально дает длполнительное условие
для определения оптимальной веоичины времени движе-
движения Г.
6. Задача на быстродействие. Требуется найти вектор
управлений u(t), соответствующее ему решение x(t) си-
системы (8.1) так, чтобы вектор x(t) за кратчайшее время
попадал на множество X.
Интервал изменения независимой переменной в этом
случае неизвестен. Поэтому, как и в трех предыдущих

§ 8] УСЛОВИЯ МИНИМУМА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ 87
случаях, введем новую фазовую переменную хп+1, перейдем
к системе (8.15), выполним замену независимой перемен-
переменной, положив /^т|, получим систему (8.18), для которой
требуется на фиксированном интервале [О, То] найти управ-
управление и(х) и параметр I так, чтобы х (Т0)?Х и функцио-
функционал хп+1(Т0) принимал наименьшее возможное значение.
Введем вспомогательную функцию /?, аналогичную (8,12):
R = qx*+i + 2 g* (х) и* + 2 Ы (х) Ы.
i \ / i
Здесь q^O, v^O. Необходимое условие минимума (8.11)
приводит к (8.19), откуда следует
Н(х(П и(Т), Т,
кроме того, появляются условия дополняющей нежестко-
нежесткости hS(x)v' = 0 и условия g(x(T)) = 0, Л(х(Г))<0.
Аналогичным образом многие другие задачи оптималь-
оптимального управления сводятся к основной задаче. Теорема 1.8.1
неприменима, однако, в том весьма распространенном и
важном случае, когда на фазовые координаты и управле-
ления наложены смешанные ограничения вдоль траектории
вида
g(x(t)9 u(t), 0 = 0, Л(*(/), и@, *)<0.
Свойства таких задач исследованы в работах А. Я. Ду-
бовицкого и А. А. Милютина [1], Э. Р, Смольякова [1],
В. П. Анорова [1]. Необходимые условия минимума здесь
записываются сложнее и малоприемлемы для создания на
их базе численных методов. Не будем останавливаться на
этих условиях, так как они не понадобятся в дальнейшем
для построения численных методов, которые будут осно-
основаны на других идеях, идущих от нелинейного програм-
программирования.

ГЛАВА II.
ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ
К ИССЛЕДОВАНИЮ ЧИСЛЕННЫХ МЕТОДОВ
В данной главе приводятся основные математические
результаты, которые будут широко использованы в даль-
дальнейшем при обосновании сходимости численных методов.
Излагаются прежде всего методы теории устойчивости:
устойчивость по первому приближению и метод функций
Ляпунова; даны теоремы о сходимости сжимающих отобра-
отображений и точечно-множественных отображений, приведены
методы решения систем нелинейных уравнений и методы
отыскания минимакса.
§'1. Устойчивость по первому приближению
1. Основные определения. Рассмотрим систему обык-
обыкновенных дифференциальных уравнений
где вектор-функция f(x, t)?C1xt(EnxI+), т.е. при каж-
каждом t^O f непрерывно дифференцируема по х всюду на Еп,
при любом х непрерывна по t на множестве /+. В этом
случае начальное условие х @) = х0 определяет единствен-
единственное решение системы A.1), которое будем обозначать
* = *(*<» *)•
Определение 2.1.1. Будем говорить, что система
A.1) устойчива по Лагранжу, если:
1) каждое решение х(х0У /), где /?/+, неограниченно
продолжимо (вправо), т. е. имеет смысл при любых /?/+;
2) норма |х(хв, Щ ограничена на /+.
Определение 2.1.2. Решение х(хЩ9 t) системы A.1)
называется устойчивым по Ляпунову при / —> оо (или,
короче, устойчивым), если для любого 8 > 0 существует
6 = 6(е) такое, что:

§ 1] УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ 89
1) все решения х(х0, t) системы A.1), удовлетворяю-
удовлетворяющие условию
К-*|< в A.2)
определены в промежутке 0^ t < оо;
2) для этих решений справедливо неравенство
\\х{х0, t)—x(x., Щ<г V<€/+. •
Другими словами, решение х(х*, f) устойчиво, если
все другие решения, начавшиеся в достаточно малой окрест-
окрестности точки хт, остаются при любых t ? /+ внутри окрест-
окрестности, построенной вокруг решения х(х*у t). Устойчивость
означает непрерывную, равномерную по t? /+ зависимость
решений x(xQ, t) системы A.1) от начальной точки х0.
Определение 2.1.3. Решение х(хф, t)@^t<oo)
называется асимптотически устойчивым (при t —+ оо) если:
1) это решение устойчиво по Ляпунову;
2) всякое решение x(xQ, t), удовлетворяющее A.2),
обладает свойством
lira \\x(x0, f)-x(x., 011 = 0. A.3)
t
Определение 2.1.4. Решение х(х«,
называется асимптотически устойчивым в целом, если оно
асимптотически устойчиво и условие A.3) имеет место для
решений х(х0, t) системы A.1) при любых хо?Еп.
Часто бывает удобно свести систему A.1) к такому
виду, чтобы точка х = 0 являлась положением равновесия,
т. е. /@, /) = 0 для любых t?l+. В этом случае система
A.1) имеет тривиальное решение л; @, t) = 0, которое будем
обозначать *(/) = (). Определения 1.2.3 и 1.2.4 можно
переформулировать следующим образом.
Определение 2.1.5. Тривиальное решение *(/)==()
системы A.1) Называется асимптотически устойчивым,
если для любого 8 > 0 существует б = б (г) такое, что для
любого решения A.1), удовлетворяющего условию || дсо|| < б,
имеет местсулг(л;0, ОЦ^е для всех t?l+J
lim x{x0, 0 = 0. 0-4)
t -*¦ оо
Определение 2.1.6. Тривиальное решение х@ = 0
системы A.1) называется асимптотически устойчивым в це-
целом, если:

90 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
1) оно устойчиво по Ляпунову;
2) для любого хо$Еп выполнено условие A.4).
Определение 2.1.7. Тривиальное решение л; (/) = ()
системы A.1) называется экспоненциально устойчивым, если
существует окрестность начала координат G такая, что
для любого xQ?G справедливо неравенство
!*(*•. <)|<JV^, A.5)
где N, к—некоторые положительные числа, независящие
от конкретного выбора точки х0.
Из экспоненциальной устойчивости тривиального реше-
решения x(t) = O следует его асимптотическая устойчивость.
Действительно, для произвольного 8 > 0 положим
тогда из A.5) будет следовать, что||д:(а:0, *)||^8 и> кроме
того, имеет место A.4).
Методы обоснования асимптотической устойчивости ока-
оказываются весьма полезными для обоснования сходимости
численных методов оптимизации. Некоторые численные ме-
методы сводятся к отысканию предельных точек для системы
обыкновенных дифференциальных уравнений вида A.1),
причем системы составляются таким образом, что их ре-
решения х(х0, t) при t—* оо стремятся к решениям исход-
исходной оптимизационной задачи. Система A.1) при этом назы-
называется численным методом решения оптимизационной за-
задачи.
2. Вспомогательная лемма.
Лемма 2.1.1 (Гронуолла—Беллмана). Пусть функции
u(t) и v(t) непрерывны при t?[a, оо), задано число С> 0,
при t^a выполнено неравенство
тогда при t^a имеет место неравенство
t

jl] УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ 91
Доказательство. Умножим обе части исходного
неравенства на |t>|
\v(t)\\u(t)\^\v(t)\\c+l\u(s)\\v(s)\ds\.
Введем обозначение w (t) = J | и (s) \ \ v (s) \ ds. Тогда полу-
a
ченное неравенство можно представить следующим образом:
или, учитывая, что 0 <C + w(t), имеем
Интегрируя обе части, находим
t
\n(C + w(t)) —
откуда следует
Учитывая исходное неравенство, получим
t
Мы пришли, таким образом, к требуемому неравенству. Щ
3. Основная теорема. Рассмотрим систему специального
вида '
^ = Л*+Ф(л;, *), A.6)
где А—квадратная матрица порядка п.
Определение 2.1.8. Функция v(x, t) имеет беско-
бесконечно малый высший предел при х—*0, если для любого
е > 0 существует б = б (е) такое, что | v (x, t) \ < е при
11*1)< б и всех t?l+.

92 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. И
Теорема 2.1.1 (Ляпунова об устойчивости по первому
приближению). Пусть в системе A.6) матрица А постоян-
постоянная, все ее характеристические числа имеют отрицатель-
ные действительные части. Функция ||ф(х, /)||/1|х\ имеет
бесконечно малый высший предел при х-+0. Тогда три-
тривиальное решение х(/)==0 системы A.6) экспоненциально
устойчиво.
Доказательство. Для системы A.6) фиксируем
начальную точку xo?Gy где G — некоторая окрестность
начала координат. Решение системы A.6) удовлетворяет
следующему интегральному уравнению:
х (х0, t) = е"х0 + S *'-•> -Ч (х (*„ s), s) da. A.7)
О
Здесь квадратная матрица Q)(f) = etA определяется по фор-
формуле
и удовлетворяет системе
Дифференцируя A.7) по / с учетом этих свойств, по-
получим, что всякое решение A.7) удовлетворяет A.6). Из
того, что характеристические числа матрицы А имеют
отрицательные действительные части, следует, что при
t^O существуют такие числа k > 0, т) > 0, что
Используя это неравенство, из A.7) получим
Для любого е > 0 существует такое б, что || ф (х,
^||х\\/k для всякого |xj < 6 и при любом ^
Пусть ||JCo||<6. Тогда найдется такое Т > 0, что при
всех 0 </< Т выполнено неравенство || х (xQ, t) || < б и
(x%9 s)\\ds.

§ Ц УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ 93
Воспользуемся леммой 2.1.1, получим оценку
", A-8)
справедливую при 0 < t < Т. Выберем & настолько малым,
что 8 < г]. Тогда из полученного неравенства следует:
jх(х0, t)||<klх01 до тех пор, пока ||х(xOi t)|| < б. Если
взять ||#о||<о/&, то A.8) имеет место для всех /^0, что
завершает доказательство теоремы. Щ
Анализ устойчивости широкого класса систем сводится
к исследованию систем вида A.6). Действительно, пусть
точка а?Еп является положением равновесия для системы
A.1), т. е. f(a, t) = 0. Сделаем замену переменных, поло-
положив х = а-\-у. Тогда приходим к системе
Предположим, что вектор-функция / (х, t) дифференцируема
по х в точке х = а, тогда систему можно представить в виде
! (fl. *)У+\У\У(У, t)=Ay + q>(y, t),
где
А=Я(а, t), Ф(У,О = МТ(У.О.
Ш\у(у, 0| = 0. A.9)
Система A.1), таким образом, сведена к виду A.6) и,
если матрица А постоянная, условие A.9) имеет место
равномерно по /, то можно воспользоваться теоремой
2.1.1. Для экспоненциальной устойчивости положения рав-
равновесия x(t) = a в системе A.1) будет достаточно, чтобы
все характеристические числа матрицы А имели отрица-
отрицательные действительные части. Задача свелась к исследо-
исследованию линеаризованной системы (системы первого прибли-
приближения или, как часто пишут, уравнений в вариациях):
Из экспоненциальной устойчивости этой системы сле-
следует экспоненциальная устойчивость положения равнове-
равновесия для системы A.1). Описанный прием часто исполь-
используется при обосновании сходимости численных методов.
Как будет показано в п. 5 § 3, из этих результатов будет
также следовать локальная сходимость дискретной аппрок-
аппроксимации системы A.1) при достаточно малом шаге интег-
интегрирования.

94 теоремы о сходимости и их приложения [гл. и
§ 2. Метод функций Ляпунова
1. Устойчивость по Лагранжу. В этом параграфе
будем обозначать \tk\ бесконечно возрастающую последова-
последовательность моментов tl стремящуюся к бесконечности, tk—
ее k-VL элемент.
Теорема 2.2.1. Пусть в системе (Ll)f(x>t)€
gC$(?nx /+). Для устойчивости системы A.1) по Лагран-
жу достаточноу чтобы на Епх1+ существовала такая
функция v(x, t), что:
1) w(x)^v(x9 t)y где w{x) —непрерывная^ бесконечно
большая функция;
2) для каждого решения х(х0У t) системы A.1) функ-
функция v(x(Xq, t), t) была невозрастающей относительно пе-
переменной t.
Доказательство. При любом tZ^O имеем
w{x{x0, t))^v(x{x0, 0, 0<о(*о, t). B.1)
Тогда решение х(хОУ t) ограничено. Действительно, если
это не так, то найдется такая последовательность {tk},
сходящаяся к Т^оо, что
lim \\ х (x0
и для бесконечно большой функции w получим
lim w(x(x^ ^)H°°>
что противоречит неравенствам B.1). Таким образом, ре-
решение х (х0, t) неограниченно продолжимо (вправо) и
sup \\х(х0, /)||<оо. Н
Замечания. Второе условие теоремы будет заведомо
выполнено, если функция v(x, t) дифференцируема всюду
по обоим аргументам и ее полная производная по / в
силу системы A.1) неположительна на ?пх/+, т. е.
*. О./(*. 0X0.
Это условие можно несколько ослабить, потребовав, чтобы
оно имело место всюду вне некоторого ограниченного
множества.

§2] МЕТОД ФУНКЦИЙ ЛЯПУНОВА 95
2. Теоремы А. М. Ляпунова об устойчивости. Рас-
Рассмотрим тот случай, когда изучаемый процесс описывает-
описывается автономной системой дифференциальных уравнений
у-/(*). B-2)
т. е. правые части системы не зависят от t. Предполага-
Предполагаем, что /@) = 0 и f(x) удовлетворяет условию Липшица
в некоторой окрестности G точки х = 0.
Непрерывную функцию v(x) назовем положительно
определенной на G, если v > 0 всюду на G, кроме точки
лг=О, где 1>(лг) = О. Аналогично, если и<0 всюду на G,
кроме точки # = 0, где v(x) = 0, то функцию v(x) будем
называть отрицательно определенной на G. Если всюду
на G имеет место неравенство v^O (i/<;0), то будем
говорить, что функция v(x) на G неотрицательна (непо-
(неположительна).
Будем обозначать 5е, Я8 соответственно сферическую
поверхность n-мерного шара с центром в начале координат
и его внутреннюю часть:
S. = {*€?": 11*11 = *}.
Теорема 2.2.2 (Ляпунова об устойчивости). Если
существует положительно определенная на G дифферен-
дифференцируемая функция v (х), производная которой по времени,
вычисленная в силу системы B.2), неположительна на G,
то тривиальное решение jt(tf)s=0 системы B.2) устойчиво
по Ляпунову.
Доказательство. Пусть г > 0, HBcG. Обозначим
X = min v (x).
5
Так как функция v (х) непрерывна и v @) = 0, можно ука-
указать число б ? @, е) настолько малое, что
sup v (х) = Яо < Я.
хен6
Пусть лго€#в, рассмотрим решение B.2) х^х(х0, t). Если
бы это решение пересекло сферическую поверхность Se

96 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
при некотором t = ti, то получили бы, что v (х (x09
С другой стороны,
Следовательно, v(x(xOi t)) является невозрастающей
функцией /, поэтому v(x(xQ, t))^v(xo)^Ko<X и, сле-
следовательно, траектория (решение) х(х09 t) ни при каких
t^O не пересечет поверхность Se. Щ
Теорема 2.2.3 (Ляпунова об асимптотической устой-
устойчивости). Если существует положительно определенная
на G дифференцируемая функция v(x), полная производ-
производная которой по ty вычисленная в силу системы B.2)—отрица-
B.2)—отрицательно определенная на G функция, то тривиальное реше-
решение *(<)== О системы B.2) асимптотически устойчиво.
Доказательство. Согласно предыдущей теореме
для любого числа R > О существует такое число г ? (О, R),
что из условия xb^HraG следует, что x(xQ> t)^H^c:G
при любых t > 0. Покажем, что для любого 8 ? @, R)
существует такое 7\ что х(х0, t)?He при всех />Т.
Для числа е можно указать 0 < б < min [e, г] такое,
что х (#0, t) g Н8 при всех t > 0, если только хо?Нб. Пусть
траектория х (xQ, t) не попадает в Н6 ни при каких / ^ 0,
тогда x(xQy t)?HR\H6,
где t= sup <vx(x)y f(x)>. Устремляя /—>«>, получим,
что lim v (x (x0, t)) < 0. Это противоречит положительной
/->со
определенности v{х) на Я^сб. Поэтому найдется Т та-
такое, что х (х0, Т) ? Яа, но тогда решение уже не пересе-
пересечет Se ни при каком / > Т. Так как в качестве 8 было
взято произвольное, сколь угодно малое число, то
Шпл;(л;0, t) = 0. Щ
t-+CD
Введенные для обоснования устойчивости функции v (x)
в дальнейшем будем называть функциями Ляпунова, а ме-
метод доказательства на основе их использования —методом
функций Ляпунова.

§2] МЕТОД ФУНКЦИЙ ЛЯПУНОВА 97
В приведенных теоремах совершенно не существенно,
что положением равновесия для системы B.2) является
начало координат. Возможно, что /(я) = 0, в этом слу-
случае функцию Ляпунова v (х) будем называть положительно
определенной, если v(a) = 0 и v(a)>0 для всех хфа,
принадлежащих некоторой окрестности точки я. Теоремы
Ляпунова дадут достаточные условия устойчивости триви-
тривиального решения х (t) e= а.
Метод функций Ляпунова широко используется при
исследовании разнообразных технических задач, в которых
система B.2) задана и требуется подобрать некоторые ее
параметры так, чтобы обеспечить устойчивость положения
равновесия. При создании численных методов оптимиза-
оптимизации ситуация другая: система B.2) подбирается таким
образом, чтобы точки решения исходной оптимизационной
задачи были бы для нее асимптотически устойчивыми
положениями равновесия. Для доказательства отрицатель-
отрицательной определенности производной функции Ляпунова при-
привлекаются обычно достаточные условия экстремума в ис-
исходной задаче.
3. Случай неавтономных систем. Полученные в п. 2
результаты переносятся на более общий случай неавтоном-
неавтономных систем вида A.1). Для этого вместо v(x) вводится
функция v (л:, t) cCDiZ), где Z = G х /+.
Определение 2.2.1. Функция v(x> t) называется
положительно определенной на Z, если существует непре-
непрерывная функция w(x), определенная на G, такая, что
0<w(x)^p(x, t) при хфО и w(O) = v(O, /) = 0.
Аналогично функция v(x, f) называется отрицательно
определенной на Z, если существует непрерывная функция
w(x) на G такая/рчто v(х, Л<w(х)< 0 при хфО л
@) @0 0 ""
() (,0
Предполагаем, что система A.1) такова, что /@, <) = 0,
f{xy t)?Cl}(Z), тогда имеют место следующие две теоре-
теоремы А. М. Ляпунова.
Теорема 2.2.4. Если существует положительно опре-
определенная на G дифференцируемая функция v(x, t)€C%(Z)%
имеющая неположительную производную в силу системы
A.1), то тривиальное решение *(/) = () системы A.1)
устойчиво по Ляпунову.
Теорема 2.2.5. Если существует положительно оп-
определенная на G дифференцируемая функция v(x, t) G%(Z)
4 ю. Г9 Евтушенко

98 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
допускающая бесконечно малый высший предел при х—+0
и имеющая отрицательно определенную производную по t
в силу системы A.1), то тривиальное решение *(?)== О
системы A.1) асимптотически устойчиво.
Доказательство в основных чертах повторяет доказа-
доказательство теорем 2.2.2 и 2.2.3 и поэтому не приводится.
4. Теоремы об асимптотической устойчивости в це-
целом. Рассмотрим систему A.1), предполагаем, что / @, f) = О,
f(x, t)?C)?t(Z). Здесь и ниже в этом пункте Z = EnxI+.
Определение 2.2.2. Будем говорить, что функция
v (x, t) ? CJS (Z) допускает бесконечно большой низший пре-
предел при х—>оо, если v (x, f)—>oo равномерно по t при
х —>оо, т. е. для любого М > О существует такое R = R (М),
что \v(x, t)\>M при всех \х\> R, t?l+.
Определение 2.2.3. Будем говорить, что функция
v(x, t)?Cl°t(Z) допускает сильный бесконечно малый выс-
высший предел при х—+0, если существует такая непрерыв-
непрерывная на Еп функция w (х)у что \v(x, t)\ ^ w (x) при [х9 t]?Z
и w@) = 0.
Теорема 2.2.6 (Барбашина—Красовского). Пусть
для системы A.1) существует положительно определен-
определенная на Z Ьифференцируемая функция v(x, ^)^СЙ(^), до-
допускающая сильный бесконечно малый высший предел при
х —> 0 и бесконечно большой низший предел при х —* оо,
причем производная v(x, f) в силу системы A Л)—отри-
Л)—отрицательно определенная на Z функция. Тогда тривиальное
решение л:(*) = 0 системы A.1) асимптотически устой-
устойчиво в целом.
Доказательство теоремы можно найти, например,
в книге Б. П. Демидовича [1].
5. Приложения к обоснованию сходимости численных
методов. Рассмотрим задачу об отыскании безусловного
минимума дифференцируемой функции f(x). Для числен-
численного решения задачи А. Коши предложил метод, в кото-
котором отыскиваются предельные точки решения следующей
системы дифференциальных уравнений:
g=-U*), *@) = *0. B.3)
Приведенные выше теоремы позволяют дать несколько
достаточных условий сходимости. Предполагаем, что су-
существует по крайней мере одно решение х = х* задачи

§2] МЕТОД ФУНКЦИЙ ЛЯПУНОВА 99
минимизации. Воспользуемся вначале методом функций
Ляпунова. Введем следующие три функции:
*i(*wm-/(*). м*)=т1м*)р. M*)=4ik-*j2-
Если считать, что хт является изолированной точкой ло-
локального минимума функции /(*), то существует окрест-
окрестность G (#„), где эти функции положительно определены.
Продифференцируем их в силу системы B.3), получим
Если в точке х = х* выполнены достаточные условия
минимума, приведенные в теореме 1.3.2, то функции vx
и v2 будут отрицательно определены по крайней мере при
х 6 G (*•) и из теоремы Ляпунова об асимптотической
устойчивости будет следовать локальная сходимость мето-
метода B.3) к точке х = хф.
Если функция / строго выпукла, то, используя тео-
теорему 1.2.5, получим, что и3</ (#•) — /(#Х0для*€ G(xm).
Производная vz таким образом, отрицательно определена
и, следовательно, метод B.3) сходится по крайней мере
локально к точке х = х*.
Воспользуемся теоремой Барбашина—Красовского.
Будем считать, что функция / (лг) строго выпукла всюду
на Еп. Тогда задача минимизации имеет единственное
решение х = х*, функция v3(x) допускает бесконечно ма-
малый высший предел при х—+х*, так как v3 (х*) = 0. Кроме
того, согласно теореме 1.1.2, v3(x)—бесконечно большая
функция и потому допускает бесконечно большой низший
предел при |*||—*оо. Производная v8 отрицательно оп-
определена всюду на Еп9 поэтому решения B.3) сходятся
к точке х = х* в целом. Метод B.3) является релакса-
релаксационным, так как в нем / (х(х0, t))—монотонно убыва-
убывающая функция t. Кроме того, в этом методе монотонно
убывает норма градиента функции / (х) и расстояние от
«текущей» точки x(xQy t) до точки минимума хч.
Если воспользоваться теоремой об устойчивости по
первому приближению, то приходим к системе
А*

100 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Если матрица fxx(x0) положительно определена, то все
характеристические корни матрицы— fxx(x^) будут дейст-
действительные, строго отрицательные. Отсюда следует локаль-
локальная экспоненциальная сходимость метода B.3)jk точке
локального минимума.
Как видно из рассмотренного примера, применение
различных теорем о сходимости или даже одной и той же
теоремы 2.2.3, но с разными функциями Ляпунова, по-
позволяет составить более полное представление об изучае-
изучаемом методе. К сожалению, далеко^не во всех случаях
удается так же просто строить функции Ляпунова.
Пусть функция f(x) всюду дважды непрерывно диф-
дифференцируема и матрица fxx (x) всюду невырождена, тогда
можно рассмотреть метод, в котором отыскиваются пре-
предельные точки следующей задачи:
Ш №Шж(*)' B-4)
Для обоснования сходимости воспользуемся функцией
Ляпунова v (х) = </* (я), fx (*)>. Дифференцируя v в силу
B.4), получим
откуда следует, что v(t) = v(Q)e~2t. Метод, таким образом
при t -+ оо сходится к стационарным точкам функции / (х)
Метод B.4) обычно называют непрерывным аналогом
метода Ньютона, описание которого будет дано в § 5.
Рассмотрим задачу об отыскании минимакса A.5.2).
Предполагаем, что функция F (х, у)—строго выпукло-
вогнутая и обладает седловой точкой [хт, уф] (см. § 5 гл. I).
Простейший численный метод решения этой задачи состоит
в отыскании предельных точек решений следующей системы:
^-F^x.y), %~Fy{x,y). B.5)
Для доказательства сходимости воспользуемся положи-
положительно определенными функциями
М*. у) «4 ИМ*. yW+\Fw(*. у)П
М*. у)«4п*-*.

$ 21 МЕТОД ФУНКЦИЙ ЛЯПУНОВА 101
Если функция F (х9 у) дважды дифференцируема на
ЕпхЕт, матрицы Fxx(x9 у) и —Fyy(x9 у) всюду положи-
положительно определены, то
$ — Я(х, y)Fxx(x9 y)Fx(x9 y) +
+ FTy{x9y)Fyy{x9y)Fy(x9y)^09
причем знак равенства имеет место лишь в точке х = х*9
У = У*-
Продифференцируем v2 в силу системы B.5), восполь-
воспользуемся условием строгой выпуклости—вогнутости и нера-
неравенствами A.5.16), получим
v2 = <Fх (х> У), хф—х> + <Fy (х, у)9 у—
y)-F(x, y)+F(x, y)-F(x9
причем знак равенства имеет место тогда и только тогда,
когда х = х*, у = у*. Используя теорему Барбашина—Кра-
совского, приходим к выводу, что в том случае, когда функ-
функция F(x9 у) дифференцируема и всюду строго выпукло-
вогнутая, метод B.5) сходится к единственному решению
задачи A.5.2) в целом.
Рассмотрим частный случай задачи A.5.2), когда л= /п=1,
F(x,y)=xy. Легко проверить, что точка [0, 0] будет седловой. Ме-
Метод B.5) приводит к следующей системе:
2F—* !=*• <2-6)
Дифференцируя положительно определенную функцию v(x, y)=x2-\-y*
в силу этой системы, получим^что Ь(х, у)<*0. Система B.6) сводит-
сводится к уравнению 'Ш"\~У—®> решение которого
не имеет предела при t—».оо. Этот пример показывает, что при исполь-
использовании метода функций Ляпунова следует тщательно проверять выпол-
выполнение всех условий. В данном случае производная i> = 0, поэтому
здесь выполнены условия теоремы 2.2.2 Ляпунова об устойчивости,
но не имеет места условие теоремы 2.2.3 Ляпунова об асимптотичес-
асимптотической устойчивости.
6. Понятие сходимости. Из рассмотренных выше двух
примеров видно, что для численных методов важно стрем-
стремление решений систем дифференциальных уравнений к
некоторому множеству Хф> т. е. их сходимость к Хт. Из

102 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
того, что точка х% является асимптотически устойчивым
положением для системы A.1), следует локальная сходи-
сходимость решений A.1) к х«. Обратное, вообще говоря, не
имеет места. Поэтому условия сходимости должны быть
слабее условий асимптотической устойчивости. В числен-
численных методах само понятие сходимости можно трактовать
более широко, чем стремление х(х0, t) к х* при t—юо.
В связи с этим дадим ряд определений.
Определение 2.2.4. Точка х?Еп есть (о-предель-
ная точка решения х(х0, t) системы A.1), если сущест-
существует последовательность {tk\, такая, что Нтлс^о, tk) = x.
Совокупность со(лго) всех со-предельных точек решении
x(xQ9 t) называется его ^-предельным множеством.
Определение 2.2.5. Метод A.1) сходится к мно-
множеству Х*с:Еп локально (или на Х9 или в целом), если
со(*0) = Х» для любых х0, принадлежащих некоторой ок-
окрестности G(X«) (или соответственно X, или Еп).
Сходимость метода на X к множеству X», таким об-
образом, означает, что для любого х0 ? X и любого г > 0
существует такое Т (х09 в), что при всех t^T(x09 г) будет
dis (лг (л:0, ?),Х«)<е.
Обозначим Q = EnxI+.
Лемма 2.2.1. Пусть для системы A.1) можно ука-
указать дифференцируемую, неотрицательную на Q функ-
функцию v (x, t) такую, что ее полная производная по времени
v(x, t), взятая в силу системы (IЛ)у неположительна на Q;
решение х(х0, t) продолжимо при t-+<x>. Тогда:
а) для любой последовательности \tk\ определен
lim v (x(x0> tk), tk)\ этот предел не зависит от конкретного
выбора подпоследовательности {tk}\
б) существует такая последовательность {//}, что
Доказательство. Так как v(x, t)^0 и v(x9
на Q, то определен lim t; (л: (лг0, /), t) = v(x0). Следователь-
но, и для любой последовательности {tk} выполнено ут-
утверждение а). Предположим, что не существует последо-
последовательности {/,-}, для которой lim v (х (хи, /,.), //) = 0. Тогда

§ 2] МЕТОД ФУНКЦИЙ ЛЯПУНОВА ЮЗ
можно указать б > 0 и Т (б) > 0 такие, что v(x(xOf t), t) <—б
при *>Т(б). Отсюда следует, что v(x(x0, t), /)—>—оо,
но это противоречит неотрицательности v (x, t) на Q. Лем-
Лемма доказана.
Введем следующие два множества:
*: dis(*f Х.)< в},
»: dis (*,*•) = в}.
Считаем, что множество X* компактно.
Теорема 2.2.7 (Ю. Г. Евтушенко [9]). Пусть реше-
решения A.1) продолжимы при t—+oo и существует такая
непрерывно дифференцируемая на Еп функция v(x), что
v(x) = 0 при х?Х* и v(x)>0 при х(?Х*\ пусть, кроме
того у производная v(x) в силу системы A.1) удовлетворя-
удовлетворяет условиям: для любого е > О существует такое t (г),
что для всех t^t(s) выполнены условия
t
p(e,t)= sup t>(*)<0, lim С p(e, s)ds = —oo. B.7)
Тогда метод A.1) сходится к множеству Хф в целом.
Доказательство. Покажем, что для любых фик-
фиксированных 8 > 0, хо?Еп существует такое 7\ что
х (х0, t) ? Ge для всех t > Т. Обозначим %е = min v (x).
д:ег8
Так как v(x) = 0 всюду на Х„, можно взять настолько
малое б?@, е), что
О < max v (х) = Хб < Хг.
Т
Покажем, что в качестве Т можно взять любое число,
удовлетворяющее следующим двум условиям:
B.8)
Покажем, что такое число существует. Предположим
противное, для всех t>t(8) x(x0J t)^G^ тогда вдоль
траектории x(xQ, t) имеем
t
о(*(*., t))-v(x(x0, <(«)))< JpF, s)ds.

104 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Устремляя t —* оо и учитывая B.7), приходим к гтому,
что v(x(xQr t))-+ — оо, что невозможно, так как v(x)^0f
поэтому найдется Т, удовлетворяющее B.8). Траектория
x(x0J t) не покинет множество G8 при *>7\ так как в
противном случае нашлись бы такие Т2>7\>7\ что
х (х0, 7\) е Гб, v (х (х0, Tt)) < Яб,
%в < v (х (*0, Г2)).
Вместе с тем при Г1<*<Г3 имеем
дг(лг0, t)cE»\G6.
Согласно первому условию из B.7) на этом участке
траектории
sup ?<0. B.9)
Учитывая, что Х& < Яе, получим противоречие с неравен-
неравенством B.9). Поэтому имеет место сходимость метода A.1)
к множеству X.. В силу произвольности начальной точки
х0 приходим к утверждению о глобальной сходимости. Щ
Предположение о продолжимости решений можно
снять, но при этом потребовать, чтобы выполнялись условия
теоремы 2.2.1, на Хт имело место равенство v(x, t) =
= w(x) = 0 и функция v (x, f) допускала бесконечно малый
высший предел при dis (дг, Хш) —* 0.
Характерно, что сходимость методов может иметь
место не обязательно4 к положениям равновесия. Более
подробно этот вопрос исследован в работе Ю. Г. Евту-
Евтушенко, В. Г. Жадана [2].
§ 3. Теоремы о сходимости итеративных процессов
I. Основные определения. Пусть всюду на Rn опре-
определено однозначное отображение Т: Rn-+Rn. Поставим
задачу об отыскании неподвижных точек этого отобра-
отображения, т. е. точек, принадлежащих множеству
Для решения этой задачи можно использовать числен-
численный метод, в котором осуществляются итерации по формуле
xk+i = T(xk). (ЗА)

§3] ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ 1(M
Этот метод в дальнейшем будем называть методом простой
итерации. Задав начальную точку х09 из C.1) однознач-
однозначным образом определим последовательность, которую обо-
обозначим {xk}.
Определение 2.3.1. Итерации, порождаемые C.1),
сходятся к точке х* локально (или на множестве X<zRn,
или2в целом), если для любой начальной точки х0, при-
принадлежащей <3(х*) (или соответственно X, или Rn), су-
существует предел последовательности {л^}, совпадающий
с точкой хф.
Далеко не во всех численных методах последователь-
последовательности {хк\ оказываются сходящимися. Тем не менее
такие методы широко используются и оказываются весьма
эффективными. Укажем, например, метод штрафных функ-
функций, который будет описан в гл. III. Методы этого типа
обладают следующим важным свойством: всякая предель-
предельная точка последовательности {хк} принадлежит искомому
множеству, благодаря чему такие методы можно назвать
сходящимися. Естественным аналогом определения 2.2.5
сходимости метода является
Определение 2.3.2. Метод C.1) сходится к мно-
множеству Х% локально (или на множестве X, или в целом),
если для любых х0, принадлежащих й(хш) (или соответ-
соответственно X, или Rn), последовательность {xk} определена,
имеет непустое множество предельных точек, каждая пре-
предельная точка принадлежит Хт.
При исследовании численных методов возникают прежде
всего следующие два вопроса:
1. При каких условиях гарантирована сходимость
метода?
2. Какова скорость его сходимости?
Следует отметить, что ответы на эти вопросы носят
не только теоретическое, но и важное практическое зна-
значение: часто либо сам метод, либо его некоторые этапы
строятся, исходя именно из условия обеспечения сходи-
сходимости; при этом теоретическое исследование методов яв-
является одновременно и способом создания самих методов.
При построении численных методов решения задач опти-
оптимизации обычно вводятся отображения, у которых мно-
множество неподвижных точек совпадает с теми точками, где
выполнены необходимые условия экстремума решаемой
оптимизационной задачи. Достаточные условия сходимости

106 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
численных методов поиска неподвижных точек совпадают
или весьма близки к достаточным условиям экстремума
в оптимизационной задаче.
В дальнейшем будет использовано два вида оценок
скорости сходимости. Предположим, что итерации, порож-
порождаемые C.1), сходятся к хт. Определим
' 0, если xk = x* для всех,
кроме конечного числа,
индексов k\
"**" если *кФ** Для всех>
cup [|****"
а-юо г 1х*_1—д^Ц* кроме конечного числа,
индексов k;
—оо в остальных случаях.
Пусть С(Т, х*)—множество всех последовательностей
с пределом #*, порождаемых итеративным процессом Т.
Тогда величины
называются С;множителем процесса Т в точке х*.
Пусть есть два метода Тг и Т2 и для них известны
Q-множители Qxp (#«.), Q2P (x*) соответственно. Если име-
имеется такое /?6[1. оо), что Qp(xm)<Q*p(Xt)9 то будем
говорить, что метод Т± Q-быстрее, чем Т2 в точке хф.
Несложно показать, что такое определение корректно,
т. е. если при некотором р метод 7\ Q-быстрее, чем Т2
в точке х*> то не существует другого р'€[1» °°) такого,
что при этом значении метод Т2 Q-быстрее, чем 7\.
Понятие «Q-быстрее» зависит от выбранной нормы и может
оказаться, что в одной норме процесс Тг Q-быстрее, в
другой норме Т2 Q-быстрее, чем 7\.
Об итеративном процессе C.1) будем говорить, что
его скорость сходимости
линейна (процесс сходится со скоростью геометри-
геометрической прогрессии), если 0 < Qx (#*)< 1;
сверхлинейна, если Qi(#««) = 0;
квадратична, если 0<:Q2 (**) < оо;
субквадратична, если Q2t*;*) = 0.
В ряде случаев можно получить другую (интеграль-
(интегральную) характеристику скорости сходимости итераций, если

§3] ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ ДО7
удается доказать, что для любых k = 1, 2, ... имеет место
оценка
*Д C.2)
у—есть некоторое постоянное число для всех последова-
последовательностей {xk\ из области сходимости итераций C.1) к
точке л:*.
Подробный анализ Q-множителей, определение других
оценок скорости сходимости содержатся в книге Дж. Ортега,
В. Рейнболдта [1].
2. Принцип сжимающих отображений.
Определение 2.3.3. Отображение Т называется
сжимающим (на X), если существует такое число О < q < 1,
что для любых точек х, у (принадлежащих X) выполнено
условие
[Т(ху-тш<9\*-уЬ C-3)
Число q называют постоянной сжатия для отображения Т.
Всякое сжимающее отображение непрерывно. Действи-
Действительно, для любого 8 > 0 можно взять б = 8/<7; тогда из
условия \\х—#|| < 6, согласно C.2), будет следовать, 'что
1Т(х)-Т(у)\]<г.
Теорема 2.3.1 (принцип неподвижной точки Банаха).
Пусть отображение Т — сжимающее на Rn. Тогда:
1) отображение Т имеет только одну внеподижную
точку х*\
2) итерации, определяемые формулой C.1), сходятся
к х* в целом;
3) скорость сходимости оценивается неравенством
\Xk-b\<?ql*t-x.l C.4)
Доказательство. Из формулы C.3) следует
Отсюда при любом s > 0 имеем
xk+s—

108 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ 1ГЛ. II
если k> N (г), где число N (в) достаточно велико. Сле-
Следовательно, последовательность {xk} фундаментальная, а
так как пространство Rn полное, то существует
lim хк=хт.
ft-»» 00
Перейдем в равенстве C.1) к пределу при ?-*оо,
учитывая непрерывность Т (х), получим lim xk =
k
*=7Ylim хЛ = хф, или х% = Т (#»). Следовательно, хш —
Vft->-oo /
неподвижная точка отображения 7\
Докажем единственность. Если быГсуществовала, по-
помимо х*, еще годна неподвижная точка у, то было бы
\\у—х* 11=1 Т(у)—Т(#*)|< qly—x*I а это возможно лишь
в случае, когда \\у—х%\=0, т. е. у = х*. Если в не-
неравенстве C.5) перейти к пределу при s—^oo, то получим
оценку C.4). Щ
Теорема 2.3.2. Пусть сжимающее на X отобраоюе-
ние Т переводит замкнутое множество X в себя
(Т: Х—+Х). Тогда отображение Т имеет только одну
неподвижную точку x*<zX; итерации, определяемые фор-
мулой C.1), линейно сходятся к х* на X, имеет место
оценка C.4). *
Доказательство почти дословно 'повторяет доказатель-
доказательство предыдущей теоремы.
3. Монотонные отображения. Пусть х, #—произволь-
#—произвольные элементы из множества ХаЕп.
Определение 2.3.4. Отображение V: Х^Х на-
называется:
ограниченным, если образ V(M) каждого ограниченного
множества МсХ ограничен;
потенциальным, если существует такая дифференци-
дифференцируемая функция f(x), что V(x) является ее градиентом,
функция / при этом называется потенциалом отображе-
отображения V(x);
монотонным, если
O«V(x)-V(y)fx-y> Vx
равномерно монотонным, если существует такое число
т (постоянная монотонности), что
-V(y), x-y> Vx,yeX; C.6)

§31 ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ Ю9
липишцевым (с постоянной /), если
\V(x)-V(y)\Kl\x-g\ Vx,y$X. C.7)
Если отображение V является одновременно сильно
монотонным и липшицевым, то из условий C.6) и C.7)
следует, что /п</.
Теорема 2.3.3. Пусть отображение V: Еп—+Еп
липшицево с постоянной I и равномерно монотонно с
постоянной монотонности т. Тогда ^отображение
Т: Еп—+Еп, определяемое формулой
T(x)=x—tV(x), C.8)
является сжимающим при т?@, 2т/12) и
\T(x)-T(y)\<q\x-yl
где
Доказательство. Для любых х, у имеем
(x)-T(y)r = \x—&(x)-y+%
^lx-y\\*-2T<V(x)-V(y), x-
При построении численных методов целесообразно
стремиться к тому, чтобы обеспечить возможно более вы-
высокую скорость сходимости. Приведенная теорема позво-
позволяет найти наилучшее значение т, исходя из минимизации
оценки отношения || Т (х)—Т (у) [|/|| х—у [|. Наименьшее
значение q по параметру т достигается при т = т//я и
равно
4. Сходимость по первому приближению. Приведем
дискретный аналог теоремы 2.1.1 об устойчивости по пер-
вому!приближению. Вначале докажем следующую лемму.
^Лемм"а 2.3.1*Пусть существует такая окрестность
G (х*) неподвижной точки х* отображения 7\ что 9для
любых x?G(x*) выполнены условия
\T{x)-x.\<q\x—x.% q<\.
Тогда итерации, определяемые формулой C.1), локально
линейно сходятся к точке х*.

НО ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Доказательство. Имеют место неравенства
Поэтому из условия х0 € G (#*) следует, что хг ? G (#*), по
индукции можно показать, что все точки xk принадлежат
G(xJ) и удовлетворяют условию
поэтому lim xk = x*. Щ
Теорема 2.3.4. Пусть отображение Т: Rn—+Rn
дифференцируемо в неподвижной точке х* и спектраль-
спектральный радиус S матрицы Тх(х*) удовлетворяет условию
S<1; тогда итерации, определяемые формулой C.1),
локально линейно сходятся к х«>
Qi{x.X\\TTx{x*)\\. C.9)
Доказательство. Воспользуемся свойством диф-
ференцируемости отображения Т, получим
, х—х,)-х.% (ЗЛО)
Здесь вектор-функция Ф такова, что
lira |Ф(*„ х—х,)|=0. C.11)
Поэтому для любого 8 > 0 существует такая окрестность
G(x«) точки #*, что для всех x?G(x*) выполнено нера-
неравенство
[|Ф( х—
Согласно известному свойству для любого г > 0 можно
подобрать такую норму матрицы T?(#*)i что || ТJ (лс%) || ^
< е + 5Г Учитывая, что Т{х*) = х*, из C.10) получим,
что для любых x^G(x^) имеет место неравенство
||Т(лг)—#*|КBs + S)\\x—дг*||. Согласно условикГтеоремы
S < 1, поэтому 8 можно считать настолько малым, что
2e+S < 1, при этом выполнены условия последней леммы,
из нее следует локальная сходимость {хк} к х*.
Из (ЗЛО) следует

§3] ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ \\\
Используя это неравенство для каждого элемента после-
последовательности {л^}, порождаемой C.1), с учетом свойства
C.11) получим
т. е. для Q-множителя имеет место оценка C.9}. Щ
Заметим, что для сходимости итераций C.1) достаточно,
чтобы какая-либо из норм матрицы Тх (л:*) была меньше
единицы, так как из этого следует, что все собственные
значения матрицы Ттх(х*) меньше единицы и, следова-
следовательно, S < 1.
Из теоремы 2.3.4 следует, что если Тх(х*) = 0, то
скорость сходимости итераций C.1) сверхлинейная. Условие
равенства нулю спектрального радиуса матрицы Тх(хф)
не гарантирует сверхлинейной скорости сходимости.
Теорема 2.3.5. Пусть отображение Т: Rn—+Rn
дифференцируемо в неподвижной точке #*, матрица Тх (х*)
симметричная. Тогда для локальной сходимости итераций
C.1) к точке х* достаточно, чтобы наибольшее по модулю
собственное число к матрицы Тх{х*) было меньше еди-
единицы. Скорость сходимости Q1(x^) = k.
Доказательство. Из симметричности матрицы
Тх (#*) следует, что ее собственные числа действительные.
Воспользуемся теоремой 2.3.4. Считаем, что норма мат-
матрицы Тх (л:*) согласована с евклидовой нормой векторов.
Тогда спектральный радиус матрицы ^(л;*) совпадает с
ее нормой и с наибольшим по модулю собственным зна-
значением х. Из условия | к \ < 1 следует, что выполнены
условия предыдущей теоремы, гарантирующие сходимость.
Симметричность матрицы Тх(х*) имеет место, в частности,
если отображение Т потенциально.
Даваемые- теоремами 2.3.4 и 2.3.5 оценки скорости
сходимости носят асимптотический характер. Оценку вида
C.2) дает
Теорема 2.3.6. Пусть отображение Т: Rn—+Rn
дифференцируемо в некоторой окрестности G (х*) непод-
неподвижной точки х* и
у= sup |]7Т(*)||<1.
xeG(x*)
Тогда итерации, определяемые формулой C.1), локально

112 теоремы о сходимости и их приложения 1гл. it
сходятся к х* и имеет место оценка скорости сходимости
ll^-^Kvll^.i-^ll = V*ll^o-^||. C.12)
Доказательство. Из того, что спектральный ра-
радиус матрицы не превосходит любую из ее норм, следует
что спектральный радиус матрицы Tl (xm) меньше единицы
и, следовательно, итерации локально сходятся к точке х*.
Оценим норму
Воспользуемся формулой Лагранжа для отображений
(см. Приложение I), получим
отсюда следует C.12). Ц
5. Связь между сходимостью дискретных и непрерыв-
непрерывных процессов. В § 1 были получены достаточные усло-
условия экспоненциальной устойчивости тривиального решения
x(t)=xm для систем вида
~ = F(x), F(x.) = 0. C.13)
Анализ проводился на основе изучения корней уравнения
|FJ(*.)-4J=O. (ЗЛ4)
Проинтегрировав C.13) по схеме Эйлера, придем к сле-
следующему итеративному процессу:
xk+t = xk+aF(xk) = T(xJ, x. = T(x.). C.15)
Согласно теореме 2.3.4 вопрос о его сходимости реша-
решается путем анализа уравнения
Преобразуем его к виду
If (,
= 0.
Сравнивая это уравнение с C.14), приходим к выводу, что
между их корнями существует простая связь |и =1"
Комплексный корень % представим в виде % = с
тогда

§31 ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ ИЗ
Условие | |х | < 1 можно записать в виде
< 0.
Если Re Я = а < 0, то у (а) < 0 при любых 0 < а < а«, где
Пусть Xj, ..., ЯЛ—корни уравнения C.14), тогда усло-
условие | (х | < 1 будет иметь место при любых а, удовлетво-
удовлетворяющих условию
0<a<a = 2min Г 7^1
Мы пришли, таким образом, к следующему результату:
Теорема 2.3.7. Пусть для системы C.13) в точке хт
выполнены достаточные условия теоремы 2.1.1 об устой-
устойчивости по первому приближению. Тогда существует
такое число а, что при любом фиксированном 0 < а < а
итерации, определяемые формулой C.15), локально линейно
сходятся к точке х*.
В частном случае, когда система C.13) реализует ме-
метод Коши B.3) безусловной минимизации функции f(x),
матрица Fx(x*) = —fxx(x*). Поэтому все %( действитель-
действительные. Если матрица fxx(x*) положительно определена, то
все kt < 0 и
a = 2 min Г—
где т)—наибольшее собственное значение матрицы fxx(xm).
Если отыскание предельных точек решений задачи
Коши для системы C.13) трактовать как численный метод
отыскания положения равновесия для системы C.13), то
C.15) является дискретным аналогом этого метода. Из при-
приведенной теоремы следует, что из обоснования экспонен-
экспоненциальной устойчивости положения равновесия для системы
C.13) автоматически следует локальная линейная сходи-
сходимость дискретного варианта метода при достаточно малом
шаге интегрирования. Этот прием широко используется
при обосновании сходимости.
Систему C.13) можно проинтегрировать и по более
точным схемам, использовав, например, метод Эйлера,
с пересчетом, метод Рунге—Кутта и т.д. Однако такой

П4 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
прием не ускоряет сходимость методов, но делает их более
трудоемкими. Это связано с тем, что применение схем
высокого порядка точности позволяет только более точно
«отслеживать»'каждое решение системы C.13), но в этом
нет никакой необходимости в связи с асимптотической
устойчивостью положения х = х^ Поэтому всюду в даль-
дальнейшем, переходя к дискретным аппроксимациям числен-
численных методов, будем пользоваться только простейшей
схемой Эйлера.
6. Приложение к задаче безусловной минимизации.
Ставится задача нахождения безусловного минимума функ-
функции f(x). Согласно теореме 1.3.5 для выпуклой дифферен-
дифференцируемой функции / эта задача эквивалентна .отысканию
стационарной точки, удовлетворяющей условию fx{x*) = Q.
Из теоремы 1.2.7 получаем, что для выпуклой функции /
отображение fx(x) монотонно. Введем отображение
Его неподвижные точки будем отыскивать с помощью
метода простой итерации C.1):
*k+i = x*-*fx(xj- C-16)
Предположим, что существуют такие числа / и т, что
при любых х, у?Еп выполнены условия
Отображение V, таким образом, равномерно монотонно,
липшицево, потенциально. Из теоремы 2.3.3 следует, что
в задаче A.3.4) существует единственное решение х = хф,
итерации, задаваемые формулой C.16), сходятся к хт
в целом при любом шаге т, удовлетворяющем условию
т?@, 2т/12) и имеет место оценка скорости сходимости
C.4), где
Локальную сходимость итераций C.16) можно обосно-
обосновать, не вводя условия выпуклости функции /. Вместо этого
потребуем, чтобы в стационарной точке х* выполнялось
достаточное условие локального минимума (см. теоре-

§3] ТЕОРЕМЫ О СХОДИМОСТИ ИТЕРАТИВНЫХ ПРОЦЕССОВ Ц5
му 1.3.2), заключающееся в том, что матрица fxx(x*)
положительно определена. Рассмотрим два характеристи-
характеристических уравнения
|/,*(*•)-Л/„ 1 = 0,
Между корнями введенных уравнений существует связь
х=1—тт). Расположим собственные значения матрицы
fxx(x*) в возрастающем порядке: 0<t]1^tj2^ .. .^t)n. Им
будут соответствовать собственные значения матрицы
Согласно теореме 2.3.5 для сходимости итераций C.16)
достаточно, чтобы кп > —1. Это условие будет иметь место
при любом 0<т<т, где t = 2/it]w. Величину т целесооб-
целесообразно выбирать из указанного интервала так, чтобы
спектральный радиус S (т) матрицы Тх (#») был наимень-
наименьшим, поэтому ищем
min S(t)= min max[|l—Щ±\> |1— Щп\\-
0<x<7 '
На интервале @, т) линейная функция 1 — гцг изменяется
от 1 до —1. Поэтому наименыпее^значение функции 5(т)
будет достигаться, когда 1—щп = —1+tt|i» т. е. при
т, = 2/(т|1 + т|д). Спектральный радиус матрицы Тх(х%) при
этом равен
Если функция / (л:) дифференцируема в окрестности G (х*)
точки х* и для всех x?G(x*)y z?En имеет место нера-
неравенство
то, согласно теореме 2.3.6, для скорости сходимости спра-
справедлива оценка
7. Один вспомогательный результат. В дальнейшем,
в гл. III, понадобится следующая

П6 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ 1ГЛ. II
Лемма 2.3.2. Пусть отображение Т(х): Еп—+Еп
таково, что 7@) = 0 и для любых х, z?En имеет место
неравенство \\Т(х)—T(z)\\^.c\\x—z||2, где с—некоторое
число. Тогда уравнение
х = Т(х+у) C.17)
при всяком векторе у, удовлетворяющем условию \у\<^
<A/2 — 1)/Bс), имеет в шаре Н"=*{х6Еп: ||*||<2cft/||2}
единственное решение.
Доказательство. Покажем, что отображение
Т(х+у) переводит Н в себя. Пусть х?Н, тогда
Таким образом, точка Т(х+у)?Н. Покажем, что отобра-
отображение Т(х-\-у) сжимающее на Н. Действительно, если
х, г?#, хфг, то
Согласно теореме 2.3.2 отображение Т(х + у) имеет только
одну неподвижную точку, соответствующую решению
уравнения C.17). В
§ 4. Сходимость процессов, порожденных
многозначными отображениями
1. Предварительные результаты. Пусть всюду на Еп оп-
определено точечно-множественное отображение W\ En —> 2ЕП
(см. Приложение III). Ставится задача об отыскании
множества всех неподвижных точек отображения W:
Предполагается, что это множество не пусто. Естест-
Естественным обобщением метода простой итерации C.1) на
многозначные отображения является следующий процесс:
). D.1)

§4] МНОГОЗНАЧНЫЕ ОТОБРАЖЕНИЯ 117
В отличие от C.1), здесь, задав начальную точку х0,
мы неоднозначным образом определим последовательность
точек atj, д:2, ... , которую будем обозначать по-преж-
по-прежнему {xk\.
Если для любой последовательности {х^у полученной
из D.1), не пусто множество предельных точек, каждая
сходящаяся подпоследовательность сходится к точке, при-
принадлежащей некоторому множеству Z, то будем говорить,
что метод D.1) сходится к множеству Z "(в целом, если
это свойство имеет~место для любых хо?Еп9 или на Х9
если это свойство^справедливо для всех хо?Х, или ло-
локально, если это свойство имеет место для всех х0, при-
принадлежащих некоторой окрестности множества Z).
Последовательность, получаемую из D.1), будем в ряде
мест также обозначать {лс^л» где Л = {0, 1, 2, . •.} — на-
натуральный "ряд. Будем обозначать Л' бесконечное "мно-
"множество неотрицательных целых чисел в их Естественной
последовательности, например Л1={1,5,7,20, ...}. Подпо-
Подпоследовательность данной последовательности {xk\, соот-
соответствующая множеству Л', обозначается {хк\л^ Обозна-
Обозначение Л' с: Л означает, что Л' является бесконечным
подмножеством Л. Запись {#;Ja+i представляет подпосле-
подпоследовательность, полученную из {#Л}л> прибавлением 1
к каждому k?A.
Обоснование сходимости рассматриваемых процессов
основано на следующей лемме, аналогичной лемме 2.2.1.
Лемма 2.4.1. Пусть на множестве X с Еп опреде-
определена непрерывная функция ~v(x) и последовательность
точек {xk}A из X такова, что для любого k?A выполнено
условие ofe+1)<nD пусть существует подпоследова-
подпоследовательность {хк}л1, Л1 с Л, сходящаяся к точке Х
Тогда
lim v(xk)= lim v(xk)=v(x*).
fefcA fcfcA*
Доказательство. Из непрерывности v(x) следует
iim v(xk) = v(xm). D.2)
Согласно условиям леммы последовательность {v(xk)\
монотонно убывает, поэтому для любого k^O имеем
v]{xo)'^v(xk)'^v(x*). Используем выражение D.2) и опре-
определение предела. Для любого е > 0 существует число

П8 теоремы о сходимости и их приложения [гл. и
NGA1 такое, что для любых k > N и
О < v (xk)—v (**) < v (xN)—v (**) < 8.
Вместе с тем для любого i?A, i^N9 выполнено условие
v(Xi)^v(xN). Поэтому для всех Х;?{хк}А таких, что
i > N, имеем
откуда следует утверждение леммы. Щ
2. Фейеровские отображения.
Определение 2.4.1. Точечно-множественное отоб-
отображение W: Еп—+2ЕП, имеющее непустое множество не-
неподвижных точек X*, называется Х*-фейеровскиму если
выполнены следующие два условия:
fl) W(y) = y Vy?X*,
2) \\г-у\\<\\х-у\\ Vy?X«f Vx$X*9 Vz?W(x).
Простейшим примером Х„.-фейеровского отображения
является рассмотренная в § 1 гл. I операция проектиро-
проектирования на компактное выпуклое множество X* (см. фор-
формулу A.1.2)). В этом случае
W(x) = Arg min ||*—у I
Теорема 2.4.1 (И. И. Еремин). Пусть точечно-
множественное отображение W (х) замкнуто и Хщгфейе-
ровское. Тогда для любой фиксированной точки х0 каждая
последовательность {xk\, определяемая из D.1), сходится
к точке х*, принадлежащей множеству X* и зависящей
только от выбора х0.
Доказательство. Пусть у—произвольная, фикси-
фиксированная точка из Х«. Обозначим v(x)=\\x—у\\. Фикси-
Фиксируем начальную точку х0. Последовательность \xk} огра-
ограничена, так как для всех k имеет место неравенство
II **—#1^ |*о—УЬ Следовательно, множество предельных
точек последовательности {xk) не пусто. Пусть р и q —
две предельные точки. Последовательность {v(xk)\ моно-
монотонно убывает и ограничена снизу нулем. Поэтому, со-
согласно предыдущей лемме,
*(Р) = НЯ) = \Р-У\ = \Я-У\- D.3)
Если р?Х* или q ?Х*, то обязательно p = q. Действи-
Действительно, пусть р?Х*у тогда в качестве у возьмем р, из
D.3) получим |/7—р|| = 0=||q—р||, т.е. p = q.

§4] МНОГОЗНАЧНЫЕ ОТОБРАЖЕНИЯ 119
Пусть подпоследовательность {.^[л1 сходится при k—>-oo
к точке р (? Хт. Рассмотрим подпоследовательность {х^лч-Г,
из ее ограниченности следует, что из нее можно выделить
подпоследовательность, соответствующую индексному мно-
множеству Л2 с Л1 + 1, такую, что
lim xk = q.
k /Л2
Если из каждого элемента множества Л2 вычесть единицу,
то получим множество Л3 с Л1, причем lim xk = p.
В силу замкнутости многозначного отображения W(х)
будем иметь q? W (р). Поэтому, взяв произвольный вектор
#€Х„ получим \\q—y\\<\\p — yl, но это неравенство
противоречит D.3). Отсюда заключаем, что последова-
последовательность *{xk\ сходится к точке, принадлежащей мно-
множеству X*. В
3. Приложение теоремы о фейеровском отображении.
Рассмотрим задачу об отыскании точки из множества
Предполагаем, что каждая из функций W (х) выпукла,
определена всюду на Еп. Из теоремы 1.1.6 тогда следует,
с
что выпуклой будет также и функция S(x)= 2 hf+(x).
Для каждой точки х?Еп определим многозначное отобра-
отображение
М(х) И(, __„ >у
W(x)=x— \ il#«ll2 W' х+ *э D.4)
если
(А
\=х—\ \н
Здесь %—некоторое число, H(x)?dS(x) (см. определе-
определение 1.2.1).
Теорема 2.4.2 (И. И. Еремин). Пусть Х*Ф0у
многозначное отображение W (х) задано формулой D.4),
где 0<Я<2. Тогда всякая определяемая из D.1) после-
последовательность {xk} сходится к множеству X* в целом.
Доказательство. Покажем, что отображение W
является Х*-фейеровским. Опустим обоснование замкну-
замкнутости (его можно найти в книге И. И. Еремина и
В. Д. Мазурова [1]), проверим выполнимость остальных
условий. Пусть х ? Х«, покажем, что [ Н (х) || Ф 0. Допустим

120 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. It
противное: (#(л;)|| = 0. Тогда, согласно формуле A.2,2),
для любого у?Еп имеет место неравенство S(x)^.S(y)f
а это противоречит тому, чтоя^Л». Поэтому \Н(хIф0
всюду вне Хт. Для произвольных у?Хф, х?Хф9 z?W(х)
имеем
<H(*) y*>+
Воспользуемся неравенством A.2.2), получим
Таким образом, при любом 0 < % < 2 многозначное отоб-
отображение W (х) является Х*-фейеровским и, согласно тео-
теореме 2.4.1, итерации D.1) сходятся к Хт. Щ
Более подробное изложение теории фейеровских отобра-
отображений и их приложения к решению прикладных задач
можно найти в книге И. И. Еремина и В. Д. Мазу*
рова [1].
4. Нестационарные процессы. Пусть процесс D.1)
определяется нестационарным многозначным отображением
W(x, k):
Ставится задача об отыскании точек
X. =
В качестве примера такого процесса приведем метод
обобщенного градиента для поиска безусловного минимума
функции f(x)f в котором
**« = *н-**У>Р (**). н W € df (х). D.5)
Здесь ак, ук—некоторые положительные коэффициенты,
возможны различные законы их изменения, укажем три

§4] МНОГОЗНАЧНЫЕ ОТОБРАЖЕНИЯ 121
ИЗ НИХ*
-\ |ал=оо, J,«2<°°. D-6)
S JS ай=оо, aft-*0, D.7)
7Л = const, 2 ал = °°> а* —* 0, D.8)
где 0 <d—произвольное число.
Ограничимся обоснованием сходимости метода D.5)
с правилом регулировки D.6).
Теорема 2.4.3. Пусть функция f{x) определена
всюду на Еп, выпукла, множество ее минимумов Хф не
пусто, тогда при использовании метода обобщенного
градиента D.5) с регулировкой D.6) из последователь-
последовательности {хк}л можно выделить такую подпоследовательность
{}», что
lim f(xk)=f(x<), x.?Xm. D.9)
Доказательство. Пусть х%?Х%, vk=\xk—
тогда
vk+i = vk-2akyk<H(xk), xk-x.>+aly%\\H(xk)f.
Отсюда следует, что
k
2 sVs(s), xs-x.>+ 2 «!1Й
s=0 s=0
D.10)
В силу выпуклости /(x) на ?"rt имеем 0 ^ <#(*), л:—
поэтому из D.10) с учетом D.6) следуют соотношения
Из ограниченности правой части константой, не за-
зависящей от fe, следует, что при k —> оо последователь-
последовательности {vh}y {xk}y {Щ(хк)\ ограничены. Из D.10) получим

122 теоремы о сходимости и их приложения [гл. и
также
к k
2а 2 as<H(xs)y xs—x*>^v0—vk+1+ 2 «!,
s=0 s=0
где постоянная а не зависит от k. Правая часть нера-
оо
венства ограничена при k—+ оо, согласно D.6) 2 а5 = оо>
s=0
но это возможно только когда <#(л:л), хк—хщ> —*0
при & —>¦ оо. Из свойства выпуклости
заключаем, что существует подпоследовательность {#Л}л*
такая, что выполнено условие D.9). Щ
Аналогично формулируются теоремы и доказывается
сходимость метода при регулировках D.7) и D.8). Методу
обобщенного градиента посвящена обширная литература;
сошлемся, например, на книги Ю. М. Ермольева [2] и
Н. 3. Шора [1].
§ 5. Методы решения систем нелинейных уравнений
1. Метод простой итерации. Пусть отображение
V: Rn —>- Rn. Ставится задача о решении системы из п
уравнений с п неизвестными
0. E.1)
По формуле C.8) определим отображение Т (х); тогда рас-
рассматриваемая задача станет эквивалентной отысканию
неподвижных точек отображения Т. Метод простой ите-
итерации C.1) приводит к следующему методу решения
системы E.1):
. E.2)
Из теорем 2.3.1 и 2.3.3 получим следующий результат.
Теорема 2.5.1. Пусть отображение V: Rn —* Rn лип-
шицево с постоянной I и равномерно монотонное с по-
постоянной монотонности т. Тогда уравнение E.1) имеет
единственное решение х — х*, и при любом т?@,2т//2)
итерации, определяемые формулой E.2), сходятся к хч

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 123
в целом. Имеет место следующая оценка скорости схо-
сходимости:
Если существует решение х — х* системы E.1) и отобра-
отображение дифференцируемо в точке х*, то, согласцо теоре-
теореме 2.3.4, для локальной, линейной сходимости итераций
E.2) достаточно, чтобы спектральный радиус матрицы
Т1(хф) = 1п—tVI(x#) был строго меньше единицы.
Введем два уравнения
Между их корнями имеет место простая связь: х=
= 1—тт). Комплексный корень tj представим в виде tj=
=a-?ib, тогда
и=1_ та—frb, |%|2 = A—тяJ + т*62.
Условие | к | < 1 запишется следующим образом:
(а2+62)т2 —2тя<0. E.3)
Если a = Ret]>0, то E.3) имеет место при любых 0<
<т<т, где T = 2Rer]/[ri|a. Если a = Reri<0, то E.3)
выполнено при любых т < т < 0.
Таким образом, спектральный радиус матрицы Т1(х*)
меньше единицы тогда и только тогда, когда выполнено
одно из следующих условий:
1) собственные значения t\u..*,i\n матрицы VI (х*)
удовлетворяют условиям Rer),. > 0, i ^ [1 :n]f и 0 < т <
2R/h|2 *6[1]
<RiJ/h/|, 6[];
2) собственные значения у\й.-.,цп матрицы VI(х*)
удовлетворяют условиям Rei^O, i € [1 :л], и 2 Rer)j/| r]z-12<
<т<0, <€[1:л].
При выполнении какого-либо из этих условий итера-
итерации E.2) локально сходятся к точке х*. Если матрица
Ух(х*) симметрическая, то все корни к\( будут действи-
действительные, а приведенные условия можно будет выполнить
только в тех случаях, когда матрица Vx(xm) либо поло-
положительно, либо отрицательно определена.

124 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ СГЛ. И
Если отображение V(x) потенциально и потенциалом
является функция / (х), то метод E.2) можно рассматри-
рассматривать как численный метод отыскания локальных экстре-
экстремумов функции / (х). Случай отыскания минимума был
рассмотрен в п. 6 § 3, метод E.2) при этом совпадает
с C.16).
2. Аналог метода обобщенного градиента. Как указы-
указывалось в п. 6 § 3, методы минимизации выпуклых функ-
функций можно трактовать как методы отыскания неподвижных
точек соответствующих монотонных отображений. Поэтому
описанный в § 4 метод обобщенного градиента эквивален-
эквивалентен итерации
xk), E.4)
где неотрицательные коэффициенты ak, yk изменяются по
какому-либо из правил D.6)—D.8). Так как доказатель-
доказательство сходимости почти дословно повторяет доказательство
теоремы 2.4.3, ограничимся лишь тем, что сформулируем
теорему о сходимости.
Теорема 2.5.2. Пусть существует решение х = хш
системы E.1). Если отображение V(x)—ограниченное и
равномерно монотонное и используется правило регули-
регулировки D.6), то* итерации^ определяемые формулой E.4),
сходятся к точке хф в целом.
3. Метод Ньютона. Наиболее распространенным мето-
методом решения системы E.1) является метод Ньютона,
в котором итерации осуществляются по формулам
E.5)
т. е. реализован метод простой итерации для нахождения
неподвижных точек отображения Т (х). Если отображение
V достаточно гладкое, то
тх (*)=№(*>]-* J; |ул> (*)]v«> (х).
Следовательно, Тх(хт) = Оу что по теореме 2.3.4 обеспе-
обеспечивает высокую скорость сходимости хк—>аг».
Основные свойства метода Ньютона отражены в сле-
следующей теореме.
Теорема 2.5.3. Пусть отображение V: Rn—+Rn
дифференцируемо в некоторой окрестности G (х9) рейхе-

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1Й>
ния х* системы E.1), причем производная Vx(x) непре-
непрерывна в хф и матрица Vx(xm) невырождена. Тогда ите-
итерации, определяемые формулами E.5), локально сходятся
к точке хт со сверхлинейной скоростью. Если, кроме того,
существует такая постоянная 1У что
\Vx(x)-Vx(x.)K4x-x.\ V*€G (*•),, E.6)
то итерации E.5) обладают локальной квадратичной
скоростью сходимости.
Это утверждение будет следовать очевидным образом
из сформулированной ниже (п. 4) теоремы 2.5.4.
Замечание. В дальнейшем теорема 2.5.3 будет
неоднократно использоваться применительно к разным
специальным задачам. При этом для простоты формули-
формулировок вместо условия, E.6). будем писать: производная
Vx (x) удовлетворяет условию Липшица в окрестности
точки xmt т. е.
\VA*)-Vx(jf)l<l\x-y\ Vx,yZG(x.).
В последующих главах в ряде случаев исследованию
метода E.5) предшествует обоснование сходимости метода
простой итерации E.2) с т==1. В процессе обоснования
доказывается, что спектральный радиус матрицы /л—VI (х«)
строго меньше единицы. Из леммы Неймана (см. Прило-
Приложение II) тогда следует невырожденность матрицы Vl(x*)
и для обеспечения квадратичной скорости сходимости E.5)
требуется только выполнимость либо E.6), либо условия
Липшица в окрестности хт.
4. Модификации метода Ньютона. Благодаря высокой
скорости сходимости метода Ньютона нашел широкое при-
применение при решении разнообразных прикладных задач.
Вместе с тем метод обладает рядом недостатков, глав-
главными из которых являются следующие:
1. Трудоемкость вычислений, связанная с необходи-
необходимостью вычислять /z? частных производных;
2. Локальный характер сходимости. При плохом на-
начальном приближении метод часто расходится;
3. Необходимость для построения ньютоновского направ-
направления рк решать систему линейных уравнений Vx"(xk)pk—
=—У(хк), что требует порядка п* арифметических опе-
операций.

126 теоремы о сходимости и их приложения [гл. и
Многочисленные работы последних лет были направ-
направлены на устранение указанных недостатков, что привело
к созданию разнообразных модификаций метода. Остано-
Остановимся на некоторых из этих результатов.
При численной реализации метода обычно вместо мат-
матрицы Vx (x) используется ее конечно-разностная аппрокси-
аппроксимация. При этом возникает вопрос о том, как выбрать
величину шага численного дифференцирования, какую
взять схему дифференцирования с тем, чтобы метод не
утратил высокой скорости сходимости. Принципиальная
возможность использования конечно-разностной аппрокси-
аппроксимации вытекает из следующей теоремы.
Теорема 2.5.4. Пусть отображение V: Rn—+Rn
дифференцируемо в некоторой окрестности G (х*) реше-
решения хт системы E.1), производная Vx(x) непрерывна в х*
и матрица Vx(x«) невырождена; имеется матрица W (х)
такая, что
lira \W(x)-Vx(*)l = 0. E.7)
Тогда последовательность
хк+1 = Т(х^ T(x) = x-[W*(x)]-*V(x)9 E.8)
локально сходится к точке х* со сверхлинейной скоростью.
Если дополнительно выполнено неравенство E.6) и
\\WT(x)-VTx(x)\\^c\\V(x)l E.9)
то итерации E.8) обладают локальной квадратичной
скоростью сходимости.
Доказательство. Покажем прежде всего, что
отображение Т(х) дифференцируемо в^и Тх(хф) = 0. Это
эквивалентно утверждению
lim 1%М=0; E.10)
Имеют место оценки
<\[WT(x)]-1\\WT(x)(x-xm)-V(x)\^l
(x) -VI {x)\ 1 *-*.| +
(*)(*-*.)-V(*)D. E.11)
Из E.7) и непрерывности производной Vx(x) в точке х.

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 127
следует
lim
* II*—*•(!
Отсюда с учетом E.7) и E.11) получаем E.10) и, ^согласно
теореме 2.3.4, имеет место сверхлинейная скорость сходи-
сходимости xk—>#*.
Пусть выполнены неравенства E.6) и E.9), тогда из
E.11) имеем
откуда вытекает квадратичная скорость сходимости, так
как
Ш
В качестве простейшей конечно-разностной аппрокси-
аппроксимации можно взять матрицу W (х), у которой i-я строка
есть
Применяя теорему 2.5.4, можно показать, что если
все /4° —>• 0 при k —> оо A ^ i ^ п)у то последователь-
последовательность E.8), использующая аппроксимацию E.12), локально
сходится к х* со сверхлинейной скоростью. Если, кроме
того, выполнено неравенство E.6) и |А^°| ^c\\V(xk)[l то
скорость сходимости квадратичная.
Для увеличения области сходимости метода обычно
на каждой итерации
)VV(xk) E.13)
производится специальная регулировка длины шага ак.
В работах В. К. Исаева, В. В. Сонина [1], В. Н. Лебе-
Лебедева [1], А. Глейзала [1], С. Хасельгрова [1] и многих
других предлагается в E.13) шаг ak дробить, начиная
от а^=1 до тех пор,Гпока не будет выполнено условие

128 теоремы о сходимости и их приложения [гл. и
|| V(*a+S)|K || V (#*)!> и только после этого переходить
к следующей итерации. Однако этот прием, вообще го-
говоря, не гарантирует сходимости метода E.13) в целом.
Ниже приведем другие способы регулировки ак9 обеспечи-
обеспечивающие глобальную сходимость и сохраняющие квадра-
квадратичную скорость сходимости вблизи точки х*.
Пусть заданы числа r>0, е?@, min{l, г}), ^?@, 1)
и выбран вид нормы J • || в Rn.
Способ 1. В качестве а взять А/, где i^O есть
наименьшее целое, удовлетворяющее неравенству
\\V(xk+Vpk)\\'<(l-sV)\\V(xk)\\r. E.14)
Способ 2. Найти целое 1^0, как и в способе 1.
Величину ак выбрать из условия
min
Способ 3. Величину ak выбрать из условия
ак = arg min || V (хк + Мрк) ||,
где i принимает всевозможные целые значения.
Способ 4; Проверить неравенство E.14) при t = 0.
Если оно выполнено, то положить ак = 1, в противном
случае продолжить поиск по способу 3.
Способ 5. Найти ак из условия
В способах 1 и 2 число i находится дроблением a = 1,
путем умножения на X, до тех пор, пока не выполнится
неравенство E.14). Характерно, что при любой заранее
заданной bTR" норме величина |V|| монотонно (от итера-
итерации к итерации) уменьшается. Это дает возможность
постановщику задачи, выбирая норму в Rn, учитывать
специфику системы E.1).
Теорема 2.5.5 (О. П. Бурдаков [2], [3]). Пусть
отображение V: Rn—*Rn дифференцируемо в R" и про-
производная Vx(x) удовлетворяет неравенствам
x,y$R», E.15)
». E.16)

§б] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 129
Тогда, какими бы ни были значения параметров г > О,
% g @, 1), 8 € @, min {1, г}), модифицированный метод
Ньютона E.13) с выбором длины шага ak no способам
1—5 сходится к единственному решению хт системы E.1)
из любой начальной точки xo?Rn, причем вблизи реше-
решения скорость сходимости квадратичная.
Доказательство. Отметим, что по теореме Ада-
мара [1] из неравенства E.16) следует существЬвание и
единственность решения системы E.1). Исключим из рас-
рассмотрения тривиальный случай, когда V(xk) = 0.
Рассмотрим сначала способ 1 при г = 1. Предполагая
а?[0, 1], воспользуемся формулой Ньютона—Лейбница
и неравенством E.15):
С учетом E.16) получаем соотношение
Видно, что неравенство E.17) будет наверняка выполнено
для всех a?[0, min{l,aft}], где aft = (l— e)//m21|F(a^)||,
тогда ал^ min {1, Яал}. Нетрудно заметить, что последо-
последовательность ak монотонно возрастает. Следовательно,
)||, E.18)
где <7 = 1 —8 min {1, Xa0} < 1. Отсюда заключаем, что
IIУ (xk) II ~* ^ ПРИ k-^oo. Значит, последовательность хк
сходится к решению х* из любой начальной точки. После-
Последовательность aft-^ оо, следовательно, начиная с некото-
некоторого номера итерации, все аА=1 и по теореме 2.5.3 ско-
скорость сходимости квадратичная. В случае г>1 неравен-
неравенство E.14) будет выполняться при всех а? [0, min{l, o^}].
Дальнейшие рассуждения аналогичны изложенным выше.
5 Ю. Г. Евтушенко

130 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. И
Пусть теперь г&(г, 1). Неравенство E.14) будет вы-
выполнено при всех а€[0, тт{1,ал}], где
Действительно, из E.17) получаем
Дальнейшие рассуждения аналогичны случаю г = 1.
Рассмотрим способы 2—5. Пусть имеются хк и pk.
Если сравнивать величины |V(x*+i)H и ||F(**+i)l> полу-
полученные соответственно по одному из способов 2—5 и по
способу 1, то нетрудно увидеть, что |V(x*+1)I<|V(*fc+1)||.
Следовательно, сохраняется оценка E.18), откуда выте-
вытекает сходимость из любой начальной точки xQ ? Rn. Заме,
им далее, что
при всех х из некоторой окрестности G(x*). Применяя
эти оценки к, неравенству
справедливому вблизи решения хт, получаем квадратич-
квадратичную скорость сходимости для способов 2—5. В
Следует подчеркнуть, что сохранить высокую скорость
сходимости метода Ньютона здесь удалось за счет того,
что способы 1—4, начиная с некоторого номера итерации,
дают ал = 1, а в способе 5аА->1 при^й —> оо.
Основные результаты этой теоремы 'остаются в силе
и при более слабых предположениях. Так, например,
глобальную сходимость можно получить, требуя непре-
непрерывность Vx(x) в Rn вместо неравенства Липшица E.15).
Можно отказаться также и от неравенства E.16). В этом
случае имеет место

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 131
Теорема 2.5.6 (О. П. Бурдаков [3]). Пусть сущест-
существует открытая выпуклая область D с Rn такая, что
отображение V: D-+Rn непрерывно дифференцируемо
в D. Пусть имеется точка x?D такая, что множество
односвязно, компактно и якобиан Vx(x) невырожден в
S(x)- Предположим, что в способах 1—5 все пробные
точки xk+<xpk выбираются из D. Тогда, какими бы ни
были значения параметров г>0, X ? @, 1), е ? @, min {1, г}),
модифицированный метод Ньютона E.13) сходится
к единственному в J?(x) решению системы E.1) при
любом xo?J?(x). Скорость сходимости сверхлинейная, а
если дополнительно выполнено неравенство E.6), то
квадратичная. , . _
Заметим, что когда множество <3?(х) не односвязно,
то его односвязные компоненты задают области притяже-
притяжения модификации E.13).
Среди способов 1—5 нельзя выделить один, который
бы во всех случаях был предпочтительнее остальных.
Каждый из них обладает своими преимуществами и недо-
недостатками. На практике выбор конкретного способа за-
зависит от того, насколько более трудоемким является
вычисление ньютоновского направления рк по сравнению
с вычислением величины ||V(#)||. Если разница в трудо-
трудоемкости велика, то более приемлемыми являются способы
3—5, если же нет, то способы 1, 2.
5. Методы квазиньютоновского типа. Отмеченные
в п. 4 недостатки 1 и 3 метода Ньютона , отсутствуют
в квазиньютоновских методах (иногда их называют мето-
методами переменной метрики). Эти методы основаны на идее
последовательной аппроксимации, либо VI, либо [FJ]".
Для аппроксимации используются только значения ото-
отображения V, вычисленные на предыдущих итерациях.
Если аппроксимируется Vj, то итерационный процесс
имеет вид
xh+1 = xk-B?V(xk). E.19)
При аппроксимации матрицы [VJ] расчеты ведутся по
формуле
х„х = хн-НкУ(хи). E.20)
5*

132 теоремы о сходимости и их приложения [гл. и
Квадратные (п х я)-матрицы Вк и Нк изменяются в соот-
соответствии с формулами, которые будут описаны ниже. При
этом Во и Нь предполагаются заранее заданными.
Если отображение V достаточно гладкое, то при малых
изменениях Ахк = хк+1—хк имеем
V(xk+1)~V(xk)+VTx(*k+i)bxk.
Естественным будет потребовать, чтобы матрица Bk+i
удовлетворяла равенству
которое указывает на близость вдоль направления Ахк
матрицы Вк+1 к Vl(xk+1). Обозначим AVk-=V(xk+1)—V(x^j
и перепишем это соотношение в виде
Bk+1Axk = AVk. E.21)
Аналогичный подход возможен и при аппроксимации
матрицы lyj^+i)]- Допустим, величина Ахк мала, тогда
Потребуем, чтобы матрица Нк+1 удовлетворяла равенству
Hk+lAVk = Axk, E.22)
свидетельствующему о достаточной близости вдоль век-
вектора AVk матрицы Нк+1 к матрице [VJO^+i)]"-
Соотношения E.21) и E.22) носят названия квазинью-
тоновских. Они не определяют однозначным образом мат-
матриц соответственно Вк+1 и Нк+1. Необходимы дальнейшие
гипотезы относительно этих аппроксимаций. Способы пере-
пересчета матрицы Вк+1 из Вк (как, впрочем, и Нк+1 из Нк)
основаны на вполне естественных требованиях. А именно,
имея Вк, необходимо построить такую матрицу Вк+1>
чтобы, во-первых, выполнялось квазиньютоновское соот-
соотношение E.21), и, во-вторых, аппроксимация В не меня-
менялась бы в некотором (п—1)-мерном подпространстве пк ? Rn,
не содержащем Ахк, т. е.
Вк+1р = Вкр Vp?nk. E.23)
Таким образом, имеется система из /г2 уравнений E.21),
E.23) относительно п2 неизвестных элементов матрицы
Вк+1. Единственным решением является

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 133
где ck?Rn—единственный (с точностью до множителя)
ортогональный к пк вектор. Каждый конкретный способ
выбора подпространства лк, а значит и вектора ск, задает
определенный квазиньютоновский метод. Так, если в ка-
качестве пк взять ортогональное дополнение к Ахк, т. е.
потребовать, чтобы аппроксимация В не менялась вдоль
любого вектора, ортогонального к Ахк> то получится пер-
первый метод Бройдена. Заметим, что в формуле E.19) можно
избавиться от обращения матрицы Вк и вести пересчет Вкг
вместо Вк. Для этого применим формулу Шермана—Мор-
рисона (см. Приложение II), которая дает соотношение
ск>
Остановимся теперь на способах пересчета Нк+1 из Нк.
Матрица Нк+1 должна удовлетворять квазиньютоновскому
соотношению E.22), совпадая при этом с матрицей Нк
в (п — 1)-мерном подпространстве xk?Rn, не содержащем
AVk, т. е.
Отсюда однозначно определяется формула пересчета
_н (Axk-HkAVk)dZ ,
- лк+—ЩГ5^— (
в которой вектор dk g Rn ортогонален к подпространству хк.
Задав конкретный вид подпространства хк (следовательно,
и вектора dk), можно получить конкретный квазиньюго-
новский метод. Если, например, в качестве хк взять орто-
ортогональное дополнение к hVk, то dk = AVk и получается
второй метод Бройдена.
Между формулами E.24) и E.26) существует опреде-
определенная связь. Так, если матрицы Вк и Нк невырождены
и Hk = Bk1, то при ck = Bldky согласно E.25), получаем
+1 ЯЙ-1«
Формулы E.24) и E.26) определяют целый класс ква-
квазиньютоновских методов. Укажем некоторые наиболее
известные:
1-й метод Бройдена (ск = Ахк):
{АН*У)А];Н E.27)
Т
<AVktH%Axk>

134 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
2-й метод Броидена (dk = AVk):
метод Пирсона (ck = AVk):
метод Мак-Кормика (dk = Axk):
Я и | (Д#ь—— Нк Дк ь) Д.ОД /г» ол\
ft+i = ^fti /л!/. лУ.ч » E"*°)
симметричный метод 1-го ранга (dk = Axk—HkAVk):
(Axk-HkAVk)(Axk-HkAVk)T
В методе Сомаса расчеты ведутся по формулам E.20)
и E.26), в которых
O^)' Et32)
где dft= (^+ 2& ^») ^**' II' |~евклиД°ва норма и
Часто матрица Vх бывает симметричная. Поэтому по-
полезно получить квазиньютоновские методы, учитывающие
эту специфику. Для них выполняется квазиньютоновское
соотношение E.21), причем, если матрица Вк симметрична,
то симметрична и Вк+1. Приведем рассуждения, исполь-
использованные сначала М. Пауэллом [2] для получения сим-
симметричного варианта 1-го метода Броидена и впоследствии
Дж. Деннисом [1] для вывода формул общего вида.
Пусть матрица Вк симметрична. Тогда аппроксимация
полученная по формуле E.24), хотя и удовлетворяет соот-
соотношению E.21), но не является симметричной. Симметрич-
Симметричности можно добиться, взяв

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 135
И, поскольку матрица Вк%2 не будет удовлетворять соот-
соотношению E.21), продолжим описанный процесс. В этом
случае получим последовательность матриц {Вк% ,}?.<> такую,
что
-й б t (AVk-Bk,2iAxk)cZ
Д* + > •
где Вк%0 = Вк. Оказывается, что {Bk%i}°?a0 имеет предел
b—BkAxk)i
A,fe> r 5
Нетрудно убедиться, что матрица Bk+1 симметрична и
удовлетворяет квазиньютоновскому соотношению E.21).
В соотношении E.19) можно избавиться от необходимости
обращать матрицу Bk. С этой целью, применив формулу
Шермана — Моррисона к E.33), получаем
Btf 1 = В?+[<ck, В**AVk>(B^ck(Axk-Bi;*AVk)T +
E.34)
Пусть имеется симметричная аппроксимация Нк матрицы
[У* (я*)]- Последовательность матриц {ЯАэ1-}^0, получен-
полученная чередованием квазиньютоновской поправки по ^фор-
^формуле E.26) и симметризацией, сходится к матрице *
(Axk-Hk AVk)T
<Axk-HkAVk,AVk>
<dkt AVk>*
Видно, что матрица Hk+1 симметрична и удовлетворяет
квазиньютоновскому соотношению E.22). Заметим, что
между формулами E.33) и E.35) нет такой очевидной связи,
какая имеется между E.24) и E.26) при ck = l

136 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Соотношения E.33) и E.35) задают два пересекающихся
(но не совпадающих) класса квазиньютоновских методов.
Конкретным значениям векторов ск и dk отвечают вполне
определенные методы:
метод Давидона —Флетчера—Пауэлла (ck = AVk):
к, /Wk> <AVk,
метод Бройдена — Флетчера — Гольдфарба — Шенно
_я ¦ {Ьхк-Нк AVft) Ьх1+Ьхк (Ьхк-Нк AVfe)r
* (&xk> ДУ*>
<Ьхк-НкЬУк,АУк>А„ . г .- q7,
<Д**, AVk>* А**й**> VO-^O
симметричный вариант Пауэлла метода Бройдена
-Вк Ьхк) A*?+A*ft (ЬУк-Вк Д^)г
5й+1 = Вк ~
<АУк-ВкАхк,
<Ьхк,
Последний метод может быть описан выражением для
по формуле E.34), в которой следует взять ск = Ахн (не
приводится в силу* громоздкости).
Перейдем к описанию свойств квазиньютоновских мето-
методов. В работе Д. Гея [1] доказана сходимость методов
E.24) и E.26) к корню системы линейных уравнений (для
любого начального приближения xQ?Rn за число шагов,
не превышающее 2п). В этой же работе для нелинейного
случая доказана локальная 2л-шаговая квадратичная ско-
скорость сходимости первого и второго методов Бройдена.
Для большинства из приведенных методов доказана ло-
локальная сверхлинейная сходимость к решению системы
нелинейных уравнений E.1). Широкие возможности для
исследования скорости сходимости представляет
Теорема 2.5.7 (Дж. Деннис, Дж. Морэ [1]). Пусть
отображение V: Rn —* Rn непрерывно дифференцируемо
на открытом выпуклом множестве D. Пусть существует
точка x*?D такая, что У(х*)^=0 и матрица Vx(x*)
невырождена. Предположим, что для некоторого xo?D

$5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 137
последовательность хкУ построенная согласно E.19),
содержится в D> хкфх* при всех k^O и сходится к хт.
В этом случае последовательность xk сходится к х* сверх-
линейно тогда и только тогда, когда
Urn Kfr-lgfe)]fa,i-^LOi E.39)
Доказательство. Пусть выполнено 'соотноше-
ние E.39). Рассмотрим
\ВШ-VI(*.)](xk+1-xk) = -V{xk)-VTx (x,)(xk+1-xk) =
~V(xk+1)-V(xk)-VTx(x.)(xk+1-xk)-V(xk+1). E.40)
Из непрерывности якобиана ^ в ^ и соотношения
E.39) вытекает
Шп JlZif^IL = 0, E.41)
а поскольку V(x*) = 0 и матрица Vx(xm) невырождена,
существует число Р > 0 такое, что
Следовательно,
jV(xk+i)\\ ^ Pl^+i—^1 =r Pfe
где Рк — \Хк+±—хА1\хк—хА- Таким образом, из E.39)
получаем сходимость A^ . —>0 при &—*оо, а значит, и
сходимость рл—^0, что и требовалось доказать.
Допустим теперь, что последовательность хк-+хт со
сверхлинейной скоростью. Тогда
поскольку
Применяя E,42) к соотношению
и используя непрерывность V^ в jc., получаем E.41). Отсюда
с учетом E.40) вытекает E.39). Щ

138 теоремы о сходимости и их приложения [гл. и
Как следует из теоремы, для сверх линейной сходимо-
сходимости хк —>хт вовсе не обязательно, чтобы Bk—+VZ(x9).
Достаточной является сходимость последовательности Вк
к VI (хт) лишь вдоль смещений Ахк итеративного процесса,
что характерно для квазиньютоновских методов.
Матрица Bk может, вообще говоря, никогда не стать
равной VI (хт) даже в линейном случае (У1(х) ss Л), когда
AV = А Ах. Так, после первой итерации имеем Bt Ах0 = AV0,
а после следующей В2 Ахг = AVU и совсем не обязательно
B2Ax0 = AV0. Иными словами, на каждой итерации в мат-
матрицу Вк+1 вкладывается текущая информация, однако при
этом теряется накопленная информация. Отсюда возни-
возникает естественная потребность в методе, который наряду
с равенством E.21) сохранял бы зависимость
т. е. удовлетворял бы для всех k соотношению
Bk+1Axj=AVi9 k—n+l^i^k, f>0. E.43)
Для методов вида E.20) это означает, что
Ял+1Д7/ = Ах/, к—п+1<*<Л, i>0. E.44)
Таким свойством обладает последовательный (п+ ^-точеч-
^-точечный метод секущих, в котором Bk+1 = [AV]k[Ax]^1 (или
Я [Д][АУЗ^), где ()
В линейном случае (VJ (я) = Л), как нетрудно убе-
убедиться, ВТп = Л (или Нтп = Л"*1). В нелинейном случае, если
матрицы [Ах]к и [AV]k невырождены, то точка хк+1 будет
единственным корнем единственного линейного отображе-
отображения, принимающего в точках {яА_/}?_<> соответственно
значения {VX**-*)}?-<>• Этот факт указывает на то, что
последовательный (п+ 1)-точечный метод секущих является
обобщением обычного (одномерного) метода секущих на
случай п переменных.
Чтобы избежать в методе секущих обращения матрицы
[Ах]к (или [ДКу, можно представить ее в квазиньютонов-
квазиньютоновской форме. Для этого в формуле E.25) вектор ск надо
выбирать так, чтобы
<ск,Ахк>ф0. E-45)

§5] МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 139
Описанный выбор ск обеспечивает выполнение соотноше-
соотношения E.43). Аналогично другое представление метода се-
секущих в форме E.26) связано с соотношением
которое гарантирует E.44).
Если якобиан Vx(x) системы E.1) симметричен, то
наиболее полно эту специфику учитывает симметричный
вариант метода секущих. В этом случае расчеты ведутся
по формулам E.19), E.34), E.45).
Теорема 2.5.8 (Л. Биттнер [1], Л. Торнхейм [1]).
Пусть отображение V удовлетворяет условиям тео-
теоремы 2.5.7. Предположим \\хо—хщ\\ достаточно мало и
при подходящих а > О, г > О итерации последовательного
(л+1)-точечного метода секущих
таковы, что ||[A#]J<r, и матрицы [&х]к равномерно
~ены, т. е.
Тогда xk-+xm со сверхлинейной скоростью. Если допол-
дополнительно выполнено неравенство Липшица E.6), то поря-
порядок сходимости выше, чем единственный положительный
корень уравнения tn+1—tn—1=0.
Доказательство мы опускаем; его можно найти, напри-
например, в монографии Дж. Ортега и В. Рейнболдта [1].
Наряду с высокой скоростью сходимости и необходи-
необходимостью вычислять на каждой итерации лишь одно значе-
значение отображения V, последовательный (я-Поточечный
метод секущих обладает существенным недостатком, за-
заключающимся в требовании равномерной невырожденности
матриц [&х]к. Последовательность хк, не удовлетворяющая
неравенству E.47), может стать источником неустойчиво-
неустойчивости метода. Исследования последних лет в этой области
направлены в основном на построение вариантов метода
секущих, устойчивых по отношению к линейной зависимо-
зависимости векторов {Aa^_,-}JL0- В этой связи следует упомянуть

140 теоремы о сходимости и их приложения [гл. и
работы Б. Грагга и Дж. Стюарта [1], Д. Гея и Р. Шна-
беля [1], Дж. Мартинца [1], О. П. Бурдакова [1].
При минимизации функции f(x) проявляются некото-
некоторые новые свойства методов квазиньютоновского типа,
имеющих вид
хк). E.48)
Оказывается, если функция / (я) квадратична, т. е.
где матрица А симметрична и строго положительно опре-
определена, а длина шага ак выбирается из условия точного
минимума
ак = arg min / (хк—аНк fx (хк)),
а
то некоторые квазиньютоновские методы такие, как, на-
например, Давидона—Флетчера—Пауэлла E.36), Брой-
дена —Флетчера—Гольдфарба—Шенно E.37), симметрич-
симметричный метод 1-го ранга E.31), генерируют последовательность
сопряженных направлений. В этом случае
и, как следствие, имеет место сходимость к точке мини-
минимума квадратичной функции за число шагов, не превос-
превосходящее п. Если методом было сделано п шагов, то Нп = Л.
При минимизации неквадратичной функции это свойство
приводит к /i-шаговой квадратичной скорости сходимости,
которая имеет вид
\\хк-х^ E.49)
Если при всех k^n направления {Ax^^Zl равномерно
линейно независимы, то может быть доказана более высо-
высокая скорость сходимости, чем E.49), с порядком, превос-
превосходящим единственный положительный корень уравнения
tn+l — tn—1=0. Такая оценка скорости сходимости ква-,
зиньютоновских методов, вырабатывающих сопряженные
направления, совпадает с оценкой, приведенной в теоре-
теореме 2.5.8 для последовательного {п + 1 )-точечного метода
секущих.

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 141
§ 6. Численные методы отыскания минимакса
Важность создания численных методов отыскания ми-
минимакса обусловлена несколькими причинами: во-первых,
многие практические задачи принятия решений в конфликт-
конфликтных ситуациях сводятся к нахождению минимакса, и
численные методы их решения требуются широкому кругу
прикладников. Во-вторых, эти методы оказываются полез-
полезными при решении задач нелинейного программирования
и оптимального управления, об этом будет неоднократно
говориться ниже.
Изложение начнем с простейшего случая, когда отыс-
отыскивается локальный минимакс (см. определение 1.5.2),
далее кратко остановимся на методах нахождения гло-
глобальных решений.
1. Методы отыскания локального минимакса. Предпо-
Предположим, что в задаче A.5.2) функция F(x, у) определена
и дифференцируема на ЕпхЕт. Будем отыскивать пре-
предельные (при t -+ оо) точки решения следующей задачи
Коши:
?. = — гРх(х, у), &L =
Дискретный вариант этой системы имеет вид
хк> ук), yk+i - yk+*Fy {хкУ ук). F.2)
Здесь 0<е<^1—малый параметр, шаг интегрирования
а > 0. Ниже покажем, что имеет место
Теорема 2.6.1 (Н. И. Грачев, Ю. Г. Евтушенко [4]).
Пусть функция F(x> у) дважды непрерывно дифферен-
дифференцируема в окрестности точки г* = [#«, */»], где выполнены
достаточные условия локального минимакса, приведенные
в_теореме 1.5.7. Тогда существуют такие числа е">0,
а > 0, что_при любых фиксированных значениях 0 < 8 < е
«0<а<а решения х(г, х0, у0У t), у (г, хОУ у0, t) систе-
системы F.1) и итерации хк(г, хи> у0), ук(е, хо> у0) по схеме
F.2) локально сходятся к точке г*.
Теорема дает сравнительно простые методы решения
задачи A.5.2). Наличие в F.1) и F.2) медленно и быстро
меняющихся переменных усложняет расчеты ? одцако в ряде

142 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
задач высокой размерности такой подход оказывается
весьма эффективным. Если в F.1) сделать замену незави-
независимой переменной x = s/, то получим
g FA», У), *jR = Ft{x,y). F.3)
Системы вида F.3) изучаются в теории сингулярных
возмущений обыкновенных дифференциальных уравнений.
Укажем работы, посвященные этому вопросу: А. Н. Ти-
Тихонов [1], А. А. Дородницын [1], Е. Ф. Мищенко,
Л. С. Понтрягин [1]. Подробная библиография содержится
в книгах А. Б. Васильевой и В. Ф. Бутузова [1],
Е. Ф. Мищенко и Н. X. Розова [1].
Следуя методам теории сингулярных возмущений,
можно рассмотреть так называемую вырожденную систему,
которая получается из F.3), при е = 0:
%~-Fx{*>y)> Fy(x,y)=0. F.4)
Если выполнены условия теоремы 1.5.8 и функция F
достаточно гладкая, то второе уравнение определяет одно-
однозначную функцию y = g(x), причем
¦ g (х) = Arg max F (*, у). F.5)
еЕ»*
Подставив это выражение в F(x, у), получим следующую
функцию максимума:
<?(x) = F(xyg(x)). F.6)
Подставляя y = g(x) в первое уравнение F.4), получим
систему
R--$в-^ (*.*(*»• F.7)
которая совпадет с методом Коши (см. формулу B.3)),
примененным к минимизации функции <р(х). Согласно
результатам § 2 для локальной сходимости метода F.7)
достаточно положительной определенности матрицы
<Pxx(*) = Fxx(Xf 8(Х)) —
-Р*ш(х, g{x))Fyl{xy g(x))Fvx(x, g(x)) F.8)
в точке х~Хщ.

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА ИЗ
В работах по теории сингулярных возмущений дока-
доказывается, что если г достаточно мало и выполнен ряд
предположений, то решение системы F.4) аппроксимирует
решение F.3). Мы совершаем обратный переход: вместо
решения вырожденной системы F.4), которая может ока-
оказаться сложной при больших значениях /п, интегрируется
система F.1), эквивалентная сингулярно возмущенной F.3).
Перейдем к доказательству теоремы. Составим урав-
уравнение в вариациях для системы F.1):
8г = М (е, z%) 6z;
здесь
bx = x{t)—x., by
Непрерывная, ограниченная (как функция г) матрица
M(s, zm) удовлетворяет следующему условию: корни ха-
характеристического уравнения
\М{г, г,)-Я/„+и| = 0 F.9)
при 8—^0 распадаются на две группы корней:
1-я группа из т корней—корни, близкие к корням
уравнения
\Fyv{z.)-Mm\ = 0;
2-я группа из п «малых» корней порядка efi, где fi —
корни, близкие к корням уравнения
Умножая нижнюю матрицу-строку слева на Fxy (гф) Fyy (z«)
и вычитая ее из верхней, получим, что ц есть корень
следующего уравнения:
Ф (z) = Fxx (z)-Fxy (г) F$ (г) Fyx (г). ^'Ш)
Согласно достаточным условиям локального минимакса
матрица Ф(г9) положительно определенная, поэтому все
корни \i действительные и строго отрицательные. Следо-
Следовательно, при достаточно малых значениях 8 все корни
уравнения F,9) имеют строго отрицательные действитель-

144 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
ные части. Согласно теореме об устойчивости по первому
приближению стационарная точка z* является асимптоти-
асимптотически устойчивым положением равновесия для системы F.1).
Отсюда следует локальная сходимость метода F.1) к г* и
сходимость разностного варианта F.2) при достаточно
малых значениях а (см. § 3). Щ
Методы F.1) и F.2) можно использовать для нахож
дения локальных максиминов в задаче A.5.1). Однако
в этом случае следует брать 8^> 1, т. е. 8 рассматривается
как большой параметр. При выполнении достаточных усло-
условий локального максимина, приведенных в теореме 1.5.9,
решения F.1) и F.2) локально сходятся к локальному
максимину, если е достаточно велико и а достаточно мало.
Введение малого параметра ев F.1) приводит к тому, что
переменные х изменяются значительно медленнее, чем пере-
переменные у. Это усложняет интегрирование F.1). В случае,
если F (*, у) строго выпукло-вогнутая функция, в задаче
A.5.1) есть седловая точка и можно положить 8=1,
упростив тем самым расчеты; метод F.1) переходит при
этом в метод B.5) отыскания седловых точек. Метод F.1)
благодаря его простоте можно использовать при решении
простейших игровых задач. (На этом вопросе мы остано-
остановимся ниже, в § 8 гл. VI.) Доказана теорема о глобаль-
глобальной сходимости F.1) и F.2) в предположении, что выпол-
выполнены требования несколько более сильные, чем условия,
приведенные в теореме 1.5.8 (см. Ю. Г. Евтушенко [12]).
«Быстрое» движение по у можно осуществить, исполь-
используя метод Ньютона:
Несложно показать, что характеристические числа матри-
матрицы, фигурирующей в уравнении в вариациях, состоят из
п чисел, близких к корням F.10), и т чисел, близких
к —1. Отсюда следует локальная сходимость метода при
стандартных предположениях.
2. Редукция к отысканию седловых точек. Произведем
в задаче A.5.2) замену, введя вместо вектора у новый
m-мерный вектор р:
P-y-gM, F.11)
где g(x) определяется из F.5).

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 145
Рассмотрим новую задачу об отыскании безусловного
минимакса:
minmaxB(x, p\ B(x9 p) = F(x9 p + g(x)). F.12)
Е*Ет
Замечательным свойством выполненного преобразова-
преобразования является то, что из существования синтеза в задаче
A.5.2) следует, что задача F.12) имеет-седловую точку.
Действительно, из теоремы 1.5.1 следует неравенство
max min В (х, р) ^ min max В (ху р).
рб Ет хеЕп Еп Ет
С другой стороны,
max min В (х, р) > min В (х, 0) =
ЕтЕп Е*
min maxF(x4 у) = min max В (х, р).
Еп'Ет ЕпЕт
Сравнивая это неравенство с предыдущим, получаем, что
max min В (х, р) = min max В (х, /?),
$Ет хеЕп ЕПеЕт
т. е. задача F.12) обладает седловой точкой.
Продифференцируем В(х, р) по л: и р, получим сле-
следующие формулы:
^-F M^F i??-F ?L-F M^
дх ~~r*'rdxV dp ~~У дхдр~~ ху^dx
p
Здесь для краткости мы не приводим аргументов функций.
Обозначим рт=*у*—g(x*)> тогда получим
Вх (*„ 0) = Fx (г.) - 0, В, (хф, 0) = Fy (z.) = 0,
В„ (х*> 0) = Fyy (z.) < 0, Вхр {х., 0) = 0,
Вхх(хт, 0) =
Найденные формулы показывают, что преобразование F.11)
обладает следующим свойством: стационарные точки [а:, у]
функции F (ху у) преобразуются в стационарные точки
[#, р] функции В (х, р)\ если в точке [#*, уф] выполнены
достаточные условия строгого локального минимакса, то

146 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
она переходит в точку \хту рт], где выполнены достаточ-
достаточные условия строгого локального седла функции В (х, р)>
и F(x%y Ут) = В(хт, 0), что дает возможность использовать
известные итеративные численные методы отыскания сед-
ловых точек для нахождения локального минимакса и
максимина. Поясним эту мысль на примере двух простей-
простейших методов.
Для нахождения седловых точек функции В (х, р) вос-
воспользуемся градиентным методом B.5). Составим систему
из п + т обыкновенных дифференциальных уравнений
Выполним в этой системе переход от переменных х,
р к первоначальным переменным х, у. Тем самым преоб-
преобразуем метод поиска седловой точки в метод нахождения
локального минимакса. Получим
* = -F*-gxFy, y = Fy+glx. F.13)
Воспользуемся другим методом. Для переменной р при-
применим метод Ньютона, а для х—градиентный метод:
х = — Вх(х,р)9 р = — В$(х,р)Вр(х,р).
В первоначальных переменных метод будет иметь вид
x = -Fx-gxFy, y = -F?yFy+glx. F.14)
Практическое использование полученных методов ослож-
осложнено тем, что в выражение
gl = -Fyl{x, g(x))Fyx(x, g(x)) F.15)
входит функция g(x), нахождение которой требует реше-
решения задачи максимизации. Однако возможны упрощенные
варианты полученных методов: в F.13) и F.14) можно
положить
8Тх~РуНх,У)Рух(х, У). F.16)
Сходимость полученных методов докажем ниже, кроме
того, обоснуем следующие методы отыскания локального
минимакса:
, F.17)
F.18)
F.19)

§ б] ЧИСЛЕННЫЕ МЕТОДЫ МИНИМАКСА ОТЫСКАНИЯ 147
Приведем дискретный вариант только для метода F.17):
xk+1 = xk—aFx(xk, ук), yk+i = yk+a.[Fy(xk, yk) +
+ Fyl (*» Ук) Fyx (**> У k) Fx (**, укI F.20)
Согласно результатам из § 5 гл. I необходимыми усло-
условиями локального минимакса в задаче A.5.2) являются
условия стационарности A.5.17). Применяя к решению
системы A.5.17) метод Ньютона, получим следующий
метод отыскания локального минимакса:
хк, ук)—
—рху (*н> Ук) руу (**, Ук) Fy (xk> УкI /б 21)
Ук+i = Ук—Fyy (Ч> У к) lFy i*k> Ук)~
3. Обоснование сходимости. Предполагая, что во всех
приведенных методах gl вычисляется по упрощенной
формуле F.16), сформулируем и докажем следующую тео-
теорему о сходимости.
Теорема 2.6.2. Пусть в точке гф = [хф, уф] выпол-
выполнены достаточные условия локального минимакса (см.
теорему 1.5.7). Тогда:
1) решения систем F.13), F.14), F.17)—F.19) локально
экспоненциально сходятся^при t —> <х> к точке г%\
2) существует такое а > 0, что при любом 0 < а < а
дискретные варианты этих систем вида F.20) локально
линейно сходятся к точке гт.
Доказательство. Воспользуемся теоремой 2.1.1
об устойчивости по первому приближению. Обозначим
Отбрасывая члены второго порядка малости, получим
уравнение в вариациях для системы F.13)
8z = Bi&z, F.22)
где Вг—квадратная матрица размера (п + тJ-, предетави-
мая с помощью четырех матриц-блоков:
в ^
1

148
ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Элементы всех матриц вычислены в точке z*. Характе-
Характеристическое уравнение матрицы Вх имеет вид
| Fn (z.)-XIm | = 0.
n
Таким образом, характеристические числа матрицы В±
состоят из характеристических чисел матриц Fyy(z#) и
—Ф(г*). Но обе эти матрицы симметричные и отрица-
отрицательно определенные. Следовательно, все собственные числа
матрицы Вг вещественны и строго отрицательны. Отсюда
заключаем, что положение равновесия г* для системы
F.13) асимптотически устойчиво.
Аналогично доказывается сходимость остальных мето-
методов. Обозначим В2У В3> Я4, Вь матрицы уравнений в ва-
вариациях F.22) для методов F.14), F.17)—F.19) соответ-
соответственно. Легко показать, что характеристические уравне-
уравнения будут следующие:
Опт
- I—Ф—X/, |. |—A+Я) /J -0,
^zIssz^LlJl z^bl
Fyx + FyyFyx Fxx; Fyy + FyyFyxFxy — \
=o,
Из этих соотношений следует, что все корни характе-
характеристических уравнений для матриц 52, В4, Вь действи-
действительные и отрицательные. Умножим верхнюю строку блоч-
ной матрицы В3—Мп+т слева на F~lFyx и сложим с ниж-
нижней, определитель матрицы при этом не изменится:
Умножим правый столбец полученной матрицы справа на
FyyFyx и вычтем из левого столбца, тогда
\В3-%1п+т\ =
\ г уу Nln

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 149
Отсюда заключаем, что характеристические числа матри-
матрицы Bs также дейстзительные, отрицательные и метод F.17)
поэтому экспоненциально сходится к стационарной точке z9.
Если величина а достаточно мала, то, согласно тео-
теореме 2.3.7, сходимость дискретных вариантов методов сле-
следует из приведенных доказательств сходимости непрерыв-
непрерывных вариантов. Щ
Заметим, что условия теоремы в случае методов F.14)
и F.19) можно ослабить и вместо отрицательной опреде-
определенности Fyy (z«) потребовать невырожденность Fyy (z«).
Однако это свойство не представляется существенным,
поэтому в дальнейшем его оговаривать не будем.
Сходимость метода Ньютона F.21) следует из общей
теоремы 2.5.3; в соответствии со сделанным к ней заме-
замечанием переформулируем эту теорему следующим образом.
Теорема 2.6.3. Пусть,в окрестности стационарной
точки z«, функция F (z) дважды дифференцируема, матри-
матрицы Ф (z,) и Fyy (z») невырождены и матрица Fzz (z) в окрест-
окрестности z» удовлетворяет условию Липшица. Тогда итера-
итерации F.21) сходятся к z» локально, с квадратичной ско-
скоростью.
Приведенные методы могут быть использованы для
получения различных модификаций. Положим, например,
в правой части первого уравнения F.13) y = g(x), тогда
получим
i = -F,(*,*(*)), y = F9(x,y)+&(x)i. F.23)
В методах F.13), F.14), F.17)—F.19) производную
функции g(x) можно находить из F.15). При выполнении
условий теоремы 1.5.7 методы по-прежнему будут схо-
сходиться к z». Это следует из того, что для уравнений
в вариациях характеристические числа будут те же, что
и при использовании формулы F.16). Численная реализа-
реализация таких методов, однако, будет более трудоемкой, так
как потребуется для вычисления правых частей систем
дифференциальных уравнений решение дополнительной
задачи максимизации F (х, у) по у.
Использование в F.13), F.14) функции g(x) не при-
приводит к качественному улучшению методов. В методе
F.23), напротив, появляется свойство сходимости в целом.
Такой же особенностью обладает следующий метод:
X = -F,(x,g(x)), У = ё(х)-у. F.24)

150 теоремы о сходимости и их приложения [гл. i
Теорема 2.6.4. Пусть F(x, у) и g(x) всюду непре-
непрерывно дифференцируемы по всем аргументам. Пусть при
любых х?Еп функция F (х, у) строго вогнута по у,
а функция F(x> g(x)) строго выпукла пох. Тогда методы
F.23), F.24) при t-+ оо сходятся в целом к стационар-
стационарной точке z*—единственному глобальному решению за-
задачи A.5.2).
Доказательство. Покажем, что стационарна я
точка z*, являющаяся положением равновесия для обеих
систем, асимптотически устойчива в целом. Составим по-
положительно определенные функции
которые обращаются в нуль только в стационарной точке
2 = 2*. Очевидно, что функция i>! бесконечно большая.
Функция v2 строго выпукла по х и у и, согласно тео-
теореме 1.1.2, также бесконечно большая.
Продифференцируем vx в силу системы F.23), v2—
в силу F.24), воспользуемся условиями выпуклости и
вогнутости, получим
y*> У), У—В(х)
x)) + F{x9y)-F{x,
причем щ = г>2 = 0 только при х = х%, y = y%=ig(xm). По-
Поэтому, согласно теореме Барбашина—Красовского, поло-
положение равновесия z = z* для систем F.23), F.24) будет
асимптотически устойчиво в целом и, следовательно, реше-
решения систем будут сходиться к zm при любых начальных
данных в задаче Коши. Q
Для реализации последних двух методов необходимо
определять значения функции g(x). Многократное вычис-
вычисление g (x) можно заменить интегрированием системы диф-
дифференциальных [уравнений. Действительно, при любом
у = g (x) должно выполняться необходимое условие экстре-
экстремума Fy(x9 g(x)) = 0. Дифференцируя это соотношение

§61 ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 151
по х, получим, что y = g(x) есть решение следующей за-
задачи Коши:
% = -FjA(x,g(*))F9X(x,g(x))9 g(xo) = yo. F.25)
Приведенные методы обладают двумя достоинствами:
во-первых, они сравнительно просты, во-вторых, позво-
позволяют найти решение с высокой точностью. Их недостаток
заключается в необходимости накладывать жесткие огра-
ограничения на функцию F (х, у). Если эти методы применить
к произвольным функциям, то результаты, полученные
с их помощью, следует рассматривать лишь как предва-
предварительные. Чтобы утверждать, что найденные решения
являются глобальными, необходимо дополнительное изу-
изучение задачи либо последующие расчеты с помощью гло-
глобальных методов.
Все методы этого . параграфа можно использовать для
нахождения седловых точек. Действительно, если в точ-
точке z« выполнены достаточные условия строгого седла:
Руу (z*) < О» Fхх (г*) > °» то в этой точке обязательно
Ф (Z,) > 0, и условия теоремы 1.5.7 заведомо выполняются.
Укажем два метода, предназначенные специально для
нахождения седловых точек:
* = - Fx (x,g (*)), y = Fy(d (у), у\ F.26)
x = d(y)—xt y = g(x)-y. F.27)
Здесь d(y) = ArgminF(x, у).
xeEn
Предположим, что для любых х?Еп, у?Ет, хфхт,
уФут имеют место условия строгого глобального седла
A.5.16). Для доказательства составим положительно опре-
определенную функцию
v{x,y) = F(x9 g{x))-F(d(y), у).
Если функция F строго выпукло-вогнутая, то функции
d(y) и g(x) дифференцируемы. Вычисляя производную
функции v в силу систем F.26) и F.27), получим соот-
соответственно
v = <Fx(x9g{x))t d(y)-x> +
+ <Fy(d(y), y\ y-g(x)>^F(d(y), g(x))-F(xt g(x)) +
+ F(d{y), y)-F(d(y), *(*))<-*(*,

152
ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Таким образом, методы сходятся, причем во втором методе
v{x(t), y(t))<:V(xOf уо)е~*.
4. Методы отыскания локальных по х, глобальных
по у решений. Если в задаче A.5.2) каким-либо способом
удается при каждом х ? Еп решать внутреннюю задачу,
то отыскание минимакса сводится к поиску безусловного
минимума функции многих переменных:
x.€Argminq>(*). F.28)
функция g(x) определяется либо аналитически, либо
из решения задачи максимизации, либо из интегрирования
системы F.25). В том случае, когда размерность вектора у
невелика, на множестве допустимых значений вектора у
можно построить некоторую сетку и значения функции
Ф (я) определить из полного перебора значений F (х, у()
на этой сетке.
Отвлекаясь от вопроса решения внутренней задачи,
мы приходим к задаче F.28), для решения которой строится
последовательность точек xk, сходящихся к хт. Рассмотрим
сначала тот случай, когда функция ф(#) дифферен-
дифференцируема, ее производные можно вычислить по формулам
F.7), F.8). Обозначим ти /п2, /п3, /л4 наименьшие соб-
собственные числа соответственно следующих симметричных
матриц: Fyy(zm), Fxx(z.)9 Fxy(z.)Fyx(z,)9 q>x*(*.).
Теорема 2.6.5. Пусть в точке z* = [x*, #«] выпол-
выполнены условия теоремы 1.5.7. Тогда имеет место соот-
соотношение
Доказательство. Если матрица Fyy(г*) отрица-
отрицательно определена, то для любых ненулевых векторов
у?Ет имеем •
Обозначив y = Fyx(z*)x, получим
Отсюда следует, что m^m2—mjm^ Учитывая, что
наименьшее собственное значение матрицы Fxy (z«) Fyx (г#)

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 153
неотрицательно и что т* < 0, приходим к требуемому
неравенству. Щ
Для многих численных методов минимизации важна
выпуклость минимизируемой функции ф(я) в окрестности
точки х*. Из полученного неравенства следует, что при
Щ > 0 функция ф (х) будет выпуклой. Это свойство может
иметь место даже в тех случаях, когда исходная функция
F (х, у*) не является выпуклой в окрестности точки #«,
и будет использоваться в гл. IV при решении задач нели-
нелинейного программирования.
Применим для решения F.28) простейшие методы безус-
безусловной минимизации:
1) Градиентный метод с постоянным шагом
xk+i = xk—aFx(xk9 g(xk)).
Если функция ф (я) дифференцируема, т4 > 0, то метод
локально сходится при любом 0<а<а. Здесь а = 2/М,
М — наибольшее собственное значение матрицы Ф
2) Метод наискорейшего спуска
где aft = Arg min ф (*ft—aF (xk> g(xk))). Считая величину
a
<px(xk) малой и отбрасывая величины третьего порядка
малости, получим
Ф(** — «Ф* (**))=*
= Ф (**)—«IIФ* (Ч) V+у Ф1 (Ч) Ух* (**) Ф^ i*k)>
минимизируя правую часть по а, получим
Отсюда следует оценка
обеспечивающая релаксационность процесса минимизации
для минимаксно определенных функций.
3) Метод Ньютона
**+i ^ Ч—[ф** W] Ф^ (^)-
Если матрица ф^^^) удовлетворяет условию Липшица и
выполнены условия теоремы 1.5.7, то метод Ньютона схо-
сходится локально с квадратичной скоростью.

154 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
4) Метод обобщенного градиента (см. формулу D.5))
(хк).
Для минимизации ф(*0 можно использовать и многие
другие численные метода безусловной минимизации.
В тех случаях, когда внутренняя задача оказывается
неоднозначно разрешимой, функция ф(х) перестает быть
дифференцируемой, метод наискорейшего спуска, метод
Ньютона оказываются неприменимыми. Необходимо поль-
пользоваться либо общими методами негладкой оптимизации,
либо создавать их версии, предназначенные специально
для минимизации функции максимума. Последнему направ-
направлению посвящены книгя В. Ф. Демьянова и В. Н. Мало-
земова [1], [2]. т
5. Методы отыскания глобальных решении. В подав-
подавляющем большинстве практических задач оптимизации
следует отыскивать глобальные решения. Однако нахож-
нахождение даже глобального экстремума функции многих пере-
переменных в общем случае представляет собой чрезвычайно
сложную задачу. Еще большие трудности возникают при
решении минимаксных задач. В вычислительной матема-
математике направление, связанное с поиском глобальных экстре-
экстремумов, развито слабо из-за большой сложности этой проб-
проблемы.
Рассмотрим вначале задачу отыскания глобального мак-
максимума функции многих переменных. Пусть на множестве
определена некоторая функция г|?(*/). Требуется найти гло-
глобальный максимум этой функции на У:
F.29)
При численных расчетах эта задача обычно упрощается,
вводится так называемое множество е-решений:
Здесь 8 > 0—заданная точность расчетов. Требуется найти
точку у*$Уг- Другими словами, необходимо с заданной
точностью е определить величину глобального максимума
функции от т переменных и найти хотя бы одну точку у*,

§ 6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА J55
где это приближенное значение достигается. Укажем не-
несколько численных методов решения сформулированной
задачи.
1) Случайный поиск. Случайным образом определим k
допустимых точек уи у2, ..., yk. В качестве решения
возьмем ту точку, в которой достигается наибольшее зна-
значение ф(^/)9 *€[1: k~\. Количество пробных точек k опре-
определяется так, чтобы была достаточно велика вероятность,
что хотя бы одна из них будет принадлежать множеству Ye.
Очевидно, метод наиболее эффективен, если функция я|э (у)
достаточно «пологая», для нее отношение меры множества
Ye K меРе множества Y не является величиной малой.
2) Случайный поиск с использованием локальных про-
процедур- Так же, как и в предыдущем случае, определим k
допустимых точек. Далее с помощью локальных методов
поиска максимума функций многих переменных отыщем
локальные максимумы функции i|)(#) на У, взяв в каче-
качестве начальных^точек у^ у2, ..., yk. В результате полу-
получим точки у19 у2, ..., ук\ в качестве решения у* возьмем
ту из найденных точек, в которой функция ty(y{) прини-
принимает наибольшее значение. Количество точек ky необхо-
необходимое для реализации метода, определяется из условия
обеспечения достаточно высокой вероятности того, что
среди начальных точек уи у2, ..., ук найдется по край-
крайней мере одна точка, попадающая в область притяжения
(область локальной сходимости) хотя бы одной точки из
множества глобальных решений задачи F.29). Метод целе-
целесообразно использовать, когда количество локальных мак-
максимумов в задаче F.29) невелико.
3) Перебор на неравномерной сетке. Чтобы строить
более - эффективные методы, необходимо вводить ограни-
ограничения на класс функций ty(y). Простейшее условие со-
состоит в том, что функция i|)(t/) удовлетворяет условию
Липшица с постоянной I.
Пусть вычислены значения функции t|) в точках у19
У2> • • •» Ун из У- Определим величину Rk и множества Ау.
Rk = max
Легко видеть, что если объединение шаров Ау (/€[^:^])
полностью покрывает множество У, то задача решена.

156 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
В качестве приближенного значения глобального экстре-
экстремума берется величина Rk. Выполнимость условия Rm—Rk^
при этом гарантирована. Возможны самые различные ва-
варианты осуществления покрытия множества Y шарами Ау.
В работах Ю. Г. Евтушенко [1], [5] приведены програм-
программы, реализующие на языке алгол алгоритмы таких покры-
покрытий с помощью m-мерных кубов, вписанных в /п-мерные
сферы, являющиеся границами шаров Ду. Чтобы покрытие
велось с возможно большими шагами, желательно, чтобы
величины Rk были как можно больше. Поэтому при реа-
реализации покрытий в точках, где удалось увеличить зна-
значение Rk на достаточно большую величину, включались
подпрограммы поиска локального максимума. Цель их
использования—возможно выше поднять «текущее» зна-
значение максимума. После работы локальных методов вклю-
включалась основная программа глобального покрытия мно-
множества Y.
г Если функция i|) (у) такова, что ее градиент удовлетво-
удовлетворяет условию Липшица с константой /, то VF V?Y
> У~У/> + ?\V-
Обозначим Sj сферу
центр которой у и радиус р^ определяются по формулам
уу%(у) p
Для точек, лежащих внутри и на поверхности сферы 5у,
выполнено неравенство f(x) <^s + Rk. Задача состоит в
покрытии множества Y последовательностью шаров, гра-
границы которых есть сферы Sj.
Методы отыскания глобальных решений требуют чрез-
чрезвычайно большого объема вычислений. Поэтому их уда-
удалось использовать лишь в случае задач невысокой раз-
размерности. Для более сложных задач приходится брать
значение /, заведомо меньшее, чем это требуется для
того, чтобы гарантировать глобальность найденного реше-
решения, и только после найденного достаточно хорошего при-
приближения пытаться увеличить /. Описанные методы успеш-
успешно использовались для решения различных задач поиска

§6] ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ МИНИМАКСА 157
глобального экстремума. Подробную библиографию по
численным методам поиска глобального экстремума можно
найти в книгах Р. Г. Стронгина [1], Л. Диксона и
Г. Сегё [1J, [2].
После того как построена программа отыскания гло-
глобального экстремума функций, можно перейти к решению
минимаксной задачи A.5.7). Согласно теореме К5.2, если
функция F(z) = F(х, у) на Q = XxY удовлетворяет усло-
условию Липшица по z с константой /, то определяемая из
A.5.8) функция ф(я) также удовлетворяет условию Лип-
Липшица на X по х с той же самой константой. Таким об-
образом, последовательная максимизация и минимизация
функции многих переменных по части ее координат не
выводит из класса функций, удовлетворяющих условию
Липшица. Это свойство открывает широкие возмож-
возможности для использования ' методов поиска глобального
экстремума в задачах о последовательном минимаксе.
В A.5.7) один и тот же метод поиска глобального экст-
экстремума можно последовательно использовать для решения
внутренней и внешней задач. Подпрограммы локального
поиска обычно берутся разные, так как функции F (х> у)
часто бывают дифференцируемы и их локальная максими-
максимизация производится с использованием свойств гладкости
F по у. Функция ф (х) дифференцируема лишь по направ-
направлению, и ее локальную минимизацию приходится выпол-
выполнять иными методами.
Сравнивая A.5.7) с задачей нахождения глобального
экстремума функции F по z на Q, приходим к выводу,
что A.5.7) обладает одним важным свойством, упрощаю-
упрощающим ее решение по сравнению с поиском глобального
экстремума. Действительно, пусть в некоторой точке хг
известно значение ф^). Если для некоторой другой точ-
точки х2 приходится отыскивать значение ф(#2), то процесс
максимизации F (х2, у) по у можно прекращать как только
найдена-хотя бы одна точка y2$Y такая, что F (х2, у2)^
^ф(*1)> так как в этом случае заведомо Ф (#2) ^ Ф (^i) и
значение ф(дс2) не улучшает текущее приближенное зна-
значение минимакса ф^). Благодаря этому свойству в ряде
случаев можно обрывать процесс решения внутренней за-
задачи.
Описанный метод использовался для решения только
тех задач, в которых размерность вектора х невелика.

158 ТЕОРЕМЫ О СХОДИМОСТИ И ИХ ПРИЛОЖЕНИЯ [ГЛ. II
Развитие методов поиска глобального экстремума и уве-
увеличение быстродействия ЭВМ,* по-видимому, позволят в
будущем достигнуть значительного прогресса в этой важ-
важной области. Работа над численными методами решения
минимаксных и игровых задач приведет, возможно, к соз-
созданию принципиально новых алгоритмов. Характерными
чертами их будет использование глобальных методов
поиска и методов построения синтезирующих управлений.

ГЛАВА III
МЕТОД ШТРАФНЫХ ФУНКЦИЙ
Одним из наиболее популярных численных методов нели-
нелинейного программирования является метод штрафных
функций. Идея метода проста и весьма универсальна;
благодаря этому метод нашел применение при решении
разнообразных экстремальных задач. Были предложены и
продолжают появляться многочисленные модификации ме-
метода. Подробную библиографию зарубежных работ, опуб-
опубликованных в этом направлении, можно найти в книге
А. Фиакко и Г. Мак-Кормика [1].
Существующие сейчас многочисленные модификации,
по-видимому, не исчерпывают всех возможностей метода,
и работы в этом направлении представляются перспектив-
перспективными. Вместе с тем следует иметь в виду, что практи-
практические расчеты разнообразных задач выявили существен-
существенный недостаток метода: он оказался неприемлемым для
решения задач с высокой точностью. Использование боль-
больших значений коэффициента штрафа приводит к миними-
минимизации функций резко выраженного овражного типа, что
существенно усложняет расчеты. В адрес метода штраф-
штрафных функций^ был высказан многими авторами целый ряд
критических замечаний. Нельзя, однако, не учитывать
сильных сторон метода. Прежде всего, метод обладает
областью сходимости часто существенно большей, чем у
других методов; вычислительные схемы, реализующие ме-
метод, отличаются исключительной простотой. Все это делает
метод штрафных функций незаменимым для нахождения
начальных, приближенных решений. Однако если от вы-
вычислений требуется более высокая точность решения, то
целесообразно обратиться к другим быстро сходящимся
методам (например, к методам, описанным в гл. IV), взяв
результаты расчетов по методу штрафных функций в ка-
качестве начального приближения. Изложение метода начнем
с традиционного варианта метода, перейдя далее к его

160 метод штрафных функций ?гл. ш
модификациям. Как будет видно из дальнейшего изложе-
изложения, к методу штрафных функций можно отнести и опи-
описанный в § 3 метод параметризации целевой функции и
его модификации.
§ 1. Метод внешних штрафных функций
1. Общая идея метода. Рассмотрим задачу нелинейно-
нелинейного программирования A.6.1). Определенную на Еп функ-
функцию S(x) будем называть штрафной, если выполнены
следующие три условия:
1) функция S(x) непрерывна всюду на Еп\
2) S(x) = 0 для любых х?Х;
3) S(x)>0 для любых х^Х.
В случае, когда допустимое множество X определяется
условием A.6.2), штрафная функция обычно строится ад-
аддитивно в виде
|W). (l.i)
Здесь непрерывная функция ф(^) такова, что <р@) = 0 и
Ф (q) > 0 для «всех q Ф 0. В качестве ф можно взять, на-
например, функции
Аддитивную штрафную функцию вида A.1) называют се-
парабельной. Простейшим примером несепарабельной функ-
функции является
S*(x)= max max [|g'(*)l> #+(*)]¦ О-2)
f€[i:]/€[i:]
Введем вспомогательную функцию:
P(x9x) = nx)+%S(x), A.3)
где т—некоторый положительный параметр, называемый
коэффициентом штрафа.
Метод штрафных функций состоит в следующем. Вы-
Выбирается некоторая монотонно возрастающая последова-
последовательность тх < т2 < т3<. •., и решаются задачи безуслов-
безусловной минимизации функции Р (лс, xk) по х для & = 1, 2, 3,...
В результате получаем последовательность точек {хк},
удовлетворяющих условию
(A;, тА). A.4)

§1] МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 161
Если тЛ—>оо, то при определенных условиях всякая схо-
сходящаяся подпоследовательность последовательности \xk)
сходится к точке из множества решений Х% задачи A.6.1).
Если при некотором конечном значении тЛ получено, что
хк?Х, то исходная задача A.6.1) решена, так как при
этом точка xk обязательно принадлежит множеству реше-
решений Х«. Такие случаи, имеющие место при использовании
специальных штрафных функций, будут рассмотрены в § 2.
В общем случае последовательность {xk} бесконечна. Стро-
Строгое обоснование сходимости метода будет следовать из
приведенного в п. 3 доказательства сходимости первой
упрощенной версии метода.
Введенная штрафная функция S(x) отлична от нуля
всюду вне допустимого множества. Поэтому такая функ-
функция обычно называется внешней штрафной функцией
(внешним штрафом), а редукция задачи A.6.1) к после-
последовательности задач безусловной минимизации вспомога-
вспомогательных функций вида A.4)—методом внешней штрафной
функции или методом внешней точки. Другой тип штра-
штрафов—внутренние штрафы будет описан ниже, в § 4.
Приведем один простейший пример, иллюстрирующий
описанный метод. Рассмотрим задачу, в которой
/(*) = *, g{x) = x\ e=l, с = 0, я=1. A.5)
Ее решением является точка х = 0. Функцию штрафа по-
построим в виде
Р(х, T) =
из необходимого условия минимума
Рх(х, t)=
находим зависимость х(х) = — Dт)/3. Отсюда видно, что
х(%)—+0 при Т-+ОО, метод действительно приводит к ре-
решению задачи.
2. Вычислительные аспекты метода. При численной
реализации метода основное время счета тратится на отыс-
отыскание точек xk, удовлетворяющих условию A.4). Чтобы
точнее решить исходную задачу, следует брать значение
коэффициента штрафа т как можно больше. Однако уве-
увеличение т приводит к тому, что Р (х, т) как функция х
начинает носить ярко выраженный овражный характер,
так как в окрестности границы допустимого множества
6 Ю. Г. Евтушенко

162 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
функция tS (x) резко изменяется от нуля (на допустимом
множестве) до больших величин вне допустимого множе-
множества. Численная минимизация таких функций чрезвычайно
сложна, поэтому более предпочтительно постепенно уве-
увеличивать коэффициент штрафа т: при некотором xk найти
точку xk, и затем, минимизируя Р(х, тл+1), взять в каче-
качестве начальной точки x = xk. Знание хорошего начального
приближения упрощает поиск безусловного минимума.
Для реализации метода штрафных функций важно
также, чтобы все функции, задающие ограничения, были
достаточно хорошо «подогнаны». Формально задача нели-
нелинейного программирования A.6.1) не изменится, если в
условиях g(x) = 0, h(x)^.O какое-нибудь из ограничений
умножить на произвольное большое положительное число.
При численной реализации метода штрафных функций
такое действие приведет к тому, что будет учитываться в
основном это ограничение, остальные будут сильно нару-
нарушены. Поэтому при работе с методом следует иметь воз-
возможность «масштабирования» ограничений путем умноже-
умножения каждого из ограничений на некоторый весовой коэф-
коэффициент. Однако в ряде случаев увеличение «веса» ограниче-
ограничений не приводит к цели. Приведем, например, задачу, в
которой
Ее решением является точка х = 0. Используем простей-
простейшую функцию штрафа:
Р(х, т) = д:5 + тд:4.
Легко видеть, что при любых т
inf Р(х, т) = — оо.
Таким образом, минимум во вспомогательной задаче не
достигается ни при каких коэффициентах штрафа. В этом
примере целевая функция / (х) на недопустимом множестве
убывает при х-+—оо значительно быстрее, чем штраф-
штрафная функция. Чтобы сделать метод работоспособным, надо
использовать более резко выраженный штраф. Например,
положить Р (х9 т) = хъ + т (ех* — 1) или Р (х, т) = хь + тх*,
тогда вспомогательные задачи будут разрешимы при т > О,
метод обеспечит"решение задачи.

§1] МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 163
Как видно из приведенного примера, для успешного
использования метода штрафных функций в ряде случаев
требуется специальный анализ задачи, иногда бывает не-
необходимо выбирать нестандартные штрафные функции.
В тех случаях, когда пользователь (математик, ведущий
расчеты) располагает готовой программой, реализующей
метод на ЭВМ, такой путь приводит к необходимости пе-
переделки программы. Проще изменять способ задания огра-
ограничений в исходной задаче. Например, в рассмотренном
последнем примере можно считать, что допустимое мно-
множество задается не условием g(x) = x2 = 0, а условием
g (х) = ех*—1=0. Допустимое множество при этом не изме-
изменяется, нет необходимости вносить какие-либо изменения
в имеющуюся программу. Вместе с тем более резко выра-
выраженная, чем в исходной задаче, зависимость g(x) позво-
позволяет обеспечить разрешимость вспомогательной задачи A.4).
Если функции, определяющие задачу A.6.1), достаточно
гладкие, то желательно, чтобы функция Р обладала той
же степенью гладкости, так как в этом случае для мини-
минимизации можно использовать методы, обладающие высо-
высокой скоростью сходимости. Можно взять, например,
Р{ху т) = /(*) +
Если функции /, g, h дважды дифференцируемы по х, то
функция Р (х, т) также дважды дифференцируема по х.
Недостаток введенной функции заключается лишь в том,
что при больших значениях \gl\ и А;+ характер зависи-
зависимости Р (ху т) от ограничений типа равенства и неравен-
неравенства различный; чтобы устранить это различие можно
строить штрафную функцию более искусно, положив, на-
например,
Здесь
( 0, если
ф (у) = j kxy\ если 0 < у < г,
[у* + к2У+кз> если г<#,
6*

164 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
г—достаточно малое число (обычно г=10~4), числа ku
k2y kd определяются из условия непрерывности первой и
второй производных функций i|?:
/г1 = 1/Зг, k2 = — r, k3 = r2/3.
При больших значениях \gl'\, h!+ зависимость «S от \g(\,
hl^ одинаковая — квадратичная. Приведенная функция ши-
широко используется при численных расчетах.
Метод штрафных функций позволяет заменить исход-
исходную задачу условной минимизации решением последова-
последовательности задач безусловной минимизации. Этот прием
расширяет область поиска минимума по х> «снимая», огра-
ограничения, что весьма удобно при отыскании локальных
решений. Если речь идет о нахождении глобальных реше-
решений, то метод приводит к необходимости отыскивать в
задаче A.4) глобальные минимумы на Еп, что является,
вообще говоря, задачей более сложной, чем решение
A.6.1). Действительно, если множество X ограничено, то
есть шанс в исходной задаче нелинейного программиро-
программирования построить покрытия множества X с помощью не-
некоторых вспомогательных множеств (см. § 6 гл II), в то
время как, используя метод штрафов, приходится искать
глобальные минимумы во всем пространстве Еп, и здесь
организовать процесс поиска экстремума сложней. Таким
образом, метод внешних штрафов целесообразно исполь-
использовать только для отыскания локальных решений, и он
не перспективен для нахождения глобальных решений.
В случае задачи нелинейного программирования A.6.29)
допустимое множество представляется как пересечение
множеств X и U. При использовании метода штрафных
функций для решения таких задач функция S (х) по-преж-
по-прежнему «штрафует» за нарушение условия х?Х, вспомога-
вспомогательная задача состоит в отыскании
{f() + ()l
хеи
Как обычно, т устремляется к бесконечности. Условие
x?U, таким образом, здесь учитывается путем замены
вспомогательной задачи безусловной минимизации на задачу
минимизации на множестве U. Такое же обобщение можно
сделать и для остальных вариантов метода штрафных
функций, приведенных в этой главе.

§ !] МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 165
2. Первая упрощенная версия метода штрафных функ-
функций* Интуитивно ясно, что при численной реализации
метода штрафных функций вспомогательные задачи безус-
безусловной минимизации можно решать приближенно. Точ-
ность расчетов при этом следует увеличивать с ростом т,
по мере приближения точек xk к множеству X*. Благодаря
этому можно несколько упростить реализацию метода. \
Введем в рассмотрение три неотрицательные, непрерыв-
непрерывные функции v(/), |ы(/), т(/) скалярного аргумента t? /+.
Вспомогательную функцию запишем в виде
P(x,t) = v(t)f(x) + x{t)S(x). A.7)
Функции v(/), \i(t), x(t) при любых *>0 и 6>0 удов-
удовлетворяют следующим условиям:
Таким образом, отношения т(?)/^(?), |*@/v@ монотонно
стремятся к бесконечности при t —+¦ оо. Определим мно-
множество
{x(t): P(x(t), t)^minP(x9 t) + v(t)}9
eEn
которое состоит из точек, доставляющих минимум вспо-
вспомогательной функции Р(ху t) по л: с погрешностью v(t)
(по значению функции).
Первый упрощенный вариант метода штрафных функ-
функций состоит в следующем. Строится последовательность
\tk), элементы которой удовлетворяют условиям
О < to < к < • • • < h, limtk = oo.
Для нее определяется последовательность произвольных
точек *? ? Q {tk)y из которой выделяются сходящиеся под-
подпоследовательности. При определенных условиях все пре-
предельные точки принадлежат множеству Хт.
Введем вспомогательное множество
В (t) = {х 6 ?•: Р (х, 0 < |i @ / (х.)+v @, х, € X.}.

166 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. Ill
Теорема 3.1.1. Пусть f (x) и штрафная функция S(x)
непрерывны [всюду на Еп, множество решений Хт задачи
A.6.1) «в пусто-, множество В@) не пусто и ограничено;
для всех t?l+ выполнены условия A.8). Тогда первая упро-
упрощенная версия метода штрафных функций сходится к Хф
в целом.
Доказательство.Покажем, что последовательность
множеств {В (t)\ при t ¦—> оо является сжимающейся, т. е.
имеет место включение B(t + 8)czB(t) для любых 6^0 и
/?/+. Пусть x?B(t-%*6), тогда, используя условия A.8),
для любого х*?Х* получим
Следовательно, x?B(t). В частности, B(t)cB@) для
всех / ^ 0, последовательность множеств В (t) ограничена
равномерно по всем t ? /+, имеет место включение Х*сB(t)a
с5@), поэтому B(t) для всех t^O не пусто и ограни-
ограничено, Хт таюке ограничено. Непрерывная по х функция
Р(х, t) достигает своего наименьшего значения на ком-
компактном множестве B(t), где определена величина р (/) =
min P(x, t)y причем выполнены условия
В(/)
= min
Таким образом, множество Q(/) также не пусто и ограни-
ограничено. В силу произвольности t для всех t ? /+ имеет место
включение Q(t)aB(t).
Обозначим р (t) расстояние между множествами B(t) и Х*:
min Ix—yl. A.9)
Уех
Из сжимаемости последовательности множеств B(t) сле-
следует, что р(/) есть монотонно убывающая функция t,
поэтому, согласно лемме 2.4.1, существует предел lim p(/) =
. Докажем, что а = 0. При каждом t^O можно
определить хотя бы одну точку x(t) € В (/), в которой реа-
реализуется максимин в A.9). Объединение всех множеств

МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 167
( при всевозможных значениях / ограничено. По-
Поэтому из ограниченного множества точек^л; (tk) можно
выделить сходящуюся к некоторой точке х подпоследова-
подпоследовательность {x(t^)\y соответствующую монотонно возраста-
возрастающей подпоследовательности {/^}с{tk}. При этом должны
выполняться условия
mini*—#|) = a, lim х{^) = х, x{tk)?B{tk).
X ^>
Для всех tf^O, x(t)?B(t) имеет место неравенство
fUjjr(ry
Отношение v(t)/\i(t) стремится к нулю при /—*оо. Уст-
Устремим t% к бесконечности, прлучим
/(*) + <*</(*•)¦ A.10)
Здесь введено обозначение
Пусть d>0, тогда из того, что lim т(/-)/и(М = оо, по-
лучим, что S(x) = 0. Но из свойств штрафной функции в
этом случае следует, что х?Х, из неравенства A.10) по-
получаем, что в допустимой точке х значение минимизируе-
минимизируемой функции / строго меньше, чем значение / (л;*), где
х*?Х*> это противоречит определению множества Х#, а
поэтому случай d > 0 невозможен. Число d не может быть
отрицательным, так как функции r(t), \i(t), S(x(t)) не-
неотрицательные при f^O, поэтому d = 0,/(я) = /(#«),
х?Хщ. Следовательно,
lim p(^)
Но если для монотонно убывающей функции р (t) найдена
частичная подпоследовательность р(%), для которой су-
существует равный 0 предел, то тот же предел имеет по-
последовательность р (tk). Отсюда следует, что lim B(tk) =-• Х%.
t I,-* СО

168 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ II!
При каждом t^O имеет место включение Q(t)aB(t),
поэтому гиз сходимости B(t) к X» следует сходимость
Й@Х ¦
0 ¦
3. Вторая упрощенная версия метода штрафных функ-
функций. Расчеты по формулам предыдущего пункта хотя и
проще, чем по исходной схеме, но обладают одним суще-
существенным недостатком: часто бывает трудно гарантировать
отыскание безусловного минимума с заданной точностью.
Поэтому предполагается по-иному проверять точность
решения задачи A.4). При каждом фиксированном ^про-
^процесс минимизации вспомогательной функции Р(х, tk) пре-
прекращается, как только найдена какая-нибудь точка xk>
удовлетворяющая условию
A.11)
Здесь приходится вводить предположение о дифференци-
дифференцируемое™ функций f (x)u S (х)у однако условие A.11) легко
проверяемо. Такая реализация метода штрафных функций
была предложена и обоснована независимо несколькими
авторами: М.А.Костиной [1], Р. Мифлиным [1], Ю.Г.Ев-
Ю.Г.Евтушенко [9]. Следуя последней работе, сформулируем и
докажем теорему о сходимости.
Считаем, что штрафная функция S(x) представима в
виде A.1), где функция ф(^) непрерывно дифференцируема
по q^E1 и такова, что
(<р(<7) = ф'(<7) = 0, если 9 = 0,
1<Р(<7)>0, ф"(<7)>0, если q^O. ( * '
Если такую функцию ф подставить в A.1), то сформули-
сформулированные в п. 1 условия на штрафную функцию S(x)
будут выполнены. Обозначим
14 *' A.13)
Теорема 3.1.2. Пусть функции f(x) и S(x) непре-
непрерывно дифференцируемы на Е", штрафная функция S(x)
сепарабельна, имеют место условия A.8) и A.12). Пред-
Предположим, что ограничения g (х) = 0, h (х) < 0 удовлетворя-
удовлетворяют условию усиленной регулярно:ти и последовательность

§ !] МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 169
{хк}> получаемая из A.11), ограничена. Тогда мнооюество
предельных точек последовательности \xk, uk, vh) при
tk —+ оо не пусто, каждая предельная точка является точ-
точкой Куна—Таккера в задаче A.6.1).
Доказательство. Используя A.13), градиент вспо-
вспомогательной функции запишем в виде
причем vk^0 для всех k.
Последовательность {xk\ ограничена, поэтому из нее
можно выделить подпоследовательность {х%}, сходящуюся
к я. Покажем, что точка х допустимая. Предположим
противное: х(^Х. Разделим обе части неравенства A.11)
на x(tk) и, устремив tk-+oo, получим, что
t V^g<(х)) gi(x) + % у' (hf+(x))hU*)==0. A.14)
Умножим A.14) скалярно на вектор z, участвующий
в определении 1.7.5 условия усиленной регулярности
ограничений. После простейших преобразований получим
Здесь введено индексное множество
Вместе с тем из условий A.12) следует, что функция ф (q)
выпукла и ф@) = 0, поэтому
ч'is?(*))&&)>** v'H&))V&)>o9
для всех t'€[l:e], j?A(x). Сравнивая эти неравенства
с A.15), приходим к выводу, что для указанных i и /
выполнены равенства
9'telW)e/(i) = 9'(AiW)*/W = 0. A.16)
Из условия х (? X следует, что найдется по крайней мере
либо одно такое it что gi(x)^Ot либо такое j?A(x)f
чтоА^(^)>0. Но тогда, согласно A.12), либо ф'(?'(*)) X
Х^/(л:)>0,либоф'(/1( (х)) У (х) > 0, что противоречит A.16).
Поэтому х 6 X.

170 метод штрафных функций [гл. ш
Докажем ограниченность последовательности {ик, vk).
Предположим противное, обозначим
е _
2 [ ul I + 2 Hkt да = lim
/=1 /=1
/с
Разделим обе части неравенства A.11) на wk и перейдем
к пределу при tk —> оо. Тогда найдутся числа а,, ру (i € [I :е],
/^а(лг)) из которых хотя бы одно не равно нулю, и та-
такие, что
'=* /6 0 п)
Это противоречит линейной независимости векторов gi (д:),
Ajt(*)» *€[be], /6ст(х). Поэтому все предельные точки
последовательности {хк, ufcy vk\ конечны. Если для неко-
некоторого /6[1:с]
lim (
то, согласно A.1в), имеем lim t;^ = 0. Поэтому в предель-
ных точках имеет место условие дополняющей нежестко-
нежесткости, и каждая предельная точка последовательности
{хк, ик, vk\ является точкой Куна—Таккера. Щ
Пусть A.6.1)—задача выпуклого программирования,
тогда из теоремы 1.1.7 следует, что вспомогательная
функция Р(х, t) выпукла по х и, согласно теореме 1.2.6,
имеет место неравенство
Р(х, t)—P(xm, t)^<Px(x, /), х—х.У.
Воспользуемся неравенством Коши—Буняковского, учтем
A.1 П, получим
В силу ограниченности {хк\ отсюда следует, что при
tk -—> оо ограничена также функция
Но из того, что т (t)/\i (t) —> оо следует, что выражение,
стоящее в квадратных скобках, стремится к нулю. По-
Поэтому х ? X. Таким образом, в случае задач выпуклого

§ j] МЕТОД ВНЕШНИХ ШТРАФНЫХ ФУНКЦИЙ 171
программирования для обоснования сходимости метода нет
необходимости привлекать условие усиленной регулярно-
регулярности—достаточно ввести условие Слейтера или Карлина и
потребовать линейной независимости векторов glx (x), ft?()
4. Третья модификация метода штрафных функций.
Приведенные выше две модификации упрощают до неко-
некоторой степени расчеты, однако в случае тех задач A.6.1),
в которых вектор х обладает большой размерностью,
многократное решение вспомогательной задачи A.4) вы-
вызывает значительные трудности. Реализация метода упро-
упрощается, если вовсе отказаться от решения задачи A.4),
а вместо этого отыскивать предельные точки решений
следующей задачи Коши:
¦$¦ — Ря(*. 0. *(<>) = *., A.17)
где Р(х, t) определяется формулой A.7). Данная версия
метода аналогична методу Коши B.2.3), отличие связано
с переменностью функций fi(/), x{t)> в результате чего
система A.17) становится неавтономной. Для обоснования
сходимости метода введем множество
B(t) = {x?E*i P(xf 0<И@/(*.)Ь
Предполагаем, что функции [i (t), x(t) непрерывные, удов-
удовлетворяют при t € /+ условиям
0, т@>0, $|*@Л=оо. A.18)
о
Теорема 3.1.3. Пусть f(x) и S(x)—выпуклые не-
непрерывно дифференцируемые всюду на Еп функции, мно-
множество Хт не пусто, множество 5@) не пусто и огра-
ограничено, непрерывные функции \i(t), r(t) при всех t?l+
удовлетворяют условию A.18), отношение -^Ц—*°° мо-
монотонно при t—+oo. Тогда метод A.17) сходится к Хф
в целом.\
Доказательство. Так же, как и при доказатель-
доказательстве теоремы 3.1.1, можно показать, что для любых /g /+,
6^0 имеют место включения XmaB(t~\-&)c:B(t). По-
Поэтому Хт компактно. Введем функцию
= [dis(x, Хт)]*

172 метод штрафных функций [гл. ш
Продифференцируем функцию w(x) в силу системы A.17),
учтем выпуклость Р (х, t) по х, получим, что для любых
х (#о, t) (? В @) выполнены неравенства
Всюду на Б @) функция до (я) ограничена. Из полученного
неравенства следует, что w(x(x0, t))—невозрастающая
функция t всюду вне В @). Рассуждая так же, как и при
доказательстве теоремы 1.1.2, можно показать, чтош(лг)—
бесконечно большая функция. Учитывая теорему 2.2.1
и замечание к ней, приходим к выводу, что система A.17)
устойчива по Лагранжу, т. е. каждое решение продолжимо
(вправо) при /-^оо и ограничено.
Воспользуемся теоремой 2.2.7. Обозначим
Xm)< е},
= inf {/>(*, t)/li(t)-f(x*)\.
Тогда для произвольного г > 0 имеем оценку
• sup w(x) <— 2ц (t)O(t).
n
Легко показать, что для любого е > 0 существует та-
такое t(e), что B(t)czGe для всех t > t(s), отсюда Ф(/) > 0
для этих же значений t. Так как Ф(/) — возрастающая
функция /, то для всех / > t (г) имеем
— lim J |*@Ф(*)Л<—ШпФ(<(в)) J |i(*)?*/ = — оо.
Все условия теоремы 2.2.7 выполнены, отсюда следует
сходимость метода A.17) к множеству Х%. Щ
При численной реализации метода A.17) возникают
определенные трудности, связанные с выбором функций
\i(t)y %(f). Поэтому метод не целесообразно использовать
в случае простых задач небольшой размерности, которые
удается решить методом штрафных функций без привле-
привлечения каких-либо упрощающих приемов.

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 173
§ 2. Оценки точности метода штрафных функций
1. Точные штрафы. Существует целый класс штрафных
функций, обладающих следующим замечательным свойст-
свойством: при всяком фиксированном, достаточно большом
значении коэффициента т множество X* решений задачи
A.6.1) и множество решений вспомогательной задачи A.4)
совпадают. Такие функции штрафа будем называть точ-
точными, при их использовании решение задачи условной
минимизации A.6.1) редуцируется к отысканию безуслов-
безусловного минимума A.4). Впервые это свойство для задач
выпуклого программирования было замечено в 1966 г.
И. И. Ереминым [1], [2], впоследствии этому вопросу
были посвящены работы У. Зангвилла [1], В. Д. Скарина [1],
Т. Петржиковского [1], К. Чараламбоса [1], С. Хана
и О. Мангасаряна [1] и многих других авторов.
Введем вспомогательные вектор-функции:
= [№(*)\* ¦•¦. 1в*(*I. #(*). ¦¦¦• #(*)]."
№(*). ..- «*(*). АИ*). •¦-.. «(*)].
отображающие Rn в Rm. Объединим двойственные векторы,
положив у = [и, v]?Rm. Если в задаче A.6.1) существует
решение х — хт и соответствующие двойственные векторы
u*?Re, Vt^Rl, то их объединение будем обозначать
*/¦ = !>•> су|€Д«.
Ниже будет показано, что точной функцией штрафа
является норма Гёльдера вектора F (х) (см. Приложение II).
Вспомогательная функция при этом имеет вид
где l^p^oo. Введем в рассмотрение множество
Z(t) = Argmin P(x, т),
зависящее от т как от параметра. Обозначим
здесь 1у*||а—норма вектора t/«, двойственная к норме
IF (*)!,, фигурирующей в B.1).
Теорема 3.2.1. Пусть в задаче A.6.1) существует
седловая точка [х*, и*У v*] функции Лагранжа L (#, м, v).
Тогда при любых значениях т > т* множества Хт и Z (т)
совпадают.

174
МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
Доказательство. Согласно теореме 1.6.1 точка**
принадлежит множеству решений Х# задачи A.6.1), в точке
[#*, v*] выполнено условие дополняющей нежесткости,
поэтому для любых х ? Rn
Из условия vm^0 следует неравенство <h(x),
^ <h+ (х), а*>, с помощью которого находим
Р (х., т) </(*) + <g (х), и,> + <h+ (x), vm> =
Воспользуемся неравенством Гёльдера (см. Приложе-
Приложение II), получим
Р(х» *)<f{x) + \y.\q \O(x)l, = f(x) + \y.\, \F(x)\p.
Учитывая, что т, < т, принимая во внимание опреде-
определение B.1), продолжим эти оценки:
т). B.3)
Это неравенство справедливо для любых x?Rn,
поэтому множество Z(r) не пусто и X*cZ(r). Докажем,
что множества Х% и Z(t) совпадают. Предположим про-
противное, т, е. чтб при некотором тх > тт найдется такая точка
2() г$Хф, тогда
Если Xx^Xj то ^б-^*» так как при этом F(x1) = 0 и
f fa) = / (atj). Если хл ^ X, то | F (хг) \\рф0 и при любом
т€(%> ^i) имеет место строгое неравенство
)|/7 = jP(a:1, t),
которое противоречит неравенству B.3). Отсюда следует,
что хг?Хт, поэтому Z(t)cX,. Учитывая ранее найденное
включение X^a.Z(i), заключаем, что множества X* и Z(т)
совпадают при всех т > т». И
Согласно теореме 1.6.7 в доказанной теореме условие
существования ограниченной глобальной седловой точки
функции Лагранжа можно в случае задач выпуклого
программирования заменить условиями существования
решения в задаче A.6.1) и условием Слейтера. В общей
задаче нелинейного программирования условие существо-

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 175
вания седловой точки в задаче A.6.1) можно заменить
выполнением достаточных условий минимума Мак-Кормика.
Имеет место
Теорема 3.2.2. Пусть в точке Куна — Таккера
[х„ w«, v*] для задачи A.6.1) выполнены условия теоремы
1.7.2 Мак-Кормика. Тогда хт является точкой локального
минимума функции Р(х, т) при любом фиксированном
т > т«, где т* определяется из B.2).
Доказательство. Определяемую из A.7.15) функ-
функцию Lx можно представить в виде
Для любого числа т > т* можно найти такой вектор
= [и, v], что v>v*, и'>|и'|, для всех /?[1:е] и
1у*\\я = **- B.4)
Согласно лемме 1.7.5 существует такая окрестность G (#*)
точки хфу что для всех х ? G (х*)> хфх% выполнены условия
Р(х„ "c) = f(xm) = L1(x., и, vXI^ix, a, v). B.5)
Используя неравенство Гёльдера, условия B.4), B.5),
получим
Мы снова пришли к неравенству B.3). Дальнейшие рас-
рассуждения ведутся точно так же, как и при доказательстве
теоремы 3.2.1. Щ
Даже в том случае, когда функции, определяющие
задачу, всюду дифференцируемы, функция B.1) не диффе-
дифференцируема в граничных точках допустимого множества X.
Поэтому такие вспомогательные функции называют не-
дифференцируемыми, их применение упрощает численную
реализацию метода штрафных функций, так как отпадает
необходимость устремлять коэффициент штрафа к беско-
бесконечности— вместо этого достаточно только один раз решить
задачу A.4) при т>т*. Однако величина т„ обычно бы-
бывает неизвестна, и поэтому приходится решать задачу
A.4) для нескольких значений т. Вместе с тем использо-
использование точных штрафов усложняет вспомогательную за-
задачу A.4), так как в этом случае приходится для безус-
безусловной минимизации применять только лишь медленно

|7б МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
сходящиеся численные методы, не использующие свойства
дифференцируемости вспомогательной функции. Поэтому
точные штрафные функции обычно применяются при ре-
решении только тех задач, в которых функции, определяю-
определяющие задачу, недифференцируемы.
Полученные результаты легко перенести на более общий
случай, когда вспомогательная функция имеет вид
Р(х9 т) = /(*) +Я (*, т), B.6)
где S(jc, x)—непрерывная функция обоих аргументов,
удовлетворяющая трем условиям:
1) В(х, x)^t\\F(x)Ip при всех x?Rn, т>т«;
2) В (х9 т) = 0 при всех х?Х\
3) В (ху т) — строго возрастающая функция т при всех
х^Х и т>т».
Этим условиям удовлетворяют, например, следующие
функции:
В(х, %) = ех
В(х, t) = t\\F(x)\\p(l+a\\F(x)\\p),
Утверждения теорем 3.2.1 и 3.2.2 остаются в силе,
если в них в качестве Р (х, т) использовать функцию B.6).
Рассмотрим'некоторые частные случаи. Будем считать,
что В(хл т) == т | F (х) 1р. Если р = 1, то q = ooy вспомо-
вспомогательная функция и величина т« определяются по фор-
формулам
B.7)
тп = max max [| ui |, v{] = || y* [».
*€[1] /€[l:]
К минимизации функции Рг(х, т) мы приходили ранее,
в гл. I (см. формулу A.6.14)), исходя из иных рассуж-
рассуждений.
Исходная и двойственная нормы совпадают в случае
евклидовых норм, когда p = q = 2,
[е с П 1/2
[е с Л 1/2

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 177
Если положить р = оо, то ? = 1,
Здесь использована несепарабельная штрафная функ-
функция A.2).
Воспользуемся приведенными в Приложении II соот-
соотношениями между различными нормами. Тогда получим,
что т»х ^ т*2 ^ т#3.
Следовательно, из трех выписанных вспомогательных
функций наименьшим минимальным коэффициентом штрафа
обладает Рг(х, т), наибольшее значение т* у функции Р3,
у которой штрафная функция является чебышевской нор-
нормой вектора F (х). ,
2. Дифференцируемые штрафы. Предположим, что
A.6.1)—задача выпуклого программирования; функции,
определяющие задачу, всюду дифференцируемы. В качестве
Р(х, т) возьмем следующую, дифференцируемую по х
вспомогательную функцию
Р(х, ^) = f(x) + T\\F(x)f. B.8)
Здесь и дальше в этом параграфе используется евклидова
норма.
Теорема 3.2.3. Пусть в задаче выпуклого програм-
программирования A.6.1) существует ограниченная седловая точка
[х*> и^ v*] функции Лагранжа L(x, и, v). Тогда при
любых значениях т > 0 имеет место оценка
Р (х, т) > /(*•)--^ [,| (uir + 2
B.9)
Доказательство. Оценим снизу Р(х, т). Из вы-
выпуклости функции f(x)y согласно формуле A.2.9), следует
Р(х, т) >/ (х.) + <fx (x.)9 x-x*> + x\\F(х)||2.
Используя A.7.1), получим

178 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
Применим формулу A.2.9) к выпуклым функциям g'(х)
и М(х), тогда
Р(х, т)-/(*.)>
Учтем, что g(x«) = 0, <у„ Л (*«)> = О, получим
Из неравенства Коши—Буняковского и определения функ-
функции F(x) следует
Выполняя далее очевидные преобразования, получим
Р(х, т)-/(*.)>
Ti
Отсюда следует B.9). Из найденных неравенств заклю-
заключаем, что при т—+оо Z(r)—+X*, погрешность в опреде-
определении величины минимизируемой^функции стремится к нулю
пропорционально величине 1/т. В
Для упрощения доказательства теоремы считалось, что
функции, определяющие задачу, дифференцируемы; вместо
этого можно ограничиться условием их выпуклости, ра-
равенство A.7.1) при этом заменится на A.7.7).
3. Дифференцируемые штрафы в случае невыпуклых за-
задач. Рассмотрим тот случай задачи A.6.1), когда допу-
допустимое множество определяется с помощью только огра-
ограничений типа равенства. Предположим, что коэффициент
штрафа т достаточно велик и 8 = 1/т можно считать малым
параметром. Пусть реализуется вторая упрощенная вер-
версия A.11), в которой точка х (г) удовлетворяет условию

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 179
Введя вспомогательный вектор и ? Ее и вектор а ? Еп,
j а ||^1, перепишем это условие в виде системы из
нелинейных уравнений
0
Исследуем зависимости х, и от малого параметра 8 > О,
порождаемые этой системой. Предположим, что в исход-
исходной задаче A.6.1) существует точка Куна—Таккера [#*, и*],
в которой выполнены достаточные условия минимума,
даваемые теоремой 1.7.2, выполнено условие регулярности
ограничений g(x*) = 0 в точке х*.
Решение B.10) при е>0 будем искать в виде фор-
формальных степенных рядов
И (8) = ^
Подставим эти ряды в B.10), предполагая, что функции
/ и g достаточное число раз дифференцируемы, разложим
их в ряд по степеням 8. Приравнивая выражения при
одинаковых степенях 8, получим систему линейных урав-
уравнений для определения членов разложения B.11). В ну-
нулевом приближении имеем
М*. и.)¦=/*(*•)+&(*•)"• = 0, *(*•)=*0, B.12)
т.е. получаем условия Куна—Таккера. Для первых чле-
членов разложения получим
Lxx{x.,um)x1+ gx(xm)u1^a>
?tf (*.)*! = «•¦ (ЛЗ)
Отсюда находим
x,^r гЬж (*•» ««)[а—ёх(х*) «J,
щ. = и. + е [2gZ (х,) Lji (х„ и,) gx (*,)]"г х B.14)
х [2gJ (х.) L^1 (х„ и,) а—и,].
Исследуем это приближение. Вычислим значения fug:
g (x,+ext) = g (др.) + zgl (x,) xt + O (e»).

180 метод штрафных функций [гл. ш
Подставим сюда найденный вектор х1У учтем B.12), по-
получим
в B.15)
g (x* + гхг) = ju*+O (e2).
Для вспомогательной функции имеем
в*). B.16)
Мы пришли к оценке, близкой к B.9). Из формул
B.15), B.16) следует, что получаемые при реализации
метода штрафных функций точки л:(е) таковы, что вычи-
вычисленные в них значения вспомогательной и минимизируе-
минимизируемой функций меньше значения /(х*) на величины порядка г.
Знаки компонент вектора g(x(e)) совпадают со знаками
соответствующих компонент вектора и». Выбор конкрет-
конкретной точки х, удовлетворяющей условию A.11), не влияет
(с точностью до величин второго порядка малости) на
значения f(x) и g(x).
Покажем, что формулы B.14) дают асимптотическое
приближение решений х(г) и и (г) системы B.10) при
е —> 0 с точностью до величин второго порядка малости, т> е.
litTI - II *• /о) , ? —— СУ II г*"*1" fV^ 11 ХХ\ —• II /У |р 1 — II __ С// II ^"*i' fv^
11111 n Л I С/I «^ф C«Ai II ^ч^ IAJ , 11111 о || И» I О I ~~~— t*j|| ^^^ CW-1 II \ <«Л^ .
B.17)
Теорема 3.2.4. Пусть [#«, м*]—точка Куна—Та/с-
кера для задачи A.6.1), в точке x = x* ограничения g (х) = О
удовлетворяют условию регулярности; функции, опреде-
определяющие задачу, дважды дифференцируемы в окрестности
точки дс», где их матрицы вторых производных удовлет-
удовлетворяют условию Липшица, матрица Lxx (x*, и*) невырож-
невырождена. Тогда формулы B.14) дают асимптотическое при-
приближение решений системы B.10) при г—+0 с точностью
до величин второго порядка малости.
Доказательство. Обозначим
х (е) = лг„ + гхг + Ьх, и (в) = и% + гиг + Ьи,

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 181
Используя дифференцируемость, систему B.10) запишем
в виде
fx (х) + 8х (х)и = Lxx (*•.- "•) {ъхг + 6х)
2g(x)—su =
Здесь введены функции Ух(г), у2(х) такие, что для любых
z?En+e, х?Еп имеют место неравенства ух (г) ^ сг \ z ||2,
y2{x)^.c2\xf, где си с2—некоторые числа. Обоснование
такого представления проводится также, как в Приложе-
Приложении I была доказана формула E). Обозначим
ft = \Lxx (**> «•) I ёх (*¦)]
Тогда с учетом B.13) соотношения B.18) можно записать
в виде
вг = Л^-1Г(ег1 + вг). B.19)
Матрица Л^ ограничена, поэтому существует такое число с,
что lN-ir(sz1 + 8z)l<c\\ez1 + 8z\\*.
Согласно лемме 2.3.2 уравнение B.19) однозначно раз-
разрешимо, если
Этого неравенства всегда можно добиться, взяв г доста-
достаточно малым. Тогда полученное из B.19) решение bz удов-
удовлетворяет условию
Или, возвращаясь к первоначальным функциям, получим
где правая часть неравенства не зависит от е. Переходя
к пределу при 8—>(), получим условия B.17), доказы-
доказывающие теорему. Q

jg2 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
4. Экстраполяция в методе штрафных функций. По-
Полученные в предыдущем пункте результаты весьма полезны
для качественного^изучения метода. Вместе с тем описан-
описанный подход можно использовать при реализации числен-
численных методов. Если величины ek=\/rk изменяются незна-
незначительно от итерации к итерации, полезно проводить
экстраполяцию векторов хк. Пусть реализуется вторая
упрощенная версия, известно значение xk, удовлетворяю-
удовлетворяющее условию A.11). Обозначим
B.20)
Здесь ||яА||^1. В качестве приближенного двойственного
вектора берется
^ B-21)
Введем малый параметр ц и рассмотрим вопрос о ре-
решении системы
/* (*) +g* (х) и = {ек—\i)ak,
{
Составим формальные ряды по степеням малого параметра ц:
+
Подставим их в систему B.22), разложим функции
в ряды по степеням ц. Приравнивая выражения при оди-
одинаковых степенях р,, получим систему линейных уравне-
уравнений для определения членов разложения в B.23). При
р = 0 получим B.20), B.21), далее имеем
Lxx (хк, uk)Xi+gx (xk) ut = — ак,
l
Решив эту систему, подставим в B.23) выражения для
xit «х, получим
x(v) = xk—\iL?(xk, ик) [ак
X(uk-2gTx(xk)L?(xk, uk)ak).

§2] ОЦЕНКИ ТОЧНОСТИ МЕТОДА ШТРАФНЫХ ФУНКЦИЙ 183
Взяв |ы = ел—eft+1, найдем приближенные векторы хк+1,
и +i, первый из них можно взять в качестве начального
при ' отыскании минимума Р(дг, 1/(х) по х?Еп. Если
расчеты по методу штрафов прекращаются после нахож-
нахождения вектора хк, то в качестве приближенного решения
целесообразно взять не векторы хк, ик, а векторы xk+1
и uh+u полученные из найденных формул путем экстра-
экстраполяции в точку (л = гк:
= xk—L^(xkJ uk)[Lx{xky uk)+gx{xk)u], B.24)
й B.25)
(xky uk)gx(xk)]'1x
)—gl(xk)Lxx(xki uk)Lx(xk, uk)l
Здесь было использовано следующее представление гра-
градиента вспомогательной функции:
Р*
справедливость которого следует из формул B.20) и B.21);
кроме того, было учтено, что величина гк малая, благо-
благодаря чему упростилось выражение для иг.
Можно отвлечься от задачи экстраполяции и рассмот-
рассмотреть формулы B.24) и B.25) как некоторый численный
метод решения задачи A.6.1); в этом методе уже не
фигурируют в явном виде ни функция штрафа, ни коэф-
коэффициент штрафа. Легко убедиться, что формулы B.24),
B.25) определяют не что иное, как метод Ньютона, при-
примененный к решению следующей системы из/г+е уравнений
Lx(x, и) = 0, g(x) = 0.
Методы вида B.24), B.25) будут получены в следую-
следующей главе из совершенно иных соображений. Изложенный
здесь подход указывает на своего рода «родство» между
этими методами, принадлежащими, казалось бы, к совер-
совершенно различным классам.
С вычислительной точки зрения использование экстра-
экстраполяции оправдано, если для решения вспомогательной
задачи A.11) применялись методы, определявшие матрицу
Lxx(xk, uk); тогда пересчет х и и несложен. В противном
случае экстраполяцию можно делать упрощенно. Согласно
полученным результатам можно считать, что функция jc(jlx)

|g4 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
линейно зависит от |х, и поэтому в качестве хк+1 берется
вектор
g^ • B-26)
5. Метод дифференцирования по параметру. Предпо-
Предположим, что система B.22) для каждого \i?[0, е*] имеет
решение [x(\i), w(fi)], непрерывно зависящее от \х. При
изменении параметра ц от 0 до гн решение B.22) \x(\i),
и (ц)] описывает некоторую пространственную кривую
в Еп+е, одним концом которой служит точка [а; @), и@)],
являющаяся решением системы B.10), другим—искомая
точка Куна—Таккера [х(гк), u(&k)] = [x*, и*].
Если выполнены условия леммы 4.1.1, то матрица
2gT(xm) | 0ее
невырождена, и по теореме о неявной функции при до-
достаточно малых значениях гк система B.22) имеет един-
единственное решение, проходящее через точку [##, «J, кроме
того, функции x(\i)t u(ii) дифференцируемы и удовлетво-
удовлетворяют следующей системе из п\-е обыкновенных диффе-
дифференциальных уравнений:
dx . / \ du
^ ()
Проинтегрируем эту систему по \л от ц = 0 до [х = гк с на-
начальными данными Коши х @) = х0, и @) = и0, где х0У и0 —
решения системы B.10). Тогда [х(гк)> и(ек)] даст иско-
искомую точку Куна—Таккера.
Описанную процедуру можно рассматривать как чис-
численный метод решения задачи A.6.1). Он состоит из двух
этапов: из приближенной минимизации функции Р (х, 1/е)
по л: и численного решения задачи Коши для системы B.27).
В отличие от метода B.2.3), здесь интегрирование си-
системы B.27) следует проводить с высокой точностью, по-
поэтому при использовании метода Эйлера приходится брать
достаточно малый шаг интегрирования, либо использовать
более точные методы (метод Эйлера с пересчетом, Рунге —
Кутта и т. д.). Погрешности интегрирования системы B.27)

§ з] МЕТОД ПАРАМЕТРИЗАЦИИ ЦЕЛЕВОЙ ФУНКЦИИ 185
приводят к тому, что решения #((i), u(\i) перестают
удовлетворять системе B.22) и требуется дополнительная
коррекция.
Описанный подход заимствован из методов решения
систем нелинейных уравнений, где его обычно называют
методом дифференцирования по параметру или методом
продолжения. Более подробное описание метода можно
найти в книге Дж. Орте га и В. Рейнболдта [1]/в статьях
Д. Ф. Давиденко [1], [2]. Широкого распространения
данный подход для решения оптимизационных задач не
получил.
§ 3. Метод параметризации целевой функции
В данном параграфе будет описан класс методов ре-
решения задачи A.6.1), весьма близкий к методам штрафных
функций, основанный на параметризации целевой функ-
функции; основное отличие состоит в том, что здесь вспомо-
вспомогательный параметр изменяется автоматически—по пред-
предписанному правилу, в то время как в методе штрафных
функций приходилось задавать политику изменения коэф-
коэффициента штрафа. Разнообразные версии метода даны в ра-
работах Б. Н. Пшеничного [1], В. В. Величенко [1], [3], [4],
Ю. П. Иванилова [1], Б. С. Разумихина [1], Д. Морри-
сона [1], Ф. Луутсмы [1], В. В. Иванова и В. А. Люд-
виченко [1] и многих других авторов. Ниже остановимся
на описании лишь некоторых вариантов метода.
1. Предварительные результаты. Пусть решается за-
задача A.6.1). Используя введенную в § 1 штрафную функ-
функцию S(x), составим вспомогательную функцию
М(х, rO = tf(*)-r,)8 + S(*). C.1)
Введем множество
, л). C.2)
( л)
хеЕ*
Лемма 3.3.1. Если х„?Хщ, f(x,)>r\, *i€X(t]), то
)f)
Доказательство. Из условия х^Х^) получим
(f(x,)-i)y = M(x«, r\)>M(xu i\)>(f (Xi)-i\)*. C.3)
Если fixj^i], то из C.3) следует

186 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
Отсюда получаем, что f (*¦)>/(#!). Если f (хг) < т), то
f(x*)^t) >/ (#i), таким образом, снова приходим к тре-
требуемому неравенству. Щ
Л е м'м а 3.3.2. Пусть т) = / (л:,), л:* ? Хф, тогда Хт =
Х() М( ) 0
(|) („ ))
Доказательство. Для любого х?Еп справедливо
соотношение М(х%, т)) = 0 <; М (#, г)), откуда следует, что
Х{)
{\)
Обратно, пусть ^^^(ti). В этом случае для любых
Е
0<М(*х, т,)<М(а:, г)).
В частности,
Но это возможно, только если S(x1) = 0J т. е. точка хг
допустимая и, кроме того, такова, что / (x1) = r\=f (хф),
поэтому хх?Хт. Отсюда заключаем, что Х» = Х(т)). В
Лемма 3.3.3. Пусть T)i<Tl2» ^le^Oli)» х%€Х(ц2),
тогда ffeX/W-
Доказательство. Для любого х справедливы не-
неравенства
, C.4)
. C.5)
Возьмем в C.4) в качестве х точку х2У в C.5)—точку хи
получим
(x2) < (f (^)-л2J + S (хг).
Сложим эти неравенства, после преобразований имеем
f (Xi) (r\2—r
откуда получаем требуемое неравенство: /A)^/B) I
Из леммы следует, что значения целевой функции f (x)
для х g X (т|) является монотонно-возрастающей функцией
параметра т|.
2. Первая версия Д. Моррисона. Предположим, что
известна некоторая нижняя оценка тH оптимального зна-
значения целевой функции f (х), т. е. Ло^/(**)> х*?Х.

§ 3] МЕТОД ПАРАМЕТРИЗАЦИИ ЦЕЛЕВОЙ ФУНКЦИИ 187
Такую оценку можно получить, например, численно решив
вспомогательную задачу безусловной минимизации A.4);
согласно B.9) тогда можно положить r\=f(xk). Метод
параметризации целевой функции состоит в последова-
последовательном нахождении точек хк и увеличении параметра г\к
таким образом, что i\k—+f(x*). Согласно доказанным
в п. 1 леммам при этом X(r\k)—>X«, что обеспечивает
сходимость метода к множеству Хт. Ключевым моментом
является способ изменения параметра ц от итерации к ите-
итерации. Д. Моррисоном [ 1 ] предложен следующий вариант.
Пусть на k-Pi итерации известно некоторое значение
параметра v\k^f(x*)- Из решения вспомогательной за-
задачи C.2) найдем точку хк^Х(у\к). Если при этом хк?Х
или М(хк, т]л) = 0, то расчеты заканчиваются, так как
при этом S(xk) = 0, xk?Xf В противном случае положим
» Ч*) . C.6)
и итеративный процесс продолжается. Докажем сходи-
сходимость описанной версии.
Лемма 3.3.4. Если т)л^/(#•), то Tlfc+i^/C**)'
Доказательство. Для любых х?Еп имеем
В частности, для х = х* получим
M(xk9 4ft)<(/(^)-
Но по условию т]л^/(^), поэтому
Теорема 3.3.1. Пусть в задаче A.6.1) множество Хт
не пусто, функция М (х, г\) .всюду непрерывна и известно
значение Ло </(*¦)• Тогда версия Моррисона сходится
к множеству X*.
Доказательство. Согласно лемме 3.3.4 монотонно
возрастающая последовательность \ч\к\ ограничена сверху
величиной /(**). Поэтому существует предел
)• C.7)

138 метод штрафных функций [гл. ш
Рассмотрим вторую вспомогательную задачу об отыскании
min /(*), Х(Х) = {хеЕ»: S(*)<ty. C.8)
€Х(Х)
Множество решений этой задачи обозначим Х*(к). Оче-
Очевидно, что Х* = Х*@), Х = Х@). Обозначим F(k)=f(x),
где х?Хт(к). Доказательство проведем в предположении,
что функция F (К) непрерывна справа в точке Х = 0, т. е.
для любого е>0 существует такое б > 0, что если 0^
<h<6, to \F(K) —F @) |< е. Здесь F@) = /(**), х*$Х%.
Чтобы доказать утверждение теоремы, покажем, что
для любых положительных чисел г19 г2 найдется такой
номер итераций N> что при всех k > N будут иметь место
неравенства
/(**)<elf S(xk)<e2. C.9)
Для ег > 0 возьмем такое бх > 0, что если 0 < X ^ 6и то
\F(K)—F @) | < гг. Из C.7) следует, что существует та-
такое N9 что при всех k > Л^ выполнено условие
откуда следует, что
VM(xk9 iQ <min
2, 6J.
Следовательно, S (*ft) < бх для всех k > Af. Поэтому
l/(**)—/(^»)l<ei Для всех k>N. Учитывая утвержде-
утверждение леммы 3.3.4, приходим к неравенствам C.9), что до-
доказывает теорему. Щ
3. Вторая версия Д. Моррисона. В статье Д. Морри-
сона [1], опубликованной в 1968 г. была высказана идея
другого способа изменения параметра тр
Впоследствии версия была исследована многими авторами.
Укажем первую из таких работ, выполненную Дж. Кова-
ликом, М. Осборном и Д. Руаном [1].

§3j МЕТОД ПАРАМЕТРИЗАЦИИ ЦЕЛЕВОЙ ФУНКЦИИ 189
4. Версия Б. С. Разумихнна. В книге Б. С. Разуми-
хина [1] предложено следующее правило определения
параметра tj:
Ч*+1 = /(**)¦ (ЗЛ1)
5. Вычислительный аспект. Сравним между собой при-
приведенные три версии метода. Обозначим А1У Д2, А3 изме-
изменения параметра ц на k-й итерации при правилах регу-
регулировки C.6), (ЗЛО) и C.11) соответственно:
Очевидно, что | Ах | ^^ | А31. Кроме того, из представления
следует, что при / (лс^) > г|^ имеют место неравенства
Д^Д^Дд.
Таким образом, наибольшее увеличение вспомогательного
параметра ц на каждой итерации происходит при исполь-
использовании версии C.10), наименьшее—в версии C.11).
Поэтому можно ожидать, что наибольшей скоростью схо-
сходимости обладает версия (ЗЛО). Численные расчеты под-
подтверждают это, однако вместе с тем численные эксперименты
заставляют обратить внимание на следующее обстоятель-
обстоятельство. Приведенные выше свойства метода параметризации
целевой функции были получены в предположении, что
вспомогательная задача минимизации функции М(ху r\k)
решается точно; погрешности расчетов могут привести
к тому, что окажется т^ >/(**)¦ В этом случае дальней-
дальнейшие расчеты по каким-либо из формул C.6), (ЗЛО), C.11)
будут лишены всякого смысла, так как они оправданы
лишь в предположении, что т)*^/(**)• Поэтому точность
решения вспомогательной задачи должна быть наибольшей
при реализации версии (ЗЛО) и наименьшей—в версии
C.11). Это обстоятельство несколько «сглаживает» время
расчетов при использовании разных версий.
Из свойств, описанных в п. 1, следует, что решение
задачи A.6Л) находится путем определения наименьшего
значения г|», для которого выполнено условие
(*, т]ф) = 0. C.12)

190 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. III
Такую редукцию можно использовать для полного реше-
решения задачи A.6.1) или частично, например, в тех случаях,
когда по каким-либо причинам получено значение т)л >/(#«)
и следует уменьшать значения r\k до выполнения усло-
условия C.12). Практическая реализация такого подхода
вызывает значительные трудности по двум причинам:
1) во-первых, при т| > r\* = f(x*) задача C.12) имеет,
как правило, континуум решений и при даже незначи-
незначительном изменении параметра г\ решение C.12) часто зна-
значительно изменяется, что усложняет расчеты;
2) во-вторых, что более важно, при численных расче-
расчетах часто бывает трудно проверить выполнимость усло-
условия C.12).
Проверка равенства нулю требует высокой точности
минимизации, что также затрудняет вычисления.
6. Связь с методом штрафных функций. Пусть штраф-
штрафная функция аддитивна и имеет вид
i = 1 / = 1
Сравним две вспомогательные задачи безусловной мини-
минимизации функций Р(х, т) и М(х, т|), задаваемых форму-
формулами A.3) и C.1). Предположим, что функции, опреде-
определяющие задачу A.6.1), всюду дифференцируемы. Тогда
необходимые условия минимума по х заключаются в сле-
следующем:
Рх(х, т) =/,(*) +2т f
+ !>'+(*)*((*)] =0, C.13)
Г2 В4х)&(х)+ .2 hUx)hUx)\ = 0. C.14)
Если в качестве коэффициента штрафа взять величину
r==wthf)> (ЗЛ5)
то условия C.13) и C.14) совпадают. Реализуя какую-
либо версию метода параметризации целевой функции, по-

§3] МЕТОД ПАРАМЕТРИЗАЦИИ ЦЕЛЕВОЙ ФУНКЦИИ 191
лучим последовательность {r\k}, по формуле C.15) опре-
определим последовательность коэффициентов штрафа тл. При
этом для обоих методов последовательности множеств ре-
решений вспомогательных задач совпадут. Метод параметри-
параметризации поэтому по существу отличается от метода внешних
штрафных функций только тем, что в нем автоматически
определена политика изменения вспомогательного пара-
параметра г], в то время как в методе внешних штрафных
функций пользователь должен специально определять
правило изменения т. Поэтому трудно сравнить эти ме-
методы: всякую реализацию метода параметризации целевой
функции можно повторить с помощью метода внешних
штрафных функций, используя формулу C.15), а при
специальном изучении решаемой задачи можно выбрать
и более удачную политику изменения коэффициента т,
что позволит методом штрафных функций получить лучшие
результаты. С другой стороны, при неудачном выборе
последовательности {хк} результаты расчетов по методу
штрафных функций будут хуже, чем при использовании
метода параметризации целевой функции. Эти обстоятель-
обстоятельства показывают, как осторожно надо относиться к так
называемым «численным экспериментам» по исследованию
сравнительной эффективности различных алгоритмов. При
желании можно построить внешне убедительные примеры
решенных задач, показывающие либо преимущество ме-
метода параметризации целевой функции перед методом внеш-
внешних штрафных функций, либо «доказывающие» обратное
утверждение.
В [заключение сделаем несколько общих замечаний.
Метод параметризации целевой функции удобнее, чем
метод внешних штрафных функций тем, что в нем, во-
первых, конкретизировано правило определения последо-
последовательности {r)k\, во-вторых, вспомогательная функция М
ограничена снизу нулем, поэтому здесь устранен один
из недостатков метода штрафных функций, связанный
с возможностью того, что вспомогательная функция ока-
оказывается иногда неограниченной снизу на недопустимом
множестве. Вместе с тем метод параметризации имеет две
слабые стороны: для его реализации надо знать нижнюю
оценку значения / (л;*), вспомогательную задачу безуслов-
безусловной минимизации обычно приходится решать более точно,
чем в методе внешних штрафных функций. В целом ме-

192
МЕТОД ШТРАФНЫХ ФУНКЦИЙ
[ГЛ. III
тоды очень близки, они лучше всего подходят для пред-
предварительных, грубых расчетов; получить высокую точность
решения с их помощью трудно.
6. Геометрическая интерпретация. Для удобства пред-
представим функцию М(ху т\) в следующем виде:
(*¦ л) = (/ (*)-
R (х) =
На рис. 1 изображена система координат, у которой по
оси абсцисс отложено R> по оси ординат—величина /.
w
Рис. 1.
Если для всевозможных значений х рассмотреть мно-
множество точек с координатами [R (x), f (#)], то они обра-
образуют некоторое множество W (на рис. 1 — заштрихованная
часть). Точка Б, имеющая координаты [0, / (х%)] соот-
соответствует решению задачи A.6.1). На плоскости [/?, /]
уравнение
(f — v\kJ + R2 = const C.16)
представляет собой окружность с центром в точке Ло,
имеющей координаты [0, r\k]. Решение вспомогательной
задачи о минимизации М(х, r\k) по х?Еп можно интер-
интерпретировать на плоскости [R, f] как отыскание проекции
точки Л 0 на множество W или как отыскание окруж-
окружности C.16) наименьшего радиуса, имеющей общую точку С
с множеством W. Полученная в результате этой операции

§4] МЕТОД ВНУТРЕННИХ ШТРАФНЫХ ФУНКЦИЙ 193
точка С имеет координаты [R (хк), f (xk)]. На рис. 1 также
изображены: точка Аг с координатами [0, t]k + ]/'M(xk9 r\k)]f
точка А2 с координатами Г О, Ш + ТТТХГТГ"! > точка ^з
с координатами [0, f(xk)].
Точка А 2 получается из условия пересечения каса-
касательной к найденной окружности в точке С с осью ор-
ординат. В первой версии метода в качестве ч\к+{ берется
ордината точки А1У во второй версии—ордината точки А 2
и в третьей версии—ордината точки А3. В каждой версии
после нахождения х\к+1 снова производится проектирова-
проектирование на множество W и так далее, до тех пор пока зна-
значение щ не станет достаточно близким к величине / (#«).
§ 4. Метод внутренних штрафных функций
1. Общая идея метода. Рассмотрим тот частный слу-
случай задачи A.6.1), когда допустимое множество опреде-
определяется только с помощью ограничений типа неравенства.
Пусть ищется
minf(x), X = {x?En: ВД<0}. D.1)
?Х
Множество решений этой задачи по-прежнему обозна-
обозначим X*. Множество внутренних точек есть Х0 — {х?Еп:
А (#)<()}, границей допустимого множества является Г=
= х\х0.
Введем вспомогательную функцию
Непрерывные функции ii(t), x(t) определены при лю-
любых /^0 и таковы, что при б > 0 выполнены условия
И@>0,,«)>0,1|>1|±|, italic. D.2)
Всюду на Хо функция b (х) непрерывна и Ь (х) > 0, для
любой бесконечной последовательности точек {х(}у принад-
принадлежащих Хо и сходящихся к точке из Г, предел
lira &(*,.) = +оо. D.3)
Ю. Г. Евтушенко

194 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. 1Ц
В качестве простейших примеров функций Ь(х), удов-
удовлетворяющих приведенному условию, можно указать
Численный метод решения задачи D.1) состоит в сле-
следующем. Для произвольной возрастающей, стремящейся
к бесконечности последовательности O^t%<t%<... ре-
решается вспомогательная задача о минимизации Р(х, tt).
В результате получается последовательность точек \xk\y
удовлетворяющих условию
xk€ArgminP(xytk). D.4)
При определенных условиях всякая предельная точка
сходящейся подпоследовательности из последовательности
{хк} принадлежит Х«, т. е. имеет место сходимость опи-
описанного метода.
Условие D.3) приводит к тому, что при приближении
точки х к границе Г значения Р (ху t) стремятся к беско-
бесконечности. Поэтому в результате минимизации Р (х, tk) no x
находятся точки хкУ принадлежащие множеству X. Вспо-
Вспомогательные задачи D.4) можно решать, используя числен-
численные методы локальной минимизации функций многих пе-
переменных, начиная поиск из произвольной точки хо?Хо.
Функция Ь (х) выполняет, таким образом, роль своеобраз-
своеобразного «барьера», в связи с чем описанный метод часто
называют методом «барьеров» или внутренних штрафных
функций.
2. Обоснование сходимости. Для произвольной точки
#о€^о определим два множества
О@«{*€#¦: Р(х9 t)
*: |*@/(*
Теорема 3.4.1. Пусть функция f (x)непрерывна наХ9
множество решений Хт задачи D.1) не пусто и существует
такая г-окрестность Ge(X#) множества X», что N —
= Ge(X,)nXo=5^0; пусть выполнены условия D.2), D.3)
и множество 5@) компактное. Тогда метод внутренних
штрафных функций сходится к X* на Хо.

§4] МЕТОД ВНУТРЕННИХ ШТРАФНЫХ ФУНКЦИЙ 195
Доказательство. Очевидно, что имеют место вклю-
включения й(/)сВ(/)сВ@), Х«сВ(/ + 8)сВ(/) для любых
5^0. Следовательно, -множество Х# и при всех / ^ 0
множества &(/), B(t) ограничены, вспомогательные задачи
минимизации D.4) имеют решения. Для любых х«?Х*,
имеем /(#*)^/(#), тем более
^ ' D.5)
Все элементы последовательности {хк\ принадлежат мно-
множеству В @), поэтому последовательность {хк} ограничена,
из нее можно выделить подпоследовательность {лс^}, схо-
сходящуюся к точке х?Х, причем из неравенства D.5) сле-
следует, что
/ (*•) < / (х) + d, d = lim Ip>
Пусть / (a:*) = / (л:) + d9 тогда d = 0, x ? X», так как
в случае d > 0 было бы / (#*) > / (#), х ? Х% что невозмож-
невозможно. Покажем, что случай
/(*•)</(*) + <* D.6)
не имеет места. Предположим противное: справедливо D.6).
Согласно условиям теоремы существует такая окрестность
Ge (Л*), что N Ф 0. Выберем 8 настолько малым, что*?#.
Всегда можно найти точку y^Ny для которой
f(**)<f(y)<f(x). D.7)
Из условия определения точек хк следует, что.
Взяв значения th> соответствующие подпоследовательности
{%}» и устремив k—^oo, получим: f(x)-\-d^f(y), что
противоречит D.6), D.7). Поэтому случай D.6) не имеет
места. Всякая предельная точка последовательности {хк\
принадлежит AV Ц
3. Вычислительный аспект. В описанном методе строится
последовательность внутренних точек \xk\ из допустимого
множества. Это может быть весьма полезным в ряде задач,
7*

196 МЕТОД ШТРАФНЫХ ФУНКЦИЙ] ГГЛ. III
где по тем или иным причинам нежелательно рассмотрение
недопустимых точек. Например, какие-либо из функций,
определяющих задачу D.1), могут быть не заданы на не-
недопустимом множестве. Вместе с тем, метод неприменим
к задаче A.6.1) в том случае, когда функции g(x) нели-
нелинейные и внутренняя часть допустимого множества пуста.
При практических расчетах обычно вводятся комбиниро-
комбинированные вспомогательные функции, в которых ограничения
типа равенства учитываются с помощью внешних штрафных
функций, ограничения типа неравенства—с помощью внут-
внутренних штрафных функций. Для задачи A.6.1) можно,
например, воспользоваться функцией
Здесь в процессе расчетов t-+0. Подробное исследование
таких комбинированных штрафных функций можно найти
в книгах А. Фиакко и Г. Мак-Кормика [I], Э. Полака [I].
В работе чешского математика М. Хамала [1] показано,
что при реализации метода внутренних штрафных функций
можно отказаться от условия стремления функции Ь(х)
к бесконечности при д:—*Г, вместо этого потребовать,
чтобы норма градиента функции Ь (х) стремилась к беско-
бесконечности при х —+ Г. При этом в качестве вспомогательной
можно использовать, например, следующую функцию:
В книге А. Фиакко и Г. Мак-Кормика [1], в статье
Ю. Г. Евтушенко [9] предложены различные «непрерыв-
«непрерывные» методы, аналогичные A.17), использующие барьер-
барьерные функции.
При численной реализации метода находятся прибли-
приближенные решения вспомогательной задачи D.4). Здесь воз-
возможны упрощенные версии, аналогичные тем, которые
были приведены при описании метода внешних штрафных
функций.
4. Оценка точности метода. Рассмотрим вспомогатель-
вспомогательную функцию

§4] МЕТОД ВНУТРЕННИХ ШТРАФНЫХ ФУНКЦИЙ 197
Воспользуемся описанным в § 2 методом асимптотических
разложений. В качестве малого параметра примем е, в ка-
качестве приближенного -решения задачи D.4) будем брать
любую точку ху удовлетворяющую условию
Для конкретной точки х = х(г) имеем
/* (х (8)) + К (х (е)) v (в) = га, R
D(v{s))h(x{E)) = -sI. V'*}
Здесь а?Еп, |ja||^l, v?Ec\ l?Ec—вектор, все компо-
компоненты которого равны единице.
Решение системы D.8) ищем в виде рядов, аналогич-
аналогичных B.11). Подставим их в D.8) и разложим функции
в ряды по степеням е; приравнивая выражения при е° и
при в1, получим
fx (х.)+hx (x,) v. = 0, »/fc/ (x.) = О,
Lxx (х„ v.) Хг + hx {хщ) vx = a, D.9)
Предполагая, что в -задаче D.1) выполнены условия
леммы 4.1.2, решим систему D.9), получим следующие
асимптотические оценки:
х (е) = х, + eL^ (*„ v,) (a—hx (ж.) о,)+0 (е2),
о (в) =»»• + «»!+ 0(в«),
Vl = - [D (h (x,))-D (о,) hTx (дсIй (х., о,) К (х,)]-1 х
Отбрасывая величины порядка г2, получим, что если
/€*(*•), то Л/() О
{ (х,), *!> = — 1, А/ (ж, + едгх) = у- < 0.
Если /^ст(д:«), то имеем
/^(ж.)<о, »:=о,
Из этих формул получим
/«*<*.)

]98 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. Ш
Здесь N — количество активных ограничений в точке хф
(т. е. число тех hJ'{x*)y для которых /€<*(*¦))•
Значение минимизируемой функции /(#(в)), таким об-
образом, больше, чем / (х+) и стремится к этой величине при
е —* 0. Интересно отметить, что здесь, как и в случае
внешних штрафов, значения /, А, Р не зависят от конкрет-
конкретного выбора вектора а (с точностью до величин^второго
порядка малости).
5. Экстраполяция. Цель экстраполяции при реализации
методов штрафных функций была разъяснена в п. 4 § 2,
что позволяет сократить изложение. Пусть при некотором
коэффициенте гк найдены векторы xk> vk, удовлетворяющие
условиям j
1^ (*» Ч) = /* (**) + К (хк) vk - гкак,
где К|<1.
Введем малый параметр ц и рассмотрим систему^
ГА*). ¦¦„.,-.-. ™- DЛ0)
Ее решение ищем в виде рядов, аналогичных B.23). Осу-
Осуществляя стандартные вычисления, находим следующие
асимптотические оценки для решений системы D.10):
х (р) = xk—iiL? (xk, vk) (ak -f hx (хку
v(\i) = vk+\w1+0(ii2),
vt = [D (h (xk))-D (vk) hi(xk)L? (xk, vk) hx (xj\-* X
> vk)ak).
Если процесс расчетов по методу внутренних штрафных
функций прекращается после нахождения хкУ то, согласно
найденным формулам, в качестве уточненных значений х
и v следует взять
=xh—Lg(xh9 vk)[Lx(xk, vk) + hx(xk)v], D.11)
D.12)
v=[D(h (xk))-D (vk) hTx{xk)Lxx (xk, vk) К (я*)]-1 х
X D Ы [hTx (xh) LH (xh9 vk) Lx (xk, vk) -D(h (xk))].

§ 5] МЕТОД ЛИНЕАРИЗАЦИИ 199
Если рассматривать эти формулы как некоторый итератив-
итеративный метод, то легко показать, что он совпадает с методом
Ньютона, примененным к решению системы Lx(x, и)=0,
D(v)h(x) = 0.
Можно воспользоваться вспомогательной функцией
zj7w- ' DЛЗ)
Тогда роль D.10) будет играть следующая система:
i(L() (ki)kt
D (w) Л (*Н — (ел —|л) /, w e Ес.
Несложно получить бее необходимые расчетные формулы,
аналогом метода D.11), D.12) для этого случая будет
метод D.1.11), который будет получен и исследован в сле-
следующей главе, исходя из других соображений.
Здесь так же, как и в § 2, можно проводить упрощен-
упрощенную экстраполяцию по формуле B.26). В случае вспомо-
вспомогательной функции D.13) использование формулы B.26)
будет соответствовать линейной зависимости х> v от корня
квадратного из истинного коэффициента штрафа, равного
в D.13) г*.
§ 5. Метод линеаризации
В настоящее время существует много версий метода
линеаризации, большинство из них можно интерпретиро-
интерпретировать как реализации метода внешних штрафных функций,
использующие недифференцируемые штрафы. Этим и объяс-
объясняется то, что описание метода линеаризации помещено
в этой главе, посвященной методу штрафных функций.
Ниже, опуская обоснование, приведем ряд версий метода.
Детальное описание всех вариантов метода, доказательства
их сходимости можно найти в первоисточниках. Изложе-
Изложение метода проведем для задачи A.6.1), используя вспо-
вспомогательную функцию B.1), хотя в большинстве перво-
первоисточников рассматривается задача D.1), в качестве вспо-
вспомогательных функций берутся либо Pt (х, т), либо Pz (х, т).

200 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. Ill
I. Общая идея метода. Для многих специалистов,
работавших в области механики, наиболее естественным
подходом к решению задачи A.6.1) представляется метод
линеаризации, который заключается в следующем. В точке
x = xk линеаризуются функции, определяющие задачу
A.6.1), и ставится задача линейного программирования
о нахождении
min<fx(xk), х—хк>, E.1)
*x
Эта задача может иметь неограниченные решения, по-
поэтому обычно вводятся дополнительные ограничения:
В результате решения вспомогательной задачи находится
вектор x^lck и осуществляется переход к точке
(Хк—Хк)> <*к>°- E.2)
Процесс повторяется в новой точке xk+1 и т. д. К сожалению,
такой метод сходится крайне медленно. Может показаться,
что для получения высокой скорости сходимости следует
использовать квадратичную аппроксимацию всех функций,
определяющих задачу. Исследования показали, что это не
так: квадратичную скорость сходимости можно получать,
ограничиваясь линейной аппроксимацией функций, задаю-
задающих ограничения, и взяв в качестве целевой функции
некоторую квадратичную форму. Вместо E.1) решается
задача
min [<M**)f x-xH>+±(x-xk)TNk(x-xk)] . E.3)
Многочисленные версии метода линеаризации отличаются
друг от друга правилами определения матриц Nk и вели-
величин ak. Укажем несколько таких вариантов. Найденный
из решения задачи E.3) вектор х обозначим xk9 соответ-
соответствующие множители Лагранжа — uk> vk, положим также
& = [«*. vk\> zk = [*k> Уь\Л(*ь, uky vk)^L(zk). Всюду пред-

§5] МЕТОД ЛИНЕАРИЗАЦИИ 201
полагается, что в задаче A.6.1) существует седловая точка
гт = [хт, ифу v*] функции Лагранжа L (х, и, v).
2. Версия Р. Уилсана. Положим в E.2) и E.3)
При стандартных предположениях Р. Уилсоном [1] дока-
доказана локальная квадратичная скорость сходимости такого
процесса. Чтобы избавиться от вычисления матриц вторых
производных, были разработаны различные упрощенные
варианты метода.
3. Версии У. Гарсия Паломарес и О. Мангасаряна [1].
Предложены следующие два способа регулировки ак и Nk:
1) a*si, матрица Nk такова, что \NL(^\^
2) a*si, матрица Nk такова, что
\\N —I lz\l<Cv lim (Nb~~
В тех случаях, когда задача E.3) неоднозначно разрешима,
в качестве zk+1 берется точка из множества решений, для
которой норма \\zk+1—zk\\ имеет наименьшее значение. Ве-
Величина v выражается через производные функций, опре-
определяющих задачу, в точке хФ. Доказано, что если выполнены
условия, близкие к условиям леммы 4.1.1, в задаче A.6.1)
присутствуют только ограничения типа неравенства, то при
использовании первого способа регулировки метод обладает
линейной скоростью сходимости, при втором способе—сверх-
способе—сверхлинейной.
4. Первая версия С. Хана. Считаем ак= 1, матрицу Nk
будем уточнять в процессе итераций, стремясь приблизить
ее к матрице Lxx(zk). Для этой цели можно использовать
различные квазиньютоновские формулы, полученные в § 5
гл. II. Воспользуемся, например, симметричным вариантом
Пауэлла метода Бройдена B.5.38). Обозначим
uk+1, vk+1)—Lx(xk, uk+1,
Тогда

202 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. Ill
Аналогичным образом можно применить многие другие
формулы пересчета матрицы Nk. В статье С. Хана [1]
доказана сверхлинейная скорость сходимости данной вер-
версии при стандартных предположениях для случая зада-
задачи D.1).
5. Вторая версия С. Хана. Все описанные выше версии
обладают только локальной сходимостью. Чтобы расши-
расширить область сходимости, следует вводить специальную
регулировку шага ак. Для этой цели можно воспользовать-
воспользоваться недифференцируемой вспомогательной функцией B.1).
Определим величину ан из условия приближенной одно-
одномерной минимизации вспомогательной функции по ак:
Р(*ы.и*)< min Р(хк + ак(хк—хк),т) + \к. E.4)
0 < ак < б
Здесь последовательность неотрицательных чисел vk такова,
оо
что 2 v*< °°; т> в—некоторые положительные числа; хк
по-прежнему обозначает решение задачи E.3), матрицы Nk
пересчитываются по каким-либо квазиньютоновским фор-
формулам. Реализация такого варианта метода не намного
сложнее предыдущей версии: тут добавилась просто реали-
реализуемая задача одномерного поиска E.4). Вместе с тем, как
показано С. Ханом [2], приведенная версия обеспечивает
глобальную сходимость метода в том случае, если D.1) —
задача выпуклого программирования, выполнено условие
Слейтера, число т достаточно веушко, в качестве Р взята
функция Р3.
Описанную схему расчетов можно рассматривать как
реализацию метода внешних штрафных функций, но вместо
минимизации недифференцируемой функции B.1) по л: по-
последовательно решаются задачи квадратичного программи-
программирования E.3) и осуществляется одномерная минимизация
E.4). С другой стороны, описанную версию С. Хана можно
рассматривать как некоторый специальный метод безуслов-
безусловной минимизации недифференцируемой функции B.1)по#.
Выпишем двойственную задачу к задаче E.3) (см. задачу
A.6.7)). Найти
max max min Г</, {хк)у Р>+\ pTNkp +
, h (xk) + hTx (xk) p>]. E.5)

§5] МЕТОД ЛИНЕАРИЗАЦИИ 203
Здесь введено обозначение р = х—хк. Если матрица Nk не
особая, то внутренняя задача решается просто:
p = ~N?Lx(x*,u,v). E.6)
Подставляя это выражение в E.5), приходим к внешней
задаче об отыскании
max max [L (xk, u,v)—f(xk)—±-1| N? Lx (хк, и, v) |||]. E.7)
Пусть [uk, vk]—решение этой задачи, тогда, согласно E.6),
имеем
**—** = — ^Lx {хк, ик, vk).
Таким образом, задачу квадратичного программирования
E.3) можно заменить решением задачи максимизации E.7)
при простейших ограничениях.
6. Версия Б. Н. Пшеничного. Считается, что Nk = In.
Шаг <хк определяется следующим образом. Находится пер-
первое значение s = 0, 1, ..., при котором выполнено нера-
неравенство
Если это неравенство впервые выполнено при s = Si, то
в E.2) полагается aJ = 2~<si. Для упрощения вспомогатель-
вспомогательной задачи E.3) в ней учитываются только те ограничения,
у которых нарушение допустимости наибольшее. Для этого
вычисляется величина Sx(**) (CM- формулу A.2)) и допу-
допустимое множество Хк в задаче E.3) определяется условиями
в1 (*к) + <8i(**), х—хк> = 0, i$Wx(xk),
V(xk) + <*i(хк), х~хк> < 0, / € W2 (xj.
Здесь введены индексные множества
(xk) - {/ € [1 ic]: V(xk) > S1 (хк)-бк\.
Начальное значение 60>0 задается пользователем,
далее оно дробится пополам каждый раз, когда вспомога-
вспомогательная задача не имеет решения. Используется следующий
способ регулировки коэффициента хн\ если сумма абсолют*

204 МЕТОД ШТРАФНЫХ ФУНКЦИЙ [ГЛ. Ill
ных величин компонент двойственного вектора, соответст-
соответствующих ограничениям E.8), меньше гк, то значение хк
удваивается, в противном случае гк+1=%к.
Сходимость метода доказана в предположении, что
в качестве вспомогательной взята функция Р3 (х, т), гра-
градиенты функций, определяющих задачу, удовлетворяют
условию Липшица. Доказательство можно найти в книге
Б. Н. Пшеничного и Ю. М. Данилина [1].
7. Версии А. И. Голикова и В. Г. Жадана. Вводится
непрерывная на Еп функция М (х)у удовлетворяющая усло-
условию: M(x)^l + Vn I fx (x) ||2. В первой версии решается
следующая задача линейного программирования о нахож-
нахождении
min min [</* (хк), x—xk> + M (xk) q\ E.9)
х q
где q€,E\> имеют место условия E.8) и, кроме того,
4. . E.10)
Обозначим xky qk — решение этой задачи, pk=^xk — xk.
Новая точка определяется по формуле, аналогичной E.2):
E.11)
Шаг ak выбирается путем дробления начального шага а
до тех пор, пока не будет выполнено условие
Рг (**+i, т) < Р3 (xk, т) +flah[<fx (*,), pk>-tS1 (xk)]. E.12)
Параметр 0<P< 1 и начальный шаг а фиксированы.
Во второй версии решается задача линейного програм-
программирования о нахождении
min min min [<fx (хк), a—b> + M (xk) q]. E\ 13)
a b q
Здесь a ? ?+, b € ?+, q € E\* допустимое множество задается
условиями
V(хк) + Фх(хк)г а-6><0, / € W2(xk),
S(^ + H<1+^. FЛ4)

§ 5] МЕТОД ЛИНЕАРИЗАЦИИ 205
Эта задача несколько проще E.9), так как здесь вместо п
условий E.10) введено лишь одно ограничение E.14); но-
новое условие неотрицательности а, Ъ сравнительно легко
учитывается. Точка хк+1 определяется из E.11), где
рk = a—й, шаг находится из E.12).
Легко проверить, что задача, двойственная к E.9),
эквивалентна (в смысле совпадения оптимальных значений
двойственных переменных, соответствующих линеаризо-
линеаризованным ограничениям) следующей задаче:
max Г 2 и*ёЧхи)+ 2 vW(xk) —
t(хк) +и 2 x ulgx (*k) + .6 ^1 v'ty (xk)l 1 , E.15)
где
, 2
*ewt(x
Также записывается двойственная к E.13) задача,
только вместо нормы Ц-^ следует использовать чебышев-
скую норму I-L. Целевые функции в E.7) и E.15) весьма
близки и отливаются только разными нормами градиента
Lx (x, u,v). К подобным методам мы придем ниже в § 6 гл. IV,
используя модифицированные функции Лагранжа. Дока-
Доказательство сходимости обеих версий дано в предположениях,
близких к использованным в предыдущем пункте.
На этом мы закончим описание различных вариантов
метода. В настоящее время мы не обладаем достаточным
экспериментальным материалом, чтобы провести сравни-
сравнительный анализ практической эффективности всех приве-
приведенных версий. В некоторых из цитированных выше пер-
первоисточников содержится информация о численных экспе-
экспериментах, но только с отдельно взятыми версиями.

ГЛАВА IV
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ,
ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ
МОДИФИЦИРОВАННЫХ ФУНКЦИЙ ЛАГРАНЖА
Значительные трудности, возникающие при попытке
решить многие практические задачи с высокой точностью
методом штрафных функций, привели к необходимости
создания нового класса численных методов, обеспечиваю-
обеспечивающих геометрическую и квадратичную скорости сходимости.
Такой класс методов был создан на базе использования
модифицированных функций Лагранжа. По-видимому впер-
впервые было предложено использовать модифицированные
функции Лагранжа для решения задач нелинейного про-
программирования в книге К. Эрроу, Л. Гурвица, X. Удзавы
[1]. В дальнейшем эта идея нашла широкое развитие и
привела к созданию метода, обладающего геометрической
скоростью сходимости. Укажем первые работы этого на-
направления, выполненные М. Хестенсом [1], М. Пауэллом
[1], П. Хаархофом и Дж. Баесом [1]. Дальнейшее разви-
развитие этот подход нашел в работах Р. Рокафеллара [2], [3],
Н. В. Третьякова [1], Б. Т. Поляка и Н. В. Третьякова
[1], Е. Г. Гольштейна и Н. В. Третьякова [1]> Д- Берт-
секаса [1]—[3], Б. Корта и Д. Бертсекаса [1] и многих
других авторов. Основное внимание в этих исследованиях
занимает описанный ниже, в § 3, метод C.21). Многие
авторы рассматривают его как самостоятельный метод
решения задач нелинейного программирования; в работах
Б. Т. Поляка и Н. В. Третьякова он назван «методом
штрафных оценок», в работах Д. Бертсекаса—«методом
множителей», во многих других—«методом модифициро-
модифицированной функции Лагранжа».
Излагаемый ниже материал будет основан на ином,
развиваемом в последние годы в ВЦ АН СССР подходе,
в основе которого лежит редукция с помощью модифици-
модифицированных функций Лагранжа исходной задачи нелинейного
программирования A,6.1) к нахождению локального мак*

§1] ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 207
сими на, минимакса, седловых точек и к решению систем
нелинейных уравнений. После этого задача решается с по-
помощью использования известных методов, разработанных
для указанных классов задач. Метод C.21) при таком
подходе представляет собой не что иное, как метод простой
итерации, примененный к решению некоторой системы
нелинейных уравнений. Предлагаемая редукция дает воз-
возможность получить широкий спектр методов решения задач
нелинейного программирования.
§ 1. Простейшая модификация функции Лагранжа
1. Предварительные результаты. Всюду в этой главе
будет рассматриваться общая задача нелинейного програм-
программирования A.6.1). Согласно теореме 1.6.1 при определен-
определенных условиях решение A.6:1) можно заменить отысканием
седловых точек функции Лагранжа. Описанные выше чис-
численные методы нахождения седловых точек оказываются
неприемлемыми для этой цели, так как они пригодны для
отыскания безусловных решений, а в A.6.9) следует учи-
учитывать условие v^O. Для преодоления этого препятствия,
следуя работам Ю. Г. Евтушенко [6], [9], [10], произве-
произведем простейшую модификацию функции Лагранжа, введя
в рассмотрение
F(x, uy w) = f(x) + <g(x), u> + 2
Обозначим
F{xy
Пусть функции, определяющие задачу, дифференци-
дифференцируемы, в задаче A.6.1) существует точка Куна—Таккера
[**, «*, iy|, тогда определим *, = [*«, ич> ау], где wL^J/vl
для /<Е[1:с]. Из условий Куна—Таккера следует, что гт
является стационарной точкой функции F (г), так как
Fz(*.) = 0n+m. A.2)
Это свойство^позволяет редуцировать задачу A.6.1) к оты-
отысканию решений системы A.2). Почти дословно повторяя

208
МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
доказательство теоремы 1.6.1, можно показать, что если
z« = [#*, umi uyj является безусловной седловой точкой
функции F, то х+^Х*, wihJ'(х*) = 0. Если функции, опре-
определяющие задачу, дифференцируемы, то седловая точка гт
функции F удовлетворяет условию A.2). Вместе с тем
использование численных методов отыскания седловых
точек затруднено тем, что функция F не является выпукло-
вогнутой, а это условие весьма существенно для обеспе-
обеспечения сходимости многих методов нахождения седловых
точек. Поэтому целесообразно рассмотреть задачу отыска-
отыскания локального максимина
maxmax minF(x> uy w).
EeEcEn
A.3)
Для ее решения можно использовать методы, описанные
в § 6 гл. II. Покажем, что при стандартных предполо-
предположениях в точках Куна—Таккера матрица Fzz(z%) невы-
невырождена и реализуется локальный максимин. Для этого
введем следующие три вспомогательные квадратные ма-
матрицы порядков, соответственно п + т, п + т и т:
Fzz(z) =
#(*) =
Г. Fxx(z)
_2D(w)hTx{x)
gxM
_2D(w)hTx(x)
fo Mi
Vee :
Осе \
-8*(x)
0ee
2hx(x)D(w)-
oec
2D(h(x)) _
\-2hx(x)L
>
)(wr
\ "ec
i 2D(h(x))
A.4)
)(z)]TF-1(z)[Fxu(z)\Fxw(z)]-
Лемма 4.1.1. Пусть в точке Куна—Таккера [#*,
и%% v*] для задачи A.6.1) выполнены достаточные условия
минимума теоремы 1.7.4, и в х* выполнено условие регу-
регулярности ограничений g(x) = 0, h(x)^Q. Тогда матрица
FZz(z*)> где 2* = [х*> и*» га>*]> невырождена.
Чтобы доказать невырожденность, достаточно показать,
что не существует ненулевого решения системы
FZz(z*)z — 0, z = [x9 и, w]. A.5)

ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 209
В подробной записи эта система выглядит так:
)u = 09 A.6)
xm))w = O. A.7)
Из A.7) следует, что для всех j ?o(x*) выполняются
условия A/ (x*) = xThJx(x*) = 0, ы/тФ0. Для jfo(xm) имеем
h/(x,)<0, xs)i = w[ = 0. В обоих случаях
Допустим, что ||х || Ф 0, тогда, умножая A.6) слева на хт
и учитывая A.7), получим
{z.)x = 0, A.8)
причем х удовлетворяет условиям
Каждой точке Куна—Таккера [а:,, и», у,] соответствует
точка г% = [хщ9 «•, w.]> поэтому F^ (гф) = L^ (^, «„, у,)
и из A.8) следует, что
xTLxx(xm, ичу v*)x = 0.
Но это равенство противоречит положительной определен-
определенности матрицы Lxx (хш, и*, vm) на К3 (х*) (см. условие A.7.16)).
Поэтому х = 0. Из A.6), A.7) тогда следует
Согласно условию строгой дополняющей нежесткости,
все у{фО для j?o(x*)9 для этих же значений хю[фО.
Учитывая условие регулярности ограничений, приходим
к выводу, что и = 0 и о^ = 0, если j?o(xm). Выше было
показано, что w-? = 0 для всех 1(?о(х*), поэтому все век-
векторы ху и, w, удовлетворяющие системе A.5), нулевые,
матрица Fzz(z+) неособая. Щ
Лемма 4.1.2. Пусть в точке Куна — Таккера [хф, и99 vm]
выполнены условия регулярности ограничений g(x) = 0,
h(x)^.O и условие строгой дополняющей нежесткости;
функции, определяющие задачу, дважды непрерывно
дифференцируемы в окрестности точки хт, матрица
Lxx(x*9 и», vm) положительно определена. Тогда:

210 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
1) матрица N (z%) положительно определена;
2) все корни X уравнения
\H(z*)-XIn+m\ = 0 A.9)
имеют строго отрицательные действительные части;
3) точка [х*у уш]> где у* = [и*у до*], является точкой
строгого у локального максимина в задаче A.3);
4) точка [хт, у*\ является седловой точкой {локальной
по х, глобальной по у) в задаче A.3);
5) х» есть локальное решение задачи A.6.1).
Доказательство. Не нарушая общности, можно
считать, что h/(xm) = 0 для 1^/^s и h/(xm)<0 для
1 -fs^Q' <с. Введем векторы q=[и1, ...,ие, до1, .. .,ws]?Ek,
k = e+s и hb (x*) = [hs+1 (**), ..., ft' (*.)]. Матрицу N B»),
определяемую формулой A.4), можно представить следую-
следующим образом:
= [Fqx (*•) Fxl M Fxq (z#) |
{Z*}" L o(~^ \
В силу условий строгой дополняющей нежесткости все
w[ Ф 0 для 1 ^„/ ^ s, поэтому из условия регулярности
ограничений следует, что столбцы матрицы Fxq (z*) линейно
независимы, ранг этой матрицы максимальный, равен k
и матрица Fqx (z%) F^x (^«) FXq iz*) размером k* положительно
определена. Диагональная матрица ~D(hb(x*)) также по
условию положительно определена. Отсюда следует поло-
положительная определенность матрицы N(z*).
Пусть ЯB«)г==Я2, вектор ? = [#, и, v] комплексно-со-
комплексно-сопряженный вектору 2. Считаем, что модуль |z|#0, тогда
RezTH (z,J = Reh|z|2 =
- Re [—xTFxx (z.)x + 2wTD (h (x.)) w] < 0.
Последнее неравенство следует из положительной опре-
определенности матрицы Fxx(zm) и из того, что в допустимой
точке h (х*) ^ 0. Пусть Re X = 0, тогда Re [—xTFxx (гф) х +
+ 2догД(/г(л:,!))до] = 0 только в том случае, если х = ® и
ш^' = 0 для / таких, что №(хт) < 0. Из системы H(z^)z=Xz9
получим уравнение
S А (х.) S' + 2 S w[wJhx (х.) = 0,
i /i

§1] ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 211
которое можно переписать следующим образом:
2gS() + 2
В силу условий строгой дополняющей нежесткости, если
/€<*(#*), то все т{фО. Из условия регулярности огра-
ограничений получаем, что векторы glx (х*) и hx (**), где / ? 0 (**),
линейно независимы. Чтобы полученное выше уравнение
имело место, необходимо, чтобы и = 0 и wJ' = 0 для всех
/?сг(л;*). Но выше мы показали, что w^ = 0 для }^о(х9).
Поэтому u = w = 0 и 2 = 0, что противоречит исходному
предположению |г|#0. Таким образом, случай ReA, = O
не имеет места и все корни A.9) обладают отрицательны-
отрицательными действительными частями.
В стационарной точке ?* = [#*, #*] матрицы FXX9 N по-
положительно определены, поэтому, согласно теореме 1.5.9,
z, является точкой строгого локального максимина в за-
задаче A.3).
Легко показать, что г, является седловой точкой (ло-
(локальной по х, глобальной по у), т. е. существует окрест-
окрестность G(x*) точки л:», такая, что для любых x?G(x%),
хфх*, и любых у$Ет выполнены неравенства
F (х., y)^F (*., Ут) <F{x, у.). A.10)
Функция F (Ху у) не является выпукло-вогнутой (вы-
(выпуклой по х при любом фиксированном у и вогнутой по у
при любом фиксированном а:). Вогнутость по w имеет место
лишь при тех фиксированных х\ для которых А(х)^0.
Из положительной определенности матрицы Fxx(zm) и
условия стационарности A.2) следует правое неравенство
A.10). Учитывая, что л:»—допустимая, стационарная точка,
получаем
для любых и?Ее, w?Ec. Отсюда следует левое нера-
неравенство A.10).
Для любого х € X Г) G (х9) из правого неравенства A.10)
имеем

212 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
т. е. Хщ является локальным решением исходной задачи
A.6.1).
В случае задач выпуклого программирования функция
F(x, у«) выпукла по х> из условия Fx(x*, у*) = 0 следует,
что F (л:*, у*) ^ F (х> у*) для любых х ? Еп.
Если выполнены условия данной леммы, то заведомо
имеют место достаточные условия минимума, даваемые
теоремой Мак-Кормика 1.7.2. Поэтому из нее также сле-
следует, что точка х% является локальным решением задачи
2. Метод Ньютона. Для нахождения решений системы
A.2) воспользуемся методом Ньютона
*k+i = zk-F?(zk)Fz(zk). ' A.11)
При реализации метода необходимо либо обращать сим-
симметричную матрицу Fгг порядка л+т, либо решать си-
систему из п + т линейных уравнений
В случае задач высокой размерности можно исполь-
использовать блочное представление матрицы вторых производных
Систему A.12) перепишем в эквивалентной форме
Рхх (Ч) (**+i —**)
РуХ (г*) (*ft+i~ 4) уУ
Предполагая, что матрица Fxx(zk) неособая, выразим из
первого уравнения разность хк+1—хк, подставим найден-
найденное выражение во второе уравнение, получим
yy4)Px(*k)l A.13)
=xk-F-Hzk) [Fx (zk) + Fxy (zk) (yk+1-yk)]. A.14)
Этот процесс можно продолжить и получить отдельные
формулы пересчета векторов ик и wk. Для этого перепишем
A.13) в виде
N{zH){yk^-yk)^Fy{zH)-Fyx{zH)F^ {zH)Fx{zH). A.15)

§ j] ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 213
Учитывая, что матрицы вторых производных Faa, Fuw
нулевые, представим N в блочном виде
Здесь введены следующие обозначения:
В = FUXF?XFXW = 2glF-lhxD И,
С = FWXF~\FXW-FWW = W (w) hZFjfrJ) (w) - 2D (А).
Предполагая, что матрица A (zk) неособая, из системы
A.15) получим
Fx]l A.16)
. A.17)
Здесь все матрицы вычислены в точке zh = \xk> uk, wk].
Эти формулы можно получить и непосредственно из A.12),
используя формулу Фробениуса для обращения блочных
матриц (см. Приложение II).
Возможны различные модификации метода. Вектор хк
можно определять из решения задачи безусловной мини-
минимизации, взяв
xk?ArgmnF(x9yk). A.18)
Предположим, что в некоторой окрестности точки уш такая
процедура определяет однозначную, дифференцируемую
функцию х(у). В этом случае необходимо найти вектор у,
являющийся решением системы
ТуР(х(у),у)=о. -
Метод Ньютона, примененный для отыскания решений
этого уравнения, приводит к следующей формуле:
^ (**. Ум)ру(*» УнУ A -19)
Эта формула следует также и из A.13), если положить
в ней Fx(xky yk)=^0. Формулу A.14) можно использовать
для экстраполяции точки хк+1 при решении задачи A.18).

214 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Для доказательства сходимости метода Ньютона A.11)
к решению системы A.2) воспользуемся теоремой 2.5.3.
С помощью леммы 4.1.1 выразим условие невырожден-
невырожденности матрицы FZ2 (г,) в терминах, используемых в теории
нелинейного программирования, придем к следующему
утверждению.
Теорема 4.1.1. Пусть в точке Куна—Таккера
[#*, #*, и*] выполнены условия леммы 4.1.1, в окрестности
точки г* = [#*, и*, w*] матрица FZ2 (z) удовлетворяет усло-
условию Липшица. Тогда метод A.11) локально сходится
к точке zm с квадратичной скоростью.
Метод A.11) обеспечивает, таким образом, при реше-
решении общей задачи нелинейного программирования квадра-
квадратичную скорость сходимости—необычно высокую для этого
класса задач. В дальнейшем мы неоднократно будем ис-
использовать метод Ньютона для таких задач. Однако метод
A.11) будет занимать особое место, так как он дает самую
простую быстросходящуюся вычислительную схему. Метод
широко используется для решения разнообразных задач
невысокой размерности. Обычно этим методом завершаются
расчеты, он применяется после того, как с помощью более
грубых методов* найдено начальное приближение для век-
вектора х и двойственных векторов.
Подобно тому как это делалось^в §Г5 гл. II "при опи-
описании метода Ньютона, здесь можно указать на ряд недо-
недостатков метода A.11), которые могут осложнить решение
задачи A.6.1):
1) в ряде случаев метод расходится;
|2) метод неприемлем для решения тех задач, в которых
размерность n + m вектора z велика, так как в этом слу-
случае приходится вычислять и обращать матрицы высокой
размерности;
3) [при неудачном, грубом начальном приближении
метод сходится к ненужным стационарным точкам (напри-
(например ,г к недопустимым);
4) если какие-либо компоненты*вектора w в начале ите-
рацийтравны нулю, то они остаются равными нулю на
всех итерациях (имеет место «прилипание» компонент век-
вектора w).
Первый из указанных недостатков может быть в ряде
случаев устранен с помощью введения переменного шага,
правила его регулировки описаны в § 5 гл. Ц,

§ !] ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 215
Второй недостаток преодолевается путем использова-
использования вместо A.11) формул A.13) и A.14), либо A.14),
A.16), A-17), либо A.1-8) и A.19). Можно также приме-
применять разнообразные квазиньютоновские методы.
Последние два недостатка свойственны всем методам,
основанным на простейшей модификации функции Ла-
гранжа вида A.1). Можно попытаться к функции F до-
добавить штрафующие слагаемые, положив, например,
Если z%—стационарная допустимая точка функции F (г),
то она будет стационарной точкой функции Р (г). Поэтому
можно отыскивать стационарные точки функции Р(г).
Такой прием несколько расширяет область сходимости,
однако не устраняет возможности того, что при фиксиро-
фиксированном значении т процесс сойдется к недопустимой точке.
3. Использование искусственных векторов. Другой
путь редукции исходной задачи 1.6.1 к решению систем
уравнений состоит во введении искусственных переменных,
позволяющих свести задачу A.6.1) к задаче нелинейного
программирования, в которой допустимое множество за-
задается только ограничениями типа равенства. Такой прием
был использован в п. 4 § 7 гл. I; он позволил редуциро-
редуцировать задачу A.6.1) к эквивалентной задаче A.7.17), для
которой функция Лагранжа L1 имеет вид A.7.18), необ-
необходимые условия минимума задаются соотношениями
A.7.20), или в более подробной записи—A.7.21). Восполь-
Воспользуемся обозначениями из § 7 гл. I; тогда метод Ньютона,
применейный к отысканию стационарных точек функции
Lx(Zy у)> будет иметь вид
{zk, yk)(yk+1—yk)= }
= -L\{zkyyk)A A.20)
Цг (г» Ук) B*+i—zk) = -LI (zk, yk). j
Матрица L\y определяется аналогично A.7.22):
Г**М ! M*)

216 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Обозначим
А(г, у) = \ •;—;—Г;
Несложно показать, что если выполнены условия леммы
4.1.1, то матрица А (z*, у*) невырождена, поэтому локаль-
локальная сходимость метода A.20) имеет место при стандарт-
стандартных предположениях.
Метод A.20) труднее реализовать, чем A.11), так как
здесь приходится обращать матрицу порядка п + т-\-с.
Однако в случае использования метода A.20) можно ут-
утверждать, что если процесс сошелся к некоторой точке
[#*> Р*, У*], то точка х* является допустимой в задаче
A.6.1). Этим свойством не обладал метод A.11). Вместе
с тем здесь не гарантируется выполнимость условия неот-
неотрицательности компонент двойственного вектора уе+1 для
1 <:/<!?. В следующих параграфах приведем более ради-
радикальные модификации функции Лагранжа, позволяющие
избавиться от этого недостатка.
4. Итеративные методы. Если в точке Куна —Так-
кера [х*> и*, V*] выполнены условия лемм 4.1.1 и 4.1.2,
то соответствующая ей точка [хФ, и«, до*] является точкой
строгого локального максимина функции F (z), и все ме-
методы, описанные в § 6 гл. II, можно использовать для
решения задачи A.6.1). Например, методы B.6.1), B.6.17),
B.6.18), B.6.24), B.2.3), примененные к решению A.3),
запишутся в виде
У=ъРу, x=-Fx9 A.21)
У = Р9, mx = -Fx-F?Fxfv9 * A.22)
y = Fy-FyxF?Fx, x = -Fx9 A.23)
y = Fv{x(y),y)9 x = x(y)-x, A.24)
Здесь зависимость х(у) определяется из условия A.18);
8—малый параметр @<е<^1); в тех случаях, когда не
указаны аргументы F, считается, что производные этой
функции вычислены в точке [x(t)y y(t)].

3 !j ПРОСТЕЙШАЯ МОДИФИКАЦИЯ ФУНКЦИИ ЛАГРАНЖА 217
г^ Теорема 4.1.2. Пусть в точке Куна—Таккера
Гх*, #*» v*l выполнены условия леммы 4 Л .2. Тогда существуют
такие г > 0, а > 0, «/то при любых фиксированных 0 < е < е,
0<a<a u при 8=1 методы A.21)—A.25) и шс диск-
дискретные варианты вида B.6.20) локально сходятся к точке
По сравнению с теоремами, приведенными в § б гл. II,
здесь добавилось утверждение о сходимости метода A.21)
прИ г = 1. Поэтому в доказательстве нуждается лишь
только оно. Составим уравнение в вариациях. Обозначим
6z = [&*r, 6иу 6w]y
здесь x(t), u(t), w{t)—решения системы A.21) с началь-
начальными условиями x@)==xo, u@)-=u0i w@) = wo. Отбрасы-
Отбрасывая члены второго порядка малости относительно 6г,
получим
Из второго утверждения леммы 4.1.2 получим, что харак-
характеристические числа матрицы Н (гф) имеют строго отрица-
отрицательные действительные части. Отсюда, согласно теореме
2.1.1, следует асимптотическая, экспоненциальная устой-
устойчивость точки 2* и, следовательно, локальная сходимость
метода A.21) и его дискретного варианта.
Если в задаче A.6.1) отсутствуют ограничения типа
неравенства, то при е=1 метод A.21) называется методом
Эрроу—Гурвица. Он обладает невысокой скоростью схо-
сходимости, поэтому им пользуются лишь в тех случаях,
когда оказываются неприменимы другие, быстросходящиеся
методы (например, при решении задач большой размер-
размерности). Заметим, что для учета ограничений типа нера-
неравенства можно вместо A.21) использовать метод, анало-
аналогичный B.4.5):
j(xk, u]v vk)],
Здесь шаг ak берется либо постоянный, либо изменяется
в соответствии с правилами B.4.6) — B.4.8).

218 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
§ 2. Модифицированные функции Лагранжа
1. Предварительные результаты. Богатый класс чис-
численных методов решения задач нелинейного программи-
программирования дает редукция к решению систем нелинейных
уравнений, идея которой была высказана в теореме 1.6.4.
Разовьем этот подход, взяв за основу следующую моди-
модифицированную функцию Лагранжа:
Я(*, и, *) = /(*) + .? V(8*(x), иО+.S ¦(#(*). vf). B.1)
i /i
Функции <р и я|) должны быть такими, чтобы обеспечить
выполнение условия A.6.18), которое запишется в виде
2 * W (*). v{) < S * (Л/ (*.), i>{), B.2)
здесь х € X. К остальным условиям на выбор функций <р
и г|) придем ниже.
При фиксированном векторе [«, у] определим множество
Х(и, v) = ArgminH(x, и, v). B.3)
Необходимое условие минимума функции Н (х, и, v)
по х состоит в выполнении условия
= 0. B.4)
Сравним его с необходимым условием минимума функции
Лагранжа по х:
Lx(x, и, v)=fA i/
Возникает мысль ввести систему уравнений
VgiS*. «0 = ^ '€[!«], B.5)
c] B.6)
и подобрать функции ф и г|) таким образом, чтобы эта
система была бы разрешима тогда и только тогда, когда

МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА 219
g , l^ ; 0. Если удается найти х*у иф1 V*,
при которых система B.5), B.6) разрешима, хт?Х(ит, i>«),
выполнены условия B.2), то, согласно теореме 1.6.4, за-
задача A.6.1) будет решена, так как лг«?Х*.
?Всюду в дальнейшем будем считать, что функции
ф(?'*, л;*'), i|)(/^, vJ') непрерывны при любых значениях
аргументов и по меньшей мере непрерывно дифференци-
дифференцируемы соответственно по g* и Ы. Обозначим J(hJ) мно-
множество действительных решений уравнения B.6), зависящих
от hJ как от параметра, а множество неотрицательных
элементов множества /(А-0 обозначим J+(h/). Наложим
дополнительные требования на функции ф и ф:
А1в Для любых действительных и1 имеют место условия:
1) Ф#@, «') = «'.
2) если ?'=й=0, то q>j(g', и1)фи1.
А2. При h/ > 0 множество / (У) пусто, при Ы < О
множество / (Ы) состоит из нуля, «/ @) совпадает с мно-
множеством неотрицательных чисел.
А3. При У > 0 множество /+ (hj) пусто, при Ы < 0
множество J+ (Ы) состоит из нуля, любое неотрицатель-
неотрицательное число принадлежит /+ @).
А4. Если в точке [я*, v*]?Ea+e выполнено условие
дополняющей нежесткости, h (хф) ^0,0^ v99 то для любых
Х имеет место неравенство
А6. При любых hJ' и любых vJ'^0 производная
Условие А4 обеспечит выполнение неравенства B.2).
Условие Аб будет полезно при реализации численных
методов. Приведем ряд функций, удовлетворяющих усло-
условию Ах:
Ф1 (*'. «О \
Ф4 (gl\ u

220 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Все эти функции относятся к широкому классу функ-
функций, представимых в виде
Ф6 (gl\ "О = g' (и1-а' @) р (и1)) + a (gi) 0 (и1).
Здесь a(g)—дифференцируемая функция такая, что
а' @) Ф а' (а) при любых афО, функция Р (а) дифферен-
дифференцируема и р (а) Ф 0 при любых а. В еще более общей форме
где для любых и1 равенство r\g{0, ui) = /v]g(giy и1) имеет
место только при g' = 0.
В качестве примеров простейших функций ф приведем
следующие:
r ((I—A/)-V если Л/<0,
t;/) - у (hi) + vf [Ы-у (-/?)],
. I АЛ если А^ > 0,
\ arctg A7", если А^ < 0.
Здесь г > 0, функция -у такова, что у @) = 0, v (я) > 0 и
Y' (я) > 0 при а > 0, у' (а) = 0 тогда и только тогда, когда
а = 0 (например, у(а) = а2, а3, а4).
Вторая и третья функции относятся к классу функ-
функций, представимых в виде
где a (a)—дважды непрерывно дифференцируемая функ-
функция такая, что 0<a'(a)<l при а < 0, l<a'(a) при
а>0.
Функции ijI—г|L, г(?6 удовлетворяют условиям А3, А4,
А5. Проверим выполнимость А3 у функции if»4. Пусть
Ау*>0, тогда уравнение B.6) имеет вид Ы+у' (Aj.) = t^f

§2] МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА 221
т. е. y'(h{)=*Of что имеет место, лишь когда /^'<0, но
это противоречит исходному предположению. Поэтому при
hJ > 0 уравнение B.6). ни при каких vJ' удовлетворить
нельзя. Пусть №<.О9 тогда
поэтому уравнение B.6) разрешимо лишь в том случае,
если vJ = Q. При hJ = 0 любое значение Ы удовлетворяет
B.6). Аналогичным образом убеждаемся в выполнимости
А3 для остальных функций.
Если в точке [#«, v*\ выполнено условие строгой до-
дополняющей нежесткости, то выполнимость условия А4
следует из неравенств
- viy (- W_ (x)) < V (V (*•), t){) = 0.
Очевидна также выполнимость А5 для функций
яр—ip. ^e.
Условие А2 выполнено для функции ojI и г)M.
2. Численные методы, основанные на использовании
модифицированных функций Лагранжа. При каждом фик-
фиксированном векторе [и, v] из B.3) определяем х(и, v)?
?Х(и, v), далее подбираем вектор [и, v] так, чтобы
удовлетворить следующую систему нелинейных уравнений:
Ф* (g (х (и, v)), и) = uf % (h (x (и, v))t v) = v. B.7)
Здесь <р,(?, u) = [yg(g\ и1), ..., cpg(ge, W)], г|)л(А, v) =
Теорема 4.2.1. Пусть функции ср и -ф построены
в соответствии с условиями кг и А2, существуют век-
векторы «*, v0, x*=x(u*, у*N^К V*), удовлетворяющие
B.7). Тогда в задаче A.6.1):
1) если выполнено А4, то Х*Ф0, x*6X*;
2) если Н(х, «*, у») дифференцируема в точке д:*, то
[д:*, и*9 v*] есть точка Куна—Таккера.
Доказательство. Из условия Аг следует, что
g(Xt) = 0, из А2 получаем, что А(#*)^;0, 0^.v* и

222 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
{) = 0, / ? [1 :с]. Поэтому имеют место условия A.6.17)
и при выполнении условия А4 из теоремы 1.6.4 следует,
Х У [ ]
р у 4 р у,
что х*?Х*. Учитывая, что в точке [#*, и*> v«] имеет
место B.4), заключаем, что [**, «*, р#]—точка Куна—-
Таккера. §j§
Теорема 4.2.1 открывает широкие возможности исполь-
использования численных методов решения систем уравнений
для решения исходной задачи нелинейного программи-
программирования A.6.1). Воспользуемся, например, методом прос-
простой итерации, получим следующий метод:
B-8)
где xk?X(Ub> х>ь). Если этот_ процесс сошелся к некото-
некоторой точке [и, и] и х?Х(иу v), то при выполнении усло-
условий Alf А2 точка х будет допустимой, [я, и, v] будет
точкой Куна—Таккера, а при выполнении А4 х?Х*.
Если вместо А2 потребовать выполнимость условия А3,
то при этом не гарантируется, что v^O. Чтобы исклю-
исключить эту возможность, вводится условие Аб, благодаря
которому из vo^0 следует, что в процессе итераций B.8),
B.9) все vk^0.
Введем сокращенные обозначения:
у = [и, v]€E", Ф(х, y) = [<Pg{g{x), и), fy(h(x)9 v)]9
Н (х9 u,v) = H (х, у), Rx (x) = [gx (x), hx (x)l
Hxy(x, y) = [gx(x)<pgu(g(x), u), hx
0 1
B(x, у) = Фу(х, y)—d>l(x, y)H?(x, y)Hxy(x, y),
B.10)
Hx(x, у) = Ы
+ i вьючим, «o+ i hxx
Hxx(x, y) = lxx(x, y) + Rx(x)<t>T(x, У). B.11)

§ 2] МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА 223
Матрицы ф^, tyhh диагональные, их *'-й диагональный
элемент есть соответственно
d2g> (g*, и1) д2^ (ft*, v1')
Матрицы Rx, Нхуу Фу, Ф?, Б, LXXJ Hxx имеют соответ-
соответственно размеры /гх/л, ях/n, тхт, тхп, тхт, пхп,
пхп. Между ними существует связь:
Нху(х, у) = ?>х(х)Фу(х, у). B.12)
Систему B.7) и метод B.8), B.9) можно записать в сжа-
сжатой форме
У = <*>{*{У), У)> BЛЗ)
Применяя для решения системы B.13) метод Ньютона,
приходим к процессу
B.15)
Можно не вводить вспомогательную задачу B.3), вместо
этого метод Ньютона применять непосредственно к реше-
решению исходной системы нелинейных уравнений B.4)—B.6).
В результате получается метод
= — Нх{хкУ yk),
Используя формулу Фробениуса, отсюда находим
Ун-{В-1т)-*[Ф-ук-<%Н?НхЪ B.16)
хк-Нх1Нх-Н^хНху (yk+1-yk). B.17)
Здесь все функции и матрицы вычислены при х = хк,
Если зависимость х(у) определять из B.3), то с уче-
учетом B.4) из B.16) следует B.15). Если в B.15) положить
ф = Ф1, опустить учет ограничений типа неравенств, то
B.15) переходит в метод, предложенный и исследованный

224 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
рядом авторов. Сошлемся, например, на работу Д. Берт-
секаса [3], где исследуется случай, когда вспомогательная
задача B.3) решается приближенно, при этом на каждой
k-n итерации \\Hx(xk, ук)\\Ф0 и в качестве расчетной
схемы используется B.16). Д. Бертсекасом показано, что
при специальной регулировке точности решения задачи
B.3) метод B.15) может обеспечить квадратичную скорость
сходимости. Не будем останавливаться на этих исследо-
исследованиях, так как они не представляют никакого практи-
практического интереса. Дело в том, что если, следуя Д. Берт-
секасу, использовать B.16), то разумно xk+1 определять
не из B.3), а из B.17), так как при этом, во-первых,
автоматически выполняются основные условия сходимости
метода Ньютона, во-вторых, значительно проще вычисли-
вычислительный процесс, ибо! после реализации одного шага по
формуле B.16) совсемТпросто из B.17) определяется хк+1.
Поэтому в дальнейшем будем рассматривать только метод
B.16)—BЛ7). По этим же соображениям нецелесообразно
пользоваться методом A.19), вместо [него следует обра-
обращаться к A.11).
§ 3. Обоснование сходимости
метода простой итерации
1. Основные теоремы о сходимости. Обозначим
АЛ*, и, *>) = min min [<р^ (?''(*)> «О»
A2(*, t>)= min
Введем дополнительное ограничение на функции ср и ф.
А6. В точке Куна—Таккера [х*, и*, v*] удовлетворена
система B.5), B.6), величина Д2(х*, а*)^0.
В дальнейшем понадобится характеристическое урав-
уравнение матрицы В:
\В{хт, и*, о.)-*/. | = 0. C.1)
Здесь и ниже при обосновании сходимости считается, что
функции ф и i|) дважды дифференцируемы по своим
аргументам.

§3] СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ 225
Теорема 4.3.1. Пусть в точке Куна—Таккера
z« = [x«, и*, v*] выполнены Ав и достаточные условия ми-
минимума из теоремы 1.7.4, кроме того, функция Н (jc, и, v)
дважды непрерывно дифференцируема в окрестности точки
zm и модули всех корней уравнения C.1) строго меньше
единицы. Тогда если величина А±(х^ м», vm) достаточно
велика, то задача B.3) локально разрешима, метод B.14)
локально сходится к точке г*.
Доказательство. В точке Куна —Таккера удов-
удовлетворена система B,5), B.6), поэтому формулу B.11)
можно записать в виде
Для соответствующей квадратичной формы имеют место
оценки
xTffxx(xm, и*,
+A, (x., u*y v.)х* \gx (x,)gTx (x*)+ S hx (x,) [hx (x.)]T] x
Согласно лемме Финслера 1.7.4 существует такое т,
что при Ai (#«, м«, V*) > т матрица Нхх (лс*, и*, v*) поло-
положительно определена. Но тогда существуют такие окрест-
окрестности G (лс*) и G (у*) точек х* и ут = [м«, t;«] соответственно,
что для x?G(xJ9 y?G(y,) матрица Нхх(хщ, и*у vm) поло-
положительно определена, для любых y?G(ym) существует
изолированное локальное решение х = х (у) ? G (х*) задачи
B.3) и выполнено необходимое условие минимума
*) = О, ^ = ^Ы. C.2)
С другой стороны, согласно теореме о неявных функциях,
можно указать такую окрестность Gt(xm) точки х» что
на Gx (x*) существует непрерывно дифференцируемая функ-
функция х(у), удовлетворяющая условиям C.2). Взяв Gl(x4)
8 Ю# Г. Евтушенко

226 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
настолько малой, что G1(xt)dG (хф), из C.2) получим
%=-Н?х{х{у),у)Нху{х{у), у).
Поэтому сложная функция Ф(х(у), у) дифференцируема
в точке у = у* к
"<<Ц>,Д(ж.,К), C.3)
,Д(ж.,К),
где матрица В определяется из B.10). Согласно теореме
2.3.4 для локальной сходимости метода B.14) достаточно,
чтобы спектральный радиус матрицы В(х*> у*) был меньше
единицы, что заведомо имеет место, если модули корней
уравнения C.1) строго меньше единицы. В
Теоремы 4.2.1 и 4.3.1 характеризуют разные свойства
метода B.14). Теорема 4.3.1 аналогична теореме 4.1.2,
обе они дают достаточные условия локальной сходимости
к точке Куна—Таккера. Теорема 4.2.1 показывает отли-
отличие B.14) от методов, описанных в § 1, здесь благодаря
условиям Аг—Аъ в случае сходимости гарантируется, что
предельные точки будут точками Куна—Таккера. Этими
свойствами не обладали методы § 1.
Анализ корней C.1) затруднителен, поэтому, введя
некоторые дополнительные предположения, преобразуем
уравнение C.1) к другому виду. Представим вектор h в
виде
h (х) - [h* (x), hb (*)], й« (х) = [/i1 (*), ..., А' (*)],
Аналогично запишем в блочном виде матрицы
Яах (х) = [gx (х), hx (x)l Rx (x) = [R* (*), hx (x
±_1
h(x),v)\'
Здесь матрицы Rxt hx, Ф?, [Ф?]г, 'Щн имеют соответст-
соответственно размеры nx{e+s), nx{c—s), (e+sJ, (e + s)xn9 sa.

§3] СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИЙ 22?
Поэтому имеют место представления
О
Пусть [#*, и*, у*]—точка Куна —Таккера; не нарушая
общности, можно считать, что первые s компонент век-
вектора к(Хщ) равны нулю. Составим уравнение
**, у.)—
* у.)]т№{х.> y*)Rax(x*>y*)-Me+s\=0- C.4)
Теорема 4.3.2. Пусть .в точке Куна—Таккера z* =
=[**> «•> ^*] выполнено А6 и условия леммы 4.1.1, функ-
функция Н(х, и, v) дважды непрерывно дифференцируема в ок-
окрестности точки г,, модули всех корней уравнения C.4)
строго меньше единицы, для всех / (?<*(#¦)
4k{h(x.)t vi) = 0, -l<^L(h(x*)t vL)<L C,5)
Тогда, если величина Ах (а:*, и*, v*) достаточно велика,
то задача B.3) локально разрешима, метод B.14) локально
сходится к точке z*.
Доказательство. Предположим, что матрицы
Нхх(х, у) и Lxx(x, у) невырождены, умножим B.11) слева
на ФТх(х, y)L?(x, у) и справа на НхЦх, у)Нху(х, у), по-
получим
= Г(*. у)Фтх(х, у)Н?(х9 у)Нху(х, у).
Здесь обозначено
Г(х, y) = /e+Oj(*. y)L?(x9 y)Rx(x).
Используя B.12), B.10), преобразуем это соотношение
к виду
(Г(*. у)-1т)Фу(х, у) = Г(х9 у)(Фу(х, у)-В(х, у)).
Отсюда следует формула
Г(*. у)В(х, у) = Фу(х,у). C.6)
я*

228 Модифицированные функции лагранжа [гл. iv
Разрешимость задачи B.3) доказывается так же, как и
в предыдущей теореме. Согласно лемме 4.1.1 матрица
Lxx(x*> y*) = Lxx(x*, у*) невырождена, поэтому матрица
Г (а:*, у*) определена и согласно C.6)
#(**, У*) = Т'1(хт, у*)Фу(х*, по-
последовательно, уравнение C.1) эквивалентно следующему:
которое с учетом C.5) можно переписать в виде
о
Таким образом, с—s корней находятся явно:
Остальные т — (с—s) корней находятся из C.4). Таким
образом, модули всех корней к строго меньше единицы.
Отсюда следует сходимость метода. ?
2. Упрощенные версии метода. Вспомогательная за-
задача B.3) обычно решается приближенно. Так же, как это
делалось во второй упрощенной версии метода штрафных
функций, процесс минимизации Н(х, yk) no x будем пре-
прекращать, как только найдена точка хк, удовлетворяющая
условию
. C.7)
Здесь последовательность {ek}-+0 при fe-*oo. Чтобы
обосновать сходимость такой версии метода, предположим,
что Ф(а:, у) удовлетворяет условию Липшица по х:
\Ф(х19у)-Ф(хЖ9у)\<1\х1-хш1 C.8)
Введем в рассмотрение нижнюю границу матрицы Нхх (х, у):
d (x9 у) - min xTHxx (х, у) х. C.9)
iun=i
Если выполнены все условия теорем 4.3.1 и 4.3.2, то
d(x, у)>0 и существуют достаточно малые окрестности
G (хф) и G (#,), такие, что
d,=- inf inf d(x, y)>0. C.10)

§з] сходимость метода простой итерации 229
Определим погрешность на &-й итерации при использова-
использовании метода B.14) с упрощенным правилом C.7) решения
вспомогательной задачи. Имеем
к9 ук)-Ф(х(ук), у*I. C.11)
С помощью формулы Ньютона—Лейбница (см. Приложе-
Приложение I) получим
1
Здесь у = у* + ъ(ук—у*)9 полная производная функции Ф
по у вычисляется аналогично C.3):
= В(х(у), у).
Воспользуемся неравенством Коши—Буняковского, норму
матрицы считаем согласованной с евклидовой нормой, тогда
|Ф(*(%). %)-Ф(*. y.)\<r\yk-y.\9
где
r= sup
Отсюда и из C.8), C.11) получим
x>\. C.12)
Оценим норму вектора q = x(yk)—хк. Используя формулу
Тейлора, получим
, ук), q>+\qTHxx(x, yk)q,
\(x, yk)q,
здесь x = xft + ei<7, x = x(yk)-B2q, 0<вх<1, 0 < 9, < 1
и учтено условие B.3). Сложим найденные формулы, тогда
<#*(**. Ун), Ч>=-\чт[НхЛх

230 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Используя неравенство Коши—Буняковского, C.9), (ЗЛО),
получим
d.\qMHx{xk9 yj\. C.13)
Учитывая условие C.7), приходим к неравенству
Подставляя это неравенство в C.12), получим следующую
оценку:
\Ун+1-У.1<г1уь-у.1 + ±ек. C.14)
Отсюда следует, что для обеспечения быстрой сходимости
необходимо специальным образом уменьшать коэффи-
коэффициент ек, устремляя его к нулю.
Другой способ регулировки точности решения задачи
безусловной минимизации B.3) состоит в нахождении точки
х = хк, удовлетворяющей условию
\Ня(х* Ук)\\<ек\\Ф(хк, ук)-ук\\. C.15)
Имеют место следующие оценки:
Ук)-Ф(х*> У*)
Используя C.13) и C.15), получим
С
Отсюда следует
Подставим это неравенство в C.15), тогда
г—d%—lek
Из C.13) получим
Из C.12) находим окончательную формулу

§3] СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ 231
Для локальной сходимости достаточно, чтобы О ^ Ь < 1,
что будет иметь место, если величина ek достаточно мала:
При выполнении этого условия метод B.14) с регулиров-
регулировкой точности решения вспомогательной задачи C.15) схо-
сходится со скоростью геометрической прогрессии. В отличие
от правила C.7) здесь нет необходимости устремлять ек
к нулю. Если в C.7), C.15) ek—>О, то, согласно C.14),
C.16), Q—множитель процесса B.14) в точке уш равен г,
что соответствует формуле B.3.9).
Найденные оценки показывают, что метод B.14) устой-
устойчив к погрешностям решения вспомогательной задачи B.3).
Это свойство, а также сравнительно высокая скорость
сходимости делают метод B.14) весьма эффективным ин-
инструментом для решения задач нелинейного программиро-
программирования. Обычно метод используется после того, как най-
найдено неплохое приближение для множителей Лагранжа.
При обосновании метода постулируется существование в задаче
A.6.1) точки Куна—Таккера. По-видимому можно доказать сходи-
сходимость метода при более слабых предположениях, не требуя, в част-
частности, существования ограниченных множителей Лагранжа. В этом
случае при использовании B.14) |]#л||—> оо при k—> оо, однако
сходимость %k к Х% будет иметь место. В качестве иллюстрации рас-
рассмотрим задачу C.1.5). Если использовать функцию ф1, то метод B.14)
приводит к следующему процессу:
uk+1==uk+xi
где хь находится из условия минимума
При малых значениях |я#|<^1 имеем
При щ —> оо имеем хк —> 0= Хт.
3. Операция масштабирования. Чтобы иметь возмож-
возможность, не изменяя вида выбранных функций ф и а|), обес-
обеспечивать условия теорем 4.3.1 и 4.3.2 о том, что вели-
величина Дх достаточно велика, и сохранить при этом эле-

232 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
менты матрицы i|^v, удобно вместо ср и а|) использовать
«промасштабированные» функции
)» tt) = z >
Производные новых функций просто выражаются через
производные исходных функций:
(g, U) = Тф~ Q, U), <fga (Я, U) = ф?ц (§, Ы).
Здесь символ g означает, что дифференцирование исход-
исходной функции (p(g, и) производится по g, а после этой
операции в полученной формуле в качестве g берется зна-
значение xg. Аналогично вычисляются производные t|). При-
Приведем основные расчетные формулы с учетом масштабиро-
масштабирования
х.)Ф1(х„ у,),
В(х„ у,)=Фу(х„ у,)—тФ!(*„ у,)Нх1(х„ yJH^ix,, у,),
Фу(^, У.) =
d.
Уравнение C.4) заменяется следующим:
(x*, y*)RUx.,y.)-Me+s\ = 0. C.17)
Вычислительная схема B.14) останется прежней с един-
единственным изменением: вместо g и А следует соответственно
брать xg и тА.
Предположим, что существует число d такое, что для
всех *€[1:«], /€*(*•)
d=4>ea@, «*)=¦*.(О, ot).

§3]
СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ
233
Сравнивая уравнения C.4) и C.17), приходим к выводу,
что между их корнями существует простая связь
^ <ЗЛ8)
причем среди корней Я нет такого, что k — d. Поэтому,
взяв т достаточно большим, можно обеспечить выполни-
выполнимость условия |1|<1. Это заведомо имеет место, если
т > max A + d)l\ ^— 1 , где X,—совокупность корней C.4).
Из формулы C.18) видно, что при т—*оо величины
\%\ стремятся к нулю, т. е. сходимость имеет сверхлиней-
сверхлинейный характер. Однако следует иметь в виду, что при
1000
больших значениях т функция Н носит ярко выраженный
овражный характер, решение задачи B.3) становится более
трудоемким и практически улучшение работы метода не
имеет места. Поэтому брать в качестве т большие вели-
величины не целесообразно. Вместе с тем при малых зна-
значениях т могут нарушаться условия теорем 4.3.1 и
4.3.2.

234 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Приведем результаты численных расчетов задачи нели-
нелинейного программировавия G.5.1). На рис. 2 представлена
зависимость N—количества обращений к вычислению функ-
функций, определяющих задачу, от параметра т, который со-
сохраняет постоянное значение в каждом отдельном расчете.
Величина N пропорциональна времени счета. Использо-
Использовался метод B.14) с функциями ф1 и "ф5, расчеты прово-
проводились для 12 различных значений т, в промежуточных
точках выполнялась интерполяция. Точность решения
вспомогательной задачи B.3) на каждой fc-й итерации
задавалась условием \\Hx(xkJ uky 0*)|Ке/9 где 8х = 0,1;
82 = 0,01. Для каждого значения т бралась одна и та же
начальная точка х09 использовались одни и те же пара-
параметры методов, задача B.3) решалась методом сопряжен-
сопряженных градиентов. Полученные зависимости носят немоно-
немонотонный характер. Наиболее быстро задача решалась при
умеренных значениях т. Вместе с тем в тех задачах, в ко-
которых не удается добиться высокой точности выполнения
условия х?Х, следует увеличивать коэффициент т; его
роль становится аналогичной коэффициенту штрафа.
4. Некоторые частные случаи. Для введенных выше
функций яр имеют место следующие формулы:
Пусть в точке [x*t v*\ выполнено условие строгой допол-
дополняющей нежесткости, тогда для приведенных функций,
/если /€а(х„), то Унн(Н/(х*), v{)>0 и для /#а(х») все
О < ФА, (*>(*•)•• t*)<lf %h(W(x,)9 oi) = 0, как и тре-
требуется в условиях теоремы 4.3.2.
Для функций ф1, ф% ф3 имеем
т, v.) = ф^а (g* {хф), ui) = 1.

$3] СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ 235
Для остальных функций получим
Отсюда следует, что для всех приведенных функций вы-
выполнены требования теорем 4.3.1 и 4.3.2 о том, что
'Ai(*»t ^*> ^*)>0> А2(**> ^*)>0 и с помощью операции
масштабирования величина Ах может быть сделана сколь
угодно большой.
Если в качестве ф, яр взять соответственно ф1 и -ф5, то
Н(х, и, v) = f
с
г
/el
если Л/(*)>0,
/tt T \arctgTA/(x)f если
Метод B.14) с учетом операции масштабирования примет
вид
C.19)
Если использовать ф1 и г|з3, взяв г = \, у(й) = а1, то
получим
Я (ж, и, о) =
i=i L J /=i
^(л;))а+(т^(л)K, если V(x)>0A
J
T \(l —тА/Сх))-1, если h/(x)<0 J
*+1 = «t+Tg' (*Д »t+1 = * [
))я, если W(xk)>0, j. C.20)
если

236 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Наиболее простые расчетные формулы получаются при
использовании функций ср1 и -ф1:
Н(х9 и, v) = f
Uk+%tf(xJt vi+1 = (vi+W(xk))+. C.21)
Этот случай особенно подробно изучен в литературе по
модифицированным функциям Лагранжа. Здесь, в отличие
от предыдущих двух случаев, функция Я не обладает
вторыми производными, что сужает класс методов безуслов-
безусловной минимизации, применимых для решения вспомогатель-
вспомогательной задачи B.3); приходится отказываться, в частности,
от использования метода Ньютона. Методы C.19) — C.21)
широко применялись для решения задач нелинейного про-
программирования, они вошли в состав библиотеки программ
ДИСО, описание которой дано в гл. VII.
§ 4. Решение задач выпуклого программирования
1. Реализация* метода простой итерации в случае задач
выпуклого программирования. В большинстве публикаций
по модифицированным функциям Лагранжа вспомогатель-
вспомогательные функции Н (х, ы, v) строятся таким образом, чтобы
точка Куна—Таккера для них была седловой. Такое
условие важно, если для решения исходной задачи пред-
предполагается использовать методы отыскания седловых точек.
Ниже для решения A.6.1) будет применен метод простой
итерации B.4), поэтому условие существования седловой
точки у модифицированной функции Лагранжа вводить
не обязательно. В частности, если воспользоваться опре-
определенной в § 2 функцией г|)*, то модифицированная функ-
функция Лагранжа будет иметь вид
Н(х, v)= ^
Легко видеть, что для нее при любых векторах х
supH(x, v)= sup#(*, и) = +оо

§4] РЕШЕНИЕ ЗАДАЧ ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ 237
и, следовательно, левое неравенство в условии седловой
точки A.6.9) никогда не имеет места, тем не менее эта
функция успешно используется для численных расчетов.
Пусть A.6.1)—задача выпуклого программирования.
Определяемое из A.6.3) множество Хо не пусто, функция
f (x) равномерно выпукла по х, т. е. существует такое
число со, что для любых х, у ? Епу /« € df (x) имеет место
неравенство
х\\*. D.1)
Чтобы упростить изложение, считаем, что в задаче
A.6.1) отсутствуют ограничения типа равенства, тогда
основные расчетные формулы B.3), B.14) будут иметь вид
**€Argmin#(#, и), D.3)
В первой упрощенной версии метода в качестве xk берется
произвольный вектор, удовлетворяющий условию
IIдхН (хк9 vk)f < б 2j hf (xk) [ih {Ы (хк\ vi) -rf] = Tl D.4)
Во второй версии вектор хк удовлетворяет неравенству
= Ib D.5)
здесь б—некоторое неотрицательное число. Ниже пока-
покажем, что
0<Г?<Г|. D.6)
Из этих неравенств следует, что всякая точка, удовлет-
удовлетворяющая D.5), будет одновременно удовлетворять усло-
условию D.4). Благодаря этому задача нахождения точки хк
в случае D.4) решается проще.
Во всех версиях метода, если получено, что vk+1 = vk9
процесс расчетов прекращается, соответствующий вектор хк
будет решением задачи A.6.1).

238 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
2. Обоснование сходимости. Рассмотрим задачу нахож
дения
Vx = sup inf L (x, v).
cEn
В случае, если в задаче A.6.1) множество X* не пусто и
выполнено условие Слейтера, то не пусто и множество
W=lv: V,= inf L(x, v), i>>0\.
\ xeEn I
Теорема 4.4.1. Пусть в задаче выпуклого програм-
программирования A.6.1) существует точка х*?Х*, выполнены
условия А3, А5, имеет место D.1), при любом v^O функ-
функция i|)(A, v) дифференцируема и выпукла по А, величина
О <; б < 4@, в качестве v0 взят любой вектор, имеющий
неотрицательные компоненты. Тогда последовательность
xk, получаемая из метода простой итерации D.2) при
любом правиле D.3)—D.5) нахождения xk, либо за конеч-
конечное число шагов попадает в точку х*, либо имеет ее своим
пределом при k—>oo. Если выполнено условие Слейтера,
то последовательность {vk\ ограничена, все ее предельные
точки принадлежат W, по крайней мере одна такая точка
существует.
Доказательство. Из условия v0^0, согласно А5, следует,
что все Vb^sO. Это свойство будем широко использовать ниже, не
оговаривая его особо. Функция t|) (Л, v) выпукла по h, поэтому, ис-
используя A.2.14), получим, что для любых hf и Ы имеют место не-
неравенства
Положим в этих неравенствах Л/ = 0, учтем, что, согласно А3,
^@, vJ)=vJ, получим
Фл (Л/, vJ) Л/^ip (Л/, w/)—-ф @, vJ) > v/hf. D.7)
Отсюда следует, что для всех
Подставляя оценку для vJ-hf из D.7), получим
Суммируя зги неравенства ло /g[l :c], приходим к неравенствам D.6).
Из D.7) и условия А5 следует, что
i>/)<i// при У < 0,
(АЛ Ы) при У > 0.

§4] РЕШЕНИЕ ЗАДАЧ ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ 239
Согласно А3, если tf/^sO, то равенство
имеет место тогда и только тогда, когда
Если выполнены последние два условия, то я|?^ (ЛА vf)=vf.
Согласно А5, г|) (ЛЛ i>i)— неубывающая функция переменной Л/.
Тогда функция ф (h (x), vk) выпукла по х. Это следует из, очевидных
неравенств
Поэтому #(#, 0*) также выпукла по jc, и в силу D.1) равномерно
строго выпукла. Для любых х, xt Н%?дхН (xt vk) выполнено нера-
неравенство
Н(х9 vk)^H(x, vk) + <H<, x-x>+(o\\x-x\\K
Отсюда заключаем, что на каждой'^-й итерации D.2) функция H(xtvk)
достигает своей нижней грани по х в единственной точке. Поэтому
правило D.3) однозначно определяет точку х& Из D.6) следует, что
существуют также х^ удовлетворяющие условиям D.4) и D.5).
Очевидны следующие формулы:
L(xkt vk+1)=L(xfct vM) + Hxk9 vk),
vk) = 2 hI (
dxH(xkt vk) = dxL(xk,
Из первого равенства и из D.7) следует, что
L (**. vk+1) ^ L (xk, vk) ^ R (vk) = mi^L (x, vk)t
причем L (xkt vk+i) > L (xkf vk) тогда и только тогда, когда имеет
место строгое неравенство хотя бы в одном из неравенств D.7).
Рассмотрим метод D.2) в случае определения хк по правилу D.3).
Функции Н (х, vk) и L (xf vk+i) выпуклы по х, поэтому можно за-
записать, что
<дхН(хк, vk)tx—xk>^H(x, vk)—H(xkf vk)f
<dxL(xkt vk+1)f x—x^^Lix, vk+1)—L(xkf vk+1).
Из правила изменения вектора v D.2) было получено равенство D.8),
согласно которому множество субградиентов функции Н в точке [хк, vk]
и множество субградиентов функции L в точке [xkt vk+1] совпадают.
Нулевой вектор принадлежит множеству дхН (хк, ?>*), так как, со-
согласно условию D.3), в точке хк достигается минимум функции
H(xtvk). Поэтому среди векторов, принадлежащих множеству
dxL (xk, vk+i)f есть нулевой. Отсюда следует важное утверждение
Arg min H(x, vk)=kxg min L(x, vk+1). /4 т\

240 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ТЛ. IV
Для любого Vk+i имеем
1=1
Учитывая D.9), D.10) и это неравенство, получим
^). D.11)
Таким образом, последовательность {R (vk)} монотонно возрастает.
Рассмотрим вопрос: можно ли сказать, что эта последовательность
строго- монотонно возрастает?
Пусть на k-м шаге итеративного процесса D.2) 0*+i = 0*, тогда
»* = ¦*(*(**)• Ч) D.12)
и, согласно А3, А5, выполнены условия
А(**)<0, 0<ufe, ft/(xfc)i4 = 0. D.13)
Кроме того, из D.11) следует, что
) = min Z, (*, ufe) /4 14\
и для любых *?Х выполнено неравенство
4
Поэтому, используя ,теорему 1.6.4, получим, что х^Х%% т. е. метод
D.2) за k шагов решает задачу A.6.1). Аналогично, если R (vk+i) =
—R (vk)> то, согласно D.11), для всех /?[1:с] выполнены условия
Но, как показано выше, из этих равенств следует D.12) и утвержде-
утверждение о том, что Xk?X*. Следовательно, если D.2) порождает беско-
беско{R ()}
, k?* д, () рд
нечную последовательность, то последовательность {R (Vk)} строго мо-
монотонно возрастает и ограничена сверху величиной / (*,). Поэтому
необходимо, чтобы значения R (Vk) стремились к некоторому пределу d,
оставаясь при каждом k меньше этого предела. Все слагаемые, состав-
составляющие функцию ?(х&, t>fe), неотрицательны, поэтому они должны
стремиться к нулю. Итак получим
\т^ R (vk) = Шп^ L(xk9vk) = d<f (xm),
Иш t(xk,vk) = Qy llmW(*fc)i4=0. DЛ5)
Из D.1) следует, что L (x, v^+i) строго выпукла по х, и для
любых х?Еп и L^dxL (x^y t>ft+i) выполнено неравенство
L(Xk, »*+i) + <I». x—xk> + G>l\x—xkf*?L(x, vk+1). D.16)
Возьмем в качестве L+ нулевой вектор, в качестве х—вектор xtt
получим
Таким образом, последовательность {хк} ограничена.

§ 4] РЕШЕНИЕ ЗАДАЧ ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ 241
Покажем, что d=f(xj. Предположим, что некоторая подпосле-
подпоследовательность {xk\ сходится к точке х Ф х9. Если hJ (х) ф 0, то
lira vL = 0, причем случай hf(x)=a > 0 невозможен, так как тогда
бы мы имели \|эд(а, 0)=0, что противоречит А8. Поэтому х"?Х,
откуда автоматически следует, что х?Х%1 f(x) = d. Те компоненты
i/ky Для которых Л/(дг#)=О, могут стремиться к бесконечности. Их
ограниченность при выполнении условия Слейтера мы докажем ниже.
Рассмотрим метод D.2) в случае, когда хк находится по способу
D.4). Фиксируем в D.16) вектор L*, минимизируем по х левую и
правую части этого неравенства. Минимум в левой части достигается
при
Поэтому из D.9) следует, что
> vk+1) — 4?J
Возьмем в качестве L* тот вектор из дхН (х& у^), при котором было
удовлетворено D.4). С учетом D.9) получим
(xkt vk)+(\-^)I (xki vk) ^ L (**, vk)^R (vk).
Как и в предыдущем случае, если vk+1 = vk или R(vk+i) = R (vk),
задача A.6.1) решена. Если последовательность {хк, vk} бесконечна,
то {R (vk)} строго монотонно возрастает и имеют место условия D.15).
Положив в D.16) x=xkt получим
Учитывая D.8), D.4), находим
Принимая во внимание D.15), приходим к выводу, что lim хк = хф.
k -+¦ оо
Пусть Хо ф 0, докажем ограниченность последовательности {иь}.
Из условий
lim /*(**)<(), lim hJ(хк) х& = 0.
k-> оо &-> оо
следует, что если для некоторой подпоследовательности < vl \ выпол-
выполнено условие lim v[_ =оо, то lim hS(x-)—hS(х#)~0, т. е. j?o(x%)
k -> Ьо fc k -> оо
(см. определение A.7.3) множества а (л:)). Согласно D.10) для произ-
произвольного вектора х имеем
Ф* (**-i)</w+ 23 Фу w.

242 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Разделим обе части этого неравенства на || v^ \. Если lim II t^ II =00,
k -¦- се ¦ "
то найдется такое множество чисел ау, 2 оь/=1» что
для любых *. Но это неравенство противоречит условию Карлина
(см. определение 1.6.7), эквивалентному в рассматриваемом случае
словию Слейтера (см. лемму 1.6.2). Поэтому последовательность
||t>fc||} ограничена. В каждой предельной точке последовательности
[xk> vk) выполнены необходимые условия минимума Куна — Таккера,
которые в рассматриваемой задаче являются одновременно и доста-
достаточными. Из неравенств D.6) следует сходимость метода D.2) и в
том случае, когда xk выбирается из условия D.5). Щ
§ 5. Редукция к максиминной задаче
1. Предварительные результаты. Описанные в §§ 2—4
методы базировались на теореме 1.6.4, функция A.6.15)
строилась таким образом, чтобы вектор у?Ет в точке
Куна—Таккера совпадал с множителями Лагранжа и чис-
численные методы были основаны на решении соотношений
(Кб. 17). В этом параграфе реализуем редукцию к макси-
максиминной задаче, аналогичной A.3), но, в отличие от послед-
последней, вместо F(x, и, w) построим модифицированную функ-
функцию Лагранжа так, чтобы для всякой точки локального
максимина гарантировалось, что соответствующая ей точка
[х9 и, v] была бы точкой Куна—Таккера для исходной
задачи A.6.1). При этом роль двойственных векторов
могут играть векторы, не совпадающие с множителями
Лагранжа, но выражающиеся через них каким-либо об-
образом. Введем векторы
\ Я1), ...,
, i|> (A, \i) = [ф (А1, ц1), ..., ф (h*9 \ic)] e Ec.
Так же, как это делалось выше, символы фя,, фя, ф
Фа*» ^IV» %» 'Фцц» tyvh будут обозначать матрицы первых
и вторых производных. Очевидно, что матрицы вторых
производных диагональные. Конкретный элемент матрицы
получается, если указать ее скалярные аргументы, напри-
например 9f(fif/, V).

§5] РЕДУКЦИЯ К МАКСИМИННОЙ ЗАДАЧЕ 243
Составим модифицированную функцию Лагранжа в виде
B.1)
е
М(х, К v)=f(x) + ? Ф <#(*). Щ+^ЪФЦх), \ft. (БЛ)
В этом параграфе индекс i пробегает целые значения
от 1 до е, индекс /—целые значения от 1 до с. Всюду
считаем, что векторы А, \л имеют только вещественные
компоненты. На функции^ ср и i|) наложим следующие
требования:
AJ. Уравнение
0 = 0 E.2)
можно удовлетворить тогда и только тогда, когда gl = 0;
уравнение E.2) вместе с условием
а' = Ф,(ОД0 . . E.3)
однозначно определяет 7J при любом заданном и'^Е1.
А7. Уравнение
^. 1*0 = 0 E.4)
можно удовлетворить тогда и только тогда, когда
Ы < 0, Ы = Ун (hf, |*0 > 0, Wv* = 0, E.5)
уравнение E.4) вместе с условием
, 1*0
однозначно определяет fx' при любых заданных значениях
h/ и Ы, удовлетворяющих E.5).
А8. Для любых х* и (Li*, таких, что для hJ'(x*) и \i[9
/g[l:c], выполнено условие E.5), и любых х?Х имеет
место неравенство
/ = 1 / = 1
Условию Ai удовлетворяют, например, определенные
в § 2 функции ф1^, А/), Ф2(^« ^0» Ф8(^» ^0- Приведем,
кроме того, функции

244 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Из E.3.) следует, что для функций ср1, <р2, <р3 Х = и9 т. е.
вектор X совпадает с множителями Лагранжа. Для функ-
функций ф8 и ф9 уравнение E.3) имеет соответственно вид
Здесь новый вектор X не совпадает с и. В качестве про-
простейшей функции, удовлетворяющей А7 и А8, приведем
следующую:
Уравнение E.4) для нее имеет вид
(Л'+^)+=ц'. E.7)
Если А'>0, то при ft' + ji/^O отсюда имеем й' = 0, что
противоречит предположению h/ > 0; при У+р* < 0 имеем
[х/=0, что противоречит условию A'+|u/<0. Поэтому
E.7) нельзя удовлетворить при У > 0. Если У < 0, то
при А/+^<0 имеем м/ = 0, если А'+ц/>0, то А' = 0,
что невозможно. Таким образом, E.7) можно удовлетво-
удовлетворить только при У ^ 0, причем если У < 0, то
если У=0, то
Таким образом, в случае разрешимости E.7) выполнены
условия E.5), соотношение E.6) определяет зависимость
fi/rrrj/tJ/ для vf^O. Следовательно, здесь вектор |х также
отличен от множителей Лагранжа v.
Обозначим q=[х9 Я, р,], <7*=[**, К, (*•]» M(q)=M(x, X, р).
Точка G* называется стационарной точкой функции
M(q)y если
Лемма 4.5.1. Пусть функции f(x), g(x), h(x), ц>
и ф непрерывно дифференцируемы по всем своим аргу-
аргументам и выполнены условия А; и А7. Если z*=[#», и», iy|—
тонка Куна—Таккера в задаче A.6.1), то из системы
, |ч) = 0 E.9)
однозначно определяются Хт и р* такие, что <7*=[#*> Я«, р«]
является стационарной точкой функции M(q).

§5] РЕДУКЦИЯ К МАКСИМИННОЙ ЗАДАЧЕ 245
Доказательство. Пусть z* — [#*, и*, iy|—точка
Куна —Таккера. Тогда
Согласно AJ и А7 в этом случае системы E.8) и E.9)
однозначно определяют Я», \1Ф такие, что Мл (q*) =
=Af|i(^)==O. Продифференцируем M(q) по х в точке
q = q*> учтем E.8) и A.7.1), получим
4*(x.)+gx(x.)u. + hx(x.)v. = Lx(z.) = 0. E.10)
Таким образом, по точке Куна—Таккера zm однозначно
определяется стационарная точка q* = [х*9 Яф, щ] функ-
функции M(q). В
2. Исследование максиминной задачи. Исходную задачу
A.6.1) заменим задачей нахождения безусловного макси-
мина функции M(q):
max max minAf (x. Я, \i). E.11)
Аналогом теоремы 4.2.1 будгт
Теорема 4.5.1. Пусть функция М(х, X, \i) непре-
непрерывно дифференцируема по своим аргументам, функции ф
и я|э удовлетворяют условиям А^, А7 и А8 и вектор
q* = [x*> Я», [1Ф]—точка строгого локального максимина
в E.11). Тогда в задаче A.6.1)
1) точка хт является локальным решением;
2) определяемые из E.8) векторы и* и у» таковы, что
г* ==[*», ы„ у»] является точкой Куна —Таккера,
доказательство. Переформулировав необходимые
условия минимакса (см. теорему 1.5.7) применительно
к максиминной задаче E.11), получаем, что в точке qm
выполнены условия E.9). Согласно AJ и А7 отсюда сле-
следует, что х*?Х. Для внутренней задачи в E.11) при
любых х € G (хф) имеем
=/W+ 2 Ф#(*•). Щ+ S ¦(A/(«,)f (xt)<
* в 1 / = 1
*. К, !*•)=/W+ S ФЙ'W. М)+ S i
t = 1 / ss 1

246 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Воспользуемся условием А8, тогда получим, что f (хф) ^
^/(лс) для всех x?G(х*)Г\Х, откуда заключаем, что
х*—локальное решение A.6.1).
Вектор q4 является стационарной точкой функции
M(q)> поэтому имеют место условия E.9), E.10), откуда
следует, что zm—точка Куна—Таккера в задаче A.6.1). Щ
Условие теоремы о том, что qm является решением
максиминной задачи, можно ослабить, потребовав, чтобы
точка <7* = [**> А,*, щ] удовлетворяла соотношениям
Фя (g W, К) = 0, % (А (*.), щ) = 0,
Для отыскания решений этой системы можно использо-
использовать подход, описанный в § 2, Здесь, мы ограничимся
рассмотрением редукции к задаче E.11).
Чтобы воспользоваться, методами отыскания локального
максимина, приведенными в § 6 гл. II, надо показать,
что функция М обладает свойствами, аналогичными тем,
которые были сформулированы для функции F(x, и, v)
в леммах 4.1.1 и 4.1.2. Для этой цели введем следующие
дополнительные 'требования на выбор функций ф, г|) и
отчасти на класс решаемых задач A.6.1).
А9. При любых значениях аргументов функция cp(g, X)
дважды непрерывно дифференцируема, удовлетворяет AJ,
в стационарной точке дт функции М (q) выполнены не-
неравенства
А10. При любых значениях аргументов функция я|) (A, \i)
дважды непрерывно дифференцируема, удовлетворяет А7,
в стационарной точке qm функции М (q) для / ? а (л:,) имеют
место неравенства
для /?<?(#*) выполнены соотношения
Условия А9 и Ai0 накладывают ограничения не только
на ф и -ф, но и на двойственные переменные, которые

§5]
РЕДУКЦИЯ К МАКСИМИННОЙ ЗАДАЧЕ
247
определяются конкретной задачей A.6.1). Условие Азо
позволяет ниже не вводить условий строгой дополняющей
нежесткости.
Построим три квадратные матрицы порядков соответ-
соответственно л + m, п + т и т:
- м
хх
ГФХХ ! °ес I
I л ! I
1%е | %„ J
Здесь все элементы матриц вычислены в стационарной
точке qm функции M(q).
Подобно тому, как это было сделано в § 3, обозначим
Ai(*. К lij^
Лемма 4.5.2. Пусть в точке Куна—Таккера z« =
=[*•» ^«» v*\ для задачи A.6.1) выполнены достаточные усло-
условия теоремы 1.7.4, в точке х* выполнено условие регулярно-
регулярности ограничений g(x)=0, h(x)^.O; точке zm соответствует
стационарная точка q*~[Xt, Х„ [л,] функции M(q), имеют
место условия А9 и Al0. Если величина Аг(хт, Я#, щ) до-
достаточно велика, то:
1) матрицы Mxx(q9) и Nt(q%) положительно опреде-
леныу матрица Mqq(q*) неособая;
2) все корни X уравнения
\Нг(д.)-М
п+т I
:0
имеют строго отрицательные действительные части;
3) точка q* является точкой строгого локального
максимина в задаче E.11).

248 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Доказательство. Дифференцирование M(q) no х
с учетом обозначений, введенных в формулировках усло-
условий А9 и А10, приводит к формуле
Мхх Ы = Lxx (*,) + t № (**) [gi (x.)]T +
2
(
Согласно А10 последняя сумма есть положительно полу-
полуопределенная матрица. Из леммы Финслера 1.7.4 получим,
что первые три слагаемых определяют положительно опре-
определенную матрицу, если значение Ах (*«, Я„ [г„) достаточно
велико. Отсюда следует положительная определенность
МХХШ-
Не нарушая общности, можно считать, что h'(x*) = 0
для 1 < / <s и W(x*) < 0 для 1 +s< / <с. Введем вспо-
вспомогательные векторы:
..., ф^ (о, М),
Ti = [4>j№ (Л1 W, rt), ...,
Г2 = [ihm (Л^+1 (*.), rt+1)f ..., V (Лс (дк.), |i8)] 6 ?<-'
Введем также матрицу размера nxk:
Rax = № (*•). • • •. Й (*•). *i W, ..., Ч (X.)].
Тогда матрицу Мг(д*) можно представить в виде
л/ / n _
NгШ _
Согласно условию А10 диагональная матрица —
положительно определена, диагональная матрица — (Х)
положительно полуопределена. Из А9 и А10 следует, что
все координаты вектора V не равны нулю, поэтому ранг
матрицы R*D(V) тот же, что ранг матрицы R%—макси-
R%—максимальный, равный k. Следовательно, левый верхний блок
представления матрицы #i(<7*) состоит из суммы двух
матриц, из которых первая положительно определена,

§ 5] РЕДУКЦИЯ К МАКСИМИННОЙ ЗАДАЧЕ 249
вторая положительно полуопределена. Их сумма есть по-
положительно определенная матрица, поэтому вся матрица
Nx(q*) положительно определена.
Используя разбиение матрицы Mqq (q*) на блоки, можно
показать, что ее определитель выражается через опреде-
определители матриц Mxx(qJ) и N1(qt) по формуле
отсюда следует, что матрица Mqq (q9) невырождена.
Доказательство того, что характеристические числа
матрицы Нх (q*) имеют строго отрицательные действитель-
действительные части, почти дословно повторяет доказательство та-
такого же свойства матрицы Н (г) (см. лемму 4.1.2). Согласно
теореме 1.5.9 q* является точкой строгого локального
максимина в задаче E.11). Щ
Воспользуемся методами A.21) — A.25) нахождения
локального максимина, взяв в качестве F (лс, у) функцию
М(х, Я, ц), в качестве у—вектор [A,, \i]?Em. Теорему
о сходимости 4.1.2 переформулируем следующим образом.
Теорема 4.5.2. Пусть в точке Куна—Таккера
z* = [*»> иф9 v*] выполнены условия леммы 4.5.2. Тогда
существуют такие е > О, а > 0, что при любых фиксиро-
фиксированных 0<8<е, 0<а<а и при 8=* 1 методы A.21)—
A.25) и их дискретные варианты вида B.6.20) локально
сходятся к стационарной точке q* функции М (q).
Аналогичным образом можно использовать метод
Ньютона и дать достаточные условия его сходимости.
3. Некоторые частные случаи. Класс функций ф,
удовлетворяющих А9, чрезвычайно широк. Укажем, напри-
например, ф1, ф2, ф8, ф8, ф9. Для ф1, ф2, ф3 выполнено условие AJ,
кроме того, для них
Ф„ @, V) = ф^ @, V) = 1, Фи @, V) = 0,
т. е. имеют место условия А9. Для ф8, ф9 условия А9
также справедливы, так как здесь
V) = ф9^ @, V) = 1, <f>ig @, У) - ch V ф 0,
О - 1 + е cos %f ф 0, Ф8и @, Щ - ф1х @, V) = 0.
Несколько сложнее строятся дважды дифференцируемые
функции i|>. Приведем один пример такой функции
V(АЛ ^-

250 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Легко видеть, что -ф8 удовлетворяет условию А7, причем
V* = №)\ при А/ = 0. Если Ъ! < 0, то yj = Ы = 0.
Вычисляя вторые производные функции г|э8, для / ? а(л:*)
получим
Л @, |х{) =
При /?<*(*») имеем
Если в точке Куна—Таккера выполнено условие стро-
строгой дополняющей нежесткости, то fx{ > 0 для /€0(х«) и
требование А10, таким образом, выполнено. Для обеспече-
обеспечения условия леммы 4.5.2 о том, что значение Д^х,, К> \i*)
должно быть достаточно велико, можно использовать опе-
операцию масштабирования, описанную в п. 3 § 2.
§ 6. Редукция к минимаксной задаче
В § б гл. Г была рассмотрена минимаксная задача
A.6.8). Ее использование для численного решения A.6.1)
осложняется тем, что для недопустимых точек внутрен-
внутренняя задача имеет решением бесконечно большие значения
двойственных векторов. Поэтому целесообразно так моди-
модифицировать функцию Лагранжа, чтобы при отыскании
минимакса внутренняя задача имела ограниченные реше-
решения. Такие функции удалось построить, однако пришлось
ввести более сложные, чем это было сделано выше, моди-
модификации, зависящие не только от вектора х и двойствен-
двойственного вектора, но и от градиентов функций, определяющих
задачу A.6,1). Полученные при таком подходе численные
методы обладают рядом новых черт и удачно дополняют
методы, описанные в предыдущих параграфах этой главы.
Более подробно на этих свойствах остановимся в конце
параграфа.
1. Предварительные результаты. Введем следующую
модификацию функции Лагранжа:
Н(х, и, w)=F{x, и, а>)-т?ф (dF(x' "' w)) , F.1)

§6] РЕДУКЦИЯ К МИНИМАКСНОЙ ЗАДАЧЕ 251
где функция F определяется формулой A.1), т—некото-
т—некоторый положительный параметр, ф(*) удовлетворяет условию
Ап. Функция скалярного аргумента ф (t) дважды не-
непрерывно дифференцируема на Е1, q>(t)^Q для любых
/0, Ф'<0) = 0, ф"@)=1.
В качестве простейших примеров функции ср укажем
<Pi('Hy'z, ф2 (') = <**,
Вычислим производные функции Н:
Нх{х, и, w)^Fx(x, и, w)—tFxx{x, w, w)<p' (Fx(xf uf w)),
Ни (х, и, w) - Fa (х, иу w)-xgTx {x) ф' (Fx (х, и, w)\ F.2)
Hw (х, иу w) = Fw (х, и, w)-2xD (w) hTx (x) ц>' (Fx (x9 u, w)).
Здесь и ниже ф' (Fx) обозначает n-мерный вектор-стол-
бец с координатами ф'( —г), i?[l:n].
Из формул F.2) и условия Ап следует, что всякая
стационарная точка функции F является стационарной
точкой функции Я. Обратное, вообще говоря, неверно.
Введем обозначения:
y = [u,w]y z = [x,y]
Соотношения F.2) запишем в виде
Нх(х, у) = Fx(х9 y)-TFxx(*, у) Ф' (Ря(х, у)),
Ну (х, у) = Fy (х, у) -xFyx (х, у) Ф' (Fx (x, у)).
В дальнейшем понадобится
Лемма 4.6.1. Пусть гф = [хФ, у*]—стационарная
точка функции F (х, у)\ функции, определяющие задачу,
дважды непрерывно дифференцируемы в окрестности
точки хт и выполнено условие Ац. Тогда функция В (х) ==
= SФ(— .у-") дважды дифференцируема по х в точ-
ке х* и имеет место формула
-^B{x»y.)==Flx{x«,y*). F.4)
Здесь и ниже Fxx{x, y) = Fxx(x, y)Fxx{x, у).

252 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Доказательство. Функция В(х) непрерывно диф-
дифференцируема в окрестности точки дс«, являющейся ста-
стационарной точкой функции В(х). Обозначим Вх(х) гра-
градиент функции В(х) в точке х и оценим норму
А (х) = || Вх (х)-Вх (*)-FL (*.) (*-*•) II =
= 1 Fxx (*. У*) Ф' (Fx (х, y*))-Flx (г*) (х—х.
+ II [Fxx (х, y*)-Fxx (г.)] Fxx (z.) (х-х.) |.
Положим Р = || Fxx (г«) ||. Так как функции f (x), g(x),
h(x) дважды непрерывно дифференцируемы, для любого
8 > 0 можно выбрать такую окрестность G (*«) точки #«,
что
II Fxx (*, y.)-Fxx (х„ у.) К е Уд: 6 G (*).
Для этих же ^ будет выполнено неравенство || Fxx (х,
Далее, в силу дифференцируемости вектор-функции
<p'(Fx(x9 у)), с учетом того, что ф"@) = 1, можно взять
окрестность E(х«) настолько малой, что
||<р' (Fx(x9 y*))-<?' (F*{гт))-Рхх(«•) (*-^)II <е!*-«• II-
Тогда для всех *6G(a;*) имеем: А(Х(р + )||*||
А так как 8 произвольно, из последнего неравенства сле-
следует формула F.4). ВЦ
2. Исследование минимаксной задачи. Рассмотрим
вспомогательную минимаксную задачу
min max H(x, у). F.5)
Еп €Ет
Теорема 4.6.1. Пусть в точке Куна—Таккера
[х9, и*, vt] для задачи 1.6.1 выполнены условия теоремы
1.7.4, в точке х» выполнено условие регулярности ограни-
ограничений g(x) = 0, h(x)^0; пусть, кроме того, функции,
определяющие задачу A.6.1), дважды непрерывно диффе-
дифференцируемы в окрестности х* и выполнено условие Аи.
Тогда существует такое т > 0, что при всех 0 < т < т
точка гф — [х*, «¦, до,], где до{ = 1Л7, /€[1:с], будет
точкой строгого локального минимакса в задаче F.5).

§61 РЕДУКЦИЯ К МИНИМАКСНОЙ ЗАДАЧЕ 253
Доказательство. Точке Куна—Таккера [х,, ищу v9]
соответствует точка z* = [x*9 ti*> w%], являющаяся стацио-
стационарной точкой функции Н. Согласно теореме 1.5.7, для
того чтобы г«. была точкой строгого локального мини-
макса, достаточно, чтобы была отрицательно определена
матрица Нуу(г*) и положительно определена матрица
Ф (г., т) = Нхх (г*)-Нху (г.) Н?у (г») Нух (г.). F.6)
Фигурирующие здесь матрицы вторых производных
получим, дифференцируя F.3) с учетом условий стацио-
стационарности и утверждения леммы 4.6.1:
Нуу
Не нарушая общности, можно считать, что А'(*«) = 0
для 1 ^ / ^ s и У (хщ) < 0 для 1 +s ^ / ^ с. Обозначим
Rax (х) - [gj {х)9 ..., й W. h\ (х), ...,«(*)]t
А.(^) = [Л1(х), ..., h'(x)]9
Учитывая условие строгой дополняющей нежесткости,
запишем матрицу Hyy(z*) в блочном виде
лГ
Здесь р есть (б + 5)-мерный вектор, у которого первые е
координат равны единице, каждая последующая (е-Н)-я
координата есть 2оЛ. Все диагональные элементы диаго-
диагональных матриц D (р) и N2 строго положительны. Поэтому,
учитывая линейную независимость векторов gx(x%), Нх(хф),
приходим к выводу, что матрица Hyy(z*) отрицательно
определена и, следовательно, имеет обратную отрицательно
определенную матрицу, которую можно представить в виде
1 .,-1
ic-s)
F.7)
Подставим это выражение в формулу F.6), учтем, что
матрица Л^1 будет при этом умножаться слева и справа

254 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
на матрицы, которые в силу условия строгой дополняющей
нежесткости являются нулевыми. Получим
Ф (г.) = (/л-тГ) [Г +1W (/й-тГ)] ,
где W = R°(x*)D(p)N?D(p)[RUx.)Y, T = Fxx(z.).
Можно показать, что при достаточно малых значениях т
матрица Ф(г») положительно определена. Используя тео-
теорему 1.5.7, отсюда заключаем, что г» есть точка строгого
локального минимакса в задаче F.5). ?
Если в условиях теоремы дополнительно потребовать
положительную определенность матрицы Lxx(x*, иф, v+),
то при достаточно малых значениях т будет положительно
определена матрица Hxx(z%) и, следовательно, в точке г«
реализуется строгое локальное седло функции Я (г). Этот
случай имеет место, например, для задачи выпуклого про-
программирования со строго выпуклой функцией f(x).
3. Численные методы. Если выполнены условия тео-
теоремы 1.7.4, то для решения задачи F.5) можно восполь-
воспользоваться методами отыскания локального минимакса. Од-
Однако функция Я» зависит не только от функций, опреде-
определяющих задачу A.6.1), но и от их производных, что су-
существенно усложняет численную реализацию методов, при-
приведенных в § 6 "гл. II. Построим методы, аналогичные
A.25), но лишенные указанного недостатка.
При фиксированном х решим вспомогательную задачу
об отыскании значения вектор-функции у(х) = [и(х), w(x)\
из условия
#(xNArgmax#(x, у). F.8)
Итерации осуществляем по какой-либо из следующих схем:
xk+i = xk—%Fx{xk, yb), F.9)
xk+1 = xk-%<f>'(Fx(xk), ук\ F.10)
где yk€y{xk). Аналогом теоремы 4.2.1 в данном случае
будет
Теорема 4.6.2. Пусть функция ф удовлетворяет
условию А и и последовательность {xk, yk\, получаемая из
F.8) и из F.9) или F.10), сходится к точке [х„, ««,, w%~\.
Тогда [#«,, и*> и«], где v[ =[a/J2, / € [1 'c]f является точкой
Куна — Таккера в задаче A.6.1).

§6] РЕДУКЦИЯ К МИНИМАКСНОЙ ЗАДАЧЕ 255
Доказательство. Согласно Ап из сходимости по-
последовательности {xky yk\ следует, что в предельной точке
выполнено условие Fx(x*, и*, w*) = 0. Кроме того, в этой
точке должно выполняться необходимое условие максиму-
максимума F{Xt, и, w) по и и w, поэтому Fa(x*> и„ ^) = 0,
Fw(x*, и*, оу») = О. Отсюда следует, что #(*¦) = О и
ц)Ш(х*) = 0 для всех / € [1 sc]. Согласно теореме* 1.3.1 не-
необходимо, чтобы матрица Fyy (#«, и«, w%) была отрицатель-
отрицательно полуопределена, откуда заключаем, что х* ? X. ?
Теорема 4.6.3. Пусть ^выполнены условия тео-
теоремы 4.6.1. Тогда найдется т>0 такое, что для всех
0<т<т итерации, задаваемые формулами F.9), F.10),
локально сходятся к х* со скоростью геометрической про-
прогрессии.
Доказательство проведем только для процесса
F,9). Для F.10) оно аналогично. Необходимое условие
максимума в F.8) состоит в следующем:
Иу(х, у(х)) = 0.
При доказательстве теоремы 4.6.1 было показано, что
матрица Нуу{хщу у*) отрицательно определена. Поэтому
существует окрестность точки х«, где локально разрешима
задача F.8), функция у(х) однозначная, дифференцируе-
дифференцируемая в точке х = х* и
*?а> = _Я?(*„ у.)Н9Х(х.. У*)- F-И)
Продифференцируем сложную функцию
Т(х, %)=x—xFx{x, y(x))
по л: в точке х = х*. С учетом F.11) получим
Т (х r)-dT(x*>x)-
= 1п-тРхх (z.)+xFxy (z.) Hyl (г.) Нух (г.).
Подставив сюда формулу F.7), приходим к следующему
результату:
Тх(х„ x)=P(In-xFxx(z.)),
где P = In—W. Введем в рассмотрение

256 МОДИФИЦИРОВАННЫЕ ФУНКЦИИ ЛАГРАНЖА [ГЛ. IV
Непосредственной проверкой убеждаемся, что симметричная
матрица Р такова, что РР = Р. Поэтому
<Я.Я> F.12)
V (+0) = - [Fxx (z.)P+PFxx (г,)].
Максимум в F.12) достигается только при тех значениях ~цч
для которых Pq = cf, т. е. когда <д?К3(х*) (см. формулу
(L7.16)). Воспользуемся теоремой 1.5.3 о дифференциро-
дифференцировании функции максимума, получим
V (+0) = 2 max fV (+0O= — 2 min ljTFxx (z*)~q < 0.
Ik ll=i Ik l!=i
Отсюда и из F.12) следует существование такого т>0,
что т](т) < 1 для всех 0 < т < т и \ТХ(х«, т)|| < 1. Учи-
Учитывая теорему 2.3.4, заключаем, что имеет место сходи-
сходимость итераций, определяемых формулой F.9). Q3
4. Вычислительные аспекты методов. В методе B.14)
решается вспомогательная задача B.3) минимизации функ-
функции Н по х9 итерации осуществляются по двойственным
векторам. Поэтому методы такого типа иногда называют
двойственными.
В методах F.9), F.10), напротив, вспомогательная
задача F.8) состоит в максимизации функции Н по двой-
двойственному вектору, итерации осуществляются по исходному
(прямому) вектору х. Ряд авторов такие методы называют
прямыми. Эта терминология не является установившейся,
тем не менее здесь будет удобно ее придерживаться.
При численных расчетах основное время тратится на
решение вспомогательных задач. Поэтому, если полное
число ограничений т значительно превосходит размерность п
вектора х, целесообразно использовать двойственные ме-
методы, так как в этом случае решение B.3) намного проще
решения задачи F.8). Если п значительно больше /л, то,
напротив, следует использовать прямые методы. В тех
задачах, где вычисление функций /, g, h требует значи-
значительного времени, также целесообразно применять прямые
методы. Это связано с тем, что при решении вспомогатель-
вспомогательной задачи изменяется лишь двойственный вектор, а пря-
прямой пересчитывается только на «внешних» итерациях, что
происходит гораздо реже.

§б] РЕДУКЦИЯ К МИНИМАКСНОЙ ЗАДАЧЕ 257
Область сходимости зависит от многих факторов, в част-
частности от вида функции ф(?), от того, какой из методов
F.9) или F.10) используется. Для ряда тестовых задач
оказалось, что она больше для метода F.10). На область
и скорость сходимости влияет выбор параметра т. Экспе-
Экспериментально обнаружено, что с уменьшением т скорость
сходимости падает, так что брать т слишком близким
к нулю оказалось невыгодным.
Если в качестве ф взять функцию ф1, то методы F.9)
и F.10) совпадают, причем вспомогательная задача F.8)
при т=1 весьма близка к задаче C.5.7), если Nk = 2ln.
Таким образом, существует связь рассматриваемых мето-
методов с методом линеаризации.
Ю. Г. Евтушенко

ГЛАВА V
РЕЛАКСАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Численные методы, у которых в процессе итераций
значение минимизируемой функции монотонно убывает,
называются релаксационными.
§ 1. Применение метода приведенного градиента
для решения задач с ограничениями типа равенства
1. Идея метода. Рассмотрим тот простейший случай
задачи нелинейного программирования A.6.1), когда отсут-
отсутствуют ограничения типа неравенств. Пусть ищется
min/(*), Y = {xeE»:g(x)^0\. A.1)
Y
В этой главе "будем предполагать, что функции, опре-
определяющие задачу, дифференцируемы пол:. Обозначимх(х0У t)
решение задачи Коши для системы обыкновенных диффе-
дифференциальных уравнений
^ = -\f*{x)+8x{x)*l *o€Y. A.2)
Правило изменения вектора и?Ее найдем из условия
обеспечения следующего требования: множество Y должно
быть инвариантно относительно системы A.2), т. е. из
условия xo?Y следует, что х(х0, t)?Y для всех t^0>
или, что то же самое, g(x(x01 ?)) = 0. Отсюда получаем
-f = -s?(*)[M*)+g*(*)«]^o. A.3)
Если матрица g% (х) gx (x) невырождена, то из условия A.3)
находим
u = -№(x)gx(x)]-lgUx)fA*)-
Подставив это выражение в A.2), получим
-§• = ~ U* (*) ~ёх (*) Ы {х) 8* (*)]"' 81 (х) fx (*)], х. € Y.
A.4)

* 1] МЕТОД ПРИВЕДЕННОГО ГРАДИЕНТА 259
Продифференцируем функцию / (х) в силу системы A.4),
получим
После ряда преобразований, учтя условие A.3), это урав-
уравнение можно преобразовать к виду
^=Н1М*)+?Л*Ы2<0- A-5)
Поэтому множество Y инвариантно относительно си-
системы A.2), вдоль любого решения x(xQ, t) системы A.4)
минимизируемая функция f(x(xOi t)) монотонно убывает.
Ниже мы докажем, что решения системы A.4) сходятся
к локальным решениям задачи A.1) при t-+oo. Таким
образом, отыскание предельных точек решений задачи
Коши A.4) дает численный метод решения задачи A.1).
Для реализации метода необходимо обращать матрицу-
Г {x)=zgl (*) ёх (*)• Ее определитель обычно называют опре
делителем Грамма, составленным для набора векторов
el (*)» el (#)* • • • i gx (x). Известно (см., например, Ф. Р. Гант-
махер [1]), что, для того чтобы определитель матрицы Г (л;)
был не равен нулю, необходимо и достаточно, чтобы век-
векторы gi(x), i'?[l:e], были линейно независимы. Поэтому
правая часть системы A.4) будет определена всюду на У,
если ограничение g(*) = 0 удовлетворяет на Y условию
регулярности (см. определение 1.7.3).
Остановимся на геометрической интерпретации метода.
Систему A.4) представим в виде
¦§- = —Л1 (х)М*),
Матрицы М(х), N (х) симметрические. Непосредственной
проверкой убеждаемся, что М2 = ММ = М, N2 = NN = N.
Матрицы, обладающие этим свойством, называются идем-
потентными. Собственные числа таких матриц равны либо 1,
либо 0, поэтому идемпотентные матрицы положительно
полуопределены (см. П. Ланкастер [1], Р. Беллман [2]).
Если х б Y и ограничения g (х) = 0 удовлетворяют ус-
условию регулярности, то конусом касательных направлений
9*

260 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
«
(касательным подпространством) к множеству У в точке х
будет множество
являющееся ортогональным дополнением подпространства,
порожденного независимыми векторами gl(x), g%(x), ...
•••» tfx(x)- Произвольный вектор z?Еп представим в виде
г = а*+Ь9 A.7)
где а—проекция вектора г на касательное подпростран-
подпространство, Ь—проекция на ортогональное дополнение. Вектор Ь
можно искать в виде линейной комбинации векторов g*x (x):
Подставив это выражение в A.7), умножая A.7) слева на
8х(х) и учитывая, что gl{x)a = 0, найдем
Следовательно, матрица М (х) проектирует каждый вектор
х?Еп на касательное подпространство, матрица N (х) —
на ортогональное дополнение. Вектор г, принадлежащий
касательному подпространству, проектируется матрицей
М (х) сам на себя, так как из г ? К (х) следует, что gl (х) г = 0
и М (х) z = г\ проекция вектора z на ортогональное допол-
дополнение N (x)z = 0. Если г—произвольный вектор из ?", то
М (х) z € К (х), так как gl (x) M (x) z = 0.
Правая часть системы A.4), таким образом, является
ортогональной проекцией антиградиента—/*(#) на каса-
касательное подпространство, благодаря чему gi(x) являются
интегралами системы A.4). Ряд авторов называют вектор,
стоящий в правой части A.4), «приведенным антиградиен-
антиградиентом». Поэтому метод A.4) будем называть методом при-
приведенного градиента. В частном случае, когда отсутствуют
какие-либо ограничения, метод A.4) переходит в градиент-
градиентный метод Коши B.2.3) безусловной минимизации функ-
функции f(x).
Пусть допустимая точка хт является положением рав-
равновесия для системы A.2). Из A.3) найдем соответствующий
вектор и*, учитывая A.5), получим соотношения

§ 1] МЕТОД ПРИВЕДЕННОГО ГРАДИЕНТА 261
Поэтому, если ограничения удовлетворяют условию регу-
регулярности, то всякому положению равновесия для системы
A.4) соответствует точка Куна—Таккера [*«., и%] в задаче
A.1). Из A.5) следует, что в положении равновесия про-
проекция вектора fx на касательное подпространство равна
нулю, что является необходимым условием экстремума
в задаче A.1).
2. Обоснование сходимости. Введем множество
& = {х?Е«: /(*)</(*•), х? Y}. A.8)
Теорема 5.1.1. Пусть функции, определяющие за-
задачу A.1), дифференцируемы на открытом множестве,
содержащем Q, где выполнено условие регулярности ограни-
чений g(x) = 0; локальный минимум функции f(x) дости-
достигается на Q в единственной точке х*. Тогда решения
системы A.4) сходятся к точке х* при t—>oo.
Доказательство. Воспользуемся функцией Ляпу-
Ляпунова v (x) = f(x)—f (х*). Для любых />0 имеем х(х0, t) с й,
v(x(x0, /))^0. Согласно A.5) v(x(xOt t)) является моно-
монотонно убывающей функцией L Рассуждая далее так же,
как и при доказательстве теоремы 2.2.3, приходим к тре-
требуемому утверждению. Ц
3. Вычислительный аспект. При реализации описанного
метода производится численное интегрирование системы
A.4). Используя, например, метод Эйлера, получим сле-
следующую дискретную аппроксимацию:
xk+1 = xk-aM(xk)fx(xk), Xo?Y. A.9)
Точность интегрирования должна быть достаточно высокой,
так как в противном случае приближенно найденная тра-
траектория выйдет из допустимого множества. Поэтому при-
приходится либо в A.9) брать малые шаги а, либо использовать
более точные схемы интегрирования.
Наиболее прост случай, когда вектор-функция g(x)
линейная. При этом матрица М постоянна, из A.9) сле-
следует, что
Mfx (xk) = gTxxk =
Таким образом, g (xk) = g (x0) при любом значении а, что
снимает с выбора шага ограничение, связанное с выпол-
выполнением условия допустимости.

262 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Ряд авторов предлагают при реализации метода делагь
на каждой fe-й итерации A.9) дополнительную корректи-
корректировку, возвращая точку хк на допустимое множество путем
решения системы уравнений g (х) = 0. При этом задаваемая
формулой A.9) точка xk берется в качестве начального
приближения. Однако такие расчеты существенно услож-
усложняют метод.
§ 2. Обобщение метода приведенного градиента
?1. Предварительные результаты. Изложенный выше
метод можно различными путями перенести на общую за-
задачу нелинейного программирования. Опишем подход, пред-
предложенный в работах Ю. Г. Евтушенко [7], Ю. Г. Евту-
Евтушенко и В. Г. Жадана [1], [3]. Воспользуемся обозначе-
обозначениями A.6.3), A.6.4). Условимся в этом параграфе точки,
принадлежащие Х09 называть внутренними точками мно-
множества X, точки из Х\Х0 называть граничными. Объединим
ограничения типа равенства и неравенства единым символом
Ф = [#> А]. Вектор-функция Ф(#), таким образом, осущест-
осуществляет отображение Еп—+Ет, где \
Обозначим у(Ф)=[у(Ф1), у(Ф2), ..., т(Фл)], Уу(—Ф)=
= [}/у(—Ф1), ..., У у (—Фж)], где функция скалярного
аргумента у (г) определена и непрерывна для всех значе-
значений z^O и удовлетворяет следующим условиям:
Y@) = 0, lim ?^>0; т(г)>0, если z > 0. B.1)
2-> +0 Z
В качестве простейших функций у можно взять у (z) = г,
z\ ez—\.
Для численного решения задачи. A.6.1) предлагается
искать предельные (при t —*- оо) точки решения задачи Коши
для системы
^г = -иЛх)+®Лх)У1 *о?Хо. B.2)
Здесь вектор у?Ет определяется из решения следующей
системы т линейных уравнений:
*) = 0, B.3)
где Г (х) = ФТХ (х) Фх (х) + D (у (- Ф (*))).

§ 2] ОБОБЩЕНИЕ МЕТОДА ПРИВЕДЕННОГО ГРАДИЕНТА 263
Найдем из B.3) у и подставим в правую часть си-
системы B.2), тогда B.2) перепишется следующим образом:
% = -M(x)fx(x), B.4)
M(x) = In-N(x), N(x) = Ox(x)T-1(x)OTx(x). B.5)
Введем индексное множество:
В частном случае, когда отсутствуют ограничения типа
неравенства, система B.4) совпадает с A.4). Ниже пока-
покажем, что в общем случае система B.4) сохраняет основные
свойства системы A.4): допустимое множество X инвари-
инвариантно относительно B.4), функция f(x(x0, t)) монотонно
убывает на всех траекториях системы B.4), удовлетворя-
удовлетворяющих условию хо?Х.о. Один из способов получения си-
системы B.4) из A.4) будет описан в п. 3 для случая, когда
у (z) = г. Дадим достаточные условия, гарантирующие раз-
разрешимость системы B.3). В соответствии с определением
1.7.3 будем говорить, что ограничения Ф(х) удовлетворяют
условию регулярности в точке х, если все векторы Ф^ (х),
j?e(x), линейно независимы. Из этого определения сле-
следует, что в случае, если ограничения удовлетворяют условию
регулярности в точке ху то число координат вектор-функ-
вектор-функции Ф(х), которые одновременно обращаются в нуль, не
превышает п.
Лемма 5.2.1. Если в каждой точке х?Х\Х0 выпол-
выполнено условие регулярности ограничений Ф (л:), то матрица
Т(х) неособая, положительно полуопределенная для всех
х?Х.
Доказательство. Матрицу Г (х) представим в виде
произведения прямоугольной матрицы В(х) (с размерами
тх(п+т)) и транспонированной к ней ВТ(х), где мат-
матрица В (х) состоит из двух матриц-блоков:
В(х) = [Фтх (х) \D (УУ(-Ф(х))I Г(х) = В(х) Вт(х).
Лемма будет доказана, если удастся показать, что для
любого х?Х ранг матрицы В(х) равен /л, так как, если
ранг матрицы В(х) максимален (равен /п), то отсюда сле-
следует, что Г (х) — неособая, положительно полуопределенная
матрица. Если отсутствуют ограничения типа равенства,

264
РЕЛАКСАЦИОННЫЕ МЕТОДЫ
[ГЛ. V
то во всякой внутренней точке х?Х0 ранг матрицы В (х)
равен /л, так как в этом случае в качестве ненулевого
минора матрицы В (х) можно взять диагональную матрицу
D(Vy(—Ф(х))). Лемма также очевидна, если Ф(лс) = О.
В силу линейной независимости векторов Ф? (я) существует
не равный нулю минор порядка т матрицы Фх(х).
Пусть в точке х ? X s компонент, е < s < /я, вектор-
функции Ф(х) обращаются в нуль. Не нарушая общности,
можно считать, что эти компоненты естьФх(х), Ф2(х), ...
..., Ф* (х). Тогда значения функций Ф*+1 (х), . •., Фт (х)
строго меньше нуля. В прямоугольной матрице
с размерами sxn выделим такую квадратную матрицу
С (а:) порядка s, что ее определитель, являющийся минором
матрицы Vi(x) порядка s, не равен нулю. Такой минор
существует в силу условий регулярности. Определитель
матрицы
»
V,(x) =
С(Х)
размера т не равен нулю. Но определитель матрицы V2 (x)
является одновременно минором т-го порядка матрицы В(х).
Поэтому ранг матрицы В (х) максимальный, т. е. равен т. QJ
Из леммы следует, что если условия регулярности ог-
ограничений выполнены в каждой граничной точке множе-
множества X, то правые части системы B.4) определены всюду
на X. В дальнейшем будем говорить, что ограничения
удовлетворяют условию регулярности всюду на X, если
они выполнены в каждой граничной точке множества X.
Лемма 5.2.2. Пусть выполнены условия леммы 5.2.1.
Тогда симметричная матрица М (х) положительно полу-
полуопределена для всех х?Х.

§2] ОБОБЩЕНИЕ МЕТОДА ПРИВЕДЕННОГО ГРАДИЕНТА 265
Введем матрицы
Г ММ 1
= —— — ,
имеющие соответственно размеры mxn и (п+т)хп. До-
Доказательство леммы следует из представления М = РТР,
справедливость которого проверяется непосредственными
вычислениями. 91
Всюду в дальнейшем будем считать, что для каждого
х0 6 X система B.2) определяет единственное решение х(х0, t).
Обозначим
Лемма 5.2.3. Пусть функции, определяющие за-
задачу 1.6.1, непрерывно дифференцируемы на открытом
множестве, содержащем компактное множество X и функ-
функция у (г) удовлетворяет условиям B.1). Тогда при любом
#о€^о решения х{х0У t) системы B.4) продолжимы при
t —> оо, множества X, Q инвариантные относительно B.4).
Доказательство. Вычислим производную вектор-
функции Ф(х) в силу системы B.2):
^=- ®lMfx=- Ф1!х-ФТхФхУ.
Воспользуемся формулой B.3), получим
^ B.6)
Вычислим квадрат нормы градиента функции Лагранжа
?( ) ^() + Ф()
= fTxMfx+yWxMfx=fTxMfx-yW (у (-Ф)) у.
Отсюда следует формула
\\(У)Т B.7)
Решение B.4) существует по крайней мере для тех
значений /, для которых х(х0, t)?X. Покажем, что реше-
решение х (xQj t) не выйдет из множества X ни при каких t ^ 0.
Допустим противное: пусть для некоторого t > 0

266 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Ф*(х(х0, /)) > 0. Тогда найдется момент tt такой, что
Ф/(*(*„> tj)) = 0 и Ф'(* (*0, tt)) > 0. Это противоречит B.6),
так как у @) = 0. Поэтому х (х0У t)?X для всех t^O. Вве-
Введенная выше функция у(—Ф) играет, таким образом, роль
«барьера», не давая возможность траектории x(xOi t) пере-
пересечь гиперповерхность Ф (х) = 0. Траектория х (xOf /) может
приблизиться к граничным точкам лишь при t—> оо. Если
начальная точка х0 является граничной, то вся траектория
системы B.4) принадлежит границе. Функции gl(x)f за-
задающие ограничения типа равенств, являются интегралами
системы B.4). Поэтому в силу ограниченности множества X
решения системы B.4) продолжимы при / —+ оо, множество X
инвариантно относительно B.4). Отсюда и из B.7) следует
инвариантность множества Q. Щ
Обозначим х* точки из X, в которых правые части
системы B.2) обращаются в нуль. Такие точки назовем
стационарными. Соответствующие значения у(х*) обозна-
обозначим #*. В точках х = х* выполнены условия
#• = 0, (9R.
Всякая точка х, являющаяся локальным решением за-
задачи A.6.1), будет стационарной. Действительно, если это
не так, то, взяв х в качестве начальной точки для си-
системы B.4), мы получили бы, что решение х(х, t)?X,
f{x(x, t))<f(x) для *>0, так как ^L < о. Но это
противоречит условию локального минимума функции / (х).
Остановимся на геометрической интерпретации. Введем
касательное многообразие к множеству активных ограни-
ограничений в точке х:
Кг (х) = {х? Е»: [Ф/ (х)]тх = 0, / € а(х)\.
Определенный из B.4) вектор х принадлежит Кх{х)
в каждой точке х. Действительно, из B.6) имеем
Если в точке х j?o(x)> то Ф^(#) = 0, правая часть при-
приведенного равенства равна нулю и, следовательно, x?Ki (x).

§2] ОБОБЩЕНИЕ МЕТОДА ПРИВЕДЕННОГО ГРАДИЕНТА 267
Пусть / (? о (л*). Согласно B.1), если z —> 0, то у (г) —± 0.
Поэтому проекция скорости движения х на градиент Ф? (Х)
неактивного ограничения стремится к нулю при прибди*
жении к гиперповерхности Ф'(л;)=:0. Благодаря этому
траектории системы B.4) не пересекают область, опреде-
ляемую ограничениями типа неравенства, траектории могут
только приблизиться сколь угодно близко к границам,
касаясь их в пределе. Введенная функция у (—Ф) автома-
автоматически изменяет направление вектора х(х0, t) вблизи гра.
ницы. Различные виды «барьерных» функций приводят
к разным характерам изменения этой скорости.
Вдали от гиперповерхности fi^(jc) = 0, когда №(х)<^0%
можно не опасаться, что траектория х(х0, t) на небольшом
интервале (t, t-\-&) пересечет ее, и в формуле для опреде.
ления М(х) можно опустить функцию hJ'(x) и ее произ-
производную, вводя их в рассмотрение лишь тогда, когда —8 <;
< h*(x(xOf t))< 0, где г > 0 выбирается в зависимости от
шага интегрирования системы B.4). Такой прием позволяет
понизить порядок системы B.3).
Вместе с тем введение барьерных функций у(—Ф) при-
приводит к «прилипанию» траектории, так как, если h/(x0) =*(),
то h*(x{x091)) = 0. Выше постулировалось, что все й'(хо)<;о.
Чтобы устранить этот недостаток, можно опустить в фор-
формулах для М функции hJ\ Ых и вычислить в силу новой
системы производную /iV = <ft/, #>. Если оказалось, что
производная отрицательная, тогда продолжаем движение
вдоль траектории этой системы. Другими словами, устра-
устраняя «барьер», мы проверяем, можно ли это сделать, не
нарушив условие допустимости траектории.
2. Обоснование сходимости.
Теорема 5.2.1. Пусть выполнены условия леммы 5.2.3,
все стационарные точки из множества X изолированы.
Тогда для любых нестационарных начальных точек х0 ? Хй
решение х(х0, t) системы B.2) и найденное из B.3) реше-
решение у(х0, t) при t-+oo сходятся к точке Куна — Такке-
[ \ [ \E+
У\ [ \
оказательство. Пусть х0—произвольная точка
из Х01 х(х0, t)—решение задачи Коши B.2). В силу ком-
компактности X множество со-предельных точек со для решения
х(х0, t) не пусто. Покажем, что со принадлежит множеству
допустимых стационарных точек. Так как /(#) ограничена

268 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
снизу на X и f(x(xo> t)) — монотонно убывающая функ-
функция t, все точки из множества со лежат на одной и той
же поверхности уровня функции f (х) (см. Е. А. Барба-
шин [1]). Пусть х ? со. Проведем через х траекторию х (х, t).
Любая ее точка также принадлежит ю, поэтому f(x (x, t))=0
и, значит, f(x) = 0. Но из B.7) видно, что это возможно
только тогда, когда х—стационарная точка для системы
B.2). Отсюда, поскольку все стационарные точки из X
изолированы, получим, что <о состоит из единственной
допустимой стационарной точки х, к которой х (xOi t) при-
приближается при t—> оо.
При каждом значении x = x(xOf t) из B.3) можно опре-
определить у = у(х0, t). Функция у от t непрерывна, поэтому
из существования предела #*= lim {x0, t) следует сущест-
вование предела у*= lim y{xQj t). Обозначим ui = y{ для
?6[1:в] и vi = yl+e для j?[l:c]. Из предыдущей леммы
следует, что х* g X. Покажем, что в точке [#*, vm] выпол-
выполнено условие дополняющей нежесткости и t>*^0. В пре-
предельной точке х* выполнены условия B.8). Учитывая B.1),
получаем, что если vl Ф 0, то Фе+* (х*) = У (х*) = 0, поэтому
имеет место условие дополняющей нежесткости A.6.5).
Из B.6) следует формула
B.9)
(@ ))
о
Если предположить, что vl < 0, то fty'(x«) = 0, сущест-
существует такое /, что для всех t > /,
Тогда lim ft(f)>ft(Q и, согласно B.9), при
/ -> оо
имеем: lim hJ'(x(xQ, t)) < 0, что противоречит условию
t ->- оо
дополняющей нежесткости, согласно которому /^ (#*) = ().
Поэтому 0*^0. Предельная точка [х*, w», i>J является,
таким образом, точкой Куна—Таккера. Ц

§2] ОБОБЩЕНИЕ МЕТОДА ПРИВЕДЕННОГО ГРАДИЕНТА 269
Легко видеть, что условия теоремы можно ослабить,
потребовав, чтобы все они выполнялись на множестве Q
(а не на X).
3. Оценка скорости сходимости. Рассмотрим для про-
простоты случай, когда у (г) —г. Запись метода B.2) и фор-
формула B.3) при этом не изменятся, формула для Г (я)
и уравнение B.6) будут иметь вид
Г (х) = Фтх (х)Фх (x)-D (Ф (*)), B.10)
M>- = -D(O(x))y. B.11)
Для дальнейших исследований оказывается весьма полезна
следующая интерпретация метода. Так же, как это было
сделано в п. 4 § 7 гл. I, введем дополнительный вектор
искусственных переменных р ? Ес и рассмотрим эквивалент-
эквивалентную A.6.1) задачу минимизации A.7.17) в пространстве Еп+С
при наличии ограничений только типа равенства. По фор-
формуле A.7.18) составим функцию Лагранжа Ьг(х, р, у).
Метод приведенного градиента A.2), примененный к реше-
решению этой задачи, запишется следующим образом:
-§- = -/,?(*, р, y) = -UA*)+gx(x)u + hx(x)vl B.12)
$ = -*Ж Р, y) = —jD(p)v. B.13)
Здесь y = [ut v]?Em. Обозначим
¦}¦ (РсJ} •
Для определения вектора у имеем уравнение, аналогичное
A.3):
= 0. B.14)
0ee\-jD{p)D(p)j
Система B.12), B.13) составлена таким образом, что R (г)
является ее интегралом. Пусть "начальная точка [х0, р0]
удовлетворяет условиям
g(*0) = 0, h{xo) + ±-D{po)pa = O. B.15)

270 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Тогда вдоль траекторий системы B.12), B.13) имеем
± 0. B.16)
Учитывая, что Rx(x, р) = Фх(х), приходим к выводу, что
система B.2) совпадает с системой B.12), B.13). Уравне-
Уравнения B.13) можно опустить, определив р из B.16). В даль-
дальнейшем считаем, что условия B.15) выполнены.
Введем обозначения
L*(z9 y) = V(x, p, у), R(z) = R(x, p),
[о \^°(Р)\ L — J
Систему B.12), B.13) и условия B.14) можно записать
в виде
-§-=-«(*, У), RTz(z)Ll(z, y) = 0. B.17)
Предполагая, что функции, определяющие задачу,
дважды дифференцируемы, продифференцируем в силу сис-
системы B.17) функцию ф(г, f/) = -g- [|Z.J BГ, t/)J2, получим
Матрица L\z задается формулой A.7.22). Предполагаем,
что выполнены условия теоремы 1.7.5 и, кроме того, мат-
матрица Lxx(xy и, v) равномерно положительно определена
на конусе /С4 (х) (см. определение 1.7.7 и формулу A.7.23)).
Согласно B.17)
переходя к первоначальным обозначениям, получим
1М*(*.. <), У(t))\\2+lD(V-h(x(x* t)))v(t)I'<
(^=TE5)iFfne-^ B.18)
Отсюда следует экспоненциальная сходимость метода к
точке Куна—Таккера,

§2] ОБОБЩЕНИЕ МЕТОДА ПРИВЕДЕННОГО ГРАДИЕНТА 271
4. Специальные случаи. Пусть решается задача A.6.29),
в которой множество X определяется условием A.6.2):
U={x?En\ *>0}, ио = {х?Е»: х>0}.
Предположим, что известна точка х0 ? Uo П Хо. Тогда
вместо B.2) интегрируется система
? *H]. BЛ9)
Вектор у?Ет определяется из системы
Г (*) Н-Ф1М О (Y (*))/*<*) = О,
Т(х)=Фтх(х)О(у(х))Фх(х) + О(у(-Ф(х))).
Исключая вектор у, придем к системе вида B.4), где
M(x) = D (у (х)) [1Я-ФХ (х) Г~* (х)фт (x)D(y (x))l
Если вместо условия х^О наложено ограничение ^
тогда в приведенных формулах вместо D (у (х)) следует пи-
писать D(y(x — а)). Если ограничения имеют вид a'^jc'^ ft'
или q? ^ Ы (х) ^ d/, тогда вводятся две барьерные вектор-
функции Yi (я), yt(h(x))% у которых i-я и /-я координаты
есть, например, - у[(х) = (х1— &)(& — xl)y yi{h(x)) =
= (hl(x)—qJ)(d/—W(x)). Системы B.2) и B.3) имеют вид
[OJD (Tl (х)) <DX + D (v, (Ф (*)))] У+Ф1О (Vi W) /» = 0я1.
Ограничения рассматриваемого вида не повышают поря-
порядок линейной системы B.3), что значительно упрощает
расчеты.
Пусть решается задача линейного программирования,
в которой требуется найти
minaTx, Х = {х: Ах = Ь, *>0}, B.20)
Х
где х9 а?Еп, b? Ееу А —матрица ехп. Двойственная
задача к B.20) состоит в отыскании
maxbTuf U = {u?Ee: Ати^а}.
«е U
Положив у(г) = гу получим, что метод B.19) для ре-
решения прямой задачи приводит к системе
x=D(x)[ATu—a]9 где AD(x)ATu = AD(x)a. B.21)

272 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
В этом случае атх = —| D (Ух) {а—А ти) f ^ О, если х0 > О
и Ахп = Ь. Аналогично, для двойственной задачи
й=Ь—Ах, где [АТА— D(ATu—a)]x = ATb, B.22)
причем имеет место неравенство
Ъ*и = \\b—Ax[\2+xTD (х)(а—
если Аит^.а. Релаксационный метод B.21) решения пря-
прямой задачи эффективен при решении задач большой раз-
размерности, но с малым числом ограничений (п^>е), так
как при реализации метода обращается матрица невысо-
невысокого порядка. Аналогично метод B.22) удобен, еслие^>п.
Методы B.21) и B.22) несущественно изменяются в слу-
случае задач квадратичного программирования.
Пусть ищется решение задачи
minf(x), Хг = {х€Еп: 2*'= а, х> 0}. B.23)
Метод B.19) приводит к следующей системе:
Если вместо Хг взять множество
?Е": |]
то система B.24) не изменится, однако в качестве на-
начальных данных для задачи Коши следует брать внут-
внутреннюю точку множества Х2.
Задача B.23) часто встречается в разнообразных при-
приложениях. Укажем два примера.
Пусть функция ty(z) определена для z$Es. Требуется
найти минимум функции if (г) на выпуклой оболочке, на-
натянутой на точки г19 г2, ..., гп. Задача сводится к отыска-
отысканию
xeX,
/ n \
Обозначив f(x) = tyi 2 ^/ )t приходим к задаче B.23).

§3] ДИСКРЕТНЫЙ ВАРИАНТ МЕТОДА 273
При решении антагонистических игр двух лиц с беско-
бесконечным числом состояний отыскиваются вероятностные
меры ц и v, определенные на а-алгебре подмножеств мно-
множеств Z и Y соответственно:
maxminjjFB, у)\х{dz)v(dy).
» v z Y
Задача сводится к следующей:
max min j F (zy у) \i (dz).
\l У € Y У
Аппроксимируя меру \i атомической, приходим к задаче,
близкой к B.25):
п
max min 2 F (zo У)х'>
Более подробно этот вопрос изучен в работе Ю. Г. Евту-
Евтушенко, В. Г. Жадана [1].
Пусть ищется решение задачи
minf(x), X4 = {
Отнесем эти ограничения к ограничениям вида ()^
воспользуемся формулами B.11), B.10) и B.3). Легко
убедиться, что в данном случае система B.3) имеет ана-
аналитическое решение. Подставив найденный из B.3) вектор
у в B.11), получим
dx*_ df(x) ( ,
При х?ХА имеем ф/(х)^0. Если х1—+а(, либо х*—+Ь1\
то ср,. (а;) —> 0, благодаря чему траектории не покидают до-
допустимое множество.
§ 3. Дискретный вариант метода
приведенного градиента
Проинтегрируем систему B.1) по схеме Эйлера
хк+г = хк—акМ (xk)fx(xk). C.1)
Ниже будет показано, что если ограничения типа ра-
равенства линейно зависят от х9 то они сохраняют постоян-
постоянное значение при любых величинах ак\ в этом случае

274 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
удается получить высокую скорость сходимости метода, так
так можно брать сравнительно большие значения ak. При чис-
численной реализации метода на каждой k-й итерации шаг
интегрирования ak обычно используется один и тот же,
но дополнительно делается проверка выполнимости усло-
условия релаксационности и допустимости точки xk+1 по ог-
ограничениям типа неравенства. Если они нарушены, то шаг
дробится до тех пор, пока эти условия не станут выпол-
выполнены. Как указывалось в § 2, при приближении к гипер-
гиперповерхности W(x) = 0 в методе C.1) автоматически умень-
уменьшается скорость движения в направлении этой гиперпо-
гиперповерхности. Благодаря этому шаг приходится дробить
сравнительно редко.
Численные расчеты показывают, что в ряде случаев
для интегрирования системы B.11) полезно бывает исполь-
использовать неявные схемы интегрирования. Некоторые резуль-
результаты таких исследований можно найти в статье В. В. Ефи-
менко и А. С. Загоруйко [1]. Если среди ограничений
типа равенства есть нелинейные, то процесс C.1) значи-
значительно замедляется, так как для обеспечения малости
| ?(**)! приходится брать достаточно малые шаги интег-
интегрирования ak.
Докажем сходимость процесса C.1), ограничившись
лишь рассмотрением случая, когда вектор-функция Ф(х)
линейно зависит от х, y(z) = z, шаг ak в C.1) постоян-
постоянный. Если выполнены условия леммы 5.2.1, тона X мож-
можно определить максимальное значение нормы матрицы М (х)
соотношением
л х ТМ (х) х .
л = max max —и —на <
Обозначим
a „ < ос.
хех t ||[|
= max тпахуЦх).
/[1] хеХ
Здесь у(х) определяется из B.3), B.10). В дальнейшем бу-
будем писать yk = y(Xk)-
Теорема 5.3.1. Пусть выполнены условия теоремы
5.2.1, вектор-функция Ф (х) линейно зависит от х, функ-
функция f (x) удовлетворяет на X условию Липшица с постоян-
постоянной I. Тогда :

§3] ДИСКРЕТНЫЙ ВАРИАНТ МЕТОДА 275
1) при О < а < min[l/v, 2/(A7)] и любых нестационар-
нестационарных начальных точках хо?Хо последовательность {xk}
сходится к точке Куна—Таккера, f(xk+1)^f(xk) для
* = 0,- 1, 2, ...;
2) если, кроме того, B\zf^zTL\z(x, y{x))z^b\zf
при всех х?Х, z?En+c, то имеет место оценка
\LX (xk9 yk)f+\]D {V^
последовательность хк—>х*, где х*—локальное решение
задачи A.6.1).
т
Здесь !(*, y) = f(x)+ Ъ&Му**
Доказательство. Из линейности функции Ф(х)
следует
Подставляя сюда выражение C.1), получим
Используя соотношения, найденные при выводе формулы
B.6), придем к следующему равенству:
Таким образом, если Ф (х0) = 0, то Ф (xk) a 0 при любых а.
Если |f/i|<v, а< 1/v и Ф^(^)<0, то
Ф/ (х>+1) = Ф' (хк) A -ау\) < Ф* (хк) A -va) < 0. C.3)
Поэтому из хо?Х следует, что все хк?Х.
Воспользуемся формулой Ньютона—Лейбница (см. При-
Приложение I), получим
f(xk+1)<f(xk)-*fTx(xk) M (xk)fx(xk) +^\\ M (xk) fx(xk)\*.
C.4)
Согласно лемме 5.2.2 симметричная матрица M(xk) не-
неотрицательно определенная, поэтому существует арифме-
арифметический квадратный корень из матрицы М. Обозначим
его УШу тогда М^УмУМ. Введя вектор a = Y
преобразуем неравенство C.4) к виду

276 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Таким образом, при а < 2l(kl) последовательность f(xk)
монотонно убывает. Из ограниченности f(x) снизу на X
следует, что существует предел f{xk). Поэтому
/(**)] = 0. C.6)
Из C.5) следует неравенство
(хк) М (xk) fx (xk)
Воспользуемся формулами, полученными при выводе B.7),
тогда неравенство C.7) запишется в виде
Устремляя k к бесконечности и учитывая C.6), получим
= 0, C.8)
т. е. в каждой предельной точке последовательности {xk\ вы-
выполнены условия стационарности B.8). В силу изолиро-
изолированности стационарных точек существуют пределы
Вместе с тем из C*3) следует
Если Ф^=0, то бесконечное произведение
П A—««/I)
s=0
должно иметь нулевое значение. Для этого необходимо
(см. Г. М. Фихтенгольц [1]), чтобы
s=0
но это возможно, только если у'^0. Согласно C.8) при
Ф'"<0 должно обязательно выполняться у/==0. Итак,
предельная точка последовательности {xk, yk} является
точкой Куна—Таккера. Оценка скорости сходимости C.2)
получается аналогично B.18). Щ

§4] МЕТОД УСЛОВНОГО ГРАДИЕНТА 277
§ 4. Метод условного градиента
1. Общее описание метода. Рассмотрим задачу мини-
минимизации дифференцируемой функции на выпуклом, ком-
компактном множестве:
min/(A;), X* = Argmin/(x). D.1)
хеХ хеХ
Пусть известна точка xk € Ху тогда из свойства дифферен-
цируемости функции f(x) следует представление
А/=/(*)-/(**) = <М**). х-хк>+\х-хк\$(хк, x-xj,
где lim fi(xk> x—xk) = 0.
X-*Xk
Определим вектор хк9 доставляющий минимум линей-
линейной части приращения А/:
хк € Argmin <fx (хк), х-хк> = W (хк). D.2)
Из замкнутости и ограниченности множества X следует,
что точечно-множественное отображение W определено для
всех хк?Х, причем
W(xk)aX, Я* = <М*Ж **
Если /?л = 0, то xki xk?W (xk) и в точке х — хк выполнено
необходимое, а в случае выпуклости / и достаточное ус-
условие минимума функции на X (см. теоремы 1.4.1 и 1.4.3).
Вычислительный процесс на этом заканчивается. Рассмот-
Рассмотрим случай, когда Rk < 0. В качестве новой точки хк+1
возьмем
k(xk—xk). D.3)
Здесь 0^ал^1. В силу выпуклости множества X точка
хк+1?Х.
Если множество W (хк) состоит из единственной точки
хкУ то вектор хк—хк называется условным антиградиен-
антиградиентом функции f (х) в точке хк. Он представляет собой век-
вектор, на который можно сместиться из точки хк, оставаясь
на множестве X, и получить наибольшую проекцию на
направление антиградиента минимизируемой функции —
fx(xk). Именно в этом направлении осуществляется сме-
смещение из точки хк в описываемом методе, называемом
обычно методом условного градиента.

278 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Возможны несколько версий метода. Наиболее распрост-
распространенная состоит в определении величины шага ak из ус-
условия минимизации значения функции / (х) на отрезке
прямой линии, соединяющей точку xk с точкой xk:
min f(xk + a(xh—xk)). D.4)
0<a< 1
Очевидно, что в этом случае последовательность {f(xk)\
не возрастает, так как
Этот первый вариант метода был предложен М. Фран-
Франком и Ф. Вольфом. Некоторые авторы называют его ме-
методом линеаризации или линейной аппроксимацией, так
как основные вычислительные трудности здесь возникают
при решении вспомогательной задачи D.2) об отыскании
минимума линеаризованной функции на множестве X. Эта
задача ненамного проще исходной задачи, и только в не-
некоторых частных случаях, когда множество X имеет про-
простую структуру,» применение описываемого метода оправ-
оправдано. Например, если множество X определяется с по-
помощью линейных ограничений типа равенства и неравен-
неравенства, то отыскание xk сводится к легко разрешимой за-
задаче линейного программирования.
Метод можно несколько упростить за счет приближен-
приближенного решения задачи D.4). В книге Б. Н. Пшеничного и
Ю. М. Данилина [1], например, предложено в качестве^
брать величину 2~\ где i0—тот первый индекс (i =
= О, 1, 2, ...,) для которого выполнено неравенство
{xk-xk))-f(xk)<^^<fx(xk), xk-xk>. D.5)
Если функция / дважды дифференцируема на JV, то для
определения направления xk—xk можно использовать бо-
более точную аппроксимацию функции
f(x)—f(xk) « <fx(xfc), х—xk>+\(x—xk)Tfxx{xk) {x—xh).
В качестве xk—хк возьмем вектор, который доставляет
минимум выражения, стоящего в правой части. После
этого по формуле D.3) находится новая точка; величина
шага ак определяется из D.4) или из D.5).

§4] МЕТОД УСЛОВНОГО ГРАДИЕНТА 279
2. Обоснование сходимости.
Теорема 5.4.1. Пусть X —компактное выпуклое мно-
множество из Еп, функция f дифференцируема на X и ее гра-
градиент удовлетворяет условию Липшица с константой L
Тогда при любом х0 ? X:
1) последовательность {xk}9 определяемая из условий
D.2)—D.4), такова, что
lim<fx(Xk)> **-**> = 0; D.6)
2) если функция f, кроме того, выпукла, то множество
предельных точек последовательности {xk\ не пусто и
принадлежит множеству Л», имеет место оценка
0 </(*)/(*)<
где С—константа, не зависящая от k, x*?X*.
Доказательство. Обозначим d диаметр множе-
множества X:
d= sup jx—yl
В соответствии с правилом D.4) выбора шага а для каж-
каждого 0 <! а ^ 1 выполнено неравенство
/ (xk+ г) —/ (хк) ^f(xk+a (xk—xk)) —f (xk).
Согласно теореме 2, приведенной в Приложении I, имеет
место неравенство
<«</*(**). хк-хк> +y\xk-xtf. D.8)
Отсюда следует, что при любом 0 < а ^ 1 справедлива
оценка
Последовательность {f(xk)\ невозрастающая и ограничена
снизу (так как все xk принадлежат компактному множе-
множеству). Поэтому последовательность {f(xk)\ сходится при
k—* оо и lim Aft = 0. Переходя в предыдущем неравенстве
к пределу при k —* оо, получим
^ k-юо k "^ 2

280 РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
Эта оценка имеет место при любых 0 < а ^ 1. Устремляя
а к нулю, получим требуемое свойстов D.6).
Если функция f(x) выпукла, то для любого х?Х
f(x)-f(xk)Xfx(x*)> х-
xeX
Следовательно, lim / {xk) ^ / (x) V x ? X, откуда заклю-
fc-»-oo
чаем, что всякая предельная точка последовательности
{xk} принадлежит множеству X».
Заметим, что в процессе расчетов можно контролиро-
контролировать точность решения исходной задачи по ошибке в оп-
определении величины целевой функции. Действительно,
учитывая выпуклость /, для х ? X, х* ? X» получим
0</(**)-/(**)<</*(**)> **-*•>-
Вместе с тем
Поэтому .
^ D.9)
Эта оценка может быть использована в критерии окон-
окончания расчетов по изучаемому методу.
Для оценки скорости сходимости перепишем D.8) в виде
Максимальное значение правой части по а будет дости-
достигаться при
При к —> оо величина ак —> 0. Поэтому найдется номер N
такой, что при всех к > N величина aft^ 1, и имеет место
оценка
Используя D.9), получим

§ 5] МЕТОД ПРОЕКЦИИ ГРАДИЕНТА 281
Обозначив ak = f(xk)—f(Xi)9 Л = l/2/d2, это неравенство
перепишем в виде
а*-а*+1>Аа1 D.10)
Пусть все ал>0, тогда из D.10) следует
>,4
ak akak + l ^ ak+l'
Просуммируем это неравенство по k от 1 до s—I, полу-
получим
1 2
Отсюда следует, что аш < jT^ZTn ^ л"» П0ЭТ0МУ D-7) име-
имеет место. Щ
Аналогично можно? обосновать сходимость в случае
регулировки шага по формуле D.5) и выбора направле-
направления из квадратичной аппроксимации.
§ 5. Метод проекции градиента
1. Идея метода. Рассмотрим задачу D.1), в которой
функцию f(x) будем считать выпуклой, дифференцируемой,
множество X—выпуклым, компактным. Тогда для каждой
точки х можно из условия A.1.2) определить ее проек-
проекцию р(х) на множество X. Метод проекции градиента
состоит в построении последовательности
xk+1 = p(xk—akfx(xk)). E.1)
Существуют различные способы изменения величины
ak\ в зависимости от этого можно получить разнообраз-
разнообразные версии метода. Ниже остановимся на простейшем
случае.
Необходимая для реализации метода вспомогательная
операция проектирования на множество X, вообще говоря,
является задачей такой же сложности, что и исходная
задача D.1). Поэтому использовать метод проекции гра-
градиента, как и метод условного градиента, целесообразно
лишь в тех случаях, когда множество X имеет простую
структуру, удобную для решения вспомогательной задачи
(например, множество X является многомерным паралле-
параллелепипедом).

РЕЛАКСАЦИОННЫЕ МЕТОДЫ [ГЛ. V
2. Обоснование сходимости.
Лемма 5.5.1. Если множество ХаЕп замкнуто и
выпукло, то для всех z?En, x?X имеет место нера-
неравенство
<р(г)—г% *-p(z)>>0. E.2)
Доказательство. Рассмотрим строго выпуклую
дифференцируемую функцию ф (л:) = || а: —л: ||3, ее производ-
производная <рх(х) = — 2(z—л;). Минимум функции <p(x) на X
достигается в единственной точке р (г), поэтому, согласно
теореме 1.4.1, необходимо, чтобы для любых х?Х вы-
выполнялось неравенство E.2). Щ
Теорема 5.5.1. Пусть X—выпуклое, компактное
множество; выпуклая, дифференцируемая функция f (x)
такова, что ее градиент удовлетворяет на X условию
Липшица с константой I. Тогда существуют такие числа
8Х, е2, что при любых ak, удовлетворяющих условию
^ E.3)
метод E.1) сходится к X*, для х*$Х* имеет место
оценка D.7).
Доказательство. Воспользуемся теоремой 2 из
Приложения I, получим
Преобразуем это неравенство к виду
Y Y l|2
Xfc + l Xfi II •
Положим в E.2) z = xk—akfx(xk), х = хк, получим, что
Регулируем ак в соответствии с правилом E.3), тогда
J L>l±2h-L-e >0
аА '2 ^ 2 2 -82>и»
. E.4)

§ 5] МЕТОД ПРОЕКЦИИ ГРАДИЕНТА 283
Таким образом, метод E.1) релаксационный, причем
xk+1 = xk тогда и только тогда, когда xk?X*. Пусть
Хф, тогда, используя формулу A.2.14), получим
Преобразуем это неравенство следующим образом:
Снова воспользуемся формулой E.2), положив в ней
z=.-.xk — ajx(xk), x = x*y тогда для ak имеем
Из ограниченности множества X следует ограниченность
величин \\fx(xk)\\, ||Jt* — xk\\ для любых k. Поэтому суще-
существует такое число Я, что cik^.'k\\xk+1—л^||. Вместе с тем
из E.4) следует
Таким образом,
Мы пришли к неравенству, аналогичному D.10), откуда
следует оценка D.7). Щ

ГЛАВА VI
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Интенсивные работы по созданию численных методов
решения задач оптимального управления начались в конце
пятидесятых годов. Эти исследования были обусловлены
двумя причинами: во-первых, в это время уже были вне-
внедрены первые электронно-вычислительные машины, пре-
предоставившие широкие возможности для реализации числен-
численных методов, во-вторых, развитие сложных технических
систем, вопросы конструирования и проектирования ракет,
самолетов и многих других технических изделий привели
к необходимости решения разнообразных задач оптималь-
оптимального управления.
Работы по созданию численных методов существенным
образом опираются на основные результаты, полученные
в области общей теории оптимального управления. Боль-
Большим продвижением в этом направлении был высказанный
Л. С. Понтрягиным «принцип максимума», позволивший
дать каноническую формулировку необходимых условий
оптимальности, заложить основу для формализации и раз-
развития нового раздела в вариационном исчислении, подго-
подготовить базу для дальнейших многочисленных и плодотвор-
плодотворных исследований.
Первые публикации по численным методам решения
задач оптимального управления выполнили Д. Е. Охоцим-
ский и Т. М. Энеев [1], Л. И. Шатровский [1], А. Брай-
сон и В. Денхем [1], А. Миеле, Г. Келли. Впоследствии
было опубликовано значительное количество статей и книг
на эту тему. Можно выделить несколько различных на-
направлений в разработке численных методов, существенно
отличающихся друг от друга. Прежде всего следует упо-
упомянуть прямые методы, основанные на спуске в простран-
пространстве управлений. Ряд исследований связан с непрямыми
методами, в которых с помощью принципа максимума
Л. С. Понтрягина исходная задача редуцировалась к крае-
краевой. Цикл работ по численным методам оптимального
управления был выполнен Н. Н. Моисеевым [2] и его

ГЛ. VI] ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 285
учениками: И. А. Крыловым, Ф. Л. Черноусько, И. А. Ва-
телем и другими. В этих работах был разработан подход,
основанный на вариациях в пространстве состояний. Дру-
Другое направление, развиваемое Р. П. Федоренко [1], бази-
базируется на использовании идей метода линеаризации.
Методы условного градиента и проекции градиента были
перенесены В. Ф. Демьяновым и А. М. Рубиновым [1J
на задачи оптимального управления. На протяжении
многих лет делаются попытки реализовать численные ме-
методы, построенные на основе динамического программиро-
программирования, наиболее подробно описанного в книге Р. Бел-
лмана [1]. Однако никаких практических задач, кроме
самых элементарных, решить таким образом не удалось.
В одной из первых монографий по численным методам
оптимального управления, написанной Н. Н. Моисеевым
[2] в 1971 г., приведено подробное изложение численных
схем, идущих от теории оптимального управления, вскользь
указано на возможность иного подхода, основанного на
методах нелинейного программирования и нашедшего
впоследствии широкое развитие, в частности, в книгах
Э. Полака [1], Ю. М. Ермольева, В. П. Гуленко,
Т. И. Царенко [11, А. И. Пропоя [21, Д. Табака и
Б. Куо [1].
В данной книге излагаются методы решения задач
оптимального управления, базирующиеся на идеях нели-
нелинейного программирования. Такой подход оказался чрез-
чрезвычайно эффективным по многим причинам: с его помощью
стали очевидными многие ранее предложенные эвристиче-
эвристические алгоритмы, возникла возможность их обобщения, он
позволил использовать богатый, всесторонне развитый
арсенал методов нелинейного программирования и безу-
безусловной минимизации, создал конструктивную основу для
построения методов оптимизации систем, проинтегрирован-
проинтегрированных по схемам высокого порядка точности; методы нели-
нелинейного программирования позволили решать сложные
задачи оптимального управления со смешанными ограни-
ограничениями.
Основные расчетные формулы, реализующие подход,
идущий от нелинейного программирования, можно найти,
например, в книге Э. Полака [1], однако приведенный
в ней вывод формул для вычисления первых производных
оказался неприемлемым в тех случаях, когда интегриро-

286 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
вание управляемых систем велось по схемам более точным,
чем метод Эйлера и когда необходимо было вычислять
вторые производные минимизируемого функционала.
В связи с этим пришлось переработать методику вывода
формул. Ниже, в § 1 на примере систем, проинтегриро-
проинтегрированных по методу Эйлера, дается схема получения основ-
основных формул вычисления производных, далее выведены
расчетные формулы для систем, проинтегрированных по
методу Рунге—Кутта, найдены формулы вычисления вто-
вторых производных целевой функции. После этого стано-
становится возможным перенести достаточные условия мини-
минимума, разработанные в теории нелинейного программиро-
программирования, на дискретные процессы, аппроксимирующие
исходные задачи оптимального управления (см. § 2).
В § 3 показано, как методы нелинейного программирова-
программирования переносятся на рассматриваемые задачи. Оказывается
возможным сохранить структурную преемственность всех
методов, изменение схем интегрирования исходных систем
дифференциальных уравнений приводит лишь к тому, что
изменяются в алгоритмах отдельные блоки вычисления
целевой функции, функций, определяющих ограничения,
и их производных.
В большинстве методов, описанных в § 3, организуется
последовательный процесс безусловной минимизации неко-
некоторой вспомогательной, изменяемой от шага к шагу функ-
функции многих переменных. В том случае, когда для решения
задачи безусловной минимизации используются локальные
методы, получаются локальные решения задач оптималь-
оптимального управления. Вспомогательные задачи безусловной
минимизации имеют свою специфику, которая позволяет,
помимо общеизвестных методов, использовать свои, спе-
специальные приемы, основанные на дискретном принципе
максимума.
Доказательства справедливости дискретного принципа
максимума даны А. И. Пропоем [1], Д. Пирсоном [1],
X. Халкиным [1] и другими авторами. Из многочислен-
многочисленных исследований, посвященных этому вопросу, укажем
работы В. Г. Болтянского [1], Р. Габасова [1], В. М. Яков-
Яковлева [1]. В этой главе в силу причин, упомянутых в §8
гл. I, «дискретный принцип максимума» назван «дискрет-
«дискретным принципом минимума», и в § 4 даны необходимые и
достаточные условия его справедливости. На базе этих

§ 1] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 287
результатов в § 5 показано, как можно использовать
методы условного градиента и проекции градиента для
решения вспомогательных задач безусловной минимизации,
решая при этом задачи оптимального управления со сме-
смешанными ограничениями.
В § 6 предлагаемые численные методы обобщаются на
задачи, содержащие управляющие параметры, запаздыва-
запаздывания, разрывные правые части, задачи на быстродействие,
с простейшими недифференцируемыми функционалами.
В § 7 решен ряд тестовых задач. Приложение к некоторым
игровым задачам содержится в § 8.
Излагаемый материал является развитием и обобще-
обобщением подхода, разрабатываемого в последние годы
в ВЦ АН СССР и опубликованного в статьях Н. И. Гра-
Грачева и Ю. Г. Евтушенко [5], [6], Ю. Г. Евтушенко [12].
§ 1. Основные расчетные формулы
1. Вычисление первых производных для схемы Эйлера.
В § 8 гл. I были приведены необходимые условия мини-
минимума для задач оптимального управления. В частности,
рассматривались процессы, описываемые неавтономной
системой обыкновенных дифференциальных уравнений
|U/(*@, 11@, t), 0</<7\ x@)=xly A.1)
где x(t)?E\ {t)?Er
() {)
При построении численных методов решения задач
оптимального управления обычно от «непрерывных» систем
A.1) переходят к их дискретным аппроксимациям. Чтобы
максимально упростить изложение, рассмотрим вначале
случай, когда система A.1) интегрируется по схеме Эйлера.
Далее будет рассмотрено интегрирование по схеме Рунге—
Кутта.
Разобьем отрезок [0, Т] на q—\ участков точками
0 = tt < /2 < • • • < tq = Т. Будем называть t-м интервалом
интегрирования отрезок [th ti+1] и величину его обозна-
обозначать hi^ti+i — t;. Положим также
t-1 q-\
ti=%hs, tq=%hs = T, *, = *(/,), и, = и(*,),
s=l s=\
f(xit «„ tt).

288 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Здесь и ниже в этой главе индекс i принимает все-
всевозможные целочисленные значения из интервала [1: q—1].
Проинтегрируем систему A.1) по формуле Эйлера, получим
Эту систему удобно будет записывать в виде
xM = F{zt), FW^Xt+htfto). A.2)
При рассмотрении «непрерывной» системы A.1) управле-
управление u(t) было некоторой вектор-функцией. При выбранной
дискретной аппроксимации управление превращается в
конечномерный вектор w = [ulf ..., ия]?ЕГ(*, который бу-
будем называть полным вектором управлений. Подставив
компоненты вектора w в систему A.2), последовательно
определим компоненты вектора
Этот вектор будем называть полным фазовым вектором.
Введем в рассмотрение функцию двух полных векторов
X И W
я %}1(В(г{). A.3)
Задав вектор w, с помощью A.2) однозначным образом
определим вектор ху учитывая эту зависимость, будем
писать x=x(w), R = R(x(w), w). Целью этого параграфа
является вывод формул для вычисления первых и вторых
производных сложной функции по компонентам вектора w.
Эти формулы потребуются в дальнейшем для реализации
разнообразных численных методов приближенного решения
задач оптимального управления. При выводе формул на
полный вектор управлений w не будет накладываться
никаких ограничений, он может быть недопустимым и
неоптимальным. Учет ограничений и численные методы
оптимизации будут описаны ниже в § 3.
Введем вспомогательный л-мерный вектор
Разъясним смысл, который вкладывается в приведен-
приведенную производную. Пусть А обозначает л-мерный вектор
приращений. Введем новый полный фазовый вектор
х = [х19 х2, ..., *,._!, xiy xi+i> ..., xq]

§ !] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 289
у которого первые i — 1 компонент совпадают с соответ-
соответствующими компонентами вектора х\ х(=х( + А, все по-
последующие компоненты получаются из рекуррентного соот-
соотношения A.2), если взять в нем в качестве*; вектор xir
далее увеличивать i до значения i = q — l. Вектор /ь,
называемый производной функции R по х{ в точке [х, w\,
определяется из условия
lim -Aj[R& w)-R(x, w) — <Pi
ЦАЦ-* О Н л и
Следует подчеркнуть, что при вычислении р( полный век-
вектор управлений w остается постоянным. Если функции
R, F непрерывно дифференцируемы по компонентам век-
вектора х{> то вектор р( существует. При i = q введенный
вектор Pi вычисляется просто:
_ dR (x; w) _ dR (х, w) _ db (zq)
Р«~ dxq - дхд -~~Ш^> V-b>
так как в силу рекуррентных соотношений A.2) ни один
из векторов хи х2> ..., х^г не зависит от хг Обозначим
%
A.6)
Учитывая формулу A.2), выражающую зависимость век-
вектора xi+1 от «предыдущего» вектора х{9 можно расписать
более подробно формулу для вычисления р(:
dR dxi+1 dR
Pt^dxt'T dxt dxi+1*
В силу формул A.2) —A.6) это выражение можно пред-
представить в следующем компактном виде:
= Hx(zif pi+1). A.7)
Здесь и всюду далее нижние индексы х и и обозначают
частные производные по, соответственно, явно входящим
компонентам векторов х и и. В частности,
Ю Ю. Г. Евтушенко

290 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Производную R в точке [х, w] по 1-й составляющей
щ € Ег вектора до обозначим
" <Ш (х (ш), w)
у*=—ш(—•
Смысл, вкладываемый в эту формулу, отличен от опре-
определения вектора pit здесь имеется в виду дифференцирова-
дифференцирование R как сложной функции до. Точнее, пусть заданы
полные векторы х и до. Введем два новых вспомогатель-
вспомогательных полных вектора
X ¦= [Xif Х2, . . ., #/
Все компоненты w совпадают с соответствующими компо-
компонентами хю, за исключением i-й, равной щ + А, здесь
AgjE'7'—вектор приращений. Первые i составляющих
вектора х совпадают с первыми i составляющими векто-
вектора х. Весь вектор х получается из A.2), если в качестве
полного вектора управлений взять вектор w. Вектор у?
определим из условия
lim тгтг [Д(*, w) — R(x9 w)-<yi9 Д>] = 0.
|| Д || -> 0 И д 11
Используя правило дифференцирования сложных функций,
получим
УA ' duq дид duq
Если в полученных формулах все ht устремить к нулю,
количество шагов q — к бесконечности, то разностное
уравнение A.7) перейдет в следующее обыкновенное диф-
дифференциальное уравнение:
. "(О. ОР(О + 5,(Д:(О, «(/), 0], A.9)
которое в случае задачи Майера (при В===0) совпадает
с уравнением A.8.3) из гл. I, описывающим изменение
импульсов в теории оптимального управления. Поэтому
в дальнейшем вектор pt будем называть импульсом.

$U ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 291
Задав полный вектор управлений w, можно, исполь-
используя A.2), последовательно определить полный фазовый
вектор х и вычислить значение функции R. В случае
непрерывной системы это соответствует интегрированию
A.1) «слева направо». Далее, с помощью A.5), A.7) вы-
вычислим последовательность р{. Эти расчеты соответствуют
в оптимальном управлении интегрированию уравнений
для импульсов «справа налево». После этого по формуле
A.8) определим производные.
Интересно сравнить формулы A.4) и A.7), дающие
выражения для одних и тех же векторов р{. Формулу
A.4) можно использовать для численных расчетов, не
вводя «уравнения для импульсов» A.7). Зафиксировав
вектор w и давая приращения вектору *,-, проинтегрируем
A.2) от 1-го шага до ^-го, вычислим изменения R и при-
приближенно найдем вектрр р{. Такие расчеты являются более
громоздкими, чем использование A.7), так как, просчитав
только один раз «справа налево» по формулам A.7), можно
сразу получить все векторы pt. Тем не менее формулу
A.4) бывает полезно использовать при отладке программ,
так как она позволяет проверить правильность запрограм-
запрограммированных формул A.7).
В этом параграфе, исходя из конечно-разностной
аппроксимации A.2) системы дифференциальных уравне-
уравнений A.1), были выведены рекуррентные соотношения для
вычисления импульсов A.7), после чего предельным пе-
переходом найдено дифференциальное уравнение A.9). Можно
было бы попытаться рассуждения вести в обратном по-
порядке, идя от «непрерывных» систем A.1) и A.9) к ди-
дискретным A.2) и A.7), но на этом пути возникает ряд
трудностей. Действительно, формальное интегрирование
системы A.9) с одной и той же погрешностью порядка h\
приводит к различным результатам. Можно написать,
например, следующие две формулы, эквивалентные в смысле
точности интегрирования A.1):
Однако только во втором случае получается та же фор-
формула, что и A.7). Вместе с тем, используя A.7), с по-
помощью A.8) можно получить точную формулу для вы-
Ю*

292 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
числения производной функции R. Поэтому предпочти-
предпочтительнее использовать формулу A.11), а не A.10), хотя
разница между ними невелика—того же порядка, что и
погрешность интегрирования. При введении схем интегри-
интегрирования системы A.1) более высокого порядка точности
различие становится более существенным. Поэтому вместо
формального интегрирования дифференциального уравнения
для импульсов следует использовать точные формулы,
которые являются прямым следствием выбранной схемы
интегрирования системы A.1). Формулы вычисления произ-
производных функции R обычно требуются для реализации раз-
различных численных методов безусловной минимизации.
Погрешности дифференцирования могут существенно услож-
усложнить расчеты. Это особенно важно, если используются
«тонкие» методы минимизации, например метод сопряжен-
сопряженных градиентов.
Необходимость исследования систем вида A.2) иногда
возникает при решении задач оптимизации объектов, пове-
поведение которых описывается только рекуррентными соотно-
соотношениями; «непрерывная» запись в виде A.1) для них не
правомочна, коэффициенты ht могут не быть малыми вели-
величинами. Для анализа таких систем особенно важно исполь-
использовать точные формулы дифференцирования.
При составлении дискретных аппроксимаций исходной
системы A.1) можно вводить специальные гипотезы
о характере изменения управления внутри интервала
интегрирования. В формуле A.2) считалось, что управ-
управление внутри интервала интегрирования постоянно. Можно
постулировать, например, что внутри каждого f-го интер-
интервала интегрирования управление есть линейная функция i\
для ti^t^ti-\-hi имеет место формула
и (t)=--u{ + '-^ (ui+i—и{).
Для схемы Эйлера расчетные формулы не изменяются, но
для более точных схем интегрирования появляются новые
слагаемые.
2. Вычисление вторых производных» Предположим,
что функции R(x> w) и F(xif uh tj) дважды непрерывно
дифференцируемы по компонентам векторов х и w. Найдем
матрицу вторых производных сложной функции R (x(w)> w)

§1] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 293
по w. Введем квадратные симметричные матрицы
р ^&R (s, w) р d?R(x,w)_d2b(zq)
^ dxidxi » ^я- dxqdxq дх* '
dyi _ d2R dyqd4(zq)
dtij ~~dujdui9 duq~~ du*
Смысл, который вкладывается в эти формулы, анало-
аналогичен определениям первых производных функции R по
компонентам векторов х и w. При дифференцировании по
компонентам вектора х вектор управлений w считается
постоянным.
Продифференцируем р{ и у( по х-ь и uh учтем A.7),
получим
. A.12)
Если 1 ^s < i ^ q— 1, то легко вывести следующие фор-
формулы:
d*R
dusdut dus dxs+id
d*R _dxs+1 d2R
u^ s
Аналогично для q> s> i имеем
d2R _ d2R
dus dU[ dus dx{+i u
dusdxi dusdx(
Из найденных формул можно последовательно определить
элементы матрицы —^^ • Ограничимся тем, что при-
приведем лишь часть этой матрицы, изобразив матрицы-блоки,
занимающие столбцы-блоки с номерами от s — 1 до +1
и строки-блоки с номерами от s —1 до s+1.

294 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
s 1
s
s+l
s— 1
d2R
dUs^dUs-!
d2R FT"(- )
dus+1dxs u s x)
s
d2R
a\zs-l) dXs(iUs
d2R
dusdus
s+l
d*R
dXsdus+1
F (-) d*R
ta(-s)dxs+1dus+1
cPR
dus+1dus+l
Таким образом, при вычислении вторых производных
необходимо «интегрировать справа налево» не только урав-
уравнение A.7) для векторов-импульсов ph но и пересчиты-
d2R
вать матрицы-импульсы Р, и матрицы ^—-г—. Возможны
(XXs UX (
случаи, когда при некоторых i вектор Pi = 0. Это соответ-
соответствует «особым» режимам в оптимальном управлении. Оче-
Очевидно, что приведенные .формулы остаются справедливыми
и их можно использовать для теоретических исследований
этих случаев.
Несмотря на громоздкость полученных формул, их роль
в ближайшем будущем будет, по-видимому, исключительно
велика, так как они открывают широкие возможности на
базе описанного в гл. IV подхода строить быстро сходя-
сходящиеся вычислительные процедуры, аналогичные методу
Ньютона. Некоторые примеры таких расчетов приведены
ниже в § 7.
3. Случай использования схем Рунге — Кутта. При
решении ряда практических задач требуется обеспечить
высокую точность интегрирования исходной системы A.1).
Простейший путь выполнения такого условия состоит
в уменьшении величин шагов интегрирования. В этом слу-
случае, однако, существенно возрастает размерность полного
вектора управлений до, что значительно усложняет процесс
оптимизации. Другой путь увеличения точности интегри-
интегрирования состоит в применении более совершенных формул
интегрирования. Ниже мы рассмотрим случай использова-
них схем Рунге—Кутта. Задача по-прежнему будет со-

§ i] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 295
стоять в отыскании формул для вычисления производных
сложной функции R(x(w), w) по компонентам вектора w.
Воспользуемся следующими формулами интегрирования
системы A.1):
/
здесь z{ = [x'h ui t\\ ui = u(ti),
^ = ^ + P/-iA,f Ы"х), rf = ^+Py-iA/f A.14)
где gj, Py_!—некоторый набор чисел, причем все О^Ру_х^
^ 1 и ро = 0, поэтому значения векторов z\ несущественны.
В A.13), A.14) и далее в этом параграфе индексы i и /
принимают целочисленные значения соответственно из ин-
интервалов [1: q—1] и [1:р].
Разным числам (параметрам) gj и ру_х будут соответ-
соответствовать различные схемы интегрирования. Поэтому фор-
формула A.13) определяет набор методов численного интегри-
интегрирования системы A.1), называемый обычно семейством
методов Рунге—Кутта. Погрешность интегрирования си-
системы A.1) на i-ы шаге оценивается разностью ^(А;)^
= *('/+i)—*/+1» гДе x(t)—решение системы A.1) с на-
начальным условием jf(/f) = Xj.. Величина г\ является функ-
функцией шага интегрирования А,-. Если / (г)—достаточно глад-
гладкая функция своих аргументов, то функция г] (А,-) предста-
вима рядом Тейлора
где 0<6< 1. Параметры метода интегрирования g/y |3y_x
подбираются так, чтобы
г,@) = т]A>@)=...='п^@)-0
для произвольных, достаточно гладких функций / (г). Если
при этом r\{s+1)@)ф0, то s называется погрешностью
метода интегрирования на одном шаге.
Подробный анализ разнообразных схем интегрирования
обыкновенных дифференциальных уравнений можно найти
во многих учебниках по численным методам. Укажем, на-
например, книгу Н. С. Бахвалова [1]. Здесь мы ограничимся
лишь тем, что приведем несколько наборов возможных
параметров из семейства методов Рунге — Кутта.

296 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Если в A.13) положить р=1, то получим рассмотрен-
рассмотренную выше схему Эйлера, которая обладает первым поряд-
порядком погрешности интегрирования.
Если положить р==2, gi = 0, g2=l» Pi = 1/2, то полу-
получим так называемую схему Эйлера с пересчетом, в которой
порядок погрешности интегрирования равен двум, вычис-
вычисления ведутся по формулам
Второй порядок погрешности имеет также модифицирован-
модифицированная схема Эйлера, в которой р = 2, gl = g%=l/2, pi=l,
Среди схем, имеющих четвертый порядок погрешности,
наиболее употребительной является схема, в которой
Перейдем к вычислению производных сложной функ-
функции R. В соответствии с формулой A.13) запишем выра-
выражение для функции R в виде
R(x9 w) = b(xv uv U) + % h
где x—полный фазовый вектор, w—полный вектор управ-
управлений:
X = [Xif Xif • • •, Xi, #2» Х%9 • • •» #2 » • • • > %q\>
Введем вспомогательные п-мерные векторы
Учцтыэая зависимости A.13), A.14), определяющие век-

§ 1] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 297
торы Х/+1, x*i+1 как дифференцируемые функции «преды-
«предыдущих» векторов xi9 x\y получим следующие формулы:
dR Л дх[ dR dxi+1 dR
Pi = ТГ + 2 +
dxi j^\ dxi dx\ dxi dxi+1
, = dR dxf1 dR dx.+1 dR
Принимая во внимание A.13), A.14), A.16), перепишем
эти выражения в виде рекуррентных соотношений
/ = 1 я дхд
Чтобы упростить формулы, удобно добавить к коэффи-
коэффициентам Ру один дополнительный коэффициент РР, считая
его равным нулю. В этом случае фигурирующий ниже
вектор pi+1 будет всюду умножаться на рр, поэтому его
значение будет не существенно. Определим функцию
Соотношения A.17) перепишем компактным образом:
р[=нхы, pi+» pi+x)-
Аналогично выводится следующая, основная формула
для вычисления компонент вектора сложных производных
функции R по w:
dR(x(w)t w)^dR . dxj+1 dR dxi+1 dR __
du\ du{ + du[ dx[+1 "*" du{ dxi+1
Приведенные формулы незначительно отличаются от
формул, найденных для схемы Эйлера. Пересчет «импуль-
«импульсов» происходит здесь по более сложным формулам.
Из найденных общих соотношений легко получить фор-
формулы вычисления производных для каждой выбранной

298 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
схемы интегрирования. Для схемы Эйлера с пересчетом
A.15), например, имеем
Р\ = \ h(fx (*,) pi p\ = ht [Вх
По сравнению со схемой Эйлера здесь число точек,
в которых ищется вектор управлений, удвоилось. Можно
положить всюду ui = u} = u] и учесть, что при использо-
использовании схемы Эйлера с пересчетом были отброшены на каж-
каждом шаге интегрирования величины порядка h]. С такой
же погрешностью определим векторы р( и производные
функции R. В результате получим:
Здесь все частныа производные fx, fuy BXJ Ba следует вы-
вычислять с погрешностью порядка h\y чтобы обеспечить
погрешность порядка Щ в определении -j—.
Для схемы Рунге—Кутта A.13) в случае, когда на
интервале интегрирования управление постоянно, получим
Pt=pt+i+ 2 лмя)+А/ SP,-iM2
s=l s=2
: 1 S = 2
4
+ hi 2 P-A-if. (*sr8) /ж (г?) Мл (zf) +
= вЛ [В (Z}) + </ (Zf),

§1] ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ 299
Аналогичным образом можно получить формулы для дру-
других схем интегрирования.
Использование схем интегрирования вида A.13) при
р ^ 2 предполагает, что на каждом интервале интегриро-
интегрирования функция / (л:, и, t) имеет ограниченные производные
по всем аргументам. Если внутри интервала интегрирова-
интегрирования управление u(t) резко изменяется (на величины по-
порядка единицы), то происходит потеря точности расчетов.
Поэтому в процессе поиска оптимального управления сле-
следует контролировать расположение узлов сетки по / и
в случае необходимости либо их изменять, либо ограничи-
ограничивать величины изменения управления на каждом интервале
интегрирования. Проще всего внутри каждого интервала
считать управление постоянным. Такой прием можно ис-
использовать при решении многих практических задач, в ко-
которых необходимо интегрировать систему A.1) с высокой
степенью точности, а нахождение оптимального управления
можно проводить грубее. Это оправдано тем, что обычно
в технических системах оптимальное управление можно
реализовать лишь приближенно, и поэтому шаг задания
управления не должен быть слишком мал.
Если на интервале интегрирования фиксировать управ-
управление, тогда щ = и) = ... = и?, вектор w можно считать
состоящим из набора [и1У u2f ..., uq]. Для вычисления
производных по щ вместо A.18) следует применять сле-
следующую формулу:
Такой подход можно развить дальше, считая, что управ-
управление постоянно на нескольких шагах интегрирования.
Благодаря этому удается понизить размерность вектора w,
понизив одновременно точность решения оптимизационной
задачи. В частности, если считать, что управление посто-
постоянно всюду, то и1 = и2= ... =и(г = и и
^^=2 2 "AzL Р,+„ РП+Ьа(г9).
Фактически в этом случае вектор и становится управляю-
управляющим параметром, а не управлением. Аналогичные формулы
для схемы Эйлера будут приведены в § 6.

300 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Формулы для вычисления производных функции R по
компонентам вектора щ потребуются в дальнейшем при
численном решении задач о минимизации R по w. Поэтому
точность определения производных целесообразно согласо-
согласовывать с точностью процесса минимизации. В частности,
при проведении грубых, предварительных расчетов в фор-
формулах для определения градиентов и импульсов можно
отбрасывать малые члены, пропорциональные высоким сте-
степеням hh облегчая тем самым вычисления. Возможны и
другие упрощающие приемы. Можно, например, считать,
что на интервале интегрирования управление и (t) является
заданной функцией t. Несложно получить формулы для
дифференцирования и в этом случае. Значительно сложнее
выглядят формулы для вторых производных функции /?;
их можно найти в работе Н. И. Гр-ч^за и Ю. Г. Евту-
Евтушенко [б].
§ 2. Необходимые и достаточные условия минимума
1. Постановка задачи. Рассмотрим задачу оптималь-
оптимального управления при наличии смешанных ограничений на
вектор фаз и управлений. Для простоты изложения будет
исследован случай, когда система A.1) проинтегрирована
по схеме Эйлера A.2), на выбор управления наложены
ограничения, которые должны быть выполнены вдоль траек-
траектории:
ГЧ*/. и/. *,) = 0, T*(xi9 ui9 *,)<0 B.1)
и в конце траектории:
гз(*„, ищ% g=o, r*(*a, uv g<o. B.2)
Каждому полному вектору управлений w=[ul9 w2, ...
• •¦¦ иА?Ег* система A.2) ставит в соответствие единст-
единственный полный фазовый вектор х — \хих2, ..., xq]?Enq.
Поэтому будем писать x = x(w). Условия B.1) и B.2)
запишем в сжатой форме:
g(x(w)fw) = 09 h(x(w),w)^09 B.3)
где вектор-функции g и h являются объединением соответ-
соответственно ограничений типа равенства и неравенства вдоль

§ 2] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 301
траектории и в конце траектории:
g(x, oO = [PBi), ГЧ*2), ..., P(Vi)* ГЗBЛ
AX*. w) = [T*(z1)y Г*(г2), ..., P(V!), Г«(г,)],
*« = [*/. "/> '/]•
He ограничивая общности, можно считать, что введен-
введенные функции осуществляют отображения g: Erq —> ?*,
Л: ?'*-^ Ес.
Вектор управлений w будем называть допустимым, если
векторы до и лс(до) таковы, что выполнены условия B.3).
Допустимое множество W полных векторов управлений
можно определить стандартным образом:
*: g(x(w), w)=*0, h(x(w),
Такая запись подчеркивает, что g и h являются сложными
функциями w. Используемые ниже частные производные
g и h по х( и щ просто выражаются через первоначальные
функции и обозначаются следующим образом:
dg __
Ъхщ- дхд -1хУгя>> duq- duq -1«W"
Кроме того, в дальнейшем будет использовано одно важ-
важное, значительно упрощающее расчеты обстоятельство, не
заметное при общей форме записи ограничений в виде
B.3) и заключающееся в том, что функции, определяющие
ограничения при t = th зависят только от xh uh t..
Задача дискретного оптимального управления процес-
процессом, описываемым соотношением A.2), заключается в отыс-
отыскании полного вектора управлений w и соответствующего
ему полного фазового вектора х таких, чтобы выполнялись
условия B.1), B.2) и^функция^цели
Rx (х, w) = Ьг (г,) + 2 /1§ВХ (г,) B.4)
принимала наименьшее возможное значение.
Вектор-функции F, g, А, функции Ь19 Вг будем в даль-
дальнейшем называть функциями, определяющими задачу дис-
дискретного оптимального управления. Предполагаем, что ре-

302 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
шение поставленной задачи существует. Аналогичную за-
задачу с фазовыми ограничениями вдоль траектории можно
сформулировать и для системы A.1). Интуитивно ясно, что
для достаточно широкого класса систем A.1) решения обеих
задач будут близкими, если шаги интегрирования системы
A.1) выбраны достаточно малыми. Не будем останавли-
останавливаться на строгом обосновании этого свойства, его иссле-
исследование содержится, например, в книгах Ю. М. Ермольева,
В. П. Гуленко, Т. И. Царенко [1], Р. П. Федоренко [1],
в статье Б. М. Будака, Е. М. Берковича, Е. Н. Соловье-
Соловьевой [1], и во многих других работах.
2. Необходимые и достаточные условия минимума.
Поставленная задача дискретного оптимального управления
является некоторой специальной задачей нелинейного про-
программирования. Поэтому формулировки условий экстремума
и численные методы решения можно получить, используя
известные результаты из нелинейного программирования.
Составим функцию Лагранжа
R(x, w, и, v) = b1(zq)+ 2 ft/?1(z/) +
* +<и, g(x, w)> + <v, h{xt w)>. B.5)
Здесь введены множители Лагранжа и?Ее> v?E%.
Определенная таким образом функция Лагранжа имеет
тот же вид, что и A.3); поэтому, если функции, определяю-
определяющие задачу, дифференцируемы по компонентам векторов х
и w, то к B.5) можно применить формулы дифференциро-
дифференцирования, полученные в предыдущем параграфе. Необходимые
и достаточные условия минимума для задач нелинейного
программирования, приведенные в §§ 6, 7 гл. I, почти
дословно переносятся на рассматриваемый случай. Поэтому
ограничимся перечислением только некоторых результатов.
Пусть существует полный вектор управлений w*y соот-
соответствующий ему полный фазовый вектор х* = х (до») и двой-
двойственные векторы м*, v*^zO такие, что для любых w9
и у v^-О выполнены условия седловой точки функции
Лагранжа:
R (*., w%9 и, v)^R (хф9 w%, um, vj < R (х (ш), w9 u*> vm).
Тогда, согласно теореме 1.6.1, вектор w* является реше-
решением задачи дискретного оптимального-управления.

§2] НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ МИНИМУМА 303
Согласно теореме 1.6.7, если задача дискретного опти-
оптимального управления является задачей выпуклого програм-
программирования и имеет место условие Слейтера или Карлина,
то существуют седловые точки функции Лагранжа R.
Согласно теореме 1.7.6, если функции, определяющие
задачу, дифференцируемы по компонентам векторов х и до,
выполнено условие Эрроу—Гурвица—Удзавы, то для того,
чтобы вектор хют был решением задачи дискретного опти-
оптимального управления, необходимо, чтобы существовали
такие множители Лагранжа и*у v*^0, что совокупность
[о>», м#, v*\ образует точку Куна — Таккера, т. е.
h(x(wm)9 -o;.)<0, vlh/(x(w,)9w,) = 0, j€[l:c]. B.6)
Здесь компоненты производной -т— вычисляются по фор-
формулам, полученным в предыдущем параграфе:
, PB,.)>, B.7)
. = —l *'^*' *' *' =Hx(z}t pl+1, uh vt),
где векторы w,-, v/ есть составляющие векторов w и v\ их
размерности совпадают с размерностями соответственно
вектор-функций Г1 и Г2 для l^t^<7—1» Г3 и Г4 для
i = q.
Введем конус
т dhJ (х (ш,), ю.)_0 г
da; '
da» "~~ /'

304 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
здесь
*, vm),
Воспользуемся теоремой Мак-Кормика 1.7.2. Предпо-
Предположим, что функции, определяющие задачу, дважды диф-
дифференцируемы по компонентам векторов х и до, существуют
векторы wm9 x*=x{w*)> иф, i>»^0 такие, что выполнены
условия B.6); определяемая с помощью формул A.12)
матрица вторых производных
dwdw
положительно определена на конусе /С(^», 0»), тогда до»
является изолированным локальным решением задачи дис-
дискретного оптимального управления.
В приведенных утверждениях единственной специфи-
спецификой, связанной с оптимальным управлением, является то
обстоятельство, что первые и вторые производные функций,
определяющих задачу, вычисляются несколько необычно
для нелинейного лрограммирования с привлечением вспо-
вспомогательных переменных (импульсов). Однако это сугубо
технический прием, не меняющий сути дела. Та или иная
схема интегрирования A.1) приведет к разным формулам
вычисления производных, не изменяя вида необходимых и
достаточных условий экстремума. Аналогичная ситуация
возникает при описании и обосновании численных методов
нелинейного программирования, примененных для решения
задачи дискретного оптимального управления. Поэтому
в следующем параграфе дадим лишь краткое описание
основных численных методов и совсем не будем останавли-
останавливаться на вопросах обоснования сходимости, предполагая,
что они исчерпывающим образом освещены в предыдущих
трех главах.
§ 3. Численные методы, основанные на редукции
к задачам нелинейного программирования
Сформулированная в § 2 задача дискретного оптималь-
оптимального управления является некоторым частным, специаль-
специальным случаем задачи нелинейного программирования. Важ-

§3] РЕДУКЦИЯ К НЕЛИНЕЙНОМУ ПРОГРАММИРОВАНИЮ 305
нейшей ее особенностью является сравнительная простота
вычисления производных функции R по компонентам век-
вектора w. Это свойство открывает широкие возможности
эффективно использовать многие методы нелинейного про-
программирования, основанные на вычислении первых произ-
производных.
В большинстве используемых методов решение задач
ведется по общей схеме: задается вектор до, вычисляются
значения целевой функции и функций, задающих ограни-
ограничения, формируется некоторая вспомогательная функция R
вида A.3), производится ее минимизация по w с помощью
методов безусловной минимизации. Различные численные
методы отличаются друг от друга способами построения
функций R, правилами их изменения в процессе итераций.
Выбор метода интегрирования системы A.1) влияет только
на формулы вычисления R, g, h и их производных. При
программной реализации методов процедуры вычисления
R, g, h и отыскания производных удобно оформлять как
отдельные модули. Тогда при изменении схем интегриро-
интегрирования системы A.1) в численных алгоритмах изменяются
только эти модули, остальные блоки программ, реализую-
реализующих такие методы, остаются прежними. Вопросы о выборе
схемы интегрирования и метода оптимизации оказываются,
таким образом, разделенными. Возможны случаи, когда
интегрирование ведется по схемам высокого порядка точ-
точности, а оптимизация проводится весьма грубыми мето-
методами, возможны противоположные ситуации.
Приведем ряд наиболее широко используемых методов
решения задач дискретного оптимального управления. Чис-
Численные расчеты тестовых задач с помощью некоторых из
них приведены в § 7. Чтобы упростить в дальнейшем
ссылки, каждому методу присвоен заголовок OPTS, где
S —номер программы, реализующей данный метод. Под
этими заголовками были составлены процедуры, вошедшие
в состав системы ДИСО, описание которой приведено
в следующей главе. При решении сложных задач оптималь-
оптимального управления обычно используется несколько различных
методов оптимизации. Вначале расчеты ведутся методами,
обладающими большой областью сходимости, и только
после попадания в достаточно малую окрестность решения
осуществляется переход к быстросходящимся методам. Для
реализации такого режима работы необходимо, чтобы каж-

306 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
дый используемый метод подготовлял необходимую инфор-
информацию для работы последующих методов.
В каждом численном методе осуществляется некоторый
итеративный процесс решения задачи, сформулированной
в § 2. Номер итерации обозначается к. Для описания ме-
метода указывается, как изменяется полный вектор управле-
управлений w на k-и итерации, в некоторых методах следует
указать правило изменения вектора двойственных пере-
переменных {и, v}.
ОРТ41. Метод внешних штрафных функций (см. § 1
гл. III). Составляется вспомогательная функция
R(x, w, x) = R1(xi w) +
е с 1
где функция цели Rt задается формулой B.4), штрафная
функция я|) определяется при описании функции C.1.6).
Для некоторой монотонно возрастающей последователь-
последовательности т0 < хг < т2 <... строится последовательность векто-
векторов w(t0), w(x1)i ..., определяемых из приближенного
решения задачи безусловной минимизации
И, w, xk). C.2)
Если функции, определяющие задачу, дифференцируемы
по компонентам вектора х, то можно приближенно опре-
определить двойственные векторы:
7Л Я (* (Щ), Щ> Ч) J №(*(Щ)> Щ>4)
Uk -= r~7 » vk = rrz >
dgl . dhJ
которые могут быть полезны для дальнейших расчетов
с помощью методов, основанных на модифицированных
функциях Лагранжа.
При выполнении условий теоремы 3.1.1 метод сходится
к решению задачи. Вычислительный процесс в значитель-
значительной степени зависит от политики увеличения коэффициента
штрафа т, от используемого метода безусловной миними-
минимизации, точности решения вспомогательных задач C.2) и
многих других факторов. Точность решения задач C.2)
интерпретируется в методах безусловной минимизации по-
разному. В частности, в методах, использующих произвол-

§3] РЕДУКЦИЯ К НЕЛИНЕЙНОМУ ПРОГРАММИРОВАНИЮ 307
ные минимизируемой функции, процесс расчетов прекра-
прекращается как только найдено управление wk9 удовлетворяю-
удовлетворяющее следующему условию:
| dR(x(wk), wkixk
Таким образом, реализуется вторая упрощенная версия
метода штрафных функций (см. § 1 гл. III).
Если функции, определяющие задачу, недифференци-
руемы по л:, и, то в качестве вспомогательной функции R
целесообразно брать функцию, зависящую от недифферен-
цируемого штрафа (см. § 2 гл. III).
ОРТ45. Первая версия метода параметризации целевой
функции (см. § 3 гл. III). Составляется вспомогательная
функция:
R(x, w, r\) = [Rt(x9 w)-^y +
+ 2 \g*(x, w)Y+ 2 W(*, w)). C.3)
Здесь функция я|э та же, что и в функции C.1), г\—нижняя
оценка оптимального значения RZ целевой функции. Сог-
Согласно результатам § 2 гл. III значение т] можно получить,
сделав по крайней мере одну итерацию по методу ОРТ41.
Пусть известно управление уокшт1 и значение r)ft, новое
управление wk определяется из решения вспомогательной
задачи
inR(x(w)y w9 цк). C.4)
Управление whmml при этом берется в качестве начального
приближения. В соответствии с формулой C.3.6) положим
Л*+1 = Л* + VR(x(wh)9 wki r\k).
Процесс расчетов прекращается, если нарушено хотя
бы одно из следующих трех условий:
* < d, S W (х («Ж wk)Y + t * W (х (wk), wk)) < e,
i = 1 / = 1
Здесь d—предписанное максимальное количество итера-
итераций, е—точность решения задачи безусловной минимиза-
минимизации. Величины d9 г задаются пользователем.

308 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Если функции, определяющие задачу, дифференцируемы
по компонентам вектора х> то можно найти двойственные
векторы
-f __ 1 dR(x(wk), wk, щ) Vt—X dR(x(wk)y wk, щ)
a dg* a dh* * n *\
OPT46. Вторая версия метода параметризации целевой
функции. Строится вспомогательная функция C.3), на k-и
итерации решается задача C.4), параметр r\k изменяется по
формуле C.3.10), которая в данном случае имеет вид
Двойственные векторы определяются по формуле C.5).
Существенным недостатком обеих версий метода пара-
параметризации целевой функции является требование, чтобы
безусловная минимизация проводилась с высокой точно-
точностью. Только в этом случае в процессе расчетов будет
выполнено необходимое условие функционирования метода:
Лл ^ R1 • Во второй версии из-за того, что изменение tj
происходит более энергично, это требование особенно важно.
Поэтому при решении вспомогательных задач безусловной
минимизации приходилось задавать более высокую^ точ-
точность расчетов, чем в остальных методах.
Метод штрафных функций и метод параметризации це-
целевой функции наиболее полезны, когда начальное прибли-
приближение известно грубо. Обычно с них начинаются расчеты
и определяются начальные значения двойственных перемен-
переменных. Решить задачу с высокой точностью этими методами
трудно.
ОРТ53. Метод модифицированной функции Лагранжа.
Реализован метод простой итерации D.3.21). Модифициро-
Модифицированная функция Лагранжа имеет вид
R (х, w9 u9v) = Ri (*, «О + ? [«' + yS( (x, w)] gl (x, w) +
i =i L J

§3] РЕДУКЦИЯ К НЕЛИНЕЙНОМУ ПРОГРАММИРОВАНИЮ 309
На 6-й итерации выполняются следующие действия:
wk?Argmm R(x(w), w, йк, vk)y
Недостатком метода является то обстоятельство, что
функция R не обладает непрерывными вторыми произ-
производными по w. Это сужает количество методов безусловной
минимизации, которые можно применять для нахожде-
нахождения wk. В этом отношении предпочтительнее использовать
последующий метод.
ОРТ55. Первый вариант метода простой итерации.
Реализован метод D.3.20). Модифицированная функция
Лагранжа имеет вид
R(x, w, и, v) =
-| < если hJ ^ (
T \[l-W{x, ш)]-А, если Л'<0.]
Метод состоит в следующем:
{x{w), w9 uk, vk),
+? [4] если Ч>0, \
[1-ЛЙ-, если Л1<0. /
Здесь hk = h(x(wk), wj.
Для реализации этого и предыдущего методов необ-
необходимо знание приближенных значений компонент двойст-
двойственных векторов. Эти методы оказались особенно эффек-
эффективными при расчетах вблизи от решения. Как показано в
гл. IV, они по существу являются некоторыми вариантами

310 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
метода простой итерации. Более высокую скорость схо-
сходимости можно получить, используя модификации метода
Ньютона.
ОРТ8. Метод Ньютона. Реализована простейшая вер-
версия D.1.11). Модифицированная функция Лагранжа имеет
вид
R (х, w, и, v) = /?! (*, w) +
+ 53 u*g*(x, w) + i; ft)*v(x, w).
Итеративный процесс осуществляется путем решения сле-
следующей системы линейных уравнений:
2
2
9 wk),
где / g [ 1:с], д;^ = л: (wk), матрица вторых производных
функции R по w определяется из рекуррентных формул
A.12). При реализации этого метода в памяти ЭВМ при-
приходится хранить симметричную матрицу размера (r-qJ,
что может наложить ограничение на размерность решае-
решаемой задачи дискретного оптимального управления.
Определенные трудности возникают при решении ли-
линейной системы C.6), когда какие-либо из ограничений
B.3) не зависят явно от компонент вектора wt так как
в этом случае определитель приведенной системы может
оказаться равным нулю. Например, если ограничение типа
неравенства имеет вид к(х)^.О, то при использовании
дискретной аппроксимации A.2) на первом шаге будем
иметь: h(xi)^.O. Таким образом, значение ^(лг^не зави-
dh (хг) л
сит от полного вектора w, градиент ^ 1; == 0, и если
= Ot то один столбец в матрице вторых производных

§3] РЕДУКЦИЯ К -НЕЛИНЕЙНОМУ ПРОГРАММИРОВАНИЮ 311
функции R по [w, и, v] равен нулю, что приводит к вы-
вырожденности этой матрицы. В рассматриваемом случае
ограничение /1(^)^0 следует опустить, а все последую-
последующие ограничения представить в виде
и„ *,)), i?[Uq-2] C.7)
и далее использовать обычные расчетные формулы.
ОРТ1. Метод линеаризации. На k-й итерации произ-
производится линеаризация функции цели B.4) и функций,
задающих ограничения:
Rl(x(w), w)^R1(x(wk), w/t) + (dR*(xB)'Wk), to)
g(x(w), w)*g(
h(x(»), w)*h(x(a*), wk) + [dh(x(wd$'Wk)]Tto,
где 8w = w—wk.
Ставится задача квадратичного программирования об
отыскании минимума по 8w функции:
Ч to)+a<to, to> C.8)
при условиях
C'9)
где а—некоторый положительный коэффициент. После
нахождения оптимального значения &у, положим: wk+1 =
= wk + a8w. Шаг а выбираем из условия минимума недиф-
ференцируемой функции штрафа
Р = Яг(х(юк+1)9 wk+1) +
y wk+1)\+ 2Ai(^(^+1), оь+
Здесь г—некоторое достаточно большое число.
Если положить # = 0, то C.8), C.9) становится зада-
задачей линейного программирования, в этом случае следует
добавить ограничения, чтобы модули компонент вектора bw

312 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
были ограничены. Можно использовать все другие версии
метода, описанные в § 5 гл. III. Специальный вариант
метода линеаризации, ориентированный на решение задач
оптимального управления, предложен Р. П. Федоренко [1].
ОРТ7. Модификация метода Эрроу—Гурвица.Слеяуя
§ 1 гл. IV, составим простейшую модификацию функции
Лагранжа, положив
R(xt w9 и, v) = Rl(x, w) + <u, g(x,w)>+ 2
Метод состоит в построении следующей последователь-
последовательности:
(и>к), wk).
Здесь шаг а должен быть достаточно мал, е либо равно
единице, либо достаточно мало. Метод обладает сравни-
сравнительно низкой скоростью сходимости.
На этом мы #закончим описание основных методов.
Многочисленные другие алгоритмы нелинейного програм-
программирования могут быть перенесены аналогичным образом
на решение задач дискретного оптимального управления.
Как указывалось в начале этого параграфа, программы,
реализующие приведенные методы, можно модифицировать
путем изменения отдельных блоков с тем, чтобы сделать
их пригодными для учета различных схем интегрирования
системы A.1). В упомянутые программах ОРТ41, ОРТ45,
ОРТ46, ОРТ53, ОРТ55, ОРТ1, ОРТ8, ОРТ7 система A.1)
интегрируется по схеме Эйлера. В § 7 будут сделаны
ссылки на программы ОРТ413, ОРТ553, в которых ре-
реализованы методы, данные при описании соответственно
программ ОРТ41 и ОРТ55, но в качестве схем интегри-
интегрирования системы A.1) использован метод Эйлера с пере-
пересчетом A.15).
§ 4. Дискретные принципы минимума
1. Основные определения. Как видно из приведенных
в § 3 численных методов, часто при решении задач ди-
дискретного оптимального управления приходится сталки-

§4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 313
ваться с необходимостью отыскания безусловного минимума
вспомогательной функции R(x(w), w). Вектор w обычно
имеет значительную размерность, поэтому минимизация
R(x(w)> w) no w является довольно сложной задачей. Для
решения можно использовать обширную библиотеку стан-
стандартных программ, реализующих самые разнообразные
методы безусловной минимизации функций многих пере-
переменных. Однако рассматриваемая задача имеет свою спе-
специфику, которая не свойственна общей задаче безусловной
минимизации и поэтому не учтена в этих методах. Тот
факт, что задача минимизации возникла в связи с реше-
решением задачи дискретного оптимального управления, поз-
позволяет в ряде случаев использовать специальные свойства,
которые для непрерывных систем отражены в принципе
максимума Л. С. Понтрягина. Их аналогом в нелинейном
программировании являются результаты, изложенные § 4
гл. I. Цель данного параграфа заключается в выводе для
системы A.2) необходимых условий минимума функции /?,
аналогичных принципу максимума Л. С. Понтрягина.
Численные методы, основанные на этих результатах, будут
описаны в следующем параграфе.
Считаем, что многошаговый процесс описывается соот-
соотношением A.2). Задача состоит в отыскании 1-й состав-
составляющей щ вектора w, доставляющей минимум сложной
функции
R{x(w)y w) = b{zq), га = [х,, uq, tq]
по всевозможным значениям ui9 принадлежащим некото-
некоторому компактному множеству U. Все остальные состав-
составляющие вектора w будем считать фиксированными. Индекс i
произвольный, меньший, чем q. Обозначим W* решение
сформулированной задачи:
№, = Argmin b{zq). D.1)
Всюду в дальнейшем считаем, что это множество не пусто.
Если отображение F{z{) и функция b(zq) непрерывно
зависят от всех своих аргументов, то для каждого век-
вектора u(^U из A.2) однозначным образом находится по-
последовательность х{+и xi+2f ..., хг Такая операция
определяет непрерывную функцию Ь от вектора ^/+1и
отображение xi+v зазисящее от вектора и(. Для упроще-

314 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
ния, дальнейших формул вектор xi+1 будем обозначать
буквой а, сложную функцию Ь от а обозначим В (#), тогда
Я(* И, w) = В (а) = В (а («,-)), a(u,) = F{xt, и„ /,).
Множество ИР* можно представить в виде
В(а(щ)).
Вместо минимизации функции В (a (ut)) по вектору управ-
управлений ut ^ U рассмотрим задачу о минимизации В (а) по
фазовому вектору a?Q = a(U) (проведем минимизацию
в пространстве состояний) и определим множество
Q# = Argmin В (а).
п
Очевидно, что й* является образом множества W* при
отображении а(и{): Qm = a(Wm).
Если вектор-функция F и функция Ь дифференцируемы
по'составляющим полного фазового вектора, то, согласно
формулам § 1, имеем
Здесь использовано обычное обозначение Н (zs, ps+1) =
(s)f Ps+
Теперь для всякого вектора и( 6 U можно вычислить
не только векторы х{+и xi+2y ..., ^, но и из D.2) по-
последовательно найти pq, pq-n ..., pi+1. Такая операция
определяет однозначные отображения
Если функция В (а) определена на открытом множестве,
содержащем й, и дифференцируема в точке agQ, то
можно ввести точечно-множественное отображение
, а—а>
или, перейдя в пространство управлений, определить для
и{ ^ U многозначное отображение
W2 (щ) = Arg min <p/+1 (а (щ)), а {и{)—а (п})>.

§4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 315
Пусть а = а{и(), тогда множество W1(a) является
образом множества W2(ui) при отображении a{ut)\
Если считать, что отображение F дифференцируемо не
только по компонентам полного фазового вектора, но и
по компонентам вектора w, то можно воспользоваться
полученной в § 1 формулой A.8), которая во введенных
здесь обозначениях перепишется в виде
Для каждого вектора ut?U определим точечно-мно-
точечно-множественное отображение
, щ-щ)
Подобно тому как это было сделано в § 4 гл. I, можно
поставить вопрос об отыскании неподвижных точек мно-
многозначных отображений W1(a)i W2(ui), Wz{ui) или о ре-
решении соответствующих им вариационных неравенств,
т. е. точек, удовлетворяющих условиям
D.3)
tt,)), f{*iL ui9 tt)—
-f(xi9 ui9 /f)»0 VW/ef/, D.4)
Va,€?/. D.5)
Если «,. ^ W*, то выполнимость условий D.4) является
дискретным аналогом принципа минимума Л. С. Понтря-
гина (см. § 8 гл. I). Условие D.3) выражает это же свой-
свойство, но в пространстве состояний. Условие D.5) является
дискретным аналогом линеаризованного принципа мини-
минимума.
Исходную задачу D.1) о численном отыскании мини-
минимума сложной функции Ь (zq) по и{ ? U заменим нахожде-
нахождением векторов, удовлетворяющих каким-либо из условий
D.3)—D.5). Прежде, однако, сформулируем условия, при
которых такая редукция оправдана.

316 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
2. Необходимые и достаточные условия минимума.
Пусть
Обозначим
A(a) = /?(*(o))f w)-R(x(w.)9 w.) = B(h)—
где все составляющие полных векторов управлений w и wm
совпадают, за исключением f-й: у вектора w берется в ка-
качестве щ вектор иь у w4—вектор и}. Величина А, таким
образом, представляет приращение целевой функции R при
замене управления и\ на щ.
Теорема 6.4.1. Пусть функция В (а) определена на
открытом множестве, содержащем Q, и существует
такая точка u^U, что функция В (а) дифференцируема
в точке а = а(и?). Тогда:
1) если ut€Wm и множество Q выпукло, то имеют
место условия D.3) и D.4);
2) если В (а) псевдовыпукла в а относительно Q и либо
в точке а выполнено условие D.3), либо в точке ut вы-
выполнено D.4), то a?Q«, u{^W%;
3) если функция В (а) выпукла на п, то для любых
a^Wxia), ui^W^^i) имеют место неравенства
0<Д(а)<<р,+1(а), а-а>> _ D.6)
О < А (Ь) < Н (*„ li% ti9 pi+1 (а {щ)))—
-H(xi9 Щ,Ь9р»г(а{щ))). D.7)
Первое утверждение является необходимым условием
минимума в задаче D.1). Его доказательство проводится
точно так же, как была доказана теорема 1.4.1. Второе
свойство, дающее достаточные условия минимума в за-
задаче DЛ)Э следует из аналогичного утверждения, приве-
приведенного в теореме 1.4.3. При этом используется следую-
следующая формула, вытекающая из дифференцируемости функ-
функции В (а) в точке а:
B(a)—B(a) = <pL+1(a), a-5>-Ha-a|]a(a, a—a), D.8)
где lima (a, a—a) = 0.

$4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 317
Если функция В (а) выпукла, то, согласно теореме
1.2.5, для любого a?Q имеем
Взяв в этой формуле в качестве а вектор a*?Q*, полу-
получим, что для любого а ? Wx (a)
Д (а) = В (а)—В (а*) < <р?+1 (а), а— а,> < <pi+1(a), a—a>
Мы пришли, таким образом, к D.6); если правую часть
этой формулы выразить через функцию Н, то получим
Необходимое условие теоремы о справедливости D.3)
можно назвать дискретным принципом минимума в про-
пространстве состояний, а утверждение о выполнимости
D.4)—дискретным принципом минимума в пространстве
управлений. Аналогичные утверждения можно получить
относительно условий D.5). Для этого определим функцию
Теорема 6.4.2. Пусть сложная функция В(а(и())
от и( определена на открытом множестве, содержащем
U и существует точка Я/ ? С/ такая, что функция
В (а (и;)) дифференцируема в и{. Тогда:
1) если Ui?Wm и множество U выпукло, то имеет
место D.5);
2) если Ui€W*t множество U выпукло, ^(и(, щ) —
псевдовыпуклая функция и( в точке ut относительно U,
то в точке щ выполнено условие D.4), а в точке а = а (и() —
условие D.3);
3) если в точке и{ выполнено либо условие D.4) и U
выпукло, либо D.5), и в ut функция B(a(ui)) псевдовы-
пукла по и{ относительно U, то ut ? W%;
4) если В (а^щ))—выпуклая функция щ на U', то для
любых и( ? Н?3 (й() имеет место оценка
0<ДE)<?*,</.(**. и„ *?)р|+1(а(и?)). щ-гщ>. D.9)

318 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Докажем первое утверждение. Из дифференцируемости
сложной функции B{a{ut)) следует, что
= <#,(*„ ui9 tit
+ \и1—щЩщ, щ — щ),
где lim_P(u;, щ— ^ = 0.
Условие и{ ? W* означает, что функция В (а (иг)) до-
достигает в точке ut минимума по щ на U. Учтем выпук-
выпуклость U, воспользуемся теоремой 1.4.1. Тогда приходим
к выводу, что для любых и( ? U должно иметь место не-
неравенство
т. е. выполняется условие D.5).
Докажем второе утверждение. Используя дифференци-
руемость функции ^(и{, и() по щ в точке и{ = и{, пере-
перепишем неравенство D.10) следующим образом:
Здесь дифференцирование ty(uiy ut) производится по вто-
второму аргументу. Но из свойства псевдовыпуклости функ-
функции я|)(а|, ид тогда следует, что
<F(xh uif tj), р,+1(ай))> = ^й, п,)<ФЙ. Щ)- DЛ1)
В силу произвольности вектора u^U, приходим к вы-
выводу, что имеют место условия D.3) и D.4).
Докажем третье утверждение. Пусть щ удовлетворяет
D.4), тогда для любых u(^U выполнено D.11). Из усло-
условия минимума ^(ио и() по и{ на выпуклом множестве U
получим, что для всякого щ ? U имеет место неравенство
о<(*^ .«,-«,) =
= <Hu(xh п„ tt, p,+1 (a(«,))). Щ—Щ>,
т.е. выполнено D.5). Из псевдовыпуклости В(а(«,)) по
щ получаем, что и,- ? W«.

§4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 319
Неравенство D.9) получается точно так же, как было
доказано D.6). Щ
Опуская условия непрерывности и дифференцируемости,
можно резюмировать утверждения, приведенные в послед-
последних двух теоремах, следующим образом:
если щ 6 W*> то для выполнимости в этой точке D.4)
достаточно либо выпуклости множества й, либо псевдо-
псевдовыпуклости H(xiy uiy th /?/+1 {a(ui))) по ui в точке ui = u?
относительно выпуклого множества U;
если в точке u^U имеет место D.4), то для выпол-
выполнимости условия u(?W* достаточно, чтобы либо функция
В (а) была псевдовыпукла в точке а = а (и;) относительно й,
либо функция В (а (щ)) была псевдовыпуклой по и{ в точ-
точке щ относительно выпуклого множества U.
При обосновании необходимых условий минимума тре-
требование о выпуклости Q можно не вводить, если вариа-
вариационные неравенства трактовать локально. Например,
вместо условия D.4) потребовать выполнимость неравенства
<Pt+i(a(ut))9 /(*?, ui9 *,)-/(*„ Ъ> *;)»0
для всех векторов иь принадлежащих U и лежащих
в достаточно малой окрестности точки щ. Утверждение
о том, что для дифференцируемой функции В (а) из усло-
условия u{GW* следует приведенное неравенство, называется
локальным принципом минимума в пространстве управ-
управлений. Не будем приводить формулировок теорем о спра-
справедливости локальных принципов минимума, так как они
аналогичны утверждению теоремы 1.4.2.
3. Принцип квазиминимума. Сравним принцип мини-
минимума, сформулированный в § 8 гл. I, с результатами
предыдущего пункта. Обоснование принципа минимума
для системы дифференциальных уравнений A.1) не тре-
требует введения условия выпуклости множества Q, в то
время как для дискретных задач оптимального управле-
управления это условие оказывается весьма существенным. Не-
Несложно привести примеры, в которых нарушение выпук-
выпуклости множества Q приводит к тому, что дискретные
принципы минимума в пространстве управлений и состоя-
состояний оказываются несправедливыми. Вместе с тем ясно,
что, взяв в численных схемах интегрирования системы

320 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. V
A.1) достаточно малые шаги интегрирования, можно при
весьма общих предположениях получить сколь угодно
точную аппроксимацию решения исходной системы A.1);
незначительно при этом должны отличаться и свойства
полученных решений. Кажущееся противоречие легко
устраняется, если дискретным принципам давать иную
трактовку, идея которой была высказана в работе
Р. Габасова и Ф. М. Кирилловой [1].
Покажем, что приближенно выполняемые дискретные
принципы минимума имею* место без предположения
о выпуклости и они выполняются тем точнее, чем меньше
шаг интегрирования исходной системы A.1). При этом
речь будет идти о принципе минимума в пространстве
управлений и состояний, так как линеаризованный прин-
принцип минимума для системы A.1) справедлив лишь при
выполнении условия выпуклости множества U.
В предыдущем пункте были введены множества W1(a),
W2{u(), которые можно представить следующим эквива-
эквивалентным образом:
{«/€*/: H(xi9 uh ti9 Л+1 (a (?,))) =
= minH(xi9 ui9 ti9 p,+i(fl
u.eu
Вместо этих множеств введем множества, которые полу-
получаются из решения аналогичных минимизационных задач,
но в них поиск минимума осуществляется приближенно,
с погрешностью, не превосходящей величины eh(:
D.12)
VI («/) = {«,• € U: Н (*„ щ, ttt pt+1 (a («,))) <
<min^(x/t й„ tt, Pt+i(a(ut)))+eh,}. D.13)
S.tV
Очевидно, что при любых е > 0 имеют место включения

§4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 321
Из D.13) следует, что если V/€ П7$ (п,), то Для любого
ut € U имеет место неравенство
#(*/. Щ> thPt+i(a(Ui)))^ff(x(,ut9 tl9 р1+1(а(щ))) + ^1{.
Верно и обратное утверждение: если это неравенство имеет
место для любых щ$и, то щ€№%{и{). Аналогичное
свойство следует из определения DЛ 2).
Введенное в D.12), D.13) произведение? еА/ связано
с тем, что если, например, неравенство, входящее в усло-
условие D.13), переписать в терминах системы A.2), то оно
примет вид
<A,min</(*/f
Отсюда, сокращая на А/, приходим к утверждению о том,
что Wl (ui) есть множество е-оптимальных точек в задаче о
минимуме скалярного произведения <f{xiy uh tt), Pi+1(a(ui))y9
т. е.
{Щ$их <f(xt9 ui% tt\ p/+1(aEf))><-
Теорема 6.4.3. Пусть MHO0fcecmeoQ = f(hi)
ограничено, функция В (а) определена на открытом мно-
множестве у содержащем множество Q, и существует такая
точка Ъ{ ^ W*, что функция В (а) дифференцируема в точ-
точке а = а(п{). Тогда для любого s>0 существует \ >0
такое, что при любом шаге интегрирования, удовлетво-
удовлетворяющем условию 0 < А/ < А/, имеют место следующие
утверждения'.
a?Wl(a)f — eh;^<pi+1(al a—a> Va?Q, D.14)
Щ € Wl (щ\ - е < <р,+1 (а (и,)), / (^ tt/t /,.)-
-/(*/. «?. W> Vtt/€t/. D.15)
11 ю Г

322 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ \.ГЛ. VI
Доказательство. В силу ограниченности множества
Q существует такое число d (диаметр множества Q), что
при любых uh щ^и выполнено условие ||/(*/, иь t() —
/(/ Щ U)\<
Для доказательства теоремы следует оценить разность
В (а)—В (а). Формулы Ньютона—Лейбница и Лагранжа
для этой цели не подходят, так как они справедливы
лишь в том случае, если множество Q выпукло. Чтобы
избавиться от этого условия, воспользуемся формулой D.8)
дифференцирования функции В (а). Из условия а?й»
следует, что для любых а?п имеет место неравенство
В(а)^В (а), которое с учетом D.8) можно записать в виде
<P/+i(«). a—a>>—ja—а\\а(а, а—а)^
^—(I а — а || • | ос (а, а—а)\.
Из свойства предела функции а (а, а—а) при
а—>а получим, что для любой величины отношения e/d
существует такое число б > 0, что \а(а9 a—a)\<e/d,
если только * *
Это неравенство будет иметь место при любом и{
если шаг интегрирования ht такой, что
D.16)
В этом случае
||а—а||- |а(а, а — а)\^.гк{.
Отсюда заключаем, что при любом hh удовлетворяющем
D.16), и при всех a?Q имеет место неравенство
— еА/<<р/+1(а), а—а>,
т. е. в точке a?Q выполнено условие D.14); переходя
в пространство управлений, получим D.15). Щ
Утверждение о справедливости D.14) можно назвать
дискретным принципом квазиминимума в пространстве
состояний, D.15)—дискретным принципом квазиминимума
в пространстве управлений.

§4j ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 323
Доказанная теорема дает объяснение тому, что при
решении многих практических задач оптимального управ-
управления можно, используя достаточно точную дискретную
аппроксимацию исходной системы A.1), вовсе игнориро-
игнорировать понятие дискретного принципа минимума и пользо-
пользоваться только принципом минимума, справедливым для
системы A.1). В книге Р. П. Федоренко [1], напри-
например, говорится, что из опыта численных расчетов «автор
не смог извлечь никаких реальных рекомендаций, которые
следовали бы из отличия дискретного принципа максимума
от принципа максимума для дифференциальных уравнений
и которые нужно было бы использовать в практических
вычислениях».
Необходимые условия минимума весьма полезны при
решении практических задач, так как позволяют «отсеять»
точки, которые не являются оптимальными. Наиболее
предпочтительными являются те необходимые условия или
их совокупность, которые дают возможность отбросить
наибольшее число ненужных точек. В этом отношении
теоремы предыдущего пункта содержательнее, чем теорема
6.4.3. Однако последняя теорема применима к существенно
более широкому классу задач. Прикладную значимость тео-
теоремы 6.4.3 можно несколько повысить, если ее применять
вместе с упомянутыми в п. 2 локальными дискретными
принципами минимума. При использовании, например,
необходимых условий минимума в пространстве управле-
управлений «подозрительными» на оптимальность будут точки
U;€Uy доставляющие с погрешностью ей/ минимум функ-
функции Я, причем среди них следует учитывать только те точки,
в которых достигается локальный минимум функции Я
по и{ на U.
4. Необходимые условия второго порядка. В некоторых
задачах выполнено условие
Я(*/. ui9 ti9 Pi+1(a(U;)))^H(xi9 ui% ti9
D.17)
для любых UfZU, IT/ ? Wm. Такие ситуации в теории опти-
оптимального управления называют особыми режимами. Подобно
тому, как это делалось в § 4 гл. I, можно получить
необходимые условия минимума и в этом случае. Если

324 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 1ХЛ. VI
функция В (а) дважды дифференцируема в точке а, то
имеет место формула
В(а)-В(а)=
+ja—afP(a, a—a), D.18)
где lira p(a, a—a) = 0.
Воспользуемся введенными в § 1 обозначениями:
- db{xq(a)) dB{l) db (x9)
da
d*B(a) n d*b(xq)
da2 • *~~~d^~
Векторы pi и матрицы Р{ определяются из рекуррентных
соотношений, приведенных в § 1. Условие особого режима
D.17) в пространстве состояний перепишется следующим
образом:
Из этого условия и D.18) следует, что если a?Q« и мно-
множество Q выпуклое, то необходимо выполнение следую-
следующего неравенства:
(a—a)T Pi+1{a) (а—а) > 0 Va 6 &
Так же, как это делалось при определении линеаризован-
линеаризованного принципа минимума, за основу можно взять функцию
В(а(щ)) от и? и особым режимом назвать тот случай,
когда
xif Hh ih pi+1 (й;))
для любых Ui?U, ~Ui?W%. Если В (а {щ))—дважды диф-
дифференцируемая функция щ в точке щ = uh выполнено усло-
условие D.19), то необходимо, чтобы для любых u^U имело
место неравенство

§4]
ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА
325
где матрица вторых производных вычисляется по фор-
формуле A.12). Аналогичным образом можно получить необ-
необходимые условия более высоких порядков.
5. Учет интегральных функционалов. Все приведен-
приведенные результаты легко обобщаются на случай, когда функ-
функция R зависит явно не только от терминального фазового
вектора xqy но и от промежуточных значений xt. Пусть
R (х (ш), w) = Ь (xq) + |J С (г,). D.20)
Расширим фазовый вектор, введя дополнительную фа-
фазовую переменную хп+1. Положим
' }
Расширенному фазовому вектору соответствует расши-
расширенный вектор-импульс^. = [/?,-, р*+1], у которого вектор pt
определяется по формулам A.4) и A.7), последняя коор-
координата есть
Pi ^р—^1- "&f^" (
Производная функции R по xi равна
dR
dR-
dxt
dR
= [
Производная функции R по щ имеет вид
и совпадает, таким образом, с A.8).
Ставится задача минимизации R(x(w,w)) по составляю-
составляющей щ вектора w. Для этого R представляется как слож-
сложная функция расширенного вектора
R(x(w)9 aO = B(a) = B(fl(n/)), D.24)
D.25)

326* ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Считаем, что функции, определяющие задачу, диффе-
дифференцируемы по х. Тогда для всякого вектора щ ? U из
A.5), A.7) и D.22) однозначно определяется последова-
последовательность «расширенных» импульсов р^, р^, •.., р/+1.
Учитывая это, будем писать
Pi+i = Pi+i(a) = pl+1 (а (щ)) = [pi+i (а (и,)), 1].
Введем обозначения, близкие к использованным:
Wm = Arg min В {а («,)),
i
Wx (a) = Arg'min <jt>,.+1(c), a—ay,
fl€Q
in <Я-+1 И"/)). а(«/)—а(«;)>.
Здесь U~d(U)—образ множества (/.
Дальнейшие рассуждения и формулировки теорем почти
дословно повторяет приведенные выше. Условие выпук-
выпуклости множества Q заменяется требованием выпукло-
выпуклости Й. В частности, необходимое условие минимума в про-
пространстве управлений D.4) примет вид: если и* ? Wmy то
для любых ui € U имеем
, uU tt)), F{xi9 ui% tt)-F(xi9 ul
+ C(xh uit ti)-
Аналогичное обобщение можно дать условиям D.3)
и D.5).
6. Учет фазовых ограничений. Вектор w считаем по-
прежнему фиксированным, за исключением его i-й составля-
составляющей щ, которую следует определить таким образом, чтобы
управление ut принадлежало ?/, были выполнены усло-
условия B.3) и функция R1{x{w), w) = b1(zq) принимала бы
наименьшее возможное значение. Предполагается, что
множество решений этой задачи Wm не пусто. Полный
вектор управлений wf у которого в качестве и{ взят век-
вектор и\^ W%, будем обозначать а/*; у вектора w все состав-
составляющие совпадают соответственно с составляющими w09 за

§4] ДИСКРЕТНЫЕ ПРИНЦИПЫ МИНИМУМА 327
исключением /-й, равной и(. Введем вспомогательную
функцию R, аналогичную A.6.25):
R(x, w) = \ib1(zq) + <u, g(xt w)>+<v, h(x, w)>. D.26)
Здесь \i?El+i u€Ee> v?E%. Обозначим
Тогда функция R (x, w) совпадает с рассмотренной выше
функцией D.20), благодаря чему можно воспользоваться
формулами и обозначениями D.21)—D.25).
От минимизации в пространстве управлений перейдем
к минимизации в пространстве состояний, тогда вектор
xi+1 следует подобрать из множества Q = a (U) таким, чтобы
функция R(x(w), w) принимала наименьшее значение и
были выполнены условия B.3); из них существенными
будут только следующие:
= 0, Г» (а,
где xi+2t xi+8, ..., xq—сложные функции вектора a — xi+1.
Тем не менее сохраним форму записи вспомогательной
функции D.26), включив в нее учет и несущественных
ограничений. Воспользуемся общей теоремой 1.7.6. Со-
Согласно формулам D.22)—D.25) условие A.7.24) запишется
в виде
-
Или, переходя в пространство управлений, получим
/f «„ t{)-F(xl9 ul
x/f uh tt)-T*(xit и , <?)> Va,6?/. D.27)

328 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Используя линеаризованный принцип минимума, получим
<Fa(xh uh tdPi+i(F(xh и], tt)) + Tlu(xh uh tt)ut +
xif ul tt)vt9 щ—и\»0 Уи(еи.
Аналогичным образом можно перенести остальные
утверждения теорем 6.4.1 и 6.4.2 на рассматриваемый
случай.
Теорему 1.7,6 можно переформулировать следующим
образом:
Теорема 6.4.4. Пусть Q—выпуклое множество,
внутренняя часть которого не пуста. Минимум сложной
функции Ъх(zq) no ut?U с учетом ограничений B.3) до-
достигается в точке и* ? Wm; функции, определяющие задачу,
непрерывно дифференцируемы по компонентам вектора х.
Тогда существуют такие \л?Е\, и{, v^O, не равные
нулю одновременно, что для любых и{ ? И имеет место
неравенство D.27) и выполнено условие дополняющей не-
нежесткости
uh *,) = 0. D.28)
Учитывая допустимость вектора w* и условие D.28),
запишем неравенство^.27) в виде
0«P,+i(F(*,, ti*, *,)), F(xl9 щ, t()-
-F{xiy ul ф + <щ9 P(jf/f щ, tt)> + <vl9 T*(xi9 ui9 ф.
Если множество U открытое, функции, определяющие
задачу, дифференцируемы по иь то, согласно теореме 1.3.1,
из D.27) следует
Fu{xt, и], ti)pi+1(F(*i> ul </)) +
+ ri(xi9 ul tifui + TKx;, ul № = 0.
Если рассматриваемая задача является задачей выпук-
выпуклого программирования, то найденные условия являются
одновременно и достаточными условиями минимума. §j
7. Некоторые обобщения. Всюду в этом параграфе
все составляющие вектора w были фиксированы, за исклю-
исключением щ. Такой прием существенно упростил изложение.
Все результаты легко переносятся на тот случай, когда
изменяется весь вектор w. Изложение проведем конспек-

§ 5J МЕТОДЫ, ОСНОВАННЫЕ НА ПРИНЦИПАХ МИНИМУМА 329
тивно, используя обозначения, по возможности близкие,
к введенным в п. 1. Условие допустимости вектора управ-
управлений w = [uu u2, ..., uq] состоит в том, что все u^U.
Каждому вектору w в силу A.2) соответствует полный
фазовый вектор а=[х19 х29 ..., xq]. Эту зависимость будем
обозначать a = a(w)f пусть Q—объединение всевозможных
полных фазовых векторов, соответствующих всевозмож-
всевозможным допустимым управлениям. Минимизируемая функция Ь
зависит явно от xq и неявно от других компонент век-
вектора а 6 ?2, поэтому можно использовать прежнее пред-
представление Ь (хй) = В (а), вкладывая в него новый смысл.
Если вектор-функция / дифференцируема по xh функ-
функция Ь—по xqy то, согласно формулам § 1, функция В (а)
дифференцируема по а, имеет место формула
, а—а)+\а—а\а(а, а—а) =
a), *j—*/>+|а—о|<х(а, а—а).
Обозначим Q* = Argmin В (а). Если множество Q выпук-
выпуклое, a?Q%f то необходимо, чтобы для всех а?й имело
место неравенство
IdB (а) Л
da ' "
Аналогичным образом можно перенести полученные выше
результаты на полные векторы w и а.
Несложно показать, что. результаты этого параграфа
переносятся и на случай интегрирования системы A.1)
по схеме Рунге—Кутта. Формулы при этом получаются
более громоздкими, поэтому здесь не приводятся.
§ 5. Численные методы, основанные
на использовании дискретных принципов минимума
Дискретные принципы минимума позволяют построить
ряд численных методов отыскания точек из множества Wm,
определяемого условием D.1). Эта задача является вспо-

330 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
могательной при реализации многих методов, описанных
в § 3 и предназначенных для решения задачи дискретного
оптимального управления.
Воспользуемся обозначениями, введенными в п. 1 § 4.
Задачу минимизации b (zq) по ut ? U можно заменить
поиском неподвижных точек многозначных отображений
W1(a), W2(u{), Ws(u{), т. е. точек, удовлетворяющих
соответственно условиям D.3)—D.5). Несложно в терми-
терминах исходной задачи сформулировать требования, гаран-
гарантирующие выполнимость условий теоремы Какутани, даю-
дающей достаточные условия существования неподвижных
точек (см. Приложение III). Для простоты рассмотрим
точечно-множественное отображение Wx{a).
Лемма 6.5.1. Пусть функция В (а) непрерывно диф-
дифференцируема и выпукла на открытом множестве, содер-
содержащем выпуклое, компактное множество Q, тогда много-
многозначное отображение Wx (а) имеет неподвижную точку ащ,
в которой имеет место D.3), множество прообразов
точки аф принадлежит W%.
Действительно, при каждом а ? Q множество Wx (а) не
пусто, выпукло, компактно и содержится в й, поэтому,
согласно теореме Какутани, Wx имеет неподвижную точку.
Вектор pi+1 является градиентом функции В по xi+l9
поэтому применявшаяся в определении множества Wx(a)
минимизация скалярного произведения <pi+u *,+i> no
xi+1?Q при фиксированном векторе р1+и есть, по су-
существу, минимизация линеаризованной функции В. Здесь
возникает связь с методом условного градиента, описан-
описанным в § 4 гл. V.
Будем предполагать, что функция В дифференцируема
по xi+1, при всех и\ € W* выполнен дискретный принцип
минимума. Пусть на k-ы шаге итеративного процесса ми-
минимизации В по и{ известен вектор и\ и соответствующие
ему векторы р^+1, xj+1. Опишем несколько вычислитель-
вычислительных процедур, реализующих метод условного градиента.
Определим вспомогательный вектор xi+1 из условия
min <pf+1> */+1>. E.1)
Q
Обозначим dk = xi+1—x$+l9 в(*?+1) = </#+1,^>. В силу E.1)
fi(?)^0 Считаем, что Q выпукло, замкнуто.

§ 5] МЕТОДЫ, ОСНОВАННЫЕ НА ПРИНЦИПАХ МИНИМУМА 331
Найдем минимум функции B(xi+1) на отрезке, соеди-
соединяющем точку х\+х и xi+u получим
Tft6Arg min B(xUi+tdk). E.2)
0<т< 1
После этого определим новый вектор
Найдем соответствующий ему градиент р^%\ и т. д. По-
Последовательность {B(xf+1)\ при этом монотонно убывает.
Действительно, если 6(#*+i)<0, то имеем
В (х?+1 + т^) = В D
Поэтому по крайней мере при достаточно малых т>0
выполнены неравенства
Если 8(я*+1) = 0, B(xl+1) псевдовыпукла, то для всех
#i+i€^ выполнено условие B(Xi+1)^B(xi+1). Таким
образом, в точке xf+1 достигается минимум В на Q и про-
процесс минимизации на этом прекращается.
При реализации описанного подхода приходится решать
задачу E.1) о минимизации линейной функции на мно-
множестве Q и после этого определить управление щ, обеспе-
обеспечивающее переход системы A.2) из точки х( в х*Х\. Струк-
Структура множества Q может оказаться весьма сложной, что
затруднит решение E.1). Проще перейти от описанной
минимизации в «пространстве состояний» к минимизации
в «пространстве управлений». Вместо E.1) будем отыски-
отыскивать
= Arg min
E.4)
Далее положим xi+1 = F (xif uiy t{). По формулам E.2) и
E.3) находим д#JJ, соответствующие ему хк и управле-
управление и\+1. Оба варианта метода порождают одну и ту же
последовательность {Xi+1\ (при условии однозначной раз-
разрешимости задач минимизации), но численно реализовать
версию «в пространстве управлений», как правило, проще.
Для обоснования, напротив, удобнее использовать «про-
«пространство состояний».

332 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
* Третью версию метода можно построить на основе
дискретного линеаризованного принципа минимума. Управ-
Управление ukt+1 будем определять из условий
|(^ ) E.5)
u E.6)
g ((
0<Т< 1
$" = и\ + чк{щ-и?). E.7)
Очевидно, что в этом случае значения функции В на каж-
каждой итерации также монотонно убывают.
Используя результаты § 4 гл. V, легко сформулиро-
сформулировать и доказать сходимость всех описанных схем, поэтому
ограничимся лишь теоремой о сходимости первой версии.
Теорема 6.5.1. Пусть функция В {а) непрерывно
дифференцируема и псевдовыпукла (относительно Q) на
открытом множестве, содержащем выпуклое, компактное
множество Q, градиент функции В (а) удовлетворяет на
Q условию Липшица. Тогда множество предельных точек
последовательности {**+i} не пусто и состоит из точек
Х{+и в которых имеет место D.3), причем соответствую-
соответствующие им управления таковы, что и{ ? W7*.
Если упростить реализацию метода условного градиента,
отказавшись от поиска шага тА, и всегда считать, что
т = 1, то получим следующие методы:
E.8)
E.9)
и?+1€^,(и?). EЛ0)
Эти модификации не приводят к монотонному убыванию
последовательных значений минимизируемой функции, фак-
фактически в них осуществляется поиск неподвижных точек
соответственно точечно-множественных отображений Wl9
W2 и W8 с помощью метода простых итераций. Для таких
задач метод часто оказывается расходящимся.
Если дискретные принципы минимума справедливы
для любых ?, то описанные методы можно использовать,
изменяя управление одновременно для всех i?[liq—l].
Очевидно, что все приведенные результаты переносятся

§6] НЕКОТОРЫЕ ОБОБЩЕНИЯ 333
на этот случай. Такие схемы минимизации Rnow позволяют
«расщеплять» исходную задачу на решение большого числа
задач минимизации по векторам Гнизкой размерности и[9
после этого выбирать каким-либо способом числа xk. Опи-
Описанные схемы привлекают простотой расчетов, однако если
начальное управление известно весьма неточно, они схо-
сходятся медленно, методы E.8)—E.10) часто расходятся.
Поэтому вначале ведется минимизация R по w каким-либо
методом безусловной минимизации и только после этого
происходит обращение к приведенным процедурам.
Если процесс E.9) применить к системе A.1), то он
совпадает с методом, предложенным И. А. Крыловым и
Ф. Л. Черноуеько [1]. Для* устранения часто возникаю-
возникающей расходимости метода в книге Ф. Л. Черноуеько и
Н. В. Баничука [1] было предложено ut определять из
E.4), а хк и uf+1—из E.6) и E.7). Сходимость такой
процедуры в случае, когда и(, получаемое из E.4), отли-
отличается от получаемого по правилу E.5), нуждается в спе-
специальном обосновании.
Заметим, что «расщепление» задачи о минимизации
функции R по вектору w можно осуществить и без исполь-
использования дискретных принципов минимума. Действительно,
проведем покомпонентную минимизацию b(zq), решая
последовательно для 1 = 1, 2, ..., q—1 задачи миними-
минимизации b(zq) по и(. Применим, например, метод проекции
градиентов в пространстве состояний и в пространстве
управлений, получим следующие численные схемы:
АХ\ = nQ (xf+1—xkpi+1 (xUi))>
uht+1 = Пи№—чНа (*/. «*. tl9 Pi fl {a(u})))].
Здесь nx(x)—проекция* вектора х на множество X. Обо-
Обоснование сходимости и свойства метода следуют из резуль-
результатов § 5 гл. V.
§ 6. Некоторые обобщения
Изложенный выше подход пригоден для решения задач
значительно более общего вида, чем это было описано.
Укажем основные возможные обобщения, используя для
простоты дискретную аппроксимацию системы A.1) по
схеме Эйлера.

334 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
1. Оптимизация по управляющим параметрам. Поста-
Постановка этой задачи для систем, описываемых обыкновен-
обыкновенными дифференциальными уравнениями и содержащих
управляющие параметры, дана в § 8, гл. I. Воспользуемся
дискретной аппроксимацией системы A.8.10):
, u(, t{, l) = F(xiy uiy tiy I). F.1)
Критерием качества управления является функция
R(x(w)y w, 6) = &(*«, uv /«, 6) + Д] Л,В(х„ uh th g).
Следует подобрать полный вектор управлений w и вектор
управляющих параметров g так, чтобы функция R прини-
принимала возможно меньшее значение. Считая, что зависимость
всех функций, определяющих задачу, от g дифференци-
дифференцируема, и используя рассуждения § 1, получим следующую
формулу для вычисления производной R по g:
dR
*i = [*t, »i> hi F.2)
здесь H(zh pi+1, l) = htB{zh \)±<F{zh 6), pi+1>. Необ-
Необходимым условием минимума является
Это условие можно получить и непосредственно из A.8.11).
Формула F.2) позволяет вычислить градиент функции R
по ?, что дает возможность применить к отысканию опти-
оптимального вектора \ тот же подход, что был использован
ранее для определения вектора w. Объединим вектор
управлений и вектор управляющих параметров единым
символом, положив w =[ш, |]. Далее процесс минимизации
R осуществим по расширенному вектору w. Таким обра-
образом, нет принципиального различия между оптимизацией
по вектору управляющих параметров и по полному век-
вектору управлений. Вместе с тем при численной реализации
такого процесса иногда возникают трудности, связанные
с «разномасштабностью» векторов w и ?. Эти векторы имеют

§6] НЕКОТОРЫЕ ОБОБЩЕНИЯ 335
обычно разный физический смысл и степень их влияния
на функцию R различна. Поэтому важно бывает проводить
специальное масштабирование вектора ?. Во многих слу-
случаях оказывается также полезным на отдельных этапах
расщеплять процесс минимизации R по до и |. Вначале
обычно проводится минимизация R по ? и только после
этого осуществляется минимизация по полному вектору до.
Вектор управляющих параметров можно вводить в си-
систему искусственно. Например, когда интервал движения
Т велик или от схем численного интегрирования си-
системы A.1) требуется большая точность, приходится исполь-
использовать малый шаг интегрирования, что приводит к высокой
размерности вектора до. В таких случаях управление ищется
в виде программы или синтеза:
и @— Tiff» О» и(/) = 7а(*@» ?• О»
Введенные функции уг и у2 зависят от t и вектора управ-
управляющих параметров. Подставив эти формулы в правую
часть системы F.1), сведем исходную задачу к оптимиза-
оптимизации только по вектору управляющих параметров. При
переходе к дискретной аппроксимации такой прием позво-
позволяет уменьшить размерность вспомогательных задач безу-
безусловной минимизации.
2. Задача с неполностью определенными начальными
условиями. Для системы A.2) часть координат начального
вектора хх может быть не задана. Доопределим A.2),
введя один дополнительный фиктивный шаг x1 = h0%9 вос-
воспользуемся формулой A.4), получим
i^ —JELi^L — A п
Снова найден градиент, далее расчеты можно вести обыч-
обычным образом, изменяя недостающие компоненты вектора хх
и улучшая полный вектор управлений w.
Полученную формулу можно использовать для решения
краевых задач, реализуя при этом метод Ньютона. Дей-
Действительно, пусть полный вектор управлений до фиксиро-
фиксирован. Векторы хг и хй состоят из двух векторов хх =
=[*i, *J, xq = [^, ?j, где х19 xq € ?v,3, хп € En'v9 причем
векторы хх и хя заданы, векторы хг и xq неизвестны.

336 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Задав произвольный вектор xlf проинтегрируем A.1) по не-
некоторой схеме и определим соответствующий вектор хг
Таким образом, существует некоторая функциональная за-
зависимость xq = ф (*х), где ф осуществляет отображение Ev
в Ev. Задача состоит в отыскании такого вектора let, что
Метод Ньютона приводит к следующей вычислительной
схеме:
-*,)• F.3)
Здесь Ак—матрица vxv первых производных вектор-функ-
вектор-функции ф (*!*), у нее /-я строка состоит из компонент вектора
d<p/ (xS) __
\ ]
dxx L dx\ dxt dxX J
Элементы матрицу Ak можно вычислить, воспользовавшись
результатами § 1. Для этого возьмем в качестве функции R
/-ю компоненту вектора xlf. Тогда, согласно A.5), вектор
импульсов pq будет иметь все компоненты, равные нулю,
за исключением /-й, равной единице. Из рекуррентного
соотношения A.7) определим вектор рх. Первые vero ком-
компонент, соответствующие xlf объединим и обозначим рг g Ev.
Из результатов § 1 следует, что
Pi
Проделав такие вычисления для /=1, 2, .. ., v, вычис-
вычислим все элементы матрицы Ak. Для этого потребуется
v раз просчитать рекуррентное соотношение A.7). После
этого можно сделать один шаг по методу Ньютона F.3).
При численной реализации этого процесса возможны опре-
определенные осложнения, связанные с расходимостью. Это
обычно бывает, если начальное приближение для вектора хх
известно грубо. Поэтому вначале используются градиент-
градиентные схемы отыскания хх и только после этого делается
переход к методу Ньютона.

§6] НЕКОТОРЫЕ ОБОБЩЕНИЯ 337
3. Задача с нефиксированным временем. Требуется для
системы A.2) найти полный вектор управлений w9 интер-
интервал движения [0, tq] так, чтобы функция R вида A.3) в ко-
конечный момент Т принимала наименьшее возможное зна-
значение.
Зададим и фиксируем последовательность шагов инте-
интегрирования hly А2, .••, Ла_!. Интервал движения будет
изменять с помощью масштабирующего числа ?. Так же,
как в § 8 гл. I, введением дополнительной фазовой пере-
переменной, превратим систему в автономную, сделаем замену
независимой переменной t = r^. Переменная т изменяется
в интервале [О, Г0], где %>Т0= 2 ht\ переменная /—в ин-
интервале [О, Т], где Т = Т0. Дискретной аппроксимацией
системы A.8.18) по схеме Эйлера будет
Минимизируемая функция A.3) запишется в виде
R = b(xr uv ^+1) + g 2J ЛД(х„ uh x?+1). F.5)
Для системы F.4), имеющей стандартный вид F.1), оты-
отыскивается полный вектор управлений w и управляющий
параметр !• такие, что функция R принимает наименьшее
возможное значение. Применим формулу F.2) к систе-
системе F.4), получим
F.6)
Условия на правом конце имеют вид
_ db (*„, uq, tq) n+i _ дЬ (

338 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Отсюда следует, что
+ <ft (*,. Us* *?+1)> Ps + l>l 1 < t < (/- 1.
Формула F.6) упрощается, если исходная система A.1)
автономная, функция В не зависит явно от t:
^(*«, uv tq).
Очевидна связь этого результата с A.8.20). Полученные
формулы позволяют строить градиентные методы миними-
минимизации по параметру ?, отыскивая тем самым величину
оптимального интервала движения Т.
4. Задача на быстродействие. Требуется найти полный
вектор управлений w и соответствующее ему решение
системы A.2), так, чтобы выполнялись условия B.3),
интервал движения был наименьшим.
Воспользуемся • представлением F.4), но, в отличие
от F.5), минимизируемой функцией будет R1 = Xg+1. Сле-
Следуя B.5), составим функцию Лагранжа
Я = *2+1 + <«, g(x, w)> + <v, h(x, w)>.
Условие F.2) для данной задачи примет вид
Условия на правом конце следующие:
Для автономной системы, в частности, получим
6 1=1
5. Учет недифференцируемых функций цели. Среди
практических задач часто встречаются случаи, когда функ-
функции цели недифференцируемы, например
т
=o max^<р(*(/), 11(9, 0, Я. = $|Ф(*(О, u(t)t t)\dt.

§ 6] НЕКОТОРЫЕ ОБОБЩЕНИЯ 339
Несмотря на то, что ср—дифференцируемая функция своих
аргументов, функционалы Rx и R2 дифференцируемы лишь
по направлению. В первом случае введем дополнительный
управляющий параметр g, по которому будем проводить
минимизацию и новое ограничение, положив
*i = E, ф (*('), «@, 0<6.
Во втором случае введем новое управление u(t) и два
дополнительных ограничения, положив
т
Я, = $«(/)Л,-Ф(*(*), «('). 0<«@>ф(*@.«@,').
о
Минимизация ведется по u(t) и u(t). Задачи в обоих
случаях сведены к стандартному виду. Недифференцируе-
Недифференцируемость, связанная с функционалами, устранена и все опи-
описанные выше методы могут быть использованы без каких-
либо дополнительных модификаций. Аналогичным образом
можно преобразовывать простейшие минимаксные задачи
(см., например, Э. Г. Давыдов [1]).
Приведенные преобразования имеет смысл выполнять,
если все функции, определяющие задачу, кроме Ry диф-
дифференцируемы по компонентам векторов х и и. В против-
противном случае нет необходимости избавляться от недифферен-
цируемых функций цели, расчеты приходится проводить,
применяя значительно менее эффективную технику, не
использующую дифференцирования.
6. Учет «параллелепипедных» ограничений. Во мно-
многих задачах оптимального управления существуют огра-
ограничения вида
0* <«/<*/. F-7)
Если для решения задачи применять методы, основанные
на использовании вспомогательных процедур безусловной
минимизации, то ограничения F.7) нецелесообразно отно-
относить к ограничениям общего типа B.3). Их проще учесть
при решении задач безусловной минимизации. Действи-
Действительно, можно показать, что большинство из приведенных
в § 3 методов остается в силе, если в них вместо вспомо-
вспомогательных задач безусловной минимизации функции R
по w решать задачу о минимизации R по w на множест-
множестве F.7). Поэтому библиотеку программ безусловной мини-
минимизации следует составлять в двух вариантах: с учетом
ограничений вида F.7) и без их учета.

340 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
7. Учет «преемистости» управления. В некоторых за-
задачах оптимального управления накладывается дополни-
дополнительное ограничение на скорость изменения управления:
\
Если t{ и ti+1—соседние точки сетки интегрирования по t,
то в дискретном варианте приведенное ограничение пере-
перепишется в виде
Полученные два ограничения можно отнести к ограниче-
ограничениям Г2^0. При использовании формул § 1 для производ-
производных следует учесть дополнительные слагаемые в связи
с*тем, что здесь ограничения на f-м шаге интегрирования
зависят не только от ^, но и от ui+1. Заметим, что огра-
ограничения F.8) можно ввести искусственно для регуляри-
регуляризации задачи.
8. Задачи с разрывными правыми частями. Если
в системе A.1) вектор-функция f (х, и, t) дифференцируема
по лг, и всюду, кроме конечного числа точек {/у}, где
имеет место разрыв первого рода, то величины шагов А,
следует подбирать* так, чтобы все точки {/у} были в узлах
основной сетки по t. Приведенные в § 1 формулы остаются
без изменений. Аналогично, если в некоторых точках tt
из основной сетки по t фазовая траектория претерпевает
заданный разрыв, не зависящий от х и и, то формулы § 1
. для вычисления производных также не изменяются. Если
разрыв зависит от #, и, т. е. х (</+) = ф(х (<?_), и(<?)),
где *(/..+)= lim *(/)• *(^-)= lim x(t)y то вэтихточ-
t^t. + Q М^-О
ках следует производить пересчет импульсов. При опреде-
определении /??_! вместо Pi следует брать вектор tyx(x(timm)9
и (/z)) pi и в формуле вычисления производной -т-у доба-
добавить слагаемое tytt(x(//_), иA;))р;. Несложно учесть раз-
разрывы более сложного вида (см., например, В. В. Вели-
ченко [2], И. П. Ченцов [1]).
9. Учет запаздывания. Пусть управляемый процесс
описывается соотношениями

§7] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 341
где s—некоторое целое положительное число, причем л^,
x2-s> ..., хг заданы и фиксированы; отыскивается полный
вектор управлений
Проводя те же рассуждения, что в § 1, получаем, что для
* = 1, 2, ..., q—\ имеют место формулы
здесь 0(а, с) = 1, если а^.с, и 0(а, с) = 0 в противном
случае; кроме того,
Положив Pqz=:-fa-> по этим формулам последовательно
определим pqmml9 ^л-2» •••» Pi- Затем вычислим необходи-
необходимые производные /? по и{\
Здесь i#€[l—s: ?—1]» причем
Аналогичным образом можно учесть и более сложные виды
запаздываний. Важно, что во всех этих случаях можно
вычислить производные функции Ry приведя тем самым
задачу к виду, удобному для использования методов не-
нелинейного программирования.
§ 7. Примеры численных расчетов
Многие из приведенных выше методов были опробованы
при решении разнообразных тестовых и практических за-
задач. Ниже даются некоторые результаты расчетов, про-
проведенных на ЭВМ БЭСМ-6. Чтобы более четко проследить

342 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 1.ГЛ. VI
процесс сходимости, для решения вспомогательных задач
безусловной минимизации всегда использовался один и тот
же метод сопряженных градиентов.
1. Простейшая задача быстродействия (задача Цер-
мело). Постановка этой задачи приведена, например,
в статье У. Пауэрса и С. Шиха [1]. Управляемый про-
процесс описывается следующей системой дифференциальных
уравнений:
dxl , dx2
На управление наложено ограничение |()|,
задано также два терминальных ограничения: х1 (Т) = 4,
х2(Т) = 3. Функционалом является время движения, т. е.
R = T. Для определенности примем, что время измеряется
в секундах.
Задача имеет наглядную физическую интерпретацию.
Пусть х1, х2—декартовые координаты материальной точки,
которая перемещается по плоскости. Ее вектор скорости
. * по модулю равен единице и об-
* Л разует угол х3 с положительным
направлением оси ОХ1 (рис. 3).
В начальный момент ? = 0 век-
вектор скорости направлен вдоль
оси ОХ1, т. е. *3@) = 0. Требу-
Требуется перевести точку из начала
координат в точку с координа-
и х' *' тами [4,3] за кратчайшее время.
Рис. 3. Если под материальной точкой
подразумевать, например, авто-
автомобиль, то управлением можно считать угол поворота
управляемых колес, и ограничение |и(/)К0,5 имеет
простой физический смысл.
При переходе к численному решению задачи сделаем
замену независимой переменной, положив г = тТ. Тогда
система примет вид
Она интегрировалась при 0 < т < 1 по схеме Эйлера с по-
постоянным шагом, равным h = 0,02, что соответствует числу

§7]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ
343
точек дискретизации q = 5l. Полное время движения Т
становится управляющим параметром.
В качестве начального приближения были взяты
и0 (т) = 0, То = 3 с. Ограничение | и (t) | < 0,5 рассматрива-
рассматривалось как «параллелепипедное»—0,5^w(<)^0,5 (см. § 6)
и учитывалось в методе сопряженных градиентов. Все
расчеты проводились в диалоговом режиме с помощью
системы ДИСО.
Решение задачи начиналось с использования первой
версии метода параметризации целевой функции ОРТ45.
Необходимую для реализации метода нижнюю оценку
оптимального значения функционала в данной задаче полу-
получить легко. Кратчайшее-расстояние между точками [0, 0]
и [4,3] равно 5 и при единичной скорости преодолевается
за 5 секунд. Так как начальное направление вектора ско-
скорости совпадает с осью ОХ1, траектория и время движе-
движения будут больше этих значений. Нижняя оценка опти-
оптимального значения функционала То = Зс удовлетворяет
условиям применимости метода ОРТ45. Им делалось две
первые итерации, после чего счет продолжался методом
ОРТ53 (метод модифицированной функции Лагранжа).
В табл. 1 представлены значения функционала на соот-
соответствующих итерациях каждого метода. По окончании
Таблица 1
Метод
Номер итерации
Значение функ-
функционала
Метод
Номер итерации
Значение функ-
функционала
ОРТ45
0
3,00000
1
3,05383
2
4,51062
ОРТ53
1
5,12532
2
5,12416
3
5,12297
4
5,12284
5
5,12277

344 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
расчетов были получены следующие результаты: R = Tmz&
& 5,12277 с, хЦТ*)^ 3,99997, х* G,) = 2,99999, которые
можно считать оптимальны-
оптимальными с достаточно высокой сте-
степенью точности. Соответст-
Соответствующие управление и траекто-
траектория показаны на рис. 4 и 5.
5 t
Рис. 4.
Рис. 5.
Задача решалась также другим сочетанием алгоритмов:
сначала «отработал» метод ОРТ41 B итерации), а завер-
завершил расчеты метод ОРТ53 E итераций). Изменения функ-
функционала в этом варианте расчетов можно проследить по
табл. 2.
Таблица 2
Метод
Номер итерации
Значение функ-
функционала
Метод
Номер итерации
Значение функ-
функционала
ОРТ41
0
3,00000
1
4,61421
2
4,78960
ОРТ53
1
5,12230
2
5,12339
3
5,12277
4
5,12266
5
5,12265

§7]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ
345
0,5
5 t
Рис. 6.
Окончательные значения функционала и фазовых коор-
координат близки к приведенным выше: R = Тт = 5,12265 с,
xi (Г„) = 3,99998, х2 G,)=2,99999. Соответствующее управ-
управление представлено на рис. 6;
оно имеет явно выраженный
релейный характер: вначале
крутой поворот в направле-
направлении терминальной точки [4,3]
с максимально возможной
угловой скоростью, далее—
движение по прямой. Пере-
Переключение происходит в мо-
момент, когда вектор скорости
впервые оказывается направ-
направленным на требуемую точку
[4,3]. Хотя конечные резуль-
результаты в обоих вариантах рас-
расчетов очень близки, графики управлений имеют различия
в моменты, последовавшие за переключением. «Дефекты»
в график на рис. 4 внес метод ОРТ45. Дальнейшие рас-
расчеты по методу ОРТ53 лишь несколько уменьшили раз-
разницу между «пиками», но не устранили ее полностью.
Управление же на рис. 6 представляется более физически
правильным. Можно сделать два вывода: во-первых, схо-
сходимость по функционалу далеко не всегда предполагает
сходимость по управлениям, во-вторых, применение раз-
различных алгоритмов весьма полезно, так как позволяет
проводить конструктивный анализ и выбор наиболее просто
реализуемых управлений.
2. Простейшая задача с фазовым ограничением. Поста-
Постановка задачи заимствована из статьи Р. Мехры и Р. Дэви-
са [1]. Там же имеются и результаты численных расчетов.
Управляемый процесс описывается уравнениями
dx* „ dx*__ v2
G.1)
dt
dt
x1@) = 0,
Задача состоит в минимизации функционала
0,005м*] dt

346 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
при ограничении вдоль траектории
Система G.1) интегрировалась по схеме Эйлера с пере-
пересчетом с постоянным шагом h = 0,02 (q — 51). Управление
на интервале интегрирования считалось постоянным. В ка-
качестве начального приближения была взята функция
ио(*)=~О. Аппроксимирующая задача нелинейного про-
программирования состоит в минимизации функции 50 пере-
переменных при наличии 50 ограничений типа неравенства:
Стратегия поиска решения аналогична той, которая
применялась в предыдущей задаче, т. е. вначале было
сделано 3 итерации методом штрафных функций ОРТ413,
а последующие расчеты проводились по первому варианту
метода простой итерации ОРТ553. В табл. 3 показано,
Таблица 3
Метод
Номер итерации
Значение функ-
функционала
Метод
Номер итерации
Значение функ-
функционала
ОРТ413
0
0,600368
1
0,163748
2
0,166120
3
0,167267
ОРТ553
1
0,169152
2
0,169468
3
0,169487
4
0,169480
5
0,169480
как изменялся функционал R в зависимости от номера
итерации. Найденная оптимальная траектория х2 (t) и соот-
соответствующий закон управления и (t) представлены на рис. 7
и 8. Нижняя кривая на рис. 7 есть траектория х* (t) при
начальном управлении uo(t). Моменты «выхода» (/х = 0,3,
x2(t1) =— 0,179077) на фазовое ограничение и «схода»
(t2 = 0,7, х2 (t2) = — 0,179997) соответствуют довольно рез-

§71
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ
347
ким изменениям («изломам») на графике оптимального
закона управления u(t). В полученном решении задачи
некоторые ограничения не выполнены, максимальное нару-
нарушение max Г,- =3-10~4.
to
4,0
Рис. 7.
1ft
_| .
OJS
Рис. 8.
Эта задача решалась также с помощью программ ОРТ41
ОРТ53, ОРТ8, в которых система G.1) интегрировалась
по схеме Эйлера. В первой серии расчетов было сделано

348 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
3 итерации по методу ОРТ41 и 8 последующих итераций
по методу ОРТ53. При этом получено значение функцио-
функционала. /?«==0,181378 и max 1^ = 3-10-*. Во второй серии
расчетов сначала была.сделана одна итерация по методу
ОРТ41, в результате которой были вычислены прибли-
приближенные значения двойственных переменных, а также полу-
получены величины #, = 0,187064, max Г, = 3,3-10~2. Далее
применялась программа ОРТ8, реализующая метод Нью-
Ньютона, с помощью которой за 8 итераций были найдены
результаты, отличающиеся высокой точностью выполнения
ограничений. Было получено, что max Г,. = 1,4-102,
Л, = 0,181378.
Найденные управления отличаются от изображенных
на рис. 8 на величины порядка 10~5, и отразить это изме-
изменение на рисунке не представляется возможным. Поэтому
в табл. 4 приведены оптимальный закон управления и зна-
значения функции, определяющей ограничения, вычисленные
по формуле C.7).. Заметим, что именно в этой задаче реа-
реализуется случай, упомянутый в § 3 при описании про-
программы ОРТ8, когда функция Г явно не зависит от
управлений. Использовав программу ОРТ8, но с количест-
количеством шагов интегрирования ^ = 70, было получено R* =
= 0,17790. Таким образом, значение Rm приближается
к значениям, найденным при интегрировании системы G.1)
по схеме Эйлера с пересчетом. Наиболее точное решение
следует искать методом Ньютона, но с применением более
точных схем интегрирования, чем A.2). В настоящее время
мы еще не располагаем такими результатами. Приведен-
Приведенные расчеты по методу Ньютона убедительно показывают
его потенциальные возможности. Рассмотренная задача
может служить хорошим тестом для проверки численных
методов, и в этом качестве она использовалась в работах
Р. Мехры и Р. Дэвиса [1], а также С. Фуджи, X. Фуд-
жимото, М. Оно [1].
3. Задача о вертикальном подъеме ракеты. Эту задачу
без преувеличения можно назвать классической тестовой
задачей оптимального управления. Ее постановка и реше-
решение приводятся в работах Д. Е. Охоцимского [1], Т. М. Эне-
ева [1], в книге Р. П. Федоренко [1]. Управляемый
процесс описывается след) ющими дифференциальными

§7]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 349
Таблица 4
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
оо
62
оо
33
34
ос
35
ос
об
37
«1
l,30039810+oi
9,75600310+00
7,2997261о+оо
5,43452510+оо
4,008026,0 +оо
2,90367310 + 00
2,О312О71О + Оо
1,31929710 + Оо
7,09720010_oi
l,526038le-ei
-3,976422lo^oi
~9,86050410-oi
-1,66077110+Оо
-2,47700310+Оо
—3,472799ю+оо
—3,22000010 + оо
—2,96080010+оо
—2,695200! 0+оо
—2,42320010+ot
—2,144800i0 + oo
—l,860000io+oo
-~1,568800ю + оо
—l,271200l0 + oo
—9,672000iO-oi
—6,568000iO-oi
—3,400000io-oi
—lf6800001(>-e.
3,128000io-oi
6,488000i0-oi
9,912000io-oi
l,34000010+oo
I,695200i0+oo
2,056800! o+oo
2,424800i0+oo
2,799200ю+оо
2,63689210 + oo
1,937987! o + oo
—2,llo + oo
—l>71o+oo
— J^lO + oo
— 1 ,1ю+оо
-9,310-oi
—7,5lo-oi
-5,910..»
—4,5iO-oi
—3,3lo-oi
—2,2i0-oi
—1,4i0-oi
—7,3lo-o2
—2,5ю«02
—2,!lo-o8
—4,5iO-i3
—2,310-i.
0,010 + oo
0,0ю+ов
9,lio-"
9,lio-"
9,lio-"
9,lio-*«
9,1ю-"
9 lm-is
l,4iO-i*
9tlio—J8
9 lin-l»
9,1ю-»
9,lie-««
9,lio-13
9,lio-»
O,Oio+««
9,lio-»'
6,8io-i»
l.lio-"
—1 ,lio-°*
—4,Зю-°*

350 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ 1ТЛ. VI
Продолжение
i
38
39
40
41
42
43
44
45
46
47
48
49
50
Ч
1,4119491о+оо
1,01613410 + оо
7,18532910_,
4,95162510_
3,28105910_
2,04049810_(
1,13198310_<
4,84727810-
4,93433810_
-2,06192810,
—2,99150010_,
-2,33452910-<
о,оооооо10+(
>i
01
01
I
I
J
03
J
>2
2
>0
г*
—9,Зю-°*
—1,6ю-в|
-2,410-о1
—3,3lo-oi
—4,210-ei
—5,3lo-oi
—6,5lo-.oi
—7,710-oi
-9,010-о,
— 1,010 + оо
— 1,210+0о
— 1,310 + оо
уравнениями:
dx*
1
dt ~~ ' dt " » dt ~LK" ^ra^i e»
0 < / < 7\
где л:1^)—масса ракеты, отнесенная к начальной массе;
x2(t)~высота над Землей (км); xz(t)—скорость (км/с);
«(/)—расход массы в единицу времени (с); V = 2 км/с —
скорость истечения газов из сопла двигателя; q =
== 0,01 км/с2—ускорение силы тяжести, которое считается
постоянным; Q(x)—величина, характеризующая аэродина-
аэродинамическое сопротивление и определяемая формулой Q(x)=
=0,05 ехр (—0, 1л:2) (л:3J.
Начальное состояние ракеты следующее: х1 @) =
= 1 f х2 @)=0, хг @)=0. Продолжительность полета Т= 100 с,
конечное значение массы должно составлять 20% от на-
начального, т. е. х1 (Т) = 0,2. На управление наложено также
«параллелепипедное» ограничение 0 ^ и (t) ^ 0,04. Тре-
Требуется найти такой закон расхода массы u(t), при кото-
котором конечная высота подъема ракеты х2(Т) будет макси-
максимальной. В соответствии с принятой в книге постановкой
общей задачи оптимального управления в качестве функцио-
функционала взят R=— kxx* G1), в качестве терминального ограниче-

§7] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 351
ния типа равенства рассматривается T=k2[x1 (Т)—0,2]=0.
Здесь введены весовые коэффициенты ?1 = 0,01 и
ft, = 10.
При переходе к численному решению отрезок [0, Т]
разбивался на 100 равных частей (q= 101) и система диф-
дифференциальных уравнений интегрировалась по схеме Эйлера
с пересчетом. Начальное управление задавалось функцией
ио(/) = 0,008. Применение системы ДИСО для решения
задач оптимального управления не требует специальных
приемов для устранения «параллелепипедных» ограни-
ограничений. Благодаря этому удалось без труда избежать таких
неприятностей, как «прилипание» управления к границе
(см. статью Т. М. Энеева [1]). Решение задачи проводи-
проводилось в диалоговом режиме, была применена хорошо зареко-
зарекомендовавшая себя последовательность методов. Первая
итерация, сделанная методом штрафных функций ОРТ413,
дала следующие результаты: х1 (Т) = 0,174711, х*(Т) =
= 133,642 км. Дальнейшие три итерации по методу ОРТ553
позволили получить окончательный ответ: х1 (Т) =
= 0,200000614, х2 (Т) =132,133 км. Оптимальный закон
управления представлен на рис. 9.
Сравнение с результатами Т. М. Энеева [1] показывает
качественное и количественное совпадение оптимальных
0,04
1
о ж wot
Рис. 9.
законов управления. В первые 6 секунд с начала движе-
движения расход массы максимален, т. е. равен 0,04 с, затем
происходит резкое снижение расхода до значений
0,013-7-0,014 с", которые сохраняются примерно до
42-й секунды. Далее следует повторное резкое падение
расхода до нуля, и с 45-й секунды до конца полета масса

352 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
ракеты уже не меняется. Согласно Т. М. Энееву [1] такой
закон управления «имеет все основные хорошо известные
особенности оптимального режима расходования массы».
В табл. 5 приведены значения функционала и конечной
массы ^1(Т), полученные в результате расчетов методами
системы ДИСО, Т. М. Энеева ГП (I) и Р/П. Федоренко
[и (id.
Таблица 5
Метод
Номер
итерации
х*(Т)
ОРТ413
0
54,687
0,20000
1
133,642
0,17471
ОРТ553
1
131,174
—
3
132,133
0,2000006
I
50
132,346
0,19967
II
12
132,180
0,20000
WO t
Результаты решения данной задачи, полученные только
методом ОРТ413, представлены в табл. 6 и на рис. 10,
где показаны графики управления u(t) после 1-й, 2-й
и 5-й итераций, а также начальное управление и0 (/) з= 0,008.
В табл. 7 помещены результаты расчетов для случая,
когда число точек дискретизации <7 = 2О1, т. е. интегриро-
интегрирование уравнений велось с шагом в два раза меньшим.
Общее время счета задачи увеличивалось по сравнению
с вариантом, представленным в табл. 5, в 1,8 раза и соста-
составило 420 с.

§7]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 353
Таблица 6
Номер
итерации
*«(Г)
0
54,687
0,20000
1 -
133,642
0,17471
2
139,270
0,18617
3
135,403
0,19333
4
133,761
0,19673
5
132,898
0,19838
Таблица 7
Метод
Номер
итерации
хЦТ)
ОРТ413
0
54,697
0,20000
1
146,519
0,170345
ОРТ553
1
131,684
2
132,167
—
3
132,167
0,199996
4. Задача об оптимальном развороте самолета. Исполь-
Используемая модель движения основана на следующих предпо-
предположениях: самолет представляет собой материальную точку,
движущуюся в трехмерной правой системе координат
связанной с Землей; суточное движение планеты не учиты-
учитывается; Земля считается плоской; ускорение силы тяжести
постоянно по высоте. Уравнения движения имеют вид
хг=х* cos (хъ) cos(A:e), *2=*4 sin (*5), #s=—я4 cos (хь) sin (л:6),
Х ~
u4) — cos (л:6)
7
ie=— g
4)
где л:1, х2, хъ—декартовы координаты самолета; х2—вы-
х2—высота над Землей; л:4—модуль вектора скорости; хь — угол
наклона траектории; #в—угол курса; х7—вес самолета;
12 Ю. Г. Евтушенко

354 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
и1 — величина тяги двигателя, отнесенная к максимальному
значению тяги Р\ и2— величина перегрузки, отнесенная
к максимальному значению перегрузки N\ иъ — величина
тормозящей силы, отнесенная к ее максимальному зна-
значению; и* — угол крена; а—угол атаки; g- = 9,81 м/с2;
S—характерная площадь самолета; q — скоростной напор,
Сх—коэффициент лобового сопротивления; Cs—секундный
расход топлива.
Использовались следующие зависимости:
- р (*»)(**)»
Ч — о »
2— 1, 155-10~5л:2
12,5
= 340,3—4,08-Ю-3*2, а =
3600
= 00
N =min( —
С помощью подхода, предложенного В. К. Исаевым
и В. В. Сониным [3], проводилось «сглаживание» функ-
функции N(x).
Помимо ограничений «параллелепипедного» типа
0,05<^(^<1, 0f01<a»(/)<l, 0<а3(/)<1, G.2)
на управления наложены ограничения по «преемистости»:
dul
dt
<0,2,
du2
dt
<0,25,
da*
dt
dt
1,57 рад/с.
G.3)
Начальное состояние следующее:
г1@) = ж3@) = 0, лгг@) = 5000 м, ж4 @) = 300 м/с,
х* @) = хв @) = 0, х1 @) = 20 000 кг.

§7] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 355
Начальные значения управлений и2 @) = 1/N (х @)),
и*@) = 0, обеспечивающие в момент t = 0 горизонтальный
полет самолета, в процессе расчетов не варьируются.
В задаче требуется, чтобы конечные значения этих же
управлений также удовлетворяли условиям горизонталь-
горизонтального полета, т. е.
и*(Т) = 0. G.4)
В конце маневра фазовые координаты самолета должны
быть такими:
х2 (Т) = 7000 м, хь (Т) = 0, v6 (T) = — я. G.5)
Сформулируем следующую задачу оптимального быстро-
быстродействия: найти управления u(t), удовлетворяющие огра-
ограничениям G.2), G.3) и переводящие самолет за кратчай-
кратчайшее время из горизонтального полета на высоте 5000 м
в горизонтальный полет на высоте 7000 м с разворотом
вектора скорости на 180°. Таким образом, в качестве
функционала выступает время движения: R — T, а усло-
условия G.4), G.5) образуют систему терминальных ограни-
ограничений типа равенства. При переходе к численному реше-
решению была сделана замена переменной t (см. § 8 гл. I) и
интегрирование дифференциальных уравнений велось на
отрезке [0, 1] по схеме Эйлера с постоянным шагом
Я = 0,02 (^ = 51). В качестве начального приближения
были взяты: Го = 21 с и функции и1 @ = 1, u2(t)^0,3y
и8@=0, tt4@ = l,5sin(-^\ .
Wo/
Задача решалась шестью различными методами. На
рис. 11 даны графики, отражающие изменение текущего
в процессе расчетов значения функционала- Т (в секун-
секундах) в зависимости от времени расчетов 7 (в минутах) на
ЭВМ БЭСМ-6. Точки — значения Т в момент окончания
каждой k-и итерации, в промежутках проводилась интер-
интерполяция. Номера кривых соответствуют следующим алго-
алгоритмам: / — методу штрафов ОРТ41, 2—методу множите-
множителей Лагранжа ОРТ7, 3—методу модифицированной функ-
функции Лагранжа ОРТ53, 4—методу простой итерации ОРТ55,
5, 6—программам ОРТ45, ОРТ46. Методы ОРТ7, ОРТ53,
ОРТ55 требовали знания двойственных переменных. По-
Поэтому они использовались после того, как был сделан
12*

356 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
один шаг по методу штрафов. Решение задачи выбранным
методом прекращалось, если два последующих значения Т
о
Рис. 11.
отличались меньше чем на 10"* либо истекало заданное
время расчетов на ЭВМ. Из рис. 11 видно, что наиболь-
наибольшей скоростью сходимости обладают методы ОРТ53,

§7} ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЁТОВ 35?
ОРТ55. Приемлемая точность решения была достигнута
за 25 минут. Метод штрафов ОРТ41 потребовал около
часа, чтобы получить близкие результаты. При использо-
использовании метода ОРТ46 точность решения вспомогательной
задачи пришлось увеличить по сравнению с методом
ОРТ45, так как в противном случае после второго шага
получалась величина Т, превосходящая оптимальное зна-
значение Т.» 16,96 с.
Данная задача потребовала для своего решения в не-
несколько раз большее машинное время, чем предыдущие
примеры. Дело в том, что после дискретизации получи-
получилась задача нелинейного программирования, в которой
отыскивался минимум по 201 переменной при наличии 5
ограничений типа равенства и 702 ограничений типа не-
неравенства, из которых 302 ограничения «параллелепипед-
ного» типа учитывалось при решении вспомогательной
задачи. Вектор двойственных переменных имел размер-
размерность, равную 405.
В заключение рассмотрим приведенные на рис. 12—15
оптимальные программы u(t) и перегрузку ny(t) —
=u*(t)N (x(t))> полученные методом ОРТ55. Соответ-
Соответствующие значения управлений и фазовых переменных
таковы, что х2 (Тф) = 7001 м, хъ (Тф) = 0, х* (Тф) = — 180,2е,
a*(^)=0f u*(T*)-N(x(T*))-l = W-*.
Управление u?(t) имеет достаточно простой вид и яв-
является граничным в смысле наложенных на него ограни-
ограничений. В начале полета @^/<. 3,39 с) u2(t) нарастает
от значения 0,133 до 1 с максимально возможной ско-
скоростью (и2 & 0,25), на завершающем этапе маневра
A3,90 с</<7\)я2(*) уменьшается от 1 до 0,226 также
с максимально допустимой скоростью (и2 ж— 0,25), в
середине полета C,39 с<*< 13,90 с) u2(t)=l. График
соответствующих значений перегрузки /г '(/) несколько
сложнее. Дело в том, что до момента tf»7,45c функция
N(x)= 150 000/а:7 и в связи с незначительным изменением
веса (Ад:7 =19 940 кг—20 000 кг = — 60 кг) практически
постоянна (Д# = 7,52—7,50 = 0,02). При значениях
/^7,45 с функция N (х) стала определяться по формуле
N (х) = qS/x7 и приобрела существенно нелинейный харак-
характер. Этот переход связан с тем, что с набором высоты
уменьшились скорость самолета и плотность атмосферы.

8-
6-
4 -
2 /
0
/г к
А Г4
4 8
Рис.
12 16 t
13.
0 4 8 12 16 t
Рис. 14.
"V/
8 12 16 t
Рис. 15.

§7] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 359
Соответствующее уменьшение скоростного напора q при-
привело к ситуации, когда qS < 150 000, и максимальная пе-
перегрузка стала вычисляться по другой формуле.
5. Задача об оптимальном распределении материала
силового шпангоута. Исторически сложилось так, чго
наиболее традиционными задачами оптимального управле-
управления оказались задачи о движении динамических объектов
типа самолета, ракеты и т. п. По мере своего развития и
усовершенствования методы теории оптимального управ-
управления стали находить широкое применение в других при-
прикладных областях. Ниже рассмотрена задача проектиро-
проектирования шпангоута минимального веса, выдерживающего
заданные нагрузки при напряжениях, не превосходящих
допустимые. При определенных предположениях поведение
таких конструкций описывается системой обыкновенных
дифференциальных уравнений, которую можно использо-
использовать для решения оптимизационных задач. Эти уравнения
составил Г. И. Пшеничнов, с которым поддерживалось
тесное сотрудничество как при постановке этой задачи,
так и при ее решении. Содержательный смысл величин,
определяющих задачу, подробно рассмотрен в работе
Н. И. Грачева, Ю. Г. Евтушенко [5] и в книге Г. М. Ка-
Кашина, Г. И. Пшеничнова, Ю. А. Флерова [1]. В этой же
книге приведены некоторые численные результаты, полу-
полученные с помощью методов из описанной здесь библио-
библиотеки. Поэтому основное внимание в дальнейшем изложе-
изложении уделим вопросам оптимизации.
Напряженно-деформированное состояние конструкции
описывается следующей системой:
dx*
-ж-
Все входящие сюда величины обезразмерены. Функции
<7@> Р@> *и@» K{t)% E(t) заданы. Управлениями u(t)
являются параметры поперечного сечения шпангоута, и
в систему G.6) они входят через площадь F(u) и момент
инерции I (и) сечения.

360 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Для системы G.6) заданы краевые условия
Незаданные при / = 0 координаты xL@), д:2@), х3@)
примем в качестве управляющих параметров, условия G.7)
отнесем к терминальным ограничениям типа равенства.
Таким образом, решение ука-
указанной краевой задачи, кото-
которое позволяет преодолеть ста-
статическую неопределимость
рассматриваемой конструк-
конструкции, укладывается в общую
схему решения задачи опти-
оптимального управления.
Для кругового шпангоута
радиуса R± на рис. 16 по-
показаны внешние нагрузки,
представляющие собой урав-
уравновешенную систему сил. Значения безразмерных парамет-
параметров внешней нагрузки равны: N = 0,5, q(t) = 2sinBnt),
/j(*) = 0, m(*) = 0. В точках/, 2, где ^ = 0,12, *а = 0,88,
сосредоточенные нагрузки N проектируются на касатель-
касательную и нормаль к контуру и учитываются по формулам
/v
cosBntf)y / = 1, 2.
Поперечное сечение шпангоута имеет вид прямоуголь-
прямоугольника с размерами игхи2у где и2—ширина сечения, и1 —
его высота (в направлении радиуса). Площадь и момент
инерции сечения вычисляются по формулам F(u)~ul-u2,
/(u) = u2(u1K/12. Требуется найти такие функции иг{1),
u2(t)y определяющие форму шпангоута, чтобы минимизи-
минимизировать объем материала:
При этом должны выполняться условия: 10^w1(/X
^ 10, 10~2^ u2(t)^ 1. Кроме того, наложены ограни-
ограничения по допустимым напряжениям в каждом сечении,

§ 7] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ 361
которые записываются следующим образом:
^№№. G.8)
Здесь а—максимально допустимое напряжение, а/Е0 =
= 10~2. Чтобы функции, определяющие ограничения, были
дифференцируемы, заменим условие G.8) эквивалентной
системой четырех неравенств
Г'(*. и, 0 = jc1 @ г/1 @ б'—6 (—1)' jc3 (О —
у Gв9)
где ?[l4] S1 62l 63 64 1
?[],
Интервал интегрирования системы G.6) был разбит на
50 участков, что привело к задаче нелинейного програм-
программирования со 103 переменными, 200 ограничениями типа
неравенства и тремя ограничениями типа равенства. В ка-
качестве начального приближения была взята конструкция
квадратного сечения: и?(/)е== Ю, и2(/) = 10~2. На пер-
первом этапе расчетов использовался линейный вариант си-
системы G.6):
jc1=/Ca:2—q, х* =
G.10)
х? = х2—т, х* = — -pj.
Интегрирование систем G.6), G.10) по схеме Эйлера
привело к большим погрешностям и дало неудовлетвори-
неудовлетворительные результаты. Использование схемы Эйлера с пере-
пересчетом, дающей погрешность^ шаге интегрирования по-
порядка О (h*), позволило решить задачу. Расчеты начина-
начинались с метода штрафов ОРТ413, далее совершался пере-
переход к двойственному методу ОРТ553. Полученные резуль-
результаты показали, что решения нелинейной G.6) и линейной
G.10) задач приводят практически к одной и той же кон-
конструкции. В частности, соответствующие значения функ-
функционала равны 1,37Ы0~4 и 1,378-10~4. Отсюда следует,
что найденная из линейной задачи конструкция шпанго-
шпангоута при заданной нагрузке устойчивости не теряет.
Как и следовало из физических соображений, ширина
сечения в результате оптимизации не увеличилась и оста-

362 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
лась равной начальному значению. Зависимость оптималь-
оптимальной высоты сечения и1 от / приведена на рис. 17. Каждое
из ограничений Г* оказалось существенным при каких-то
0,020
0,015
0,0/0
о*
0,5
Рис. 17.
/ t
/ 1
€
-0,05
Ч),10
0,5
Г \ f ' \ f
\\ \ Л
I / \] \
Y
\ г
/ t
г
I
Рис. 18.
значениях t. На рис. 18 показано, как ведут себя функ-
функции Г1 и Г4 вдоль оптимальной траектории. Из графика
на рис. 17 заключаем, что начальная конструкция была
взята слишком облегченной для данной нагрузки и опти-
оптимизация привела к увеличению веса; вместе с тем есть
участки, где м1(/)=10~2, на них высота сечения могла

§8] ПРИЛОЖЕНИЕ К ДИФФЕРЕНЦИАЛЬНЫМ ИГРАМ 363
быть и меньше, что облегчило бы шпангоут. Однако ниж-
нижнее «параллелепипедное» ограничение оказалось здесь су-
существенным. В реальных конструкциях эти ограничения
диктуются, как правило, технологическими соображениями.
Сравнение рисунков показывает, что увеличение высоты
сечения и1 вызвано требованиями прочности. В терминах
нелинейного программирования полученное оптимальное
решение является граничной точкой допустимого множе-
множества, заданного как «параллелепипедными» ограничениями,
так и ограничениями G.9) вдоль траектории. Если бы в
задаче не было первых из этих ограничений, то в каждом
сечении реализовалось бы максимально допустимое напря-
напряжение. Это утверждение соответствует гипотезе равно-
прочности, которая в данном случае оказалась справед-
справедливой. Описанный подход применим для проектирования
конструкций, контуры которых могут быть незамкнутыми,
многосвязными, иметь более сложные поперечные сечения
в виде тавра и двутавра.
§ 8. Приложение к дифференциальным играм
1. Постановка задачи. В последние годы опублико-
опубликовано большое число статей и книг, посвященных диффе-
дифференциальным играм. Подробную библиографию по этому
вопросу можно найти в книгах Р. Айзекса [1], Н. Н. Кра-
совского и А. И. Субботина [1]. Значительно меньше
исследований проведено в области создания численных
методов решения игровых задач. Объясняется это боль-
щими вычислительными трудностями, связанными с оты-
отысканием глобальных экстремумов функций многих пере-
переменных. Этот вопрос кратко обсуждался в § 6 гл. II.
Пусть игра описывается системой обыкновенных диф-
дифференциальных уравнений
w=
Считая для простоты интервал Т фиксированным, перей-
перейдем к дискретной аппроксимации этой системы по схеме
Эйлера
zxc=[xh щу *,], (8.2)
*jf = [y,, vi% ti\. (8.3)

364 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
В системе учитываются смешанные ограничения
Г1 (*„«,)< О, Г2(#/, «КО, 1 </<</. (8.4)
Здесь для упрощения изложения опущены ограничения
типа равенства, и не выделяются специально терминаль-
терминальные ограничения.
Качество игры оценивается функцией R(xq> yq), зави-
зависящей только от терминальных фазовых координат. Пред-
Предположим, что функции /, g, Г1, Г2, R, определяющие
задачу, всюду непрерывно дифференцируемы по xi9 у{,
и{, vt. Введем полные фазовые векторы х, у и полные
векторы управлений и и v:
x=[xlt х2, ..., xq], и = [ии ui9 ..., uQ],
У = [Уи #2, ..-, yq], v = [vu i>2, ...,vq].
Следует отличать введенные полные векторы х, у9 и, v от
функций x(t)9 y(t)t u(t), v(t), входящих в систему (8.1).
Задав векторы и и v, однозначным образом определим
xq = xq(u) и yq = yq{v)\ используя формулы § 1, получим
(8'5)
Здесь векторы р\ и р\ имеют те же размерности, что и
соответственно хг и у{.
Задача I заключается в отыскании величины Vx—наи-
Vx—наилучшей гарантированной оценки сложной функции
R (xqy yq) для игрока, поведение которого описывается
системой (8.3):
V1 = tn'dxmmR(xq{u), yq(v)). (8.6)
V U
Задача II состоит в нахождении наилучшей гаранти-
гарантированной оценки для другого игрока:
V2 = min max R (xq (u\ yq (v)). (8.7)
и v
В обеих задачах экстремумы ищутся с учетом ограниче-
ограничений (8.4).

<8J ПРИЛОЖЕНИЕ К ДИФФЕРЕНЦИАЛЬНЫМ ИГРАМ 365
Сформулированные задачи обычно называются задачами
отыскания максиминных и минимаксных оценок в про-
программных стратегиях. Строгий смысл, вкладываемый в
записи (8.6) и (8.7), разъяснен в § 5 гл. I. Для задачи
(8.7), в частности, из решения «внутренней» задачи опре-
определяется точечно-множественное отображение
v (и) = Argmax R (xq (и), yq (v)); (8.8)
V
после этого решается «внешняя» задача о нахождении
a.€Argmtaq>(n)f <p(u) = R(xq(u)9 yq{v(u)))t
У2 = ФЫ. (8.9)
Согласно результатам § 5 гл. I между решениями за-
задач (8.6) и (8.7) имеет место оценка: Ki^VV
2. Глобальные методы решения задач. Простейший
метод отыскания минимакса V2 базируется на использо-
использовании методов минимизации в пространстве пониженной
размерности (см. § 6 гл. II). Согласно этому подходу
при фиксированном и решается внутренняя задача, опре-
определяется v ? v (и). Это—рассмотренная выше в этой главе
обычная задача дискретного оптимального управления.
Считаем, что при каждом и задача разрешима, тогда при-
приходим к задаче минимизации сложной функции <р (и), ко-
которая сводится к нахождению последовательности и, схо-
сходящейся к и*. Если для решения внутренней и внешней
задач используются глобальные методы, то получается
глобальное решение задачи (8.7). Однако "численная реа-
реализация такого подхода сопряжена с огромным объемом
вычислений, и на современных ЭВМ таким способом уда-
удается решить лишь самые простые игровые задачи. По-
Поэтому целесообразно вводить упрощающие предположения,
которые позволяют решать задачи высокой размерности,
но, к сожалению, за счет сужения класса задач, к кото-
которым такой подход применим.
3. Численные методы отыскания локального мини-
минимакса. Следуя подходу, развитому в § 6 гл. II, будем
решать внутреннюю и внешнюю задачи (8.8) и (8.9), ис-
используя локальные методы, в результате найдем локаль-
локальный минимакс. Такой подход требует тщательного ана-
анализа получаемых решений, он применим лишь при доста-
достаточно хорошем начальном приближении и при существо-

366 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
вании однозначной, непрерывной зависимости v(u). При
каждом полном векторе управлений ик решается внутрен-
внутренняя задача (8.8). Считаем, что ее решение vk?v(uk) су-
существует; кроме того, есть двойственный вектор Kk = к (uk)
и в точке Куна — Таккера [vk, Xk] выполнены необходи-
необходимые условия максимума:
Г2 (У К), i>*)<0,
Здесь T2S есть s-я координата вектора Г2.
Для решения внутренней задачи (8.8) можно приме-
применить любой из описанных в § 3 методов. Обычно исполь-
используется комбинация разных методов: вначале несколько
шагов делается методом штрафных функций и далее про-
производится обращение к двойственным методам. Таким об-
образом, значения функции ф(и) становятся известны. Ус-
Условная минимизация <р {и) ведется этими же методами.
В тех случаях, когда функция ц>(и) недифференцируема,
при решении внешней задачи (задачи нелинейного про-
программирования) применяется, например, вариант метода
штрафных функций, использующий недифференцируемые
штрафные функции.
Для реализации методов, использующих производные,
вводится предположение о дифференцируемости функций
v(u), 'к (и), что будет иметь место, в частности, при вы-
выполнении условий теоремы 1.7.7. Из дифференцируемости
v (и), К (и) следует дифференцируемость функции yq{v(u)).
Системы (8.2) и (8.3) интегрируются независимо и свя-
связаны между собой только через терминальный функцио-
функционал R. Поэтому вместо функций v(u), Я (и), yq(u) можно
говорить о зависимостях v(xq), %(xq)y yq(xq). Чтобы вос-
воспользоваться формулами (8.5), следует вычислить
х _dR(xqy yq) dR(xqi yq) dyq OR (xq, yq)
pi~~ d^ ~ Wq *~~dx~q Wq '
В п. 6 § 7 гл. I показано, что последнее слагаемое равно
нулю, поэтому
dR (Xq, yq)

§8] ПРИЛОЖЕНИЕ К ДИФФЕРЕНЦИАЛЬНЫМ ИГРАМ 367
Заметим, что если бы функция Г2 зависела явно от и, то
в этой формуле появились бы дополнительные слагаемые.
Приведенная процедура решения задачи (8.7) реализу-
реализуема в рамках описанного в этой главе подхода, однако
она тоже может привести к значительному объему вычис-
вычислений. Поэтому может оказаться целесообразным исполь-
использовать метод B.6.2), не требующий решения внутренней
задачи. В этом случае осуществляется одновременное из-
изменение управлений и и v:
), yq(vk))
dR(xq(uk),yq(vk))
Здесь для простоты опущен учет ограничений (8.4),
0<8<1.
Используя результаты § 6 гл. II, несложно строго
сформулировать достаточные условия для того, чтобы
такой подход приводил к решению задачи II.
4. Необходимые условия минимакса. Выше были опи-
описаны глобальные и локальные процедуры решения за-
задачи (8.7). Возможен промежуточный вариант, когда
внутренняя задача решается с помощью глобальных мето-
методов, внешняя задача—на основе применения локальных
процедур. Для этой цели можно использовать свойства,
аналогичные дискретному принципу минимума, приведен-
приведенные в § 4. Кратко остановимся на этом вопросе, опуская
учет ограничений (8.4).
Пусть управляемый процесс описывается разностными
соотношениями (8.2) и (8.3). На выбор управлений нало-
наложим ограничения Vj?V9 /€[l-<7]» которые будем записы-
записывать в краткой форме следующим образом: v ? V. Фикси-
Фиксируем в полном допустимом векторе управлений и все
компоненты, кроме и{, рассмотрим задачу определения
V2 = min max R (xq (и), yq (v)). (8.11)
Во внутренней задаче определяется
,(a)f yq(v)). (8.12)
vev

368 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Во внешней задаче множеством решений является
<p(u) = R(x0(u)t yg(v(u))).
Будем предполагать, что выполнены следующие условия:
1) вектор-функция F (xh uh tt)> и функция R(xqt yq) не-
непрерывно дифференцируемы по компонентам вектора х\
2) при каждом и{ € U внутренняя задача разрешима,
из условия (8.12) определяется точечно-множественное
отображение v{u()y которому соответствует множество
терминальных точек yq(ti().
Задав допустимый вектор щ ? U, из (8.2) однозначным
образом определим xv решив внутреннюю задачу, найдем
уя {щ). Задача (8.11) становится эквивалентной следующей:
V i max R(xq(ui)9 ущ). (8.13)
)
Фиксируем точку и,?1/ и точку yq€yq{Ui), тогда,
используя формулы (8.5), последовательно определим век-
векторы р*, /?*_!, ..., pj+1, зависящие от xi+1=^F(xh ui9 t()
и уд как от параметров. В частности, получим
х ч dR (xqt yq)
Pi+i (*i+i> yq) — dx.+i •
Так же, как это делалось в § 4, перейдем при реше-
решении внешней задачи в пространство состояний, тогда
задача (8.13) будет эквивалентна следующей:
У2= min max R{xq9 yq).
x*uy*y(u)
Здесь введено множество Q = /r(x/, U, t()9 которое считаем
выпуклым, компактным. Согласно теореме 1.5.4, для того
чтобы Xt+1 = F(xh u\y if), u\ ?Wt, необходимо выполнение
условия
Ui, Уд), *т—*?+
для любых xl+1?Q, или, переходя в пространство управ-
управлений, получим, что для всех u^U имеет место нера-
неравенство
max ^ <pf+t(F(xi9 и], /,), yq), F{xh uh tt)—
(8.14)

§ 8] ПРИЛОЖЕНИЕ К ДИФФЕРЕНЦИАЛЬНЫМ ИГРАМ 369
Мы пришли к следующему утверждению, называемому
дискретным принципом минимакса.
Теорема 6.8.1. Пусть для систем (8.2), (8.3) вы-
выполнены условия 1) и 2), множество Q = F (xh U, t-) выпукло
и компактно. Тогда, для того чтобы u*t ? W*, не-
необходимо, а в случае выпуклости <р(и/) и достаточно
выполнение условия (8.14) для любых U;?U.
Аналогом линеаризованного принципа минимума будет
следующее утверждение: для любых и( ? U выполнено
неравенство
max <Fa (xh и), tt) рхш {F (*/> ui > h)> Vq)> Щ—Ф > 0.
()
Полученные результаты позволяют для численных
расчетов использовать варианты метода условного гра-
градиента и проекции градиента подобно тому, как это де-
делалось в § 5. Рассматриваемая задача, однако, сложнее.
Если раньше /?/+1 определялось из соотношений A.5), A.7),
то здесь в случае неоднозначного решения внутренней
задачи следует рассмотреть совокупность векторов pxUly
определяемых из (8.5) при различных значениях уг
Используя изложенный подход, нетрудно принять во
внимание фазовые ограничения и получить необходимые
условия минимакса.
5. Пример численных расчетов. Приведенные методы
переносятся на случай, когда уравнения (8.1) не разделены
и отсутствуют фазовые ограничения. В качестве простей-
простейшего решенного примера такого типа приведем задачу
о долихобрахистохроне, взятую из книги Р. Айзекса [1].
Игра описывается системой
Здесь и и v—управления, удовлетворяющие ограничениям:
02 11
Первый игрок, управляющий функцией и, стремится
за кратчайшее время провести фазовый вектор на мно-
множество
М = {х,у: jc = O

370 ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ [ГЛ. VI
Второй игрок, распоряжающийся функцией v, стре-
стремится не допустить попадания на М или по крайней мере
отсрочить его. Численное решение задачи начиналось с ис-
использования метода (8.10), далее продолжалось методом
условного градиента в соответствии с подходом, описан-
описанным в предыдущем пункте.
Результаты расчетов приведены на рис. 19, где изобра-
изображены фазовые траектории в плоскости [х, у]. Изломы
Рис. 19.
траектории лежат на так называемой параболе переключе-
переключений, где управление второго игрока релейно изменяется
от —1 до +1. Интересно сравнить этот рисунок с ана-
аналогичным рис. 5.2.2, приведенным на с. 127 книги Р. Ай-
зекса [1], где ищется решение игры в позиционных
стратегиях. Фазовые траектории в области, лежащей выше

§ 8] ПРИЛОЖЕНИЕ К ДИФФЕРЕНЦИАЛЬНЫМ ИГРАМ 371
параболы переключений, в точности соответствуют анали-
аналитическому решению, полученному Р. Айзексом. Однако
фазовые траектории, лежащие ниже параболы, имеют иной
вид. В статье С. А. Чигиря [1] было указано на неточ-
неточности в качественном описании Р. Айзексом поля траек-
траекторий. Вместе с тем в этой статье неточно изображены
вблизи множества М фазовые траектории, которые должны
подходить к оси ординат под прямым углом. Это следует
из аналитических формул и численного решения приве-
приведенного на рис. 19.

ГЛАВА VII
ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ
§ 1. Общие принципы построения диалоговых систем
При использовании численных методов оптимизации
для решения практических задач приходится проводить
огромный объем вычислений. Поэтому широкое внедрение
методов оптимизации стало возможным лишь сейчас, бла-
благодаря созданию современных мощных быстродействующих
электронно-вычислительных машин третьего поколения.
При работе на машинах первого и второго поколений
пользователь обычно составлял одну-две программы опти-
оптимизации и пытался »с их помощью решить поставленную
задачу. Если ему это не удавалось, то он программировал
новый метод и делал новую попытку решить эту же за-
задачу. Появление ЭВМ третьего поколения открыло воз-
возможность по-новому организовать внешнее математическое
обеспечение, вместо стандартных программ сейчас стало
реальным использовать пакеты прикладных программ, т. е.
комплекс программных средств, включающих в себя биб-
библиотеку разнообразных алгоритмов для решения данного
класса задач, вспомогательные программы и управляющую
программу (монитор), организующую на ЭВМ решение
задач с учетом их специфики. Опыт работы показывает,
что использование пакетов программ значительно увели-
увеличивает возможности применения ЭВМ.
Создание эффективно действующих и достаточно уни-
универсальных пакетов программ представляет собой большую
научно-техническую задачу. К их разработке привлечены
большие коллективы ученых-математиков и специалистов
по вычислительной технике. После создания первых ва-
вариантов пакетов проводится их опытная эксплуатация
и в процессе решения практических задач накапливаются
различные замечания, уточнения, которые учитываются
при создании последующих версий.

§1] ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 373
Сейчас перед учеными стоят проблемы резкого повы-
повышения эффективности всего общественного производства,
ускорения научно-технического прогресса. Для их успеш-
успешного решения необходимо научиться создавать системы
планирования и автоматизированного проектирования
сложных комплексов, уметь рассчитывать социальные,
экономические и экологические последствия принимаемых
решений. Опыт работы по созданию таких систем пока-
показывает, что эти задачи нельзя ставить и решать как еди-
единую оптимизационную задачу. Методы оптимизации,
имеющие большое значение при решении частных задач
управления и проектирования, становятся, как правило,
неприемлемыми при проектировании сложных комплексов.
Можно указать две основные причины такого явления.
Во-первых, математические модели (т. е. математические
описания) социально-экономических процессов, достаточно
адекватно отражающие основные закономерности, чрезвы-
чрезвычайно сложны. Трудности их расчета возникают прежде
всего из-за высокой размерности, свойственной большин-
большинству практически важных задач (укажем, например, эко-
экономическую задачу оптимизации межотраслевого баланса,
техническую задачу проектирования самолета). Поэтому
решение единой оптимизационной задачи в рамках этих
моделей становится невозможным даже с привлечением
самых мощных ЭВМ.
Вторая не менее важная причина заключается в воз-
возникновении принципиальных трудностей при формализации
целей и критериев проектирования. Часто бывает так, что
проектировщик, изготовляя новую конструкцию, стремится
создать многоцелевой объект, причем ему необходимо
выполнить ряд требований, являющихся «внешними» по
отношению к данному, проектируемому объекту. Напри-
Например, конструкторы, проектирующие пассажирский самолет,
стремятся спроектировать прежде всего наиболее эконо-
экономичный вариант. Вместе с тем они должны учитывать
факторы, связанные с надежностью самолета, с созданием
условий, способствующих простоте и удобству его эксплуа-
эксплуатации, самолет должен быть приспособлен к тем взлетно-
посадочным полосам, где он будет использоваться, соот-
соответствовать пассажирским потокам и т. д. Как правило,
выполнение «внешних» требований приводит к ухудшению
основных показателей. Необходимо вместе с тем достичь

374 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
некоторого компромисса. Решить этот вопрос в рамках
математических моделей трудно, поэтому обычно в таких
случаях привлекают экспертов-специалистов, обладающих
содержательными знаниями о решаемой задаче. Используя
опыт практической работы, эксперты приходят к некото-
некоторому соглашению.
Все это заставляет в практике управления и плани-
планирования сложных социально-экономических, технических
систем наряду с классическими методами оптимизации
использовать такие приемы, как эвристические подходы,
основанные на интуиции и опыте экспертов. Для реали-
реализации такого подхода создаются так называемые имита-
имитационные системы, в которые входят математическое
описание проектируемого объекта, электронно-вычисли-
электронно-вычислительная машина и системное обеспечение, позволяющее
группе специалистов (экспертов) в режиме непосредст-
непосредственного диалога с ЭВМ рассчитывать возможные послед-
последствия принимаемых решений, анализировать результаты
и вырабатывать наилучший вариант проектируемого объ-
объекта. Электронно-вшчислительные машины третьего поко-
поколения создали техническую базу для построения таких
систем, позволив легко вводить в ЭВМ данные, необхо-
необходимые для воспроизведения исследуемого процесса, опе-
оперативно получать из ЭВМ информацию о его течении
в форме, удобной для дальнейшего анализа, непосредст-
непосредственно управлять исследуемым процессом. По приказу
экспертов осуществляется изменение искомых параметров
и функций, изучается реакция на них системы. Экспертам
принадлежит ведущая роль в процессе принятия решений
на базе неформальных, плохо поддающихся алгоритмизации
рассуждений. Таким образом, создается симбиоз человека
и электронно-вычислительной машины.
Использование имитационных систем в практике про-
проектирования сложных комплексов не только не означает
отказа от решения точных оптимизационных задач, но
опирается на эту технику. В имитационную систему целе-
целесообразно включить пакеты программ, предназначенные
для поиска оптимальных решений. С их помощью можно
отыскать решение вспомогательных задач, упрощая работу
с системой. Например, в имитационную систему, создан-
созданную для проектирования самолета, можно включать блок
оптимизации для отыскания силовой конструкции само-

§1] ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 375
лета, обладающей наименьшим весом и выдерживающей
заданные нагрузки. Физически ясно, что уменьшение веса
самолета, не идущее в ущерб его прочностным свойствам,
приводит только к его улучшению. Аналогичная ситуация
имеет место почти всюду в задачах машиностроения (про-
(проектирование автомобилей, кораблей, ракет и т. д.).
По мере развития методов оптимизации, более глубо-
глубокого понимания сущности управляемых процессов роль
оптимизационных блоков будет, естественно, возрастать.
Управления, получаемые в результате численного решения
оптимизационных задач, из вспомогательной информации,
помогающей принимать решения, будут все более превра-
щаться в основу для принятия решений. Возникают
вопросы, каким образом создать эффективно действующие
пакеты программ, предназначенные для решения широкого
класса разнообразных оптимизационных задач? Каковы
должны быть основные принципы построения таких па-
пакетов, какие методы оптимизации должны быть в них
включены? В настоящее время разработано большое число
методов оптимизации. Математик при решении конкретной
задачи стремится выбрать наилучший метод, позволяющий
за наименьшее время использования электронно-вычисли-
электронно-вычислительной машины получить решение с заданной точностью.
Но как найти наилучший метод, какие взять параметры
в выбранном методе?
Качество численного метода характеризуется многими
факторами: областью сходимости, скоростью сходимости,
временем выполнения одной итерации, объемом памяти
машины, необходимым для реализации метода, классом
решаемых задач и т. д. Решаемые задачи также обладают
большим разнообразием. Среди них встречаются гладкие
и негладкие задачи, высокой и малой размерности, овраж-
овражного типа, унимодальные и многоэкстремальные и т. д.
Поэтому один и тот же метод может оказаться эффектив-
эффективным для решения одного типа задач и совершенно непри-
неприемлемым для другого типа. В связи с этим сейчас не суще-
существует, да, по-видимому, и не будет существовать наилуч-
наилучшего во всех отношениях универсального численного
метода. Ясно, что не поиск универсального метода, а
разумное сочетание разнообразных методов позволит с наи-
наибольшей эффективностью решать поставленные задачи.
Поэтому для создания пакета необходимо прежде всего

376 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
иметь обширную библиотеку разнообразных программ,
реализующих методы разных классов и позволяющих
решать задачи различного типа. Вместе с тем необходимо
иметь программное обеспечение, позволяющее на ЭВМ
вести расчеты с последовательным использованием раз-
различных методов, осуществляя, таким образом, режим
многометодной оптимизации. Такой подход приводит к но-
новому взгляду на оценку эффективности численных методов.
Раньше при тестировании методов ставился вопрос:
насколько быстро и точно решалась определенная задача
с начала и до конца одним выбранным методом? Резуль-
Результат в значительной степени зависел от типа тестируемой
задачи и от выбора начального приближения.
Поклонники быстро сходящихся методов брали доста-
достаточно хорошие начальные приближения и с помощью
результатов численных расчетов «доказывали» преимуще-
преимущества этих методов над методами, не обладающими высокой
скоростью сходимости. Разработчики последних методов
предпочитали брать весьма грубые начальные приближения
и благодаря этому» получать лучшие результаты. При
ориентации на многометодный режим расчетов от методов
требуется высокая эффективность по крайней мере на
каком-либо этапе расчетов или для какого-либо класса
задач. Роль метода штрафов, например, становится весьма
велика, так как он эффективен на начальном этапе рас-
расчетов. Метод Ньютона,'напротив, эффективен при завер-
завершении вычислений. Новый подход к качественной оценке
методов ослабляет остроту споров между разработчиками
различных методов, требуя от них только одного—при-
одного—признания преимущественной ориентации создаваемых ими
методов на какой-либо этап численных расчетов или класс
решаемых задач.
Многометодный режим расчетов поставил новую задачу
об управлении процессом вычислений, привел к необхо-
необходимости создания алгоритмов работы с алгоритмами.
Управление процессом оптимизации можно осуществлять
статически, когда пользователь заранее задает сценарий
расчетов, т. е. определяет последовательность применяемых
методов, их параметры, вводит эту информацию в ЭВМ
и получает результаты только после завершения всех
расчетов. Этот подход, однако, может привести к значи-
значительному объему вычислений, поскольку, часто бывает

§1] ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 377
трудно предугадать ход вычислительного процесса. Более
целесообразным представляется осуществлять управление
в диалоговом режиме, когда пользователь в процессе
расчетов получает сведения о текущих результатах, изме-
изменяет параметры методов, осуществляет целенаправленный
переход от одного метода к другому. Такой динамический
режим работы дает возможность в максимальной степени
использовать опыт и интуицию математика-пользователя.
Для успешной работы с диалоговой системой желательно,
чтобы пользователь знал основные свойства, специфику
используемых методов, правильно ориентировался в новых
ситуациях. В противном случае пользователю приходится
тратить определенное время на обучение.
В настоящее время во многих организациях ведутся
работы по созданию и внедрению в эксплуатацию диало-
диалоговых систем. Это связано со многими причинами и прежде
всего с разработкой терминальных устройств и операцион-
операционных систем, позволяющих осуществить диалоговое взаимо-
взаимодействие пользователя с электронно-вычислительными
машинами. Построение диалоговых систем началось с со-
создания систем, предназначенных для отладки программ,
запуска их в счет с терминала. В качестве примера для
ЭВМ БЭСМ-6 можно указать системы ПУЛЬТ (ВЦ АН
СССР) и ДИМОН (ИПМ АН СССР). Целью последующих
диалоговых систем было построение человеко-машинных
средств для решения содержательных задач. Такие системы
составляют важную часть программного обеспечения
в системах автоматизированного проектирования и управ-
управления сложными техническими комплексами. Созданные
первые, далеко не совершенные и не универсальные диало-
диалоговые системы показывают, что их использование сущест-
существенно упрощает и ускоряет расчеты по сравнению с тради-
традиционными методами эксплуатации ЭВМ. Организация диа-
диалога значительно снижает непроизводительные затраты
времени пользователя, наличие в системе библиотеки
разнообразных алгоритмов оптимизации освобождает поль-
пользователя от трудоемкой работы по программированию
численных методов. Диалоговый сервис позволяет быстро
переходить от одного метода к другому, изменять пара-
параметры методов, корректировать текущее состояние, опре-
определять условия очередного прерывания расчетов, иниции-
инициировать продолжение вычислительного процесса.

378 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
В ряде случаев важно иметь автоматический пакет,
содержащий библиотеку программ оптимизации, вспомо-
вспомогательные и управляющую программы, которые обеспечи-
обеспечивают выбор наиболее подходящей последовательности
используемых алгоритмов и их параметров для решения
каждой конкретной задачи без участия пользователя.
Такие пакеты необходимы в двух случаях: если с системой
работает пользователь, не являющийся специалистом в об-
области методов оптимизации; если процесс расчетов должен
по каким-либо причинам протекать автономно, без уча-
участия человека. Это может иметь место, например, когда
эксперты используют имитационную систему для принятия
решений на высоком уровне, а вспомогательные задачи
оптимизации должны решаться без их участия.
Несложно составить удовлетворительно работающие
управляющие программы для решения однотипных задач.
Вопрос о создании автоматически работающей управляю-
управляющей программы в общем случае является чрезвычайно
сложным по следующим причинам: слишком разнообраз-
разнообразными могут быть "решаемые задачи и слишком слабо
изучены методы их решения. Первые управляющие про-
программы создаются на основе эвристических рассуждений.
Первым шагом для практического создания управляющей
программы является разработка специальной информаци-
информационно-логической системы, которая, используя разнообраз-
разнообразную информацию о конкретной задаче, результаты про-
проделанных расчетов, отбраковывает наименее подходящие
методы и сужает, таким образом, число конкурентоспо-
конкурентоспособных методов.
Возможны и более сложные комбинированные пакеты,
в которых, по желанию пользователя, можно применять
режимы диалога и автоматической работы. В перспективе
желательно создание «интеллектуальных пакетов», которые
будут обладать знаниями о предметной области, смогут
идентифицировать характер процесса расчетов и, исполь-
используя хранящиеся в базе данных правила предпочтения,
оценивать ситуацию, избирать стратегию и тактику реше-
решения задач. Человек при этом может наблюдать за дейст-
действиями системы, при желании лишь корректируя процесс.
Если пользователь решает вести расчеты самостоятельно, то
такая система в свою очередь может выдавать рекомендации
пользователю о продолжении расчетов как на базе введен-

§ 1] ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 379
ных априори описаниях объектов и «теорем», так и на
текущей «ситуационной» информации, характеризующей
динамику вычислительного процесса.
Современное состояние разработок диалоговых систем
можно назвать этапом эмпирического накопления опыта
создания первых систем и их эксплуатации. В последние
годы в научной литературе появилось много сообщений
о созданных диалоговых системах, есть работы, посвя-
посвященные теоретическим вопросам построения таких систем,
их архитектуре, реализации, психологическим аспектам
человеко-машинного взаимодействия. Сравнительный ана-
анализ созданных систем затруднителен из-за того, что системы
были разработаны для разных машин, реализованы на
разных алгоритмических языках и их создатели часто
ставили различные цели.
Приведем короткую информацию о некоторых оптими-
оптимизационных системах. В Институте кибернетики АН УССР
создана диалоговая система планирования ДИСПЛАН
(см. В. М. Глушков, Г. Б. Олеярш [1]). Система пред-
предназначена для оперативного решения задач текущего пла-
планирования на этапе согласования плана. В ней осущест-
осуществляются балансовые расчеты с учетом ограничений на
ресурсы путем решения системы линейных алгебраических
уравнений (размерность переменных должна не превосхо-
превосходить 1200). Система ориентирована на ЭВМ БЭСМ-6,
позволяет решать в диалоговом режиме задачи линейного
программирования.
В Институте математики и механики УНЦ АН СССР
для ЭВМ БЭСМ-6 создан пакет ОПТИМА-2 (см. Г. Ф. Кор-
Корнилова и др. [1]). Пакет имеет двухцелевое назначение:
с одной стороны, как комплекс прикладных программ
для решения задач линейного программирования и, с дру-
другой стороны, как средство автоматизации программирова-
программирования для экспериментальных исследований алгоритмов.
Пакет содержит развитое программное обеспечение для
решения различных производственных задач; среди них
важное место занимает задача оптимального объемно-ка-
объемно-календарного планирования, решение которой проводится
в автоматическом режиме, начиная с формирования инфор-
информационных массивов и кончая выходной документацией.
В пакете используется модифицированный симплекс-метод
с мультипликативным представлением обратной матрицы

380 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ tl\fl. Vll
и процедурой повторения. Для задач большой размерности
разработан механизм стыковки итерационного метода ре-
решения и симплекс-метода.
В ВЦ АН СССР создана система ЛП БЭСМ-6
(Н. К. Бурова и др. [1]), предназначенная для решения
задач линейного и сепарабельного программирования,
содержащих до 2000 условий общего вида и до 30 000
переменных. Система состоит из библиотеки модулей,
реализующих некоторые специфические операции (ввод
данных, проверка и модификация данных, решение задачи
линейного программирования симплекс-методом, исследо-
исследование чувствительности и устойчивости решения, вывод
промежуточных данных, результатов), и аппарата, реали-
реализующего управляющий язык системы (ЛП-язык). Этот
язык позволяет осуществить взаимодействие не только
между пользователем и системой, но и между отдельными
модулями системы. В ЛП-языке имеется достаточно бога-
богатый набор средств для программирования различных
нестандартных операций. Система содержит метод Франка
и Вольфа для решения задачи квадратичного программи-
программирования, метод ветвей и границ для решения частично-
целочисленной задачи линейного программирования, метод
минимизации алгоритмически вычисляемой кусочно-линей-
кусочно-линейной функции, возникающей при двойственной формули-
формулировке задач блочного программирования и т. д. Возмож-
Возможность относительно простого доступа ко всем входным и
выходным данным позволяет легко программировать на
ЛП-языке формирование очередной задачи линейного про-
программирования.
Для ЭВМ БЭСМ-4 разработана диалоговая система
автоматизации процесса принятия оптимальных решений
САППОР (см. Д. И. Батищев [1]). Система ориентирована
на решение трех классов задач: безусловная минимизация
функций многих переменных, нелинейное программирова-
программирование и многокритериальная (векторная) оптимизация.
В Харьковском университете разработан пакет программ
для решения задач безусловной минимизации функций
многих переменных для ЭВМ М-222 (см. В. И. Мелешко
и Р. И. Лесина [1]).
В Институте кибернетики АН УССР разработано се-
семейство пакетов ВЕКТОР, предназначенных для реше-
решения оптимизационных задач комбинаторного типа (см.

§ 1| ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 381
В. М. Глушков и др. [1]). Реализованы версии для ЭВМ
серии ЕС, М4030 и БЭСМ-6. Пакеты дают возможность
пользователю вести расчеты в диалоговом режиме, опера-
оперативно пополнять, модифицировать и настраивать пакеты
на особенности решаемых задач, генерировать версии пакета
для разных типов ЭВМ, производить сопряжение с дру-
другими программами, осуществляющими продолжение
счета.
Ниже мы остановимся на описании проблемно-ориен-
проблемно-ориентированной диалоговой системы оптимизации ДИСО, раз-
разработка которой началась в ВЦ АН СССР в 1975 г. Система
представляет собой комплекс из оптимизационных программ
и диалогового монитора, позволяющих управлять процессом
расчетов в пакетном и диалоговом режимах. Во время работы
над этой системой были найдены основные принципы по-
построения, функционирования и эксплуатации таких систем,
опыт практических расчетов способствовал развитию чис-
численных методов оптимизации, выработке наиболее рацио-
рациональных форм организации диалогового взаимодействия.
Расчеты велись на ЭВМ БЭСМ-6. Система ДИСО функциони-
функционирует в рамках мониторной системы ДУБНА, управляющая
программа (монитор) написана на языках алгол и фортран.
ДИСО реализована в рамках разработанной в ВЦ АН СССР
инструментальной системы ДИАЛОГ, предназначенной для
построения диалоговых пакетов программ научного харак-
характера. Для оперативного ввода информации используется
алфавитно-цифровое терминальное устройство типа «дис-
«дисплей» с пишущей машинкой «Видеотон-340». При работе
с ДИСО пользователь в соответствии со стандартными
требованиями оформляет задачу оптимизации на языках
алгол или фортран, вводит ее в систему либо с перфокарт,
либо с магнитной ленты, либо непосредственно с буквенно-
цифровой клавиатуры терминала; с помощью директив
(команд) вызывает из библиотеки программ наиболее под-
подходящие (с его точки зрения) алгоритмы, подбирает их
параметры. Управляющая программа организует взаимо-
взаимодействие модулей из тела пакета, управляет вводом исходной
и текущей информации, интерпретирует директивы поль-
пользователя, динамически загружает ЭВМ оптимизационными
модулями, выводит результаты счета в предписанном поль-
пользователем виде на экран дисплея (одновременно можно
получать результаты и на алфавитно-цифровом печатающем

382 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
устройстве). Анализируя результаты вычислений, пользо-
пользователь принимает решения о дальнейших расчетах, полу-
получая, таким образом, возможность следить за ходом решения
задачи, оперативно вмешиваться в процесс расчетов, выби-
выбирать методы, корректируя в случае необходимости их пара-
параметры. ДИСО является системой с директивным входным
языком. Пользователь определяет, как часто и в каком
виде должны выдаваться результаты на экран дисплея,
и далее, используя заранее определенный набор директив,
ведет расчеты. В процессе работы были выработаны и реа-
реализованы следующие основные принципы построения диа-
диалоговой системы.
В пакете должны быть заложены возможности модерни-
модернизации программного обеспечения, расширения функциональ-
функциональных возможностей добавления новых режимов эксплуатации.
Пакет должен иметь иерархическую структуру, отдель-
отдельные его программы строятся по модульному принципу.
Описание задач оптимизации должно быть простым
и приемлемым для ^ использования любого алгоритма из
библиотеки программ.
Система должна позволять выводить на экран дисплея
любые данные о текущем процессе расчетов, об управля-
управляющих параметрах, представляя пользователю всю нужную
информацию для управления.
Пользователь должен иметь возможность осуществлять
диалог по выбору методов их параметров, т. е. управлять
любыми параметрами процедур, просто переходить от одного
алгоритма к другому.
У пользователя должна быть возможность вести диалог
по параметрам задачи (модели) путем изменения масшта-
масштабирующих коэффициентов. Желательно обеспечить возмож-
возможность оперативно корректировать постановки задач. Дирек-
Директивы пользователя должны быть близкими к естественным
и вместе с тем не быть слишком длинными, чтобы умень-
уменьшить возможные ошибки, неизбежные при вводе длинных
текстов с буквенно-цифровой клавиатуры.
Библиотека методов оптимизации должна иметь иерар-
иерархическую структуру. При введении новой группы методов
для решения нового класса задач должна быть преду-
предусмотрена возможность использования в качестве вспомо-
вспомогательных процедур всех программ, существующих в биб-
библиотеке.

«1] ПРИНЦИПЫ ПОСТРОЕНИЯ ДИАЛОГОВЫХ СИСТЕМ 383
Система должна замечать по крайней мере самые про-
простые ошибки пользователя и сообщать ему об этом (на-
(например, с терминала введена неправильная директива).
Вместе с тем система должна допускать возможность того,
что пользователь не определяет все или некоторые пара-
параметры процедур; при этом учитываются параметры, пре-
предусмотренные для режима работы «по умолчанию».
Систему следует строить так, чтобы ее можно было
использовать для решения задач в пакетном режиме по
предписанному сценарию. Расчеты в этом случае проходят
без непосредственного участия пользователя.
При создании ДИСО возникли противоречивые требо-
требования: с одной стороны, было бы желательно, чтобы поль-
пользователь мог как можно более существенно влиять на процесс
решения задачи. Для этого следовало увеличить библиотеку
программ, расширить список параметров процедур, ввести
сюда все вспомогательные коэффициенты, предусмотреть
как можно большее число возможных вариантов алгорит-
алгоритмов. Но для работы с такой системой требуется хорошая
подготовка пользователя. С другой стороны, чтобы рас-
расширить круг пользователей, следует упростить работу
с ДИСО, автоматизировать процесс принятия решений,
ограничить набор алгоритмов. Другая трудность связана
с детализацией человеко-машинного взаимодействия. Диалог
можно оформить так, чтобы система задавала человеку
весьма подробные вопросы об организации расчетов и давала
комментарии и разъяснения по этим вопросам. Это упро-
упростило бы работу начинающего пользователя, но удлинило
бы время расчетов опытного пользователя. В процессе
создания ДИСО был достигнут некоторый компромисс в этих
вопросах.
В настоящее время ДИСО дает возможность решать
задачи следующих трех классов: безусловная минимизация
функций многих переменных (БМ), нелинейное програм-
программирование (НЛП), оптимальное управление системами
с фазовыми ограничениями (ОПТ). Основу библиотек алго-
алгоритмов для последних двух классов задач составили при-
приведенные в предыдущих главах методы.
В процессе эксплуатации системы происходит чередова-
чередование режимов активности пользователя и системы. В моменты
прерывания расчетов пользователь выполняет любые из
следующих действий:

384 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
анализ и коррекция текущего состояния,
вычисление значений целевой функции, ограничений,
их градиентов в текущей точке,
выбор метода решения,
настройка управляющих параметров метода,
спецификация критериев остановки и форм выдачи ин-
информации,
запуск метода на счет,
фиксация текущего состояния в базе данных.
Структура большинства методов НЛП и ОПТ двух-
двухуровневая, так как йозникает дополнительный уровень
управления, состоящий в решении подзадачи БМ. Пере-
Перечисленные выше возможности управления распространяются
на оба уровня. Пользователь может установить автомати-
автоматический или диалоговый режим решения любой подзадачи.
Важной чертой системы ДИСО является ее расширяе-
расширяемость, обеспечиваемая специальным инструментальным
блоком. Вычислительные возможности могут наращиваться
в различных направлениях путем введения как новых ме-
методов, так и добавления новых классов решаемых задач.
Планируется в дальнейшем в систему включить блоки ре-
решения минимаксных задач, поиска глобального экстремума
и управления системами с распределенными параметрами.
Предполагается также создать комбинированный пакет,
позволяющий проводить диалог, рассчитанный не только
на управление процессом оптимизации, но и на динамиче-
динамическое изменение постановки задачи.
В последующих параграфах будут приведены основные
сведения о реализации методов решения задач безусловной
минимизации функций многих переменных и задач нели-
нелинейного программирования. В качестве примеров будут
даны протоколы расчетов простейших тестовых задач.
Протоколы решения задач оптимального управления гораздо
более громоздкие, поэтому здесь не приводятся; некоторые
результаты решения этого класса задач с помощью ДИСО
были изложены в § 7 гл. VI.
§ 2. Библиотека программ решения задач
безусловной минимизации
В библиотеку ДИСО входят: программы оптимизации,
набор стандартных программ вычисления с разными сте-
степенями точности градиентов функций и матриц вторых

§2] БИБЛИОТЕКА БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ 385
производных, вспомогательные программы вывода инфор-
информации. Вся библиотека написана на языке алгол и создана
на основе модульного принципа. Такая организация допу-
допускает взаимозаменяемость модулей; изменение одного из
них не приводит к изменению других. Это позволяет, со-
сохраняя в целом систему, производить постепенную пере-
переработку отдельных блоков, включать новые и исключать
неудачные варианты.
Программы, предназначенные для решения задач опти-
оптимизации, имеют стандартную форму записи и унифициро-
унифицированную структуру. Задача безусловной минимизации функ-
функций многих переменных состоит в отыскании
minf(x). B.1)
Многие методы решения этой задачи переносятся на
случай нахождения
B.2)
Поэтому в библиотеке БМ содержатся программы, реша-
решающие задачи B.1) и B.2). Каждая программа в библиотеке
имеет свой заголовок. Программы, реализующие методы
решения задачи B.1), имеют заголовки, начинающиеся
с буквы А, далее идет цифра, предписанная для каждого
конкретного метода. Если программа позволяет решать
задачу B.2), то после буквы А ставится буква Р. Ана-
Аналогично в случае программ решения задач нелинейного
программирования вначале пишется буква С, в случае
задач оптимального управления—ОРТ, далее указывается
значащий код программы в данном классе.
Для решения поставленных задач созданы программы,
реализующие следующие методы: API—шесть версий по-
покоординатного спуска; А2, АР2—две версии наискорейшего
спуска; А31, АР31—метод сопряженных градиентов Флет-
чера — Ривса и его модификации; АР4 — метод Хука
и Дживса; А5—метод Пауэлла; АР6—метод случайного
поиска; А8, А80, А89—модификации метода Ньютона;
А9—метод эллипсоидов Н. 3. Шора; А81—четыре версии
квазиньютоновского метода.
Собранные методы можно классифицировать по различ-
различным признакам. Простейшим признаком является наиболь-
наибольший порядок производных функции /(*), необходимый для
13 ю. Г. Евтушенко

386 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ - [ГЛ. VII
реализации метода. Не требуется вычисления производных
в программах АР4, А5, АР6; в программе А9 следует
определять производные по направлению. В большинстве
программ вычисляются только первые производные, к этому
классу относятся API, А2, АР2, А31, АР31, А89, А81.
Вторые производные вычисляются в А8, А80. Наибольший
объем памяти требуется для работы программ А5, А8,
А80, А81, А9, что делает их малоприемлемыми для ре-
решения задач высокой размерности.
Программы оформлены в соответствии с требованиями
языка алгол. Каждая программа представляет собой про-
процедуру со следующим списком формальных параметров:
п, х, а, 6, /, fgr, fhess, у, g, q, par.
Разъясним их смысл:
п—целое число, размерность вектора х;
х—массив [1:я], перед расчетами в него помещается
начальная точка х0, последующие векторы xk записы-
записываются в х;
а, Ь—массивы [Г:л], определяющие ограничения в за-
задаче B.2);
f—процедура-функция с одним формальным парамет-
параметром х\
fgr—процедура для вычисления градиента минимизи-
минимизируемой функции;
fhess—процедура для вычисления матрицы вторых
производных минимизируемой функции;
у—вещественное число, равное значению функции f (x)\
g—массив [1:/г], хранящий градиент минимизируемой
функции / в точке х;
par—информационный массив, предназначенный для
передачи процедуре значений управляющих параметров,
которые записываются в массиве последовательно, распо-
расположение первого из них определяется индексом q.
Все элементы массива par имеют некоторые названия.
Обычно они представляют сокращенные названия парамет-
параметров на русском языке. Приведем описания тех элементов
массива, которые являются общими для всех программ:
ЧИСШАГ—целое число, максимальное число шагов
(итераций), которое можно сделать выбранным методом;
ВЫПШАГ—целое число, количество фактически сде--
ланных итераций;

§3] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ БМ 387
ТОЧ—точность решения задачи; в случае методов,
использующих производные, расчеты оканчиваются, когда
норма градиента минимизируемой функции меньше вели-
величины ТОЧ, в случае задачи B.2) при определении нормы
учитываются производные лишь вдоль возможных на-
направлений;
ШАГПЕЧ—целое число, определяет через сколько
итераций производить очередную выдачу результатов счета;
ПОДР—целое число, код подробности выводимой ин-
информации.
В тех программах, где используется вычисление про-
производных, присутствуют также следующие параметры:
ШАГДИФ—вещественное число, номинальный шаг для
численного дифференцирования;
ПОРДИФ—целое число, определяет используемую
разностную схему численного дифференцирования.
Пользователь системы может либо описать свои спе-
специальные процедуры дифференцирования (основанные на
аналитических формулах или конечно-разностных аппрок-
аппроксимациях), либо воспользоваться стандартными процеду-
процедурами, хранящимися в библиотеке ДИСО.
§ 3. Примеры численных расчетов задачи
безусловной минимизации
Результаты расчетов в значительной степени зависят
от значений управляющих параметров; путем тщательного
их подбора можно существенно повлиять на ход вычислений
и получить некоторые «рекордные» результаты. Ниже будут
приведены протоколы расчетов, выполненных в диалоговом
режиме и, кроме того, даны таблицы, иллюстрирующие
решения тестовой задачи, проведенные с помощью только
одного метода оптимизации от начала до конца расчетов.
В последнем случае расчеты велись в основном с исполь-
использованием параметров методов, предусмотренных для режи-
режима работы «по умолчанию»; только в нескольких случаях
делалось дополнительно два-три просчета с другими па-
параметрами и лучший результат был представлен в таблице.
Приведенные данные, таким образом, являются далеко не
«рекордными». Чтобы упростить описание численных экспе-
экспериментов, бралась простейшая тестовая задача. Поэтому
результаты расчетов мало говорят об эффективности
13*

388 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VH
используемых методов. Сравнительный анализ методов
следует проводить на основе решения разнообразных и
более сложных задач. Чтобы в некоторой степени при-
приблизить расчеты к реальности, везде используется чис-
численное дифференцирование функций, определяющих зада-
задачу. Трудоемкость расчетов определяется в основном числом
Ny равным количеству обращений к вычислению функции
(обращения, необходимые для вычисления производных,
при этом также учитываются).
В качестве тестовой задачи возьмем так называемую
функцию Розенброка
Начальная точка всегда берется л:0 = [1,2, 1]. В методах,
предназначенных только для решения задачи B.2), пола-
полагается ail} = а{2) = —2, Ь{1) = 2, 6B) = 1. Решением задачи
является точка лг« = [1, 1], в которой / (д:^) = 0.
Результаты решения задачи Розенброка приведены
в табл. 8, где указано число N, количество итераций /С,
сделанных методом, значение функции /, норма ее гради-
градиента в результирующей точке. В тех методах, где не вы-
вычисляется градиент, его норма не дается. В случае про-
программы А81 приведены последовательно следующие варианты
квазиньютоновских методов: метод Пауэлла — Бройдена
B.5.48), B.5.38); Давидона —Флетчера—Пауэлла B.5.48),
B.5.36); симметричный метод первого ранга B.5.48), B.5.31)
и метод Бройдена — Флетчера — Гольдфарба — Шенно
B.5.48), B.5.37).
В данной сравнительно простой задаче малой размер-
размерности очевидно преимущество быстро сходящихся методов.
Одинаковый, хороший результат получен методом Ньютона
по программам А8 и А80, причем в последнем случае,
благодаря более экономной организации вычислений про-
производных, число N на 100 меньше, чем при использовании
программы А8. Еще лучшие результаты можно получить
с помощью многометодного режима оптимизации. В каче-
качестве примера приведем расчеты по простейшему сценарию.
В начале делается 3 итерации методом эллипсоидов и затем
из найденной точки делаются итерации по программе А80
до тех пор, пока норма градиента функции / (х) не станет
меньше 10~8. Параметры в обеих программах взягы «по
умолчанию» и совпадают с соответствующими параметрами,

§3]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ БМ 389
Таблица 8
Програлша
API
АР2
А31
АР4
А5
АР6
А8
А80
А89
А81
А9
N
151
544
296
435
186
233
276
176
299
347
198
329
269
644
К
4
50
16
91
15
31
25
25
21
50
32
48
38
50
fix)
2,5110_6
5,01910_02
3,72610_„
9,56110-..
Ю-20
7,2210.12
7,85610-15
7,85610_16
7,77010_16
1,74410_1?
3,12010_16
2,65410.1в
2t988l0-tt
3,680Х0_7
И fx (х) [\
—
2,51510-01
6,78410.в
—
—
1,85910-в
1,8591о-.
1,12610..
2,22710.7
1,43310.в
1,60610-?
5,47410.в
2,88410_3

390 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
использованными при расчетах, приведенных в табл. 8.
Комбинированная стратегия поиска, при которой вначале
использовался метод, подходящий для проведения предва-
предварительных расчетов, и только после этого осуществлялся
переход к быстросходящемуся методу, позволил добиться
наилучших результатов как по точности, так и по трудо-
трудоемкости расчетов. Действительно, было получено N = 95,
!/*(*)(= 1,220-10"9, время расчетов и величину N удалось
сократить почти в два раза по сравнению с использованием
только одной программы А80 и в шесть раз по сравнению
с использованием только программы А9. Еще лучшие ре-
результаты можно получить, применяя аналитические фор-
формулы для вычисления производных и с помощью подбора
управляющих параметров. Эти расчеты приводить не будем,
так как их изложение потребует более детального описа-
описания используемых программ, разъяснения смысла всех
управляющих параметров.
Приведем протокол реализации простейшего многоме-
тодного режима работы, выведенный на алфавитно-цифро-
алфавитно-цифровое печатающее устройство. Здесь и ниже черта в начале
строки указывает, что содержимое строки—информация,
сообщаемая системе пользователем. Директива вида:
ТОЧКА = 2 3 означает, что у двумерного вектора в каче-
качестве координат взяты числа 2 и 3. Слово РЕСУРС обозна-
обозначает количество обращений к функции f (х) (выше это
было N).
Протокол № 1
— ОТКРЫТЬ БЛОК БМ
— ВЗЯТЬ ТЕСТОВУЮ ЗАДАЧУ РОЗЕНБРОКА
— ВЗЯТЬ МЕТОД А9
УСТАНОВЛЕН МЕТОД А9
-ЧИСШАГ = 3; ТОЧКА = -1,2 1;
-СЧЕТ
НАЧАЛ СЧЕТ МЕТОД А9
БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ
[АГ
0
1
2
3
ФУНКЦИЯ
2,42010 + 01
8,05510-oi
3,22310-02
3,22310_02
РЕСУРС
3
21
30
33
НОРМА
ГРАДИЕНТА
2,32810 + 08
3,3381О + Оо
6,72410 + 00
6,72410 + 00

§4] БИБЛИОТЕКА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 391
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ЗАКОНЧИЛ СЧЕТ МЕТОД А9
— ВЗЯТЬ МЕТОД А80
УСТАНОВЛЕН МЕТОД А80
-СЧЕТ
НАЧАЛ СЧЕТ МЕТОД А80
БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ
ШАГ
0
1
2
3
4
5
6
7
8
функция
3,22310_О2
9,43410_08
7,09910_о,
1,63010-о,
2,47610_в4
7,9771О-о.
2,28510.0в
1,51410.1$
0,000
РЕСУРС
38
47
56
65
71
77
83
89
95
HOPM^V
ГРАДИЕНТА
6,72410+в0
4,72710-О1
3,54410.О1
1,05010+„
1,21010.в1
7,77910.08
1,8661О-о.
9,24010_о.
1,22010-о.
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ЗАКОНЧИЛ СЧЕТ МЕТОД А80
— КОНЕЦ РАСЧЕТОВ
§ 4. Библиотека программ для решения задач
нелинейного программирования
В системе ДИСО общая задача нелинейного програм-
программирования A.6.1) ставится следующим образом: найти
min/@, х), D.1)
где Х = {хеЕп: f(i, x) = 0, ( j
1^/^^}- Созданы версии методов, решающие задачу
нахождения
min /@, х), D.2)
хр
где Р = {х?Еп: <<}
Для решения этих задач в системе ДИСО собраны
программы, реализующие следующие методы:

392 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
СР41—метод внешних штрафных функций (в первой
версии функция штрафа имеет вид C.1.6), во второй вер-
версии—C.2.7));
СР45—метод параметризации целевой функции (штраф-
(штрафная функция строится по формуле C.1.6), в первой версии
реализовано правило C.3.6), во второй—C.3.10), в третьей—
C.3.11));
СР53—метод модифицированной функции Лагранжа
(см. D.3.21));
СР55—первый вариант метода простой итерации (см.
D.3.20));
СР5—второй вариант метода простой итерации (см.
D.3.19));
С6—метод приведенного градиента (см. E.2.2), E.2.3),
E.2.10));
С1—метод возможных направлений;
С2—метод линеаризации (см. формулы C.5.8)—C.5.12));
СЗ—две версии прямого метода модифицированной
функции Лагранжа (см. D.6.8), D.6.10));
С8 — модификация метода Ньютона (см. формулу
D.1.11));
С7—модифицированный метод Эрроу—Гурвица (см.
D.1.21)).
Буква Р в заголовке программы указывает на то, что
реализована модификация соответствующего метода, при-
приспособленная для решения задачи D.2). Многие программы
могут быть использованы как для решения D.1), так и для
D.2) без каких-либо переделок. В этих программах исполь-
используются вспомогательные процедуры безусловной миними-
минимизации, с помощью которых осуществляется, если это нужно,
учет ограничений х?Р. Так, например, программа СР41,
реализующая метод штрафов, будет решать задачу D.1),
если в качестве программ решения задач БМ взяты А31,
А8, и задачу D.2), если в качестве программ БМ взяты
АР4, АР31 или какие-либо другие, учитывающие парал-
лелепипедные ограничения. При задании системе ДИСО
задачи D.2) пользователь имеет две возможности. Первая—
отнести параллелепипедные ограничения к общим ограни-
ограничениям типа неравенства, числам а', V приписать фиктивные
значения и для расчетов использовать процедуры, не учи-
учитывающие параллелепипедные ограничения. Вторая возмож-
возможность состоит в учете параллелепипедных ограничений

§4] БИБЛИОТЕКА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 393
с помощью программ группы СР. Преимущество первого
подхода состоит в том, что он позволяет использовать
более широкий набор методов, представленных в библио-
библиотеке. Преимущество второго подхода заключается в том,
что при этом удается сравнительно просто учитывать па-
раллелепипедные ограничения.
В библиотеке ДИСО содержится также программа
ВНУТР, с помощью которой отыскиваются внутренние
точки множества X. В методах С1 и С6 требуется, чтобы
начальная точка была внутренней, поэтому перед началом
счета по этим программам обычно делается обращение
к программе ВНУТР.
Все программы, предназначенные для решения задач
D.1), D.2), и программа ВНУТР оформлены в виде про-
процедур со следующим списком формальных параметров:
п, е, т, х, а, &, /?, /, fgr9 fhess, у, q, par.
Разъясним их смысл:
п—целое число, размерность вектора х\
е—целое число, количество ограничений типа равенства;
т—целое число, полное количество ограничений типа
равенства и неравенства;
х—массив [1:я]; перед расчетами начальная точка х^
помещается в этот массив, последующие точки xk хранятся
в массиве х\
а, Ь—массивы [1:я], определяющие параллелепипедные
ограничения;
р—массив [1:т], определяет двойственный вектор;
/ — процедура, задающая набор функций, определяющих
задачу;
fgr—процедура для вычисления градиентов функций
fhess—процедура для вычисления матриц вторых про-
производных функций /(/, я);
у—массив [0:m], y[i] = f{i, х) для всех O^i'^m;
par—информационный массив, предназначен для пере-
передачи процедуре значений управляющих параметров, кото-
которые записываются в массиве последовательно, расположе-
расположение первого из них определяется индексом q.
Общие элементы массива par обозначаются так же
и имеют тот же смысл, что и приведенные в § 2.

394 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
Задание функций, определяющих задачу D.1), осуществ-
осуществляется с помощью процедуры, имеющей заголовок
/ (*, У. О-
Массивы х, у описаны выше; i—целое число, если
i < 0, то при обращении к процедуре f определяются все
элементы массива у> при O^i^m определяется только
элемент y[i].
Вычисление градиента функции f(i9 x) осуществляется
с помощью процедуры, имеющей заголовок
fgr(f, *, у, m, ?, f, hy ас).
Здесь /—процедура вычисления функций /(*,#); h—но-
h—номинальный шаг численного дифференцирования; g—мас-
g—массив [1:п], определяющий градиент функции f{i>x)\ i —
целое число (O^t^m); ас—номер схемы дифференци-
дифференцирования. Если ас=1, то частная производная функции
/ (i, х) по л/ вычисляется по формуле
8ii] = jjUii. x+eW)-f(i, x)]. D.3)
Здесь eJ'—единичный вектор, направленный по /-й оси,
шаг дифференцирования равен
в/ = ЛA + 1О-1*[/]|). D.4)
Если ас = 2, то используется более точная схема диф-
дифференцирования
Погрешность вычисления производной по формуле D.3)
имеет порядок 6'', по формуле D.4) — (б'J.
В соответствии с приведенными стандартами пользова-
пользователь может оформить свои процедуры дифференцирования
или доопределить процедуру fgr для случая ас > 2. Ана-
Аналогичная ситуация имеет место для вычисления вторых
производных.

§5]
ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ НЛП
395
§ 5. Примеры численных расчетов задачи
нелинейного программирования
Общее описание подхода к численным расчетам было
дано в § 3, поэтому сразу перейдем к описанию тестовой
задачи, в которой
п = 3, e=l, m = 5,
/ @, х) = (х1 + 3jc2+*3J + 4 (л:1 —л:2J — 1,8309996947;
*~l; /B, *) = -**, E.1)
В качестве начальных векторов ху р брались следующие:
Значение минимизируемой функции в точке решения
задачи близко к нулю.
Производные всюду считаются численно. Полное коли-
количество обращений к каждой из функции / (/, х) обозна-
обозначается по-прежнему N, в протоколах называется РЕСУРС.
Количество выполненных итераций обозначается буквой /С.
Мерой нарушения ограничений является значение штраф-
штрафной функции S(x), вычисленной по формуле C.2.7).
В табл. 9 приведены результаты решения тестовой задачи.
Таблица 9
Прог-
Программа
СР41
СР45
СР53
СР55
СР5
СР6
С1
С2
СЗ
С8
N
1254
1728
2154
1254
1404
482
313
402
126
177
К
6
12
6
6
6
12
15
16
5
3
/ @, х)
о
Z10~4
л
10~4
710-з
-2ю-
6ю-
О
Ю-3
510_6
4ю-'
S
4ю-
«го —
310-4
5ю-'
Чо-12
510_5
2ю-»
0,29465
0,29429
0,29362
0,29433
0,29434
0,29428
0,29575
0,29525
0,29427
0,29429
а:2
0,10204
0,10125
0,10328
0,10129
0,10124
0,10133
0,10580
0,10312
0,10129
0,10131
0,60327
0,60440
0,60165
0,60443
0,60443
0,60439
0,5984
0,60163
0,60442
0,60440

396 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VI!
В качестве программы, решающей вспомогательные задачи
безусловной минимизации в методах СР41, СР53, СЗ,
бралась программа А31, реализующая метод сопряженных
градиентов. В случае применения методов СР45, СР55,
СР5 использовался метод Ньютона А80.
Наилучший по точности результат получен методом
Ньютона (программа С8), после него можно указать на
С6, СР55, СЗ. Надо иметь в виду, что в рассматриваемой
задаче ограничение типа равенства линейно зависит от *,
что существенно повышает эффективность метода приве-
приведенного градиента (программа С6). Лучший результат по
количеству обращений к функциям, определяющим задачу
(N=126), получен с помощью программы СЗ. Однако
следует заметить, что в программах Cl, C2, СЗ число N
в слабой степени отражает трудоемкость расчетов, так
как в них считаются вспомогательные задачи, не содер-
содержащие обращений к вычислению значений функции f(i, х).
Поэтому время решения данной задачи методами СЗ и
СР55 оказывается примерно одинаковым, несмотря на
десятикратное отличие в величинах N.
При проведении расчетов, помещенных в табл. 9, было
взято хорошее начальное приближение для множителей
Лагранжа, что упростило задачу. Дадим два примера
решения этой же задачи в диалоговом режиме, взяв в ка-
качестве начальных условий менее благоприятные точки.
После краткого описания диалога приведем протоколы
расчетов.
Пример 1. Пользователь в качестве х задал вектор
[5,3,4] и дал системе директиву вызвать метод СР41.
Система выполнила приказ, пользователь указал, чтобы
были выполнены две итерации. Пользователь решил не
менять параметров процедуры и взять метод решения
задачи безусловной минимизации, предусмотренный «по
умолчанию». Поэтому на директиву ОТКРЫТЬ МЕТОД
БМ система указала, что установлен метод А31 (сопря-
(сопряженных градиентов). Пользователь установил точность
решения задачи БМ, равную 0,5, что соответствует
в программе А31 прекращению расчетов после того, как
найдена точка, где норма градиента минимизируемой функ-
функции становится меньше 0,5. Подробность выводимой ин-
информации в методе БМ соответствует двум. Далее была
дана директива начать счет.

$5] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ НЛП 397
В начальной точке значение минимизируемой функции
оказалось равным 326, 169, штрафная функция S(x)= 105.
При первом обращении к методу А31 сделано 9 итераций,
норма градиента вспомогательной функции доведена до
0,353, при этом число N, которое в диалоге называется
«РЕСУРС» стало равным 1026. На второй итерации реше-
решения задачи НЛП программа А31 выполнила одну лишь
итерацию, несмотря на то, что коэффициент штрафа уве-
увеличился в 10 раз и стал равным 30. После второй
итерации решения задачи НЛП получено /@, *)=
= —0,02317, S(х) =0,02034, TV = 1230, кроме того, были
определены множители Лагранжа, что позволило перейти
к методам, основанным на использовании итераций по
двойственным векторам. Была вызвана программа СР5,
для нее заданы три итерации. В качестве метода решения
задачи безусловной минимизации использовался метод
Ньютона (программа А80), точность расчетов 0,01, под-
подробность вывода информации соответствовала двум. После
трех итераций по программе СР5 получено /@, х)=
=0,001848, S(*) = 0,0002967, W = 1992.
Чтобы завершить расчеты, пользователь обратился
к методу Ньютона С8. Все параметры метода были взяты
из режима работы «по умолчанию», в частности, точ-
точность была равной 10~4. В данной программе это значит,
что расчеты прекращаются как только найдена точка
z = [x, и, и], удовлетворяющая условию |F,B)|^ 10~4,
где F(z) определяется формулой D.1.1). Метод Ньютона
«сработал» исключительно эффективно: после второй ите-
итерации было получено /@, x) = 4,474iO-«, S(#)=10-u,
N = 2334. Пользователь дал команды ДВОЙСТВ, ОГРРАВ
и ОГРНЕР, по которым были выведены компоненты
двойственного вектора, значения ограничений типа ра-
равенства и неравенства. На этом расчеты были прекра-
прекращены .
Протокол № 2
— ОТКРЫТЬ БЛОК НЛП; ТЕСТОВАЯ ЗАДАЧА № 1;
— ТОЧКА = 5 3 4
— ВЗЯТЬ МЕТОД CP4I
УСТАНОВЛЕН МЕТОД СР41
— ЧИСШАГ = 2;
— ОТКРЫТЬ МЕТОД БМ

398 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ 1ГЛ. VII
ОТКРЫТ МЕТОД А31
-ТОЧ = 0,5; ПОДР==2; СЧЕТ
ИСХОДНОЕ СОСТОЯНИЕ НЛП
ФУНКЦИЯ = 3,26210+02
РЕСУРС = 6
ШТРАФ = 105
БЕЗУСЛОВНАЯ <
ШАГ
0
1
2
3
4
5
6
7
8
9
ФУНКЦИЯ
2,71910+04
4,00110+0,
3,58310+01
3,26110+00
8,05610-01
-2,68910-02
—3,78210_02
• ^®
-9,13110.02
-l,09710-oi
МИНИМИЗАЦИЯ
РЕСУРС
30
222
402
516
606
702
774
864
948
1026
НОРМА
ГРАДИЕНТА
4,25810+04
1>57210+0,
3,997lo + oi
3,4421О+О1
7,74810+0.
2,60610+0»
9,01610_„,
1,2931О+.№
1,07310+00.
3,53110_„
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ШАГ НЛП=1
ФУНКЦИЯ =-2,2141О_о1
РЕСУРС =1032
ШТРАФ = 2,22410_01
БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ
НОРМА
ШАГ ФУНКЦИЯ РЕСУРС ГРАДИЕНТА
0 8,94910_01 Ю56 7,68210f01
1 —1,1121О.ов 1224 2,379lo.oi
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ШАГ НЛП=2
ФУНКЦИЯ = -2,3171О_о,
РЕСУРС =1230
ШТРАФ = 2,03410_о*
ЗАКОНЧИЛ СЧЕТ МЕТОД СР41

§5J ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ НЛП 399
— ВЗЯТЬ МЕТОД СР5
УСТАНОВЛЕН МЕТОД
— ЧИСШАГ = 3
— ВЗЯТЬ МЕТОД БМ А80
УСТАНОВЛЕН МЕТОД
— ТОЧ = 0,01; СЧЕТ
НАЧАЛ СЧЕТ МЕТОД
СР5
А80
СР5
ИСХОДНОЕ СОСТОЯНИЕ НЛП
РЕСУРС =1236
ШТРАФ = 2,03410-02
БЕЗУСЛОВНАЯ J
МИНИМИЗАЦИЯ
ШАГ ФУНКЦИЯ РЕСУРС
0 2,2251О-о.
1 4,77410_0*
2 -7,69010_0«
3 -1,6651О_о,
4 -1,8561О_оз
5 -1,87210_03
1278
1356
1434
1494
1572
1632
НОРМА
ГРАДИЕНТА
2
2
1
2
7
6
,836lo_oi
,38310_О1
»831 lo-oi
,07210_01
,3411О_о2
»79310_q»
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ШАГ НЛП=1
ФУНКЦИЯ =1,О52ю-о«
РЕСУРС- 1638
ШТРАФ = 2,18210_м
БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ
НОРМА
ШАГ ФУНКЦИЯ РЕСУРС ГРАДИЕНТА
0 3,1781О_оз 1680 2,48010_ei
1 9,1Ю1О-о4 1740 4,10810_оа
2 9,01410.о4 1800 3,89810_0*
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ШАГ НЛП = 2
ФУНКЦИЯ = 4,6541О_о.
РЕСУРС = 1806
ШТРАФ =2,04910_оа

400 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ. VII
БЕЗУСЛОВНАЯ МИНИМИЗАЦИЯ
НОРМА
ШАГ ФУНКЦИЯ РЕСУРС ГРАДИЕНТА
0
1
2
9
9
9
,50110_04
,2961О_о4
>2441О_О4
1848
1908
1986
2
1
4
,74910
,04710
,75910
— 02
— 03
КОНЕЦ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ЗАКОНЧИЛ СЧЕТ МЕТОД СР5
— ВЗЯТЬ МЕТОД С8
УСТАНОВЛЕН МЕТОД С8
— СЧЕТ
ИСХОДНОЕ СОСТОЯНИЕ НЛП
ФУНКЦИЯ = 1,8481О-О,
РЕСУРС = 2034
ШАГ НЛП=1
РЕСУРС-2186
ШТРАФ = 1,2691О.от
ШАГ НЛП = 2
ФУНКЦИЯ = 4,47410_1О
РЕСУРС^ 2334
ШТРАФ=1,00010.„
ЗАКОНЧИЛ СЧЕТ МЕТОД С8
— ДВОЙСТВ -2,26910.о, 9,1241в.„ 2,13810_le lt221ie.tt
lf165ie+w
— ОГРРАВ
-1,0001в_»
- ОГРНЕР
-2,94310_о, —1,01310.„ -6,04410_О1
-2,38810.„
- КОНЕЦ РАСЧЕТОВ
Пример 2. Пользователь задал начальную точку
[5, 3, 4] и двойственный вектор [3, 3, 3]. Система указала,
что вторая директива задана неверно. Дело в том, что
двойственный вектор пятимерный, а не трехмерный, как
его определил пользователь. Поэтому в последующей
команде в качестве двойственного вектора был задан вектор

§5] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ НЛП
401
[3, 3, 3, 3, 3]. Учтя хорошие результаты, полученные
методом Ньютона в предыдущем примере, пользователь
решил начать расчеты с него, ограничив число итераций
пятью. Судя по результатам, приведенным в протоколе,
метод быстро сошелся и уже после второй итерации мини-
минимизируемая функция не изменялась (с точностью до четы-
четырех значащих цифр), однако большая величина штрафа,
равная 89,31 указывала на то, что метод сошелся к не-
недопустимой точке. Ранее в § 1 гл. IV указывалось на
этот недостаток метода D.1.11), связанный с узкой об-
областью его сходимости. Проделанный неудачный экспери-
эксперимент потребовал значительных вычислений, число N стало
равным 3396. После этого пользователь обратился к про-
программе С2 (метод линеаризации), задав число итераций
равным пяти. После завершения расчетов получено
f@, х) = 0,002921, S (х) = 0,002089, // = 4416. Добиться
высокой точности методом линеаризации трудно, поэтому
пользователь обратился к программе СЗ (прямой метод
модифицированной функции Лагранжа), по которой пред-
предполагалось сделать пять итераций. Однако расчеты пре-
прекратились после третьей итерации из-за выполнения усло-
условия окончания расчетов по точности. Было получено
f@, x) = 9,7710-», S(x) = 8,20310-o., ЛГ = 4494. На этом
расчеты закончились.
Протокол № 3
— ОТКРЫТЬ БЛОК НЛП; ТЕСТОВАЯ ЗАДАЧА № 1;
ТОЧКА=5 3 4
— ДВОЙСТВ = 3 3 3
ОШИБКА: НЕ СОВПАДАЮТ РАЗМЕРНОСТИ МАССИВОВ
— ДВОЙСТВ = 3 3 3 3 3
-ВЗЯТЬ МЕТОД С8
УСТАНОВЛЕН МЕТОД С8
— ЧИСШАГ = 5
-СЧЕТ
ИСХОДНОЕ СОСТОЯНИЕ НЛП
ФУНКЦИЯ = 3,2611О+О,
РЕСУРС = 42
ШТРАФ = 1,05010+0,
14 Ю. Г. Евтушенко

402 ДИАЛОГОВЫЕ СИСТЕМЫ ОПТИМИЗАЦИИ [ГЛ VI
ШАГ НЛП=1
ФУНКЦИЯ =5,79810 +
РЕСУРС = 234
ШАГ НЛП = 2
ФУНКЦИЯ = 1,56810+м
РЕСУРС = 426
ШТРАФ = 8,93110+в»
ШАГ НЛП=3
ФУНКЦИЯ- !,15810+08
РЕСУРС = 1416
ШТРАФ = 8,93110+01
ШАГ НЛП = 4
ФУНКЦИЯ = 1,15810+§1
РЕСУРС = 2406
ШТРАФ = 8,93110+о1
ШАГ НЛП = 5
ФУНКЦИЯ- 1,15810+м
РЕСУРС = 3396
ШТРАФ =8,93110+01
ЗАКОНЧИЛ СЧЕТ МЕТОД С8
- ВЗЯТЬ МЕТОД С2
УСТАНОВЛЕН МЕТОД С2
— ЧИСШАГ = 5
-СЧЕТ
ИСХОДНОЕ СОСТОЯНИЕ НЛП
ФУНКЦИЯ- 1,15810+и
РЕСУРС = 3402
ШТРАФ = 8,9311О+О1
ШАГ НЛП=1
ФУНКЦИЯ-3,1691О+оо
РЕСУРС = 4314
ШТРАФ = 4,00010+00
ШАГ НЛП = 2
ФУНКЦИЯ--7,49410.«I
РЕСУРС = 4338
ШТРАФ = 7,93110_01

j 5] ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ НЛП 403
ШАГ НЛП = 3
ФУНКЦИЯ-1,34610_01
РЕСУРС = 4362
ШАГ НЛП = 4
ФУНКЦИЯ = 2,75810_0,
РЕСУРС = 4386
ШТРАФ = 2,8691О_оз
ШАГ НЛП = 5
ФУНКЦИЯ = 2,92110_ оз
РЕСУРС = 4416
ЗАКОНЧИЛ СЧЕТ МЕТОД С2
ВЗЯТЬ МЕТОД СЗ
УСТАНОВЛЕН МЕТОД СЗ
СЧЕТ
ИСХОДНОЕ СОСТОЯНИЕ НЛП
ФУНКЦИЯ = 2,92110_08
РЕСУРС = 4422
ШАГ НЛП=1
ФУНКЦИЯ =2,75010-о*
РЕСУРС = 4446
ШАГ НЛП = 2
ФУНКЦИЯ = 8,60010-.с.
РЕСУРС = 4470
ШТРАФ =l,17310..i
ШАГ НЛП = 3
РЕСУРС = 4494
ШТРАФ = 8,20310_0,
ЗАКОНЧИЛ СЧЕТ МЕТОД СЗ
КОНЕЦ РАСЧЕТОВ
14*

ПРИЛОЖЕНИЕ I
ДИФФЕРЕНЦИРУЕМОСТЬ
1. Дифференцируемые функции. Пусть функция / (х) от «-мер-
«-мерного вектора x?Rn определена на некотором открытом множестве X.
Будем говорить, что функция f (х) дифференцируема в точке х?Х,
если существует такой ограниченный вектор p(zRn, что для всех
h?Rn удовлетворяющих условию х-\-п?Х справедлива формула
где функция а обладает свойством:
lim a(x, h) = 0.
Пусть функция / дифференцируема в точке х, тогда она непре-
непрерывна в этой точке, у нее существуют частные производные по всем
координатам и определен я-мерный вектор
df(x) df(x)
который называется градиентом функции / в точке х. В формуле A)
можно положить p = fx(x).
Функцию / будем называть дифференцируемой на открытом мно-
множестве Ху если она дифференцируема в каждой точке х?Х.
Если говорится, что функция / дифференцируема на множестве X
(возможно, замкнутом), то имеется в виду, что / дифференцируема на
некотором открытом множестве, содержащем X.
Функцию f (х) будем называть дифференцируемой (всюду), если
она дифференцируема в каждой точке x?Rn.
Функция /(*), имеющая в некоторой точке х (или на открытом
множестве X) непрерывные частные производные, называется непре-
непрерывно дифференцируемой в этой точке (соответственно на множестве X).
Обозначим h я-мерный вектор, норма которого равна единице.
Предел
*
если он существует, называется производной функции / (х) в точке х
по направлению h и обозначается S .
он
Если функция f дифференцируема в точке #, то в этой точке
функция / имеет производные по любому направлению.

ДИФФЕРЕНЦИРУЕМОСТЬ 405
Теорема 1. Если функция f (x) дифференцируема на откры-
открытом выпуклом множестве X?Rn и хъ х2?Х, то существует такое
число 0 < т < 1, что имеют место следующие равенства:
*i)). a:2-^>, B)
C)
Формулу B) обычно называют формулой Лагранжа, а C) — фор-
формулой Ньютона—Лейбница.
Будем говорить, что функция /(*)> определенная на Ху удовлет-
удовлетворяет на X условию Липшица с постоянной /, если для любых xlt
х2?Х имеет место неравенство
Очевидно, что функция, удовлетворяющая на X условию Липшица,
непрерывна на X.
Теорема 2. Пусть функция f (x) дифференцируема на откры-
открытом выпуклом множестве Х> где ее градиент fx (x) удовлетворяет
условию Липшица с постоянной I. Тогда для любых хъ х2?Х и лю-
любого 0 ^ т ^ 1 имеют место формулы
где функция ц (z) такова, что т) @) = 0 и \х\ (г)\ < /1| г ||2.
2. Дважды дифференцируемые функции. Пусть функция / (х) оп-
определена на открытом множестве X<zRn. Будем говорить, что функ-
функция f (х) дважды дифференцируема в точке х?Х, если для всех
h?R удовлетворяющих условию х-\-1г?Х, справедлива формула
/ <*+*)-/(*> = /* М h+Y hTfxx (x) h+\ h f p (x, A),
где функция р обладает свойством
lim 6(jc, h) = 0.
ЦЛ||->0
Здесь fxx(x)—матрица пХп вторых производных функции / в точке х
(гессиан), у которых всякий (/, /)-й элемент есть
d2f(x)
dx*dxi'
Теорема 3 (формула Тейлора). Если функция f дважды диф-
дифференцируема на открытом выпуклом множестве XczRn и хъ х2?Х,
то существует такое число 0 < т < 1, что имеет место равенство
f (x2) — f(xi) =fl (*i) (x2x)+

406 ПРИЛОЖЕНИЕ I
3. Дифференцируемость отображений. Пусть задано отображение
g: X—> /?**, где X множество в Rn. Будем говорить, что отображе-
отображение g дифференцируемо во внутренней точке х множества X, если
существует матрица А размером пХт такая, что для всех h?R
удовлетворяющих условию х + п?Х, справедлива формула
xt Л),
где вектор-функция Ф обладает свойством:
lim |ф(х, к) || = 0.
Матрица А называется производной отображения g(x) в точке х
и обозначается gx(x).
Так определенная дифференцируемость часто называется диффе-
ренцируемостью по Фреше. Из этого определения следует, что если
отображение g: X—> R™ дифференцируемо в точке *?intX, X<zRn,
то выполнено условие
Формула Ньютона—Лейбница C) переносится на случай отобра-
отображений, а формула B) неверна. Поэтому формулой Лагранжа для ото-
отображений будем называть следующее неравенство:
Теорема 4. Пусть отображение g: X—>Rm дифференци-
дифференцируемо на открытом выпуклом множестве X. Тогда для любых х, у?Х
имеет место неравенство F).
Если для любых xlt x2?Rn имеет место неравенство
то отображение ^(л:) называется липшицевым с постоянной I.
4. Дифференцируемость сложных функций
Теорема 5. Пусть т-мерная функция g определена на откры-
открытом множестве XcRn, функция <р определена на Rm. Тогда, если g
дифференцируема в точке 1с?Х, ф дифференцируема в точке */=?{*•)>
то сложная функция у (х) = <р (g (x)) дифференцируема в точке х и
Этот результат переносится на случай, когда у(х) = Ц>(х, ^(х))»
где функция ф определена на декартовом произведении RnxRm. Фор-
Формула для вычисления производной сложной функции у(х) имеет вид
Здесь фх—частная производная ф по явно входящему вектору я,
ф^—частная производная ф(дг, g) по вектору g.

ПРИЛОЖЕНИЕ II
НЕКОТОРЫЕ СВОЙСТВА МАТРИЦ
1. Матрицей А называется прямоугольная таблица чисел
и, а12, ..., а1п ~
21» а22> • • • > а2п
Если т~пу то матрица называется квадратной, число /тг = /г на-
называется ее порядком. В общем случае, когда m может быть не
равно п, матрица называется прямоугольной размера тхп. Числа,
образующие матрицу, называются ее элементами. На пересечении
1-й строки и /-го столбца матрицы расположен элемент й/у, который
называется (i, /)-м элементом матрицы А. Главной диагональю квад-
квадратной матрицы А называют совокупность элементов а,-/, t?[l:n].
Пусть у матриц А и В элементами являются a-ti, bji соответ-
соответственно, где i?[l:/rc], /?[1:п]. Тогда произведением матриц
АВ называется матрица С, у которой (i, д)-м элементом является
п
Ciq = S
k l
Обозначим D(z) диагональную матрицу, у которой все элементы,
расположенные вне главной диагонали, равны нулю, каждый 1-й диа-
диагональный элемент есть г{ (i-я компонента вектора г). Порядок ма-
матрицы D (г) определяется размерностью вектора г.
Если C=AD(z)t B = D(z)A, то с/у=а/у2/, Ь^^г{а^. Таким
образом, при умножении прямоугольной матрицы А размера тхп
справа на диагональную матрицу D (г) порядка п все столбцы ма-
матрицы А умножаются на числа г1, г2, ..., гп. При умножении ма-
матрицы А слева на диагональную матрицу D (г) все строки матрицы А
умножаются на числа г1, г2, ..., zn.
Матрица размера mX/г, все элементы которой равны нулю, назы-
называется нулевой и обозначается 0тп. Квадратная матрица порядка я,
у которой все элементы равны нулю, кроме элементов главной диа-
диагонали, равных единице, называется единичной матрицей и обозна-
обозначается /„,
Квадратная матрица А порядка п называется симметричной, если
djj^aji для всех ?, / из [1:я]. Такая матрица совпадает с транспо-
транспонированной к ней матрицей: Л = ЛГ.

408 ПРИЛОЖЕНИЕ II
Пусть А — квадратная матрица порядка п. Матрица Л называется
вырожденной (особой), если ее определитель равен нулю: |Л| = 0.
Корни уравнения
|Л-Я/„|=0 A)
называются характеристическими числами или собственными значе-
значениями матрицы А. Уравнение A) называется характеристическим
уравнением матрицы А. Определитель и собственные значения матрицы
являются непрерывными функциями элементов матрицы. Если урав-
уравнение
Ах = Хх B)
имеет отличное от нуля решение х?Еп, то л; называется собственным
вектором матрицы Л, соответствующим собственному значению Я.
Матрицы А и АТ имеют одинаковые собственные значения.
Если А—действительная симметричная матрица, то все ее собст-
собственные значения действительные и выполняются неравенства
%xxTx < хтАх < %пхтх Чх?Еп,
где Xi^^2^.. .<%„,—собственные значения матрицы А. Если Xi > 0,
то матрица А положительно определена (А > 0), если Ях^О, то ма!
трица А положительно полуопределена (Л^=0).
Лемма (Р. Ф и н с л е р а). Если хтАх > 0 для всех х, удо-
удовлетворяющих условию хТВх = 0, где В—неотрицательно определен-
определенная квадратная матрица, то существует такое число т*, что квад-
квадратичная форма хТАх\-%хТВх положительно определена при т > т„.
Матрица В называется квадратным корнем из матрицы Л, если
Л=??. У каждой положительно полуопределенной матрицы есть
квадратный корень.
Если квадратная матрица А положительно определена, матрица В
невырождена, то матрица ВТАВ положительно определена. В част-
частности, для любой невырожденной матрицы В матрица ВВ положи-
положительно определена.
Если А и В — квадратные матрицы одного порядка, то имеют
место формулы
\ = \А\-\В\,
Матрица А называется обратной к матрице Л, если АА~х~1п.
Всякая неособая матрица имеет обратную. Если Л и В — невырож-
невырожденные матрицы одинакового порядка, то
2. Отображение )•( из Rn в R1 называется нормой, если для
любого x?Rn выполнены следующие три условия:
1) 0^||*[|, причем ||*||=0, тогда и только тогда, когда х = 0;
2)\\\\ \\\\l?Ri
. )\\\\ \*\\\xl?R;
3) 1* + 0|<|*|+Ш Для любых х, y?Rn.
Для скалярного произведения в Еп выполнено неравенство Коши —
Буняковского
|<*, у>\<\\х\\г\\у\\г.

НЕКОТОРЫЕ СВОЙСТВА МАТРИЦ 409
Для векторной нормы ||«||^ в Rn существует векторная норма ||«||^,
называемая двойственной или сопряженной к ||»||^, которая опреде-
определяется из условия
1*1*= sup <х, у>.
1Ы11
Если в качестве ||*||^ взять норму Гёльдера
\1/р
то двойственной к ней будет норма
In
1 , 1
Имеет место следующее неравенство Гёльдера (см. В. В. Воеводин [1]):
К*, У> К1*1ИЫв-
В частности, для так называемой октаэдрической нормы
двойственной является норма
||a;[U= max
называемая обычно чебышёвской или кубической. Исходная и двойст-
двойственная нормы совпадают, когда p = q==2
|1/2
l*li= " "'
[п
Такая норма называется евклидовой или сферической. Она может быть
получена, исходя из скалярного произведения
|*б=<*, *>=Л.
Для введенных норм л-мерных векторов имеют место оценки:
Поэтому
3. Каждая норма любой матрицы А размера тхп должна удо-
удовлетворять следующим трем условиям:
1) 0<] А ||, причем И Л Ц= 0 тогда и только тогда, когда A = 0mnt
2) laAl=\a\.lAla?R4**<*a
3) | А + В |]<|| А | + || В || для~[любой матрицы В размера тхп.
Будем говорить, что норма ||«|| матрицы согласована с данной нор-
нормой ||«|| вектора, если для любой матрицы А размера тхп и любого
/г-мерного вектора х выполняется неравенство
\\Ах\\<\\А\\-\\х\\.

410 ПРИЛОЖЕНИЕ II
Приведем правило построения наименьшей нормы матрицы, согла-
согласованной с данной нормой вектора. Примем за норму матрицы Л
максимум норм векторов Ах, когда вектор х пробегает множество
всех векторов, имеющих единичную норму:
|| Л ||= max || Ах\.
0*11=1
Исходя из этого правила, можно показать, что нормам векторов
ll'lli II'IU» На соответствуют следующие согласованные с ними нормы
матриц:
п
У\ \аи\,
5
где К—максимальное собственное значение матрицы АТА. В част-
частности, если А — квадратная матрица пхп с собственными значениями
%i, Я2, ..., %п> то
. ||Л||2= max |X,|. C)
«[1]
= max
Спектральным радиусЪм S (А) квадратной матрицы А называется
наибольший из модулей собственных значений матрицы Л. Из B)
с учетом свойств норм получим
В силу произвольности использованных здесь согласованных норм
приходим к выводу, что любая из норм матрицы не меньше ее спект-
спектрального радиуса. Из C) следует, что S (Л)=|] Л|]2. Вместе с тем
можно показать, что для любого заданного числа е > 0 всегда сущест-
существует такая норма || А (б, что имеет место неравенство 5 (Л) + 8^1ИКв.
Лемма (Неймана). Пусть спектральный радиус квадратной
матрицы А строго меньше единицы. Тогда матрица 1п — Л невырож-
невырождена и
4. Пусть даны матрицы Л, В и С размеров соответственно nXnt
т, riixn; ма Л < М А\ВС
ождена тогд
рдена, и в э
сона —Вудбери
у д рц , В и раеров сесе Xt
пхт, riixn; матрица Л невырождена и т<п. Матрица А-\-ВС не-
невырождена тогда и только тогда, когда матрица /^-(-СЛ"^ невы-
невырождена, и в этом случае имеет место формула Шермана—-Морри-
Вб
. D)
В частном случае, когда т —1, в качестве В и С берутся векторы Ь
и с соответственно; тогда из D) получаем так называемую формулу
Шермана—Моррисона:

НЕКОТОРЫЕ СВОЙСТВА МАТРИЦ 411
5. Пусть невырожденная матрица М разбита на блоки
М--
,-fiui.
[с { р\
где матрицы Л, В, С, Р имеют соответственно размеры nXnt nXq>
qXn> qXq. Пусть квадратная матрица А невырождена. Имеет место
следующая формула Фробениуса для вычисления обратной матрицы
I »
J
/И""
где H = P-CA-iB.
С помощью этой формулы обращение квадратной матрицы по-
порядка n-\-q сводится к обращению двух матриц порядка п и q и
к операциям сложения и умножения матриц размеров пхп, qXq,
nxq, qxn.
Если вместо условия | А | Ф 0 ввести предположение, что | Р \ Ф О,
то получим другой вид формулы Фробениуса:
где/С=Л—ВР-^.
Более подробные сведения о свойствах матриц можно найти,
например, в книгах Ф. Р. Гантмахера [1], П. Ланкастера [1], Р. Белл-
мана [2], В. В. Воеводина [1], Э. А. Коддингтока и Н. Левинсона [1].

ПРИЛОЖЕНИЕ III
НЕКОТОРЫЕ СВОЙСТВА ОТОБРАЖЕНИЙ
1. Однозначные отображения. Пусть каждому элементу х множе-
множества X а Еп сопоставлен единственный элемент Т (х) множества
Y<zEm. В этом случае будем говорить, что задано отображение
(однозначное) Т множества X в множество У, и будем записывать
Т: X—+Y. Для любого множества S CZ X определяется его образ:
такое, что у = Т(х)}.
Существуют две эквивалентные формулировки понятия непрерыв-
непрерывности для отображений — в терминах сходимости и в смысле Коши:
1. Отображение Т непрерывно в точке х, если для любой после-
последовательности {xk} из X, сходящейся к пределу х при k —¦* оо,
Иш T(xh) = T(x).
Ъ-+ оо
2. Отображение Т непрерывно в точке х, если для любой окрест-
окрестности V точки Т (х) найдется окрестность G точки х такая, что
Т (G) с V.
Особый интерес представляют неподвижные точки отображений,
т. е. точки, принадлежащие следующему множеству:
х = Т (*)}, где Т: Еп —* Еп.
При построении численных методов решения систем уравнений, задач
нелинейного программирования, оптимального управления часто бы-
бывает целесообразно производить редукцию к задаче нахождения непод-
неподвижных точек некоторых отображений. Один из первых результатов
о" существовании неподвижных точек отображений был получен
в начале XX века голландским математиком Брауэром.
Теорема Брауэра. Пусть X — непустое компактное выпук-
выпуклое множество в Еп, а отображение Т: X —*- X непрерывное, перево-
переводящее каждую точку х множества X в точку Т (х) этого же множе-
множества. Тогда отображение Т имеет неподвижную точку.
2. Точечно-множественные отображения. Пусть определено неко-
некоторое правило W, ставящее каждой точке пространства Еп некоторое
подмножество пространства Ет. Такое соответствие называется много-
многозначным или точечно-множественным отображением и обозначается
W: Еп —>¦ 2Ет. Множество W (х) называется образом точки х. Оче-
Очевидно, что однозначное отображение является частным случаем точечно-
множественного, при] котором образ каждой точки является'множе-
является'множеством, состоящим из одной точки. Возможны случаи, когда отображение

НЕКОТОРЫЕ СВОЙСТВА ОТОБРАЖЕНИЙ 413
W определено на множестве X с Еп и каждой точке х?Х ставит
в соответствие подмножество множества X, в этом случае обозначаем
W: X-+2X.
Если приведенные в п. 1 понятия непрерывности в терминах схо-
сходимости и в смысле Коши леренести на многозначные отображения,
то придем к следующим двум различным понятиям.
Многозначное отображение W: Еп —
в точке х, если из условий lim х^ = х, lim Уь — у и
k -*• оо k -*• оо
следует, что y?W (x).
Многозначное отображение W: Еп —>¦ 2ЕТП называется полунепре-
полунепрерывным сверху в точке х, если для любой окрестности V множества
образа W (х) найдется окрестность G точки х такая, что W (G) а V.
Многозначное отображение W называется замкнутым на множе-
множестве ХаЕпу если оно замкнуто в каждой точке х?Х. Будем гово*
рить, что отображение W замкнуто, если оно замкнуто во всех точ-
точках, где оно определено. Аналогично доопределяется понятие полу-
полунепрерывности сверху.
Точка Хщ. называется неподвижной точкой точечно-множественного
отображения Т: Еп—^2^", если
*•€*(*.)•
Обобщением теоремы Брауэра на многозначные отображения явилась
Теорема Какутани. Пусть X — непустое компактное вы-
выпуклое множество в Еп, a W: X —*¦ 2%—многозначное отображение,
удовлетворяющее условиям:
а) для каждой точки х?Х множество W (х) является непустым
выпуклым подмножеством множества X;
б) отображение W замкнуто.
Тогда отображение W имеет неподвижную точку.
Доказательство теорем Брауэра и Какутани можно найти в книге
X. Никайдо [1].

КОММЕНТАРИИ И БИБЛИОГРАФИЯ
Глава I
К §§ 1—4. Теория выпуклых функций и множеств, необходимые
и достаточные условия экстремумов функций подробно описаны в много-
многочисленных публикациях. Сошлемся на книги Ф. П. Васильева [1],
Е. Г. Гольштейна [1], И. И. Еремина и Н. Н. Астафьева [1], В. Г. Кар-
манова [1], О. Мангасаряна [1], Р. Рокафеллара [1], Б. Н. Пшенич*
ного [3].
К § 5. Первой публикацией по исследованию общих свойств мини-
минимаксных задач была, по-видимому, статья Н. Г. Чеботарева [1].
Подробную библиографию последующих исследований можно найти
в книгах В. Ф. Демьянова и В. Н. Малоземова [I], [2], Дж. Дан-
скина [1]. Теоремы 1.5.7—1.5.8 взяты из статьи Ю. Г. Евтушенко [3].
К § 6. Теорема 1.6.1 является очевидным обобщением результата,
полученного X. Удзавой (дм. гл. 3 в книге К. Дж. Эрроу и др. [1]).
Теорема 1.6.4 принадлежит Ю. Г. Евтушенко [12]. Лемма 1.6.1 взята
из статьи К. Фана и др. [1]. Утверждение теоремы 1.6.7 о существо-
существовании седловой точки без учета ограничений типа равенства впервые
было установлено Г. Куном и А. Таккером [1]; учет ограничений типа
равенства был выполнен X. Удзавой (см. гл. 3 в книге К. Дж. Эрроу
и др. [1]).
К § 7. Более подробное описание различных определений условий
регулярности ограничений, связи между ними приведено в книге
О. Мангасаряна [П. Доказательство теоремы 1.7.2 можно найти в статье
Г. Мак-Кормика [1] и в книге А. Фиакко и Г. Мак-Кормика [1].
Доказательства теоремы 1.7.3 и леммы 1.7.5 взяты из статьи С. Хана
и О. Мангасаряна [1]. Формулировка теоремы 1.7.5 взята из статьи
Ю. Г. Евтушенко и В. Г. Жадана [3].
К § 8. Подробное изложение теории оптимального управления
содержится в книгах Л. С. Понтрягина и др. [1], Н. Н. Моисеева [2],
Р. Габасова и Ф. М. Кирилловой [2].
Глава II
К §§ 1, 2. Основополагающие теоремы теории устойчивости были
получены в конце прошлого века А. М. Ляпуновым [1]. Подробное
изложение этого материала можно найти в многочисленных публика-
публикациях по теории устойчивости, укажем, например, книги Е. А. Барба-
шина [1], Б. П. Демидовича [1], Н. Н. Красовского [1], И. Г. Мал-
кина [1].
Теорема 2.2.6 доказана Е. А. Барбашиным и Н. Н. Красовским.
Теорема 2.2.7 принадлежит Ю. Г. Евтушенко [9], близкий результат
приведен в статье В. И. Венец, М. В. Рыбашова [1]. Ряд теорем по

КОММЕНТАРИИ И БИБЛИОГРАФИЯ 415
исследованию сходимости решений систем обыкновенных дифферен-
дифференциальных уравнений содержится в статье Ю. Г. Евтушенко, В. Г. Жа-
дана [2]. Вопросам применения методов теории устойчивости к иссле-
исследованию сходимости методов оптимизации посвящены работы М. В. Ры-
башова [1], [2].
К § 3. Весьма обстоятельное изучение вопросов сходимости ите-
итеративных процессов содержится в книгах Дж. Ортега и В. Рейн-
болдта [1], Д. К. Фаддеева и В. Н. Фаддеевой [1], А. Халаная и
Д. Векслера [1], X. Гаевского, К- Грёгера, К. Захариаса [1] и многих
других. Утверждение теоремы 2.3.7 высказывалось многими*авторами.
Укажем, например, статью М. А. Скалкиной [1].
К § 4. Теория фейеровских отображений развивается И. И. Ере-
Ереминым и его учениками. Библиографию этих работ можно найти
в книге И. И. Еремина и В. Д. Мазурова [1]. Исследование различ-
различных вирсий метода обобщенных градиентов содержится, в частности,
в работах Ю. М. Ермольева [1], [2], Н. 3. Шора [1].
К § 5. Весьма подробное обсуждение методов решения систем
нелинейных уравнений с обширной библиографией имеется в книгах
Дж. Ортега и В. Рейнболдта [1], В. Рейнболдта [1].
Исследования метода Ньютона имеются в монографии Л. В. Кан-
Канторовича и Г. П. Акилова [1]. Дискретный вариант метода Ньютона
рассматривался в статье В. Е. Шаманского [2]. Более детально этот
вопрос изложен в книге Дж. Ортега и В. Рейнболдта [1]. Что касается
способов 1—5 регулировки длины шага в методе Ньютона, то их
некоторые частные случаи, отвечающие конкретному виду норм, рас-
рассматривались в работах Ю. М. Данилина и В. М. Панина [1],
В. И. Купцова и Е. Г. Шуршковой [1], В. М. Панина [1], Б. Н. Пшенич-
Пшеничного [2], Э. Полака и И. Теодору [1], Дж Стоера [1]. Способы 1—5
с нормами произвольного вида предложены и исследованы О. П. Бур-
даковым [2], [3]. Обзор по методам квазиньютоновского типа имеется
в статьях Дж. Денниса и Дж. Морэ [2], Е. Спедикато [1]. Как свидетель-
свидетельствуют результаты численных экспериментов Е. Спедикато [1], [2],
Е. Спедикато и Дж. Гринстадта [1], Д. Шенно и К. Фу [1] и многих
других, эти. методы являются весьма эффективными при решении систем
уравнений и минимизации функций. Методы E.27), E.28) были пред-
предложены С. Бройденом [1]; E.29)—Дж. Пирсоном [2]; E.30) —Г. Мак-
Кормиком (см. Дж. Пирсон [2]); E.31) —В. Давидоном [1], С. Бройде-
Бройденом [2] и другими; E.32) —С. Сомасом [1]; E.36) —В. Давидоном [1],
Р. Флетчером и М. Пауэллом [1]; E.37) — С. Бройденом [3], Р. Флет-
чером [1], Д. Гольдфарбом [1], Д. Шенно [1]; E.38)—М. Пауэллом [2].
В работе Н. Адачи [1] был предложен целый класс квазиньютоновских
методов, которые при минимизации квадратичных функций генерируют
сопряженные направления и содержат в себе некоторые из методов,
приведенных в § 5. Доказательство «-шаговой квадратичной скорости
сходимости методов с такими свойствами к минимуму не квадратичной
функции имеется в статьях Г. Мак-Кормика и К- Риттера [1], Л. Дик-
Диксона [1], Ю. М. Данилина [1], Дж. Стоера [2], П. Баптиста и
Дж. Стоера [1] и др. Оценки скорости сходимости такие же высокие,
как и в (я+1)-точечном методе секущих (с порядком сходимости,
являющимся корнем уравнения tn+1 — tn —1=0), были получены
Г. Шуллером [1]. Метод секущих для решения систем нелинейных
уравнений был впервые предложен Л. Биттнером [1] и Ф. Вольфом [1].

416 КОММЕНТАРИИ И БИБЛИОГРАФИЯ
Исследованию методов, использующих идею метода секущие, посвящены
также работы Л. Торнхейма [11, Д. Андерсона [1], Дж./Барнеса [1],
В. Е. Шаманского [1], С. Ю. Ульма [1], [2]. Метод секущих также
использовался Э. Полаком [2], Ю. М. Данилиным и Б. Н. Пшеничным
[1], [2], Б. Н. Пшеничным иЮ. М. Данилиным [1] для решения задач
математического программирования. Симметричный вариант метода
секущих предложен О. П. Бурдаковым [1].
К § 6. Численным методам отыскания минимакса посвящены мно-
многочисленные публикации, сошлемся на книги В. Ф. Демьянова и
В. Н. Малоземова [1], [2], В. Ф. Демьянова и А. М. Рубинова [1],
Ю. Б. Гермейера [1], Н. 3. Шора [1]. Обзор методов поиска седловых
точек можно найти в статье В. Ф. Демьянова и А. Б. Певного [1].
Теорема 2.6.1 взята из статьи Н. И. Грачева и Ю. Г. Евтушенко [4].
Результаты пп. 2, 3 взяты из статей Ю. Г. Евтушенко [3], [4]. Многие
из этих методов обобщены на решение игровых задач с непротивопо-
непротивоположными интересами в статье Н. И. Грачева и Ю. Г. Евтушенко [1].
Метод F.27) был предложен В. А. Волконским [1].
Методы поиска глобального экстремума описаны в книгах
Р. Г. Стронгина [1], Л. Диксона и Г. Сегё [1]. Кратко упомянутые
в п. 5 методы поиска глобального экстремума путем перебора на не-
неравномерной сетке более подробно описаны в статьях Ю. Г. Евту-
Евтушенко [1], [5].
Глава III
К § 1. Наиболее подробное описание метода штрафных функций
содержится в книге А. Фиакко и Г. Мак-Кормика [1]. Метод штрафных
функций входит во многие книги, посвященные численным методам
нелинейного программирования. Укажем, например, книги Ф. П. Ва-
Васильева [1], У. Зангвилла [2], В. Г. Карманова [1], Э. Полака [1],
Б. Н. Пшеничного и Ю. М. Данилина [1]. При описании метода
штрафных функций автор отступил от традиционного изложения, изло-
изложение проведено на основе статьи Ю. Г. Евтушенко [9], из этой же
статьи взята теорема 3.1.3. Аналогичный результат был получен
М. А. Шепиловым [1].
К § 2. Впервые на возможность использования точных штрафных
функций для решения задач выпуклого программирования указал
И. И. Еремин [1], [2]. Из последующих работ укажем статьи У. Занг-
Зангвилла [1], В. Д. Скарина [1], Т. Петржиковского [1], К- Чаралам-
боса [1], С Хана и О. Мангасаряна [1]. Из последней статьи взята
теорема 3.2.2. При доказательстве теоремы 3.2.1 в § 2 удалось осво-
освободиться от традиционных условий выпуклости. Оценка B.9) приве-
приведена во многих работах (см., например, В. Д. Скарин [1]). Исследо-
Исследования оценки точности метода штрафных функций с помощью метода
асимптотических разложений публикуются в § 2 впервые. Близким
вопросам посвящена статья Б. Т. Поляка [2].
К § 3. Целый ряд ссылок по излагаемому материалу содержится
в тексте.
К § 4. Метод внутренних штрафных функций более подробно
описан в книге А. Фиакко, Г. Мак-Кормика [1].
К § 5. Библиография по излагаемому материалу содержится
в тексте.

КОММЕНТАРИИ И БИБЛИОГРАФИЯ 417
Глава IV
Во введении к этой главе указан ряд работ, посвященных моди-
модифицированным функциям Лагранжа.
К § 1. Описание простейшей модификации функции Лагранжа A.1)
основывается на статьях Ю. Г. Евтушенко [6], [8], [9], [10]. Иссле-
Исследование метода Ньютона A.11) и метода A.21) при 8 = 1, но без учета
ограничений типа неравенства было проведено Б. Т. Поляком [1].
Одна из первых численных реализаций метода Ньютона A.11) дана
в работе Н. И. Грачева, Ю. Г. Евтушенко [2].
К §§ 2—5. Изложение этого материала основано на работах
Ю. Г. Евтушенко [11], [12], А. И. Голикова и Ю. Г. Евтушенко [1],
Ю. Г. Евтушенко и Ю. Н. Павловского [1]. Результаты, близкие
к описанным в § 4, получены Б. Кортом и Д. Бертсекасом [1]. Подход,
близкий к описанному в § 5, развивался О. Мангасаряном [2].
К § 6. Материал, приведенный в этом параграфе, взят из статьи
А. И. Голикова и В. Г. Жадана [1]. Другой подход к исследованию
прямых методов содержится в работе А. С. Антипина [1].
Глава V
К § 1. Идея метода приведенного градиента A.4) высказывалась
многими авторами. Укажем, например, статью К. Эрроу и Р. Солоу,
приведенную в книге К. Дж. Эрроу, Л. Гурвица и X. Удзавы [1].
К §§ 2, 3. Изложение проводится на базе статей Ю. Г. Евту-
Евтушенко [7], Ю. Г. Евтушенко и В. Г. Жадана [1], [3]. Некоторые
результаты численных расчетов с использованием метода B.4) приве-
приведены в статье В. В. Ефименко и А. С. Загоруйко [1]. Иное перенесе-
перенесение метода приведенного градиента на случай задач, содержащих огра-
ограничения типа неравенства, можно найти в работах Дж. Розена [1].
Близкий подход использован в работах Э. Л. Акима и Т. М. Энеева [1],
Т. М. Энеева [1].
К §§4, 5. Более подробное изучение свойств методов проекции
градиента и условного градиента можно найти в книгах В. Г. Кар-
манова [1], В. Ф. Демьянова и А. М. Рубинова [1] и Ф. П. Васильева [1].
Глава VI
Некоторые из направлений в разработке численных методов реше-
решения задач оптимального управления описаны во введении к этой главе.
Дать подробный перечень ведущихся здесь исследований исключительно
трудно из-за большого количества существующих публикаций.
К §§ 1, 2, 3. Эти параграфы написаны на основании работ
И Г Ю Г Е [5 [6 Ю Г Е [12
К §§ , , ррф р
Н. И. Грачева и Ю. Г. Евтушенко [5], [6] и Ю. Г. Евтушенко [12].
Иной подход к выводу формул A.7) изложен в книге Э. Полака [1].
К §§ 4, 5. Материал этой статьи написан на основе подхода, пред-
предложенного Ю. Г. Евтушенко [12]. Понятие принципа квазиминимума
и его обоснование были даны в работе Р. Габасова и Ф. М. Кирил-
Кирилловой [1]. Здесь интерпретация и доказательство принципа квазими-
квазиминимума несколько видоизменены. Иной подход к выводу дискретного
принципа максимума дан в книгах В. Г. Болтянского [1] и А. И. Про-
Пропоя [2].
К § 6. Помимо упомянутых в тексте работ, укажем статью
В. Ф. Демьянова [1] и книгу В. Ф. Демьянова и А. М. Рубинова [1].

418 КОММЕНТАРИИ И БИБЛИОГРАФИЯ
К § 7. Излагаемый материал написан совместно с Н. И. Граче-
Грачевым. Результаты расчетов задачи G.1) при помощи метода Ньютона
были предоставлены В. А. Пуртовым.
К § 8. Результаты решения задачи Р. Айзекса взяты из работы
Н. И. Грачева и Ю. Г. Евтушенко [5]. Особенно просто отыскиваются
решения игровых задач р том случае, когда существует седловая точка
в программных стратегиях, при этом становятся применимыми многие
известные методы (см. В. Ф. Демьянов и А. Б. Певный [1], Н. И. Гра-
Грачев и Ю. Г. Евтушенко [3]).
Глава VII
К § 1. В тексте упомянуты лишь некоторые из существующих
пакетов прикладных программ, предназначенных для оптимизационных
расчетов. Важное место при создании автоматических пакетов имеет
проблема определения стратегии последовательного использования ал-
алгоритмов. По-видимому, впервые этот вопрос был поставлен Н. Н. Мои-
Моисеевым [1]. Укажем одну из последних работ в этой области, выпол-
выполненную Г. М. Адаменко [1]. Общие принципы построения пакетов
прикладных программ обсуждаются в статье В. Я. Карпова и др. [1].
К § 3. Результаты расчетов, приведенные в Протоколе № 1, были
получены М. А. Потаповым.

ЛИТЕРАТУРА
А д а м а р Дж. (Hadamard J.)
1. Sur les transformations ponctuelles Bull.—Soc. Math. France, 1906,
34, 71—84.
Адаменко Г. М.
1. О решении классов задач минимизации.— Препринт ИМ АН БССР
№ П.—Минск, 1976.
Адачи Н. (Adachi N.)
1. On variable metric algorithm.—J. Optim. Theory Appl., 1971, 7,
391—409.
Айзеке Р.
1. Дифференциальные игры. — M.: Мир, 1967.
Аким Э. Л., Энеев Т. М.
1. Определение параметров движения космического летательного
аппарата поданным траекторных измерений.— Космические иссле-
исследования, 1963, 1, № 1, 5—28.
Андерсон Д. (Anderson D.)
1. Iterative procedures for nonlinear integral equations.—J. Assoc.
Comput. Mach., 1965, 12, 547—560.
АноровВ. П.
1. Принцип максимума для процессов с ограничениями общего вида.—
Автоматика и телемеханика, 1967, № 3, 5—15.
Антипин А. С.
1. Методы нелинейного программирования, основанные на прямой
и двойственной модификации функции Лагранжа.— Препринт
ВНИИСИ.—Москва, 1979.
Баптист П., Стоер Дж. (Baptist P., Stoer J.)
1. On the relation between quadratic termination and convergence
properties of minimization algorithms.— Numer. Math., 1977, 28,
№ 4, 367—391.
Барбашин Е. A.
1. Введение в теорию устойчивости.— М.: Наука, 1967.
Б а р н е с Дж. (Barnes J.)
1. An algorithm for solving nonlinear equations based on the secant
method.—Сотр. J., 1965, 8, 66—72.
Батищев Д. И.
1. Поисковые методы оптимального проектирования.— М.: Сов.
радио, 1975.
Бахвалов Н. С.
1. Численные методы.— М.: Наука, 1973.
Беллман Р.
1. Динамическое программирование.— М.: ИЛ, 1963.
2. Введение в теорию матриц.—М.: Наука, 1969.

420 ЛИТЕРАТУРА
Бертсекас Д. (Bertsekas D.)
1. Combined primal-dual and penalty methods for constrained mini-
minimization.—SIAM J. Control, 1975, 13, 521—544.
2. Multiplier Methods: A survey.—Automatica, 1976, 12, 133—145.
3. On the convergence properties of second-order multiplier methods.—
J. Optim. Theory Appl., 1978, 25, № 3, 443—449.
Биттнер Л. (Bittner L.)
1. Eine Verallgemeinerung des Sekantenverfahrens zur naherungsweisen
Berechnunng der Nullstellen eines nichtlinearen Gleichungssystems.—
Wiss. Z. Tech. Univ. Dresden, 1959, 9, 325—329.
Болтянский В. Г.
1. Оптимальное управление дискретными системами.— М.: Наука,
1973.
Брайсон А., Денхем В.
1. Применение наискорейшего спуска к задачам оптимального управ-
управления.— Ракетная техника и космонавтика, 1964, № 2.
Бройден С. (Broyden С.)
1. A class of methods for solving nonlinear simultaneous equations.-—
Math. Сотр., 1965, 19, № 92, 577—593.
2. Quasi-Newton methods and their application to function minimiza-
minimization.—Math. Compt., 1967, 21, № 99, 368—381.
3. A new double-rank minimization algorithm.— Notices Amer. Math.
Soc, 1969, 16, № 4, 670.
Будак Б. M,, Беркович* Е. М., Соловьева Е. Н.
1. О сходимости разностных аппроксимаций для задач оптимального
управления.— ЖВМ и МФ, 1969, 9, № 3, 522—547.
Бурдаков О. П.
1. Об одном принципе построения квази-ньютоновских методов
решения систем уравнений.— В кн.: Всесоюзный научно-техни-
научно-технический семинар «Численные методы нелинейного программирова-
программирования»: Тезисы докладов. Ч. I.—M.: 1979, 38—40.
2. О некоторых способах выбора длины шага в методе Ньютона.—
В кн.: Исследования операций. Вып. 7.—М.: ВЦ АН СССР, 1979,
111-115.
3. Некоторые глобально сходящиеся модификации метода Ньютона
для решения систем нелинейных уравнений.—ДАН СССР, 1980,
254, № 3, 521—523.
Бурова Н. К., Станевичене Л. И., Станевичюс А.—
И. А., Шкляр П. Э.
1. Система линейного программирования ЛП/БЭСМ-6.— М.:
ВЦ АН СССР, 1981.
Васильев Ф. П.
1. Численные методы решения экстремальных задач.—М.: Наука,
1980.
Васильева А. Б., Бутузов В. Ф.
1. Асимптотические разложения решений сингулярно возмущенных
уравнений.— М.: Наука, 1973.
Величенко В. В.
1. Численный метод решения задач оптимального управления.—
ЖВМ и МФ, 1966, 6, № 4, 635—647.
2. О задачах оптимального управления для уравнений с разрывными
правыми частями.—Автоматика и телемеханика, 1966, № 7,20—30.

ЛИТЕРАТУРА 421
3. Способ определения условного минимума функций многих пере-
переменных.—Автоматика и телемеханика, 1967, № 2, 171—172.
4. К задаче о минимуме максимальной перегрузки.— Космические
исследования, 1972, 10, № 5, 700—710.
Венец В. И., Рыба шов М. В.
1. Метод функций Ляпунова в исследовании непрерывных алгорит-
алгоритмов математического программирования.— ЖВМ и МФ, 1976,
16, № 3, 622—633.
Воеводин В. В.
1. Линейная алгебра.— М.: Наука, 1980.
Волконский В. А.
1. Оптимальное планирование в условиях большой размерности.—
Экономика и матем. методы, 1965, 1, № 2, 195—219.
Вольф Ф. (Wolf P.)
1. The secant method for simultaneous nonlinear equations. — Comrn.
ACM, 1959, 2, 12-13.
Габасов Р.
1. К теории оптимальных процессов в дискретных системах.— ЖВМ
и МФ, 1968, 8, № 4, 780—796.
Габасов Р., Кириллова Ф. М.
1. К вопросу о распространении принципа максимума Л. С. Понтря-
гина на дискретные системы.—Автоматика и телемеханика, 1966,
№ И, 46—51.
2. Принцип максимума в теории оптимального управления.— Минск:
Наука и техника, 1974.
Гаевский X., Грегер К., Захариас К.
1. Нелинейные операторные уравнения и операторные дифференциаль-
дифференциальные уравнения.— М.: Мир, 1978.
Гантмахер Ф. Р.
1. Теория матриц.— М.: Наука, 1967.
Гарсиа Поломарес У., Мангасарян О. (Garcia Paloma-
res'JJ., Mangasarian О.)
1. Superlinearly convergent quasi-Newton algorithms for nonlinearly
constrained optimization problems.-—Math. Prog., 1976, 11, № 1,
1-13.
Гей Д. (Gay D.)
1. Some convergence properties of Broyden's method.— SIAM J. Numer.
Anal., 1969, 16, № 4, 623—630.
Гей Д., Шнабель P. (Gay D., Schnabel R.)
1. Solving systems of nonlinear equation by Broyden's method with
projected updates. In: Nonlinear programming З./Ed. O. Mangasa-
Mangasarian, S.* Robinson, R.Meyer.—N.Y.Academ. Press, 1978, 254—
281.
Гермейер Ю. Б.
1. Введение в теорию исследования операций.— М.: Наука, 1971.
Глейзал A. (Gleyzal A.)
1. Solution of nonlinear equations.—Quart. J. Appl. Math., 1959, 17,
95—96.
Глушков В. М., Каспшицкая М. Ф., Сергиенко И. В.
1. Вопросы формализации и решения одного класса задач дискрет-
дискретной оптимизации.—ЖВМ и МФ, 1980* 20, № 6, 1384—1399.

422 литература
Глушков В. М., Олеярш Г. Б.
1. Диалоговая система планирования ДИСПЛАН.— Управляющие
системы и машины, 1976, № 4, 123—124.
Голиков А. И., Евтушенко Ю. Г.
1. Об одном классе методов решения задач нелинейного програм-
программирования.—ДАН СССР, 1978, 239, № 3, 519—522.
Голиков А. И., Жадан В. Г.
1. Итеративные методы решения задач нелинейного программиро-
программирования с использованием модифицированных функций Лагранжа.—
ЖВМ и МФ, 1980, 20, № 4, 874—888.
Гольдфарб Д. (Goldfarb D.)
1. A family of variable-metric methods derived by variational means.—
Math. Сотр., 1970, 24, № 109, 23—26.
Гольштейн Е. Г.
1. Теория двойственности в математическом программировании и ее
приложения.—М.: Наука, 1971.
Гольштейн Е. Г., Третьяков Н. В.
1. Модифицированные функции Лагранжа.— Экономика и матема-
математические методы, 1974, 10, № 3, 568—591.
Грагг Б., Стюарт Г. (Gragg В., Steward G.)
1. A stable variant of the secant method for solving nonlinear equa-
equations.—SIAM J. Numer. Anal., 1976, 13, № 6, 889—903.
Грачев Н. И., Евтушенко Ю. Г.
1. Некоторые численные методы решения игр с непротивополож-
непротивоположными интересами.— В кн.: Исследование операций.— М.: ВЦ
АН СССР, 1974, вып. 4, 219—235.
2. Вариант метода Ньютона для решения общей задачи нелинейного
программирования.— В кн.: Исследование операций.— М.: ВЦ
АН СССР, 1976, вып. 5, 54—58.
3. Численные методы отыскания седловых точек.— В кн.: Числен-
Численные методы нелинейного программирования. Тезисы II Всесоюз-
Всесоюзного семинара.— Харьков: 1976, 138—142.
4. Применение метода сингулярных возмущений для решения ми-
минимаксных задач.—ДАН СССР, 1977, 233, № 3, 277—280.
5. Пакет программ для решения задач оптимального управления.—
М.: ВЦ АН СССР, 1978.
6. Библиотека программ для решения задач оптимального управ-
управления,—ЖВМ и МФ, 1979, 19, № 2, 367—387.
Давиденко Д. Ф.
1. Об одном новом методе численного решения систем нелинейных
уравнений.—ДАН СССР, 1953, 88, 601—602.
2. О применении метода вариации параметра к построению итера-
итерационных формул повышенной точности для определения элемен-
элементов обратной матрицы.—ДАН СССР, 1965, 162, 743—746.
Давидон В. (Dayidon W.)
1. Variable metric method for minimization.— Argonne Nat. Lab.
Rep. NANL-5990, 1959.
Давыдов Э. Г.
1. О распределении ресурсов на графах.— В кн.: Системы распре-
распределения ресурсов на графах.— М.: ВЦ АН СССР, 1970.
2. Методы и модели теории антагонистических игр.— М.: МГУ, 1978.

ЛИТЕРАТУРА 423
Данилин Ю. М.
1. Скорость сходимости методов сопряженных направлений.— Кибер-
Кибернетика, 1977, № б, 97—105.
Данилин Ю. М., Панин В. М.
1. О некоторых методах поиска седловых точек.— Кибернетика,
1974, № 3, 119—124.
Данилин Ю. М., Пшеничный Б. Н.
1. О методах минимизации с ускоренной сходимостью.— ЖВМ и
МФ, 1970, 10, № 6, 1341—1354.
2. Оценка скорости сходимости одного класса алгоритмов оптими-
оптимизации.—ДАН СССР, 1973, 213, № 2, 270—273.
Д а нскин Дж.
1. Теория максимина.— М.: Сов. радио, 1970.
Д ем и дович Б. П.
1. Лекции по математической теории устойчивости.— М.; Наука,
1967.
Демьянов В. Ф.
1. К решению оптимальных задач в нелинейных системах автома-
автоматического управления.—ЖВМ и МФ, 1966, 6, № 2, 218—228.
2. Пакетный принцип минимакса.— Л.: Вестник ЛГУ, 1976, № 6,
35—39.
Демьянов В. Ф., Малоземов В. Н.
1. Введение в минимакс.— М.: Наука, 1972.
2. Вопросы теории и элементы программного обеспечения минимакс-
минимаксных задач.—Л.: ЛГУ, 1977.
Демьянов В. Ф., Певный А. Б.
1. Численные методы разыскания седловых точек.— ЖВМ и МФ,
1972, 12, № 5, 1099—1127.
Демьянов В. Ф., Рубинов А. М.
1. Приближенные методы решения экстремальных задач.— Л.: ЛГУ
1968.
Деннис Дж. (Dennis J.)
1. On some methods based on Broyden's secant approximation to
the Hessian.— In: Numerical methods for nonlinear optimiza-
optimization/Ed. Lootsma F., London: Academic Press, 1972.
Деннис Дж., Морэ Дж. (Dennis J., More J.)
1. A caracterization of superlinear convergence and its application
to quasi-Newton methods.—Math. Сотр., 1974, 28, № 126,
549—560.
2. Quasi-Newton methods motivation and theory.— SI AM Review,
1977, 19, № 1, 46—89.
Джон Ф. (John F.)
1. Extremum problems with inequalities as side conditions.— Studies
and essays. Courant anniversary volume. New York: 1948, 187—
204.
Диксон Л. (Dixon L.)
1. On quadratic termination and second order convergence: two pro-
properties of unconstrained optimisation algoritms. In: Towards
global optimisation/Ed. L. Dixon, G. Szego.— Amsterdam: North-
Holl., 1975, 211—228.
Диксон Л., Сегё Г. (Dixon L., Szego G.)
1. Towards global optimisation.—Amsterdam: North-Holl, 1975.

424 ЛИТЕРАТУРА
Дородницын А. А.
1. Асимптотическое решение уравнения Ван -дер-Пол я.— ПАШ, 1947
11, № 3, 313-328.
Дубовицкий А. Я.,1Милютин А. А.
I. Задачи на экстремум при наличии ограничений.— ЖВМ и Мф
1965, 5, № 3, 395—453.
Евтушенко Ю. Г.
1. Численный метод поиска глобального экстремума функций/пере-
функций/перебор на неравномерной сетке/.—ЖВМ и МФ, 1971, И, № 6
1390—1403.
2. Численный метод отыскания наилучших гарантированных оце-
оценок.—ЖВМ и МФ, 1972, 12, № 1, 89—104.
3. Некоторые локальные свойства минимаксных задач.— ЖВМ и
МФ, 1974, 14, № 3, 669—679.
4. Итеративные методы решения минимаксных задач.— ЖВМ и
МФ, 1974, 14, Ко 5, 1136—1149.
5. Методы поиска глобального экстремума.— В кн.: Исследование
операций.—М.: ВЦ АН СССР, 1974, вып. 4, 39—68.
6. Некоторые численные методы нелинейного программирования.—
Доклады конференции ИФИП по методам оптимизации, Ново-
Новосибирск, 1974.
7. Два численных метода решения задач нелинейного программи-
программирования.—ДАН СССР/1974, 215, № 1, 38—40.
8. Численные методы нелинейного программирования.—ДАН СССР,
1975, 221, № 5, 1016—1019.
9. Численные методы решения задач нелинейного программирова-
программирования.—ЖВМ и МФ, 1976, 16, № 2, 307—324.
10. Generalized Lagrange multiplier technique for nonlinear program-
programming.—J. Optim. Theory Appl., 1977, 21, № 2, 121—135.
I1. Применение обобщенных функций Лагранжа для решения
задач нелинейного программирования.— В кн.: Исследование
операций.—М.: ВЦ АН СССР, 1979, вып. 4, 3—23.
12. Численные методы решения экстремальных задач и их приме-
применение в системах оптимизации: Автореферат докторской дис-
диссертации.—М.: ВЦ АН СССР, 1980.
Евтушенко Ю. Г., Жадан В. Г.
1. Численные методы решения некоторых задач исследования
операций.—ЖВМ и МФ, 1973, 13, № 3, 583—598.
2. Применение метода функций Ляпунова для исследования схо-
сходимости численных методов.— ЖВМ и МФ, 1975, 15, № 1,
101—112.
3. Релаксационный метод решения задач нелинейного программи-
программирования.—ЖВМ и МФ, 1977, 17, № 4, 890—904.
Евтушенко Ю. Г., Павловский Ю. Н. (Evtushenko Yu.f
Pavlovsky Yu.)
1. Integrated optimization-simulation system for industry and regional
planning.—IFIP, 1980, North-Holl, 651—658.
Еремин И. И.
1. О методе «штрафов» в выпуклом программировании.—Тезисы
кратких научных сообщений Международного математическо-
математического конгресса. Секция 14, Вычислительная математика.— М.*
1966.

ЛИТЕРАТУРА ' 425
2. Метод «штрафов» в выпуклом программировании.— ДАН СССР,
1967, 173, № 4, 748—751.
Еремин И. И., Астафьев Н. Н.
1. Введение в теорию линейного и выпуклого программирования.—
М.: Наука, 1976.
Еремин И. И., Мазуров В. Д.
1. Нестационарные процессы математического программирования.—
М.: Наука, 1979.
Ермольев Ю. М.
1. Методы решения нелинейных экстремальных задач.— Киберне-
Кибернетика, 1966, № 4, 1—17.
2. Методы стохастического программирования.— М.: Наука, 1976.
Ермольев Ю. М., Гуленко В. П.
1. Конечно-разностный метод в задачах оптимального управле-
управления.— Кибернетика, 1967, № 3, 1—20.
Ермольев Ю. М., Гуленко В. П., Царенко Т. И.
1. Конечно-разностный метод в задачах оптимального управле-
управления.— Киев: Наукова думка, 1978.
Ефименко В. В., Загоруйко А. С.
1. О программной реализации методов прямого интегрирования
для задач многомерной минимизации.— ЖВМ и МФ, 1980, 20,
№ 3, 615—622.
Зангвилл У. (Zangwill W.)
1. Non-linear programming via penalty function.— Management Sci.,
1967, 13, Nq 5, 344—358.
2. Нелинейное программирование. Единый подход.— М.: Сов.
радио, 1973.
Иванилов Ю. П.
1. Два алгоритма решения задачи выпуклого программирования.—
В кн. Теория оптимальных решений. Киев: Изд-во ИК АН УССР,
вып. 4, 1968.
Иванов В. В., Людвиченко В. А.
1. Об одном методе последовательной безусловной минимизации
решения задач математического программирования.— Киберне-
Кибернетика, 1977, № 2, 1—8.
Исаев В. К.» Сонин В. В.
1. Об одной модификации метода Ньютона численного реше-
решения краевых задач.—ЖВМ и МФ, 1963, 3, № 6, 1114—
1116.
2. Вычислительные аспекты задачи об оптимальном перелете как
краевой задачи.—ЖВМ и МФ, 1965, 5, № 2, 252—261.
3. Новый подход к проблеме аппроксимации и его приложения к
вариационным и минимаксным задачам. Труды ЦАГИ, 1975,
вып. 1646, 3—23.
Канторович Л. В., Акилов Г. П.
1. Функциональный анализ.— М.: Наука, 1977.
Карпов В. Я., Корягин Д. А., Самарский А. А.
1. Принципы разработки пакетов прикладных программ для задач
математической физики.—ЖВМ и МФ, 1978, 18, № 2, 458—
467.
Карманов В. Г.
1. Математическое программирование.— М.: Физматгиз, 1975.

426 ЛИТЕРАТУРА
Кашин Г. М., Пшеничное Г. И., Флеров Ю. А.
1. Методы автоматизированного проектирования самолета.—М.:
Машиностроение, 1979.
Ковалик Дж., Осборн М., Руан Д. (Kowalik J., Osborne M
Ryan D.)
1. A new method for constrained optimization problems.—Math
Progr., 1969, 17, № 6, 973—983.
Коддингтон Э. А., Левинсон Н.
1. Теория обыкновенных дифференциальных уравнений.— М.: ИЛ,
Корнилова Г. Ф, и др.
1. Пакет «Оптима-И» решения задач оптимального планирования
для машины БЭСМ-6.—В кн.: Программы оптимизации.—
Свердловск: Изд-во ИММ УНЦ АН СССР, 1974, вып. 5.
Корт Б., Бертсекас Д. (Kort В., Bertsekas D.)
1. Combined primal-dual and penalty methods for convex program-
programming.— SIAM J. Control, 1976, 14, № 2, 268—294.
Костина М. A.
1. Некоторые способы управления итерационными процедурами в
методах типа штрафных функций.— В кн.: Методы выпуклого
программирования и приложения.— Свердловск: Изд-во ИММ
УНЦ АН СССР, 1973, 32—41.
К р асовск и й Н. Н.
1. Некоторые задачи теории устойчивости движения.— М.: Физ-
матгиз, 1959.
Красовский Н. Н., Субботин А. И.
1. Позиционные дифференциальные игры.— М.: Наука, 1974.
Крылов И. А., Черноусько Ф. Л.
1. О методе последовательных приближений для решения задач
оптимального управления.—ЖВМ и МФ, 1962, 2, №6,1132—
1139.
Кун Г., Таккер A. (Kuhn H., Tucker А.)
1. Nonlinear programming. Proc. Second Berkeley Symp. Math.
Statistics, Probability.— Berkeley and Los Angeles Univ. Calif.
Press, 1951, 481—492.
2. Линейные неравенства и смежные вопросы.— М.: ИЛ, 1959.
Купцов В. И., Шуршкова Е. Г.
1. О сходимости модифицированного метода Ньютона.— В кн.:
Вычислительные методы и программирование. Вып. 14.— М.:
Изд-во МГУ, 1970.
Ланкастер П.
1. Теория матриц.— М.: Наука, 1978.
Лебедев В. Н.
1. Расчет движения космического аппарата с малой тягой.— М.:
ВЦ АН СССР, 1963.
Луутсма Ф. (Lootsma F.)
1. Convergence rates of quadratic exterior penalty-function method
for solving constrained-minimization problems.— Philips research
reports, 1974, 29, JVb 1, 2—12.
Ляпунов А. М.
1. Общая задача об устойчивости движения.— М.— Л.: Гостехиз-
дат, 1950.

ЛИТЕРАТУРА 427
М а к-К о р м и к Г. (McCormick G.)
1. Second order conditions for constrained minima.—SIAM J. Appl.
Math., 1967, 15, № 3, 641—652.
Мак-Кормик Г., Рит тер К. (McCormick G., Ritter К.)
1. Methods of conjugate directions versus quasi-Newton methods.—
Math. Progr., 1972, 3, № 1, 101—116.
Maлкин И. Г.
1. Теория устойчивости движения.— M.: Наука, 1966.
Мангасарян О. (Mangasarian О.)
1. Nonlinear programming.— Me. Graw-Hill Book Comapny, N. Y.,
1969.
2. Unconstrained Lagrangians in nonlinear programming.— SIAM J.
Control, 1975, 13, № 4, 772—791.
Мартинец Дж. (Martinez J.)
1. Three new algorithms based on the sequential secant method.—
BIT, 1979, 19, № 2, 236—243.
Мищенко Е. Ф., Понтряг.ин Л. С.
1. Доказательство некоторых асимптотических формул для реше-
решения дифференциальных уравнений с малым параметром.—ДАН
СССР, 1958, 120, № 5, 643—660.
Мищенко Е. Ф., Розов Н. X.
1. Дифференциальные уравнения с малым параметром и релакса-
релаксационные колебания.—М.: Наука, 1975.
Мелешко В. И., Песина Р. И.
1. Разработка пакетов программ безусловной оптимизации на мо-
модульном принципе. — Управляющие системы и машины, 1977.
№ 2, 35—40.
Мех ра Р., Дэви с P. (Mehra R., Davis R.)
1. A generalized gradient method for optimal control problems with
inequality constraints and singular arcs. — IEEE Trans. Automa-
Automatic Control, 1972, № 1, 69—79.
Мифлин Р. (Mifflin R.)
1. Convergence bounds for nonlinear programming algorithms. —
Math. Prog., 1975, 8, № 3, 251—271.
Моисеев Н. H.
1. Методы оптимизации.—М.: ВЦ АН СССР, 1969.
2. Численные методы в теории оптимальных систем.—М.: Наука,
1971.
Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М.
1. Методы оптимизации,—М.: Наука, 1978.
Моррисон Д. (Morrison D.)
1. Optimization by least squares.—SIAM J. Numerical Analysis,
1968, 5, № 1, 83—88.
Нейман Д., Морген штерн О.
1. Теория игр и экономическое поведение.—'М.: Наука, 1970.
Никайдо X.
1. Выпуклые структуры и математическая экономика. — М.: Мир,
1972.
Ортега Дж., Рейнболдт В.
1. Итерационные методы решения нелинейных систем уравнений
со многими неизвестными.—М.: Мир, 1975.

428 ЛИТЕРАТУРА
О ходи м ский Д. Е.
1. К аеории движения ракет. —ПММ, 1946, 10, № 2, 251—272.
Охоцимский Д. Е., Энеев Т. М.
1. Некоторые вариационные задачи, связанные с запуском искус-
искусственного спутника Земли.—УФН, 1957, 63, № 1а, 36—51.
Панин В. М.
1. Решение систем нелинейных уравнений демпфированным мето-
методом Ньютона при условии продолжимости. — В кн.: Теория оп-
оптимальных решений. —Киев: Изд-во ИК АН УССР, 1976, 39—51.
Пауэлл М. (Powell M.)
1. A method for nonlinear constraints in minimization problems. —
In: Optimization.— London: Acad. Press, 1969, 283—298.
2. A new algorithm for unconstrained optimization. — In: Nonlinear
programming/ Ed. J. Rosen, O. Mangasarian, K. Ritter. N. Y.:
Acad. Press, 1969.
ПауэрсУ., ШихС. (Powers W., Shich C.)
1. Convergence of gradient-type methods for free final time prob-
problems,—AIAA J. Numer. Anal., 1976, 14, № 11, 1598—1603.
Петржиковский Т. (Pietrzykowski Т.)
1. An exact potential method for corstrained maxima.—SIAM J.
Numer. Anal., 1969, 16, 299—304.
Пирсон Д. (Pearson J.)
1. The discrete maximum principle. — Int. J. Control, 1965, 11,№2.
2. On variable metric methods of minimization.—Сотр. J., 1971,
12, № 2, 171—178.
Полак Э. (Polak E.)
1. Численные методы оптимизации. Единый подход. —М.: Мир,
1974.
2. A modified secant method for unconstrained minimization. — Math.
Progr., 1974, 6, № 4, 264—280.
Полак Э., Теодору И. (Polak E., Teodoru I.)
1. Newton derived methods for nonlinear equations and inequalities.—
In: Nonlinear programming 2/Ed. O. Mangasarian, R. Meyer,
S. Robinson,—Academic Press, 1975, 255—277.
Поляк Б. Т.
1. Итерационные методы, использующие множители Лагранжа,для
решения экстремальных задач с ограничениями типа равен-
равенства.— ЖВМ и МФ, 1970, 10, № 5, 1098—1108.
2. О скорости сходимосги метода штрафных функций.—ЖВМ и
МФ, 1971, 11, № 1, 3—11.
Поляк Б. Т., Третьяков Н. В.
1. Метод штрафных оценок для задач на условный экстремум.—
ЖВМ и МФ, 1973, 13, № 1, 34-46.
Понтрягин Л. С, Болтянский В. Г., Г ам к р е л и дзеР. В.,
Ми ще н ко Е. Ф.
1. Математическая теория оптимальных процессов.—М.: Физмат-
гиз, 1961.
Пропой А. И.
1. О принципе максимума для дискретных систем управления. —
Автоматика и телемеханика, 1965, № 7, 1177—1187.
2. Элементы теории оптимальных дискретных процессов.—М.:
Наука, 1973.

ЛИТЕРАТУРА 429
Пшени ч н ый Б. Н.
1. Об одном алгоритме решения нелинейной задачи оптимального
управления.—ЖВМ и МФ, 1965, 5, № 2, 236—241.
2. Метод Ньютона для решения систем равенств и неравенств. —
Матем. заметки, 1970, 8, № 5, 635—640.
3. Выпуклый анализ и экстремальные задачи.—М.: Наука, 1980.
Пшеничный Б. Н., Данилин Ю. М.
1. Численные методы в экстремальных задачах.—М.: Наука, 1975.
Раздольский А. Р.
1. Схема решения задачи нелинейного программирования при уни-
унимодальной целевой функции. —Изв. АН СССР. Сер. Техничес-
Техническая кибернетика, 1973, № 4.
Разумихин Б. С.
1. Физические модели и методы теории равновесия в программи-
программировании и экономике.—М.: Наука, 1975.
РейнболдтВ. (Rheinboldt W.)
1. Methods for solving systems of nonlinear equations.—Philadel-
equations.—Philadelphia: Soc. Ind. Appl. Math., 1974.
Розен Дж. (Rosen J.)
1. The gradient projection method for nonlinear programming. —
J. Soc. Ind. Appl., 1961, 9, № 4, 514—532.
Рокафеллар P. (Rockafellar R. T.)
1. Выпуклый анализ.—M.: Мир, 1973.
2. A dual approach to solving nonlinear programming problems by
unconstrained optimization.—Math. Prog. 1973, 5, 354—373.
3. Augmented Lagrange miltiplier functions and duality in noncon-
vex programming.—SI AM J. Control, 1974, 12, № 2, 268—285.
Рыба шов М. В.
1. Метод дифференциальных уравнений в задаче отыскания экстре-
экстремума функций с помощью аналоговых вычислительных машин.—
Автоматика и телемеханика, 1969, № 5, 181—194.
2. Непрерывные алгоритмы продолжения решения конечных урав-
уравнений, зависящих от параметров. — Автоматика и телемеханика,
1975, № 4, 11—18.
Скалкина М. А.
1. О связи между устойчивостью решений дифференциальных и
конечно-разностных уравнений. — ПММ, 1955, 19,3,287—294.
С к а ри н В. Д.
1. О методе штрафных функций для задач нелинейного програм-
программирования.—ЖВМ и МФ, 1973, 13, № 5, 1186—1199.
Смольяков Э. Р.
1. Принцип максимума для задач с фазовыми ограничениями.—
В кн.: Исследование операций. — М.: ВЦ АН СССР, 1971,
вып. 2, 136—155.
Сомас С. (Thomas S.)
1. Sequential estimation techniques for Quasi-Newton algorithms. —
Cornell Univ., 1975, TR 75—227.
Спедикато Е. (Spedicato E.)
1. Quasi-Newton methods for nonlinear unconstrained minimization:
a review. —In: Toward global optimisation 2/Ed. L. Dixon—Am-
Dixon—Amsterdam: North-Holl., 1978, 191—207.

430 ЛИТЕРАТУРА
2. Computational expirience with Quasi-Newton algorithms for mi-
minimisation problems of moderately large size.— In: Toward glo-
global optimisation 2/Ed. L. Dixon —Amsterdam: North-Holl., 1978,
209-213.
Спедикато Е., Гринстадт Дж. (Spedicato E., Greenstadt J.)
1. On some classes of variationally derived Quasi-Newton methods
for systems of nonlinear algebraic equations. — Numer. Math.,
1978, 29, № 4, 363—380.
Стоер Дж. (Stoer J.)
1. Einfunhrung in die Numerische Mathematik. — Berlin: Springer,
1976.
2. On the relation between quadratic termination and convergence
properties of minimization algorithms. —Theory Numer. Math.,
1977, 28, № 3, 343—366.
Стронгин Р. Г.
1. Численные методы в многоэкстремальных задачах.-—М.: Наука,
1978.
Табак Д., Куо Б.
1. Оптимальное управление и математическое программирование.—
М.: Наука, 1975.
Тихонов А. Н.
1. Системы дифференциальных уравнений, содержащие малые пара-
параметры при производных.—Матем. сб., 1952, 31, № 3, 576—
586.
Торнхейм Л. (Tornheim L.)
1. Convergence of multipoint iterative methods. — J. Assoc. Comput.
Mash., 1964, 11, № 2, 210—220.
Третьяков Н. B.
1. Метод штрафных оценок для задач выпуклого программирова-
программирования.—Экономика и математические методы, 1972, 8, №5,740—
751.
У и л сон P. (Wilson R.)
1. A simplicial algorithm for concave programming—Boston: Harvard
Univ., 1963.
УльмСЮ.
1. Обобщение метода Стеффенсена для решения нелинейных опе-
операторных уравнений.—ЖВМ и МФ, 1964, 4, № 6, 1093—1097.
2. Об обобщенных разделенных разностях. — Изв. АН ЭССР, Сер.
физ.-мат. наук, 1967, 16, № 1, 13—26.
Фаддеев Д. К., Фаддеева В. Н.
1. Вычислительные методы линейной алгебры.—М.: Физматгиз,
1960.
Фан К., Гликсберг И., Гоффма н A. (Fan K.,Glicksberg I.,
Hoffman A.)
1. Systems of inequalities involving convex functions.—Proc. Amer.
Math. Soc, 1957, 8, 617—622.
ФедоренкоР. П.
1. Приближенное решение задач оптимального управления. --М '
Наука, 1978.
Ф и а к к о А., М а к-К о р м и к Г.
1. Нелинейное программирование. Методы последовательной безу-
безусловной минимизации.—М.: Мир, 1972.

ЛИТЕРАТУРА 431
Фихтенгольц Г. М.
1. Курс дифференциального и интегрального исчисления.—М.:
Наука, 1959, т. II.
Флетчер P. (Fletcher R.)
1. A new approach to variable metric algorithms.—Сотр. J., 1970,
13, 317—322.
Флетчер Р., Пауэлл M. (Fletcher R., Powell M.)
1. A rapidly convergent descent method for minimization.—Сотр.
J., 1963, 6, № 2, 163—168.
Франк М., Вольф Ф. (Frank M., Wolf P.)
1. An algorithm for quadratic programming.—Nav. Res. Log. Quart.,
1956, 3, 95—110.
Фуджи С, Фуджимото X., Оно М. (Fujii S., Fujimoto H.,
Ono M.)
1. Shifting method for constrained optimal control problems.—Bull.
JSME, 1977, 20, № 140, 176—182.
ХаархофП., БаесДж. (Haarhoff P., Buyes J.)
1. A new method for the optimization of a nonlinear function sub-
subject to nonlinear constraints.—Сотр. J., 1970, 13, № 2, 171 —
177.
Халанай А., Векслер Д.
1. Качественная теория импульсных систем.—М.: Мир, 1971.
Халкин X. (Halkin H.)
1. A maximum principle of the Pontryagin type for systems desc-
described by nonlinear difference equations,—SIAM J. Control, 1966,
4, № i.
Хама л а М. (Hamala M.)
1. Quasibarriar method for convex programming.—Abstracts IX Int.
Symp. Math. Prog. —Budapest: Bolyay math, soc, 1976, 110—
111.
X а н С (Han S.)
1. Superlinearly convergent variable metric algorithms for general
nonlinear programming problems.—Math. Prog., 1976, 11, № 3,
263-281.
2. A globally convergent method for nonlinear programming.—J.
Optim. Theory Appl., 1977, 22, № 3, 297—309.
Хан С, Мангасарян О. (Han S., Mangasarian О,)
1. Exact penalty functions in nonlinear programming.—Math. Prog.,
1979, 17, 251—269.
Хасельгров С. (Haselgrove С.)
1. The solution of nonlinear equations with two-point boundary
conditions.—Сотр. J., 1961, 4, № 3, 255—259.
Хестенс М. (Hestenes M.)
1. Multiplier and gradient methods.—J. Opt. Theory Appl., 1969,
4, № 5, 303-320.
Чараламбос К. (Charalambous С.)
1. A lower bound for the controlling parameters of the exact penalty
functions.—Math. Prog., 1978, 15, 278—290.
Чеботарев H. Г.
1. Об одном критерии минимакса.—ДАН СССР, 1943, 39, 373—
376 (см. также Собр. соч., т, 2, Изд-во АН СССР, 1949).

432 ЛИТЕРАТУРА
Ченцов И. П.
1. О применении градиентных методов к решению некоторых раз-
разрывных задач оптимального управления.—Кибернетика, 1976,
№ 1, 87-91.
Черноусько Ф. Л., Баничук Н. В.
1. Вариационные задачи механики и управления.—М.: Наука,
1973.
Чигирь С» А.
1. Об игровой задаче о долихобрахистохроне.—ПММ, 1976, 40,
№ 6, 1003—1013.
Шаманский В. Е.
1. Методы численного решения краевых задач на ЭЦВМ,—Киев:
Наукова думка, 1966.
2. Об одной модификации метода Ньютона.—Укр. матем. ж., 1967,
19, 133—138.
Шатровский Л. И.
1. Об одном численном методе решения задачи оптимального управ-
управления.— ЖВМ и МФ, 1962, 2, № 3, 488—490.
Шенно Д. (Shanno D.)
1. Conditioning of Quasi-Newton methods for function minimiza-
minimization.—Math. Сотр., 1970, 24, 647—656.
ШенноД.,ФуК. (Shanno D., Phua K.)
I. Numerical comparison of several variable metric algorithms.—
J. Opt. Theory Appi., 1978, 25, JVb 4, 507—518.
ШепиловМ. А.
1. Непрерывные аналоги метода штрафов для задач выпуклого
программирования.—Экономика и математические методы, 1975,
11, № 3, 130—341.
Шор Н. 3.
1. Методы минимизации недифференцируемых функций и их при-
приложения.—Киев: Наукоза думка, 1979.
Шулл ер Г. (Shuller G.)
1. On the order of convergence of certain Quasi-Newton methods.—
Numer. Math. 1974, 23, 181—192.
Энеев Т. М.
1. О применении градиентного метода в задачах теории оптималь-
оптимального управления. — Космические исследования, 1966, 4, № 5,
651—669.
Эрроу К. Дж., ГурвицЛ., Удзава X.
1. Исследования по линейному и нелинейному программированию. —
М.: ИЛ, 1962.
Яковлев В. М.
1. О дискретном принципе максимума.—Проблемы кибернетики,
1978, вып. 34, 247—257.