Мемуар о компактных топологических пространствах - Александров П.С., Урысон П.С.

Глава I. Основные определения и общие теоремы

§ 3. Пространства, компактные в данном отрезке мощностей

Глава II. О строении и мощности бикомпактных пространств

§ 2. Совершенные множества в компактных пространствах

§ 3. Об одном усилении первой аксиомы счетности в бикомпактных пространствах

Глава III. Об абсолютно замкнутых пространствах

§ 2. Компактные топологические пространства с точки зрения их замкнутости в объемлющих пространствах

Глава IV. Локально компактные пространства

Глава V. Метризация компактных и локально компактных пространств

§ 2. Метризация пространств со счетной базой, метризация компактных пространств

§ 3. Метризация локально компактных пространств

Список литературы, цитированной в предисловии и примечаниях

Author: Александров П.С. Урысон П.С.

Tags: математика топология

Year: 1971

Similar

Теория функций действительного переменного и теория топологических пространств

Топологические векторные пространства и их приложения

Топология

Топологические теоремы двойственности. Незамкнутые множества. Часть 2

Text

П. С. АЛЕКСАНДРОВ и П. С. УРЫСОН
МЕМУАР
О КОМПАКТНЫХ
ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВАХ
ИЗДАНИЕ ТРЕТЬЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1971

517.6
А 46
УДК 513.83
Павел Сергеевич Александров
и Павел Самуилович Урысон
Мемуар о компактных
топологических пространствах
М., 1971 г., 144 стр. с илл.
Редакторы В. В. Федорчук, В. В. Донченко
Техн. редактор В, И. Кондакова
Корректор В. П. Горячева
Сдано в набор 25/1 1971 г. Подписано к печати I3/V 1971 г.
Бумага 84xl08'/si. Физ. печ. л. 4,5. Условн. печ. л. 7,56. Уч.-изд.
л. 7,93. Тираж 9900 экз. Т-06575. Цена книги 74 коп. Заказ £66.
Издательство сНаукаэ
Главная редакция
физико-математической литературы.
Москва В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении Соколовой
Главполиграфпрома Комитета по печати при Совете Министров
СССР. Измайловский проспект, 29,
30-71

ОГЛАВЛЕНИЕ
Предисловие 4
Глава I. Основные определения и общие теоремы .... 13
§ 1. Предварительные понятия 13
§ 2. Бикомпактные пространства 23
§ 3. Пространства, компактные в данном отрезке мощностей 34
Глава II. О строении и мощности бикомпактных пространств 40
§ 1. Регулярные и нормальные пространства 40
§ 2. Совершенные множества в компактных пространствах 47
§ 3. Об одном усилении первой аксиомы счетности в
бикомпактных пространствах 53
Глава III. Об абсолютно замкнутых пространствах .... 62
§ 1. Определения. Условия для абсолютной замкнутости . 62
§ 2. Компактные топологические пространства с точки
зрения их замкнутости в объемлющих пространствах . . 69
Глава IV. Локально компактные пространства 80
§ 1. Бикомпактность в данной точке. Характер сходимости 80
§ 2. Локально бикомпактные пространства 88
Глава V. Метризация компактных и локально компактных
пространств 93
§ 1. Вопросы метризации и вторая аксиома счетности . . 93
§ 2. Метризация пространств со счетной базой, метризация
компактных пространств . 99
§ 3. Метризация локально компактных пространств . . . 107
Примечания к главе I 117
Примечания к главе II 122
Примечания к главе III 128
Примечания к главе IV 132
Примечания к главе V 134
Список литературы, цитированной в предисловии и примечаниях 139

ПРЕДИСЛОВИЕ
Эта монография представляет собою третье русское
издание *) работы, оригинал которой был опубликован
под заглавием Memoire sur les espaces topologiques
compacts, dedie a M. D Egoroff par P. Alexandroff et P. Ury-
sohn (Verhandelingen der Kon. Akademie van Weten-
schappen te Amsterdam, Afdeeling Naturkunde, eerste
sectie, deel XIV, 1929, стр. VIII + 96). Она содержит
изложение результатов по теории компактных и
бикомпактных топологических пространств, полученных
П. С. Урысоном и мною летом 1922 г. и доложенных
Московскому математическому обществу 8 июня и 17
октября 1922 г. Подготовка к печати была закончена 3 февраля
1923 г. Тогда же, в 1923 г. работа была принята к напе-
чатанию редакцией журнала Fundamenta mathematicae,
однако была издана лишь в 1929 г. и в другом
журнале**), после того как краткое изложение ее основных
*) Первое русское издание было опубликовано в 1950 г. в
Трудах Математического института им. В. А. Стеклова Академии
наук СССР, т. 31, а второе — являющееся перепечаткой первого —
в «Трудах П. С. Урысона», т. 2, стр. 854—956.
**) Задержка с публикацией совершенно готового текста этого
Мемуара произошла по следующим причинам. Так как в журнал
Fundamenta mathematicae незадолго перед этим поступила рукопись
весьма обширной работы П. С. Урысона о канторовых
многообразиях (Memoire sur les multipliers cantoriennes), печатание которой
и без того растянулось на два тома (седьмой и восьмой), то,
естественно, редакция Fundamenta не могла приступить к
немедленному печатанию также весьма обширного Мемуара о компактных
топологических пространствах. Вследствие этого по инициативе
Брауэра (L. Е. J. Brouwer) возник вопрос о перенесении печатания
в другой журнал. Однако везде с печатанием столь большой
работы возникали трудности. В результате, уже после смерти Урысона,
следуя настоятельной рекомендации Брауэра, работу передали в
Verhandelingen Амстердамской Академии наук, где печатание (при
необходимости пересылать корректуры из Амстердама в Москву и
обратно) также затянулось и в конце концов продолжилось
дальнейшие три года (1926—1929). В результате произошло значительное
запоздание по сравнению с тем, которое возникло бы, если бы
работа была оставлена в Fundamenta.

ПРЕДИСЛОВИЕ
5
результатов было опубликовано (в марте 1923 г.) в
Бюллетене Польской академии наук и в 1924 г. в Mathemati-
sche Annalen [в работах, помещенных в списке
литературы под номерами*) [1], [2] (Александров и Урысон),
[6], [8] (Александров) и [1], [2] (Урысон)].
Основателями теории топологических пространств
(общей топологии**)) являются, как известно, Фреше
(Maurice Frechet) и Хаусдорф (Felix Hausdorff, 1868—1943),
причем ни один из них, по-видимому, не ставил своей
задачей создание новой математической дисциплины.
Фреше, введя в математику (в своей основной работе
[1], 1906 г.) фундаментальные понятия метрического
пространства ***), его компактности и полноты, к сколько-
нибудь окончательной идее топологического
пространства тогда не пришел****).
Побужденный к своим исследованиям великими
аналитиками своего времени, прежде всего Адамаром (J. На-
damard), Фреше, как это видно даже из заглавия его
работы [1] — Sur quelques points du calcul fonctionnel,
рассматривал свои исследования как составную часть только
зарождавшегося тогда функционального анализа, а не
как построение новой теоретико-множественной
дисциплины. И последующая монография Фреше — «Les espa-
ces abstraits» (1926)—не изменяет положения вещей:
это скорее каталог большого числа «абстрактных
пространств», чем систематическая теория каких-нибудь
особенно важных среди них.
Если Фреше исходил из нужд математического
анализа в широком смысле слова, то Хаусдорф стоял
целиком на почве собственно теории множеств. Его прежде
*) Работы в списке литературы (в конце монографии)
помещены в алфавитном порядке авторов с отдельной нумерацией работ
каждого автора (или коллектива авторов).
**) Во времена, когда писался этот Мемуар, термина «общая
топология» вообще не существовало. Но был распространен — по
крайней мере в московских математических кругах — термин
«абстрактная топология».
***) Термин «метрическое пространство» принадлежит Хаус-
дорфу. Фреше называл открытые им метрические пространства
«классами D» (от слова «distance»).
****) Далеко идущие идеи в этом направлении, также не
получившие полного завершения, высказал Ф. Рисе (F. Riesz) ц
1907—1908 гг.

6
ПРЕДИСЛОВИЕ
всего интересовала логическая структура теории
точечных множеств, как она сложилась к концу первого
десятилетия текущего столетия. Своими знаменитыми
четырьмя аксиомами топологического пространства Хаус-
дорф попал в самую цель, выделив вместо большого
набора различных возможных построений один достаточно
широкий и в то же время действительно
«жизнеспособный» класс пространств, известных теперь под названием
хаусдорфовых *). Четыре аксиомы и последующее
присоединение к ним аксиом счетности позволило Хаус-
дорфу в своей замечательной книге «Grundzuge der
Mengenlehre» (1914) достаточно полно решить задачу
логического анализа и аксиоматического обоснования
основных топологических предложений теории точечных
множеств**).
В этом Мемуарё П. С. Урысон и я стояли всецело на
почве хаусдорфовой «Теории множеств», но в отличие от
Хаусдорфа мы интересовались не вопросами логического
анализа классических теорем, а —видя в определенных
им топологических пространствах увлекательный новый
объект математического исследования — решили
действительно предпринять это исследование с возможной
систематичностью, начав его с того конца, который
казался нам наиболее обещающим, — с понятия
компактности ***).
*) Теперь некоторые авторы стали называть хаусдорфовы
пространства «отделенными» или «отделимыми» пространствами. Не
говоря о логической несостоятельности этого термина («отделены»
или «отделимы» не сами пространства — неизвестно от чего, — а
лежащие в них точки друг от друга), хотелось бы заметить, что Хаус-
дорф право же заслужил, чтобы открытый им класс пространств
носил его имя, как это всегда и было до сих пор!
**) При дальнейшем (после Хаусдорфа) развитии аксиоматики
топологических пространств в основу были поставлены
последовательно понятия: замыкания множества (Куратовский [1]),
открытого множества (Александров [13]), замкнутого множества
(Серпинский [1]). Вес эти различные подходы привели к одному
и тому же универсально принятому сейчас понятию топологического
пространства (или Г-пространства), и Куратовскому в этом
отношении принадлежит бесспорный приоритет. См. также примечания2-3
к гл. I.
***) Аналогичную задачу, по-видимому, ставил себе и Виеторис
(Vietoris): его статья [1] в нескольких местах пересекается с нашим
Мемуаром. Статья Виеториса была нам неизвестна (и недоступна)'

ПРЕДИСЛОВИЕ
7
Дальнейшее развитие общей теории топологических
пространств может быть названо стремительным. За
нашим Мемуаром — и примыкая к нему —прежде всего
последовала замечательная работа А. Н. Тихонова [1].
В ней —две вещи, оказавшие огромное влияние на
дальнейшее развитие общей топологии (и не только ее одной):
во-первых, открытие класса вполне регулярных
(«тихоновских») пространств; во-вторых, введение общего
понятия топологического (или «декартова» или
«тихоновского») произведения (с последовавшей за ним
«тихоновской» топологией в самых различных функциональных
пространствах) и доказательство теоремы о
бикомпактное™ произведения любого числа бикомпактных
пространств. Кроме этой «первой теоремы» Тихонова в той же
его работе доказана и вторая — о погружении любого
вполне регулярного пространства (данного веса т) в
тихоновский куб Iх того же веса т, т. е. в произведение т
экземпляров отрезка / = [0; 1] числовой прямой.
Определение тихоновских пространств основано на
урысоновской идее функциональной отделимости
(«Большая лемма» Урысона — см. гл. V, § 2), одной из самых
плодотворных идей общей топологии. Эта идея внесла
в общую топологию понятие действительного числа —
в применении к гораздо более широкому классу
пространств, чем класс метризуемых пространств*).
На этой почве возникла теория колец непрерывных
действительных функций, определенных на
топологических пространствах, —теория,являющаяся одновременно
и плодотворным методом, и обширной областью
исследования, в которой общая топология соприкасается с
во время работы над этим Мемуаром; мы познакомились с ней
значительно позже.
Нашему Мемуару предшествовала также работа К у р а т о в-
ского и С е р п и н ско г о [1].
*) Заметим, что введение в общую топологию действительного
числа неизбежно влечет за собою и инвазию «паразита счетности».
Поэтому сейчас же после определения тихоновских пространств
возникла задача так называемого внутреннего (т. е. свободного от
пользования действительными числами) определения этих
пространств. См. по этому поводу примечание3 к гл. I.

8
ПРЕДИСЛОВИЕ
функциональным анализом и топологической алгеброй;
ей посвящена обстоятельная монография Гилмана и
Джерисона [1], к которой я и отсылаю читателя; см.
также работу Хьюитта [1].
Наряду с тихоновским кубом фундаментальное
значение в топологии (и в теории топологических групп)
приобрело пространство Dx — «канторовский
дисконтинуум», т. е. топологическое произведение т экземпляров
пространства D, состоящего из двух изолированных
точек. Непрерывные образы канторовских дисконтинуумов
(любого веса) суть так называемые диадические
бикомпакты (диадическими бикомпактами счетного веса
являются просто метризуемые компакты)*).
Следующий этап в развитии общей топологии связан
с работами Чеха [2] и М. Стоуна [1]. В обеих работах
среди многих других важных результатов содержится
построение знаменитого максимального
(«стоун-чеховского») расширения рХ для любого тихоновского
пространства X. После этих работ теория бикомпактных (и
близких к ним) расширений топологических пространств
становится одной из центральных тем общей топологии.
Особый интерес приобретает эта теория после того, как
Ю. М. Смирнов поставил бикомпактные (хаусдорфовы)
расширения данного пространства во взаимно
однозначное соответствие с близостями в смысле В. А.
Ефремовича, которые можно определить на данном
топологическом пространстве (см. примечание4 к гл. III и мои
статьи [3], [4], [5]).
Значение работы М. Стоуна не ограничивается
содержащимися в ней замечательными результатами, из
которых кроме упомянутого выше построения
максимального бикомпактного расширения рХ, скажу здесь лишь
*) Тот факт, что каждый (метризуемый) компакт есть
непрерывный образ канторова совершенного множества, сделал
естественной гипотезу, что каждый бикомпакт веса т есть непрерывный
образ обобщенного канторова дисконтинуума D\ Эта гипотеза была
опровергнута Шпильрайном-Марчевским [1], доказавшим,
что всякий диадический бикомпакт обладает свойством Суслина
(гл. V, § 1, п. 2, свойство 1°), поэтому уже пространство всех
порядковых чисел ^ (i)i с естественной порядковой топологией в нем
(гл. I, § 1, конец п. 5) является недиадическим бикомпактом.

ПРЕДИСЛОВИЕ
9
о решении поставленной в гл. III этого Мемуара задачи,
а именно доказательства бикомпактности хаусдорфова
пространства, все замкнутые подпространства которого
Я-замкнуты. Работа М. Стоуна внесла в топологию
новый метод — метод булевых алгебр, возможности
которого еще далеко не исчерпаны и только в наши дни
начинают оцениваться по достоинству. Я думаю, ни один
молодой тополог не должен пройти мимо
фундаментальной работы М. Стоуна*).
Основным продвижением в общей топологии,
сделанным в течение военных лет, было открытие в 1943 г. па-
ракомпактных пространств**).
Замечательные теоремы А. Стоуна (А. Н. Stone)
о паракомпактных пространствах (см. примечание *
к гл. V) несомненно принадлежат к самым выдающимся
достижениям послевоенного времени в общей топологии.
За ними последовали метризационные теоремы Бинга и
Нагата — Смирнова; я напоминаю их в примечании1
к гл. V, где говорю и о других метризационных
критериях, полученных в последнее время.
Наряду с этими продвижениями в старых проблемах
общей топологии (к которым принадлежит проблема
метризации и вся проблематика бикомпактных и близких
к ним расширений топологических пространств), наряду
с созданной за последние десятилетия теорией диадиче-
ских бикомпактов, к самым значительным продвижениям
всей общей топологии в целом принадлежит несомненно
построение общей теории непрерывных отображений
топологических пространств. В этом Мемуаре, да и вообще
в довоенной литературе не сделано в сущности никаких
шагов в направлении создания этой теории (кроме кни*
ги Александров и Хопф [1] и моей работы [10]),
где введены понятия замкнутого, а также факторного
отображения). Поэтому, хотя теория непрерывных
отображений топологических пространств и занимает
сейчас центральное положение в общей топологии, я не
могу здесь на ней останавливаться, отсылая читателя
*) Кстати, если я не ошибаюсь, именно в заглавии работы
М. Стоуна [1] термин «общая топология» впервые появляется в
математической литературе.
**) См. примечание на стр. 136.

10
ПРЕДИСЛОВИЕ
к моим обзорным статьям [4] и [5], а главным образом к
основным работам А. В. Архангельского и В. И.
Пономарева—авторов, которым теория непрерывных
отображений обязана, может быть, самыми значительными
своими результатами.
В то время когда писался этот Мемуар, теория
размерности только еще создавалась; при этом П. С. Уры-
сон в своих работах по теории размерности ограничивался
метризуемыми пространствами со счетной базой,
главным же образом — компактами. Поэтому в те времена
теория размерности вообще не считалась частью общей
топологии и даже в некоторой степени противополагалась
ей (как глава «конкретной», геометрической теоретико-
множественной топологии). Построение теории
размерности более общих пространств (главным образом
бикомпактов и далее финально компактных, паракомпакт-
ных и даже просто нормальных пространств) началось
значительно позже и с этим Мемуаром не связано.
Некоторое представление о развитии общей теории
размерности читатель может получить из моих статей [4] и [5].
В этом предисловии я хотел коснуться некоторых
примеров тех направлений общетопологических работ,
которые могут считаться связанными с тематикой Мемуара.
Выбор этих направлений, конечно, субъективен и не
может ни в какой мере рассматриваться как попытка
обзора развития какой бы то ни было части общей
топологии— я имел в виду лишь примеры, иллюстрирующие
основную мысль, руководившую авторами Мемуара при
работе над ним, а именно, что общая топология имеет не
только «подсобное», но и вполне самостоятельное
значение математической дисциплины, составляющей
неотъемлемую часть общей сокровищницы математической
мысли, какой она представляется нам сейчас.
В заключение несколько слов об этом издании.
Основной текст Мемуара остается по существу почти
неизменным во всех трех русских изданиях. При переходе
от французского оригинала к первому русскому изданию
некоторой переработке подвергся конец § 1, а также § 3
гл. V.

ПРЕДИСЛОВИЕ
11
Однако фактическое содержание и здесь не
претерпело существенных изменений.
Что касается самого начала Мемуара, то в оригинале
оно состояло из формулировок четырех аксиом Хаус-
дорфа, тогда как начиная с первого русского издания
приводится современное определение топологического
пространства (в форме, данной мною в работе [13] и
являющейся теперь наиболее распространенной).
В предлагаемом вниманию читателя третьем издании
некоторому сокращению и несущественной модернизации
подвергся § 1 гл. III и заново доказана наследственная
финальная компактность пространства А7 («две
стрелки»). Наконец, в целом изложение во всех русских
изданиях стало несколько более сжатым, чем в оригинале,
насколько это было возможно достигнуть, не нарушая
стиля всей работы.
Что касается моих примечаний к этому изданию, то
я написал их почти целиком заново. Однако задача этих
примечаний осталась прежней: в них указываются
непосредственно примыкающие к данным местам текста
новые результаты, представляющиеся мне наиболее
важными. Иногда указываются и более простые варианты
доказательств.
В настоящее время существует много книг, в которых
излагаются основы общей топологии. Одной из
наилучших среди них является, по моему мнению, книга Р. Эн-
гелькинга, изданная на польском и английском языках
соответственно под заглавиями Zarys topologie ogolnej
(Warszawa, 1965) и Outline of general topology
(Amsterdam, 1968). Надо надеяться, что она скоро будет
переведена на русский язык. См. также классическую
монографию Куратовского по теоретико-множественной
топологии (Топология, т. 1, «Мир», 1966; т. 2, «Мир», 1969).
Всеобщую известность приобрели выпуски трактата
Бурбаки, посвященные общей топологии. Однако книга
эта написана в другом стиле и других традициях, чем те,
которые нашли свое отражение в настоящем издании.
Широкое распространение получила «Общая топология»
Келли («Наука», 1968).
Сошлюсь и на свою старую книгу [1]. В ней (в гл. 6
и 7 и главным образом в Прибавлениях к этим главам)

12
ПРЕДИСЛОВИЕ
доступно изложена элементарная теория метрических и
топологических пространств. Дополнением к моей
книге [1], а также и к этому Мемуару может служить моя
статья [3].
В статьях [4] и [5] я старался дать обзор (без
доказательств) тех общетопологических результатов,
полученных в послевоенные годы (по 1964 г.), которые казались
мне наиболее важными. При всей неизбежной
субъективности такой попытки обзора, я думаю, тем не менее,
что некоторую ориентацию в прогрессе общей топологии
примерно за два первых послевоенных десятилетия
читатель из этих статей сможет получить. Хорошим
дополнением к ним могут служить статьи В. И. Пономарева,
С. Илиадиса и С. В. Фомина и А. В. Архангельского,
напечатанные в Успехах математических наук, 21, №4 0966).
От читателя этого Мемуара требуется лишь знание
элементарной классической теории множеств, включая,
однако, трансфинитные числа любой мощности. Никакой
подготовки в области собственно
теоретико-множественной топологии от читателя не требуется, изложение
везде элементарно и подробно.
Как мне кажется, эта монография может
рассматриваться и сейчас (как и сорок лет тому назад) в качестве
одного из вариантов «первой книги для чтения» по
общей топологии. Поэтому мне хотелось бы надеяться, что
новое русское издание Мемуара, как и
предшествовавшие, найдет своих читателей, главным образом среди
молодых людей, начинающих заниматься общей топологией
и ищущих изложения возможно более простого,
конкретного и снабженного большим числом примеров. Может
быть, его перелистают и те специалисты, которые
пожелают вспомнить первоначальные формулировки
определений и доказательства некоторых теорем, им давно и
хорошо известных.
П. Александров
Москва, 25 марта 1971 г.

ГЛАВА I
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
§ 1. Предварительные понятия1 *)
1. Под пространством во всем последующем будет
пониматься хаусдорфово топологическое
пространство, т. е. множество R (элементов
произвольной природы, называемых точками), в котором
выделены некоторые подмножества, называемые открытыми
множествами пространства /?, так что при этом
выполнены следующие условия («аксиомы пространства»):
1° Сумма любого числа и пересечение конечного числа
открытых множеств есть открытое множество.
2° Все пространство и пустое множество открыты2.
3°2 Ко всяким двум различным точкам х и у
пространства имеются два непересекающихся открытых
множества Ох и Оуу содержащих соответственно эти точки'6.
Любое открытое множество, содержащее данную
точку х, называется окрестностью этой точки. Иногда,
однако, бывает удобно рассматривать не все окрестности
данной точки, а только некоторые, и, с другой стороны,
данное открытое множество относить в качестве
окрестности не ко всем точкам этого множества. Так, например,
рассуждая о числовой прямой, мы часто под
окрестностями какой-либо точки понимаем среди открытых
множеств, содержащих эту точку, преимущественно
интервалы или даже только интервалы вида (* ~ 7Г» х^~т)'
где п — натуральное число. Таким образом, приходим
к понятию определяющей системы (окрестностей)
данного пространства. Предположим, что для каждой точки
х пространства R среди всех окрестностей этой точки
отмечены некоторые, причем таким образом, что, какова
*) Ссылки, помеченные цифрами *•2 и т. д., относятся к
примечаниям в конце книги. — Прим. ред.

14 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
бы ни была точка х и ее произвольная окрестность Ох
(т. е. произвольное, содержащее точку х открытое
множество), имеется по крайней мере одна отмеченная
окрестность О'х точки х, удовлетворяющая включению
х е О'х ^ Ох. В этом случае множество всех отмеченных
окрестностей (вместе с указанием того, окрестностью
каких именно точек является данная отмеченная
окрестность) называется определяющей си ст е м о й
данного пространства. С понятием определяющей системы
тесно связано более простое и по существу более
удобное понятие базы пространства. Под базой
пространства R понимается всякое множество 33 открытых
множеств пространства /?, такое, что каждое открытое
множество пространства R может быть представлено как
сумма некоторых множеств, являющихся элементами
множества 334.
Нетрудно видеть, что множество 33 открытых
множеств U пространства R тогда и только тогда является
базой этого пространства, когда для каждой точки хе/?
и каждого содержащего эту точку открытого множества
Г можно найти такое U е 33, что
XGt/сГ,
Отсюда легко выводим следующее предложение:
Множество всех элементов любой определяющей
системы 2 пространства R есть база этого пространства;
обратно, если дана база 33 пространства R и если каждый
элемент U этой базы признается окрестностью всякой
точки хе(/, то получим определяющую систему
окрестностей пространства R.
Отсюда, в свою очередь, вытекает такое замечание:
если имеем какую-нибудь определяющую систему
окрестностей пространства R и если каждое множество £/,
являющееся элементом этой системы, будем
рассматривать как окрестность любой точки хе(/, то получим
снова определяющую систему пространства /?.
Отсюда видно, что рассмотрение баз и определяющих
систем окрестностей по существу сводится к одному и
тому же5.
Пример. Пусть Rx — множество всех действительных чисел
с его естественной топологией. Рассматривая в качестве окрестно-

§ 1. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
15
стей точки х е R все интервалы вида ( х , *Н—),где п = 1,
2, 3 получим определяющую систему окрестностей
пространства RK Соответствующая база состоит из всех интервалов, длины
которых имеют вид 2/л, где п — любое натуральное число. Считая
за окрестности точки х все интервалы вида (х — е, х + е), где е —
любое положительное число, также получим определяющую систему
окрестностей (соответствующая база состоит из всех вообще
конечных интервалов). Базой пространства R1 является и множество всех
интервалов с рациональными концами.
Для всякого пространства без труда вводятся
основные топологические понятия, известные читателю из
элементарного курса теории точечных множеств. Так, точка
I е R называется точкой прикосновения
множества М ^ /?, если любая окрестность точки g (т. е. любое
содержащее эту точку открытое множество) содержит
хотя бы одну точку множества М\ точка | называется
предельной точкой множества М9 если любая ее
окрестность*) содержит бесконечное множество точек
множества М\ множество всех точек прикосновения
множества М называется замыканием множества М и
обозначается через [М], иногда **•) через [M]R; множество
всех предельных точек множества М называется
производным множеством множества М и обозначается
через М'\ очевидно,
[М] = М U М'9
причем точки множества М\М' называются
изолированными точками множества М. Если М есть
множество всех точек пространства /?, то изолированные
точки множества М характеризуются тем, что каждая
такая точка образует открытое множество пространства
R. Множества, совпадающие со своим замыканием или,
что то же самое, содержащие все свои предельные точки,
называются замкнутыми (в данном пространстве/?).
Легко доказать, что замкнутые множества суть не что
*) При этом, если мы в основу определения точек
прикосновения (соответственно предельных точек) положим не все
окрестности, а лишь окрестности, взятые из данной определяющей
системы, то результат получится тот же; это и дает право вместо
максимальной определяющей системы пользоваться любой другой.
**) Если надо подчеркнуть, что замыкание делается в
пространстве R.

16 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
иное, как множества, дополнительные к открытым.
Множество М называется всюду плотным в пространстве R,
если его замыкание совпадает со всем пространством /?,
и т. д.
Важно заметить, что каждое множество М, лежащее
в пространстве R, само естественным образом
превращается в пространство, если открытые в М множества
определять как множества, являющиеся пересечением
с М открытых в R множеств.
2. Понятие топологического пространства есть
совокупность двух понятий: данного множества X элементов
(«точек») пространства и топологии £, введенной
в этом множестве: под нею понимается та совокупность
лежащих в X множеств, которые определены как
открытые множества данного пространства R = (Х,Х).
Наиболее удобный способ определить топологию дается
следующей теоремой.
Теорема 1. Пусть дано множество Е каких угодно
элементов, называемых точками. Пусть для каждой
точки хеЕ определены некоторые подмножества Ох^Е,
называемые «окрестностями» данной точки и
удовлетворяющие следующим условиям (обычно называемым
аксиомами Хаусдорфа):
A. Каждая точка имеет хотя бы одну «окрестность» и
содержится во всякой своей «окрестности».
B. Пересечение двух «окрестностей» данной точки
содержит «окрестность» этой точки.
C. Какова бы ни была «окрестность» Ох какой-либо
точки х^Е и точка у е Ох, существует «окрестность»
точки у, содержащаяся в Ох.
D. Для всяких двух различных точек х и у множества
Е можно найти две непересекающиеся «окрестности»
этих точек.
Тогда, называя открытыми множествами все
множества, являющиеся «окрестностями» точек xg£, и суммы
всевозможных таких множеств, а также пустое
множество, получим хаусдорфово пространство, в котором
система всех «окрестностей» является определяющей
системой. Очевидно, что и, наоборот, всякое хаусдорфово
пространство может быть получено таким образом (до-

§ 1. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
17
статочно в пространстве R определить в качестве
«окрестности» произвольной точки х любую окрестность этой
точки, т. е. любое содержащее ее открытое множество).
Для доказательства этой теоремы достаточно
убедиться в том, что открытые множества, определенные,
как указано выше, на основе «окрестностей»,
удовлетворяют сформулированным в начале п. 1 трем аксиомам
хаусдорфова пространства. Но это совсем легко, так как
по самому определению открытых множеств сумма
любого числа открытых множеств есть открытое множество.
Далее, пусть Г и Г" — два непустых открытых
множества; для доказательства того, что Г П Г7 открыто, т. е.
является суммой некоторого множества «окрестностей»,
достаточно показать, что для каждой точки х е Г П Г'
существует «окрестность» О'х^ГПГ". Но по определению
Г и Г" как открытых множеств имеется «окрестность»
Ох ^ Г и «окрестность» О'х ^ Г'; пересечение этих
«окрестностей» содержит по хаусдорфовой аксиоме В
«окрестность» 0"х и эта последняя, очевидно, лежит
в Г П Г.
Таким образом, аксиома Г топологического
пространства выполнена. Аксиома 2° непосредственно следует из
хаусдорфовой аксиомы А (и из того, что пустое
множество было принято в число открытых). Наконец, ак-
о
сиома Зг вытекает из хаусдорфовой аксиомы D.
3. Весом пространства R называется наименьшее из
таких кардинальных чисел ш, что пространство R имеет
базу, мощность которой равна ш.
Таким образом, пространства счетного веса суть
пространства, имеющие счетную базу («пространства со
счетной базой» или «пространства, удовлетворяющие
второй аксиоме счетности»).
Назовем базой пространства R в точке х. всякое
множество Sjc окрестностей точки х, обладающее тем
свойством,, что для любой окрестности Ох точки х найдется
содержащаяся в ней окрестность О'х е 93*.
Наименьшее кардинальное число, являющееся
мощностью какой-либо базы пространства R в точке х,
называется характером пространства R в точке х и
обозначается через %XR>

18 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Назовем псевдобазой пространства Re точке х всякое
множество 33* окрестностей точки х, обладающее тем
свойством, что пересечение всех Ох е 33* состоит из
одной лишь точки х.
Наименьшее кардинальное число, являющееся
мощностью какой-либо псевдобазы пространства R в точке х,
называется псевдохарактером пространства R в точке х
и обозначается через ybxR.
Из аксиомы отделимости Зг (и даже из 3ij следует,
что всякая база пространства R в точке х есть вместе
с тем и псевдобаза; поэтому всегда tyxR ^ %xR-
Единственное конечное число, могущее быть
характером или псевдохарактером пространства в какой-либо
точке, есть, очевидно, 1; каждое из равенств tyxR = 1 или
XxR = 1 равносильно тому, что точка х есть
изолированная точка пространства /?. Если %xR ^ **о для любой
точки хе/?, то говорят, что пространство R
удовлетворяет первой аксиоме счетности.
Заметим еще, что каждая точка хеЛ является
пересечением открытых множеств R\x', где хг —
какая-нибудь точка /?, отличная от точки х. Отсюда следует, что
псевдохарактер пространства R в любой точке х не
превосходит мощности множества всех точек пространства $в.
Теорема 2Х. Во всякой базе 93х пространства R
в точке х содержатся некоторая псевдобаза мощности
фх/? и некоторая база мощности %XR.
Доказательство обоих утверждений очень просто и
протекает параллельно. Пусть 33*—псевдобаза,
соответственно база, пространства R в точке х, имеющая
мощность фх/?, соответственно faR. Для каждой окрестности
Ох е S3» имеется содержащаяся в ней окрестность О'х е
е 33х, и эти О'х образуют псевдобазу, соответственно
базу, R в х, имеющую искомую мощность.
Приведем пример пространства, которое обозначим
пространством Я; для него в каждой точке хеЯ имеем
фх# = Ко, х*# = с
Точками пространства Я являются все точки числовой
прямой. Окрестность*) Ох любой точки х получим, если
*) Здесь и далее слово «окрестность» (понимаемое в смысле
теоремы 1) заключать в кавычки не будем.

§ 1. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
19
из любого содержащего точку х интервала числовой
прямой вычтем произвольное не более чем счетное
множество точек, отличных от точки х. Так как для любой
точки хеЯ интервалы вида 1х — —, х + — J образуют
псевдобазу, то фх// = Ко. Предположим теперь, что для
какой-нибудь точки хеЯ имеем %ХН = m < с, и
покажем, что это предположение приводит к противоречию.
Для этого воспользуемся теоремой 2Х. Из сделанного
предположения и этой теоремы следует, что существует
база 33х пространства Н в точке ху имеющая мощность m
и состоящая из тех окрестностей, которые были
выделены при определении пространства Н. Другими
словами, каждая окрестность О е 93х имеет вид
0 = U\D0t
где U — какой-либо интервал, содержащий точку xyaD0 —
конечное или счетное множество точек, отличных от
точки х. Сумма множеств Do, взятых по всем Ое93х,
есть множество Е мощности ^т*К0 = т < с, так что
множество Н\Е имеет во всяком интервале мощность с.
Можно поэтому найти счетное множество точек
Х = {хи хъ ..., хп$ ...}<= Н\Е
таких, что хп^ 1х — —, х + —). Но тогда каждая
окрестность О е 9ЭХ точки х в пространстве Н должна
содержать все точки хп за исключением, быть может,
конечного числа, что, очевидно, противоречит определению
этого пространства. Полученное противоречие доказывает
равенство %ХН = с.
Замечание 1. Не во всякой псевдобазе 93х
пространства R в данной точке х непременно содержится
псевдобаза мощности фх/?. Например, если R— числовая
прямая, х — какое-либо действительное число, а 93х —
псевдобаза R в точке ху состоящая из всех множеств
вида Ох = R \ х\ где х' Ф х, то Sx, очевидно, не
содержит никакой счетной псевдобазы R в ху хотя фх/? = Ме.
Теорема 2. Если пространство R имеет вес тп, то
всякая база 33 пространства R содержит подмножество
мощности m, являющееся базой пространства R.

20 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Доказательство. Возьмем какую-нибудь базуЗЭ0
пространства /?, имеющую мощность т. Обозначим через
и элементы этой базы. Назовем пару (Uat £/3), где Ua^
^330, ^е ^ ЗЭо, отмеченной, если существует хотя бы
одно V е 33, удовлетворяющее включению
tfesKs£/p. (1)
Множество всех отмеченных пар имеет мощность, не
большую, чем множество всех вообще пар элементов
множества Э30, а эта последняя, как известно, равна т.
Для каждой отмеченной пары выберем по одному
элементу VgS, удовлетворяющему условию (1).
Множество S37 отобранных элементов имеет также мощность
^ m; поэтому достаточно доказать, что 33' есть база
пространства R (этим, в частности, будет доказано, что
мощность множества 33' в точности равна т).
Итак, пусть дана какая-нибудь точка x^R и какая-
нибудь окрестность Ох этой точки; требуется найти V е
е 33', удовлетворяющее условию
xeV s Ох. (2)
Так как 330 — база, то существует такое U$ е 330, что х е
б(/р£ Ох. Но базой является и 33, поэтому существует
УеЭЗ, удовлетворяющее включению
Наконец, можно найти Ua е 330 с условием
xe=UasV.
Отсюда следует, что пара (£/а, U$)—отмеченная;
поэтому существует У'еЗЗ', удовлетворяющее условию
и тем более условию (2), что и требовалось доказать.
Замечание 2. Если M^R, то, очевидно, вес
пространства М не превосходит веса /?; кроме того, для х е
gAI всегда %ХМ ^ %xRt ухМ ^ yxR. Отсюда, в частности,
следует, что как первая, так и вторая аксиомы счетности
выражают наследственные свойства пространства.
4. Хаусдорфовы пространства, единственные
изучаемые в этой работе, называются также Гг-пространствами.

§ 1. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
21
Ослабляя аксиому 32, получим так называемые
^-пространства; в них открытые множества, кроме аксиом 1°
и 2°, удовлетворяют аксиоме 3° (см. примечание 4). Для
всяких двух различных точек хну можно найти
открытое множество Ох, содержащее точку х, но не
содержащее точки у, и открытое множество Оу, содержащее
точку у, но не содержащее точки х*).
Можно, наоборот, усилить требование отделимости,
содержащееся в аксиоме 32. Так приходим к
следующему определению:
Пространство R называется регулярным в точке х,
если для любого замкнутого множества A czR, не
содержащего тонки х, можно найти два непересекающихся
открытых множества Ох и О А, из которых первое
содержит точку х, а второе — множество А **).
Это же определение можно высказать и в такой
форме:
Пространство R называется регулярным в точке х,
если каждая окрестность точки х содержит замыкание
некоторой окрестности той же точки.
Докажем эквивалентность обоих определений. Пусть
выполнено требование, содержащееся во втором
определении. Возьмем замкнутое множество А, не содержащее
точки х\ тогда R\A есть окрестность точки х\ значит,
существует окрестность Ох той же точки,
удовлетворяющая включению [Ол:]^/?\Л. Но тогда открытые
множества Ох и /?\[Ох] не пересекаются и содержат
соответственно точку х и множество А.
Пусть, наоборот, выполнено требование первого
определения. Возьмем произвольную окрестность Ох.
Замкнутое множество А = R \ Ох не содержит точки х\ беря
непересекающиеся открытые множества 0& и ОА,
видим, что [0{х] П О А пусто; значит, [Otx] ^R\A = Ox,
что и требовалось доказать.
*) В первоначальном французском тексте «Мемуара» этого
абзаца не было, он прибавлен в первом русском издании 1950 г.
**) Всякое открытое множество, содержащее данное множество
М a R, называется окрестностью множества М (в
пространстве R); поэтому наше условие можно сформулировать так:
точка х и не содержащее ее замкнутое множество А имеют
непересекающиеся окрестности.

22 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Хаусдорфово пространство, регулярное в каждой
своей точке, называется регулярным пространством, или
Тз-прост ранетвом7.
5. Приведем несколько примеров нерегулярных
пространств. (При построении этих примеров и вообще почти
всех примеров, данных в этом сочинении, мы будем
пользоваться теоремой 1, т. е. определять систему
окрестностей, удовлетворяющих аксиомам А — D.)
Г Точками пространства R являются все точки
сегмента [0; 1]. Окрестности для всех точек хФО те же, что
У* У $ х _ h
a i i« »| 1 » »>0
1 ! ■ !
2 ! i i
Рис. 1.
и на полуинтервале [0; 1] (т. е. для 0 < х < 1 —
содержащие точку х интервалы, лежащие в (0; 1), а для точки
1 — полусегменты вида (1— е; 1], где 0<е<1). Для
точки х = 0 определяем в качестве окрестностей
множества вида [0; e)\D, где D есть множество всех точек -
(п = 1,2, 3, ... и 0 < е < 1). Легко видеть, что
полученное таким образом пространство не регулярно в
точке О (множество D в пространстве R замкнуто, и всякие
две окрестности точки О и множества D пересекаются)^.
2° Построим пространство, нерегулярное во всякой
своей точке. Пространство R состоит из всех точек
плоскости. Окрестность любой точки х получим, если из
любого открытого круга с центром х удалим все отличные
от самой точки х точки, лежащие на вертикальном
диаметре этого круга.
3° Пространство R состоит из всех точек
полуинтервалов [а; Ь) и (с\ d\ (рис. 1). Для точек £, лежащих в [а, 6),
окрестности суть полуинтервалы [£;*), имеющие ^своим
левым концом. Произвольную окрестность какой-либо
точки £*, лежащей в (с; d\, получим, если возьмем сумму
произвольного полуинтервала (**; VI имеющего точку I*
своим правым концом, и интервала (*/*;л*)> являюще-

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА
23
гося ортогональной проекцией интервала (х*\ £*) на
прямую ab.
Легко видеть, что пространство R нерегулярно во всех
точках, лежащих в [а\Ь)\ эти точки образуют открытое
множество G, плотное в R и обладающее следующими
свойствами:
а) множество G, не имея ни одной изолированной
точки, не содержит также и никакого совершенного
множества;
б) множество G компактно в пространстве R (т. е.
всякое бесконечное подмножество множества G имеет
в R хотя бы одну предельную точку), тогда как
производное множество G' = R множества G не компактно
в себе*).
Только что построенное пространство назовем
пространством А\.
Примерами регулярных пространств могут служить
все метризуемые пространства. Примеры другого рода
можно получить так:
Пусть W — какое-либо упорядоченное множество.
Возьмем за окрестность Ох произвольной точки x^W
любой содержащий эту точку интервал упорядоченного
множества W. Таким образом, во всякое упорядоченное
множество вводится «естественная» топология;
полученное пространство будем называть пространством данного
упорядоченного множества W или просто пространством
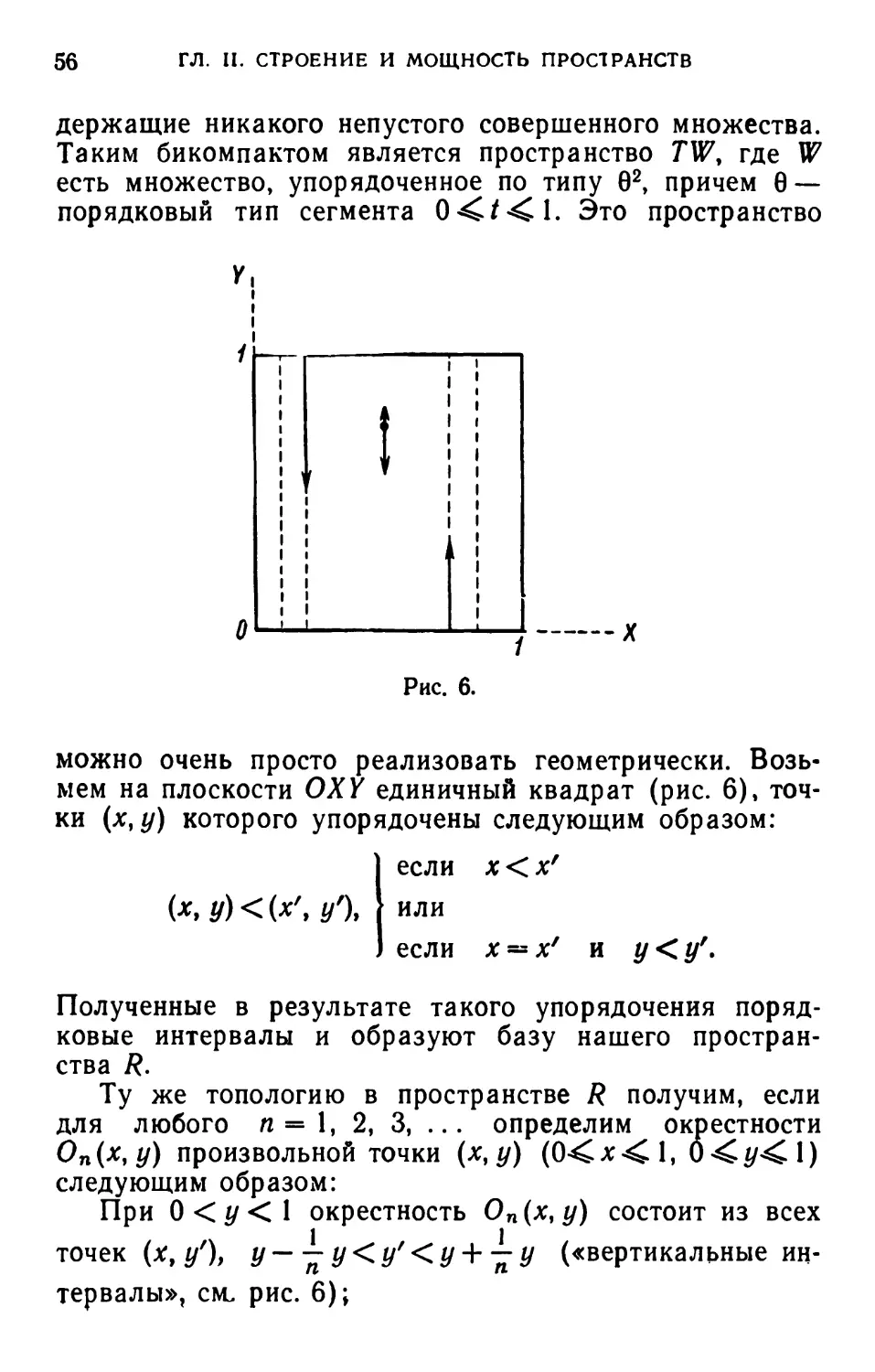
TW\ легко видеть, что все такие пространства регулярны.
§ 2. Бикомпактные пространства8
6. Как известно, пространство R называется
компактным, если в нем каждое бесконечное множество имеет
хотя бы одну предельную точку.
Введем сразу же следующее основное определение:
Точка I пространства R называется точкой полного
накопления бесконечного множества М ^ /?, если для
каждой окрестности 0% точки £ множество М [) 0\ имеет
ту же мощность, что и все множество М.
*) То есть в R = G' имеются бесконечные множества,
лишенные предельных точек.

24 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Следующее предложение доказывается без всякого
труда. Каждое из нижепоименованных условий а), б), в)
является условием, необходимым и достаточным для ком-
пактности пространства:
а) всякое счетное множество М имеет хотя бы
одну точку полного накопления-,
б) всякая счетная убывающая последовательность
непустых замкнутых множеств
Л, => i42=> ... => AnzD ...
имеет непустое пересечение-,
в) в каждом счетном открытом покрытии
пространства R содержится конечное покрытие*) этого
пространства.
Необходимость и достаточность условия а) очевидна, так как
каждое бесконечное множество содержит счетное подмножество и
для счетных множеств понятия предельной точки и точки полного
накопления совпадают.
Необходимость условий б) и в) хорошо известна. Для того
чтобы убедиться в достаточности условия б), предположим, что
пространство R не компактно, и покажем, что тогда условие б) не
выполнено. Но если R не компактно, то существует счетное
множество
Х\у *2. • • •! Хп, ...»
не имеющее ни одной предельной точки; обозначая через Ап
множество точек хп, Хп+и ..., видим, что все Ап замкнуты и образуют
убывающую последовательность с пустым пересечением.
Пусть выполнено условие в); покажем, что пространство
компактно. В противном случае по только что доказанному
существовала бы убывающая последовательность непустых замкнутых
множеств
^э^з ... ^ Ап^ ...
с пустым пересечением. Тогда множества
Tl-R\AU T2 = R\A2, .... Tn-R\An, ...
открыты и образуют покрытие пространства /?, не содержащее
никакого конечного покрытия того же пространства.
*) Множество я, элементами которого являются некоторые
множества Р пространства R, называется покрытием множества М, если
Af £М Я; покрытие называется открытым, соответственно замкну-
тым, если все его элементы суть открытые, соответственно
замкнутые, множества пространства R\ покрытие я' содержится в
покрытии я, если я' £ я.

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА
25
7. Из только что доказанного следует, что понятие
компактности тесно связано с теми или иными счетными
конструкциями (счетное множество точек, счетные
последовательности замкнутых множеств, счетные покрытия).
С другой стороны, нельзя отрицать некоторого, пока еще
совсем неясного, интуитивного содержания понятия
компактности, которое возникает перед нашим сознанием,
когда мы думаем, например, о сегменте числовой
прямой, о сферической поверхности и т. п. Это пока еще не
выясненное нами интуитивное содержание сводится к
некоторой полноте, к некоторой, в каком-то смысле
абсолютной, замкнутости рассматриваемых геометрических
образований, к невозможности естественным образом
пополнить их новыми элементами. Мы надеемся в
настоящем сочинении представить эти туманные соображения
в свете полной логической отчетливости (см. гл. III); но
уже сейчас мы хотим заметить, что для приведения всего
в ясность понятия компактности, во всяком случае,
недостаточно. Подумаем, в самом деле, о пространстве
TW((ui) всех порядковых чисел*) < «i и о пространстве
TW((ut + 1) порядковых чисел ^ ог, оба пространства
компактны, между тем второе из них этой искомой
замкнутостью, по-видимому, обладает, а первое весьма
чувствительным образом ею не обладает (именно ввиду
возможности совершенно естественно присоединить к
пространству rW(a)i) еще и точку coi).
Наконец, заметим, что и преимущественная роль,
которую в понятии компактности играет счетная мощность,
наполняет нас некоторым чувством неудовлетворенности.
Из этих весьма еще, впрочем, неясных соображений
рождается интерес, представляемый, быть может,
следующим предложением:
Основная теорема (теорема 3). Следующие три
свойства пространства R эквивалентны между собою:
*) Через <Di обозначаем первое несчетное порядковое число
(обозначаемое часто через Q; первое бесконечное порядковое число,
обычно изображаемое буквой со, мы будем обозначать через о)о).
Если а — какое-нибудь порядковое число, то через W(a)
обозначаем вполне упорядоченное множество всех порядковых чисел < а;
тогда TW(a), естественно, означает соответствующее
топологическое пространство.

26 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
A. Всякое бесконечное множество, лежащее в
пространстве /?, имеет хотя бы одну точку полного
накопления.
Б. Всякая (не непременно счетная) вполне
упорядоченная последовательность непустых убывающих
замкнутых множеств имеет непустое пересечение.
B. Всякое открытое покрытие пространства содержит
конечное покрытие9.
Прежде чем переходить к доказательству этой
теоремы, напомним10, что порядковое число называется
нерегулярным, если оно конфинально какому-нибудь
меньшему порядковому числу; в противном же случае (т. е.
если оно не конфинально никакому меньшему
порядковому числу) порядковое число называется регулярным.
Из этого определения следует, что всякое регулярное
порядковое число является начальным порядковым числом
(т. е. наименьшим порядковым числом данной
мощности)*). С понятием регулярного порядкового числа тесно
связано понятие регулярного кардинального числа:
кардинальное число ш называется регулярным, если
регулярно первое порядковое число мощности ш. Для
бесконечных кардинальных чисел это же понятие может быть
определено и гак: кардинальное число ш регулярно, если
оно не может быть представлено в виде суммы меньших,
чем т, кардинальных чисел, взятых в количестве, также
меньшем, чем т**). В дальнейшем понятие регулярности,
соответственно нерегулярности, будет рассматриваться
лишь в применении к бесконечным порядковым и
кардинальным числам.
После этого обозначим через Лг, £>г, Вт те свойства,
в которые перейдут свойства Л, £, 5, если потребовать,
чтобы рассматриваемые в них множества (множества
точек в Л, множества открытых множеств в В) имели
*) Согласно этому определению, среди конечных порядковых
чисел регулярными являются лишь числа 0 и 1.
**) Доказательство этого факта и другие сведения о
регулярности можно найти, например, в книге П. С. Александрова [1]
(гл. 3, § 7). Там же читатель найдет и доказательство весьма
важной и применяемой в дальнейшем теоремы Хаусдорфа о том, что
всякое упорядоченное множество мощности Кт конфинально
некоторому своему вполне упорядоченному множеству, порядковый
тип которого есть регулярное порядковое число ^о)т.

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА 27
регулярную мощность, а последовательности (в Б) —
регулярный порядковый тип. Интересно заметить, что
при доказательстве теоремы 3 само собою получится, что
каждое из свойств Лг, Бг, Вг эквивалентно всем
свойствам Л, Б, В.
План доказательства ясен из схематического чертежа
(рис. 2), на котором стрелки означают логическое
следование.
Так как утверждения В-+Вг
и А-+Аг очевидны, то можно
ограничиться доказательством
остальных указанных в нашей
схеме утверждений.
5->Л. В самом деле,
предположим, что свойство В имеет
место; а свойство Л — нет. Тогда
существует бесконечное множество
М, не имеющее в R ни одной
точки полного накопления, так что
каждая точка х е R обладает
окрестностью Охх для которой с#
мощн. (М П Ох) < мощн. М.
В силу условия В существует конечное число таких
окрестностей:
Охи ..., Oxsy
дающих в сумме все пространство /?. Но тогда
М = {М[\Охх)\) ... \}(M[\Oxs\
чего не может быть11, так как бесконечное множество
нельзя представить в виде суммы конечного числа
слагаемых (в данном случае множеств М[\Охи ..., М(]Ох8),
каждое из которых имеет мощность, меньшую, чем
мощность М.
ЛГ->БГ. Пусть Лг выполнено. Рассмотрим вполне
упорядоченную последовательность
А{^А2з ... э^в2... (1)
регулярного порядкового типа о)т (где сот есть первое
порядковое число некоторой регулярной мощности Кт),
состоящую из непустых замкнутых множеств Ла.

28 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Переходя, если надо, к конфинальной
последовательности, имеющей (в силу регулярности (От) тот же порядковый
тип сот, можно предположить, что либо все Аа совпадают
между собою (и тогда, очевидно, имеют непустое
пересечение), либо все они попарно различны. Тогда для
каждого а < (От можно взягь точку ха^Аа\ Аа+{.
Множество X всех отобранных таким образом точек ха имеет
регулярную мощность Кт, так что согласно условию Аг
существует точка полного накопления g множества X.
Если бы точка g не принадлежала какому-нибудь
множеству Аа последовательности (1), то R\Aa было бы
окрестностью 01 точки £, причем в эту окрестность Og =
= R\Aa могут попасть лишь те точки х$, для которых
Р < а. Но в этом случае мощность множества X П 0|
была бы меньше, чем Кт = мощн. X, вопреки определению
точки £. Итак, l^f]Aay так что свойство Бт имеет место.
а
БГ-*Б. Это утверждение сразу следует из того, что
каждая последовательность вида (1) какого угодно
порядкового типа содержит конфинальную
подпоследовательность некоторого регулярного порядкового типа озт,
которую получим, если возьмем наименьшее порядковое
число 0т, обладающее тем свойством, что в (1)
существует конфинальная подпоследовательность.
Ла.=> Ла,=> ... =>Aav=> ... (1')
типа (от. Так как (от по самому своему определению
регулярно, то (Г) есть искомая последовательность.
В силу этого пересечение всех Аа^ не пусто, а так как
ГМа = ГМ<Ч' Т0 И ПИ<* Не ПУСТ0-
а v а
Б-*В. Пусть дано бесконечное открытое покрытие
пространства R. Предполагая условие Б выполненным,
обозначим через m наименьшее такое кардинальное
число, что я содержит покрытие я' мощности т. Если ш
бесконечно, т = fc*T, то все элементы покрытия я' можно
упорядочить по типу (От, так что
я/-{0„ G2, ..., Ga, ...} (a<(oT). (2)
Отсюда и из определения числа (от следует, что при лю-

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА
29
бом а < сот замкнутое множество Ла = /?\ (J Gp не
пусто. Так как множества Аа образуют убывающую
вполне упорядоченную последовательность, то в силу
условия Б их пересечение не пусто; а это значит, что
сумма их дополнений R \ Ла, равная сумме всех Ga
последовательности (2), есть собственное подмножество
пространства /?, вопреки тому что (2) есть покрытие
этого пространства. Полученное противоречие
показывает, что Til конечно и что В выполнено.
Изложенные утверждения и доказывают теорему 3,
а также эквивалентность свойств Лг и Бг каждому из
свойств Л, Б, В. Кроме того, так как из В следует Вг, то
остается лишь доказать утверждение 5Г-*БГ. Тогда
эквивалентность всех трех свойств Л, 5, В между собою,
а значит, и эквивалентность каждого из них свойствам
Л, ZJ, В будет доказана.
Для доказательства утверждения Вг-+Бг возьмем
какую-нибудь вполне упорядоченную последовательность
непустых замкнутых множеств
Л,эЛ2э ... эЛаэ .... (1)
имеющую регулярный порядковый тип ot. Если бы f]Aa
а
было пусто, то множества Га = R\Aa образовывали бы
покрытие я пространства /?. Взяв конечное покрытие
я'an (существующее в силу 5Г), состоящее из
множеств
Га,, ..., Га5,
видим, что Аах П • • • П Ла5 пусто, что вследствие
включений Ла, ^ ... ^ Aas приводит к пустоте множества Аа$.
Полученное противоречие завершает наше
доказательство.
Доказанные результаты оправдывают, как нам
кажется, введение следующего определения:
Пространство R называется бикомпактным, если
в нем имеет место одно какое-нибудь (а следовательно%
и каждое) из свойств Л, Б, В.
При этом нами доказана:

30 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Теорема 3'. Каждое из условий Агу Бг, Вг является
достаточным (и, очевидно, необходимым) для биком-
пактности пространства R.
Важно заметить, что как доказанные результаты, так
и определение бикомпактности остаются в силе не только
для хаусдорфовых, но и для любых Ггпространств8.
Хаусдорфовы бикомпактные пространства называются
просто бикомпактами*).
8. Приведем несколько
примеров. Обозначая через
W(a) вполне упорядоченное
множество всех порядковых
чисел < а, мы легко
убеждаемся в том, что для
всякого начального числа азт
пространство TW(<x)x +1)
бикомпактно, а пространство
TW((ut) при т>0
компактно, но не бикомпактно.
Вставим между любыми двумя
Рис. 3. числами вида а и а + 1 по
множеству, подобному
числовой прямой; точнее, рассмотрим множество всех пар
вида (а, 0» гДе 0 <; f < 1, и положим
( aw ' i'\ \ если (ПРИ Л1°бых /, ?) имеем а<а',
1а, г;«ма, I) у a ?акже если ава/ и t<t,
Если у — предельное число, то полученное
упорядоченное множество обозначаем через А (у). В случае у вида
Y = у/+ 1 к упорядоченному множеству A(y') добавим
точку у\ полагая (a, t)<y' для любых а < у' и /(0^
^/< 1). Полученное упорядоченное множество A(y')U
U у' обозначим через A(y) = A(y' + 1). Пространства
ТА((йх + 1) и ГА(о)т) связны и компактны, при этом
ГД(а)т + 1) бикомпактно, а ГА((от) —нет.
Бикомпакт совершенно другого рода получим
следующим образом. Рассмотрим на плоскости две концентри-
*) Метризуемые бикомпактные пространства называются
компактами; как мы увидим в § 2 гл. V, они тождественны с
бикомпактами (а также с компактными хаусдорфовыми пространствами),
имеющими счетную базу («удовлетворяющими второй аксиоме счет-
ности»). — Прим. ред.

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА
31
ческие окружности Ci и С2 (рис. 3). Пространство R
состоит из точек обеих этих окружностей, причем если х
лежит на С2, то объявляем точку х изолированной в R
(т. е. множество, состоящее из одной точки х, объявляем
открытым). Окрестности точек £,. лежащих на
внутренней окружности Си определяем так: берем произвольную
открытую дугу alb окружности С{ и, обозначая через а*,
£*, Ь* проекции точек а, g, Ъ на С2 из общего центра О
окружностей С{ и С2, определим окрестность 0% точки £
как множество, состоящее из всех точек дуги а\Ь
окружности С^ и открытых дуг а*1* и |*Ь* окружности С2 так,
что
Построенные таким образом окрестности превращают,
согласно теореме 1, множество всех точек окружностей
Ci и С2 в хаусдорфово пространство R. Пространство это
бикомпактно. Чтобы в этом убедиться, заметим, что
всякое замкнутое в R множество Л распадается на два
множества Л1 и Л2, где Л* (i = 1, 2) состоит из всех точек Л,
лежащих на Сь причем Л1 замкнуто на С{ в смысле
обычной топологии, данной на этой окружности*). При
этом, если А бесконечно, то Л1 не может быть пусто.
Пусть нам дана вполне упорядоченная
последовательность непустых убывающих замкнутых множеств
А{=>А2=> ... =>Ла=> ...
Если хотя бы одно из множеств Ла конечно, то все эти
множества начиная с некоторого непременно совпадают
между собою, а значит, и с пересечением Р) Ла, которое,
а
таким образом, оказывается не пусто. Если же все Ла
бесконечны, то имеем вполне упорядоченную
последовательность
Л|эЛ1>=2 ... эЛ^э ...
*) Это следует из того, что, рассматривая С\ как множество,
лежащее в пространстве R, и как множество, лежащее на
обыкновенной плоскости, получим одно и то же топологическое
пространство.

32 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
непустых замкнутых на окружности Gi множеств,
которые в силу бикомпактности окружности имеют непустое
пересечение. Так как f)Ala^f]Aai то и f]Aa не пу-
а а а
сто и бикомпактность пространства R доказана.
Среди свойств этого пространства, которое назовем
пространством Л2, отметим следующие:
во-первых, пространство А2 удовлетворяет первой
аксиоме счетности;
чС во-вторых, так как
все точки, лежащие па
Сг, изолированы, то
пространство А2у
содержащее множество
мощности континуума
изолированных точек,
не удовлетворяет
второй аксиоме счетности
(следовательно, как
мы увидим в гл. V, не
метризуемо)*);
в-третьих,
множество всех точек,
лежащих на Сг, есть
открытое множество
мощности континуума, плотное во всем пространстве А2 и не
содержащее никакого бесконечного замкнутого в А2
множества (откуда, в частности, следует, что это открытое
множество не является суммой счетного числа
замкнутых множеств)12.
Построим еще один бикомпакт, который будем
называть пространством £Д.
Точками пространства £Д являются все точки
квадрата abed (рис. 4), причем берутся как граничные, так и
внутренние точки этого квадрата.
Окрестности строятся так:
для точек |, лежащих внутри квадрата, но не
лежащих на диагонали (а; с), а также для точек интервалов
*) Пространства TW((dx)t TW(uyx+ 1), построенные выше,
также не удовлетворяют второй аксиоме счетности: будучи
компактными, они не метризуемы.
Рис. 4.

§ 2. БИКОМПАКТНЫЕ ПРОСТРАНСТВА
33
(a; d) и (Ь\ с) окрестности определяются как
вертикальные интервалы, содержащие данную точку £;
для точек £*, лежащих на полусегментах (а; Ь] и
[d\ с), окрестности определяются как вертикальные
полусегменты [£*; 1')\
окрестности точек х, лежащих на диагональном
интервале (а; с), определяются так: берется произвольный,
СОДерЖаЩИЙ ТОЧКу X ОТКРЫТЫЙ ПрЯМОуГОЛЬНИК X2*l*/l*/2
(см. рис. 4) с вершинами, лежащими на (a; d) и {Ь\с),
и из этого прямоугольника удаляется произвольное
конечное число не содержащих точку х вертикальных
интервалов (z\\ z"), ..., (z'n; z£), причем z\ лежат на
(*р Ух\ a z'( на (х2; у2)\
наконец, окрестности точек а и с аналогичны только
что построенным с той лишь разницей, что к
прямоугольнику ХоаЬуо причисляются две его стороны, а
именно, сегмент [а; Ь] и полусегмент [я;*о), точно так же к
прямоугольнику x'Qdcy'0 причисляются стороны [d\ с] и
[г; у'0]\ что же касается вычитающихся из этих
прямоугольников вертикальных интервалов, то они не должны
лежать в первом случае на стороне [a; d], а во втором —
на стороне [Ь; с].
Первая аксиома счетности не выполнена в
пространстве Ui ни для одной из точек диагонали [а\ с]. Нетрудно
доказать, что характер пространства в каждой из этих
точек равен мощности континуума с (в остальных точках
он, очевидно, равен К0).
Заметим, что всякое бесконечное множество М ^ Uif
лежащее на какой-либо горизонтальной прямой, сходится
к точке пересечения этой прямой с диагональю [а\ с]
(множество М называется сходящимся к точке ху если каждая
окрестность точки х содержит все точки множества М, за
исключением, может быть, конечного числа этих точек).
Для доказательства бикомпактности пространства Ut
воспользуемся условием Лг13. Покажем, что всякое
множество £, лежащее в пространстве £Л и имеющее
регулярную мощностьт, имеет в [Д хотя бы одну точку
полного накопления.
Это так, если имеется хотя бы один вертикальный
сегмент, пересекающийся с Множеством Е по множеству

34 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
мощности тп (утверждение следует из того, что каждый
сегмент является бикомпактом).
Итак, пусть для каждого вертикального сегмента v
множество Е Л v имеет мощность < т. Отсюда следует,
что для любого конечного множества вертикальных
сегментов 01, ..., va
мощн. (е \ (J vt) = m. (3)
Обозначим через Е' проекцию множества Е на сегмент
[a; d]. Если мощн. Е' < тп, то в силу регулярности
кардинального числа тп имеется по крайней мере одна
горизонтальная прямая, пересекающаяся с множеством Е
по множеству Н мощности ш; тогда, как мы уже
упоминали, все множество Н сходится к точке пересечения х
этой горизонтальной прямой с диагональю [а; с] и точках
есть точка полного накопления множества Я, а значит, и
равномощного с ним множества Е.
Остается рассмотреть случай, когда мощн. Е' = т.
Но тогда на [а\ d] имеется точка полного накопления р
множества Е'. Проведем через точку р горизонтальную
прямую; эта последняя пересечет диагональ в некоторой
точке х, которая в силу равенства (3) есть точка полного
накопления множества Е.
Заметим, наконец, что бикомпакт Ui есть связное
пространство.
§ 3. Пространства, компактные в данном отрезке
мощностей
9. Имеет место следующее предложение:
Теорема За,в- Пусть а==Ка"Ь=Кр— два
кардинальных числа (а^Ь ). Следующие три свойства
пространства R эквивалентны между собою.
А[, ь. Всякое множество Е произвольной регулярной
мощности тп, удовлетворяющей неравенству а^т^Ь,
имеет в Rno крайней мере одну точку полного накопления.
Бга, ь. Всякая вполне упорядоченная
последовательность регулярного порядкового типа*) а)Т(о)а^а)Т^(оз),
*) Напоминаем, что всякое регулярное порядковое число > 1
есть начальное число.

§ 3. КОМПАКТНОСТЬ В ДАННОМ ОТРЕЗКЕ МОЩНОСТЕЙ 35
состоящая из непустых убывающих замкнутых множеств
Д,эЛ2э ... э^з ... (v<oT) (1)
пространства /?, имеет непустое пересечение.
В[, е. Всякое открытое покрытие п пространства Rt
имеющее произвольную регулярную мощность т,
удовлетворяющую неравенству а ^ m ^ Ь, содержит
покрытие мощности < т.
Прежде чем переходить к доказательству этой
теоремы14, введем следующие определения:
Пространство, удовлетворяющее какому-нибудь
одному, а следовательно, и каждому из условий A[t f, Ба, ♦
Вга, е, называется компактным в отрезке мощностей [а; Ь]
или просто [й; Ъ]-компактным. При этом случай а = Ь не
исключается.
Если а = Ко, то пространство называется инициально
компактным вплоть до мощности Ь. Очевидно, просто
компактные пространства инициально компактны вплоть
до мощности К0, т. е. [К0; К0]-компактны.
Если для некоторого а и любого Ь^а пространство
R является [а; Ь]-компактным, то оно называется фи-
нально компактным начиная с мощности а или а
-финально компактным; пространства, Ki-финально
компактные, называются просто финально компактными.
Так, например, из известных теорем следует, что
всякое пространство со счетной базой является финально
компактным.
Наконец, бикомпактные пространства инициально
компактны вплоть до любой бесконечной мощности и
одновременно финально компактны начиная с любой
мощности; отсюда и название «бикомпактные пространства».
Переходим теперь к доказательству теоремы 3£t ьОно
представляет значительную аналогию с доказательством
теоремы 3.
Докажем сначала эквивалентность условий 6а, ь и Вга, ь.
Предположим выполненным условие Вга, ь и докажем,
что в этом случае имеет место и БГ, *. Пусть
А{=>А2^ ... 2/lv2 ... (v<<DT) (1)

36 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
вполне упорядоченная последовательность регулярного
порядкового типа о)т(соа ^ o)t ^ сор), состоящая из
непустых замкнутых множеств. Положим
Если бы пересечение всех Av было пусто, то Tv
образовывали бы покрытие пространства R и тогда в силу Ва, ъ
из этого покрытия можно было бы выделить покрытие
мощности Кт,< Кт. Множества Ауу соответствующие
элементам этого покрытия, составили бы
подпоследовательность (некоторого порядкового типа 6 < сат,
мощности Кх,)
Avx => Av2 => ... => AV(J => ... (<т<9) (2)
последовательности (1) ив силу предположенной
регулярности порядкового типа сот последовательность (1) не
может быть конфинальной последовательности (2). Но
тогда последовательность (2) не может иметь пустого
пересечения вопреки тому, что соответствующие rV(j =
e R \ Rva образуют покрытие пространства R.
Полученное противоречие доказывает утверждение
Предположим теперь, что выполнено условие Бга, ь>
покажем, что тогда пространство обладает и
свойством Вга, в.
Возьмем произвольное открытое покрытие я
пространства /?, имеющее регулярную мощность Кт(а^ **т ^
^Ь). Занумеруем элементы покрытия я во вполне
упорядоченную последовательность
Г,, Г2, ..., Tv, ... (v<coT)
типа о)т; положим
AV = R\ (J^
Тогда Av образуют убывающую последовательность
замкнутых множеств, имеющих пустое пересечение. Так
как порядковое число сот, являющееся типом этой после-

§ 3. КОМПАКТНОСТЬ В ДАННОМ ОТРЕЗКЕ МОЩНОСТЕЙ 37
довательности, регулярно, то из пустоты пересечения
Р) Av следует, что пусто и некоторое Av(v < о)т), т. е. со-
v
вокупность тех Гц, у которых \i < v, образует покрытие
пространства /?, имеющее, очевидно, мощность,
меньшую Кт.
Докажем теперь эквивалентность условий Ага, ь и Бга, ь-
Бга, ь -> Аа, &. Пусть Е есть произвольное множество,
лежащее в R и имеющее регулярную мощность Кт( &^
^ Их ^ Ь). Точки множества Е занумеруем по
порядковому типу (от:
£ = {*„ хъ ..., xv, ...} (v<coT). (3)
Обозначим через Ец множество всех xv, для которых
v ^ р. Положим, наконец, Лц = £д. Тогда
Л, э Л2 э ... Лц э ... (и, < cot).
Предположим теперь, что условие />£. ь выполнено, и
докажем, что тогда множество £ имеет хотя бы одну точку
полного накопления (этим и будет доказано, что Бга, ь -*
-> Аа, б). Из />£, ь следует существование точки
и
Мы утверждаем, что £ есть точка полного накопления
множества Е.
В самом деле, пусть 0| — произвольная окрестность
точки |. Так как при любом \х < о)т имеем £еЛц = 2?ц,
то 0£ П £ц =£ Л; значит, для каждого \л < сот существует
наименьшее vu > ц, такое, что *v е 0£. Получаем
последовательность
(30
конфинальную последовательности (3) и состоящую из
некоторых точек множества ЕЛО£; так как шт регулярно,
то последовательность (3) имеет тот же порядковый тип
сот, значит, мощность Кт. Так как 0£ — произвольная
окрестность точки g, то эта точка есть действительно
точка полного накопления множества Е.

38 ГЛ. I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ОБЩИЕ ТЕОРЕМЫ
Остается доказать, что из Ага, ь следует Бга, ь-
Пусть условие A[t ь выполнено. Рассмотрим какую-
нибудь последовательность
Ах ^ А2 s ... ^ Av ^ ...
регулярного порядкового типа (от(о)а ^ о)т ^ сор),
составленную из непустых замкнутых множеств. Надо
доказать, что пересечение всех Av не пусто. Это очевидно,
если все Av совпадают между собою начиная с
некоторого. Если же после каждого v имеется jnv, такое, что
Да с= ЛУ, то можно перейти к конфинальной
подпоследовательности, имеющей (в силу регулярности о)т) тот
же тип сот и состоящей из попарно различных множеств.
Поэтому можно с самого начала предположить, что все
Av различны между собою. Но тогда для каждого v < o)t
можно взять точку л;уеЛу\Лу+1. Множество X всех
полученных точек xv имеет регулярную мощность Кт,
а следовательно, имеет и точку полного накопления g.
Эта точка I принадлежит всем множествам Avt в чем
можно убедиться, дословно повторяя рассуждения,
сделанные в соответствующем месте доказательства
утверждения Аг-+Бг в п. 7 предыдущего параграфа.
Теорема 3^ ь полностью доказана.
Заметим, что отказаться в формулировке теоремы
За.ь от требования регулярности фигурирующих в ней
кардинальных и порядковых чисел невозможно, как
показывает пример пространства ГИ^сош). Пространство
это финально компактно, между тем в нем существует
убывающая последовательность типа (Оаъ состоящая из
непустых замкнутых множеств с пустым пересечением.
Это пространство, имея мощность K<d, лишено точки
полного накопления. Между тем легко видеть, что в
пространстве Т№((йц>) каждое несчетное открытое покрытие
содержит счетное покрытие. Таким образом, без
предположения регулярности из условия Ва, ь условия Ай, * и
Ба, ь не следуют.
В случае инициально компактных пространств
положение более удовлетворительно. Именно, теми же
методами, какими мы доказывали теорему 3, можно доказать
и следующее предложение:

§ 3. КОМПАКТНОСТЬ В ДАННОМ ОТРЕЗКЕ МОЩНОСТЕЙ 39
Теорема 3&. Для того чтобы пространство R было
инициально компактно вплоть'до мощности Ъ, каждое из
следующих трех условий является необходимым и
достаточным:
А б. Каждое множество Е мощности ^ b имеет в R
по крайней мере одну точку полного накопления.
Бь. Каждая вполне упорядоченная
последовательность мощности ^ Ь, состоящая из непустых убывающих
замкнутых множеств, имеет непустое пересечение:
Вь. Каждое открытое покрытие пространства /?,
имеющее мощность ^ О, содержит конечное покрытие
пространства /?.
10. В заключение приведем некоторые примеры.
Очевидно, пространство Tw((da+i) может служить примером
пространства, инициально компактного вплоть до
мощности Ка, но не до мощности Ка+ь Мы уже говорили, что
всякое пространство со счетной базой финально
компактно. Примером финально компактного пространства,
имеющего в каждой точке характер, равный мощности
континуума с, может служить пространство Я,
построенное в § 1, п. 3. Заметим, что если при построении
окрестностей в пространстве Н удалять вместо множеств
мощности ^ К0 произвольные множества первой категории,
то получим пространство, которое не будет компактно ни
в каком отрезке мощностей.

ГЛАВА И
О СТРОЕНИИ И МОЩНОСТИ
БИКОМПАКТНЫХ ПРОСТРАНСТВ
§ 1. Регулярные и нормальные пространства
1. Среди особенностей, которые могут представиться
в нерегулярных пространствах, одной из наиболее
интересных является существование неотделимых точек.
Две точки pup' называются неотделимыми в данном
пространстве, если, каковы бы ни. были их окрестности
Ор и Ор', замыкания [Ор] и [Ор'] имеют непустое
пересечение.
Регулярное пространство, очевидно, не может
содержать неотделимые точки; нерегулярные пространства,
приведенные в предыдущей главе в качестве примеров,
также не обнаруживают этой особенности. Вот пример
нерегулярного пространства, содержащего две
неотделимые точки. Это пространство — назовем его U*— состоит
из двух точек р и р' и из всех точек плоскости оху, кроме
начала координат.
Окрестности Опр(п = 1,2,3,...) точки р составлены
из точки р и из тех точек (ху у) плоскости оху, для
которых х2 + у*<± (у>0).
Окрестности Опр' точки р' составлены из точки р' и
из тех точек (х, у) плоскости оху, для которых
*2 + У2<-^ (У<0).
Окрестности всех остальных точек пространства t/2
суть обычные окрестности, которые те же точки имели
на плоскости оху.
Сразу видно, что точки р и р' неотделимы в
пространстве £/г.
Приведем пример пространства, называемого
пространством Лз, в котором имеется несчетное множество
мощности континуума, состоящее из попарно неотдели-

§ 1. РЕГУЛЯРНЫЕ И НОРМАЛЬНЫЕ ПРОСТРАНСТВА
41
мых точек. Пространство Аз имеет в качестве своих
точек:
Г Все точки сегмента 0 ^ у ^ 1 оси ординат данной
плоскости OXY (рис. 5).
2° Все точки открытых прямоугольников anbncndn,
расположенных, как указано на рис. 5; прямоугольники
,У
х3 хг
! а3 &за2 d2 а<
dt
i£l
Ьз сз b<
'2 С2
ь,
с<
Рис. 5.
эти, не имея попарно общих точек, имеют основания
(Ьп\сп) длины -jpr, тогда как длина их вертикальных
сторон (ап\ Ьп) равна 1.
3° Точки
*ь *ъ • • •» %ъ • • •»
которые могут быть взяты где угодно вне наших
прямоугольников и отрезка 0 ^ у ^ 1, например, там, где они
изображены на рис. 5.
Окрестности определяются следующим образом:
Г Если точка \ лежит на отрезке O^f/^1 оси
ординат, то окрестностью этой точки является пересечение
любого открытого круга £/(5, е) со множеством всех
точек категорий Г и 2°.
2° Для точки £, лежащей в каком-либо
прямоугольнике anbncndn, окрестности суть обычные окрестности на
плоскости, содержащиеся в этом же прямоугольнике.

42 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
3° Окрестностью Опхл точки Xh категории 3° является
открытый прямоугольник UhbhSkh (см. рис. 5, k = 2),
основание (Ьк\ sk) которого имеет длину j-.
Легко убедиться, что каковы бы ни были точки р и р'
отрезка 0 ^ у ^ 1 и их окрестности Ор и Ор', все точки
Xh с достаточно большим номером k содержатся в [Ор] и
[Ор% так что р и р' неотделимы.
Читатель может найти в другом месте пример
пространства, состоящего из счетного множества попарно
неотделимых точек; пространство это, кроме того,
связно1. Нам не удалось построить несчетное пространство,
представляющее ту же особенность. Существование
такого пространства кажется нам, однако, довольно
вероятным 4.
2. Первая идея отделимости содержится в четвертой
аксиоме Хаусдорфа; как показывает возможность
наличия неотделимых точек в хаусдорфовых пространствах,
степень отделимости, даваемая названной аксиомой, не
может почитаться вполне удовлетворительной. Усиление
отделимости осуществляется в регулярных
пространствах, в которых точка и не содержащее ее замкнутое
множество отделены непересекающимися окрестностями.
Между тем, например, в метрических пространствах
любые два замкнутых множества, без общих точек,
обладают непересекающимися окрестностями: достаточно для
двух непересекающихся замкнутых непустых множеств Л
и В, лежащих в метрическом пространстве /?, определить
окрестности ОА и ОБ следующим образом:
О А = О U (х, гх\ где гх = -| р (х9 В),
О В - (J U (у, г у), где г у = у р (у, А).
уев
Естественно поэтому ввести следующий новый класс
пространств:
Определение. Пространство R называется
нормальным, если всякие два лежащих в нем непересекаю-

§ I. РЕГУЛЯРНЫЕ И НОРМАЛЬНЫЕ ПРОСТРАНСТВА 43
щихся замкнутых множества имеют непересекающиеся
окрестности *).
Из этого определения и первого из данных в п. 4
предыдущей главы определений регулярного пространства
следует, что всякое нормальное пространство и подавно
является регулярным.
Замечание. Мы не получим никакого дальнейшего
сужения класса пространств, если потребуем, чтобы
любые два замкнутых непересекающихся множества А и В
имели окрестности ОА и ОВ, замыкания которых [ОА] и
[ОВ] не пересекаются: во всяком нормальном
пространстве только что сформулированное условие всегда
выполнено. В самом деле, взяв сначала две
непересекающиеся окрестности ОИ и О^В данных замкнутых
множеств Л и В, замечаем, что [ОИ] П 0\В = Л так, что
замкнутые множества [0{А] и В не пересекаются, значит,
имеют непересекающиеся окрестности, которые могут
быть обозначены через 02А и 02В. Тогда вновь
ОИП[02ЯЬЛ,
а значит, и2
[01А](][02В]= А.
3. Важность класса нормальных пространств
подтверждается уже тем, что, как мы только что видели, всякое
метризуемое пространство нормально. Но с точки
зрения, положенной в оскову настоящего сочинения,
основное значение имеет следующая
Теорема 1. Всякий бикомпакт является
нормальным пространством.
Доказательство. Пусть А и В — два
непересекающихся замкнутых множества, лежащих в бикомпакте
/?. Построим для каждой пары точек хеД и(/ей пару
непересекающихся окрестностей Оух и Оху соответственно
точек х и у. Так как В (рассматриваемое как
пространство) бикомпактно, то, оставляя точку х постоянной и
заставляя у пробегать все множество В, мы можем
*) Еще раз напоминаем, что окрестностью множества Mt
лежащего в данном пространстве, называется всякое открытое
множество этого пространства, содержащее данное множество М.

44 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
в покрытии бикомпакта В, состоящем из всех полученных
таким образом Оху, найти конечное покрытие
ОхУи •••> ОхУт
так что
В s 0,01 и ... \}Охуи = ОхВ.
Вместе с тем положим
Ох = 0Ухх[\ ... ПО,/,
замечая в то же время, что
Ох[\ОхВ = Д.
Пусть теперь х пробегает все множество А. В покрытии
этого множества, состоящем из всех Ох, содержится
конечное покрытие того же множества
иХ\у . •., OxS9
причем
Л£0х,11 ••• \JOxs = OA.
Положим, наконец,
ОВ-ОххВ[\ ... (\0ХВ\
тогда О А П ОВ = Л, что и требовалось доказать.
4. Теорема, аналогичная теореме 1 для компактных
пространств, уже не имеет места. Более того, существуют
компактные нерегулярные пространства; примером таких
пространств может служить пространство U3.
Точки пространства U3 распределяются на
следующие шесть категорий:
Г Две точки р и р'.
2° Точки (0, у), где 0 < у ^ 1.
3° Точки (0, у), где — 1 < f/< 0.
4° Точки (а,0), где а — порядковое число первого
или второго класса, 1 ^ а < coi.
5° Точки (а,у) (1 < а<а)1,— 1 < у <0).
6° Точки (а, у) (1 <а<а)1, 0< у ^ 1).
Окрестности всех этих точек определяются так:

§ 1. РЕГУЛЯРНЫЕ И НОРМАЛЬНЫЕ ПРОСТРАНСТВА 45
1° 0$,пР состоит из точки /?, из всех точек (а,у),
таких, что р<а<(0! и 0<у<-> и из всех точек (0, у)
Аналогичным образом окрестность 0$,пр' состоит из
точки //, из всех точек (а, у), для которых р < а < со4 и
~^<у<0, и из точек (0, у) (~^<#<о).
2° и 3° Оз,п(0, уо) состоит из всех точек (у, у), таких,
что P<Y<®i> Уз-~\Уо\<У<Уо + -\Уо\> и из всех
точек^, у), таких, что Уо--\Уо\<У<Уо + -\у01
4° Оз,п(а,0) состоит из всех точек (у,у), таких, что
p<Y<a, -±<у<±.
5° и 6° Op,n(a, уо) состоит из всех точек (y, у), таких,
что P<Y<«, Уо-~\Уо\<У<Уо + -\Уо1
Пространство U3 компактно. В самом деле, пусть
D = {x{, х2, ..., хП9 ...}
— произвольное счетное множество в l/з, причем хп =
= (an, f/n). Без ограничения общности мы можем
положить, что всегда ап ^ an+i и что все уп, не равные нулю,
имеют, один и тот же знак и образуют сходящуюся
последовательность с пределом у<>.
Если lim a„ = a0 (1 <а0<со1),то точки хп = (ап,*/п)
rt-»oo
сходятся к точке (ао, */о), которая и является в этом
случае (единственной) предельной точкой множества D.
Если lima„ = 0 (чго возможно лишь в том случае,
когда все an начиная с некоторого суть нули), то
единственной предельной точкой множества D является точка
р или точка р' в зависимости от того, будут ли все уп
положительными или отрицательными.
Итак, множество D во всяком случае имеет
предельную точку, что и доказывает компактность
пространства U3.
Для доказательств нерегулярности этого пространства
достаточно убедиться, что точки р и р' неотделимы. Но

46 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
это следует из того, что Ор,пр и Ор', п*р' имеют в
качестве общих предельных точек все точки вида (а, 0), где
а больше любого из двух порядковых чисел р и Р'.
5. Пространство, полученное удалением из
пространства Us точек р и //, обозначим через l/з. Пространство
f/з, очевидно, регулярно. Докажем, что оно не является
нормальным. Для этого рассмотрим замкнутые в 1/з
множества Л и В, причем А состоит из всех точек вида
(а, 0) (l^a<coi), а В— из всех точек вида (0, у)
(О < \у\ <Л). Покажем, что всякие две окрестности О А
и ОВ имеют общие точки. Для этого достаточно найти
точку I е А П [ОВ]. Рассмотрим последовательность
х0 = (0, 1), *i = (o, у), ..., xm=(o, gin"), ...
Каждая из точек этой последовательности принадлежит
В\ поэтому можно для каждого натурального числа т
найти окрестность 0$т>птхт точки хт, лежащую в ОВ.
Если р ^ Рш при любом т, то при любом т
(bl)^0K.nmxm^OB.
Поэтому (р,0)е[ОЯ]. Но в то же время (р, 0)еЛ и
наша цель достигнута3.
6. Компактное нерегулярное пространство U3 не
удовлетворяет первой аксиоме счетности, и это не случайно,
так как имеет место
Теорема 2. Всякое компактное пространство /?,
удовлетворяющее первой аксиоме счетности, регулярно.
Доказательство. Пусть
О,*, 02х, ..., Опх, ... (1)
— счетная система окрестностей точки х такая, что для
любой окрестности Ох точки х найдется Опх^ Ох.
Заменяя каждую Опх пересечением первых п элементов
последовательности (1), получим убывающую
последовательность окрестностей точки х, обладающую
по-прежнему тем свойством, что каждая окрестность Ох
содержит некоторую окрестность, принадлежащую нашей

§ 2. СОВЕРШЕННЫЕ МНОЖЕСТВА
47
последовательности. Поэтому можно с самого начала
предположить, что последовательность (1) убывающая:
0{х з 02х з ... 3 Опх => ...
Если бы пространство R не было регулярно в точке ху го
существовала бы окрестность Опх, не содержащая
замыкания никакой окрестности точки х.. Другими словами,
любое из замкнутых множеств
®k = [On+kX]\Onx (Л-1, 2, 3, ...)
было бы не пусто. Но эти множества образуют
убывающую последовательность и, следовательно, имеют непу-
00
стое пересечение, так что существует точка у е Р)Ф* и
эта точка, очевидно, отлична от точки х. Так как Фл^
оо
е [Оп+ьх], то гем более у е Р)[0Лл:]. Но из аксиомы от-
оо
делимости D следует, что f}[0*x] = x, так как для
уфх можно найти непересекающиеся окрестности Оу и
Отх, из чего следует, что у не содержится в [Отх], тем
оо
более не содержится в Р|[0Ллг].
§ 2. Совершенные множества в компактных
пространствах
7. Начнем со следующей теоремы:
Теорема 3. Всякое совершенное множество,
лежащее в регулярном компактном пространстве, имеет
мощность, не меньшую, чем мощность континуума.
Так как всякое совершенное множество, лежащее
в компактном регулярном пространстве, представляет
собою компактное регулярное пространство, го достаточно
доказать предложение:
3х. Всякое компактное регулярное пространство /?, не
содержащее изолированных точек, имеет мощность ^с.

48 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
Доказательство. Так как данное компактное
регулярное пространство /?, по предположению, не
содержит изолированных точек, то тем же свойством обладает
и всякое открытое в R множество Г, а также замыкание
[Г] всякого открытого множества.
Пусть х0 и Xi — две различные точки пространства /?,
а Охо и Oxi — две окрестности этих точек с
непересекающимися замыканиями R0 = [Ох0] и R\ = [Ох{\. В Oxi (i = 0
или 1) берем снова две точки Xi9 и xi} и заключаем их
в окрестности Oxi9 и О*/, с непересекающимися
замыканиями Ru = [Oxiu] и /?*, = [OxJ и т. д. Получим для
любой комбинации индексов k ... in, равных 0 или 1,
замкнутое множество Ri0...in, являющееся замыканием
некоторого открытого в R множества, причем Ri0... *„=э
^^'o-'n'/i+i и Л*,... *яоП&!...*„!= Л. Так как/?
компактно, всякая последовательность вида
Ri =э R( i zd .., Г) Ri i ... f =d ...
имеет непустое пересечение, в котором выбираем точку
*/,.../„... Разным последовательностям индексов
соответствуют таким образом различные точки Xix .../..,
так что множество этих точек имеет мощность
континуума, и теорема 3 доказана.
Следствие. Всякий бикомпакт, не содержащий
изолированных точек, имеет мощность ^ с.
8. Большое значение в теории бикомпактных
пространств имеет следующая
Теорема 4. Для любой точки х бикомпакта R
имеем %xR = q>xR.
Доказательство. Пусть 93* — какая-либо база
пространства R в точке х, а 33* — какая-либо
содержащаяся в 93* псевдэбаза мощности ^XR (см. гл. I, § 1, п. 3,
теорема 2*). Для каждого элемента Оахе93* возьмем
окрестность 0'ах, удовлетворяющую условию[Оа*| £ Оах\
отобранные таким образом 0'ах образуют множество 23*,
не только являющееся псевдобазой R в х, но
удовлетворяющее более сильному условию: пересечение всех [0'ах]
состоит из одной лишь точки х. Обозначим теперь через
Г зсевозможные множества, являющиеся пересечением

§ 2. СОВЕРШЕННЫЕ МНОЖЕСТВА
49
конечного числа множеств 0'ах. Каждое Tv есть
окрестность точки х\ множество 33* всех Гу имеет мощность
\|ix/?. Покажем, что 33* есть база пространства R в
точке х. Для этого достаточно показать, что всякая
окрестность Ох точки х содержит некоторое Гу. Считая
окрестность Ох выбранной раз навсегда, положим
Фа = [Оах] \ ОХ.
Так как пересечение всех \о'ах] состоит из одной лишь
точки х, то пересечение всех Фа пусто. Следовательно,
существует конечное число множеств Фа, положим
Фа , ..., Фа5, с пустым пересечением. Для
соответствующих Oatx имеем:
Гу=Оа/П ... [\OasX=\0'axx\{\ ... П [0а5*| S
<=Ох\}{Фах{\ ... ПФа5)=0*,
чем все доказано.
Аналогично доказывается
Теорема 4о. Если компактное пространство R
регулярно в точке х и tyxR = Ко, то и %xR = Ко-
Следствие. Какова бы ни была точка х
бикомпакта R и ее окрестность Ох, число %XR не превосходит
мощности множества всех точек окрестности Ох.
В самом деле, точка х является, очевидно,
пересечением открытых множеств вида Ох\у, где у —
какая-нибудь отличная от х точка множества Ох. Значит,
Х*# = *Ы? < мощн. Ох.
(Неравенство ф*/? ^ мощн. Ох имеет, очевидно, место во
всяком ^-пространстве.)
9. Теперь естественно ввести следующее
Определение. Точка х топологического
пространства R называется особой точкой этого пространства,
если, каково бы ни было кардинальное число и, меньшее
чем мощность множества всех точек пространства /?,
в любой окрестности точки х имеются точки, в которых
характер пространства превосходит число и. Тогда х
называется простой особой точкой пространства /?, если

50 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
число %xR равно мощности множества всех точек
пространства /?.
Множество всех особых точек пространства, очевидно,
замкнуто. Мы сейчас увидим, что множество всех
простых особых точек может быть и незамкнутым. Но
прежде всего рассмотрим примеры.
1° Пусть m—произвольное бесконечное кардинальное
число. Обозначим через Ат пространство, состоящее из
множества мощности ш изолированных точек и еще из
одной точки |, окрестности которой получаются
вычитанием из нашего пространства любого конечного числа
точек, отличных от точки |. Очевидно, точка £ есть
простая особая точка пространства Лт. Возьмем теперь
несчетное m и изготовим счетное число экземпляров
пространства Ат: Am, Am, ..., Am, ..., которые мыслим по-
оо
парно без общих точек. Возьмем A = \jAm, причем все
А{т сохраняют в А свою топологию (так что они
одновременно открыты и замкнуты в пространстве А).
Присоединяем к А новую точку е, определяя ее окрестности
оо
Опе (п= 1,2,3,...) гак: Опе = е U (J А{£\ В простран-
k-n
стве A U е имеется счетное число простых особых точек
£(ft), множество этих точек не замкнуто в A U е, так как
имеет предельную точку е, которая является особой, но
не простой особой точкой этого пространства.
2° Точка a>j в пространстве TW(®i + 1) есть простая,
а точка (о© в пространстве TWfaa + 1) —непростая
особая точка.
3° Пространство U{ (см. гл. I, п. 8) может служить
примером бикомпакта с совершенным множеством
простых особых точек: таковы все точки, лежащие на
диагонали [а\ с] (см. рис. 4).
Теорема 5о. Если бикомпакт R имеет регулярную
мощность m и точка х есть точка полного накопления
пространства /?, изолированная в множестве всех точек
полного накопления /?, то х есть простая особая точка
пространства R.

§ 2. СОВЕРШЕННЫЕ МНОЖЕСТВА
51
Доказательство. Заменяя R через [0{х], где
[0\х] ^ Ох, а Ох не содержит никакой отличной от точки
х точки полного накопления пространства R, можем с
самого начала предположить, что х есть единственная
точка полного накопления пространства /?.
Имеем:
R\x = \J(R\Oax), (1)
а
где суммирование производится по всем окрестностям
Оах точки х, образующим базу 93ж пространства R
в точке ху имеющую мощность х*Я. Так как х —
единственная точка полного накопления /?, то мощность
каждого слагаемого /?\ Оах в сумме (1) меньше, чем
мощность тп всего пространства /?. Так как ш — регулярное
кардинальное число, то число слагаемых (равное %xR)
не может быть меньше тп, но оно (по следствию из
теоремы 4) и не больше тп; значит, %XR = тп = мощн./?,
что и требовалось доказать.
Из теоремы 5о вытекает
Теорема 5Г. Если бикомпакт регулярной мощности
не содержит никакого совершенного множества, то он
содержит простую особую точку (изолированную в
множестве всех особых точек).
В самом деле, если бикомпакт R регулярной
мощности не содержит совершенного множества, то множество
его точек полного накопления, будучи замкнутым,
непременно содержит изолированную точку х, которая по
предыдущему является простой особой точкой.
10. Если мощность бикомпакта R есть нерегулярное
кардинальное число, то, как показывает уже пример
пространства Г№(о)а, + 1), в R может не содержаться ни
совершенного множества, ни простой особой точки. Однако
имеет место общая
Теорема 5. Всякий бикомпакт, не содержащий не-
пустого совершенного множества, содержит особую
точку, изолированную в множестве всех особых точек.
Доказательство. В силу теоремы 5 можно
ограничиться случаем, когда мощность данного бикомпакта
R есть нерегулярное кардинальное число m = »;; так
как, по предположению, R не содержит никакого

52 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
непустого совершенного множества, то среди точек
полного накопления пространства R имеется изолированная
(в множестве всех точек полного накопления) точка £.
Возьмем окрестность 0£, не содержащую никакой
отличной от I точки полного накопления, и такую окрестность
Oi|, что /?i=[Oi£]s Og; при этом мощн./?1 = мощн./?=т.
Берем начальное число щ мощности m = К;, и пусть
сот — наименьшее порядковое число, конфинальное числу
©;. Тогда о; есть предел упорядоченной по типу он
возрастающей последовательности регулярных начальных
порядковых чисел
<o<V <S, ..., (0av, ..., Hm (0av = ©;. (2)
Занумеруем далее все точки множества R\ в
последовательность типа со;:
хи хъ ..., ха, ... (1<а<©^, (3)
и обозначим через Лу множество регулярной мощности
Kav всех точек ха, для которых a<cottv.
Пусть п — произвольное кардинальное число,
меньшее чем т. Пусть v < сот — первое такое порядковое
число, что Nav>n (такое число существует ввиду
соотношений (2) и п<тп = К;).
Так как R не содержит непустого совершенного
множества, то в множестве точек полного накопления
множества А можно найти изолированную точку; обозначим
ее через х. Пусть Ох — окрестность точки ху не
содержащая никакой точки полного накопления множества Лу,
отличной от точки лс, и пусть [0\х] ^ Ох.
Докажем теперь, что %XR^ **о> и- Обозначим
через ф мощность какой-либо базы 83* = {Оах}
пространства R в точке х. Тогда, полагая Еа = Ау\Оах, видим,
что, во-первых, Av\x = [jEa и, во-вторых, мощность
и
каждого из множеств Еа меньше, чем fc*av (так как
в противном случае всякая принадлежащая множеству
R\Oax точка полного накопления множества Еа была
бы и точкой полного накопления множества Лу,
вопреки определению точки х и ее окрестности Оах). Так

§ 3. СОВЕРШЕННО НОРМАЛЬНЫЕ ПРОСТРАНСТВА 53
как К а — регулярное кардинальное число, то
кардинальное число ф [т. е. число слагаемых в сумме U^<0
не меньше чем Kav. Неравенство Хх#>пэтим
доказано. Так как х лежит в произвольной окрестности 0|, то
t — особая точка и теорема 5 доказана.
Следствие. Всякий бикомпакт, удовлетворяющий
первой аксиоме счетности, или состоит не более чем из
счетного множества точек (и в этом случае по теореме 4
удовлетворяет и второй аксиоме счетности) 4, или
содержит непустое совершенное множество и, следовательно,
имеет мощность >с.
Замечание 1*). Было бы заблуждением думать,
что бикомпактные пространства с первой аксиомой
счетности могут быть, в общем случае, представлены как
сумма совершенного множества и счетного множества;
противоречащим примером может служить пространство
Аг\ оно бикомпактно и содержит множество
изолированных точек мощности континуума.
Замечание 2. Мы пришли к тому выводу, что
мощность континуума является нижней гранью
мощностей несчетных бикомпактов, не содержащих особых
точек. Но мы ничего не знаем о верхней грани мощности
бикомпактов даже в случае, когда выполнена первая
аксиома счетности. Возникает задача общей теории
множеств, кажущаяся столь же интересной, как и
трудной**).
§ 3. Об одном усилении первой аксиомы счетности
в бикомпактных пространствах
И. Как следует из теоремы 4, в бикомпактах первая
аксиома счетности равносильна требованию, чтобы
каждая точка была пересечением не более чем счетного
числа открытых множеств. Естественным усилением этого
требования является следующее
*) Текст замечаний 1 и 2 восстановлен по французскому
оригиналу; в первых двух русских изданиях он печатался в сильно
сокращенном виде.
**) Эта задача решена лишь в 1969 г. А. В. Архангельским;
см. примечание9 к этой главе.

54 гл. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
Условие (Я). Всякое замкнутое множество
пространства R является пересечением счетного числа
открытых множеств.
Следуя установившейся терминологии, мы будем
называть совершенно нормальными нормальные
пространства (в частности, бикомпакты), удовлетворяющие
условию (Я) 5.
Мы покажем, что совершенно нормальные
бикомпакты обладают многими замечательными свойствами.
Прежде всего для таких бикомпактов естественно
ставить вопросы, относящиеся к дескриптивной теории
множеств: в них всякое замкнутое множество есть G6,
значит, всякое открытое множество есть F0\ поэтому
классификации борелевских множеств, отправляющиеся
от замкнутых и от открытых множеств, сливаются, как
и в случае метрических пространств, в одну
классификацию. Можно было бы, кроме того, легко доказать, что
мы получим в совершенно нормальных пространствах
один и тот же класс Л-множеств независимо от того,
будем ли прилагать Л-операцию к замкнутым или к
открытым множествам 6.
Докажем, что всякое несчетное А-множество,
лежащее в совершенно нормальном бикомпакте /?, содержит
непустое совершенное множество7.
Для доказательства рассмотрим несчетное Л-множе-
ство £, определенное Л-системой {Ф^ ... ^},
составленной из замкнутых множеств. Вычеркивая в Л-системе
l^'i •••'*} все элементы Ф*,... *Л1 содержащие не более
счетного множества точек £, мы изменяем ядро
системы Е не более чем на счетное множество точек.
Поэтому можно с самого начала предположить, что все
множества E[\<l>i ...tk несчетны. В этом
предположении рассмотрим какое-либо множество Ф/, первого
ранга (т. е. с одним индексом i\). Возможны два
случая:
1° Существует начинающаяся с Ф*. цепь
Ф^аФ^э... аФ,1|1...,Аа... (i)
с несчетным ядром fl^i'i•••'*• ^ этом слУчае эт0 ЯДР°
к

§ 3. СОВЕРШЕННО НОРМАЛЬНЫЕ ПРОСТРАНСТВА 55
(будучи несчетным бикомпактом с первой аксиомой
счетности) содержит непустое совершенное множество,
содержащееся в £, и наше предложение доказано.
2° Всякая цепь (1), начинающаяся с Ф,,» имеет не
более чем счетное ядро.
Тогда существует такой номер k, что имеются два
множества Ф, / / и Ф, .» ,% удовлетворяющие усло-
l\l2'"lk \l2"'lk
вию: множество Е{\(Ф, ,» i»\Q>ll' А несчетно (это
V 12" k l\l2'"lk/
утверждение проще всего доказать от противного). Но
оо
из условия (Я) следует, что Ф, .» ,» \Ф, ,г ,> = \\Ап,
где все Ап замкнуты в /?. Положим П0 = Ф, ./ {> и обо-
12'" k
значим через nt первое Ап, содержащее несчетное
множество точек Е. Очевидно, По Л lit = Л и оба множества
По П Е и П1 П Е несчетны.
Продолжая рассуждать аналогичным образом, мы
придем к системе замкнутых множеств ПШ1 ...mk\ индексы
tnu ... , trik принимают независимо друг от друга два
значения 0 и 1, причем всегда П^... ^гэП^ . ^ ,_
П||...^оПП|1... tk\ = Л и Rt „ikf\E несчетно. Полагая
Х = () U П,, ...,, = /?,
* 'i <*-°
видим, что содержащееся в Е замкнутое множество X
имеет мощность континуума и, следовательно, содержит
в себе совершенное множество, что и требовалось
доказать.
Легко видеть, что изложенное в этом подразделении
теряет силу при отказе от условия (Я), даже если при
этом сохраняется первая аксиома счетности. Так,
пространство А2 (см. гл. I) есть бикомпакт с первой
аксиомой счетности, в котором имеется открытое множество
мощности континуума, состоящее из точек внешней
окружности (см. рис. 3) и не содержащее никакого
бесконечного замкнутого множества. Построим бикомпакт /?,
в котором имеются несчетные множества типа G6, не со-

56 гл. И. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
держащие никакого непустого совершенного множества.
Таким бикомпактом является пространство TW, где W
есть множество, упорядоченное по типу в2, причем 0 —
порядковый тип сегмента 0-^/^1. Это пространство
!
Т
! 1
Рис. 6.
можно очень просто реализовать геометрически.
Возьмем на плоскости OXY единичный квадрат (рис. 6),
точки (х,у) которого упорядочены следующим образом:
|если х<х'
или
если х~х' и у<у'.
Полученные в результате такого упорядочения
порядковые интервалы и образуют базу нашего
пространства R.
Ту же топологию в пространстве R получим, если
для любого п=1, 2, 3, ... определим окрестности
Оп{х,у) произвольной точки (х,у) (0<x<l, 0<t/<l)
следующим образом:
При 0 < у < 1 окрестность Оп (х, у) состоит из всех
точек (лг, г/0> У У<У'<У + ~У («вертикальные
интервалы», см. рис. 6);

§ 3. СОВЕРШЕННО НОРМАЛЬНЫЕ ПРОСТРАНСТВА 57
0(х, 0) состоит из всех точек (*',#'), для которых
х < х'Кх + ^-^-у 0<*/'<1, и из всех точек (х, у')
0(лг, 1) состоит из всех точек (*',*/'), для которых
х х<х'<х, 0<#'<1, и из всех точек (х\у')>
для которых 1 — —<у'< 1.
Легко видеть, что, например, множество всех точек
вида (jc, -о)» гДе х пробегает все значения сегмента
0<jc^1, есть множество типа G6, не содержащее
никакого совершенного непустого множества. Точки вида
(х, -о), рДе х пробегает совершенно произвольное
множество в сегменте 0^*-< 1, также образуют множество
типа G6 в пространстве R. Отсюда видна вся
безнадежность занятий дескриптивной теорией множеств в
бикомпактах (даже являющихся пространствами
непрерывных порядковых типов и удовлетворяющих первой
аксиоме счетности), не удовлетворяющих условию (Я).
Наоборот, в совершенно нормальных бикомпактах
построение дескриптивной теории множеств, по-видимому,
обещает вполне серьезный успех6.
12. В совершенно нормальных бикомпактах имеет
место следующее свойство, известное под названием
свойства Линделёфа:
Каждая система а открытых множеств {Га}
содержит конечную или счетную подсистему, имеющую то же
тело*), что и вся данная система.
Для доказательства рассмотрим открытое множество
Г = 5. В силу условия (Н) множество Г есть сумма
счетного числа замкнутых множеств:
T-OjUOsU ... ио„и ...
В силу бикомпактности пространства R каждое из
множеств Фп покрыто конечным числом множеств Га е а;
значит, все Г покрыто счетным числом наших Га.
*) Телом системы а множеств называется объединение всех
множеств — элементов системы о, оно обозначается через а.

68 гл. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
Верно и обратное предложение: бикомпакт /?,
обладающий свойством Линделёфа, совершенно нормален.
В самом деле, пусть в бикомпакте /?, обладающем
сформулированным выше свойством, дано открытое
множество Г. Для каждой точки хеГ возьмем окрестность
Ох с замыканием [Ох] ^ Г. Эти Ох образуют систему
с суммой Г; следовательно, некоторая счетная
подсистема Ох\у ..., Охп, ... имеет ту же сумму Г; но так
как [Ох] ^ Г, то и
(j[Oxn] = Y9
т. е. Г есть множество типа Fa\ другими словами,
пространство R совершенно нормально.
Итак, доказана следующая
Теорема 6. В классе бикомпактов свойство
совершенной нормальности эквивалентно свойству Линделёфа8.
Мы видели, что бикомпакт /?, удовлетворяющий
условию (Я), удовлетворяет и первой аксиоме счетности.
Но для пространств с первой аксиомой счетности (и
даже для более широкого класса пространств) Серпинским
и Куратовским была доказана *) эквивалентность
свойства Линделёфа каждому из следующих свойств:
1. Каждое несчетное множество содержит по
крайней мере одну точку конденсации.
2. Всякое разреженное множество (т. е. множество,
не содержащее никакого непустого плотного в себе
подмножества) не более чем счетно.
3. Всякая строго убывающая вполне упорядоченная
последовательность замкнутых множеств состоит из не
более чем счетного числа элементов (свойство Бэра).
Эти свойства оказываются, таким образом, не
только выполненными в совершенно нормальных
бикомпактах, но и характеризующими их.
Далее, так как каждое множество есть сумма
плотного в себе множества и множества разреженного, то в
совершенно нормальных бикомпактах всякое множество
есть сумма плотного в себе множества и множества не
более чем счетного.
*) Fundam. math. 2 (1921), 172-188.

§ 3. СОВЕРШЕННО НОРМАЛЬНЫЕ ПРОСТРАНСТВА 59
В частности, всякое замкнутое множество есть
сумма совершенного и не более чем счетного множества.
Заметим, что в пространстве Лг, являющемся
бикомпактом с первой аксиомой счетности, только что
высказанные свойства не имеют места: пространство Лг
содержит множество мощности с, состоящее из
изолированных точек, и разлагается в совершенное множество
и множество изолированных точек, имеющее мощность с
(внутренняя и внешняя окружности на рис. 3).
Закончим эту главу доказательством следующей
теоремы:
Теорема 7. Совершенно нормальный бикомпакт
имеет мощность, не превосходящую мощности
континуума 9.
Доказательство этого предложения начнем со
следующего замечания, применимого к любому Гг-простран-
ству: всякое замкнутое множество Ф, содержащее более
одной точки, может быть представлено как сумма двух
собственных замкнутых подмножеств. В самом деле,
взяв в Ф две различные точки х и у и две
непересекающиеся окрестности Ох и Оу этих точек, положим
Фо = Ф\Оу, Ф1 = Ф\Ох. Множества Ф0 и Ф1 дают в
сумме Ф и являются собственными подмножествами
множества Ф.
Теперь мы построим последовательность типа а»:
20, 2|э ..., 2а, ... (а<со1), (1)
элементы которой суть системы 2а замкнутых множеств,
причем система 2а состоит из замкнутых множеств
имеющих последовательность индексов
lu h> •••» *х> • ••
типа а, а каждый из индексов есть 0 или 1. В силу
тождеств
2»о = с, с К, = с
в каждой системе 2а содержится не более чем с
замкнутых множеств, а следовательно, и во всех наших
системах общее число замкнутых множеств будет не
более с. Поэтому наша цель будет достигнута, если нам

60 ГЛ. II. СТРОЕНИЕ И МОЩНОСТЬ ПРОСТРАНСТВ
удастся построение наших систем осуществить таким
образом, чтобы в числе наших множеств Ф?г.. /х... были
все одноточечные множества (т. е. все множества,
каждое из которых содержит лишь одну какую-нибудь
точку пространства R).
Переходим к самому построению
последовательности (1). Оно осуществляется посредством индукции. Мы
начнем с множества Ф° = /?, последовательность
нижних индексов которого пуста и, следовательно, имеет
порядковый тип 0, являющийся верхним индексом
множества Ф°. Множество Ф° и является единственным
элементом системы 20.
Предположим, что построены все системы 2р для
Р < а. Построим 2а.
Первый случай: а есть число первого рода: а = а' + 1.
Если произвольно выбранное множество Ф^... ik ... е 2а'
содержит более одной точки, то мы представляем
множество Ф?[... ik... в виде суммы двух его собственных
подмножеств, которые и обозначаем через Ф^...^..^
и Ф?...|. ...1 (так как последовательность индексов
iu 1ъ ..., *х У множества Ф?^..^... была
последовательностью типа а', то последовательности iu h i\, ...
..., 0 и fi, f2f /ь ..., 1 имеют тип о! + 1 = а). Если же
множество Ф^...^... состоит из одной лишь точки, то
полагаем
Второй случай: а есть число второго рода. Тогда
полагаем
фУ,...|Х...|,-ДЧ ...ifc...
(Мы помним, что у каждого Ф^... f ., стоящего под
знаком пересечения, последовательность индексов имеет
тип р, у Ф*г...и...9 стоящего слева и являющегося
пересечением всех этих Ф^ .../х..., в последовательность

§ 3. СОВЕРШЕННО НОРМАЛЬНЫЕ ПРОСТРАНСТВА 61
индексов войдут все индексы, стоящие справа в их
естественном порядке, и этот порядок будет иметь тип а.)
Из нашего построения непосредственно вытекает, что
иза<р следует Ф?, ... ,к... =>Ф^ ... tk....
Пусть х — произвольная точка пространства R. Без
труда получаем посредством трансфинитной индукции
последовательность содержащих эту точку множеств
Ф^Ф^а ... =Ф?|в..,х...а •••
Так как эта последовательность несчетна (типа coi),
то начиная с некоторого порядкового числа а ее
элементы совпадают между собою, что, согласно нашему
построению, может произойти лишь тогда, когда Ф?|#../х...
(для некоторого a<o)i) состоит лишь из одной точки,
в данном случае из точки х.
Таким образом, любое множество, состоящее из
одной лишь точки пространства /?, есть одно из наших
множеств Ф?1... i ,9 и теорема доказана.
Подведем итог основным результатам этого
параграфа.
Теорема 8. Пусть R есть совершенно нормальный
бикомпакт. Тогда каждое несчетное А-множество,
значит, в частности, каждое несчетное В-множество
пространства R содержит совершенное множество и имеет
мощность континуума. В частности, каждое несчетное
замкнутое множество пространства R есть сумма
совершенного множества и не более чем счетного множества,
а каждое непустое совершенное множество имеет
мощность континуума.
Замечание. В наших последних рассуждениях,
касающихся неравенства мощн. /?4^с, мы фактически
не пользовались бикомпактностью пространства R.
Поэтому имеет место предложение:
Всякое пространство, обладающее свойством Бэра
(а значит, — в силу результатов Куратовского и Серпин-
ского — всякое финально компактное совершенно
нормальное пространство), имеет мощность, не
превосходящую мощность континуума10.

ГЛАВА HI
ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
§ 1. Определения.
Условия для абсолютной замкнутости
1. Определение. Пространство R называется
абсолютно замкнутым, если во всяком пространстве /?U£,
полученном присоединением к пространству R одной
точки |, эта точка оказывается изолированной.
Другими словами, пространство R называется
абсолютно замкнутым, если оно замкнуто во всяком
объемлющем пространстве, или (понимая под расширением
данного пространства R всякое пространство /?0,
содержащее пространство R в качестве всюду плотного
множества) пространство R абсолютно замкнуто, если
оно не имеет никакого не совпадающего с ним
расширения1.
2. Дадим два критерия абсолютной замкнутости
пространства. Для этого назовем центрированной системой
множеств всякую такую систему множеств- U = {Аа},
что пересечение
Аах П • • • П Aas
любого конечного числа элементов этой системы не
пусто.
3. Теперь мы можем следующим образом
сформулировать первый критерий абсолютной замкнутости
пространства:
Теорема 1. Для того чтобы пространство R было
абсолютно замкнутым, необходимо и достаточно, чтобы
для каждой центрированной системы © = {Га}
открытых множеств пространства R пересечение Q [Г J было
не пусто.

§ 1. УСЛОВИЯ ДЛЯ АБСОЛЮТНОЙ ЗАМКНУТОСТИ 63
Доказательство. Условие необходимо. В самом
деле, пусть дана такая центрированная система © = 1^
открытых множеств пространства /?, что f] 1Га]=Л.
Присоединим к пространству R новую точку £
посредством окрестностей вида
os-gu^n ... ПГал). (1)
Покажем, что при таком присоединении аксиомы А, В,
С, D (см. гл. I, § 1, п. 2) выполнены. Достаточно
проверить выполненность аксиомы отделимости D
(выполненность остальных аксиом очевидна). Пусть точка
jigJJ выбрана произвольно. Так как f] [Га]= Л, то
гае®
существует такое Га) е ©, что х.^ё[Га,]. Полагаем Ох =
= *\[Га,], 01 = 1 U Га,. Тогда Ох и 01 образуют пару
непересекающихся окрестностей точек х и £.
Докажем, что точка £ в пространстве R U £ не
является изолированной. Но это следует из того, что ни
одна из окрестностей (1), образующих базу
пространства R U I в точке |, не совпадает с точкой |.
Условие достаточно. Требуется доказать, что во
всяком пространстве /?, не являющемся абсолютно
замкнутым, можно найти центрированную систему © = {Га}
открытых множеств, для которой f) [Га]=Л. Так как,
га€=©
по предположению, пространство R не абсолютно
замкнуто, то существует пространство R U £, в котором £
не есть изолированная точка. Рассмотрим открытые в R
множества Га вида
где Оа1 — какая-либо окрестность точки £ в
пространстве R U £. Множества Га образуют центрированную
систему множеств — центрированность этой системы
сразу следует из того, что точка £ не изолирована в /?U|.
В силу аксиомы отделимости Хаусдорфа, выполненной
в пространстве R U £, для любой точки x^R существует

64 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
окрестность Ох, не пересекающаяся с некоторой
окрестностью 0а1 точки g. Поэтому
а а
значит,
П1ГаЬ=Л,
а
что и требовалось доказать.
4. Второй критерий абсолютной замкнутости дается
следующей теоремой:
Теорема 2. Для того чтобы пространство R было
абсолютно замкнутым, необходимо и достаточно, чтобы
всякое открытое покрытие Q = {Га} пространства R
содержало конечное число элементов
Taj, 1а2, . . ., * ast
сумма замыканий которых есть все пространство R.
Доказательство. Необходимость. Предположим,
что наше условие не выполнено. Докажем, что
пространство R не абсолютно замкнуто. Пусть Q = {Га} есть
открытое покрытие пространства /?, обладающее тем
свойством, что для любого конечного числа элементов
r<V Га2> .. ., Га$
покрытия Q множество #<*, ...^^R \ ([^ajU ... U[raJ)
не пусто. Присоединяем к пространству R точку £, делая
ее окрестностями множества 0|= Оаг..аДяБ11/Л1 ...а,-
Докажем, что аксиома отделимости D при этом
выполнена (выполнение остальных аксиом очевидно). В самом
деле, какова бы ни была точка xei?, существует
содержащее эту точку множество Га и [Гр] ^ Га. Окрестности
Ох = Га и 0$Ъ — I U (/?\[Гр]), очевидно, не
пересекаются. Заметим, наконец, что никакое из множеств #a,...as
не пусто (так как иначе мы имели бы[Га1]и ... и[Га5] =
= R вопреки предположению). Итак, точка | не
изолирована в R U |; значит, R не абсолютно замкнуто.
Достаточность. Пусть наше условие выполнено.
Докажем, что во всяком пространстве R вида R = R П £

§ 1. УСЛОВИЯ ДЛЯ АБСОЛЮТНОЙ ЗАМКНУТОСТИ 65
точка I изолирована. В самом деле, для каждой точки
хей имеются непересекающиеся окрестности 0\х и 0*£.
Отсюда следует, что
[О^ПОх|=Л;
поэтому замыкание [О^х]^ множества 0%х в пространстве
R не содержит точки £, т. е. лежит в R и, значит,
совпадает с замыканием [0$х]д = [0$х] того же множества
в R. Строим окрестности 0\х для всех хе/?. В силу
нашего условия существует такое конечное число точек
Х{ х8 пространства /?, что
[Oix{]() ... [)[Oixs) = R.
Так как по доказанному каждое из множеств [0^]
замкнуто в R U I, то замкнута в R U £ и сумма этих множеств,
т. е. R замкнуто в R U £; значит, £ есть изолированная
точка пространства R U £.
Из только что доказанной теоремы непосредственно
вытекает
Следствие 1. Всякий бикомпакт является
абсолютно замкнутым пространством.
Далее, имеет место
Следствие 2. Если R — абсолютно замкнутое
пространство и Е — какое-нибудь лежащее в R бесконечное
множество, то существует по крайней мере одна такая
точка хо е /?, что для любой окрестности Ох0 точки хо
множество Е П [Ох0] имеет ту же мощность, что и все
множество2.
В противном случае для каждой точки х можно найти
такую окрестность Ох, что
мощн. (Е П [Ох]) < мощн. Е.
Выбирая конечное число окрестностей этого рода, именно
Охь ..., Oxs
с замыканиями, дающими в сумме все пространство /?,
видим, что множество Е есть сумма конечного числа
своих подмножеств Е П [0*i], ..., £ П [OxJ, каждое из
которых имеет мощность, меньшую, чем все множество Е.
Но это противоречит тому, что множество Е бесконечно.
Из следствия 2 выводим, наконец,

66 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
Следствие 3. Всякое регулярное абсолютно
замкнутое пространство R бикомпактно3.
В самом деле, пусть Е — любое бесконечное
множество в R. Берем такую точку х0 е /?, что для всякой
окрестности Ох0 мощность множества Е П [Охо] равна
мощности всего множества Е. Так как R регулярно, то
во всякой окрестности Ох0 содержится замыкание
некоторой окрестности OiX0, и так как мощн. (Е П [О{х0]) =
= мощн. £, то и мощн. (Е П Ох0) = мощн. Е. Так как это
верно для любой окрестности Ох0 точки jc0, то Хо есть
точка полного накопления множества £, и бикомпакт-
ность пространства R доказана.
В следствиях 1 и 3 и в теореме 1 гл. II содержится
предложение, принадлежащее (вместе с теоремой 3 гл. I)
к самым главным результатам всего этого сочинения:
Основная теорема (теорема 3). Для того чтобы
пространство было бикомпактом, необходимо и
достаточно, чтобы оно одновременно было регулярным и
абсолютно замкнутым4.
Замечание 1. В формулировке этой теоремы
можно, очевидно, требование регулярности заменить
требованием нормальности5.
Замечание 2: Наша основная теорема дает
исчерпывающий ответ на вопрос, поставленный в § 2, п. 7 гл. I,
и возвращает понятие бикомпактности к его
непосредственным, наглядно-геометрическим истокам.
5. Дадим несколько примеров нерегулярных и,
следовательно, небикомпактных абсолютно замкнутых
пространств. Это тем более легко, что многие нерегулярные
пространства, приведенные выше в качестве примеров,
сами оказываются абсолютно замкнутыми или делаются
таковыми после небольших видоизменений. Так,
например, нерегулярное пространство, приведенное под
номером 2° в п. 5 гл. I, делается абсолютно замкнутым после
присоединения к плоскости единственной бесконечно
удаленной точки, за окрестности которой принимаются
внешние области к кругам, имеющим своим центром одну
определенную точку плоскости («начало координат»).
Пространство, описанное в п. 5 гл. I под номером 1°,
само является абсолютно замкнутым, как легко
убедиться, применяя теорему 2. По этому поводу заметим, что

§ 1. УСЛОВИЯ ДЛЯ АБСОЛЮТНОЙ ЗАМКНУТОСТИ 67
теорема 2 остается в силе, если рассматривать в ней не
произвольные открытые покрытия, а лишь покрытия,
элементами которых являются элементы некоторой базы
данного пространства: в этом виде теорему 2 особенно
удобно применять к исследованию различных примеров.
Пространство Аз превращается в абсолютно
замкнутое пространство А3, если его видоизменить следующим
образом:
Г В каждом прямоугольнике anbnCndn удаляется
лишь одна сторона [ап\ Ьп] (вместе с концами);
остальные стороны сохраняются; окрестности неудаленных
точек элементарны (т. е. вытекают из топологии плоскости,
в которой лежат наши прямоугольники).
2° Когда имеют дело с прямоугольниками ahbkSktk
(см. условие 3° на стр. 42), то предполагаются
удаленными стороны [а*; &*] и [S*; th], а стороны (bh\ Sh) и
(ah\ th) (без их концов) сохранены.
Докажем абсолютную замкнутость пространства А3.
Применим теорему 2 к какому-либо покрытию й
пространства Аз, элементами которого являются элементы той
базы пространства А3, которая служила нам для
определения этого пространства. Прежде всего заметим, что
всякое множество вида Хп U апЬ бикомпактно (оно
гомеоморфно обыкновенному замкнутому треугольнику).
Поэтому из покрытия Й можно выделить конечное
подмножество, состоящее из элементов
о?,..., огп
нашей базы, покрывающее множество хп U anbnCndn.
Далее, можно из покрытия Й выделить конечное
множество элементов
0\, • • •> Ov
покрывающих предельный сегмент [0; 1] оси ординат.
Легко убеждаемся в том, что сумма этих элементов
содержит все прямоугольники anbnCndn> номера п которых
превосходят некоторое достаточно большое т. Отсюда
выводим, что множество fO?]U ••• U[o2J содержит не
только все прямоугольники anbnCndn, но и все точки хп,

68 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
для которых п> т. Поэтому конечная сумма
UИ и 0 иДО
покрывает все пространство Аз, чем его абсолютная
замкнутость доказана.
В заключение этого параграфа приведем пример
компактного, но не бикомпактного абсолютно замкнутого
пространства А^
Точками пространства А4 являются все точки (a, t)
пространства A(coi), определенного в п. 8, § 2 гл. I, и еще
одна присоединенная точка \. Точки пространства A(o)i)
сохраняют в пространстве Л4те окрестности, которые они
имеют в пространстве A(o)i). Что же касается точки £,
то ее окрестности Ор£, где 1 ^ р < соь определяются так:
Ов&-6 U (J U (*.').
Э<а<©, 0<*<1
Пространство Ak компактно. Оно нерегулярно в точке £,
следовательно, не бикомпактно. Докажем, что это
пространство абсолютно замкнуто.
Пусть дано какое-нибудь покрытие Q пространства А4,
составленное из только что определенных окрестностей
различных его точек. Так как точка £ не содержится ни
в одной из окрестностей точек х Ф £, то в числе
элементов покрытия Q, несомненно, находится некоторое 0$%.
Имеем:
[оэа-Би (J U («. «•
6<а<й), 0<*<1
тогда как множество
Л4\Ор£= (J (J (а, О
1<а<3 0<*<1
гомеоморфно прямолинейному сегменту и, следовательно,
бикомпактно. Поэтому множество А4\Оз§ покрыто
конечным числом элементов покрытия Q, которые вместе
с множеством [Ор£] покрывают все пространство А4,
абсолютная замкнутость которого таким образом и
доказана.

§ 2. КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
69
§ 2. Компактные топологические пространства
с точки зрения их замкнутости
в объемлющих пространствах
6. Вернемся к главному результату всей этой главы:
Бикомпакты суть не что иное, как абсолютно
замкнутые регулярные пространства.
Значит, для регулярных пространств понятия
абсолютной замкнутости и бикомпактности совпадают.
В общем случае взаимоотношение между абсолютной
замкнутостью и бикомпактностью особенно полно
выясняется теоремой 2 предыдущего параграфа,
представляющей абсолютную замкнутость как своего рода
«испорченную бикомпактность». Между прочим, невозможно
сделать формулировку этой теоремы более
симметричной: уже для интервала R = (—1; 1) числовой прямой
легко построить систему открытых множеств, именно
Г0-(-1;0), r.-^Lp;!) (л-1,2,3,...).
сумма замыканий которых покрывает все пространство
/?, в то время как сумма замыканий никакого
конечного числа этих Тп(п = 0, 1,2, ...) пространства R не
покрывает.
Из доказанного вытекает, что для множеств,
лежащих в бикомпактах /?, относительная замкнутость
(т. е. замкнутость в/?) совпадает с абсолютной
замкнутостью. Мы не знаем, имеет ли место обратное
предложение, т. е. будет ли непременно бикомпактным
пространство, в котором всякое замкнутое (в R) множество
абсолютно замкнуто6. Докажем это предложение для
пространств, удовлетворяющих первой аксиоме счетно-
сти. Итак, пусть R — пространство с первой аксиомой
счетности, в котором всякое замкнутое множество
абсолютно замкнуто. Отсюда, в частности, следует, что в R
не может быть счетных расходящихся (т. е. не имеющих
ни одной предельной точки) множеств, так как такие
множества, будучи в R замкнутыми, очевидно, не
обладают свойством абсолютной замкнутости. Итак, R
компактно. Но, удовлетворяя первой аксиоме счетности,
компактное пространство R регулярно (по теореме 2 гл. II,

70 ГЛ. 111. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
§ 1, п. 6), а будучи регулярным и абсолютно замкнутым,
пространство R бикомпактно.
Итак, для того чтобы пространство с первой аксиомой
счетности было бикомпактным, необходимо и достаточно,
чтобы все замкнутые множества этого пространства были
абсолютно замкнутыми.
Имея в виду центральное место, занимаемое в
настоящем исследовании теоремой 3 предыдущего
параграфа, дадим этой теореме еще одно доказательство,
независимое от данных выше критериев абсолютной
замкнутости.
Пусть R — регулярное, не бикомпактное пространство.
Докажем, что оно не является абсолютно замкнутым. Так
как R не бикомпактно, то существует вполне
упорядоченная убывающая последовательность непустых
замкнутых в R множеств
А, zd А2 :=э ... :=> Аа => ... (а < сот)
с пустым пересечением. Для каждого а < сот выбираем
раз навсегда точку ха^Аа\Аа+{. Присоединяем к
пространству R новую точку |, определяя ее окрестности
следующим образом. Берем какое-нибудь порядковое
число X < о)т и для каждой точки ха с индексом а > к
берем произвольную окрестность Оха. Этими данными
определяется окрестность
ОЕ = g U (J Оха\
варьируя число К < о)т и выбор окрестностей Оха для
а > X, будем получать различные Og.
В полученном таким образом пространстве R U £
аксиомы А, В, С, очевидно, выполнены. Докажем, что
выполнена и аксиома отделимости D. Пусть х —
произвольная точка пространства R. Берем такое А,, чтобы хе
е/?\Ль и находим такую окрестность Ох, чтобы было
[Oa:]s/?\ Лх. Так как все точки ха с индексами а > Я
лежат в А^ а следовательно, в /?\[Ох], то можно для
всех этих ха найти окрестность Oxa<=R\[Ox], Но тогда и
Ol-ll)\JOxa

§ 2. КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
71
не пересекается с Ох, что и требовалось доказать. Так
как все определенные нами окрестности 0£ содержат
точки пространства /?, то g не изолирована в R U £ и /?
не абсолютно замкнуто.
Остается доказать абсолютную замкнутость всякого
бикомпакта R. Это делается легко: берем какое-нибудь
пространство R U I и для каждой точки xeR
определяем непересекающиеся окрестности 0%х и Ох\. Таким
образом, замыкание каждой окрестности О^х в R U £ не
содержит точки g и, следовательно, совпадает с
замыканием [О^х] того же множества О^х в /?. Беря в покрытии
й пространства /?, состоящем из всех 0$х, конечное
число элементов
также образующих покрытие пространства /?, видим, что
R = [Olxl][) ... U[0**J
замкнуто в R U |, так что £ есть изолированная точка
пространства R U £. Теорема 3 полностью доказана.
7. Рассмотрим в качестве элементарного приложения
теоремы 3 пространство TW какого-либо упорядоченного
множества W (см. гл. 1, § 1). Докажем, что пространство
TW тогда и только тогда бикомпактно, когда
упорядоченное множество W не имеет щелей (под щелью
упорядоченного множества понимают, как известно, такое его
сечение
W = A\}B,
что в нижнем классе А нет наибольшего, а в верхнем
классе В нет наименьшего элемента; при этом не
исключается случай, когда один из двух классов является
пустым множеством).
Необходимость только что высказанного условия
вытекает из того, что всякую щель в упорядоченном
множестве можно «заполнить» присоединением нового, не
изолированного в TW элемента; достаточность следует
из того, что всякая вполне упорядоченная
последовательность
i4j2 Л2э ... ^Аа^ ...

72 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
непустых замкнутых в TW множеств с пустым
пересечением определяет в W щель, нижний класс которой
состоит из всех хеУ, для которых существует такое а,
что х ^ у для любого J/G/4a.
Из доказанного вытекает, что всякое небикомпактное
пространство, являющееся пространством некоторого
упорядоченного множества W, является всюду плотным
подмножеством некоторого бикомпакта: именно бикомпакта,
полученного заполнением всех щелей упорядоченного
множества W. Возникает весьма интересный и
кажущийся очень трудным вопрос:
всякое ли пространство является всюду плотным
подмножеством некоторого абсолютно замкнутого
пространства7?
8. Переходим к исследованию компактных
пространств, не являющихся бикомпактными. Нам придется
рассматривать понятие замкнутости
пространства R по отношению к точкам того или
иного типа (например, по отношению к точкам
счетного характера или псевдохарактера, по отношению
к точкам, в которых пространство регулярно, и т. п).
Предположим, что нам дано некоторое определенное
свойство Р, характеризующее некоторый тип точек
топологических пространств. Мы скажем, что пространство R
замкнуто по отношению к точкам, обладающим
свойством Р, если невозможно к пространству R присоединить
точку I таким образом, чтобы в пространстве R U I точка
была неизолированной и обладала свойством Р.
Введем еще следующие обозначения. Точки, в
которых пространство R имеет счетный характер, назовем
для краткости \,-точками, точки счетного псевдохарактера
назовем 6-точками. Наконец, мы скажем, что точка х
есть к-точка пространства R, если существует счетное
множество Е, сходящееся к точке х (как известно,
множество Е сходится к точке х, если в любой
окрестности точки х содержатся все
точки множества Е, за исключением, быть
может, конечного числа точек этого
множества).
Как известно, всякая i-точка является в
то же время и б-точкой и х-точкой. В про-

§ 2. компактность И ЗАМКНУТОСТЬ
73
странстве СЛ все точки суть х-точки, хотя вес и псевдовес
пространства в точках, не лежащих на диагонали [а; с],
равен So, а в точках, лежащих на диагонали [а; с], равен
мощности континуума. Напомним, наконец, доказанную
в гл. II теорему 4 (§ 2, п. 8), утверждающую, что в
бикомпактных пространствах характер точки равен ее
псевдохарактеру и поэтому понятия б- и i-точек
совпадают между собою. После этих замечаний докажем
следующее предложение:
Теорема 4. Для того чтобы регулярное прост ран-
ство было компактным, необходимо и достаточно, чтобы
оно было замкнуто по отношению к к-точкам.
Доказательство очень просто. Необходимость нашего
условия имеет место даже без предположения
регулярности пространства /?. В самом деле, предположим, что
к компактному пространству /? можно присоединить
точку £ так, что эта точка в R U £ оказывается х-точкой.
Тогда в /? существует счетное множество
{Хь Х2> • • •> хп> • • •/» (О
сходящееся в точке £. Но в силу предположений
компактности пространства R в нем имеется точка
накопления х множества (1) и тогда точки £. и х, очевидно, не
могут иметь в R непересекающихся окрестностей.
Докажем достаточность нашего условия для
компактности регулярного пространства R. Итак, пусть
регулярное пространство R некомпактно; требуется доказать,
что оно не замкнуто по отношению к х-точкам. Так как/?
некомпактно, то в нем существует счетное множество
(1), не имеющее ни одной точки накопления.
Присоединим к пространству R новую точку £, беря в качестве ее
окрестностей всевозможные множества вида
06-6U U 0хп>
где Охп — произвольные окрестности точки хп-
Как обычно в таких случаях, в справедливости
аксиом А, В, С убеждаемся автоматически. Проверим
аксиому D. Пусть х —произвольная точка пространства/?.
Возьмем окрестность Оху не содержащую никакой
отличной от х точки Хп\ в силу регулярности пространства R

74 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
существует окрестность 0& точки х с замыканием,
содержащимся в Ох. Возьмем столь большое ky чтобы в Ох
не содержалось ни одной точки хп с индексом п ^ к
(если х не совпадает ни с одной точкой хп, то можно
положить k = 1). Берем, далее, для каждой точки xn(n^k)
окрестность Охп ^ R \ [OiX] и окрестность точки |
Окрестности 01 и 04х не пересекаются; кроме того, так
как множество (1) сходится к точке |, то £ есть х-точка
в R U £, и теорема 4 доказана.
Следствие. Всякое компактное пространство
замкнуто по отношению к i -точкам.
9. Наиболее интересным нам представляется вопрос
о том, в каких случаях это следствие допускает
обращение. Мы имели выше примеры даже абсолютно
замкнутых и в то же время некомпактных нерегулярных
пространств (таково, например, пространство, приведенное
в гл. I, § 1, п. 5 под номером Г). Однако существуют и
регулярные некомпактные пространства, замкнутые по
отношению к i-точкам; таково пространство t/з,
определяемое как множество, лежащее в пространстве С/3
(гл. II, п. 4) и состоящее из точек этого пространства,
названных нами при определении пространства С/3
точками типов 2°, 4°, 6°. Пространство U$ некомпактно, так
как счетное множество, состоящее из точек хл=(0; —)>
не имеет в нем никакой точки накопления.
Пространство l/з регулярно. Докажем, что
невозможно присоединить к пространству U$ точку | таким
образом, чтобы в этой точке пространство U^lji, имело
характер К0. Предположим, что такое присоединение
возможно. Тогда существует счетное множество
Л|, Л2» • • •» **п» • • • >
сходящееся в точке £. Предположим, что для
бесконечного числа значений п, скажем п = пи п2у ..., пи мы
имеем:
хп = (аЯ1 уп) К Ф 0)*

$ 2. КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
75
Заменяя, если надо, последовательность {nk)
подпоследовательностью, можно предположить, что lim artft = а и
что Пт */=*/.
Обозначим через х точку (а,у). Очевидно, что
аксиома отделимости D не удовлетворена для пары точек
|, х. Из полученного противоречия следует, что все точки
Хп> за исключением, быть может, конечного числа этих
точек, принадлежат к типу 2°, т. е. имеют вид хп=(Оууп).
Заметим теперь, что точка £ есть точка накопления
множества всех точек типа 6°. В самом деле, каждая
окрестность точки £ содержит точки типа 2°, а следовательно,
и типа 6°. Теперь остается только заметить, что никакая
счетная последовательность точек типа 6° не сходится
к точке |, и противоречие с предположением, что R U £
имеет в точке | счетный характер, налицо!
10. После всех этих замечаний доказываем, наконец,
следующее предложение:
Теорема 5. Для того чтобы нормальное
пространство R было компактным, необходимо и достаточно,
чтобы оно было замкнуто по отношению к точкам счет-
ного характера.
Доказательство. Необходимость этого условия
уже была отмечена (см. следствие из теоремы 4).
Докажем достаточность. Пусть R— нормальное некомпактное
пространство и А = {хи хъ ..., хПУ ...} есть счетное
множество, не имеющее в R ни одной точки накопления.
Множество А и всякое его подмножество замкнуты в R.
Замкнуто, в частности, и множество Л\^. Поэтому,
имея в виду нормальность пространства /?, можно
найти такую окрестность O0Xi точки хи что ее
замыкание [O0Xi] не содержит ни одной из точек х2у х3,
Можно, далее, найги окрестность ОоХ2 такую, что
[OqX2]s R\([Ouxl][i{A\x2))9
и окрестность О0х3 такую, что
[О0х3] s R \ ([О0х{] U [О0х2] U (А \ *3));
можно продолжать рассуждение таким образом без-

76 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
гранично. В результате получим окрестности
OqXi, OqX2, . . ., ОоХп, ...
такие, что
[O0Xi] П [O0xf] = Л для любых /, / (/ Ф /).
Обозначим через В замкнутое множество
[оо "I оо
U°o^ Ки°о^.
Замкнутые множества А и В не имеют общих точек,
поэтому они могут быть заключены в непересекающиеся
окрестности ОА и ОВ.
Так как хп е ОоХп П ОЛ, то существует окрестность
Оп точки xnt удовлетворяющая условию
хп<=Оп<=[Оп]я=О0хп()ОА.
оо
Докажем, что для любого т множество (J [Оп] замк-
нуто.
Сделаем противоположное допущение. Тогда
множество
^—Г и t°«il ^ йю„]
не пусто. Пусть xg£, Тогда любая окрестность Ох
пересекается с бесконечным числом различных Оп, значит,
с бесконечным числом различных OoJtn. Отсюда выте-
оо
кает, что х не принадлежит множеству [JO0xn (так
как в противном случае было бы *е OoXi при некотором
единственном i, и множество Оо** было бы окрестностью
точки jc, не пересекающейся ни с одним ОоХп при пФ1).
Итак,
/оо Woo Г оо 1 оо
Vt-l / л-1 Lrt-l J n-l

§ 2. КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
77
С другой стороны,
Х(
Г О Ю„]1 \ (J[0„]c:[(J[On]
L/i—m J л—m »-п— 1
£[ОЛ],
так что х е [ОА] П 05, а это противоречит тому, что
ОА и ОВ суть непересекающиеся открытые множества.
оо
Итак, множество \J [оп] замкнуто.
Присоединим теперь к пространству Р точку |,
полагая в качестве окрестностей этой точки:
оо
Om5 = IUU°n (m-1, 2, 3,...).
Аксиомы А, В, С выполнены.
Для того чтобы убедиться, что выгкинена и аксиома
D, возьмем какую-нибудь точку х е R. Возможны два
случая:
[оо 1 оо
U [Оп] = (J [Оп]- Тогда существует единст-
л-1 J Л-1
венное множество [От], содержащее точку дг, и замкну-
оо
тое множество (J [Оп] эту точку не содержит. По-
Л-Ш + 1
этому можно найти окрестность О*, не пересекающуюся
оо оо
с (J [0J, а следовательно, и с 0W+1£ = £U (J On,
я—m+1 л-m+l
так что в этом случае точки | и jc имеют
непересекающиеся окрестности.
00 оо
2° х е= R \ [J [Оп]. Тогда существует Ox s /? \ (J [0„J
л-1 л-1
и Ох П Oi£ = Л, так что точки | и х снова имеют
непересекающиеся окрестности. Так как очевидно, что
характер пространства R U | в точке I равен Ко, то
теорема 5 полностью доказана.
Можно, слегка видоизменяя определение
окрестностей От|, достигнуть того, чтобы пространство R UI
было регулярно в точке £. Для этого достаточно

78 ГЛ. III. ОБ АБСОЛЮТНО ЗАМКНУТЫХ ПРОСТРАНСТВАХ
ПОЛОЖИТЬ
где On удовлетворяют условию Х^ On ^ [On] ^ On"1
и Оп = Оп» Доказательство регулярности пространства
R U | в точке £ не представляет затруднений.
Итак, можно сказать:
Для того чтобы нормальное пространство было
компактно, необходимо и достаточно, чтобы оно было
замкнуто по отношению к регулярным i-точкам.
11. Метод, которым мы пользовались при
доказательстве теоремы 5, позволяет доказать и следующее
предложение:
Теорема 6. Если Е есть множество, компактное
в нормальном пространстве R, то и производное
множество Е', и замыкание [Е] суть компактные пространства.
Обозначим через Е* какое-нибудь из множеств £'
или [Е] и предположим, что £*, рассматриваемое как
пространство, некомпактно. Так как Е* замкнуто в R, то
существующее в Е* и расходящееся в нем (т. е. не
имеющее в Е* ни одной точки накопления) счетное
множество Х = {х{, х2, ..., хп, ...} расходится в /?.
Поэтому, применяя рассуждения предыдущего
пункта, можно построить окрестности Охи Охъ ..., ОхПУ ...
точек Хи *2> ..., хп, ... такие, что
[Ох(] П [Oxk] = Л при 1фк
оо
и что (J [Охп] есть замкнутое множество. Отсюда сле-
дует, что, как бы ни были выбраны точки уп е Ох,
множество У = {у\, Уъ •••» Уп> •••} расходится в R. Так как
хп е £*, то точки уп можно выбрать соответственно
в Е П Охп, так что Y будет расходящимся в R
подмножеством множества Е вопреки компактности
множества Е в R. Теорема доказана.
12. Назовем счетно нормальным всякое пространство,
обладающее следующим свойством (являющимся
очевидным ослаблением свойства нормальности): любые
два множества, из которых одно есть не более чем счет-

§ 2. КОМПАКТНОСТЬ И ЗАМКНУТОСТЬ
79
ное расходящееся множество, а другое —произвольное
замкнутое множество, не пересекающееся с первым,
имеют непересекающиеся окрестности.
Все рассуждения пп. 10 и 11 применимы к любым
счетно нормальным (а не только к нормальным)
пространствам. Итак, мы доказали, что для счетно
нормальных пространств компактность совпадает с
замкнутостью по отношению к (регулярным) сточкам и что
в счетно нормальном пространстве всякое компактное
(в данном пространстве) множество имеет компактное
в себе замыкание и производное множество.
Дальнейшее обобщение поименованных теорем уже
не представляется -возможным, так как, с одной
стороны, пространство V3 регулярно, замкнуто по отношению
к i-точкам, но не компактно. С другой стороны,
множество всех точек типов 4° и 6° компактно и всюду плотно
в Uy следовательно, его замыкание и его производная,
совпадая со всем пространством 1Г„ не являются
компактными пространствами.
13. Класс счетно нормальных пространств не
совпадает ни с классом регулярных, ни с классом нормальных
пространств. Только что рассмотренное пространство
U\ регулярно, но не счетно нормально. Вот пример
пространства счетно нормального, но не нормального. Это
пространство (назовем его U^) имеет своими точками
всевозможные пары вида (а, Р), где a^coi и р^сог*
кроме пары (coi, 0)2), которая исключается. Окрестности
^а'р' (а, р) точек (а, р) определены следующим образом:
«/«И*.»- (J (J (Y,*).
a'<v<a Р'<б<3
Это пространство регулярно, компактно [оно было бы и
бикомпактно, если бы мы не исключили пару (0)1,0)2)] и
счетно нормально (так как не содержит вовсе
расходящихся множеств). Но оно не нормально: замкнутые
множества А = (J (а, <о2) и В« (J (о),, р) не
пересек©, 1<Р<о>,
секаются, но не имеют непересекающихся окрестностей.
Если удалить точку (о)0, со0), то получится
некомпактное пространство, счетно нормальное, но не нормальное
и содержащее расходящееся счетное множество8.

ГЛАВА IV
ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
§ 1. Бикомпактность в данной точке.
Характер сходимости
1. Назовем замкнутой окрестностью какой-
либо точки х пространства R замыкание [Ох] любой
окрестности Ох этой точки. Основными для всей этой (и
значительной части следующей) главы настоящей
работы являются следующие определения:
Пространство R называется бикомпактным
(соответственно компактным) в данной точке xgJ?, если у этой
точки имеется окрестность Ох, замыкание которой [Ох]
является бикомпактом (соответственно компактным
пространством) .
Замечание. Может возникнуть вопрос: почему
в этом определении мы пользуемся замкнутыми
окрестностями, а не требуем, чтобы существовала обычная,
открытая окрестность Ох точки ху бикомпактная
(соответственно компактная) в данном пространстве*) Ю
Следующий пример убедительно, как нам кажется,
показывает, что такое видоизменение нашего определения
было бы неблагоразумным. Пространство R состоит из
всех точек плоскости оху. Все точки, кроме начала | =
= (0,0), получают обычные окрестности (т. е. те,
которые они имеют на плоскости). Окрестность 0„|
начала координат | состоит из всех точек открытого круга
радиуса — с центром в £, кроме лежащих в нем
точек положительной полуоси абсцисс.
В смысле нашего определения пространство R не только
не бикомпактно, но даже и не компактно в точке g; оно,
*) Множество £ г R естественно называть бикомпактным в
пространстве /?, если каждое бесконечное множество Е\ s Е имеет
в пространстве R хотя бы одну точку полного накопления !.

§ 1 БИКОМПАКТНОСТЬ В ДАННОЙ ТОЧКЕ
81
кроме того, нерегулярно в точке £. Между тем любая
окрестность Оп£ бикомпактна в пространстве R.
2. Введем, наконец, следующее определение:
Пространство R называется локально бикомпактным
(соответственно локально компактным), если оно
бикомпактно (соответственно компактно) в каждой своей
точке.
Приведенные определения позволяют сразу же
перенести на локально бикомпактные пространства
доказанные в гл. II локальные свойства бикомпактов.
Например, если пространство R бикомпактно в точке дг, то
y\)xR = XxR (теорема 4 гл. II), откуда следует, что (в этом
же предположении бикомпактности пространства R
в точке х) имеет место неравенство %XR ^ мощн. Ох, где
Ох — любая окрестность точки х в R. Для
доказательства последнего* утверждения достаточно (заметив, что
пространство, бикомпактное в данной точке, очевидно,
регулярно в этой точке) применить следствие из
теоремы 4 гл. II к какому-либо бикомпакту вида [Oix]^Ox.
Подобным же образом теорема 40 гл. II применима
к пространствам, компактным в данной точке х: если R
компактно и регулярно в точке х и г|)х/? = Ко, то %xR =
= К0.
В связи с изложенным заметим еще следующее:
Теорема 1. Всякое компактное пространство
замкнуто по отношению к регулярным Ь-точкам.
В самом деле, пусть пространство R U £ регулярно
в своей б-точке \. Тогда, так как пространство Rs а
значит, и R\}\ компактно, то %\{R О I) = \Ы# U |) = К0,
что противоречит следствию теоремы 4 гл. III, § 2, п. 8.
3. В дополнение к только что установленному
предложению построим следующие примеры:
а) пример компактного пространства, не замкнутого
по отношению к нерегулярным б-точкам;
б) пример компактного нерегулярного пространства
/?, в котором для некоторой точки g имеем \|>$/? = Ко,
XiR = Hi;
в) пример регулярного некомпактного пространства,
замкнутого по отношению к регулярным б-точкам.
Пример а) дается пространством ГД((01),
определение которого приведено в гл. I, § 3, п. 8; присоединим

82 ГЛ. IV. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
к этому пространству новую точку I посредством
окрестностей
Ок.пЪ- U U («.о,
х<а<<%<*<-1
п
где
f А- 1, 2, ..., р, ... <(Dj; 1
1 я = 1, 2, ..., m, ... <а>0. J
оо
Точка I не изолирована в rA(e>i)Ug; далее |= f^Oi,n|f
так что £ есть б-точка в jTA(g)i)U|. Полученное
пространство 77^(0)1) U| компактно и поэтому может
служить нам примером б).
Примером в) может служить пространство £/з.
Это пространство не компактно. Докажем, что оно
замкнуто по отношению к регулярным б-точкам.
Предположим противное, и пусть точка \ есть регулярная б-точка
в пространстве #з11£- Обозначим через А множество
всех точек £/з, имеющих вид (а, /) при а ^ 1, 0 ^ t ^ 1.
Так как Л, рассматриваемое как пространство,
компактно и потому замкнуто по отношению к регулярным
б-точкам, то I не входит в замыкание множества А
в пространстве ^US- Поэтому £ есть точка производной
(UzUi) от множества U= V\ \ А, состоящего из всех
точек вида (0,/). Обозначим через Un множество всех
точек (0,/), для которых —^7<1. Так как Un есть
бикомпакт, то I не может быть точкой накопления
множества Un и поэтому входит в производную множества
£7\ Un. Значит, каждая окрестность Og содержит точки
(О,/) со сколь угодно малыми /, а следовательно, и точки
вида (a, t) также со сколь угодно малыми t. Отсюда
вытекает, что 0| содержит точки вида (а, 0) при а^1.
Так как это верно для любой окрестности точки £, то,
взяв окрестность Oig, не содержащую ни одной точки
множества Л, видим, что для всякой окрестности 01
имеем [01] П А Ф Л; поэтому в Oig не может
содержаться замыкание никакой окрестности 0|, так что, вопреки

§ 1. БИКОМПАКТНОСТЬ В ДАННОЙ ТОЧКЕ
83
предположению, g не есть регулярная точка
пространства t/з U 6-
4. Введем теперь следующее новое и, как нам
кажется, важное понятие: скажем, что бесконечное множество
Е пространства R сходится по мощности к точке х е /?,
если при любом выборе окрестности Ох имеем2:
мощн. (Е П Ох) > мощн. (£ \ О*)
(и значит, в частности, мощнл (Е О Ох) = мощн. Е);
скажем, далее, что в (неизолированной) точке х
пространства R определен характер сходимости, если
существует бесконечное множество E<=zR, сходящееся по
мощности к точке х, — в этом случае характером
сходимости kxR пространства R в точке х называется
наименьшее такое бесконечное кардинальное число т, что
в R существует множество Е мощности т, сходящееся
по мощности к точке х. Кроме того, мы положим, что во
всякой изолированной точке пространства R характер
сходимости определен и равен числу 1.
Очевидно, точки, в которых характер сходимости
равен Ко, суть не что иное, как к-точки данного
пространства.
Известно, что в пространстве R с первой аксиомой
счетности для любой точки х имеем:
С другой стороны, полагая R = TW(o)i +1), имеем для
точки (oiG/?:
5. Мы видели (гл. I, § 1, п. 3), что для любой точки
пространства Н, определенного в только что указанном
месте главы I, имеем:
Что касается характера сходимости х*//, то легко
доказывается следующее предложение:
Если мощность континуума с меньше, чем Ко, то
характер сходимости пространства Н не определен ни
в какой точке; если же с ^ К^ (и, значит, как известно>
с > **©), то кхН = К0 в каждой точке х^Н.

84 ГЛ. IV. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
Доказательство основывается на следующем почти
очевидном предложении:
Лемма. Пусть бесконечное кардинальное число m
не есть сумма счетного числа меньших кардинальных
чисел. Если точка х пространства R есть Ь-точка этого
пространства, то никакое множество Е мощности m не
может сходиться по мощности к точке х.
В самом деле, имеем:
оо
*- f)°nX
г»-1
значит, полагая
El = E\Olx, E2 = E()(OiX \02х), ....
£„ = £П(0„х\0„+|х), ••-.
имеем:
E\x=f)En.
Но если Е сходится по мощности к точке х и имеет
мощность тп, то, обозначая через mn мощность множества
£п, имеем:
00
mn<m, m=2mrt,
n-l
что противоречит нашим предположениям.
Так как всякое бесконечное кардинальное число
го < &*<•> удовлетворяет условию нашей леммы, то при
с < К © в пространстве Н (состоящем из одних 6-точек)
никакое несчетное множество не может сходиться по
мощности ни к какой точке; а так как счетные
множества в пространстве Н вообще не имеют предельных
точек, то в предположении с < Кш характер сходимости
не определен ни в какой одной точке х^Н.
Если же с> К©, то можно получить множество Е
мощности Ко,, сходящееся по мощности к любой точке
оо
хеЯ, полагая E — [jEn, где Еп есть множество мощ-
ности Кп, помещенное на интервале (х +—у; х — —-А.

§ 1. БИКОМПАКТНОСТЬ В ДАННОЙ ТОЧКЕ
85
Так как (независимо от всякой гипотезы, касающейся
мощности континуума) никакое множество мощности
<Ксо в Н не может сходиться по мощности, то в
предположении с > К(о характер сходимости пространства Н
в каждой точке х равен К<».
6. Построим пространство R = Л5, в котором для
некоторых точек х будем одновременно иметь:
Точками пространства Л5 являются все точки
обыкновенной плоскости, в которой для удобства введем
полярную систему координат г, ф с полюсом в точке а.
Окрестности различных точек х = (г, ф) определим
следующим образом:
Г Если ф рационально и г Ф О, то окрестность Опх
состоит из всех точек х' = (г', ф'), для которых ф' « ф и
r-±<r'<r + ~.
П п
2° Если ф иррационально, то окрестности Ох состоят
из открытых кругов с центром в х = (г, ф) по удалении
из каждого из них не более чем счетного множества
точек х' = (г', ф'), где ф' = ф, г' Ф г.
3° Окрестности точки о суть произвольные открытые
круги с центром в этой точке.
Все точки пространства А5 суть одновременно б- и
х-точки. Между тем характер этого пространства в
любой точке типа 2° равен с.
Заметим еще, что для пространства R = Ат (см. гл. II,
§ 2, п. 9, пример 1°) имеем в точке |:
♦*Яв»Я-го, **/?= К0.
7. Основным результатом этого параграфа является
следующая
Теорема 2. Пространство R, бикомпактное в
данной своей точке х, имеет в этой точке определенный
характер сходимости kxR, не превосходящий характера
XxR пространства R в точке х.
Доказательство. Очевидно, можно ограничиться
случаем, когда х — неизолированная точка пространства
R. Заменяя, если надо, пространство R некоторой
бикомпактной замкнутой окрестностью точки х, можно

86 ГЛ. IV. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
предположить, что все пространство R есть бикомпакт.
Пусть
%XR = К о*
Возьмем какую-нибудь базу пространства R в точке *,
имеющую мощность Ка, и запишем ее в виде
последовательности типа о)0:
0„ 02, ..., Оа, ... (1<а<со0). (1)
Положим теперь для любого а < со0
Фа=ГН°р].
Тогда, очевидно,
Ф,ЗФ23 ... ^Фа3 ... (1<а<соД (2)
причем
П Фа = *>
а<©а
и при а < 0а всегда Фа =£ х (так как в противном
случае, вследствие того что мощность порядкового числа
а < (Оо меньше чем Ка, мы бы имели tyxR < **а = Х*#Ь
Положим теперь ai = 1. Предположим, что все aw
для ц, меньших чем конкретное А, < ша, уже определены.
Если к = [х + 1, то обозначим через а*, первое такое
порядковое число, что Фа \ Фа, =?*= Л. Такое ах непре-
менно существует, так как в противном случае было бы
Фа = Фа + 1 = ... = П Ф<* в X* чт0 Противоречит ДО-
Ц * а>ан
казанному неравенству Фа Ф х для любого а. Если же
К—предельное трансфинитное число, то берем в
качестве ах первое порядковое число, следующее за всеми
ац(|л< X), если только оно <со0. В результате получаем
последовательность
а,<а2< ... <ах< ... (3)
порядковых чисел, конфинальную последовательности
всех порядковых чисел <о)0, причем по самому
построению всегда
Фая\Фа,+,^Л.

§ 1. БИКОМПАКТНОСТЬ В ДАННОЙ ТОЧКЕ 87
Переходя, если надо, к подпоследовательности, конфи-
нальной всей последовательности (3), можем
предположить, что порядковый тип последовательности (3) есть
регулярное начальное число сот.
Возьмем теперь для каждого К < сот точку
и обозначим через X множество (мощности Кт) всех
отобранных таким образом точек *х. Докажем, что
множество X сходится по мощности к точке х. Пусть Ох —
произвольная окрестность точки х\ эта окрестность (как
всякая окрестность точки х) содержит некоторую
замкнутую окрестность [ОуХ], где Оух взято из
последовательности (1); поэтому Ох содержит и Фау, где aY есть
первое порядковое число из последовательности (3),
превосходящее у. Значит, Ох содержит все Фах, а
потому и все Хь с индексами А,>у, так что
мощн.(XП Ох)« Nт, мощн. (X \ Ох)< Кт,
что и требовалось доказать3.
Замечание 1. Даже в бикомпактных
пространствах на легких примерах осуществляется неравенство
kxR < %XR\ так, например: если R = U{ (см. гл. I, § 2,
п. 8), то для всех точек х диагонали [а; с] имеем Хх R =
= с, kxR = «о.
В любых пространствах (не непрерывно локально
бикомпактных) имеет место следующее легко доказуемое
соотношение:
Если KxR есть регулярное кардинальное число, то
*xR<$xR-
Мы видели, что в пространстве Я в предположении, что
с > К©, имеют место соотношения кхН= К^, фх//== N0 *)•
*) Видоизменяя пространство Я, легко построить пространство
Я*, в котором независимо от какой-либо гипотезы, касающейся
мощности континуума, характер сходимости не определен ни в какой
точке, хотя в то же время фжЯ* = Н0 для всех х е Я*.
Пространство Я* (как и пространство Я) строится из множества всех
действительных чисел, но окрестности Ох точек х получаются, если из
любого содержащего точку х интервала вычесть любое множество
мощности < с, В пространстве Я* множества мощности с вообще

88 ГЛ. IV. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
Построим (не опираясь ни на какие недоказанные
гипотезы) пространство R = Ubl для которого в
некоторой его точке £ имеют место соотношения
+**-*<>. х^-к,, *s#=*W W
Пространство Иъ строится следующим образом.
Обозначим через Ма какое-нибудь множество мощности
К<мл-о+а, где порядковое число a<coi.
Множества Ма с несовпадающими парами индексов считаем не
имеющими общих точек. После этого положим
Af-6U U U м«
1<л <<d 1<а<со,
и введем в множество М топологию следующим
образом. Все точки х е М \ | считаем изолированными;
окрестности 0| определяем так:
om.„i=iu U U м$.
m<n<(0 a<3<<o,
Легко видеть, что в полученном пространстве R = 1/5
имеем соотношения (4).
Замечание 2. В связи с введенными здесь
понятиями, естественно, возникает следующий вопрос:
существует ли бикомпакт, не содержащий никакой к-точки
(и, следовательно, не содержащий никакой состоящей из
попарно различных точек сходящейся счетной
последовательности)? Если бы такой бикомпакт удалось построить,
он должен был бы быть существенно иной природы, чем
все до сих пор известные примеры бикомпактов4.
§ 2. Локально бикомпактные пространства
8. Основным результатом этого параграфа является
следующая
Теорема 3. Всякое локально бикомпактное
пространство, которое само не является бикомпактным,
может быть, и притом единственным способом,
присоединением одной точки превращено в бикомпакт,
не имеют точек накопления. Ни одно множество Е мощности С не
сходится по мощности, что легко доказать применением леммы,
изложенной в п. 5 настоящей главы, имея в виду, что кардинальное
число С не может быть представлено как сумма счетного числа
кардинальных чисел <С.

§ 2. ЛОКАЛЬНО БИКОМПАКТНЫЕ ПРОСТРАНСТВА 89
Доказательство. Пусть R не бикомпактное, но
локально бикомпактное пространство. Присоединим к R
точку I посредством окрестностей
0£ = |1Н/?\Ф),
где Ф есть любой бикомпакт, лежащий в /?. Докажем
прежде всего, что в полученном пространстве Л = R U £
выполнены все аксиомы А, В, С, D окрестностей. Для А
это очевидно. Аксиома В выполнена, так как сумма двух
лежащих в R бикомпактов Oi и Ф2 есть бикомпакт
Ф111Ф2^#; аксиома С выполнена, так как /?\Ф
открыто в /?, каков бы ни был бикомпакт Ф. Выполнена
и аксиома D, так как для любой точки х е R. имеется
окрестность Ох с бикомпактным замыканием [Ох], и
тогда, полагая Og = £ U (R\ [Ох]), имеем 0£ П Ох = Д.
Покажем, что полученное пространство Л = R U |
бикомпактно. Для этого возьмем какое-нибудь
бесконечное множество £сД. Если Е пересекается с каким-либо
бикомпактом Ф ^ R по множеству той же мощности, что
и £, то точка полного накопления множества Е Г) Ф
в бикомпакте Ф является и точкой полного накопления
множества Е в /?, а значит, и в Л. Если же для любого
бикомпакта Ф ^ R множество Е П Ф имеет мощность,
меньшую чем £, то для всякой окрестности 0\ =
= I U (/?\ Ф) имеем: мощн. (Е П Og) = мощн. £, т. е.
I есть точка полного накопления множества £, чем би-
компактность пространства Л доказана.
Докажем, наконец, что всякий бикомпакт /?\
полученный присоединением к пространству R одной точки,
гомеоморфен, а если считать, что присоединяется всегда
одна и та же точка £, то и тождествен пространству Л.
Для этого достаточно показать, что во всяком
бикомпакте /?*, полученном присоединением
к пространству R точки |, открытые
множества, содержащие точку |, суть все
множества вида |и(/?\Ф) (где Ф есть бикомпакт,
лежащий в/?) итолькоони (а открытые множества, не
содержащие точки £, совпадают с открытыми
множествами пространства /?; последнее утверждение
очевидно, так как означает, что пространство R сохраняет
в R* свою топологию). Почти очевидно и первое утвер-

90 ГЛ. IV, ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
ждение: если Я открыто в R* и содержит точку £, то
множество /?*\// = /?\# замкнуто в бикомпакте /?*,
т. е. является бикомпактом Ф, содержащимся в /?, н
// = !U(/?\0>).
Таким образом, топология в /?* однозначно
определена требованием, чтобы /?* было бикомпактом, и
теорема 3 полностью доказана.
9. Заметим, что если R есть локально бикомпактное
пространство, то можно, вообще говоря, многими
способами дополнить его присоединением одной точки до
абсолютно замкнутого пространства. Так, например,
полусегмент (0; 1] присоединением точки О дополняется до
сегмента [0; 1]. Но можно присоединить точку О и
существенно иным способом, а именно так, чтобы получилось
нерегулярное абсолютно замкнутое пространство,
рассмотренное нами в гл. I, § 1, п. 5 под номером 1°.
10. Для локально компактных пространств имеет
место следующее предложение, аналогичное теореме 3.
Теорема Зо. Всякое локально компактное
пространство R, не являющееся компактным, может быть
присоединением одной точки £ превращено в компактное
пространство R U|; такие присоединения, однако,
возможны многими различными способами, так что
топология в /? U £ не является однозначно определенной
требованием, чтобы R U I было компактным.
Доказательство. Присоединим к локально
компактному пространству R новую точку £ посредством
окрестностей
0£ = |и(/?\Ф)>
где Ф есть произвольное лежащее в R компактное
замкнутое множество. Аксиомы А, В, С проверяются
автоматически (ср. доказательство теоремы 3). Аксиома D
является следствием локальной компактности
пространства R. Полученное пространство R U £ компактно. В
самом деле, пусть Е — произвольное бесконечное
множество в R. Если Е П Ф бесконечно хотя бы для одного
компактного замкнутого Ф ^ /?, то Е имеет точку
накопления в /?. Если для любого компактного замкнутого
Ф множество Е П Ф конечно, то множество Е П 0|
бесконечно при любом выборе окрестности 0£, так что |
является точкой накопления множества Е в R U £.

§ 2. ЛОКАЛЬНО БИКОМПАКТНЫЕ ПРОСТРАНСТВА 91
Покажем, что топология в R U £ не является
однозначно определенной. Для этого рассмотрим, например,
локально компактное пространство /?, полученное
удалением из компактного пространства TW((x)i) точки со0.
Пространство R не только локально компактно, но и
локально бикомпактно, поэтому оно может быть дополнено
одной точкой I до бикомпакта R = R U £. Легко видеть,
что точка I при этом вводится посредством окрестностей
ok,«t=i{i (J wи U <ю-
n-k+\ Э-а+1
Но можно получить из R присоединением одной точки
| = ©о и пространство 7lF(o)i), являющееся компактным,
но не бикомпактным. При этом точка g получает
окрестности
0*Б-£ U (J (")•
11. Из теоремы 3 следует, что всякое локально
бикомпактное пространство может быть рассматриваемо
как открытое множество, лежащее в некотором
бикомпакте (например, в бикомпакте Я = /?Щ). С другой
стороны, легко видеть, что всякое открытое множество Г
произвольного бикомпакта X есть локально
бикомпактное пространство. Для того чтобы убедиться в этом,
достаточно для любой точки х е Г взять окрестность Ох,
замыкание которой (в X) содержится в Г. Тогда Ох
имеет и в Г то же замыкание [Ох], что и в Ху и это
замыкание есть бикомпакт. Итак:
Теорема 3'. Локально бикомпактные пространства
могут быть определены, во-первых, как множества,
получаемые вычитанием одной точки из бикомпактов, во-
вторых, как открытые множества, лежащие в
бикомпактах.
Заметим, наконец, что из теоремы 3 и из теоремы 3
гл. II (§ 2, п. 7) сразу вытекает
Теорема 4. Всякое непустое совершенное
множество локально бикомпактного пространства имеет
мощность, не меньшую, чем мощность континуума.
Теорема о наличии совершенного ядра в fi-миоже-
ствах для локально бикомпактных пространств уже

92 ГЛ. IV. ЛОКАЛЬНО КОМПАКТНЫЕ ПРОСТРАНСТВА
теряет, вообще говоря, силу; достаточно взять
пространство, состоящее из множества (например, мощности
tfi) изолированных точек.
12. Согласно теореме Зо, всякое локально компактное
пространство R может быть рассматриваемо как
открытое множество, лежащее в некотором компактном
пространстве (например, в пространстве /?U|). Однако не
всякое открытое множество, лежащее в компактном
пространстве, локально компактно. В самом деле,
рассмотрим пространство С/31 состоящее из некоторой точки |
и точек х = (а, 0» где l^a<(ot и 0-</<1, с окрест*
ностями
для х = (а, /)
и данных
I п<(о0, К<щ\
Ох,„* = (J U (<*>')
*<*'<« ,_-L<r<*+-L
п п
о*,»!- U U (М).
X<0<e>'o<«-L
П
Пространство U$ компактно. Открытое множество Г,
состоящее из точки | и из всех точек (а, /),
удовлетворяющих условиям l^a<(oi, 0 < / ^ 1, в точке g не
компактно, так как любая окрестность Г П Окп I точки
I в Г содержит не имеющее в Г предельных точек
бесконечное множество £, состоящее из всех точек хт вида
(а, — и где а > к фиксировано, а т пробегает все целые
значения.
С другой стороны, всякое открытое множество,
лежащее в регулярном компактном пространстве, локально
компактно. В частности, локально компактным является
всякое открытое множество, лежащее в компактном
пространстве, удовлетворяющем первой аксиоме счетности.
Подводя итоги, можем сказать:
Теорема Зо. Локально компактные пространства
могут быть определены как пространства, получаемые
вычитанием одной точки из компактных пространств.
Вычитание замкнутого множества из регулярного
компактного пространства также приводит к локально
компактным пространствам.

ГЛАВА V
МЕТРИЗАЦИЯ КОМПАКТНЫХ
И ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ
§ 1. Вопросы метризации и вторая аксиома счетности
1. Эта глава посвящена следующей задаче,
известной под названием проблемы метризации топологических
пространств:
Найти необходимые и достаточные условия для того,
чтобы топологическое пространство было гомеоморфно
метрическому пространству *.
Мы дадим решение этой задачи:
для всех пространств со счетной базой;
для всех компактных пространств;
для всех локально компактных пространств.
Во всех вопросах, связанных с проблемой
метризации, большое значение имеет вторая аксиома счетности.
Мы начнем поэтому с некоторых рассуждений,
посвященных этой аксиоме.
2. Как известно, следующие свойства пространства
являются следствиями второй аксиомы счетности:
1° Отсутствие несчетного множества попарно не
пересекающихся открытых множеств («свойство Су-
слина»).
2° Теорема о стационарности несчетных монотонных
последовательностей замкнутых и открытых множеств
[для всякой несчетной вполне упорядоченной
последовательности убывающих (возрастающих) замкнутых или
открытых множеств можно указать порядковое число
а < (Oi, начиная с которого все множества этой
последовательности совпадают между собою].
3° Теорема Кантора — Бендиксона: всякое
замкнутое множество есть сумма совершенного
множества и множества не более чем счетного.
4° Финальная компактность (см. гл. I, § 3).
5° Наличие в пространстве всюду плотного
множества мощности К0.

94
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
6° Свойство Линделёфа (каждая система открытых
множеств содержит подсистему с той же суммой).
Докажем теперь следующее предложение:
Теорема 1. В метризуемом пространстве
каждое из свойств Г—6° эквивалентно наличию счетной
базы.
Доказательство. Мы начнем со свойства 5°.
Пусть D — счетное всюду плотное в метрическом
пространстве R множество. Тогда открытые множества
Old,г), где d пробегает все точки счетного множества
D, а г — все рациональные числа, образуют счетную базу
пространства R. В самом деле, какова бы ни была
сферическая окрестность 0(х, е) произвольной точки хе/?,
беря точку d так, чтобы р(х, d)<-^, и рациональное г,
е 2е
удовлетворяющее неравенству у<г<~з~э получим
xs=0(d,r) с=0(х, е).
Переходим к свойству Г. Вместе с Хаусдорфом
назовем е-сетью метрического пространства R всякое
лежащее в нем множество Л/, обладающее тем
свойством, что для любой точки x^R имеем р(х, N) <е.
Достаточно из свойства 1° вывести существование в R
при любом е > 0 конечной или счетной е-сети. В самом
деле, если такая сеть построена для любого е > 0, то,
давая числу е значения гк =* -г и беря не более чем
счетную еь-сеть Л/*, будем иметь в R счетное всюду
плотное множество (J Nk.
к
Построим при данном произвольном е > 0 б данном
метрическом пространстве, удовлетворяющем условию
Г, конечную или счетную е-сеть. Для этого берем
произвольную точку *о, далее точку х{ с условием
р(*ь Хо) ^ е, точку Хг с условием р(х2у х0 U х{) ^еи т. д.,
пока мы не столкнемся с невозможностью найти точку,
отстоящую от множества всех уже построенных точек
на расстояние ^е. Эта остановка процесса непременно
произойдет на некотором конечном или счетном шаге,
так как в противном случае мы построили бы множество
мощности 6*f, состоящее из точек *a(a<coi), попарно
отстоящих друг от друга на расстояние >е. Положим

§ 1. МЕТРИЗАЦИЯ И СЧЕТНАЯ БАЗА
95
Га=0 [ха, ||, и мы получим несчетное множество
попарно не пересекающихся открытых множеств в
пространстве /?, вопреки условию Г. Итак, процесс
обрывается на некотором а < cot. Но тогда построенные точки
хр(Р^а) образуют счетное множество Nf обладающее
тем свойством, что расстояние любой точки х от
множества N меньше е, другими словами, N есть е-сеть,
которую нам и требовалось построить.
Теперь остается лишь показать, что свойство Г
является следствием каждого из свойств 2°, 3°, 4°, 6°. Это
очевидно для свойства 6°. Если выполнено 2°, то
выполнено и 1°; в противном случае, взяв попарно не
пересекающиеся непустые открытые множества Га, где а
пробегает множество всех порядковых чисел <o)i, и
положив Ga= (J Гр, соответственно Ga= \J Гр, получим
несчетную возрастающую, соответственно убывающую,
последовательность открытых множеств, которые все
различны.
Далее, беря в каждом Га по точке ха, получим
несчетное множество Ху обладающее тем свойством, что
все числа
е„ = р(*„,М\*)
положительны; так как индекс а принимает несчетное
число значений, то существует такое е > 0 и такое
несчетное подмножество Х0 ^ X, что для всех ха е Х0
будем иметь:
9(хФ[Х]\Х)>в9 т.е. 9(Х0,[Х]\Х)^г.
Множество Хо не только состоит из изолированных то-
ч*ек, но, кроме того, замкнуто: если бы оно имело
предельную точку х, то было бы *е[А']\Х, что
противоречит условию р(Х0, [Л]\Я) >е.
Наличие в пространстве несчетного замкнутого
множества, состоящего из изолированных точек,
противоречит каждому из условий 3° и 4°, таким образом, если
какое-нибудь из этих условий выполнено, то выполнено

96
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
и условие 1°, а значит, и вторая аксиома счетности.
Теорема 1 полностью доказана.
3. Построим теперь, во-первых, бикомпакт R со
счетным всюду плотным множеством, содержащий точку £,
для которой %iR = с ; во-вторых, бикомпакт, совершенно
нормальный (а значит, удовлетворяющий первой
аксиоме счетности) и, кроме того, обладающий всеми
свойствами Г—6°, но не имеющий счетной базы и, значит,
(см. § 2) не метризуемый.
Для построения первого из этих двух бикомпактов
рассмотрим все действительные числа и для каждого
нерационального числа х выберем определенную
сходящуюся к нему (в обычном арифметическом смысле)
последовательность
г(*> г(*) г(*)
'1 » f2 » ' * *» 'k > * * *
рациональных чисел.
Построим теперь из всех действительных чисел
локально бикомпактное пространство Ле, объявляя все
рациональные точки изолированными точками
пространства А^ и определяя для каждой иррациональной точки
х окрестности Опх так: Опх состоит из точки х и из всех
r{k\ для которых k > п. Пространство Ав определяется
как бикомпакт, получающийся присоединением к
пространству Лв одной точки £. Счетное множество всех
рациональных точек плотно в пространстве Лб, а
значит, и в пространстве А6. Чтобы вычислить характер
пространства Ав в точке £, заметим, что каждая
окрестность 01 непременно содержит все иррациональные
точки, за исключением, быть может, конечного
множества этих точек. Так как, с другой стороны, для каждого
х е Ав можно найти не содержащую точки х окрестность
0£, то множество / всех иррациональных точек есть
сумма конечных множеств вида 1\ОаЬ где Оа1 суть
окрестности точки |, взятые из определенной базы Э&
пространства А% в точке \. Отсюда следует, что
мощность множества этих слагаемых, равная мощности базы
S9fc, равна и мощности множества всех нерациональных
чисел, т. е. мощности континуума. Итак, х&Ав=с.

§ I. МЕТРИЗАЦИЯ И СЧЕТНАЯ БАЗА
97
Второй бикомпакт строится так. Точками
пространства A7*) являются все точки двух полусегментов,
изображенных на рис. 7.
Определение окрестностей: произвольная
окрестность 0| какой-либо точки | верхнего
полусегмента состоит из всех точек полусегмента [£; х) (где х—
любая точка, лежащая вправо от £) и из всех точек
интервала (£'; х') — проекции интервала (1\х) на нижний
полусегмент.
4
X у' ,/
Рис. 7.
Произвольная окрестность Ох\ какой-либо точки
нижнего полусегмента (см. рис. 7) состоит из всех точек
полусегмента (у; у\] (где у —любая точка, лежащая
влево от т]) и из всех точек интервала (у*\ ц') — проекции
интервала (у; ц) на верхний полусегмент. База, состоящая
из только что определенных окрестностей, называется
основной базой бикомпакта Л7.
Замечание. Легко убедиться, что пространство Л7
есть не что иное, как пространство TWy где W —
упорядоченное по типу 1 + 2К + 1 множество (X— порядковый
тип числовой прямой).
Бикомпактность пространства может быть доказана
разными способами (например, опираясь на только что
сделанное замечание и на результат гл. III, § 2, п. 5).
Весьма легко доказать бикомпактность пространства
Л7 непосредственным применением критерия Ат (гл. I,
§2, стр. 26). Пусть М — произвольное бесконечное
множество регулярной мощности ш, лежащее в
пространстве Л7. Без ограничения общности можно
предположить, что множество Ми состоящее из всех точек
*) За пространством At в настоящее время утвердилось
название «две стрелки».

$8 ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
множества Af, лежащих на верхнем полусегменте, имеет
мощность га. Если р— какая-нибудь точка полного
накопления множества М, рассматриваемого в
топологии эвклидовой прямой, отличная от точки а*), то либо
точка р, либо ее проекция рг на нижнюю прямую будет
точкой полного накопления множества М в
пространстве А?, что и требовалось доказать.
Докажем, что пространство А7 наследственно
финально компактно2, т. е. что в нем выполнена
Теорема Линделёфа. Каждая система открытых
множеств у = {Га} содержит счетную подсистему у0
с тем же телом у0, что и вся система у: у0 = у.
Можно ограничиться случаем, когда все Га£у СУТЬ
элементы оснований базы пространства Л7.
Пусть y=MiUM2, где Ми М2 — множество всех
точек х е у, лежащих соответственно на верхнем и
нижнем сегментах. Докажем, что каждое из множеств М1у
М2 содержится в сумме счетного числа множеств Гаеу.
Достаточно ограничиться множеством М\.
Точку xgMj назовем точкой первого рода, если она
содержится (хотя бы) в одном из интервалов,
являющихся верхней половиной какого-нибудь Га *= у. В
противном случае точка х называется точкой второго рода.
Точка второго рода есть левый конец интервала о(х),
являющегося верхней половиной некоторого Га, и не
содержится внутри интервала, составляющего верхнюю
половину какого бы то ни было Га. Поэтому интервалы
а(х) и о(х')у соответствующие различным точкам вто-
рого рода х и х\ дизъюнктны, откуда вытекает, что
множество всех точек второго рода не более чем счетно.
Множество же всех точек первого рода в силу теоремы
Линделёфа, выполненной для числовой прямой,
содержится в объединении не более чем счетного множества
*) Такая точка существует — это вытекает из следующего
предложения:
Пусть М — некоторое множество регулярной мощности ш,
лежащее в пространстве со счетной базой. Тогда множество Мс всех
точек полного накопления множества М не содержит изолированных
точек; кроме того, множество М\МС имеет мощность < ш.
Доказательство совершенно аналогично доказательству
элементарной теоремы о точках конденсации vcm., например, П. С.
Александров [1], гл. V).

§ 2. МЕТРИЗАЦИЯ КОМПАКТНЫХ ПРОСТРАНСТВ 99
верхних половин окрестностей ГаЕу, а значит, и
в объединении счетного числа самих этих Га.
Итак, для пространства А1 имеет место теорема Лин-
делёфа — наследственная финальная компактность и
совершенная нормальность этого пространства доказаны.
§ 2. Метризация пространств со счетной базой;
метризация компактных пространств
4. Первая основная теорема (теорема 3).
Для того чтобы пространство со счетной базой было
метризуемо, необходимо и достаточно, чтобы оно было
нормально.
Только достаточность высказанного условия
нуждается в доказательстве. Докажем, что всякое
нормальное пространство со счетной базой
метризуемо.
Лемма 1. Для нормальности пространства R
необходимо и достаточно, чтобы для любой окрестности ОФ
любого замкнутого множества Ф ^ R существовала
окрестность 0{Ф множества Ф с замыканием [О1Ф],
содержащимся в Оф.
Если R нормально, то существуют непересекающиеся
окрестности О^Ф и 0(R\ ОФ) замкнутых множеств Ф
и R\OФ. Тогда [0{ф] не пересекается с 0(/?\ОФ),
а значит, и подавно не пересекается с /?\ОФ, т. е.
лежит в ОФ. Итак, условие необходимо. Оно достаточно,
так как если Ф0 и Ф1 — непересекающиеся замкнутые
множества в R и [ОФ0] ^ R \ Фи то ОФ0 и R \[ОФ0]
суть непересекающиеся окрестности множеств Ф0 и Фь
Только что доказанная лемма 1 позволяет доказать
следующее основное предложение (следствием которого
явится изложенная выше метризационная теорема):
Основная лемма (лемма 2) *). Для всяких двух
непересекающихся замкнутых множеств Ф0 и Ф{
нормального пространства R можно построить непрерывную
во всем R функцию f, удовлетворяющую неравенству
*) Это давно уже ставшее классическим предложение
общеизвестно в настоящее время под названием леммы (или Большой
леммы) Урысона.

100 ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
0</(дс)^1 для всех хе/?, равную нулю на Ф0 и
единице на Ot.
Доказательство леммы 2. Положим Г\ =
= R\Q)i. Очевидно, 1\ есть некоторая окрестность
множества Фо. По лемме 1 существует окрестность ОФо =
= Го, удовлетворяющая условию [Го] ^ П. Предположим,
что при данном целом л>0 построены открытые
множества Гт для всех целых т (0 ^ т ^ 2П), причем при
т' < т" имеем:
[TV] с= IV
L 2я J 2я
(О
(для п = 0 имеем Г0 и Ti, [Г0]^ П). На основании
леммы 1 можно построить такие открытые Г2т+1, что
2я+1
[Гт 1 ^ Г2т-и ^ ГГгт-и] ^ Гт + |,
2я J 2rt+1 L 2n + 1J 2я
так что условие (1) выполнено и при замене п на п + 1,
и наша индукция идет дальше.
В результате этого построения получаем множество
окрестностей Гг множества Фо, занумерованных всеми
двоично-рациональными числами г, лежащими на
сегменте [0; 1] (включая его концы), причем для г'< г"
имеем:
Положим для любого не двоично-рационального /(0<
r<t
Если / < ? — две какие-нибудь точки на [0; 1], то всегда
[Г/]Е1>;
достаточно взять двоично-рациональные гиг' так, чтобы
t < г < г' < t\ тогда [Г,] с= [Гг] s Гг, s Г,,.
Пусть, наконец, для *<0
1>Л,
а для / > 1
Г,-Л.

§ 2. МЕТРИЗАЦИЯ КОМПАКТНЫХ ПРОСТРАНСТВ \Q\
Каждая точка x^R определяет сечение (Лх, Вх)
в множестве всех действительных чисел: нижний класс
Ах состоит из всех /, для которых Г* не содержит лг, и,
следовательно, Вх состоит из всех t, для которых Г*
содержит точку х. Число, определяемое этим сечением,
обозначим через f(x). Так как для любого хе/?
множество Г/(х)+е\[Г/(х)_8] есть окрестность точки х, для
всех точек х' которой f(x) — е </(*') <f(x) + е, то
функция f(x) непрерывна во всем пространстве R. При
этом, очевидно, f(x) = 0 для *еФ0, f(x) = 1 для х&
gOi и 0 -*Cf(x) < 1 для любого xg/?; основная лемма
доказана.
Переходим к доказательству теоремы 3. Пусть R—
пространство со счетной базой S3, элементы которой
обозначим через
Я,, Я2, • • •» Hk, ...
Занумеруем в виде последовательности
пи л2, ..., яП) ... (2)
все пары вида яп = (НиНь), удовлетворяющие условию
[Hi] ^ Ял. Такие пары называем каноническими. Для
каждой канонической пары пп = (Ни Hh) построим
непрерывную во всем R функцию fn, удовлетворяющую
неравенству 0 4^fn(x) 4>\ для всех x^R, а также
равенствам fn(x) = 0 для всех xe[Hi] и fn(x) = 1 для всех
xs=R\Hk.
Положим для любых двух точек х, у пространства R
оо
р(х,у) = %-$г\Ш-Ш\' О)
Функция р(х, (/), очевидно, удовлетворяет аксиомам
симметрии и треугольника. Если х и у — две различные
точки /?, то, взяв Hi и Hk так, чтобы было хеЯАд/?\.
\у, xg//iC [Hi] £ Ял, получим каноническую пару
Яп = (НиНк)у причем fn(x) = 0, fn(#) = 1. Отсюда
следует, что при хфу имеем р(хщу)Ф0. Итак, функция
Р(Х>У) удовлетворяет всем трем аксиомам расстояния и
превращает пространство R в метрическое пространство

102
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
/?*. Остается доказать, что тождественное отображение
пространства R на пространство /?* есть отображение
топологическое.
Для этого достаточно доказать следующие два
утверждения:
1. Пусть ag/? и е>0 выбраны произвольно.
Существует такое #щ, что а е Нт s U(ay г).
2. Если сеЯлеЯ, то существует такое е > 0, что
U(a,e)<=Hh.
Первое утверждение непосредственно следует из
непрерывности функции ф(лс) = р(а, *), которая в свою
очередь вытекает из того, что все функции fn
непрерывны, а ряд (3) равномерно сходится.
Второе утверждение докажем от противного: пусть
для данной точки аеЯа и для всякого целого т>1
существует точка xm^R\Hk с расстоянием р(а, х)<
<-уп- Берем Я* так, чтобы ае Н{<=:[Н\]<= Я*. Тогда
пара (Яг, Ни) есть некоторая каноническая пара яЛ,
причем для любого т имеем fn(xm) = К fn(a) = 0,
а значит,
р(я, *т)>~2п>
что при т> п противоречит определению точек хт.
Полученное противоречие завершает доказательство
первой основной теоремы3.
Вторая основная теорема (теорема 4). Для
того чтобы компактное пространство было мет ризу емо,
необходимо и достаточно, чтобы оно имело счетную базу.
Необходимость условия давно известна: если в
метрическом пространстве R нет счетной базы, то нет и
счетного всюду плотного множества; значит, при
некотором е > 0 нет счетной е-сети (так как, если бы для
всякого натурального п в R существовала счетная —-сеть
Лп, то счетное множество 4 = (J.4n было бы плотно
п
в /?). Но если для данного е>0 в метрическом
пространстве R не существует г-сети, то, взяв точку а\
произвольно, можно найти точку а2, отстоящую от а{ на
расстоянии ^ е, затем точку а3, отстоящую от обеих

§ 2. МЕТРИЗАЦИЯ КОМПАКТНЫХ ПРОСТРАНСТВ ЮЗ
точек а{ и а2 на расстоянии ^ е, и т. д. В результате
получится последовательность точек
ах> а2, . .., ат> ...
с попарными расстояниями >е. Из этой
последовательности, очевидно, нельзя выбрать сходящейся
подпоследовательности, что несовместимо с компактностью
пространства R.
Остается доказать, что всякое компактное
пространство R со счетной базой метризуемо. Но из наличия в R
счетной базы следует финальная компактность. Так как
пространство /?, кроме того, компактно, то оно
бикомпактно и, следовательно, нормально, а потому, по
теореме 3, метризуемо. Теорема 4 доказана.
5. Сделаем несколько замечаний относительно не-
метризуемых компактных пространств.
Первая возможность, которая может представиться,
заключается в том, что пространство метризуемо вблизи
каждой своей точки*), не будучи мегризуемым в целом.
Таково, например, пространство nS?((oi), каждая точка
которого имеет окрестность, гомеоморфную некоторому
множеству, лежащему на числовой прямой, или
пространство jTA((di), окрестности точек которого гомео-
морфны прямой линии **).Между тем ни одно из двух
пространств TW(cui) и ГД(coi) не метризуемо (так как
эти пространства, будучи компактными, не обладают
счетной базой). Упомянутое положение вещей не может
иметь места в бикомпактах. Докажем, что из
метризуемости бикомпакта R вблизи каждой точки jce/? следует,
что все пространство R метризуемо.
В самом деле, из нашего предположения следует, что
каждая точка х имеет окрестность Ох, замыкание
которой (и тем более сама окрестность Ох) обладает счет-
*) То есть что для каждой точки х данного пространства R
имеется окрестность Ох, замыкание которой представляет собою
метризуемое пространство. Так как о метризуемости вблизи данной
точки имеет смысл говорить лишь в предположении регулярности
пространства в данной точке, то требование метризуемости
замкнутой окрестности [Ох] можно заменить тем же требованием в
применении к самой окрестности Ох. Пространство, метризуемое
вблизи каждой своей точки, называется локально метризуемым.
**) См. гл. I, п. 8.

104
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
ной базой. Выбрав конечное число этих окрестностей
так, чтобы они покрывали все пространство /?, и взяв
сумму построенных в них счетных баз, получим счетную
базу всего бикомпакта /?.
Замечание. Только что доказанное предложение,
очевидно, справедливо и для финально компактных
пространств.
Итак, множество точек, вблизи каждой из которых
данный бикомпакт R неметризуем, есть, очевидно,
замкнутое множество я, которое назовем множеством точек
неметризуемости бикомпакта R. Докажем, что в
бикомпакте R не может существовать изолированная точка
неметризуемости х со счетным характером %XR.
Переходя, если надо, к бикомпакту [Ох], не содержащему
никакой отличной от точки х точки неметризуемости
бикомпакта /?, можем с самого начала предположить, что
х — единственная точка неметризуемости бикомпакта /?,
и это предположение надлежит привести к противоречию
с условием %xR = Ко. Из этого условия следует
существование счетного числа окрестностей Опх, таких, что
х = \*\Опх, причем Опх ^ [Оп+\х] (это предположение
п
законно в силу регулярности пространства R). Мы
имеем право предположить, что все бикомпакты [0{х] \
\ Опх метризуемы, так что в [Охх] \ Опх имеется
счетная база. Тем более имеется счетная база 9П в О^х \
\ [Опх\ а сумма всех 9П образует вместе со счетной
базой пространства OiX в точке х счетную базу в OiX.
Значит, и бикомпакт [Огх\^0\Х имеет счетную базу и
потому метризуем, вопреки предположению, что х есть
точка неметризуемости бикомпакта R.
Мы доказали следующее предложение:
Теорема 5. Неметризуемый бикомпакт,
удовлетворяющий первой аксиоме счетности, содержит совершен-
ное множество (мощности > Ь) точек неметризуемости.
Структура множества точек неметризуемости может
быть весьма разнообразна. Так, например, это
множество само может быть метризуемым пространством, как
показывает бикомпакт Аи множество точек
неметризуемости которого есть обыкновенная окружность. Но,
с другой стороны, на примере пространства Г82, где 8
есть порядковый тип прямолинейного сегмента, мы

§ 2. МЕТРИЗАЦИЯ КОМПАКТНЫХ ПРОСТРАНСТВ 105
видим, что множество точек неметризуемости бикомпакта
может быть нигде не плотным совершенным множеством
я, которое само является бикомпактом, не содержащим
точек метризуемости (и, следовательно, совпадающим
со своим собственным множеством неметризуемости).
Например, пространство TW((oi+l) есть бикомпакт,
в котором имеется одна-единственная точка
неметризуемости, являющаяся, естественно, и единственной точкой,
в которой не выполнена первая аксиома счетности.
6. Основное утверждение теоремы 4 легко поддается
следующему обобщению:
Теорема 6. Всякое локально компактное
пространство со счетной базой метризуемо.
Доказательство. Пусть R— локально
компактное пространство со счетной базой. Так как каждая
точка хе/? имеет окрестность Ох, замыкание которой
компактно и имеет счетную базу, следовательно,
представляет собою бикомпакт, то R локально бикомпактно
и, значит, единственным образом дополняется до
бикомпакта R U g. Счетная база
#,, #2, • • •, Нп> • • •
пространства R может быть выбрана так, чтобы
замыкание в R U g каждого множества #„ лежало в R. В самом
деле, сохраняя в какой-либо базе R лишь те элементы,
для которых выполнено только что сформулированное
условие, получим базу пространства R. Положим теперь
0„& = (*U6)\([tf,]U ■■■ и[/ш
Очевидно, f]Onl=-l\ значит, g есть б-точка бикомпакта
п
R U g, а потому в точке g бикомпакт R U g удовлетворяет
первой аксиоме счетности. Дополнив счетную базу
пространства R счетной базой пространства R 0 g в точке g,
получим счетную базу всего R О g, откуда следует, что
бикомпакт R U g метризуем, поэтому метризуемо и
пространство R.
Из нашего доказательства вытекает
Следствие 1. Всякое локально компактное
пространство со счетной базой может бцть одной точкой
дополнено до компакту.

106
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
Другими словами:
Локально компактные пространства со счетной базой
суть не что иное, как открытые множества, лежащие в
компактах.
Следствие 2. Всякое удовлетворяющее второй
аксиоме счетности множество Г, открытое в некотором
(хотя бы и нерегулярном) компактном пространстве R,
метризуемо.
В самом деле, так как в точках хеГ компактное
пространство R удовлетворяет первой аксиоме
счетности, то в этих точках R регулярно*). Следовательно, Г
есть локально компактное пространство и метризуемо
по теореме 6.
Следствие 3. Если в компактном неметризуемом
пространстве R дано открытое множество Г,
удовлетворяющее второй аксиоме счетности, то множество Ф =
= R \ Г несчетно **).
Предположим противное: пусть Ф счетно. Так как
в Г имеется счетная база и, следовательно, выполнено
свойство финальной компактности, то финально
компактным является и все пространство /?, полученное
присоединением к финально компактному Г счетного
множества Ф. Пространство /?, будучи компактным и
вместе с тем финально компактным пространством,
является бикомпактом. Докажем, что в каждой точке
хей выполнена первая аксиома счетности. Достаточно
рассмотреть точки хеФи доказать, что каждая такая
точка есть б-точка бикомпакта R. Для этого берем
счетную базу Ни Н2, ..., #п, ••• пространства Г<=/?,
состоящую из множеств НПу замыкания которых (в R)
лежат в Г. Пусть Ф состоит из точек хи хг, ..., хп,
Для данной точки £ е Ф обозначаем через Оп|
окрестность, удовлетворяющую условию [On£] S R \(хп П [пп]).
Очевидно, f] Оп1 = I.
п
*) См. гл. II, § 6, теорему 2. Эта теорема доказана в
предположении, что характер пространства R счетен во всех точках;
рассуждения, однако, остаются теми же и для случая счетного
характера в данной точке х.
**) Весьма вероятно, что Ф не может быть пространством со
счетной базой, однако мы не умеем этого доказать4.

§ 3. МЕТРИЗАЦИЯ ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ 1Q7
§ 3. Метризация локально компактных пространств
7. Основным предметом этого параграфа является
доказательство следующего предложения:
Третья основная теорема (теорема 7). Для
того чтобы локально компактное пространство было ме-
тризуемо, необходимо и достаточно, чтобы оно было
суммой (какого-нибудь числа ^1) попарно не
пересекающихся открытых множеств*), каждое из которых
удовлетворяет второй аксиоме счетности (т. е. является
пространством со счетной базой).
Достаточность высказанного в этой теореме условия
легко устанавливается на основании теоремы 6. В самом
деле, если локально компактное пространство R есть
сумма попарно не пересекающихся открытых множеств
Га, то каждое из этих Га также и замкнуто,
следовательно, локально компактно. Имея счетную базу,
каждое Га метризуемо, причем можно предположить, что
в каждом Га выбрана метрика ря, удовлетворяющая
условию ра(х,у)<1 для любых точек х и у
множества Га (если ра — какая-нибудь метрика, то получим
метрику, удовлетворяющую нашему условию, полагая
Теперь остается положить р(х, у) = ра(х> У), если
точки х и у пространства R принадлежат одному
какому-нибудь Га, и р(х,у) = 1, если эти точки принадлежат
разным Га. Метризация пространства R этим
осуществлена.
Замечание 1. Наличие счетной базы во всем
пространстве /?, будучи достаточным для метризуемости
локально компактного пространства, отнюдь не является
необходимым условием; достаточно взять пространство
/?, состоящее из несчетного множества изолированных
точек.
8. Доказательство необходимости условия,
высказанного в теореме 7, требует значительно более
пространных рассуждений. Мы получим завершение
доказательства теоремы 7 в качестве заключительного звена цепи
*) Они, очевидно, оказываются и замкнутыми.

108
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
предложений, некоторые из которых представляют и
самостоятельный интерес.
Прежде всего заметим, что всякое локально
компактное метризуемое пространство удовлетворяет условию,
которое естественно называть локальным условием или
локальной аксиомой спетости.
Определение 1. Регулярное пространство
удовлетворяет локальной аксиоме счетности, если каждая
его точка имеет окрестность, являющуюся
пространством со счетной базой.
Введем еще несколько определений. Скажем, что
данная система множеств 23, лежащих в пространстве
/?, является точечно счетной, соответственно звездно
счетной, если каждая точка пространства R содержится
не более чем в счетном числе элементов системы 93,
соответственно если каждый элемент системы S3
пересекается не более чем со счетным числом других
элементов этой системы*). Наконец, назовем множество D
локально счетно плотным в пространстве /?, если
пересечение множества со всяким непустым открытым
множеством пространства /?, удовлетворяющим второй
аксиоме счетности, есть непустое, не более чем счетное
множество. Очевидно, если пространство удовлетворяет
локальной аксиоме счетности, то всякое локально счетно
плотное множество в нем будет плотным во всем
пространстве.
Далее очевидно, что всякая звездно счетная система
множеств и подавно является точечно счетной. Легко
видеть также, что всякое пространство, имеющее звездно
счетную базу, удовлетворяет локальной аксиоме
счетности. В самом деле, каждый элемент Н базы 93 есть
пространство, имеющее не более чем счетную базу,
состоящую из всех непустых множеств, являющихся
пересечениями множеств Н со всевозможными элементами
базы 93. С другой стороны, пространства TWfai) и
ГД(о>1) удовлетворяют локальной аксиоме счетности, но
не имеют никакой точечно счетной базы, значит, и
подавно не имеют звездно счетной базы. Легко построить
также пример метрического пространства, имеющего
*) В первоначальной редакции условие точечной счетности на-
зывадось условием Л, а условие звездной счетности — условием 4'.

§ 3. МЕТРИЗАЦИЯ ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ 109
точечно счетную базу, но не являющегося пространством
с локальной аксиомой счетности. Такое пространство
получим, если возьмем множество всех точек плоскости,
выделим среди этих точек одну определенную точку о
и, обозначая через d(xyy) расстояние между двумя
точками х и у па обыкновенной эвклидовой плоскости,
положим р(х, у) =d(xyy), если прямая ху проходит через
точку о, и р(х, у) = d(x, о) + d(yy о), если прямая ху
через точку о не проходит.
9. Докажем прежде всего следующее предложение:
Теорема 8. Всякое пространство,
удовлетворяющее локальной аксиоме счетности, содержит локально
счетно плотное множество.
Для доказательства теоремы 8 обозначим через ф
множество всех открытых множеств пространства /?,
удовлетворяющих локальной аксиоме счетности, и
расположим все элементы множества ф во вполне
упорядоченную последовательность типа о)т (обозначая
через Кт мощность множества ф):
$-{Я„ Я2, .... Яа, ...} (а<сот).
Обозначим через Z>i какое-нибудь не более чем
счетное множество, плотное в Я4; положим П = Н\.
Пусть X — порядковое число <o)t; предположим, что
Da и Га построены для всех а < X.
Положим
г*=я*х[иЯ
и обозначим через £>*, какое-нибудь не более чем счетное
множество, плотное в 1\. Положим, наконец,
D= (J Д.-
о<©т
Очевидно, D плотно во всем пространстве /?.
Остается доказать, что для любого X < сот множество
D П Ях не более чем счетно.
Прежде всего имеем:
La<X J
- (Г* U JJ (Га П HJ) U (^ П ( [U^ Га] \ U Га)) .

110
ГЛ. V. МЕТРИЗАЦИИ ПРОСТРАНСТВ
Так как множества Га открыты и попарно не
пересекаются, а данное //*, — пространство со счетной базой,
то #х имеет непустое пересечение лишь с конечным или
счетным числом множеств Га, которые мы и обозначим
через
1а,, 1о2, • • •, ' ап,
Так как
а«ох
и D П Га = Da, то
ЯхЛ£>= U (ЯлПГ.ПЯ)-
а<©т
л \ п I п
т. е. НХГ\ D не более чем счетно. Теорема 8 доказана.
Замечание. Нами доказана следующая, более
сильная
Теорема 8'. Если каждая точка пространства R
имеет окрестность, содержащую конечное или счетное,
плотное в этой окрестности множество, то пространство
R содержит локально счетно плотное множество.
Из теоремы 8 вытекает такое
Следствие. Если в пространстве с локальной
аксиомой счетности имеется точечно счетная база, то
имеется и звездно счетная база.
Другими словами: наличие в данном пространстве
звездно счетной базы эквивалентно совокупности двух
условий: локальной аксиоме счетности и наличию
точечно счетной базы*).
Доказательство. Пусть в пространстве /?,
удовлетворяющем локальной аксиоме счетности, имеется
точечно счетная база 230. Сохраняя в базе 330 лишь те
элементы, которые сами удовлетворяют второй
аксиоме счетности, получим базу 93 пространства R. Мы
*) Поэтому в оригинале (и в предшествующих русских
изданиях) пространства, имеющие звездно счетную базу, назывались
пространствами, равномерно удовлетворяющими второй аксиоме
счетности.

§ 3. МЕТРИЗАЦИЯ ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ Ц1
утверждаем, что база 23 является звездно счетной. В
самом деле, пусть D есть локально счетно плотное в R
множество (существующее в силу теоремы 8). Возьмем
какой-нибудь элемент Я базы 33. Так как Я
удовлетворяет второй аксиоме счетности, то множество Я Л D есть
не более чем счетное множество, плотное в Я. Если
Яае8 и Я П На = Л, то в На имеется хотя бы одна
точка множества Я П D. Так как множество Я П D не
более чем счетно, то из предположения, что существует
несчетное множество элементов Яае23, пересекающихся
с Я, следовало бы, что по крайней мере одна точка
множества HOD содержится в несчетном числе этих
Яа, а это противоречит тому, что 53 — точечно счетная
база. Следствие доказано.
10. Следующее предложение является в нашем
исследовании основным.
Теорема 9. Всякое пространство R, имеющее
звездно счетную базу, есть сумма (некоторого карой-
нального числа ^1) попарно не пересекающихся
открытых (а следовательно, одновременно и замкнутых) в R
множеств, каждое из которых является пространством
со счетной базой.
Доказательство. Возьмем звездно счетную базу
23 пространства R. Назовем цепью базы 23,
связывающей элементы Hi и Я8, всякую конечную
последовательность
Яь Я2, ..., H9-lf Hs (s>l)
элементов этой базы, удовлетворяющую условию
ЯгПЯг+1=£Л для всех * = 1, 2, ..., s— 1. Назовем
компонентой в 23 элемента Яа базы 23 множество
©а тех элементов этой базы, которые могут быть
связаны с элементом На цепями базы 23. Очевидно, что вся
база 23 распадается на компоненты своих элементов,
причем компоненты двух различных элементов либо
тождественны, либо не имеют ни одного общего элемента.
Более того, если @а и ©р — две различные компоненты,
то никакие два элемента Ях^©а и Яце@р не могут
иметь общих точек; поэтому тела Га = (§а
различных компонент суть попарно не
пересекающиеся открыто замкнутые множества, на
которые распадается все пространство R.

112
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
Остается доказать, что тело каждой компоненты
удовлетворяет второй аксиоме счетности. Но так как все
элементы базы 33 удовлетворяют второй аксиоме счетности,
то достаточно доказать, что каждая компонента ©а
состоит из не более чем счетного числа элементов.
Доказываем это последнее утверждение.
Пусть рассматриваемая компонента есть компонента
элемента #аеЗЗ. Обозначим через ©2 множество всех
ЯеЗЗ, которые могут быть связаны с На цепями,
состоящими не более чем из п элементов («звеньев»).
Очевидно, ®Ъ состоит из одного лишь элемента На и ©а =
оо
= (J©2. Предположим доказанным, что ©2 состоит
не более чем из счетного числа элементов (для п = 1
это верно). Так как каждый элемент Яе®2+|
пересекается по крайней мере с одним элементом из ©2 и
с каждым элементом базы 33 пересекается вообще не
более чем счетное число элементов этой базы, то число
элементов, пересекающихся хотя бы с одним элементом
из ©2, т. е. число элементов, входящих в ©2+\ также
не более чем счетно. Итак, каждое ©2 состоит не более
чем из счетного числа элементов. Но тогда и множество
@a = (J@2 не более чем счетно. Теорема 9 полностью
п
доказана.
11. Переходим к рассмотрению метрических
пространств.
Теорема 10. Всякое метрическое пространство,
удовлетворяющее локальной аксиоме счетности, имеет
звездно счетную базу (и, значит, —в силу теоремы 9 —
является суммой попарно не пересекающихся открыто
замкнутых множеств, каждое из которых есть
пространство со счетной базой).
Так как всякое локально компактное метрическое
пространство удовлетворяет локальной аксиоме
счетности, то еще не доказанная часть теоремы 7
(необходимость!) является непосредственным следствием
теоремы 10.
Доказательство теоремы 10. Ввиду следствия
теоремы 8 нам требуется только доказать, что всякое

§ 3. МЕТРИЗАЦИЯ ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ ИЗ
метрическое пространство R с локальной аксиомой счет-
ности имеет точечно счетную базу5.
Возьмем какую-нибудь точку дге/? и обозначим
через рх верхнюю грань тех положительных е, для
которых окрестность U(xte) есть пространство со счетной
базой (или, что в нашем случае есть то же самое, со*
держит счетное всюду плотное множество). Обозначим
через D какое-нибудь локально счетно плотное
множество в R. Тогда множество D, пересекаясь с каждым
U(x, е) (е < рзс) по не более чем счетному множеству,
имеет и со множеством U(xtpx) не более чем счетное
пересечение.
Обозначим через 59 множество всех £/(*, г), где
r< yPx рационально и x^D. Докажем, во-первых, что
S3 есть база и, во-вторых, что эта база удовлетворяет
условию Л.
Для доказательства первого утверждения требуется
к любой заданной окрестности U(a,e) любой точки
ag/? найти такое V(х, г)е 39, что ае U(х, r)^U(а, е).
Для этого возьмем прежде всего положительное а,
меньшее чем ра и чем е, и точку * е D, удовлетворяющую
условию р(а, *)<-£ а. Тогда
u(x9±o)sU(a9o)sU(a,*), (1)
так как из у е U ix, -j а) следует, что
р{а,у)<Р{а, х) + р{*, y)<-Q<J+j<J<o.
Из первого включения (1) и определения числа а следует,
что U fx,-j о) есть пространство со счетной базой, так что
Р*^"4"а> "з Р*^ 4~а>"б а* Обозначим через г
рациональное число, лежащее между -g-a и наименьшим из
двух чисел -jp* и ~. Тогда U(x, г)еЭ9 и по выбору

114
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
точки х и в силу формулы (1)
eel/(x,j)sl/ (х, г) s £/(*,£) sU(a9a)sU (а, е),
чем доказано, что 93 есть база пространства /?.
Докажем, наконец, что каждая точка ае1?
содержится не более чем в счетном числе множеств U(x, г) ее
е8. Для этого рассмотрим какую-нибудь точку ag/?
и какое-нибудь содержащее эту точку множество
U(x, г)е 93. Тогда г < у р^ и а е U (х, г) ^ U (х, у Р*) •
Возьмем произвольно ^ е (/ а, у pJ. Имеем:
р(*, У)<9(х, а) + р(а, y)<jpx.
Итак,
С/ (a, -J- рж) s I/ (х, |- рх) s I/ (х, р ,),
а потому U (а, -=- р J удовлетворяет второй аксиоме
счетности, так что
Ра>^Рх ихе tf (a,r)s£/(a,yp,)s=I/(a, pe).
Таким образом, если а е £/(х, г)е 93, то XG(/(a,pfl).
Так как при этом хеД а множество DC\U(a, pa) не
более чем счетно, то множество тех £/(х,г), для
которых xeDfl t/(a,pa), а г, как всегда, рационально,
также не более чем счетно. Теорема 10 этим доказана.
Доказана и теорема 7.
12. Сделаем несколько последних замечаний:
Теорема 11. Для того чтобы пространство,
удовлетворяющее локальной аксиоме счетности, было мет-
ризуемоу необходимо и достаточно, чтобы оно было
нормально и имело точечно счетную (значит, и звездно
учетную) базу6.
Необходимость условия следует из теоремы 10 (и из
нормальности всякого метрического пространства),
достаточность— из теоремы 9 (и рассуждения, сделанного
в п. 7).

§ з. МЕТРИЗАЦИЯ ЛОКАЛЬНО КОМПАКТНЫХ ПРОСТРАНСТВ Ц5
В частности:
Теорема 12. Для того чтобы локально компактное
пространство было метризуемым, необходимо и
достаточно, чтобы оно имело звездно счетную базу.
Теорема 11 ввиду теоремы 9 может быть
сформулирована и так:
Теорема И'. Для того чтобы нормальное
пространство с локальной аксиомой счетности было метри-
зуемо, необходимо и достаточно, чтобы оно было суммой
(некоторого числа ^ 1) попарно не пересекающихся от-
крыто замкнутых множеств, каждое из которых
удовлетворяет второй аксиоме счетности1.
Отсюда имеем:
Следствие 1. Для того чтобы связное нормальное
пространство с локальной аксиомой счетности было ме-
тризуемо, необходимо и достаточно, чтобы оно имела
счетную базу.
Следствие 2. Для того чтобы связное локально
компактное пространство было метризуемо, необходимо
и достаточно, чтобы оно имело счетную базу.
Мы уже давали в п. 8 пример метрического связного
пространства без счетной базы, которое, следовательно,
и не локально компактно и не удовлетворяет локальной
аксиоме счетности, причем обе эти особенности
осуществляются лишь в одной точке. Там же мы
упомянули, что пространство 7"А (coi) неметризусмо, хотя и
локально бикомпактно и удовлетворяет локальной аксиоме
счетности (даже локально гомеоморфно обыкновенной
прямой), откуда следует, что в этом пространстве не
существует точечно счетной базы. Остается открытым
вопрос о существовании локально компактного (и,
разумеется, неметризуемого) пространства, имеющего
точечно счетную базу (не удовлетворяющую локальной
аксиоме счетности)8.
ДОПОЛНИТЕЛЬНОЕ ЗАМЕЧАНИЕ ОБ ОДНОМ СВОЙСТВЕ
ТРАНСФИНИТНЫХ ЧИСЕЛ
В этом замечании доказывается следующая
Теорема. Предположим, что для каждого
порядкового числа а < coi определено порядковое число ц,(а)

116
ГЛ. V. МЕТРИЗАЦИЯ ПРОСТРАНСТВ
с единственным условием \i(a) <а для любого а < coi.
Тогда существует несчетное множество порядковых
чисел at < сс2 < ... <»ах < ... (X < o)i), для которых
H(ai)= И(аг)= ••• = М<(ах) = •••
Доказательство. Предположим, что для
каждого а < coi определено |i(a)<a. Имеются две логические
возможности:
1° Для каждого а < coi существует такое первое
v(ex)> а, что для всех р > v(a) имеем ц(р)> а.
2° Существует первое такое а, для которого
предположение 1° не имеет места и, следовательно, для
каждого р > а имеется такое у > р, что м<(у)^а-
Разберем сначала случай Г. Положим
a0=l, a2 = v(a0), ..., an = v(an.1), ...
Пусть а© есть предел возрастающей последовательности
a0<a!< ... <art< ...
Так как а© > ап+ь то м,(а<о)> ап для любого л; поэтому
^(асй)^»©, что противоречит основному свойству
функции м-- Итак, первая возможность неосуществима.
Рассмотрим вторую возможность. Пусть ао — первое
порядковое число, для которого гипотеза 1° не имеет
места. Пусть at — первое порядковое число, большее
чем ао и для которого fi(ai)^ ао. Предположим, что
построено ах; определяем a^+i как первое порядковое
число, большее чем а*, и такое, что ji(ax+i)^ao.
Предположим, что X второго рода и что построены все a0(a < X);
пусть т—первое порядковое число, большее, чем все аа\
существует первое порядковое число ах>т, такое,
что м,(аО<ао. Таким образом, процесс продолжается
трансфинитно и мы получаем несчетное множество
возрастающих порядковых чисел
a0<aj< ... <au)< ... <ax< ... (А,<ю,),
обладающих тем свойством, что \ь.(а%) < ао. Но так как
всех чисел <ао лишь счетное множество, то для
несчетно многих ах значение функции \л должно быть
одним и тем же числом а' < ао, чем наша теорема доказана.
Москва, 3 февраля 1923 г,

ПРИМЕЧАНИЯ К ГЛАВЕ I
1 (стр. 13). Вопросы, изложенные в этом, а отчасти и в
следующем параграфе, в настоящее время подробно излагаются в
любом из многочисленных учебников общей топологии; некоторые из
них указаны в конце предисловия.
2 (стр. 13). Если потребовать лишь соблюдения условий Г и
2°, то получим топологические пространства в наиболее общем
смысле (так называемые Г-пространства).
3 (стр. 13). Обозначение 32 вызвано тем, что изложенная под
этим номером «хаусдорфова аксиома отделимости» при ее
ослаблении переходит в аксиомы 3! и 30, а при усилении — в аксиомы
З3 и 3J. Тогда вместо хаусдорфовых (или Г2-пространств) получаем
соответственно Гг и Го-пространства (более Общие, чем хаусдор-
фовы), а с другой стороны, более специальные: Г3- (или регулярные)
и Та- (или нормальные) пространства. Определения Т\- и Гз-про-
странств даны в § 1, п. 4 этой главы. Нормальные пространства
определены в гл. 2, § 1. Определение Го-пространств получим, если
к аксиомам 1° и 2° топологического пространства прибавим еще
аксиому 3q (А. Н. Колмогорова) *): Если х и у — различные точки
пространства, то по крайней мере одна из этих точек принадлежит
открытому множеству, не содержащему вторую хочку. Как известно,
условия Го, Гь Гг, /з, Г4 образуют линейный ряд строго
усиливающихся аксиом отделимости. К ним присоединяется еще аксиома
отделимости существенно нового типа, а именно, аксиома Тихонова
Г j , утверждающая функциональную отделимость **) любой точки
32
х пространства от любого не содержащего ее замкнутого
множества F. Пространства, удовлетворяющие этому условию, называются
*) Впервые опубликовано в книге: P. Alexandroff,
Н. Нopf, Topologie I* Berlin, 1935, гл. 1, § 4.
**) Говорят, что два непересекающихся множества А и В
функционально отделимы в пространстве X, если существует
определенная на всем X непрерывная функция /, для которой 0 ^ f(x) ^ 1
при любом х^Х w которая принимает значение 0 во всех точках
х е А и значение 1 во всех точках xsfi, Содержанием знаменитой
Большой леммы Урысона является утверждение, что пространство
нормально тогда и только тогда, когда в нем любые два
дизъюнктных замкнутых множества функционально отделимы (см. ниже,
гл. V, § 2, лемма 2).

118
ПРИМЕЧАНИЯ
вполне регулярными или тихоновскими пространствами. Они обра
зуют класс пространств, более узкий, чем класс регулярных, и более
широкий, чем класс нормальных пространств.
Из классических результатов А. Н. Тихонова следует, что
тихоновские пространства могут быть определены как всюду плотные
подпространства бикомпактов (т. е. бикомпактных хаусдорфовых
пространств; см. § 2 этой главы).
Уже в эпоху первых результатов А. Н. Тихонова возникла
задача дать открытому им классу вполне регулярных пространств
прямое и внутреннее определение (т. е. определение, не содержащее
понятия действительной функции и не рассматривающее данное
пространство как подпространство некоторого другого, объемлющего
его). Этой задачей занимались Ю. М. Смирнов [1], [2], О. Фринк
[1] и другие. Вполне удовлетворительное и окончательное решение
этой задачи получено лишь недавно В. Зайцевым [1]. К этой
работе мы еще сейчас же вернемся в примечании5 и в примечаниях
к гл. III.
4 (стр. 14). В последнее время вошли в употребление два
очень важных обобщения понятия базы.
1. Понятие сети (в смысле А. В. Архангельского [1]):
сетью в пространстве X называется любая система % = {А}
множеств, лежащих в пространстве X, такая, что для любой точки
х & X и любой ее окрестности Ох найдется такое А е Ш, что
х е А г Ох (таким образом, база — это сеть, состоящая из
открытых множеств).
2. Понятие я-базы (В. И. Пономарев [6]): я-базой
называется любая плотная система открытых множеств данного
пространства X, причем система 8t = {А} множеств называется плотной
в пространстве X (Пономарев), если каждое открытое в X
множество содержит хотя бы одно А е %.
5 (стр. 14). Принадлежащая Хаусдорфу идея «отмеченных»
окрестностей (прикрепленных к данной точке) уже давно казалась
имеющей лишь исторический интерес — казалось, окончательно
восторжествовало «более простое и по существу более удобное
понятие базы пространства». Однако старая хаусдорфова идея
неожиданно зажила новой и плодотворной жизнью в упомянутой в
примечании 3 работе В. Зайцева, в которой рассматриваются впервые
отмеченные окрестности не только точек, но и замкнутых множеств.
На стр. 54 своей работы [1] В. Зайцевым доказывается следующая
теорема:
Для того чтобы Т\-прост ранет во X было тихоновским,
необходимо и достаточно, чтобы для всех его замкнутых множеств F
можно было отобрать окрестности U(F) таким образом, чтобы система
отобранных окрестностей удовлетворяла следующим условиям:
1° каждая окрестность любой точки хеХ (т. е. каждое
открытое множество, содержащее эту точку) есть ее отобранная
окрестность *);
*) Можно было бы ограничиться требованием, чтобы все
окрестности точки xt принадлежащие како.и иибудь базе, были
отобранными.

К ГЛАВЕ !
119
2° всякое замкнутое множество F и дополнение F\ = X\U(F)
ко всякой его отобранной окрестности U(F) имеют
непересекающиеся отобранные окрестности U\(F) и Ui(Fi). Систему окрестностей
замкнутых множеств, удовлетворяющую этим двум условиям,
В. Зайцев называет хаусдорфовой системой окрестностей. Наличие
такой системы окрестностей в ^-пространстве необходимо и
достаточно для того, чтобы это пространство было вполне регулярным.
6 (стр. 18). П. С. Урысону принадлежит изложенный ниже
пример регулярного пространства, состоящего из счетного
множества точек и тем не менее не удовлетворяющего первой аксиоме
счетности (очевидно, что счетное пространство, удовлетворяющее
первой аксиоме счетности, удовлетворяет и второй аксиоме
счетности). Изложению этого примера П. С. Урысона предпошлем
несколько замечаний, касающихся последовательностей натуральных
чисел..
Мы будем рассматривать лишь строго возрастающие
последовательности {ап} натуральных (т. е. целых и положительных) чисел:
ах<а2<аг< ... <ап< ... (1)
Суммой двух таких последовательностей {ап) и {Ьп} назовем
последовательность {сп} в {ап) U {Ьп}, элементы которой суть элементы
множества {ап} U {Ьп}, написанные в порядке их возрастания. Если
при этом для каких-нибудь /, k окажется я* -= bk, то
соответствующий элемент будем считать в последовательности {сп} лишь один раз.
Последовательность (1) назовем быстро растущей, если
П-»оо Я
Лемма. Сумма двух быстро растущих последовательностей
есть быстро растущая последовательность.
Доказательство. Пусть {сп} = {ап} U {Ьп}. Наша цель
будет достигнута, если для любого наперед заданного числа q > О
с о
мы сможем найти такое Nq > 0, что для всех m > Nq имеем—~^4-.
Итак, пусть q > О задано. Берем такое Nq, чтобы для п> Nq
было ап> nq, bn> nq, и пусть m > 2Nq. Так как каждое из m
чисел
сх<с2< ... <ст (2)
является элементом последовательности {ап}, или
последовательности {Ьп}, или обеих этих последовательностей, то среди чисел (2)
найдется по крайней мере -=- чисел, входящих в одну из
последовательностей {ап} или {Ьп}. Пусть, например, среди чисел (2) имеется
ПХ . %
не менее -=- чисел, принадлежащих последовательности {ап}, и
пусть Ck — aj есть последнее в ряду (2) число, принадлежащее
последовательности {ап}. Тогда j ^ -х- > Nq, а значит, 0/ >jq^-^- q.

120
ПРИМЕЧАНИЯ
Гак как, с другой стороны, с* содержится среди (2), то Ch ^ ст;
поэтому для нашего т (которое было произвольным m > 2Nq) имеем
cm>ck-ai>Ttq'
lim 1Г>Ь
что и требовалось доказать.
Переходим теперь к построению пространства П. С. Урысона.
Точками пространства R являются все неотрицательные целые
числа. При этом положительные целые числа полагаем изолированными
точками пространства /?, что же касается числа 0, то мы получим по
определению произвольную окрестность этой точки, если удалим из
множества всех неотрицательных целых чисел элементы любой
быстро растущей последовательности натуральных чисел. Легко
видеть, что это определение окрестностей удовлетворяет всем четырем
аксиомам Хаусдорфа. (Справедливость аксиомы о следует из
только что доказанной леммы.) Для доказательства того, что характер
пространства R в точке 0 несчетен, достаточно заметить, что,
во-первых, точка 0 в пространстве R не является изолированной (так как
дополнение ко всякой быстро растущей последовательности
представляет собою бесконечное множество) и, во-вторых, не существует
никакой счетной последовательности точек пространства /?,
сходящейся к точке 0. Но последнее утверждение следует из того, что
каждая последовательность попарно различных натуральных чисел
содержит растущую подпоследовательность
ах<а2< ... <ап< ..., (3)
которая, в свою очередь, содержит быстро растущую
подпоследовательность (достаточно положить Ь\ *= а\ и обозначить вообще через
Ьп первое число в последовательности (3), которое больше чем 2n_1,
тогда — ^ ► оо I.
п п
7 (стр. 22). Весьма важным обобщением регулярных
пространств являются так называемые полурегулярные или
/£-пространства, впервые введенные М. Стоуном в его работе [1].
Го-пространство X называется полурегулярным, если в нем
канонические открытые множества *) образуют базу. Исследования
М. Стоуна, М. Катетова, В. Зайцева, Е. Щепина и др. показали, что
полурегулярные пространства несомненно заслуживают дальнейшего
*) Множество Н называется каноническим открытым или
хо-множеством пространства X, если Н совпадает с открытым
ядром своего замыкания: Н •» /[//]. Множества, дополнительные к
каноническим открытым множествам, называются каноническими
замкнутыми или ха-множествами; это множества Л, являющиеся
замыканиями своего открытого ядра: А «= [IA]. Обозначения
^-пространств, а также ха- и хомножеств введены В. Зайцевым [21.

К ГЛАВЕ I
121
изучения, несмотря на то что они, вообще говоря, не являются даже
^-пространствами.
Важность этих пространств становится особенно ясной после
работ В. Зайцева [2]—[4] о проекционных спектрах. В этих
работах доказывается, что полные пределы спектров во всех сразум-
ных> случаях полурегулярны и лишь в совершенно исключительном
случае так называемых экстремально несвязных пространств
являются ^-пространствами.
В. Зайцев [2], [3] ввел следующий очень интересный и важный
подкласс класса полурегулярных пространств, названный им
классом 7\-пространств. Пространство X называется 7\ -пространством,
если оно полурегулярно и если, какова бы ни была точка х и ее
окрестность их, найдется такое конечное число ха-множеств А\> ...
..., А9, что х е А\ Г) ... ГИ, s Ох. Называя я-множествами
множества, являющиеся пересечением конечного числа ха-множеств, можно
сказать, что 7\-пространства суть полурегулярные пространства, в
которых л-множества образуют сеть в смысле Архангельского.
Зайцев доказал, что 7\-пространства могут быть определены
как всюду плотные подпространства бикомпактных полурегулярных
пространств — совершенно так же, как вполне регулярные
пространства могут быть определены как всюду плотные подпространства
бикомпактных регулярных пространств.
8 (стр. 23). Все теоремы этого и в значительной степени
следующего параграфа вместе с их доказательствами остаются в силе
не только для любых ^-пространств (как указывается в конце п. 7),
но и для любых топологических пространств (т. е. для Г-пространств
в смысле примечания8).
9 (стр. 26). Очевидно, условие В при переходе к
дополнительным множествам превращается в следующее условие:
В'. Всякая центрированная система *) замкнутых множеств
пространства X имеет непустое пересечение.
Так как в полурегулярном пространстве каждое замкнутое
множество есть пересечение всех содержащих его ха-множеств, то
полурегулярное (в частности, регулярное) пространство тогда и только
тогда бикомпактно, когда всякая центрированная система его
ха-множеств имеет непустое пересечение.
Заслуживает быть отмеченным и следующий критерий
бикомпактное™ (В. Зайцев [5]). Регулярное пространство X тогда
и только тогда бикомпактно, когда всякая направленная по
включению **) система £ = {А} его непустых канонических замкнутых
множеств имеет непустое пересечение.
10 (стр. 26). См., например, Александров [1], гл. 3, § 7.
11 (стр. 27). См. Александров [1], гл. 6, теорема 220 на
стр. 109.
*) Как известно (гл. III, § 1, п. 2), система множеств £ = {А)
называется центрированной, если любая конечная подсистема
системы £ имеет непустое пересечение.
**) Система | — {А} множеств называется направленной по
включению, если для любых двух элементов А\, А2 этой системы
имеется третий элемент А& содержащийся в них обоих: Аз £ Ai f) А*

122
ПРИМЕЧАНИЯ
12 (стр. 32). Принципиально важные обобщения примера А2,
приводящие к установлению новых интересных результатов,
содержатся в работе Р. Энгелькинга [1].
13 (стр. 33). Бикомпактность пространства U{ легко
устанавливается непосредственным применением критерия В.
14 (стр. 35). Свойство Й£ ь есть, конечно, не то свойство,
эквивалентность которого свойствам АглЬ и БгаЬ естественно доказывать.
Сама собою напрашивается гипотеза, что свойства АгйЬ и Бга ь
эквивалентны следующему свойству: В[ъ. Всякое открытое покрытие
пространства R, имеющее регулярную мощность ш, а^т^Ь,
содержит покрытие мощности <а.
А. С. Мищенко [2] показал, что в таком общем виде только
что высказанная гипотеза неверна, даже если ограничиться
важнейшим случаем финально компактных пространств (для
инициально компактных пространств все доказано в основном тексте гл. I,
теорема 3).
Введем следующую терминологию, которая в настоящее время
может считаться общепринятой.
Назовем пространство финально компактным в смысле
точек полного накопления, если всякое лежащее в нем
несчетное множество имеет хотя бы одну точку полного накопления
(без ограничения общности можно при этом ограничиться лишь
несчетными множествами регулярной мощности).
Назовем пространство финально компактным в смысле
покрытий или просто финально компактным, если каждое
его открытое покрытие содержит счетное покрытие. Аналогично
[а, Б]- компактность, как она сформулирована в Мемуаре, естественно
назвать[а, Б]-компактностью в смысле точек полного накопления,
оставив термин [а, Бикомпактного пространства для пространств,
удовлетворяющих условию ВгаЬ (т. е. для пространств [а, Б]
-компактных в смысле покрытий).
Из результатов § 3 этой главы вытекает, что всякое
пространство, финально компактное в смысле покрытий, будет финально
компактным и в смысле точек полного накопления.
А. С. Мищенко [2] строит вполне регулярное пространство,
финально компактное в смысле точек полного накопления, не
являющееся финально компактным в смысле покрытий.
ПРИМЕЧАНИЯ К ГЛАВЕ II
1 (стр. 42). Речь идет о знаменитом урысоновском примере
счетного связного пространства (см. П. С. Урысон, Труды по
топологии и другим областям математики, Гостехиздат, 1951, том I,
стр. 189).
В настоящее время имеются гораздо более простые примеры
этого рода, построенные Хьюиттом [2] и Бингом [1]. Е. Щепин
только что построил пример счетного связного хаусдорфова
пространства, в котором любое конечное число ха-множеств имеет не-

К ГЛАВЕ II
123
пустое пересечение. Пример пространства, состоящего из несчетного
множества попарно неотделимых точек, равно как и пример связного
компактного пространства мощности »it построила И. Л. Раухвар-
гер [1].
2 (стр. 43). Из этого рассуждения следует:
Если G и Н — два дизъюнктных открытых множества в любом
топологическом пространстве, то дизъюнктны и хо-множества
1[д] и /[//]• В самом деле, из G Г) Н =* Л последовательно вытекает
[0]ПЯ-Л, '[Я]П#=Л,
/[0]П[ЯЬЛ, /[0]П/[Я]-Л.
Отсюда, в свою очередь, следует:
Если два множества М и N в любом топологическом
пространстве имеют дизъюнктные окрестности ОМ и ON, то они имеют и
дизъюнктные канонические окрестности 1[ОМ] и I[ON] (заметим, что
для открытого G множество I[G] есть наименьшее каноническое
открытое множество, содержащее множество G).
3 (стр. 46). Дальнейшие интересные примеры регулярных, в
том числе и вполне регулярных ненормальных пространств,
построили А. Н. Тихонов [1], В. В. Немыцкий [1], [2], Ю. М.
Смирнов [1], [2], Е. Щепин [1] и другие. В работе Ю. М. Смирно-
ва [2] содержится, в частности, подробное исследование пространства
Немыцкого. В самое последнее время определены различные
естественно возникающие и потому интересные классы пространств,
«близких к нормальным». Это прежде всего квазинормальные
пространства Зайцева и далее полунормальные и х-нормальные
пространства *), определенные Е. Щепиным [1].
4 (стр. 53). Отсюда следует, что всякий счетный бикомпакт
метризуем (это означает в данном случае, что он гомеоморфен
некоторому замкнутому ограниченному множеству на числовой прямой).
5 (стр. 54). В предыдущих изданиях этого Мемуара термина
«совершенно нормальное пространство» не было — эти пространства
так и назывались «пространствами, удовлетворяющими условию
(Я)». Лишь значительно позже, в 1932 г., эти пространства были
названы совершенно нормальными Э. Чехом [1], который изучал
их в связи с проблемами теории размерности (см. ниже,
примечание10). В настоящее время сохранять первоначальное название
«пространств, удовлетворяющих условию (Я)» было бы
нецелесообразно. Совершенно нормальные пространства и, в частности,
совершенно нормальные бикомпакты оказались важным и интересным
предметом исследования в общей топологии. Они породили
обширную литературу (в том числе работы Э. Чеха [1], Даукера [2],
*) Пространство квазинормально (В. Зайцев [2]), если в нем
всякие два дизъюнктных я-множества имеют дизъюнктные
окрестности; заменяя в этом определении я-множества хй-множествами,
получим х-нормальные пространства (Е. Щепин), образующие
класс, более обширный, чем класс квазинормальных пространств.
Наконец, Е. Щепин называет пространство полунормальным, если
в нем всякие два дизъюнктных замкнутых множества содержатся
в дизъюнктных я-множествах.

124
ПРИМЕЧАНИЯ
А. В. Архангельского и В. Голштинского [1], В. И.
Пономарева [6], [7], В. Филиппова [1] и др.).
Совершенно нормальные бикомпакты образуют класс
бикомпактов, как бы непосредственно следующий (по сложности) за
компактами. Однако все компакты лежат в гильбертовом кирпиче и,
следовательно, распадаются на множество топологических типов,
имеющее мощность континуума, тогда как существует (В.
Филиппов [1]) множество попарно негомеоморфных совершенно
нормальных бикомпактов, мощность которого равна 2е. Этим В. Филиппов,
в частности, доказал, что среди совершенно нормальных
бикомпактов нет универсального (т. е. содержащего топологический образ
любого совершенно нормального бикомпакта) — решение задачи,
поставленной В. И. Пономаревым.
Отметим еще следующие интересные задачи, касающиеся
совершенно нормальных пространств; они также поставлены В. И.
Пономаревым и решены в самое последнее время.
1. Всякий ли совершенно нормальный бикомпакт содержит
счетное всюду плотное множество (является «сепарабельным»)? Юхас
(I. Juhasz) *) только что доказал, что утвердительный ответ на
этот вопрос В. И. Пономарева совместим с обычными аксиомами
теории множеств (так что, во всяком случае, все попытки
построения совершенно нормального несепарабельного бикомпакта
являются безнадежными).
2. Существует ли локально связный неметризуемый совершенно
нормальный бикомпакт?
В предположении что 2**° = кь В. Филиппов [1] построил
пример такого бикомпакта. В силу одной теоремы С. Мардешича этот
бикомпакт не может быть непрерывно отображен ни на какой
компакт У так, чтобы прообразы всех точек ^еУ при этом
отображении были нульмерны (чем решается еще одна задача В. И.
Пономарева). Однако остается нерешенным вопрос о построении
аналогичного примера без каких-либо предположений о. мощности
континуума.
6 (стр. 54). Естественность построения дескриптивной теории
множеств в несчетных совершенно нормальных бикомпактах стала
особенно убедительной после того, как В. И. Пономарев [7]
доказал для этих бикомпактов теорему о непустоте классов борелев-
ской классификации множеств (решив тем самым задачу,
поставленную еще со времени написания этого Мемуара).
7 (стр. 54). Нижеследующее рассуждение в основном
воспроизводит доказательство этой теоремы, данное в 1916 г. в моей
работе [9] для борелевских множеств.
8 (стр. 58). В любых топологических пространствах свойство
Линделёфа эквивалентно, во-первых, свойству наследственной
финальной компактности**), а во-вторых, следующему свойству Бэра—
Хаусдорфа:
*) Bull. Acad. Sci. Pol., ser. mathem., astron., phys. 18, No. 2
(1970), 71-74.
**) Пространство X наследственно финально компактно, если
всякое его подпространство финально компактно. При этом, если

К ГЛАВЕ II
125
Всякая вполне упорядоченная последовательность строго
убывающих замкнутых множеств состоит не более чем из счетного числа
элементов.
Доказательство*). Пусть в наследственно финально
компактном пространстве X дана несчетная система 2 = {Га}
открытых множеств. Тогда из покрытия 2 финально компактного
пространства Х0 в \Л Га можно выделить счетное подпокрытие того
же подпространства, т. е. свойство Линделёфа имеет место в X.
Обратно, если в X выполнено свойство Линделёфа, то всякое
открытое подпространство ГеХ, очевидно, финально компактно,
а тогда по только что сделанному замечанию финально компактно и
всякое подпространство пространства X.
Докажем эквивалентность свойства Линделёфа свойству Бэра.
Пусть пространство X обладает свойством Линделёфа и пусть
ф! zd ф2 ^ ... :эФа:э ... — вполне упорядоченная
последовательность строго убывающих замкнутых в л множеств. Требуется
доказать, что она не более чем счетна. Предположим противное — пусть
последовательность {Фа} несчетна. Если она имеет иррегулярную
мощность, то в ней содержится подпоследовательность несчетной
регулярной мощности, занумерованная всеми порядковыми числами,
меньшими чем некоторое несчетное начальное регулярное число сог»
Итак, можем с самого начала предположить, что наша
последовательность имеет вид
(1) Ф, :эФ2=> ... =>Фа=> ..., а<сот,
где со х — регулярное несчетное начальное число. Открытые
множества Та = Х\Фа образуют строго возрастающую
последовательность
(2) Г,сГ2с ... сгГас: ...,
занумерованную теми же a < cot. Но так как X обладает свойством
Линделёфа, то некоторая счетная подпоследовательность
(3) Га , ..., Га , ...
финально компактны все открытые подпространства Г£Х, то
финально компактно и всякое подпространство Хо с: X. В самом деле,
пусть a = {tfa} — какое-нибудь покрытие произвольного
пространства Х0 с X открытыми в нем множествами На. Берем для
каждого Я a какое-нибудь открытое в X множество Га с условием
Яа=ХП Га. Так как Г = (J Га — открытое и, значит, по предпо-
a
ложению финально компактное подпространство пространства Х% то
существует счетная подсистема 20 = {^ап) системы 2 — {Га},
покрывающая все Г; но тогда a0 = [Х0 (] rQ/j} есть счетная подсистема
системы а, покрывающая все пространство Хо.
*) См. Ю. М. Смирнов [3].

126
ПРИМЕЧАНИЯ
последовательности (2) должна покрывать все объединение Г =1|Га.
Но это невозможно: сот—регулярное начальное число, поэтому
существует а<сот, превосходящее все ап, и тогда (так как
последовательность (2) строго возрастающая) множество Га и тем более
все Г не может содержаться в объединении множеств,
составляющих последовательность (3).
Обратно из свойства Бэра следует свойство Линделёфа. В
самом деле, пусть в пространстве X со свойством Бэра дана несчетная
система а открытых множеств; объединение всех Га£о обозначим
через Г. Элементы Ga системы а можем считать занумерованными
посредством всех порядковых чисел, меньших некоторого
начального числа сот. Из полученной последовательности G\t G2, ...,Ga,...
... , a < o)t, выделяем подпоследовательность Gal, Gar ..., Ga^t ...
следующим образом: полагаем ai = 1 и, предполагая все а^, для
\' < Я выбранными, обозначаем через а^ первое такое число, что
Ga^ не содержится в М Ga , Пусть Г^ « М Ga ,. Очевидно,
Г\ « (J Оа; поэтому Г — (I Г\. Так как в пространстве X
свойской к
ство Бэра выполнено и последовательность открытых множеств {Га}
Строго возрастающая, то она счетная. Таким образом, счетной
является последовательность порядковых чисел ai, о&2, ..., a*,, ... и
множеств Ga^, дающих в сумме все Г, т. е. в пространстве X
свойство Линделёфа оказывается выполненным.
Итак:
8 классе бикомпактов совершенная нормальность эквивалентна
не только свойству Линделёфа (т. е. наследственной финальной
компактности), но и свойству Бэра.
Эта теорема обобщена Ю. М. Смирновым на класс регулярных
финально компактных пространств.
9 (стр. 59). Введение класса совершенно нормальных
бикомпактов произошло следующим образом. С самого начала совместной
работы над бикомпактными топологическими пространствами, в
1922 г., П. С. Урысоном и мною было высказано предположение, что
всякий несчетный бикомпакт с первой аксиомой счетности имеет
мощность континуума. То, что мощность такого бикомпакта не
меньше мощности континуума, было доказано легко (это утверждение
содержится в теореме 3 гл. II, § 2). Доказательство того, что
мощность всякого бикомпакта с первой аксиомой счетности не
превосходит мощности континуума, наталкнулось на трудности, которые
мы так и не смогли преодолеть. Поэтому в нашей совместной
работе [1] 1923 г. (а также в замечании 2 в конце § 2 этой главы)
была поставлена задача: доказать или опровергнуть это
предположение. Тем временем П. С. Урысон и я решили попытаться
определить более узкий класс бикомпактов, для которого проблема
мощности допускала бы решение. Так как бикомпакты с первой
аксиомой счетности характеризуются тем, что в них каждое
одноточечное множество есть пересечение счетного числа открытых множеств,

К ГЛАВЕ II
127
то естественно было перейти к бикомпактам, в которых пересечением
счетного числа открытых множеств является всякое замкнутое
множество. А это и есть совершенно нормальные бикомпакты. Для
них нам удалось решить проблему мощности (доказав теорему 7
гл. II).
Что же касается превоначальной проблемы о мощности любого
бикомпакта с первой аксиомой счетности, то, несмотря на
многочисленные усилия, она оставалась нерешенной в течение 45 лет. Лишь
в 1969 г. А. В. Архангельскому [5] удалось доказать, что
бикомпакт с первой аксиомой счетности имеет мощность, не
превосходящую мощность континуума.
Год спустя В. И. Пономарев [8] дал второе доказательство
этой теоремы, применив методы, разработанные им по другому
поводу, см. В. И. Пономарев [6]. Отметим в связи со сказанным
результат Б. Поспишила [1]: бикомпакт, ни в какой своей
точке не удовлетворяющий первой аксиоме счетности, имеет
мощность ^s 2*'. Так как мощность бикомпакта с первой аксиомой
счетности не может превосходить мощность континуума, а совершенно
нормальные (и даже метризуемые) пространства могут иметь
любую мощность, то возникает задача топологической характеристики
подпространств бикомпактов с первой аксиомой счетности (в
частности, подпространств совершенно нормальных бикомпактов).
10 (стр. 61). В предыдущих примечаниях указаны некоторые
связи, существующие между совершенно нормальными (в частности,
бикомпактными) пространствами и вопросами общей и
дескриптивной теории множеств. Совершенно нормальные пространства тесно
связаны также с построением теории размерности в достаточно
общих предположениях: именно по этому поводу они исследовались
Чехом и Даукером. Ю. М. Смирнов [4] доказал, что не только
для бикомпактов (как упомянуто в конце примечания6), но даже
для регулярных финально компактных пространств свойство
совершенной нормальности эквивалентно свойству наследственной
финальной компактности. Это заставляет нас здесь вернуться к
финально компактным (регулярным) пространствам и упомянуть еще
об одной их характеристике, данной также Ю. Смирновым (и
связанной с теорией размерности).
Еще в 1940 г. я заметил, что во всяком нормальном
пространстве X всякое замкнутое множество F является «совершенно
нормально расположенным> в том смысле, что каждая окрестность OF
множества F содержит меньшую окрестность 0[F, являющуюся
/^-множеством. Это замечание позволило мне доказать для случая
любых нормальных пространств основные теоремы теории
размерности (теоремы о «малых сдвигах», о «существенных отображен
ниях»), что в свою очередь позволило перенести на общий случай
нормальных пространств основные теоремы гомологической теории
размерности (см. П. С. Александров [11]).
Ю. М. Смирнов называет произвольное множество М
пространства X нормально расположенным в этом пространстве, если
каждая окрестность OF содержит /^-множество А = М (при этом в
определении Ю. М. Смирнова множество А может не быть
открытым). Ю. М. Смирнов доказывает следующую теорему:

128
ПРИМЕЧАНИЯ
Для того чтобы вполне регулярное пространство было
финально компактным, необходимо и достаточно, чтобы оно было
нормально расположенным в некотором бикомпакте (тогда оно будет
нормально расположенным и во всяком бикомпакте). Мы знаем, что
вполне регулярные пространства веса ^ т — это множества,
лежащие в тихоновском кирпиче /х; в силу теоремы Ю. М. Смирнова
финально компактные пространства — это в точности те множества,
лежащие в /т, которые нормально расположены в /т, а совершенно
нормальные пространства суть не что иное, как те множества
А £ /т, все подмножества которых нормально расположены в /т.
Добавим к этому еще и следующий результат Ю. М.
Смирнова*). Если X нормально, а Х0 нормально расположено в Я, то
dim Х0 £ dim X.
ПРИМЕЧАНИЯ К ГЛАВЕ III
1 (стр. 62). Термин «абсолютно замкнутый» мы применяем
здесь вполне последовательно, исходя из того, что никакие
пространства, кроме хаусдорфовых, в этом сочинении не
рассматриваются. В настоящее время пространства, названные здесь
абсолютно замкнутыми, обычно называются //-замкнутыми; литература,
относящаяся к ним, очень обширна. Среди самых
фундаментальных работ, имеющих дело с этими пространствами, назовем лишь
указанные в списке литературы работы А. Н. Тихонова, М. Ка-
тетова, С. В. Фомина, С. Илиадиса, Ю. Флаксмейера, Н. В.
Величко и др.
2 (стр. 65). В то же время существуют неабсолютно замкнутые
пространства, обладающие только что сформулированным (в
следствии 2) свойством. Первое такое пространство построил Г.
Киртадзе [1].
3 (стр. 66). Это следствие можно очень просто доказать,
опираясь на определение бикомпактности посредством свойства В
(«каждое открытое покрытие пространства содержит конечное
покрытие этого пространства»), В самом деле, пусть у — {Оа}— какое-
нибудь открытое покрытие регулярного абсолютно замкнутого
пространства R. Для каждой точки х е R берем некоторое содержащее
эту точку множество Оа (х) е Y и такую окрестность Ох, что
[Ох]^Оа(Х). По теореме 2 существует такое конечное множество
этих Ох — пусть это будут 0*1, ..., Ох„ — что [Oxi] U ... U [Оха]=*
-#; так как [Oxt]sOa^ при /-I, 2,..., s, то Оа^х^ (J ...
... [}Оа/х ч»/?. Итак, R бикомпактно.
4 (стр. 66). Эта теорема может быть сформулирована и так:
Среди всех регулярных (соответственно вполне регулярных,
соответственно нормальных) пространств бикомпакты суть
единственные пространства, не имеющие никакого регулярного (даже
*) Который и был основным поводом к введению понятия
нормального расположения.

К ГЛАВЕ III
129
хаусдорфова) — соответственно вполне регулярного, соответственно
нормального — расширения (отличного от исходного пространства).
В следующей главе будет доказано, что локально бикомпактные
пространства суть единственные пространства, имеющие
минимальное (т. е. получаемое присоединением единственной точки)
бикомпактное расширение. Эти результаты (а также проблемы,
поставленные в комментируемой главе) позволяют считать, что большой
отдел общей топологии, известный под названием стеории
бикомпактных (а также //-замкнутых) расширений», ведет свое начало от
комментируемой сейчас главы. Однако собственно развитие теории
бикомпактных расширений открывается несомненно
фундаментальными работами А. Н. Тихонова, в которых доказывается
существование бикомпактных расширений у всех вполне регулярных, и
только у этих, пространств и при этом доказывается существование у
вполне регулярного пространства данного веса т бикомпактного
расширения того же веса т. Далее (1936) следуют работы М. Стоуна
и Чеха, строящих для каждого вполне регулярного пространства X
единственное его максимальное или стоун-чеховское расширение fiX.
При построении расширения рХ Чехом применяется метод А. Н.
Тихонова*). Совсем другим методом (оказавшимся впоследствии
весьма плодотворным во многих общетопологических исследованиях)
расширение X строится в 1939 г. в моей работе [2].
В 1951 г. Ю. М. Смирнов строит для любого вполне
регулярного пространства X все его хаусдорфовы бикомпактные
расширения ЬХ. Ю. М. Смирнов достигает этой цели, показывая, что
бикомпактные расширения данного пространства X находятся в
естественном взаимно однозначном соответствии с так называемыми
«близостями» в смысле Ефремовича, которые можно определить в
пространстве X (т. е. которые согласуются с топологией этого
пространства). Данную В. А. Ефремовичем аксиоматику «пространств
близости» можно перефразировать различными способами. Одной
из наиболее удобных перефразировок представляется мне
предложенная В. И. Пономаревым (в совместных со мною работах [1], [2])
и заменяющая понятие близости между двумя (замкнутыми)
множествами F и Ф понятием подчинения (или усиленного включения)
одного из этих замкнутых множеств, скажем Z7, открытому
множеству Н - Х\Ф.
При этом подчиненность замкнутого множества F открытому
множеству Н обозначается через F < Н и удовлетворяет
следующим аксиомам:
К1. Если F<H, то Х\Н <X\F.
К2. Если F < Я, то F <= //.
КЗ. Если F,cF<//c//broF,< //,.
К4. Если Fi < Ни F2 < #2, то F, (J F2 < Нх U //*
К5. Если F < Н, то существует такая окрестность OF
множества F, что F <OF^ [OF] < И.
Кб. Для пустого множества Л имеем Л < Л.
*) Восходящий — в частном случае пространств со счетной
базой—еще к П. С. Урысону (см. выше гл. V, § 2).

130
ПРИМЕЧАНИЯ
К7. Для каждой точки х и произвольной ее окрестности Ох
имеется такая окрестность 0\Х, что [0\х] < Ох*).
Первыми примерами подчинений было введенное мною в 1939 г.
в работе [2] «вполне регулярное подчинение»: F < Я, если
множества F и Х\ Я функционально отделимы.
Каждому подчинению v, удовлетворяющему условиям К1—К7,
соответствует однозначно определенное бикомпактное (хаусдорфово)
расширение vX пространства: точками пространства vX, по
определению, являются так называемые и-концы, т. е. максимальные
центрированные семейства £ — W открытых множеств,
удовлетворяющих следующему условию: для каждого Яе5 имеется Hi е £ с
[НЛ < Я.
Множество vX всех и-концов тополигизируется так же, как в
указанной работе [2], а именно: если Я открыто в X, то через Ун
обозначается множество всех концов, содержащих Я в качестве
элемента. Обратно, каждое бикомпактное расширение ЬХ вполне
регулярного пространства X получается как пространство vX при
однозначно определенном подчинении и: надо положить F < Я, если
[F]bx^T, где Г — какое-нибудь (например, наибольшее) такое
открытое в X множество, что X (] Г = Я. Это и есть — с точностью до
словесной переформулировки — основная теорема Ю. М. Смирнова
о бикомпактных расширениях.
Еще один шаг в смысле наглядного истолкования этой теоремы
сделал В. Зайцев в уже цитированной работе [1] (см. примечание4
к гл. I): Всякая хаусдорфова система окрестностей замкнутых
множеств во вполне регулярном пространстве определяет подчинение
v (и следовательно, бикомпактное хаусдорфово расширение vX
пространства X): подчинение v получаем, положив сначала F<U(F),
где 0(F)—произвольная отобранная окрестность множества F, и
затем F < Я, если найдется такое замкнутое множество F\ и такая
отобранная окрестность U(F\), что Fг F\ <U(F\) £ Я. Обратно,
всякое подчинение определяет систему отмеченных окрестностей:
достаточно считать окрестность Н — U(F) отмеченной, если F < Я.
5 (стр. 66). Как известно, класс ЭР топологических пространств
называется наследственным (соответственно наследственным «по
множествам данного типа», — например, по замкнутым, открытым,
по Fa-множествам, по всюду плотным множествам и т. п.), если
все подпространства всякого пространства класса Ж
(соответственно подпространства, являющиеся множествами данного типа) также
принадлежат классу Jif. Так, класс 7\-пространств, /«О, 1, 2, 3, 3—,
есть наследственный класс; класс (нормальных пространств)
наследствен лишь по F а -множествам. Класс полурегулярных
пространств наследствен по всюду плотным множествам, так же как и
введенный В. Зайцевым класс 7\-пространств (см. примечание7
к гл. I).
*) Вместо этого можно было бы просто потребовать, чтобы
х < Ох\ однако иногда данная в тексте формулировка аксиомы К7
предпочтительнее (она позволяет, например, рассматривать
подчинения в «ограниченном запасе» множеств).

К ГЛАВЕ III
131
Назовем класс Ж топологических пространств
^'-унаследованным (В. Зайцев), если Х'^Ж и каждое пространство X
класса Ж имеет расширение X е Ж'. Особенно важен, конечно, случай,
когда Ж' есть подкласс класса Ж, состоящий из всех бикомпактных
пространств, принадлежащих классу Ж, — тогда говорим, что
класс Ж бикомпактно унаследованный.
А. Н. Тихонов доказал, что классы вполне регулярных и
нормальных пространств являются бикомпактно унаследованными
(таковы классы Т\ и Го-пространств, а также класс всех Г-пространств).
При этом класс вполне регулярных пространств является
наибольшим бикомпактно унаследованным подклассом в классе хаусдорфо-
вых и в классе регулярных пространств (которые сами не являются
бикомпактно унаследованными).
Как показал В. Зайцев, класс Гх-пространств является
бикомпактно унаследованным, и притом наибольшим бикомпактно
унаследованным подклассом в классе полурегулярных пространств: это
следует из того, что Г х,-пространства и только они имеют
полурегулярные бикомпактные расширения и всякое бикомпактное
полурегулярное пространство есть /^-пространство. Сам же класс
полурегулярных пространств не является бикомпактно унаследованным
(это следует из существования построенного Е. Щепиным примера
полурегулярного пространства, не являющегося 7\-пространством).
Наконец, назовем класс Ж бикомпактно полным, если
бикомпактное пространство X класса Ж не имеет отличного от самого
X бикомпактного расширения, принадлежащего классу Ж. Если
данный класс Ж топологических пространств бикомпактно полон, то
тем же свойством обладает и всякий подкласс Жо класса Ж. Класс
хаусдорфовых пространств (в отличие от класса Ггпространств)
бикомпактно полон, поэтому тем же свойством обладают классы
регулярных, вполне регулярных, нормальных пространств и т. д.
Из результатов В. Зайцева вытекает, что класс полурегулярных
(а значит, введенный Зайцевым меньший класс 7\-пространств)
бикомпактно полон.
6 (стр. 69). Это вопрос, действительно, оказался трудным. Его
утвердительное решение получили: сначала М. Стоун [1], потом
Катетов [1] и С. В. Фомин [1]. Обзор некоторых основных
относящихся сюда результатов см. в моей работе [4], § 4, п. 4.
7 (стр. 72). А. Н. Тихонов, доказав существование для
каждого вполне регулярного пространства бикомпактного расширения,
доказал в той же работе [1], что каждое хаусдорфово пространство
X содержится в некотором абсолютно замкнутом Х\. Но он не
доказал существования абсолютно замкнутого расширения
пространства X, т. е. не построил абсолютно замкнутого пространства Хи
содержащего X в качестве всюду плотного подпространства. Этот
последний результат получили Катетов [1], [2] и С. В. Фомин [1].
8 (стр. 79). Понятие счетно нормального пространства*)
осталось в стороне от основного направления развития теории тополо-
*) В первоначальном тексте Мемуара эти пространства
назывались квазинормальными.

132
ПРИМЕЧАНИЯ
гических пространств, вызвавшего те обобщения нормальных
пространств, о которых шла речь в примечании2 к гл. II.
Заметим, что счетнонормальное пространство UAt о котором
говорится в тексте, вполне регулярно (как подпространство
бикомпакта). Я не знаю, существуют ли не вполне регулярные счетно
нормальные пространства. С другой стороны, известное
пространство Немыцкого является примером вполне регулярного не счетно
нормального пространства.
ПРИМЕЧАНИЯ К ГЛАВЕ IV
1 (стр. 80). Понятие локальной компактности впервые введено
мною в работе [8].
Вопрос о том, когда множество Е «естественно назвать»
бикомпактным в пространстве X, не так прост, как кажется с первого
взгляда. В. И. Пономарев предлагает называть множество
бикомпактным в X, если каждая последовательность *) {*$}, 9е9, точек
xq ^ Е по любому направленному множеству 0 содержит
подпоследовательность, сходящуюся к некоторой точке xga, это
определение эквивалентно следующему: Множество £ = Х бикомпактно в X
тогда и только тогда, когда его замыкание [Е] ъ X есть бикомпакт.
Эта эквивалентность нарушается (как показал А. В.
Архангельский), если определять бикомпактность множества в пространстве
посредством точек полного накопления.
В эпоху, когда писался этот Мемуар, т. е. почти полстолетия
тому назад, теорема Больцано — Вейерштрасса (ее называли и
«принципом Больцано — Вейерштрасса») занимала в сознании
математиков гораздо более значительное место, чем скромная «лемма
Бореля — Лебега» Поэтому и для авторов этого Мемуара
определение бикомпактных пространств посредством точек полного
накопления было бесспорно первым и основным среди трех эквивалентных
определений, порядок которых — Л, Б, В—в формулировке
основной теоремы 3 гл. I как бы отражает сравнительный «вес» каждого
из этих определений. Однако дальнейшее исследование понятия
бикомпактное™ и ее последовательных обобщений заставляло все
более убеждаться в том, что основной подход к понятию биком-
пактности дается открытыми покрытиями или, что то же,
центрированными семействами замкнутых множеств, а не точками полного
накопления: это мы прежде всего видим в таких обобщениях
понятия бикомпактности, какими является [а, Б]- компактность, в
частности, финальная компактность, Я-замкнутость (которую так и не
*) О последовательностях по данному направленному
множеству, их подпоследовательностях и их сходимости см., например,
мою работу [4], § 1; п. 8 или книгу Келли, Общая топология,
«Наука», 1968. Там же приводится.
Теорема. Топологическое пространство бикомпактно тогда и
только тогда, когда каждая последовательность его точек по
любому направленному множеству содержит сходящуюся
подпоследовательность.

К ГЛАВЕ IV
133
удается определить посредством точек полного накопления), биком-
пактность множества £ в пространстве X и наконец, важнейшее из
всех обобщений бикомпактности — паракомпактность.
Тем более замечателен тот факт, что сама бикомпактность
может быть выражена и через точки полного накопления,
существование которых для любого бесконечного множества пространства
есть и остается не только исторически первым, но и самым
наглядным и — вместе с замкнутостью во всяком объемлющем
пространстве — самым ярким выражением бикомпактности топологического
пространства.
2 (стр. 83). Проще было бы сказать: Множество Е сходится по
мощности к точке х е /?, если для любой окрестности Ох этой
точки имеем
мощн. {Е \ Ох) < мощн. Е.
Множество £, лежащее в бикомпакте /?, сходится по мощности
к точке х тогда и только тогда, когда х есть единственная точка
полного накопления множества Е. Доказательство проводится
автоматически и может быть предоставлено читателю.
3 (стр. 87). Ю. М. Смирнов предложил следующее очень
простое доказательство основного утверждения теоремы 2:
Если пространство R бикомпактно в своей неизолированной
точке xt то существует бесконечное множество Е, сходящееся по
мощности к точке х.
Без ограничения общности можно предположить (как и в
основном тексте), что R— бикомпакт. Так как х — неизолированная точка,
то /?\* не бикомпактно (если бы пространство R \х было
бикомпактным, то оно было бы абсолютно замкнутым, между тем как его
можно пополнить неизолированной точкой х до пространства R),
Так как пространство /?\ х не бикомпактно, то в нем существует
бесконечное множество £, не имеющее ни одной точки полного
накопления в пространстве R. Но тогда х есть единственная точка
полного накопления множества Е в пространстве R и, значит, Е
(см. предыдущее примечание) сходится по мощности в R к точке х.
4 (стр. 88). Задача действительно оказалась и трудной и
важной — последнее потому, что она оказалась связанной с изучением
целого класса так называемых экстремально несвязных *)
пространств, а эти последние суть не что иное, как абсолюты
топологических пространств. См. по этому поводу, кроме
основополагающей работы В. И. Пономарева [4], также работы С.
Илиадиса [1], В. И. Пономарева [5], а также мою обзорную статью [5],
где подробно изложена и история вопроса.
Однако первый пример бикомпакта, не содержащего ни одной
х-точки, построил А. Н. Тихонов (1935 г.) в работе [2]. Этот пример
изложен в моей книге [1], стр. 403—406.
Пространство |W, где N состоит из счетного множества
изолированных точек, построенное Чехом в 1936 г. (см. [2]), также
отвечает на этот вопрос.
*) Пространство называется экстремально несвязным (Хьюитт),
если в нем замыкание каждого открытого множества открыто.

134
ПРИМЕЧАНИЯ
ПРИМЕЧАНИЯ К ГЛАВЕ V
1 (стр. 93). Проблема метризации со времени первых
специальных работ по теории топологических пространств принадлежала к
центральным проблемам общей топологии, определившим во многих
отношениях пути ее развития.
В настоящее время дано несколько решений этой проблемы,
т. е. несколько (естественно, эквивалентных между собою)
формулировок условий, необходимых и достаточных для того, чтобы
данное топологическое пространство было гомеоморфно метрическому.
Приведем основные из этих решений.
1) Назовем множество покрытий 2 = {у) пространства X
измельчающимся, если, какова бы ни была точка х и ее окрестность
Ох, в множестве 2 найдется такое у» что звезда точки х
относительно покрытия у (т- е. объединение всех элементов этого
покрытия, содержащих точку *) лежит в Ох. Первое решение общей
проблемы метризации, впервые данное П. С. Урысоном и мною в
работе [1], состоит в следующем. Пространство X тогда и только
тогда метризуемо, когда в нем существует счетное измельчающееся
множество 2 (открытых) покрытий, удовлетворяющее следующему
условию:
(Д) Покрытия у» образующие множество 2, могут быть
занумерованы в виде последовательности
Y1.Y2,..., Yn. ...
таким образом, что объединение любых двух пересекающихся
элементов (п -Ь 1)-го покрытия содержится в некотором элементе л-го
покрытия (при любом п = 1, 2, 3, ...).
П. С. Урысон и я воспринимали условие (А) как существенный
недостаток данного нами критерия метризуемости: наши
возражения вызывал тот факт, что в условие Д входит некоторая
определенная нумерация множества покрытий, превращающая это множество
в последовательность.
Но вот двадцать лет спустя после опубликования первого
решения общей проблемы метризации и введения (в моей работе [7])
понятия локально конечного покрытия Дьедонне [1] определяет
понятие паракомпактного пространства, сразу делающееся одним
из основных понятий общей топологии*). Это позволяет Бингу [1]
*) Покрытие пространства называется локально конечным, если
каждая точка пространства имеет окрестность, пересекающуюся
лишь с конечным числом элементов данного покрытия. Это понятие
позволило подойти к обобщению бикомпактности в совершенно
новом направлении и получить следующие определения:
Пространство X называется паракомпактным (Дьедонне [1]),
если во всякое его открытое покрытие можно вписать локально
конечное открытое покрытие (говорим, что покрытие а' вписано в
покрытие а, если каждый элемент покрытия а' содержится хотя бы
в одном элементе покрытия а).

К ГЛАВЕ V
135
и В. И. Пономареву [2] заменить в приведенном только что
критерии метризуемости условие (Л) требованием паракомпактности
пространства X и тем самым этому критерию следующую
окончательную форму:
Первый общий критерий метризуемости (AU).
Топологическое пространство А метризуемо тогда и только
тогда, когда оно является паракомпактом (т. е. парокомпактным хаус-
дорфовым пространством), содержащим счетное измельчающееся
множество открытых покрытий.
Открытие паракомпактных пространств произвело решительный
сдвиг во всех исследованиях, связанных с общей проблемой
метризации. Произошло это посредством следующих двух замечательных
теорем, доказанных А. Стоуном [1].
Для формулировки первой теоремы А. Стоуна надо ввести
следующее определение. Скажем, что покрытие а' пространства X
является звездным измельчением покрытия а (или звездно вписано
в него), если звезда всякой точки х относительно покрытия а'
содержится в некотором элементе покрытия а. Первая теорема
А. Стоуна состоит в том, что пространство X тогда и только тогда
является паракомпактом, когда оно регулярно и обладает тем
свойством, что для каждого открытого покрытия а имеется
открытое покрытие а', являющееся звездным измельчением покрытия а.
Вторая теорема А. Стоуна легко следует из первой; она
утверждает, что всякое метрическое пространство паракомпактно.
Ясно, что «условие А» в первой общей метризационной теореме
является некоторым ослаблением условия звездной вписанности; из
первой теоремы А. Стоуна легко следует, что условие А всегда
осуществимо в паракомпактных пространствах. Но связь
паракомпактности с метризуемостью гораздо глубже. Оказывается, регулярное
пространство X паракомпактно тогда и только тогда, когда для
всякого открытого покрытия © пространства X имеется
©-отображение этого пространства на некоторое метрическое
пространство *).
2) Последующие общие метризационные критерии — это прежде
всего критерии Бинга и Нагата — Смирнова (полученные почти
одновременно в 1950—1951 гг.): условиями метризуемости
топологического пространства являются следующие условия:
(NS) (Нагата [1] — Смирнов [5]). Пространство X
должно быть регулярным и иметь а-локально конечную базу (т. е. базу,
являющуюся объединением счетного числа локально конечных
систем открытых множеств).
*) Отображение / пространства X в пространство Y
называется ©-отображением (где © — некоторое покрытие пространства X),
если каждая точка уеУ имеет окрестность Оу, полный прообраз
f~lOy которой лежит в некотором элементе покрытия со. Эта
теорема впервые доказана (но даже не сформулирована!)
Даукером [1]; впервые сформулирована и доказана М. Катетовым [3]
а примечаниях к книге Э. Чеха, вновь сформулирована и доказана
В. И. Пономаревым [3].

136
ПРИМЕЧАНИЯ
(В) (Бинг [1]). Пространство X должно быть регулярным и
иметь базу, являющуюся объединением счетного числа дискретных
систем множеств*).
Казалось, что этими критериями проблема метризации
исчерпана до конца. Однако в 1960 г. я предложил [11] еще один общий
критерий метризуемости, позволяющий, как мне кажется, подойти
к проблеме метризации с существенно новой стороны. Я называю
базу ЯЗ топологического пространства X равномерной, если
каковы бы ни были точка х и ее окрестность Ох, в базе SB имеется лишь
конечное число элементов, содержащих точку х и пересекающихся
сХ \Ох.
Оказывается:
(А) Для того чтобы пространство X было метризуемым,
необходимо и достаточно, чтобы оно было паракомпактом и имело
равномерную базу.
Связь между свойствами паракомпактности и метризуемости
пространств достаточно выяснена теоремой об ©-отображениях
паракомпактов на метризуемые пространства (см. выше). Эта
теорема делает естественным вопрос: что надо прибавить к
паракомпактности, чтобы получить метризуемость?
Из сказанного в этом примечании следует, что достаточно
прибавить любое из двух условий:
1) существование счетной измельчающейся системы покрытий;
2) существование равномерной базы.
Заметим, что второе условие является усилением первой
аксиомы счетности. В самом деле, легко видеть, что база равномерна
тогда и только тогда, когда всякое бесконечное (в частности, всякое
счетное) множество ее элементов, содержащих данную
(произвольную) точку, образует базу пространства в этой точке**).
Что касается связи между самой первой аксиомой счетности и
метризуемостью, то ее до конца выясняет следующая замечательная
Теорема Пономарева. Топологическое пространство
удовлетворяет первой аксиоме счетности тогда и только тогда, когда
оно является образом некоторого метрического пространства при
некотором непрерывном открытом отображении***).
Это положение вещей позволило мне-легко закончить работу [12]
следующими словами:
«П. С. Урысон в самом начале своих занятий проблемой
метризации высказал гипотезу, что условие метризуемости должно
получиться в результате одновременного усиления с одной стороны
аксиом отделимости, а с другой — первой аксиомы счетности. Наш
*) Система 2 множеств, лежащих в пространстве X,
называется дискретной, если каждая точка пространства X имеет
окрестность, пересекающуюся не более чем с одним элементом данной
системы 2.
**) Более того, всякая равномерная база является точечно
счетной (см. мою работу [12],стр. 136).
***) Как известно, отображение f: X-+Y называется открытым,
если образ /Г всякого открытого в пространстве X множества Г
есть множество, открытое в пространстве Y.

К ГЛАВЕ V
137
результат придает точное содержание этой гипотезе П. С. Урысона
и доказывает ее спустя 35 лет после его смерти».
Замечание. Интересно было бы посредством специализации
теоремы Пономарева охарактеризовать совершенно нормальные
бикомпакты, а также все бикомпакты с первой аксиомой счетности.
Несколько усилив понятие равномерной базы, А. В.
Архангельский [2] смог заменить в формулировке моей теоремы
требование паракомпактности аксиомой отделимости Т\ и, не меняя
существа дела, придать только что изложенному критерию следующую
форму. Архангельский называет базу SB пространства X регулярной,
если, каковы бы ни были точка х и ее окрестность Ох, существует
такая окрестность 0\Х s Ох, что в базе имеется лишь конечное
число элементов, одновременно пересекающихся с 0\Х и с Х\Ох.
Оказывается, из существования в ^-пространстве X регулярной
базы вытекает паракомпактность и регулярность этого пространства
(тогда как из существования равномерной базы следует лишь
слабая паракомпактность*) этого пространства). Таким образом,
предложенный мною критерий переходит в следующий:
(А') 7>пространство X метризуемо тогда и только тогда, когда
в нем имеется регулярная база.
Архангельскому принадлежат и другие критерии метризуемости,
с которыми читатель может познакомиться в его работах.
В этом Мемуаре общие критерии метризации не
рассматриваются, а доказываются лишь классические метризационные теоремы
для бикомпактных, локально бикомпактных пространств, а также
для пространств со счетной и локально счетной базой.
2 (стр. 98). Как мы знаем, наследственная финальная
компактность бикомпакта эквивалентна его совершенной нормальности
(см. гл. II, § 3, п. 12, теорема 6 и примечание8 к гл. II).
3 (стр. 102). По существу здесь построено топологическое
отображение x-*-f(x) в основной параллелепипед гильбертова про-
странства **), где
#ги_Ш*1 Mi ЬМ. \в*
V 2 * 22 ••••' оп ••••lc=i •
Это построение, обобщенное на случай несчетного множества
канонических пар Лп и функций /п» составляет основу результатов
А. Н. Тихонова (о топологическом отображении любого вполне
регулярного пространства X веса т в «тихоновский кирпич» /т) и
*) Система 2 множеств, лежащая в пространстве X, называется
точечно конечной (точечно счетной), если каждая точка
пространства принадлежит лишь конечному (не более чем счетному) числу
элементов системы 2. Пространство называется слабо (или
точечно) паракомпактным, если во всякое его открытое покрытие
можно вписать точечно конечное (открытое) покрытие.
**) Состоящий из всех точек у = (у\, у2, . .., уп, ...) гильбертова
пространства, для которых О^уп^-^г; см., например, мою книгу
[1], гл. 6, § 2, стр. 232.

138
ПРИМЕЧАНИЯ
Чеха (о существовании максимального бикомпактного расширения
рХ). См., например, мою книгу [1], Прибавление I к гл. 7, теоремы
11 и 12 (стр. 392—402) и в особенности мою статью [3], § 4, где
подробно изложена теория пространства рХ.
4 (стр. 106). Поставленная здесь задача решена Ю. М.
Смирновым [7], доказавшим следующую теорему: Если бикомпакт X
есть объединение двух (любых) подпространств со счетной базой, то
он сам имеет счетную базу и, следовательно, метризуем. Этот
результат очень усилен А. В. Архангельским [1], доказавшим
следующую общую аддиционную теорему: Если бикомпакт X есть
объединение не более чем т слагаемых (т —любое бесконечное
кардинальное число), каждое из которых есть подпространства веса
^ т пространства X, то X имеет вес ^ т.
5 (стр. 113). Это предложение верно и без предположения
локальной аксиомы счетности: всякое метризуемое пространство имеет
точечно счетную базу — это вытекает как из метризационной
теоремы Нагата — Смирнова, так и из предложенного мною
метризационного критерия *). В самом деле: и всякая а-локально конечная
база (Нагата — Смирнова), и всякая равномерная база являются
точечно счетными. Поэтому интерес приводимого ниже
доказательства состоит лишь в его элементарности (и в том, что оно было
первым по времени). Заметим еще, что равномерная база характе-
изуется тем, что всякое бесконечное счетное множество элементов
азы, содержащих данную произвольную точку х, образует базу
этой точки в данном пространстве.
6 (стр. 115). Требование нормальности может быть здесь
заменено требованием регулярности, так как всякое регулярное
пространство со счетной базой нормально (А. Н. Тихонов — см.,
например, Ф. Хаусдорф [1], стр. 138).
7 (стр. 115). Как заметил впервые Ю. М. Смирнов [5],
теоремы И, 12, 1Г могут быть дополнены следующим предложением:
Для того чтобы регулярное пространство одновременно было
метризуемым и удовлетворяло локальной аксиоме счетности,
необходимо и достаточно, чтобы оно имело звездно счетную базу.
8 самом деле, условие достаточно, так как из него следует,
что пространство распадается в дискретную сумму регулярных
подпространств, каждое из которых имеет счетную базу и,
следовательно, метризуемо. А тогда и все пространство метризуемо (см. § 3,
п. 7, доказательство теоремы 7). Необходимость условия вытекает
из следствия теоремы 8.
8 (стр. 115). Ответ на этот последний поставленный в Мемуаре
вопрос дан А. С. Мищенко [1], доказавшим, что всякий
бикомпакт, имеющий точечно счетную базу, метризуем, и, следовательно,
имеет счетную базу. Мищенко доказал даже больше, а именно, что
всякая точечно счетная база в бикомпакте является счетной.
Отсюда следует, что и всякое локально бикомпактное пространство
с точечно счетной базой является локально метризуемым
пространством с точечно счетной базой и, следовательно, метризуемо (по
теореме И).
*) См. примечание ! к этой главе.

СПИСОК ЛИТЕРАТУРЫ, ЦИТИРОВАННОЙ
В ПРЕДИСЛОВИИ И ПРИМЕЧАНИЯХ
Александров П. С.
[1] Введение в общую теорию множеств и функций, Гостехиздат,
1948.
[2] О бикомпактных расширениях топологических пространств,.
Матем. сб. 5 (47) (1939), 403—424.
[3] О понятии пространства в топологии, УМН 1 (17) (1947),
5—57.
[4] О некоторых новых результатах в теории топологических
пространств, полученных за последние двадцать пять лет,
УМН 15, №2 (92) (1960).
(5] О некоторых основных направлениях в общей топологии,
УМН 19, №6 (1964), 3—46.
[5а] К пономаревской теории абсолютов, ДАН СССР 161 (1965),
263-266.
[6] Sur les proprietes locales des ensembles et la notion de com-
pacticite, Bull. Acad. Polonaise, ser. A. 1923, 9—12.
[7] Sur les ensembles de la premiere classe et les espaces abstraits,
Compt. rend. Acad. Sci. Paris 178 (1924), 185—187.
[8] Ueber die Metrisation der im kleinen kompakten topologischen
Raumen, Math. Ann. 92 (1924), 294—301.
[9] Sur la puissance des ensembles mesurables В, С R. Acad. Sci.
Paris 162 (1916), 323—326.
[10] Ueber stetige Abbildungen kompakter Raume, Proc. Acad. Sci.
Amsterdam 28 (1925), 997—999; Math. Ann. 96 (1927), 555—
571.
[11] On the dimension of normal spaces, Proc. Roy. Soc. London
189 (1947), 11-39.
[12] О метризации топологических пространств, Бюлл. Польской
Акад. наук, сер. матем., 8 (1960), 135—140.
[13] Zur Begrundung der /i-dimensionalen mengentheoretischen To-
pologie, Math. Ann. 94 (1925), 296—308.
[14] О размерности бикомпактных пространств, ДАН СССР 26
(1940), 627—630.
Александров П. С. и Урысон П. С.
[1] Sur les espaces topologiques compacts, Bull. Acad. Sci.
Polonaise., ser. A, 1923, 5—8.
[2] Zur Theorie der topologischen Raume, Math. Ann. 92 (1924),
258—266.
[3] Une condition necessaire et suffisante pour qu'une classe (L)
soit une classe (D), C. R. Acad. Sci. Paris 177 (1923), 1274—1277.
Александров П. С. и Хопф (Hopf H.)
[1] Topologie I, Berlin, Springer, 1935-

140
СПИСОК ЛИТЕРАТУРЫ
Архангельский А. В.
[1] Аддиционная теорема для веса множеств, лежащих в
бикомпактах, ДАН СССР 126 (1959), 239—240.
[2] О внешних базах множеств, лежащих в бикомпактах, ДАН
СССР 132 (1960), 495—496.
[3] О метризации топологических пространств, Бюлл. Польской
Акад. наук, сер. матем., 8, № 9 (1960), 589—595.
[4] Новые критерии паракомпактности и метризуемости
произвольного 7Упространства, ДАН СССР 141 (1961), 13—15.
[5] Бикомпактные множества и топология пространства, ДАН
СССР 150 (1963), 9—12.
[6] О мощности бикомпактов с первой аксиомой счетности, ДАН
СССР 187 (1969), 967—970.
Архангельский А. В. и Голштинский В.
(Holsztynski W.)
[1] Sur les reseaux dans les espaces topologiques, Bull. Acad. Pol.
Sci., ser. math., 11, № 8 (1963), 493—497.
Б инг (Bing R. H.)
[1] Metrization of topological spaces, Canad. Math. J. 3 (1951),
175—186.
Величко H. B.
[1] Я-замкнутые топологические пространства, Матем. сб. 70,
No 1 (1966), 98—112.
[2] К теории //-замкнутых топологических пространств, Сиб.
матем. ж. 8, № 4 (1967), 754—763.
Виеторис (Viеtоris L.)
[1] Stetige Mengen, Monatsh. f. Math. u. Phys. 31 (1921).
[2] Bereiche zweiter Ordnung, Monatsh. f. Math. u. Phys. 32
(1922).
Гельфанд И. M. и Колмогоров A. H.
[1] О кольцах непрерывных функций на топологических
пространствах, ДАН СССР 22 (1939), 11—15.
Генриксен и Исбелл (Henriksen М. and Isbell J. R.)
[1] Some properties of compactifications, Duke math. J. 25 (1958),
83—106.
Гилман и Джерисон (Gillman L. and Jerison M.)
[1] Rings of continuous functions, Princeton, 1960.
Даукер (DowkerG. M.)
[1] An extension of Alexandroffs mapping theorem, Bull. Amer.
math. soc. 64 (1951), 219—229.
[2] С. H. Dowker, Local dimension of normal spaces, Quart. J.
Math. Oxford (2) 6 (1955), 101-120.
Дьедонне (Dieudonne J.)
[1] Une generalisation des espaces compacts, J. math, pures
appl. 23 (1944), 65—76.
Зайцев В.
[1] К теории тихоновских пространств, Вестн. Моск. ун-та, сер.
матем. и мех., 1967, 48—57.
[2] О некоторых классах топологических пространств и их
бикомпактных расширениях, ДАН СССР 178 (1968), 778—
779.

СПИСОК ЛИТЕРАТУРЫ
[3] Finite spectra of topological spaces and their limit soaces
Math. Ann. 179 (1969), 153-179. P S'
[4] О бикомпактных полурегулярных и хаусдорфовых оасшиое-
ниях, ДАН СССР 182 (1968), 27-30. F И
[5] Бесконечные спектры топологических простраств и их
предельные пространства, ДАН СССР 185 (1969), 20—23.
[6] О спектральной теории абсолютов топологических
пространств, их полноте и бикомпактности, ДАН СССР (1970)
(в печати).
Илиадис С.
[1] Абсолюты хаусдорфовых пространств, ДАН СССР 149 (1963),
22—25.
[2] О некоторых свойствах абсолютов, ДАН СССР 152 (1964),
798—800.
[3] Характеризация пространств при помощи Я-замкнутых
расширений, ДАН СССР 149 (1963), 1015—1018.
Илиадис С. и Фомин С. В.
[1] Метод центрированных систем множеств, УМН 21, № 4
(1966), 47—76.
Исбел (Isbell J. R.)
[1] Uniform spaces, Providence, 1964.
Катетов (Katetov M.)
[1] Uber tf-abgeschlossene und bikompakte Raume, Casopis mat.
fys. 69 (1940), 36—49.
[2] On Я-closed extensions of topological spaces, Casopis mat. fys.
72 (1947), 17—32.
[3] Fully normal spaces (прибавление к книге Э. Чеха
«Topological spaces»), Prague, 1966.
Киртадзе Г.
[1] О различных видах полноты топологических пространств,
Матем. сб. 50, № 1 (1960), 67—90.
Куратовский (Kuratowski K.)
[11 Sur l'operation A de l'analysis situs, Fundam. math. 3 (1922),
182—199.
Куратовский и Серпинский (Kuratowski K-, Sier-
p i n s k i W.)
1] La theoreme de Borel — Lebesgue dans la theorie des ensembles
abstraits, Fundam. math. 2 (1921), 172—178.
Мищенко A. С
[1] О пространствах с точечно счетной базой, ДАН СССР 144
(1962), 985—988.
[2] О финильно компактных пространствах, ДАН СССР 145
(1962), 1224—1227.
Нагата (Nagata J.)
[1] On a necessary and sufficient condition of metrizability, J. Inst.
Polytechn. Osaka City University 1 (1950), 93—100.
Немыцкий В. В.
[1] On the «third axiom of metric space», Trans. Amer. Math. Soc.
29, №3 (1927), 507—513.
[2] Uber die Axiome des metrischen Raumes, Math. Ann. 104, № 5
(1931), 666—671.

142
СПИСОК ЛИТЕРАТУРЫ
Пономарев В. И.
[1] Нормальные пространства как образы нульмерных, ДАМ
СССР 132 (1960), 1269-1272.
[2] Аксиомы счетности и непрерывные отображения. Бюлл. Поль
ской Акад. наук 8, № 3 (1960), 127—134.
[3] О паракомпактных и финально компактных пространствах,
ДАН СССР 141 (1962), 46—49.
[4] Паракомпакты, их проекционные спектры и непрерывные
отображения, Матем. сб. 60 (1963), 89—119.
[5] Об абсолюте топологических пространств, ДАН СССР 149
(1963), 26—28.
[6] О пространствах, соабсолютных с метрическими, УМН 21, №4
(1966), 101—132.
[7] О борелевских множествах в совершенно нормальных
пространствах, ДАН СССР 170 (1966), 520—523.
[8] О мощности бикомпактов с 1-й акс. счетности, ДАН СССР
(1970) (в печати).
Пономарев В. И. и Александров П. С.
[1] О бикомпактных расширениях топологических пространств,
ДАН СССР 121 (1958), 575—578.
[2] О бикомпактных расширениях топологических пространств,
Вестник МГУ, сер. матем., № 5 (1959), 93—108.
Поспишил (PospiSil B.)
[1] Sur la puissance..., 6as. mat. a fys. 67 (1938), 89—96.
Раухваргер И. Л.
[1] К вопросу о мощности связных множеств, УМН 2, № 2
(1947), 195.
С ерпинский (Sierpiriski W.)
[1] General Topology, 1927.
Скляренко Е. Г.
[1] О совершенных бикомпактных расширениях, ДАН СССР 137
(1961), 39—41.
[2] Некоторые вопросы теории бикомпактных расширений, Изв.
АН СССР, сер. матем., 26 (1962), 427—452.
Смирнов Ю. М.
[1] К теории вполне регулярных пространств, ДАН СССР 62
(1948), 749—752.
[2] К теории вполне регулярных пространств, Уч. зап. Моск. ун-та,
сер. матем., 155, N° 5 (1952), 137—155.
[3] О топологических пространствах, компактных в данном отрезке
мощностей, Изв. АН СССР, сер. матем., 14 (1950), 155—178.
[4] О нормально расположенных множествах нормальных
пространств, Матем. сб. 29 (1951), 173—176.
[5] О метризации топологических пространств, УМН 6, № 6
(1951), 100—111.
[6] О пространствах близости, Матем. сб. 31 (1952), 543—576.
[7] О метризуемости бикомпактов, разлагаемых в сумму множеств
со счетной базой, Fundam. math. 43 (1956), 387—393.
Стоун A. (Stone А. Н.)
[1] Paracompactness and product spaces, Bull. Amer. Math. Soc. 54
(1948), 977—982,

СПИСОК ЛИТЕРАТУРЫ
143
Стоун М. (Stone М. Н.)
[1] Application of the theory of Boolean rings to general topology,
Trans. Amer. Math. Soc. 41 (1937), 375-481.
[2] On the compactification of topological spaces, Ann. Soc. Polon.
Math. 21 (1948), 153—160.
ТихоновА. H.
[1] Ober die topologische Erweiterung von Raumen, Math. Ann. 102
(1929), 544—561.
[2] Ober einen Funktionenraum, Math. Ann. HI (1935), 762—
766.
[3] Ober einen Metrisationssatz von P. Urysohn, Math. Ann. 95
(1925), 139—142.
Уpысон П. C.
[1] Sur la metrisation des espaces topologiques, Bull. Acad.
Polonaise, ser. A, 1923, 13—16.
[2] Ober die Metrisation der Kompakten topologischen Raume, Math.
Ann. 92 (1924), 275—293.
[3] Zum Metrisationsproblem, Math. Ann. 94 (1925), 309—315.
Филиппов В.
[1] О совершенно нормальных бикомпактах, ДАН СССР 189
(1969), 36-39.
Флаксмейер (FlachsmeyerJ.)
[1] //-abgeschlossene Raume als schwachstetige Bilder kompakter
Raume, Math. Z. 91 (1966), 336—343.
[2] Zur Theorie der tf-abgeschlossenen Erweiterungen, Math. Z. 94
(1966), 349—381.
Фомин С. B.
[1] Extensions of topological spaces, Ann. math. 44 (1943), 471—
480.
Фреше (Frechet M.)
[1] Sur quelques points du calcul fonctionnel, Rend. Circ. Mat.
Palermo 22 (1906), 1—74.
[2] Les espaces abstraits, Paris, 1926.
Фринк (Frink О.)
[1] Compactifications and semi-normal spaces, Amer. J. math. 86,
№ 3 (1964), 602—608.
Хаусдорф (Hausdorff F.)
[1] Теория множеств, ОНТИ, 1937.
Хьюитт (Hewitt Е.)
[1] Rings of real-valued continuous functions, Trans. Amer. Math.
Soc. 64 (1948), 45—99.
[2] On two problems of Ugysohn, Ann. math. 47 (1946), 503—
509.
Чернавский A. B.
[1] Замечание к теореме Шнейдера о существовании в совершенно
нормальных бикомпактах Л-множеств, не являющихся Б-мно-
жествами, Вестн. Моск. ун-та, сер. матем., 2 (1962), 20.
Чех (Cech Е.)
[1] Sur la dimension des espaces parfaitement normaux, Bull. Acad.
Sci. Boheme, 1932, 1—18.
[2] On bicompact spaces, Ann. math. 38 (1937), 823—844.

144 СПИСОК ЛИТЕРАТУРЫ
Шанин Н. А.
[1] О произведении топологических пространств. Тр. Матем. ин-та
АН СССР им. В. А. Стеклова, XXIV, Изд-во АН СССР, 1948.
Шнейдер В. Е.
[1] Непрерывные образы суслинских и борелевских множеств,
ДАН СССР 50 (1945), 77-79.
Шпильрайн (SzpilrajnE.)
[1] Заметка о декартовых произведениях топологических
пространств, ДАН СССР 31, № 6 (1941), 525—527.
Щепин Е.
[1] О пространствах, близких к нормальным, и их бикомпактных
расширениях, ДАН СССР 191 (1970), 295—297.
Энгелькинг (Engelking R.)
[1] On the double circonference of Alexandroff, Bull. Acad. Polon.
Sci., ser. Main., 16 (1968), 629—637.
Юxac (Juhasz I.)
[1] Martin's Axiom Solves Ponomarev's Problem, Bull. Acad. Polon,
Sci, ser. Math, 18, № 2 (1970), 71—74.

П.С. АЛЕКСАНДРОВ
П.С.УРЫСОН
МЕМУАР
О КОМПАКТНЫХ
ТОПОЛОГИЧЕСКИХ
ПРОСТРАНСТВАХ