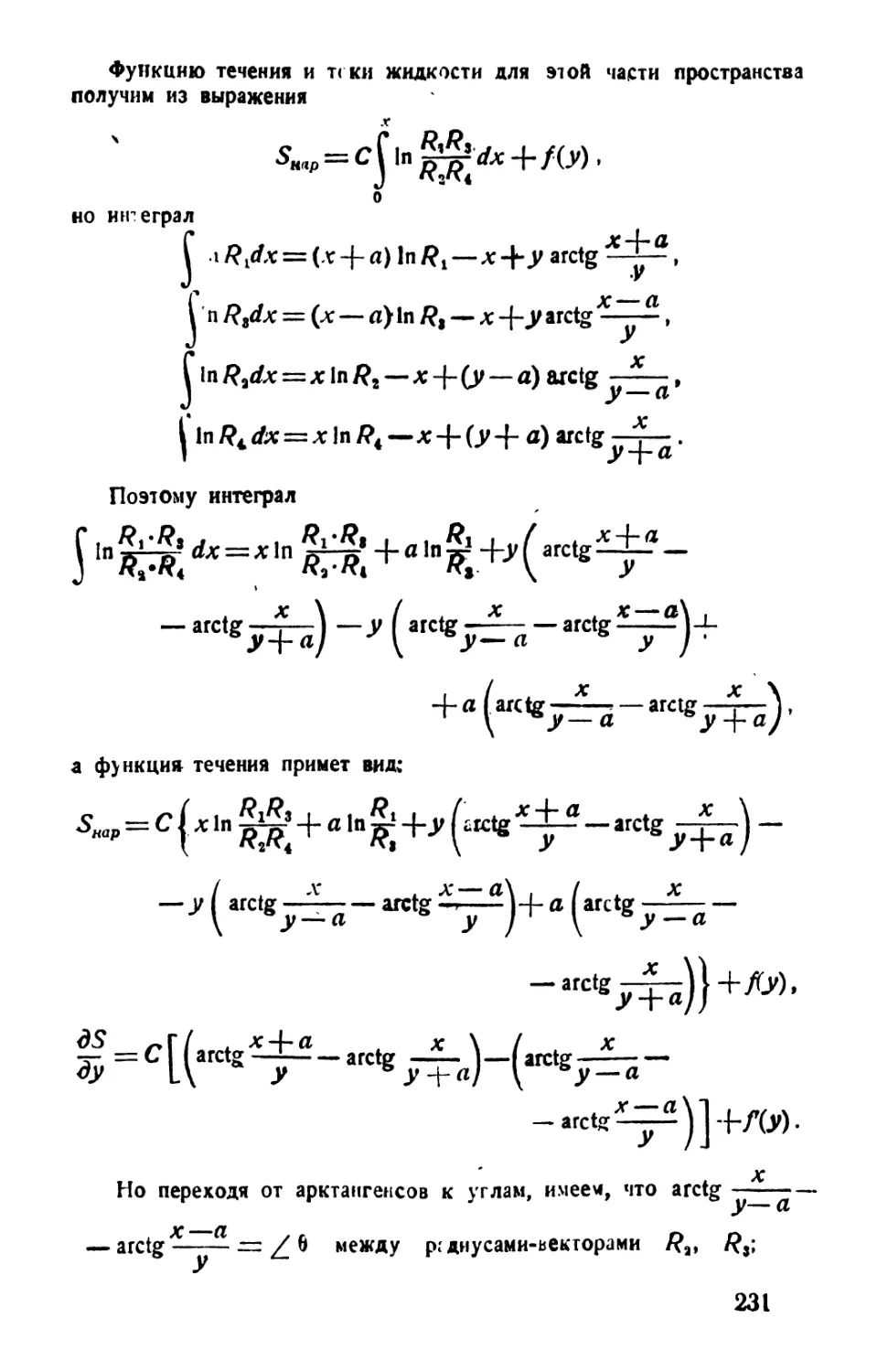Text
А. Я- МИЛОВИЧ
ТЕОРИЯ ДИНАМИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ ТЕЛ И ЖИДКОСТИ
НКЭП СССР
ГОСУДАРСТВЕННОЕ ЭНЕРГЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО МОСКВА 1 9 4 0 ЛЕНИНГРАД
Другу моей жизни, жене моей Марии Андреевне Милович, посвящаю я этот труд.
ПРЕДИСЛОВИЕ
Вопрос о величине сопротивления, испытываемого неподвижным телом в движущейся жидкости или, наоборот, движущимся телом в неподвижной жидкости, относится к древнейшим задачам гидродинамики г.
Несмотря на это, до настоящего времени не удалось достигнуть его общего теоретического решения, что и привело к попыткам прямого экспериментального определения сопротивления, дав тем самым толчок к развитию экспериментальной гидро- и аэродинамики.
Но и теперь при наличии громадного экспериментального материала не уменьшилась необходимость в его общем теоретическом обосновании и освещении, без которого он всегда будет представлять собой только собрание наблюдений над отдельными случайными явлениями природы.
В чем же заключается основная причина такого отсутствия успеха в развитии общего теоретического учения о сопротивлении движению тел в жидкости, или иначе, учения о динамическом взаимодействии тел и жидкости. На наш взгляд эта причина лежит в отсутствии до настоящего времени в гидродинамике ясного и простого учения о механизме восприятия и передачи силы безграничной непрерывной жидкой средой, ибо сущность взаимодействия тел и жидкости станет понятна нам только тогда, когда нам будет известно, каким образом непрерывная масса жидкости может воспринимать и передавать внутри себя импульсы сил.
В целях обоснования подобного учения мы должны обратить внимание на то, что во всех случаях взаимодействия тела и жидкости мы имеем перед собой одно и то же явление обтекания тела жидкостью.
1 См. О. Flachsbart .Geschichte der experimentellen Hydro- und Aero-mechanik, insbesondere der Widerstandsforschung*. Handbuchder Experimental-physlk, 2 Tell, Leipzig, 1932.
Это обтекание тел окружающей их жидкостью, обусловливаемое непроницаемостью для жидкости пространства, занятого телом, необходимо вызывает изменения в движении набегающего на него потока.
Поверхность тела, прямо обращенная к набегающему потоку, замедляет или тормозит движение набегающих на нее частиц жидкости.
Она как бы стремится отбросить их назад. Наоборот, остальная часть поверхности тела, от которой сами частицы жидкости стремятся отойти, двигаясь по инерции, притягивает или подсасывает к себе эти частицы. Поэтому во всех случаях обтекания тел жидкостью поверхность тела по своим свойствам всегда делится на две части: на часть поверхности, отбрасывающую или выбрасывающую из себя жидкость, и на поверхность, всасывающую жидкость.
Осуществить свойство первой части поверхности тела гидродинамически мы можем, только представив ее себе покрытой непрерывным слоем положительных или выбрасывающих из себя жидкость источников-точек.
Свойство второй части поверхности тела представляется непрерывным слоем отрицательных или всасывающих источников-точек.
Но из отдела I настоящей работы видно, что при наличии в жидкости системы источников разных знаков и напряжений выполнение условия сохранения постоянства всего объема жидкости в пространстве требует, чтобы источники-точки разных знаков и напряжений были связаны между собой попарно элементарными прямолинейными трубками, концы которых представят источники-точки разных знаков, но одного и того же напряжения.
Далее доказывается, что каждая такая трубка по своему направлению действует на жидкость с определенной силой, почему они и называются силовыми трубками.
Совокупное действие системы силовых трубок, возбуждаемых в обтекаемом теле набегающим на него потоком жидкости, должно быть равно и прямо противоположно по направлению действию на тело самого потока жидкости, почему силовые трубки всегда направлены по направлению движения набегающего потока.
Поле токов жидкости, возникающее в результате воздействия на нее системы силовых трубок, вполне аналогично полю магнитных линий, возникающих под действием электромагнитов. Ибо, как доказывается далее, действие на жидкость всякой системы силовых трубок всегда может быть заменено действием на нее определенной системы вихрей, неизбежно возникающих на поверхности обтекаемого тела и аналогичных электрическим токам.
Но тогда теоремы Н. Е. Жуковского о количестве движения, сообщаемого безграничной массе жидкости системой двух параллельных вихрей или плоским замкнутым вихрем, а также моя теорема о количестве движения, сообщаемом жидкости вихревым соленоидом, дают возможность найти величину силы, вызывающей рассматривав-, мое движение жидкости, или силы искомого взаимодействия тел и жидкости.
Вместе с тем вскрывается и замечательная связь теории источни ков-точек с теорией вихрей. Так, система силовых трубок бесконечно малой длины или диполей, распределенная по какой-либо поверхности, оказывается эквивалентной вихревому шнуру, идущему по контуру этой поверхности, что вполне аналогично двойному магнитному листку и электрическому току, пробегающему по его контуру*
Система силовых трубок конечной длины эквивалентна вихревому соленоиду, расположенному на боковой поверхности тела, что аналогично действию электромагнита. Более того, развитие анализа диполей и вихрей по § 2, 3 и 4 приводит нас еще и к принципиально важному результату, заключающемуся в том, что сам диполь может быть рассматриваем как система двух бесконечно близких друг другу вихревых шнуров с прямо противоположным вращением или как вихревое кольцо бесконечно малого диаметра.
Поэтому диполь несет в себе определенный запас количества движения или иначе действует на окружающую его жидкость с определенной силой. Но тогда вихревое кольцо, возникающее и движущееся в жидкости как самостоятельное жидкое тело, является вполне определенным и единственным механизмом восприятия и передачи внутри себя непрерывной жидкой средой импульса сил.
А запас его количества движения дает нам точную величину самой силы.
Чтобы обладать этим количеством движения, вихревое кольцо должно содерж ать в себе определенный запас кинетической энергии.
Последнюю оно получает или извне в случае рассеяния добавочной для данной среды энергии, передаваемой движущимися в жидкости посторонними ей телами, тогда мы будем иметь общее увеличение запаса энергии частиц жидкой среды, или за счет начального запаса энергии частиц самой жидкости при обтекании ею неподвижных тел,
В этом случае мы будем иметь общее уменьшение начального запаса энергии частиц жидкой среды, „потерю энергии жидкости*, не зависимую ни от трения, ни от вязкости и происходящую в самой идеальной жидкости.
В обоих случаях запас энергии частиц жидкой среды явится величиной переменной и интеграла Д. Бернулли не будет существовать, почему в различных частях пространства мы должны будем постоянному уравнения Бернулли приписывать не одно и то же, но различные значения.
Параграфы 4 и 5 показывают на примере теории обтекания бесконечно длинной плоской пластинки, что в тех случаях, когда, идя намеченным выше путем, мы сможем довести решение вопроса до конца, мы получим картину взаимодействия между телом и жидкостью, вполне совпадающую со всеми результатами экспериментальных исследований как с качественной, так и с количественной стороны. Кроме того, предлагаемая теория позволила впервые установить полное тождество механизмов явлений обтекания тел и протекания через отверстия вплоть до тождественности коэфициентов сопротивления коэфи-циентам расхода.
Опубликовывая настоящим трудом уже имеющийся материал по развитию и приложению предлагаемой теории динамического взаимодействия тел и жидкости, я надеюсь вызвать им интерес у читателей к подобному методу исследования относящихся сюда вопросов, предполагая в ближайшем будущем дать дальнейшее их развитие.
А. Милован
СОДЕРЖАНИЕ
Предисловие . ,.................................................. 3
Отдел I. Основные понятия....................................... 11
§ 1. Источник-точка. Системы источников и силовые трубки. Вихри и вихревые слои .................................................. 11
I. Система двух источников-точек с напряжениями, равными по величине, но обратными по знаку; элементарная силовая трубка 16
Диполь (Dipol) или дублет................................. 19
II. Источник-точка в пространстве трех измерений............. 21
Система двух источников-точек с напряжениями, равными по величине, но обратными по знаку........................... 23
Дйполь или дублет в трех измерениях....................... 24
Ш. Плоское динамическое вращение жидкости вокруг оси или прямолинейный вихревой шнур........................................ 27
Циркуляция скорости по контуру........................... 29-
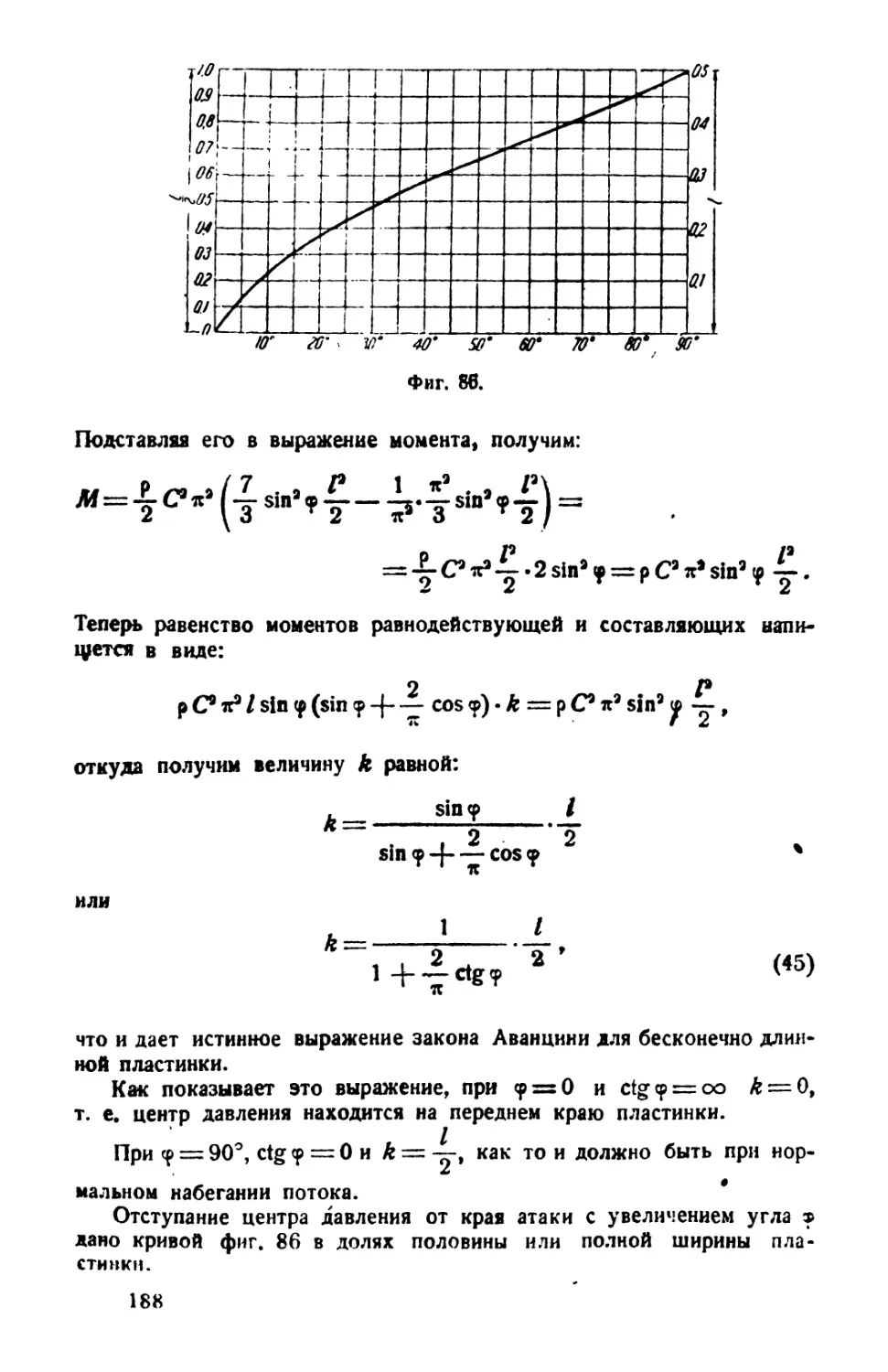
Однородный конечный цилиндрический вихрь кругового сечения ................................................- . . 31
IV. Движение жидкости под действием непрерывного вихревого слоя конечной ширины....................................... 33
Функция течения и токи жидкости........................... 35
Отдел И. Механизм восприятия и передачи силы безграничной непрерывной массой жидкости..................................... 38
§ 2. Действие на жидкость прямой-гдиполя или системы параллельных вихрей.......................................................... 38
I. Тождественное!» функции потенциала скоростей прямой-диполя потенциалу пары параллельных вихрей ......................... 38
И. Форма движения жидкости, вызываемая прямой-диполем или парой параллельных вихревых шнуров................................ 44
III. Количество движения прямой-диполя или пары параллельных
вихрей.......................................................... 52
Первая сеорема Н. Е. Жуковского, ее следствия.............. 52
Вторая теорема Н. Е. Жуковского............................ 56
Количество движения, сообщаемое безграничной жидкости вихревым соленоидом. Третья теорема........................... 58
§3. Нормальное давление потока на плоские пластинки или отверстия 62
Экспериментальное подтверждение справедливости теории диполя как силовой трубки.................................... 64
Отдел ///. Теория нормального обтекания плоской пластинки ... 69
§ 4. Нормальное обтекание безграничным потоком жидкости бесконечно длинной плоской пластинки конечной ширины................. 69
Течение I.................................................. 71
Течение II................................................ 74
Течение III................................................ 76
Функция течения.................................: *. •..... 83
Уравнение предельного тока ................................ 88
§ 5 Кривые равной полной скорости, равного давления и сила давления потока на плоскую пластинку............................ 90
Кривые равных полных скоростей частиц жидкости............. 90
Кривые равных давлений или уровней ........................ 93
Распределение давления и величина силы давления потока на поверхность пластинки..................................• . 95
Следствие I. Потери энергии потока, обтекающего пластинку. . . 100
Следствие II. Применение метода зеркальных изображений . • 103
Действие бесконечно близких непрерывных вихревых слоев обратного вращения..................................... 106
Отдел IV. Теория плоской решетки и истечения из отверстий. . . ПО
§ 6. Система пластинок. Теория нормального протекания потока жидкости через щели плоской решетки................................. ПО
Нормальное набегание безграничного потока жидкости на систему двух пластинок.......................................... ПО
К Истечение жидкости из щели в стенке бесконечно широкого бассейна (случай совершенного сжатия)............................ П2
Функция течения............................................. П4
Распределение скоростей и давлений.......................... П9
Величина ускорения по оси струи............................ 1^3
II. Случай равномерного движения щели........................ 1^6
III. Истечение жидкости из отверстия в стенке бесконечно длинного канала (концентрация струи) ............................ 126
Функция течения.........................................
Уравнение предельного тока и коэфициент сжатия струи .... 134
Распределение скоростей и давлений..................... 137
Ускорение по оси струи................................... 139
Полная величина давления потока.......................... 140
IV. Истечение жидкости из щели в стенке бассейна конечной ширины...................................................... 141
Поле скоростей........................................... 141
Функция течения.......................................... 144
Уравнения предельного тока............................... 151
Ускорение движения струи по осн УК....................... 152
Распределение и величина давления потока жидкости на систему двух пластинок с дцедью между ними................. 154
Отдел К Теория косого обтекания плоской пластинки.............. 156
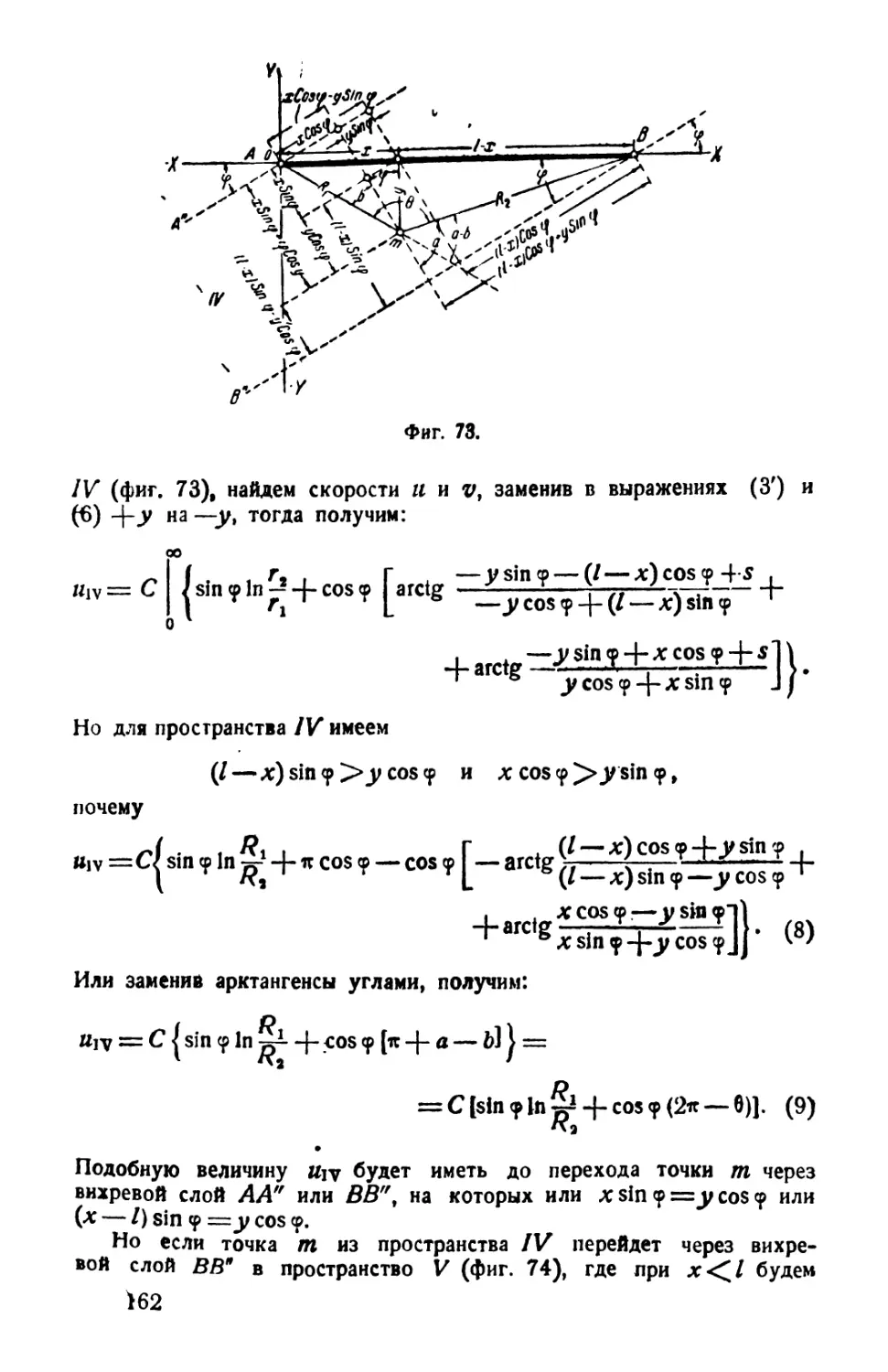
§ 7. Косое набегание потока жидкости на плоскую пластинку бесконечной длины ................................................... 156
I. Граничные условия........................................ 166
II. Функция течения и токи жидкости........................... 168
III. Общая схема движения жидкости при косом набегании потока на пластинку............................................... 176
§ 8. Величина и распределение давления жидкости при косом набегании потока на пластинку ....................................... 179
I. Центр давления............................................. 182
Величина среднего отрицательного давления на нижней поверхности пластинки . ..................................... 183
Центр давления при среднем давлении на нижнюю поверхность пластинки............................................ 186
II. Подъемная сила и лобовое сопротивление плоской пластинки бесконечной длины................................................ 189
Замечание о причине вибрации плоских пластинок ........... 189
Положение точки нулевого давления на верхней поверхности пластинки.................................................. 190
III. Сравнение результатов предлагаемой теории с имеющимися данными испытаний плоских пластинок........................... 191
IV. Сравнение предлагаемой теории с теорией Кутта-Жуковского 193
Отдел VI. Теория деления потока жидкости......................... 195
§ 9. Косое набегание потока жидкости на плоскую решетку. Основы теории деления потока жидкости........................... .... 195
I. Основы теории деления потока .......................... . 195
II. Функции течения и тока жидкости........................... 199
Функция течения и тока жидкости в пространстве /........... 199
Положение точки нулевой скорости или раздела течения М в пространстве /............................................. 209
Уравнение предельного тока в пространстве / ............... 201
Функция течения и токи жидкости в пространстве II........ 201
Предельные токи в пространстве II.......................... 202
Функция течения и токи жидкости в пространствах III и IV 203
П1. Схема движения жидкости при делении потока................ 204
IV. Распределение скоростей и давлений........................ 205
Отдел VII. Теория обтекания жидкостью твердых тел конечных размеров........................................................ 208
§ 10. Общие свойства движения жидкости при обтекании ею прямоугольного бесконечно длинного бруса нормально к его боковой грани 208
I. Функция потенциала скоростей.............................. 208
II. Поле скоростей соленоида................................. 214
III Функция течения и токи соленоида......................... 215
§11 . Общие свойства движения жидкости при обтекании ею бруса квадратного сечения по направлению его диагонали................ 221
I. Функция потенциала скоростей.............................. 221
II. Скорости, параллельные осям координат.................. 225
Ш. Функция течения и токи жидкости вихревого соленоида .... 230
Заключение.................................. . .............. 236
ОТДЕЛ I
ОСНОВНЫЕ ПОНЯТИЯ
§ 1. ИСТОЧНИК-ТОЧКА. СИСТЕМЫ ИСТОЧНИКОВ И СИЛОВЫЕ ТРУБКИ. ВИХРИ И ВИХРЕВЫЕ СЛОИ
При всяком непрерывном движении жидкости должно удовлетворяться уравнение непрерывности или неразрывности жидкой среды:
др . д(рм) , д(р^) , d(pw)
~д1 + ~дГ^~дГ + ~дГ-^ (1)
где р — плотность жидкости; t—время, а и9 v и w— компоненты скорости частицы в произвольной точке пространства т (фиг. 1) по направлению прямоугольны^ осей координат Х9 Y и Z.
Для жидкостей несжимаемых р = const и уравнение (1) примет вид:
ди . да ! dw дх ‘ ду ‘ dz
(2)
Наконец, в случае движения установившегося с потенциалом скоростей—движения невихревого при наличии функции потенциала скоростей <р (х, у, z) такой, что
(3)
дъ дер дер
дх ду dz
уравнение (2) переходит в уравнение Лапласа (3):
Дф=Й+-Й.+^-=Ь. дх2 djr ' dz*
Всякая функция координат ср (х, у, z), удовлетворяющая последнему уравнению, дает нам одну из форм возможного при данных условиях движения несжимаемой жидкой среды.
При плоском движении жидкости параллельно плоскости координат XOY скорость w = 0, почему равна нулю и производная этой dw скорости по координате z9 -5— = 0.
az
Фиг. 1. Фиг. 2.
В этом еще более частном случае движения жидкости уравнения (2) и (3) напишутся в виде
ди . dv
+ -з- = 0 дх ' ду
н
д-f .
дх-^ду3
(4)
(5)
Источник-точка в пространстве двух измерений. В случае движения жидкости, совершенно симметричном относительно какой-либо точки пространства О, принимаемой нами за начало координат, мы можем найти частный интеграл уравнений (5) и (3) путем прямого их интегрирования следующим образом:
При плоском движении жидкости, совершенно симметричном относительно начала координат О (фиг. 2), функция потенциала скоростей <р (х, у) должна явиться функцией только одной переменной г расстояния произвольной частицы жидкости т от этого начала, причем
__dq дг d? у
ду dr ду dr г
\ # д’<р_d3<o у3 . d^> / 1
dy3~dr3 У3'~5г\г
Но тогда rf? дг dv х дх____________________dr дх_dr г ’
д^у__d3<f х3 .d<f> Z x3
дх3 dr3"^3' dr k
Поэтому уравнение (5) может быть написано в этом случае как уравнение
I X *?=о,
dr'1' г dr ’
Интегрируя последнее уравнение один раз, получим z/ф Л г -г- = Q = const, dr
или
d^=Q~-.
4 г
Интегрируя второй раз, найдем функцию ср в виде ф = Q In г. (6)
Последнее выражение показывает, что в случае плоского движения жидкости потенциал скоростей дается логарифмом расстояния частицы от начала координат.
Но тогда' слагающие скорости частицы по осям и и v будут
равны:
дх х г- г
ду г1 г
(О
где а — угол радиуса вектора г с осью ОХ.
Поэтому полная скорость частицы W равна
И7=—. (8)
Она обратно пропорциональна расстоянию частицы от начала коорди* нат О и направлена по ее радиусу-вектору.
Уравнение тока' найдем, интегрируя выражение
dx dy
или
dlnx = d\nyt или din —= 0, У откуда получим
In — = const или — = const = ctg а, У У *
почему окончательно уравнению тока может быть придан вид
у = tg а х.
О)
Это уравнение показывает, что ток жидкости представляет прямую линию, проходящую через начало координат и образующую с осью ОХ угол а. Он совпадает с радиусом-вектором г точки т. Изменяя величину угла а от 0 до 2 получим все токи исследуемого движения жидкости в виде комплекса радиальных прямых, исходящих из точки О или в ней сходящихся, смотря по направлению движения.
Точка пространства, наполненного жидкостью, выбрасывающая или всасывающая эту жидкость полученным выше образом, называется источником-точкой.
Источник-точку, выбрасывающую из себя жидкость во внешнее пространство, мы будем далее считать положительным. Наоборот, источи и к-точка, всасывающая в себя всю окружающую жидкость, будет считаться отрицательным.
Уравнение (6) показывает, что поверхность равного потенциала скоростей ср = const в данном случае будет иметь уравнение
г = const,
т. е. представит собой боковую поверхность прямого кругового цилиндра с осью, проходящей через начало координат. Во всех плоскостях, параллельных плоскости координат XOY, мы будем иметь течений жидкости, тождественные рассмотренному. Поэтому прямая, проходящая через начало координат и нормальная к плоскости чертежа фиг. 2, является здесь совокупностью непрерывного ряда источников-точек одного и того же знака и представляет собой прямолинейный источник.
Расход прямолинейного источника. Напряжение. Расход подобного прямолинейного источника q на единицу ширины слоя жидкости получим как расход через боковую поверхность прямого кругового цилиндра единицы высоты равным
q = 2тс г • у- = 2z Q, о:куда
<?=-£• 0 °)
Выражение (10) показывает, что постоянное Q, входящее во все предыдущие выражения, представляет собой расход жидкости, вызываемый действием прямолинейного источника, через боковую поверхность кругового цилиндра с осью, совпадающей с прямой источника и радиусом основания, равным единице.
Этот расход Q называют напряжением источника.
Знак напряжения обусловливает собой и знак источника. Источник положителен, выбрасывает жидкость, когда положительно его напряжение Q, и отрицателен, всасывает жидкость, когда напряжение его Q отрицательно.
Система источников. Если в просхранстве, заполненном движущейся жидкостью, имеется не один источник в точке О, а целая система их, находящихся в точках О, Ох, О2 и т. д. с напряжениями Q, Qp 14
Qa и т. д., то функцию потенциала скоростей, движения жидкости, ими вызываемого, всегда можно представить в виде алгебраической суммы потенциалов каждого отдельного источника:
9 — Q in г-J- Qi 1° г\ 4* Qi 1° гг +•••» 0 0
где Q9 Qv Q2,... — напряжения источников в точках О, О2,..., а rv rv» — расстояния от этих точек произвольно взятой частицы жидкости, так как уравнение непрерывности (5) будет при этом, очевидно, удовлетворено.
Расход жидкости, вызываемый всей системой источников, очевидно, будет равен алгебраической сумме расходов всех источников:
4 = 2* (Q + Q1 + Q. 4-...). (12>
Но удовлетворяя формально уравнениям гидродинамики, так изложенная теория источника-точки не может еще соответствовать реальным явлениям природы, ибо она молчаливо допускает возможность физически невозможного явления: полного уничтожения или создания материи в точках источников из ничего, так как ясно, что всасывать в себя всю жидкость из окружающего пространства точка источника могла бы только при условии исчезновения в ней всей этой жидкости вследствие превращения ее в ней в ничто. Или, наоборот, непрерывно выбрасывать из себя жидкость точка источника могла бы только при условии непрерывного возникновения в ней самой жидкости из ничего» В обоих случаях мы неизбежно пришли бы к увеличению или уменьшению всего объема жидкости в пространстве, т. е. к его непостоянству. Это изменение общего начального объема жидкости и выражается уравнением (12\
А так как при движении реальных жидкостей их начальный объем должен сохраняться неизменным, то для восстановления реальности теории источников необходимо выполнение ею кроме уравнения непрерывности (5) еще одного добавочного условия, выражающего собой условие неизменности или постоянства начального объема жидкости.
По уравнению (12) это условие может быть представлено в виде уравнения:
Ч = 2к (Q + Q. + (?,+„.) = 0. (13)
Оно требует равенства нулю алгебраической суммы напряжений системы источников
U Q + Qi+Qa+... = o (14)
и тем самым показывает нам, что реальным может быть не один изолированный источник-точка, а минимум система из двух источников-точек с напряжениями, равными по величине, но обратными по знаку, выполняющими условие
Q — Q = O и q = 0.
К рассмотрению теории подобной простейшей системы источников, играющей особо важную роль во всем последующем, теперь и перейдем»
I. Система двух источников-точек с напряжениями, равными по величине, но обратными по знаку; элементарная силовая трубка
Пусть имеется система, состоящая из двух источников-точек Otn О2, расположенных на расстоянии 2а друг от друга по оси XX.
Напряжения этих источников Q пусть будут
равны между собой по величине, но обратны по знаку.
Тогда, согласно фиг. 3, функцию потенциала скоростей ср ими вызываемого, можно написать в виде:
течения.
? — Q In rt — Q In ra = Q In -Г2
где
г,2
G = /j2 + (^ + a)3; г2=|/уЧ-(х-а)\
Компоненты скорости частицы по осям X и У будут равны:
B==^=Qx + a _Qx-a 1 дх v г/ v г/ ’ J
ду ** г/ " г92 *
Диференциальное уравнение тока жидкости dx dy , ,
— — — или v dx — udv = 0. u v л
(15)
(16)
напишется в виде:
Поэтому для функции течения S будем иметь: ,с OS . . dS , dS=fa dx + dydy = vdx~udy = 0>
откуда получим равенства:
dS dS
-r- = vt .- = —U.
dx dy
Интегрируя выражение
dS = v dx
2
от нуля до х, получим:
JT X
~ fl . х^а | . х — а 1 , ,, ч
= Q Л arete ---------I arete —-----J +/(у) =
<в X о
(х х-\-а . х— а \ , ,, .
«etg —f--------arctg —-— ) 4- f(v)>
где / (у) — неизвестная еще пока функция у. п dS
Для ее определения сравним выражения с
выраженном — и
тогда получим
п(Х + а ду ~
7 4 г 1 Г1 /
откуда видны, что /(у) = 0 или f(y) = const.
Поэтому окончательно будем иметь функцию течения в виде:
о = Q arete —~-----arctg ——— ). (Щ
Но arctg —у— — 90° — ар а arctg *—у— = 90° — а,, поэтому, переходя от арктангенсов к углам, найдем, что
arctg — arctg = (90° — aj — (90° — at) = — a, at — У V
= — «l + « —₽!=«-- (»i + Pl) = 0« где 0 — угол, под которым из точки т видно расстояние мемац> источниками 2а, а выражение (17) примет вид
5=Q[«-(«1+P1)] = Q0. (18)
На основании последнего выражения уравнение токов рассматриваемого движения жидкости 5=const напишется в виде;
оц 4“01 = K=const или в = const. (19)
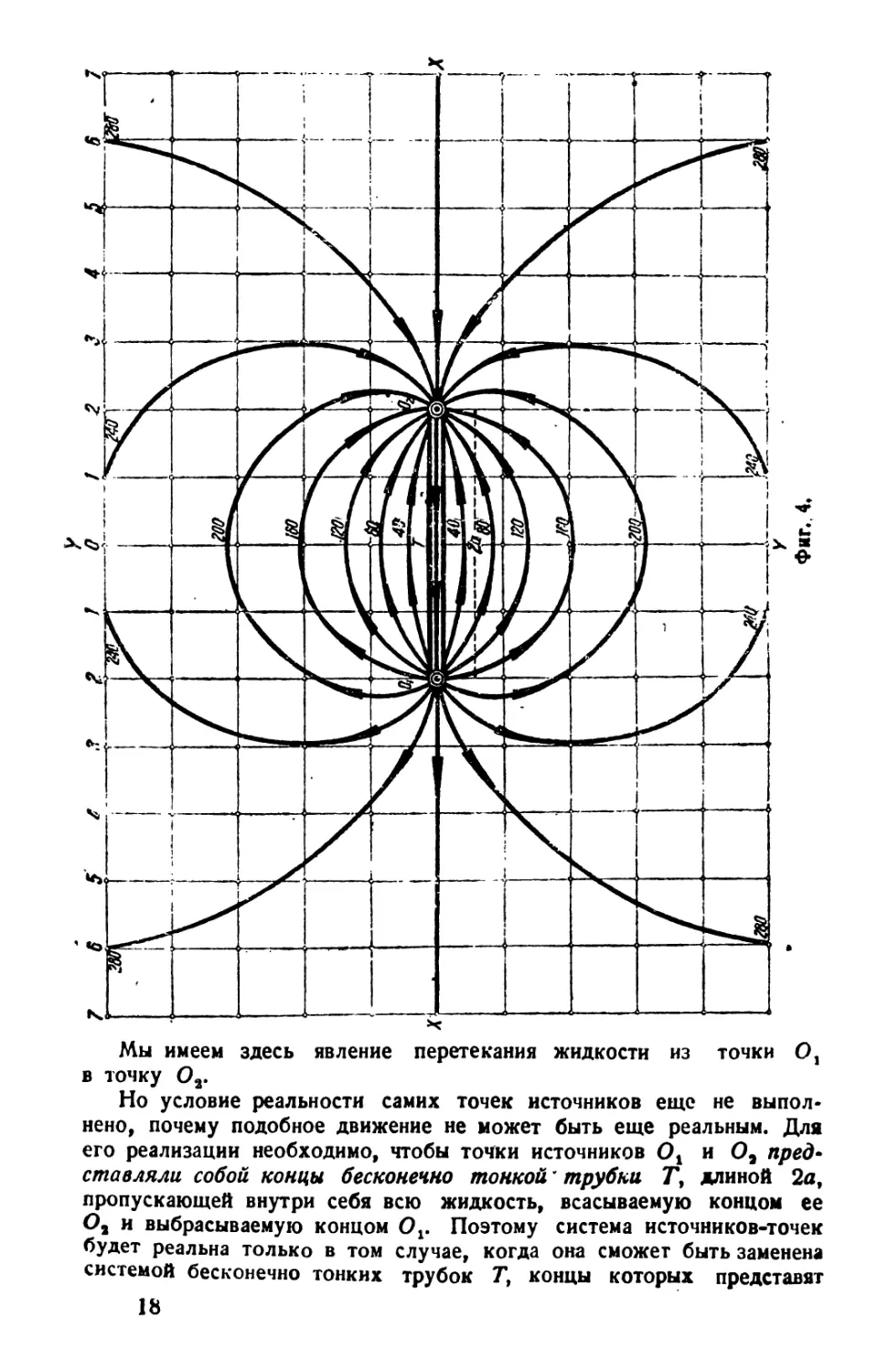
Фиг. 4 дает точную картину движения жидкости по уравнению (19).
О а
Мы имеем здесь явление перетекания жидкости из точки в точку О2.
Но условие реальности самих точек источников еще не выполнено, почему подобное движение не может быть еще реальным. Для его реализации необходимо, чтобы точки источников Ох и Оэ пред* ставляли собой концы бесконечно тонкой' трубки Т, длиной 2а, пропускающей внутри себя всю жидкость, всасываемую концом ее О2 и выбрасываемую концом Ov Поэтому система источников-точек будет реальна только в том случае, когда она сможет быть заменена системой бесконечно тонких трубок Г, концы которых представят 18
данные источники-точки. Отсюда следует, что всякая реальная система источников-точек может состоять только из одинакового числа источников, противоположных по знаку и равных по величине напряжения. С другой стороны, движение жидкости вдоль по элементарным трубкам Г, необходимое для действия их концов как источников-точек, возможно только при условии наличия у этих концов разности давлений, дающей начало возникновению движущей жидкость силы. Сэто1 силой каждая из элементарных трубок дей-
Фиг. 5.
ствует на окружающую ее жидкость или, наоборот, окружающая жидкость действует на элементарную трубку с силой, равной первой по величине, но прямо обратной по направлению.
На основании изложенного мы будем в дальнейшем трубки Т,
соединяющие два источника-точки с напряжениями, равными по величине и обратными по знаку, называть силовыми трубками.
Длина силовой трубки, обусловленная расстоянием источников-точек, ею соединяемых, может быть как} конечна, так и бесконечно мала.
Трубки конечной длины дают основу теории обтекания тел конечных размеров по направлению движения набегающего на них потока
жидкости.
Трубки бесконечно малой длины дают основу теории обтекания потоком жидкости бесконечно тонких пластинок.
Диполь (Dipol) или дублет. Функцию потенциала скоростей этого предельного случая системы двух источников или силовой трубки можно получить следующим образом:
При бесконечно малом расстоянии между источниками Ог и О2, равном Дх (фиг. 5), функция потенциала скоростей течения, ими вызываемого, имеет вид: 9
причем
поэтому
т=?i (*» у)—<р 1 (*—Д
и чтобы найти, к какому виду придет функция ср при уменьшении Дх Ф
до нуля, необходимо будет найти предел отношения .
Но применяя формулу Тэйлора, имеем:
Д
? = <Р» (•*»/) — [Ф1 (— Д*<Р1' (х,у) + • • • ] =
= Дхер/ (х,у) — -рз ф/ (х,у) +. . .,
лде ср/' и т. д. — первая, вторая и т. д. производные функции <pt по х.
2* 19
Поэтому
т. е. искомая функция потенциала скоростей равна первой производной по х от функции потенциала источника-точки (6), при условии QAx = const.
Точка пространства, наполненного жидкостью, являющаяся совмещением двух источников-точек с напряжениями, равными по величине, но обратными по знаку, или силовой трубки бесконечно малой длины, называется источником-парой, диполем или дублетом. А на основании изложенного функция потенциала скоростей диполя или дублета плоского движения жидкости будет равна:
или
д ~ f ~ х T1=KQlnr=Qr!
?,=/ Qlnr=Q 4.
*" ди Г2
(20)
смотря по оси расположения начальной системы источников-точек, •си X или F.
Компоненты скорости частицы жидкости для расположенного ко оси X диполя найдем из выражений:
(21)
а функцию течения 5 получим, интегрируя уравнение
dS=vdx = — Q ,
г4
в виде
или
S=Q^.
(22)
Согласно такому выражению S уравнение токов жидкости может быть представлено в виде
г = Dsincp = 2 Z?sln<p, (23)
где D = 2R — постоянное тока.
Уравнение (23) есть уравнение круга радиуса R, касающегося оси X в начале координат, с центром на оси Y. Фиг. 6 дает картину подобного течения жидкости.
ол
Полная скорость частицы жидкости равна ______________________________Q
UZ=)/ =77. (24)
Она обратно пропорциональна квадрату расстояния частицы от точки-диполя. Диполь <р2, ориентированный не по оси XX, а по оси YY, даст относительно этой оси ту же картину движения, что и диполь <рг относительно оси XX,
II. Источник точка в пространстве трех измерений
В пространстве трех измерений необходимо удовлетворять уравнению Лапласа (3).
Частный интеграл этого уравнения, соответствующий источнику-точке, получим аналогично плоскому течению жидкости следующим образом:
Для течения вполне симметричного относительно точки О начала координат фвг. 7 искомая функция потенциала скоростей источника-
точки должна являться функцией одного расстояния г произвольной точки жидкости т от начала О, причем г=)/х*-}-у*-{-г*.
Поэтому
ду___dy х
дх~~ dr'V*
д*у d*y х* . dy(l_______х* \
dy у ду dr г ’
д'-у_</-’<? у' \dyr t у’\
ду* dr* г* ' dr\ г г* / ’
<J’<p_d*y z2 .dyf 1
dz* ~^r* ’7^' dr\r r* / ’
ду___dy z
dz~~ dr г ’
Уравнение (3) может быть написано теперь, как уравнение:
_L\_n
dr* * dr\r г)
или
Ё*? j Ё? —о
dr^ г dr 9
или
r dr* ' 2r dr •
или
0.
Интегрируя один раз, получим г2 = const = Q, dr х
или
Наконец, интегрируя второй раз, получим функцию потенциала скоростей источника-точки в трех измерениях в виде:
(25)
Поверхность равного потенциала скоростей
<? =— — = const или г = const
представляет собой поверхность сферы радиуса г. 22
Компоненты скорости частицы по осям координат равны:
Фиг. 8.
Поэтому полная скорость частицы UZ=Va*-|-v,-|-ws = Q . (27)
Она обратно пропорциональна квадрату расстояния частицы от на -чала координат и направлена по ее радиусу-вектору.
Уравнение тока найдем, интегрируя выражение dx______________________dy____dz
х ~ у ~~z'
распадающееся на два уравнения:
dx dy dx dz
— = — и — ——,
X у X z
которые после интегрирования приведут нас к уравнениям: y = tgxr, z = tgix, (28)
представляющим прямую линию, проходящую через начало координат и совпадающую с радиусом-вектором частицы.
Расход через поверхность сферы радиуса г будет равен:
^ = 4№^=4kQ,
откуда напряжение источника-точки в трех измерениях равно: Я
4к
(29)
Система двух источников-точек с напряжениями, равными по величине, НО обратными ПО знаку. Пусть согласно фиг. 8 мы имеем на оси XX два источника-точки Ot и Ог с напряжениями -f- Q и — Q.
Тогда, исходя из выражения (25), функция потенциала скоростей течения, ими вызываемого, напишется в виде:
? =
-Q-+-2.
(30)
где /?! и — расстояния произвольной точки жидкости т от точек источников Ot и Эти расстояния, очевидно, равны
/?, = /(х-|-а)*4-г«; /?, = /(х —а)’+?’. (31)
Скорости частиц жидкости параллельно осям координат ОХ и 02 будут равны:
*?_ п(х + а а\ д<₽ Л / г z \
V~dz~QVR? 7^)'
(32)
Все течение симметрично относительно оси XX, почему скорость v = 0.
Уравнение тока в плоскости Z0X напишется в виде:
или
dx__dz
wdx — adz = 0.
При симметрии течения относительно оси XX множителем, ннтег» рирующим последнее выражение, будет по Стоксу я, так что
dS = zwdx — zudz = О,
откуда имеем равенства: dS д$
-— — Z W, 3 - = — яи. дх dz
Поэтому
dS = — zudz = — Qz(j^—’ откуда
S=-Q(*+e)^+Q(*-e) j$+JW.
Выполнив интегрирование по z9 найдем:
S=Q*±f_Q^ = COn8t. (33)
Но по фиг. 8 имеем: х+а х—а
-a_=cosa1; = cosa2>
почему уравнение тока жидкости можно писать в виде: cos 04 — cos a2 = const или
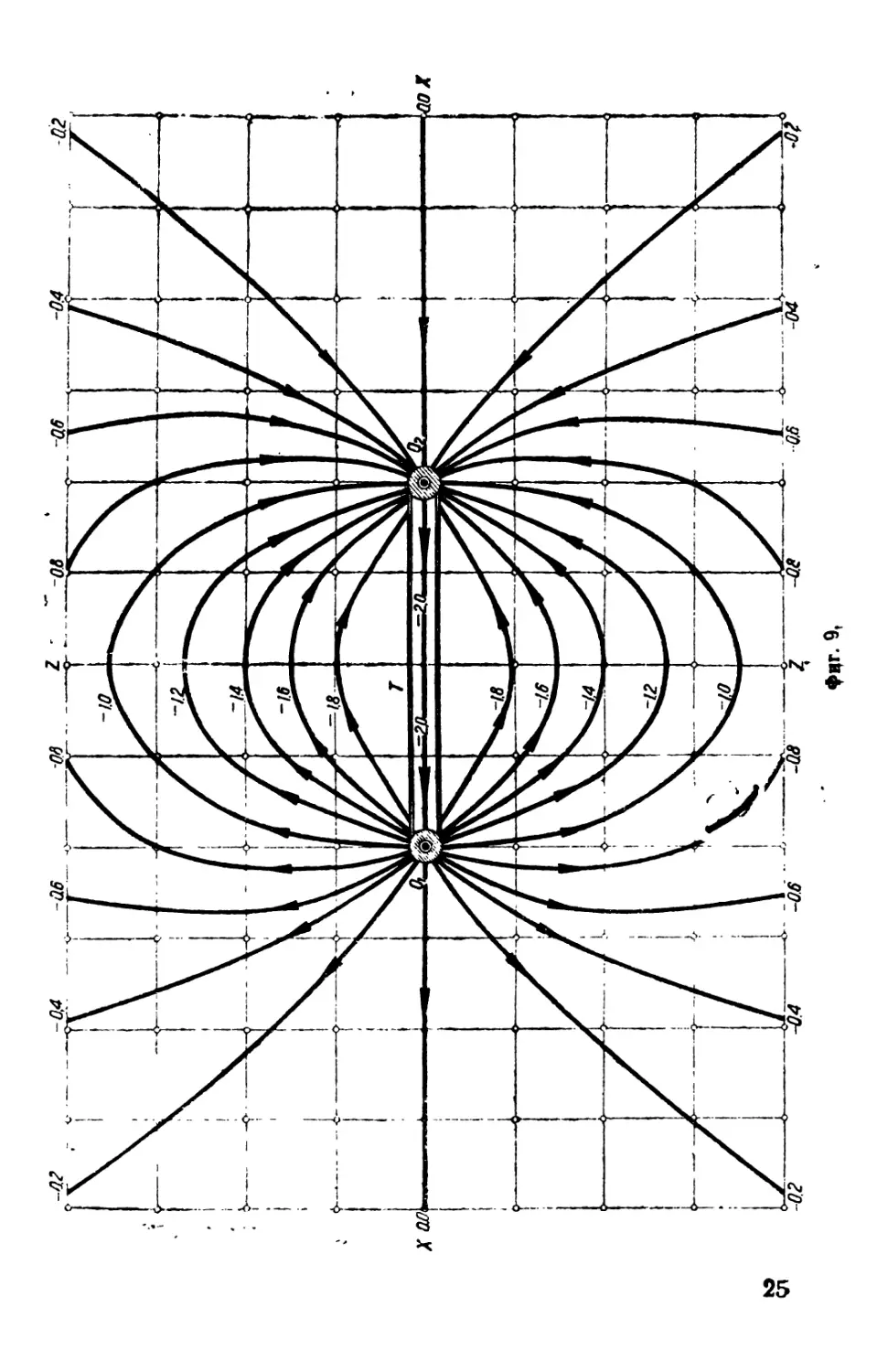
cos 04 cos = const. (34)
Фиг. 9 дает точную картину исследуемого движения жидкости. Диполь или дублет в трех измерениях. Применяя анализ, подобный изложенному при выводе Функции потенциала скоростей диполя 24
♦иг.
в двух измерениях, получим для диполя в трех измерениях, ориентированного по оси XX, функцию потенциала скоростей:
д д Q Qx —дхТ — дх г г* (Зб)
Компоненты скорости частицы по осям XX и ZZ равны:
_ z’ — 2х* | “ = <? г> 1 _ 3xz ( (36) ^=<?7Г- 1
Функцию течения S найдем, интегрируя уравнение dS=Q^dx,
в виде
почему уравнение токов жидкости
е ~ sin’ ф
S = Q —— — const
может быть представлено в виде r==D sin’<р.
(37 г
Фиг. 10 дает точный чертеж подобного течения и соответствует полю силовых линий элементарного магнита. Очевидно, что функции потенциала скоростей диполей, ориентированных по оси УУ или ZZ, будут иметь выражения:
<n —Qy <о
(38)
III. Плоское динамическое вращение жидкости вокруг оси или прямолинейный вихревой шнур
Вторым видом плоского потенциального движения жидкости, симметричного относительно точки, является ее вращение вокруг оси, проходящей через эту точку, параллельное плоскости нормальной к оси вращения.
Полагая, что подобное вращение совершается вокруг осн ZZ или параллельно плоскости координат ХО Y (фиг. 11), возможно далее рассматривать движение только в этой плоскости.
А так как при вращении частицы жидкости т в плоскости X0Y вокруг точки О как центра со скоростью W, очевидно, будет изменяться величина угла а ее радиуса-вектора г с осью 0Х9 то и найдем функцию потенциала скоростей <р как функцию угла а.
Но по фиг. 11 имеем, что у — г sin а; х = г cos а и
-- = tga, х ь
почему у а = arctg —.
*
Полагая теперь С постоянным, напишем искомую нами функцию потенциала скоростей в виде:
? = Са= Carctg^- (39)
X
и проверим, удовлетворяет ли она уравнению Лапласа.
Компоненты скорости точки т по осям координат будут равны:
<*?_ Су _ Су |
дх x’+j*2 г2 ’ I
_ д?___ Сх ______Сх ( (40)
ду~ х’+У г*' J
Поэтому
<?*<? 2Сху <?2<? 2Сху
дх? г* И ду*~ г*
Дф = О.
Полная скорость ч.'етицы жидкости
(41)
она изменяется обратно пропорционально расстоянию частицы до оси вращения.
На самой оси вращения при rt=O W=oo.
Во всем остальном пространстве она везде конечна и однозначна и уменьшается с удалением от осн в
бесконечность до нуля, при г=оо 47=0. Имея выражение полной скорости (41), можно выражения
компонентов ее по осям координат написать в виде:
и = — W — — — W sin а, 1
г Г ! (42)
v = 47 — = W cos а, I
указывающем на то, что полная скорость частицы жидкости 47 нормальна к ее радиусу-вектору г, т. е. является касательной или окружной скоростью частицы.
Траекторию частицы найдем, интегрируя уравнение тока
dx ____ dy
__Су Сх
~~ F 7»
или
xdx -f - ydy — О,
что дает уравнение траектории в виде:
xi -|- у1 =г* — const. (43)
Выражение (43) показывает, что при подобном вращении частицы жидкости движутся по окружностям различных радиусов.
А так как окружные скорости частиц различны для различных расстояний их от оси вращения (41), то и угловые скорости их будут также различны и равны:
со =------
Г
(44)
Последнее выражение показывает, что угловая скорость со изменяется здесь обратно пропорционально квадрату расстояния частип от оси вращения.
Частицы, различно удаленные от оси вращения, вращаются вокруг нее с различными угловыми скоростями и потому смещаются относительно друг друга.
Жидкое тело не вращается здесь, как тело твердое, вследствие чего в отличие от статического вращения жидкости подобное вращение называют динамическим вращением.
Выражение полной скорости (41) показывает наиболее характерную особенность такого движения жидкости, состоящую в том, что произведение из скорости частицы жидкости на ее расстояние до оси вращения остается величиной постоянной:
почему постоянна для всей жидкости и площадь прямоугольника со сторонами W и г.
На основании сказанного динамическое вращение характеризуют также наименованием вращения по закону постоянства площадей.
Оно дает нам закон Кеплера для частиц непрерывной жидкой среды и выражает собой результат действия на материальную частицу центробежной силы при полном сохранении запаса ее энергии.
Как движение с потенциалом скоростей, динамическое вращение является движением невихревым и нетрудно видеть, что все компоненты вихря по осям координат X, Y и Z, равные:
,_ 1 / dw ду\
~"2
___ 1 (ди ду)\ 4__2 хог дх ) ’
Г_ 1 (dv ди\
^~~2\дх ду)'
в данном случае равны нулю, так как: 1) w = 0, почему равны нулю
dw dw ,.ЛЧ
ду И дх"' 2' скорости р и в по (40) не зависят от z, почему dv
равны нулю также
величину С, получим:
и (следовательно, Е = tj = 0), 3) вычисляя
1 Г д Сх д С/| _С [Р —2х* . Г*—2/ I _ ^—lldx'r' ду гг J al Г1 Г г4 J
Таким образом все три компонента вихря ( = т] = С — О, почему и движение является невихревым.
Однако анализ этого движения помощью циркуляции скорости по контуру приводит нас к иному весьма важному результату.
Циркуляция скорости по контуру. Циркуляцией скорости по контуру АВ (фйг. 12) называют по Томсону выражение
в Г= fvcosO^,
(где v — скорость частицы т. а 0 угол ее с касательной mt). которое в прямоугольных осях координат может быть представлено в виде:
в
что в случае движения невихревого с потенциалом скоростей ср приводит к выражению:
в
Г== рф = — <?а , (45)
или в функции компонентов вихрей для замкнутого контура £ (фиг. 13), ограничивающего площадь S, в виде:
Г= j (udx + + *wdz)= 2 J j(Ba + 4“ Ctf)d8, (46)
где В, 7), С—компоненты вихря, а а, Ь. с—косинусы углов нормали к элементарной площадке площади 5. Пользуясь этими выражениями циркуляции скорости по замкнутому контуру, увидим, что в случае движения невихревого, когда одновременно все компоненты вихря равны нулю, B = tj = C = O, по выражению (46) будем иметь и циркуляцию Г5=0.
Тот же результат получим из выражения (45) при однозначной функции потенциала скоростей ср, ибо при совпадении точек А и В и равенстве срд = срд будем иметь
Г$ = срв—<рд = О.
Но если функция потенциала скоростей ср многозначна. как в случае рассматриваемого нами динамического вращения, где по (39)
ср = Са = С arctg е
почему ср возрастает при каждом полном обороте частичы вокруг оси вращения на 2к, то циркуляция скорости по целой окружности пути будет равна не нулю* но 2кС:
Гдв = <fB — <р л = 2я С» (47)
Этот результат показывает нам, что в случае многозначности функции потенциала скоростей движение жидкости не может быть чисто невихревым.
Оно необходимо должно совершаться в присутствии вихря. А так как по фиг. 11 угол а будет возрастать на 2тстолько при замкнутом контуре, включающем в себя ось вращения всей массы жидкости OZ, то и искомый нами вихрь должен совпадать или располагаться по этой оси.
Но тогда величина циркуляции по (46) будет равна
r = 2jjws
или яри постоянстве напряжений С
Г = 2СИЛ, (48)
S
где S—площадь, ограниченная замкнутой кривой циркуляции.
Однородный конечный цилиндрический вихрь кругового се.чения. Пусть совокупность вихревых нитей бесконечно малого поперечного сечения di9 параллельных оси OZ и имеющих одно и то же напряжение С, заполняют пространство прямого кругового цилиндра с осью OZ и радиусом круга поперечного сечения R (фиг. 14). Тогда циркуляция по граничной окружности I поперечного сечения конечного вихря будет равна Г = 2кС = 2£гс/?а, откуда
С= №/? = £/?* или
HZ = W. „ (49,
Беря циркуляцию по окружности /2 радиуса г,<7?» снова получим-.
2кС=2Сяг,» или
= <>,’, откуда
1Р, = Оа. (50)
Выражения (49) и (50) показывают, что внутри конечного вихря частицы жидкости вращаются вокруг оси с постоянной угловой скоростью С вокруг оси вращения, иными словами, жидкость, составляю-тая однородный, конечный цилиндрический вихрь, вращается вокруг оси как твердое тело.
Но если бы мы взяли циркуляцию по окружности радиуса r^R. т. е. взяли циркуляцию по кривой, проходящей вне пространства, занятого конечным вихрем, то должны были бы писать, что:
2кС = 2Ск/?» или
Фиг. 14.
Фиг. 15.
откуда
1 G G ’
г. е. снова пришли бы к распределению скоростей по (41). На поверхности вихря при rt = R получим
т. е. начиная от оси вращения, где скорость W=9 до бесконечности, скорость частиц жидкости везде конечна и изменяется непрерывно.
После изложенного вся картина плоского динамического вращения жидкости может быть представлена в следующем виде:
При каждом динамическом вращении жидкости на оси вращения появляется однородный, конечный, цилиндрический вихрь кругового сечения, вихревой шнур (фиг. 15), внутри которого жидкость вращае-„ с
тся как твердое тело с угловой скоростью С = р-,. Вне этого вих
ревого шнура во всем остальном пространстве до бесконечности вращение жидкости выполняет закон площадей и движение ее является мевихревым.
На основании сказанного говорят, что динамическое вращение вызывается действием на массу жидкости вихревого шнура.
Постоянное закона площадей С, выраженное через циркуляцию Г скорости по контуру в виде
(51)
называют напряжением им интенсивностью вихря.
Радиус круга поперечного сечения вихревого шпура /?0 может быть в каждом отдельном случае найден из условия разрыва сплошности движения жидкости им равенства нулю абсолютного давления в рассматриваемом ее месте.
Так, для движений в воздухе атмосферы, вблизи земной поверхности, где можно пренебречь действием объемных сил, будем иметь:
4- = Н — const,
С
что при р = 0 и гг=С/?0=ту приведет нас к выражению:
откуда _____
Последнее выражение показывает, что /?0 пропорционально напряжению вихревого шнура С.
IV. Движение жидкости под действием непрерывного вихревого слоя конечной ширины
Пусть мы имеем непрерывный вихревой слой (фиг. 16), бесконечно длинные прямолинейные вихри которого нормальны к плоскости чертежа. Все вихри расположены вдоль по оси ОХ и занимают на ней ширину /. " Возьмем произвольную точку пространства т координат х и у и * л найдем слагающие скорости ее и и v, параллельные осям координат ОХ и OF, возбуждаемые в ней действием рассматриваемого вихре* ♦. . вого слоя.
** С этой целью выделим у точки п в расстоянии х от начала беско« нечно малый элемент слоя ds.
В точке т этот элемент будет возбуждать скорость dW9 нормаль* ную к радиусу-вектору г и равную
dW = — ds, г ’
где г —расстояние точки т от точки п, а С— напряжение вихрей слоя* Полагая угол между г и ОХ равным а, получим слагающие СИО* роста dW по ОХ и OY равными:
dll — dWsina; dv =— dWcosai.
Hojr = rsina; x — s = rcosa; r*=y*-]-(x — s)*;
i У x —s
sfaa = j-; cosa = —-—,
Потому выражения тех же скоростей можно писать в виде:
<г«=£.2л=а,Л=_^’, Г Г Г* —
Г г Г* .У* й~ (х *)*
8 Я Мааломач
Полную величину составляющих получим, интегрируя от и выражения по всей ширине вихревого слоя от 0 до I, в виде:
।
I Z»
о
I
— С | arctg - =
о
= — С ( arctg — arctg = С ( arctg * + arctg j = ^С(?4Ч-ра) = Св, (53)
где 6 — угол, под которым из точки т видна ширина вихревого слоя Z.
Аналогично изложенному для скорости v будем иметь:
„ _ О (X-S)ds _crd[y^±(x-sf]_
J ? + (*-*)’“ 2 J >’ + (x — s)a “ 0 0
I
т 4/+(* - s)’l = f (М/ 4Л' - - Hr+X1)' av I J
0
Но из фиг. 16 имеем:
Л’ +/=:/?/; у + (/-л-)’^/?Л
где /?! и /?а — расстояния точки т от концов вихревого слоя 1 и 2.
Теперь выражение скорости v возможно представить в виде:
С Р
т» = -^(1пЛ1’-1п/?г) = -С1п^. (54)
Чтобы проверить, удовлетворяют ли полученные скорости уравнению Лапласа, возьмем производные от них по х и у, тогда получим
$=-с i|л й=- v ^['"0"+*’> - - ^’1] -
__ С / 2у 2у \ “~ 2\х®+У ~+ —х)7 ’
поэтому
। __ п
уравнение Лапласа удовлетворено.
Выражения (53) и (54) показывают, что скорость и, параллельная вихревому слою, изменяется пропорционально величине угла 0.
Она непрерывна во всем пространстве, положительна выше оси XX н отрицательна ниже этой осн.
На самом слое она равна Стг сверху осн* XX и — Сгс снизу ее, так что, проходя через вихревой слой, она изменяется скачком на 2тгС. Вне вихревого слоя на оси XX она везде равна нулю. Скорость
и, пропорциональная In , равна нулю во всех точках Пространства, **з
равно отстоящих от концов вихревого слоя, т. е. во всех точках плоскости, нормальной к плоскости слоя и проходящей через его середину. Она отрицательна вправо от этой плоскости и, наоборот, положительна влево от нее.
Скорости v стремят^т вращать весь вихревой слой по стрелке часов, т. е. по направлению вращения элементарных вихрей, вокруг его середины. Последнее обстоятельство особенно ясно видно из формы движения жидкости, вызываемого действием подобного вижревого слоя.
Функция течения и токи жидкости. Функцию течения получим, интегрируя выражение
5= J vdx — — С J In dx = —Jln/?22dx + у J ln/?2arfx. Но
J \nR2dx = Jln(y2 xQ)dx = x ln(yr9 x2) — J x —
=x ln - 2 JO -yr^dx =
Г d —
=x ln(j»2-f-As)—2x-±2yI-~x ln(/"T*’)—Ъс -f-arctg £,,
V-M — I У
J \yJ
= — (/—х)1п[/ 4- (/—*)*] + 2(/—х) — 2у arctg .
Поэтому
С In dx = х In/?,’ — 2x4- 2у arctg^- + (f — к) In Rt — 4-
J У
4-2yarctg^y?.
Внося полученное значение интеграла в выражение функции течения, получим ее равной:
5 = — С {х 1 п /?, — х 4-у arctg у 4- (/—х)1п R, — (I — х) 4-
4~_у arctg—у—.
Для проверки правильности выражения S посмотрим, выполняется ли . равенство:
<?S Л l x । I— x\
— = - и = -Св = - C^ arctg у 4-arctg — ).
Беря производную S по у, получим:
as_ cr xy । arct * xy । (!-x)y .
+arctgLL5] =
= — C(arctg у 4- arctg= — Св,
т. e. предыдущее равенство действительно выполняется.
Полученное нами выражение функции течения можно преобразовать в следующее:
5 = — с [х 1п£ 4- / In /?,—14- у ( arctg -у 4- arctg =
= — С [х In 4-jfl 4- /(In /?, - 1) j =
= — С Gh - (at 4- а,)] 4-X In 4- /(In Rt - 1Й . (55)
♦иг. 17 дает точный чертеж подобного движения жидкости.
Из него ясно видно, что подобный вихревой слой будет стремиться свернуться в конечный, цилиндрический вихрь кругового сечения.
ОТДЕЛ II МЕХАНИЗМ ВОСПРИЯТИЯ И ПЕРЕДАЧИ СИЛЫ БЕЗГРАНИЧНОЙ НЕПРЕРЫВНОЙ МАССОЙ ЖИДКОСТИ
§ 2. ДЕЙСТВИЕ НА ЖИДКОСТЬ ПРЯМОЙ-ДИПОЛЯ ИЛИ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ВИХРЕЙ
Т. Тождественность функции потенциала скоростей прямой-диполя потенциалу пары параллельных вихрей
Из выражения (20) § 1 нам известно, что плоское течение жидкости, вызываемое наличием в ней источника-пары (диполя) О, сри-ентиро ванного по оси YY, имеет потенциал
(1)
где Q—напряжение диполя; у — ордината какой либо произвольной точки жидкости т (фиг. 18); г — расстояние этой точки до начала координат или точки-диполя О. Диполь О выбрасывает из себя и всасывает частицы жидкости по направлению осн YY. Если теперь мы вместо одной точки пожелаем иметь выбрасывание и всасывание жидкости по длине I прямой АВ (фиг. 19) в целях получения плоского движения ее как при истечении через отверстие ширины АВ, так и при обтекании пластинки той же ширины, то мы можем достигнуть желаемого, вообразив прямую АВ равномерно покрытой точ-
ками диполей одного и того же напряжения и знака.
Полагая напряжение прямой АВ равным Q, получим напряжение
Q I ’
се на единицу длины равным
а функцию потенциала скоростей
течения прямой диполя
? /Jr* о
(2)
где согласно фиг. 20 ds = т'т4 представляет бесконечно малый элемент прямой-диполя, взятый у точки ее iri на расстоянии s от начала прямой А, а ^=^-{-(5—х)2—квадрат расстояния до него какой-либо произвольной точки жидкости т.
Поэтому выражение (2) можно представить в виде: i i
__ QT yds _________ Q Г ds
Ч — ~ I ($ — x)2 ly J (s — x\* 0 0 / $__X ' J '
Полагая ---= £, будем иметь s— x=yt и ds=ydt, почему
предыдущее выражение с? напишется в виде: i ' i i
QC л Q хх Qi । *
----7jrp5=~ 11arctg * = " 7 arclg ~'
о О О
Y
V
Фиг. 18.
Фиг. 19.
Подставляя пределы интеграции, получим функцию потенциала скоростей прямой-дщюля <р в виде:
ч = -т [ ? ».«tg -2^7 •
У У откуда
? = — Я arctg —у-. (3)
* УА~Х—Iх
Подобное выражение функции <р удовлетворяет уравнению Лапласа для плоского течения жидкости.
В самом деле, беря первые и вторые производные <р по к и у,
получим:
^?_Г)_____У&Х — 1)
дх~ч (У4-х2-/х)’4-/>2 ’
(4)
(/+ х'- lx) (У- Зх2 + 3/х) - ГхЧ 1*х дх2 “ уч [(У4- хъ—/х)24- /’У]2
_ о **-1х-у*_________ (5)
ду~ 4 (у'-^х'—^У^Гу *
д»<Р — (у*4~ х'— 1х) (у2— Зха+ 3/х) 4- Гха— 1»х
dyi — *уч КУЧ-*’—Z*)a+W * почему
дх'^ду1
Полученное нами выражение функции ф может быть представлено и в другом особо простом виде.
I__х х
А именно, замечая, что по фиг. 20 arctg ——— = a arctg— =
= / р, получим:
'F = — 7 ( arctg 4- arctg у) = — ® (« + ₽) = ~ 7 •0- <3’>
Последнее выражение показывает, что функция потенциала скоростей прямой-диполя пропорциональна углу 6, под которым из рассматриваемой точки т видна длина прямой I.
Но ту же функцию потенциала скоростей <р мы можем найти, исходя из совершенно иного представления о рассматриваемом нами здесь явлении протекания жидкости через пространство 00 (фиг. 21).
В самом деле, положим, что на краях отверстия или пластинки прежней ширины I мы имеем прямолинейные параллельные вихревые шнуры в точках О и Ох фиг. 21 прямо, обратного направления вращения и равного напряжения.
Найдем функцию потенциала скоростей течения жидкости, вызываемого означенной парой вихревых шнуров, полагая вращение шнура в точке О по направлению часовой стрелки, а в точке Ох—против стрелки.
Для произвольной частицы жидкости, расположенной в точке т, с координатами х и у будем иметь расстояния ее до вихревых шнуров О и Ох равными:
г.= у/{1- х)34-л (6)
у = г sin л — fjSin 04; x = rcosa; I — x = r1cosa1,
где а и а,— углы радиусов векторов г и Л. с осью х. Одинаковое по величине напряжение вихревых шнуров О и Ot обозначаем через С, Тогда, зная, что каждый из этих вихрей будет стремиться вращать вокруг себя частицы жидкости по кругам со скоростями, выполняющими закон площадей1:
С= W-r,
1 Отдел I, выражение (41). ап
найдем, что в точке т вихрь О возбуждает скорость W, нормальную к радиусу-вектору г и рав-
ную IF= —.
Одновременно с этим в той же точке т вихрь Ог возбуждает скорость UZp нормальную к направлению радиуса вектора и рав-С nyroPZj = —. Поэтому слагающие скорости точки т по направлению осей координат ОХ и ОУ, и и ф будут равны:
а = = IF cos (90 — а) — W\cos (90 — at) = W sin « — JPjSin at=
.»• _ C x Cl x_____
о=^=-Гсо.«-1Г1И»«1=---у--.—=
— I l~x\
V ‘ r* )'
Подставляя в полученные выражения скоростей значения радиусов векторов г и гх из выражений (6), можем написать их в виде:
<?ср &У
х*— 1х—у*
или, наконец, в виде:
ц_*р_ а y№x~i)______________ 1
дх~ (у' + х1— /х)’ + /У ’ I
v - _ а х2-1х-у* (
v—dy — ^iy’-^ — txf + W j
так как
(7)
Но выражения скоростей (7) тождественны выражениям (4) и (5) при условии, что С = — у- .
На основании всего изложенного функция потенциала скоростей плоского движения жидкости, вызываемого парой параллельных
сихревых шнуров противоположного направления вращения, будет равна
<Р = С arctg = СО. (8)
Она тождественна функции потенциала скоростей прямой-диполя п
при условии С = — -у, т. е. при равенстве напряжения вихревых шнуров напряжению прямой-диполя на единицу шцрины пластинки с обратным знаком.
Тождественность теории прямой-диполя и пары параллельных вихревых шнуров противоположного вращения легко развить теперь и далее и показать, что сам диполь представляет собой не что иное, как систему двух бесконечно близких параллельных вихрей противоположного вращения.
С этой целью положим, что пара рассматриваемых вихревых шнуров находится на бесконечно близком расстоянии друг от друга А/, и посмотрим, к какому виду придет функция (8) при уменьшении Д/ до нуля. Называя этот предел функцией срп получим, что
ср д ф
<р = lim тт=х-т-г-
Но
_ . Му
ср = С arctg —о -77—,
т * — Д/х ’
поэтому
У (*2 * * +.У2 — Д/х)-|-Д 1ух
с ~х2+У-Д/х)а
дД/ / Му V
— мх)
= Су(?-|-У)(ха4-у — 2Д/х4- Д/5) =Су Д/Л'4-д/1
lim д/ —* о
ду _ ___ Су ___Су
1ГК1—?»— х2 4-j7 ~ 7’~'
(9)
Последнее выражение тождественно выражению (/) диполя плоского движения жидкости при условии равенства С = — Q напряжения диполя напряжению вихревых шнуров с обратным знаком.
Совершенно аналогично всему изложенному беря диполь для движения в трех измерениях
(фиг. 22) и покрывая ими всю площадь какой-либо ограниченной поверхности S (фиг. 23), мы получим функцию потенциала скоростей
движения жидкости при протекании ее через ату поверхность тождественной функции потенциала скоростей течения ее, вызываемого действием замкнутого вихря А, идущего вдоль по контуру поверхности S. И обратно, уменьшая величину площади поверхности S до нуля и тем самым стягивая контур вихря* А в точку, мы в пределе получим для движения в трех измерениях тождество точки-ди-поля вихревому кольцу бесконечно малого диаметра с напряже-нием вихря, равным напряжению диполя и обратным ему по знаку.
Выясненное нами тождество теории диполя теории замкнутого вихря или пары параллельных, бесконечно длинных вихрей, сводящееся по гидроэлектрической аналогии к тождеству действия двойного магнитного листка действию электрического тока, пробегающего по кривой его контура \ сразу освещает и решает все вопросы как протекания потоков жидкости через отверстия, так и взаимодействия жидкой среды и движущейся в ней поверхности произвольного вида. Оно показывает нам, например, что во всех случаях протекания потока жидкости через отверстия струя жидкости неизбежно одевается на краях отверстия системой вихрей, препятствующей быстрому расширению ее по выходе из отверстия, что вполне соответствует данным непосредственного опыта. Такой же вихревой поверхностью одевается и внутренняя часть потока, обтекающая края твердого тела, движущегося в неограниченной жидкой среде, так как явление, здесь происходящее, подобно явлению протекания части потока через отверстие контура, нормального к потоку сечения тела в направлении, прямо обратном направлению реального потока. Но чтобы все дальнейшее было вполне ясно, мы прежде всего найдем форму движения жидкости, вызываемого действием прямой-диполя или парой параллельных вихревых шнуров.
1 Р. A ppalle. Tra!te‘de M^canlque Rationnelle, Tome Ш, § 574.
II. Форма движения жидкости, вызываемая прямой-диполем или парой параллельных вихревых шнуров
Пусть согласно фиг. 24 мы имеем два вихревых шнура в точках Oj и Оа на оси XX в расстоянии I друг от друга.
Полагая напряжение их С одинаковым по величине, но обратным по знаку, мы, очевидно, бу-
Фиг. 24.
дем иметь картину движения жидкости, ими вызываемую, симметричной относительно оси YY\ проходящей черев середину расстояния I между вихрями, т. е. через точку О.
Поэтому для упрощения результатов отнесем все движения к началу координат в точке О вместо точки Оп как то принималось нами на фиг. 21.
Новая абсцисса точки т будет связана со старой равенством:
х' = х—— ИЛИ Х = —
£
Подставляя его в выражение функции потенциала скоростей течения (8), получим:
Или опуская значок' у х, окончательно для новых осей будем иметь:
ср = С arctg
(10)
Вместе с тем при новом начале координат имеем соотношения:
А слагающие скорости частицы по осям координат будут равны:
Функцию течения S искомого движения жидкости найдем из сравнения уравнения тока:
dx__dy
и v
или
с выражением полного
vdx— udy=0
диференциала функции течения:
dS - . dS - л dS=-^-dx -+-3—dy = О, дх ' ду
откуда имеем, что д<? dS
и = —
дх ду
ду~дх ’ Почему
$ = -Curfy +/(*) = 2 C/xfr-------------------+/(*)•
Но
на основании чего подинтегральное выражение возможно представите в виде:
Пользуясь последним выражением, мы «ожем писать, что
Подставляя полученное выражение интеграла в выражение функции течения, найдем, что
где f(x) — неизвестная еще нам функция х.
Для определения ее сравним между собой выражения с выра* женнем V, тогда найдем, что
откуда имеем, что
/(х) = 0 или f{x)~ const.
Поэтому окончательно можем функцию течения 5 представить в виде:
(13)
На основании выражения (13) мы можем уравнение токов жидкости написать в виде:
D = const
ИЯМ
У+(4-л)’ = 0У + 0(^- + х)’
или
или, наконец,
/ 1+DV DP
2 '1— D) — (1—D)a
(14)
Уравнение (14) показывает, что токи жидкости представляют собой окружности с централи, расположенными но оси XX.
Координаты центров этих окружностей будут равны:
У о —
_ I 14-0 *0“ 2"’ 1 — D '
Величии раднусов их
R = l
(15)
(16)
При D — 0 х0—g- и /? — 0; при D = 1 хв=оо и R = oo.
Постоянное D изменяется от единицы до нуля; оно равно единице в середине расстояния между вихрит и равно нулю на концах его в точках вихрей Оу н OY
Точный чертеж полученного нами плоского движения жидкости представлен на фиг. 25. На нем постоянное D изменяется при переходе от одной цилиндрической поверхности токов к другой, ей ближайшей, на одну и ту же величину в 0,1, почему между двумя последовательными поверхностями протекает один и тот же расход, равный
Поэтому фиг. 25 кроме картины линий токов дает нам точную картину и распределения всего расхода q по ширине отверстия или пластинки Z. Так из фиг. 25 мы видим, что интенсивнее всего расход в середине ширины отверстия и что он быстро уменьшается в величине от середины к его краям. Обращая внимание на самую внутреннюю окружность токов с постоянным D = 0,l, увидим, что 0,9 расхода проходит здесь приблизительно через половину ширины отверстия в его средней части. Остальная половина к его краям пропускает только 0,1 расхода, причем на самих краях, где D — 0, и расход также равен нулю.
Указанное выше распределение расхода вдоль по ширине отверстия или пластинки с полной ясностью представлено на фиг. 26, где расход в ее середине принят за единицу сравнения.
&
M (LQ IQ 09 W
Фаг» 25.
Но чтобы вполне убедиться в том, что мы имеем здесь соответствие реальному явлению природы, найдем уравнение кривой распределения расхода вдоль по ширине отверстия или пластинки и по ней вычислим величину самого расхода.
С этой целью отнесем согласно фиг. 27 кривую распределения расхода АВ, А'В к началу координат в точке О середины отверстия. Ось абсцисс ОХ возьмем по прямой ширины отверстия и ось ординат OD нормально к ней. Тогда координаты произвольной точки т кривой АВ согласно фиг. 25 и выражениям (15) и (16) будут равны:
Фиг 25.
х — х0 — R — |
( 2 1— D Ч-ГНу ' y = D.* .)
а уравнение кривой АВ может быть представлено в виде:
I 1—/О 2^1+/р’
Фиг.. 27.
Чтобы найти теперь величину расхода при средней чения равной 1 м[сек для каждой половины ширины
скорости исте-I отверстия - f
т. е. расход, проходящий через половину ширины его, \ 2
рируем
выражение элементарного
расхода
а--, равного £
проинтег-
заштрихо-
ванной на изменения
фиг. 27 элементарной площадке (1—D)dx в пределах I '
X от нуля до —, тогда полусим:
J<- = U-D)dX,
_L L
2 2
f-=f(l-D)rfx = L-f£M*
A J Z J
0 0
= 21
Но последний интеграл после ввода новой переменной г, равной г=—4-х, dz = dxl x = z — ^ и (у+х) = г’»
может быть приведен к виду: / \. г г
2/ \dz I \ dz
~z~ У iz2
I 1 2 Z * •
Xdx нт
z2
Поэтому, внося снова вместо z и подстав’ляя значение
£
интеграла в уравнение расхода, получим:
2
In
2 /
= 2/(In 2 — 0,5) =
о
1 ' ±4.
2 ' 0
= 4 (0,692369 — 0,5) = 0,769476-^-
Фиг. 28.
и окончательно
q = Q,77l.
Или для .средней скорости истечения w q=6,77lw. (19)
Таким образом для истечения из отверстия в виде бесконечно длинной щели шириной I мы получили здесь коэфициент расхода равным 0,77, Вычисление того же коэфициента более простым способом прямолинейного источника, лежащего в середине щели, дает коэфициент расхода, равный 0,7851, т. е. коэфициент больший на 1,5°/0. Столь ничтожная разница результатов подсчетов одной и той же величины весьма различными между собой методами указывает нам на близость этой величины коэфициента расхода его истинному фачению, что хорошо подтверждается и результатами непосредственного опыта. Ясно также, что, уменьшая на фиг. 25 расстояние между вихрями I до нуля и сближая тем самым токи жидкости между ними, мы в пределе придем снова к точке диполя фиг. 18 и притом с весьма малым изменением картины расположения токов, что прямо видно из сравнения обеих фигур.
В заключение должно быть еще раз отмечено то замечательное свойство подобных движений жидкости, по которому, несмотря на наличие на краях отверстия или пластинки в центрах вихревых шнуров бесконечно больших скоростей, даваемых выражениями (12)npHj = 0 и х = —, равенство нулю для этих точек расхода или массы проте-z &
кающей здесь жидкости приводит к тому, что как полный расход потока через отверстие, так и количество движения этого рас-хода остаются величинами конечными и вполне определенными.
1 См. А. Я. М и л о в и ч, Основы динамики жидкости, стр. 45. ЭнеРго-издат, 1933 г.
4е * 51
Фиг. 29.
Фиг. 28 дает нам фотографию формы силовых линий магнитного поля электрического тока, пробегающего в прямо противоположном направлении по двум параллельным проводникам, нормальным плоскости фигуры и проходящим через точки Ох и О2 в расстоянии / друг QT друга.
J Мы имеем здесь картину, совершенно тождественную чертежу течения жидкости прямой-диполя фиг. 25.
Фиг. 29 дает картину силовых линий магнитного поля того же электрического тока при сближении проводников почти до соприкосновения для получения картины поля магнитного диполя-точки или элементарного магнита. Эта картина тождественна течению диполя-точки плоского движения жидкости фиг. 18.
1П.Ф(оличество движения прямой-диполя или пары параллельных вихрей
, В предыдущем мы исследовали вопрос о расходе или секундной массе жидкости, протекающей через прямую-диполь.
Но чтобы определить силу, порождающую это явление, необходимо найти величину секундного количества движения этого расхода или массы.
Последнее мы можем выполнить, пользуясь теоремами проф. Н. Е. Жуковского, к изложению которых и перейдем.
Первая теорема Н. Е. Жуковского, ее следствия. Количество движения, сообщаемое безграничной массе жидкости парой в проти-,воположные стороны вращающихся, параллельных, прямолинейных вихрей равного напряжения, равно плотности жидкости, умноженной на циркуляцию вихрей и расстояние между ними.
Пусть согласно фиг. 30 мы имеем пару параллельных, прямолинейных вихрей О и Oj равного напряжения, вращающихся в противоположных направлениях и отстоящих друг от друга на расстояние /. «в
Обозначим напряжение Этих вихрей, через С, тогда циркуляция их равна Г=2кС, и отнесем всю систему к осям координат YOX, с началом в центре вихря О, осью ОХ9 идущей по линии центров вихрей О и и осью OF, направленной вертикально вверх.
Тогда, как нам уже известно, в произвольной точке /и с координатами х и у вихрь О будет вызывать своим действием скорость W, нормальную к направлению радиуса-вектора г точки и
равную
Полагая г наклоненным к оси ОХ под углом ср, будем иметь следующую связь всех потребных далее нам величин:
у = г sin ср; х = г cos ср; г = j/х* + 5 *£ »
X
. у у х
cp = arctg^; sincp = ~; coscp = — .
Возьмем теперь бесконечно тонкую полоску жидкости ab, проходящую через точку т и нормальную к оси £)Х. Ширина полоски пусть будет равна dx и толщина равна единице. Вычислим количество движения, сообщаемое жидкости такой полоски вихрем О, в направлении, параллельном оси OY (иначе вдоль по самой полоске). С этой целью выделим в полоске «6 у точки т бесконечно малый объем жидкости с площадью основания dxdy и толщиной, равной единице. Масса жидкости этого объема равна
dm = fidxdy.
Количество движения его в направлении, параллельном оси QF, равно:
dM=pdxdy. HZcoscp —— pdxdy — • ~ =
Г Л
Чтобы найти теперь количество движения, сообщаемое полоске ab на всем ее протяжении от —со до -f-oo, проинтегрируем полу-
ценное выражение элементарного количества движения по у в пределах изменения его от — оо до-|-оо, тогда найдем:
arctg У- = — 2 pCrfx
ср = — pnCdx.
Количество движения, сообщаемое вихрем О р направлении, параллельном оси OY, бесконечно длинной и тонкой полоске ab9 равно поэтому
dM = — pnCdx.
Оно не зависит от величины х, т. е. от расстояния полосы ab от > ихря О, и для всех полосок, расположенных вправо от вихра, будет отрицательно,*а влево от него положительно, '/го обусловлено знаком компонента скорости Ww даваемой вихрем.
Для вихря Ох мы получим ту же величину количества движения, но только с обратным знаком, т. е. отрицательную влево от вихря и, наоборот, положительную вправо от него. В результате этого изменения знака количества движения второго вихря получим, что все полоски жидкости, проходящие между обоими вихрями на протяжении расстояния между ними Z, будут иметь количество -движения одного знака и потому от обоих вихрей полоска ab получит количество движения, равное сумме их,
dM= — 2?nCdx.
Наоборот, для всех полосок, проходящих с одной стороны обоих вихрей, как например, для полоски^с^ количества движения будут гавны по величине, но обратны по знаку и потому взаимно уничтожатся и в сумме дадут нуль.
На основании сказанного полное количество движения, сообщаемое жидкости парой вихрей обратного вращения, но равного напряжения будет равно:
t
М= — 2 *Ср ^dx = — 2 кС[Л = — [ЛЧ, (20)
*0
что и. доказывает жалаемое.
Но это количество движения от пары вихрей сообщается жидкости только в направлении, нормальном к прямой, их соединяющей. В направлении, параллельном этой прямой, как например, ’ля полоски ef знаки количеств движения, сообщаемых различными
вихрями, будут различны, и при суммировании эти количества движения взаимно сократятся.
Следствие!. Важнейшее следствие доказанной теоремы, прямо вытекающее из самого метода ее доказательства, состоит в том, что один изолированный, прямолинейный вихревой шнур не может сообщить жидкости какого-либо количества движения ни по какому направлению. Он не дает никакой силы и может только вращать массу жидкости симметрично вокруг своей оси.
Следствие II. Количество движения, сообщаемое жидкости точкой-диполем при ее плоском движении, по оси течения равно произведению из плотности жидкости на циркуляцию вихрей, его образующих. Ибо при сохранении напряжения вихрей и постепенном сокращении расстояния между нимй I до нуля, для перехода к точке-диполю, мы будем иметь количество движения последней равкмм:
— lim=-^- = —2лСр = —pl. (21)
Второе следствие показывает нам, что диполь плоского движения сообщает жидкости по оси им вызываемого течения (по оси OY на фиг.' 18) совершенно определенное и конечное количество движения, т, е. действует на жидкость с совершенно определенной силой.
Таким образом точка-диполь или силовая трубка бесконечно малой длины представляет собой силу или центр энергии, рассеиваемой им в окружающей его жидкой среде \
Вполне ясно теперь, что подобно одному прямолинейному, изолированному вихрю бесконечной длины один изолированный источник-точка не может сообщить жидкости никакого количества движения, т, е. не дает еще никакой силы воздействия на жидкую среду.
Изложенным, как видит читатель, я принципиально расхожусь со взглядами проф. Прандтля (Prandtl), развитыми им в §§ 8 7, 88 и далее во втором томе его .Hydro- und Aeromechanik" von О. Tie-tiens, Berlin, 1931 r. .
Вполне определенную силу и количество движения может дать,\ как нам теперь ясно, только система двух источников или двух вихрей противоположных знаков.
Только эти системы и системы, из них образуемые, приводят нас к результатам теории, хорошо соответствующим результатам непосредственного, реального опыта. А между тем в § 87 проф. Прандтль предлагает для определения количества движения или силы пользоваться импульсом только одного источника-точки.
1 Сказанное дает нам новое доказательство правильности свойств, приписываемых точке-диполю и изложенных с совершенно иной точки зрения в моем предыдущем труде: .Основы динамики жидкости*, Москва, 1933 г., сгр. 59 в разделе .Замечание о динамическом эффекте введения в жидкость систем источников*. ;
Там же на стр. 135, пример Ш, приведен и метод, коим мы моИсем оп- | редел и ть величину силы давления диполя на окружающую его жидкость.;
Фиг. 31.
Следствие III. Невихревое или чисто потенциальное движек ie жидкости, подобно прямолинейному равномерному движению твердого тела по инерции, осуществимо только при полном отсутствии каких-либо сопротивлений ему, требующих для своего преодолев, я затраты энергии потока.
Оно не может дать никакой силы, почему и невозможно основывать на нем теорию взаимодействия тел и жидкости.
Для распространения всего сказанного выше на движение жидкости в трех измерениях докажем вторую теорему Н. Е. Жуковского Ч Вторая теорема Н. Е. Жуковского. Количество движения, сообщаемое беспредельной жидкой массе замкнутым, плоским вихревым шнуром, равно циркуляций скорости вихря, умноженной на ограничиваемую им площадь и плотность жидкости.
Вообразим согласно фиг. 31 плоский, замкнутый вихрь КК, лежащий в горизонтальной плоскости.
Построим у точки п на элементе df, ограничиваемой им площади F, бесконечно тонкую призму ZZ, нормальную к площади/7 и распространяющуюся своими концами в бесконечность.
У произвольной точки т оси Z с ординатой z выделим бесконечно малый объем призмы ZZ, равный df-dz, и найдем количество движения, сообщаемое массе жидкости этого объема элементом вихря ВС = ds.
С этой целью найдем прежде всего величину скорости, сообщаемой точке т по вертикальному направлению снизу вверх рассматриваемым элементом вихря ds.
Для этого примем направление элемента вихря ds, О'О” за ось вращения в направлении, обратном часовой стрелке; расстояние точки тц от ds, т. е. Вт, обозначив через /?, а, угол тВО9 между прямыми О'О" и Вт через ср.
1 Трудц, ЦДГИ, вып. I, 1919.
56
Тогда по закону Био-Савара *, элементарная скорость dW, сообщаемая элементом вихря ds точке т по направлению, нормальному оси вращения О'О", будет равна:
г sin»<fc
г
где ds — элемент вихря; —---напряжение вихря; /? = тВ — расстоя-
4 тс
ние точки т от ds* ср — угол тВ(У. Скорость dW лежит в плоскости треугольника тАп, проходящей через ось ZZ и перпендикуляр А, опущенный из точки п на прямую 0'0", и нормальна к прямой mA. Пространственное расположение всех этих величин для наглядности дано отдельно на фиг. 32.
Из нее прямо видно, что искомая нами вертикальная составляющая скорости dW равна:
cos 0 = ^4-.
Но из треугольника АтВ имеем, что 1 = R sin ср, почему
dW' = dW-^— = 4“ • ~Sr-KSincp 4тс
Поэтому количество движения, сообщаемое элементом вихря ds массе жидкости р dfdz, выделенной у точки т по направлению вертикальной оси ZZ, будет равно:
dM~ 17f hds ~7F~=77р hdsdf (zHL>77r ’ так как
R* = z' + r\
Проинтегрировав это выражение во всей бесконечной длине призмы ZZ, получим
поэтому
... Л Г „his dM=2^dfjr,
1 См. А. Я». Ми ловил .Основы днввмшив жидкости/. стр.. Z3.
S7
с другой стороны, из подобия треугольников АпВ й DBC Следует, что, h______________________________rd^i .
г ds
< или •
hds=r~dt\.
На основании последнего равенства предыдущее выражение dM можно написать в виде:
Интегрируя по всему замкнутому контуру вихря и по всей площади его, получим
2г. F
тИ=2^-р [rfri i df=?VF
4к J J *
о о
для суммы количеств движения всех призм, пересекающих площадь F. Для всех призм, не пересекающих площади F, получим сумму, равную нулю, ибо для всякой внешней призмы пределы изменения угла т| равны нулю.
Поэтому окончательно имеем, что
* Af=rPF, (22)
*1т» и требовалось доказать. ‘
Согласно последнему выражению для точки-диполя в трех измерениях, как для вихревого кольца бесконечно малого диаметра, будем 4меть
Силы взаимодействия безграничной жидкости и пары прямолинейных ^параллельных «вихрей или замкнутого вихря, даваемые изложенными выше теоремами Н. Е. Жуковского, были получены на основании закона Био-Савара, примененного к гидродинамическому полю. Поэтому они являются вполне аналогичными силам взаимодействия между электрическим током и магнитным полем Ампера.
Количество движения, сообщаёмое безграничной жидкости вихревым соленоидом. v
Третья теорема; Количество движения, сообщаемое безграничной массе жидкости двумя параллельными между собой, прямолинейными и непрерывными вихревыми слоями конечной ширины равного напряжения и прямо обратного вращения, равно плотности жидкости, умноженной на циркуляцию вихрей, расстояние между слоями и на их ширину.
Для доказательства этой теоремы вообразим вихревой соленоид ABCD (фиг. 33), состоящий из двух параллельных между собой, непрерывных вихревых слоев AD и ВС ширины Н, образованных и?
прямолинейных вихрей прямо обратного направления вращения и равного напряжения, и найдем, какую скорость каждый из этих слоев сообщает произвольной точке пространства т (х, у) параллельно своему направлению или оси YY.
С этой целью выделим у Точки а бесконечно малый элемент слоя /4D, равный ds в расстоянии s от начала координат, и посмотрим, какую скорость'Л? сообщает он частицам жидкости в произвольной точке пространства т с координатами х и у. Вихрь в точке а сообщает точке т скорость dW, равную:
Фиг. 33.
Г
где г — расстояние точки а до точки т, а С — постоянное напряжение вихрей слоя AD.
Эта скорость нормальна к направлению Г. Обозначая угол между направлением г и осью ОХ через <р, будем иметь, что *
dv = dW cosep. f
Но из треугольника amb имеем:
х х — Г cos <р, откуда соъ <? = —.
Поэтому
. „xds ~ xds = С~ъ- = ~ •
г * + (У —S)
О
Теперь для нахождения полной скорости гт, сообщаемой в точке т «семи элементами вихревого слоя AD, должно проинтегрировать выражение d*v в пределах от нуля до Н9 тогда получим:
и
। xds
V =С \ ~2~ I /----
U2 + (y—$)’
О
н
= —С arctg^^,
откуда
V = —С ( arctg ---------arctg . (24)
Но
arctg = / ntAB = a, a arctg = / tn.DC — ар
поэтому выражение'(24) возможно представить в виде:
t’ = — С(а— а1) = С(а1 — ?) = <??, (25)
У а
8
Фиг. 34.
где y = / AmD есть угол, под которым из точки т видна ширина вихревого слоя AD.
Зная все сказанное, возможно приступить и к определению количества движения, сообщаемого жидкости вихревым слоем AD по направлению оси УК Для удобства выполне-* ния анализа отнесем вихревой слой AD к осям координат с началом в точке О его середины, осью ОХ. нормальной к слою (фиг. 34), и осью УК, совпадающей с направлением слоя AD.
Положим H=2h равной ширине слоя и I расстояние между слоями AD и ВС. Выделим в безграничной жидкости бесконечно шириной dx. параллельную вихревым слоям, т элемент высотой dy и толщиной, равной.
тонкую полоску ab и возьмем у ее точки
единице. Тогда масса элемента полоски жидкости будет равна
dm = р dxdy. где р — плотность жидкости. Элементарное же количество движения параллелЛьно оси УУ равно
х dM = р Cdxdy -f,
. J' + A a y — h где -[ — а, — 04 = arctg <4----arctg ?
Поэтому
dM = p Cdxdy ( arctg - '
arctg —
Для получения полного количества движения, сообщаемого слоем AD всей полоске ab, проинтегрируем . это выражение по у1 от — оо до Tflhia получим:
+оо
dM = р Cdx С / arctg Ki* — arctg~~ dy =
J \ х х I
—со v
Интегрируя, получим: оо
dM—fyCdx о оо л „. I ( ( . y-\-h
=2р Cdx I < у I arctg^-arctg.
arctg ^4
1 x у—А
|arctg -----х In
У-Ь\
—х lni^|= 2р Cdx hn=&Cit Hdx, dM=^CHdx. (26)
Выражение (26) показывает, что величина dM независима от координаты х. Справа от слоя AD она положительна, слева от него отрицательна. Для слоя ВС, наоборот, она положительна слева и отрицательна справа от него.
Поэтому между слоями величины dM суммируются для каждой элементарной полоски и в этом пространстве:
i
М = 2пСрН^Х=2т:СрН1.
О
Но 2тсС=Г есть циркуляция вихрей соленоида, почему окончательно будем иметь: '
М=?ГН4, (27)
что и требовалось доказать. Вне слоев М=0.
Из всего изложенного видно, что относительно количества движения, сообщаемого жидкости вихревым соленоидом» состоящим из двух параллельных вихревых слоев конечной ширины, может быть повторено все то, что излагалось нами относительно количества движения, сообщаемого жидкости парой вихрей (§ 2, первая теорема и ее следствия).
Так, например, один изолированный вихревой слой конечной ширины не сообщает жидкости никакого количества движения. Он не действует на жидкость как сила. Силу мы получаем только при наличии вихревого соленоида, т. е. двух параллельных между собой вихревых поверхностей взаимно обратного вращения.
Эта сила М = pVHl нормальна к плоскостям концов соленоида . АВ и DC или параллельна направлению вихревых слоев или их J продолжению. Величина ее пропорциональна длине рихревого солено- И ида Н, совершенно так же как сила электромагнита пропорциональна | числу ампервитков. г
Если силу Л1 написать в виде:
Л4=рГ7, (28)
где Р = то станет ясно, что действие каждого вихревого солено-
ида всегда возможно заменить действием только одной пары вихрей с циркуляцией, в Н раз большей.
Наконец, сближая вихревые слои соленоида, уменьшая расстояние между ними до нуля, получим в пределе силу М, равную:
М = ^=рш, (29)
с которой действует на жидкость элементарная силовая трубка длины Н.
Иными словами, система двух источников-точек напряжения, равного по величине, но обратного по знаку, отстоящих друг от друга на расстоянии Н, действует на окружающую жидкость с силой M' = ?VH.
Подобно диполю такая система двух источников-точек есть сила, почему трубка, соединяющая эти источники, и называется нами силовой трубкой конечной длины. *
Изложенная теорема дает основу теории динамического взаимодействия жидкости и обтекаемого ею тела конечной ширины по направлению движения. fil
§ 3. НЭ?VIАЛЬНЭЕ ДАВЛЕНИЕ ПОТОКА НА ПЛОСКИЕ ПЛАСТИНКИ ИЛИ ОТВЕРСТИЯ
. Теоремы Н. Е. Жуковского, изложенные в § 2, позволяют нам в: самом общем виде решить вопрос о величине силы давления неограниченного потока жидкости на плоские пластинки, расположенные нормально к направлению его движения, или о силе давления при истечении жидкости из отверстий.
В самом деле, из гидродинамики нам известно, что согласно закону количества движения или импульса сил величина силы динамического давления, производимая потоком жидкости в направлении его движения, равна секунднрму количеству движения потока по этому направлению.
Поэтому согласно первой теореме Н. Е. Жуковското величина силы давления Р потока жидкости, создаваемая парой параллельных, прямолинейных вихревых шнуров, расположенных в расстоянии Z друг от друга и вращающихся в противоположных направлениях, по направлению, нормальному к плоскости вихрей, будет равна секундному количеству движения жидкости, ими вызываемого, т. е.
Р = Л1хе = р • I,
где представляет величину секундной циркуляции жидкости вокруг вихрей.
Но для прямолинейного вихревого шнура, вращающего вокруг себя частицы жидкости по окружностям с окружной скоростью W9 путь, проходимый частицей в 1 сек., равен скорости UZ, почему
P = piriZ = p/IF- W=pqW = mW, (30)
где q = lW есть расход жидкости, протекающей между вихрнми в 1 сек., a tn = pq— проходящая вю же время между ними ее масса. Выражение (30) показывает нам, что сила давления Р потока, создаваемого парой вихрей, равна произведению из секундной массы жидкости, проходящей между ними, на .ее скорость, т. е. равна количеству движения проходящей массы жидкости, как то и должно было быть.
Кроме того, оно указывает нам и на то, что сила давления на пластинку или отверстие может одинаково выражаться как через квадрат скорости набегания жидкости, так и через секундную циркуляцию вихрей на ее краях. На том же основании сила давления на жидкость диполя, рассматриваемого как система двух вихрей, по выражению (21) равна:
Р = Мхс = 9УГ-=^-2%-. (31)
Эта величина силы давления диполя на* окружающую его жидкость, полученная из соображений разности давлений в жидкой среде, им вызываемой, и определяется мной в моих .Основах динамики жидкости14, Ар. 135. ,
Аналогично сказанному согласно второй теореме Жуковского, будем иметь, что сила давления потока жидкости, создаваемого« замкнутым плоским вихревым шнуром, равна по выражению (23)
P^W3F=?WFw = wW=mW, (32)
т. е. равна секундной массе жидкости, протекающей через площадь, ограниченную замкнутым вихревым шнуром, на скорость ее протс кания, иначе равна количеству движения протекающей жидкости.
Таким образом теоремы Жуковского сводят задачу определение величины давления от потоков, создаваемых системой двух параллельных вихрей “или плоским замкнутым вихрем, к чисто гидравлической задаче определения величины расхода жидкости при протекании* ею площади, ограниченной этими вихрями.
Так, например, для протекания жидкости через бесконечно длинную щель ширины I мы по формуле (19) § 2 имели расход- ее равным^
<7 = 0,77/117.
Поэтому для такой щели будем иметь величину силы давления на нее неограниченного потока жидкости, движущегося нормально к ней со скоростью W, равной:
p=?qW = ^,lllW\ (33)'
И вообще нормальная сила давления неограниченного потока жидкости на отверстия или пластинки произвольной формы будет равна:
P = WFW?
(34)
гдер—коэфициент расхода жидкости при протекании ее через отверстие в тонкой стенке, F—площадь отверстия и W—скорость истечения. Эта сила всегда нормальна к плоскости отверстия или пластинки. В случае истечения жидкости из отверстия в стенке сосуда формула (34) прямо дает нам величину давления жидкости в плоскости отверстия, необходимую для получения данного расхода ее. Именно, написав формулу (34) в виде
Гр
P=2^F^- = ^F-H, (35)
где
что
Н — — , получаем известное всем из гидравлики сила динамического' давления вытекающей струи
выражение, жидкости
равна удвоенной силе статического давления на площадь попереч-
ного сечения сжатой струи.
Для силы давления неограниченного потока жидкости, набегающего нормально на бесконечно длинную плоскую пластинку, будем иметь:
Uz^ w*
P=w FW*= 2tiFP j- = c№ ?F-^ . (36).
Иными словами, соответственно тому, относим ли’ мьк давление прямо к квадрату скорости, подобно принятому в Англии и Франции, или к половине квадрата скорости подобно Германии, мы должны будем вводить или чистый коэфициент расхода р. или его удвоенную величину:
сю = 2р. или р. = . (37)
£
Формулы (37) дают нам связь между коэфициентом расхода р. и коэфициентом сопротивления сш.
Данные непосредственного опыта подтверждают рбщую правильность подобного чисто теоретического заключения, как то видно из следующей таблицы коэфициентов. •
ТАБЛИЦА!
Форма пластинки или отверстия ’ Коэфициент расхода р Коэфициент сопротивления cw = 2р. Прямое определение cw Авторы
Круг Квадрат . . • • Прямоугольник <1:20) 0,62 0,62 .. 0,75 (для газа) 0,77 (для жид- кости) 1,24 1,24 1,50 1,54 0,61 Х2 = 1,22 йг1'23 }1,50 Эйфель, 1907 г. Геттинген Эйфель, 1907 г. Геттинген
Таким образом мы можем вообще с достаточной степенью точности считать коэфициент расхода тождественным коэфициенту со-противления, что прямо вытекает из тождественности механизма обоих явлений, ясного из содержания отделов Ш и IV, между тем как до настоящего времени они считались весьма отличными друг от друга. Такое обобщение приводит к интересным и важным следствиям.
Так, например, изменение формы отверстия, ведущее к увеличению коэфициента расхода, приводит нас к форме пластинки большего сопротивления при обтекании ее потоком, что видно из данных таблицы относительно квадратных и прямоугольных отверстий и пластинок. Поэтому задача об отыскании формы пластинки наибольшего сопротивления является тождественной задаче об определении формы отверстия наибольшего расхода.
Понятно, что во всех тех частных случаях, в которых мы сможем, применяя изложенные выше общие идеи, довести решение до конца, мы получим ответ также вполне ясный, простой и точно соответствующий данным непосредственного опыта.
С целью подтверждения всего сказанного ниже приведен пример выяснения взаимодействия ‘ между безграничным потоком жидкости и плоской пластинкой конечной ширины и бесконечной длины.
Экспериментальное подтверждение справедливости теории диполя как силовой трубки. Изложенная выше теория диполя как центра энер-64
' тин, действующего- Cg вполне определенной силой на окружающую, его безграничную массу жидкости, 1 оказалась столь непривычной нашему современному мышлению, что даже лица, весьма компетентные в гидродинамике, отнеслись к ней с большим недоверием.
Это недоверие особо сильно касалось моего утверждения, что диполь есть сила. способная на взаимодействие окружающей его жидкостью, и что поэтому, будучи сво-боден^он должен двигаться в жидкой среде.
Фиг. 35.
' С целью исчерпать всякие сомнения в полной реальности диполя
или силовой трубки как главной основы учения о взаимодействии тел и жидкости ,яо моему предложению Государст^нный энергетический институт построил прибор, демонстрирующий его действие. ” .
Идея этого прибора состоит в следующем.
Чтобы осуществить основную особенность диполя, состоящую в* одновременном всасывании и выбрасывании им одного и Того же количества жидкости.^ о^Ааковыми скоростями, выполнен петлеобразный канал АВС (фй^5) прямоугольного поперечного сечения.
Всасывающий и вбрасывающий концы этого канала А и С имеют одну и ту же площадь F поперечного сечения и расположены прямо обратно друг другу в одной горизонтальной плоскости, так что продолжение их,*показанное пунктиром, образует как бы одну прямую трубу АС. • •
Для возбуждения движения воздуха в этом канале в верху, в расширенной его части В, помещен пропеллер К, вращающийся вокруг оси 00. Весь канал подвешен на горизонтальную ось, проходящую через точку О' и нормальную к плоскости чертежа. Вокруг этой оси кауал АВС может свободно вращаться под действием силы Р, развивающейся у его концов А и С при работе пропеллера, причем конструкция исключает' влияние на это вращение тяги самого пропеллера. Сила Р измеряется весом G, стоящим на чашке весов Е. Чашка Е подвешена к концу канала С цомощью тонкой проволоки, огибающей подвижный блок D.
Основной вопрос, подлежащий здесь разрешению путем опыта,
Ь А. Я. Мвловжч
f 5
состоял в том, что появится или не появитсяйсила Р, действующая 1 на концы канала' ЛВС, при работе пропеллера и движении потока воздуха вдоль по каналу? Ибо по обычному мышлению, опирающемуся на неправильное применение уравнения Д. Бернулли, величина давления в концах канала Л и С, где скорость входа и выхода потока одинакова и равна v, должна быть также одинакова и равна:
На — рй — И Hc^o — Pj.- (а)
где р0— давление в окружающей прибор жидкости. Из выражений же (а) следует, что Ha = Hci почему и сила Р=0.
Но падЛное суждение, очевидно, полагает, что работа пропел-
лера, движущая поток воздуха по каналу, исчезает бесследно и не передает этому потоку никакой добавочной энергии. Иными словами, подобное мышление допускает отмену закона сохранения энергий и возможность превращения ее в ничто. Наоборот, не допуская
возможности бесследного исчезновения Энергии передаваемой жидкости работой пропеллера, мы должны будем величину давлений в кон-
•
цах канала На и Нс принимать равными На—р^ — р —
(так как
жидкость у этого конца канала всасывается им внутрь, что возможно
только при понижении давления . в нем по сравнению
в окружающей жидкой
среде) и Нс=р0-]~?^ ,
т.
с давлением
е. большим
наружного давления на скоростный напор, так как в противном случае жидкость не сможет вытекать из конца С.-Но тогда разность давлений
окажется равной не нулю, а двойному скоростному напору, или рЛ Поэтому и искомая нами сила Р, действующая на концы канала ЛВС» будет также равна не нулю, а ; *
P=pFv* = mv, (b)
т. е. секундному количеству движения потока жидкости, протекающего по каналу.
Непосредственный опыт, произведенный с "описанным выше прибором* вполне подтвердил все наши положения.
, Формула (Ь) тем точнее дает Ьеличину веса Р груза, лежащего на чашке весов, чем точнее будет измерена средняя скорость вытекающего из конца С потока воздуха, т. е. расход потока. Но уже при выполненных измерениях скоростей у выходного конца канала получено, что
Р'=0,8Р.
Фиг. elk.
Помощью пьезометрических трубок, идущих от концов канала > А и С, возможно наблюдать также и разность давлений в этих местах потока. i
Выработку конструкции прибора, его выполнение и опыты с его-работой вел инженер б. Научно-исследовательского гидроэнергетического института (ГЭИ) Б. Э. Глезер, которому я и приношу здесь, благодарность за его труды.
Фиг. 36 дает конструктивный чертеж прибора.
1.0 0,8 0,6 0,4 02 О
\тич. кривая давления мая кривая давления
0,8 М 0,4 Д2 О
Ю 08 06 04 02 О
IS)
То явление выбрасывания или отбрасывания жидкости передней идо носовой частью тела и, наоборот, всасывания его- кормовой частью, которое мы наблюдаем на приборе для демонстрации диподя| мы будем ^наблюдать также и при движении всякого твердого тела в я^доой среде.^Лоэтому каж- , I <юе твердое тел^ движущееся в жидкости^ представляет собой также диполь, рассеи-I вающий свою энергию в окру- > 1жающей его среде, { * ’ На основании предыдущего мы должны будем запасы энергии у его носойоЛ и кормовой части принимать пропорцией
/1 ' । V2
валяными сумме /?0 "г Р “у или
Qfi , V1 '
разности Ро-—р— (где р0— давление окружа(бЩей среды, •, V— скорость движения тела), а разность давлений, вызываемую движением тела, пропор-е. пропорциональной количеству движр-
Фиг. 37. f
циона/гьиой 2 р—, или р-zr.
ния, сообщаемому им жидкости, как то И должно 'быть по закону импульса сил. ' u /
ежду тем, в книге Проф. Прандтля (Prandtl — Tittjens 'Hydro-Aeromechanik*, том И, стр. 152) приведены Как вполне правиль-
un ныё диаграммы Фурмана (G. Fuhrmann) обтекания тела дирижабля (фиг. 84 и 85), чккое дарение
’Офуг. 37, а).
При таком
кзность давлений у носа и кормы равна нулю, почему и никакого сопротивления подобное тело в жидкости не должно было бы испыт^пъ. 1 И хотя опыт совершенно не подтвердил теоретического ожидания величины давления у кормы, авторы остались при своем заблуждении и не перешли к единственно правильной нашей диаграмме (фиг. 37, Ь) с отрицательным, а не положительным давлением у кормы, где увеличение давления обязано своим происхождением обратному кормовому течению жидкости за телом, “что ясно показано в изложенной далее теории обтекания плоской пластинки.
на которых как у носа, так и кормы тела теорети-& принято одинаковым, положительным и равным р
представлении явления обтекания тела жидкостью
.ОТДЕЛИ! -ТЕОРИЯ НОРМАЛЬНОГО ОБТЕКАНИЯ ПЛОСКОЙ ПЛАСТИНКИ <
, § 4. НОРМАЛЬНОЕ ОБТЕКАНИЕ БЕЗГРАНИЧНЫМ ПОТОКОМ
ЖИДКОСТИ БЕСКОНЕЧНО ДЛИННОЙ ПЛОСКОЙ ПЛАСТИНКИ КОНЕЧНОЙ ШИРИНЫ
t (
Пусть мы имеем бесконечно дЛИйну^о плоскую пластинку ширины АВ=*2а> нормальную к плоскости чертежа (фиг. 38).
Безграничный по ширине поток жидкости пухль-набегает на пластинку параллельно^ оси УК, или нормально к ее ширине АВ, со
скоростью — VQ. 4 ’
Тогда вследствие невозможности для части потока жидкости шириной 2а протекать сквозь пластинку масса жидкости p2az/0 принуждена будет обтекать ее снаружи, проходя мимо ее краев А и В, где согласно § 2^Л0лжны будут появиться прямолинейные вихревые шнуры Ог и Oi9 параллельные между собой и вращающиеся в противоположных направлениях, как показано на фиг. 38, изнутри наружу. Поэтому Движение потока жидкости вблизи пластинки мы можем найти, прибавив к течению, вцДкваемому прямой-диполем или парой параллельных вихрёвых шнуров § 2, поступательное движение среды с постоянной скоростью — v0, параллельной оси YY.
Аналогично выражениям (Ы) и (12) § 2 в рассматриваемом случае будем иметь:
G = /y + |o-|-x)’, га = |/у4-(а —х)\ У — t\ sin pj =ч г, sin f
л4-х = Г1 COS0J; а — x = r3cosp2.
(О
А слагающие скорости частицы жидкости tno осям координат X и Y 'будут равны: .
?_____________У
а—х\ _________г Г а-\-х ,
г? / ~ [ у + (а х)J Т
( (2)
! а — х ~|
+ ^+(Д_Х)2]-г'°
Функцию течения искомого движения жидкости найдем, интегрируя выражение
5 =
ydy________ydy
-У-На — х)? у’ + М
У + (М
х,
Фиг. 38.
или
In +/(х).
2 у-|-(а-чс)2 r'v 7
ф Для определения неизвестной пока функции /(х) возьмем производную S по х и сравним ее с выражением для V, тогда получим:
dS ГГ а-}-х .
dx~'VL/ + (a-FxFT
-сГ .“+*_______+
-cljr+(a+x)J
— 4 а—х 1
откуда будем иметь, что
Функция течения напишется
—
или = — v#x.
поэтому окончательно в виде:
S—'-[„Д' +(д+*х)3 5 —2 —х)а 0
или
5= Cln-1— vQx,
(3)
а уравнение токов в виде:
(4)
’ С1п^ — vox = D = const.
Это уравнение показывает нам, что форма токов зависит от^отно-шения постоянных Си , т. е. отношения скорости движения^рвхрей к скорости движения жидкой среды.
В самом д^ле, для системы вихрей фиг. 38 маг имеем, что каждый из них стремится двигать другой по направлению оси YY со скоростью
^-^2-2а’ • » в то время как середина расстояния между ними, точка О, имеет скорость'
^о = 2 — = 4—= 4г,1’ а 2а 1
£ в четыре раза большую.
Иными словами, система вихрей Ох, движется параллельно оси YY в четыре раза медленнее середины расстояния между ними, т. е. точки О.
Течение 1. Поэтому вихри или концы пластинки А и В останутся неподвижными в пространстве при условии
, 2а
и скорости в середине
<—‘Ув = Э-^-=Зх'о.
С другой стороны, для середины или начала координат при х =у =0 и гг == г„ = а по выражениям (2) имеем: .
А 2dQ' ” 'С zt==0 и V — —-3-----*р0 = 2 —----^0’
а . с* ч
почему мы имеем равенство
• С
2 — — г/0 г= Зг»0,
• и
откуда ’ * 1
С— 2ая0 , (5)
т. е. в этом случае напМ^сение вихрей прямо пропорционально скорости набегания v$Ku Лирине пластинки 2а.
Подставляя значение С из равенства (5) в ^равнение токов' (4), получим последнее в виде: ' *
/•
• 2а In—1—х =« D = const .
< • G .
ИЛИ * :
’ x = 2aln —— D. , (6)
Течение жидкости, соответствующее этому уравнению, дано на фиг. 39. Ихнее мы видим, что в рассматриваемом нами случае движения жидкости пара вихрей и\О2, вместе с вращающейся вокруг них массой жидкости, оказывается изолированной от всей остальной жидкости, замкнутой поверхностью предельного тока, проходящего через точки нулевой скорости М.
Чтобы найти положение этих точек, необходимо приравнять нулю выражения (2) компонентов скорости частицы, что дает равенства:
« 4 Г1 Г2 '
• \
, Первое из «их возможно при j = 0 или при г2 = гр указывающем на то, что точки нулевой скорости могут лежать только на осЦ УУ, т. е. для них х = 0.
Но тогда второе равенство примет вид:
2дС
V V0 — 0
или, заменив С через 2a^0 и сократив на придадим ему следующий вид: у2 = За2,откуда
у = ±уг3-а = ±},73а.
Случай х — 0 иу = О, т. е. расположения точки нулевой скорости в начале координат, рассмотрен ниже (см. течение II). Таким образом координаты точек нулевой скорости М и М9 в данном случае равны:
х = 0 и у ~ ± 1,73 а.
Но если точки нулевой Скоррсти лежат на оси . УУ, то Согласно уравнению (6) постоянное тока жидкости, через' них^проходящего, равно ж .• - - _. $* ' <
0 = 0,
а потому уравнениеЪфедей^)го тока напишется в виде;
x = 2aln.— . (7)
и точки пересечения его с осью Х& найдем, ^^гая уравнение ' *г. •*
* ь , х^=2а 1п —i—%, » >.
которое Мает величину абсциссы х 'равной ... , <
* х=.2$фа. *
к* показывает фиг. w, ча?ги ^ёдельйЬго^уока/окружающие вихрй, имеют форм£ овала, весьма близкую к форме эйлипсас полуосями 1,73а и 2,09а. Этот эллипс сжат по направлению движения, линии мертвых точек и растянут в направлении, нормальном к движению вихрей или среды, их сгкружающей.
Пространство, ограниченное цилиндрической замкнутой поверхностью предельного тока, В/Томсон называет .атмосферой вихрей*.
Предыдущий анализ течения показывает нам, что часть жидкости, заключающая в себе вихри и их атмосферу,, движется в остальной е массе жидкости как совершенно самЬстоятельное, отдельное от нее, жидкое тело с постоянной относительной поступательной скоростью:
С
' 2а ’
обусловливаемой величиной напряжения вихрей Q Количество движения (или импульс силы), переносимое вместе с собой этим жидким телом по направлению его движения, мы. сейчас же найдем по первой теореме Н. Е. Жуковского в виде:
М = 2~Ср2а = 2~(2a)2pv0 = 2xpf2v0, (8).
где f=2ah есть плошадь,Ограниченная вихрями. Фиг. 39 показывает нам тот единственный для жидкости механизм, помощью которого непрерывная жидкая среда воспринимает и передает далее внутри себя импульс силы.
Рассматривая его, мы видим, что жидкость протекает здесь через плоскость между вихрями ОгО.2, почему сможем осуществить подоб* ное явление, передав жидкости ймпульс силы движением в ней пластинки ОгО2 на коротком пути и затем мгновенно удалив или остановив саму пластинку, т. е. выполнив то, что мы делаем, гребя/ веслом. •
<1 иг. 4?.
Фиг. 40 дает нам снид ок подобного явления, выполненный в лаборатории проф. Прандтля.
Между прочим формула (8) показывает, что величина силы, передаваемая площадью пластинки жидкости и от нее воспринимаемая, пропорциональна квадрату площади пластинки и скорости ее движения. В пространстве трех измерений подрбный механизм восприятия и передачи силы образуется замкнутым вихрем и далее движется в виде вихревого кольца.
Течение П. Мы видели, что течение I не дает еще нам картины взаимодействия м*ежду пластинкой и потоком потому, что при нем не выполняется основное условие наличия пластинки в жидкости: ее непроницаемость, препятству!фцая жидкости двигаться сквозь пластинку.
Очевидно, для того, чтобы приблизиться к искомой форме движения жидкости, нам необходимо перейти от течения I, при котором точки нулевой скорости М и ЛГ лежат на оси YY вдали от плоскости пластинки, к новому виду движения ее с точкой нулевой скорости М на самой пластинке в ее середине или начале координат (фиг. 41). А так как по предыдущему точка в середине пластинки движется в четыре раза скорее ее концов, то вместо условия (5) мы должны положить скорость набегания потока на пластинку
или
C=0,25-2uvo.
(9)
Фиг. 41,
т. е. вихри на краях пластинку будут сноситься вниз по течению со скоростью, равной 0.75 скорости набегания.
Очевидно, что это обстоятельство приводит нас к тому, что уравнение токов (4) будет справедливо только в на чайный момент движения жидкой среды, пока зарождающиеся на краях пластинки Ьихри не успеют еще отойти от нее. Мы получим подобную начальную картину движения жидкости вблизи пластинки, положив в уравнении (4) согласно равенству (9) С 0,25 -2 av0.
Фаг. 42^
краях эти вихри будут таюке непрерыйЙо
" Тогда уравнение токов жидкости, будет дано в виде: _
\=0,5ato -1 — D (10) z « ^*2
и приведет нд& к течению, показанному на фиг. 41.
Рассматривая его, мы снова увидим, что хотя предельный ток значительно приблизился к плос-кости пластинки по срав-. нению с течением I, но все-таки и здесь он не идет, еще по самой пластинке и она протекается жидкостью;- Протекание прекратится, если вихри, ; образующиеся на ее краях, будут оА'оситься течением со скоростью 0,75 %. Но если при непрерывном набегании потока на пластинку и непрерывном образовании вихрей на ее зноситься вниз по течению,
то от схемы явления фиг7'*41 мы должры будем 'перейти к схеме фиг. 42 и представить себе все явление происходящим нижеописанным образом. \
Течение III. При непрерывном набегании потока жидкости на пластинку АС (фиг. 42) и непрерывном давлении потока на нее это давление потока выразится таким же непрерывным возникновением на краях пластинки пар бесконечно тонких вихрей постоянного напряжения, но взаимно обратного вращения. Количество движения, ими сообщаемое жидкости, будет равно и прямо обратно по направлению силе давления потока на пластинку. Вихри будут непрерывно сноситься вниз по течению за пластинку и образуют за ней два непрерывных, вихревых слоя (АВ и CD), уходящие в бесконечность. Поэтому, чтобы найти, наконец, форму движения потока жидкости, обтекающего пластинку, мы должны будем выяснить, какое движение сообщается окружающей жидкости этими вихревыми слоями,.или, иными^риовами, найти то движение жид-ж кости, которое приводит к образованию указанных вихревых слоев.
С этой целью найдем прежде всего скорости, сообщаемые различным точкам окружающей жидкости, совместным действием обоих слоев \ начав исследования с точек пространства, лежащих выше оси XX в области положительных у.
1 См. Н. Е. Жуковский, Насадки и диффузоры аэродинамических труб.
76
При у положительном и в точке т координат х и у бесконечно-малые элементы слоев ds, взятые у точек а и с, в расстоянии <5 от начала, возбуждают бесконечно малые скорости dW и dIFlt равные
1 jivs £ds лтхг (^ds
dW =— и aWi = — ч r fi
где С—напряжение вихревых слоев, аги — расстояния точки т от точек с и а, равные:
. r = /(s-{-j)a4-(a4-x)\
G = +(«—*)’ •
•
Эти скорости нормальны к соответствующим радиугам-векторам г и г1э почему, обозначив углы последних с прямой ас через а и. а^, будем иметь элементарные слагающие скорости точки т по осям координат* равными:
du=: dWtSina.! — dUZsina, , '*
%
= dFFj cosa! -f-dUZcosa.
Но ив фиг. 42 имеем:
s -|- У = r sin a = rt sin ap
a -f- x = r c°s a; a x = r t cos ax.
Поэтому слагающие элементарной скорости точки in по осям коор-* динат можно писать в виде^
, Л,=с(ф!-’-фг)л,1
; ‘ г > (Н)
, ^/a-4-x । а—х\. 1 4 ’
dv = C[-II-4. — )ds,J
а сами скорс^ти найдем, проинтегрировав выражения (11) в пределах изменения длины вихревых слоев 5 от нуля до бесконечности:
оо
оо
с I f 3 ’(s-H0<fc г _
,(J (s + »х)9 J (s+j)!!4-(a4-*)2
0 ° , oo -
2 (S + y) .+ (a + *) Vy* + (a — X)?
(12)
Эти выражения слагающих скорости в точке т возможно гфедста-вить и в другом более простом виде, заметив, что ' * •
rme^R и R{ — расстояния точки т до краев пластинки, точек Си А, y — R sin P = sin pjH a-}-x=/?cos£; a — x = /?1cos49I;
почему ф . м
arctg;rH=z^: arc,STx^=Zlv Uf “I Af ' Ulf Л»
Заменяя в выражениях (12) все входящие в них величины новыми, получим, что ' »
г 1 R И —► С In у)- , v = C[zl(l3 + pi)] = C6, J (13)
где 0 =.тг — (Р 4" 01) = / АтСу т. е. представляет собой угол, под которым видна из данной точки ширина пластинки,
Но если от точки т с абсциссой х<а мы перейЛм к трчке с абсциссой х>я, иными словами, зайдем за линии АА' илиг СС, продолжения вверх направления вихревых слоев, то разность а — xs станет отрицательной л равной — (х— а). Вследствие^ого скорость v в выражении (12) представится не суммой, но разностью интегралов, и станет равной:
со •
V—C Г a rclg --arctg 1= cf arc tg arctg——\ L ъх4-а fe x — a J < 8 x — a 6x+a> о . 1
или замечая, что arctg —= Z Т,
* v=c(7-p)=c[/-(?+₽l)i=ce,' (и).
получаем выражение, тождественное (13).
Из сказанного видно, что .сражения (13) с особой простотой и ясностью указывают нам на следующие основные свойства компонентов скорости частиц жидкости во всем пространству выше оси XXz Скорость и, параллельная оси ХХК непрерывна во всем пространстве, занятом жидкостью. Она равна нулю на оси YY, где R = R„ и стремится к нулю при удалении от пластинки по любому направлению в бесконечность, ибо при этом R стремится стать равным Наоборот, с приближением к краям пластинки она возрастает по величине и на самых краях в точках А и С становится бескднечно болАиой.
Скорость v, параллельная оси YY, выше оси XX изменяется непрерывно во всем пространстве. Вдо^ь по оси XX, между точками А и СУ т. е. на плоскости пластинки, скорость v постоянна и равна Ск, ибо здесь углы |3 = — 0, а 6 = z. Наоборот, вне этого отрезка она везде на оси XX равна нулю, ибо один из углов всегда равен нулю, а другой а 6 = 0. С удалением от пластинки в бесконечность по любому направлению скорость v стремится к нулю, ибо 9 стремится к нулю.
Иную и более сложную картину распределения скоростей v мы получим для пространства, расположенного ниже оси XX, в области отрицательных ординат у.
. Так, для точек пространства ниже оси XX, находящихся между вихревыми слоями, т. е. при х<а, получий скорость v для точки /иг, если в выражении (12) заменим у на —у и вынесем минус за знак арктангенса, тогда найдем, что
г»! = с| z 4-arctg—%— 4-arctg1 (15)
или^снова заменяя арктангенсы соответствующими им углами 3 и (фиг. 43), получим:
^=q54-?4-?1)=c(z4-w-81)=c(2S-61), (16)
т. е. ниже оси XX, между вихревыми слоями, скорость, параллель’ I ная оси YY, пропорциональна внешнему углу, под которым из данной точки тх видна ширина пластинки., Выражение (16) сейчас же показывает нам, что при удалении точки т1 вниз на бесконечно большое расстояние от пластинки, при у=—ос, 0t будет стремиться к нулю и — к пределу ‘ 1
lira == 2 ТгС,
в то время как на поверхности пластинки при01 = тс мы попрежнему будем иметь ' f
Vj = v = О,
Из сказанного видно, что вдоль по осн YY, между вихревыми слоями частицы жидкости, подходя из бесконечности к пластинке,^движутся замедленно и скорость их уменьшается в два раза, оставаясь все время положительной.
Интересно отметить, что при распространении вихревых слоев в бесконечность в обоих напра-
влениях скорость между ними u = 0, a v = 2vC и остается постоянной во всем пространстве. •*
Такое движение жидкости будет* происходить в прямолинейном канале бесконечной длинр, ограниченном с боков двумя вертикальными и параллельными между собой плоскостями. А так как ширина канала равна 2а, то расход жидкости в нем на единицу высоты равен:
Q = 2а • v = 2а • 2кС = 4а кС,
откуда
4атс ’
т. е. напряжение вихревого. слоя, образующегося при этом у боковых стенок канала, пропорционально расходу Q и обратно пропорционально удвоенной ширине канала.
Но если от точки тх перейти через вихревой слой к точке «ц и в выражении (14) переменить у на — у, то для скорости в точке Пц. получим выражение:
/У у \
„,[=С(агс1е^-аге1г^, ^17)
или, вновь заменяя арктангенсы углами, — выражение:
^i=c(ft—+ —тг)=—соп. (18)
Это выражение показывает нам, что за вихревым слоем скорость Фи опять становится пропорциональной углу 8, как выше оси XX, но при этом еще и отрицательной. Последнее приводит к тому, что на поверхности самого вихревого слоя скорость v будет изменяться скачком на величину 2~С, *ибо
Vi — Vii = С (2тс — 8) 4- се = 2*С.
Очевидно также, что с удалением от пластинки, т. е. с уменьшением угла 8ц, скорость vn уменьшается и в бесконечном * расстоянии от нее сгремится к нулю:
*>11 lim = 0.
Вышг МЫ ВЫЯСНИЛИ' распределение скоростей, вызываемое в безграничной массе жидкости наличием в ней двух непрерывных и параллельных вихревых слоев с напряжениями, равными по величине, но обратными по знаку. Теперь мы можем перейти к выяснению окончательной картины распределения скоростей в массе жидкости в случае нормального набегания ее на плоскую пластинку.
Действительно, мы видели, что непрерывные вихревые слои образуются за пластинкой вследствие непре^ рывного сноса набегающим потоком жидкости вихрей с краев пластинки.
При этом снос вихрей с краев пластин
фиг. 44
ки должен происходить
при такой скорости набегания на нее потока жидкости, которая равна и прямо противоположна скорости протекания жидкости через Пластинку, вызываемой действием вихревых слоев, е тем чтобы обе эти
скорости взаимно уничтожали друг друга и тем самым стала возможной действительная реализация пластинки как твердого, непроницаемого для жидкости тела.
Но теперь нам известно, что нормальная скорость протекания жидкости сквозь плоскость пластинки, вызываемая действием вихревых слоев, положительна и равна
V ~ Clt.
Поэтому для ее уничтожения необходимо, чтобы скорость набегания потока жидкости на пластинку из бесконечности была бы равна
Vo = —Стс.
Прибавив эту поступательную скорость вдоль оси YY набегающего на пластинку потока жидкости ко всему полученному нами полю скоростей, параллельных той же оси и вызываемых действием вихревых слоев, мы в результате сложения скоростей придем к следующему рас-
6 А Я Мвловвч 81
тределению их во всем пространстве, схематически показанному на фиг. 44.
В пространстве /, ограниченном снизу плоскостью пластинки АС и с боков прямыми АА' и СС, продолжающими вверх направления вихревых слоев, согласно выражению (13) имеем
v i=C0 —Ск = - 8). (а)
Скорость Vi отрицательна и пропорциональна разности г: — 6, почему движение набегания на пластинку является замедленным.
В бесконечном удалении от нее скорость равна —Ск, а на самой пластинке равна нулю.
В пространстве// под пластинкой, ограниченном плоскостями вихревых слоев, согласно выражению (16)
-= С(2тс — 0J — Ск = + С (к — 8J. (Ь)
Скорость ттц положительна, направлена вверх к пластинке и пропорциональна разности к — 0р как и скорость . В бесконечном расстоянии от пластинки она равна-j-Стг; на плоскости пластинки она равна нулю.
Движение подсасывания является движением замедленным в тождественным движению набегания.
В пространстве ///, ограниченном снизу осью XX, а со стороны пластинки плоскостью АА! или СС, согласно выражению (13) имеем:
= С9 — Ск — — С (тг — 6). (с)
В бесконечности скорость = — Ск; с приближением к пластинке скорость тгщ уменьшается пропорционально разности к — 0, затем снова увеличивается и на самой оси ОХ достигает своей начальной величины — Сгс, оставаясь все время отрицательной.
В пространстве IV, ограниченном сверху осью ОХ, а со стороны пластинки плоскостью вихревого слоя АВ или CD, согласно выражению (18) имеем:
viv=— СО — Ск = — С (к 4-0), W
т. е. скорость все время остается отрицательной и пропорциональной сумме 0. На оси ОХ скорость 77lv = — Сл, затем она сначала возрастает, а с удалением в бесконечность снова, уменьшаясь, приходит к начальной величине Vw = — Стг.
Установив окончательную картину всего поля скоростей, мы можем уяснить себе и реальный смысл входящего во все выражения ^скоростей напряжения вихревого слоя С. В бесконечном удалении от пластинки в пространстве / или //, т. е. между вихревыми слоями или продолжением их направлений, скорость
и = 0, а =
Поэтому расход жидкости через поперечное сечение этого пространства на единицу высоты равен:
Q = 2а • Стг,
откуда имеем, что
С —
Q 2а к
Cw =
Q
2о *
и
(Э9
т. е. произведение жС представляет собой расход жидкости, набс~ гаюигей на единицу ширины пластинки. Но для полной наглядност! вида всего движения жидкости вблизи пластинки найдем и построим всю систему токов последовательно во всех перечисленных выше частях пространства.
функция течения. В пространстве/^—положительно, х < а. Согласно выражению (12) имеем:
v — С | п — arctg —у-arctg ——— ) — Ск = — С | arctg —-U
\ а-[-х ^а — х] \ ьй4~х?
Поэтому функцию течения 5 для этой части пространства мы можем представить в виде: Я л
S = Ivdx = — СI I arctg —=т— J \J «4-лс
о о
Но
Г _у _у , Г ydx и
larctg—-— dx = xarctg —---Pi х . ।—?1 = xarctg —=7-P
J a-|-x 6 a-[-x * J y+(fl + x) x'
1 1 frffr’+ (« + *)*!• Г ** A У ;
+ x
У )
-f- (a 4- *)*] — a arctg
Замечая, что
arc,eJT3 +аг«г^=у. почему
. a-f-x к A у
arctg—— = ----arctg —у—9
У 2 fea+x получим окончательно:
Jarctgr^ dx=(x + °)arctg^r¥“Ta+ f lnb’+(«+*)’!•
Точно так же найдем, что
С arctg —— dx = {x — в) arctg —+ у « — 4 ,п [У + (а—х)1]. J а — X а — X * *
Подставляя теперь найденные нами величины в выражение функции течения, найдем:
S = — c|{(x4-a)arctg-^--|-(x — a) arctg -^-4-II Л “Г” С* <* Лг
О
+rIn4±£+4’i.
' 2 у* + (а — xf ) Или
$=— С
(х 4- a) arctg 4- (х — a) arctg 4 С4" Л Mr Л
Из выражения (20)
При х = 0
видно, что для крайних значений х будем иметь:
5о = 0.
При х — а
S.= -C{2aarct6Z + Z,„>!±^}.
(21(
В пространстве III. При переходе тока жидкости из пространства I в пространство^ III, за линию ДД* (фиг. 44); где х > а, мы должны будем писать функцию течения в виде:
X
S = Sa 4- I vdx,
где величина Sa известна уже нам из выражения (21).
Но для пространства /// согласно выражению (14) будем иметь:
• = С( a,cls,K'S^Га ) -С”=-С { '+’ге(е VTi ~
-аг^тЪ)'
Поэтому функция тока для этой части пространства напишется в виде:
я
Но
^arctg ^-(ir/x = (x4-a)arctg — 2 а+т ln.IZ4-<*.+ «)*L
j arctS 7Z^ <*x = (x-a) arctg 4- -o-|- ~ in [^ + (x — a)’]. Почему
U «4-arctg TXT—arctg-^- h/x = rx + (x + a)arctg-X- —
— f °+у lnlv’+ (x — a) arctg—V— — -a-^ £ a —u z
— 2 МУ -H*—Л)Ч == « 0*—<») 4- (x 4- a) atcig —
/ \ . У I У . У3 4- (х4- а)9
— (x—a)arctg —— 4-<- ln„ j-)—u--Z.
v 7 x—a 1 2 У4"(<“та)
На основании последнего выражения будем иметь:
5=-С 2«^+<>»Ц^
— (х — а) arctg 4- hr Л 1Ь £
• ' ' ^ХфЛ
>а п р-2аа'С'»й-
--Л- 1п<-_» 2 у
Или окончательно для пространства 111 получим:
5 = —С { гг(х — а)4-(х4-a)arctg -X-—(х — а)arctg X Л —U л—lb
У1пУ + ОН-а) (22)
2 у 4~(х —а) ) J
В пространстве II, ниже оси XX, прих•<а согласно выражению (15) имеем:
( * + а'с,г й + х + 1гс,8 44) - С- = С (arctg +
+ ’ГС,«?Ъ)-
Поэтому для функции течения будем иметь выражение:
• др
s= )<лг=4( +ак,г
« о
(нтеграл, входящий в это выражение, тождественен с интегралом, входящим в выражение функции течения для пространства /. Вся разнила выражений функции S в обоих случаях состоит только в знаке, эторый для пространства выше оси XX отрицателен, а ниже ее положителен.
На основании сказанного выражение функции течения S для прост-анства II напишется в виде:
‘=С ((x-j-a)arctg——|-(х—a)arctg —Ч~ I *(23)
С ‘ ' а 4~х а — х'2 у *+(а—х)) 4 7
Лрн Х = 0 St — Q.
Лря х = a Sa — C ^2а arctg j J (24)
В пространстве /К Для пространства IV, ниже осн XX при х>а, согласно выражению (17) имеем:
7—с( arctg —=7----arctg ——— ) — Стс — — С ( тс—arctg —у--1-
\ *х + а ^x~aj \ X-[-a '
4-arctg ).
' x—aj
Поэтому выражение для функции течения напишется в виде:
0 0
5 = so + \vdx — Sa —С ((тс—arctg + arctg )<fx. J J \ Л -j- u л — u /
0 0
Ио по предыдущему
\ I тс—arctg —=т (- arctg ? I dx = тсх — (х 4- a)arctg — к J\ ° x-f-a 1 6 х—а/ ‘ п x-j-a 1
+ 4 а— 2-1п1у* + (^ + «)’1+(^ — а)агс&,НЧ+1 а +
+ Inb*-H-<-<I)’]=i:(-«+a)-~(x+a)afCtg7^4-
+ (х—(i)arctg ---In Л Дуг •
’ 4 . х—а 2 у -Н* — <0
На основании последнего выражения получим:
С { — 2а arctg In У +4а -{-тс(х+а)—
- (х + a) „etg + (X - а) arctg - fl» -
- ' Я 2а Т- 2а arctg9^--|- In .
Или окончательно для пространства IV получим:
5 =— к(х — о)—(х -f- a) arctg 4.
4~ (х — a) arctg —---£ 1пЛ~ФгЖ Д?г) • (25)
. х—а 2 У4-(л —a)*J ' '
Но полученные нами выражения функции течения неудобны для построения системы токов жидкости вблизи пластинки. Поэтому аналогично выражениям скоростей заменим в них все арктангенсы соответствующими углами, а суммы у* (х а)’ и у9 (х — а)1 — квадратами расстояний частицы от краев пластинки, сообразно схеме, изображенной на фиг. 45. Тогда вместо выражений (20), (22), (23) и (25) получим:
для пространства /
+ (а)
для пространства III
( R \
Sm = — c (к(х —a)4<x4-a)p—(х —aft 4*J
но 7 = к — р,, почему окончательно имеем?
5Ш =-с|(х-|-а) р+ (х-о) In (b)
для пространства И
SB = + c{(x + e)? + (<--«)₽i+J'b» (О
для пространства /V
• Siv = —с{*(х —a) —(x-f-a)p-Hx —а)т —ylri£-| .
или заменяя 7 = тс— рп имеем:
Slv = — С^2 ft (х — а) — рх 4~ a) Р 4- (х — a) 4-у In j. (d)
Просматривая теперь ряд полученных выражений, мы видим, чао все они являются функциями одной и той же суммы
(x-hrt)Pf(x-tf)pJ4-jm^=4. (Ж
причем
Si=Sm=—С.4; Sh=4-CAjj Slv = — <Д2к(х — а) —Л].
87
Выше этого тока YOCE или
Поэтому определив значения М для ряда точек пространства, заключенного в одном прямом угле координат, мы построим все токи искомого течения, соединяя между собой точки одного и того же значения S.
Фиг, 46 дает нам точную картину токов жидкости искомого ками движения.
Рассматривая ее, мы видим, что все движение неограниченной жидкой среды, набегающей на пластинку, делится поверхностью граничного или предельного тока на две весьма различные части.
YOAF поток жидкости движется
в прямом направлении, огибая пластинку, и уходит в бесконечность за нее, будучи всегда ограничен поверхностью предельного тока со своей внутренней стороны.
Наоборот, в пространстве под пластинкой, ограниченном предельным током, мы имеем самостоятельную циркуляцию жидкости. Между вихревыми слоями АВ и CD поток жидкости из—оо движется к пластинке в направлении прямо обратном направлению движения основ-
ного потока.
Обратная поверхность пластинки подсасывает жидкость. Эта подсасываемая масса жидкости, как показывают ее токи, протекает постепенно через вихревые слои, где резко изменяет направление своего движения опять на прямо обратное и в пространстве между поверхностями вихревого слоя и предельного тока снова вся сполна уходит в — оо.
Уравнения предельного тока. Предельный ток, разграничивающий движение основного потока и потока, подсасываемого пластинкой, идет к ней по оси YO и — YO, затем от точки О середины пластинки расходится по ней к ее краям Л и С и далее идет по кривым СЕ и AF в —оо.
Поэтому уравнение предельного тока согласно (26) до схода его с края пластинки напишется в виде:
р
(х + а)Р + (х_я)Р1+>.1п^- = О. (27)
Оно удовлетворяет точкам оси YO или — УО, для которых х = 0, и /? = #!, а также и точкам поверхности пластинки у = 0, 8 = = 0, до ее краев. Но начиная с «рая пластинки, ветви предельного тока должны удовлетворять уравнению токов пространства 1У лри постоянном, равном нулю. Здесь уравнение предельного тока напишется поэтому в виде:
(х + а) р + (х - а) р, 4-у In £ = 2 z (х - а). (28)
фиг. 46.
Это уравнение показывает нам, что, уходя в бесконечность, дпя которой a p=.|j = —, кривая предельного тока будет удовлет-
ворять уравнению
(*+«) ’+(х_а)’=2л(х_а)>
откуда получим, что х = 2сц т. е. сам предельный ток будет асимптотически приближаться к прямой, параллельной оси КУ, отстоящей от нее на расстояние 2 а, равное ширине пластинки.
А так как вихревой слой отстоит от оси YY на расстоянии, равном а, то в бесконечности ширина подсасываемого пластинкой потока экидкости будет в точности равна ширине потока, оттекающего от пластинки в пространстве между поверхностями предельного тока и вихревыми слоями. Поэтому в бесконечном расстоянии от пластинки скорость подсасывания будет точно равна скорости отбрасывания и обе скорости равны по величине и прямо обратны по направлению:
— оо
Но кроме указанного выше необходимо обратить внимание еще на одну принципиальную особенность полученного нами решения вопроса об обтекании плоской пластинки. Как уравнения токов жидкости в ^пространствах / и //, так и чертеж течения фиг. 46 показывают нам, что движение жидкости между вихревыми слоями под пластинкой совершенно тождественно по отношению к ней движению потока яад пластинкой в пространстве, ограниченном плоскостями, являющимися продолжением плоскостей вихревых слоев.
Одно течение является точным зеркальным изображением другого, где роль зеркала играет сама пластинка.
Сказанное позволяет нам все вопросы обтекания тел неограниченным потоком жидкости решать, польфясь методом зеркальных изображений, как вопросы взаимодействия двух потоков, идущих навстречу друг другу, иными словами, как вопросы формы соединения двух прямо противоположных друг другу потоков, причем форма тела обусловливает собой форму зеркала и тем самым форму зеркального изображения второго потока.
Ниже показано, как это обстоятельство расширяет и углубляет смысл и значение развитого нами здесь метода решения вопросов обтекания тел неограниченным потоком жидкости.
§ 5. КРИВЫЕ РАВНОЙ ПОЛНО! СКОРОСТИ. РАВНОГО ДАВЛЕНИЯ И СИЛА ДАВЛЕНИЯ ПОТОКА НА ПЛОСКУЮ ПЛАСТИНКУ
Форма движения потока жидкости, набегающего на плоскую пластинку, изображенная на фиг. 46, дает нам только чисто кинематическую картину этого явления.
Для выяснения его динамического характера приступим теперь к изучению распределения полных скоростей и давлений во всем поле окружающей пластинку жидкости.
Кривые равных полных скоростей частиц жидкости. По выражениям (13) и фиг. 44 полная скорость W частицы жидкости во всем пространстве выше оси XX, пространства / и ///, ноже г быть представлена в виде:
w = С j/ (.In (н- &)’ . (29)
Поэтому кривые равней помой скорости W = const будут даны здесь уравнением:
(1П /?;)'+ <₽+=D’=const» (3°)
а величина скорости на каждой кривой будет равна
W—CD. (31)
Ниже оси XX между вихревыми слоями пространства // мы будем иметь те же выражения для кривых равной скорости и ее величины. Только направление ее будет противоположно скорости в пространстве /. Наконец, в пространстве IV за вихревым слоем и.лесм:
(in ^)’+ [2К- (₽ + ₽,)]’ = £«. (32)
Правая сторона фиг. 47 дает нам точную картину вида и распределения кривых равной полной скорости частиц жидкости. На каждой кривой указано значение соответствующей ей постоянной величины D, почему известна для нее и величина полной скорости.
Рассматривая фиг. 47, мы с полной ясностью видим, какое возмущение в состоянии начального однородно-поступательного движения л ндкой среды вносит наличие в ней неподвижной, плоской пластинки. Впереди нее движение потока становится замедленным, и на поверхности самой пластинки в ее середине скорость его равна нулю.
Это торможение потока ослабевает от середины к его краям, и форма кривых равной полной скорости показывает, как распространится изменение скорости во всем окружающем пространстве.
Торможение прекращается на кривой, для которой D = rc = 3,14, т. е. кривой начальной скорости потока W—Vq = Ck. Эта кривая, помеченная на фиг. 47 как .граница торможения4, начинаясь вблизи края пластинки, круто отходит от нее в сторону и быстро превращается в прямую, параллельную оси XX или плоскости пластинки и расположенную выше нее на 0,3 а.
Выше границы торможения все скорости частиц жидкости меньше начальной скорости потока Сте, ниже ее — больше той же скорости. При этом скорости быстро возрастают с приближением к краю пластинки. Но какова бы ни была скорость по абсолютной величине, се кривая всегда начинается с передней стороны плоскости пластинки, ибо на плоскости пластинки, т. е. при у = 0 и мы имеем
Р = рх = 0 и скорость частицы по выражению (29) равной:
1Г = С1п.{?-==С1п (33)
/?1 а—х '
А последнее выражение показывает нам, что, начиная от середины пластинки, при х = 0, где скорость W = 0, к ее краю, где х = а, a U7 —со, мы вдоль по пластинке будем иметь все скорости от нуля до бесконечности, почему и все кривые скоростей вачцн^ютси с передней стороны пластинки. ,
Фиг. 47
Уравнение (33) дает нам возможность найти положение точки начала кривой .границы торможения*. Для этой кривой W= Ск, почему мы будем иметь уравнение:
In iLT_r = 3,i4 а — х
рения которое, получим
х = 0,92 а.
Полученная величина х показывает, что хотя кривая .границы торможения* начинается очень близко от края пластинки, но все же не на самом краю и за ней скорость быстро возрастает к краю до бесконечности.
Далее мы увидим, какие принципиально важные следствия вытекают из указанного обстоятельства. Ниже пластинки, между вихревыми слоями, распределение скоростей тождественно распределению их в подобном же пространстве с ее передней стороны.
Вся разница заключается здесь только в направлении скоростей. Поэтому вдоль по вихревому слою разность скоростей-'равна их сумме, т. е. 2 к — 6,28. *
Кривые равных давлений или уровней. Для всего пространства выше и в стороне от пластинки за исключением пространства между вихревыми слоями мы по уравнению Д. Бернулли можем писать, что
P.a.WL=Po I лл
Т ‘2g Т ' 2 g 1 '
где р и W—давление и полная скорость произвольной частицы жидкости, а и Wo—начальные величины давления и скорости в набегающем на пластинку потоке жидкости.
При потоках тяжелой жидкости конечной глубины уравнение бу» дет иметь вид:
I ' 2g 7 + 2g ' ’
где г —ордината рассматриваемых частиц.
Поэтому для исследуемого нами случай плоского двмжени# жидкости бесконечной глубины будем иметь по уравнению (а).
--------------------tp»-----------------0 Д=Ро4-Р ^~2_________=А>+
или
р—Ро=^г(*3 — О3), (34)
где D — попрежнему коэфициент полной скорости частицы.
Уравнение кривых равного давления получим, приравнивая вторую часть выражении (34) постоянному, в виде:
= D’= const—£*. (35)
р
Кривые равных давлений, соответствующие уравнению (35), даны на левой половине фиг. 47.
Во всем пространстве выше пластинки и кривой .границы торможения* имеем почему разность ка — D3 положительна, а следовательно, положительна и разность давлений р —р^, т. е. здесь РУ'Рл или мы имеем подпор, повышение давления или уровня.
Максимум подпора получим в середине пластинки, где/) —0> почему здесь
Р =Ро+ J С*=А)+ | *<Л
Подпор исчезает на .границе подпора*, где D = * и гс* — D9 =0, почему по этой линии р=р& т. е. имеем начальный уровень или начальное давление потока.
Наоборот, ниже этой линии и р—р$ отрицательно. Да-
вление падает здесь ниже начальной величины. Особо сильное падение давления у края пластинки, где оно теоретически доходит до—оо, т. е. до разрыва сплошности течения.
Переходя теперь к пространству между вихревыми слоями и обращенной к нему обратной стороной пластинки, мы будем иметь иную картину давлений:
По предыдущему при переходе через вихревой слой скорость изменяется скачком на
2 к С = 2
т. е. на удвоенную скорость в бесконечности.
Для создания подобной разности скоростей необходим напор А, равный:
А=(2^-4-^
2g ~ 2g'
А так как в пространстве между вихревыми слоями движение жидкости прямо обратно движению ее над пластинкой и скорость набегания сверху точно равна скорости подсасывания снизу, то на самой пластинке, с различных ее сторон мы будем иметь два равных и прямо обратных скоростных напора взаимно уничтожающихсяу
почему остающееся давление потока на пластинку равно:
Л1 = й-2^=2 1 2g 2g
(36)
т. е. равно двойному скоростному напору от начальной скорости набегания жидкости.
К этому результату мы можем притти и иным путем. Если в пространстве выше пластинки мы начальный запас энергии частицы жидкости представляем согласно фиг. 48 суммой ^=-4-^.
I 2g ' то начальный запас энергии частицы жидкости ниже пластинки, между вихревыми слоями или в области всасывания, мы должны представить разностью:
ну-=~—-£
7 2g
Поэтому разность давлений с обеих сторон пластинки в ее центре? равна 1
т. е. результат, тождественный предыдущему. Выражение (37) показы* вает, что давление между вихревыми слоями везде отрицательно и увеличивается с удалением от пластинки в бесконечность в два раза.
Постоянные кривых равного давления над пластинкой равны тс1 — D\ а под ней -f-D3, почему сумма постоянных равна:
и’ — Оа + (к, + Р2) = 2к\
Распределение Давления и величина силы давления потока н& поверхность пластинки. Найдем теперь как распределение давления, так и величину силы давления потока на плоскую пластинку вдоль по ее ширине. Скорость. частицы жидкости, лежащей на ее поверхности в точке т (фиг. 49) в расстоянии х от середины пластинки, по выражению (33) равна
r=Cln^i5.
а — х
Поэтому, относя, как принято, изменение давления в различных точках по* ширине пластинки к скоростному напору от скорости в бесконечности*
2 2 *
Фиг. 49.
распределение давления Ех вдоль по ширине пластинки с ее передней стороны мы сможем согласно выражению (35) представить в виде:
(38)
а распределение давления Et с обратной ее стороны по выражекшо (37) в виде:
•___Р Ро
2 рх’С2
9
(39)
Поэтому ровность давлений на одну и ту же точку т пластинки с двух противоположных сторон ее будет пропорциональна:
т. е. разность давлений постоянна по всей ширине пластинки.
Взяв у точки т бесконечно малую площадь поверхности пластинки 1 -dx. найдем, что элементарная сила давления потока на.эту площадь будет равна:
,я _ рк’С2 . dP=2'—— dx
и полная сила давления:
' р=2 f2 S^dx = 2 l^.2a = 2^lf=f.f.^ (40)
О
т. е. равно количеству движения набегающей массы жидкости. К тому же результату мы придем и применяя закон количества движения. С этой целью заключим пластинку АС (фиг. 50) в бесконечно удаленную от нее замкнутую поверхность S в виде призмы MN0P, плоскости которой и ОР нормальны к оси YY, а МР и NO параллельны ей.
На бесконечном расстоянии от пластинки скорости, параллельные оси XX. как то мы*видели, равны нулю. Поэтому через плоскость ALV Жидкость будет втекать в объем MNOP с постоянной и нормальной к ней скоростью — С той же скоростью она будет нормально вытекать из объема MNOP через части плоскости РО, PC" и А"О. Но на части А"С мы будем снова 'иметь втекание жидкости в объем MNOP со скоростью ^о- Применяя теперь закон импульса сил, получим силу давления потока на пластинку равной:
Р= [{jv2cos(v21N)v2dS-- jp^cos^^^dS-j- f p2dS— \ptdS, s s s s
где значками 1 и 2 обозначены места входа и выхода потока из поверхности 5.
В рассматриваемом нами случае имеем:
cos(tf3,/V) — cos(vvN) = 1; ф., = фх — ф0 ; • t
Fl—rOT 2 ’ —P® 2 ’
w
Поэтому здесь будем иметь:
Р= ?v0*dS- ргг03Л5+ (ро - ^)dS- ;
s а» а"С"
Ча •
Д'С' о
результат, тождественный выражению (40), ибо знак минус дает направление силы Р давления потока на пластинку, противоположное положительному направлению o^i OY. *
Кроме того, сам вывод снова показывает нам, что в случае нормального набегания пбтока на пластинку сила взаимодействия между потоком и пластинкой появляется в результате разности давлений по обе ее стороны, а не скоростей.
Посмотрим теперь, в какой мере вся изложенная вьпйе теория соответствует данным прямых опытных наблюдений того же явления.
С этой целью на фиг. 51 точно построено как распределение давлений на прямой и обратной стороне пластинки согласно выраже-ниямш (38) и (39), так, и распределение давления, найденное Фэйгом и Джохансеном (Fage и Johansen) из опытов и опубликованное в Лондоне "в 1927 г. и с возможной точностью перенесенное мной на фйг. 51 из „Handbuch der Experimentalphysik", 2 Teil. Hydro- und Aerodynamik за 1932 г., стр. *321. t
На фиг. 51 теоретическая кривая давления дана непрерывной линией, опытная кривая дана пунктиром.
Сравнение обеих кривых показывает нам их полное совпадение с передней стороны пластинки в области положительного давления. Здесь теория вполне соответствует реальному явлению.
На обратной ее стороне ’• области отрип9тельных давлений мы не имеем столь полного совпадения.
Здесь вместо теоретической кривой распределения давлений опыт дает давление почти постоянное, равное—1,33. Это расхождение результатов теории и опыта происходит вследствие неустойчивости положенных в основу теории непрерывных вихревых слоев, сходящих с краев пластинки. £>пыт показывает, что эти непрерывные вихревые
слои всегда разлагаются на ряды отдельных вихрей конечных размеров, дающих начало „дороге Кармана*.
Фиг. 52 представляет три последовательных снимка киноленты с проме
жуткам времени ме-
жду ними в 1 сек.
Она показывает нам, что за пластинкой обычно существует один вихрь, занимающий всю ее ширину, почему и давление с ее обрат-, ной стороны почти постоянно по вели-s чине (фиг. 52, /). Удаляясь от пластин
Фиг. 52.
ки, он дает место
для такого же, но обратного вихря (фиг. 52, 3). Фиг. 52, 2 дает промежуточный момент отхода от пластинки первого вихря и развитие* второго. И если в настоящее время мы не можем еще дать полного анализа этого весьма сложного явления, то во всяком случае наша теория показывает, что разложение непрерывного вихревого слоя связано с выравниванием давления на обратной стороне пластинки.
Но указанная разница в конечном виде движения жидкости за пластинкой весьма мало отражается на величине давления на нее отока.
Так, прямой подсчет опытной площади давления с передней стороны пластинки до точки переселения с ней кривой давления (точки, лежащей, как нам теперь известно, в расстоянии 0,92 а от ее сере-дины^ дает величину силы положительного давления равной 4-0,733^, £
а для отрицательного давления с ее обратной стороны величину, равную
— 0,92 • 1,33 ^°- = — 1,2^3 .
Поэтому полная сила давления на пластинку по опытным данным равна /
1,956^'. ь
Теоретические силы давлений, определенные подобным же методам, дадут нам:
*
давление положительное = 4“ 0,733 ;
давление отрицательное — — 1,267 ;
сила полного давления = 2,00 .
Прямые измерения силы давления потока на бесконечно длинную, .плоскую пластинку в Геттингене дали:
\ Р^
а) старые Измерения 2,00
I I
, б) новые измерения 1,95^- .
Столь малые колебания в конечной величине давления, обусловливаемые колебанием в величине отрицательного давления максимум в 2,2°/0, показывают нам, что данные непосредственных опытных из.-мерений вполне подтверждают правильность развитой нами теории рзаимодействия потока и плоской пластинки. Но если излагаемую адесь теорию возможно признать правильной, то должны быть справедливы и ее следствия.
Следствие I. Потеря энергии потока, обтекающего пластинку. Одним из следствий этой теории является возможность точного подсчета потери энергии потоком жидкости, обтекающим пластинку, или, наоборот, затрата энергии на ее движение в неподвижной жидкой среде. Действительно, мы видели, что при обтекании потоком жидкости плоской пластинки последняя своей обратной стороной-подсасывает и снова выбрасывает согласно схеме фиг. 53 количество* жидкости, равное количеству ее, набегающему ма пластинку из бесконечности..
Но тогда по закону Карно энергия, теряемая или затрачиваемая Ъкидкостью на эту циркуляцию ее под пластинкой, будет равна живой силе потерянной скорости.
• Для единиц^ массы жидкости мы в бесконечности получим ее равной:
h *р[+ (—Мэ _ . (2wo)2 — 4 о
й.,=----2----р^2“Р2 *
1 См. HandbucA der Expen'mentalphyslk, стр. 321.
ЮО
Для всей площади /пластинкй эта потеря равна:
г /71 2
Я, = 4/^-=2/рг^=
= 2/pv0v0- (41)
Но есть не что иное, как „количество движения** набе-тающей или подсасываемой массы. жидкости.
Поэтому согласно закону К*ар-но энергия, теряемая потоком / жидкости при обтекании плас- / тинки, равна удвоенному колике- I ству движения набегающей на I нее массы жидкости^ I
Фиг. 53 показывает, что одна половина Ни затрачивается^ подсасывание жидкости пластинкой
+ И .
и вторая на обратное ее отбра- Фиг. 53.
рывание.
Секундная работа, затрачиваемая потоком на преодоление сопротивления его движению пластинкой, будет поэтому равна:
N=H„v()=2pfv99. ' (42)
Она равна той работе, которую необходимо будет затрачивать, чтобы двигать плоскую пластинку в неподвижной жидкости со скоростью v0.
Изложенное показывает нам, что сила давления потока на пластинку по формуле (40) равА
^=2^-f=pfv0v0, £
а потеря энергии по (41) равна *
Ц, = 4 {'V"- f= 2pfvaVQ,
т, е. сила давления потока* равна количеству движения, а потеря энергии —удвоенному количеству движения набегающей массы жидкости. Иными словами, потеря энергии по величине вдвое больше силы давления потока ,на пластинку, И если бы величину силы давления на пластинку мы считали бы ее полезным для нас сопротивлением, то для достижения этой силы мы должны были бы расходовать работу, соответствующую удвоенной сиве давления.
Поэтому совокупность жидкости и плоской пластинки представляет собой машину с коэфициентом полезного действия, рас-ным 50°'0, или половине.
С этой точкой зрения определение лобового сопротивления по способу Мариотта (Mariott) {1686 г.) весами или динамометром в действительности является только определением величины силы давления потока на пластинку, но не работы или затраты энергии, необходимой для ее получения, величина которой и должна была бы на наш взгляд с большим правом считаться величиной истинного лобового сопротивления.
К нашему удовольствию этот принципиально важный результат изложенной теории нашел полное и интересное в смысле выяснения истины подтверждение в работах Кармана (K&rmfin) и Н. Е. Жуковского. На стр. 180 курса Н. Е. Жуковского „Теоретические основы воздухоплавания*, Москва, 1925 г., приведена формула лобового сопротивления Кармана
R=0,592 — ?Fv2 S
(где 5 — ширина пластинки, a h — расстояние между рядами вихрей), вычисленная по потерянному количеству движения „вихревой дороги* за пластинкой. Приводя ее, Н. Е. Жуковокий на стр. 188 и далее говорит, что „Определение силы сопрЬтивления с помощью динамо-.Uempa приводит нас к меньшему числу*, и, принимая во внимание не только изменение величины скоростей, но и давлений, выводит формулу величины сопротивления в виде
/? = 0,296 (l+|i)p
где р— весьма малая величина.
После чего на стр. 190 Н. Е. Жуковский говорит: „Таким образом получаются довольно близкие к действительности результаты, если к формуле Кармана прибавить множител!^- •.
h
Там же для плоской пластинки по опытам дана величина.— =3,6. s
Но если мы умножим коэфициенты формулы Кармана и Н. Е. Жуков-h
•гкого на43,6= —, то получим:
лобовое сопротивление по Карману
R — 0,592 • 3,6 pFo’ = 2,13 р Fv\ *
лобовое сопротивление по Н. Е. Жуковскому
/? = 0,296 • 3,6 (1 + р) p/V = 1,07 (1 + р) рАЧЛ
А так как pFn9 есть количество движения набегающей на пластинку массы жидкости, то мы видим, что у Н. Е. Жуковского, так же как и у нас, динамометрическая сила давления потока на пластинку измеряется количеством*движения набегающей массы жидкости, а у Кармана она равна удвоенному количеству движения. Но эта
величина измеряет не давление на пластинку, а потерю энергии потока при обтекании пластинки, величина которой действительно в два раза больше силы давления, даваемой динамометром.
Проф. Прандтль и проф. Карман в своей теории лобового сопро-7 тивления как силы давления на пластинку, несомненно, впали в ошибочное его представление, отождествив две весьма различные по своему смыслу величины силы давления потока на пластинку и потерю потоком энергии при обтекании пластинки или сопротивление движению потока. Но, вскрывая эту неясность существующей теории, мы должны обратить внимание на ошибочность и другого представления. А именно, весьма распространено убеждение, что в идеальной жидкости, с которой оперирует гидродинамика, не может быть никаких потерь энергии потока, почему энергия ее частиц остается всегда величиной постоянной и уравнение Д. Бернулли всегда существует.
Полученная Прандтлем, Карманом и нами величина потери количества движения или энергии потока идеальной жидкости, обтекающего пластинку, показывает нам на неправильность подобного взгляда.
В самой идеальной жидкости, лишенной вязкости и трения, всегда возможна как потеря, так и увеличение энергии ее частиц, или изменение запаса их энергии вследствие превращения ^асти энергии потока в энергию вихревую или рассеяния последней. И $сли само движение жидкости не будет при этом винтовым, то не будет существовать и интеграл Д. Бернулли, т. с. запас энергии частицы жидкости явится величиной переменной1. *
Пример подобного движения жидкой среды мы имеем при взаимодействии потока и пластинки. Когда поток обтекает пластинку, энергия/ его частиц уменьшается вследствии общей потери энергии, равной удвоенному количеству движения набегающей на пластинку массы •жидкости. Наоборот, когда 1? Жидкой среде движется пластинка, она, рассеивая энергию своего движения, испытает тем самым запас энергии окружающей среды на удвоенное количество движения встречаемой ею массы жидкости. В обоих случаях интеграла Д. Бернулли существовать не будет, почему мы при развитии настоящей теории и были вынуждены приписывать постоянному уравнения Бернулли различные значения в разных местах пространства, окружающего нашу пластинку.
Наше механическое представление явления станет гораздо более ясным и правильным, если в случаях, подобных здесь излагаемому, мы, отбросив пластинку, заменим ее вторым потоком жидкости с запасом энергии, отличным от запаса ее в первом потоке, а взаимодействие потока и пластинки заменим соединением двух указанных потоков, что и приведет нас к замене реального Ала системой силовых трубок, т. е. к чисто фарадеевскому представлению явления.
Следствие II. Применение метода зеркальных изображений. В кон-4 не § 4 указывалась возможность применения метода зеркальных изображений к решению вопросов обтекания тел жидкостью. Из начала § 5 нам известно, что сила давления потока жидкости, нормально
1 См. А. Я. Милович, Основы динамики жпдюд’гн. § 11. стр. «4
набегающего на плоскую пластинку, измеряется количеством движения этого потока [выражение (40)]:
Р=р.2а-тг0\
Зная все сказанное, применим метод зеркальных изображений к решению вопроса о том^ как изменится величина силы давления потока жидкости, если вместо плоской пластинки АВ шириной 2а поток будет
набегать на цилиндри-
ческую поверхность ANB (фиг. 54) с радиусом основания, равным а, С этой целью вообразим себе, что поверхность ANB представляет собой поверхность цилиндрического зеркала, радиус кривизны кото-
рого равен а. ~
Тогда зеркальное изображена прямой MNP ширины набегающего потока жидкости, равного 2а, представится в виде кривой mNp, \ ширина которой тр будет равна 0,58-2а, Поэтому сила давления потока на цилиндрическую поверхность с диаметром основания, # равным 2а, будет равна 0,58 от силы давления его на плоскую пластинку АВ той же ширины: > ш •
Р' = 0,!>8Р=0,58р-2< v£. (41')
Если бы вместо бесконечной пластинки ширины АВ = 2а взяли плоский диск того же ди'аметра, а потом заменили его сферическим зеркалом ANB и построили в нем изображение площади круга МР набегающего потока Жидкости, то получили бы круг тр, диаметр которого был бы равен 0,58 МР. Площадь круга зеркального изображения была бы тогда равна (0,58)* = 0,33 площади набегающего потока жидкости и во столько же раз сила давления на шаровую поверхность будет меньше силы давления на плоский диск
Р" = 0,ЗЗР, (42') #
ибо зеркальные изображения в выпуклых зеркалах всегда меньше действительных предметов.
Непосредственный опыт показывает справедливоеть выводов и возможность применения подобного метода.
Так, например, если коэфициент силы давления потока жидкости на бесконечно длинную плоскую пластинку равен 2, то такой же коэфициент силы дарении на цилиндрическую поверхность будет- равен 1Ъ4
2*0,58=1,16. По измерениям в Геттингене коэфициент давления на бесконечно длинный цилиндр равен 1,20.
Принимая силу давления на диск рав- * ной единице", силу давления на сплошное полушарие получим равной 0,33. Непосред-^ ственный опыт дает коэфициент, рав- » ный 0,32. Вместе с тем применение подобного метода впервые дает нам понятие как о связи между коэфициентами силы давления потока жидкости на тела различной геометрической формы, 'так и о влиянии изменения формы тела на величину силы давления на нею жидкости. Для нас понятно теперь, почему округление торцевых поверхностей тела умень
шает величину давления на него уотока.
Особенно интересно в этом отношении дальнейшее развитие метода зеркальных изображений. Так, из ^теории зеркал нам известно, что сферически зеркала дают нам неясные изображения вследствие аберрации, что ведет к увеличению и коэфициентов силы давления. Аберрация отсутствует только у гиперболических, выпуклых зеркал, почему и все торцевые поверхности тел должны иметь гиперболические очертания.
Действие бесконечно близких непрерывных вихревых слоев обратного Вращения. На фиг. 42, § 4 мы имели два вихревых слоя* бесконечной длины, отходящих от концов А и В плоской, пластинки..
Расстояние между ними, равное ширине пластинки АВ, равнялось-2а. Совместное действие этих слоев вызывало в окружающем пространстве поле скоростей, даваемых выражениями (12) —(18).
Посмотрим теперь, как изменится это поле скоростей при уменьшении ширины пластинки 2а до нуля, т. е. при сближении вихревых слоев на бесконечно малое расстояние между ними.
По схеме фиг. 55, полагая ширину ‘ пластинки бесконечно малой; и равной 2Да, будем иметь:
я=С1п^+(х-+Д-.“Г
, + —Ла)2 ’
V = С ( arctg —-arctg —.
•Л х — А а 6
При уменьшении Да до нуля мы найдем предельные значения функций и и V, взяв производные от них по Да. и приравняв затем Да нулю. Тогда для скорости и новое выражение п0 будет равно:
,, lim ди lim г ( д г „ ,--------
wo == да._0 — да—*0 G I ^да In у у + (х -f- Ла/ —
___L.I ./-5-Г7-ГтЛ— lim с( х + Да | х —Да Ч dba ln I У' । И м) да_о |у4-(х4_дар~гу._|_J
или
2х __2Сх
и°~ г+*а— %* '
Но х = R Cos s, почему можно писать, чта
2 С coscp tt°——/?”"•
1ля скорости v получим:
„ _ lim lim c/_jLarct{?_____________У . _ _ arete—__________1 =
н» - дв^о д1а - с ( dla g X - Да дЛа g х -f- Да )
__ lim (J (______У_________|__л----У.----— I, Да—>0 ( у2 + (х — Да)’ у2 + (х -f- Да) J
.или
2у 2Су
Но y = R sin ср, почему окончательно;
2 С sin ср
• С'о — 7Г^
Полная скорость частицы т равна:
W? — и<) + ^03 = 4 0-^5 или
• 5
* *
(44)
(45)
Сравнивая выражения (43), (44) и (45) с. выражениями (7) и (8) § 1, увидим, что два бесконечно близкие, вихревые слоя действуют на всю окружающую их массу жидкости как прямолинейный, положительный источник, проходящий через точку О их начала с напряжением Q=2C. Они выбрасывают из точки О жидкость, подсасываемую между вихревыми слоями из бесконечности (фиг. 56), и дают нам, наконец, истинную картину элементарного движения с сопротивлением (Widerstandssiroiiiung), которое помощью только одного изолированного источника точки пытается представить себе проф. Прандтль в § 88 своей ,Hydio- und Aeromechanik", 11 Band, 1931 г. Но так как вихревые слои и создаваемый ими на их конце прямолинейный источник сами являются результатом набегания потокй на торец тела со скоростью — vu (фиг. 57), то действительное движение жидкости, здесь
происходящее, мы получим, сложив движение, вызываемое источником
точкой Ос поступательным движением вдоль оси УК, со — va. Слагающие скоростей подобного движения по осям будут равны;
_2Сх 2 С cos ср
“°— R2 R ’
2 Су 2Csincp
скоростью
XX и YY
(46)
V
Фиг. 57.
Функцию течения найдем, интегрируя выражение:
Г d-
= 2С\ ---A-j — vax = 2 Сarctg J — vax = 2 C0 — va x.
Лч-У
Поэтому уравнение токов жидкости рассматриваемого течения напишется в виде:
2 СО — vaRsin 0 = const. ‘ (47)
Но выражения (46) показывают, что на положительном направлении оси OY при ср = 90° мы будем иметь точку нулевой скорости М в таком расстоянии /?0 от начала, при котором
2C = vaRQ.
А на основании уравнения (47) предельный mote жидкости, проходящий через точку нулевой скорости Л/, должен удовлетворять уравнению: V, •
• Va ------VaR sin ® = cortst
или
/?о 0 — R sin 0 = const.
Но для точки M угол 6=0, почему мы должны иметь уравнение пре-
дельного тока в виде:
/?о0 — sin 6 = 0
или окончательно
,481
Подобно уравнению представленного тока (48) урав! ение всякого другого тока возможно представить в виде:
где т—постоянное тока. •
Для токов, идущих вне предельного для пределы ого пг=О и для токов, идущих внутри предельного т < 0.
• Написав уравнение*предельного тока в форме
х = /?sin6 = /?0 6 ,
сейчас же увидим, что при 6 = 0 х = 0 и предельный ток идет по положительному направлению оси OY, наоборот, с приближением угла Окт: он' уходит бесконечность параллельно отрицательному направлению OY на расстоянии от этой оси *
Хте=7г/?0.
А так как в бесконечном расстоянии от источника-точки О при /? = оо компоненты (жорости частицы по = О и ^0=;— va9 то между осью OY и предельным током проходит расход
— = к/?ог!ц.
Поэтому полный расход источника-точки равен:
• . q = 2KR0va. (51)
Последнее количество жидкости и подается ему в единицу времени из бесконечности между вихревыми слоями. Сила действия потока жидкости на подобный источник-точку согласно выражению (40), § 5 равна количеству движения набегающего потока, что по выражению (51) дает силу ч
Р= ?qva = p2vR0va2. (52)
Потеря энергии согласно выражению (41), §5 равна двойному количеству движения
Нр42Р=2р.2к/?0ггД ' (Q3)
Фиг. 58 дает точный чертеж исследуемого нами движения жидкости» /?о=1О мм, а фотография (фиг. 59), взятая из „Hydro- und Aerome-chanik* проф. Прандтля, изображает случай обтекания жидкостью тонкой пластинки.
Мы видим полное подобие обеих картин движения жидкости, указывающее нам на сущность явления, именуемого нами трение.^ 108
жидкости о поверхность твердого тела. Выполненный анализ показывает, что при движении потока жидкости вдоль по поверхности твердого тела, необходимо являющейся поверхностью разрыва сплошностей функции скорости, эта поверхность будет покрыта непрерывной вихревой поверхностью жидкости, проходя через которую, частицы ее будут изменять свою скорость скачками на 2 vai где va — скорость движения потока. Эффект вихревого слоя сводится поэтому к движению жидкости у поверхности тела в направлении прямо обратном движению остального потока со скоростью — va. Такая подача жидкости в направлении прямо' обратном направлению / движения потока поведет к образованию у стенки слоя ее толщиной с внутренней циркуляцией в нем жидкости.
На эту циркуляцию и затрачивается энергия, теряемая потоком на трение о поверхность тела. С другой стороны, тот же анализ говорит нам, что источник-точка является концом Шиловой трубки бесконечной длины.
ОТДЕЛ IV
ТЕОРИЯ ПЛОСКОЙ РЕШЕТКИ И ИСТЕЧЕНИЯ ИЗ ОТВЕРСТИЙ
w
§ 6. СИСТЕМА ПЛАСТИНОК. ТЕОРИЯ НОРМАЛЬНОГО ПРОТЕКАНИЯ ПОТОКА ЖИДКОСТИ ЧЕРЕЗ ЩЕЛИ ПЛОСКОЙ РЕШЕТКИ
Теория нормального набегания потока жидкости на плоскую пластинку конечной ширины и бесконечной длины, развитая нами в § 4 и 3, дает все необходимое для постановки и решения вопроса о взаимодействии друг на друга ряда пластинок, расположенных в одной и той же плоскости и параллельных друг другу.
Если учение об обтекании потоком жидкости одной пластинкЛ» представляет, главным образом, интерес чисто теоретический в смысле простейшего выяснения характерных особенностей механизма подобных явлений, то теория обтекани%системы пластинок представляет интерес прямо прикладной, давая решения ряда вопросов, важных для гидротехники и гидравлики, как, например, протекание потока между быками через мостовые отверстия дамб, через предохранительные решетки, через щели в дне сосуда и т.д.
Для ясности и простоты всего последующего начнем изучение с простейшего случая системы двух пластинок.
Нормальное набегание безграничного потока жидкости на систему двух пластинок. Вообразим две пластинки бесконечной длины АВ и CD (фиг. 60), параллельные между собой и лежащие в плоскости XX.
Пусть ширина пластинок будет равна 2а; а расстояние между ними ЛС=±26. Начало координат возьмем в точке О середины расстояния- АС и положим, что безграничный поток жидкости набегает па пластинки #по направлению оси YY со скоростью — Тогда на основании § 4 можем компоненты скорости частицы жидкости в произвольной точке пространства т выше оси XX написать в виде:
и = С1п — — С1п — = Cta, G г г. R'
v=С61+со—v0=с(о -|- GJ—V& где
R = 1/_Уа-j-(2а— х)а; г = /у—х)3,'
Ri=И У4- (2л ч- /»+•*)*; п= /У+(*+х)3, 0 = я — (а1 + аа); в1=те —(₽1+Ра)- >
Поэтому
04-61 = 2к-(а1 + а2 + ₽14-ра) И
v = С [2л — (а, + а2 + 0, -f- р2)] — v0.
(О
(2)
(3)
Для произвольной точки поверхности пластинки АВ будем иметь: -
Фиг. 6й
почему на поверхности пластинок скорость tr = Ск— и чтобы он> была равна нулю, необходимо, чтобы г>0 = Сгс. Внося эту величину скорости набегания в выражение (3), окончательно получим, что
к v — С[~—(04 а2 + “Ь «].
(4>
Выражения (1), (2) и (4) показывают нам, что компоненты скорости частицы жидкости при постоянной ширине щели между пластинками 2Ь зависят от ширины пластинок 2а. Чем больше эта ширина, тем больше
R
длина R и и меньше величина отношения ~ вблизи оси FK, а R
также меньше и величина углов аг и 1
При пластинках бесконечно большой ширины 2а = 00, /?t = /? = оо,
= 1 и «i = ?i = 0.
•
Этот простейший по анализу случай физически представляет собой явление истечения жидкости из бесконечно длинной щели шириной 2Ь в плоской стенке бесконечно широкого бассейна в бесконечную массу жидкости меньшего давления.
Мы начнем развитие анализа с этого простейшего случая, так как он позволит далее легко переходить к случаям, более сложным, не теряя ясности в физическом представлении исследуемых нами реальных явлений.
I. Истечение жидкости из щели в стенке бесконечно широкого бассейна (случай совершенного сжатия)
В этом случае согласно фиг. Q1 2а = оо, почему прямые R и/?г
становятся параллельными orti XX и бесконечными по величине, а отно-
шение их
= 1. Углы 04 = 11^ = 0, а
аа = гс— 6 и Р2 —
R
Поэтому компоненты скорости частицы будут равны:
и — С\п — = — С1п —, г, г
zr = -C[K-(6 + 61)]=-C60J
(5)
где гх и г суть расстояния рассматриваемой частицы жидкости от краев отверстия А и С, а 0О— угол, под которым из точки т видна ширина его 2b.
Выражения (5) показывают, что выше оси XX величина обоих компонентов скорости частицы жидкости изменяется непрерывно во всем пространстве. *
\ Скорость и равна нулю на оси YY и в бесконечности и, наоборот, бесконечно велика на краях отверстия в точках Л и* С.
Скорость v равна нулю в бесконечности и на плоскости стенок, ибо здесь 0о = О.
Наоборот, в плоскости отверстия по всей длине’отрезка АС, где = скорость v постоянна и равна:
' V — —
Но если из ирострамства выше оси XX с положительным у мы перейдем в пространство ниже оси XX. где у стгрицателен, то для точек /п', находящихся между вихревыми слоями А А' и СС в пространстве ///, получим, что 60 = 2к — 0О', а дЛя тб’чёк znr', или в пространстве IV', Оо = 0о', почему ниже оси XX в пространстве III будем иметь скорость
. ^ш= —C(2--^609f - - ; < (6).
9 вне вихревых слоев в пространстве IV « •
C4v = + ^0ог. * (7)
При переходе через вИхревой слой скорость изменяется здесь скачком на—2тгС» ибо
• ^1И — tfIV =— С (2г — 0'о) — С0О'= — 2гС.
Между вихревыми слоями скорость v все время остается отрицательной и с удалением в бесконечность при 0О' =Ю увеличивается в два раза:
- ^Ш,оо — 2гС.
Вне вихревых слоев скорость v положительна и в бесконечности равна нулю, так же как и на нижней поверхности стенки.
1 1 n i
Фиг. 61.
Скорость и остается неизменно непрерывной и во всем пространстве ниже оси XX* Имея выражения скоростей (5), (6) и (7), на основании соотношений (2), мы можем все поле скоростей дать в функции координат частицы жидкости в виде:
V >'+(» — -Ч (8)
п = - С [ к + arete arete
для пространства I фиг. 61;
и, = -С [atclg_^-arctg-i.] для пространства //;
™ =~ 4'~ Иг - arctg ^)] (S')
для пространства ///;
Viv = + С [arctS 7Z7& ~arctg
для пространства IV.
8 А. Я. Мило.нч
Выражения (8) показывают, что скорости v в различных частях пространства являются функциями одной и той же суммы:
«48^=*.
обозначив которую через К, возможно будет все скорости v написать в сокращенном виде:
t'l — — С 4" АГ), ^ш = — С (тс— К), ^iv — -\~CK-j ' '
Функция течения. На основании приведенных выражений скоростей функцию течения жидкости для различных пространств возможно писать в виде:
Для пространства / имеем:
S, = — С^(тс4-К)Лс = — Стсх— C^Kdx.
Но
\ Kdx = i arctg ~z~b d X — \ arctg dx,
где
( arctg dx=(x — 6)arctg — у b 4- £ In Г y’+( x—6)2l, J X ““ U Л U £ л L J
J arc‘s Тира dx =^x+*)arctg*T* ~ 3 6+fln I?’+
Поэтому
jK<fa=(x-t)aree-^-(x+Ha.dg^-|ln>;+^+^.
Подставляя найденное значение последнего интеграла в выражение функции течения, найдем:
51 = — сГкх4-(л — 6) arctg —— (х 4-6) arctg —=т-7 — L X — U X О
_ J’ |пУ+(х + И'1
2 >’ + (х-»)] ',0>
При х = Ь величина Si равна:
Sb = — C(nb — 2b arctg £ — £ ) •
\ £U £ jr J
Для пространства //:
Sji=St> 4~ $ = Sft — C f Kdx.
0 b
Поэтому
5U = -с[кЬ-2Ь arctg — у •" У ут?- +(* — *) arctg —
— (x-}-d) arctg
In
2 ,ny + (x_*)»
2b^ .a ль*
2
Или
Sh = — C | vb 4- (x — b) arctg : — (x + b) arctg L X и
2
Для плоскости стенки при у = 0 5ц равно:
50 = — СкЬ = const,
(12)
показывающее, что токи жидкости, идущие по стенке, суть прямые линии. Постоянное их — СъЬ представляет произведение скорости v истечения а плоскости отверстия на половину его ширины и равно поэтому половине расхода жидкости через отверстие. Вместе с тем выражение (12) дает нам величину постоянного предельного или граничного тока жидкости, вытекающей из отверстия. Для пространства ///:
5Ш= — С j (я — К) dx = — С Г ™ — (к — b) arctg 4-
О L
ИЛИ
$ш = — С |ях — £(х — 6) arctg — (х 4- f>)arctg —
2 nj»4-(x— b)' JJ <13)
При х — Ь
8, = — с(кЬ-^2Ьarctg£4"41П,У i'")’ \ Л у J
Для пространства IV*.
Sjv == 4“ I vdx = Sb 4* С ^Kdx9
поэтому
5iv = — с/ кЬ + 2b arctg Л + f -ln V ~tr')+ \ 4 У J
-f- C (x—b) arctg
- (x + J) ardg - f l°X+<^;+
откуда окончательно получим:
5iv = — С {«* — [ (* — b) arctg — (x 4- b) arctg
У + +
— 2 my-|-(x —0‘JJ’
(14)
Но согласно фиг. 61 сумму членов
(л-- (,) arctg-(X4-» arctg 1
для всех четырех частей пространства возможно представить в виде:
I -(х-г>)в—(х+^в*—^1ц-^=—[(х—^)в+(х+^)о1+ +J'ln7i] = А-
II к(х— Ь)—[(х-6)9(х6)®i4-jln yj =л(х —^)4-^«
III —(х——(х 4-W — у In-£ = 4',
где знаком прим обозначено пространство ниже оси XX.
IV к(х — £)+ А'.
Очевидно, что для точек пространства, симметричных относительно оси XX, значения A = A't почему окончательно выражения функций течения могут быть написаны в виде:
=_с(тгх+Л), Sin=—с(кх-Д), \
5ц = — С(гл + Л), . SIV = — С[^(2Ь — л) — Л],/ 1 '
где
л=—[(х—£)«4Лх4-&)014\у1п71]- (16)
Выражения (15) и (16) позволяют построить без затруднений токи всего поля движения жидкости. Точный чертеж течения дан на фиг. 62. Струя жидкости, вытекающая из отверстия щели, ограничена 116
Фиг. 62.
поверхностью предельного или граничного тока, уравнение которого на основании выражений (15) и (12) напишется в виде:
— С(кх— Л) = — кСЬ,
или
(* + 0Н-(*4-^4\у1п-7 = о. (17)
Это уравнение, как и чертеж течения, показывает, что, уходя в бесконечность, при в = в1 = -^-и — = 1, предельный ток приближается к i г
оси Y7 на расстояние х = —.
Иными словами, в бесконечности ширина вытекающей струй жидкости равна половине ширины отверстия.
Поток, вытекающий из отверстия, уходя в бесконечность в жидкости нижнего бьефа, сжимается в два раза, почему коэфициент ежа* тия в этом случае необходимо считать равным:
а =0,5.
В соответствии с этим скорость движения частиц жидкости в нем непрерывно увеличивается также в два раза, на что уже указывалось выше.
Таким образом развитая здесь нами теория указывает на то, что струя жидкости в случае истечения ее из сосуда бесконечной ширины, т. е. в случае, совершенного сжатия, движется по выходе из отверстия в плоской стенке ускоренным движением, причем ускорение прекращается только в бесконечно большом удалении от плоскости отверстия.
Следовательно, на частицы жидкости подобной струи кроме силы инерции начального движения действует еще и другая сила, под в ли* янием которой скорость их по мере удаления в бесконечность уве* личивается в два раза. Этой силой может быть здесь только сила давления. Откуда следует, что в случае истечения жидкости из отверстия в плоской стенке с совершенным сжатием струи ’ скорость в плоскости отверстия соответствует только части, а не всему напору или разности давлений, вызывающих само движение.
Далее мы ближе исследуем этот вопрос в связи с анализом рас* пределения скоростей и давлений по всей массе жидкости.
Но течение, изображенное на фиг. 62, кроме картины движения жидкости при истечении из отверстия и формы вытекающей струи показывает нам, что струя по выходе из отверстия приводит в движение всю массу жидкости за стенкой. Она подсасывает к себе эту жидкость, заставляет ее протекать через вихревой слой и резко менять здесь направление своего движения тем энергичнее, чем ближе рассматриваемое место к краю отверстия. А так как в бесконечности ширина основной струи равна только половине ширины между вихревыми слоями, а вторая половина занята жидкостью, ею подсосанной и движущейся здесь с той же скоростью, то мы имеем, что масса подсосанной жидкости точно равна массе жидкости основной струи. А о!сюда следует, во-первых, что поверхность основной струи не является в данном случае поверхностью постоянного давления, как то обычно принято предполагать, а во-вторых, что вся энергия основной струи в точности поглощается движением жидкости за стенкой и в ней рассеивается, образуя вихревую дорогу Кармана, одевающую основную струю в случае истечения жидко
сти из отверстий совершенно подобно подсасываемой струе в случае обтекания пластинки или тела.
Все только что изложенное совместно с указанной в § 3 тождественностью коэфициентов истечения из отверстий коэфициентам сопротивления при обтекании приводит к заключению о полной тождественности механизма истечения жидкости из отверстий механизму обтекания ею твердых тел.
Изложенный ниже случай истечения из отверстия потока конечной ширины, который мы можем наблюдать уже на реальном опыте, еще более подтвердит это единство механизма двух явлений, рассматриваемых ныне, как совершенно отличные друг от друга.
Распределение скоростей и давлений. Выражения компонентов скорости частицы (5J, (6) и (7) показывают, что величина полной скорости ее для всего пространства, занятого жидкостью, за исключением пространства между вихревыми слоями может быть дана выражением:
W = 1/ Са^1п^У + С90о’ = С1/ + , (18)
где W—полная скорость частицы.
Для пространства между вихревыми слоями
(19)
Поэтому кривые равной полной скорости будут иметь уравнения:
I) для всего пространства за исключением пространства между вихревыми слоями:
(in £)’ 4- 60»= № = const; (20)
II) для пространства между вихревыми слоями:
(in уУ + (2к — 0о)’ = № = const. (21)
А полная скорость частицы будет равна:
W=ск.
(22)
Имея выражения полной скорости частицы жидкости в каждой точке поля, найдем величину давления в ней помощью уравнения Д. Бернулли. Для всего пространства выше стенки или оси XX будем иметь, что
р 4- р-=- =Н = const,
где р — давление; р — плотность среды; Н— запас энергии.
Поэтому
или
p = H—^-C‘Ki, (23)
£t
где К* для пространства выше стенки дается выражением (20), а ниже ее для частиц вытекающей струи (21). Для жидкости, заполняющей пространство ниже стенки оси XX, исключая основную струю, будем иметь выражение для давления в виде:
р'=Н’ — ^W2=H'—(24) z z
где H'— запас энергии жидкости ниже стенки. Неизвестные постоянные, входящие в уравнения (23) и (24), можем определить Следую* щим образом:
Удаляясь от отверстия в бесконечность в простра аве выше оси XX, получим,
/С=0 и р_роо = //,
почему для всего пространства выше оси XX можем писать, что
Р=Р+*-%сч<\
Но перейдя за стенку по вытекающей струе, мы в бесконечности, где /С = 2тг, получим да’вление в ней равным
Р-* —Р+* — у<^(2^)а. А
Если теперь давление между вихревыми слоями вниз от стенки на бесконечном расстоянии от нее равно р0, т. е.
Р- . = р0, то р+ „=С\2к)а
И
• P=P(A-^{^-Ki). (25)
Поэтому кривые равного давления р== const для пространства выше оси XX и между вихревыми слоями будут даны уравнением
4т? — № = const = h\ (26)
Во всем остальном пространстве ниже оси XX давление р’ будет равно
Р'=Р<Г-^К\ (27)
Для одного и того же значения К разность давлений в пространствах выше и ниже стенки постоянна и равна
Р - Р' =Ро + (4л’ - №)-р0+ = -fac? = 4 , (28)
т. е. равна четырем скоростным напорам от скорости истечения в центре отверстия.
Вне вихревых слоев, ниже стенки, кривые равного давления будут даны уравнением
— № = const. (29)
Фиг. 63 дает точный чертеж расположения поверхностей равного давления во всем пространстве.
Фиг. 63 показывает, что при истечении жидкости из отверстия в стенке бассейна бесконечной ширины изменение давления стацрвится
заметным только вблизи самого . отверстия (кривая равного давления с постоянным 380, тогда как в бесконечности постоянное равно 394).
Но зато от этого места давление по оси вытекающей струи YY начинает быстро падать до кривых с постоянными 220—240, т. е. до расстояния, равного 0,25 ширины отверстия, после чего изменение давления снова замедляется и с расстояния, равного двойной ширине отверстия, струя жидкости движется в бесконечность почти равномерным движением.
В пространстве между вихревыми слоями, равном по ширине отверстию, давление везде положительно и больше давления за стенкой pQ, приближаясь к последнему только в бесконечности.
Поэтому причиной ускоренного движения струи жидкости по выходе ее из отверстия является избыток давления в ней относительно давления в окружающей ее среде.
Фиг. 63 прямо показывает, что наибольшее падение давления происходит у краев отверстия, где оно приобретает характер ямы с почти вертикальными стенками и весьма малым диаметром, что вполне подтверждается данными всех опытов.
На самом краю отверстия, где скорость движения частиц жидкости равна бесконечности, давление равно — оо, т. е. мы всегда получаем здесь разрыв сплошности течения, почему оно и является местом наибольшего всасывания в поток окружающей среды и местом наибольших разрушений всех гидротехнических сооружений.
Расположение и вид кривых равного давления в пространстве ниже стенки, за вихревыми слоями, дают особо наглядную картину этого места наиболее интенсивного подсасывания к себе жидкости за стенкой вытекающей струи.
Теперь для нас становится, наконец, вполне ясным, что как в случае обтекания пластинки безграничным потоком, так и в случае истечения жидкости из отверстий подсасывание жидкости за стенкой производится не стенкой, как мы обычно говорим, а струей у ее схода с края отверстия или пластинки.
Это подсасывание обтекающей или вытекающей струей жидкости окружающей ее среды (безразлично, будет ли жидкость этой среды однородна или неоднородна ей) всегда наблюдается в действительности и, как показывает фиг. 63, имеет свою причину в том, что поверхность обтекающей или вытекающей струи жидкости не является поверхностью равного давления, как то до настоящего времени всегда принималось, следуя предположению Кирхгофа \
Вместе с тем фиг. 63 показывает, что на поверхности вихревых слоев в соответствии со скачком скорости происходит также и скачок давления, причем величина давления повышается.
Основная струя жидкости передает здесь свою энергию жидкости, ею подсасываемой, резко изменяя при этом направление движения последней.
1 О-Kirchhoff .Zur Theoriefreier Flflssigkeitsstrahlea", Crelle's Journla lar reine und angew. Mathematlk, Bd. 70, 1869.
Величина ускорения Пб оси струи. Выражения (5) и (6) скорости частиц жидкости, движущихся вдоль по оси YYt позволяют легко найти и выражения величины ускорения в каждой точке этой оси.
Обозначая ускорение через j\ для положительной части оси YY будем иметь:
Л=$=й<-С’"»-
Но00=«— 2 arctg почему
2С arctg 4 = SC-j-J-r-, • Q .
dt 6 b у’4-6* di
Выше отверстия движение направлено обратно положительному направлению оси YY, т. е.
= —гг = С90,
и потому выше отверстия ускорение равно:
r _ 2С2*
1—%
(30)
где г — расстояние рассматриваемой точки оси YY от края отверстия, а 60 — угол, под которым из нее видна ширина отверстия. Подобно изложенному, для точек оси YY, расположенных ниже плоскости отверстия, будем иметь:
= v = — С (2к — 0'о) = — С (к + 2arctg почему
f —dv— 2С —_________— — (2т: V ) <3 О
dt~ dt~ Г2 ( °'*
Выражения (30) и (31) показывают, что на бесконечно большом расстоянии от плоскости отверстия, г = оо, ускорения и /2 равны нулю, т. е. жидкость остается там или неподвижной или движется равномерно. Ускорение все время остается положительным, но переменно по величине. Оно равно нулю в бесконечности и возрастает с приближением к плоскости отверстия.
Своей максимальной величины оно достигает ниже отверстия, там, где
,. — 2у (к -f- 2arctg — }
= -------Цт-------— = 0
ду г*
или
ir4-2arctg^=y. (32)
Максимальная величина ускорения равна здесь:
_2W У г2 '
Для полной ясности представления всего сказанного об ускорении движения жидкости вдоль по оси струи или оси YY на фиг. 63 дана кривая изменения величины ускорения вдоль оси YY. Рассматривая ее, мы видим, что максимум ускорения лежит ниже плоскости отверстия, хотя и близко к ней (на расстоянии 0,135 ширины отверстия).
Ясно также, что причиной непостоянства величины ускорения или силы, действующей вдоль по вытекающей из отверстия струе жидкости, точно так же, как и причиной сжатия струи является давление на нее токов жидкости, направление которых сильно отклоняется от направления ее оси.
Поэтому рассматриваемый здесь нами случай совершенного сжатия, соответствующий истечению жидкости из бассейна бесконечной ширины, при котором предельный ток лежит в плоскости отверстия и нормален к оси вытекающей струи, даст нам наибольшую величину сжатия, повышения давления и неравномерности движения при истечении из отверстия в плоской стенке. С выходом из отверстия струя начинает подсасывать к себе жидкость за стенкой. Избыток давления в ней, ускоряющий ее движение, начинает расходоваться на приведение в движение этой подсосанной жидкости, иными словами, движущая сила распределяется здесь на большую массу жидкости, почему величина ускорения начинает понижаться.
Полную величину движущей силы мы легко найдем, определив количество движения, сообщаемое в единицу времени безграничной массе жидкости при истечении ее из отверстия в плоской стенке бесконечно широкого бассейна. Но из предыдущего нам известно, что на бесконечно большом расстоянии от отверстия, вне вихревых слоев, скорость движения жидкости везде равна нулю, а между слоями постоянна и равна
Х/-оо = — 2-^-
Поэтому искомое количество движения или сила будет равна:
; м = р • 2b — 2кС — 2*С = р2* (2* С)\ (34)
А так как струя, вытекающая из отверстия, в бесконечном удалении от него имеет ширину, равную половине ширины отверстия, то найденное количество движения делится между струей и подсосанной жидкостью на две равные части.
Таким образом, совершенно подобно тому, как при обтекании пластинки сила давления на нее жидкости равна половине силы давления потока между вихревыми слоями, за ней образующимися, при истечении жидкости из отверстия в тонкой плоской стенке с совершенным сжатием сила давления вытекающей струи равна половине силы давления потока, движущегося между вихревыми слоями.
Наконец, определяя величину потерянной энергии по закону Карно, найдем, что она в обоих случаях равна;
(35)
где v — скорость протекания в плоскости отверстия*
Сопоставляя все сказанное о явлениях обтекания плоской пластинки и протекания через отверстие в ней, увидим полную тождественность механизмов обоих явлений, что и приводит к равенству коэфициенгпа расхода коэфициенту сопротивления, указанному в табл. 1, § 3.
Но рассмотренный здесь случай истечения жидкости из бассейна бесконечной ширины представляет собой случай, не выполнимый в действительности; он интересен нам как случай предельный*
Он с большей рельефностью позволит нам понять далее влияние ограничения ширины бассейна на форму истечения жидкости из отверстия в его стенке*
II. Случай равномерного движения щели
В разделе I мы имели случай истечения жидкости из неподвижной щели, так как согласно выражениям (8) все скорости жидкости в бесконечном удалении от щели везде равны нулю, за исключением пространства между вихревыми слоями.
Но если начало этих слоев само будет двигаться в жидкости параллельно оси YY с постоянной скоростью
Vq = Cut, где t может иметь все положительные значения от нуля до бесконечности, то относительное движение жидкости и вихревых слоев будет таково, как если бы слои оставались неподвижными, а вся окружающая их масса жидкости набегала бы на них паралелльно оси YY с прямо обратной скоростью
— vQ = — Cut. (36)
Очевидно, что искомое здесь движение жидкости мы найдем, прибавив к выражениям компонентов скорости v по оси YY постоянную скорость — Cut, после чего вместо выражений (8) и (9) будем иметь по фиг. 61:
u=_cin^-, vi=-с [к (1+04-к], ] ®к=- С И-{-/<], ( (37)
фш==-С[к(1-Н)-К], viV = — Cfrt-K], )
снова переходящие в выражения (9) при / = 0.
Подобное изменение постоянного скорости Ф поведет к изменению величины первого члена скобок в выражениях функции течения
-(15). Руководствуясь выражениями (10), (И), (13)и(14), легко получим новый вид функций течения:
5, =_С[к(1+/)х + Л] , 5П=-С[к(1 +0х + -4], V
5Ш = — U(к(1 4- t)x — Л], 5IV= — С [26 4-х(t-1)] — А }. ](38)
При / = 0 выражения (38) возвращаются к выражениям (15).
Очевидно, что при / отрицательном, изменяющемся ог нуля до — оо, выражения (37) и (38) дадут нам форму движения жидкости при
движении начала вихревых слоев параллельно отрицательному направлению оси FK Во всех выражениях (37) и (38), как и ранее,
4 = -[(x-6)6 + (x4-d)ei+j 1гЛ].
Случай I, /=1. Если щель будет двигаться по положительному направлению оси YY со скоростью, равной скорости протекания жидкости по YY на плоскости щели, т. е. /=1, мы получим форму
движения жидкости, вызываемую действием на нее пропеллера, движущегося в пространстве со скоростью
^о = -Нс-
Фиг. 64 дает нам картину подобного плоского течения жидкости со скоростью в щели =— 2 к С.
Предельные токи выполнены более толстыми линиями, проходящими через края щели АВ-
Случай II, t = —1. Но если щель будет со скоростью — к С двигаться по отрицательному направлению оси УК, т. е. t = —1, что соответствует набеганию всей массы жидкости из бесконечности со скоростью vQ = к С на заднюю сторону плоскости пропеллера, то в плоскости пропеллера или щели скорость протекания станет равной нулю ^ = 0.
Картина подобного движения пропеллера или щели АВ дана на фиг. 65.
III. Истечение жидкости из отверстия в стенке бесконечно длинного канала (концентрация струи)
Изученный нами случай истечения жидкости из щели в стенке бесконечно широкого бассейна, § 6, I, показал нам, что струя, вытекающая из отверстия, движется ускоренно.
Причину наличия этого ускорения и вызываемого им сжатия струи мы полагали в давлении на нее струек жидкости, сильно отклоненных в начале своего движения от направления, нормального к плоскости отверстия.
Но чтобы доказать с полной ясностью справедливость подобного утверждения, а вместе с тем и возможность получения сколь угодно сильного сжатия струи, исключим влияние нормального подтекания жидкости к плоскости отверстия, введя плоскую непроницаемую для жидкости стенку, ограничивающую высоту бассейна,
С этой целью вместо течения жидкости по схеме фиг. 61 исследуем движение ее при наличии стенки АВ (фиг. 66), параллельной плоскости вихрей или отверстия 00 х и отстоящей от нее на расстоянии а. Мы найдем искомое течение помощью метода зеркальных изображений, удалив стенку АВ. а ее воздействие на форму движения жидкости, заменив действием на все частицы жидкости кроме пары реальных вихрей О и Ои возникающих на краях отверстия 00v еще и их зеркальных изображений в плоскости стенки О’ и О/.
Таким образом каждая произвольно взятая частица в точке т будет подвержена здесь воздействию системы четырех вихрей О, Ov О’, О\, или, что то же, воздействию двух пар вихрей О, Ох и О', О\, удаленных друг от друга на расстояние, равное 2а.
Полагая ширину отверстия равной 2Ь и замечая, что расстояния точки т от краев отверстия и его зеркального изображения равны:
г* 4- (х Ь)\ г12 = (2а — у? + (х — Ь)\
г1а +(Х + W, Г» - (2а - уГ -Их 4- Ь}\
а углы, под которыми из той же точки видно отверстие и его зеркальное изображение, равны 0е и 6е', согласно выражениям (5), получим компоненты скорости частицы в точке т равными:
C!n-> = —С1п г г гг
ti=_cot4-c8<><=-.C(e0.-o0>
Эти выражения показывают, что ка плоскости стенки АВ, где угол 60 всегда равен 0/, г^г/ и г = У, будем иметь
(39)
tf = 0 и а —— 20 In---, г
т. е. стенка АВ остается непроницаемой для жидкости, которая может только скользить по ней со скоростью и. Но в точке М пересечения плоскости стенки с осью ОУ, rt = r и я = 0, почему точка М является точкой нулевой скорости или вмертвой точкой* исследуемого течения жидкости.
Пользуясь общим выражением компонентов скоростей (39), легко написать выражения скорости, параллельной оси УУ, для пространств /, 7/, /// и IV.
Пространство /, между осью ОХ, стенкой АВ и прямыми 0,0/ и ОО'; х<Ь. По фиг. 66 имеем:
6 = arctg ; 0. = arctg ; 0' = arctg ;
ЪЬ- х 1 * Ь±х 6 Ь — х
Поэтому
е0 = Я - (е-I-6,) = К - arctg - arctg ,
»о' = п - (6' + е/) = « - arctg - arctg
и, следовательно,
п =_с [_arclSyz__„ag^_+««K^’+. 4-arctg2^~^l. (40)
V “ф" X J
В пространстве fl, при х>Ъ '
vn— — С (arctg -^-7 —arctg -Д-т—-arctg4-
+ "ctgTT^)' (41)
В пространстве ///, при л-^6, но у отрицательном, угол •ф=2«—в<у, почему
ош = — С [2к — (®о,.1-|-®еИ или
viu — — С ( arctg + arctg _|1 arctg ?£±£
+ arctg2^j~x)'(42)
В пространстве /V, при х>Ъ и у отрицательном
„>.=+c(.rCtgriJ-.Kig-^+«-dg?^:--“*£+») <43)
Имея выражения скорости v для всех частей пространства, возможно найти выражения для них и функции течения.
Функция течения. Для пространства / функция течения Si будет равна:
° о о
, Г л 2а —у . . Г х 2а— у .
+ J arctg ^з^-Лг+larctg dx
о о
Но интегралы, входящие в это выражение/ptfBhwf:
I 3iC^'^-bdx jaretg^-^jAr =(*;—b>arctg—
— yb >n [У + (x - b> ]:
j ™^^bdx = (x+Z>) *ctg7+a^ Tb + i ln{^+
+(х+*)г ;
f . 2a—у . С > 2a-у . , ... 2a— у
J arctgdx = J arctg b — x dx~(x — *)arctg x^lb “
- 4 * + ,n K2e - & -H* “
Z tX
JaKt8'^M’ <йг=(х+*) M(:,BT+> “I "+
+ 1” К2Л - J'i’+(* + *h.
z
Поэтому будем иметь:
X
S\ = — С I {(x — b)arctg-^-T — |н41п;[У1+(х-I Л и л ш
О
-(* । »>«^--4^+4 »-4jft(v’+(x+.»H- " л I - с/х х
- (х- «)a,cig + ' ь _^Zln [(2а +(х- »)>1 +
Л J U Z Z
или
Si=-— С((х —- Л.) arctg —
—!{х 4- J).arctg—— (х — b) arctg +
’ I 2а^У In _(2q-j)a4-(x4-f>y . 2а-у -|
+ 2 (2а— j)2 + (x — by +(x + b.)arctg x^b J.
Вводя вместо арктангенсов соответствующие им углы, то же выражение получим в виде: * ; ,
5, = - С - х) (6 - 6') - {Ь + хДб, - 0/) —Ш 4-
Прй x = b будем иметь:
s“=-c [fln -24 a,cts и +
20-, + M*>=/].
' 2 (2a —y) 1 2b J
В пространстве 11 функция течения равна:
5и=5!,*4-|®и dx = Si.b— с|{ (x — b) arctg у& +
* ь
+ у In [Vs-ь (X — ft)2] — (x+b) arctg ^у4-уй~ у,п 1/4-4- (х 4- *)21 - (X - b) arctg 4-1 b - 1П [(2а - у)’ 4-4- (* - *)*] 4- (X 4- b) arctg ?£=£ - ± b 4- 2-^=±1 п [(2а - j)‘ 4~ 4-(* 4-*)*)}•
Подставив пределы интегрирование и сделав приведение всех чле* нов, окончательно получим;
Л=-с[(.х-'’)агс,ггЬ+4|"7тет^~ ’
—(х 4- &) arctg —(x — b) arctg у 4-
, 2a^-yt (?d— _y)’4~(*4-fe)’ 1 / . .4 2a — vl
+ 2 n ^а—у)*+(х—ьу + (x+&) “с‘е V4=y}
ИЛИ
я, =-с[(*-Ч(в’~ oj + Or+mo,"-»,)-I- 2
+ ?±fZ,“£r]- (45)
В пространстве III, при x<b-
Sm=P„,<ix = -c[jarclS^+Jarcig^e +
+f arc's + J dx].
0 0 1 J
Но интегралы соответственно равны:
J *= = -.) 4л: = (л:-б;агс1е^±^+
+ | I" [(2о +>)’ + (*- »№
! "с,г ттУ ix =(х + 41 а,с1в - ’2 4 +
+ 1» i(2o НО" + (X + »)’!
Поэтому'окончательно будем иметь: *
•Sin = — СI (х b) arctg —jpj + пг,п м» —
I? 1 . bx-\-b 1 2 у 44х— ft)
— (.х — b) arctg 4- (х 4- b) arctg 4- ’
। ^±У in (2±±jO2 +(*4-6)2 _(х _ м arct„ 2о±2 I + 2 1 (2а+_у)а4-(х—d)a > C g х — ft Г
Или, заменяя арктангенсы углами, получим:
sm = -c[(x4-d)(o14-e1')4-jin^-4-(x-6)0-e')4-
442а 4-,v)ln р ] . (46)
В пространстве /И, при х>Ь, получим:
5IV ^iv
ь Но при х = Ъ S\\\tb равно:
=
— c\2b arctg 4" £ |п> + 2ft arc‘g^£
4&С/
2а
Поэтому будем иметь:
Siv= 5ш.» 4- с {(* — ft) afctg -^-т—ft 4- тг1п Ь*’ 4-О
+ (X - ft)3] - (X 4- ft) arctg ^-b 4- b - f in[У 4- (X 4- ft)’) -"
4- (X - ft) arctg - V ft + in [(2« 4-J)’ + (X - ft)’] -
- ;x J- ft) arctg 4- у ft “ »n «2а ]-jr)« 4~ (x 4- ft)’l )
или окончательно
S,v = + C[(x-
- (* + &) arctg (* — b) arctg 4-
2а+j (2a4-^)l4-(x-^'( , ^ За+^1
Нводя углы, получим:
5IV= - с £(х - ь) (0'4- в- 2к) 4- (к 4- эде/4-Л) 4-у ш £+ 4-(2a4-j)ln^]. (47) выражения (44), (45), (46) и (47) позволяют построить всю систему токов жидкости исследуемого течения* точный чертеж которого дан на фиг. 67.
Уравнение предельного тока и коэфициент сжатия струи. Течение фиг. 67 показывает нам, что оно ограничено ч: одной стороны Стенкой АВ и осью YY, вдоль которых постоянное тока везде равно нулю. Этот ток проходит через точку нулевой скорости Af. С другой стороны вытекающая из отверстия DJ струя ограничена током, проходящим через точку края отверстия.
Этот предельный ток дает нам как контур вытекающей струи DE, JK9 так и контур второй стенки канала DC и JF.
Постоянное этого предельного тока найдем, подставив в выражения (46) или (47) все величины для точки края отверстия D или J, т. е.
J = O; х = £; Ох = 0; 0 = у4 0/=у-; / = 21;г\ = 2 у7 а®
Тогда получим:
Sin,/ = Siv,/ = -с[гд0\,о4-2a in jZа-у*]
Подставив это значение постоянного в выражение (46), получим уравнение । раничного тока вытекающей из отверстия струя жидкости в виде:
- с [2^,0 4- 2a In р/ = - С [(X 4- Ь) (0\ - вх) -f-
+(Х-Ч (О' 4- 0) 4-У toy 4- (2 а 4- _у)1п .
Или окончательно уравнение предельного тока струи будет иметь выражение:
(X 4- Ь) (0\ 4- 0Х) 4- (X - Ь) (0’ 4- 0) 4->1п4- (2a 4->о»п =
= 2Ь О'ьо 4- 2a in 1/ . (48)
г **
где Г1Л = arctg •£. ,
В бесконечности будем иметь:
I in'j- = ш J = o; = о, = е»=е = г г9 1 1 2
и; уравнение (48) приводит к равенству:
1 г а , 1 ZoM-V 1
хоо =— ftarctg — 4-a in I/-------Ч—, (49)
к L о I Л" J
дающему величину расстояния предельного тока от оси YY в беско-нечно'большом удалении от плоскости отверстия. 'Поэтому коэфи-циент сжатия струи получим равным:
' Хоо 1 Г а а / , / ft \2 я
т = —=-[aIdgy + y|nj/l + (-) ]_• (SO) Течение жидкости фиг. 67 построено в предположении а = &, почему в этом случае получим коэфициент сжатия струи равным:
<p = l^ + ln^-2 j = 0,36.
Формула (50) дает величину сжатия струи в функции отношения -у , что для различной величины этого отношения от нуля до бесконечности приводит к изменению коэфициента сжатия по приводимой ниже таблице от нуля до 0?50.
ТАБЛИЦА 2
а ~Ь 0 0,01 0,10 0,20 1,00 2,00 1 00 1
<Р 0 0,02 0,10 0,16 0,36 0.42 0,50
Данные таблицы показывают, что, увеличивая размер Ь по сравнению с а, можно достигнуть сколь угодно большого сжатия вытекающей из отверстия струи жидкости. А так #ак увеличение сжатия струи приводит, как то ясно из изложенного ниже, к увеличению ускорения движения массы жидкости струи при удалении от отверстия, т. е. к увеличению движущей частицы жидкости силы, то увеличение сжатия струи необходимо приводит к большей устойчивости самой струи при движении ее в той же или иной жидкости.
На сказанное необходимо обратить внимание для правильной конструкции фонтанных или пожарных струй, где высота подъема струи или дальность ее боя имеют столь большое значение. Приравнивая постоянное предельного тока выражению (47), получим уравнение контура стенки в виде:
(* + *) (e’^ej-Hx-bxo'+o-a^+jin £- +
К а 1 / а2 -|-6’
+ (2<i4-^)ln- =26arctg — 4-2л 1п|/ —. (51)
Распределение скоростей и давлений. Выше мы видели, что слагающие скорости частицы по осям коорДиНат равны:
Vj = Vn — t'in — — С (Оо — О'о ), tfjv = -|“ С (0о — 6Г$ ).
Поэтому полную скорость частицы жидкости можно представить одной формулой:
IF= = С (in + (0о - 60')3 = СК, (52> где
К= j/(ln^T + (e»“eo')a- (53>
Поверхности равной полной скорости будут даны уравнением:
К= const. (54}
В точке М при х = 0 и у = а будем иметь К = 0 и 117 = 0.
В струе при бесконечном удалении от плоскости отверстия имеем:
Г • Г I
8в = 2к; 6о' = 0; In 1-J- = 0 и /С=2гс.
9 0 r-f
В бесконечности скорость движения струи равна:
1Гоо = 2кС.
А так как в бесконечности ширина струи
I = 2хоо — 2<fb,
где ср— коэфициент сжатия, то расход потока Q будет равен: ' ш Q = <f-2b-2nC. (55)
Последнее выражение дает величину постоянной течения С равной:
Зная* величину коэфициента сжатия ср и ширину отверстия 26, найдем для данного расхода Q величину С и по выражению (52) скорость в каждой точке пространства.
Обращаясь теперь к, распределению давлений, мы для канала и струи, а также для всего пространства между вихревыми слоями будем иметь:
ГР р+?— = Н = const л
Л1ЛИ
Для всего остального пространства
, р' = Н' —
Полные запасы энергии Н и Н’ можем найти следуют^ образом» •В точке нулевой скорости М с координатами х = 0 и j/=±a имеем UZ = O, почему давление в ней рм равно полному запасу энергии жидкости в канале Я, т. е. # ✓
Рм = Н.
У
Следовательно, давление во всем пространстве кдндла и струи равно;
м
На бесконечном расстоянии от отверстия скорость в схруе равна, 4<ак мы видели, 2кС, и если давление там обозначим через р^ то
Р - со = Ро = Рм — ~ (2кС)* £г
ИЛИ
Лн=А) + у(21гС)’. А
Поэтому
P=Po + -|-K2«C)1-IF«1
Ж л и
Р=Р^^-^-К'\ ' ' (57)
А о
W.
Вне канала и пространства между вихревыми слоями давление // равно:
р'^Ръ-^К\ <58)
А
откуда ясно, что р§ есть давление в окружающей канал жидкости. Разность давлений по обеим сторонам стенки канала
есть величина постоянная.
138
Поверхности, равного давления,. канале и пространств* между вихревыми слоями будут даны уравнением:
4гс*—fC = const. (59)
Во всем остальном пространстве уравнением:
— № = const. (60)
На фиг. 67 даны эти поверхности равного давления; Их взаимное расположение с полной ясностью дает картину распределения давления во всем пространстве.
Подобно случаю истечения из отверстия в плоской стенке (фиг. 62) на фиг. 67 мы видим быстрое и сильное понижение давления только вблизи плоскости самого отверстия и особенно у его краев. Ясна неравномерность давления в струе и непостоянство его величины по ее поверхности.
Результатом последнего является всасывание ею и увлечение за собой жидкости, наполняющей пространство, в котором она движется. Подсасывающее действие особенно интенсивно у края отверстия.
Ускорение ПО оси струи. Быстрое изменение давления в жидкости у отверстия порождает силу, действующую на вытекающую из отверстия струю. Ускорение этой силы по оси струи получим следующим образом:
По выражению (40) скорость движения частиц по оси OY выше плоскости отверстия равна:
Vi = — С 2 arctg у 4-2 arctg ,
поэтому ускорение / по той же оси будет равно:
/— dv — 9Г ( Ь I Ь _ \ ЛУ
J~ dt + *’ ^4-^7 dt ’
|| = - Vi = 4- С (2 arctg 4- 2 arctg 2Д^ = С(90 —
следовательно,
J=2C'b(± 4-^(60-вД (61)
Ниже плоскости отверстия, на отрицательной части оси ОУ, ускорение* можно представить тем же выражением при условии, что угол 0о будет внешним углом, под которым из данной точки оси видна ширина отверстия. Выражение (61) показывает, что ускорение остается всегда положительным. В точке 7И, где ea = 0of, оно равно нулю и быстро возрастает с приближением к плоскости отверстия. Максимум находится ниже плоскости отверстия. Далее величина ускорения начинает медленно. уменьшаться и в бесконечности, где ®0 = 2к, = 0; r = r, = oot
стремится к нулю.
На фиг. 67 дана кривая ускорения в том же масштабе, как и на фиг. 63.
Сличение обеих кривых между собой показывает их почти полное тождество, несмотря на отсутствие во втором случае токов, нормальных к плоскости отверстия, что и подтверждает справедливость мысли о причине наличия ускорения от действия токов, параллельных плоскости отверстия.
Отличие состоит только в том, что при истечении из отверстия в стенке бесконечно широкого и длинного бассейна абсолютная величина максимума немного больше «‘течения из бассейна конечной длины. Наоборот, уменьшение ускорения с удалением от отверстия во втором случае происходит медленнее, чем в первом.
Сказанное видно и из сличения выражений ускорения (31) и (61). Но если ускорение при увеличении сжатия струи падает медленнее, то сильно сжатая струя, находясь под действием более постоянной силы, должна быть и более устойчива в своем движении в пустоте или жидкости меньшего удельного веса, ибо увеличение сжатия повышает и всасывающую способность струи.
Полная величина давления потока, определяемая по количеству движения жидкости между вихревыми слоями в бесконечности, равна, как и в первом случае:
/И = р-2д-(2тгС)2.
Но теперь мы имеем коэфициент сжатия ср '=0,36 вместо прежнего ср = 0,50. Влияние величины сжатия станет ясно, если давление жидкости в бесконечности выразить в функции коэфициента сжатия, подставив в выражение давления величину
по выражению (18). Тогда ^рлучим: л,=₽^- «*>
Для одного и того же расхода Q и ширины отверстия 2b, но разных ср, будем иметь:
Qa Оа
^ = Рср22^ И ср'2 • 2d
поэтому Af /ср\* Af \<Р7
или (63)
Так при ср = 0,50 и ^' = 0,36 получим: М' = (1,96 со 2) М.
Увеличение сжатия увеличивает давление потока в бесконечности. Но при ср = 0,36 площадь подсосанной струи равна 0,64*26, т. е. струя подсасывает энергичнее, чем прежде, и ее разрушительное действие увеличивается.
Фотография фиг. 68 показывает, как близко изложенная теория соответствует результатам непосредственного’ опыта. На ней видна картина истечения из отверстия в боковой стенке прямого канала при встрече двух потоков. Ясно видны как форма вытекающей струи, так и резкое изменение направления движения струй подсасываемой жидкости
Фиг. 68.
на линии, вихревых поверхностей. Снимок, сделан аспирантом Жулене-вым в Гидравлической лаборатории Института инженеров водного хозяйства в Москве. ж
IV. Истечение жидкости из щели в стенке бассейна конечной ширины
Для решения поставленного здесь вопроса вернемся снова к началу настоящего параграфа и исследуем до конца явление набегания потока безграничной ширины на систему двух пластинок конечной ширины 2а по фиг. 60. ш
Поле скоростей. Скорость и. Принимая во внимание выражения (1), (2) и (4), будем иметь, что скорость и, параллельная плоскости пластинок или оси XX, непрерывна во всем поле и равна;
Она равна нулю в точках пространства, для которых
Ri.L-i
Г\ /г"1’
'Очевидно, ч-о равенство :(ЗД) .удов ЛСТворяетсйдля Всех точек оси УУ, для которых мы имеем:
— Р и т, — г,
почищу я в ^рассматриваемом случае ось YY останется -осью -симме-Ифии всего течения. Но кроме оси ГГ, скорость и = 0 ив других точках, найти которые мы сможем, решая уравнение:
7?/=/?^ или = Т?^!2
или, наконец,
Цу2 4Ч2а + * + х)2] • (-Н& — Х)21=
-[^ -К2а + b - х)2] • [у* +(Ь 4- х)Н.
Но последнее .равенство по раскрытии скобок н приведении членов дает 'равенство:
x24-jr«=(2a4-i).^ (65)
представляющее уравнение окружности с центром« начале координат и радиусом
(66)
Построение Этой окружности легко выполняется следующим графическим спос(йк)м:
На прямой ВС == 2а 2Ь, как на диаметре, строим пунктирную
полуокружность и находим точку пересечения ее п осъю YY.
Тогда Ол = р = |/ (2a-f-^)-d и окружность с центром в О и радиусом On будет искомой. Во всех точках этой окружности скорость и = 0, почему токи жидкости при пересечении с нёй будут иметь направления, параллельные оси YY. «
Пересечение ее с плоскостью пластинок дает нам две точки О9, ' в которых не только скорость и, но также и скоростью равна нулю, т. е. точки О9 являются точками нулевой полной скорости частиц или иначе мертвыми точками или точками раздела течения,
С другой стороны, струя жидкости, протекающая через щель между пластинками, в месте своего пересечения с этой окружностью будет состоять из токов, параллельных оси YY и между собой.
Здесь сжатие струи прекратится и за окружностью струя начнет расширяться. Таким образом окружность н = 0 дает нам не только точки раздела течения, но и границу или место наибольшего сжатия струи.
Из сказанного видно, что при конечной ширине бассейна струя жидкости, вытекающая из отверстия в плоской стенке, испытывает максимальное сжатие на конечном расстоянии от центра отверстия, равном р.
В соответствии со всеми выясненьями свойствами окружности и = 0 в дальнейшем мы будем называть ее .окружностью максимального сжатия*.
При переходе через эту окружность знак или направление скорости и меняется на прямо обратный.
С к<ор^с тъ Д лч! про с тр а н с т в а I, выше осн XX при скорость V равна:
01=-c|«-x»4-«j)=c(—с.+».+Л+М)=-с[«+
+«*;£5- "с'е;ф-“с|ег-(н-*.) + +*di!7+0+U' (в7>
Для пространства Я, выше осн XX при х>Ь\
** = -cfardg —£р^+
+ ^ГН6 + 2а)1 <“>
Для пространства 7/7, выше оси XX, x>b-f~2a:
«™ = - С [а + ardg - «cig - «dg +
+1К*;?+(£рй)]- <69>
Дяя пространства ниже оси XX, где у отрицателен, будем «меть:
+»мг<+(а+2а)]' <™>
= + С ["с*8 A~‘gtg^+t^i,,dex-(/,+ 2a) + +”ct8^+(H-2aJ: (71>
,и=_ С[. _ (aKlg _2_ _ ,rclg _ a„tg +
+ »dSx+(t + 2a)]- <72>
Выражения скорости v в различных пространствах по выражеАиям (67)—(Т2) показывают, что все они являются функциями одной и той же величины:
I = arctg - «dg - »^,_(/+2а) +
+ ис,«4+(42«)-
поэтому все эти скорости, подобно выражениям- (9), могут представлены выражениями: >г
т,1=-С(к+/), f и — — С/,
f ш = — с (к 4" О»
viv = — С (тс — /), f V —- “Ь С1,' f VI = — с (тс — /).
быть
(73)
Или вводя угол 60 = (аа-}~?а) — к> откуда
«а “Ь Ра — к + %. * f
получим, что выше оси XX скорость v равна: •
V=-C(0o4-a1 + pi). Л. (74)
Ниже оси XX, между вихревыми слоями, в пространстве IV'.
fiv = — С[2я — (60 + а1 + Р1)]- (7S)
Ниже оси XX под пластинкой скорость
fv = + C(0o + «i + P.) (*)
и, наконец, в пространстве VI имеем:
*vi = - С [2тс - (60 + a, + pJJ. (77)
Выражения (74) —(77) показывают, что в бесконечней удалении от пластинок, когда 0о = 0, а углы 04 = пе выражениям (74), (75)
я (77) будем иметь:
V±oo = — С ТС.
А для пространства V по (76):
—СО --С тс.
На плоскости оси XX, между пластинками, на прямой ДСуглы ^ = р1 = 0, а О0 = тс, почему скорость v здесь постоянна и равна:
V — — Стс.
За пластинками 0о = О и один из углов 04 или равен нулю, а другой равен к, почему здесь
v = — Стс.
' Наконец, на плоскости пластинки 0o = a1»pi = O и v = 0.
Имея теперь все поле скоростей, можем перейти к получению уравнений токов и построению всего течения жидкости.
Функция течения. Для пространства /, выше оси XX, функ* имя течения Si согласно (73) будет равна:
•Si = j v\ dx = — С ( (тс0dx — — С тс л: — С С Idx. о 5 а
НО
\ldx =j.rclg ^-bix -jardg ^dx -jardg-^^.rfx +
А интегралы, входящие в это выражение, разны:
1 arctg 1Г~Ь ах = (х — b)arctg b 4- ~ In [у’ + (х — ft)9];
f arctff7+3rfx~^+^arctgr+4?~¥Z' +2^1п ^’ + <х + ^: j а"'г ^й^га) Л='х-<4+2“Иа'с,«^=(Щ5) - ? (*+2‘” + +fi" {’’’ + Iх- (4+2“>l’).-
f ardB?HH^)‘fa“[J'+|i+2“>1"c'g^4fe_^<S + 2a) +
Поэтому:
px=(x-4)ardg -J-b - (x + 4) arctg - £ 1»^^ -
_(л: _ 4_2a),rdg—J^ +(X + 4 + 2a) arclgj-j-^pj-f
J ,„У+(х + 4 + 2а)> 2 Ли’+(«—b—2a)9*
(78)
Принимая во внимание выражение (78), функцию течения Si получим в виде:
St = — Спх — СН.г — Z>)arctg
^-(x + 4)arctg^
4’,пУ + (х + 4У 2 *П J9 + (x — b)2
-(x-4-2r.)ardgA,_-B_2|i-t
+ (x + 4 + 2r.)ardg-.+ x+2<|
/+(х+4+2а)»
JZ94-(X— b—2a)9
• (79)
При x = b
^1,»= ——26afctg^——
2airctg^+
+^+»‘rc4i^FF)
Для пространства// функция течения напишется в виде:
•$п*= S&
,» — С \ Idx.
Или подставляя выражения обоих членов в виде:
•$п = - с — 2Ь arctglnJ +/- —:
+ 2(о + Ь) arctg In
— с/(х — ^)arctg ~—г— (*-W) 7
I Л ' и л
2а
1'"
- (х - 6 - 2а) ^х_6_2я Н
У I у /+(х+^+2д)~
+2darctgi + -ln^_ + 2aarctg^-
-2(а + М arctg- - Z.in^±*^±^ 1 + D) arclg 2(a 4- b) 2 у 4.4aJ
что по приведении дает для 5ц выражение:
5п= — С|яЬ + (х — b) arctg
_»_2а)а1с,я_ v +
2 У4~(х — by 4 ' 6 х — Ь — 2а~
Г * 4- 2а\arctr У । -У 1п -У84-(^ + ^4-2а)«\
lX4-* + 2 ) fcX4-*4_2a+ 2 У4-(х—й—2a)’J При х = ^4-2а функция 5ц получает значение:
•Sb,»+ 2в= — с < nb 4- 2а arctg — 2 (а 4- b) arctg — I * [fl -f- и)
v <»а -L 4 (л -L- h\* ,v
<-2(* + 2‘,),к|»2(42аН
-fn
1 2
Для пространства /// получим:
•Siu = Sir, b + 2e 4” j “Odx = $ц, b + ta
Или подставляя значения всех величин:
У
-<-1п
Sin = — С | arctg — 2 (а Ц- ft) arctg
^2(4 + 2o).rtlg27R;^)T ’ —C{rtx4-(x—4)arctg-^j
— (х + b) arctg Пг\Т/
Ч Т ) sX-j-3 2 у3^-(Х—1>)2
_ (x _ b _ a,) arctg _JL_ 4. (x 4.4 4- 2а) arctg +
4- % In \ a я (4 4“ 2а) — 2а arctg 4-
1 2 _у’ + (х — ft — 2а)2 6 2а 1
что по сокращении приводит к выражению:
Sm = — C|ir(x — 2а)-)-(х— ft) arctg *
— (х 4-ft) arctg —
У ьУ9+(*+*У 2 У + (х—б)2
-(x-ft-2a)arCtg—£—
+ {х + й +2д) arctg
У [n^ + (x + ft + 2g)al
2 У + (х —ft—2а)а /’
(81)
Аналогично изложенному для пространства ниже оси будем иметь В пространстве /И:
х а
Siv =У vdx — — С\ (л—/) dx,
или
SjV = — С — (x — b) arctg -j~-b + (* + ft) arctg +
+f +^-*-М«ЯКх-4--2а~
— (X 4- 4 4- 2а) arctg —Inуср(х - 4^2а)5}' (82)
При к = b:
Syv, ь — — С nb 4- 2b arctg ~ 4" *n ^~y»
+ 2<-«ctg£-2(a + 6),rctg^^!-?)—In >1 + *^±га,|.
В пространстве V
Sy — S\ v,»4* =•Siv.b 4“ Idx,
ь b
или
5V = — С
—2(аb) arctg =‘У- . —ln-У
' 1 7 2 (а 4-д) 2 j’4-4a
~£__(x4-b)arctg
2 1П^+(Х-*)’
_ (х _ ь - 2а) arctg —+(х + »+ 2а)arctg
, у 1п-Уа + <х+/’ + 2а)’ I у I У 1П-У4 + 4*’ I
+ ¥'”Z+^-»-2»)’ + 2Sa,ctgS+T1п +
-|- 2а arclg -— 2(а ~ й) arctg ? — - In * I,
2а 1 в2(а4-д) 2 У4-4а» [’
что по сокращении дает
Sy = — C —[jx — b) arctg-—-^—(x 4- £)arctg —
“ f'" y+(xi*)’ - (Л - 4 - 2“) тЧ х-й—2a+ + lx + i + 2a^^s+|ln/^ + ^^]}. <33)
При x — b-\-2a получим:
5v.*+2aC^kb-^2narctg — 2(a4-6)arctg^(^b)~
-|'"^Ш^+^+М.«|в2-^:+ +zi„.!ay°q}.
ч48
В пространстве VI'
5vi = ~ /) *d
Ъ+2а
что приводит к выражению:
Svi= — b — ^2а arctg — 2(а 4- b) arctg —
- f1"J,’t’ + 4t',), + 2(t + 2a)ari:lg2(t+^j +
-[(х - 4)a,ctg _2_ - (х + 4) arctg -
-(х-Ь- 2а)arctg + (х + 4 + 2<r)arctg ~^_р^4
+ -ПЛ ~1~ /Х qgL — 2а arct£ ~ + 2(а 4~ &) “Cte о?' j_ /л +
2 >’ + (* — Ъ — 2а)’ 2а &2(а4-/>)'
I Z ь£±^£±*1’ _ 2(Л 4- 2a)arcta У -
+ 2 У4-4а« l+ ' g2(d4-2a)
_ У. |пУ + <(^4-2а)31 )
2 У3 I/
или, по приведении, к выражению:
SVi = — С / к (х — 2а) — ^(х- d)arctg^-g—(х 4- b) ar cig
^1п.Уа + (х4-»)8 2 ,ПУ+(*-*)’
-(Х-4-2П) arctg х_^_2а
+ (*4-b + 2а)arctg
Л " Г U ХС4
У_
2
>»4-(х+^4-2ау-|у у’4-(х-д4-2а)«]]
.(84)
Полагая
= (X - 4) arctg ^-ь - (х + 4) arctg 1 -
- (X-4-2«) >'Cter^KZ2j + (x + b + 2<,)“c®i + ^p2S +
2 -У34~(* — Ь — 2а)’ ’
получим выражение t через углы ар §1, а,, 0, и расстояния частицы до краев пластинок /?, /?„ г, г.
для пространств / и /V: D г t = — 2*х+(х—ft)а,-И*+ *)?*+-У I» + <**"* -2а) «44.
-4* (х 4” Ь + 2а) ри для пространств /7 и V: 7=-«(x + t) + (x-.^)«. + (x4.fr)p14-jrln^+
4- (х — Ь — 2а) а, 4- (х b -f- 2а) &,
для пространств П1 и V7:
* = — 2к (х — а)4-(х — Ь) «, + (х + ^)?24-^1п ^4-“{" («^ — Ь — 2л) ocj (х b -|“ 2л) Р|
Назвав сумму членов этих выражений, кроме первых через р, т. е. положив
р = (х — Ь) а2 + (* 4-*)?» + (* — Ь — 2а) «14-(л4-^4-2а)р14-
4-У In (85)
получим: Для пространств I и IV: t = — 2кх-\-р.
Для пространств II и V: 7 = —я(х4-^)4-а Для пространств III и VI'. t=z — 2к(х — а)-\-р. Пользуясь последними выражениями функции t, возможно написать выражения функции течения в различных частях пространства в виде: $1 = 5ц = = С (к х —р), S4 = — С [я (х 4- 2Ь) —р], )
Svf = — C(3nx— р), Syn = — С[я(3х — 4а)— р],) v$0'
где для различных точек пространства р вычисляется по формуле (85). В пространствах /7 и V* для плоскости пластинок будем иметь
®1 = ?i = х2 — °> = п> У = °-
почему здесь /> = к(х 4"^)> а величины 5H=SV= — кСЬ, (87)
т. е. предельный ток идет по пластинке и постоянная его равна расходу через половину ширины щели, как то и должно быть. 150
Уравнения Предельного тока. Постоянная предельного тока по (87) равна — пСЬ, а значение р в бесконечном расстоянии от плоскости
Л Л я /?.г
пластинок, т. е. при а1 = аа = р1 = р3 = ~ и ^- = 1, равно
2 /V 1
Роо = 2 ?-х.
Поэтому выше оси XX уравнение предельного тока получим в виде:
P — t.{x,-\-V). (88)
Уходя в бесконечность, этот ток приближается к оси YY на расстояние х = Ь, т. е. в бесконечном расстоянии от пластинки ширина потока, проходящего через щель, в точности равна ширине щели.
Ниже оси XX для пространства IV уравнение предельного тока напишется как
р = к(3х — Ь\ (89)
что для бесконечности снова дает х — Ъ. т. е. по проходе через щель поток расширяется в бесконечности до ширины щели.
Изложенное дает нам полную картину явления протекания потока жидкости через отверстие в стенке бассейна конечной ширины и рациональное объяснение наблюдаемой в этих случаях малой устойчивости струй.
Для пространства VI уравнение предельного тока примет вид:
р = я(3х— 4а — Ь) (90)
и в бесконечности даст
х = 4а-\-Ь.
Ио абсцисса края пластинки В или D
х^ b 2а, почему предельный ток, удаляясь в бесконечность, отступит от края пластинки на расстояние
х —х' = 2а, как то мы имели уже в § 4 для предельного тока, обтекающего одну пластинку.
Точный чертеж исследованного течения дан на фиг. 69.
Предельные токи играют здесь роль боковых стенок, ограничивающих ширину бассейна. Это ограничение ширины сказывается на уменьшении сжатия протекающей через щель струи жидкости, приближении места наибольшего сжатия к плоскости щели и уменьшении величины ускорения вытекающей струи. Сжатие и ускорение струи исчезают при сближении боковых стенок до расстояния, равного ширине щели, т. е. при истечении из конца прямого канала.
Ускорение Движения струи ио оси YY. Скорость частиц жидкости о оси гК согласно выражениям (67) и (70) равна:
Vi = — С (тг - 26) = — С [к - 2 (arctg — arctg .
i?jV= — С (к -f- 26) = — С [it -J-2 (arctg у— arctg ^_р2а)] •
Поэтому выше оси XX ускорение j\ будет равно:
. _ dv\ __9ГГ ь____________b-j-2a I 4У
Jl~ dt ~i 1у4-*» У4-(^4-2л)».1 <й *
Но
dt ~
— С [к — 29], почему будем иметь
(91)
Аналогично сказанному ниже оси XX ускорение /1V получим равным;
^=+2^[34^-?т(Шф]|’+2в)- (92)
Угол 6 между радиусами-векторами Rar всегда меньше прямого и к > 2б, следовательно, окончательный знак ускорения обусловливается, знаком разности величин, стоящих в первых скобках выражений (91) и (92).
Ускорение равно нулю, когда
b _ Ь-±2а
у1 b1 “*/+ (/> 4- 2а)1
или когда
или к >гда
y = ±l/(2a-j-b)‘b.
(93)
Но по выражению (66) последняя величина у равна р радиусу окружности максимального сжатия.
Таким образом ускорение равно нулю в точках пересечения окружности максимального сжатия с осью YY.
Оно отрицательно выше и ниже этой окружности и положительно только внутри нее (фиг. 69).
Последнее обстоятельство бросает яркий свет на всю область учения об истечении жидкости из отверстий в стенках сосудов. Так, из выражения (93) следует, что положение места наибольшего сжатия зависит от положения по отношению к краям отверстия боковых стенок, ограничивающих ширину бассейна, или от величины ширины пластинок 2а по отношению к ширине отверстия 2Ь. При 2а = О, что соответствует истечению из конца прямолинейного канала или трубы,
у=ь,
*69 ЧИФ
т. е. расширение вытекающей струи начинается с расстояния, равного половине ширины отверстия.
С увеличением 2а до бесконечности у также увеличивается до бесконечности и место максимального сжатия и начала расширения струи уходит в бесконечность.
Коэфициент сжатия изменяется при этом от единицы до 0,5, как то мы видели выше.
В соответствии с изложенным величина ускорения при выходе
струи из отверстия изменяется согласно выражению (91) от нуля при 2а = 0 до
2<?S*a
о
при 2а = оо [выражение (30)]
Иными словами, наличие и величина ускорения при истечении жидкости из отверстий в стенках сосудов прямо и непосредственно связаны с величиной сжатия вытекающей струи, т. е. с воздействием на нее токов жидкости, сильно отклоненных вначале от направления вытекающей струи.
Присоединяя сюда наш анализ величины коэфициента сжатия для случая истечения жидкости из отверстия в боковой стенке канала ограниченной ширины, увидим, что все здесь нами изложенное охватывает все возможные величины сжатия струи от единицы до нуля.
А последнее впервые в истории развития гидравлики дает ей ясную и рациональную основу для развития учения об устойчивости струй, столь важное по своим непосредственным практическим приложениям.
Распределение и величина давления потока жидкости на систему двух пластинок с щелью между ними. Подобно тому как в § 5 мы находили распределение и величину силы давления потока жидкости на одну изолированную плоскую пластинку, возможно найти распределение и величину силы давления потока жидкости на систему из двух параллельных, плоских пластинок следующим образом.
Скорость жидкости вдоль по плоскости пластинок равна:
и л
-с in + + —
(2а4-^ — х)(х + Ь)'
(94)
В бесконечном расстоянии от них она равна:
г’0~ — г.С,
Поэтому давление р потока жидкости на переднюю сторо .у каждой пластинки равно:
2
“лл*
(95)
млн
1___L Fin (2д4-^+*) (* —£)1а
Р _ЗГ2 L (2a-f-6 — х)(х-г £)J
Давление р' с обратной стороны пластинки равно:
Р'^Рп — Р
или
/—А>
Л/
1 Г1п (2а + &4-х)(х-^)Т) к* L (2а + & — х)(х-\-Ь)\ )’
(96)
где pQ—давление в бесконечности и все давления отнесены к скоростному напору набегающего потока.
Фиг. 70 дает точную картину распределения давления вдоль по пластинкам, с обеих сторон их, согласно выражениям (95) и (96). Она показывает, что в случае системы двух пластинок максимум давления смещается от середины пластинки к краю щели между ними. Величина этого смещения я равна:
е = а + Ь — р = а + Ь — /(2а+ 6).6. (97)
При а = 0 е — 0. С увеличением а увеличивается и е до бесконеч-* ности. Распределение давлений при системе двух пластинок дано на фиг. 70 сплошными кривыми. Пунктирные кривые дают распределение давлений при одной изолированной пластинке.
Относительное расположение обеих систем кривых показывает, что приближение второй пластинки к первой вызывает увеличение положительных давлений на край пластинки, близкий к щели между ними,
и уменьшение давлений на противоположном крае и, наоборот, вызывает уменьшение отрицательных давлений у щели и увеличение их вдали от нее.
Но все эти изменения в распределении давлений не изменяют величины силы давления потока на каждую пластинку, ибо согласно выражениям (95) и (96) разность давлений с двух противоположных сторон пластинки при одном и том же х равна:
—- =2 ил» Р—P' = pv0*, (98)
2'К'С2
т. е. равна количеству движения потока жидкости, набегающего на каждую пластинку.
Неизменной остается также и величина потери энергии потока жидкости, обтекающего систему пластинок, так как для каждой пластинки она снова равна:
Л = р = 4р Ц = 2pv0’, (99)
т. е. удвоенному количеству движения набегающей на пластинку массы жидкости.
Этот принципиально важный результат выполненного анализа показывает, что;
а) полная, нормальная сила давления потока жидкости на плоскую решетку равна сумме сил давления его на отдельные ее пластинки, взятые изолированно-,
Ь) потеря энергии потока, нормально протекающего плоскую решетку, равна сумме потерь, вызываемых в нем обтеканием отдельных пластинок ее, взятых изолированно.
Последнее дает ясную и простую основу для подсчета как величины давления потока жидкости на плоскую решетку, так и потери его энергии при протекании решетки.
ОТДЕЛ V
ТЕОРИЯ КОСОГО ОБТЕКАНИЯ ПЛОСКОЙ ПЛАСТИНКИ
§ 7. КОСОЕ НАБЕГАНИЕ ПОТОКА ЖИДКОСТИ НА ПЛОСКУЮ ПЛАСТИНКУ БЕСКОНЕЧНОЙ ДЛИНЫ
Во всех предыдущих параграфах исследовались случаи нормального набегания потока жидкости на плоскость пластинки или их системы, причем вихревые шнуры, возникающие на краях пластинки, образовывали за ней две непрерывные, вихревые плоскости, также нормальные к плоскости пластинки.
Понятно, что подобное направление потока и расположение вихревых поверхностей являются только одним из возможных частных случаев направлений потока относитльно плоскости пластинки. Поэтому для освещения всей области вопросов, связанных с теорией обтекания
плоской пластинки, необходимо сейчас приступить к развитию теории косого набегания потока жидкости на плоскую пластинку или набегания под произвольным углом, меньшим прямого.
Эту теорию мы будем развивать на нашей прежней основе непрерывного возникновения на краях обтекаемой пластинки вихревых шнуров прямо обратного вращения и одинакового напряжения и непрерывного сноса набегающим потоком пар этих шнуров, дающих силу давления на пластинку, за плоскость пластинки по направлению самого потока.
Вследствие этого плоскости непрерывных вихревых слоев АА" и ВВ" будут наклонены к плоскости пластинки АВ фиг. 71 под тем же углом, как и набегающий поток.
Найдем движение жидкости, вызываемое наличием в ней подобной скошенной системы вихревых слоев.
С этой целью найдем подобно § 4 скорости и и V, параллельные осям координат ОХ и ОК, сообщаемые произвольной точке т -нжкко-сти вихревыми слоями А А" и ВВ' (фиг. 71).
Элементы этих слоев ds} взятые у точек а и Ь, по направлению слоев, на расстояниии 5 от пластинки будут возбуждать в точке т элементарные скорости dwx и dw2, равные:
. Cds . Cds dw. =----- и dw~ =-----,
G G
где С—напряжение вихревых слоев, a rt и г, — расстояния элемен-тов слое» ds от точки т.
Скорости dWi и dwt нормальны к соответствующим радиусам rt и rt, почему слагающие их по направлению осей ОХ и ОУ будут равны:
du — dllf — dut = dwt cos (P — 90°) — sin a, dv =s dVi —dvt = rf»jC0i a— dwtsln (0 — 90°)
или
du = sin p — dwv sin a, dv = Ar, cos a dw9 cos 0,
где a и 0 — углы радиусов-векторов г, и г, с прямой ab, параллельной оси ОХ.
Но из треугольников атт” и Ьтт" имеем:
г/ = (у 4- s sin <р)’+(х 5 cos <р)2;
г,’ = {у 4- s sin <р)’ 4- (х—I+s cos <р)’;
j4-ssin<p = fiSina; x4-^cos«p = r1scosa,
у 4* s sin <р = r9 sin (тс — Р) = rt sin р,
X — / 4-s cos <р = га cos (я — Р) = —r2cosp, '
поэтому ' '
, у -I- s sin Ф х -4- s cos ф
sin a = —!------J-; cos a = —1-------;
. о _P4-Jsin<? о x—Z 4-5 COS?
sin p = ---i; cos P =----------L-----T
ra r 9
Подставляя в выражения скоростей du и dv все эти величины, получим:
du = С (^+7'-Т _ SL-Нлм) \ G G /
x4~5CQS?* — / 4~ 5 C0S ?
\ Г 3 Г Ъ
\ Г\ ГЪ
ds.
)
Скорости и и v получим, интегрируя выражения (2) по $ от нуля до бесконечности:
(3)
j 4“ sJn ф г 2 JT2
x4~5c0s<p___х — z -|" *cos w
G3 — гаа Jas-
О
Но интеграл
fj>4-ssin<p , _ Г____________y4~5sin?_________________
J G2 J(у-нsin<р)»4- [(X-/) 4-5cos?]«05“
Slnfl 9 1
— —~ In г* 4" cos ? агс*£
у sin у 44* — /) cos ?4~ у cos ф — (х — I) sin ср
Точно так же интеграл i v4-s sino f f
-ds = 2
sln<f>, , . . jsin <p-|-XC0S®4
-77-1- in r? 4- cos Ф arctg -—J-----j—-
2 i г т jcos<p — xsin?
Внося найденные значения интегралов в выражение скорости и, получим:
u = C
{^l»4
I 2 Tj о
Г arctg >sin<p4-(x —Z)coscp + 5
L • у cos <p — {x — I) sin f
+ arctg
у sin у —|—лс cos ср —|— -У x sin <p —у cos <p
Подставив пределы интегрирования и замечая, что
х’+/ = /?/, (/-х)» 4-= /?,*,
где /?г и /?, суть расстояния рассматриваемой точки т от краев пластинки Лий, получим:
“=С{Ч-Т|л^ V “ 'Va
, Г . vsin<p4-(x — /)cos®
4- it cos ф — cos ф arctg —;-к—:—-
1 т т L у cos <р — (х — /) sin f
4-arctg>Siny-+XC0S?lk
1 bxsincp—jcosfJJ
Наконец, заменив в последнем выражении арктангенсы соответственными углами по фиг. 72, получим его в виде:
п = С {sin <Р 1п ~ 4- cos « [к — (а 4- 6)] } =
р
— С (sin <р In 4“ cos ? в)» (5)
где в — угол, под которым из точки т видна ширина пластинки I.
Выражения (4) и (5) справедливы для всей части пространства выше оси ОХ, ограниченной с боков прямыми АА' и Bff, продолжающими вверх направления вихревых слоев АА" и ВВ".
Эту часть пространства будем называть пространством /. Но если перейти из пространства / в пространство II, за линию В В', для всех точек которой (х —/) sin ср =j>cosp, то будем нметы
(х— /) sin ср >_у cos <р, х sin ср cos ср.
Тогда выражение (3') напишется в виде:
00
~ fsincp , г,2 . Г . vsincp-4-xcos<p-|-^
Uu = С J !п-\- 4-cos ф arctg <—/-t------Z-L- —
I 2 r* 1 L XSlncp—ycoscp -
0
-агае^'^+^+ГП. (зэ (x — /) sin cp — JCOScp J J
В квадратных скобках вместо суммы арктангенсов здесь входит их разность, почему, переходя к пределам, получим:
, Rt Г , vsin®4-xcos«
sin ср in yr- — cos ср arctg—', 1-- —
\ Rt L xsincp—jcoscp
-aag;x-{>c”'>+-|,5lsxiL (4-j
8(x— /)sin<p —-.ycos ? J/ 4 7
Или переходя к углам, выразим эту скорость в виде: р
U п = С (sin ср In -|- cos срб). (5Г)
Наоборот, переходя из пространства / через линию АА', на которой у cos ср = х sin ср, в пространство III, при х положительном и меньшем /, будем иметь:
xsin <р<_у cos р, (х — /)coscp> j sin Ср
и скорость Uni будет для этого пространства дана выражением:
Т|_ 8 —X sin ср-[-J cos <р
__,гС^/~х)сО8<Р~-у51пУ~Д 8 (I — х) sin р У cos ?
или, перейдя к пределам: / о
U[|( = С {sin ср In СО! 1 П2
, X COS <Р 4~-У Sin ? |
_у-COS ср — х sin ср • (/-x)coscp-jsin?-|1
8 (I—х) sin ср 4-JC cos ср J J * '
Введение в это выражение углов вместо арктангенсов придаст ему вид:
р
Um = С (sin pin -fA- 4- cos <? 6) *^2
Наконец, за осью ОУ, в пространстве отрицательных х, получим выражение и'ш, заменив в (4")-|-х на — х, в виде;
, z4 , /?. . Г * (ZH-x)coscp—JSln ф
C^-smTln^+cMT^cIg (<^x)tlnT+j,CMT-_arc| „
b ATSlIl ф-j-y COSCp J J
которое в углах приведет нас снова к выражению (5"'). Таким образом во всем пространстве выше оси ОХ скорость и дается выражением (5).
Чтобы получить для той же части пространства выражение скорости v по (3), заметим, что интеграл:
X 4~ 5 COS ф
. __________* I ° ° Т_____ ________
| (у + s sin 4" 5 cos ?)s
cos cp , . . t v sin ср -|- x cos Ф 4- • — —к- ln Г.*4- sm cp. arctg <-----------4-^--------—L-
2 T x sin cp —у cos cp
а интеграл:
+ = eosj у з!п т-Н*-0созт-Н
J г,- 2 a 1 T (x — /)sin<p—jcoscp
Подставляя выражения интегралов в (3), получим:
[х v sin © 4-х cos ©4-$ arctg ----г—!-----—-------
х sin ср — у cos ср
— arctg ysin?+(*~0 cos <p-f- 5
* (x— /) sin ср—j, cos ср
Поэтому:
. /?э । . Г V sin ср 4-x cos ср
v = C{ cos ср In pc—4~^ sincp — smcp I arctg --I--------1
I Ki 1 L x sin cp —у cos <p
(I — х) sin ср -f-у cos ср
Или заменив арктангенсы углами, получим:
( р г -п
v = С| cos ср ln~4 + sin <р — (а 4~ J > =
о
= С (cos ? In 4- sin ср 6). (7)
Выражение (7) справедливо для всего пространства выше оси А’А'. Ниже оси XX, между вихревыми слоями АА" и ДВ", в пространстве
11 Л. Я. Мндоаяч 161
IV (фиг. 73)t найдем скорости и и v, заменив в выражениях (3') и (6) на —у. тогда получим:
00
Z» ( , , Г. . г —у sin® — (/—x)cos<p4s .
«1V = С / sin ф In — + cos ф I arctg —--1—7-75——-\—r----h
I T fj 1 L —JCOS<p-|-(Z — x)sin<p
0 *
4- arcto — JSin? + ^cos?4-^l I ’ ® у cos <p x sin <p J J
Но для пространства IV имеем (Z—x) sin <p >у cos <p и x cos <p >ysin <p, почему . /?i - Г . (I — x)cos<p4-vsincp .
«iv =Cl sm<p In4-n cos <? — cos <p — arctgу.-; . T +
I T Rt 1 T T |_ (I—x) sin <p —у cos tp 1 . . ХСО8Ф:—v staff!
“barc gjfsinf-j-ycoscpjj’ (8)
Или заменив арктангенсы углами, получим: . о .
«IV = С | sin (р In .cos ?(’* + « — bl у —
= С [sin <р In —tcos <р (2« — 0)]. (9)
•
Подобную величину «jy будет иметь до перехода точки тп через вихревой слой АА,Г или ВВ'\ на которых или х sin ср —у cos ср или (* — I) sin ср =у cos ср.
Но если точка m из пространства IV перейдет через вихревой слой ВВ” в пространство V (фиг. 74), где при х<^1 будем 162
"* Фиг. 74.
иметь ~х) sin ср cos ср, то выражение скорости Ду получим в виде;
J |sin <р In о
или
Ду = C]sin<p in
JI sin ср У— х) COS ср — 5 у cos ср — (/ — х) sin ср
iarctg XC0S(P— Js»n?4-г Б х sin ср -|- у cos ср
У Sin ф (/ — х) COS ф у cos <р — (/ — х) sin у
.2222^1 г --.1 I НО'»
XSin<p4*JC0S? J/ V '
Наконец, заменяя арктангенсы углами, найдем, что Ду равно:
Uy — С [sin ср in —cos <р (a-|"^)j=C(sin ф1® ту1 — cos ср 6). (11)
Из выражений (9) и (11) следует, что при переходе через вихревой слой скорость и изменяется скачком на 2к С cos <р, ибо Нту — Ну = — 2ft Ceos <р. Скорость в пространстве VI получим, заменив в выра* жении (10) ординату 4”* на —х, в виде:
. 1 /?1 Г . (Z4-x)cos?-l~Jsin ? ।
= C {sm ч In jjl- cos T [- ardg +
^arclgi5^T±J^D. ()2)
' ° x sm <p —у cos <p J J ' '
Обращаясь теперь к скорости v, получим:
? ( г. , , Г —У sin Ф — (I—х) C0S(₽ + 5 ।
v„ = С | |cos т In Л’ + sin ч [«ole _J,co,y_t.(<_Je)siroT Н
-ysInT + ^osf+sn
1 & у COS Ср х siu <р J J
Сравнивая это выражение с соответственным выражением для Uiv, видим, что оба выражения имеют одну и ту же сумму арктангенсов, почему можем прямо написаты
„ 1 Ri । , Г 1 G—х) cos ф-р у sin ф
=с|«» , i„ +. „„ f - si» т [- .rctg (f_x)5ln;^cos;
+ (,
1 ь л: sin ф 4“ > cos 4
Или переходя к углам, получим:
p
vIV = C [cos ф In 4- sin ф (2k —0)]. (14)
Точно так же соответственно выражениям (11) получим:
р
w = С (созф1п^ —sincpO), (15)
а из двух последних имеем:
^iv — = 2к С sin ф,
т. е. при переходе вихревого слоя скорость изменяется скачком на 2тсСзшф.
Собрав теперь всю систему полученных нами выражений скоростей, мы можем представить ее в виде:
Для всего пространства выше плоскости пластинки или выше оси XX р \
и = С (sin ф In S-14~ cos ф 6), Г
R °6)
V = С (— COS ф In 4" sin ? I
Для пространства ниже плоскости пластинки или оси XX. между вихревыми слоями,
V
[р
sin ф In 4- cos ф (2 к —
Аз
Р
cos ф In 4” s*n ? (2 тс
К* •
Для пространства ниже оси XX. за вихревыми слоями,
/ R \
и = С sin ф In — cos фб J,
\ А2 /
(О
— cos ф In •— — sin фб
(17)
(18)
Рассматривая эту систему скоростей, видим что она получилась в результате проектирования параллельно и нормально к плоскости
Ф*.г. 75.
пластинки двух скоростей, сообщаемых частице жидкости скошенной системой вихревых поверхностей (фиг. 75):
1) Скорости С6, параллельной направлению вихревых поверхностей и пропорциональной углу 6, под которым из данной точки жидкости видна ширина пластинки АВ.
р
2) Скорости С1п^, нормальной к направлению вихревых по-^2
верхностей и пропорциональной логарифму отношения расстояний данной точки до краев пластинки. И теперь, когда выражения (16), (17) и (18) получены прямым интегрированием действия элементов скошенной системы вихревых слоев, возможно показать, как просто получить ту же систему скоростей на основании известных уже нам из предыдущих параграфов свойств поля скоростей вихревых слоев.
В самом деле, по фиг. 75 видно, что каждую скошенную систему вихревых поверхностей АА' и ВВ” всегда возможно представить себе как бы состоящей из двух систем:
а) системы из двух параллельных, бесконечных вихревых поверхностей ДД* и СВ* с началом по прямой АС, нормальной направлению набегающего потока;
б) конечного по длине отрезка вихревого слоя ВС, параллельного
направлению набегающего потока.
Но по выражению (13) § 4, а также по выражению (53) и (54) § 1, нам уже известно, что первая система вихревых поверхностей
сообщает точке т параллельную себе скорость Свх и нормальную р
к слоям скорость С1пуу,а вихревой слой конечной длины ВС сооб-
щает параллельно себе той же точке т скорость Св, и нормально
по направлению к слою скорость ClnS^. Поэтому одновременное действие в точке т обеих систем вихрей сообщает ей:
а) параллельно вихревым слоям скорость
С01-|-Св2 = С6;
б) нормально к вихревым слоям скорость
С In bJ + CI«& =С1П&.
Г\$ lx* r\2
что и соответствует полученной нами системе скоростей (16). Для точки п, находящейся под пластинкой между вихревыми слоями, найдем скорость, параллельную вихревым слоям, равной:
С(2к — в1 + в2) = С[21Г — (О,— 02)] = С(2к — в), что соответствует выражениям (17).
Наконец, для точки р ниже оси XX за вихревым слоем ВВ” получим:
— соа4-се1==—с(о2—6t)=—со, соответствующую системе (18).
Наоборот, скорость, нормальная к слоям, во всех точках пространства имеет одно и то же выражение
СДп^р или С* In.
Очевидно, что уменьшение угла набегания или атаки увеличивает влияние слоя ВС и уменьшает действие вихревых слоев АА” и СВ'.
А из § 1 (фиг. 17) известно, что вихревой слой конечной длины вращает вокруг себя окружающую его жидкость, поэтому действие слоя ВС с уменьшением угла ср должно под пластинкой выразиться интенсивным развитием односторонней циркуляции или вращения жидкости. Наконец, должно быть замечено, что в системе двух взаимно ортогональных скоростей
се и С1пф, управляющей рассматриваемыми здесь движениями жидкости, скорость р
С In — является производной скорости СО. Она проявляется нормально только тому направлению, по которому изменяется величина скорости СО.
Мы имели уже подобное явление в § 4 (фиг. 46) при нормальном набегании потока жидкости на пластинку.
I. Граничные условия
Полученные нами общие выражения поля скоростей скошенной системы вихревых слоев значительно упрощаются в случае обтекания потоком жидкости плоской пластинки.
В самом деле, во всех точках плоскости плоской пластинки АВ (фиг. 76) угол 6 = it, почему выражения (16) и (17) дают для всех точек плоскости пластинки одну и ту же постоянную скорость, параллельную плоскостям вихревых поверхностей, Стг, которая должна быть равна и прямо противоположна скорости набегания жидкости на пластинку из бесконечности v0.
Разлагая теперь скорость под пластинкой С it на скорость, параллельную плоскости пластинки —Citcoscp и нормальную к ней 4~Citsin<p, а скорость набегания жидкости — на скорость над пластинкой, параллельную ей 4-vocos<? и нормальную к ней—sin 9, увидим, что условие непроницаемости для жидкости плоскости пластинки требует во всех точках этой плоскости равенства величин нормальных к ней скоростей
С it sin ? = Vq sin р, или
^0 = Cit. (19)
Что же касается до компонента скорости набегания жидкости, параллельного плоскости пластинки cos с? = 4“ С it cos ср, то нет никаких причин для изменения его величины и направления во всем пространстве за исключением пространства под пластинкой, ограниченного с боков вихревыми слоями ААп и ВВи. В этом пространстве параллельно плоскости пластинки будем иметь скорость также постоянную и равную по величине скорости над пластинкой, но обратную ей по знаку:
— С к cos у.
А постоянство во всем пространстве скоростей, параллельных пластинке, приводит к тому, что нормальная к ним скорость
р
Cln^-’cos<p 5=0.
На основании сказанного обтекание плоской пластинки будет ддно полем скоростей:
1. Во всем пространстве / выше оси ХХ\ о «I =C(itcos<p4-ln^-’sin<p), z/i=—С(л — 6)sincp,
На плоскости пластинки, где 6 = тг, =0.
За краем пластинки, где 6 = 0, vj = —Cirsincp.
2. В пространствах II и IV ниже оси XX, ограниченных вихревой поверхностью АА" или ВВ4,
р л
ип = С (к cos <р -I- In sin ф), Ъ | (21)
Vii = — С (тг 6) sin ср, J
3. В пространстве /// под пластинкой и между вихревыми слоями: р
Нп1=С(— ж cos <р-f-In sin <р),
Vin = С (тг — 6) sin ср.
Выражения (20), (21) и (22) в случае <р = 90°, т. е. нормального набегания потока на пластинку, приводятся к выражениям (а), (Ь) и (d) § 4. Наоборот, при <р = 0 получим одну скорость жидкости во всем пространстве:
vo = u — 4-Стг,
как то и должно быть, ибо при ср = 0 пространство III исчезает и мы имеем только пространства / и //, где скорость Ст: cos ср положительна.
11. Функция течения и токи жидкости
1. Пространство / выше оси XX. Во всем пространстве I выше оси XX (фиг. 77) имеем:
р П) = С т: cos ср + С In sin ср,
= — С(тг — 6) sin <р. Поэтому функцию течения для этой части пространства получим, интегрируя выражение
X
S] = j -udy-\-f{x) о
или
V Г р
Si=—Cl (xcos<p-|-ln о1 sin<р)4у+ /(х),
о где
/?1’ = Д;2+У; =
Фиг. 77
Но интеграл:
я cos <р dy = тг cos у у,
а интеграл:
у Г J? v v
I In тУ sin<pdy = sin<p lyln^1 -f-xarctg^- —(/ — x)arcfg . J L r\i X I—X
о
Поэтому функция течения будет равна:
{ГР у
к cos у у sin ? ly In 4- х arctg — —
L Aj X
— (I — х) arctg } +/ to-
Для определения неизвестной пока функции /(х) берем производную 51 по х и приравниваем ее скорости trx =— С (тс—в) sin ср, получаем:
?'-=-cSinT [ + ,4;~х> +MIlg г—<£-,+
дх Lj*a4-xa ‘у ’-[-(/—х)1 6 х уа-|-ха 1
+ afC<g/ (Jl^)a] +/to=-Csin?(arctS х +
+ arctg Г^х] +/'(х) = — Csin <р (я — 6)+/'(х).
Приравнивая теперь полученное выражение скорости vit найдем, что — С sin <р (я — 0) 4~/ to = — sin ? (к — ®).
откуда
f (х) = 0 или /(х) == const.
Теперь возможно выражение для «St написать окончательно в виде:
= — С f гс cos у у -{- sin ср
—(l — x) arctg
-а уравнение токов жидкости представить здесь выражением:
[R 1
jHn^ -f-xax— (Z — х)а2 j =const. (23)
Ha плоскости пластинки имеем у = 0; ах = а^ = 0, почему здесь const = 0, ток идет по пластинке.
Положение точки нулевой скорости М или раздела течения найдем, решая уравнение:
гс cos ср -|- In -*— sin ср = 0, 4 х
ИЛИ
I — X
In—^-=irctg?.
(24)
I___х I
При ср = 90° ctg ср = 0 и-----= 1 или х = , т. е. точка нулевой
X 2»
скорости лежит в середине ширины пластинки, что нам уже известно. / — х
При ср = 0 ctgcp = ooH -------= оо, почему х = 0, в этом случае
точка раздела течения лежит на переднем краю пластинки или на краю атаки. С изменением величины угла атаки от 90° до 0° точка М нулевой скорости по верхней поверхности пластинки перемещается от ее середины к краю атаки.
Предельный ток в пространстве /. Уравнение предельного тока для пространства / получим, положив в уравнение токов этого пространства (23) const = 0, в виде:
[р т
JFln^ +*ai.— —х)аа|=0.
Кг J
Но чтобы сумма двух членов этого уравнения могла равняться нулю, необходимо, чтобы второй член ее был отрицателен. Последнее указывает нам на то, что кривая предельного тока должна по фиг. 77 итти влево от оси ОУ, в пространстве отрицательных х. А тогда для точек этой кривой /?х<7?2 и предыдущее уравнение возможно написать в виде:
*1
гс cos с? у — sin <р ly In
JC -(-(/-4- х) аа = 0.
(24')
На бесконечном расстоянии от пластинки точки кривой предельного тока должны будут удовлетворять уравнению (24') при условии, что
/?,==/?„ at=ir — <р, а4=ср,
что приводит к уравнению j cos ?—х sln?= -2-1 sin?. (25) ТС
Но по фиг. 78 разностьу cos?— — xsin ср есть ни что иное, как расстояние от прямой АА\ направления набегающего из бесконечности потока на передний край пластинки, до параллельной ей прямой КК. Поэтому, уходя в бесконечность, предельный ток пространства I приближается к прямой КК9 параллельной прямой АА9 и отстоя
Л
Фиг. 78.
щей от последней на расстояние ~ Z sin ср. На фиг. 78 видно, что Zsin? есть проекция ширины пластинки I на направление, нормальное к напра
влению набегающего потока, а дает часть этой длины. Из равенства (25) видно, что разность у cos ?—-х sin ср всегда положительна, т. е. предельный ток идет всегда выше прямой ЛЛГ- Придя на плоскость пластинки в точку нулевой скорости М9 он идет от »нее вдоль по пластинке к ее концам В и А. При нормальном набегании потока, к
когда <р = —, будем иметь:
I coscp = 0, sincp = l, —л = х и x = -g-,
т. е. предельный ток проходит через середину ширины пластинки. При ср = 0, cos ср = 1, sin ср = 0 получим у — 0, т. е. предельный ток идет по оси ХХ9 как то и должно быть.
Изложенный анализ расположения кривой предельного тока в пространстве I показывает, что эта кривая, подходя к пластинке, всегда загибается к краю атаки, точке А.
2. Пространство II. В пространстве //ниже оси XX, ограниченном справа вихревым слоем АА" (фиг. 77), имеем:
р \
Иц= С(тс cos ср -{- In^-1 sin ср), I
г
Ян = — С(к 4- 0) sin ср . J
Здесь для точки п обе координаты отрицательны, —хи —у, и равны /?/ = / + ха, /?/ — у* + (/ 4- х)а. Имея это в виду, получим функцию течения для пространства //, интегрируя выражение:
у у
5ц= J— udy + /(х) = — С j cosf 4-ln^ sin <p 1 &У +/(*) о о J
или
Sn= — С тг cos <p у — Csin <p£ у ln^ + x aTC*S —
— (*+*) "c*g +/(*) •
Определение неизвестной функции f(x) дает:
dS„ „ . Г J* y(^4~x) i v
-a— = — C sin ф —,«5—5-------r.\,\t -4- arctg ——
dx T Lj +* у 4-G+*) *
— arete У— — yX 4- <Z+*)j 1 । ft (xx tg 14- x у+x* + y* 44/ 4- x)« J + " w
ИЛИ
= — Csin <p (7 — a2) 4-/(x) = — Csin ? (it — ax — aa)4~/(x) =
= — C sin Cp6 4*/ (*)•
Поэтому имеем равенство:
— C sin <рв 4- f'(x) = — С(тг 4- 6) sin ср, откуда следует, что
f(x) = — Cusincp и f(x) =—Csintprcx.
Теперь выражение для 5*ц окончательно напишется в виде: о
Sii = — С я cos <р у — С sin ср [j In 4"х (* — а1)—G4- х) а2 4" я *1» а уравнение токов жидкости в пространстве отрицательных х напишется в виде:
Г R1
— я cos ср у — sin <р^2 я х —х ах —(/ 4- х) <4 4"У1п I = const. (26)
В пространстве положительного х, вправо от оси YY, получим уравнение токов, заменив в выражении (26)4-* на —*, в виде:
— я cos ср у 4" s’n ? Г2 * х— xal-\-(l — х)а2—у In = const
L ^2J
или
I г R
2 к х sin { пу cos <р 4- sin ? У In -в* 14-*ai —
( L ^2
— (Z — х)а4 J | = const. (27)
Уравнение предельного тока в пространстве У/. Соответственно уравнению (27) уравнение предельного тока в пространстве // напишется в виде:
2 к х sin ср — cos cp4~sin ср Гу In ^4"*ai—(^—*)aa 11 =О- (28)
L /<2 JI
Удаляясь в бесконечность, точки этого тока АК" (фиг. 79) должны удовлетворять уравнению (28) при условии а2=тс—ср, а1 = ?, = что приводит
нас к уравнению:
Т =у cos ср — х sin ср =
= I sin ср. (29)
Последнее выражение вместе с фиг. 79 показывает, что, удаляясь в бесконечность, предельный ток АК" асимптотически приближается к прямой АТС,
паралллельной плоскости вихревого слоя АА" и отстоящей от него на расстояние
тс— срх .
----- I sin ср.
Фиг. 79.
При ср = 90° = ^- по выражению (29) будем иметь: I ~х—2 ’
что мц имели уже в случае нормального набегания потока жидкости на пластинку.
тс— ср
С уменьшением угла ср величина -- стремится к единице, т. е.
• тс
расстояние предельного тока до вихревого слоя стремится стать равным I sin ср, вся циркуляция жидкости под пластинкой смещается в сторону края атаки.
При ср = 0 получим
_у=о,
т. е. предельный ток идет по нижней стороне пластинки, как то и должно быть.
3. Пространство III. Для пространства III под пластинкой и между вихревыми слоями скорости частицы жидкости даются выражениями:
(р \
—тс cos ср -|- In sin ср |,
/
= С(тс — 0) sin ср.
Кроме того, по фиг. 77 в этом пространстве отрицательна одна ордината у, поэтому функцию течения найдем здесь по выражению:
-j -у &
Sin = f — udy-\-f{x) = C V ^KCoscp — ln^sincf>]rfy-f-/(x).
о о
Выполнив интегрирование, получим: [R v
jln-p-1 -j-xardg^- — Aj X
— (l — x) arctg +/(*)•
Ho
dSin dx
— C sin <p( arctg — -|- arctg
У \ I — x]
+/’(x)=Csin?(x-e)+f(x).
Тогда из равенства
C sin ср (it — 9)+/ (х) — Сsin <р (it — 6) получим
f(x) = 0 или /(х) —const.
После изложенного можем выражение функции течения писать в виде:
Г R
= — Circoscpj-|“ С sin ср I х«ц— (/ — х) а3-\-у In g-1 L *\2
а уравнение токов жидкости пространства 111 в виде.* г R ”1
к cos ср у — sin гр I х ах — (Z — х) аа -]- у In = const. (30)
Положение точна нулевой скорости М или раздела течения найдем, решая уравнение
х — тг cos <р -|“1п --sin ср = О
4 — X
или
ln-^—= itcotg<p. (31)
I ~ л
Уравнение (31) показывает, что на нижней стороне пластинки точка нулевой скорости перемещается от середины пластинки при ср ±=90° к ее хвосту при ср = 0, х = 1.
Кроме того, сравнивая между собой уравнения (24) и (31), увидим, что сверху и снизу пластинки точки нулевой скорости расположены симметрично относительно ее середины.
Уравнение предельного тока в пространстве///.
В пространстве III уравнение предельного тока напишется в виде: •
[R 1
X 04 —(Z — ас) а2 У In & — 0. (32)
При удалении точек кривой МК предельного тока в бесконечность (фиг. 80) их координаты должны будут удовлетворять уравнению (32) при условии, что
а2 = ср, а2 = тс — ср, /?! — /?а.
Но подстановка этих предельных значений в уравнение (32) приводит его к виду:
xsincp—jcoscp =
_ ILZT.? I Sjn m (33) 7Г
показывающему, что предельный ток МК9 в пространстве ///, уходя в бесконечность, асимптотически приближается к прямой КК, параллельной направлению вихревого слоя АА" и
Фиг. 80.
отстоящей от прямой АА" на расстояние -—5 / sin ср.
тс
4. Пространство IV. В пространстве IV (фиг. 77), ниже осн XX за вихревым слоем ВВ\ имеем:
/ R
U\ v = С (тс cos ср -J- Jn sin ср
Viv = — С (я + 0) sin ср.
Функцию течения Siv получим, выполнив интегрирование выражения;
Sjy=—тс cos cp 4* о Тогда будем иметь: [R jln^
— (K—l} arctg —j -I- / (x).
У
А так как
= С sin <Р (arctg _ arctg (х) = — С sln?0 +f(x),
TO
откуда
— Сsin ср в +/' (х) = — С(тс 4- 6) sin ср, /'(*) = — С sin сртг и /(х) = — Сsin сртс (х — Z). Теперь выражение функции течения окончательно напишется в виде:
3iv = С тс cos <ру 4“ С sin <р I — 2 и (х — I) 4“ х ai +
Фиг. 81.
Сообразно такому выражению функции течения уравнение токов жидкости примет вид: wcosfyr—sintp ^2к(х—I)— — 0«s +
p -l\
|= const. (34)
Уравнение предельного тока в пространстве IV. Предельный ток ВК в пространстве IV (фиг. 81) будет иметь урав-
нение:
Г Г R 1)
itcos<p.y — sin ср I 2ге(х—I)—|^х«14-(х — I) а2 -|- у In J | =0. (35)
В бесконечности при а, = ср, а, = гс— ср,оно примет вид:
(х — I) sin <р—-J/ cos <t = ^l sin ср, (36)
который показывает, что, уходя в бесконечность, предельный ток приближается к прямой КК> отстоящей от вихревого слоя ВВ" на
расстояние —I sin ср.
III. Общая схема движения жидкости при косом набегании потока на пластинку
Весь выполненный анализ указывает нам на весьма ясную и простую схему движения жидкости вблизи плоской пластинки при косом набегании на нее потока под углом ср.
Если на пластинку АВ (фиг. 82) будет набегать поток жидкости под углом ср, с начальной скоростью ^0 = Ск, то на ее концах А и В он будет непрерывно возбуждать пары вихрей с напряжением С, секундное количество движения которых будет равно и прямо противоположно действию потока на пластинку.
Эти пары вихрей будут сноситься набегающим потоком за пластинку, по направлению его начального движения, и образуют там две параллельные, непрерывные, вихревые поверхности АА" и ВВ". Жидкость, находящаяся между этими вихревыми поверхностями, нач-нет под их действием двигаться по направлению к пластинке с начальной скоростью — — С к, будет как бы подсасываться пластин-
кой. Эта подсасываемая пластинкой жидкость будет протекать через вихревые слои и с другой стороны их будет менять направление своего движения на прямо обратное, т. е. будет снова двигаться по направлению набегающего потока.
Набегающая на пластинку жидкость и подсасываемая ею отделены друг от друга поверхностями предельных или граничных токов, AG и ВН, отходящих от краев пластинки. Наконец, в одном и том . же пространстве распределение движения жидкости дается поверхностями предельных токов КМ и КМ9 проходящих через точки нулевой скорости на поверхности пластинки М и М.
На фиг. 82 видно, что вся жидкость, набегающая на пластинку «иже предельного тока КМВН, протекает и уходит в бесконечность ниже пластинки. Наоборот, жидкость, движущаяся выше тока KMAG, протекает выше пластинки.
С обратной стороны пластинки мы имеем также два определенных пространства, в которых циркулирует подсасываемая пластинкой жидкость: пространство, ограниченное поверхностью предельного тока K’MA’G, с циркуляцией жидкости по движению стрелки часов и пространство, ограниченное токами К'МВ'Н, с циркуляцией против часовой стрелки.
В достаточном удалении от пластинки, там, где кривые предельных токов близки к прямым, параллельным направлению набегающего потока, расстояния между ними имеют вполне определенную величину.
Так, ширина пространства между токами AG и BHt отделяющими подсасываемую жидкость от набегающей, равно:
2 —I sin © 2 1 sin © — 21 sin ср.
Оно равно двойной ширине проекции ширины пластинки на направление, нормальное направлению набегающего потока.
Эта ширина делится на две равные части:
а) между вихревыми слоями шириной I sin ср, занятой жидкостью подсасываемой, движущейся к пластинке со скоростью —
12 А Я. Милович 1 / I
Фиг. 83.
б) между вихревыми слоями и предельными токами AG и ВН шириной
- -1 sin Zsincp=
= Z sin ф,
занятых жидкостью, оттекающей от пластинки со скоростью равной и прямо противоположной скорости подсасывания. Но ширины, захватываемые прямой циркуляцией _ ~ — ф .
2------- / sin ср и обрат-
ен *
ной 2 — Zsin?, в от-тг 1
дельности могут быть весьма отличны друг от друга, в особенности при малых углах атаки ф.
Фиг. 83 дает точный чертеж течения жидкости при набегании потока на пластинку под углом ф — 35°. А фиг. 84 дает фотографический снимок подобною обтекания
плоской пластинки, снятый в Гидротехнической лаборатории Строительства канала Москва — Волга в г. Дмитрове.
Тождественность общей картины явления показывает, насколько близко предлагаемая здесь теория соответствует реальному Явлению природы, но с другой стороны, с полной ясностью подчеркивает и недостаток теории, вводящей в анализ явления непрерывность вихревого слоя, который в действительности всегда разлагается на отдельные вихри, как то было уже нами отмечено в § 5(V), фиг. 51 и 52.
§ 8. ВЕЛИЧИНА И РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ ПРИ КОСОМ НАБЕГАНИИ ПОТОКА НА ПЛАСТИНКУ
Из § 7. нам известно, что при косом набегании потока жидкости на плоскую пластинку компонент скорости набегания тг Ceos <?, параллельный плоскости пластинки, остается величиной постоянной, откуда следует, что никакого давления на пластинку он произвести прямо не
может. Его роль сводится только к изменению распределения давления вдоль по ширине пластинки.
Давление же на пластинку обусловливается только вторым компонентом скорости набегания, нормальным к плоскости пластинки тс С sin ср (фиг. 85). Поэтому для всего пространства, за исключением пространства /// между вихревыми слоями, постоянный запас энергии жидкости в бесконечности следует представить суммой — -~
I С2 ТС2 COS2 Ср v
Н------—-, а полный запас суммой'.
р0. С2 тс2 cos2 ср . С2 тс2 sin2 ср_р0 . С2 тс2
7 ' 2g ’ 2g ~ 7+ ~2g~ ’
а уравнение Д. Бернулли для пространства /^ад пластинкой должно писать в виде:
7 "Г 2g 7
- In т--sin ср)1
I— х 2g
(37)
где р — давление в точке т верхней стороны пластинки, а С(тссовср4-х
—|—In -j---sin ср) — скорость жидкости в ней.
4 X
Из уравнения (37) получим:
Р— Ро =
X • \«1
s,nT)- .
(38)
дающее нам закон распределения давления в каждой точке верхней поверхности пластинки.
Для нижней поверхности пластинки, подсасывающей к себе жидкость пространства ///, между вихревыми слоями, постоянный запас энергии жидкости, как и для верха пластинки, представится суммой рь . С2 тс2 cos2 ср .
I-----—----1, но полный запас будет равен:
. С2 ж2 cos2 ср С2 к2 sin2 ср 2g 2g ~ ~
С2 тс4
2g
а cos’ ср 2g
— — —2 cos2 <р).
7 2g 4
Поэтому для нижней поверхности пластинки, в пространстве между вихревыми слоями, уравнение Д. Бернулли напишется в виде:
х
С2 (— тс cos ср In -т_ sin ср)2
.(39)
^-^-(1 -2 0084)=^
2g
откуда
р' - Fo = —2~ С* к2 [1 —2 cosVH—cos?4- 4",n sin ?)*] (40)
—выражение, дающее распределение давления во всех точках п нижней поверхности пластинки.
Для одного и того же х получим разность давлений с двух сторон пластинки, по выражениям (38) и (40) равной: р—р'= С2 к2 ^2— 2 cos2 ср—(cos ср-{--Ь In sin ср)2-|-
• 1 V 3
-I- (— cos ? -!-In -т-— sin <p)*
1 ' ‘ 1 к I—x ™ J
или
p —ff=z y~Ci‘Ki(2 sin2 <p — in -X— sin ? cos ?),
2 к 4 — X
или, наконец,
2 x p—p, = ?Cin2 (sin2 <p---In -----sin <p cos <p). (41)
7Г I —X
Равенство (41) показывает, что при ср = 90° или нормальном набегании потока на пластинку *
р — р' = р С2 к2 = const,
как то мы уже имели в § 5. 4
При ср = О р—р’— 0, т. е. при направлении пластинки по направлению набегающего потока последний не оказывает на нее никакого давления, как то и должно быть.
Полную силу давления потока на пластинку Р, по нормали к ней, найдем из выражения:
i i
Р —Р9} dx — pC2 к2 о о
Но интеграл
1п т~Х dx — х lnx-f- (/ — х) In (I — х) — /, поэтому
I
^\n~^dx-l}nl—l\al — l = — l. о
Интегрируя теперь выражение силы давления Р, получим:
2
Р= р С3 л3 / sin ср (sin ср Ц- —cos ср). (42)
2 х
(sin2 ср--In ----sin ср cos ср) dx,
К I —X
Pk=
I ,п 7-
] I—х
I. Центр давления
Точку приложения равнодействующей силы давления Р получим из равенства моментов равнодействующей и составляющих:
(р—p')xdx„
о
где k — абсцисса центра давления. Но интеграл:
JC2 X2
х In xdx — I x In (I — x)dx — — In x — — —
.• J Л & T &
, (x + /)J ,• l\ „ ‘ ч 7^, X3 , /2-ха, n 4 , (x-H)3
ь 7 + уln (/—x)== у|п х ~ т+~т~1п (/ “х) ",4 •
Поэтому интеграл:
f. х . Г , , I3 I3 ' I3 ') I3
\XnT^-xxdx^-2 •«*-Т~ о ....
Принимая во внимание полученный результат, найдем, что
'Г./' - ’ Г* < J ‘
—Р ) х&х = р С3 тс2 J(siп- ср — In ix sin ? соз ср) =ь
о о
/ Z2 2 Р \
= р С2 тс2 ( sin2 ср —-— sin ср cos ср— I =
2 к 2 /
Z2 2
= р С° — sin ср (sin ср — — cos ср).
А уравнение моментов равнодействующей и составляющих примет вид:
2 Z2 2
р С2 тс2 Z sin ср k (sin ср -J- — cos ср) = р С2 к2 — sin ср (sin ср — cos ср) j
откуда ордината центра давления Получится равной:
2
, sin ср----- COS ср
_______
Л 2 2
’ ’• ' sin ср Ц——cos ср
Выражение (43) iпоказывает* что при ср = 90° т. е. при нрр-
мальном набегании потока центр давления лежит на половине, ширины пластинки.
I
Цри ср = 0 выражение (43) дает k = т. е. центр давления лежит впереди края атаки на расстоянии половины ширины пластинки; = т. е. центр давления лежит на краю атаки, тогда когда sin ср = 2 2 *!
— cos ср или tg ? = — = 0,637, что дает ср = 32°30'. Последнее противоречит опыту, так как прямая пластинка с^ осью вращения, расположенной на краю атаки, как флюгер, всеГд^ устанавливается по направлению набегающего потока, а не под углом ср = 32°30' к нем У я Это ^противоречие опыту выводов теории/, показывает, что нами не учтено пока одно явление, играющее здесь решающую роль, — явление, с которым мы познакомились у^ке в§5 (фиг. 52 и 53), состоящее в том, что движение вихрей с задней стороны пластинки выравнивает там давления и мы наблюдаем Здесь не определенное неподвижное распределение давления, а давление среднее.
Понятно, что с уменьшением угла атаки, ср < движение вихрей и выравнивание им отрицательного давления у спины пластинки будет сказываться все сильнее на -положении 'центра давления, не изменяя при этом величины самого давления, даваемой выражением (42). Поэтому правильное определение центра давления или правильное выражение закона Аванцини (Avanzini, 1804 г.) будет достигнуть нами только при том условии, когда на верхней поверхности пластинки распределение давления потока оставим по выражению (38), а на нижйей ее поверхности вместо распределения по выражению (40) вычислим соответствующее ему /среднее отрицательное давление {р*—Ро)Ср-И только после этого снова определим положение центра давления, ,
Величина среднего отрицательного давления нанйжнёй поверхности пластинки. Среднее отрицательное .давление на нижней поверхности пластинки получим по выражению:
(р. —.р0)ср — _ JL са л2 / С[Т 2 с oS8 <р 4- (— cos 4-
• t Q
I
4-“,n ///sin?)'i —----------ж5* j-Jtsin’? —
и
2 х • Г / х \
— к ln C0S ? + — t,n T^x} s1"9 dx'
В этом выражении значение ише.р;ла: t ‘ . к
л.л, о
нам уже известно и требуется только найти значение интеграла
‘ С( In dx.
J\ I — XJ
0
Но интеграл
j (,n Г^~х) j lln Л — In — *))’<& =
= J[in3x—2 in x In (I—x) 4- In’ ({— x)J dx =
= J In’ xdx—2^1n x • In (I—л) dx 4- J In’ (Z— x) dx.
Первый из этих интегралов равен:
jin® xdx = х in® x — 2x In x 4~ 2x.
Последний интеграл равен:
jin3(Z — x)dx —— (I — x) ln®(Z—x)4-2(/ —x)ln(Z — x)—2(Z—x).
Поэтому сумма первого и последнего интегралов после подстановки пределов даст:
i i i
§ ln2xdx 4~ П"’(Z— х) dx— |[xln®X—2xlnx4~2x—
0 0 о
- (Z -х) in’(Z -х) 4- 2(/-х) 1п(/-х)—2 (Z—х)] = 21 in’ I-4/ In 14- 4Z.
Второй интеграл приводится к виду:
\lnxia(Z— x)dx = xlnxln(Z— x)4~(Z — x)ln(Z — х) — {I—х) — — л 1пх4-х — Zlnx-ln(Z—x)4-Z Jin(Z—x)dlnx =
— —(Z — x)fnxln(Z—x)4-(Z — x)ln(Z — x) — (Z — x)—xinx-]-4-x4- Z^ln {l — x)dln x.
Последний интеграл этого выражения может быть представлен в виде;
или
Поэтому интеграл
С1и (Z — x)dlnx = | ln/-lnx— (1 +*gi+^-b‘'| • о о 4
7Г*
Выражение в фигурных скобках, как известно, равно > почем]
имеем:
a* I
kin (Z — x)dlnx = InZlnx—
о 0
Но тогда интеграл
i i
J In x in (Z —x) dx = Ц— (Z — x) In x In (Z x) 4- (Z — x) In (Z — x) —
• .° l
— (I—x)—xlnx-J-x-f-ZlnZlnxj— i
— p In Z — (Z — x) In (Z — x) j In x — I In I 4-1—I In I 4~1 —
— ^Z = ZlnaZ4-2Z — 2ZlnZ—-£-/ .
Окончательно получим1, что искомый интеграл
J(ln 7^)’ dx = 21 In’Z — 4Z In 14- 4Z — 21 ln« I — 4Z -f-0
+ UI.Z+2 £./=£(, или
(('"^хУЛ = Тг- ’ о
После всего изложенного величину среднего отрицательного давл -ния на нижней поверхности пластинки получим равной:
(X — Ро)ср=— -у С ~2 7"(sini ?1+"7 sin ? cos <Р I -f- Д, .у I sin3 ? j или
о / 4 2 \
(X—Ро)ер = 2 С’ ” \"3 si°2 ? + — Sin ® • cos <? j . (44)
Выражение среднего отрицательного давления нц нижней дцрер^ ности пластинки (44), полученное нами чисто теоретическим путем, дает возможность проверить справедливость всей теории сравнением вытекающих из нее результатов с данными непосредственно^ опыта.
Так, выражение (44) в случае нормального набегания потока на пластинку, т. е. при ср = 90°, когда sin ср =1 и cos ср = 0, дает
</’’-Ро)ср = —уСЗ’'94==~133‘2<?’'2 .
X О & - * S
Но, как известно, Фэйдж и Джохансен (Fage и Johansen) в Лондоне чисто экспериментальным путем нашли (см. § 5,. фиг. 51) величину этого отрицательного, среднего давления равной L
— 1,33-|-C3^, ,пл4... •;
что является лучшим подтверждением правильности всей предлагаемой : нами теории. ;’
Центр давления при среднем давлении на нижнюю поверхности пластинки. Принимая во внимание выражение (38), дающее величину давления потока в каждой точке х верхней поверхности пластинки, $ выражение (44) среднего давления на ее нижней поверхности, будем иметь разность давлений в каждой точке поверхности пластинки, по ее ширине равной: • Ji
<Р —Ро) — (Р' —Ро)ср = |С* НI — (cos ? In sin*®)3 +
J +4si"a? + 4sin?cos?].
ИЛИ ,.4(
(р—Ро) — (Pr-Po)cp= 2 ......V- ’
• . 2 . / х \ 1 /, х V . 3 Т-I’
t -sin? cos ? I 1 — In ---------- — —J In -j—- sin3 ? .
; , Г У 4 “““ X / Г у 4 X / J
Поэтому сумма моментов, составляющих Л), будет равна: t
i
= —• тс2 С° И sin3 ср — $in ® cos ср (1 — |п . Х -) —
’(.о к * \ 4 X /
о
1 / х у . т.
------1 In , r sin’s f xdx.
Г-Д L --- X/ ?i 4.‘.J Н : -
Но мы уже имеем, что интеграл
С । х . I2 I In т---хах = тг ,
J I — х 2 о поэтому интеграл
О откуда получим, что I лл Р zn 9 Г 7 • 9 ? Sin9 Ф СЛ X V , 1 M=-2Cr- | 3s'" "N-
О
Величину последнего интеграл^ возможнб найти следующим образом:
— х/ 2\ 1—х) jl—х 1 — х
г2 / х \3 Г г / 1 х
= 4-(1П7т^-| -/ Г-1 + Н—] \nr^-dx =
2 I—х) JL I — х] I—х
х \3
I п 7—7 ) Ч- * (х,п X —• г) 1[(1—х) In (I—х) — (I—x)J —
— Z’ -i In’ (Z — х) +/’ ta x In (Z—x)—j In (4— x) d In x.
Поэтому интеграл
— l(Zs —x’)lnxta(Z —x)—£9ln’(Z —x) + ^ln’x — 0
— Z’ InZlnx] 4- ^-.p.
О
Или подставив пределы и раскрыв неопределенности, окончательно получим1:
1 Это значение интеграла было найдено Ю. Д. Городковым, за что я приношу ему благодарность.
Подставляя его в выражение момента, получим:
ы Р гч » / ? • a Z9 1 к’ . . /’\ (та" »г~?-з“ »т)=
= -СС1 я*~-2sin*, = рС*я*sin’, £ 4 &
Теперь равенство моментов равнодействующей и составляющих напи-1уется в виде:
2 Р
р С8 к21 sin ср (sin 4“ — cos ср) • k — р С9 тг8 sin8 у —, откуда получим величину k равной:
sin ср I
* 2 2
sin ср 4- — cos Т 4
или
*=-Ч— 1 + vdgt?
что и дает истинное выражение закона Аванцини для бесконечно длинной пластинки.
Как показывает это выражение, при ср = 0 и ctg ср = оо А = 0, т. е. центр давления находится на переднем краю пластинки.
При ср = 90°, ctg ср = 0 и k — как то и должно быть при нормальном набегании потока. *
Отступание центра давления от края атаки с увеличением угла ® дано кривой фиг. 86 в долях половины или полной ширины пластинки.
II. Подъемная сила н лобовое сопротивление плоской пластинки бесконечной длины
Выражение (42) дает силу полного нормального давления потока на плоскость пластинки в виде:
2
P=pv04sin?(sin©4"“cos ’f) >
где v0—скорость набегания в бесконечности. Разложив эту силу на две слагающих нормально к направлению набегающего потока и fto его направлению, получим две силы (фиг. 85), подъемную си/iy Pcos f и силу лобового сопротивления Рsin ср, равные: а) подъемная сила
2
Ра= Pcos э = р T/o21 sin ср cos cp(sin ср Ц- — cos ср), (46)
б) лобовое сопротивление
2
Pc = Psincp= р v*01 sin3 ср (sin ср -]-cos ср).
Последние выражения показывают, что наличие подъемной силы возможно только при наличии лобового сопротивления. Но если р
обратить внимание на отношение эти); сил = ср, то увидим, что при малых углах атаки ср оно, выражаясь через ctgcp, может быть сколько угодно велико, в пределе при
? = о; / =
‘с
Понятно, что таких результатов возможно достигать только за счет использования весьма малой части силы полного давления на пластинку Р» Все подобные соображения с ясностью и простотой вытекают из рассмотрения фиг. 87, на которой дана совокупность трех кривых: силы полного давления на пластинку Р, подъемной силы Р(1 и лобового сопротивления Рс в зависимости от угла атаки ср.
Из фиг. 87 видно, что своего максимума кривая силы полного давления достигает при ср = 70°, где коэфициент ее равен 1,09; ко-эфициент равен 1,0 при ср = 90° и ср = 58°. Как видно из кривых, для судовых р^ей при ср=^50° возможно воспринимать на ось вращения 0,9 силы нормального давления.
Кривая подъемной силы имеет максимум при ср = 45°, где она равна лобовому сопротивлению и использует, таким образом, 0,58 силы нормального давления. Лобовое сопротивление имеет максимум при ср = 80°, когда коэфициент равен 1,05; оно равно 1,0 при ср = 90° и ср = 68°.
Замечание о причине вибрации плоских пластинок. Непосредственные наблюдения над пластинками флюгерами, флагами и крыльями аэропланов показывают, что при обтекании их потоком жидкости
они никогда не остаются совершенно неподвижны-ми, а, нарборот, всегда колеблются или вибрируют вблизи определенного положения равновесия, обусловленного положением их оси вращения относительно краев пластинки.
Теперь, имея полную теорию обтекания потоком жидкости плоской
пластинки, нетрудно понять причину подобного явления. Точная диаграмма давлений С передней и задней сторон пластинки, данная Фэйджем и Джохансеном (см. § 5, фиг. 51), дает отрицательное давление у спины пластинки не в виде строгой прямой, но в виде волнистой линии, для которой прямая давления, равного—1,33, является давлением средним.
Эти колебания давления по фиг. 52 обусловлены движением вихрей за пластинкой и непрерывным перемещением по ее ширине точки минимального отрицательного давления.
Сравнивая теперь между собой два полученные нами выражения ординаты центра давления (43) для неподвижных вихрей и (45) — для среднего отрицательного давления, будем иметь две величины ординаты центра давления:
о 9 ’ 2 2
1 + — cts? 1 + — ctg?
При колебании величины отрицательного давления у спинки пластинки центр давления не будет оставаться неподвижным и ордината его k2 будет указывать только среднее его положение.
Колебание величины отрицательного давления поведет за собой непрерывное смещение или колебание центра давления, а последнее вызовет колебание или вибрацию самой пластинки около ее среднего положения. •
Таким образом, причиной вибрации пластинки является движение вихрей у ее спинки.
Положение точки нулевого давления на верхней поверхности пластинки. Согласно выражению (38) давление на верхней поверхности плоской пластинки, вдоль по ее ширине, распределяется по закону:
Р~Ро = V Са -а Г1 — (cos ? + 4-ln sin • z К 4 —- л J
В зависимости от величины и знака выражения в квадратных скобках оно может быть положительным, нулем или отрицательным. Ординату
трч!си нул< вог давления, т. е. давления/? — р$-—0, найдем из выражения: ..
• (cos? 4-— In-. х - sin о)3 = 1
* * Tt L 1 Л
или 1 X 1 — COS Ф
r In 7--- =ГС-----:----•
I — X sin ?
(47;
При Н( рмальн >м I аргании потока ср = 90° будем иметь:
In j-—=*=3,14,
I— X
почему точки нулевого давления будут всегда близки краям пластинки, как то мы уже имели в § 5.
.Наоборот, при ср = 0 получим:
Раскрывая неопределенность, получим: ( 1 —cos ср sin 0
пт i к,—L. I = к----------
I sin ср \ cos 0 или
откуда
т. е. точка нулевого давления расположена в середине ширины пластинки.
Таким образом с уменьшением угла атаки ср от 90° до 0° точка нулевого давления перемещается от края пластинки к ее середине.
*
III. Сравнение результатов предлагаемой теории с имеющимися данными испытаний плоских пластинок.
Развитая нами выше теория обтекания потоком жидкости плоской пластинки конечной ширины, но бесконечной длины, является понятно предельным случаем теории обтекания плоской пластинки вообще. Так как в реальности все исследуемые нами пластинки всегда конечны по длине.
Но сопоставление результатов экспериментальных данных по исследованию плоских пластинок конечной длины, с различным отношением ширины их к длине, с чисто теоретическими выводами для пластинки бесконечно длинной позволяет нам с полной ясностью судить как о правильности предлагаемой теории, так и о влиянии конечно-
сти пластинки и пути к окончательному созданию теории обтекания плоской пластинки произвольной конечной длины.
С этой целью в на фиг. 88 даны три кривые силы полного давления потока жидкости на единицу площади плоских пластинок различного удлинения, от 1 до 6 в зависимости от угла атаки, по опытам Эйфеля1. Четвертая кривая для бесконечно длинной пластинки дана по выражению (42).
Ф ’г. 89 •
Фиг. 88 показывает, что с возрастанием длины пластинки закон изменения величины силы давления постепенно приближается к закону, данному нами для бесконечно длинной пластинки.
Для углов атаки, меньших 65°, сила давления на пластинки конечной длины становится тем больше силы давления на пластинку бесконечно длинную, чем короче сама пластинка. Наоборот, для углов атаки, бблыпих 65°,
сила давления на плас-
тинки конечной длины
меньше, чем на бесконечно длинную пластинку. Таким образом конечность длины пластинки повышает разрежение у ее спины при углах атаки, меньших 65°, и, наоборот, уменьшает разрежение для углов, ббльших 65°.
Для небольших углов атаки, от 0° до 20°, пластинки с удлинением в 2- или ~ будут давать величину силы давления, весьма близ-8 10
кую к таковой для пластинки бесконечной длины. Кривая изменения давления для бесконечно длинной пластинки дает ясную границу эф-
1 £• В. Красноперов, Экспериментальная аэродинамика, 193.5, стр. 126.
1 по
фекта конечности пластинок. Вместе с тем намечается и вполне определенный путь развития теории обтекания плоских пластинок конечной, произвольной длины. В самом деле, исследуя явление обтекания пластинки бесконечной длины (фрг. 89, /), мы рассматривали сбегание с ее краев ab и cd только двух непрерывных и параллельных между собой вихревых поверхностей aa'bb' и cc'dd'. Если же пластинка abdca (фиг. 89, //) имеет конечную длину, то с ее краев будет сноситься замкнутый вихрь abdca, afixd^Cya^ и т. д. Теория обтекания подобной пластинки должна основываться на теории поля замкнутой, бесконечно длинной вихревой поверхности. Только этим она и будет отличаться от вышеприведенной нами теории. Ее оформление не представит никаких принципиальных затруднений.
IV» Сравнение предлагаемой теории с теорией Кутта-Жуковского
Изложенная выше теория динамического взаимодействия тел и жидкости опирается на положение, что жидкость может воспринимать и передавать внутри себя импульсы внешних ей сил только одним единственным способом, а именно — образуя пару вихрей или один замкнутый вихрь, количество движения которых в точности равно подействовавшей на жидкость силе.
При длительном периоде времени получения импульсов, как то имеет место при обтекании потоком твердых тел или движении этих тел в покоящейся жидкости, пары вихрей или замкнутые вихри, возникающие на переферии пластинок или поверхности тел, будут сноситься набегающим на них потоком жидкости и образовывать за телом вихревой хвост или тень.
Этот непрерывный снос вихрей за обтекаемое тело, являясь необходимым следствием непрерывности взаимодействия между телом и жидкостью, выражает наличие силы этого непрерывного взаимодействия. И, наоборот, отсутствие за телом подобной вихревой тени или хвоста при совершенном без отрывов потенциальном обтекании тела жидкостью возможно только в случае полного отсутствия каких-либо силовых взаимодействий между телом и жидкостью.
Таким образом при силовом взаимодействии тела и жидкости состояние движения жидкости перед телом будет всегда отлично от состояния движения ее за ним.
Если теперь мы обратимся к известному всем выводу основной теоремы проф. Н. Е. Жуковского о поперечной поддерживающей силе в плоском потенциальном потоке1, с особой ясностью, простотой и критическим отношением к ней изложенной проф. А. А. Саткевичем2, то увидим нижеследующее:
При выводе теоремы о поперечной (нормальной к направлению скорости в бесконечности) поддерживающей силе, проф. Н. Е. Жуковский предполагает неотрывное, потенциальное обтекание тела жид
1 Н. Е. Жуковский, О присоединенных вихрях, Москва, 1906.
2 А. А. С а т к е в и ч, Теоретические основы гидро- и аэродинамики, ч. П. Динамика жидких тел, ОНТИ, стр. 130, § 22, 1934.
костью, т. е. одинаковое состояние потока жидкости как перед телом, так и за ним, вдали от него. А далее доказывает теорему, что при таком обтекании сила взаимодействия между жидкостью и телом может появиться только при наличии циркуляции Г, т. е. вихря, вращающего всю массу жидкости вокруг тела по закону прямолинейного, вихревого шнура:
Г _ 2 тг v г, где г — радиус окружности циркуляции, a v — касательная к ней скорость. Этот вихрь автор называет присоединенным.
Сила взаймодействия по величине будет тогда равна на единицу длины тела:
Р— рг'соГ.
Она нормальна к направлению скорости в бесконечности и не дает никакой составляющей по этой скорости, т. е. лобового сопротивления. Очевидно, что в потоке потенциальном и нециркуляционном никаких силовых взаимодействий между потоком и телом при такой теоретической постановке вопроса не получается1 2.
Таким образом независимо от вида контура обтекаемого тела подобная поперечная сила будет появляться только тогда, когда будет появляться присоединенный к телу вихрь. А этот последний может появиться только при вращении самого обтекаемого тела, приводящем во вращение окружающую его жидкость. Но тогда поперечная сила Жуковского является не чем иным, как силой эффекта Магнуса, которая точно выражается той же формулой3 и не имеет продольной составляющей.
Следовательно, подъемная сила Жуковского не является силой взаимодействия телй и жидкости, а его теория представляет собой совершенно искусственный прием определения одной из составляющих силы этого взаимодейстия, годный только для весьма малых углов атаки от 0° до 15°.
Возможность применения подобного приема прямо видна из фиг. 87, на которой мы видим, что до угла атаки ср =10° подъемная сила равна силе полного давления, а лобовое сопротивление почти равно нулю. Но оперируя подобным приемом, нельзя забывать его условность и стремиться весьма туманными и неубедительными рассуждениями доказывать необходимость появления такой циркуляции вокруг обтекаемого тела, которой в действительности не существует и существовать не может, пока же вращается само тело.
Не выражается формулой Жуковского и истинная величина подъемной силы, как то легко видеть на примере плоской пластинки. Так, выше мы имели по выражениям (20) и (22), что скорость жидкости на верхней поверхности пластинки равна:
Ui — С к coscp -j- С In
sin ср,
1 А. А. С а т к е в и ч, там же, стр. 135.
2 А. А. Саткевич, там же, стр. 127, ур-ние (92).
а на нижней поверхности
»ш = — с 1Г cos <р -}- С1л -jr^— Sin <р .
4 Ль
Поэтому циркуляция Г по поверхности пластинки .будет равна;
Г = j*C |\cos<p-{- In о
о
— sin ср |С|—Ttcoscp-f-i
sin ср Лег =2Ст:/cosср = 2^оо/cosср
По Жуковскому мы имели бы величину подъемной силы равной:
Р — р -Псо Г = р -Лоо 2Voo / cos ср = 2 р v?oo / cos ср.
При угле атаки ф = 0 и cos ср = 1 получим:
Рmax —“ 2р t^oo2 I >
тогда как в действительности сила Р равна здесь нулю. Для прямого рыбообразного профиля Жуковского1 имеем величину подъемной силы равной:
Sin ср.
При ср = 0 и Р — О, но при ср = 90°
Р=кр7^оо2»
т. е. мы имеем здесь подъемную силу при нормальном к профилю набегании потока, что тоже не соответствует опыту. На основании всего изложенного можно заключить, что, отдавая должное историческому значению теории Кутта-Жуковского, необходимо пойти по новому пути в дальнейшем развитии теории взаимодействия тел и жидкости.
ОТДЕЛ VI
ТЕОРИЯ ДЕЛЕНИЯ ПОТОКА ЖИДКОСТИ
§ 9. КОСОЕ НАБЕГАНИЕ ПОТОКА ЖИДКОСТИ НА ПЛОСКУЮ РЕШЕТКУ. ОСНОВЫ ТЕОРИИ ДЕЛЕНИЯ ПОТОКА ЖИДКОСТИ
I. Основы теории деления потока
В § 7 нами была изложена теория косого набегания потока жидкости на одну бесконечно длинную, плоскую пластинку ширины Z. Пользуясь достигнутыми там результатами анализа явления, легко распространить теперь эту теорию и на какую угодно систему плоских пластинок.
1 А. А. Саткевич, там же, стр. 142, формула (114).
Простейшей, а вместе с тем и особо важной по следствиям, является система двух параллельных, плоских, бесконечно длинных пластинок конечной ширины а, расположенных в одной и той же плоскости. Поэтому мы и приступим сейчас к развитию анализа обтекания потоком подобной системы пластинок и в частности пласти
нок бесконечно большой ширины а = оо. w
Пусть мы имеем две плоские пластинки АВ и CD шириной а, лежащие параллельно друг другу в плоскости XX (фиг. 90). Ширина щели между пластинками пусть будет равна /, а поток жид-
кости набегает на них под углом ср.
Тогда согласно § 7 в произвольной точке пространства т систему скошенных вихревых слоев АА", ВВ" и СС\ DD” будут возбуждать скорость, параллельную вихревым слоям и равную С (0 — где 6 и Oj—углы, под которыми из точки т видна ширина пластинок R R АВ и CD, и скорость, нормальную вихревым слоям, С1п^«=^.
одесь G — попрежнему напряжение вихрей. Положим теперь, что
ширина пластинок а стала бесконечно большой и края их В и D удалились в бесконечность.
Тогда расстояния точки т от этих краев /?а и /?8 станут также бесконечно большими, а направление их будет параллельно плоскостям пластинок или оси XX, и вместо схема фиг. 90 мы придем к схеме фиг. 91.
В этом случае сумма углов 6 6* = *^— 0О, где 0О— угол, под
которым из точки т видна ширина щели Z, а /?2 =/?3 = оо. Поэтому вихревые слои АА" и СС, отходящие от концов щели АС, будут возбуждать в произвольной точке пространства т скорости:
а) параллельно вихревым слоям
С(Л-в0);
б) нормально к ним • I : '
На плоскости пластинок в точке п угол 0& —0 и скорость, параллельная слоям, равна Стс. Разлагая эту скорость на слагающие параллельно плоскости пластинок — Ст? cos ср и нормально к ним Стс sin ср, увидим, что условие непроницаемости пластинок требует, чтобы набегающий поток на их плоскостях давал нормальную к ним слагающую, равную — С тс sin ср.
Что же касается до второй слагающей, параллельной плоскостям пластинок, то она остается постоянной по величине и равна -|~ С тс cos ср, во всем пространстве выше оси XX и в пространстве между вихревыми слоями II ниже оси XX. Наоборот, за вихревыми слоями в пространствах III и IV параллельно оси XX имеем постоянную скорость — Стс cos ср. Прибавив по вертикальному направлению ко всем скоростям слагающую скорости* набегания — Crcsintp, получим поле скоростей всего движения жидкости в виде:
Выше оси XX в пространстве / имеем:
р
щ = С (тс cos ср In -^1 sin ср);
Vi =— C0osincp.
На плоскости пластинок, где 0о = О, ^1=0, наоборот, по всей ширине щели АС, где 0О = тс, скорость Vi = — С тс sin ср.
Ниже оси XX, между вихревыми слоями, в пространстве //: р Un =*= C(TCCoscp4-ln-^sincp),
Vii — —С (2тс — 0Д sfc <р. '
В пространствах /// и IV, ниже оси XX, ограниченных вихревым слоем АА" или СС", имеем:
р
«ш = С (— Я cos ? 4- In sin ср), (3)
Выражения (2) и (3) показывают, что при переходе через вихревой слой ААи скорость частицы изменяется скачком в вертикальном направлении на
Фн—Фщ = — 2 Сте sin ср,
в горизонтальном направлении на
«п — «ш + 2С к cos ср,
а полная скорость частицы W изменяется на
W=2C*.
(3^)
С другой стороны, выражение для фц показывает, что, начиная с плоскости щели АС, где -6о' = тс, а V» = — Ск sin <р, скорость Vn непрерывно растет и в бесконечности, где 60' — 0, становится равной ^ц,оо= — 2Crrsinf> т. е увеличивается в два раза.
Движение между вихревыми слоями является ускоренным, жидкость находится здесь под действием силы внутреннего давления.
Поэтому направление движения в пространстве И, в бесконечности, будет происходить под углом ср к оси XX только в том случае, когда параллельно этой оси мы будем иметь скорость не Crccoscp, a 2Crccos<p.
Для получения подобной постоянной скорости, параллельной оси XX, в пространстве II мы должны всей массе жидкости ниже оси XX сообщить параллельно этой оси постоянную скорость + С тс cos <р.
Тогда окончательно ниже оси XX будем иметь скорости в пространстве // равными:
R '
«п — С(2тс cos <р 4- In ^sin ф), = — С (2тс — 60') sin ср,
(2')
а в пространствах III и IV'.
А
П
Ищ = С1п-^sin tp, 1 =4-C80'sln <p.j
Последние выражения показывают, что ниже оси XX в бесконечном расстоянии от щели частицы жидкости в пространствах /// и IV неподвижны, а все явление состоит в истечении жидкости через щель в пространство, наполненное неподвижной массой жидкости.
Имея выражения (1), (2') и (З'г), легко представить те же скорости в функции координат произвольной точки пространства и перейти к получению функций течения и уравнениям токов.
II. Функции течения и тока жидкости
Функция течения и тока жидкости в пространстве I. Во всем пространстве /, выше оси XX (фиг. 92), имеем:
[R 1
т: cos ср111 ТУ sin ?
J ’
vx =— C60sincp.
Поэтому функцию течения 5i для этой части пространства получим из выражения:
у
Si = \ — udy-{-f(x) О
или
St = — я cos <рInsin cpj о
где
RS + (х - /)’; RS =.-/• + х*.
Но интеграл
j In dy =у In R, — у _ dy =
= ^10/?!—,у4-(д:—/)arctg^j; ✓
У In Ridy = ylnRt— j-|-xarctg-^ .
П оэтому
j ,n dy ~у ,п "Ь—Z) arc,gХ^1 ~х arctg х’’
а ( г R v
5. — — C{^jcos<p-f-sin<p у ln~-J-(x— tyirctg-^-——
I L *м ’ * x —
— X arctg -^-]l+/(x),
Ии | I
— Csin <p (arctg — arctg-£j 4-Дх) =
= — C sin ? (7 - a2)+/(x) = — C 60 sin ? +/ (x).
Приравнивая это выражение выражению v , получим:/(х) = О или /(х) = const. Окончательно имеем:
/ г R ‘П
5| = —C{njcos<p4-sin(plyln + —/)(я —aj —xaa } . (4)
I L J J
Для плоскости стенки AB при у = 0, х> /, = тг и а2=0
Si = 0.
Для плоскости щели АС при J = 0, X<^Z, aj = а2 = 0
Si = -j- C?r sin ср (I — x).
Для пространства слева от оси YY, заменяя х на —х, будем иметь:
( ГР 14
51 = — С{ куcos?4-sin? Nlngi- —(/4-х)(- —aj)4-xaa В (4') \ L fQ Jf
Поэтому для плоскости стенки CD при j = 0, ^ = 0 и = т
Si = -1- С z I sin ср.
Это постоянное равно расходу жидкости через щель АС.
Положение точки нулевой скорости или раздела течения М в пространстве /. В пространстве I скорость вдоль плоскости пластинок АВ и CD имеет выражение:
। t х — I • 7Г COSCp 1П — Sin ?•
Для того чтобы эта величина могла стать равной нулю, необходимо, чтобы
1 х К COS Ф = 1п --г Sin ф,
‘ X — I т
откуда
In j^j = «ctg?. (5)
Фиг. 93.
Уравнение (5) показывает, что точка нулевой скорости М лежит справа от оси ГУ (фиг. 93).
При <р = О, ctgcp = oo их = /, т. е. точка раздела течения М лежит на краю щели в точке Л.
С увеличением угла ср от нуля до 90° она, двигаясь по плоскости АВ, удаляется от края А и при ср = 90°, когда ctg ср = 0 или
х
-—уходит в бесконечность, ибо при этом х = сю.,
Таким образом точка нулевой скорости М может занимать на плоскости АВ в зависимости от величины угла ср все положения от края щели А до бесконечного удаления от него.
Уравнение предельного тока в пространстве/. Для получения уравнения предельного тока надо в выражениях (4) рт (4Г) положить const = 0.
Уходя в бесконечность в направлении отрицательных х, точки предельного тока должны будут удовлетворять выражению (4Г) при условии: = а2 = гс и ^ = 0, т. е. равенству
у cos ср = I sin ср. (6)
На фиг. 93 указано построение этого равенства, а само равенство показывает нам, что, уходя в бесконечность, предельный ток асимптотически приближается к прямой ЯХ, параллельной оси XX и отстоящей от нее на расстояние
j = /tg©. (7)
Последнее выражение дает нам прямую связь между шириной потока, попадающего в отверстие щели, углом набегания ср и шириной щели I.
Функция течения я токи жидкости в пространстве //. Ниже оси XX, между вихревыми слоями, в пространстве // (фиг. 92) скорости частицы жидкости равны:
п
цп = С (2 гс cos ср -f- In sin ср);
Ян = — С (2 гс—90') sin ср.
Поэтому функцию течения получим здесь равной:
Г Г Р 1
5ц = — С I 12 тс cos ср In sin ср hty + f(x)
J 1 Hi j
о или
Si! = C {2 я у cos tp -|- sin In (x — I) arctg -37^ —
— x arctg ^J|+/(x).
5* * \ '
= Csin <P ^arctg — arctg j+/* (x) = Csin <p (7' — a2) -J-+/' (x) = C sin <p0o'+/(x).
Приравнивая последнее выражение скорости ^ц , получим, что /(х) =— 2rcCsin<p и /(х) =— 2irCsincp(x — /).
Теперь функция течения 5ц напишется окончательно в виде:
/ Г р -л
5ц = С I 2 пу cos ср -|- sin ср — (х— /) (« —at) ~ xaij г (8)
Для плоскости щели при jz = O, a1 = aa = 0 получим: Sn = + Стс (/ — х) sin ср.
В начале координат, точке С, при х = 0 имеем: 5ц =Cnl sin ср, т. е. полному расходу через щель. В точке А при х = / 5ц = О.
Предельные токи в пространстве //. Жидкость пространства /, втекая в пространство II, будет ограничена здесь с боков двумя предельными токами, идущими от краев щели А и С.
Постоянное этих токов равно:
а) для тока, проходящего через A, const = 0;
b) для тока, проходящего через точку С, const = Citi sin ср. Предельный ток, проходящий через точку А, будет поэтому выражаться уравнением:
г Р 1
2 к у cos ср -f- sin срIniL1— (х—0(K-Fai)—^a2j = 0« (9)
Уходя в бесконечность, точки этого тока должны удовлетворять уравнению (9) при условии:
/?1=/?4 = оо, аг = тс— ср, ав = ср или уравнению:
2 тсу cos ср — sin <р [2 тс (х —ср]==О, которое можно написать в виде:
1 ©
_ycos« — (х — /)sin<p = — sin<p. (10)
Фиг. 94.
На фиг. 94 дано построение этого уравнения, показывающее, что предельный ток, проходящий через точку А, асимптотически приближается в бесконечности к прямой d'd", параллельной вихревому
1 ф
слою АА" и отстоящей от него на расстояние - - — I sin ср.
Предельный ток, проходящий через точку С, имеет уравнение:
р
2ку cos ср 4* sin ф [у In — (х — /) (тс 4" ai) — х а3] = тс Z sin ср,
которое для точек, бесконечно удаленных от щели, т. е. при Rt = = /?4 = оо, ах = тс-—ср и а, = ср, приводит к уравнению:
у cos ср—(х — I) sin ср = ~ I sin ср . (11)
£ тс
Последнее выражение показывает, что ток, проходящий через край щели С, в бесконечности асимптотически приближается к прямой Vl\ параллельной вихревому слою АА" и отстоящей от него на расстоя-1 тс -к- co f ние — —— Z sin ср.
2 тс т
Из выражений (1'0) и (tl) видно; что расстояние между прямыми ГГ и d'd" равно —/sinср, что дает нам ширину протекающего через л
отверстие щели потока жидкости в бесконечности.
Функция течения и токи жидкости в пространствах III и /К Ниже оси XX, за вихревым слоем ЛЛ1', в пространстве ///, скорости частицы жидкости имеют выражение:
р
«ш = С In sin ср, z/щ = С G'o sin <р, где
Поэтому функцию течения получим здесь из выражения:
7 R
Shi =зд- С sin <р I In dy-\rf(x\
О
или
Siu = <— С sin ср
с
jin ^-’+(x — Z) arctg — X arctg *
Вводя пределы интегрирования, получим:
5ш = С sin «р Г у In (х — /) arctg - У — х arctg у "I +/(х); I *'4 ™ ~~ * X J
~J~ = Csin ? (агс&т^7~агс‘£ х ) +/(Л') = СО',sin .?+/'(х).
Приравнивая последнее выражение выражению скорости, г/щ, най-дем, что f(x) — O и /(х) = const. Поэтому окончательно имеем:
[Р т
J — 0(к — я1) — хяа1 • (12)
Для плоскости АВ при j/ = 0, 04 = 1: и а2 = 0 получим 5ш=0.
Слева от оси УК, в пространстве IV, мы получим токи жидкости, заменив в уравнении (12) х на—хи прибавив постоянное 2 к Cl sin ср, тогда
р
Siv = С sin <р I + у in 4- (х 4- Z) ах — х (т: — а3)]. (13)
На плоскости стенки CD, при j=0, ах = 0 и аа = гс
SIV = 4- С п I sin <р, как то и должно быть.
III. Схема движения жидкости цци делении потока
Принимая во внимание все ранее выясненное, мы можем теперь дать общую схему формы движения жидкости при делении потока.
Так, если через щель АС (фиг. 95) ширины I вытекает струя жидкости под углом <р'к плоскости отверстия, то из потока пространства / будет в отверстие поступать его часть шириной, равной /tgcp.
От всей остальной массы жидкости эта часть будет отделена предельным током КМ, упирающимся в точке нулевой скорости М в плоскость стенки АВ.
Струя, протекающая через щель АС в пространство II между вихревыми слоями АА" и СС’\ будет при этом ограничена двумя предельными токами, проходящими через края щели точки А и С.
В бесконечном расстоянии от щели ширина струи будет
-^-Zsin<p, а ее расстояния от вихревых слоев А А" и СС" будут
равна равны
1 ? > .
— — /smcp
1 * — ?/ е
и -т-------— Z sin •
2 к
Эти пространства заполняются жидкостью, всасываемой началом вытекающей из щели струи из окружающей ее массы неподвижной жидкости.
Точный чертеж всего течения при ср = 35° дан на фиг. 96. Из него видно, что наиболее интенсивно всасывает точка С, начало щели, наоборот, точка А лежит в области повышенного давления.
IV. Распределение скоростей и давлений
Сообразно выражениям компонентов скоростей (1), (2Г) и (3") будем иметь выражения полной скорости частиц жидкости для различных частей пространства в виде:
1) для пространства /, выше оси XX или щели
= С2 3 ((к cos ®+In sin ср)2 4- 0о2 sin2 р]; (14)
^4
2) для пространства //, ниже оси XX, между вихревыми слоями, вдоль по вытекающей струе
1Г22 = С2 [(2ir cos ср + In ф sin ср)2 4- (2* - 60')2 sin2 ср]; *(15)
3) для пространств /// и /I/, ниже оси XX, за вихревыми слоями
*
В бесконечном расстоянии от щели будем иметь те же скорости равными:
^l.eo =C«C°S<p, = 2Ск, ^s..=0.
(17)
Последние выражения показывают, что если ниже оси XX, за вихревыми ’ слоями, в пространствах Ш и IV, в бесконечном расстоянии от щели, там, где масса жидкости остается неподвижной, мы давление или
полный запас энергии ее будем иметь равным р0, то давления ps во всех остальных точках тех же пространств будут равны:
Рз=Рь ^з** Л 8)
Запас энергии жидкости пространства II, между вихревыми слоями, будет равен:
Л + у(2С')’.
почему давления в каждой точке пространства // будут равны:
л=л+|(«?«’-гЛ (is)
В середине щели при = и 6'0 = тг имеем:
A=/’o + y3C3ir3sin3?.
Давления в точках пространства /, выше оси XX, будут равны:
Aa=A + f(4Ca«,-Wrl’). ' (20)
&
В бесконечности:
Pi =Ро + у С* (3 + sin3 ?).
В середине щели при = и 60 = я:
А=А+£ ЗСЛ
Таким образом на плоскости щели мы имеем изменение давления в жидкости, равное для ее середины:
Pi— Рг = J- ЗС2 к3 cos3?. (21)
Это внезапное изменение давления будет равно нулю, исчезнет при ср = 90° и cos ср = О, т. е. при нормальном истечении струи жидкости. Наоборот, при ср = 0 и cos ср =1 оно достигнет своего максимального значения:
G»i—А)аах = уЗС,я2. (22)
Но при ср = 0 вихревой слой СС11 будет лежать в плоскости отверстия СА (фиг. 97) и согласно теории вихревого слоя конечной длины Г (отдел I, § It п. IV, фиг. 17) вызовет в плоскости щели циркуляцию жидкости. Подобная циркуляция, всегда наблюдаемая в жидкости
над впадиной стенки или углублением берега, вызывает в потоке, движущемся над щелью, волнообразный подъем жидкости, похожий на явления прыжка.
Указанное выше повышение давления над плоскостью стенки дает объяснение этому явлению.
Заканчивая на этом краткое изложение основ теории деления потока жидкости, я надеюсь вызвать им интерес читателя к подобному анализу явлений деления, и соединения потоков жидкости, развитие теории которых столь важно для науки и техники.
ОТДЕЛ VII
ТЕОРИЯ ОБТЕКАНИЯ ЖИДКОСТЬЮ ТВЕРДЫХ ТЕЛ КОНЕЧНЫХ РАЗМЕРОВ
£ 10. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЯ ЖИДКОСТИ ПРИ ОБТЕКАНИИ ЕЮ ПРЯМОУГОЛЬНОГО, БЕСКОНЕЧНО ДЛИННОГО БРУСА, НОРМАЛЬНО К ЕГО БОКОВОЙ ГРАНИ
I. Функция потенциала скоростей
Положим, что на вертикально стоящий бесконечно длинный брус (фиг. 98) поперечного сечения в виде прямоугольника ABCD шириной I и толщиной h набегает поток жидкости со скоростью нормальной к ширине бруса Z.
Тогда согласно основному представлению развиваемой здесь нами теории взаимодействия тела и жидкости воздействие на тело набегающего потока жидкости выразится в появлении в теле системы прямолинейных элементарных силовых трубок ab бесконечно малой толщины ds. Направление каждой трубки будет совпадать с направлением набегающего потока. Их длина А будет равна толщине тела по этому направлению в данной точке поверхности тела а. А концы этих трубок, точки а и А, представят собой источники’тонки с напряжениями, равными по величине, но обратными по знаку. Совместное действие всех этих элементарных трубок должно быть равно и прямо противоположно действию набегающего на тело потока жидкости, почему на передней грани тела АВ должны быть расположены положительные или выбрасывающие источники-точки а, а на его за*
ли ей гран» DC отрицательные или всасывающие источники -точки —Ь. Движение жидкости внутри элементарных силовых трубок будет происходить в направлении от* b к а, т. е. прямо обратно набеганию потока.
Функция потенциала скоростей отдельной, элементарной, силовой трубки нам известна из § 1, выражение (15) в виде функции
ф — С1«7 , гч
где С—постоянное напряжение точек-источников, а гг и г2 — расстояния их до произвольной точки пространства т. Зная это, лайдем функцию потенциала скоростей всей системы элементарных трубок ср, интегрируя действия трубок по всей ширине бруса Z, в виде:
ф = С
где 5 — расстояние трубки от начала координат. По фиг..98 имеем;
—s)\ I (
rJ=(y+W+(x— 1 ’
Вычислим интеграл, входящий в выражение (1):
I Inds = 4- fInrtQ ds —~ tinr22ds.
J гч 2 J 2 J
Но первый интеграл равен:
7 f In r? ds = s In r,a — -1 f Л “*,n r• +
, f (x — s)ds . f y*'ds
= 5lnr‘-s + xJ y* + (x~s)"+JУЧ-(* — ’
14 а. Я. Миювнч 209
или
(In г,ds = s In fj — s — -7Г tn G’ — У arctg =
J & у
= ^1плх —5 —xln^—jarctg —- =
• = — (x — s) In rt — s —у arctg ——.
Точно так же найдем, что
С In r^ds = — (х — s) 1 п га — 5 — (у A) arctg —.—г.
J УЛ~п
Поэтому функция потенциала скоростей равна '
Г X ' £
I — (X — s) In Г! - 5 — у arctg-у—
/ I
<f = c{ln^ds = C J <3 о о
-Их —s) lnra-H4-O' + A)arctgj^=£| =
= С рх —5)ln^—jarctg-^£ + (j + A)arctgj^ ) ♦
или
<F = (х — 0 In —у arctg+ (j-|-A)arctg^ — х 1 n -hy arctgy — (у A) arctg
или
Т = c[- (l — x) In —x In 4-у (arctgZ-y -f- arctgy ) —
•-(5’ + A)(arctg^4-arctg^)]J (3)
/?/ = х’4-У, /?1'’ = x’+^ + A)3I’ t (
/?2’ = (Z-x)3+js, y ^=(/-x)9+(j + A)2 /
и представляют собой расстояния точки т от углов Л, В9 D и С прямоугольного сечения бруса.
Имея функцию потенциала скоростей, возможно сейчас же найти и поле скоростей, вызываемое в жидкости совокупным действием всей системы силовых трубок.
Так, скорость и, параллельная осн координат ОЛ, будет равна
Эх [*“/?, /?, у'-н/-х)»^су4-а)’+(/-х)
х% у* у*
~ (^Н-А)4 + л* + ~j’ + (/-xj4 “Гун-л» +
W • „ (j-w 1 _ г Лп Я/
(^ + А)3 + (/-х)4 СН-Л)г+<1 V Яз
и = с(|п§-' —1п^) = С1пЛ^&-. (5)
\ t\2 KJ
Как показывает выражение (5), скорость и непрерывна во всем пространстве. Она равна нулю на осях Х,Х9 и Y9Y9 (фиг. 99) и изменяет свой знак при переходе частицы через эти линии. В углах Y'OX' и — XfО9 — Y9 скорость и положительна, в противоположных накрест — отрицательна. Скорость v, параллельная оси YY, равна производной функции ср по у, т. е. равна
.. _ _ г Г _ <z~л)Су+а) । (I —х)у _
“ ду L (y + W + U-xy^y' + U-x)* x{y-\-h) ху i arct z~* ardc* <l-x)y _ g у g у У + (/-х)2
ху . I — х . X .
-у+^~агс^ агс^я=А+;
, (/—х)(у-|-А) . x(y+h) 1
или
^c[arctg^4-arctg^--arctg.^-arctgy^]. . (6)
Но по фиг. 98
, I — х
ardg •-----
= / т'тВ = arctg
— / Атт' = pi
и & +
arctg —т-, ‘’J' + A
точно так же
= /_ т"т С — p'j; arctg —Dmm” =
и ?'1+₽', = 6'.
Поэтому выражение (6) можно писать в виде:
ф = С(в —б'),* (7)
С»
где 9 и (И суть углы, под которыми видны из произвольной точки пространства т длины граней АВ и DC.
Фиг. 99. поставив выражения скоростей и и ника ABCD (фиг. 100),
Но разность углов 6 — 6' = / СтВ 4-+ /4/710 = 1,4-^, почему имеем также, -X что
® = С(71 + Тг)» (8)
где углы Yj и являются углами, под которыми из точки т видны длины граней AD и ВС. Теперь мы имеем все выражения для замены системы наших воображаемых силовых трубок соответствующей ей системой вихрей.
В самом деле, со-; Полученные для прямоуголь-
п = с( 1п§.'-1п4И,
V Ri Rj (9)
^ = C(y1H-73), ,
• *
с выражениями скоростей § 1, (53) и (54), сообщаемых жидкости непрерывным вихревым слоем длины Л, увидим, что выражения (9) являются алгебраической суммой скоростей, сообщаемых точке т действием двух параллельных между собой непрерывных вихревых слоев AD и ВС длины h прямо противоположного вращения.
Отсюда является доказанной следующая теорема относительно связи уежду системой элементарных силовых трубок конечной постоянной длины h и ограничивающих ее непрерывных вихревых слоев прямо обратного вращения.
Первая теорема» Поле скоростей, вызываемых в жидкости непрерывной системой элементарных силовых трубок конечной и постоянной длины, тождественно полю скоростей, вызываемому в ней действием двух параллельных между собой непрерывных вихревых слоев той же длины и прямо обратного вращения, ограничивающих ширину системы силовых трубок.
Таким образом толщина тела по направлению набегания на него потока жидкости действует как система двух вихревых слоев, расположенных на граничных поверхностях тела по тому же направлению. Это действие аналогично действию соленоида длиной, равной толщине тела Л.
Но механический смысл результатов предыдущего анализа стдрет для нас еще более ясным, если вместо силовкх трубок (фиг. 100) мы по фиг. 101 представим себе площадь прямоугольника ABCD раз-
Фиг. 100.
битой рядом бесконечно близких горизонтальных линий, соединяющих центры вихрей бокового соленоида (фиг. 1О1>. Тогда мы получим, что дей-
ствие системы силовых трубок, возбуждаемых в теле набегающим на него потоком жидкости, эквивалентно действию системы беско-
нечно большого числа вихревых пар, вихри которых находятся здесь на постоянном расстоянии друг от друга I и вращаются в прямо обратных направлениях. Согласно первой теореме Н. Е. Жуковского (§ 2, раздел Itt) каждая такая пара вихрей будет сообщать полосе жидкости между ними шириной I совершенно апреле ленное коли-
чество движения
zn = 2zCp/ = p/»
Совокупное действие всех таких вихревых пар должно сообщить бесконечно длинной полосе жидкости ширины I количество движения М, равное и прямо противоположное по направлению количеству движения потока жидкости, набегающего на плоскость тела АВ, ибо действие равно и прямо противоположно противодействию. А противодействие тела давлению на него потока жидкости выражено нами теперь действием вихревого соленоида. Последним мы снова приводим к правильности нашего утверждения (§• 4, фиг. 39), что .единственным для жидкости механизмом, помощью которого непрерывна» жидкая среда воспринимает и передает внутри, себя импульсы сил, является пара вихрей*. Теперь мы с полной ясностью и простотой видим, что /калздщг тела на давление набегающего на него потока жидкости неизбежно должна выражаться количеством движения вихревых пар, возбуждаемых потоком на поверхности тела.
Для тела прямоугольного сечения АВ СР. на сторону которого АВ цорцально к ней набегает поток жидкости со скоростью будем иметь постоянную силу давления потока равной
Р^р/г'о9.
С другой стороны, по теореме Ш § 2 количество движения, сообщаемое вихревым соленоидом [см. выражение (27)], равно:
7И = рГ'й/.
Для равенства обеих сил необходимо, чтобы циркуляция вихрей соленоида Г была в h раз слабее циркуляции эквивалентного ей одного вихря Г (как то имело бы место при набегании потока на бесконечно тонкую плоскую пластинку), т. е.
Г = ГА или Г' = 4, h
где попрежнему Г — vj.
Принимая, кроме того, во внимание, что hl ~f есть площадь поперечного сечения нашего тела, получим силу давления потока жидкости на тело равной
P=jf=Pr2=p^^. (10)
Выражение (10) показывает, что при одной и той же площади поперечного сечения f — const сила. давления потока обратно пропорциональна толщине бруса* >
II. Поле скоростей соленоида Г
Отнесем по фиг. 102 поперечное сечение бруса ABCD к его осям симметрии ОХ и ОК и положим, что его толщина равна 21, а ширина 2h. Скорости, сообщаемые произвольной точке пространства т вихревым соленоидом AD, ВС, согласно выражениям (5) и (7) будут равны:
Ц=С(,П^“,П7Г')’ zf = C(O-O').
(Ц)
Тогда по выражениям (11) видим, что скорости и непрерывны во всем пространстве и равны нулю на осях координат, где они меняют свой знак. С удалением точки т в бесконечность по любому направлению скорости и стремятся к нулю.
Скорость v\ Пространство /. Во всем пространстве /, выше прямой АВ, между продолжением направления вихревых слоев ВВЪ и АА*, угъл 6 всегда больше угла 6', почему и скорость v здесь всегда положительна. В бесконечности 0 = 0' = 0 и v-д = 0. Наоборот, на прямой АВ угол к и скорость = — О'). В различных точ-
ках прямой АВ она непостоянна и наименьшее значение имеет в'середине, на оси OY, где угол 6' наибольший. 9
Пространство //.В пространстве //, выше прямой АВ и справа от ВВ\ угол 0 >0' и скорость v положительна. Она равна нулю на линии ВВ’\ наклоненной под углом около 45° к продолжению пря-
мой ЛВ, для точек которой 6 = 6'. Ниже прямой ВВ9' угол 6<6' и скоростью отрицательна.
Пространство ///. В пространстве ///, справа от вихревого слоя ВС и между продолжением линий АВ и DC, для произвольной точки п будем иметь скорость.
V = — Ct,+ C^ = = —С(Т2 —Ti) = =-С(е-|-п
Скорость v здесь всегда отрицательна. Она остается отрицательной до прямой СС\ в точках которой v = 0.
Прфтранство IV. Ниже прямой CD и прямых СС9 и DD" для точки р имеем:
y = 4-C(T,4-Y2) = = + C(6'1-6j =
• =4-C(6—6’).
Фиг. 102.
Скорость V здесь положительна и одинакова со скоростями пространства /.
Пространство V. Внутри вихревого соленоида ABCD, в пространстве V скорость v положительна и по величине равна:
v - + С (Т1 + Ь) =+С - 6' - 6 J = С (6 - 6'),
•так как 2к—6'= 6. Она больше скоростей пространства /. В начале координат (точке О) имеем 6' = 6Р почему скорость v равна здесь:
^0 = + 2С(«-6'). ‘
Скорость v достигает здесь своего максимального значения. Изучив поле скоростей, возбуждаемое соленоидом, мы легко получим и картину возбуждаемого им движения окружающей его жидкости.
III. Функция течения и токи соленоида
Пространство /; Л: <^1 и у 4 (фиг. ЮЗ). В пространстве У скорости произвольной точки т даются выражениями:
"=б?( ,nz?7—
г^с(е-е').-.С(ь-Н1),
где
/?1« = (х + /)3 + О'-А)2: ^12=(^4-034-(^4-a?j; Я4’ = (/-х/ + Су-ЛЛ
. 1-\-х , /-’гх
^ardg^-aKtg^;
х I—X 1—х b = a„tg—^-arcig^.
Поэтому функцию течении в этой части пространства можно писать в виде:
X
5, =cj[aKtgj±^-.re<g|±^+«dey=<-
<)
> -arctg^Ux+VO’).
У-гп J
Но интеграл »
J arcte = 0 4~ Л) a(C‘g — (з> — *)1в 1!
arcte^ifZ^ dx—V 4- *) агеЧ —(J'+А)te
J arctgy_5^<^c = — — x)arctgy——A)ln /?.;
Jarctejq?|rfx ~~(z~*)«cfg^rj4-(.y+A)ln/?£
Подставляя эти значения интегралов в выражение функции терния, получим: •
5, = С (У — A) In
+ (У 4- A) In +(/ + -O(arctg
/4- v
y—h
~ar*^^) -Н' - Л'Хагс*^ jrp~arctg7=^)+/'-v)-
• При х=0 S( = 0; кроме того, нетрудно убедиться, что f(y)~ = coftst, почему окончательно имеем:
5, = с[(У- л> ы +СУ+Л) ш (/ 4- -
. /4-.Г\ ... ч/ . I—X . I—Л\1
- arcte jzp)+<z - x><arc,g JTp -arctg y=h) I • ! 12)
При x — l будем иметь:
S,.,= С [(у - 4) in + (,+ 4) l„*A' + 21 (arctg ^4 -
. - j i
Пространство II; x^> I, y^> h. Для пространства // скорое i г имеет выражение:
С(Т1 -7,) = С(arctg ХЛ±-arctg- - arctg J±_' -f-
+ ‘“‘444 '
Поэтому будем иметь функцию течения для этого пространства по выражению:
51I=S:5U4-C —(J' —А)1п₽! —
— (/ — л) arctg 4- (у—A) In /?а—(I 4- х) arctg 4.
4- (У + *)ta Я/+Ц — х) arct£— ,п /?3* |
или окончательно
5„ = С[(у - 4) In ^+(j,+ 4) + (х +<X««tgi±)i'-7
-™*74*Z)+(J'_/x,B’eyTi~*”:,g^4)1' (12)
Пространство IV; х<^1. Скорость частиц* этого
пространства равна:
i/lv = -(- СЧъ Н“ ъ)= (2* (014~ О1)]=
= cpn-arctg <^-arctg^^-arctg(-+4-ar<:,SZ4+4
=с [s« + +"'‘4^ * - "dg4H _ arc,g !
Поэтому функция течения Siv будет здесь равна: *
х х
Slv = c\vdx = C [2^x4-О'—Л) In 4-(J 4-Л) In ^4-00 1 *
4-(/4-x)(arctg|±^- arctgj^) + ('—*) (arctg £=^-. I—x\1 ♦ — arctg-7 1 .
У — A/J
При x = 0 Siv = 0, почему окончательно имеем: 5JV=c[2Kx + (j-A)ln^ + (y4-A^n^4-4- (/ 4- х) (arctg - arctg + (/ - л) (arctg -- - arcfgj^)]- <,a) При x = l получим: • -
sw=sc[2«/4-a-A)ii>^ 4-(j4-A)ln
Пространство ///; y<Zh, х^>1. Скорость частиц пространства ///равна:
„П1 = - С(6 4- О') = - С [arctg £±2-arctg£^ + 1 х x-j-l . x —U1 >*гс1”Л+5“"гМ^]'
Поэтому функция Shi будет равна
= Stv,! + С [о-A) in^2-'4-(j4- А)^4-
4-(/Т*) (arctgarctg L^)4-(/- х) (arctgj^-
- arc‘gj^) - (у -А)1п етН-у+А) ,n “
* 2/ t 2/ \
’ — 2/(arctSj—arctg JT-ГГа) >
или
5ui = c[2K/ + (j-4)ln^+(jr4-A)ln^+ Ч-ifZ + x) (arctg <±^_аге|(Л±£
I
। ✓ j \ / . / —— x . I лс\ "1 z
+ (Z-x)(«ctg^-j-arctg —,)]•• (14)
Вводя теперь в выражение функции течения углы вместо арктангенсов, получим уравнения токов жидкости для различных пространств в виде:
Пространство /; х</, ^>Л:
c['(> + A)lng-(jz-A)ln^4-(/+A;)(?1-a1)-
— {I — х) (?а — a2)j = const. "
Пространство II; х>1, y>h:
с[(^4-Л)1п^-(^-Л)1п^4-(/4-х)(?1-а1)-
— (/—х) (?3 — аа) J — const.
Пространство IV; х<1, •< А:
c[Cy4-A)lng-(j-A)ln^-+(/ + A0(?1 + a1')-
• — (I—х) (?2 a/) J = const.
Пространство III; х^>1, у<h’
сГ2*(/-х)+О, + А)1п^-(^-А)1п^ +
+ (I + х) (?) + а/) — (Z — л) (?, + a.j')! = const.
Точный чертеж течения, вызываемого в жидкости вихревым соленоидом, дан на фиг. 104. Она дает нам картину поля магнитных линий плоского электромагнита конечной длины 2А.
Самой характерной особенностью исследуемого нами движения жидкости является протекание ее не только через торцевые плоскости, но и через боковые плоскости, на которых расположены вихревые слои. Через эти плоскости, как видно из чертежа, протекает совершенно определенный объем жидкости, ограниченный током, проходящим через концы бокового вихревого слоя. Поэтому непроница-
емость для жидкости боковых поаерхносте1Г нашего твердого бруса возможно осуществит*, только отодвинув весь вихревой ело* от боковой плоскости тела на расстояние, достаточное и необходимое для пропуска между ним и телом указанного выше расхода жидкости. Это раздвигание вихревых слоев, происходящее и в реальном явлении (фиг. 105), производит эффект увеличения ширины бруса /, а тем самым приводит к увеличению и сопротивления.
Практика дирижаблестроение непосредственным опытом пришла за последнее врейя к твердому убеждению о вреде прямых цилиндрических вставок между носом и кормой корабля. Излагаемая теория дает ответ на это столь странное на первый взгляд явление.
& И. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЯ ЖИДКОСТИ ПРИ ОБТЕКАНИИ ЕЮ БРУСА КВАДРАТНОГО СЕЧЕНИЯ ПО НАПРАВЛЕНИЮ ЕГО ДИАГОНАЛИ
I. Функция потенциала скоростей
Пусть поток жидкости, движу? щийся из бесконечности со скоростью,^, параллельной оси РУ, набегает на бесконечно длинный
брус квадратного сечения ABCD (фиг. 106), параллельно его диагонали АС. Тогда для получения функции ср потенциала скоростей обтекания бруса проинтегрируем действие системы элементарных силовых трубок cl бесконечно малой ширины Л, параллельных направлению набегающего потока*
Искомая функция потенциала скоростей ср будет равна:
•2« а • 2а
(1)
где rt2 = (x— s)2-|-(y — $)*, = — sf -|- (J -|- s)2 для измене
ния f от 0 до а.
Интеграл jin равен: I
jin г,ds = s In г, + ds =s I nr. - s +'
, x—y . 2s — (x-j-y) '2 x— у
Точно так же получим:
Г. . 2s —(х— у), । х-4-у . 2s — (х—у)
I щ rads = ------_ s 4- arctg----------------------.
I-----x-a —:—>4
У
* Фаг. iOS.
Поэтому интеграл
г. , 2s — (x4-v) , I x—у . 25—(хЦ-jO
\n-+ds =-----lnri — 5H-----------2^"Cg-------x-y ~
_ 25-(x-j>) , _xjt_J 2y-(x-j0
2 lnra-j-5 2 arctg .
Подставив пределы, найдем, что
? f in ds = C /yin /?! + 2a~ <* + /) ,n ₽2 _
A r’ I 2
-^^In^ + ^arctg2^^ di & A У
•*+.У .
-y2-arctg
2д—(x—j>), x+y
l X— у . x+jt X-l-J x— JO
i arctg ——-------------ar<*g —?
1 2 6 x—у 2 6 x-t-yf
, ио
arctg
— arctg —— -, 2 °х — у
почему окончательно имеем:
2
о
2а — (х— Н. п . х—у . 2а — (х4-у) -------lnR‘ + ' 2 a'dg Т-у х4-у . 2а — (х—у) x-f-y w .
---Р - Д У>------------p-^+xarctg
X— yj ’
где /?12 = х24->2, = a)4 + (j—а)2, #4» = (x—а)2 4-
+ (у 4- л)1— расстояния точки /п от вершин квадрата D, Л и С. Но при дальнейшем увеличении расстояния силовой трубки $ от начала координат, переходя за линию диагонали ЛС, как, например, для трубки (fl9 будем иметь!
г Л = (х — s)2 4- ( у — 2а 4- s)a, г/ = (х — s)’ 4- О' 4- 2а — $)2.
Поэтому теперь будем иметь: f, _ . 2s— (х—v4-2a) , ,
I In г, ds =---------—1----1 In r — « -i-
2 ,"'1
_____arct£r 2s-(x-j>4-2a) 2 arCt£ x4-v — 2a
|«г,Л =
2 -'э --г
х—у — 2а 25-(Jc4-j4-2a) 2 s x—y —2а ’
Второй интеграл, входящий в Выражение функции потенциала скоростей, получит выражение:
2a
С С in£ ds^cfy 1Л /?#4-х-^1п /?2R4 + J * а И £
4 --------arctg--—L-Z-X-----XL-----arctg —4—
' 2 x-j-y—2a 2 x4~J — 2а
x—у—2a . —x— v4-'2a , x—у — 2a , —x— у t
-----1----"C,g -i-y-la + ~2--------”“SJ ’
где Rt3 = (x — 2а)2 +У-
2
После всего полученного функция потенциала скоростей напишется в виде:
<р = Ср/ In R, -|- у In /?3 + (а — у) In /?г — (а у) In /?4 -|-
. х — у . 2а — (х4~у) x+j,„^tT 2<г—(х — з»)
-4----— arete------—L-=L-'--z— arctg----,-----*—
“ 2 a x—y 2 ° х-f-J/
x -!- v • к , , x 4-у . x-\-y — 2a . 2a —(x —y)
-----—-------- x arctg —4------------ arctg-:—-—
2 2 ' x — yT 2 x-\-y—
x—y x—y —2a 2Я —(x-j-j/) _ x-]-y — 2a 2 • ® x—у — 2a
x—y —2a , x-j-y 'I
------1----a"'Sj7Z7Z--2„)-
x-f-y — 2a 2
arctg
Или, выполнив приведение членов с арктангенсами, получим:
С
i 4~у In /?3 4- (а — у) In /?а —(а у) In Rt—
р^-у-ЬСх —a) arctg
—у к 2~~ ’ 2
— (х - a) arctg
v ' 6 х—у—2а' 2 2
। / п \ х-1-у — 2а х-4-у — 2а я ’
——2-------
Окончательно выражение для <р примет вид:
? = СI у In Rt 4-у In Rs 4- (а — у) !n R2 — (а 4-.у) In Rt 4~ , , it х—у . . . х+у
+(J - “>a,clB X +>- & ~<1Г ~ а> "с1е ^=4-^ ~
— (•« — <")4 + (» — 2а) arctg+ хarc,g ®
Л V 1 ^(€> •Л». 1
Для проверки, удовлетворяет ли выражение (2) уравнению Лапласа, возьмем- от пего псрмис- я вторые производные по х и у, тогда получим:
, <?у _г / ___х х — 2а ,
U дх^ [•Уха4-У (х — 2д)24~У~^
1 У\х — а)2 + (^ — аУ (а+У\х — а)* 4’(Д'4-а)а~^
+ ’««7^7=25-^
x-j-y х—у — 2а
х4~.У —2« х—у.— 2а
1 х4-у , , . —(а—у) • .
4- arctg —— 4- (х — а) г-4~
1 ьх—у 1 v . 7(х—а)а4-(у-“Л)2 1
агс(£ ±=Е__________(v_.2a)_____У______V—1;
1 cg(x—<i)°4 -(y pi)2 v 4 ) (х—2»)24-у х24-у /
„Г l x—У i *-l~y «
и = C arctg —:--------arctg-------------—
L x-^-y—2a x—у — 2a 2
। . x4-v — 2a . . x4-j>]
+а"'к^Г7^+амг^]: <’)
За_гГ У—a. । y + a
fa 1(х-аГ+(у-а)'~Г(х-аУ + (у + а)’
_____у___________у 1 .
(x—2а)’+У л*+УГ
®=-=jp = c[ ln/?x + In/?, — in/?,— ln/?4 J; (4) fa _ r Г У j_____У_________у —а _
ду ~ь Lx’+У -|"(х—2а)’О’ (х — a)«+(jz—а)»
Поэтому
ди . fa_
дх'ду —
(х-а)’4-(^4-д)’
т. е. уравнение Лапласа удовлетворено.
II. Скорости, параллельные осям координат
Согласно выражениям (3) и (4) скорости ину, параллельные осям координат, имеют выражения: а) параллельно оси XX
.. /-’Г < *—у 1 х—у । t х~1-у—2а ।
« = С arctg —: arctg------------— — 4- arctg —1 — 4-
L х~ЬУ — 2а х—У—2л ' х —у — 2а '
। i *-Ку 1
4-arctg —:
~ х — у 2 j
б) параллельно оси ГУ
V = С (tn 4- In /?,—ln/?a—In R<] = C in . (5)
A 1^4
Последняя скорость имеет уже свой окончательный вид, являяс! функцией логарифма от отношений расстояния частицы жидкости от вершин квадрата поперечного сечения бруса. Но выражение скорости и требует еще преобразования, чтобы стать столь же понятным Оно может быть написано в виде:
и — С arctg
х у X —I— у . . X у 2(1
~+у-2а ~ "гс«-^7=27. +
— arclg^TZ^
Но разность
4 Х~У . х—У i а(х—У)
arctg —:-----arctg —= arctg -х—:—s =
/f. —2а Х+У 6 л2-}-/-a'x-f-j)
. х —а . х, = arctg----arctg —.
* У — а У
С другой стороны, разность
>3rctrX ~-V~2a --arctgx>4-j«-a(3x-j-2a)_ S_
+ arctS x^y 2 g a(x—y — 2a) 2 ~~
, a(x—у — 2a) . x—a , x — 2a
0 . х — 2а .
= р; arctg-----— =3И
На основании изложенного получим выражение для скорости и в виде:
L х — а . х . . х— а . х — 2а 1 /£?.
» = С [arctg —- — arctg у -f- arctg — arctg — ----- I. (6)
Переводя арктангенсы в углы, по фиг. 106 получим:
х х — а . х . х—а
arctgyqr=a; arctg у—“v arct£yp^
Поэтому:
и = С(а-а1 + р-р1) = С(тГ + 71) = С(в_е1). (7)
Окончательно для всего внешнего пространства скорости, параллельные осям XX и УУ, получат выражения:
а = С(74--[1) = С(6 —6J ;
г' = С1П'ВД- (8)
Эти выражения скоростей дают нам возможность заменить рассматриваемую нами систему воображаемых силовых трубок эквивалентной ей системой вихрей.
В самом деле, представим себе, что на гранях бруса АВ, ВС, CD и DA расположены непрерывные вихревые слои (фиг. 107) с вращением по часовой стрелке справа от оси YY и обратно часовой стрелке слева от нее. Тогда согласно выражению (53) отдела I будем иметь, что в произвольной точке пространства т конечные вихревые слои АВ и CD будут возбуждать параллельно себе скорость С (0 — 0J. Одновременно с этим слои AD и ВС будут в точке иг возбуждать параллельно себе скорость Поэтому полная
скорость точки /и, расположенной выше оси XX, по направлению этой оси будет равна:
а = С/Т (б - 0J = С/Т (-г + Ъ),
что дает нам первую из скоростей выражения (8). Нетрудно тем же приемом найти, что на самой оси ОХ скорость U — Q, а ниже ее в точке mf отрицательна. Далее найдем, что и —~0 на оси YY и сле-
ва от этой оси меняет свой знак на обратный. Переходя теперь к скоростям, параллельным оси YY, по выражению (54) отдела I, найдем, что в точке т (фиг. 108) вихревые слои AD и ВС нормально /? •/?
к себе возбуждают скорость С'1п =у—зД и слои АВ и CD скорость
R R
СТп tf'ry . Поэтому полная скорость по оси YY будет равна: Па^4
v = C 2 In
R,R3
R2R4
что дает нам вторую из скоростей (8). Эта скорость равна нулю на прямых — XX и Y'Y', наклоненных к осям координат XOY под углом в 45°. На этих прямых она меняет и свой знак. В угле—XOY’ она положительна, так же как в угле—Y'OX'. Наоборот, в углах — Y'OX и XOY1 она отрицательна.
Весь выполненный анализ показывает, что действие на окружающую жидкость системы силовых трубок, возбуждаемых в теле набегающим на него потоком жидкости, тождественно действию на нее системы вихрей, покрывающих собой всю поверхность тела при обтекании ее потоком.
Эта система вихрей дает ту систему элементарных вихревых пар, количество движения которой должно быть оавно и ппамл -------
Фиг. 108.
положно количеству движения набегающей на тело массы жидкости. Поэтому подобная система должна состоять из равного числа вихрей прямо противоположного вращения. И мы видим, что при отсутствии плоского торца, на который поток набегает нормально, как в примере § 9, вихревой соленоид занимает всю поверхность тела.
Изложенное доказывает следующее принципиально важное, основное положение всей теории динамического взаимодействия тел и жидкости.
Вторая теорема. Поле скоростей, вызываемое в жидкости непрерывной системой элементарных силовых трубок, возбуждаемых в теле набегающим на него потоком, тождественно полю скоростей вихревого соленоида, возбуждаемого на боковой поверхности тела обтекающей его жидкостью, количество движения которого равно и прямо противоположно количеству движения набегающего на тело потока жидкости.
Количество движения вихревого соленоида на боковой поверхности квадратного бруса при набегании потока параллельно его диагонали.
Пусть фиг. 109 дает нам поперечное сечение бесконечно длинного квадратного бруса, на который поток жидкости набегает со скоростью vQ параллельно диагонали АС.
Тогда по второй теореме этот поток возбудит на всей боковой поверхности бруса вихревой соленоид с вращением вихрей по часовой
Фиг. 109.
стрелке на части поверхности АВС и против стрелки часов на части ADC.
На расстоянии у от начала координат выделяем в сечении бруса полоску ab, бесконечно малой толщины dy и длины 2(а —у). параллельную оси XX. Такая полоса вырежет на боковых поверхностях АВ и AD части вихревых поверхностей длиной ds = р^2 dy. Чтобы получить теперь количество движения, сообщаемое такой полоской жидкости параллельно оси YY. применим первую теорему Н. Е. Жуковского, по которой элементарное количество движения, даваемое полоской, будет равно:
dM=рГ2 (а — у) ds = 2/f рГ' (а — у) dy.
Полное количество движения тогда будет равно: а
М=2 /2рг — у) dy = /2 рГ2а2, (9)
О
где Г' — циркуляция вихрей на поверхности бруса.
Для бесконечно тонкой плоской пластинки ширины 2й мы имели
М = р 2аГ, -f
где Г — циркуляция вихрей на концах пластинки. Поэтому при равенстве сил получим, что
Г = /2аГ' или (Ю)
а/2 '
т. е. по сравнению q плоской пластинкой циркуляция, а следовательно, и напряжение виф&й соленоида обратно пропорциональны длине сторон квадрата.
Если мы будем сравнивать теперь между собой сопротивления пластинки и квадрата, расположенного своей диагональю параллельно направлению набегающего потока, то последнее окажется в /2 раза меньше первого, т. е. при одной и той же ширине пластинки и длине диагонали квадрата сила давления на последний Р будет равна:
где Р—сила давления
на пластинку.
Но по § 5 Р = 2, по-
-Ц у
у чему
4 иг. ПО. 2 /—
Р'=-Я==1/2 — 1,41.
/2
Совершенно подобным образом найдем, что сопротивление пластинки
Л
и круглого цилиндра должны относиться друг к другу, как 2:-^-,т. е. Л»
/*чил=4=1’27-
Измерения в Геттингене дали для круглого бесконечно длинного цилиндра сопротивление, равное 1,20. Вместе с тем в согласии с опытом мы получили, что сопротивление квадрата больше сопротивления круга. <
Вообще изложенная нами теория показывает, что сопротивление тел уменьшается с уменьшением напряжения вихрей поверхности ного соленоида, почему и полезно увеличивать боковую поверхность тела, вытягивая его в направлении набегания потока, но понятно до известного предела, так как с приближением к форме вытянутого цилиндра сопротивление по § 9 начнет снова увеличиваться.
к \
III. Функции течения и токи жидкости вихревого соленоида
Пространство /. Для всего пространства /, внешнего сечению
Кондрата или соленоида, мы имеем скорости частиц жидкости по осям XX и УУ (фиг, 110) равными:
u=C(b-bt), v = Cln^.
Функцию течения и теки жидкости для этой части пространства получим из выражения
.Г
S„p = cjlng^^+/W. О
но интеграл
j i/?1</x = (.t + a) In/?^ хarctg
j п Rtdx = (х—a) In R, — х -{-.у arctg ,
11п/?а</х=х1п/?г—х4-(у—a) arctg ——-, । у ““ С1
j in/?4rfx=xln/?4—х4-(^4-а)arctgjqzy •
Поэтому интеграл
f Ins1-2?rfx=xln £^* + aln)F+^(arctg:4r “
. x \ / . x . x—aX .
-У (arctg^-arctg—J-H
(X X \
arctg--> — arctg —j— ),
У—a У + а} а функция течения примет вид:
_ , R1R» । , /?i । [' х 4-а . х \
s-»=с |х |л я+у vkib у—arctg -
/ . х . х— а\ . I . х
- У (arctg J-3 - ~)+ а (агс g у^ ~
-afc‘Sj4^)}+/Cv)’
= С Г ( arctg —— arctg —~ /arctg —-— —
1\ У 6У + <Ч \ у —а
X *“*“ Л \ ”1 । л/ %
-arctg-y—jj-HV)-
W д X
Но переходя от арктангенсов к углам, имеем, что arctg ——— У
— arctg -—— — / 6 между рг днусами-векторами /?а, /?5;
arctg
др
arctg = / 6, между радиусами-векторами Rv R,
x
= / 0o . между радиусами-векторами Rt, Rit
•rctg7^-arcts почему
g=C(et-e)+/cy)=-c(8-el)+ro)=-«> откуда
/'(j) = 0 и f(y) = const.
Теперь окончательно мы можем написать функцию течения для всего внешнего квадрату пространства в виде:
= с[х in +а Ш - у (8 - 8J + а80], (18)
где
Выражение (13) показывает, что величина во всем пространстве J вплоть до точек грани квадрата ВС везде конечна и определенна за исключением одной точки Ct где
/?в = 0 и SMap = оо — оо.
Чтобы найти истинное значение функции SHav в точке С, с координатами х — а и j = 0, раскроем неопределенность следую цим образом: lim Гх 1п вгф- + а In^1] =,im Г(х~а) In /?8 + х In у—*0 >—*0
Но при л' = а и _у = 0 имеем: Rt = 2a; Rt = Rt = a]^2, /?я = 0. почему lim | х In р3 -j- a In
х—»aL *4*4
v—*0
j-aln/?! .
f-aln
lim (x. — a) In R3 -I- a in ~ -|-a In 2a =
<^0 2ай
= lim (x — a) In /?, -|- a In 2.
Ho
Нт (X - Л) to Rt = lim = l|m - =
1 *—a У + (Л —a)2
x — a
3(х —a)2
— ,im ~^7---Г=0-
*—a 2(x — a)
Поэтому
Яж Гх In б1] = ° 1п2
г—ди
и истинную величину функции SNap в точке С получим равной:
lim SMp = С(а^- + а In 2) = 2,26 С а. (14>
X—»д *
На фиг. 111 дан точный вид поля наружных токов, возбуждаемых квадратным соленоидом в окружающей его жидкости.
Пространство//. При переходе от точек пространства /, внешнего квадратному вихревому соленоиду, к точкам пространства //, расположенным внутри его (фиг. 112), т. е. перехода грань квадрата ВС с ее внешней стороны на внутреннюю, мы попадаем в пространство, для точек которого компоненты скорости частицы, параллельные вихревым слоям ВС и AD, суммируются и равнодействующая их равна:
С'(6'4-51) = С'[2к-(9-е1].
Равнодействующая же компонентов, параллельных слоям АВ и DC, остается попрежнему равной:
; С'(т+Г1) = С'(9-S).
Это обстоятельство приводит к тому, что, как видно из фиг. 112, компоненты скорости частиц жидкости получат здесь добавочные слагаемые, параллельно оси YY слагаемую -j-C* j/sTi: и параллельно оси XX— С |/2 к, почему для точек внутри соленоида будем иметь:
« = С[(0 — О,) — к], | = (15)
где С=С^2 ; /?,• = у’ + (а4.x)>, =>> + (<т
С другой стороны, имеем, что угол в равен: в = тс-[-а — 8, а = Р — е, почему
6 - в1 = « 4-(« + в) — ( 8 + ?) = Я + arctg + arctg - —
Л <* ""у" Л
1 У L а~]-у — arctg — ' * — arctg —~ •
Поэтому окончательно будем иметь:
И = с (arctg 4- arctg — *=c('+inW-
Функцию течения для внутреннего пространства II получим из
выражения:
X X
— С J vdx +f(y) — С ^[я 4- In
О о
где интегралы соответственно равны:
j"ln /?! dx = (а 4- х) In Rt — х 4-У arctg .
j In Rt dx — — (а — х) In Rs — х — у arctg ~р*,
!п Rt dx = х In R, — x 4- (a — у) arctg .
jln/?4dx = xln/?4 —x4-(a 4-j)arctg^-~j, почему выражение для функции течения примет вид: о , RiRt I , R, , , / х а-4-х . а—х\
StH = С In + a In 4- я х 4-у arctg —у— arctg —у J —
— {а—у} arctg — (а + у) arctg -^—14-/0');
и — у I* I У J
С (arctS - arctg^ 4-arctg - arctg -f-4-/ О') = “ С (arctg °~У 4- arctg - arctg -
— arctg 4- 7(у)= — и4-/' 0^
Приравнивая ее скорости и с обратным знаком, найдем, что /’Су) = О и /(.у) = const. С другой стороны, заменяя арктангенсы углами, получим окончательное выражение для функции течения в виде:
S.H = С р In + a In -у (0-&,)+ а ео- к (а -х - j)]. (17)
Фиг. 111 дает точную картину этих внутренних токов квадратного вихревого соленоида.
Помня, что набегающий на тело поток возбуждает на его боковой поверхности вихревой соленоид, мы должны будем поле токов этого соленоида рассматривать как эффект реакции между телом и жидкостью, а задачу об обтекании тела решать теперь как задачу сложения двух движений жидкости: а) движения, вызываемого вихревым соленоидом; Ь) поступательного движения жидкой среды со скоростью набегания.
Граничные условия непроницаемости поверхности тела дают условия расположения и вида вихревого соленоида по отношению к телу.
Все изложенное в настоящем отделе дает общую основу теории обтекания жидкостью тел конечных размеров и произвольной формы.
Эта общая основа заключается в положении, что поток, набега* ющий на тело, в случае силового взаимодействия с ним, возбуждает на его боковой поверхности вихревой соленоид, количество движения которого равно и прямо противоположно количеству движения набегающей на тело массы жидкости.
Пары вихрей или замкнутые вихри этого соленоида будут сноситься с поверхности тела за него и образовывать там вихревой хвост или вихревую тень, к каковым относится и .вихревая дорога Кармана*.
Поэтому теория обтекания тел жидкостью должна базироваться на свойствах ее движения, обусловленного наличием на поверхности тела вихревого соленоида и за телом вихревой тени. Только теория, развиваемая на этой основе, приблизит нас к истинному пониманию динамического взаимодействия тел и жидкости и всех явлений, при этом нами наблюдаемых.
Наоборот, теория обтекания тела чисто потенциальным потоком, исключая вихревой соленоид и вихревую тень за телом, тем самым исключает и возможность силового взаимодействия между телом и жидкостью. Такая теория по необходимости приводит нас к парадоксальному заключению о возможности отсутствия силового взаимодействия между телом и набегающей на него массой жидкости, чему противоречит весь опытный материал экспериментальной гидродинамики.
ЗАКЛЮЧЕНИЕ
Представляя вниманию читателей свою .Теорию динамического взаимодействия тел и жидкости", я считаю необходимым с возможной ясностью отметить, что на мой взгляд она дает положительного
по сравнению со всеми существующими теориями подобного рода, в чем она еще несовершенна и какие перспективы она может открыть для науки при своем дальнейшем развитии. Со времени Ньютона, впервые ясно выразившего мысль о том, что взаимодействие между твердым телом и окружающей его непрерывной жидкой средой может быть опрЕЛЕлено количеством движения массы жидкости, набегающей на тело в их относительном движений^иёхЗнйка~взаимодействия тела и жидкости не дала более никаких ясных и простых представлений о сущности и механизме этого взаимодействия.
В этом отношении предлагаемая мной теория, базируясь на понятии .силовой трубки* как элементарной силе взаимодействия тела и жидкости, вносит полную ясность в сущность самого процесса взаимодействия.
Сущность, заключающуюся в том, что каждая система силовых! трубок, возбуждаемых в теле набегающим на нее потоком жидкости,) во всех случаях приводит нас к одному единственному результату: у возбуждения на боковой поверхности обтекаемого тела системы вихрей, образующих вихревой соленоид, эквивалентный по своему действию на жидкость системе силовых трубок и сообщающий ей количество движения, равное и прямо противоположное количеству движения набегающей на тело жидкости.
Изложенная в этом труде теория обтекания жидкостью бесконечно тонкой пластинки бесконечной длины и конечной ширины, а также и основа теории обтекания тел конечных размеров отдела VII дает убедительные примеры справедливости этого положения.
Для бесконечно тонкой пластинки вихревой соленоид стягивается на ее краях в один замкнутый вихрь при пластинке конечной длины или в пару параллельных вихрей при бесконечной длине пластинки, особо сильного напряжения, так как он один должен сообщить жидкости все количество движения набегающего на пластинку потока.
При телах конечной толщины, по направлению набегания, напряжен-нбсть вихрей бокового соленоида уменьшается обратно пропорционально длине контура боковой поверхности. В таком же отношении сопротивление тел конечной толщины уменьшается по сравнению с сопротивлением тонкой пластинки. Вихревой соленоид на боковой поверхности тела, выражающий силовое взаимодействие между телом и жидкостью для единицы времени, в случае продолжительного периода времени этого взаимодействия постоянно сносится обтекающей тело жидкостью за тело по направлению набегания, уступая место для соленоида, вновь возбуждаемого.
Этот процесс постоянного возбуждения вихревых соленоидов на боковой поверхности тела и постоянного сноса их за тело и является основной характеристикой наличия продолжительного силового взаимодействия тела и жидкости. Поэтому все теории совершенного невихревого или потенциального обтекания тела жидкостью неизбежно приводят к парадоксальному заключению о возможности отсутствия взаимодействия тел и жидкости, т. е. отсутствия сопротивления. Вихри, сносимые с поверхности тела, образуют за ним вихревую тень или хвост.
Исследование движения жидкости здесь особо трудно и недоступно пока для нас по следующим причинам.
При непрерывности взаимодействия между телом и жидкостью снос вихрей с поверхности тела мы принуждены считать также непрерывным и происходящим в направлении набегающего на тело потока жидкости.
Тогда за телом мы получаем непрерывную вихревую поверхность, простирающуюся в бесконечность по направлению набегания. Движение жидкости внутри этой поверхности направлено к телу, т. е. прямо обратно направлению движения ее в остальном пространстве. Давление внутри такой поверхности всегда меньше наружного давления и с удалением от тела понижается на четырехкратный скоростной напор от скорости набегания. Понятно, что реальное существование подобной поверхности невозможно. Внешняя жидкость прорывает ее9 и вихревая поверхность разлагается на ряд отдельных, конечных вихрей, примером чего является вихревая дорога Кармана.
Но механизм этого разложения непрерывной вихревой поверхности на отдельные вихри нам еще совершенно неизвестен и ждет талантливого исследователя для своего объяснения. В настоящее время на основании изложенной здесь теории обтекания плоской пластинки мы можем только сказать ему, что расход жидкости внутри вихревой поверхности равен расходу набегающего на тело потока, почему появляющиеся отдельные вихри должны уносить с собой весь этот расход. Только в этом пункте изложенная мной теория должна быть далее развита и усовершенствована, чтобы мы могли окончательно подойти к пониманию всех наблюдаемых явлений природы.
Но это выясненное нами несовершенство теории совсем не влияет на достижение при ее помощи ответов на все особо важные для нас вопросы теории взаимодействия тела и жидкости, ибо точное определение величины давления потока на тело, как и величины потери энергии жидкости при его обтекании, совершенно не зависит от того или иного механизма распадения непрерывной вихревой поверхности на отдельные вихри и дальнейшей формы движения жидкости за телом. В этом отношении введенная нами гипотеза непрерывной вихревой поверхности вполне достаточна для достижения всех важных для нас результатов, а изложенная здесь мной теория обтекания плоской пластинки дает наглядный и убедительный пример справедливости всего сказанного.
Мы должны здесь решительно отойти от введенного Кирхгофом понятия о „мертвой жидкости" за обтекаемым телом, так как скорости за телом по величине равны скоростям набегания на него, а отрицательные давления для плоской пластинки доходят до величин вдвое больших давлений положительных.
Вот почему правильное очертание кормы воздушного корабля важнее, как говорит проф. Прандтль1, очертания его носа.
Но достигнутая нами правильность взглядов на сущность и механизм динамического взаимодействия тел и жидкости основана, как то видит читатель, на чисто фарадеевском представлении всего явления, на поня-
1 Проф. В. Дюрэнд, Аэродинамика, 1937, стр. 389.
тпи силовых трубок и неразрывно связанном с ним понятии вихревых соленоидов, аналогичных линиям магнитного поля и электрического тока1 2 *.
В заключение скажем, что если наше стремление приблизиться к познанию истины заставляет нас иногда сомневаться в справедливости общепризнанных положений и понятий, то здесь я полагаю, исследователь природы должен всегда руководствоваться великим поучением Галилея, что .там, где дело идет о законах природы, доступных духов-ным очам каждого, тот или другой авторитет теряет силу убедительности, уступая место силе разума9®.
1 Здесь невольно возникает мысль о возможности существования аналогичных явлений в области электромагнетизма, над чем весьма желательно была бы работа физиков.
Так, например, если наш земной шар, как и всякое другое тело, двигаясь в мировом пространстве, испытывает со стороны среды, его заполняющей, сопротивление своему движению, то по изложенной здесь теории это сопротивление будет возбуждать на его поверхности соленоид электрических токов, который выразится появлением магнитного поля.
Не в этом ли лежит причина наличия подобного поля у земного шара?
Что же касается до возможности существования сопротивления движению земли в мировом пространстве, то оно прямо вытекает из факта динамического равновесия в движении земли вокруг солнца при постоянной потере еге массы через излучение.
Но если бы подобное явление электризации поверхности земного шара действительно существовало, то он должен был бы оставлять за собой в пространстве электрическую тень или хвост, а направление его магнитной оси должно было бы совпадать с направлением абсолютного движения земного шара в галактике.
2 Архимед, Стевин, Галилей, Паскаль, Начала гидростатики^
Москва, 1932, стр. 161.
ВТКК № 2# от TTJYL !2^±, '5-5-3(4)
Редактор инж В. К. Рерих Техред. А. Д. Ч а р о в
Сдано в производство 8/XII 1938 г. Формат 60 X 921/1* Тираж 3000 экз. Изд. № 228 Уполномоченный Главлита № А-9826 Подписано к печати 18/Ш 1940 г. Печ. л. 15 Уч. авт. листов 18 Учет. № 7630 Заказ №2355
Отпечатано с матриц в 13-й тип. ОГИЗа треста «Полиграфкнига* Москва, Денисовский 30. Зак. '2923.
ОПЕЧАТКИ
Строка Напечатано Следует читать.
По чьей вине
сверху V=5 w =
юрмула (34) /И = р. 2Ь — 2пС—2иС - ... М = р • 2b(—2кС)(-2пС) =... авт.
!сверху (фиг. 52 и 53), (фиг. 51 и 52),
12 и 13 сверху Я'2 Г 1 <Р = СI (ж—Z) In -5——. . . . ; L J
1 сверху т = . Г . . = р 1. т = . . . . = рГ Z. тип.
Под чертежом пропуа ^но: Фиг. 111
Нилович.