Author: Фаддев М.А. Чупрунов Е.В.
Tags: ядерная, атомная и молекулярная физика механика физика микроэлектроника молекулярная физика
ISBN: 9785-94052-162-4
Year: 2008
Text
М.А. ФАДДЕЕВ
Е.В. ЧУПРУНОВ
ЛЕКЦИИ
ПО
АТОМНОЙ
ФИЗИКЕ
Рекомендовано УМС по физике УМО по классическому
университетскому образованию в качестве учебника для
студентов высших учебных заведений, обучающихся по
специальностям 010400 — физика и 010600 — физика
конденсированного состояния вещества и по направлению
510400 — физика
Фундаментальная
библиотека
ФИ
ФИЗМАТЛИТ
Мо с к в а
2008
ББК 22.29
Ф 15
УДК 539.18+539.19
Ре цензе пт:
доктор физико-математических наук А. А. Фраерман (ИФМ РАН)
ФАДДЕЕВ М. А., ЧУПРУНОВ Е.В. Лекции по атомной физике:
Учебник для вузов.—М.: Издательство физико-математической литера-
туры, 2008.—612 с.—ISBN 9785-94052-162-4.
Последовательное изложение экспериментальных основ и принципов кван-
товой физики в применении к строению атомов и молекул. Рассматриваются
оптические и рентгеновские спектры, а также поведение атомов во внешних элек-
трических и магнитных полях. Описываются приближенные методы расчета
электронной структуры молекулярных систем.
Для студентов физических факультетов университетов, а также других выс-
ших учебных заведений, изучающих физику атома, физику конденсированного
состояния, микроэлектронику и нанотехнологии.
Учебное издание
ФАДДЕЕВ Михаил Андреевич
ЧУПРУНОВ Евгений Владимирович
ЛЕКЦИИ ПО АТОМНОЙ ФИЗИКЕ
Редактор Л. А. Панюшкина
Компьютерная графика М. Н. Грицук
Компьютерная верстка Г. М. Красниковой
ИД №01389 от 30.03.2000
Гигиеническое заключение № 77.99.10.953.Д.005466.07.03
от 25.07.2003
Подписано в печать 12.08.2008. Формат 60x90/16.
Бумага офсетная № 1. Печать офсетная.
Усл. печ. л. 38,25. Уч.-изд. л. 41,075.
Тираж 1500 ЭКЗ. Зак. 178
Издательство Физико-математической литературы
123182 Москва, ул. Щукинская, д. 12, к. 1
Отпечатано с готовых диапозитивов
ГП «Облиздат»
248640 Калуга, пл. Старый торг, 5
ISBN 9785-94052-162-4
© Физматлит, 2008
© М.А. Фаддев, Е.В. Чупрунов, 2008
СОДЕРЖАНИЕ
Предисловие ................................................ 9
Лекция 1. Атом — структурная единица вещества ............. 11
1.1. Эволюция классических представлений об атомном стро-
ении вещества 11
1.2. Электрон........................................... 14
1.3. Заряд электрона. Метод Милликена................... 18
1.4. Массы атомов....................................... 21
1.5. Размеры атомов..................................... 26
Дополнения к лекции 1 (29). 1.1. Определение постоян-
ной Авогадро методом электролиза солей металлов (29).
1.2. Определение размеров атомов по столкновениям в га-
зовой фазе (30).
Лекция 2. Законы излучения абсолютно черного тела ......... 34
2.1. Тепловое излучение................................. 34
2.2. Закон Кирхгофа..................................... 38
2.3. Абсолютно черное тело.............................. 40
2.4. Закон Стефана-Больцмана. Формула и закон Вина .... 41
Дополнения к лекции 2 (47). 2.1. Экспериментальные
установки для исследования теплового излучения (47).
Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка 49
3.1. Формула Рэлея-Джинса............................... 49
3.2. Гипотеза и формула Планка.......................... 56
Дополнения к лекции 3 (63). 3.1. Реликтовое излучение
(63).
Лекция 4. Фотоны .......................................... 67
4.1. Фотоэффект......................................... 67
4.2. Фотонная теория фотоэффекта........................ 72
4.3. Импульс фотона..................................... 76
4.4. Эффект Комптона.................................... 78
Дополнения к лекции 4 (85). 4.1. Невозможность фотоэф-
фекта на свободном электроне (85). 4.2. Оценка времени
выхода электрона из металла при фотоэффекте на металле
(86). 4.3. Поляризация фотона (87). 4.4. Угловое распреде-
ление фотоэлектронов (88). 4.5. Уравнение Вульфа-Брэгга
(89).
4
Содержание
Лекция 5. Волновые свойства частиц........................ 92
5.1. Гипотеза де Бройля................................. 92
5.2. Экспериментальные исследования дифракции массивных
частиц.................................................. 93
5.3. Статистическая интерпретация волн де Бройля....... 101
Дополнения к лекции 5 (105). 5.1. Волновой пакет (105).
Лекция 6. Соотношения неопределенностей .................. 111
6.1. Интерференционный опыт Юнга на электронах......... 111
6.2. Соотношения неопределенностей Гейзенберга......... 115
6.3. Корпускулярно-волновой дуализм.................... 121
Дополнения к лекции 6 (124). 6.1. Эксперименты, ил-
люстрирующие выполнение соотношений неопределенно-
стей (124). 6.2. О возможности делимости фотона (127).
Лекция 7. Планетарная модель атома ....................... 130
7.1. Проблема структуры атома.......................... 130
7.2. Опыты Резерфорда по рассеянию альфа-частиц........ 131
7.3. Модель атома Резерфорда .......................... 138
Дополнения к лекции 7 (142). 7.1. Рассеяние положи-
тельных заряженных частиц на тяжелых атомных ядрах
(142). 7.2. Опыт Чедвика (144). 7.3. Состав атомного ядра
(146).
Лекция 8. Спектр излучения атома водорода и постулаты Бора 148
8.1. Спектральные серии атома водорода................. 148
8.2. Постулаты Бора ................................... 151
8.3. Энергетическое соотношение неопределенностей и есте-
ственная ширина спектральной линии .................... 155
Лекция 9. Волновая функция и операторы квантовой
механики ................................................. 158
9.1. Волновая функция и уравнение Шредингера........... 159
9.2. Операторы физических величин...................... 161
9.3. Коммутативность операторов........................ 164
9.4. Оператор момента импульса......................... 166
9.5. Собственные значения и собственные функции операто-
ров проекций момента импульса.......................... 168
9.6. Собственные значения и собственные функции оператора
квадрата момента импульса.......................... 170
Дополнения к лекции 9 (176). 9.1. Коммутационные со-
отношения для операторов квадрата модуля и проекций
момента импульса (176). 9.2. Средние значения физиче-
ских величин (179).
Содержание
5
Лекция 10. Стационарные состояния........................... 183
10.1. Уравнение Шредингера для стационарных состояний . . 183
10.2. Движение частицы в одномерной бесконечно глубокой по-
тенциальной яме.......................................... 185
10.3. Движение частицы в одномерной потенциальной яме ко-
нечной глубины .......................................... 189
Дополнения к лекции 10 (198). 10.1. Проникновение ча-
стиц в классически запрещенную область пространства
(198). 10.2. Прохождение частиц сквозь потенциальный
барьер (202). 10.3. Автоэлектронная эмиссия электронов
с поверхности металла (206).
Лекция 11. Атом водорода ................................... 210
11.1. Гамильтониан атома водорода........................ 210
11.2. Решение уравнения Шредингера для атома водорода ... 211
11.3. Основное состояние атома водорода.................. 218
11.4. Возбужденные состояния атома водорода.............. 220
Дополнения к лекции 11 (225). 11.1. Радиальные вол-
новые функции стационарных состояний атома водо-
рода (225). 11.2. Спектр излучения дейтерия (226).
11.3. Оценка неопределенности координаты электрона в
атоме водорода (229). 11.4. Водородоподобные атомы
(230).
Лекция 12. Магнитные свойства атома водорода................ 232
12.1. Классическое гиромагнитное отношение............... 232
12.2. Опыт Штерна-Герлаха и магнито-механические эф-
фекты ................................................... 235
12.3. Спин............................................... 239
12.4. Полный момент импульса электрона.................. 241
Дополнения к лекции 12 (247). 12.1. Сила, действующая
на магнитный момент в неоднородном магнитном поле
(247). 12.2. Классическая модель вращающегося элек-
трона и ее несостоятельность (248). 12.3. Оператор спина
(251).
Лекция 13. Тонкая структура спектра атома водорода ......... 254
13.1. Энергия'тонкой структуры........................... 254
13.2. Правила отбора..................................... 257
13.3. Тонкая структура энергетического спектра атома водо-
рода .................................................... 258
13.4. Тонкая структура серии Лаймана..................... 260
13.5. Тонкая структура серии Бальмера.................... 262
6
Содержание
Дополнения к лекции 13 (266). 13.1. О тонкой структуре
водородоподобных атомов (266). 13.2. Лэмбовский сдвиг
энергетических уровней (266).
Лекция 14. Многоэлектронный атом............................. 272
14.1. Опыты Франка-Герца.................................. 272
14.2. Уравнение Шредингера для стационарных состояний
многоэлектронного атома................................ 275
14.3. Тождественность частиц.............................. 277
14.4. Самосогласованное поле.............................. 281
14.5. Электронные слои и оболочки......................... 284
Дополнения к лекции 14 (288). 14.1. Аналитические ап-
проксимации волновых функций (288).
Лекция 15. Периодическая таблица химических элементов
Менделеева............................................... 290
15.1. Периодический закон Менделеева...................... 290
15.2. Внешние и внутренние электронные оболочки атомов . . 292
15.3. Электронные конфигурации основных состояний атомов
химических элементов................................... 295
15.4. Связь свойств химических элементов и электронных кон-
фигураций их атомов.................................... 303
15.5. Сродство к электрону................................ 308
Дополнения к лекции 15 (310). 15.1. Некоторые специфи-
ческие свойства химических элементов (310). 15.2. Эф-
фект Рамзауэра (320).
Лекция 16. Атомные термы .................................... 329
16.1. Сложение моментов импульса для многоэлектронных
атомов................................................. 329
16.2. Атомные термы ...................................... 334
16.3. Терм основного состояния атома. Правило Хунда... 338
16.4. Полный момент импульса многоэлектронного атома . . . 339
Лекция 17. Оптические спектры многоэлектронных атомов . . 347
17.1. Радиационные переходы в многоэлектронных атомах . . 347
17.2. Формирование спектров излучения атомов щелочных ме-
таллов ................................................ 350
17.3. Тонкая структура оптических спектров атомов щелочных
металлов............................................... 352
Дополнения к лекции 17 (360). 17.1. Спектр излучения
атома гелия (360).
Содержание
7
Лекция 18. Рентгеновские лучи................................. 365
18.1. Открытие и основные свойства......................... 365
18.2. Измерение длин волн рентгеновских лучей ............. 368
18.3. Тормозное рентгеновское излучение.................... 371
18.4. Линейчатый спектр рентгеновских лучей................ 376
Дополнения к лекции 18 (381). 18.1. Уравнения Лауэ
(381). 18.2. Синхротронное излучение (384).
Лекция 19. Закон Мозли, тонкая структура характеристичес-
кого рентгеновского излучения и эффект Оже 391
19.1. Закон Мозли.......................................... 391
19.2. Механизм образования характеристического рентгеновс-
кого излучения.......................................... 394
19.3. Тонкая структура характеристического рентгеновского
излучения............................................... 399
19.4. Эффект Оже........................................... 405
Дополнения к лекции 19 (411). 19.1. Нарушения монотон-
ной зависимости атомной массы от порядкового номера
элемента в таблице Менделеева (411). 19.2. Взаимодей-
ствие рентгеновского излучения с веществом (413).
Лекция 20. Атомы во внешних полях ............................ 423
20.1. Эффект Зеемана и триплет Лоренца..................... 423
20.2. Квантовый анализ эффекта Зеемана..................... 428
20.3. Наблюдение простого эффекта Зеемана.................. 436
Дополнения к лекции 20 (440). 20.1. Теорема Лармора
(440). 20.2. Классическая энергия магнитного момента во
внешнем магнитном поле (441). 20.3. Расчет магнитного
момента атома по векторной модели (443).
Лекция 21. Атомы во внешних полях (продолжение)............... 447
21.1. Эффект Пашена-Бака................................... 447
21.2. Эффект Штарка........................................ 450
21.3. Электронный парамагнитный резонанс................... 458
21.4. Автоионизация атома во внешнем электрическом поле . . 464
Дополнения к лекции 21 (467). 21.1. Создание экстре-
мально сильных магнитных полей (467). 21.2. Магнит-
ные моменты атомных ядер (469).
Лекция 22. Молекулы........................................... 478
22.1. Общие свойства ...................................... 478
22.2. Принцип образования ионной химической связи...... 482
22.3. Уравнение Шредингера для многоатомных молекул . . . 486
8
Содержание
22.4. Адиабатическое приближение........................ 488
22.5. Ион молекулы водорода............................. 490
Лекция 23. Метод молекулярных орбиталей ................... 498
23.1. Молекулярные спин-орбита л и и орбитали........... 498
23.2. Линейные комбинации атомных орбиталей............. 499
23.3. Применение метода МО ЛКАО к иону молекулы водорода 502
23.4. Применение метода МО ЛКАО для двухатомных гомо-
ядерных молекул...................................... 507
Дополнения к лекции 23 (516). 23.1. Основные типы
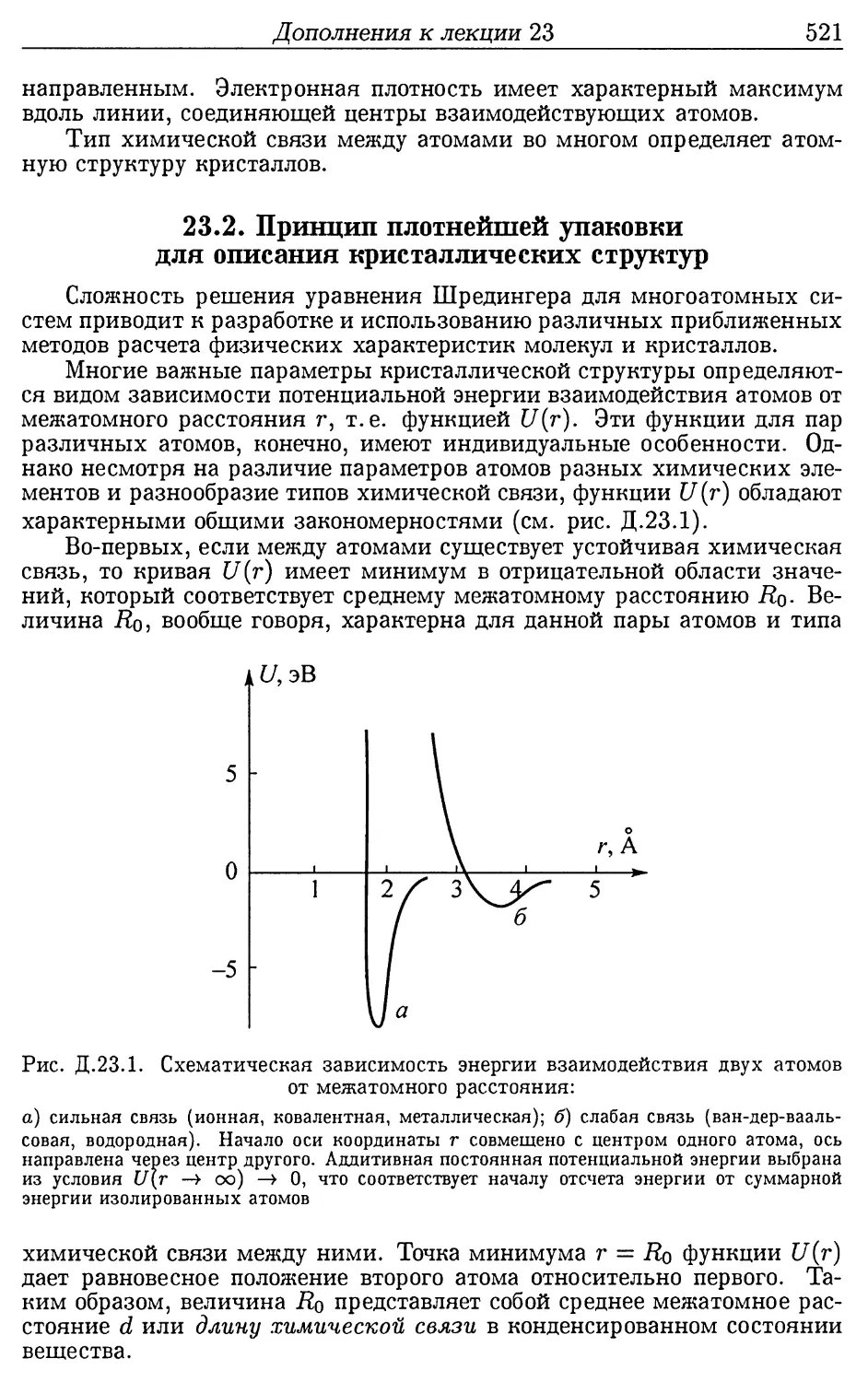
химической связи (516). 23.2. Принцип плотнейшей
упаковки для описания кристаллических структур (521).
23.3. Теорема Купмэнса (525).
Лекция 24. Вариационный метод и молекулярные термы . . . 528
24.1. Вариационный метод для молекул и секулярное урав-
нение ............................................... 528
24.2. Расчет молекулярных орбиталей вариационным методом 531
24.3. Молекулярные термы двухатомной молекулы........... 536
Дополнения к лекции 24 (544). 24.1. Метод валентных
связей (544).
Лекция 25. Молекулярные спектры............................ 553
25.1. Составные части энергии молекулы.................. 553
25.2. Вращательные спектры.............................. 554
25.3. Колебательно-вращательные спектры................. 560
25.4. Принцип Франка-Кондона и полосатые оптические спек-
тры ................................................. 569
25.5. Рентгеновские молекулярные спектры................ 576
Дополнения к лекции 25 (580). 25.1. Комбинационное рас-
сеяние света (580).
Приложение ................................................ 583
Список литературы ......................................... 611
Если бы в результате мировой катастрофы все накопленные
научные знания оказались бы уничтожены и к грядущим поколе-
ниям людей перешла бы только одна фраза, то какое утвержде-
ние принесло бы наибольшую информацию? Я думаю, что это
атомная гипотеза: все тела состоят из атомов — маленьких
частиц, которые находятся в беспрерывном движении, при-
тягиваются на небольшом расстоянии, но отталкиваются,
если одно прижать к другому. В этой фразе содержится неве-
роятное количество информации о мире, стоит лишь приложить
к ней немного воображения и чуть соображения.
Ричард Фейнман
ПРЕДИСЛОВИЕ
Развитие экспериментальных и теоретических методов иссле-
дований в важнейших областях физики и химии требуют от спе-
циалистов владения современными представлениями квантовой
физики на уровне применения их в повседневной практической
работе. Это связано с тем, что, с одной стороны, принципы, на ко-
торых базируется работа современных экспериментальных уста-
новок, являются прямым следствием законов атомной физики, а
с другой, — интерпретация полученных результатов может прово-
диться лишь на основе современных квантовых представлений.
Сказанное в полной мере относится к таким приоритетным напра-
влениям современного естествознания, как нанофизика и всевоз-
можные нанотехнологии. Наноразмерные объекты описываются
законами квантовой физики, и владение квантовыми законами
и представлениями является неотъемлемой частью профессиона-
лизма современного физика-исследователя и технолога.
Атом и молекула — это «природные» нанообъекты, поэтому
изучение законов квантовой физики в университетах начинается,
как правило, с изучения атомной физики.
Настоящий учебник содержит описание законов квантовой фи-
зики в применении к строению атома водорода и многоэлектрон-
ных атомов, их оптических и рентгеновских спектров, а также по-
ведению атомов во внешних электрических и магнитных полях.
Часть книги посвящена описанию свойств простейших молекул,
их оптических и рентгеновских спектров, приближенным мето-
дам расчета электронной структуры молекулярных систем. Рас-
смотрены экспериментальные методы атомной физики и резуль-
таты фундаментальных опытов, на которых базируются основные
принципы квантовой физики.
Исходной базой данного учебника является курс общей физики
(раздел «физика атома»), который в течение многих лет читался
авторами студентам 3-го курса физического факультета Нижего-
родского государственного университета им. Н.И. Лобачевского.
Отличительной особенностью данного учебника является пре-
жде всего его структуризация. Основной его частью являются 25
лекций. Лекции содержат определенный минимум материала, ко-
10
Предисловие
торый необходимо усвоить студенту для понимания последующих
разделов атомной физики и для последующего систематического
изучения методов квантовой механики. Кроме того, эти знания
пригодятся и при изучении других курсов, где используются кван-
товые представления.
Кроме обязательных лекций студенту предлагаются многочис-
ленные дополнения, которые могут представлять интерес для наи-
более подготовленных студентов, а также для тех, для кого эта
книга будет не первой прочитанной по физике атома книгой. В на-
стоящем учебнике можно также найти биографии физиков (в ос-
новном нобелевских лауреатов), внесших значительный вклад в
развитие квантовой физики. Предлагаемое небольшое количество
задач также определяет тот минимум, которым должен овладеть
студент при изучении данного курса.
Данная книга ориентирована прежде всего на студентов-фи-
зиков. Предполагается, что читатель освоил все разделы клас-
сической общей физики, а также владеет необходимым матема-
тическим аппаратом. Она может служить также пособием для
аспирантов, молодых преподавателей и научных сотрудников, од-
ним словом, для тех, кто хочет просто «освежить» свои знания в
области физики атома и атомных явлений.
Данный учебник разработан в процессе деятельности Образо-
вательно-научного центра «Информационно-телекоммуникацион-
ные системы: физические основы и математическое обеспече-
ние. Повышение качества и увеличение масштабов подготовки
специалистов на основе интеграции образовательной, научной и
инновационной деятельности», созданного в Нижегородском госу-
дарственном университете в результате победы в конкурсе инно-
вационных вузов в рамках приоритетного национального проекта
«Образование» в 2006 г.
Авторы благодарят своих коллег — сотрудников физического
факультета и Научно-исследовательского физико-технического
института (НИФТИ) Нижегородского государственного универси-
тета им. Н.И. Лобачевского (ННГУ) за прочтение рукописи, со-
веты, рекомендации и обсуждение, которое сопровождало напи-
сание данной книги. Особую благодарность авторы выражают
заместителю директора ИФМ РАН доктору физ.-мат. наук Фра-
ерману А. А., доценту Мордовского государственного университета
Рябочкиной П.А., заведующему кафедрой теоретической физики
ННГУ Демиховскому В. Я., профессору Вугальтеру Г. А., доцен-
там Бурдову В. А. и Максимовой Г. М., старшему преподавателю
Хомицкому Д.В., заведующему лабораторией физики металлов
НИФТИ профессору Чувильдееву В.Н., доценту кафедры элек-
троники твердого тела Маркову К. А., профессору кафедры фи-
зики полупроводников и оптоэлектроники Ежевскому А. А., до-
центу кафедры кристаллографии и экспериментальной физики
Сафьянову Ю.Н., старшему преподавателю Марычеву М. 0.
Лекция 1
ATOM — СТРУКТУРНАЯ ЕДИНИЦА ВЕЩЕСТВА
1.1. Эволюция классических представлений
об атомном строении вещества
Весь период развития физико-химических представлений об
атомном строении вещества можно условно разделить на два пе-
риода. В первый период разрабатывались идеи об атомном стро-
ении вещества и структуре атома на основе принципов классиче-
ской физики. Этот период простирается от античности до начала
XX века. Для второго периода развития атомной физики харак-
терно развитие квантовых представлений о строении микромира
и, в частности, о строении атомов. Начало этого периода можно
датировать 14 декабря 1900 г., когда Макс Планк выступил на за-
седании Немецкого физического общества с изложением квантовой
гипотезы, с помощью которой удалось построить теорию теплового
излучения.
Трудно указать дату и автора первого учения об атомах. Нам
известно, что идея атома впервые в наиболее отчетливой форме
была сформулирована Левкиппом и его учеником Демокритом в
V веке до н.э.
Одним из основных вопросов, который решали древнегрече-
ские философы, заключался в установлении предела делимости
вещества. Атом появился как элемент структуры вещества, как
естественный предел делимости, дробления (по-древнегречески
«атом» — неделимый). В отличие от своих предшественников,
Левкипп и Демокрит исходили из того, что множественность ве-
щей в природе обусловлена не составом, а строением. По их мне-
нию, тела отличаются друг от друга формой простейших частиц
(атомов) и их взаимным расположением. Между атомами нахо-
дится пустота, а сами атомы совершают определенные движения.
«Как трагедия, так и комедия могут быть написаны одними и теми
же буквами, так и все разнообразие существующего в мире осу-
ществляется одними и теми же атомами, поскольку они имеют
различные положения и выполняют различные движения».
12 Лекция 1. Атом — структурная единица вещества
Сторонником атомной теории был греческий философ Эпикур
(ок. 342-270 гг. до н.э.), а в I веке до н.э. один из его последо-
вателей, римский поэт и философ Лукреций Кар изложил учение
Эпикура в поэме «О природе вещей». Благодаря этому труду уче-
ние Эпикура сохранилось для следующих поколений. К сожале-
нию, один из крупнейших ученых древности, Аристотель (384-
322 гг. до н.э.) атомистические представления не принимал, а
поскольку его научные взгляды преобладали в Средневековье, то
идеи атомарного строения вещества были забыты до конца эпохи
Возрождения, когда на смену умозрительным философским рас-
суждениям пришел физический эксперимент.
По-видимому, одним из первых мыслителей Нового времени,
кто вновь вернулся к идее атомного строения вещества, был фран-
цузский теолог и философ П. Гассенди (1592-1655). Гассенди пред-
ставлял различные вещества в виде смесей атомов подобно смеси
песчинок в горстке песка или камня. При этом с помощью ха-
рактера движений атомов он пытался описывать различные агре-
гатные состояния вещества. Реакцией на гипотезу Гассенди было
запрещение французским парламентом в 1624 г. распространения
учения об атомах под страхом смертной казни.
Р. Бойль (1627-1691) и И. Ньютон (1643-1727) исходили в сво-
их рассуждениях из представления о существовании неделимых
частиц вещества. Однако ни Бойлю, ни Ньютону не потребовалось
детальной атомистической теории для объяснения интересовав-
ших их явлений, и результаты проведенных ими экспериментов
не дали ничего нового атомной теории.
Лишь в начале XIX века экспериментальная химия пришла к
выводу о неизбежности существования атомов. Выяснилось, что
в химических реакциях сложные вещества можно разлагать на
составляющие не беспредельно. Были обнаружены простые веще-
ства — химически неразложимые субстанции, названные химиче-
скими элементами. Существование химических элементов позво-
лило успешно объяснить многие экспериментально установленные
закономерности. Убежденным сторонником атомного (корпуску-
лярного) строения вещества был М.В. Ломоносов (1711-1765).
Первым действительно научным обоснованием атомистической
идеи явилась работа английского школьного учителя математики
Дж. Дальтона (1766-1844), которая была опубликована в 1803 г.
Дальтон изучал свойства газов, в частности, измерял отношения
объемов и масс газов, вступавших в реакцию образования химиче-
ского соединения. Примером такой реакции является образование
воды из водорода и кислорода. В ходе своих исследований Даль-
тон установил, что отношения масс прореагировавших исходных
веществ всегда выражаются отношениями небольших целых чи-
сел. Так (по современным данным, более точным, чем измерения
Дальтона), при образовании воды ЩО с 16г кислорода в реак-
1.1. Эволюция классических представлений об атомном строении 13
цию вступают 2,016 г водорода, а при образовании перекиси водо-
рода Н2О2 с 2,016 г водорода соединяются 32 г кислорода. Массы
кислорода, реагирующие с одной и той же массой водорода при
образовании этих двух соединений, соотносятся между собой как
16:32 = 1:2.
На основе полученных результатов Дальтон сформулировал
свой «закон кратных отношений». Согласно этому закону, если
два элемента соединяются в разных пропорциях, образуя разные
соединения, то массы одного из элементов, соединяющиеся с од-
ним и тем же количеством второго элемента, соотносятся как не-
большие целые числа. Убедительное подтверждение этого закона
дают соединения кислорода с азотом. В пяти разных оксидах
азота массы кислорода на единицу массы азота относятся как
1:2: 3:4: 5.
По второму закону Дальтона — «закону постоянных отноше-
ний» — в любом химическом соединении соотношение масс вхо-
дящих в него элементов всегда одно и то же.
На основе своих исследований Дальтон постулировал, что
1) все атомы одного и того же химического элемента тожде-
ственны во всех отношениях, в частности, одинаковы их массы;
2) атомы разных химических элементов имеют неодинаковые
свойства, в частности, неодинаковы их массы;
3) в вещество, представляющее собой химическое соединение,
в отличие от элемента, входит определенное целое число атомов
каждого из составляющих его элементов;
4) в химических реакциях может происходить перераспределе-
ние атомов, но ни один атом не разрушается и не создается вновь.
Кроме того, Дальтон первым ввел понятие «атомный вес» («ато-
мная масса»).
Основанная на этих четырех постулатах атомная теория Даль-
тона давала простое объяснение законов постоянных и кратных
отношений. Постулаты Дальтона имели преимущество перед аб-
страктными рассуждениями древнегреческих атомистов, так как
эти постулаты позволяли объяснить и увязать между собой резуль-
таты реальных опытов, а также предсказать результаты новых
экспериментов.
Большое количество экспериментальных данных, относящих-
ся не только к газам, но также и к жидкостям и твердым соеди-
нениям, собрал Й. Берцелиус (1779-1848), который провел точные
измерения реагирующих масс элементов для многих соединений.
Его данные подтвердили сформулированные Дальтоном законы
и убедительно продемонстрировали наличие у каждого элемента
наименьшей единицы массы.
Итальянский химик А. Авогадро (1776-1856) ввел понятие эле-
ментарной единицы вещества — молекулы, которая состоит из
атомов. Молекулы простых веществ состоят из одинаковых ато-
14 Лекция 1. Атом — структурная единица вещества
мов, молекулы сложных веществ — из разных. В 1811 г. Аво-
гадро выдвинул гипотезу, которая имела огромное значение для
развития атомных представлений в физике и химии. Эта гипо-
теза состояла в том, что равные объемы газов, находящиеся при
одинаковых температуре и давлении, содержат одно и то же
число молекул.
Развитие атомной теории вещества выдвинуло проблему опре-
деления масс атомов и молекул. Количество молекул, содержа-
щихся в макроскопическом объеме вещества, чрезвычайно велико.
Измерения масс веществ, участвующих в реакциях, давало хими-
кам данные лишь об относительных значениях масс атомов. Для
связи микроскопических и макроскопических величин оказалось
очень ценным понятие моль. Первоначально моль был определен
как количество вещества, содержащее столько же молекул, сколько
атомов водорода содержится в 1г водорода. Затем по ряду при-
чин, которые будут изложены далее, было принято иное, более
корректное определение. Моль — это количество вещества, в ко-
тором содержится столько же молекул, сколько атомов углерода
содержится в 12 г изотопа углерода 12С. Определение изотопа при-
ведено в конце данной лекции.
Количество молекул, содержащееся в одном моле, названо по-
стоянной Авогадро N&. Расчет этой фундаментальной величины
являлся одной из самых сложных задач физики и химии на про-
тяжении десятков лет. Один из самых точных методов измерения
постоянной Авогадро — рентгенографический — описан в допол-
нении 18.1 к лекции 18 данной книги. В настоящее время принято
значение Na = 6,0221367(36) • 1023 моль-1.
Было измерено, что один моль идеального газа при нормаль-
ных условиях (т.е. при температуре 0°С и давлении 1атм) за-
нимает объем приблизительно 22,4 литра. Эта важная физиче-
ская величина часто называется объемом Авогадро Рд- Можно
вычислить, что 1л воздуха при нормальных условиях содержит
примерно 3 • 1022 молекул кислорода, азота и некоторых других
газов.
Прямое экспериментальное доказательство атомного (дискрет-
ного) строения вещества было получено в 1914 г., когда М. Лауэ
с сотрудниками открыл дифракцию рентгеновских лучей на кри-
сталлических решетках.
1.2. Электрон
Идея «атомов электричества» определенно следует из анализа
законов электролиза, открытых М. Фарадеем (1791-1867). Если
пропускать одно и то же количество электричества через различ-
ные электролиты, то количество одновалентного вещества (эле-
мента), которое выделяется на электродах, пропорционально атом-
1.2. Электрон
15
ной массе. Например, если некоторое количество электричества
способствует выделению 35,45 г хлора, то при таком же количе-
стве электричества всегда выделится 107,87 г серебра.
Таким образом, один грамм-атом любых одновалентных ато-
мов в растворе (ионов) всегда несет с собой одно и то же коли-
чество электрического заряда. Эта величина заряда F названа
числом (постоянной) Фарадея, которое равно приблизительно
96485 Кл/моль или 2,893 • 1014ед. зар. CGSE/моль (см. дополне-
ние 1.1). Если при пропускании тока на электроде выделяется
двухвалентный элемент, то один заряд F переносится половиной
грамм-атома этого вещества и т. д.
По закону Авогадро 1 моль вещества содержит Na частиц. Счи-
тая, что заряд всех частиц одинаков, можно найти элементарный
заряд («атом электричества»)
F
Na
9,65 • 104
6,022 • 1023
« 1,603 • 10"19 Кл к
« 4,803 • 10"10 ед. зар. CGSE.
Уместно вспомнить, что убежденным сторонником атомарного
строения электричества был один из первооткрывателей закона
сохранения энергии Г. Гельмгольц (1821-1894), который опубли-
ковал свои идеи по данной проблеме в 1881 г.
В середине XIX века был выполнен ряд интересных экспери-
ментов, в которых исследовался электрический ток в стеклянных
трубках, наполненных газом при низких давлениях. Такие изде-
лия назывались трубками Гейсслера, по имени немецкого стекло-
дува Г. Гейсслера (1815-1879), который, сконструировав ртутный
насос, сумел добиться сильного разрежения газа внутри сосуда.
В трубке Гейсслера, содержащей очень разреженный газ, рас-
полагались два электрода с проделанными в них отверстиями, как
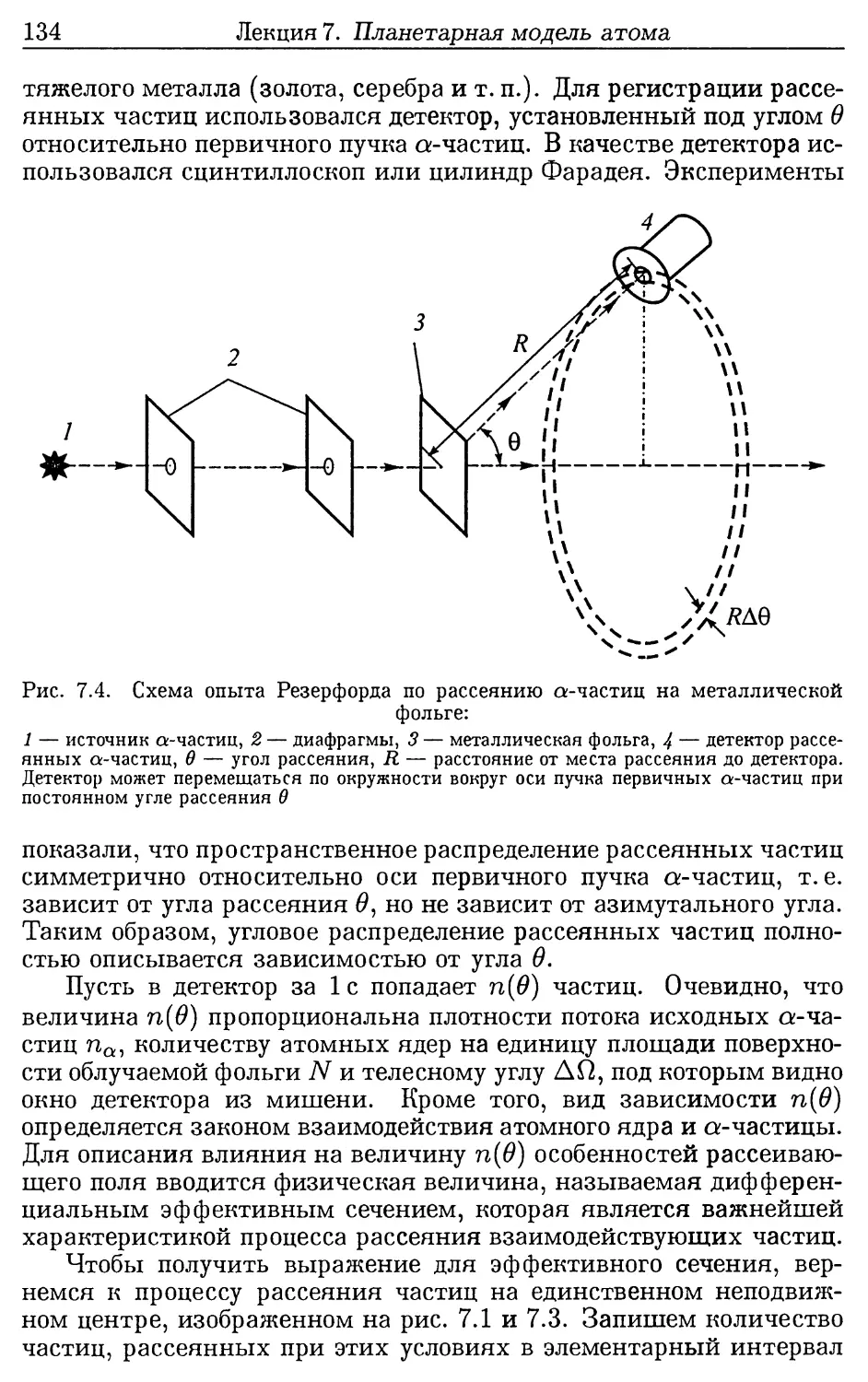
Рис. 1.1. Схема газоразрядной трубки для наблюдения катодных лучей:
Е — источник высокого напряжения, R — реостат. Знаки «+» и «—» указывают поляр-
ность электродов. Штриховые линии — траектории катодных лучей
это показано на рис. 1.1. На электроды подавалось высокое элек-
трическое напряжение.
16 Лекция 1. Атом — структурная единица вещества
При подключении трубок к высоковольтной обмотке индукци-
онной катушки (источнику высокого напряжения) они испускали
яркое свечение. Было обнаружено, что сквозь каналы, просверлен-
ные в аноде, проходят потоки «лучей», которые вызывают флуорес-
ценцию на внутренней поверхности стенок трубки.
Наблюдаемое свечение Э. Гольдштейн (1850-1930) назвал «ка-
тодными лучами», полагая, что оно испускается поверхностью
катода в направлении перпендикулярном ей. Тщательные исследо-
вания катодных лучей провел У. Крукс (1832-1919), который уста-
новил, что характер разряда в трубке зависит от давления и что
разряд полностью исчезает при высоком вакууме. Крукс обнару-
жил механическое и флуоресцирующее действие катодных лучей,
а также их отклонение в магнитном поле.
Природа «катодных лучей» оставалась загадкой. Крукс предпо-
лоркил, что открыл «четвертое состояние вещества». Гольдштейн
полагал, что это волны, но продольные, в отличие от поперечных
световых.
Более поздние исследования Ж. Перрена (1870-1942) показали,
что вызывающие свечение «катодные лучи» представляют собой
отрицательно заряженные частицы, которые движутся прямоли-
нейно, но могут отклоняться магнитным полем. Однако некото-
рые физики отрицали связь отрицательно заряженных частиц с
наблюдаемым свечением. Оставались неизвестными заряд и масса
частиц.
Только в 1897 г. Дж. Дж. Томсон (1856-1940) эксперименталь-
но доказал, что все частицы, образующие катодные лучи, тожде-
ственны друг другу. С помощью разрядной трубки особого типа,
изображенной на рис. 1.2, Томсон измерил скорость и отноше-
ние заряда к массе частиц катодных лучей, названных электро-
нами. Заметим, что трубка Томсона была первой «электронно-
лучевой трубкой» с экраном, предшественницей телевизионного
кинескопа. Электроны вылетали из нагретого катода и ускоря-
лись высоким напряжением С7, созданным в трубке между като-
дом и анодом. Через диафрагмы проходили только те частицы,
которые двигались вдоль оси трубки (см. рис. 1.2). После этого
электроны попадали на экран, вызывая его свечение.
Работа электрического поля приводит к увеличению кинетиче-
ской энергии заряженной частицы на величину
ДЕ = qU, (1.1)
где q — заряд частицы.
Напряжение J7, разгоняющее частицы в трубке, было столь ве-
лико, что их конечная скорость на несколько порядков превышала
начальную. Тогда с приемлемой точностью можно полагать, что
все частицы, прошедшие через диафрагмы, имеют приблизительно
одинаковую скорость.
1.2. Электрон
17
В трубке Томсона была установлена пара пластин электриче-
ского конденсатора, которые, если на них подавалось разность по-
тенциалов, могли отклонять электроны. Кроме того, Томсон ис-
пользовал пару катушек с током, с помощью которых можно было
Рис. 1.2. Схема электронно-лучевой трубки Томсона
создавать магнитное поле (см. рис. 1.2), способное также откло-
нять движущиеся электроны, но в противоположную сторону.
Электрическая сила F#, действующая на заряд q со стороны
электрического поля Е, равна
Fe = qF. (1.2)
Сила Лоренца Fp^ действующая со стороны магнитного поля
В, при данном взаиморасположении векторов скорости частицы v
и индукции поля В равняется
FB = -vB,
С
(1.3)
где с — скорость света в вакууме.
Изменяя напряжение на конденсаторе и ток в катушках, Том-
сон отрегулировал электрическое и магнитное поля так, чтобы ре-
зультирующее отклонение электронов было равно нулю. В такой
ситуации электронный пучок (точнее, его след на экране трубки)
находился в таком же положении, как и при отсутствии обоих по-
лей. Поскольку в этом случае модули обеих сил Fe и Fp^ действую-
щих на электрон, равны друг другу, величина скорости электронов
равна следующему выражению:
v = (1.4)
фундаментальная
библиотека
18
Лекция 1. Атом — структурная единица вещества
Так как начальной кинетической энергией электронов в опыте
Томсона можно пренебречь, то уравнение (1.1) записывается в сле-
дующем виде:
массе:
с2 (Е\2
2U \В
(1-6)
где тпе — масса электрона, е — абсолютная величина его заряда.
Подставляя в (1.5) выражение для скорости (1.4), получим от-
ношение заряда частицы к ее
е _
те
Следует учесть, что уравнение (1.5), а следовательно и (1.6),
справедливо для частиц нерелятивистской энергии. Легко пока-
зать, что при ускоряющем напряжении в несколько десятков ки-
ловольт электроны можно рассматривать как нерелятивистские.
Измерения в экспериментах величин Е, В и U позволяют вы-
числить отношение е/те для исследуемого электрона. По измере-
ниям, проведенным в конце XX века, оно равно 1,75881962(53) х
хЮ11 Кл/кг. Для перевода в систему Гаусса необходимо эту вели-
чину умножить на 10-4с, где с — скорость света в вакууме, рав-
ная с = 2,99792458 • Ю10см/с. Таким образом, е/те ~ 5,2728 х
х1017ед. зар. CGSE/r.
Эксперименты Томсона показали, что электроны в электронно-
лучевых трубках возникают при изготовлении катодов из различ-
ных металлов.
Так как электроны, несомненно, появлялись из атомов, то ре-
зультаты опытов позволяют сделать следующие выводы:
1. Атомы обладают сложной структурой.
2. Электроны входят в состав атомов.
3. Методы экспериментальной физики позволяют разделять
атомы на составные части.
1.3. Заряд электрона. Метод Милликена
Первое экспериментальное определение заряда электрона было
проведено американским физиком Р.Э. Милликеном (1868-1953) в
ходе исследований 1908-1911 гг. Схема установки приведена на
рис. 1.3.
В область пространства между пластинами плоского конденса-
тора с помощью пульверизатора впрыскиваются маленькие капли
масла. К пластинам прикладывается разность потенциалов Uy.
Для наблюдения за поведением маленьких капель служит оптиче-
ский микроскоп.
При распылении масла отдельные капли могут случайным об-
разом приобретать различные электрические заряды (как поло-
1.3. Заряд электрона. Метод Милликена 19
жительные, так и отрицательные). В микроскоп видно, что при
определенном значении электрического поля Е некоторые капли
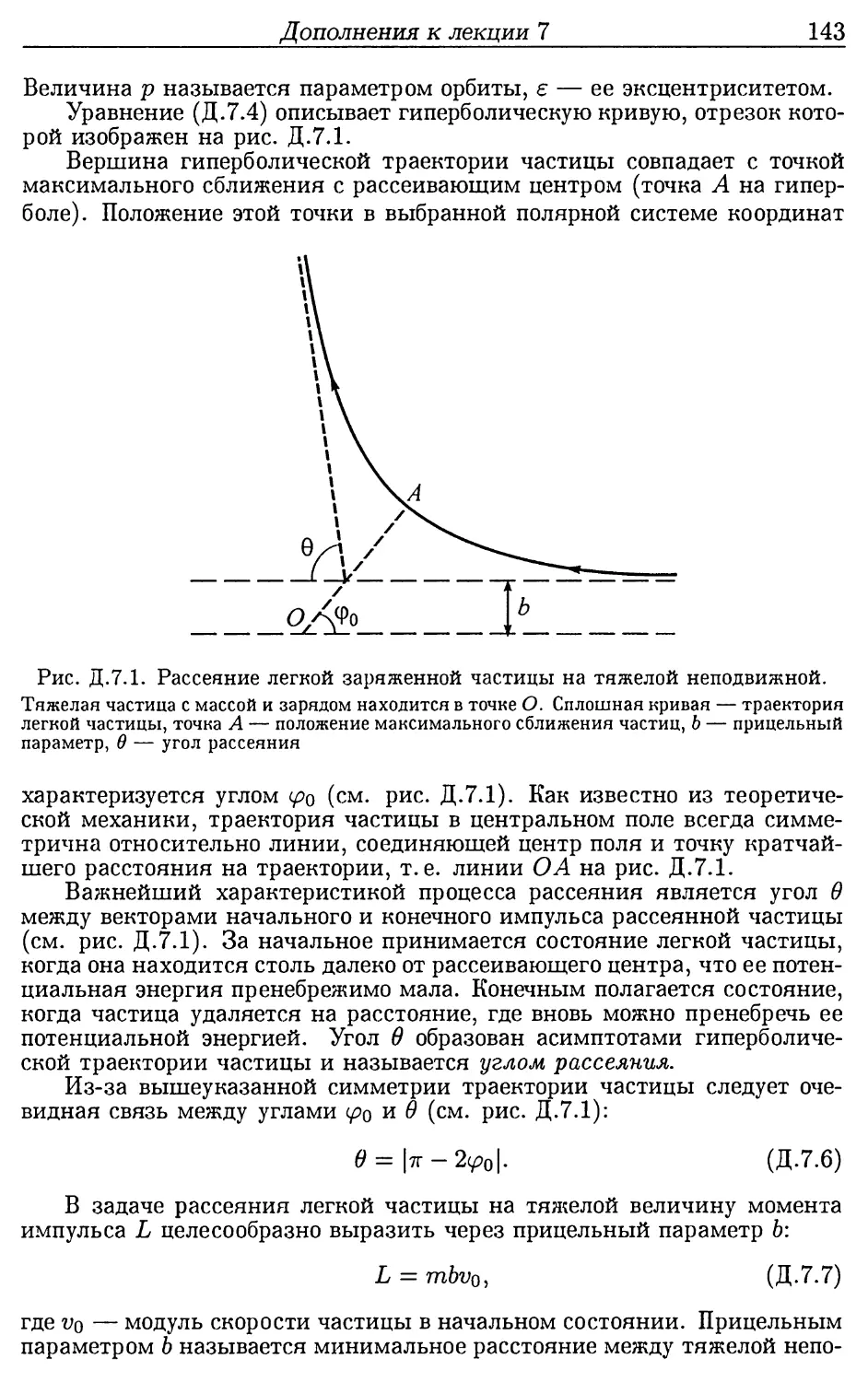
Рис. 1.3. Схема установки Милликена для определения заряда электрона:
1,2 — пластины плоского конденсатора, 3 — сопло пульверизатора, 4 — рентгеновская
трубка в защитном кожухе, 5 — окуляр микроскопа, 6 — электрическая батарея, 7 —
делитель напряжения. Штриховые линии между пластинами конденсатора ограничивают
поле наблюдения движущихся капелек
поднимаются вверх, другие опускаются вниз, что свидетельствует
о различии их электрических зарядов.
Допустим, что электрическое поле Е между пластинами кон-
денсатора будет направлено вниз. Рассмотрим каплю, которая
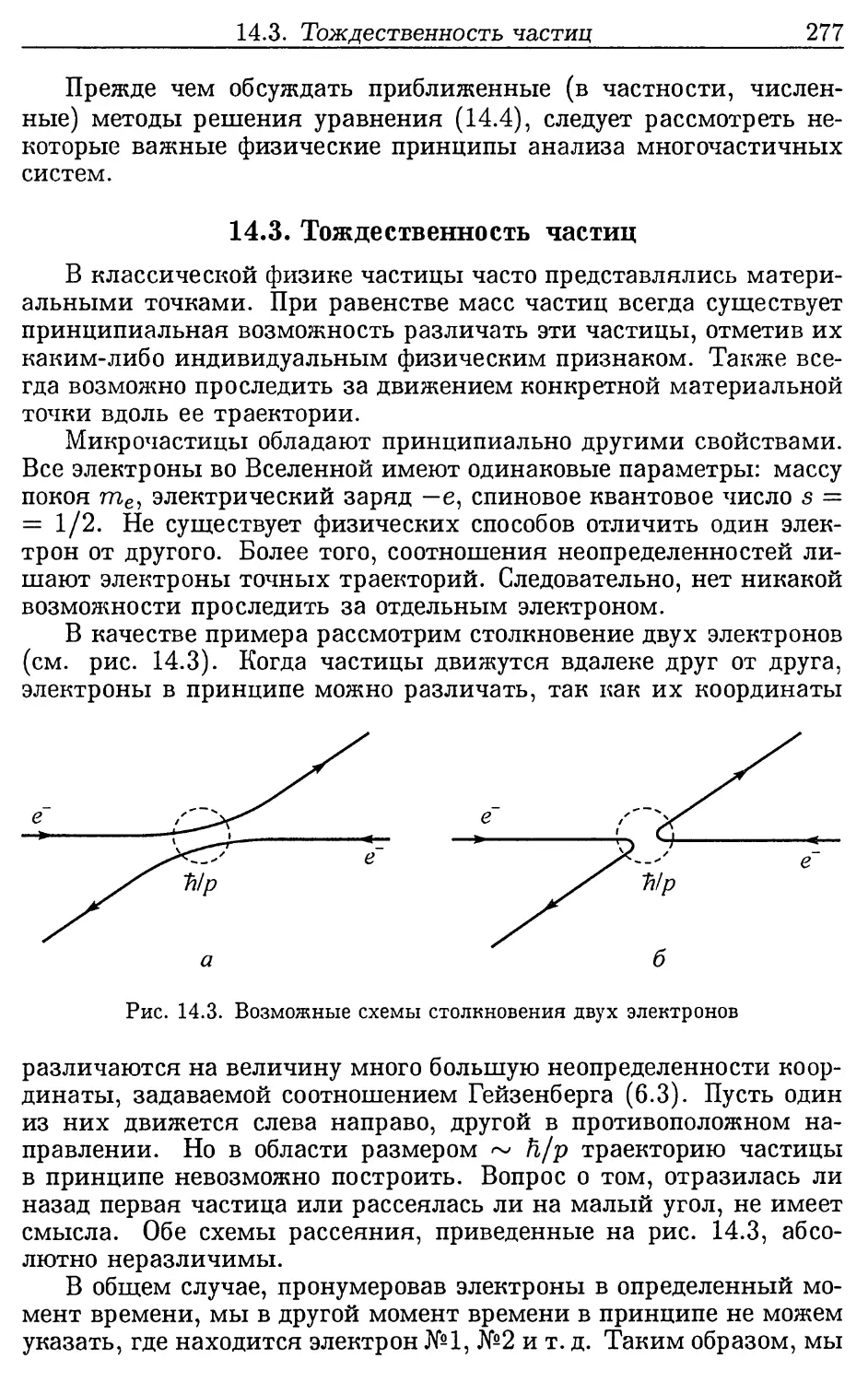
Рис. 1.4. К описанию опыта Милликена по определению заряда электрона:
а) конденсатор и электрическое поле между его пластинами; б) силы, действую-
щие на движущуюся каплю
поднимается вверх с постоянной скоростью v (см. рис. 1.4). Этого
всегда можно добиться подбором величины напряжения Uj_.
wg
б
V
20
Лекция 1. Атом — структурная единица вещества
На каплю будут действовать 4 силы. Вверх направлены элек-
трическая сила Fe и сила Архимеда Ед, вниз — сила тяжести FT
и сила вязкого трения Fv. Модули этих сил выражаются следую-
щими формулами:
„ 4 ч
FT = mg = ~тгглрд,
Fv = (yjuqrV)
г. 4 ч
Fa = ^глрод,
О
(1-7)
где m — масса капли, г — радиус капли, р — плотность капли, q —
электрический заряд капли, ро — плотность воздуха, р — вязкость
воздуха, d — расстояние между пластинами конденсатора, д —
ускорение свободного падения.
Капля движется с постоянной скоростью, если векторная сумма
сил (1.7), действующих на каплю, равняется нулю. Это равенство
в проекции на вертикальную ось можно записать в следующем
виде:
= ^тгг3(р - Ро)9 + бтгтупл (1.8)
a 3
Движение капли наблюдается в оптический микроскоп. По из-
меренному пройденному расстоянию As за интервал времени Ai
вычисляется скорость подъема капли
Затем из уравнения (1.8) вычисляется величина электрического
заряда капли.
Вблизи плоского конденсатора располагается рентгеновская
трубка. Кратковременная вспышка рентгеновских лучей ионизует
воздух и изменяет заряд капли q. Измерения повторяются. Совер-
шенствуя свою установку, Милликен добился продолжительности
наблюдения капли до 4,5 часов.
В результате многократных измерений Милликен установил,
что электрический заряд капли всегда кратен величине 1,6 х
х10’19 Кл « 4,8 • КГ10 ед. зар. CGSE.
Несмотря на неоднократные и тщательные поиски, в природе
до сих пор не обнаружено электрических зарядов меньшей вели-
чины. Все электрические заряды могут быть представлены в виде
q = пе, где множитель п является целым числом.
Положительная величина е называется элементарным заря-
дом. Заряд электрона является отрицательной величиной, рав-
ной —е.
1.4. Массы атомов
21
Зная величину заряда электрона и отношение заряда элек-
трона к его массе, можно легко вычислить массу электрона. При-
ведем современные значения этих фундаментальных постоянных:
е = (1,60217733 ± 0,00000049) • 10"19 Кл,
те = (9,1093897 ±0,00000054) • 10“31 кг.
Единица электрического заряда в системе Гаусса меньше ку-
лона в с/10 раз, следовательно, элементарный заряд приблизи-
тельно равен 4,80324 • 1О“10 ед. зар. CGSE.
1.4. Массы атомов
Вычисления масс молекул газов можно провести, зная постоян-
ную Авогадро TVa- Например, тщательное измерение массы объ-
ема Авогадро (22,4 л) газообразного водорода (достаточно разре-
женного, чтобы его можно было полагать идеальным газом) дает
значение 2,016г. Разделив эту величину на 7Va> получим массу
молекулы водорода, равную 3,346-10-24 г. Так как молекула водо-
рода двухатомная, масса одного атома 1,673 • 10-24 г.
Универсальный и достаточно точный метод измерения масс
атомов базируется на законах движения заряженных частиц в
электромагнитных полях. Атом электронейтрален, что устано-
влено с колоссальной точностью. Действительно, рассмотрим, на-
пример, 1 моль одноатомного газа. Факт электронейтральности
этого количества газа базируется на том, что во всех экспери-
ментах не наблюдается действия электрических полей, которые
создаются этим газом. Это говорит о том, что величины поло-
жительного и отрицательного заряда в одном атоме одинаковы с
погрешностью, равной приблизительно
1
от погрешности, с
6 • 1023
которой можно измерить заряд данного количества газа. С уве-
личением количества газа соответственно уменьшится и погреш-
ность утверждения об электронейтральности отдельного атома.
В состав атомов входят электроны. Следовательно, атом со-
стоит из электронов и положительно заряженного остатка, кото-
рый называется положительным ионом.
Уже первые эксперименты с газоразрядными трубками пока-
зали, что если в катоде сделать отверстия («каналы»), то через
эти каналы проходят какие-то «лучи», которые вызывают свече-
ние люминесцентного экрана, расположенного в противоположном
от анода конце трубки. Эти лучи, названные «каналовыми», тоже
отклонялись магнитным полем, но в направлении, противополож-
ном электронам. Это говорит о том, что каналовые лучи предста-
вляют собой поток положительно заряженных частиц. После того
как было доказано, что «катодные лучи» — это потоки электронов,
22 Лекция 1. Атом — структурная единица вещества
естественно предположить, что «каналовые лучи» представляют
собой потоки положительных ионов.
Дж. Дж. Томсон измерил массу и заряд «каналовых лучей»,
также используя для отклонения частиц электрическое и магнит-
ное поля. В установке Томсона для исследования частиц «кана-
ловых лучей» электрическое и магнитное поле были направлены
параллельно друг другу и, следовательно, отклоняли частицы во
взаимно перпендикулярных направлениях.
Атомы на пути между анодом и катодом могут потерять один
или несколько электронов, и по этой причине образовавшиеся ио-
ны могут ускоряться до различных энергий. Ионы одного типа
с одинаковыми зарядом и массой, но с некоторым разбросом ко-
нечных скоростей, вычертят на люминесцентном экране или фо-
топластинке кривую линию. Можно рассчитать, что эта кривая
представляет собой отрезок параболы. Если в пучке присутствуют
ионы различной массы, то более массивные (с тем же электриче-
ским зарядом) будут отклоняться от центральной оси слабее, чем
более легкие. Измерение кривизны полученных отрезков парабол
в принципе позволяют провести расчеты удельного заряда иона,
т. е. отношения заряда частицы к ее массе. Однако этот способ
расчета характерен значительными погрешностями результатов,
что привело к разработке более точных методов.
Надежная методика измерения масс электрически заряжен-
ных частиц, основанная на определении их удельных зарядов по
их траектории движения в электрических и магнитных полях,
реализуется на установках, получивших общее название масс-
спектрометров. Первый такой прибор создал в 1920 г. Ф. Астон
(1877-1945), назвав его масс-спектрографом, и добился относи-
тельной погрешности измерения массы иона порядка 10-3. В сле-
дующие годы были построены масс-спектрометры различных
конструкций, которые обеспечивали все большую точность изме-
ряемых масс. В качестве примера рассмотрим принципиальную
схему масс-спектрометра Демстера (рис. 1.5).
Источник ионов (ИИ) содержит газ исследуемого химического
элемента, а также нагреваемый катод. Катод, вследствие тер-
моэмиссии, испускает электроны, которые ускоряются электриче-
ским полем и ионизуют атомы газа. Электрическое поле вытяги-
вает положительные ионы в ускоряющую камеру.
Из источника ионы выходят с малой кинетической энергией
порядка 1эВ. Затем они ускоряются электрическим полем с раз-
ностью потенциалов U в несколько тысяч вольт. При этом од-
нократно заряженные ионы за счет работы электрического поля
приобретают кинетическую энергию, определяемую в нереляти-
вистском приближении уравнением
^v2 = qU, (1.10)
1.4. Массы атомов
23
где Mi — масса иона, v — скорость иона в конце ускоряющей
камеры, q — заряд иона.
Векторы скоростей ионов после ускорения имеют значитель-
ный разброс направлений. Для формирования узкого пучка ио-
нов используется фильтр скоростей ФС. Принцип работы филь-
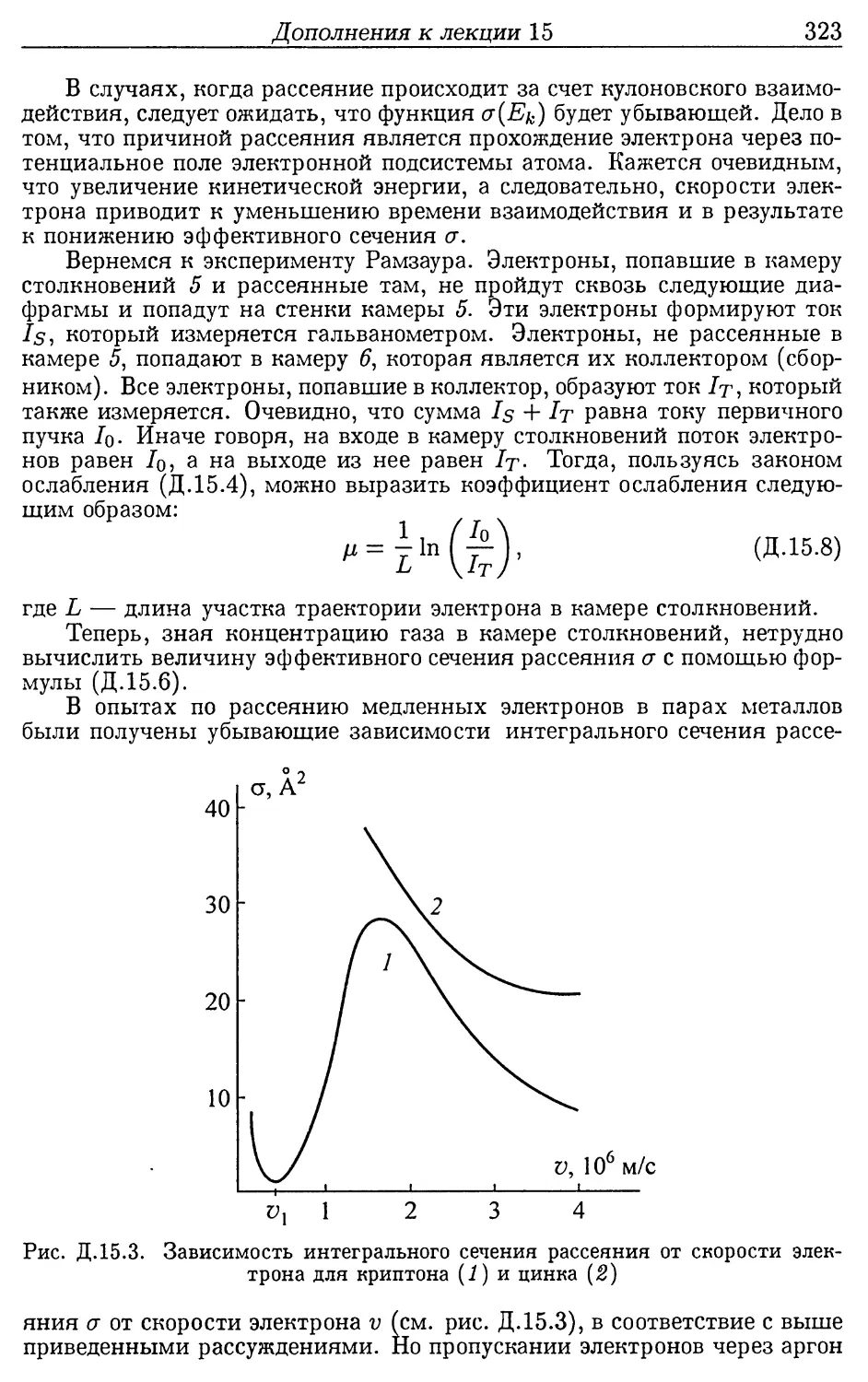
Рис. 1.5. Схема масс-спектрометра Демстера:
ИИ — источник ионов, УК — ускоряющая камера, ФС — фильтр скоростей, U — ускоря-
ющая разность потенциалов, ВК — вакуумная камера, В — магнитное поле отклоняющей
системы, R — радиус траектории иона, Д — детектор ионов
тра основан на отклонении пучка зараженных частиц в скре-
щенных электрическом и магнитном полях, аналогичном тому,
который использовался в электронно-лучевой трубке Томпсона (см.
рис. 1.2). Сквозь выходную щель фильтра скоростей выходят
только ионы с почти параллельными векторами скоростей.
Далее ионы попадают в вакуумную камеру ВК, которая имеет
форму полуцилиндра. Внутри камеры создано магнитное поле В,
направление которого перпендикулярно основаниям полуцилиндра
(т. е. перпендикулярно плоскости рис. 1.5).
Скорость ионов в камере v ориентирована перпендикулярно
вектору магнитного поля В. Ионы движутся под действием силы
Лоренца по дуге окружности. Уравнение движения иона в пер-
пендикулярном магнитном поле в рассматриваемом случае легко
привести к следующему скалярному виду:
= ^vB, (1.11)
где R — радиус траектории иона в области перпендикулярного маг-
нитного поля.
2 1
Лекщш 1. Атом — структурная единица вещества
Траектории ионов в магнитной камере представляют собой по-
луокружности. Из соотношения (1.11) следует, что радиус окруж-
ности зависит от массы иона.
Из системы уравнений (1.10) и (1.11) выводится выражение
для массы иона:
Mi =
qB2R2
2Uc2 '
(1-12)
Измерение радиуса траектории ионов позволяет вычислить
массу этих ионов.
В правую часть уравнения (1.12) входит заряд иона д, который,
вообще говоря, кратен элементарному, т. е. q = пе. Однако в
экспериментах обычно создаются условия, при которых в камере
ИИ образуются преимущественно однократно заряженные ионы,
и в (1.12) следует полагать q — е.
В одном из вариантов методики масс-спектрометрических ис-
следований устанавливаются определенные величины В и J7, а де-
тектор ионов перемещается вдоль радиуса вакуумной камеры. При
некотором значении радиуса R регистрируется ионный ток. Для
полученного значения радиуса R проводится вычисление массы
иона по формуле (1.12). Заметим, что наличие в пучке многоза-
рядных ионов (q = пе, п > 1) не мешает описанной методике.
Дело в том, что n-кратное увеличение заряда ионов приводит к
n-кратному уменьшению радиуса траектории, согласно уравнению
(1.11). Следовательно, многозарядные ионы значительно откло-
няются от анализируемого пучка и не попадаю! во входное окно
детектора.
В качестве примеров приведем измеренные значения масс од-
нократно заряженных положительных ионов гелия (6,64 • 10“24 г)
и золота (3,27 • 10-22г). Таким образом, оказывается, что массы
атомов на 3-5 порядков превышают массу электрона. Поэтому при
вычислениях с точностью до трех значащих цифр можно пола-
гать массу атома равной массе однократно заряженного по-
ложительного иона.
Задолго до масс-спектрометрических исследований химики
пришли к выводу, что из-за малости атомов и молекул грамм явля-
ется неудобной единицей измерения масс атомов. Еще в 1828 г.
великий химик И.Я. Берцелиус (1779-1848) в качестве атомной
единицы массы (а.е.м) принял 1/16 массы атома кислорода. При
этом масса самого легкого атома — водорода — оказалось прибли-
зительного равной 1 а.е.м. Числовое значение а.е.м. в граммах
химики вычисляли с помощью постоянной Авогадро, которая в
XIX веке была известна со значительной погрешностью.
В 1912 г. Дж.Дж. Томсон, исследуя движение ионов неона в
электрическом и магнитном полях, обнаружил, что атомы хими-
чески чистого неона различаются по своим массам. Оказалось,
1.4. Массы атомов
25
что примерно 90% атомов имеют массу 20 а.е.м., а 10% — массу
22а.е.м. Это удивительно, так как, согласно химии XIX века,
атомы определенного простого вещества должны быть абсолютно
одинаковыми.
Зависимость ионного тока, регистрируемого масс-спектромет-
ром, от массы частиц называется масс-спектрограммой веще-
ства. Исследования Астона и его коллег показали, что масс-спект-
рограммы большинства химически чистых простых веществ
содержат несколько узких пиков (см. рис. 1.6). Величина ионного
/, отн. ед.
30 I-
М, а.е.м.
Рис. 1.6. Масс-спектрограмма химически чистого кадмия. По вертикали отло-
жены значения ионного тока в относительных единицах
тока в максимуме пика прямо пропорциональна количеству атомов
определенной массы в исследуемом веществе. Ширина пика опре-
деляется разрешающей способностью масс-спектрометра. Диск-
ретный характер спектра масс чистого простого вещества объяс-
няется существованием у определенного химического элемента
атомов с различными массами.
Атомы определенного химического элемента, имеющие раз-
личные массы, называются изотопами, по предложению Ф. Содди
(1877-1956), который вместе с Э.Резерфордом (1871-1937) зани-
мался исследованием радиоактивных элементов.
В частности, природный углерод состоит из смеси двух изо-
топов с атомными массами 12а.е.м. и 13 а.е.м., которые кратко
называются углерод-12 (12С) и углерод-13 (13С). Процентная доля
изотопа 12С в природе составляет 98,9%.
Рисунок 1.6 демонстрирует, что природный кадмий состоит,
по крайней мере, из восьми различных изотопов. По положению
пиков масс-спектрограммы можно установить, что массы изотопов
равны 106, 108, 110, 111, 112, ИЗ, 114 и 116 а.е.м.
Дробные значения атомных масс элементов, полученные хи-
мическими методами и записанные в таблице Менделеева, объяс-
няются тем, что химический элемент представляет собой смесь
26 Лекция 1. Атом — структурная единица вещества
изотопов, входящей в состав газопылевого облака, из которого об-
разовалась Солнечная система. Например, согласно точным хими-
ческим измерениям, атомная масса хлора составляет 35,45 а.е.м.
Масс-спектроскопические исследования установили, что природ-
ный хлор состоит примерно из четвертой части изотопа хлора-37
и трех четвертей хлора-35. В 1932 г. Г. Юри (1893-1981) обна-
ружил, что природный водород, помимо изотопа с массой 1 а.е.м.,
содержит 0,015% изотопа с массой 2 а.е.м., названного дейтерием,
В 1929 г. У. Джиок (1895-1982) нашел у кислорода, кроме изотопа
с массой 16 а.е.м., еще два: кислород-17 (0,038% в химически чи-
стом кислороде) и кислород-18 (0,2%).
Из-за открытия изотопов кислорода пришлось изменить опре-
деление атомной единицы массы. С 1961 г. атомная единица
массы принята равной 1/12 массы атома углерода-12, которая
была вычислена по результатам масс-спектрометрических иссле-
дований:
1 а.е.м. = 1,6605402 • 1СГ24 г. (1.13)
Имея числовое значение (1.13), можно массы атомов, измеренные
химиками в атомных единицах массы, пересчитать в граммы.
Интересным результатом масс-спектрометрических исследова-
ний оказалось то, что массы отдельных изотопов всех химических
элементов с точностью до 0,1% кратны а.е.м. Может создаться
впечатление, что атомы сложены из «кирпичиков» массой 1 а.е.м.
Этот факт исторически оказался весьма полезным при выяснении
внутренней структуры атома.
Приведенные выше числовые значения показывают, что масса
электрона много меньше массы любого из атомов. Масса самого
легкого — атома водорода — приблизительно в 1837 раз больше
массы электрона.
1.5. Размеры атомов
Измерения размеров атомов проводятся различными экспери-
ментальными методами. Наиболее точные методики базируются
на анализе картин рассеяния на атомах пучков электронов, ней-
тронов и рентгеновских лучей. Один из наиболее простых для
понимания способов получения радиусов атомов, основанный на
пропускании пучков атомов через газовую среду, приведен в до-
полнении 1.2. Более точным и универсальным методом является
дифракция рентгеновских лучей на кристаллических образцах, ко-
торая описывается в лекции 18.
Приблизительную оценку размеров атомов можно дать с по-
мощью закона Авогадро, используя известную молярную массу
химического элемента и плотность соответствующего простого ве-
щества. Предположим, что в твердом теле атомы расположены
1,5. Размеры атомов
27
вплотную друг к другу. Для примера возьмем алюминий, у ко-
торого масса одного моля приблизительно равна 27 г, а плотность
р ~ 2,7г/см3. Запишем выражение массы моля как суммарную
массу однородных шариков с плотностью р и радиусом г:
WA (|7гг3 ) р « 27 г. (1.14)
Решив это уравнение, получим г « 1,3 • 10-8 см.
Измерения радиусов атомов различными методами дают уди-
вительный результат. Оказывается, что размеры всех атомов от
водорода до урана имеют один порядок и, в большинстве, лежат
в интервале от 10~8 см до 2 • 10-8 см, что демонстрирует рис. 1.7.
Рис. 1.7. Соотношение радиусов атомов и их масс
Такой диапазон размеров атомов химических элементов обусло-
вил широкое употребление внесистемной единицы длины, равной
10~8 см = 10-1Ом. Эта единица называется ангстрем и обозна-
чается символом А.
Полученные размеры атомов интересно сравнить с результа-
тами спектрометрических исследований, которые показали, что
массы атомов различных химических элементов могут различать-
ся в 200 с лишним раз. Например, масса наиболее распростра-
ненного изотопа урана превышает массу атома водорода в 238 раз.
При этом зависимость радиуса атома от массы имеет довольно при-
чудливый немонотонный вид с пиками и провалами (см. рис. 1.7).
Разумеется, удивительно, что объекты одинакового размера разли-
чаются по массе более, чем на два порядка.
Полученные результаты приводят к неизбежности предположе-
ния, что атомы имеют сложное и существенно неоднородное вну-
треннее строение. Исследования структуры атома, описанные в
следующих лекциях, показали, что атом не является твердым ша-
риком, и понятие радиуса атома нуждается в уточнении.
28
Лекция 1. Атом — структурная единица вещества
Задачи к лекции 1
1. Отшить количество молекул в 1 см3 воздуха при нормальных усло-
виях.
2. Оцепить величину ускоряющего напряжения, при котором элек-
трон следует рассматривать как релятивистский. То же самое рассчи-
тан» для протона.
3. При измерениях на масс-спектрометре Демстера были получены
траектории:
а) с радиусом 11,52 см при ускоряющей разности потенциалов 10 кВ
п индукции магнитного поля 5000Гс;
б) с радиусом 6,46 см при ускоряющей разности потенциалов 50 кВ и
индукции магнитного поля 5000 Гс;
в) с радиусом 9,7 см при ускоряющей разности потенциалов 4,5 кВ и
индукции магнитного поля 1000 Гс.
Вычислить массы ионов, полагая их заряды равным элементарному. .
4. В опыте по пропусканию пучка ускоренных электронов через скре-
щенные электрическое и магнитное поля было обнаружено, что пучок не
отклоняется при следующих значениях параметров: ускоряющая раз-
ность потенциалов Uq = 300 В, индукция магнитного поля В — 1,2 х
х10-3Тл, поперечная разность потенциалов U± = 185 В, расстояние
между пластинами конденсатора отклоняющей системы d = 15 мм.
5. Доказать, что величина, обратная атомной единицы массы (а.е.м.),
выраженной в граммах, численно равна постоянной Авогадро.
6. Оценить радиусы атомов, исходя из модели соприкасающихся ша-
ров по известной плотности р и молярной массе р для следующих хи-
мических элементов: а) магний, р = 1,74г/см3, р = 24,3г; б) никель,
р = 8,91 г/см3, р = 58,7г, в) висмут, р = 9,78г/см3, ^ = 209г.
7. В опыте Милликена наблюдалось движение капли масла между
рисками, расположенными на расстоянии 6,0 мм друг от друга по верти-
кали. Среднее время падения капли в отсутствие электрического поля
равнялось 21,2 с. При различных зарядах этой же капли были зареги-
стрированы следующие времена подъема: 46,1; 15,6; 28,0; 13,0; 45,2 и
20,1с. При этом к пластинам конденсатора было приложено напряже-
ние 4,55 кВ, расстояние между пластинами 16,0 мм. Плотность масла
0,858г/см3, вязкость воздуха 1,83 • 10“5кг-м-1 ♦ с-1. Вычислить по
результатам опыта заряд электрона.
8. Вычислить энергии покоя электрона, протона и атома водорода.
Результаты выразить в электрон-вольтах.
9. Вычислить скорость электрона, который был ускорен равностью
потенциалов: а) 5000 В; б) 5 • 104 В; в) 3 • 105 В; г) 2 • 106 В; д) 107 В.
10. Найти отношение кинетической энергии к энергии покоя элек-
трона, если электрон был ускорен равностью потенциалов: а) 1000 В;
б) 2 • 104 В; в) 5 • 105 В; г) 5 • 106 В; д) 107В.
Аналогичные вычисления провести для протона.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 1
1.1. Определение постоянной Авогадро
методом электролиза солей металлов
Еще в своих пионерских работах А. Вольта обнаружил, что растворы
солей металлов являются хорошими проводниками электрического тока.
В многочисленных опытах по пропусканию постоянного тока через такие
жидкости (электролиты) было установлено, что на катоде (на электроде с
отрицательным потенциалом) происходит осаждение металла, входящего
в состав используемой соли.
Законы электролиза, экспериментально установленные М. Фарадеем,
связывают массу М осажденного металла с величиной заряда д, прошед-
шего через электролит, следующим уравнением:
M = q-^, (Д.1.1)
ЬГ
где /1 — молярная масса металла, l — его химическая валентность, F —
универсальная постоянная, названная числом Фарадея. Размерность
этой величины — электрический заряд, приходящийся на 1 моль веще-
ства (Кл/моль).
Согласно атомной теории, ток через электролит создается ионами ме-
талла, каждый из которых имеет массу тп и заряд равный ле, где е —
элементарный заряд. Следовательно, полный перенесенный электриче-
ский заряд q равен
q = Nbe, (Д.1.2)
где N — число ионов, достигших катода. На катоде каждый ион присо-
единяет к себе l электронов проводимости и превращается в нейтраль-
ный атом металла. Отсюда следует, что
М
N=—. (Д.1.3)
тп
Согласно определению постоянной Авогадро,
m = (Д.1.4)
Iva
При этом пренебрегается различием масс атома и иона, так как оно со-
ставляет примерно от 10-1% до 10-3% (см. § 1.4 лекции 1).
Подставив выражения (Д.1.2)-(Д.1.4) в уравнение (Д.1.1), получим
связь между тремя константами:
Na = -• (Д.1.5)
30
Дополнения к лекции 1
Число Фарадея измерялось в многочисленных экспериментах по
электролизу различных растворов солей. В результате было получено
значение F = 96485,3 Кл/моль — 2,89253 ед. зар. CGSE/моль. Разде-
лив число Фарадея на элементарный заряд е, измеренный в независи-
мых экспериментах, получим числовое значение постоянной Авогадро
Na = 6,022137-1023 моль-1.
1.2. Определение размеров атомов
по столкновениям в газовой фазе
Для измерения размеров изолированных атомов применяется метод,
основанный на процессе столкновений атомов в газовой фазе. Схема
установки приведена на рис. Д.1.1.
Рис. Д.1.1. Схема установки для определения размеров атомов газов:
1 — источник атомов, 2 — камера, наполненная газом (диафрагмы формируют узкий
пучок атомов), 3 — детектор атомов
С помощью небольшой печки, снабженной узкой щелью, формируется
направленный пучок атомов определенного химического элемента. Мо-
дули скоростей этих атомов определяются температурой внутри печки и
описываются распределением Максвелла. Но размеры щели таковы, что
векторы скоростей приближенно направлены параллельно друг другу.
Узкий пучок атомов пропускается через камеру, в которую закачан
газ другого или того же химического элемента. Регистрация атомов
производится с помощью детектора, который регистрирует количество
атомов, попавших в его входное окно. Один из типов детекторов пред-
ставляет собой раскаленную нить, у которой измеряется электрическое
сопротивление. При попадании атомов на нить она охлаждается. Сопро-
тивление нити зависит от ее температуры, поэтому изменяется в зави-
симости от потока (количества в единицу времени) атомов, приходящих
в детектор.
Атомы исходного пучка попадают в детектор, если не сталкиваются с
атомами газа в камере. Концентрация атомов в камере подбирается так,
что вероятность более чем одного столкновения мала. Иначе говоря,
атомы пучка или пролетают беспрепятственно в детектор, или претерпе-
вают одно столкновение, рассеиваются на некоторый угол и не попадают
в окно детектора.
Дополнения к лекции 1
31
Целесообразно полагать атомы твердыми шариками с определенным
радиусом г. Атомы различных химических элементов различаются сво-
ими радиусами. Обозначим ri и Г2 — радиусы атома пучка и атома газа
камеры соответственно.
Тогда столкновение атомов произойдет, если вектор скорости атома
пучка пересекает круг радиуса г\ + г2, очерченный вокруг атома газа,
находящегося в камере (см. рис. Д.1.2).
Рис. Д.1.2. Геометрическое условие столкновения двух атомов:
b — расстояние между продолжением вектора скорости атома пучка и параллельной ли-
нией, проходящей через центр атома-мишени
Круг радиуса и 4-Г2, расположенный перпендикулярно векторам ско-
ростей атомов, называется эффективным сечением столкновений.
Рассмотрим тонкий слой газа толщиной dx, перпендикулярный век-
торам скоростей атома пучка. Пусть S — площадь поперечного сечения
камеры столкновений. В выделенном тонком слое находятся число ато-
мов газа, равное
” (Д.1.6)
N — nS dx,
где п — концентрация газа, заполняющего камеру.
В тонком слое газа сечения столкновений отдельных атомов не пе-
рекрываются. Отсюда следует, что вероятность столкновения атомов в
таком слое равна отношению суммы площадей сечений всех атомов в
слое к площади поперечного сечения S камеры столкновений:
7V7r(ri 4- г2)2 , .2 ,
------------- = П7Г(Г1 + Г-2) dx.
S
При каждом столкновении атом выбывает из пучка.
Плотностью потока J называется количество атомов пучка, пересека-
ющих за 1с площадку в 1см2, ориентированную перпендикулярно век-
тору скорости. При прохождении слоя толщиной dx поток убывает на
величину пропорциональную вероятности столкновения. Тогда для плот-
ности потока можно записать следующее дифференциальное уравнение:
—dJ = «7п7г(г1 4- Г2)2 dx. (Д.1.7)
Интегрирование уравнения (Д.1.7) позволяет получить зависимость
плотности потока от расстояния ж, пройденного атомами:
J(x) = Jq exp [~п7г(г1 4- г2)2х], (Д.1.8)
где Jq — плотность потока атомов на входе в камеру столкновений.
32
Дополнения к лекции 1
Таким образом, плотность потока атомов экспоненциально ослабля-
ется при прохождении через газ, причем характер ослабления определя-
ется размерами сталкивающихся атомов.
Разреженность газа в камере столкновений позволяет использовать
уравнение Менделеева-Клапейрона
г>
Р = Р-Т, (Д.1.9)
А6
где р — плотность газа, р, — молярная масса, R — газовая постоянная.
Воспользуемся известными соотношениями
p = mna, p> = Npjn^ R = N^kB,
где ma — масса атома, N& — постоянная Авогадро, кв — постоян-
ная Больцмана, и получим связь давления Р и температуры Т в камере
столкновений в следующем виде:
Р = пквТ, (Д.1.10)
Из последнего уравнения можно вычислить концентрацию атомов газа
п по измеренным давлению Р и температуре Т в камере столкновений.
Величину Jo можно измерить с помощью детектора, предварительно
выкачав газ из камеры столкновений.
Тогда измерения плотности потока атомов J(x) для известной кон-
центрации п и расстояния х между источником и детектором с помощью
зависимости (Д.1.8) позволят вычислить сумму радиусов атомов и -Ьгд.
Проводя опыты с различными комбинациями химических элемен-
тов, можно составить систему уравнений, решение которой позволит по-
лучить радиусы атомов каждого элемента. Например, вычислив суммы
радиусов ri 4- Г2, ri 4- гз, Г2 4- гз, нетрудно рассчитать ri, Г2 и Г3. Не-
которые результаты приведены в табл. Д.1.1.
Таблица Д.1.1. Радиусы некоторых атомов,
измеренные методом столкновений
Химический элемент Радиус атома (А)
Гелий (Не) 1,1
Неон (Ne) 1,3
Ртуть (Hg) 2,1
В данном методе атомы каждого химического элемента рассматри-
вались как твердые шарики определенного радиуса г. Как будет пока-
зано в лекциях 11 и 14, атом представляет собой систему электронов и
ядра, состояние которой описывается законами квантовой физики. Сле-
довательно, атомы, строго говоря, не имеют резких границ. Значения
г, измеренные выше описанным методом, представляют собой размеры
(которые должны были бы иметь) твердых шаров, необходимые для того,
чтобы наблюдался закон ослабления (Д.1.8). Эти радиусы называются
Дополнения к лекции 1
33
эффективными, так как они наглядно характеризуют определенный эф-
фект, в данном случае явление столкновения атомов в газовой среде.
Такие величины являются хорошим приближением размеров атома и
полезными параметрами для описания механизма межатомных упругих
взаимодействий.
Развитие понятия радиуса атома будет изложено в лекции 11 после
описания его внутреннего строения.
4 Зак. 178
Лекция 2
ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
Попытки описания свойств атомов, электронов и других ми-
кроскопических объектов, пользуясь законами и представлени-
ями классической физики, оказались неудачными. Эти проблемы
конца XIX - начала XX века получили название «кризис физики».
Успешное его разрешение стало возможным только с созданием
принципиально новой физики — квантовой. Важным этапом в
развитии атомной физики явилось создание теории теплового из-
лучения.
2.1. Тепловое излучение
Экспериментальные исследования показали, что все тела, тем-
пература которых отлична от абсолютного нуля, излучают элек-
тромагнитные волны. Кусок металла, нагретый до достаточно вы-
сокой температуры, излучает электромагнитные волны видимого
(оптического) диапазона. Тела с меньшей температурой излучают
в инфракрасном диапазоне и т.д. Диапазон испускаемых волн,
вообще говоря, неограничен, но при этом непрерывный спектр из-
лучения имеет характерный максимум. Если нагревать кусок ме-
талла, то видно, что с ростом температуры металл сначала начи-
нает светиться темно-красным цветом, затем красно-оранжевым,
далее раскаляется добела. Следовательно, при повышении темпе-
ратуры тела максимум излучения смещается в направлении более
коротких длин волн, т. е. более высоких частот.
Эти экспериментальные результаты были получены к концу
XIX века, но их теоретическое объяснение, а также описание с
классических позиций процесса излучения электромагнитной вол-
ны отдельным атомом привели к парадоксальным результатам и
завели классическую физику в тупик, выход из которого дала
только квантовая теория.
Данная лекция посвящена описанию параметров электромаг-
нитного излучения, которое названо тепловым и вызывается ха-
отическим движением ионов, атомов и молекул в нагретом теле.
2.1. Тепловое излучение
35
Рис. 2.1. К описанию равновес-
ного теплового излучения в за-
мкнутой полости
Излучение с характерным линейчатым спектром, которое сопро-
вождается изменением внутреннего состояния атома, рассматри-
вается в лекции 8 и следующих лекциях.
Рассмотрим несколько тел с конечной теплоемкостью, которые
помещены в массивную замкнутую оболочку со стенками, имею-
щими постоянную температуру Tq
(см. рис. 2.1).
Предположим, что в начальный
момент времени все тела имели раз-
ную температуру, т. е. Т\ Ф Т<2 Ф
. Теплообмен между те-
лами и оболочкой путем излучения
и поглощения приводит к тому, что
температура тел будет изменяться
со временем. Опыты показывают,
что через некоторое время темпера-
тура всех тел станет одинаковой и
равной То. После установления тем-
пературы То каждое тело в единицу
времени излучает и поглощает оди-
наковое количество энергии. Но то-
гда для описания излучения в по-
лости все тела можно убрать и оставить пустую полость, где за-
ключено излучение, которое излучается и поглощается стенками
оболочки.
Установившееся излучение в полости можно описать следую-
щим образом. Для произвольной площадки ds на внутренней
поверхности оболочки за произвольный интервал времени dt в
любом интервале частот dw для каждого направления и опреде-
ленной поляризации количество поглощенной энергии равно ко-
личеству излученной. Такое излучение называется равновесным.
Равновесное излучение характеризуется единственной величи-
ной — температурой Го, равной температуре тела, с которым про-
исходит теплообмен посредством излучения.
Введем основные характеристики равновесного излучения.
Распределение электромагнитной энергии теплового излучения
в пространстве описывается плотностью излучения и, которая
представляет собой энергию электромагнитного поля в единице
объема. Размерность величины и Дж-м-3 или эрг-см-3.
Из опытов известно, что тепловое излучение содержит непре-
рывную совокупность волн с разными длинами Л, что требует
использования спектральных характеристик. Рассмотрим беско-
нечно малый интервал длин волн равновесного излучения от Л до
A-f-dA. Тогда плотность равновесного излучения в этом интервале
длин волн можно представить как и\ dX, где их называется спек-
тральной плотностью излучения. Размерность этой величины
4*
36 Лекция 2. Законы излучения абсолютно черного тела
Дж-м-4 или эрг-см-4. Плотность равновесного излучения может
быть представлена в виде
оо
и = у* их dX. (2.1)
о
Аналогично можно рассмотреть бесконечно малый интервал ча-
стот (cu, си + dcu) и ввести другую спектральную характеристику
следующей формулой:
оо
и = У иш dev. (2.2)
о
Функция также называется спектральной плотностью излуче-
ния, но имеет размерность Дж • м-3 • с или эрг • см-3 • с, т. е. от-
личается по размерности от функции и\.
Найдем соотношение между величинами иш и и\. Пусть ин-
тервал dX — интервал длин волн, соответствующий интервалу ча-
стот dcu. Тогда количество энергии излучения в данном интервале,
выраженное через разные спектральные плотности, должно быть
одинаковым, т. е.
\иш dcv\ = dX\. (2.3)
Запишем связь длины волны Л с частотой си электромагнитного
излучения:
Л = —с, (2.4)
CU
где с — скорость света в вакууме, и возьмем дифференциалы от
обеих частей (2.4). Для модулей дифференциалов получим соот-
ношение
2тг
\dX\ = — cdcv ,
что позволит уравнение (2.3) переписать в виде
\ии dcu| =
2тг
ux—^cdw
Используя соотношение (2.4) и принимая во внимание, что все
входящие в последнее уравнение величины положительны, полу-
чаем связь обеих функций спектральных плотностей излучения ии
и их:
- -их- (2.5)
CU
2.1. Тепловое излучение 37
Если рассматриваемая полость содержит только вакуум, то
спектральная плотность и\ для равновесного излучения является
функцией только длины волны и температуры, т. е. их = ид (Л, Г).
Аналогично спектральная плотность также является функцией
только частоты и температуры
Найдем энергию dW равновесного теплового излучения, прохо-
дящего за время.^ через произвольно выделенную в пространстве
площадку ds внутри телесного угла c/Q, ось которого перпендику-
Рис. 2.2. К определению удельной интенсивности излучения
лярна площадке. Очевидно, что через окрестность каждой точки
излучение через площадку проходит во всех направлениях, в том
числе и внутри телесного угла dQ (рис. 2.2).
Величину искомой энергии dW можно записать в виде
dW = Idsdttdt, (2.6)
где I — удельная интенсивность излучения (или поверхност-
ная плотность потока излучения). Величина I имеет размерность
Дж • м-2 • с-1 или эрг • см-2 • с-1. Аналогично тому, как это было
сделано для плотности равновесного излучения, можно ввести
функции 1Х и 1Ш спектральной интенсивности излучения с помо-
щью следующих интегралов:
оо оо
1 = j Iudv = f IxdX. (2.7)
О о
Если ось телесного угла c/Q составляет с нормалью к площадке
угол (/?, то уравнение (2.6) примет вид
dW = I cos <р ds dQ dt. (2.8)
Произведение cos (p ds для краткости называют видимой вели-
чиной площадки ds. Смысл термина становится очевидным при
рассматривании площадки под углом ср к ее нормали.
38
Лекция 2. Законы излучения абсолютно черного тела
Найдем связь между величинами и и I для равновесного из-
лучения в вакууме. Пусть излучение внутри телесного угла dQ па-
дает на площадку ds (рис. 2.3). За время dt на площадку ds пада-
ет излучение с энергией I ds dQ, dt.
Пусть dl — расстояние, которое
свет проходит за время dt. Тогда
dt = dl/с, и
Рис. 2.3. К выводу связи удельной
интенсивности и плотности энер-
гии равновесного теплового излу-
чения
гии внутри телесного угла c/Q.
Idsdttdt = Idsdtt— = IdV —,
с с
где dV = ds dl — элемент объема
пространства. Сравнивая послед-
нее выражение с определением
плотности энергии излучения
dW = udV, получаем, что вели-
чина 1— равна плотности энер-
с
Так как равновесное излучение
является изотропным, то интегрирование
углу дает искомое уравнение связи
4тг/
-----= и.
с
по полному телесному
(2-9)
Аналогичные соотношения можно получить и для спектральных
характеристик:
4тг^ 4тг/л
= иш или = и\.
с--------------------с
(2.10)
Важность соотношений (2.9) и (2.10) заключается в том, что
они связывают экспериментально измеряемые характеристики те-
плового излучения /, 1\ и с величинами и, и^ п их, получае-
мыми методами теоретической физики.
2.2. Закон Кирхгофа
Рассмотрим общие свойства излучения и поглощения теплового
излучения. Пусть излучающие и поглощающие тела полностью
непрозрачны. Этого можно добиться, например, если взять тела
достаточных размеров. Величину энергии в интервале частот от
си до cu + dw, излучаемой за время dt с площадки ds тела внутрь
телесного угла c/Q, ось которого составляет угол ср с нормалью к
площадке ds, можно записать в виде
dW^v+dw — Еш cos ср dQ. ds dt du. (2.11)
Величина Eu называется излучательной способностью тела в
интервале частот от и до и + du в направлении, определяемом
2.2. Закон Кирхгофа
39
Рис. 2.4. К выводу закона Кирх-
гофа
углом ср. Размерность величины Еш совпадает с размерностью
спектральной интенсивности 1Ш.
Введем поглощающую способность Аи тела в интервале ча-
стот от и до и + du) в направлении, определяемом углом (/?, как
долю энергии падающего излучения, которое поглощается телом.
Величина Аш безразмерна.
Найдем связь между величинами и Аш для определенного
тела. Обе эти величины характеризуют лишь поверхности из-
лучающего и поглощающего тела и
не зависят от внешних условий, в
частности, от излучения, которое
окружает это тело. Следовательно,
при рассмотрении связи между Еш
и Аш мы можем ввести любые усло-
вия, касающиеся излучения, в ко-
тором находится рассматриваемое
тело.
Пусть рассматриваемое тело ок-
ружено равновесным излучением,
температура которого равна темпе-
ратуре тела. Как мы видели выше
(см. рис. 2.1), этого можно добиться,
поместив тело на достаточно боль-
шое время внутрь ящика с массив-
ными стенками, температура кото-
рых поддерживается постоянной. Рассмотрим площадку площа-
дью ds поверхности тела настолько малую, что ее можно считать
частью плоскости (рис. 2.4).
В интервале частот (си, си + dcu) на площадку ds за время dt
падает энергия, равная
cos ср ds d£l dt dw.
(2.12)
Часть ее, равная АШ1Ш cos ipdsdft dtdw, поглощается, a (1 - AJ x
x Iu cos (p ds dQdt dw отражается. Кроме этого, за то же время
dt площадка ds тела излучает энергию Еш cos ср dCl ds dt dw. Та-
ким образом, полная энергия излучения с частотой в интервале
(си, си + с/си), которая за время dt исходит от площадки ds внутри
телесного угла c/Q, равна
[(1 — Аш)1м + Еш] cos tpdft ds dtdw. (2.13)
Так как окружающее излучение является равновесным, то ве-
личина (2.13) равна падающей на эту же площадку ds за то же
время dt энергии (2.12). Приравнивая выражения (2.12) и (2.13),
получим
[(1 — АШ)1Ш + Ещ\ = Iqj
40
Лекция 2. Законы излучения абсолютно черного тела
или
L (2-14)
Величина характеризует равновесное излучение в полости
и не зависит от присутствия каких-либо тел, а является функ-
цией лишь частоты и температуры. Следовательно, отношение
излучательной способности к поглощающей способности тела
Еш/Аш для всех тел одинаково и зависит только от темпера-
туры и частоты. Это важное уравнение было впервые получено
Г. Кирхгофом (1824-1887) в 1859 г. и называется законом Кирх-
гофа.
2.3. Абсолютно черное тело
Рассмотрим некоторое идеализированное тело, для которого
поглощательная способность Аи — 1. Это означает, что все из-
лучение, которое падает на тело, поглощается им. Такое тело на-
зывается абсолютно черным.
Абсолютно черное тело, как и любое другое нагретое тело,
является источником теплового излучения. Обозначим излуча-
тельную способность абсолютно черного тела через е^. Тогда по-
______________ лучим 1и — еы. С учетом этого
соотношения закон Кирхгофа
можно сформулировать как
ш X/Xlw / (2-15)
ИХ / X. / т.е. отношение излучательной
ч/ X. способности к поглощатель-
Wk /X ^Х/] н°и способности для любого
X. уХыЮг тела есть универсальная функ-
Х-Хи^Ог й/ия температуры и частоты
eCJ(T,си), равная излучательной
Шож способности абсолютно черно-
Рис. 2.5. Принципиальная модель аб- &О тела.
солютно черного тела Абсолютно черное тело (АЧТ)
является, вообще говоря, идеа-
лизированным телом. Простейшей моделью АЧТ является с ма-
ленькое отверстие в полости со стенками, имеющими определен-
ную температуру (рис. 2.5).
Если стенки полости непрозрачны, а отверстие очень мало, то
внутри полости установится электромагнитное поле, практически
не отличимое от равновесного излучения. Каждый луч, вошедший
в полость, многократно отражается от внутренней поверхности сте-
нок. При каждом отражении часть энергии луча поглощается.
В результате луч поглощается полностью, или через отверстие
2.4. Закон Стефана-Больцмана. Формула и закон Вина 41
выйдет ничтожная часть начальной энергии. В то же время вну-
тренние поверхности стенок испускают тепловое излучение, кото-
рое быстро становится равновесным.
Через отверстие полости будет выходить такое же излучение,
которое бы испускалось абсолютно черной площадкой той же фор-
мы и размера.
В природе к АЧТ по свойствам близки сажа, черный бархат,
черная шерсть животных, поглощающие свойства которых обу-
словлены их пористостью.
С одной из моделей АЧТ столкнулся Карабас-Барабас в хар-
чевне «Три пескаря», пытаясь разглядеть Буратино внутри кув-
Рис. 2.6. Наблюдения Карабаса-Барабаса
шина (см. рис. 2.6). Несмотря на «научный» диспут с продавцом
пиявок Дуремаром, ничего, кроме теплового излучения, из кув-
шина извлечь не удалось.
2.4. Закон Стефана-Больцмана. Формула и закон Вина
Рассмотрим более подробно излучательную способность абсо-
лютно черного тела. В 1893-1894 гг. В. Вин (1864-1928) теорети-
чески установил, что спектральная плотность равновесного тепло-
вого излучения может быть представлена в виде
u)3F
(2.16)
где F — некоторая универсальная функция, аргументом которой
является отношение частоты к температуре.
Несмотря на то, что методами классической физики устано-
вить вид функции F(w/T) не удалось, формула (2.16) позволяет
3 Зак. 178
12 Лекции 2. Законы излучения абсолютно черного тела
сформулировать два важных закона теплового излучения. Запи-
шем плотность излучения с помощью уравнений (2.2) и (2.16)
U =
У u^j div
о
(2.17)
Проведем замену переменной £ = cu/Т. Тогда div = Т d£, и
последний интеграл можно преобразовать в виду
и
оо оо
у T^3F(£)T<X = Т4 У £3F(£) d£.
О о
оо
Определенный интеграл f £3F(£)d£ представляет собой неко-
о
торое число, которое мы обозначим через а. Тогда получаем,
Рис. 2.7. К вычислению энерге-
тической светимости:
что плотность излучения пропорцио-
нальна 4-й степени температуры:
и = аТ4. (2.18)
Используя уравнение (2.9), получим
выражение для удельной интенсив-
ности излучения АЧТ:
I = ^-аТ4. (2.19)
4тг
На практике часто используется
величина энергетической светимо-
сти S, которая определяется как
количество энергии, излучаемой в
единицу времени с единицы поверх-
п — вектор нормали к площадке пло-
щадью ds. Излучение распространя-
ется под углом О к нормали п
ности тела в одну сторону, т. е. в те-
лесный угол Q = 2тг. Получим связь
энергетической светимости S с удель-
ной интенсивностью излучения I.
В соответствии с определением видимой величины площадки (2.8),
энергия, испускаемая в единицу времени с единичной площадки
в телесный угол c/Q, ось которого образует угол в с нормалью,
равна
I cos в d£l.
(2.20)
Чтобы вычислить энергетическую светимость, требуется про-
интегрировать величину (2.20) по полусфере, т. е. по телесному
2.4. Закон Стефана-Больцмана. Формула и закон Вина
43
углу Q = 2тг:
I cos в dCl.
Q=2tt
К вычислению энергетической светимости:
Элементарный телесный угол dCl равен smO dO dp, где в —
угол между направлением излучения и нормалью к площадке (по-
лярный угол), р — азимутальный угол, отсчитываемый вокруг
вектора нормали. Тогда предыдущий интеграл для энергетиче-
ской светимости S выразится так:
27Г 7г/2
S — J dp f IcosOsinOdO. (2.21)
о о
Вследствие изотропии излучения величина удельной интенсив-
ности выносится из-под знака интеграла, и интегрирование дает
искомую связь:
S = л1. (2.22)
Сравнивая последнее выражение с (2.19), убеждаемся, что
энергетическая светимость АЧТ также пропорциональна 4-й сте-
пени температуры:
S = сгТ4, (2.23)
(2.24)
где a — константа, которая, как следует из сравнения уравнений
(2.19)—(2.21), связана с параметром а следующим соотношением:
ас
а = Т
Уравнения (2.18), (2.19), (2.23) представляют собой различ-
ные варианты записи закона Стефана-Больцмана. Заметим, что
во всех указанных выше уравнениях температура выражается по
шкале Кельвина и называется термодинамической температурой.
Й. Стефан (1835-1893) в 1879 г. в результате анализа экспери-
ментальных данных установил, что интегральная излучательная
способность тела пропорциональна 4-й степени термодинамиче-
ской температуры. В дальнейшем в результате эксперименталь-
ных проверок было установлено, что зависимость (2.19) имеет
место только для тел, свойства которых близки к свойствам АЧТ.
Л. Больцман (1844-1906) в 1884 г. на основе термодинамических
законов вывел соотношение, согласно которому излучательная спо-
собность АЧТ пропорциональна 4-й степени термодинамической
температуры, т. е. теоретически обосновал закон Стефана.
44
Лекция 2. Законы излучения абсолютно черного тела
Константа а первоначально определялась экспериментально,
затем ее величина была рассчитана. Ее современное значение
равно
о Вт
ст = (5,67032 ± 0,00071) • 1(Г8 —-т.
м2 • К
В начале данной лекции сообщалось о существовании макси-
мума спектральной плотности теплового излучения. В эксперимен-
тах традиционно исследовалась зависимость плотности излучения
от длины волны, поэтому перейдем от функции uu к функции и\
с помощью уравнения (2.5). Используя формулы (2.16) и (2.4),
выразим спектральную плотность и\ через длину волны:
их =
(2«)4 „
~>TF
2тгс\
АТ/ *
(2.25)
Для нахождения максимума спектральной плотности излуче-
ния необходимо исследовать функцию и\ на экстремум при фикси-
рованной температуре. Вычислим производную dux/dX, для ком-
пактности записи используя обозначение
2тгс
АТ’
(2.26)
и приравняем производную нулю. В результате получим уравнение
5F(7)+7~^=0. (2.27)
«7
Это нелинейное уравнение имеет решение, которое будет при-
ведено ниже (в лекции 3), после выяснения явного вида функции
Т(7). Пока, опираясь на результаты экспериментов, можно утвер-
ждать, что для заданной температуры Т найдется определенное
значение длины волны Атах, при которой функция их достигает
максимума. Обозначив корень уравнения (2.27) символом 70, мо-
жем записать
2тгс
~ А Т
лтах2
Отсюда следует, что температура АЧТ и длина волны максимума
спектральной плотности излучения связаны обратно пропорцио-
нальной зависимостью
АтахТ = Ь. (2.28)
Уравнение (2.28) представляет собой закон смещения Вина.
Значение константы 5, полученное из экспериментов, равно
0,29 см • К.
2.4. Закон Стефана-Больцмана. Формула и закон Вина 45
Существование экстремума спектральной плотности излучения
иш и их и формула Вина (2.28) позволяют сделать заключение о
виде спектральных функций удельной интенсивности излучения
/д и
Из соотношений (2.10) следует, что существование максимума
у функции и\ (или и^) обусловливает наличие максимума у спек-
X, нм
Рис. 2.8. Вид зависимости спектральной интенсивности излучения от длины
волны при разных температурах абсолютно черного тела:
УФ — ультрафиолетовый диапазон, ИК — инфракрасный диапазон
тральной характеристики 1\ (или причем положение макси-
мума, согласно (2.28), зависит от температуры нагретого тела (см.
рис. 2.8).
Из рис. 2.8 видно, что максимум функции удельной интенсив-
ности излучения АЧТ при повышении температуры смещается в
сторону все более коротких волн, что полностью согласуется с экс-
периментальными данными.
Задачи к лекции 2
1. Оценить длину волны максимума спектра:
а) излучения фотосферы Солнца (температура 6000К),
б) излучения центра Солнца (температура ~ 1,6 • 107 К), полагая
спектр излучения близким к равновесному.
2. Нить лампы накаливания разогревается до температуры 2400 °C.
Вычислить длину волны максимума спектра излучения.
3. Температура тела, которое можно полагать абсолютно черным, воз-
росла со 100 °C до 800 °C. Во сколько раз увеличилась его энергетическая
светимость?
46 Лекция 2. Законы излучения абсолютно черного тела
4. Температура ранней Вселенной Т и время прошедшее после
Большого взрыва, связаны следующим приближенным соотношением:
Т(К) =
1Q10
У* (лет)
Примерно через миллион лет после Большого взрыва началась ре-
комбинация плазмы с образованием нейтральных атомов водорода и ге-
лия. Полагая равновесным излучение, заполняющее Вселенную, оценить
длину волны максимума спектра в указанное время.
5. Вычислить длину волны максимума спектра излучения туго-
плавкого металлического образца, нагретого до: а) 100 °C, б) 500 °C,
в) 1000 °C, г) 2000 °C, д) 3000 °C.
6. Чугунная сковорода разогрета до температуры 300 °C. Можно ли
ее увидеть в темноте невооруженным глазом?
ДОПОЛНЕНИЯ К ЛЕКЦИИ 2
2.1. Экспериментальные установки
для исследования теплового излучения
В лекции 2 было показано, что хорошей моделью абсолютно черного
тела (АЧТ) является полость, нагретая до определенной температуры
и имеющее отверстие диаметра, малого по сравнению с размерами по-
лости. Для высокоточных экспериментальных исследования спектров
теплового излучения и проверки выводов теории необходимы специаль-
ные установки. Важнейшими требованиями к моделям АЧТ являются:
1) равномерный нагрев стенок полости, 2) высокая стабилизация тем-
пературы излучающих стенок, 3) малый диаметр отверстие для вывода
потока исследуемого излучения.
В ходе экспериментов выяснилось, что для различных диапазонов
температур следует использовать различные конструкции моделей АЧТ.
Рис. Д.2.1. Установка с температурной баней:
1 — жидкость с определенной температурой, 2 — поток теплового излучения
На рис. Д.2.1 изображена установка для получения равновесного излуче-
ния для сравнительно низких температур.
Основная часть установки представляет собой металлический сосуд
с двойными стенками. Пространство между стенками заполняется жид-
48
Дополнения к лекции 2
костью с определенной температурой Т. В зависимости от требуемой
температуры используется кипящая вода, жидкий газ (азот, кислород,
гелий), вода с тающим льдом и т.п. Таким образом, полость, окру-
женная жидкостью, поддерживается при определенной температуре Т и
является источником теплового излучения с соответствующей темпера-
турой. Такие установки называют температурной баней.
Для ликвидации конденсата в излучающей полости через нее непре-
рывно прокачивается вентилирующий газ.
При температурах порядка комнатной тепловое излучение, в основ-
ном, принадлежит инфракрасному диапазону.
Для разложения инфракрасного излучения в спектр используются ди-
фракционные решетки с периодом, близким к длине волны исследуемого
излучения. Кроме того, применяются диспергирующие системы, содер-
жащие призмы, изготовленные из кристаллов галогенидов щелочных ме-
таллов (NaCl, КВг, CsI, LiF и т.д.).
Простейшим детектором интенсивности инфракрасного излучения
является фотоэмульсия, нанесенная на прозрачную пленку или плас-
тинку.
Для исследования теплового излучения при высоких температурах
может использоваться модель АЧТ, показанная на рис. Д.2.2.
Рис. Д.2.2. Установка для генерации теплового излучения высокой температуры:
1 — спай термопары, 2 — поток теплового излучения
Установка состоит из двух коаксиальных цилиндров. Внутренний
изготовлен из фарфора, внешний — из платины, через который про-
пускают электрический ток. Из-за эффекта Джоуля-Ленца платиновый
цилиндр нагревается, что приводит к разогреву фарфорового до опреде-
ленной температуры. Внутренние диафрагмы затрудняют проникнове-
ние внутрь окружающего воздуха и препятствуют охлаждению полости.
Температура внутри полости измеряется термопарой.
При температурах, значительно превышающих комнатную, диапа-
зон теплового излучения захватывает видимую и ультрафиолетовую об-
ласти. Спектрометрия видимого и ультрафиолетового излучения была
хорошо разработана еще в начале XX века и подробно описана в курсах
оптики.
Лекция 3
«УЛЬТРАФИОЛЕТОВАЯ КАТАСТРОФА»
И ФОРМУЛА ПЛАНКА
3.1. Формула Рэлея-Джинса
В рамках классической физики не удалось получить явный
вид универсальной функции F(cu, Т), а следовательно, и зависимо-
сти спектральных плотностей равновесного теплового излучения
и гбд(А, Т). Дж.Рэлей (1842-1919) в 1900 г. и Дж. Джинс
(1877-1946) в 1905 г. попытались найти вид этих функций, при-
менив к равновесному тепловому излучению известную в термо-
динамике теорему о равном распределении энергии по степеням
свободы. Это была, по-видимому, одна из последних серьезных
попыток решить проблему равновесного теплового излучения ме-
тодами классической физики.
Рэлей предложил для решения задачи о тепловом излучении
тела использовать вместо термодинамического статистический
подход. Равновесное электромагнитное излучение в замкнутой по-
лости с постоянной температурой стенок он рассматривал как си-
стему стоячих волн различных частот в трех измерениях. Джинс,
следуя идее Рэлея, провел точные электродинамические расчеты.
Как известно из молекулярно-кинетической теории идеального
газа, на каждую степень свободы молекулы приходится кинети-
ческая энергия, равная къТ/2, где кв — постоянная Больцмана.
Рассмотрим равновесное тепловое излучение в кубической полости
с ребром L (см. рис. 3.1). Введем декартову систему координат,
оси которой направим вдоль ребер куба.
Тепловое излучение представляет собой совокупность электро-
магнитных волн. Запишем волновое уравнение для ж-компоненты
вектора электрического поля Е:
= (3-1)
с2 dtz
Введем граничные условия для электромагнитных волн на
внутренних стенках куба. Равновесное излучение однородно, по-
50 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
этому значения напряженности электрического поля на всех стен-
ках должно быть одинаковым. Положим его равным Eq. Это озна-
чает, что граничные условия должны быть циклическими, т. е.
= Ex(L,y,z) = Eq,
Ех(х, 0, z) — Ех(х, L, z) — Eq,
Ех(^, Уч 0) Ех(х, у, L) Eq.
Рассмотрим физическую картину, когда электромагнитные
волны теплового излучения проникают в глубь стенок на прене-
Рис. 3.1. Куб с ребром L, заполненный равновесным тепловым излучением
брежимо малую величину, а напряженность электрического поля
внутри стенки равна нулю. Тогда граничные условия (3.1) можно
записать в виде
Ех№ Уч *) = ЕХ(Ь, у, z) = 0,
Ex(x,0,z) = Ex(x,L,z) = 0, (3.2)
Ех(х, у, 0) = Ех(х, у, L) = 0.
Будем искать решение уравнения (3.1) с граничными услови-
ями (3.2) в виде следующей функции:
Ех = X(x)Y(у)Z(г) exp (iwt). (3.3)
Вычислим вторую частную производную от функции (3.3) по
координате х:
f)2 Е
—- X"(a;)Y(y)Z(^) exp (М =
0X2
Х"(т} Х"(х}
= ^Y(y)Z(z) exp M) =
X \x) X(x)
3.1. Формула Рэлея-Джинса
51
Вычислим вторые частные производные величины Ех по дру-
гим координатам и времени:
^Ex_z\zy э2ех 2
ду2 Y (у) х' dz2 Z(z) х' dt2 x
Подставим выражения производных в волновое уравнение (3.1)
и получим
, Y"(y) Z"(z) =
Х(х) Y(y) Z(z) с2’ { ’
Все три слагаемых в левой части (3.4) — функции разных пе-
ременных, т. е. совершенно независимы друг от друга. Уравнение
(3.4) должно выполняться в любой точке внутри кубика, т. е. при
любых значениях координат я, j/, z и в любой момент времени.
Это может быть только в том случае, если каждое слагаемое в ле-
вой части равно некоторой константе. Обозначим эти константы
следующим образом:
о?)* = «а
Х(х) УЩ 2(г) 1 '
Z"
Тогда уравнение (3.4) примет вид
. fl
q2x + q2y + q2z = ^. (3.6)
Первое из уравнений (3.5) имеет решение
Х(х) = Axsin(qxx + <px), (3.7)
где величины Ах и <рх являются постоянными интегрирования.
Решения других уравнений системы (3.5) запишутся в анало-
гичном виде:
Y(у) = Aysm(qyy + фу), Z(z) = Az sin (qzz + tpz). (3.8)
Тогда решение волнового уравнения (3.1) представится произве-
дением функций:
Ех = В sin (qxx 4- (рх) sin (qyy + tpy) sin (qzz + ipz) exp (iut). (3.9)
Нетрудно видеть, что решения (3.7)-(3.9) представляют собой
стоячие электромагнитные волны. Иначе говоря, равновесное те-
пловое излучение в кубической полости можно представить в виде
суперпозиции стоячих электромагнитных волн.
Из граничного условия Ех(х = 0) = 0 следует, что <рх — 0.
Аналогично граничные условия Ех(у = 0) = 0 и Ex(z — 0) = 0
52 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
определяют, что сру = <pz = 0. Таким образом, выражение (3.9)
упрощается:
Ех = В sin (qxx) sin (qyy) sin {qzz) exp (iwt). (3.10)
Граничное условие на противоположной грани кубической по-
лости Ех(х = L) = 0 дает нетривиальное соотношение qxL = лтх.
Аналогично получим qyL = лту и qzL = тгт2, где тж, ту, mz —
целые неотрицательные числа.
Следовательно, каждой стоячей волне, суперпозицией которых
является тепловое излучение в кубике, ставится в соответствие не-
которая тройка целых неотрицательных чисел тх, ту, mz и со-
ответствующие им волновые числа
qx = 7^, Яу = yrny, qz = yrnz. (3.11)
Li 1j Jj
Минимальные значения чисел qx, qy, qz равны 7г/Т, макси-
мальные значения — неограниченны.
Мы получили выражение только для одной компоненты элек-
трического поля Ех. Нетрудно проверить, что решение волно-
вых уравнений для остальных компонент Еу и Ez даст функции,
аналогичные (3.10) и, главное, те же соотношения для волновых
чисел (3.11). Величины qx, qy, qz представляют собой проекции
волновых векторов q стоячих волн, заполняющих куб, на оси ко-
ординат (см. рис. 3.1).
Отметим важное обстоятельство, что в классической физике у
стоячих волн, находящихся в кубической полости, волновые век-
торы не могут принимать непрерывный ряд значений. Их значе-
ния дискретны.
Набор волновых векторов стоячих волн в кубе удобно предста-
вить графически, используя обратное пространство, в котором
задана прямоугольная система координат. Начала всех волновых
векторов q, чьи проекции заданы выражениями (3.11), совместим
с точкой начала координат. Тогда концы этих векторов изобра-
зятся точками обратного пространства (рис. 3.2), которые будем
называть изображающими точками.
Как видно из рис. 3.2, множество волновых векторов системы
(3.11) образует собой решетку, построенную на базисе трех вза-
имно перпендикулярных векторов, модули которых равны л/L.
Эта решетка называется обратной решеткой.
Теперь найдем число стоячих волн, которые содержатся в ку-
бическом ящике размером L х L х L. Для этого зададим неко-
торую величину волнового вектора q и опишем им как радиусом
сферу, приняв за центр начало координат обратного пространства.
Мы будем рассматривать лишь один октант построенной сферы,
так как все числа тх, ту, mz — неотрицательные. Число изо-
3.1. Формула Рэлея-Джинса
53
бражающих точек (концов волновых векторов, узлов обратной ре-
шетки) 7V, лежащих внутри этой сферы, будет равно целой части
отношения объемов 1/8 части сферы и элементарного куба с ре-
бром 7г/£, т. е.
лг Г1 4 з 1
N = целая часть < - • -тгд -——
1^8 3 (тг/ь)6
[ 7Г з L3 1
= целая часть < — q — >
(6 7Гб J
= целая часть
где V — объем куба с излучением, равный L х L х L,
Будем полагать, что длина ребра ящика L много больше длины
волны излучения Л. Тогда модули волновых векторов q = 2тг/Л »
тг/L, и в построенный октант сферы войдет большое количество
Рис. 3.2. Фрагмент обратного пространства.
На осях отложены проекции волновых векторов. Точки изображают концы волновых век-
торов стоячих волн, заполняющих кубический объем, т. е. обратную решетку
изображающих точек. Вследствие этого величину q можно пола-
гать квазинепрерывной, а число волновых векторов N — квази-
непрерывной функцией аргумента д, определенной выражением
(3.12)
Продифференцируем выражение (3.12) по параметру q\
dN=^2g2dg-
54 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
Используем связь модуля волнового вектора q с частотой си
си dcu
dq =—
с с
и получим
V и?
dN=——du. (3.13)
2тГ2 С6
Для того чтобы получить число стоячих волн, приходящихся
на интервал частоты dcu, необходимо учесть, что электромагнит-
ные волны — поперечные. Тепловое излучение неполяризовано,
поэтому каждую такую волну можно представить в виде супер-
позиции двух плоскополяризованных волн. Каждому волновому
вектору соответствуют две независимые поляризации, и поэтому
число (3.13) необходимо удвоить.
Теперь оценим энергию, приходящуюся на одну стоячую волну.
Мы приняли, согласно гипотезе Рэлея-Джинса, что на одну сте-
пень свободы (т. е. на волну определенной поляризации) прихо-
дится энергия, равная к^Т/2. Если мы учтем, что электромаг-
нитная волна имеет также магнитную составляющую, то средняя
энергия, приходящаяся на одну стоячую волну определенной по-
ляризации, будет равна к&Т. Тогда на интервал частоты dcu при-
ходится энергия
dW = 2квТ—^
с3
Отсюда следует, что спектральная плотность энергии излучения
равна
си2
— квТ-у-^. (3.14)
(3.15)
Используя соотношение между и и\ (2.5) и связь параметров
(2.4), получаем выражение для другой функции спектральной
плотности:
8лквТ
их = ~Х^
Выражения (3.14) и (3.15) представляют собой два варианта фор-
мулы Рэлея-Джинса для спектральной плотности энергии тепло-
вого излучения абсолютно черного тела.
Анализ формулы Рэлея-Джинса показывает полную несостоя-
тельность классического подхода к описанию равновесного тепло-
вого излучения.
Во-первых, при возрастании частоты (или при уменьшении
длины волны) излучения спектральная плотность электромагнит-
ной энергии монотонно неограниченно растет, что не согласуется
3-1. Формула Рэлея-Джинса
55
с экспериментом (рис. 3.3). Неограниченное возрастание плотно-
сти энергии теплового излучения с уменьшением длины волны,
которое следует из формулы (3.15), получило название «ультрафи-
олетовая катастрофа».
Во-вторых, для получения полной энергии электромагнитного
излучения, находящегося в равновесии с нагретым твердым те-
Рис. 3.3. Иллюстрация «ультрафиолетовой катастрофы».
По вертикальной оси отложена спектральная интенсивность излучения в относительных
единицах. Точки, соединенные сплошной линией, — экспериментальные результаты.
Штриховая линия — результаты расчета по формуле Рэлея-Джинса
лом, требуется проинтегрировать функцию (3.14) по диапазону
всевозможных частот. Интеграл от функции спектральной плот-
ности энергии расходится:
квТ
л2 с3
и =
(3.16)
Следовательно, нагретое твердое тело должно излучать, в ос-
новном, на высоких частотах, до тех пор, пока не охладится до
абсолютного нуля. Таким образом, равновесие между твердым те-
лом и электромагнитным излучением в принципе невозможно. Эти
выводы свидетельствуют о неприменимости классической теории
к проблеме излучения твердого тела.
Нетрудно, однако, заметить, что с увеличением длины волны
кривая Рэлея-Джинса все ближе подходит к кривой, полученной
экспериментально. Это позволяет предположить, что классиче-
ский подход и формула Рэлея-Джинса справедливы для частного
случая — длинноволнового теплового излучения.
56 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
3.2. Гипотеза и формула Планка
Задача описания теплового излучения была решена выдаю-
щимся немецким физиком М. Планком (1858-1947). В своем вы-
ступлении на заседании Немецкого физического общества 14 дека-
бря 1900 г. он заявил, что проблема непротиворечивого описания
излучения абсолютно черного тела может быть решена на основа-
нии следующей гипотезы.
Излучение и поглощение света происходит не непрерывно, а
порциями с энергиями Wq, 2P7q, ..., причем энергия РИо линейно
зависит только от частоты колебаний волны со так:
Wq = hco.
(3-17)
Постоянная величина h была также введена М. Планком и но-
сит название постоянной Планка.
Получим в явном виде выражение для спектральной плотности
энергии иш равновесного теплового излучения, базируясь на гипо-
тезе Планка. Вновь рассмотрим систему стоячих волн в ограни-
ченном объеме, как это было сделано при выводе формулы Рэлея-
Джинса. Но теперь, следуя гипотезе Планка, полагаем, что энергия
волн в ящике может быть равна Wq, 2P7q, •••, а вероятности су-
ществования волн с определенной энергией подчиняются распре-
делению Больцмана, т. е. равны
А, А ехр
Wq \
kBTJ
, А ехр
2УУ0\
квт)’
. / пЖЛ
А ехо — -—— , ..
' \ квТ J
Сумма вероятностей для всевозможных энергий волн равна еди-
нице, поэтому коэффициент А может быть найден из условия нор-
мировки
оо
22 А ехр
п=0
=
kBTj
следовательно,
ОО
Е ехр
п=0
пР70\
квт)
(3.18)
Среднее значение энергии волн в замкнутом объеме вычисляется
суммированием энергий отдельных волн, умноженных на соответ-
ствующие вероятности:
W =
ОО
2 пРИрехр
п=0
оо
Е ехР
п=0
nWp\
ьёт)
пТУр\
квт)
3.2. Гипотеза и формула Планка
57
Для краткости введем безразмерную переменную х = W^/k^T и
перепишем последнее выражение:
оо
^2 пехр (—пх)
W = W0^--------------. (3.19)
^2 ехР (~nx)
n=0
Среднюю энергию W вычислим следующим способом. Во-
оо
первых, заметим, что выражение ^2 ехР (—nx) = 1 + ехр (—х) +
п=0
+ ехр (—2х) + ..., стоящее в знаменателе (3.19), представляет со-
бой бесконечную геометрическую прогрессию, знаменатель кото-
рой равен ехр (—ж). Пользуясь формулой суммы бесконечной гео-
метрической прогрессии, запишем:
ОО 1
22 ехр (-пх) = ----------(3.20)
l-exp(-x)
Продифференцируем выражение (3.20) по параметру х:
~ £пехр =_ и - е*р (-я»2 (3,21)
Теперь видно, что левая часть в (3.21) совпадает с числителем
в выражении (3.19) с точностью до знака. Подставляя правые
части соотношений (3.20) и (3.21) в правую часть формулы (3.19),
получаем выражение для средней энергии волн в данном объеме:
1 — ехр (—ж) _
Ту = IV, ехр
(1 — ехр (—ж
1
= W. ехр(~.-Ц = Wo------7^-—,
1 - ехр (-х) ехр (х) - 1
или
W = W0----
ехр
(3.22)
Вернемся к выводу функции спектральной плотности энергии
равновесного излучения. Можно воспользоваться полученной ра-
нее формулой (3.14) и заменить в ней энергию к&Т на среднюю
58 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
энергию W, данную выражением (3.22). Тогда мы получим иско-
мую функцию в следующем виде:
— 1 со2 ттг 1 со2 1
““= = IV“jr2<3' / Wo \ ' (3'23)
ехр (w) -1
(3.24)
1
Теперь в последнее выражение подставим (3.17), и спектральная
плотность энергии примет вид
/kJ3 1
о о / \
7Г2Сб / ПЫ \
ехр fe; -
Выражение (3.24) называется формулой Планка для спектральной
плотности энергии равновесного излучения.
Прежде всего заметим, что формула Планка соответствует уни-
версальной функции Вина. Сравнение (2.16) и (3.28) дает явный
вид функции:
WT) =
h
7Г2С3
(3.25)
Исследуем полученную формулу Планка (3.24). Сначала рас-
смотрим область предельно низких частот. Возникающая при
cj —> О неопределенность раскрывается по правилу Лопиталя диф-
ференцированием числителя и знаменателя по частоте cj:
/kJ3 1 3/kj2 1
11Ш -----Т— г-------- = 11Ш --------7—г Г- = 0.
CJ->O ( ГШ) \ си->0 h ( ГШ \
ехр -—— — 1 —— ехр -——
\kBT J квТ \квТ J
Следовательно, спектральная плотность энергии излучения (3.24)
стремится к нулю при со —> 0.
В области низких частот выполняется соотношение hco/квТ
<С 1. При этом условии экспоненту, находящуюся в знаменателе
формулы Планка, можно разложить в ряд Тейлора, ограничиваясь
линейным членом. В результате выражение (3.24) упрощается и
превращается в формулу Рэлея-Джинса (3.14):
~ /kJ3 1 _ cj2
UuJ Л2С3 1 /kJ _ в 7Г2С3
квТ "
3.2. Гипотеза и формула Планка
59
.. /kJ3 1
lim ------------г-г—7------:
j->oo 7Г2Сй [ ПЫ \
ехр (-1
.. 6/kj
= lim
Далее найдем предел функции (3.24) при и —> оо:
3/kj2 1
J—>оо 7Г2С3 h f fiw \
______1____________
2c3 / h \2 / hw \
= lim -yj—-------3——~-------— = 0.
U->OO tJc3 f h \ ( Нш \
exp\k^r)
Таким образом, и при неограниченном возрастании частоты функ-
ция Планка (3.24) стремится к нулю.
Для высоких частот выполняется условие tuv/kT 1. При
этом в знаменателе формулы (3.24) можно пренебречь единицей.
Тогда формула Планка приобретает следующий вид:
/kJ3 ( /kJ \
= Тз ехР *
ivzc6 \ квТ J
Этот частный случай формулы Планка можно использовать в
области высоких частот cj k^T/h. Видно, что зависимость
(3.26) тоже является частным случаем универсальной функции
Вина (2.16). Явный вид этой функции в данном случае выражается
следующей формулой:
(3.26)
(3.27)
= ехр [~^т)’
Вид спектральной плотности энергии равновесного теплового
излучения (3.24) представлен графиком на рис. 3.4.
Из рис. 3.4 видно, что формула Планка, в отличие от формулы
Рэлея-Джинса, не приводит к «ультрафиолетовой катастрофе».
Многократные эксперименты подтвердили правильность подхода
Планка к описанию теплового излучения абсолютно черного тела
и справедливость формулы (3.24).
Постоянная Планка относится к важнейшим фундаменталь-
ным константам, и ее числовое значение измерялось различными
экспериментальными методами. Согласно современным измере-
ниям h = 1,0545887(57) • 10“27 эрг-с. Размерность постоянной
Планка можно непосредственно получить из формулы (3.1) и она
совпадает с размерностью действия. По этой причине постоянную
Планка называют иногда квантом действия.
60 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
Заметим, что часто в расчетах и формулах используется также
константа h = 2тгЙ = 6,6260755(40) • 10-34 Дж • с.
Рис. 3.4. Спектральная плотность излучения абсолютно черного тела.
Сплошная линия — расчет по формуле Планка (3.10), штриховая — по формуле Рэлея-
Джинса (2.42)
Пользуясь формулой Планка можно найти значения постоян-
ных в законе Стефана-Больцмана (2.18)—(2.20) и в законе сме-
щения Вина (2.25), которые первоначально определялись экспери-
ментально.
Для вычисления постоянной а в формуле Стефана-Больцмана
(2.18) получим выражение для плотности энергии равновесного
излучения tz, проинтегрировав функцию Планка (3.24) по всему
частотному диапазону:
оо
(3.28)
“ = 7
о
dw =
/• 1
J 7Г2С3 ( fiW \
° ехр\йг/ 1
Снова используем обозначение х = -г—=. Тогда си = ——х и
квТ П
квТ
= —г— dx. Подставляя эти выражения в интеграл (3.28), получим
Гь
о° Л оо
„= ____1___dx=J^T< _________________dx.
J fi37T2c3 h ехр (ж) — 1 Л37г2с3 J ехр (ж) — 1
о
о
3.2. Гипотеза и формула Планка
61
оо
Несобственный интеграл f------—---- dx представляет собой
о ^ХР \х) ~ I
оо хр~^
частный случай интегралов вида f-----—г-----dx, который вы-
о ехр (ax) — 1
ражается через специальные функции:
f X?-1 Г(р)
/ ----7--\---7 dX = ----
J ехр (ах) — 1 ар
о
1 1 1 Г(р)Л. .
+ 2Р + 3? + ’ ‘ ” аР Р ’
ар
1
Здесь Г(р) — гамма-функция, Q(p) — дзета-функция Римана.
В нашем частном случае при параметрах р = 4 и а — 1 этот не-
собственный интеграл равен тг4/15.
В результате выражение (3.28) для плотности энергии излуче-
ния приводится к следующему виду:
к4 тг2
т4
15Л3с3
(3.29)
Таким образом, мы из формулы Планка (3.24) теоретически
вывели закон Стефана-Больцмана в форме (2.18). Сравнение со-
отношений (2.18) и (3.29) дает нам выражение для постоянной а
через фундаментальные константы:
15Л3с3
(3.30)
Вычисления дают приближенное значение а~7,566-10 16 —т.
м3- К
Полученное в предыдущей лекции соотношение (2.21) позво-
ляет вычислить константу а для закона Стефана-Больцмана, за-
писанного в форме (2.23):
С Ajg7T2
а 4^ 60Л3с2
(3.31)
Расчеты дают значение константы ст, совпадающее с приведенным
в предыдущей лекции.
Из формулы Планка может быть получен также закон смеще-
ния Вина (2.28) и рассчитана постоянная Вина Ь. Так как закон
смещения Вина связывает температуру с длиной волны, то целе-
сообразно использовать функцию спектральной плотности ^д(А),
которую можно получить из функции (3.24) с помощью уравнений
(2.4) и (2.5):
1б7Г2Лс
“Pljsfj-1
(3.32)
и =
=
1
62 Лекция 3. «Ультрафиолетовая катастрофа» и формула Планка
Теперь найдем экстремум функции (3.32) и длину волны АтаХ5
на которой достигается этот экстремум. Для этого необходимо вы-
числить производную du\(X)/d\ и приравнять ее нулю. Исполь-
зуем для краткости обозначение
D _ 2тгЛс
ХквТ
и выразим функцию и\ через переменную /3:
- Д5 feB*5 1
Ux 2%3/14с4 ехр (/3) — 1 ’
(3.33)
Теперь вычислим производную du\/dfl и приравняем ее нулю. Со-
кратив на ненулевой множитель и выполнив несложные преобра-
зования, получим уравнение
5ехр(-/3) 4-/3-5 = 0. (3.34)
Это трансцендентное уравнение решается численными методами,
и его единственный положительный корень с точностью до восьми
значащих чисел равен /Зо = 4,9651142. Теперь с помощью фор-
мулы (3.33) можно получить константу Вина:
7 m 2л he
— АтахТ = — (3.35)
Вычисления дают следующее значение константы b = (2,89779 ±
± 0,00009) • 10“3м-К, что хорошо согласуется с эксперименталь-
ными результатами.
Задачи к лекции 3
1. Рассчитать количество стоячих волн в объеме, имеющем форму
прямоугольного параллелепипеда с длинами ребер, выражаемыми вза-
имно простыми числами Li, £2? Тз- Показать, что и в этом случае для
плотности энергии излучения получается формула Рэлея-Джинса.
2. Полагая спектр излучения Солнца близким к тепловому равновес-
ному с температурой ~ 6000 К, вычислить долю энергии, принадлежащей
видимому диапазону.
3. Нить лампы накаливания разогревается до температуры « 2400 °C.
Вычислить, какая доля излучаемой энергии приходится на видимый диа-
пазон.
4. Температура абсолютно черного тела возросла с 200 °C до 2000 °C.
Во сколько раз увеличилась спектральная плотность излучения на длине
волны: а) А = 1мкм; б) А = Юмкм; в) А = 0,1 мкм?
5. Вычислить отношение энергий, излучаемых абсолютно черным
телом в интервалах длин волн 1мкм < А < 2мкм и Юмкм < А <
< 11 мкм. Температура тела: а) 300 К; б) 1000 К; в) 3000 К.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 3
3.1. Реликтовое излучение
В 1964 г. американская научно-исследовательская фирма «Белл Теле-
фон Лабораторис» изготовила 6-метровую рупорную антенну со сверхниз-
ким уровнем шумов для связи со спутником «Эхо». Сотрудники фирмы
А.А.Пензиас и Р.В. Вильсон использовали эту антенну для измерения
интенсивности радиоизлучения нашей Галактики на длине волне 7,35 см.
В ходе этих исследований в 1965 г. было обнаружено микроволновое
излучение, заполняющее космическое пространство и обладающее прак-
тически полной изотропией. В первую очередь это означало, что ис-
точником данного излучения являются не определенные части нашей
Галактики, а вся Вселенная. По этой причине обнаруженное излучение
было названо фоновым.
Измерения на разных длинах волн позволили установить, что ми-
кроволновое фоновое излучение имеет непрерывный спектр, хорошо со-
впадающий по форме со спектром теплового излучения, описываемым
формулой Планка (3.24) или (3.32).
Оценки, выполненные по первым измерениям спектрального состава
фонового излучения, дали значение характерной температуры Т прибли-
зительно равной трем кельвинам. По закону Вина (3.35) легко вычи-
слить приближенное положение максимума спектра теплового излучения
при такой характерной температуре, т. е. длину волны
Атах = ~ 0,1 СМ = 1 ММ. (Д.3.1)
J- о
Электромагнитное излучение с длиной волны более Змм интенсивно
ослабляется земной атмосферой, поэтому в последующие годы исследо-
вания фонового излучения проводились с помощью специализированных
спутников Земли и орбитальных лабораторий. Работа космического ра-
диотелескопа WMAP, запущенного в 2001 г., позволила получить значе-
ние характерной температуры равное 2,728 К.
Существование микроволнового фонового излучения явилось прек-
расным подтверждением концепции горячей ранней Вселенной, выдви-
нутой Г.А. Гамовым (1904-1968) еще в 1946 г., и находится в согласии с
теорией Большого взрыва (Big Bang).
Согласно современной космологии, после Большого взрыва Вселен-
ная, расширяясь, остывала, причем ее температура Т на раннем этапе
эволюции подчинялась следующей приближенной зависимости:
Ю10
Г - (Д.3.2)
64
Дополнения к лекции 3
где время £, прошедшее с момента Большого взрыва, выражено в секун-
дах, а температура Вселенной — в кельвинах.
Ранняя Вселенная представляла собой высокотемпературную плаз-
му, содержащую различные частицы и античастицы. Когда температура
понизилась до ~ 108 К, все античастицы аннигилировали, а во Вселен-
ной остались фотоны, электроны, нейтрино, протоны и альфа-частицы.
Рис. Д.3.1. Один из первых спектров фонового космического излучения, получен-
ный внеатмосферным аппаратом.
По горизонтальной оси отложена длина волны в см, по вертикальной — спектральная плот-
ность потока излучения в 10“12 Вт/см2/стер/см. Обе шкалы — логарифмические. За-
штрихованная полоса — коридор экспериментальных погрешностей, штриховая линия —
спектр равновесного излучения с характерной температуры Т = 3 К
При этом количество фотонов примерно на девять порядков превышало
количество массивных частиц. Фотоны интенсивно взаимодействовали с
электрически заряженными частицами — поглощались, переизлучались
и в результате сформировали равновесное тепловое излучение с харак-
терной температурой, выраженной формулой (Д.3.2).
Примерно через миллион лет после Большого взрыва температура
Вселенная упала настолько, что тепловая энергия k&T стала значительно
ниже энергии Ридберга Ry. Тогда плазма рекомбинировала — электроны
присоединились к протонам и альфа-частицам, и образовались нейтраль-
ные атомы водорода и гелия.
Дополнения к лекции 3
65
Интенсивность взаимодействия фотонов (количество актов взаимо-
действия в единице объема за единицу времени) с нейтральными ато-
мами на несколько порядков меньше, чем с электрически заряженными
частицами плазмы. Как следствие, после образования нейтральных ато-
мов водорода и гелия Вселенная стала почти прозрачной для фотонов.
Иначе говоря, число фотонов практически не изменялось с течением вре-
мени.
Таким образом, экспериментально обнаруженное фоновое микровол-
новое излучение образовалось миллиарды лет назад в ранней горя-
чей Вселенной. По предложению известного российского астрофизика
И.С. Шкловского (1916-1985) это излучение было названо реликтовым.
После рекомбинации плазмы реликтовое излучение практически пе-
рестало взаимодействовать с атомами Вселенной. Но в период реком-
бинации характерная температура излучения Т, согласно соотношению
(Д.3.2), имела порядок тысяч кельвинов, т.е. много больше современ-
ного значения « ЗК.
Дальнейшее охлаждение реликтового излучения (после образования
нейтральных атомов) происходило из-за космологического расширения
Вселенной, которое было открыто Э. Хабблом по смещению в сторону
больших значений спектральных линий оптического диапазона, излуча-
емых галактиками.
Изменение длин волн А фотонов может быть описано классическим
эффектом Доплера:
где ДА — регистрируемое смещение спектральной линии, v — скорость
удаляющегося источника излучения с длиной волны А.
При относительном удалении источника излучения от наблюдателя
регистрируемая длина волны возрастает на величину ДА, а энергия фо-
тонов соответственно уменьшается. Следовательно, при космологиче-
ском расширении не только разбегаются галактики, но и увеличивается
длина волны фотонов, заполняющих Вселенную.
Согласно закону Вина (3.34), увеличение длины волны Агпах макси-
мума спектра теплового излучения соответствует понижению его харак-
терной температуры. Таким образом, современное значение характер-
ной температуры реликтового излучения является еще одним доказа-
тельством космологического расширения Вселенной.
По измеренной длине волны Агпах максимума спектра можно оценить
среднюю энергию фотона реликтового излучения:
ё = ~ 1(Г3 эВ ~ 10-15 эрг. (Д.3.4)
Ащах
Маленькая величина энергии ё является одной из причин, по которой
реликтовое излучение не было открыто раньше.
Измерения плотности энергии реликтового излучения дали прибли-
женное значение « 5 • 10-13 эрг/см3. Следовательно, концентрация ре-
ликтовых фотонов во Вселенной составляет около 500 в 1см3. Эта нео-
жиданно большая величина кажется еще более грандиозной, если
6 Зак. 178
Дополнения к лекции 3
знать, что во Вселенной в среднем на один протон (или электрон, так
как Вселенная электронейтральна) приходится несколько кубических
метров.
Астрофизики называют реликтовое излучение «эхом Большого взры-
ва». Исследование физических характеристик реликтового излучения
позволяет получить информацию о состоянии Вселенной на раннем этапе
ее существования и совершенствовать теорию эволюции Космоса.
Лекция 4
ФОТОНЫ
4.1. Фотоэффект
Одним из физических явлений, непонятных с точки зрения
классической физики, является фотоэффект. В 1887 г. Г. Герц
(1857-1894) обнаружил, что если осветить шарики электроискро-
вого разрядника ультрафиолетовым светом, то процесс получения
искры между ними значительно облегчается. Ряд закономерно-
стей этого явления был установлен в работах русского физика
А.Г. Столетова (1839-1896) в период 1888-1890 гг. Наиболее пол-
ное исследование характеристик фотоэффекта было выполнено
Ф. Ленардом (1862-1947) в 1900 г. Существенно, что к этому вре-
мени уже был открыт электрон.
В первых опытах использовалось несложное оборудование —
электрометр и источник света, например, электрическая дуга.
К электрометру присоединялась цинковая пластинка. Если пла-
стина предварительно заряжалась положительно, то при ее осве-
щении светом электрической дуги пластина почти не разряжается.
Но если пластину зарядить отрицательно, то световой пучок от
дуги разряжает электрометр очень быстро. Именно это явление
было названо фотоэффектом. Однако, когда на пути пучка света
поставлено обыкновенное стекло, отрицательно заряженная пла-
стина уже не разряжалась, какова бы ни была интенсивность из-
лучения. Известно, что стекло поглощает ультрафиолетовые лучи,
поэтому можно заключить, что фотоэффект вызывает именно уль-
трафиолетовый участок спектра.
Систематическое исследование фотоэффекта можно проводить
с помощью установки, схема которой показана на рис. 4.1.
В колбе, прозрачной для видимого и ультрафиолетового света,
из которой откачан воздух до высокого вакуума, находятся два
металлических электрода: эмиттер и коллектор. Эта колба с впа-
янными электродами называется вакуумным фотоэлементом.
Фотоэлемент включен в электрическую цепь, которая позволяет по-
давать на впаянные электроды регулируемую разность потенциа-
68
Лекция 4. Фотоны
лов U и измерять протекающий через фотоэлемент электрический
ток I. На эмиттер направляется поток ультрафиолетового излуче-
ния интенсивности L и частоты и. При этом с поверхности облуча-
емого эмиттера вылетают электроны, которые для краткости часто
Рис. 4.1. Схема установки для исследования фотоэффекта:
/т,А — микроамперметр, V — вольтметр
называют фотоэлектронами. Подчеркнем, что фотоэлектроны —
это обычные электроны, и название характеризует не параметры
частиц, а только их происхождение. Часть фотоэлектронов попа-
дают на коллектор, и в результате возникает электрический ток У,
который регистрируется микроамперметром.
Для исследования свойств фотоэффекта измеряются зависимо-
сти тока I от напряжения (7, т.е. вольт-амперные характеристики
(ВАХ) вакуумного фотоэлемента при различных значениях осве-
щенности эмиттера и частоты падающего света. Качественный
вид типичной вольт-амперной характеристики вакуумного фото-
элемента при определенной интенсивности L и заданной частоте
излучения си показана на рис. 4.2.
Из рис. 4.2 видно, что ток течет через фотоэлемент только в од-
ном направлении. Это обусловлено тем, что источником носителей
заряда (электронов) является эмиттер.
Если потенциал коллектора больше потенциала эмиттера, то
фотоэлектроны притягиваются к коллектору. При увеличении по-
ложительного потенциала коллектора ток достигает максималь-
ного значения /щах- Это происходит, когда все электроны, ис-
пущенные эмиттером, достигают коллектора. Величина тока /тах
прямо пропорциональна числу фотоэлектронов (т.е. электронов,
испущенных эмиттером).
4.1. Фотоэффект
69
Если разность потенциалов между коллектором и эмиттером
равна нулю, то ток не равен нулю и поддерживается за счет кине-
тической энергии электронов, с которой они выходят из эмиттера.
При изменении разности потенциалов U на обратную (т. е. ко-
гда потенциал коллектора ниже потенциала эмиттера) ток умень-
шается. Ток прекращается при определенном значении потен-
циала коллектора. Этот потенциал имеет отрицательный знак
Рис. 4.2. Типичный вид ВАХ вакуумного фотоэлемента:
U — разность потенциалов между электродами (коллектором и эмиттером), I — ток на
коллекторе, /max — ток насыщения, Ug — потенциал запирания
относительно потенциала эмиттера. Абсолютную величину напря-
жения между эмиттером и коллектором Ug, при которой прекра-
щается электрический ток в фотоэлементе, принято называть за-
пирающим потенциалом (см. рис. 4.2).
Форма ВАХ в отрицательной части напряжения U легко объ-
ясняется, если предположить, что при облучении эмиттера светом
с фиксированными интенсивностью и частотой из эмиттера вы-
ходят электроны с разными энергиями. Тогда при уменьшении
напряжения U ниже нуля между электродами возникает электри-
ческое поле, тормозящее вышедшие из эмиттера электроны. Если
работа поля — eU превысит начальную кинетическую энергию фо-
тоэлектрона, то он вернется на эмиттер и не даст вклад в реги-
стрируемый ток I. При определенном значении напряжения — Ug
работа поля eUg достигает максимальной начальной кинетической
энергии фотоэлектронов jEmax, и они все возвращаются на эмит-
тер. Ток в цепи фотоэлемента становится равным нулю. Следова-
тельно, максимальная кинетическая энергия фотоэлектронов, по-
кинувших эмиттер, определяется уравнением
^max — ^Ug. (4-1)
Плавный вид ВАХ в отрицательной области напряжения U
свидетельствует о том, что фотоэлектроны, покинувшие эмиттер,
имеют практически непрерывный спектр кинетической энергии в
интервале от 0 до eUg.
70
Лекция 4. Фотоны
Таким образом, характерные особенности ВАХ фотоэлемента,
изображенной на рис. 4.2, удается объяснить в рамках классиче-
ской физики.
При увеличении интенсивности L облучения эмиттера светом
фиксированной частоты си сила тока I возрастает. Однако при этом
значение запирающего потенциала Ug остается неизменным. Ти-
пичные вольт-амперные характеристики вакуумного фотоэлемента
при различных значениях интенсивности L падающего на эмит-
Рис. 4.3. ВАХ вакуумного фотоэлемента для различной интенсивности L моно-
хроматического падающего излучения
тер монохроматического излучения приведены на рис. 4.3. Экс-
перименты показывают, что величина запирающего потенциала
Ug вообще не зависит от интенсивности излучения, падающего на
эмиттер.
Еще более странно с точки зрения классической физики вы-
глядит экспериментальная зависимость запирающего потенциала
Ug от частоты излучения си при неизменной его интенсивности L
(см. рис. 4.4).
Рис. 4.4. ВАХ вакуумного фотоэлемента для различных частот падающего излу-
чения си при постоянной интенсивности L
С ростом частоты си запирающий потенциал Ug возрастает,
причем строго линейно при любых значениях освещенности эмит-
4.1. Фотоэффект
71
тера. Свободные члены этих линейных функций Ug(w) являются
характеристиками материала эмиттера, но угловой коэффициент
всех зависимостей Ug((v) один и тот же (см. рис. 4.5). Логично
Рис. 4.5. Зависимость запирающего потенциала Ug от частоты излучения си для
различных материалов эмиттера
предположить, что этот неизменный угловой коэффициент опреде-
ляется какими-то фундаментальными константами и не зависит
от вещества, из которого изготовлен эмиттер.
Наконец, наиболее удивительной особенностью фотоэффекта
является наличие «красной границы». Опытным путем было по-
лучено, что для каждого металла (материала эмиттера) существу-
ет определенная частота излучения cuq, такая, что при меньших
частотах и < а?о фотоэффект не наблюдается при сколь угодно
большой интенсивности излучения L. Эта «красная граница» у
большинства металлов лежит в ультрафиолетовой части спектра,
поэтому для наблюдения фотоэффекта требуется использовать уль-
трафиолетовое излучение. «Красная граница» в видимом диапа-
зоне находится лишь у щелочных металлов. Поэтому наблюдать
фотоэффект в видимом свете можно только на эмиттере, изгото-
вленном из щелочного металла, приняв меры, препятствующие его
окислению.
Свойства фотоэффекта, иллюстрированные рис. 4.3-4.5, и су-
ществование «красной границы» противоречат выводам классиче-
ской теории. Это видно из следующих рассуждений.
Во-первых, интенсивность света прямо пропорциональна энер-
гии электромагнитной волны, которая взаимодействует с электро-
нами, находящимися внутри эмиттера. Поэтому с точки зрения
классической физики с увеличением интенсивности L должна ра-
сти начальная кинетическая энергия фотоэлектронов и, следова-
тельно, величина запирающего потенциала Ug, что противоречит
результатам опытов, изображенных на рис. 4.3.
72
Лекция 4. Фотоны
Во-вторых, энергия электромагнитной волны определяется ква-
дратом ее амплитуды и не зависит от частоты. Следовательно,
кинетическая энергия фотоэлектронов и запирающий потенциал
Ug в рамках классических представлений не должны зависеть от
частоты света. Таким образом, рис. 4.4 демонстрирует еще одно
противоречие классической теории и результатов опыта.
В-третьих, наличие «красной границы» вообще кажется пара-
доксальным. Монохроматический поток света с большой интен-
сивностью и частотой и < ц?о, облучающий поверхность эмитте-
ра в течение длительного времени, казалось бы, должен передать
электронам металла значительную энергию. Тем не менее, в та-
ких опытах не наблюдается ни одного фотоэлектрона!
Еще одно несоответствие получается при классическом подходе
расчета среднего времени выхода фотоэлектронов из эмиттера при
заданной интенсивности излучения. Например, согласно клас-
сической теории, при интенсивности порядка 10-2Вт/см2 фото-
электроны из цинкового эмиттера должны начать выходить через
несколько секунд после начала облучения (см. дополнение 4.2).
С другой стороны, в экспериментах было обнаружено, что время
задержки времени выхода фотоэлектронов заведомо меньше 10“9 с
при потоке облучающего света ~ 1О-10 Вт/см2.
Многочисленные попытки объяснить свойства вакуумного фо-
тоэффекта на базе классической физики не увенчались успехом.
4.2. Фотонная теория фотоэффекта
Теоретическое объяснение наблюдаемых закономерностей фо-
тоэффекта было дано А. Эйнштейном (1879-1955) в 1905 г. Это
объяснение базировалось на гипотезе М. Планка, согласно которой
электромагнитное излучение испускается и поглощается опреде-
ленными порциями, причем энергия каждой такой порции опреде-
ляется формулой
е = fiw. (4.2)
Развивая идеи М. Планка, Эйнштейн пришел к выводу, что
электромагнитное поле имеет дискретную структуру. Электромаг-
нитная волна может состоять из отдельных частиц — квантов,
впоследствии названных фотонами. Фотоны могут излучаться
и поглощаться веществом. Первым приложением фотонной тео-
рия было объяснение физического механизма вакуумного фотоэф-
фекта.
Согласно теории П.Друде (1863-1906), созданной в 1900 г., в
металлах содержится большое количество электронов проводимо-
сти, которые могут свободно перемещаться по всему объему метал-
лического тела, что и обеспечивает хорошую электропроводность
металлов. Эйнштейн предположил, что в вакуумном фотоэффекте
фотон из пучка света, падающего на эмиттер, поглощается каким-
4.2. Фотонная теория фотоэффекта
73
либо электроном проводимости и передает ему всю свою энергию.
Благодаря полученной энергии электрон может выйти из металла
во внешнюю среду.
При комнатной температуре и отсутствии освещенности элек-
трон проводимости самопроизвольно не может выйти из металла,
так как на границе металл-вакуум (или металл-воздух) существу-
ет потенциальный барьер. Экспериментальные исследования по-
казали, что для удаления электрона проводимости из металла тре-
буется затратить определенную энергию. Минимальное значение
этой энергии (высота потенциального барьера) называется рабо-
той выхода Ав. Эта величина является характеристикой металла
и существенно зависит от его кристаллической структуры. Чи-
словые значения Ав удобно измерять в электрон-вольтах (эВ). По
определению электрон-вольт представляет собой кинетическую
энергию, которую приобретает электрон, ускоренный разностью
потенциалов 1 вольт (1эВ = 1,602177 • 10-12эрг). Измерения по-
казали, что для большинства металлов работа выхода Ав лежит в
интервале 2-5 эВ.
Энергия фотоэлектронов в вакууме
-------г----------г----- Энергия фотоэлектронов в вакууме
Энергия
фотона
7700
= Лео -Лп
пл ах в
Энергия
------ фотона
7?оо
£,„ах
£,л
Зона
проводимости
Зона
проводимости
Металл | Вакуум
Металл [ Вакуум
Рис. 4.6. Энергетическая схема фотоэффекта:
Высота потенциального барьера на границе «металл-вакуум» равна работе выхода Ав.
Ноль отсчета энергии соответствует неподвижному электрону, находящемуся вне металла.
Положительные энергии имеют свободные электроны вне металла, обладающие кинетиче-
скими энергиями. Энергии электронов проводимости в металле Еэл имеют отрицатель-
ные значения: а) фотон поглотился электроном проводимости с максимально возможной
энергией. Фотоэлектрон получает максимально возможную энергию Ешах! б) фотон погло-
тился электроном проводимости с произвольной энергией. Фотоэлектрон получает энергию
Е < -Етпах
Явление вакуумного фотоэффекта удобно рассмотреть с помо-
щью энергетической диаграммы, приведенной на рис. 4.6.
Электроны проводимости металла имеют различные энергии,
лежащие в диапазоне, называемом зоной проводимости. Элек-
5 Зак. 178
74
Лекция 4. Фотоны
трон проводимости, поглощая фотон, увеличивает свою энергию.
Если этой энергии достаточно, чтобы преодолеть потенциальный
барьер на границе, то электрон покидает металл, теряя энергию
равную Ав- Остаток представляет собой кинетическую энергию
свободного (вышедшего из металла) электрона.
Если фотон поглощается электроном проводимости, который
обладает наибольшей энергией, то его кинетическая энергия после
выхода из металла будет иметь максимально возможное значение
#тах (см. рис. 4.6а).
Уравнение Эйнштейна для вакуумного фотоэффекта записыва-
ется в виде
£ ~ Ав + Етгсх-) (4.3)
где е — энергия поглощенного фотона, Втах — максимальная ки-
нетическая энергия фотоэлектрона.
Можно сказать, что уравнение Эйнштейна представляет собой
закон сохранения энергии для системы фотон-электрон.
Из диаграммы на рис. 4.6 также очевидно, что при энергии
фотона ё = hw меньшей, чем работа выхода Ав, фотоэффект в
принципе невозможен. Энергии, полученной электроном от фо-
тона, недостаточно для преодоления потенциального барьера. Та-
ким образом, уравнение (4.3) применимо, если энергия фотона е
превышает работу выхода Ав данного металла (материала эмит-
тера).
Форма ВАХ вакуумного фотоэффекта определяется распределе-
нием плотности состояний электронов проводимости в зоне про-
водимости. Расчет этой плотности состояний является одной из
важных задач квантовой физики твердого тела. Кроме того, на
форму регистрируемой ВАХ влияет то, что часть энергии элек-
троны теряют при столкновениях с атомами вещества.
Уравнение Эйнштейна (4.3) позволяет объяснить все законо-
мерности фотоэффекта, обнаруженные в экспериментах. Сопоста-
вление (4.2) и (4.3) сразу дает линейную зависимость максималь-
ной кинетической энергии фотоэлектронов от частоты си:
-S'max — ^CU — Ав. (4-4)
Последнее уравнение доказывает независимость кинетической
энергии фотоэлектронов от интенсивности излучения, падающего
на эмиттер.
Существование «красной границы» объясняется наличием для
электронов потенциального барьера высотой Ав. Для вычисле-
ния граничной частоты cuq следует в уравнении (4.4) положить
EmQiX = 0. Это описывает ситуацию, когда вся энергия электрона
расходуется на совершение работы выхода. Частота электромаг-
нитного излучения, соответствующая «красной границе» фотоэф-
4.2. Фотонная теория фотоэффекта
75
фекта, равна
W0 = ф. (4.5)
h
При частоте излучения cu > cuq фотоэффект происходит, при си <
< сио фотоэффект невозможен.
С уменьшением интенсивности потока монохроматического из-
лучения уменьшается только количество фотонов, а их энергия
остается неизменной. Малая инерционность фотоэффекта обусло-
влена тем, что взаимодействие происходит между двумя части-
цами. Поглотив фотон, электрон проводимости практически мгно-
венно увеличивает свою энергию на величину е, иначе говоря, не
требуется большого времени для накопления энергии электроном
проводимости (см. дополнение 4.2).
Для оценки времени выхода фотоэлектрона из металла при вы-
полнении условия cu > cuq сначала выразим энергию фотона через
длину волны, пользуясь связью (2.4) величин А и си:
Отсюда видно, что при длине волны ультрафиолетового излуче-
ния Л ~ 0,1 мкм энергия фотонов приблизительно равна ~ 10 эВ.
Следовательно, энергии фотоэлектронов, вышедших из металла
при cu > cuq, составляют несколько электрон-вольт. По извест-
ной массе покоя электрона те легко вычислить его энергию покоя
тесЕ 2 * * * * * « 511 кэВ. Сравнивая эти энергии, мы видим, что фотоэлек-
троны, возникшие при облучении металлов ультрафиолетовым из-
лучением, можно считать нерелятивистскими, и их кинетическая
энергия пропорциональна квадрату скорости:
Е = —-и2.
2
Последняя формула позволяет получить оценку скорости та-
ких фотоэлектронов v ~ 108см/с. Уравнения электродинамики
позволяют вычислить, что фотоны ультрафиолетового диапазона
проникают в металл на глубину не превышающую 1 мкм. Следо-
вательно, время вылета фотоэлектронов из столь тонкого припо-
верхностного слоя и время движения до коллектора так мало, что
его трудно зарегистрировать.
Далее заметим, что общее число фотоэлектронов, выходящих
из металла через поверхность эмиттера за 1 с, должно быть про-
порционально числу фотонов, падающих за то же время на эту
поверхность. Из этого следует, что ток насыщения /тах должен
быть прямо пропорционален интенсивности светового потока, что
и подтверждается экспериментами (см. рис. 4.3).
Перейдем к анализу углов наклона графиков по отношению к
оси абсцисс на рис. 4.5. Подстановка в уравнение Эйнштейна (4.4)
76
Лекция 4. Фотоны
выражения (4.1) дает теоретическую зависимость запирающего
потенциала Ug от частоты излучения:
U, = - Y- (4-7>
которая соответствует экспериментальной. Тангенс угла наклона
зависимости Ug((v) равен отношению постоянной Планка h к за-
ряду электрона е и не зависит от условий эксперимента:
/z
tga = -. (4.8)
е
Анализ зависимостей Ug(w), полученных при исследовании ва-
куумного фотоэффекта с помощью уравнения (4.8), позволяет по-
лучить числовое значение постоянной Планка К. Такие измерения
были выполнены Р. Милликеном в 1914 г. и дали хорошее согла-
сие со значением величины Л, входящей в формулу Планка (3.8) и
в выражение для константы в законе Стефана-Больцмана (3.15).
Измерения зависимостей Ug(w) позволили также получить
значения работы выхода Ав для многих металлов. Выяснилось,
что среди металлов наименьшей работой выхода обладают щелоч-
ные металлы. Например, для натрия Ав — 1,9 эВ, что соответст-
вует красной границе фотоэффекта Ло = 2тгА/сио ~ 680 нм. По-
этому соединения щелочных металлов используют для создания
катодов в фотоэлементах, предназначенных для регистрации ви-
димого света.
В заключение данного параграфа заметим, что в числителе
формулы (4.6) стоят лишь фундаментальные константы. Поэтому
полезно для практических расчетов эту величину вычислить и вы-
разить в удобных для вычислений единицах. Например, полезно
знать наизусть, что произведение констант 2тгЛс ~ 12400 эВ • А.
4.3. Импульс фотона
Итак, явление фотоэффекта полностью объясняется, если при-
нять, что свет представляет собой поток частиц — фотонов. Фо-
тоны движутся в вакууме со скоростью света с. В соответствии с
теорией относительности это может быть лишь в том случае, если
фотон не имеет массы покоя.
Запишем известное соотношение специальной теории относи-
тельности, которое связывает массу покоя то, импульс р и полную
энергию Е свободной частицы:
Е2 = тдс4 + р2с2. (4.9)
Полагая массу покоя фотона равной нулю, получаем
Е2 =р2с2.
4.3. Импульс фотона
77
Отсюда следует, что фотон должен обладать импульсом, модуль
которого равен
р = —. (4.10)
с
Заметим, что первым, кто достаточно обоснованно высказался
в пользу корпускулярной природы света, был Исаак Ньютон. Та-
ким образом, учение о свете, совершив после И. Ньютона виток
длительностью в два столетия, вновь возвратилось к представле-
ниям о световых частицах — фотонах.
Используя выражение для энергии фотона (4.2), получим из
формулы (4.10) выражение модуля импульса фотона через волно-
вое число к:
р — — = fik. (4.11)
с
В монохроматической волне фотоны летят в направлении, за-
данном волновым вектором к, который перпендикулярен поверх-
ности постоянной фазы волны. Тогда вектор импульса фотона р
можно записать в виде
р = Лк. (4.12)
Уравнения (4.2) и (4.12) определяют важнейшие характери-
стики фотона и связывают их с параметрами волны: частотой и
и волновым вектором к, следовательно, и с длиной волны Л.
Наличие ненулевого импульса фотона должно проявляться в
возникновении сил давления при отражении света от какого-либо
твердого тела. Рассмотрим площадку, перпендикулярно которой
падает поток монохроматического света. Удельную интенсивность
этого излучения, введенную уравнением (2.6), можно записать в
виде
I = Nhu, (4.13)
где N — число фотонов, падающих на площадку площадью 1 смI 2
за 1 с.
Если площадка полностью отражает свет, то по закону сохра-
нения импульса каждый фотон, падающий на площадку, сообщит
ей импульс, равный
А Леи / Л/j
Др=--------------=2—.
с \ с J с
Поскольку при отражении происходит передача импульса от-
ражающей поверхности, то, следовательно, свет должен оказывать
давление на эту поверхность. Давление света равно полному им-
пульсу, передаваемому отражающей площадке единичной площа-
дью N фотонами за одну секунду:
2/kj 21
Р = N-----= —
с с
(4.14)
78
Лекция 4. Фотоны
Экспериментально давление света было обнаружено и измерено
в 1900 г. русским физиком П.Н. Лебедевым (1866-1912). Расчеты
по фотонной теории света дают результаты, совпадающие с дан-
ными экспериментов.
4.4. Эффект Комптона
Поскольку фотоны обладают ненулевым импульсом (4.12), то
при столкновениях фотонов с массивными частицами должен вы-
полняться не только закон сохранения энергии, но и закон со-
хранения импульса при равенстве нулю суммы внешних сил, дей-
ствующих на систему взаимодействующих частиц. В связи с этим
противники фотонной теории выдвигали следующее возражение.
Рассмотрим рассеяние фотона на какой-либо частице (элек-
троне, атоме, молекуле). Внешними силами являются силы грави-
тации, которыми из-за малости гравитационной постоянной G =
= 6,6726 • 10“8 см3 • г-1 • с-2 можно пренебречь. Тогда суммарный
импульс фотона и частицы должен сохраняться.
При рассеянии света на частицах вещества фотоны, сталки-
ваясь с электронами, должны терять часть своей энергии. Потеря
энергии, согласно соотношению (4.10), должна приводить к умень-
шению импульса фотона. Далее, из уравнения (4.11) следует, что
у фотона должна изменяться частота и, естественно, длина волны.
А это значит, что при рассеянии света на предметах должна обя-
зательно изменяться длина волны, т. е. его цвет. Однако в опытах
такого изменения цвета не наблюдается. Таким образом, имеются
сомнения в том, что в процессе рассеяния фотона на электроне вы-
полняется закон сохранения импульса, который является одним из
фундаментальных законов Природы.
Только через 18 лет после публикации Эйнштейном фотон-
ной теории, т.е. в 1923 г., в результате тщательно выполненных
экспериментов А. Комптон (1892-1962) обнаружил эффект, кото-
рый являлся прямым подтверждением наличия импульса фотона,
определяемого уравнением (4.12). Независимо от Комптона в том
же году теорию рассеяния фотонов на свободных электронах по-
строил П. Дебай (1884-1966), поэтому обнаруженное явление ино-
гда называют эффектом Комптона-Дебая.
Схема установки для наблюдения эффекта Комптона приведена
на рис. 4.7.
В качестве источника электромагнитного излучения исполь-
зовалась рентгеновская трубка. Рентгеновская трубка Комптона
излучала электромагнитные волны с длиной волны Aq « 0,71 А.
Иначе говоря, Комптон работал с коротковолновым (по сравнению
с видимым светом) электромагнитным излучением. Свинцовые
диафрагмы формировали узкий пучок рентгеновских лучей, кото-
рые направлялись на исследуемый образец. Рассеяние рентгенов-
4.4. Эффект Комптона
79
ских лучей на исследуемом образце происходило во всех направле-
ниях. С помощью других свинцовых диафрагм вырезался узкий
пучок излучения, рассеянного под углом в. Установка Комптона
позволяла изменять угол рассеяния в в широких пределах.
Анализ спектра рассеянного рентгеновского пучка производил-
ся с помощью рентгеновского спектрометра (см. рис. 4.7). Основ-
ным элементом спектрометра является кристаллическая пластин-
ка, которая ориентируется по отношению к падающему на нее
Рис. 4.7. Схема эксперимента Комптона:
1 — рентгеновская трубка, 2 — образец, на котором рассеивались рентгеновские лучи,
3 — свинцовые экраны, поглощающие рентгеновские лучи, 4 — блок рентгеновского спек-
трометра, 5 — кристалл спектрометра, 6 — устройство регистрации рассеянных лучей,
О — угол рассеяния, — угол скольжения
рентгеновскому пучку таким образом, чтобы в этом кристалле ре-
ализовались условия фраунгоферовой дифракции. При падении
пучка монохроматического рентгеновского излучения на высокосо-
вершенный кристалл в его периодической атомной структуре фор-
мируется дифракционный пучок, который распространяется под
углом 2(/9 относительно первичного пучка (см. рис. 4.7). При этом
угол скольжения 99 и длина волны А излучения связаны уравне-
нием Вульфа-Брэгга
2dsin(/? = nA, (4.15)
где d — расстояние между атомными плоскостями в кристалле,
п — целое число (см. дополнение 4.5).
Согласно уравнению (4.15), узкие пучки рентгеновского излуче-
ния с разными длинами волн Л дифрагируют под разными углами
скольжения 99. Измерения углов 99 при известных значениях ве-
личин d и п позволяет вычислить длину волны Л.
В качестве измерительного устройства часто используют фо-
топленку с нанесенной шкалой длин волн. Спектральная интен-
сивность регистрируемого излучения определяется по плотности
засветки фотопленки. В первых опытах Комптона вместо фото-
80
Лекция 4. Фотоны
пленки использовалась подвижная ионизационная камера, которая
позволяла измерять электрический ток, пропорциональный интен-
сивности попадающего в нее излучения.
Пример типичных результатов измерений Комптона приведен
на рис. 4.8. Если угол рассеяния в равен нулю, то рентгеновский
спектрометр показывает обычный спектр излучения рентгеновской
Рис. 4.8. Спектры рассеянного электромагнитного излучения в эксперименте
Комптона для разных углов рассеяния 0:
По горизонтали отложена длина волны рассеянного рентгеновского излучения, по верти-
кали — интенсивность этого излучения в относительных единицах
трубки с максимумом Aq (рис. 4.8а). Но при углах в отличных от
нуля в спектрах рассеянного рентгеновского излучения наблюда-
ется два максимума: с длиной волны первичного излучения Aq и
с несколько большей А' > Aq (рис. 4.8б-г). Характерной особен-
ностью обнаруженного эффекта является увеличение расстояния
между максимумами ДА = А' — Aq с ростом угла рассеяния в.
Именно появление в спектре рассеянного рентгеновского излуче-
ния максимума с длиной волны А' > Aq называется эффектом
Комптона-Дебая.
Опыты показали, что разность длин волн (комптоновское сме-
щение) ДА = А' — Aq не зависит от состава вещества рассеиваю-
щего образца и длины волны Aq первичного излучения.
Согласно классической волновой теории, при рассеянии элек-
тромагнитных волн их частота (и длина волны) не должны из-
4.4. Эффект Комптона
81
меняться. Волна с частотой cuq «раскачивает» электроны, которые
излучают вторичные (рассеянные) волны с той же частотой. Сле-
довательно, классическая физика не могла объяснить наличия в
спектрах рассеянного рентгеновского излучения максимума с дли-
ной волны А' > Aq. Напротив, все особенности эффекта Комптона
можно объяснить на основе упругого столкновения фотонов рент-
геновского излучения с электронами вещества.
Существенно, что Комптон обнаружил эффект при рассеянии
рентгеновских лучей на материалах, состоящих из атомов с ма-
лыми химическими номерами (графит, парафин и т.д.). Фо-
тоны, испускаемые рентгеновской трубкой, имели длину волны
Aq ~ 0,71 А и, согласно соотношению (4.6), энергию е ж 17,5кэВ,
что много больше энергии связи электронов в легких атомах, ко-
торая имеет порядок нескольких десятков эВ (см. лекцию 15).
Рис. 4.9. К описанию рассеяния фотона на электроне:
а) геометрическая схема процесса, б) векторная диаграмма импульсов частиц. Ао и А' —
длины волн первичного и рассеянного фотонов, /iko и Лк' — их импульсы соответственно,
ре — импульс электрона отдачи
Таким образом, данный процесс можно рассматривать как упру-
гое столкновение фотонов со свободным электроном, в результате
которого фотон рассеивается на угол в относительно первоначаль-
ного направления движения (см. рис. 4.9а).
Полагаем, что процесс столкновения фотона и электрона про-
исходит по модели абсолютно упругого удара с сохранением энер-
гии и импульса. После рассеяния фотона электрон получает кине-
тическую энергию и импульс и называется электроном отдачи.
Запишем законы сохранения для системы «фотон + электрон» в
релятивистском виде, так как энергия первичных фотонов Hcoq
„ 2
сравнима с энергией покоя электрона тес :
2
+ гаес2 = hw -I—z еС ., (4.16)
л/1 “7
ТГ)
Ako = /ikz Н— v, (4-17)
л/1 -7
где шо и ко — частота и волновой вектор первичных фотонов, ш'
и к' — те же величины рассеянных фотонов, 7 = (v/c)2, v —
82
Лекция 4. Фотоны
скорость электрона после рассеяния. Вектор
является импульсом электрона отдачи.
В уравнениях (4.16), (4.17) электрон до взаимодействия с фо-
тоном полагается неподвижным.
Получим из системы (4.16), (4.17) выражение разности длин
волн ДА = А' — Aq. Сначала перепишем уравнения в виде
= (4.18)
ft \vl~7 /
k0 - к' = 1= v (4.19)
п у/1 - 7
и возведем их в квадрат. Скалярное произведение волновых векто-
ров kgk' выразим, используя формулу (4.11) и диаграмму рис. 4.9d:
kgk' = Д-cuoo/ cos в.
cz
Возведенное в квадрат уравнение (4.19) домножим на с2, исполь-
зуем связь модуля волнового вектора с частотой к = w/c, соотно-
шение 7 = (v/c)2 и приведем к виду
Wq — 2wqw' cos в + w2 = —• ———. (4.20)
ft2 1 — 7
Теперь вычтем из (4.20) квадрат уравнения (4.18) и преобразуем
правую часть:
2cW(l “ cos 0) = 2^- (-^= - 1 ) . (4.21)
ft2 \ у 1 - 7 J
Сравнивая правые части уравнения (4.18) и (4.21), получим
77?2 /?
uW(l - COS0) = - wf).
nr тпес£
Теперь надо разделить последнее уравнение на произведение wqw'
и использовать связь частоты и длины волны (2.4):
l-cos0=^(A'-Ao).
Z7Tft
Таким образом, мы получили формулу Комптона
Л'-Ао = —(l-cos0), (4.22)
TTLqC
которая связывает разность длин волн ДА = А' — Ао с углом рас-
сеяния в.
4.4. Эффект Комптона 83
Формула Комптона (4.22) с хорошей точностью подтверждает-
ся в экспериментах и показывает, что разность длин волн АЛ =
= А' — Ао действительно не зависит от материала, на котором рас-
сеиваются фотоны, но возрастает с увеличением угла рассеяния в.
Постоянная величина
Лс =----« 2,43 • 10-12 м = 0,0243 А (4.23)
тес
называется комптоновской длиной (точнее, комптоновской дли-
ной электрона).
Числовое значение константы Лс объясняет ненаблюдаемость
эффекта Комптона в видимом и радиодиапазонах электромагнит-
ных волн. В реальных условиях генерируемые волны всегда име-
ют разброс длин волн. Для световых и, тем более, радиоволн этот
разброс дХ много больше постоянной Лс. Следовательно, компто-
новское смещение АА не может быть зарегистрировано на фоне
сравнительно большего значения SX. Наблюдать эффект Комп-
тона практически можно лишь для электромагнитных волн, име-
ющих величину разброса JA, сравнимую с постоянной Лс или
меньшую. Таким условиям удовлетворяют рентгеновские лучи и,
тем более, гамма-излучение.
Подытоживая сказанное можно констатировать, что экспери-
менты Комптона убедительно подтвердили представление электро-
магнитной волны как потока частиц — фотонов, которые обладают
энергией (4.2) и импульсом (4.12).
Возвращаясь к рис. 4.8, обратим внимание на то, что в спект-
рах рассеянного рентгеновского излучения, помимо пика фотонов,
рассеянных вследствие эффекта Комптона, присутствует макси-
мум, соответствующий длине волны Ао первичных рентгеновских
лучей. Наличие этого максимума объясняется процессом упругого
рассеяния излучения на атомах.
Согласно классической электродинамике, электромагнитная
волна с определенной частотой cuq, действуя на электроны в атоме,
приводит их в колебательное движение с той же частотой cuq.
Как следствие, электроны излучают вторичные электромагнитные
волны с частотой cjq в различных направлениях. Такой процесс
назван упругим рассеянием, так как частота (и длина волны) пер-
вичного и рассеянного излучения совпадают.
Фотонная теория приводит к тому же выводу. При упругом
рассеянии фотон взаимодействует с атомом как с единым объек-
том. Легко оценить, что фотон рентгеновского диапазона даже
при рассеянии на максимальный угол (0 = 180°) передает им-
пульс порядка 10“18 г • см/с. При этом легкий атом, например атом
углерода, получит кинетическую энергию ~ 10“18 эрг, что на пять
порядков меньше энергии первичного фотона. Более массивные
атомы приобретут еще меньшую энергию. Следовательно, потерей
84
Лекция 4. Фотоны
энергии фотона при упругом рассеянии на атомах можно прене-
бречь. Иначе говоря, в этом процессе длина волны рентгеновских
лучей практически не изменяется.
В заключение лекции заметим, что открытие фотонов не озна-
чает возвращения к классической корпускулярной теории света
и отбрасывания волновой теории электромагнитного излучения.
Фотонная теория не опровергает справедливость уравнений Макс-
велла. Фотон не является корпускулой в классическом смысле.
Уравнения (4.2) и (4.12) демонстрируют, что фотон обладает как
корпускулярными, так и волновыми свойствами. В классической
физике существование таких объектов считалось принципиально
невозможным, поэтому фотонная теория является одним из этапов
построения современной квантовой физики.
Задачи к лекции 4
1. Ультрафиолетовое монохроматическое излучение с длиной волны
500 А попадает на платиновую пластинку. Найти максимальную кине-
тическую энергию фотоэлектронов и их скорость. Работа выхода для
платины равна 5,32 эВ.
2. Длина «красной границы» фотоэффекта для данного металла равна
2900 А. Найти максимальную кинетическую энергию фотоэлектронов
при облучении металлической пластины ультрафиолетовым излучением
с длиной волны 2000 А.
3. Фотон с энергией Е рассеялся на свободном электроне на угол 3.
Найти длину волны и энергию рассеянного фотона, а также скорость
электрона после рассеяния при следующих значениях: а) Е = 5 МэВ,
3 = 45°; б) Е = 1 МэВ, 3 = 60°; в) Е = 2 МэВ, 3 = 30°.
4. Фотон длиной волны А рассеялся на свободном электроне на угол 3.
Найти энергию электрона после рассеяния Ее и угол ср между импуль-
сами первичного фотона и электрона отдачи при следующих значениях:
а) А = 2 • 10-3 А, в = 45°; б) А = 3 • 10-3 А, 6 = 60°; в) А = 5 1СГ3 А,
0 = 30°.
5. Вычислить энергии фотонов для границ видимого диапазона элек-
тромагнитных волн.
6. Найти скорость электрона, если его импульс равен импульсу фо-
тона с длиной волны: а) 1А; б) 10 А; в) 1 мкм.
7. Найти длину волны фотона, если его импульс равен импульсу
электрона, кинетическая энергия которого равна: а) 1кэВ; б) 50 кэВ;
в) 1МэВ.
8. Найти длину волны фотона, если его энергия равна энергии покоя:
а) электрона; б) протона.
9. Вычислить изменение длины волны фотона в эффекте Комптона,
если рассеяние происходит на угол 90°.
10. Оценить количество фотонов в электромагнитной волне с энер-
гией 1 Дж: а) для радиоволны метрового диапазона; б) для излучения
видимого диапазона; в) для рентгеновского излучения.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 4
4.1. Невозможность фотоэффекта на свободном электроне
Помимо фотоэффекта на электронах проводимости, описанного в лек-
ции 4, существуют и другие разновидности явления, в котором поглоща-
ется фотон и образуется свободный электрон. До поглощения фотона
электрон может быть связан в атоме, молекуле или в кристалле. Однако
невозможно поглощение фотона свободным электроном, что доказыва-
ется ниже.
Предположим, что свободный электрон поглощает фотон с энергией е.
Рассмотрим этот процесс в системе координат, где электрон до поглоще-
ния был неподвижен. Запишем законы сохранения энергии и импульса
для данной пары частиц в релятивистском виде
г 4- тес2 =
тес2
V1 - (v/c)2 ’
г _ mev
С у/1 - (v/c)2’
(Д.4.1)
где те — масса покоя электрона, с — скорость света, v — скорость элек-
трона после поглощения фотона. Исключив энергию фотона из системы
уравнений (Д.4.1), перейдем к единственному уравнению
2 тесм тес2
тес -\---===== — ——.
д/1 - (^/с)2 \/1 - (у/с)2
Разделив последнее уравнение на его правую часть, получим
(Д-4.2)
(Д.4.3)
Последнее уравнение имеет два корня v = 0 и v = с. Первый
является физически бессмысленным, так как после поглощения фотона
электрон должен получить кинетическую энергию и, следовательно, при-
обрести определенную скорость. Второй корень также должен быть от-
брошен, так как электрон обладает ненулевой массой покоя и поэтому
не может двигаться со скоростью света. Таким образом, выдвинутое
в начале предположение о возможности поглощения фотона свободным
электроном привело к физически неверному результату.
Поглощение фотонов происходит всегда электронами, которые взаи-
модействуют с окружающими объектами. В вакуумном (внешнем) фо-
тоэффекте электрон проводимости получает практически всю энергию
поглощенного фотона, что выражается уравнением Эйнштейна (4.3). Од-
нако при этом значительная часть импульса фотона передается ионам ме-
86
Дополнения к лекции 4
талла, с которыми взаимодействует этот электрон проводимости. Энер-
гия, получаемая ионами, пренебрежимо мала из-за различия масс покоя
электрона и ионов.
Расчеты с помощью уравнения Эйнштейна показывают, что при
длине волны фотона типичной для ультрафиолетового диапазона (А ~
~1000А) фотоэлектроны получают скорости на два порядка меньше ско-
рости света. Иначе говоря, при облучении металлов ультрафиолетовым
излучением образуются нерелятивистские электроны.
В других разновидностях фотоэффекта часть импульса фотона пере-
дается окружающим атомам или ионам.
4.2. Оценка времени выхода электрона из металла
при фотоэффекте на металле
Рассмотрим эксперимент по исследованию вакуумного фотоэффекта,
описанный в лекции 4. Пусть источник ультрафиолетового излучения
с интенсивностью I находится на расстоянии г от эмиттера. Согласно
классической теории, электрон в атоме постепенно получает энергию от
электромагнитной волны, падающей на эмиттер.
Исследования электрофизических свойств металлов позволили уста-
новить, что концентрация электронов проводимости примерно равна кон-
центрации атомов в металле. Иначе говоря, каждый атом металла от-
дает в среднем один электрон в совокупность электронов проводимости.
Следовательно, концентрация электронов проводимости п может опреде-
ляться по плотности р и молярной массе р, металла:
pNa
(Д.4.4)
где ТУд — постоянная Авогадро. Подставляя в (Д.4.4) числовые значения
характеристик р и у, получим, что концентрация электронов проводимо-
сти у большинства металлов имеет порядок 1022 см-1.
По известной концентрации можно оценить средний размер области,
приходящийся на один электрон проводимости:
х ~
(Д.4.5)
и убедиться, что величина х примерно равна 1 А.
За время t электрон получит энергию, равную
9
47ГГ2
(Д.4.6)
Приравняв энергию (Д.4.6) работе выхода Ав, мы получим уравне-
ние, которое можно использовать для вычисления времени, за которое
электрон получит от электромагнитной волны энергию, достаточную для
выхода из металла:
4тгг2Ав
1х2
(Д.4.7)
Весьма важно, что, согласно (Д.4.7), время накопления энергии, не-
обходимой для фотоэффекта, обратно пропорционально интенсивности
Дополнения к лекции 4
87
источника света. При вычислениях возьмем работу выхода Ав, равную
« 4 эВ, что справедливо для многих металлов. При мощности источника
I = 100 Вт, находящегося на расстоянии г = 30 см от облучаемой метал-
лической пластинки, расчет по формуле (Д.4.7) дает время « 0,75 с. Но
эксперименты показали, что фотоэффект наблюдается также при гораздо
меньшей интенсивности света. Например, плотности потока излучения
~ 10-5Вт/см2, согласно формуле (Д.4.7), фотоэлектроны должны реги-
стрироваться примерно через 2 ч после включения светового потока.
Однако многократно проведенные прецизионные эксперименты дока-
зывают, что фотоэлектроны выходят из металла практически мгновенно
после начала облучения эмиттера даже при очень слабой интенсивности
светового потока (конечно, если длина волны короче «красной границы»
данного металла). Эти исследования свидетельствуют в пользу фотонной
теории, которая объясняет вылет фотоэлектрона из металла отдельным
актом поглощения фотона электроном проводимости.
Оценку времени такого процесса можно провести по энергетическому
соотношению неопределенностей (см. лекцию 6) и получить величину
~ h/AB ~ 10“15 с (где А3 — работа выхода электрона проводимости из
металла). С помощью уравнения Эйнштейна (4.3) нетрудно вычислить,
что при облучении металла ультрафиолетом фотоэлектроны получают ки-
нетическую энергию, равную нескольким электрон-вольтам, т.е. ско-
рость ~108см/с. Классическая электродинамика позволяет оценить,
что толщина слоя металла, в который проникает электромагнитная вол-
на ультрафиолетового диапазона, составляет по порядку величины не
более 1 мкм. Следовательно, при этом время выхода фотоэлектрона из
металла ~ 10-12 с, что вполне согласуется с результатами экспериментов.
4.3. Поляризация фотона
Фотон, помимо энергии и импульса, характеризуется определенным
состоянием поляризации.
Рассмотрим монохроматическую плоскую линейно поляризованную
электромагнитную волну. Согласно классической электродинамике, по-
ляризация волны определяется по направлению вектора электрического
поля £ волны. В квантовой теории электромагнитная волна представля-
ется совокупностью фотонов. Следовательно, все фотоны плоской моно-
хроматической линейно поляризованной волны должны обладать одина-
ковыми энергией, импульсом и состоянием поляризации, которая может
быть задана единичным вектором е, параллельным вектору электриче-
ского поля £ данной волны. Отсюда следует, что каждому значению
импульсу фотона hk соответствуют две линейно независимые поляри-
зации, характеризуемые взаимно перпендикулярными векторами е^) и
е(2\ Эти векторы выбираются таким образом, чтобы тройка и
к/к образовывали орты правой системы координат:
е(О х е(2) = у. (Д.4.8)
к
С другой стороны, в качестве базиса также можно использовать век-
торы круговой поляризации и которые связаны с векторами
88
Дополнения к лекции 4
еС1) и следующими формулами:
е(+) = е(1) + г'е(2)
\/2
— ie^
е' 7 =------7=---
х/2
(Д.4.9)
Состояние, характеризуемое вектором называется правой круговой
поляризацией, а состояние с вектором — левой круговой поляриза-
цией.
Для квантовой физики важно, что фотон в состоянии с круговой по-
ляризацией обладает определенным значением проекции собственного
момента импульса Sz на направление волнового вектора фотона к. Эта
проекция Sz равняется Й, или — h в случаях правой или левой круговой
поляризации соответственно.
4.4. Угловое распределение фотоэлектронов
Фотоны ультрафиолетового диапазона имеют энергии порядка десят-
ков электрон-вольт, т.е. много меньше энергии покоя электрона. Как
следствие, фотоэлектроны, выходящие из металла при облучении уль-
трафиолетовым излучением, имеют нерелятивистские энергии.
В дополнении 4.1 было показано, что суммарный импульс системы
«электрон проводимости 4-фотон» не сохраняется, так как часть им-
пульса передается ионам металла. В то же время энергия системы «элек-
трон 4-фотон» сохраняется с высокой точностью, потому что ионы полу-
чают ничтожно малую энергию из-за их сравнительно большой массы.
Рис. Д.4.1. Геометрическая схема взаиморас-
положения векторов при фотоэффекте на элек-
троне проводимости:
Лк — импульс фотона, ре — импульс фотоэлек-
трона, е — вектор поляризации фотона
По этим причинам вектор импульса фотоэлектрона, вообще говоря,
не параллелен импульсу поглощенного фотона. Угловое распределение
нерелятивистских фотоэлектронов зависит от их скорости v и может
быть приближенно описано следующим выражением:
Idfl ~ sin2 3 cos2 fl 4- 4- cos#") dQ, (Д.4.10)
\ с /
где I — плотность потока фотоэлектронов, d£l — элемент телесного угла,
с — скорость света.
Угол 3 образован векторами импульсов фотона hk и фотоэлектрона
ре, — угол между плоскостью, в которой лежат эти векторы hk и ре,
и направлениехМ вектора поляризации фотона е (см. рис. Д.4.1).
Дополнения к лекции 4
89
Согласно выражению (Д.4.10) максимум интенсивности потока не-
релятивистских фотоэлектронов наблюдается в направлении перпенди-
кулярном импульсу фотона (0 = тг/2) и в плоскости его поляризации
(</? = 0). При скорости фотоэлектронов, много меньшей скорости света
(v с), угловое распределение фотоэлектронов практически симмет-
рично относительно угла рассеяния 3 = тг/2.
С увеличением кинетической энергии фотоэлектрона максимум угло-
вого распределения фотоэлектронов смещается в область меньших углов
Рис. Д.4.2. Полярные диаграммы углового распределения плотности потока фото-
электронов при фотоэффекте на электронах проводимости для различных энер-
гий фотонов е (Лк — импульс поглощаемого фотона):
1 — е = 20 кэВ, 2 — 8 — 100 кэВ, 3 — 8 — 5 МэВ
рассеяния 3. На рис. Д.4.2 приведены полярные диаграммы углового
распределения фотоэлектронов, рассчитанные для фотонов высокой энер-
гии, принадлежащих рентгеновскому и гамма-диапазону.
4.5. Уравнение Вульфа-Брэгга
Обнаружение дифракции рентгеновских лучей на кристаллах яви-
лось экспериментальным доказательством волновой природы рентгенов-
ских лучей и атомарного строения вещества, что подробно излагается
в лекциях 18 и 19. Разработанная в ходе рентгеновских исследований
теория дифракции оказалась применимой для рассеяния волн любой фи-
зической природы на периодических структурах при условии, что про-
странственные периоды имеют порядок длины волны.
Первая теория рассеяния волн на трехмерной периодической струк-
туре была предложена Максом Лауэ в 1912 г. (см. дополнение 18.1).
Практически в то же время Л. Брэгг (1890-1971) и, независимо от него,
Ю. Вульф (1863-1925) предложили более простой вариант теории, кото-
рый успешно используется при решении множества физических задач.
Рассмотрим трехмерный объект, содержащий множество точечных
рассеивателей, которые периодически расположены в пространстве. При-
мером может служить монокристалл, состоящий из одинаковых атомов.
90
Дополнения к лекции 4
На поверхность объекта падает плоская монохроматическая волна.
Взаимодействие волны с каждым рассеивателем порождает вторичные
волны. Суперпозиция вторичных волн образует отраженный (рассеян-
ный) волновой поток, который может быть обнаружен с помощью какого-
либо детектора исследуемого излучения.
Предположим, что детектор рассеянного излучения расположен на
расстоянии, значительно превышающем размер облучаемого объекта.
Тогда все вторичные волны, попадающие в детектор, можно рассматри-
вать как плоские. Падающую и регистрируемую (рассеянную) волны
удобно изобразить системой пучков, направленных параллельно соответ-
ствующим волновым векторам (см. рис. Д.4.3).
Согласно теории Брэгга, рассеянную волну можно представить супер-
позицией волн, рассеянных плоскостями, каждая из которых содержит
—е----е-----в-----©----•----•-----е—
—0----0 0 0----0----0 0—
Рис. Д.4.3. Схема отражения пучков волн от атомных плоскостей кристалла:
АА' и ВВ' — две атомные плоскости, МО и М'О' — пучки падающих волн, ON и
О'N' — пучки отраженных волн, ip — угол скольжения, d — межплоскостное расстояние
множество атомов. Точнее говоря, картина рассеянного излучения обра-
зуется интерференцией пучков монохроматических когерентных волн,
отраженных отдельными атомными плоскостями (см. рис. Д.4.3).
Очевидно, что наиболее интенсивные пучки отраженного излучения
формируются конструктивной (положительной) интерференцией отдель-
ных рассеянных волн. Известно, что условием положительной интерфе-
ренции является разность фаз интерферирующих волн кратная 2тг. При
этом разность хода таких когерентных волн равняется целому числу
длин волн А.
Ограничимся самым распространенным в практике случаем симме-
тричной геометрии Брэгга. В этом случае регистрируется волна, отра-
женная от поверхности объекта под углом, равным углу падения пер-
вичной волны (см. рис. Д.4.3). Угол ip между плоскостью облучаемой
поверхности и волновым вектором падающей волны называется углом
скольжения.
Дополнения к лекции 4
91
По геометрической схеме легко вычислить, что разность хода коге-
рентных волн, отраженных соседними атомными плоскостями, равня-
ется 2cZsin где d — расстояние между соседними атомными плоско-
Рис. Д.4.4. К расчету разности хода когерентных волн, отраженных соседними
атомными плоскостями.
Треугольники ОСО1 и ODO' — прямоугольные. Углы СО(У и DOO1 равны Разность
хода волн NO'N1 и МОМ1 равна сумме длин отрезков СО' и DO1
стями (так называемое межплоскостное расстояние), — угол между
облучаемой поверхностью объекта и направлением падающей волны, ко-
торое задается ее волновым вектором (см. рис. Д.4.4).
Условие конструктивной интерференции запишется в виде
2dsin<£ = пХ, (Д.4.11)
где п — произвольное натуральное число. При этом из геометрической
схемы на рис. Д.4.4 очевидно, что число п равно отношению разно-
сти хода волн, отраженных соседними атомными плоскостями, к длине
волны А.
Соотношение (Д.4.11) называется уравнением Вульфа-Брэгга. Углы
удовлетворяющие этому уравнению, задают направления распростра-
нения интенсивных пучков рассеянного излучения. Число п называется
порядком отражения для системы атомных плоскостей с определенным
межплоскостным расстоянием d.
Лекция 5
ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ
5.1. Гипотеза де Бройля
Обнаружение корпускулярных свойств электромагнитного из-
лучения вызвало к жизни принципиально новые идеи, которые
ранее показались бы парадоксальными. В 1923 г. французский
физик Луи де Бройль (1892-1987) выдвинул гипотезу о существова-
нии волновых характеристик у массивных частиц, т. е. у частиц,
масса покоя которых не равна нулю (электронов, протонов, ато-
мов, молекул и т. д.). Луи де Бройль предположил, что если волны
обладают корпускулярными свойствами, то корпускулы должны
обязательно иметь волновые свойства. Эта концепция получила
название корпускулярно-волнового дуализма.
Согласно гипотезе де Бройля, соотношения, полученные для
фотонов (4.2) и (4.12):
Е = hw и р = Лк, (5.1)
являются универсальными, т. е. справедливыми не только для
фотонов, но и для любых массивных частиц. Это означает, что
каждая частица наряду с энергией Е и импульсом р должна харак-
теризоваться частотой со и длиной волны А. Гипотеза де Бройля
впоследствии была подтверждена многочисленными эксперимен-
тами, некоторые из которых будут описаны ниже.
Прежде всего, используя известную связь волнового числа с
длиной волны, получим для модуля импульса частицы соотно-
шение
2тгЛ
р= W
где величина Ар называется длиной волны де Бройля. Следова-
тельно, дебройлевская длина волны обратно пропорциональна мо-
дулю импульса частицы:
2тгЛ
Ар =------•
Р
(5-2)
5.2. Экспериментальные исследования дифракции 93
Оценим длину волны де Бройля макроскопических объектов.
Пусть шарик массой 1г движется со скоростью 1м/с. Величина
его импульса р = mv = 102г-см/с, и таким образом, из (5.2)
следует, что длина волны де Бройля этого шарика равна
х 2 • 3,14 • 1,05 • 10~27
Ad ~
7 • IO’29 см.
102
Такую маленькую длину зафиксировать в опытах на сегод-
няшний день невозможно. Современный предел эксперименталь-
ных методик по оценке линейных размеров ограничен порядком
~ 10-16 см.
Легко видеть, что малая величина длины волны де Бройля
определяется, в первую очередь, малостью постоянной Планка в
числителе (5.2). Отсюда очевидно, что экспериментально искать
волновые свойства следует у частиц с очень малым импульсом, в
первую очередь, у микрочастиц, например у электронов.
Оценим длину волны де Бройля для электрона, обладающего
кинетической энергией 100 эВ. Так как эта величина много меньше
9
энергии покоя электрона тес , то для оценки воспользуемся нере-
лятивистской формулой связи энергии и импульса
= 2тгП (5 ,з)
Вычисления дают длину
~ 2 • 3,14 1,05 • 10-27 8
х/2 • 0,911 • 10-27 • 102 • 1,6 • 10-12
т. е. величину, сравнимую с размерами атома. Отсюда следует,
что наблюдать волновые свойства электронов в принципе можно в
опытах по их дифракции на атомных структурах кристаллов, так
как межатомные расстояния в кристаллах имеют порядок диаме-
тра атома.
5.2. Экспериментальные исследования дифракции
массивных частиц
Первое экспериментальное подтверждение гипотезы де Бройля
было получено в 1927 г. американскими физиками К. Девиссоном
(1881-1958) и Л. Джермером (1896-1971), которые исследовали
рассеяние пучка электронов на монокристалле никеля. Схема экс-
перимента Девиссона и Джермера приведена на рис. 5.1.
Электронная пушка формировала узкий пучок электронов, ко-
торый, пройдя ускоряющую разность потенциалов J7, падал на
94
Лекция 5. Волновые свойства частиц
плоскую отшлифованную грань кристалла никеля. В качестве
детектора использовался цилиндр Фарадея, соединенный с чув-
ствительным гальванометром. В опытах измерялось угловое рас-
пределение рассеянных электронов, т. е. количество частиц, отра-
женных от кристалла под разными углами в. Было обнаружено,
Рис. 5.1. Схема эксперимента Девиссона и Джермера по обнаружению дифракции
электронов на кристалле:
1 — электронная пушка, 2 — пучок электронов, 3 — кристалл, 4 — детектор рассеянных
электронов, 5 — вакуумный баллон, 6 — ось поворота кристалла, G — гальванометр
что угловое распределение имеет характерные максимумы, похо-
жие на дифракционные пики, которые возникают при рассеянии
на кристалле коротковолнового рентгеновского излучения.
Дифракционный характер рассеяния электронов свидетельст-
вует об их волновых свойствах. Атомная структура кристалла ни-
келя в опыте Девиссона и Джермера играла роль объемной отра-
жательной дифракционной решетки. Если, согласно гипотезе де
Бройля, электроны обладают волновыми свойствами, то положе-
ние дифракционных максимумов может быть рассчитано путем
решения уравнения Вульфа-Брэгга (см. (Д.4.11) дополнения 4.5).
Электроны, ускоренные разностью потенциалов С7, имеют ки-
нетическую энергию Е = eU. В опытах Девиссона и Джермера
использовалось напряжение U порядка десятков вольт, таким об-
разом, с кристаллом взаимодействовали нерелятивистские элек-
троны. Следовательно, согласно формуле (5.3), длина волны де
5.2. Экспериментальные исследования дифракции 95
Бройля выразится формулой
\ /Г
Л° = (5-4)
Один из результатов экспериментальных исследований Девис-
сона и Джермера представлен на рис. 5.2. Полярная диаграмма
интенсивности отраженных электронов (т.е. распределение ко-
Рис. 5.2. Угловое распределение потока электронов, отраженных кристаллом ни-
келя, полученное в экспериментах Девиссона и Джермера:
U — разность потенциалов, ускоряющая первичные электроны, 0 — угол между падающим
и отраженным пучками отраженных электронов
личества электронов, попавших в детектор при разных углах от-
ражения 0) имеет немонотонный характер, что явно свидетель-
ствует о дифракционных явлениях. При ускоряющем напряжении
U = 54 В наблюдался резкий дифракционный максимум под углом
0 = 50°.
По формуле (5.4) легко вычислить длину волны де Бройля элек-
трона, ускоренного разностью потенциалов U. При U = 54 В зна-
чение Ad приближенно равно 1,67 • Ю-10м = 1,67 А.
С другой стороны, расчеты по формуле Вульфа-Брэгга, прове-
денные для условий эксперимента и п — 1, дали при угле в = 50°
длину волны 1,65 А. Это значение удовлетворительно совпадает с
длиной волны де Бройля Ad, вычисленной выше, если учитывать
точность экспериментальной методики Девиссона-Джермера.
При сопоставлении результатов экспериментов и расчетов сле-
дует учесть, что электроны проникают внутрь кристалла, взаи-
модействуют с электрически заряженными частицами его крис-
таллической структуры. Электрон внутри металла движется в
электрическом поле, создаваемом положительными ионами. Этим
определяется различие дифракции электронов на кристалле от ди-
фракции рентгеновских лучей, которые не обладают электриче-
96
Лекция 5- Волновые свойства частиц
ским зарядом. Влияние внутреннего электрического поля кри-
сталла на дифракцию электронов можно описать эффективным
внутренним потенциалом и внесением поправки в уравнение Вуль-
фа-Брэгга. Учет поправок привел к тому, что различие между зна-
чениями длины волны де Бройля, вычисленной по формуле (5.4), и
длиной волны, получаемой при решении уравнения Вульфа-Брэгга
(Д.4.11) для зарегистрированного максимума в спектре рассеян-
ных электронов, стало меньше погрешности измерений.
В ходе опытов Девиссон и Джермер изучали также зависимость
интенсивности потока рассеянных электронов от азимутального
угла 99 при фиксированном полярном угле в. Для этого при неиз-
менном положении детектора кристалл поворачивался вокруг оси,
перпендикулярной облучаемой отшлифованной грани.
Полученное угловое распределение (см. рис. 5.3) характерно
для пространственной интерференционной картины, образован-
ной волнами, рассеянными атомами кристаллической структуры
0° 90° 180° 270°
Рис. 5.3. Примеры зависимостей интенсивности потока рассеянных электронов
от азимутального угла ср при фиксированных полярных углах 0.
По вертикали отложено количество рассеянных электронов, попавших в детектор за еди-
ницу времени
металла. В частности, расположение на рис. 5.3а максимумов с пе-
риодом 120° объясняется тем, что ось первичного пучка электронов
была направлена вдоль поворотной оси симметрии 3-го порядка об-
лучаемого кристалла никеля.
5.2. Экспериментальные исследования дифракции
97
Кроме того, в ходе экспериментов Девиссон и Джермер наблю-
дали смещение дифракционных максимумов при изменении уско-
ряющего напряжения J7, которое соответствовало уравнению (5.4).
Согласие результатов опытов с расчетами по формуле де Бройля вы-
полнялось для максимумов различных порядков вплоть до п = 8.
В 1928 г. английский физик Дж. Томсон (1892-1975), сын
Дж.Дж. Томсона, открывшего электрон, получил новое подтвер-
ждение гипотезы де Бройля. В своих экспериментах Дж. Томсон
наблюдал дифракционную картину, возникающую при прохожде-
нии пучка электронов через тонкие поликристаллические фольги
(рис. 5.4).
Дж. Томсон использовал коллимированный (узкий) пучок мо-
ноэнергетических электронов с энергиями от 17,5 до 56,5 кэВ (см.
Рис. 5.4. Схема опыта Дж. Томсона по обнаружению дифракции электронов на
поликристаллической пластинке золота: К — электронная пушка
рис. 5.4). Ускоренные электронной пушкой К электроны падали
нормально на тонкую поликристаллическую фольгу из золота. Про-
ходящие через фольгу электроны попадали на фотопластинку и
вызывали почернение фотопластинки в местах попадания.
В экспериментах Дж. Томсона было обнаружено, что электрон-
ные пучки рассеиваются на металлических микрокристаллах ана-
логично рентгеновским лучам, образуя типичные дифракционные
кольца, центр которых находился на оси первичного пучка элек-
тронов.
Поликристаллическая металлическая фольга состоит из мно-
жества маленьких монокристаллов хаотически ориентированных
относительно друг друга. При падении на фольгу монохромати-
ческой плоской волны большое количество монокристаллов ока-
зываются в отражающем положении, т. е. рассеянные вторичные
волны, рассеянные атомами, интерферируют и образуют дифрак-
ционные пучки. Углы, под которыми наблюдаются дифракцион-
ные максимумы, определяются уравнением Вульфа-Брэгга (4.15),
которое выведено в дополнении 4.5.
Так как микрокристаллы, находящиеся в отражающем поло-
жении, располагаются симметрично относительно оси первичного
пучка, то дифракционные пучки распространяются вдоль поверх-
8 Зак. 178
98 Лекция 5. Волновые свойства частиц
ностей набора коаксиальных конусов. Регистрируемые дифракци-
онные кольца образуются сечением конических поверхностей плос-
костью фотопленки.
В исследованиях Дж. Томсона выяснилось, что углы 99, кото-
рые определяют направления дифракционных максимумов, удо-
влетворят уравнению Вульфа-Брэгга (4.15), если длина волны Л
вычислена по формуле де Бройля (5.2).
Создавая в области пролета электронов сильное магнитное по-
ле, Дж. Томсон добивался заметного искажения дифракционной
картины. Это послужило доказательством того, что дифракция
создавалась заряженными частицами — электронами, а не вто-
ричными рентгеновскими лучами, которые образуются при взаи-
модействии ускоренных электронов с атомами металла.
Эксперименты по рассеянию электронов проводил в те же годы
П.С. Тартаковский (1895-1939). Он применял геометрию опыта,
аналогичную использованной Дж. Томсоном, но использовал элек-
троны с энергией свыше 1 кэВ и алюминиевую фольгу. В этих опы-
тах также были получены характерные дифракционные кольца,
изображенные на рис. 5.5в.
Все эксперименты как на монокристаллах, так и на поликри-
сталлах показали качественное совпадение дифракционных кар-
тин для электронов (электронограмм) и для рентгеновских лучей
(лауэграмм и дебаеграмм). На рис. 5.5 приведены некоторые ха-
рактерные примеры.
Рис. 5.5. Дифракционные картины рентгеновских лучей (лауэграмма) на кри-
сталле дигидрофосфата калия (а) и электронограммы от монокристаллической
пленки PbS (5) и поликристалла алюминия (в)
Дальнейшие эксперименты показали, что дифракционные яв-
ления свойственны не только электронам, но и другим массивным
микр оча стицам.
В 1929 г. И.Эстерман (1900-1973) и 0. Штерн (1888-1969)
обнаружили на опыте дифракцию частиц, которые уже нельзя на-
звать элементарными. В этих экспериментах газ нагревался в спе-
циальной печи до заданной температуры. Затем создавался узкий
5.2. Экспериментальные исследования дифракции
99
пучок атомов, исходящих из отверстия в стенке печки, и напра-
влялся на монокристалл. При рассеянии пучков атомов гелия Не и
молекул водорода Н2 на кристаллах фторида лития LiF были полу-
чены характерные дифракционные
максимумы (см. рис. 5.6). Изме-
ренные по дифракционным карти-
нам длины волн совпадали с рас-
считанными по формуле де Бройля
(5.2).
Рис. 5.6. Угловое распределение атомов гелия на кристалле LiF. Температура газа
295 К. Кроме центрального максимума дифракционной картины наблюдаются два
побочных
Рис. 5.7. Картина дифракции пучка нейтронов на кристалле NaCl
После создания ядерных реакторов и получения мощных пуч-
ков нейтронов было экспериментально обнаружено, что нейтроны
дифрагируют на кристаллах как объекты с длиной волны, опреде-
ляемой формулой де Бройля (5.2). На рис. 5.7 приведен пример ди-
фракционной картины, полученной при рассеянии пучка моноэнер-
гетических нейтронов на кристалле хлорида натрия NaCl. Видно,
что картина похожа на типичную лауэграмму — результат рассе-
яния рентгеновских лучей на монокристалле.
Нейтроны не имеют электрического заряда и поэтому не взаи-
модействуют с электронами вещества. Но за счет сил межнуклон-
ного взаимодействия происходит рассеяние нейтронов на протонах
и других атомных ядрах. Если атомы в веществе расположены
периодически, атомные ядра образуют для нейтронов дифракци-
онную решетку. Так как нейтроны с определенным импульсом
имеют длину волны де Бройля (5.2), то рассеяние пучка моноэнер-
гетических нейтронов на кристалле дает дифракционную картину.
100
Лекция 5. Волновые свойства частиц
В настоящее время дифракция нейтронов является основой
структурной нейтронографии, представляет собой эффективный
метод исследования атомных структур, существенно дополняя
методы рентгенографического и электронографического анализа.
В частности, именно по дифракции нейтронов удалось определить
положения атомов водорода в кристаллах сложных веществ.
Таким образом, многочисленные опыты показали, что волно-
выми свойствами обладают не только электроны, а любые массив-
ные частицы. Трудности наблюдения дифракции тяжелых атомов,
многоатомных молекул и более массивных частиц объясняются
лишь тем, что их длины волн де Бройля слишком коротки, чтобы
их можно было наблюдать при современном состоянии экспери-
ментальной техники.
Для выяснения физического смысла волн де Бройля оказался
очень важным эксперимент, проведенный в 1949 г. В.А. Фабрикан-
том (1907-1991), Л.М. Биберманом и Н.Г. Сушкиным. В этих опы-
тах, как и в экспериментах Томсона-Тартаковского, пропускались
ускоренные электроны через фольгу, но использовались пучки
очень слабой интенсивности. Интервал времени между двумя по-
следовательными прохождениями электронов через фольгу в сред-
нем был примерно в 30000 раз больше времени прохождения
электрона от источника до детектора. В качестве детектора исполь-
зовалась фотопластинка. Попадание электрона в определенное ме-
сто фотоэмульсии вызывало химическую реакцию восстановления,
и в этом месте фотопластинки после химической обработки воз-
никало маленькое черное пятно металлического серебра. Таким
образом, в этом опыте исследовалось взаимодействие отдельного
Рис. 5.8. Картина дифракции электронов на поликристаллическом образце при
длительной экспозиции (а) и при короткой экспозиции (5). На рисунке (5) видны
точки попадания отдельных электронов на фотопластинку
электрона с кристаллической структурой металла. В результате
длительного облучения фотопластинки потоком электронов были
получены такие же дифракционные кольца (см. рис. 5.8а), как
5.3. Статистическая интерпретация волн де Бройля 101
и в опытах Дж. Томсона и Тартаковского. Таким образом было
доказано, что волновые свойства присущи отдельному элект-
рону.
Следует упомянуть, что после опубликования результатов вы-
шеописанных экспериментов Девиссона и Дж. Томсона противни-
ками гипотезы де Бройля было высказано предположение о том,
что явление дифракции объясняется рассеянием «коллективных
электронных волн». По этой гипотезе пучок летящих моноэнерге-
тических электронов образует «коллективную волну», которая при
взаимодействии с периодической атомной структурой порождает
пучки рассеянных электронов в направлениях, определяемых за-
конами классической интерференции. Иначе говоря, отдельные
электроны не имеют волновых свойств, а коллектив электронов
обладает некоторой длиной волны. Опыт группы В.А. Фабриканта
позволил отвергнуть эту идею.
Кроме того, в тех же опытах была получена еще более важ-
ная информация. При сравнительно коротком времени пропус-
кания электронов через фольгу на фотопластинке точки попада-
ния располагались нерегулярным образом, хотя все ускоренные
электроны имели одинаковые импульс и кинетическую энергию.
Казалось, что места попадания рассеянных электронов имеют слу-
чайное распределение (см. рис. 5.86). Но если предварительно рас-
считать расположение кольцевых областей дифракционных макси-
мумов и минимумов по формулам классической интерференции, то
можно обнаружить в хаотическом распределении точек попадания
электронов некоторую закономерность. При увеличении времени
опыта количество попаданий электронов возрастало в области ко-
лец дифракционных максимумов. В области же дифракционных
минимумов попаданий практически не наблюдалось.
Обнаруженный случайный характер точек попаданий отдель-
ных электронов явился одним из обоснований статистической ин-
терпретации волн де Бройля.
5.3. Статистическая интерпретация волн де Бройля
Обнаружение дифракции массивных частиц породило множе-
ство попыток объяснить их волновые свойства на базе классиче-
ской физики.
В частности, была высказана идея о том, что все массивные
(имеющие ненулевую массу покоя) частицы не являются «корпус-
кулами», а в принципе представляют собой волновые образования,
иначе говоря, волновые пакеты очень малого размера. Однако тео-
ретический анализ показал, что волновые пакеты, построенные
для массивных частиц, с течением времени расплываются (см.
дополнение 5.1). Время расплывания t волнового пакета, описы-
вающего движение массивной частицы массы т, можно оценить
102
Лекция 5. Волновые свойства частиц
по следующей формуле:
t ~ ^(Дя)2, (5.5)
п,
где Дж — характерный размер волнового пакета.
Если частица макроскопическая, например, имеет массу покоя
m = 1г и диаметр Дж = 1мм, то оценка по формуле (5.5) дает
порядок 1025 с. Это должно говорить о стабильности волнового па-
кета, которым описывается данная массивная частица. Однако для
атомной физики этот вывод мало полезен. Выше было показано,
что длина дебройлевской волны макроскопической частицы очень
мала, поэтому волновые свойства такой частицы практически не
проявляются в физических процессах.
Если мы рассмотрим электрон, находящийся в атоме, то в
качестве максимально возможного размера соответствующего вол-
нового пакета следует взять диаметр атома. Следовательно, m ~
~ 10“27 г, Дж ~ 1А = 10“8 см и оценка времени расплывания t
волнового пакета электрона дает 10“17 с. Столь малое время сви-
детельствует о нестабильности такого волнового пакета.
Волновой пакет свободного электрона должен иметь еще мень-
ший размер, что дополнительно уменьшает время расплывания t.
Полученные оценки времени расплывания означают, что если
бы массивные микрочастицы представляли собой волновые па-
кеты, они были бы нестабильны, причем обладали бы ничтожно
малым временем жизни. Следовательно, от такой идеи описания
электронов, протонов и других микрочастиц пришлось отказаться.
В течение нескольких десятилетий обсуждалась модель, кратко
называемая «волна-пилот». Сторонниками этой концепции был
сам Луи де Бройль и известный физик-теоретик Д.Бом (1917—
1992). Основная идея состоит в том, что частица является класси-
ческой «корпускулой» с определенной массой покоя и малыми раз-
мерами. С частицей всегда связана волна, которая представляет
собой колебание некоторого «пси-поля». Движение частицы упра-
вляется силами этого «пси-поля», которые направляют частицу в
точки пространства, где интенсивность «пси-поля» максимальна.
Все волновые явления, в том числе дифракция частиц, описыва-
ются интерференцией волн «пси-поля» на атомных периодических
структурах.
В рамках этой модели может быть разработан математический
аппарат, который позволяет описать наблюдаемые явления. Но
экспериментальный поиск гипотетического «пси-поля» не дал ре-
зультатов, поэтому от предложенной модели «волна-пилот» совре-
менная физика отказалась.
Кроме того, до сих пор не выяснен физический смысл частоты
волны де Бройля.
5.3. Статистическая интерпретация волн де Бройля 103
Остается предположить, что волны де Бройля — это волны
нового типа, который не был известен в классической физике.
После многих выдвинутых и отвергнутых гипотез весьма пло-
дотворной для развития квантовой физики оказалась статисти-
ческая интерпретация волны де Бройля, сформулированная в
1926 г. Максом Борном (1882-1970). Согласно этому постулату,
квадрат амплитуды волны де Бройля в какой-либо области про-
странства пропорционален вероятности обнаружить микрочастицу
в этой области. Точнее, квадрат амплитуды А(г) прямо пропор-
ционален плотности распределения вероятности /(г) нахождения
частицы в данной точке г. При этом вероятность регистрации ча-
стицы в области пространства объема ДУ, окружающего точку г,
равна /(г)ДУ.
Таким образом, движение каждого электрона имеет недетер-
минированный (случайный) характер. Но эта случайность не оз-
начает полного произвола. Электроны движутся, в основном, в
направлениях, для которых амплитуда волны де Бройля имеет
наибольшее значение. Расчет пространственного распределения
амплитуд волн де Бройля позволяет определить области простран-
ства, в которых можно зарегистрировать потоки дифрагированных
частиц.
В частности, результаты опыта Бибермана-Сушкина-Фабри-
канта успешно описываются на основе статистической интерпре-
тации. Расчеты дифракции волн с длиной (5.2) дают максимум
амплитуды волнового поля в местах максимального почернения
фотопластинки. Иначе говоря, именно в эти места попадает пре-
валирующее число электронов, рассеянных на кристаллической
структуре металла. Число попаданий пропорционально квадрату
амплитуды волны де Бройля.
С другой стороны, опыты с малым временем облучения фольги
демонстрируют случайный разброс точек попадания электронов
на фотопластинку. С увеличением времени экспозиции случай-
ное распределение точек попадания сходилось к своему среднему
значению (системе дифракционных колец), так же как частота слу-
чайного события с ростом числа опытов сходится к соответствую-
щей вероятности.
Статистической интерпретации не противоречат результаты
всех экспериментов по дифракции массивных частиц, что явля-
ется ее несомненным достоинством. Принципиальная новизна
такой интерпретации состоит в том, что согласно ей поведение от-
дельных частиц подчиняется в принципе вероятностным законо-
мерностям. Для сравнения вспомним, что в классической физике
газов частицы полагаются движущимися по траекториям, опре-
деляемым решением уравнения движения Ньютона. Статистиче-
ские (вероятностные) закономерности вводились в теорию из-за
огромного количества (порядка числа Авогадро) частиц газа.
104
Лекция 5. Волновые свойства частиц
Согласно статистической интерпретации, волны де Бройля не
представляют собой распространяющиеся возмущения какого-
либо физического поля. Иначе говоря, амплитуда волны де Бройля
обладает лишь вероятностным смыслом.
Отметим, что волны де Бройля описывают движение только
свободных частиц с определенным импульсом. Полная квантовая
теория должна быть пригодна для частиц, движущихся в произ-
вольных внешних полях. Как будет показано в следующих лек-
циях, волновая функция, характеризующая состояние электро-
нов в атомах, является по своему смыслу обобщением волны де
Бройля.
Статистическая интерпретация волн де Бройля оказалась очень
полезной для создания квантовой теории на базе уравнения Шре-
дингера (см. лекцию 9).
Задачи к лекции 5
1. Оценить длину дебройлевских волн молекул водорода, азота и ки-
слорода при комнатной температуре.
2. Вычислить длину дебройлевской волны электрона с кинетической
энергией: а) 5 эВ, б) 5 кэВ, в) 5 МэВ, г) 5 ГэВ.
3. Оценить длину дебройлевских волн атомов гелия: а) при ком-
натной температуре, б) температуре Т = —100 °C, в) температуре Т =
= 1000°С.
4. Вычислить длину дебройлевской волны нейтронов, имеющих
среднюю тепловую энергию к&Т при комнатной температуре.
5. Вычислить длину дебройлевской волны: а) Луны, движущейся
по орбите вокруг Земли, б) земного шара, летящего по орбите вокруг
Солнца.
6. Найти кинетическую энергию электрона, у которого дебройлейв-
ская длина волны равна комптоновской длине. Можно ли рассматривать
такой электрон как нерелятивистский ?
7. Оценить время расплывания волнового пакета, которым описыва-
ется протон.
8. Вычислить длину дебройлевской волны пули «Магнум» для ре-
вольвера «Смит-Вессон». Масса пули 8,1г, скорость 442 м/с.
9. Вычислить длину дебройлевской волны артиллерийского снаряда
германской дальнобойной пушки «Дора». Масса снаряда 4800 кг, ско-
рость 820 м/с.
10. Протон с кинетической энергией Е = 1 МэВ рассеивается на не-
подвижной альфа-частице на угол 90°. Вычислить длину дебройлевской
волны рассеянного протона.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 5
5.1. Волновой пакет
Плоская монохроматическая волна может быть описана функцией ко-
ординат г и времени t:
Ф(ж, t) — Aexp[z(cji - kr 4- <£0)], (Д-5.1)
где А — амплитуда, cj — частота, к — волновой вектор, ср0 — началь-
ная фаза, которую смещением начала отсчета координаты или времени
можно сделать равной нулю.
Выбрав ось координат X в направлении волнового вектора, функцию
(Д.5.1) можно переписать в виде
Ф(ж, i) = А ехр [г(cut — кх + </>о)], (Д-5.2)
где к — волновое число, х — координата.
Строго говоря, плоская монохроматическая волна вида (Д.5.2) явля-
ется объектом бесконечным в пространстве и вечным во времени, по-
этому представляет собой математическую идеализацию реальных волн.
Для описания волны, ограниченной в пространстве, можно использовать
суперпозицию плоских волн, различающихся волновыми числами. Та-
кие волновые образования имеют амплитуду отличную от нуля в конеч-
ной области координаты х и называются волновыми пакетами. На-
пример, волновой пакет можно образовать суммированием непрерывного
набора плоских волн, имеющих одинаковые амплитуды А/Хк и волно-
вые числа в интервале [&о — ДА:/2, ко 4- ДА:/2]:
Аго4"Д^/2
^4 Г
Ф(ж, t) = / ехр [z(cji — кх)] dk,
ko-^k/2
(Д-5.3)
где ко и ДА: — постоянные величины.
Частота cj, вообще говоря, является функцией волнового числа к.
Разложение функции cj(A:) в ряд Тейлора вблизи точки к — ко имеет вид
ш(к) = w(Ao) + и'(к0)(к - ко) + lw"(fco)(fc - fco)2 + ... (Д.5.4)
Ограничимся разложением ряда (Д.5.4) до линейного члена:
и>(к) ~ и(ко) + (к - ко)и'(ко). (Д.5.5)
106
Дополнения к лекции 5
При этом оценка погрешности разложения (Д.5.5) будет определяться по
порядку величины отброшенным квадратичным членом:
|w"(M^ - fc0)2 ~ ш"(к0)(Ак)2. (Д.5.6)
Введем для сокращения записей обозначения cjq = <^(&о) и Uq =
= о/(А;о). Подставив линейный закон дисперсии (Д.5.5) в интеграл
(Д.5.3), получим волновое поле вида
Ф(я,£) = Bexp[i(coot — А;о:г)], (Д-5.7)
где множитель В имеет смысл амплитуды волнового пакета и выра-
жается интегралом
&О A fc/2
А Г
В = — / ехр [i(k - ko)(u/Qt - я)] dk. (Д.5.8)
Za/ъ J
ko-^k/2
Введем новую переменную, зависящую от координаты и времени:
дь
С =-2-(wot-x). (Д.5.9)
Тогда амплитуда волнового пакета В выразится в компактной форме:
В = А^-. (Д.5.10)
Отсюда видно, что, в отличие от плоской волны, амплитуда волнового
пакета (Д.5.10) является функцией координаты и времени.
Постановка амплитуды (Д.5.10) в формулу (Д.5.7) дает следующее
выражение для волнового поля:
Ф(а;,£) = ехр [г(сио£ — ^о^)]- (Д.5.11)
Формулу (Д.5.11) можно интерпретировать как произведение мед-
ленно меняющейся во времени и пространстве (при условии ДА; ко)
амплитуды (Д.5.10) и быстро изменяющейся гармонической функции
ехр [i(coot — кох)]. При этом «медленная» амплитуда играет роль плав-
ной огибающей, а «быстрая» гармоника — роль заполнения, как пока-
зано на рис. Д.5.1, где приведена реальная часть кохмплексной функции
Ф(ж, t).
Огибающая задается функцией (Д.5.10). Функции ±1?(£) имеют цен-
тральный экстремум при = 0 и нули в точках £ = пл, где п — целое
число. Модули значений функций ±В(£) в точках экстремумов моно-
тонно убывают при удалении от точки £ = 0 (см. рис. Д.5.1). Можно
сказать, что амплитуда волнового пакета |В| заметно отличается от нуля
в области —7г/2 < £ < тг/2, т.е. в качестве ширины волнового пакета
можно принять величину Д£ = л.
Дополнения к лекции 5
107
Рассматривая момент времени t = 0, из соотношения (Д.5.9) полу-
чим £ = х^к/2. Тогда оценка пространственного размера имеет вид
л 2А£ 2тг
АА; АА;
Иначе говоря, ширйна волнового пакета Аж и диапазон волновых
чисел АА; связаны обратно пропорциональной зависимостью
АжАА; = 2тг. (Д.5.12)
Это означает, что для формирования узкого волнового пакета необ-
ходимо просуммировать множество гармонических волн, которые запол-
няют широкий интервал волновых чисел АА;.
Рис. Д.5.1. Мгновенная «фотография» волнового пакета.
Сплошная линия — заполняющая гармоническая функция, штриховая линия — огибаю-
щая ±В при А — 1
Зависимость величины £ от времени определяет скорость распро-
странения волнового пакета. Возьмем производную по времени от вели-
чины £ и приравняем нулю:
АА; (dx ,\
Решение последнего уравнения дает скорость распространения максиму-
мов огибающей и, следовательно, скорость распространения амплитуды
(Д.5.10):
« = • (Д-5-13)
\dkJk=k0
108
Дополнения к лекции 5
Так как интенсивность волны пропорциональна квадрату амплиту-
ды, то величина (Д.5.13) является скоростью распространения энергии
в пространстве, т.е. групповой скоростью волнового пакета.
Заполняющая гармоника ехр [г— Azq^)] также является функцией
координаты и времени. Взяв производную от аргумента coot — k$x по
времени и приравняв ее нулю:
~ = 0’
at
мы получим выражение для фазовой скорости, т.е. скорость распро-
странения в пространстве, заполняющая гармоники:
dx loq
dt ко
(Д-5.14)
Эта величина отличается от групповой скорости (Д.5.13) и не определяет
скорость распространения энергии в пространстве.
Таким образом, при описании движения массивных частиц с помо-
щью пакетов волн де Бройля следует полагать скорость частицы равной
групповой скорости волнового пакета (Д.5.13), а не фазовой (Д.5.14).
Волновой пакет вида (Д.5.11) локализован не только в пространстве,
но и во времени, образуя импульс некоторой длительностью At Вели-
чина £, согласно формуле (Д.5.9), линейно зависит от координаты х и от
времени t. Запишем величину £ в точке х = 0 и воспользуемся опреде-
лением групповой скорости (Д.5.13) как скорости изменения величины
(Д-5.9):
A A: dw Acj /тт „
^=~~2dkt = ~~2^ (Д-5Л5)
где Acj — интервал частот, соответствующий диапазону волновых чисел
АА: при линейном законе дисперсии (Д.5.4). Теперь по ширине волно-
вого пакета А£ = тг можно, пользуясь соотношением (Д.5.15), оценить
длительность импульса At. Мы получаем, что диапазон частот Ас^ и
интервал времени At также связаны обратно пропорциональной зависи-
мостью
Аа;АА = 2тг. (Д.5.16)
Таким образом, для получения более короткого импульса требуется
сложить гармонические волны с частотами, заполняющие более широ-
кий диапазон Аси. В оптике соотношение (Д.5.16) связывает ширину
спектральной линии Acj с длительностью излучения At
Итак, если частота cj и волновое число к связаны линейным законом
дисперсии (Д.5.5), то длительность импульса At (и ширина волнового
пакета А А:) не изменяются с течением времени. Если же закон диспе-
рсии нелинейный и разложение (Д.5.4) содержит квадратичный член
(а может быть, и следующие), то волновой пакет вида (Д.5.3) с течением
времени постепенно расплывается. Время расплывания можно оценить
из следующих соображений.
Предположим, что волновой пакет был образован в момент времени
t = 0. Тогда, очевидно, время расплывания td можно найти из условия
дополнительного набега фазы волны (Д.5.11), сопоставимого с числом тг.
Дополнения к лекции 5
109
Набег фазы возникает от слагаемого второго порядка (Д.5.6) в разложе-
нии (Д.5.4) частоты по разности к — к®. Таким образом, мы получаем
соотношение
(A^^id-Tr. (Д.5.17)
акт
Отсюда следует, что
7Г
td ~
(ДА:)2^
ПК,
(Д.5.18)
Воспользовавшись соотношением (Д.5.12), запишем время расплывания
в виде
id ~ (Д.5.19)
а ш
Из последней формулы следует, что время расплывания существенно за-
висит от второй производной dw2/dk2, а следовательно, от закона диспе-
рсии ш(к).
Применим полученные результаты к реальным частицам. Характе-
ристики фотонов описываются соотношениями (4.2) и (4.11), что позво-
ляет записать для них закон дисперсии в виде ш = ск, где с — ско-
рость света. Следовательно, вторая производная d2w/dk2 равна нулю, и
время расплывания (Д.5.19) обращается в бесконечность. Это означает,
что импульсы электромагнитных волн любых диапазонов могут успешно
описываться устойчивыми волновыми пакетами.
Для дебройлевских волн закон дисперсии можно получить из урав-
нения, связывающего энергию и импульс частицы (4.9) и соотношений
(5-1):
I
ш(к) = 1/с2/;2 + (Д.5.20)
V nr
Нелинейный характер закона дисперсии обусловлен ненулевой массой
покоя то частиц.
При нерелятивистских энергиях частиц величина
h2k2
2mgC2
<£ 1. Раз-
ложим закон дисперсии (Д.5.20) в ряд Тейлора по малой величине
до квадратичного члена включительно:
И2 к2
2m^c2
w(k) «
9
mocz
h
/ h2k2 \
\ + 2mgC2/ ’
(Д.5.21)
Вычислим вторую производную от функции (Д.5.21):
d2w h
dk2 mo
по
Дополнения к лекции 5
и подставим ее в формулу (Д.5.19):
id ~
(Аж)2т0
(Д.5.22)
Таким образом, время расплывания волнового пакета дебройлевских
волн, описывающего движение нерелятивистской частицы, определяется
ее массой и размером.
Например, рассмотрим электрон с массой покоя те ~ 10-27 г. В ка-
честве исходного размера волнового пакета возьмем Аж ~ 10-8 см, т. е.
размер атома. Подстановка величин те и Аж в формулу (Д.5.22) дает
время расплывания td ~ 10-17с. Если величину Аж взять порядка
е2
«классического» радиуса электрона го = ---т = 2,8179 • 10“13 см, то
mecz
время td уменьшится до ~ 10-26 с. Это доказывает невозможность опи-
сания электронов волновыми пакетами.
Подставляя в выражение (Д.5.22) массы протона, нейтрона и других
микрочастиц, мы будем получать также чрезвычайно малые времена.
Это означает, что нельзя для объяснения волновых свойств массивных
микрочастиц заменять их волновыми пакетами дебройлевских волн.
Лекция б
СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ
6.1. Интерференционный опыт Юнга на электронах
Для формулировки базовых принципов квантовой физики по-
лезно рассмотреть опыт по рассеянию электронов на системе из
двух отверстий в непрозрачном экране. Схема опыта показана на
рис. 6.1. Видно, что этот опыт похож на знаменитый экспери-
мент Томаса Юнга по интерференции света на двух щелях, выпол-
ненный им в 1802 г. Этот замечательный эксперимент наглядно
иллюстрировал законы интерференции и явился эксперименталь-
ным обоснованием волновой теории света.
Аналогичный эксперимент на пучках электронов был действи-
тельно выполнен в 1961 г. К. Ионссоном, хотя все его результаты
были теоретически предсказаны и проанализированы на много лет
раньше.
Источником электронов является электронная пушка, которая
испускает пучок электронов с определенной энергией. На пути
электронов находится перегородка с двумя отверстиями. При про-
хождении через отверстие из-за взаимодействия с его краями (точ-
нее, с атомами, из которых сделана перегородка) электрон рассе-
ивается на некоторый угол. За ней расположена стенка, вдоль
которой перемещается детектор. Детектор регистрирует количе-
ство попавших в него электронов за единицу времени, т. е. интен-
сивность потока рассеянных электронов I. Будем рассматривать
положения детектора на прямой, проходящей через отверстия, и
характеризовать его положение координатой ж, которая отсчиты-
вается вдоль поглощающей стенки. Таким образом, может быть
измерена интенсивность I как функция координаты х. Зависи-
мость /(ж) является распределением интенсивности рассеянных
электронов вдоль заданной прямой.
Результаты экспериментов можно подытожить следующим об-
разом. Когда открыто лишь отверстие I, то распределение 1\(х)
содержит один широкий максимум, положение которого опреде-
ляется взаимной ориентацией открытого отверстия и источника
112 Лекция 6. Соотношения неопределенностей
электронов. При открывании только отверстия 2 получается ана-
логичное распределение — функция /2(^) также имеет единствен-
ный широкий максимум, естественно смещенный относительно
максимума функции Д(ж). Но при открывании обоих отверстий
Рис. 6.1. Интерференция электронов в схеме Юнга
регистрируется типичная картина интерференции Д2 (х) — функ-
ция со множеством максимумов и минимумов (см. рис. 6.1). При
этом выполняется неравенство
Ш / /1(х) + 12(х). (6.1)
Все интерференционные картины света, рассматриваемые в
классической физике, формируются наложением, по крайней мере,
двух когерентных волн, исходящих из пространственно разделен-
ных источников (например, классический опыт Юнга). Но при
анализе результатов опыта по рассеянию электронов возникает во-
прос — что с чем интерферирует? В опытах с пучками слабой
интенсивности электроны проходят через рассеивающее препят-
ствие поодиночке. Если бы электрон мог разделиться на две части,
а каждая часть проходила бы через свое отверстие, можно было
бы выдвинуть гипотезу об интерференции частей электрона. Но
электрон является неделимой частицей. Во всех экспериментах
регистрируются попадания в детектор целого количества элект-
ронов.
Но если некоторые электроны проходят через отверстие 7, а
другие — через отверстие 5, то в эксперименте должна регистри-
роваться сумма унимодальных функций
I0(x) = Ых) + 12(х), (6.2)
которая не содержит интерференционных максимумов.
Кроме того, сравнивая кривые I12(#) и Iq{x\ можно видеть,
что в некоторых точках /12(ж) > /о(^)5 в других Т12(я) < Л)(я).
6.1. Интерференционный опыт Юнга на электронах
113
Это значит, что, закрывая одно из двух отверстий, увеличиваем
потоки электронов, рассеянных в некоторых направлениях, и при
этом уменьшаем потоки, рассеянные в других направлениях. Но
как электроны, проходящие через определенное отверстие, могут
«знать» о том, что другое отверстие закрыто (или открыто)?
Таким образом, если электрон не разделится на части, то, с
точки зрения классической физики, интерференция электронов
кажется невозможной. Но она наблюдается в эксперименте!
Для разрешения этого парадокса естественно попытаться про-
следить за движением электронов вблизи перегородки — может
быть, удастся выяснить, как именно электроны проходят через
отверстия? Чтобы зафиксировать местонахождение электрона,
можно использовать рассеяние фотонов, т.е. эффект Комптона,
описанный в лекции 4. Рассмотрим модификацию вышеописан-
ного опыта. Вблизи отверстий в перегородке разместим источник
Рис. 6.2. Рассеяние фотонов на электронах в схеме Юнга
света Р и поставим фотоприемники Ф1 и Ф2 (см. рис. 6.2). Пред-
положим, что установка настроена таким образом, что при прохо-
ждении электрона сквозь отверстие 1 фотон, испущенный источни-
ком света, рассеется на этом электроне и попадет в фотоприемник
Ф1. Аналогично, при прохождении электрона сквозь отверстие 2
произойдет попадание рассеянного фотона в фотоприемник Ф2.
Эксперименты на установке, приведенной на рис. 6.2, показы-
вают, что фотоприемники Ф1 и Ф2 не срабатывают одновременно.
Это значит, что электрон не делится на части и не проходит че-
рез оба отверстия одновременно. Регистрация рассеянных фото-
нов фотоприемниками свидетельствует о том, что некоторые элек-
троны проходят через отверстие 7, другие — через отверстие 2,
Но при этом детектор электронов регистрирует кривую попаданий
вида /0(я). Иначе говоря, электроны не интерферируют, а про-
ходя через различные отверстия, формируют в области стенки
114 Лекция 6. Соотношения неопределенностей
суммарный поток /о(^) — Л(^) + ^2(2)- Ликвидировав одну па-
радоксальную ситуацию, мы получили другую. Оказывается, при
наблюдении за прохождением электронов через отверстия интер-
ференционная картина исчезает!
В классической физике подобные ситуации не встречались. За-
коны движения макроскопических тел не изменялись при наблю-
дениях за этими телами. Камни, брошенные под углом к гори-
зонту, летят по баллистической траектории независимо от того,
глядим ли мы на них или нет.
В опытах с электронами наблюдение проводилось с помощью
рассеяния фотонов. Следовательно, в процессе наблюдения на
электрон осуществлялось воздействие, которое изменяло харак-
теристики этого электрона. В опыте 2 на стенку с детектором
попадают электроны, проходящие через отверстия и взаимодей-
ствующие с фотонами. В опытах, схематично изображенных на
рис. 6.1, 6.2, реализуются различные физические процессы, что
приводит к различным результатам. Но в опыте 2 (рис. 6.2) пла-
нировалось наблюдение за прохождением электронов без искаже-
ния этого процесса!
Попытаемся максимально ослабить воздействие фотонов на
движущиеся электроны. Чтобы обнаружить месторасположение
электрона, но не изменить существенно характеристики его дви-
жения, можно уменьшить энергию и импульс рассеиваемых фо-
тонов. Идея кажется плодотворной, для этого следует понизить
частоту излучения источника Р. Например, вместо видимого из-
лучения использовать инфракрасное или СВЧ и в схеме на рис. 6.2.
поставить детекторы соответствующего излучения. Но при умень-
шении частоты электромагнитного излучения си увеличивается его
длина волны Л, согласно (2.4). Ясно, что погрешность определения
координаты электрона будет не меньше длины волны рассеиваю-
щегося фотона. К нашему удивлению (или огорчению), опыты
показывают, что воздействие фотонов на электроны становится
малым, когда длина волны А фотонов превышает расстояние L
между отверстиями в перегородке. В такой ситуации фотоприем-
ник фиксирует попадание рассеянного фотона, но остается неиз-
вестным, около какого отверстия произошло это рассеяние. При
такой большой длине волны (Л > L} по результатам рассеяния фо-
тонов невозможно определить местонахождение электрона с необ-
ходимой точностью. Остается неизвестным, через какое отверстие
проходит электрон.
Кроме того, при длине волны фотонов Л > L детектор рассеян-
ных электронов вновь регистрирует интерференционную картину
/12(ж). Вновь возникает прежняя ситуация: когда не отслеживает-
ся прохождение электронов через отверстия, они интерферируют.
Подобные эксперименты проводились в действительности, хотя
в установках более сложных, чем изображенная на рис. 6.2.
6.2. Соотношения неопределенностей Гейзенберга 115
Результаты последних опытов могут навести на мысль о за-
говоре Природы против физиков.. Оказывается, экспериментально
не удается про.следить за траекторией электронов и выяснить при-
чины возникновения интерференционной картины. Предположе-
ние о том, что электрон делится на части, которые представляют
собой когерентные волны, также экспериментально не установ-
лено. Пока физикам не удалось разделить электрон на части, и
он считается элементарной частицей.
Множество удивительных фактов, полученных при исследова-
нии свойств микрочастиц, должны привести к мысли о необходи-
мости формулировки новых фундаментальных принципов физики,
т.е. о разработке новой теории. Это не является отказом от клас-
сической физики. Новая теория может лишь установить границы
применимости классических принципов, как, например, специаль-
ная теория относительности не опровергла механику Ньютона, а
ограничила ее нерелятивистскими скоростями тел.
6.2. Соотношения неопределенностей Гейзенберга
Множество экспериментов с электронами и другими микроча-
стицами дали результаты, являющиеся парадоксальными с точки
зрения классической физики (например, дифракция массивных
частиц на монокристаллах). Один из создателей квантовой тео-
рии В. Гейзенберг (1901-1976) в 1927 г. выдвинул предположение,
что все трудности, возникшие в интерпретации этих эксперимен-
тов, должны быть следствием некоторого фундаментального за-
кона Природы, который до XX века не был еще обнаружен. Этот
закон Гейзенберг назвал принципом неопределенности, который
ограничивает применение к микрообъектам классических поня-
тий и представлений.
Количественно принцип Гейзенберга выражается в виде соот-
ношений неопределенностей. Первое из них можно записать в
виде неравенства
Дж £±рх > 2тг/г, (6.3)
где Дж и Држ — неопределенности координаты ж и проекции им-
пульса рх соответственно. Под неопределенностями следует пони-
мать минимально возможные погрешности одновременного изме-
рения величин, связанных соотношением (6.3). Знак > означает
неравенство по порядку величины.
Соотношение (6.3) означает, что если некоторая материальная
точка имеет неопределенность проекции импульса Држ, т0 невоз-
можно измерить или вычислить координату этого тела с точностью
большей, чем Дж = 2тгЛ/Држ. С другой стороны, если координата
тела ж задана с неопределенностью Дж, то в принципе невозможно
получить проекцию импульса рх с погрешностью меньшей, чем
2тгЛ/ Дж.
116 Лекция 6. Соотношения неопределенностей
Воспользовавшись изотропией пространства, можно записать
аналогичные соотношения неопределенностей для ортогональных
направлений:
Ду Дру > 2тгЛ, (6.4)
Дг Дрг > 2тг/г. (6.5)
Следует обратить внимание, что соотношения (6.3)-(6.5) свя-
зывают неопределенности координат и соответствующей проекции
импульса. Напротив, координаты и проекции импульса для раз-
ных осей (например, х ыру) могут быть одновременно определены
сколь угодно точно.
Заметим, что часто при записи соотношений неопределенно-
стей опускают множитель 2тг в правых частях выражений (6.3)-
(6.5). Это никак не влияет на выводы этой лекции и следующих,
так как соотношения (6.3)-(6.5) выполняются только по порядку
величины. Кроме того, строгое математическое определение не-
определенностей координат, проекций импульса и других физиче-
ских величин можно дать только на базе квантовой механики.
Из соотношений Гейзенберга следует, что любое тело не мо-
жет в определенный момент иметь точные значения координат и
импульса. Абсолютно точные координаты тело получит, если его
импульс абсолютно не определен, т. е. неопределенности проекций
импульса бесконечны.
В подавляющем количестве физических ситуаций неопределен-
ности проекций импульса имеют конечную величину, в некоторых
случаях они могут быть уменьшены до нуля. Но тогда, согласно
соотношениям Гейзенберга (6.3)—(6.5), неопределенности коорди-
нат имеют конечное (не нулевое) значение, а при уменьшении
неопределенности проекций импульса до нуля неопределенности
координат возрастают до бесконечности. Отсюда следует, что дви-
жение частицы, вообще говоря, не описывается классической тра-
екторией материальной точки, которая понималась в классической
механике как математическая линия.
Таким образом, соотношения Гейзенберга вынуждают физиче-
скую теорию отказаться от классических траекторий тел, описыва-
емых векторными функциями г(£). Траектория должна рассмат-
риваться как макроскопическое приближение описания движения
частицы.
Отсутствие классических траекторий снимает «парадокс» про-
хождения электронов через перегородку с двумя отверстиями в
схеме Юнга, который был описан в предыдущем разделе. Вопрос
«через какое отверстие проходит электрон?» является некоррект-
ным, так как электрон не движется по траектории. Точнее, не-
определенность координаты х превышает расстояние между отвер-
стиями L, Расчеты показывают, что действительно в этом опыте
Дх > L. С другой стороны, рассеяние фотонов на электронах в
6.2. Соотношения неопределенностей Гейзенберга 117
схеме Юнга позволяет установить отверстие, через которое про-
шел электрон. Но при этом электрон получает значительный им-
пульс отдачи (как в опыте Комптона) и неопределенность проек-
ции импульса сильно возрастает. Можно вычислить, что в
этом опыте произведение Др.т • d по порядку величины превышает
2тгЛ, где d — диаметр отверстия.
Анализ показывает, что результаты всех экспериментов по рас-
сеянию микрочастиц, описанные ранее, вполне укладываются в
соотношения Гейзенберга (см. дополнение 6.1).
Соотношения неопределенностей Гейзенберга являются важ-
ной частью современной квантовой теории. Заметим, что в соот-
ношениях (6.3)—(6.5) понятие неопределенности сформулировано
недостаточно четко. В квантовой механике этот недостаток ликви-
дирован.
Соотношения неопределенностей находятся в соответствии со
статистической интерпретацией волн де Бройля. В конце преды-
дущей лекции было указано, что амплитуда волны де Бройля по-
зволяет вычислить вероятность нахождения частицы в различных
точках пространства, но не дает точной координаты в данный мо-
мент времени.
Рассмотрим сначала частицу, которая характеризуется волной
де Бройля в виде комплексной гармонической функции
А ехр [i(wt — kr)] (6.6)
с постоянной амплитудой А = const. Волновой вектор к напра-
влен в сторону движения частицы, т.е. параллелен ее импульсу,
согласно (5.1).
Расположим ось координат X в направлении волнового век-
тора к. Тогда функция (6.6) примет вид
А ехр [i(wt — fc#)], (6.7)
где к — модуль волнового вектора (волновое число).
Гармоническая функция вида (6.7) имеет определенную длину
волны Л = 2л/к и, следовательно, определенный импульс с моду-
лем р = 2лН/Х = hk. Так как, согласно (5.1), импульс частицы р
параллелен волновому вектору к ее волны де Бройля, то у рассма-
триваемой частицы имеется определенная проекция импульса на
ось координат X:
2лК
Рх = —
Следовательно, неопределенность проекции импульса /\рх равна
нулю.
С другой стороны, гармоника (6.7) с постоянной амплитудой
бесконечно растянута вдоль оси координат X, следовательно, не-
определенность координаты Хх бесконечна. Видно, что даже в
118
Лекция 6. Соотношения неопределенностей
этом предельном случае характеристики частицы не противоречат
соотношениям Гейзенберга.
Далее, согласно статистической интерпретации, квадрат ам-
плитуды волны де Бройля пропорционален вероятности нахожде-
ния в данном месте пространства. Постоянство амплитуды озна-
чает, что частица с одинаковой вероятностью может иметь любое
значение координаты —оо < х < оо, а это соответствует бесконеч-
ной неопределенности координаты х. Это означает, что частица с
волной де Бройля вида (6.6) может быть с одинаковой вероятно-
стью обнаружена в любой точке оси X (как говорят, «размазана»
по бесконечному интервалу одномерного пространства).
Теперь рассмотрим другую, противоположную ситуацию. Пусть
частица движется вдоль оси X, причем ее координата х известна
с большой точностью, т. е. имеет малую неопределенность Хх.
Волна де Бройля такой частицы имеет амплитуду не равную нулю
только в области пространства размером Хх. Ясно, что такая
волна непохожа на гармоническую и, следовательно, не имеет опре-
деленной длины волны. Так как длина волны де Бройля одно-
значно связана с величиной импульса частицы соотношением
(5.2), то наша частица должна иметь ненулевую неопределенность
импульса Хрх.
Для оценки величины неопределенности представим волну де
Бройля частицы в виде волнового пакета следующего вида:
д С
<р(х, t) = — / ехр [i(wt — кх)] dk.
ко-^к/2
(6-8)
Величина Дк задает интервал волновых чисел к интегрируемых
гармоник, необходимых для формирования волнового пакета (6.8).
Вид зависимости <р(х, t) от координаты х в некоторый момент
времени t показан на рис. 6.3.
Огибающая осциллирующей функции ср(х^ t) ограничивает ха-
рактерные максимумы, которые разделены нулями. Центральный
максимум имеет ширину Xxq. В дополнении 5.1 показано, что в
качестве характерной ширины волнового пакета Хх целесообразно
взять половину расстояния между первыми нулями огибающей,
т.е. Джо/2. Вычисления, приведенные в дополнении 5.1, дают
следующую связь ширины волнового пакета Хх с диапазоном ин-
тегрирования /\к:
ХхХк = 2л. (6.9)
На рис. 6.3 видно, что за пределами главного максимума ам-
плитуда волнового пакета, вообще говоря, не равна нулю. Но ам-
плитуды побочных максимумов быстро уменьшаются при удале-
нии от главного максимума. Разумной является оценка ширины
6.2. Соотношения неопределенностей Гейзенберга
119
Рис. 6.3. Фотография волнового пакета, распространяющего вдоль оси коор-
динат X. Штриховая линия — огибающая отдельных экстремумов волнового
пакета.
Джо — расстояние между первыми нулями огибающей, которые ограничивают централь-
ный (главный) максимум
волнового пакета несколько большая, чем данная соотношением
(6.9). Иначе говоря, для размера волнового пакета целесообразно
использовать следующее неравенство:
ДжД/с > 2тг. (6.10)
Размер волнового пакета задает неопределенность координаты
Дж частицы, движущейся вдоль оси X.
С другой стороны, ненулевая ширина диапазона интегрирова-
ния Хк в (6.8) означает, что движущаяся частица имеет неопре-
деленность проекции импульса
Хрх = КХк. (6.11)
Сопоставление (6.10) и (6.11) дает неравенство, совпадающее с
соотношением неопределенностей Гейзенберга (6.3).
Если рассмотреть волновые пакеты, описывающие движение
частиц вдоль осей У и Z, то аналогичным образом можно получить
другие соотношения неопределенностей (6.4), (6.5).
Соотношение неопределенностей Гейзенберга является фунда-
ментальным законом Природы, т.е. выполняется не только для
микрочастиц, но для любых тел. Но почему же этот всеобщий за-
кон не был обнаружен до XX века в ходе развития классической
физики?
Дело в том, что произведение неопределенностей координаты
и проекции импульса, согласно соотношениям Гейзенберга, очень
мало — порядка постоянной Планка И. В физических эксперимен-
тах любые измерения проводятся с погрешностями (прямыми или
120 Лекция 6. Соотношения неопределенностей
косвенными). Если произведение погрешностей измерения коор-
динат и проекций импульса значительно превышает величину Л,
то соотношение неопределенностей в опытах не будет обнаружено.
Можно показать, что при исследовании макроскопических тел про-
изведение этих погрешностей много больше постоянной Планка Л,
поэтому соотношения неопределенностей экспериментально не на-
блюдаются.
В качестве примера рассмотрим некоторое движущееся макро-
скопическое тело (биллиардный шар, пулю и т. п.). Предположим,
что измерения проводятся со следующими погрешностями:
Дж ~ 1 мкм = 10“4 см,
Дт ~ 0,1 мг = 10-4 г,
Д^ж ~ 1 мкм/с — 10-4 см/с.
Вычисления дают Дж Држ ~ 10-12эрг-с. Эта величина почти
на 15 порядков больше произведения 2тгЛ ~ 10-27 эрг • с. Таким
образом, измерения характеристик макроскопической частицы
дают результаты, которые не противоречат соотношению неопре-
деленностей.
Иначе говоря, соотношения неопределенностей для макроско-
пических тел выполняются «с большим запасом», поэтому соотно-
шения Гейзенберга были сформулированы после многочисленных
опытов с электронами и другими микрочастицами.
Когда в классической физике используются такие понятия, как
траектория, луч, бесконечно узкий пучок частиц, подразумевается,
что объекты, характеризуемые этими абстракциями, имеют, хотя
и очень малую, но конечную толщину. Но термин «малость» имеет
физический смысл только в сравнении. Если для опытов Гали-
лея погрешность измерения координат Дж ~ 1 мкм кажется очень
малой, то в сравнении с размером атомов эта величина является
очень большой. Можно сделать вывод о том, что открытие соот-
ношений неопределенностей не отменяет понятий и идеализаций
классической физики, которая занимается исследованием макро-
скопических объектов. С другой стороны, при изучении процес-
сов, происходящих с микрочастицами, использование соотноше-
ний Гейзенберга необходимо.
Соотношения неопределенностей во многих важных случаях
позволяют выполнить оценки параметров физических микроси-
стем. Некоторые характерные примеры приведены в дополне-
нии 6.1.
В заключение параграфа заметим, что было бы неверно тракто-
вать соотношения неопределенностей как результат несовершен-
ства современной техники эксперимента. Согласно современным
воззрениям, именно невозможность одновременного измерения
координаты ж и соответствующей проекции импульса рх соста-
вляет смысл соотношений неопределенностей.
6.3. Корпускулярно-волновой дуализм 121
6.3. Корпускулярно-волновой дуализм
Подведем итог предыдущих лекций. В экспериментах начала
XX века было обнаружено, что электромагнитные волны предста-
вляют собой ансамбли частиц (фотонов), а массивные частицы
(имеющие ненулевую массу покоя) обладают явными волновыми
свойствами. Эти удивительные сочетания корпускулярных и вол-
новых физических характеристик были названы корпускулярно-
волновым дуализмом.
Корпускулярная структура электромагнитного излучения озна-
чает, что электромагнитная волна представляет собой поток фо-
тонов, каждый из которых обладает энергией е и импульсом р.
С другой стороны, фотон имеет волновые характеристики: опре-
деленную частоту и, длину волны Л и волновой вектор к, причем
перечисленные физические величины связаны простыми соотно-
шениями:
е = Ла;, р = Лк, Л = . (6.12)
Р
С точки зрения классической физики совокупность этих урав-
нений представляется парадоксальной. Также классическая фи-
зика не в состоянии объяснить наличие волновых свойств у мас-
сивных частиц. Эти частицы как классические корпускулы обла-
дают определенной энергией и импульсом. Но кроме этого, они
интерферируют на периодических атомных структурах как волны
с длиной волны, определенной формулой (5.2). Волновые и кор-
пускулярные характеристики массивных частиц также оказались
связанными уравнениями (6.12).
Для анализа возникшей проблемы прежде всего следует вспо-
мнить, что и корпускула, и волна являются определенными идеа-
лизациями — абстрагированными объектами.
Классическая корпускула имела определенные размеры, она
четко ограничена в пространстве, ее движение полностью описы-
валось траекторией — определенной кривой в пространстве. В ка-
ждый момент времени положение корпускулы задавалось тремя
числами — координатами ее центра масс.
Классическая волна в принципе не имеет определенных гра-
ниц, ее движение не описывается траекторией. Когда в частных
случаях используется лучевое приближение распространения вол-
ны, то принимается во внимание, что луч в реальности не является
бесконечно тонким. Классические волны описываются гармониче-
скими функциями вида (6.6) или их суперпозицией (6.8).
Все физические объекты, изучаемые классической физикой, от-
носились либо к корпускулам, либо к волнам, но эти идеализиро-
ванные объекты полагались взаимоисключающими.
Квантовая теория утверждает, что совокупность уравнений
(6.12) не является парадоксальной. Частицы обладают как корпус-
122 Лекция 6. Соотношения неопределенностей
кулярными, так и волновыми характеристиками. Дело в том, что
электроны, фотоны и другие микрочастицы не являются класси-
ческими корпускулами. В частности, невозможно указать точные
размеры (например, диаметр) этих частиц. Следует помнить, что
корпускулярные свойства микрочастиц лишь похожи на свойства
классических корпускул.
Из предыдущего анализа экспериментов было видно, что вол-
новые свойства массивных частиц описываются не классическими
волнами. Амплитуда волн де Бройля имеет вероятностный харак-
тер. Таким образом, волновые характеристики микрочастиц лишь
похожи на свойства классических волн.
Следует полагать, что электрон, фотон и прочие микрочастицы
представляют собой физические (материальные) объекты, облада-
ющие набором внутренне непротиворечивых свойств и характе-
ристик. Некоторые из этих характеристик сходны со свойствами
классических корпускул, другие — с классическими волновыми
свойствами. Именно это положение составляет смысл термина
«корпускулярно-волновой дуализм».
В рамках корпускулярно-волнового дуализма полезно рассмо-
треть вопрос о возможности «расщепления» микрочастиц на ча-
сти. При анализе опыта Юнга с электронами было установлено,
что всегда детектор электронов регистрирует целое число частиц.
Ни в одном из экспериментов не было зафиксировано попадания
в детектор части электрона. В этом смысле электрон является не-
делимой частицей. Что касается интерференционных свойств от-
дельных электронов, то это явление не описывается классической
физикой (и наглядными механическими моделями), но прекрасно
укладывается в квантовую теорию, благодаря волновым свойствам
массивных микрочастиц и соотношениям неопределенностей.
В дополнении 6.2 изложены рассуждения, которые доказывают,
что фотон также не «расщепляется» в процессах рассеяния.
В начале данного раздела были приведены уравнения, связы-
вающие корпускулярные и волновые свойства микрочастиц, ко-
торые применимы и к фотонам, и к массивным частицам. При
этом не следует преувеличивать сходства микрочастиц разных ти-
пов, а напротив, обратить внимание на некоторые принципиаль-
ные физические различия. Это, в первую очередь, отсутствие
массы покоя и электрического заряда у фотонов. Во-вторых, ам-
плитуды электромагнитных и дебройлевских волн имеют прин-
ципиально различный смысл, как было показано в предыдущих
лекциях.
Важным уравнением, характеризующим основные свойства ча-
стицы, является закон дисперсии, т.е. связь энергии и импульса
частицы этого типа. Согласно уравнению (4.10), энергия фотона
прямо пропорциональна модулю его импульса: е = рс, где с —
скорость света в вакууме. С другой стороны, связь энергии и
6.3. Корпускулярно-волновой дуализм 123
импульса свободной массивной частицы выражается нелинейным
уравнением (4.9):
Е = yj77ZqC4 + р2с2,
где то — масса покоя частицы. Величина Е в последнем урав-
нении представляет собой сумму кинетической энергии и энер-
гии покоя тос2. Различие законов дисперсии разного типа частиц
является источником важных физических следствий.
В заключение можно сказать, что многие свойства микрочастиц
и их сочетания не могут быть объяснены в рамках классической
физики. Для этого создается квантовая теория, которая дополняет
классическую, не разрушая ее, и устанавливает границы приме-
нимости классической физики. Аналогичная ситуация сложилась,
когда специальная теория относительности А. Эйнштейна допол-
нила механику, созданную И. Ньютоном.
Задачи к лекции 6
1. Оценить с помощью соотношений Гейзенберга неопределенности
кинетической и потенциальной энергий электрона, входящего в состав
атома водорода.
2. Оценить неопределенность скорости электрона в атоме водорода,
полагая размер атома порядка 1 А.
3. Среднее время жизни возбужденного состояния атома т ~ 10-8 с.
При переходе в основное состояние испускается фотон энергией 10,2 эВ.
Оценить естественную ширину соответствующей спектральной линии.
4. Оценить с помощью соотношения неопределенностей Гейзенберга
порядок энергии нулевых колебаний гармонического осциллятора.
5. Объяснить на основе соотношения неопределенностей, почему
электрон в атоме водорода не падает на атомное ядро.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 6
6.1. Эксперименты, иллюстрирующие выполнение
соотношений неопределенностей
Эксперимент 1. Рассмотрим свободный электрон с определен-
ным импульсом р. Расположим перпендикулярно вектору импульса элек-
трона непрозрачную перегородку со щелью шириной d. За перегородкой,
параллельно ей поставим экран, регистрирующий попадания электронов.
Это может быть слой сцинцилирующего вещества или фотоэмульсии.
Рис. Д.6.1. Схема прохождения электронов через щель:
1 — непрозрачная перегородка со щелью, 2 — экран, регистрирующий электроны, 3 —
главный максимум дифракционной картины; р — начальный импульс электрона, d —
ширина щели
Введем плоскую систему декартовых координат. Ось X направим вдоль
перегородки со щелью, ось Y — вдоль вектора импульса электрона р
(см. рис. Д.6.1).
Наблюдение прохождения электрона через щель представляет собой
измерение его координаты х в некоторый момент времени. Очевидно,
что погрешность измерения Хх не менее ширины щели <7, т. е. Хх d.
Сужая щель, мы, в принципе, можем неограниченно уменьшать неопре-
деленность координаты Хх,
Движение свободного электрона описывается монохроматической
волной де Бройля с волновым вектором k = p/h и длиной волны А =
= 2тг/г/р. При соответствующей ширине щели взаимодействие электрона
с краями щели можно интерпретировать как дифракцию Фраунгофера
волны де Бройля на щели. Как известно из классической волновой тео-
рии, дифракционная картина на экране содержит главный максимум и
множество побочных. Главный максимум ограничен первыми нулями,
Дополнения к лекции 6
125
положение которых на экране определяется условием деструктивной ин-
терференции:
dsina = A. (Д.6.1)
Угол а определяет угловую ширину главного максимума дифракцион-
ной картины на экране (см. рис. Д.6.1). Как следствие, ширина глав-
ного максимума превышает ширину щели d. Рассматривая электрон как
частицу, это можно интерпретировать таким образом, что при взаимо-
действии электрона с краями щели он получил некоторое приращение
проекции импульса
= psina. (Д.6.2)
Выражая sin си из уравнения (Д.6.1), а модуль импульса — через длину
волны де Бройля, получим
л 2тгЛ
Арх = -J".
d
(Д.6.3)
Заменяя ширину щели d на неопределенность координаты Аж, мы
получим равенство = 2тг/г/Аж. Теперь вспомним, что оценка прира-
щения проекции импульса (Д.6.2) была проведена по ширине главного
максимума дифракционной картины. Учет побочных максимумов при-
водит к увеличению возможного приращения величины Арх, которая
определяет неопределенность проекции импульса. Следовательно, со-
гласно уравнению (Д.6.3), неопределенность координаты Аж и неопреде-
ленность проекции импульса Дрх связаны уже знакомым соотношением
Гейзенберга
Аж Арх > (Д.6.4)
Из уравнения (Д. 6.3) следует, что при уменьшении ширины щели d
(и уменьшении неопределенности координаты Аж) неопределенность
проекции импульса Арх возрастает обратно пропорционально. С другой
стороны, для уменьшения неопределенности Арх необходимо увеличи-
вать ширину щели т.е. неопределенности координаты Дж. Таким
образом, невозможно неограниченно уменьшать обе неопределенности
Аж и Арж в условиях данного опыта.
Эксперимент 2. В этом опыте, предложенным Гейзенбергом, ко-
ордината частицы измеряется с помощью микроскопа. Пусть свободный
электрон имеет определенный импульс р и движется в направлении на-
блюдателя (см. рис. Д.6.2).
Измерение координаты электрона осуществляется с помощью рассе-
яния на нем монохроматического света. При этом точность определе-
ния координаты ограничивается уширением изображения объекта из-за
явления дифракции. Согласно классической оптике, размер изображения
зависит от длины волны света А и апертуры объектива микроскопа. Для
погрешности Аж измеряемой координаты точечного объекта в оптике вы-
ведена следующая формула:
Дж = ———
2 sin О
(Д.6.5)
где 0 — угол, определяющий апертуру объектива (см. рис. Д.6.2).
126
Дополнения к лекции 6
Разрешающая способность микроскопа, кроме апертуры объектива,
зависит также от качества линз и различных особенностей аппаратуры.
На практике погрешность измерения координаты всегда превышает ве-
личину (Д.6.5). Для нас важно, что, вследствие волновой природы света,
smoc
2nh
Рис. Д.6.2. Схема опыта Гейзенберга по измерению координаты частицы:
а) апертура объектива микроскопа, б) векторная диаграмма импульсов рассеяния
фотона на электроне
величина (Д.6.5) является минимальным пределом погрешности измере-
ния координаты точечного объекта при фиксированных значениях А и 0.
Из уравнения (Д.6.5) следует, что точность определения координаты
Аж имеет порядок длины волны А света, используемого для освещения
объекта. Таким образом, для уменьшения погрешности измерения ко-
ординаты объекта следует использовать свет с более короткой длиной
волны.
Величина Дж задает неопределенность координаты частицы. От-
сюда следует, что, уменьшая длину волны света А, можно, в принципе,
неограниченно уменьшать неопределенность координаты Аж.
Теперь рассмотрим точность измерения проекции импульса частицы
рх. На первый взгляд кажется, что погрешность проекции импульса Држ
также можно уменьшать неограниченно. Для этого надо поточнее из-
мерить координаты электрона для двух различных моментов времени,
вычислить проекцию его скорости vx и получить значение проекции им-
пульса рх с малой погрешностью.
Однако при измерении координаты объекта вышеизложенным спо-
собом на этом объекте рассеивается фотон. Ясно, что если фотон не
взаимодействует с частицей, то мы вообще не получим информации о ее
координате. Для обнаружения частицы в определенном месте простран-
ства необходимо зарегистрировать фотон, рассеянный на этой частице.
При этом согласно законам сохранения импульса и энергии, часть им-
пульса фотона передастся наблюдаемой частице. Следовательно, ее им-
пульс изменится, что приведет к возникновению неопределенности Држ.
Оценим величину Др^. Пусть в качестве частиц используются элек-
троны. В рассматриваемом эксперименте (см. рис. Д.6.2) свет пред-
ставляет собой поток фотонов с параллельными импульсами, направлен-
ными вертикально вверх. Модуль импульса каждого фотона равен 2тгЛ/А.
Чтобы получить информацию о координате электрона, рассеянный
фотон должен попасть внутрь апертуры микроскопа. Если бы был изве-
Дополнения к лекции 6
127
стен угол рассеяния фотона, то можно было бы вычислить изменение им-
пульса электрона, используя уравнения сохранения энергии и импульса
для системы «фотон4-электрон». Однако известно только, что рассеян-
ный фотон попал в систему линз микроскопа. Иными словами, рассеян-
ный фотон, зарегистрированный микроскопом, двигался внутри конуса с
углом раствора 20 (см. рис. Д.6.2а). Следовательно, составляющая им-
пульса рх в направлении оси X рассеянного фотона может иметь любое
27r/isin0 27rftsin0 . _ Л .
значение в пределах от----------до 4------г--- (см. рис. Д.6.2о).
А Л
Согласно геометрии рассматриваемого процесса, перед столкнове-
нием с электроном проекция импульса фотона на ось X равнялась нулю.
Поэтому приобретенная электроном составляющая импульса рх может
2тгЛ sin 0 2тгЛ sin 0 __
иметь любое значение в интервале от-----------до 4----------. Иначе
А А
говоря, измерив у электрона координату ж, мы получили неопределен-
ность проекции его импульса, равную
А 47rftsin0
=------7---
(Д.6.6)
Отсюда видно, что для получения малой неопределенности проекции им-
пульса необходимо увеличивать длину волны света А.
Но с другой стороны, из соотношения (Д.6.5) следует, что для умень-
шения неопределенности координаты Аж, напротив, необходимо умень-
шать длину волны А.
Таким образом, мы приходим к выводу, что невозможно одновре-
менно сделать малыми обе неопределенности Аж и Хрх. Любые дей-
ствия, которые уменьшают одну неопределенность, при этом увеличи-
вают другую. К примеру, для уменьшения Хрх следует уменьшать
импульс фотона и, следовательно, увеличивать его длину волны А. При
этом будет расти неопределенность координаты электрона Дж, и нао-
борот.
Произведение величин неопределенностей (Д.6.5) и (Д.6.6) дает со-
отношение
Аж Хрх = 2тгЛ. (Д.6.7)
Выше было сказано, что оценки (Д.6.5) и (Д.6.6) являются иде-
альными, а в условиях реальных экспериментов величины Дж и Дрх
приобретают существенно большие значения. Следовательно, равенство
(Д.6.7) необходимо заменить неравенством по порядку величины
Аж Хрх > 2тгН. (Д.6.8)
Таким образом, мы опять приходим к соотношению неопределенностей
Гейзенберга.
6.2. О возможности делимости фотона
Рассмотрим вопрос о возможности «расщепления» фотона с энергией
hw на два таким образом, чтобы суммарная энергия оставалась равной
величине Ли, и при этом оба фотона, возникшие в результате «расщеп-
ления», обладали бы частотой ш начального фотона. Для этого про-
128
Дополнения к лекции 6
анализируем результаты эксперимента, схема которого изображена на
рис. Д.6.3.
Пусть источник И испускает видимый свет с определенной часто-
той cj. Непрозрачный экран с отверстием Д (диафрагма) формирует уз-
кий пучок излучения, который попадает на полупрозрачное зеркало 3.
Рис. Д.6.3. Схема прохождения фотонов через полупрозрачное зеркало:
И — источник монохроматических фотонов, Д — диафрагма, 3 — полупрозрачное зеркало,
Ф1 и Ф2 — фотоэлементы
В результате взаимодействия с веществом часть излучения рассеивается
под прямым углом, часть проходит насквозь. Для регистрации интен-
сивности потоков прошедшего и рассеянного излучения используются
два детектора — фотоэлементы Ф1 и Ф2.
Пусть первичное излучение имеет достаточно высокую интенсив-
ность Iq. Варьируя параметры установки, можно добиться, чтобы ин-
тенсивности прошедшего и рассеянного потоков были равны друг другу.
Это значит, что оба фотоэлемента регистрируют одинаковые значения.
С точки зрения классической физики ситуация понятная: падающая
электромагнитная волна делится на две части, создавая прошедшую и
отраженную волны одинаковой интенсивности.
Согласно квантовой теории, пучок излучения, падающий на зеркало
3, состоит из фотонов с одинаковой энергией Тты. Так как фотоны при-
надлежат видимому диапазону, то можно полагать, что на атомах проис-
ходит только упругое рассеяние, при этом частота рассеянных фотонов
остается равной и.
Пусть фотоэлементы настроены таким образом, что могут регистри-
ровать фотоны только с энергией, превышающей -/ku. Это сделано для
о
того, чтобы фотоэлементы не реагировали на попадание в них фотонов с
1,
«половинной» энергией, равной -/ku.
Наблюдения показывают, что в данном эксперименте оба детектора
регистрируют некоторую интенсивность излучения. Это означает, что
отдельные фотоны не делятся пополам. При «расщеплении» фотона на
две части каждая из них получила бы энергию, равную -/ku, и оба де-
тектора ничего бы не зарегистрировали. Кроме того, деление фотона
пополам привело бы к уменьшению вдвое его частоты, что наблюдалось
бы по изменению цвета рассеянного и прошедшего пучков по сравнению с
Дополнения к лекции 6 129
цветом первичного. Этого изменения цвета в опытах не наблюдается, что
свидетельствует против гипотезы о делении фотона на две части. Равен-
ство интенсивностей, регистрируемых фотоэлементами, означает, что за
единицу времени оба фотоэлемента регистрируют одинаковое количество
фотонов.
В пользу неделимости фотонов на части в данном опыте свидетель-
ствуют наблюдения при уменьшении интенсивности Iq потока первич-
ного излучения. При этом, естественно, уменьшаются и регистрируемые
интенсивности прошедшего и рассеянного потоков. Но если величина
/0 становится очень малой, то фотоэлементы регистрируют отдельные
фотоны. При этом попадания в разные детекторы распределяются во
времени случайным образом, хотя средние количества фотонов, попав-
ших в детекторы Ф1 и Ф2, остаются равными. Это означает, что фотон,
проходя через полупрозрачное зеркало, с равной вероятностью может
рассеяться и попасть в детектор Ф1 или пройти насквозь и зарегистриро-
ваться фотоэлементом Ф2. При этом у каждого фотона энергия остается
неизменной. Таким образом, рассеяние фотона в полупрозрачном зер-
кале является случайным событием, но фотон не делится на части.
Подводя итог анализу данного эксперимента, можно сделать вывод,
что фотон не является классической волной, которая может делиться
на части.
Лекция 7
ПЛАНЕТАРНАЯ МОДЕЛЬ АТОМА
7.1. Проблема структуры атома
До самого конца XIX века подавляющее большинство химиков
полагало атомы неделимыми и вечными. В многообразии хими-
ческих реакций атомы образуют различные молекулярные струк-
туры, которые могут разрушаться. Но при этом сами атомы не
могут исчезать, также не могут возникать новые атомы. Эти по-
ложения соответствовали закону сохранения вещества Лавуазье-
Ломоносова. Вопрос о структуре атома признавался праздным.
Открытие электрона Дж. Дж. Томсоном означало, что атом име-
ет сложную структуру. Очевидно, что электрон является частью
атома. Исследования, проведенные в первые годы XX века, пока-
зали, что атомы могут содержать, вообще говоря, большое количе-
ство электронов. Таким образом, атом из неделимого превратился
в сложную структурную единицу вещества.
Из ранних теоретических моделей атома наибольшую извест-
ность получила структура, предложенная самим Дж.Дж. Томсоном
в 1903 г. и названная впоследствии «пудинг с изюмом». Атом Том-
сона представлял собой положительно заряженное «облако» диаме-
тром около 0,1 нм (т. е. 1 А), в котором находятся электроны. Раз-
работка модели столкнулась с проблемой устойчивости системы
электронов, также неясна была физическая природа положитель-
ного «облака».
Важный шаг в изучении внутренней структуры атома был сде-
лан в ходе исследования явления радиоактивности, обнаружен-
ного Анри Беккерелем (1852-1908) при исследовании флуоресцен-
ции солей урана в 1896 г.
Трудами А. Беккереля, Марии Склодовской-Кюри (1867-1934)
и Пьера Кюри (1859-1906) было обнаружено, что уран, радий, по-
лоний и другие химические элементы с химическими номерами
Z 84 испускают ранее неизвестное науке излучение, названное
радиоактивным, свойства которого несколько похожи на свойства
рентгеновских лучей. Радиоактивное излучение ионизовало воз-
7.2. Опыты Резерфорда по рассеянию альфа-частиц 131
дух и другие газы, вызывало флуоресценцию некоторых веществ
и почернение фотоэмульсий.
Исследования влияния электрических и магнитных полей на
радиоактивное излучение показали, что оно является смесью из
трех составляющих потоков, которые были названы тремя пер-
выми буквами греческого алфавита: а, /5, 7.
Альфа-излучение представляет собой поток массивных поло-
жительно заряженных частиц. Заряд а-частицы равен удвоен-
ному элементарному 2е, масса составляет 4 а.е.м. Характерно, что
кинетические энергии а-частиц, испускаемых атомами разных ра-
диоактивных химических элементов, лежат, в основном, в срав-
нительно узком диапазоне 4-9 МэВ.
Бета-излучение состоит из быстрых электронов, кинетиче-
ские энергии которых (у различных радиоактивных изотопов)
находятся в пределах от десятков кэВ до нескольких МэВ. Следова-
тельно, /5-электроны преимущественно являются релятивистски-
ми частицами.
Гамма-излучение — это коротковолновых электромагнитные
волны, длина которых еще меньше, чем у рентгеновских лучей.
Фотоны 7-лучей обычно имеют энергии от десятков кэВ до не-
скольких МэВ.
Измерения характеристик радиоактивных излучений дало бо-
гатую информацию о внутреннем строении атомов. Кроме того,
пучки а-частиц оказались эффективным инструментом для иссле-
дования внутренней структуры атома.
7.2. Опыты Резерфорда по рассеянию альфа-частиц
Э. Резерфорд (1871-1937) с группой сотрудников в 1906 г. на-
чал эксперименты по облучению тяжелых металлов а-частицами.
Единственными источниками а-частиц в то время были соли ра-
дия, полония и некоторых других радиоактивных элементов. Уз-
кий пучок а-частиц формировался диафрагмами и направлялся
на тонкую металлическую фольгу перпендикулярно ее плоскости.
Уже в первых опытах были получены поразительные результаты.
Хотя большинство а-частиц проходило через фольгу, практически
не отклоняясь или рассеиваясь на малые углы, небольшая доля
а-частиц (примерно одна из нескольких тысяч) изменяла напра-
вление движения более чем на 90° (иногда почти на 180°). Этот
факт противоречит модели атома Дж. Дж. Томсона. Электроны,
имеющие массу почти на 4 порядка меньше массы а-частицы, не
могут рассеять тяжелые а-частицы на большие углы.
Для объяснения характера рассеяния а-частиц Э. Резерфорд
в 1913 г. выдвинул смелую гипотезу о существенно неоднород-
ной структуре атома. Согласно этой идее, в центре атома нахо-
132
Лекция 7. Планетарная модель атома
дится массивное, положительно заряженное ядро малого размера.
Вокруг ядра движутся электроны. Масса ядра практически со-
впадает с массой всего атома (m/у ~ тД так как суммарная
масса даже сотни электронов дает малый вклад в массу атома тпд.
Пусть, например, рассеивателем служит ядро атома золота с мас-
сой ~ 200 а.е.м. Альфа-частица, имеющая массу в 50 раз меньше,
вполне может отразиться назад (рассеяться на 180°) при лобовом
столкновении с ядром атома золота.
На основе выдвинутой гипотезы Резерфорд разработал теорию
рассеяния а-частиц на атомных ядрах. Рассеяние происходит
вследствие кулоновского отталкивания двух положительно заря-
женных частиц с зарядами qi и 92- Более массивная частица с
зарядом q2 полагается неподвижной. Более легкая движется с на-
чальной кинетической энергией jEq, исходное взаиморасположение
частиц задается прицельным параметром b (см. рис. 7.1).
Геометрию рассеяния можно рассчитать с помощью классиче-
ской механики (см. дополнение 7.1). Проходя мимо массивной не-
подвижной частицы-мишени, более легкая рассеивается на угол в
Рис. 7.1. Траектория кулоновского рассеяния легкой частицы на более массивной:
Ь — прицельный параметр, gi и <?2 — электрические заряды частиц
(см. рис. 7.1). При этом важным параметром является расстояние
максимального сближения Lmin. Если в процессе движения наи-
меньшее расстояние между центрами частиц превышает сумму
радиусов Г1 + Г2 этих частиц, то связь угла рассеяния в с при-
цельным параметром b выражается следующим уравнением (см.
дополнение 7.1):
<7'!>
При этом траектория рассеивающейся частицы представляет собой
гиперболу.
Так как значения угла рассеяния в лежат в интервале (0, тг),
то зависимость угла в от прицельного параметра b является моно-
7.2. Опыты Резерфорда по рассеянию альфа-частиц 133
тонно убывающей (см. рис. 7.2). На рис. 7.3 изображены рассчи-
танные траектории для частиц с одинаковой начальной кинети-
ческой энергией Eq и различными прицельными параметрами.
Рис. 7.2. Зависимость прицельного параметра b от угла отклонения 0 рассеива-
ющейся частицы
Очевидно, что для определенной а-частицы невозможно изме-
рить величину прицельного параметра Ь, соответствующую изме-
ренному значению угла рассеяния в. По этой причине, чтобы про-
Рис. 7.3. Примеры траекторий рассеивающихся частиц с одинаковой началь-
ной кинетической энергией Ео и различными прицельными параметрами
bi < 62 < Ьз < Ьа
верить справедливость уравнения (7.1) и на его основе определить
количественные параметры атомного ядра, Резерфорд провел тща-
тельные измерения углового распределения рассеянных а-частиц.
Схема экспериментальной установки Резерфорда приведена на
рис. 7.4. Узкий пучок, содержащий множество а-частиц с одинако-
вой кинетической энергией Eq, направлялся на тонкую фольгу из
134 Лекция 7. Планетарная модель атома
тяжелого металла (золота, серебра и т. п.). Для регистрации рассе-
янных частиц использовался детектор, установленный под углом в
относительно первичного пучка а-частиц. В качестве детектора ис-
пользовался сцинтиллоскоп или цилиндр Фарадея. Эксперименты
Рис. 7.4. Схема опыта Резерфорда по рассеянию а-частиц на металлической
фольге:
1 — источник а-частиц, 2— диафрагмы, 3— металлическая фольга, 4 — детектор рассе-
янных а-частиц, О — угол рассеяния, R — расстояние от места рассеяния до детектора.
Детектор может перемещаться по окружности вокруг оси пучка первичных а-частиц при
постоянном угле рассеяния 0
показали, что пространственное распределение рассеянных частиц
симметрично относительно оси первичного пучка а-частиц, т.е.
зависит от угла рассеяния 0, но не зависит от азимутального угла.
Таким образом, угловое распределение рассеянных частиц полно-
стью описывается зависимостью от угла 0.
Пусть в детектор за 1 с попадает п(0) частиц. Очевидно, что
величина п(0) пропорциональна плотности потока исходных а-ча-
стиц nQ, количеству атомных ядер на единицу площади поверхно-
сти облучаемой фольги N и телесному углу AQ, под которым видно
окно детектора из мишени. Кроме того, вид зависимости п($)
определяется законом взаимодействия атомного ядра и а-частицы.
Для описания влияния на величину особенностей рассеиваю-
щего поля вводится физическая величина, называемая дифферен-
циальным эффективным сечением, которая является важнейшей
характеристикой процесса рассеяния взаимодействующих частиц.
Чтобы получить выражение для эффективного сечения, вер-
немся к процессу рассеяния частиц на единственном неподвиж-
ном центре, изображенном на рис. 7.1 и 7.3. Запишем количество
частиц, рассеянных при этих условиях в элементарный интервал
7.2. Опыты Резерфорда по рассеянию альфа-частиц
135
углов (0, в + d6), в следующем виде:
dn(0) = na da, (7.2)
где na — плотность потока исходных частиц, da — некоторый
коэффициент, смысл которого сейчас будет установлен. Легко ви-
деть, что величина da имеет размерность площади.
Из-за монотонной связи (7.1) прицельного параметра Ь и соот-
ветствующего угла рассеяния 0 следует, что все а-частицы, рассе-
янные в элементарный интервал углов {в, 0 + de), обладали перед
рассеянием прицельными параметрами в интервале (b, b — db), что
Рис. 7.5. К выводу эффективного дифференциального сечения рассеяния:
1 — положение рассеивающего центра (атомного ядра)
иллюстрируется на рис. 7.5. Иначе говоря, все частицы, рассе-
янные под углами ф, в + dO), пересекли в своем полете кольцо,
ограниченное радиусами b и b — db. Таким образом, поток частиц
dn(0) равняется
dntf) = na27rbdb. (7.3)
Из сравнения выражений (7.2) и (7.3) следует, что величина
da равна площади этого кольца:
da = 2irbdb. (7.4)
По этой причине величину (7.4) называют эффективным се-
чением рассеяния (или элементарным эффективным сечением).
Так как в экспериментах измеряются не прицельные параме-
тры, а углы рассеяния 0, то эффективное сечение (7.4) также сле-
дует выразить через углы в. Для этого дифференциал прицельного
параметра db достаточно представить в виде
db =
dbtf)
de
dO,
(7-5)
136
Лекция 7. Планетарная модель атома
где зависимость Ь(в) прицельного параметра от угла рассеяния
задана уравнением (7.1). Тогда эффективное сечение (7.4) выра-
зится следующей функцией угла рассеяния в:
do- —
db(O)
(7-6)
Диапазону углов рассеяния (0, в + dd) соответствует элемен-
тарный телесный угол c/Q образованный конусами с растворами в
и в + dd. Величина этого телесного угла равна
dQ = 2л smd dd. (7.7)
Отношение величин (7.6) и (7.7) называется эффективным
дифференциальным сечением:
do _ Ь(0) dbtf)
dQ sin e de
(7-8)
Дифференциальное сечение do/d£l описывает неоднородность
углового распределения рассеянных частиц. Величина do интер-
претируется как площадка в пространстве, которую пересекают ча-
стицы, рассеянные в телесный угол c/Q. Дифференциальное сече-
ние (7.8) является функцией угла рассеяния в.
Используя уравнение (7.1) получим следующее выражение эф-
фективного дифференциального сечения рассеяния при кулонов-
ском взаимодействии между частицами:
/ Q1Q2 \2 1
c/Q \ Eq / 16 sin4 (0/2)
Выражение (7.9) часто называют формулой Резерфорда.
Так как число электронов в атоме целое, то заряд ядра кратен
элементарному заряду, т.е. q2 = Ze, где Z — некоторое целое
число. Учитывая, что заряд а-частицы равен 2е, перепишем фор-
мулу (7.6) в виде
(7-9)
(7-10)
do / Ze2\2 1
dQ \ Eq ) 4sin4(0/2)
Теперь следует учесть, что рассеяние а-частиц происходит на
множестве атомных ядер, а телесный, угол AQ окна детектора
имеет конечную величину. Это означает, что количество зареги-
стрированных в единицу времени рассеянных а-частиц п(0) мо-
жет быть выражено следующим образом:
п(0) = САПаА(1 = CAnaN (-X/9V (7-П>
d\l \ Eq / 4sm (0/2)
7.2. Опыты Резерфорда по рассеянию альфа-частиц 137
где N — поверхностная плотность распределения атомных ядер
на мишени. Коэффициент Сд < 1, называемый эффективностью
регистрации, характеризует неизбежные просчеты детектора при
проведении эксперимента.
Основным достижением выше проведенного анализа является
вывод о том, что при кулоновском взаимодействии между a-части-
цами и атомными ядрами регистрируемая детектором величина
обратно пропорциональна четвертой степени синуса половины
угла рассеяния в:
"(«) ~ ~ Р-12)
all sm (6//2)
Для подтверждения гипотезы Резерфорда о маленьком, положи-
тельно заряженном и массивном атомном ядре существенно, что
экспериментальное исследование углового распределения рассеян-
ных a-частиц дало зависимость, совпадающую (с учетом погреш-
ностей измерений) с функцией (7.11) для углов 0° 9 150°.
Из формул (7.10)—(7.12) следует, что количество рассеянных
a-частиц квадратично зависит от целого числа Z, которое опре-
деляет заряд ядра Ze. Подбором величины Z можно попытаться
Рис. 7.6. Угловое распределение рассеянных a-частиц. Сравнение результатов
экспериментов с расчетами для разных значений заряда атомного ядра Ze
добиться совпадения теоретической кривой п(9) с результатами
экспериментов (см. рис. 7.6). На основе анализа результатов опы-
138 Лекция 7. Планетарная модель атома
тов Резерфорда в 1913 г. А. Ван ден Брук (1870-1926) обнаружил,
что наилучшее согласие теории и опыта наблюдается, если чи-
сло Z равно порядковому номеру химического элемента в таблице
Менделеева.
Методика Резерфорда не позволяла с достаточной точностью
измерить заряды атомных ядер у различных химических элемен-
тов. Дж. Чедвик (1891-1974) в 1920 г. создал более совершенную
экспериментальную установку, на которой измерил заряды ядер
у атомов меди, платины и серебра (см. дополнение 7.2). Точные
измерения зарядов атомных ядер практически у всех химических
элементов были проведены с помощью регистрации характеристи-
ческого рентгеновского излучения, что будет изложено в лекции 19.
В результате было подтверждено предположение Ван ден Брука.
Но так как атом электронейтрален, то оказывается, что поряд-
ковый номер химического элемента равен числу электронов в
атоме! Трудно переоценить важность полученного результата для
дальнейшего развития физики.
Помимо этого, исследования рассеяния а-частиц на атомных
ядрах позволили Резерфорду сделать оценку размера атомного яд-
ра. При лобовом соударении а-частицы и атомного ядра закон
сохранения энергии принимает вид
где Lmin — кратчайшее расстояние, на которое сближаются ча-
стицы.
Расчеты дают, что для ядер атомов серебра и золота (химиче-
ских элементов с атомными номерами Z = 47 и Z = 79) расстоя-
ние Lmin имеет порядок 10“12 см.
В опытах Резерфорда не было замечено отклонений зависимо-
сти от функции (7.11). Поэтому можно утверждать, что радиус
атомного ядра Яя по порядку величины не превышает 10“12см.
Таким образом, оказывается, что радиус атомного ядра на 4 по-
рядка меньше радиуса атома.
Последующие исследования, проведенные на ускорителях за-
ряженных частиц, позволили получить следующую приближенную
формулу для оценки радиуса атомного ядра:
Ля « {Атм(а.е.м.) • 10“13 см. (7.14)
7.3. Модель атома Резерфорда
Базирусь на результатах проведенных экспериментов и расче-
тов, Резерфорд предложил отказаться от модели атома Дж. Дж. Том-
сона («пудинга с изюмом») и выдвинул планетарную модель атома.
Согласно этой модели, атом содержит в центре ядро, вокруг ко-
7.3. Модель атома Резерфорда
139
торого вращается Z электронов, где Z — порядковый номер хи-
мического элемента (см. рис. 7.7). Ядро имеет положительный
электрический заряд Ze, что обеспечивает электронейтральность
Рис. 7.7. Схема планетарной модели атома.
В центре находится массивное (по массе), но
относительно маленькое (по размерам) ядро.
Вокруг ядра движутся электроны по круго-
вым или эллиптическим орбитам
атома. В ходе дальнейших исследований было обнаружено, что
заряд ядра объясняется содержанием в нем Z протонов, каждый
из которых имеет элементарный положительный заряд е и массу
1 а.е.м. Радиус ядра примерно на 4 порядка меньше радиуса
атома.
Масса ядра равна
тпя = mA — Zme
(7-15)
т.е. практически совпадает с массой всего атома Суммарная
масса всех электронов даже у урана (Z = 92) значительно меньше
атомной единицы массы и, следовательно, является малой добав-
кой к массе ядра тпя.
Движение электронов вокруг ядра в планетарной модели обес-
печивается силами Кулона, которые подчиняются закону обратных
квадратов, как и сила гравитационного притяжения. Таким обра-
зом, вращение электронов вокруг ядра аналогично движению пла-
нет вокруг Солнца, что объясняет название модели Резерфорда.
Орбиты электронов должны иметь вид окружностей или эллипсов.
Модель атома, предложенная Резерфордом, верно описывает со-
став и строение атома. Но в то же время у планетарной модели
имеются серьезные трудности при описании динамики движения
электронов и характера спектров излучения.
Движение частицы в ограниченном объеме атома (финитное)
обязательно происходит с ускорением. В классической электро-
динамике установлено, что любая ускоренно движущаяся заря-
женная частица излучает электромагнитные волны непрерывного
спектра. При этом электрон должен непрерывно терять энергию и
в результате упасть на ядро. Таким образом, получается, что мо-
дель Резерфорда описывает в принципе нестабильный атом. Чис-
ленные оценки времени падения электрона на ядро дают очень ма-
лые значения, противоречащие наблюдаемой стабильности атома.
138 Лекция 7. Планетарная модель атома
тов Резерфорда в 1913 г. А. Ван ден Брук (1870-1926) обнаружил,
что наилучшее согласие теории и опыта наблюдается, если чи-
сло Z равно порядковому номеру химического элемента в таблице
Менделеева.
Методика Резерфорда не позволяла с достаточной точностью
измерить заряды атомных ядер у различных химических элемен-
тов. Дж. Чедвик (1891-1974) в 1920 г. создал более совершенную
экспериментальную установку, на которой измерил заряды ядер
у атомов меди, платины и серебра (см. дополнение 7.2). Точные
измерения зарядов атомных ядер практически у всех химических
элементов были проведены с помощью регистрации характеристи-
ческого рентгеновского излучения, что будет изложено в лекции 19.
В результате было подтверждено предположение Ван ден Брука.
Но так как атом электронейтрален, то оказывается, что поряд-
ковый номер химического элемента равен числу электронов в
атоме\ Трудно переоценить важность полученного результата для
дальнейшего развития физики.
Помимо этого, исследования рассеяния а-частиц на атомных
ядрах позволили Резерфорду сделать оценку размера атомного яд-
ра. При лобовом соударении а-частицы и атомного ядра закон
сохранения энергии принимает вид
^min
где Lmin — кратчайшее расстояние, на которое сближаются ча-
стицы.
Расчеты дают, что для ядер атомов серебра и золота (химиче-
ских элементов с атомными номерами Z = 47 и Z = 79) расстоя-
ние Lmin имеет порядок 10-12 см.
В опытах Резерфорда не было замечено отклонений зависимо-
сти п(0) от функции (7.11). Поэтому можно утверждать, что радиус
атомного ядра Пя по порядку величины не превышает 10“12 см.
Таким образом, оказывается, что радиус атомного ядра на 4 по-
рядка меньше радиуса атома.
Последующие исследования, проведенные на ускорителях за-
ряженных частиц, позволили получить следующую приближенную
формулу для оценки радиуса атомного ядра:
Ля ж (а.е.м.) • 10“13 см. (7.14)
7.3. Модель атома Резерфорда
Базирусь на результатах проведенных экспериментов и расче-
тов, Рез ер форд пр ед л ожил отказаться от модели атома Дж. Дж. Том-
сона («пудинга с изюмом») и выдвинул планетарную модель атома.
Согласно этой модели, атом содержит в центре ядро, вокруг ко-
7.3. Модель атома Резерфорда
139
торого вращается Z электронов, где Z — порядковый номер хи-
мического элемента (см. рис. 7.7). Ядро имеет положительный
электрический заряд Ze, что обеспечивает электронейтральность
Рис. 7.7. Схема планетарной модели атома.
В центре находится массивное (по массе), но
относительно маленькое (по размерам) ядро.
Вокруг ядра движутся электроны по круго-
вым или эллиптическим орбитам
атома. В ходе дальнейших исследований было обнаружено, что
заряд ядра объясняется содержанием в нем Z протонов, каждый
из которых имеет элементарный положительный заряд е и массу
« 1 а.е.м. Радиус ядра примерно на 4 порядка меньше радиуса
атома.
Масса ядра равна
тя — тпа — Zmei
(7-15)
т. е. практически совпадает с массой всего атома Суммарная
масса всех электронов даже у урана (Z = 92) значительно меньше
атомной единицы массы и, следовательно, является малой добав-
кой к массе ядра тя.
Движение электронов вокруг ядра в планетарной модели обес-
печивается силами Кулона, которые подчиняются закону обратных
квадратов, как и сила гравитационного притяжения. Таким обра-
зом, вращение электронов вокруг ядра аналогично движению пла-
нет вокруг Солнца, что объясняет название модели Резерфорда.
Орбиты электронов должны иметь вид окружностей или эллипсов.
Модель атома, предложенная Резерфордом, верно описывает со-
став и строение атома. Но в то же время у планетарной модели
имеются серьезные трудности при описании динамики движения
электронов и характера спектров излучения.
Движение частицы в ограниченном объеме атома (финитное)
обязательно происходит с ускорением. В классической электро-
динамике установлено, что любая ускоренно движущаяся заря-
женная частица излучает электромагнитные волны непрерывного
спектра. При этом электрон должен непрерывно терять энергию и
в результате упасть на ядро. Таким образом, получается, что мо-
дель Резерфорда описывает в принципе нестабильный атом. Чис-
ленные оценки времени падения электрона на ядро дают очень ма-
лые значения, противоречащие наблюдаемой стабильности атома.
140
Лекция 7. Планетарная модель атома
В качестве примера рассмотрим одноэлектронный атом с кру-
говой орбитой электрона радиусом г (см. рис. 7.8а). Ядро атома
водорода — протон — имеет элементарный заряд +е и массу в
1 а.е.м. На электрон действует сила Кулона величиной е2/г2, при
Рис. 7.8. К вопросу о классической модели атома водорода: а) круговая орбита
электрона, б) падение электрона на ядро.
Крестиком обозначено положение ядра атома (протона), F — сила Кулона, действующая
на электрон
этом электрон движется с центростремительным ускорением v2 /г.
Запишем, полагая ядро неподвижным, для электрона второй за-
кон Ньютона в проекции на мгновенную ось, направленную вдоль
силы Кулона:
е2 гпе 9
72 = ’
и выразим из него модуль скорости электрона
е
v = ..
(7-16)
(7-17)
у/тпег
Мы уже знаем из лекции 1, что радиус атома имеет порядок
г ~ 1А = КГ8 см. По формуле (7.17) можно получить оценку ве-
личины скорости электрона в атоме водорода v ~ 108см/с. Сле-
довательно, электроны в данной модели атома являются нереля-
тивистскими, что чрезвычайно важно для дальнейшего развития
теории.
Период кругового движения Т электрона по орбите радиуса г
равен отношению длины окружности к величине скорости. Ис-
пользуя (7.17), получим
_ 2тг /------
Т = —ymer\
е
Следовательно, частота кругового движения электрона
р
" = -== (7.18)
у/тет6
зависит от радиуса его орбиты.
7.3. Модель атома Резерфорда 141
Потенциальная энергия электрона на круговой орбите равна
—е2/г. Так как такой электрон нерелятивистский, то его кине-
тическая энергия запишется как mev2/2. Используя (7.17), выра-
зим полную механическую (потенциальную плюс кинетическую)
энергию в виде
е2
(7.19)
2г
Согласно классической электродинамике, электрон, двигаясь
на круговой орбите, непрерывно излучает и, следовательно, теряет
свою энергию. Из уравнения (7.19) следует, что при этом радиус
орбиты должен непрерывно уменьшаться (см. рис. 7.86). Частота
излучения, совпадающая с частотой кругового движения (7.18),
является непрерывной функцией радиуса. Таким образом, атом
водорода должен испускать непрерывный спектр, что находится в
противоречии с результатами спектроскопических исследований,
которые рассматриваются в следующей лекции.
Неизбежно следует вывод, что классическая механика и элек-
тродинамика не в состоянии построить модель стабильного
атома, не противоречащую результатам экспериментальных
исследований.
Задачи к лекции 7
1. Альфа-частица с начальной кинетической энергией Е сближается
с неподвижным атомным ядром массы М, электрический заряд которого
Ze, где е — элементарный заряд. Полагая столкновение центральным
(прицельный параметр равен нулю), вычислить расстояние максималь-
ного сближения для следующих значений физических величин: а) Е —
= 5МэВ, М = 197 а.е.м., 7 = 79; б)Е = 4МэВ, М = 209 а.е.м., 7 =
= 83; в) Е = 4,5 МэВ, М = 181 а.е.м., 7 = 73.
2. Альфа-частица с начальной кинетической энергией Е рассеивается
на атомном ядре с массой М с электрическим зарядом Ze на угол 0.
Полагая ядро первоначально покоящимся, вычислить расстояние мак-
симального сближения для следующих значений физических величин:
а) Е = 5 МэВ, М = 16 а.е.м., 7 = 8, 0 = 90°; б) Е = 4 МэВ,
М = 20 а.е.м., 7 = 10, 0 = 60°; в) Е = 4,5 МэВ, М = 27 а.е.м.,
7 = 3, 0 = 45°.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 7
7.1. Рассеяние положительных заряженных частиц
на тяжелых атомных ядрах
Рассмотрим систему, состоящую из двух электрически зараженных
частиц с массами т и М. Силы взаимодействия частиц описываются
законом Кулона, а потенциальная энергия взаимодействия выражается
формулой
*7 = —, (Д.7.1)
Г
где q и Q — электрические заряды частиц, г — расстояние между ними.
В теоретической механике доказано, что задача о взаимодействии
двух частиц сводится к описанию движения частицы приведенной массы
то =
тМ
т + М
(Д.7.2)
во внешнем центральном потенциальном поле, которое заданно функ-
цией (Д.7.1). Центр поля находится в центре масс системы частиц.
Мы здесь ограничимся важным случаем, когда масса первой частицы
много меньше массы второй, т.е. т М. Тогда центр масс системы
совпадает с местоположением более массивной частицы, а приведенная
масса практически неотличима от массы т легкой частицы. В таких
случаях целесообразно начало координат совместить с массивной части-
цей и полагать ее неподвижной. При этом легкая частица рассматрива-
ется движущейся издалека с начальной кинетической энергией Eq-
Траекторию частицы удобно выразить в полярных координатах г
и В курсе теоретической механики подробно показано, что интегри-
рование уравнения движения частицы дает следующую связь координат:
L/r — mqQ/L /тт „
ср = arccos , . = 4- const, (Д.7.3)
У2т£?о + (m9Q)2/L2
где L — модуль момента импульса движущейся частицы.
Начало отсчета угла ср можно выбрать так, чтобы константа интегри-
рования в предыдущей формуле равнялась нулю. Тогда выражение для
траектории можно представить в виде
- = ecos(£ - 1, (Д.7.4)
г
где введены следующие обозначения:
_ L2
Р mqQ’
1 +
8 =
2EqL2
mqQ
(Д.7.5)
Дополнения к лекции 7
143
Величина р называется параметром орбиты, е — ее эксцентриситетом.
Уравнение (Д.7.4) описывает гиперболическую кривую, отрезок кото-
рой изображен на рис. Д.7.1.
Вершина гиперболической траектории частицы совпадает с точкой
максимального сближения с рассеивающим центром (точка А на гипер-
боле). Положение этой точки в выбранной полярной системе координат
Рис. Д.7.1. Рассеяние легкой заряженной частицы на тяжелой неподвижной.
Тяжелая частица с массой и зарядом находится в точке О. Сплошная кривая — траектория
легкой частицы, точка А — положение максимального сближения частиц, b — прицельный
параметр, 0 — угол рассеяния
характеризуется углом сро (см. рис. Д.7.1). Как известно из теоретиче-
ской механики, траектория частицы в центральном поле всегда симме-
трична относительно линии, соединяющей центр поля и точку кратчай-
шего расстояния на траектории, т. е. линии О А на рис. Д.7.1.
Важнейший характеристикой процесса рассеяния является угол О
между векторами начального и конечного импульса рассеянной частицы
(см. рис. Д.7.1). За начальное принимается состояние легкой частицы,
когда она находится столь далеко от рассеивающего центра, что ее потен-
циальная энергия пренебрежимо мала. Конечным полагается состояние,
когда частица удаляется на расстояние, где вновь можно пренебречь ее
потенциальной энергией. Угол в образован асимптотами гиперболиче-
ской траектории частицы и называется углом рассеяния.
Из-за вышеуказанной симметрии траектории частицы следует оче-
видная связь между углами <^0 и 3 (см. рис. Д.7.1):
3 = |тг-2^о|. (Д-7.6)
В задаче рассеяния легкой частицы на тяжелой величину момента
импульса L целесообразно выразить через прицельный параметр Ь:
L = mbvo, (Д.7.7)
где vq — модуль скорости частицы в начальном состоянии. Прицельным
параметром b называется минимальное расстояние между тяжелой непо-
144
Дополнения к лекции 7
движной частицей и направлением вектора начальной скорости легкой
частицы (см. рис. Д.7.1).
Подставив (Д.7.7) в уравнение траектории (Д.7.3), получим для угла
в точке максимального сближения следующее выражение:
Vo
= arccos
qQ
2b Ер
(Д.7.8)
Пользуясь выражением тангенса через косинус, преобразуем выра-
жение (Д.7.8) к следующему виду:
tgVo =
2ЬЕ0
qQ
(Д.7.9)
Воспользовавшись соотношением (Д.7.6) и формулой приведения, по-
лучим искомую связь между углом рассеяния в и прицельным параме-
тром Ь:
Ctgl = ^6 ИЛИ tSl = 2b£~' (Д-7.10)
2 qQ 2 20jC/q
Согласно последней формуле, при нулевохм прицельном параметре
угол рассеяния равен тг, т. е. частица отражается назад. С ростом при-
цельного параметра угол рассеяния постепенно уменьшается до нуля.
Формула (Д.7.10) справедлива для описания рассеяния таких поло-
жительных заряженных частиц, как протоны и альфа-частицы на тяже-
лых атомных ядрах, которые содержат более сотни нуклонов (протонов
и нейтронов).
7.2. Опыт Чедвика
Опыты Резерфорда по рассеянию а-частиц на атомных ядрах позво-
ляют определить электрический заряд ядра eZ и, как следствие, поряд-
ковый номер Z химического элемента. При этом для вычислений ис-
пользуется знаменитая формула Резерфорда (7.9). Однако следует обра-
тить внимание, что в левой части данной формулы стоит эффективное
дифференциальное сечение dcr/dSl, которое является функцией угла рас-
сеяния 0. В экспериментах значения этой функции для определенных
углов 0 рассчитываются с помощью соотношения (7.2).
Таким образом, для вычисления искомого порядкового номера Z
исследуемого химического элемента требуются тщательные измерения
плотности потока а-частиц падающих на металлическую фольгу, и
потоков рассеянных а-частиц п(0) для ряда угла рассеяния 6. Глав-
ная трудность данной экспериментальной методики заключается в том,
что измеряемое количество частиц, попавших в детектор за единицу вре-
мени, на несколько порядков меньше числа падающих на фольгу в тот же
интервал времени. По этой причине Резерфорду пришлось измерять ве-
личины n(ff) и па на различных установках, что привело к значительной
погрешности измеряемого дифференциального сечения dcr/dSl. В резуль-
Дополнения к лекции 7
145
тате методика Резерфорда не позволила добиться желаемой погрешности
определения порядкового номера химического элемента AZ = 1.
Первооткрыватель нейтрона Дж. Чедвик (1891-1974) разработал
принципиально усовершенствовал методику определения порядкового
номера Z химического элемента, в которой величины п(3) и nQ измеря-
лись на одной и той же установке, схема которой приведена на рис. Д.7.2.
Рис. Д.7.2. Схема опыта Чедвика:
S — источник а-частиц, D — детектор, расстояния SO и OD равны L, 0 — угол рассе-
яния. Рассеивающее кольцо АА' расположено перпендикулярно плоскости рисунка
Рассеиватель а-частиц — металлическая фольга — имела форму
кольца А А'. Источник а-частиц S и детектор D располагались на оси
кольца и на одинаковом расстоянии L от него (см. рис. Д.7.2). В каче-
стве детектора использовался сцинтиллоскоп.
При измерении величины п(0), точнее потока а-частиц, рассеянных
в диапазон углов [0 — Д0, 3 4- Д0], внутри кольца А А’ устанавливался
свинцовый экран в форме круга с радиусом, равным внутреннему ради-
усу рассеивающего кольца. Толщина экрана была достаточно большой
для поглощения всех а-частиц, попавших на него.
Для измерения плотности потока nQ, испускаемых источником а-ча-
стиц, закрывалась кольцевым свинцовым экраном рассеивающая фольга.
При этом рассеянные а-частицы поглощались, а частицы, испускаемые
источником, могли беспрепятственно попадать в детектор. В установке
Чедвика плотности потоков первичных и рассеянных частиц различа-
лись примерно на 4 порядка. Вследствие этого для уменьшения количе-
ства сцинтилляций при измерении па перед детектором дополнительно
устанавливался вращающийся поглощающий диск с прорезью. Регу-
лировка скорости вращения позволяла уменьшить проходящий поток
а-частиц в определенное количество раз.
Методика Чедвика позволила значительно уменьшить погрешность
измерения порядкового номера Z химических элементов. С помощью
своей установки Чедвик для меди получил значение Z = 29,3, что с точ-
ностью до целого числа совпадает порядковым номером меди Z = 29.
Для серебра и платины Чедвик получил немного заниженные значения
46,3 и 77,4 (точные значения 47 и 78). Однако работы Чедвика яви-
лись серьезным экспериментальным подтверждением гипотезы о том,
что заряд атомного ядра равен eZ, где Z — порядковый номер данного
химического элемента.
146
Дополнения к лекции 7
Точный экспериментальный метод измерения порядковых номеров
химических элементов основан на законе Мозли, который описан в лек-
ции 19.
7.3. Состав атомного ядра
Состав, строение и свойства атомного ядра являются объектами изу-
чения ядерной физики и излагаются в соответствующем учебном курсе.
Однако для лучшего понимания ряда важных вопросов физики атома це-
лесообразно привести здесь краткие сведения о составе атомного ядра.
В ходе экспериментов по облучению атомных ядер а-частицами, на-
чатых в 1919 г., Э. Резерфорд и Блэккет обнаружили, что в состав атом-
ных ядер входят протоны — положительно заряженные частицы с эле-
ментарным зарядом и массой тр = 1,67265 • 10-24г = 1,0072765 а.е.м.
Ядро самого легкого атома — водорода — состоит из единственного про-
тона. Так как атом электрически нейтрален, то количество протонов в
атомном ядре равно числу электронов в атоме и, следовательно, поряд-
ковому номеру химического элемента Z.
В 1932 г. Дж. Чедвик на основе анализа экспериментов Боте и Бек-
кера, Ирэн и Жолио Кюри и собственных опытов открыл нейтрон —
еще одну частицу, входящую в состав атомных ядер. Нейтрон предста-
вляет собой электрически нейтральную частицу с массой тп = 1,67495 х
х10"24г = 1,008665 а.е.м.
Гипотезу о том, что атомные ядра состоят только из протонов и ней-
тронов независимо выдвинули В. Гейзенберг и Д. Иваненко. Частицы,
составляющие ядро атома, получили общее название нуклоны. Число
нуклонов в ядре называется массовым числом А. Обозначив символом
N количество нейтронов, можем записать
A = Z + N. (Д.7.11)
Целесообразность введения термина «массовое число» обусловлена
тем, что массы протона и нейтрона близки друг к другу. Если к тому же
учесть, что масса электрона (те = 0,910939 • 10-27 г) почти в 2000 раз
меньше масс нуклонов, то масса атома Мд приближенно выражается
произведением массового числа на атомную единицу массы
МА « А а.е.м = А 1,66054 • 10-24 г. (Д.7.12)
Изотопы определенного химического элемента имеют определенное
число протонов Z в ядре и различаются количеством нейтронов N.
Основная трудность в теории атомного ядра заключалась в объясне-
нии природы сил притяжения между нуклонами. На пути решения этой
проблемы было открыто фундаментальное сильное взаимодействие, тео-
рия которого весьма сложна и в настоящее время еще не закончена.
Прецизионные масс-спектр о скопиче ские исследования позволили об-
наружить удивительный факт: масса атомного ядра Мя заметно мень-
ше суммы масс нуклонов, входящих в это ядро. Разность масс (Zmp 4-
+ Nmn — Мя), умноженная на квадрат скорости света, равна энергии
связи нуклонов в ядре:
Есв = (Zmp 4- Nmn - Мя)с2. (Д.7.13)
Дополнения к лекции 7
147
В результате экспериментов было установлено, что величина энергии
связи Есв в первом приближении возрастает пропорционально количе-
ству нуклонов в ядре. Среднее значение удельной энергии связи, т.е.
энергии связи на один нуклон Есв/А составляет около 8 МэВ. Пропорци-
ональность энергии связи Есв массовому числу обусловлена короткодей-
ствующим характером межнуклонного притяжения.
Лекция 8
СПЕКТР ИЗЛУЧЕНИЯ АТОМА ВОДОРОДА
И ПОСТУЛАТЫ БОРА
8.1. Спектральные серии атома водорода
Важнейшую информацию об атомах физики получают при
исследовании их спектров электромагнитного излучения и погло-
щения.
Многочисленные опыты показывают, что оптические спектры
излучения (т.е. принадлежащие видимому диапазону, ближним
УФ и ИК областям) веществ, состоящих из одноатомных молекул,
являются линейчатыми. Это означает, что спектры излучения
атомов представляют собой дискретный набор частот (или длин
волн). Так как в спектрометрах и спектроскопах каждая опре-
деленная длина волны обычно дает изображение входной щели в
виде узкой вертикальной полоски, то эти фиксированные длины
волн исторически стали называться спектральными линиями.
Атомы каждого химического элемента обладают своим харак-
терным линейчатым оптическим спектром.
Первый спектроскоп был сконструирован Р. Бунзеном (1811—
1899) и Г. Кирхгофом в 1859 г. С тех пор исследователи разных
стран составляли специальные таблицы, в которые сводились зна-
чения длин волн и соответствующей интенсивности спектральных
линий излучения химических элементов. К 1913 г. число работ,
посвященных исследованию спектров различных веществ, дости-
гало уже 50000! Однако поиски закономерностей оптических спек-
тров оказались трудной физической проблемой.
Оптические спектры химических элементов содержат, вообще
говоря, большое количество спектральных линий. Наиболее про-
стым по своей структуре является спектр излучения атомов водо-
рода. В результате экспериментальных спектрометрических иссле-
дований было установлено, что в видимой области этого спектра
атомов водорода наблюдаются 4 узкие спектральные линии (ярко-
красная, бирюзовая, сине-фиолетовая и темно-фиолетовая), кото-
8.1. Спектральные серии атома водорода
149
рые обозначаются символами HQ, Н^, Н7 и Щ (см. рис. 8.1).
Этим линиям соответствуют длины волн приблизительно равные
6562 А, 4860 А, 4340 А и 4101А соответственно.
Первая успешная попытка установления закономерности в рас-
положении спектральных излучений атомарного водорода принад-
лежит швейцарскому учителю И. Бальмеру (1825-1898). В 1885 г.
Яр Ну Нь
7000 6000 5000 4000
Рис. 8.1. Спектр атома водорода в видимом диапазоне, наблюдаемый в спек-
троскоп (линии HQ — ярко-красная, — бирюзовая, Н7 — сине-фиолетовая,
Н<5 — темно-фиолетовая)
Бальмер заметил, что длины волн этих линий относятся друг к
другу как целые числа и могут быть выражены одной формулой:
п2
Х = Ь-^-Л. (8.1)
п2 - 4
где b — константа, равная приближенно 3646 А, а целочисленный
параметр п для линий HQ, Нд, Н7 и Щ принимает соответственно
значения 3, 4, 5, 6. Сравнение результатов расчетов по формуле
(8.1) с экспериментом дало Бальмеру совпадение с относительной
погрешностью 10“5-10“6. Позже спектроскопические исследова-
ния показали, что спектр атомарного водорода содержит линии
в ультрафиолетовой области, длины которых также выражаются
формулой (8.1) при значениях п = 7,8,9,...
В современной физике формула Бальмера представляется в не-
сколько ином виде:
1 = п = 3,4,5,6,..., (8.2)
А у 4 J
где константа Rh = 109677,58 см-1 называется постоянной Рид-
берга (или обратной длиной Ридберга). Все спектральные линии,
длина волны которых определяется формулой (8.2), называются
серией Бальмера. Очевидно, что с ростом числа п длина волны со-
ответствующей спектральной линии уменьшается. Было уже ука-
зано, что 4 первые линии серии Бальмера принадлежат видимому
диапазону, остальные — ультрафиолетовому. В ходе спектроско-
пических исследований не было обнаружено максимальное значе-
150 Лекция 8. Спектр излучения атома водорода и постулаты Бора
ние параметра п, поэтому теоретически серию Бальмера можно
считать бесконечной. Однако из формулы (8.2) видно, что с уве-
личением параметра п разность соседних длин волн быстро сокра-
щается. Это значит, что при достаточно большом значении числа
п разрешающей способности спектрометра будет недостаточно для
того, чтобы зафиксировать отдельные спектральные линии. Сле-
довательно, практически наблюдается лишь конечное количество
спектральных линий. Теоретически, однако, можно вычислить
наименьшую длину волны серии Бальмера, устремив в (8.2) чи-
сло п в бесконечность:
Rh
Аоо 4
Величина Aqq называется пределом серии Бальмера и равна
3647,053 А (с точностью до 9 значащих цифр). Нетрудно убе-
диться, что этот предел совпадает с параметром b в первоначальной
формуле Бальмера (8.1).
Сравнение результатов измерений и расчетов по формуле (8.2)
приведено в табл. 8.1.
Таблица 8.1. Длины волн спектральных линий
серии Бальмера (А)
п Эксперимент Расчет
3 6562,8473 6562,798
4 4861,3578 4861,327
5 4340,497 4340,466
6 4101,7346 4101,738
7 3970,074 3970,075
8 3889,0575 3889,052
9 3835,397 3835,387
10 3797,910 3797,900
Дальнейшие исследования показали, что спектр атома водорода
в инфракрасном (ИК) и ультрафиолетовом (УФ) диапазоне содер-
жит множество спектральных линий, длины волн которых могут
быть описаны следующей единой формулой:
1 = (8.4)
где параметры пит могут принимать только значения натураль-
ных чисел, при выполнении условия п > т. Формула (8.4) часто
называется обобщенной формулой Бальмера.
8.2. Постулаты Бора
151
Таблица 8.2. Спектральные серии атома водорода
т п Название Диапазон
1 2,3,4,5,... Серия Лаймана Ультрафиолетовый
2 3,4,5,6,... Серия Бальмера п 6 — видимый, п > 6 — ультрафиолетовый
3 4,5,6,7,... Серия Пашена Инфракрасный
4 5,6,7,8,... Серия Брэкета Инфракрасный
5 6,7,8,9,... Серия Пфунда Инфракрасный
Значения целочисленного параметра m определяют различные
спектральные серии. Первые пять серий (т = 1,2, 3,4,5) полу-
чили собственные названия по именам их исследователей. Каж-
дая серия имеет свой предел (наименьшую длину спектральной
линии), выражаемый формулой
Лоо ГП2 '
(8-5)
Напомним, что данное строение оптических спектров харак-
терно лишь для атомов водорода. Остальные химические эле-
менты, находящиеся в состоянии атомарного газа, испускают ли-
нейчатые спектры более сложной структуры, которые не удалось
выразить простыми эмпирическими формулами. Число спект-
ральных линий, вообще говоря, увеличивается с химическим но-
мером элемента и может достигать десятков тысяч в видимом диа-
пазоне.
Для сопоставления спектроскопических данных с планетарной
моделью атома важно, что атомарные спектры не содержат сплош-
ных участков. На основе этого экспериментального факта можно
сделать вывод, что классическая теория неприемлема для объяс-
нения строения атома и механизма его излучения. Требуется раз-
работка новой теории, которая на базе небольшого количества но-
вых постулатов позволила бы объяснить все многообразие свойств
атомов и внутриатомных процессов.
8.2. Постулаты Бора
Первую неклассическую теорию атома водорода предложил
Нильс Бор (1885-1962) еще в 1913 г. Теория базировалась на двух
постулатах, которые целесообразно рассмотреть в целях ознаком-
ления с неклассическими идеями квантовой физики.
1-й постулат. Существуют стационарные состояния ато-
ма, в которых движущиеся электроны не излучают.
152 Лекция 8. Спектр излучения атома водорода и постулаты Бора
Энергии стационарных состояний образуют дискретный набор
El, jE?2, Е3. Еп, ..., (8.6)
где п — целое число, которое называется квантовым числом ста-
ционарного состояния (или номером стационарного состояния),
которое, в принципе, может принимать любое значение из ряда
натуральных чисел. Для атома водорода энергия стационарного
состояния Еп выражается формулой
Еп = -^- п = 1,2,(8.7)
где Ry — характерная энергия (энергия Ридберга), равная при-
близительно 13,6 эВ.
Выражение (8.7) означает, что энергия стационарного состоя-
ния однозначно определяется квантовым числом этого состояния.
Заметим, что понятие стационарного состояния является прин-
ципиально неклассическим. В конце предыдущей лекции (§ 7.3)
подробно объяснялось, что финитное движение электронов в атоме
происходит с ускорением, и согласно классической электродина-
мике, должно сопровождаться непрерывной потерей энергии.
2-й постулат. Атом излучает или поглощает энергию, пе-
реходя из одного стационарного состояния в другое. При этом
испускается (или поглощается) фотон с энергией
£ — Еп1 Еп2>
(8-8)
Иначе говоря, энергия фотона равна разности энергий ста-
ционарных состояний атома.
Выразим частоту излучаемого (или поглощаемого) фотона че-
рез его энергию и воспользуемся формулой (8.8). Тогда мы полу-
чим связь частоты фотона с энергиями стационарных состояний
атома:
ЕП1 Еп2
(8.9)
{Eni > ЕП2).
Переходя в (8.9) от частоты со к длине волны Л излучения,
сопоставляя уравнения (8.9) и (8.7), получим соотношение
Л
Ry
2лсК
\n2
_1_\
Ц)
(ni > n2),
(8.10)
которая совпадает с обобщенной формулой Бальмера (8.4).
Сравнение формул (8.4) и (8.10) позволяет выразить постоян-
ную Ридберга (имеющую размерность обратной длины) следую-
щим образом:
о Ry
Н 2тгс/г
(8.И)
8.2. Постулаты Бора
153
Вычисление величины (8.11) дает отличное совпадение с эм-
пирическим значением постоянной Ридберга Ли, полученной по
спектроскопическим данным и приведенным в предыдущем пара-
графе.
В атоме водорода ядро (протон) на 3 порядка массивней элек-
трона, поэтому атомное ядро можно полагать неподвижным. То-
гда энергии стационарных состояний (8.6) представляют собой
энергии единственного электрона атома водорода. Таким обра-
зом, электрон в атоме водорода может принимать дискретный ряд
энергий (8.7). Следует иметь в виду, что каждое значение энергии
Еп (п = 1,2,...) представляет собой сумму кинетической энер-
гии движущегося электрона и потенциальной энергии его взаимо-
действия с атомным ядром (протоном). Отрицательные значения
соответствуют связанным состояниям, как и в классической тео-
ретической механике.
Самая низкая из допустимых энергий Е\ = — Ry = —13,6057 эВ
соответствует основному состоянию атома водорода. Прочие стаци-
онарные состояния (с п > 1) являются возбужденными и обладают
более высокой энергией.
Значения энергий стационарных состояний атома водорода
и переходы между ними, сопровождающиеся излучением фото-
нов, наглядно изображаются на энергетической диаграмме (см.
рис. 8.2).
Прекрасным подтверждением идей, высказанным Бором, яви-
лась интерпретация серии Пикеринга. В 1887 г. астроном Пике-
ринг, изучая спектры звезд, обнаружил в них дискретную после-
довательность длин волн, которые укладывались в формулу Баль-
мера (8.2), если положить, что параметр п может принимать не
только целые, но и полуцелые значения: п = 2,5; 3; 3,5; 4; 4,5; ...
Впоследствии выяснилось, что источником серии Пикеринга явля-
ется гелий. Бор убедительно показал, что спектральные линии
серии Пикеринга испускаются однократно ионизированными ато-
мами гелия, т. е. одноэлектронными ионами.
Формула (8.7) может быть обобщена для любых одноэлектрон-
ных ионов введением дополнительного множителя Z2, где Z —
количество протонов в атомном ядре (или порядковый номер хи-
мического элемента):
Таким образом, теория Бора, не отвергая гипотезу Резерфорда
о наличии атомного ядра, позволила объяснить дискретный спектр
излучения и стабильность атома.
К сожалению, Бору не удалось разработать методику вычисле-
ний энергий стационарных состояний многоэлектронных атомов,
даже двухэлектронных.
154 Лекция 8. Спектр излучения атома водорода и постулаты Бора
Недостатком теории Бора является отсутствие объяснения при-
чины существования стационарных состояний, осталась неизвест-
ной динамика электронов в этих состояниях.
Остался нерешенным в теории Бора вопрос о времени пере-
хода Ai электрона из одного стационарного состояния в другое.
Если предположить, что Ai = 0, то мы получим противоречие со
Рис. 8.2. Энергетическая диаграмма стационарных состояний атома водорода.
Горизонтальные отрезки изображают энергии состояний, справа от них поставлены соот-
ветствующие квантовые числа. Вертикальные стрелки изображают переходы электрона
между стационарными состояниями. Длина стрелки пропорциональна энергии испускае-
мого фотона
специальной теорией относительности, согласно которой не могут
происходить мгновенные процессы (с бесконечно большой скоро-
стью). Если, напротив, предположить, что время перехода конечно
(Af >0), то возникает вопрос о возможности существования про-
межуточных состояний со значениями энергий Е / Еп, которые
не присутствуют в дискретном наборе энергий (8.7).
Э. Резерфорд высоко оценил значение постулатов Бора для тео-
рии атома, но в письме к Бору сформулировать еще одну воз-
никшую проблему: «Как может электрон знать, с какой частотой
8.3. Энергетическое соотношение неопределенностей
155
он должен излучать, когда он переходит из одного стационарного
состояния в другое? Мне кажется, что Вы вынуждены предпо-
ложить, что электрон знает заблаговременно, где он собирается
остановиться».
Следует признать, что, с одной стороны, теория Бора отлича-
лась эклектизмом и непоследовательностью. С другой стороны,
идея стационарных состояний оказалась весьма плодотворной для
дальнейшего развития физики. Кроме того, отказываясь от мно-
гих важных положений классической физики, Бор полагал закон
сохранения энергии одним из важнейших принципов.
На пути преодоления недостатков теории Бора была создана
современная квантовая теория, основные положения которой из-
лагаются в следующей лекции.
8.3. Энергетическое соотношение неопределенностей
и естественная ширина спектральной линии
В процессе разработки квантовой теории выяснилось, что, по-
мимо соотношений неопределенностей Гейзенберга (6.3)-(6.5), су-
ществует соотношение, связывающее неопределенности энергии и
времени:
А£? • At > 2тг7ъ, (8.13)
где At — неопределенность времени жизни объекта в некотором
состоянии, А2? — неопределенность энергии объекта в этом со-
стоянии.
В задаче о квантовых скачках неопределенностью времени At
является среднее время жизни стационарного состояния. Атом
находится в стационарном состоянии (кроме основного) конеч-
ное время, которое называется временем жизни этого состояния.
Атом, находясь в любом из своих возбужденных состояний, че-
рез некоторый промежуток времени понижает свою энергию, пере-
ходя в более низкоэнергетическое состояние. Переход в основное
состояние может осуществляться не напрямую, а через несколько
промежуточных возбужденных состояний. Характерно, что время
жизни стационарного состояния является случайной величиной,
поэтому в экспериментах определяется, как правило, среднее вре-
мя жизни т возбужденного состояния. Исследования показали,
что это время т имеет порядок 1О“8-1О-10 с.
Согласно соотношению неопределенностей (8.13), энергия воз-
бужденного стационарного состояния характеризуется неопреде-
ленностью порядка
Напротив, в основном состоянии атом может оставаться не-
ограниченно долго и его время жизни можно полагать бесконеч-
156 Лекция 8. Спектр излучения атома водорода и постулаты Бора
ным. Следовательно, неопределенность энергии основного сос-
тояния равна нулю, т.е. энергия основного состояния атома
определена точно.
Неопределенности энергий возбужденных состояний атомов,
согласно (8.14), имеют порядок 10-19-10“17 эрг, т. е. 10-7-10-5 эВ,
что позволяет во многих задачах ими пренебрегать. Но, вообще
говоря, из-за ненулевой величины AjE (неопределенности энергии
возбужденного состояния) энергии фотонов, которые испускаются
атомом при переходе из возбужденного состояния в основное, име-
ют некоторый разброс энергий Де, равный неопределенности АЕ.
Рис. 8.3. Энергетическая схема, поясняющая формирование естественной ши-
рины спектральной линии:
Ei — энергия основного состояния, Еп — энергия возбужденного состояния, ДЕ — не-
определенность энергии возбужденного состояния, £i и £2 — минимальная и максималь-
ная энергия излучаемых фотонов
Вычислим разность длин волн ДА, соответствующую разно-
сти энергий фотонов Де. Для этого используем энергетическую
диаграмму на рис. 8.3 и следующие обозначения:
Де — £2 ~ £1, £1 — £о-----------> £2 — £о н----------^0 — Еп ~
£ £
Принимая во внимание, что Де eq, получим
ДА = At — А2 = 2тг/гс
_1_
£1
1
£2
2 л/гс .
-72-Д£ =
£0
(2л/г)2с
(Еп-Е^т‘
(8.15)
8.3. Энергетическое соотношение неопределенностей 157
Величина АЛ называется естественной шириной спектральной
линии.
Сделаем численную оценку естественной ширины первой ли-
нии серии Лаймана. Полагая в (8.15) Еп = Е% = —Ry/4, вы-
числим, что величина АЛ имеет порядок ~ 10“5 А. С помощью
формулы (8.4) легко получить, что АЛ/Л составляет ~ 10“8. Та-
ким образом, естественная ширина спектральной линии является,
вообще говоря, очень малой и трудно измеримой величиной. С дру-
гой стороны, следует помнить, что никакая совершеннейшая экс-
периментальная техника не может зафиксировать длину волны
излучения атома с погрешностью меньше естественной ширины
АЛ соответствующей спектральной линии.
Задачи к лекции 8
1. Рассчитать длины волн первых четырех спектральных линий се-
рии Лаймана и предел серии.
2. Вычислить длины волн первых трех спектральных линий серии
Пашена и предел серии.
3. Рассчитать длину волны первых спектральных линий серий Брэ-
кета и Пфунда и их пределы серий.
4. Оценить разрешающую способность спектрометра, необходимую
для регистрации:
а) 15-и первых спектральных линий серии Бальмера,
б) 10-и первых спектральных линий серии Лаймана,
в) 5-и первых спектральных линий серии Пашена.
5. Рассчитать длины волн первых трех спектральных линий серии
Пикеринга, полагая, что они порождаются переходами в основное состо-
яние однократно ионизированного атома гелия.
6. Вычислить:
а) разность длин волн второй линии серии Лаймана для обычного
водорода и дейтерия,
б) разность длин волн первой линии серии Бальмера для обычного
водорода и дейтерия.
7. Оценить естественную ширину первой спектральной линии серии
Бальмера.
Лекция 9
ВОЛНОВАЯ ФУНКЦИЯ
И ОПЕРАТОРЫ КВАНТОВОЙ МЕХАНИКИ
Анализ результатов экспериментов по дифракции электронов
и других микрочастиц доказывает, что движение частиц происхо-
дит не по траекториям, а описывается вероятностными законами.
При этом возможность физическим величинам иметь определен-
ные значения ограничена соотношением неопределенностей.
Эти утверждения принципиально противоречат положениям
классической физики. В классической механике движение ча-
стицы может быть рассчитано путем решения основного уравне-
ния механики — второго закона Ньютона. Для расчета требуется
знать суммарную силу F, действующей на частицу, и начальные
условия, т. е. координаты и скорость в момент времени t = 0:
Го = r(t = 0), Vo = v(i = 0). (9.1)
Решения уравнения динамики можно записать в следующем
векторном виде:
r(f + dt) = r(i) + v(£) dt,
v(i + dt) = v(i) + —F(r(i), t) dt, (9 )
m
где m — масса частицы, F(r(£), t) — сила, действующая на ча-
стицу в момент времени t в точке с радиус-вектором г (2). Сила,
вообще говоря, может сложным образом зависеть от времени и
координат.
Уравнения (9.2) с условиями (9.1) однозначно описывают тра-
екторию частицы, а также изменение координат и скорости этой
частицы с течением времени. Это составляет полную информацию
о движении частицы в классическом смысле. Поэтому в классиче-
ской физике утверждается, что состояние частицы в данный мо-
мент времени полностью определяется ее координатами r(t)
и скоростью v(f).
9.1. Волновая функция и уравнение Шредингера 159
Однако величины г и v не могут одновременно иметь опреде-
ленные значения вследствие соотношения неопределенностей Гей-
зенберга (6.3)-(6.5). Классические траектории несовместимы с
волнами де Бройля, которые описывают вероятностный характер
движения свободных микрочастиц.
Таким образом, необходимо сформулировать понятие состо-
яния частицы в рамках квантовой теории.
Общая неклассическая теория должна давать распределение
вероятностей местонахождения микрочастиц, находящихся в про-
извольных внешних силовых полях, а также вычислять возмож-
ные значения физических величин (импульса, энергии, момента
импульса и т. д.) и вероятности их получения в результате из-
мерения в данном состоянии системы. Кроме того, эта теория
должна давать спектры энергий и других физических величин,
которые наблюдались в экспериментах, описанных в предыдущей
лекции. Квантовая теория должна объяснить также стабильность
атомов, линейчатый характер их спектров излучения, а также по-
лучить из своих базовых принципов соотношения неопределенно-
стей. Кроме всего прочего, квантовая физика должна включать в
себя законы классической физики некоторое предельное прибли-
жение и частный случай. Такая теория была создана и получила
название квантовой механики.
Основы квантовой теории были заложены работами М. Планка
и Н. Бора. Замкнутая внутренне непротиворечивая квантовая ме-
ханика и ее математический аппарат были разработаны в конце
20-х годов XX века в основном трудами В. Гейзенберга, Э. Шредин-
гера (1887-1961), В. Паули (1900-1958), П. Дирака (1902-1984) и
ряда других выдающихся физиков.
9.1. Волновая функция и уравнение Шредингера
Заранее оговорим, что далее будет рассматриваться движение
частиц со скоростями много меньшими скорости света, т. е. нере-
лятивистская квантовая теория.
Основные принципы квантовой теории кратко можно сформу-
лировать в следующих утверждениях.
Состояние микрочастицы (или системы частиц) описывается
некоторой, вообще говоря, комплексной функцией координат и
времени Ф(г,£), которую называют волновой функцией или ам-
плитудой вероятности. Волновая функция обладает свойствами
однозначности, конечности и непрерывности по всем своим пере-
менным во всей области определения. Волновую функцию можно
рассматривать как обобщение волны де Бройля для частиц, дви-
жущихся в силовых полях.
Физический смысл волновой функции связан с вероятностью
местонахождения частицы. Для финитных движений вероятность
160 Лекция 9. Волновая функция и операторы квантовой механики
нахождения частицы в объеме dV в окрестности точки г в момент
времени t равна
|Ф(г, t)|2 dV. (9.3)
Иными словами, выражение (9.3) означает, что в случае фи-
нитного движения частиц квадрат модуля волновой функции яв-
ляется плотностью вероятности распределения частицы в прост-
ранстве для данного момента времени. Отсюда следует условие
нормировки для волновой функции:
У |Ф(г, t)|2 tZV = 1. (9.4)
все прост-
ранство
Знание волновой функции позволяет предсказать результаты
измерений не только координат, но и других физических величин.
При этом вероятности различных результатов измерений опреде-
ляются выражениями, билинейными по Ф* и Ф. Отсюда следует,
что волновая функция данной физической системы определена с
точностью до произвольного фазового множителя ехр (га).
Одним из важнейших положений квантовой механики явля-
ется принцип суперпозиции. Его содержание сводится к следую-
щему утверждению.
Если система может находиться в нескольким состояниях, опи-
сываемых ВОЛНОВЫМИ функциями Ф1(г,^), Ф2(г,£), ..., Ф&(г,£),
..., то она может находиться и в состоянии с волновой функцией
Ф(гЗ) = С1Ф1(г,t) + С2Ф2(г,t) + ... + + . . ., (9.5)
где ci, С2, ..., Ск — постоянные коэффициенты, смысл которых
будет выяснен ниже.
Базируясь на физическом смысле волновой функции можно
сформулировать ее общие свойства.
1. Волновая функция должна быть непрерывной. Нарушение
этого свойства может привести к несохранению электрического за-
ряда или энергии.
2. Волновая функция должна иметь непрерывную производную
по координате. Можно показать, что это свойство обусловлено ко-
нечной величиной сил, действующих на частицу.
3. Волновая функция должна быть ограниченной. Неограни-
ченное возрастание волновой функции приводит к потере ее веро-
ятностного смысла.
4. Волновая функция должна быть однозначной.
В квантовой механике волновая функция Ф(г, t) полностью
определяет состояние физической системы. Это означает, что за-
дание функции Ф (г, t) не только характеризует свойства системы
9.2. Операторы физических величин 161
в данный момент времени, но и определяет ее поведение в после-
дующие моменты времени. Математически это означает, что зна-
чение производной <ЭФ/dt в каждый момент времени должно опре-
деляться самой функцией Ф(г, £), причем эта зависимость должна
быть линейной, что вытекает из принципа суперпозиции. Эта за-
висимость записывается в следующем общем виде:
г/i—= ЯФ(г,<), (9.6)
(J ь
где Н — оператор, называемый оператором Гамильтона или га-
мильтонианом.
Соотношение (9.6) является фундаментальным уравнением не-
релятивистской квантовой теории и называется уравнением Шре-
дингера.
Следует усвоить, что уравнение (9.6) не выводится, а явля-
ется постулатом, т. е. формулируется на базе множества экспе-
риментальных данных, полученных при исследовании поведения
микрочастиц в различных условиях. Аналогичными базовыми
постулатами в классической физике являются законы Ньютона и
уравнения Максвелла.
Гамильтониан Н является квантовым аналогом функции Га-
мильтона, используемой в классической физике. Прежде чем уста-
новить явный вид гамильтониана для заданной системы частиц,
следует рассмотреть использование операторов физических вели-
чин в квантовой теории.
9.2. Операторы физических величин
Каждой физической величине, характеризующей состояние
микрочастицы (или их системы), ставится в соответствие опре-
деленный линейный оператор. Оператор (правило, преобразова-
ние) /, действуя на какую-либо функцию ^(д), дает, вообще го-
воря, другую функцию 99(g), что записывается в виде
/W) = y’(g),
где q — совокупность аргументов функций и (р.
Операторы физических величин далее обозначаются теми же
символами с «крышкой» наверху. Например, оператор коорди-
наты х обозначается х.
Операторы квантовой физики позволяют находить возможные
значения соответствующих физических величин частицы (или си-
стемы частиц). Утверждается, что в результате измерения физиче-
ской величины f может быть получено только одно из собственных
значений fn оператора f этой физической величины. Для получе-
162 Лекция 9. Волновая функция и операторы квантовой механики
ния этих значений необходимо решить уравнение вида
/Фп = /л, (9.7)
где Фп — собственная функция оператора /.
При этом, если квантовая система находится в состоянии, ко-
торое совпадает с одной из собственных функций оператора /, т. е.
Ф(г) = Фп, то результат измерения физической величины f с до-
стоверностью (с вероятностью равной единице) дает значение
fn. В таких случаях говорят, что физическая величина f имеет
определенное значение f = fn. Если же волновая функция со-
стояния системы является суперпозицией собственных функций
оператора /:
Ф(г)=^спФп, (9.8)
п
то в результате измерения физической величины f может быть по-
лучено какое-либо из собственных значений fn с вероятностями
W(f = fn) — |сп|2, где сп — коэффициенты разложения функ-
ции (9.8). Таким образом, в состоянии, заданном волновой функ-
цией (9.8), физическая величина f не имеет определенного значе-
ния. При этом следует помнить, что коэффициенты разложения
сп должны удовлетворять условию
Z>i2 = i. (9.9)
п
Совокупность собственных значений fn оператора / образует
спектр, который может быть как непрерывным, так и дискретным.
Если данному собственному значению fn соответствует s линейно
независимых функций Фп1, ФП2? • • • , Фп$> то собственное значение
fn называется 5-кратно вырожденным.
Следует помнить, что для таких параметров микрочастицы,
как электрический заряд или масса покоя, операторы не вводятся,
так как эти величины не определяют квантового состояния.
Далее приводится явный вид операторов основных физических
величин.
1. Оператор координаты х представляет собой операцию умно-
жения на значение координаты х:
£Ф(я) = жФ(ж). (9.10)
2. Оператор любой функции координат сводится к умножению
на эту функцию. В частности, оператор потенциальной энергии
определяется уравнением
С/(г)Ф(г) = [/(г)Ф(г). (9.11)
9.2. Операторы физических величин
163
3. Оператор проекции импульса рх является дифференциаль-
ным и задается формулой
(9.13)
Рх = -^-7^-. (9.12)
ОХ
Операторы других проекций импульса имеют аналогичный вид:
9 д
Отсюда следует, что оператор вектора импульса может быть выра-
жен с помощью оператора V («набла») следующим образом:
р = -zTiV. (9.14)
В качестве примера найдем спектр собственных значений и со-
ответствующие собственные функции для проекции импульса ча-
стицы рх, для чего решим уравнение (9.7), используя оператор
(9.12):
7ГФ
-г/г— = рхФ.
Ох
Решением этого уравнения является функция
Ф(т) - Аехр ( ^рхх ),
/
где А — некоторая константа. Решение (9.16) описывает состо-
яние частицы, которая имеет определенную проекцию импульса
рх. Подстановка собственной функции (9.16) в уравнение (9.15)
показывает, что оно удовлетворяется при любом вещественном соб-
ственном значении рх^ т.е. спектр собственных значений опера-
тора рх является непрерывным. Это значит, что изучаемая ча-
стица может двигаться вдоль оси X с произвольным значением
проекции импульса.
4. Оператор нерелятивистской кинетической энергии можно
получить, заменяя в классическом выражении для кинетической
энергии Т = р2/2т импульс р на его оператор р. Согласно пра-
вилам квантовой механики, оператор квадрата импульса получа-
ется формальным возведением в квадрат оператора (9.14). Тогда
для нерелятивистской частицы с массой т оператор кинетической
энергии может быть записан в следующем виде:
т = -^-д,
2т
где Д — оператор Лапласа (лапласиан):
g2 д2 д2
дх2 ду2 dz2
(9.15)
(9.16)
(9-17)
(9.18)
164 Лекция 9. Волновая функция и операторы квантовой механики
5. Аналогично можно ввести оператор энергии (гамильтониан)
для частицы, движущейся во внешнем поле, которое задано потен-
циальной энергией U(г). Сначала следует записать классическую
функцию Гамильтона для этой системы:
а затем от классического выражения перейти к операторам, ис-
пользуя соотношения (9.11) и (9.14). При этом кинетическая энер-
гия заменится на оператор вида (9.17).
Например, гамильтониан свободной частицы совпадает с опе-
ратором (9.17). Гамильтониан частицы с массой т, находящейся
в поле с потенциальной энергией U(г), имеет вид
(9.19)
h2
H = --^ + U^.
Другой важный пример — гамильтониан системы двух заряжен-
ных частиц с массами mi, m2 и зарядами gi, — записывается
в виде
н = --^д, - -^д2 +
2mi 2m2 Г12
(9.20)
где Г12 — расстояние между частицами, а в лапласианах Ai и Д2
проводится дифференцирование по координатам первой #i, 3/1, z\
и второй Х2, у2, Z2 частиц соответственно:
_ д2 д2 д2 _ д2 д2 д2
1 дх2 + ду2 + dz^ ’ 2 дх^ ду^ dz2
Третье слагаемое в (9.20) представляет собой оператор потенци-
альной энергии взаимодействия данных заряженных частиц.
Гамильтонианы более сложных систем частиц рассматрива-
ются ниже.
9.3. Коммутативность операторов
С операторами физических величин квантовой физики можно
проводить некоторые математические действия.
Суммой операторов является также оператор, определяемый
следующим соотношением:
(/ + 5)Ф = /Ф + £Ф. (9.21)
Произведением двух операторов f и g является оператор, кото-
рый представляет собой последовательное действие операторов f
и g на функцию, т. е.
(/•р)ф = /(рф).
(9.22)
9.3. Коммутативность операторов
165
Для квантовой физики существенно, что умножение операто-
ров физических величин в общем случае некоммутативно. Это
значит, что, вообще говоря,
(/•?)Ф/(£•/)*• (9-23)
Оператор, равный разности произведений f д — д • /, называ-
ется коммутатором операторов f и д и обозначается с помощью
квадратных скобок:
f-9~9-f = [/,£]• (9-24)
Для примера рассмотрим коммутацию операторов координаты
х (9.10) и проекции импульса рх (9.12). Сначала вычислим
( Э \ <ЭФ
)Ф = х(рх Ф) = х I — ih—Ф = — ihx—. (9.25)
\ ox J ох
Теперь переставим местами операторы х и рх и вновь подействуем
на функцию Ф:
д 5Ф
(рх ж)Ф = рх{х Ф) = —г’Л—(жФ) = —гЛФ — ihx-y—. (9.26)
(J JU (JJb
Различие полученных выражений в правых частях (9.25) и (9.26)
означает, что операторы координаты х и проекции импульса рх
не коммутируют. Пользуясь определением (9.24) и выражениями
(9.25) и (9.26), вычислим коммутатор этих операторов:
[я, рх] = ih. '(9.27)
Нетрудно установить, что операторы других координат не ком-
мутируют с операторами соответствующих проекций импульса.
С другой стороны, легко показать, что аналогичные операторы раз-
ных переменных коммутируют, например, (рху)^ = (урх)^, т.е.
[у, Рх] = 0- (9.28)
Аналогично получается
[ж, Ру] = [х, pz] = [у, Рг] = [z, рх] = [z, Ру\ = 0.
Рассмотрим два оператора /ид, которые обладают общими
собственными функциями. Это значит, что система уравнений
/Ф = /Ф, д* = дЪ
имеет общие решения Ф. Подействуем на левую часть первого
уравнения оператором д, а на левую часть второго уравнения —
166 Лекция 9. Волновая функция и операторы квантовой механики
оператором /, затем вычтем из первого уравнения второе. При
этом учтем, что собственные значения операторов /ид — это
числа, которые можно выносить за символ линейного оператора.
Получим
9(f Ф) - Д9 Ф) = f9 Ф " 9f Ф = № - 5/)Ф = 0.
Это означает, что операторы f ид коммутируют.
В квантовой механике доказывается и обратная теорема: если
операторы физических величин коммутируют между собой, то
эти физические величины в некоторых состояниях данной си-
стемы могут иметь одновременно определенные значения.
Некоммутативность двух операторов означает, что не суще-
ствует, вообще говоря, таких состояний, в которых обе соответст-
вующие физические величины имеют одновременно определенные
числовые значения. В частности, отсутствие коммутативности
операторов координаты х и проекции импульса рх означает, что
координата х и проекция импульса рх не могут быть одновременно
измерены. То же самое утверждает соотношение неопределенно-
стей Гейзенберга (6.3).
9.4. Оператор момента импульса
Момент импульса является одним из основных интегралов
движения классической механики. Рассмотрим операторное пред-
ставление этой важной физической величины в квантовой физике.
Классическое выражение для момента импульса частицы за-
писывается в виде символического определителя:
L = [г, р] =
i j k
X у z
Рх Ру Pz
(9.29)
где тир — радиус-вектор и импульс частицы соответственно, i,
j, к — единичные векторы системы координат. Отсюда следуют
выражения для отдельных проекций момента импульса:
Lx = PzV ~ PyZ,
Ly = pxz - pzx, (9.30)
Lz — Py% ~ РхУ'
Используя описанный выше метод квантовой механики, заме-
ним координаты и проекции импульса соответствующими опера-
торами и тем самым получим следующие операторы проекций
9.4. Оператор момента импульса
167
момента импульса:
I^X 2/Z> 1 ( d ^у- d \ dyZJ = —ih ( d 9 \ Zdy) ’
Lt у — —1“1 (d ^dzx d A dxZ) = +ih | ( d \^dz ZdxJ’ (9.31)
Lz — —ih 1 < d d \ = — ih | ( d d \
—x — \dy я~У дх J \ dy -yTx)-
Для квантовой физики атома важное значение имеет квадрат
модуля момента импульса L2. Введем оператор квадрата мо-
мента импульса частицы, согласно методу квантовой механики,
следующим образом:
L2=L2 + L2y + L2 = -h2
( д д\2
+
( д д\2 ( д а\21
+ ( ) +(жл-----) • (В 9-32)
\ oz дх J \ ду дх )
В выражения (9.32) входят координаты и соответствующие
проекции импульса, которые связаны соотношениями неопреде-
ленностей. Уже это ставит вопрос об одновременной измеримости
разных проекций момента импульса. Для ответа рассмотрим ком-
мутативность операторов (9.31) и (9.32). Вычисления соответству-
ющих коммутаторов приведены в дополнении 9.1. В результате
расчетов выясняется, что любая пара операторов (9.31) не комму-
тирует:
(9.33)
LxLy LyLx — ihLz,
LyLz LzLy — ihLx,
LZLX LXLZ = ihLy.
Это означает, что две компоненты момента импульса не могут
иметь определенные значения в одном состоянии.
С другой стороны, оператор квадрата момента импульса ком-
мутирует с любой из своих проекций:
LXL2 - L2Lx = О,
LyL2 - L2Ly = О,
LZL2 - L2Lz = 0.
(9.34)
168 Лекция 9. Волновая функция и операторы квантовой механики
Следовательно, существуют квантовые состояния, в которых опре-
делен квадрат момента импульса и одна (любая) из его проекций.
Эти состояния должны характеризоваться собственными функци-
ями операторов соответствующих физических величин.
9.5. Собственные значения и собственные функции
операторов проекций момента импульса
Для нахождения системы собственных функций операторов
проекций момента импульса удобно использовать сферическую си-
стему координат. Связь декартовых и сферических координат вы-
ражается известными формулами:
х = г sin 9 cos (/?, у = г sin 9 sin (/?, z = г cos 0, (9.35)
где г — модуль радиус-вектора материальной точки, 9 — ее по-
лярный угол, ф — азимутальный угол.
Применяя преобразование координат (9.35), выразим частные
производные по декартовым координатам в выражениях (9.31) че-
рез частные производные по сферическим координатам г, 0, (/?.
Тогда операторы проекций момента импульса приобретут следую-
щий вид:
Lx
Ly
f. д п д\
= in sin 9? • — + ctg 9 cos ф • — ,
\ 39 дф J
/ 3 3 \
= in I - cos (/?• — + ctg 6/ sin (/?• — ,
\ д9 Зф J
(9.36)
Lz
-
дф
Оператор квадрата модуля момента импульса в сферических
координатах может быть получен непосредственно как сумма ква-
дратов операторов (9.36). После несложных преобразований полу-
чаем
sin 9 39 \ П $ 39 ) sin2 9 дф2
(9.37)
Последнее выражение полезно сравнить с оператором Лапласа,
выраженным в сферических координатах:
£ д_ ( 2д_\ £ Г 1 а 1____
г2 дг \ дг / г2 sin 9 39 \ 39 / sin2 9 дф2
(9.38)
Этот оператор состоит из двух слагаемых:
А = Дд + 1ДУ, (9.39)
9.5. Оператор проекций момента импульса
169
где оператор
Ад = (9-40)
г 2 dr \ or J
является радиальной частью оператора Лапласа, а
1 д f д \ 1 д2
Sin<? • + —2^ТГ2 <9-41)
sm v ov \ ди J sm в д(рЛ
его угловой частью.
Сравнение выражений (9.37) и (9.41) показывает, что опера-
тор квадрата модуля момента импульса может быть представлен в
кратком виде:
L2 = -/г2Ду. (9.42)
Теперь найдем собственные функции и собственные значения
операторов квадрата модуля момента импульса L2 и одной из его
проекций, в качестве которой можно выбрать Lz. Напомним, что
операторы квадрата модуля момента импульса и любой из его про-
екций коммутируют, т. е. значения соответствующих физических
величин могут быть измерены одновременно в принципе с любой
точностью. Следовательно, эти операторы обладают одинаковым
набором собственных функций. Спектры собственных значений
являются, естественно, различными.
Заметим, что операторы (9.36) и (9.37) зависят только от угло-
вых координат. Следовательно, уравнения на собственные функ-
ции операторов Lz и L2 можно записать в следующем виде:
М(^МЖН (9.43)
£2Ф(0,</?) = £2Ф(0,<Д), (9.44)
где Lz и Z2 — собственные значения операторов Lz и L2.
Система уравнений (9.43) и (9.44) решается методом разделе-
ния переменных. Будем искать решение системы в виде произве-
дения функций
Ф(0,у>) = Р(0)ф(<^). (9.45)
Подставляя это выражение в уравнение (9.43), получим
_=
dtp
Решение последнего уравнения запишем в виде
Ф((/?) = С ехр , (9.47)
\ h j
170 Лекция 9. Волновая функция и операторы квантовой механики
где С — постоянная интегрирования. Так как состояния физиче-
ской системы, различающиеся на азимутальный угол = 2тг,
неразличимы, то функция Ф((/?) должна быть периодической с пе-
риодом 2%:
Ф(</>) = Ф((/> + 2тг).
Из вида функции (9.47) следует, что это условие периодичности
выполнится, если собственные значения Lz квантуются по сле-
дующему правилу:
Lz = hm, (9.48)
где m = 0, ±1, ±2, ... Иначе говоря, спектр собственных значе-
ний оператора проекции момента импульса является дискретным,
причем эти значения Lz кратны постоянной Планка. Целое число
m в квантовой физике обычно называется магнитным кванто-
вым числом.
Каждая волновая функция (9.47) характеризуется определен-
ным значением магнитного квантового числа т. Постоянную С
для этой функции можно вычислить из условия
2тг
У Ф*Ф dtp = 1.
о
Таким образом, собственные функции оператора проекции мо-
мента импульса на ось Z, соответствующие собственным значе-
ниям (9.48), записываются в виде
(</>) =-7= ехр (гт</2). (9.49)
V 2л
9.6. Собственные значения и собственные функции
оператора квадрата момента импульса
Для вычисления собственных функций и собственных значе-
ний оператора квадрата момента импульса обратимся к уравнению
(9.44). Оператор L2 запишем в виде (9.42), а функцию Ф(0,<^)
представим произведением (9.45) с учетом (9.49):
—Й2АуР(0)-у= ехр (гт</?) = £2Р(0)—5= ехр (гт</?). (9.50)
у2тг у2тг
Напомним, что, согласно постулатам квантовой механики, вол-
новая функция должна быть однозначной, ограниченной, непре-
рывной и иметь непрерывную производную. Дифференциальное
9.6. Оператор квадрата момента импульса 171
уравнение (9.50) хорошо изучено в математической физике, имеет
ограниченные решения только в тех случаях, когда собственные
значения оператора квадрата момента импульса принадлежат сле-
дующему дискретному множеству:
L2 = h2l(l + 1), (9.51)
где величина I пробегает ряд целых значений: 0, 1, 2, ... В кван-
товой физике безразмерный параметр I называется орбитальным
квантовым числом. Величина I ограничивает возможные абсо-
лютные значения параметра т следующим образом: |m| < I,
Функции Р(0), которые удовлетворяют уравнению (9.50), пред-
ставляют собой присоединенные полиномы Лежандра (cos 0).
Эти полиномы являются специальными функциями, определяе-
мым следующим соотношением:
4|m|(f) = - 1)', (9.52)
где £ = cos в.
Вид функции Ф((/?) был получен выше и выражен формулой
(9.49). В результате решение системы (9.43), (9.44) представля-
ется в виде нормированных определенным образом сферических
функций, содержащих два квантовых числа I и т:
Ф«т(0,¥>) = =
= lJ(”+Р|1т'(‘:°5 6ХР (”"Н (9'53)
где I = 0,1,2,..., и
т = 0, ±1, ±2, ..., ±Z. (9.54)
Параметр к равен числу т при т 0 и к = 0 при т < 0. Коэф-
фициент перед полиномом Лежандра обеспечивает нормировку ква-
драта модуля функции (9.53) на единицу. Непосредственно можно
убедиться, что
7Г 2?Г
У J Yim^y(P)Yi,m'^,(p)sin.ed0dtp = 5и>6тт>, (9.55)
о о
т.е. функции Yim(6) 99) являются нормированными на единицу.
172 Лекция 9. Волновая функция и операторы квантовой механики
Таблица 9.1. Вид сферических функций Yim(О, ср) для малых значений
квантовых чисел I и тп
Состояние I m
S 0 0 1 ч/4^
Р 1 -1 i\l-7- sin9exp (—icp) V О7Г
0 — COS 0 V 47Г
+1 —iyjsin 9 exp (icp)
d 2 —2 - У sin2 e exp (-2iy>)
-1 /15 — cos 9 sin 9 exp (—icp) V О7Г
0 J^(l-3coS20) V 1О7Г
1 /15 \ cos # s^n # exP (^) V О7Г
2 ~V ^T"sin2(?exP(2i<^ V OZ7F
f 3 -3 / 35 ——— sin3 9 exp (—3icp) V 647Г
—2 —ц/cos 9 sin2 9 exp (—2icp) V 327Г
-1 1 21 —ц/ 7— sin 0(5 cos2 0 — 1) exp (—icp) V 64тг
0 —i\lcos 0(5 cos2 0 — 3) V 1О7Г
1 / 21 ц/ —— sin 0(5 cos2 0 — 1) exp (icp) V 64тг
2 —ц/cos 0 sin2 0 exp (2icp) V 327Г
3 • / • 3 n /0• \ г\/ —— sin 0 exp (Згср) у 647Г
9.6. Оператор квадрата момента импульса 173
Явный вид функций Yim(6,99) для ряда значений квантовых
чисел I и m приведен в табл. 9.1.
Заметим, что определенному значению квадрата момента им-
пульса L2, которое задано орбитальным квантовым числом Z, со-
гласно (9.51), соответствуют 21 + 1 различных линейно независи-
мых функций Y/m(0,99), иначе говоря, 2Z +1 различных состояний
физической системы, различающихся значениями квантовых чи-
сел m = 0, ±1, ±2, ..., ±Z. Это означает, что каждое состояние
с определенным квадратом момента импульса (2Z + 1)-кратно вы-
рождено по магнитному квантовому числу (или по проекциям мо-
мента импульса).
Квантовые состояния с определенными значениями орбиталь-
ного квантового числа I исторически принято обозначать строч-
ными буквами латинского алфавита согласно табл. 9.2.
Таблица 9.2. Обозначения состояний с определенными
значениями орбитального квантового числа
Орбитальное число 1 0 1 2 3 4 5
Обозначение S Р d f 9 h
По принятому правилу состояния с орбитальными числами
I 3 обозначаются латинскими литерами в алфавитном порядке.
Заметим на будущее, что в физических системах (атомах, молеку-
лах и т.п.) состояния со значениями орбитального числа больше
пяти реализуются очень редко.
Из соотношения (9.48) следует, что максимальное значение
проекции момента импульса достигается при m — I и равно
£(тах) = (9,5б)
Следовательно, £,(тах) всегда меньше модуля момента импульса,
равного
|L| = y/L2 = Ну/ЦГ+Т). (9.57)
Соотношения неопределенностей говорят о том, что в физи-
ческой системе могут одновременно существовать (быть измерен-
ными) лишь значения квадрата момента импульса и одна из его
проекций на выбранную ось координат. Это означает, что, в отли-
чие от классических представлений, момент импульса в квантовой
физике не является векторной величиной. Геометрическая интер-
претация (весьма условная!) квантового момента импульса может
быть следующей. Геометрическое место радиус-векторов опреде-
ленной длины \L\ с их постоянной проекцией Lz на выбранную ось
174 Лекция 9. Волновая функция и операторы квантовой механики
представляет собой конус. Измерение в любой момент времени мо-
мента импульса дает одну из произвольных образующих данного
конуса. При повторении измерений момента импульса в том же
состоянии будут получаться случайным образом другие образую-
щие. Усреднение результатов измерений проекций Lx и Ly даст
нулевые значения в полном соответствии с выводами квантовой
теории (см. дополнение 9.2).
Геометрические соотношения между модулями и проекциями
момента импульса можно наглядно проиллюстрировать с помощью
«векторной модели». Величина \L\ изображается длиной символи-
ческого вектора, начало которого совмещается с началом коорди-
Рис. 9.1. Изображение проекций момента импульса с помощью векторной мо-
дели: а) проецирование символического вектора с модулем L = |L| на ось Z;
б) проецирование символического вектора для орбитального числа I = 1; в) про-
ецирование символического вектора для орбитального числа I = 2
нат. Этот «вектор» ориентируется в плоскости, содержащей ось Z,
таким образом, чтобы его проекции принимали значения из ряда
(9.48).
На рис. 9.1 приведены изображения проекций момента им-
пульса с помощью векторной модели для орбитальных квантовых
чисел I = 1 и I = 2.
Подчеркнем, что стрелки, приведенные на рис. 9.1, не явля-
ются векторами момента импульса, а лишь наглядным способом
изображения дискретных проекций Lz момента импульса при за-
данной величине модуля момента импульса |£|.
9.6. Оператор квадрата момента импульса
175
Задачи к лекции 9
1. Вычислить коммутатор следующих операторов:
а) гамильтониана свободной частицы и координаты х;
б) гамильтониана свободной частицы и проекции импульса рх,
в) кинетической энергии и потенциальной энергии кулоновского
поля;
г) координаты z и проекции импульса pz;
д) проекции импульса рх и проекции момента импульса Lx.
2. Непосредственно доказать ортогональность сферических функций
со следующими квантовыми числами:
а) I = 1, тп = 0 и I = 1, m = 1;
б) I = 0, тп = 0 и I = 1, тп = 0;
в) I = 0, тп = 0 и I = 2, тп = 0;
г) I = 1, тп = 1 и I = 2, тп = 0.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 9
9.1. Коммутационные соотношения для операторов
квадрата модуля и проекций момента импульса
Прежде всего покажем, что операторы разных компонент момента
импульса не коммутативны. Запишем:
LxLy — К
. 2 г д2 д ( д\
h
д2 2 д2 1
zxdydz+z дудх_
= h2
д2 д д2 д2 2 д2 1
ухдГ2 ~уТх~ yzd^x ~ zxd^z + *
(Д.9.1)
Аналогично получаем
’ д2 9 ( д\ д2
yXd^~XWz \ZVy)~Zy^dz
д2 '
дх ду
= П2
' д2 д д2 д2 2 д2 1
yxdz'i Хду xzdzdy zydxdz+z дхду.
(Д.9.2)
Непосредственно сравнивая полученные произведения операторов,
можно убедиться, что они не совпадают, т.е. LxLy / LyLx. Аналогично
можно убедиться, что LzLy / LyLz и LZLX / LXLZ, Это означает, что
никакие две компоненты момента импульса в физической системе не мо-
гут быть измерены одновременно. Исключение составляет тривиальный
случай, когда все три компоненты равны нулю. Из этого следует, что
классическое понятие вектора момента импульса в квантовой физике не
имеет аналога.
Дополнения к лекции 9
177
Вычислим коммутатор
— LxLy LyL% —
г д2 д д2 д2
[yXd72-yTx-yZd7d-x-ZXd^z
г д2 д д2 д2
[ухд^-хд^-хгд^-гуд^-
' д 5 1 ,t f ,t Г д С
хя---Уя~ =гп\-гП, х--у—
оу ох\ [оу ох
= h2
-h2
= Н2
д2
.2
ду дх
д2 1
.2______ _
дх ду
= -ihLz. (Д.9.3)
' д д'
*ду У дх
Аналогично можно получить соотношения LyLz —LzLy = ihLx и LZLX —
LXLZ — ihLy.
Рассмотрим свойства коммутативности операторов проекций момен-
та импульса и оператора квадрата момента импульса. Во-первых, убе-
димся, что LXL2X = L2LX. Запишем:
,t3 / д д\2 ( д д\
+Л \yai-zau) =
-iS3 -’T-) 6'F I "'' (Д-94)
\ dz ду J \ dz dy J
Свойства коммутативности оператора квадрата момента импульса с
операторами компонент момента импульса нетрудно получить непосред-
ственно, однако короче это можно сделать, используя уже полученные
свойства коммутативности операторов компонент момента импульса. За-
пишем:
LxLy LyLx — ihL z
и подействуем на это соотношение справа и слева оператором Ly:
LxLyLy LyLxLy — ihL zLy,
LyLxLy LyLyLx — iHLyLZl
или
LxLy LyLxLy — ihLzLy,
LyLxLy LyLx — ihLyL z.
Складывая уравнения, получим
LxLy LyLx — ih(LzLy 4~ LyLz}.
(Д.9.5)
178
Дополнения к лекции 9
Аналогично, умножение обеих частей уравнения
LZLX LXLZ ~ ihJ-jy
на оператор Lz дает следующие соотношения:
ТуzLxLz LXLZ — iJxLyLz^
LZLX L ZLXL z = ihLzLy.
Складывая два последних уравнения и умножая обе части на —1, по-
лучим
LXL2Z — L2ZLX — —ih(LyLz 4~ LzLy). (Д.9.6)
Сложим выражения (Д.9.4), (Д.9.5) и (Д.9.6):
LXL^. — L^LX 4- LxL%j — L^LX 4- LXL2Z — L2ZLX —
— zfb^Lz^y 4* LyLz LyLz LzLy^ — 0
или
^(^2 4- L2y 4- L2Z} — (L2 4- L2 4- L2Z)LX = 0.
Это означает, что
LXL2 - L2Lx = 0,
т. e. оператор ^-компоненты момента импульса коммутирует с операто-
ром квадрата момента. Аналогичное соотношение можно получить и для
других компонент момента импульса.
Итак, подведем итоги. Полученные свойства коммутативности
LxLy LyLx — ilbLzi
LyLz LzLy — i^LXj
LZLX LXLZ — iJiLy)
LXL2 - L2Lx = 0,
LyL2 - L2Ly = 0,
LZL2 - L2Lz = 0
(Д.9.7)
говорят о том, что у квантовой частицы одновременно можно измерить
квадрат модуля момента импульса и одну из его компонент.
Теперь мы можем доказать, что сферические функции
Кп1(0, ¥>) = (~^kJ4^+ |^|)! pz”l(cosехР
Дополнения к лекции 9
179
являются также собственными функциями оператора Lz. Для этого за-
пишем
I у 47г(/ 4- |т|Д I и<р )
= tim j (-1)*/' Fzm(cos61) I ехР (z'w) = hrnYim(6,(p).
I у 47г(/ 4- |т|Д I
Итак, мы убедились, что сферические функции являются также соб-
ственными функциями оператора проекции момента импульса на ось Z.
9.2. Средние значения физических величин
В лекции 9 было показано, что в данном состоянии частицы (или сис-
темы частиц), характеризуемом волновой функцией Ф(г, t) (или Ф(гг, £)),
не все физические величины имеют определенные значения. Например,
свободная частица в состоянии с определенной проекцией импульса рх
не имеет определенного значения координаты х.
В квантовой механике среднее значение физической величины А в
момент времени t в системе, которая описывается волновой функцией
Ф(г,£), определяется как
At= Ф*(г,£)АФ(г, £)dV.
(Д.9.8)
В качестве первого примера рассмотрим нерелятивистскую частицу,
которая совершает одномерное движение на отрезке длины L. Ее нор-
мированная волновая функция записывается в следующем виде:
( [2 ( iEt\ . (рх\
\ — ехр------— sin — при 0 < х L,
Ф(г,£) = «{У£ \ h J (Д.9.9)
. О, если х < 0 или х > L,
где Е — энергия частицы, р — модуль ее импульса. Такая волновая
функция описывает движение частицы в бесконечно глубокой потенци-
альной яме, которая подробно рассматривается в лекции 10. Свойство не-
прерывности волновой функции приводит к тому, что модуль импульса
частицы может принимать только следующие квантовые значения:
лКп
Р=~Г’
(Д.9.10)
где п — любое натуральное число.
180
Дополнения к лекции 9
Найдем среднее значение кинетической энергии частицы на интер-
вале [0,L]. Запишем, используя определение (Д.9.8) и выражение опе-
ратора (9.17):
Ф*(г,£)Т Ф(г,£) =
L
2 Г /iEt\ , /рх\ ( h2 _Л ( iEt\ . fpx\ ,
- / exp — sin I —) Vz exp —— sin — ) dx =
L J \ h J \ П J \ 2m J \ h J \ h /
= ~T^ [exp (°)sin (i)sin (jr)dx =
Jj 2m J \ Тъ ' dx J Л ✓
о
2 p2
(Д.9.11)
Вычисление интеграла с использованием соотношения (Д.9.10) дает зна-
L
чение —. Таким образом, среднее значение кинетической энергии ча-
стицы получается равным
__ 2
T=f-, (Д.9.12)
что совпадает с известным классическим выражением.
Аналогично можно вычислить среднее значение координаты час-
тицы, описываемой волновой функцией (Д.9.9). Запишем по определе-
нию (Д.9.8) и вычислим:
L L
х = f Ф*(г,£)£Ф(г,£) =-| х sin2
-l о
dx =
Таким образом, среднее значение координаты соответствует положению
частицы в центре отрезка длины L,
В качестве еще одного полезного примера вычисления средних значе-
ний рассмотрим состояния физической системы, в которых имеют опре-
деленные значения квадрат момента импульса L2 и одна из его проекций
Lz. В этих состояниях, как показано в § 9.4 и в дополнении 9.1, две дру-
гие проекции Lx и Ly не имеют определенных значений.
Вычислим средние значения этих проекций Lx и Ly в заданных со-
стояниях, пользуясь определением (Д.9.8). Согласно §9.6 собственными
функциями этих состояний являются сферические функции
выраженные формулами (9.53).
Для вычисления средних значений Lx и Ly целесообразно исполь-
зовать операторы L+ и L_, которые выражаются линейными комбина-
Дополнения к лекции 9
181
циями операторов Lx и Ly:
Z% = Lx + iLy, L_ = Lx — lLy. (Д.9.13)
Операторы (Д.9.13) замечательны тем, что, действуя на сферическую
функцию они увеличивают или уменьшают на единицу пара-
метр т по следующим правилам:
L+Ylm(0^ = (Д.9.14)
= C2Yi^e^\ (Д.9.15)
где постоянные коэффициенты С\ и С2 выражаются через параметры I
и т сферической функции:
Cl = hy/(l-m + l)(l + m), С2 = V(/ + m + l)(/-m). (Д.9.16)
Теперь запишем выражение для среднего значения Lx:
Lx = f У Y£n(0,p)LxYlm(0,^sm0d0dv. (Д.9.17)
О о
Используя определение (Д.9.13), представим оператор Lx в виде линей-
ной комбинации операторов L+ и L_:
Lx = L+ + L~ (Д-9.18)
и подставим (Д.9.18) в (Д.9.17):
7Г 27Г
Lx = 111 Yjm ^)-j-Ylm (3y?) sin 3 d3 dtp~\~
о 0
+^l I Yfm(0,<p)L_Yim(9,rf sin0 d9 d<p.
0 0
Воспользуемся свойствами операторов (Д.9.14) и (Д.9.15):
Lx = У J~ Yl*m(e,cp)Yi<m+i(<e,tp')sin9d0dip+
О о
// Yi*m(e,<p)Yl>m_1(e,v)sined0d^.
О о
182
Дополнения к лекции 9
Из-за свойства ортогональности сферических функций (9.55) оба инте-
грала в предыдущем уравнении равны нулю. Следовательно,
Lx = 0. (Д.9.19)
Аналогично вычисляется среднее значение Ly. Для этого оператор Ly с
помощью определений (Д.9.13) представляется в виде
Ц = L+~L~ (Д.9.20)
и подставляется в выражение
7Г 2тг
LV = I У Yt*m(9, v)LyYim(9,<p) sin $ dddp. (Д.9.21)
О о
Далее нетрудно вычислить, что
Ly = 0. (Д.9.22)
Таким образом, средние значения проекций момента импульса Lx и
Ly в состояниях, где квадрат момента импульса L2 и проекция Lz имеют
определенные значения, равны нулю. Это означает, в частности, что при
измерениях проекций Lx и Ly с одинаковой вероятностью получаются
как положительные, так и отрицательные значения.
Лекция 10
СТАЦИОНАРНЫЕ СОСТОЯНИЯ
10.1. Уравнение Шредингера
для стационарных состояний
Для атомной физики особое значение имеет исследование ста-
ционарных состояний физических систем. Стационарными на-
зываются состояния, в которых энергия частицы (или системы
частиц) имеет определенное значение. Стационарные состояния
вводятся в тех случаях, когда гамильтониан системы Н не за-
висит явно от времени. Например, это условие выполняется для
движения системы частиц в потенциальном поле, не зависящем
явно от времени.
Волновая функция Ф(г, t) системы в стационарных состояниях
может быть представлена произведением координатной ^(г) и вре-
менной x(t) частей:
Ф(г,0 = ^(r)x(i). (10.1)
(10.2)
Подстановка функции (10.1) в уравнение Шредингера (9.6) дает
W(r)^^ = х(<)Я^(г).
at
Перепишем полученное уравнение в виде
ft dx(t) = Нф(г)
\(<) dt V’(r)
Правая часть последнего уравнения зависит только от координат,
а левая только от времени. Поскольку уравнение (10.2) должно
выполняться для всех возможных значений координат и времени,
то правая и левая части должны быть равны некоторой константе
Е, т. е.
И dx(t) _ Я^(г) _ „
(10.3)
184 Лекция 10. Стационарные состояния
Решение первого уравнения с точностью до постоянного множи-
теля записывается в виде
( Е \
(Ю-4)
где А — константа. Так как нормировка (9.4) проводится для пол-
ной волновой функции (10.1), то без потери общности можно по-
ложить А = 1. Нормировка (9.4) полной волновой функции Ф(г, t)
проводится подбором коэффициента перед координатной частью
волновой функции V>(r), как это будет показано ниже в данной
лекции.
При А = 1 всегда выполняется равенство |х|2 = 1. В начале
предыдущей лекции было отмечено, что волновые функции одной
и той же системы в одном и том же состоянии могут отличаться
на множитель ехр (га), где а — произвольное комплексное число.
Это означает, что в стационарных состояниях временная часть
волновой функции xW не дзет информации о пространственном
распределении ме стона хождения частицы в стационарном состоя-
нии.
Второе уравнение системы (10.3) можно переписать в виде
Я^(г) = £л0(г). (10.5)
Это уравнение представляет собой уравнение на собственные функ-
ции и собственные значения гамильтониана. В соответствии со
смыслом оператора Н множество его собственных значений обра-
зует спектр возможных значений энергии Е рассматриваемой си-
стемы в соответствующих состояниях, которые задаются волно-
выми функциями V’(r)- Решения уравнения (10.5) дают волновые
функции V;(r) стационарных состояний данной системы и значе-
ния энергии jE, которые может иметь система, характеризуемая
гамильтонианом Н.
Уравнение (10.5) называется уравнением Шредингера для
стационарных состояний. Квадрат модуля координатной части
волновой функции |^(г)|2 описывает пространственное распреде-
ление вероятности системы (или частицы) в данном стационарном
состоянии с определенной энергией Е. Состояние с минимально
возможной энергией для данной системы называется основным.
Спектр собственных значений физических характеристик
квантовой системы может быть как непрерывным, так и дискрет-
ным. Это в полной мере относится и к стационарным состояниям,
определяемым уравнением (10.5). Можно показать, что если дви-
жение системы финитно (происходит в конечном объеме простран-
ства), то спектр стационарных состояний дискретный. Иначе го-
воря, системы, совершающие финитные движения, могут иметь
10.2. Движение частицы в одномерной потенциальной яме 185
только дискретные значения энергии. Если же движение частиц
системы инфинитно (когда хотя бы одна частица системы уходит
в бесконечность), то спектр энергий стационарных состояний не-
прерывен.
Отсюда, в частности, следует, что электрон в связанном со-
стоянии (например, в атоме) должен обладать дискретным спек-
тром стационарных состояний с определенными энергиями, что
и декларировали постулаты Бора. Напротив, энергии свободных
электронов, рассеивающихся на атомах, могут иметь любые дей-
ствительные значения энергий из заданного интервала.
10.2. Движение частицы в одномерной
бесконечно глубокой потенциальной яме
Для того чтобы выяснить некоторые общие свойства стацио-
нарных состояний, обратимся сначала к простым одномерным за-
дачам, в которых рассматривается движение частиц вдоль прямой
линии.
Пусть частица с массой m движется в области постоянной по-
тенциальной энергии, на границах которой находятся абсолютно
отражающие стенки. Расположим ось координат X вдоль напра-
вления движения частицы. При этом функция потенциальной
энергии может быть записана в виде
О,
оо,
0 х а,
х < 0, х > а.
(10.6)
Рисунок 10.1 иллюстрирует физическую ситуацию, когда дви-
жение частицы ограничено идеально твердыми непроницаемыми
Рис. 10.1. Одномерная бесконечно глубокая потенциальная яма
стенками, расположенными в точках х = 0 и х = а. Функцию вида
(10.6) называют бесконечно глубокой одномерной потенциальной
ямой.
186
Лекция 10. Стационарные состояния
В классической физике аналогом данной системы является
движение небольшого тела внутри горизонтального ящика с высо-
кими упругими стенками и гладким дном. Как известно, движение
такого тела является финитным, спектр энергии непрерывным, а
тело может находиться с равной вероятностью в окрестностях лю-
бой точки своей траектории.
Для исследования законов движения квантовой частицы най-
дем волновые функции стационарных состояний частицы в за-
данной потенциальной яме и энергии частицы в этих состояниях.
Гамильтониан частицы внутри ямы содержит лишь оператор ки-
нетической энергии и имеет вид
(Ю.7)
(10.8)
2m 2m dx2 *
Запишем для частицы в яме уравнение Шредингера для стацио-
нарных состояний (10.5) и преобразуем его к виду
2mE t
ф +"^2_V’ = 0.
Решение этого однородного уравнения запишем в виде
= Asin^kx) + В cos {кх\
где А, В — постоянные, и введено обозначение
_ /2тЕ
к = у-р-
(10.9)
(10.10)
Стенки в нашей физической системе являются идеально твер-
дыми, согласно заданным условиям (10.6). Это обусловливает не-
возможность проникновения частицы в области вне потенциальной
ямы (х < 0 и х > а), поскольку для этого необходимо совершить
бесконечно большую работу. Следовательно, для волновой функ-
ции имеем соотношения ^(x < 0) = ^{x > a) = 0, откуда в силу
свойства непрерывности волновой функции получаем для нее гра-
ничные условия
*ф(х = 0) = ^(х = о) = 0. (10.11)
Из этих граничных условий следует, что постоянная В в функции
(10.9) равна нулю. Кроме того, второе условие из (10.11) дает
важное соотношение
sin (ко) = 0.
Отсюда получается, что величина к может принимать лишь дис-
кретный ряд значений:
кп = — п, п = 1,2,... (10.12)
а
10.2. Движение частицы в одномерной потенциальной яме 187
Значение п = 0 отбрасываем, так как при этом к — 0 и волно-
вая функция (10.9) становится тождественно равной нулю. Этот
случай не реализуется в нашей физической системе (вероятность
нахождения частицы в любой точке потенциальной ямы равна
нулю) и поэтому может быть исключен из рассмотрения.
Из соотношений (10.10) и (10.12) следует, что значения энер-
гий частицы в потенциальной яме (10.6) имеют дискретный спектр
тг2Л2
£п = -^п2, п = 1,2,... (10.13)
Каждому значению энергии Еп соответствует своя волновая функ-
ция
I / \ А * / 1 \ А • ТСТЬХ
'фп(х) = Asm (knx) = Asm-------, n = 1, 2,...
a
Поскольку движение частицы финитно, коэффициент А нахо-
дится с помощью следующего условия нормировки:
а а
|^п(ж)|2 dx = А2 у* sin2 (knx) dx = 1.
о о
Выполняя интегрирование, получаем А = у/2/a.
Таким образом, стационарные состояния частицы, находящей-
ся в бесконечно глубокой потенциальной яме, описываются дис-
кретным набором волновых функций
V’n(^) = n = l,2,... (10.14)
V a a
Целое число n нумерует дискретные стационарные состояния ча-
стицы и называется квантовым числом. Согласно (10.13), с уве-
личением квантового числа п значения энергии возрастают ква-
дратично.
Мы получили, что для рассмотренной физической задачи вы-
полняется ранее указанное свойство квантовых систем — финит-
ное движение описывается дискретным спектром стационарных
состояний и соответствующих энергий. Следует для сравнения
вспомнить, что, согласно классической физике, частица в потен-
циальной яме может иметь любую энергию из непрерывного мно-
жества значений.
тт -г / ч [% . кпх ( .Е \
Полные волновые функции Фиг, t) = w-sin-----ехр I — г-г-t
у а а \ П J
рассматриваемых стационарных состояний представляют собой
стоячие волны, причем величина (10.12) имеет смысл волнового
числа. Дискретный набор волновых чисел кп (п = 1,2,3,...)
188
Лекция 10. Стационарные состояния
делает эти функции в математическом смысле аналогичными сто-
ячим волнам в кубе, которые мы получали при выводе формулы
Релея-Джинса (см. лекцию 3).
Полезно рассмотреть несколько конкретных состояний части-
цы в заданном потенциальном поле (10.6). Во-первых, заметим,
что, в отличие от классической частицы, кинетическая энергия
квантовой частицы в глубокой потенциальной яме не может быть
равна нулю. Выше уже было установлено, что для стационарных
состояний частицы п 0 и ее энергия Еп 0. Фигурально выра-
жаясь, квантовая частица не может покоиться на дне потенциаль-
ной ямы.
Пусть п = 1. Это состояние с наименьшей кинетической энер-
гией
El = 2та2’ (10‘15)
т. е. основное состояние. Оно характеризуется волновой функцией
V’i(z) = \ - sin (—(10.16)
V й > о '
Плотность вероятности обнаружения частицы внутри потенци-
альной ямы вида (10.6) выражается тригонометрической функ-
цией координаты х\
1^1 (ж) |2 — - sin2 (—ж) .
О \ Q, /
Видно, что плотность вероятности максимальна для точки х = a/2
и уменьшается до нуля у краев потенциальной ямы (см. рис. 10.2).
Теперь рассмотрим состояние с п = 2. Это первое возбужден-
ное состояние согласно общей формуле (10.13) имеет энергию
2тг2Й2
Е2 =----5-=4£?i, (10.17)
то/
т.е. в 4 раза больше энергии Е± основного состояния. Волновая
функция первого возбужденного состояния
^(^) = \ ~ sin (2—х} (10.18)
V Oi \ a /
имеет пространственный период в 2 раза меньше по сравнению с
волновой функцией 'ф1(х) основного состояния.
При вычислении плотности вероятности распределения коор-
динаты частицы в яме получается удивительный результат:
|^2(^)|2 = - sin2 Г2—яЛ .
О \ CL /
10.3. Движение частицы в одномерной яме конечной глубины 189
Эта функция имеет ноль при х = а/2, т. е. вероятность нахожде-
ния частицы в окрестностях центра потенциальной ямы практи-
чески равна нулю! (См. рис. 10.2.)
Аналогично можно написать выражения для энергии и плот-
ности вероятности частицы в других состояниях (рис. 10.2) и убе-
Рис. 10.2. Дискретные значения энергии и плотности вероятности для частицы в
одномерной потенциальной яме с бесконечными стенками. Показаны состояния
с квантовыми числами п = 1,2,3
диться в неоднородном распределении плотности вероятности ко-
ординаты частицы внутри потенциальной ямы.
В классической механике вероятность нахождения частицы в
различных точках внутри потенциальной ямы может быть выра-
жена следующей функцией:
j г> ( \ 2 dx
dP(x) = ~ = moi’
где dt — время, за которое частица проходит отрезок длиной dx,
Т — период колебаний частицы в потенциальной яме, v — ско-
рость частицы. Множитель 2 обусловлен тем, что частица отрезок
dx за период проходит дважды (в двух противоположных напра-
влениях). У частицы в потенциальной яме (10.6) скорость не за-
висит от координаты ж, следовательно, вышеприведенные вероят-
ности для различных точек внутри ямы одинаковы.
10.3. Движение частицы в одномерной
потенциальной яме конечной глубины
Во многих физических задачах рассматривается движение ча-
стицы во внешнем поле, которое описывается потенциальной ямой
конечной глубины.
190
Лекция 10. Стационарные состояния
Пусть одномерная потенциальная яма имеет прямоугольную
форму, изображенную на рис. 10.3. В этом случае зависимость
потенциальной энергии от координаты можно записать в виде
О,
и0,
0 х < а,
х < 0, х > а.
(10.19)
Как и в предыдущем параграфе, будем искать волновые функ-
ции стационарных состояний данной частицы и энергии частицы
в этих состояниях.
Рис. 10.3. Функция потенциальной энергии для «одномерной ямы» конечной
глубины:
Uq — глубина ямы, а — ширина ямы. Цифрами 7, 2 и 3 обозначены области одномерного
пространства х < 0, 0 $аих> а соответственно
В отличие от предыдущей задачи, для потенциальной ямы
конечной глубины возможны две различные физические ситуа-
ции.
1. Энергия частицы Е меньше Uq. Как говорят, частица на-
ходится в потенциальной яме. Движение частицы при этом фи-
нитно.
2. Энергия частицы Е больше Uq. При этом движение частицы
становится инфинитным.
Сначала рассмотрим первый случай, когда Е < Uq. Для реше-
ния поставленной задачи целесообразно разбить весь бесконечный
интервал изменения координаты —оо < х оо на три области,
как это показано на рис. 10.3.
Прежде всего видно, что гамильтониан для области 2 имеет
вид отличный от остальных областей:
f h2 d2
2m dx2
< 2m dx2
+ Uq
для области 2,
для областей 1 и 3.
(10.20)
10.3. Движение частицы в одномерной яме конечной глубины 191
Подстановка гамильтониана (10.20) в (10.5) дает два уравнения
Шредингера для разных областей:
'ф" + к2/ф = 0 для области 2,
(10.21)
— х2,ф — 0 для областей 1 и 3,
где величина к задана формулой (10.10), а положительный пара-
метр х определен следующим образом:
х = J2m^U°~E\ (10.22)
V Й2
Решения уравнений (10.21) для разных областей целесооб-
разно записать в следующем виде, что облегчает дальнейший ана-
лиз:
= Л1 ехр (хж) + Az ехр (—ха:),
^2 = Aq sin (кх + 5),
фз = Bi ехр [—х(ж — а)] + Bz ехр [х(ж — а)],
х<0, (10.23)
О^ж^а, (10.24)
х > а. (10.25)
Выражение (10.24) означает, что в центральной области (0 С
х С а) полная волновая функция построена в виде стоячей
волны.
Коэффициенты Ai, Bi, Az, Bz, Aq и 6 в функциях (10.23)-
(10.25) являются константами интегрирования, которые должны
определяться из граничных условий, а также в случае финитного
движения (Е < Uq) из условия нормировки.
Если коэффициент Az имеет ненулевое значение, то при стрем-
лении координаты х —> —оо функция неограниченно возра-
стает. Так как, согласно общим свойствам, волновая функция
должна быть ограниченной, то коэффициент Az должен равняться
нулю. По той же причине коэффициент Bz — 0.
Для вычисления оставшихся констант следует воспользовать-
ся свойством непрерывности волновых функций и их производ-
ных. «Сшивание» функций и их производных на границах обла-
стей, т.е. в точках х — 0 и х = а, дает следующую систему
уравнений:
V’i(o) = -02(0), Ao sin 6 = А, (10.26)
^1(0)=^2(0), AqA;cos5 = хА, (10.27)
^2 (а) = "03 (а), Aq sin (ка + 6) = В, (10.28)
^(а) = ’/’з(а), AqAjcos (ка + 6) = —хВ. (10.29)
192
Лекция 10. Стационарные состояния
Деление (10.26) на (10.27) и (10.28) на (10.29) дает два следующих
уравнения:
_ к z, к
tgd = —, tg (ka + о) =------.
Выражая тангенсы через синусы, получим эквивалентную систему
уравнений
к к
sin 6 = —, sin (ка + 5) =-----
х0 х0
где введено новое обозначение
(10.30)
(10.31)
=
2т/7о
Л2
Запишем систему уравнений (10.30) для обратных тригонометри-
ческих функций:
х . к
о = arcsin —,
х0
к
ка + 6 = пк — arcsin —, п = 1,2,3,...
х0
(10.32)
Во втором уравнении системы (10.32) появился дискретный пара-
метр п, который может принимать произвольные целочисленные
значения.
Подстановка первого уравнения системы (10.32) во второе дает
единственное уравнение
к
ка — пк — 2 arcsin —, п = 1, 2,3,... (10.33)
Xq
относительно величины к.
Прежде чем решать это трансцендентное уравнение, заметим,
что при Е Uq оно превращается в уравнение (10.12) для беско-
нечно глубокой потенциальной ямы. Действительно, при Е Uq
отношение /с/xq = \/E/Uq становится много меньшим единицы
и arcsin (к/иц) можно положить равным нулю. Тогда 6 = 0 и
уравнение (10.33) становится совпадающим с (10.12).
Нелинейное уравнение (10.33), вообще говоря, решается чи-
сленными методами. Пример графического решения, приведен-
ный на рис. 10.4, позволяет сделать некоторые важные выводы.
На рис. 10.4 изображены графики зависимостей от величины
к правой и левой частей уравнения (10.33). Каждое пересечение
графиков дает определенное значение волнового числа кп, которое
является корнем уравнения (10.33). Ряд значений дискретного
параметра п = 1,2,3,... обусловливает существование нескольких
различных решений кп данного уравнения.
10.3. Движение частицы в одномерной яме конечной глубины 193
Найденные волновые числа кп, согласно соотношению (10.10),
определяют энергии стационарных состояний частицы в потен-
циальной яме (10.19). Таким образом, количество пересечений
графиков на рис. 10.4 равно числу стационарных состояний ча-
стицы.
Приведенный пример наглядно демонстрирует, что спектр вол-
новых чисел кП} которые получаются решением уравнения (10.33),
Рис. 10.4. Пример графического нахождения волновых чисел кп для частицы,
находящейся в потенциальной яме конечной глубины при условии Е <Uq. Раз-
меры потенциальной ямы Uq и а и масса частицы тп определяют величину xq
и, следовательно, количество пересечений графиков, которое при данных пара-
метрах равно трем
остается дискретным для потенциальной ямы любой глубины.
А это означает, согласно (10.21), что при Е < Uq спектр значе-
ний энергий частицы, находящейся внутри ямы, также остается
дискретным. Различные стационарные состояния частицы нуме-
руются квантовым числом п.
Волновая функция (10.24) стационарного состояния частицы
внутри потенциальной ямы является отрезком синусоиды. В отли-
чие от случая бесконечно глубокой ямы, эта синусоида не зануля-
ется в точках х = 0 и х = а. В областях 1 и 3 (т. е. вне ямы) та же
194 Лекция 10. Стационарные состояния
волновая функция представляется экспонентами (10.23) и (10.25),
убывающими при удалении от стенок потенциальной ямы.
На рис. 10.5 приведен качественный вид зависимости квадрата
модуля волновых функций от координаты (т.е. распределения
Рис. 10.5. Качественный вид распределения плотности вероятности двух ста-
ционарных состояний с квантовыми числами п = 1 и п = 2 для частицы в
потенциальной яме конечной глубины при Е < Uo
плотности вероятности нахождения частицы в потенциальной яме)
для двух стационарных состояний с квантовыми числами п = 1 и
п = 2.
Так как волновые функции в областях 1 и 3 экспоненциально
убывают при неограниченном возрастании модуля координаты |ж|,
движение частицы в потенциальной яме конечной глубины при
Е < Uq является финитным.
Таким образом, вновь финитное движение частицы характери-
зуется дискретным спектром стационарных состояний и соответ-
ствующих значений энергии.
10.3. Движение частицы в одномерной яме конечной глубины 195
Из рис. 10.4 ясно, что при конечных значениях ширины a
и глубины Uq ямы (в случае Е < С7о) количество пересечений
прямой ka и ветвей функции пл — 2 arcsin (fc/xo), где п = 1, 2, 3,...
конечно. Следовательно, количество стационарных состояний с
различной энергией для частицы с Е < Uq также конечно.
С уменьшением ширины ямы угол наклона прямой ka на
рис. 10.4 уменьшается. При этом также уменьшается количество
стационарных состояний. Однако по рисунку видно, что сколь
угодно узкая потенциальная яма содержит одно стационарное со-
стояние. Аналогично можно показать, что в сколь угодно «мелкой»
яме образуется хотя бы одно стационарное состояние с Е < Uq.
Теперь перейдем к физической ситуации, когда энергия ча-
стицы Е превышает величину Uq. Этот случай соответствует ин-
финитному движению частицы. Пусть при этом частица движется
с кинетической энергией Е — Uq из области 1 вдоль оси коорди-
нат х.
Вновь будем искать стационарные состояния с помощью урав-
нения Шредингера (10.5). Прежде всего заметим, что вид гамиль-
тониана частицы (10.20) не изменяется при условии Е > Uq. Од-
нако уравнения Шредингера для случая Е > Uq целесообразно
записать в следующем виде:
'ф" + к?"ф = 0 для области 2, z Л Л
(10.34)
'ф" + kl'ip = 0 для областей 1 и 3,
несколько отличном от (10.21). В уравнениях (10.34) использо-
ваны обозначения
kl=2m(Ef-U°}. (10.35)
Видно, что в области 2 уравнения Шредингера для случаев Е > Uq
и Е < Uq имеют идентичный вид. Однако решения уравнений
(10.34) целесообразно записать в форме, соответствующей бегу-
щим волнам:
= Ai ехр (ikix) + ехр (—ik\x), х < 0, (10.36)
^2 = Ci ехр (ifcirc) + С2 ехр (—zfcr), 0 х а, (10.37)
= В\ ехр [iki(х — а)] + В2 ехр [—iki(x — а)], х > а. (10.38)
Экспоненты с положительным аргументом изображают волны,
бегущие в положительном направлении оси X, с отрицательным
аргументом — в противоположном направлении.
Для нахождения констант интегрирования Л1, Bi, Л2, В2, Ci,
С2 используются граничные условия. Предположим, что частица
движется из —оо в положительном направлении оси X. Тогда
196
Лекция 10. Стационарные состояния
в области 3 наличие отраженной волны невозможно, что обусло-
вливает равенство В? = 0. Требование непрерывности волновой
функции (10.36)—(10.38) и ее производной дает возможность со-
ставить 4 уравнения «сшивания» в точках х = 0 и х = а, анало-
гичные уравнениям (10.26)—(10.29). Чтобы определить константу
Л1, требуется задать некоторое дополнительно граничное условие.
В нашей задаче существенно, что движение частицы при усло-
вии Е > Uq инфинитно и волновая функция не нормируется на
единицу. Кроме того, в процессе решения уравнений Шредин-
гера (10.34) нигде не накладывались никакие условия, приводя-
щие к дискретности значений волновых чисел к и к±. Иначе го-
воря, спектр волновых чисел к и к± и соответствующих волновых
функций (10.36)—(10.38) является непрерывным. Как следствие,
уравнения (10.35) обусловливают непрерывный спектр энергий ча-
стицы Е в случае Е > Uq.
Таким образом, в данной задаче показано, что инфинитному
движению с энергий частицы Е > Uq соответствует непрерывный
спектр стационарных состояний. Заметим, что при этом для опре-
деленного значения энергии Е существует два различных состо-
яния, характеризующие движение частицы справа налево и слева
направо. Следовательно, каждому значению энергии Е соответ-
ствует две разные волновые функции, что свидетельствует о дву-
кратном вырождении спектра.
Задачи к лекции 10
1. Зависимость потенциальной энергии от координаты имеет вид
«ступеньки»
тп у-fU = Q> х<^
( и = Uo, X 0.
Частица с импульсом р и энергией
х из области отрицательных координат
Е < Uq движется вдоль
(см. рисунок). Вычислить
оси
ха-
рактерную глубину проникновения частицы массы тп внутрь области
х > 0. Расчеты провести для массы электрона и «ступенек» высотой:
10.3. Движение частицы в одномерной яме конечной глубины 197
1) С7о — 5 эВ, 2) 10 эВ, 3) 20 эВ. Для каждой высоты взять значения
энергии: 1) Е = 0,1 UQ- 2) Е = 0,5 %; 3) Е = 0,9 Uo.
2. Вычислить коэффициент прохождения сквозь прямоугольный од-
номерный потенциальный барьер для энергии частицы равной высоте
барьера Uq. Провести расчеты для толщины барьера 2 А, 5 А, 10 А и
высоты барьера 5 эВ, 10 эВ, 20 эВ.
3. Вычислить среднюю кинетическую энергию электрона, находяще-
гося в одномерной бесконечно глубокой потенциальной яме шириной L,
в стационарном состоянии с квантовым числом: a) n = 1; б) п = 2;
в) п — 4.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 10
10.1. Проникновение частиц
в классически запрещенную область пространства
Рассмотрим одномерную потенциальную яму конечной глубины Uq и
ширины а. Для более удобного представления результатов расчетов
выберем начало координат в центре ямы, как показано на рис. Д.10.1.
Рис. Д.10.1. Одномерная потенциальная яма, симметричная относительно начала
координат
Зависимость потенциальной энергии от координаты записывается в
следующем виде:
U(x) = < 0,
%,
(Д.10.1)
Пусть в потенциальной яме (Д.10.1) находится частица с массой тп
и энергией Е меньшей величины Uq. При этом, согласно классической
теории, частица может двигаться только в пределах ямы, т. е. иметь
координаты в интервале [—а/2,а/2]. Невозможность проникновения ча-
стицы за эти границы в классической физике формально выражается
тем, что в области [—а/2 < х < а/2] кинетическая энергия становится
отрицательной.
В § 10.3 было показано, что в областях пространства, где энергия
частицы Е < Uq, частица характеризуется волновой функцией не рав-
ной тождественно нулю. Для потенциальной ямы, изображенной на
рис. Д.10.1, это области (х < -а/2) и (х > а/2).
Дополнения к лекции 10
199
Уравнение Шредингера для частицы в потенциальной яме конечной
глубины в случае Е < Uq было рассмотрено в лекции 10 и записано в
виде (10.21). Решение уравнения проводится аналогично изложенному
в этой лекции. Однако симметрия границ потенциальной ямы (Д.10.1)
обусловливает два типа решений: четные и нечетные. Рассмотрим чет-
ные решения, которые записываются в следующем виде:
где
-0 — А ехр [х ’ а Х<~2’ (Д.10.2)
-0 = В cos (kx), а а — < х < 2 2 (Д.10.3)
-0 = С ехр х (я — , е |см Л Н (Д.10.4)
1 /2тЕ t=V к *=’ 12т{Ца - Е) \1 Н2 (Д.Ю.5)
а коэффициенты А, В и С определяются из граничных условий, ана-
логичных уравнениям (10.26)-(10.29). В частности, получается, что
А = С, это также следует из симметрии потенциальной ямы (Д.10.1).
Квадрат модуля волновой функции пропорционален плотности веро-
ятности нахождения частицы в данной точке пространства, поэтому из
(Д.10.2) и (Д.10.4) следует, что частица может проникать в «классически
запрещенную» область пространства.
Экспоненциальные функции (Д.10.2) и (Д.10.4) очень быстро стре-
мятся к нулю при удалении от границ потенциальной ямы х = —а/2 и
х — а/2. Оценим характерную глубину проникновения частицы в «клас-
сически запрещенную» область как расстояние 6 от границ потенциаль-
ной ямы, на котором плотность вероятности местонахождения частицы
уменьшается в е раз. Выражая эту плотность вероятности, как квадрат
модуля функций (Д.10.2) и (Д.10.4), получим, что расстояние S опреде-
ляется уравнением
ехр (—2xJ) = е,
решение которого имеет вид
r 1 h
о = -— = —=====.
2х 2л/2т(С/0 - Е)
(Д.10.6)
Малая величина постоянной Планка в числителе (Д.10.6) обусловли-
вает очень малые значения расстояния 6. Очевидно, что наибольшие
значения 6 достигаются для частиц малой массы. Для электрона при
разности энергий Uq—E = 1 эВ получаем 6 ~ 1 А. Следовательно, в подоб-
ных физических системах размер «классически запрещенной» области
имеет порядок атомного радиуса, что влечет нетривиальные трудности
экспериментальной проверки обсуждаемого эффекта.
200
Дополнения к лекции 10
Проведем расчеты вероятности проникновения частиц на различные
расстояния в глубь «классически запрещенной» области. Прежде всего
заметим, что результат существенно зависит от соотношения между
энергиями Е и Uq.
Потенциальная яма называется глубокой, если выполняется нера-
венство
h2
Uq » —-. (Д.10.7)
8ma2
Если энергия частицы Е <$С Uq и потенциальная яма достаточно глу-
бокая, то из соотношений (Д.10.6) и (Д.10.7) следует, что расстояние
6 пренебрежимо мало по сравнению с шириной ямы а. В этом случае
волновая функция частицы практически равна нулю вне границ ямы,
а внутри ямы близка к гармоническим функциям вида (10.14). Можно
сказать, что проникновения в «классически запрещенные» области про-
странства не происходит.
Теперь рассмотрим противоположный случай, когда энергия частицы
Е, оставаясь меньше величины Uq, близка к ней, т. е. Е ~ Uq. При
этом характерная длина 6, согласно (Д.10.6), становится много больше
ширины потенциальной ямы а. Тогда можно пренебречь гармоническим
характером волновой функции в области 2 (Д.10.3) и волновую функцию
основного состояния частицы на всей числовой оси аппроксимировать
экспонентами вида
-0 = А ехр (хж), х < 0, (Д.10.8)
ф = Аехр (—хж), х > 0. (Д.10.9)
Нормировка волновой функции (Д.10.8), (Д.10.9) на единицу
оо
У [ф(х)\2 dx = 1 (Д.10.10)
—ОО
позволяет вычислить предэкспоненциальный множитель А = \/ж.
Плотность вероятности /(ж) иметь частице координату х выражается
квадратом модуля волновой функции (Д.10.8), (Д.10.9)
f(x) = хехр (2хт), х < 0, (Д.10.11)
f(x) = хехр (—2хж), х > 0. (Д.10.12)
Тогда вероятность того, что частица проникнет в «классически запре-
щенную» область, расположенную справа от потенциальной ямы, на рас-
стояние большее, чем L равна
сю
Р(х > L) = У f(x) dx = | ехр (-2xL). (Д.10.13)
L
Вероятность проникновения частицы в классически запрещенную
область слева от ямы на такое же расстояние равна той же величине
(Д.10.13). Эта вероятность является быстро убывающей функцией рас-
стояния L. В табл. Д.10.1 приведены значения вероятности (Д.10.13)
для электрона и разности энергий Uq — Е = 1 эВ.
Дополнения к лекции 10
201
Таблица Д.10.1. Вероятности проникновения электрона в классически
запрещенную область для различных расстояний
при разности энергий Uo — Е = 1 эВ
ь(А) 1 2 3 5 10 20
ЛИ > L) 0,18 0,065 0,025 0,003 1,8 • 10-5 6,5 • Ю-10
Из табл. Д.10.1 видно, что для расстояний порядка десятков ангстрем
вероятность проникновения в классически запрещенную область стано-
вится исчезающе малой. Однако на расстояниях порядка нескольких
ангстрем вероятностью данного неклассического эффекта пренебрегать
уже нельзя.
Можно проверить, что при анализе нечетных решений уравнения
Шредингера получаются аналогичные оценки глубины проникновения и
соответствующие вероятности.
При интерпретации явления проникновения в классически запре-
щенную область пространства нет оснований полагать, что частица в
классически запрещенной области имеет отрицательную кинетическую
энергию. Дело в том, что микрочастица не движется по определенной
траектории (см. лекцию 6), а уравнение Шредингера дает возможность
рассчитать лишь распределение вероятностей ее местонахождении. При
этом характерную глубину проникновения (Д.10.6) можно интерпрети-
ровать как неопределенность координаты
Аз: « 5. (Д.10.14)
Тогда, согласно соотношению (6.3), неопределенность проекции импуль-
са имеет порядок
Др.т > 7 = 2У2т(С70 - Е). (Д.10.15)
О
Последняя величина в случае одномерного движения задает неопределен-
ность кинетической энергии
АТ = > 4({7о _ Еу (Д.10.16)
2т
Таким образом, неопределенность кинетической энергии внутри
классически запрещенной области превышает величину \Е — Uo\. Следо-
вательно, в рассматриваемой области координат нет оснований полагать
кинетическую энергию отрицательной.
Неопределенности проекции импульса Арх и кинетической энергии
АТ могут быть также интерпретированы с помощью следующего рас-
суждения. Обнаружение частицы в классически запрещенной области
производится путем измерения ее координаты. Любое измерение со-
пряжено с некоторым воздействием на исследуемый объект, которое не
может быть сделано пренебрежимо малым (см. лекцию 6 и дополне-
ние 6.1). Например, для измерения кинетической энергии частицы не-
обходимо осуществить ее взаимодействие с другой микрочастицей. При
этом процесс измерения приводит к значительному изменению кинети-
ческой энергии и импульса микрочастицы.
202
Дополнения к лекции 10
10.2. Прохождение частиц
сквозь потенциальный барьер
Рассмотрим прямолинейное (одномерное) движение частицы в потен-
циальном поле, энергия которого выражается функцией U(х) следующего
вида:
'0,
U(x) = < Uo,
(о,
х < 0,
0 х С а,
х > а,
(Д.10.17)
где Uq и а — постоянные величины. Потенциальное поле вида (Д.10.17)
называется одномерным прямоугольным потенциальным барьером.
Энергия Uq называется высотой потенциального барьера, расстояние а —
шириной (или толщиной) барьера.
Рис. Д.10.2. График потенциальной энергии U(x) одномерного прямоугольного
потенциального барьера
Пусть частица массы т движется вдоль оси X из области отрица-
тельных значений координат в положительном направлении. Рассмо-
трим случай, когда энергия частицы Е меньше высоты потенциального
барьера Uq.
Согласно классической теории, в этом случае частица должна в точке
х = 0 изменить свой импульс р на противоположный — р и уйти в на-
правлении х -> —оо. В область х > 0 частица не должна попасть, так
как формальное использование закона сохранения энергии дает отрица-
тельную кинетическую энергию в интервале координат [0 х а].
В квантовой теории поведение частицы описывается решением урав-
нения Шредингера. Методика его решения для одномерных движений
микрочастиц была описана в лекции 10 и дополнении 10.1. Ось коор-
динат разбивается на три интервала: (—оо < х < 0), [0 х а],
(О < х < оо). Для каждого интервала записывается гамильтониан ча-
стицы, затем — уравнение Шредингера. Решения — волновые функ-
ции — целесообразно представить в следующем виде:
0i = Al ехр (ikx) + A<z ехр (—ikx), х < О, (Д.10.18)
02 = Bi ехр (хт) + В2 ехр (-хж), 0 х а, (Д.10.19)
0з = Ci ехр [ik(x - а)] 4- С? ехр [—ik(x — а)], х > а, (Д.10.20)
Дополнения к лекции 10
203
где
i = (д1021)
п, п,
В первой и третьей области решения уравнения Шредингера имеют
вид бегущих волн. Коэффициент С2 = 0, так как при заданных на-
чальных условиях в области (х > а) нет отраженной волны. Однако
коэффициент Ci, вообще говоря, не равен нулю, следовательно, частица
с определенной вероятностью может из области (х < 0) попасть в область
(х > а), т. е. преодолеть потенциальный барьер, обладая начальной энер-
гией Е меньшей, чем высота барьера Uq. Такое прохождение частиц
через потенциальный барьер называется туннельным эффектом.
Сшивание волновых функций (Д.10.18)—(Д.10.20), полученных для
разных интервалов координаты, и их производных в точках х = 0 и
х = а на границах этих интервалов дает 4 уравнения для неизвестных
коэффициентов:
^1(0) = ^2(0) -> А 4- А2 = В. 4- В2, (Д.10.22)
0i(O) = 0'(0) ikAi - ikA2 = >cBi - *В2, (Д.10.23)
02(a) = фДа) -» Bi ехр (ха) 4- В2 ехр (-ха) = (71, (Д.10.24)
-02(a) =0з(а) —> Bi ж ехр (ха) — В2хехр(—ха) — ikCi. (Д.10.25)
Для прикладных задач физики важна не судьба отдельной частицы,
а относительная доля частиц, прошедших через потенциальный барьер.
Эта характеристика, называемая коэффициентом прохождения D, есть
отношение модуля плотности потока частиц, прошедших через потенци-
альный барьер к модулю плотности потока падающих частиц:
_Jnp_
Тпад
(Д.Ю.26)
В классической физике плотность потока частиц с одинаковой скоро-
стью v выражается произведением концентрации частиц п на скорость v:
j = nv.
(Д.10.27)
Согласно квантовой теории, концентрация частиц п определяется
пространственным распределением плотности вероятности и, следова-
тельно, выражается через квадрат модуля волновой функции частицы.
Скорость частицы v может быть выражена через ее импульс р и, со-
гласно (Д. 10.21), через волновой вектор волны де Бройля к:
р Лк
v = — = —.
т т
(Д.Ю.28)
Сравнение волновых функций (Д.10.18) и (Д.10.20) показывает, что
волновые векторы первичной (падающей на барьер) Ai ехр (ikx) и про-
ходящей (71 ехр [г/и(ж — а)] волн одинаковы. Это означает, что коэф-
фициент прохождения выражается отношением концентраций частиц в
204
Дополнения к лекции 10
падающей и прошедшей волне:
С1СГ _ IGI2
лм; |Л|2-
(Д.10.29)
Из последнего выражения следует, что при вычислении коэффици-
ента прохождения через потенциальный барьер без потери общности
можно положить Ai = 1, иначе говоря, нормировать падающий поток на
единицу. Тогда уравнения сшивания (Д.10.22) и (Д.10.23) упростятся,
и коэффициент прохождения выразится следующим произведением:
D = C1C1\ (Д.10.30)
Пользуясь уравнениями сшивания (Д. 10.24) и (Д. 10.25), представим ко-
эффициенты Bi и В2 через Ci*.
Bi = Ci ехр (-ха), В2 = Ci-—ехр (ха). (Д.10.31)
& и
Уравнения (Д.10.22) и (Д.10.23) преобразуем к виду
1 + А2 = в1+в2, 1-Л2 = ^(В1-В2). (Д.10.32)
гк
Сложив уравнения (Д.10.32), а затем, подставив выражения (Д.10.31),
получим коэффициент Ci в следующем виде:
2ch (ха) 4-г(х//с — Zc/x) sh (ха) ’
Умножая последнюю величину на комплексно сопряженную Cf, найдем
искомый коэффициент прохождения:
4 А*2
D = 2>2 К2/ 2’ (Д'10'34)
(к2 4- х2)2 sh (ха) 4- 4/с2х2
где величины к и х определяются формулами (Д.10.21).
Для исследования зависимости коэффициента прохождения D от
энергии частицы Е целесообразно разделить числитель и знаменатель
формулы (Д.10.34) на 4&2х2 и подставить выражения (Д.10.21):
D =-------------------, --------------(Д.10.35)
Ц2 2 ( ay/2m(U0-E)\
4Е(£/0 - Е) ft )
Очевидно, что при Uq > Е коэффициент прохождения D < 1. Это
означает, что в данной физической ситуации лишь некоторая доля частиц
участвует в туннельном эффекте.
Дополнения к лекции 10
205
Из выражения (Д. 10.35) следует, что коэффициент прохождения уве-
личивается с возрастанием энергии частицы Е при фиксированных раз-
мерах потенциального барьера (см. рис. Д.10.3) и достигает максималь-
ного значения при Е = Uq.
Рис. Д.10.3. Зависимость коэффициента прохождения через прямоугольный од-
номерный потенциальный барьер от энергии частицы. Высота барьера Uq = 5 эВ.
Ширина барьера: 1 — а = 2 А, 2 — а = 3 А, 3 — а = 5 А
Раскрытие неопределенности в выражении (Д. 10.35) при равенстве
Е = Uq дает формулу для коэффициента прохождения в этом частном
случае:
D(E = = l4.Jn2/^- (Д.Ю.36)
1 4- mUQ(r'/
Последняя формула показывает, что вероятность туннельного эффекта в
указанных условиях возрастает с уменьшением высоты барьера Uq и его
ширины а.
Если энергия частицы Е много меньше высоты потенциального ба-
рьера Uq, а его ширина а достаточно велика, так что справедливо нера-
венство ха 1, то выражение (Д. 10.34) для коэффициента прохождения
значительно упрощается:
4&х \2
р+х2;
ехр (—2ха)
или
D « 4g(tZ° ехр Г-^У2т(С7о-£) •
Ц) L
(Д.Ю.37)
(Д.10.38)
Иначе говоря, вероятность прохождения через «широкий» потенциаль-
ный барьер (ха 1) экспоненциально уменьшается с ростом его ши-
рины а.
Вопрос о знаке кинетической энергии частицы в диапазоне коорди-
нат 0 х а разрешается также, как аналогичный вопрос для «клас-
сически запрещенной» области (см. дополнение 10.1). Измерение ко-
ординаты микрочастицы (например, электрона) всегда сопряжено с
воздействием на эту частицу, что вызывает изменение ее импульса и
206
Дополнения к лекции 10
энергии. Можно показать, аналогично выполненному в дополнении 10.1,
что минимальное изменение энергии частицы будет превышать абсолют-
ную величину разности |Е - £7о | •
Туннельный эффект объясняет множество удивительных физиче-
ских явлений, которые невозможно объяснить в рамках классической
теории. Это, например, автоэмиссия электронов из металла (см. до-
полнение 10.3), альфа-распад атомных ядер, термоядерные реакции в
центрах звезд и т. д. Туннельный эффект широко используется в совре-
менной наноэлектронике при создании сложных гетер о структур в инте-
гральных схемах для микропроцессоров.
10.3. Автоэлектронная эмиссия электронов
с поверхности металла
Экспериментальные исследования показали, что если приложить
перпендикулярно поверхности металла постоянное внешнее электриче-
ское поле достаточно большой напряженности 8, то происходит выход
электронов из металла через его поверхность при комнатной темпера-
туре. Это явление называется автоэлектронной или холодной эмис-
сией.
Для осуществления холодной эмиссии вектор напряженности внеш-
него электрического поля 8 должен быть направлен из окружающего
пространства к поверхности металла. Тогда электрическое поле создает
силу, приложенную к электрону проводимости, равную F = —е8, и на-
правленную изнутри металла к его поверхности. Можно предположить,
что при достаточно большой силе F электрон проводимости может пре-
одолеть потенциальный барьер, созданный ионами металла, который
описывался в лекции 4. Таким образом возникнет эмиссионный ток
электронов с поверхности металла.
Для вычисления формы потенциального барьера на поверхности
металла примем во внимание, что при удалении электрона в металле
остается нескомпенсированный положительный электрический заряд е,
который взаимодействует с уходящим электроном. Этот вклад во вза-
имодействие может быть учтен с помощью так называемой силы элек-
!-, х „ х н
1 А
+е -е
Металл Вакуум
Рис. Д.10.4. Схема образования силы электрического изображения, действующей
на электрон проводимости, уходящий из металла
трического изображения между выходящим из металла электроном и
симметрично расположенной «дыркой» — положительным элементарным
зарядом е (см. рис. Д.10.4).
Дополнения к лекции 10
207
Таким образом, на электрон проводимости, уходящий из металла,
действует суммарная сила, направленная перпендикулярно поверхности
металла, модуль которой равен
е2
(Д.10.39)
где х — расстояние от электрона до поверхности металла.
Можно полагать, что электрон находится в поле с эффективной по-
тенциальной энергией вида
е
U = UQ-e£x-—.
4х
(Д.10.40)
Это означает, что внешнее электрическое поле £, накладываясь на поля
ионов металла, превращает прямоугольную потенциальную «ступень»
(см. рис. 4.6 в лекции 4) в барьер, изображенный на рис. Д.10.5. Этот
Рис. Д.10.5. Потенциальный барьер для электронов проводимости вблизи по-
верхности металла при наложении внешнего электрического поля.
Жирной штриховой линией изображена функция (Д.10.40). Ав — работа выхода, Ер —
энергия Ферми, а — толщина потенциального барьера для энергии электрона Е = Ер
потенциальный барьер имеет треугольный профиль с закругленной вер-
шиной из-за последнего члена в функции (Д. 10.40).
Взяв производную от функции (Д. 10.40), приравняв ее нулю и решив
получившееся уравнение, мы найдем координату xq вершины потенци-
ального барьера, препятствующего выходу электронов проводимости из
металла:
х0 = ^£~1/2. (Д.10.41)
208
Дополнения к лекции 10
Подставляя координату (Д. 10.41) в выражение (Д. 10.40), мы получим
максимальное значение потенциальной энергии:
и = и0 - \/ёз 51/2.
(Д.10.42)
По рис. Д.10.5 видно, что электрон проводимости, обладающие мак-
симально доступной энергией должен для выхода из металла пре-
одолеть потенциальный барьер высотой
Ав
(Д-10.43)
Из выражений (Д.10.42) и (Д.10.43) следует, что с ростом напряжен-
ности £ приложенного электрического поля потенциальный барьер пони-
жается. Таким образом, при некотором значении £о барьер должен ис-
чезнуть и начаться эмиссия электронов из металла. Оценки по формуле
(Д. 10.43) дают для большинства металлов значения Eq порядка 108 В/см.
Например, в результате экспериментальных исследований фотоэффекта
была определена работа выхода для поликристаллического вольфрама
равная 4,3 эВ. Приравняв нулю выражение (Д.10.43) при Ав = 4,3 эВ,
получим соответствующее пороговое значение напряженности электри-
ческого поля £о ~ М • Ю8 В/см, при котором должна начаться эмиссия
электронов из вольфрама. Однако, согласно опытам Милликена, замет-
ный ток холодной эмиссии наблюдался уже при напряженности электри-
ческого поля ~ 106 В/см, т.е. на два порядка меньше.
Согласие с результатами экспериментов достигается, если объяснить
холодную эмиссию туннельным эффектом, т.е. прохождением электро-
нов проводимости сквозь потенциальный барьер на поверхности металла,
изображенный на рис. Д.10.5. В дополнении 10.2 было получено выра-
жение коэффициента прохождения через прямоугольный потенциальный
барьер (Д. 10.35). В случаях, когда напряженность электрического поля
значительно меньше значения £о> можно воспользоваться приближен-
ной формулой (Д. 10.38) и проинтегрировать коэффициент прохождения
по толщине барьера:
D = Dq ехр
d(F)
I х/вд
о
— Edx
(Д.10.44)
Интегрирование проводится по диапазону координаты ж, правая гра-
ница которого d зависит от энергии Е туннелирующего электрона. Ко-
ордината правой границы d определяется уравнением
U(x = d)=E.
(Д.Ю.45)
Пренебрегая последним членом в выражении (Д. 10.40), что незначи-
тельно влияет на окончательный результат, получим решение уравнения
(Д.10.45):
d = (С70 ~Е)/е (Д.10.46)
О
Дополнения к лекции 10
209
Вычисление интеграла (Д. 10.44) дает коэффициент прохождения
D = Do ехр
4(С70 - Д)3/2
ЗеК8
= ехр
(Д.10.47)
где £т — константа, зависящая от работы выхода данного металла.
Плотность тока автоэмиссии j пропорциональна коэффициенту про-
хождения (Д. 10.44), поэтому может быть выражена в виде экспоненци-
альной зависимости от величины внешнего электрического поля:
j = jo ехр
£т А
(Д.Ю.48)
Экспериментальные исследования подтвердили экспоненциальный
характер зависимости j(£), которая обусловлена туннельным эффектом
через потенциальный барьер на поверхности металла. Таким образом,
механизм холодной эмиссии объясняется квантовой теорией.
Лекция 11
АТОМ ВОДОРОДА
11.1. Гамильтониан атома водорода
Принципы квантовой механики, изложенные в предыдущих ,
лекциях, позволяют перейти к анализу свойств и характеристик
атомов. Начнем с наиболее простого — атома водорода.
Атом водорода имеет самый простой состав — он содержит
1 электрон, его ядро (протон) имеет положительный элементар-
ный заряд и массу приблизительно в 1836 раз больше массы элек-
трона те.
В лекции 7 было показано, что размер атомного ядра примерно
на 4 порядка меньше размера атома, поэтому будем полагать элек-
трон и ядро точечными частицами. Взаимодействие между элек-
троном и ядром описывается сферически симметричной функцией
потенциальной энергии:
Ц(г) = --, (11.1)
г
где г — расстояние между электроном и ядром.
Из теоретической механики известно, что задача о взаимодей-
ствии двух частиц сводится к задаче движения одной частицы с
приведенной массой в центральном поле 17(г). Приведенная масса
системы «электрон+атомное ядро» выражается формулой
ТП^ ТП N
------------------------------------
me + win
где win — масса атомного ядра.
Функция Гамильтона такой системы записывается в виде сум-
мы кинетической и потенциальной энергий:
Я=£- + Я(г). (11.3)
zmg
Так как у атома водорода win = 1836 те, то приведенная масса то
приближенно равна массе электрона те с относительной погреш-
(И.2)
11.2. Решение уравнения Шредингера для атома водорода 211
ностью « 5-10“4. Отсюда следует, что с этой точностью в функции
Гамильтона (11.3) величину р можно рассматривать как импульс
электрона, а приведенную массу mg заменить на массу электрона
те. Кроме того, центр масс атома можно полагать совпадающим
с ядром (протоном), которое остается практически неподвижным.
Начало отсчета координаты г совмещено с центром масс.
11.2. Решение уравнения Шредингера для атома водорода
Рассмотрим стационарные состояния атома водорода. Для это-
го требуется сначала составить уравнение Шредингера (10.5), ре-
шение которого должно дать волновые функции стационарных со-
стояний и значения энергии в этих состояниях.
Оператор Гамильтона атома водорода получается заменой в
функции (11.3) кинетической и потенциальной энергий соответ-
ствующими операторами, согласно (9.17) и (9.11):
Л2 е2
2mg г
(И-4)
Уравнение Шредингера для стационарных состояний атома во-
дорода в декартовых координатах имеет вид
Л2 / д2,ф д2,ф д2,ф\ е2 \
(^2 + d^+dz^)~ y^2—y2~z2 ~ ( -5)
Аналитическое решение этого дифференциального уравнение
второго порядка в частных производных возможно в сферической
системе координат, где максимально используется сферическая
симметрия атома. При замене декартовых координат на сфери-
ческие уравнение Шредингера (11.5) преобразуется к следующему
виду:
Щ> + К2(г)ф = 0, (11.6)
где величина К2 (г) является функцией только радиальной коор-
динаты г:
К\г) = ^(е + -\. (11.7)
п,£ \ Г J
Лапласиан А в сферических координатах выражается формулами
(9.38)-(9.41) в лекции 9.
Использование сферических координат позволяет разделить
переменные. Представим искомую волновую функцию стационар-
ного состояния в виде произведения
^ = аду(б,^), (И.8)
212
Лекция 11. Атом водорода
где -Н(г) — радиальная часть, a Y(0, ср) — угловая часть волновой
функции.
Волновая функция в виде (11.8) подставляется в (11.6) и
г2
обе части этого уравнения умножаются на величину —-.
B(r) У(0,<р)
В результате получается
г*Д^(г)
Я(г) +гл У((М ’ 111Я)
где Д/? — радиальная часть (9.40) оператора Лапласа, Ду — его
угловая часть (9.41).
Левая часть последнего уравнения зависит только от расстоя-
ния электрона до ядра г, правая — только от углов 0 и (/?. Для
того чтобы уравнение (11.9) удовлетворялось во всех точках про-
странства, правая и левая часть должны равняться одной и той же
константе. Каждую часть приравняем некоторой постоянной £.
Таким образом, уравнение (11.6) превращается в систему двух
уравнений:
ДдЯ(г) + (к2 - R(r) = 0, (11.10)
ДуУ(0,<^)+ £У(0,у>) = 0. (11.11)
Согласно соотношению (9.42), оператор Ду отличается от опера-
тора квадрата момента импульса L2 лишь постоянным множите-
лем —Л2. Следовательно, уравнение (11.11) с точностью до посто-
янного множителя совпадает с уравнением (9.44) на собственные
функции оператора L2. Его решением в виде ограниченных функ-
ций являются сферические функции (9.53), рассмотренные в лек-
ции 9, примеры которых приведены в табл. 9.2. Точнее говоря,
угловая часть волновой функции Y(0, (/?) представляет собой сфе-
рическую функцию Yim(0,(p), которая содержат два дискретных
параметра — квантовые числа I и т.
Из сравнения уравнений (9.44) и (11.11), а также соотношений
(9.42) и (9.51) следует, что постоянная интегрирования £ выра-
жается через орбитальное квантовое число
£ = Z(Z + 1). (11.12)
Подставим постоянную (11.12) в радиальное уравнение (11.10)
и преобразуем его к следующему виду:
d2R 2dR 2m0 („ е2 Л2Ш + 1)\ п 1О.
ТТ + -7" + -^ \Е+--------------Т^-22 Д = 0- ПЛЗ
drz г dr riz \ г 2mor2 J
11.2. Решение уравнения Шредингера для атома водорода 213
Подробное решение радиального уравнения (11.13) изложено в
курсах квантовой механики. Здесь приведем основные результаты
решения, которые потребуются для описания физических свойств
атома водорода.
Вид решения уравнения (11.13) зависит от знака энергии Е
электрона. Для положительного значения Е > 0 спектр энергии
непрерывный. В частности, в стационарные состояния с энер-
гией Е > 0 электрон переходит при ионизации атома водорода.
При этом электрон может удалиться от протона на неограничен-
но большое расстояние. В таких состояниях кинетическая энер-
гия электрона может принимать в принципе любые значения из
континуума Е > 0. Заметим, что и в этой физической системе
инфинитному движению соответствует непрерывный спектр энер-
гий.
Если Е < 0, то спектр стационарных состояний является дис-
кретным. Эти состояния характеризуют финитное движение элек-
трона внутри атома водорода.
Решения радиального уравнения — радиальные волновые
функции связанных состояний электрона в атоме водорода — мо-
гут быть выражены следующим образом:
RM = Сп|ехр (-0MJM (И.14)
где для краткости записи введена замена переменной
2г
Р=— • (П-15)
пао
Параметр
а0 =----? и 0,529 • 1СГ8 см (11.16)
meez
называется первым воровским радиусом, его физический смысл
изложен ниже.
Функции (р) являются обобщенными полиномами Лагер-
ра. Эти специальные функции подробно рассматриваются в курсе
математической физики, далее будут приведены в явном виде
частные случаи для состояний, наиболее часто встречающихся в
физических задачах. Наконец, постоянные Cni — коэффициенты
нормировки, которые также приводятся ниже.
Заметим, что радиальные волновые функции зависят от двух
целых параметров — квантовых чисел пи/. Параметр I был вве-
ден в ходе решения исходного уравнения Шредингера в радиаль-
ное уравнение (11.13). Второй дискретный параметр п появился
при решении уравнения (11.13) из-за условия ограниченности (ко-
нечности) волновой функции при 0 г оо.
214
Лекция 11. Атом водорода
Параметр п называется главным квантовым числом и может
принимать в принципе любые значения из натурального ряда
п= 1, 2, 3, ... (11.17)
В ходе решения уравнения (11.13) выясняется, что орбиталь-
ное квантовое число I в радиальной волновой функции (11.14) мо-
жет иметь лишь конечное количество значений, ограниченное ве-
личиной главного квантового числа:
I = 0, 1, 2, ..., n- 1. (11.18)
Теперь можно записать общий вид волновой функции (11.8):
фп1т(.гД,1р) = Rnltr'iYhn&ip). (11.19)
Так как волновая функция (11.19) характеризует финитное
движение электрона внутри атома, то она должна нормироваться
на единицу. Применим правило нормировки (9.4) к функции
V?(r, 0,99), используя разделение радиальной г и угловых 0, ср ко-
ординат. Элементарный объем трехмерного пространства dV вы-
разим через сферические координаты:
dV = г2 sin# dr dd dip. (11.20)
Тогда уравнение нормировки
ty(r,0,4>)\2dV = l
все прост-
ранство
разобьется на два независимых уравнения: (9.55) и
оо
R2nl(r)r2 dr = 1. (11.21)
о
Уравнение (9.55) свидетельствует, что угловая часть волновой
функции Yim уже нормирована на единицу. Вычисление ин-
теграла (11.21) дает явный вид коэффициента Cni радиальной ча-
сти (11.14), который можно записать в виде
2 \3 (^ — Z — 1)!
тшо / 2п[(п + Z)!]3 ’
(11.22)
Подставив (11.22) в (11.14), мы получим явное выражение для
радиальной части волновой функции 2^/(г). Несколько радиаль-
11.2. Решение уравнения Шредингера для атома водорода 215
ных волновых функций для малых значений квантовых чисел п
и I приведены в дополнении 11.1.
Теперь, используя выражения (11.19), (11.14), (11.22) и (9.53),
можно записать явный вид волновой функции стационарного со-
стояния электрона в атоме водорода:
I з
^п/т(г,ад = (-i)fc+1y(—) 2(n[(n + z)q3ехр(-0х
XplQn^(р)У'Z 4%(?+P/|m|(C0S ехр
где переменная р связана координатой г выражением (11.15).
Мы получили, что эта волновая функция зави-
сит от трех дискретных параметров: квантовых чисел n, I и т,
возможные значения которых заданы наборами значений (11.17),
(11.18) и (9.54). Часто для краткости говорят, что тройка кванто-
вых чисел n, I и m определяет стационарное состояние электрона
в атоме водорода.
Перейдем к собственным значениям оператора Гамильтона
(11.4), т.е. к энергиям найденных стационарных состояний. Тре-
бование ограниченности волновой функции V>nfrn(r> 0, V7) приводит
к следующему значению энергии электрона в стационарном состо-
янии: j
Следует помнить, что эта величина является суммой кинетической
и потенциальной энергий электрона в атоме водорода.
Расчет коэффициента тое4/2Л2 показывает, что он совпадает с
характерной энергией Ридбрега Ry « 13,6 эВ, которая входит в вы-
ражение для энергии атома водорода в первом постулате Бора (8.7).
Таким образом, при решении уравнения Шредингера о стационар-
ных состояниях атома водорода получен результат, уже подтвер-
жденный экспериментами. Иначе говоря, общий метод квантовой
теории позволил обосновать существование стационарных состоя-
ний, которые ранее постулировались Бором при создании им пер-
вой неклассической модели атома водорода.
Дискретный спектр отрицательных значений Еп соответствует
тому, что эти энергии характеризуют связанные состояния элек-
трона.
Выражения (8.7) и (11.23) означают, что с ростом главного
квантового числа энергии стационарных состояний возрастают не-
равномерно, значение Е = 0 является точкой сгущения энерге-
тических уровней. Характер спектра определяется формой функ-
216
Лекция 11. Атом водорода
ции потенциальной энергии (7(г) = — е2/г, что иллюстрируется
рис. 11.1.
Важной особенностью спектра (11.23) является то, что энер-
гии стационарных состояний зависят только от одного квантового
Рис. 11.1. Энергии стационарных состояний (энергетические уровни) атома во-
дорода и зависимость потенциальной энергии электрона от расстояния до центра
атома
числа — главного, в то время как волновые функции этих состо-
яний — от трех квантовых чисел. Другими словами, несколько
разных состояний электрона в атоме водорода характеризуются
одинаковой энергией.
Можно подсчитать количество разных состояний, имеющих
совпадающие величины энергии. Для фиксированного орбиталь-
ного числа I количество разных значений магнитного числа равно
21+1. Но так как при заданном главном числе п орбитальное число
I принимает ряд значений (11.18), то искомое количество состоя-
ний выражается суммой арифметической прогрессии
п-1
52(2/ + 1) = п2. (11.24)
1=0
Таким образом, одинаковую энергию имеют п2 различных стацио-
нарных состояний. Говорят, что стационарные состояния атома
9
водорода п -кратно вырождены по энергии.
Естественно поставить вопрос: чем отличаются вырожденные
состояния, обладающие одинаковой энергией? Для этого прежде
всего следует выяснить, какие физические величины (кроме энер-
гии) имеют определенные значения в стационарных состояниях
атома водорода. В лекции 9 было установлено, что одновремен-
11.2, Решение уравнения Шредингера для атома водорода 217
но измеримые величины обладают общей системой собственных
функций, а их операторы коммутируют.
Подействуем на волновую функцию стационарного состояния
(11.19) оператором квадрата момента импульса (9.38). Этот опе-
ратор L2 содержит производные только по угловым переменным, и
радиальную часть волновой функции можно вынести из-под знака
оператора:
L2^nim(r, 0, <р) = Rni(r) L2Yim(0, <p).
Но, согласно лекции 9, угловая часть волновой функции
Yiml&p) является собственной функцией оператора L2. Таким
образом, волновая функция стационарного состояния
является одновременно собственной функцией оператора квадрата
момента импульса. Это значит, что в стационарных состояниях
электрон, кроме энергии Еп, выраженной формулой (11.23), имеет
определенное значение квадрата момента импульса L2 = Л2/(/ + 1),
значение которого определяется орбитальным квантовым числом Z.
В лекции 9 было доказано, что операторы квадрата момента
импульса L2 и проекции момента импульса Lz обладают общей си-
стемой собственных функций. Можно непосредственно подейство-
вать оператором Lz на волновую функцию (11.19) и убедиться, что
функции ,фп1т(г) 6, ¥>) также являются собственными функциями
оператора проекции момента импульса. Следовательно, в стацио-
нарных состояниях электрон обладает определенным значением
одной из проекций импульса Lz = hm, величина которой задана
магнитным квантовым числом т. Таким образом, вырожденные
состояния электрона с одинаковой энергией могут отличаться зна-
чениями квадрата момента импульса L2 и проекции момента им-
пульса Lz на некоторую выбранную ось Z.
Для сравнения заметим, что по классической теории у ча-
стицы, движущейся в центральном поле, сохраняется вектор мо-
мента импульса L (т.е. все 3 проекции). Согласно квантовой фи-
зике, у частицы в стационарных состояниях сохраняется квадрат
момента импульса и только одна из проекций момента импульса.
Мы установили физический смысл трех квантовых чисел ста-
ционарного состояния с волновой функцией 'фп1т(г^ в, главное
квантовое число п определяет значение энергии Еп, орбитальное
квантовое число I задает квадрат момента импульса L2, магнитное
квантовое число т дает величину проекции момента импульса Lz.
Еп = L2 = Н21(1 + 1), Lz = hm,
где квантовые числа могут принимать следующие значения:
п = 1,2,3,..., I = 0,1,2,..., п — 1, т = 0, ±1, ±2,..., ±Z.
218
Лекция 11. Атом водорода
Заметим, что квантовые числа являются независимыми вели-
чинами, хотя главное число ограничивает максимальное значение
орбитального, а орбитальное — максимальное значение магнит-
ного.
11.3. Основное состояние атома водорода
Рассмотрим стационарное состояние электрона в атоме водо-
рода с наименьшей энергией, т. е. основное состояние. Это состо-
яние задается следующими значениями квантовых чисел: п = 1,
I = 0, m = 0. Волновая функция основного состояния получается
подстановкой данных значений квантовых чисел в общее выраже-
ние (11.19):
2 / г \ 1
V’ioo(r) - Rio (г) Уоо = ~т^ ехР----“7== -
л/ \ 0,0 J у/4тг
= -Д— ехр (-—) • (11.25)
у 7гад \ «о /
Видно, что волновая функция основного состояния обладает
сферически симметричным распределением вероятности нахожде-
ния электрона в пространстве.
Энергия основного состояния равна Еп — —Ry « 13,6 эВ. Сле-
довательно, минимальная энергия, необходимая для того, чтобы
перевести электрон из основного состояния в свободное, равна
Ei = — Еп ~ 13,6 эВ. Эта величина называется энергией иониза-
ции атома водорода.
Заметим, что в состоянии, заданном волновой функцией
(11.25), квадрат момента импульса L2 и его проекции Lz могут
иметь только нулевые значения. Следовательно, основное состоя-
ние атома водорода кажется невырожденным. В следующей лек-
ции будет получено, что основное состояние двукратно вырождено
из-за квантования проекции спина.
В основном состоянии орбитальное число I = 0, следовательно,
модуль момента импульса также равен нулю. В классической фи-
зике нулевой момент импульса согласно определению L = [г, р]
возможен в следующих случаях: 1) г = 0, 2) р = 0, 3) векторы г и
р параллельны (или антипараллельны). Таким образом, согласно
классической теории электрон или находится в центре ядра, или
неподвижен, или постоянно удаляется от центра атома, или, нако-
нец, совершает колебания вдоль прямой линии, проходящей через
ядро. На самом деле ни один из перечисленных вариантов не реа-
лизуется. Таким образом, остается сделать вывод, что классиче-
ской интерпретации основного состояния не существует. Иногда
говорят, что электрон делокализован в пространстве. Во всяком
случае, орбиты электрона в виде окружностей и эллипсов, которые
часто рисуют, не имеют никакого отношения к действительности.
11.3. Основное состояние атома водорода
219
Волновая функция (11.25) позволяет получить распределение
вероятностей нахождения электрона на различных расстояниях
от центра атома (от атомного ядра). Согласно физическому смы-
слу модуля волновой функции (9.3), вероятность нахождения элек-
трона в сферическом слое, ограниченного радиусами г и г + dr,
равна
( ‘It \
|V>ioo (г)|24тгг2 dr = -пг-ехр I-]dr.
а0 \ ао /
Следовательно, функцию
4г2 ( 2,г \
£>ю(г) = —г ехр I-----) (11.26)
ао \ ао /
можно назвать плотностью радиального распределения место-
расположения электрона в основном состоянии атома водорода.
Вид функции _Z?io(r) приведен на рис. 11.2.
Рисунок 11.2 поясняет физический смысл первого боровского
радиуса. Величина ао представляет собой расстояние от центра
атома водорода, на котором плотность радиального распределения
Рис. 11.2. Плотность радиального распределения для электрона в основном со-
стоянии атома водорода 2?ю(г). По горизонтали отложена величина г в единицах
первого боровского радиуса ао
Рю (г) достигает максимума. Другими словами, первый боров-
ский радиус является наивероятнейшим расстоянием электрона
до ядра в атоме водорода. По рис. 11.2 также видно, что вероят-
ность нахождения электрона на расстоянии от ядра г > а$ экспо-
ненциально уменьшается с ростом расстояния г.
Вполне определенной величиной является среднее расстояние
г электрона от центра атома. Вновь пользуясь вероятностным
220
Лекция 11. Атом водорода
смыслом волновой функции, вычислим величину г для основного
состояния атома водорода:
оо
г = [ г|^юо|2 dV = X [ г3 ехр \——]dr — 1,5 Go- (11.27)
J J \ «о /
0
Среднее расстояние г превышает величину gq из-за асимметрии
радиального распределения (см. рис. 11.2).
11.4. Возбужденные состояния атома водорода
Все стационарные состояния с главным квантовым числом
п > 1 являются возбужденными, так как имеют энергию, боль-
шую, чем в основном состоянии. Энергии возбужденных состоя-
ний выражаются формулой
Еп = -Ц (п>1),
совпадающей с (8.7) первого постулата Бора. Как уже было пока-
зано в лекции 8, этот дискретный набор энергий позволяет теоре-
тически рассчитать длины волн всех спектральных серий излуче-
ния атома водорода (см. табл. 8.1 и рис. 8.2).
Для анализа пространственного распределения координат
электрона в различных стационарных состояниях воспользуемся
вероятностным смыслом волновой функции (11.8). Величина
|^п/т(^5 #5 <^)|2r2 sin 0 dr dd dtp (11.28)
представляет собой вероятность нахождения электрона в окрест-
ности точки с координатами (г, #,99), в области пространства с
объемом
dV = г2 sin#dr d0dtp. (11.29)
Обозначим dQ телесный угол, соответствующий элементар-
ному объему (11.29), т.е. угол, под которым виден объем dV из
начала координат:
dQ ^smededtp (11.30)
и перепишем вероятность (11.28) в виде
\Rni(r)\2r2dr -|У/т(0,<< dtl. (11.31)
Интегрирование по полному телесному углу дает нам вероят-
ность обнаружения электрона в сферическом слое, ограниченном
радиусами г и г + с/r, которую выразим через функцию плотности
вероятности радиального распределения Dni(r) следующим обра-
зом:
\Rnltr)\2r2dr = Dnl(r)dr. (11.32)
11.4. Возбужденные состояния атома водорода 221
Примеры функций радиального распределения для малых зна-
чений квантовых чисел п и I приведены на рис. 11.3.
Для стационарных состояний исторически сложилась система
кратких обозначений, в которой главное квантовое число п вы-
ражается цифрой, а орбитальное число I обозначается латинской
Рис. 11.3. Функции плотности вероятности радиального распределения Dni(r)
электрона в стационарных состояниях атома водорода:
1s (п = 1, I = 0), 2s (п = 2, I = 0), 3s (п = 3, I = 0), 4s (п = 4, I = 0), 2р (п = 2,
I = 1), Зр (п = 3, I = 1), 4р (п = 4, I = 1), 3d (п = 3, I = 2), 4d (п = 4, I = 2), 4/
(п = 4, I = 3). По горизонтали отложена радиальная координата г в единицах ао
буквой согласно табл. 9.1 (см. лекцию 9). В частности, основное
состояние обозначается 15. Магнитное квантовое число в таких
кратких обозначениях не указывается.
Интересной особенностью графиков на рис. 11.3 является на-
личие узлов функции радиального распределения Dni(r). Иначе
говоря, для определенных значений координаты г функция Dni(r)
принимает нулевые значения. Эти значения являются радиусами
сфер, вблизи которых вероятность нахождения электрона близка
к нулю. Количество узловых сфер равно п — I — 1, что следует
из анализа радиальных волновых функций и просматривается на
рис. 11.2.
Среднее расстояние электрона г от центра атома в возбужден-
ных стационарных состояниях вычисляется аналогично (11.27) и
222
Лекция 11. Атом водорода
выражается общей формулой, содержащей квантовые числа п и I:
Г = I r^rtfr2 dr = у [Зп2 - 1(1 + 1)]. (11.33)
Числовые значения среднего расстояния г для нескольких возбу-
жденных состояний приведены в табл. 11.1.
Таблица 11.1. Средние расстояния электрона от центра атома
в возбужденных стационарных состояниях
Главное квантовое число п Орбитальное квантовое число 1 Среднее расстояние, выраженное в боровских радиусах г/ао
2 0 6
2 1 5
3 0 13,5
3 1 12,5
3 2 10,5
4 0 24
4 1 23
4 2 21
4 3 18
Формула (11.33) и данные табл. 11.1 демонстрируют, что рас-
стояние электрона от центра атома квадратично возрастает с уве-
личением главного квантового числа п. Это значит, что с ростом
энергии Еп стационарного состояния атом «распухает», что должно
сказываться на его химической активности.
Теперь рассмотрим угловое распределение вероятности место-
нахождения электрона. Запишем вероятность того, что электрон
находится в телесном угле c/Q, т. е. вблизи луча, заданного углами
в и (р. Для этого следует проинтегрировать выражение (11.31) по
радиальной координате в интервале 0 г < оо и получить
|У/то(0)¥>)|2<Ю. (11.34)
Таким образом, квадрат модуля угловой части волновой функции
является плотностью вероятности углового распределения элек-
трона в атоме водорода. Из вида сферических функций (см.
табл. 9.2) следует, что величина |У/т(0,</>)|2 не зависит от азиму-
тального угла </?. Это означает, что угловое распределение вероят-
ности местонахождения электрона обладает симметрией вращения
11.4. Возбужденные состояния атома водорода 223
относительно оси Z, для которой определена проекция импульса
Lz данного стационарного состояния. Обратим внимание, что вид
функции углового распределения 9?)|2 не зависит от глав-
ного квантового числа.
Плотность вероятности углового распределения (/>)|2
удобно изображать в полярной системе координат. При этом по
направлению, заданному углами в и 99, откладывается величина
m = +1
m = +2 m = +1
w = +3 w = +2 w = +l
Рис. 11.4. Полярные диаграммы углового распределения местонахождения элек-
трона в стационарных состояниях атома водорода. На рисунке изображены се-
чения тел вращения, проходящие через ось Z
|У/т(0, (/?)|2. На рис. 11.4 приведены полярные диаграммы плот-
ности вероятности углового распределения для стационарных со-
стояний с орбитальными числами I = 0,1, 2, 3.
Стационарные состояния с орбитальным числом I = 0 назы-
ваются ^-состояниями. По рис. 11.4 видно, что они все обладают
сферической симметрией, независимо от величины главного кван-
тового числа.
Угловые распределения |У/т(0,^)|2 с орбитальным числом I >
> 0 характеризуются анизотропией. В частности, состояния с
магнитным числом \m\ = I обладают максимумом плотности ве-
роятности в плоскости, перпендикулярной оси Z. Форма углового
распределения не зависит от знака магнитного квантового числа.
Функции (0, <р) |2 с I > 0 имеют узловые поверхности (т.е.
поверхности, на которых плотность вероятности нахождения элек-
трона равна нулю) в виде конусов, причем количество этих поверх-
224
Лекция 11. Атом водорода
ностей, как следует из свойств сферических функций, равно I — |т|,
что наблюдается на рис. 11.4.
Совокупность конических и сферических узловых поверхно-
стей и пространственное распределение вероятности
</?)|2Г2 Sin0
характеризует неклассическое поведение электрона в атоме водо-
рода.
В заключение лекции заметим, что теория атома водорода лег-
ко распространяется на одноэлектронные ионы, называемые водо-
родоподобными атомами (см. дополнение 11.4).
Задачи к лекции 11
1. Вычислить первый боровский радиус ао, энергию Ридберга Ry и
постоянную Ридберга в обобщенной формуле Бальмера, пользуясь фун-
даментальными константами.
2. Вычислить постоянные Ридберга для обычного вородода и дейте-
рия, пользуясь фундаментальными константами.
3. Найти максимум радиального распределения электронной плотно-
сти в основном состоянии атома водорода.
4. Вычислить среднее расстояние электрона от ядра атома водорода
в основном состоянии.
5. Вычислить среднее расстояние электрона от ядра атома водорода в
стационарном состоянии, заданнохм квантовыми числами п = 2 и I = 0.
6. Атом водорода, переходя из возбужденного состояния в основное,
испускает последовательно два фотона с длинами волн 6563 А и 1216 А.
Найти главное квантовое число исходного состояния.
7. Поток свободных электронов с кинетической энергией 13 эВ стал-
кивается с атомами водорода. Рассчитать спектр излучения.
8. Вычислить энергию связи единственного электрона двухкратно
ионизированного атома лития.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 11
11.1. Радиальные волновые функции
стационарных состояний атома водорода
Решение радиальной части стационарного уравнения Шредингера
для атома водорода
ДлЯ(г) + [к2 - R(r) = О
выражается через обобщенные полиномы Лагерра:
Т?п/(Р) = Cnl ехр (Д.Ц.1)
где аргумент р связан с координатой г формулой (11.15).
Обычные полиномы Лагерра р-й степени определяются следующей
формулой:
dp
ьР(х) = ех—(е.-“хР). (Д-11.2)-
При этом для значения параметра р = 0 полагается, что L$(x) = 1.
Для примера запишем несколько полиномов Лагерра низших степе-
ней в явном виде:
L\(x) = 1 — х, L2(x) = х2 — 4ж+2, L3 = —т3 + 9з:2 —18т+6. (Д.11.3)
Обобщенный полином Лагерра может быть определен через обычные
полиномы Лагерра следующим выражением:
dk
Q*(x) = -^Lp{x). (Д.11.4)
Как видно из (Д.11.4), обобщенный полином Лагерра характеризу-
ется двумя целочисленными параметрами, которые указываются в виде
верхнего и нижнего индексов. Для вычисления явного вида обобщенных
полиномов Лагерра можно использовать следующую формулу:
тэ’ dp k
= (-l)k7-^exx-k-—e~xx’> (Д.11.5)
H (p — к)\ axp K
или представление этих полиномов в виде ряда
Qp(X) = §(~1)J+1 (P-fc-J)!(^ + W (ДЛ1’6)
226
Дополнения к лекции 11
Легко вычислить, например, что
С|(я) — “1> • ••, “ 4, ...
..., Q^x) = —Зя2 4- 18я — 18, ..., <Э|(я) =-6я4-18. (Д.11.7)
Для того чтобы получить радиальные части волновых функций
(Д.11.1) в явном виде, следует воспользоваться выражениями для обоб-
щенных полиномов Лагерра (Д.11.5) или (Д.11.6). Верхний индекс по-
линома к берется равным 21 4- 1, а нижний р — равным п 4- Z, где п и
I — главное и орбитальное квантовые числа соответственно.
Нормировочный коэффициент Cni определяется нормировкой волно-
вой функции на единицу (11.21) и выражается формулой (11.22).
Подставляя значения квантовых чисел пи!, запишем радиальные
части волновых функций стационарных состояний атома водорода для
нескольких низших значений главного и орбитального квантовых чисел:
2 / т \
Rio(r) = —7= ехр (---), (Д.11.8)
V«о V ао/
1 ( т \ ( Т \
7?2o(r) = “^(1_2^_)exp(_2^-)’ (Д-11-9)
у/2а§ \ / \ у
1 г ( т \
Й21^ = ^=?7'ехр (“тГ)’ (Д-11-10)
2у/6ад^о \ 2ао/
2 ( 2т 2т2 \ / т \
д30(г) = (1 - х— + д?д)ехр(_^Г )> (Д-11-11)
ЗуЗ(2д \ Зйо 2*ао/ \ Зао/
8 т ( т \ ( т \
Д31(Г) = ——- 1-_ ехр , (Д.11.12)
27у/6а%ао \ 6a0J \ Зао /
4 т2 ( г \
R32(r) =---===-7 ехр . (Д.11.13)
81^30^«о \ Зао/
11.2. Спектр излучения дейтерия
При описании атома водорода в лекции 11 задача о взаимодействии
двух частиц (электрона и протона) была сведена к задаче движения одной
частицы с приведенной массой
memp
т0 =-------
те 4- тр
(Д.11.14)
в центральном поле с потенциальной энергией вида
е2
U(r) =-----, (Д.11.15)
Г
где те и тр — массы электрона и протона соответственно, г — рассто-
яние между частицами.
Дополнения к лекции 11
227
В результате решения уравнения Шредингера для атома водорода
(11.5) были получены энергии стационарных состояний в виде дискрет-
ного спектра:
Еп = -Ц, (Д.11.16)
где характерная энергия Ридберга
Ry = (Д-11-17)
& П
выражается через приведенную массу ttiq.
Из-за значительного различия масс электрона и протона (тр &
~ 1836 те) приведенная масса (Д.11.14) мало отличается от массы элек-
трона, поэтому можно записать
те А тпе \
mQ = —------— « me 1-------.
l + me/mp \ rripj
(Д.11.18)
Во многих задачах такое различие масс в четвертом знаке несуществен-
но, и тогда приведенная масса (Д.11.14) заменяется массой электрона.
Интерес к расчету приведенной массы возник в ходе эксперимен-
тов по измерению точного значения массы атома водорода тн- Масс-
спектрометрия, описанная в лекции 1, и прецизионные методы аналити-
ческой химии давали различие в 0,0145%, что значительно превышало
погрешность измерения массы атомов. Для объяснения возникшей не-
увязки была выдвинута гипотеза о существовании тяжелого изотопа во-
дорода, атомы которого имеют массу вдвое большую, чем у атомов обыч-
ного водорода.
Методы ядерной физики позволили установить, что этот изотоп, на-
званный дейтерием, имеет атомное ядро, содержащее 1 протон и 1 ней-
трон. Этот изотоп оказался столь интересным, что получил особый хи-
мический символ D. Совокупность физических и химических методов
позволили установить, что доля дейтерия составляет примерно 1,5% в
естественной смеси изотопов водорода.
Масса ядра дейтерия — дейтрон — получена путем масс-спектро-
метрических исследований и составляет ntd ~ 2,0141 а.е.м ~ 3672 те.
Приведенная масса для атома дейтерия выражается аналогично фор-
мулам (Д.11.14) и (Д.11.18):
(ТП \
1------ ) . (Д.11.19)
mdJ
Несовпадение приведенных масс (Д.11.18) и (Д.11.19) влечет разли-
чие энергий Ридберга (Д.11.17) для обычного водорода и дейтерия, что
приводит к некоторому сдвигу их спектров излучения.
Как следует из анализа результатов оптической спектрометрии и ре-
шения уравнения Шредингера, длины волн спектральных линий атома
водорода выражаются формулой
А \п{
(Д.11.20)
228
Дополнения к лекции 11
где Hi и П2 — главные квантовые числа стационарных состояний, между
которыми происходит радиационный переход. Постоянная R связана с
энергией Ридберга прямо пропорциональной зависимостью (8.11):
(Д.11.21)
2тгс/г
Выражая энергию Ридберга через приведенную массу, получим, что кон-
станты R различаются для обычного водорода и дейтерия. Вычисления
дают, что
е^тР ( тПр \ л
Rh = -—1-----------е- ) « 109677 см-1,
4тгс/г \ Trip J
4 ~~~
е тпе
Rd = ~
4л сп?
(Д.11.22)
(Д.11.23)
109 707 см
Подставляя величины (Д.11.22) и (Д.11.23) в формулу (Д. 11.20) мы
обнаружим различие длин волн для двух изотопов водорода при фиксиро-
ванных значениях квантовых чисел и П2- Это означает, что спектры
обычного водорода и дейтерия сдвинуты относительно друг друга. Так
как Rb > Ян, то, в соответствии с (Д. 11.20), спектральные линии дей-
терия имеют более короткую длину волны.
Разность обратных длин волн пропорциональна разности постоян-
ных Ридберга:
11 ( 1 1 \
V- “ v- = («D - Ян) — - — Г (Д.11.24)
Ad Ан \п{ n^J
Следовательно, сдвиг длины спектральной линии дейтерия выразится
так:
ЛА = AhAd(#D - Ян) ( —2 2 )
\П1 п2/
Rd ~ Ян (П1П2)2
RdRh n2 “ ni *
(Д.П.25)
Для примера рассмотрим красную линию серии Бальмера, которая
образуется при переходе между стационарными состояниями с главными
квантовыми числами = 2 и п2 = 3. Вычисления по формуле (Д.11.25)
дают разность длин волн ДА « 1,8 А. Современные оптические спек-
трометры имеют достаточно высокую разрешающую способность, чтобы
надежно регистрировать такое различие длин волн.
Относительный сдвиг спектров излучения двух изотопов водорода
наблюдается экспериментально, причем измеряемая величина сдвига со-
впадает с результатами расчетов по вышеприведенной формуле (Д. 11.25).
Примечание. На Земле дейтерий, в основном, присутствует в со-
ставе тяжелой воды D2O, которая была открыта и изучена Гаральдом
Юри в 1932 г. Выделение тяжелой воды из природной смеси до сих пор
является сложной научно-технической задачей. Однако применение тя-
желой воды оказалось весьма важным для осуществления управляемой
цепной реакции деления атомных ядер.
Дополнения к лекции 11
229
11.3. Оценка неопределенности координаты электрона
в атоме водорода
Обозначим Аж неопределенность координаты электрона, входящего
в состав атома водорода. Значение Аж выразим из соотношения неопре-
деленностей Гейзенберга (6.3). Естественно, минимуму неопределен-
ности координаты (Аж)т1п соответствует максимум неопределенности
проекции импульса (Арж)тах. Если нас интересует оценка по порядку
величины, то можно записать:
(Arr)min ~ . (Д.11.26)
(^АРж)тах
В качестве оценки неопределенности (Арж)тах можно взять вели-
чину модуля импульса р, что соответствует 100%-ной неопределенности.
Электрон атома водорода является нерелятивистской частицей, поэтому
его импульс связан с кинетической энергией Екип следующим соотноше-
нием:
Р — \/2шеЕ,кин. (Д. 11.27)
В классической теоретической механике доказано, что для матери-
альной точки, движущейся в кулоновском поле, справедлива теорема ви-
риала, которая связывает кинетическую и потенциальную энергию про-
стым соотношением
U - -2ЕКИН. (Д.11.28)
Потенциальная энергия электрона U в атоме водорода зависит от
расстояния г до центра атома, т. е. от расстояния между электроном и
атомным ядром:
U = -~. (Д.11.29)
г
Однако как кинетическая, так и потенциальная энергия электрона
в атоме обладают неопределенностями. Это обусловлено тем, что кине-
тическая энергия является функцией импульса (Д.11.27), а потенциаль-
ная — функцией координат (Д. 11.29).
В квантовой механике доказано, что теорема вириала (Д.11.28) вы-
полняется для средних значений энергий:
и = -2ЁКИН. (Д.11.30)
С другой стороны, первый постулат Бора (8.7), изложенный в §8.2,
дает энергию электрона в основном состоянии (состоянии с самой низкой
энергией) атома водорода:
Е = -Ry « -13,6 эВ, (Д.11.31)
где величина Е включает в себя кинетическую и потенциальную энергию
и может быть представлена суммой
Е = й + Ёкин. (Д.И.32)
230
Дополнения к лекции 11
Отрицательный знак энергии (Д.11.31) означает, что абсолютная вели-
чина потенциальной энергии |С7| превышает кинетическую.
Из сравнения уравнений (Д. 11.30) и (Д.11.32) следует, что средняя
кинетическая энергия Еккн имеет тот же порядок, что и абсолютная
величина полной энергии электрона в атоме водорода:
Ёкин ~ \Е\ = Ry. (Д.11.33)
Тогда, заменив величину Екин в формуле (Д.11.27) на энергию Ry,
получим оценку
(Apz)max ~ x/2meRy. (Д.11.34)
Наконец, для искомой неопределенности координаты запишем
(A^)min ~ /9уп pv (Д.11.35)
V ^meRy
и вычислим порядок величины (Дт)1П1П ~ 10 27/\/10_27 • 10 • 10-12 ~
~ 10-8 см = 1 А. Это означает, что неопределенность координаты элек-
трона в атоме водорода совпадает по порядку величины с размером всего
атома. Как следствие, рисование орбит электронов внутри атома красиво,
но не имеет физического смысла.
11.4. Водородоподобные атомы
Вышеизложенная теория легко обобщается для водородоподобных
(или одноэлектронных) атомов, которые содержат один электрон и име-
ют ядро с электрическим зарядом Ze. Такие атомы, за исключением
атома водорода, являются, строго говоря, положительными ионами с
электрическим зарядом (Z — 1)е. Примерами водородоподобных ионов
являются однократно ионизированный атом гелия Не+, двукратно ио-
низированный атом лития Li+2 и т. д.
Единственный электрон в таких системах движется в поле с потен-
циальной энергией
Ze2
U(r) =------. (Д.11.36)
г
Следовательно, для нахождения стационарных состояний водородоподоб-
ных атомов гамильтониан (11.4) необходимо заменить на следующий:
Н = (Д.11.37)
2m г
Решение стационарного уравнения Шредингера аналогично вышеприве-
денному решению для атома водорода. Угловые части волновых функций
стационарных состояний также будут выражаться сферическими функ-
циями (9.53). Радиальные части волновых функций водородоподобных
атомов могут быть выражены в виде (11.14), если параметр (11.15) за-
Дополнения к лекции 11
231
менить на
2Zr
пао ’
(Д.11.38)
а нормировочный множитель (11.22) заменить следующим:
Z2Z\3 (тг —Z — 1)!
\тшо / 2п[(п 4- Z)!]3 ’
(Д.И.39)
Можно показать, что в стационарных состояниях с теми же кванто-
выми числами п и I средние расстояния электрона от центра атома г в
водородоподобных атомах уменьшатся в Z раз по сравнению расстояни-
ями (11.33) в атоме водорода:
Г = ^[Зп2 - /(/ + 1)].
(Д.И.40)
Это означает, что с ростом заряда ядра размеры водородоподобных ато-
мов уменьшатся обратно пропорционально числу Z.
Энергии стационарных состояний водородоподобных атомов предста-
вятся выражением
_m0Z2e4 = Z2Ry
2h2n2 n2
(Д.11.41)
Квадратичная зависимость энергии Еп от заряда атомного ядра при-
водит, в частности, к тому, что энергия ионизации однократно ионизиро-
ванного атома гелия Не+ составляет 4 Ry « 54,4 эВ, что подтверждается
экспериментами.
Теория водородоподобных атомов объясняет закономерности спек-
тральной серии Пикеринга, о которой упоминалось в лекции 8.
Помимо прочего, решение задачи о стационарных состояниях водоро-
доподобных атомов дает некоторую полезную информацию о характери-
стиках многоэлектронных атомов, для которых аналитическое решение
стационарного уравнения Шредингера не существует.
Лекция 12
МАГНИТНЫЕ СВОЙСТВА АТОМА ВОДОРОДА
12.1. Классическое гиромагнитное отношение
Рассмотрим классическую частицу (материальную точку) мас-
сы rriQ с электрическим зарядом д, которая равномерно движется
по окружности радиуса R. Ограничимся нерелятивистскими ско-
ростями, тогда момент импульса частицы, согласно определению,
представится следующим классическим выражением:
L = 777q[Rv],
где v — скорость частицы, R — ее радиус-вектор в системе коор-
динат, центр которой совмещен с центром окружности.
Модуль момента импульса этой частицы выражается так:
L = mQvR^ (12.1)
где v — модуль скорости частицы.
Направление вектора момента импульса L определяется по пра-
вилу правого винта так, как это показано на рис. 12.1.
Рис. 12.1. К выводу классического гиро-
магнитного отношения:
R — радиус-вектор частицы, v — скорость ча-
стицы. Нерелятивистская частица движется по
окружности радиуса R = |R|
Круговое движение заряженной частицы можно рассматривать
как виток с током, следовательно, движущаяся таким образом ча-
стица обладает магнитным моментом у,. Вектор магнитного мо-
12.1. Классическое гиромагнитное отношение
233
мента перпендикулярен плоскости витка с током, т. е. окружности,
по которой движется частица. Направление вектора /л определя-
ется по правилу правого винта относительно направления тока.
Таким образом, если заряд частицы q положительный, то векторы
L и /1 параллельны, если отрицательный — антипараллельйы.
Вычислим модуль магнитного момента, пользуясь его класси-
ческим определением:
1 q
Ц = -S,
с
где с — скорость света в вакууме.
Ток I выразим как заряд частицы, деленный на период ее вра-
щения:
(12.2)
1=1
где период Т представим отношением
_ 2kR
Т =-----.
v
Подстановка двух последних выражений в (12.2) дает модуль маг-
нитного момента в следующем виде:
qR
^TcV-
Теперь найдем отношение модулей магнитного момента клас-
сической ~
поделить
(12.3)
частицы и ее момента импульса. Для этого достаточно
уравнение (12.3) на (12.1):
Д = д
L 2тос
того, что векторы магнитного момента и момента им-
(12-4)
(12.5)
(12.6)
С учетом
пульса колинеарны, запишем связь этих векторов в виде
Q т
М 2т0с
Таким образом выяснилось, что векторы магнитного момента /л и
механического момента импульса L заряженной частицы, движу-
щейся по окружности, прямо пропорциональны друг другу. Коэф-
фициент пропорциональности является скалярной величиной
я
7 = о---’
2то с
которая называется гиромагнитным отношением.
Характерно, что величина 7 не зависит от радиуса траектории
и скорости движения, а определяется только массой то и элек-
трическим зарядом q частицы, т. е. собственными параметрами
объекта.
234 Лекция 12. Магнитные свойства атома водорода
Более подробные исследования показывают, что при произ-
вольной форме замкнутой траектории и неравномерном движении
частицы связь магнитного момента и момента импульса сохра-
няет вид (12.5). Более того, гиромагнитное отношение (12.6) со-
храняется и для тел произвольной формы, если пространственное
распределение в них массы и электрического заряда имеет одина-
ковый вид.
Движение электрона внутри атома не описывается траекто-
рией, поэтому вопрос о наличии у электрона магнитного момента
решается с помощью квантовой механики. Мы будем рассматри-
вать стационарные состояния, в которых у электрона атома водо-
рода одна из проекций орбитального момента импульса Lz имеет
определенное значение. При этом соответствующая проекция маг-
нитного момента равна
—е
Мг = 2^1'2’ (12’7)
где Lz — проекция орбитального момента на ось Z. Аналогично
связаны модули магнитного и орбитального (механического) мо-
ментов.
По причинам, которые выяснятся в следующих лекциях, наи-
более важной характеристикой магнетизма атомов является не мо-
дуль, а проекция магнитного момента на выделенное направление
в пространстве. Это направление, в частности, может быть задано
внешним электрическим или магнитным полем.
Выражение (12.7) означает, что для электрона, движущегося
в атоме, справедливо классическое гиромагнитное отношение, не-
смотря на неклассический характер движения электрона.
Величина проекции орбитального момента в стационарных со-
стояниях атома водорода имеет дискретный спектр значений Lz =
= hm, где m — магнитное квантовое число. Согласно (12.7), про-
екция магнитного момента также квантуется, т. е. принимает ряд
значений, пропорциональных магнитному квантовому числу
Hz = (12.8)
где параметр
eh
Mb = ~---
2mec
(12.9)
называется магнетон Бора,
Величина /хв определяется только фундаментальными конс-
тантами и равна приблизительно 0,927 • 1О-20 эрг/Гс.
Из формулы (12.8) становится ясным, почему квантовое число
т было названо магнитным. Проекция магнитного момента Hz,
согласно (12.8), может принимать 21 + 1 различных значений, из
которых I положительных и столько же отрицательных.
12.2. Опыт Штерна-Герлаха и магнито-механические эффекты 235
Эти выводы квантовой теории нуждаются в эксперименталь-
ном подтверждении. Необходимо обнаружить магнитный момент
электрона в стационарном состоянии атома и характер квантова-
ния его проекции.
12.2. Опыт Штерна-Герлаха
и магнито-механические эффекты
Опыты по измерению магнитного момента электрона базиру-
ются на том, что частица (или система частиц) с магнитным мо-
ментом при попадании в неоднородное магнитное поле начинает
двигаться ускоренно, что может быть зафиксировано регистрирую-
щими приборами.
Из классической электродинамики известно, что на систему,
обладающую магнитным моментом р, и помещенную в однородное
внешнее магнитное поле В, действует момент сил М, равный
М = [/1В]. (12.10)
Макроскопическая система с магнитным моментом р, (напри-
мер, виток с током или магнитная стрелка) в магнитном поле В
под действием момента сил М поворачивается. Для электрона в
атоме аналогичный эффект наблюдать не представляется возмож-
ным.
В классической физике установлено (см. дополнение 12.1), что
если внешнее магнитное поле В неоднородно, то на тело с маг-
нитным моментом действует сила
F = (mV)B, (12.11)
где скалярное произведение (jitV) представляет собой дифферен-
циальный оператор
/ 9 д д
Это значит, что проекция силы Fz имеет вид
„ _ дв, dBz dBz
Fz~^x дх +р,у ду + l2z dz‘
(12.12)
(12.13)
Аналогично с помощью выражений (12.11) и (12.12) записываются
остальные проекции силы: Fx и Fy.
Для измерения магнитного момента атома в стационарном со-
стоянии используется метод пропускания узких пучков атомов че-
рез неоднородное магнитное поле. Впервые эта методика была раз-
работана П.Л. Капицей и Н.Н. Семеновым в 1920 г. Эксперименты
по обнаружению магнитных моментов атомов были проведены в
236 Лекция 12. Магнитные свойства атома водорода
Германии в 1922 г. 0. Штерном (1888-1969) и В. Герлахом (1889—
1979). Принципиальная схема экспериментальной установки при-
ведена на рис. 12.2.
Прибор находился в сосуде, где предварительно создавался вы-
сокий вакуум. Исследуемое вещество помещалось в печку. Атомы
вещества из-за нагрева получали скорости порядка нескольких
Рис. 12.2. Схема эксперимента Штерна и Герлаха:
N и S — северный и южный полюсы постоянных магнитов, а) Проекция XZ. Пучки
атомов изображены штриховыми линиями. Угол расхождение пучков сильно преувеличен;
1 — печка (источник пучка атомов), 2 и 3 — диафрагмы, 4 — стеклянная пластина или
фотоэмульсия, б) Проекция YZ, 5— след нерасщепленного пучка атомов на фотоэмульсии
сотен метров в секунду и разлетались в разные стороны. Си-
стема диафрагм позволяла вырезать узкий пучок, который про-
ходил через область сильно неоднородного магнитного поля (см.
рис. 12.2а). Неоднородность поля должна быть существенной на
расстояниях порядка атомных размеров, т.е. 10-8см. Для со-
здания высокой степени неоднородности магнитного поля исполь-
зовалась специальная форма полюсных наконечников магнитов.
Один из них имел форму призмы с острым ребром, другой имел
проточенную канавку (см. рис. 12.26). Атомы, прошедшие через
область неоднородного магнитного поля, осаждались на стеклян-
ной пластине или оставляли след на фотоэмульсии.
Для описания движения атомов необходимо ввести систему ко-
ординат. Ось X совместим с пучком атомов, ось Z направим по
магнитному полю В, которое определяет ось физической анизо-
тропии пространства. Атомы, находящиеся в этом поле, должны
иметь определенную проекцию орбитального момента Lz.
На атомы, движущиеся между полюсами магнита, действует
сила (12.11). Для исследования свойств магнитного момента наи-
более существенна компонента силы (12.13), т.е. проекция силы
на направление магнитного поля. Компонента силы Fx ускоряет
или тормозит пучок, компонента Fy его расширяет вдоль оси Y, и
лишь компонента Fz может дать искомое расщепление пучка.
12.2. Опыт Штерна-Герлаха и магнито-механические эффекты 237
Величина расщепления пучка определяется средней проекцией
силы ____
= (12.14)
az
которая связана с усреденным градиентом компоненты поля Bz.
Атомы с определенной энергией, т. е. находящиеся в стационар-
ном состоянии, обладают только одной измеримой проекцией ор-
битального момента Lz, и следовательно, только одной проекцией
магнитного момента /j,z. Проекции Lx и Ly не имеют определен-
ных значений в стационарном состоянии атома и их средние зна-
чения Lx и Ly равны нулю, как это было показано в дополне-
нии 9.2. То же самое справедливо и для проекций магнитного
момента: ~jax =~ру = 0- Таким образом, выражение для отклоняю-
щей силы принимает вид (12.14).
Атомы, проходящие между полюсами магнита, обладают маг-
нитными моментами произвольной ориентации. Отклоняющая
сила (12.14) зависит от ориентации магнитного момента, следо-
вательно, от величины проекции магнитного момента p,z на на-
правление магнитного поля В.
Если проекция магнитного момента p,z квантуется по закону
(12.8), то пучок атомов водорода должен разделиться на 21 + 1
отдельных пучков, где I — орбитальное квантовое число. Пучок
атомов, находящихся в состоянии с квантовыми числами I = 0 и
m = 0, не должен отклоняться от первоначального направления.
Для атомов в возбужденных состояниях с I 0 количество пучков
должно быть обязательно нечетным.
Если же, согласно классической механике, проекция магнит-
ного момента /az принимает непрерывное множество значений в
интервале [—/х, р], то пучок атомов должен «размазаться», т. е. про-
сто ушириться вдоль направления оси Z.
Опыты, проведенные Штерном и Герлахом, дали результаты,
противоречащие обоим вышеприведенным предсказаниям. Пучок
атомов водорода, заведомо находящихся в основном состоянии
(т. е. не обладающих орбитальным моментом), расщеплялся в не-
однородном магнитном поле симметрично на два пучка. Анализ
результатов показал, что проекция магнитного момента pz ато-
мов водорода в основном состоянии равнялась магнетону Бора дщ-
Таким образом, было экспериментально доказано квантование
проекции магнитного момента, но характер квантования не
определялся проекциями орбитального момента.
Дополнительная информация о величине гиромагнитного отно-
шения для электрона была получена в исследованиях связи между
механическим и магнитным моментами атомов. Еще в 1915 г.
В. де Гааз (1878-1960), воспользовавшись идей А. Эйнштейна,
провел эксперимент, схема которого приведена на рис. 12.3.
238
Лекция 12. Магнитные свойства атома водорода
На тонкой кварцевой нити подвешивался тонкий образец в
форме цилиндра диаметром примерно 0,03 см и длиной 10 см. Об-
разец, изготовленный из ферромагнетика или парамагнетика, по-
мещался внутри соленоида, по которому пропускался ток. При до-
Рис. 12.3. Схема опыта Эйнштейна-де Гааза:
1 — цилиндрический образец, 2 — соленоид, 3 — кварцевая нить, 4 — зеркальце, 5 —
луч света, 6 — экран
статочно сильном токе магнитные моменты атомов в образце ори-
ентируются в направлении магнитного поля соленоида. Если из-
менить направление тока в соленоиде, то все магнитные моменты
меняют свою ориентацию на противоположную. При этом, со-
гласно классическому гиромагнитному отношению, механические
моменты атомов тоже должны изменить свое направление. Вслед-
ствие закона сохранения момента импульса цилиндрик, как целое,
должен повернуться и закрутить кварцевую нить. Этот эффект, в
принципе, похож на известный опыт с вращающимся велосипед-
ным колесом на скамье Жуковского, но во много раз более слаб.
Для усиления эффекта закручивания нити через соленоид про-
пускался переменный ток с частотой, равной собственной частоте
крутильных колебаний цилиндра. К нити крепилось маленькое
зеркальце, на которое направлялся узкий пучок света. По ампли-
туде колебаний светового пятна на экране можно определить угол
закручивания нити, а по измеренному углу рассчитать крутящий
момент силы и изменения момента импульса цилиндра.
В результате экспериментов де Газа на разных материалах
была обнаружена прямо пропорциональная связь между магнит-
ными и механическими моментами, но их отношение оказалось
вдвое больше классического гиромагнитного!
12.3. Спин
239
В том же 1915 г. С. Барнетт (1873-1956) обнаружил эффект
намагничивания быстро вращающихся стержней. При закручи-
вании их в противоположном направлении происходило их пере-
магничивание. Измеренное Барнеттом отношение магнитных и
механических моментов тоже дало величину, вдвое большую клас-
сического гиромагнитного отношения.
12.3. Спин
К 1925 г., кроме результатов опытов Штерна-Герлаха, Эйнш-
тейна-де Гааза и Барнетта, в атомной физике накопилось много
необъяснимых фактов.
С увеличением разрешающей способности спектроскопов было
обнаружено, что большинство спектральных линий представляют
собой мультиплеты — группы близко расположенных спектраль-
ных линий. Были открыты дублеты, триплеты и т.д. Иначе го-
воря, спектральные линии оказались образованными излучением,
состоящим из потоков фотонов с очень близкими длинами волн.
Эта особенность спектра была названа тонкой структурой. Тон-
кая структура была найдена даже в спектре атома водорода. Ли-
нии серии Лаймана оказались дублетами, линии серии Бальмера
демонстрировали еще более сложную тонкую структуру.
Еще более сложные спектральные картины возникали при воз-
действии на излучающий атом внешнего магнитного поля. Экспе-
риментальные исследования эффекта Зеемана, который будет рас-
смотрен в лекции 20, дали результаты, радикально отличающиеся
от предсказанных теорией Лоренца.
Все перечисленные трудности атомной физики были разре-
шены после того, как в 1925 г. С. Гаудсмит (1902-1979) и Дж. Улен-
бек (1900-1988) выдвинули гипотезу о вращении электрона вокруг
своей оси. Эта идея в принципе объясняла наличие у электрона
собственного механического момента (не зависимого от орбиталь-
ного), который получил название спин. Английское слово spin
означает «вращение» или «верчение». Вращение электрически за-
ряженного шарика должно обеспечить существование собственного
магнитного момента электрона.
Однако сразу же выяснилась несостоятельность классического
представления спина. Для того чтобы электрон обладал наблюда-
емыми параметрами (электрическим зарядом, массой покоя, соб-
ственным магнитным моментом), оказалось, что поверхность вра-
щающегося шарика должна иметь скорость значительно большую
скорости света (см. дополнение 12.2). Попытки модифицировать
классическую модель вращающегося электрона приводили к не-
преодолимым противоречиям с результатами экспериментов.
Таким образом, спин не может быть интерпретирован в рам-
ках классической теории как момент импульса вращающегося ша-
240 Лекция 12. Магнитные свойства атома водорода
рика и, следовательно, не является классическим вектором с тремя
определенными проекциями.
Согласно современным воззрениям спин является сугубо кван-
товым понятием. В. Паули ввел спин в квантовую механику, но
исключил в принципе возможность классического представления
спина.
В 1928 г. П. Дирак (1902-1984) показал, что существование
спина непосредственно следует из релятивистской теории элек-
трона. Явный вид оператора спина получен в квантовой меха-
нике (см. дополнение 12.3). Установлено, что каждая из элемен-
тарных частиц (и систем частиц) характеризуется определенным
квантовым числом 5, которое может принимать полуцелые и це-
лые положительные значения, включая ноль. В частности, для
электрона (а также для протона и нейтрона) спиновое квантовое
число 5 = 1/2.
Проекция спина на заданное направление в пространстве мо-
жет принимать 2s + 1 различных значений:
Sz = hms — —hs, —h(s -hl),..., hs. (12.15)
Для электрона (протона и нейтрона) ms равно 1.2 или —1/2,
следовательно,
Sz = ±J. (12.16)
Проекция модуля спина является дополнительной (внутрен-
ней) степенью свободы электрона.
Таким образом, стационарное состояние электрона в атоме во-
дорода характеризуется не тремя, а четырьмя независимыми кван-
товыми числами:
n, Z, т, Ш5, (12.17)
физический смысл которых определяется выражениями (8.7),
(9.51), (9.48) и (12.15).
Квантовое число s = 1/2, определяющее модуль спина, явля-
ется инвариантом и одним из важнейших параметров электрона,
наравне с его массой покоя и электрическим зарядом.
Существование спина обусловливает наличие у электрона соб-
ственного магнитного момента, величина которого не зависит от
орбитального квантового числа. Величина собственного магнит-
ного момента связана со спином не классическим гиромагнитным
отношением, а удвоенным. Иначе говоря, в стационарном состо-
янии проекция собственного магнитного момента электрона p,sz
выражается через проекцию спина Sz следующим образом:
(12.18)
- ~е Q
P'Sz —
mec
12.4. Полный момент импульса электрона 241
Учитывая квантование проекции спина (12.17) получаем
VSz = (12.19)
где /хв — магнетон Бора (12.9).
Это означает, что атом водорода даже в основном состоянии
обладает магнитным моментом. Если орбитальное квантовое чи-
сло равно нулю, то модуль орбитального момента электрона L ра-
вен нулю, следовательно, его проекция Lz = 0 и соответствующий
магнитный момент (12.4) также равен нулю. При этом магнитный
момент электрона определяется только спином, а его проекция nsz
на выделенное направление принимает два различных значения
противоположных знаков: ±//в- Этот вывод подтверждается ре-
зультатами опытов Штерна-Герлаха. Атомы водорода, в которых
электрон находится в состоянии с ms — 1/2, будут иметь проек-
цию магнитного момента —//в и в неоднородном магнитном поле
отклоняться от направления прямолинейного движения атомного
пучка. Другие атомы, в которых электрон находится в состоянии
с ms — —1/2, будут иметь проекцию магнитного момента про-
тивоположного знака и отклоняться в противоположную сторону.
В результате сформируются два пучка, наблюдаемые в экспери-
менте.
Таким образом, наличие спина у электрона и удвоенное ги-
ромагнитное отношение объясняет результаты опытов Штерна-
Герлаха, Эйнштейна-де Гааза и Барнетта.
Если же атом водорода находится в возбужденном стационар-
ном состоянии с орбитальным квантовым число I 0, то электрон
должен обладать не только собственным, но и орбитальным маг-
нитным моментом. Возникает вопрос о том, чему равна величина
полного магнитного момента, который будет зарегистрирован в
экспериментах.
Для решения этого вопроса следует вначале рассмотреть пол-
ный механический момент электрона в стационарном состоянии
атома водорода.
12.4. Полный момент импульса электрона
Выше было выяснено, что электрон в стационарном состоя-
нии атома обладает двумя моментами импульса: орбитальным и
собственным (спином). Первый может принимать различные зна-
чения, включая и равное нулю, второй имеет постоянный квадрат
модуля, согласно формуле (Д.12.26) дополнения 12.3. Введем пол-
ный момент импульса электрона, который складывается из орби-
тального и собственного.
В классической физике моменты импульса можно складывать
как векторы
J = L + S, (12.20)
242
Лекция 12. Магнитные свойства атома водорода
причем угол между складываемыми векторами может быть лю-
бым.
Задача сложения моментов импульса электрона осложняется
тем, что в стационарных состояниях каждый из моментов — ор-
битальный и спин — имеет только одну определенную проекцию:
Lz и Sz.
Метод сложения моментов излагается в курсе квантовой ме-
ханики. Здесь ограничимся изложением результатов, получен-
ных для суммирования орбитального момента и спина электрона
в атоме водорода.
В стационарных состояниях имеют определенное значение
квадрат модуля полного момента J2 и одна из его проекций Jz.
Квадрат модуля полного момента J2 квантуется по закону
J2 = + 1), (12.21)
где j — квантовое число модуля полного момента. Число j зависит
от орбитального числа I и связано с ним следующим образом:
3 =
при I О,
при I = О,
(12.22)
где s — квантовое число модуля спина, тождественно равное 1/2.
Очевидно, что все значения квантового числа j — полуцелые.
Таким образом, согласно (12.22), в состояниях с определенным
орбитальным числом I 0 квантовое число j для электрона может
принимать только два различных значения. Следовательно, при
заданном модуле орбитального момента L модуль полного момента
J может иметь только два различающихся значения:
Ji = h
Можно сказать, что, в отличие от классических векторов, ор-
битальный момент и спин могут складываться лишь двумя спосо-
бами.
Вторая строка в выражении (12.22) означает, что при нулевом
орбитальном моменте полный момент равен спину.
Связь модулей орбитального момента, спина и полного момента
иллюстрируется на рис. 12.4 с помощью векторной модели.
На рис. 12.4 приведен пример для электрона с орбитальным
квантовым числом I = 2, когда модуль орбитального момента L =
= hy/б. Величина hy/fi « 2,45 Л изображена вертикальным
отрезком, из верхнего конца которого как из центра проведена
дуга окружности радиусом S = Л\/3/2 « 0,866 Л, равным мо-
12.4. Полный момент импульса электрона
243
дулю спина. Из нижнего конца вертикального отрезка проводятся
дуги окружностей, радиусы которых равны всевозможным моду-
лям полного момента. Эти величины определяются по формуле
(12.21) при подстановке в них зна-
чений квантового числа j = 1/2,
3/2, 5/2 и т. д. Легко получить
геометрическим построением, что
только две такие дуги пересекут
дугу с радиусом S. Точки пере-
сечения ограничат отрезки, кото-
рые изображают модули полного
момента. В данном случае они
равны Ji « 2,96 h и J2 — 1,94 Л.
Вычисления по формулам (12.23)
дают совпадающие значения Ji =
= h.V^/2 И J2 = V15/2, чему,
согласно (12.21), соответствуют
значения j = 3/2 и j = 5/2. Та-
ким образом, векторная модель
Рис. 12.4. Схема сложения орбитального
момента и спина электрона, согласно век-
торной модели. Орбитальное число I = 2.
Штриховые дуги имеют радиусы, равные
модулю спина |S| и возможным значе-
ниям модулей полного момента |Ji|, | J2I,
которые определяются формулами (12.23)
иллюстрирует два возможных значения модуля полного момен-
та электрона при заданном модуле его орбитального момента.
Проекция полного момента Jz квантуется по правилу
Л = hmj. (12.24)
Квантовое число mj пробегает ряд значений от — j до j с ша-
гом 1, т. е.
mj = -j, -j + 1, • •-1, 1, • • j - 1, j- (12.25)
Так как, согласно (12.22), все значения квантового числа j —
полуцелые, то и все значения квантового число mj также полу-
целые.
244
Лекция 12. Магнитные свойства атома водорода
Можно вычислить, что при фиксированном значении кванто-
вого числа j число mj может принимать 2j +1 различных значе-
ний. Это означает, что для заданного значения модуля проекция
полного момента электрона проекция полного момента Jz может
иметь 2j + 1 различных значений.
На рис. 12.5 приведен пример построения проекции полного
момента импульса электрона по векторной модели для случая, ко-
гда квантовое число j = 7/2. При этом модуль полного момента
Рис. 12.5. Пример квантования проекции полного момента импульса электрона
с помощью векторной модели. Ось Z задает определенное направление в про-
странстве. Длины стрелок равны модулю полного момента импульса J
J — Л\/бЗ/2 « 3,97 К. Отрезок с такой длиной одним концом за-
крепляется в начале координат и поворачивается, причем фикси-
руются его проекции на ось, кратные величине К. Такое геометри-
ческое построение, выполненное на рис. 12.5 наглядно демонстри-
рует 8 возможных проекций полного момента импульса электрона
на направление, заданное осью Z. Такое же количество проекций
дает формула (12.25).
12.4. Полный момент импульса электрона 245
Используя данную векторную модель, следует помнить, что
векторы полного момента импульса в стационарных состояниях
атома водорода не располагаются в определенной плоскости, а мо-
гут занимать любое случайное положение на поверхности конуса.
Теперь можно вернуться к задаче вычисления магнитного мо-
мента электрона в атоме водорода.
Из предыдущего материала этой лекции следует, что в ста-
ционарных состояниях имеют определенные значение модуль J
и одна из проекций полного механического момента Jz. Следует
ожидать, что проекция полного магнитного момента p>z пропор-
циональна проекции полного механического момента Jz. Вопрос
о величине коэффициента пропорциональности возникает потому,
что для орбитального момента этот коэффициент представляет со-
бой классическое гиромагнитное отношение, а для собственного
момента — удвоенное гиромагнитное отношение.
В квантовой механике получено, что связь полного (эффектив-
ного) магнитного момента электрона и полного механического мо-
мента может быть записана в следующем виде:
—е
= дъ— Л, (12.26)
2тес
где безразмерный множитель перед гиромагнитным отношением
называется ^-фактором или множителем Ланде. Расчет показы-
вает, что ^-фактор для атома водорода определяется квантовыми
числами I и j:
. , 3(3 + 1) - 1(1 + 1) + s(s + 1)
9 = 1 +---------адП)------------
где квантовое число s = 1/2.
Например, в состоянии с/ = 1иу = 1/2 g-фактор равен 2/3,
а при I = 1 и j — 3/2 множитель д = 4/3. Очевидно, что при
I = 0 фактор д = 2, так как, в соответствии с ранее изложенным,
магнитный момент в этом случае определяется только спином.
Вычисления ^-фактора необходимы при анализе характери-
стик атома, находящегося во внешнем магнитном поле, что рас-
сматривается в лекциях 20 и 21.
Задачи к лекции 12
1. Вычислить классическое гиромагнитное отношение для частицы
с удвоенным элементарным зарядом и массой, равной 4 а.е.м.
2. Поток нейтральных частиц с нулевым спином в опыте Штерна-
Герлаха расщепился на 5 пучков. Найти квантовое число орбитального
момента импульса частицы.
(12.27)
246 Лекция 12. Магнитные свойства атома водорода
3. Вычислить магнетон Бора, пользуясь фундаментальными констан-
тами.
4. Найти возможные значения модуля полного момента импульса
электрона в атоме водорода, если его орбитальное квантовое число при-
нимает значения: а) I = 2, б) I = 3.
5. Перечислить возможные значения проекции полного момента им-
пульса электрона в атоме водорода, если его орбитальное квантовое число
принимает значения: а) I = 1, б) I = 2, в) I = 3.
6. Вычислить возможные значения множителя Ланде для электрона
в атоме водорода, если его орбитальное квантовое число принимает зна-
чения: а) I = 1, б) I = 2, в) I = 3.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 12
12.1. Сила, действующая на магнитный момент
в неоднородном магнитном поле
Произвольный объект, обладающий магнитным моментом, может
быть представлен кольцевым током (витком с током). Рассмотрим ма-
ленький виток с площадью AS, в котором циркулирует ток I. Пусть ви-
ток находится в неоднородном магнитном поле, при этом характерные
размеры витка с током много меньше длины, характеризующей неод-
нородность магнитного поля. Виток перемещается на малое расстояние
dx вдоль направления, которое мы определим осью X. Вследствие не-
однородности поля, магнитный поток через виток изменяется на вели-
чину с/Ф.
В классической электродинамике доказано, что при этом произво-
дится работа сил поля, действующих на виток, равная
8 А = - </Ф.
С
(Д.12.1)
Дифференциал магнитного потока с/Ф через виток постоянной пло-
щади AS выражается через скалярное произведение:
d$ = AS(dB-n),
(Д.12.2)
где п — нормаль к площадке, охваченной витком с током. Вектор dB
представляет собой изменение индукции магнитного поля в центре
витка, обусловленное его перемещением. Подставим (Д.12.2) в (Д.12.1)
и используем выражение магнитного момента витка с током
ц= i/ASn.
С
(Д.12.3)
Тогда работа dA представится следующим скалярным произведением:
6А = (Д.12.4)
С другой стороны, работу поля над объектом можно выразить с по-
мощью силы:
8A = Fxdx. (Д.12.5)
Сопоставление соотношений (Д.12.4) и (Д.12.5) и элементарное пре-
образование дают выражение для проекции искомой силы
Fx
дв
/ дВх дБ,, дВД
\^х дх +tiy дх + дх ) ‘
(Д.12.6)
248
Дополнения к лекции 12
Рассматривая перемещения витка с током в направлениях других
осей координат, можно аналогично получить выражения для других про-
екций:
( <ЭВ\ ( дВх дВу дВЛ Fy~ У* ду)~ \?х ду ру ду ду )' (Д.12.7)
Fz~{IJ'dz)~ Г* dz + Ру dz dz ) • (Д.12.8)
Выражения (Д.12.6)-(Д.12.8) можно записать в общем векторном
виде: F = (mV)B, где введен дифференциальный оператор (/zV) (Д.12.9)
, д д д (Д.12.10)
Используя оператор (Д.12.10), например, проекцию вектора силы на ось
Z можно записать в виде
dBz dBz dBz Fz-»x Эх + ру~д^ + pz~dT (Д.12.11)
Заметим, что формулы (Д.12.8) и (Д.12.11) не противоречат друг
другу. Так как наш виток с током находится в безвихревом внешнем
магнитном поле (rot В = 0), то выполняются равенства
дВх _ dBz дВу _ dBz
dz дх ' dz dy '
Таким образом, сила, действующая на магнитный момент в неодно-
родном магнитном поле, зависит от величины этого момента и его ори-
ентации относительно направления, в котором изменяется неоднородное
магнитное поле.
Из общей формулы (Д.12.9) очевидно, что в однородном поле сила,
действующая на магнитный момент, становится равной нулю.
12.2. Классическая модель вращающегося электрона
и ее несостоятельность
Представим электрон в виде шара радиуса 7?, вращающегося вокруг
оси, проходящей через его центр, с частотой cj. Предположим, что элек-
трический заряд шара равномерно распределен по его объему. Тогда
абсолютная величина плотности электрического заряда выразится отно-
шением - Зе Р ~ 4тг7?3 ’ (Д.12.12)
где е — элементарный заряд.
Дополнения к лекции 12
249
Свяжем с шаром сферическую систему координат, начало которой
совместим с центром шара, а полярную ось — с осью вращения.
Выберем внутри шара произвольную точку с координатами г, в и
где г — расстояние до точки от начала координат, 0 — полярный угол,
Рис. Д.12.1. Сечение шара плоскостью, проходящей через его центр. Заштрихо-
вано сечение элементарного кольца с радиусом г±
— азимутальный угол (см. рис. Д.12.1). Простроим в ее окрестности
элементарный объем
dV = г2 sine dr de dp. (Д.12.13)
Интегрирование объема (Д.12.13) по азимуту р в пределах от 0 до 2тг
дает элементарное кольцо, расположенное перпендикулярно оси враще-
ния шара. Радиус кольца
r± = rsin#, (Д.12.14)
а площадь поперечного сечения элементарного кольца равняется
da = г d3 dr. (Д.12.15)
Следовательно, объем элементарного кольца равен 2тгг2 sin е dr de, а его
электрический заряд
dq = р • 2тгг2 sine dr de. (Д.12.16)
Эквивалентный ток элементарного кольца получается делением за-
ряда (Д.12.16) на период вращения шара:
2тг
Т = —, (Д.12.17)
где си — частота вращения шара. Таким образом, ток dj, создаваемый
вращением заряженного элемента шара с объемом dV, выразится в виде
dj = pur2 sin# dr de. (Д.12.18)
250
Дополнения к лекции 12
Согласно классической электродинамике, любой замкнутый ток со-
здает магнитный момент пропорциональный произведению силы тока на
площадь, охватываемую контуром тока. Следовательно, каждый кольце-
вой ток дает вклад в магнитный момент вращающегося шара, равный
с1ц = —ттг2± = sin3 в dr d0. (Д.12.19)
с с
Здесь 1/с — коэффициент пропорциональности в абсолютной (гауссовой)
системе единиц, где с — скорость света в вакууме.
Модуль магнитного момента всего шара вычисляется интегрирова-
нием:
R 7Г
/Z = [г4 dr f sin3 0dO = ^—R5. (Д.12.20)
c J J 15c
о о
Подставим объемную плотность заряда р, выраженную формулой
(Д.12.12), в правую часть (Д.12.20):
м = f-Я2- (Д.12.21)
ОС
Для оценки положим, что максимальное значение магнитного мо-
мента вращающегося шара, выраженное формулой (Д.12.21), достига-
ется, если скорость движения точек на экваторе шара сравняется со ско-
ростью света с. Тогда модуль магнитного момента представится простым
соотношением
eR
(Д.12.22)
о
Элементарный заряд е (равный заряду электрона с обратным зна-
ком) к настоящему времени измерен с высокой точностью е = 4,80324 х
х1О“10 ед-CGSE.
В квантовой механике установлено, что проекция магнитного мо-
мента электрона на направление внешнего магнитного поля равна
где //в — магнетон Бора:
№ = (Д.12.23)
2тес
Этот вывод подтвержден многочисленными экспериментами. Кроме
того, согласно квантовой теории, модуль магнитного момента свобод-
ного электрона равен ц = д/Зх^в, т.е. имеет порядок величины
~ 1О-20 ед-CGSE. Подставив это выражение модуля магнитного момента
в соотношение (Д. 12.22) мы получаем следующую оценку радиуса элек-
трона:
R ~ 1О“10 см, (Д.12.24)
что на три порядка больше размера протона или нейтрона. Однако мно-
гочисленные эксперименты по рассеянию, проводимые на ускорителях
элементарных частиц, показали, что радиус электрона не превышает
10"16 см.
Дополнения к лекции 12
251
Теперь вспомним, что соотношение (Д. 12.22) было получено при ус-
ловии предельно возможной скорости точек на экваторе шара — скоро-
сти света. Из выражения (Д. 12.21) следует, что при уменьшении угловой
скорости вращения ш радиус электрона должен дополнительно увеличи-
ваться относительно оценки (Д. 12.24).
Если, напротив, исходить из малого радиуса электрона (например,
R ~ 10-16см), то соотношение (Д.12.22) даст величину магнитного мо-
мента на 6 порядков меньше измеренного экспериментально. Таким
образом, предложенная классическая модель электрона в виде враща-
ющегося электрически заряженного шара является несостоятельной.
Заметим, что любая классическая модель электрона в виде заряжен-
ного шара конечного радиуса ставит важный вопрос о его стабильности.
Отдельные части заряженного шара должны расталкиваться электри-
ческими силами. А какая же физическая причина делает такой шар
устойчивым? (Просьба не привлекать в качестве объяснения божий про-
мысел.)
Из вышеизложенного следует вывод, что физические характерис-
тики электрона должны описываться не классической, а квантовой тео-
рией.
12.3. Оператор спина
Последовательная теория спина является частью квантовой меха-
ники и не рассматривается в данном курсе лекций. Ниже приводятся
без вывода некоторые элементарные сведения о спине, т.е. о собствен-
ном моменте импульса микрочастицы.
Спин обладает общими свойствами квантовомеханического момента,
которые рассматривались в лекции 9 и в приложении 9.1 на примере
орбитального момента импульса. В частности, собственные значения
оператора квадрата спинового момента
S2 = S2 + S2 + S2Z (Д. 12.25)
выражаются формулой
S2 = h2s(s + 1), (Д.12.26)
где безразмерный параметр s называется спиновым квантовым числом.
При этом количество возможных проекций спина на произвольно ориен-
тированную ось равно 2s 4-1.
Значение квантового числа з для каждой частицы определяется в
экспериментах. Так, для наиболее распространенных частиц, из кото-
рых состоят атомы, т.е. для электронов, протонов и нейтронов з = 1/2.
Возможные значения проекции спина на произвольную ось равны
Sz = ±^. (Д.12.27)
Оператор спина S для частицы с з = 1/2 может быть выражен через
матрицы Паули
S = (Д.12.28)
252
Дополнения к лекции 12
где
/О 1\ ~ _ /О -А л _ /1 О\
^1 о) ’ ay\i О/’ аг-^О -1J ‘
(Д.12.29)
Следовательно, операторы проекций спина имеют вид
Sy — 2 672/5 $z ~ 2 °z'
(Д.12.30)
с
L^X -- 2
Можно убедиться в том, что
^2 ^2 ^2 / 1
= ( 0
0\
1J
(Д.12.31)
Таким образом, оператор квадрата спина имеет вид
3/г2 /1 0\
5 =тЧо 1/
(Д.12.32)
Операторы проекций спина удовлетворяют тем же перестановочным
соотношениям, что и операторы проекций момента импульса (Д.9.7), что
и доказывается непосредственными вычислениями с помощью выраже-
ний (Д.12.30) и (Д.12.29):
SxSy - SySx
= ihSz,
SySz - SzSy
— i liS x,
(Д.12.33)
szsx — sxsz
— z l~i>Sy.
Соотношения (Д. 12.33) означают, что в данном состоянии спин может
иметь только одну определенную проекцию.
Также нетрудно убедиться, что операторы каждой проекции спина
коммутируют с оператором квадрата спина:
SXS2 - S2SX = О,
SyS2 - S2Sy = О,
SZS2 - S2SZ = 0.
(Д.12.34)
Коммутационные соотношения позволяют корректно ввести кванто-
вый полный момент импульса как сумму орбитального момента и спина
(см. лекцию 12).
Существование спина приводит к необходимости представления вол-
новой функции электрона в виде произведения координатной и спиновой
частей (при отсутствии спин-орбитального взаимодействия). Спиновую
часть волновой функции Ха удобно представить в виде столбца
Ха =
СЛ
с2)'
(Д.12.35)
Дополнения к лекции 12
253
где Ci и С?2 — вообще говоря, комплексные числа. При этом |Ci|2 —
это вероятность того, что в данном состоянии проекция спина равна
Sz = h/2, а |С*212 — это вероятность того, что Sz = — h/2. Отсюда следует
соотношение
|С1|2 + |С2|2 = 1. (Д.12.36)
В частности, спиновая волновая функция
(Д.12.37)
описывает частицу с определенной проекцией спина на ось Z, равной
Sz = h/2. Соответственно, в состоянии, заданном волновой функцией
. (Д.12.38)
проекция спина на ось Z равна Sz = — h/2.
Действительно, используя вид опреатора Sz (Д.12.30), нетрудно убе-
диться, что волновые функции (Д. 12.37) и (Д. 12.38) удовлетворяют со-
ответственно следующим уравнениям:
а с
SzX+ = 2^+ и SzX- = -?X--
(Д.12.39)
Лекция 13
ТОНКАЯ СТРУКТУРА СПЕКТРА АТОМА ВОДОРОДА
13.1. Энергия тонкой структуры
При исследовании излучения атома водорода с использованием
спектрометров достаточно высокой разрешающей способности бы-
ло обнаружено, что вместо одной спектральной линии, определя-
емой обобщенной формулой Бальмера (8.4), наблюдается мульти-
плет: две, три или больше близко расположенные спектральные
линии. Близость расположения означает малое различие их длин
волн. Подобная особенность была обнаружена и в спектрах излу-
чения других атомов и была названа тонкой структурой.
Наличие тонкой структуры спектра атома водорода свидетель-
ствует о том, что выражение энергии стационарных состояний
(11.23) является приближенным и нуждается в уточнении.
Во-первых, следует вспомнить, что гамильтониан (11.4) ста-
ционарного уравнения Шредингера (11.5) для атома водорода был
записан в нерелятивистском приближении. Хотя скорости элек-
трона в атоме водорода можно в хорошем приближении полагать
нерелятивистскими, для объяснения тонкой структуры следует к
гамильтониану (11.4) добавить релятивистские поправки.
Во-вторых, гамильтониан (11.4) уравнения (11.5), кроме опе-
ратора нерелятивистской кинетической энергии, содержал только
оператор потенциальной энергии вида —е2/г. Это означает, что
при решении уравнения Шредингера учитывалось только взаи-
модействие между электрическими зарядами электрона и ядра.
С другой стороны, в предыдущей лекции было установлено, что
электрон из-за наличия спина в любом состоянии имеет собствен-
ный магнитный момент, проекции которого выражаются форму-
лой (12.9). Таким образом, электрон в стационарном состоянии
атома водорода с орбитальным числом I 0 обладает как орби-
тальным, так и собственным магнитным моментом.
В классической физике известно, что взаимодействие двух
магнитных моментов обладает определенной энергией, величина
которой зависит от взаимной ориентации этих моментов (допол-
13.1. Энергия тонкой структуры
255
нение 13.1). Так как орбитальный и собственный магнитные мо-
менты принадлежат одной и той же частице, то классическая
аналогия в данном случае неприменима. Однако собственный маг-
нитный момент электрона, движущегося в атоме, взаимодействует
с электрическим полем атомного ядра. Это специфическое взаимо-
действие традиционно называется спин-орбитальным, которому
соответствует определенная энергия спин-орбитального взаимо-
действия.
Для расчета тонкой структуры спектра атома водорода ис-
пользуется релятивистская квантовая теория, разработанная Ди-
раком. Решение уравнения Дирака для электрона в кулоновском
поле протона дает следующие значения энергии стационарных со-
стояний атома водорода:
Ry 2 Ry ( 1 3
n2 a n3 \j 4-1/2 4n
(13.1)
Первое слагаемое было получено сначала в теории Бора, а за-
тем при решении стационарного уравнения Шредингера (11.5), в
котором учитывалось лишь электрическое взаимодействие (11.1)
между электроном и протоном в атоме водорода. Первый член фор-
мулы (13.1) совпадает с выражением (11.23) и часто называется
основным, боровским или бальмеровским.
Второе слагаемое в формуле (13.1) называется энергией тон-
кой структуры. Безразмерная константа
называется постоянной тонкой структуры.
Энергия тонкой структуры иногда в литературе называется
спин-орбитальной энергией. Это, строго говоря, неверно, так как
она, помимо энергии спин-орбитального взаимодействия, содержит
и другие релятивистские поправки.
Согласно формуле (13.1), энергия тонкой структуры зависит от
двух квантовых чисел п и j:
Можно сказать, что энергия тонкой структуры связана с полным
моментом импульса электрона (12.21), величина которого выра-
жается через квантовое число j.
Для сравнения заметим, что нерелятивистская энергия стаци-
онарного состояния (11.23) зависит только от главного квантового
числа п, т.е. вырождена по орбитальному квантовому числу I и
по направлениям спина. Спин-орбитальное взаимодействие ча-
256 Лекция 13. Тонкая структура спектра атома водорода
стично снимает вырождение энергии, но не полностью. Остаются
двукратно вырожденными уровни энергии с одинаковыми значе-
ниями квантовых чисел п и j, но с различными орбитальными
числами I = j ± 1/2.
Малая величина безразмерного множителя о? ~ 5 • 10“5 1
обусловливает значительное различие бальмеровского слагаемого
энергии (13.1) и энергии тонкой структуры:
Ry» ./—7 1 3'i.
п2 п3 \ j 4-1/2 4п)
Следовательно, энергия тонкой структуры (13.1) является от-
носительно малой поправкой к основному члену (11.23) энергии
стационарного состояния атома водорода.
В основном состоянии атома водорода орбитальное квантовое
число I = 0 и квантовое число j может принять единственное зна-
чение, равное 1/2. Следовательно, учет энергии тонкой структуры
приводит к сравнительно небольшому понижению энергии основ-
ного состояния, которая становится равной
£1,1/2 = "Ry-а2^- (13-4)
Легко вычислить, что относительная поправка к формуле Бора
(8.7) для основного состояния атома водорода составляет около
10“5.
В предыдущих лекциях спин-орбита л ьное взаимодействие не
рассматривалось. В нерелятивистском приближении стационар-
ные состояния атома водорода описываются четырьмя квантовы-
ми числами п, Z, m, ms- Четыре независимых квантовых числа
соответствуют четырем степеням свободы электрона — трем про-
странственным и одной неклассической, обусловленной различ-
ными ориентациями спина.
Согласно выводам квантовой теории, спин-орбитальное взаи-
модействие приводит к тому, что проекции орбитального и спи-
нового момента Lz и Sz по отдельности в стационарных состоя-
ниях не сохраняются. Следовательно, квантовые числа m и ms
не имеют определенных значений в этих состояниях и не могут
быть их характеристиками. Однако при этом сохраняется ква-
драт полного момента импульса электрона J2 и одна из его про-
екций Jz. Следовательно, и при учете спин-орбитального взаимо--
действия электрон также обладает четырьмя степенями свободы
и его стационарное состояние описывается четырьмя квантовыми
числами п, Z, j, mj.
Учет релятивистских поправок (в том числе спин-орбитального
взаимодействия) приводит к усложнению спектров излучения ато-
ма водорода. Спектральные серии излучения атома водорода, рас-
13.2. Правила отбора
257
смотренные в лекции 8, формировались переходами между ста-
ционарными состояниями с определенными значениями главного
квантового числа п. При пренебрежении слагаемым (13.3) энер-
гии излучаемых фотонов е определяются разностями выражений
(8-7):
£ = Eni Еп2> (13.5)
При учете релятивистских поправок к гамильтониану атома во-
дорода энергии излучаемых фотонов е должны определяться раз-
ностями
£ = £(nj)l “ ^(nj)2> (13.6)
где величины #(nj)i и ^(nj)2 выражаются формулой (13.1). Оче-
видно, что спектры должны содержать больше спектральных ли-
ний, чем приведено на рис. 8.2.
Подсчитаем количество различных значений квантового чи-
сла j при фиксированном главном квантовом числе п. При п =
= const орбитальное число I пробегает п различных значений I =
= 0,1,...,п — 1. При I = 0 квантовое число j принимает един-
ственное значение s = 1/2 согласно (12.22). Каждому из осталь-
ных п — 1 значений орбитального числа I 0 соответствует два
значения j = I ± 1/2. Таким образом, при п = const кванто-
вое число j может принимать 2(п — 1) 4- 1 = 2п — 1 различных
значений. Можно сказать, что при учете релятивистских попра-
вок энергетический уровень расщепляется на 2п — 1 подуровней
тонкой структуры. Однако для расчета количества спектральных
линий спектра излучения необходимо также выяснить, между ка-
кими стационарными состояниями возможны переходы с излуче-
нием фотонов.
13.2. Правила отбора
Как известно, любые спектральные линии поглощения и из-
лучения фотонов соответствуют переходам атома из одного ста-
ционарного состояния в другое. Обратное утверждение, вообще
говоря, не верно — не каждый переход атома из одного стационар-
ного состояния в другое сопровождается излучением или поглоще-
нием фотона.
Переходы между стационарными состояниями, сопровождаю-
щиеся излучением фотонов, называются радиационными. Кван-
товая теория излучения устанавливает определенные ограничения
на возможность радиационных переходов. Наиболее вероятными
и наблюдаемыми в опытах являются переходы, для которых вы-
полняются следующие правила:
AZ = ±1, AJ = 0, ±1, = 0, ±1, Ап — любое. (13.7)
258 Лекция 13. Тонкая структура спектра, атома водорода
Знак А означает разность между конечным и начальным значе-
ниями соответствующего квантового числа.
Соотношения (13.7) исторически названы правилами отбора.
Основной причиной существования правил (13.7) является то,
что фотон также обладает собственным моментом импульса — спи-
ном. Модуль спина квантуется по тем же правилам, что и мо-
менты электрона, но с существенным отличием — квантовое число
спина фотона является целочисленным. С наибольшей вероятно-
стью в радиационных переходах излучаются фотоны с квантовым
числом спина равным единице. С другой стороны, закон сохра-
нения момента импульса является одним из фундаментальных
законов природы. Можно сказать, что правила отбора являются
следствиями закона сохранения момента импульса для системы
«электрон 4- фотон».
Так, например, радиационный переход из стационарного состо-
яния с li = 0 в другое стационарное состояние с I2 = 0 невозможен,
так как излученный фотон обязательно уносит ненулевой момент
импульса.
Следует заметить, что правила отбора (13.7) не являются аб-
солютно точными. Иногда наблюдаются радиационные переходы
очень малой интенсивности с изменением орбитального числа
на два, т.е. AZ = 2. Это может происходить в переходах с ис-
пусканием двух фотонов или одного фотона с квантовым числом
момента импульса равным двум. Такие процессы в принципе
возможны, но имеют очень малую вероятность, что и обуслов-
ливает малую интенсивность соответствующей спектральной ли-
нии.
Однако следует принять во внимание, что в современных мощ-
ных лазерах формируется высокая плотность излучения, при кото-
рой многофотонные процессы характеризуются значительной ве-
роятностью и поэтому надежно регистрируются.
13.3. Тонкая структура
энергетического спектра атома водорода
Выражение для энергии стационарных состояний (13.1) и пра-
вила отбора (13.7) позволяют теоретически рассчитать тонкую
структуру спектра водорода.
Для уточнения энергетической структуры спектра водорода,
прежде всего, заметим, что для всех s-состояний (с I = 0) кванто-
вое число j имеет единственное значение j = 1/2. Энергии
s-состояний можно записать в общем виде:
= ' = <>• (1.3.8)
13.3. Тонкая структура энергетического спектра атома водорода259
Второе слагаемое быстро убывает с ростом главного кванто-
вого числа п. Следовательно, учет релятивистских поправок лишь
немного уменьшает ранее вычисленное значение энергии s-сос-
тояний.
Стационарные состояния с ненулевым значением орбитально-
го момента импульса (Z 7^ 0) подразделяются на состояния с j =
= I — 1/2 и j = I 4-1/2. Их энергии, согласно (13.3), различаются
при фиксированном значении главного квантового числа. Говорят,
что каждый боровский энергетический уровень разбивается на два
близких различных по энергии уровня с энергиями
р = 1_________3 A f1 о m
ЕП, 1+1/2 n2 a пз ^i + i/2) + l/2 4п / ’ ( 3'9'
_ Ry 9 Ry / 1 3 \ /чп
^n,Z-l/2 = --^2 - 01 ^3 ((/ — 1/2) + 1/2 “ 4п/ ( 3’ 0)
Из последних выражений следует, что уровень располо-
жен выше на оси энергий, чем уровень 1/2 на величину
^п,1+1/2 ~ 1-1/2 — + -qj* (13.11)
Очевидно, что разность уровней энергии (13.11) мала по сравне-
нию с энергией Ридберга Ry и резко убывает с ростом главного
квантового числа.
Для краткого обозначения состояний с тремя определенными
квантовыми числами n, Z, j принята следующая символика. На
первом месте ставится главное квантовое число, затем орбиталь-
ное квантовое число, обозначенное латинской буквой в соответ-
ствии с табл. 9.1 (лекция 9). Квантовое число j ставится в конце
в виде нижнего индекса. Например, состояние с квантовыми чис-
лами n = 1, I = 0, j = 1/2 обозначится так: lsi/2-
Для анализа тонкой структуры спектра излучения атома водо-
рода удобно использовать энергетическую диаграмму, приведен-
ную на рис. 13.1. От схемы на рис. 8.1 эта диаграмма отличается
тем, что энергии состояний с различными значениями орбиталь-
ного квантового числа изображены в отдельных столбцах. На та-
кой диаграмме правило отбора для орбитального квантового числа
(AZ = ±1) графически представляется переходами между сосед-
ними столбцами уровней энергии.
На рис. 13.1 хорошо видно, что влияние спин-орбитального
взаимодействия приводит к «расщеплению» энергетических уров-
ней всех состояний с определенными квантовыми числами п и I
(кроме, естественно, s-состояний) на два близких подуровня. Так-
260 Лекция 13. Тонкая структура спектра атома водорода
Z=1 / = 2 / = 3
/=1/2 у = 3/2, 5/2
7= 1/2, 3/2 7 = 5/2, 7/2
п = 2
п - 1----
a
Рис. 13.1. Схема энергетических уровней стационарных состояний атома водо-
рода: а) без учета тонкой структуры; б) при учете энергии тонкой структуры.
Расстояния между уровнями с различными значениями квантового числа j по-
казаны в существенно увеличенном масштабе
же видно, что энергии состояний с одинаковыми квантовыми чи-
слами п и j не зависят от орбитального квантового числа I. На-
пример, энергии состояний 2si/2 и 2р^/2 совпадают.
13.4. Тонкая структура серии Лаймана
Серия Лаймана в спектре излучения образуется при переходе
атома водорода в основное стационарное состояние с главным
квантовым числом n = 1 из возбужденного с любым числом n > 1.
Основное состояние является s-состоянием и характеризуется
квантовыми числами n = 1, I = 0, j = 1/2. Следовательно, в
соответствии с правилом отбора AZ = ±1 все переходы происхо-
дят из p-состояний (с орбитальным квантовым числом Z = 1).
В p-состояниях (Z = 1) квантовое число j может принимать
значения 3/2 и 1/2. Это означает, что каждый р-уровень воров-
ской модели атома водорода расщепляется на два близких под-
уровня Еп^/2 и ЕП£/2 (см. рис. 13.1). Переходы из соответствую-
щих состояний в основное не запрещены правилами отбора для
квантового числа j (Aj = 0, ±1). Следовательно, все спектраль-
ные линии серии Лаймана представляют собой дублеты. Энергии
13.4. Тонкая структура серии Лаймана
261
фотонов таких дублетов представляются выражениями
„ А 1 > £1 = Ry l 2 \ п / 1 Л _ JLA п3 \ 4п у п > 1. (13.12)
£2 = Ry ( 1 - Л ] \ п2 у । _ 2^у ( a п3 \ 2 4п /
Схема переходов, которые соответствуют спектральным лини-
ям серии Лаймана в спектре водорода, приведена на рис. 13.2.
Рис. 13.2. Энергетическая схема переходов, генерирующих спектральные линии
серии Лаймана. Разности энергий состояний, различающихся только квантовым
числом J, на рисунке значительно преувеличены
Разность энергий фотонов лаймановского дублета зависит от
главного квантового числа возбужденного стационарного р-состоя-
ния и равна
Дб =
g2Ry
2п3
(13.13)
262 Лекция 13. Тонкая структура спектра атома водорода
Видно, что все дублеты состоят из очень близких линий и разность
(13.13) резко уменьшается с номером линии серии Лаймана. Если
для первого дублета As = a2 Ry/16 « 4,5 • 10“5 эВ, то уже для че-
твертого дублета As = a2 Ry/250 « 2,9-10“6 эВ. При неограничен-
ном увеличении главного квантового числа п исходного состояния
величина расщепления энергетических уровней (13.13) уменьша-
ется до нуля. Таким образом, тонкую структуру спектральных
линий серии Лаймана удобнее наблюдать на первых линиях этой
серии, образованных переходами электронов из стационарных со-
стояний с малым значением главного квантового числа.
13.5. Тонкая структура серии Бальмера
Серия Бальмера образуется радиационными переходами в ста-
ционарное состояние с главным квантовым числом п = 2 из со-
стояний с п > 2.
Изобразим на энергетической диаграмме (рис. 13.3) всевоз-
можные переходы между стационарными состояниями с главными
Рис. 13.3. Энергетическая схема радиационных переходов, образующих первую
спектральную линию серии Бальмера
квантовыми числами п = 2 и п = 3 (первая линия серии Баль-
мера), а затем найдем разрешенные с точки зрения правил отбора.
В соответствии с правилами отбора, имеем 7 следующих раз-
решенных радиационных переходов между стационарными состо-
13.5. Тонкая структура серии Бальмера
263
яниями:
3-51/2 2р!/2, 33!/2 2р3/2, 3pi/2 —> 2s!/2,
Зрз/2 2s!/2,
3^3/2 2р!/2,
3^5/2 2РЗ/2>
3^3/2 2р3/2.
(13.14)
Переход Зр5/2 %Pi/2 запрещен правилами отбора, так как при
этом Aj = 2.
Энергия стационарного состояния с учетом спин-орбитального
взаимодействия не зависит от орбитального числа, поэтому пере-
ходы 3<§!/2 ^Р\/2 и 3pi/2 —> 2si/2 сопровождаются испусканием
фотонов одинаковой энергии. Аналогично переходы Зр3/2 —> 2s 1/2
и Зс/3/2 —> 2р1/2 также генерируют фотоны с совпадающими энер-
гиями.
Напомним, что по теории Бора первая спектральная линия се-
рии Бальмера образуется при переходе электрона с третьего энерге-
тического уровня (с главным квантовым числом п = 3) на второй
(с главным квантовым числом п = 2). Из приведенного выше ана-
лиза следует, что релятивистские поправки (13.3) к энергии стаци-
онарных состояний атома водорода приводят к тому, что нижний
энергетический уровень (п = 2) разделяется на два с энергиями
гп Л 5 2\
В2,1/2 - -Ry (4 + 64a J ’
„ Г. /1 1 2^\
^2,3/2 - “RY ( 4 + ) •
(13.15)
Аналогично при этом верхний энергетический уровень с п = 3
превратится в три со следующими значениями энергии:
^3,1/2 - -Ry (g + ,
^3,3/2 = -Ry Q + l^"2)’
^3,5/2 = “Ry (j + ^«2) •
(13.16)
На рис. 13.4 приведена схема уровней энергии, между кото-
рыми происходят переходы, образующие компоненты тонкой
структуры первой линии серии Бальмера. Длина вертикальной
стрелки, изображающей радиационный переход, пропорциональна
энергии излучаемого фотона.
264 Лекция 13. Тонкая структура спектра атома водорода
По рис. 13.4 видно, что наиболее длинноволновую компоненту
первой линии серии Бальмера образует переход между уровнями
^3,1/2 и ^2,3/2:
(5 7 \
77 “ ктд6*2 ) * (13.17)
Зо о7о J
Расчет показывает, что наиболее коротковолновая компонента
образуется при переходе между уровнями Е3д/2 и Е2д/2-.
Smax = #3,3/2 - Е2д/2 = Ry f— 4- • (13.18)
у 00 1 ( 2jO /
Разность энергий фотонов коротковолновой и длинноволновой
компонент характеризует характерную ширину спин-орбитального
расщепления первой линии серии Бальмера:
35
Де = Стах - Emin = Ry 77^«2 ~ 0,081 Ry О'2 « 5,9 • 10~5 эВ.
Аналогичные рассуждения можно провести и для других спек-
тральных линий серии Бальмера. Каждая линия серии Бальмера
Рис. 13.4. Энергетическая схема формирования тонкой структуры первой линии
серии Бальмера
содержат 5 компонент тонкой структуры. У любой линии этой
серии длинноволновая компонента тонкой структуры образует пе-
реходом между уровнями энергии Епд/2 и 7?2,з/2> а наиболее ко-
ротковолновая — при переходе между уровнями Еп,3/2 и Е2д/2,
13.5. Тонкая структура серии Бальмера
265
где п — главное квантовое число начального стационарного состо-
яния. Энергии фотонов обеих указанных компонент вычисляются
по формулам аналогичным (13.17) и (13.18). Разность энергий
фотонов этих компонент представляются в следующем виде:
Дб — Стах ^min ~ Ry ( 77 Н о ) , П > 2, (13.19)
\8 п6 J
где п — главное квантовое число верхнего энергетического уровня.
Таким образом, расщепление спектральных линий серии Баль-
мера, обусловленное энергией тонкой структуры, медленно умень-
шается с ростом главного квантового числа начального стацио-
нарного состояния, так как определяется, в основном, разностью
энергий конечных состояний ^2,1/2 и ^2,3/2- Из (13.19) следует,
что при п -4 оо разность энергий фотонов компонент тонкой струк-
туры для спектральных линий серии Бальмера (13.19) стремится
к величине Де = a2 Ry/8 « 0,9 • 10-4 эВ.
Задачи к лекции 13
1. Оценить энергию тонкой структуры:
а) в основном состоянии атома водорода;
б) в первом возбужденном состоянии (п = 2) атома водорода.
2. Получить общую формулу для вычисления разности длин волн
лаймановских дублетов. Рассчитать разности длин волн компонент тон-
кой структуры для:
а) второй спектральной линии серии Лаймана;
б) третей спектральной линии серии Лаймана.
3. Вычислить разность длин волн самой длинноволновой и самой
коротковолновой компонент тонкой структуры:
а) второй спектральной линии серии Бальмера;
б) третей спектральной линии серии Бальмера.
4. Вычислить разность длин волн самой длинноволновой и самой ко-
ротковолновой компонент тонкой структуры спектральной линии серии
Пашена.
5. Вычислить разность длин волн первого дублета спектральной ли-
нии серии Лаймана для дейтерия.
6. Получить общую формулу для вычисления разности длин волн
лаймановских дублетов для однократно ионизированного атома гелия.
Рассчитать разности длин волн компонент тонкой структуры для первого
дублета.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 13
13.1. О тонкой структуре водородоподобных атомов
Релятивистская квантовая теория позволяет получить выражение
для энергии стационарных состояний водородоподобных атомов, о ко-
торых упоминалось в дополнении 11.4 к лекции 11:
Z2Ry 2Z4Ry / 1 3\
п2 а п3 \ j 4-1/2 4п) ’
(Д.13.1)
Энергия (Д.13.1) зависит от двух квантовых чисел п и j. Основ-
ной член выражается формулой (Д.11.41). Второе слагаемое в (Д.13.1),
как и в случае атома водорода, обусловлено релятивистскими эффектами
(включая спин-орбитальное взаимодействие) и называется энергией тон-
кой структуры. Влияние релятивистских эффектов приводит к расщеп-
лению каждого энергетического уровня, определенного основным членом
формулы (Д. 11.41) на 2j 4-1 подуровней тонкой структуры.
Энергия тонкой структуры, согласно (Д.13.1), пропорциональна че-
твертой степени заряда ядра. Вследствие этого разности соседних энер-
гетических подуровней тонкой структуры резко увеличиваются с ростом
числа Z. Это означает, что тонкую структуру спектра легче экспери-
ментально обнаружить у водородоподобных атомов с большим зарядом
атомного ядра.
Пользуясь выражением (Д.13.1) нетрудно получить, что разность
энергий фотонов дублетов серии Лаймана (13.13) для водородоподобных
атомов примет следующий вид:
А£ = (Д-13.2)
где п — главное квантовое число исходного состояния.
Аналогично тонкое расщепление спектральных линий серии Баль-
мера (13.19) для водородоподобных атомов преобразуется к виду
Дг = a2Z4Ry (1 + V) > п > 2- (Д.13.3)
\О TV5 J
Таким образом, тонкое расщепление спектральных линий иона гелия
Не+ в 16 раз (!) больше соответствующих величин для атома водорода.
13.2. Лэмбовский сдвиг энергетических уровней
Согласно изложенному в лекции 11, энергии стационарных состоя-
ний атома водорода в первом приближении зависят от одного квантового
числа — главного. Следовательно, состояния с фиксированным главным
Дополнения к лекции 13
267
квантовым числом п, но с различными орбитальными квантовыми чис-
лами I обладают одинаковой энергией. В квантовой механике показано,
что простой вид формулы (11.23) для энергии стационарных состояний
Еп атома водорода (т. е. вырождение по орбитальному квантовому чи-
слу) обусловлен кулоновским видом потенциального электрического поля,
в которохм движется электрон. Электрическое поле, действующее на элек-
трон, изменяется по закону обратных квадратов, если на поле, создава-
емое атомным ядром, не накладываются поля других электронов атома.
Таким образом, вырождение по орбитальному квантовому числу I наблю-
дается только в одноэлектронных атомах, в частности, в атоме водорода.
Спин-орбитальное взаимодействие и другие релятивистские эффекты
усложняют спектр энергий стационарных состояний атома водорода, при
этом вырождение энергетических уровней частично снимается, как это
описано в лекции 13. Дополнительная энергия тонкой структуры (13.3)
зависит от двух квантовых чисел: п и j. Однако, согласно выраже-
нию (13.1), энергия стационарного состояния атома водорода не зависит
явным образом от орбитального квантового числа I. Это означает, что
энергии состояний с одинаковыми квантовыми числами п и j совпадают
независимо от значения орбитального квантового числа I.
Например, стационарные состояния атома водорода с главным кван-
товым числом п = 2 могут иметь орбитальные квантовые числа I = О
и I = 1. Квантовое число у, в соответствии с правилом (12.22), может
принимать значения j — 1/2 и j = 3/2. Тогда, согласно формуле (13.3),
стационарные состояния 2si/2 и 2ру2 должны иметь одинаковую энер-
гию.
Экспериментальные исследования тонкой структуры спектров излу-
чения не дают надежную информацию об энергиях стационарных состо-
яний 2si/2 и 2р1/2, так как спектральные линии обладают значитель-
ной аппаратной шириной, что не позволяет различать малые различия
между энергиями состояний.
В 1947 г. американские физики У. Лэмб и Р. Ризерфорд провели экс-
перимент, который позволил обнаружить и измерить различие энергий
вышеуказанных стационарных состояний атома водорода.
Оба стационарных состояния 2s1/2 и 2pi/2 являются возбужденны-
ми. Среднее время жизни состояния 2ру2 имеет порядок 10“8 с. Че-
рез это характерное время атом водорода спонтанно переходит в основ-
ное состояние lsi/2 с испусканием фотона, так как этот радиационный
переход 2pt/2 —> lsj/2 разрешен правилами отбора (13.7). Стационар-
ное состояние 2si/2 является метастабильным, так как радиационный
переход 2si/2 —> l«Si/2 запрещен правилом отбора Д/ = ±1. Переход
2^1/2 —> 1^1/2 осуществляется, в основном, за счет двухфотонных про-
цессов, которые имеют малую вероятность по сравнению с испусканием
одного фотона. Как следствие, среднее время жизни состояния 2$i/2 при-
мерно на 8 порядков превышает среднее время жизни состояния 2рг/2.
Схема экспериментальной установки приведена на рис. Д.13.1. Моле-
кулы водорода Н2 в печке под действием высокой температуры подверга-
лись диссоциации на отдельные атомы. С помощью системы диафрагм
формировался узкий пучок атомов водорода, находящихся в основном
состоянии lsi/2. Пучок атомов направлялся на металлическую пластину
(мишень), которая была соединена с гальванометром G.
268
Дополнения к лекции 13
Для возбуждения атомов водорода использовался пучок электронов,
направленный перпендикулярно пучку атомов. При столкновениях элек-
троны передавали часть своей энергии атомам и переводили их в раз-
личные возбужденные состояния. Правило отбора Д/ = ±1 выполняется
Молекулярный
водород
Генератор
ВЧ-поля
1 Пучок атомов водорода
I в основном состоянии
Печь
Пучок
электронов
Металлическая
пластина (мишень)
Рис. Д.13.1. Схема эксперимента по обнаружению лэмбовского сдвига энергети-
ческих уровней в атоме водорода:
А — область возбуждения атомов, В — область вынужденных переходов, G — гальвано-
метр
только для радиационных переходов (с излучением или поглощением фо-
тона), поэтому часть атомов водорода из-за столкновений с электронами
переходит в возбужденные состояния 2s 1/2 и 2рг/2- Энергия возбужде-
ния, согласно формуле (11.23), равна приблизительно
Е* = Е2 - Ei = « 10,2 эВ. (Д.13.4)
Атомы в состоянии 2р1/2 не успевают достичь мишени по причине
короткого времени жизни. Они испускают фотоны с энергией равной
(Д.13.4), переходят в основное состояние lsi/2 и в таком состоянии по-
падают на металлическую мишень.
Если атомы водорода находятся в основном состоянии, то они не
могут передать электронам проводимости металла энергию, достаточную
для эмиссии. Следовательно, металлическая пластина не изменяет свой
электрический заряд, и гальванометр G не регистрирует прохождение
электрического тока.
Возбужденные атомы, находящиеся в мета стабильном состоянии
2^1/2, достигают мишени и переходят в основное состояние lsi/2, от-
давая свою энергию возбуждения Е* электронам проводимости. Так как
энергия (Д.13.4) значительно превышает работу выхода, будет проис-
ходить эмиссия электронов с поверхности металлической мишени. Как
следствие через гальванометр G будет проходить электрический ток, сила
Дополнения к лекции 13
269
которого пропорциональна количеству атомов водорода, достигших ми-
шени в возбужденном состоянии 2«Si/2-
Экспериментальная установка содержит устройство, создающее вы-
сокочастотное электромагнитное поле в области пространства, через ко-
торую проходят возбужденные атомы (см. рис. Д.13.1). Если энергии
стационарных состояний 2s1/2 и 2Р1/2 различаются, то подбором ча-
стоты электромагнитного поля можно добиться вынужденных перехо-
дов между данными состояниями. В таких процессах атом водорода
переходит из одного состояния в другое, поглотив или испустив фотон с
энергией, равной разности энергий этих состояний.
В эксперименте Лэмба-Ризер форда исследовалась зависимость силы
тока, проходящего через гальванометр, от частоты электромагнитного
поля СВЧ-диапазона, воздействующего на возбужденные атомы водорода.
В ходе опытов было обнаружено, что при частоте электромагнитного поля
уг = 1057,90 ± 0,06 МГц наблюдается минимум тока. Этот результат
можно интерпретировать следующим образом. Абсолютная величина
разности энергий состояний 2si/2 и 2pi/2 равна энергии фотона с ча-
стотой д/г, т.е.
|£(2$1/2) - Е(2Р1/2)| = 2лЪиг. (Д.13.5)
В результате взаимодействия с высокочастотным электромагнитным
полем атомы из состояния 2si/2 переходят в состояние 2pi/2, а затем
практически мгновенно возвращаются в основное состояние, излучив
фотон с энергией (Д.13.4). В результате этого количество возбужден-
ных атомов, доходящих до мишени, значительно уменьшается. Следова-
тельно, уменьшается эмиссия электронов из металла и регистрируемый
ток через гальванометр.
По измеренной частоте z/r, воспользовавшись уравнением (Д.13.5),
легко вычислить, что абсолютная величина разности энергий состояний
2si/2 и 2р1/2 составляет приблизительно 4,377- 10-6эВ. Эта величина
примерно на порядок меньше разности энергий стационарных состояний
2р!/2 и 2р3/2 атома водорода, которая определяет тонкое расщепление
первого лаймановского дублета a2Ry/16 « 4,5 • 10-5 эВ (см. § 13.4).
Обнаруженное явление, заключающееся в различии энергий стацио-
нарных состояний с различными орбитальными квантовыми числами I
при фиксированных квантовых числах п и у, было названо лэмбовским
сдвигом энергетических уровней.
Лэмбовский сдвиг не является уникальным для атомов водорода.
В ходе последующих экспериментов был обнаружен лэмбовский сдвиг
и в других атомах. Для дейтерия эффект наблюдался на частоте элек-
тромагнитного поля иг — 1058,9 Мгц, для иона гелия — на частоте
иг = 14046,3 Мгц.
Лэмбовский сдвиг существует не только для состояний с главным
квантовым числом п = 2, но его экспериментальное наблюдение при
п > 2 сопряжено со значительными техническими трудностями.
Обнаружение лэмбовского сдвига одним из важных экспериментов,
подтверждающих теоретические выводы квантовой электродинамики,
которая бурно развивалась после второй мировой войны. Теоретиче-
ское значение резонансной частоты вынужденных переходов составляет
1057,91 ± 0,01 МГц, что оказывается в согласии с результатами экспе-
римента Лэмба-Ризер форда. Расчеты показали, что энергия стационар-
270
Дополнения к лекции 13
ного состояния 2si/2 превышает энергию состояния 2р1/2- Относитель-
ное расположение соответствующих энергетических уровней показано на
рис. Д.13.2.
Теоретическое объяснение лэмбовского сдвига требует применения
математического аппарата квантовой электродинамики, поэтому в дан-
ном приложении приходится ограничиться некоторыми качественными
разъяснениями.
Согласно квантовой электродинамике, любое электромагнитное поле,
в том числе и электростатическое, представляется ансамблем фотонов.
Е
‘1 ^Рз/2
2S]/2
\е2
1Р\/2
Рис. Д.13.2. Энергетическая схема энергетических уровней стационарных сос-
тояний атома водорода с учетом лэмбовского сдвига:
Д2?1 — разность энергий тонкой структуры первого лаймановского дублета (~ 4,5 х
хЮ-5 эВ), Д£?2 — величина лэмбовского сдвига (~ 4,4 • 10-6 эВ)
Электрическое поле, окружающее электрический заряд, состоит из фото-
нов, которые случайным образом испускаются и поглощаются этим за-
рядом. В связи с тем, что каждый фотон обладает энергией, возникает
вопрос о выполнении закона сохранения энергии в таких процессах. Эта
проблема может быть решена с помощью энергетического соотношения
неопределенностей Д£ • Ai > 2тг/1, которое обсуждалось в §8.3. В соот-
ветствии с этим соотношением, может возникнуть фотон с энергией е на
время г, которое подчиняется неравенству (по порядку величины)
2тгН
е
(Д.13.6)
Это означает, что фотоны с большой энергией могут существовать в
течение столь малого времени, что их невозможно зарегистрировать в
эксперименте. Например, энергии 1эВ соответствует время т ~ 10-15с.
Дополнения к лекции 13
271
Такие возникающие и исчезающие фотоны называются виртуальными.
Можно сказать, что электростатическое поле образовано виртуальными
фотонами.
Кроме того, квантовая теория утверждает, что в любой точке про-
странства может возникнуть пара, состоящая из частицы и античастицы
(например, электрон и позитрон) на короткое время г, а затем исчезнуть
(аннигилировать). Время т определяется энергетическим соотношением
не опр еделенно стей:
(Д.13.7)
. 2тгН
где Е — суммарная энергия пары частиц, включающая их энергию по-
коя. Такие частицы также называются виртуальными.
Из соотношения (Д.13.7) очевидно, что время т очень мало даже для
таких маломассивных частиц, как электрон и позитрон.
Несмотря на малое время существования виртуальных частиц, они
взаимодействуют с электронами атома. Расчеты, выполненные методами
квантовой электродинамики, показывают, что различный вид волновых
функций стационарных состояний электрона в оболочках 2s и 2р обу-
словливает различие в энергии взаимодействия с виртуальными части-
цами. В результате энергии стационарных состояний 2s и 2р становятся
не одинаковыми, что объясняет явление лэмбовского сдвига.
Лекция 14
МНОГОЭЛЕКТРОННЫЙ АТОМ
В предыдущих лекциях рассматривались основные физичес-
кие свойства и характеристики атома водорода и других одно-
электронных (водородоподобных) атомов и ионов. Напомним,
что решение стационарного уравнения Шредингера для водоро-
доподобных атомов проводилось аналитически. Это значит, что
полученные волновые функции стационарных состояний и соот-
ветствующие значения энергий являются точными в рамках ис-
пользованных идеализаций.
Атомы всех химических элементов, кроме водорода, содержат
более одного электрона. Число электронов в нейтральном атоме
равно Z — порядковому номеру элемента в таблице Менделеева.
Для создания теории атома водорода оказался очень важным
анализ его спектра излучения. Если в трубке, наполненной газом,
создать электрический разряд, то атомы газа будут получать энер-
гию, а затем испускать электромагнитное излучение. Наблюдения
оптических спектров многоэлектронных атомов показывают, что
их спектры излучения являются линейчатыми, подобно спектру
атома водорода. Число спектральных линий в видимом диапазоне
порядка десяти у гелия и сотни тысяч у элементов с большими
атомными номерами. При этом дискретный набор длин волн су-
губо индивидуален для каждого элемента, на чем и базируется
метод спектрального анализа — один из самых точных экспери-
ментальных методов физики.
14.1. Опыты Франка-Герца
Важные свойства многоэлектронных атомов были получены в
знаменитых опытах Франка-Герца. Джеймс Франк (1882-1964)
и Густав Герц (1887-1975), племянник Генриха Герца — первоот-
крывателя электромагнитных волн, в течение 1912-1914 гг. зани-
мались исследованием столкновений электронов с атомами газов.
В качестве газов использовались пары металлов и инертные газы.
14.1. Опыты Франка-Герца
273
Схема экспериментальной установки Франка-Герца приведена на
рис. 14.1.
Установка состоит из трех основных частей.
1. Электронная пушка. Источником электронов является ме-
таллическая проволока, нагреваемая проходящим через нее элек-
трическим током, т.е. термокатод. Электроны ускоряются элек-
трическим полем цилиндрического анода, и энергия ускоренного
Камера
Рис. 14.1. Схема экспериментальной установки Франка-Герца
электрона на выходе электронной пушки определяется разностью
потенциалов между катодом и анодом. Разброс энергий ускорен-
ных электронов уменьшается с помощью фильтра скоростей. Диа-
фрагмы, установленные в электронной пушке, позволяют форми-
ровать узкий пучок моноэнергетических электронов.
2. Камера столкновений. Она содержит одноатомный газ
исследуемого элемента при оптимальном давлении. В камере про-
исходят столкновения ускоренных электронов с атомами газа.
Оптимальным полагается давление, при котором двукратные
столкновения электронов с атомами газа маловероятны. Таким
образом, электроны, ускоренные пушкой, либо достигают анали-
затора без столкновений, либо претерпевают однократное столк-
новение с атомом газа.
3. Анализатор. В анализаторе измеряются энергии электро-
нов, попавших в него, методом задерживающего потенциала. За-
держивающий потенциал подается на сетку анализатора. В качест-
ве детектора используется цилиндр Фарадея. Электроны, попавшие
в цилиндр, формируют ток, регистрируемый гальванометром.
Электрический ток на выходе пропорционален количеству элек-
тронов, попавших в анализатор. Плавное изменение задерживаю-
щего потенциала позволяет получить зависимость тока от энергии
электронов, т.е. энергетический спектр достигших анода элек-
тронов.
274
Лекция 14. Многоэлектронный атом
Результаты экспериментов показывают, что спектры рассеян-
ных электронов имеют дискретный вид — состоят из отдельных
пиков. На рис. 14.2 схематически изображен типичный спектр
Рис. 14.2. Спектр электронов, полученный в опыте Франка-Герца. Камера столк-
новений заполнена натрием в газовой фазе. Энергия первичных электронов
Ео = 3,5 эВ. В спектре наблюдаются пики с энергиями 0,3 эВ, 1,4 эВ и 3,5 эВ.
Первые два пика образованы неупруго рассеянными электронами на атомах на-
трия, третий пик — упруго рассеянными или нерассеянными электронами
энергий электронов, зарегистрированных анализатором, при опре-
деленной энергии ускоренных электронов, в случае, когда камера
столкновений заполнена разреженными парами натрия.
Спектры электронов, прошедших через камеру, заполненную
атомами натрия, обладают следующими характерными особенно-
стями. При энергии исходных электронов Eq, не превышающей
величину = 2,1 эВ, спектр зарегистрированных электронов со-
держит единственный пик с энергией Е = Eq. Если энергия исход-
ных электронов лежит в интервале Е\ < Eq < где Е2 = 3,2 эВ,
то в спектре, помимо пика с энергией Eq, появляется дополнитель-
ный пик, энергия которого равна разности Eq — Ei = Eq — 2,1 эВ.
При дальнейшем увеличении энергии исходных электронов Eq
спектры рассеянных электронов содержат уже три пика с энер-
гиями Eq, Eq — El = Eq — 2,1 эВ И Eq — Е2 = Eq — 3,2 эВ (см.
рис. 14.2). С ростом энергии Eq спектры становятся все более
сложными, в них появляются новые пики.
Для объяснения вида вышеописанных спектров учтем, что при
прохождении ускоренного электрона через газовую среду проис-
ходят его столкновения с атомами газа. Кинетической энергией
атома перед столкновением можно пренебречь, так как при ком-
натной температуре средняя тепловая энергия составляет к&Т «
14.2. Уравнение Шредингера для стационарных состояний 275
« 0,025 эВ, что много меньше энергий электронов Eq, используе-
мых в опытах.
Столкновение исходного электрона с атомом может быть упру-
гим, при этом внутренняя энергия атома не изменяется. Энергия
рассеянного электрона Е из-за разницы масс электрона и атома
(тпе тпа) практически совпадает с энергией исходного элек-
трона Eq.
При неупругом столкновении электрона с атомом часть кине-
тической энергии исходного электрона Eq пойдет на возбуждение
атома. Эта энергия равна
Eq = Е + Е*, (14.1)
где Е* — энергия возбуждения атома (разность энергии основного
и возбужденного состояния).
Из вышеприведенных экспериментальных результатов следу-
ет, что при исходной кинетической энергии Eq < Е\ = 2,1 эВ все
столкновения электронов с атомами натрия являются упругими.
Два пика спектра, которые наблюдались при энергиях Е\ <
< Eq < Е2 = 3,2 эВ, объясняются следующим образом. Один пик
(с энергией Е = Eq) образован нерассеянными и упруго рассе-
янными электронами, другой (с энергией Е = Eq — Е±) — элек-
тронами, претерпевшими неупругое рассеяние и потерявшими в
столкновениях энергию Е± = 2,1 эВ. В соответствии с (14.1) это
значит, что при этом атом получил определенную энергию возбу-
ждения Е* = Е\ = 2,1 эВ.
Три пика на рис. 14.2 объясняются тем, что часть электро-
нов, зарегистрированных анализатором, потеряла энергию Е± =
= 2,1 эВ, а другая часть — энергию Е% = 3,2 эВ. Следовательно,
атомы натрия могут получать энергии возбуждения 2,1 эВ и 3,2 эВ.
Энергия возбуждения равна разности энергий возбужденного
стационарного состояния и основного. Таким образом, вышеопи-
санные эксперименты показывают, что атом натрия обладает дис-
кретным спектром стационарных состояний. Эксперименты по
рассеянию электронов на многоэлектронных атомах других хи-
мических элементов дали аналогичные результаты.
Основным итогом опытов Франка-Герца является доказатель-
ство существования дискретных стационарных состояний у
многоэлектронных атомов.
14.2. Уравнение Шредингера для стационарных состояний
многоэлектронного атома
Дискретные оптические спектры излучения, опыты Франка-
Герца и другие экспериментальные данные свидетельствуют в
пользу дискретного спектра стационарных состояний у многоэлек-
тронных атомов. Для получения волновых функций стационар-
276
Лекция 14. Многоэлектронный атом
них состояний и соответствующих энергий в принципе следует ис-
пользовать уравнение Шредингера (10.5). Однако гамильтониан
неподвижного многоэлектронного атома имеет весьма громоздкий
вид:
Z Z
Z Z
.. -1
k'>k
4-2 z z 1 z z
I bp I
e k=l k=l K k=l k'=l
I 1 ,, (14.2)
|r/c “Г/Н
где Z — число электронов, или порядковый номер химического
элемента.
Первое слагаемое представляет собой оператор кинетической
энергии, куда входит сумма операторов Лапласа, каждый из кото-
рых содержит вторые частные производные по координатам к-го
электрона:
д2 д2 д2
^ = a^t + att + aj: (14'3)
Вторая сумма в (14.2) является оператором потенциальной
энергии кулоновского взаимодействия всех электронов с атомным
ядром. Здесь гь — расстояние А;-го электрона до центра ядра.
Наконец, последняя сумма в (14.2) — оператор потенциальной
энергии межэлектронного кулоновского взаимодействия. Двойное
суммирование производится по всем парам электронов. Количе-
ство слагаемых в этой сумме равно Z(Z — 1)/2.
Расстояние между электронами не превышает размера атома,
поэтому энергия межэлектронного взаимодействия по порядку ве-
личины сравнима с энергией кулоновского взаимодействия элек-
тронов с ядром. Следовательно, невозможно пренебречь двойной
суммой в операторе (14.2) и тем самым несколько упростить га-
мильтониан.
Следует заметить, что гамильтониан (14.2) не учитывает спин-
орбитальное взаимодействие различных электронов, спин-спино-
вое межэлектронное взаимодействие, взаимодействие магнитного
момента электрона с магнитным моментом атомного ядра (кото-
рый существует у ядер многих изотопов) и т. п. При учете этих
взаимодействий гамильтониан многоэлектронного атома еще бо-
лее усложняется.
Подытоживая вышеизложенное, можно констатировать, что
уравнение Шредингера
ЯФл = ЕдФд (14.4)
для волновой функции Фд стационарных состояний многоэлек-
тронного атома с гамильтонианом вида (14.3) не имеет аналити-
ческого решения.
14.3. Тождественность частиц
277
Прежде чем обсуждать приближенные (в частности, числен-
ные) методы решения уравнения (14.4), следует рассмотреть не-
которые важные физические принципы анализа многочастичных
систем.
14.3. Тождественность частиц
В классической физике частицы часто представлялись матери-
альными точками. При равенстве масс частиц всегда существует
принципиальная возможность различать эти частицы, отметив их
каким-либо индивидуальным физическим признаком. Также все-
гда возможно проследить за движением конкретной материальной
точки вдоль ее траектории.
Микрочастицы обладают принципиально другими свойствами.
Все электроны во Вселенной имеют одинаковые параметры: массу
покоя те, электрический заряд —е, спиновое квантовое число s =
= 1/2. Не существует физических способов отличить один элек-
трон от другого. Более того, соотношения неопределенностей ли-
шают электроны точных траекторий. Следовательно, нет никакой
возможности проследить за отдельным электроном.
В качестве примера рассмотрим столкновение двух электронов
(см. рис. 14.3). Когда частицы движутся вдалеке друг от друга,
электроны в принципе можно различать, так как их координаты
Рис. 14.3. Возможные схемы столкновения двух электронов
различаются на величину много большую неопределенности коор-
динаты, задаваемой соотношением Гейзенберга (6.3). Пусть один
из них движется слева направо, другой в противоположном на-
правлении. Но в области размером ~ h/p траекторию частицы
в принципе невозможно построить. Вопрос о том, отразилась ли
назад первая частица или рассеялась ли на малый угол, не имеет
смысла. Обе схемы рассеяния, приведенные на рис. 14.3, абсо-
лютно неразличимы.
В общем случае, пронумеровав электроны в определенный мо-
мент времени, мы в другой момент времени в принципе не можем
указать, где находится электрон №1, №2 и т. д. Таким образом, мы
278
Лекция 14. Многоэлектронный атом
не можем контролировать однотипные микрочастицы по их тра-
екториям и поэтому их следует считать не просто одинаковыми, а
тождественными, т.е. принципиально неразличимыми.
Вышесказанное относится и к микрочастицам других типов:
протонам, нейтронам и т. п.
Свойство тождественности микрочастиц обусловливает харак-
терные особенности многочастичных систем.
Рассмотрим сначала систему, содержащую две тождественные
частицы. Если мы поменяем их местами, то получим нс новое
состояние системы с совпадающими характеристиками, а то же
самое физическое состояние. Это утверждение обусловлено тем,
что не существует никаких физических способов различить эти
состояния системы.
Волновая функция данной системы в определенном состоянии
может быть записана в виде где — совокупность коор-
динат и проекции спина (x,y,z,ms) 1-й частицы, & — аналогич-
ные характеристики 2-й частицы. Переставив частицы местами,
мы получим систему, описываемую волновой функцией ^(£2>£1)-
Как было указано выше, взаимная перестановка частиц в силу
их тождественности приводит к физически неразличимому состо-
янию данной системы. Согласно лекции 9, физический смысл
имеет лишь квадрат модуля волновой функции. Следовательно,
неразличимость двух состояний при перестановке частиц должна
выражаться тем, что волновая функция может измениться только
на фазовый множитель еш, модуль которого равен 1:
Ж(1) = е^(6,е2). (14.5)
Повторив перестановку частиц еще раз, мы вернемся к исход-
ному состоянию с волновой функцией ^(С1,^2)- Следовательно,
е2ш = 1, откуда ега = ±1. Отсюда следует важный вывод: си-
стемы, состоящие из тождественных частиц, описываются волно-
выми функциями только с определенной симметрией.
Функция может быть симметричной, не меняющейся при пе-
рестановке любой пары частиц, или антисимметричной, которая
при перестановке двух любых частиц меняет только знак.
В ходе разработки квантовой теории было установлено, что
два типа перестановочной симметрии волновых функций соответ-
ствуют двум типам микрочастиц.
Частицы, которые описываются симметричными волновыми
функциями, называются бозонами. Частицы, описываемые ан-
тисимметричными волновыми функциями, называются фермио-
нами.
Релятивистская квантовая механика установила, что тип ча-
стиц однозначно определяется их спином. Частицы, у которых
квантовое число спина является полуцелым: 1/2, 3/2, ..., яв-
ляются фермионами. В частности, электроны, протоны и ней-
14.3. Тождественность частиц 279
троны имеют спиновое квантовое число s = 1/2 и относятся к
фермионам.
Частицы с целым или нулевым значением спинового кванто-
вого числа s являются бозонами. Представителем бозонов явля-
ется фотон, у которого квантовое число s = 1.
Часто для краткости терминологии говорят вместо «спиновое
квантовое число» просто «спин». Тогда фермионы характеризуют
полуцелым спином, а бозоны — целым.
Перейдем к анализу систем, состоящих из конечного числа ча-
стиц одного типа. Вообще говоря, такие системы описываются
единой волновой функцией, которая зависит от координат всех
частиц. Решение стационарного уравнения Шредингера для мно-
гочастичной системы должно давать волновую функцию стацио-
нарного состояния всей системы и энергию этой системы. При
этом возникает вопрос о существовании стационарных состояний
отдельных частиц системы. В квантовой механике установлено,
что если между частицами системы взаимодействие отсутствует,
то состояние системы представляются совокупностью стационар-
ных состояний отдельных частиц системы. В этих состояниях
каждая частица описывается своей волновой функцией и обладает
определенной энергией. Энергия системы составляется из энергий
отдельных частиц.
Пусть имеется система, содержащая N тождественных частиц,
причем взаимодействием между частицами можно пренебречь.
Предположим, что каждая из частиц системы находится в одном
из своих стационарных состояний. Тогда легко доказать непосред-
ственной подстановкой в уравнение Шредингера (10.5), что в та-
кой ситуации произведение волновых функций отдельных частиц
будет являться решением этого уравнения, при этом энергия си-
стемы равна сумме энергий стационарных состояний отдель-
ных частиц.
Рассмотрим сначала систему, состоящую из двух тождествен-
ных невзаимодействующих частиц 1 и 2. Если частицы являются
бозонами, то волновые функции их системы должны быть сим-
метричными относительно перестановки частиц. Очевидно, что
произведение ^(£1) ^(£2) этим свойством не обладает. Вследствие
этого волновая функция системы двух бозонов должна быть запи-
сана в следующей линейной комбинации произведений:
Ф(£1, &г) = 4=[Фр1(6)ФР2(е2) + ’Ы£2)ФР2(6)], (14.6)
V "
где pi и р2 — наборы квантовых чисел, определяющих стационар-
ные состояния, в которых находятся частицы системы. Так как
полные наборы квантовых чисел однозначно задают стационарное
состояние частицы, то величины р\ пр2 можно принять за номера
стационарных состояний частиц.
280 Лекция 14. Многоэлектронный атом
Волновая функция системы фермионов должна быть построена
из волновых функций отдельных частиц так, чтобы выполнялось
свойство ее антисимметричности относительно перестановки ча-
стиц. Можно непосредственно убедиться, что антисимметричной
волновой функцией системы из двух невзаимодействующих фер-
мионов является следующая линейная комбинация:
ф(С1,е2) = 4['М£1)’Ы&) - Фр1(е2)фр2(б)]- (и.7)
V "
Множитель 1/\/2 в формулах (14.6) и (14.7) возникает вследствие
условия нормировки. Нетрудно заметить, что волновую функцию
(14.7) можно записать в эквивалентной форме в виде определителя
Ф(£1 &)=:-— Фр2^2) (14 8)
V2 фр2(б) фр1(е2) • ( J
Допустим, что обе частицы находятся в одинаковых состоя-
ниях, т. е. обладают одинаковыми наборами квантовых чисел
Р1 — Р2- Тогда волновая функция для системы из двух тожде-
ственных бозонов запишется в виде произведения
Ф(£1,£2) = Фр1(£1)Фр2(&).
Волновая функция системы двух тождественных фермионов (14.8)
при том же условии равна нулю. Это означает, что в
двухчастичной системе фермионов частицы никогда не могут на-
ходиться в одинаковых состояниях.
Разумеется, речь идет о достаточно компактной системе частиц,
характерный размер которой не превышает величины h/p, где р —
импульс частицы в системе центра масс. Пара фермионов, находя-
щихся на большом расстоянии друг от друга, может описываться
совершенно одинаковыми наборами квантовых чисел. Примером
могут служить два электрона в электронно-лучевых трубках ос-
циллографов, стоящих на соседних столах в лаборатории. Так
как в данном примере электроны практически не взаимодействуют
друг с другом, они не представляют собой квантомеханическую
систему. Заметим, что волновые функции данных электронов не
совпадают, так как частицы находятся в разных областях про-
странства.
Обобщим полученные результаты на системы из произвольного
количества невзаимодействующих частиц. Пусть ФрД£г) — вол-
новая функция г-й частицы в состоянии Pi (т. е. в стационарном
состоянии, определяемом полным набором квантовых чисел Pi).
Предположим, что все волновые функции всех частиц в стационар-
ных состояниях нормированы.
14.4. Самосогласованное поле
281
Если частицы — бозоны, то волновая функция системы
Ф(£1, £2? • • •> Сдг) представляется суммой произведений вида
фР1(£1)фр2(£2)- • .ФруДСдг):
ф = V w Еф^(е1)фр2(е2)---фр^(Ы- (14.9)
Сумма содержит произведения, образованные всевозможными пе-
рестановками пар частиц. Числа Ni равны количеству частиц,
находящихся в одинаковых состояниях Р^, и подчиняются оче-
видному соотношению
Для системы из N невзаимодействующих фермионов волновая
функция может быть записана в виде определителя TV-го порядка,
аналогичного (14.8) и называемого определителем Слэтера:
фР1(6) ФрДбг) ••• ФрДСлг)
Фр2(6) Фр2(Сг) ••• Фр2(£лг)
(14.10)
фРлД6) Фр/Лбг) ... ^pn(£n)
Взаимная перестановка любых двух частиц выражается пере-
становкой двух столбцов определителя. Как известно из линейной
алгебры, при этом определитель меняет знак. Также известно, что
определитель с двумя одинаковыми строками равен нулю. Отсюда
следует, что если две любые частицы системы тождественных фер-
мионов окажутся в одинаковых состояниях, то волновая функция
системы частиц (14.9) обратится в нуль. Таким образом, в си-
стеме тождественных фермионов все частицы должны нахо-
диться в различных состояниях. Это важное для квантовой фи-
зики утверждение называется принципом Паули.
14.4. Самосогласованное поле
Многоэлектронный атом представляет собой сложную систему
взаимодействующих друг с другом электронов, которые движутся в
электрическом поле атомного ядра. Вид гамильтониана системы
атомных электронов (14.2) исключает возможность аналитичес-
кого решения стационарного уравнения Шредингера (14.4) и по-
лучения волновых функций стационарных состояний многоэлек-
тронного атома.
В процессе развития квантовой теории оказалось целесообраз-
ным ввести понятие стационарных состояний электронов, находя-
щихся в атоме. Каждый электрон рассматривается движущимся в
поле, создаваемом ядром и всеми остальными электронами. Дей-
282 Лекция 14. Многоэлектронный атом
ствие Z — 1 электронов характеризуется некоторым эффективным
полем которое приближенно полагается центрально-симмет-
ричным. Эти эффективные поля для разных электронов (находя-
щихся в различных состояниях), вообще говоря, имеют различ-
ный вид. Вычисляться эти поля должны одновременно, так как
все они зависят от состояний всех остальных электронов. Сово-
купность всех эффективных функций называется самосо-
гласованным полем атома.
Введение самосогласованного поля позволяет записать стацио-
нарные уравнения Шредингера для отдельных электронов атома:
(14.11)
где k = 1,2,..., Z — номер электрона, — гамильтониан к-го
электрона, Д — волновая функция одноэлектронного стационар-
ного состояния fc-го электрона, — энергия этого состояния.
Одноэлектронный гамильтониан Нь имеет вид
Hk = - — + и^\ (14.12)
2те гк К
где Д^ — оператор Лапласа (14.3), — эффективное поле для
fc-го электрона.
Таким образом гамильтониан атома (14.2) разбивается на Z
одноэлектронных гамильтонианов (14.12), причем двойная сумма
межэлектронного взаимодействия разделяется на Z операторов
умножения на энергию эффективного поля Щ, .
Следовательно, задача решения сложного уравнения (14.4) све-
лась к решению системы Z менее сложных уравнений (14.11).
Результатом решения уравнений (14.11) являются одноэлектрон-
ные волновые функции и энергии отдельных электронов в
стационарных состояниях, где к = 1,2,..., Z.
Важным достоинством такого пути решения проблемы мно-
гоэлектронного атома является следующее. Выбор одноэлектрон-
ного гамильтониана в виде (14.12) приводит к тому, что волновая
функция стационарного состояния атома Фд представляется через
одноэлектронные волновые функции {к = 1,2, ...,Z) в виде
определителя Слэтера (14.10), записанного для Z частиц:
фР1(£1) ••• ФР1(£?)
ФР2(?1) ФР2(^) ••• ФР2(^)
(14.13)
фР2(6) ФРИ(6) ••• ^Pz(Cz)
14.4. Самосогласованное поле 283
Таким образом удовлетворяется свойство антисимметричности
волновой функции системы фермионов относительно перестановок
тождественных электронов атома. При этом энергия атома в этом
стационарном состоянии равна сумме энергий одноэлектронных
состояний:
Z
ЕА = ^Ек. (14.14)
k=l
В предыдущем параграфе указывалось, что подобными свой-
ствами обладают системы невзаимодействующих тождественных
фермионов. Именно приближение самосогласованного поля и
представление одноэлектронных гамильтонианов в виде (14.12),
содержащем функции эффективного взаимодействия (к —
= 1,2,..., Z), позволяет получить решение задачи о стационарных
состояниях многоэлектронного атома в виде выражений (14.13) и
(14.14). При этом энергии одноэлектронных состояний Ek (к =
= 1,2,..., Z) содержат не только кинетическую энергию и потен-
циальную энергию взаимодействия к-го электрона с атомным
ядром, но и энергию взаимодействия с остальными электронами.
Следует учесть, что решение системы уравнений (14.11) со-
, rr(eff)
пряжено со значительными трудностями, так как функции Uj: 7
(к = 1,2,...,Z) не определены исходными данными и должны
вычисляться в ходе решения.
Выше упоминалось, что в первом приближении самосогласо-
ванное поле полагают центрально-симметричным. Иначе говоря,
потенциальная энергия электрона в самосогласованном поле
f/(eff)(r) зависит только от одной скалярной координаты г — рас-
стояния электрона от центра атомного ядра. Это означает, что
каждое одноэлектронное состояние характеризуется определенным
значением орбитального квантового числа I. Стационарные состо-
яния отдельного электрона при заданном числе I нумеруются в
порядке возрастания их энергии с помощью главного квантового
числа п. При этом главное квантовое число пробегает значения
тг = /4-1, Z + 2, ... Такой порядок нумерации соответствует при-
нятому ранее для стационарных состояний атома водорода (см.
(11.17) и (11.18) в лекции 11). При определенных значениях
главного и орбитального квантовых чисел электрон может обла-
дать различными значениями магнитного квантового числа т =
= 0, ±1, ±2,..., ±1 и квантового числа проекции спина ms =
= ±1/2. Таким образом, одноэлектронное стационарное состоя-
ние характеризуется четырьмя квантовыми числами, аналогично
состояниям атома водорода.
Вычисления явного вида одноэлектронных волновых функций
и энергий отдельных электронов в их стационарных состояниях
284
Лекция 14. Многоэлектронный атом
выполняются приближенными методами квантовой механики.
Как правило, эти методы используют последовательные прибли-
жения. В качестве нулевого приближения можно выбрать водо-
родоподобные функции, описанные в лекции 11. Приближенное
решение, полученное на определенной итерации, служит для уточ-
нения вида оператора Гамильтона и соответствующих ему соб-
ственных волновых функций. При этом осуществляется поэтап-
ный учет имеющихся в атоме взаимодействий по мере убывания
их энергии.
На приближении самосогласованного поля базируется метод,
разработанный Д.Р. Хартри (1897-1958) и В.А. Фоком (1898-1974).
Методом Хартри-Фока рассчитаны одноэлектронные функции для
основных состояний атомов всех химических элементов, а также
для многих возбужденных состояний атомов и ионов. Недостат-
ком метода является то, что решения проводятся численно и по-
лученные функции представляются в виде таблиц чисел. Однако
современная вычислительная техника позволяет выполнять рас-
четы таблиц функций с достаточной точностью и за приемлемое
компьютерное время.
Кроме того, широко используются различные аналитические
аппроксимации одноэлектронных функций (см. дополнение 14.1).
В заключение данного параграфа еще раз повторим, что, строго
говоря, необходимо рассматривать стационарные состояния атома
в целом. Говорить об определенном стационарном состоянии от-
дельного электрона в системе тождественных взаимодействующих
частиц, характеризовать это состояние определенным набором
квантовых чисел можно только в определенном приближении.
Представление стационарного состояния атома совокупностью од-
ноэлектронных функций является приближенной математичес-
кой моделью многоэлектронного атома. Однако с помощью этого
подхода оказывается возможным вычислять значения измеряе-
мых физических величин, удовлетворительно совпадающие с
экспериментальными данными. Следовательно, описание атома
одноэлектронными волновыми функциями оправдано и целесооб-
разно.
14.5. Электронные слои и оболочки
Рассмотрим многоэлектронный атом в пренебрежении спин-
орбитальным взаимодействием электронов. Представим стацио-
нарное состояние атома совокупностью одноэлектронных волно-
вых функций, согласно изложенному в предыдущем параграфе.
Каждое одноэлектронное состояние характеризуется четырьмя
квантовыми числами n, Z, тп и ms-
Результаты расчетов методом Хартри-Фока показывают, что в
данном приближении энергия одноэлектронного состояния зави-
14.5. Электронные слои и оболочки
285
сит от квантовых чисел пи/, причем более резко изменяется при
изменении главного квантового числа п.
Введем определения, которые позволяют в рамках модели
самосогласованного поля классифицировать электроны в много-
электронном атоме по основным физическим характеристикам.
Набор состояний (электронов) с фиксированными квантовыми
числами п и I называется электронной оболочкой. Можно ска-
зать, что понятие электронной оболочки базируется на величине
энергии электрона, а не на геометрических параметрах. Оболочки
обозначаются символом, на первом месте которого записывается
значение главного квантового числа п, а на втором месте указы-
вается символ з, d, ..., обозначающий орбитальное квантовое
число Z, в соответствие с табл. 9.1 в лекции 9. Для чисел I > 4 ис-
пользуются следующие буквы латинского алфавита. Количество
состояний в электронной оболочке определяется диапазонами воз-
можных вариаций квантовых чисел т и ms и равно 2(2/ 4- 1),
т.е. не зависит от значения главного квантового числа п (см.
табл. 14.1).
Таблица 14.1. Обозначения электронных оболочек и количество
стационарных состояний в них
Орбитальное квантовое число 1 0 1 2 3 4
Символ электронной оболочки S Р d f 9
Количество стационарных состояний в электронной оболочке 2 6 10 14 18
Набор состояний с фиксированным главным квантовым чис-
лом п называется электронным слоем. Исторически сложилось
обозначение заглавными латинскими буквами в алфавитном по-
рядке, начиная с буквы К (см. табл. 14.2).
Таблица 14.2. Обозначения электронных слоев и количество
стационарных состояний в них
Главное квантовое число 1 2 3 4 5 6 7
Символ электронного слоя К L М N О Р Q
Число состояний в слое 2 8 18 32 50 72 98
Очевидно, что электронный К-слой содержит единственную
электронную оболочку Is. Электронный L-слой состоит из двух
электронных оболочек: 2з и 2р, третий электронный слой
(М-слой) имеет 3 оболочки (Зз, Зр, 3d) и т. д.
286 Лекция 14. Многоэлектронный атом
Распределение электронов атома по электронным оболочкам
(т. е. по состояниям с различными квантовыми числами пи/)
называется электронной конфигурацией.
Так как энергия одноэлектронного состояния в данном при-
ближении зависит только от квантовых чисел п и /, то задание
электронной конфигурации полностью определяет энергию атома
Ед. Выражение (14.14) в приближении электронных конфигура-
ций можно переписать в следующем виде:
EA = ^QniEni. (14.15)
Здесь коэффициент qni равен количеству электронов, находящих-
ся в оболочке nl. Величины Eni представляют собой энергии од-
ноэлектронных состояний, которые в сумме (14.14) обозначались
как Е^- Суммирование в (14.15) проводится по всем оболочкам,
содержащим электроны.
Рассмотрим несколько примеров электронных оболочек в ато-
мах.
1. Оболочка Is (n = 1, 1 = 0). Данная оболочка содержит
два одноэлектронных состояния со следующими квантовыми чи-
слами: т = 0, ms = 1/2 и т = 0, ms = —1/2.
2. Оболочка 2s (п = 2, I = 0) также содержит 2 состояния,
различающиеся квантовыми числами т = 0, ms = 1/2 и т =
= 0, ms = —1/2. Очевидно, что любая s-оболочка содержит два
одноэлектронных состояния.
3. Оболочка 2р (п = 2, I = 1) содержит 6 состояний с кванто-
выми числами: т = —1,0,1 и ms = ±1/2. Нетрудно убедиться,
что любая р-оболочка содержит шесть одноэлектронных состоя-
ний.
Так как электронная оболочка с орбитальным числом I содер-
жит 2(21 + 1) состояний, то количество состояний в электронном
слое с определенным значением номера п равно
2(2/ + 1) = 21 + 2(П~1) + 1 п = 2п2. (14.16)
z=o
Согласно принципу Паули в одноэлектронных состояниях не
может быть более одного электрона. Следовательно, существуют
заполненные и пустые одноэлектронные состояния. В основном
состоянии атома заполненными должны быть одноэлектронные
состояния с наинизшей энергией.
Таким образом, электронные конфигурации многоэлектронно-
го атома определяются принципом Паули и величиной энергии
атома в стационарном состоянии.
14.5. Электронные слои и оболочки
287
Задачи к лекции 14
1. На установке Франка-Герца проводились эксперименты по рассе-
янию электронов с энергией 7 эВ на атомах ртути. В спектре рассеян-
ных электронов были зарегистрированы максимумы, соответствующие
энергиям 1,5 эВ, 2,1 эВ и 2,3 эВ. Зная, что энергия ионизации ртути со-
ставляет « 10,4 эВ, рассчитать энергии трех первых возбужденных ста-
ционарных состояний атома ртути.
2. Записать в явном виде гамильтониан: а) атома гелия, б) атома
лития, в) иона лития Li+.
3. Перечислить всевозможные электронные оболочки электронных
слоев: а) М и N, б) О и Р.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 14
14.1. Аналитические аппроксимации волновых функций
К настоящему времени методом Хартри-Фока вычислены одноэлек-
тронные волновые функции не только для всех атомов, но и для мно-
гих ионов. Однако работа с такими функциями не всегда удобна из-за
того, что они представляются не аналитическими формулами, а в виде
числовых таблиц. По этой причине широко используются различные
аналитические аппроксимации одноэлектронных волновых функций, из
которых наиболее употребительной является система функций Слэтера.
Эти функции представляются следующей общей формулой
✓ \ п* —1 / \
Фп(т = Мг( —) ехр (-£—)У(т(61,</9), (Д-14.1)
\ а0 / \ а0 /
где г, 0, — полярные координаты электрона, ао —боровский радиус, п,
1,т — квантовые числа (главное, орбитальное, магнитное). Параметр п*
получил название эффективного квантового числа, метод его вычисления
описан ниже.
Коэффициент Nn = (2£)n+1/2[(2n)]-1/2 обеспечивает нормировку
функции (Д.14.1), экспоненциальный множитель
Z-Se
П*
зависит от порядкового номера химического элемента Z, постоянной
экранирования Se и эффективного квантового числа п*.
Угловая часть волновой функции Слэтера (Д.14.1) представляется
сферическими функциями (9.53), некоторые из которых приведены в
табл. 9.2 лекции 9.
Построение явного вида функции (Д.14.1) сводится к вычислению
постоянных экранирования Se и эффективных квантовых чисел п*. Слэ-
тер разработал такую методику расчета величин Se и п*, чтобы резуль-
таты согласовывались с данными оптической и рентгеновской спектро-
скопии атомов. Этот метод изложен ниже.
Эффективное квантовое число п* определяется главным квантовым
числом п согласно табл. Д.14.1.
Таблица Д.14.1. Значения эффективных квантовых чисел
для волновых функций Слэтера
п 1 2 3 4 5 6
п* 1 2 3 3,7 4 4,2
Дополнения к лекции 14
289
Электронные оболочки разбиваются на последовательные группы:
(Is), (2s2p), (3s3p), (3d), (4s4p), (4d), (4/), (5s5p) и т.д. Все состоя-
ния в определенной группе характеризуются одинаковыми радиальными
функциями Слэтера (Д.14.1).
Значение постоянной экранирования Se для данной электронной обо-
лочки равно сумме вкладов, вносимых отдельными заполненными одно-
электронными состояниями. Вклад в величину Se равен:
1) нулю для любых электронов, расположенных в группах более
внешних электронных оболочек;
2) 0,35 от каждого электрона в той же группе, кроме рассматривае-
мого; в группе 1s вместо этого значения берется 0,3;
3) для s- и р-электронов по 0,85 от каждого электрона с главным кван-
товым числом на единицу меньше, чем у рассматриваемого электрона,
и по 1,0 от всех электронов, расположенных в группах более внутренних
электронных оболочек;
4) для d- и /-электронов по 1,0 от каждого электрона, расположенного
в группах более внутренних электронных оболочек.
В качестве примера рассмотрим расчет постоянных экранирования
Se и экспоненциальных множителей £ для заполненных электронных
оболочек атома углерода в основном состоянии. В таком состоянии элек-
троны распределяются по двум группам: (1s) и (2s2p). Для оболочки 1s
константа экранирования Se = 0,3 и множитель £ = 5,7. Для оболочек
2s и 2р константа Se = 3 • 0,35 + 2 • 0,85 = 2,75, а экспоненциальный
множитель £ = 1,625.
Подстановка функций (Д.14.1) в уравнение Шредингера для водоро-
доподобного атома дает следующие значения энергий одноэлектронных
состояний:
g=_Ry (Д.14.2)
(п*)2
Недостатком волновых функций типа (Д.14.1) являются значитель-
ные погрешности при малых расстояниях г <£ ао, т. е. в области вну-
тренних электронных оболочек. Этот недостаток частично устраняется
составлением линейных комбинаций нескольких слэтеровских функций
с различными экспоненциальными множителями.
Для аппроксимации одноэлектронных волновых функций также ис-
пользуются функции, содержащие гауссовый множитель:
Фп/m = ^n(«)rn-1exp(-ar2)YZm(^,^), (Д.14.3)
где а — подгоночный параметр. Линейные комбинации функций (Д.14.3)
позволяют конструировать аппроксиманты, удовлетворительно описыва-
ющие одноэлектронные волновые функции в приближении самосогласо-
ванного поля.
Лекция 15
ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
ХИМИЧЕСКИХ ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА
15.1. Периодический закон Менделеева
К середине XIX века успехи химии, в том числе открытие но-
вых химических элементов, позволили накопить большой фак-
тический материал и выявили необходимость его систематиза-
ции. Большое значение имело то обстоятельство, что к этому
времени были проведены достаточно точные измерения атомной
массы многих элементов. В качестве основы практически всех
попыток систематизации химических элементов использовалась
общность их химических свойств. Элементы подразделялись на
группы в соответствии с их общими свойствами. Так, наиболее
резко выраженный основной характер был обнаружен у соедине-
ний элементов, названных щелочными металлами, а способность
к проявлению кислотных свойств — у галогенов. Задачу систе-
матизации химических элементов полностью решил великий рус-
ский химик Д.И. Менделеев (1834-1907).
Идея Д.И. Менделеева состояла в том, что в основу классифика-
ции химических элементов должна быть положена фундаменталь-
ная количественная характеристика элементов — атомная масса,
от которой должны зависеть все другие их свойства.
Д.И. Менделеев сопоставил между собой элементы, расположив
все известные в то время химические элементы в порядке воз-
растания их атомных масс. Фрагмент этой последовательности
выглядел следующим образом:
Ослабление металлических свойств
Li-Be-B-C-N-0-F-.....
Na-Mg-Al-Si-P-S-Cl-...
К-Са.................
15.1. Периодический закон Менделеева 291
От лития Li к фтору F происходит постепенное ослабление ме-
таллических свойств и усиление неметаллических с одновремен-
ным увеличением валентности. Переход от фтора F к следую-
щему по значению атомной массы натрию Na происходит при
скачкообразном изменении свойств и валентности. При этом на-
трий во многом повторяет свойства лития, будучи типичным од-
новалентным металлом, только более химически активным. При
движении от натрия к хлору также происходит ослабление ме-
таллических свойств и усиление неметаллических. Следующий
за натрием магний Mg во многом сходен с бериллием Be. Оба
элемента двухвалентны, проявляют металлические свойства, но
химическая активность обоих выражена слабее, чем у лития и
натрия. Алюминий А1, следующий за магнием, напоминает бор В
(валентность равна трем). Следующие элементы попарно похожи
друг на друга: кремний Si и углерод С, фосфор Р и азот N, сера
S и кислород О, хлор С1 и фтор F. При переходе к следующему за
хлором в последовательности увеличения атомной массы элементу
калию К опять происходит скачок в изменении валентности и хи-
мических свойств. Калий, подобно литию и натрию, открывает
ряд элементов (третий по счету), представители которого демон-
стрируют аналогию с элементами первых двух рядов.
Таким образом, Д.И. Менделеев установил, что в ряду элемен-
тов, расположенных по мере возрастания атомной массы (т. е. по
естественному физическом параметру) их химические свойства
изменяются периодически. Иначе говоря, сходные в химическом
отношении элементы встречаются в естественном ряду через пра-
вильные интервалы и, следовательно, повторяются периодически.
Эта замечательная закономерность, обнаруженная Д.И. Менделе-
евым и названная им законом периодичности, была сформулиро-
вана следующим образом: «Свойства простых тел, а также форма
и свойства соединений элементов находятся в периодической за-
висимости от величины атомных весов элементов».
Периодический закон Д.И. Менделеев использовал для созда-
ния периодической системы элементов. Периодическая система
химических элементов была в основном создана 1 марта (17 фе-
враля по ст. стилю) 1869 г., так как в тот день Менделеевым был
предложен первый вариант таблицы.
Весь ряд элементов, расположенных в порядке возрастания
атомных масс, Менделеев разбил на периоды, внутри которых
свойства элементов изменяются последовательно, разметив перио-
ды так, чтобы выделить сходные элементы.
Открытие периодического закона и создание периодической та-
блицы позволили Менделееву предсказать существование и физи-
ко-химические свойства трех еще тогда неизвестных химических
элементов, в том числе их атомный вес. Менделеев назвал эти
гипотетические элементы экабор, экаалюминий и экасилиций и
292
Лекция 15. Периодическая таблица Менделеева
указал клетки периодической таблицы, в которых должны они
располагаться. В течение последующих 15 лет все эти элементы
были обнаружены. Экабор был назван скандием, экаалюминий —
галлием, а экасилиций — германием. Это было триумфом пе-
риодического закона, так как даже количественные предсказания
Менделеева оказались весьма точными.
До открытия Менделеева бериллий считался аналогом алюми-
ния, ему приписывалась валентность равная трем и атомная масса
13,5 а.е.м. Менделеев на основе периодического закона предсказал,
что валентность бериллия равна двум, а атомная масса 9 а.е.м.
Вскоре экспериментальные исследования подтвердили правоту
Менделеева. Аналогично Менделееву удалось теоретически испра-
вить атомные массы цезия и урана.
Открытие периодического закона дало мощный толчок раз-
витию химии и физики XIX и XX веков. Знаменитый амери-
канский астроном X. Шелл и (1885-1972) о периодическом законе
Менделеева сказал так: «Это самый компактный и полный зна-
чения сгусток знания, когда-либо изобретенный человеком». Сам
Д.И. Менделеев был уверен, что «периодическому закону не грозит
разрушение, а обещаются только надстройка и развитие». Слова
оказались пророческими.
В последние годы XIX века исследованиями У. Рамзая (1852—
1916) и Дж. Релея (1842-1919) были открыты инертные газы, ко-
торые нашли свое место в таблице Менделеева в качестве нулевой
группы (столбца) между галогенами и щелочными металлами.
В результате работ Резерфорда и Бора было установлено, что
номер химического элемента в таблице Менделеева строго опреде-
ляется дискретной физической величиной — количеством электро-
нов в атоме. Поэтому открытие изотопов — атомов определенного
химического элемента с различными массами — не поколебало
периодический закон.
Синтез атомных ядер трансуранов — химических элементов с
номерами, превышающими Z = 92, — показал, что особенности
их строения и физических свойств также укладываются в перио-
дическую таблицу Менделеева.
15.2. Внешние и внутренние
электронные оболочки атомов
Рассмотрим периодический закон и таблицу Менделеева с точ-
ки зрения квантовой физики атома. В соответствии с приближени-
ем самосогласованного поля электрон в любом одноэлектронном
стационарном состоянии характеризуется четырьмя квантовыми
числами n, Z, m, ms и, следовательно, имеет определенные энер-
гию, квадрат момента импульса, проекцию момента импульса на
выбранную ось и проекцию спина. Многоэлектронный атом в
15.2. Внешние и внутренние электронные оболочки атомов 293
стационарном состоянии представляется совокупностью одноэлек-
тронных состояний и также обладает набором перечисленных фи-
зических величин.
В основном состоянии многоэлектронный атом должен иметь
минимальное значение собственной энергии. Поэтому электрон-
ные конфигурации основных состояний атомов можно построить,
исходя из принципа Паули и принципа минимума энергии. В ос-
новном состоянии атома электроны заполняют стационарные од-
ноэлектронные состояния с самой низкой энергией, с учетом того,
что, согласно принципу Паули, в каждом одноэлектронном состо-
янии атома не может быть более одного электрона. При расчете
электронных конфигураций следует учитывать, что энергия од-
ноэлектронного состояния возрастает с ростом главного кванто-
вого числа п (т.е. от слоя к слою). Внутри электронного слоя
(n = const) энергия одноэлектронного состояния растет с увели-
чением орбитального квантового числа Z, т. е. с увеличением мо-
мента импульса электрона. В используемом приближении кон-
фигураций энергия одноэлектронного состояния не зависит от
квантовых чисел тп и ms-
Для анализа одноэлектронных состояний важной характери-
стикой является среднее расстояние электрона от атомного ядра
г, величина которого может быть рассчитана по волновой функ-
ции одноэлектронного состояния, аналогично формулам (11.27) и
(11.33). По величине г электроны атома могут условно подразде-
ляться на «внутренние» и «внешние».
Физический смысл такой классификации электронов основан
на том, что квантомеханические расчеты волновых функций одно-
электронных состояний доказывают тенденцию возрастания сред-
него расстояния г с увеличением энергии данного одноэлектрон-
ного состояния.
Эта зависимость в принципе объясняется тем, что плотность
пространственного распределения «внутренних» электронов час-
тично экранирует электрическое поле положительного ядра атома,
действующее на «внешние» электроны. Заметим еще раз, что так
как в приближении электронных конфигураций энергия электро-
нов зависит только от квантовых чисел п и Z, то среднее рас-
стояния г является характеристикой электронной оболочки и не
зависит от квантовых чисел тп и ms-
Энергии стационарных состояний для электронов, связанных
в атомах, имеют отрицательные знаки, согласно выбранному ра-
нее началу отсчета потенциальной энергии (см. лекцию 11). При
этом энергия ионизации или энергия связи (т.е. минимальная
энергия, необходимая для отрыва электрона от атома) равна энер-
гии стационарного состояния с обратным знаком. Отсюда следует,
что наименьшую энергию ионизации имеют внешние электроны
атома.
294 Лекция 15. Периодическая таблица Менделеева
Самосогласованное поле, которое действует на внешний элек-
трон, конечно, зависит от вида волновых функций заполненных
одноэлектронных состояний. Но, грубо говоря, внешний электрон
движется в электрическом поле, созданном положительным заря-
дом ядра +Ze и отрицательным зарядом — (Z — 1)е всех осталь-
ных электронов. В результате энергия ионизации атома, т.е. энер-
гия связи самого слабо связанного внешнего электрона, имеет для
атомов всех химических элементов одинаковый порядок. Экспери-
—'-А.
Ее (Ry)
2,0
1,5
1,0
0,5
-----------1---------1----------1---------1----------L_ Z
0 20 40 60 80 100
Рис. 15.1. Зависимость энергии ионизации (энергии связи внешних электро-
нов) от атомного номера химического элемента. Энергия выражена в единицах
энергии Ридберга Ry
ментальные исследования показали, что эта энергия связи лежит в
пределах от 3,9 эВ для цезия до 24,6 эВ для гелия, т. е. в интервале
примерно от 0,2 Ry до 1,8 Ry, что видно на рис. 15.1.
Напротив, внутренние электроны имеют максимальную энер-
гию связи среди остальных электронов атома данного химического
Рис. 15.2. Зависимость энергии связи внутренних электронов (электронов обо-
лочки Is) от атомного номера химического элемента. На вертикальной оси —
логарифмическая шкала. Энергия выражена в единицах энергии Ридберга Ry
элемента. Экранировка их от поля атомного ядра минимальна.
Расчеты и эксперименты показывают, что энергия связи внутрен-
15.3. Электронные конфигурации основных состояний атомов 295
них электронов (т.е. электронов оболочки 1s) растет, грубо го-
воря, пропорционально квадрату порядкового номера атома Z (см.
рис. 15.2).
Таким образом, подразделение электронов на внутренние и
внешние отражается, в первую очередь, на их энергетических, т.е.
измеримых характеристиках.
На основе вышеизложенных принципов и свойств электрон-
ных оболочек можно построить электронные конфигурации для
основных состояний всех химических элементов, располагая их
в порядке увеличения заряда ядра и заполняя электронами одно-
электронные состояния с постепенно увеличивающейся энергией.
Электронные конфигурации записываются в виде символов оболо-
чек, содержащих электроны. Количество электронов в каждой обо-
лочке изображается в виде верхнего правого индекса. Например,
электронная конфигурация, содержащая два электрона в оболочке
1s и один электрон в оболочке 2р, запишется в виде ls22p1.
15.3. Электронные конфигурации основных состояний
атомов химических элементов
В данном параграфе мы ограничимся конструированием элек-
тронных конфигураций только основных состояний атомов раз-
личных химических элементов таблицы Менделеева.
Водород. Химический символ Н, порядковый номер Z — 1.
Единственный электрон занимает одноэлектронное состояние
с минимально возможным значением квантовых чисел пи/, т.е.
п = 1, I = 0. Следовательно, магнитное квантовое число может
иметь единственное значение тп = 0. Квантовое число ms мо-
жет принимать любое из значений ±1/2, так как в приближении
конфигураций энергия зависит только от чисел п и Z, а в атоме
водорода в пренебрежении спин-орбитальным взаимодействием —
лишь от квантового числа п. Электронная конфигурация основ-
ного состояния атома водорода запишется в виде 1s1. Энергия со-
стояния единственного электрона равна энергии Ридберга с обрат-
ным знаком —Ry « —13,606 эВ.
Гелий. Химический символ Не, порядковый номер Z — 2.
Два электрона атома гелия полностью заполняют электронную
оболочку 1s, которая имеет минимальную энергию. Эта оболочка
содержит два одноэлектронных состояния со значениями кванто-
вых чисел, приведенными в табл. 15.1.
Следовательно, электронная конфигурация основного состоя-
ния атома гелия 1s2. Энергии этих одноэлектронных состояний
одинаковы, так как одинаковы их числа п и I. Величину этой
энергии можно получить экспериментально, ионизируя атом ге-
лия. При этом получается ион гелия и свободный электрон: Не —>
296
Лекция 15. Периодическая таблица Менделеева
-> Не+ 4- е~. Эта энергия равна приблизительно —24,6 эВ. Таким
образом, энергия ионизации атома гелия почти вдвое больше, чем
энергия ионизации атома водорода. Этим объясняется низкая хи-
мическая активность гелия, который относится к инертным газам.
Таблица 15.1. Квантовые числа электронов
в основном состоянии атома гелия
71 1 тп ms
1 0 0 1/2
1 0 0 -1/2
Отметим следующий интересный факт. Энергия электрона в ос-
новном состоянии иона гелия Не+ вычисляется по общей формуле
для энергии электронов водородоподобных атомов (см. (Д.11.41))
и равна — 4Ry « —54,4 эВ. Сравнивая эту величину с энергией од-
ноэлектронного состояния нейтрального атома гелия, мы видим,
что добавление второго электрона уменьшает энергию связи почти
в два раза! Это связано с тем обстоятельством, что электронная
плотность обоих электронов распределена по объему атома и элек-
троны «экранируют друг друга» от положительного атомного ядра.
Состояния двух электронов в атоме гелия отличаются только
знаком проекции спина. В приближении электронных конфигу-
раций эти состояния обладают одинаковыми энергиями.
Литий. Химический символ Li, порядковый номер Z = 3.
Нейтральный атом лития содержит три электрона. Два элек-
трона заполняют оболочку 1s. Так как энергия электронных со-
стояний оболочки 2р выше энергии электронных состояний 2s, то
третий электрон находится в оболочке 2s. Электронная конфигу-
рация основного состояния атома лития ls22s.
Квантовые числа электронов в основном состоянии атома ли-
тия приведены в табл. 15.2.
Таблица 15.2. Квантовые числа электронов
в основном состоянии атома лития
п 1 тп ms
1 0 0 1/2
1 0 0 -1/2
2 0 0
Квантовомеханические расчеты показывают, что среднее рас-
стояние от ядра г у электрона в стационарном состоянии, грубо го-
воря, пропорционально квадрату главного квантового числа. Сле-
довательно, электроны ls-оболочки в среднем в 4 раза ближе к
15.3. Электронные конфигурации основных состояний атомов 297
ядру, чем 25-электрон. Таким образом, в атоме лития 15-элек-
троны являются внутренними, а 25-электрон — внешним. При
этом электроны 15- оболочки эффективно экранируют 25-электрон
от электрического поля ядра. Это значит, что на внешний элек-
трон действует не поле заряда 4-Зе, а некоторое самосогласованное
поле положительного заряда, значительно уменьшенного двумя
отрицательными элементарными зарядами. Величина этого сум-
марного поля определяется пространственным распределением
электронов, т.е. квадратом модуля одноэлектронных волновых
функций. Экранировка приводит к слабой связи 25-электрона с
ядром по сравнению с 15-электронами, которые, находясь ближе к
ядру, имеют значительно большую энергию связи. Энергии элек-
тронов разных оболочек атома лития различаются более чем на
порядок, что показано на рис. 15.3.
|£, эв
о------------
2р (пустая)
-5,3 -----------
2s
м Е, эВ
О------------
2р (пустая)
-9,3 -----------
2s
-67,5
15
-129
Рис. 15.3. Схема энергий электронных оболочек атома лития
Рис. 15.4. Схема энергий электронных оболочек атома бериллия
Бериллий. Химический символ Be,порядковый номер Z — 4.
Два электрона заполняют 15-оболочку. Остальные два нахо-
дятся в 25-оболочке. При этом обе оболочки оказываются полно-
стью заполненными. Электронная конфигурация основного состо-
яния атома бериллия 152252. Соответствующий набор квантовых
чисел электронов бериллия приведен в табл. 15.3.
298
Лекция 15. Периодическая таблица Менделеева
Таблица 15.3. Квантовые числа электронов
в основном состоянии атома бериллия
71 1 тп ms
1 0 0 1/2
1 0 0 -1/2
2 0 0 1/2
2 0 0 -1/2
Энергии электронов в соответствующих оболочках почти вдвое
ниже по сравнению с атомом лития из-за увеличения заряда ядра
с ростом порядкового номера элемента (см. рис. 15.4).
Бор. Химический символ В, порядковый номер Z = 5.
В атоме бора 4 электрона полностью заполняют оболочки 1s
и 2s, а пятый электрон размещается в 2р-оболочке. Электронная
конфигурация ls22s22p. Схема энергий одноэлектронных состоя-
ний атома бора приведена на рис. 15.5.
Е, эВ
Е, эВ
О
О
8/
13,:
2р
2s
-21,6
-52,5
2s
-192-----—
-874
Is
Рис. 15.5. Схема энергий электронных оболочек атома бора
Рис. 15.6. Схема энергий электронных оболочек атома неона
Из диаграммы на рис. 15.5 видно, что разница энергий одно-
электронных состояний между оболочками одного электронного
15.3. Электронные конфигурации основных состояний атомов 299
слоя много меньше, чем разница энергий одноэлектронных состо-
яний, принадлежащих разным электронным слоям.
Таким образом, после рассмотрения электронных конфигура-
ций и энергетических диаграмм первых пяти элементов таблицы
Менделеева мы можем подытожить, что энергия связи с ядром
электронов первого слоя (n = 1) быстро растет с увеличением по-
рядкового номера химического элемента.
У следующих элементов вплоть до Z = 10 продолжается запол-
нение 2р-оболочки, которая, согласно табл. 14.1, содержит шесть
одноэлектронных состояний.
Неон. Химический символ Ne, порядковый номер Z — 10.
Электронная конфигурация основного состояния атома неона
ls22s22p6. У этого атома полностью заполнены два электронных
слоя: первый (К-слой, содержащий единственную оболочку 1s2) и
второй (L-слой, состоящий из двух оболочек: 2s2 и 2р6).
Атомы с полностью заполненными s- и ^-оболочками обладают
аномально низкой энергией внешних электронов (т. е. повышен-
ной энергией связи). Это определяет химические свойства неона
как инертного газа. Схема энергий одноэлектронных состояний
атома неона в основном состоянии приведена на рис. 15.6.
Натрий. Химический символ Na, порядковый номер Z — 11.
Распределение одиннадцати электронов в атоме натрия по од-
ноэлектронным состояниям для атома натрия следующее: 10 элек-
тронов заполняют 2 первых слоя, последний одиннадцатый элек-
трон размещается в s-оболочке третьего электронного слоя (М-слоя
с п = 3). Таким образом, электронная конфигурация основного
состояния атома натрия имеет вид ls22s22p63s. Среднее рассто-
яние от ядра г у электронов электронных слоев К (n = 1) и L
(п = 2) значительно меньше, чем у единственного 35-электрона.
Таким образом, десять электронов двух внутренних слоев эффек-
тивно экранируют поле ядра от внешнего Ss-электрона, поэтому
энергия связи внешнего электрона мала: всего 5,14 эВ. Именно это
обусловливает химическую активность натрия как одновалентного
металла.
Магний. Химический символ Mg, порядковый номер Z = 12.
Для атома магния характерно продолжение заполнения обо-
лочки 3s электронного слоя М (п = 3). Но так как любая s-обо-
лочка содержит только два одноэлектронных состояния, то у ато-
ма магния в основном состоянии 35-оболочка заполняется пол-
ностью. Электронная конфигурация атома магния имеет вид
ls22s22p63s2.
Алюминий. Химический символ А1, порядковый номер
Z = 13.
300 Лекция 15. Периодическая таблица Менделеева
В атоме алюминия тринадцатый электрон попадает в оболочку
Зр. В М-слое начинает заполняться его вторая электронная обо-
лочка. Электронная конфигурация основного состояния атома
алюминия ls22s22p63s23p.
Далее вплоть до порядкового номера Z — 18 продолжает запол-
няться электронная оболочка Зр.
Аргон. Химический символ Аг, порядковый номер Z = 18.
У атома аргона в основном состоянии полностью заполнены
электронные слои К и L, а также две оболочки М-слоя: 3s и Зр.
Электронная конфигурация записывается в виде ls22s22p63s23p6.
Далее для сокращения записей для многоэлектронных атомов пол-
ностью заполненные слои в электронных конфигурациях будут
обозначаться символами электронных слоев, заключенными в
квадратные скобки. Например, электронная конфигурация атома
аргона в основном состоянии запишется в следующем сокращен-
ном виде: [К, L] 3s23p6.
Расчеты показывают, что основное состояние атома аргона
отличается сравнительно низкой энергией внешних электронов,
которая равна —15,7 эВ. Это означает относительно высокую энер-
гию ионизации атома. Такая особенность аргона обусловливает его
сходство с рассмотренным выше неоном, который тоже относится
к инертным газам.
Калий. Химический символ К, порядковый номер Z = 19.
В результате вычислений по методу Хартри-Фока выяснилось,
что электронная конфигурация атома калия в основном состоянии
имеет следующий вид: [К, L] 3s23p64s. Иначе говоря, в этом атоме
при незаполненной оболочке 3d в электронном слое М (п = 3)
начала заполняться s-оболочка следующего, четвертого, N-слоя.
Это обусловлено тем, что в основном состоянии атома калия энер-
гия 45-оболочки ниже, чем энергия оболочки 3d. Поэтому 19-й
электрон размещается в оболочке 4s, т.е. в электронном слое N
(п = 4). Среднее расстояние 45-электрона от ядра г в основном
состоянии атома калия значительно больше аналогичных расстоя-
ний для остальных электронов. Следовательно, 45-электрон явля-
ется внешним и отличается пониженной энергий связи, которая в
данном случае составляет 4,34 эВ. Это объясняет химические свой-
ства калия как активного металла, подобные натрию и литию.
Кальций. Химический символ Са, порядковый номер Z =
= 20.
В атоме кальция полностью заполняется электронная оболочка
4s, и электронная конфигурация основного состояния атома каль-
ция имеет вид [К, L] 3s23p64s2. Конфигурация внешних оболочек
(3s23p64s2) имеет сходство с конфигурацией внешних оболочек
атома магния (2s22p63s2), а именно — заполнена s-оболочка во
15.3. Электронные конфигурации основных состояний атомов 301
внешнем электронном слое, а в предыдущем (с квантовым чис-
лом меньшим на единицу) заполнены s- и р-оболочки. Сходство
конфигурацией внешних электронных оболочек обусловливает по-
хожие химические свойства этих металлов.
Скандий. Химический символ Sc, порядковый номер Z =
= 21.
Начиная с этого атома, происходит заполнение оболочки 3d.
Электронная конфигурация основного состояния атома скандия
[K,L] 3s23p64s23<L
Любая d-оболочка содержит 10 одноэлектронных состояний,
поэтому заполнение электронной оболочки 3d продолжается вплоть
до атома цинка.
Цинк. Химический символ Zn, порядковый номер Z = 30.
Электронная конфигурация основного состояния атома цинка
[К, L] 3s23p64s23d10. Третий электронный слой заполнен полно-
стью. Заметим, что энергия ионизации атома цинка составляет
9,39 эВ и не является экстремальной. Иначе говоря, полное запол-
нение электронного М-слоя не приводит ни к аномально понижен-
ной, ни к аномально повышенной энергии внешних электронов.
У атомов следующих химических элементов происходит запол-
нение оболочки 4р, начиная с галлия.
Галлий. Химический символ Ga, порядковый номер Z = 31.
Электронная конфигурация основного состояния атома имеет
вид [К, L, М] 4s24p.
Криптон. Химический символ Кг, порядковый номер Z —
= 36.
Электронная конфигурация основного состояния атома кри-
птона [К, L, М] 4s24p6. Вновь мы стакиваемся с ситуацией, когда
при заполнении s- ир-оболочек очередного электронного слоя обра-
зуется атом с повышенной энергией связи внешних электронов —
около МэВ. Криптон является инертным газом, как аргон и неон.
Рубидий. Химический символ Rb, порядковый номер Z =
= 37.
Если бы с ростом порядкового номера химического элемента
последовательно заполнялись бы все оболочки очередного элек-
тронного слоя, то в основном состоянии атома рубидия 37-й элек-
трон должен бы находиться в оболочке 4d. Однако хотя в четвер-
том электронном слое свободны оболочки 4d и 4/, 37-й электрон
располагается в бз-оболочке, т. е. в пятом электронном слое. Это
означает, что одноэлектронные состояния в оболочке 5s в атоме
рубидия имеют более низкую энергию, чем состояния в оболочках
4d и 4/. Таким образом, электронная конфигурация основного
состояния атома рубидия имеет вид [К, L, М] 4s24p65s.
302 Лекция 15. Периодическая таблица Менделеева
Энергия связи внешнего электрона приблизительно равна
4,18 эВ, что ниже энергии ионизации атома калия. Следовательно,
рубидий является еще более активным металлом, чем калий.
Стронций. Химический символ Sr, порядковый номер Z =
= 38.
В атоме этого элемента полностью заполнена электронная обо-
лочка 5s и электронная конфигурация основного состояния атома
имеет вид [К, L, М] 4s24p65s2. Наблюдается аналогия конфигура-
ций внешних оболочек атомов стронция, кальция и магния.
У атомов десяти химических элементов от иттрия (Z = 39) до
кадмия (Z = 48) включительно заполняется электронная оболочка
4с/. Затем начинает заполняться не последняя оболочка 4/ четвер-
того электронного слоя, а вторая оболочка пятого электронного
слоя, т. е. 5р-оболочка. Эта оболочка заполняется электронами
вплоть до атома ксенона (Z = 54). Электронная конфигурация
основного состояния атома ксенона [К, L, М] 4s24p65s24c/105p6.
В атомах следующих химических элементов — цезия и ба-
рия, — несмотря на наличие незаполненных оболочек в четвертом
(4/) и пятом (5с/, 5/ и 5g} электронных слоях, начинает запол-
няться 65-оболочка шестого электронного слоя. Причиной этого
является более низкая энергия одноэлектронных состояний обо-
лочки 6s. Электронная конфигурация основного состояния атома
бария [К, L, М] 4s24p65s24c/105p66s2.
С дальнейшим увеличением порядкового номера химических
элементов реализуется еще более причудливый порядок заполне-
ния электронных оболочек.
В атоме лантана (Z = 57) в основном состоянии 56 электронов
формируют конфигурацию бария, а 57-й электрон размещается в
оболочке 5с/. А затем у атомов следующих элементов с ростом хи-
мического номера Z начинает заполняться оболочка 4/, которая,
в соответствии с табл. 14.1, содержит 14 одноэлектронных состо-
яний. 14 химических элементов от церия (Z = 58) до лютеция
(Z = 71), у атомов которых последовательно заполняются состо-
яния 4/-оболочки, называются лантаноидами, т.е. подобными
лантану. Таким образом, в атомах лютеция наконец-то запол-
нился целиком четвертый электронный слой.
Далее от гафния (Z = 72) до ртути (Z = 80) в атомах продол-
жает заполняться оболочка 5с/. Затем у атомов от таллия (Z = 81)
до радона (Z = 86) происходит заполнение бр-оболочки.
С атома франция (Z = 87) начинается заполнение 7-го элек-
тронного слоя. Электронная конфигурация основного состояния
атома радия (Z = 88) содержит заполненную оболочку 7s и может
быть записана в виде [К, L, M,N] 6s25c/106p67s2.
Основное состояние атома актиния (Z = 89) имеет электрон-
ную конфигурацию основного состояния атома радия плюс еще
15.4. Свойства химических элементов и конфигурации их атомов 303
один электрон в оболочке 6d. У атомов следующих 14 элементов —
актиноидов — происходит заполнение 5/-оболочки.
Начиная с атома резерфордия (Z = 104) должно продолжаться
заполнение 6</-оболочки. Серьезной трудностью исследования
электронных состояний атомов трансурановых элементов явля-
ется то, что их изотопы радиоактивны и в большинстве обладают
очень малым временем жизни. Однако имеющиеся эксперимен-
тальные результаты свидетельствуют о том, что закономерности
заполнения электронных оболочек сохраняются и у атомов самых
последних элементов таблицы Менделеева.
15.4. Связь свойств химических элементов
и электронных конфигураций их атомов
Химические реакции осуществляются за счет взаимодействия
внешних электронов атомов, участвующих в реакции. Как след-
ствие, все химические свойства и значительная часть физических
свойств элементов определяются электронными конфигурациями
внешних оболочек атомов. В предыдущем параграфе настоящей
лекции было показано периодическое изменение этих конфигура-
ций с возрастанием атомного номера химического элемента. Пери-
оды (строки) и группы (столбцов) таблицы Менделеева отражают
строение внешних электронных оболочек.
Разными авторами было предложено более 400 вариантов та-
блицы Менделеева, из которых получили практическое примене-
ние только четыре. Решением ШРАС (Международного союза
теоретической и прикладной химии) в качестве основной при-
нята длиннопериодическая таблица, состоящая из семи периодов и
18-и столбцов (групп) (см. табл. 15.4).
Первый период — очень короткий — состоит только из двух
элементов: водорода и гелия. В атомах этих элементов происходит
заполнение единственной оболочки 1s электронного К-слоя.
Все остальные периоды начинаются с элементов, у атомов ко-
торых находится один электрон в s-оболочке электронного слоя,
причем номер слоя совпадает с номером периода. Эти элементы
образуют первый столбец (первую главную группу) и называются
щелочными металлами. Их атомы имеют во внешнем электрон-
ном слое единственный электрон, который характеризуется срав-
нительно большим средним расстоянием от ядра г и, как след-
ствие, малой энергией связи (3,9-5,4эВ). В результате атом легко
превращается в положительный ион с зарядом 4-1, что обусловли-
вает высокую химическую активность щелочных металлов: оки-
сление в воздухе, горение в воде, бурные реакции со многими неме-
таллами и т. д. Щелочным металлам соответствуют характерные
минимумы графика на рис. 15.1.
Все периоды заканчиваются элементами, которые образуют
18-й столбец (группу VIIIA) и называются инертными газами.
304
Лекция 15. Периодическая таблица Менделеева
Таблица 15.4. Длиннопериодическая система Менделеева
Периоды ГРУППЫ
1 2 3
IA ПА in В
1 1 н
2 3 Li 4 Be
3 11 Na 12 Mg
4 19 К 20 Ca 21 Sc
5 37 Rb 38 Sr 39 Y
6 55 Cs 56 Ba 57 La 58 Ce 59 Pr 60 Nd 61 Pm 62 Sm 63 Eu 64 Gd 65 Tb 66 Dy 67 Ho 68 Er 69 Tm 70 Yb 71 Lu
7 87 Fr 88 Ra 89 Ac 90 Th 91 Pa 92 U 93 Np 94 Pu 95 Am 96 Cm 97 Bk 98 Cf 99 Es 100 Fm 101 Md 102 No 103 Lr
Периоды ГРУППЫ
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
IV В VB VI в VII В VIII В I В II В III A IVA V A VIA VII A VIII A
1 2 He
2 5 В 6 c 7 N 8 0 9 F 10 Ne
3 13 Al 14 Si 15 P 16 S 17 Cl 18 Ar
4 22 Ti 23 V 24 Cr 25 Mn 26 Fe 27 Co 28 Ni 29 Cu 30 Zn 31 Ga 32 Ge 33 As 34 Se 35 Br 36 Kr
5 40 Zr 41 Nb 42 Mo 43 Tc 44 Ru 45 Rh 46 Pd 47 Ag 48 Cd 49 In 50 Sn 51 Sb 52 Tc 53 I 54 Xe
6 72 II f 73 Ta 74 W 75 Re 76 Os 77 Ir 78 Pt 79 Au 80 Hg 81 Tl 82 Pb 83 Bi 84 Po 85 At 86 Rn
7 104 Rf 105 Db 106 Sg 107 Bh 108 Hs 109 Mt
15.4. Свойства химических элементов и конфигурации их атомов 305
Их атомы (кроме гелия) имеют электронные конфигурации внеш-
них оболочек вида ns2np6, где п — номер периода, иначе говоря,
их внешние оболочки полностью заполнены. Такая электронная
структура отличается повышенной энергией ионизации (25-12 эВ),
на графике рис. 15.1 инертным газам соответствуют резкие пики.
Сравнительно высокая энергия ионизации препятствует химиче-
ским реакциям с отделением электронов. С другой стороны, атомы
с конфигурацией внешних оболочек вида ns2npe не обладают спо-
собностью присоединять дополнительные электроны. В резуль-
тате инертные газы практически не участвуют в химических ре-
акциях и характеризуются валентностью равной нулю. Лишь к
концу XX века было синтезировано несколько десятков соедине-
ний криптона, ксенона и радона. Оказывается, атомы перечислен-
ных газов могут отдавать электроны из р-оболочек внешнего элек-
тронного слоя.
У атома гелия электронная конфигурация 1s2 (т. е. у него пол-
ностью заполнен только первый электронный слой), но его свойс-
тва близки к свойствам остальных инертных газов. Гелий и неон
по современным представлениям не могут образовывать химиче-
ских соединений.
Таким образом, на сегодняшний день известно 6 химических
элементов, являющихся инертными газами. Седьмым инертным
газом должен быть элемент с номером Z = 118, которым закан-
чивается седьмой период, но этот элемент пока не синтезирован.
Элементы второго столбца (группы ПА) имеют во внешнем
электронном слое единственную заполненную s-оболочку, т. е.
электронную конфигурацию ns2, где п — номер периода. Энергия
связи внешних электронов невелика (9-5эВ). Эти элементы на-
зываются щелочноземельными, химически активны, в реакциях
обычно теряют два электрона, т. е. проявляют валентность 4-2.
Элементы групп IIIA-VIIA (т.е. столбцов 13-17 табл. 15.4)
имеют электронную конфигурацию внешнего слоя ns2npg~2^ где
д — номер группы, п — номер периода. Эти элементы могут
демонстрировать переменную валентность, но при этом высшая
валентность совпадает с номером группы д.
Остановимся особо на галогенах — элементах группы VIIA,
т.е. 17-го столбца. Атомы галогенов имеют электронные конфи-
гурации внешних оболочек вида ns2np5, где п — номер периода.
Единственная вакансия во внешней ^-оболочке приводит к значи-
тельной энергии «сродства к электрону». Это означает, что атомы
галогенов обладают характерной энергией (~ 2-4 эВ) присоедине-
ния электрона к нейтральному атому. Сродство к электрону, ко-
торое подробнее описано в следующем параграфе настоящей лек-
ции, объясняется тем, что, присоединив еще один электрон, атом
понижает свою энергию и приобретает устойчивую электронную
306 Лекция 15. Периодическая таблица Менделеева
конфигурацию инертного газа (ns2npQ). При этом атом превра-
щается в отрицательный ион, что обусловливает высокую химиче-
скую активность галогенов и их отрицательную валентность —1.
Заметим, что значительное «сродство к электрону» проявляют
атомы кислорода, что позволяет ему демонстрировать отрицатель-
ную валентность —2. Энергия присоединения дополнительного
электрона к атому кислорода составляет около 1,5 эВ.
Элементы групп IB--VIIIB табл. 15.4 (в химической терминоло-
гии — побочных групп) иногда называются переходными. Атомы
переходных элементов определенного периода различаются коли-
чеством электронов в d-оболочке предыдущего периода, причем
внешние электроны имеют конфигурацию вида ns2 (п — номер
периода). Так как химические свойства элементов определяются
в основном з- и р-электронами внешнего слоя, то переходные эле-
менты определенного периода сравнительно слабо отличаются по
химическим свойствам друг от друга. Эти элементы демонстри-
руют, в основном, положительную переменную валентность 4-1,
4-2, иногда 4-3, т. е. в химических реакциях отдают электроны,
однако их химическая активность гораздо ниже активности ме-
таллов групп IA-IIA.
Электронные конфигурации атомов лантаноидов различаются
лишь количеством электронов в /-оболочке, что практически не
влияет на химические свойства элементов. Расчеты показывают,
что у лантаноидов средние расстояния от ядра г для электронов
4/-оболочки значительно меньше, чем для оболочек Ьр и 6з. Это
означает, что внешними электронами атомов лантаноидов явля-
ются Ьр- и 6з-электроны, которые образуют химические связи и
обусловливают все химические особенности этих элементов. Как
следствие, лантаноиды столь схожи по своим химическим свойс-
твам, что для них часто употребляется общий химический сим-
вол Ln.
Результаты расчетов методом Хартри-Фока позволяют обна-
ружить любопытное свойство лантаноидов — с ростом атомного
номера Z электроны заполняют 4/-оболочку не строго последо-
вательно (см. табл. 15.5). Оказывается, не существует атомов,
которые бы в основных состояниях имели 2 или 8 электронов в
оболочке 4/.
Электронные конфигурации атомов актиноидов различаются
лишь числом электронов в 5/-оболочке. Исследование химических
свойств актиноидов затруднено их радиоактивностью и высокой
дороговизной их синтеза. Времена жизни у наиболее стабильных
изотопов массивных актиноидов монотонно убывают с ростом по-
рядкового номера Z химического элемента, уменьшаясь до трех
минут у Однако, преодолевая перечисленные трудности,
удалось накопить информацию о сходстве химических свойств ак-
тиноидов.
15.4. Свойства химических элементов и конфигурации их атомов 307
Таблица 15.5. Распределение электронов по оболочкам 6d и 4f в основных
состояниях атомов лантана и лантаноидов
Хими- ческий элемент La Се Рг Ne Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu
Атомный номер Z 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
Число элек- тронов в оболочке 5d 1 1 1 1
Число элек- тронов в оболочке 4/ 1 3 4 5 6 7 7 9 10 11 12 13 14 14
На рис. 15.1 видно, что график зависимости энергии иониза-
ции Ei химического элемента от его порядкового номера Z со-
стоит из нескольких частей сходного мотива. Каждая такая часть
графика Ei(Z) начинается щелочным металлом и заканчивается
инертным газом, следовательно, соответствует определенному пе-
риоду таблицы Менделеева. Сравнивая фрагменты графика Ei(Z),
можно заметить, что с ростом номера периода у повторяющегося
мотива постепенно понижается энергия ионизации Е{, Это озна-
чает, что внутри каждой группы таблицы Менделеева величина Е^
монотонно уменьшается с ростом номера периода. Например, у
щелочных металлов энергия ионизации изменяется от 5,3 эВ у ли-
тия до 3,26 эВ у франция. У инертных газов величина Ei также
монотонно уменьшается от 25,4 эВ у гелия до 11,7 эВ у радона.
Отсюда следует вывод, что при определенном типе электронной
конфигурации внешних электронов (т.е. в определенной группе
таблицы Менделеева) их энергия связи постепенно падает с ро-
стом номера периода, т. е. с увеличением количества электронов
в атоме. Как следствие, с ростом порядкового номера у элементов
фиксированной группы все сильнее проявляются металлические
свойства, т. е. способность отдавать электроны в химических ре-
акциях. Ярким примером этого утверждения являются свойства
элементов группы IVA. Углерод и кремний — неметаллы, олово и
свинец — металлы. Аналогично, в группе VA азот и фосфор —
неметаллы, висмут — металл. Еще более удивительный пример
дают элементы группы VIIA — галогены. Первые три — активные
неметаллы. Однако пятый — астат — демонстрирует ряд типично
металлических свойств. Этот факт малоизвестен, так как астат ра-
диоактивен, его самый долгоживущий изотоп 210At имеет период
полураспада 8,1ч.
Для объяснения индивидуальных свойств отдельных химиче-
ских элементов необходимо проводить расчеты волновых функций
308 Лекция 15. Периодическая таблица Менделеева
соответствующих атомов. Эта работа, вследствие математической
сложности, еще далека до завершения.
15.5. Сродство к электрону
Квантовая теория многоэлектронного атома позволила объяс-
нить явление, названное химиками сродством к электрону. Экс-
периментально в начале XX века было обнаружено, что электро-
нейтральные атомы многих химических элементов присоединяют
к себе свободный электрон и образуют устойчивый отрицательный
ион. Процесс присоединения является экзоэнергетическим, иначе
говоря, для отрыва электрона от отрицательного иона требуется
затратить определенную энергию Еа — энергию сродства к элек-
трону.
Таблица 15.6. Сродство к электрону некоторых химических элементов
Химический элемент Энергия сродства к электрону (эВ) Химический элемент Энергия сродства к электрону (эВ)
Н 0,754 Ge 1,20
F 3,40 As 0,80
С1 3,62 Zr 0,8
Вг 3,37 Nb 1,3
I 3,07 Mo 1,0
0 1,465 Ru 1,5
S 2,077 Ag 1,30
Se 2,021 In 0,5
Те 1,9 Sn 1,25
Si 1,394 Sb 1,05
Р 0,77 La 0,5
Ti 0,2 Ta 0,8
V 0,7 W 0,5
Сг 0,66 Pt 2,13
Fe 0,16 Au 2,31
Со 0,66 Tl 0,5
Ni 1,15 Pb 1,2
Си 1,23 Bi 1,0
Решение уравнения Шредингера показало, что для нейтраль-
ных атомов некоторых химических элементов добавление еще
одного электрона приводит к перестройке волновых функций,
вследствие которой суммарная энергия атома понижается. Рас-
четы показали, что наибольшее понижение энергии происходит,
когда внешние электронные оболочки достраиваются до конфигу-
рации атома инертного газа ns2np6, где п — главное квантовое
число. Следовательно, максимальным сродством к электрону (пре-
вышающим 3 эВ) обладают атомы галогенов. Несколько меньшую
15.5. Сродство к электрону 309
величину Еа имеют химические элементы группы VIA таблицы
Менделеева, что иллюстрируется табл. 15.6.
У химических элементов побочных групп (в частности, у пере-
ходных металлов) сродство к электрону лишь иногда превышает
1 эВ, у большинства из них энергия Еа составляет несколько де-
сятых долей электрон-вольта.
У инертных газов, как следует из изложенного выше, сродство
к электрону равно нулю.
Задачи к лекции 15
1. Записать конфигурации трех наиболее низкоэнергетических воз-
бужденных состояний атома гелия.
2. Записать конфигурацию первого возбужденного состояния атома
бериллия.
3. Записать конфигурации основных состояний атомов: а) углерода,
б) азота, в) кислорода, г) фтора.
4. Записать конфигурации основных состояний атомов: а) кремния,
б) фосфора, в) серы, г) хлора.
5. Записать конфигурации основных состояний атомов: а) титана,
б) ванадия, в) железа, г) кобальта, д) никеля.
6. Записать конфигурации основных состояний атомов: а) прометия,
б) самария, в) европия.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 15
15.1. Некоторые специфические свойства
химических элементов
В даннохм дополнении приведены (весьма отрывочно) некоторые све-
дения о химических элементах, которые, по мнению авторов, могут ока-
заться полезными студентам-физикам.
Хотя водород входит в состав воды океанов, его общее количество в
составе земной коры не превышает 1% (по массе). С другой стороны, он
составляет около 3/4 массы наблюдаемого вещества Вселенной. Энер-
говыделение Солнца и большинства других звезд происходит за счет
синтеза альфа-частиц из протонов — атомных ядер водорода. Юпи-
тер и подобные ему планеты состоят, в основном, из водорода. Этому
элементу предстоит в ближайшем будущем важная роль в человеческой
цивилизации. Во-первых, водород представляет собой экологически чи-
стейшее горючее. При его окислении выделяется энергия, а продуктом
горения является вода. При образовании 1 моля (18 г) водяного пара
выделяется около 240 кДж тепловой энергии. Запасы этого горючего
огромны, если учитывать воды океанов. Развитие водородной энерге-
тики пока тормозят трудности хранения водорода. Молекулы Щ столь
малы, что диффундируют даже сквозь стенки металлических резерву-
аров. Во-вторых, теория предсказывает, что при высоких давлениях
водород должен перейти в металлическую фазу. Теоретики предсказы-
вают металлическому водороду сверхпроводящие и другие интересные
физические свойства. Возможно, металлический водород находится в
центральной области Юпитера и других подобных планет.
Щелочные металлы (элементы подгруппы IA), помимо своей хи-
мической активности, отличаются аномально низкой работой выхода
электронов проводимости. Их красная граница лежит не в ультрафио-
летовом, а видимом диапазоне электромагнитного излучения. Первые
фотоэлементы, реагирующие на видимый свет, содержали эмиттеры из
щелочных металлов или их сплавов.
Элементы подгруппы ПА представляют собой типичные химически
активные металлы. Бериллий отличается сочетанием низкой массовой
плотности (р = 1,848 г/см3) и высокой твердости. На воздухе он по-
крывается тончайшей пленкой оксида, который защищает его от кор-
розии. Малая масса атомов бериллия (9,012 а.е.м.) обусловливает их
использование в качестве замедлителей нейтронов в ядерных (урано-
вых и плутониевых) реакторах. Отражатели нейтронов из бериллия
отличаются прочностью, малым весом и химической стойкостью. Ма-
лый порядковый номер (Z = 4) и, как следствие, малый коэффициент
поглощения рентгеновских лучей, делает бериллий уникальным мате-
риалом для фольги входного окна газовых спектрометров мягкого рент-
геновского излучения и выходного окна рентгеновских трубок. Малые
Дополнения к лекции 15
311
добавки (доли процента) бериллия к меди дают бериллиевые бронзы,
обладающие прочностью, упругостью и износостойкостью сталей. Воен-
ные самолеты содержат множество деталей из бериллиевых бронз.
Магний из-за высокой окислительной способности был непремен-
ным атрибутом фотографов в начале прошлого века. Тонкая магниевая
лента на воздухе сгорала почти мгновенно с ослепительным светом и
поэтому использовалась в качестве фотовспышки. В настоящее время
магниевые стержни используются как элемент электролитической пары
для уменьшения коррозии стальных и медных деталей в нагревателях
воды и стиральных машинах.
Кальций является пятым по распространенности химическим эле-
ментом земной коры (4,1% по массе). Карбонат кальция СаСОз образует
залежи мела, известняка и мрамора. Гидраты сульфата кальция: гипс
(природный гипс CaSO4 -2Н2О) и алебастр (жженый гипс 2CaSO4 -Н2О)
широко используются в строительстве и скульптуре. Смесь силикатов и
алюмосиликатов кальция образует цемент. Затвердевание смеси цемента
с водой происходит из-за процессов гидролиза и гидратации этих соеди-
нений. Ортофосфат кальция Саз(РС>4)2 обеспечивает прочность костей.
Барий — самый тяжелый из стабильных щелочноземельных метал-
лов (элементов подгруппы ПА), его порядковый номер Z = 56. Добавле-
ние бария в состав стекла дает прозрачные экраны, эффективно защи-
щающие от потоков рентгеновских лучей.
Радий принадлежит к подгруппе щелочноземельных элементов ПА,
но все его изотопы радиоактивны. Изотоп 2|sRa был открыт супругами
Кюри в 1898 г. Переработав почти тонну урановой руды, они получили
0,1 г хлорида радия. Этот изотоп радия возникает из-за альфа-распада
урана-238. Сам изотоп 2ggRa с периодом полураспада 1600 лет, испуская
альфа-частицу, превращается в изотоп радона 2g|Rn.
Подгруппа ША содержит как металлы, так и неметаллы. Бор явля-
ется типичным неметаллом и имеет структурную единицу Bi2 в форме
икосаэдра — правильного двадцатигранника. Прочность связей между
икосаэдрами Bi2 обусловливают высокую твердость бора и его темпера-
туру плавления 2075 °C. Бор с водородом образует множество соедине-
ний, состав которых можно выразить общими формулами: ВпНп+4 и
ВпНп+б, где п — целое число. Бороводороды имеют высокую теплотвор-
ную способность и используются в качестве ракетного топлива.
Алюминий является третьим по распространенности химическим
элементом земной коры (8% по массе) и входит в состав множества алю-
мосиликатов. Кристаллический оксид А120з — корунд — уступает по
прочности только алмазу. Микропримеси в корунде образуют рубин и
сапфир. Металлический алюминий был получен в начале XIX века и
долго стоил дороже золота. Лишь в 1886 г. Ч.М.Холл и П.Эру неза-
висимо друг от друга разработали сравнительно дешевый метод получе-
ния алюминия в больших количествах. Алюминий является активным
химическим элементом, из его сплавов изготовляют корпусы зажига-
тельных бомб, его соли входят в состав напалма. Однако на воздухе
алюминий моментально покрывается тонкой пленкой оксида, что пре-
пятствует дальнейшему окислению. По этой причине алюминий и его
сплавы принадлежат к самым распространенным металлам современной
технологии. Сочетание пластичности, легкости и электропроводности
обусловило применение алюминиевых проводников для электропередачи
на большие расстояния.
312
Дополнения к лекции 15
Галлий по внешнему виду напоминает алюминий, но отличается ано-
мально низкой температурой плавления: 29,8 °C. Таким образом, гал-
лий можно расплавить в ладони. Высокочистый галлий используется
в детекторах солнечных нейтрино. Почти весь добываемый галлий ис-
пользуется для изготовления арсенида галлия GaAs — одного из самых
востребованных полупроводников.
Индий, как и галлий, в основном, используется для получения полу-
проводников InAs, InSb и т. п.
Таллий известен ядовитостью своих соединений. Основные сим-
птомы отравления: выпадение волос и нервные расстройства.
Подгруппа IVA также отличается разнообразием свойств элементов.
Углерод является основным элементом всех органических соединений.
Он образует несколько аллотропных модификаций, из которых давно из-
вестны алмаз и графит. Алмаз отличается не только прозрачностью,
высокой прочностью, но и самым высоким показателем преломления
п — 2,417. Именно эти качества обусловили ценность бриллиантов —
ограненных алмазов. Кроме того, алмаз имеет высокую теплопровод-
ность (в 4 раза больше меди!) и практически не проводит электрический
ток. Графит обладает характерной слоистой структурой, что позволяет
делать из него карандаши. Третьей модификацией углерода считалась
сажа, как аморфизованная форма графита. В 60-х годах XX века были
открыты карбины — кристаллические структуры, состоящие из упоря-
доченных цепочек атомов углерода. А с 1985 г. начался синтез фуллере-
нов — молекул, содержащих различное количество атомов углерода: Сео,
С70, С72, •.Сю8 и т. Д- Все эти молекулы имеют форму близкую к сфе-
рической. Молекула Сео поразительно напоминает футбольный мяч — ее
каркас состоит из 12 пятиугольников и 20 шестиугольников. Молекулы
фуллеренов могут упаковываться в кристаллические структуры с раз-
личной симметрией. Первооткрыватели фуллеренов (Г. Крото, Р.Керл,
Р. Смелли) были удостоены Нобелевской премии по химии 1996 г. Но
это еще не все! В 1991 г. в Японии при синтезе фуллеренов были полу-
чены первые нанотрубки — цилиндрические структуры из атомов угле-
рода диаметром порядка нанометра. В настоящее время ведутся интен-
сивные работы по увеличению длины нанотрубок и их упорядочению.
Волокно из нанотрубок должно иметь ранее невиданную прочность.
По распространенности в земной коре кремний уступает только ки-
слороду и составляет 28% по массе. Оксид кремния SiC>2 (кварц) с не-
большими примесями образует кварцевый песок, цитрин, аметист, сердо-
лик, халцедон, агат, опал, яшмы и т. д. Кремний высокочистый, а также
легированный донорными или акцепторными примесями является са-
мым распространенным полупроводниковым материалом. Процессоры
компьютеров и платы оперативной памяти изготавливаются, в основном,
из высокочистого кремния. Кристаллический кремний имеет структуру
алмаза. Однако кремний, в отличие от углерода, не образует длинных
молекул. По этой причине не существует кремниевой жизни. Одна из мо-
дификаций карбида кремния SiC — карборунд — образует алмазоподоб-
ную кристаллическую структуру, отличается высокой прочностью и ис-
пользуется для изготовления абразивных материалов. Аморфный сплав
кварца с оксидами натрия и кальция образует обычное оконное стекло.
Присадки оксидов других элементов дают стекла различной окраски.
Германий по многим химическим свойствам является аналогом
кремния. Германий также является хорошим полупроводником. Од-
Дополнения к лекции 15
313
нако германия в земной коре почти в 40000 раз меньше, чем кремния,
поэтому он очень дорог.
Олово имеет две аллотропные модификации. Белое олово является
типичным металлом с хорошей тепло- и электропроводностью. Сплавы
белого олова со свинцом имеют низкую температуру плавления (ниже
200 °C) и используются для пайки металлов. При температуре ниже
— 13,2 °C белое олово может спонтанно переходить в другое стабильное
состояние — серое олово — неметалл. Эта модификация имеет алмазопо-
добную кристаллическую структуру, но при фазовом переходе из белого в
серое олово рассыпается в порошок. Это явление называется оловянной
чумой.
Последний элемент в подгруппе IVA — свинец — типичный металл.
Древние римляне использовали высокую пластичность свинца, изгота-
вливая из него водопроводные трубы и посуду. Взаимодействие с угле-
кислым газом приводило к образованию углекислого свинца, который
является медленно действующим ядом, что привело к постепенному со-
кращению средней продолжительности жизни римлян. Из-за высокой
массовой плотности (р = 11,34 г/см3) свинец рассматривался средневе-
ковыми алхимиками как первый кандидат для превращения (трансму-
тации) в золото. В настоящее время свинец широко используется в каче-
стве защитного материала от различных ионизирующих излучений по
причине большого коэффициента поглощения и легкости обработки.
Подгруппа VA начинается с азота. Этот элемент в виде двухатом-
ных молекул составляет 78% (объемных) земной атмосферы. Молекулы
N2 характерны химической инертностью, но атомарный азот активен
и проявляет переменную валентность. Существует 5 оксидов азота: от
веселящего газа N2O до азотного ангидрида N2O5. Это означает, что
в образовании химических связей могут участвовать все 5 электронов
L-слоя атома азота: 2s22p3. Некоторые химические соединения азота
являются хорошими минеральными удобрениями, другие служат осно-
вой мощных взрывчатых веществ. В частности, порох представляет со-
бой смесь калийной селитры KNO3, угля и серы. Нитрид бора BN при
высоком давлении приобретает алмазоподобную кристаллическую струк-
туру, которая называется боразон. Это вещество по твердости превосхо-
дит алмаз и используется как огнеупорный и абразивный материал.
Фосфор хорошо известен в трех аллотропных модификациях. Че-
тырехатомные молекулы белого фосфора имеют форму тетраэдра со сто-
роной 2,21 А. Эти молекулы непрочны, что обусловливает высокую реак-
ционную способность белого фосфора и, в частности, его ядовитость.
Вследствие медленного окисления в воздухе белый фосфор светится в
темноте (фосфоресцирует). В XIX веке головки спичек делали из белого
фосфора. Кристаллическая структура черного фосфора состоит из упа-
кованных гофрированных слоев, состоящих из шестиугольников. Тер-
мин красный фосфор на самом деле объединяет несколько аллотропных
модификаций, различающихся кристаллическим строением с довольно
сложной структурой. Коричневое покрытие боков спичечных коробок со-
держит аморфизованный красный фосфор. Черный и красный фосфор
отличаются пониженной химической активностью и меньшей ядовито-
стью по сравнению с белым.
Мышьяк также существуют в виде различных аллотропных моди-
фикаций. Наиболее устойчив серый мышьяк, имеющий структуру сход-
314
Дополнения к лекции 15
ную с черным фосфором. Оксид мышьяка AS2O3 в средневековье часто
использовался как яд. Вероятно, им были отравлены французский ко-
роль Карл IX (организатор Варфоломеевской ночи) и узурпатор трона
великого князя московского Дмитрий Шемяка. В XX веке на основе
мышьяка были созданы боевые отравляющие вещества, например, лю-
изит. В настоящее время, помимо прочего, мышьяк используется как
донорная примесь при легировании германия.
Чистая сурьма обладает металлическим блеском, хорошо проводит
электрический ток, но имеет низкий коэффициент теплопроводности и
отличается высокой хрупкостью. Оксид сурьмы ВЬгОб проявляет ки-
слотные свойства. Таким образом, сурьма обладает свойствами как ме-
таллов, так и неметаллов. Еще в древнем Вавилоне сурьма применялась
женщинами для подведения бровей.
Висмут является последним элементом в таблице Менделеева, ко-
торый имеет стабильные изотопы. Он по своим химическим свойствам
сходен с сурьмой, но отличается низкой температурой плавления 271 °C.
Сплав Вуда (50% Bi, 25% Pb, 12,5% Cd, 12,5% Sb) плавится уже при
69 °C, поэтому используется в плавких предохранителях электроаппара-
туры.
Первый элемент подгруппы VIA — кислород составляет 21% (объем-
ных) атмосферы и 47% (массовых) земной коры. Таким образом, кисло-
род является самым распространенным химическим элементом на на-
шей планете. Конфигурация внешних электронных оболочек атома ки-
слорода 2s22р4 объясняет его химическую валентность, равную —2, так
как является энергетически выгодным привлечение еще двух электронов
от другого атома для заполнения р-оболочки. В нормальных условиях
(т.е. при температуре 20°C и атмосферном давлении 101 кПа) кисло-
род образует двухатомные молекулы. При пропускании электрических
разрядов через кислород (или воздух) образуется трехатомные молекулы
Оз озона. Характерный запах озона ощущается во время грозы. Озон
является очень сильным окислителем, поэтому используется для дезин-
фекции воды и воздуха.
Сера интересна тем, что в нормальных условиях состоит из 8-атом-
ных молекул, имеющих форму гофрированного кольца с межатомными
расстояниями 2,07 А. Многочисленные аллотропные модификации серы
различаются, в основном, способами упаковки этих молекул в кристалли-
ческую структуру. Конфигурация внешних электронных оболочек атома
серы 3s2Зр4 аналогична электронной конфигурации атома кислорода, од-
нако сера демонстрирует валентность не только —2, но и 4-2, 4-4, 4-6. Это
означает прежде всего, что теория валентности не сводится к формиро-
ванию заполненных оболочек типа ns2np6, а требует более глубокого
развития теории химической связи на базе квантовой физики.
Селен — один из первых открытых полупроводников. Его характер-
ным свойством является резкая зависимость электропроводимости от
освещенности. Используется при изготовлении выпрямителей и фото со-
противлений.
Теллур является редким элементом с полупроводниковыми свойст-
вами. В основном используется для приготовления теллуридов CdTe,
PbTe, HgTe, которые применяются в термо- и фотоэлектронных пре-
образователях. Теллуроводород НзТе представляет собой газ, который,
по словам химиков, отличается ужасным, невыносимым запахом.
Дополнения к лекции 15
315
Полоний завершает подгруппу VIA. Все его изотопы нестабильны
и радиоактивны. Изотоп полоний-210 был впервые выделен в 1898 г.
Марией Склодовской-Кюри из урановой руды в результате двухлетнего
ежедневного труда. С периодом полураспада 138 суток он превращается
в свинец 282?Ь.
Элементы подгруппы VIIA (галогены) демонстрируют сходные хи-
мические, но весьма разные физические свойства. Чистый фтор пред-
ставляет собой газ ярко-желтого цвета. Из-за высокой химической ак-
тивности фтор реагирует почти со всеми элементами и воспламеняет
многие вещества (даже воду!) при контакте. Очень ядовит. С другой
стороны, если содержание фтора в питьевой воде падает ниже 5 • 10-5%,
то происходит разрушение эмали зубов у человека. Политетрафторэтилен
(СзКОп отличается высокой химической и термической устойчивостью
и является основой тефлонов.
Хлор — газ желто-зеленого цвета. Из-за своей ядовитости использо-
вался в годы первой мировой войны как боевое отравляющее вещество.
Химически активен, демонстрирует в соединениях различные валентно-
сти: — 1, +1, +3, +5, +7. Является основой такого распространенного
полимера, как поливинилхлорид (С2НзС1)п.
Бром в нормальных условиях представляет собой темно-красную не-
прозрачную жидкость с резким запахом. Хорошо растворяется в воде.
Температура кипения 59 °C. Пары брома очень ядовиты, ожоги от брома
болезненны и долго не заживают. Бромид серебра AgBr используется
в фотографии, так как обладает светочувствительностью. Соли брома
используются в медицине, бромистый калий применяется как успокои-
тельное средство.
Иод в нормальных условиях образует темные кристаллы с металли-
ческим блеском. При нагревании кристаллы легко сублимируют, обра-
зуя пар фиолетового цвета. 5%-ный водо-спиртовой раствор иода ши-
роко используется как антисептическое средство. В организме человека
содержится около 20 мг иода, который, в основном, концентрируется в
щитовидной железе. Иод входит в состав тиреоглобулина — белка, син-
тезирующего некоторые необходимые человеку гормоны. При недостатке
иода у человека развиваются тяжелые заболевания, в частности, базедова
болезнь.
История открытия инертных (благородных) газов удивительна. Еще
Г. Кавендиш в 1785 г., проводя опыты по окислению азота, открыл «де-
флогистонированный воздух» — газ, который не вступал в реакции с дру-
гими веществами. Но так как Г. Кавендиш не публиковал своих трудов,
то его открытие осталось неизвестным. В 1888 г. Д.У. Релей, измеряя
молекулярные массы газов, обнаружил заметное различие значений для
атмосферного азота и азота, полученного разложением нитрита аммония.
У. Рамзай предположил, что в воздухе присутствует еще неизвестный на-
уке газ, отличаемый абсолютной химической инертностью. 12 августа
1894 г. Релей выступил с докладом об открытии нового химического эле-
мента, который представляет собой газ, состоящий из одноатомных мо-
лекул. Газ был назван аргоном. Оказалось, что его в земной атмосфере
почти 1% (по объему), т.е. его больше, чем углекислого газа и водяного
пара.
Гелий был открыт методом спектрального анализа в солнечном про-
туберанце в 1868 г. двумя астрономами. Однако это открытие полу-
316
Дополнения к лекции 15
чило официальное признание после 1888 г., когда Рамзай обнаружил
присутствие гелия в ур ано содержащем минерале. Гелий обладает самой
низкой температурой кипения —269 °C. Жидкий гелий впервые получил
голландский физик X. Камерлинг-Оннес в 1908 г., за что был удостоен
Нобелевской премии 1913 г. Перевести гелий в твердую фазу удалось
только при давлении свыше 2,5 МПа. Работы с жидким гелием позво-
лили открыть явление низкотемпературной сверхпроводимости метал-
лов. В 1938 г. П.Л. Капица открыл сверхтекучесть гелия при темпера-
туре ниже 2,71 К. За исследования сверхтекучести гелия П.Л. Капица был
награжден в 1978 г. Нобелевской премией. Так как гелий при нормаль-
ных условиях имеет массовую плотность в 7 раз меньше, чем у воздуха,
и к тому же негорюч, он используется для наполнения метеозондов и
аэростатов.
Аргон служит для создания инертной атмосферы в химических и
металлургических процессах, при электросварке. Ускоренные пучки ио-
нов аргона используются для очистки поверхностей полупроводников в
технологии создания микро- и наногетероструктур.
Криптон и ксенон применяются в мощных газонаполненных ис-
точниках света.
Химическая инертность элементов группы VIIIA обусловлена их
электронной конфигурацией. Однако в 1962 г. канадский химик Н. Барт-
летт получил желтые кристаллы состава XePtFe- В следующем году
были синтезированы фториды ксенона: XeF2, XeF4 и XeFe- К концу
XX века были созданы более сотни соединений ксенона и более двух
десятков соединений криптона (KrF2, KrF4 и др.).
Все химические элементы побочных групп (IB-VIIIB) представляют
собой типичные металлы. Каждый из них обладает уникальными свой-
ствами, которые описаны в специальной литературе.
Еще в начале XX века химики полагали, что титан не может иметь
практического применения из-за высокой хрупкости. Лишь в 1925 г.
было обнаружено, что хрупкость титана обусловливалась примесями. Чи-
стый титан очень пластичен, по твердости превосходит железо, при этом
имеет почти вдвое меньшую массовую плотность р = 4,5 г/см3. Кроме
того, титан тугоплавок и устойчив к коррозии. В настоящее время тита-
новые сплавы используются в судостроении, реакторостроении, авиаци-
онной и космической технике. Пары титана активно поглощают кисло-
род и азот, поэтому применяются при создании сверхвысокого вакуума.
Нитрид титана TiN является одним из самых прочных химических со-
единений. Слой TiN толщиной 2-3 мкм, нанесенный на металлорежу-
щие инструменты, значительно повышает их износостойкость. К тому
же нитрид титана имеет красивый золотой оттенок. По этой причине
купола восстановленного храма Христа Спасителя в Москве покрыты ни-
тридом титана.
Хром получил свое название (от греческого «хрома» — «цвет») из-за
поразительного разнообразия окраски солей этого элемента. В зависимо-
сти от проявляемой валентности хрома его соединения имеют голубой,
зеленый, фиолетовый, оранжевый или желтый цвет. Сплавы хрома с
железом представляют собой нержавеющие стали. Сплавы хрома с ни-
келем — нихромы — обладают высоким электрическим сопротивлением
и применяются для изготовления электронагревательных приборов. По-
крытие стальных изделий тонким (~ 0,1 мкм) слоем хрома (хромирова-
ние) надежно защищает их от коррозии.
Дополнения к лекции 15
317
Марганец химики называют «хамелеоном» из-за проявления всех
промежуточных величин степеней окисления от +1 до +7. Соединения
марганца демонстрируют различные оттенки красного, а также синий,
зеленый и черный цвета. Сплав железа с марганцем дает стали особой
прочности. Широко распространенное дезинфицирующее средство —
перманганат калия КМпСЦ («марганцовка») — представляет собой силь-
ный окислитель, что объясняет его бактерицидное действие.
Большинство переходных металлов — парамагнетики. Элементы
4-го периода группы VIIIB: железо, кобальт и никель демонстрируют
ферромагнитные свойства.
Самородная медь является, видимо, первым из металлов, используе-
мым древними людьми для изготовления орудий. В начале III тысячеле-
тия было случайно обнаружено, что малые добавки олова к меди (5-10%)
значительно повышают прочность металла. Так была открыта бронза,
и начался бронзовый век человечества, который длился около двух ты-
сяч лет. Чистая медь отличается низкой твердостью и малым удель-
ным электросопротивлением. Бронзы и латуни (сплавы меди с цинком)
являются прочными металлами с малым коэффициентом трения, что
позволяет их использовать для изготовления подшипников.
Кадмий представляет собой легкоплавкий и пластичный металл. Ха-
рактерно, что он в природе не образует собственных минералов и встре-
чается в виде примеси к цинковым рудам. Примерно две трети общеми-
ровой добычи кадмия расходуется на производство никель-кадмиевых
(щелочных) аккумуляторов. Кадмий обладает очень большим коэффи-
циентом поглощения нейтронов, поэтому кадмиевые стержни являются
регуляторами и аварийной защитой урановых и плутониевых ядерных
реакторов.
Вольфрам, тантал и рений являются самыми тугоплавкими метал-
лами. Их сплавы сохраняют прочность вплоть до температур ~ 3000 °C
и используются для изготовления носовых частей ракет и сверхзвуковых
самолетов. Так как вольфрам имеет температуру плавления 3410 °C, то
из него изготавливают катоды рентгеновских трубок и нити ламп на-
каливания, которые разогреваются в процессе работы до температуры
« 2500 °C. Карбид вольфрама WC является веществом особой твердости
и служит для изготовления режущих инструментов.
Шесть металлов группы VIIIB периодов 5 и 6 — рутений, родий,
палладий, осмий, иридий, платина — получили название благородных
за особо низкую химическую активность. Кроме того, осмий и иридий
обладают самой высокой массовой плотностью среди химических эле-
ментов: 22,57 г/см3 и 22,42 г/см3 соответственно.
Также низкой химической активностью обладают серебро и золото,
издавна используемые для изготовления монет и драгоценностей. Самые
древние из известных монет были отчеканены в VII веке до н.э. из при-
родного сплава золота и серебра (электрума).
Палладий обладает уникальной способностью поглощать в значи-
тельных количествах водород и удерживать его в пустотах своей кристал-
лической структуры. При атмосферном давлении и температуре 80 °C
один объем металла может поглотить 900 объемов водорода. При на-
гревании примерно до 250 °C палладиевая фольга пропускает водород,
но удерживает другие газы. Этим свойством пользуются для высокой
очистки водорода от газовых примесей.
318
Дополнения к лекции 15
Среди переходных металлов резко выделяется ртуть, которая при
нормальных условиях находится в жидком состоянии. Температура пла-
вления ртути —39 °C, поэтому у полярных путешественников иногда за-
мерзали ртутные термометры. Ртуть является самой тяжелой жидко-
стью, ее массовая плотность р = 13,6 г/см3 — почти вдвое больше, чем
у железа. Почти все металлы могут растворяться в ртути, образуя амаль-
гамы (жидкие сплавы).
В природе, как правило, все лантаноиды встречаются совместно в
составе одного минерала. Разделение редкоземельных элементов явля-
ется сложной технологической задачей, так как различие физических
свойств лантаноидов обусловлено только их относительно малой разни-
цей атомных масс. К примеру, при получении чистой соли туллия при-
шлось провести процесс перекристаллизации 15 000 раз!
Некоторые лантаноиды обладают ферромагнитными свойствами,
например, гадолиний. Но самыми сильными ферромагнитными свой-
ствами обладают интерметаллиды (химические соединения различных
металлов) лантаноидов. Из соединения SmCos изготавливаются самые
сильные постоянные магниты.
Церий и его сплавы обладают пирофорными свойствами — мелкие
частицы металла самовоспламеняются в воздухе. Это свойство исполь-
зуется в зажигалках. Сплав церия с железом (ферроцерий) при трении
о стальное колесико дает сноп искр, поэтому он входит в состав оболочек
трассирующих пуль и снарядов. Воспламенение происходит при трении
о воздух. Кстати, первооткрыватель пирофорных свойств церия — Карл
Аэур (1858-1929) — построил завод по производству зажигалок, а на по-
лученные доходы основал НИИ лантаноидов, причем сам открыл три из
них: празеодим, неодим и лютеций.
Все изотопы прометия радиоактивны, самый долгоживущий 145Рш
имеет период полураспада 17,7 года. Прометий выделяют из продук-
тов урана в ядерных реакторах. Из-за случайного характера процесса
деления среди осколков присутствуют и ядра изотопов прометия, кото-
рые захватывают электроны, превращаются в ионы и отделяются маг-
нитной сепарацией, аналогично используемой в масс-спектрометрии (см.
лекцию 1). Радиоактивность прометия позволяет использовать его при
изготовлении миниатюрных источников электропитания.
Соединения на основе сульфидов (ЬпзБз) и оксисульфидов (ЬпзОзЗ)
лантаноидов служат люминофорами в экранах дисплеев и телевизоров.
В галогенные лампы вводят люминофоры на основе иодидов лантано-
идов, что обеспечивает свечение различных цветов. Оксиды некоторых
лантаноидов используются как катализаторы крекинга нефти.
Все актиноиды радиоактивны, т. е. не имеют стабильных изотопов.
Среди актиноидов встречаются изотопы с большими временами жизни
(периодами полураспада), что позволило им не распасться полностью
за время существования Земли. Долгоживущие актиноиды являются
тугоплавкими серебристыми металлами.
Уран характерен низкой тепло- и электропроводностью. Природный
уран состоит из смеси трех изотопов 234U (0,006%), 235U (0,72%), 238U
(99,274%). Для нужд ядерной энергетики в основном необходим уран,
обогащенный изотопом 235U, что требует применения сложной техноло-
гии разделения изотопов с относительно близкими массами.
Дополнения к лекции 15
319
Начиная с кюрия Cm (Z = 96), у актиноидов периоды полураспада
Туг наиболее долгоживущих изотопов монотонно убывают с ростом по-
рядкового номера химического элемента (см. табл. Д.15.1).
Таблица Д.15.1. Периоды полураспада наиболее долгоживущих
изотопов актиноидов
Порядковый номер Z Химический символ Массовое число A Период полураспада T\/2
89 Ас 227 21,8 лет
90 Th 232 1,4 • 1О10 лет
91 Ра 231 32760 лет
92 и 238 4,47 • 109 лет
93 Np 237 2,14 • 106 лет
94 Pu 244 8,08 • 107 лет
95 Am 243 7340 лет
96 Cm 247 1,56 • 107 лет
97 Bk 247 1380 лет
98 Cf 251 898 лет
99 Es 254 258 сут.
100 Fm 257 100,5 сут.
101 Md 258 55 сут.
102 No 259 1 ч
103 Lr 260 3 мин
У химических элементов, стоящих в таблице Менделеева после ак-
тиноидов (Z > 103), время жизни наиболее долгоживущих изотопов не
превышает секунд и даже миллисекунд. По этой причине их физические
и химические свойства пока мало изучены.
К концу XX века были синтезированы и получили общепризнанные
названия трансактиноиды, приведенные в следующей табл. Д.15.2. По
имеющимся сведениям все они являются металлами.
Таблица Д.15.2. Названия и химические символы
тр ансактиноидов
Порядковый номер Z Название и химический символ
104 Резерфордий Rf
105 Дубний Db
106 Сиборгий Sg
107 Борий Bh
108 Хассий Hs
109 Мейтнерий Mt
ПО Дармштадтий Ds
111 Рентгений Rg
Ко времени редактирования данного учебника были получены изо-
топы химических элементов с порядковыми номерами 112, 114, 116 и
118.
320
Дополнения к лекции 15
15.2. Эффект Рамзауэра
В 1921 г. Карл Рамзауэр (1879-1955) проводил исследования прохо-
ждения медленных электронов с энергией около 1 эВ через различные
газы. Схема установки Рамзауэра приведена на рис. Д.15.1.
Рис. Д.15.1. Принципиальная схема экспериментальной установки Рамзауэра:
1 — пучок монохроматического света, 2 — фотокатод, 3— батарея, 4 — первая диафрагма,
5— камера, заполненная исследуемым газом, 6— коллектор электронов (камера поглоще-
ния), 7— патрубок для откачки воздуха и подачи газа в камеру столкновений; Is — ток
рассеянных электронов, 1т — ток нерассеянных электронов. Направление индукции од-
нородного магнитного поля В перпендикулярно плоскости рисунка. Штриховая линия —
траектория пучка моноэнергетических электронов
Источником электронов являлся фотокатод 2, освещаемый пучком
монохроматического света 1. На катод, посредством батареи У, подан
отрицательный потенциал относительно корпуса аппарата, который за-
землен.
Скорость фотоэлектрона зависит от длины световой волны Л и может
быть вычислена с помощью уравнения фотоэффекта (4.3). Так как в
опытах Рамзауэра использовался видимый свет, то фотоэлектроны имели
нерелятивистские энергии. Тогда максимальная скорость фотоэлектрона
выражается формулой
v —
(Д.15.1)
Изменяя длину световой волны А, Рамзауэр получал фотоэлектроны
различной энергии.
Электроны, выходящие из фотокатода, попадали в камеру, которая
была откачана до столь малого давления, что длина свободного пробега
электрона много больше размеров аппарата. На начальном участке тра-
Дополнения к лекции 15
321
ектории электроны ускорялись разностью потенциалов между фотокато-
дом и первой диафрагмой 4-
В вакуумной камере создавалось однородное магнитное поле В (см.
рис. Д.15.1). Электроны, имеющие начальную скорость v, перпенди-
кулярную вектору В, двигались под действием силы Лоренца по дугам
окружностей, аналогично движению ионов в масс-спектрометре Демстера
(см. лекцию 1). Радиус окружностей R определяется уравнением дви-
жения
^-v2 = -vB, (Д.15.2)
JLL С
которое аналогично уравнению (1.11).
Установка сконструирована таким образом, что электроны должны
пройти через систему узких диафрагм, расположенных на окружности
определенного радиуса Rq. Система диафрагм предназначена для того,
чтобы в камеру столкновений 5 попадали практически моноэнергетиче-
ские электроны, скорость которых, согласно уравнению (Д.15.2), равна
Описанная процедура формирования узкого моноэнергетического
пучка (называемая магнитной сепарацией) необходима, так как фо-
тоэлектроны, выходящие из фотокатода, обладают некоторым разбро-
сом энергий. Электроны, имеющие величину скорости, отличную от
(Д.15.3), будут двигаться по дугам окружностей с радиусами R Rq и
будут отсечены от пучка одной из диафрагм (см. рис. Д.15.1).
Легко вычислить, что электрон с кинетической энергией 1 эВ (за-
ведомо нерелятивистский!) имеет скорость ~ 5,9 • 107 см/с. Согласно
уравнению (Д.15.3), в однородном магнитное поле с индукцией 1Гс та-
кой электрон движется по окружности радиуса « 3,37 см. Таким обра-
зом, в установке Рамзаура траектории малого радиуса обеспечивались с
помощью относительно слабого магнитного поля.
Камера столкновений 5 наполнялась исследуемым газом до требуе-
мого давления, которое контролировалось специальным манометром.
Кратко рассмотрим процесс прохождения электронов через газовую
среду, в ходе которого они сталкиваются с атомами газа. При комнатной
температуре практически все атомы газа находятся в основном стацио-
нарном состоянии. Если кинетическая энергия электронов меньше
энергии возбуждения Е* первого возбужденного состояния, то столкно-
вения будут упругими (см. описание опыта Франка-Герца в § 14.1 лек-
ции 14). Такие столкновения приводят к изменению направления век-
тора скорости электрона. В результате каждого столкновения электрон
выбывает из первичного узкого пучка. Как следствие, электронный пу-
чок приобретает широкий угловой разброс, а поток в первоначальном
направлении постепенно уменьшается. При таких физических условиях
ослабление первичного узкого пучка можно удовлетворительно описать
экспоненциальной функцией типа (Д.1.8)
I(x) = Iq ехр (-рх), (Д.15.4)
где Iq — поток электронов на входе в камеру столкновений, 1(х) — поток
электронов, прошедших расстояние ж, р — коэффициент ослабления.
322
Дополнения к лекции 15
Средняя длина свободного пробега электрона в газе определяется как
величина обратная коэффициенту ослабления:
Lq = i (Д.15.5)
р
Коэффициент р зависит концентрации атомов газа п и представляется
произведением
р = па, (Д.15.6)
где параметр а называется интегральным эффективным сечением рас-
сеяния.
Из формул (Д.15.5) и (Д.15.6) очевидно, что величина а имеет раз-
мерность площади, поэтому может интерпретироваться в виде круговой
площадки, содержащей в центре атом и расположенной перпендикулярно
Рис. Д.15.2. Геометрическая интерпретация интегрального эффективного се-
чения:
а) проекция в плоскости рассеивающихся частиц; стрелки показывают направления дви-
жения частиц; б) проекция, перпендикулярная скоростям налетающих частиц; заштрихо-
вана площадка, изображающая интегральное эффективное сечение сг
векторам скорости электронов первичного пучка. Согласно этой интер-
претации, электроны, пересекающие площадку, рассеиваются, а не пе-
ресекающие — не изменяют своего направления движения и величины
скорости (см. рис. Д.15.2).
Справедливость такой геометрической интерпретации интегрального
эффективного сечения доказывается в теоретической механике. Там по-
казано, что величина а равна определенному интегралу от дифференци-
ального эффективного сечения, взятому по всевозможным направлениям
в пространстве:
7Г 27Г
сг — ^^sinOdOdcp. (Д.15.7)
о о
Интегральное сечение ст является важнейшей количественной харак-
теристикой процесса рассеяния в тех случаях, когда угловое распределе-
ние рассеянных частиц не представляет интереса. Эта величина для
фиксированных типов сталкивающихся частиц, как правило, не кон-
станта, а функция кинетической энергии налетающих частиц.
Дополнения к лекции 15
323
В случаях, когда рассеяние происходит за счет кулоновского взаимо-
действия, следует ожидать, что функция сг(^) будет убывающей. Дело в
том, что причиной рассеяния является прохождение электрона через по-
тенциальное поле электронной подсистемы атома. Кажется очевидным,
что увеличение кинетической энергии, а следовательно, скорости элек-
трона приводит к уменьшению времени взаимодействия и в результате
к понижению эффективного сечения а.
Вернемся к эксперименту Рамзаура. Электроны, попавшие в камеру
столкновений 5 и рассеянные там, не пройдут сквозь следующие диа-
фрагмы и попадут на стенки камеры 5. Эти электроны формируют ток
Is, который измеряется гальванометром. Электроны, не рассеянные в
камере 5, попадают в камеру 6, которая является их коллектором (сбор-
ником). Все электроны, попавшие в коллектор, образуют ток 1т, который
также измеряется. Очевидно, что сумма Is + 1т равна току первичного
пучка /о- Иначе говоря, на входе в камеру столкновений поток электро-
нов равен /0, а на выходе из нее равен 1т- Тогда, пользуясь законом
ослабления (Д.15.4), можно выразить коэффициент ослабления следую-
щим образом:
M = (Д.15.8)
L \1т /
где L — длина участка траектории электрона в камере столкновений.
Теперь, зная концентрацию газа в камере столкновений, нетрудно
вычислить величину эффективного сечения рассеяния а с помощью фор-
мулы (Д.15.6).
В опытах по рассеянию медленных электронов в парах металлов
были получены убывающие зависимости интегрального сечения рассе-
Рис. Д.15.3. Зависимость интегрального сечения рассеяния от скорости элек-
трона для криптона (1) и цинка (2)
яния а от скорости электрона v (см. рис. Д.15.3), в соответствие с выше
приведенными рассуждениями. Но пропускании электронов через аргон
324
Дополнения к лекции 15
зависимость ct(v) оказалась нелинейной (см. рис. Д.15.3). Наиболее
удивительным было при скорости электронов vi « 4 • 107 см/с падение
интегрального сечения рассеяния а практически до нуля! Иначе говоря,
при определенной скорости электронов vi атомы газа стали для них со-
вершенно прозрачными!
Для криптона и ксенона получались подобные результаты, которые
оказалось невозможным истолковать на основе классической физики.
Эффект Рамзауэра удалось объяснить только после создания кванто-
вой теории. Необходимыми условиями для возникновения эффекта яв-
ляются, во-первых, характерное пространственное распределение элек-
тронной плотности р(г) атомов инертных газов, во-вторых, волновые
свойства электронов.
В § 15.4 указывалось, что электронные конфигурации внешних обо-
лочек атомов инертных газов имеют вид ns2np\ где п — номер периода
(исключением является гелий с конфигурацией 1s2). Иначе говоря, у
этих атомов полностью заполнены внешние электронные оболочки. Как
следствие, у таких атомов функция электронной плотности р(г) убы-
вает более резко, чем у других атомов. По этой причине эффективное
поле электронной оболочки атома инертного газа, описывающее взаи-
модействие с налетающими медленными электронами, можно успешно
аппроксимировать сферической потенциальной ямой следующего вида:
= Г -и„ пр» г а,
v 7 [0 при г > a, v 7
где г — расстояние от центра атома, а — радиус потенциальной ямы.
Выражение (Д.15.9) означает, что на расстоянии г > а взаимодействие
электрона с атомом пренебрежимо мало. Понижение потенциальной энер-
гии на расстояниях г < а можно качественно объяснить тем, что при
проникновении внутрь атома электрон взаимодействует с суммарным
зарядом атомного ядра и внутренних электронных оболочек, который
имеет положительный знак. Влияние внешних электронных оболочек
равно нулю из-за сферической симметрии электронной плотности атома
инертного газа.
Качественное объяснение эффекта Рамзауэра можно провести, поль-
зуясь следующей одномерной моделью. Рассмотрим движение электрона
вдоль оси ж, проходящей через центр атома инертного газа. Взаимо-
Рис. Д.15.4. Прямоугольная потенциальная яма, характеризующая взаимодей-
ствие электрона с атомом инертного газа в одномерном приближении
действие электрона с атомохм можно описать функцией потенциальной
энергии, которая изображена на рис. Д.15.4. Можно сказать, что потен-
циальная яма на рис. Д.15.4 получена сечением функции (Д.15.9).
Дополнения к лекции 15
325
В данном приближении электрон, имеющий координату х < —а или
х > а, имеет нулевую потенциальную энергию, т.е. является свободным.
В диапазоне координат — а < х < а из-за взаимодействия с атомом по-
тенциальная энергия электрона понижается до величины — Uq. Гамиль-
тониан электрона записывается в виде
для областей х < — а и х > а,
Н =
2т dx2
h2 d2
----— — Uq для области — а < х < а.
2т dxz
(Д.15.10)
Решение уравнения Шредингера проводится аналогично изложен-
ному в лекции 10. Мы рассматриваем задачу о рассеянии электрона
на атоме, т. е. случай инфинитного движения. Для этого случая волно-
вые функции целесообразно записать в виде, соответствующем бегущим
волнам:
-01 = Ai ехр (ikx) + Аъ ехр (—ikx),
-02 = Ci ехр (ikix) + С2 ехр (—ikix),
fa = Bi ехр (ikx) 4- В2 ехр (—ikx),
х < —а, (Д.15.11)
х > а,
(Д.15.12)
(Д.15.13)
(Д.15.14)
(Д.15.15)
где
к = ^-у/2теЕ,
П
кг = ^\/2те(Е + U0).
Величина Е представляет собой начальную кинетическую энергию
электрона. Функции (Д.15.11)-(Д.15.13) являются дебройлевскими вол-
нами, а параметры к и ki — их волновыми числами. Следователь-
но, длины волн, распространяющихся в пределах потенциальной ямы,
равны
_ 2лП _ 2л h
1 ~ V “ ^2те(Е + ио)’
(Д.15.16)
а для волн вне ямы
2irh _ 2irli
к у/2теЕ
(Д.15.17)
Из сравнения (Д.15.14) и (Д.15.15) следует, что А > Ai, что соответствует
увеличению кинетической энергии рассеиваемого электрона внутри по-
тенциальной ямы.
Как было указано в § 10.3 лекции 10, экспоненты с положительным
аргументом описывают волны, бегущие в положительном направлении
оси х, с отрицательным аргументом — в противоположном направлении.
Если для определенности рассматривать электрон, движущийся из обла-
сти отрицательных координат вдоль оси х, то коэффициент В2 следует
приравнять к нулю, так как в области (х > а) не возникает отраженной
волны.
326
Дополнения к лекции 15
Коэффициенты перед экспонентами в функциях (Д. 15.11)-(Д. 15.13)
являются амплитудами волн. Величины амплитуд находятся из условий
непрерывности волновой функции на границах потенциальной ямы:
V’i(-a) = ф2(-а), ^2(а) = ^з(а),
V’l(-a) = ф'2(а) = ф'3(а).
(Д.15.18)
Используя уравнения (Д.15.18), вычислим отношение амплитуды
волны, отраженной от первой стенки потенциальной ямы (х = —а), к
амплитуде волны, падающей на эту стенку ямы:
Л2 _ к — кг
Ai ki + к'
(Д.15.19)
Аналогично получим отношение амплитуд отраженной и падающей волн
для второй стенки потенциальной ямы \х = а):
С2 _ ki-k
(7i ki + к
(Д.15.20)
Видно, что из-за неравенства ki > к отношение амплитуд (Д.15.19)
имеет отрицательный знак, а отношение (Д. 15.20) — положительный.
Умножение на —1 амплитуды гармонической волны эквивалентно изме-
нению фазы волны на тг (по формуле Эйлера ехр (гтг) — —1). Следо-
вательно, при отражении от первой стенки потенциальной ямы фаза де-
бройлевской волны получает приращение Д</> — тг. Напротив, при отра-
жении от второй стенки в точке х = а фаза волны не изменяется.
Аналогичное явление хорошо известно в оптике. При отражении
от границы раздела с более оптически плотной средой (т.е. средой с
большим показателем преломления) происходит изменение фазы волны
на тг. При отражении от границы раздела с менее оптически плотной сре-
дой (т. е. средой с меньшим показателем преломления) изменения фазы
не происходит. Так как волновое число гармонической волны прямо
пропорционально показателю преломления среды, в которой распростра-
няется волна, аналогия является полной.
В рамках рассматриваемой одномерной модели рассеяние электронов
эквивалентно их отражению от потенциальной ямы. Интерференция де-
бройлевских волн может привести к ослаблению отраженной волны, что
эквивалентно уменьшению коэффициента ослабления р и интегрального
эффективного сечения рассеяния а. Очевидно, что максимальное осла-
бление достигается при отрицательной (деструктивной) интерференции,
когда разность фаз волн равна тг.
Волна, рассеянная потенциальной ямой (Д.15.9), формируется нало-
жением волн, отраженных обеими стенками. При отражении на первой
границе (х = —а) волна приобретает приращение фазы Д</?1 = тг. При
отражении на второй границе (х = а) фаза волны не изменяется. Но не-
обходимо учитывать, что с волной, отраженной от первой стенки, интер-
ферирует волна, которая, отразившись от второй стенки, прошла допол-
нительное расстояние, равное удвоенной ширине потенциальной ямы.
Это расстояние 4а является разностью хода интерферирующих волн и
Дополнения к лекции 15
327
приводит к дополнительному набегу фазы второй волны Д992 = 4a&i.
Уравнение деструктивной интерференции можно записать в виде
Ду?2 - Д^1 = тг- (Д.15.21)
Решение последнего уравнения Ai = 4а целесообразно переписать, ис-
пользуя выражение (Д.15.16) для длины дебройлевской волны внутри
потенциальной ямы:
2а = ...—.........= . (Д.15.22)
У27Пе(Ех + Uo)
Кинетическая энергия Е\ в последнем соотношении соответствует экспе-
риментально измеренной скорости электрона Vi, при которой наблюда-
ется минимум эффективного сечения рассеяния а (см. рис. Д.15.3):
E1~TVC
(Д.15.23)
При соотношении (Д. 15.22) между кинетической энергией электрона и
параметрами потенциальной ямы достигается минимум коэффициента
ослабления р. Говорят, что при этом электроны практически перестают
«замечать» атомы на своем пути.
Максимум эффективного сечения рассеяния ст, наблюдаемый на экс-
периментальных графиках (см. рис. Д.15.3), также можно интерпре-
тировать в рамках одномерной модели. При постепенном возрастании
начальной скорости электрона возрастает волновое число ki и, следова-
тельно, набег фазы Д992 второй интерферирующей волны. Тогда при
определенной скорости электрона разность фаз интерферирующих волн
станет равной 2тг и осуществится условие конструктивной (положитель-
ной) интерференции. Запишем уравнение конструктивной интерферен-
ции
Д</?2 — Д<£1 = 2тг (Д.15.24)
и его решение 3Ai = 8а или
у/2те(Е2 + Uq)
Начальная кинетическая энергия Еъ, которая обращает в тождество
последнее уравнение, определяет скорость V2, при которой эффективное
сечение рассеяния а достигает максимума (см. рис. Д.15.3).
В принципе, можно экспериментально измерить характерные энер-
гии Ei и Е2 для определенного инертного газа, решить систему уравне-
ний (Д.15.22) и (Д.15.24) и вычислить параметры потенциальной ямы
(Д.15.9). Однако описание процесса рассеяния электронов атомами с по-
мощью одномерного приближения слишком грубо для вычисления фи-
зических характеристик атомов. Рассмотренное приближение служит
лишь для принципиального объяснения эффекта Рамзауэра. В то же
время, оценки параметров потенциальной ямы, выполненные решением
системы уравнений (Д.15.22) и (Д.15.24), дают разумные результаты,
328
Дополнения к лекции 15
что свидетельствует о применимости вышеприведенной одномерной мо-
дели.
Анализ физической картины рассеяния электронов атомами в трех-
мерном пространстве и расчеты эффективного сечения а выполняются в
рамках квантовой теории рассеяния.
В заключение необходимо отметить, что независимо от Рамзауэра
эксперименты по рассеянию медленных электронов на атомах примерно
в то же время были проведены Таунсендом (1868-1957) — знаменитым
исследователем электрических разрядов в газах. По этой причине рас-
смотренное явление часто называют эффектом Рамзауэра-Таунсенда.
Лекция 16
АТОМНЫЕ ТЕРМЫ
В предыдущей лекции показано, что расчет основных состоя-
ний многоэлектронных атомов в приближении электронных кон-
фигураций позволяет объяснить структуру таблицы Менделеева и
многие свойства химических элементов.
При возбуждении атома один или несколько электронов пере-
ходят в свободные одноэлектронные состояния с большей энер-
гией. Возбужденные состояния атома обладают средним време-
нем жизни ~ 10“8 с и менее. Переход в основное состояние (или
в возбужденные состояния с меньшей энергией) может сопрово-
ждаться испусканием фотонов. Следует помнить, что переходы
между стационарными состояниями атома могут быть безизлу-
чательными, при этом разность энергий может превращаться в
кинетическую энергию сталкивающихся атомов или передаваться
внешнему электрону при эффекте Оже, описанном в лекции 19.
Спектры излучения многоэлектронных атомов можно описать
переходами отдельных электронов между одноэлектронными сос-
тояниями. Однако переходы электронов между оболочками не
могут объяснить наличие множества спектральных линий в на-
блюдаемых спектрах излучения многоэлектронных атомов. Сле-
довательно, для описания оптических спектров недостаточно
приближения электронных конфигураций. Требуется более по-
дробное описание стационарных состояний многоэлектронных
атомов, в частности, расчет суммарного орбитального момента им-
пульса и суммарного спина всех электронных оболочек атома.
16.1. Сложение моментов импульса
для многоэлектронных атомов
Согласно нерелятивистской квантовой теории, многоэлектрон-
ный атом в стационарном состоянии обладает определенным моду-
лем суммарного орбитального момента импульса La и определен-
ным модулем суммарного спина Sa всех электронов атома. Эти
330
Лекция 16. Атомные термы
величины определяются моментами отдельных электронов и их
взаимной ориентацией.
Как было показано в лекции 14, в приближении самосогласо-
ванного поля каждое одноэлектронное состояние характеризуется
квантовыми числами Z, тп и тп$. Число I задает модуль орби-
тального момента импульса электрона, а числа тп и ms опреде-
ляют ориентации орбитального момента и спина электрона соот-
ветственно. Суммирование орбитальных моментов импульса всех
электронов с учетом их взаимной ориентации должно давать ор-
битальный момент импульса атома. Если же сложить спины всех
электронов атома, то получится, вообще говоря, не спин атома,
а суммарный спин электронной системы атома (множества всех
электронов атома). Дело в том, что атомное ядро также обладает
собственным моментом импульса — спином ядра. Однако по при-
чинам, изложенным в лекции 21, во многих физических задачах
спином атомного ядра можно пренебречь. Тогда суммарный спин
атома полагается равным сумме спинов всех электронов атома.
Различные распределения электронов определенной оболочки
по одноэлектронным состояниям с разными квантовыми числами
тп и ms будут давать разные значения модулей суммарных мо-
ментов импульса атома — орбитального La и спинового Sa- Вы-
числение величин La и Sa по квантовым числам заполненных
одноэлектронных состояний атома является одной из задач кван-
товой механики.
Рассмотрим сначала двухэлектронный атом в стационарном со-
стоянии. Пусть один электрон атома находится в состоянии с
орбитальным числом Zi, а другой — в состоянии с орбитальным
числом Z2. Квадраты модулей моментов импульса электронов вы-
ражаются следующими формулами:
L2 = ^2Zi(Zi + l), L2 = + 1). (16.1)
Квадрат суммарного момента импульса Lq также квантуется по
аналогичному закону и характеризуется квантовым числом Iq:
Lq = h2lo(lo + 1). (16.2)
Следовательно, задача суммирования двух моментов импульса
сводится к вычислению квантового числа Zq суммарного момента
импульса по известным квантовым числам Zi и Z2 складываемых
моментов. Согласно квантовой теории, правило сложения момен-
тов импульса выглядит таким образом, что квантовое число сум-
марного момента импульса Iq может принимать значения только
из следующего конечного множества:
Zo = h + h + h ~ ---) |^i “Z2I. (16.3)
Различные значения числа Zq при заданных числах Zi и I2 обу-
словлены различной взаимной ориентацией суммируемых момен-
тов импульса.
16.1. Сложение моментов импульса
331
В классической физике количество взаимных ориентаций двух
векторов моментов импульса бесконечно и несчетно, угол между
векторами моментов может меняться непрерывно. Напротив, ко-
личество взаимных ориентаций квантовых моментов импульса
дискретно и конечно. Например, при Zi = 3 и 1% = 2 кванто-
вое число Iq может принимать пять различных значений: 5, 4, 3,
2, 1. Соответственно, модуль суммарного момента импульса может
иметь величину
|L0| = Л\/30, Йх/20, йх/12, йТб, Йх/2.
Заметим, что максимальное значение модуля суммарного мо-
мента импульса несколько меньше суммы модулей складываемых
моментов:
Йх/ЗО < Йх/12 + Йх/б.
С другой стороны, минимальное значение |Zo| превышает
|£i — L2I:
Лу/2 > Йх/12 - Йх/б.
Два последних неравенства доказывают, что моменты импуль-
са электронов не могут располагаться строго параллельно или ан-
типараллельно.
Данную процедуру сложения моментов импульса можно на-
глядно продемонстрировать с помощью векторной модели (см.
рис. 16.1). Суммируемые моменты условно изображаются на плос-
кости символическими векторами, длины которых равны
х/ф + 1), где 1 = 1,2,... (16.4)
Иначе говоря, длина символического вектора равна модулю
момента импульса в единицах Л. В декартовой системе коорди-
нат проводятся концентрические дуги с радиусами, определен-
ными формулой (16.4). Символические векторы, изображающие
моменты импульса, складываются как классические векторы, но
с условием, чтобы суммарный вектор имел длину из того же ряда
значений (16.4). В результате начало суммарного вектора нахо-
дится в начале координат, а конец — на одной из построенных
дуг (см. рис. 16.1).
При сложении трех моментов импульса можно к полученной
сумме двух добавить третий с помощью той же процедуры. Опи-
санный метод можно распространить на любое количество слагае-
мых.
Заметим, что изложенный способ сложения пригоден не только
для вычисления орбитальных моментов импульса, но и для спи-
нов, а также для полных моментов импульса многоэлектронных
атомов.
332
Лекция 16. Атомные термы
Набор квантовых чисел одноэлектронных состояний дает ин-
формацию не только о модулях, но и о проекциях моментов элек-
трона. Известные значения проекций орбитального момента и
спина электрона упрощают вычисления суммарных моментов
атома.
Модуль спина у всех электронов одинаков, а проекции на опре-
деленное направление в пространстве могут принимать только
Рис. 16.1. К правилу сложения двух моментов импульса с помощью векторной
модели. Квантовые числа суммируемых моментов равны h = 3 и I2 = 2. Видно,
что возможно пять различных значений модуля суммарного момента импульса
с квантовыми числами Iq = 1,2,3,4,5. Изображены векторы максимального и
минимального значений суммарного импульса Lq
одно из двух возможных значений: Й/2 или —Й/2. Отсюда сле-
дует, что спины двух электронов с противоположными значениями
квантовых чисел ms (1/2 или —1/2) полностью компенсируют
друг друга и дают суммарный спин равный нулю. Таким обра-
зом, для вычисления спина атома достаточно найти количество
некомпенсированных спинов, при этом сумма квантовых чисел ms
заполненных одноэлектронных состояний совпадает с квантовым
числом so, которое определяет квадрат модуля спина атома:
S2a =/i2so(so + 1). (16.5)
В частности, у двухэлектронного атома в стационарном состо-
янии модуль спина может быть или равным нулю (если проекции
спинов электронов имеют разные знаки), или равным Ну/2 (если
проекции спинов электронов имеют одинаковые знаки). Эти со-
16.1. Сложение моментов импульса
333
стояния характеризуются квантовыми числами so == 0 и so = 1.
Часто физики говорят о «параллельных» и «антипараллельных»
спинах электронов. Строго говоря, это неверно, так как у всех
квантовых моментов импульса (в том числе, у спина) в стацио-
нарных состояниях две проекции являются неопределенными.
Соответствующие значения модуля спина Sa = 0 и Sa = h\/2
определяют две разновидности гелия: парагелий и ортогелий
(см. дополнение 17.1).
У атомов с химическим номером Z > 2 электроны распреде-
лены по нескольким электронным оболочкам. Покажем, что сум-
марный орбитальный момент импульса любой заполненной элек-
тронной оболочки равен нулю. В соответствии с принципом Паули
полностью заполненная оболочка содержит 2(2/4-1) электронов, где
I — орбитальное квантовое число, характеризующее данную элек-
тронную оболочку. Половина электронов имеет квантовое число
ms = 1/2 (т.е. положительную проекцию спина), причем магнит-
ное квантовое число т пробегает ряд значений: —Z, — (Z — 1), ..., О,
1, ..., Z. Иначе говоря, каждой положительной проекции орбиталь-
ного момента импульса электрона соответствует равная ей по мо-
дулю отрицательная проекция. Таким образом, орбитальные мо-
менты .импульса электронов полностью компенсируют друг друга.
Вторая половина электронов оболочки характеризуется квантовым
числом ms = —1/2, при этом квантовое число т пробегает тот же
ряд значений и также дает нулевой вклад в суммарный орбиталь-
ный момент. Таким образом, у заполненной электронной оболочки
модуль суммарного орбитального момента импульса равен нулю.
С другой стороны, в заполненной оболочке число электронов с
проекциями спина Й/2 и —Й/2 одинаково. Следовательно, суммар-
ный спин такой оболочки также равен нулю. В качестве иллю-
страции приведем табл. 16.1, в которой указаны квантовые числа
всех одноэлектронных состояний в электронной оболочке 2р.
Таблица 16.1. Квантовые числа одноэлектронных
состояний оболочки 2р
п 1 т ms
2 1 1 1/2
2 1 0 1/2
2 1 -1 1/2
2 1 1 -1/2
2 1 0 -1/2
2 1 -1 -1/2
334
Лекция 16. Атомные термы
16.2. Атомные термы
В современной научной и учебно-методической литературе тер-
мин терм употребляется в различных (хотя и связанных между
собой) значениях. Часто термами называют энергетические уров-
ни стационарных состояний атомов, иногда — сами стационарные
состояния. Встречаются и другие употребления этого термина.
В данном курсе лекций атомным термом называется сово-
купность физических характеристик атома, которая включает в
себя модули орбитального момента импульса La и спина Sa- Ниже
(в § 16.4) к ним добавится модуль полного момента импульса ато-
ма. Стационарные состояния атома обладают определенными зна-
чениями величин модулей моментов La и Sa-, поэтому можно
говорить о термах атомных состояний. В современной научной
литературе постоянно используются термины: терм основного со-
стояния, термы возбужденных состояний и т. п. Энергия стацио-
нарного состояния с определенными значениями величин La и Sa
называется энергией соответствующего терма. Часто в научной и
учебно-методической литературе под термом понимается совокуп-
ность стационарных состояний атомов, которые характеризуются
величинами суммарных моментов импульсов La и Sa (а также
полного электронного момента импульсов Уд, который определя-
ется в § 16.4 данной лекции).
Подчеркнем различие атомного терма от электронной конфи-
гурации атома, которая ранее была определена как распределе-
ние электронов по электронным оболочкам. Далее будет показано,
что определенной электронной конфигурации могут соответство-
вать несколько атомных термов.
Значения модулей орбитального момента импульса La и спина
Sa атома, определенные в предыдущем параграфе, согласно фор-
мулам (16.2) и (16.5), выражаются через соответствующие кван-
товые числа Iq и sq:
La = ^y/lQ^Q + 1), Sa = ^\/ «$о(5о + 1)- (16.6)
Атомные термы обозначаются по исторически сложившейся
терминологии. Квантовое число Iq выражается латинской заглав-
ной буквой в соответствие со следующей таблицей.
Таблица 16.2. Символы для обозначения атомных термов
Квантовое число 1о 0 1 2 3 4 5 6
Символ S Р D F G Н I
Для более высоких значений квантового числа Iq используются
последующие буквы латинского алфавита. Видно сходство с табли-
цей обозначений электронных оболочек 14.1, различие заключа-
ется в замене латинских строчных букв на заглавные.
16.2. Атомные термы 335
Величина спина атомного терма характеризуется верхним ле-
вым индексом у обозначения терма. Этот индекс равен 2зо 4- 1 и
исторически называется мулътиплетностпъю. Например, терм с
квантовыми числами Iq = 1 и sq = 1/2 обозначается символом 2Р.
Как будет показано в следующей лекции, в случаях, когда so
величина 2so +1 равна количеству подуровней, появляющихся из-
за спин-орбитального взаимодействия.
Выше было показано, что у атома с полностью заполненными
электронными оболочками суммарный орбитальный момент им-
пульса Ьд = 0 и спин Sa = 0. Это значит, в частности, что
термы основных состояний атомов всех инертных газов и щелоч-
ноземельных металлов имеют вид 15.
Очевидно, что суммарный орбитальный момент La и спин
атома Sa определяются только частично заполненными электрон-
ными оболочками.
Пока пренебрежем спин-орбитальным взаимодействием, так
как оно значительно слабее электрического взаимодействия между
электронами и атомным ядром. В этом случае, согласно квантовой
теории, атом в стационарном состоянии обладает не только опре-
деленными модулями моментов La и но и определенными
проекциями этих моментов на некоторое направление Z в про-
странстве, т.е. величинами Laz и Saz- Как и в атоме водорода,
определенное значение имеет только одна из трех проекций мо-
ментов. Проекции моментов квантуются по законам сходным с
(9.48) и (12.16):
Laz = hmo, то = Zo, Zo - 1, ..-к,
Saz = Zimso, rnSo — so, so — 1, ..., — sq.
Квантовое число то определяет проекцию суммарного орби-
тального момента атома Laz и может принимать 2Zq + 1 разных
значений, различающихся на единицу. Аналогично, квантовое
число mso определяет проекцию суммарного спина атома Saz и
может иметь 2зо 4-1 значений, также различающихся на единицу.
Как будет показано в лекциях 20 и 21, квантовые числа то и mso
характеризуют магнитные свойства атома.
Теперь можно перейти к расчету суммарных моментов импуль-
са атома с частично заполненными электронными оболочками.
Для проекций моментов импульса правило сложения очень про-
стое: квантовое число то равно сумме магнитных квантовых чи-
сел всех электронов в оболочке. Аналогично, квантовое число mso
равно сумме квантовых чисел ms отдельных электронов. Если у
атома несколько частично заполненных электронных оболочек, то
это правило суммирования распространяется и на них.
Общая методика сложения квантовых моментов импульса и
вычисления излагается в курсах квантовой механики. Здесь мы
ограничимся следующим типичным примером.
336
Лекция 16. Атомные термы
Рассмотрим атом углерода, содержащий шесть электронов.
Электронная конфигурация его основного состояния имеет вид
ls22s22p2. Оболочки 1s и 2s полностью заполнены, все четыре
квантовых числа электронов однозначно определяются табл. 15.3,
составленной для основного состояния атома бериллия (см. лек-
цию 15). Оставшиеся два электрона можно распределить по ше-
сти одноэлектронным состояниям 2р-оболочки несколькими спо-
собами. Эти варианты имеют одинаковые квантовые числа п и I,
но различаются квантовыми числами m и ms-
При I = 1 возможны три разных значения магнитного кванто-
вого числа т, характеризующего проекцию орбитального момента
импульса, равные тп = —1,0,1. Соответственно, каждый из двух
р-электронов может находиться в одном из шести одноэлектрон-
ных состояний с парами квантовых чисел тп и ms, приведенными
в следующей таблице.
Таблица 16.3. Возможные значения квантовых чисел тп и ms
в одноэлектронных состояниях р-оболочки
Обозначание состояния а) Ь) с) d) е) f)
Магнитное квантовое число тп 1 0 -1 1 0 -1
Квантовое число проекции спина ms 1/2 1/2 1/2 -1/2 -1/2 -1/2
В силу принципа Паули каждое из состояний табл. 16.3 может
быть занято только одним электроном. Состояния многоэлектрон-
ной системы характеризуются проекцией суммарного орбиталь-
ного момента атома Laz и проекцией суммарного спина атома
SaZi которые выражаются посредством формул (16.7) через соот-
ветствующие квантовые числа то и т^о- Для двухэлектронной
системы квантовые числа проекций суммарных моментов равны
mo = mi4-m2, mse = mSi 4- mS2, (16.8)
где mi и m2 — магнитные квантовые числа одноэлектронных со-
стояний, в которых находятся электроны, msi и т$2 — соответ-
ственно квантовые числа проекций спина электронов.
Рассмотрим, например, случай, когда электроны занимают од-
ноэлектронные состояния a) nd). Тогда
то = 2, mso = 0. (16.9)
Различным вариантам распределения электронов по состоя-
ниям табл. 16.3 соответствуют пары значений квантовых чисел
то и т^о, сведенные в следующую таблицу.
16.2. Атомные термы
337
Таблица 16.4. Возможные варианты значений квантовых
чисел то и mso системы двух р-электронов
Номер состояния Квантовые числа т и ms пары р-электронов 7710 = mi 4- 7712 т so = msi 4- ms2
1 (1, 1/2), (1,-1/2) 2 0
2 (1, 1/2), (0,-1/2) 1 0
3 (1,-1/2), (0, 1/2) 1 0
4 (1, 1/2), (—1,—1/2) 0 0
5 (1.-1/2), (-1,1/2) 0 0
6 (0, 1/2), (0,-1/2) 0 0
7 (1, 1/2), (0, 1/2) 1 1
8 (1, 1/2), (-1,1/2) 0 1
Для определения терма достаточно рассмотреть только состоя-
ния с неотрицательными значениями квантовых чисел mg и mso,
которые приведены в табл. 16.4.
В рассматриваемом случае системы двух р-электронов из дан-
ных табл. 16.4 следует, что максимальному значению квантового
числа то = 2 соответствует квантовое число mso — 0. Это озна-
чает, что для данной системы сущетвует терм 1Р, который вклю-
чает в себя по одному из состояний mo = 1, mso — 0 и то = 0,
mso — 0 табл. 16.4.
Четыре состояния, отвечающие значениям mo = 1, mso = 1;
то = 1, mso = 0; то = 0, mso = 0 и то = 0, mso = 1, со-
ответствуют значениям квантовых чисел Iq = 1 и so = 1, кото-
рые определяют суммарные орбитальный и спиновый моменты,
согласно (16.2) и (16.5). Следовательно, эти состояния принадле-
жат терму 3Р.
Наконец, последнее оставшееся из восьми состояний табл. 16.4
с то = 0 и mso = 0 отвечает терму 15.
Заметим, что среди состояний, перечисленных в табл. 16.4,
присутствуют состояния с одинаковыми парами квантовых чисел
mg и mso- В частности, в состояниях 4, 5, 6 квантовые числа
то = 0 и mso = 0. Если теперь составить линейную комбинацию
волновых функций, то для этих состояний также будет то = 0 и
mso = 0. При этом одна линейная комбинация соответствует кван-
товым числам Zq = 2 и so = 0, т. е. терму другая — квантовым
числам Iq = 1 и so = 1 (терму 3Р), а третья — числам Iq = 0 и
So = 0 (терму 1S). Аналогично, из двух состояний 2 и 3 с кван-
товыми числами mg = 1 и mso = 0 можно составить линейную
338 Лекция 16. Атомные термы
комбинацию волновых функций, соответствующую квантовым чи-
слам Zq = 2, So = О И Zq = 1, Sq — 1.
Результаты, полученные для системы двух р-электронов, при-
менимы к атому углерода в основном состоянии, которое задано
электронной конфигурацией ls22s22p2. Дело в том, что две за-
полненные s-оболочки дают нулевой вклад в суммарные моменты
атома углерода в данной электронной конфигурации. Следова-
тельно, в основном состоянии атома углерода при электронной
конфигурации ls22s22p2 возможно существование трех различных
атомных термов: rD (so = 0, Zo = 2), 3F (so = 1, Zq = 1) и rS
(so = 0, Zo = 0).
16.3. Терм основного состояния атома.
Правило Хунда
При расчете энергий одноэлектронных состояний в первом при-
ближении полагалось, что все самосогласованные поля, в каждом
из которых движется отдельный электрон, обладают центральной
симметрией. Учет нецентральной части у самосогласованного поля
и решение уравнения Шредингера методом Хартри-Фока приво-
дит к тому, что энергия стационарного состояния атома стано-
вится зависящей не только от электронной конфигурации, но и от
модулей суммарного орбитального момента импульса La и спина
Sa атома. Следовательно, при фиксированной электронной конфи-
гурации различные термы имеют несовпадающие значения энер-
гии. На рис. 16.2 приведены результаты расчета энергий атомных
термов электронной конфигурации ls22s22p2 атома углерода.
Квантомеханические расчеты показывают, что в большинстве
случаев энергии различных атомных термов в рамках определен-
ной электронной конфигурации различаются на величину порядка
Рис. 16.2. Энергетическая схема низших термов атома углерода
электронвольта (см. рис. 16.2). Следовательно, разность энер-
гий термов определенной электронной конфигурации несколько
меньше, чем различие энергий конфигураций. Однако расстояние
между энергетическими уровнями термов для данной конфигура-
ции имеет тот же порядок, что и расстояние между энергетиче-
скими уровнями различных электронных конфигураций.
16.4. Полный момент импульса многоэлектронного атома 339
Для исследования оптических спектров атомов и решения мно-
гих других задач атомной физики важно знать атомный терм с
низшей энергией, т.е. терм основного состояния атома. В 1927 г.
Ф. Хунд (1896-1997) сформулировал эмпирические правила реше-
ния поставленной задачи, которые впоследствии были подтвер-
ждены квантовой теорией.
Из всех термов заданной электронной конфигурации самой
низшей энергией обладает атомный терм с:
1) максимальным значением суммарного спина Sa = Smax;
2) максимальным значением суммарного орбитального момен-
та La при спине Sa = S'max-
Иначе говоря, сначала среди всех возможных атомных тер-
мов данной электронной конфигурации необходимо отыскать терм
с максимальным значением спина атома Sa = S'max- Если та-
ких термов больше одного, то среди них наименьшей энергией
обладает терм с максимальным значением суммарного орбиталь-
ного момента La- В приведенном выше примере основное состоя-
ние атома углерода описывается термом 3Р с квантовым числом
<§0 = 1-
К сожалению, правило Хунда не позволяет находить последо-
вательность термов в порядке возрастания их энергии, т. е. это
правило не пригодно для анализа термов возбужденных состоя-
ний. Энергии термов вычисляются методами квантовой механики
и уточняются с помощью спектрометрических измерений.
16.4. Полный момент импульса многоэлектронного атома
Прецизионные спектроскопические исследования показали, что
спектры излучения многоэлектронных атомов обладают характер-
ной тонкой структурой. При увеличении разрешающей способ-
ности спектрометров выяснилось, что большинство спектральных
линий состоит из нескольких компонент, немного различающихся
по значениям длин волн. В оптических спектрах наблюдаются
дублеты, триплеты и более высокие мультиплеты, хотя некоторые
спектральные линии являются синглетами, т. е. не демонстрируют
тонкой структуры.
В лекции 13 было установлено, что природа возникновения
тонкой структуры атома водорода обусловлена релятивистскими
добавками к гамильтониану атома. В той же лекции показано, что
поправка к энергии стационарных состояний (т. е. энергия тонкой
структуры) зависит от квантового числа у, которое определяет ве-
личину полного механического момента импульса электрона.
Аналогично, энергия тонкой структуры многоэлектронных ато-
мов связана с величиной полного момента импульса всей электрон-
ной системы атома СЦ. Эта физическая величина представляет со-
бой сумму орбитальных моментов и спинов всех электронов атома.
340
Лекция 16. Атомные термы
Следует иметь в виду, что полный момент импульса атома со-
стоит из суммарного момента импульса всех электронов Лд и мо-
мента импульса (спина) атомного ядра, который обсуждается в
дополнении 21.2. В последующих лекциях рассматриваются эф-
фекты, в которых спин ядра не участвует (за исключением допол-
нения 21.2). Величина Лд далее называется полным электрон-
ным моментом импульса атома.
В стационарных состояниях многоэлектронного атома полный
электронный момент импульса обладает определенным квадратом
модуля, который квантуется по следующему закону:
Ji = ^oOo + l), (16.10)
где jo — квантовое число, аналогичное квантовому числу у, опре-
деляющему квадрат модуля полного механического момента им-
пульса электрона формулой (12.21).
Квантовое число у’о, а следовательно, и модуль полного элек-
тронного момента импульса атома Лд может определяться двояко.
Во-первых, величину Лд можно получить, складывая по пра-
вилу сложения квантовых моментов модуль суммарного орбиталь-
ного момента импульса атома Ьд и модуль спина атома вд
(точнее, модуль суммарного спина всех электронов атома, о чем
упоминалось в § 16.1) . Этот способ получил название связи Рас-
села-Саундерса или, короче, LS'-связи.
При этом квантовое число jo выражается с помощью квантовых
чисел суммарного спина so и суммарного орбитального момента Iq
по правилу суммирования, аналогичному правилу (16.3), и может
принимать следующий ряд значений:
jo = Zo + lo + «50 ~ 1> • • •> Ro ~ «so|• (16.11)
Физический смысл квантовых чисел Iq и so определяется соотно-
шениями (16.2) и (16.5).
В квантовой теории доказано, что IDS'-связь осуществляет-
ся, когда энергия спин-орбитального взаимодействия значительно
меньше разности энергий соседних энергетических уровней, вы-
численных без учета спин-орбитального взаимодействия. Иначе
говоря, спин-орбита л ьное взаимодействие дает малые поправки
к энергии стационарного состояния атома. В таких физических
ситуациях стационарные состояния атомов характеризуются опре-
деленными величинами модулей моментов импульса Ьд и Зд.
Экспериментальные исследования показывают, что в атомах с
небольшим порядковым номером Z реализуется IDS'-связь. С уве-
личением химического номера Z атома влияние спин-орбитально-
го взаимодействия усиливается, и приближение связи Рассела-Са-
ундерса становится неприемлемым.
16.4. Полный момент импульса многоэлектронного атома 341
Во-вторых, модуль полного электронного момента импульса
атома Ja можно, в принципе, получить из полных моментов им-
пульса отдельных электронов по методике, изложенной в § 16.1 для
суммарного орбитального момента импульса. Для одноэлектрон-
ных состояний полный электронный момент импульса квантуется
по правилу (12.21), приведенному в §12.4 лекции 12. Электрон
в одноэлектронном состоянии обладает определенными модулем
полного момента импульса и одной из проекций на некоторое на-
правление Z в пространстве. Правила квантования и возможные
значения квантовых чисел выражаются соотношениями (12.21),
(12.22) и (12.24), (12.25). Методика сложения моментов, изло-
женная в §16.1 и 16.2 данной лекции, позволяет вычислить мо-
дуль полного электронного момента импульса атома Jд с помощью
квантовых чисел j и mj отдельных электронов. Данный способ
суммирования моментов называется jj-связью.
Можно вычислить, что при данной электронной конфигурации
количество стационарных состояний атома с определенным значе-
нием модуля суммарного полного электронного момента импульса
Ja одинаково как в случае 77-связи> так и в случае IDS'-связи.
Согласно квантовой теории, уу-связь возможна, когда энергия
спин-орбита л ьного взаимодействия существенно превышает раз-
ности энергий атомных термов в рамках определенной электрон-
ной конфигурации. Иначе говоря, физическая картина противопо-
ложна той, в которой осуществлялась LS'-связь, описанная выше.
В чистом виде jj-связь в атомах не встречается.
В третьих, возможны различные смешанные способы сложе-
ния моментов импульса, которым соответствуют различные сме-
шанные типы связи.
Тяжелые атомы (с большим порядковым номером Z) описы-
ваются смешанными типами связи. В частности, разновидность
смешанного типа связи наблюдается в сильно возбужденных состо-
яниях атомов, состоящих из электрона в высокоэнергетическом
одноэлектронном состоянии и положительно заряженного атом-
ного остатка. В таких системах атомный остаток характеризуется
определенными величинами модулей орбитального момента L и
спина S. Полный электронный момент атомного остатка описы-
вается связью Рассела-Саундерса. Но полный момент всего атома
определяется jj -связью полных электронных моментов атомного
остатка и возбужденного электрона. Это объясняется ослабленным
кулоновским взаимодействием электрона с атомным остатком, так
как с ростом энергии одноэлектронного состояния увеличивается
среднее расстояние электрона от центра атома.
Характерные особенности различных типов связи целесооб-
разно рассмотреть на примере системы, состоящей из двух элек-
тронов. Для определенности положим, что один электрон при-
надлежит р-оболочке, а другой — d-оболочке. Это означает, что
342
Лекция 16. Атомные термы
электронные состояния описываются следующими квантовыми
числами: = 1, Si = 1/2, I2 = 2, s% = 1/2.
Если в данной двухэлектронной системе реализуется IDS'-связь,
то, используя правила сложения моментов (16.3), легко получить
всевозможные значения квантовых чисел суммарного орбиталь-
ного момента: Zq = 1; 2; 3 и суммарного спина: so = 0; 1. Кван-
товые числа Iq и sq позволяют по правилу (16.11) вычислить все
значения квантового числа Jo? характеризующего полный элек-
тронный момент импульса атома (16.10). В результате получа-
ются 12 стационарных состояний, каждое из которых обладает
определенными тремя суммарными моментами импульса: орби-
тальным, спиновым и полным электронным. Каждое из этих со-
стояний характеризуется тремя квантовыми числами: Zq, «so и Jo>
значения которых приведены в табл. 16.5.
Таблица 16.5. Квантовые числа Zo? so и jo стационарных состояний
двухэлектронной системы в случае LS'-связи при орбитальных
квантовых числах электронов /1 = 1 и I? = 2
№ 1 2 3 4 5 6 7 8 9 10 11 12
/о 1 1 1 1 2 2 2 2 3 3 3 3
«0 0 1 1 1 0 1 1 1 0 1 1 1
JO 1 0 1 2 2 1 2 3 3 2 3 4
Таким образом, в рассматриваемом примере квантовое число
jo может принимать 5 различных значений: jo = 0, 1, 2, 3, 4. По
табл. 16.5 видно, что определенному значению полного электрон-
ного момента импульса атома Ja соответствуют, вообще говоря,
несколько стационарных состояний, различающихся суммарным
орбитальным моментом La и суммарным спином Sa-
Теперь предположим, что в данной двухэлектронной системе
реализована jj-связь. Тогда сначала следует определить возмож-
ные значения квантовых чисел, характеризующих полные элек-
тронные моменты импульса обоих электронов. Используя пра-
вило сложения, аналогичное (16.3), получим, что у р-электрона
квантовое число может принимать значения ji = 1/2 или 3/2, а у
d-электрона соответственно j2 = 3/2 или 5/2. В случае jj-свя-
зи стационарные состояния двухэлектронной системы описыва-
ются квантовыми числами отдельных электронов j\ и j‘2, а также
квантовом числом jo полного электронного момента атома (16.10).
Складывая квантовые числа j\ и j2 по общему правилу сложения
моментов (т.е. правилу, аналогичному (16.3) и (16.11)), мы полу-
чим 12 стационарных состояний, различающихся наборами кван-
товых чисел ji, j2 и jo, которые сведены в табл. 16.6.
16.4. Полный момент импульса многоэлектронного атома 343
Таблица 16.6. Квантовые числа ji, J2 и jo стационарных состояний
двухэлектронной системы в случае jj-связи при орбитальных
квантовых числах электронов li = 1 и I2 = 2
№ 1 2 3 4 5 6 7 8 9 10 11 12
ji 1/2 1/2 3/2 3/2 3/2 3/2 1/2 1/2 3/2 3/2 3/2 3/2
h 3/2 3/2 3/2 3/2 3/2 3/2 5/2 5/2 5/2 5/2 5/2 5/2
jo 1 2 0 1 2 3 2 3 1 2 3 4
Нетрудно заметить, что при j’J-связи квантовое число полного
электронного момента атома принимает те же значения: jo =
= 0, 1, 2, 3, 4, как и в случае связи Рассела-Саундерса. При этом
количество нулей, единиц и т. д. одинаково. В квантовой механике
приведенный выше пример обобщается до следующего утвержде-
ния: при заданных орбитальных квантовых числах отдельных
электронов модуль полного электронного момента импульса атома
Ja имеет определенный набор возможных значений, независимо
от типа связи.
Далее в данной лекции рассматриваются многоэлектронные
атомы, в которых осуществляется IDS'-связь. Выражения (16.10) и
(16.11) означают, что при определенных значениях модулей сум-
марных моментов атома La и Sa модуль полного электронного
момента импульса атома Ja может иметь только конечное коли-
чество различных значений. Это существенно для анализа тон-
кой структуры спектров излучения атомов, так как энергия спин-
орбитального взаимодействия зависит от величины полного элек-
тронного момента атома точнее, выражается через квантовое
число jo- Следовательно, при учете спин-орбитального взаимодей-
ствия для определенной электронной конфигурации энергии стаци-
онарных состояний атома зависят не от двух, а от трех квантовых
чисел: Zo, $0, Jo-
Необходимо уточнить понятие атомного терма в случаях, когда
нельзя пренебрегать релятивистскими эффектами (в том числе и
спин-орбитальным взаимодействием). Для этого целесообразно к
понятию терма дополнительно присовокупить величину полного
электронного момента импульса Ja- Таким образом, далее под
определенным атомным термом понимается множество стационар-
ных состояний атома, которые характеризуются фиксированными
величинами суммарных моментов импульсов La, Sa и Ja-
Соответственно в обозначение терма вводится правый нижний
индекс, который представляет собой квантовое число jo-
Двенадцать термов, приведенных в табл. 16.5, запишутся в
виде следующих символов: 1Pi, 3Ро, 3Р1, 3Р2, 3Рь 3Т>2, 3Дь
^3, 3F2, 3F3, Зг4.
344
Лекция 16. Атомные термы
Выше в данной лекции рассматривались атомные термы основ-
ной электронной конфигурации ls22s22p2 атома углерода. Низ-
ший (основной) терм 3Р (с квантовыми числами so = 1, Zq = 1)
при учете спин-орбитального взаимодействия, согласно правилу
(16.11), расщепляется на три с квантовыми числами jo = 2, 1, 0.
Эти стационарные состояния атома записываются в виде 3Р2> 3А>
3Р0, ПРИ этом иногда говорится, что атомный терм 3Р предста-
вляет собой триплет.
Терм iD характеризуется квантовыми числами so — 0, Zo — 2
и может иметь единственное значение квантового числа Jo — 2.
Следовательно, терм lD не расщепляется из-за спин-орбитального
взаимодействия и записывается в виде 11?2- Аналогично, не рас-
щепляется третий терм электронной конфигурации ls22s22p2, за-
данный квантовыми числами so = 0, Zq = 0, Jo = 0 и обозначае-
мый символом т50.
Обобщая рассмотренный пример, далее будем называть син-
глетами атомные термы, которые не расщепляются при учете
энергии тонкой структуры. Термы с нулевым суммарным спином
(so = 0) представляют собой синглеты, например, для электронной
конфигурации ls22s22p2 таковыми являются термы 11?2 и 1S'o-
Влияние спин-орбитального взаимодействия и других реляти-
вистских эффектов заключается в том, что уровень энергии атом-
ного терма расщепляется на несколько подуровней по числу воз-
можных значений числа Jo- Величина этого расщепления, которое
часто называется спин-орбитальным, мала по сравнению с разли-
чием энергии атомных термов с неодинаковыми значениями кван-
товых чисел Zq и so-
Для анализа тонкой структуры спектральных линий необхо-
димо расставить спин-орбитальные подуровни по шкале энергий.
Пример расщепления уровня энергии атомного терма вследствие
спин-орбитального взаимодействия приведен на рис. 16.3.
Е
АЕ2
Зр
Л£1 : Зр
Рис. 16.3. Энергетическая схема расщепле-
ния терма 3Р в конфигурации ls22s22p2
атома углерода при учете энергии тонкой
структуры: ДВ1 = 2 • 10-3 эВ, Д2?2 =
= 5,4 • 10"3 эВ
Расчет энергий атомных термов с учетом тонкой структуры (в
частности, спин-орбитального взаимодействия) является сложной
задачей квантовой механики. Однако для нахождения терма с
16.4. Полный момент импульса, многоэлектронного атома 345
минимальной энергией при заданной электронной конфигурации
можно воспользоваться дополнительным правилом Хунда.
Если электронная оболочка заполнена меньше чем наполо-
вину, то квантовое число jo терма с низшей энергией равно
jo — Ro~«so|- Если же оболочка заполнена больше чем наполови-
ну, то терм с минимальной энергией характеризуется числом
jo = Ro + «5о|-
Определим квантовое число jo терма с низшей энергией, если
электронная оболочка с определенным орбитальным квантовым
числом I заполнена точно наполовину. Прежде всего по правилу
Хунда, приведенного в предыдущей лекции, суммарный спин дол-
жен быть максимальным, что достигается при одинаковой ори-
ентации спинов всех электронов данной оболочки. Иначе говоря,
проекции всех спинов электронов этой оболочки должны иметь
одинаковые проекции, равные Л/2. Как следствие, согласно прин-
ципу Паули, проекции орбитальных моментов этих электронов
должны быть различными, а магнитные числа электронов выну-
ждены принимать всевозможные значения т = —I, —I + 1, ..., I.
В результате суммарный орбитальный момент электронной обо-
лочки становится равным нулю. Таким образом, у терма с мини-
мальной энергией в этих случаях квантовое число Iq = 0. Тогда,
согласно правилу сложения, квантовое число jo становится равным
квантовому числу so- Иначе говоря, суммарный полный момент
совпадает со спином атома.
В основном состоянии атома углерода (электронной конфи-
гурации ls22s22p2) оболочка 2р заполнена меньше чем наполо-
вину. Следовательно, согласно вышеприведенному правилу, наи-
меньшую энергию имеет атомный терм 3Ро (см. рис. 16.3).
Задачи к лекции 16
1. Записать термы возбужденных состояний атома водорода с глав-
ными квантовыми числами: а) п = 2, б) п = 3, в) п = 4.
2. Найти все термы основной электронной конфигурация атомов:
а) азота, б) кислорода, в) фтора. Определить термы основных состоя-
ний.
3. Найти термы основных состояний атомов третьего периода таб-
лицы Менделеева (от натрия до аргона).
4. Найти термы основных состояний атомов: а) ванадия, б) железа,
в) никеля.
5. Найти термы основных состояний атомов: а) циркония, б) гаф-
ния, в) вольфрама.
6. Найти термы основных состояний атомов редкоземельных эле-
ментов: а) лантана, б) церия, в) самария.
7. Найти количество различных значений модуля суммарного пол-
ного момента импульса атома в случае LS-связи. Квантовые числа сум-
346
Лекция 16. Атомные термы
мерного орбитального момента и суммарного спина атома равны: а) /о =
— 1, so — 1; б) Iq — 2, So — 1/2; в) Iq — 2, so — 3/2.
8. Перечислить все проекции суммарного полного момента импульса
атома при следующих значениях квантового числа jo, определяющего
модуля суммарного полного момента импульса атома: а) у‘о =3/2; б) jo =
= 5/2; в) уо = 2; г) у0 = 7/2.
9. Пользуясь правилом Хунда, вычислить квантовые числа /о тер-
мов основных состояний атомов второго периода таблицы Менделеева
(от лития до неона).
10. Пользуясь правилом Хунда, вычислить квантовые числа у’о тер-
мов основных состояний атомов третьего периода таблицы Менделеева
(от натрия до аргона).
Лекция 17
ОПТИЧЕСКИЕ СПЕКТРЫ
МНОГОЭЛЕКТРОННЫХ АТОМОВ
17.1. Радиационные переходы в многоэлектронных атомах
Экспериментальные исследования показывают, что спектры
излучения и поглощения многоэлектронных атомов являются дис-
кретными и содержат множество спектральных линий в видимом,
ультрафиолетовом и инфракрасном диапазонах.
Дискретный характер спектров многоэлектронных атомов ус-
пешно объясняется в приближении атомных термов. Точнее гово-
ря, можно полагать, что наблюдаемые спектральные линии форми-
руются при радиационных переходах между различными термами
многоэлектронного атома.
Спектроскопические исследования показывают, что между про-
извольно выбранной парой термов с различной энергией радиа-
ционный переход может не происходить. Ограничения обусло-
влены различными законами сохранения, которым подчиняется
квантовая система «атом+фотон». Необходимые условия возмож-
ности радиационного перехода между различными атомными тер-
мами были сначала выражены эмпирическими правилами, полу-
ченными в атомной спектроскопии на основе анализа оптических
спектров, а затем строго выведены методами квантовой электро-
динамики.
Для формулировки этих условий, называемых правилами от-
бора, прежде всего следует принять во внимание, что фотон обла-
дает моментом импульса, квадрат модуля которого квантуется по
общему правилу квантовомеханического момента
4 = W + 1), (17.1)
где квантовое число jf может принимать целые значения 1, 2, ...
Правило сложения квантовых моментов импульса, выражаю-
щее закон сохранения момента импульса квантовой системы
«атом+фотон» может быть выражен в виде правила сложения, ана-
348 Лекция 17. Оптические спектры многоэлектронных атомов
логичного (16.3):
702 = Joi + Joi + 3 - 1, • • I Joi + (17.2)
где joi и jo2 — квантовые числа jo, определяющие квадрат модуля
полного электронного момента импульса многоэлектронного атома
в начальном и конечном состоянии соответственно.
Наиболее вероятными являются процессы излучения с испус-
канием дипольных фотонов, которые обладают квантовым числом
/ = 1. Отсюда следует правило отбора по квантовому числу jo:
Ajo = ±1, 0. (17.3)
Кроме того, радиационные переходы из состояний с joi — 0 в
состояния с jo2 = 0 являются запрещенными.
Заметим, что правило (17.3) сформулировано для дипольных
фотонов. При излучении квадрупольных фотонов, которые обла-
дают квантовым числом / = 2, величина Ajo может равняться
±2. Однако вероятность испускания квадрупольного фотона воз-
бужденным атомом примерно на 5-6 порядков меньше вероятно-
сти испускания дипольного фотона. По этой причине радиацион-
ные переходы с изменением квантового числа Ajo = ±2 форми-
руют спектральные линии с очень малой интенсивностью, которые
трудно наблюдать в экспериментах.
Взаимодействие электромагнитной волны с атомом можно ус-
ловно разделить на две основные части: действие электрического
поля на заряды электронов и взаимодействие магнитного поля с
магнитными моментами электронов. Интенсивность второго вза-
имодействия на несколько порядков меньше первого. Как след-
ствие, для оптического диапазона электромагнитного излучения в
первом приближении суммарный спин многоэлектронного атома
не изменяется, что выражается следующим правилом отбора для
радиационных переходов:
Аз0 = 0. (17.4)
Если выполняется последнее соотношение, то изменение кванто-
вого числа суммарного орбитального момента импульса Iq опреде-
ляется изменением квантового числа jo. Таким образом, получа-
ется следующее правило отбора для наиболее вероятных радиаци-
онных переходов многоэлектронного атома:
AZ0 = ±1, 0. (17.5)
Подавляющее большинство процессов излучения и поглоще-
ния многоэлектронными атомами (исключениями могут быть про-
цессы взаимодействия атомов с мощными потоками лазерного
излучения) может быть рассмотрено в одноэлектронном прибли-
жении. Это означает, что при испускании или поглощении фо-
17.1. Радиационные переходы в многоэлектронных атомах 349
тона изменяется стационарное состояние только одного электрона
атома.
При формулировке правил отбора для радиационных перехо-
дов в многоэлектронном атоме целесообразно сначала ввести по-
нятие четности как одноэлектронных, так и фотонных состоя-
ний.
Волновая функция электрона (а также любой массивной час-
тицы) называется четной, если она не изменяется при смене знака
всех трех координат частицы. Нечетной называется волновая
функция, которая при замене г на —г изменяет только свой знак.
Четные функции обозначаются индексом #, нечетные — индексом
и. Количественно величина четности для таких волновых функ-
ций определяется числами 1 и —1 соответственно.
Четность фотона может быть определена по его круговой по-
ляризации (см. приложение 4.3). Состояние с правой круговой
поляризацией полагается четным, а состояние с левой круговой
поляризацией нечетным. Числовое значение четности обоих со-
стояний определяется равным 1 и —1 соответственно.
Для описания процессов излучения используется классифика-
ция состояний фотонов по четности и величине момента импульса.
Фотон в состоянии с квантовым числом j1 и четностью (—I)7 на-
зывается электрическим 27 -польным, в состоянии с j и четностью
(—I)7 +1 — магнитным 27 -польным. В частности, нечетное состо-
яние с / = 1 определяет электрический дипольный фотон, четное
состояние с / = 1 — магнитный дипольный фотон, четное состо-
яние с j1 = 2 — электрический квадрупольный фотон и т. д.
В 1924 г. О. Лапорт (1902-1971), анализируя спектры излуче-
ния многоэлектронных атомов, сформулировал эмпирическое пра-
вило, которое явилось выражением закона сохранения четности
квантовой системы. В современной терминологии это правило мо-
жет быть выражено в следующих утверждениях. Радиационные
дипольные переходы возможны между состояниями с различной
четностью и запрещены между состояниями с одинаковой четно-
стью. Напротив, радиационные квадрупольные переходы разре-
шены между состояниями с одинаковой четностью и запрещены
между состояниями с различной четностью.
Таким образом, наиболее интенсивные спектральные линии
дают переходы между состояниями с различной четностью.
Если многоэлектронный атом во внешней оболочке имеет один
электрон, то, согласно правилу Лапорта, наиболее интенсивные
спектральные линии формируются радиационными переходами,
которые подчиняются следующему правилу отбора для орбиталь-
ного квантового числа Z, характеризующего одноэлектронное ста-
ционарное состояние
(17-6)
AZ = ±1.
350 Лекция 17. Оптические спектры многоэлектронных атомов
В оптических спектрах иногда наблюдаются очень слабые спек-
тральные линии, образованные радиационными переходами с
изменением орбитального квантового числа AZ = ±2. Согласно
вышеизложенному, такие процессы отвечают испусканию квадру-
польных фотонов и характеризуются очень малой вероятностью.
17.2. Формирование спектров излучения
атомов щелочных металлов
Сравнительно простой структурой обладают спектры излуче-
ния атомов щелочных металлов. Такие атомы в основном состоя-
нии, как было показано в лекции 15, имеют несколько полностью
заполненных оболочек и единственный s-электрон в верхнем элек-
тронном слое. Этот внешний электрон, переходя в возбужденные
состояния, обусловливает возникновение оптического спектра из-
лучения атома. В результате все радиационные переходы реали-
зуются между стационарными состояниями, которые характеризу-
ются различными электронными конфигурациями. Иначе говоря,
оптические спектры щелочных металлов успешно интерпретиру-
ются в приближении конфигураций. Кроме того, в этом случае
электронные конфигурации полностью задаются квантовыми чи-
слами п и I внешнего электрона. Таким образом, радиационный
переход может быть задан в виде (n'Z') —> (nZ), где штрихами
обозначены квантовые числа исходного стационарного состояния
внешнего электрона. Орбитальное квантовое число обозначается
латинской буквой, согласно табл. 9.1.
Правила отбора по орбитальному числу (17.6) приводят к раз-
биению спектра излучения атомов щелочных металлов на следую-
щие спектральные серии.
Главная серия образуется переходами в основное состояние
атома из возбужденных p-состояний. В общем виде такие пере-
ходы записываются так: (п'р) —> (ns), где п' п.
Резкая (вторая побочная) серия образуется переходами типа
(n's) —> (пр), где п' > п.
Диффузная (первая побочная) серия формируется переходами
вида (n'cZ) —> (пр), где п' > п.
Фундаментальная серия возникает при радиационных перехо-
дах типа (п'/) —> (nd), где п' > п.
В качестве типичного примера на рис. 17.1 приведена энер-
гетическая схема низших возбужденных термов атома лития и
возможных радиационных переходов между ними.
Энергия электронных конфигураций по определению зависит
от квантовых чисел п и Z, следовательно, энергия возбужденных
стационарных состояний атомов щелочных металлов определяется
только двумя квантовыми числами п и Z внешнего электрона. Ана-
лиз спектров излучения щелочных металлов позволил получить
17.2. Формирование спектров излучения атомов 351
простое приближенное выражение для энергий этих состояний:
Enl = (17-7)
(п — 0)z
где Ry — энергия Ридберга, 5 — параметр, зависящий в первом
приближении от орбитального квантового числа I.
Рис. 17.1. Энергетическая схема низших термов атома лития и спектральных
линий излучения.
Горизонтальные черточки изображают энергии электронных оболочек. Наклонные ли-
нии — возможные радиационные переходы, числа — длины волн (А). Главная серия:
переходы пр —> 2s (п 2), резкая серия: ns —> 2р (п > 2), диффузная серия: nd —> 2р
(п > 2), фундаментальная серия: nf —> 3d (п > 3). Переход 2р —> 2s дает характерную
красную линию излучения лития
Числовые значения, полученные обработкой результатов спек-
тральных измерений, сведены в табл. 17.1.
352 Лекция 17. Оптические спектры многоэлектронных атомов
Таблица 17.1. Параметр 8 для расчета энергий стационарных
состояний атомов щелочных металлов
Элемент 1 = 0 1 = 1 1 = 2 I = 3
Li 0,412 0,041 0,002 0,000
Na 1,373 0,883 0,010 0,001
К 2,230 1,776 0,146 0,007
Rb 3,195 2,711 1,233 0,012
Cs 4,131 3,649 2,448 0,022
Выражение энергии стационарного состояния (17.7) является
приближенным, так как более тщательный анализ показывает, что
параметр 8 зависит не только от орбитального Z, но и от главного
квантового числа п стационарного состояния внешнего электрона
атома щелочного металла. В табл. 17.1 приведены числовые зна-
чения параметра 5, соответствующие наименьшему возможному
главному квантовому числу, т. е. п = 2 для атома лития, п = 3
для атома натрия и т. д.
В качестве примера в табл. 17.2 приведена зависимость вели-
чины поправки 8 в формуле (17.7) от главного квантового числа
для S'-термов атома натрия (т.е. для стационарных состояний
внешнего электрона с орбитальным квантовым числом 1 = 0}.
Таблица 17.2. Параметр 8 для расчета энергий S'-термов атома натрия
Главное квантовое число п = 3 п = 4 п = 5 п = 6 п = 7 п = 8
Параметр 6 1,373 1,357 1,352 1,351 1,350 1,350
Видно, что при возрастании главного квантового числа п по-
правка 8 сначала несколько убывает, а затем становиться практи-
чески постоянной. Аналогичная зависимость наблюдается и для
атомов остальных щелочных металлов.
17.3. Тонкая структура оптических спектров
атомов щелочных металлов
Расщепление уровней энергии атомных термов на подуровни,
вследствие учета релятивистских поправок к гамильтониану ато-
ма, приводит к возникновению тонкой структуры оптических
спектров многоэлектронных атомов.
Величина 2sq + 1 называется мультиплетно стъю терма. При
выполнении неравенства Iq sq мультиплетность равна числу
17.3. Тонкая структура оптических спектров 353
подуровней тонкой структуры энергии атома. Можно непосред-
ственно убедиться, что из правила сложения моментов (16.11) сле-
дует, что, при Zq «5о количество различных значений квантового
числа jo равно 2so + 1-
Если выполняется обратное неравенство so Zo, то количество
подуровней тонкой структуры равно 2Zq 4-1, что также следует из
правила сложения моментов (16.11).
Сравнение рис. 16.2 и 16.3 показывает, что разность энергий
между энергетическими подуровнями тонкой структуры при фик-
сированных квантовых числах Zq и so значительно меньше, чем
между энергиями термов с различными числами Zq и sq (т.е. в
случае пренебрежения релятивистскими эффектами). Однако с ро-
стом порядкового номера атома разность энергий между подуров-
нями тонкой структуры постепенно возрастает. Следовательно,
тонкую структуру спектров излучения легче наблюдать у тяжелых
многоэлектронных атомов.
Общим свойством является уменьшение разности энергий ме-
жду подуровнями тонкой структуры с ростом главного квантового
числа стационарного состояния. Это означает, что тонкая струк-
тура спектральных линий более четко проявляется при переходах
между низкоэнергетическими термами, т. е. с относительно малым
главным квантовым числом.
Характер тонкого расщепления спектральных линий определя-
ется правилами отбора, которые приведены выше в § 17.1.
Вычисление длин волн компонент тонкой структуры оптиче-
ских спектров может, в принципе, проводиться с помощью уравне-
ния, выражающего закон сохранения энергии (иначе говоря, вто-
рого постулата Бора):
=Еп2-Еп1, (17.8)
где ЕП2 и Eni — энергии стационарных состояний, между ко-
торыми произошел радиационный переход. При расчете тонкой
структуры в выражениях для энергии стационарных состояний
атома необходимо учитывать релятивистские члены (в том числе,
обусловленные спин-орбитальным взаимодействием). В случае во-
дородоподобных атомов величина энергии стационарного состоя-
ния выражается формулой (Д.13.1) приложения 13.1 к лекции 13.
В этой физической системе квантовые числа пи j состояний пол-
ностью определяют длины волн радиационных мультиплетов. Для
многоэлектронных атомов расчет энергии стационарных состоя-
ний, как уже неоднократно упоминалось, является очень сложной
задачей.
Наименее трудный частный случай представляет собой расчет
тонкой структуры спектров атомов щелочных металлов.
354 Лекция 17. Оптические спектры многоэлектронных атомов
Основной (бальмеровский) член энергии выше был записан в
виде (17.7), а числовые значения поправок 8i приведены в табл. 17.1
и 17.2. Дополнительное слагаемое — энергия тонкой структуры —
выражается в виде аналогичном водородоподобному (Д.13.1), но
атомный номер Z заменяется на эффективный атомный номер
Z*, который меньше Z на определенную константу с, т.е.
Z* = Z - с.
(17-9)
Таким образом, релятивистская поправка к основному члену
энергии стационарного состояния атома щелочного металла (17.7)
представляется следующим выражением:
'с.о.
р = ( '______-П
с’0’ n3 \jo4-l/2 4п)
(17.10)
Величину поправки с к атомному номеру в формулах (17.9) и
(17.10) приходится рассчитывать, используя как эксперименталь-
ные данные, так и приближенные методы квантовой механики.
Проведем качественный анализ тонкой структуры спектраль-
ных линий главной серии. Переходы, генерирующие эту серию
(п'р) —> (ns), где п' п, при учете спин-орбитального взаимо-
действия превратятся в дублеты, аналогично серии Лаймана для
п'Рз/2
п'Р\п
nsm
n's\!2
ПРЗ!2
ПР\!2
ПРЗГ2
в
n'd5/2
«4/2
ПР\!2
Рис. 17.2. Энергетические схемы спин-орбитального расщепления спектральных
линий излучения атомов щелочных металлов:
а) линия главной серии п' п, 5) линия резкой серии п' > п, в) линия диффузной
серии п' п
атома водорода. Исходные p-состояния расщепляются на два (с
квантовыми числами j = 1/2 и j = 3/2), а конечные s-состояния
не расщепляются (см. лекцию 13, §13.4).
Каждая спектральная линия главной серии превращается в две
с близкими длинами волн (см. рис. 17.2а). Нетрудно подсчитать,
17.3. Тонкая структура оптических спектров 355
что энергии фотонов этих дублетов различаются на величину
у*4
Ае = «2Яу^з- (17.И)
Отдельные линии главной серии характеризуются главным
квантовым числом nf верхнего энергетического уровня (см.
рис. 17.2а). Согласно выражению (17.11), с ростом квантового
числа п' различие энергий фотонов дублета уменьшается. Иначе
говоря, спектральные линии главной серии определенного щелоч-
ного металла представляют собой сужающиеся дублеты.
Величина разности энергий (17.11) пропорциональна квадрату
постоянной тонкой структуры, которая является весьма малой ве-
личиной (а2 « 5-10“5 1). С другой стороны, четвертая степень
эффективного атомного номера Z* приводит к сильному возраста-
нию тонкого расщепления дублетов главной серии с увеличением
химического номера Z щелочного металла.
Рассмотрим для примера первую линию главной серии атома
натрия (см. рис. 17.3).
Эта спектральная линия образуется при радиационном пере-
ходе атома натрия из возбужденного состояния с электронной
конфигурацией ls22s22p63p1 в основное состояние, имеющее кон-
фигурацию 1s22s22;j63s1. Можно этот процесс интерпретировать
как переход внешнего электрона между оболочками Зр и 3s. Спин-
орбитальное взаимодействие превращает эту яркую желтую линию
в дублет, обусловленный переходами Зр1у/2 Зз^ и %Рз/2
—> 35^2- Спектрометрическая аппаратура регистрирует две близ-
кие линии с длинами волн 5895,92 А и 5889,95 А. Таким образом,
тонкое расщепление этой линии составляет около 6 А. Следует упо-
мянуть, что этот дублет столь широко используется в физических
исследованиях, что получил собственное имя: D-дублет натрия.
На рис. 17.3 наблюдаются и другие дублеты линий главной се-
рии излучения атома натрия, а именно: дублеты второй (4р!/2 —>
—> 3si/2 и 4р3/2 —> 3«§!/2) и третьей (переходы 5pi/2 ^si/2 и
5рз/2 —> 3s|/2) спектральных линий этой серии.
Теперь рассмотрим тонкое расщепление первой линии главной
серии атома цезия, которая излучается при радиационном переходе
внешнего электрона атома из оболочки 6р в оболочку 6s. Вслед-
ствие спин-орбитального взаимодействия эта спектральная линия
превращается в дублет, компоненты которого образуются перехо-
дами 6рх/2 6Si/2 и 6рз/2 —> 6s!/2- Длины компонентов дублета
равны 8943,48 А и 8521,15 А (см. рис. 17.4), т. е. релятивистские
эффекты обусловливают расщепление более 422 А. Следовательно,
разность длин волн по сравнению с аналогичной величиной для
натрия увеличилась в 70 раз!
356 Лекция 17. Оптические спектры многоэлектронных атомов
Рис. 17.3. Энергетическая схема низших термов атома натрия и спектральных
линий излучения.
Цифры у энергетических уровней — главные квантовые числа стационарных состояний
внешнего электрона. Наклонные линии — возможные радиационные переходы, числа —
длины волн (А)
Второй дублет главной серии атома цезия (7р1/2 —> бз^,
7р%/2 6s!/2) также демонстрирует более сильное тонкое расщеп-
ление по сравнению с разностью длин волн компонент второго ду-
блета главной серии атома натрия (см. схемы на рис. 17.3 и 17.4).
Перейдем к анализу тонкой структуры спектральных линий
резкой серии атомов щелочных металлов. Переходы типа (n's —>
—> пр, где п1 > п), образующие эти линии, также являются дублет-
ными. Спин-орбитальное взаимодействие приводит к расщепле-
нию конечных p-состояний на два с квантовыми числами j = 1/2
и j = 3/2, при этом исходные s-состояния не расщепляются. Сле-
довательно, любая спектральная линия резкой серии является ду-
блетом (см. рис. 17.26).
17.3. Тонкая структура оптических спектров 357
Энергии фотонов компонент этого дублета вычисляются как
разности энергий электронных состояний, определяемых форму-
Е9 эВ
О
2о 2д 2р 2гч 2гч 2т?
И/2 *1/2 *3/2 U3/2 U5/2 Г 5/2,7/2
Рис. 17.4. Энергетическая схема низших термов атома цезия и спектральных
линий излучения.
Цифры у энергетических уровней — главные квантовые числа стационарных состояний
внешнего электрона. Наклонные линии — возможные радиационные переходы, числа —
длины волн (А)
лой (17.10). Можно вычислить, что различие энергий фотонов
(ширина дублета) равняется
<7*4
А£ = а2Яу^з, (17.12)
где п — главное квантовое число нижнего стационарного состо-
яния радиационного перехода, образующего спектральную линию
резкой серии. Таким образом, величина (17.12) не зависит от глав-
ного квантового числа верхнего состояния, следовательно, спек-
358 Лекция 17. Оптические спектры многоэлектронных атомов
тральные линии резкой серии определенного щелочного металла
представляют собой эквидистантные дублеты.
Сравним тонкое расщепление спектральных линий резкой се-
рии разных щелочных металлов. Дублет первой линии резкой
серии натрия возникает при переходах 4s1/2 %Рз/2 и ^si/2
—> Зрх/2 И имеет длины волн 11403,8 А и 11381,5 А. Разность
длин волн компонент равна 22,3 А. Для цезия соответствующие
переходы 7s1/2 —> 6р3/2 и 7si/2 —> 6р1у/2 и длины волн 14694,9 А и
13588,3 А дают ширину дублета 1106,6А, т.е. большую в 50 раз
по сравнению аналогичной величиной для натрия. Сравнение схем
на рис. 17.3 и 17.4 позволяет убедиться в значительном различии
величины тонкого расщепления и для второй спектральной линий
резкой серии атомов цезия и натрия.
Тонкая структура спектральных линий диффузной серии бо-
лее сложна. Согласно § 17.2, линии этой серии образуются при
радиационных переходах типа (n'd —> пр), где п' п. Спин-
орбитальное взаимодействие приводит к расщеплению энергети-
ческих уровней как p-состояний на два подуровня (с квантовыми
числами j = 1/2 и j = 3/2), так и d-состояний на два подуровня
(с квантовыми числами j = 3/2 и j = 5/2). Следовательно, тон-
кому расщеплению подвергаются как исходный, так и конечный
энергетический уровень (см. § 13.4 лекции 13). В результате спин-
орбитального взаимодействия спектральные линии диффузной се-
рии становятся триплетами (см. рис. 17.2в), так как радиаци-
онный переход с изменением квантового числа j на 2, согласно
правилам отбора, является «запрещенным», точнее весьма мало-
вероятным.
Расчеты по формуле (17.10) показывают, что энергии электрон-
ных d-состояний с одинаковым главным квантовым числом и раз-
личными числами j различаются очень мало. Как следствие, у
большинства монохроматоров (оптических спектрометров) недо-
статочно разрешающей способности для наблюдения отдельных
компонент триплетов спектральных линий диффузной серии. В та-
ких случаях линии диффузной серии наблюдаются размытыми,
что и явилось причиной названия данной серии.
На рис. 17.3 энергетические уровни термов 2Р3/2 и 2^5/2 атома
натрия не разрешены из-за малости релятивистских добавок, по-
этому наблюдается расщепление спектральных линий диффузной
серии только на две компоненты. Спин-орбитальное взаимодей-
ствие в атоме цезия более велико (по сравнению с атомом натрия),
поэтому на рис. 17.4 видно расщепление спектральных линий диф-
фузной серии на три компоненты, в соответствие с энергетической
схемой на рис. 17.2в.
Тонкую структуру спектральных линий, возникающих при ра-
диационных переходах между F-термами и Р-термами, наблю-
17.3. Тонкая структура оптических спектров 359
дать еще более трудно, чем тонкую структуру линий диффузной
серии, поскольку различие между спин-орбитальными энергети-
ческими подуровнями тонкой структуры ^-термов составляет ты-
сячные доли электрон-вольта.
Задачи к лекции 17
1. Длина волны первой спектральной линии резкой серии лития
равна 8126,4 А, а предел резкой серии равен 3505 А. Вычислить зна-
чения параметра 5 в формуле энергии стационарных состояний атома
щелочного металла для орбитальных чисел I = 0 и I = 1 в случае атома
лития.
2. У атома лития энергия ионизации основного состояния 5,39 эВ,
а энергия возбуждения первого возбужденного состояния 1,85 эВ. Вычи-
слить значения параметра 6 в формуле энергии стационарных состояний
атома щелочного металла для орбитальных чисел I = 0 и I = 1 в случае
атома лития.
3. Первая спектральная линия резкой серии представляет собой ду-
блет с длинами волн 14695 А и 13588 А. Найти разность энергий излу-
чаемых фотонов.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 17
17.1. Спектр излучения атома гелия
Наблюдаемый спектр излучения атома гелия может быть интерпре-
тирован на базе энергетической схемы низших атомных термов этого
инертного газа.
Электронная конфигурация атома гелия в основном состоянии имеет
вид 1s2. При этом квантовые числа обоих электронов определены одно-
значно, согласно табл. 15.1. Это значит, что основному состоянию атома
гелия соответствует только один атомный терм xSo с нулевыми момен-
тами La = 0, Sa = 0, Ja — 0, как и должно быть для атома с полностью
заполненными электронными оболочками. Термы возбужденных состо-
яний отличаются большим разнообразием.
При возбуждении атома гелия один из электронов может перейти в
пустые оболочки электронного L-слоя. Так образуются самые низкоэнер-
гетические электронные конфигурации возбужденных состояний атома
гелия: Is12s1 и Is1 2рх.
В лекции 16 было показано, что квантовое число суммарного спина
двухэлектронной системы может принимать только два значения: sq = 1
и So — 0. Это справедливо при любом расположении электронов по элек-
тронным слоям, т.е. при любых значениях главных квантовых чисел
электронов. Следовательно, возбужденные состояния атома гелия обла-
дают мультиплетно стью 1 или 3. Атомы гелия с различной величи-
ной суммарного спина столь заметно различаются по своим физическим
свойствам, что получили специальные названия. Атомы с нулевым сум-
марным спином (so = 0), когда спины электронов «антипараллельны»,
образуют парагелий. Атомы с ненулевым спином Sa = (so — 1),
т.е. когда спины электронов «параллельны», образуют ортогелий.
Ясно, что наиболее низкоэнергетическая электронная конфигурация
1s2 реализуется только в виде парагелия.
Пользуясь вышеизложенным методом сложения квантовых момен-
тов импульса, получим, что в электронной конфигурации гелия Is12s1
квантовое число атома равно Iq = 0. При этом формируется терм rS
парагелия и терм 3S ортогелия. Для электронной конфигурации ls12p1
квантовое число может принимать значения Iq = 0 или 1. Следовательно,
существуют терм гР парагелия и терм 3Р ортогелия. Аналогично можно
найти термы и для конфигураций с более высокой энергией.
Спектр излучения атома гелия формируется переходами между тер-
мами, разрешенными правилами отбора, изложенными в § 17.1 лек-
ции 17.
Основное состояние парагелия (ls2)1^ имеет энергию —24,59 эВ.
В это состояние возможны радиационные переходы из Р-термов, кото-
рые образуют серию спектральных линий, принадлежащих ультрафио-
летовому диапазону.
Дополнения к лекции 17
361
Энергия самого низкоэнергетического терма ортогелия (ls12s1)3S со-
ставляет около —4,77 эВ. Как следствие, спектр ортогелия лежит в более
длинноволновом участке (см. рис. Д.17.1).
Рис. Д.17.1. Энергетическая схема низших термов атома гелия и спектральных
линий излучения.
Горизонтальные линии изображают уровни энергии стационарных состояний, цифры около
них — главные квантовые числа. Наклонные линии — возможные радиационные пе-
реходы, числа — длины волн (А). Штриховой линией обозначен интеркомбинационный
переход
Видимые и инфракрасные спектральные линии образуются перехо-
дами с Д/q = ±1 между возбужденными состояниями как парагелия,
так и ортогелия. Правило отбора Д$о — 0 препятствует радиационным
переходам между состояниями парагелия и ортогелия.
Однако в спектре возбужденных атомов гелия наблюдаются линии
с длинами волн 591,44 А и 538,96 А, которые образуются переходами
между состояниями (ls^p1)3/3 -> (ls2)1^ и {ls13p1)3P -> (ls2)1^ со-
ответственно. Подобные переходы с нарушением правила отбора Д$о = О
362
Дополнения к лекции 17
в спектроскопии называются интеркомбинационными. Они возникают
из-за спин-орбитального взаимодействия, при котором величина спина
атома может измениться. Приведенные примеры радиационных перехо-
дов между состояниями парагелия и ортогелия иллюстрируют прибли-
женный характер правил отбора (17.4).
Низший терм ортогелия (ls^s1)3^ является метастабильным состо-
янием, так переход в более низкоэнергетическое состояние — терм па-
рагелия (Is2)1 S — запрещен не только правилом отбора Aso = 0, но
правилом Д/о = ±1. Однако исследования излучения Солнца, которое
содержит большое количество гелия, показали, что переход между тер-
мами (ls^s1)3^ и (Is2)1S возможен, хотя имеет малую вероятность.
Среднее время жизни терма (ls^s1)3^ весьма велико по сравнению
с характерным временем радиационных переходов (10“8-10-9 с) и су-
щественно зависит от температуры и концентрации газа окружающей
среды.
Образование ортогелия в Солнце и других звездах происходит в два
этапа. Сначала атом гелия ионизуется, т.е. теряет один электрон при
столкновениях с другими частицами. При последующей рекомбинации
(присоединения электрона) с равной вероятностью образуется как атом
парагелия, так и ортогелия. Также атом ортогелия может образоваться
из атома парагелия при столкновениях частиц, в которых происходит
обмен не только импульсами и энергиями, но и моментами импульса.
Наиболее яркие спектральные линии излучения гелия в видимом
диапазоне изображены на рис. Д.17.2.
400 450 500 550 600 700
—1_________J________—JL_____1 _|________1
X, нм
Рис. Д.17.2. Спектр излучения гелия в видимом диапазоне
Сравнив рис. Д.17.2 с энергетической схемой на рис. Д.17.1 нетрудно
идентифицировать радиационные переходы, генерирующие три самые
длинные спектральные линии в видимом спектре атома гелия:
{ls13d1)1D (ls^p1)1/3 6678А (красная),
(Is^rf1)3/? (ls12p1)3P 587бА (желтая),
(ls^p1)1^ (ls12s1)1S 5016 А (зеленая).
Остальные спектральные линии, видимые на рис. Д.17.2 в сине-
зеленом диапазоне, образуются при следующих радиационных перехо-
дах:
(IsMd1)3/? -» (ls^p1)3^ 4472 А,
(ls14s1)3S -» (ls^p1)3^ 4713 А,
(IsMd1)1/? (ls^p1)1^ 4922 A.
Дополнения к лекции 17
363
Рассмотрим теперь тонкую структуру спектра гелия.
Все термы парагелия являются синглетами, так как спин атома в
этих стационарных состояниях равен нулю: Sa — 0, а модуль пол-
ного момента импульса атома Ja этих совпадает с модулем его орбиталь-
ного момента La- Низкоэнергетические стационарные состояния пара-
гелия с учетом значения модуля полного электронного момента импульса
атома запишутся в виде: (ls2)1So, (ls12s1)1So, (ls12p1)1 J3!, (ls13s1)1So,
(ls^d1)1^, и т.д. Таким образом, каждому терму параге-
лия с определенным орбитальным числом Iq соответствует единственное
значение квантового числа jo = Iq, так как во всех стационарных состо-
яниях парагелия число so = 0- Как следствие, спин-орбитальное вза-
имодействие не приводит к «расщеплению» энергий термов парагелия
на спин-орбитальные подуровни, и спектральные линии парагелия не
демонстрируют тонкой структуры.
Перейдем к анализу тонкой структуры спектра излучения ортогелия.
S-термы ортогелия также являются синглетами. Хотя в этих ста-
ционарных состояниях спин атома не равен нулю (so — 1), но из-за
нулевого орбитального момента (Iq — 0 у S-термов) квантовое число мо-
дуля полного электронного момента импульса атома может принимать
единственное значение у0 — sq = 1. Тонкое расщепление энергий этих
термов не происходит.
Остальные термы ортогелия претерпевают тонкое расщепление. Так,
терм 3Р дает три спин-орбитальные компоненты: 3Ро, 3Л, раз-
личающиеся энергиями, терм 3D — тоже три: 3J9i, 3/?2, 3/?з, и т.п.
Пример, демонстрирующий величину тонкого расщепления энергии тер-
мов, приведен на рис. Д.17.3. Характерно, что разность энергий между
энергетическими уровнями термов 3Pi
и 3Р2 на порядок меньше, чем между
энергетическими уровнями термов 3Pi
и 3Р0.
Е
___________________
М го
Рис. Д.17.3. Энергетические уровни термов (15х2р1)3Fo,i,2 ортогелия. AFoi = 1,2х J : : 3р
JaSj 2
X10"4 эВ, ДЕ12 = 9,7 • 10-6 эВ 1 2
При радиационных переходах между S-термами и Р-термами ор-
тогелия должны генерироваться триплеты, так как из-за влияния
спин-орбитального взаимодействия верхний или нижний энергетический
уровень (соответствующий Р-терму) расщепляется на три, а S-терм ос-
тается нерасщепленным. При этом, согласно правилам отбора (17.3),
разрешены радиационные переходы из S-терма в любой Р-терм: 3Ро,
3Р1 и 3Рг. Аналогично, возможны переходы из любого Р-терма в
S-терм с испусканием фотонов. Примеры формирования триплетов ор-
тогелия приведены на рис. Д.17.4.
Тонкую структуру спектральных линий ортогелия (из-за малой раз-
ности энергий между спин-орбитальными подуровнями) эксперимен-
тально удается наблюдать только при переходах между термами с низ-
364
Дополнения к лекции 17
кой энергией. Например, переход между термами (1s12f1)3Po,i,2
-> (ls12s1)3Si дает триплет в инфракрасном диапазоне с длинами волн
10829,1 А, 10830,2 А и 10830,3 А. Столь близкие значения длин волн
обусловлены малой разницей энергий термов 3Ро, 3Pi, 3Р? (см.
рис. Д.17.4а).
Электронной конфигурации 1s1 Зр1 соответствуют более высокие
значения энергии термов ортогелия по сравнению с энергиями тер-
мов конфигурации ls12p1. Как следствие, радиационные переходы
Рис. Д.17.4. Энергетические схемы радиационных переходов, генерирующих
триплеты, в атоме ортогелия:
a) (ls12p1)3Po,i,2 —> (ls12s1)3Si, б) (ls13s1)3Si —> (ls12p1)3Fo,i,2- Масштаб по оси
энергий не соблюден. Вертикальными стрелками обозначены переходы между энергетиче-
скими уровнями. Около стрелок указаны длины волн спектральных линий
(ls13p1)3Po,i,2 (ls12s1)3Si дают триплет, принадлежащий области
близкого ультрафиолета (А « 3888 А). Для термов 3Ро,1,2 электронной
конфигурации 1s1 Зр1 энергетическая схема спин-орбитальных подуров-
ней имеет вид, аналогичный изображенному на рис. Д.17.3, но разно-
сти энергий соседних подуровней имеют значения ДРох — 2,5 • 10-5 эВ
и ДР12 = 2,0 • 10-5 эВ. Нетрудно вычислить, что различие длин волн
компонент тонкой структуры триплета (ls13p1)3Po,i,2 (ls12s1)3Si со-
ставляет несколько сотых долей ангстрема.
Лекция 18
РЕНТГЕНОВСКИЕ ЛУЧИ
18.1. Открытие и основные свойства
В 1895 г. немецкий физик Вильгельм Конрад Рентген (1845-
1923) проводил исследования электрического тока в сильно раз-
реженных газах. Для опытов Рентген использовал стеклянную
трубку, из которой предварительно был выкачен воздух с помо-
щью ртутного насоса. В трубку были впаяны два электрода, к
которым прикладывалась разность потенциалов в несколько ки-
ловольт. Первый прибор Рентгена представлял собой газоразряд-
ную трубку, описанную в лекции 1, и его работа начиналась с
изучения свойств катодных лучей. В ходе своих экспериментов
Рентген обнаружил, что трубка становится источником лучей, ко-
торые он назвал «икс-лучами» (см. рис. 18.1а). Основные свойства
Рис. 18.1. Схемы рентгеновских трубок: а) одна из первых трубок Рентгена,
б) рентгеновская трубка конца XX века:
К — термокатод, А — высоковольтный анод, Т — накал термокатода, Э — пучки ускоряе-
мых электронов (штрихпунктирные линии), Р — потоки рентгеновских лучей (штриховые
линии), О — окна в корпусе трубки для выхода рентгеновских лучей
Р>»0
б
«икс-лучей» изучил сам Рентген в результате трехлетней работы,
за которую в 1901 г. был удостоен Нобелевской премии — пер-
вым среди физиков. Открытые им лучи впоследствии справедливо
были названы рентгеновскими.
366
Лекция 18. Рентгеновские лучи
Уже в первых опытах было установлено, что поток рентгенов-
ских лучей исходит из анода трубки. Как было выяснено в экспе-
риментах с газоразрядными трубками (см. лекцию 1), от катода
к аноду движется поток электронов, который вызывает возникно-
вение рентгеновских лучей. Впоследствии прибор для получения
рентгеновских лучей был существенно усовершенствован. Воздух
откачивался до высокого вакуума (порядка 10“7 атм), а в каче-
стве источника электронов стал использоваться термокатод (см.
рис. 18.16}. Корпус стал изготавливаться не из стекла, а из стали.
Для вывода рентгеновских лучей предназначались специальные
окна, закрытые тонкими пластинками, которые препятствовали
разгерметизации прибора. За устройством подобного вида закре-
пилось название рентгеновской трубки.
Важнейшими свойствами рентгеновских лучей являются сле-
дующие.
1. Лучи проходят через все материалы, в том числе непро-
зрачные для видимого света. Интенсивность проходящих лучей
I уменьшается экспоненциально с толщиной х слоя вещества:
1(х) = /о ехр (—/xz), (18.1)
где Iq — интенсивность рентгеновских лучей, падающих на слой
облучаемого материала.
Коэффициент /х характеризует ослабление потока рентгенов-
ских лучей веществом и зависит от плотности материала р и его
химического состава. Величина обратная коэффициенту /х назы-
вается средней длиной пробега I = 1//х рентгеновских лучей в
данном веществе. На расстоянии х = I интенсивность потока
уменьшается в е раз.
Многочисленные эксперименты показали, что для рентгенов-
ских лучей, испускаемых трубкой, и простых веществ в первом
приближении наблюдается зависимость
/х - pZn, (18.2)
где Z — порядковый химический номер простого вещества. Пока-
затель степени п для разных веществ может принимать значения
в интервале 4 < п < 5.
Потоки рентгеновских лучей проходят сквозь толстые доски,
металлические листы, человеческое тело и т. д. Значительная про-
никающая способность рентгеновских лучей в настоящее время
широко используется в дефектоскопии, медицине и различных на-
учных исследованиях.
Для вывода пучков рентгеновских лучей из рентгеновской
трубки в ее стенках конструируются окна, обычно два (см.
рис. 18.16} или четыре. Окна закрываются тонкой пластинкой из
вещества, слабо поглощающего рентгеновское излучение. В каче-
18.1. Открытие и основные свойства 367
стве таких материалов используются, в соответствие с формулой
(18.2), алюминий, бериллий, пластик с напыленной пленкой гра-
фита и т. д.
2. Рентгеновские лучи вызывают люминесценцию некоторых
химических соединений. Например, экран, покрытый солью
BaPt(CN)4-4Н2О при попадании рентгеновских лучей светится
желто-зеленым цветом.
3. Рентгеновские лучи, попадая на фотоэмульсии, вызывают их
почернение. Следовательно, рентгеновские лучи вызывают фото-
химические реакции.
4. Рентгеновские лучи ионизуют воздух и другие газы, делая
их электропроводными. Это свойство используется в детекторах,
позволяющих обнаружить невидимые рентгеновские лучи и изме-
рить их интенсивность.
5. Рентгеновские лучи обладают сильным физиологическим
действием. Длительное облучение живых организмов интенсив-
ными потоками рентгеновских лучей приводит к возникновению
специфических заболеваний (так называемая лучевая болезнь) и
даже к летальному исходу. Для защиты от влияния рентгенов-
ских лучей используются экраны, изготовленные из материалов,
содержащих, согласно (18.2), химические элементы с большим по-
рядковым номером Z, например свинец.
Открытие рентгеновских лучей и их последующие исследова-
ния были для развития атомной физики не менее важны, чем
гипотеза Планка, обнаружение электрона и радиоактивности ато-
мов. Удивительные свойства рентгеновских лучей поразили во-
ображение современников и дали мощный толчок развитию всего
естествознания.
Природа лучей в течение ряда лет оставалась загадочной. В хо-
де экспериментов было выяснено, что пучки рентгеновских лучей
распространяются прямолинейно, не отклоняясь электрическими
и магнитными полями, как и направленные потоки электромаг-
нитных волн. С другой стороны, рентгеновские лучи не отража-
лись от зеркал, не преломлялись в стеклянных (флинтгласовых)
призмах, не давали интерференционной картины на дифракцион-
ных решетках.
Лишь в 1912 г. Макс Лауэ (1879-1960) со своими сотрудниками
доказал, что рентгеновские лучи представляют собой электромаг-
нитные волны очень малой длины — порядка ангстрем.
Известно, что характерные волновые эффекты хорошо наблю-
даются, если размеры рассеивающих объектов имеют порядок
длины волны (т.е. в условиях дифракции Фраунгофера). Для
наблюдения дифракции рентгеновских лучей Макс Лауэ предло-
жил воспользоваться естественной дифракционной решеткой —
периодической структурой, которую образуют атомы в совершен-
ном кристалле. В то время уже было установлено, что расстояния
368
Лекция 18. Рентгеновские лучи
между соседними атомами в кристаллах имеют порядок несколь-
ких ангстрем. По идее Лауэ его ученики Книппинг и Фридрих
провели опыт по пропусканию узкого пучка рентгеновских лучей
через кристалл (см. рис. 18.2а).
В результате опыта на фотопластинке, расположенной позади
кристалла, зафиксировалась картина пятен, образованная дифра-
гированными пучками рентгеновских лучей (см. рис. 18.26}.
Рентгеновские лучи, рассеянные отдельными периодически
расположенными атомами, являются когерентными. Как следст-
вие. 18.2. Опыты по дифракции рентгеновских лучей:
а) схема установки Фридриха и Книппинга. 1 — пучок рентгеновских лучей, 2 — свин-
цовый экран, 3 — свинцовые диафрагмы, 4 — кристалл, 5 — фотопластинка; б) следы
дифрагированных рентгеновских пучков на фотоэмульсии
вие, при выполнении условий конструктивной интерференции в
определенных направлениях формируются дифрагированные пуч-
ки значительной интенсивности.
В ходе интерпретации результатов опытов Лауэ разработал
математическую теорию рассеяния рентгеновских лучей на иде-
альном кристалле (см. дополнение 18.1). Работы Макса Лауэ, ко-
торые убедительно доказали волновой характер рентгеновских лу-
чей, были удостоены в 1914 г. Нобелевской премии.
18.2. Измерение длин волн рентгеновских лучей
Практически в то же время два английских физика (отец и
сын) У.Г. Брэгг (1862-1942) и У.Л. Брэгг (1890-1971) занимались
исследованием рассеяния рентгеновских лучей на кристаллах.
Они показали, что рентгеновская дифракция может быть успешно
описана как результат интерференции волн, отраженных отдель-
ными плоскостями, заполненными атомами. К тем же выводам
пришел профессор Московского университета Г.В. Вульф (1863—
1925), поэтому полученное основное соотношение часто называется
18.2. Измерение длин волн рентгеновских лучей
369
уравнением Брэгга-Вульфа:
2d sin 0 = пХ,
(18.3)
где d — расстояние между соседними атомными плоскостями, на
которых происходит рассеяние, А — длина волны рентгеновских
лучей. Угол между первичным и дифрагированным пучками ра-
вен 20. Число п может принимать целые значения 1, 2 и т.д. и
называется порядком отражения (см. дополнение 4.5 к лекции 4).
Отец и сын Брэгги первыми использовали явление рентгенов-
ской дифракции на кристаллах для измерения длин волн рент-
геновских лучей. На рис. 18.3 изображена схема рентгеновского
спектрометра Брэгга.
Рис. 18.3. Схема рентгеновского спектрометра
Брэгга:
1 — пучок рентгеновских лучей, выходящий из
рентгеновской трубки, 2 и 3 — диафрагмы, фор-
мирующие узкий пучок лучей, 4 — кристалл, 5 —
изогнутая фотопленка, 6 — цилиндрический кожух
камеры, 7 и 8 — места попадания прошедших и ди-
фрагированных рентгеновских лучей на фотоэмуль-
сию соответственно
Узкий пучок рентгеновских лучей с длиной волны А направля-
ется на кристалл, который укреплен на поворотном столике. Часть
потока падающих рентгеновских лучей проходит сквозь кристалл
и оставляет след на фотоэмульсии в точке 7. Кристалл 4 медленно
поворачивается, при этом угол скольжения 0 постепенно изменя-
ется. Когда кристалл займет положение, при котором выполнятся
условия дифракции (18.3), сформируется дифрагированный пучок
рентгеновских лучей, попадающий на фотоэмульсию в точку 8.
Длина дуги L между точками 7 и 8 измеряется непосредствен-
но, и угол 0 может быть вычислен достаточно точно из уравнения
= 20, (18.4)
гС
где R — радиус цилиндрический камеры, т. е. расстояние от кри-
сталла до фотопленки.
Интенсивность рассеянных рентгеновских лучей определялась
по плотности почернения фотоэмульсии. В другой модификации
спектрометра Брэгга фотопленка была заменена ионизационной
камерой. Регистрируемый ток пропорционален интенсивности
370
Лекция 18. Рентгеновские лучи
Рис. 18.4. Фрагмент атомной
структуры поваренной соли.
Черными кружками обозначено
положение атомов натрия, бе-
лыми — атомов хлора. Эле-
ментарная ячейка имеет форму
куба
рентгеновских лучей, попадающих в камеру. Ионизационный спек-
трометр позволил значительно уменьшить погрешность измере-
ния интенсивности рентгеновских лучей.
Для вычисления длины волны, соответствующей измеренному
углу 0, с помощью уравнения (18.3) требуется знать расстояние
d между атомными плоскостями, которые формируют регистриру-
емый дифракционный пучок. В на-
стоящее время эти расстояния очень
точно измеряются именно рентгено-
дифракционным методом. Так как
Брэгги еще не имели этих данных,
они остроумно вычислили межплос-
костное расстояние d, пользуясь фи-
зико-химическими свойствами ис-
следуемых кристаллов. В частности,
поваренная соль имеет химическую
формулу NaCl и плотность р =
= 2,165г/см3. Огранка кристаллов
поваренной соли позволяет предполо-
жить атомную структуру, показан-
ную на рис. 18.4 (что впоследствии
было доказано экспериментально).
Это означает, что на каждый атом
натрия или хлора приходится объем
с/3, где d — минимальное расстояние
между плоскостями, заполненными атомами. Атомные массы на-
трия и хлора равны соответственно т^а — 22,99 а.е.м. и ?zici =
= 35,45 а.е.м. Искомое расстояние d получается решением следу-
ющего уравнения:
2d3 р = т^а + тпсь (18.5)
Вычисления дали d = 2,814 А. Это позволило каждому изме-
ренному значению угла 0 поставить в соответствие определенную
длину волны рентгеновских лучей.
Таким образом, работы отца и сына Брэггов дали возможность
количественных измерений спектров рентгеновских лучей. Кроме
того, в спектрометрах Брэггов первичное рентгеновское излучение
с различными длинами волн рассеивалось на различные углы.
Следовательно, установки Брэггов нетрудно переделать в монохро-
маторы, которые дают пучки монохроматических рентгеновских
лучей. Использование монохроматического рентгеновского излу-
чения чрезвычайно важно для решения многих научно-исследова-
тельских и прикладных физических задач. Работы У.Г. Брэгга и
У.Л. Брэгга благодарная научная общественность отметила Нобе-
левской премией 1914 года.
18.3. Тормозное рентгеновское излучение
371
18.3. Тормозное рентгеновское излучение
Спектрометрические исследования излучения, генерируемого
рентгеновскими трубками, позволили выявить некоторые общие
закономерности. Еще в начале своих исследований Брэгги обнару-
жили, что излучение, испускаемое анодами рентгеновских трубок,
обладает спектром весьма сложного вида. На фоне непрерывного
спектра различаются резкие максимумы, которые появляются при
определенной разности потенциалов между анодом и катодом.
Для любого материала анода спектр рентгеновских лучей все-
гда содержит непрерывную составляющую, имеющую максимум и
резкую границу со стороны коротких волн (см. рис. 18.5).
Измерения показали (см. рис. 18.5), что высота максимума и
интегральная интенсивность рентгеновского излучения монотонно
Рис. 18.5. Непрерывная составляющая спектров рентгеновских лучей при раз-
ных ускоряющих напряжениях U: A) U = 20 кВ, В) U = 25 кВ, С) U = 30 кВ,
D) U = 35 кВ, Е) U = 40 кВ, F) U = 50 кВ. Вольфрамовый анод. По верти-
кальной оси отложена спектральная интенсивность излучения в относительных
единицах
растет с увеличением ускоряющего напряжения С7, т. е. разностью
потенциалов между анодом и катодом рентгеновской трубки.
Положение коротковолновой границы непрерывного рентгенов-
ского спектра не зависит от материала анода и определяется только
напряжением U. Длина волны коротковолновой границы выража-
ется следующей эмпирической формулой:
Amin « (18.6)
372
Лекция 18. Рентгеновские лучи
где напряжение U измеряется в киловольтах, а длина волны вы-
ражается в ангстремах.
Рентгеновские лучи с непрерывным спектром образуются при
торможении электронов в материале анода. Электроны, испущен-
ные катодом рентгеновской трубки, ускоряются электрическим
полем и достигают поверхности анода, получив кинетическую энер-
гию eU. Попав внутрь анода, эти электроны испытывают дей-
ствие электрических полей ядер и электронов атомов вещества
анода. Электрические силы придают электронам ускорение, а
ускоренно движущиеся заряженные частицы излучают электро-
магнитные волны непрерывного спектра. Этот механизм излуче-
ния называется тормозным.
Согласно классической электродинамике, интегральная ин-
тенсивность тормозного излучения заряженной частицы (т. е.
энергия, излучаемая в единицу времени во всех направлениях)
равна
2 о2 о,2
W = -1-^, (18.7)
где q — электрический заряд, а — ускорение частицы, с — ско-
рость света.
Заметим, что ускорение тормозящегося электрона вызывается
кулоновской силой, модуль которой пропорционален произведению
электрических зарядов взаимодействующих частиц. Следователь-
но, тормозное излучение генерируется, в основном, за счет взаи-
модействия электрона с атомными ядрами атомов металла анода.
В электродинамике показано, что вероятность излучения на фик-
сированной длине волны при торможении электрона в электриче-
ском поле атомного ядра пропорционально квадрату порядкового
номера атома, а при электрон-электронных столкновениях — по-
рядковому номеру атома.
Чтобы выяснить хотя бы приближенную связь интегральной
интенсивности W с ускоряющим напряжением U рентгеновской
трубки, предположим, что электрон в материале анода тормозится
полностью на прямолинейном отрезке длиной х. Рассматривая ве-
личину а как среднее ускорение на отрезке торможения, запишем
известное кинематическое уравнение
2ха = v2, (18.8)
где v — скорость электрона, ускоренного разностью потенциалов
непосредственно перед входом в анод (начальной скоростью
электрона пренебрегаем). Так как у обычных рентгеновских тру-
бок величина U не превышает нескольких десятков киловольт,
то кинетическая энергия электрона eU значительно ниже его энер-
гии покоя тпес2. Следовательно, ускоренные электроны можно счи-
тать нерелятивистскими и их кинетическую энергию записать в
18.3. Тормозное рентгеновское излучение
373
виде
ТТ те 2
(18.9)
Выразив ускорение а и скорость v из уравнений (18.8) и (18.9) и
подставив в (18.7), получим
2 е4{72
3 с3х2т2 ’
(18.10)
Несмотря на приближенный характер выполненной оценки, фор-
мула (18.10) дает нелинейную (квадратичную) зависимость инте-
гральной интенсивности W тормозного излучения от ускоряющего
напряжения £7, которая прослеживается на рис. 18.5.
Регистрируемая интегральная интенсивность излучения рент-
геновской трубки WR должна быть пропорциональна анодному
току /е, т.е. количеству электронов, которые в единицу времени
тормозятся в аноде, генерируя электромагнитное излучение.
Экспериментально установлено, что
WR = kZIeU2, (18.11)
где к — аппаратурный коэффициент пропорциональности. Это
означает, что интегральная интенсивность рентгеновского тормоз-
ного излучения пропорциональна атомному номеру Z материала
анода.
Расчет формы спектра электромагнитного излучения, генери-
руемого тормозящимися в металле электронами, является слож-
ной задачей электродинамики. В массивных анодах рентгенов-
ских трубок тормозящийся электрон, многократно рассеивается
на заряженных частицах (атомных ядрах и электронах) и его
траекторию нельзя считать прямолинейной. Кроме того, на вид
регистрируемого спектра тормозного излучения существенно вли-
яют процессы комптоновского и упругого рассеяния фотонов, а
также их поглощение на атомах вещества анода. В частности,
низкоэнергетическая часть спектра значительно поглощается стен-
ками рентгеновской трубки, что объясняет понижение кривых на
рис. 18.5 в области длинных волн. Экспериментальные исследо-
вания показывают, что обычно максимум непрерывного спектра
рентгеновской трубки находится в области длин волн приблизи-
тельно в полтора раза больших коротковолновой границы спектра
(см. рис. 18.5).
Положение коротковолновой границы непрерывного рентгенов-
ского спектра легко вычислить с помощью закона сохранения энер-
гии. Максимальная энергия фотона бтах тормозного излучения
определяется простым выражением
Стах = еи. (18.12)
374
Лекция 18. Рентгеновские лучи
Последнее уравнение описывает предельный случай, когда вся ки-
нетическая энергия электрона eU излучается в виде единственного
фотона с энергией £тах.
Понятно, что при торможении электрона атом получает им-
пульс и, следовательно, кинетическую энергию. Однако можно
показать, что в случае нерелятивистских электронов эта энергия
пренебрежимо мала по сравнению с величиной еС/, так как тормо-
жение происходит, в основном, из-за взаимодействия с массивным
атомным ядром. Как следствие, равенство (18.12) выполняется с
хорошей точностью.
Максимальной энергии smax соответствует минимальная длина
волны фотона Amin? которая, согласно (4.6), выражается так:
_ 2тгсЛ
^min ~ тг"'
eU
При подстановке числовых значений в (18.13) мы получаем сов-
падение с эмпирической формулой (18.6) для коротковолновой гра-
ницы непрерывного рентгеновского спектра.
Согласно выражению (18.13), коротковолновая граница Amin
при определенном ускоряющем напряжении U не зависит от мате-
(18.13)
Рис. 18.6. Сравнительные спектры тормоз-
ного излучения для разных материалов
анода при одинаковом ускоряющем напря-
жении и одинаковом токе электронов в
рентгеновской трубке. Спектральная ин-
тенсивность излучения 1\ выражена в от-
носительных единицах. Материал анода:
1 — алюминий, 2 — молибден, 3 — пла-
тина
риала анода, что иллюстрируется рис. 18.6. Площади под кривыми
на рис. 18.6 пропорциональны атомному номеру материала анода
в соответствии с выражением (18.11).
Разрешающая способность современных рентгеновских спек-
трометров позволяет проводить измерения длины волны коротко-
волновой границы непрерывного рентгеновского спектра с высокой
точностью. Это в свою очередь позволяет по формуле (18.13) вы-
числить постоянную Планка h с малой погрешностью. Оказалось,
что этот метод получения значения h является одним из самых
точных.
Большинство электронов, тормозящихся в аноде рентгеновской
трубки, теряет свою энергию, излучая последовательно несколько
фотонов с различными энергиями е < бШах- Соответствующие
18.3. Тормозное рентгеновское излучение 375
длины волн заполняют интервал значений А > Amin, что обусло-
вливает непрерывный характер спектра.
Следует иметь в виду, что значительная часть кинетической
энергии электронов затрачивается на ионизацию и возбуждение
атомов вещества анода. Последующая рекомбинация и снятие
возбуждения порождает излучение с длинами волн много больше
рентгеновских.
Кроме того, в многочисленных актах рассеяния электронов
на атомных ядрах некоторая доля кинетической энергии превра-
щается в тепловую, что приводит к сильному разогреву анода.
В современных рентгеновских установках используются устрой-
ства принудительного охлаждения, чаще всего потоком холодной
воды.
Как следствие, в среднем лишь небольшая часть энергии уско-
ренных электронов превращается в энергию рентгеновского из-
лучения. Коэффициент полезного действия (к.п.д.) равен отно-
шению величины (18.11) к мощности тока рентгеновской трубки,
равной
WQ = IeU. (18.14)
Следовательно, к.п.д. рентгеновской трубки пропорционален атом-
ному номеру Z материала анода и ускоряющему напряжению U:
77 = = kZU. (18.15)
Wo
Для напряжений U порядка де-
сятков киловольт к.п.д. т] обыч-
но не превышает одного про-
цента.
Рис. 18.7. Полярная диаграмма рас-
пределения интенсивности тормоз-
ного излучения, генерируемого элект-
ронами.
Вектор Ре — импульс тормозящихся
электронов. Цифрами обозначены кривые
для различных ускоряющих напряжений:
1 — ЗкВ, 2 — ЮкВ, 3 — ЗОкВ, 4 —
60 кВ
Угловое распределение интенсивности тормозного излучения
анизотропно и существенно зависит от энергии электронов, т. е. от
ускоряющего напряжения рентгеновской трубки (см. рис. 18.7).
376
Лекция 18. Рентгеновские лучи
При малых энергиях eU <£С тпес2 большая часть потока излу-
чения испускается в направлениях перпендикулярных импульсам
Ре тормозящихся электронов. С увеличением энергии электронов
максимум потока излучения постепенно приближается к направле-
нию вектора Ре.
По этой причине в первых рентгеновских трубках для увели-
чения потока рентгеновских лучей, выходящих наружу, анод был
развернут, как это показано на рис. 18.1а. Очевидно, что вид угло-
вого распределение интенсивности тормозного излучения следует
принимать во внимание при конструировании размеров и формы
окон рентгеновской трубки, служащих для вывода потоков рент-
геновских лучей (см. рис. 18.16).
18.4. Линейчатый спектр рентгеновских лучей
В 1906 г. английский физик Чарльз Баркла (1877-1944) прово-
дил исследования рассеяния рентгеновских лучей на различных
веществах. Схема экспериментальной установки Баркла приве-
дена на рис. 18.8.
Изменяя материалы рассеивателей и поглотителей, Баркла об-
наружил, что физические характеристики вторичного (рассеянно-
го) рентгеновского излучения значительно отличаются от свойств
Рис. 18.8. Схема экспериментальной установки Ч. Баркла:
1 — пучок первичных рентгеновских лучей, 2 и 5 — свинцовые диафрагмы, 3 — рассеи-
ватель, 4 — пучок вторичных (рассеянных) рентгеновских лучей, 6— поглотитель, 7 —
детектор (ионизационная камера)
первичных (падающих на рассеиватель) рентгеновских лучей.
Вторичные рентгеновские лучи, образованные в рассеивателях из
разных химических элементов, значительно различаются по по-
глощающей способности, т.е. коэффициентом /л.
18.4. Линейчатый спектр рентгеновских лучей
377
Исследование спектров вторичных рентгеновских лучей позво-
лило обнаружить, что при достаточно большом ускоряющем напря-
жении между электродами рентгеновской трубки в спектре рент-
Рис. 18.9. Спектры рентгеновских лучей для разных ускоряющих напряже-
ний U. Родиевый анод:
1 — U = 23,2 кВ, 2 — U = 31,8 кВ, 3 — U = 40,0 кВ. На горизонтальной оси ука-
заны значения коротковолновых границ. По вертикальной оси отложена спектральная
интенсивность излучения в относительных единицах. Около пиков записаны длины волн
спектральных линий
геновских лучей на фоне непрерывной составляющей появляются
узкие пики высокой интенсивности (см. пример на рис. 18.9).
Эти пики были названы рентгеновскими спектральными ли-
ниями (по аналогии с оптическими спектральными линиями). Со-
вокупность рентгеновских спектральных линий образует линейча-
тый спектр рентгеновских лучей.
В экспериментах было установлено, что вид линейчатого спек-
тра вторичных рентгеновских лучей существенно зависит от хи-
мического состава рассеивателя.
В установке Баркла использовалась рентгеновская трубка с
анодом, изготовленным из определенного металла. Первичное
рентгеновское излучение генерировалось в аноде трубки потоком
ускоренных электронов. Затем пучок первичных рентгеновских
378
Лекция 18. Рентгеновские лучи
лучей попадал на рассеиватель — тело, состоящее из атомов, во-
обще говоря, других химических элементов. Первичные рентге-
новские лучи — фотоны высокой энергии — генерировали вторич-
ные рентгеновские лучи (механизм этого процесса изложен в конце
§19.3 и дополнении 19.2). Впоследствии для изучения линейча-
тых спектров рентгеновских лучей различных химических эле-
ментов стали использоваться рентгеновские трубки со сменными
анодами.
Таким образом, спектр излучения рентгеновской трубки явля-
ется, вообще говоря, суперпозицией непрерывной и линейчатой
частей (см. рис. 18.9). Механизм генерирования непрерывного
рентгеновского излучения был изложен в предыдущем параграфе.
Линейчатые рентгеновские спектры демонстрируют ряд общих за-
кономерностей, описанных ниже.
В ходе экспериментов было установлено, что расположение
спектральных линий на оси длин волн определяется элементным
составом материала анода. При этом каждому химическому эле-
менту соответствует определенный индивидуальный набор
длин волн линейчатого рентгеновского спектра. Интересно, что
числовые значения этих длин волн не зависят от вида химиче-
ского соединения, в который входит данный химический элемент.
По этой причине рентгеновское излучение, имеющее линейчатый
спектр, называется характеристическим. Этим рентгеновские
линейчатые спектры принципиально отличаются от оптических
спектров атомов, которые существенно изменяются при объеди-
нении атомов в молекулы (см. лекцию 25).
Ч. Баркла за открытие характеристического рентгеновского
излучения (ХРИ) был в 1917 г. награжден Нобелевской пре-
мией.
Линейчатый рентгеновский спектр, в отличие от атомных оп-
тических спектров, состоит из небольшого числа резких пиков.
Еще до того как был выяснен механизм образования ХРИ пики
линейчатого спектра объединялись в серии по близости значений
длин волн.
В экспериментах сначала была открыта и промерена самая ко-
ротковолновая серия ХРИ, которая была названа А?-серией. Для
большинства химических элементов хорошо разрешаются 3 пика
этой серии: Ka, Кр, Ку, где греческие буквы расставлены в по-
рядке убывания интенсивности спектральных линий. Для длин
волн спектральных линий /С-серии у всех атомов выполняется со-
отношение
Хка>Хк0>Хк,- (18-16)
Кроме того, в линейчатых рентгеновских спектрах была об-
наружена более длинноволновая серия спектральных линий, на-
званная L-серией. Эта серия, вообще говоря, содержит большее
18.4. Линейчатый спектр рентгеновских лучей 379
количество линий, чем JC-серия. Для любого химического эле-
мента длины волн L-серии в несколько раз больше, чем длины
волн /С-серии. Интенсивность линий L-серии, как правило, мень-
ше, чем интенсивность линий /С-серии того же химического эле-
мента, находящегося в тех же условиях эксперимента.
Постепенно в ходе исследований ХРИ возрастала разрешающая
способность рентгеновских спектрометров и просматривались все
более длинноволновые участки рентгеновского диапазона. В ре-
зультате были открыты рентгеновские спектральные серии, обо-
значенные буквами М, N и О. Каждая из этих серий состоит
из спектральных линий более длинных волн, которые постепенно
смещаются в направлении коротковолнового участка ультрафио-
летового диапазона шкалы электромагнитных волн. С помощью
рентгеновских спектрометров характеристические линии этих се-
рий можно наблюдать лишь у химических элементов, расположен-
ных в конце таблицы Менделеева.
Длинноволновые серии ХРИ отличаются более сложным соста-
вом и меньшей интенсивностью спектральных линий по сравне-
нию с коротковолновыми сериями для того же химического эле-
мента.
Важной особенностью спектральных серий ХРИ является на-
личие порога возбуждения. Каждая серия возникает лишь тогда,
когда ускоряющее напряжение между электродами рентгеновской
трубки U превысит определенную величину [7%, где индекс X обо-
значает определенную спектральную серию ХРИ. Для всех хими-
ческих элементов выполняются соотношения
UK>UL>UM> ... (18.17)
Таким образом, с увеличением ускоряющего напряжения U
сначала происходит возникновение более длинноволновых серий
ХРИ.
Интенсивность спектральных линий ХРИ зависит от перена-
пряжения, т. е. от разности анодного U и порогового Ux напряже-
ний. Для интенсивности линий /С-серии наблюдается следующая
зависимость:
/ (7 \5/3
1к ~ ( ТГ" -1 , U>UK. (18.18)
\ик )
Интенсивность спектральных линий остальных серий также
является возрастающей функцией перенапряжения U — Ux-
Объяснение природы и закономерностей спектра ХРИ оказа-
лось возможным лишь на основе квантовой теории атома, что бу-
дет продемонстрировано в следующей лекции.
380
Лекция 18. Рентгеновские лучи
Задачи к лекции 18
1. Вычислить угол Брэгга при рассеянии рентгеновских лучей с дли-
ной волны А на кристалле с межплоскостными расстояниями d: а) А =
= 0,71 A, d = 3,61 А; б) А = 1,54 A, d= 2,87 А; 30 кВ; в) А = 1,79 А,
d = 3,92 А.
2. Найти коротковолновую границу непрерывного рентгеновского
спектра, если ускоряющая разность потенциалов на электродах рент-
геновской трубки равна: а) 20 кВ; б) 30 кВ; в) 50 кВ.
3. Электроны, ускоренные в рентгеновской трубке, подлетают к аноду
со скоростью v, равной: a) v = с/5; б) v = с/3; в) v = с/2, где с —
скорость света. Найти коротковолновую границу непрерывного рентге-
новского спектра.
4. Электрон, ускоренный в рентгеновской трубке разностью потен-
циалов U, теряет при взаимодействии с атомным ядром всю свою кине-
тическую энергию на излучение тормозного фотона. Найти импульс и
кинетическую энергию, которую получает ядро, если до взаимодействия
с электроном оно было неподвижным. Заряд ядра Ze, масса М. Про-
вести вычисления для следующих атомных ядер: a) 209Bi; б) 197Au;
в) 1271; г) 107Ag.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 18
18.1. Уравнения Лауэ
Рассмотрим распространение плоской монохроматической волны
внутри кристалла в направлении, задаваемом единичным вектором so.
Волновое возмущение, создаваемое этой волной в точке кристалла с ра-
диус-вектором г, можно описать в виде комплексной функции
А = Ао ехр [г(ког — u>Z)], (Д.18.1)
где Ао — комплексная амплитуда падающей волны в случаях скаляр-
ных волн или одна из компонент вектора амплитуды Ао для векторных
волн, ко -— волновой вектор волны, со — частота колебаний, t — время.
Волновой вектор можно представить как ко = &oso, где ко — модуль
волнового вектора.
Примером скалярной волны является распространение звука в кри-
сталле. Векторными волнами описывается распространение электромаг-
нитных волн, в частности, рентгеновского излучения в кристалле. В слу-
чае векторных волн функции вида (Д.18.1) описывают три проекции
вектора возмущения А на оси выбранной системы координат.
Первичная рентгеновская волна, созданная каким-либо источником,
взаимодействует с рассеивающими центрами в кристалле: с электро-
нами, атомами, молекулами.
Известно, что идеальный кристалл представляет собой периодиче-
скую структуру конденсированного состояния вещества. Пространствен-
ная периодичность кристалла описывается с помощью кристаллической
решетки, как подробно изложено в курсах кристаллографии.
Совокупность узлов кристаллической решетки задается системой век-
торов трансляции
Т = из. -I- цЬ + we, (Д.18.2)
где а, Ь, с — базисные векторы элементарных трансляций, u, v, w —
произвольные целые числа.
Для подавляющего большинства кристаллических структур длина
волны рентгеновских лучей по порядку величины совпадает с длинами
элементарных трансляций а, Ь, с.
Сравнение экспериментальных и расчетных результатов показало,
что рассеяние рентгеновских лучей на кристалле успешно описывается,
если рассеивающие центры полагать расположенными в узлах кристал-
лической решетки. Хотя каждому узлу соответствует один или несколько
атомов, для описания дифракции рентгеновских лучей на кристалле мож-
но такие рассеиватели полагать точечными.
В первом приближении можно предположить, что рассеяние не со-
провождается дисперсией и, следовательно, частота рассеянных волн со-
впадает с частотой первичной волны. Если рассеяние является упругим,
то не изменяется также и модуль волнового вектора.
382
Дополнения к лекции 18
Электрически заряженные частицы, входящие в состав кристалла,
при взаимодействии с электромагнитным полем падающей волны явля-
ются источниками вторичных (рассеянных) волн. В нашей прибли-
женной физической картине каждый точечный рассеивающий центр с
радиус-вектором pj порождает вторичную (рассеянную) сферическую
волну вида
(j
—Ао ехр (гкор7) ехр [г(кугу - cot)], (Д.18.3)
гз
где гу — вектор, соединяющий произвольный у-й центр рассеяния (ис-
точник у-й вторичной волны) и точку наблюдения, а ку — волновой
вектор волны, рассеянной у-м центром. Коэффициент С характеризует
особенности рассеивающего центра, который, как было упомянуто выше,
может быть атомом или группой атомов.
Рассмотрим результат интерференции рассеянных волн в точке, уда-
ленной от всех рассеивающих центров на расстояние много большее, чем
межатомные расстояния в кристалле. Обозначим через R радиус-вектор
точки наблюдения, где находится детектор, в котором складываются ко-
лебания, вызванные пришедшими в эту точку рассеянными волнами (см.
Рис. Д.18.1. Геометрическая схема дифракции рентгеновских лучей на кристалле
рис. Д.18.1). Единичный вектор s задает направление от кристалла к де-
тектору. Тогда радиус-вектор R можно представить произведением Rs,
где R — модуль вектора R.
Если величина R значительно больше модулей векторов pj (как это
выполнено в оговоренных выше условиях), то от разных центров рассея-
ния в месторасположение детектора приходят волны, которые с достаточ-
ной точностью можно считать плоскими. Тогда все векторы гу (Д.18.3)
можно приближенно заменить одним вектором г (см. рис. Д.18.1).
Волновые векторы ку всех рассеянных волн, регистрируемых детек-
тором, можно считать приблизительно равными и параллельными век-
тору R. Так как рассеяние полагается упругим, то все модули векторов
ку равны ко, и волновые векторы регистрируемых всех волн можно вы-
разить как k = kos.
Из рис. Д.18.1 непосредственно следует, что
г = R-P>.
(Д.18.4)
Дополнения к лекции 18
383
Подставив (Д.18.4) в выражение (Д.18.3), получим представление
рассеянной волны, приходящей в точку наблюдения с радиус-вектором
R, в виде
Q
Ej(R) = Ао—ехр [г(к0 — k)py] ехр [z(kR — (Д.18.5)
Учтем, что векторы к и R параллельны, и в знаменателе (Д.18.5)
заменим модуль вектора г на R, величины которых мало отличаются.
В результате функция рассеянной волны примет вид
(j
= Aq— ехр (ikoR) ехр [г(к0 - k)pj] ехР (~^0- (Д.18.6)
Введем вектор разности волновых векторов рассеянной и первичной
волн:
Лк = к -к0. (Д.18.7)
Тогда комплексную амплитуду волны, рассеянной j-м центром в
точке наблюдения, можно записать в виде
А = Л0§ехр(-гДк-р,), (Д.18.8)
R J
где Ао — постоянная величина, равная Aq ехр
Угол между волновыми векторами ко и к (или между векторами so
и s) называется углом рассеяния. Этот угол в кристаллографии обычно
принято обозначать 20.
Амплитуда суммарной волны, возникшей вследствие интерферен-
ции, в точке наблюдения выразится суммой
Л(К) = £>хр (—гДк • Pj), (Д.18.9)
j
где суммирование проводится по всем центрам рассеяния.
Очевидно, что величина амплитуды суммарной волны зависит от
координат рассеивающих центров, угла рассеяния 20, а также от мо-
дуля волнового вектора ко (или от длины волны А). Таким образом,
вследствие интерференции отдельных вторичных волн, в разных на-
правлениях распространяются как усиленные, так и ослабленные пучки
рассеянного излучения.
Если начало координат выбрано в каком-либо узле кристаллической
решетки, то радиус-векторы рассеивающих центров pj совпадают с век-
торами трансляций (Д.18.2).
Так как любой реальный кристалл имеет конечные размеры, то ко-
личество рассеивающих центров в подобном кристалле конечно, и числа
u, v, w будут лежать внутри ограниченного (пусть и очень большого)
множества значений М. Тогда комплексная амплитуда суммарной рас-
сеянной волны, распространяющейся в заданном направлении s, может
384
Дополнения к лекции 18
быть записана в виде
Д(И) = С^ £ ехр(-гТДк) =
u,v,wGAf
= ехр [—i(ua. + vb + wc)Ak]. (Д.18.10)
u,v,wEM
Теперь очевидно, что амплитуда (Д.18.10) будет достигать макси-
мального значения при выполнении условия
ТДк = 2тг?Л (Д.18.11)
где N — любое целое число.
Из выражения (Д.18.2) следует, что условие дифракции (Д.18.11) вы-
полняется, если совместно удовлетворяются три следующих уравнения:
а Дк = 2тгЛ, b Дк = 2тг/с, с Дк = 2тг/, (Д.18.12)
где h, k, I — некоторые целые числа.
Векторное уравнение (Д.18.11) или система трех уравнений (Д.18.12)
называются условиями Лауэ. Они являются условием конструктивной
интерференции, при которой фазы слагаемых волн в сумме ?Д.18.10)
сдвинуты на целое число периодов гармонической функции. При этом
интерферирующие волны сформируют в данном направлении волну зна-
чительной интенсивности. Эта волна, которая приближенно может счи-
таться плоской, распространяется в направлении единичного вектора s
под углом 20 к направлению первичной волны, заданного единичным
вектором So- Описанное явление рассеяния рентгеновских лучей на кри-
сталле по аналогии с оптикой можно назвать рентгеновской дифракцией
Фраунгофера.
18.2. Синхротронное излучение
Рассмотрим частицу с массой т и электрическим зарядогл q, нахо-
дящуюся в однородном магнитном поле с индукцией В. На частицу
действует сила Лоренца, равная
FL = - [vB], (Д.18.13)
С
где v — скорость частицы, с — скорость света в вакууме.
Уравнение движения частицы можно записать в следующем виде:
4p = “[vB], (Д.18.14)
dt с
где р — импульс частицы.
Так как мы будем рассматривать частицы с различной кинетической
энергией, в том числе и превышающую энергию покоя тс2, то импульс
целесообразно записать в релятивистском виде:
Е
p=-rv, (Д.18.15)
с2
Дополнения к лекции 18
385
где Е — полная энергия частицы, равная сумме кинетической энергии
Екин и энергии покоя тс2. В магнитном поле В энергия частицы Е не
меняется, поэтому уравнение движения (18.2.2) примет вид
(Д.18.16)
Выберем декартову систему координат, направив ось Z вдоль вектора
однородного магнитного поля В. Введем обозначение
где В — модуль магнитного поля В, и перепишем векторное уравнение
(Д.18.16) в отдельных проекциях:
vx — vy = -wvx, vz = О, (Д.18.18)
где vx, vy, vz — проекции вектора скорости v частицы.
Для интегрирования уравнений (Д.18.18) следует сначала сложить
первое со вторым, умноженным на мнимую единицу г:
— \ух + ivy) = -гш\ух + ivy).
Решение последнего уравнения записывается в виде
vx + ivy — а ехр (—iwf), (Д.18.19)
где а — комплексная постоянная, t — время. Запишем величину а в
виде vorexp(—ш), где vqt и а — вещественные параметры. Тогда в
уравнении (Д.18.19) можно разделить действительную и мнимую части
и получить функции двух проекций скорости частицы:
vx = vqt cos (wt + a), vy = -vor sin (u>t + a). (Д.18.20)
Параметр а является начальной фазой. Величина vqt вычисляется из
выражений (Д.18.20):
vor = (Д.18.21)
и имеет смысл модуля проекции скорости частицы на плоскость XY,
перпендикулярной вектору магнитного поля В. При движении частицы
величина vqt остается постоянной.
Решение третьего уравнения (Д.18.18) дает постоянную проекцию
скорости частицы vqz на направление магнитного поля В.
Интегрирование по времени уравнений (Д. 18.20) дает зависимости
координат частицы от времени, которые целесообразно записать в сле-
дующем виде:
х — хо + .ftsin (cvt + а), у = уо + Rcos (cvt + а), (Д.18.22)
386
Дополнения к лекции 18
где параметр R равен
R = — = (Д.18.23)
со qcB
Интегрирование уравнения vz = vqz дает линейную функцию для тре-
тьей координаты:
Z = z0 + vOzt- (Д.18.24)
Уравнения (Д. 18.22) и (Д.18.24) описывают движение электрически
заряженной частицы в однородном магнитном поле по винтовой линии,
ось которой направлена по вектору поля В, а радиус витка R опреде-
ляется формулой (Д. 18.23). В частном случае, когда voz = 0, частица
движется по окружности радиуса R в плоскости, перпендикулярной век-
тору магнитного поля В.
Частота вращения выражается формулой (Д.18.17) и обратно про-
порциональна полной энергии частицы Е. В нерелятивистском случае,
когда кинетическая энергия частицы много меньше ее энергии покоя
(#кин гас2), частота вращения становится не зависящей от кинетиче-
ской энергии частицы:
wc = (Д.18.25)
те
Величина (Д. 18.25) называется циклотронной частотой, которая опи-
сывает вращение нерелятивистских частиц в однородном магнитном
поле.
В противоположном случае, когда кинетическая энергия ЕКИН части-
цы много больше ее энергии покоя, в знаменателе выражения (Д.18.17)
можно пренебречь энергией покоя тс2 ЕКИН. В этом случае (который
называют ультрарелятивистским) частота вращения становится обратно
пропорциональной кинетической энергии частицы:
w (Д.18.26)
•^КИН
Далее рассматривается электрон е, который вращается по окруж-
ности в постоянном однородном магнитном поле В. Ясно, что при
этом вектор скорости v электрона остается перпендикулярным вектору
поля В. Радиус окружности R и частота вращения со, согласно (Д.18.23)
и (Д.18.17), выражаются следующим образом:
R = v, и = (Д-18.27)
еВу/1 — тс
введено обозначение
/ v \
7=1-1 . (Д.18.28)
\с/
Круговое движение электрически заряженной частицы во внешнем
магнитном поле является ускоренным. Как известно из классической
электродинамики, любая ускоренно движущаяся частица излучает элек-
Дополнения к лекции 18
387
тромагнитные волны с интенсивностью, которая выражается формулой
(18.7) лекции 18. В нашего случае интенсивность излучения равняется
Зт2с5(1 — 7)
(Д.18.29)
Угловое распределение излучаемой энергии анизотропно и выражается
следующей формулой:
_ е4В27(1 - 7) (2 - cos2 0 - 7(1 + З7) cos4 0/4)
8тгт2с3 (1 — 7 cos2 0)7/2
(Д.18.30)
где 0 — угол между волновым вектором излучения и плоскостью орбиты
электрона, dQ — элемент телесного угла.
Спектр излучения должен представляться разложением в ряд Фурье
по частотам соп = tw, где частота со задана второй формулой из (Д. 18.27),
а п — натуральное число. Спектральная плотность выражается через
специальные функции Бесселя и имеет весьма громоздкий вид, приво-
димый в курсах теории поля.
Для нас особый интерес представляет ультрарелятивистский случай
(^кин когда скорость вращающегося электрона очень близка к
скорости света в вакууме. В этом случае испускаемое излучение называ-
ется синхротронным и обладает интересными специфическими харак-
теристиками.
Во-первых, интенсивность излучения (Д.18.29) в ультрарелятивист-
ском случае становится пропорциональной квадрату энергии электрона:
2е4#2 ( Е \
3m2c3 \тес2/
(Д.18.31)
причем Е ~ £?кин.
Во-вторых, практически вся энергия синхротронного излучения со-
средоточена в узком угловом интервале Д0 вблизи плоскости орбиты
электрона, который по порядку величины равен отношению энергий
Д0«
о
тес£
Е ’
(Д.18.32)
Максимум спектральной плотности синхротронного излучения ле-
жит в области высоких частот = псо, где натуральное число п имеет
следующий порядок:
( Е \3
п ~ . (Д.18.33)
\тес2 J
При этом превалирующая часть энергии излучения сосредоточена в обла-
сти частот
Е \
тес2 J
2
^шах
еВ
тес
(Д.18.34)
388 Дополнения к лекции 18
Спектр синхротронного излучения состоит из множества близко располо-
женных спектральных линий, т. е. имеет квазинепрерывный характер.
Синхротронное излучение получило свое название от одного из типов
ускорителей электронов — синхротрона. Этот циклический ускоритель
предназначен для получения мощных импульсов ультрарелятивистских
электронов с энергией 100 МэВ и выше. Принципиальная конструкция
ускоряющей системы синхротрона приведена на рис. Д.18.2.
Электроны приобретают энергию несколько раз за оборот, проходя
через резонаторы, питаемые высокочастотным напряжением. Резона-
тор представляет собой цилиндрическую металлическую трубку, внутри
Рис. Д.18.2. Принципиальная схема синхротрона:
1 — ускоряющие резонаторы, 2 — отклоняющие магниты, 3 — фокусирующие магниты,
4 — инжектор электронов. Штриховая линия — орбита ускоряемых электронов. Жирные
стрелки указывают направление ускоряющего электрического поля
которой с помощью высокочастотного генератора возбуждаются электро-
магнитные волны. Режим работы синхротрона таков, что ускоряемый
сгусток электронов проходит через резонатор в тот интервал времени,
когда вектор электрического поля направлен вдоль оси резонатора в опре-
деленную сторону. После получения импульса в резонаторе сгусток элек-
тронов движется под действием магнитного поля, а затем входит в сле-
дующий резонатор. Для того чтобы электроны вновь получили импульс
в том же направлении, необходимо совпадение частоты генератора с ча-
стотой вращения электронов.
В синхротронах магнитное поле создается в вакуумной камере, име-
ющей форму тора. В процессе ускорения сгусток электронов движется по
окружности постоянного радиуса R. Так как ускоряемые в синхротроне
электроны являются ультрарелятивистскими, то их скорость практиче-
ски совпадает со скоростью света, а радиус круговой траектории, в со-
ответствии с формулами (Д. 18.23) и (Д. 18.27), пропорционален энергии
частицы:
Е
Я=~Б- (Д.18.35)
Дополнения к лекции 18 389
Период вращения ультрарелятивистской частицы
Т = (Д.18.36)
не зависит от ее энергии при фиксированном радиусе траектории. Для
удержания на такой траектории ускоряемого ультрарелятивистского
электрона необходимо увеличивать индукцию магнитного поля пропор-
ционально его энергии Е во время всего процесса ускорения.
Принцип работы синхротрона требует инжекции электронов, перво-
начально ускоренных до энергии порядка 10 МэВ. Для этого использу-
ются линейные ускорители, бетатроны или микротроны. Чтобы напра-
вить пучок ускоренных электронов в определенную цель, достаточно в
надлежащий момент времени отключить магнитное поле, удерживаю-
щее электроны на круговой траектории, или включить дополнительное
отклоняющее магнитное поле.
На рис. Д.18.2 изображены, кроме отклоняющих, фокусирующие
магниты. Они с помощью неоднородных магнитных полей специаль-
ной конфигурации позволяют уменьшать угловую расфокусировку пучка
электронов.
Синхротроны прежде всего строились для решения проблем физики
элементарных частиц высоких энергий. С помощью синхротронов прово-
дились исследования столкновений ультрарелятивистских электронов с
другими элементарными частицами. Количество электронов в отдельном
импульсе может превышать ~ 1О10, а количество импульсов достигает
несколько десятков в секунду. Эксплуатация синхротронов показала, что
при энергии электронов, превышающей 100 МэВ, ее значительная часть
теряется на электромагнитное излучение, описанное выше в данном до-
полнении. Это обстоятельство является главным ограничением на рост
энергии ускоряемых частиц. Альтернативой синхротронам являются
большие линейные ускорители, в которых электроны движутся по пря-
мой линии и потери энергии на излучение сведены к минимуму. К при-
меру, линейный ускоритель в Стенфорде (США) имеет длину около Зкм
и служит для ускорения электронов вплоть до энергии 50 ГэВ.
С другой стороны, синхротроны в настоящее время широко исполь-
зуются в качестве мощных источников рентгеновского излучения с раз-
личными длинами волн. В таких синхротронах мощный поток электро-
нов ускоряется до энергий порядка 100 МэВ. При этом происходит генери-
рование синхротронного излучения, которое, в соответствии с (Д. 18.34),
охватывает рентгеновский диапазон. Согласно формуле (Д. 18.32), прак-
тически весь поток излучения локализован вблизи плоскости орбит уско-
ряемых электронов. Коллиматоры формируют узкие пучки излучения,
которые выходят по касательным к электронным орбитам и направля-
ются на кристаллы-монохроматоры. В результате брэгговского отраже-
ния от монокристалла рентгеновское излучение разлагается в спектр.
Системы поглощающих диафрагм позволяют «вырезать» любой доста-
точно узкий интервал длин волн рентгеновских лучей, который, в свою
очередь, направляется на исследуемый объект.
Кроме того, мгновенное отключение одного из отклоняющих магни-
тов позволяет вывести пучок электронов с круговой орбиты и направить
его на массивную мишень, изготовленную из тугоплавкого металла с
большим химическим номером Z. Взаимодействие быстрых электро-
нов и атомных ядер с электрическим зарядом Ze порождает генерацию
390
Дополнения к лекции 18
мощного потока тормозного излучения широкого спектра, которое ис-
пользуется в физических исследованиях.
В Российском научном центре «Курчатовский институт» функциони-
рует источник синхротронного излучения, представляющий собой ин-
женерный комплекс, в состав которого входит форинжектор — линей-
ный ускоритель на энергию до 100 МэВ, малое накопительное кольцо на
энергию 450 МэВ и большое накопительное кольцо на энергию 2,5 ГэВ.
Комплекс предназначен для генерации мощных пучков электромагнит-
ного излучения в диапазоне от 0,1 до 2000 А. Ток электронов составляет
300 мА. Таким образом, синхротронный комплекс «Курчатовского ин-
ститута» позволяет подвергать исследуемые объекты воздействию мощ-
ных потоков электромагнитного излучения от инфракрасного до жесткого
рентгеновского диапазона.
Синхротронное излучение может быть не только рукотворным, но и
иметь природное происхождение. В ходе астрофизических исследова-
ний после второй мировой войны было обнаружено, что многие косми-
ческие объекты испускают мощное электромагнитное излучение, облада-
ющее линейной поляризацией и имеющее характерный синхротронный
спектр, который по своей форме принципиально отличается от спектра
теплового излучения, определяемого формулой Планка. В первую очередь
было зарегистрировано синхротронное излучение от радиотуманностей,
которые являются остатками взрывов Сверхновых. При этом синхро-
тронный характер спектра наблюдается не только в метровом радиодиа-
пазоне, но и в оптическом и даже рентгеновском и гамма-диапазоне. Та-
ким образом, было открыто, что остатки взрывов Сверхновых содержат
огромные облака горячей намагниченной плазмы, наполненные ультра-
релятивистскими электронами.
Например, Крабовидная туманность представляет собой остаток
взрыва Сверхновой 1054 г., подробно описанной в китайских хрониках.
Анализ спектров излучения в разных диапазонах позволил установить,
что внутренние области Крабовидной туманности обладают магнитным
полем порядка 10-3Гс. Тогда по уравнению (Д. 18.34) легко оценить,
что наблюдаемое синхротронное излучение с длиной волны А 0,1 А
генерируется электронами с энергией порядка 1014 эВ!
Впоследствии было обнаружено синхротронное излучение радиога-
лактик, квазаров, джетов и т.д. В настоящее время исследование син-
хротронного излучения является одним из важных методов астрофизики
и космологии.
Лекция 19
ЗАКОН МОЗЛИ, ТОНКАЯ СТРУКТУРА
ХАРАКТЕРИСТИЧЕСКОГО РЕНТГЕНОВСКОГО
ИЗЛУЧЕНИЯ И ЭФФЕКТ ОЖЕ
19.1. Закон Мозли
Спектральные исследования рентгеновских лучей позволили
обнаружить монотонные зависимости длин волн характеристиче-
ских линий от порядкового номера химического элемента Z (см.
рис. 19.1).
Рис. 19.1. Диаграмма расположения характеристических линий рентгеновских
лучей для различных химических элементов.
Вертикальными черточками обозначены спектральные линии ХРИ отдельных элементов.
По вертикали отложены атомные номера. Буквами обозначены спектральные серии
392 Лекция 19. Закон Мозли, эффект Оже
В 1913 г. ученик Э. Резерфорда Генри Мозли (1887-1915) про-
вел тщательные измерения длины волны спектральной линии Ка
для 33-х химических элементов и после обработки результатов
предложил эмпирическую формулу, связывающую длину волны
Ака с порядковым химическим номером Z:
-^- = C{Z-a)\ (19.1)
где С и а — эмпирические константы. Мозли положил а = 1,
константа С, вычисленная по эмпирическим данным, равнялась
8,23 • 104 см"1.
Закон Мозли (19.1) позволяет выразить порядковый номер Z
химического элемента через измеренную длину волны Хка спек-
тральной линии Ка характеристического рентгеновского излуче-
ния этого элемента. Ближайшее целое от величины
ж+1 (19-2)
дает значение атомного номера Z. При этом точность определения
эмпирических констант такова, что погрешность величины (19.2)
значительно меньше единицы. Следовательно, используя закон
Мозли, можно по измеренной длине волны Ака вычислить точно
атомный номер любого химического элемента, который входит в
состав анода.
Для спектральных линий других серий ХРИ Г. Мозли получил
приближенные соотношения, аналогичные формуле (19.1). Разли-
чие заключалось лишь в величине констант С и а, входящих в
формулу. Но при этом для всех спектральных линий наблюдалась
линейная зависимость между атомным номером химического эле-
мента и величиной 1/vCx (см. рис. 19.2).
К 1914 г. в таблице Менделеева оставались пустые места, отве-
чающие еще не открытым элементам. Кроме того, расположение
некоторых элементов, основанное на значениях их атомных масс
и химических свойствах, оставалось сомнительным. Например,
элементы с номерами от Z = 58 до Z = 71 (лантаноиды) обладают
практически одинаковыми химическими свойствами, а трудность
измерения атомных масс обусловлена их сложным изотопным со-
ставом и технологическими сложностями разделения элементов.
Как следствие, до работ Мозли расположение ряда химических
элементов в таблице Менделеева было предметом дискуссий хи-
миков. Закон Мозли впервые позволил достоверно расставить все
химические элементы по клеткам таблицы Менделеева.
Кроме того, Г. Мозли убедительно доказал, что Д.И. Менделеев
был прав, когда при составлении таблицы в первую очередь ори-
19.1. Закон Мозли
393
ентировался на химические свойства элементов, иногда нарушая
тенденцию последовательного увеличения атомной массы М с воз-
растанием порядкового номера Z соответствующего химического
i/Vx
Рис. 19.2. Зависимость величины 1 / а/А от атомного номера химического эле-
мента (диаграммы Мозли) для спектральных линий Ka (1), La (2) и Ма (<?)
элемента. Ниже приведены фрагменты таблицы Менделеева, в ко-
торых не выполняется монотонная зависимость M(Z).
Из табл. 19.1 видно, что, если следовать тенденции монотон-
ного возрастания атомной массы с ростом химического номера
Z, калий (щелочной металл) и аргон (инертный газ) должны по-
меняться в таблице местами. Но тогда калий попадет в группу
благородных газов, а аргон в группу щелочных металлов, что на-
ходится в противоречии с общими положениями Периодического
закона.
Таблица 19.1. Фрагменты таблицы Менделеева
Химический элемент Порядковый номер Масса атома (а.е.м)
Аг 18 39,95
К 19 39,10
Со 27 58,9
Ni 28 58,7
Те 52 127,6
I 53 126,9
После работ Мозли и прецизионных спектрометрических ис-
следований вышеприведенные особенности таблицы Менделеева
были объяснены неоднородным изотопным составом естествен-
ной смеси химических элементов на нашей планете (см. дополне-
ние 19.1).
394 Лекция 19. Закон Мозли, эффект Оже
Из вышеизложенного ясно, что трудно переоценить значение
работы Г. Мозли для развития фундаментальной физики и химии.
Лишь преждевременная смерть Г. Мозли (он погиб в первую миро-
вую войну, не дожив до своего 30-летия) не позволила ему стать
лауреатом Нобелевской премии.
На базе работ Г. Мозли разработан метод рентгеноспект-
рального анализа, который позволяет, не разрушая объект ис-
следования, обнаруживать наличие определенного химического
элемента, даже если его относительная концентрация составляет
10“4% (т.е. один атом на миллион).
Использование рентгеноспектрального анализа позволило в те-
чение двух десятилетий заполнить все пустые клетки таблицы
Менделеева. Сам Г. Мозли пытался по спектрам ХРИ обнаружить
неизвестный элемент с номером от Z — 72, который был най-
ден только в 1923 г. и назван гафнием. Тщательные поиски не
привели только к обнаружению химического элемента с номером
Z — 43, который был предсказан Д.И. Менделеевым под условным
названием «экамарганец». Он был синтезирован искусственно ме-
тодами ядерной физики в 1937 г. и назван технецием. Впослед-
ствии выяснилось, что все изотопы технеция радиоактивны и не-
стабильны.
Наконец, работа Г. Мозли сделала несостоятельными псевдона-
учные спекуляции об открытиях новых стабильных химических
элементов. Г. Мозли установил, что между водородом и ураном
может располагаться точно 90 других элементов. Все трансура-
новые химические элементы (с порядковым номером Z > 92) не
имеют стабильных изотопов.
19.2. Механизм образования
характеристического рентгеновского излучения
Механизм возникновения линейчатого спектра характеристи-
ческого рентгеновского излучения был впервые разработан В. Кос-
селем (1888-1956) в 1916 г. на основе квантовой теории Бора.
Необходимой причиной образования ХРИ является образова-
ние вакансий во внутренних электронных оболочках атома. Элек-
троны, ускоренные в рентгеновской трубке, получают кинетиче-
скую энергию порядка десятков килоэлектрон-вольт. С такой
высокой энергией они проникают во внутренние области атома и
взаимодействуют с электронами внутренних оболочек, у которых
главное квантовое число п имеет малое значение (n = 1,2,3,...).
В квантовой механике доказано, что вероятность взаимодействия
электрона-снаряда и внутреннего электрона атома растет с увели-
чением плотности пространственного распределения электронной
плотности, т. е. с величиной квадрата модуля волновой функции
одноэлектронного состояния |Ф|2. Следовательно, наиболее ве-
19.2. Механизм образования рентгеновского излучения 395
роятным будет взаимодействие электрона-снаряда с электронами
оболочки Is, у которого главное квантовое число п = 1. Если при
этом кинетическая энергия электрона, бомбардирующего атом,
превышает энергию связи внутреннего электрона, то последний
может оторваться от атома. Произойдет ионизация атома на элек-
тронном /С-слое, и в электронной оболочке 1s образуется вакансия.
При ионизации атом получает энергию, равную энергии связи
удаленного электрона, и поэтому атом переходит в возбужденное
состояние. Возбуждение атома может сняться путем заполнения
вакансии электроном из другой оболочки, обладающей большей
энергией, а разность энергий может быть унесена из атома фо-
тоном. Энергия такого фотона е дается уравнением сохранения
энергии
e = En2-Eni, (19.3)
где ЕП2 и Eni — энергии стационарных состояний, между кото-
рыми произошел переход. При этом энергия атома уменьшится
на разность энергий верхнего и нижнего стационарных состоя-
ний. Так как каждый атом обладает определенным дискретным
набором одноэлектронных стационарных состояний, то спектр ис-
пускаемых фотонов имеет линейчатый вид. Таким образом, ХРИ
образуется радиационными переходами электронов при запол-
нении вакансий во внутренних электронных оболочках.
Рассмотрим механизм образования отдельных серий ХРИ.
Пусть вакансия образовалась в первом электронном слое (с глав-
ным квантовым числом п = 1). Тогда становятся возможными
переходы электронов из более высокоэнергетических электронных
слоев (с главными квантовыми числами п > 1) в образованные
вакансии. При этих переходах генерируются характеристические
линии Jf-серии.
Энергетическая схема образования /С-серии приведена на
рис. 19.3а. Очевидно, что каждой линии соответствует переход из
очередного электронного слоя.
Квантовомеханические расчеты показывают, что вероятность
радиационных переходов в вакансию /С-слоя резко уменьшается
с увеличением главного квантового числа верхнего электронно-
го слоя. -Иначе говоря, интенсивность /С^-линии значительно
меньше интенсивности JCq-линии, а интенсивность /С7-линии го-
раздо меньше интенсивности К^-линии, что хорошо видно на
рис. 18.9.
Ясно, что число спектральных линий в спектральной серии ха-
рактеристического рентгеновского излучения, в принципе, опреде-
ляется количеством электронных слоев атома, содержащих элек-
троны. Но с ростом квантового числа п энергии слоев сближаются,
и отдельные спектральные линии могут уже не разрешаться рент-
геновским спектрометром.
396
Лекция 19. Закон Мозли, эффект Оже
На рис. 19.3а хорошо видно, что разность энергий электрон-
ных слоев Еп — Е\ увеличивается с ростом главного квантового
Рис. 19.3. Схема образования спектральных линий характеристического рент-
геновского излучения JC-серии (а) и L-серии (б). Сплошные горизонтальные
линии обозначают средние энергии электронных слоев. Различием энергий элек-
тронных оболочек в данной схеме пренебрегается
числа п верхнего электронного слоя. Отсюда следует ранее от-
меченная эмпирическая закономерность (18.5) А/<а > А^ > А/<7,
которая видна на рис. 18.9.
Так как для образования /С-серии необходимо создание вакан-
сии в электронном /С-слое, то очевидно, что пороговое напряже-
ние возбуждения /С-серии определяется энергией связи электронов
этого слоя:
eUK = \Ev\. (19.4)
Для вычисления порогового напряжения возбуждения /С-серии
можно использовать значения энергий связи электронов оболочки
1s, изображенные на рис. 15.2.
Если ускоряющее напряжение рентгеновской трубки недоста-
точно велико и eU < |£\|, то характеристическая /С-серия не мо-
жет возникнуть. Но если при этом eU > |L?2| (т.е. кинетическая
энергия электрона-снаряда превышает энергию связи атомного
электрона второго электронного слоя), то возникают вакансии в
оболочках электронного L-слоя. Заполнение этих вакансий пере-
ходами электронов из более высокоэнергетических слоев (с глав-
ными квантовыми числами п > 2) приводит к генерированию
L-серии ХРИ. Переходы из слоев с главными квантовыми числами
п = 3,4,... генерируют спектральные линии LQ, L@ и т. д. Энер-
гетическая схема образования L-серии приведена на рис. 19.36
с указанием обозначений характеристических спектральных ли-
ний. Из-за роста энергии электронных слоев с главным кванто-
19.2. Механизм образования рентгеновского излучения
397
вым числом п длины волн L-серии последовательно уменьшаются
> ^^/3 > * * *
М-серия ХРИ образуется аналогично после заполнения вакан-
сий в электронном слое атома с главным квантовым числом п = 3.
При электронной бомбардировке в атомах с большим поряд-
ковым номером возможно образование вакансий в электронных
слоях с главными квантовыми числами п = 4,5 и 6 с последую-
щим заполнением их электронами из более высокоэнергетических
слоев. При этом радиационные переходы генерируют характери-
стические линии, которые можно, в принципе, объединить в 7V-,
О-, F-серии. Например, в атоме урана (и других атомах 7-го пери-
ода таблицы Менделеева) возможно образование вакансии в Р-слое
(главное квантовое число п = 6), которая может заполниться пере-
ходом электрона из Q-слоя (с главным квантовым числом п = 7).
Испущенные при этом фотоны образуют характеристическую спек-
тральную линию, которую, согласно вышеописанной терминоло-
гии, следует отнести к F-серии ХРИ.
Очевидно, что при энергии ускоренных электронов е£7, превы-
шающих энергию ионизации Р?-слоя, происходит образование не
только /f-серии, но всех остальных серий ХРИ, которые, в прин-
ципе, может генерировать данный химический элемент.
Расчет длин волн спектра ХРИ, в принципе, возможен
нове уравнения (19.3):
2тгЛс
^п2 ~~ Еп1
Следовательно, для вычисления длин волн спектральных
ХРИ требуется знать энергии электронов для всех электронных
слоев атома.
Экспериментальные результаты (см. рис. 15.2) показывают,
что энергии электронов /С-слоя (n = 1) плавно изменяются с ро-
стом порядкового номера Z химического элемента. Аппроксима-
ция результатов позволяется приближенно выразить энергию этих
электронов в следующем виде:
Е. = -Ry(Z-5i)2, (19.6)
где для всех химических элементов можно приближенно положить
S1 = l.
Представим энергии остальных электронных слоев атома в во-
дородоподобном виде, вводя дополнительно поправки Sn на экра-
нирование электрического поля атомного ядра электронами вну-
тренних оболочек. Тогда эти энергии могут быть представлены
следующей приближенной формулой:
на ос-
(19.5)
ЛИНИЙ
Ry(Z-Sn)2
(19-7)
п = 1,2,...
398
Лекция 19. Закон Мозли, эффект Оже
Выразим обратную длину волны ХРИ спектральной линии Ка
с помощью выражений (19.5) и (19.7), используя постоянную Рид-
берга (8.11):
1 Е2 — Е\
XKa 2л7гс
= RH (Z-Si)2-1(Z-S2)2 .
(19.8)
Если положить константы Si и S2 одинаковыми (т. е. Si = S2 =
= S), то последнее выражение совпадет с формулой Мозли (19.1):
xb>(z-s)2
(19.9)
Нетрудно убедится в том, что величина 3Rh/^ близка к эмпириче-
ской константе С в формуле (19.1). Таким образом, закон Мозли
является следствием квантовой теории атома и имеет приближен-
ный характер, т.е. дает приближенное значение длины волны
спектральной линии Ка характеристического рентгеновского из-
лучения.
Анализ экспериментальных спектров ХРИ показывает, что
S2 7^ Si. Данные экспериментов позволяют с определенным при-
ближением положить S2 = 3,5 и S3 = 10,5. Это означает, что
закон Мозли для Ка линии ХРИ приобретает вид
-^- = Rh [(Z-l)2-|(Z-3,5)2
L 4
(19.10)
Используя вышеприведенные числовые значения констант экра-
нирования Si, S2 и S3, можно, комбинируя формулы (19.5) и
(19.7), вычислить длины волн спектральной линий Ка, К@ и La
для химических элементов с заданным порядковым номером Z.
Однако сравнение результатов расчетов с экспериментальными
данными показывает расхождение на 10-20%. Причина столь зна-
чительного различия заключается прежде всего в том, что, со-
гласно формуле (19.7), энергия стационарного состояния электрона
зависит только от главного квантового числа, хотя для многоэлек-
тронных атомов эта энергия (даже в приближении конфигураций!)
зависит еще и от орбитального числа Z, что обсуждалось в лек-
ции 14.
После заполнения вакансии вследствие электронного перехода
возникает новая вакансия в более высокоэнергетическом электрон-
ном слое. Следовательно, возникают условия для генерирования
спектральной линии ХРИ более длинноволновой серии. Таким
образом, электронные вакансии перемещаются из слоя в слой
вверх по оси энергий. При этом может испускаться каскад спек-
тральных линий ХРИ различных серий, атом в результате оста-
ется в ионизованном состоянии.
19.3. Тонкая структура рентгеновского излучения 399
19.3. Тонкая структура
характеристического рентгеновского излучения
В процессе совершенствования экспериментальной техники
рентгеновской спектрометрии было обнаружено, что спектральные
линии ХРИ, как и оптические спектры, обладают тонкой структу-
рой. Например, самая интенсивная линия рентгеновских харак-
теристических спектров представляет собой дублет, компоненты
которого были названы Ка\ и Ка2- Структура остальных линий
ХРИ оказались более сложной, причем L-серия оказалась более бо-
гатой компонентами тонкой структуры, чем /С-серия (см. пример
на рис. 19.4).
Предыдущая классификация спектральных линий ХРИ на ос-
нове теории Косселя является довольно грубой, так как энергия
стационарного состояния электрона принимается зависящей толь-
ко от главного квантового числа.
Ранее было выяснено (см. лекции 14-17), что в многоэлектрон-
ных атомах энергия стационарного состояния электрона сущест-
венно зависит от орбитального числа Z, а при учете спин-орбиталь-
ного взаимодействия — дополнительно от квантового числа j. При
этом зависимость энергии от орбитального числа I гораздо более
резкая, чем от числа j (см. рис. 16.2, 16.3, 17.3 17.4, Д.17.1).
Это означает, что при анализе оптических спектров атомов спин-
орбитальное взаимодействие можно рассматривать как малое воз-
мущение.
Исследование спектров ХРИ доказывает, что влияние спин-
орбитального взаимодействия на энергии одноэлектронных состо-
яний с низким главным квантовым числом (особенно в тяжелых
атомах) столь велико, что его уже нельзя считать малым возмуще-
нием. Сдвиг энергии одноэлектронного состояния при изменении
на единицу как числа Z, так и числа j имеет одинаковый порядок.
Как следствие, при анализе тонкой структуры ХРИ необходимо
ввести понятие электронной подоболочки.
400 Лекция 19. Закон Мозли, эффект Оже
Электронной подоболочкой называется набор одноэлектрон-
ных состояний с фиксированными квантовыми числами n, I и j.
Для обозначения используется символ оболочки с дополнительным
нижним субиндексом равным квантовому числу j. Такие символы
уже использовались в лекции 13 при анализе тонкой структуры
спектра атома водорода. В отсутствие внешних электромагнит-
ных полей электроны в подоболочке вырождены по квантовому
числу mj. Количество одноэлектронных состояний в подоболочке
определяется только квантовым числом j и равняется 2j 4- 1 (см.
§ 12.4 лекции 12).
При учете спин-орбитального взаимодействия спектральную
линию ХРИ следует рассматривать как результат радиационного
перехода между двумя электронными подоболочками. Электрон
из более высокоэнергетической подоболочки заполняет вакансию в
подоболочке, лежащей ниже по оси энергий.
Каждой подоболочке соответствует определенная энергия (энер-
гетический уровень). Исторически в рентгеновской физике сложи-
лась система обозначений энергетических уровней, которая при-
ведена в табл. 19.2.
Таблица 19.2. Рентгеновские символы уровней энергии
электронных подоболочек
Электронная подоболочка Рентгеновский символ Электронная подоболочка Рентгеновский символ
1^1/2 К 4A/2 Nvil
251/2 и ^51/2 Ol
2Р1/2 Ln 5pi/2 Он
2рз/2 Lni 5рз/2 Ош
351/2 Mi 5с?3/2 Oiv
ЗР1/2 Мп 5с?5/2 Оу
Зрз/2 Мт 5/5/2 Ovi
Зб?3/2 Mw 5/7/2 Ovu
Зс?5/2 My 651/2 Pi
451/2 Ni 6pi/2 Ри
4Р1/2 Nn 6рз/2 Рщ
4рз/2 Nin бс?3/2 Pw
4с?3/2 Mv 6с?5/2 Fv
4с?5/2 Ny 751/2 Qi
4/б/2 N\i
Из табл. 19.2 следует, что первый электронный слой содержит
одну подоболочку, второй электронный слой — три (Li, Lu, Lm),
третий — пять подоболочек (Mi, Мц, Мщ, Мр/, Му) и т.д. При
анализе тонкой структуры ХРИ следует учитывать правила от-
19.3. Тонкая структура рентгеновского излучения 401
бора для радиационных переходов, которые описаны в предыду-
щих лекциях.
Например, Ка-линия представляет собой дублет, состоящий
из Kai и Ка2-линий, который образуются заполнением вакансии
в К-слое (подоболочке 1<§1/2) переходами электронов с уровней Lni
и Ьц (т. е. подоболочек 2р3/2 и 2^1/2) соответственно. При этом ор-
битальное число изменяется на единицу. Переход L\ —> К (без из-
менения орбитального квантового числа) является запрещенным
и имеет пренебрежимо малую вероятность по сравнению с указан-
ными выше переходами.
В табл. 19.3 приведены радиационные переходы электронов,
образующие наиболее интенсивные спектральные линии /С-серии,
которые регистрируются в экспериментах.
Таблица 19.3. Переходы, генерирующие спектральные линии К-серии
Переход электрона в вакансию Название спектральной линии Переход электрона в вакансию Название спектральной линии
Ln - > К Mi -> К К0"2
Lin - -> к ка1 Мп -> К к0,2
Мп - -> к К0з Mv -+К 4х
Мщ - -> к к01 Ny -> К К04
Mw - -> к К0"Ь On -> К Ki2
Му - -> к К0Ч> Ош -> К Кб1
Заметим, что в табл. 19.3 некоторые спектральные линии яв-
ляются неразрешенными дублетами. Например, разность длин
волн, образованных при переходах М\у К и Му —> /С, слиш-
ком мала, чтобы быть уловленной современными рентгеновскими
спектрометрами.
Влияние спин-орбитального взаимодействия разделяет L-се-
рию ХРИ на 3 подсерии, в соответствии с тремя подоболочками
(Li, Ln, Lni), которые могут содержать вакансии. Наиболее ин-
тенсивные спектральные линии L-серии сведены в табл. 19.4.
Видно, что табл. 19.4 также содержит пока еще неразрешенные
спректральные линии ХРИ.
Различие энергий подоболочек Lj, Ln и Lin означает, что ка-
ждой подсерии L-серии ХРИ соответствует свое пороговое напря-
жение. Эти три величины определяются следующими уравнени-
ями:
eUL1 = |S(2s1/2)|,
eUL11 = |£(2pi/2)l, (19.И)
sUlui = |Г(2р3/2)|,
402 Лекция 19. Закон Мозли, эффект Оже
где в правых частях стоят энергии связи электронов в соответст-
вующих подоболочках.
Таблица 19.4. Переходы, генерирующие спектральные линии L-серии
Переход электрона Название линии Переход электрона Название линии Переход электрона Название линии
Mu L\ L/34 Mi —> Li i Lrj Мш -> Lin Ls
Mui Li Lp3 Mm Ln L/317 M\y -> Lui Lq2
Afiv ~Li Lp iq Mw —> Ln Lpi My —> Lin Lal
Му —> Li L/39 M -» Ln M -> Lui Lp6
Mi -> Li L^2 Mv -» Li i L-yi Mv -» Lui L(315
Мп -> Li L^3 Oi -> Ln Ly8 Ny -> Lui L(32
TVv -> Li L7h Ow -» Ln Nyi-yu —> Lui Lu
Oii-iii —> Li L74 Mi —> Lin Li Oi -> Lui L(37
Ph-ш Li L7i3 Mu —> Lin Lt Oiv v —> Lui L/35
На рис. 19.5 приведены зависимости пороговых энергий возбу-
ждения Lj, Lu и Lni серий ХРИ от атомного номера химического
элемента.
Влияние спин-орбитального взаимодействия, вообще говоря,
разделяет М-серию ХРИ на 5 подсерий (Mj, Мп, Мщ, Mjy, Му)
Рис. 19.5. Зависимости энергий возбуждения серий ХРИ от атомного номера
химического элемента: 1 — Li, 2 — Ln, 3 — Lin
с пятью различными пороговыми энергиями возбуждения. Од-
нако спектральные линии М-серии даже у тяжелых химических
элементов имеют близкие длины волн, которые трудно разреша-
ются современными рентгеновскими спектрометрами. Поэтому в
табл. 19.5 указаны лишь наиболее интенсивные спектральные ли-
нии М-серии, которые используются в научных исследованиях.
19.3. Тонкая структура рентгеновского излучения
403
Таблица 19.5. Переходы, генерирующие наиболее интенсивные
спектральные линии TVf-серии
Переход электрона в вакансию Название спектральной линии Переход электрона в вакансию Название спектральной линии
Nv - > Мш My Mi - > Му М^
Мп — > Miv MS Мп - -> Му М$2
Mv-v - -> Miv M0 Мп - -> Му ма2
Оп-ш - -» Miv My Мш - -> Му Ма1
Энергетическая схема электронных переходов, сопровождаю-
щихся излучением самых интенсивных линий ХРИ, изображе-
на на рис. 19.6. Названия спектральных линий приведены в
табл. 19.3-19.5. Расчет относительной интенсивности спектраль-
ных линий определенной серии ХРИ является достаточно трудной
задачей квантовой механики. Усредненные значения по всем хи-
мическим элементам для К- и L-серий, полученные в эксперимен-
тах, сведены в табл. 19.6 и 19.7.
Таблица 19.6. Приближенные значения относительных
интенсивностей важнейших спектральных линий К-серии ХРИ
Спектральная линия ХРИ Ка1 ка2 к01 к02 К03
Относительная интенсивность 100 50 15-30 1-10 6-15
Таблица 19.7. Приближенные значения относительных интенсивностей
некоторых спектральных линий L-серии ХРИ
Спектральная линия ХРИ Lq 1 LQ2 Lpi Т(32 Дзз L7 i L72
Относительная интенсивность 100 10 50 20 1-5 3-5 1-10 0,5-2
Интенсивность линии Мр составляет 3/5 от суммарной интен-
сивности линий Ма\ и Ма2-
Более точные значения относительных интенсивностей спек-
тральных линий ХРИ отдельных серий для различных химиче-
ских элементов приведены в специальной литературе.
Заметим, что после испускания фотона спектральной линии
Ка\ или Ка2 заполняется вакансия в первом электронном слое,
но образуется электронная вакансия в подоболочке Ln или Lin
(см. рис. 19.6). Таким образом, создаются условия для генериро-
404
Лекция 19- Закон Мозли, эффект Оже
вания спектральных линий Lqi, LQ2> Lpi и других, указанных в
табл. 19.4. При испускании фотонов других линий К- и L-серий
также возникают вакансии в более высокоэнергетических элек-
тронных подоболочках и, следовательно, необходимые условия для
Рис. 19.6. Схема образования наиболее интенсивных спектральных линий К-,
L- и М-серий ХРИ с учетом тонкой структуры. Названия спектральных линий
приведены в табл. 19.3-19.5
формирования более длинноволновых спектральных линий ХРИ.
Это означает, что образование вакансии во внутренних электрон-
ных слоях может приводить к каскадному испусканию фотонов
различных спектральных линий ХРИ.
В настоящей и предыдущей лекциях рассматривалось форми-
рование спектральных линий ХРИ из-за образования вакансий во
внутренних электронных оболочках путем бомбардировки атомов
электронами достаточно высокой энергии. Однако образование
19.4. Эффект Оже
405
электронных вакансий возможно и другими способами. В дополне-
нии 19.2 описан фотоэффект на внутренних атома, что также при-
водит к возникновению вакансий. Образование вакансии в опре-
деленной электронной подоболочке возможно, если энергия фотона
превышает энергию связи данной подоболочки. Таким образом,
существует метод генерирования спектральных линий ХРИ пу-
тем возбуждения атомов достаточно коротковолновым («жестким»)
рентгеновским или гамма-излучением. Этот процесс называется
рентгеновской флуоресценцией. В экспериментах Баркла про-
исходила именно рентгеновская флуоресценция, т. е. образование
вторичных рентгеновских лучей в рассеивателе под действием пер-
вичных, исходящих из рентгеновской трубки (см. рис. 18.8).
Еще одним способом образования электронных вакансий яв-
ляется ионизация атомов потоком предварительно ускоренных
ионов. Кинетическая энергия ионов должна превышать энергию
связи электронной оболочки, вакансии в которой ответственны за
формирование определенной спектральной серии ХРИ. Особенно-
стью генерирования рентгеновского излучения ионным возбужде-
нием является относительно низкая интенсивность непрерывной
составляющей спектра. Согласно (18.7), интенсивность тормоз-
ного излучения W пропорциональна квадрату ускорения, следо-
вательно, при прочих равных условиях бомбардировка протонами
дает величину интенсивности W в (mp/me)2 « 3,37-106 раз мень-
шую, чем при бомбардировке электронами той же кинетической
энергии. В результате при ионном возбуждении в спектре рент-
геновского излучения почти отсутствует горб непрерывной соста-
вляющей, показанный на рис. 18.6, 18.7 и 18.9. Таким образом,
бомбардировка ионами исследуемого вещества дает практически
чистый линейчатый рентгеновский спектр, состоящий только из
узких пиков ХРИ.
19.4. Эффект Оже
Как было показано выше, при образовании вакансии во внут-
ренней электронной подоболочке атом переходит в возбужденное
состояние. Энергия возбуждения равняется энергии ионизации
данной подоболочки. Снятие этого возбуждения (понижение энер-
гии атома) происходит заполнением вакансии электроном из ка-
кого-либо более высокоэнергетического состояния. При этом раз-
ность энергий электронных состояний может испуститься в виде
фотона характеристической спектральной линии.
Однако возможен альтернативный вариант снятия возбужде-
ния атома — без испускания фотона ХРИ. В 1925 г. французский
физик Пьер Оже (1899-1993) в ходе своих экспериментов обнару-
жил явление автоионизации возбужденного атома. Этот процесс,
названный впоследствии эффектом Ожеь заключается в том, что
избыток энергии атома передается одному из внешних электронов.
406
Лекция 19. Закон Мозли, эффект Оже
Энергетическая схема типичного процесса Оже изображена на
рис. 19.7. Необходимым условием возникновения эффекта явля-
ется наличие вакансии во внутренней электронной оболочке атома.
Е
Ап
Ai
А
В случае, изображенном на рис. 19.7,
была образована вакансия в электрон-
ном /С-слое. При этом атом получил
энергию возбуждения равную энергии
связи А-электрона, т.е. —Е(К) > 0.
Затем вакансия была заполнена перехо-
дом электрона из подоболочки L\. В рас-
смотренном случае высвободившаяся
энергия E(L{) — Е(К) передалась элек-
трону подоболочки Ln- Энергии связи
электронов в L-слое значительно мень-
7
Рис. 19.7. Энергетическая схема оже-процесса
JCLiLn:
1 — переход электрона из Li-подоболочки, заполня-
ющий вакансию в К-слое, 2 — выход электрона из
________________К Ьц-подоболочки, Те — кинетическая энергия оже-
л электрона
ше энергии связи /С-электронов. Следовательно, произойдет иони-
зация атома по Ln-подоболочке, а освободившийся электрон полу-
чит кинетическую энергию
ТЕ = Е(й) - Е(К) 4- E(Ln). (19.12)
Напомним, что все энергии в правой части (19.12) имеют отрица-
тельные значения, как энергии стационарных состояний электро-
нов в атоме. Соответствующие энергии связи равны им по абсо-
лютной величине и имеют положительные значения.
В общем случае кинетическую энергию оже-электрона обычно
выражают через энергии связи трех подоболочек:
Те = Е1-Е2-Е3, (19.13)
где Ei — энергия связи электрона в подоболочке, содержащей пер-
воначальную вакансию, Е2 — начальная энергия связи электрона,
заполняющего вакансию, Е% — энергия связи электрона в подобо-
лочке, из которой выбрасывается оже-электрон.
Процесс Оже, изображенный на рис. 19.7, кратко обозначается
KLiLn. Заметим, что на переход электрона L\ —> К не наклады-
вается никаких ограничений, так как этот переход не радиацион-
ный.
19.4. Эффект Оже
407
Каждая подоболочка содержит несколько электронов, поэтому
возможны переходы /CLiLm, КЬцЬц и т.п. Все подобные оже-
процессы обозначаются символом KLL. Очевидно, что также воз-
можны оже-переходы LMM, MNN и другие.
Энергии электронных подоболочек имеют фиксированные зна-
чения, характерные для атомов определенного химического эле-
мента. Следовательно, спектры оже-электронов, в принципе,
являются линейчатыми, а их вид специфичен для данного хими-
ческого элемента. Это означает, что возможно исследование хи-
мического состава вещества не только по спектрам ХРИ, но и по
спектрам оже-электронов. Метод элементного анализа на основе
регистрации спектров электронов Оже называется электронной
оже-спектроскопией.
Существенной трудностью оже-спектроскопии является то,
что электроны в исследуемом материале на пути к энергоанализа-
тору могут терять часть своей энергии. В результате пики спек-
тра электронов Оже получают уширение. Широкое применение
на практике оже-спектроскопии для количественного химического
анализа началось после того, как была разработана методика ап-
Рис. 19.8. Спектров электронов Оже палладия. Энергия первичных электронов
равна 2,5 кэВ. На вертикальной оси левого графика — число отсчетов детектора
в 1 с. На правом графике дифференцированный спектр оже-электронов
паратного дифференцирования спектров электронов, что позволяет
уточнить энергию регистрируемых Оже-электронов (см. рис. 19.8)
и подавить фон неупруго рассеянных электронов.
На практике в элементном анализе регистрируются спектры
оже-электронов, возникающих в переходах KLL, LMM, MNN,
NOO и ООО. На рис. 19.9 приведена диаграмма энергий оже-
электронов для различных химических элементов.
Из приведенной диаграммы следует, что для обнаружения лег-
ких элементов целесообразно регистрировать электроны оже-про-
цессов KLL, для элементов с Z = 14-40 анализировать оже-про-
цессы LMM, для элементов с Z = 40-79 — процессы MNN, и
для более тяжелых элементов — NOO.
408
Лекция 19. Закон Мозли, эффект Оже
На рис. 19.8 просматриваются 3 пика электронов Оже с энерги-
ями приблизительно 240, 275 и 330 эВ. Энергия первичных элек-
тронов 2,5 кэВ недостаточна для ионизации оболочек электронных
Z
Рис. 19.9. Зависимость энергии электронов типичных оже-процессов от атом-
ного номера элемента.
Заштрихованные зоны содержат значения энергий оже-электронов. Крупные точки соот-
ветствуют оже-переходам, наиболее часто используемым в элементном анализе
слоев К- и L-атомов палладия, поэтому наблюдаемый спектр обра-
зован оже-электронами переходов серии MNN.
Ясно, что в результате оже-процесса заполняется одна элек-
тронная вакансия и образуются две новые в более высокоэнер-
Е, эВ
2400 *
19.4. Эффект Оже
409
гетических подоболочках. Следовательно, атом остается в воз-
бужденном состоянии. Снятие возбуждения должно происходить
заполнением новых вакансий. При этом возможно излучение рент-
геновских характеристических длинноволновых серий или эмис-
сии оже-электронов меньшей энергии. Как следствие, электронные
вакансии перемещаются в состояние вверх по оси энергий. В ре-
зультате атом может оказаться многократно ионизованным.
Из вышеизложенного следует, что при наличии вакансии во
внутреннем электронном слое атома возможны два конкурирую-
щих процесса: эффект Оже и испускание фотона характеристиче-
ского рентгеновского излучения. Следовательно, после электрон-
ного перехода с заполнением вакансии вероятность испускания
характеристического фотона и вероятность эмиссии электрона
Оже в сумме равны единице. Эти вероятности значительно за-
висят от химического номера атома Z.
Рассмотрим атом с вакансией в электронном Jf-слое. Веро-
ятность заполнения этой вакансии с испусканием рентгеновского
фотона (иначе говоря, вероятность рентгеновской флуоресцен-
ции) от порядкового номера химического элемента Z является
Рис. 19.10. Зависимость вероятности рентгеновской флуоресценции шк от
атомного номера химического элемента Z
нелинейной монотонно возрастающей функцией, представленной
на рис. 19.10. Например, вероятность и>к для атома углерода со-
ставляет 1,8 • 10“3, для урана вероятность шк « 0,97.
Вероятности испускания рентгеновских фотонов при заполне-
нии вакансий в L-подоболочках также являются резко возрастаю-
щими функциями атомного номера Z.
Таким образом, заполнение электронных вакансий в легких
атомах, в основном, сопровождается выходом электронов Оже. На-
против, ионизация внутренних электронных оболочек тяжелых
410
Лекция 19. Закон Мозли, эффект Оже
атомов влечет за собой интенсивную рентгеновскую флуоресцен-
цию. Следовательно, в веществе сложного химического состава
поиск легких химических элементов целесообразно проводить с
помощью электронной оже-спектроскопии, а тяжелых — путем ре-
гистрации и анализа спектров ХРИ.
Задачи к лекции 19
1. Вычислить длины волн характеристических линий Ка и К@ сле-
дующих химических элементов: а) магния, б) никеля, в) молибдена,
г) вольфрама.
2. Вычислить длины волн характеристической линии L& следующих
химических элементов: а) алюминия, б) железа, в) серебра, г) платины.
3. Найти кинетическую энергию, которую получает атом углерода 12С
при упругом рассеянии на нем фотона с энергий е, если угол рассеяния
в лабораторной системе координат 0 = 90°: а) е = 5 кэВ, б) е = 10 кэВ,
в) е — 20 кэВ, г) е — 50 кэВ. Вычислить энергию рассеянного фотона.
4. Вычислить энергию фотона, упруго рассеянного на атоме железа
56Fe на угол в = 180°. Длина волны первичного фотона: а) А = 0,2 А,
б) А = 0,5 А, в) А = 1 А, г) А = 2 А.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 19
19.1. Нарушения монотонной зависимости атомной массы
от порядкового номера элемента в таблице Менделеева
При составлении Периодической таблицы Менделеев размещал хи-
мические элементы в порядке возрастания атомной массы. В то же
время, эту последовательность он подразделял на периоды, располагая
в столбцах элементы со сходными химическими свойствами в столбцах,
которые были названы группами. Повторяемость свойств элементов в
группах таблицы Менделеева является основой Периодического закона,
поэтому Менделеев в некоторых местах таблицы нарушал последователь-
ность возрастания атомных масс М с увеличением порядкового номера
Z химического элемента.
Впоследствии с увеличением точности измерения атомных масс
удалось добиться большего соответствия с монотонностью зависимости
M(Z). Однако несколько нарушений монотонности остались (см.
табл. 19.1 в лекции 19).
Исследования Резерфорда, Мозли и других физиков показали, что
порядковый номер Z совпадает с количеством электронов в атоме этого
химического элемента. Именно число электронов (и их распределение
по оболочкам) определяет химические свойства элемента. С ростом чи-
сла электронов увеличивается и количество протонов. В ядерной физике
было установлено, что с числом протонов увеличивается и число нейтро-
нов в атомном ядре. Таким образом, масса атома М оказалась вторичной
химической характеристикой атома.
Нарушения монотонности зависимости M(Z) в таблице Менделеева,
приведенные в табл. 19.1, объясняются изотопным составом естествен-
ной смеси изотопов химических элементов.
Изотопы определенного химического элемента различаются массо-
вым числом Л, которое равно сумме количества протонов и нейтронов в
ядре атома (см. дополнение 7.3). При этом масса атома, выраженная в
а.е.м., приближенно равна массовому числу А данного изотопа. Следова-
тельно, изотопный состав химического элемента может быть выражен
набором массовых чисел, для каждого из которых указана распрост-
раненность — относительная доля изотопа в химически чистом эле-
менте.
В табл. Д.19.1 представлены изотопные составы аргона и калия,
полученные усреднением по множеству образцов, взятых в различных
частях коры земного шара. Видно, что аргон практически полностью
состоит из изотопа аргон-40. У калия наиболее распространенным явля-
ется изотоп калий-39. Как следствие, масса атома калия, усредненная по
его изотопному составу, значительно меньше усредненной массы атома
аргона.
В табл. Д.19.2 проведено сравнение изотопных составов кобальта и
никеля, теллура и иода. Естественный кобальт состоит из единственного
412
Дополнения к лекции 19
изотопа с массовым числом А = 59. У никеля самым распространенным
является изотоп никель-58, что обусловливает меньшую атомную массу
никеля, по сравнению с атомной массой кобальта.
Таблица Д.19.1. Изотопные составы природных аргона и калия
Химический элемент и его порядковый номер Атомное число изотопа Доля изотопа в естественной смеси (%) Средняя атомная масса химического элемента
Аргон 36 0,337 39,94
Z = 18 38 0,063
40 99,600
Калий 39 93,258 39,10
Z = 19 40 0,012
41 6,730
Таблица Д.19.2. Изотопные составы природных кобальта,
никеля, теллура и иода
Химический элемент и его порядковый номер Атомное число изотопа Доля изотопа в естественной смеси (%) Средняя атомная масса химического элемента
Кобальт Z = 27 59 100 58,93
Никель 58 68,27 58,70
Z = 28 60 26,10
61 1,13
62 3,59
64 0,91
Теллур 120 0,096 127,6
Z = 52 122 2,60
123 0,908
124 4,816
125 7,14
126 18,95
128 31,69
130 33,80
Иод Z = 53 127 100 126,9
Аналогично, иод имеет один стабильный изотоп иод-127. Наибо-
лее распространенными изотопами теллура являются более массивные
теллур-128 и теллур-130. Таким образом, атомная масса природного тел-
лура превышает атомную массу иода.
Дополнения к лекции 19
413
19.2. Взаимодействие рентгеновского излучения
с веществом
Экспериментальные исследования показывают, что при прохожде-
нии узкого пучка рентгеновских лучей через вещество его интенсивность
убывает по экспоненциальному закону (18.1). Коэффициент ослабления
р зависит от ряда физических характеристик среды и от длины волны
А рентгеновского излучения. Уменьшение интенсивности потока обусло-
влено как поглощением рентгеновских лучей, так и их рассеянием на
углы 0 в диапазоне 0 < 0 2тг. Кроме того, на интенсивность потока
существенно влияют различные вторичные процессы, наиболее важные
из которых рассмотрены ниже.
Рентгеновскую монохроматическую волну можно представить как по-
ток фотонов с одинаковыми энергиями в = 2irhc/X. В рамках квантовой
теории уменьшение интенсивности рентгеновской волны при прохожде-
нии через вещество объясняется отдельными актами взаимодействия фо-
тонов с атомами среды. Эти элементарные процессы описываются кван-
товой электродинамикой и имеют статистический характер. Каждый
акт взаимодействия происходит независимо от других и приводит к уда-
лению фотона из первичного узкого пучка.
Прежде всего покажем, что коэффициент р в законе ослабления (18.1)
можно интерпретировать как вероятность взаимодействия рентгеновс-
кого фотона с атомами вещества на единице длины. Будем полагать,
что при любом виде взаимодействия фотон выбывает из пучка фотонов
с параллельными импульсами. Тогда вероятность взаимодействия dN
фотонов с атомами на длине dx при прохождении рентгеновского пучка
через вещество можно записать в виде
В результате взаимодействия с атомами количество фотонов в пучке
убывает, поэтому изменение числа фотонов является отрицательной ве-
личиной. Обозначив N(x) количество фотонов в пучке, который прошел
в веществе расстояние х, можно записать следующее дифференциальное
уравнение:
-dN = N(x)pdx. (Д.19.1)
Интенсивность излучения 1(х) прямо пропорциональна количеству
фотонов N(x), поэтому для интенсивности узкого рентгеновского пучка
справедливо аналогичное уравнение
—dl — l(x)pdx. , (Д.19.2)
Интегрирование уравнения (Д.19.2) с учетом начального условия
/(ж = 0) = /0 дзет зависимость интенсивности пучка рентгеновского
излучения от пройденного расстояния в веществе:
1(х) = Iq ехр (-рх), (Д.19.3)
совпадающую с законом ослабления (18.1). Таким образом, доказан ве-
роятностный (статистический) смысл коэффициента ослабления р.
414
Дополнения к лекции 19
Для связи коэффициента ц с характеристиками атомов среды сна-
чала рассмотрим вещество, состоящее из атомов только одного химиче-
ского элемента (точнее, из атомов одного определенного изотопа). Целе-
сообразно представить коэффициент ослабления в следующем виде:
ДГд
М = ~ГР^ (Д.19.4)
где N& — постоянная Авогадро, р — массовая плотность вещества,
А — молярная масса. Параметр ст характеризует процесс взаимодей-
ствия электромагнитной волны с отдельным атомом и называется эф-
фективным атомным сечением (точнее, интегральным эффективным
атомным сечением).
Величина ст имеет размерность площади и допускает наглядную
геометрическую интерпретацию. Представим себе, что с каждым атомом
связан кружок площадью ст, параллельный поверхности постоянной фазы
электромагнитной волны, распространяющейся в веществе. Будем рас-
сматривать фотоны как поток точечных частиц с одинаковыми импуль-
сами, перпендикулярными поверхности постоянной фазы волны. Если
такая прямолинейно летящая частица пересечет кружок, то произойдет
взаимодействие фотона с данным атомом. Несмотря на механистичность
данной интерпретации, она позволяет оценить ослабление потока фото-
нов. (Интегральное сечение ст использовалось в дополнении 15.2 при
интерпретации эффекта Рамзауэра.)
Легко убедиться в том, что множитель перед величиной сечения ст
в выражении для коэффициента ослабления (Д.19.4) представляет собой
концентрацию атомов, т. е. количество атомов в единице объема (см.
формулу (Д.15.6)).
Для сложного вещества с известным химическим составом коэффи-
циент ослабления может быть представлен суммой
= (Д.19.5)
J=i Aj
где 8j — относительная доля атомов у-го химического элемента в данном
веществе (безразмерная величина), Aj и сту — молярная масса и сечение
для атомов у-го химического элемента соответственно, п — количество
различных химических элементов в данном веществе.
Величина а является суммарной характеристикой всевозможных
процессов взаимодействия фотонов с атомом определенного химического
элемента и поэтому часто называется полным сечением. Пользуясь неза-
висимостью различных элементарных процессов взаимодействия, можно
полное сечение представить в виде суммы
ст = (71 + 02 4" СГз + ..., (Д.19.6)
где каждое слагаемое называется парциальным сечением соответствую-
щего процесса.
Статистический характер элементарных процессов выражается в
том, что, вообще говоря, результат взаимодействия фотона с атомом яв-
Дополнения к лекции 19
415
ляется неоднозначным. При фиксированной энергии фотонов в возмож-
ны различные процессы взаимодействия с тождественными атомами,
причем каждый процесс характеризуется определенной вероятностью.
Теория позволяет лишь в принципе вычислить вероятность каждого про-
цесса, которая равняется отношению
Pk = (Д.19.7)
а
где к — номер элементарного процесса.
Слагаемые в сумме (Д.19.6) являются, вообще говоря, нелинейными
функциями порядкового номера химического элемента и длины волны
рентгеновского излучения и поэтому могут значительно различаться по
величине. Количество различных элементарных процессов взаимодей-
ствия рентгеновских фотонов с атомами может быть велико. В каждой
физической задаче следует ограничиваться членами суммы (Д.19.6), да-
ющими существенный вклад в линейный коэффициент ц.
Для рентгеновского диапазона электромагнитного излучения наибо-
лее существенными процессами являются фотопоглощение (или фото-
эффект), упругое и неупругое рассеяние фотонов на электронах атомов.
Следовательно, полное сечение (Д.19.6) с хорошей точностью может быть
представлено суммой трех слагаемых:
a = crPh Н- as + asc, (Д.19.8)
где стрь, crs и ctsc — интегральные сечения фотопоглощения, упругого и
неупругого рассеяния соответственно.
Фотоэффектом называется поглощение фотона с энергией е одним из
электронов, принадлежащих атому. При этом энергия электрона увели-
чивается на величину е, он освобождается от атома и переходит в одно из
состояний непрерывного спектра. Атом превращается в положительный
ион. Этот процесс реализуется, если энергия фотона е превышает энер-
гию связи такого электрона Е{. Освобожденный электрон приобретает
кинетическую энергию
Те=е-Ег. (Д.19.9)
Энергия связи электрона равна его энергии в исходном стационар-
ном состоянии с обратным знаком. Поглощение фотонов может про-
исходить на электронах в различных стационарных состояниях. Для
анализа процесса фотопоглощения целесообразно использовать прибли-
жение электронных подоболочек, описанное в лекции 19. Каждой подо-
болочке, характеризуемой тремя квантовыми числами n, I и у, соответ-
ствует определенный энергетический уровень Enij. Часто для обозначе-
ния электронных подоболочек и их энергий используют рентгеновские
обозначения, определенные в лекции 19 (см. табл. 19.2 и рис. Д.19.1).
Если энергия фотона в превышает энергию ионизации электронной
подоболочки то фотоэффект может происходить на этой подобо-
лочке. Следовательно, сечение фотопоглощения сгрь может быть предста-
влено в виде суммы, каждое слагаемое которой характеризует фотоэф-
фект на соответствующей электронной оболочке:
стрь = crph(lsi/2) + o-Ph(2s1/2) 4- crph(2p!/2) 4- сгрь(2р3/2) 4-... (Д.19.10)
416
Дополнения к лекции 19
Исследования показали, что максимальную величину имеет сече-
ние фотопоглощения стри (lsi/2) на электронах внутреннего электронного
слоя, т.е. на подоболочке lsi/2- Расчет зависимости сечений crph(ls^)
Рис. Д.19.1. Энергетическая схема ионизации внутренних подоболочек атома
рентгеновскими фотонами.
Горизонтальные линии — энергетические уровни подоболочек. Штрих-пунктирные вер-
тикальные стрелки — энергии поглощаемых фотонов £i и £2- Штриховые вертикальные
стрелки — кинетические энергии освобожденных электронов Tei и Те2\ Ек и Ецп —
энергии связи электронов подоболочек lsi/2 и 2р3/2 соответственно
от энергии фотона в и химического номера атома Z в общем случае
весьма сложен, но при выполнении условий е Ек и е тес2 се-
чение фотопоглощения на /С-слое выражается формулой
/ е \ -7/2
fph(IS1/2) = Oov2®a2Z5 I----------- I
\ TTleC j
(Д.19.11)
где a — постоянная тонкой структуры.
Величина сто называется сечением томсоновского рассеяния:
о-о
8тг 2
— "7“ ге-
3 е
(Д.19.12)
Параметр
р2
ге =------- « 2,818 • 10"5 А (Д.19.13)
тес2
исторически называется классическим радиусом электрона.
Дополнения к лекции 19
417
Из формулы (Д.19.11) следует, что с ростом энергии фотонов сечение
фотопоглощения на /f-слое резко убывает. Если энергия фотона е <
< Ек — —E(1$i/2), т.е. недостаточна для ионизации подоболочки lSi/2,
то фотопоглощение на этой оболочке невозможно. Величина
2тгНс
(Д.19.14)
называется К-краем поглощения. Таким образом, при длине волны рент-
геновского излучения А > Хк фотопоглощение на электронном /С-слое
не происходит.
Энергия электронов подоболочки lsi/2 выражается приближенной
формулой (19.6), которая, в принципе, позволяет вычислить /<-края по-
глощения (Д.19.14) различных атомов. Исследования показали, что для
легких атомов формула (19.6) дает заметную погрешность. Величины
/<-края поглощения для ряда элементов, полученные экспериментально
для ряда элементов, приведены в табл. Д.19.3.
Таблица Д.19.3. JFC-края поглощения
для некоторых легких элементов
Химический элемент Атомный номер JC-край поглощения (ангстрем)
С 6 43,68
N 7 30,99
О 8 23,32
Na 11 15,69
Al 13 7,948
Si 14 6,738
Р 15 5,784
S 16 5,019
К 19 3,437
Са 20 3,070
Zn 30 1,283
Для рентгеновских лучей с длиной волны А > А/< поглощение фо-
тонов может происходить на любой из подоболочек L-слоя или других,
энергии которых расположены еще более высоко на оси энергии.
Сечения фотоэффекта на подоболочках L-слоя обладают общими тен-
денциями резкого возрастания с химическим номером атома Z и дли-
ной волны А рентгеновских лучей. Каждая подоболочка характеризуется
своей энергией ионизации и соответствующим краем поглощения (см.
рис. Д.19.2).
При длине волны А > Аып фотопоглощение происходит на подобо-
лочках М-слоя и т. д.
Для описания экспериментальных результатов иногда используются
приближенные зависимости вида сгрь = CXpZq, где показатель степени
q лежит в интервале 4 < q 5; показатель р с ростом А принимает зна-
418
Дополнения к лекции 19
чения от 1 до 3,5; С — постоянный коэффициент. Конкретные значения
параметров дир зависят от химического номера атома Z и диапазона
длин волн А.
При переходе через любой край поглощения суммарное сечение фо-
топоглощения изменяется скачком. При фиксированной длине волны А
рентгеновских лучей величина сечения фотопоглощения (если оно воз-
можно) резко падает с ростом главного квантового числа подоболочки.
К важным процессам взаимодействия рентгеновских лучей с веще-
ством относится упругое рассеяние фотонов на электронных оболочках
атома. При этом виде рассеяния происходит обмен импульсов между фо-
тоном и атомом как целым, а внутренняя энергия атома не изменяется.
Рис. Д.19.2. Типичный вид зависимости сечения фотопоглощения от длины
волны электромагнитного излучения в рентгеновском диапазоне:
Л;< — /С-край поглощения, величины Лц, и — края поглощения трех подобо-
лочек 2s!/2, 2р1/2 и 2р3/2 соответственно электронного L-слоя
Нетрудно показать, пользуясь законами сохранения энергии и импульса
для системы «фотон + атом», что после упругого столкновения атом полу-
чает пренебрежимо малое приращение кинетической энергии, а энергия
фотона практически не изменяется. В то же время, угол рассеяния фо-
тона 0 может принимать значения в интервале 0° < 0 180°.
Согласно классической электродинамике, дифференциальное сечение
упругого рассеяния неполяризованных рентгеновских лучей на свобод-
ном электроне выражается следующей формулой:
^ = ^(l + cos20). (Д.19.15)
Последнее выражение задает распределение вероятностей рассеяния под
разными углами 0, т. е. определяет угловое распределение упругого рас-
сеяния фотонов. Видно, что это распределение зеркально симметрично
относительно плоскости, перпендикулярной импульсу первичных фото-
нов, и имеет минимум для угла рассеяния в = 90°.
Интегрирование по полному телесному углу показывает, что интег-
ральное сечение упругого рассеяния на электроне представляется фор-
мулой (Д.19.12).
Дополнения к лекции 19
419
При расчете сечения упругого рассеяния на атоме, содержащем Z
электронов, следует учитывать, что атом имеет размер порядка длины
волны А рассеивающегося рентгеновского излучения. Это значит, что
нельзя полагать электроны находящимися в одной точке, и сечение упру-
гого рассеяния на атоме не равно произведению величины (Д.19.15) на
число электронов в атоме. Расчет корреляции между среднестатистиче-
скими положениями электронов, движущихся внутри атома, приводит к
следующему представлению дифференциального сечения упругого рассе-
яния на атоме:
§ = ^/2(0)’ (ДЛ9Л6)
где функция /(0) называется атомным фактором (или атомной ам-
плитудой). Из выражения (Д.19.16) следует, что функция является
безразмерной. Величина атомного фактора обусловлена разностью фаз
вторичных волн, генерированных отдельными электронами атома, и су-
щественно зависит от угла рассеяния в и длины волны рентгеновского
излучения А. Функции атомного фактора f(0) для всех атомов имеют
вид, показанный на рис. Д.19.3.
При угле 0 = 0° функция достигает максимального значения
Z, равного количеству электронов в атоме. С ростом угла рассеяния
sin(0)/X
Рис. Д.19.3. Общий вид зависимости атомного фактора от аргумента sin(0)/A:
Z — химический номер атома
функция f(0) монотонно убывает. Таким образом, угловое распределе-
ние фотонов, упруго рассеянных на атоме, существенно анизотропно:
рассеяние на малые углы является более вероятным.
Упругое рассеяние рентгеновских лучей на атомах используется для
исследования структуры кристаллов и других конденсированных сред.
Рентгеноструктурные методы базируются на том, что упругое рассея-
ние на атомах обладает свойством когерентности. Рентгеновские волны,
упруго рассеянные периодически расположенными атомами кристалла,
формируют дифракционные пучки.
Длина волны А рентгеновского излучения имеет, вообще говоря, по-
рядок размера атомов. По этой причине для описания зависимости ин-
тенсивности упругого рассеяния от длины волны А неприменим закон
Релея, который требует выполнения условия А а, где а — размер рас-
сеивающего объекта. Интегральное сечение упругого рассеяния рентге-
новских лучей на атоме может быть рассчитано интегрированием выра-
жения (Д.19.16) по всевозможным углам рассеяния. В результате рас-
420
Дополнения к лекции 19
четов получается, что интегральная интенсивность упругого рассеяния
является нелинейной возрастающей функцией длины волны А рентге-
новских лучей.
Заметим, что вид зависимости интенсивности упругого рассеяния
рентгеновских лучей от длины волны Z(A) существенно зависит от струк-
туры вещества. Для рентгеновских дифракционных максимумов идеаль-
ного кристалла Z(A) ~ А3, для мозаичного /(А) ~ А2.
При возрастании энергии рентгеновских фотонов увеличивается ве-
роятность неупругого рассеяния на атомах вещества. В этом процессе
электроны атома переходят в возбужденные состояния или даже проис-
ходит ионизация атома. При этохм фотон не исчезает, а рассеивается на
угол в относительно направления первоначального импульса.
Энергия рентгеновского фотона е значительно превышает энергию
связи внешнего электрона атома Ei, которая имеет порядок энергии Рид-
берга Ry ~ 13,6 эВ. Следовательно, для излучения рентгеновского диапа-
зона неупругое рассеяние на внешних электронах атомов можно прибли-
женно описывать элементарной теорией эффекта Комптона, изложенной
в лекции 4. В таком приближении можно пренебречь потерей энергии
фотона на ионизацию атома и энергией отдачи атома при рассеянии фо-
тона. Тогда длина волны рассеянного фотона может быть вычислена по
формуле Комптона (4.22).
Угловое распределение неупруго рассеянных фотонов неполяризован-
ного рентгеновского излучения описывается формулой Клейна-Ниши-
ны-Тамма:
(дл917)
аз I & \л / \ л л у
где А и А' — длины волн первичного и рассеянного фотона соответ-
ственно.
Рис. Д.19.4. Диаграммы углового распределения неупругого рассеянных фотонов
на свободном электроне.
Буквами обозначены кривые для различной начальной энергией фотона е\ а) £ = 10 кэВ,
б) е = 60 кэВ, в) е = 200 кэВ, г) е = 500 кэВ, д) е = ЗМэВ
Вид функции (Д.19.17) задает анизотропию углового распределения
неупругого рассеянных фотонов, которая растет с уменьшением длины
волны рентгеновских лучей (см. рис. Д.19.4).
Дополнения к лекции 19
421
Интегрирование функции (Д.19.17) по полному телесному углу с уче-
том соотношения (4.22) дает зависимость интегрального сечения неупру-
гого рассеяния от длины волны первичного рентгеновского излучения
<7sc(A), которое можно преобразовать в зависимость от энергии первич-
ных фотонов crsc(^)- Эти функции имеют достаточно сложный вид и
приводятся в специальных курсах, посвященных взаимодействию рент-
геновского и гамма-излучения с веществом.
Теория неупругого рассеяния фотонов на внутренних электронах
атома является весьма сложной проблемой электродинамики и выходит
за рамки данного учебного пособия.
Для физики взаимодействия рентгеновских лучей с веществом су-
щественным является то, что сечение неупругого рассеяния а$с, грубо
говоря, пропорционально количеству электронов в атоме, т.е. химиче-
скому номеру атома Z. С другой стороны, сечение фотопоглощения сгрь
возрастает с числом Z гораздо более резко (см., например, (Д.19.11)).
Как следствие, в рентгеновском диапазоне вероятность фотопоглощения
на тяжелых атомах (с большим числом Z) значительно превышает ве-
роятность сечение неупругого рассеяния. Для легких атомов (с малым
номером Z) наблюдается противоположное соотношение между вероят-
ностями этих двух процессов.
Из предыдущего ясно, что при прохождении узкого пучка рентге-
новского излучения через вещество его интенсивность ослабляется не
только из-за поглощения фотонов, но также из-за рассеяния. Рассеян-
ные фотоны отклоняются от первоначального направления и выходят из
первичного узкого пучка. Кроме того, при неупругом рассеянии фотоны
теряют, вообще говоря, значительную часть своей энергии. Из-за этого,
в частности, возрастает вероятность поглощения фотона при следующем
элементарном акте взаимодействия с атомом.
При неупругом рассеянии отсутствует корреляция между углами рас-
сеяния отдельных фотонов, рассеянных на разных атомах, поэтому дан-
ный процесс часто называют некогерентным рассеянием. Если упру-
гое когерентное рассеяние рентгеновских лучей на кристалле приводит
к формированию дифракционных пупков, то неупругое рассеяние дает
вклад в диффузную составляющую рассеянного рентгеновского излуче-
ния.
Рассмотренные процессы поглощения и рассеяния рентгеновских
фотонов вызывают ряд вторичных эффектов.
Как было показано выше (см. рис. Д.19.2), фотопоглощение наиболее
вероятно на внутренних электронных подоболочках атома (конечно, при
энергии фотонов, достаточной для ионизации этих подоболочек). Погло-
тив фотон с энергией е атом увеличивает свою энергию на величину е и
переходит в возбужденное состояние со средним временем жизни т по-
рядка 10“8—10”10 с. Так как при этом в подоболочке образуется электрон-
ная вакансия, то энергия возбуждения может быть потеряна либо флуо-
ресценцией (испусканием характеристического фотона), либо выбросом
из атома оже-электрона (см. §19.4 лекции 19). Таким образом, процесс
фотопоглощения сопровождается последующим испусканием характери-
стических фотонов, иначе говоря, рентгеновской флуоресценцией.
Из энергетической схемы рис. 19.3 и Д.19.1 очевидно, что энергии
образованных характеристических фотонов заведомо меньше, чем энер-
гия первичного поглощенного фотона. Это обусловлено тем, что энергия
422 Дополнения к лекции 19
первичного фотона е должна превышать энергию ионизации подоболочки
Ei, а энергия характеристических фотонов, возникшая при радиацион-
ном переходе электрона в эту оболочку, — меньше Е^ так как переход
осуществляется из одноэлектронного состояния с отрицательной энер-
гией.
Таким образом, рентгеновское излучение с длиной волны А может
быть использовано для генерирования спектральных линий характери-
стического рентгеновское излучение с длиной волны меньше, чем А.
Такое излучение часто называют вторичным. Для увеличения интен-
сивности потока вторичного рентгеновского излучения следует выбирать
возбуждающее излучение и материал рассеивателя таким образом, чтобы
длина волны первичного излучения А была близка к краю поглощения
возбуждаемой серии, но при этом была несколько меньше его. Например,
для генерирования /С-серии ХРИ определенного химического элемента
целесообразно использовать рентгеновские лучи с длиной волны А не-
много меньше /С-края поглощения Хк- При этом сохраняется возмож-
ность ионизации /С-слоя атомов данного элемента, а сечение фотопогло-
щения близко к максимально возможному (см. рис. Д.19.2).
Лекция 20
АТОМЫ ВО ВНЕШНИХ ПОЛЯХ
Действие внешних электромагнитных полей на атомы явля-
ется причиной различных эффектов, которые очень важны для
развития квантовой физики. В данной лекции мы рассмотрим
характер оптического излучения атомов в постоянном магнитном
поле.
20.1. Эффект Зеемана и триплет Лоренца
С 1896 г. П. Зееман (1865-1943) проводил исследования спек-
тра излучения атомов, помещенных в сильное постоянное маг-
нитное поле. По словам Зеемана, для него мощным побудитель-
ным стимулом являлись работы М. Фарадея 1862 г., в которых
тот пытался экспериментально обнаружить связь между светом и
магнетизмом. Справедливо полагая, что за прошедшие годы зна-
чительно увеличилась разрешающая способность спектрометров и
индукция постоянных магнитов, Зееман приступил к своим экспе-
риментам. Высокотемпературное пламя горелки Бунзена помеща-
лось между полюсами сильного магнита с зазором в 14 мм. Ток в
обмотках магнита мог изменяться от нуля до 35 А. В пламя вводи-
лось асбестовое волокно, пропитанное поваренной солью. В спект-
роскоп с дифракционной решеткой Зееман наблюдал четкие линии
D-дублета натрия. (Формирование D-дублета натрия на основе
квантовой теории изложено в конце лекции 17.) При включе-
нии магнитного поля обе линии дублета расширялись, причем
это расширение увеличивалось с величиной индукции магнитного
поля В.
Аналогичное явление Зееман обнаружил на красных линиях
в спектре лития. Заметим, что в первых экспериментах четкого
расщепления спектральных линий не наблюдалось из-за недоста-
точной разрешающей способности спектроскопа Зеемана.
Эффектом Зеемана сразу же заинтересовался X.А. Лоренц
(1853-1928), который к тому времени уже был крупнейшим физи-
ком-теоретиком. Лоренц разработал классическую теорию эффек-
424
Лекция 20. Атомы во внешних полях
та, базирующуюся на представлении атомных электронов клас-
сическими осцилляторами. Частота излучения атома полагалось
равной частоте электронного осциллятора. В отсутствие внешнего
поля уравнение колебаний электрона имеет вид
г + с^г = 0, (20.1)
где и?о — собственная частота колебаний. При наличии внешнего
магнитного поля В на электрон действует дополнительно сила Ло-
ренца. Тогда уравнение движения электрона приобретает вид
г 4- и?дГ = —- [гВ], (20.2)
тпес
где сила Лоренца записана в системе Гаусса. Преобразования при-
водят уравнение (20.2) к виду
г + 2[rQ]+^r = 0, (20.3)
где введена величина
Q = —— В. (20.4)
2тес
которая называется ларморовой частотой (см. дополнение 20.1).
Для решения уравнения (20.3) выберем декартову систему ко-
ординат, ось Z направим по вектору внешнего магнитного поля В.
Проецирование уравнения (20.3) на оси координат дает систему
х 4- 2Q?/ 4- WqX = 0,
у — 2Qi 4- ШцУ = 0, (20.5)
z 4- WqZ = 0.
Из последнего уравнения следует, что внешнее магнитное поле
не влияет на движение электрона в направлении параллельном
вектору В. Для интегрирования первых двух уравнений целесо-
образно ввести комплексную координату £ = х 4- iy, которая опре-
деляет положение электрона на плоскости XY. Умножив второе
уравнение системы (20.5) на мнимую единицу и сложив с первым,
получим
с - i2QC + = 0. (20.6)
Решение однородного уравнения (20.6) ищется в гармониче-
ской форме:
( = ехр (iwt). (20.7)
Подстановка (20.7) в (20.6) дает уравнение для величины аг.
—ш2 4- 2Qu? 4~ = 0, (20.8)
20.1. Эффект Зеемана и триплет Лоренца 425
которое имеет два решения:
w = Q ± + Q2. (20.9)
Теперь оценим величину частоты Q для реальных физических
ситуаций. Воспользовавшись формулой (20.4), легко вычислить,
что при величине магнитного поля В ~ Ю4 Гс параметр Q имеет
порядок 1011с“1. Используя экстремально сильные магнитные
поля, которые создаются в импульсном режиме, можно добиться
увеличения величины Q на два порядка. С другой стороны, час-
тоты видимого света лежат в диапазоне и?о ~ (1015-1016) с-1. Сле-
довательно, в пределах видимого диапазона всегда выполняется
неравенство Q 4с coq. Это значит, что соотношение (20.9) с боль-
шой точностью можно заменить следующим: со = Q ± cjq-
Для выяснения физического смысла решения (20.7) целесо-
образно определить следующие величины:
~ (20.10)
Тогда решения уравнения (20.6) запишутся в виде
£1 = ехр (zu?i^), ^2 = ехр (—й^)- (20.11)
Первое из решений (20.11) можно интерпретировать как круговое
движение электрона против часовой стрелки с угловой скоростью
(частотой) u?i, второе — круговое движение по часовой стрелке с
частотой coz-
Согласно классической электродинамике, движущиеся таким
образом электроны излучают электромагнитные волны с часто-
тами собственных колебаний (20.10).
Колебания электронов вдоль оси Z, т. е. описываемые третьим
уравнением системы (20.5), генерируют электромагнитную волну
частоты и?о, электрический вектор которой параллелен магнит-
ному полю В. Подобные волны в электродинамике называются
тг-компонентами.
Круговые движения электронов в плоскости XY можно разло-
жить на суперпозицию гармонических колебаний в двух взаимно
перпендикулярных направлениях. При этом генерируются волны
с частотами = coq 4- Q и u?2 = ~ электрические векторы
которых перпендикулярны полю В, т.е. а-компоненты.
Угловое распределение интенсивности излучения неоднородно.
Максимум достигается в направлении перпендикулярном ускоре-
нию электрона; в направлении ускорения интенсивность излуче-
ния равна нулю. Так как электрический вектор волны параллелен
ускорению электрона, то а- и тг-компоненты обладают не только
различной поляризацией, но и демонстрируют зависимость интен-
сивности излучения от направления наблюдения.
426
Лекция 20. Атомы во внешних полях
При регистрации излучения в направлении перпендикулярном
внешнему магнитного поля В, согласно теории Лоренца, должен
наблюдаться триплет с частотами и ^2 = ~
В = 0
Рис. 20.1. Схема расщепления спектральных линий во внешнем магнитном поле,
согласно теории Лоренца.
Спектральные линии изображены вертикальными отрезками прямых. 1 и 2 — положения
спектральных линий в отсутствие внешнего магнитного поля, 3 и 4 — то же во внешнем
магнитном поле для различных ориентаций вектора индукции В относительно направле-
ния наблюдения. На вертикальных отрезках условно обозначено состояние поляризации
соответствующих спектральных линий
Все компоненты триплета линейно поляризованы, причем плос-
кость поляризации крайних cr-компонент с частотами и о?2 пер-
пендикулярна плоскости поляризации центральной тг-компоненты
частоты с^о-
При наблюдении излучения вдоль магнитного поля В должны
наблюдаться только две cr-компоненты триплета с частотами
и u?2 с круговой поляризацией во взаимно противоположных на-
правлениях. Если излучение распространяется в направлении
вектора В, то поляризация первой компоненты с частотами
является левой, а второй компоненты — правой. При измене-
нии направления поля В на противоположное изменятся на про-
тивоположные круговые поляризации cr-компонент. Несмещенная
тг-компонента частоты cjq не наблюдается.
Таким образом, по теории Лоренца характер расщепления спек-
тральной линии во внешнем магнитном поле различается в за-
висимости от направления регистрации относительно вектора по-
ля В. В физике закрепились термины поперечный и продольный
эффекты Зеемана.
20.1. Эффект Зеемана и триплет Лоренца
427
Экспериментально линейная поляризация определяется с по-
мощью поворачивания поляризатора. Для обнаружения круговой
поляризации излучения его пучок пропускается через четвертьвол-
новую пластинку, вследствие чего поляризация становится линей-
ной и фиксируется поляризатором. Принципиальная схема уста-
новки для изучения поляризации спектральных линий в эффекте
Зеемана показана на рис. 20.2.
Соотношение Q и?о объясняет то, что Зееман в своих первых
опытах, имея спектроскоп со слабой разрешающей способностью,
Рис. 20.2. Схема установки для исследования поляризации спектральных линий,
наблюдаемых в эффекте Зеемана:
1 — источник излучения (пламя горелки, электрическая дуга, газоразрядная трубка и
т.п.), N и S — полюса электромагнитов, в которых просверлены каналы для вывода
пучков излучения, 2 и 3 — коллимирующие линзы, 4 — четвертьволновая пластинка, 5 и
6 — поляризаторы, 7 и 8 — оптические спектрометры
наблюдал не дискретные спектральные линии с частотами
а только уширение линий. Но исследования поляризации краев
и центра расширенной линии дали результаты, совпадающие с
предсказаниями теории Лоренца.
В начале XX века были созданы интерференционные спектро-
метры высокой разрешающей способности (пластина Луммера-
Герке, интерферометр Фабри-Перо, большие дифракционные ре-
шетки и т. д.), которые позволили измерять длины волн с точ-
ностью до сотых долей ангстрема. Тогда было обнаружено, что
теория Лоренца дает правильные предсказания лишь для отно-
сительно небольшого числа спектральных линий. Действительно,
всегда разность частот возникающих компонент спектральной ли-
нии пропорциональна величине индукции магнитного поля В, но
эта разность лишь в отдельных случаях равна ларморовской ча-
стоте Q. Главное, что триплет Лоренца наблюдался для срав-
нительно небольшого количества спектральных линий. Гораздо
428
Лекция 20. Атомы во внешних полях
чаще спектральная линия расщеплялась на большее число компо-
нент. В частности, длинноволновая компонента Р-дублета натрия
= 5895,92 А) расщепилась в магнитном поле на 4 спектраль-
ные линии, а коротковолновая компонента (А/)2 = 5889,95 А) —
на 6 линий. Были обнаружены и более сложные картины расщеп-
ления. Разности частот соседних компонент также отличались
разнообразием.
Картины расщепления спектральных линий во внешнем маг-
нитном поле, отличающиеся от триплета Лоренца, были названы
сначала аномальным, затем сложным эффектом Зеемана. От-
сюда неизбежно следовал вывод, что теория Лоренца имеет част-
ный характер, а полное объяснение эффекта Зеемана должно ба-
зироваться на квантовой физике.
20.2. Квантовый анализ эффекта Зеемана
Из предыдущих лекций ясно, что любое изменение длины вол-
ны (или частоты) излучения атома является следствием изме-
нения энергии стационарных состояний, так как энергия испус-
каемого фотона равна разности энергий начального и конечного
стационарного состояния атома, согласно второму постулату Бора.
Во всех предыдущих задачах энергии стационарных состояний
атома находились как собственные значения уравнения Шредин-
гера (10.5). Но при расчете характеристик атома во внешнем маг-
нитном поле следует вспомнить, что уравнение Шредингера (10.5)
справедливо для нерелятивистских систем, а магнитное взаимо-
действие по своей природе является релятивистским. Следова-
тельно, последовательная теория эффекта Зеемана должна бази-
роваться на релятивистском уравнении Дирака.
Однако В. Паули показал, что в случае однородных магнит-
ных полей со сравнительно слабой индукцией, т.е. вплоть до
104 Гс, можно использовать следующее модифицированное урав-
нение Шредингера, которое было названо уравнением Паули:
(НЛ-р3ВУф = Е^. (20.12)
Оператор НА представляет собой гамильтониан атома, в котором
операторы импульсов электронов р заменены на операторы р —
— - А, где А — вектор-потенциал внешнего магнитного поля.
с
Оператор собственного момента атома ps пропорционален опера-
тору спина (Д. 12.25)
ps = 275,
где 7 — классическое гиромагнитное отношение (12.6) для элек-
трона.
20.2. Квантовый анализ эффекта Зеемана 429
Как уже было показано в лекции 12, магнитный момент атома
обусловлен как орбитальным движением электронов, так и их соб-
ственными моментами. Оператор полного магнитного момента
атома может быть представлен в виде
(L + 25), (20.14)
С
где LnS — операторы орбитального и собственного механического
момента импульса атома соответственно. Множитель 2 перед опе-
ратором S в (20.14) возникает из-за удвоенного гиромагнитного
отношения для спина (см. лекцию 12).
Решение уравнения Паули (20.12) с оператором (20.13) явля-
ется задачей квантовой механики. Важным результатом реше-
ния является следующий факт. Если атом попадает в постоянное
внешнее магнитное поле В, то его энергия изменяется на вели-
чину
Em = -p>ZB, (20.15)
где /j>z — проекция полного магнитного момента атома на напра-
вление внешнего магнитного поля, В — модуль этого поля.
Величина p>z пропорциональна проекции полного механиче-
ского момента импульса атома Jaz'-
P>z = -(hJaz, (20.16)
где д — безразмерный спектроскопический фактор, который, как
показано в лекции 12, характеризует способ суммирования орби-
тальных моментов и спинов электронов, в том числе и при учете
спин-орбитального взаимодействия.
Выражение (20.15) становится несправедливым только в очень
сильных внешних магнитных полях, когда уже нельзя пренебре-
гать в уравнении Паули квадратичным членом по векторному по-
тенциалу.
Заметим, что формула (20.15) является квантовым аналогом
классической энергии частицы с магнитным моментом д, находя-
щейся во внешнем магнитном поле В, которая равна
Ет — “(М®)*
Вывод последнего соотношения приведен в дополнении 20.2.
Полный механический момент импульса всех электронов ато-
ма, описанный в § 16.4 лекции 16, в стационарном состоянии обла-
дает не только определенным модулем но и одной из проек-
ций. Вектор внешнего магнитного поля В задает направление, для
которого существует измеряемая проекция Jaz- Правило кван-
тования проекции Jaz аналогично правилу (12.24), сформулиро-
ванному для проекции полного механического момента импульса
430 Лекция 20. Атомы во внешних полях
электрона. Величина проекции Jaz'-
Jaz = hmj, (20.17)
определяется магнитным квантовым числом mj, которое может
принимать дискретные значения из множества
mj = -jo, -jo + 1, jo - 1, Jo, (20.18)
где jo — квантовое число, определяющее модуль полного электрон-
ного механического момента импульса атома, согласно (16.10).
Ограничимся случаем LS'-связи (см. §16.4 лекции 16). То-
гда величина квантового числа jo определяется правилом (16.11).
В этом случае безразмерный спектроскопический фактор д выра-
жается формулой Ланде (12.27), но с заменой квантовых чисел для
моментов импульса электрона на квантовые числа для моментов
импульса атома:
п -i . JoOo + 1) “ ^oGo + 1) + 5о(«5О + 1) /9П 1(П
9 = 1 +-----------ШЙТч-----------------’ (2019)
где Iq и so — квантовые числа, определяющие модули орбитального
момента импульса и спина атома по формулам (16.6).
Тогда проекция полного магнитного момента атома на напра-
вление внешнего магнитного поля В квантуется по правилу
Hz = g^BTnj, (20.20)
где //в — магнетон Бора (12.9), mj — магнитное квантовое число
(20.18). Знак минус в правой части (20.20) нет смысла ставить
в явном виде, так как квантовое число mj принимает и положи-
тельные, и отрицательные значения, согласно (20.18).
Сложный вид выражения (20.19) для спектроскопического фак-
тора связан с тем, что вследствие спин-орбитального взаимодей-
ствия стационарные состояния атомов не характеризуются опре-
деленными значениями проекций орбитального момента и спина,
а обладают только измеряемой проекцией полного момента (20.17).
Аналогичная ситуация обсуждалась при рассмотрении магнитных
свойств одноэлектронного атома водорода в лекции 12.
Таким образом, дополнительная энергия (20.15), которую при-
обретает атом во внешнем магнитном поле, выразится следующим
образом:
Em = (20.21)
Значение проекции полного магнитного момента атома (20.20),
а следовательно, и выражение для дополнительной магнитной
энергии (20.21), может быть формально получено с помощью век-
торной модели, которая приводится в дополнении 20.3.
20.2. Квантовый анализ эффекта Зеемана
431
Полученное выражение (20.21) означает, что влияние внешнего
магнитного поля приводит к снятию вырождения по магнитному
квантовому числу. В частности, в случае одноэлектронных атомов
вырождение снимается полностью. Полезно заметить, что снятие
вырождения связано с понижением симметрии системы. В эф-
фекте Зеемана внешнее поле с аксиальной симметрией наклады-
вается на сферически симметричное самосогласованное поле.
Проведем оценку величины дополнительной энергии Ет в
обычных лабораторных условиях. Формула (20.19) ясно демон-
стрирует, что ^-фактор имеет порядок единицы, то же самое видно
из приведенных ниже примеров этого параграфа. Тот же поря-
док имеет магнитное квантовое число mj. Следовательно, вели-
чина энергии Ет, в основном, определяется произведением
Для магнитных полей В ~ 104 Гс величина Ет имеет порядок
~ 10“1б-10-15 эрг, или ~ 10“4-10“3эВ. Это означает, что типич-
ная энергия спин-орбитального взаимодействия (см. лекцию 17)
может значительно превышать дополнительную магнитную энер-
гию Ет. Отсюда следует, что при анализе эффекта Зеемана не-
льзя, вообще говоря, пренебрегать тонкой структурой спектраль-
ных линий.
Таким образом, если атом находится во внешнем магнитном
поле, то энергию его стационарного состояния можно представить
в виде суммы
Е = Eq 4- Ет, (20.22)
где Eq — энергия стационарного состояния атома в отсутствие
внешнего магнитного поля. Величина Eq представляет собой энер-
гию атомного терма, включающую энергию тонкой структуры.
Иначе говоря, энергия Eq определяется не только электронной кон-
фигурацией атома, но и квантовыми числами Zq, «so, jo суммарных
моментов импульса атома.
В отсутствие внешнего магнитного поля частота излучения оп-
ределяется формулой
где Ei и Е2 — энергии начального и конечного атомных термов,
между которыми происходит радиационный переход. Соответст-
вующие стационарные состояния характеризуются квантовыми
числами Zi, si, ji и Z2, <§2, 72 суммарных моментов импульса
атома.
При включении внешнего магнитного поля энергии термов Ei
и Е2 получат добавки Ет, и выражение для частоты примет сле-
дующий вид:
(Ei 4- Emi) — (Е2 4- Emz) Ei — E2 Emi — Em2
u =------------------------=---------4-----------.
n n n
432 Лекция 20. Атомы во внешних полях
Первое слагаемое представляет собой частоту (20.23), второе по-
лезно переписать, используя (20.21). Тогда частота излучения
атома выразится так:
- ff2mJ2)
Ш = О?о Н----------Z---------
п
Прежде всего ясно, что зеемановское расщепление спектраль-
ных линий определяется дискретным спектром дополнительной
магнитной энергии (20.21). Сложный характер расщепления обу-
словлен возможными значениями разностей произведений gmj,
стоящих в скобке формулы (20.24).
Напомним, что радиационные переходы подчиняются прави-
лам отбора (17.3)-(17.5), которые должны быть дополнены прави-
лом для магнитного квантового числа. Возможные изменения чи-
сла mj при радиационных переходах обусловлены тем, что кван-
товое число спина подавляющего числа фотонов, генерируемых в
радиационных переходах, равно единице (см. §13.2 лекции 13).
Это означает, что спин фотона может иметь три разные проекции
на определенное направление: —Л, 0, Л. Направление в данном
случае задано вектором магнитной индукции В. Вследствие сохра-
нения суммарного момента импульса системы «электрон 4- фотон»
при испускании фотона проекция момента импульса электрона
должна изменяться на Л, 0, —h соответственно. При этом кванто-
вое число mj не изменяется или изменяется на единицу. Таким
образом, согласно квантовой теории излучения, зеемановские пе-
реходы должны подчиняться дополнительному правилу отбора:
Amj = 0, ±1. (20.25)
Кроме того, является запрещенным радиационный переход из со-
стояния с квантовым числом jo = 0 в состояние с квантовым чи-
слом jo = 0.
Спектроскопический ^-фактор (20.19) зависит от трех кванто-
вых чисел Zo> «$о> определяющих величины суммарных момен-
тов импульса атома. Из правил отбора (17.3) и (17.5) следует,
что в большинстве случаев радиационный переход происходит с
изменением квантовых чисел Iq и jo, что в свою очередь влечет
неравенство ^-факторов для начального и конечного состояния из-
лучающего атома (gi дъ). Так как, согласно (20.24), сдвиг ча-
стоты пропорционален разности произведений A(gmj), то коли-
чество различных частот в эффекте Зеемана может быть гораздо
больше трех.
В квантовой теории излучения получено, что радиационные
зеемановские переходы без изменения магнитного квантового чи-
сла mj генерируют тг-компоненты, а переходы с изменением mj
на ±1 дают сг-компоненты. Это полностью определяет тип реги-
стрируемой поляризации магнитных компонент как в продольном,
20.2. Квантовый анализ эффекта Зеемана
433
так и в поперечном эффекте Зеемана. Интенсивности отдельных
компонент существенно зависят от квантовых чисел jo и mj. Зна-
чения регистрируемых относительных интенсивностей компонент
спектральной линии для поперечного и продольного эффекта Зее-
мана, вычисленные с помощью квантовой теории излучения, при-
ведены в табл. 20.1 и 20.2.
Таблица 20.1. Относительные интенсивности компонент
спектральной линии для поперечного эффекта Зеемана
Ajo = -1 Ajo = 0 Ajo = 1
Amj = — 1 (joH-mj)(jo+mj-l) 4 (jo+mj)(jo-mj + l) 4 (jo-mj +2)(j0-mj + 1) 4
Дт; = 0 (jo + rnj)(j0 - mj) (jo+mj + l)(jo-mj + l)
Amj = 1 (jo-mj)(jo-mj-l) 4 (jo-mj)(jo+mj + l) 4 (jo4-mj-t-2)(jo4-mj + l) 4
Таблица 20.2. Относительные интенсивности компонент
спектральной линии для продольного эффекта Зеемана
Ajo = -1 Ajo = 0 Ajo = 1
Am; = — 1 (joH-mj)(jo+mj-l) 2 (jo+rnj^jp-mj + l) 2 (jo-mj +2)(j0-mj + 1) 2
Amj = 0 0 0 0
Amj = i (jo-mj)(jo-mj-l) 2 (jo-mj^jo+mj + l) 2 (jo+mj +2)(jo + mj + 1) 2
Вернемся к первым опытам Зеемана и рассмотрим расщепле-
ние Р-дублета натрия во внешнем магнитном поле. Этот зна-
менитый дублет, описанный в лекции 17, характеризуется двумя
верхними (начальными) и одним нижним (конечным) термами,
квантовые числа которых приведены на рис. 20.3.
Действие внешнего магнитного поля изменяет энергию стаци-
онарного состояния атома на величину Ет, определяемую общей
формулой (20.21). В результате энергетические уровни всех трех
термов «расщепляются». Число возникающих магнитных под-
уровней для каждого терма равно 2 jo + 1, в соответствии с прави-
лом квантования (20.18). Следовательно, энергетические уровни
верхних термов «расщепляются» на два и четыре подуровня, ниж-
него — на два (см. рис. 20.4).
Количество радиационных переходов подсчитывается с учетом
правил отбора по магнитному квантовому числу. Легко убедиться,
что спектральная линия расщепляется на 4 магнитные ком-
434
Лекция 20. Атомы во внешних полях
понентпы, линия — на 6 (а не на 8!) магнитных компонент.
Следовательно, Р-дублет натрия во внешнем магнитном поле пре-
вращается в 10 спектральных линий с близкими длинами волн.
Е
so Jo S
_______Г— 2Р
1 1/2 3/2 4/3 3/2
1 1/2 1/2 2/3 —I---------2Р1/2
0 1/2 1/2 2
Рис. 20.3. Энергетическая диаграмма D-дублета натрия в отсутствие внешнего
магнитного поля.
Горизонтальные линии изображают энергетические уровни атомных термов натрия.
Слева — квантовые числа термов и значения ^-фактора, справа — обозначения термов.
Разность энергий F-термов сильно преувеличена
Существенно, что произведения gmj для всех 10-и магнитных
подуровней различаются, поэтому длины волн всех 10-и магнит-
ных компонент различны.
Таблица 20.3. Параметры магнитных компонент D-дублета натрия.
Два последних столбца содержат интенсивности в случае поперечного
и продольного эффектов соответственно
Номер компоненты Поляризация (в единицах Q) 1± (отн.ед.) 7ц (отн.ед.)
1 а -4/3 1/4 1/2
2 7Г 2/3 1/4 0
3 7Г -2/3 1/4 0
4 а 4/3 1/4 1/2
5 а -1 3/2 3
6 а -5/3 1/2 1
7 7Г 1/3 2 0
8 7Г -i/з 2 0
9 а 5/3 1/2 1
10 а 1 3/2 3
20.2. Квантовый анализ эффекта Зеемана
435
Состояния поляризации магнитных компонент определены из-
менением квантового числа mj и приведены в табл. 20.3. Как
было изложено при анализе триплета Лоренца, в продольном эф-
фекте Зеемана тг-компоненты не наблюдаются, а сг-компоненты
Е
2
2/3
-2/3
-2
1/3
-1/3
1
-1
Рис. 20.4. Энергетическая диаграмма D-дублета натрия во внешнем магнитном
поле.
Горизонтальные линии изображают энергетические уровни атомных термов натрия.
Слева — обозначения термов, справа — квантовые числа mj магнитных подуровней и
значения произведений gmj. Масштаб по оси энергии сильно искажен
демонстрируют круговую поляризацию. В поперечном эффекте ре-
гистрируются а- и тг-компоненты, линейно поляризованные во вза-
имно перпендикулярных направлениях.
Нумерация компонент спектральной линии в табл. 20.3 совпа-
дает с нумерацией на рис. 20.4. Частоты компонент ш удобно вы-
разить через сдвиги частот До;, пользуясь формулой (20.24). Для
436
Лекция 20. Атомы во внешних полях
4-х первых компонент частоты равны w = 4- Aw, для осталь-
ных 6-и: w = W£>2 + Aw. Числовые значения сдвигов частот Aw,
выраженные в единицах ларморовской частоты Q:
Aw = (20.26)
приведены в 3-м столбце табл. 20.3.
Величины Aw, согласно табл. 20.3, имеют порядок ларморов-
ской частоты Q. Следовательно, во внешнем поле с магнитной ин-
дукцией В = 104 Гс сдвиги Aw имеют порядок 1011 с-1. С другой
стороны, разность частот спектральных линий Р-дублета натрия
W£>i и W£>2 в отсутствие внешнего поля определяется длинами волн
и А/22 и составляет приблизительно 3,3 • 1012с-1, т.е. на по-
рядок больше. Таким образом, в магнитных полях В ~ 104 Гс и
менее рассматриваемый дублет превращается в 2 изолированные
группы спектральных линий.
Относительные интенсивности магнитных компонент Р-дуб-
лета натрия для поперечного и продольного эффектов Зеемана при-
ведены в двух последних строках табл. 20.3. Видно, что интен-
сивности отдельных компонент различаются незначительно и все
наблюдаются при достаточной разрешающей способности спектро-
метра.
20.3. Наблоюдение простого эффекта Зеемана
Сложный характер эффекта Зеемана в разобранном выше при-
мере обусловлен наличием спина и собственного магнитного мо-
мента атома. Если в формулах (20.19)-(20.24) положить спин рав-
ным нулю, то зеемановское расщепление превратится в триплет
Лоренца.
Для состояний с нулевым спином g-фактор равняется единице,
в чем можно убедиться подстановкой значения sq = 0 в формулу
(20.19). Тогда выражение для частоты (20.24) упростится:
цвВ(тл - mJ2) . wBAmj
w = а>о d---z------= wo d--z---
n n
(20.27)
Разность магнитных квантовых чисел начального и конечного
терма, согласно правилу отбора (20.25), может принимать одно
из трех возможных значений. Следовательно, выражение (20.27)
разбивается на три варианта:
w = Wo, w — wq i “т—, (20.28)
h
что полностью совпадает с триплетом Лоренца.
Таким образом, триплет Лоренца (т.е. простой эффект Зее-
мана) наблюдается на спектральных линиях, обусловленных ра-
20.3. Наблюдение простого эффекта Зеемана
437
диационными переходами между стационарными состояниями с
нулевыми спинами. Все три линии триплета наблюдаются, если
направление наблюдения перпендикулярно магнитному полю. При
наблюдении вдоль поля несмещенная линия с частотой cjq отсут-
ствует. Состояния поляризации совпадают с изображенными на
рис. 20.1.
В частности, простой эффект Зеемана можно наблюдать в слу-
чаях, когда одно из стационарных состояний атома, между кото-
рыми происходит радиационный переход, имеет квантовое число
jo = 0, а второе jo = 1, причем оба состояния характеризуются
квантовыми числами so = 0. Примером является эффект на яркой
желтой спектральной линии неона с длиной волны А = 5852,5 А,
энергетическая схема которого изображена на рис. 20.5. Исход-
ный атомный терм характеризуется квантовыми числами Iq = 0,
Рис. 20.5. Энергетическая схема эффекта Зеемана для желтой линии неона:
а) в отсутствие внешнего магнитного поля; б) при наличии внешнего магнитного поля
5о — 0, jo = 0, конечный терм — числами lo = 1, so = 0,
jo = 1. Во внешнем магнитном поле верхний энергетический уро-
вень не изменится, а нижний расщепится на три с магнитными
квантовыми числами mj = —1,0,1. Все три перехода с верх-
него энергетического уровня разрешены правилами отбора (20.25).
Частоты переходов даются значениями (20.28). Рассматриваемая
спектральная линия относительно яркая и достаточно удаленная
от ближайших соседей, поэтому на ней легко наблюдать простой
эффект Зеемана.
Другой пример простого эффекта Зеемана демонстрирует жел-
тая линия излучения атомов ртути с длиной волны 5790 А. Ха-
438
Лекция 20. Атомы во внешних полях
рактеристики атомных термов, между которыми происходит ра-
диационный переход, приведены на рис. 20.6а. Квантовые числа
jo как начального, так и конечного состояний не равны нулю,
однако существенно, что оба терма являются синглетными, т. е.
б
а
Рис. 20.6. Энергетическая схема эффекта Зеемана для желтой линии ртути:
а) в отсутствие внешнего магнитного поля; б) при наличии внешнего магнитного поля
Е
имеют нулевые спины. При включении внешнего магнитного
поля верхний энергетический уровень с joi — 2 расщепляется
на 5 магнитных подуровней, а нижний с 7’02 = 1 — на 3 под-
уровня. Правила отбора разрешают 9 радиационных переходов
(см. рис. 20.66).
Частоты излучения для перехода между синглетными термами
рассчитываются по формуле (20.27). Вычисления дают только
три различные величины — классический триплет Лоренца. На
рис. 20.66 заметно, что 9 разрешенных переходов разбиваются на
три подмножества, в каждом из которых энергии испускаемых фо-
тонов одинаковы. Это переходы с увеличением магнитного числа
на 1, с уменьшением на 1 и без изменения mj. Следовательно,
все переходы каждого такого подмножества сопровождаются излу-
чением одной и той же частоты. Таким образом, вновь получен
триплет Лоренца или простой эффект Зеемана.
Значение работ по исследованию излучения атомов, находя-
щихся во внешнем магнитном поле, для развития атомной фи-
зики столь велико, что П. Зееман и Х.А. Лоренц были удостоены
Нобелевской премии 1902 года.
20.3. Наблюдение простого эффекта Зеемана 439
Задачи к лекции 20
1. Вычислить ларморову частоту электрона в магнитном поле с ин-
дукцией: а) В = 102 Гс; б) В = 103 Гс; в) В = 104 Гс.
2. Вычислить фактор Ланде для термов: а) 2 Si/2; б) т5о; в) 3Pi/2;
г) 3Ро; д) 451/2; е) 3Р2; ж) 2Р3/2-
3. Вычислить фактор Ланде для термов: а) 2Р3/2; б) 3F2; в) 3F3/2;
г) 7S3; д) 6S5/2; е) 5Р4; ж) 4F9/2.
4. Рассчитать расщепление спектральной линии, возникающей при
радиационном переходе между термами: a) 3/?i -> 3Pi; б) 2Р3/2
2Si/2;b) 2jD3/2 2Pi/2-
5. Желтая спектральная линия (Л — 5852,5 А) испускается атомом
неона при радиационном переходе между термами -> 1Sq. Вычи-
слить длины волн компонент, возникающих в магнитном поле с индук-
цией В = 104 Гс.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 20
20.1. Теорема Лармора
Теоретический анализ, проведенный Лоренцем, наглядно подкрепля-
ется классической моделью прецессии электронной орбиты во внешнем
магнитном поле. В классической электродинамике движение электрона
в атоме описывается замкнутой орбитой. Как следствие, электрон обла-
дает моментом импульса L и магнитным моментом дл.
Предположим, что атом помещается во внешнее магнитное поле с
индукцией В. Тогда на атомный электрон будет действовать момент
сил М, определяемый векторным произведением
М = [мВ]. (Д.20.1)
Классическое уравнение движения имеет вид
= М. (Д.20.2)
at
Отсюда следует, что векторы dL и М коллинеарны. Взаиморасположение
векторов В, L, у, М и dL приведено на рис. Д.20.1.
Рис. Д.20.1. К описанию ларморовой прецессии электронной орбиты во внешнем
магнитном поле
Проецируя уравнение (Д.20.2) на направление вектора М, получаем
= цВ sin а, (Д.20.3)
at
где а — угол между направлениями векторов L и В.
Дополнения к лекции 20
441
С другой стороны, модуль вектора dL можно выразить через проек-
цию вектора L на направление вектора магнитного поля В:
dL = L sin a d0, (Д.20.4)
где dd — угол, на который повернется вектор L за время dt под действием
момента силы М.
Комбинируя соотношения (Д.20.3) и (Д.20.4), получаем
f = LB- (Д-20'5)
Последнее уравнение означает, что вектор момента импульса L и кол-
линеарный ему вектор магнитного момента р осуществляют прецессию
вокруг направления магнитного поля В. Слева в (Д.20.5) стоит частота
прецессии, которую мы обозначим символом Q. В правой части (Д.20.5)
находится гиромагнитное отношение p/L, умноженное на модуль маг-
нитной индукции В. Гиромагнитное отношение выразим с помощью
классической формулы (12.6), применив ее к электрону. Тогда выраже-
ние для частоты прецессии примет следующий вид:
О = —— В. (Д.20.6)
2тес v '
Таким образом, согласно классической теории, электронная орбита
вращается вокруг направления магнитного поля В с постоянной угловой
скоростью (Д.20.6). Это утверждение называется теоремой Лармора,
так как оно было получено в 1895 г. английским физиком и математиком
Дж. Лармором (1857-1942).
По формуле (Д.20.6) нетрудно оценить, что для обычных лаборатор-
ных магнитных полей В ~ 104 Гс частота Q (угловая скорость прецес-
сии) имеет порядок 1011 Гц. Частота вращения электронов на своих ор-
битах в классической теории полагается равной частоте излучения
испускаемого атомом. Для видимого света с длиной волны А ~ 0,5 мкм
частота а>о ~ 4 • 1015 Гц. Таким образом, частота прецессии Q на не-
сколько порядков ниже частоты вращения электронов на их классиче-
ских орбитах. Поэтому сравнительно медленная частота прецессии на-
кладывается на быстрое вращение электронов. Следствием является то,
что электроны атома, находящегося во внешнем магнитном поле, из-
лучают не только на собственной частоте ojq, но и на дополнительных
частотах ujq ± Q.
Следовательно, в рамках классической физики эффект Зеемана объ-
ясняется как превращение спектральных линий в триплеты под дей-
ствием внешнего магнитного поля.
20.2. Классическая энергия магнитного момента
во внешнем магнитном поле
Любой объект, обладающий определенным магнитным моментом р,
в классической физике может быть представлен в виде замкнутого про-
водника, по которому протекает постоянный ток (короче — витка с
током).
442
Дополнения к лекции 20
Найдем классическое выражение для энергии витка с током, харак-
теризующимся магнитным моментом д, во внешнем магнитном поле с
индукцией В.
Момент сил М, действующих на виток с током, находящимся во
внешнем магнитном поле В, определяется следующим векторным про-
изведением:
М = [дВ]. (Д.20.7)
Это означает, что момент сил М равен нулю, когда магнитный момент д
параллелен или антипараллелен вектору индукции В, и достигает мак-
симального значения, когда магнитный момент м перпендикулярен на-
правлению внешнего магнитного поля.
На рис. Д.20.2а показан пример относительного расположения векто-
ров В, у и М, а также пары сил, создающих момент сил М. Видно, что
пара сил, действующих на магнитный момент у со стороны внешнего
магнитного поля, стремится повернуть его параллельно вектору магнит-
ной индукции В. Нетрудно убедиться, что это происходит при любом
В
Рис. Д.20.2. Поворот магнитного момента у во внешнем магнитном поле В:
а) произвольное положение магнитного момента: в — угол между векторами В и у, по-
казана пара сил, поворачивающая магнитный момент и направление вектора момента
силы М; б) У1 и у2 — начальное и конечное положение вектора магнитного момента,
а — угол поворота, п — единичный вектор, указывающий направление поворота по пра-
вилу правого винта
взаиморасположении векторов Вид. Следовательно, при параллельно-
сти векторов у ft В объект с магнитным моментом у занимает положе-
ние устойчивого равновесия, а при антипараллельности векторов у 11 В
объект находится в неустойчивом равновесии.
Положение магнитного момента относительно вектора индукции В
внешнего магнитного поля охарактеризуем углом 0 между векторами В
и у (см. рис. Д.20.2а).
Как известно из классической механики, работа, совершаемая над
объектом при его повороте на элементарный угол da, выражается с по-
мощью скалярного произведения
dA = (Мп) da, (Д.20.8)
Дополнения к лекции 20
443
где п — единичный вектор поворота, направленный по правилу правого
винта.
Вычислим работу сил, действующих на виток, при его повороте на
произвольный угол а. Для определенности положим, что при пово-
роте угол а увеличивается. Начальное положение магнитного момента
обозначим углом конечное положение — углом 02 = #1 + а (см.
рис. Д.20.26).
Заметим, что при данном направлении поворота векторы М и п ан-
типараллельны. Тогда искомая работа выразится следующим опреде-
ленным интегралом:
02 02
А — у*(Мп)с?0 = — [iBAnOdO = — [/zBcos#i — дВсозбг]- (Д.20.9)
01 01
Минус перед интегралом возникает именно из-за антипараллельности
векторов М и п.
Можно сказать, что работа (Д.20.9) производится за счет запаса энер-
гии Ет, которую объект с магнитным моментом ц имеет во внешнем
магнитном поле. Следовательно, работа (Д.20.9) и энергия Ет связаны
соотношением
А = -ДЕт. (Д.20.10)
Сравнение уравнений (Д.20.9) и (Д.20.10) позволяет записать вы-
ражение для классической энергии магнитного момента /1 во внешнем
магнитном поле В в виде следующего скалярного произведения:
Ет = -(МВ). (Д.20.11)
Под действием момента сил М (Д.20.7) объект с магнитным момен-
том м переходит в более устойчивое положение и уменьшает свою энер-
гию (Д.20.11). При параллельности векторов g и В энергия Ет прини-
мает свое минимальное значение.
20.3. Расчет магнитного момента атома
по векторной модели
Расчет магнитного момента атома является задачей квантовой фи-
зики. Как было показано в лекциях 9 и 12, орбитальный момент им-
пульса и спин электрона не являются обыкновенными векторами, ко-
торые имеют по три определенные проекции. То же самое справедливо
для полного момента импульса электрона и суммарных моментов им-
пульса атома. Как следствие, обыкновенными векторами не являются
магнитные моменты электрона и атома. Вычисления магнитного мо-
мента атома осложняются тем, что гиромагнитные отношения для орби-
тального и собственного моментов различаются в два раза.
Следует иметь в виду, что, в первую очередь, представляет инте-
рес проекция суммарного магнитного момента атома /iz на направление
внешнего магнитного поля В, так произведение этой величины на мо-
дуль магнитной индукции В равно дополнительной энергии Ет) которую
приобретает атом во внешнем магнитном поле.
444
Дополнения к лекции 20
В рамках векторной модели, которая уже описывалась в лекциях 9
и 12, можно получить правильную формулу для величины p,z, включа-
ющую сложное выражение спектроскопического фактора (20.19).
В стационарном состоянии атом характеризуется определенными мо-
дулями орбитального момента импульса La и спина Sa (имеются в виду
суммарные моменты импульса всего атома). Кроме того, в данном со-
стоянии атом имеет определенный модуль полного момента импульса
Ja, который вычисляется по правилам сложения моментов, описанном в
лекции 16.
В векторной модели три момента импульса атома изображаются сим-
волическими векторами, длины которых равны модулям Тд, Sa и Дд.
Начала векторов Ьд, 8д, Дд совмещаются, а их взаимоориентация под-
чиняется соотношению
Дд =Ьд + 8д. (Д.20.12)
Далее на векторной диаграмме строятся также символические век-
торы магнитных моментов ijls, которые полагаются прямо пропор-
циональными соответствующим моментам импульса атома:
Рис. Д.20.3. К расчету маг-
нитного момента многоэлек-
тронного атома по векторной
модели. Модули магнитных
моментов изображены в мас-
штабе 7 = 1
Ml = -7L4, Ms = “27sa, (Д-20.13)
где 7 — классическое гиромагнитное отно-
шение для электрона:
е
<Д-2ОЛ4>
Затем векторы nL и* fis формально
складываются по правилам векторной ал-
гебры:
M = Ml + Ms- (Д.20.15)
Важно, что из-за различия классиче-
ского и спинового гиромагнитных отноше-
ний векторы д и Дд не коллинеарны (см.
рис. Д.20.3).
Теперь опустим перпендикуляр из кон-
ца суммарного вектора д на направление
вектора Дд и получим новый, вектор /ieff
(см. рис. Д.20.3), который в векторной мо-
дели называется эффективным магнитным
моментом. Этот вектор антипараллелен
символическому вектору полного момента
импульса атома Дд.
Вычислим модуль эффективного маг-
нитного момента Обозначим углы
между парами символических векторов (Ьд и Дд) и (8д и Дд) буквами
а и /3 соответственно. Тогда, согласно рис. Д.20.3, величина /zeff может
быть представлена следующей суммой:
Meff = HL cos а + Us COS
(Д.20.16)
Дополнения к лекции 20
445
Косинусы углов а и (3 легко вычислить, применяя теоремы косинусов к
треугольникам, составленным из векторов Ьд, 8д, Лд:
S2A = J2A + L2a — 2JaLa cos ci,
L2a - J2 + S2A - 2JASA cos/3.
(Д.20.17)
Выразим из соотношений (Д.20.17) косинусы углов а и /3:
cos а —
J2a + L2a-S2a
2LaJa
cos/3 =
J2a + S2a-L2a
2SaJa
и подставим их в (Д.20.16). Модули магнитных моментов ць и fis вы-
разим, согласно (Д.20.13), через модули моментов импульса LA и SA.
Тогда модуль эффективного магнитного момента представится следую-
щей суммой:
= 7 (1 + JA- (Д-20.18)
\ 2<4 /
Коэффициент в скобках содержит квадраты модулей моментов им-
пульса, которые целесообразно выразить через соответствующие кванто-
вые числа согласно формулам (16.6) и (16.10). Очевидно, что эта вели-
чина точно совпадает со спектроскопическим (/-фактором (20.19). Таким
образом, мы получаем выражение для модуля эффективного магнитного
момента:
Л , Jo(jo + 1) + <$о(5о + 1) - Wo -г Щ т т
ы = Ч1 +-----------------шТч------------------J Ja = ,9Ja-
(Д.20.19)
В векторной модели для вычисления дополнительной энергии Ет,
которую приобретает атом во внешнем магнитном поле, используется
классическая формула
Ет = -MeffB. (Д.20.20)
Скалярное произведение (Д.20.20) целесообразно представить в виде
Ет = ~(м)гВ,
(Д.20.21)
где (^eff)z — проекция эффективного магнитного момента /ieff на на-
правление магнитного поля В, а В — модуль индукции этого поля.
Согласно выражению (Д.20.19), проекцию эффективного магнитного мо-
мента (^eff)z можно выразить через проекцию полного момента им-
пульса на направление магнитного поля, т. е.
(Meff)z = -ygJAZ-
(Д.20.22)
446
Дополнения к лекции 20
Так как последний сомножитель в правой части (Д.20.22) квантуется по
правилу (20.17), то проекция эффективного магнитного момента выра-
жается в виде
(Meff)z — (Д.20.23)
где mj — магнитное квантовое число, определяющее проекцию полного
момента импульса, могущее принимать любое из 2jo + 1 значений, со-
гласно правилу (20.18). Знак минус в правой части (Д.20.23) не указан,
потому что квантовое число mj принимает как положительные, так и
отрицательные значения.
Сравнение выражений (Д.20.23) и (20.20) показывает, что проекция
эффективного магнитного момента (^eff)z, полученная с помощью век-
торной модели, совпадает со значением проекции полного магнитного
момента атома pz на направление внешнего магнитного поля В, полу-
ченной методом квантовой механики.
Следовательно, дополнительная энергия (Д.20.20), которую приобре-
тает атом во внешнем магнитном поле, представляется в виде
Ет = pngBrnj, (Д.20.24)
совпадающим с формулой (20.21).
Лекция 21
АТОМЫ ВО ВНЕШНИХ ПОЛЯХ (ПРОДОЛЖЕНИЕ)
21.1. Эффект Пашена-Бака
В 1912 г. Ф.Пашен (1865-1947), который обнаружил спек-
тральную серию излучения водорода в инфракрасном диапазоне,
и Э.Бак (1881-1959) открыли эффект, вошедший в физику под их
именем. Эффект заключался в том, что при резком увеличении
индукции магнитного поля сложный эффект Зеемана на некото-
рых спектральных линиях превращался в триплет Лоренца.
Внешнее магнитное поле В можно полагать слабым, если маг-
нитная энергия Ет (энергия магнитного момента атома во внеш-
нем поле) значительно меньше энергии спин-орбитального взаимо-
действия Esl, т.е. Ет Esl- Пользуясь выражениями (17.10)
и (20.21), можно критерий слабого магнитного поля представить
в виде следующего неравенства:
„ a2RyZ*4 ГП1 ч
цвВ «С----, (21.1)
где п — главное квантовое число стационарного состояния атома,
Z* — эффективный атомный номер, определяемый формулой
(17.9).
Легко получить граничное значение слабого магнитного поля
для спектральных линий атома водорода, у которого Z = 1. В част-
ности, для первой линии серии Бальмера имеем В а2 Ry/8/хв ~
- 104 Гс.
В случаях, когда вычисление эффективного атомного номера
Z* затруднительно, можно воспользоваться экспериментальными
данными о тонкой структуре оптических спектров. Например,
для Р-дублета натрия оценку величины спин-орбитальной энер-
гии можно сделать по известным длинам волн компонент Adi =
= 5889,95 А и А^2 = 5895,92 А. Разность энергий верхних термов
Р-дублета равна 2tt/zc(1/Adi — 1/Ad2) ~ 2-10“3 эВ. Тогда критерий
Ет Esl дает неравенство В 3 • 105 Гс.
448 Лекция 21. Атомы во внешних полях {продолжение)
Таким образом, для D-дублета натрия магнитное поле с ин-
дукцией В ~ 104 Гс можно рассматривать как слабое. Подтверж-
дением этого является совпадение результатов расчетов в прибли-
жении слабого поля, приведенных выше, и экспериментальных
спектрометрических данных. Но для спектральных линий се-
рии Бальмера такое поле В уже нельзя полагать слабым и про-
водить расчеты магнитного расщепления энергетических уровней,
используя формулы (20.24) и (20.19).
Вычисление энергии стационарных состояний атома, находя-
щегося во внешнем магнитном поле, является сложной задачей
квантовой механики, которая в общем виде пока не решена. Од-
нако при выполнении условия
(21.2)
nA
противоположного неравенству (21.1), задача упрощается. В силь-
ных магнитных полях, когда магнитная энергия значительно
превышает спин-орбитальную, можно полагать, что стационарное
состояние атома характеризуются не проекцией полного момента
Jaz (20.17), а определенными проекциями орбитального момента
Laz и спина Saz- Эти проекции принимают дискретные значе-
ния, согласно правилам, аналогичным (20.17):
Laz = ftmL, Saz = hms, (21.3)
где квантовые числа ть и ms пробегают ряды значений, в со-
ответствии с общими правилами квантования механических мо-
ментов
m^ = —Iqi —Io + 1, ..., Io ~ 1, lot (21-4)
ms = -<$o- -«so 4-1, ...so - 1, s0. (21.5)
В такой ситуации проекция полного магнитного момента атома
pz выразится суммой проекций Laz и Saz> каждая из которых
умножена на соответствующее гиромагнитное отношение
l^z = ^Laz + 27SUZ, (21.6)
где 7 — классическое гиромагнитное отношение (12.6). Следова-
тельно, величина проекции магнитного момента pz квантуется по
правилу
Vz = Р>в(ть + 2ms), (21.7)
а дополнительная магнитная энергия выражается так:
Em = + 2ms)B = Q/i(mL 4- 2ms). (21.8)
Таким образом, в сильном магнитном поле энергия стационар-
ного состояния атома представляется в виде трех слагаемых, при-
21.1. Эффект Пашена-Бака
449
чем каждое из них много меньше предыдущего:
Еа = Eq 4- Em 4- Esl, (21.9)
Eq 3> Em Esl- (21.10)
В двух последних выражениях Eq — энергия атомного терма без
учета спин-орбитального взаимодействия.
Рассмотрим расщепление спектральной линии в сильном маг-
нитном поле, подчиняющемся условию (21.2). Частота излучения
равна разности энергий Ед, деленной на постоянную Планка, т.е.
АЕа Д#0 , A^m , ^Esl
W — ----- =----------------------
h h h h
Первое слагаемое в (21.11) представляет собой частоту излучения
wq в отсутствие внешнего магнитного поля, третьим слагаемым,
вследствие (21.10), можно пренебречь. Тогда
ш = шо + ^в(Ат£ + 2Ат5)В = + + 2Дт5). (21.12)
(21.11)
h
Для получения спектральной картины требуется учесть пра-
вила отбора, которые отсекают маловероятные радиационные пе-
реходы. К правилам (20.24) добавляются следующие условия для
квантовых чисел тп^ и ms’
&mL = 0, ±1, Ams = 0. (21.13)
Тогда частота (21.12) может принимать только три следующих
значения:
I ^0,
1 CUq i
(21.14)
Это не что иное, как триплет Лоренца. Следовательно, в сильных
магнитных полях сложный эффект Зеемана должен превращаться
в простой.
Учет отброшенного третьего слагаемого в (21.11) приведет к
появлению спин-орбитальных добавок = ^Esb/h в
выражениях частот (21.14). Если в отсутствие внешнего магнит-
ного поля спектральная линия обладала тонкой структурой, то при
включении сильного поля возникает триплет, каждая из компо-
нент которого обладает той же тонкой структурой. В частности,
дублет с разностью частот в сильном магнитном поле пре-
вращается в три дублета с тем же расщеплением Au>sl, которые
различаются на величину Q.
Исследования эффекта Пашена-Бака требуют создания в ла-
бораторных условиях постоянных магнитных полей с индукцией,
450
Лекция 21. Атомы во внешних полях (продолжение)
по крайней мере, в несколько сотен тысяч гаусс. Решение этой за-
дачи оказалось связанной с рядом принципиальных трудностей,
которые в полной мере не преодолены до настоящего времени.
Первый результативный метод получения сильных магнитных по-
лей был предложен в 1922 г. П.Л.Капицей (1894-1984). Этим
методом создавался импульс магнитного поля с индукцией около
5 • 105 Гс длительностью « 0,01 с. За это время нетрудно сфотогра-
фировать картину расщепления спектральной линии (см. допол-
нение 20.1).
Из условия (21.1) следует, что эффект Пашена-Бака легче на-
блюдать на легких атомах с малым эффективным атомным но-
мером Z* и на радиационных переходах между состояниями с
низким главным квантовым числом п, В частности, эффект на-
дежно наблюдается на некоторых спектральных линиях излучения
атомов лития, натрия и кислорода во внешних магнитных полях
с индукцией порядка нескольких десятков тысяч гаусс. Резуль-
таты экспериментов продемонстрировали согласие с вышеприве-
денными выводами.
21.2. Эффект Штарка
Рассмотрим влияние внешнего электрического поля на энергию
стационарных состояний атомов и возникающие при этом изме-
нения в спектре излучения этих атомов.
Согласно классической электродинамике, воздействие внешне-
го электрического поля на атом не должно изменять частоты соб-
ственных колебаний внутриатомных электронов и, следовательно,
искажать спектр излучения атома.
Пусть атом находится в постоянном однородном внешнем элек-
трическом поле с напряженностью 5. Направим ось Z декартовой
системы координат вдоль вектора поля 5. Проекции напряжен-
ности £ примут вид 8Х = 8у = 0, 8Z = 8, где 8 — модуль
напряженности внешнего электрического поля. На электрон бу-
дет действовать дополнительная сила, равная — е£ и направленная
антипараллельно оси Z.
По классической теории движение атомного электрона пред-
ставляется суперпозицией трех ортогональных колебаний. Во
внешнем электрическом поле движение электрона вдоль осей X
и У не изменится, а движение вдоль оси Z будет описываться
уравнением
mez 4- meufiz = —е8, (21.15)
где z — координата электрона, wq — собственная частота коле-
баний электрона в атоме, е — элементарный (положительный)
электрический заряд. Решение неоднородного уравнения (21.15)
может быть записано в виде суммы гармонической функции и по-
21.2. Эффект Штарка
451
стоянного члена:
z(£) =----—^£ + A cos + </?), (21.16)
где А — амплитуда возникших колебаний.
Решение (21.16) означает, что действие внешнего электриче-
ского поля лишь смещает положение равновесия, но не меняет
частоту колебаний электрона. Следовательно, согласно классиче-
ской теории, спектр излучения атома не должен изменяться, если
атом попадает во внешнее постоянное электрическое поле.
В 1913 г. И.Штарк (1874-1957) занимался эксперименталь-
ными исследованиями излучения атомов водорода, помещенных
в постоянное электрическое поле (см. рис. 21.1). В установке
Рис. 21.1. Схема экспериментальной установки для наблюдения эффекта Штарка:
Т — газоразрядная трубка, А — анод, К — катод, Э — дополнительный электрод, С —
спектрометр. Стрелкой указано направление регистрируемого излучения
Штарка использовалась газоразрядная трубка, наполненная раз-
реженным водородом. Между катодом и анодом устанавливалась
разность потенциалов порядка нескольких киловольт. Атомы во-
дорода переводились в возбужденные состояния из-за соударений с
ускоренными ионами и электронами. В трубку был впаян допол-
нительный электрод, на который подавался положительный по-
тенциал ~ 104 В. Расстояние между электродами К и Э составляло
около 1 мм, что обеспечивало в межэлектродном пространстве элек-
трическое поле напряженностью ~107В/м. Излучение возбуж-
денных атомов анализировалось с помощью оптического спектро-
метра.
В ходе опытов Штарк обнаружил, что спектральная линия HQ
серии Бальмера в электрическом поле расщепляется на 15 отдель-
ных компонент. Остальные видимые линии серии Бальмера пре-
терпевали еще более сложное расщепление. Разность частот край-
них компонент оказалась прямо пропорциональной модулю напря-
женности электрического поля 8. При наблюдении в направлении
перпендикулярном вектору напряженности 8 все компоненты де-
452 Лекция 21. Атомы во внешних полях (продолжение)
монстрировали линейную поляризацию. Эти характерные явле-
ния получили название эффекта Штарка.
Использование спектрометров ультрафиолетового излучения
позволило обнаружить эффект Штарка на спектральных линиях
серии Лаймана. В частности, первая линия этой серии расщепля-
ется в электрическом поле на три компоненты. Дальнейшие экс-
перименты показали, что эффект Штарка возникает, в принципе,
на всех спектральных линиях любых атомов.
Первый вариант теории эффекта Штарка был предложен в
1916 г. К. Шварцшильдом (1873-1916) и П.С. Эпштейном (1883—
1966). Последовательная теория базируется на решении уравне-
ния Шредингера в рамках квантовой теории атома.
Рассмотрим сначала эффект Штарка для одноэлектронного
атома — атома водорода. Единственный электрон атома движется
в кулоновском поле ядра, величину которого легко оценить, ис-
пользуя первый боровский радиус а^:
£N~ 1011 В/м. (21.17)
ао
Для наблюдения эффекта Штарка в лабораторных эксперимен-
тах обычно используются однородные постоянные электрические
поля с величиной напряженности ~ 107В/м. Следовательно, дей-
ствие внешнего электрического поля на атом водорода можно рас-
сматривать как малое возмущение.
Из классической электродинамики известно, что электриче-
ский дипольный момент de во внешнем электрическом поле при-
обретает энергию, равную
Ue = -£de. (21.18)
В квантовой механике для вычисления энергии стационарных
состояний атома во внешнем электрическом поле решается соот-
ветствующее уравнение Шредингера. К гамильтониану атома во-
дорода добавляется энергия электрона Ue в электрическом поле с
напряженностью 5, которую можно записать в виде
Ue = ez£. (21.19)
Гамильтониан теряет сферическую симметрию, которая пони-
жается до аксиальной. Решение уравнения Шредингера для ста-
ционарных состояний атома водорода во внешнем электрическом
поле целесообразно проводить, перейдя от декартовых к специаль-
ным параболическим координатам
л . . У
£ = г 4- г, rj = г — z, ср = arctg —,
х
где £ и г] пробегают значения от 0 до оо, а координата <р — от О
до 2тг.
21.2. Эффект Штарка 453
В результате решения уравнения Шредингера, изложенного в
курсе квантовой механики, получено, что каждое стационарное со-
стояние атома водорода во внешнем электрическом поле харак-
теризуется четырьмя квантовыми числами: npi, nP2, ms-) где
m — магнитное число, npi и пр2 — числа, названные параболиче-
скими. Главное квантовое число п в данном случае представляется
линейной комбинацией п = пр\ 4- пр2 4- \тп\ 4- 1. Энергии стацио-
нарных состояний в первом приближении представляются в виде
суммы двух слагаемых:
Rv 3
Е'п = Еп + Ее =---+-ea0£n(npi - пР2). (21.20)
П
Первый член представляет собой энергию изолированного ато-
ма водорода, второй возникает из-за влияния внешнего электриче-
ского поля. Разность параболических квантовых чисел npi — пР2
пробегает 2п—1 значений, различающихся на единицу, от — (n—1)
до п — 1, где п — главное квантовое число.
Действие внешнего электрического поля на атом водорода при-
водит к частичному снятию вырождения стационарных состоя-
ний. Одинаковыми энергиями обладают состояния, которые раз-
личаются только знаком магнитного квантового числа тп.
Основное состояние атома водорода с п = 1 не изменяет свою
энергию, так как при этом разность npi — пР2 принимает един-
ственное значение равное нулю, и согласно (21.20), дополнитель-
ная электрическая энергия Ее = 0. При п = 2 разность пара-
болических квантовых чисел принимает три разных значения:
— пР2 = 1, 0, — 1, а дополнительная энергия Ее соответственно
может быть равна
Ее = Sea^S, 0, - Зеа0£. (21.21)
Иначе говоря, энергетический уровень с Еп=2 = —Ry/4 при
воздействии внешнего электрического поля 5 расщепляется на
три. Разность энергий АЕе между соседними подуровнями, со-
гласно (21.21), равна Зеао£, т.е. пропорциональна модулю напря-
женности электрического поля.
Энергия Ее = при величине напряженности внешнего
поля 8 ~ 107В/м имеет порядок 10-3эВ. Спин-орбитальное рас-
щепление энергетического уровня атома водорода сп = 2/согласно
(13.13), составляет a2 Ry/16 « 4,5-10“5 эВ, т. е. много меньше Ее.
Следовательно, при рассмотрении эффекта Штарка во внешних
электрических полях порядка 107В/м и более спин-орбитальным
взаимодействием можно пренебречь.
Из формулы (21.20) следует, что разность между крайними
энергетическими уровнями равна 3eao£n(n — 1). Можно сказать,
что максимальное значение дополнительной электрической энер-
454 Лекция 21. Атомы во внешних полях (продолжение)
гии Ее с увеличением главного квантового числа п возрастает ква-
дратично (при фиксированной напряженности внешнего электри-
ческого поля). Из-за такой нелинейной зависимости Ее(п) эффект
Штарка должен быть более заметен для сильно возбужденных со-
стояний атома водорода.
С другой стороны, абсолютная величина энергии тонкой струк-
туры Esl, в соответствии с выражениями (13.3) и (17.10), убы-
вает пропорционально п“3. Следовательно, в достаточно сильных
внешних электрических полях, когда
\Ее\ » \ESL\, (21.22)
можно анализировать эффект Штарка, пренебрегая спин-орби-
тальным взаимодействием.
Характер расщепления спектральной линии определяется па-
раметрами стационарных состояний, между которыми происходит
радиационный переход. Из вышеизложенного следует, что в силь-
ном электрическом поле первая линия серии Лаймана превраща-
ется в триплет (см. рис. 21.2). Тип поляризации компонент три-
плета вычисляется методами квантовой электродинамики. Как и в
Рис. 21.2. Энергетическая схема расщепления первой спектральной линии серии
Лаймана в сильном внешнем электрическом поле, m — магнитное квантовое
число
зеемановских переходах (см. лекцию 20), при изменении магнит-
ного квантового числа m на единицу генерируются сг-компоненты,
в переходах с Am = 0 образуются тг-компоненты.
Энергии испускаемых фотонов выражаются разностями энер-
гий (21.20):
6 = Еп-2 — En-\ + Ее = - Ry 4- Eej (21.23)
где энергия Ее принимает значения (21.21). При этом разность
энергий крайних компонент штарковского триплета первой линии
серии Лаймана равна
As = 6еао£.
(21.24)
21.2. Эффект Штарка
455
Таким образом, расщепление спектральной линии прямо про-
порционально модулю напряженности внешнего электрического
поля 8. Такой вид эффекта Штарка называется линейным.
Для описания эффекта Штарка на других спектральных ли-
ниях серии Лаймана следует сначала рассчитать расщепление
энергетических уровней с фиксированным главным квантовым
числом п > 2. Из выражения (21.20) для дополнительной энергии
Ее следует, что штарковские подуровни являются эквидистант-
ными (равноотстоящими) и их количество равно 2п — 1. Разность
энергий соседних подуровней равна Зеао£п/2, т. е. растет линейно
с главным квантовым числом п.
При этом следует учесть, что количество компонент расщеп-
ления спектральной линии ограничивается правилами отбора по
магнитному квантовому числу тп. В частности, вторая линия се-
рии Лаймана в сильном внешнем электрическом поле разделяется
на четыре компоненты, а не пять, так как правила отбора (Am =
= 0, ±1) запрещают центральную компоненту, соответствующую
переходу между состояниями с нулевой дополнительной энергией
Ее = 0 (см. рис. 21.3).
Третья линия этой серии расщепляется на семь компонент и
т. д. Нечетные линии серии Лаймана расщепляются на 2п — 1
штарковских компонент, четные линии серии Лаймана — на 2п
пр\ ~Пр2 I Е
Рис. 21.3. Энергетическая схема расщепления второй спектральной линии серии
Лаймана в сильном внешнем электрическом поле
компонент, где п — главное квантовое число исходного стацио-
нарного состояния. Квантовая электродинамика дает результаты,
совпадающие с данными, полученными экспериментально.
Штарковское расщепление спектральных линий серии Баль-
мера имеет более сложный вид, так как во внешнем электрическом
456 Лекция 21. Атомы во внешних полях {продолжение)
поле расщепляются и верхний, и нижний энергетические уровни,
между которыми происходит радиационный переход. Например,
первый бальмеровский переход из состояния с п = 3 в состояние
с п = 2 разбивается на 15 различных переходов (см. рис. 21.4).
Так как расстояние между соседними штарковскими подуров-
нями ДЕе зависит от главного квантового числа п, то все 15 ради-
ационных переходов на рис. 21.4 генерируют фотоны различных
-Ry/9
(" = 3)
-Ry/4
(л = 2)
А Е
Рис. 21.4. Энергетическая схема расщепления первой спектральной линии серии
Бальмера в сильном внешнем электрическом поле
энергий. Таким образом, первая спектральная линия серии Баль-
мера в сильном электрическом поле расщепляется на 15 штарков-
ских компонент.
Так как число штарковских энергетических подуровней равно
2п — 1, то в сильном внешнем электрическом поле каждый баль-
меровский переход должен разбиться на 3(2п' — 1), где nf — глав-
ное квантовое число исходного состояния. Вследствие различного
расщепления верхнего и нижнего энергетических уровней, штар-
ковские радиационные переходы, вообще говоря, дают фотоны с
несовпадающими энергиями. Однако правила отбора запрещают
генерацию центральных компонент для спектральных линий и
Щ. Иначе говоря, в сильном внешнем электрическом поле бальме-
ровские линии Н^, Н7 и Н$ расщепятся на 20, 27 и 32 компоненты
соответственно. Таким образом, нечетные линии серии Бальмера
расщепляются на 3(2п' — 1) штарковских компонент, четные ли-
нии этой серии — на 3(2п' — 1) — 1 компоненту.
21.2. Эффект Штарка
457
Вышеприведенный анализ был выполнен в приближении силь-
ного внешнего электрического поля. Для слабых внешних элек-
трических полей, когда имеет место условие противоположное
(21.22), т.е.
|£?е| « (21.25)
эффект Штарка в данной задаче накладывается на спин-орбиталь-
ное расщепление. В частности, во внешнем электрическом поле
S ~ 104В/м каждая компонента первого лаймановского дублета
должна превратиться в триплет.
Решение стационарного уравнения Шредингера для атома
водорода во втором приближении обнаруживает квадратичный
эффект Штарка. В выражении для дополнительной энергия Ее по-
является член пропорциональный квадрату напряженности элек-
трического поля. Вклад квадратичной составляющей становится
существенным в сильных полях.
Расчет эффекта Штарка на многоэлектронных атомах является
более сложной задачей квантовой физики, поэтому здесь следует
ограничиться качественным описанием. Согласно (21.18), эффект
существенно зависит от величины электрического дипольного мо-
мента атома de. Известно, что в отсутствие внешнего электриче-
ского поля среднее квантовомеханическое значение дипольного мо-
мента многоэлектронного атома в стационарном состоянии равно
нулю. Действие внешнего электрического поля приводит к сме-
щению пространственного распределения электронной плотности
относительно положительного атомного ядра, т. е. к поляризации
атома. При этом наведенный дипольный момент de в первом при-
ближении прямо пропорционален напряженности поля 8. Следова-
тельно, дополнительная электрическая энергия (21.18) пропорцио-
нальна квадрату напряженности поля 5, и величина расщепления
спектральных линий Дб ~ £2. Таким образом, эффект Штарка
на многоэлектронных атомах является квадратичным.
Линейный же характер эффекта Штарка в атоме водорода обу-
словлен специфическим кулоновским вырождением, связанным с
существованием дополнительного интеграла движения в данной
системе — вектора Рунге-Ленца, рассматриваемого в теоретиче-
ской механике. Это специфическое вырождение проявляется в том,
что энергия электрона не зависит от модуля орбитального момента
импульса (от орбитального квантового числа Z). Как следствие, в
атоме водорода существуют состояния с отличным от нуля сред-
ним значением электрического дипольного момента.
Следует учитывать, что в стационарных состояниях эта вели-
чина не имеет определенного значения в отличие, например, от
модуля или проекции орбитального момента импульса. Средняя
его величина вычисляется по правилу квантовой механики, опи-
санном в дополнении 9.2. Среднее значение модуля дипольного мо-
458 Лекция 21. Атомы во внешних полях (продолжение)
мента de свободного атома водорода может быть выражено через
главное квантовое число и разность параболических квантовых
чисел:
- 3
de = - eaon(npi - пр2)- (21.26)
Взаимодействие среднего дипольного момента с внешним элек-
трическим полем приводит к линейному эффекту Штарка, описан-
ному выше.
21.3. Электронный парамагнитный резонанс
Как было показано в предыдущей лекции, действие внешнего
магнитного поля приводит к снятию вырождения по магнитному
квантовому числу mj (20.18). Стационарные состояния атома с
различными числами mj приобретают дополнительную энергию
Emi значения которой квантуются, согласно формуле (20.21). Экс-
периментальные исследования показали, что возможны радиаци-
онные переходы между состояниями, которые различаются только
квантовым числом mj. Такие переходы подчиняются правилу от-
бора
Amj = ±1. (21.27)
В таких переходах не изменяется электронная конфигурация
атома и квантовые числа Zq? «5о и Ль определяющие атомный терм.
Радиационные переходы, подчиняющиеся правилу отбора (21.27),
сопровождаются испусканием или поглощением магнитных ди-
польных фотонов.
При радиационных переходах между состояниями, различаю-
щимися только квантовым числом mj, поглощаются или испуска-
ются фотоны с энергией
е = АЕт = дрвВ kmj = дрвВ. (21.28)
Эта величина равна разности энергий соседних магнитных
подуровней, на которые внешнее магнитное поле расщепляет энер-
гетический уровень атомного терма. Энергия фотона (21.28) прямо
пропорциональна магнитному полю и при индукции В ~ 104 Гс
имеет порядок 10“4 эВ. Пример схемы расщепления энергетиче-
ских уровней атомов во внешнем магнитном поле и возможных
радиационных переходов между магнитными подуровнями приве-
ден на рис. 21.5.
Если выразить энергию фотона е через его длину волны А, то
уравнение (21.28) можно переписать в виде
(21.29)
21.3. Электронный парамагнитный резонанс
459
Следовательно, при В ~ 104 Гс обсуждаемые переходы должны
происходить при поглощении электромагнитного излучения сан-
тиметрового диапазона.
Понятно, что расщепление во внешнем магнитном поле претер-
певают энергетические уровни атомных термов с квантовым чис-
лом jo 7^ 0. В противном случае, как следует из (20.18), возникает
---1---1~ 3/2
• = ?/9 ---1Г—Г— 1/2
/о 3/2 -----t , .. f -1/2
----*-----3/2
В=0 В^О
Рис. 21.5. Энергетическая схема расщепления энергетического уровня атомного
терма на магнитные подуровни во внешнем магнитном поле В.
Все расстояния между соседними магнитными подуровнями одинаковы. Стрелки изобра-
жают радиационные переходы между соседними магнитными подуровнями как с поглоще-
нием, так и с испусканием фотонов
только один магнитный подуровень. Таким образом, переходы
между подуровнями осуществляются для стационарных состояний
с ненулевым магнитным моментом. В первую очередь такие пере-
ходы наблюдаются у атомов, которые являются парамагнетиками
в основном состоянии.
Мы приходим к выводу, что если на парамагнитные атомы, на-
ходящиеся во внешнем магнитном поле В, направить поток элек-
тромагнитного излучения с длиной волны А, то при выполнении
равенства (21.29) должно наблюдаться интенсивное поглощение
электромагнитных волн атомами.
Существенно, что при заданной величине индукции В погло-
щение происходит при строго определенной длине волны А (или
частоте со = 2тгс/А) электромагнитного излучения, т. е. имеет ре-
зонансный характер. Так как при этом изменяется стационарное
состояние электронной оболочки облучаемых атомов, то рассма-
триваемое явление получило название электронный парамагнит-
ный резонанс или сокращенно ЭПР.
Электронный парамагнитный резонанс был открыт в 1944 г.
советским физиком Е.К. Завойским (1907-1976). В своих первых
опытах Завойский имел в своем распоряжении генератор дециме-
тровых радиоволн, поэтому резонансное поглощение впервые было
обнаружено во внешних магнитных полях с индукцией В ~ 103 Гс.
По нижеизложенным причинам ЭПР целесообразно наблюдать в
сантиметровом диапазоне, используя более сильные магнитные
поля.
Обычная принципиальная схема наблюдения ЭПР приведена
на рис. 21.6.
460
Лекция 21. Атомы во внешних полях (продолжение)
В качестве источника электромагнитного излучения может ис-
пользоваться клистрон или другое устройство, генерирующее
электромагнитные волны определенной длины волны Ао сантиме-
трового диапазона (так называемое СВЧ-излучение). Такие волны
Рис. 21.6. Принципиальная схема радиоспектрометра для исследования элек-
тронного парамагнитного резонанса:
1 — клистрон, 2— блок питания, 3— волновод, 4 — резонатор, 5 — исследуемый образец,
N и S — полюсы постоянного электромагнита, 6— модулирующие катушки, 7— детектор
СВЧ-волн, 8 — усилитель, 9 — осциллограф
с малыми потерями передаются по полому металлическому волно-
воду в резонатор, где достигается значительная пространственная
плотность электромагнитного поля. В резонатор помещается обра-
зец, содержащий исследуемые атомы. Поток СВЧ-волн частично
поглощается в образце и по другому волноводу попадает в детектор,
измеряющий интенсивность излучения.
Условие резонанса достигается путем подбора величины ин-
дукции внешнего магнитного поля В. Это поле складывается из
двух составляющих. Сильное постоянное поле, создаваемое между
полюсами электромагнита, модулируется с помощью дополнитель-
ных катушек, через которые пропускается переменный ток низкой
частоты (обычно 50Гц).
Сигнал с детектора через усилитель поступает на вертикальные
пластины осциллографа. На горизонтальные пластины подается
напряжение пропорциональное мгновенному значению индукции
внешнего магнитного поля В. В результате на экране осцилло-
графа формируется кривая, изображающая зависимость интенсив-
ности СВЧ-излучения /, прошедшего через образец, от величины
индукции В. При выполнении соотношения (21.29) на кривой
образуется резкий провал, соответствующий резонансному погло-
щению электромагнитного излучения. Измерив индукцию Bq в
этом минимуме, по известной длине волны Ао СВЧ-генератора
можно вычислить величину спектроскопического ^-фактора:
2тгйс
/zbAqBq
(21.30)
21.3. Электронный парамагнитный резонанс 461
Электронный парамагнитный резонанс используется, в первую
очередь, для измерения магнитных моментов атомов, ионов, мо-
лекул, радикалов и других микрочастиц.
В физике часто используется понятие скалярного магнитного
момента /л, который определяется как максимальное значение
проекции магнитного момента на заданное направление в про-
странстве. Из выражений (20.16)—(20.18) следует
V = Mzmax = = РДвУо- (21.31)
Направление оси Z определяется вектором внешнего магнитного
поля В.
Таким образом, для определения магнитного момента /л ча-
стицы, кроме измерения ^-фактора, необходимо знать квантовое
число jo стационарного состояния, для которого требуется полу-
чить значение величины /х.
Следует иметь ввиду, что в полный магнитный момент атома
дают вклад не только электроны, но и атомное ядро. Экспери-
ментальные исследования позволили установить, что ядра мно-
гих изотопов атомов обладают магнитными моментами /ля, но их
величина примерно на 3 порядка меньше магнетона Бора (см. до-
полнение 21.2). Атомные ядра ряда изотопов имеют нулевой маг-
нитный момент.
Рассмотрим атом изотопа 7Li, ядро которого содержит 3 про-
тона и 4 нейтрона. Скалярные магнитные моменты атомного ядра
принято выражать в единицах ядерного магнетона /лк, который
определяется выражением
eh
UN = ------« 5,0508 • 10~24 эрг/Гс, (21.32)
ZiTTlp с
где е — элементарный заряд, тр — масса протона. Магнитный
момент атомного ядра изотопа 7Li измерен экспериментальными
методами ядерной физики (см. дополнение 21.2) и равен ря =
= 3,26/хдг « 1,65 • 10"23 эрг/Гс.
Конфигурация электронной оболочки атома лития ls22s по-
зволяет легко определить терм основного состояния 25,1/2- Ис-
пользуя квантовые числа механических моментов атома Iq = 0,
so = 1/2, jo = 1/2, легко по формуле (20.19) вычислить, что
спектроскопический фактор равен g = 2. Следовательно, скаляр-
ный магнитный момент электронной оболочки (21.31) составляет
/л = /л& « 0,927 • 10“2° эрг/Гс, что почти на 3 порядка больше маг-
нитного момента ядра /ля ~ 1,65 • 10“23 эрг/Гс атома 7Li. Таким
образом, с точностью до трех значащих цифр можно полагать, что
магнитный момент атома изотопа 7Ы определяется только момен-
том электронной оболочки /л = /Л&.
462 Лекция 21. Атомы во внешних полях (продолжение)
Пусть образец, содержащий атомы 7Ы, облучается потоком
СВЧ-излучения с длиной волны Ао = 10 см. Уравнение (21.30)
позволяет получить, что ЭПР наступит при величине внешнего
магнитного поля Bq « 1070 Гс.
Для анализа результатов экспериментов по ЭПР существенно,
что для лабораторных магнитных полей В ~ Ю3 Гс разность энер-
гий (21.28) соседних магнитных подуровней дрвЕ ~ 10“5 эВ, что
обычно значительно меньше характерной тепловой энергии квТ.
Например, при комнатной температуре квТ « 0,025 эВ, при тем-
пературе кипения молекулярного азота квТ « 6,6 • 10“3 эВ.
Это означает, что во внешнем магнитном поле атомы (или мо-
лекулы) находятся в стационарных состояниях с разными энерги-
ями, точнее говоря, на разных магнитных подуровнях. Как возра-
стание, так и уменьшение энергии происходит, в основном, из-за
столкновений с соседними частицами, т.е. эти переходы между
стационарными состояниями являются безрадиационными. Ста-
тистический характер переходов приводит к установлению дина-
мического равновесия.
Относительное количество частиц в разных состояниях (на
разных магнитных подуровнях) описывается распределением
Больцмана. Если Ni — количество атомов в состоянии с энергией
£1 и — количество атомов в состоянии с энергией то их
отношение
TVi f Е2 — Ei \
7V2=eXPV“fc^/
(21.33)
Если данные состояния соответствуют соседним магнитным под-
уровням, то обычно Е2 — Ei = дрвВ кяТ, и отношение (21.33)
приближенно равно
N1 ~ , Е2 ~ Ej = , . дръВ
TV2 ~ квТ “ квТ ’
(21.34)
При комнатной температуре и индукции магнитного поля В «
« 103 Гс относительное различие чисел Ni и Л^2 составляет около
0,1%. Количество актов поглощения и вынужденного излучения в
единицу времени прямо пропорционально числу атомов, находя-
щихся в данном стационарном состоянии. Малая разница между
числами Ni и 7V2 означает, что количество актов поглощения не-
значительно превалирует над числом актов вынужденного излу-
чения.
В экспериментах по ЭПР обычно используются макроскопиче-
ские образцы, содержащие количество исследуемых атомов или
молекул порядка постоянной Авогадро Лд- Следовательно, даже
при малом относительном различии заселенности соседних маг-
21.3. Электронный парамагнитный рез онанс 463
нитных подуровней явление ЭПР надежно регистрируется. Совре-
менные радиоспектрометры позволяют обнаруживать ЭПР в образ-
цах, содержащих даже ~ 109 парамагнитных частиц.
При электронном парамагнитном резонансе частицы поглоща-
ют фотоны и переходят в более высокоэнергетические стационар-
ные состояния, при этом относительная заселенность магнитных
подуровней изменяется. Параллельно происходят процессы релак-
сации, при которых энергия частиц уменьшается. Основным ме-
ханизмом релаксации являются межатомные столкновения, при
которых магнитная энергия частиц переходит в тепловую. Кроме
того, существенный вклад в релаксацию дает взаимодействие меж-
ду магнитными моментами различных частиц. В результате при
постоянной интенсивности потока СВЧ-излучения вновь насту-
пает динамическое равновесие заселенности магнитных поду-
ровней.
Если ЭПР наблюдается в конденсированных средах, то меж-
атомное взаимодействие существенно изменяет условия резонанса.
Действие электрических полей электронных оболочек соседних
атомов приводит прежде всего к дополнительному штарковскому
расщеплению энергетических уровней. Для примера рассмотрим
ЭПР на ионах марганца Мп+2, которые находятся в окружении
диамагнитных атомов кристалла. Атом марганца имеет химиче-
ский номер Z — 25 и в основном состоянии обладает электронной
конфигурацией ls22s22p63s23p64s23d5. При ионизации атомы по-
теряли электроны 45-оболочки, следовательно, ионы Мп+2 имеют
только одну частично заполненную электронную оболочку с кон-
фигурацией 3d5. Используя правила Хунда, легко установить, что
в основном состоянии этот ион имеет следующие квантовые чи-
сла механических моментов: Iq = 0, so = 5/2, jo = 5/2. Иначе
говоря, это стационарное состояние иона характеризуется термом
6 S^/2- В отсутствие внешнего магнитного поля действие окружа-
ющих атомов (так называемое кристаллическое поле) приводит
к расщеплению энергетического уровня на три штарковских под-
уровня (см. рис. 21.7). При включении внешнего магнитного
поля В к энергии стационарных состояний добавляются значения
магнитной энергии (20.21), зависящей от квантового числа mj.
Шесть различных значений числа mj равных ±1/2, ±3/2, ±5/2
задают шесть магнитных подуровней. Штарковское расщепление
приводит к неодинаковым разностям энергий соседних магнит-
ных подуровней. В результате при постоянном поле В резонанс-
ное поглощение будет происходить на пяти различных частотах
(см. рис. 21.7). Таким образом, линия поглощения оказывается
состоящей из пяти близких компонент. Эта характерная особен-
ность ЭПР-спектров поглощения называется тонкой структурой
линий ЭПР.
464
Лекция 21. Атомы во внешних полях (продолжение)
Если в экспериментальной установке используется радиоспек-
трометр, типа изображенного на рис. 21.6, то ЭПР регистрируется
при пяти различных значениях индукции магнитного поля В.
В современной экспериментальной физике широко использу-
ются эффекты, родственные ЭПР: ядерный магнитный резонанс
№
В = 0
5/2
3/2
1/2
Рис. 21.7. Схема формирования тонкой структуры линии ЭПР иона марганца
Мп+2, находящегося внутри кристалла. Все расстояния между соседними маг-
нитными подуровнями различны
(ЯМР), двойной электронно-ядерный резонанс (ДЭЯР), магнит-
ный резонанс молекулярных пучков и другие, описанные в специ-
альной литературе.
21.4. Автоионизация атома
во внешнем электрическом поле
В сильных внешних электрических полях (8 > 107В/м) на-
блюдается явление автоионизации атомов, т. е. отрывание от них
электронов. Квантовую теорию механизма автоионизации разра-
ботал в 1931 г. венгерский физик-теоретик Корнелий Ланцош
(1893-1974).
Направим координатную ось Z вдоль вектора напряженности
электрического поля 5, выбрав начало координат в центре атома.
Тогда электрон в атоме, помещенный во внешнее электрическое
поле 5, согласно изложенному в §21.2, приобретает дополнитель-
ную энергию f7e, которая выражается формулой (21.19). Следо-
вательно, потенциальная энергия электрона в атоме может быть
представлена в виде
Uee(r) = Ueff(r) + ezS, (21.35)
где C7eff(r) — энергия электрона в самосогласованном поле (см.
§14.4), г — расстояние электрона от центра атома, е — элемен-
тарный заряд.
21.4. Автоионизация атома во внешнем электрическом поле 465
Функция J7eff(r) отрицательна в объеме атома и быстро стре-
мится к нулю, когда расстояние г превышает несколько ангстрем.
Для атомов водорода и одноэлектронных ионов энергия f7eff(r) со-
впадает с кулоновской (Д.11.36). Дополнительная энергия Ue =
= ez8 обусловливает возрастание потенциальной энергии элек-
трона при его смещении в направлении вектора напряженности
электрического поля 5.
Согласно (21.35), потенциальная энергия электрона в атоме, по-
мещенном во внешнее электрическое поле, при z —> — сю неогра-
ниченно убывает. Это означает, что внешнее электрическое поле
8 создает потенциальный барьер для электрона, находящегося в
атоме (см. рис. 21.8).
Из энергетической схемы на рис. 21.8 следует, что электрон
с энергий Ef < Um находится в потенциальной яме, но для него
Рис. 21.8. Образование потенциального барьера для электрона, находящегося в
атоме, помещенном во внешнее электрическое поле 5.
Сплошная линия — энергия Uee, штриховые линии — ее составляющие, согласно фор-
муле (21.35), Um — высшая точка потенциального барьера при заданной напряженности
электрического поля 5, zq — координата вершины барьера, Ei — энергия электрона в
основном состоянии атома
возможен туннельный эффект. Видно, что с ростом модуля напря-
женности электрического поля 8 толщина барьера быстро умень-
шается, кроме того, понижается высшая точка барьера Um = Uee
(z = zq). При этом вероятность туннельного эффекта возрастет
экспоненциально. В достаточно сильном внешнем электрическом
поле должен наблюдаться выход электронов из атомов, иначе го-
воря, ионизация.
466
Лекция 21. Атомы во внешних полях (продолжение)
Напротив, в слабых внешних электрических полях вероят-
ность туннелирования настолько мала, что автоионизация прак-
тически не наблюдается.
Если при экспериментальном исследовании эффекта Штарка
постепенно увеличивать напряженность внешнего электрического
поля 5, то сначала наблюдается расщепление спектральных ли-
ний, а затем уменьшение их интенсивности из-за превращения
части атомов в ионы.
При наблюдении эффекта Штарка на спектральных линиях
серии Бальмера отчетливо видно, что с ростом внешнего поля £
вначале исчезают компоненты линий, образованных радиацион-
ными переходами из более высокоэнергетических стационарных
состояний. Это объясняется тем, что с ростом энергии состояния
(и главного квантового числа п) уменьшается толщина потенци-
ального барьера и возрастает вероятность ионизации. Иначе го-
воря, электрон, находящийся на высоком энергетическом уровне,
выходит из атома, а не переходит на более низкий уровень с из-
лучением фотона.
Из рис. 21.8 также следует, что для атома, находящегося в
стационарном состоянии с энергией электрона Е" > Um вероят-
ность автоионизации равна единице. Следовательно, в сильном
внешнем электрическом поле спектральные линии, образованные
переходами из состояний с большим значением главного кванто-
вого числа п, вообще не могут генерироваться, что подтверждается
экспериментами.
Задачи к лекции 21
1. Рассчитать разность длин волн штарковского триплета для пер-
вой линии серии Лаймана в однородном электрическом поле напряжен-
ностью 107 В/м.
2. Вычислить длины волн компонент штарковского расщепления
второй линии серии Лаймана в однородном электрическом поле напря-
женностью 107В/м.
3. Найти длину волны, на которой может происходить ЭПР на атомах
изотопа 16О, находящихся в основном стационарном состоянии, если
индукция внешнего магнитного поля равна 1000 Гс.
4. Вычислить величину однородного внешнего магнитного поля, в
котором может происходить ЭПР на атомах алюминия в основном ста-
ционарном состоянии при длине волны СВЧ-излучения 10 см.
5. Найти отношение заселенности соседних магнитных подуровней
для следующих значений индукции внешнего магнитного поля В и тем-
пературы окружающей среды Т: а) В = 103 Гс, Т — 20 °C; б) В =
= 104 Гс, Т = 20°С; в) В = 103 Гс, Т = -120°С; г) В = 104Гс, Т =
= -219 °C.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 21
21.1. Создание экстремально сильных
магнитных полей
Исследование воздействия на атомы, молекулы и кристаллы очень
сильных магнитных полей имеет важнейший научный интерес. Кроме
того, для современной астрофизики актуальна проблема поведения плаз-
мы и газа в аномально сильных магнитных полях в связи с изучением
солнечных пятен, пульсаров и других экзотических объектов. Однако
создание сильных магнитных полей в лабораторных условиях наталки-
вается на ряд принципиальных препятствий.
При увеличении силы тока в соленоиде квадратично растет мощ-
ность выделяемого тепла, согласно закону Джоул я-Ленца, что приводит
сначала к увеличению электросопротивления, а затем и к расплавле-
нию проволоки соленоида. Использование ферромагнитных сердечников
также накладывает ограничения на рост индукции магнитного поля из-
за явления насыщения. В результате наиболее мощные электромагниты
дают постоянное магнитное поле с индукцией порядка 50000 Гс.
Прорыв в решении проблемы создания сильных магнитных полей
совершил П.Л. Капица, когда еще будучи молодым физиком работал в Ка-
ведишской лаборатории у Э. Резерфорда. В 1924 г. Капица предложил в
соленоид посылать ток короткого замыкания. При этом в соленоиде дол-
жен сформироваться короткий импульс очень сильного магнитного поля.
Первые опыты Капица предусмотрительно провел, когда Резерфорд во
время своего отпуска уехал в Каир. Заряженный аккумулятор с малым
внутренним сопротивлением замыкался на концы соленоида диаметром
в 1 см и длиной 4,5 см. Затем Капица в письме к Резерфорду с удо-
вольствием сообщал: «...катушка разрушилась со страшным грохотом,
что Вас бы, несомненно, позабавило. Теперь мы знаем, как выглядит
электрическая дуга в 13000 ампер... Мы ухитрились при этом получить
магнитное поле в 270000 гаусс в течение 0,01 секунды...».
В дальнейшем Капица заменил аккумулятор мощным генератором
постоянного тока, который мгновенно разряжался на катушку, которая
помещалась в стальную оболочку, для противодействия возникающим
разрывным усилиям. В результате удавалось получать импульсы маг-
нитной индукции до 5 • 105 Гс длительностью около 0,02 с. Даже в начале
XX века спектроскопическая техника позволяла за это короткое время
сфотографировать спектры излучения исследуемых атомов в созданном
экстремально сильном магнитном поле и наблюдать эффект Пашена-
Бака.
В 50-х годах XX века А.Д. Сахаров (1921-1989) предложил создавать
сверхсильные магнитные поля путем быстрой деформации взрывом то-
конесущих контуров. Этот метод получил название магнитной куму-
ляции. Работы по разработке и совершенствованию магнитной кумуля-
ции для получения сильных полей проводились в течение многих лет во
468
Дополнения к лекции 21
ВНИИЭФ (ныне Российский федеральный ядерный центр, г. Саров) под
руководством академика А.И. Павловского (1927-1992).
Первый генератор МК-1 представлял собой короткую металлическую
трубу радиуса 7?о, окруженную зарядом взрывчатого вещества (ВВ). Вну-
три трубы помещался соленоид из алюминиевой фольги. В соленоид по-
давался мощный импульс тока путем разряда батареи большой емкости,
что приводило к возникновению внутри соленоида аксиального магнит-
ного поля Bq. В момент времени, когда импульс тока достигал мак-
симума, проводился подрыв заряда ВВ, и труба подвергалась быстрому
Рис. Д.21.1. Схема генератора МК-1 для получения сверхсильного магнитного
поля:
1 — соленоид, 2 — изолятор, 3 — металлическая труба, 4 — заряд взрывчатого вещества
симметричному сжатию (см. рис. Д.21.1). При этом площадь ее попе-
речного сечения уменьшалась, и в стенках трубы индуцировались элек-
трические токи, стремящиеся сохранить постоянным поток магнитного
поля Ф в трубе. Если стенки трубы полагать идеально проводящими, то
по теореме постоянства магнитного потока имеем
Ф = тг^Во = тгВ2В, (Д.21.1)
где R и В — радиус трубы и индукция магнитного поля в процессе
сжатия трубы.
Из (Д.21.1) следует, что при взрыве индукция магнитного поля В
возрастает обратно пропорционально квадрату внутреннего радиуса
трубы:
В = Во||. (Д.21.2)
Вследствие конечной проводимости металла трубы часть энергии
из-за эффекта Джоуля-Ленца переходит в тепловую форму. В процессе
сжатия внутренняя поверхность трубы разогревается до столь высокой
температуры (~ 104 К), что происходит частичное испарение металла и
образование плазмы. При этом теряется часть магнитного потока через
сечение сжимающейся трубы.
Уже в первых опытах группе А.И. Павловского удалось получить маг-
нитные поля с индукцией свыше мегагаусса. Потери магнитного потока
совпадали с расчетными и составляли около 70%. Однако вскоре было
обнаружено, что установка МК-1 не дает надежной воспроизводимости
Дополнения к лекции 21
469
результатов. Дело в том, что при взрывном сжатии очень быстро нару-
шается аксиальная симметрия металлической оболочки, что приводит к
развитию неустойчивостей. В результате струи плазмы уносят значи-
тельную часть кинетической энергии, и процесс магнитной кумуляции
прекращается.
В дальнейшем для стабилизации процесса магнитной кумуляции
были разработаны более сложные установки, в которых взрывное сжа-
тие магнитного потока проводилось системой коаксиальных токонесу-
щих оболочек. Кроме того, для инициирования начального магнитного
потока были созданы генераторы, способные формировать импульсы то-
ков с энергией ~ 107 Дж и длительностью 10-4-10”5 с.
В настоящее время установки магнитной кумуляции во ВНИИЭФ
(г. Саров) позволяют получать магнитные поля с индукцией свыше
28МГс в цилиндрических объемах диаметром « 4 мм.
Несмотря на малое время существования сверхсильного магнитного
поля (~ 10“6 с), современная измерительная техника позволяет надежно
регистрировать различные магнитооптические эффекты, например, по-
ворот плоскости поляризации, открытый М. Фарадеем.
Таким образом, метод магнитной кумуляции дает уникальную воз-
можность исследований физических свойств различных веществ в сверх-
сильных магнитных полях.
Представляется весьма вероятным, что явления магнитной кумуля-
ции происходят в звездах. Сильные токи в водородной плазме могут об-
жиматься при взрывном характере реакции синтеза ядер гелия из про-
тонов, при этом возможно образование магнитных полей с индукцией
порядка гигагаусс.
По представлениям астрофизиков на поверхности пульсаров (быстро
вращающихся намагниченных нейтронных звезд) существуют области
с магнитным полем ~ 1012 Гс. В настоящее время не существуют обще-
признанной теории генерации столь грандиозных магнитных полей.
21.2. Магнитные моменты атомных ядер
Впервые гипотезу о существовании у атомного ядра спина и магнит-
ного момента высказал В. Паули в 1928 г. Впоследствии удалось экс-
периментально подтвердить это предположение и измерить магнитный
момент ядер большинства изотопов всех химических элементов, за ис-
ключением самых короткоживущих.
В первую очередь, прецизионные исследования оптических спектров
излучения атомов позволили, помимо тонкой структуры, обнаружить еще
и сверхтонкую структуру спектральных линей. Например, Р-дублет
спектра излучения натрия, который рассматривался в § 17.2 лекции 17,
состоит из двух компонент тонкой структуры с длинами волн Ai =
= 5889,9 А и А2 = 5895,9 А. Спектрометрия с высокой разрешающей спо-
собностью позволяет обнаружить, что каждая составляющая Р-дублета
демонстрирует расщепление еще на две очень близкие сверхтонкие ком-
поненты, разности длин волн которых равны ДА1 = 0,021 А и ДА2 =
= 0,023 А соответственно.
Сверхтонкое расщепление, объясняется аналогично спин-орбиталь-
ному расщеплению, описанному в лекциях 13 и 17. Взаимодействие
магнитного момента системы электронов атома с магнитным моментом
470
Дополнения к лекции 21 •
ядра дя характеризуется определенной дополнительной энергией, кото-
рую можно выразить скалярным произведением
Ej = -цяВЕ, (Д.21.3)
где — среднее магнитное поле, создаваемое всеми электронами ато-
ма, в месте расположения атомного ядра.
Дискретный спектр энергии (Д.21.3) обусловлен квантованием про-
екции магнитного момента ядра на направление магнитного поля В#.
Магнитный мохмент атомного ядра пропорционален спину ядра I, ко-
торый образуется орбитальными моментами импульса нуклонов и их соб-
ственными спинами.
Суммарный момент импульса атома F может быть представлен сум-
мой
F = J + I, (Д.21.4)
где J — полный момент импульса всех электронов атома, введенный в
§ 16.4 лекции 16. В стационарных состояниях модуль момента импульса
атома квантуется по общему правилу
|F| = Hy/FfF+l), (Д.21.5)
где квантовое число F может принимать следующий ряд значений:
F = jo+I, Jq + I-1, ..., |у0 - /|. (Д.21.6)
Квантовое число у’о определяет модуль момента импульса J выраже-
нием (16.10), а квантовое число I характеризует модуль спина ядра по
правилу, аналогичному (16.10) и (Д.21.5):
|1| = /ц//(7+1). (Д.21.7)
Взаимодействие между магнитными моментами электронов и ядра
приводит к тому, что каждый энергетический уровень с определенным
значением квантового числа jo расщепляется на 21 +1 подуровней (если
jo > I) или на 2у*о + 1 подуровней (если I > у’о). Переходы с разных
подуровней (и/или на разные подуровни) формируют сверхтонкую струк-
туру оптических спектров излучения. Величина сверхтонкого расщепле-
ния спектральных линий определяется разностями энергий (Д.21.3). Ис-
следования сверхтонкой структуры оптических спектров количественно
подтверждают вышеприведенные утверждения и дают доказательства су-
ществования магнитных моментов у атомных ядер.
Магнитный момент ядра обусловлен, во-первых, движением внутри
ядра протонов — положительно заряженных частиц. Во-вторых, есте-
ственно ожидать, что протоны обладают собственным магнитным момен-
том, аналогично электронам. Протоны, являясь фермионами, обладают
спином с квантовым числом s = 1/2, как и электроны. В лекциях 20 и
21 было показано, что проекции магнитного момента электрона в стаци-
онарных состояниях квантуются и имеют порядок магнетона Бора дв-
Экспериментальные исследования показали, что сверхтонкое расщепле-
ние спектральных линий (разность длин волн соседних компонент) при-
мерно на три порядка меньше тонкого расщепления. Базируясь на этих
Дополнения к лекции 21
471
данных, Паули предположил, что величина магнитных моментов атом-
ных ядер, в том числе, протона должна иметь порядок ядерного магне-
тона, который определяется следующим выражением:
MN = о----’ (Д-21-8)
2трс
где тр — масса покоя протона.
Для измерения магнитных моментов протона и других атомных ядер
используются резонансные методы, из которых наиболее простым явля-
ется ядерный магнитный резонанс (ЯМР).
Процесс ядерного магнитного резонанса сходен с электронным пара-
магнитным резонансом, рассмотренным в §21.3 лекции 21.
Согласно квантовой теории, поведение магнитных моментов атома
существенно зависит от величины внешнего магнитного поля. Если
энергия взаимодействия внешнего магнитного поля Во с полным маг-
нитным моментом всех электронов атома pLj по абсолютной величине
значительно превышает энергию (Д.21.3), то такое поле Во в ЯМР на-
зывается сильным. Иначе говоря, критерием сильного внешнего магнит-
ного поля является неравенство
IMjBqI |д^В£;|. (Д.21.9)
Квантовомеханические расчеты дают, что величина внутреннего по-
ля B# для разных атомов лежит приблизительно в интервале 105-106 Гс.
Например, для основного состояния атома 3Li величина поля Бе ~ 1,3 х
х 105 Гс, для атома 55Cs поле Be ~ 2,1 • 106 Гс.
Магнитные моменты pbj по имеют порядок магнетона Бора (см. § 20.2
лекции 20), а магнитные моменты ядер — порядок ядерного магнетона
(Д.21.8). Следовательно, согласно критерию (Д.21.9) сильными явля-
ются внешние поля с индукцией Bq 102—103 Гс. Для легких атомов
(в том числе для атома водорода) поле с индукцией Bq ~ 104 Гс является
сильным в смысле критерия (Д.21.9).
Во внешнем поле такой величины независимо квантуются проекции
магнитных моментов электронной оболочки и атомного ядра на напра-
вление внешнего магнитного поля. Количество различных проекций
равно 2jo + 1 и 2/ 4- 1 соответственно. Каждой проекции соответствует
дополнительная энергия, которую приобретает атом во внешнем магнит-
ном поле. Дискретный спектр энергии взаимодействия внешнего поля с
электронным магнитным моментом выражается формулой (20.21). Энер-
гия взаимодействия магнитного момента атомного ядра ця с внешним
магнитным полем Во может быть представлена произведением
Ux=-»hzBq, (Д.21.10)
где цяг — проекция магнитного момента ця на направление внешнего
поля Во-
Введем ядерное гиромагнитное отношение уя аналогично классиче-
скому (12.6). Коэффициент ^я связывает проекции магнитного момента
цЯг и спина Iz ядра соотношением, аналогичным (12.7):
Цяг = (Д.21.11)
472
Дополнения к лекции 21
Проекция спина атомного ядра в стационарных состояниях кванту-
ется по правилу
Iz = hmj, (Д.21.12)
где квантовое число mj может принимать дискретные значения из мно-
жества
т/ = -/, - I + 1, ..., I - 1, I. (Д.21.13)
Определим скалярный магнитный момент атомного ядра ця как
максимальное значение его проекции на заданное направление в про-
странстве, т.е. на направление внешнего магнитного поля Во-
Из выражений (Д.21.11)—(Д.21.13) следует
Р'Я = (мя^)тах = (Д.21.14)
Эта величина аналогична скалярному магнитному моменту элект-
ронной оболочки атома, определеннохму формулой (21.31). Целесообраз-
ность использования скалярных магнитных моментов обусловлена тем,
что эти величины имеют определенные значения в стационарных состо-
яниях атома; с их помощью вычисляется дополнительная энергия атома
во внешнем поле и проекции силы, действующей на магнитный момент
в неоднородном внешнем поле.
Сравнение выражений (Д.21.9)—(Д.21.11) показывает, что дополни-
тельная магнитная энергия (Д.21.10) имеет дискретный спектр значе-
ний:
ия = чяЬВът!. (Д.21.15)
Различие величин электронного и ядерного магнетонов (которое сле-
дует из различия масс электрона и протона) обусловливает неравенство
£Мв » 7яй. (Д.21.16)
Отсюда следует, что магнитный подуровень, возникший из-за кванто-
вания энергии (20.21), описанного в лекциях 20 и 21, при учете взаи-
модействия магнитного момента атомного ядра с внешним магнитным
полем расщепляется на 21 +1 более близких подуровней. Как было уста-
новлено в §21.3 лекции 21, разность энергий соседних «электронных»
магнитных подуровней равняется дцвВо. Разность энергий соседних
«ядерных» магнитных подуровней гораздо меньше:
&ия = 7яЬВ0. (Д.21.17)
Целесообразно выразить величину (Д.21.17), используя выражение
(Д.21.14), через магнитный (скалярный) момент ядра:
^ия = ^Во. (Д.21.18)
Между соседними «ядерными» магнитными подуровнями возможны
радиационные переходы как с испусканием, так и с поглощением фо-
тонов. При этом энергии фотонов должны равняться разности энергий
(Д.21.18).
Дополнения к лекции 21
473
Рис. Д.21.2. Схема энергетических магнитных подуровней стационарных состо-
яний атома, возникающих под влиянием внешнего магнитного поля:
а) без учета взаимодействия с магнитным моментом атомного ядра; б) с учетом взаимо-
действия с магнитным моментом атомного ядра в случае сильного внешнего магнитного
поля
Если на атомы, находящиеся во внешнем магнитном поле Во? напра-
вить поток электромагнитного излучения с определенной частотой wr, то
при выполнении равенства
hwR = ^-Во (Д.21.19)
должно наблюдаться интенсивное поглощение электромагнитных волн
атомами.
Уравнение (Д.21.19) является условием ядерного магнитного резо-
нанса, которое аналогично уравнениям (21.28) и (21.29) для ЭПР (см.
§ 21.3 лекции 21).
Полагая, что величина магнитного момента ця имеет порядок ядер-
ного магнетона (Д.21.7) и квантовое число спина ядра 7 ~ 1, нетрудно
вычислить, что при Во ~ Ю4 Гс резонансная частота должна составлять
десятки МГц, что соответствует длине волны в несколько десятков ме-
тров. Это означает, помимо прочего, что диапазоны ЭПР и ЯМР не пе-
рекрываются.
Принципиальная схема установки ЯМР изображена на рис. Д.21.3.
Образец, содержащий исследуемые атомные ядра, помещается в область
сильного постоянного магнитного поля с индукцией Во порядка 104 Гс.
Атомы подвергаются воздействию высокочастотного электромагнитного
поля, осциллирующего с резонансной частотой wr. При выполнении
равенства (Д.21.19) наблюдается резонансное поглощение энергии высо-
кочастотного поля, что фиксируется с помощью осциллографа. Низкоча-
стотное электромагнитное поле с частотой 50 Гц служит для модуляции
474
Дополнения к лекции 21
высокочастотного поля, чтобы условия резонанса повторялись 50 раз в
секунду, что необходимо для получения стационарной картины на осцил-
лографе.
Рис. Д.21.3. Принципиальная схема устано-
вки ядерного магнитного резонанса:
1 — полюса магнитов, создающих сильное посто-
янное магнитное поле, 2 — образец, содержащий
исследуемые атомные ядра, 3— контур, в котором
создается высокочастотное электромагнитное поле,
4 — катушки, создающие низкочастотное электро-
магнитное поле, 5 — генератор высокочастотного
электромагнитного поля, 6 — осциллограф
Исследования методом ЯМР показали, что предположение В. Паули
было справедливым — магнитные моменты атомных ядер ця имеют
порядок ядерного магнетона /хдг. Однако величины дя не выражаются
целым числом магнетонов ^дг. Более того, магнитный момент протона
приблизительно равняется
« 2,79285 т (Д.21.20)
т.е. не равен ядерному магнетону //дг. Полученный результат свиде-
тельствует о том, что протон не является элементарной частицей, по-
добно электрону. Значение магнитного момента протона (Д.21.20) было
использовано при разработке кварковой теории строения нуклонов.
Таблица Д.21.1. Магнитные моменты некоторых атомных ядер
Изотоп Квантовое число спина ядра I Магнитные моменты ядер в ядерных магнетонах цн
7Ы 3/2 3,2564
14n 1 0,40376
i9p 1/2 2,6289
23Na 3/2 2,2175
27 Al 5/2 3,6415
31 p 1/2 1,1316
35 Cl 3/2 0,82187
37 Cl 3/2 0,68412
45 Sc 7/2 4,756
5!y 7/2 5,151
“Mn 5/2 3,47
59 Co 7/2 4,6
93Nb 9/2 6,17
n5In 9/2 5,54
127j 5/2 2,81
133 Cs 7/2 2,582
139La 7/2 2,78
197 Au 3/2 0,146
209Bi 9/2 4,3
Дополнения к лекции 21
475
В табл. Д.21.1 приведены измеренные значения магнитных момен-
тов различных атомных ядер. Из таблицы видно, что магнитные мо-
менты атомных ядер не превышают нескольких ядерных магнетонов.
Магнитные моменты у многих атомных ядер с четным числом нуклонов
равны нулю, например, у изотопов 4Не, 12С, 16О, 20Ne, 28Si, 32S, 40Са,
52Cr, 56Fe, 140Ce, 184W, 202Hg, 208Pb, 238U и др.
Для измерения магнитного момента нейтрона выше описанная схема
метода ЯМР не пригодна. Свободные нейтроны являются нестабиль-
ными частицами, их среднее время жизни составляет около 10 мин. Од-
нако можно с помощью радиоактивных изотопов создать источники, ис-
пускающие интенсивные потоки нейтронов.
Для измерения магнитного момента нейтрона можно использовать
радиочастотный метод (метод магнитного резонанса пучков), который
в 1937 г. был разработан И. Раби (1898-1988). Этот метод предназначен
для работы с электрически нейтральными частицами. Принципиальная
схема экспериментальной установки приведена на рис. Д.21.4.
Узкий пучок нейтронов, выходящий из источника, формируется с
помощью коллиматора и направляется в область сильно неоднородного
магнитного поля. Нейтрон является фермионом со спиновым квантовым
Рис. Д.21.4. Принципиальная схема установки Раби для измерения магнитного
момента нейтрона:
1 и 2 — полюсы магнитов, создающих неоднородные магнитные поля с взаимно проти-
воположными направлениями градиентов, 3 — полюсы магнита, создающего однородное
магнитное поле, 4 — контур, генерирующий высокочастотное электромагнитное поле, 5 —
генератор высокочастотных колебаний с резонансной частотой, 6 — источник нейтронов,
7— траектория пучка нейтронов, 8 — детектор нейтронов. Стрелками показано направле-
ние сил, действующих на нейтроны в неоднородных магнитных полях
числом s = l/2 (как протон и электрон), следовательно, проекция спина
нейтрона на определенное направление пространства может принимать
два значения: h/2 и —h/2. Если нейтрон обладает собственным магнит-
ным моментом /zn, то во внешнем магнитном поле этот момент может
иметь одну из двух возможных проекций:
MnZ - ±~^-,
(Д.21.21)
476
Дополнения к лекции 21
где 7п — гиромагнитное отношение для нейтрона, т.е. коэффициент
пропорциональности, который связывает магнитный момент нейтрона с
его спином.
В неоднородном магнитном поле на частицы с магнитным моментом
действует сила (12.11), описанная в § 12.2 лекции 12 и дополнении 12.1.
Направление этой силы зависит от знака проекции магнитного момента
и направления градиентов проекций индукции магнитного поля.
На рис. Д.21.4 показана траектория пучка нейтронов с определенной
проекцией /znz. При прохождении между полюсами первого и последнего
магнитов на эти частицы действуют силы противоположных направле-
ний, средние значения которых выражаются следующей формулой:
__ до
Fz=»z^. (Д.21.22)
OZ
В результате траектория нейтронов с определенной проекцией маг-
нитного момента pnz имеет вид, изображенный на рис. Д.21.4 сплошной
линией.
В области однородного магнитного поля Во, создаваемого централь-
ным магнитом нейтроны приобретают дополнительную энергию
Un — -PnzBv, (Д.21.23)
величина которой зависит от знака проекции магнитного момента
(Д.21.21).
Если нейтрон получит энергию, равную 2р,пгВъ, то знак проекции
его магнитного момента сменится на противоположный. Тогда изме-
нится на противоположное направление отклоняющей силы (Д.21.22),
действующей между полюсами последнего магнита установки Раби. В ре-
зультате последний участок траектории получит отклонение в противо-
положную сторону, что изображено на рис. Д.21.4 штриховой линией.
Энергию, необходимую для переориентации магнитного момента,
нейтроны получают от высокочастотного электромагнитного поля. При
этом энергия поглощаемых фотонов должна быть равной энергии 2цпгВ^.
Таким образом, условие переориентации магнитного момента записыва-
ется в виде
Itwr = 2цпгВъ, (Д.21.24)
где u>r — резонансная частота, при которой происходит поглощение фо-
тонов и переориентация магнитного момента нейтрона в центральной
области установки Раби.
Когда частота высокочастотного электромагнитного поля совпадает
с резонансной ujr, то пучок нейтронов не попадает в детектор. Таким
образом, условие переориентации магнитного момента (Д.21.24) экспе-
риментально обнаруживается по резкому уменьшению потока нейтронов,
попадающих в детектор.
Аналогично тому, что было сделано выше для атомных ядер и про-
тона, определим скалярный магнитный момент нейтрона рп как макси-
мальное значение его проекции. Из (Д.21.21) следует, что pn — ^nh/2.
Тогда условие резонанса (Д.21.24) переписывается в виде уравнения,
которое можно использовать для вычисления магнитного момента ней-
трона:
hwR = 2рпВ$. (Д.21.25)
Дополнения к лекции 21
477
В установке Раби создавалось однородное магнитное поле Bq ~ 104 Гс
и использовалось высокочастотное электромагнитное поле с частотой не-
сколько десятков МГц. Был получен удивительный результат: нейтрон,
несмотря на отсутствие электрического заряда, обладает магнитным мо-
ментом. Более того, этот момент имеет отрицательный знак, т. е. его
направление антипараллельно спину нейтрона:
-1,913/zjv. (Д.21.26)
Существование отрицательного магнитного момента нейтрона объясня-
ется в рамках кварковой теории строения нуклонов.
Магнитные моменты атомных ядер складываются из магнитных мо-
ментов протонов и нейтронов, из которых состоит ядро. Как следствие,
существуют атомные ядра с отрицательным магнитным моментом, при-
меры которых приведены в табл. Д.21.2.
Таблица Д.21.2. Отрицательные магнитные моменты
некоторых атомных ядер
Изотоп Квантовое число спина ядра I Магнитные моменты ядер в ядерных магнетонах цм
3Не 1/2 -2,1276
9Ве 3/2 -1,178
25 Mg 5/2 -0,8554
95Мо 5/2 -0,914
103Rh 1/2 -0,088
107 Ag 1/2 -0,1137
109 Ag 1/2 -0,1307
129Хе 1/2 -0,778
147Sm 7/2 -0,81
179Hf 9/2 -0,64
201 Hg 3/2 -0,56
235u 7/2 -0,35
Впоследствии метод Раби был модернизирован и использован для
прецизионных измерений магнитных моментов атомных ядер, молекул
и других частиц. Совершенствование этого метода впоследствии позво-
лило довести точность измерений спектроскопических ^-факторов, а сле-
довательно, магнитных моментов частиц до 12-и значащих цифр (т.е.
до 10“1О%). В частности, именно радиочастотным методом был измерен
лэмбовский сдвиг (см. дополнение 13.2).
Лекция 22
МОЛЕКУЛЫ
22.1. Общие свойства
Молекула в химии определяется как наименьшая часть веще-
ства, для которой характерны все химические свойства данного
вещества.
В течение нескольких веков химики накапливали результаты
экспериментов по разложению и синтезу самых различных ве-
ществ. В частности, было обнаружено, что физико-химические
свойства сложных веществ (окислов, солей, щелочей и т.д.) очень
не похожи на свойства простых, из которых образовано данное
сложное вещество. Для примера приведем водород, хлор и хлорид
водорода, водный раствор которого называется соляной кислотой.
Это означает, что сложное вещество не является смесью простых.
Еще в 1624 г. Пьер Гассенди предположил, что тела состоят
не из первичных атомов, а из их соединений, которые он назвал
молекулами. Это слово Гассенди образовал от латинского moles
(масса), добавив уменьшительный суффикс cula. М.В. Ломоносов
(1711-1765) в своей теории строения материи утверждал, что все
вещества состоят из «корпускул» (молекул), которые представляют
собой разнообразные сочетания «элементов» (атомов). Сторон-
ники молекулярного строения вещества утверждали, что физико-
химические свойства молекул могут резко отличаться от свойств
атомов ингредиентов. Физические методы исследования микро-
структуры вещества в XX веке подтвердили истинность этих умо-
зрительных идей.
Многолетние экспериментальные исследования химиков и фи-
зиков показали, что подавляющее большинство молекул являются
многоатомными. При нормальных условиях одноатомные моле-
кулы образуют только инертные (благородные) газы — элементы
группы VIIIA таблицы Менделеева. С одной стороны, существуют
около ста видов стабильных атомов (не считая изотопов). С дру-
гой стороны, к началу XXI века было обнаружено и синтезировано
свыше 18 млн различных молекул. Столь огромное разнообразие
22.1. Общие свойства
479
обусловлено различными сочетаниями атомов в молекуле. Особый
интерес вызывает существование молекул, состоящих из несколь-
ких одинаковых атомов. Например, при нормальных условиях
молекулы таких газов, как водород, азот, кислород содержат по
два атома. Электрические разряды в атмосфере (молнии) приво-
дят к образованию озона — газа с характерным резким запахом,
имеющего трехатомную молекулу кислорода О3.
Прежде чем обсуждать природу межатомных связей в молеку-
лах, целесообразно кратко описать некоторые характерные физи-
ческие свойства молекул.
Молекулы в газообразном состоянии вещества состоят из ко-
нечного числа атомов. Если же рассматривать конденсированное
состояние, то удобно ввести понятие формульной единицы. Фор-
мульной единицей является группа атомов, обозначенная химичес-
кой формулой данного вещества. Например, формульной единицей
серной кислоты является совокупность двух атомов водорода, че-
тырех атомов кислорода и одного атома серы, выражаемая форму-
лой H2SO4. Дело в том, что обычно под молекулой понимают атом-
ную группировку, внутри которой силы атомного взаимодействия
гораздо сильнее, чем с атомами, расположенными вне молекулы.
В газе всегда можно выделить такую группу атомов. Например, во-
дяной пар состоит из практически изолированных молекул Н2О.
Однако в кристаллическом состоянии складывается иная ситуа-
ция. Так, например, кристалл кремния или поваренной соли пред-
ставляет собой такую структуру, в которой каждый атом связан с
другими приблизительно одинаковыми связями, и выделить мо-
лекулу в вышеприведенном смысле невозможно. В таких случаях
состав вещества характеризуется формульной единицей, которая
определяет относительное количество атомов различных элемен-
тов в данном веществе. Например: Si, NaCl, ВаТЮз (титанат
бария) и т. д.
Молекулы обладают симметрией отличной от сферической (кро-
ме, естественно, одноатомных). Так, например, молекула водорода
Н2 представляет собой «гантель» с аксиальной симметрией и опи-
сывается предельной группой Кюри Точечная симметрия
молекулы определяет сохраняющиеся величины и тем самым на-
бор квантовых чисел, которыми характеризуется молекула в ста-
ционарном состоянии. Из-за отсутствия сферической симметрии
следует, что у молекул не сохраняется определенное значение ква-
драта полного момента импульса. Если молекула обладает осью
симметрии бесконечного порядка, то у нее в стационарных сос-
тояниях имеется определенная проекция момента импульса на
эту ось.
При образовании молекулы изменяется пространственное рас-
пределение электронной плотности составляющих ее атомов. В ре-
зультате молекула может получить электрический дипольный мо-
480
Лекция 22. Молекулы
мент de. Такие молекулы называются полярными. Удобной еди-
ницей измерения величины момента de является дебай D, равный
10“18ед. СГСЭ (т.е. 10“18ед. СГСЭ заряда-см).
Все молекулы обладают поляризуемостью. Это свойство со-
стоит в том, что под действием внешнего электрического поля
молекула изменяет (или приобретает, если молекула неполярная)
электрический дипольный момент de. При этом величина момента
de зависит от напряженности 5 внешнего электрического поля,
что можно записать в виде
de = f(£). (22.1)
Векторная функция f зависит от строения молекулы, состояния
составляющих ее атомов и т. д. ив общем случае не может быть
записана аналитически.
Исследования показали, что функция f достаточно гладкая, по-
этому можно считать, что она дифференцируема и имеет достаточ-
ное число непрерывных производных. Тогда ее можно разложить
в ряд Тейлора вблизи точки 5 = 0. Для молекул направления
векторов de и £ совпадают, поэтому можно записать
, , (dd\ „ 1 /d2d\
4 = 4(5 = 0) + \эё)£=о£+2 \dS^)£=0£ +’” (22’2)
Если молекула неполярна, то нулевой член разложения (22.2)
de(5 = 0) равен нулю. При небольших значениях напряженно-
сти электрического поля £ можно ограничиться линейным чле-
ном разложения (22.2), пренебрегая всеми последующими. Тогда,
обозначая величину первой производной в точке 5 = 0 через cve,
получаем следующее выражение для электрического дипольного
момента: , ч
de = ае£. (22.3)
Параметр ае называется линейной поляризуемостью молекулы.
В отличие от поляризуемости среды, величина ае имеет размер-
ность см3. Для большинства молекул поляризуемость ае имеет
порядок нескольких А3.
Рентгеновские спектры молекул сложных веществ являются су-
перпозицией рентгеновских спектров отдельных атомов, составля-
ющих данное вещество. Оптические спектры радикально отлича-
ются от оптических спектров атомов, входящих в состав данной
молекулы. Описание молекулярных спектров молекул приводится
ниже в лекции 25.
Методами рентгеноструктурного анализа установлено, что рас-
стояния между соседними атомами в молекулах лежат в интер-
вале приблизительно от 1А до 3 А. Химические методы позволяют
также определить типичные энергии связи атомов в молекулах.
Они имеют порядок нескольких электрон-вольт.
22.1. Общиесвойства
481
Важнейшим является вопрос о природе сил, связывающих ато-
мы в молекулы.
Из четырех фундаментальных взаимодействий мы сразу дол-
жны отбросить сильные и слабые, которые эффективно действуют
только на расстояниях на несколько порядков меньше ангстрема.
Величина энергии межатомного гравитационного взаимодействия
определяется известным выражением
го
где G — гравитационная постоянная, mi и m2 — массы взаимо-
действующих атомов, го — межатомное расстояние.
Для оценки гравитационной энергии возьмем атомы с массой
порядка 100 а.е.м., находящихся на расстоянии го = 2 А. Получим
Ш1Ш2 8Ю02 • (!>6 • IO’24)2
« 101-8+4-48+8 10-43 gpr 10~31 gB
Ничтожно малая энергия гравитационного взаимодействия
атомов в молекуле позволяет сделать вывод, что силы, объединя-
ющие атомы в молекулы, порождаются электромагнитным фунда-
ментальным взаимодействием.
Прежде чем рассматривать различные способы объединения
электронейтральных атомов в молекулу, следует заметить, что
независимо от механизма межатомной связи, молекула будет ус-
тойчивой, если ее энергия Ем будет меньше суммы энергий со-
ставляющих ее изолированных атомов. Иначе говоря, должно вы-
полняться неравенство
Na
Ем<^Ек, (22.4)
к=1
где Na — число атомов в молекуле, Ek — энергия fc-ro атома мо-
лекулы, находящегося в свободном состоянии (А; = 1,.. .,7Va). Та-
ким образом, при образовании устойчивой молекулы суммарная
энергия атомов понижается.
Многочисленные эксперименты показали, что для разделения
молекул на отдельные атомы требуется затрата определенной энер-
гии, которая называется энергией диссоциации D.
Измерения различными физико-химическими методами поз-
волили установить, что величина энергии диссоциации для двух-
атомных молекул имеет порядок нескольких электрон-вольт. Ха-
рактерные примеры приведены в табл. 22.1.
482
Лекция 22. Молекулы
Таблица 22.1. Параметры некоторых двухатомных молекул
Молекула Энергия диссоциации (эВ) Межатомное расстояние (А)
н2 4,48 0,74
n2 9,76 1,09
о2 5,11 1,21
f2 1,6 1,42
CsCl 4,58 2,91
CaO 4,3 1,82
HBr 3,75 1,41
LiF 5,89 1,56
22.2. Принцип образования ионной химической связи
Молекулы значительного числа веществ, в основном неоргани-
ческих, состоят из положительных и отрицательных ионов, кото-
рые связаны между собой кулоновскими силами. Это означает, что
при образовании подобных молекул электронейтральные атомы пе-
реходят в заряженное состояние. В качестве типичного примера
рассмотрим образование двухатомной молекулы КС1. Заметим,
что молекулы этого вещества как изолированные образования су-
ществуют лишь в газообразном состоянии. В кристаллическом
состоянии хлористый калий образует атомную структуру, в кото-
рой невозможно выделить отдельные молекулы.
В качестве начального состояния системы возьмем неподвиж-
ные нейтральные атомы калия и хлора, удаленные друг от друга
на такое большое расстояние, чтобы можно было пренебречь меж-
атомным взаимодействием. Таким образом, потенциальная энер-
гия взаимодействующих атомов в начальном состоянии выбрана
равной нулю.
Для наглядности разобьем образование молекулы на отдельные
этапы. На ионизацию атома калия необходимо затратить энергию
Ei = 4,34 эВ. При этом образуется положительный ион калия К+ и
электрон. Присоединение электрона к атому хлора высвобождает
энергию Еа = 3,62 эВ, которая представляет собой энергию срод-
ства хлора к электрону. Иначе говоря, присоединение электрона к
атому хлора уменьшает энергию нашей системы атомов на вели-
чину Еа. Следовательно, для образования пары ионов К+ и С1“
из пары электронейтральных атомов К и С1 требуется затратить
энергию АЕ = Ei — Еа = 4,34 — 3,62 = 0,72 эВ (см. рис. 22.1).
Электронные конфигурации нейтральных атомов калия и хло-
ра имеют вид
К : (Z = 19) ls22s22p63s23p64s1
Cl: (Z = 17) ls22s22p63s23p5
22.2. Принцип образования ионной химической связи 483
После обмена электроном электронные конфигурации возникших
ионов К+ и С1“ полностью совпадают:
К+ : ls22s22p63s23p6
СГ : 1з22з22рб3з23рб
Эти ионы с заполненными внешними з- и р- электронными
оболочками обладают сферической симметрией. Кроме того, такие
электронные конфигурации, совпадающие с конфигурацией атома
Е
Рис. 22.1. Энергетическая схема об-
разования пары ионов К+ и С1“ из
электро-нейтральных атомов калия и
хлора:
Ei(K) — энергия ионизации атома калия,
2?а(С1) — энергия сродства хлора к элек-
трону, AF = ЕДК) - Еа(С1)
£,(С1)
г-4-
I АЕ
аргона (инертного газа), обусловливает резкую границу простран-
ственного распределения электронной плотности р(г). На расстоя-
ниях от центра иона г > гд, функция р(г} становится практически
равной нулю. Следовательно, ионы К+ и С1“ можно приближенно
представить заряженными шарами с определенными радиусами
гд, взаимодействие которых описывается законом Кулона. При
взаимном притяжении ионов их суммарная энергия уменьшается
на величину —е2/г, где г — расстояние между их центрами, что
повышает устойчивость образующейся молекулы (см. рис. 22.2).
Сближение атомов под действием кулоновских сил происходит
до тех пор, пока силы притяжения не скомпенсируются силами от-
талкивания, которые резко возрастают при перекрытии внешних
электронных оболочек. Причиной возникновения этих сил явля-
ется меж электронное кулоновское взаимодействие. С энергетиче-
ской точки зрения явление отталкивания связано с тем, что ионы
К+ и СГ объединяются в единую квантовую систему. У каждого
из ионов уже заполнены все низкоэнергетические одноэлектронные
состояния и поэтому, согласно принципу Паули, при дальнейшем
сближении некоторые электроны должны перейти в свободные (не-
заполненные) оболочки, например, 3d или 4s, которые имеют более
высокие энергии. Это приведет к повышению энергии системы в
целом и сделает невыгодным дальнейшее сближение ионов, что и
проявляется как возникновение сил отталкивания.
Расчет зависимости энергии отталкивания от расстояния г
между центрами ионов должен проводиться методами квантовой
484
Лекция 22. Молекулы
механики. Трудности расчета обусловлены искажением одноэлек-
тронных волновых функций из-за перекрестного взаимодействия
электронов сближающихся ионов. Однако очевидно, что резкий
Рис. 22.2. Зависимость энергии молекулы КС1 от расстояния г между центрами
ионов.
Пунктирная линия — энергия отталкивания, штриховая линия — энергия кулоновского
притяжения плюс величина AF = Е{ — Еа, сплошная линия — полная энергия Е системы
атомов. На выноске показана зависимость энергии Е(г) вблизи минимума. Величина
Ег — энергия отталкивания на равновесном расстоянии г = Rq
вид зависимости энергии отталкивания от межионного расстоя-
ния г приводит к появлению минимума на кривой зависимости
полной энергии Е системы ионов от расстояния г. Этот минимум
определяет равновесное расстояние Ro между атомами (точнее,
ионами) в молекуле и соответствующую энергию диссоциации D.
На рис. 22.2 видно, что при г = Rq энергия образовавшейся мо-
лекулы равна —Р, т.е. на величину D меньше исходной энергии
системы атомов калия и хлора. Таким образом, выполняется не-
обходимое условие (22.4). Потенциальная яма на кривой функции
Е(г) обеспечивает устойчивость молекулы. При любом отклонении
расстояния г от равновесного Rq возникают межатомные силы, ко-
торые возвращают молекулу в состояние с г = Rq и Е = —D.
Величины Rq и D определяются экспериментально различ-
ными физико-химическими методами, в частности, из анализа
молекулярных спектров, описанных ниже. Для молекулы хлорида
калия получены значения Ro = 2,67 А и D = 4,37 эВ.
22.2. Принцип образования ионной химической связи
485
В реальных условиях образование молекулы не разбивается
на вышеописанные последовательные этапы. Процесс объедине-
ния атомов в молекулу зависит от множества параметров окру-
жающей среды и идет весьма сложным путем. Но в любом случае
на начальной стадии сближения ато-
мов им необходимо преодолеть не-
который потенциальный барьер (см.
рис. 22.3). Для этого исходным ато-
мам требуется иметь определенную
кинетическую энергию. В частно-
сти, при образовании молекулы КО
из нейтральных атомов К и С1 вы-
сота потенциального барьера опреде-
ляется величиной = Ei — Ea =
= 0,72 эВ, которая равна затрате
энергии на образование пары ионов
К+ и СГ. Эта энергия, называе-
мая энергией активации реакции,
для большинства простых реакций
имеет порядок долей электрон-воль-
та. Как известно из эксперимента л ь-
Рис. 22.3. Схематическая за-
висимость энергии двухатомной
системы при образовании моле-
кулы. На графике виден потен-
циальный барьер, препятствую-
щий образованию устойчивого
состояния молекулы
ной химии, активация реакций осуществляется нагреванием ис-
ходных веществ, воздействием видимого или ультрафиолетового
света, рентгеновского или гамма-излучения. Хорошо известно,
что скорость химических реакций обычно возрастает с повыше-
нием температуры вещества.
После преодоления потенциального барьера взаимодействую-
щие атомы попадают в область потенциальной ямы, где под дей-
ствием сил притяжения сближаются на равновесное расстояние,
которому соответствует минимум энергии данной системы.
Рассмотренный здесь механизм объединения атомов в моле-
кулу называется ионной химической связью, которая объясняет
устойчивость молекул электрическим притяжением ионов разного
знака. Ионный характер связи атомов осуществляется в других
щелочно-галоидных молекулах (NaCl, LiF, КВг и т.д.). Ионная
связь реализуется также в оксидах щелочноземельных металлов
(MgO, СаО, ВаО и т.д.) и в других соединениях элементов
II группы таблицы Менделеева с элементами VI группы (напри-
мер, в сульфидах).
В то же время ионный механизм связи не может объяснить
существование двухатомных молекул газов Н2, N2, О2, F2 и т.п.,
которые состоят из пары одинаковых атомов. В подобных молеку-
лах атомы удерживаются ковалентной связью, механизм которой
описывается ниже на базе квантовой физики.
Для количественного описания способности к образованию
молекул с ионной связью используется понятие электроотрица-
486
Лекция 22. Молекулы
телъности. В настоящее время применяется несколько различ-
ных шкал электроотрицательности (по Полингу, Олреду-Рохову и
др.), каждая из которых обладает определенными достоинствами и
недостатками. До сих пор ни одну из шкал не удалось согласовать
со всем объемом накопленной экспериментальной информации о
химических соединениях. Наиболее простой из них является
шкала Малликена, предложенная американским физико-химиком
Р.С. Малликеном, лауреатом Нобелевской премии по химии 1966 г.
Электроотрицательность по Малликену хм для данного
химического элемента определяется как среднее арифметическое
энергии ионизации атома Ei и энергии его сродства к электрону Еа'.
Ei 4- Еа
Хм =
(22.5)
2
Смысл формулы Малликена состоит в том, что способность атома к
обмену электронами с соседом определяется двумя факторами: воз-
можностью отдать собственный электрон (что определяется энер-
гией ионизации и принять дополнительный электрон (что ха-
рактеризуется энергией сродства к электрону Еа).
Анализ экспериментальных данных свидетельствует о том, что
способность к образованию ионной связи в двухатомных моле-
кулах увеличивается с величиной разности электроотрицательно-
стей хм химических элементов, атомы которых объединяются в
молекулу. Например, величины хм в табл. 22.2 свидетельствуют
об ионном характере связи щелочных и щелочноземельных метал-
лов с галогенами и кислородом.
Таблица 22.2. Электроотрицательности по Малликену
для некоторых легких химических элементов
Элемент Н Li С О F Na Al Р S Cl
хм (эВ) 6,42 2,25 4,87 7,63 8,23 2,17 2,61 4,38 4,74 5,06
К сожалению, количественная корреляция физических свойств
молекулы и электроотрицательности наблюдается не всегда. Обна-
ружено, в частности, что электроотрицательность некоторых эле-
ментов зависит от вида химической связи. Трудности с постро-
ением единой количественной шкалы приводят к использованию
различных определений электроотрицательности.
22.3. Уравнение Шредингера для многоатомных молекул
Основной задачей квантовой химии является нахождение па-
раметров стационарных состояний молекул. Для этого требуется
записать и решить уравнение Шредингера для стационарных со-
стояний (10.5).
22.3. Уравнение Шредингера для многоатомных молекул 487
Пусть молекула состоит из Na атомов в общем случае различ-
ных химических элементов. Даже если число атомов невелико, то
гамильтониан молекулы имеет устрашающий вид. Этот гамиль-
тониан должен содержать прежде всего операторы кинетической
энергии Na атомных ядер и Ne электронов. Полное количество
электронов в молекуле равно
Na
Ne = ^Z^ (22.6)
П=1
где Zn — порядковый химический номер n-го атома данной моле-
кулы. Оператор кинетической энергии электронов Те выражается
суммой
ь2 Ne
е к=1
причем каждый лапласиан Д^ (к = l,...,7Ve) выражается через
вторые производные по координатам соответствующего fc-ro элек-
трона:
а2 д2 д2
(22'8)
Оператор кинетической энергии атомных ядер Тп представляется
аналогичной суммой
fc2
^ = -7Ej^An> (22-9)
п =1
где Мп — масса n-го атомного ядра, а лапласианы Дп (п =
= выражается через вторые производные по координа-
там соответствующих атомных ядер:
д2 д2 д2
+ (22Л0)
Кроме того, в гамильтониан молекулы должны входить операторы
меж электронного взаимодействия С7ее, межядерного взаимодейст-
вия Unn и взаимодействия электронов с ядрами Uen. Так как
основной вклад в межчастичные взаимодействия дает кулоновское,
то вышеуказанные операторы записываются в виде следующих
двойных сумм, которые выражаются через координаты электро-
нов (к = 1,..., Ne ) и атомных ядер rn (n = 1,..., Na) соответ-
488
Лекция 22. Молекулы
ственно:
иее = 2 Ne Ne 2 g g 1—i’ (22.11)
k'^k
Unn = „2 Ng Ng у у g ^n1 2 |rn-rn/|’ (22.12)
n~1 n — 1
n'^n
Na Ne
Uen “ Ms O) QJ 1 (22.13)
Таким образом, гамильтониан молекулы представляется сум-
мой вышеприведенных операторов:
Нм = Те 4- Тп 4- Uee 4- Unn 4- Uen. (22.14)
Уравнение Шредингера для стационарных состояний молеку-
лы записывается в обычном виде:
ЯмФ(гй,гп) = E^(rk,rn), (22.15)
где Ф(г£,гп) — волновая функция стационарного состояния, а ве-
личина Е — энергия этого состояния.
Как было показано в лекции 14, гамильтониан многоэлектрон-
ного атома имеет столь громоздкий вид (14.2), что соответствую-
щее уравнение Шредингера невозможно решить аналитическими
методами. Очевидно, что гамильтониан (22.14) молекулы, содер-
жащей множество взаимодействующих электронов и атомных
ядер, принципиально гораздо сложнее, что требует специальных
подходов к решению уравнение Шредингера для стационарных
состояний молекулы.
Следует заметить, что в гамильтониане (22.14) не учтено спин-
орбитальное взаимодействие электронов, взаимодействие между
магнитными моментами отдельных частиц (электронов и ядер),
влияние внешних электрических и магнитных полей и т. д. По-
нятно, что перечисленные факторы еще более усложняют проблему
решения уравнения Шредингера для многоэлектронной молекулы.
22.4. Адиабатическое приближение
Первый шаг к упрощению уравнения Шредингера для стацио-
нарных состояний молекулы обоснован сильным различием масс
электронов и атомных ядер. Неравенство
Мп » тпе (22.16)
справедливо для любых ядер, так как даже для атома водорода
Мн ~ 1836 тпе.
22.4. Адиабатическое приближение 489
Из неравенства (22.16) следует, что средняя скорость движе-
ния ядер много меньше средней скорости электронов. Тогда ча-
стицы молекулы можно условно подразделить на электронную под-
систему, состоящую из быстро движущихся легких частиц, и
ядерную подсистему, образованную сравнительно медленно движу-
щимися тяжелыми атомными ядрами. Можно сказать, что элек-
тронная подсистема быстро перестраивается, следуя за более мед-
ленными ядрами атомов молекулы.
Такой подход к анализу движения частиц молекулы был пред-
ложен в 1927 г. Максом Борном (1882-1970) и Робертом Оппен-
геймером (1904-1967) и получил название адиабатического при-
ближения. Идея этого метода (называемого также приближением
Борна-Оппенгеймера) заключатся в том, что электроны молекулы
рассматриваются движущимися в кулоновском поле атомных ядер
с определенными значениями координат rn (п = 1,.. .,Na). При
этом гамильтониан (22.14) представляется суммой
Ям = Я0 + Тп, (22.17)
где оператор
Hq = Те 4- Uee 4- Unn 4- Uen (22.18)
является гамильтонианом молекулы в нулевом приближении.
В адиабатическом приближении волновая функция молекулы
Ф(г^,гп) представляется произведением
Ф(гьгп) =^(гьгп)Ф(гп), (22.19)
где ^(г^,гп) — волновая функция определенного стационарного
состояния электронной подсистемы молекулы при определенных
положениях атомных ядер, Ф(гп) — волновая функция, характе-
ризующая ядерную подсистему. Обе волновые функции содержат
квантовые числа, физический смысл которых обсуждается ниже.
Волновая функция электронной подсистемы рассматривается
в данном приближении как собственная функция гамильтониана
(22.18):
Я0^(га;,гп) = £?(гп)^(гьгп). (22.20)
Подстановка волновой функции (22.19) в (22.15) дает следующее
уравнение:
Ng -I fc2 1 fc2 1
-л2 E - у E й-фД^ - E и-д"*~
n=l n п=1 Мп п=1 Мп
h2 Ne
-----Ф V + (Uee + Unn + иепуф$ = Е<фФ.
2ГПе
490
Лекция 22. Молекулы
Различие в скоростях движения атомных ядер и электронов
молекулы обусловливает то, что электронная волновая функция
^(гЬгп) является медленно изменяющейся функцией координат
атомных ядер. По этой причине в последнем уравнении можно
пренебречь двумя первыми суммами. Последующие алгебраиче-
ские преобразования с использованием (22.20) дают уравнение для
волновой функции Ф(гп), характеризующей ядерную подсистему
молекулы:
(Тп + Е(гп))Ф(гп) = Ем^Гп). (22.21)
Уравнение (22.20) описывает стационарное состояние элект-
ронной подсистемы молекулы, поэтому оператор Hq называют
адиабатическим (иногда, менее удачно, электронным) гамиль-
тонианом молекулы, хотя он, согласно (22.18), содержит слагае-
мое межядерного кулоновского взаимодействия (22.12). Величина
Е(гп) является энергией электронной подсистемы, к которой до-
бавлена энергия межядерного отталкивания Unn. Волновые функ-
ции ^(1>,гп) и энергии Е(гп) зависят от координат ядер гп (п =
= l,...,7Va) как от параметров. Следует подчеркнуть, что если
для атомов энергии стационарных состояний представляли собой
числа, то энергии стационарных состояний молекулы Е(гп) явля-
ются функциями координат атомных ядер гп, в частности, зависят
от межядерных расстояний в молекуле.
Уравнение (22.21) описывает движение атомных ядер моле-
кулы в электрическом поле, задаваемом функцией Е(гп). Согласно
(22.21), полная энергия молекулы Ем существенно зависит от
энергии электронной подсистемы Е(гп).
Методы квантовой механики позволяют оценить погрешнос-
ти использования приближения Борна-Оппенгеймера. Например,
расчет энергии диссоциации молекулы водорода Щ в этом прибли-
жении дает отличие от экспериментальных результатов 0,016%.
С увеличением массы атомов, входящих в состав молекулы, по-
грешность приближения Борна-Оппенгеймера быстро уменьша-
ется.
22.5. Ион молекулы водорода
Использование адиабатического приближения для решения
уравнения Шредингера целесообразно начать с иона молекулы во-
дорода Н^. В предыдущих лекциях квантовое описание физиче-
ских свойств атомов начиналось с анализа простейшего одноэлек-
тронного атома — атома водорода. Аналогично, при исследовании
молекул следует вначале рассмотреть одноэлектронную молекулу
Нд", состоящую из двух протонов и единственного электрона.
Обозначим ri и Г2 — расстояния до электрона от протонов
молекулы, R — расстояние между протонами.
22.5. Ион молекулы водорода
491
Ось Z проведем через протоны молекулы Н^. Центр коорди-
нат выберем в центре масс молекулы, находящемся на середине
отрезка, соединяющего протоны (см. рис. 22.4).
Рис. 22.4. Геометрическая схема иона мо-
лекулы водорода Н^.
Протоны расположены в точках А и В. Центр
масс молекулы находится в точке О. Расстоя-
ния О А и О В равны R/2, где R — расстояние
между протонами
Уравнение Шредингера для стационарных состояний единст-
венного электрона записывается в виде
= Ее<ф, (22.22)
2те Г1 Г2
где Де — лапласиан, выраженный через координаты электрона,
Ее — энергия электрона в стационарном состоянии молекулы Н^.
В соответствии с адиабатическим приближением протоны полага-
ются неподвижными.
Уравнение (22.22) имеет аналитическое решение. Для этого
следует перейти в этом уравнении от декартовых координат элек-
трона к сферическим £, С, 99, которые определяются следующим
образом:
е = С = (22.23)
где 99 — угол поворота вокруг оси Z (оси симметрии молекулы).
Сферические координаты позволяют в уравнении (22.22) про-
извести разделение переменных. В результате волновая функция
электрона в стационарных состояниях молекулы представля-
ется произведением
V’ = V’l(0^2(0 ехр (гА<р), (22.24)
где ^1($) и ^2(0 выражаются через специальные функции, значе-
ния которых можно вычислить с требуемой точностью.
Полученные волновые функции (22.24) обладают симметрией
относительно инверсии в центре масс молекулы и описываются
предельной группой Pqo/i- Эти функции либо не изменяются при
инверсии, либо меняют только знак. Первые называются чет-
ными и обозначаются индексом д, вторые называются нечетными
и обозначаются индексом и.
Связанным (инфинитным) стационарным состояниям элект-
рона соответствуют отрицательные значения энергии Ее, причем
спектр энергии электрона дискретный. Энергии состояний зави-
сят от квантового числа А, которое может принимать значения О,
492 Лекция 22. Молекулы
±1, ±2, ... и четности состояния. Для значений А, равных по мо-
дулю, энергии Ее совпадают, т. е. соответствующие стационарные
состояния двухкратно вырождены. В атомной спектроскопии для
состояний с различными значениями квантовых чисел |А| при-
няты обозначения, приведенные в табл. 22.3.
Таблица 22.3. Обозначение состояний электрона
с различными значениями проекции момента импульса
на ось симметрии молекулы
Квантовое число А Обозначение Проекция момента импульса
0 а 0
±1 7Г
±2 6 ±2П
Квантовое число А = 0, ±1, ±2, ... определяет проекцию ор-
битального момента импульса электрона на ось симметрии моле-
кулы:
Lz = hX.
(22.25)
Стационарные состояния с определенным квантовым числом
А и четностью различаются по своей энергии и характеризуются
главным квантовым числом п, которое может принимать значения
из натурального ряда. Энергии состояний возрастают с ростом
числа п (при фиксированным числе А и определенной четности).
В ходе решения уравнения (22.22) получено, что существуют
стационарные состояния 1ад, 1аи, 1тги, 2ад и т.д. Для краткости
этими же символами обозначаются волновые функции соответст-
вующих состояний.
На рис. 22.5 изображены зависимости волновых функций со-
стояний 1ад и 1сгп от координаты z для различных межядерных
расстояний R. Эти две функции замечательны тем, что описы-
вают состояния с наименьшей энергией. Из рис. 22.5 видно, что
с ростом расстояния R обе волновые функции 1ад и 1аи превра-
щаются в волновые функции состояния 1s для атома водорода.
Точнее, функция 1ад представляется суммой двух атомных функ-
ций 1s, а функция 1аи — их разностью. В пределе R —> 0 вол-
новая функция 1ад стремится к волновой функции состояния 1s
для одноэлектронного иона гелия Не+, функция 1аи — к функции
2р того же иона. При любых конечных расстояниях R в состоя-
нии Io-р электронная плотность р = [ф\2 в области между ядрами
значительно отличается от нуля. Напротив, в состоянии 1сгп вол-
новая функция имеет узел (нулевое значение) в центре молекулы.
Как следствие, в межядерном промежутке электронная плотность
имеет пониженное значение.
22.5. Ион молекулы водорода
493
АТ
-6 vzi 4) 2 4 6
-0,4 г R = 4ao
Рис. 22.5. Зависимости волновых функций состояний 1сг^ (сплошная линия)
и 1аи (штриховая линия) молекулы от координаты z для различных меж-
ядерных расстояний R.
По горизонтальной оси отложены значения координаты z в единицах воровского радиуса ао
На рис. 22.6 приведены зависимости энергии Ее нескольких
низших стационарных состояний электрона в молекуле от
межпротонного расстояния R. Видно, что с увеличением R не-
прерывные функции Ee(R) стремятся к значениям —Ry/n2, т.е.
к энергиям электрона в стационарных состояниях атома водорода.
При R —> 0 функции Ee(R) стремятся к значениям —4Ry/n2, т.е.
к аналогичным величинам для одноэлектронного иона гелия Не+.
Устойчивость молекулы характеризуется видом функции Е(тп\
которая является решением уравнения (22.20). В данном случае
молекулы эта функция зависит только от межпротонного рас-
стояния R и получается добавлением к функции 2?е(/?) потенци-
альной энергии кулоновского отталкивания протонов:
е2
E(R) = Ee(R) + -. (22.26)
jTL
494 Лекция 22. Молекулы
Напомним, что первое слагаемое в правой части (22.26) было полу-
чено решением уравнения Шредингера (22.22) и является энерги-
ей единственного электрона в стационарном состоянии молекулы
Рис. 22.6. Зависимости энергии электрона в низших стационарных состояний
молекулы от межпротонного расстояния R, выраженого в единицах боров-
ского радиуса ао
Н^. Величина E(R}, согласно адиабатическому приближению, ха-
рактеризует поле электрических сил, действующих на каждое из
атомных ядер. В данной системе эти силы создаются электроном
и другим ядром молекулы. Энергия Е(Е£), вообще говоря, является
собственным значением уравнения (22.20), которое для молекулы
принимает вид
+ -ф = (22.27)
2те Г\ Г2 R
22.5. Ион молекулы водорода
495
Очевидно, что уравнения (22.22) и (22.27) удовлетворяются оди-
наковыми волновыми функциями а соответствующие значения
энергий связаны соотношением (22.26).
Зависимости функций E(R) от межпротонного расстояния R
для различных состояний молекулы приведены на рис. 22.7.
При R —> оо энергия E(R) совпадает с Ee^R\ т.е. стремится
к значениям —Ry/n2, как показано на графиках рис. 22.7, так
Рис. 22.7. Зависимость энергии E(R) = Ee(R) 4- е2/R от расстояния R между
протонами для низших стационарных состояний молекулы Н^". Расстояние вы-
ражено в единицах боровского радиуса ао
как при увеличении расстояния между протонами энергия их
кулоновского отталкивания неограниченно убывает до нуля.
Видно, что самое низкоэнергетическое (основное) состояние
lag обладает минимумом энергии при расстоянии Rq « 2ао- Глу-
496
Лекция 22. Молекулы
бина потенциальной ямы определяет энергию диссоциации D «
« 0,2 Ry. Следовательно, состояние 1ад является устойчивым.
Напротив, кривая E(R) для волновой функции 1аи монотонно
убывающая. Это означает, что в состоянии 1аи молекула не-
стабильна, вследствие чего распадается или переходит в другое
(стабильное) состояние. Рисунок 22.7 демонстрирует, что состоя-
ния 1тги и Зсгр также являются стабильными. Однако характер-
но, что минимумы соответствующих функций E(R) наблюдаются
лишь при межпротонных расстояниях значительно больших, чем
Rq. Энергии этих минимумов лежат заметно выше кривой E(R)
основного состояния 1ад. Следовательно, состояния 1тгп и Зсгр
являются возбужденными, в которых молекула «распухает».
Кроме того, потенциальные ямы этих возбужденных состояний
весьма «мелкие», что определяет их низкую энергию диссоциации.
Монотонно убывающий вид функций E(R) для состояний 2сгп,
1?Гр и Зсгп свидетельствует о нестабильности этих состояний моле-
кулы Н^".
Исследование пространственного распределения электронной
плотности р(г) в стационарных состояниях молекулы позво-
ляет обнаружить ряд важных закономерностей. Прежде всего ста-
бильные состояния характеризуются повышенной электронной
плотностью в межядерной области пространства. Это означает,
что в этих состояниях электрон движется, в основном, вблизи цен-
тра молекулы и его электрическое поле удерживает положительные
атомные ядра на определенном равновесном расстоянии Rq. На-
против, нестабильные состояния отличаются пониженной (в неко-
торых точках до нуля!) электронной плотностью в центральной
области молекулы. При этом отталкивание атомных ядер не ком-
пенсируется, что и приводит к распаду молекулы.
Таким образом, решение уравнения Шредингера для молекулы
привело к обнаружению нового вида химической связи, от-
личного от ионной. Во всех устойчивых состояниях молекулы
пространственное распределение электронной плотности р(г) сим-
метрично относительно отражения в плоскости, перпендикуляр-
ной оси симметрии молекулы и проходящей через ее центр масс.
Иначе говоря, симметрия функции р(г) описывается надгруппами
точечной группы Съь- Можно сказать, что электрон молекулы в
устойчивом стационарном состоянии в равной степени принадле-
жит обоим ядрам, т.е. в среднем находится около каждого ядра
одинаковое время. В таких состояниях электрический диполь-
ный момент молекулы равен нулю и химическая связь не имеет
ионного характера. Тип химической связи, описанный в данном
параграфе, называется ковалентной. Теория ковалентной связи
не имеет классического объяснения и может быть построена лишь
в рамках квантовой физики.
22.5. Ион молекулы водорода
497
Задачи к лекции 22
1. Рассчитать энергию связи молекулы CsCl, базируясь на ионном
характере связи. Энергия сродства к электрону приведена в табл. 15.5,
равновесное расстояние см. в табл. 22.1.
2. Пользуясь табл. 22.2, вычислить разность электр о отрицательно-
стей: а) у лития и фтора; б) у натрия и хлора; в) у кислорода и углерода;
г) у кислорода и водорода. Сделать вывод о возможности образования
ионной связи между данными парами атомов.
3. Найти энергию отталкивания Ег для молекулы NaCl в равновес-
ном состоянии. Энергия ионизации атома натрия 5,14 эВ, остальные
необходимые параметры см. в табл. 15.5 и 22.1.
4. Вычислить энергию взаимодействия двух протонов, находящихся
на расстоянии двух первых боровских радиусов. Сравнить полученную
величину с энергией диссоциации молекулы в основном состоянии
P«0,2Ry.
5. Записать значения проекции орбитального момента импульса Lz
электрона на ось симметрии молекулы для молекулы Н^- в состояниях
1О"р, 1б7"|2, 17Г|2, ^^9^ ^^9 3o"t4«
Лекция 23
МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ
23.1. Молекулярные спин-орбитали и орбитали
Решение уравнения Шредингера для одноэлектронной системы
убедительно продемонстрировало трудности задач квантовой
физики молекул. Очень сложный вид гамильтониана (22.14) для
многочастичных систем не позволяет получить аналитическое ре-
шение уравнения Шредингера даже при использовании адиабати-
ческого приближения.
Следующий важный шаг в развитии методов физики молекул
базируется на приближении самосогласованного поля, аналогично
тому, как это было проделано в квантовой физике многоэлектрон-
ных атомов (см. §14.4 лекции 14). Каждый электрон молекулы
представляется движущимся в некотором усредненном эффектив-
ном поле атомных ядер и остальных электронов этой молекулы.
Многоэлектронная волновая функция стационарного состояния
молекулы выражается линейной комбинацией произведений од-
ноэлектронных волновых функций, точнее — их детерминан-
том Слэтера (14.10). Каждая одноэлектронная волновая функция
^(rjcr) представима произведением
^(г,ст) = ^(г)х(^)- (23.1)
Первый сомножитель ?/>(г) зависит только от пространствен-
ных координат г электрона, а второй х(сг) — от спиновой пе-
ременной ст. Спиновая переменная а и спиновый сомножитель
х(сг) определяются значением проекции спина электрона на не-
которую пространственную ось. Это означает, что спиновый со-
множитель может принимать только два разных значения х~ и
Х+, соответствующих двум разным квантовым числам проекции
спина ms = ±1/2 (см. приложение 12.3). В большинстве практи-
чески важных случаев в качестве этой оси целесообразно выбрать
ось симметрии молекулы.
Функции вида (23.1) называются в квантовой химии (т.е. в
квантовой физике молекул) спин-орбиталями. Каждая из этих
23.2. Линейные комбинации атомных орбиталей 499
волновых функций характеризует одноэлектронное состояние, со-
вокупность которых определяет стационарное состояние всей мо-
лекулы. Согласно принципу Паули, в каждом одноэлектронном со-
стоянии не может находиться более одного электрона (см. § 14.3
лекции 14). Следовательно, любое стационарное состояние мо-
лекулы (основное и возбужденные) может быть описано набором
заполненных и пустых спин-орбиталей. Каждой спин-орбитали
ставится в соответствие определенная энергия, которой обладает
электрон, заполняющий эту спин-орбиталь.
В отсутствие внешних полей энергия спин-орбитали не зависит
от знака квантового числа проекции спина ms, т.е. от ориента-
ции спина электрона. Следовательно, все одноэлектронные стаци-
онарные состояния молекул двукратно вырождены. Точнее говоря,
определенное значение энергии имеют две спин-орбитали, разли-
чающиеся знаком проекции спина электрона. Таким образом,
в огромном множестве задач квантовой физики, когда исследуе-
мые молекулы не подвергаются действию значительных внешних
электромагнитных полей, целесообразно описывать стационарные
состояния молекулы детерминантами Слэтера, составленными из
волновых функций V’(r), зависящих только от координат электро-
нов. Такие функции ?/>(г) принято называть орбиталями. В соот-
ветствии с принципом Паули, в состояниях, характеризуемых лю-
бой орбиталью, могут находиться не более двух электронов, при-
чем они должны иметь проекции спинов различных знаков. Иначе
говоря, существуют пустые орбитали, орбитали с одним электро-
ном и полностью заполненные орбитали. Энергия электронной
подсистемы молекулы складывается из энергий заполненных ор-
биталей.
Следует помнить, что устоявшийся термин «орбиталь» не озна-
чает, что электрон в молекуле движется по определенной орбите.
Координаты каждого электрона характеризуются лишь плотно-
стью вероятности пространственного распределения, которое зада-
ется квадратом модуля соответствующей волновой функции ^(г),
т. е. соответствующей орбитали.
23.2. Линейные комбинации атомных орбиталей
Расчет спин-орбиталей и орбиталей может быть в принципе осу-
ществлен с помощью метода Хартри-Фока. Однако следует иметь
в виду, что к использованию приближенных численных методов
следует относиться с осторожностью. Предположим, что в ходе
численного решения уравнения Шредингера получена некоторая
волновая функция ?/>(г) стационарного состояния в виде таблицы
значений. Так как функция ?/>(г) зависит от трех пространствен-
ных координат т, у, г, то таблица должна иметь большой объем.
Например, если на каждой оси декартовой системы взять 100 зна-
500 Лекция 23. Метод молекулярных орбиталей
чений соответствующей координаты, то в пространстве будет за-
дано 10б точек г. Вычислив во всех этих точках волновую функ-
цию V’(r), мы получим таблицу, содержащую миллион чисел, если
функция ?/>(г) действительная, или два миллиона, если эта функ-
ция комплексная. С таким представлением волновой функции ра-
ботать практически невозможно. С другой стороны, иногда тре-
буется более подробное описание волновой функции, для которого
ста точек на одной пространственной оси координат недостаточно.
Эти обстоятельства привели к альтернативной идее, которая
заключается в представлении сложной функции в виде линейной
комбинации базовых, выраженных через элементарные или хо-
рошо изученные специальные функции. В качестве базовых функ-
ций оказалось целесообразным брать волновые функции изолиро-
ванных атомов — водородоподобные или функции Слэтера (см.
дополнение 14.1). Кроме того, волновые функции атомов кон-
струируются без спиновой части, иначе говоря, описывающие
состояния с произвольной проекцией спина электрона. Такие вол-
новые функции называются атомными орбиталями^ в соответ-
ствующих состояниях могут размещаться два электрона с про-
тивоположно ориентированными спинами. Атомные орбитали
характеризуются тремя квантовыми числами. В случае прене-
брежения спин-орбитальным взаимодействием (и другими реля-
тивистскими эффектами) такими числами являются главное п,
орбитальное I и магнитное т квантовые числа. Одноэлектронные
волновые функции, которые обсуждались в лекции 14 и зависят
от четырех квантовых чисел, в данном контексте могут по анало-
гии называться атомными спин-орбиталями. Каждой атомной
орбитали соответствуют две атомные спин-орбитали, которые раз-
личаются только знаком квантового числа проекции спина ms-
Таким образом, молекулярные орбитали должны быть выра-
жены в виде линейной комбинации атомных орбиталей. В кванто-
вой физике такой подход кратко называется МО ЛКАО, т.е.
молекулярные орбитали как линейные комбинации атомных ор-
биталей.
Понятно, что предлагаемый метод является приближенным, но
его практическое использование позволяет добиться достаточной
точности результатов при решении многих задач физики молекул.
На этом пути часто встречаются трудности чисто технического
характера, которые постепенно преодолеваются с ростом возмож-
ностей компьютерных систем.
Подробно метод МО ЛКАО излагается и обосновывается в специ-
альных курсах квантовой химии. Здесь мы ограничимся кратким
перечислением важнейших положений этого метода.
Молекула рассматривается как единая квантовая система. Ка-
ждый электрон, принадлежащий молекуле, движется в самосогла-
сованном поле всех ее ядер и остальных электронов.
23.2. Линейные комбинации атомных орбиталей 501
Стационарные состояния молекулы описываются набором ор-
биталей, каждая из которых характеризуется тремя квантовыми
числами. На любой орбитали может размещаться по два электрона
в соответствии с принципом Паули. Заполнение молекулярных ор-
биталей электронами определяет конфигурацию стационарного со-
стояния молекулы.
Каждой молекулярной орбитали соответствует определенное
значение энергии. Электроны могут переходить на свободные
спин-орбитали (одноэлектронные стационарные состояния). При
этом возможно испускание или поглощение фотонов в соответствии
с правилами отбора, которые изложены ниже при описании моле-
кулярных спектров.
Выше на примере молекулы уже было показано, что вид
волновой функции электрона в молекуле существенно зависит от
расстояния между центрами атомов молекулы. Это накладывает
определенные требования на форму МО ЛКАО. Во-первых, при не-
ограниченном взаимном удалении атомов молекулярные орбитали
должны превращаться в сумму атомных орбиталей отдельных ато-
мов, так как при этом взаимодействие атомов уменьшается до
нуля. Во-вторых, молекулярная орбиталь вблизи любого атомного
ядра должна практически совпадать с атомной орбиталью соответ-
ствующего атома. Это объясняется тем, что в центральной области
атома электрон подвергается действию самосогласованного поля
ядра и внутренних электронов этого же атома. При этом влия-
ние остальных заряженных частиц молекулы пренебрежимо мало.
Обе указанные особенности молекулярных орбиталей можно про-
следить для молекулы на рис. 22.5.
Согласно изложенному в лекциях 11 и 14, количество различ-
ных атомных орбиталей, вообще говоря, бесконечно. Следова-
тельно, при применении метода МО ЛКАО требуется задать конеч-
ный набор базовых атомных орбиталей, линейной комбинацией
которых выразится молекулярная орбиталь. Точнее говоря, задача
метода МО ЛКАО состоит в получении молекулярной орбитали 'ф
в виде следующей конечной суммы:
лг
(23-2)
5=1
где ips ($ = 1,2,.. .,7V) — базовые атомные орбитали, N — ко-
личество базовых АО. Ясно, что для получения явного вида МО
следует вычислить коэффициенты разложения cs ($ = 1,2,..., TV).
В многолетнем процессе разработки и совершенствования ме-
тода МО ЛКАО были сформулированы следующие рекомендации,
позволяющие упростить задачу нахождения базового набора АО.
1. Базовые атомные орбитали должны быть близки по энер-
гиям. Если энергия какой-либо АО резко отличается от осталь-
502
Лекция 23. Метод молекулярных орбиталей
ных, то соответствующий коэффициент разложения пренебрежи-
мо мал.
2. Комбинируемые АО должны «перекрываться». Это означает,
что интегралы вида
(ps(pt dV, s/t, (23.3)
v
где V — объем, в котором движутся электроны молекулы, должны
заметно отличаться от нуля. Следовательно, в молекуле должна
существовать достаточно обширная область пространства, где ба-
зовые АО обладают значительной плотностью вероятности |?/>|2.
3. В первую очередь должны комбинироваться базовые АО с
одинаковой симметрией.
Вышеперечисленные условия взаимосвязаны и обеспечивают
делокализацию построенных МО относительно отдельных атомов.
Иначе говоря, молекулярная орбиталь должна охватывать несколь-
ко или все атомы данной молекулы. В двухатомных молекулах
электроны, заполняющие МО, движутся вокруг обоих атомных
ядер, обеспечивая устойчивую химическую связь.
23.3. Применение метода МО
ЛКАО к иону молекулы водорода
Прежде чем рассматривать общие аспекты метода МО ЛКАО,
проиллюстрируем его преимущества на примере молекулы Н^.
Напомним, что, несмотря на аналитическое решение уравнения
Шредингера для этой молекулы, волновые функции стационар-
ных состояний выражаются в очень сложном виде и количественно
представляются таблицами значений, о неудобстве чего уже упо-
миналось выше.
Если нас интересует основное состояние исследуемой моле-
кулы, то в качестве базового набора АО достаточно взять коорди-
натные части волновых функций основного стационарного состо-
яния атома водорода (11.25). Тогда искомую МО можно записать
в следующем виде:
'Ф = С1^1(п) +с2</?2(г2), (23.4)
где и у>2(г2) — волновые функции основного состояния
(11.25) для двух атомов водорода, входящих в молекулу:
, ч 1
W1) = ^=ехр
V7ro0
¥>2(г2) = ,—ехр
(23.5)
23.3. Применение метода МО ЛКАО к иону молекулы водорода, 503
Г1 и Г2 — расстояния электрона до ядер молекулы в определен-
ный момент времени (см. рис. 22.4). Для получения МО основного
состояния молекулы требуется вычислить коэффициенты ci и С2-
Пространственное распределение электрона задается квадра-
том модуля молекулярной орбитали (23.4):
IV'l2 = ClV’l + <%Ч>2 + 2ciC2^i<^2- (23.6)
Симметрия основного состояния молекулы описывается точеч-
ной группой Pqo/i? что может быть обеспечено при равенстве
2 2
С1 = с2.
Отсюда следует, что для коэффициентов ci и С2 возможны два
различных соотношения:
С1 = с2, Cl = -С2. (23.7)
Таким образом, получаются две МО, которые можно записать в
виде
Фд = Cg(<pi +</>2), Фи = Cw(^l - Ы- (23.8)
Первая из этих функций является симметричной, а вторая анти-
симметричной относительно перестановки АО.
Для нахождения коэффициентов сд и си воспользуемся норми-
ровкой молекулярных орбиталей (23.8) на единицу, что соответ-
ствует финитному движению электрона в молекуле. Полагая, что
коэффициенты сд и си имеют действительные значения, а атомные
орбитали заданы функциями (23.5), условие нормировки можно
записать в виде
У |<Wi + c2tp2\2dV = 1, (23.9)
v
где интегрирование, как и в (23.3), проводится по всему объему V
трехмерного пространства, в котором движется электрон. Подста-
новка функций (23.8) в интеграл (23.9) дает два уравнения:
J‘фдНУ = с2д I^1 + ^1 +2^2) dV = 1, (23.10)
V V
Jip2dV = c2J^+ ^ - 2^2) dV = 1. (23.11)
V V
Вспомним, что базовые АО (23.5) нормированы (см. лекцию 11) и
введем обозначение для интеграла перекрытия вида (23.3) базовых
функций (23.5):
S12 = / ViVbdV.
(23.12)
504
Лекция 23. Метод молекулярных орбиталей
Тогда уравнения (23.10) и (23.11) могут быть представлены в сле-
дующей форме:
С2(2 + 2S12) = 1, C2U(2 - 2S12) = 1.
Отсюда получаются искомые коэффициенты для молекулярных ор-
биталей (23.8):
с‘= = ^тЙзЗ' (23ЛЗ)
Выбор знака коэффициентов произволен, так как физический
смысл имеет только квадрат модуля волновой функции. Поэтому
без потери физической общности можно оба коэффициента (23.13)
брать положительными. Тогда искомые молекулярные орбитали
могут быть записаны в виде
V2 + 2S12’ ’
Интеграл перекрытия (23.12) зависит от расстояния R между
протонами молекулы Но, поэтому полученные МО ЛКАО являются
функциями параметра К.
Важнейший результат, достигнутый в этом параграфе, заклю-
чается в том, что функции МО ЛКАО фд и имеющие весьма
простой вид, очень близки к точным решениям 1ад и lau соответ-
ственно уравнения Шредингера для молекулы Н^. На рис. 23.1
приведены графики этих волновых функций для равновесного
межядерного расстояния Rq. Видно, что МО ЛКАО фд хорошо
совпадает с волновой функцией 1сгд основного состояния данной
молекулы.
Из рис. 23.1 видно, что приближенная МО ЛКАО фд имеет не-
сколько заниженные значения по сравнению с точной волновой
функцией 1сгд, а орбиталь фи — напротив, завышенные значения
относительно соответствующего точного решения lau. Для более
лучшего приближения АО вида (23.5) заменяются на более слож-
ные функции и используется вариационный метод, изложенный
в следующей лекции. Сведения о методах уточнения МО можно
получить в специальных курсах по теории химической связи.
Теперь найдем энергии стационарных состояний, описывае-
мых функциями фд и фи, полученными в приближении МО ЛКАО.
В квантовой механике доказывается, что для этого не обяза-
тельно прямое решение уравнения Шредингера для стационарных
состояний (10.5) с нахождением собственных значений оператора
Гамильтона. Умножим обе части уравнения Шредингера
Нф = Еф
23.3. Применение метода МО ЛКАО к иону молекулы водорода 505
Рис. 23.1. Профили волновых функций (зависимости от координаты г) молекулы
: а) четная волновая функция б) нечетная lcru(0u).
Сплошные линии — точные решения уравнения Шредингера, штриховые линии — при-
ближенные решения методом МО ЛКАО
на комплексно сопряженную волновую функцию стационарного со-
стояния 0* и проинтегрируем по всей области изменения аргумен-
тов волновой функции:
У ip*HipdV = ЕУ Tl^dV.
Если волновая функция нормирована, то последнее уравнение
дает выражение для энергии соответствующего стационарного со-
стояния
Е = Ji/>*HipdV. (23.15)
Таким образом, если функция 0 — точное решение уравнения
Шредингера, то формула (23.15) дает точное значение энергии со-
стояния. Если же 0 — приближенная (но нормированная на еди-
ницу) волновая функция, то интеграл (23.15) позволяет вычислить
приближенное значение энергии этого состояния.
Подстановка функций (23.14) в формулу (23.15) дает энергии
стационарных состояний lcrq и 1сгп молекулы в приближении
МО ЛКАО:
Eg,и = 9 , tc [ (<Р1 ± W1 ± <^2) dV, (23.16)
Z ± 2^12 J
где положительный знак отвечает l(jg орбитали, а отрицательный
знак — орбитали 1сги.
506
Лекция 23. Метод молекулярных орбиталей
Для молекулы оператор Н представляет собой адиабатиче-
ский гамильтониан вида (22.18), используемый выше в уравнении
(22.27):
4 7 ’ ° 2 2 2
е е
Г\ Г2 R
h2
Н = --—Де
2тпе
(23.17)
Интеграл в формуле (23.16) выражается через следующие вели-
чины:
Нп= j dV,
Н12 = / 4>iHy>2 dV,
Н22 = У ^Н(р2 dV\
Н21 = / dV,
(23.18)
которые в квантовой теории называются матричными элемен-
тами.
Функции (/>1 и 992 (23.5) являются эквивалентными атомными
орбиталями, записанными для двух одинаковых атомов, поэтому
выполняются равенства Нц = Н22 и Я12 = Я21. При этих усло-
виях вычисление интеграла (23.16) дает следующий результат:
Яц±Я12
9'и 2 ±2512 ’
(23.19)
где, как и в (23.16), верхний знак соответствует четному ^-состоя-
нию, нижний знак — нечетному гб-состоянию.
Для гамильтониана (23.17) и функций (23.5) интегралы (23.12)
и (23.18) могут быть вычислены аналитически и выражены через
межядерное расстояние R:
S12 =
ехр
R
ао
Я12 = 2Ну
\
1 7R
2 бао
бао/
ехр
R
ао
(23.20)
(23.21)
Яц = 2 Ry (1 + ехр
\ IX /
2Л\
ао /
-Ry.
(23.22)
+ ао + За^ )
Зависимость величин (23.20)-(23.22) и энергий Яр, Еи от
межядерного расстояния R приведены на рис. 23.2. Видно, что с
ростом R величины 512 и Н\2 экспоненциально спадают до нуля,
а значение Яц стремится к —Ry, что равно энергии атома водо-
рода в основном состоянии. При R —> 0 интеграл перекрытия 512
стремится к единице.
23.4. Метод МО ЛКАО для двухатомных гомоядерных молекул 507
Рис. 23.2. Зависимости интеграла перекрытия S12, матричных элементов Иц,
Н12 и энергий Ед, Еи от межядерного расстояния R для молекулы Н^-. Интеграл
S12 безразмерен, прочие величины имеют размерность энергии
Энергии состояний и фи, вычисленные по формулам
(23.19)-(23.22), являются функциями межядерного расстояния R
близкими к зависимостям E(R} для состояний 1ад и lau моле-
кулы Н^, изображенным на рис. 22.7. График функции Eg(R)
обладает минимумом в области « 2ао, что характеризует устойчи-
вость основного состояния фд молекулы и определяет равновесное
межядерное расстояние Rq « 2ао- Кривая EU(R) является мо-
нотонно убывающей, что соответствует неустойчивости состояния
фи. Заметим, что минимум на графике функции Eg(R) определя-
ется, в основном, видом зависимости H^R)-
Подводя итог данного параграфа, констатируем, что метод МО
ЛКАО дает волновые функции стационарных состояний и их энер-
гии с приемлемой точностью. Для уменьшения погрешностей в
атомные орбитали вводят различные корректирующие факторы,
что позволяет повысить точность расчетов методом МО ЛКАО до
требуемого уровня.
23.4. Применение метода МО ЛКАО
для двухатомных гомоядерных молекул
Гомоядерными называют молекулы, состоящие из атомов од-
ного химического элемента. Простейшей из них является моле-
кула водорода Н2, содержащая 2 электрона и 2 протона. Гомоядер-
508 Лекция 23. Метод молекулярных орбиталей
ными являются двухатомные молекулы азота N2 и кислорода О2,
которые в сумме образуют 99% атмосферы Земли.
Метод МО ЛКАО позволяет, не решая уравнения Шредингера
для многоэлектронной системы, рассчитать основные физические
параметры многих гомоядерных молекул с точностью достаточной
для практических приложений.
Согласно вышеизложенному, молекулярные орбитали строятся
с помощью минимального базиса атомных орбиталей. Получен-
ные МО заполняются электронами в соответствии с принципом
Паули, т. е. на каждой орбитали могут размещаться два электрона
с проекциями спинов различных знаков. Для конструирования
основного состояния молекулы заполнение орбиталей проводится
в порядке возрастания их энергий, аналогично проделанному для
основных состояний атомов в лекции 15.
В предыдущем параграфе были построены методом МО ЛКАО
приближенные орбитали lag и 1сгп для иона молекулы водорода
на базе атомных орбиталей 1s. Из-за того что АО 1s являются
самыми низкоэнергетическими в атоме, то МО lag и lau имеют
наиболее низкие энергии в молекуле, причем E(lau) > £Д1сгр).
Поэтому в основном состоянии любой молекулы рассматриваемого
типа сначала заполняется орбиталь lag, далее орбиталь 1сгп, затем
остальные, обладающие большими энергиями.
Ранее было установлено, что в основном состоянии молекулы
единственный электрон располагается на орбитали lag. При
этом молекула обладает спином с квантовым числом s = 1/2.
Наиболее низкоэнергетическое стационарное состояние моле-
кулы Н2 будет достигнуто, если оба электрона молекулы разме-
стятся на орбитали lcr^. Электронная конфигурация молекулы
запишется в виде (1сг^)2. Так как МО lag характеризуется повы-
шенной электронной плотностью р(г) в пространстве между про-
тонами (см. рис. 22.5), то заполнение орбитали lag двумя электро-
нами дополнительно увеличит значения функции р(г) в централь-
ной области молекулы. Это приводит к возрастанию энергии связи
(энергии диссоциации D) и уменьшению равновесного межядер-
ного расстояния Rq по сравнению с параметрами одноэлектронной
молекулы (см. табл. 23.1).
Электроны в основном состоянии молекулы Н2 имеют про-
екции противоположного знака, поэтому суммарный спин такой
молекулы равен нулю. Так как оба электрона находятся в s-co-
стоянии, то суммарный орбитальный момент также равен нулю.
Как следствие, молекулы Н2 в основном состоянии не обладают
собственным магнитным моментом и проявляют диамагнитные
свойства.
Экспериментальные исследования доказали существование
трехэлектронной молекулы Не^, которая содержит два ядра гелия
23.4. Метод МО ЛКАО для двухатомных гомоядерных молекул 509
и обладает суммарным электрическим зарядом 4-е. Минимальный
базис ЛКАО этой системы может быть составлен из двух атомных
орбиталей состояний Is, которые целесообразно выбрать в виде
слэтеровских функций вида = Nехр (—&г), где коэффициент к
имеет оптимальное значение 1,6875, а величина N определяется
нормировкой АО на единицу. Наиболее низкоэнергетическими МО
ЛКАО молекулы Не^" являются функции lag и 1сгп, которые опре-
деляются формулами (23.8), имеют энергии (23.19) и обладают
симметрией аналогичных орбиталей молекул и В основ-
ном состоянии два электрона заполняют МО lcr^, а третий на-
ходится на орбитали 1сги. Электронная конфигурация молекулы
может быть записана в виде (1сгр)2(1сгп)1.
Таблица 23.1. Физические характеристики простейших двухатомных
гомоядерных молекул
Молекула Электронная конфигурация Кратность связи Равновесное расстояние (А) Энергия диссоциации (эВ)
н+ (l^)1 1/2 1,06 2,65
н2 (la9)2 1 0,74 4,478
Не+ (l£7s)2(lau)1 1/2 1,08 2,47
Не2 (l<79)2(ltTu)2 0 - -
Существенно, что МО lag имеет энергию меньшую, чем энер-
гия АО 1s атома, входящего в молекулу. Напротив, МО 1аи имеет
энергию большую, чем энергия АО 1s соответствующего атома (см.
рис. 22.7 и 23.1). Как видно по табл. 23.1, заполнение МО 1сгд
двумя электронами привело к значительному понижению энергии
молекулы Н2 по отношению к энергии изолированных атомов. Од-
нако размещение третьего электрона на МО 1сгп приводит к возра-
станию энергии системы и, следовательно, к уменьшению энергии
диссоциации (см. табл. 23.1).
Таким образом, имеет смысл классифицировать МО по их
вкладу в энергию электронной подсистемы молекулы. Молекуляр-
ные орбитали, заполнение электронами которых приводит к пони-
жению энергии молекулы (т.е. к усилению межатомной связи),
называются связывающими МО. Если заполнение электронами
орбитали вызывает возрастание энергии и уменьшение межатом-
ной связи, то такая орбиталь называется дестабилизирующей или
разрыхляющей.
Для количественной оценки межатомного взаимодействия в
молекуле X. Херцберг (1904-1999) ввел понятие кратности связи,
величина которой определяется так:
k = Щ-П2, (23.23)
510 Лекция 23. Метод молекулярных орбиталей
где ni — количество электронов в молекуле на связывающих МО,
П2 — количество электронов в молекуле на разрыхляющих МО.
Рассмотрим систему частиц, полученную при добавлении еще
одного электрона к молекуле Не^.. Требование минимальности
энергии системы обусловливает размещение этого электрона на МО
1сгп, так как МО lag заполнена, а прочие МО имеют более высокие
энергии. Но тогда количества электронов на связывающих и раз-
рыхляющих МО совпадают и порядок связи (23.23) равен нулю.
Как следствие, молекула Не2 не существует в стационарном состо-
янии с электронной конфигурацией (1сгр)2(1сгп)2.
Характерной особенностью параметров табл. 23.1 являются
близкие значения равновесных расстояний Rq и энергий диссоци-
ации D для молекул с одинаковой кратностью связи к. Видно, что
с уменьшением к возрастает расстояние Rq и падает энергия D.
Говорят, что с ростом кратности связи увеличивается прочность
молекулы.
Перейдем к построению двухатомных молекул, составленных
из одинаковых атомов химических элементов второго периода та-
блицы Менделеева. В основных состояниях атомы элементов с
химическими номерами Z от 3 до 10 имеют заполненными элек-
тронные оболочки Is, 2s и 2р. Это означает, что минимальный
базис АО должен комбинироваться из орбиталей перечисленных
оболочек.
Орбитали оболочек 1s и 2s имеют сферическую симметрию (см.
рис. 11.4). Водородоподобные АО с орбитальным числом I = 1
описывают вырожденные состояния, т. е. обладающие одинаковой
энергией. Из табл. 9.2 видно, что эти волновые функции ком-
плексные. Квадраты их модулей, определяющие пространствен-
ное распределение электронной плотности, обладают аксиальной
симметрией относительно поворота вокруг оси Z (см. рис. 11.4).
При использовании метода МО ЛКАО целесообразно сначала
ввести новые АО в виде следующих линейных комбинаций:
2р% = R21~t=(Yii + ^1,-1)>
V "
О о 1 /V V \ (23.24)
2ру = J?21-7“7^(^ll - У1,—1), V 7
zv 2
2pz = ^21^10,
где Rni и Yim — радиальные и угловые части волновых функ-
ций атома водорода (11.14) и (9.53) соответственно. Нетрудно
убедиться, что любая линейная комбинация волновых функций
вырожденных стационарных состояний удовлетворяет уравнению
Шредингера (10.5) и также описывает состояние с определенной
энергией.
23.4. Метод МО ЛКАО для двухатомных гомоядерных молекул 511
Все волновые функции (23.24) действительные. Каждая из
них определяет пространственное распределение электронной
плотности в форме «гантели» вытянутой вдоль соответствующей
оси декартовой системы координат. Опыт, накопленный кванто-
вой химией, показывает, что в методе МО ЛКАО удобнее строить
молекулярные орбитали из атомных волновых функций (23.24),
чем из водородоподобных АО с орбитальным числом I = 1.
Таким образом, минимальный базис АО для конструирования
МО основных состояний молекул из атомов с химическими номе-
рами Z от 3 до 10 состоит из пяти пар орбиталей Is, 2s, 2рх, 2ру,
2pz-
Далее, для краткости, приближенные молекулярные орбитали,
полученные методом ЛКАО, будут обозначаться символами точных
МО, введенных в §22.5 предыдущей лекции.
Для получения приближенных МО ЛКАО можно, воспользо-
вавшись правилами 1-3, изложенными в конце § 23.2, каждую из
молекулярных орбиталей составить только из двух атомных. То-
гда наиболее низкоэнергетические молекулярные орбитали можно
представить следующими формулами:
lag = lsi + 1S2, 1сгп = bi - 1S2, (23.25)
2^ = 2si + 2s2, 2cru = 2si - 2s2. (23.26)
В этих и следующих обозначениях АО последний нижний индекс
задает номер атома.
Из атомных р-орбиталей составляются следующие МО:
3crg = 2pzi + 2pZ25
1тг^(ж) = 2pxi - 2рх2,
1тг^(у) = 2pyi - 2ру2,
Зсгп = 2pzi ~ 2pz2,
1тф) = 2pxi + 2рх2,
1тги(у) = 2pyi +2ру2-
(23.27)
(23.28)
(23.29)
Молекулярные орбитали (23.27) описываются симметрией то-
чечной группы РооА- Орбитали (23.28) и (23.29) инвариантны
относительно поворота вокруг оси Z на угол л/2 с одновременной
переменой знака волновой функции. Эти орбитали обладают сим-
метрией черно-белой группы mm'2', хотя соответствующее распре-
деление электронной плотности имеет симметрию 2?2Д- Энергия
молекулярных тг-орбиталей не зависит от их ориентации в про-
странстве, поэтому МО 1тг^(ж) и 1тг^(у), а также 17ггб(ат) и 1ли(у)
соответственно обладают одинаковыми энергиями.
Результаты расчетов энергий МО (23.25)-(23.29) для молекул
С>2 и F2 представлены на рис. 23.3. Видно, что каждая комбинация
АО дает две МО, причем одна из них имеет энергию большую отно-
сительно порождающей АО, а другая — меньшую. Следовательно,
формулы (23.25)-(23.29) задают 5 связывающих и 5 разрыхляю-
512
Лекция 23. Метод молекулярных орбиталей
щих орбиталей. Прочность молекулы и ее физические характе-
ристики определяются, в первую очередь, порядком заселения МО
электронами.
При расчете электронных конфигураций основных стационар-
ных состояний молекул, сведенных в табл. 23.1, достаточно было
Е
Атом 1 Молекула Атом 2
Рис. 23.3. Качественная энергетическая схема формирования МО ЛКАО для мо-
лекул Ог и F2.
По вертикальной оси отложена энергия. АО 2р трижды вырождены по энергии, МО 1тг —
дважды
применить принцип Паули и требование минимальности энергии
системы. В молекулах, где заполняются вырожденные МО, выпол-
нения этих двух условий недостаточно.
Рассмотрим для примера основное стационарное состояние мо-
лекулы О2, которая содержит 16 электронов. Электроны после-
довательно заполняют орбитали 1сг^, 1сги, 2сг^, 2сги, 1сг^, 1тги(ж),
1тги(у). Каждый из двух оставшихся электронов может разме-
ститься в любом их 4-х одноэлектронных состояний (спин-орби-
талей), объединенных в орбитали 1тг^(ж) и 1тг^(у), имеющих в
приближении конфигураций одинаковые энергии. Такое распреде-
ление имеет, вообще говоря, С% = 6 вариантов, которые в исполь-
зуемом приближении являются равновероятными. Таким обра-
зом, в рамках приближения электронных конфигураций вопрос
об основном состоянии молекулы О2 не может решиться. Более
детальный анализ взаимодействия электронов и ядер в молекуле
позволяет обнаружить зависимость энергии молекулы от величины
23.4. Метод МО ЛКАО для двухатомных гомоядерных молекул 513
суммарного спина Sq электронной подсистемы и ее суммарного мо-
мента импульса Lq.
Совокупность экспериментальных результатов показала спра-
ведливость распространения правила Хунда (см. § 16.3 лекции 16)
на молекулы. Согласно этому правилу, при фиксированной элек-
тронной конфигурации наинизшей энергией обладает стационар-
ное состояние с максимально возможной величиной суммарного
спина So = Smax электронной подсистемы. Если равенство So =
— Smax выполняется для нескольких состояний, то основным яв-
ляется состояние с максимально возможной величиной суммар-
ного момента импульса L$ = Lmax.
Из правила Хунда следует, что в основном состоянии молекулы
О2 электронная конфигурация имеет вид
(1<т9)2(1сги)2(2сг9)2(2<т„)2(1ст9)2(17ги(я:))2(17г„(?/))2(17г9(я:))1(17г9(?/))1.
(23.30)
Таким образом, на орбиталях 1тг^(ж) и 1тгр(у) размещаются по
одному электрону, которые имеют проекции спина одного знака.
При этом модуль спина электронной подсистемы молекулы опреде-
ляется формулой So = + 1), где квантовое число so = 1.
Как следствие, молекула О2 в основном состоянии обладает маг-
нитным моментом, что подтверждается экспериментально. Моле-
кулярный кислород демонстрирует свойства типичного парамагне-
тика, например, втягивается в область более сильного магнитного
поля. Важно, что парамагнетизм молекулы О2 получил объяснение
только после создания квантовой теории.
Электроны, размещенные по одному в состояниях, характери-
зуемых МО 1тг^(ж) и 1тг^(у), в химии называются неспаренными.
Электроны в таких состояниях играют важную роль в механизме
многих химических реакций.
Переходя к молекуле F2, заметим, что электронная конфигура-
ция основного состояния содержит только заполненные МО:
(1<т9)2(1сги)2(2сг9)2(2<ти)2(1<т9)2(17г„(я:))2(17ги(?/))2(17г9(а:))2(17г9(2/))2.
(23.31)
Следовательно, молекула F2 обладает нулевым суммарным спином.
При исследовании других двухатомных гомоядерных молекул
выяснилось, что для построения их МО базис АО необходимо рас-
ширить. Например, нельзя пренебрегать интегралом перекрытия
орбитали 2s одного атома с орбиталью 2pz другого. Тогда МО 2ад
должна записываться в виде
2(jg = ci(2si + 2^2) 4- 02(2^71 — Zpzz)- (23.32)
514
Лекция 23. Метод молекулярных орбиталей
Рис. 23.4. Качественная энергетическая схема формирования МО ЛКАО для
двухатомных молекул от Li2 до N2.
По вертикальной оси отложена энергия. АО 2р трижды вырождены по энергии, МО 1тг —
дважды
Таблица 23.2. Физические характеристики некоторых двухатомных
гомоядерных молекул
Молекула Электронная конфигурация Кратность связи Равновесное расстояние (А) Энергия диссоциа- ции (эВ)
Li2 [lW,)1 1 2,67 1,1
Вег [l](2a9)2(2au)2 0 - -
в2 [1][2](1тг„)2 1 1,59 3,0
с2 [1WW 2 1,24 6,4
N? 5/2 1,12 8,9
n2 [1][2](1тги)4(3<т9)2 3 1,1 9,9
О? [1](2](1тг„)4(3<т9)2(17г9)1 5/2 1,12 6,6
о2 [1][2](17Ги)4(3<79)2(17Г9)2 2 1,21 5,2
f2 [1][2](17Ги)4(3<79)2(17Г9)4 1 1,42 1,4
Ne2 [1][2](17Ги)4(3<79)2(17Г9)4(3<7и)2 0 - -
Символами [1] и [2] для краткости обозначены электронные конфигурации (1<т^)2(1<ти)2 и (2<т^)2(2<ти)2 соответственно.
23.4. Метод МО ЛКАО для двухатомных гомоядерных молекул 515
Расчеты показали, что для молекул О2 и F2 в грубом приближе-
нии можно пренебречь малым коэффициентом С2, однако для более
легких двухатомных гомоядерных молекул МО конструируются на
базисе из нескольких АО. Выражения аналогичные (23.32) соста-
вляются и для более высокоэнергетических МО. Результаты вы-
числений качественно представлены в виде энергетической схемы
на рис. 23.4.
Результаты расчета методом МО ЛКАО основных параметров
двухатомных гомоядерных молекул, состоящих из атомов легких
химических элементов, приведены в табл. 23.2. Видно, что с уве-
личением кратности связи происходит монотонный рост энергии
диссоциации D и монотонное уменьшение равновесного расстоя-
ния Rq, Молекулы, у которых на связывающих и разрыхляющих
молекулярных орбиталях размещено по равному количеству элек-
тронов (т.е. кратность связи равна нулю), являются нестабиль-
ными и самопроизвольно диссоциируют на отдельные атомы.
Задачи к лекции 23
1. Пользуясь правилом Хунда, найти суммарный спин двухатомных
гомоядерных молекул второго периода таблицы Менделеева в их основ-
ном состоянии.
2. Рассчитать коэффициент корреляции между равновесным рассто-
янием и энергией диссоциации двухатомных гомоядерных молекул вто-
рого периода таблицы Менделеева, пользуясь табл. 23.2.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 23
23.1. Основные типы химической связи
Сложность гамильтониана (22.14), описывающего многоатомные си-
стемы, обусловливает непреодолимые трудности точного решения урав-
нения Шредингера для стационарных состояний молекул. Как показано
в лекциях 22-24, прямые методы квантовой физики не позволяют анали-
тически вычислять физические характеристики многоатомных молекул
и кристаллов.
В ходе разработки приближенных методов расчета (которые явля-
ются предметом квантовой химии и кристаллохимии) были сформули-
рованы некоторые важные принципы, идеи и закономерности, оказавши-
еся полезными для развития современной физики, химии и технологии.
Одним из важнейших является понятие химической связи.
Все многообразие межатомных взаимодействий сводится к несколь-
ким наиболее типичным видам химической связи. Для каждого типа хи-
мической связи разрабатывается приближенная математическая модель,
базирующаяся на определенных физических предположениях. Грубо го-
воря, в основе каждого типа химической связи лежит некоторый пре-
валирующий физический механизм или процесс. Влияние прочих про-
цессов полагается пренебрежимо малым или учитывается впоследствии в
виде поправок. Для расчетов характерных параметров межатомной связи
используется математический аппарат квантовой механики. Сопоста-
вление результатов расчетов с экспериментальными данными позволяет
совершенствовать разработанную модель.
Наиболее распространенными являются ионная, ковалентная (с дву-
мя разновидностями — гомеополярной и гетерополярной), металличе-
ская, ван-дер-ваальсовская и водородная химические связи.
Ионная связь. Механизм ионной связи базируется на специфических
свойствах атомов химических элементов. Атомы активных (щелочных)
металлов имеют сравнительно низкую энергию отрыва валентного элек-
трона (Е; ~ 4-5 эВ). С другой стороны, атомы галогенов и элементов
главной подгруппы VI группы (кислород, сера, ...) обладают заметной
положительной энергией присоединения электрона (т. е. энергией срод-
ства к электрону Е’д). Эта энергия, определенная в § 15.5 лекции 15, для
галогенов особенно велика и, согласно табл. 15.5, превышает ЗэВ.
В результате межатомного взаимодействия (например, столкнове-
ния) атом щелочного металла может потерять электрон, а атом гало-
гена присоединить. При этом образуются положительный ион металла
и отрицательный ион галогена. Эти ионы имеют заполненные внеш-
ние электронные s- и р-оболочки, вследствие чего обладают повышен-
ной устойчивостью. Из-за различия знаков ионы будут притягиваться
друг к другу. Сближение ионов будет происходить до тех пор, пока пере-
крытие волновых функций внешних электронов не приведет к возник-
Дополнения к лекции 23
517
новению сил меж электронного отталкивания, которые уравняют силу
кулоновского притяжения. Равенство сил отталкивания и притяжения
определяет среднее расстояние между ионами, которое называется рав-
новесным.
Количество теряемых (или приобретаемых) электронов в процессе
формирования межатомной связи определяет величину положительной
(или отрицательной) химической валентности атомов.
Пример формирования ионной связи между атомами щелочного ме-
талла и галогена рассматривался в § 22.2 лекции 22.
В кристалле, содержащем огромное количество упорядоченно распо-
ложенных ионов, расчет энергии является более сложной математичес-
кой задачей. Но необходимым условиям устойчивости кристаллической
структуры является понижение энергии системы взаимодействующих
ионов, по отношению к системе изолированных атомов, что характе-
ризуется неравенством (22.4).
Характерные энергии ионных связей в кристаллах составляют не-
сколько эВ. Межатомные равновесные расстояния существенно зависят
от геометрии кристаллической структуры и, в основном, изменяются в
пределах 1-3 А.
Ковалентная связь. Существование устойчивых кристаллических
структур простых веществ показало, что одинаковые атомы тоже спо-
собны образовывать прочные химические связи. Этот тип связи, ко-
торый невозможно объяснить притяжением разноименных ионов, полу-
чил название ковалентной. Теория ковалентной связи была разработана
лишь с помощью квантовой механики. Ковалентная связь обеспечивает
существование не только простых, но и многих сложных химических
соединений и их кристаллов.
Когда атомы сближаются на расстояние порядка нескольких ангст-
рем, на их электроны начинают существенно действовать электрические
поля, создаваемые ядрами и электронами других атомов. Результатом
является перестройка волновых функций одноэлектронных стационар-
ных состояний взаимодействующих атомов, при этом наиболее сильно
искажаются волновые функции внешних электронов. Как следствие,
формируются молекулярные орбитали, которые являются общими для
нескольких атомов. Иначе говоря, электроны, заполняющие такие орби-
тали, движутся в области пространства, охватывающей два или больше
атомных ядер.
Квантовая теория позволила установить, что среди молекулярных
орбиталей всегда имеются связывающие, при заполнении которых ва-
лентными электронами общая энергия системы атомов понижается, что
обеспечивает стабильность данной структуры. Пространственное распре-
деление связующих молекулярных орбиталей таково, что в пространстве
между атомами образуются области повышенной электронной плотно-
сти. Грубо говоря, эти области избыточного отрицательного заряда свя-
зывают положительные ионы атомов посредством электрических сил
притяжения.
Чаще всего при этом образуется электронная пара, волновые функ-
ции которых «размазаны» на два взаимодействующих атома. Соответ-
ствующий максимум электронной плотности локализован в межатомном
пространстве. Энергия такой электронной пары значительно меньше
энергии двух валентных электронов изолированных атомов. Таким спо-
собом формируется одинарная ковалентная связь.
518
Дополнения к лекции 23
Заполнение электронами разрыхляющих молекулярных орбиталей
(см. § 23.4 лекции 23) ослабляет межатомное притяжение и может при-
вести к дестабилизации системы атомов. Прочность ковалентной связи
количественно характеризуется кратностью связи (23.23). Удвоенное
значение кратностью связи равно разности электронов, находящихся на
связывающих и разрыхляющих молекулярных орбиталях соответствен-
но. Нечетное значение этой разности обусловливает полуцелую кратность
ковалентной связи.
Энергии ковалентных связей, в основном, лежат в диапазоне 1-10 эВ.
Разброс энергий объясняется в первую очередь различной кратностью
связи. Межатомные расстояния имеют тот же порядок, что и у ион-
ных связей. Например, в кристалле кремния энергии одной межатомной
связи равна 3,7 эВ, а равновесное расстояние Rq = 2,35 А.
Если функция электронной плотности р(г) заполненной молекуляр-
ной орбитали симметрична относительно средней точки межатомного
промежутка, то такая ковалентная связь называется гомеополярной.
Если максимум электронной плотности сдвинут к одному из связанных
атомов, то связь называется гетер ополярной.
Например, атомы в структуре алмаза объединены ковалентной свя-
зью, причем максимумы функции электронной плотности совпадают с
центрами межатомных расстояний. В бинарных химических соедине-
ниях типа антимонида индия In As, состоящих из атомов третьей и пя-
той главных групп таблицы Менделеева, максимум электронной плот-
ности сдвигается к атомам пятой группы. В соединениях типа AnBIV
аналогичное смещение электронной плотности увеличивается. Отсюда
следует, что с увеличением полярности ковалентной связи она посте-
пенно становится неотличимой от ионной. Таким образом, не существует
строгой границы между ионной и гетерополярной ковалентной связью,
что иллюстрирует приближенность понятия химической связи.
Следует отметить, что в некоторых молекулах формируются связу-
ющие молекулярные орбитали, которые делокализованы («размазаны»)
по трем и более атомам. При заполнении электронами таких орбита-
лей возникают ковалентные связи, объединяющие вместе несколько ато-
мов. Такие многоцентровые связи существуют, например, в бензольных
кольцах.
Металлическая связь. Металлы, сплавы, интерметаллические соеди-
нения образуют кристаллы с особым видом химической связи, которую
называют металлической. Особенность металлической связи заключа-
ется в том, что при объединении в кристаллическую структуру образу-
ются специфические орбитали, делокализованные по всему объему кри-
сталла. Собственная энергия этих делокализованных орбиталей такова,
что при переходе на них валентных электронов атомов энергия всей
структуры понижается, что и обеспечивает стабильность и прочность ме-
таллических структур.
«Обобществленные» электроны, заполняющие делокализованные ор-
битали, называются электронами проводимости, так как именно они
обеспечивают высокую электропроводность металлов. Плотность элек-
тронов проводимости примерно постоянна по всему металлическому об-
разцу.
Так как все атомы металлов отдают электроны на заполнение дело-
кализованных орбиталей, можно сказать, что металл состоит из упорядо-
Дополнения к лекции 23
519
ченно расположенных положительных ионов и электронов проводимости,
легко мигрирующих по всему объему металлического кристалла.
Для металлических связей характерны несколько большие межатом-
ные (точнее, межионные) равновесные расстояния Rq по сравнению с ко-
валентной и ионной связями. Прочность металлических структур обеспе-
чивается большим количеством ближайших соседей Ni у каждого атома.
При Ni = 12 величина расстояния Rq лежит в интервале 2,6-2,9 А, при
Ni = 8 величины Rq могут превышать 3 А.
Заметим, что эффект делокализации электронов, вообще говоря, раз-
мывает строгую границу между ковалентной и металлической связями.
Три перечисленных типа химической связи являются сильными.
Кристаллические структуры с этими типами химической связи обладают
устойчивостью в широком интервале температур.
Ван-дер-ваальсовская связь. Ван-дер-ваальсовские силы притяже-
ния между электронейтральными частицами обусловливаются диполь-
дипольным взаимодействием.
Если молекулы обладают постоянным электрическим дипольным мо-
ментом de, то между ними возникает диполь-дипольное притяжение,
хорошо изученное в классической физике. Сила взаимодействия двух
дипольных моментов (короче, диполей) зависит от их взаимной ориен-
тации и расстояния между ними. Тепловое движение молекул приводит
к разориентации диполей, и их энергия взаимодействия определяется
выражением
иДг) = -
2^
Зг6/свТ’
(Д.23.1)
где г — среднее расстояние между диполями, кв — постоянная Больц-
мана, Т — температура. Величина (Д.23.1) дает заметный вклад в
энергию межмолекулярного взаимодействия для молекул со сравнительно
большим электрическим дипольным моментом de, напцимер, ЩО или
NH3.
Электронейтральный атом (или молекула), не имеющий дипольного
момента в свободном (изолированном) состоянии, может его приобре-
сти под действием электрического поля другой молекулы, обладающей
электрическим дипольным моментом de. Этот эффект называется поля-
ризацией, а возникающие диполи — наведенными (индуцированными).
Энергия взаимодействия постоянного дипольного момента с индуциро-
ванным выражается формулой
С72(г) =
2а
^•6
(Д.23.2)
где коэффициент ае называется поляризуемостью частицы.
Исследования показали, что основной вклад во взаимное притяжение
электронейтральных атомов (или молекул) дает так называемое дис-
персионное взаимодействие. Оно осуществляется из-за образования
в нейтральных атомах мгновенных диполей, возникающих вследствие
случайного (вероятностного) характера движения электронов. Энергия
дисперсионного взаимодействия рассчитывается методами квантовой ме-
ханики и оказывается обратно пропорциональной г6.
520
Дополнения к лекции 23
Суммарная энергия взаимодействия электронейтральных атомов или
молекул может быть выражена приближенной формулой
t7(r) = + Вехр(-Сг), (Д.23.3)
где А, В и С — константы, характерные для взаимодействующих ато-
мов. Экспоненциальное слагаемое в (Д.23.3) описывает отталкивание
атомов при их сближении из-за перекрывания внешних электронных
оболочек.
Баланс сил диполь-дипольного притяжения и межэлектронного от-
талкивания обеспечивает минимум энергии системы атомов или молекул
при определенных равновесных расстояниях между ними.
Ван-дер-ваальсовская химическая связь возникает, в частности,
между атомами инертных газов при низких температурах. Эти же вза-
имодействия обеспечивают устойчивость кристаллов, образованных ор-
ганическими молекулами.
Энергии ван-дер-ваальсовских связей в среднем на порядок ниже,
чем энергия сильных химических связей. Характерные равновесные
расстояния Rq ван-дер-ваальсовской связи превышают соответствую-
щие величины для сильных химических связей и в среднем равняются
3,5-4 А. Например, в кристалле аргона Rq = 3,75 А, а энергия межатом-
ной связи составляет около 0,1 эВ.
Водородная связь. Специфическая разновидность химической свя-
зи — водородная — возникает, если при образовании ковалентной связи
единственный электрон атома водорода переходит на связующую моле-
кулярную орбиталь. Если вблизи расположены другие атомы, то между
ядром атома водорода (протоном) и электронными оболочками соседних
атомов действуют силы кулоновского притяжения. Рентгенографические
и нейтронографические исследования показали, что протон атома водо-
рода весьма слабо экранирован электронами молекулярной орбитали и
образует устойчивую связь. Этот тип связи атомов водорода формиру-
ется чаще всего с атомами 7-й и 6-й групп таблицы Менделеева, которые
имеют сравнительно большое количество электронов во внешнем элек-
тронном слое.
Энергии водородных связей в среднем несколько выше, чем ван-дер-
ваальсовских и могут варьироваться в пределах 0,1-0,5 эВ. Равновесные
расстояния Rq водородных связей превышают величины Rq для силь-
ных связей.
В частности, благодаря водородным связям, молекулы воды Н2О,
атомы внутри которой объединены ковалентной связью, образуют гек-
сагональную структуру льда. Длина ковалентной связи равна 1,01 А,
а длина водородной связи (равновесное расстояние между протоном и
ядром атома кислорода соседней молекулы) равняется 1,75 А.
Водородные связи стабилизируют форму длинных органических мо-
лекул белков, нуклеиновых кислот, в том числе двойную спираль ДНК.
Подводя итог краткому обзору основных типов химических связей,
отметим, что ионная, металлическая и ван-дер-ваальсовская связь не от-
личаются направленностью. Это значит, что электронная плотность в
окрестности связанных атомов приблизительно сохраняет сферическую
симметрию. Напротив, ковалентная и водородная связи относятся к
Дополнения к лекции 23
521
направленным. Электронная плотность имеет характерный максимум
вдоль линии, соединяющей центры взаимодействующих атомов.
Тип химической связи между атомами во многом определяет атом-
ную структуру кристаллов.
23.2. Принцип плотнейшей упаковки
для описания кристаллических структур
Сложность решения уравнения Шредингера для многоатомных си-
стем приводит к разработке и использованию различных приближенных
методов расчета физических характеристик молекул и кристаллов.
Многие важные параметры кристаллической структуры определяют-
ся видом зависимости потенциальной энергии взаимодействия атомов от
межатомного расстояния г, т.е. функцией U(r). Эти функции для пар
различных атомов, конечно, имеют индивидуальные особенности. Од-
нако несмотря на различие параметров атомов разных химических эле-
ментов и разнообразие типов химической связи, функции U(г) обладают
характерными общими закономерностями (см. рис. Д.23.1).
Во-первых, если между атомами существует устойчивая химическая
связь, то кривая U(f) имеет минимум в отрицательной области значе-
ний, который соответствует среднему межатомному расстоянию Rq. Ве-
личина Rq, вообще говоря, характерна для данной пары атомов и типа
Рис. Д.23.1. Схематическая зависимость энергии взаимодействия двух атомов
от межатомного расстояния:
а) сильная связь (ионная, ковалентная, металлическая); б) слабая связь (ван-дер-вааль-
совая, водородная). Начало оси координаты г совмещено с центром одного атома, ось
направлена через центр другого. Аддитивная постоянная потенциальной энергии выбрана
из условия U{r —> оо) —> 0, что соответствует началу отсчета энергии от суммарной
энергии изолированных атомов
химической связи между ними. Точка минимума г = Rq функции U(r)
дает равновесное положение второго атома относительно первого. Та-
ким образом, величина Rq представляет собой среднее межатомное рас-
стояние d или длину химической связи в конденсированном состоянии
вещества.
522
Дополнения к лекции 23
Во-вторых, при уменьшении межатомного расстояния г —> 0 функ-
ция U(г) резко и практически неограниченно возрастает. Это означает,
что независимо от механизма межатомного взаимодействия (типа хи-
мической связи) при сближении атомов возникают силы отталкивания,
которые очень резко возрастают при сближении атомов. Расстояние, на
котором силы отталкивания становятся преобладающими, определяется
перекрыванием волновых функций внешних электронов взаимодейст-
вующих атомов.
Вышеприведенные особенности межатомной связи обусловливают
эффективность описания кристаллических структур с ненаправленными
связями с помощью модели твердых шаров. В этом приближении пре-
небрегается тепловыми колебаниями атомов и проводится замена атомов
несжимаемыми шарами, которые касаются друг друга. Касание соответ-
ствует такому расположению взаимодействующих атомов, которое обес-
печивает минимум потенциальной энергии кристалла.
Для использования предложенной модели необходимо каждому атому
поставить в соответствие определенный радиус твердого шара Яд. Из
вышеизложенного следует, что длины химических связей должны выра-
жаться суммой радиусов твердых шаров, характеризующих взаимодей-
ствующие атомы. Если ДА, В) — расстояние между взаимодействую-
щими атомами Л и В, то
ДА, В) = Ra+Rb, (Д.23.4)
где Ra и Rb — радиусы атомов А и В соответственно.
В частности, радиус шара, изображающего атом благородного (инерт-
ного) газа, принимается равным половине равновесного расстояния меж-
ду ближайшими атомами ДА, А) в кристалле, образованном атомами
этого газа:
Ra = (Д.23.5)
Радиусы атомов в модели твердых шаров должны обладать свойст-
вом аддитивности. Это означает, что радиусы, определенные на основе
анализа межатомных расстояний в некоторой кристаллической струк-
туре, являются пригодными для описания других кристаллов, содержа-
щих данные атомы.
Основная трудность разработки аддитивной системы радиусов ато-
мов заключается в следующем. Когда атом вступает во взаимодействие
с другими, т.е. образует химическую связь, то волновые функции его
внешних (валентных) электронов претерпевают значительную перест-
ройку. Размер взаимодействующего атома по сравнению с радиусом изо-
лированного может заметно меняться.
Экспериментальные исследования структур множества кристаллов
показали, что не удается охарактеризовать атом данного химического
элемента определенным радиусом твердого шара, который был бы при-
годен для описания всех известных кристаллических структур. С дру-
гой стороны, выяснилось, что, оставаясь в рамках определенного типа
химической связи, можно взаимодействующим атомам поставить в соот-
ветствие определенные эффективные радиусы так, чтобы приближенно
выполнялось свойство аддитивности (Д.23.4). Иначе говоря, можно со-
ставить набор металлических, ван-дер-ваальсовых и других эффектив-
Дополнения к лекции 23
523
ных радиусов, обладающих свойством аддитивности. Будучи однажды
вычисленными, они наблюдаются в новых открываемых или синтези-
рованных кристаллических структурах. Определенные таким образом
радиусы называются кристаллохимическими. Зависимость эффектив-
ных радиусов от типа химической связи обусловливает существование и
использование нескольких наборов эффективных размеров взаимодей-
ствующих атомов, которые сводятся в систему кристаллохимических
радиусов. Точность определения кристаллохимического радиуса обычно
ограничивается одной сотой ангстрема.
Наряду с системой атомных эффективных радиусов построена си-
стема ионных радиусов Ri. Анализ кристаллических структур показал,
что величина ионного радиуса для определенного химического элемента
существенно зависит от заряда иона. Например, для иона V2+ эффек-
тивный радиус равен Ri = 0,93 А, для иона V3+ радиус Ri = 0,78 А.
Заметим, что, вообще говоря, полная энергия кристаллической
структуры обусловлена взаимодействием всевозможных пар атомов.
Однако в рассматриваемом приближении основной вклад в энергию кри-
сталла дает взаимодействие ближайших соседей, т.е. пар соприкасаю-
щихся атомов — твердых шаров. Как было показано выше, касание
твердых шаров соответствует расположению взаимодействующих ато-
мов, которое обеспечивает минимум потенциальной энергии. Следова-
тельно, с наибольшей вероятностью стабильные кристаллические
структуры образуются, если каждый атом будет взаимодействовать с
наибольшим числом соседних, или, иначе говоря, каждый твердый шар
будет касаться максимального количества соседних твердых шаров. Та-
ким образом, требование наименьшей потенциальной энергии взаимо-
действия атомов может быть в данной модели переформулировано в
принцип максимальности числа касаний твердых шаров, описываю-
щих атомы. При этом отношение объема шаров ко всему объему кристал-
лического пространства, так называемый коэффициент заполнения, бу-
дет максимальным. Упаковки твердых шаров с максимально возможным
коэффициентом заполнения называются плотнейшими упаковками.
Таким образом, модель твердых шаров приводит к выводу, что наи-
более стабильные кристаллические структуры химических соединений с
ненаправленными связями должны описываться плотнейшими упаков-
ками. Такой подход к описанию кристаллических структур называется
принципом плотнейшей упаковки.
Следует иметь в виду, что этот подход является лишь геометриче-
ским принципом, и его недостаточно для полного описания атомных
структур кристаллов. Однако кристаллографические исследования по-
казали, что принцип плотнейшей упаковки успешно описывает огром-
ное множество кристаллических структур, особенно в случаях «ненапра-
вленных» ‘ химических связей — металлических, ван-дер-ваальсовых,
ионных. «Ненаправленные» связи могут быть представлены взаимодей-
ствием атомов со сферически симметричной электронной плотностью.
В таких случаях требование максимального числа касаний соседей для
образования наиболее стабильной кристаллической структуры является
естественным.
Число касаний шара с соседними (т.е. количество ближайших со-
седей у атома) называется координационным числом данного атома.
В частности, анализ структур с ионным типом связи позволил выяс-
нить, что ионный кристаллохимический радиус для определенного хи-
524
Дополнения к лекции 23
мического элемента существенно зависит не только от заряда иона, но и
от его координационного числа (к.ч.). В табл. Д.23.1 приведены примеры
ионных радиусов для разных значений координационных чисел.
Таблица Д.23.1. Ионные радиусы (А) для различных
координационных чисел
Ион Координационное число
2 4 6 7 8 9 12
Na1+ - 1,13 1,16 1,26 1,32 1,38 1,53
К1+ - 1,51 1,52 1,60 1,65 1,69 1,78
F1- 1,15 1,17 1,19 - - - -
С17+ - 0,22 0,44 - - - -
о2- 1,21 1,24 1,26 1,28 - - -
S6+ - 0,26 0,43 - - - -
и4+ - - 1,03 1,10 1,14 1,19 1,31
и6+ 0,59 0,66 0,87 0,95 1,00 - -
Таблица Д.23.2. Сравнительные значения ковалентных радиусов
для некоторых химических элементов. Первое число — тетраэдрический
радиус, второе — октаэдрический (в ангстремах)
C 0,77/0,97 N 0,70/0,95 0 0,66/0,90
Mg 1,46/1,42 Al 1,26/1,41 Si 1,17/1,37 P 1,10/1,35 S 1,04/1,30
Си 1,35/1,25 Zn 1,31/1,27 Ca 1,26/1,35 Ge 1,22/1,43 As 1,18/1,43 Se 1,14/1,40
Ag 1,53/1,43 Cd 1,48/1,45 In 1,44/1,53 Sn 1,40/1,60 Sb 1,36/1,60 Те 1,32/1,56
Аи 1,50/1,40 Hg 1,48/1,45 T1 1,47/1,73 Pb 1,46/1,67 Bi 1,46/1,65
Ковалентные связи, в отличие от вышеперечисленных, являются «на-
правленными». Это означает, что максимумы электронной плотности ва-
лентных электронов этих связей располагаются в межатомных областях.
Тем не менее, модель твердых шаров оказалась полезной и для опи-
сания кристаллических структур с ковалентными связями. Оказалось
возможным разработать систему эффективных ковалентных радиусов,
обладающих свойством аддитивности. Экспериментальные исследова-
ния показали, что существует заметное различие между ковалентными
Дополнения к лекции 23
525
и металлическими радиусами одного и того же химического элемента.
Например, атомы серого олова (a-Sn) связаны ковалентными связями,
их атомный радиус равен 1,4 А. Межатомное расстояние в белом олове
(/?-Sn), которое является типичным металлом, равно 3,03 А. Следова-
тельно, металлический радиус атома олова превышает ковалентный.
Величины ковалентных радиусов зависят от координационного чи-
сла. Наиболее употребительными на практике являются «тетраэдриче-
ские» (координационное число 4) и «октаэдрические» (координационное
число 6) ковалентные радиусы. Примеры таких радиусов приведены в
табл. Д.23.2.
Кроме того, ковалентные радиусы сильно зависят от кратности связи.
Например, для атомов углерода, азота, кислорода и серы сокращение ко-
валентного радиуса по сравнению с одинарной связью составляет для
двойных связей 12-14%, для тройных — 20-22%. Для «нецелочислен-
ных» связей ковалентные радиусы принимают промежуточные значе-
ния.
23.3. Теорема Купмэнса
Одной из важных характеристик молекулы является ее энергия ио-
низации Ei, т.е. энергия, необходимая для отрыва электрона от моле-
кулы и превращения ее в однократно заряженный положительный мо-
лекулярный ион. Электроны молекулы, вообще говоря, размещены на
нескольких молекулярных орбиталях, которые различаются энергиями.
Каждому энергетическому уровню соответствует своя энергия ионизации.
Набор энергий ионизации определяет способности молекулы к пере-
ходу в окисленные состояния и, следовательно, характеризует ее реак-
ционную способность.
Широко распространенным экспериментальным методом измерения
энергий ионизации Ei является фотоэлектронная спектроскопия. В этом
методе молекулы, находящиеся в газовой фазе, подвергаются воздей-
ствию монохроматического электромагнитного излучения с частотой си.
При достаточно большой частоте си энергия фотонов /ки превышает энер-
гию ионизации Ei, и от молекул отрываются электроны. Эксперимен-
тальная установка снабжена энергоанализатором, который позволяет из-
мерять кинетическую энергию освобожденных электронов Те. Искомая
энергия ионизации Ei вычисляется из уравнения сохранения энергии
tiw = Te+Ei. (Д.23.6)
Эксперименты показали, что при определенной частоте излучения си
регистрируется линейчатый спектр электронов, содержащий иногда до-
вольно много узких пиков. Максимум с наибольшей энергией Те обусло-
влен ионизацией внешней молекулярной орбитали — наиболее высоко-
энергетической из заполненных. Остальные пики объясняются отрывом
электронов с более низкоэнергетических (внутренних) молекулярных ор-
биталей. Электроны, полученные ионизацией молекулы с помощью об-
лучения потоком фотонов, называются для краткости фотоэлектронами.
В фотоэлектронной спектроскопии для ионизации молекул обычно
используется пучок монохроматического излучения ультрафиолетового
диапазона. Например, часто для ионизации внешних электронов приме-
няется спектральная линия возбужденного атома гелия с длиной волны
526
Дополнения к лекции 23
А = 584 А (см. рис. Д.17.1 дополнения 17.1). Для отрыва электро-
нов, размещенных на внутренних орбиталях, молекула подвергается воз-
действию какой-либо спектральной линии мягкого характеристического
рентгеновского излучения.
Регистрация спектра фотоэлектронов позволяет на основе уравнения
(Д.23.6) вычислить набор энергий ионизации Ei исследуемой молекулы.
На рис. Д.23.2 приведены фрагменты спектра фотоэлектронов для мо-
лекулы N2. Каждому пику на графике соответствует ионизированный
1аа
415 405
45 35
б
2og
а
Рис. Д.23.2. Спектр фотоэлектронов молекулы азота N2, пересчитанный в энер-
гии ионизации Ег.
По вертикальной оси отложено количество зарегистрированных электронов Ne на интер-
вал энергий Те. По горизонтальной оси отложены значения энергий ионизации Е^ вычи-
сленных по формуле (Д.23.6). Участки спектра а и б получены при облучении молекулы
рентгеновскими лучами характеристической спектральной линии Ка магния, участок в —
при ионизации молекулы излучением спектральной линии А = 584 А гелия
энергетический уровень стационарных состояний молекулы. Измерения
энергий ионизации Ei позволяют получить значения энергий молекуляр-
ных орбиталей с помощью ниже изложенной теоремы Купмэнса.
Теоремой Купмэнса называется утверждение, что измеренная энер-
гия ионизации равна энергии электронов еп (с обратным знаком), нахо-
дящихся на определенной молекулярной орбитали
Ei = -еп, (Д.23.7)
где п — набор квантовых чисел, полностью характеризующий данную
молекулярную орбиталь. Отсчет энергий орбиталей еп производится от
нуля, за который принята энергия свободной неподвижной частицы. На
рис. Д.23.3 изображена схема, иллюстрирующая связь энергий фотонов,
фотоэлектронов и молекулярных орбиталей.
Фактически теорема Купмэнса базируется на предположении, что
после отрыва одного электрона энергии орбиталей молекулы не изме-
няются, несмотря на изменения потенциала электронной оболочки,
потерявшей один электрон. Иначе говоря, предполагается, что спектр
энергий молекулярных орбиталей для однократно заряженного положи-
тельного иона таков же, что и для соответствующей нейтральной моле-
кулы.
Дополнения к лекции 23
527
В квантовой теории доказано, что теорема Купмэнса верна, если
орбитали молекулы пусты или заполнены двумя электронами с проти-
воположными проекциями спинов. В случаях молекул с частично запол-
ненными орбиталями в уравнение (Д.23.7) следует вводить поправки.
Рис. Д.23.3. Энергетическая диаграмма формирования линейчатого спектра
электронов при воздействии монохроматического излучения на молекулу.
За ноль отсчета энергии принята энергия свободного неподвижного электрона. Горизон-
тальные сплошные линии — энергетические уровни заполненных молекулярных орбита-
лей с энергиями €i, €2, £з- Штрихпунктирные вертикальные стрелки изображают энергию
фотонов /kJ, ионизирующих молекулу. Вертикальные сплошные стрелки — кинетические
энергии Tgi, Те2, Тез оторванных от молекулы электронов
Энергии молекулярных орбиталей, рассчитанные на основе теоремы
Купмэнса, являются хорошим приближением и часто используются из-за
простоты вычислений.
Лекция 24
ВАРИАЦИОННЫЙ МЕТОД
И МОЛЕКУЛЯРНЫЕ ТЕРМЫ
24.1. Вариационный метод для молекул
и секулярное уравнение
В предыдущих лекциях показано, что для вычисления волно-
вых функций, энергий стационарных состояний и других физи-
ческих характеристик многоэлектронных систем приходится ис-
пользовать приближенные численные методы квантовой физики.
При этом усилия физиков должны быть направлены на увеличение
точности расчетов и уменьшение их трудоемкости. Одним из об-
щих подходов к исследованию многоэлектронных систем является
вариационный метод, предложенный в 1908 г. Вальтером Ритцом
(1878-1909).
Метод основан на следующей важной теореме квантовой ме-
ханики. Пусть электронная система (атом, молекула, ион и т.п)
описывается гамильтонианом Н. Основное стационарное состо-
яние системы характеризуется точной волновой функцией Фо и
обладает энергией Eq. Тогда для любой нормированной прибли-
женной волновой функции Ф выполняется соотношение
Ё = У J ^H^odV = Ео, (24.1)
где интегрирование проводится по всему пространству.
Доказательство приводится в курсах квантовой механики. По
определению величина Е представляет собой среднюю энергию со-
стояния, характеризуемого волновой функций Ф. Согласно соотно-
шению (24.1), энергия состояния, вычисленная с помощью при-
ближенной волновой функции, всегда превышает точное значение
энергии основного состояния. Если волновая функция Ф неогра-
ниченно приближается к точной волновой функции Фо, то энергия,
выраженная левым интегралом в соотношении (24.1), стремится
24.1. Вариационный метод для молекул 529
к точному значению Eq энергии основного состояния данной элек-
тронной системы. Иначе говоря, замена функции Ф на функцию
Фо в левом интеграле обеспечивает достижение экстремума вели-
чины Е.
На теореме (24.1) базируется вариационный метод Ритца для
молекул. По причине невозможности получить точное решение
уравнения Шредингера волновая функция основного состояния
молекулы выбирается в виде линейной комбинации п независи-
мых функций epi (г = 1,..., п):
п
Ф = ^сЖ. (24.2)
г=1
В качестве функций tpi (г = 1,..., п) могут быть выбраны, вообще
говоря, любые определенные функции, т. е. не обязательно АО. Ко-
эффициенты Ci (i = 1,...,п) вводятся сначала как неопределен-
ные параметры, предназначенные для варьирования. Величины Ci
(г = 1,...,п) подбираются так, чтобы функция (24.2) наилучшим
образом приближала точную волновую функцию Фо- Критерием
наилучшей аппроксимации, согласно теореме (24.1), является ми-
нимальность величинь1_Е.
Запишем энергию Е в виде левого интеграла (24.1), подста-
вив в него выражение (24.2). Примем во внимание, что функ-
ция (24.2) не обязательно нормирована на единицу, а функции epi
(г = 1,..., п) не обязательно ортогональны. Тогда энергия Е пред-
ставится следующим отношением двойных сумм:
Е Е CiCjfPiH'PjdV
Ё = , (24.3)
Е Е
г=1 j=l
где индексы i и j независимо пробегают набор значений 1, ..., п.
Введем обозначения (подобно тому, как это было сделано в
§23.3 для молекулы Н^) для матричных элементов гамильто-
ниана
Hij = J^HcpjdV (24.4)
и интегралов перекрытий
Sa —
<Pi<PidV.
(24.5)
530 Лекция 24. Вариационный метод и молекулярные термы
Это позволяет переписать (24.3) в виде уравнения
п п п п
£ £ - Ё£ £ d^cjSij = о.
i=l j=l г=1 j=l
(24.6)
Будем рассматривать величину Е как непрерывную функцию
£/(ci,..., сп) коэффициентов Ci (г = 1,..., п). Необходимым усло-
вием минимальности функции F(ci,..., сп) является равенство
нулю всех частных производных вида
— =0, i =
(24.7)
Продифференцируем уравнение (24.6) по параметрам с* (г =
= 1,..., п) и получим систему из п уравнений:
п п п п
— У? у cj$ij cj$ij + ~ Q? г = 1,...,П.
г i=l j—1 j=l j=l
(24.8)
Условия (24.7) обеспечивают равенство нулю первого слагае-
мого во всех вышеприведенных уравнениях (24.8), и система
(24.8) становится однородной относительно искомых коэффици-
ентов Cj (j = 1,..., n):
Y'CjlHij-ESij) = 0, j = (24.9)
J=1
Как известно, система однородных уравнений типа (24.9) име-
ет нетривиальное решение, если ее детерминант равен нулю, т. е.
det (Hij - ESij) = 0. (24.10)
Уравнения системы (24.9) называются секулярными или ве-
ковыми, а детерминант этой системы называется секулярным.
Приравнивание секулярного детерминанта нулю дает уравнение
(24.10), которое имеет, вообще говоря, имеет п корней ..., Еп.
Наименьший из корней jEmin является искомой энергией основного
состояния молекулы, остальные корни соответствуют некоторым
возбужденным состояниям.
Далее следует найденное значение -Emin подставить в систему
уравнений (24.9) и, решив ее, вычислить коэффициенты Cj (j =
= 1,..., п). Подстановка найденных значений в разложение (24.2)
даст явный вид волновой функции основного состояния молекулы.
24.2. Расчет молекулярных орбиталей вариационным методом 531
Заметим, что полученная вышеописанным вариационным ме-
тодом волновая функция соответствует минимально возможной
энергии молекулы (основному стационарному состоянию), однако
может быть непригодна для вычисления других физических ха-
рактеристик этой молекулы.
24.2. Расчет молекулярных орбиталей
вариационным методом
Проиллюстрируем вариационный метод на примере расчета
энергии основного состояния произвольной двухатомной молеку-
лы. Волновую функцию молекулы зададим в виде
'Ф = 4- С2<Р2, (24.11)
который является частным случаем линейной комбинации (24.2).
Однако, вообще говоря, в отличие от случая, рассмотренного в
§23.3, коэффициенты с\ и С2 не связаны определенными симме-
трическими соотношениями. Секулярные уравнения имеют вид
С1(Яц - ESn) + C2(#12 - Я$12) = О,
С1(Яг1 — ES21) + £2(^22 — ES22) — 0.
Из симметрии интегралов (24.4) и (24.5) следует Н\2 = Я21
и S12 = S21- Без потери общности можно полагать, что базисные
функции и ф2 нормированы, тогда
Sil = У dV = S22 = У <^2^2 dV = 1.
При этом детерминант системы уравнений (24.12) принимает вид
Яц - Е Я12 - Я512
Я12 — ES\2 Я22 — Е
Приравнивая этот детерминант нулю, получим квадратное уравне-
ние для энергии
(Ни - H)(H22 - Е) - (Hi2 - ES12)2 = 0. (24.14)
Не представляет труда записать в общем виде выражения для
обоих корней полученного уравнения, хотя это выглядит несколько
громоздко.
Рассмотрим практически важную ситуацию, когда интеграл пе-
рекрытия S12 мал по сравнению с единицей. Тогда корни уравне-
ния (24.14) могут быть записаны в следующей форме:
Е = 1 ((Иц + Н22) ± л/(Н11-Н22)2 + 4Н122 ) . (24.15)
(24.13)
532 Лекция 24. Вариационный метод и молекулярные термы
Теперь интересно остановиться на двух частных случаях.
В первом рассмотрим гомоядерные молекулы, для которых спра-
ведливо равенство Ни = #22- Тогда решение (24.15) запишется
в простом виде
Е = Нп±Н12, (24.16)
где энергия Hu — Н\2 соответствует основному состоянию моле-
кулы.
Выражение (24.16) означает, что энергия одной из МО выше
энергии АО, энергия другой — ниже, при этом разность энергий
МО равна 2Я12. Говорят, что атомная орбиталь симметрично рас-
щепляется на 2 молекулярные, из которых одна связывающая с
энергией Ни — Н\2, другая — разрыхляющая, имеющая энергию
Ни +Я12. Примеры таких расщеплений наблюдаются на рис. 23.3.
Второй интересный частный случай касается гетероядерных
молекул и определяется условием
|Я12| «|Яп-Я22|. (24.17)
В этом случае радикал в (24.15) можно разложить в ряд до ли-
Н12
нейного члена по степеням малого параметра —----—Тогда
Ни — Н22
энергии (24.15) приближенно выразятся следующим образом:
тт2 тт2
Е = Нп+„ 12 , Е = Н22- 12 (24.18)
/1ц — ±/22 Пц — ^22
Это означает, что в данном случае энергии МО смещены отно-
сительно энергий АО на величину Я^ДЯц — Я22), при этом энер-
гия одной МО смещается вверх, другая — вниз. Условие (24.17)
обусловливает относительно небольшую величину смещений энер-
гетических уровней. Следует заметить, что если Ни > Я22, то
энергетический уровень первой орбитали поднимается, а уровень
второй — понижается. В квантовой химии принято говорить, что в
данном случае при взаимодействии атомов энергетические уровни
орбиталей отталкиваются.
Смещение энергии Н^2/(Ни — Н22) может быть мало вслед-
ствие малости величины |Я12| или большого значения разности
|Яц — Н22\. Из уравнений системы (24.12) можно получить два
отношения коэффициентов ci/c2:
ci _ HSj2 - Н12 ci _ Е - Я22 , .
с2 Ни — Е ’ с2 Я12 — ES12
Если полученные величины энергий (24.18) подставить в
(24.19), то легко убедиться, что отношение коэффициентов с\/с2
24.2. Расчет молекулярных орбиталей вариационным методом 533
либо очень мало, либо очень велико. Это означает, что превали-
рующий вклад в волновую функцию молекулы (24.11) дает лишь
одна из атомных орбиталей. Таким образом, подтверждается при-
веденное в предыдущей лекции первое правило составления ми-
нимального набора АО: энергии АО не должны значительно раз-
личаться. Кроме того, теперь можно сформулировать еще одно
полезное утверждение: в минимальный набор АО не следует вклю-
чать орбитали и (pj, для которых перекрестный матричный эле-
мент Hij имеет относительно малое значение.
Расчет молекулярных орбиталей и энергий стационарных со-
стояний гетероядерных молекул (по сравнению с гомоядерными)
представляет собой гораздо более громоздкую задачу, несмотря на
введенные выше приближения. Подробная методика расчетов и по-
лученные результаты приводятся в специализированных курсах
квантовой химии. В качестве примера приведем некоторые ре-
зультаты расчетов для молекулы фторида водорода HF в основном
состоянии.
Эта гетероядерная молекула содержит 10 электронов, которые
распределены по 5-и молекулярным орбиталям. Расчеты были про-
ведены с помощью минимального базиса, состоящего из волновой
функции ls-орбитали атома водорода ls(H), Is, 2s и 2р орбита-
лей атома фтора: 15(F), 2s(F), 2px(F), 2py(F) и 2p2(F). Наибо-
лее низкоэнергетические МО (заполнение которых соответствует
основному состоянию молекулы HF) имеют вид
la = 0,997 • ls(F) + 0,013 • 2s(F) + 0,002 • 2p2(F) - 0,031 • ls(H),
2a = -0,24 • ls(F) + 0,955 • 2s(F) + 0,11 • 2p2(F) + 0,16 • ls(H),
3(7 = 0,076 • ls(F) - 0,429 • 2s(F) + 0,717 • 2p2(F) + 0,52 • ls(H),
1тгж = 2pz(F), 17^. = 2py(F).
(24.20)
Ось координат Z направлена вдоль оси симметрии молекулы, про-
ходящей через ядра атомов водорода и фтора.
Как и ранее, молекулярные орбитали для краткости обозна-
чаются квантовыми числами. Гетероядерные молекулы не имеют
центра инверсии, поэтому их МО классифицируются по значениям
квантового числа |Л|, согласно табл. 22.3, и главного квантового
числа, изображаемого цифрой. Но так как гетероядерные моле-
кулы обладают аксиальной симметрией, то тг-орбитали вырождены
по взаимно перпендикулярным направлениям X и У, ортогональ-
ными оси симметрии молекулы.
Три первые МО в списке (24.20) обладают аксиальной симме-
трией (ось Z направлена вдоль оси молекулы) и являются (7-ор-
биталями, согласно определению в §22.5 (см. табл. 22.3). Осталь-
ные две МО представляют собой тг-орбитали, согласно тому же
определению.
534 Лекция 24. Вариационный метод и молекулярные термы
На рис. 24.1 изображена контурная карта распределения раз-
ностной электронной плотности молекулы фторида водорода в ос-
новном состоянии. Электронная плотность молекулы вычислена
как квадрат модуля молекулярных орбиталей (24.20), затем из нее
Рис. 24.1. Контурная карта пространственного распределения разностной элек-
тронной плотности молекулы фторида водорода в основном состоянии.
Сплошные линии — уровни избыточной электронной плотности в молекуле относительно
электронной плотности в атомах Н и F, штриховые линии — уровни дефицитной элек-
тронной плотности. Цифрами и буквами обозначены значения электронной плотности:
0 — 0; 1 — 0,001; 2 — 0,002; 3 — 0,004; 4 — 0,02; 5 — 0,04; 6 — 0,08; 7 — 0,2; А —
-0,001; В-----0,002; С----0,003; D----0,004; Е----0,02
вычтена электронная плотность изолированных атомов водорода и
фтора, расположенных на равновесном расстоянии молекулы фто-
рида водорода. На рис. 24.1 видно, что электронная плотность р(г)
при объединении атомов водорода и фтора в молекулу фторида
водорода сместилась из периферийных областей в межядерное про-
странство, это обусловливает устойчивость данной молекулы, энер-
гия диссоциации которой равна D = 5,8 эВ. Расчеты для отдель-
ных МО показывают, что связывающим орбиталям соответствует
повышение плотности р(г) в межядерном промежутке, разрыхля-
ющим — ее понижение.
Молекулярные орбитали, полученные вариационным методом
позволяют рассчитывать энергию диссоциации, равновесное рас-
стояние, электрический дипольный момент, потенциал ионизации
и другие физические характеристики молекул.
24.2. Расчет молекулярных орбиталей вариационным методом 535
Интересные результаты дает расчет молекулярных орбиталей
гетероядерной молекулы оксида углерода СО и сравнение их с МО
гомоядерной молекулой азота N2. Обе молекулы имеют по 14 элек-
тронов, поэтому называются изоэлектронными. Приближенные
квантовомеханические методы расчета показывают, что вид моле-
кулярных орбиталей и соответствующие энергии их изоэлектрон-
ных молекул обладают некоторым сходством, что подтверждается
результатами экспериментальных исследований.
Ее, Ry
За
ба
1л
2л
- -0,4
- -0,8
g
3°g
2а„
4а
- -1,2
Рис. 24.2. Сравнительная схема энергетических уровней МО молекул N2 и СО
На вертикальной оси отложены энергии МО в единицах энергии Ридберга Ry. Штриховыми
линиями соединены энергетические уровни орбиталей одинаковой симметрии и с близкой
энергией. Все тг-орбитали дважды вырождены, так как 7г(ж) и 7г(у) имеют одинаковые
энергии при фиксированных четности и главном квантовом числе. Уровни энергии АО 1s
не показаны, как не участвующие в образовании МО
Орбитали как гомоядерной молекулы N2, так и гетероядерной
молекулы СО характеризуются квантовым числом А, определяю-
щим проекцию орбитального момента импульса электрона на ось
симметрии молекулы, и обозначаются символами в соответствии
с табл. 22.3.
536 Лекция 24. Вариационный метод и молекулярные термы
Электроны ls-оболочек всех атомов образуют МО вида А.сгд и
lau, которые практически не участвуют в образовании химиче-
ской связи (см. рис. 23.3 и 23.4). На рис. 24.2 показано, что МО
молекул N2 и СО с одинаковой симметрией (т. е. сг- и тг-орбитали
соответственно) обладают близкой энергией.
Различие МО рассматриваемых изоэлектронных молекул за-
ключается в том, что у гомоядерной молекулы N2 орбитали обла-
дают определенной симметрией относительно инверсии в центре
масс молекулы (см. §22.5 лекции 22). В зависимости от четности
МО указывается нижним индексом д или и.
Молекулярные орбитали гетероядерной молекулы СО одинако-
вой симметрии нумеруются главным квантовым числом в порядке
возрастания энергии соответствующего стационарного состояния
(см. рис. 24.2).
В основном состоянии молекулы оксида углерода заполнены
молекулярные орбитали до 5сг включительно, так как на выро-
жденных орбиталях 1тг(ж) и 1тг(у) размещаются по 2 электрона.
По рис. 24.2 видно, что все заполненные орбитали имеют отрица-
тельную энергию, что соответствует понижению энергии молекулы
относительно энергии изолированных атомов, образующих дан-
ную молекулу. В результате, как и в основном состоянии молекулы
N2, количество заполненных связывающих МО больше заполнен-
ных разрыхляющих на три. Отсюда следует вывод, что кратность
химической связи (23.22) молекулы оксида углерода равна трем,
что обусловливает высокую прочность этой молекулы (энергия дис-
социации D = 11,09 эВ).
Электронная плотность в гетероядерной молекуле СО не инва-
риантна относительно отражения в плоскости, перпендикулярной
молекулярной оси. Как следствие, молекула СО обладает элек-
трическим дипольным моментом de, который удалось рассчитать,
значительно расширив минимальный базис АО. Интересно, что
направление вектора de соответствует смещению электронной
плотности от атома кислорода к атому углерода, хотя оценка по
значениям электроотрицательности (см. табл. 22.2) дает противо-
положный результат. Это свидетельствует еще раз о справедливо-
сти квантовых методов молекулярной физики, базирующихся на
решении уравнения Шредингера.
24.3. Молекулярные термы двухатомной молекулы
Охарактеризуем стационарное состояние отдельного электрона
в двухатомной молекуле, которое описывается определенной спин-
орбиталью. Такое состояние должно, вообще говоря, задаваться
четырьмя независимыми квантовыми числами.
В §22.5 уже было введено квантовое число А, определяющее,
согласно (22.25), проекцию орбитального момента импульса элек-
трона на ось симметрии молекулы.
24.3. Молекулярные термы двухатомной молекулы
537
Вторым выбирается квантовое число ms, характеризующее
проекцию спина электрона на ось симметрии молекулы:
Sz = hms, (24.21)
и принимающее только два различных значения: ms = 1/2 или
ms = -1/2.
В качестве двух остальных обычно берутся квантовые числа п
и Z, которые соответствуют главному и орбитальному числам со-
стояния электрона в атоме при неограниченном увеличении меж-
ядерного расстояния R -> оо или при неограниченном сближении
атомов молекулы R -> 0. Как продемонстрировано в предыдущих
лекциях (см. рис. 22.5, 22.6), при Л —> 0 или Л —> сю молекуляр-
ные волновые функции непрерывно переходят в атомные.
В отсутствии внешних полей энергия электрона не зависит от
квантового числа ms, поэтому стационарные состояния электро-
нов в молекулах обычно характеризуют тремя квантовыми чи-
слами n, Z, А. Эти три числа однозначно определяют МО, на
которой могут размещаться 2 электрона с квантовыми числами
ms = ±1/2. Различные значения орбитального квантового числа
I обозначаются символами, согласно табл. 14.1. В такой символике
МО, в том числе рассмотренные в предыдущих лекциях, обозна-
чаются как lscr, 2ртг и т. д.
Кроме того, МО гомоядерных двухатомных молекул обладают
дополнительной симметрией относительно инверсии в центре масс
молекулы, как это было показано на примере молекулы в § 22.5
лекции 22. Если волновая функция (орбиталь) симметрична от-
носительно инверсии, то она называется четной и обозначается
дополнительным индексом </, например Если волновая функ-
ция антисимметрична, т.е. меняет при инверсии только знак, то
она называется нечетной и обозначается индексом и, в частности
2p7ru. Характерно, что четным состояниям соответствуют четные
значения орбитального числа I (включая 0), а нечетным состоя-
ниям — нечетные орбитальные числа. Следует помнить, что МО
строятся, как правило, в виде линейных комбинаций водородо-
подобных или слэтеровских функций. Таким образом, МО явля-
ются действительными функциями, вообще говоря, знакоперемен-
ными.
Следует заметить, что данная классификация стационарных
состояний электронов является строгой только для двухатомных
молекул. В более сложных системах уже нельзя, вообще говоря,
полагать, что отдельный электрон движется в аксиально-симмет-
ричном поле ядер и остальных электронов. При этом проекция
орбитального момента импульса (22.25) не сохраняется и кванто-
вое число А не имеет определенного значения. Для трехатомных и
более сложных молекул используются другие классификации одно-
электронных состояний, с которой можно ознакомиться в учебни-
538 Лекция 24. Вариационный метод и молекулярные термы
ках по теории строения молекул и квантовой химии. Здесь упо-
мянем, что система обозначений определяется в первую очередь
пространственной симметрией волновых функций.
Для анализа оптических, магнитных и других физических
свойств молекул необходимо разработать классификацию стаци-
онарных состояний всей электронной подсистемы в целом. Эта
классификация тесно связана с симметрией молекулы.
Пространственное распределение электронной плотности двух-
атомных молекул инвариантно относительно поворота на любой
угол вокруг оси, проходящей через центры ядер (так называемой
главной молекулярной оси). Относительно маленькие атомные
ядра можно полагать сферическими. Это означает, что двухатом-
ные молекулы описываются предельной точечной группой CooV-
Очевидно, что гомоядерные двухатомные молекулы имеют более
высокую симметрию группы Pqo/i, так они дополнительно инва-
риантны относительно отражения в плоскости, проходящей через
геометрический центр молекулы и перпендикулярной молекуляр-
ной оси. С геометрическим центром гомоядерной двухатомной мо-
лекулы совпадает центр масс и центр инверсии.
Вышесказанное не противоречит тому, что отдельные молеку-
лярные орбитали имеют гораздо более низкую симметрию. Напри-
мер, в данной и предыдущей лекциях использовались орбитали
1тг(ж) и 1тг(у), характеризуемые черно-белой группой т'т2'. Эта
группа задана тремя генераторами, где операция тп — отражение в
плоскости, mf — отражение в перпендикулярной плоскости с изме-
нением знака функции, 2' — поворот на 180° вокруг оси, проходя-
щей через линию пересечения плоскостей, со сменой знака. Ква-
драт модуля таких волновых функций имеет симметрию (?2У, т. е.
соответствующая электронная плотность имеет максимумы в двух
взаимно ортогональных направлениях X и У, перпендикулярных
главной молекулярной оси. Но для изолированной молекулы оси
X и У не имеют физически определенных направлений, и в ре-
зультате статистического усреднения пространственное распреде-
ление электронной плотности двухатомной молекулы приобретает
симметрию предельной группы С^у.
Аксиальная симметрия влечет сохранение проекции суммар-
ного орбитального момента импульса Lqz на ось молекулы.
В стационарных состояниях эта величина квантуется и принимает
значения
LqZ = ±ЙЛ, (24.22)
где Л — соответствующее квантовое число, принимающее значе-
ние 0, 1, 2, ...
Состояния двухатомных молекул с различными значения-
ми Л обозначаются большими греческими буквами, согласно
табл. 24.1.
24.3. Молекулярные термы двухатомной молекулы
539
Таблица 24.1. Обозначения стационарных состояний двухатомных молекул
с различными значениями проекции суммарного орбитального
момента импульса Lqz на ось молекулы
Проекция суммарного орбитального момента импульса на ось молекулы Значения квантового числа А Обозначение состояния молекулы
0 0 S
1 П
±2П 2 А
Симметрия группы CqoV включает инвариантность относи-
тельно отражения в плоскостях симметрии, проходящих через
центры ядер молекулы. При отражении знак проекции Lqz ме-
няется на противоположный, так как момент импульса является
не полярным, а аксиальным вектором. В квантовой механике это
доказывается на основе вида оператора проекции суммарного ор-
битального момента импульса Lqz. Прояснить смену знака проек-
ции Lqz возможно по следующей классической модели. Ненулевая
проекции Lqz обусловлена вращением электрона вокруг оси сим-
метрии молекулы, проходящей через центры атомных ядер. Знак
проекции Lqz определяется направлением вращения (по правому
винту или наоборот). При отражении в плоскости симметрии,
параллельной оси вращения, направление вращения изменяется
на противоположное, что эквивалентно изменению знака проек-
ции LqZ.
Волновые функции стационарных состояний Ф, построенные
как линейные комбинации спин-орбиталей, могут быть как сим-
метричными, так и антисимметричными относительно отражения
в таких V-плоскостях. Однако пространственное распределение
квадрата модуля |Ф|2 идентично для состояний с проекциями Lqz
противоположных знаков. Как следствие, состояния с квантовыми
числами ±Л двукратно вырождены, т.е. обладают одинаковой
энергией.
Стационарные состояния молекул характеризуются определен-
ной величиной суммарного спина всех электронов молекулы. Ква-
драт модуля суммарного спина Sq квантуется как в многоэлектрон-
ном атоме по правилу
Sq = /i25o(so + 1). (24.23)
Квантовое число sq определяется количеством электронов мо-
лекулы и порядком заполнения ими орбиталей. Оно может при-
нимать как полуцелые, так и целые значения, включая ноль. При
анализе спектроскопических данных выяснилось, что значение
квантового числа sq существенно влияет на структуру оптических
540 Лекция 24. Вариационный метод и молекулярные термы
спектров молекулы, поэтому величина 2sq + 1, как и для отдельных
атомов, в спектроскопии называется мультиплетно стью.
При исследовании многоэлектронных атомов выяснилось, что
их оптические, магнитные и другие физические свойства суще-
ственно зависят от величин их суммарного орбитального момента
импульса Lq и суммарного спина Sq (см. лекцию 16). Совокуп-
ность определенных значений Lq и Sq были названы атомными
термами. Аналогично для молекул целесообразно ввести понятие
молекулярного терма, которое включает в себя прежде всего аб-
солютную величину проекции суммарного орбитального момента
импульса L$z на ось симметрии молекулы и суммарный спин мо-
лекулы.
Для обозначения молекулярных термов используются кванто-
вые числа А и so, которые определяют величины |Lqz| и So, со-
гласно формулам (24.22) и (24.23) соответственно. Основной сим-
вол молекулярного терма, который задает величину |Lqz|, выби-
рается из табл. 24.1. У символа ставится верхний левый индекс,
равный мультиплетности 2sq + 1. Например, терм с квантовыми
числами А = 0 и sq = 0 обозначается символом 1S, при А = 1 и
so = 1 символ терма 3П и т. д.
Для состояний с А = 0 распределение электронной плотно-
сти не меняется при отражении в У-плоскости, проходящей через
ось симметрии молекулы, и волновая функция при этом может
лишь сменить знак. Следовательно, существуют стационарные
состояния молекулы симметричные и антисимметричные относи-
тельно отражения в V-плоскости. Такие состояния обозначаются
верхним правым индексом «+» или «—» у символа молекулярного
терма. Например, существуют термы XS+, 3S“ и т.п.
У гомоядерных молекул имеется дополнительный вид симме-
трии относительно центра инверсии. Следовательно, существуют
состояния с волновыми функциями четными или нечетными
относительно инверсии. Соответствующие термы помечаются сим-
волами g и и, которые записываются справа внизу основного сим-
вола. В качестве примеров обозначения можно привести следую-
щие молекулярные термы: 13^’, 3S+, 3S“, 3Пи, 3Щ и т.д.
Стационарные состояния молекулы с одинаковыми проекци-
ями суммарного орбитального момента импульса Lqz, суммарного
спина So и одинаковой пространственной симметрией могут разли-
чаться энергией. Чтобы различать такие состояния, перед симво-
лом терма основного состояния ставится буква X, возбужденные
состояния нумеруются латинским буквами из начала алфавита.
При этом обычно состояния с мультиплетностью, совпадающей
с мультиплетностью основного состояния, обозначаются заглав-
ными буквами А, В, С, ..., состояния с другой мультиплетно-
стью — строчными а, Ь, с, ...
24.3. Молекулярные термы двухатомной молекулы
541
Для примера запишем термы нескольких стационарных со-
стояний молекулы водорода Н2. Согласно табл. 23.1, электрон-
ная конфигурация основного состояния имеет вид (1сгр)2. Ясно,
что проекция орбитального момента на ось симметрии молекулы
в этом состоянии равна нулю, следовательно, данное состояние
характеризуется термом S. Проекции спинов обоих электронов в
соответствии с принципом Паули должны иметь различные знаки,
следовательно, суммарный спин Sq молекулы водорода равен нулю.
В § 22.5 лекции 22 было указано, что состояние 1ст^ является чет-
ным относительно инверсии в центре молекулы (см. рис. 22.5 и
23.1). Таким образом, терм основного состояния молекулы водо-
рода запишется как 1S^.
Термы нескольких возбужденных стационарных состояний мо-
лекулы водорода приведены в табл. 24.2. Видно, что одинаковым
электронным конфигурациям МО могут соответствовать различ-
ные термы. Энергия терма зависит от величины проекции сум-
марного орбитального момента импульса и от значения суммар-
ного спина.
Таблица 24.2. Молекулярные термы молекулы водорода Н2
Молекулярный терм Электронная конфигурация МО Энергия возбуждения (эВ) Равновесное расстояние между ядрами атомов (А)
ал1е+ (Isa)2 0 0,741
в^+ (1$сг)(2рбт) 11,18 1,292
с3Пи (1$сг)(2ртг) 11,75 1,038
a3S+ (1$сг)(2$сг) 11,79 0,989
С'Пи (1$сг)(2ртг) 12,28 1,031
Е1^ (lscr)(2scr) 12,29 1,012
е3Е+ (1$сг)(3рсг) 13,23 1,107
d3nu (1$сг) (Зрл) 13,85 1,05
Обращает на себя внимание, что энергии возбуждения термов,
указанные в табл. 24.2 значительно превышают энергию диссо-
циации молекулы. Эта особенность осложняет экспериментальное
исследование возбужденных состояний молекул.
Система термов гетероядерной молекулы показана в табл. 24.3
на примере оксида углерода СО.
Во втором столбце табл. 24.3 записаны электронные конфигу-
рации высокоэнергетических молекулярных орбиталей молекулы
оксида углерода. Орбитали с меньшей энергией описываются кон-
фигурацией 1сг22сг23сг24сг2.
542 Лекция 24. Вариационный метод и молекулярные термы
Таблица 24.3. Молекулярные термы молекулы оксида углерода СО
Молекулярный терм Электронная конфигурация МО Энергия возбуждения Е* (эВ) Равновесное расстояние между ядрами атомов (А)
x‘s+ 17г4 бег2 0 1,128
а3П 17Г45сГ127Г1 6,01 1,206
</3Д 17Г35сГ227Г1 7,52 1,37
е3£“ 17Г35сГ227Г1 7,90 1,383
17Г35о-227Г1 8,00 1,391
л‘п 17Г45сГ127Г1 8,03 1,236
Таблицы 24.2 и 24.3 демонстрируют, что наименьшее равно-
весное межядерное расстояние Rq молекула имеет в основном со-
стоянии. Однако зависимость равновесного расстояния от энергии
возбуждения молекулы, вообще говоря, не является монотонно воз-
растающей.
Данные табл. 24.2 и 24.3 показывают, что энергии возбужден-
ных конфигураций молекул имеют тот же порядок, что и у ато-
мов — величину несколько меньше энергии Ридберга Ry.
Экспериментально обнаружено, что у большинства двухатом-
ных молекул терм основного состояния 1S+, а у гомоядерных —
В таких высоко симметричных состояниях спин молекулы
равен нулю. Интересным исключением является молекула О2.
терм основного состояния которой Наличие спина в основ-
ном состоянии обусловливает сильный парамагнетизм молекулы
О2, который обсуждался в предыдущей лекции. Другим исключе-
нием является гетероядерная молекула окиси азота NO с термом
основного состояния 2П.
В лекциях 16 и 17 было показано, что для описания многоэлек-
тронных атомов (в частности, для объяснения тонкой структуры
оптических спектров) в характеристики атомных термов необхо-
димо включить величину полного момента импульса электронной
оболочки атома. Аналогично, при изучении молекул выясняется,
что при учете спин-орбитального взаимодействия энергия стаци-
онарного состояния двухатомной молекулы зависит не только от
квантовых чисел А и so, ноиот проекции суммарного спина Sqz
электронной подсистемы молекулы на главную ось симметрии мо-
лекулы, проходящей через центры атомов. Эта проекция кванту-
ется по правилу
(24.24)
Sqz =
24.3. Молекулярные термы двухатомной молекулы
543
где квантовое число проекции суммарного спина S пробегает
2sq + 1 значений:
S = So, So - 1, -SO. (24.25)
Иначе говоря, спин-орбитальное взаимодействие снимает выро-
ждение по проекции суммарного спина электронной подсистемы
молекулы.
Для описания физических характеристик молекул весьма важ-
на проекция полного момента импульса электронной подсистемы
двухатомной молекулы на главную ось симметрии, равная /iQ.
Квантовое число проекции полного момента импульса Q получа-
ется суммированием чисел А и S:
Q = А 4- S. (24.26)
При фиксированном значении числа А величина Q может при-
нимать 2sq + 1 разных значений. Таким образом, терм с опреде-
ленным числом А расщепляется на несколько компонент, количе-
ство которых равно мультиплетности.
В обозначении молекулярного терма квантовое число Q ста-
вится нижним правым индексом. Например, 2П1/2, 2П3/2, 2Д5/2
и т. д.
В качестве примера рассмотрим терм 2П, который описывает
состояние с квантовыми числами А = 1 и sq = 1/2. При учете
спин-орбитального взаимодействия терм 2П с мультиплетностью
2sq + 1 = 2 расщепляется на два: 2П1/2 и 2П3/2, которые разли-
чаются взаимной ориентацией суммарного орбитального момента
импульса и суммарного спина всех электронов молекулы. У моле-
кулярных термов, различающихся только значением квантового
числа Q, разность энергий составляет обычно сотые доли электрон-
вольта и менее.
Задачи к лекции 24
1. Записать термы основных состояний двухатомных гомоядерных
молекул первого периода таблицы Менделеева, приведенных в табл. 23.1
лекции 23.
2. Записать термы основных состояний двухатомных гомоядерных
молекул второго периода таблицы Менделеева, приведенных в табл. 23.2
лекции 23.
3. Рассчитать коэффициент корреляции между равновесным рассто-
янием и энергией возбуждения возбужденных состояний следующих мо-
лекул: а) молекулы водорода Н2; б) молекулы окиси углерода СО. Необ-
ходимые данные взять из табл. 24.2 и 24.3.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 24
24.1. Метод валентных связей
Первый квантовомеханический расчет химической связи молекулы
водорода Н2 был выполнен в 1927 г. В.Гайтлером и Ф. Лондоном. Ис-
пользуемый ими подход впоследствии стал основой метода валентных
связей (метод ВС). В настоящее время в квантовой химии большее рас-
пространение получил метод МО ЛКАО, но для некоторых разновидно-
стей химической связи метод ВС обладает определенными преимуще-
ствами.
Идея метода ВС состоит в том, что при образовании молекулы из
атомов последние в значительной степени сохраняют свою электрон-
ную конфигурацию. Химическая связь осуществляется объединением
валентных электронов атомов. Из-за тождественности электронов их
специфически квантовый характер взаимодействия обусловливает пони-
жение энергии системы частиц, составляющих молекулу, что эквива-
лентно возникновению сил притяжения между атомами. В методе ВС
волновая функция молекулы строится на базисе волновых функций от-
дельных атомов, причем вблизи атомных ядер волновая функция моле-
кулы должна быть очень близка к волновым функциям соответствующих
Рис. Д.24.1. Геометрическая схема молекулы водорода Нг. Точками обозначены
положения частиц: а и b — протоны, 1 и 2 — электроны
изолированных атомов. Напомним для сравнения, что в методе МО вол-
новая функция молекулы строится из молекулярных двухэлектронных
орбиталей, которые являются многоцентрованными, т.е. делокализо-
ванными по двум или более атомам.
Рассмотрим применение метода ВС к расчету молекулы водорода Н2.
Эта система состоит из четырех частиц: двух протонов и двух электро-
нов. Геометрическая схема молекулы представлена на рис. Д.24.1. Как
Дополнения к лекции 24
545
принято в квантовой химии, точки местонахождения электронов обозна-
чены цифрами 1 и 2.
Запишем адиабатический гамильтониан (22.18) для молекулы водо-
рода:
Я = Яа + Я6 + На6, (Д.24.1)
где отдельные слагаемые имеют следующий вид:
яа = -—Д1-—, Я6 = -—Д2-—, (Д.24.2)
2те Rai 2те Rb2
e% e? e2 e%
Hab = — + — - — . (Д.24.3)
П2 rtab ^a2 Щ1
Операторы Ai и Д2 — лапласианы по координатам первого и второго
электронов соответственно. Обозначения расстояний между частицами
приведены на рис. Д.24.1.
Гамильтонианы (Д.24.2) характеризуют изолированные атомы водо-
рода. Гамильтониан (Д.24.3) содержит кулоновские энергии взаимодей-
ствия двух электронов, двух протонов и каждого протона с электроном
другого атома. Заметим, что, согласно адиабатическому приближению,
в гамильтониане (Д.24.3) отсутствуют операторы кинетической энергии
протонов.
В соответствии с идеей метода ВС волновая функция молекулы водо-
рода составляется из волновых функций атомов водорода.
Если первый атом содержит протон а и электрон 1, а второй — про-
тон b и электрон 2, волновая функция двух невзаимодействующих атомов
водорода может быть представлена в виде
Ф1 = <Ра(У1)(рЬ(г2),
(Д.24.4)
где </’а(г1) — волновая функция электрона первого атома водорода,
у?(,(г2) — волновая функция электрона второго атома, и и г2 — ко-
ординаты электронов 1 и 2 соответственно в системе центра масс моле-
кулы. Если рассматривается основное состояние молекулы водорода, то
обе функции <А1(Г1) и <^(г2) являются атомными орбиталями (23.5).
Из-за тождественности электронов волновую функцию системы не-
взаимодействующих атомов водорода можно записать в следующем экви-
валентном виде:
$2 = ^a(r2)^(ri).
(Д.24.5)
Волновые функции (Д.24.4) и (Д.24.5) описывают состояния, различаю-
щиеся перестановкой координат электронов 1 и 2.
В методе ВС волновая функция основного состояния молекулы водо-
рода строится в виде линейной комбинации волновых функций электро-
нов невзаимодействующих атомов:
Ф = С1Ф1 + с2Ф2 = сцра (Г1 )¥>(,(г2) + c2¥>a(r2)</?(,(ri). (д.24.6)
Для вычисления коэффициентов ci и с2 удобно использовать вариа-
ционный метод Ритца. Запишем функционал энергии (24.1) для гамиль-
тониана (Д.24.1) и функции (Д.24.6) в виде
Е =
ff Ф*НФ dVi dV2
ГГФ*ФЩ/1Щ/2 ’
(Д.24.7)
546
Дополнения к лекции 24
где dVi = dxi dyi dzi и dV2 = dx% dy2 dz% — объемы атомов, по которым
проводится интегрирование.
Подставив функцию (Д.24.6) в выражение (Д.24.7), перепишем его в
виде
С1 Ц <Pa(r1)i/>b(r2)H<pa(r1')<pb(r2)dV1dV2 +
+С1С2 II <Pa(r1)ipb(r2')H(pa(r2')<Pb(.ri')dVidV2 +
+С1С2 II <ра(г2)<Рь(Г1)Н(ра(Г1)<ръ(г2) dVl dV2 +
+С2 II <Pa(r2')<Pb(r1)H<pa(r2)<pb(r1)dV1dV2 =
= #<< II ^o(ri)^(r2) dVr dV2 +
+2£?C1C2 II <pa(r1)<pb(r2)<pa(r2)<pb(r1) dVj. dV2 +
+Ecl II <p2M<pl(r1)dV1dV2. (Д.24.8)
В выражении (Д.24.8) было использовано, что атомные орбитали основ-
ного состояния атома водорода (23.5) являются действительными функ-
циями.
Для сокращения записей введем обозначения:
Яц = II <Pa(ri)<Pb(r2)H<Pa(r1)<Pb(r2)dV1dV2, (Д.24.9)
#12 = II <Pa(ri)<Pb(.r2')H<Pa(r2)<Pb(r1)dVidV2, (Д.24.10)
#21= II <Pa(.r2)>Pb(r1)H^a(r1>)(pb(r2>)dV1dV2, (Д.24.11)
#22 = II iPa^ipb^Hipa^ipbin) dVX dV2, (Д.24.12)
Sil- II ip2(ri)ip2b(r2)dVidV2, S22 = II (р2а(г2)(р2(г1) dVi dV2,
(Д.24.13)
512 = II lPa(ri)<Pb(.r2)<Pa(.r2)<Pb(.ri)dV1dV2. (Д.24.14)
Тогда уравнение (Д.24.8) можно переписать в кратком виде:
Нц + С1С2-Н12 + С1С2-Н21 + ^2^22 — ^(ciSu + 2C1C2S12 + C2S22) — 0.
(Д.24.15)
Дополнения к лекции 24 547
Поскольку оба электрона и оба протона в молекуле водорода взаимна
неразличимы (тождественны), то выполняются следующие соотноше-
Ац = А22, Н12 = Н21. (Д.24.16)
Согласно вариационному методу, проводится вычисление частных
производных от левой части уравнения (Д.24.15) по параметрам а и С2-
Используя необходимые условия минимума функционала (Д.24.7), т.е.
равенство нулю частных производных дЕ/дс\ = дЕ/дсъ = 0, получаем
однородную систему уравнений относительно искомых коэффициентов
ci и С2:
Cl (fl’ll - ESU) + C2(fli2 - ESi2) = 0,
C1(fl12 - ES12) + с2(Ац - ES22) = 0.
Так как атомные орбитали ipa и сръ нормированы на единицу:
I ^(п) dVi = 1, I<pl(r2) dV2 = 1, (Д.24.18)
то интегралы
5ц = S22 = 1. (Д.24.19)
Величина (Д.24.14) выражается квадратом
S12 = S2ab (Д.24.20)
интеграла перекрывания функций <ра и ерь-
Sab = У <ра(Г1)(рЬ(Г1) dVi = J pa(r2)ipb(r2) dV2. (Д.24.21)
Приравнивая к нулю детерминант системы (Д.24.17), получим се-
кулярное уравнение (24.10) для энергии стационарных состояний моле-
кулы водорода:
flu -Е H12-ES2b
fl12 - ES2b flu - Е
ИЛИ Нп - Е = ±(fl12 - ES2ab), (Д.24.22)
решения которого имеют вид
Es = Нц + Н12 1+526 ’ (Д.24.23)
Ед = Ап - А12 1-5о2& ’ (Д.24.24)
548
Дополнения к лекции 24
Вычисления матричных элементов Нц, Н12 и интеграла перекрыва-
ния Sab показывают, что Es < Ед. Это означает, что величина (Д.24.23)
представляет собой энергию основного состояния молекулы водорода, а
величина (Д.24.24) — энергию первого возбужденного состояния.
Подставив значение энергии (Д.24.23) в однородную систему
(Д.24.17), мы получим, что отношение коэффициентов
— = 1. (Д.24.25)
С2
Для вычисления числовых значений коэффициентов ci и С2 исполь-
зуем нормировку волновой функции (Д.24.6) на единицу, т. е.
УФ*Ф dVi dV2 = 1. (Д.24.26)
Подстановка линейной комбинации (Д.24.6) в нормировочный ин-
теграл (Д.24.26) и использование соотношений (Д.24.18), (Д.24.21) и
(Д.24.25) позволит получить уравнение
c?(2 + 2S^) = l,
откуда следует
(Д'24-27>
Теперь можно записать волновую функцию основного состояния мо-
лекулы водорода в явном виде:
= /<> [^(Г1)уь(г2) + <ра(г2)у>ь(г1)]. (Д.24.28)
V2 + гЬаЬ
Далее следует повторить аналогичные математические операции для
значения энергии (Д.24.24). Для этого случая получается ci = —С2 и
а = (Л24'29>
Следовательно, волновая функция данного состояния молекулы водорода
имеет вид
Фл = /О 1оо2 [Уа(г1)<рь(г2) - Va(r2)^(ri)]. (Д.24.30)
V 2 ”
Выражения (Д.24.28) и (Д.24.30) свидетельствуют, что функция Ф$
симметрична, а функция Фд антисимметрична относительно переста-
новки координат электронов.
Дополнения к лекции 24
549
Вернемся к энергиям состояний, которые описываются волновыми
функциями Ф$ и Фд. Для этого сначала преобразуем выражение для
матричного элемента Нц:
Нц = // <Pa(r1)<pb(r2)[Ha + НЬ + Habjtpa^r^tpbiri) dVi dV2 =
= // ^ri^b^r2^ab^ri^b^dVldV2 +
+ У <Pa(r1)Ha(pa(ri)dV1 У </>ь(г2) dv2+
+ У <Pb(r2)Hb<Pb(r2)dV2 J<pl(n)dVi
Орбитали ipa и <pb являются собственными функциями атома водо-
рода, т.е. удовлетворяют уравнениям Шредингера
Д^а(гх) = ЯН<А1(Г1), Нь<рь^2) = £нЫг2), (Д.24.31)
где — энергия атома водорода в основном состоянии, равная —Ry.
Тогда матричный элемент Нц можно выразить так:
Нц =Q + 2EH, (Д.24.32)
где величина
<2 = УУ <Pa(ri)<pb(r2)Hab<pa(ri)(pb(.r2)dV1dV2 (Д.24.33)
называется кулоновским интегралом.
Проведем аналогичное преобразование матричного элемента Нц-
Я12 = УУ 'Ра(г1')<рь(г2)[На +Нь + Наь]<Ра(г2)<рь{гх) dVi dV2 =
= УУ 4>a{Tl)<Pb{r2)Hafpa(r2)ipb{ri) dVi dV2 +
+ УУ <Pa (г 1) Vb (r2 ) Hb <pa (r2) '-fib (r 1) dVx dV2 +
+ УУ ^a{rl)<Pb{r2)Hab<pa(r2)ipb{ri')dVidV2 =
= У <Pb(r2)<Pa(r2)dV2 У Pa(r1)Ha<Pb(ri)dV1 +
+ У <Ра(п)<Р(>(Г1)Л1 У <Pb(r2)Hb<Pa(r2) dV2 +
+ I[ Vair^ipb^Habtpa^tpbiri) dVi dV2 = A + ЪЗ^Ен, (д.24.34)
550
Дополнения к лекции 24
где введено обозначение обменного интеграла:
А = // (Д.24.35)
Подставим выражения матричных элементов (Д.24.32) и (Д.24.34) в
(Д.24.23) и (Д.24.24) получим энергии симметричного (Д.24.28) и анти-
симметричного (Д.24.30) состояний молекулы водорода:
ES = 2£?н + (Д.24.36)
1 + bab
Еа = 2£?н + Т—^Г- (Д-24.37)
1 "" bab
Расчет зависимости энергий (Д.24.36) от межядерного расстояния
Rab дает кривую с характерным минимумом при значении Rab = 0,86 А
(см. рис. Д.24.2). Это означает, что в состоянии с симметричной волно-
вой функцией молекула водорода устойчива. Положение минимума
Рис. Д.24.2. Зависимости энергий стационарных состояний молекулы водорода
от межядерного расстояния R. Штриховая линия построена на базе результатов
экспериментов
функции Es(Rab) приближенно равно равновесному межядерному рас-
стоянию молекулы водорода Rq = 0,74 А. Энергия связи молекулы в
этом стационарном состоянии определяется глубиной минимума, т.е. аб-
солютной величиной энергии \Es(Rab = 0,86 А)| = 3,14эВ. Эта величина
заметно меньше энергии диссоциации молекулы водорода D = 4,74 эВ,
что является недостатком метода ВС.
Зависимость Ед(Д1аь) является монотонно убывающей (рис. Д.24.2).
Это означает, что состояние с антисимметричной волновой функцией Фд
молекулы водорода является неустойчивым. В этом состоянии атомы
водорода отталкиваются друг от друга и молекула разрушается.
Дополнения к лекции 24
551
Теперь построим полные волновые функции двух вышерассмотрен-
ных стационарных состояний молекулы водорода. Для этого координат-
ные волновые функции и Фд необходимо домножить на спиновые
части. Так как электроны являются фермионами, то их полные вол-
новые функции должны быть антисимметричными относительно пере-
становки пространственных и спиновых координат. Следовательно, ко-
ординатную часть Ф$ надо домножить на антисимметричную спиновую
функцию, а функцию Фд — на симметричную спиновую часть.
Используем обозначения дополнения 12.3. Спиновая функция
описывает состояние с положительной проекцией спина на выделенное
направление в пространстве (на главную ось симметрии молекулы, про-
ходящей через протоны), функция х- — состояние с отрицательной про-
екцией спина.
Для системы из двух электронов нормированную на единицу анти-
симметричную спиновую функцию можно построить единственным об-
разом:
ХА = ^k-(l)X-(2) - X-(2)х-(1)], (Д.24.38)
где цифры в круглых скобках нумеруют электроны молекулы.
Следовательно, полная волновая функция основного состояния запи-
шется в виде
X [^а(г1)^(г2) + ¥>а(г2)¥>»(г1)][х+(1)х-(2) -х+(2)х_(1)]. (Д.24.39)
В этом состоянии спины электронов имеют проекции разных знаков,
и суммарный спин электронной подсистемы молекулы водорода равен
нулю. Такое состояние называется синглетным.
Симметричная спиновая функция двухэлектронной системы может
быть построена тремя разными способами:
( Х+(1)х+(2),
Xs = <
-^[Х+(1)х-(2) + х+(2)х-(1)],
(Д.24.40)
1х-(1)Х-(2).
Следовательно, состоянию молекулы водорода с координатной волно-
вой функцией Фд соответствуют три разные полные волновые функции
следующего вида:
ФлХз =
1
х/2^2^;
[^а(Г1)^г,(г2) - <ро(г2)у>(>(Г1)] X
fX+(l)x+(2),
-Ьх+(1)х_(2) + х+(2)х-(1)],
V
1х_(1)Х_(2).
(Д.24.41)
552
Дополнения к лекции 24
Такую совокупность трех состояний называют триплетом. Во всех
этих состояниях электронной подсистемы молекула водорода имеет спин
с квантовым числом, равным единице. Состояния различаются проек-
циями спина Sz на молекулярную ось, которые принимают значения /г,
О, — h. Энергии трех состояний триплета (Д.24.41) при пренебрежении
спин-орбитальным взаимодействием равны между собой.
Лекция 25
МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
25.1. Составные части энергии молекулы
Атомные оптические и характеристические рентгеновские
спектры образуются при радиационных переходах между стацио-
нарными состояниями электронной системы атома, что обусловли-
вает линейчатый характер спектров. Спектры излучения и погло-
щения молекулярных газов в видимой области состоят из более
или менее широких полос, поэтому получили название полоса-
тых спектров. Спектрометры с высокой разрешающей способ-
ностью позволили обнаружить, что полосы состоят из огромного
количества очень близких спектральных линий. Некоторые по-
лосы имеют явно выраженный край с одной стороны \кант по-
лосы), причем на другой стороне интенсивность полосы посте-
пенно снижается до нуля. Причиной сложности молекулярных
спектров является то, что в энергию стационарных состояний мо-
лекулы вносит значительный вклад не только энергия электрон-
ной подсистемы, но и энергия движущихся ядер.
Молекула может двигаться поступательно и вращаться относи-
тельно своего центра масс. Кроме того, атомы молекулы при лю-
бой температуре совершают колебания. Поступательное движение
молекулы как целого не рассматривается, так как кинетическая
энергия не квантуется и не влияет на характер полосатых спек-
тров. Движение излучающей молекулы относительно наблюда-
теля приводит к эффекту Доплера, вследствие которого происходит
смещение всего спектра по оси частот. Это явление используется
в астрофизике для определения скоростей космических объектов.
В данной лекции влияние поступательного движения молекулы на
спектр ее излучения не рассматривается.
Будем полагать, что в нашей системе координат центр масс мо-
лекулы неподвижен. В рамках адиабатического приближения (см.
§22.4 лекции 22) движение ядер описывается уравнением (22.21).
Согласно этому уравнению, ядра движутся в эффективном потен-
циальном поле, определенном функцией Е(гп), которая, в свою
554
Лекция 25. Молекулярные спектры
очередь, получается решением уравнения (22.20). Решение урав-
нения для ядер (22.21) в принципе дает энергию молекулы Ем,
однако в предыдущих лекциях уже обсуждались чрезвычайные
трудности решения уравнений Шредингера для многочастичных
систем.
Важный результат теоретического анализа уравнения Шре-
дингера для молекулы можно сформулировать следующим обра-
зом. Если колебания атомов не имеют экстремально больших
амплитуд, то в первом приближении энергию молекулы можно
представить в виде суммы трех слагаемых:
EM = Ee + Ev + ER. (25.1)
Первое слагаемое представляет собой энергию электронной под-
системы, к которой добавлена энергия кулоновского отталкивания
атомных ядер молекулы, т.е. функция, 7?(гп), стоящая в пра-
вой части уравнения (22.20). У двухатомных молекул эта энергия
является функцией межядерного расстояния R. Для устойчивых
состояний двухатомных молекул функция E(R) обладает харак-
терным минимумом в точке равновесного расстояния Rq. Иначе
говоря, в этих случаях функция E(R) представляет собой потен-
циальную яму характерного вида. Глубина ямы, т.е. значение
функции E(R) в точке R = Rq, равна энергии диссоциации D с
обратным знаком. Примеры графиков потенциальных ям для ион-
ных молекул приведены на рис. 22.2 и 22.3. На рис. 22.7 и 23.2 по-
казано, что функции E(R) для связующих орбиталей ковалентной
связи имеют аналогичный вид. Следовательно, для стационарных
состояний любых двухатомных молекул функция E(R) имеет вид
потенциальной ямы, причем при 7? —> 0 энергия E(R) неограни-
ченно возрастает, а при 7? —> сю функция E(R) стремится к нулю.
Это означает, что за нулевую точку отсчета энергии принято значе-
ние энергии изолированных неподвижных атомов, составляющих
данную молекулу.
Второе слагаемое в (25.1) является энергией колебаний ато-
мов молекулы. У двухатомных молекул присутствует единствен-
ная мода, соответствующая движению атомов вдоль молекулярной
оси.
Третье слагаемое задает энергию вращения молекулы вокруг
своего центра масс. Эта величина определяется, в основном, дви-
жением ядер, так как масса электронов на несколько порядков
меньше (22.16).
25.2. Вращательные спектры
Выражение для вращательной энергии молекулы существенно
зависит от ее формы и симметрии, так как момент инерции мо-
лекулы представляет собой, вообще говоря, тензор 2-го ранга. Мо-
25.2. Вращательные спектры
555
мент импульса молекулы складывается из соответствующих орби-
тальных моментов и спинов как ядер, так и электронов. Общий
подход к решению данной нетривиальной задачи изложен в курсах
квантовой механики.
У двухатомной молекулы момент инерции Iq относительно пря-
мой, перпендикулярной оси симметрии молекулы и проходящей
через ее центр масс, выражается произведением
/0 = M0R2, (25.2)
где Mq — приведенная масса, R — расстояние между ядрами ато-
мов. Приведенная масса двухатомной молекулы выражается через
массы ядер М\ и
= мгм2
° м1 + м2'
(25.3)
Решение уравнения Шредингера (22.21) для двухатомной мо-
лекулы показало, что вращательная (или ротационная) энергия
Ер молекулы может быть представлена в виде
Er = (25.4)
где Jm — модуль полного момента импульса молекулы относи-
тельно ее центра масс. Выражение (25.4) совпадает с формулой,
полученной в классической механике для макроскопического твер-
дого тела. Однако квадрат модуля полного момента импульса мо-
лекулы квантуется по правилу, общему для всех квантовых
моментов:
J2M = h2K(K + 1), (25.5)
где К — квантовое число, принимающее значения 0, 1, 2, ...
Подставляя выражения (25.2) и (25.5) в формулу (25.4), полу-
чаем выражение для энергии вращения двухатомной молекулы:
Er = h2
K(K + Q
2M0R2 ’
(25.6)
Таким образом, вращательная энергия Ер молекулы прини-
мает дискретный ряд значений.
Стационарные состояния молекулы с определенным значением
вращательной энергии Ер будет далее называть вращательными
состояниями.
Введем постоянную вращательной энергии для молекулы:
/г2
2MqR2'
(25.7)
556 Лекция 25. Молекулярные спектры
Тогда ряд последовательных значений вращательной энергии мо-
жет быть записан в следующем виде:
Er = 0,2В, 6В, 12В, 20В, ... (25.8)
Таким образом, спектр энергии вращения молекулы не обладает
свойством эквидистантности.
Если электронная подсистема находится в основном состоя-
нии, то расстояние R равно равновесному Rq. Эксперименты
позволяют утверждать, что при небольшом увеличении враща-
тельной энергии межядерное расстояние R практически не изме-
няется. Однако с ростом квантового числа К межядерное рас-
стояние R постепенно увеличивается, а при достаточном большом
значении числа К молекула может распасться.
Переходы между состояниями с различными энергиями (25.8)
могут сопровождаться поглощением или излучением фотонов.
Экспериментальные исследования показывают, что вращательное
движение гомоядерных двухатомных молекул (т.е. молекул, со-
стоящих из одинаковых атомов) не сопровождается излучением.
Это объясняется тем, что согласно классической электродинамике,
генерирование электромагнитных волн происходит при измене-
нии электрического дипольного момента источника или его про-
екции на направление излучения. Следовательно, вращающиеся
гомоядерные двухатомные молекулы, у которых электрический
дипольный момент de равен нулю, в первом (дипольном) прибли-
жении не должны излучать.
Эксперименты демонстрируют поглощение и излучение фото-
нов вращающихся гетероядерных двухатомных молекул, которые
обладают ненулевым электрическим дипольным моментом de и
называются полярными.
Правила отбора для радиационных переходов зависят, вообще
говоря, от симметрии молекулы. Однако наиболее интенсивными
спектральными линиями являются те, которые удовлетворяют сле-
дующему правилу отбора для изменения квантового числа К:
&К = ±1. (25.9)
Легко вычислить, что разность энергий (25.6) при выполнении
условия (25.9) равняется
&Er = ER(K + 1) - ER(K) = 2В(К + 1), (25.10)
где К — квантовое число нижнего энергетического уровня, соот-
ветствующего конечному вращательному состоянию. При перехо-
дах молекулы из состояний с большей энергией ER в состояния
с меньшей происходит испускание фотона определенной энергии.
Излучаемые частоты образуют дискретный набор эквидистантных
25.2. Вращательные спектры
557
значений:
и,г = ^л = _^_(^ + 1)) к = 0,1,2,..., (25.11)
которые составляют вращательный спектр двухатомной моле-
кулы.
Определив минимальную частоту
ШОг = WR2’ (25‘12)
спектр частот (25.11) можно записать в виде
— OJQp 5 2ti?Qy», 3cl^Qj», ... (25.13)
Энергетическая схема формирования вращательного спектра двух-
атомной молекулы приведена на рис. 25.1.
Е
Sh(aQr
Рис. 25.1. Энергетическая схема формирова-
ния вращательного спектра двухатомной мо-
лекулы.
Горизонтальные отрезки — энергетические уровни
стационарных состояний, цифры справа — со-
ответствующие значения квантового числа К.
Стрелки, направленные вниз, изображают радиа-
ционные переходы, величины слева — энергии фо-
тонов вращательного спектра
4to0r
2/zco0r
fico0r
3
2
1
0
Выражение (25.12) позволяет оценить типичный диапазон вра-
щательного спектра. Так как для большинства двухатомных моле-
кул равновесное расстояние Rq ~ 1 А, а приведенная масса Mq ~
~ 10 а.е.м., то частота саог имеет порядок 1012с-1. Соответству-
ющие длины волн А принадлежат миллиметровому диапазону,
558
Лекция 25. Молекулярные спектры
иначе называемому далеким инфракрасным. При этом энергии
излучаемых фотонов имеют порядок 10-3 эВ.
В молекулярной спектроскопии в основном регистрируются
вращательные спектры поглощения. Пучок электромагнитных
волн непрерывного спектра миллиметрового диапазона пропуска-
ется через объем, заполненный исследуемыми молекулами в газо-
образной фазе. Минимумы (провалы) в зависимости интенсивно-
сти прошедшего излучения от частоты соответствуют дискретным
частотам (25.13) поглощенных фотонов.
В молекулярной спектроскопии обычно принято представлять
спектры в виде зависимости интенсивности от обратной длины
волны излучения, выраженной в обратных сантиметрах. Согласно
(2.4), 1 см-1 соответствует частоте си « 1,885с-1 и энергии фотона
Нш « 1,24 • 10-4 эВ.
Типичный пример вращательного спектра поглощения приве-
ден на рис. 25.2. Минимумы обладают значительной шириной,
опр еде л яемой погр ешно стями экспериментальной аппар ату ры.
Тем не менее, эквидистантный характер спектра частот очеви-
ден. Различие интенсивности отдельных линий объясняется, в
первую очередь, разной заселенностью энергетических вращатель-
ных уровней. При комнатной температуре тепловая энергия к&Т
значительно превышает расстояния между вращательными уров-
нями (см. (25.12) и схему на рис. 25.1). Таким образом, тепловое
движение молекул приводит к возбуждению нескольких нижних
энергетических вращательных уровней. Вероятность возбуж-
дения уровня с энергией Ег описывается распределением Больц-
мана
По ехр (-^;),
(25.14)
где по — нормировочный множитель.
При расчете заселенности вращательных уровней следует при-
нять во внимание, что они являются вырожденными. Опреде-
ленную энергию Er имеет несколько стационарных состояний с
различными проекциями полного момента импульса молекулы.
Количество различных проекций равное 2К + 1 является стати-
стическим весом энергетического уровня. Следовательно, число
молекул N с энергией Ер определяется формулой
Er \
N = 7Vo(2# + l)exp
(25.15)
где Nq — полное число молекул. С ростом квантового числа К
энергия Ер увеличивается согласно (25.6), а экспоненциальный
множитель (25.14) уменьшается. В результате зависимость коли-
25.2. Вращательные спектры
559
чества возбужденных молекул N от квантового числа К обладает
максимумом, зависящим от характерной вращательной частоты
cuor и температуры среды Т.
На рис. 25.2 приведен случай, когда наибольшую заселенность
имеет энергетический уровень с квантовым числом К = 6. С ро-
стом частоты (или обратной длины) интенсивность излучения
Рис. 25.2. Вращательный спектр поглощения молекулы НС1.
По оси ординат отложена интенсивность проходящего излучения в относительных едини-
цах. Минимумы соответствуют частотам, на которых происходит интенсивное поглоще-
ние. Цифры у минимумов — вращательные квантовые числа состояний, между которыми
происходит радиационный переход
падает, так как вероятность возбуждения более высоких энерге-
тических уровней вращательной энергии Ер экспоненциально
убывает.
Измерения расстояний между соседними минимумами Д(1/А)
во вращательных спектрах поглощения позволяют вычислить ми-
нимальную частоту съ>ог = 2тгс Д(1/А). Для примера приведем ряд
измеренных длин волн вращательного спектра излучения молеку-
лы окиси углерода СО:
А = 2,61 мм, 1,3 мм, 0,87 мм, 0,65 мм, ...
Самая большая длина волны в данной последовательности по-
зволяет вычислить по формуле (2.4) минимальную частоту ы$г =
= 0,723 • 1012с-1. По известным массам ядер Mi = 12 а.е.м. и
М2 = 16 а.е.м. легко вычислить приведенную массу молекулы
окиси углерода: Mq = 1,138 • 10-23г. Теперь соотношение (25.12)
позволяет рассчитать равновесное расстояние этой молекулы Rq «
«1,13 А.
Измеренные частоты a>Qr и рассчитанные равновесные рассто-
яния некоторых двухатомных молекул приведены в табл. 25.1.
560
Лекция 25. Молекулярные спектры
Таблица 25.1. Параметры вращательных состояний двухатомных молекул
Молекула Частота uqt (xlO12 c"1) Вращательная постоянная В (х10-4эВ) Равновесное расстояние Rq (А)
CN 0,7154 2,354 1,172
HF 7,8965 25,987 0,917
LiH 2,8293 9,311 1,595
NO 0,6423 2,114 1,151
PN 0,2962 0,9748 1,487
SO 0,2716 0,8937 1,492
Современная молекулярная спектроскопия позволяет с высокой
точностью измерять частоты (25.11) вращательных спектров моле-
кул. По полученным результатам с помощью соотношения (25.12)
вычисляются межядерные расстояния с точностью до тысячных
долей ангстрема (см. табл. 25.1).
25.3. Колебательно-вращательные спектры
В начале данной лекции упоминалось, что для устойчивых со-
стояний двухатомных молекул функция £/(Д), исполняющая роль
потенциальной энергии при описании движения ядер, имеет ха-
рактерный минимум в точке равновесного расстояния Rq.
Разложим эту функцию E(R) в окрестности точки R = Rq
в ряд Тейлора по параметру R — Rq. Нулевой член — Dq имеет
отрицательный знак и определяет глубину потенциальной ямы.
Первый член равен нулю, так как в точке R = Rq функция E(R)
имеет минимум.
Если ограничиться малыми отклонениями от равновесного
расстояния то функция E(R) удовлетворительно аппроксими-
руется разложением в ряд Тейлора до второго члена включительно:
1 /гРе\
E(R)^-Do + - — (Я-До)2- (25.16)
2 \dR2 J R=Ro
Иначе говоря, вблизи точки равновесного расстояния R = Rq по-
тенциальная яма E(R) описывается квадратичной функцией.
Известно, что движение частицы в потенциальном поле, задан-
ном квадратичной функцией отклонения от положения равнове-
сия, представляет собой колебания гармонического осциллятора.
Частота колебаний, согласно классической теории, определяется
выражением
=\Ж’ <25-17>
25.3. Колебательно-вращательные спектры
561
где Mq — приведенная масса, kv — динамическая (или силовая)
постоянная равная
kv = (dip)R_R • (25-18)
В квантовой теории установлено, что гармонический осцилля-
тор обладает дискретным спектром энергий
Ev = (v + |, (25.19)
где частота cuqv определяется выражением (25.17), параметр и на-
зывается колебательным (или вибрационным) квантовым чис-
лом, которое может принимать значения 0, 1, 2, ...
Таким образом, двухатомная молекула, совершающая гармони-
ческие колебания, согласно формуле (25.19), характеризуется на-
бором эквидистантных колебательных энергетических уровней.
В стационарных состояниях с малыми значениями колеба-
тельного квантового числа и происходят гармонические колеба-
ния. При этом равновесное расстояние 7?о и параметр В (25.7)
остаются неизменными.
С увеличением квантового числа v колебательная энергия
(25.19) и, следовательно, энергия стационарного состояния воз-
растает. При этом функция E(R) уже не может адекватно вы-
ражаться квадратичным приближением (25.16) и в разложение
функции E(R) в ряд Тейлора необходимо включать кубичный и
следующие члены. Потенциальная яма теряет параболическую
симметрию, а колебания атомов молекулы в такой потенциальной
яме становятся ангармоническими. При этом равновесное меж-
ядерное расстояние увеличивается.
В ходе исследований было обнаружено, что колебания двух-
атомной молекулы успешно описываются с помощью потенциаль-
ной энергии в виде функции Морзе
E(R) = Bq [ехр (—2ах) — 2 ехр (—а.т)], (25.20)
где
х =
R — Rq
Rq
(25.21)
Dq и а — константы.
На больших расстояниях (ж > 0) потенциальная энергия
(25.20) описывает силы притяжения. При х = 0 (т.е. при R = Rq)
функция (25.20) имеет минимум равный — Dq. При дальнейшем
сближении атомов (х < 0) потенциальная энергия (25.20) харак-
теризует их сильное отталкивание. Схематичный вид функции
Морзе (25.20) изображен сплошной линией на рис. 25.3.
562
Лекция 25. Молекулярные спектры
Рис. 25.3. Схема колебательных энергетических уровней двухатомной молекулы:
D — энергия диссоциации, Rq — равновесное расстояние в основном стационарном со-
стоянии. Сплошная линия — график функции E(R), штриховая линия — график квадра-
тичного приближения (25.16). Горизонтальные черточки — энергетические уровни, справа
от них — соответствующие значения колебательного квантового числа v
Разложение функции (25.20) в ряд Тейлора до квадратичного
члена включительно дает квадратичную зависимость вида (25.16)
E(R) = -Do + - До)2, (25.22)
£
где
2 _ 2Г>0а2
W°v “ MoR% '
(25.23)
Следовательно, спектр колебаний с малой амплитудой описыва-
ется формулой (25.19), задающей эквидистантные энергетические
уровни. Выражения (25.17) и (25.23) определяют одну и ту же
частоту.
Если решить уравнение Шредингера с потенциальной энер-
гией, заданной функцией (25.20), то энергии колебательных ста-
ционарных состояний выразятся следующей формулой:
(25.24)
где величина в квантовой химии называется постоянной
ангармонизма, а безразмерный параметр хе — коэффициентом
ангармонизма. Коэффициент энгармонизма выражается через па-
раметры функции Морзе:
ha
р ~~ / •
2ЯО\/ШоЖ
(25.25)
25.3. Колебательно-вращательные спектры
563
Экспериментальные исследования показали, что у всех устой-
чивых молекул выполняется неравенство хе 1 (см. табл. 25.2).
Из вида формулы (25.24) следует, что в области ангармонизма
колебательные энергетические уровни перестают быть эквидис-
тантными (см. рис. 25.3). Расстояния между ними уменьшаются
с ростом квантового числа и.
При очень больших значениях квантового числа v молекула
может диссоциировать, т.е. распасться на составные части.
Подстановка v — 0 в выражение (25.19) показывает, что в низ-
шем энергетическом состоянии молекула совершает колебания, ко-
торые называются нулевыми. Это означает, что даже при абсо-
лютном нуле молекулы должны иметь ненулевую кинетическую
энергию колебательного движения атомных ядер. (Заметим, что
отсутствие нулевых колебаний противоречило бы соотношению не-
определенностей.) Следовательно, нулевые колебания уменьшают
энергию диссоциации на величину нулевой энергии Hivqv/2 (см.
рис. 25.3). Энергия диссоциации D связана с глубиной потенци-
альной ямы Dq соотношением
D = р0 -
(25.26)
Колебательное состояние молекулы в значительной степени оп-
ределяется температурой Т вещества. При выполнении условия
k&T hwQV/2 молекулы совершают только нулевые колебания.
Измерение частот колебаний cvqv проводится путем регистра-
ции спектров излучения и поглощения, образующихся при перехо-
дах между колебательными стационарными состояниями. В кван-
товой теории установлено, что возможны радиационные переходы
с различным изменением колебательного квантового числа Av =
= ±1, ±2, ±3, ... Однако вероятность излучения (или поглоще-
ния) резко уменьшается с ростом величины |Av| и наиболее ве-
роятными являются процессы с |Av| = 1.
Существенно, что радиационные переходы между колебатель-
ными стационарными состояниями наблюдаются лишь у поляр-
ных, т. е. гетероядерных двухатомных молекул. Эта особенность
объясняется изменениями электрического дипольного момента de
полярной молекулы, возникающими при колебаниях атомов. У го-
моядерных двухатомных молекул электрический дипольный мо-
мент равен нулю, и как следствие, излучение или поглощение элек-
тромагнитных волн при колебаниях атомов в молекуле в первом
(дипольном) приближении не происходят.
Экспериментальные исследования показали, что характерные
колебательные частоты cuov имеют порядок ~ 1014 с-1 и принад-
лежат ближнему инфракрасному диапазону спектра. Измеренные
значения cjq и рассчитанные приведенные массы Mq двухатом-
ных молекул позволяют вычислять динамические постоянные kv
564
Лекция 25. Молекулярные спектры
с помощью соотношения (25.17). Оказалось, что для большинства
двухатомных молекул величины kv имеют порядок 105-106 дин/см
или 102—103 Н/м. Вычисленные значения kv. определяющие фор-
мулой (25.18) кривизну потенциальной ямы E(R) в точке равнове-
сия, необходимы для согласования с результатами теоретических
расчетов функции E(R).
Параметры колебательных состояний некоторых двухатомных
молекул приведены в табл. 25.2. Заметим, что в химии и моле-
кулярной спектроскопии характерные частоты cuqv и постоянные
энгармонизма cuova;e принято выражать в обратных сантиметрах.
Для единообразия изложения в табл. 25.2 частоты cjq представлены
в обратных секундах. Вместо постоянных wqvxg приведены без-
размерные коэффициенты ангармонизма хе.
Таблица 25.2. Параметры колебательных состояний двухатомных молекул
Молекула Частота ivqv (xlO14 c-1) Коэффициенты ангармонизма xe (xlO-3) Динамическая постоянная kv (xlO5 дин/см)
CN 3,900 6,33 17,0
HF 7,802 21,74 9,66
LiH 2,650 16,5 1,02
NO 3,589 7,35 15,9
PN 2,520 5,22 10,2
SO 2,166 4,9 8,31
Из данных табл. 25.2 следует, что расстояния между соседними
колебательными энергетическими уровнями £±EV составляют до-
ли электрон-вольта, т.е. на 2-3 порядка больше расстояний меж-
ду соседними вращательными энергетическими уровнями ДЕр
(25.10), которые оценивались в предыдущем параграфе. Таким
образом, из-за AEV ^Ер между соседними колебательными
уровнями в принципе могут разместиться много вращательных
уровней.
Отсюда следует важный вывод, что чисто колебательных спек-
тров не существует, так как при переходах между колебатель-
ными стационарными состояниями возможны изменения враща-
тельного состояния (т.е. изменения квантового числа К).
Запишем выражение для энергии излучаемого фотона при пе-
реходе между двумя колебательными состояниями с квантовыми
числами Vi и V2:
^ = Ev(vl)-Ev(v2)+ER(Kl)-ER(K2). (25.27)
Согласно правилам отбора (25.9) вращательное квантовое чи-
сло К может как увеличиться, так и уменьшиться на единицу.
25.3. Колебательно-вращательные спектры
565
Следовательно, при определенной разности Av — Vi — V2 (vi > V2)
формируются две ветви спектральных частот. Разделим уравнение
(25.27) на постоянную Планка h и воспользуемся выражениями
(25.19), (25.6) и (25.12). Для переходов с увеличением вращатель-
ного числа {К —> К + 1) частоты выражаются формулой
cvi = - щг(К + 1), К = 0,1,2,..., (25.28)
где a>y = cUfryAv.
При переходах с уменьшением вращательного числа (К
К — 1) получаем второй набор частот:
CJ2 — cv-y -{ К — 1,2,3,... (25.29)
Выражения (25.28) и (25.29) определяют две ветви колеба-
тельно-вращательного спектра. Набор частот (25.28) называ-
ется F-ветвью, совокупность частот (25.29) составляет Я-ветвь
Р-ветвь
v = v2
2
О
Рис. 25.4. Энергетическая схема формирования ветвей колебательно-вращатель-
ного спектра излучения
колебательно-вращательного спектра. Энергетическая схема ради-
ационных переходов, формирующих две ветви колебательно-вра-
щательного спектра излучения, приведена на рис. 25.4.
566 Лекция 25. Молекулярные спектры
Из формул (25.28) и (25.29) видно, что частоты обеих ветвей
являются эквидистантными, разность соседних частот равна а?ог,
определяемой выражением (25.12). Интервал между ветвями со-
ставляет 2tJor5 так как частота ojv в колебательно-вращательном
спектре не наблюдается.
Если при радиационном переходе колебательное квантовое чи-
сло изменяется на единицу (Аг> = 1), то выражения (25.28) и
(25.29) принимают вид
— cjQr(jFC ~г 1), К — 0,1,2,..., (25.30)
и?2 = Н" cuor-fC, К = 1,2,3,..., (25.31)
где частота cuqv определена формулой (25.17).
Для спектров поглощения выражения (25.28), (25.29) также
справедливы, только параметр К является вращательным числом
конечного стационарного состояния.
Как было показано выше, колебательно-вращательные спект-
ры принадлежат инфракрасному диапазону и поэтому кратко на-
зываются ИК-спектрами. Регистрация ИК-спектров поглощения
является одним из важных физических методов исследования мо-
лекул. В качестве источника излучения часто используется так
называемый глобар, изготовленный, например, из карбида крем-
ния, через который пропускается электрический ток. Вследствие
эффекта Джоуля-Ленца глобар нагревается до температуры свыше
1000 °C и испускает тепловое излучение непрерывного спектра (см.
лекции 2 и 3), которое, согласно закону Вина, имеет максимум
интенсивности в инфракрасном диапазоне. Пучок первичного
ИК-излучения проходит через камеру (кювету), наполненную ис-
следуемыми молекулами, и направляется на детектор через дис-
пергирующую систему. Стекло и кварц, используемые для разло-
жения в спектр видимого света, сильно поглощают инфракрасное
излучение, поэтому призмы ИК-спектрометров изготавливаются из
кристаллов галогенидов щелочных металлов (NaCl, KBr, CsI, ...).
Прошедшее излучение, разложенное в спектр, регистрируется де-
текторами, которые представляют собой терморезисторы или фо-
торезисторы, работающие в инфракрасном диапазоне.
На рис. 25.5 приведен пример колебательно-вращательного
спектра поглощения, содержащего две ветви и принадлежащего
ИК-диапазону. Наблюдается отсутствие центрального минимума.
Относительная интенсивность минимумов колебательно-враща-
тельного спектра обусловлена различной заселенностью враща-
тельных энергетических уровней как исходного, так и конечного
колебательных состояний. Зависимость заселенности уровней от
вращательного квантового числа была описана в § 25.2 данной лек-
ции (см. рис. 25.2).
Исследование колебательно-вращательных спектров позволяет
вычислять динамические постоянные kv и приведенные массы
25.3. Колебательно-вращательные спектры 567
двухатомных молекул. Зависимость регистрируемых частот ко-
лебательно-вращательных спектров от масс атомов, входящих в
молекулу, позволяет исследовать их изотопный состав.
Например, еще в ходе масс-спектрометрических исследований
(см. лекцию 1) было обнаружено, что природный хлор предста-
вляет собой смесь изотопов 35С1 и 37С1. При образовании химиче-
ских соединений хлора его изотопы входят в молекулы в той же
Рис. 25.5. Колебательно-вращательный спектр поглощения молекулы оксида
углерода СО.
Цифры у минимумов — вращательные квантовые числа конечного стационарного состоя-
ния. Разности частот соседних минимумов (кроме центральной части) равны cuor
пропорции. Разрешающая способность инфракрасных спектроме-
тров позволяет разделить минимумы в ИК-спектрах поглощения,
образованных колебаниями изотопов хлора различной массы, что
хорошо просматривается на рис. 25.6.
Анализ полученных ИК-спектров позволяет не только обнару-
жить сложный изотопный состав элементов исследуемого хими-
ческого соединения, но и по величине минимумов измерить про-
центное содержание каждого изотопа.
Увеличение разрешающей способности регистрирующей аппа-
ратуры позволяет обнаружить отклонение частот обеих ветвей ко-
лебательно-вращательных спектров от эквидистантности. Это
объясняется тем, что при переходах между стационарными состо-
яниями с высокими значениями колебательных квантовых чисел
568
Лекция 25. Молекулярные спектры
v равновесное межядерное расстояние заметно изменяется. На
рис. 25.3 это наблюдается при v > 3. Рост равновесного рас-
стояния влечет, согласно выражению (25.7), уменьшение враща-
тельной постоянной В. Следовательно, большему колебательному
2700 2800 2900 3000 „ ,
1/л,см
Рис. 25.G. Колебательно-вращательный спектр поглощения молекул хлорово-
дорода НС1, полученного из естественной смеси изотопов хлора (35 *С1 — 76%,
37С1 — 24%). Более глубокие минимумы образованы колебаниями атомов 3оС1,
менее глубокие — атомами 37С1
квантовому числу v соответствует меньшее значение постоян-
ной В. С другой стороны, при выводе формул (25.28) и (25.29),
которые дают эквидистантность частот ветвей ИК-спектра, исполь-
зовалось равенство вращательных постоянных для начального и
конечного колебательных состояний. Нетрудно провести вычисле-
ния частот в случае, когда вращательная постоянная В± верхнего
колебательного уровня меньше постоянной В2 нижнего уровня.
При этом выясняется, что эквидистантность частот колебательно-
вращательных спектров нарушается. С возрастанием вращатель-
ного квантового числа конечного стационарного состояния мини-
мумы F-ветви спектра поглощения постепенно расходятся, а ми-
нимумы В-ветви — сходятся (см. рис. 25.6).
Более подробное исследование колебательно-вращательных
спектров, возникающих при переходах с высоких колебатель-
ных энергетических уровней, позволяет рассчитывать отклонение
функции E(R) от квадратичного приближения (25.16) и, в прин-
ципе, построить профиль потенциальной ямы E(R).
Колебательно-вращательные спектры многоатомных молекул
также принадлежат инфракрасному диапазону, хотя имеют бо-
лее сложную структуру. Однако установлено, что определенные
группы атомов в молекулах приводят к появлению в спектрах по-
глощения характерных полос (см. рис. 25.7).
25.4. Принцип Франка-Кондона
569
HF
НС1
НВг -------------,
HI
ОН
I-----1
HSe
NH
СН
I------1
HAs
*SiH ’
GeH
1/X, cm-1
4000 3500 3000 2500 2000
Рис. 25.7. Диапазоны характерных частот колебательно-вращательных спек-
тров, генерируемых определенными группами атомов, входящих в состав мно-
гоатомных молекул
Следовательно, исследования ИК-спектров поглощения много-
атомных молекул позволяют обнаружить химические связи между
определенными атомами, что важно для установления структуры
сложной молекулы и ее химических свойств.
25.4. Принцип Франка-Кондона
и полосатые оптические спектры
При небольших энергиях передаваемых молекуле (порядка де-
сятых долей электрон-вольта) происходит возбуждение колеба-
тельных и вращательных энергетических уровней. В конце преды-
дущей лекции (§ 24.3) было показано, что для перехода молекулы
в стационарное состояние, характеризуемое другим молекулярным
термом, требуется энергия порядка нескольких электрон-вольт.
Рассмотрим радиационные переходы между различными элек-
тронными стационарными состояниями (молекулярными терма-
ми). При этом происходит излучение или поглощению фотонов,
принадлежащих видимому, ближним ультрафиолетовому или ин-
фракрасному диапазонам, что объясняется характерной величиной
энергии возбужденных термов. При переходах между термами воз-
можны изменения колебательных и вращательных состояний мо-
лекулы. Иначе говоря, в выражении энергии (25.1) изменяются
570 Лекция 25. Молекулярные спектры
все три слагаемых, что обусловливает сложный характер молеку-
лярных спектров.
Основные особенности спектров молекул успешно интерпрети-
руются на базе принципа Франка-Кондона, который был сфор-
мулирован в 1926 г. Джеймсом Франком (1882-1964) и Эдвардом
Кондоном (1902-1974). Смысл принципа заключается в утвержде-
нии, что из-за значительной разницы масс электронов и атом-
ных ядер за время перехода электрона между молекулярными тер-
мами (электронными стационарными состояниями) межядерные
расстояния практически не изменяются.
Стационарные состояния электронной подсистемы молекулы,
задаваемые электронными конфигурациями МО и молекулярными
термами, характеризуются функциями Е(гп), которые вычисля-
ются при решении уравнения (22.20) в рамках адиабатического
приближения. В разных электронных состояниях, согласно урав-
нению (22.21), атомные ядра движутся в эффективных потенци-
альных полях jE(rn), различающихся равновесными расстояни-
ями и другими характеристическими величинами. Следовательно,
при расчете молекулярных спектров необходимо учитывать разли-
чия вращательных постоянных (25.7), динамических постоянных
(25.18), постоянных ангармонизма и других вращательных и ко-
лебательных параметров молекулы в исходном и конечном стаци-
онарном состоянии.
Применение принципа Франка-Кондона для описания спектра
излучения целесообразно рассмотреть для двухатомных молекул.
Теоретические расчеты и анализ экспериментальных данных по-
казали, что функция эффективного потенциального поля E(R) для
возбужденных молекулярных термов заметно отличается от ана-
логичной функции Eq(R) основного состояния молекулы. Потен-
циальная яма сдвигается вверх по оси энергии, а точка мини-
мума смещается в сторону больших межядерных расстояний. Из
табл. 24.2 и 24.3 видно, как увеличиваются равновесные расстоя-
ния R для возбужденных термов по сравнению с равновесным рас-
стоянием Ro основного состояния молекулы. Кроме того, при воз-
буждении молекулярных термов изменяется форма кривой E(R)
вблизи минимума, что, согласно (25.18) и (25.17), вызывает изме-
нение динамических постоянных kv и характерных частот коле-
баний CUQ.
На рис. 25.8 качественно изображены типичные кривые функ-
ций E(R) основного и возбужденного молекулярных термов. Пред-
положим для определенности, что разность энергий термов
Ei(R)— Eq(R) такова, что радиационные переходы между ними со-
провождаются испусканием и поглощением фотонов видимого диа-
пазона.
В случае, изображенном на рис. 25.8а, равновесные расстоя-
ния обоих термов приблизительно равны. Так как, согласно прин-
25.4. Принцип Франка-Кондона
571
ципу Франка-Кондона, при возбуждении верхнего терма межатом-
ное расстояние не изменяется, то при этом переходе колебатель-
ное состояние молекулы остается практически неизменным. На
Рис. 25.8. Энергетическая схема возбуждения молекулярных термов и высоко-
энергетических колебательных состояний: a) R\ ~ Яо, б) Ri > Rq:
Eq(R) и Ei(R) — потенциальные ямы для основного и возбужденного термов, Rq и Ri —
соответствующие равновесные расстояния. Горизонтальные отрезки внутри потенциаль-
ных ям — энергетические уровни колебательных состояний. Сплошные стрелки, напра-
вленные вверх, изображают переход из равновесного расстояния Rq. Штриховые стрелки
ограничивают диапазон межядерных расстояний при возбуждении молекулы, находящейся
в нулевом колебательном состоянии. В правой части — потенциальная яма возбужденного
терма в увеличенном виде с указанием переходов между колебательными состояниями
рис. 25.8а переход в возбужденное состояние изображен верти-
кальными стрелками. Видно, что у возбужденного терма колеба-
тельное состояние молекулы остается неизменным. При обратном
переходе из возбужденного состояния в основное произойдет излу-
чение видимого фотона с энергией Ei(R) — Eq(R').
В случае, показанном на рис. 25.86', при возбуждении верхнего
терма межатомное равновесное расстояние значительно увеличи-
вается: Ri > Rq. Как следствие, молекула оказывается в колеба-
тельном состоянии с высоким значением квантового числа v. При
обратном переходе молекула, кроме оптического фотона, испустит
каскад инфракрасных фотонов при переходах в более низкоэнер-
гетические колебательные состояния.
Таким образом, на видимый спектр излучения, образован-
ный радиационными переходами между молекулярными терма-
ми, накладывается линейчатый спектр ИК-диапазона, возникаю-
щий из-за переходов между различными колебательными состоя-
ниями.
Кроме того, необходимо учитывать, что энергия оптического
фотона зависит от квантовых чисел vi и vq верхнего и нижнего
572
Лекция 25. Молекулярные спектры
колебательных уровней, между которыми происходит радиацион-
ный переход. На рис. 25.9 изображена схема наиболее вероятных
радиационных переходов между двумя молекулярными термами,
которые сопровождаются изменением колебательного квантового
Е
5
4
3
2
1
О
^2
5
4
3
2
1
О
У е2
J
Рис. 25.9. Энергетическая схема излучательных переходов между двумя молеку-
лярными термами с изменением колебательного состояния молекулы:
и Е2 — группы энергетических уровней, относящихся к начальному и конечному тер-
мам соответственно. Слева от энергетических уровней указаны значения колебательных
квантовых чисел соответствующих состояний. Показаны лишь уровни с колебательными
квантовыми числами вплоть до 5 и переходы с изменением колебательного числа Av = ±1
числа на единицу. Видно, что при этом возникает не определен-
ная оптическая спектральная линия, а серия, обусловленная мно-
жеством возбужденных колебательных уровней как верхнего, так
и нижнего термов.
Разрешенные переходы между различными вращательными
состояниями дополнительно усложняют оптический спектр излу-
чения молекулы.
25.4. Принцип Франка-Кондона
573
Спектры, возникающие при совместном изменении электрон-
ного, колебательного и вращательного состояний молекулы, назы-
ваются электронно-колебателъно-вращателъными или просто
электронными. Наличие трех составных частей энергии молекулы
(25.1) приводит к тому, что в электронно-колебательно-вращатель-
ных переходах излучаются фотоны, энергию которых можно пред-
ставить в виде
hwm = АЕе + AEV + AER. (25.32)
Первое слагаемое представляет собой разность энергий моле-
кулярных термов, второе — разность энергий колебательных со-
стояний, соответствующих разным термам. Обозначим здесь
символом п совокупность квантовых чисел молекулярного терма.
Энергию стационарного состояния молекулярного терма с опреде-
ленным колебательным квантовым числом v обозначим Env. То-
гда можно записать
АТ?е + ^Ev — En\,v\ — Еп2^у2ч (25.33)
где индексы 1 и 2 относятся к начальному и конечному состоя-
ниям молекулы соответственно, т. е. верхнему и нижнему энерге-
тическим уровням.
Возможные значения энергии (25.33) изображены на рис. 25.9
стрелками, направленными вниз.
Изменение вращательного состояния усложняет выражение
для энергии излучаемых фотонов. Введем обозначение о/ частоты
радиационного перехода без учета вращательного состояния:
. А£/е 4“ ^Еу
ш = h
(25.34)
Величина си' в молекулярной спектроскопии называется электрон-
но-вибрационной частотой.
Излучаемая молекулой частота спектральной линии выра-
жается из (25.32) с помощью (25.34) следующим образом:
— oj1 ---—, (25.35)
А
где A£7r = Eri — ER2.
Энергии вращательных состояний ER\ и ER2 относятся к раз-
личным молекулярным термам — начальному и конечному. В со-
ответствии с (25.6) и (25.7) запишем:
ЕЯ1 = + 1), ER2 = В2К2(К2 + 1), (25.36)
где К\ и К2 — вращательные квантовые числа начального и ко-
нечного вращательных состояний, В\ и В2 — соответствующие
постоянные (25.7), причем, вообще говоря, В± В2.
574
Лекция 25. Молекулярные спектры
Рисунок 25.1 и табл. 24.3 демонстрируют значительное увели-
чение равновесных расстояний у возбужденных термов по сравне-
нию с основным. Следовательно, при переходах из возбужденного
терма в основное состояние В\
Обозначив ЛЕр/h = К2, запишем выражение для излуча-
емой частоты (25.35) в виде
= о/ + o>ki, К2- (25.37)
В случае переходов между различными молекулярными тер-
мами правила отбора для вращательного квантового числа прини-
мают вид
ДК = ±1, 0. (25.38)
Таким образом, разрешенные изменения вращательных состо-
яний приводят к тому, что при фиксированной частоте о/ частоты
молекулярного спектра а>т образуют три ветви, соответствующие
трем правилам отбора (25.38):
=о;' + а;к,к-1, ЛК = -1, (25.39)
cu° = J + uKi к, ЛК = 0, (25.40)
= и)1 + к+1, ЛК = 1. (25.41)
В формулах (25.39)-(25.41) параметр К представляет собой
вращательное квантовое число начального стационарного состо-
яния. Так как это число может принимать различные значения
(см. рис. 25.1), то каждая из ветвей (25.39)-(25.41) состоит из
большого количества спектральных линий. Исторически эти на-
боры линий получили названия В-, Q- и F-ветвей соответственно.
С помощью (25.36) выразим частоты ветвей через вращатель-
ные постоянные В± и В2 начального и конечного стационарных
состояний:
w+=u/ + i[(Bi -В2)Кг + {В1 + В2)К] (Я-ветвь), (25.42)
и° = а/ + |[(В1-В2)(Я2 + Я)] (Q-ветвь), (25.43)
п
w" = w/ + ^[(B1-B2)F2 + (B1-3B2)F-2B2] (F-ветвь), (25.44)
где К — вращательное квантовое число исходного состояния.
Согласно формулам (25.42)-(25.44), частоты всех трех ветвей
квадратично зависят от вращательного квантового числа К. Эти
зависимости в молекулярной спектроскопии принято изображать
диаграммами Фортра. Пример таких диаграмм для спектра из-
лучения в случае, когда В\ < В?, приведен на рис. 25.10. Следует
иметь ввиду, что в переходах между различными молекулярными
25.4. Принцип Франка-Кондона
575
Рис. 25.10. Диаграммы Фортра для спектров излучения в случае Bi < В2.
По вертикальной оси отложены вращательные квантовые числа исходного стационарного
состояния молекулы. Жирные линии соединяют значения частот для трех ветвей (25.42)-
(25.44) полосатого спектра. Ниже отдельно изображены наборы частот отдельных ветвей
термами возможны ситуации, когда В\ > В2. При этом вид диа-
грамм Фортра существенно изменится, так как ориентация ветвей
парабол си(А') зависит от знака разности By — jE?2-
576 Лекция 25. Молекулярные спектры
Отдельные спектральные линии ветвей (25.42)-(25.44) распо-
ложены очень тесно, так как разность соседних частот имеет
порядок cuor ~ 1012с-1. В оптических спектрах эти линии сли-
ваются в полосы, которые, согласно рис. 25.10, имеют резкие низ-
кочастотные границы и размытые высокочастотные. По этой
причине электронно-колебательно-вращательные спектры молекул
получили название полосатых. Резкие границы полос называ-
ются кантами.
Экспериментальные исследования молекулярных спектров де-
монстрируют полное согласие с выводами теории.
25.5. Рентгеновские молекулярные спектры
Экспериментальные исследования показали, что К-серии спек-
тров характеристического рентгеновского излучения (ХРИ) почти
всех молекул являются наложением рентгеновских К-серий спек-
тров атомов, входящих в состав данной молекулы. Это объяс-
няется тем, что рентгеновские К-линии возникают вследствие
образования вакансий в электронном К-слое — самом низкоэнер-
гетическом. В лекции 23 было показано, что атомные орбитали
ls-оболочки практически не участвуют в формировании молеку-
лярных орбиталей. Это означает, что при объединении атомов в
молекулы, волновые функции и энергии электронов К-слоя прак-
тически не изменяются.
Конечно, исключениями являются молекулы, состоящие из
атомов первого периода таблицы Менделеева (см. табл. 23.1). Но
эти атомы в принципе не могут генерировать спектральные линии
ХРИ, так как имеют электроны только в К-слое электронном слое,
что исключает заполнение вакансий переходами электронов из бо-
лее высокоэнергетических электронных слоев (см. лекцию 19).
Однако спектры ХРИ молекул обладают существенными осо-
бенностями, которые важны для экспериментального исследова-
ния химических соединений. Ясно, что различия молекулярных
и атомных рентгеновских спектров должны наблюдаться при за-
полнении вакансий внутренних электронных оболочек в резуль-
тате радиационных переходов электронов с самых внешних из за-
полненных молекулярных орбиталей.
Рассмотрим для примера двухатомную молекулу хлорида во-
дорода НС1. В первом приближении можно полагать, что хими-
ческая связь образуется с помощью Зр-электронов атома хлора и
ls-электрона атома водорода. Остальные атомные орбитали (АО)
хлора не участвуют в формировании молекулярных орбиталей
(МО).
При построении МО методом ЛКАО в качестве минимального
базиса можно взять орбиталь атома водорода 1з(Н) и орбиталь
атома хлора 3pz(Cl), которая характеризуется квантовыми чис-
25.5. Рентгеновские молекулярные спектры 577
лами п = 3 и I = 1. Квадрат модуля Зр/(С1)-орбитали дает про-
странственное распределение электронной плотности, обладающей
аксиальной симметрией относительно оси, соединяющей центры
атомов молекулы НС1. Линейные комбинации данных АО обра-
зуют связывающую и разрыхляющую молекулярные орби-
тали:
Фа = СРР1 + С2ср2, фа* = С3</?1 + С4(/?2, (25.45)
где = ls(H), = Зр/(С1) — атомные орбитали, ci, с2, с3,
с4 — коэффициенты ЛКАО.
Атомные орбитали Зр%(С1) и Зру(С1) атома хлора определяют
пространственное распределение электронной плотности, облада-
ющей аксиальной симметрией относительно осей, перпендикуляр-
ных оси симметрии молекулы НС1. Три орбитали Зр%(С1), Зру (С1)
и 3pz (Cl) выражаются линейными комбинациями волновых функ-
ций Зр-оболочки атома хлора, аналогичными преобразованиям
(23.24).
Орбитали Зрх(С1) и Зру(С1) имеют нулевые интегралы пере-
крытия с АО 15(H) и поэтому не входят в ЛКАО, образующую меж-
атомную химическую связь. Энергии этих орбиталей в молекуле
практически совпадают с АО изолированного атома. Такие АО, не
искажающиеся при объединении атомов в молекулу, называются
несвязывающими.
Эти несвязывающие орбитали в молекуле НС1 характеризуются
квантовыми числами |А| = 1 и, в соответствие с табл. 22.3, обозна-
чаются Зртг(ж) и Зртг(?/). Эти МО вырождены, их энергии равны
энергиям АО Зрх и Зру ‘изолированного атома хлора. Энергети-
ческие уровни МО молекулы НС1 изображены на рис. 25.11а.
Пять Зр-электронов атома хлора и единственный электрон ато-
ма водорода размещаются на МО фа^ Зрл(х) и Зртг(?/), как показано
на рис. 25.11а. Разрыхляющая орбиталь фа* остается пустой в
основном состоянии молекулы НС1, что обеспечивает понижение
энергии системы по сравнению с изолированными атомами Н и
С1 и, следовательно, устойчивость данной молекулы.
Спектр ХРИ молекулы НС1 целесообразно сравнить со спек-
тром изолированного атома хлора. Самая коротковолновая линия
ХРИ атома хлора — линия К@ с длиной волны 4,403 А и энергией
фотонов 2,816 кэВ — образуется переходом электрона в вакансию
ls-оболочки. Экспериментальные исследования спектра ХРИ мо-
лекулы НС1 позволили обнаружить на указанном участке энергии
два близких пика и приведенные на рис. 25.1161
Спектральная линия К@(В} образуется при заполнении вакансии
в ls-оболочке атома хлора любым электроном из несвязывающих
МО Зртг(ж) и Зртг(?/). Эта линия совпадает с К^-линией изоли-
рованного атома хлора. Менее интенсивный пик спектра
578
Лекция 25. Молекулярные спектры
с энергией фотонов приблизительно 2,813 кэВ возникает из-за
перехода в такую же вакансию электронов из связывающей ор-
битали Можно сделать вывод, что энергетический уровень
орбитали x[)a находится ниже уровня орбиталей Зр на ЗэВ.
Рис. 25.11. Формирование спектральной линии Кр характеристического рентге-
новского излучения молекулы хлорида водорода НС1:
а) схема уровней энергии МО и переходы электронов в вакансию оболочки 1s хлора, уровни
энергии оболочек 3s, 2р и 2s хлора не показаны; б) спектр линии ХРИ Кр молекулы НС1
Меньшая высота пика спектра Кр(А') по сравнению с пиком
объясняется тем, что интенсивность данной спектральной
линии пропорциональна статистическому весу, с которым АО
3pz(Cl) входит в МО ^<т, т.е. величине |с2р < 1.
Таким образом, регистрация спектра ХРИ молекулы позволяет
не только измерить энергии МО, но и получить коэффициенты в
ЛКАО.
Энергии разрыхляющих МО экспериментально определяются
по рентгеновским спектрам поглощения. При облучении молекул
рентгеновским излучением непрерывного спектра электроны 1s-
оболочки с большой вероятностью поглощают рентгеновские фо-
тоны и переходят на свободные места разрыхляющих МО. Напри-
мер, в рассмотренном выше примере электроны из ls-оболочки
хлора перемещаются на незаполненную орбиталь При этом
молекула НС1 поглощает энергию, равную разности энергетиче-
ских уровней состояний и ls(Cl). В соответствующем месте
спектра поглощения образуется минимум. Глубина минимума по-
25.5. Рентгеновские молекулярные спектры
579
зволяет вычислить модуль коэффициента С4 в выражении второй
волновой функции из (25.45).
В современных рентгеновских спектрометрах используются
полупроводниковые детекторы, обеспечивающие высокую разре-
шающую способность в области так называемого «мягкого» рент-
геновского излучения с длиной волны порядка нескольких десят-
ков ангстрем и более. Анализ спектров мягкого ХРИ позволяет
измерять энергии МО и коэффициенты разложения в ЛКАО мно-
гоатомных молекул.
Задачи к лекции 25
1. Вычислить моменты инерции двухатомных молекул, перечислен-
ных в табл. 22.1 лекции 22.
2. Рассчитать постоянную вращательной энергии и три низших вра-
щательных энергетических уровня для следующих двухатомных моле-
кул: а) КС1, б) НВг, в) MgO, г) Nal.
3. Вычислить разность постоянных вращательной энергии для мо-
лекул обычного водорода и дейтерия.
4. Во вращательном спектре молекулы НС1 присутствуют спект-
ральные линии с длиной А = 120,3 мкм, 96,0 мкм, 60,4 мкм, 68,9 мкм,
60,4 мкм. Рассчитать межатомное расстояние в данной молекуле, пола-
гая, что в ее состав входит только обычный водород и изотоп 35С1.
5. Вычислить энергию нулевых колебаний молекул, перечисленных
в табл. 25.2.
6. Рассчитать энергии трех низших колебательных стационарных со-
стояний с учетом энгармонизма для молекул, перечисленных в табл. 25.2.
ДОПОЛНЕНИЯ К ЛЕКЦИИ 25
25.1. Комбинационное рассеяние света
В 1928 г. было обнаружено характерное явление преобразования
спектра видимого света при его рассеянии на некоторых кристаллах и
жидкостях. Если первичное излучение имеет линейчатый спектр, то
в рассеянном излучении появляются дополнительные спектральные ли-
нии, называемые сателлитами. При этом каждой спектральной линии
с частотой о?о соответствует две группы сателлитов с частотами cu < cuq
И CU > CUq.
Это явление было открыто в России Л.И. Мандельштамом (1879-
1944) и Г.С. Ландсбергом (1890-1957) и практически одновременно в
Индии Ч.В. Раманом (1888-1970) и К.С. Кришнаном (1898-1961). Явле-
ние получило название Раман-эффект, или комбинационное рассеяние
света.
В ходе экспериментальных исследований были установлены следую-
щие основные закономерности комбинационного рассеяния.
1. Пусть cuj — частота сателлита, где j — номер сателлита. Абсо-
лютные величины разностей |cuj — cuo| при фиксированном номере j оди-
наковы для всех спектральных линий первичного излучения. Величины
|cuj — cuo| являются характеристиками вещества рассеивателя.
2. Для определенной частоты первичного излучения cuo каждому са-
теллиту с частотой cuj = cuq — Acuj сопутствует сателлит с частотой
cuj = cuo + Acuj. Сателлиты с частотами cu < cuo называются красными
или стоксовыми, сателлиты с частотами cu > cuo называются фиолето-
выми или антистоксовыми.
3. Количество сателлитов для определенной спектральной линии пер-
вичного излучения и их относительная интенсивность при фиксирован-
ной температуре зависят от рассеивающего вещества. При этом интен-
сивности сателлитов уменьшаются с ростом разностей |cuy — cuo|, т.е. с
увеличением номера сателлита. Для пары сателлитов j интенсивность
красного сателлита значительно больше, чем фиолетового.
4. Абсолютные значения разностей |cuj - cuq| частот сателлитов и
частоты первичного излучения обычно имеют порядок ~ 1013-1014 с-1.
Раман-эффект в жидкостях и газах может быть схематично объяс-
нен взаимодействием первичной электромагнитной волны с изолирован-
ными молекулами. Рассмотрим монохроматическую волну с частотой
cuo- Фотон такой волны, обладающий энергией Zkuo, при взаимодействии
с молекулой может перевести ее в другое колебательное состояние. Пусть
в начальном стационарном состоянии молекула характеризовалась коле-
бательным квантовым числом v, а в конечном — числом v'. В процессе
рассеяния молекула поглощает фотон с энергией Tkuo, а затем испускает
фотон с энергией /ки'. Сохранение энергии системы «фотон + молекула»
Дополнения к лекции 25
581
обеспечивает следующее равенство:
/кио + Ev = tuv1 + Evf, (Д.25.1)
где Еу и Еу> — колебательные энергии молекулы в начальном и конечном
стационарных состояниях соответственно.
Из соотношения (Д.25.1) следует, что частота рассеянного (переиз-
лученного) фотона равна
о/ = о/0 + Ev~hEv'. (Д.25.2)
Очевидно, что если первоначально молекула находилась в основном
состоянии с нулевой колебательной энергией huj$y/2 (см. §25.3 лек-
ции 25), то разность колебательных энергий в (Д.25.2) всегда будет от-
рицательной. Тогда частота рассеянного излучения cu' < сио, т.е. ниже
частоты первичного излучения. Дискретный характер спектра колеба-
тельных энергий Еу (25.20) обусловливает дискретный набор стоксовых
сателлитов.
Если первоначально молекула находилась в одном из своих возбу-
жденных колебательных состояний, то разность Ev — Ev> может прини-
мать любой знак в зависимости от соотношения между квантовыми чис-
лами v и vf. Как следствие, появляется возможность возникновения как
стоксовых, так и антистоксовых сателлитов. При одинаковой абсолют-
ной величине разности |v — v'| образуются стоксовый и антистоксовый
сателлиты
J = cuq ± Аси (Д.25.3)
с равными сдвигами частот
Да/ = (Д.25.4)
Наиболее вероятными являются радиационные переходы с измене-
нием колебательного квантового числа Av = ±1. При этом абсолют-
ная величина разности колебательных энергий |jEv — Ev> | имеет поря-
док ~ hujQy, где характерная частота cuqv определяется формулой (25.17).
Пользуясь данными табл. 25.2, можно убедиться в том, что сдвиги частот
(Д.25.4) по порядку величины совпадают с наблюдаемыми в эксперимен-
тах разностями частот |cuj — cuo | сателлита и первичного излучения.
Множество пар сателлитов наблюдается, когда из-за теплового дви-
жения молекул возбуждается значительное количество различных коле-
бательных стационарных состояний. Каждой паре сателлитов соответ-
ствует определенная пара колебательных квантовых чисел v и г/.
Вероятности возбуждения колебательных энергетических уровней
описываются распределением Больцмана. Это означает, что относитель-
ное число молекул с определенной колебательной энергией Ev уровней
экспоненциально спадает с ростом этой энергии.
Пусть ансамбль молекул находится в тепловом равновесии. Обозна-
чим TVi — количество молекул в колебательном состоянии с квантовым
числом v, N2 — количество молекул в состоянии с колебательным кван-
582
Дополнения к лекции 25
товым числом v'. Тогда, согласно распределению Больцмана,
Ni
N2
Ev — Ev> \
kBT /
(Д.25.5)
Для определенности положим, что v' > v. Тогда при переходе vr —> v
формируется фиолетовый сателлит, а при переходе v —> v' — красный.
Тогда из соотношения (Д.25.5) следует, что Ni > N2. При этом правая
часть уравнения (Д.25.5) равна отношению интенсивности красного са-
теллита Ii к интенсивности фиолетового сателлита 12. Выразив разность
колебательных энергий через сдвиг частот, получим
Ii / /гДаА
T2=expVwr
(Д.25.6)
Последнее соотношение означает, что Д > 12, следовательно, интен-
сивность красного сателлита превышает интенсивность фиолетового, что
согласуется с результатами экспериментов.
В заключение следует упомянуть, что комбинационное рассеяние све-
та на кристаллах объясняется в рамках физики твердого тела и кристал-
лооптики.
Приложение
КРАТКИЕ БИОГРАФИЧЕСКИЕ СПРАВКИ О ФИЗИКАХ,
ВНЕСШИХ ВАЖНЫЙ ВКЛАД В РАЗВИТИЕ
АТОМНОЙ ФИЗИКИ
АНГСТРЕМ Андерс Йонас (13.VIII 1814 - 21.VI 1874) — шведский
физик и астроном. Родился в Лёгдё. Окончил ун-т в Упсале (1839), где
работал (с 1858 г. — профессор, в 1870-71 гг. — ректор).
Физические исследования посвящены спектральному анализу. Явля-
ется одним из основоположников спектроскопии. Изучал спектры пла-
мени, электрической дуги, Солнца, планет. С большой точностью из-
мерял длины волн солнечного излучения и составил в 1868 г. первый
подробный атлас спектральных линий солнечного спектра. Открыл в
1862 г. водород в солнечной атмосфере. Работы Ангстрема относятся
также к теплоте, магнетизму и изучению металлов. Именем Ангстрема
названа единица длины, равная 10“8 см. Член ряда научных обществ.
Медаль Б.Румфорда (1872).
АСТОН Фрэнсис Уильям (1.IX 1877 - 20.XI 1945) — английский
физик и химик, член Лондонского королевского общества (1921). Ро-
дился в Харборне. Окончил Бирмингемский ун-т (1898), где работал в
1903-09 гг., в 1910-19 гг. — в Кавендишской лаборатории, с 1919 г. —
в Тринити-колледж Кембриджского ун-та.
Исследования относятся к атомной и ядерной физике и радиохимии.
В 1919 г. сконструировал масс-спектрограф и с его помощью в том же
году убедительно доказал наличие изотопов у хлора и ртути. В после-
дующие годы открыл большое количество (212) стабильных изотопов у
многих химических элементов и изучил их закономерности (Нобелев-
ская премия по химии, 1922). Показал, что большинство устойчивых
элементов является смесью изотопов. В 1913 г. предложил метод газо-
вой диффузии для разделения изотопов, а в 1919 г. — электромагнитный
метод. В 1927 г. сконструировал второй спектрограф еще большей раз-
решающей силы, а в 1937 г. — третий, точность которого была еще
выше. Измеряя атомные массы, показал, что атомная масса ядра не
равна сумме масс, входящих в него частиц, а меньше этой величины на
несколько десятых процента. Измерив массы ряда изотопов и определив
дефекты их масс, в 1927 г. построил первую кривую упаковочных ко-
эффициентов, характеризующую энергию связи атомных ядер. Открыл
(1931) изотоп уран-238.
Иностранный чл.-корр. АН СССР (1924).
БАЛЬМЕР Иоганн Якоб (1.V 1825 - 12.III 1898) — швейцарский фи-
зик и математик. Родился в Лозанне. Учился в Базеле, Карлсруэ, Бер-
лине. В 1849 г. получил степень доктора в Базельском ун-те. С 1859 г.
преподавал в средней школе и в 1865-90 гг. — в Базельском ун-те.
Физические работы в области спектроскопии. Обнаружил законо-
мерность в спектральных линиях атома водорода, показав в 1885 г., что
длины волн линий видимой части спектра атома водорода связаны между
собой простой зависимостью (формула Бальмера), которая дает возмож-
584 Приложение. Краткие биографические справки о физиках
ность вычислить длины волн всех линий спектральной серии (серия
Бальмера). Это открытие послужило толчком для обнаружения других
серий в спектре атома водорода — серий Лаймана, Пашена, Брэкетта и
Пфунда в ультрафиолетовом и инфракрасном диапазонах.
БАРКЛА Чарлз Гловер (27.VI1877- 23.Х 1944) — английский физик,
член Лондонского королевского общества (с 1912). Родился в Уиднесе.
Окончил Ливерпульский ун-т (1899). В 1905-09 гг. работал в Ливер-
пульском, в 1909-13 гг. — в Лондонском ун-те. С 1913 г. — профессор
Эдинбургского ун-та.
Основные работы посвящены физике рентгеновских лучей. Первый
экспериментально осуществил в 1904 г. поляризацию рентгеновских лу-
чей, доказав тем самым их волновую природу. В 1906 г. открыл ха-
рактеристические рентгеновские лучи. За исследования рентгеновских
лучей удостоен в 1917 г. Нобелевской премии.
БЕККЕРЕЛЬ Антуан Анри (15.XII 1852 - 25.VIII 1908) — француз-
ский физик, член Парижской АН (1889), президент в 1908. Родился в
Париже. Окончил Политехническую школу в Париже (1874), с 1876 г. —
лектор этой школы, с 1895 г. — профессор (с 1892 г. — также зав. ка-
федрой физики в Музее естественной истории и Консерватории искусств
и ремесел).
Основные работы посвящены оптике (магнитооптика, фосфоресцен-
ция, инфракрасные спектры) и радиоактивности. В 1896 г., изучая
действие различных люминесцирующих веществ на фотопластинку, в
частности солей урана, открыл неизвестное излучение, присущее самой
урановой соли и ничего общего не имеющее с люминесцирующим излу-
чением. Это явление самопроизвольного излучения солями урана лучей
особой природы было названо радиоактивностью. За открытие явле-
ния естественной радиоактивности урана Беккерель в 1903 г. удостоен
Нобелевской премии. Пропуская бета-лучи через пересекающиеся элек-
трическое и магнитное поля, первый измерил отношение заряда к массе
бета-частиц и установил, что оно такого же порядка, как и для частиц
катодных лучей (1900). Обнаружил в 1901 г. (независимо от П.Кюри)
физиологическое действие радиоактивного излучения, а также его спо-
собность ионизировать газ.
Член ряда академий наук.
БОР Нильс Хендрик Давид (7.Х 1885 - 18.XI 1962) — выдающийся
датский физик-теоретик, один из создателей современной квантовой фи-
зики, член Датского королевского общества (1917), президент с 1939.
Родился в Копенгагене. Окончил Копенгагенский ун-т (1908). В 1911—
12 гг. работал в Кембридже у Дж. Дж. Томсона, в 1912-13 гг. — в Манче-
стере у Э. Резерфорда. С 1916 г. — профессор Копенгагенского ун-та и с
1920 г. — директор созданного им Института теоретической физики, ко-
торый стал международным центром физиков-теоретиков и сыграл боль-
шую роль в международном общении ученых (Ин-т Нильса Бора).
Как ученый Бор формировался в очень острый для физики период,
когда она вплотную подошла к изучению мира атомных процессов. Ра-
боты М. Планка, А. Эйнштейна, анализ спектров излучения атомов уже
показали необычность закономерностей микромира. Был накоплен ог-
ромный экспериментальный материал, весьма противоречивый в свете
ранее известных законов. Важная заслуга Бора состояла в том, что он
Приложение. Краткие биографические справки о физиках 585
нашел новый подход для создания физической картины атомных процес-
сов. Бор сформулировал идею о дискретности энергетических состояний
атомов, в свете новых идей построил атомную модель, открыв условия
устойчивости атомов, и объяснил большой круг явлений.
В 1913 г., исходя из идеи М. Планка о квантовании энергии, Бор
на основе модели атома Резерфорда создал свою теорию водородоподоб-
ного атома, основанную на двух постулатах, которые прямо противоре-
чили классическим представлениям и законам. Бор установил наличие в
атоме стационарных разрешенных орбит, двигаясь по которым электрон,
вопреки законам классической электродинамики, не излучает энергию,
однако может скачком перейти на более близкую к ядру также разрешен-
ную орбиту, испустив при этом квант энергии, равный разности энергий
атома в стационарных состояниях. Теория Бора позволила объяснить
целый ряд сложных вопросов строения атома и фактов, чего не в со-
стоянии была сделать классическая физика. В частности, Бор нашел
основные законы спектральных линий и электронных оболочек атомов,
объяснил (1923) особенности периодической системы химических эле-
ментов, предложив свой вариант изображения периодической системы
элементов, и в том же году пришел к представлению об оболочечной
структуре атома, основанной на классификации электронных орбит по
главному и азимутальному квантовым числам. За создание квантовой
теории планетарного атома в 1922 г. удостоен Нобелевской премии.
В 1918 г. сформулировал важный для новой атомной теории прин-
цип соответствия, показывающий, когда именно существенны квантовые
ограничения, а когда достаточно и классической физики. Многое сделал
Бор для становления и интерпретации квантовой механики, возникшей
в 20-х годах XX века. Усилиями Бора и его сотрудников и учеников была
создана система физических идей квантовой механики. В 1927 г. сфор-
мулировал важный для ее понимания принцип дополнительности, что
привело к его известным дискуссиям с А.,Эйнштейном о детерминизме.
Бор много сделал для развития ядерной физики. Он — автор теории
составного ядра (1936), один из создателей капельной модели ядра (1936)
и теории деления атомного ядра (1939). Совместно с Дж. Уилером (неза-
висимо от Я.И. Френкеля) дал количественную интерпретацию деления
ядра, введя так называемый параметр деления, предсказал спонтанное
деление урана.
Создал большую интернациональную школу физиков (Ф. Блох,
О.Бор, В.Вайскопф, X. Казимир, 0. Клейн, X. Крамере, Л.Д. Ландау,
К. Мёллер, У. Нишина, Л. Розенфельд, С.Росселанд, Дж. Уилер и др.).
Почетный член более 20 академий наук мира, в том числе иностран-
ный член АН СССР (1929).
БОРН Макс (11.XII 1882 - 5.1 1970) — немецкий физик-теоретик,
один из пионеров квантовой физики. Родился в Бреслау (ныне Вроц-
лав). Окончил Гёттингенский ун-т (1907). В 1915-20 гг. - профессор
Берлинского и Франкфуртского ун-тов, в 1921-33 гг. — Гёттингенского.
В 1933 г. эмигрировал в Англию, где работал до 1936 г. в Кембридже.
На протяжении 1936-53 гг. возглавлял кафедру теоретической физики
в Эдинбургском ун-те (Шотландия). С 1954 г. жил в Гёттингене (ФРГ).
Основные работы посвящены динамике кристаллической решетки,
термодинамике кристаллов, квантовой теории, кинетической теории
конденсированных газов и жидкостей, теории относительности, атом-
586 Приложение. Краткие биографические справки о физиках
ной физике. Один из создателей квантовой (матричной) механики, со-
вместно с В. Гейзенбергом и П. Иорданом разработал формализм мат-
ричной механики (1926). Дал (1926) статистическую интерпретацию
волновой функции, показав, что квадрат ее модуля следует понимать как
меру плотности вероятности нахождения частицы в данной точке про-
странства (Нобелевская премия, 1954). М. Борн и его школа сразу же
применили новую квантовую механику к различным проблемам стро-
ения атома, молекулярной физики, физики твердого тела. Предложил
способ расчета электронных оболочек атома, разработал в 1926 г. ме-
тод решения квантовомеханических задач о столкновении частиц, осно-
ванный на теории возмущений (борновское приближение). Совместно
с Н. Винером ввел (1926) в квантовую механику понятие оператора. Со-
вместно с Р. Оппенгеймером разработал в 1927 г. теорию строения двух-
атомных молекул, с Л. Инфельдом в 1934 г. — феноменологическую
модель классической электродинамики, устраняющей бесконечность
энергии точечного заряда (теория Борна-Инфельда). Является одним
из создателей современной теории жидкостей.
Борн всегда видел связь физики с принципиальными философскими
проблемами, много занимался анализом вклада физики в теорию позна-
ния, стремился философски осмыслить новый этап развития физиче-
ской науки. Все это сделало Борна пионером новой физики и одним из
ее создателей. Создал гёттингенскую физическую школу (В. Гейзенберг,
В. Паули, В.Гайтлёр, Ф. Хунд, П. Иордан, М. Гёпперт-Майер, Г. Герцберг,
Э. Хюккелъ, М. Дельбрюк, Л. Нордгейм, Ю. Вигнер и др.).
Почетный член многих академий наук и научных обществ, в том
числе иностранный член АН СССР (1934).
БРЭГГ Генри (2.VII 1862 - 12.III 1942) — английский физик, член
Лондонского королевского об-ва (1907), его президент в 1935-40 гг. Ро-
дился в Уигтоне. Окончил Кембриджский ун-т 1885). В 1885-1908 гг. —
профессор Аделаидского (Австралия), в 1909-15 гг. — Лидского, в 1915—
23 гг. — Лондонского ун-тов. С 1923 гг. — профессор и директор Коро-
левского ин-та (Лондон).
Работы посвящены исследованию рентгеновских лучей, проникаю-
щей и ионизирующей способности быстрых заряженных частиц, рент-
геноструктурному анализу, рентгеновской спектроскопии. Используя
явление дифракции рентгеновских лучей на кристаллах, совместно со
своим сыном Л. Брэггом впервые осуществил (1912) исследование кри-
сталлических структур, дал экспериментальное доказательство перио-
дичности атомной структуры кристаллов. Анализируя отражение мо-
нохроматического рентгеновского излучения от различных кристаллов,
определил длину волны излучения, тип симметрии и параметры кристал-
лической решетки исследуемой структуры. Разработал метод рентгено-
графического анализа кристаллических структур — метод вращающе-
гося кристалла. Для экспериментального исследования рентгеновских
спектров сконструировал рентгеновский спектрометр (1913). Экспери-
менты Брэггов по изучению структур кристаллов положили начало рент-
геноструктурному анализу и рентгеновской спектроскопии. За большой
вклад в изучение структуры кристаллов с помощью рентгеновских лучей
Г. Брэгг (вместе с сыном) удостоен в 1915 г. Нобелевской премии. Изу-
чал тормозную способность различных элементов, установил, что альфа-
частицы имеют определенный пробег; исследовал удельную ионизацию,
Приложение. Краткие биографические справки о физиках 587
создаваемую альфа-частицами в воздухе на различных расстояниях от
источника.
Автор нескольких научно-популярных книг, в т. ч. переведенных
на русский язык. Член ряда академий. Медали Б.Румфорда (1916),
Копли (1930). В 1923-30 гг. — президент Международного союза чистой
и прикладной физики.
БРЭГГ Лоуренс (31.III 1890 - 1.VII 1971) — английский физик,
член Лондонского королевского общества (1921). Сын Г. Брэгга. Ро-
дился в Аделаиде (Австралия). Окончил Аделаидский (1908) и Кем-
бриджский (1911) ун-ты. В 1919-37 гг. — профессор Манчестерского
ун-та, в 1937-38 гг. — директор Национальной физической лаборато-
рии, с 1938-53 гг. — профессор и директор Кавендишской лаборатории,
в 1954-66 гг. — директор Королевского ин-та.
Научные исследования относятся к теории дифракции рентгеновских
лучей, рентгеноструктурному анализу, металлургии, вопросам полимор-
физма и фазовых переходов в металлах и сплавах, химии белка, исто-
рии физики. В 1912 г., независимо от Ю.В. Вульфа, вывел уравнение,
связывающее длину волны рентгеновского излучения с периодом кри-
сталлической решетки кристалла (формула Брэгга-Вульфа) и лежащее в
основе спектроскопии рентгеновских лучей. Усовершенствовал методы
рентгеноструктурного анализа, разработал методы расшифровки слож-
ных кристаллических структур, определил структуры многих силикатов.
Используя рентгеновские лучи, получил в 1939 г. оптическое изобра-
жение атомной структуры кристалла. Рентгеновский микроскоп Брэгга
послужил отправной точкой при разработке идей Д. Габора по созданию
голографии. Л. Брэгг совместно с Дж. Берналом и Л. Полингом заложил
фундамент структурного анализа белка.
Возглавляя Кавендишскую лабораторию, способствовал развитию в
послевоенные годы новых научных направлений — радиоастрономии и
молекулярной биологии.
Нобелевская премия (1915). Медали Д.Юза (1931), Копли (1966),
Королевская медаль (1946).
ВИН Вильгельм (13.1 1864 - 30.VIII 1928) — немецкий физик, чл.-
кор. Берлинской АН. Родился в Гафкене. Окончил Берлинский ун-т
(1886). В 1890-1902 гг. был ассистентом Г. Гельмгольца в Физико-
техническом ин-те (Берлин), в 1900-20 гг. — профессор Вюрцбургского,
в 1920-28 гг. — Мюнхенского ун-тов.
Работы относятся к теории теплового излучения, оптике, термо-
динамике, гидродинамике, изучению электрических разрядов в газах.
В 1893 г. распространил понятия температуры и энтропии на тепло-
вое излучение, показал, что максимум излучения в спектре абсолютно
черного тела с увеличением температуры смещается в сторону коротких
волн (закон смещения Вина). В 1895 г. совместно с О. Люммером развил
идеи Г. Кирхгофа об абсолютно черном теле, показал, что его можно реа-
лизовать в виде полости с внутренними зеркальными стенками и узким
отверстием. В 1896 г., исходя из классических представлений, вывел
закон распределения энергии в спектре черного тела (закон излучения
Вина), который оказался правильным лишь в случае коротких волн. Эти
два закона Вина сыграли значительную роль в развитии квантовой тео-
рии (Нобелевская премия, 1911).
588 Приложение. Краткие биографические справки о физиках
В 1902 г. установил отклонение каналовых лучей в электрическом и
магнитном полях и измерил величину отношения их заряда к массе, до-
казал также, что их заряд положительный. Исследовал электрическую
проводимость в металлах и в 1913 г. пришел к выводу, что скорость
свободных электронов в металлах не зависит от температуры. Изучал
катодные и рентгеновские лучи, в 1907 г. измерил длину волны рентге-
новского излучения.
ВУЛЬФ Георгий (Юрий) Викторович (22.VI 1863 - 25.XII 1925) —
российский кристаллограф и кристаллофизик, чл.-кор. АН СССР (1921).
Родился в Нежине. Окончил Варшавский ун-т (1885), где работал до
1909 г. (в 1907-08 гг. — профессор Казанского ун-та). С 1909 г. — в
Московском ун-те. В 1911 г. оставил ун-т в знак протеста против реак-
ционных действий министра просвещения Кассо и перешел в Народный
ун-т им. А.Л. Шанявского. Возвратился в Московский ун-т профессором
в 1917 г.
Основные работы в области кристаллографии, кристаллофизики, кри-
сталлооптики, рентгеноструктурного анализа, минералогии. Предложил
способ вывода всех видов симметрии кристаллов, разработал графиче-
ский метод обработки результатов измерения кристаллов с помощью сте-
реографической сетки (сетка Вульфа). Обнаружил (1895) влияние силы
тяжести на форму кристалла во время его роста из раствора, изобрел
вращающий кристаллизатор и разработал метод получения кристаллов
правильной формы. Установил закон процесса роста кристаллов, со-
гласно которому скорости роста граней кристалла пропорциональны их
удельным поверхностным энергиям (закон Вульфа). В 1913 г. незави-
симо от Л. Брэгга вывел условия интерференционного отражения рент-
геновских лучей от кристаллов (формула Брэгга-Вульфа), положенные в
основу рентгеновской спектроскопии. Первый в России начал рентгено-
структурные исследования.
ГААЗ (де Гааз) Вандер Иоханес (2I.III 1878 - 26.IV 1960) — ни-
дерландский физик, член Нидерландской АН (1922). Родился в Лисе.
В 1895-1917 гг. работал в Лейдене, Берлине, Потсдаме, в Тейлоров-
ском музее в Гарлеме, в 1917-22 гг. — профессор Высшей техниче-
ской школы в Делфте, в 1922- 24 гг. — Гронингенского ун-та, в 1924-
48 гг. — профессор Лейденского ун-та и директор криогенной лаборато-
рии им. X. Камерлинг-Оннеса.
Работы посвящены физике низких температур и сверхпроводимо-
сти. Исследовал эффекты при низких температурах, сверхпроводимость
магнетиков, достиг рекордно низкой температуры 0,0002 К. В 1915 г. со-
вместно с А. Эйнштейном экспериментально обнаружил и теоретически
объяснил явление, заключающееся в том, что тело при намагничива-
нии вдоль некоторой оси приобретает относительно нее вращательный
импульс, пропорциональный намагниченности (эффект Эйнштейна-де
Гааза). В 1930 г. вместе с Л.В. Шубниковым открыл при низких темпе-
ратурах зависимость электрического сопротивления висмута от обратной
величины магнитного поля (эффект Шубникова-де Гааза), а в 1931 г. с
П. ван Альфеном — зависимость магнитной восприимчивости металлов
от напряженности магнитного поля (эффект де Гааза-ван Альфена).
Медаль Б.Румфорда (1934).
Приложение. Краткие биографические справки о физиках 589
ГАМИЛЬТОН Уильям Роуан (4.VIII 1805 - 2.IX 1865) — ирланд-
ский математик и физик, член Ирландской АН (1832), президент в 1837-
45 гг. Родился в Дублине. Окончил Тринити-колледж Дублинского ун-та
(1827). С 1827 г. профессор Дублинского ун-та и директор астрономи-
ческой обсерватории.
Физические исследования в области оптики и механики. Разрабо-
тал теорию оптических явлений («математическую оптику»). Установил
(1834) аналогию между классической механикой и геометрической опти-
кой. Иными словами, показал, что математический аппарат, разрабо-
танный им для решения задач геометрической оптики, основанной на
применении так называемой характеристической функции (функции Га-
мильтона), можно использовать в механике. Предсказал в 1828 г. явле-
ние конической рефракции в кристалле, которое было вскоре доказано
экспериментально и сыграло определенную роль в утверждении волновой
теории света. Аналогия между корпускулярной и волновой оптикой, раз-
витая Гамильтоном, долгое время была почти совсем забыта, и только
через 100 лет ее использовал Э. Шредингер при разработке волновой ме-
ханики.
Гамильтон распространил свою теорию оптических явлений на меха-
нику, разработав ее новые общие принципы, в частности вариационный
принцип. Аналитический аппарат механики, открытый Гамильтоном на
основе синтеза проблем оптики и механики, получил дальнейшее раз-
витие в работах немецкого математика К. Якоби и М.В. Остроградского.
Матричный аппарат Гамильтона используется при решении задач кван-
товой механики. В 1839 г. ввел понятие групповой скорости (дол-
гое время этот факт приписывался Дж. Стоксу и Дж. Рэлею). Построил
теорию гиперкомплекных чисел — кватернионов, которая в настоящее
время используется в теории симметрии. Член ряда академий наук, в
том числе Петербургской АН (1837).
Королевская медаль (1836).
ГЕЙЗЕНБЕРГ Вернер Карл (5.XII 1901 - 1.II 1976) — немецкий
физик-теоретик, один из создателей квантовой механики. Родился в
Вюрцбурге. Окончил Мюнхенский (1923) и Гёттингенский (1924) ун-ты.
В 1927-41 гг. — профессор теоретической физики Лейпцигского ун-та,
в 1941-45 гг. — директор Ин-та физики кайзера Вильгельма и профес-
сор Берлинского ун-та. В 1946-58 гг. — директор Физического ин-та и
профессор Гёттингенского ун-та. С 1958 г. — директор Ин-та физики и
астрофизики и профессор Мюнхенского ун-та.
Работы относятся к квантовой механике, квантовой электродина-
мике, релятивистской квантовой теории поля, теории ядра, магнетизму,
физике космических лучей, теории элементарных частиц, философии
естествознания. В 1925 г. разработал матричную механику — первый
вариант квантовой теории (Нобелевская премия, 1932). В 1926 г. объ-
яснил отличие двух систем термов для пара- и ортогелия: паратермы
соответствуют симметричным, а ортотермы — антисимметричным ре-
шениям волнового уравнения. В 1927 г. сформулировал принцип не-
определенностей, ограничивающий применение к микрообъектам клас-
сических понятий и представлений.
Совместно с П. Дираком выдвинул в 1928 г. идею обменного взаимо-
действия, введя обменные силы, и независимо от Я.И. Френкеля разра-
ботал первую квантовомеханическую теорию ферромагнетизма, основан-
590 Приложение. Краткие биографические справки о физиках
ную на обменном взаимодействии электронов (модель локализованных
спинов). В 1929 г. совместно с В.Паули предпринял попытку дать фор-
мулировку квантовой электродинамики, введя общую схему квантования
полей. Развил (1934-36) теорию дырок Дирака. Вслед за ним постули-
ровал (1934) существование эффекта поляризации вакуума.
Независимо от Д.Д. Иваненко пришел к протонно-нейтронной модели
ядра (1932). В 1932 г. ввел понятие изотопического спина и построил
теорию ядерных сил, развив идею обменного взаимодействия. В 1943 г.
в квантовой теории поля ввел матрицу рассеяния (S-матрицу), явля-
ющуюся важным инструментом для описания взаимодействия частиц.
В последние годы усилия Гейзенберга были направлены на создание еди-
ной теории поля. В 1958 г. проквантовал нелинейное спинорное уравне-
ние Иваненко-Гейзенберга. Немало его работ посвящено философским
проблемам физики, в частности теории познания.
Почетный член многих академий наук и научных обществ. Медали
М. Планка, К. Маттсучи и др.
ГЕРЦ Густав Людвиг (22.VII 1887 - 30.X 1975) — немецкий физик,
член АН ГДР. Племянник Генриха Герца. Родился в Гамбурге. Окон-
чил Мюнхенский и Берлинский (1911) ун-ты. В 1913-20 гг. работал
в Берлинском ун-те; в 1920-25 гг. — в лаборатории завода Филлипса
(Эйдховен), в 1925-27 гг. — профессор ун-та в Галле, в 1928-35 гг. —
Высшей технической школы в Берлине, в 1935-45 гг. возыавлял научно-
исследовательскую лабораторию Сименса в Берлине, в 1945-54 гг. рабо-
тал в СССР, в 1954-62 гг. — профессор и директор Физического ин-та
Лейпцигского ун-та.
Основные исследования в области спектроскопии. В 1912-14 гг. со-
вместно с Дж. Франком проводил эксперименты по столкновению элек-
тронов с атомами газа (опыты Франка-Герца), в результате которых
впервые было доказано существование в атомах дискретных уровней
энергии, что непосредственно подтверждало квантовую теорию атома
Бора (Нобелевская премия, 1925).
Изучал рентгеновские спектры поглощения. Установил в 1920 г. пра-
вило для иррегулярных дублетов (правило Герца). Выполнил ряд иссле-
дований по диффузии, электронной эмиссии, разрядам в газах, физике
плазмы, ультразвуку и полупроводникам. Разработал метод разделения
изотопов путем диффузии.
Член академий наук ряда стран, иностранный член АН СССР (1958).
Государственная премия СССР (1951). Национальная премия ГДР (1955).
ДАЛЬТОН Джон (6.IX 1766 - 27.VII 1844) — английский химик
и физик, член Лондонского королевского общества (1822). Родился в
Иглсфилде. Образование получил самостоятельно. Был учителем мате-
матики в Манчестере.
Физические исследования в области молекулярной физики. Наблю-
дал (1800) повышение температуры воздуха при его адиабатическом сжа-
тии и понижение — при расширении. Исследовал свойства водяного
пара, первый указал (1801) на различие паров насыщенных и перегре-
тых. В 1801 г. открыл закон парциальных давлений газов, в 1803 г. —
закон зависимости растворения газов от их парциального давления (за-
кон Дальтона), в 1801 г. независимо от Ж. Гей-Люссака — один из га-
зовых законов: при постоянном давлении все газы с повышением тем-
пературы расширяются одинаково.
Приложение. Краткие биографические справки о физиках 591
Большая заслуга Дальтона в развитии атомистических представле-
ний применительно к химии. Установил, что атомы одного и того же хи-
мического элемента имеют одинаковые свойства. Ввел понятие атомного
веса и составил первую таблицу атомных весов (атомных масс) элемен-
тов (1803). Предложил обозначения для атомов химических элементов,
которые не получили распространения. В 1794 г. впервые описал дефект
зрения, получивший название дальтонизма.
Член Парижской АН.
ДЕВИССОН Клинтон Джозеф (22.Х 1881 - 1.II 1958) — американ-
ский физик, член Национальной АН. Родился в Блумингтоне. Окончил
Чикагский (1908) и Принстонский (1911) ун-ты. В 1911-17 гг. рабо-
тал в Технологическом ин-те Карнеги, в 1917-46 гг. — в лабораториях
Бэлл-Телефон, в 1946-54 гг. — визит-профессор Виргинского ун-та.
Работы относятся к термоэлектронной и термоионной эмиссии, элек-
тронной микроскопии, тепловому излучению, физике кристаллов, кван-
товой теории. Вместе со своим сотрудником Л. Джермером открыл в
1927 г. явление дифракции электронов (независимо от Дж.П. Томсона)
на кристалле никеля, что было экспериментальным подтверждением
теории де Бройля о волновых свойствах материи (Нобелевская премия,
1937). Развил метод электронной фокусировки.
Медали Д. Юза (1935), Э.Грессона (1931) и др.
ДЕМПСТЕР Артур Джеффри (14.VIII 1886 - 11.III 1950) — канад-
ский физик и химик. Родился в Торонто (Канада). Окончил ун-т в
Торонто (1909). В 1911-14 гг. совершенствовал знания в Гёттингене,
Мюнхене, Вюрцбурге. С 1914 г. жил в США. С 1919 г. работал в Чикаг-
ском ун-те (с 1927 г. — профессор).
Работы относятся к масс-спектрометрии, химии изотопов, электри-
ческим разрядам в газах, физике ускорителей. Построил первый масс-
спектрометр (1918) и первый масс-спектрограф с двойной фокусиров-
кой, открыл ряд изотопов (калия, лития, магния, кальция и цинка),
в 1935 г. — уран-235. Построил кривую упаковочных коэффициентов
для тяжелых элементов. Предложил вариант прямого метода ускорения
ионов (1932).
ДЖИНС Джеймс Хопвуд (11.IX 1877 - 16.IX 1946) — английский
физик и астрофизик, член Лондонского королевского общества (1906).
Родился в Лондоне. Окончил Кембриджский ун-т (1900), работал там же
в 1901-04 гг. и 1910-12 гг.; в 1905-09 гг. — профессор Принстонского
ун-та, в 1923-44 гг. — научный сотрудник обсерватории Маунт-Вилсон
(США); в 1924-29 гг. и 1934-39 гг. — профессор Королевского ин-та
(Лондон).
Основные физические исследования посвящены кинетической тео-
рии газов и теории теплового излучения. Широкой популярностью в свое
время пользовалась его работа «Динамическая теория газов», выдержав-
шая несколько изданий (первое в 1904). В теории теплового излучения
абсолютно черного тела, использовав метод Рэлея равномерного распре-
деления энергии, вывел в 1905 г. формулу для плотности энергии (закон
Рэлея-Джинса). Эта формула, построенная на основе классической фи-
зики, оказалась неприменимой ко всему спектру излучения, но не про-
тиворечила эксперименту в диапазоне длинных волн. Работы Джинса
592 Приложение. Краткие биографические справки о физиках
посвящены также квантовой теории, математической теории электриче-
ства и магнетизма, теоретической механике, теории относительности.
Астрофизические исследования Джинса относились к фигурам рав-
новесия вращающихся жидких тел, строению и эволюции звезд и их си-
стем, происхождению Солнечной системы. В 20-30-е годы XX столетия
широкую известность приобрела его космогоническая гипотеза происхо-
ждения нашей планетной системы. Согласно этой гипотезе, Солнечная
система образовалась вследствие того, что другая звезда, проходя близко
от Солнца, вырвала из него сгусток материи, из которого впоследствии
сформировались планеты.
Написал много научно-популярных книг.
Королевская медаль (1919), медаль Б. Франклина (1931) и др.
ДИРАК Поль Адриен Морис (8.VIII 1902 - 20.Х 1984) — английский
физик-теоретик, один из создателей квантовой механики, член Лондон-
ского королевского общества (1930). Родился в Бристоле. Окончил Бри-
стольский (1921) и Кембриджский (1926) ун-ты. В 1932-68 гг. — про-
фессор Кембриджского ун-та.
Работы относятся к квантовой механике, квантовой электродина-
мике, квантовой теории поля, теории элементарных частиц, теории гра-
витации. Разработал (1926-27) математический аппарат квантовой ме-
ханики — теорию преобразований, предложил (1927) метод вторичного
квантования. В 1927 г. применил принципы квантовой теории к элек-
тромагнитному полю и получил первую модель квантованного поля, по-
ложив начало квантовой электродинамике. Предсказал тождественность
квантов вынужденного и спонтанного излучений, лежащую в основе
квантовой электроники (1927). Совместно В. Гейзенбергом в 1928 г. от-
крыл обменное взаимодействие, введя обменные силы.
Построил в 1928 г. релятивистскую теорию движения электрона,
предложив волновое уравнение, описывающее движение электрона и удо-
влетворяющее релятивистской инвариантности (релятивистская кван-
товая механика). В теории Дирака гармонически объединяются теория
относительности, кванты и спин, казавшиеся до этого понятиями неза-
висимыми. Из теории Дирака следовал важный вывод, что электрон
может иметь отрицательные значения энергии. Исходя из этого, предпо-
ложил существование положительно заряженного электрона, или пози-
трона, который был открыт в 1932 г. Построил теорию дырок (1930), в
1931 г. предсказал существование античастиц, рождение и аннигиляцию
электронно-позитронных пар. В 1931 г. выдвинул гипотезу о существо-
вании элементарного магнитного заряда (монополь Дирака), в 1933 г. —
антивещества. Постулировал эффект поляризации вакуума (1933). За
создание квантовой механики вместе с Э. Шредингером в 1933 г. был
удостоен Нобелевской премии.
Независимо от Э. Ферми разработал в 1926 г. статистику частиц с
полуцелым спином (статистика Ферми-Дирака). В 1942 г. ввел понятие
индефинитной метрики с целью устранения бесконечности собственной
энергии электрона. В 1962 г. разработал теорию мюона, в которой мюон
описывается как колебательное состояние электрона. Работал над про-
блемой квантования гравитационного поля.
Почетный член ряда академий наук и научных обществ, иностран-
ный член АН СССР (1931). Королевская медаль (1939), медаль Копли
(1952), премия Р. Оппенгеймера и др.
Приложение. Краткие биографические справки о физиках 593
ЗАВОЙСКИЙ Евгений Константинович (28.IX 1907 - 9.Х 1976) —
советский физик-экспериментатор, академик (1964, чл.-корр. 1953). Ро-
дился в Могилеве-Подольском. Окончил Казанский ун-т (1930), где в
1933-47 гг. заведовал кафедрой физики. С 1947 г. работал в Ин-те
атомной энергии им. И.В. Курчатова.
Работы относятся к радиоспектроскопии, проблемам новой техники,
физике плазмы. Изучал различные физические явления при помощи ра-
диотехнических методов, в частности поглощение энергии радиочастот-
ного поля растворами электролитов и газами. В 1944 г. открыл элек-
тронный парамагнитный резонанс (Ленинская премия, 1957) и затем
(1944-47) установил его основные закономерности, изучил различные
типы парамагнетиков. В 1947 г. независимо от Дж. Гриффитса обнару-
жил ферромагнитный резонанс.
Вместе с М.М. Бутсловым разработал метод электронно-оптической
хронографии для исследования сверхбыстрых процессов (10“12-10-14 с).
Предложил и построил первую люминесцентную камеру для изучения
ядерных процессов, разработал способы регистрации ионизирующих из-
лучений, метод поляризации ядер с использованием сдвига Лэмба.
С 1958 г. занимался изучением плазмы в связи с проблемой упра-
вляемого термоядерного синтеза. Независимо от Я.Б. Файнберга и дру-
гих открыл (1961) эффекты аномально высокого сопротивления плазмы
при больших плотностях тока и ее быстрого (турбулентного) нагрева.
Независимо от У. Беннета указал (1968) на возможность осуществления
управляемого термоядерного синтеза с помощью релятивистских элек-
тронных пучков.
Герой Социалистического Труда (1969). Государственная премия
СССР (1949).
ЗЕЕМАН Питер (25.V 1865 - 9.Х 1943) — нидерландский физик,
член Нидерландской АН. Родился в Зоннемайре. Окончил Лейденский
ун-т (1890), где преподавал. С 1897 г. работал в Амстердамском ун-те
(с 1900 г. — профессор и с 1908 г. — директор Физического ин-та).
Работы относятся к оптике, магнитооптике, атомной спектроскопии.
В 1896 г. открыл эффект Зеемана — явление расщепления спектраль-
ных линий под влиянием магнитного поля (Нобелевская премия, 1902).
Измерял (1914-15) скорость света в быстро движущемся стержне, экспе-
риментально доказал (1917) с высокой точностью равенство инертной и
гравитационной масс. Определил удельный электрический заряд. Раз-
работал метод измерения коэффициента поглощения электромагнитных
волн. Исследовал броуновское движение.
Медаль Б. Франклина.
КИРХГОФ Густав Роберт (12.III 1824 - 17.Х 1887) — немецкий фи-
зик, член Берлинской АН (1875). Родился в Кенигсберге. Окончил Ке-
нигсбергский ун-т (1846), профессор Бреславльского (с 1850), Гейдель-
бергского (с 1854) и Берлинского (с 1875) ун-тов.
Работы посвящены электричеству, механике, оптике, математиче-
ской физике, теории упругости, гидродинамике. В 1845-47 гг. открыл
закономерности в протекании электрического тока в разветвленных элек-
трических цепях (правила Кирхгофа), в 1857 г. построил общую теорию
движения тока в проводниках. Совместно с Р. Бунзеном в 1859 г. разра-
594 Приложение. Краткие биографические справки о физиках
ботал метод спектрального анализа и открыл новые элементы — цезий
(1860) и рубидий (1861). Установил (1859) один из основных законов
теплового излучения, согласно которому отношение испускательной спо-
собности тела к поглощательной не зависит от природы излучающего
тела (закон Кирхгофа), предложил (1862) концепцию черного тела и дал
его модель. Открыл обращение спектров (1860), объяснил происхождение
фраунгоферовых линий, высказал предположение, что Солнце состоит из
раскаленной жидкой массы, окруженной атмосферой пара.
Развил (1882) строгую теорию дифракции. Усовершенствовал тео-
рию магнетизма Пуассона. Исследовал также упругость твердых тел, ко-
лебания пластин и дисков, форму свободной струи жидкости, движение
тела в жидкой среде.
Член Петербургской АН (1862).
КОМПТОН Артур Холли (10.IX 1892 - 15.III 1962) — американский
физик, член Национальной АН, 1927). Родился в Вустере (Огайо). Окон-
чил Вустерский колледж (1913) и Принстонский ун-т (1914). В 1920—
23 гг. и 1953-61 гг. — профессор ун-та Дж. Вашингтона (Сент-Луис),
в 1923-45 гг. — профессор Чикагского ун-та, в 1942-45 гг. возглавлял
Металлургическую лабораторию. Работы посвящены атомной и ядерной
физике, физике космических лучей. Открыл в 1922 г. явление измене-
ния длины волны рентгеновского излучения вследствие рассеяния его
электронами вещества (эффект Комптона) и независимо от П. Дебая по-
строил его теорию (Нобелевская премия, 1927). Тем самым было полу-
чено прямое доказательство существования импульса фотона. Наблюдал
явление полного внутреннего отражения рентгеновских лучей и разрабо-
тал метод измерения длины волны рентгеновского излучения. В 1932 г.
открыл (независимо от Я. Клея) широтный эффект космических лучей
и наличие в них заряженных частиц.
Член многих академий наук. Медали Б. Румфорда (1927), К. Маттеу-
чи (1933), Б. Франклина (1940, 1945), Д.Юза (1940) и др.
КЮРИ Пьер (15.V 1859 - 19.IV 1906) — французский физик, один из
основателей учения о радиоактивности, член Парижской АН (1905). Ро-
дился в Париже. Окончил Парижский ун-т (1877), где в 1878-83 гг. рабо-
тал ассистентом, в 1883-1904 гг. — в Школе физики и химии (с 1895 г. —
зав. кафедрой). В 1895 г. женился на М. Склодовской. С 1904 г. — про-
фессор Парижского ун-та.
Важнейшие исследования посвящены физике кристаллов, магнетиз-
му, радиоактивности. В 1880 г. вместе со своим братом минерало-
гом Ж. Кюри открыл пьезоэлектрический эффект, а также обратный эф-
фект — возникновение упругой деформации кристалла при сообщении
ему электрического заряда. Используя открытый пьезоэлектрический
эффект, они сконструировали высокочувствительный прибор для изме-
рения малых количеств электричества и слабых токов. В 1884-85 гг.
П. Кюри развил теорию образования кристаллов и исследовал законы
симметрии в них, в частности впервые ввел (1885) понятие поверхност-
ной энергии граней кристалла и сформулировал общие закономерности
роста кристаллов. Предложил (1894) принцип, дающий возможность
определить симметрию кристалла, находящегося под внешним воздей-
ствием (принцип Кюри).
Приложение. Краткие биографические справки о физиках 595
Осуществил исследования магнитных свойств, тел в широком диа-
пазоне температур. Установил в 1895 г. независимость магнитной вос-
приимчивости диамагнетиков от температуры и ее обратно пропорцио-
нальную зависимость от температуры для парамагнетиков (закон Кюри).
Открыл для железа существование температуры, выше которой у него ис-
чезают ферромагнитные свойства (точка Кюри) и скачкообразно изменя-
ются некоторые другие свойства, например удельная электропроводность
и теплоемкость (1895).
С 1897 г. научные интересы П. Кюри сосредоточиваются на изуче-
нии радиоактивности, где он вместе с М. Склодовской-Кюри сделал ряд
выдающихся открытий. В 1898 г. они открыли новые радиоактивные
элементы — полоний и радий, в 1899 г. — наведенную радиоактивность
и установили сложный характер радиоактивного излучения и его свойс-
тва. В 1901 г. Кюри обнаружил биологическое действие радиоактивного
излучения, в 1903 г. открыл количественный закон снижения радиоак-
тивности, введя понятие периода полураспада, и показал его независи-
мость от внешних условий. Исходя из этого, предложил использовать
период полураспада как эталон времени для установления абсолютного
возраста земных пород. В том же году вместе с А. Лабордом обнаружил
самопроизвольное выделение тепла солями радия, что явилось первым
наглядным свидетельством существования ядерной энергии. Выдвинул
гипотезу радиоактивного распада. Организовал промышленную добычу
радия на основе разработанной технологии извлечения радия из урано-
вой руды.
За исследования радиоактивности и открытие радия П. Кюри и
М. Склодовская-Кюри (вместе с А. Беккерелем) в 1903 г. были удосто-
ены Нобелевской премии.
Медаль Г. Дэви (1903). В честь Пьера и Марии Кюри назван искус-
ственный химический элемент — кюрий.
ЛАУЭ (фон ЛАУЭ) Макс Феликс Теодор (9.Х 1879 - 24.IV 1960) —
немецкий физик-теоретик, член Берлинской АН (1921). Родился в Пфаф-
фендорфе. Окончил Берлинский ун-т (1903), где работал ассистентом у
М. Планка, в 1909-12 гг. — в Мюнхенском ун-те, в 1912-14 гг. — про-
фессор Цюрихского ун-та, с 1919 г. — профессор Берлинского ун-та и с
1921 г. — заместитель директора Ин-та физики кайзера Вильгельма (до
октября 1943 г.). В 1945-46 гг. был интернирован в Англию. В 1946 г.
возвратился в Гёттинген, где до 1951 г. был заместителем директора Фи-
зического ин-та, а в 1951-59 гг. — директор Ин-та физической химии и
электрохимии (Берлин).
Работы относятся к оптике, кристаллофизике, сверхпроводимости,
теории относительности, квантовой теории, атомной физике, физике
твердого тела. В 1912 г. разработал теорию интерференции рентге-
новских лучей на кристаллах, предложив использовать кристаллы как
дифракционные решетки для рентгеновских лучей. В том же году тео-
рия получила экспериментальное подтверждение в опытах В. Фридриха и
П. Книппинга. Открытием явления интерференции (дифракции) рентге-
новских лучей была подтверждена их электромагнитная природа и уста-
новлено их место на шкале волн, доказана периодическая атомная струк-
тура кристаллов. Это открытие привело к созданию мощного способа
исследования структуры вещества — рентгене структурного анализа. За
открытие дифракции рентгеновских лучей Лауэ в 1914 г. удостоен Нобе-
596 Приложение. Краткие биографические справки о физиках
левской премии. Был активным популяризатором теории относительно-
сти и автором многих работ, особенно по теории тяготения. Занимался
также историей физики.
Иностранный член АН СССР.
ЛОРЕНЦ Хендрик Антон (18.VII 1853 - 4.II 1928) — нидерландский
физик-теоретик, создатель классической электронной теории, член Ни-
дерландской АН. Родился в Арнеме. Учился в Лейденском ун-те, в 1875 г.
защитил докторскую диссертацию «К теории отражения и преломления
света». В 1878-1913 гг. — профессор Лейденского ун-та и заведующий
кафедрой теоретической физики. С 1913 г. — директор физического ка-
бинета Тейлеровского музея в Гарлеме.
Работы в области электродинамики, термодинамики, статистической
механики, оптики, теории излучения, теории металлов, атомной физики.
Исходя из электромагнитной теории Максвелла-Герца и вводя в учение
об электричестве атомистику, создал (1880-1909) классическую элек-
тронную теорию электрических, магнитных и оптических свойств ве-
щества и электромагнитных явлений, базирующуюся на динамике дис-
кретных электрических зарядов (уравнения Лоренца-Максвелла). На
основе электронной теории объяснил целый ряд физических фактов и
явлений и предсказал новые.
Вывел формулу, связывающую диэлектрическую проницаемость с
плотностью диэлектрика, и зависимость показателя преломления веще-
ства от его плотности (формула Лоренца-Лоренца), дал выражение для
силы, действующей на движущийся заряд в электромагнитном поле (си-
ла Лоренца), объяснил зависимость электропроводности вещества от те-
плопроводности, развил теорию дисперсии света. Предсказал явление
расщепления спектральных линий в сильном магнитном поле и, когда
оно в 1896 г. было открыто П. Зееманом, разработал (1897) его теорию
(Нобелевская премия, 1902).
Для объяснения опыта Майкельсона-Морли выдвинул (1892) неза-
висимо от Дж. Фитцджеральда гипотезу о сокращении размеров тел в
направлении их движения (сокращение Лоренца-Фитцджеральда), ввел
(1895) понятие о местном времени, которое в движущихся телах про-
текает иначе, чем в покоящихся. Разработал электродинамику движу-
щихся тел. В 1904 г. вывел формулы, связывающие между собой про-
странственные координаты и моменты времени одного и того же события
в двух различных инерциальных системах отсчета (преобразования Ло-
ренца), которые позволяют получить все кинематические эффекты спе-
циальной теории относительности. В 1904 г. получил формулу зависи-
мости массы электрона от скорости.
Исследования Лоренца посвящены также кинетической теории газов,
кинетике твердых тел, электронной теории металлов, созданной им в
1904 г. Оказал значительное влияние на молодое поколение физиков. По
мировоззрению был материалистом, активно боролся против проявлений
идеализма в физике.
Член многих академий наук и научных обществ, в частности ино-
странный член АН СССР (1925). Организатор и председатель (1911-27)
Сольвеевских конгрессов физиков.
МАЛЛИКЕН Роберт Сандерсон (07.VI 1896 - 31.X 1986) — амери-
канский физик и химик. Родился в Ньюберипорте (Массачусетс).
Приложение. Краткие биографические справки о физиках 597
Интерес к атомной физике проявлял с детства, при окончании сред-
ней школы написал сочинение «Электрон: что это такое и как он себя
ведет».
После окончания Массачусетсского технологического ин-та (1917) ра-
ботал в Горном бюро США, в войсках химической защиты и в «Нью-
Джерси цинк компани». В 1919 г. поступил в аспирантуру по химии в
Чикагском ун-те, а в 1921 г. получил докторскую степень по физической
химии, защитив диссертацию на тему о разделении изотопов ртути мето-
дом фракционной перегонки. Затем в Гарвардском университете исследо-
вал линейчатые спектры двухатомных молекул. Изучал спектроскопию
в Европе (1925). В 1926 г. возвратился в США в качестве ассистент-
профессора физики Нью-Йоркского ун-та. С 1928 г. адъюнкт-профессор,
профессор физики Чикагского ун-та (1928), с 1931 г. — полный профес-
сор, 1957-61 гг. — заслуженный профессор Чикагского ун-та. Во время
второй мировой войны занимал пост директора по учебной информаци-
онной работе над плутониевым проектом в Чикагском ун-те, а в 1955 г.
был атташе по науке в посольстве США в Лондоне.
Проводил исследования механизмов молекулярной структуры, соче-
тая спектроскопический анализ с теоретическими расчетами. Эта ра-
бота значительно расширила границы знаний об образовании химиче-
ских связей и особенно о поведении молекул, когда много электронов
и молекулярных групп активно взаимодействуют друг с другом. После
создания первых компьютеров Малликен с коллегами создали первыми
программы для расшифровки молекулярных структур. Разработал ко-
личественную теорию образования молекулярных химических связей,
установил форму и энергии орбиталей для многих соединений. В 1966 г.
Малликену была присуждена Нобелевская премия по химии за фунда-
ментальную работу по химическим связям и электронной структуре мо-
лекул, проведенную с помощью метода молекулярных орбиталей.
Медали Г.Н. Льюиса (1960), Т.У. Ричардса (1960), У. Гиббса (1965).
Член американской Национальной АН, Американской ассоциации со-
действия развитию науки и Американской академии наук и искусств,
иностранный член Лондонского королевского общества.
МИЛЛИКЕН Роберт Эндрус (22.III 1868 - 19.XII 1953) — американ-
ский физик-экспериментатор, член Национальной АН (1915). Родился
в Моррисоне. Окончил Оберлинский колледж (1891), продолжал учебу
в Колумбийском и Чикагском ун-тах, в последнем в 1895 г. получил
степень доктора философии. В 1896-21 гг. работал в Чикагском ун-те
(с 1910 г. — профессор), в 1921-45 гг. — в Калифорнийском технологи-
ческом ин-те.
Работы в области атомной физики, спектроскопии, физики космиче-
ских лучей. В 1906 г. разработал метод капель, который дал возмож-
ность измерять заряд отдельных электронов, и провел (1910-14) боль-
шое количество опытов по точному определению заряда электрона. Тем
самым экспериментально была доказана дискретность электрического
заряда и впервые достаточно точно измерена его величина. Проверил
уравнение Эйнштейна для фотоэффекта в области видимых и ультра-
фиолетовых лучей и определил постоянную Планка (1914). За работы в
области элементарных зарядов и фотоэлектрического эффекта удостоен
в 1923 г. Нобелевской премии.
598 Приложение. Краткие биографические справки о физиках
Выполнил большой цикл исследований космических лучей, в частно-
сти опыты (1921-22) с воздушными шарами с самопишущими электрос-
копами на высотах около 15,5 км. В 1925-27 гг. показал, что ионизиру-
ющее действие космического излучения уменьшается с глубиной, и с
определенностью подтвердил его внеземное происхождение, предложил
название «космические лучи». Исследуя траектории космических частиц
и их искривление, один из первых установил сложный характер косми-
ческих лучей, обнаружив в них альфа-частицы, быстрые электроны, про-
тоны, нейтроны, позитроны и гамма-кванты. Независимо от С.Н.Вер-
нова, открыл широтный эффект космических лучей в стратосфере.
В 1916-18 гг. — президент Американского физического общества.
Почетный член многих академий наук и научных обществ, том числе
иностранный чл.-корр. АН СССР (1924).
МОЗЛИ Генри (23.IX 1887 - 10.VIII 1915) — английский физик,
один из основоположников рентгеновской спектроскопии. Родился в Уэй-
муте. Окончил Оксфордский ун-т (1910). В 1910-14 гг. работал в Манче-
стерском ун-те под руководством Э. Резерфорда, а затем в Оксфордском.
Погиб в первую мировую войну.
Работы в области бета-, гамма- и рентгеновской спектроскопии. Ис-
следуя рентгеновские спектры химических элементов, открыл в 1913—
14 гг. закон, связывающий частоту спектральных линий характеристи-
ческого рентгеновского излучения с порядковым номером излучающего
элемента (закон Мозли). Этот закон имел большое значение для утвер-
ждения периодического закона химических элементов и установления
физического смысла атомного номера элемента. Измерил длины волн
рентгеновских лучей, предсказал рентгеновские спектры некоторых эле-
ментов. Проводил исследования радиоактивности.
ОЖЕ Пьер Виктор (14.V 1899 - 25.XII 1993) — французский физик,
член Парижской АН (1977). Родился в Париже. В 1926 получил сте-
пень доктора в Парижском ун-те, где работал в 1927-69 гг. (с 1937 г. —
профессор). В 1941-44 гг. работал в США и Англии. Возвратившись во
Францию, в 1945-48 гг. был комиссаром по атомной энергии, в 1948-
59 гг. — директор Департамента естественных наук ЮНЕСКО, в 1959—
62 гг. был президентом Французского комитета космических исследова-
ний, в 1962-67 гг. — генеральным директором Европейской организации
космических исследований.
Работы посвящены атомной и ядерной физике, физике космических
лучей, философии науки. Исследуя фотоэффект в газах, выполнил точ-
ные измерения углового распределения вылетающих фотоэлектронов,
чем подтвердил квантовую теорию фотоэффекта. Открыл в 1925 г. явле-
ние автоионизации возбужденного атома в результате внутреннего пере-
распределения энергии возбуждения (эффект Оже) и в 1938 г. — широ-
кие атмосферные ливни (ливни Оже).
ПАУЛИ Вольфганг (25.IV 1900 - 14.XII 1958) — физик-теоретик.
Родился в Вене. Окончил Мюнхенский ун-т (1921). В 1921-22 гг. рабо-
тал в Гёттингенском ун-те ассистентом у М. Борна, в 1922-23 гг. — у
Н. Бора в Ин-те теоретической физики в Копенгагене, в 1923-28 гг. —
доцент Гамбургского ун-та, с 1928 г. — профессор Политехникума в Цю-
рихе (кроме 1935-36 гг., 1940-45 гг., 1949-50 гг., 1954 г., когда работал
в США в Принстонском ин-те перспективных исследований).
Приложение. Краткие биографические справки о физиках 599
Работы относятся ко многим разделам современной теоретической
физики, в развитии которых он принимал непосредственное участие, в
частности к квантовой механике, квантовой электродинамике, теории
относительности, квантовой теории поля, теории твердого тела, ядер-
ной физике, физике элементарных частиц. В 1924 г. для объяснения
сверхтонкой структуры спектральных линий выдвинул гипотезу ядер-
ного спина, предложив существование спинового и магнитного моментов
атомных ядер. В 1924-25 гг. сформулировал один из важнейших прин-
ципов современной теоретической физики, согласно которому две тожде-
ственные частицы с полуцелыми спинами не могут находиться в одном
состоянии — принцип Паули (Нобелевская премия, 1945). Объяснил па-
рамагнетизм электронного газа в металле (1927), структуру электронных
оболочек атомов. Совместно с Э. Ферми ввел представление о сильно вы-
рожденном электронном газе в металлах. В 1927 г. ввел в квантовую
механику спин, а для описания спина электрона — матрицы (спиновые
матрицы Паули). Совместно с В. Гейзенбергом предпринял в 1929 г. по-
пытку формулировки квантовой электродинамики, введя общую схему
квантования полей, заложив тем самым основы систематической теории
квантования поля.
Высказал в 1931 г. гипотезу о существовании нейтрино и сформули-
ровал в 1933 г. основные свойства нейтрино. Является автором фунда-
ментальных исследований по теории элементарных частиц и квантовых
полей, а также мезонной теории ядерных сил. В 1940 г. доказал тео-
рему о связи статистики и спина, в 1941 г. показал, что закон сохране-
ния электрического заряда связан с инвариантностью относительно ка-
либровочных преобразований. В 1955 г. сформулировал СРТ-теорему,
отражающую симметрию элементарных частиц.
Член Лондонского королевского общества. Медали X. Лоренца (1930),
Б. Франклина (1952), М. Планка (1958) и др.
ПЛАНК Макс Карл Эрнст Людвиг (23.IV 1858 - 4.Х 1947) — немец-
кий физик-теоретик, основоположник квантовой теории, член Берлин-
ской АН (1894), непременный секретарь в 1912-38 гг. Родился в Киле.
Окончил Мюнхенский ун-т (1878), где в 1879 г. получил степень доктора
философии. В 1880-85 гг. работал в Мюнхенском ун-те, 1885-88 гг. —
профессор теоретической физики Кильского, 1889-1926 гг. — Берлин-
ского ун-тов.
Работы относятся к термодинамике, теории теплового излучения,
теории относительности, квантовой теории, истории и методологии фи-
зики, философии науки. В 1900 г., исходя из чуждого для классической
физики предположения, что атомные осцилляторы излучают энергию
лишь определенными порциями — квантами, причем энергия кванта
пропорциональна частоте колебания, вывел закон распределения энер-
гии в спектре абсолютно черного тела. Ввел фундаментальную посто-
янную (постоянная Планка) с размерностью действия. Формула закона
Планка сразу же получила экспериментальное подтверждение. Оценивая
значение открытия Планка, А. Эйнштейн писал: «Именно закон излуче-
ния Планка дал первое точное определение абсолютных величин атомов,
независимо от других предложений. Более того, он убедительно показал,
что, кроме атомистической структуры материи, существует своего рода
атомистическая структура энергии, управляемая универсальной посто-
янной, введенной Планком. Это открытие стало основой для всех иссле-
600 Приложение. Краткие биографические справки о физиках
дований в физике XX века и с того времени почти полностью обусловило
ее развитие. Без этого открытия было бы невозможно установить насто-
ящую теорию молекул и атомов и энергетических процессов, управляю-
щих их превращениями. Более того, оно разрушило остов классической
механики и электродинамики и поставило перед наукой задачу: найти
новую познавательную основу для всей физики».
Постоянная Планка, или квант действия, является одной из универ-
сальных постоянных в физике. День 14 декабря 1900 г., когда Планк
доложил в Немецком физическом обществе о теоретическом выводе за-
кона излучения, стал датой рождения квантовой теории (Нобелевская
премия, 1918).
Большое значение имели работы Планка по теории относительно-
сти. В 1906 г. вывел уравнения релятивистской динамики, получив
выражения для энергии и импульса электрона, и тем самым завершил
релятивизацию классической механики. Он же ввел термин «теория от-
носительности» (1906). В 1907 г. провел обобщение термодинамики в
рамках специальной теории относительности.
Дал общий вывод законов химического равновесия в газах и разба-
вленных растворах (1887).
В решении конкретных научных проблем стоял на материалистиче-
ских позициях, выступал против «энергетиков», защищая атомистику.
Активная борьба Планка против физического идеализма на рубеже XIX-
XX веков сыграла важную роль в истории развития познания.
Иностранный член АН СССР (1926), Лондонского королевского обще-
ства (1926). Именем Планка названо научное общество в ФРГ. Немецким
физическим обществом учреждена медаль М. Планка.
РАМЗАЙ Уильям (2.Х 1852 - 23.VII 1916) — английский ХИМИК
и физик, член Лондонского королевского общества (1888). Родился в
Глазго. В 1866-70 гг. учился в ун-те Глазго, в 1871 г. — в Гейдельберг-
ском, в 1872 г. — в Тюбингенском ун-тах, в последнем получил в 1872 г.
степень доктора философии. В 1872-80 гг. работал в ун-те в Глазго, в
1880-87 гг. — профессор Бристольского, в 1887-1913 гг. — Лондонского
ун-тов.
Открыл и исследовал инертные газы: в 1894 г. (с Дж. Рэлеем) от-
крыл аргон, в 1895 г. — гелий, в 1898 г. — криптон, ксенон и неон (с
М. Траверсом). Изучал молекулярную структуру чистых жидкостей, в
1893 г. предложил способ определения молекулярной массы жидкостей
по величине их поверхностного натяжения. Определил в 1903 г. плот-
ность эманации радия (радона), в 1903 г. доказал (вместе с Ф. Содди)
наличие гелия в продуктах излучения радона (образование гелия из ра-
дона). Это было первое экспериментальное доказательство превраще-
ния одного элемента в другой. Вместе с О. Ганом в 1905 г. открыл
радиоторий. Проводил исследования трансмутации химических элемен-
тов. В 1910 г. изобрел микровесы, в 1912 г. предложил подземную
газификацию каменного угля (эта идея еще в 1888 г. была высказана
Д.И. Менделеевым). В 1904 г. за открытие инертных газов и определе-
ние их места в периодической системе удостоен Нобелевской премии по
химии.
Член ряда академий наук и научных обществ, иностранный член
Петербургской АН (1913). Медаль Г. Дэви (1895) и др.
Приложение. Краткие биографические справки о физиках 601
РАМЗАУЭР Карл (6.II 1879 - 24.XII 1955) — немецкий физик. Ро-
дился в Ольденбурге. В 1902 г. получил степень доктора философии
в Кильском ун-те. В 1907-28 гг. работал в Гейдельбергском ун-те
(с 1915 г. — профессор), в 1928-45 гг. — профессор Высшей техниче-
ской школы в Данциге (ныне Гданьск, Польша), с 1945 г. — Берлинского
ун-та (в 1950-51 гг. — ректор).
Работы в области атомной физики. Исследовал взаимодействие мед-
ленных электронов и протонов с атомами газа. В 1921 г. при изуче-
нии рассеяния медленных электронов в аргоне обнаружил аномальный
характер их взаимодействия с нейтральными атомами (эффект Рамза-
уэра). В 1914 г. разработал новый метод исследования фотоэффекта —
метод отклонения фотоэлектронов в магнитном поле, с помощью которого
подтвердил квантовую теорию фотоэффекта (опыт Рамзауэра).
РЕЗЕРФОРД Эрнест (30.VIII 1871 - 19.Х 1937) — английский фи-
зик, основоположник ядерной физики, член Лондонского королевского
общества (1903), президент в 1925-30 гг. Родился в Спринг-Броуве (сей-
час Брайтуотер) в Новой Зеландии. Окончил Кентерберийский колледж
Новозеландского ун-та в Крайстчерче (1894). В 1895-98 гг. работал в
Кавендишской лаборатории под руководством Дж. Дж. Томсона, в 1898-
1907 гг. — профессор Мак-Гиллского ун-та в Квебеке (Канада), в 1907-
19 гг. — профессор Манчестерского ун-та и директор физической ла-
боратории. С 1919 г. — профессор Кембриджского ун-та и директор
Кавендишской лаборатории.
Исследования посвящены радиоактивности, атомной и ядерной фи-
зике. Своими фундаментальными открытиями в этих областях заложил
основы теории радиоактивности и строения атома. В 1899 г. открыл
альфа- и бета-лучи, в 1900 г. — эманацию тория и ввел понятие пери-
ода полураспада. Вместе с Ф. Содди в 1902-03 гг. разработал теорию
радиоактивного распада и открыл закономерности радиоактивных пре-
вращений. В 1903 г. доказал, что альфа-лучи состоят из положительно
заряженных частиц.
Предсказал существование трансурановых элементов. В 1903 г.
Э. Резерфорд писал: «Если существуют элементы тяжелее урана, то впол-
не вероятно, что они окажутся радиоактивными. Исключительная чув-
ствительность методов химического анализа, основанных на радиоак-
тивности, дает возможность обнаружить эти элементы, даже если они
будут присутствовать в ничтожно малых количествах. Поэтому можно
ожидать, что в будущем число радиоактивных элементов увеличится».
За исследования по превращению элементов и химии радиоактивных
веществ Резерфорду в 1908 г. была присуждена Нобелевская премия по
химии.
В 1908 г. вместе с Г. Гейгером сконструировал прибор для регистра-
ции отдельных заряженных частиц (счетчик Гейгера) и с его помощью
доказал (1909), что альфа-частицы являются дважды ионизированными
атомами гелия. Изучая явление прохождения альфа-частиц через ве-
щество, установил закон рассеяния альфа-частиц атомами различных
элементов (формула Резерфорда), что привело в 1911 г. к открытию в
атоме массивного ядра диаметром около 10-12 см, заряженного положи-
тельно, и созданию новой модели атома — планетарной (модель атома
Резерфорда).
602 Приложение. Краткие биографические справки о физиках
Выдвинул идею об искусственном превращении атомных ядер (1914),
предсказал внутреннюю конверсию. Совместно с Э. Андраде в 1914 г. до-
казал идентичность рентгеновских спектров изотопов, чем окончательно
подтвердил равенство порядковых номеров у изотопов данного элемента,
наблюдал дифракцию гамма-лучей на кристалле, доказав их электромаг-
нитную природу. В 1919 г. осуществил первую искусственную ядерную
реакцию, превратив азот в кислород, заложив тем самым основы совре-
менной физики ядра, открыл протон. В 1920 г. предсказал существо-
вание нейтрона и дейтрона. С М. Олифантом экспериментально доказал
(1933) справедливость закона взаимосвязи массы и энергии в ядерных
реакциях, в 1934 г. осуществил реакцию синтеза дейтронов с образова-
нием трития.
Создал большую школу физиков (Г. Гейгер, Э. Марсден, Дж. Нэттол,
О.Ган, Г. Мозли, Дж. Чедвик, Э. Андраде, Ч.-Г. Дарвин, Н.Бор, Д.Хеве-
ши, П. Блеккет, Дж. Кокрофт, Э. Уолтон, С. Пауэлл, М. Олифант, У. Вус-
тер, Г. Месси, X. Баба и др.). У Резерфорда учились советские физики
П.Л. Капица, Ю.Б. Харитон, А.И. Лейпу некий и др. Член всех академий
наук мира, в том числе иностранный член АН СССР (1925).
РЕНТГЕН Вильгельм Конрад (27.III 1845 - 10.11 1923) — немец-
кий физик-экспериментатор, чл.-корр. Берлинской АН (1896). Родился
в Леннепе. Окончил Цюрихский политехникум (1868). В 1871-73 гг.
работал в Вюрцбургском ун-те, в 1874-79 гг. — в Страсбургском, в 1879-
88 гг. — профессор ун-та в Гиссене и директор Физического ин-та, в
1888-1900 гг. — профессор Вюрцбургского ун-та (в 1894 г. избран рек-
тором), в 1900-20 гг. — профессор Мюнхенского ун-та и директор Фи-
зического ин-та.
Научные исследования относятся к электромагнетизму, физике кри-
сталлов, оптике, молекулярной физике. В 1895 г. открыл коротковол-
новое электромагнитное излучение (Х-лучи), названное в дальнейшем
рентгеновскими лучами, и исследовал их свойства: способность рассе-
иваться, поглощаться, ионизировать воздух и т.д. Предложил конст-
рукцию трубки для получения Х-лучей с наклонным платиновым анти-
катодом и вогнутым катодом, первый сделал фотографии при помощи
рентгеновских лучей. Открыл в 1885 г. магнитное поле диэлектрика,
движущегося в электрическом поле (так называемый рентгенов ток). Его
опыт наглядно показал, что магнитное поле создается подвижными за-
рядами, и имел важное значение для создания X. Лоренцем электронной
теории. Значительное число работ Рентгена посвящено исследованию
свойств жидкостей, газов, кристаллов, электромагнитных явлений, от-
крыл взаимосвязь электрических и оптических явлений в кристаллах.
За открытие лучей, носящих его имя, Рентгену в 1901 г. первому среди
физиков была присуждена Нобелевская премия.
Учениками Рентгена были М.Вин, А.Ф. Иоффе, П.Книппинг, Р.Ла-
денбург, П. Прингсгейм, В. Фридрих и др.
Медаль Б.Румфорда.
РИДБЕРГ Иоганнес Роберт (8.XI 1854 - 28.XII 1919) — шведский
физик и математик, член Шведской АН (1919). Родился в Хальмстаде.
Окончил Лундский ун-т (1879), где работал (с 1897 г. — профессор).
Основные работы посвящены систематике атомных спектров и атом-
ной физике. Первый начал оперировать волновым числом, ввел универ-
Приложение. Краткие биографические справки о физиках (>()3
сальную константу Ry (постоянная Ридберга), установил связи мгжл.у
различными сериями, образующими спектр элемента, дал формулу, они
сывающую любую спектральную линию (1890). Идеи Ридберга сыграли
значительную роль в установлении в 1908 г. В. Ритцем так называемого
комбинационного принципа, согласно которому волновое число любой
линии спектра может быть представлено в виде разности двух членов из
множества спектральных термов, характеризующих элемент. Этот за-
кон известен сейчас в физике как комбинационный принцип Ридберга-
Ритца. В 1889 г. предположил, что спектры испускания химических
элементов должны привести к пониманию периодической системы Мен-
делеева. Выдвинул идею, что независимой переменной является не атом-
ная масса элемента, а его порядковый номер.
РИТЦ Вальтер (22.11 1878 - 7.VII 1909) — швейцарский физик-
теоретик и математик. Родился в Сионе. Окончил Цюрихский ун-т
(1900). Работал в Геттингене, Бонне, Париже, Цюрихе, Тюбингене.
Работы по физике посвящены спектроскопии, теории теплового излу-
чения, электродинамике. В 1908 г. открыл закон, согласно которому вол-
новое число любой спектральной линии равно разности двух термов из
множества термов, присущих данному элементу. Закон получил назва-
ние «комбинационный принцип Ридберга-Ритца». Сформулировал (1908)
метод решения вариационных задач (метод Ритца).
РЭЛЕЙ (СТРЕТТ) Джон Уильям (12.XI 1842 - 30.VI 1919) — ан-
глийский физик, член Лондонского королевского общества (1873), пре-
зидент в 1905-08 гг. Родился в Ленгфорд-Грофе. Окончил Кембриджс-
кий ун-т (1865), где работал в Тринити колледж до 1871 г. Оборудовал
в 1871 г. в своем родовом имении в Терлинзе собственную лаборато-
рию. В 1873 г., после смерти отца, унаследовал титул лорда Рэлея.
В 1879-84 гг. — профессор и директор Кавендишской лаборатории, в
1887-1905 гг. — профессор Королевского ин-та в Лондоне. С 1908 г. —
президент Кембриджского ун-та. Работы посвящены теории колебаний,
одним из основоположников которой он является, акустике, теории те-
плового излучения, молекулярной физике, гидродинамике, электромаг-
нетизму, оптике. Исследовал колебания упругих тел (струн, стержней,
пластин), установил ряд свойств колебательных систем, первый обратил
внимание на автоколебания. Изучал дифракцию, рассеяние и поглоще-
ние волн, волны конечной амплитуды и поверхностные волны, пред-
сказал (1885) особый вид поверхностных волн (волны Рэлея). Развил
понятия о фазовой и групповой скорости волн и установил соотношение
между ними, дал формулу для групповой скорости.
Заложил основы теории молекулярного рассеяния света, установил
(1871) закон, согласно которому интенсивность рассеянного средой света
обратно пропорциональна четвертой степени длины волны возбуждаю-
щего света (закон Рэлея), объяснил голубой цвет неба. В 1894 г. вместе
с У. Рамзаем открыл новый химический элемент — аргон и определил
его свойства и место в периодической системе элементов (Нобелевская
премия, 1904). В 1900 г. вывел закон распределения энергии излуче-
ния в спектре абсолютно черного тела в зависимости от температуры
(закон Рэлея-Джинса). Независимо от 0. Хевисайда построил теорию
скин-эффекта. Известен также законом намагничивания Рэлея (1887),
обнаружил явление магнитного последействия или магнитной вязкости.
604 Приложение. Краткие биографические справки о физиках
Сконструировал рефрактометр (рефрактометр Рэлея), установил разре-
шающую силу призменных и дифракционных приборов, изобрел диффе-
ренциальный манометр (манометр Рэлея), прибор для измерения силы
звука (диск Рэлея).
Медали Б.Румфорда, Копли, М. Фарадея.
СЛЭТЕР Джон Кларк (22.XII 1900 - 25.VII 1976) — американский
физик-теоретик, член Национальной АН (1932). Родился в Оук-Парке.
Окончил Рочестерский (1920) и Гарвардский (1923) ун-ты. В 1924-30 гг.
работал в Гарвардском ун-те, в 1930-66 гг. — профессор Массачусетс-
ского технологического ин-та. С 1964 г. — профессор Флоридского ун-та.
Работы посвящены квантовой теории и ее применению к физике
атомов, молекул и кристаллов, химической физике, магнетизму, теории
экситонов. В 1929 г. показал, что детерминант, составленный из от-
дельных электронных волновых функций, можно использовать как мно-
гоэлектронную волновую функцию, удобную для вариационных расчетов
в задачах по электронной структуре атомов и молекул (детерминанты
Слэтера). В 1930 г. предложил полярную модель кристаллов и неза-
висимо от Ф. Блоха ввел спиновые волны. Развил коллективизирован-
ную модель ферромагнитных металлов и сплавов. В 1937 г. построил
теорию ферромагнетизма в металлах, частично основанную на исполь-
зовании функций Ванье. Развил теорию валентных связей, основные
представления о барьерном механизме фотопроводимости, теорию атом-
ных мультиплетов. В 1934 г. обобщил метод ячеек Вигнера-Зейтца, в
1937 г. для расчета многоэлектронных систем предложил метод присо-
единенных плоских волн.
Создал школу физиков. Национальная медаль за науку и др.
ТОМСОН Джозеф Джон (18.XII 1856 - 30.VIII 1940) — англий-
ский физик, член Лондонского королевского общества (1884), президент
в 1916-20 гг. Родился в Четхем Хилле. Учился в Манчестерском ун-
те, окончил Кембриджский ун-т (1880). В 1884-1919 гг. — профессор
Кембриджского ун-та и директор Кавендишской лаборатории, в 1905—
18 гг. — также профессор Королевского ин-та. С 1918 г. возглавлял
Тринити колледж в Кембридже.
Работы посвящены изучению прохождения электрического тока че-
рез разреженные газы, катодных и рентгеновских лучей, атомной фи-
зике. В 1897 г., исследуя отклонения катодных лучей в магнитном и
электрическом полях, показал, что они представляют собой поток отри-
цательно заряженных частиц, измерил удельный заряд этих частиц и
нашел, что их масса приблизительно в 1837 раз меньше массы атома
водорода. Это было прямым и надежным открытием электрона (Нобе-
левская премия, 1906). В этом же году выдвинул гипотезу об электрон-
ном составе атомов (внутриатомных электронах). В 1899 г. обнаружил
электроны в фототоке и эффект термоэлектронной эмиссии. Разрабо-
тал теорию движения электрона в магнитном и электрическом полях.
Изучил многие особенности электрического разряда в газах. Объяснил
происхождение сплошного спектра рентгеновских лучей.
Предложил в 1903 г. одну из первых атомных моделей, согласно ко-
торой атом представлял собой положительно заряженную сферу с вкра-
пленными в нее электронами, суммарный отрицательный заряд кото-
рых равен положительному заряду сферы (модель «пудинг с изюмом»).
Приложение. Краткие биографические справки о физиках 605
В 1904 г. ввел представление о том, что электроны в атоме разделяются
на группы, образуя различные конфигурации, обусловливающие перио-
дичность химических элементов. В 1907 г. предложил принцип дей-
ствия масс-спектрометра. Разработал в 1911 г. метод парабол для опре-
деления относительных масс частиц ионных пучков (ионов различных
газов), что имело важное значение для исследования изотопов; получил
в 1912 г. первые экспериментальные данные о существовании изотопов,
обнаружив атомы неона с массой 20 и 22 а.е.м. В классической теории
рассеяния дал выражение для эффективного сечения в случае рассеяния
света свободными электронами (формула Томсона). Является одним из
основоположников классической электронной теории металлов (1900).
Член многих академий наук, в частности АН СССР (1925). Создал
большую интернациональную школу физиков-экспериментаторов (Ф. Ас-
тон, Ч. Баркла, Ч. Вильсон, Э. Резерфорд, О. Ричардсон, Дж.П. Томсон,
П. Ланжевен, Дж. Таунсенд, X. Каллендар, Дж. Мак-Леннан, Т. Лайман,
В. Натансон, Дж. Тейлор, Э. Эпплтон, У. Никольсон, Р.Стрэтт, Дж. Сирл
и др.).
Медали Б.Франклина (1923), М.Фарадея (1938), Д.Юза (1902), Ко-
пли (1914) и др.
ТОМСОН Джордж Паджет (3.V 1892 - 10.IX 1975) — английский фи-
зик, член Лондонского королевского общества (1930). Сын Дж.Дж. Том-
сона. Родился в Кембридже. Окончил Кембриджский ун-т (1914), там
же работал в 1919-22 гг. В 1922-30 гг. — профессор Абердинского ун-та
(Шотландия), в 1930-52 гг. — Имперского колледжа науки и технологии
(Лондон), в 1952-62 гг. возглавлял один из колледжей в Кембридже.
Работы относятся к атомной .и ядерной физике, квантовой меха-
нике, аэродинамике, электрическим разрядам в газах. Независимо от
К. Дэвиссона и Л. Джермера открыл в 1927 г. явление дифракции элек-
тронов, чем была экспериментально доказана волновая природа элек-
тронов (Нобелевская премия, 1937). Проводил исследования геометрии
электронограмм и теории рассеяния.
Медали Д.Юза (1939), Королевская (1949), М.Фарадея (I960).
ФОК Владимир Александрович (22.XII 1898 - 27.XII 1974) — со-
ветский физик-теоретик, академик (1939; чл.-корр. с 1932 г.). Родился
в Петербурге. Окончил Петроградский ун-т (1922), там же работал (с
1932 г. — профессор). Одновременно работал в 1924-36 гг. в Ленин-
градском физико-техническом ин-те и в 1928-41 гг. — в Государствен-
ном оптическом ин-те, в 1934-41 и в 1944-53 гг. — в Физическом ин-те
АН СССР, в 1954-64 гг. — в Ин-те физических проблем АН СССР.
Работы относятся к квантовой механике, квантовой электродина-
мике, квантовой теории поля, теории многоэлектронных систем, ста-
тистической физике, теории относительности, теории гравитации, ра-
диофизике, математической физике, философским вопросам физики.
В 1930 г. для объяснения спектров атомов разработал метод приближен-
ного описания и расчета системы взаимодействующих тождественных
фермионов, который получил широкое применение в теории многоэлект-
ронных систем, так называемый метод самосогласованного поля, или ме-
тод Хартри-Фока. Разработал теорию атома водорода, использовав мето-
ды теории групп, первый открыл скрытую симметрию в атоме водорода.
606 Приложение. Краткие биографические справки о физиках
В 1932 г. предложил метод рассмотрения систем с переменным чи-
слом частиц в конфигурационном пространстве (метод вторичного кван-
тования в пространстве Фока). Разработанные Фоком два вышеупомя-
нутых метода оказались плодотворными для построения и развития
квантовой теории многочастичных систем. В 1934 г. предложил осо-
бый способ формулировки уравнений квантовой теории поля и кванто-
вой теории многих тел — метод функционалов Фока. За исследования
по квантовой теории поля, в частности по вторичному квантованию и
квантовой электродинамике, проведенные в 1928-57 гг., в 1960 г. был
удостоен Ленинской премии.
Исследовал ряд важных задач теории тяготения и предложил при-
ближенный метод решения уравнений Эйнштейна для сферических масс
в допущении евклидовости пространства на бесконечности (1939), рас-
смотрел вывод уравнений движения тел с учетом их структуры и враще-
ния, получение десяти интегралов движения и т.д. Широко известны
также «представления Фока», «условия симметрии Фока», «преобразова-
ния Фока», «формулы Фока». Огромное теоретическое и практическое
значение имеют труды Фока по теории дифракции, в частности он раз-
работал теорию распространения радиоволн над земной поверхностью
(Государственная премия СССР, 1946).
Значительное внимание уделял философским вопросам физики, в
частности методологии квантовой механики. Принимал активное уча-
стие в дискуссиях по принципиальным вопросам квантовой механики и
теории относительности.
Герой Социалистического Труда (1968). Член ряда академий наук и
научных обществ. Премия Д.И. Менделеева (1936), член ряда академий
и научных ин-тов.
ФРАНК Джеймс (26.VII 1882 - 21.V 1964) — немецкий физик. Ро-
дился в Гамбурге. В 1901-02 гг. учился в Гейдельбергском ун-те, окон-
чил Берлинский ун-т (1906), там же работал до 1917 г. (с 1916 г. —
профессор), в 1917-21 гг. возглавлял физическое отделение в Ин-те фи-
зической химии (Берлин). В 1921-34 гг. — профессор Гёттингенского
ун-та и директор Физического ин-та. В 1935 г. эмигрировал в США.
В 1935-38 гг. — профессор ун-та Дж. Гопкинса, в 1938-47 гг. — Чикаг-
ского ун-та.
Работы посвящены атомной и ядерной физике, молекулярной спек-
троскопии и ее применению к химии, фотосинтезу. Вместе с Густавом
Герцем осуществил (1912-14) ряд экспериментов по возбуждению и ио-
низации атомов паров ртути ударами электронов (опыты Франка-Герца)
и открыл законы столкновений электронов с атомами, что послужило
доказательством дискретности уровней энергии атомов и подтвердило
теорию атома Бора (Нобелевская премия, 1925). Изучал уровни энергии
в атомах, передачу энергии в атомных системах при флюоресценции,
развил спектральный метод исследования химических сил, исследовал
фотохимические процессы в молекуле хлорофилла. В 1925 г. предложил
механизм, объясняющий фотохимическую диссоциацию молекул иода,
развитый впоследствии Э. Кондоном (принцип Франка-Кондона). Вы-
ступал (1945) против применения атомной бомбы.
Член ряда академий наук и научных обществ, в частности, ино-
странный чл.-корр. Академии наук СССР (1927). Медали М. Планка,
Б.Румфорда (1955).
Приложение. Краткие биографические справки о физиках 607
ХАРТРИ Дуглас Рейнер (27.III 1897 - 12.11 1958) — английский
?1изик-теоретик и математик, член Лондонского королевского общества
1932). Родился в Кембридже. В 1926 г. получил степень доктора фило-
софии в Кембриджском ун-те, где работал. В 1929-46 гг. — профессор
Манчестерского ун-та, с 1946 г. — Кембриджского.
Работы относятся к численному математическому анализу, кванто-
вой теории, атомным структурам, вычислительным машинам, распро-
странению радиоволн. В 1928 г. разработал метод самосогласованного
поля, развитый в дальнейшем В.А. Фоком (метод Хартри-Фока), имею-
щий важное значение в квантовой теории многих тел. Применил свой
метод для расчета волновых функций многоэлектронных атомов, а также
к задачам баллистики, атмосферной физики, гидродинамики. Ввел ма-
тематическое определение количества информации (1928). Построил
первый в Англии дифференциальный анализатор и явился пионером во
внедрении в Англии цифровых вычислительных машин.
ХУНД Фридрих (4.II 1896 - 31.III 1997) — немецкий физик-теоре-
тик, член Гёттингенской АН. Родился в Карлсруэ. Окончил Гёттинген-
ский ун-т (1922). В 1925-27 гг. работал в Гёттинтенском ун-те, 1927-
29 гг. — профессор Ростокского ун-та, 1929-46 гг. — Лейпцигского,
1946-51 гг. — Йенского ун-та, 1951-56 гг. — Франкфуртского, 1956-
64 гг. — Гёттингенского ун-тов.
Работы посвящены квантовой механике, квантовой теории атомов,
молекул и твердых тел, общим вопросам квантовой теории, квантовой
химии, истории физики. Совместно с Р. Малликеном и Ю. Вигнером раз-
работал метод молекулярных орбиталей и заложил основы теории моле-
кулярных спектров. Предложил в 1927 г. эмпирический способ определе-
ния термов основного стационарного состояния атомов (правила Хунда).
Исследовал закономерности взаимодействия угловых моментов в двух-
атомных молекулах.
ЧЕДВИК Джеймс (20.Х 1891 - 24.VII 1974) — английский физик-
экспериментатор, член Лондонского королевского общества (1927). Ро-
дился в Веллингтоне. Окончил Манчестерский и Кембриджский ун-ты.
В 1923-35 гг. преподавал в Кембриджском ун-те и был заместителем
директора Кавендишской лаборатории, в 1935-48 гг. — профессор Ли-
верпульского ун-та, в 1948-58 гг. возглавлял Гонвилл и Кайус колледжи
Кембриджского ун-та.
Работы в области радиоактивности и ядерной физики. В 1914 г.
открыл непрерывный спектр энергии бета-излучения. В 1920 г. иссле-
довал рассеяние альфа-частиц ядрами платины, серебра и меди и непо-
средственно измерил заряды ядер, чем окончательно подтвердил теорию
атома Резерфорда и вывод о том, что заряд ядра равен порядковому
номеру элемента. В 1932 г., исследуя излучение, возникающее при об-
лучении бериллия альфа-частицами, показал, что оно является потоком
электрически нейтральных частиц — нейтронов (Нобелевская премия,
1935).
Исследовал искусственное превращение элементов под действием
альфа-частиц (совместно с Э. Резерфордом) и образование электрон-по-
зитронных пар гамма-квантами (совместно с П. Блэккетом и Дж. Ок-
киалини). В 1934 г. совместно с М. Гольдхабером впервые обнаружил
расщепление ядра под действием гамма-квантов (ядерный фотоэффект),
бомбардируя гамма-квантами энергии 2,62 МэВ, они расщепили дейтрон,
608 Приложение. Краткие биографические справки о физиках
предсказали бета-распад нейтрона. Исследования посвящены также осу-
ществлению цепной ядерной реакции деления. Один из первых рассчи-
тал критическую массу урана-235.
Член ряда академий наук. Медали Д.Юза (1932), Копли (1950),
М. Фарадея (1950), Б.Франклина (1951).
ШРЕДИНГЕР Эрвин (12.VIII1887 - 4.1 1961) — австрийский физик-
теоретик, один из создателей квантовой механики. Родился в Вене.
Окончил Венский ун-т (1910). Работал в Венском и Йенском ун-тах,
в 1920-21 гг. — профессор Высшей технической школы в Штуттгарте
и ун-та в Бреслау, 1921-27 гг. — профессор Цюрихского ун-та, 1927—
33 гг. — Берлинского, в 1933-36 гг. — Оксфордского, 1936-38 гг. —
Грацского ун-тов. В 1941—55 гг. — директор Ин-та высших исследова-
ний в Дублине, с 1956 г. — профессор Венского ун-та.
Основные работы в области статистической физики, квантовой тео-
рии, квантовой механики, обшей теории относительности, биофизики.
Исходя из идей де Бройля о волнах материи и принципа Гамильтона,
разработал (1926) теорию движения микрочастиц — волновую механику,
в основу которой положил уравнение (уравнение Шредингера), играю-
щее в атомных процессах такую же фундаментальную роль, как законы
Ньютона в классической механике, и ввел для описания состояния ми-
крообъекта волновую функцию (^-функцию). В 1926 г. доказал экви-
валентность своей волновой механики и матричной механики, разрабо-
танной В. Гейзенбергом, М. Борном и П. Иорданом. В 1926 г. построил
квантовую теорию возмущений — приближенный метод квантовой ме-
ханики. Пытался (1926) представить частицу как группу волн, занима-
ющую определенную часть пространства и движущуюся целиком (вол-
новой пакет). За создание волновой механики в 1933 г. (с П. Дираком)
удостоен Нобелевской премии.
Однако воспитанный на традициях классической физики, основан-
ной на полном детерминизме, Шредингер пытался построить теорию ис-
ключительно в терминах волн. Это привело его к дискуссии с другими
ведущими физиками, в частности с Н. Бором. «Если мы собираемся со-
хранить эти проклятые квантовые скачки, — сказал как-то в отчаянии
Шредингер, — то я вообще жалею, что имел дело с атомной теорией!»
Дальнейшие исследования Шредингера посвящены теории мезонов,
термодинамике, нелинейной электродинамике Борна-Инфельда, общей
теории относительности. В частности, он сделал несколько попыток по
разработке единой теории поля. Интересы Шредингера были чрезвы-
чайно разнообразны: он занимался лепкой, написал книгу по греческой
философии, исследовал проблемы генетики и т.д.
Член ряда академий наук и научных учреждений, иностранный член
АН СССР (1934).
ЮРИ Гарольд Клейтон (29.IV 1893 - 6.1 1981) — американский фи-
зик и физико-химик, член Национальной АН (1935). Родился в Уолкер-
тоне. Окончил Монтанский ун-т (1917), там же преподавал в 1919-21 гг.
В 1924-29 гг. работал в ун-те Дж. Гопкинса, в 1929-45 гг. — в Колум-
бийском ун-те (с 1934 г. — профессор), возглавлял в нем в 1940-45 гг.
научно-исследовательскую лабораторию по разделению изотопов урана.
В 1945-58 гг. — профессор Ин-та ядерных исследований им. Э. Ферми
Чикагского ун-та, в 1958-70 гг. — Калифорнийского ун-та (в Сан-Диего).
Приложение. Краткие биографические справки о физиках 609
Работы посвящены атомной физике, спектроскопии, квантовой ме-
ханике, химии изотопов, геохимии, космохимии. В 1932 г. открыл тя-
желый водород, назвав его дейтерием (Нобелевская премия по химии,
1934). Проводил исследования по получению тяжелой воды, разделению
изотопов урана, в частности с целью получения изотопа урана-235.
В послевоенные годы научные интересы Юри сосредоточились в гео-
химии и космохимии. Осуществил измерение палеотемператур меловых
белемнитов, что было одним из значительных успехов геофизики. Рабо-
тал над развитием нового направления — геохимии стабильных изото-
пов, исследовал проблемы астрофизики, геохронологии, возникновения
жизни. Доказал (1950), что аминокислоты образуются при электриче-
ских разрядах в атмосфере. Вышедшая в 1952 г. его книга «Планеты,
их возникновение и развитие» содержала первую систематическую хро-
нологию Солнечной системы. Исследования относятся также к происхо-
ждению метеоритов, структуре Луны, распределению и возникновению
элементов и их изотопов в природе. В 1956 г. совместно с Г. Зюссом
построил таблицу относительной распространенности химических эле-
ментов.
Член многих академий наук и научных обществ. Медали Дж. Гиббса
(1934), Г. Дэви (1940), Б. Франклина (1943), Национальная медаль за
науку (1964) и др.
ЭЙНШТЕЙН Альберт (14.III 1879 - 18.IV 1955) — выдающийся
физик-теоретик, один из создателей современной физики. Родился в
Ульме (Германия). Четырнадцати лет переехал в Швейцарию, где окон-
чил Цюрихский политехникум (1900). В 1902-08 гг. работал экспертом
в патентном бюро в Берне, в 1909—13 гг. — профессор Цюрихского по-
литехникума (в 1911 г. — профессор Немецкого ун-та в Праге), в 1914—
33 гг. — профессор Берлинского ун-та и директор Ин-та физики. После
установления власти нацистов покинул Германию. В 1933 г. переехал в
США, где до конца жизни работал в Принстонском ин-те перспективных
исследований.
Создатель специальной и общей теорий относительности, коренным
образом изменивших представления о пространстве, времени и мате-
рии. В 1905 г. в статье «К электродинамике движущихся тел» разрабо-
тал основы специальной теории относительности, изложив новые законы
движения, которые обобщали ньютоновские и переходили в них в случае
малых скоростей (много меньше скорости света в вакууме) тел. В основу
своей теории положил два постулата: специальный принцип относитель-
ности, являющийся обобщением механического принципа относительно-
сти Галилея на любые физические явления, и принцип постоянства ско-
рости света в вакууме (скорость света в вакууме не зависит от движения
источника света или наблюдателя и одинакова во всех направлениях,
т.е. одинакова во всех инерциальных системах и равна 3 • 101Осм/с).
Оба постулата и теория, построенная на их основе, привели к ломке
многих установившихся классических понятий (абсолютное пространст-
во, абсолютное время), заставили пересмотреть ряд основных положений
классической физики Ньютона, установили новые пространственно-вре-
менные представления (относительность длины, времени, одновремен-
ности событий). Однако эта теория не отбросила совсем закономерно-
стей, установленных классической механикой, а уточнила их в случае
движения со скоростями, соизмеримыми со скоростью света в вакууме.
610 Приложение. Краткие биографические справки о физиках
Исходя из своей теории, в том же 1905 г. Эйнштейн открыл закон
взаимосвязи массы и энергии. Это соотношение Эйнштейна (Е = тс2)
лежит в основе расчета энергетического баланса ядерных реакций, в
основе всей ядерной физики. Все положения и выводы специальной
теории относительности подтвердились в многочисленных эксперимен-
тах, поэтому она стала мощным инструментом в физических исследова-
ниях, в частности в физике микромира.
Эйнштейн ввел в 1905 г. представление о дискретной, квантовой
структуре самого светового излучения, рассматривая последнее как по-
ток фотонов (фотонная теория света). Исходя из квантовой теории света,
Эйнштейн объяснил такие явления, как фотоэффект, правило Стокса
для флюоресценции, фотоионизацию и др., которые не могла объяснить
электромагнитная теория света (Нобелевская премия, 1921). В 1907 г.
распространил идеи квантовой теории на физические процессы, непо-
средственно не связанные со светом. В частности, рассмотрев тепловые
колебания атомов в твердом теле и использовав идеи квантовой теории,
объяснил уменьшение теплоемкости твердых тел при понижении темпе-
ратуры, разработав первую квантовую теорию теплоемкости твердых тел
(1907). В 1909 г. впервые рассмотрел корпускулярно-волновой дуализм
для излучения, а также флуктуации энергии равновесного излучения, по-
лучив формулу для флуктуации энергии. В 1912 г. установил основной
закон фотохимии: каждый поглощенный фотон вызывает одну элемен-
тарную фотореакцию (закон Эйнштейна). Предсказал в 1916 г. явление
индуцированного излучения, ввел вероятности спонтанного и вынужден-
ного излучений (коэффициенты Эйнштейна).
В статистической физике развил в 1905 г. молекулярно-статистичес-
кую теорию броуновского движения, в 1924-25 гг. создал квантовую ста-
тистику частиц с целым спином (статистика Бозе-Эйнштейна). В 1915 г.
предсказал и совместно с В. де Гаазом экспериментально обнаружил эф-
фект изменения механического момента при намагничивании тела (эф-
фект Эйнштейна-де Гааза).
В 1915 г. завершил создание общей теории относительности, или со-
временной релятивистской теории тяготения, установившей связь между
пространством-временем и материей. К ее созданию Эйнштейна при-
вел анализ равенства отношения инертной массы тела к гравитацион-
ной для всех тел (принцип эквивалентности). Этот принцип вместе с
принципом относительности лег в основу общей теории относительно-
сти, объяснившей сущность тяготения, состоящую в искривлении четы-
рехмерного пространства-времени вокруг тел, которые образуют грави-
тационное поле. Вывел уравнение, описывающее поле тяготения (урав-
нение Эйнштейна). Для проверки своей теории предложил три эффекта:
искривление светового луча в поле тяготения Солнца, смещение периге-
лия Меркурия и гравитационное красное смещение. Впоследствии эти
эффекты были обнаружены и показали количественное совпадения с
выводами теории. В 1916 г. постулировал гравитационные волны и
в 1918 г. вывел формулу для мощности гравитационного излучения.
В 1917 г. Эйнштейн предложил модель стационарной Вселенной. Начи-
ная с 1933 г. работы Эйнштейна были посвящены вопросам космологии
и единой теории поля.
Член многих академий наук и научных обществ, в частности ино-
странный член АН СССР (1926).
СПИСОК ЛИТЕРАТУРЫ
1. Шпольский Э.В. Атомная физика. Т. 1,2.—М.: Наука, 1974.
2. Сив у хин Д.В. Атомная и ядерная физика. Ч. 1.—М.: Наука, 1986.
3. Вихман Э. Квантовая физика.—М.: Наука, 1977.
4. Матвеев А.Н. Атомная физика.—М.: Высшая школа, 1985.
5. Спроул Р. Современная физика.—М.: Наука, 1974.
6. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 8,9.—М.: Мир,
1977.
7. Борн М. Атомная физика.—М.: Мир, 1967.
8. Блохинцев Д.И. Основы квантовой механики.—М.: Наука, 1976.
9. Ландау Л. Д., Лифшиц Е. М. Квантовая механика.—М.: Наука, 1974.
10. Маррел Дж., Кеттл С., Теддер Дж. Химическая связь.—М.: Мир,
1980.
Дополнительная литература
1. Левич В. Г., Вдовин Ю.А., Мямлин В. А. Курс теоретической физики.
Т. 2.—М.: ФМ, 1962.
2. Давыдов А. С. Квантовая механика.—М.: ФМ, 1963.
3. Ландау Л.Д., Лифшиц Е.М. Квантовая электродинамика.—М.: Наука,
1980.
4. Ландау Л.Д., Лифшиц Е.М. Теория поля.—М.: Наука, 1973.
5. М а з а л о в Л. Н. Рентгеновские спектры и химическая связь.—Новосибирск:
Наука, 1982.
6. Сайто К. Химия и периодическая таблица.—М.: Мир, 1982.
7. С л стер Дж. Электронная структура молекул.—М.: Мир, 1965.
8. Леше А. Физика молекул.—М.: Мир, 1987.
9. Ландау Л. Д., Лифшиц Е.М. Механика.—М.: Наука, 1973.
10. Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А. Основы кристаллогра-
фии.—М.: ФМ, 2004.
11. Стародубцев С.В., Романов А.М. Взаимодействие гамма-излучения с
веществом.—Ташкент: Фан, 1971.
12. Коляда В.М., Зайченко А.К., Дмитриенко Р.В. Рентгеноспек-
тральный анализ с ионным возбуждением.—М.: Атомиздат, 1978.
13. Вольдсет Р. Прикладная спектрометрия рентгеновского излучения.—М.:
Атомиздат, 1977.
14. Вертхайм Г., Хаусман А., Зандер В. Электронная структура точеч-
ных дефектов.—М.: Атомиздат, 1977.
612 Список литературы
15. Методы анализа поверхности / Под ред. А.Задерны.—М.: Мир, 1979.
16. Степанов Н.Ф., Пупышев В.И. Квантовая механика молекул и кван-
товая химия.—М.: Изд-во Моск, ун-та, 1991.
17. Мальцев А.А. Молекулярная спектроскопия.—М.: Изд-во Моск, ун-та,
1980.
18. Накамото К. Инфракрасные спектры неорганических и координацион-
ных соединений.—М.: Мир, 1966.
19. Урусов В. С. Теоретическая кристаллохимия.—М.: Изд-во Моск, ун-та,
1987. 276 с.
20. Фриш С. Э. Оптические спектры атомов.—М.-Л.: ФМ, 1963.
21. Радциг А.А., Смирнов Б.М. Справочник по атомной и молекулярной
физике.—М.: Атомиздат, 1980.
22. Храмов Ю. А. Физики. Биографический справочник.—М.: Наука, 1983.
23. Мухин К.Н., Суставов А.Ф., Тихонов В.Н. Российская физика Но-
белевского уровня.—М.: ФМ, 2006.