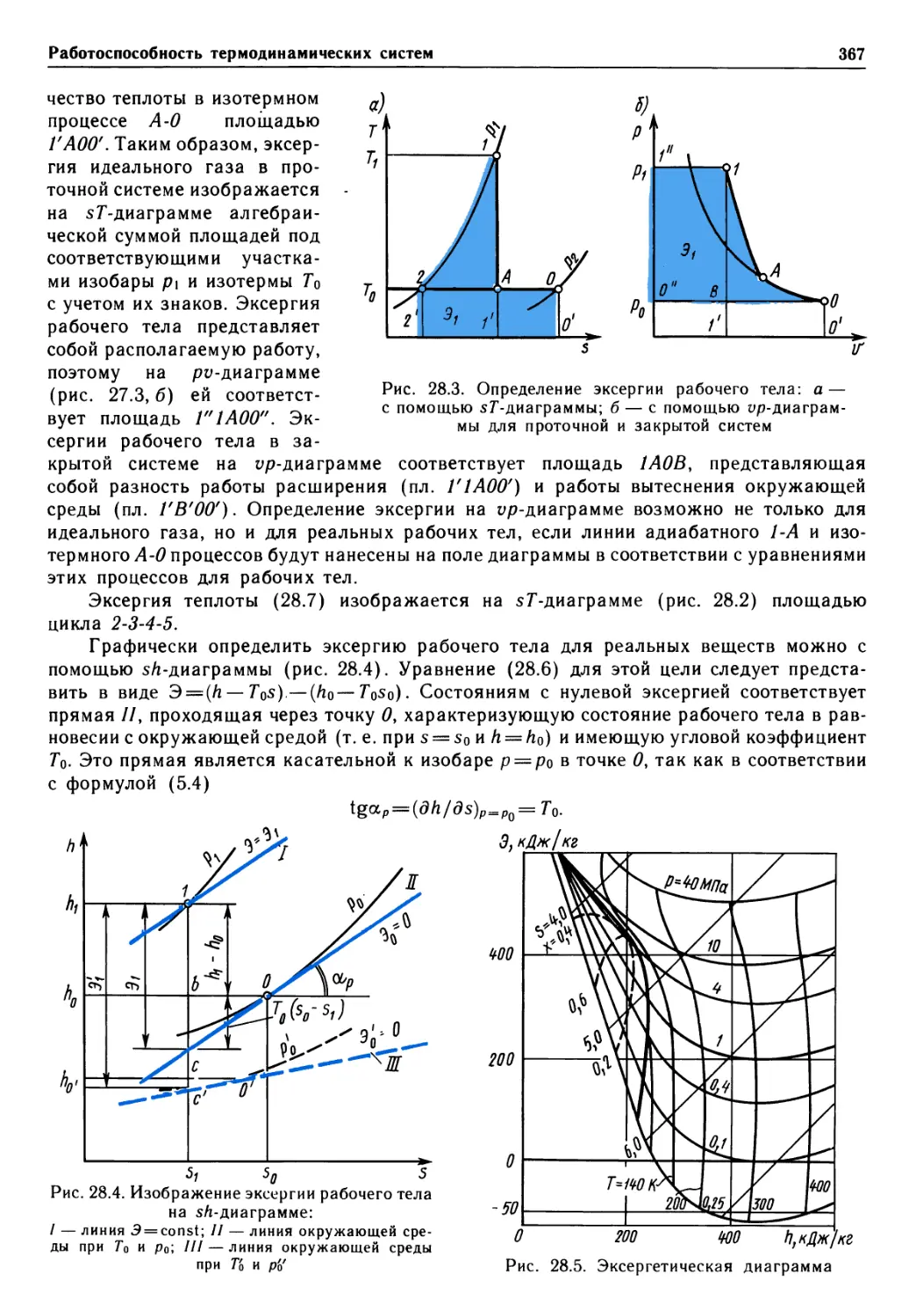
Author: Крутов В.И. Исаев С.И. Кожинов И.А.
Tags: тепловые двигатели в целом получение, распределение и использование пара паровые машины паровые котлы теплоэнергетика теплотехника термодинамика тепловые двигатели
ISBN: 5-06-002045-2
Year: 1991
ТЕХНИЧЕСКАЯ
Под редакцией В. И. Крутова
Третье издание,
переработанное и дополненное
Допущено Государственным комитетом СССР
по народному образованию
в качестве учебника для студентов
машиностроительных специальностей вузов
Москва
«Высшая школа*
1991
ББК 31.31
Т 38
УДК 621.1.016.7
Авторы:
В. И. Крутое, С. И. Исаев, И. А. Кожинов, Н. П. Козлов,
В. И. Кофанов, Б. М. Миронов, В. М. Никитин,
Г. Б. Петражицкий, А. М. Пылаев, В. И. Хвостов,
Е. В. Шишов
Рецензент — д-р техн. наук, проф. В. К. Кошкин (Московский
авиационный институт им. Серго Орджоникидзе)
Техническая термодинамика: Учеб. для машиностроит.
Т 38 спец. вузов/В. И. Крутов, С. И. Исаев, И. А. Кожинов
и др.; Под ред. В. И. Крутова.— 3-е изд., перераб. и доп.—
М.: Высш. шк., 1991.— 384 с: ил.
ISBN 5-06-002045-2
В учебнике изложены основные законы термодинамики и их применение
к идеальным и реальным рабочим телам. Уделено внимание основным положениям
о прямых и обратных циклах, эксергии, непосредственному преобразованию
теплоты в электрическую энергию, основам химической термодинамики растворов.
В третьем издании (2-е— 1981 г.) дополнительно изложены основы
термодинамики плазмы и твердого тела, циклы с реальными рабочими телами, элементы
статистической термодинамики, истечение из сосудов и другие вопросы.
2203020000(4309000000)—332
Т 147-91 ББК 31.31
001(01)—91 6П2.2
Учебное издание
крутов Техническая
Виталий Иванович терМОДИНЗМИКа
исэев
Сергей Иванович
Кожинов
Иван Александрович
и др.
Заведующий редакцией А. В. Дубровский. Редактор
Л. Н. Шатунова. Младший редактор Т. Ф. Артюхина.
Художник В. М. Боровков. Художественный
редактор С. Г. Абелин. Технический редактор Л. А.
Муравьева. Корректор Г. И. Кострикова
ИБ № 9107
Изд. N9 ОТ-746. Сдано в набор 31.07.90. Подп. в печать 04.06.91. Формат
70X100/16. Бум. офс. № 2. Гарнитура литературная. Печать офсетная.
Объем 31,2 усл. печ. л. 62,4 усл. кр.-отт. 31,28 уч.-изд. л. Тираж 15 000 экз.
Зак. № 584. Цена 2 руб.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул., д. 29/14.
Московская типография N9 4 Госкомпечати СССР
129041, Москва, Б. Переяславская, 46.
ISBN 5-06-002045-2 © Коллектив авторов, 1991
Предисловие
Важнейшая роль в решении народнохозяйственных задач принадлежит энергетике,
в теоретическую базу которой входит термодинамика. Изучив термодинамику,
студенты энергетических, машиностроительных и отчасти приборостроительных
специальностей получат хорошую основу для усвоения специальных дисциплин учебного
плана. В свою очередь, материал технической термодинамики опирается на знание
математики, физики, химии, алгоритмических языков и программирования.
Предлагаемый учебник по технической термодинамике подготовлен в
соответствии с утвержденной учебной программой на основе лекций, прочитанных авторами
студентам различных специальностей Московского государственного технического
университета им. Н. Э. Баумана.
В учебнике в сжатой форме раскрыт предмет термодинамики. Термодинамика
изучает фундаментальные законы природы о превращениях энергии в различных
процессах, а также вопросы повышения эффективности работы машин и аппаратов,
использующих эти процессы. Уделено внимание основным положениям о прямых и
обратных циклах, эксергии, непосредственному преобразованию теплоты в
электрическую энергию. Изложены основы химической термодинамики растворов, теории
истечения идеальных и реальных рабочих тел.
В отличие от многих изданных учебников в данном рассмотрены
термодинамические свойства плазмы, истечение из сосудов ограниченных и неограниченных
размеров, элементы статистической, неравновесной термодинамики и термодинамики
твердых тел.
Методологической основой познания общих законов взаимодействия в материальном
мире является диалектический материализм. Студенты могут убедиться в этом
прочитав изложение основных законов термодинамики и, в частности, второго
закона — его отношения к принципам существования и возрастания энтропии, связи
деградации энергии с проблемами теплового загрязнения атмосферы Земли.
Целью обучения термодинамике является привитие студентам умений и навыков,
необходимых для выполнения термодинамических расчетов, связанных с анализом
эффективности различных теплоэнергетических машин и установок.
Для этого студенты должны усвоить и знать:
основные принципы оценки эффективности теплоэнергетических установок и машин,
работа которых базируется на фундаментальных законах термодинамики;
методы математического и физического моделирования тепловых процессов;
должны уметь:
формулировать цель проблемы, связанной с расчетом и проектированием
теплоэнергетической установки или машины определенного назначения (в соответствии со
специальностью);
разработать физическую модель процесса;
ПРЕДИСЛОВИЕ
применять математическое моделирование термодинамического процесса для оценки
эффективности теплоэнергетической установки или машины.
Для хорошего усвоения материала учебника необходимо применять активные
формы обучения, а именно:
семинарские занятия с использованием учебного пособия «Задачник по
технической термодинамике и теории теплообмена» под ред. В. И. Крутова и Г Б. Петражицкого
(М., 1986);
лабораторные работы с использованием учебного пособия «Лабораторный
практикум по термодинамике и теплопередаче» под ред. В. И. Крутова, Е. В. Шишова
(М., 1988);
домашние задания (задания приведены в вышеназванном задачнике); часть
домашних заданий должна выполняться с применением ЭВМ.
Эффективность усвоения возрастает при использовании технических средств
обучения, аналоговых и цифровых ЭВМ, а также типовых лабораторных
установок, описанных в вышеназванном практикуме.. Лабораторные установки
обеспечивают экспериментальную проверку достоверности изучаемых законов и
процессов. Проводя лабораторные работы, студенты усваивают основные теплофизические
методы измерений, приобретают навыки испытаний теплоэнергетических установок
и участия в научных исследованиях.
Выполняя домашние задания, студенты решают конкретные теплотехнические
задачи, что способствует систематизации, закреплению и расширению теоретических
знаний, развитию навыков самостоятельной работы с технической литературой.
Авторами учебника являются В. И. Крутов (Предисловие, Введение, гл. 9, 23 и
25), С. И. Исаев (гл. 3, 4, 16, 17, § 18.1 — 18.7), И. А. Кожинов (гл. 20, 21, 22, § 27.1,
27.3, 27.4), Н. П. Козлов (гл. 13, § МЛ —14.5), В. И. Кофанов (гл. 19, § 18.8, 24.9, 27.2),
Б. М. Миронов (гл. 11), В. М. Никитин (§24.1—24.8), Г. Б. Петражицкий (гл. 8, 10, 12,
§ 26.3—26.5, 26.7), В. И. Хвостов (гл. 1, 2, § 26.1, 26.2, 26.6, 26.8, 26.9, гл. 28), Е. В. Шишов
(гл. 5, 6, 7, § 14.6—14.8); гл. 15 написана Г. Б. Петражицким и А. М. Пылаевым
совместно.
Авторы выражают благодарность профессору В. К. Кошкину за ценные
замечания и пожелания, которые были учтены при доработке рукописи и позволили
повысить ее качество.
Авторы обращаются к читателям с просьбой присылать замечания и
предложения, появившиеся при чтении учебника, по адресу: 101430, Москва, ГСП-4,
ул. Неглинная, д. 29/14, издательство «Высшая школа».
Авторы
ВВЕДЕНИЕ
Теория производит тем большее
впечатление, чем проще ее предпосылки,
чем разнообразнее предметы,
которые она связывает,
и чем шире область ее применения.
Отсюда глубокое впечатление, которое
произвела на меня термодинамика.
Это единственная физическая теория
общего содержания, относительно которой
я убежден, что в рамках применимости
ее основных понятий
она никогда не будет опровергнута.
А. Эйнштейн
Введение
Исторический очерк. История человеческого общества неразрывно связана с
развитием энергетики. Сначала человек использовал лишь собственную мускульную силу/
затем мускульную силу домашних животных, затем энергию ветра, воды, пара и т. д.
Источники энергии, которые человек использовал в своих целях, постепенно
становились все более мощными. Создание тепловых двигателей в XIX в. знаменовало
качественный скачок в техническом прогрессе, так же как открытие ядерной реакции
в нашем столетии.
Достижения промышленности, авиации, космонавтики оказались возможными
в результате освоения таких мощных источников энергии, как гидравлические,
паровые и газовые турбины, двигатели внутреннего сгорания, ракетные и реактивные
двигатели, атомные реакторы, холодильники и криогенные установки.
Стержневое значение в развитии энергетики имела и имеет термодинамика,
являющаяся теоретической базой создания теплоэнергетических машин и установок.
Прел мегом термодинамики является изучение наиболее общих свойств
макроскопических материальных систем, проявляющихся в равновесных (и неравновесных)
процессах обмена энергией между ними. Значение термодинамики среди других
наук весьма велико, так как почти все явления природы в той или иной степени
связаны с процессами преобразования энергии. Поэтому область применения методов,
которыми пользуется термодинамика, весьма обширна.
Термодинамика как наука возникла в начале XIX в. в связи с необходимостью
теоретического обоснования тепловых процессов в паровых поршневых машинах.
Поэтому первоначально, в середине XIX в., основным содержанием термодинамики
было изучение процессов взаимного превращения теплоты и механической работы
как двух форм обмена энергией, отражением чего явилось и само название
науки, составленное из двух слов греческого языка: thefme — тепло, dynamis — сила
(сила как средство совершения работы). Этим же объясняется и то обстоятельство,
что открытие и обоснование важнейших понятий термодинамики — термодинамической
температуры и энтропии — оказались исторически связанными с исследованиями
работы тепловой машины.
Однако по мере углубления знаний о явлениях, сопровождающих процессы
передачи энергии от одних тел к другим, становилось ясно, что, несмотря на
большое разнообразие таких процессов, они обнаруживают много общих,
универсальных свойств, не зависящих ни от конкретной формы обмена энергией, ни от
физических свойств тех конкретных тел, которые обмениваются энергией. Вследствие
универсальности этих свойств их изучение оказалось возможным с одних и тех же
позиций, одними и теми же методами, с применением одинакового физического и
математического аппарата.
в ВВЕДЕНИЕ
Существенный вклад в развитие термодинамики внес М. В. Ломоносов (1711 —
1765) — первый русский ученый-естествоиспытатель. Его открытия обогатили многие
отрасли знаний, а идеи далеко определили науку того времени и практически
предвосхитили достижения физики XIX в.
Ломоносов открыл и экспериментально доказал закон сохранения вещества;
является одним из основоположников молекулярно-кинетической теории теплоты. Свою теорию
теплоты он изложил в работе «Размышления о причинах теплоты и стужи»
(1747—1748), где высказал убеждение в том, что теплота является формой
движения мельчайших частиц тела, и, таким образом, он не только определил сущность
теплоты как внутреннего движения материи, но и сущность разработанных
впоследствии законов термодинамики.
Так, например, в работе «Рассуждения о твердости и жидкости тел» (1760)
Ломоносов так сформулировал одно из этих положений:
«Ежели где убудет несколько материи, то умножится в другом месте... Сей всеобщий
естественный закон простирается и в самые правила движения, ибо тело, движущее
своею силой другое, столько же оное у себя теряет, сколько сообщает другому, которое
от него движение получает».
В основе этого положения лежит представление о первом законе термодинамики,
являющемся законом сохранения энергии.
В работе «Размышления о причинах теплоты и стужи» Ломоносов подчеркнул,, что:
«Если более теплое тело А приходит в соприкосновение с другим телом Б, менее
теплым, то находящиеся в точке соприкосновения частички тела А быстрее вращаются,
чем соседние с ним частички тела Б. От более быстрого вращения частички тела А
ускоряют вращательное движение частичек тела Б, т. е. передают им часть своего
движения; сколько движения уходит от первых, столько же прибавляется ко вторым.
Поэтому когда частички тела А ускоряют вращательное движение частичек тела Б,
то замедляют свое собственное. А отсюда, когда тело А при соприкосновении
нагревает тело Б, то само оно охлаждается... Поэтому холодное тело Б, погруженное
в тело А, не может воспринять большую степень теплоты, чем какую имеет тело А».
В приведенных соображениях раскрывается сущность процесса теплообмена,
заключающаяся в том, что движение, а значит и теплота, может передаваться лишь
от тела более нагретого к телу менее нагретому и что эта передача может
происходить лишь до тех пор, пока не сравняются скорости движения частичек обоих
тел. Отсюда следует, что обратный естественный процесс передачи движения от менее
нагретого тела к более нагретому невозможен. Указанные сображения Ломоносова
составляют содержание второго закона термоднамики, сформулированного Р. Клаузиу-
сом (1822—1888) только в 1850 г., т. е. спустя примерно 100 лет после Ломоносова.
Большой интерес представляют высказывания Ломоносова о «наибольшей и
последней степени холода», стоящие в непосредственной связи с третьим законом
термодинамики. Ломоносов пишет:
«...нельзя назвать какую-нибудь определенную скорость движения, чтобы
мысленно нельзя было представить себе .^большую скорость. Это надо отнести и к
тепловому движению, поэтому высшая и последняя"^сг'ёп'ёнь'ТЙЬ^кег- настолько
уменьшиться, что наконец тело достигает состояния совершенного покоя и никакое
дальнейшее уменьшение движения невозможно. Следовательно, по необходимости должна
существовать наибольшая и последняя степень холода, состоящая в полном покое
частичек, в полном отсутствии вращательного движения их».
И далее:
«Так как воздух всюду и везде наблюдается газообразным, т. е. теплым, то все
тела, окруженные земной атмосферой, хотя бы и казались чувствам холодными,—
теплы и поэтому высшей степени холода на нашей планете не может быть».
Много позже это положение Ломоносова было сформулировано в виде принципа
Введение 7
недостижимости абсолютного нуля температур, вытекающего в качестве одного из
следствий тепловой теоремы Нернста.
Среди работ, появившихся в пору широкого распространения паровых машин и
заложивших основы термодинамики как науки, необходимо отметить прежде всего
работу выдающегося французского ученого С. Карно (1796—1836) «Размышления о
движущей силе огня и о машинах, способных развить эту силу» (1824), содержащую
фактически формулировку второго закона термодинамики. В работе были
сформулированы идеи, создавшие впоследствии основу технической термодинамики. Он ввел
такие основополагающие понятия термодинамики, как равновесный процесс, круговой
процесс, сформулировал принцип (принцип Карно), определивший работоспособность
теплоты и явившийся в дальнейшем фундаментом для обоснования понятий
термодинамической температуры и энтропии, показал, что коэффициент полезного
действия всех тепловых машин зависит от разности температур внутренней и
окружающей сред.
В 1816 г. в Великобритании Стирлингом была запатентована «машина, которая
производит движущую силу посредством нагретого воздуха». Предложенный для этой
машины цикл занимает в термодинамике важное место, так как автором впервые
была предложена регенерация теплоты, получившая впоследствии широкое
распространение в теплотехнике. Циклы с полной регенерацией теплоты, по экономичности
равные циклу Карно, стали часто называться обобщенными циклами Карно.
Большое значение для становления термодинамики имело открытие основных
газовых законов: Бойля — Мариотта (1661), Гей-Люссака (1802), Дальтона (1802),
Авогадро (1811), Клапейрона (1834), давшего окончательное выражение уравнения
состояния идеального газа. В работах Ю. Р. Майера (1814—1878), опубликованных
в 1842 и 1845 г., Дж. Джоуля (1818—1889) —в 1843 г. и Г. Гельмгольца (1821 — 1894) —
в 1847 г., был установлен принцип эквивалентности теплоты и работы и на его
основе в окончательной форме сформулирован закон сохранения и превращения
энергии — первый закон термодинамики. У. Томсон (Кельвин) (1824—1907) на основе
принципа Карно ввел понятие и создал шкалу термодинамической температуры
(1848), не зависящую от свойств вещества, с помощью которого измеряется
температура.
Выдающийся вклад в развитие термодинамики внес Р. Клаузиус (1822—1888).
На основе эквивалентности теплоты и работы он ввел понятие внутренней энергии
рабочего тела и дал уравнение первого закона термодинамики (1850), а на основе
принципов Карно и эквивалентности теплоты и работы обосновал понятие энтропии
(принцип существования энтропии), им же сформулирован принцип возрастания
энтропии в необратимых процессах (1865).
На основе анализа свойств веществ вблизи абсолютного нуля немецкий
физик В. Нернст (1864—1941) обосновал третий закон термодинамики (1906). В
соответствии с этим законом энтропия конденсированных веществ при абсолютном нуле
является величиной постоянной, а М. Планк (1858—1947) предложил принять ее
равной нулю. Следует также отметить труды Дж. В. Гиббса (1839—1903), в которых
разработан метод потенциалов, создан законченный аппарат химической
термодинамики с рядом важных выводов и заложены основы статистической физики. Русский
химик Г. И. Гесс (1802—1850) экспериментально установил закон (1840) о тепловом
эффекте химической реакции, зависящем лишь от начального и конечного состояний
реакции. Большой вклад в развитие термодинамики внесли отечественные ученые.
Профессор Киевского университета Н. Н. Шиллер (1848—1910) дал более строгое
обоснование второго закона термодинамики. Профессор Т. А. Афанасьева-Эренфест
впервые показала целесообразность раздельного толкования второго закона
термодинамики для равновесных и неравновесных процессов.
В Московском высшем техническом училище им. Н. Э. Баумана, переименованном
ВВЕДЕНИЕ
в 1989 г. в Московский государственный технический университет, закладывались
теоретические основы теплоэнергетического машиностроения. Термодинамические
исследования возглавлялись профессорами В. И. Гриневецким (1871 —1919), К. В.
Киршем, Н. И. Мерцаловым (1866—1948), Л. К. Рамзиным (1887—1948), Б. М. Ошурковым
(1887—1927) и др.
В период 1901 —1908 гг. Гриневецкий опубликовал ряд работ, в которых изложил
термодинамический расчет паровых котлов, методы анализа рабочего процесса паровых
машин (с применением энтропийной диаграммы) и исследования общих уравнений
термодинамики применительно к водяному пару. В 1907 г. им был опубликован
капитальный труд «Тепловой расчет рабочего процесса». Профессор А. С. Ястржембский
так характеризует этот труд: «Этой глубокой работой, построенной на общих
положениях термодинамики, Гриневецкий заложил начало научно обоснованной теории
двигателей внутреннего сгорания и теплового расчета их рабочего процесса. Эта
работа Гриневецкого оказала огромное влияние на развитие отечественного двигате-
лестроения». Большое значение имели также труды профессоров К. В. Кирша и
Л. К- Рамзина в области термодинамического исследования топок паровых котлов,
котельных установок и происходящих в них тепловых процессов.
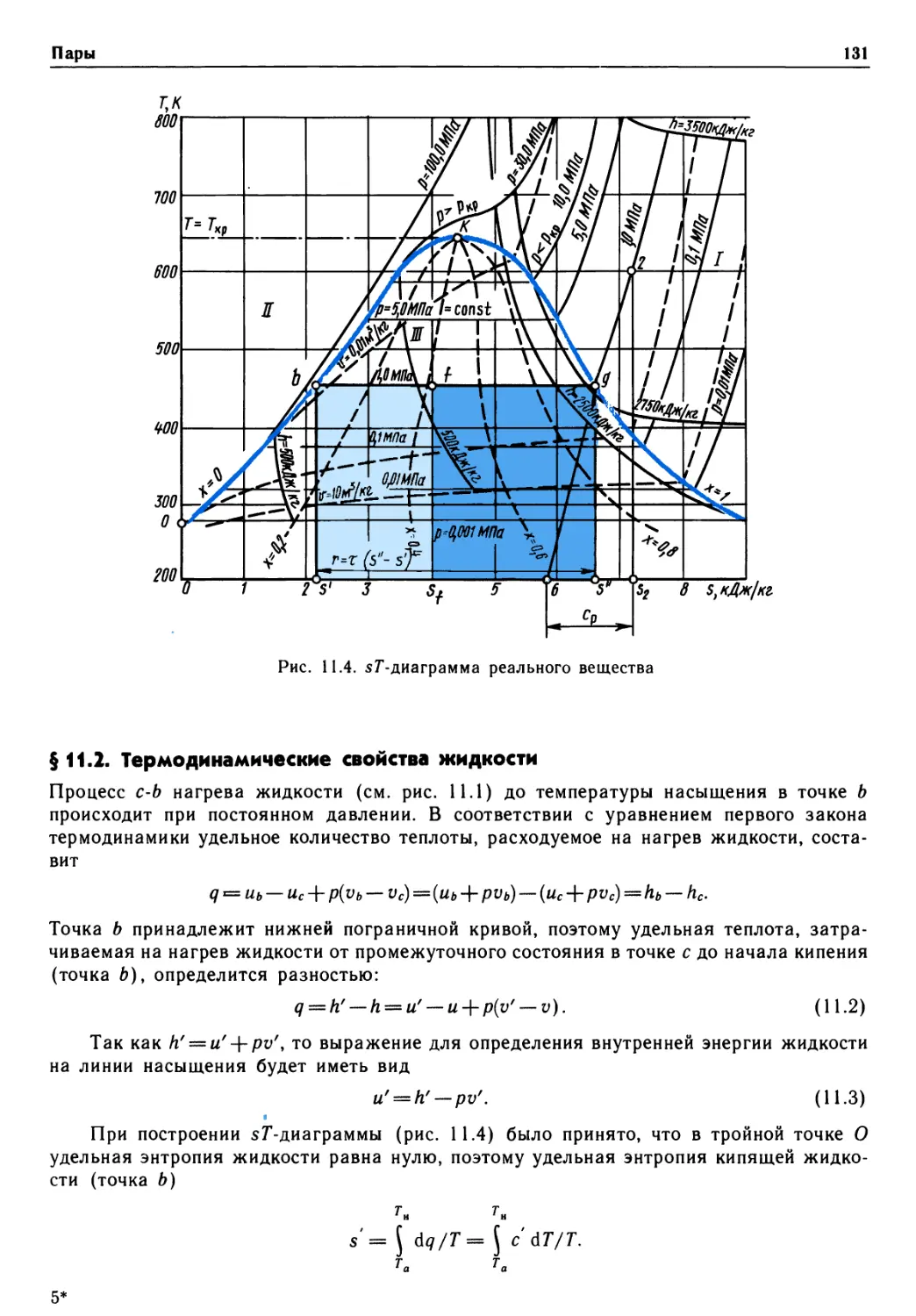
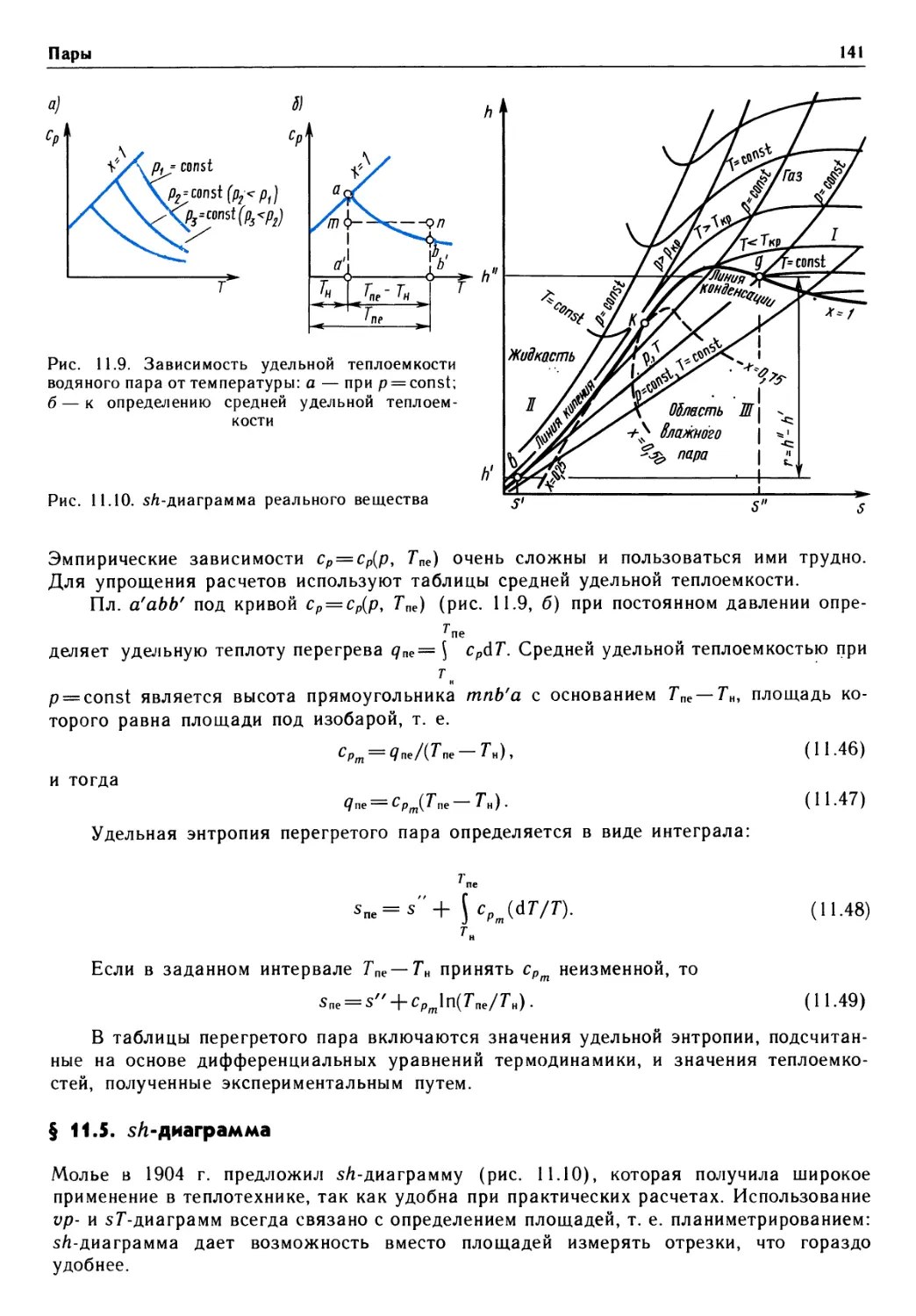
Л. К. Рамзин разработал и опубликовал в 1918 г. tfd-диаграмму для влажного
воздуха, которая широко применяется и в настоящее время для расчета
термодинамических процессов с влажным воздухом. Профессора Н. И. Мерцалов и Б. М.
Ошурков известны своими учебниками по термодинамике. Так, учебник профессора
Б. М. Ошуркова был первым советским учебником по термодинамике, а первый
советский задачник по технической термодинамике выпустил профессор МВТУ
М. В. Носов (1887—1968).
В СССР проводятся большие теоретические и экспериментальные исследования
в области термодинамики. В первую очередь следует отметить исследования
Всесоюзного теплотехнического института (ВТИ) им. Ф. Э. Дзержинского,
Центрального котлотурбинного института (ЦКТИ) им. И. И. Ползунова, Энергетического
института им. Г. М. Кржижановского АН СССР, Московского энергетического
института (МЭИ) и др.
Эти исследования привели к созданию теории рабочих процессов и циклов
тепловых двигателей, применяемых в современной теплоэнергетике. Важное значение имели
обширные работы, связанные с получением теплофизических свойств новых рабочих
тел. Приоритет в этой области принадлежит коллективу ученых МЭИ и ВТИ и в первую
очередь профессорам М. П. Вукаловичу (1899—1970), В. А. Кириллину, И. И. Новикову,
Д. А. Тимроту и Н. В. Иноземцеву (1902—1956), В. К. Кошкину и др.
Развитие термодинамики способствовало дальнейшему развитию теплотехники.
Так, в начале этого столетия появилась холодильная техника, обеспечивающая
возможность получения глубокого холода. Стали строиться мощные двигатели
внутреннего сгорания, паровые котлы, паровые и газовые турбины. Успехи термодинамики
способствовали развитию ракетостроения, машин и установок атомной энергетики.
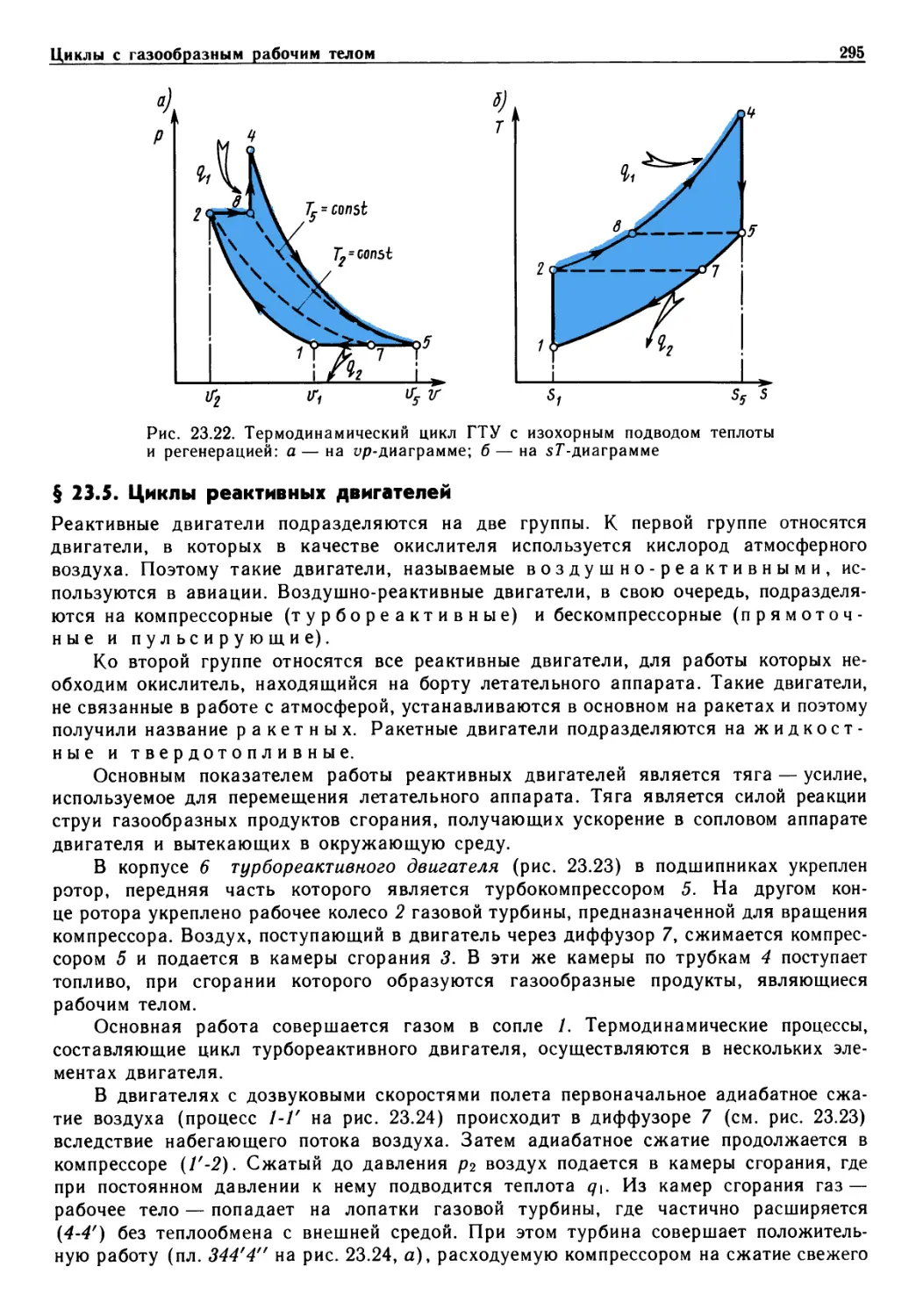
Энергетика и пути ее развития. Энергия для удовлетворения нужд народного
хозяйства и социальных потребностей общества вырабатывается на энергетических
станциях: тепловых (ТЭС), атомных (АЭС), гидравлических (ГЭС), а также за счет
возобновляемых источников энергии (ВИЭ). Так, например, в 1985 г. вся первичная
энергия в стране (100%) была получена за счет нефти (примерно 38%), угля
(20 %), газа (35 %). Около 2 % энергии была выработано на АЭС и около 4 % на ГЭС.
За счет различных ВИЭ было получено энергии в пределах 1 % (рис. В.1).
Перспективы развития энергетики в стране определяются энергетической
программой. Такая программа была разработана и утверждена в 1983 г., но так, что в
зависимости от складывающейся ситуации предусматривалась возможность
корректировки ее показателей через каждые пять лет. И, действительно, такая корректировка
Введение
100°/
20
1970
1990
2010
Годы
Рис. В. 1. Перспективы развития
энергетики
оказалась необходимой. Сегодня при формировании
энергетической политики в стране стало недопустимым
исходить только из задачи выработки необходимого
количества энергии, нужно при этом учитывать
экологические и социальные факторы, нравственные
соображения.
В разработке проекта новой скорректированной
энергетической программы приняли участие многие
научные коллективы и, в частности, Института
энергетических исследований АН СССР и
Государственного комитета СССР по науке и технике, результаты
их некоторых исследований использованы ниже.
Для получения целостного представления о
проблемах энергетики на ближайшую перспективу
целесообразно проанализировать и оценить возможности
каждого из направлений ее развития, определяемых
видом первичного источника.
Такими источниками являются органические
топлива (нефть, уголь, газ), а также ядерное топливо,
гидроэнергетические и возобновляемые ресурсы.
Нефть. По оценкам ученых, нефти в недрах
планеты имеется порядка 200 млрд. т, из них твердо
разведанных запасов 110 млрд. т. Ежегодное мировое
потребление нефти приближается к 3 млрд. т.
Добыча нефти постепенно усложняется. Уже в
настоящее время примерно треть всей нефти
добывается со дна морей. Глубина подводных скважин
достигает 2 км, увеличивается глубина скважин и на земле. Установлено, что
целесообразная глубина скважин для поиска нефти находится в интервале от 4 до 8 км.
Энергетика нашей страны до недавнего времени развивалась за счет наращивания
расходования нефти в качестве энергетического топлива (рис. В.1), так как это топливо
наиболее высококалорийное, удобное в транспортировке и эксплуатации.
Однако ограниченность запасов нефти на планете и целесообразность
использования нефти в качестве сырья для химической промышленности привели к
необходимости ограничения расходования нефти в качестве энергетического топлива. Вначале
это расходование будет стабилизироваться, а затем, с началом будущего века, и
снижаться (рис. В.1).
Уголь. Разведанные запасы угля в стране значительны, в особенности на
востоке страны в Канско-Ачинском и Экибастузском бассейнах. Так, например,
только в Канско-Ачинском бассейне находится 24 крупных месторождения угля с
мощностью пластов от 6 до 96 м. Однако низкая калорийность этих углей затрудняет
их использование. Так, в европейскую часть страны, где потребность в энергии
особенно высока, эти угли невыгодно транспортировать, так как значительную долю
перевозимого угля составляют отходы (и тем не менее доля топлива в таких перевозках
в настоящее время составляет около 40 %). Если же перерабатывать эти угли
в электрическую энергию на месте, то потребуется строительство сверхдальних
линий электропередачи (ЛЭП), в магистралях которых теряется до 10 % энергии и в
распределительных сетях еще около 40 %. Тем не менее в ближайшей перспективе
количество угля, используемого в качестве энергетического топлива, будет хотя и медленно,
но возрастать. Предполагается, что к 2000 г. добыча угля в мире превзойдет
отметку 9 млрд. т.
В СССР увеличение добычи угля будет происходить преимущественно за счет
открытых месторождений (до 50...60 % против 38 % в 1980 г.). Часть угля будет
10 ВВЕДЕНИЕ
перерабатываться в электрическую энергию непосредственно в районах добычи., Для
передачи энергии планируется строительство мощных ЛЭП, продолжится
формирование Единой энергетической системы страны с созданием межсистемных ЛЭП
напряжением переменного тока 500, 750 и 1150 кВ и постоянного тока напряжением
1500 кВ. В настоящее время плотность ЛЭП в СССР намного ниже, чем в странах
Западной Европы и США. Часть угля станет сырьем для производства на месте
синтетического жидкого топлива. В связи с этим идет активный поиск более
перспективных способов газификации углей и долговечных катализаторов для этих целей.
Газ. В настоящее время считают, что запасы природного газа на Земле
составляют примерно 2,5-1014 м3, причем твердо разведанных— (8...9)1013 м3.
Это самый чистый вид органического топлива, запасы которого на территории
страны значительны. Подсчитано, что за всю историю страны эти запасы были
израсходованы лишь на 4 %. Кроме обычного природного газа имеются большие запасы
еще газовых гидратов (газ, связанный с водой в зонах вечной мерзлоты и океане).
Расчеты и практика показали, что применение газа в качестве энергетического
топлива в европейской части страны оказалось эффективнее на 10... 15 % по
сравнению со всеми другими энергетическими ресурсами. Газ, кроме того, может существенно
повысить мобильность Единой энергетической системы при резких изменениях нагрузки
(по времени суток, по временным поясам), если организовать в стране производство
в достаточном количестве мощных энергетических газовых турбин и строительство
на их базе пиковых электростанций. Дело в том, что газовые турбины могут
значительно интенсивнее изменять или сбрасывать нагрузку по сравнению с паровыми
конденсационными станциями. Использовать газ можно также в парогазовых
циклах.
Все вышесказанное свидетельствует о том, что в ближайшей перспективе в
развитии энергетики приоритет будет отдаваться газу. В связи с этим необходимо
обеспечить производство 1 трлн. м3 газа не к 2000 г., как предусматривалось прежней
программой, а уже в тринадцатой пятилетке. При этом нужно знать, что добыча газа
усложняется из-за неблагоприятных климатических условий (особенно Севера),
строительства газопроводов в европейскую часть страны, необходимости все более углублять
газовые скважины (есть скважина, дающая газ с глубины 8088 м), что, естественно,
удорожает его поиск и добычу.
Практика эксплуатации газопроводов показала необходимость существенного
повышения качества их прокладки, монтажа и усиления контроля за значениями
параметров, за герметичностью стыков в процессе эксплуатации. Пренебрежение этими
требованиями может приводить (и уже приводило) к снижению безопасности работы
газопроводов и авариям.
АЭС. В настоящее время около 15% энергии в мире вырабатывается на АЭС,
эксплуатация которых началась с 1975 г. Однако опыт, накопленный за этот период,
оказался слишком малым (по сравнению с эксплуатацией ТЭС) настолько, что не
смог предотвратить крупные аварии АЭС вначале в Пенсильвании (США), а затем
в Чернобыле. Эти аварии вызвали определенный спад в развитии атомной энергетики.
Неоднозначно отношение к развитию атомной энергетики в различных государствах.
Если во Франции на АЭС вырабатывается около 70 % энергии без тенденции к
снижению, то в Швеции и Италии строительство АЭС прекращено. Атомная энергетика
США втрое мощнее советской и вдвое — французской. Ее доля в национальной
выработке энергии составляет 18 % и в 1991 г. достигнет 20% при 124 действую-,
щих энергетических блоках общей мощностью свыше 100 ГВт. В настоящее время
большие средства направляются на развитие научно-исследовательских и опытно-
конструкторских работ в области атомной энергетики с целью создания
необходимого задела на будущее. Изменила свое отношение к атомной энергетике и Япония,
построившая в одной из зеленых долин на побережье крупнейшую в мире АЭС
«Фукусити» (10 блоков общей мощностью 9 млн. кВт). Зеленая зона вокруг АЭС
Введение Ц
сохраняется в неприкосновенности, что было бы невозможным, если бы вместо АЭС
функционировала ТЭС.
Анализ перспектив развития энергетики в СССР, проведенный в последние годы,
показал, что наше народное хозяйство не сможет обойтись без определенного развития
атомной энергетики. Однако наращивание ее мощности предлагается осуществлять
примерно вдвое медленнее, чем это предусматривалось энергетической программой
1983 г. Одновременно предприняты значительные усилия к обеспечению безопасности
работы АЭС. Изменена конструкция поглощающих стержней и увеличено их количество.
Внесены существенные изменения в систему управления, внедряются средства
технической диагностики, вводятся новые автоматизированные системы контроля и анализа
параметров АЭС. Пассивная система охлаждения при необходимости будет
автоматически включаться в отвод теплоты от активной зоны реактора. Появились идеи
строительства маломощных АЭС с небольшими модульными реакторами. С 1995 г.
планируется оснащать АЭС реакторами нового поколения, которые будут обладать
«внутренней» безопасностью, предотвращающей возможность расплавления активной
зоны.
Фирма «Дженераль атомикс» из Сан-Диего разрабатывает небольшой
энергетический реактор, который намечено строить под землей. Охладителем в нем будет
инертный газ — гелий.
К новому перспективному направлению развития атомной энергетики повышенной
безопасности следует отнести также разработку и применение реакторов на быстрых
нейтронах с натриевым наполнителем: в первом реакторном контуре давление
среды составляет всего около 0,15 МН/м2 (в тепловых реакторах с водяным и газовым
охлаждением — десятки МН/м2), что практически исключает механические
повреждения корпуса и трубопроводов. Сталь при таком контакте с натрием не корродирует.
Натрий второго контура и рабочий пар, получающий теплоту от второго контура,
не радиоактивны.
Специалисты утверждают, что атомная энергетика с помощью быстрых реакторов
способна обеспечить человечество теплом и светом на ближайшее тысячелетие.
Кроме того, ученых все больше тревожат проблемы потепления климата
вследствие парникового эффекта. Атомная энергетика на этот процесс не влияет.
Повышению безопасности работы АЭС способствует также моделирование на ЭВМ
рабочих процессов АЭС. Пока надежно моделируются лишь переходные процессы,
что очень важно для создания совершенных систем автоматического регулирования.
Перед специалистами-разработчиками моделей стоит задача столь же надежно
моделировать экстремальные и аварийные ситуации, что позволит выявлять условия и причины
возникновения аварийных ситуаций, наиболее целесообразные средства борьбы с ними,
а главное, более уверенно определять требования, исключающие возникновение
аварии. В мае 1989 г. в Москве была учреждена Всемирная ассоциация организаций,
эксплуатирующих АЭС. Создан банк данных, который поможет принимать более
верные решения в вопросах развития атомной энергетики.
ГЭС. Гидростанции в нашей стране дают в настоящее время лишь 15...16%
электроэнергии и 4% общего производства энергетических, ресурсов (рис. В.1).
В связи с этим значение ГЭС для Единой энергетической системы страны не
столько в количестве производимой энергии, сколько в основном в возможности снятия
пиковых нагрузок, мобильного автоматического включения ГЭС в непредвиденных
обстоятельствах. Дело в том, что ТЭС и АЭС значительно инерционнее при смене
режимов и работают наиболее экономично на одном заданном установившемся
режиме. В связи с этим ГЭС работают в качестве регуляторов Единой энергетической
системы.
В нашей стране построены наиболее мощные ГЭС, но крупные ГЭС с большими
по площади водохранилищами нарушают экологическое равновесие и приводят к
значительным неблагоприятным последствиям в окружающей среде. В связи с этим в
12 ВВЕДЕНИЕ
перспективе предполагаются более медленные темпы строительства ГЭС в основном
в горных условиях (Тянь-Шань, Кавказ, Тунгуска). Следует также отметить
целесообразность использования энергии малых водных потоков (практически ручьев) с помощью
рукавных переносных гидроэлектростанций. Ручей (или его часть) забирается в
брезентовый рукав, подводящий воду к турбине, связанной с генератором. Мощность
такой установки до 1,5 кВт (имеются модификации), вырабатывается переменный
ток напряжением 220 В с частотой 50 Гц. Вес установки 85 кг. Себестоимость
1 кВт-ч рукавной ГЭС всего 0,5 коп., в то время как бензоэлектростанция
такой же мощности дает ток себестоимостью 35 коп. Длина рукава 100 м (10 секций
по 10 м) при уклоне потока 4° и 30 м при уклоне 10°. Потребность в таких
рукавных ГЭС в стране очень велика (для высокогорных пастбищ, геологических
партий и т. п.).
ВИЭ. К числу возобновляемых источников энергии обычно относят:
солнечную энергию;
ветровую энергию;
геотермальные источники энергии;
прирост биомассы на земле;
биогаз из отходов животноводства;
энергию приливов и отливов морей и океанов, энергию морских волн и др.
До настоящего времени количество энергии, полученное за счет ВИЭ, в общем
энергетическом потоке незначительно. В нашей стране за счет ВИЭ вырабатывается
всего 1 млн. т условного топлива. И тем не менее опыт использования ВИЭ в мире
постепенно накапливается. Специалисты, например, убеждены, что к 2060 г. доля энергии
Солнца в общем потреблении может превысить 50 %.
Фирма «Арко Солар» (США) еще в 1983 г. начала эксплуатировать солнечную
электростанцию мощностью 1 МВт и строит в Калифорнии фотоэлектрическую
станцию мощностью 6,5 МВт. В нашей стране длительное время работает гелиостанция
в Крыму.
Ведутся большие работы по совершенствованию кремниевых солнечных элементов
(кремниевые пластинки преобразуют солнечный свет в электричество), в результате
чего за последние 10 лет цена на них снизилась в 3,5 раза. Значительное внимание
уделяется более дешевому поликристаллическому и аморфному кремнию в виде пленки.
Коэффициент полезного действия элементов на аморфном кремнии составляет 6... 10 %
против 12... 16 % монокристаллических элементов.
В перспективе будет расширяться использование геотермальных источников энергии,
в особенности в районах, богатых ими. Так, например, на Камчатке известно свыше
140 таких источников. Более 10 лет вырабатывает ток Паужстская геотермальная
электростанция. Создается Мутновская геоТЭС мощностью более 100 тыс. кВт. Более
20 тыс. квартир в городе Видин (НРБ) отапливаются геотермальными водами.
Внимание ученых-энергетиков привлекают и перспективы использования ежегодно
возобновляемой биомассы. Дело в том, что каждый год на планете прирастает
117 млрд. т биомассы (в сухом весе) и в том числе 80 в лесах, 18 в степях и саванне,
9 на обрабатываемых полях. Энергия, которой обладает такое количество биомассы,
эквивалентна 40 млрд. т нефти.
Переработка зеленой биомассы в топливо осуществляется газификацией древесины
и ферментацией Сахаров, причем в качестве целевого продукта не обязательно
получать только углеводороды. Известны и другие органические вещества — эфиры
и спирты (метанол, этанол, бутанол), которые по своим энергетическим свойствам
близки к нефти. Уже накоплен положительный опыт их получения. Так, например,
ферментация отходов сахарного тростника в Бразилии в 1981 г. дала 4,2 млн. т этанола.
В период с 1977 по 1982 г. Япония снизила количество нефти для топлива с 74,5 до
62 % с тенденцией к дальнейшему снижению за счет получения этанола из рисовой
соломы, ацетона и бутанола из сельскохозяйственных отходов. Фирма «Сан даймонд
Введение 13
гроверс» (Калифорния) производит 4,5 МВт Электроэнергии за счет сжигания скорлупы
грецких орехов, что за год экономит 11 тыс. т. нефти. Фирма «Гемотек
инкорпорейшен» вырабатывает 8,5 МВт электроэнергии, сжигая миндальную скорлупу,
косточки персиков и слив. В США этанол получают из отходов кукурузы.
Получен некоторый опыт по преобразованию в электроэнергию морских волн.
Так, в Киевском политехническом институте была создана установка, подающая
морскую воду за счет энергии волн на некоторую высоту с последующим использованием
ее для привода гидротурбинки.
Одна из установок, созданных румынскими учеными, представляет собой буй с
открытым дном. При качании на волнах уровень воды в буе изменяется, что вызывает
движение воздуха через верхнее отверстие. Этот поток воздуха и использовали для
привода турбинки, ротор которой вращается всегда в одну сторону независимо от
направления движения воздуха. Пусть это пока только отдельные примеры, но и они
свидетельствуют о возможности этого направления развития энергетики.
В проекте новой энергетической программы СССР предусматривается к 2000 г.
получить за счет ВИЭ 20...25, а к 2010 г.—50...60 млн. т условного топлива. Это
экономически чрезвычайно трудная задача, так как стоимость энергии, полученной за счет
ВИЭ, пока слишком велика. Так, например, себестоимость 1 кВт-ч, выработанного
на Крымской гелиостанции, составляет — 26 руб., а на ТЭС и АЭС — всего 1,2 коп.
Следовательно, использование ВИЭ пока требует вложения больших средств, которые
могут окупиться лишь в отдаленной перспективе.
Для повышения эффективности использования ВИЭ, концентрации и
конкурентоспособности получаемой таким образом энергии необходимо проведение большого
объема научно-исследовательских работ.
Энергосбережение. Если поставить задачу обеспечения развития экономики страны
только путем наращивания энергетического потенциала, то уже в тринадцатой
пятилетке потребовалось бы условного топлива на 520...530 млн. т, а в 16 — на
1,4 млрд. т больше, чем в двенадцатой пятилетке. Задача развития энергетики
такими темпами для страны непосильна.
Для того чтобы темпы развития энергетики были реальными, необходимо проводить
активную энергосберегающую политику и прежде всего уменьшить потери
энергоресурсов. А они в стране весьма велики. Коэффициент полезного использования
энергоресурсов составляет в стране примерно 40 %, следовательно, 60 % составляют потери, из
которых примерно 20 % могут быть отнесены к предотвратимым. Только в факелах
сгорает 12... 15 млн. т условного топлива, которые могли бы дать для народного
хозяйства 8 млн. кВт электроэнергии. Именно часть предотвратимых потерь и
необходимо всемерно сокращать.
Расчеты показывают, что энергоемкость национального дохода должна обязательно
снижаться: так к 2000 г. энергоемкость должна снизиться в полтора раза, а к 2010 г.—
в два раза. Задача очень трудная и может быть решена только путем осуществления
общегосударственных мероприятий, таких, как снижение в структуре народного
хозяйства доли энергоемких отраслей за счет наращивания наукоемких.
Так, внедрение уже известных энергосберегающих технологий и оборудования
дало бы экономию 750...800 млн. т условного топлива. Можно обеспечить
значительную экономию энергии и в социально-бытовой сфере, если, например, усилить
теплозащитную способность строящихся зданий. В настоящее время разрабатывается новый
строительный материал, который может сэкономить до 50 % теплоты, расходуемой на
обогрев зданий. Стены здания, покрытые прозрачными панелями из этого материала,
воспринимают теплоту лучей солнца, пропускаемых панелями, и не отдают теплоту
наружу, так как панели являются хорошим теплоизоляционным материалом. Даже в
холодное время года солнечная энергия подогревает эти здания.
Люминесцентные лампы потребляют примерно в восемь раз меньше электричес-
И ВВЕДЕНИЕ
кой энергии по сравнению с лампами накаливания. Сбережение энергоресурсов
является делом всенародным и должно активно проводиться в жизнь как во всех отраслях
народного хозяйства, так и в быту.
Проблемы экологической* защиты окружающей среды. Применительно к
энергетике задачи экологической защиты окружающей среды особенно актуальны. Предприятия
топливно-энергетического комплекса выбрасывают в атмосферу около 33 млн. т
токсичных отходов. По сравнению с лучшими электростанциями мира наши выбрасывают
на порядок больше твердых частиц, в три раза больше серы, в два — оксидов азота.
Особенно вредны выбросы сернистых газов.
Совершенствование технологии и оборудования требует огромных средств.
Получить экологически «чистую» энергетику бесплатно невозможно. Передовые
промышленно развитые страны уже в настоящее время тратят на эти цели около 5 %
совокупного общественного продукта.
Серьезные экономические проблемы возникают также в связи с необходимостью
качественного захоронения на длительный («геологический») срок отходов атомной
энергетики. Определенные перспективы в этом деле откроет применение быстрых
реакторов. Многократное использование вторичного ядерного горючего в таких
реакторах приводит к выгоранию в потоке быстрых нейтронов самых тяжелых изотопов,
трансактинидов, испытывающих альфа-распад и спонтанное деление с очень большими
периодами. При оптимальной организации использования быстрых реакторов уровень
остаточной активности, получаемый в хранилище отходов тепловых реакторов через
миллион лет, может быть достигнут уже через двести лет.
Серьезные проблемы на планете возникают в связи с задачей сохранения
запасов пресной воды, широко используемой в качестве теплоносителя в
энергетических системах. Известно, что в настоящее время запасы пресной воды на земле
составляют всего 2,8 % и только 0,3 % ее запасов доступны для использования
человеком. Следовательно, задача экономии пресной воды при создании и эксплуатации
различных энергетических систем, использующих воду, замены ее опресненной водой
морей и океанов является крайне актуальной.
Все вышесказанное свидетельствует о том, что подходить к развитию энергетики
только с позиций экономических в настоящее время недопустимо. Необходимо
увязывать экономические аспекты с социальными и экологическими.
В целях улучшения экологической обстановки в стране предполагается
осуществить комплекс мероприятий, который позволит к 2000 г. сократить вредные выбросы
примерно на 30 % и в 1,5 раза — к 2010 г.
Человек сможет назвать себя действительным хозяином планеты только тогда, когда
он научится не истощать ее богатства, а приумножать их.
* От греч. эко — дом.
Термодинамика — это наука
с прочными основаниями,
ясными понятиями и меткими границами
Дж. К. Масквелл
В^ЗОЕЛ
ОСНОВНЫЕ
ПОНЯТИЯ ЗАКОНЫ
И УРАВНЕНИЯ
Законы термодинамики
представляют собой научные обобщения
экспериментальных данных,
наблюдений за явлениями природы
и работой машин, созданных человеком.
Достоверность законов подтверждена
согласием вытекающих из них выводов
с результатами опыта —
единственного критерия их истинности.
Путем математических преобразовании
уравнений, выражающих
законы термодинамики, получают
соотношения, необходимые для
термодинамического расчета
машин, аппаратов,
а также свойств веществ.
16 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Глава 1
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
§1.1. Предмет термодинамики
Предметом современной термодинамики является изучение тех наиболее общих
свойств макроскопических тел, которые не зависят от конкретного микрофизического
строения этих тел и которые проявляются в процессах обмена энергией между телами.
Любые явления в природе и технике сопровождаются обменом энергией, поэтому
термодинамика, разрабатывая общие методы изучения энергетических явлений, имеет
всеобщее методологическое значение и ее методы используются в самых различных
областях знания.
Разделы термодинамики, в которых методы, определения, математический аппарат
разрабатываются безотносительно к какому-либо конкретному приложению, часто
называют общей (или физической) термодинамикой.
В технической термодинамике общие методы применяют для
исследования явлений, сопровождающих обмен энергией в тепловой и механической формах.
Техническая термодинамика дает возможность построить теорию тепловых машин,
составляющих основу современной энергетики.
Химическая термодинамика представляет собой приложение общих
термодинамических положений к явлениям, в которых процессы обмена энергией
сопровождаются изменениями химического состава участвующих тел.
Указанное деление термодинамики в значительной степени условно. Так, выводы
общей термодинамики справедливы для всех других ее разделов; процессы горения
топлива в тепловых двигателях описываются методами химической термодинамики и т. д.
Термодинамика как наука характеризуется своим специфическим методом
описания изучаемых явлений. Главные особенности термодинамического метода
состоят в следующем.
1. Термодинамический метод построен на использовании небольшого числа
обобщенных закономерностей, установленных в результате накопления и научного
анализа огромного количества опытных фактов, что позволяет рассматривать эти
закономерности как объективные законы природы.
Эти обобщенные закономерности были сформулированы в форме так называемых
трех законов или трех начал термодинамики.
Первый закон термодинамики вытекает из всеобщего закона сохранения
и превращения энергии, выраженного в специальных термодинамических понятиях,
и обеспечивает возможность составления баланса энергии в термодинамических
процессах.
Понятия и определения Г7
Второй закон термодинамики устанавливает условия для взаимного
превращения работы и теплоты, а также указывает определенную направленность
изменений, возникающих во всех реальных процессах обмена энергией.
Третий закон термодинамики объясняет поведение веществ при
температуре, стремящейся к абсолютному нулю.
Иногда к числу законов термодинамики относят также существование
термического равновесия между телами, имеющими одинаковую температуру (так называемый
«нулевой» закон термодинамики).
Использование универсальных законов природы придает выводам и
соотношениям термодинамики достоверный характер.
2. Для описания процессов обмена энергией и свойств различных тел в
термодинамике используются физические понятия и величины, не связанные с существующими
представлениями о микроскопическом (молекулярном, атомарном и т. д.) строении
материи. Эти величины могут быть либо непосредственно измерены, либо вычислены
по термодинамическим соотношениям с использованием измеренных величин. Они
характеризуют итоговые результаты действия огромного числа микрочастиц вещества,
когда влияние каждой отдельной частицы становится неразличимым. Подобного
рода величины называются макроскопическими, феноменологическими,
или термодинамическими в отличие от микроскопических, характеризующих
поведение отдельных молекул, атомов и других частиц. Примерами феноменологических
величин являются температура, давление, плотность.
Преимущество феноменологического подхода состоит в том, что справедливость
термодинамических соотношений и выводов не нарушается, когда в ходе развития
физики непрерывно углубляются или даже в корне изменяются представления о
строении вещества. Общие термодинамические соотношения, записанные через
феноменологические величины, применимы к веществам в любом состоянии — газообразном,
твердом, жидком, а также к электромагнитному излучению, несмотря на большие
различия в физических свойствах этих форм материи.
Недостаток феноменологического метода состоит в том, что для его применения
требуется знание физических свойств конкретных рабочих тел. Эти свойства не могут
быть определены методами термодинамики и требуют поэтому экспериментального
исследования.
В конце XIX в. стала развиваться так называемая статистическая
термодинамика, являющаяся разделом статистической физики. В статистической
термодинамике свойства макроскопических тел вычисляются исходя из модельных
представлений о строении вещества (идеальный газ рассматривается как
совокупность невзаимодействующих частиц, твердое тело — как идеальная кристаллическая
решетка и т. п.). Поведение элементарных частиц описывается методами
классической либо квантовой механики, а макроскопические свойства получают статистическим
усреднением действия всех частиц, составляющих тело. Статистический метод
позволяет проникнуть в физическую сущность изучаемых явлений и вычислить значения
физических свойств конкретных веществ. Однако правильность таких расчетов зависит
от того, насколько совершенна используемая физическая модель строения вещества и
как точно известны величины, характеризующие поведение и свойства микрочастиц.
Поэтому результаты статистической термодинамики также требуют экспериментального
подтверждения.
При изложении феноменологической (классической) термодинамики нет
принципиальной необходимости прибегать к микрофизическим представлениям. Использование
некоторых элементарных моделей (например, молекулярно-кинетической модели
идеального газа) позволяет лишь пояснить связь таких макроскопических величин, как
температура; давление, энтропия и др., с исходными микроскопическими величинами.
Иногда статистические методы получают практическое. jmejij£YliLecTBO 1Щред феномено-
18 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
логическими, например при описании свойств веществ при предельно низких или
максимально высоких температурах и давлениях, когда непосредственное измерение
термодинамических величин становится весьма трудным и неточным. Термодинамика и
статистическая физика как науки о свойствах вещества и энергии взаимно дополняют
одна другую.
3. Термодинамический метод не является абсолютно универсальным. Область
его приложения ограничивается указанными ранее особенностями. С одной стороны,
в силу своей феноменологичности термодинамические методы исследования можно
применять только к макроскопическим телам, т. е. состоящим из весьма большого
числа элементарных частиц. С другой стороны, количество этих тел или их
совокупностей должно быть ограниченным. Выводы термодинамики нельзя распространять на
бесконечную Вселенную, так как основные положения термодинамики
сформулированы в результате наблюдения явлений лишь в ограниченной ее части.
§1.2. Виды энергии и формы обмена энергией
Материалистическая философия определяет энергию как меру различных видов
материального движения в процессах взаимного превращения одних форм движения в
другие. Движение, понимаемое в широком смысле, есть способность материи к
изменению и является ее неотъемлемым свойством.
Формы движения материи и виды энергии. Первой формой, изученной наукой
качественно и количественно, была механическая форма движения, состоящая в
изменении пространственного расположения макроскопических тел. К середине XIX в.
были изучены тепловая, электрическая, химическая, магнитная и
другие формы движения и найдены количественные меры для каждой из них. При
этом установлено, что
передача движения от одних тел к другим может происходить как без изменения,
так и с изменением формы движения. В первом случае уменьшение движения
некоторой формы в одном теле сопровождается таким же увеличением движения той же
формы в другом (принцип сохранения движения). Во втором случае уменьшение
движения некоторой формы в одном теле приводит к увеличению в другом теле
движения иной формы (принцип превращения движения).
Опыт показал, что такие превращения всегда происходят с одинаковым
отношением количеств взаимно превращающихся форм движения (выраженных каждая
своими единицами). Количественная эквивалентность различных форм движения
послужила основанием для введения единой, общей для всех форм движения материи
меры — энергии.
Энергия — общая количественная мера для всех форм движения материи,
способных превращаться одна в другую.
Любое материальное тело в зависимости от его физической структуры обладает
способностью к различным изменениям, т. е. может обладать движением различных
форм. Так, например, в смеси газообразных кислорода и водорода возможны
механические изменения (сжатие, ускорение потока), химические (горение),
электрические (поляризация при помещении в электростатическое поле), магнитные
(магнитная поляризация молекул кислорода в магнитном поле).
В связи с этим в качестве характеристики вида движения используют
понятие вида энергии (кинетическая, гравитационная, химическая, электрическая
энергия и др.). Следует иметь в виду, что энергия «данного вида» не является чем-то,
что передается от одних тел к другим в своем неизменном качестве. При передаче
движения может происходить как исчезновение прежней, так и появление новой формы
движения, но при этом энергия как общая мера любых форм движения едина по
своей сущности, она не создаваема и неуничтожима.
Особую роль в термодинамике играет понятие теплового движения материи.
Понятия и определения И)
Тепловым движением называют хаотическое механическое движение большой
совокупности микрочастиц, составляющих макроскопические тела.
В отличие от прочих видов движения (механического, электрического и др.).
характерных как для макроскопических тел, так и для элементарных частиц, понятия
тепловое движение и тепловая энергия имеют смысл только для большой совокупности
микрочастиц.
Установление количественной эквивалентности разных форм движения материи при
взаимных превращениях привело, как известно, к открытию закона сохранения
энергии. Этот закон стал универсальным после того, как в 40-е годы XIX в. в него
была включена тепловая форма движения материи. Основоположниками этого закона
считают немецких ученых Ю. Р. Майера и Г. Гельмгольца, английских
исследователей Дж. Джоуля и У. Томсона (Кельвина), но выводы этих ученых были подготовлены
трудами многих их предшественников.
От понятия вид энергии следует отличать понятие форма передачи энергии (или
способ обмена энергией).
Передача движения (энергии) от одних тел к другим происходит в результате
взаимодействия этих тел. Современная физика различает четыре фундаментальных
вида взаимодействия: электрическое, гравитационное, ядерное и слабое. Во всех
явлениях неастрономических и неядерных масштабов на микроскопическом уровне
проявляется лишь одно из них — электрическое. Однако макроскопические проявления этого
взаимодействия весьма разнообразны, и именно они определяют многие
наблюдаемые формы движения материи и соответствующие виды энергии. Так,
например, явления упругости обусловлены электрическим взаимодействием между
одноименно заряженными электронными оболочками соседних атомов твердого тела,
электромагнитное излучение нагретого тела — электрическим взаимодействием между
ядрами и их электронными оболочками, химические изменения — электрическим
взаимодействием ядер и электронных оболочек различных химических элементов
и т. д.
Такое разнообразие макроскопических проявлений фундаментального
микроскопического взаимодействия приводит и к большим различиям в изменениях, наблюдаемых
в телах при различных способах передачи энергии.
В ходе развития науки об энергии было, однако, установлено, что все виды
термодинамических взаимодействий, т. е. все формы обмена энергией, сводятся к двум
принципиально различным способам: совершению работы и теплообмену.
Работа. Передача энергии в результате макроскопического, упорядоченного,
направленного движения называется работой.
Количество передаваемой при этом энергии называют работой процесса или
просто работой.
Простейшим, наиболее наглядным видом работы является механическая
работа, совершаемая механической силой, которая перемещает в пространстве
макроскопическое тело или некоторую часть тела. Кроме того, существуют различные
виды немеханических работ. Так, электрическая работа совершается,
когда некоторое количество носителей электрического заряда переносится в
электрическом поле (при течении тока по проводнику, накоплении зарядов на обкладках
конденсатора и т. д.). При совершении магнитной работы происходит
организованный, соответствующий ориентации магнитного поля поворот в пространстве
всех элементарных магнитов, присутствующих в намагничиваемом материале.
Общим для всех видов работы свойством является принципиальная возможность
их полного количественного преобразования друг в друга.
Теплообмен. Передача энергии в результате теплообмена не связана с какими-либо
направленными перемещениями макроскопических количеств материи. Передача энергии
происходит под воздействием хаотического, т. е. теплового, движения микрочастиц,
20 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
составляющих макроскопические тела. Для этого между телами должен существовать
так называемый тепловой контакт, осуществляемый либо непосредственным
соприкосновением тел, либо переносом энергии беспорядочных электромагнитных колебаний,
а тела должны иметь различную температуру.
Передача энергии в результате обмена хаотическим, ненаправленным движением
микрочастиц называется теплообменом; а количество передаваемой при этом
энергии — кол и ч ест во м теплоты, теплотой процесса или теп л от ой *.
Работа (любого вида) и теплота не являются ни энергией (как общей мерой
движения), ни видом энергии (как мерой движения какой-либо определенной формы);
они являются лишь количествами, выражающими изменение материального движения
во взаимодействующих телах, а различные названия этих величин подчеркивают
различия в способах (формах) обмена энергией.
И работа, и теплота могут вызывать во взаимодействующих телах изменение
движения любой формы. Например, передача энергии в механической форме путем
совершения работы деформации над газом приводит к увеличению его теплового движения.
Электрическая работа, совершаемая аккумулятором, сопровождается химическими
изменениями его элементов.
Итак, существует множество различных форм движения материи и соответственно
множество различных видов энергии. Однако имеется лишь два принципиально
различающихся способа передачи энергии (формы обмена энергией): работа и
теплообмен .
Если не требуется указывать форму обмена энергией, то количество энергии,
передаваемое от одного тела к другому тем или иным способом, называют
количеством внешнего воздействия.
§1.3. Термодинамические системы, окружающая среда
и взаимодействия между ними
Термодинамической системой называется та совокупность
макроскопических тел, которая является объектом термодинамического анализа в каждом
конкретном случае.
В качестве термодинамической системы может, например, рассматриваться
земная атмосфера (в метеорологии), комплекс машин электростанции или узел
теплового двигателя (в энергетике) и т. д.
Объектом изучения в технической термодинамике часто является какое-либо
вещество, выполняющее главную функцию в тепловой машине: пар, продукты сгорания
топлива, сжатый газ и т. п. Такое вещество называется рабочим телом (рабочим
веществом, агентом) машины и рассматривается как частный случай
термодинамической системы.
Тела, не входящие в состав изучаемой термодинамической системы,
объединяются общим понятием «окружающая среда». Границу между термодинамической системой
и окружающей средой называют контрольной поверхностью. Это условное
понятие; лишь в ряде случаев контрольная поверхность может совпадать с некоторой
реальной физической поверхностью. Например, для газа в цилиндре контрольная
поверхность совпадает с внутренними поверхностями поршня и цилиндра (рис. 1.1, а).
На контрольной поверхности происходит
взаимодействие термодинамической системы и окружающей среды, которое состоит в
передаче энергии или вещества в систему или из нее. Конкретный способ или форму
передачи энергии называют родом взаимодействия,а количество
различающихся между собой родов взаимодействия, к которым по своей физической структуре
* Другие названия способа обмена энергией — «передача теплоты», «тепловое
взаимодействие», «термическое воздействие».
Понятия и определения
21
способна данная система,— числом
термодинамических степеней свободы
системы.
Примером термодинамической
системы с двумя степенями свободы
является газ /, заключенный в цилиндре 3
с подвижным поршнем 4 (рис. 1.1, а).
Энергию газа можно изменить
посредством совершения механической работы,
т. е. вдвигая или выдвигая поршень 4,—
это механическая, или деформационная,
степень свободы. Вторая степень
свободы (тепловая, или термическая)
проявляется при изменении энергии газа
путем теплообмена, например при
подводе теплоты от нагревателя 2 через
стенку цилиндра 3.
Ь)
V,
т П/в
Ьтт
К
da
Ц-
F
Рис. 1.1. Термодинамические системы: а — с
двумя степенями свободы (термической и
деформационной); б — с четырьмя степенями свободы
(термической, деформационной, электрической и
магнитной):
/ — рабочее тело; 2 — нагреватель; 3 — цилиндр; 4—
поршень
Системы, обладающие двумя степенями свободы (термической и деформационной),
называют простыми или термодеформационными.
На рис. 1.1,6 представлена схема сложной термодинамической системы с четырьмя
степенями свободы: деформационной, термической, электрической и магнитной. Рабочим
телом этой системы является газ с диэлектрическими и парамагнитными свойствами
(например, кислород). Его энергию можно изменить сжатием, подводом теплоты,
изменением электрического заряда на поршнях 4, являющихся одновременно
обкладками конденсатора, и намагничиванием во внешнем магнитном поле.
В технической термодинамике обычно рассматриваются простые
(термодеформационные) системы.
Характер взаимодействия между термодинамической системой и окружающей
средой зависит также от свойств контрольной поверхности.
Система называется закрытой (замкнутой), если контрольная поверхность
непроницаема для вещества, т. е. между системой и средой отсутствует обмен массой
(рис. 1.1, а). Открытой система называется в том случае, когда при взаимодействии
через контрольную поверхность переходит вещество.
Частным случаем открытой системы является так называемая проточная
система, когда на одних участках контрольной поверхности вещество входит в
систему, а на других — выходит из нее.
Термодинамическая система называется изолированной, если контрольную
поверхность не могут пересекать ни потоки вещества, ни потоки энергии.
Это понятие является научной абстракцией, так как идеальной изоляции не
существует. Практически идеальна деформационная изоляция газа (газ в жестком
сосуде или в цилиндре с закрепленным поршнем). Существуют также способы создания
весьма совершенной тепловой изоляции. Системы, находящиеся в тепловой изоляции
и потому не обменивающиеся с окружающей средой теплотой, называются
адиабатными.
§ 1.4. Состояние термодинамической системы, параметры
и функции состояния
Состояние термодинамической системы. Совокупность физических величин, по которым
мо,жно отличить данную систему от других, а также проследить за изменениями,
возникающими в системе при ее взаимодействии с окружающей средой, характеризует
состояние термодинамической системы. Опыт показывает, что
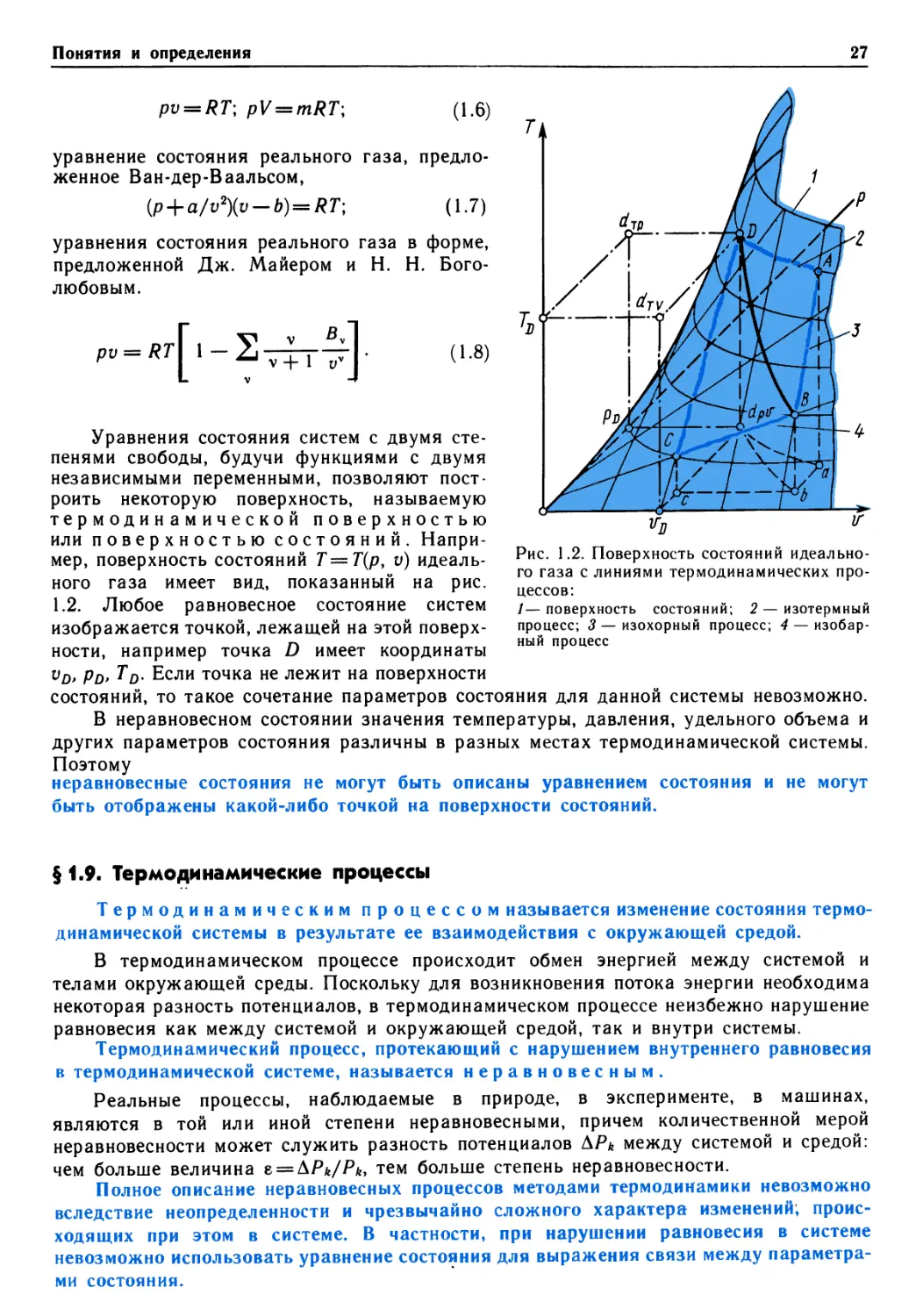
22 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
в изолированной системе с течением времени прекращается видимый
макроскопический обмен энергией и веществом между различными ее частями и система приходит
в состояние, которое называется равновесным.
Условием равновесности состояния является равномерное распределение по системе
тех физических величин, различие в которых является причиной обмена энергией.
Так, для равновесия термодеформационной системы во всех ее точках должны быть
одинаковая температура и одинаковое давление. Если система изолирована от
внешних воздействий, то равновесное состояние системы сохраняется неизменным
неограниченно долго, т. е. система не может самопроизвольно выйти из состояния
внутреннего равновесия. Для изменения состояния системы необходимо устранить изоляцию и
допустить взаимодействие между системой и окружающей средой, т. е. обмен энергией
между ними в тех или иных формах.
Равновесное состояние системы следует отличать от стационарного состояния,
которое также остается неизменным во времени, но характеризуется наличием в
системе потоков энергии или массы, как, например, при установившейся
(стационарной) теплопроводности в твердом теле.
Понятие равновесного состояния играет в термодинамике чрезвычайно важную
роль:
только равновесные состояния термодинамических систем и их изменения могут быть
количественно описаны методами классической термодинамики.
Параметры и функции состояния. В качестве характеристик состояния системы
используются лишь такие физические величины, значения которых не зависят от
предыстории системы, т. е. от того, по какому «пути» система пришла в данное состояние,
какие изменения она претерпела до этого.
Физические величины, значения которых однозначно определяются состоянием
системы и не зависят от ее предыстории, называются параметрами состояния
или функциями состояния системы.
При одинаковых состояниях одинаковые системы имеют равные значения
одноименных параметров состояния. Часто параметрами состояния называют лишь те
величины, которые имеют простую физическую природу и могут быть непосредственно
измерены. Такими величинами являются, например, температура, давление, плотность
вещества, напряженность электрического поля и т. п. Функциями состояния
в этом случае называют величины более сложной природы, недоступные для прямого
измерения. Они могут быть выражены через параметры состояния, которые в таких
случаях используются в качестве аргументов в функциональных зависимостях.
Например, значение энергии идеального газа можно вычислить, если известна его температура.
Вместе с тем следует подчеркнуть, что понятия параметр состояния и функция состояния
в принципе равнозначны.
§ 1.5. Внутренняя энергия термодинамической системы
Любая термодинамическая система обладает определенным запасом энергии. Некоторая
часть этого запаса зависит только от собственных, внутренних свойств системы,
другая — от внешних условий, в которых находится система. Так, если система
подвержена действию внешних силовых полей (гравитационного, магнитного и др.), то часть
полной энергии системы составляет ее потенциальная энергия в силовом поле. Если
вся система как целое участвует в поступательном или вращательном движении
относительно наблюдателя, в состав полной энергии входит кинетическая энергия
системы.
Та часть полного запаса энергии термодинамической системы, которая не
связана с положением системы в поле внешних сил и с ее движением относительно
тел окружающей среды, называется внутренней энергией термодинамической
системы.
Понятия и определения 23
Внутренняя энергия является функцией состояния неподвижной замкнутой
термодинамической системы. При рассмотрении открытых систем их кинетическая и
потенциальная энергии должны вводиться в термодинамические соотношения в виде
самостоятельных выражений дополнительно к внутренней энергии.
§1.6. Координаты термодинамического состояния
и потенциалы взаимодействий
Среди параметров состояния можно выделить две группы в соответствии с той ролью,
которую они играют в термодинамической характеристике систем.
Координаты термодинамического состояния. Как правило, при взаимодействии
какого-либо рода в системе одновременно изменяются значения нескольких параметров
состояния. Однако опыт показывает, что среди параметров состояния всегда имеется
один (и только один) такой параметр, изменение которого в так называемых
равновесных процессах вызывается взаимодействием только одного определенного рода.
Именно наличие таких параметров состояния, однозначно связанных с соответствующим
родом взаимодействия, и дает возможность отличать одни взаимодействия от других,
различать между собой разные формы обмена энергией.
Параметры состояния, обязательно изменяющиеся при наличии взаимодействия
данного рода и не изменяющиеся под влиянием взаимодействия иных родов, называются
координатами термодинамического состояния.
Изменение некоторой координаты состояния говорит о том, что происходит обмен
энергией в соответствующей форме, т. е. взаимодействие данного рода. Для некоторых
родов взаимодействия координаты состояния (признаки взаимодействия) можно легко
наблюдать' и измерять. Так, в случае деформационного взаимодействия (рис. 1.1, а)
необходимым условием передачи энергии в форме механической работы является
перемещение поршня, на который действует сила давления газа. Отсутствие перемещения
поршня говорит об отсутствии передачи энергии в форме работы. Перемещение
поршня приводит к изменению объема рабочего тела в цилиндре.
Следовательно, координатой деформационного состояния однородного рабочего
тела является его объем.
Значение электрического заряда тела является координатой электрического
состояния системы, изменяющейся в результате электрического взаимодействия.
Признаком наличия магнитного взаимодействия является изменение координаты
магнитного состояния — намагниченности тела.
Если рабочее вещество системы является твердым телом или же система
представляет собой некоторый механизм, то обмен работой при деформации системы
оказывается связанным с изменением не объема, а геометрических координат точек
приложения сил и моментов. В механике такие координаты называют обобщенными.
В термодинамике, по аналогии, также используют этот термин.
Значительно сложнее было выявить величину, которая является координатой
термического (теплового) состояния системы, т. е. найти такой параметр, изменение
которого следует считать признаком изменения состояния термодинамической системы
в результате передачи энергии в форме теплоты. Затруднения эти были вызваны тем,
что физическая величина, являющаяся координатой термического состояния системы,
не оказывает воздействия ни на органы чувств человека, ни на измерительные
приборы, т. е. величина эта оказалась неизмеряемой. Причиной невозможности
измерить эту величину является хаотичность, ненаправленность теплового движения
материи, не способного оказать направленное силовое воздействие на чувствительный
элемент прибора.
Глубокий анализ тепловых взаимодействий термодинамических систем привел
немецкого физика Р. Клаузиуса в 1852 г. к выводу о том, что
существует функция состояния, изменение которой (в равновесных процессах) одно-
24 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
значно связано с количеством энергии, передаваемым в форме теплоты. Эта функция
состояния была названа Клаузиусом энтропией.
Хотя прямое измерение значения энтропии невозможно, Клаузиус указал способ
вычисления ее изменения через другие наблюдаемые в опыте и измеряемые величины.
Таким образом, энтропия является параметром состояния, выполняющим роль
координаты термического состояния термодинамической системы.
Этот факт подтвердился всем последующим опытом использования в науке
понятия энтропии: ни одно термодинамическое соотношение, полученное с применением
энтропии, не вступает в противоречие с наблюдаемыми фактами.
Потенциалы взаимодействий. Другую важную для термодинамического анализа
группу величин, характеризующих состояние системы, составляют так называемые
потенциалы термодинамических взаимодействий.
Потенциалом взаимодействия некоторого рода называют параметр
состояния, различие значений которого между системой и окружающей средой на
контрольной поверхности приводит к возникновению взаимодействия данного рода, т. е.
к передаче энергии в данной форме между системой и окружающей средой.
При равенстве потенциалов в системе и окружающей среде соответствующее
взаимодействие отсутствует. Например, при равенстве внешней и внутренней сил не
возникает деформации, при равенстве электрических потенциалов невозможно
электрическое взаимодействие, равенство температур исключает передачу энергии в форме
теплового взаимодействия. Наоборот, наличие разности указанных величин на
контрольной поверхности является необходимым условием возникновения в неизолированной
системе процессов деформации, электрической работы, теплообмена.
Потенциалами термодеформационной термодинамической системы являются: для
теплового взаимодействия — термодинамическая температура, для
деформационного механического взаимодействия — давление.
Большинство известных в термодинамике потенциалов доступно измерению
приборами, так как между прибором и системой возникает взаимодействие, интенсивность
которого тем больше, чем больше разность потенциалов. Исключением является
химический потенциал: его значение вычисляется по значениям других, измеряемых
величин.
§ 1.7. Единицы термодинамических величин
Применяемые в термодинамике макроскопические (феноменологические) величины
принято делить на калорические и термические, интенсивные и экстенсивные, полные
и относительные.
Калорическими называют термодинамические величины, выражаемые в
единицах энергии. Такими величинами являются сама энергия, количество теплоты,
количество работы, энтропия и др.
Термическими являются величины, физический смысл которых не связан
непосредственно с понятием энергии и которые выражаются через температуру, силы,
размеры и т. п. Термическими величинами являются, например, температура,
давление, коэффициент термического расширения и др.
Интенсивными называют величины (параметры состояния), значения которых
не изменяются, если рассматривать какую-либо часть системы, отделив ее (мысленно)
от системы. Примерами интенсивных величин являются температура, давление,
напряженность силового поля и вообще все потенциалы взаимодействий.
Экстенсивными или аддитивными (суммируемыми) называют величины,
значения которых пропорциональны количеству вещества, находящемуся в данной
части системы или во всей системе. Экстенсивными величинами являются внутренняя
энергия, количество энергии, передаваемой при взаимодействии (т. е. работа,
количество теплоты), энтропия, объем и др. Если система рассматривается состоящей из отдель-
Понятия и определения 25
ных частей, то значение экстенсивной величины для системы равно сумме значений
этой величины для всех частей.
Если термодинамическая система физически однородна во всех своих частях
(гомогенна), то удобно все расчеты проводить для некоторой единичной части
этой системы. В зависимости от того, какие единицы используют для выделения
такой единичной части, различают: удельные величины, отнесенные к 1 кг вещества;
объемные величины, отнесенные к 1 м3 вещества; молярные величины, отнесенные к
1 кмоль вещества.
Будучи отнесены к единичной части системы, экстенсивные величины перестают
зависеть от размеров системы и приобретают свойства интенсивных величин.
Для выражения значений термодинамических величин следует использовать
основные и производные, кратные и дольные величины Международной системы
единиц (СИ).
В термодинамическом анализе применяется термодинамическая температура 7\
значение которой выражается в Кельвинах (К). Разрешается также выражать
температуру / в градусах Цельсия (°С), но при условии, что во всех термодинамических
соотношениях используется только термодинамическая температура, выраженная в кельви-
нах. Связь между температурами, выраженными по двум шкалам, определяется
соотношением
Г = * + 273,15. (1.1)
Одним из параметров состояния равновесной термодинамической системы является
термодинамическое (абсолютное) давление р, представляющее собой силу, действующую
по направлению нормали на единичную площадку некоторой поверхности, находящейся
в системе. Единицей давления служит паскаль (Па) —давление, вызываемое силой
1 Н, равномерно распределенной по поверхности площадью 1 м2 и нормальной к ней.
Для измерения давления газов и жидкостей в различных технических системах
применяют приборы, на чувствительный элемент которых (упругая мембрана,
трубка Бурдона, столб жидкости и т. д.) с одной стороны воздействует измеряемое
давление, а с другой — атмосферное (барометрическое) давление. Таким образом,
прибор (манометр) показывает не абсолютное давление р, а лишь разность между
абсолютным р и атмосферным (барометрическим) рбаР. давлениями — так называемое
избыточное ризб (или манометрическое) давление. В термодинамических соотношениях
используется абсолютное давление, представляющее собой сумму манометрического
и барометрического давлений:
Р = Ризб + Рбар. (1.2)
Для выражения значения таких экстенсивных величин, как энергия, работа,
теплота, в СИ применяется джоуль (Дж) — производная единица, определяемая
через механические величины как работа, совершаемая при перемещении точки
приложения силы 1 Н на расстояние 1 м в направлении действия силы. Для
обозначения полных величин используют заглавные буквы: внутренняя энергия U,
работа L, количество теплоты Q. Удельные значения обозначают строчными
буквами, соответственно и, qy /, и выражают в Дж/кг.
Энтропия также является экстенсивной величиной. Полная величина обозначается
буквой S и выражается в Дж/К, а удельная — буквой s и выражается в
Дж/(кг-К).
Объем V системы выражается в м3. Для выражения координаты состояния
однородных систем используют удельный объем v (м3/кг). Иногда в
термодинамических соотношениях вместо удельного объема применяется обратная величина —
плотность р (кг/м3).
26 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
§ 1.8. Уравнения состояния
Количество параметров, присущих термодинамической системе в некотором ее
равновесном состоянии, может быть весьма большим. Однако
число независимых параметров, значения которых полностью и однозначно
определяют данное равновесное состояние, значительно меньше и равно числу
термодинамических степеней свободы системы.
В самом деле, изменение равновесного состояния термодинамической системы
возможно только в результате внешних воздействий, а воздействие каждого рода
изменяет значение одной из координат состояния. Значит, для определения состояния
системы и, следовательно, значений всех параметров состояния достаточно указать
значения всех координат состояния. Все остальные параметры системы имеют
значения, соответствующие данному состоянию, т. е. данным значениям координат
состояния. Таким образом,
каждый параметр равновесного состояния системы является однозначной функцией
всех координат состояния.
Во многих случаях удается установить вид этой функциональной зависимости
в форме некоторого уравнения.
Уравнения, представляющие зависимость параметров (функций) состояния
равновесной системы от независимых параметров состояния, называются уравнениями
состояния термодинамической системы.
Если обозначить произвольную функцию состояния системы через ф, а координаты
состояния — через х\, х% ..., хп (п — число координат состояния, т. е.
термодинамических степеней свободы), то уравнение состояния можно представить в виде
ф=ф(Х|, JC2, -.., Хп). (1.3)
Например, состояние однородной термодеформационной системы описывается
уравнениями, содержащими две независимые переменные: координату деформационного
состояния — удельный объем и, координату термического состояния — удельную
энтропию 5. Потенциалы термодеформационной системы (температура и давление)
связаны со значениями координат соответствующими уравнениями состояния в виде
T=T{s, v); p = p(s, v). (1.4)
Использовать уравнения в указанной форме затруднительно, так как энтропия —
неизмеряемая величина. Однако, решая совместно систему уравнений (1.4), мджно
исключить энтропию выразив ее через объем и температуру или через объем и давление.
В результате получается уравнение
F(p, v, Г) = 0, (1.5)
связывающее давление, объем и температуру однородного рабочего тела и называемое
термическим уравнением состояния.
Для газообразного состояния вещества уравнения типа (1.5) являются
однозначными. Однако замена одной или нескольких координат состояния (в рассмотренном
случае — энтропии) через другие параметры состояния может в некоторых случаях
привести к потере однозначности определения состояния через новые независимые
переменные. Так, например, в области температур от 0 до 9 °С одинаковым значениям
давления и удельного объема соответствуют два разных значения температуры воды.
Примерами термических уравнений состояния могут служить: уравнение состояния
вещества массой 1 и м кг в идеально-газовом состоянии* (уравнение Клапейрона)
* Идеально-газовым называют в термодинамике такое состояние вещества, при котором
произведение давления на удельный объем, а также удельная внутреняя энергия вещества
зависят только от температуры (но не зависят ни от объема, ни от давления, взятых в
отдельности).
Понятия и определения
27
(1.6)
уравнение состояния реального газа,
предложенное Ван-дер-Ваальсом,
(p + a/v2)(v-b) = RT; (1.7)
уравнения состояния реального газа в форме,
предложенной Дж. Майером и Н. Н.
Боголюбовым.
pv •■
(1.8)
Уравнения состояния систем с двумя
степенями свободы, будучи функциями с двумя
независимыми переменными, позволяют
построить некоторую поверхность, называемую
термодинамической поверхностью
или поверхностью состояний.
Например, поверхность состояний Т=Т(р, v)
идеального газа имеет вид, показанный на рис.
1.2. Любое равновесное состояние систем
изображается точкой, лежащей на этой
поверхности, например точка D имеет координаты
vD, pD, TD. Если точка не лежит на поверхности
состояний, то такое сочетание параметров состояния для данной системы невозможно.
В неравновесном состоянии значения температуры, давления, удельного объема и
других параметров состояния различны в разных местах термодинамической системы.
Поэтому
неравновесные состояния не могут быть описаны уравнением состояния и не могут
быть отображены какой-либо точкой на поверхности состояний.
Рис. 1.2. Поверхность состояний
идеального газа с линиями термодинамических
процессов:
/— поверхность состояний; 2 — изотермный
процесс; 3 — изохорный процесс; 4 —
изобарный процесс
§ 1.9. Термодинамические процессы
Термодинамическим процессом называется изменение состояния
термодинамической системы в результате ее взаимодействия с окружающей средой.
В термодинамическом процессе происходит обмен энергией между системой и
телами окружающей среды. Поскольку для возникновения потока энергии необходима
некоторая разность потенциалов, в термодинамическом процессе неизбежно нарушение
равновесия как между системой и окружающей средой, так и внутри системы.
Термодинамический процесс, протекающий с нарушением внутреннего равновесия
в термодинамической системе, называется неравновесным.
Реальные процессы, наблюдаемые в природе, в эксперименте, в машинах,
являются в той или иной степени неравновесными, причем количественной мерой
неравновесности может служить разность потенциалов ДР* между системой и средой:
чем больше величина е = ДЯ*/Рл, тем больше степень неравновесности.
Полное описание неравновесных процессов методами термодинамики невозможно
вследствие неопределенности и чрезвычайно сложного характера изменений;
происходящих при этом в системе. В частности, при нарушении равновесия в системе
невозможно использовать уравнение состояния для выражения связи между
параметрами состояния.
28 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Анализ принципиальных особенностей неравновесных процессов выполняется на
основе второго начала термодинамики.
Опытом установлено, что по мере уменьшения разности потенциалов поведение
системы в процессе значительно упрощается: эффекты, вызванные нарушением
равновесия, уменьшаются и проявляются наиболее существенные, принципиальные
особенности, присущие конкретным формам обмена энергией. В пределе, при
стремлении разности потенциалов к нулю, нарушение равновесия в системе становится
пренебрежимо малым.
Термодинамический процесс, протекающий с бесконечно малым отклонением
состояния системы от равновесного состояния, называется, равновесным.
Равновесные процессы являются научной абстракцией, идеализацией реальных
процессов, позволяющей изучить главнейшие, принципиальные свойства систем при
обмене энергией. В равновесном процессе термодинамическая система проходит ряд
бесконечно близких состояний, каждое из которых является равновесным. Поэтому
равновесные процессы называют также квазистатическими*.
Каждое промежуточное состояние системы в процессе описывается уравнением
состояния и изображается соответствующей точкой, например D, на
термодинамической поверхности / диаграммы состояний (рис. 1.2). Эту точку называют
фигуративной или изображающей. Совокупность таких точек образует на поверхности
состояний линию (в общем случае пространственную), называемую линией
процесса.
В термодинамике широко используются графические методы анализа процессов.
При этом удобнее использовать не пространственные трехмерные изображения линий
процессов, а их двумерные проекции на координатные плоскости, получаемые,
например, в виде проекций сечений термодинамической поверхности плоскостями,
перпендикулярными одной из координатных осей. Так, сечение поверхности / (рис. 1.2)
плоскостями, перпендикулярными оси v, дает на плоскости рТ изохорные процессы
p = f(T) при y = const (линия 3)\ сечение плоскостями, перпендикулярными оси 7\
дает на плоскости pv изотермные процессы p = f(v) при 7 = const (линия 2); сечение
плоскостями, перпендикулярными оси р, дает на плоскости vT изобарные процессы
v — f(T) при p = const (линия 4).
В общем случае может быть получен термодинамический процесс и при иных
условиях, например при отсутствии теплообмена с окружающей средой. В этом случае
каждая точка такого процесса должна удовлетворять условию f(p> v, Г) = 0 при
d<7 = 0, где q — удельное количество теплоты. Такой процесс называется адиабатным.
Изображение линии термодинамического процесса на плоскости vp называется
z/p-д иаграммой или рабочей диаграммой процесса.
Каждый термодинамический процесс, изображенный линией на плоскости,
отображает совокупность последовательных равновесных состояний системы, выраженных в
виде зависимости одного параметра от другого при постоянстве значения третьего
параметра или при каких-то других определенных условиях.
Вопросы 1. Дайте краткую характеристику трех начал термодинамики.
2. Что называется внутренней энергией системы?
3. В чем состоит различие между теплотой и работой?
4. Каковы свойства координат термодинамического состояния?
5. Какие величины называют потенциалами термодинамических взаимодействий?
г * Равновесные, термодинамические процессы являются и обратимыми: как
термодинамическую систему, так и окружающую среду можно вернуть после окончания процесса в
исходное состояние, повторив последовательно в обратном направлении все равновесные
состояния, которые система имела в прямом термодинамическом процессе.
Глава 2
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
§2.1. Первый закон термодинамики как форма закона
сохранения энергии при ее превращениях
Термодинамический метод основан на использовании всеобщего закона сохранения
энергии при ее превращениях, согласно которому
энергия изолированной системы тел сохраняется при всех процессах, происходящих
в системе: она может лишь передаваться от одних тел другим (с сохранением или
изменением формы движения материи).
Теория относительности устанавливает эквивалентность взаимных превращений
не только энергии Д£, но и массы Am в соответствии с уравнением Д£ = с2Ат,
где с — скорость света в вакууме. В процессах, рассматриваемых в технической
термодинамике, изменения энергии таковы, что сопровождающее их относительное
изменение массы, выражаемое соотношением Дт/т = ДЕ/(тс2), оказывается
пренебрежимо малым. Поэтому масса закрытой термодинамической системы принимается
неизменной и учитывается только изменение энергии.
В термодинамике рассматриваются термодинамические системы (ТС) (рис. 2.1) не
изолированные, а напротив, взаимодействующие с окружающей средой, т. е.
обменивающиеся энергией с внешними телами. Чтобы применить закон сохранения и
превращения энергии, рассмотрим расширенную систему, которая состоит из
неподвижной термодинамической системы (ТС) и тех тел /, 2, ... окружающей
среды, с которыми происходит обмен энергией. Такая расширенная система в целом
может рассматриваться как изолированная, и в применении к ней закон сохранения
энергии может быть записан в виде
'=/
U+ 2 Ei=E= const, (2.1)
i=i
где Е — полная энергия расширенной системы; U — внутренняя энергия
термодинамической системы; £, — энергия /-го тела окружающей среды; у — число таких тел.
Если Д(У и ДЕ — изменения энергий в термодинамическом процессе, то с учетом
уравнения (2.1) для изолированной системы получим
Д(У + 2 Д£,= 0. (2.2)
/=1
Уравнение (2.2), являющееся прямым выражением закона сохранения и
превращения энергии, не может быть, однако, использовано для нахождения изменения Д(У
внутренней энергии термодинамической системы. Это потребовало бы изучения
изменения энергии Д£( всех / тел, взаимодействующих между собой и с системой, что может
создать непреодолимые трудности. Поэтому изменение Д1/ внутренней энергии системы
в термодинамике определяют изучая взаимодействие системы с окружающей средой.
Действительно, так как возникновение и исчезновение энергии невозможно, то
энергия системы может измениться только в результате обмена воздействиями между
системой и телами окружающей среды. При этом существенно, что характер
изменений в термодинамической системе зависит не от свойств окружающих тел, а
исключительно от способа передачи энергии, т. е. от рода взаимодействия. Поэтому при
составлении баланса энергии термодинамической системы алгебраически суммируются
воздействия каждого рода, исходящие от всех тел окружающей среды. Если через
Qk обозначить количество воздействия &-го рода (рис. 2.2, а), то уравнение сохранения
энергии можно представить в виде
30
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Рис. 2.1. Расширенная
термодинамическая
система:
ТС — термодинамическая
система; Из — изоляция;
1,2,..., /, ..., I — тела
окружающей среды
L>0 Q>0
Рис. 2.2. Внешние воздействия на
термодинамическую систему: а — п родов
взаимодействий; б — теплоты и работы
(2.3)
где п — число родов взаимодействий, т. е. число термодинамических степеней свободы
системы.
Уравнение (2.3) является формой выражения первого закона
термодинамики для произвольной термодинамической системы с многими степенями свободы,
который может быть сформулирован так:
изменение внутренней энергии термодинамической системы равно алгебраической
сумме внешних воздействий.
Применяя первый закон термодинамики к системам определенного класса,
обычно вводят специальные названия для взаимодействий различных родов,
используют отдельные обозначения для соответствующих количеств воздействий и
устанавливают правила знаков, характеризующие направление воздействий. Так, в
технической термодинамике количество термического воздействия (количество
теплоты) обозначается Q и считается положительной величиной, когда в результате
теплового взаимодействия внутренняя энергия возрастает (рис. 2.2, б).
Остальные воздействия называются работой (механической или немеханической).
В технической термодинамике отдельно рассматривают работу объемной деформации
системы и работу, не связанную с объемной деформацией. Механическая работа,
совершаемая при объемной деформации, обозначается L.
Работа считается положительной величиной, когда деформация системы
происходит с уменьшением внутренней энергии, т. е. когда система совершает
работу над окружающей средой (рис. 2.2, б). Такое же правило знаков применяется
и для других видов работ, в связи с чем знаки количеств нетермических воздействий
всегда противоположны знакам количеств соответствующих работ.
С учетом введенных обозначений и правила знаков уравнение первого закона
термодинамики для термодеформационной системы получит вид
A(; = Q-L, (2.4)
а первый закон — следующую формулировку:
изменение внутренней энергии термодинамической системы равно разности между
количеством теплоты и работой.
Первый закон термодинамики
Уравнение (2.4) определяет изменения в термодинамической системе, происшедшие
в конечном термодинамическом процессе. В случае элементарного, бесконечно
малого процесса теплота, работа и, следовательно, изменение внутренней энергии
системы бесконечно малы. Тогда
dU = dQ-dL (2.5)
В тех случаях, когда термодинамическая система представляет собой однородное
рабочее тело, свойства которого не изменяются от точки к точке,, Оывает удобно в
расчетах использовать удельные величины: удельную энергию, удельную теплоту и удельную
работу. Уравнение первого закона термодинамики для однородной
термодеформационной системы, участвующей в элементарном термодинамическом процессе, в
удельных величинах получит вид
du = dq — d/. (2.6)
При наличии немеханических работ уравнение первого закона термодинамики
для элементарного процесса имеет вид
dw = d^-d/-2d/HeMex. (2.7)
В сумму могут войти электрическая работа, работа намагничивания и др.
§ 2.2. Работа. Свойства работы как формы обмена энергией
Техническая термодинамика рассматривает в основном такие термодеформационные
системы, рабочими телами которых являются газы, пары и жидкости. Чтобы определить
работу деформации замкнутой неподвижной системы с однородным газообразным
(или жидким) рабочим телом, следует рассмотреть бесконечно малое расширение
объема V, занимаемого рабочим телом, в элементарном термодинамическом процессе
(рис. 2.3). Газ, заключенный в оболочку, способную деформироваться без
сопротивления, имеет давление р и находится в равновесии с окружающей средой. При
бесконечно малом расширении газа оболочка (контрольная поверхность) системы
смещается в сторону окружающей среды на бесконечно малое расстояние dx, которое
может быть различным на разных участках поверхности. При этом на каждом участке
с элементарной площадью d/ поверхности F бесконечно малая сила pdf совершает
над окружающей средой бесконечно малую работу pdfdx. Для вычисления
элементарной работы dL, совершаемой всей термодинамической системой, необходимо
вычислить интеграл по всей поверхности Ft поэтому
\fdx. (2.8)
Давление р выносится за знак интеграла, так как давление газообразных
или жидких рабочих тел не зависит от ориентации площадки (закон Паскаля), а
размеры системы предполагаются небольшими, что позволяет пренебречь изменением
гидростатического давления. Интеграл в выражении (2.8) представляет собой
бесконечно малое приращение dV объема всей системы в результате деформации, т. е. объем
бесконечно тонкого слоя (показан более, темным цветом на рис. 2.3). Следовательно,
элементарная работа объемной деформации физически однородной системы
dL = pdV. (2.9)
Разделив полученное выражение на массу т однородного рабочего тела,
заключенного в объеме V, получим выражение для элементарной удельной работы объемной
деформации:
d/=pdu, (2.10)
32 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
где v= V/m — удельный объем рабочего тела.
^ ^ В конечном термодинамическом процессе давление
в общем случае не остается постоянным, поэтому для
вычисления работы процесса требуется интегрирование
выражения (2.9) по всему процессу. Если / — начальное,
2 — конечное состояние системы, то удельная работа
процесса 1-2
2 2
l\-2 = \ dl=\pdv. (2.11)
Рис. 2.3. Схема объемной дефор- l l
мации рабочего тела
Знак а/ определяется знаком da. Так как абсолютное
давление — существенно положительная величина, то при
da> 0 (расширение системы) работа производится
системой над окружающей средой и считается положительной, при da<0 (сжатие
системы) работа совершается окружающей средой над системой и считается
отрицательной.
Для вычисления интеграла (2.11) необходимо знать зависимость (рис. 2.4)
давления в системе от ее объема в данном термодинамическом процессе:
P = P{v). (2.12)
Уравнение, выражающее зависимость давления от объема в процессе, называется
уравнением процесса в переменных а, р.
Площадь заштрихованной плоскости, равная pdv, в масштабе ар-диаграммы
представляет собой бесконечно малое количество работы на элементарном участке
процесса 1-2, а вся площадь под кривой 1-2—полную работу процесса.
Важнейшим свойством работы как формы обмена энергией является
зависимость количества работы от характера термодинамического процесса. Для
термодинамических систем, обладающих более чем одной степенью свободы, вид уравнения
процесса (2.12) определяется не только деформационным воздействием, которое
непосредственно отражено в уравнении через изменение объема, но и одновременно
протекающим термическим воздействием, т. е. теплообменом (а для сложных систем также
и другими воздействиями). Это выражается зависимостью давления от двух
переменных — объема и, например, температуры, а действительная линия такого процесса
представляет собой пространственную кривую в координатах р, a, T (например, линия
BD на рис. 1.2).
Одно и то же конечное состояние системы может быть достигнуто в ходе различных
термодинамических процессов, изображающихся различными пространственными
линиями на поверхности состояний F(p, a, Г) = 0.
Проекции этих линий на плоскость ар различны, различны и
уравнения процессов (2.11). В связи с этим различные термодинамические
процессы при одинаковых начальном и конечном состояниях дают различные
количества работы, которыми система в этих процессах обменивается с окружающей
средой.
Так, например, работа процесса 1-2-3 (рис. 2.4, б) больше работы процесса
1-3, а работа процесса 2-3 равна нулю.
Таким образом, работа термодинамического процесса не может быть вычислена
по начальному и конечному состояниям системы, она зависит от вида
термодинамического процесса, в результате которого система переходит из начального состояния в
конечное.
В связи с этим не может существовать функция, выражающая работу только
через параметры состояния;
Первый закон термодинамики
33
Рис. 2.4. Рабочие диаграммы термодинамических процессов: а —
графическое определение работы; б — термодинамический цикл, работа
цикла и располагаемая работа
элементарная работа не обладает математическими свойствами полного дифференциала.
Это — бесконечно малое (элементарное) количество энергии, переданной рабочим телом
окружающей среде определенным способом.
Зависимость работы от характера процесса приводит к ряду важных физических
и математических следствий. Действительно, если подынтегральное выражение не
является полным дифференциалом некоторой функции, то интеграл по замкнутому
контуру от такого выражения в общем случае не равен нулю. Следовательно, в
замкнутом термодинамическом процессе (цикле) 1-2-3-1 (рис. 2.4, б) система получает
от окружающей среды (или отдает ей) некоторое конечное количество энергии в
форме работы цикла /ц, причем в состоянии системы никаких изменений не
остается:
/ц = фа7 = фрсЬ. (2.13)
Графически указанная работа выражается площадью, ограниченной замкнутой
кривой 1-2-3-1, полученной алгебраическим суммированием положительных (при
&v~> 0) и отрицательных (при d^<<0) площадей, соответствующих процессам
расширения и сжатия.
При термодинамическом анализе более сложных систем необходимо учитывать
немеханические виды работ, а также механическую работу при деформациях других
видов (помимо объемной). Так, например, вал / машины 2 (рис. 2.5, а) при повороте
на элементарный угол dcp совершает механическую работу dLM = MAd(p, где Мя —
крутящий момент на валу. Электрическая работа, являющаяся работой переноса
заряда, совершается в электрической цепи (рис. 2.5, б), например при зарядке
аккумулятора или разрядке конденсатора. Она равна произведению напряженности ЕЭЛ
электрического поля, в котором переносится заряд (или напряжению на зажимах
устройства), на количество перенесенного электричества d/эл- Следовательно,
dL3JI=—Egjid/sji- Магнитная работа (работа намагничивания магнетика в магнитном
поле) производится при изменении силы тока в катушке (рис. 2.5, в). При этом
изменяются напряженность магнитного поля #маг и намагниченность сердечника,
измеряемая магнитным моментом Ммаг. Если не учитывать работу, пошедшую на
создание магнитного поля в объеме сердечника, то работа изменения намагниченности
материала сердечника, рассматриваемого в качестве термодинамической системы,
определится произведением: dLMar= — #ма^Ммаг. Таким образом, работа LM имеет
2 Зак. 584
34
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Рис. 2.5. Термодинамические системы с
недеформационной работой: а — работа крутящего
момента; б — электрическая работа при заряде
конденсатора; в — магнитная работа при
намагничивании тороидального сердечника
механическую природу, но не является
работой объемной деформации, а работы
^эл и LMar являются немеханическими.
Выражения для определения работ
dL, dLM, dL3ji, dLMar оказываются сходными
между собой не только по форме, но и по
физическому содержанию. Элементарная
работа любого рода получается
умножением интенсивной величины, выполняющей
роль движущего фактора процесса (давление, крутящий момент, напряженность
поля), на изменение экстенсивной величины, характеризующей меру взаимодействия
(изменение объема, угла поворота, заряда, магнитного момента). Первые величины
получили в механике название обобщенных сил Xk, вторые — обобщенных координат
Xk. При этом
элементарная работа любого рода выражается в виде произведения обобщенной
силы на изменение обобщенной координаты: dLk = Xkdxk.
В термодинамике вместо обобщенной силы используется понятие потенциала
взаимодействия Р*, причем Pk=—Xk> а понятие обобщенной координаты совпадает
с понятием координаты термодинамического состояния. Учет принятого в технической
термодинамике правила знаков для работы (работа противоположна по знаку
количеству нетермического воздействия) приводит к выводу, что
для всех родов взаимодействия, сопровождающихся передачей энергии в форме работы
любого вида, количество воздействий выражается произведением потенциала данного
взаимодействия на изменение соответствующей координаты термодинамического
состояния:
dQk = Pkdxk. (2.14)
Следует при этом иметь в виду, что выражения (2.9), (2.14) и выражения для
немеханических работ справедливы только в случае равновесных процессов.
§ 2.3. Теплота. Свойства теплоты как формы обмена энергией
Важнейшим результатом теоретического анализа тепловых явлений, проведенного
немецким физиком Р. Клаузиусом в 1852—1864 гг., был вывод о том, что
элементарное количество теплоты в равновесном процессе может быть выражено
в виде (2.14), так же как и количество воздействия любого иного рода, а именно
в виде произведения потенциала термического взаимодействия (температуры Т)
на изменение координаты термического состояния (энтропии S):
(2.15)
или для удельного количества теплоты
= Tds.
(2.16)
Так как термодинамическая температура всегда положительна, то
алгебраический знак количества теплоты в выражении (2.16) совпадает со знаком
изменения энтропии: при подводе теплоты (dqz> 0) энтропия системы возрастает
(ds;> 0), при отводе теплоты (dq<cO) энтропия убывает (ds<cO).
Первый закон термодинамики
35
В произвольном термодинамическом процессе температура изменяется как под
действием теплообмена, так и в результате обмена работой. Поэтому с определенностью
судить о том, получает или отдает система теплоту в некотором процессе, можно лишь по
изменению энтропии, но не по изменению температуры.
Для вычисления полного количества теплоты конечного процесса необходимо
проинтегрировать выражение (2.16) от начального состояния / до конечного
состояния 2:
2 2
(2.17)
Чтобы осуществить интегрирование, необходимо знать функциональную связь
температуры с энтропией в данном процессе в виде уравнения процесса
T = T{s). (2.18)
Графическое изображение уравнения (2.18) называется тепловой или энтропийной
sT-диаграммой процесса. Площадь выделенной цветом полоски на энтропийной
диаграмме (рис. 2.6,а) процесса 1—2 определяется произведением Tds и поэтому
представляет собой бесконечно малое количество теплоты dq на элементарном участке
процесса. Площадь под кривой 1-2 (линией процесса) представляет собой полное количество
теплоты, которым обмениваются между собой система и окружающая среда в процессе
1-2.
Как и количество работы,
количество теплоты зависит от вида термодинамического процесса, переводящего
систему из начального состояния в конечное.
Поскольку изменение температуры происходи? не только в результате
теплообмена, но и под действием одновременно протекающей деформации системы (т. е. в
результате совершения работы), то в зависимости от соотношения между количествами теплоты
и работы на последовательных элементарных участках процесса получаются
различные законы изменения температуры в процессе. Таким образом, в зависимости от
вида процесса могут быть получены различные уравнения процесса (2.18) и,
следовательно, различные количества теплоты (2.17) при одинаковых начальном и конечном
состояниях системы. Зависимость количества теплоты от характера процесса (зависимость
интеграла (2.17) от пути интегрирования) говорит о том, что
количество теплоты.не является функцией состояния системы, а элементарное
количество теплоты d<7 не может быть получено дифференцированием какой-либо функции
параметров состояния и поэтому не обладает свойствами полного дифференциала.
Г s
Рис. 2.6. яГ-диаграмма: а — процесса; б — цикла
36 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Как и в случае работы, результат интегрирования выражения (2.17) по замкнутому
контуру (рис. 2.6,6) в общем случае дает величину теплоты цикла, не равную нулю:
= §Tds =
Это означает, что в замкнутом термодинамическом процессе (цикле) система получает из
окружающей среды (или отдает ей) некоторое количество энергии ^ц в форме теплоты,
причем в состоянии системы при этом не остается никаких изменений.
Между математическими свойствами выражений для теплоты и работы имеется
большое сходство. Это обусловлено тем, что обе величины выражают лишь различные
стороны энергии — общего свойства материи, проявляющегося при обмене движением в
различных его формах. Однако между теплотой и работой имеется и принципиальное
различие, вызванное различием между направленным и хаотическим движениями материи.
Это различие проявляется в неравновесных процессах.
§ 2.4. Теплоемкость
Так как ни энтропия, ни ее изменение не могут быть измерены, выражение (2.16) нельзя
непосредственно использовать для вычисления количества теплоты по изменению
параметров состояния системы. Напротив, уравнения вида (2.16) применяют для
вычисления изменения энтропии по измеренному или вычисленному иными способами количеству
теплоты.
Для вычисления количества теплоты в термодинамике используется понятие
теплоемкости.
Истинная теплоемкость есть отношение количества теплоты d Q в бесконечно
малом термодинамическом процессе к изменению температуры с1Г в том же процессе:
Для конечного процесса 1-2 вводится понятие средней теплоемкости как
отношения полного количества теплоты Qi-2 к изменению температуры:
^-y^V- (2-20)
7 2 У 1
Если система представляет собой однородное вещество (рабочее тело), то применяют
понятия:
удельной теплоемкости
молярной теплоемкости
..„_ ля
или объемной (при нормальных условиях) теплоемкости
где т — масса; \л — количество вещества; V — объем рабочего тела, приведенный к
нормальным условиям (давление 101 325 Па, температура 273,15 К). Единицы этих тепло-
емкостей соответственно: Дж/(кг-К), Дж/(кмоль-К) и Дж/(м3-/С).
Количество теплоты в элементарном процессе выражается произведением
теплоемкости на изменение температуры:
(2.24)
Первый закон термодинамики
37
а в конечном процессе — в виде интеграла:
2
ИЛИ
(2:25)
(2.26)
Как было показано, для термодинамической системы с двумя (и более) степенями
свободы количество теплоты является функцией процесса, а не функцией состояния
системы. Следовательно, и
теплоемкость данного рабочего тела характеризует не только его собственное физическое
свойство, но и зависит от того, в каком конкретном термодинамическом процессе рабочее
тело получает или отдает энергию в форме теплоты.
Эта зависимость обусловлена тем, что изменение температуры, входящее в
выражение (2.24), вызвано изменением энергии не только на величину dq вследствие
теплообмена, но одновременно и на величину d/ вследствие совершения работы. Если рабочее
тело, имеющее в начальном состоянии А (рис. 2.7) температуру Т д , получает в разных
процессах АВ, AC, AD одинаковое количество теплоты dq, то изменение энтропии во
всех процессах с точностью до бесконечно малых высшего порядка будет одинаковым
и равным ds = dq/Tд .
Однако в зависимости от совершаемой в этих процессах работы произойдут разные
изменения объема, что в соответствии с (1.4) приведет к разным конечным значениям
температуры и, следовательно, к разным значениям теплоемкости. В процессе АВ
температура возрастает и теплоемкость рабочего тела в этом процессе имеет конечное
положительное значение: Сдв — dq/dT дв ~> 0. В процессе АС температура не изменяется
(например, при испарении жидкости под постоянным давлением) и теплоемкость в таком изо-
термном процессе формально следует считать равной бесконечности: слс = dq/0=oo.
В процессе AD температура понижается, несмотря на подвод теплоты, что может быть в
том случае, когда рабочее тело совершает достаточно большую работу. При этом dTAQ<c
<0 и теплоемкость оказывается отрицательной: Сд£> =dq/dTAQ <<0. Таким образом,
в зависимости от характера термодинамического процесса, в котором участвует рабочее
тело, его теплоемкость может принимать любое значение от -f «-х. до — оо.
Приравнивая (2.16) и (2.24), получим выражение для теплоемкости через изменения
параметров системы: с— Tds/dT. Полная производная ds/dT в этом выражении является
характеристикой процесса. Если термодинамический процесс протекает при
постоянном значении некоторого параметра х, то полная производная заменяется частной
производной (ds/dT)х, а теплоемкость в таком процессе обозначают соответствующим
индексом. Так, для процесса при постоянном объеме рабочего тела получаем изохорную
теплоемкость:
(2.27)
ат
т<
для процесса при постоянном давлении —
изобарную теплоемкость:
(2.28)
Истинную теплоемкость рабочего тела в
каком-либо состоянии в ходе данного
термодинамического процесса можно определить
графически, построив линию процесса в sT-диаграмме
(рис. 2.7). Проведя в точке А касательную АЕ к
линии процесса и учитывая, что AF=TA , tga =
= dT/ds, получим EF = AF/tga = TA ds/dT = c.
Та
и
Е\
"7
4*-
m с
А
/
'L
N
F
В
С '
[
D
ds
КкЛ
5
Рис. 2.7. Теплоемкость как функция
процесса
38 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Таким образом, значение теплоемкости на sT-диаграмме изображается длиной подка-
сательной к линии процесса.
Для вычисления количества теплоты по выражениям (2.25), (2.26) необходимо знать
зависимость теплоемкости данного рабочего тела от температуры вданном
термодинамическом процессе в виде с — с(Т). При этом средняя теплоемкость
выражается в виде
= г2 - т, \
Зависимости истинных и средних изохорных и изобарных теплоемкостей от
температуры для конкретных рабочих тел, представленные в виде формул, графиков или
таблиц, имеются в справочной литературе.
§ 2.5. Основное уравнение термодинамики
Закон сохранения и превращения энергии, аналитическим выражением которого для
термодинамических систем является уравнение (2.6), соблюдается как в равновесных,
так и в неравновесных термодинамических процессах.
Для равновесных процессов оказывается возможным выразить элементарные
количества теплоты и работы через параметры состояния термодинамической системы в виде
произведений (2.10) и (2.16).
Путем подстановки этих выражений в уравнение (2.6) и учета возможных работ
немеханического характера можно получить
уравнение первого закона термодинамики для равновесных термодинамических
процессов в закрытой термодинамической системе в виде
du = Tds -pdv- 2 Xk dxki (2.30)
где 2 Xdxk — сумма работ немеханического характера, совершаемых системой и
выраженных произведениями обобщенной силы Xk на изменение обобщенной
координаты dxk.
Если работы немеханического характера отсутствуют, то
du=Tds — pdv. (2.31)
Это уравнение называют основным уравнением термодинамики.
Ни теплота, ни работа, стоящие в правой части этого уравнения, не являются
функциями состояния системы. Определенные их количества лишь выражают изменения
энергии системы, вызванные разными по своей физической природе способами передачи
энергии.
Внутренняя энергия в отличие от теплоты и работы является свойством системы,
параметром ее состояния и может рассматриваться в качестве функции других
параметров состояния, принятых за независимые переменные.
Бесконечно малое изменение этой функции du обладает свойствами полного
дифференциала, поэтому интегрирование от начального до конечного состояния системы в
некотором процессе сводится к вычислению разности значений внутренней энергии в этих
двух состояниях, т. е. 2
u = и2 — и{ = Да, (232)
независимо от характера термодинамического процесса.
Первый закон термодинамики 39
§2.6. Особенности открытых систем
Открытые (в частности, проточные) термодинамические системы имеют ряд
особенностей, отличающих их от закрытых систем.
1. Поток рабочего тела несет с собой кроме внутренней энергии также и
кинетическую энергию своего движения относительно границ системы. Изменение
кинетической энергии рабочего тела следует учитывать в балансе энергии дополнительно
к изменению внутренней энергии.
2. При вводе рабочего тела необходимо преодолевать действие внутреннего давления
■в системе. Следовательно, над рабочим телом, поступающим в систему, должна быть
совершена некоторая работа внешней силой —работа ввода, которая увеличивает
полную энергию системы. При выводе рабочего тела из системы ею должна
затрачиваться работа по преодолению давления внешней среды — работа вывода рабочего
тела*.
3. Рабочее тело, находясь в пределах системы, может производить работу, не
связанную с деформацией системы, т. е. с изменением ее объема. Эта работа, например,
совершается газом при вращении ротора турбины или при получении электрической
работы в канале магнитогидродинамицеского генератора.
Работа рабочего тела в проточной системе, не связанная с деформацией границ,
называется технической работой LT.
4. В некоторых случаях может играть существенную роль изменение
потенциальной энергии рабочего тела в поле внешних сил, например в атмосферных
процессах, когда массы воздуха перемещаются в поле сил тяготения Земли на большие
расстояния по вертикали, или в процессах теплообмена при так называемой естественной
конвекции, когда основным источником энергии для создания потока рабочего тела
является разность потенциальных энергий холодного (тяжелого) и нагретого (легкого)
газов.
5. В открытую систему могут поступать (или выходить из нее) одновременно
несколько потоков рабочего тела с различающимися параметрами. Термодинамическое
описание открытых систем возможно только при условии, что процессы ввода — вывода
рабочих тел являются равновесными. Для этого необходимо, чтобы параметры вводимых и
выводимых рабочих тел были такими же, как и параметры рабочего тела в системе в
соответствующих местах ввода и вывода.
§2,7. Уравнение первого закона термодинамики
для открытых систем
Для учета особенностей открытых систем в уравнении первого закона термодинамики
рассмотрим условную схему такой системы (рис. 2.8). Границы системы образованы
сечением /—/ (вход рабочего тела з систему), сечением 2-^2 (выход рабочего тела),
жесткими стенками 3 и сечением 4 вращающегося вала. Вал передает в окружающую
среду (потребителю) техническую работу LT, совершаемую в системе при взаимодействии
потока рабочего тела с лопатками 5 ротора турбины. Рабочее тело может получать
некоторое количество теплоты Q, например, за счет сжигания топлива в камере сгорания
6. Потенциальная энергия рабочего тела при его движении изменяется, так как центры
тяжести входного и выходного сечений расположены на разной высоте (у\ и уч на
рисунке).
Изменение энергии системы за малый промежуток времени dx составит d£ —d£n—
— d£p, где d£ — изменение полной энергии системы; d£n — количество энергии,
поступающей в систему из внешней среды; d£p — расход энергии.
За рассматриваемый промежуток времени в систему через сечение /—/ со скоростью
* Работу ввода — вывода рабочего тела называют иногда работой проталкивания.
40
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЕ
Рис. 2.8. Схема проточной
термодинамической системь
w\ входит рабочее тело массой dmi, обладающее удельной внутренней.энергией и\, и
вносит в систему собственную внутреннюю энергию u\dm\y кинетическую энергию
dnt\w2i/2 и потенциальную энергию gy\dm\.
При вводе рабочего тела силы внешнего давления р\ совершают над системой
работу ввода dLBB. Давление pi, действуя на сечение площадью f\, создает силу pi/i, точка
приложения которой перемещается на расстояние dxi, необходимое для того, чтобы
элементарная масса dm\ оказалась введенной в систему через сечение / — /. Таким
образом, работа ввода dLBB = p\f\dx\= p\dV\, где dVi —объем, занимаемый массой dm\.
Находясь в системе, рабочее тело за время dx получит количество теплоты
dQ.
В итоге количество энергии, поступающей в систему, выразится суммой:
? (2.33)
Аналогично определяется и расход энергии, с той лишь разницей, что место
подведенной теплоты займет отводимая техническая работа, а произведение p2d V2 будет иметь
смысл работы вывода.
Если одновременно с совершением технической работы dLj происходит смещение
границ системы, то при этом система совершает и работу деформации, рассмотренную
ранее (см. § 2.2.): dL = pdV, где р — давление в том месте системы, где происходит
смещение ее границы, a dV — изменение объема, вызванное этим смещением.
Следовательно,
dEp = и2 dm2 + dm2 w\/2
Изменение полной энергии системы
gy2 dm2 + p2 dV2 + dLT
p2v2
w\/2
gy2) dm2
dQ — dLT — dL,
(2.34)
где v\ = dV\/dm\ и v<i = dV<2.ldm2 — удельные объемы рабочего тела во входном и
выходном сечениях.
Уравнение (2.34) применимо как для стационарных, так и для нестационарных
процессов, происходящих в системе. Процесс будет нестационарным, если поступление
энергии или массы рабочего тела за каждый промежуток времени не будет равно расходу
энергии и массы. В этом случае скорость изменения энергии системы выразится как
(" + P + >/2 + g</) m, — (u2 + p2v2 + w22/2 + gy2) rh2+Q — LT— L,
(2.35)
Первый закон термодинамики 41
где mj, m<i — массовые расходы рабочего тела на входе и выходе, кг/с; Q — поток
подводимой теплоты, Дж/с; LT и L — мощности, отводимые от системы, Дж/с.
§ 2.8. Уравнение первого закона термодинамики
для стационарной проточной системы.
Энтальпия и располагаемая работа
В стационарном процессе поступление массы рабочего тела и энергии в систему
равно их расходу, а объем системы постоянен:
d£ = 0; dm,
При этих условиях деление всех членов уравнения (2.34) на dm дает удельные объемы
v\ = dKi/dm и V2 = dV2/dm и удельные количества q = dQ/dm и /T=dLT/dm, отнесенные к
1 кг рабочего тела, прошедшего через систему*.
С учетом полученных соотношений уравнение (2.34) получит вид
yi). (2.36)
В уравнениях баланса энергии рабочего тела в проточной системе (2.35), (2.36)
обязательно присутствует сумма внутренней энергии рабочего тела и работы ввода или
вывода. Эта сумма выражена через параметры состояния и сама, таким образом, является
функцией состояния.
Функция состояния, равная сумме внутренней энергии и произведения давления на
объем рабочего тела, называется энтальпией h:
h = u + pv. (2.37)
Физический смысл этой функции обнаруживается при анализе конкретных явлений. Так,
например, при анализе процессов в проточных системах энтальпия является суммой
внутренней энергии рабочего тела и той работы, которая необходима, чтобы ввести
рабочее тело в данном его состоянии в систему или вывести его оттуда.
С учетом (2.37) уравнение первого закона термодинамики для конечного изменения
состояния рабочего тела в проточной термодинамической системе можно представить в
виде
ДЛ = q- /т- Д(ш2/2) -Д(дг). (2.38)
В этом уравнении: Ah = h2 — h\ — изменение удельной энтальпии; Д(до2/2) =до22/2 —
— w\/2— изменение удельной кинетической энергии; &{gy) =gy2 — gy\ — изменение
удельной потенциальной энергии рабочего тела.
. Для бесконечно малого изменения состояния в элементарном процессе уравнение
(2.35) имеет вид
dh = dq — d/T — d(w2/2)— gdy. (2.39)
Техническая работа /т, изменение кинетической энергии Ддо2/2 и изменение
потенциальной энергии &(gy) представляют собой величины механической природы. В
пределах термодинамической системы эти количества могут претерпевать взаимное
преобразование. Так, например, техническая работа в турбине может совершаться за счет
уменьшения кинетической энергии потока или уменьшения его потенциальной энергии
(при падении с верхнего уровня на нижний). Если затратить техническую работу
в колесе компрессора, то это приведет к увеличению кинетической энергии газа и т. д. В
связи с этим
* Эти величины (q и /т) отличаются от удельных количеств и работы, входящих в
уравнения для закрытых систем; там эти величины находят как отношение ко всей массе рабочего тела,
находящегося в системе. г
42 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
сумму технической работы, изменения кинетической энергии и изменения потенциальной
энергии называют располагаемой работой /():
2 (2.40)
или
d/0=d/T+d (w2/2) +gdy. (2.41)
Распределение располагаемой работы между составляющими зависит от назначения
и конструкции системы (машины). Во всех тепловых машинах изменение потенциальной
энергии, как правило, совершенно несущественно (A(gt/)«0). В турбинах почти вся
располагаемая работа расходуется на внешнюю техническую работу (d/o«d/T), в соплах
располагаемая работа полностью превращается в кинетическую энергию потока и в этом
случае
d/0 = d(w2/2) - (2.42)
и т. д.
С учетом (2.40) и (2.41) уравнения (2.38) и (2.39) для проточной системы примут
вид
\h = q — /о, или dh==dq — dk. (2.43)
При выводе уравнений (2.34), (2.38), (2.43) использовались параметры состояния
только во входных и выходных сечениях потока, где состояния рабочего тела
предполагались равновесными. Поэтому
эти уравнения остаются справедливыми и в тех случаях, когда внутри системы рабочее
тело претерпевает и неравновесные изменения состояния, например если в системе
имеются трение, турбулентность, химические реакции и т. п.
Если неравновесные процессы в системе отсутствуют (т. е. там происходят только
обратимые процессы), то располагаемую работу процесса и количество теплоты можно
выразить через изменение параметров состояния рабочего тела в процессе. Для этого
достаточно уравнение (2.37) продифференцировать и затем учесть соотношения (2.6) и
(2.10):
Сопоставив полученный результат с (2.43), видим, что
элементарная располагаемая работа определяется произведением объема на изменение
давления, взятым с обратным знаком, т. е.
d/0= — vdp. (2.44)
В конечном процессе располагаемая работа находится интегрированием
2 2
/o=fd/o=-bdp (2.45)
от начального / до конечного 2 состояния рабочего тела в процессе. При одних и тех же
начальных и конечных состояниях, но при разных процессах будут различны законы
изменения объема по мере изменения давления. Поэтому для вычисления значения
располагаемой работы необходимо знать уравнение термодинамического процесса в виде
v — f(p). Следовательно,
располагаемая работа является функцией процесса (но не функцией состояния рабочего
тела).
Графически располагаемая работа изображается на ур-диаграмме (см. рис. 2.4, б)
площадью, ограниченной осью давлений, линией процесса 1-2 и абсциссами начального
/ и конечного 2 состояний рабочего тела. Площадь следует считать положительной при
убывании давления и отрицательной при возрастании давления в процессе.
Количество теплоты в равновесном процессе выражается уравнением (2.16). Соот-
Замкнутые термодинамические процессы 43
ношения (2.16) и (2.43) дают возможность уравнение первого закона
термодинамики для проточной системы представить в форме
dp. (2.46)
Уравнения (2.43) и (2.46) представляют второй вид уравнений первого закона
термодинамики.
Вопросы 1. Объясните различия между законом сохранения и превращения энергии и первым
началом термодинамики.
2. Дайте определение уравнения процесса.
3. Почему выражение для элементарной работы не является полным дифференциалом?
4. Объясните различие между уравнением первого закона и основным уравнением
термодинамики.
5. Укажите особенности, отличающие баланс энергии открытой термодинамической
системы по сравнению с закрытой.
6. Дайте определение понятия располагаемой работы.
Глава 3
ЗАМКНУТЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
§ 3.1. Прямой цикл
Термодинамическим циклом или круговым процессом называется
термодинамический процесс, в котором термодинамическая система, претерпев ряд
изменений, возвращается в исходное состояние.*Все параметры и функции состояния,
изменяясь в процессе, в конце цикла принимают свое первоначальное значение. На
диаграмме состояний такой процесс изображается замкнутой линией. Следовательно, в
результате замкнутого термодинамического процесса внутренняя энергия системы не
изменяется, т. е.
Диц = фс1м = М1 — Mi =0.
Отсюда следует, что в соответствии с уравнением (2.31) для цикла
/ц = <7и, (3.1)
т. е. работа, совершаемая термодинамической системой за цикл, должна быть равна
суммарному количеству теплоты, полученному и отданному системой в течение цикла.
Замкнутые термодинамические процессы имеют очень большое практическое
значение, так как они позволяют непрерывно использовать теплоту для совершения работы, а
также передавать теплоту с низшего температурного уровня на высший. На рис. 3.1, а
изображен произвольный цикл в координатах v, p, в котором последовательность
процессов показана стрелкой. Из ур-диаграммы видно, что на участке цикла ADB работа
/i положительна (объем системы увеличивается, т. е. газ расширяется) и численно
равна площади eADBf. На участке ВСА работа /2 отрицательна и равна площади
eACBf. Так как площадь под линией ADB больше, чем площадь под линией
ВСА, то, следовательно, суммарная работа за цикл в рассмотренном примере
положительна. Она равна площади замкнутой линии ADBCA. За цикл
термодинамическая система отдает окружающей среде некоторое количество работы:
[ = пл.АОВСА> 0.
44
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
/77
Рис. 3.1. Замкнутые термодинамические процессы (циклы): а, б — прямой;
в, г — обратный
Так как в рассмотренном цикле /ц> 0, то и суммарное количество теплоты должно
быть положительным. Поэтому на яГ-диаграмме (рис. 3.1,6) этот цикл должен быть
представлен таким образом, чтобы подведенное к системе количество теплоты по
абсолютной величине было больше, чем отведенное. Для этого линия процесса CAD, в котором
теплота подводится (т. е. процесса, в котором происходит увеличение энтропии от
начального значения sc до конечного значения sD), должна располагаться выше,
чем линия процесса DBC, в котором теплота отводится (а энтропия от значения sD
возвращается к первоначальному значению sc).
Обозначая подведенное количество теплоты через q\ = nn.mCADn, а отведенное
количество теплоты через ^2=пл.тСВО/г, можно записать
qll = ql — \q2\ = nA.mCADn — пл.тСВОп = пл.САОВС> 0. (3.2)
Так как за время цикла термодинамическая система получает из окружающей
среды теплоту, эквивалентную работе, совершенной системой за цикл, то можно сказать, что
в рассмотренном цикле израсходовано определенное количество теплоты для получения
механической работы. Именно в этом смысле иногда говорят, что в данном цикле
произошло превращение теплоты в работу. Такие циклы совершает рабочее тело в тепловых
двигателях, а сами циклы называют циклами двигателей или прямыми циклами.
Из уравнений (3.1) и (3.2) видно, что количество работы, полученное от системы в
прямом цикле, меньше количества теплоты, подведенного к системе. Часть энергии
отводится от системы в виде теплоты q2> а в работу оказывается превращенной лишь
разность между q\ и q2.
Эффективность превращения теплоты в работу в цикле характеризуется
термическим кпд цикла т]/, который представляет собой отношение работы /ц, совершен-
Замкнутые термодинамические процессы 45
ной системой за цикл, к подведенному к системе количеству теплоты q\\
r\t = ljq\=q*/q\=(q\ — Ы /q\ = 1 — q<ilq\. (3.3)
Термический кпд всегда меньше единицы, так как осуществление цикла неизбежно
связано с отводом определенного количества теплоты (q2) от системы и поэтому отношение
q2/q\ в уравнении (3.3) всегда больше нуля.
§ 3.2. Обратный цикл
Последовательность процессов в цикле может быть обратной, такой, что расширение
рабочего тела термодинамической системы происходит при более низком давлении, чем
сжатие (рис. 3.1, в). В этом случае работа на участке BDA (l2 = nA.eADBf) отрицательна,
а на участке ЛСВ (1\ = пл.еЛСВ}) положительна. Так как UA.eADBf^nA.eACBf, то
работа за цикл отрицательна: /Ц=Л — \12\ = ua.ACBDA<zO.
В соответствии с уравнением (3.1) суммарное количество теплоты в этом цикле
также должно быть отрицательно: qa<c0. Для этого необходимо, чтобы теплота подводилась
к термодинамической системе при более низкой температуре (линия CBD на рис. 3.1, г), а
отводилась при более высокой температуре (линия DAC). В этом случае ^u = ^i — q2 =
= YiA.CBDAC<CO. При осуществлении такого цикла (в какой-либо машине) на участке
CBD рабочее тело машины отбирает теплоту q\ от некоторых тел в окружающей среде, а
на участке CAD отдает теплоту q2 другим телам в окружающей среде, имеющим более
высокую температуру, чем первые тела. Таким способом передается теплота с низшего
температурного уровня на высший, т. е. охлаждаются некоторые тела окружающей
среды. Это охлаждение обязательно сопровождается превращением работы, подведенной
к машине, в теплоту. Одновременно с охлаждением одних тел в окружающей среде
обязательно нагреваются другие тела, которые получают как теплоту, взятую у холодного
тела, так и теплоту, в которую превратилась работа цикла: q2 — q\ + |<7ul = <7i + |/ц|.
Циклы, в которых теплота переносится от холодного тела к нагретому, называют
холодильными или обратными циклами.
Эффективность холодильного цикла характеризуется холодильным
коэффициентом ех, который представляет собой отношение количества теплоты qu
воспринятого системой на низшем температурном уровне, к работе /ц, воспринятой системой
за цикл:
ex = <7i//u = <7i/<7u=<7i/(l<72| —<7i). (3-4)
Холодильный коэффициент может быть как меньше, так и больше единицы, это
зависит от соотношения между количествами теплоты q\ и q2 в цикле. Обратный
цикл может использоваться как цикл теплового насоса — машины, предназначенной
для отбора теплоты от менее нагретого тела (q\) и передачи ее более нагретому
телу (q2) за счет затраты работы цикла. Эффективность цикла теплового насоса
характеризуется отопительным коэффициентом ф/, представляющим собой
отношение количества теплоты q2y передаваемого отапливаемому помещению, к
затраченной работе цикла lil=\q2\— q{:
ql). (3.5)
Отопительный коэффициент всегда больше единицы, так как |<72l
Значение характеристики, r\h ex или ф,, определяющей эффективность цикла,
зависит от температур, при которых подводится и отводится теплота, а также от
характера термодинамических процессов, составляющих конкретный цикл. При прочих равных
условиях наибольшее значение кпд имеют такие циклы, в которых все процессы являются
равновесными (обратимыми). По отношению к процессам подвода и отвода теплоты это
означает, что температура рабочего тела системы в процессах теплообмена должна
46 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
быть практически равна температуре тел окружающей среды, с которыми
осуществляется теплообмен.
Циклы, состоящие из обратимых (равновесных) процессов, называются
обратимыми (равновесными) циклами.
§ 3.3. Цикл и теорема Карно
Французский ученый Сади Карно впервые предложил и проанализировал наиболее
экономив ii.iii термодинамический цикл, получивший впоследствии его имя*. При
совершении инк.i«i Карно термодинамическая система взаимодействует только с двумя телами,
имеющими постоянную температуру.
Так как имеется два тела с постоянными, но разными температурами
Т\ и T2(T\Z> Т2), то одно из них должно быть использовано для подвода теплоты
q\ к системе, а другое — для отвода теплоты q2 от системы. Так как температуры тел
постоянны, а процессы подвода и отвода теплоты должны быть равновесными, то эти
процессы могут быть только изотермными, т. е. протекать при постоянных
температурах Ti=const и Т2 = const. Температура рабочего тела в цикле должна изменяться от
Т\ до Т2 без теплообмена с окружающей средой, т. е. в адиабатных
процессах. Таким образом,
цикл Карно состоит из двух изотерм и двух адиабат (рис. 3.2).
В процессе АВ (рис. 3.2) рабочее тело получает количество теплоты qlt в результате
его энтропия возрастает от значения sA до значения sB на величину &sAB = q\/T\. Далее
следует адиабатное расширение (линия ВС), в ходе которого температура рабочего
тела уменьшается от Т\ до Т2. При темперутаре Т2 протекает изотермный процесс (линия
CD), в ходе которого рабочее тело отдает приемнику такое количество теплоты q2t что
энтропия тела от значения sc = sB снова возвращается к значению sA = sD\
следовательно, AsCD= — &sAB — q2/T2. Цикл завершается адиабатным сжатием (линия
DA), в ходе которого температура повышается от Т2 до Tiy принимая
первоначальное значение.
Выражение для термического кпд равновесного цикла Карно получается из общего
выражения (3.3) подстановкой в него величин q\ и l^l, выраженных через температуру
и изменение энтропии на участках АВ и CD:
r\i= I — \q2\/q\ = 1 — T2\^sCD\/(Ti^sAB ).
Так как \&sCD\ = ksAB, то
(3.6)
Кпд цикла Карно зависит только от температуры Т\ источника и Т2 приемника
теплоты и не зависит от рода рабочего тела. Этот вывод составляет содержание так
называемой теоремы Карно.
Цикл Карно имеет наибольший термический кпд по сравнению с другими циклами
в интервале температур Т\ — Т2. Для доказательства этого утверждения следует
сравнить на sT-диаграмме (рис. 3.3) цикл Карно ABCD с произвольным циклом
abed, проходящим между теми же температурными границами. Для цикла Карно
r\tK— 1 —\q2K\/qiK- Из диаграммы видно, что q2K = nA.eDCf, a q\K = nA.eABf.
Соответственно для произвольного цикла r\t= 1 — \q2\/q\, где q2 = nA.eadcf, a q\ — nA.eabcf. Сравнивая
соответствующие площади, замечаем, что q2K<Cq2y a <7iK> qi- Отсюда q2K/q\K<Zq2/q\.
Следовательно, Т]/к> Л'-
Эффективность превращения теплоты в работу (термической кпд) в любом другом
цикле не может быть больше, чем в цикле Карно, осуществляемом в том же интервале
температур.
* На русском языке работа С. Карно напечатана в сборнике: Второе начало термодинамики.
М., ГТТИ. 1934. С. 17—61.
Замкнутые термодинамические процессы
47
А
Л
«,
А*сш-А*лв
В
С
Vs* h=5c s
Рис. 3.2. Цикл Карно на sT-
диаграмме (идеальный газ)
А
а
В
b В
V J
d
с
С
i s
Рис. 3.3. К доказательству
максимальности термического кпд цикла
Карно
Фундаментальное значение полученного результата состоит в том, что он
устанавливает предел кпд тепловых двигателей.
Взяв частные производные от r\tK соответственно по Т\ и Г2, можно получить
выражения, показывающие влияние изменения температур Т\ и Т2 источников
теплоты на кпд цикла Карно:
?
Так как Г,>Г2, то, следовательно, \ {dr\t/dTi)T2\ <:\ (dr\t/dT2)Tl. Это значит, что
изменение температуры Т\ источника теплоты влияет на кпд меньше, чем изменение
температуры Т? приемника теплоты.
Так как не существует ни источников теплоты с бесконечно высокой
температурой (Г=оо), ни приемников теплоты с температурой, равной абсолютному нулю
(Г2 = 0), то отношение Т2/Т\ всегда больше нуля. Следовательно, кпд цикла Карно и тем
более любого другого цикла всегда меньше единицы.
Кпд цикл Карно тем больше, чем меньше отношение Т2/Т\у т. е. чем ниже
температура Т2 и выше температура Т\. Хотя в настоящее время технически возможно
получение очень высоких температур (сотни тысяч градусов), однако в реальных
двигателях использовать эти температуры невозможно, так как материалы, из которых
изготовлены детали двигателей, не способны выдерживать такие температуры.
Максимальная практически реализуемая в большинстве двигателей температура близка
к 1000...2000 К. Имеются двигатели (например, ракетные), в которых используются
более высокие температуры (до 4000 К). Однако эти двигатели рассчитаны на
очень короткий срок службы.
Температура Т2 составляет приблизительно 300 К, поскольку приемником теплоты
для всех двигателей, работающих в наземных условиях, является либо атмосферный
воздух, либо вода в реках, морях и других водоемах. Может быть получена и
температура, близкая к абсолютному нулю, однако получение температур ниже температуры
окружающей среды связано с затратой работы. Затрата работы оказывается больше,
чем выигрыш в кпд, поэтому такой путь увеличения кпд неприемлем.
§ 3.4. Цикл Карно как инструмент для построения шкалы
термодинамической температуры
С помощью цикла и теоремы Карно может быть построена шкала
термодинамической температуры, на что впервые (1848 г.) указал В. Томсон. Для создания
такой шкалы использовалось равенство, вытекающее из сопоставления выражений (3.3)
и (3.6), т. е. Г2/Г1 = <7i/<72. Следовательно, измеряя отношение количеств теплоты,
взятой от источника с температурой Т\ и отданной приемнику с температурой
Тч (или, что то же, измеряя отношение работ в двух изотермных процессах цикла
48 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Карно), можно получить отношение температур. Шкала температуры, определенная на
этой основе, и является шкалой термодинамической температуры. Важно при этом
подчеркнуть, 4to такая термодинамическая шкала температуры, так же как и
термический кпд цикла Карно, не связана со свойствами вещества.
Чтобы сама термодинамическая температура (а не только отношение температур)
имела определенное значение, надо выбрать (произвольно) какое-то число для одной
точки шкалы. Тогда все остальные значения определятся с помощью цикла Карно. За
опорную (эталонную) точку термодинамической шкалы была выбрана легко
воспроизводимая экспериментальным путем температура тройной точки воды, при которой
сосуществуют в равновесии три ее фазы: пар—вода—лед. Температура в этой тройной
точке была принята равной 273,16 К. Такой выбор сделан для того, чтобы значение
температуры в тройной точке по новой шкале практически не отличалось от
значения ее по ранее принятой шкале Цельсия с двумя опорными точками (точки
плавления льда и кипения воды при нормальном давлении).
§ 3.5. Условия равновесной передачи энергии между телами
с разной температурой и взаимопревращения теплоты и работы
Совершая цикл Карно, термодинамическая система осуществляет равновесный
(обратимый) теплообмен между телами окружающей среды, имеющими разную температуру.
При этом в окружающей среде происходят равновесный отвод теплоты от тела с одной
температурой и равновесный подвод теплоты к телу с другой температурой.
Следовательно, происходит равновесный теплообмен между телами с разной
температурой. Если бы этот теплообмен между ними осуществлялся непосредственно, он
мог бы быть только необратимым. Направление равновесного теплообмена между
телами с разной температурой определяется направлением цикла (прямой или
обратный), совершаемого посредником между этими телами. Таким образом, из анализа
цикла Карно (прямого и обратного) следует, что обратимо, т. е. с помощью одних
только равновесных процессов, передавать энергию можно с одинаковым успехом как
от тела с большей температурой к телу с меньшей температурой, так и наоборот.
Такая равновесная передача энергии между телами с различными температурами
возможна только с помощью посредника (термодинамической системы) и обязательно
сопровождается превращением работы в теплоту или теплоты в работу. Так, для
того чтобы передать теплоту от тела с более высокой температурой Т\ к телу
с более низкой температурой Т2 обратимым путем, необходимо иметь в качестве
посредника между телами термомеханическую систему, изменяющую свое состояние по
прямому циклу Карно. Тогда, как это следует из анализа термодинамических
циклов, термодинамическая система получает от тела с температурой Т\ количество
теплоты q\ в изотермном обратимом процессе и отдает телу с температурой Т2
количество теплоты q2 тоже в изотермном обратимом процессе. Все процессы,
происходящие при такой передаче энергии между телами с разными температурами, будут
обратимыми.
Термодинамическая система может совершать между телами с температурами
Т\ и Т2 обратный цикл Карно. В таком случае, как было установлено, от тела
с температурой Т2 будет отбираться количество теплоты q2, а телу с температурой Т\
будет отдаваться количество теплоты q\, т. е. произойдет обратимая передача теплоты
от тела с меньшей температурой Т2 к телу с большей температурой Т|. При этом
разность q\—q2 представляет собой работу, которую необходимо совершить над
системой в обратном цикле.
Итак, без термодинамической системы, совершающей цикл Карно, а поэтому и без
процессов взаимного превращения работы и теплоты обратимо передать теплоту
между двумя телами с разными температурами невозможно.
Имея в виду условия, необходимые для осуществления цикла Карно, можно
Второй закон термодинамики 49
сформулировать следующие важные положения, связанные с обратимыми процессами
передачи теплоты между телами с разными температурами и взаимным
превращением теплоты и работы.
1. Невозможно обратимо передать теплоту от тела с большей температурой к
телу с меньшей температурой без совершения работы. При этом телу с меньшей
температурой будет обязательно сообщено меньше теплоты, чем взято у тела с большей
температурой, на то количество теплоты, которое неизбежно превращается в работу в
процессе обратимого теплообмена.
2. Невозможно обратимо передать теплоту от тела с меньшей температурой к
телу с большей температурой без затраты работы. При этом телу с большей температурой
будет обязательно сообщено больше теплоты, чем взято у тела с меньшей
температурой, на количество работы, которое неизбежно превращается в теплоту в процессе
обратимого теплообмена.
3. Невозможно обратимо непрерывно превращать теплоту в работу и работу
в теплоту при наличии одного лишь источника теплоты.
4. Невозможно обратимо превратить всю теплоту, подведенную к рабочему
телу, в работу и соответственно всю работу, совершенную над рабочим телом, в
теплоту.
Вопросы!. Какой термодинамический процесс называется циклом?
2. Сформулируйте теорему Карно.
3. Можно ли осуществлять передачу теплоты от тела с большей температурой к телу
с меньшей температурой с помощью только равновесных (обратимых) процессов? Если
можно, то как?
4. Можно ли всю теплоту, взятую от тела с большей температурой, передать с помощью
равновесных процессов (обратимо) телу с меньшей температурой?
Глава 4
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
§4.1. Принцип существования энтропии
Второй закон термодинамики состоит из двух самостоятельных положений, или
закономерностей, являющихся следствием независимых опытных фактов.
Одно из них называют вторым законом термодинамики для обратимых процессов
или принципом существования энтропии (2.14), второе — вторым
законом термодинамики для необратимых процессов или принципом возрастания
энтропии.
Принцип существования энтропии относится к равновесному состоянию системы и
состоит, по существу, в утверждении (доказательстве) существования энтропии как
функции состояния. Он может быть сформулирован следующим образом:
для каждой термодинамической системы существует физическая величина (энтропия),
значение которой зависит от состояния системы (функция состояния) и изменение
которой происходит только под действием энергии, передаваемой в виде теплоты
(тепловая координата состояния).
Аналитическим выражением принципа существования энтропии является уравнение
(2.14), связывающее изменение энтропии в равновесном процессе с количеством
теплоты, передаваемым в процессе:
ds = dq/T. (4.1)
Энтропия была введена как тепловая координата состояния при рассмотрении
особенностей функций состояния, проявляющихся в процессах взаимодействия системы
с окружающей средой (см. § 2.3). Подтверждает существование энтропии опыт,
которому соответствуют все выводы, полученные на основе выражений (2.14) или (4.1).
50 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
§ 4.2. Принцип возрастания энтропии
Принцип возрастания энтропии относится к неравновесным процессам и отражает
особенности этих процессов. Поэтому, чтобы понять проблему возрастания энтропии,
сформулировать принцип возрастания энтропии и получить его аналитическое
выражение, необходимо рассмотреть особенности неравновесных (необратимых) процессов.
Особенности неравновесных процессов. Опыт показывает, что реальные процессы
передачи энергии с одного уровня давления и температуры на другой, являясь
процессами неравновесными, имеют определенную направленность и сопровождаются
необратимыми явлениями, т. е. такими изменениями, которые не могут быть устранены
противоположными процессами такого же характера.
1. Из опыта известно, что непосредственная самопроизвольная передача энергии
между двумя системами в виде работы происходит только тогда, когда давление в
системах разное и направлена она от системы с большим давлением к системе с
меньшим давлением и никогда наоборот. Аналогичная картина наблюдается и при
передаче энергии в форме теплоты: теплота сама собой переходит только от тела с
большей температурой к телу с меньшей температурой. Процессы эти являются
неравновесными и тем больше, чем больше разность давлений или соответственно
температур между взаимодействующими телами.
Таким образом, при непосредственном взаимодействии между телами с разными
давлениями и температурами энергия передается только необратимо и обязательно
в направлении меньшего давления (передача энергии в форме работы) и меньшей
температуры (передача энергии в форме теплоты).
Равновесная (обратимая) передача энергии между телами с разными
температурами, как было установление выше, возможна как в одном, так и в другом направлении.
Но такая передача энергии оказывается возможной только с помощью посредника —
промежуточной термодинамической системы. Так, равновесная передача теплоты между
телами с разными температурами требует наличия термомеханической системы,
совершающей цикл Карно, и сопровождается взаимными превращениями теплоты и
работы.
2. Опыт показывает, что в необратимых процессах передачи энергии в форме
работы часть этой работы неизбежно самопроизвольно превращается в теплоту. При
этом доля работы, превратившаяся в теплоту, тем больше, чем больше степень
неравновесиости процесса. Так, при разных давлениях в термодинамической системе
и окружающей среде (ри)Фр(е)) в теплоту превращается часть работы /н,
равная разнице между работой, «отданной» окружающей средой (ге' = р^е'№е'),
и работой, «воспринятой» термодинамической системой (№ = p^Av^), и определяемая
произведением разности давлений (Ар= \р{е) — pU) I) на изменение объема
термодинамической системы или окружающей среды | Ди(£>)| = | Ди(|)| :qH = lll = l(e) — /(/) = ДрДу. В
предельном случае вся работа может превратиться в теплоту. Например, хорошо
известно, что при трении два твердых тела нагреваются. Так как объем тел при этом
практически не изменяется, то изменение их внутренней энергии происходит не за счет
совершения над ними работы. Следовательно, в результате трения работа внешних
сил целиком превращается в теплоту, которая и воспринимается телами. Таким
образом, при неравновесной передаче механической работы непосредственно в самом
процессе передачи происходит самопроизвольное превращение части работы (или всей
работы) в теплоту.
Равновесное же превращение работы в теплоту обязательно требует наличия
тел с разной температурой, наличия посредника между этими телами в виде
термодинамической системы, совершающей обратный круговой процесс, и обязательно
сопровождается переносом теплоты от холодного тела к нагретому.
3. Опыт показывает, что в отличие от того, что происходит при неравновесной
«передаче» механической работы, неравновесная «передача» теплоты при непосредст-
Второй закон термодинамики
венном взаимодействии тел с разными температурами не сопровождается, на первый
взгляд, никакими превращениями: одно тело отдает только теплоту, а второе тело
получает также только теплоту, причем в том же количестве. Однако с помощью
посредника между телами в виде термодинамической системы, совершающей прямой
равновесный цикл Карно, часть теплоты, отданной телом с более высокой температурой,
можно превратить в работу (см. § 2.7).
Следовательно, при необратимой передаче теплоты от тела с большей температурой
к телу с меньшей температурой происходит превращение потенциально возможной
работы в теплоту. Другими словами, то количество внутренней энергии тела с
более высокой температурой, которое могло бы быть передано другим телам (при
наличии разности температур) в виде работы, в необратимом процессе энергообмена
оказывается переданным в виде теплоты телу с меньшей температурой. Количество
этой потенциально возможной работы, превращающейся в теплоту из-за
необратимости теплообмена между телами с разными температурами (Т\ФТ2), определяется
произведением разности температур (Д7*= | Т\ — 7^1) на изменение энтропии тел / или 2,
Aso= IAsi| =t= |As2l в обратимом теплообмене: qH = tu=^^TAso (см. § 3.3). . 'v
Рассмотренные явления свидетельствуют о качественной неравноценности теплоты
и работы как форм обмена энергией. Эта неравноценность проявляется только в
необратимых процессах. Теплота является как бы низшей, менее совершенной формой
обмена энергией, в которую при малейшей возможности (неравновесности процесса)
самопроизвольно превращается работа. Таким образом,
характерной особенностью необратимых процессов передачи энергии является их
определенная направленность — от большего потенциала взаимодействия к меньшему —
и неизбежное самопроизвольное превращение работы (действительно совершаемой
в процессе или потенциально возможной) в теплоту.
Количество работы, которое превращается в теплоту из-за необратимости,
неравновесности процесса, протекающего при конечной разности потенциалов
взаимодействия, равно количеству работы, которое может быть получено за счет этой
разности при равновесной передаче энергии между системами с разными потенциалами,
и определяется произведением разности потенциалов, под действием которой протекает
неравновесный процесс, на изменение соответствующей координаты состояния.
Односторонний характер изменений в реальных неравновесных процессах влечет
за собой одностороннее изменение энтропии. Так как в неравновесном процессе
хотя бы часть работы обязательно превращается в теплоту, то
энтропия, отражая свойство тепловой координаты состояния изменяться под
действием теплоты, при этом неизбежно увеличивается (пропорционально количеству
образовавшейся теплоты) или, как говорят, возрастает вследствие необратимости
процесса.
В этом, по существу, состоит физический смысл принципа возрастания энтропии.
Принцип возрастания энтропии может быть сформулирован и выражен
аналитически как для термодинамической, так и изолированной системы, представляющей
собой совокупность всех взаимодействующих между собой тел.
Возрастание энтропии термодинамической системы. Теплота, образовавшаяся
при неравновесном взаимодействии термодинамической системы со средой, как
показывает анализ, воспринимается термодинамической системой («подводится» к
термодинамической системе) независимо от знака разности потенциалов этого взаимодействия и,
следовательно, от направления неравновесного энергообмена между ними. Энтропия
термодинамической системы увеличивается за счет этой теплоты, и изменение ее в
термодинамической системе (с учетом знака) становится большим по сравнению с
изменением при отсутствии неравновесности; б последнем изменение энтропии
системы разно изменению энтропии окружающей среды с обратным знаком.
Покажем справедливость вышесказанного и получим аналитическое выражение
принципа возрастания энтропии применительно к термодинамической системе.
52 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Количества теплоты и работы, определяющие изменение внутренней энергии
термодинамической системы в уравнении первого закона термодинамики (2.29), должны
выражаться через параметры состояния окружающей среды, так как в соответствии
с законом сохранения энергии du(i) = — du{e\ a du{e) = T{e)ds{e) — p{e)dv{e\ где ds(<?) и
dv{e) — изменение энтропии и объема окружающей среды с соответствующими
знаками. Таким образом,
du{i)= - Т(еШе)-р(е№\ (4.2)
Параметры окружающей среды в правой части уравнения можно выразить через
параметры термодинамической системы с помощью соотношений 7^ — 7^ + АГ;
p{e) = p{l)-\-/\p; ds(p)= — ds^; di/e)= — dv^l\ где dstf— изменение энтропии
термодинамической системы в том случае, если бы процесс был равновесным, т. е. при
рп=Т(е) и р(о = р(е) в результате
du(i) = - T{i) dstf - p{i) dv{i) + Ar - Лр, (4.3)
где A^^AIds^ — разность между количествами теплоты, определяемыми через
параметры окружающей среды и системы; Ap = A/?dy(/)— разность между количествами
работы, определяемыми через параметры окружающей среды и системы. Величина
А7- всегда положительна, так как при АГ;> 0 энтропия системы увеличивается, т. е.
dsftb* О, а при АГ<0 энтропия уменьшается, т. e. dsi)}<0. Величина Ар всегда
отрицательна, так как при Ар> 0 объем системы уменьшается, т. е. d^(/)<<0,
а при dp<0 значение di/'b> 0.
Общее несоответствие в количествах теплоты и работы, найденных через параметры
окружающей среды и через параметры системы, оказывается всегда положительным:
А7- — А^ = А> 0. Разность А представляет собой количество работы, которое
превращается в теплоту вследствие необратимости процессов взаимодействия (теплового
и механического), поэтому ее можно представить в виде
А = 6^ = Г(0 dsj?, (4.4)
где dsi,0 — дополнительное изменение энтропии термодинамической системы вследствие
неравновесности. Так как А> 0, то dstf всегда положительно.
Это свидетельствует о том, что теплота, образовавшаяся вследствие
необратимости энергообмена между термодинамической системой и окружающей средой
(<7н), воспринимается термодинамической системой или «подводится» к
термодинамической системе независимо от направления энергообмена между термодинамической
системой и окружающей средой (qu = q$> 0).
Подставляя в уравнение (4.3) вместо Дг —Ар = А выражение (4.4) и опуская индексы
(/), поскольку теперь все величины относятся к системе, получим dw = r(dso+dsH) —
— pdv = Tds — pdv, где ds0 — изменение энтропии термодинамической системы в случае
равновесного процесса, т. е. при Т^=Т^ и р(/) = р(е); dsH — дополнительное
изменение энтропии вследствие неравновесности; ds = dso + dsH — общее изменение энтропии
термодинамической системы в неравновесном процессе. Так как всегда dsH> 0,
то также всегда ds:> ds0 (с учетом знака). Но dsb/)== — ds(e), ds^ = 6q^/T^e\
a bqie)= — dq{'\ Следовательно, опуская индексы у величин ds(/) и 6q{i\ относящихся
к термодинамической системе, можно записать
ds> bq/T{e\ (4.5)
Это неравенство является аналитическим выражением принципа возрастания
энтропии применительно к термодинамической системе, который может быть
сформулирован следующим образом:
изменение энтропии термодинамической системы в неравновесном процессе всегда
больше изменения энтропии в равновесном процессе; в последнем изменение
энтропии термодинамической системы равно изменению энтропии окружающей среды с
обратным знаком.
Второй закон термодинамики 53
В выражение (4.5) входит не температура системы, а температура окружающей
среды. Поэтому данное выражение может быть использовано для анализа поведения
термодинамической системы в неравновесном процессе только тогда, когда теплообмен
между системой и окружающей средой является обратимым, т. е. когда 7(/)=Г(е), так
как только тогда все величины выражения (4.5) будут относиться к
термодинамической системе. Это следует иметь в виду, так как индекс у температуры в данном
неравенстве обычно опускается.
Объединяя выражения (4.1) и (4.5), получим аналитическое выражение второго
закона термодинамики в виде
ds>6<7/7\ (4.6)
В выражении знак равенства относится к равновесным процессам (принцип
существования энтропии), а знак неравенства — к неравновесным процессам (принцип
возрастания энтропии).
§ 4.3. Энтропия изолированной системы и деградации энергии
Изолированная система представляет собой совокупность взаимодействующих тел.
При рассмотрении взаимодействия термодинамической системы с окружающей
средой изолированной системой является их совокупность
и изменение ее энтропии представляется суммой dsH.c = ds(0 + ds(e).
Изменение энтропии термодинамической системы в соответствии с выражением
(4.5) ds(0> bq{i)/T(e\ а изменение энтропии окружающей среды ds^^dq^/^.
Так как 6q{l)= — 6q{e\ то, следовательно,
dsHC> 0. (4.7)
Это неравенство является аналитическим выражением принципа возрастания
энтропии применительно к изолированной системе, который формулируется следующим
образом:
энтропия изолированной системы при наличии в ней неравновесных процессов всегда
возрастает.
Поэтому в применении к изолированной системе принцип возрастания энтропии
выглядит проще и нагляднее, чем в применении к термодинамической системе.
Различие в поведении энтропии изолированной системы при неравновесных и
равновесных процессах в ней можно показать на следующем примере.
Пусть два тела / и 2 с разными температурами (Г|> Г2), представляющие
собой изолированную систему, приведены в тепловой контакт (рис. 4.1). Будет
происходить неравновесный теплообмен, при котором изменение энтропии системы
где q — количество теплоты, переданное от тела / к телу 2. Так как Т\> Гг, то
AsH.e> 0» т- е- энтропия изолированной системы при наличии в ней необратимого
теплообмена возрастает.
Для того чтобы теплообмен между телами / и 2 осуществлялся равновесно,
необходим посредник — термодинамическая система (ТС), которая могла бы совершить
цикл Карно (рис. 4.2), взаимодействуя с телами / и 2 как с источником и приемником
теплоты. В этом случае изолированная система должна состоять из тела /, тела 2,
ТС и некоторого тела <?, которое могло бы равновесно воспринять от ТС механическую
работу.
В результате совершения цикла Карно тело / отдаст теплоту q\, а тело 2 воспримет
теплоту <72- Изменение энтропии тела / будет Asi = — q\/T\, а тела 2 соответственно
As2 = <72/7"2. Изменение энтропии ТС AsTC = 0, так как после совершения цикла система
возвратится в исходное состояние. Энтропия тела 3 не изменится (As3 = 0), так как
54
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Рис. 4.1. К доказательству возрастания
энтропии изолированной системы при
наличии в ней необратимого
теплообмена между телами
Рис. 4.2. К доказательству неизменности
энтропии изолированной системы при
наличии в ней обратимого теплообмена
между телами
это тело не участвует в теплообмене, а обмен работой между ТС и телом 3 происходит
равновесно. Изменение энтропии изолированной системы AsH.c = Asi +As2 + AsTc +
+ As3 = — q\/T\ + q2/T2. Но кпд цикла Карно r\lK=l — q2/q\ = \ — T2/T\, поэтому по
абсолютной величине отношения q\/T\ и q2/T2 равны. Следовательно, энтропия
изолированной системы при наличии в ней только равновесных процессов остается
неизменной (AsHt=0).
Из рассмотренного выше следует, что переход изолированной системы из одного
состояния в другое с помощью неравновесных процессов сопровождается
выравниванием потенциалов (давлений, температур и т. п.) в системе. При этом энергия
изолированной системы, оставаясь количественно неизменной (закон сохранения
энергии), теряет способность передаваться от одних тел к другим, т. е. совершать
работу. Утрата энергией изолированной системы способности совершать работу
рассматривается как обесценивание ее — деградация.
Увеличение энтропии изолированной системы, характеризующее неравновесность
протекающих в ней процессов, отражает в то же время потерю ее энергией
работоспособности: Выражение, связывающее потерю работоспособности с увеличением энтропии
изолированной системы, может быть записано на основе следующих рассуждений.
В неравновесных процессах работа самопроизвольно превращается в теплоту, которая
также самопроизвольно переходит от горячих тел к холодным. Таким образом, в
изолированной системе теплота, в которую превратилась работа вследствие
неравновесности процессов, окажется в конце концов воспринятой телом, имеющим
наименьшую температуру. При этом изменение энтропии этого тела, вызванное только
неравновесностью процессов, будет, очевидно, равно изменению энтропии изолированной
системы. Имея в виду, что теплота выражается в форме произведения абсолютной
температуры тела на изменение его энтропии, можно равенство, отражающее
необратимое превращение работы в теплоту, представить в виде
/H = roA5H.c=roAsH, (4.8)
где Го — низшая температура в изолированной системе; AsH.c = AsH — изменение
энтропии изолированной системы вследствие необратимости.
Таким образом, потеря работы вследствие необратимости пропорциональна
изменению энтропии вследствие необратимости. Коэффициентом пропорциональности
является наименьшая абсолютная температура в изолированной системе (температура
стока теплоты). При анализе технических процессов в качестве такой температуры
обычно принимают температуру окружающей среды.
Второй закон термодинамики J55
§4.4. Формулировки второго закона термодинамики
Принципы существования и возрастания энтропии отражают самостоятельные
положения, вытекающие из опытных фактов. Объединены они во втором законе
термодинамики, в связи с тем что существование энтропии было методически впервые показано
на основе формулировок второго закона термодинамики, отражающих свойства
неравновесных процессов, т. е. на основе принципа возрастания энтропии.
Существует много различных формулировок второго закона термодинамики,
отражающих свойства необратимых процессов, но подчеркивающих только какую-либо
одну их сторону. Наиболее распространенными формулировками являются:
1. «Теплота не может сама собой переходить от холодного тела к горячему»
(Р. Клаузиус).
2. «Теплоту какого-либо тела невозможно превратить в работу, не производя
никакого другого действия, кроме охлаждения этого тела» (В. Томсон).
3. «Невозможно построить периодически действующую машину, которая
производила бы только поднятие груза и охлаждение источника теплоты» (М. Планк).
В первой формулировке подчеркивается только необратимость непосредственного
теплообмена между телами с разными температурами. В двух других формулировках
наряду с категорическим отрицанием возможности полного превращения теплоты в
работу содержится неявное указание на возможность полного превращения работы в
теплоту. В них, следовательно, подчеркивается, что работа необратимо превращается
в теплоту весьма просто и для этого достаточно иметь в окружающей среде
единственное тело (приемник теплоты), которое воспринимало бы эту теплоту. Для
превращения же теплоты в работу необходимы специальные искусственно созданные условия:
наличие по крайней мере двух тел с разными температурами, между которыми
посредник (термодинамическая система) мог бы осуществить цикл и произвести работу.
Для достижения некоторой общности в формулировках законов
термодинамики второй закон термодинамики был сформулирован так:
«Невозможно создать вечный двигатель (perpetuum mobile) второго рода»
(В. Оствальд).
Вечным двигателем второго рода называют двигатель, который мог бы работать с
одним источником теплоты, т. е. двигатель, превращающий теплоту в работу при
отсутствии разности температур в окружающей среде. Если бы такой двигатель был
возможен, то, используя в качестве источника теплоты окружающую нас атмосферу или
воду океанов, обладающих громадными, практически неограниченными запасами
энергии, этот двигатель работал бы сколь угодно длительное время, т. е. был бы практически
вечным. Рассматриваемая формулировка второго закона, как и две предыдущие,
отражает только характер необратимых процессов.
Таким образом, наиболее распространенные формулировки второго закона
термодинамики отражают именно характер необратимых процессов (принцип
возрастания энтропии) и практически не касаются проблемы существования функции
состояния—энтропии (принцип существования энтропии). Поэтому
второй закон термодинамики, по существу, определяет одностороннюю направленность
естественных, самопроизвольных, неравновесных процессов и одностороннее
необратимое превращение энергии, которое сопровождает эти процессы.
Аналитическое выражение второго закона термодинамики используется обычно в
виде (4.6), объединяющем аналитические выражения обоих принципов — принципа
возрастания энтропии (знак неравенства) и принципа существования ее (знак
равенства).
Для " классической термодинамики — науки, занимающейся анализом только
равновесных состояний и равновесных процессов, наибольшее значение имеют принцип
существования энтропии и его аналитическое выражение (4.1). Принцип возрастания
энтропии (4.5), отражающий свойства неравновесных самопроизвольных ^
56 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УПРАВЛЕНИЯ
используется для качественного анализа при рассмотрении вопросов, связанных с
работоспособностью и условиями равновесия термодинамических систем.
Количественные данные с помощью этого принципа получить невозможно.
Таким образом, объединяя принципы существования энтропии и возрастания её во
втором законе термодинамики, можно утверждать:
во-первых, существует функция состояния — энтропия, изменение которой в
равновесных процессах происходит только под действием энергии, передаваемой в форме
теплоты (принцип существования энтропии), и,
во-вторых, явления, сопровождающие реальные, неравновесные процессы
(самопроизвольное превращение работы в теплоту), приводят к тому, что изменение
энтропии термодинамической системы в этих процессах всегда оказывается больше
того изменения, которое имело бы место в равновесном процессе, \иЛ\ что энтропия
изолированной системы при неравновесных процессах в ней увеличивается (принцип
возрастания энтропии).
С учетом выражения (4.6) уравнение (2.28) первого закона термодинамики
можно представить в обобщенном виде
к = п
du < Tds — pdv — 2 Pk dxk, (4.9)
k=\
объединяющем первый и второй законы термодинамики.
Выражение (4.9) может быть использовано для анализа поведения
термодинамической системы в необратимых процессах только при равновесном тепловом и
механическом взаимодействиях между системой и окружающей средой, так как только тогда
все величины обобщенного уравнения будут относиться к термодинамической системе.
§ 4.5. Энтропия и вероятность состояния
Ограниченность принципа возрастания энтропии. Самопроизвольное превращение
работы в теплоту, сопровождающее неравновесные процессы, связано, как уже
отмечалось, с переходом упорядоченного, организованного движения частиц системы в
беспорядочное, хаотическое движение. Увеличение энтропии в такого рода процессах
дает основание усмотреть связь ее со степенью беспорядка в системе. Часто
оказывается возможным даже оценить направление изменения энтропии системы на
основе только внешних признаков, отражающих степень беспорядка частиц в ней.
Так, например, переход твердого тела в жидкое состояние сопровождается
увеличением беспорядка в системе частиц и поэтому можно ожидать увеличения энтропии
при плавлении. Это увеличение равно отношению теплоты плавления к температуре.
Развивая анализ в этом направлении, можно установить количественную связь
энтропии с так называемой вероятностью состояния системы. Беспорядочное движение
частиц, когда в каждый момент для каждой частицы все направления движения в
равной мере возможны, является более вероятным движением, чем организованное,
вызванное определенными условиями. Поэтому организованное движение стремится
перейти в неорганизованное и соответственно изолированная система стремится
перейти из менее вероятного состояния, при котором возможно организованное
движение, в более вероятное — хаотическое. Это и отражается принципом возрастания
энтропии. Отсюда следует, что энтропию можно рассматривать как характеристику
вероятности состояния изолированной системы. Сказанное можно пояснить
следующим примером.
Допустим, имеется два одинаковых сосуда, разделенных краном (рис. 4.3). Один
из них содержит газ, другой пустой. Если кран открыть, то под действием разности
давлений (в соответствии с принципом возрастания энтропии) газ распределится
равномерно в обоих сосудах. Можно полагать, что последнее состояние газа, равномерно
распределенного в двух сосудах, является более вероятным, чем первое, когда газ
Второй закон термодинамики 57
находится в одном сосуде при открытом кране.
Доказать это можно с помощью теории
вероятности.
Математическая вероятность появления
случайного события представляет собой отношение
числа случаев, которые благоприятствуют
рассматриваемому событию, к числу всех возмож- Рис- 4-3- К доказательству связи энтро-
/ * \ г- пии с вероятностью состояния систе-
ных случаев (всегда правильная дробь). Если v мы
предположить, что вся система, т. е. вещество,
находящееся в двух сосудах, состоит из одной молекулы, то будет, очевидно,
равная вероятность того, что эта молекула будет найдена в любом из
двух сосудов. Математическая вероятность нахождения молекулы в определенном
сосуде будет равна 1/2. Если система состоит из двух одинаковых молекул, то
легко показать, что имеется один шанс из четырех, что обе молекулы будут
обнаружены в определенном сосуде. Таким образом, вероятность такого распределения
будет 1/4 или (1/2)2. Из теории вероятности следует, что вероятность сложного
события равна произведению вероятностей простых событий, независимых друг от
друга. Для системы, состоящей из N молекул, вероятность того, что все молекулы
окажутся в одном определенном сосуде, равна (1/2)^.
Вероятность того, что все молекулы системы, состоящей из очень большого
числа молекул, останутся в исходном сосуде при открытом кране, чрезвычайно
мала. Такова же вероятность самопроизвольного возвращения всех молекул,
равномерно распределенных в двух сосудах, в один из них. Вероятность же равномерного
распределения газа в обоих сосудах велика. Следовательно, самопроизвольный
необратимый процесс перехода системы из неравновесного состояния в равновесное
представляет собой переход из менее вероятного состояния в более вероятное. А так
как такой неравновесный процесс сопровождается увеличением энтропии, то есть
основание утверждать, что между энтропией системы в определенном состоянии и
вероятностью этого состояния существует связь.
Стремление определить вероятность существования термодинамической системы в
данном состоянии привело к понятию термодинамической вероятности W.
Макросостояние системы может быть определено двумя способами: 1) совокупностью
макропараметров состояния (давление, температура и т. п.) и 2) совокупностью величин,
характеризующих состояние каждой молекулы (таких, как координаты, скорости).
Другими словами, макросостояние системы может быть определено фиксированием
так называемого микросостояния. Одному и тому же макросостоянию может, очевидно,
соответствовать очень большое число различных микросостояний. Неизменность
макросостояния не означает, следовательно, неизменности микросостояния. В
результате хаотического движения молекул и непрерывных их столкновений
происходит непрерывная смена микросостояний, и если они эквивалентны с точки зрения
реали.члцми определенного макросостояния, то это состояние останется неизменным.
Термодинамическая вероятность макросостояния есть число микросостояний,
которые |н\1.шзуют данное макросостояние; это число очень велико. Термодинамическая
и математическая вероятности связаны друг с другом. Впервые связь энтропии s
с термодинамической вероятностью состояния W была высказана Л. Больцманом.
Вид аналитической зависимости s = s(tt?) может быть получен следующим образом.
Положим, что имеются две системы, содержащие энтропии si и s<> и термодинамические
вероятности W\ и W2. Объединяя эти системы в одну, можно утверждать, что
термодинамическая вероятность ее будет равна произведению вероятностей №|2 =
— W\W2 (на основе теории вероятности), а энтропия ее — сумме энтропии
s,2 = 5i+52 (на основе свойства аддитивности). Отсюда, имея в виду, что
Sl = s(Wi), s2 = s(W2), a si2 = s(Wi2) = s(W\W2), можно записать s(WiW2) = s(Wl) +
58^ РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
+ s(W2). Дифференцируя это выражение сначала по W\ (полагая №2 = const),
а затем по W2 (при №i= const), имеем W2s'(WiW2) = s'(W]yt №,s'(№, UP2) = s'( №2).
Умножая первое ураиы-пие на Wu а второе на W2, получим выражения W\W2s'(W\W2) =
= s'(Wi)Wu W]W2s\WiW2) = s!{W2)W2. Они равны между собой, поэтому s'(W<)W\ =
= s'(W2)W2\ или s'(W)W=const = k. Отсюда s'(W) = k/W.
С другой стороны, так как s = s(W), то ds/&W = s'(W). Сравнивая выражения,
имеем ds = kdW/W или после интегрирования s = k\nW-{-c. Как показывает
дополнительный анализ (квантовая теория), коэффициент пропорциональности k —
= 1,38-10 23 Дж/К в этой формуле есть постоянная Больцмана, не зависящая от
свойств вещества. Значение постоянной интегрирования с, как было установлено
М. Планком, может быть принято равным нулю. Таким образом, уравнение,
связывающее энтропию с термодинамической вероятностью, получает вид
s=*kh\W. (4.10)
Из статистического толкования энтропии следует, что
возрастание энтропии изолированной системы в необратимых процессах отражает
только наиболее вероятное течение реальных процессов, переход системы из менее
вероятного состояния в более вероятное.
Однако так же, как малая математическая вероятность случайного события не
исключает возможности его появления, статистическое толкование энтропии не
исключает возможности перехода системы из более вероятного состояния в менее вероятное,
т. е. не исключает возможности процессов, сопровождающихся уменьшением
энтропии изолированной системы, хотя вероятность таких процессов в системах, состоящих
из большого числа частиц, чрезвычайно мала. Например, расчеты М. Смолуховского
показали, что при нормальных условиях в 1 см3 газа только один раз в течение 10140 лет
можно наблюдать I % отклонения плотности газа от равновесного значения.
Неизбежное возрастание энтропии изолированной системы при самопроизвольных
необратимых процессах в ней было необоснованно возведено Клаузиусом в
универсальный физический закон, не знающий ограничений, и поставлено в ряд с законом
сохранения энергии. Оба этих закона, по Клаузиусу, в равной мере определяют
состояние Вселенной: «Энергия Вселенной остается постоянной, энтропия Вселенной
стремится к максимуму». Это значит, что всегда и везде во Вселенной происходят
превращения всех видов энергии в теплоту и постепенное выравнивание температур.
Это утверждение Клаузиуса дало почву для появления теории «тепловой смерти»
Вселенной. Такая теория, опирающаяся на авторитет термодинамики, имеющая
видимость строго обоснованного научного результата, вытекающего из второго
«универсального» закона термодинамики, явилась орудием в руках идеалистов и религии
в их борьбе против материалистического мировоззрения. Концепция «тепловой
смерти» неминуемо приводит к признанию начала в существовании Вселенной.
«Эта неизбежная судьба, предвидимая для Вселенной, красноречиво свидетельствует
о существовании Высшего Существа»,— заявил папа Пий XII на заседании
Ватиканской Академии наук (ноябрь 1951 г.).
В противоположность этому диалектический материализм учит, что богатство
форм движения материи и непрерывная взаимопревращаемость их являются
неотъемлемыми свойствами приводы и ее жизнь не может иметь ни начала, ни конца во времени.
Ф. Энгельс в работе «Диалектика природы» обращает внимание на то, что второе
начало термодинамики, понимаемое как универсальный закон, несовместимо с законом
сохранения и превращения энергии и противоречит ему, так как, не требуя изменения
энергии в количественном отношении, оно утверждает качественное вырождение
энергии, потерю энергией основного ее свойства — способности к превращениям.
Принцип возрастания энтропии может существовать рядом с законом сохранения
энергии только при том условии, что он понимается как ограниченный принцип,
Второй закон термодинамики 59
т. е. верный в определенных физических условиях. В других условиях может быть
справедлив противоположный принцип. Только такая комбинация прямого и обратного
принципов совместима с законом сохранения и превращения энергии.
Теория «тепловой смерти» противоречит статистическому толкованию энтропии.
Поэтому если и термодинамика, и статистика в равной мере применимы к бесконечной
системе, которой является Вселенная, то и тогда на их основе невозможно прийти
к выводу о «тепловой смерти»; Действительно, в такой системе имели бы место
флуктуации, т. е. случайные отклонения системы от равновесного состояния, размеры
которых в масштабе Вселенной могли бы быть значительными.
Американский ученый Д. Льюис сказал по этому поводу: «Термодинамика не
дает оснований для предположения, что Вселенная гибнет. Выигрыш в энтропии
всегда означает проигрыш в осведомленности и ничего больше». Проблема энтропии
Вселенной состоит в определении особенностей физических условий, в которых верен
один и другой принцип, и выяснении условий, при которых один из них переходит
в другой. Можно полагать, что для решения этой проблемы, далеко выходящей за
пределы термодинамики, современный уровень знания еще недостаточен.
§ 4.6. О доказательстве существования энтропии
Впервые понятие энтропии было введено Клаузиусом. Он показал существование ее на основе
доказательства теоремы Карно, в соответствии с которой термический кпд цикла Карно не зависит
от природы рабочего тела, совершающего цикл, а определяется только температурами источника
и приемника теплоты: r}u = f(t\,t2) (см. § 3.3). Это, во-первых, показывает, что правильность
теоремы, сформулированной Карно (1824), не вызывает сомнений. Во-вторых, это дает основание
полагать, что теорему Карно можно рассматривать как следствие принципа существования
энтропии. На последнее указывает тот факт, что, располагая понятием энтропии, доказать
теорему Карно очень просто. Пересмотр учения Карно потребовался Клаузиусу для приведения
его в соответствие с установленным к тому времени принципом эквивалентности теплоты и работы,
на основе которого теплоту, как и работу, стали рассматривать как форму передачи энергии.
Долгое время считалось, что доказательство Карно этой теоремы с помощью понятия теплорода
неверно.Однако позднее было обращено внимание на то, что в представлении Карно теплород
выступал в качестве носителя теплоты: количество теплорода остается неизменным в круговых
обратимых процессах и таким образом энтропия Клаузиуса является не чем иным, как
«теплородом» Карно. С точки зрения Карно, работа, совершаемая теплородом (энтропией),
зависит от количества теплорода и разности температур, между которыми существует равновесная
передача теплорода, что аналогично водопаду, работа которого определяется количеством воды и
разностью уровней.
Таким образом, доказательство теоремы Карно, выполненное им на основе понятия теплорода,
эквивалентного по смыслу понятию энтропии, верно. Это значит, что теорема Карно является
следствием принципа существования энтропии и может рассматриваться как одна из
формулировок этого принципа. Понятие теплорода в смысле, эквивалентном понятию энтропии, оказалось
полезным только для доказательства теоремы Карно. Это понятие, конечно, неверно в
применении к теплоте как форме передачи энергии.
Клаузиус предпринял попытку доказать теорему Карно отбросив понятие теплорода.
Оказалось, что теорема не может быть доказана без дополнительного постулата. Для Карно таким
постулатом было признание существования теплорода — нематериального носителя теплоты,
количество которого не изменяется при обратимых процессах в изолированной системе.
Клаузиус для доказательства использовал в качестве постулата опытный факт, что «теплота не
может сама собой переходить от холодного тела к горячему». Применяя этот постулат,
отражающий характер неравновесного теплообмена, к рассмотрению обратимых процессов с
использованием всех особенностей этих процессов, Клаузиус доказал теорему Карно и на этой
основе ввел понятие энтропии. Это привело к тому, что факт существования энтропии стал
неразрывно связываться с законом, отражающим особенности неравновесных процессов, с
фактом возрастания энтропии. Однако доказательство теоремы Карно получилось кажущимся,
или некорректным, на что обращается внимание в работах многих ученых (Н. Шиллер, К. Каратео-
дори, Т. Афанасьева-Эренфест, М. Борн, А. Гухман и др.).
Действительно, пусть две системы А и В с различными рабочими веществами совершают
60
Р АЗД ЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Рис. 4.4. К доказательству
теоремы Кар но
обратимый цикл Карно между источниками теплоты с
температурами Т\ и Т2 (рис. 4.4). Машина А является тепловым
двигателем с газом в качестве рабочего вещества; газ
совершает прямой цикл Карно. Система В является холодильной
машиной с другим рабочим веществом (например, паром),
совершающим обратный цикл Карно. Обе машины связаны
между собой одним валом так, что количество работы,
потребляемое холодильной машиной, равно количеству работы,
производимому двигателем, т. е. /' = /".
Предположим, что термический кпд равновесного
цикла системы A r\i = I'/ q\ = (q\— qr2)lq'\ больше соотношения
между соответствующими величинами для равновесного
обратного цикла системы В: т\" = I" / q'\ = (qY — q")/qY, т. е.
Л/>л" Гак как // = ///, то q\—<?2 = q'\ —q'{ или q\—q\' =
= q2 — q2. Так как х\\~> л", то q'\<Cq" или q\ — q" <CO.
Следовательно, q^ — q'KO или qf2<Cq2 ■
Неравенства q\<q" и qf2<Cq2 указывают на то, что при
сделанном предположении теплота переходит от холодного тела
к горячему. Это противоречит постулату, и поэтому сделанное предположение не может иметь
места.
Рассуждение можно повторить поменяв местами системы А и В, т. е. заставив систему В
работать как двигатель, а систему А — как холодильную машину. Полагая затем, что
л£> Ль можно снова прийти к противоречию с принятым постулатом «теплота не может сама
собой переходить от холодного тела к горячему». Отсюда можно сделать вывод, что
термические кпд цикла Карно для систем А и В равны и, следовательно, кпд цикла Карно не зависит
от природы рабочего тела, а зависит только от температур источников теплоты.
При таком доказательстве необходимо всегда исходить из посылки, что термический кпд
прямого цикла больше, чем обратного, иначе доказательство не получится. Убедимся в этом.
Пусть система А работает по прямому циклу, а система В — по обря- юму. Предположим,
что л><Л/' т- е- сделаем противоположное предположение. При этом, очевидно, мы получим
неравенства, противоположные предыдущим: q\> q'{ и q'2> q'{. Но эти неравенства указывают на
то, что теплота переходит от горячего тела к холодному, что не противоречит принятому постулату.
Таким образом, теорема Карно может быть доказана только в предположении, что кпд
это указывает на погрешность системы
прямого цикла больше, чем обратного {у^> г\Г
доказательства.
Аналогично теорема Карно может быть доказана с совершенно противоположным
постулатом «теплота не может сама собой переходить от горячего тела к холодному»,
абсурдность которого очевидна. В этом случае необходимо только полагать при доказательстве
л?б> л?р.
Получить аналитическое выражение теоремы Карно, т. е. вид функции r\t = f(t\, t2), и
ввести понятие энтропии можно следующим образом.
На основе теоремы Карно r\t= I — q2/q\=f(t\, t2). Отсюда q\/q2 = f{t\, h)- Уточним вид этой
зависимости. Для этого рассмотрим три цикла Карно, полученные при пересечении трех
изотерм (/i=const, /2 = const, /3 = const) и двух адиабат на ир-диаграмме (рис. 4.5, а).
Для этих циклов можно записать: для цикла abed q\/q2 = q>(t\, /2); для цикла dcef qi/q?,—
= /(*2,*з); Для цикла abef q\/qz = y (t\,U) • Имея в виду, что (71/^3 = ^1^2/(72^3), запишем
<p(i,,/3) =<pUi,*2) ф(/2,*з)- Но это выражение справедливо, если функция ср имеет вид
ф(/,,*2) =ii)(/i)/\|)(/2). Вид функции г|)(/) зависит от особенностей температурной шкалы.
Однако отношение q\/q2 = 'ty(t\)/'ty{t2) имеет одинаковое значение в любой температурной шкале.
Поэтому можно выбрать такую температурную шкалу, в которой функция г|) сама является
мерой температуры г|)(/)=Г. Это шкала термодинамической температуры. Отсюда аналитической
выражение теоремы Карно л>к= 1 —q2/q\ = 1 — Т2/Т\. Из полученного выражения имеем
q\/T\ — q2/T2 = 0. Имея в виду, что количества теплоты q\ и q2 входят в выражение для кпд
по абсолютному значению, и учитывая их знаки (q\> 0, ^2<0), можно получить для цикла
Карно выражение
Второй закон термодинамики
Рис. 4.5. К иллюстрации связи теоремы Карно с энтропией; а — к нахождению
аналитического выражения теоремы Карно; б — к доказательству существования
энтропии
Отношение q/T называют приведенной теплотой. Следовательно, алгебраическая сумма
приведенных теплот в обратимом цикле Карно равна нулю: 2(^/7) = 0.
Произвольный цикл (рис. 4.5, б) может быть разбит адиабатами и изотермами на множество
элементарных циклов Карно, для каждого из которых можно записать 6</i/7\ + 0^2/7*2 = 0.
Суммируя выражения для элементарных циклов при стремлении их числа к бесконечности, т. е.
интегрируя, получим
где первый интеграл берется вдоль линии MaN, а второй — вдоль линии NbM. Сумма этих
интегралов может быть записана в форме интеграла по замкнутому контуру:
Но если интеграл по замкнутому контуру равен нулю, это значит, что подынтегральное
выражение является полным дифференциалом функции. Эта функция состояния была названа
энтропией s.
Рассмотрев вопросы, связанные с классическим методом введения понятия энтропии, можно
сделать следующие замечания.
1. Существование энтропии и справедливость теоремы Карно — жестко связанные друг с
другом положения, каждое из которых может быть легко получено из другого, и поэтому каждое из
них можно рассматривать как следствие другого.
2. Получилось так, что постулат, на основе которого доказывается теорема Карно,
относится к самопроизвольным неравновесным процессам, а следствие из него — к свойствам
веществ и имеет смысл только для равновесных состояний и равновесных процессов, ибо
следствием является утверждение о возможности представить количество теплоты в виде
уравнения (2.14); это утверждение эквивалентно утверждению о существовании энтропии как
функции состояния.
3. Так как энтропия была введена с помощью постулата, отражающего особенности
неравновесных процессов, два совершенно независимых положения — существование функции
состояния (принцип существования энтропии) и существование определенных особенностей у
необратимых процессов (принцип возрастания энтропии) — оказались связанными между собой в
одном законе.
4. Доказательство теоремы Карно на основе постулата, отражающего неравновесные
процессы, оказалось несостоятельным. Это произошло потому, что к анализу равновесного
процесса (равновесный цикл Карно) применялся постулат, отражающий неравновесный процесс.
Для успешного доказательства положений, относящихся к равновесным состояниям и равновесным
62 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
процессам, необходимо располагать постулатом, отражающим особенности таких процессов.
Однако такой постулат оказывается неочевидным, так как в природе равновеных процессов
нет, и получает он ясный смысл, по существу, только после установления положения,
для доказательства которого применен. Другими словами, исходная посылка доказательства
основывается в известной мере на том, что необходимо доказать. Так, постулат К. Каратеодори,
с помощью которого строго доказывается существование энтропии, утверждает: «В окрестности
любого состояния имеются другие состояния, недостижимые равновесным адиабатным путем».
Этот постулат едва ли можно считать очевидным.
Такими же неочевидными являются и утверждения, симметричные в отношении
равновесного взаимопревращения теплоты и работы, сформулированные выше на основе рассмотрения
равновесного цикла Карно (см. § 3.5) с помощью принципа существования энтропии.
Исходя из этих постулатов тоже, конечно, можно корректно доказать существование энтропии.
Однако с их помощью, как и с помощью постулата К. Каратеодори, нельзя показать
возрастание энтропии в неравновесных процессах, так как постулаты не содержат сведений об
особенностях неравновесных процессов.
Отмеченные выше особенности, связанные с проблемой доказательства существования
энтропии, привели к возникновению направления в термодинамике, которое отвергает
необходимость специального доказательства существования энтропии с помощью каких-либо постулатов.
Фактически предлагается непосредственно постулировать существование энтропии как функции
состояния. При этом отпадают необходимость в аналитическом доказательстве на основе
принятого постулата, необходимость обосновывать справедливость одного неочевидного
положения с помощью другого столь же неочевидного. В качестве доказательства существования
энтропии предлагается рассматривать опыт, который подтверждает все выводы и уравнения,
полученные на основе использования аналитического выражения принципа существования
энтропии (2.14).
Одним словом, предлагается в отношении энтропии поступить так же, как поступил В. Гиббс
с химическим потенциалом,— введя это понятие без какого-либо доказательства по интуиции и
логике исследования, т. е. непосредственно постулировав его существование. Опыт подтвердил
существование химического потенциала, и вопроса о доказательстве его не возникало.
Рассмотрев несостоятельность классического доказательства теоремы Карно, полезно привести
замечательные слова известного физика М. Борна: «Неизбежна критика классических
доказательств, но это не означает принижения великолепных достижений мастеров науки, чья
интуиция вывела нас на правильный путь». Таким образом,
второй закон термодинамики в обычно принятых формулировках отражает только особенность
неравновесных процессов — принцип возрастания энтропии.
Вопросы|. Назовите основные особенности неравновесных (необратимых) процессов. ■
, £. В чем состоит физический смысл и каково аналитическое выражение принципов
существования и возрастания энтропии?
3. Может ли в процессе без теплообмена (адиабатном) изменяться энтропия?
4. В чем выражается деградация энергии изолированной системы при наличии в ней
необратимых процессов?
Глава 5
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 5.1. Основные характеристические функции
Необходимость введения характеристических функций в термодинамику впервые была
теоретически обоснована Масье (1869), однако наиболее строгое и полное изложение
метод характеристических функций получил в работах Дж. В. Гиббса (1873—1878).
Гиббс показал, что из всего множества термодинамических функций можно выбрать
такие, через частные производные которых наиболее просто выражаются
термодинамические параметры. Построение термодинамического анализа на особых свойствах
таких функций и составляет основу метода характеристических функций.
Характеристические функции 63
В термодинамическом анализе используют несколько характеристических функций.
Основными из них являются внутренняя энергия, энтальпия, свободная энергия и
свободная энтальпия. Характеристические функции являются производными функциями
от внутренней энергии и потому, как и внутренняя энергия, представляют собой
функции состояния термодинамической системы. Однако все они обладают свойствами
характеристических функций только при определенных условиях сопряжения
(взаимодействия) термодинамической системы с окружающей средой.
Если выбрать в качестве независимых переменных энтропию s и удельный объем и,
то полное изменение удельной внутренней энергии можно представить в виде суммы:
du = (du/ds)vds + (du/dv)sdu. (5.1)
Сопоставление полученного выражения с уравнением (2.29) показывает, что
(du/ds)v=T\ (du/dv)s=—p. (5.2)
Таким образом, при выбранных переменных s \i v абсолютная температура Т и давление
р могут быть наиболее просто выражены с помощью частных производных внутренней
энергии по энтропии и удельному объему. Следовательно,
внутренняя энергия является Характеристической функцией при независимых
переменных S И V.
Характеристической функцией является также энтальпия с независимыми
переменными s и р. Действительно, полный дифференциал функциональной зависимости
h — f(s, p) имеет вид
p. (5.3)
Сопоставление с уравнением (2.43) показывает, что
(dh/ds)p=T\ (dh/dp)s = v\ (5.4)
энтальпия является характеристической функцией при независимых переменных sup.
При независимых переменных Г, v характеристической функцией является разность
F = u—Ts, (5.5)
введенная в термодинамику Г Гельмгольцем и названная им свободной
энергией. С учетом уравнения (2.28) дифференциал этой функции имеет вид
dF=— sdT — pdu. (5.6)
В изотермных процессах в соответствии с уравнением (5.6) работа может совершаться
только за счет убыли этой функции. Действительно, при Т = const
dF=-pdv=-dl.
Часть функции Ts, согласно (5.5), представляет собой количество теплоты, которым
обменивается система с окружающей средой в изотермпом процессе. Таким образом,
уравнение (5.6) показывает, что дифференциал функциональной зависимости
F — f(T, v), имеющий вид
dF = (dF/dT)vdT+(dF/dv)1dv, (5.7)
включает частные производные
(dF/dT)v= -s; (dF/dv)T= -p, (5.8)
которые определяются из сопоставления полученного выражения с уравнением (5.6).
Следовательно,
свободная энергия является характеристической' функцией 'при ^зависимых
переменных Т и v.
По аналогии со свободной энергией Дж. Гиббс ввел в термодинамику
64 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
свободную энтальпию
G = h — Ts = u + pv—Ts, (5.9)
называемую иногда термодинамическим потенциалом Гиббса. Дифференциал свободной
энтальпии с учетом уравнения (2.28) имеет вид
dG= — sdT + vdp. (5.10)
Так как полный дифференциал этой же функции в соответствии с выражением
(5.9) при независимых переменных Тир
dG = (dG/dT)pdT + (dG/dp)Tdp, (5.11)
то сопоставление выражений (5.10) и (5.11) показывает, что частные производные
свободной энтальпии определяют соответствующие термодинамические параметры в виде
{dG/dT)p= -s; (dG/dp)T = v; (5.12)
свободная энтальпия является характеристической функцией при независимых
переменных Тир.
Итак, мы установили четыре характеристические функции u(s, v), h(s, p),
F(T, v) и G(7\ p), частные производные которых по термодинамическим параметрам
равны значениям сопряженных термодинамических параметров при определенных
условиях сопряжения термодинамической системы с окружающей средой.
§ 5.2. Свойства характеристических функций
Частные производные характеристических функций w(s, v), h(s, p), F(T, v\ G(Ty p) no
независимым переменным могут быть выражены через сопряженные термодинамические
параметры согласно соотношениям (5.2), (5.4), (5.8) и (5.12). Это свойство
характеристических функций существенно упрощает весь термодинамический анализ.
Так как характеристические функции являются функциями состояния, то их
дифференциалы в математическом смысле являются полными дифференциалами, а
уравнения вида d\b = (()y\')/dXk)xldxk + (dyi>/dxi)Xkdxi представляют собой линейные
дифференциальные соотношения.
Согласно свойству полного дифференциала, вторая производная от функции г|э
не зависит от порядка дифференцирования
д (dyt>/dxk)/dxt = d(dyt>/dxi)/dxk, (5.13)
поэтому смешанные производные, например производные от внутренней энергии
(2.29), можно записать в виде [d(du/ds)/dv]s = [d(du/dv)/ds]v или после замены
частных производных (du/ds)v и (du/dv)s через термодинамические параметры,
согласно выражениям (5.2), в виде (дТ/dv)s= —(dp/ds)v. Остальные дифференциальные
соотношения можно получить, если воспользоваться уравнениями (5.3), (5.7), (5.11) и
соответствующими соотношениями (5.2), (5.4), (5.8) и (5.12).
Таким образом, для термодеформационной системы могут быть получены
следующие соотношения между частными производными:
(dT/dv)s= -(dp/ds)v- (dT/dp)s = (dv/ds)p;
(ds/dv)T =(dp/dT)v\ (ds/dp)T= -(dv/dT)p.
Уравнения (5.14) называются дифференциальными соотношениями
взаимности или уравнениями Максвелла и широко используются в
термодинамическом анализе, так как, являясь следствием первого и второго начал
термодинамики, в такой же степени достоверны, как и сами эти начала.
В дифференциальных уравнениях (5.14) связываются частные производные
одного термодинамического параметра по другому при определенных условиях
сопряжения термодинамической системы с окружающей средой. Эти производные
Характеристические функции 65
характеризуют некоторые вполне определенные макроскопические свойства системы.
С помощью соотношений взаимности становится возможным выразить одни
макроскопические свойства системы через другие, а также использовать
экспериментальные исследования одних свойств для выявления других, т. е. можно заменить
исследования одного процесса исследованием другого при соответствующих условиях
и обеспечить получение того же результата. Поэтому дифференциальные
соотношения широко применяются для вычисления величин, непосредственно не изменяемых
в опытах; так, например, можно определить производные по энтропии через
известные термодинамические характеристики вещества — термическую расширяемость
(dv/dT)p и упругость (dp/dT)v.
Через характеристические функции могут быть выражены как термодинамические
характеристики вещества, так и теплоемкости. Так, например, вторая производная
(d2u/ds2)v, согласно уравнению (5.2), преобразуется: (d2u/ds2)v = (dT/ds)v=TX
X(dT/Tds)v=T(dT/dq)v. Удельная теплота dqy полученная системой в изохорном
процессе и при элементарном изменении температуры дТ, может быть определена в виде
произведения dqv = cvdTy где cv — удельная теплоемкость системы при v = const.
Следовательно, (dq/dT)v = cv и тогда (d2u/ds2)v=T/cv и cv=T/(d2u/ds2)v. Аналогично из
соотношения (5.2) следует, что (d2u/dv2)s= — (dp/dv)s. Деление полученного соотношения на
удельные объем vq системы при нормальных условиях дает коэффициент адиабатной
сжимаемости ps = — (dv/dp)s/vo = (l/vo)(d2u/dv2)s.
Характеристические функции обладают еще одним замечательным свойством,
которое в полной мере проявляется лишь при анализе сложных
термодинамических систем. Применяя преобразование Лежандра к уравнению (2.28), т. е. вычитая из
левой и правой частей уравнения дифференциалы произведения сопряженных
термодинамических параметров d( — pv)y d(Ts) и d(Ts — pv)y можно представить
дифференциалы характеристических функций в виде выражений
п
du = Tds — pdv — 2 Xk d**;
k=\
n
dh = Tds + vdp — 2 Xk dxk\
(5.15)
dF= — sdT — pdv— 2 Xk dxk\
k=\
n
dG = — sdT + vdp — 2 Xk dxky
k=i
где Xk — обобщенные силы; Xk — обобщенные координаты.
Нетрудно заметить, что по изменению характеристических функций при
соответствующих условиях сопряжения с окружающей средой можно определить
максимальную работу немеханического характера. Действительно,
при
5 = const и v = const du = — 2-Х* dxk;
k=\
при s = const и р = const dh = — 2 Xk dxk;
k=\
(5.16)
при T = const и v = const dF = — 2 Xk dxk;
k=\
n
при T = const и p = const dG = — 2 Xk dxk.
3 Зак. 584 k~l
66 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Следовательно,
сумма элементарных работ немеханического характера может быть определена через
изменение характеристических функций при соответствующем выборе условий
сопряжения с окружающей средой.
В аналитической механике функции, дифференциал которых с обратным знаком
равен элементарной работе, называются потенциалами. По аналогии,
характеристические функции в термодинамике также называют термодинамическими
потенциалами: изохорно-изоэнтропийный потенциал (и), изобарно-изоэнтропий-
ный потенциал (/i), изохорно-изотермный потенциал (F), изобарно-изотермный
потенциал (или потенциал Гиббса) (G).
§ 5.3. Дифференциальное уравнение состояния
Термодинамика не дает конкретного вида уравнения состояния, но исходя из
общих физических представлений позволяет выявить условия, которым должно
удовлетворить это уравнение. Так, например, дифференцируя уравнение p — f(T,v),
получим dp — (dp/dT)vdT-\-(dp/dv)Tdv. Если принять условие p = const, то соотношение
приобретает вид O — (dp/dT)vdTp + (dp/dv)TdvPi откуда
(dv/dT)p(dT/dp)v(dp/dv)T= -1. (5.17)
Полученное соотношение между частными производными параметров часто
называют дифференциальным уравнением состояния, а входящие в, него частные
производные — термодинамическими характеристиками рабочего тела. №
Каждая термодинамическая характеристика, входящая в уравнение (5.17), имеет
свой физический смысл. При расчетах удобнее использовать величины, получаемые
делением выражений (dv/dT)p> или (dp/dT)v на давление р0 при тех же условиях
и (dv/dp)T на удельный объем газа v0 при Г0 = 273 К и р0— 101,325 кПа, а именно:
коэффициент термического расширения
a = (dv/dT)p/v0; (5.18)
коэффициент термической упругости
y = (dp/dT)v/p0\ (5.19)
коэффициент изотермной сжимаемости ^
(5.20)
Подстановка выражений (5.18) —(5.20) в уравнение (5.17) показывает, что
(5.21)
Любое уравнение состояния рабочего тела должно удовлетворять не только условию
(5.17), но и условию устойчивости равновесного состояния (критерию
стабильности)
(5.22)
где Pk — потенциалы; Xk — термодинамические координаты.
В частности, для случая термодеформационной системы (Р\ =—р, Р2=
X\ = v, x2 = s) получим следующие критерии стабильности:
(dp/dv)T<0;
При выполнении условий (5.23) любые случайные отклонения от состояния
равновесия вызывают в термодинамической системе такие процессы, которые
восстанавливают равновесие. Условие dPk/dxk — О отвечает «безразличному» равновесию, когда
прежнее состояние не восстанавливается, но и нарушения равновесия не происходит.
Дифференциальные уравнения 67
Рассмотрим, например, рабочее тело (газ), находящееся в цилиндре двигателя
под поршнем в условиях адиабатной изоляции. Если его вывести из состояния
равновесия, приложив дополнительную силу F к поршню (см. рис. 1.1, а), то его удельный
объем уменьшится, что, согласно (5.23), приведет к увеличению давления газа под
поршнем. Когда давление газа сравняется с давлением, создаваемым приложенной
к поршню силой, то процесс прекратится и рабочее тело придет в состояние
равновесия, характеризующееся новыми значениями давления и удельного объема.
Так как производная (dp/dv)T, согласно (5.23), всегда должна быть меньше нуля,
то из соотношения (5.17) следует, что для всех веществ, встречающихся в природе,
должно соблюдаться неравенство (dv/дТ')^дТ/др)у> 0. И действительно, опыт
показывает, что термическая расширяемость и упругость могут быть одновременно либо
положительными, либо отрицательными. В первом случае состояние вещества
называется нормальным, во втором — аномальным. Одно и то же вещество в зависимости
от физических условий может находиться как в нормальном, так и в аномальном
состоянии. Примером тому может служить вода, которая при давлении 0,1 МПа и
температуре, меньшей 277 К, обладает аномальными свойствами, а при температуре
выше 277 К — нормальными.
§ 5.4. Дифференциальные уравнения внутренней энергии,
энтальпии и энтропии
Уравнения в частных производных характеристических функций, называемые
дифференциальными уравнениями термодинамики, однозначно определяют физические
свойства вещества и поэтому, по существу, отражают связи между различными
физическими эффектами, вытекающими из первого и второго законов термодинамики.
Они позволяют, в частности, выразить величины du, dA, ds, входящие в уравнение
первого закона термодинамики, через основные термодинамические характеристики
вещества и использовать основное уравнение термодинамики для термодинамического
анализа и практических расчетов. При составлении основных дифференциальных
уравнений термодинамики выбираются системы, состояния которых определяют двумя
термодинамическими параметрами: р, Т\ vy T\ и, р.
Дифференциальные уравнения в независимых переменных v, Т. Если рассматривать
внутреннюю энергию как функцию независимых переменных v и Г, то ее дифференциал
можно представить в виде суммы:
du = {du/dT)vdT + (du/dv)Tdv. (5.24)
Частные производные, входящие в это выражение, можно найти через
термодинамические параметры и их производные. Так, из уравнения (2.29) следует, что
при T = const изменение внутренней энергии duT—TdsT — pdvT, откуда
(du/dv)T= T(ds/dv)T-p, (5.25)
или с учетом соотношения взаимности (5.14)
(du/dv)T= T(dp/dT)v-p. (5.26)
Производную (du/dT)v можно определить следующим образом. Количество теплоты
Tds, входящее в уравнение (2.29), определяется удельной теплоемкостью с так, что
du = cdT — pdv, (5.27)
или (при v — consi)duv = cvdTv. Отсюда
duv/d Tv = (ди/дТ) v = cv. (5.28)
Подставив (5.26) и (5.28) в (5.24), получим дифференциальное уравнение
внутренней энергии
3*
68 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
p]dv. (5.29)
Дифференциальное уравнение энтропии можно получить совместным решением
уравнений (2.29) и (5.29):
ds = codT/T + (dp/dT)vdv. (5.30)
Дифференциальные уравнения в независимых переменных р и Т. Дифференциал
функциональной зависимости h = f(p, T) имеет вид
dh = {dh/dT)pdT + (dh/dp)Tdp. (5.31)
Частная производная (д/г/др)т может быть определена из уравнения (2.43), если
его рассматривать при условии T = const. Так как в этом случае dhT = TdsT-\-vdpT, то
(д/г/др)т= T(ds/dp)T+ vy (5.32)
или с учетом (5.14)
(dh/dp)T= — T(dv/dT)p+v. (5.33)
Частная производная (д/г/дТ)р уравнения (5.31) также определяется из уравнения
(2.43) при условии р = const. В этом случае
dhp=Tdsp = dqp.
Элементарное количество удельной теплоты dqp, полученное системой в процессе при
p = const и элементарном изменении температуры d7\ может быть определено как
произведение dqp = cpdT, где ср — удельная теплоемкость системы в процессе при
постоянном давлении. Следовательно,
(дН/дТ)р = ср. (5.34)
Дифференциальное уравнение энтальпии получается из уравнения (5.31) с учетом
(5.33), (5.34):
dh = cpdT— \T(dv/dT)p — v\dp. (5.35)
Дифференциальное уравнение удельной энтропии в переменных р и Т получается
при подстановке соотношений (5.35) в уравнение (2.43):
ds = cpdT/T- (dv/dT)pdp. (5.36)
Дифференциальные уравнения в независимых переменных v и р. Если в качестве
независимых переменных выбрать v и р, то дифференциал удельной внутренней
энергии можно представить в виде
du=(du/dp)vdp + (du/dv)pdv. (5.37)
Так как (du/dp)v = (du/dT)v(dT/dp)Vy то в соответствии с выражением (5.28)
(du/dp)v = cv(dT/dp)v. (5.38)
Производную (du/dv)p можно определить из уравнения (5.27), если в последнем
учесть условие р = const. В этом случае dup = cpdTp— pdvp, откуда
(du/dv)p = cp(dT/dv)p — p. (5.39)
Подставляя частные производные (5.38), (5.39) в выражение (5.37), получим
дифференциальное уравнение удельной внутренней энергии в переменных vy p:
du = cv(dT/dp)vdp + [cp(dT/dv)p-p]dv. (5.40)
Приращение энтропии можно получить подстановкой выражения (5.40) в уравнение
(2.29):
dv.- (5.41)
Дифференциальные уравнения 69
Дифференциальное уравнение удельной энтальпии в переменных v и р может
быть получено, если подставить выражение (5.41) в уравнение (2.43):
dA = cp(dT/dv)pdv + [cv(dT/dp)v + v]dp. (5.42)
Дифференциальные уравнения термодинамики позволяют вычислить изменение
внутренней энергии, энтальпии и энтропии, если известно уравнение состояния или
имеются экспериментальные данные по основным термодинамическим характеристикам
вещества и теплоемкостям.
§ 5.5. Дифференциальные уравнения
удельных теплоемкостей с„ и ср
Для определения связи между cv и ср следует воспользоваться уравнением (2.29),
которое можно представить в виде dq = cdT = du + pdv. Здесь с — удельная
теплоемкость системы в произвольном процессе. Подставив в полученное уравнение
соотношения (5.29) cdT = cvdT+ T(dp/dT)vdv, при условии p = const получим уравнение
Майера:
Cp — cv=T(dp/dT)v(dv/dT)p. (5.43)
Соотношение (5.43) показывает, что разность ср — cv определяется термической
упругостью (dp/dT)v и термической расширяемостью (dv/dT)p рабочего тела. Ранее
отмечалось, что алгебраические знаки производных, входящих в выражение (5.43),
могут быть либо оба положительными (нормальное состояние вещества), либо оба
отрицательными (аномальное состояние вещества), поэтому произведение этих
производных всегда положительно. Вследствие этого ср всегда больше cv.
Зависимость теплоемкостей от давления и объема можно установить с помощью
уравнений (5.30) и (5.36). В этих уравнениях дифференциал удельной энтропии
является полным, поэтому смешанные производные, построенные согласно правилу
(5.10), должны быть равны между собой, т. е.
Следовательно,
(dcP/dp)T=-T(d2v/dT2)p- (5.44)
(dcv/dv)T=T(d2p/dT2)v. (5.45)
Соотношения (5.44), (5.45) позволяют вычислить зависимость теплоемкостей от
давления и удельного объема. С этой целью их необходимо проинтегрировать с учетом
постоянства температуры:
p/dT2)v dv] T + f{T); (5-46)
ср = \ | Т (с?2 v/дТ2 )р dp] т + / (Т). (5.47)
Р
Если известно уравнение состояния или опытным путем определены производные
от изобарной расширяемости и изохорной упругости
jL/_^_\ I - Г д ( др\
дт\ат)р\; \бт{дт)
то интегрирование выражений (5.46), (5.47) должно привести к зависимостям
ср и cv от термодинамических параметров р, v и Т в виде функциональных зависи-
70 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
мостей cv — cv(vy Т) и ср'=ср(р, Т). Можно решить и обратную задачу, т. е. по
экспериментальным данным с помощью соотношений (5.44), (5.45) построить эмпирическое
уравнение состояния реального рабочего тела F(p, v, T) — 0.
Вопросы 1. Назовите основные свойства термодинамических характеристических функций.
2. Почему характеристические функции называют также термодинамическими
потенциалами?
3. Докажите, что разность между теплоемкостями ср — cv для всех веществ,
встречающихся в природе, всегда положительна.
Глава 6
ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
§ 6.1. Общие условия термодинамического равновесия
Любая термодинамическая система может находиться как в равновесном, так и
неравновесном состоянии, но если устранить причины, вызвавшие отклонение
термодинамической системы от состояния равновесия, то она самопроизвольно вернется в
состояние равновесия и будет сохранять его неопределенное время. Общим условием
равновесия в механике является требование равенства нулю суммы работ по так
называемым виртуальным (малым) перемещениям, не противоречащим основным
связям системы:
п
6LM= 2 Xkdxk\ L = 0. (6.1)
k=\
Условию (6.1) соответствует экстремум потенциальной энергии. Если это минимум,
то при смещении от состояния равновесия расходуется положительная работа
(62LM;> 0) и состояние равновесия является устойчивым. Если 62LM<0, то состояние
равновесия неустойчиво', и если 62LM = 0, то безразлично. Условия равновесия
механических систем являются частным случаем равновесия более сложных
термодинамических систем.
В термодинамике роль потенциальной энергии выполняют характеристические
функции, дифференциалы которых (4.15) в общем случае могут быть представлены
в форме
п
du <; Tds — pdv — 2 Xk dxk\
k=\
n
dh^Tds + vdp— 2 Xk dxk;
(6.2)
П
dF^-sdT-pdv- 2 Xkdxk\
k=\
n
dG< -sdT + vdp- 2 Xkdxk.
k=i
В соотношениях (6.2), согласно уравнению (4.9), знак равенства относится к
обратимым процессам, а знак неравенства — к необратимым.
Условия равновесия для различных сопряжений термодинамической системы с
окружающей средой можно сформулировать для термодеформационной системы,
Термодинамическое равновесие
п
для которой 2 Xk&Xk — O. В этом случае система уравнений (6.2) принимает вид
— pdv; d/i<I
— sdT + vdp.
Эти условия сопряжения системы с окружающей средой можно конкретизировать.
Так, например, пусть в системе совершаются термодинамические процессы при
постоянных значениях и и v. Этот случай соответствует полной изоляции системы от
внешнего воздействия. В этом случае, согласно первому неравенству, Tds^O.
Это неравенство свидетельствует о том, что
при протекании необратимых процессов в изолированной системе ее энтропия
увеличивается (ds;> 0) до тех пор, пока не будет достигнуто условие устойчивого состояния
равновесия, т. е. условие максимума (ds = 0, s = smax).
Никакие отклонения от этого состояния равновесия самопроизвольно возникнуть
не могут, так как энтропия при таких отклонениях системы должна была бы принимать
значения, меньшие максимального, что противоречит второму закону термодинамики.
В тех случаях, когда процессы в термодинамической системе происходят при
постоянных s и vy то из первого соотношения (6.3) следует, что du^O. В этих условиях
внутренняя энергия убывает и при достижении состояния равновесия принимает
свое минимальное значение (dw = 0 w = wmin).
При этом необходимо иметь в виду, что условие s = const в данном случае не
означает адиабатной изоляции системы от окружающей среды, так как вследствие
протекания в системе необратимых процессов для поддержания постоянства
энтропии теплоту от системы необходимо отводить.
Если термодинамические процессы протекают в системе при постоянных 5 и р,
то из второго соотношения (6.3) следует условие d/i^0. Таким образом, при принятых
ограничениях
энтальпия системы будет уменьшаться и в состоянии равновесия примет свое
минимальное значение (d/z = O, h = hm]n).
При термодинамических процессах, протекающих в условиях постоянства 7\ s,
можно использовать третье уравнение (6.3). Это приведет к неравенству df^O. Таким
образом, при выбранных условиях
приближение термодинамической системы к состоянию равновесия характеризуется
стремлением свободной энергии к своему минимальному значению. В состоянии
равновесия d/r==0, F = Fmin.
При постоянных Г, р следует использовать четвертое неравенство (6.3), из
которого следует dG<I0, a
условием равновесия является минимум свободной энтальпии (dG = 0, G = Ginin).
Таким образом, при достижении термодинамической системой состояния
устойчивого равновесия в зависимости от условий сопряжения системы с окружающей
средой соответствующая характеристическая функция принимает свое минимальное
значение.
Уравнения (6.2) дают возможность рассмотреть равновесие сложных
термодинамических систем, у которых кроме перечисленных выше условий сопряжения
сохраняются постоянными значения Pk и xki характеризующие работу немеханического
характера.
1. При условиях сопряжения s = const, y = const, x* = const первое уравнение
системы (6.2) свидетельствует о том, что в этом случае dw^O, т. е. внутренняя
энергия при приближении к состоянию равновесия, как и для простой
термодеформационной системы, убывает и достигает минимума в состоянии равновесия (dw = 0,
2. При условиях сопряжения s = const, p = const, Xfe = const второе уравнение
72 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
п
(6.2) показывает, что "^ k xk- Сумма работ немеханического характера
с помощью преобразования Лежандра может быть представлена в виде
2 ХкАх„= 2 d(Xkxk) - 2 хкйХк.
k=l k=\ k=\
С учетом полученного соотношения и Х* = const условие равновесия принимает вид
d ( h + 2 Xk xk 1 <I 0. Этот критерий равновесия отличается от критерия, полученного
\ *=i /
онной системы.
( h + 2 XkxA
\ *=i /
ранее для простой термодеформационной системы.
Физический смысл выражения ( h + 2 XkxA можно выяснить, если учесть, что
/
энтальпия Л, определяемая соотношением (2.34), физически представляет собой
энергию открытой термодинамической системы (внутренняя энергия плюс работа
п
проталкивания). Следовательно, выражение и + pv + 2 Xk xk можно рассматривать
k=i
в качестве энтальпии /г* сложной расширенной системы, которая связана с «обычной»
п
энтальпией соотношением А*=А+ 2 Xkxk. Таким образом, условие равновесия
к=\
может быть записано в виде d/i*<I0, совпадающем по форме с условием
равновесия простой системы.
3. При условиях сопряжения T = const, y = const, x* = const третье уравнение
(6.2) показывает, что dF^.0. Это совпадает с условием равновесия простой
термодинамической системы.
4. При условии сопряжения r = const, /? = const, jf* = const преобразование
Лежандра применительно к четвертому уравнению системы (6.2) дает d
f G + 2 Xkxkj.
Величину Q* — Q + 2 Xkxk можно рассматривать в качестве изобарно-изотермного
k=\
потенциала сложной термодинамической системы.
Таким образом, условие равновесия может быть записано в виде dG*<0,
совпадающем по форме с условием равновесия простой термодеформационной
системы.
§ 6.2. Основное уравнение термодинамики
для неоднородных систем
Химический потенциал. Системы, к которым применим термодинамический метод
исследования, в общем случае являются неоднородными, состоящими из тел
различного химического состава, находящихся в различных агрегатных состояниях.
При этом между телами, образующими термодинамическую систему, могут протекать
различные химические реакции и переходы веществ из одних фаз в другие. В связи
с этим анализу условий равновесия неоднородных систем должно предшествовать
введение ряда новых понятий и определений.
Термодинамическое равновесие 73
Всякое независимое химически различное вещество, входящее в систему,
содержание которого не зависит от других составляющих называется
компонентом. Например, раствор хлорида натрия в воде состоит из двух компонентов NaCl и
Н2О, причем молекулы NaCl диссоциированы в водном растворе на ионы Na+ и С1".
Однако ионы нельзя рассматривать в качестве компонентов, так как число их
(Na+ и С1~~) взаимозависимо.
Различные формы одного и того же вещества, отличающиеся физическими
свойствами и ограниченные друг от друга видимыми макроскопическими поверхностями
раздела, называются фазами. Понятие фазы не следует отождествлять с понятием
агрегатного состояния вещества. В то время как в природе существует всего три
агрегатных состояния (газообразное, жидкое и твердое), число фаз может быть
неограниченным. Например, твердое вещество может существовать в нескольких фазах,
отличающихся различными кристаллическими модификациями.
Гомогенная система — это физически однородная система, состоящая из
одного или нескольких компонентов, находящихся в одинаковых агрегатных состояниях,
и обладающая одинаковыми физическими свойствами во всех своих частях.
Примерами гомогенной системы являются смесь газов или раствор.
Гетерогенная система — это физически неоднородная система, состоящая
из одного или нескольких компонентов, находящихся в различных фазах. Как
гомогенная, так и гетерогенная системы могут состоять из химически активных
компонентов.
Характерным признаком неоднородных термодинамических систем является
изменение массы веществ, входящих в систему, в результате протекания
химических реакций и фазовых переходов, так как в конечном счете процессы
химического или фазового превращения состоят в перераспределении массы между
фазами или веществами, составляющими систему. Следовательно, масса играет роль
координаты состояния в этих процессах. Процессы перераспределения массы могут
протекать и в системах, полностью изолированных от окружающей среды, если
предварительно будут созданы необходимые условия.
Гиббс показал, что причину возникновения фазовых и химических превращений
следует искать в неоднородностях, возникающих в самой системе, и ввел в
термодинамику понятие химического потенциала. Гиббс показал, что неоднородность
поля химических потенциалов приводит к процессам перераспределения массы.
Интенсивной величиной (потенциалом) в выражении работы химических сил в
рассматриваемых процессах химических и фазовых превращений являются химические
потенциалы компонентов ц,*.
Пусть имеется неоднородная термодинамическая система, которая ограничена
контрольной поверхностью, непроницаемой для веществ, составляющих систему.
Энергетическое взаимодействие такой системы с окружающей средой вызывает
перераспределение веществ в системе в процессах фазовых и химических превращений.
Если мысленно разбить систему на подсистемы, число которых равно числу веществ,
участвующих в химических реакциях или фазовых переходах, и взаимодействие
системы с окружающей средой считать равновесным, то для системы в целом
изменение удельной внутренней энергии определится уравнением (2.29).
Так как система в целом находится в равновесии с окружающей средой, то
обмен количеством теплоты и работы каждой из подсистем с окружающей средой
носит также равновесный характер, поэтому неравновесность химических процессов
может выражаться только в перераспределении массы внутри системы. Тогда для
каждой из подсистем
duk=Tdsrk — pdvk + Vkdnik, (6.4)
где drrik—изменение массы подсистемы. Так как процесс переноса массы неравно-
74 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
весен по своей природе, то в выражении (6.4) учтено значение внешнего химического
потенциала (if.
Связь между внешним \к% и внутренним \ik потенциалами рассматриваемой
подсистемы устанавливается уравнением
(6.5)
С учетом соотношения (6.5) уравнение (6.4) получит вид
(6.6)
Дополнительное слагаемое Дц*с1т* вызвано неравновесностью процесса
перераспределения массы и предствляет собой некомпенсированную часть взаимодействия.
Оно всегда положительно. Действительно, если A|i*;> 0 (|л£;>|л*), то имеется приток
массы в подсистему и dm*> 0, если же Дц,*<0 (ц!<ц,*), то и dm*<0.
Суммируя уравнения (6.6) для всех подсистем системы, получим
п п п п п
2 duk = Т 2 dsr — р 2 dvk -f- 2 и** dmk -f- 2 Дщ dmk. (6.7)
k=\ k 1 k=\ k=\ /e=1
л
Если Zi duk— полное изменение внутренней удельной энергии системы, то
k=\
в случае равновесного обмена теплотой и работой уравнение(6.7) примет вид
л л
du = Tdsr — pdv + 2 \ik &mk + 2 Дм-* dmft. (6.8)
k=i k=\
Опыт показывает, что единственная форма энергии, в которую превращается
л
некомпенсированная часть взаимодействия 2 &\ikdmkt— это теплота, т. е.
л
% &\ikdmk = Tdsir. Поэтому уравнение (6.8) можно представить в форме зависи-
k=\
мости
л
du < Tds — pdv + 2 \ik dmk. (6.9)
Здесь ds представляет собой обратимую dsr и необратимую dsir части изменения
удельной энтропии. Уравнение (6.9) показывает, что
в термодинамических системах, в которых происходит перераспределение масс
вследствие химических реакций или фазовых переходов, происходят три рода
взаимодействия: термическое, механическое и химическое, которые определяют изменение
внутренней энергии системы.
В дальнейшем при анализе таких термодинамических систем удобнее
использовать вместо масс компонентов число молекул (частиц) Nk компонентов и молярные
значения как характеристических функций ((У, Я, /\ G), так и экстенсивных
термодинамических параметров состояния (S, V). В этом случае выражения для
дифференциалов характеристических функций примут вид
п
dU=TdS-pdV+ 2 \ikdNk; (6.10)
Термодинамическое равновесие 75
п
dH = TdS + Vdp + 2 \ik dNk\
/г= 1
(6.10)
a
df = - SdT - pdV + 2 \ik dNk;
a=i
n
dG = - SdT + Vdp + 2 м* d^A-
a=i
Уравнения (6.10) позволяют выяснить физический смысл химического потенциала
и указать пути его определения. Так как дифференциалы характеристических функций
обладают свойствами полного дифференциала, то из уравнений (6.10) следует, что
Nk=(dF/dNk)TXN¥: Nk=(
а это значит, что при определенных условиях сопряжения системы с окружающей
средой химический потенциал компонента представляет собой меру изменения
соответствующей характеристической функции в зависимости от изменения числа молекул
этого компонента.
Аналогично, уравнения (6.10) позволяют выразить термодинамические параметры
через частные производные характеристических функций:
T = (dU/dS)v,N=VH/dS)p§Ne; р = -(dU/dV) StNk= -pF/dV)rtN;,
S=-(dF/dT)ViN = -(dG/dT)PtNk;
V = (dH/dp)StN=(dG/dp)TtN, (6.12)
Характеристические функции, являясь производными от внутренней энергии, обладают
свойством аддитивности, т. е. их значения зависят от числа частиц, составляющих
систему.
В отличие от интенсивных величин (давление, температура) аналогичными
свойствами обладают экстенсивные величины (объем и энтропия). В связи с этим
функциональная зависимость характеристических функций от молярных значений
термодинамических параметров простейших однородных систем, состоящих из N частиц,
может быть представлена в виде
1 V/N)=N<px(s9 v)\ H = Nq>2(S/Ny p) = %2(s, p);
T9 v)\ G = Nip(Tt p) = N<tfT, p). (6.13)
Таким образом, все характеристические функции сложным образом зависят от
числа частиц, составляющих систему, за исключением свободной энтальпии G, для
которой сама функциональная зависимость ср не включает число частиц N и является
интенсивной величиной.
С учетом последнего выражения (6.13) химический потенциал (6.11) получает вид
И* = Ф(Р. 7"); (6.14)
химический потенциал компонента при постоянных температуре и давлении численно
равен молярному значению свободной энтальпии.
§6.3. Условия термодинамического равновесия
неоднородных систем
Так как было принято, что взаимодействие неоднородной термодинамической системы
с окружающей средой носит равновесный характер, то для системы в целом
изменение удельной внутренней энергии определяется уравнением (2.29). Таким образом,
сопоставление уравнений (2.29)- и (6.8) с одновременной заменой масс компонентов
76 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
п п
mk на число частиц Nk показывает, что 2 \ikd Nk= — 2 h\ikdNk, причем сумма
п
2j &\ik dNk в процессе перераспределения массы больше нуля. Поэтому
k=\
п
I> \ikdNk<0. (6.15)
k=\
Следовательно, в процессе перераспределения массы вследствие химических реакций
или фазовых переходов всегда выполняется условие (6.15), а окончание процесса
произойдет в момент выравнивания химических потенциалов, когда Д^ = 0, т. е.
п
2 (1,(1^ = 0. (6.16)
k=\
Объединяя условия (6.15) и (6.16), получим
п
2 \ikdNk^0. (6.17)
Таким образом, условие (6.17) означает, что
при химических или фазовых превращениях в системе алгебраическая сумма количеств
воздействии, которыми обмениваются между собой различные однородные подсистемы,
убывает и обращается в нуль при достижении состояния равновесия.
Условие (6.17) можно связать с поведением характеристических функций при
химических и фазовых превращениях. Согласно уравнениям (6.10), с учетом
неравенства (6.17) общие условия термодинамического равновесия сложных
неоднородных систем при соответствующем выборе условий сопряжения могут быть представлены
так:
п
если S,V — const, то dU = 2 \ik d Nk < 0;
k=i
n
если S,p — const, то d# = 2 \ikd Nk^. 0;
kT (6.18)
если T,V — const, то dF = 2 M-* d N < 0;
k=i
n
если Typ — const, то dG = 2 M-* d Nk ^ 0.
k=\
Эти выражения показывают, что химические реакции и фазовые переходы при
определенных условиях сопряжения с окружающей средой возможны только при
уменьшении соответствующих характеристических функций. При этом в состоянии равновесия
соответствующая характеристическая функция достигает своего минимального значения
(U=Umin, H=Hmin, F=Fmin, G = Gmin).
Таким образом, исследуя поведение характеристических функций, можно судить о
направлении химических реакций и фазовых превращений и условиях их
равновесия.
Термодинамическое равновесие 77
§ 6.4. Условия фазового равновесия
Правило фаз Гиббса. Пусть гетерогенная система состоит из Ф фаз и п
компонентов, так что в каждой фазе находятся все п компонентов. В этом случае условие
равновесия (6.16) получит вид
Ф л
2 2 ni<wi = ii',d#; +... + ^d< + ... + n;dyv; + ... + ^d<=o
/=i k=i
(6.19)
и может быть дополнено п уравнениями сохранения массы компонентов:
d#i + ... + (!<' = 0;
(6.20)
Совместное решение уравнений (6.19) и (6.20) даст конкретные условия
равновесия гетерогенной системы.
Если предположить, что только /г-й компонент претерпевает фазовые превращения,
а остальные остаются неизменными, то система уравнений (6.19) и (6.20) принимает вид
lii d N'k + ... + |i? d Nk = 0; dNk + ... + d< = 0.
Решая их совместно, получим
В общем случае dNi, ..., d/V0"1 не равны нулю, поэтому
' Ф /Л Ф 1 Ф /Л ' " Ф
М-* — М-* = 0;...; \ik — \ik = 0, или ^Л = М-л = ••• = М-* •
Аналогичные предположения для остальных компонентов дают следующие условия
равновесия гетерогенной системы:
мч = мч = ... = in;-; м^л= м^л = • = м^л- (6-21)
Таким образом, в равновесной гетерогенной системе переход компонента из одной
фазы в другую должен происходить при равенстве химических потенциалов этого
компонента во всех фазах.
Условия (6.21) позволяют установить число независимых параметров (число
степеней свободы) гетерогенной системы в состоянии равновесия. Это число
определяется правилом фаз Гиббса.
В общем случае, для того чтобы определить число степеней свободы системы
С, необходимо из общего числа переменных Л/, характеризующих систему, вычесть
число уравнений Z, связывающих эти переменные: C = N — Z. По сравнению с гомогенной
системой общее число переменных в гетерогенной системе возрастает, так как возможно
перераспределение между массами компонентов, находящихся в различных фазах.
Согласно уравнениям сохранения масс (6.20), число дополнительных переменных
определяется числом п масс компонентов, находящихся в различных фазах
(N\, N\\ ...), т. е. пФ. Следовательно, общее число N переменных с учетом к внешних
78 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
независимых параметров равно Л/ = 2/г + /гФ. Для определения числа уравнений,
связывающих эти переменные, следует учесть число внешних параметров.
Так, например, если для термодеформационной системы общее число
термодинамических параметров равно четырем (S, V, Г, р), то число связывающих эти
параметры уравнений равно двум: p = p(S, V), T=T(Sy V). Дополнительными
уравнениями, связывающими новые переменные, являются уравнения сохранения масс фаз,
находящихся в равновесии, dN\ +... + dN'n = 0\ dN'{+... + dN'r!=0\ ...; dN?+... + dN?=
= 0, число которых равно числу фаз Ф, и уравнения сохранения масс, вытекающие
из условий равновесия гетерогенной системы (6.21),
d N\ +. d N\' = 0,..., d N'n + d ЛС = 0;
d N\ + d N\" = 0,..., d AC + d ЛС = 0;
число которых равно /г(Ф—1).
Таким образом, общее число степеней свободы гетерогенной системы равно
C—N — Z — 2k-\-n<$> — {/г + Ф + /г(Ф—1)}, откуда получаем правило фаз Гиб-
бса :
C = k — Ф + /г; (6.22)
число степеней свободы гетерогенной системы, находящейся в состоянии равновесия,
равно числу независимых внешних параметров (внешних степеней свободы) к плюс
число компонентов п минус число фаз Ф.
В случае термодеформационной системы правило фаз Гиббса принимает вид
С = 2 — Ф + п. (6.23)
В отличие от неравновесной системы, состоящей из п компонентов, где число
фаз может быть произвольным, в равновесной системе, согласно правилу фаз
Гиббса, число фаз связано вполне определенным соотношением с числом компонентов.
Действительно, так как число степеней свободы термодинамической системы не может
быть отрицательным, то в условиях равновесия, согласно (6.22), должно соблюдаться
условие
Ф</г + /г, (6.24)
т. е. число фаз, находящихся в равновесии, должно быть меньше или равно числу
компонентов п плюс число внешних независимых параметров k.
Правило фаз Гиббса универсально, оно выполняется для любых сложных
термодинамических систем, в которых происходит химические реакции и фазовые переходы.
Это правило сохраняется и в том случае, когда часть компонентов отсутствует
в некоторых фазах (при этом число уравнений при сохранении массы сократится как
раз на число отсутствующих компонентов).
§6.5. Фазовые переходы 1-го рода
Переход вещества из одного фазового состояния в другое носит название
фазового перехода. Отличительной особенностью фазовых переходов 1-го рода
является скачкообразное изменение удельного объема и удельной энтропии:
Au = i;// — v'\ /is = s" — s'. (6.25)
Вследствие скачкообразного изменения энтропии фазовые переходы 1-го рода
протекают с поглощением или выделением теплоты, называемой теплотой
фазового перехода. К таким переходам относятся процессы изменения агрегатного
Термодинамическое равновесие 79
состояния вещества (испарение, конденсация, плавление, сублимация, затвердевание,
возгонка) или переход вещества в различные кристаллические модификации.
Пусть, например, гетерогенная система, состоящая из одного компонента
(/г=1), находится в изобарно-изотермных условиях сопряжения с окружающей
средой. В этом случае условие (6.2) получит вид
(j/-(!" = (). (6.26)
При дальнейшем анализе этого условия удобнее использовать молярные значения
свободной энтальпии yk=Gk/Nk = q)k(p, Т). Согласно (6.14), величины ср* представляют
собой химические потенциалы, поэтому условие фазового равновесия (6.26) может быть
представлено в виде
ф'(р,Г)-ср"(р, Г) = 0. (6.27)
Соотношения (6.12) показывают, что
(dq>/dp)T = v\ (d<p/dT)p=-sy (6.28)
поэтому соотношения (6.25) могут быть записаны в виде
Так как значения Ду и As конечны, то, значит, и первые производные свободной
энтальпии меняются скачкообразно при фазовых превращениях, поэтому и принято
называть такие превращения фазовыми переходами 1-го рода.
Вторые производные от свободной энтальпии по температуре и давлению, согласно
соотношениям (6.28), имеют вид
(д\/дТ\ = -(ds/dT)p\ (d\/dp2)T = (dv/dp)T;
(d2q>/dTdp)p = {dv/dT)p. (6.30)
Отсюда следует, что в условиях фазового перехода, когда давление и температура
остаются постоянными, эти производные обращаются в бесконечность, а соотношения
(6.30) получают определенный физический смысл: в соответствии с соотношениями
(5.36), (5.18) и (5.20) (при p = const) имеем: (ds/dT)p = cp/T\ (dv/dT)p = (xvoy
(dv/dp)T=—$Tv0.
Таким образом, фазовые превращения 1-го рода обладают следующими
особенностями, вытекающими из приведенного анализа:
при переходе в новую фазу затрачивается или выделяется теплота фазового перехода;
при переходе в новую фазу происходит скачок удельного объема и энтропии веществ;
теплоемкость и коэффициенты термической расширяемости и изотермной сжимаемости в
точке перехода обращаются в бесконечность.
Правило фаз Гиббса (6.23) свидетельствует о том, что равновесная гетерогенная
система, образованная из двух фаз чистого вещества, обладает всего одной степенью
свободы. В этом случае давление должно быть однозначной функцией температуры,
которую в дифференциальном виде можно получить из условия фазового равновесия
(6.27). Дифференцируя (6.27) по р и Ту получим
откуда
или после подстановки производных (6.29)
др/дТ = (s" - s')/{v» - v') = W№" - v')\, (6.31)
где qn — удельная теплота фазового перехода.
80
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Уравнение (6.31), определяющее зависимость давления от температуры при
равновесном существовании двух фаз, называется уравнением Клапейрона —
Клаузиуса.
§ 6.6. Фазовая Гр-диаграмма
Число фаз, возможных в состоянии равновесия однокомпонентной термодинамической
системы, согласно правилу фаз, должно удовлетворять неравенству Ф^З. Это значит,
что однокомпонентная равновесная термодинамическая система в зависимости от
физических условий может существовать как одно-, двух- или трехфазная.
Пусть, например, однокомпонентная система (я=1) является одновременно и
однофазной: Ф=1. Уравнение (6.23) показывает, что такая система обладает двумя
степенями свободы, т. е. в пределах этой системы независимо могут изменяться два
термодинамических параметра: давление р и температура Т. Если же в такой системе
(/г=1) фаз две (Ф = 2), то, согласно правилу фаз (6.23), система обладает только
одной степенью свободы и произвольно может меняться только один
термодинамический параметр, т. е. должна существовать однозначная зависимость между давлением
и температурой р = р(Г) (уравнение Клапейрона — Клаузиуса). При наличии трех
фаз (Ф = 3), согласно (6.23), число степеней свободы однокомпонентной системы
(лг = 1) равно нулю, т. е. равновесное существование трех фаз данного вещества
возможно лишь при определенных давлении и температуре. Это состояние вещества принято
называть тройной точкой.
Рассмотренные выше состояния равновесия однокомпонентных термодинамических
систем могут быть представлены в виде Гр-диаграммы (рис. 6.1, а). На этой диаграмме
в тройной точке О (равновесное существование трех фаз) пересекаются три линии,
соответствующие изменению состояния равновесных двухфазных систем. На линии
p = pi(T) (кривой испарения) находятся в равновесии жидкая и паровая фазы.
Линия р = р2(Т) соответствует равновесному существованию твердой и паровой фаз,
и ее называют кривой сублимации. И наконец, на линии р = Рз (Т) равновесно
существуют твердая и жидкая фазы, и она называется кривой плавления. Эти
кривые разграничивают плоскости диаграммы на области, соответствующие паровой,
жидкой и твердой фазам.
Внешние крайние точки кривых сублимации и плавления для некоторых веществ,
способных образовывать несколько твердых или жидких фаз, могут представлять собой
новые тройные точки. Так, например, на рис. 6.1, б представлена Гр-диаграмма
воды, имеющая несколько твердых модификаций, а следовательно, и несколько
тройных точек.
АЛЛ
г
Рис. 6.1. Гр-диаграмма: а — вещества с одной тройной точкой; б — воды; в — гелия
Термодинамическое равновесие 81
Кривые испарения для всех веществ оканчиваются при определенных значениях
давления и температуры. Это состояние, называемое критическим, обозначается
на Г/?-диаграммах точкой К. В состоянии, соответствующем критической точке,
пропадает различие между физическими свойствами паровой и жидкой фаз.
Конкретный вид кривых равновесия не может быть найден с помощью
термодинамического метода, так как вид кривых зависит от особенностей молекулярной
структуры индивидуальных веществ. Однако форма кривых, а также их взаимное
расположение на Гр-диаграмме могут быть установлены на основании анализа уравнения
Клапейрона — Клаузиуса (6.31). Запись этого уравнения можно конкретизировать
для рассмотренных случаев равновесного существования двухфазной однокомпонент-
ной системы (рис. 6.1, а):
для кривой испарения
-v')]; (6.32)
для кривой плавления
dp/dT = \m/[TJp' - vTB) ]; (6.33)
для кривой сублимации
= Xc/[Tc(vTB-v")]. (6.34)
Здесь г, А,™, К — соответственно скрытые удельные теплоты испарения, плавления
и сублимации; v", v', vTB — удельные объемы паровой, жидкой и твердой фаз;
Ts, ТпЛу Тс — температуры испарения, плавления и сублимации.
В соответствии с уравнением (6.31) производная dp/dT в (6.32) положительна,
так как для всех веществ г>0, Г5;>0 и v" — v'>0. Следовательно, кривая испарения
от тройной точки О направлена вверх и вправо. Так как разлчие между удельными
объемами паровой и жидкой фаз уменьшается быстрее, чем растут Гиг при
приближении к критической точке, то кривая испарения обращена выпуклостью вниз. Кривая
плавления (6.33) круче кривой испарения, так как изменение удельных объемов фаз при
плавлении на несколько порядков меньше, чем при испарении, при незначительной
разнице значений скрытых теплот и температур.
Знак производной dp/dT зависит от свойств самого вещества. Если состояние
вещества оказывается нормальным, то dp/dr>0, если аномальным, то dp/dT<<0.
Кривая сублимации (6.34) при dp/dr>0 (A,c>0, Гс>0, v" — утв>0) круче
кривой испарения, так как А,с = А,™ + г и v" — vTBzzv"—v'.
§ 6.7. Фазовые переходы 2-го рода
Фазовые переходы 2-го рода совершаются в процессах перехода некоторых металлов
в сверхпроводящее состояние (при очень низких температурах превращение гелия
Не(1) в Не(П)), перехода металлов из ферромагнитного в парамагнитное состояние,
некоторых превращений в кристаллических телах и, наконец, фазовых переходов
веществ в критических точках. В отличие от фазовых переходов 1-го рода при фазовых
переходах 2-го рода скачкообразного изменения удельного объема и удельной энтропии
не наблюдается, а следовательно, и теплоты фазового перехода.
Характерным признаком фазового перехода 2-го рода (название введено П. С. Эрен-
фестом) является скачок удельной теплоемкости, а также коэффициентов термической
расширяемости и сжимаемости.
Отмеченные особенности фазового перехода 2-го рода приводят к тому, что в
точках перехода не только удельное значение свободной энтальпии ср, но и ее первые
производные, согласно (6.29), меняются плавно. Поэтому
82 РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Вместе с тем вследствие скачкообразного изменения значений Сру а, рг в точках
перехода скачкообразно изменяются и вторые частные производные свободной
энтальпии. Действительно, согласно (6.30), (6.36), (6.18) и (6.20),
{д\/дТ2)р=-ср/Т, (d\/dp2)T = -pTv0; (d2<p/dpdT)p = av0y (6.36)
(д\"/дТ2)р - (д\'/дТ2)р = Д {д\/дТ2)р = - (1/Г) (с; - ср) = - Дс,/Г; (6.37)
(д\"/др2)т - (д2у'/др2)т = Д {д2ц>/др2)т = - ио( Pi-' - Рг) =
откуда следует
(д\"/др дТ)р - (д2у'/др дТ)р = Д (д2ц>/дрдТ)р = у0 (а" - а) =
Полученные соотношения подтверждают, что вторые частные производные от
свободной энтальпии при фазовых переходах 2-го рода меняются скачкообразно.
П. С. Эренфест получил уравнения, связывающие величины Дср, Да, Дрг при
фазовых переходах 2-го рода. Чтобы получить эти уравнения, необходимо
продифференцировать выражения (6.35) по р и Г, т. е.
р&Т + Цд2у/др2)т(\р = 0;
) pdT + Цд2у/дрдТ) р=О,
и учесть соотношения (6.37):
(\c/T)dT + v\adp = O\ (б38)
Решая последние уравнения совместно, получим
2 = О. (6.39)
Уравнения (6.38) являются аналогами уравнения Клапейрона — Клаузиуса
(6.31) для фазовых переходов 2-го рода. Они позволяют найти производную
dp/dT в каждой точке фазового перехода и построить граничную кривую на фазовой
диаграмме так, что dp/dT= — \cp/(Tvoka) и dp/d7' = Aa/Ap7.. Фазовые переходы 2-го
рода не сопровождаются изменениями агрегатного состояния вещества и происходят
в пределах определенной фазы. Их механизм состоит в перегруппировке атомов и
молекул.
На рис. 6.1, в приведена диаграмма фазового перехода 2-го рода
жидкого гелия при 29 К и атмосферном давлении из одной жидкой фазы Не(1) в
другую Не(Н), при котором исчезает вязкость и гелий Не(Н) становится
сверхтекучим.
Вопросы 1. Для какой характеристической функции химический потенциал равен его удельному
значению и почему?
2. Сформулируйте общее условие термодинамического равновесия для любых
термодинамических систем.
k = n
3. Объясните, как связано неравенство 2 \ikdNk<0 для сложных термодинамических
систем со вторым законом термодинамики (принципом возрастания энтропии).
4. В чем отличие между понятиями фаза и агрегатное состояние?
Физический закон должен быть
математически изящным.
П. Дирак
СВОЙСТВА
И ПРОЦЕССЫ
ИДЕАЛЬНЫХ ГАЗОВ
Чтобы выявить фундаментальные
закономерности в работе тепловых
машин и установок, нужно пренебречь
второстепенными факторами,
т. е. идеализировать поставленную задачу.
С этим связано использование
в термодинамике понятия идеального газа.
Так как свойства реальных газов
в широкой области состояний
оказываются достаточно близкими
к свойствам идеального газа,
то уравнения,
полученные для идеального газа,
применяются для расчета процессов
с реальными рабочими телами.
Однако получаемые при этом результаты
являются приближенными,
поэтому идеализация задачи должна
определяться требуемой точностью
расчета.
РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Глава 7
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА И ТЕПЛОЕМКОСТЬ
§7.1. Термодинамические характеристики
Идеальным называется газ, подминающийся уравнению состояния (1.6). Для
1 кмоль газа это уравнение получит вид
PV=vlRT, (7.1)
где V — объем 1 кмоль газа, м3/кмоль; \iR — универсальная газовая постоянная,
Дж/(кмоль-К), значение которой можно определить из уравнения (7.1). Так, при
нормальных физических условиях (р = 0,1013 МПа, Г = 273,15 К, V = 22,4 м3/кмоль)
(Ll^ = pt7/7'= 101325.22,4/273,15 = 8314,4 Дж/(кмоль-К). (7.2)
Таким образом, уравнение (7.1) с учетом (7.2) принимает вид
? Т (7.3)
и называется уравнением состояния Клапейрона — Менделеева.
Идеальное газовое состояние является пределом, к котором^- приближается
соседние газов при безграничном снижении давления.
Идеальный газ в действительности не существует, однако его свойства справедливы
и для реальных газов при низких давлениях и высоких температурах.
Анализ дифференциальных уравнений термодинамики совместно с уравнением (1.6)
состояния идеального газа позволяет выявить специфические термодинамические
свойства идеального газа и получить необходимые расчетные соотношения. Так,
например, производные, входящие в выражения (5.18) — (5.20), с учетом уравнения
(1.6) получают вид
(dp/dT)v = R/v; (dv/dp)T=-RT/p2. (7.4)
В связи с этим для идеального газа:
коэффициент термического расширения
a = R/(vop); (7.5)
коэффициент термической упругости
y = R/(povo)\ (7.6)
коэффициент изотермной сжимаемости
2. (7.7)
Термодинамические свойства 85
Соотношения (7.4) удовлетворяют условиям (5.17) и (5.23). Действительно, с
учетом выражений (7.4) соотношение (5.17) получит вид
(dv/dT)p (dT/dp)v(dp/dv)T= -pv/(RT) = - 1.
При этом, согласно третьему равенству (7.4), удовлетворяется условие стабильности
(5,23), так как RT/p2 всегда больше нуля.
§ 7.2. Внутренняя энергия, энтальпия и энтропия
Основным термодинамическим свойством идеального газа является независимость его
внутренней энергии от объема и давления. Это свойство может быть выявлено опытным
путем при расширении газа в пустоту. Такой опыт впервые был проведен Ж. Гей-
Люссаком, а затем Дж. Джоулем. Два сосуда, соединенных трубкой с краном,
помещались в ящик с хорошей термоизоляцией. В одном из сосудов был исследуемый
газ, а в другом создавалось разрежение. При открытии крана газ из первого сосуда
перетекал во второй до тех пор, пока не устанавливалось состояние равновесия.
Стенки сосудов выбирались достаточно жесткими, поэтому суммарный объем системы
в опыте не изменялся, следовательно, работа расширения не производилась.
Вследствие адиабатной изоляции газ при расширении не мог обмениваться теплотой
с окружающей средой. В этих условиях в соответствии с первым законом
термодинамики (2.29) внутренняя энергия газа не должна изменяться. И действительно,
опыты Джоуля показали, что температура газа при его перетекании из одного
сосуда в другой и расширении остается неизменной. Соотношение (5.24) в этом случае
показывает, что при dr = O du — (du/dv)Tdv. Так как удельный объем газа в
рассматриваемом процессе менялся dvфO1 то (du/dv)T = O и, следовательно, внутренняя энергия
от объема при постоянной температуре не зависит.
Независимость внутренней энергии идеального газа от объема может быть
строго установлена с помощью дифференциального уравнения (5.26), если учесть в нем
второе соотношение (7.4). Можно также показать, что внутренняя удельная энергия
идеального газа не зависит и от давления: (ди/др)т = 0. С этой целью производную
(ди/др)т следует представить в виде произведения:
= (du/dv)j{dv/dp)T.
Третье соотношение (7.5) показывает, что (ди/др)тФ0. Так как {du/dv)T=0,
то (ди/др) т=0. Таким образом,
удельная внутренняя энергия идеального газа не зависит ни от объема, ни от давления
к является однозначной функцией температуры.
Учет этого свойства идеального газа в выражении (2.34) показывает, что
энтальпия также является однозначной функцией температуры.
Действительно, с учетом уравнения (1.6)
(7.8)
поэтому для идеального газа h — h(T). Учет второго соотношения (7.4) в уравнениях
(5.29), (5.30) позволяет определить при независимых переменных v и Т изменение
удельной внутренней энергии идеального газа
du = cvdT + [RT/v — p]dv = cvdT (7.9)
и изменение удельной энтропии
(7.10)
Если в качестве независимых переменных выбрать р и 7\ то в соответствии с
первым соотношением (7.4) уравнения (5.35) и (5.36) позволяют определить изменение
энтальпии идеального газа
86 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
dh = cpdT-[(RT)/p-v]dp = cpdT (7.11)
и изменение энтропии
ds = cp(dT/T)-R(dp/p). (7.12)
Таким образом, изменения внутренней энергии и энтальпии идеального газа при
выбранных выше независимых переменных определяются удельными теплоемкостями
системы соответственно при v = const и р = const.
При независимых переменных v и р уравнения (5.40) —(5.42) с учетом первого и
второго соотношений (7.5) и уравнений Майера (5.43) могут быть представлены в
виде
du = cv(v/R)dp + cv(p/R)dv\ (7.13)
ds = cvdp/p + cpdv/v\ (7.14)
dh = cp(p/R)dv + Cp(v/R)dp. (7.15)
Так же как и в случае реальных газов, полученные дифференциальные
уравнения служат основой построения аналитического аппарата термодинамики
идеального газа и позволяют вычислить при использовании уравнения состояния (7.1)
изменение внутренней энергии, энтальпии и энтропии в исследуемых процессах.
§ 7.3. Теплоемкость
Как уже отмечалось, в термодинамическом анализе используют истинную удельную
теплоемкость (2.19), истинную молярную теплоемкость (2.20) и истинную объемную
теплоемкость (2.21), причем объем вещества принимается при нормальных физических
условиях ро— 101,325 кПа, Г0 = 273,15 К. Молярная, удельная и объемная теплоемкости
связаны соотношением
jic = qi = 22,4с', (7.16)
где \i — молярная масса вещества, кг/моль; 22,4 м3/кмоль — молярный объем газа
при нормальных условиях. Из соотношения (7.16) также следует, что
= cpo, (7.17)
где ро — плотность газа при нормальных условиях, кг/м3.
По аналогии с истинными теплоемкостями различают среднюю удельную
теплоемкость
^-l/(^~^.); (7.18)
среднюю молярную теплоемкость
^i.2==Q2.i/M'2--;.)] (7.19)
и среднюю объемную теплоемкость при нормальных условиях
t{)]. (7.20)
Значения средних теплоемкостей в заданном диапазоне изменения температуры
можно вычислить, если известна зависимость истинной теплоемкости от температуры.
Для большинства газов, подчиняющихся уравнению состояния идеального газа,
зависимость удельной теплоемкости от температуры близка к линейной:
(7.21)
Подставив зависимость (7.21) в (2.17) и проинтегрировав по температуре,
получим
Теплоемкость
87
= (cd/= \ (a + bt) dt = с
где
(7.22)
(7.23)
— средняя удельная теплоемкость в диапазоне изменения температуры от t\ до t%
Обычно значения теплоемкостей приводятся в таблицах термодинамических свойств
веществ. Однако для сокращения объема исходных данных в таблицах приводятся
значения средних теплоемкостей, определенных в диапазоне изменения температуры
от 0 до / °С. Если необходимо вычислить значение средней теплоемкости в другом
(заданном) диапазоне изменения температуры, то это можно сделать по формуле
(7.24)
Площадь 0511' под кривой c = f(t) (рис. 7.1) в соответствии с выражением (7.23)
соответствует удельному количеству теплоты q\, необходимому для повышения
температуры газа от 0 до /|°С. Это количество теплоты можно определить через среднюю
удельную теплоемкость do1 в виде qx — c\^t\. Аналогично (площадь 0522')
определяется количество теплоты <72 = с1о2^2, необходимое для повышения температуры
газа от 0 до ^2ОС. Таким образом, разность q2 — Qi=:Q2i (площадь 1422') может
быть представлена в виде соотношения
?2-1 =
которое с учетом (7.19) приводит к выражению (7.24). Формулы, аналогичные
(7.24), могут быть получены для средних молярной и объемной теплоемкостей.
Значение теплоемкости зависит от процесса подвода (или отвода) теплоты.
Поэтому в практике термодинамических расчетов используют теплоемкости cv и ср,
характерные для нагревания газа в условиях постоянства объема и давления
соответственно. С помощью этих теплоемкостей могут быть вычислены любые другие
теплоемкости.
С учетом второго и третьего соотношений (7.5) уравнение Майера (5.43) для
идеального газа примет вид
cp — cv = R. (7.25)
Следовательно, теплоемкость ср
идеального газа всегда больше теплоемкости cVy
так как при нагревании газа в условиях
р = const теплота расходуется как на
увеличение внутренней энергии газа, так и
на совершение внешней работы расширения,
в то время как при нагревании в условиях
v = const теплота расходуется только на
увеличение внутренней энергии газа.
Теплоемкости ср и cv идеального газа
являются однозначными функциями
температуры. Действительно, для идеального
газа справедливы соотношения (7.4), а по-
Рис. 7.1. Определение средней удельной
теплоемкости газа и количества теплоты в
координатах /, с
88
РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
этому уравнения (5.44) и (5.45) принимают вид
(dcP/dp)T=T[d(dv/dT)p/dT]p=T[d(R/p)/dTIP =
(dcv/dv)T=T[d(dp/dT)v/dT]v=T[d(R/v)/dT]v = O.
(7.26)
С помощью соотношений (dcp/dv) T= (dcp/dp)T(dp/dv)T; (dcv/dp)T=(dcv/dv)TX
X(dv/dp) T и выражений (7.26), (7.5) можно также показать, что теплоемкость ср
не зависит от объема, а теплоемкость cv — от давления.
Если части уравнения (7.25) умножить на молярную массу вещества ц, то
получим \кср — \xcv = \iR— соотношение между молярными теплоемкостями, где \iR—
универсальная газовая постоянная (7.2). Следовательно, для всех идеальных газов
licp—iicv = 8314 Дж/(кмоль-К), (7.27)
или
ср —
(7.28)
Для объемных теплоемкостей ср и c'v можно также получить аналогичную
зависимость. Разность ср — c'v в соответствии с уравнением Майера (7.25) можно
записать в виде
ср - c'v = рср - pcv = р (ср - cv) = p/?, (7.29)
показывающем, что разность c'p — c'v зависит от плотности газа. Так как плотность
газа зависит от давления и температуры, то при определении разности (7.29) надо
указывать условия, в которых находится газ. Если это нормальные условия, то
cp — cv = (\icp — \icv)/22A = 8,314/22,4 « 0,371 кДжДм' . к). (7.30)
Таким образом, у газов с одинаковыми молярными теплоемкостями объемные
теплоемкости также равны.
В термодинамике и ее приложениях большое значение имеют не только разности
теплоемкостей ср и cv [см. (7.25), (7.27), (7.28)) или (7.29)], но и их отношение
= cp/cv = \icp/(\icv) = c'p/c'v.
(7.31)
Значения k могут быть определены по формуле (7.27), если воспользоваться
данными табл. 7.1.
Таблица 7.1
Наименование газа
Аргон Аг
Гелий Не
Пары ртути Hg
Кислород Ог
АУзот N2
Число
степеней
свободы
3
3
3
5
5
Молярная
теплоемкость
\1СОъ
кДж/(кмоль- К)
12,48
12,60
12,52
20,85
20,72
Наименование газа
Водород Н2
Диоксид углерода СО2
Водяной пар НгО
Диоксид серы SO2
Число
степеней
свободы
5
6
6
6
Молярная
теплоемкость
\ic0,
кДж/(кмоль«К)
20,26
28,13
28,47
32,24
Расчеты показывают, что для одноатомных газов приближенно можно принять
k ж 1,67, для двухатомных к «1,4, для трехатомных к «1,29.
Значения /г, \icp и \icv можно найти также опытным путем измеряя скорость
распространения звука в среде данного газа.
Нетрудно заметить, что значение к зависит от температуры. В самом деле, из
уравнений (7.25) и (7.31) следует, что
Теплоемкость
k=\+R/cVy (7.32)
или
k=\+8314/(\lcv). (7.33)
Так как с увеличением температуры газа теплоемкость cv увеличивается, то значение
k уменьшается, приближаясь к единице, но всегда остается больше нее.
Если зависимость k = f(t) принять линейной, то k — k0 — at, где k0 — отношение
теплоемкостей, взятых при О °С; а — коэффициент, постоянный для данного газа.
Так, например, для двухатомных газов в диапазоне температур от 0 до 2000 °С
приближенно £«1,4 — (5-10~~5)/.
Зная k из опыта, можно определить значение соответствующей теплоемкости.
Так, например, из выражения (7.32) имеем
cv = R/(k-\). (7.34)
Но так как cp=kcVy то удельную теплоемкость при постоянном давлении определим
по формуле
cp=Rk/(k-\). (7.35)
Молярные теплоемкости определяются выражениями
|ыс„ = yiR/(k - 1) = 8314/(к - 1); (7.36)
М,Ср = 8314Л/(Л-1). (7.37)
В соответствии с выражениями (6.29) и (6.31) объемные теплоемкости
ci = po/?/(*-l); (7.38)
c'p = PoRk/(k-\). (7.39)
Таким образом, формулы (7.34) — (7.39) показывают, что найденные
экспериментальным путем значения k дают возможность определить значения теплоемкостей.
§ 7.4. Основы кинетической теории теплоемкости
Кинетическая теория газов позволяет вычислить теплоемкость идеального газа.
В соответствии с выражением (7.9) для количества вещества идеального газа
1 кмоль du = \icvdTt откуда \icv=du/dT. Внутренняя энергия идеального газа
представляет собой энергию движения составляющих его молекул. В свою очередь,
полная энергия молекулы состоит из энергии поступательного движения, вращения и
колебания ее атомов.
Эти виды энергии обычно ассоциируются с понятием числа степеней свободы
молекулы. Поступательное движение центра масс молекулы в пространстве можно
задать составляющими скорости движения вдоль трех взаимно перпендикулярных
осей координат, поэтому говорят, что молекула обладает тремя поступательными
степенями свободы. Вращательное движение молекулы задается составляющими
угловой скорости вдоль тех же осей координат и молекула может также обладать
тремя вращательными степенями свободы. К указанным степеням свободы в общем
случае добавляются колебательные степени свободы.
Энергия молекулы каким-то образом распределена между указанными степенями
свободы. В простейшем случае можно предположить, что энергия молекулы равномерно
распределена между всеми возможными степенями свободы. Эта гипотеза носит название
принципа равномерного распределения энергий.
По кинетической теории газов, давление, оказываемое идеальным газом на стенки
сосуда, определяется соотношением
90 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
где N — число молекул, сдержащихся в объеме V; т — масса молекулы; W — средне-
квадратическая скорость молекулы газа.
Для количества вещества газа 1 моль это уравнение принимает вид
PV ТП ~Г"% (7*40)
где V — молярный объем; п — число молекул в количестве вещества газа 1 моль.
Приравнивая правые части уравнений (7.3) и (7.40), получим
2 mW2
откуда можно определить кинетическую энергию поступательного движения молекулы
газа:
mW2 _ 3 \xRT _ 3 , т
2 ~" 2 п ~" 2 '
где /г = ц,/?/гс — константа Больцмана, представляющая собой универсальную газовую
постоянную, отнесенную к одной молекуле. На каждую степень свободы
поступательного движения приходится часть кинетической энергии (1/3) (mW2/2) =kT/2. И
наконец, если через / обозначить полное число степеней свободы, то при соблюдений
принципа равномерного распределения энергии суммарная энергия молекулы
определится выражением (f/3)(mW2/2) = fkT/2. Энергия п молекул, содержащихся в
количестве вещества идеального газа 1 моль, или его внутренняя энергия, определяется
из выражения u = (f/2)nkT = (f/2)\iRT или с учетом (7.9):
\icv = fiiR/2. (7.41)
Из уравнения Майера (7.27) и соотношения (7.41) следует, что
(7.42)
(7.43)
Таким образом, используя принцип равномерного распределения энергии по
степеням свободы, а также кинетическую модель идеального газа, теплоемкости
\xcPi \icv и показатель адиабаты k могут быть выражены через степени свободы.
Можно предположить, что молекулы одноатомных газов ведут себя как молекулы
идеального газа, массы которых сосредоточены в геометрических точках. Поэтому
молекулы одноатомных газов должны обладать только тремя поступательными
степенями свободы. В связи с этим в уравнениях (7.41) и (7.43) можно принять
/ = 3, тогда \icv = Зц/?/2 = 3-8,314/2«12,48 кДж/(кмоль- К); k= (3 + 2)/3= 1,667.
Следует ожидать, что молекулы двухатомных газов (Ог, N2, Н2 и т. д.) обладают
пятью степенями свободы: тремя поступательными и двумя вращательными. Здесь
не учитывается третья вращательная степень свободы, так как момент инерции
относительно оси, на которой расположены атомы, намного меньше, чем моменты
инерции относительно перпендикулярных осей. Если / = 5, то из уравнений (7.41) и
(7.43) получим значения ^^ = 5-8,314/2»20,8 кДж/(кмоль-К); /г = (5 + 2)/5= 1,4.
Трехатомные и многоатомные молекулы имеют три степени свободы
поступательного движения и три степени свободы вращательного движения. В этом случае
расчет по формулам (7.41) и (7.43) дает р,су = 24,99 кДж/(кмоль-К); Дг = 1,33.
Экспериментальные значения теплоемкостей (см. табл 7.1) качественно подтверж-
Смеси идеальных газов
дают значения молярных теплоемкостей, найденных расчетным путем по формулам
(7.41) и (7.43).
Однако имеющиеся расхождения, а также экспериментально наблюдаемая
зависимость теплоемкости от температуры свидетельствуют о том, что кинетическая
теория газов не учитывает колебания атомов сил взаимодействия между молекулами.
Влияние указанных эффектов может быть объяснено лишь с помощью квантовой
теории.
Вопросы 1. Докажите, что теплоемкости ср и cv идеального газа зависят только от температуры.
2. Покажите связь показателя адиабаты с теплоемкостями ср и cv идеального газа.
3. Сформулируйте основные свойства идеального газа и покажите их связь с его
физической моделью.
Глава 8
СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ
§8.1. Парциальные давления компонентов смеси
Механические смеси различных газов, называемые газовыми смесями, часто
являются рабочими телами тепловых машин. Примерами газовых смесей могут служить
атмосферный воздух, состоящий из азота, кислорода, водяного пара и других
компонентов, продукты сгорания твердых, жидких и газообразных топлив, содержащие
углекислый газ, азот, водяной пар и другие газы. Для многих реальных газовых
смесей при невысоких давлениях представление о компонентах газовой смеси как об
идеальных газах является хорошим приближением. При этом каждый газ.
распространяется по всему объему так, как будто бы других газов вовсе не существует. Для
идеальных газов имеет место аддитивность термодинамических свойств при смешении.
Газ, входящий в газовую смесь, оказывает на стенки сосуда давление, которое
не зависит от присутствия в этом объеме других газов.
Давление, называемое парциальным, равно давлению данного компонента
газовой смеси при условии, что компонент занимает весь объем, предназначенный для
смеси при температуре смеси.
Опыт показывает, что в газовой смеси каждый из компонентов занимает весь
объем смеси. В случае смеси идеальных газов в соответствии с уравнением
состояния (1.6), записанным для /-го газа массой mt, его парциальное давление в
газовой смеси Pi — rriiRiTCM/VCM, где /?, — газовая постоянная /-го компонента газовой
смеси.
Согласно закону Дальтона, полное давление смеси рсм химически не реагирующих
между собой газов равно сумме парциальных давлений отдельных газов, входящих в
смесь:
п
Рем = Р\ + Pi + - + Рп = 2 Ph (8.1)
/=1
где п — число компонентов газовой смеси.
Выражение (8.1) называется также законом парциальных давлений.
§ 8.2. Состав газовой смеси
Для проведения термодинамических расчетов, связанных с газовыми смесями,
необходимо знать состав газовой смеси. Состав смеси может быть задан массовыми
gi, объемными г/ или молярными долями компонентов.
Массовая доля /-го компонента газовой смеси представляет собой отношение
массы т1 /-го компонента к массе тсм всей смеси:
92 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
п
g. = mjm^ = mj 2 mh (8.2)
п
Очевидно, что 2g/=l. Например, массовые доли азота, кислорода, аргона
и углекислого газа в сухом воздухе составляют:
£N2 = 0,7553; £o2=0,2314; ^Аг = 0,0128 и gCO2 = 0,0005.
Объемная доля ^-го компонента газовой смеси определяется отношением
парциального объема Vt /-го компонента к объему VctAf занимаемому всей смесью:
(8.3)
(парциальный объем — это объем /-го компонента газовой смеси при температуре и
давлении смеси. Поэтому в соответствии с уравнением состояния К4 = т47?4Тсм/рСм).
Так как р(Усм = ап,7?/Гсм и рСмУ/ = т,/?,ТСм, to ptVCM = Рем Vi и, следовательно,
парциальные объемы газов прямо пропорциональны парциальным давлениям:
(8.4)
Так как VCM 2 pt = Рем 2 V^,то сумма парциальных объемов газов, составляющих
i=i 1
смесь, равна полному объему смеси:
2^=КСМ, (8.5)
<=1
а сумма объемных долей компонентов равна единице: 2 /*,- = 1.
/=1
Молярная доля /-го компонента газовой смеси определяется отношением количества
вещества /-го компонента /г, к количеству вещества смеси псм.
Количество вещества /-го компонента газовой смеси /zt = mt/(j,t, где р,- — молярная
масса /-го компонента газовой смеси. За единицу количества вещества в Международной
системе единиц принят моль. В количестве вещества 1 кмоль содержится столько
молекул (или каких-либо других структурных элементов вещества), сколько атомов
содержится в 12 кг углерода |2С.
Из закона Авогадро следует, что при одинаковых температуре и давлении
молярные объемы (\iv)i всех компонентов газовой смеси равны и не зависят от
химического состава газа, поэтому
п
П= Vi/VCM=ni(\Lv)i/'£ ni(iiv)i= nJnCM, (8.6)
i= 1
где (\iv)i = const. Из равенства видно, что молярные и объемные доли численно
равны. Так как Vi/VCM = Pi/PcM, то состав смеси можно задать также через парциальные
давления отдельных компонентов, что равносильно заданию объемных или молярных
долей.
§ 8.3. Свойства идеальных газовых смесей
Для каждого компонента газовой смеси уравнение состояния идеального газа может
быть записано в следующей форме:
Смеси идеальных газов 93
Суммируя уравнения состояния отдельных компонентов, получим
п п
2дУа,= 2т1-/?,Гси. (8.7)
/= 1 i= 1
С учетом соотношений (8.1) и (8.2) уравнение (8.7) примет вид
п
Рем VCM = тсм Гсм 2 giRi.
i=i
Если принять, что газовая постоянная смеси подчиняется правилу аддитивности
и определяется суммой произведений массовых долей компонентов газовой смеси на
соответствующие газовые постоянные компонентов, то по аналогии с уравнением
состояния отдельного газа связь величин рсм, Усм и Тсм выразится уравнением состояния
идеального газа
Рсм^см=^см^см^см» (8-8)
п
где /?см = gl Л, + g2 R2 + - + g-t Rt + ... + gn Rn = 2 {gt /?,).
t=i
Для каждого из газов в смеси справедливо соотношение (7.2), поэтому формулу
для /?см можно представить в виде
п
/?„= 8314 2 («,/(!,). (89)
1=1
Например, газовая постоянная воздуха
+ 0,2314/31,999+ 0,0128/39,948+ 0,0005/44,010) = 8314- 3,453-10"2 = 287,1 Дж/(кг-К).
Таким образом, для определения газовой постоянной смеси необходимо знать
массовый состав смеси и молярные массы компонентов.
§8.4. Кажущаяся молярная масса
Определяя параметры газовой смеси, удобно пользоваться некоторой условной
величиной, называемой кажущейся (средней) молярной массой газовой смеси.
Понятие кажущейся молярной массы смеси позволяет условно рассматривать
смесь как однородный газ, что существенно упрощает расчеты.
Количество вещества (моль) каждого компонента газовой смеси может быть
определено по формуле
...; /i/ = m,-/|il-; ...; nn = mn/\in. (8.10)
Считая, что смесь обладает свойствами идеального газа с молярной массой \iCMy
по аналогии с соотношениями (8.10) можно записать
пСм = тсм/\1см, (8.11)
где (1см — кажущаяся молярная масса газовой смеси. Так как количество вещества сме-
п п
сипсм= ZjfiiyTo с учетом соотношений (8.10) и (8.11) получимтсм/цсм = 2 (mf/(i(-)H
94 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
следовательно,
п
|*ем =!/(«! 1*1 +*И**+-+«'.11«)= 1/2 в, |1,. (8-12)
Так, например, кажущаяся молярная масса воздуха \iCM= 1/ (£n2/M'N2 +£02/^02 +
+ Яаг/^Аг + Ясо2/м-соо) = 1 / (0,7553/28,013 + 0,2314/31,999 + 0,0128/39,948 + 0,0005/
44,01) =28,964 кг/кмоль.
С учетом (8.12) формула (8.9) примет вид
п
tfCM=8314 2g,/n,= 8314/,xCMl (8.13)
т. е. для определения газовой постоянной смеси достаточно знать кажущуюся
молярную массу смеси.
Из равенств (8.10), (8.11) следует, что молярные массы компонентов и смеси
определяются отношениями
М.1 = /Л|/Л|; \Х2 = пг2/п2; ...; \n = nii/nr9 ...; \in = mn/nn; (8.14)
(Хсм = тсм/«см. (8.15)
п п
Так как тсм— 2 wt , то с учетом (8,14) и (8.15) цсм /гсм = 2 м*/л/ и» следовательно,
1= 1 i=i
M-o^'lM-l + Г2Р2+ - + ri\Li+ - + ГпРп= 2 rf.|Xf.t (8.16)
/=
где г, — объемная (молярная) доля /-го компонента газовой смеси.
§ 8.5. Соотношения между массовыми, объемными
и молярными долями компонентов газовой смеси.
Плотность газовой смеси
Объемные доли компонентов газовой смеси однозначно связаны с массовыми долями.
Эта связь может быть установлена исходя из следующих соображений.
Если учесть соотношения (8.10), (8.11), из формулы (8.2) получим
п
gi= \lini/(\lCMncM)= [iiri/\Lcu= Hi'//2 M-i'/. (8-17)
i=I
С учетом соотношений (8.14) и (8.15) уравнения состояния 1-го компонента и смеси
можно представить в форме
M; (8-18)
rCM. (8.19)
Выше было показано, что объемные и молярные доли численно равны. По
массовому составу смеси можно определить объемный. Так как ri=Vi/VCM = ni/nCM =
= ni/(n\ + n2+... + nn), то с учетом соотношения (8.10) n = (mi/\ii)/(mi/\ii + m2/\i2 +
+ ... + т„/|х„). Поделив числитель и знаменатель правой части этого равенства
на тсм, получим формулу, выражающую соотношение между массовыми и объемными
(молярными) долями в виде
О =(«//!*,)/( Sft/nA
(8.20)
Смеси идеальных газов 95
Так, например, пользуясь формулой (8.20), по заданному массовому составу
воздуха (см. § 8.2) можно определить объемный: rN2=0,7809; гОг=0,2095; гАг==0,0093;
гС02= 0,0003.
Плотность газовой смеси
pCM = mCM/VCM (8.21)
можно определить через объемные и массовые доли компонентов, если их плотности
известны. Так как pi = mt/Vt-, то
п п п
Рем = ^см/^см = 2 Щ = -п— 2 Pi Vi = 2 9i Гц (8.22)
CM " CM
где pt = pCM/(RJcm). Подставляя в формулу (7.21) значения парциальных объемов
У,- = т//р,-, получим
1 1
" ° (8.23)
л • п \~ / п \~
/1/ /\^ 1/ / 1 \^ j_ \ / V ^j_ \
i=\ \ С ' i= 1 ' / \ i•— 1 /
Формулы (8.22) и (8.23) позволяют определить плотность газовой смеси при
заданных давлении и температуре смеси, если известны объемные или массовые доли
компонентов смеси, а также их плотности.
Плотность смеси может быть также определена, если известны парциальные
плотности компонентов смеси. Плотность /-го компонента газовой смеси при его
парциальном давлении и заданной температуре смеси называется парциальной
плотностью. Таким образом, парциальные плотностии компонентов смеси равны
pi=ml/Vcu. (8.24)
Суммируя равенства (8.24). при /, изменяющемся от 1 до /г, получим формулу
П П
для определения плотности газовой смеси 2j pi = -п— 2 mi = тсм/^см * или с учетом
соотношения (8.21) /=1 см •==1
где в соответствии с определением парциальной плотности р/=р//(/?/Тсм), /?t = 8314/(j,t.
При известных объемных или массовых долях парциальные давления компонентов
смеси могут быть определены на основании формул (8.3), (8.4) и (8.20):
^^-, (8.26)
/= 1
где rt и gi — объемная и массовая доли компонента газовой смеси.
§ 8.6. Теплоемкость газовой смеси
Для определения теплоемкости газовой смеси необходимо знать состав смеси, который
может быть задан массовыми, объемными или молярными долями, и теплоемкости
компонентов смеси, которые берутся из таблиц.
Для нагревания смеси массой тсм на 1 К необходимо температуру каждого из
компонентов также повысить на 1 К. При этом на нагревание 1-го компонента смеси
массой mi затрачивается количество теплоты, равное Citrii. Для всей смеси количество
96 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
л
теплоты составит ссм тсм = 2^/Л;, где с,- и ссм— массовые теплоемкости /-го
/=i
компонента и смеси.
Таким образом, если смесь задана массовыми долями, то
л
с«=2с<«/. (8.27)
Л
Так как c'cmVCm= 2 с,■ V,, где с,- и с£м—объемные теплоемкости /-го компонента
i=i
и смеси, a V,- и VCM — приведенные объемы /-го компонента (К/ = т,7?,Тсм/Рсм) и
смеси соответственно, то при задании смеси объемными долями объёмная
теплоемкость смеси может быть определена по формуле
с«=2с>, (8.28)
Так как в соответствии с уравнением состояния, записанным для 1 кмоль газа,
рсм(м<1>)/ = 8314Гсм; рсм(м<у)см = 8314Гсм, то молярный объем /-го компонента газовой
смеси (\iv)i при заданном давлении и температуре смеси равен молярному объему
смеси (\xv)CM. С учетом этого формулу (8.28) можно представить в виде
где с/(\iv)i = (\ic)i и CcM(\iv)CM= (цс)см — молярные теплоемкости /-го компонента и смеси.
С учетом принятых обозначений
л
(цс)см= 2(цс),.г;. (8.29)
Формулы (8.27), (8.28) и (8.29) справедливы лишь для смесей постоянного
состава, т. е. без химических реакций. В формулах для химически реагирующих
газовых смесей должны учитываться затраты теплоты на изменение состава смеси,
который зависит от температуры. Так, например, для химически реагирующей газовой
смеси в случае процесса р = const формула (8.27) примет вид
i= I /= 1
где hi — энтальпия /-го компонента смеси.
§ 8.7. Внутренняя энергия, энтальпия и энтропия газовой смеси
При изобарно-изотермном смешении идеальных газов, имеющих одинаковые
температуру и давление, температура и давление смеси не изменяются. Так как смешение
происходит без подвода теплоты и отсутствует внешняя работа, то внутренняя
энергия при этом также остается неизменной. Следовательно,
Аналогичное соотношение справедливо и для объема (8.5). Газовая смесь с такими
свойствами называется идеальной газовой смесью.
Смеси идеальных газов 97
Аддитивность объема и внутренней энергии смеси идеальных газов означает, что
эта закономерность распространяется и на энтальпию смеси:
Так как (/, = т|и|/тСм и Я/=тЛ/АПСм, то для соответствующих удельных величин
полученные соотношения примут вид
п
cu= 2 g,u,(T);
i=\
п
си= 2 ft АДГ).
/=1
В соответствии со вторым законом термодинамики при обратимом адиабатном
смешении отдельных компонентов энтропия остается постоянной и, следовательно,
энтропия газовой смеси равна сумме энтропии отдельных газов, составляющих
смесь.
В обратимом адиабатном процессе смешения сохраняется механическое равновесие
и процесс протекает без затраты работы, т. е. при постоянных внутренней энергии
и температуре системы. При этом парциальные давления компонентов смеси до
смешения должны быть равны соответствующим парциальным давлениям после
смешения и каждый из компонентов до смешения должен занимать объем, равный объему
смеси. Такой, в действительности неосуществимый, обратимый процесс можно себе
представить используя понятие полупроницаемой перегородки, пропускающей только
определенный компонент газовой смеси и задерживающей все остальные.
Так как рассматриваемый процесс обратим, энтропия такой идеальной газовой
смеси определяется суммой энтропии компонентов смеси, вычисленных для условий,
когда каждый из компонентов занимает объем, равный объему смеси при температуре
смеси. Тогда энтропия компонента газовой смеси, находящегося в смеси под своим
парциальным давлением, определится по формуле
Si = cpi\n(T/T0) — Ri\n(p/po) + siO. (8.30)
Это соотношение может быть получено путем интегрирования уравнения (2.43) с
учетом уравнения состояния идеального газа. Здесь индексом 0 отмечено некоторое
исходное значение энтропии (при Го и р0), соответствующее началу отсчета.
Так как в 1 кг смеси содержится gi кг данного компонента, то
п
*см = 2 g,[cpi In (Г/Го) - R, In (Pt/Po) + s,0]; (8.31)
/=l
энтропия идеальной газовой смеси равна сумме энтропии компонентов, взятых при
парциальных давлениях компонентов и температуре смеси.
С помощью формулы (8.31) можно определить приращение энтропии в каком-либо
процессе, например в процессе смешения компонентов газовой смеси, протекающем
при постоянном давлении: р = const. Если перед смешением все компоненты находятся
при равных давлениях р и имеют одинаковую температуру Г, то сумма энтропии
отдельных газов до смешения
п п
2 s, = 2 g,[ cpi 1гГ(Г/Г0) - /?,- In (p/p0) + s,0]. (8.32)
i== 1 /= I
4 За к. 584
98 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Значение энтропии системы после смешения (sCM) может быть определено по
формуле (8.31). Следовательно, приращение энтропии в рассматриваемом необратимом
процессе определится разностью:
п п п
Д*с« = *с« - 2 s, = 2 g,[ ср In (Г/Го) - Ri In (P,/Po) + *ю] - S ft [cpi In (Г/Го) -
/= I /= 1 /= 1
п п
- /?, In (р/р0) + si0] = 2 £//?,[ In (p/p0) - In (p,//?<>)] = 2 g/#/ In (p/p,),
/= 1 i= I
где p — давление компонентов до смешения; р/ — парциальное давление /-го компонента
после смешения. »
В рассмотренном выше обратимом процессе компоненты газовой смеси перед
смешением имеют давления, равные соответствующим парциальным давлениям после
смешения, и для каждого из компонентов p = pit a AsCM = 0. В необратимом процессе,
протекающем при р = рсм = const, давления Pi<p, a AsCM>0. С учетом соотношений
gi = yan/\icM и Ri = S3\4/\ii приращение энтропии смеси
п
A5CM=~/?CMS r.-ln/v (8.33)
/=i
Это приращение называется энтропией смешения газовой смеси и
характеризует меру необратимости адиабатного процесса получения идеальной газовой
смеси из чистых компонентов. Так как объемные доли о<1 и 1пг/<0, энтропия
смешения всегда положительна. Реальный процесс смешения газов всегда необратим.
Величина AsCM не зависит ни от давления, ни от температуры и определяется только
составом газовой смеси. При изменении физического состояния газовой смеси состав
смеси не изменяется и величина AsCM остается постоянной. Следовательно, при
определении разности энтропии в процессах изменения физического состояния газовой
смеси величина AsCM сокращается.
Для каждой газовой смеси AsCM имеет определенное значение. Так, например,
энтропия смешения сухого воздуха (см. § 8.3, 8.5) AsCM= — #cM(/'N2lnrN2+''o2ln/'o2+
+ гАг1пгАг+Гсо21пгСО2) = 287,1(0,1931 +0,3275+.0,0435+ 0,0024)= 162,6 Дж/(кг-К).
Вопросы!• Как вычислить парциальное давление /-го компонента газовой смеси, если известны
масса и газовая постоянная этого компонента, а также температура и объем смеси?
2. Каковы соотношения между массовыми, объемными и молярными долями компонентов
газовой смеси?
3. Что называется кажущейся молярной массой газовой смеси?
4. Как вычисляется газовая постоянная смеси газов?
Глава 9
ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
§9.1. Задачи изучения термодинамических процессов
Исследование термодинамических процессов идеальных газов ставит своей целью
разработать методы расчёта параметров состояния системы в процессе, а также
методы определения теплообмена q системы с внешней средой и.количества работы
/, свершаемой ее рабочим телом. В этих целях на основе уравнения первого
закона термодинамики, записанного для условий рассматриваемого процесса,
определяется уравнение самого процесса, характеризующее изменение состояния рабочего
Основные термодинамические процессы
99
тела. На основе уравнения процесса можно получить функциональные зависимости
pz=f(p)\ s = f(T) и т. д. и выявить особенности расходования подведенной к рабочему
телу теплоты на изменение внутренней энергии и совершение рабочим телом внешней
работы.
Изменение внутренней энергии рабочего тела определяется для всех
термодинамических процессов одинаково в соответствии с выражением (7.9), если известна
удельная теплоемкость cv. Внешняя / и располагаемая /о удельные работы определяются
по формулам (2.10) и (2.42), также общим для всех термодинамических процессов.
Подсчитанные таким образом изменение внутренней энергии и совершенная
внешняя работа дают возможность по уравнению (2.29) первого закона термодинамики
определить подведенное к рабочему телу или отведенное от него количество теплоты.
Эта же задача может быть решена, если известна теплоемкость рабочего тела в
исследуемом, процессе.
Характер распределения подведенной энергии в виде теплоты в термодинамическом
процессе можно изобразить схемой (рис. 9.1, б) в соответствии с тремя частями
уравнения первого закона термодинамики. На схеме подведенное или отведенное от
рабочего тела количество теплоты изображено кружочком, изменение внутренней
энергии — треугольником, внешняя работа, совершаемая рабочим телом,—квадратом.
Стрелки (рис. 9.1, б), связывающие эти три составные части уравнения первого
закона термодинамики, показывают лишь направления передачи энергии в
рассматриваемом процессе и не затрагивают количественной стороны процесса.
а)
К—.
*#/
7"
А
^£v
-Л
S/
JN
п,
т1
•у
г
к
St
В Ctr
t
j
Si
ъ
s
Рис. 9.1. Изохорный процесс: а—на ур-диаграмме; б —схема
распределения теплоты; в — на sT — диаграмме; г — графическое
определение изменения удельной внутренней энергии по sT-диаграмме
100 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Выполнение условий термодинамического равновесия в каждый данный момент
времени в течение всего процесса позволяет рассматривать термодинамические
процессы в качестве равновесных и изображать их в виде кривых на vp- или
sT-диаграммах, причем координаты и, р удобны при определении работы, совершаемой
рабочим телом в процессе, а координаты s, T дают возможность графически
определить подведенное или отведенное от рабочего тела в процессе количество
теплоты.
В общем случае любые два термодинамических параметра из трех в процессе
могут изменяться произвольно (независимо). Однако изучение работы тепловых машин
показывает, что наибольший интерес для практики представляют некоторые частные
случаи, к которым относятся рассмотренные ниже процессы.
§ 9.2. Изохорный процесс
В изохорном процессе выполняется условие du = 0, или v = const.
Такой процесс совершается рабочим телом (газом), находящимся в цилиндре
(рис. 9.1, а), при неподвижном поршне, если к рабочему телу подводится теплота от
источника теплоты / или отводится теплота к холодильнику //.
Уравнение изохорного процесса может быть получено из уравнения
состояния идеального газа (1.6), если принять v = const. В этом случае
р/Г = /?/и = const, или рч/р\ = Тч1Ти (9.1)
т. & в изохорном процессе давление газа пропорционально температуре.
Удельная работа газа определяется выражением (2.10). Так как в
изохорном процессе du = 0, то и d/ = 0, т. е. внешняя работа не совершается.
Располагаемая удельная работа (например, процесса 1-3) (рис. 9.1, а)
определяется выражением (2.42), интегрируя которое получим
Рз
lo=-\vdp=v(pl-p3). (9.2)
Р\
В координатах vy р располагаемая удельная работа изохорного процесса численно
равна площади V133' (рис. 9.1, а).
Уравнение первого закона термодинамики (2.29) с учетом выражения (7.9) для
изохорного процесса получает вид
dq = du = cvdT; (9.3)
в изохорном процессе все количество теплоты, подводимое или отводимое от
рабочего тела, расходуется на изменение внутренней энергии (рис. 9.1, б).
Удельное количество теплоты, подводимое к рабочему телу в процессе
1-2 при Cu = const, определяется интегрированием выражения (9.3):
q = j dw = и2 - их = cv (T2 - Г,). (9.4)
71,
Если теплоемкость в процессе изменяется, то
Основные термодинамические процессы *'■' 101
где cv
средняя удельная изохорная теплоемкость в интервале температур от
Т\ до Г*.
Изменение удельной энтропии в изохорном процессе можно получить
интегрированием уравнения (7.10):
Asv = s2 — sx= $ cvdT/T.
Если же с0 = const, то
ksv = cv\n(T2/Tl). (9.5)
Полученное соотношение показывает, что изохорный процесс, изображенный в
координатах s, T (рис. 9.1, в), являясь логарифмической кривой, протекает так,
что при увеличении энтропии увеличивается и температура.
Изображение термодинамического процесса в координатах s, T имеет ряд удобств.
Элементарная площадь T\ds (на рис. 9.1, в), построенная на абсциссе ds при
температуре Т\, в масштабе показывает элементарный теплообмен с внешней средой.
Следовательно, площадь под процессом 1-2 или 1-3 на sT-диаграмме численно равна
подведенному (при увеличении s) или отведенному (при уменьшении s) количеству
теплоты. В соответствии с выражением (9.4) эта же площадь в данном процессе
v = const показывает также изменение внутренней энергии рабочего тела. Если в точке
/ изохорного процесса (рис. 9.1, в) провести касательную 1А, то подкасательная
АВ в определенном масштабе для этого процесса представляет собой величину cv.
Действительно, отложив от точки / отрезок 1С, соответствующий элементарному
изменению температуры d7\ и проведя горизонталь CD до пересечения с касательной
1А, получим AD/C, подобный Л А1В.
Из подобия треугольников имеем AB/DC= IB/1С. Так как 1В = ТУ lC — dT,
DC=dsy то ABdT=Tds=dq. Сопоставление полученного соотношения с выражением
(9.3) показывает, что AB — cVi что и требовалось доказать.
Изохорные процессы газов, имеющих большую теплоемкость (например,
трехатомных по сравнению с двухатомными), изображаются на зГ-диаграмме более
пологими кривыми, определяемыми соотношением (9.5).
Так как во всех термодинамических процессах идеальных газов, протекающих
в одном и том же интервале температур, внутренняя энергия изменяется на одно и то же
значение, то
площадь под изохорным процессом на si -диаграмме показывает в интервале температур
Т2—Т\ изменение внутренней энергии в любом другом термодинамическом процессе,
протекающем в этом же интервале температур.
Так, например, если в интервале температур от Т\ до Т2 протекает произвольный
обратимый процесс, показанный кривой 1-2 на рис. 9.1, г, то для определения изменения
внутренней энергии Д^|.2 в этом процессе достаточно провести кривую изохорного
процесса 2-3 того же рабочего тела и в том же интервале температур и измерить
под этим процессом площадь (на рис. 9.1, г заштрихована). В выбранном процессе
1-2 внутренняя энергия уменьшается, так как температура снижается.
* В дальнейшем формулы, в которые входят удельные или объемные теплоемкости,
не приводятся, так как они идентичны написанным выше. Далее везде в формулах теплоемкость
принята постоянной.
102
РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
§ 9.3. Изобарный процесс
В изобарном процессе выполняется условие dp = 0, или р = const.
Такой термодинамический процесс может протекать в цилиндре, поршень которого
перемещается без трения так, что давление в цилиндре равно постоянному давлению
окружающей среды, действующему на поршень с внешней стороны (рис. 9.2, а).
Уравнение изобарного процесса может быть получено из уравнения
состояния идеального газа (1.6) при р = const. В этом случае
v/T = R/p — const, или V2/v\ = T2/T\, (9.6)
т. е. в изобарном процессе объем газа пропорционален абсолютной температуре.
Количество работы в изобарном процессе определяется интегрированием
выражения (2.10) при p = const:
(9.7)
На ур-диаграмме работа газа изображается в виде площади V122' под процессом
1-2 (рис. 9.2, а), причем /:>0, если v2>V\.
Так как pv\ — RT\ и pv2 = RT2, то
Г.). (9.8)
Следовательно, работа газа в изобарном процессе положительна только в том
случае, если температура газа увеличивается.
L —
1
7
v>
Asir
19
AsP
7
1
s
T< —
Рис. 9.2. Изобарный процесс: а — на ир-диаграмме; б — на яГ-диаграмме; в —
графическое определение изменения удельной энтальпии по sT—диаграмме; г —
графическое определение работы по яГ-диаграмме; д — схема распределения удельной
теплоты
Основные термодинамические процессы 103
Положив в формуле (9.8) разность температур Т2—Т\ равной одному градусу,
найдем 1—R.
Удельная газовая постоянная представляет собой работу 1 кг газа в изобарном
проЦессе при увеличении температуры на один градус.
Располагаемая работа /0, определяемая выражением (2.42), в изобарном
процессе (dp = O) равна нулю (/0р=0).
При известном значении удельной теплоемкости изобарного процесса ср
удельное количество теплоты qt подводимое к рабочему телу (или
отводимо), определяется уравнением (7.12). При dp = O
Tds = dq = cpdT, (9.9)
откуда
Сравнение выражения (3.9) с выражением (7.11) показывает, что в изобарном
процессе
dq = dh (9.10)
и, следовательно, при ср= const
q=zCp(T2—T\) = h2 — h\. (9.11)
Из соотношения (9.11) видно, что теплота, подведенная к рабочему телу в изобарном
процессе, расходуется на увеличение его энтальпии.
В изобарном процессе меняется температура рабочего тела и, следовательно, его
внутренняя энергия. Поэтому
на совершение внешней работы расходуется лишь часть теплоты, подведенной к
рабочему телу извне.
Преобразование энергии при изобарном расширении газа иллюстрируется схемой
на рис. 9.2, д.
Для определения доли теплоты, затрачиваемой в изобарном процессе на внешнюю
работу, следует все члены уравнения (2.29) разделить на dq:
. du . d/
dq dq*
откуда с учетом выражения (7.31)
— = 1 ILZ== \ 1 _- 1 1__ 1 L
aq dq ср dT cp k'
или
du _ 1
dq ~" k '
Если принять k =1,4, что соответствует двухатомным газам, то d//d^ = 0,285 и
Следовательно, 28,5 % всего подведенного к рабочему телу количества теплоты
в изобарном процессе двухатомного газа расходуется на совершение внешней работы
и 71,5 % — на изменение внутренней энергии.
Изменение энтропии в изобарном процессе можно определить из уравнения
(7.12). При p = const ds — CpdT/T или после интегрирования
Asp=s2 — si = cpln(T2/Ti). (9.12)
104 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Таким образом, изобара на sT-диаграмме является некоторой логарифмической
кривой.
Если Т2>Т\У то в соответствии с выражением (9.12) Asp>0, т. е. изобарный
процесс на sT-диаграмме (рис. 9.2, б) протекает так, что при увеличении энтропии
увеличивается и температура. Если провести аналогичные рассуждения, проведенные
применительно к изохорному процессу (рис. 9.2, б), то нетрудно доказать, что
подкасательная к кривой изобарного процесса равна ср. Так как cp>cVy то
изобарный процесс на sT-диаграмме протекает более полого, чем изохорный процесс
того же газа (рис. 9.2, г).
Из рис. 9.2, б с учетом уравнения (9.11) следует, что площадь под изобарным
процессом численно равна изменению энтальпии. Так как изменение энтальпии
рабочего тела определяется изменением только его температуры, то в любых
термодинамических процессах, протекающих в одном и том же интервале температур, энтальпия
изменяется на одно и то же значение. Поэтому
площадь под изобарным процессом на si-диаграмме в интервале температур Т2—Т\
равна изменению энтальпии в любом другом термодинамическом процессе,
протекающем в этом же интервале температур.
Следовательно, для определения изменения энтальпии в произвольном процессе
1-2 (рис. 9.2, в) необходимо этот процесс изобразить в sT-диаграмме, определить
Т2 и Ти выбрать в этом интервале любой изобарный процесс (например, 1-3) и тогда
площадь под процессом 1-3 (на рис. 9.2, в заштрихована) покажет изменение
энтальпии в процессе 1-2.
Так как при изобарном расширении газа Т2>Ти то Д/г|2>0.
§9.4. Изотермный процесс
При изотермном процессе выполняются условия dr = O, или Theorist.
Такой термодинамический процесс протекает, например, в цилиндре поршневой
машины, когда по мере подвода теплоты и рабочему телу поршень машины
перемещается, увеличивая объем настолько, что температура остается неизменной.
Уравнение изотермного процесса может быть получено из уравнения
(1.6), если принять Т=const. В этом случае
pv = RT= const. (9.13)
Следовательно, на ир-диаграмме изотерма является равнобокой гиперболой (рис.
9.3, а). Из уравнения изотермы (9.13) следует
P2/p\ = v\/v2y (9.14)
т. е. при постоянной температуре давление и объем рабочего тела обратно
пропорциональны. Отношение (9.14) является следствием закона Бойля — Мариотта.
Соотношения (7.9) и (7.11) показывают, что
изотермный процесс идеального газа одновременно является процессом при постоянной
внутренней энергии (du = 0) и при постоянной энтальпии (d/г = 0).
Применительно к изотермному процессу уравнение (2.29) получает вид d^ = d/.
Из данного выражения видно, что
все сообщенное газу количество теплоты в изотермном процессе затрачивается на
совершение внешней работы (рис. 9.3, в).
Работу при изотермном процессе определяют по формуле
v2 l v2
/= ( pdv= \ RT(dv/v) = RT\n(v2/vl).
Основные термодинамические процессы
105
Следовательно,
Рис. 9.3. Изотермный процесс:
а — на ир-ди а грамме; б — на sT-
диаграмме; в — схема
распределения удельной теплоты
(9.15)
Располагаемая работа /0 изотермного процесса на i/p-диаграмме численно
равна площади V122' (рис. 9.3, а), поэтому
/о = р 11; i + / — p2v2y
откуда с учетом уравнения (9.13) lo=l=RT\n(p\/p2). На зГ-диаграмме изотермный
процесс изображается горизонтальной прямой (Т = const). Площадь под процессом
(рис. 9.3, б) численно равна теплообмену рабочего тела с внешней
средой и совершенной в процессе работы:
si). (9.16)
Изменение энтропии в изотермном процессе определяется отношением
ds=dq/T
и тогда в соответствии с выражениями (9.15)
&sT = s2 — Sx = R\n(v2/v{) = R\n(px/p2). (9.17)
Полученное соотношение показывает, что расстояние между изобарами p2 = const
и pi = const, так же как и между изохорами v2 = const и yi = const, по оси абсцисс
106 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
на sT-диаграмме не зависит от температуры. Следовательно, как изобары, так и
изохоры в координатах s, T эквидистантны между собой. Расстояние между
эквидистантными изобарами или эквидистантными изохорами зависит лишь от
отношения давлений р\/р2 или объемов v2/v\. По мере увеличения давлений изобары
приближаются к оси ординат, так как &ST<z0 при р2>р\. Изохоры по мере
увеличения объема, наоборот, удаляются от оси ординат, так как Д5т->0 при vt>v\.
Удельная теплоемкость изотермного процесса может быть определена из общего
соотношения c — dq/dT. Так как при изотермном процессе dq=£Oy a d7n = 0, то с== ± оо.
Следовательно, определить количество теплоты, подведенное к рабочему телу в
изотермном процессе, с помощью удельной теплоемкости невозможно.
§ 9.5. Адиабатный процесс
В адиабатном процессе изменение состояния рабочего тела происходит без теплообмена
с внешней средой, т. е. при условиях d<7 = 0 и q = 0.
Следует при этом отметить, что условие q — О для адиабатного процесса является
необходимым, но не достаточным. Действительно, в начале сжатия га^а в цилиндре
дизеля температура стенок цилиндра выше температуры рабочего тела, в связи с чем
теплота передается от стенок цилиндра рабочему телу. По мере сжатия газа температура
его повышается настолько, что в конце сжатия стенки цилиндра оказываются холоднее
газа, в связи с чем тепловой поток меняет свое направление: теплота передается
от рабочего тела стенкам цилиндра дизеля. В частном случае количество теплоты,
полученное газом от стенок цилиндра в начале сжатия, может оказаться равным
количеству теплоты, отданному газом стенкам цилиндра в конце сжатия.
Следовательно, суммарный теплообмен рабочего тела с внешней средой окажется равным
нулю (<7 = 0), хотя процесс сжатия был явно не адиабатным.
Таким образом, необходимым и достаточным для адиабатного процесса является
условие dq = O.
Уравнение адиабатного процесса может быть получено из уравнения
(2.29) при d<7 = 0. Если использовать соотношение (7.9), то уравнение (2.29) можно
представить в виде \
cvdT + pdv = 0, (9.18)
или с учетом выражения (7.34)
RdT+(k—\)pdv = 0. (9.19)
Дифференцирование уравнения состояния идеального газа (7.9) дает выражение
(9.20)
подставив которое в уравнение (9.19) получим vdp-\-kpdv = 0. После разделения
переменных
i£_ + *il=0 (9.21)
р v
и интегрирования при k = const имеем \np-\-k\nv = const, откуда
pvk = const. (9.22)
Полученное уравнение является уравнением адиабаты идеального газа при постоянных
теплоемкостях (cv= const и ср=const).
Сопоставление уравнений (9.13) и (9.22) показывает, что на i/p-диаграмме
адиабата расположена круче изотермы (k>\) и является неравнобокой гиперболой
(рис. 9.4, а).
Основные термрди нам и ческие, процессы
107
^J pir=consi 1
V2 У
i)
Рис. 9.4. Адиабатный процесс: а — на ур-диаграмме; б — на sT-
диаграмме; в — схема распределения удельной теплоты
Из уравнения (9.22) следует, то
P2/pi=(vi/v2)k. (9.23)
С помощью уравнений состояния, написанных для состояний 1 и 2 адиабатного
процесса (рис. 9.4, а),
/?Г1 и p2v2 = RT2 (9.24)
из выражения (9.23) можно получить соотношения между температурами и удельными
объемами
T2/Tl=(vl/v2)k-1
или между температурами и давлениями
(9.25)
(9.26)
При dq = O уравнение (2.29) первого начала термодинамики получит вид
d/=— du. (9.27)
108 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Работа в адиабатном процессе совершается только за счет уменьшения внутренней
энергии (рис. 9.4, в).
Проинтегрировав выражение (9.27) при co = const, имеем
"2
/ = - \ du = - (и2 - иг) = их - и2 = cv(T{ - T2). (9.28)
«I
После подстановки (7.34) в (9.28) приходим к выражению
7-2), (9.29)
или с учетом уравнений (9.24)
l = [\/(k-\)](p{v{-p2v2). (9.30)
Вынесем p\V\ за скобки, тогда
/ = |р|1м/(Л-1)](1-7УГ|), (9.31)
а с учетом соотношений (9.22) и (9.23)
/ = [Piv{/(k - 1)] [ 1 - (v{/v2)k-1], (9.32)
или
1=[р «1/(л-1)][1-(р2/р|)(*"|)/А]- (9-33)
Располагаемая удельная работа /о адиабатного процесса на ур-диаг-
рамме численно равна площадке V122' (рис. 9.4, а), поэтому
Принимая во внимание формулу (9.30), располагаемую удельную работу можно
определить по соотношению
lo = kl. (9.34)
Так как в адиабатном процессе d^ = 0, то энтропия рабочего тела в обратимом
процессе не изменяется (ds = 0 и s = const).
На sT-ди а грамме адиабатный процесс изображается вертикальной линией
(рис. 9.4, б), причем падение температуры происходит при расширении рабочего тела,
а увеличение температуры — при его сжатии.
Выражение с = dq/aT показывает, что теплоемкость адиабатного
процесса равна нулю. Об этом же свидетельствует адиабатный процесс, например
1-3, изображенный на sT-диаграмме (рис. 9.4, б), так как подкасательная к нему,
дающая представление о теплоемкости, также равна нулю. Для определения
изменений внутренней энергии и энтальпии в адиабатном процессе, например 1-3 на
рис. 9.4, б, достаточно в том же диапазоне изменения температуры Г3—Т\ построить
изохору и изобару и измерить под ними площади (на рис. 9.4, б заштрихованы).
Постоянство показателя адиабаты, принятое выше, во многих случаях
оказывается весьма приближенным. Оно справедливо лишь в том случае, когда диапазон
изменения температуры рабочего поля в адиабатном процессе таков, что зависимостью
теплоемкостей cv и ср от температуры можно пренебречь. В действительности
показатель адиабаты, определяемый выражением (7.31), зависит от температуры. Эта
зависимость в некоторых случаях может быть принята линейной cv = av + bT и тогда
уравнение (9.18) получает вид
или с учетом уравнения (9.20)
Основные термодинамические процессы 109
— '
(av + bT)d(pv)
Разделим члены уравнения на произведение pvy тогда
откуда после интегрирования
av\n(pv)-{-bT-\- R\nv = const
или
aV а« + ^ ЬТ А
р vv e° = const.
Введем обозначение ap=av + R, тогда
р\аре*т= COnst. (9.35)
Полученное таким образом уравнение адиабаты при переменных теплоемкостях
включает три параметра состояния рабочего тела: р, v и Т.
При постоянных теплоемкостях уравнение (9.35) преобразуется к виду (9.22).
Действительно, в этом случае коэффициенты соответственно равны av = cv\ b = 0;
ар=ср, поэтому после извлечения корня с„-й степени уравнение получает вид (9.22).
Удельная работа, совершаемая рабочим телом в адиабатном процессе при
переменных теплоемкостях, может быть подсчитана по соотношениям d/ = pcb= —dw =
= —cvdT= —(av + bT)dT. Интегрирование в пределах изменения температуры от Т\
до Гг приводит к выражению
1=с.
Т\ТХ - Т2) = К + (Ь/2) (Г, + Т2)] (Г, - Т2). (9.36)
Правая часть этого равенства представляет собой изменение внутренней энергии
рабочего тела без теплообмена с внешней средой, что выражает суть адиабатного
процесса:
Когда температура процесса изменяется от нуля до нескольких сотен градусов,
допустимо принимать cv^av и тогда выражение (9.36) совпадает с (9.28).
§ 9.6. Политропный процесс*
Свое название «политропный» процесс получил от сочетания греческих слов: «поли» —
много, «тропос» — путь.
Если с — удельная теплоемкость политропного процесса, то dq = cdT и уравнение
(2.29) преобразуется к виду
cdT=cvdT + pdvy (9.37)
или
(с — cv)dT = pdv.
* Впервые в отечественной литературе по термодинамике политропный процесс был
рассмотрен в учебнике Ф. Е. Орлова «Термодинамика» (М., 1890).
ПО РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Из уравнения (9.20) следует, что dT = (pdv-\-vdp)/R. Поэтому
(с — сУ) (pdv -f vdp)/R — pdv = 0,
или после некоторых преобразований
(с — cp)pdv + (с — cv)vdp = 0.
Разделив оба члена полученного уравнения на выражение (c — cv)pv и
проинтегрировав
[(с — Ср)/(с — cv)]\n u-f-lnp = const,
получим уравнение политропы в виде
„„<'"'''<'-''>« const,
или
pvn = const, (9.38)
где п — показатель политропы, определяемый отношением
n = (c-cp)/(c-cv). (9.39)
Выражение (9.39) свидетельствует о том, что показатель политропы п может
иметь любое значение в пределах от —оо до +оо. Действительно,
п-*~ —оо при с-*сУ, если cp>ocv\
п-> +°° при £-►£„, если c<cv<Zcp.
Уравнение (9.38) показывает, что политропным является такой
термодинамический процесс изменения параметров состояния рабочего тела, в котором в течение всего
процесса показатель политропы п остается постоянным.
Политропный процесс является обобщающим по отношению к уже рассмотренным
четырем процессам (изохронному, изобарному, изотермному и адиабатному).
Действительно, уравнение (9.38) становится уравнением изохоры (v = const), если в
уравнении pl/ny = const принять п— ±оо. При /г = 0 уравнение (9.38) есть уравнение
изобары (р = const); при п—\ — изотермы и при /z = /j = const — адиабаты. Интересен
также политропный процесс при п= — 1, представляющий собой в координатах v, p
прямую, исходящую из начала координат. Действительно, при п= — 1 уравнение
(9.38) получает вид pv~l = const, откуда р = v-const.
Сравнивая уравнения (9.22) и (9.38), видим, что в соответствии с
соотношениями (9.23), (9.25) и (9.26) для политропного процесса (при k = n) можно
записать
sGRGf^er1-
Для определения работы политропного процесса по аналогии
выражениями (9.29), (9.30), (9.32) и (9.33) могут быть записаны формулы:
(9,42)
Основные термодинамические процессы
111
/ = •
/'л(я~1)/я1
U/ J
(9.43)
(9.44)
Располагаемая удельная работа
ется по формуле, аналогичной (9.34), так что
/0 политропного процесса
определя(9.45)
Удельная теплоемкость
шению [см. (9.39)]
политропного процесса определяется по
соотно(9.46)
показывающему, что удельная теплоемкость идеального газа в каждом
термодинамическом процессе имеет свое значение.
С помощью формулы (9.46) можно проследить за изменением удельной
теплоемкости рабочего тела в политропном процессе в зависимости от показателя политропы п.
График на рис. 9.5 показывает, что удельная теплоемкость с в диапазоне изменения
показателя политропы 1<п</г оказывается отрицательной величиной. Это
свидетельствует о том, что
в таких процессах значения dq и dT имеют различные алгебраические знаки, т. е. при
подводе теплоты к рабочему телу температура последнего снижается, а при отводе
теплоты — повышается.
Подставив в формулу (9.46) значения /г, соответствующие частным
термодинамическим процессам, получим значения удельных теплоемкостей этих процессов:
Процесс
Изохорный
Изобарный
Изотермный
п
±оо
0
1
с
Cv
ср
оо
Процесс
Адиабатный
Политропный
Прямолинейный (в
координатах у, р)
п
k
п
— 1
с
0
cv(n-k)/(n-\)
cv(k+[)/2
Если удельная теплоемкость с политропного процесса известна, то количество
теплоты, подведенное к рабочему телу в этом процессе,
dq = cdT. (9.47)
Подставив в это выражение соотношения (9.46) и проинтегрировав, получим
q = cv-j^-(T2--Tl). (9.48)
Вся теплота, подведенная к рабочему телу в политропном процессе, в общем
случае расходуется как на изменение внутренней энергии, так и на свершение внешней
работы.
Долю теплоты, расходуемой на изменение удельной внутренней энергии рабочего
тела, можно представить в виде отношения
или с учетом соотношения (9.46)
(9.49)
112
РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Так как du — ydq, то после интегрирования
(9.50)
Подстановка в выражение (9.50) формул (9.48) и (9.49) приводит его, как и следовало
ожидать, к виду (9.4).
Изменение удельной энтальпии рабочего тела в политропном процессе
при cp = const в интервале температур от Т\ до Т2 определяется по формуле
Tl), (9.51)
справедливой для всех термодинамических процессов.
Доля теплоты, идущей на свершение внешней работы,
t|> = d//d<7= \ — du/dq= 1 — <р= 1 — (п— \)/(п — k).
Следовательно,
(9.52)
Подставляя в формулы (9.49) и (9.52) значения показателя политропы /г, можно
определять доли теплоты, расходуемой на изменение внутренней энергии и свершение
внешней работы, в рассмотренных выше термодинамических процессах:
Процесс
Изохорный
Изобарный
Изотермный
Ф
1
\/k
0
ч>
0
1 — 1/*
1
Процесс
Адиабатный
Политропный
Прямоинтегральный
(в координатах и, р)
Ф
(n-\)/(n-k)
2/(*+1)
(\-k)/(n-k)
(*_!)/(* + !)
Таким образом, при /i = const и fc = const политропному процессу может быть
дано и другое определение:
политропным процессом является такой термодинамический процесс изменения
параметров состояния рабочего тела, при котором в течение всего процесса во
внутреннюю энергию превращается одна и та же доля подведенной от горячего источника
теплоты и имеется вполне определенный закон распределения энергии не только для
конечного процесса, но и для каждого бесконечно малого участка его.
Если же яФconst и пФconst, т. е. cv = f(T)y то в политропном процессе ц>Фconst и
Ч1"Фconst. Следовательно, первое определение политропы, связанное с требованием п =
= const, в уравнении (9.38) является более общим.
Значение показателя политропы п определяет расположение и характер линии
политропного процесса на ур-диаграмме (рис. 9.6, а). Если выбрать некоторую
произвольную точку А и провести через нее все рассмотренные выше кривые частных
термодинамических процессов как в сторону расширения, так и в сторону сжатия, то все
поле построенной таким образом диаграммы разделится на восемь областей, каждая
из которых объединяет все располагающиеся в ее пределах термодинамические
процессы общностью определенных свойств. Так, все процессы, исходящие из точки А и
располагающиеся в областях V—V7//, имеют отрицательную работу, так как
сопровождаются сжатием рабочего тела. Наоборот, процессы, начинающиеся в точке А
и расположенные в областях / —/V, сопровождаются расширением рабочего тела и
поэтому совершают положительную работу. Процессы, начинающиеся в точке А и
располагающиеся в областях / — /// и VIII (заштрихованные), протекают с подводом
теплоты извне, а в областях IV—VII — с отводом теплоты. Изотерма (п=\) делит
все поле координатной плоскости на области, в пределах которых протекают
термодинамические процессы с повышением (области VII, VIII, I w II) и с понижением
температуры рабочего тела (области ///—VI). Особый интерес представляет область ///,
Основные термодинамические процессы
113
в пределах которой протекают процессы с подводом теплоты и с падением
температуры рабочего тела. В пределах области VI температура рабочего тела в процессе
растет, а теплота отводится.
Изменение удельной энтропии в политропном процессе можно
определить по формулам (7.9), (7.12) и (7.14), проинтегрировав которые получим:
(9.53)
Рис. 9.5. Зависимость удельной
теплоемкости от показателя политропы
Рис. 9.6. Области возможных политроп-
ных процессов: а — на ур-диаграмме; б —
на sT-диаграмме
с i
4/4
г
5)
с=0 v= const
const
c-d
Рис. 9.7. К определению теплообмена
рабочего тела с внешней средой,
изменений удельной внутренней
энергии, энтальпии и совершаемой
работы в политропном процессе по
sr-диаграмме
114
РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
52 — 5, = ср1 п(Г2/Г,) — /?ln(p2/pi);
(9.54).
(9.55)
Подставив выражение (9.46) в соотношение ds = dq/T = cdT/Ty получим
. п — к dT
A c
интегрирование которого дает уравнение политропного процесса в координатах s, T
п к , Т2
As = s2 — 5,
^ п- 1
или с учетом выражений (9.39) и (9.40) — в ином виде
А
s2 — s, = cv (п — k) In -J- = --f (n — k) In -i.
v2 n p,
(9.56)
(9.57)
Известный показатель политропы п дает возможность с помощью формулы (9.56)
построить на яГ-диаграмме соответствующий политропный процесс. На рис. 9.6, б
показаны те же термодинамические процессы, что и на рис. 9.6, а с одинаковой
нумерацией областей. Полученная, таким образом, диаграмма в ^^-координатах показывает,
что все термодинамические процессы, начинающиеся в точке Ау с увеличением энтропии
протекают с подводом теплоты извне. В областях, расположенных левее адиабаты,
процессы, начинающиеся в точке Л, протекают с уменьшением энтропии, т. е. с отводом
теплоты от рабочего тела.
SB SA S, 5
tgir
Рис. 9.8. Определение показателя по-
.литропы: а—по точкам и
площадям ур-диаграммы; б — по углу
наклона кривой процесса в
логарифмических координатах; в — по
sT -диаграмме при л>1; г — по
'яГ-диаграмме при я>0; д — по
sT-диаграмме при п<С0
т\
i i ;
Основные термодинамические процессы 115
На рис. 9.6, б заштрихованы области, в пределах которых либо одновременно
увеличивается температура (dT>0) и подводится теплота (d<7>0) (области VIII, I и
//), либо одновременно понижается температура (с1Г<0) и отводится теплота (d<7<0)
(области IV—VI). Соотношение (9.47) показывает, что теплоемкости
термодинамических процессов, располагающихся в областях VIII, I, //, IV, V и VI, положительны,
в областях /// и VII — отрицательны.
Если политропный процесс 1-2 (рис. 9.7) с любым показателем политропы
изображен на sT-диаграмме, то по ней могут быть определены значения Дм, ДА, qy l и /о.
Изменение удельной внутренней энергии Дм численно равно площади под кривой
изохорного процесса, проходящего в том же интервале температур, что и политропный
процесс 1-2. При выбранном направлении процесса температура рабочего тела
увеличивается, поэтому Дм>0. Если пренебречь криволинейностью изохорного процесса, то
^ = AsrlTl + T2)/2. (9.58)
Изменение энтальпии рабочего тела в политропном процессе численно равно
площади 2'ЬВ2 под кривой изобарного процесса, проходящего в том же интервале
температур, что и политропный процесс 1-2, т. е.
Ah = Asp(Tl + T2)/2. (9.59)
Так как Т2>Т\, то Д/г>0.
Теплообмен q рабочего тела с внешней средой численно равен площади под
процессом 1-2. Если заменить кривую 1-2 прямой, то
<7 = Д51.2(Г, + Г2)/2. (9.60)
Так как энтропия в выбранном политропном процессе уменьшается, то теплота от
рабочего тела отводится, т. е. q<CO. В соответствии с уравнением (2.29) определим
удельную работу, совершаемую рабочим телом в процессе 1-2: l — q — \u. В
политропном процессе Л-2 (рис. 9.7) <7<0, а Дм>0, поэтому в соответствии с формулами
(9.58) и (9.60) имеем
/== -(Д51.2 + Д5у)(Г, + Г2)/2.
Следовательно, удельная работа, совершаемая рабочим телом в политропном процессе
1-2, измеряется площадью V 12Аа.
Уравнение первого закона термодинамики может быть представлено в виде
выражения (2.40), интегрирование которого позволяет определить располагаемую
удел ьную работу:
/0 = <7 — ДА.
Так как в выбранном политропном процессе 1-2 q<.0, а ДА>0, то располагаемая
удельная работа выразится формулой
и численно равна площади V12В.
Следует, однако, отметить, что применение приближенных формул (при замене
кривых процессов прямыми) приводит при расчетах к определенной ошибке, тем
большей, чем больше разность начальной и конечной температур. Поэтому при желании
получить более точный результат расчета пользоваться этими формулами недопустимо.
В тех случаях, когда термодинамический процесс задан кривой в vp- или sT-коор-
динатах, иногда возникает необходимость определения показателя политропы такого
процесса. Для определения показателя политропы п можно использовать несколько
способов.
116 РАЗДЕЛ 2. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
1. Известны параметры двух различных состояний данного политропного
процесса (рис. 9.8, а), в этом случае можно воспользоваться уравнением (9.38):
После логарифмирования
l
показатель политропы п определяется в виде отношения:
(9.61)
2. Площадью а12Ь под процессом 1-2 (рис. 9.8, а) определяется удельная работа /
политропного процесса, а площадью cl2d слева от процесса 1-2 — располагаемая
удельная работа /0. Согласно формуле (9.45), имеем
3. Политропа изображена в логарифмических координатах (рис. 9.8, б).
Логарифмирование уравнения (9.38) \gp + n\gv = const показывает, что в
логарифмических координатах \gv, \gp политропа является наклонной прямой, определяемой
уравнением
\g p = const —n\gv.
Из этого уравнения следует, что /z = tga, где a — угол наклона политропы в
логарифмических координатах.
Отклонение экспериментально полученного процесса от прямолинейного,
построенного в логарифмических координатах (рис. 9.8, б), свидетельствует о том, что данный
процесс не является политропным. Иногда такие процессы можно приближенно
изображать несколькими последовательными прямолинейными участками, имеющими
разные углы а. Такие процессы часто называют кусочно-политропными, так как на
каждом таком участке показатель политропы п имеет свое, отличное от других значение.
В частном случае для изотермы а = 45°, для адиабаты (при £=1,4) а = 54°28/.
4. Задан политропный процесс на яГ-диаграмме. Расстояния по абсциссе между
изобарами и изохорами в координатах s, T определяются формулами (9.17).
Отношение этих формул применительно к графику на рис. 9.8, в дает
(5, — sB)(si — sA) = \n(pi/p2)/\n(v2/vl) = \g(pi/p2)/\g(v2/vi).
Сравнивая полученное выражение с (9.61), имеем
n = (Si-sB)/(si-sA). (9.62)
Показатель политропы положителен, если точки Л и В располагаются по одну
сторону от точки /. Так, например, для политропы 1-2 (рис. 9.8, в) /г>1; для
политропы 1-2 (рис. 9.8, г) 0<Zn<Ci. Если точка / расположена между точками Л и В
(рис. 9.8, д), то /г<0.
Вопрось/* Какие термодинамические процессы идеального газа изучаются в термодинамике?
Их специфические особенности. Почему они являются равновесными?
2. В каком термодинамическом процессе можно получить механическую работу без
подвода теплоты? За счет чего это происходит?
3. В каком термодинамическом процессе все подведенное к рабочему телу количество
теплоты полностью расходуется на получение механической работы? Почему?
4. Изобразите термодинамические процессы на vp- и яГ-диаграммах; определите область,
ограниченную процессами, в которой рабочее тело совершает положительную работу
при подводе теплоты и снижении температуры.
5. Назовите способы определения показателя политропы.
Принципы термодинамики бросают свет
не все явления природы.
Дж. К. Максвелл
СВОЙСТВА
И ПРОЦЕССЫ
РЕАЛЬНЫХ ГАЗОВ
Для расчета рабочих процессов
в тепловых машинах и установках
необходимо знать термодинамические
свойства реальных рабочих тел —
газообразных, жидких, плазменных,
твердых. Эти свойства
могут быть определены с помощью
термических уравнений состояния,
таблиц, диаграмм,
полученных на основе, статистической
обработки экспериментальных данных.
Диаграммы позволяют наглядно
представлять и рассчитывать, процессы,
протекающие в машинах и установках.
118
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Глава 10
РЕАЛЬНЫЕ ГАЗЫ
§ 10.1. Качественные особенности реальных газов
Исследования свойств реальных газов в широком диапазоне изменения
термодинамических параметров показали, что свойства реальных газов отклоняются от законов,
справедливых для идеальных газов, тем значительнее, чем выше их плотность. При
условиях, близких к нормальным, углекислый газ, а затем кислород, воздух и азот
наименее, а аргон, водород и гелий наиболее близки по своим свойствам к свойствам
идеального газа. Молекулы реальных газов в отличие от воображаемых частиц,
составляющих идеальные газы, имеют определенные (конечные) размеры, и между ними
существуют силы межмолекулярного взаимодействия. При определенных условиях эти
силы могут приводить к ассоциации или диссоциации молекул, что существенно
отражается на свойствах газа. При малых межмолекулярных расстояниях внутренние
силы могут действовать как силы отталкивания и создавать внутреннее давление.
А jnvПхи При значительных расстояниях между
молекулами действуют главным образом силы
взаимного притяжения (ри£. ,10.1)., В связи с этим
значение произведения давления реального газа
на его удельный объем (pv) при изменении
давления и сохранении постоянства температуры, как
правило, не остается постоянным.
В случае уменьшения произведения pv с
ростом давления реальный газ оказывается более
сжимаемым, чем идеальный, и, наоборот, при
увеличении pv с ростом давления реальный газ
оказывается менее сжимаемым по сравнению с
идеальным газом.
Результаты измерений показывают, что газы
в некотором интервале температур обнаруживают
оба эти отклонения от свойств идеального газа
и кривые z = pv/(RT)=f(p) имеют экстремум
(рис. 10.2). Параметр z даже у гелия и водорода
при определенных условиях существенно
отличается от единицы, но по мере повышения
температуры и уменьшения давления он приближается
к единице.
I
1 /
2
5
4-
W
\
-1
-J
в г-10+мкм
Рис. 10.1. Изменение энергии
взаимодействия молекул реальных газов в
зависимости от расстояния между
молекулам^: /—СО; 2 — Аг; 3 — Н2; 4 — Не
Особенности реальных газов
119
10 12 M 16 Id р,МПа
0,5\
г
w
г
/
/
/у
>
Jk
у
/
/*1б 1
Sk:
^^
R
Я02
^s
г^—
""ш
-Af
1
8
9 pt МП а
Рис. 10.2. Зависимость коэффициента сжимаемости реального газа от давления:
а —Н2;б—Не
Особенности поведения реальных газов можно проследить при сравнении
изотерм реального и идеального газов, построенных в координатах и, р. Так, в области
малых значений удельного объема газа (точка а на рис. 10.3) изотерма идеального
газа (py = const) более полога, чем изотерма реального газа (r=const). Это связано с
тем, что при большой плотности (значение v мало) молекулы реального газа, имеющие
конечные размеры, находятся друг от друга на небольших расстояниях и их влияние на
сжимаемость становится существенным. Коэффициент изотермной сжимаемости газа
(4.20) характеризуется тангенсом угла ф или г|э между касательной в данной точке
изотермы и отрицательным направлением оси ординат. Так как ср — угол между осью
р и касательной в точке а, проведенной к, изотерме реального газа r = const, а г|? —
120
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
угол между осью р и касательной в точке а, проведенной к изотерме идеального газа
pv = const, то сжимаемость реального газа меньше сжимаемости идеального газа
(tg<p<tgi|>).
В точке Ьу лежащей в области больших значений удельного объема v,
сжимаемость реального газа оказывается более высокой вследствие влияния сил взаимного
притяжения между молекулами: tgq>;> tg-ф.
Можно продолжить изотермы, проходящие через точку Ь в область малых
удельных объемов, и найти точку с их пересечения.
Следовательно, при некотором давлении, большем, чем в точке /;, и меньшем,
чем в точке с, сжимаемости реального и идеального газов одинаковы.
Если соответствующие состояния реального и идеального газов обозначить
точками d и е, то касательные к изотермам в этих точках должны быть параллельны
В области еще более высоких значений удельного объема и низких значений
давления изотермы реального газа имеют горизонтальный участок — такова,
например, изотерма Т = const, проходящая через точку /. При этом точка g соответствует
началу конденсации газа, в то время как в точке h газ полностью превращается в ка-
пельно-жидкое состояние. Изменение физического состояния вещества на участке gh про1
исходит при условии T = const и p = const и характеризуется наличием как
газообразной, так и жидкой фаз (область насыщения). Сравнивая изотермы реального и
идеального (ру = const) газов, проходящих через точку /, можно заметить, что
сжимаемость реального газа или жидкости на участке fgh больше, а на участке hi меньше,
чем у идеального газа. Из-за слабой сжимаемости для жидкостей характерно лишь
незначительное уменьшение удельного объема при значительном повышении
давления.
\\ V
*?4S
^4=90°
onst
7"= const
T>ff
const
— pV- const
v pir= const
h / ^^^
Theorist ^"^^^
Рис. 10.3. Сопоставление изотерм
реального газа с изотермами идеального газа
гРис. 10.4. р — ру-диаграмма реального
газа
Особенности реальных газов
121
В области насыщения gh при соответствующем изменении параметров состояния
происходит постепенное сжижение газа по мере уменьшения удельного объема v.
На р — ру-диаграмме (рис. 10.4) видно, что по мере повышения давления и
температуры участок сжижения gh будет сокращаться, постепенно превращаясь в точку К.
Кривая KN, на которой располагается точка g, называется верхней
пограничной кривой. Состояние газа, соответствующее точкам на этой кривой, называется
сухим насыщенным паром.
При этом следует иметь в виду, что между паром и реальным газом нет
принципиального различия. Паром называется любой реальный газ в состоянии, близком к
верхней пограничной кривой и в области ниже нее.
Кривая КМ (рис. 10.4), на которой располагается точка h, называется нижней
пограничной кривой. Она соответствует состояниям вещества, характерным
для кипящей жидкости. Точка К, в которой исчезает различие между жидкой и
газовой фазами, называется критической.
Состояние вещества при критическом давлении ркр, критической плотности ркр и
критической температуре Ткр называется критическим (табл. ЮЛ).
Таблица 10.1
Вещество
Азот N2
Аммиак ЫНз
Водород Н2
Водяной пар ЬЬО
Гелий-4 Не
Кислород Ог
Натрий Na
Неон Ne
Оксид углерода СО
Ртуть Hg
Углекислый газ СО2
Этиловый спирт С2Н5ОН
Критические параметры
7\<р, К
126
405
33,2
647
5,20
154
2570
44,4
133
1763
304
516
Ркр, МПа
3,40
11.3
1,29
22,1
0,229
5,05
35,0
2,65
3,49
151
7,38
6,38
Ркр, кг/м3
313
235
30
307
69,3
435
—
483
301
—
468
276
Критическое давление и температура являются максимальными в области
двухфазного состояния.
В критической точке К удельная теплота парообразования г обращается в нуль.
Это следует из уравнения (6.31) Клапейрона—Клаузиуса, так как в точке К v'—
= v", а величина dps/dT не может быть бесконечно большой.
Критическая изотерма, проходящая через точку /(, имеет точку перегиба. При
температурах выше критической изотермы не имеют горизонтальных касательных
(см. рис. 10.3). Это означает что ПРИ сверхкритических температурах осуществить
сжижение газа невозможно. Только при температурах выше критической характер
изотерм реального газа близок к характеру изотерм идеального газа.
На р — ру-диаграмме (рис. 10.4) показаны три характерные области,
отличающиеся различным состоянием вещества. В гомогенной области / вещество находится
в газообразном состоянии. Газ в состояниях, близких к верхней пограничной
кривой KN> принято называть перегретым паром. В изотермных процессах,
протекающих в области /, по мере повышения давления наблюдается монотонное изменение
произведения pv без скачкообразного изменения этого параметра, характерного для
фазового перехода. Область // соответствует капельно-жидкому состоянию. Как в
области /, так и в области // вещество находится в гомогенном однофазном состоянии
и граница между этими областями в значительной мере условна. Эта граница, при
122
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Т=ТК? и р> ркр совпадающая с критической изотермой (rKp = const), на рис. 10.4
показана пунктиром. В процессе испарения, соответствующем, например, линии х — у,
происходит непрерывное накапливание качественных различий между жидкостью и
паром. Переход от жидкости к пару происходит постепенно. Если в точке х вещество
обладает свойствами жидкости, то в точке у появляются свойства газа. Здесь в
отличие от процессов, протекающих при давлениях ниже критических, не наблюдается
скачкообразного изменения физических свойств испаряющейся жидкости.
В гетерогенной (двухфазной) области /// сухой насыщенный пар и кипящая
жидкость находятся в термодинамическом равновесии. По мере приближения к верхней
пограничной кривой содержание жидкости уменьшается, в то время как содержание
сухого насыщенного пара возрастает.
Эту смесь кипящей жидкости и сухого насыщенного пара принято называть
влажным паром.
Особенности фазовых переходов были рассмотрены в гл. 5.
Из изложенного следует, что любой реальный газ путем изотермного сжатия мож-
Рис. 10.5. Зависимость изобарной теплоёмкости воздуха от температуры и
давления
Особенности реальных газов 123:
но перевести в капельно-жидкое состояние. Однако это возможно лишь при
температурах ниже критической.
Отношение RTKp/(pKpvKp) для реальных газов в несколько раз больше единицы.
Это свидетельствует о том, что
поведение реальны* газов в окрестности критической точки существенна отклоняется
от поведения идеальных газов (для которых RT/(pv)=\).
Отклонение свойств реальных газов от свойств идеальных газов становится
особенно заметным на р— ру-диаграмме (рис. 10.4). В системе координат р, pv изотермы
реальных газов (Т — const) имеют минимум, изотермы идеальных газов (pv=?= const)
изображаются отрезками горизонтальных прямых. На участке bd коэффициент
сжимаемости реального газа z уменьшается, в то время как на участке
dc возрастает. В точке минимума d сжимаемость реального и идеального газов
одинакова.
Кривая Ad, соединяющая точки минимума реальных изотерм, называется
линией Бо й л я.
Температура, соответствующая изотерме с точкой минимума А на оси ординат,
называется температурой Бойля. Вблизи точки А реальный газ обладает всеми
свойствами идеального газа (в самой точке А р = 0, а удельный объем бесконечно
велик). При температурах, больших температуры Бойля (изотермы тМ),
произведение pv увеличивается по мере роста р.
Показанная на рис. 10.4 р — ру-диаграмма является диаграммой состояния.
Каждой точке на ней соответствуют три термодинамических параметра: р, v и Т.
Об особенностях изменения основных термодинамических параметров реальных
газов — водорода и гелия — в области низких температур можно судить по sT-ди-
аграммам. Эти газы широко используются в технике низких температур.
Об отклонении свойств реальных газов от свойств идеальных можно судить и по
их теплоемкостям. О характере зависимости изобарной теплоемкости воздуха от
температуры и давления можно судить по данным, приведенным на рис. 10.5. Если
теплоемкости идеальных газов зависят только от температуры, то теплоемкости реальных
газов существенно зависят не только от температуры, но и от давления или объема.
Так, например, по мере приближения к критической точке теплоемкость ср некоторых
веществ, например водяного пара, водорода и воздуха, начинает неограниченно
возрастать, что объясняется большим расходом тепловой энергии на распад крупных
молекулярных ассоциаций.
§ 10.2. Уравнение Ван-дер-Ваальса
Состояние реального газа качественно характеризует уравнение
(p + a/v2)(v-b) = RT, (10.1)
известное под названием уравнения Ван-дер-Ваальса. В уравнении (10.1) а и b—
две численно малые величины, постоянные для данного газа.
Член a/v2 характеризует внутреннее давление газа или жидкости, появляющееся
вследствие наличия сил сцепления между молекулами, а величина b учитывает
уменьшение объема, в котором движутся молекулы реального газа, за счет объема самих
молекул и объема промежутков между молекулами при их плотной упаковке.
Уравнение Ван-дер-Ваальса может быть представлено в виде
v3-(b + RT/p)v2 + (a/p)v-ab/p = 0. (10.2)
Если обозначить через vj, vu и иь возможные три корня этого уравнения, то урав.-
нение (10.2) можно записать в следующей форме:
124
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Рис. Ю.6. Геометрическая интерпретация уравнения Ван-дер-Ваальса: а — в
координатах у, р\ б — в координатах ср, л
(V — Vf)(v — Vd) (V — Vb) = 0.
(10.3)
Уравнение имеет три действительных корня при сравнительно низких температурах
(Т<сТк[>)у а один действительный и два комплексных корня — при температурах
Г> Гкр.
Изотермы, соответствующие этому уравнению, показаны на ур-диаграмме (рис.
10.6, а). Точки, соответствующие корням Vfy Vdt vt уравнения (10.3), найдены при
давлении pf и некоторой температуре Т. В критической точке К корни оказываются
действительными и равными между собой.
На изотерме abcdefg нанесены характерные точки. В окрестности точки а вещество
обладает свойствами газа (перегретого пара), в то время как в точке g — капельной
жидкости.
Если при Т~> Ткр изотермы, построенные по уравнению (10.1), качественно
соответствуют изотермам реального газа, то докритические изотермы при T<zTKp вместо
горизонтального участка bf, соответствующего реальному газу, имеют волнообразный
участок bcdef.
Точки b и /, через которые проходят пограничные кривые, могут быть определены
при сопоставлении реальной изотермы и изотермы Ван-дер-Ваальса при одном и том
же значении температуры. Из них можно составить круговой замкнутый процесс
b-c-d-e-fy который можно было бы обратимо провести при наличии лишь одного
источника теплоты с температурой, равной температуре на изотермах. В этом случае
можно получить работу, характеризуемую разностью площадок внутри кругового
процесса, ибо алгебраические знаки работ, измеряемых полученными таким образом
площадками, разные. Однако получить работу при одном источнике теплоты
невозможно. Это противоречит второму закону термодинамики. Вследствие этого
горизонтальная (реальная) изотерма должна быть выбрана таким образом, чтобы
результирующая работа оказалась равной нулю (пл. bcdb = i\A. defd)\ это требование
определяет расположение на изотермах точек b и / пограничных кривых. Выбор нескольких
изотерм обеспечивает построение пограничных кривых.
По линии be процесс может идти лишь при отсутствии в газе центров конденсации
Особенности реальных газов 125
(пылинок, капелек тумана или ионов). На линии be газ находится в относительно
устойчивом (метастабильном) состоянии, которое называется пересыщенным
паром. Участок fe соответствует метастабильному состоянию жидкости
(перегретая жидкость). Перегретое состояние жидкости соответствует расширению
жидкости за пределы точки /. Давление перегретой жидкости при данной температуре
ниже давления насыщения. В этом неустойчивом состоянии давление жидкости может
стать отрицательным, однако при малейшем возмущении она скачком перейдет в
термодинамически устойчивое состояние, соответствующее прямой bf. Области метаста-
бильных состояний / и // на рис. 10.6, а заштрихованы. Участок cde соответствует
состояниям, в действительности не реализуемым, так как на этом участке (dp/dv)T~> 0.
На участках ab и fg экспериментальная изотерма качественно согласуется с изотермой
Ван-дер-Ваальса.
Постоянные а и b в уравнении (10.1) вычисляются с помощью уравнения (10.3),
написанного для условий критической точки /С, когда все три корня равны между
собой (vf=Vd = Vb = vKp). В этом случае уравнение (9.3) получит вид (v — укр)3 = 0, или
32 2-v3Kp = 0. (10.4)
Для условий критической точки уравнение (10.2) может быть записано в форме
v3 - (Ь + R TKp/pKp)v2 + (a/pKp)v - ab/pKp = 0. (10.5)
Уравнения (10.4) и (10.5) тождественны, поэтому
3vKp = b + RTKp/pKp\ 3vlp = a/pKpy vip = ab/pKp.
Полученные соотношения дают возможность определить значения a, b и R через
критические параметры:
a=Zv2KppKp; b=vKp/3; R = SvKppKp/(3TKp). (10.6)
Подстановка этих выражений в уравнение (10.1) дает возможность привести его
к безразмерной форме
(л + 3ф2)(3ф-1) = 8т, (10.7)
где п = р/ркру y = v/vKpt т=Т/Ткр — безразмерные переменные, называемые
приведенными параметрами (рис. 10.6, б).
Если разные газы имеют одинаковые я, <р и т, то их состояния называются
соответственными. Так как уравнение (10.7) не содержит каких-либо констант,
связанных с индивидуальными свойствами вещества, то можно сделать предположение
о том, что все газы в соответственных состояниях ведут себя одинаковым образом.
Закон соответственных состояний приближенно справедлив для ряда веществ,
в том числе и таких, поведение которых заметно отклоняется от уравнения (10.1).
Пользуясь этим подобием свойств, можно оценить свойства какого-либо газа по
известным свойствам другого.
По правилу Гульдберга и Гюи, отношение температуры кипения при атмосферном
давлении к критической температуре одинаково для всех веществ и равно «0,6.
Это правило и некоторые другие, основанные на подобии свойств, в
действительности выполняются приближенно и могут быть отнесены лишь к определенным группам
близких по свойствам веществ. Так, например, отношение RTKp/(pKpvKp)y по Ван-дер-Ва-
альсу, равно 2,67. Экспериментально полученные для некоторых веществ значения
этого отношения находятся в пределах 3,2...5.
Уравнение Ван-дер-Ваальса дает количественное представление о поведении
газов, плотность которых не очень велика, и лишь качественное представление о конден-
126 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
сации и критическом состоянии веществ. Поэтому этим уравнением нельзя пользоваться
для количественной оценки явлений, протекающих в газе с высокой плотностью.
Большинство других существующих уравнений состояния применимы лишь в
узком интервале переменных либо имеют значительно более сложный вид. В связи с этим
в инженерной практике широкое распространение получили различные таблицы и
диаграммы.
§ 10.3. Уравнение состояния в вириальной форме
Известно большое число попыток составления уравнений состояния реальных газов.
Так, например, методами статистической физики было показано, что уравнению
состояния реального газа в наиболее общей форме может быть придан вид
1- 2 kfa/(k+l)vk\ (10.8)
k=\ /
где Ра — так называемые вириальные коэффициенты, зависящие от температуры
рабочего тела (k=\y 2, ...). В области высоких значений удельного объема v (низкой
плотности) для описания поведения реального газа можно ограничиться меньшим
числом членов ряда п по сравнению с областью малых значений v. В предельном случае
при у->-оо уравнение (10.8) принимает вид уравнения (1.6). По мере уменьшения v
(повышения плотности) число членов ряда должно увеличиваться. Однако
практическое использование уравнения (10.8) наталкивается на определенные трудности.
В общем случае для получения приемлемой точности число членов ряда в уравнении
(10.8) должно быть значительным. Кроме того, для вычисления коэффициентов р* нужны
экспериментальные данные. Во многих случаях трудности определения коэффициентов
Ра настолько велики, что оказываются более приемлемыми таблицы и диаграммы,
составленные непосредственно по экспериментальным данным. На основе таких
данных нередко составляются эмпирические формулы и уравнения, которые при
определенных условиях дают возможность ограничить количество экспериментов.
Для составления эмпирических уравнений состояния необходимо получить опытные
данные, устанавливающие связь трех параметров состояния р, v и Г, или выявить
зависимости теплоемкости от температуры и давления. Можно также воспользоваться
данными о температурном эффекте дросселирования или данными о скорости
распространения звука.
Так, например, если на основании экспериментальных исследований установлены
зависимости удельной теплоемкости при постоянном давлении ср и ее частной
производной (дср/др)т от р и 7\ то уравнение состояния можно получить путем интегрирования
по Т дифференциального уравнения (4.44) при условии p = const:
откуда
v = _ JJ J-j^i^dr] AT + TUip) + Ш-
Если р-+0 (или и-*»), то в соответствии с уравнениями (4*44), (6.4) и (1.6)
(дср/др)т = 0, (dv/dT)p=R/p, v = RT/p. Из этих предельных условий следует, что
функция f\(p) = R/p, а функция f2(p) = O. Уравнение (10.9) применимо только в
области / (см. рис. 10.4). ,
Особенности реальных газов ' HJ7
Большой объем измерений, выполняемых в последнее время с целыЪ получения
данных о термодинамических свойствах веществ, свидетельствует о том, что основным
источником надежной информации в этой области по-прежнему остается эксперимент.
Для составления уравнений, пригодных для расчета таблиц термодинамических
свойств, используют статистические методы обработки результатов измерений.
Применение этих методов в общем случае связано с решением систем нелинейных
алгебраических уравнений с большим числом неизвестных, поэтому значительные успехи в
этом направлении были достигнуты с помощью ЭВМ. " ■ '
Единые уравнения состояния, описывающие термодинамические свойства веществ
в жидком и газообразном состояниях, а также на линиях равновесия фаз, содержат
от 40 до 60 коэффициентов, определяемых при обработке экспериментальной
информации методами математической статистики, и используются для расчета таблиц.
Сложность уравнений этого типа обусловлена различием механизма
межмолекулярного взаимодействия в газах и жидкостях. В газах при высоких температурах и
умеренных давлениях преобладают парные и тройные взаимодействия молекул, в то время
как в жидкостях наблюдается коллективный характер взаимодействия молекул.
Например, единое уравнение состояния для расчета термодинамических свойств
газообразного и жидкого азота, полученное профессором В. В. Сычевым и др., имеет
следующий вид:
/ /-г/-/ \
Pv = RT[ 1 + 2 2 МПР)/(гУкр), '(ю.10)
\ i=\ /=0 /
где / и / — целые положительные числа, причем г= 10, а значение st определяется
выбором / и может принимать значения 4...8. При определении коэффициентов Ьц
использовался метод наименьших квадратов.
В простейшем случае процедура определения коэффициентов Ьц состоит в следующем Если
из эксперимента известны значения функций, выражающих зависимость, например, сжимаемости
z от приведенной плотности рпр при данной приведенной температуре Гпр, то задача определения
неизвестных постоянных Ь\, &2, ..., Ьт в выражении
решается в следующем порядке. Для определения Ь\, &2, ..., Ьт составляется система условных
уравнений:
вид:
i, &2, .... br) — 2* = 0 (fc=l, 2 m).
Если эти уравнения линейны относительно bit то такая система имеет следующий
(Pnpi b\ + pnpi ^2+... + Pnpi br) — z\ =0;
(Рпр m&l+pnp /n &2 + ... + рпр/n&r) —2m = 0,
причем 2|, г, ..., zm, соответствующие каждому из значений pnpi, р„р, ..., рпрт, берутся из
экспериментальных данных.
Если ошибки в определении величин z\, 22, .... zm имеют нормальный закон распределения,
то для наиболее вероятной системы значений неизвестных сумма квадратов отклонений е* =
=Ф* — 2* должна быть наименьшей. \
Требование минимума суммы квадратов отклонений приводит к системе линейных
уравнений, решение которых дает возможность определить значения неизвестных величин Ь\% Ьч Ьг.
При составлении уравнений состояния типа (10.10) процедура определения постоянных Ьц
128 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
принципиально сохраняется. По экспериментальным значениям сжимаемости в пространстве
переменных z, рПр, Гпр строится совокупность поверхностей z = z(pnp, 7\,р, 6|, 62, ..., Ьг)у причем каждой
из таких поверхностей соответствует свое уравнение состояния. Окончательные значения
постоянных b[j в едином уравнении состояния определяются усреднением соответствующих постоянных по
всей совокупности уравнений состояния.
Полученное таким образом уравнение (10.10) удовлетворяет соотношению (5.32) и надежно
отображает экспериментальные данные по азоту в интервале температур 63,1...1500 К и
давлений 0,01...100 МПа. При расчете коэффициентов Ьц используются экспериментальные значения
р, у, Т.
Статистические методы обработки экспериментальной информации при составлении
уравнений типа (10.10) позволяют использовать не только данные р, у, 7\ но также и данные о
теплоемкости, энтальпии, энтропии, теплоте испарения и других свойствах исследуемого рабочего тела.
Кроме того, эти методы дают возможность оценить и учесть достоверность используемой
первичной информации. Располагая сведениями о погрешности экспериментальных данных и их
согласуемости между собой, оказывается возможным построить таблицы наиболее вероятных
значений термодинамических функций и оценить границы их рассеяния.
ФОРТРАН-программа, предназначенная для расчета термодинамических свойств азота,
в указанном диапазоне температур и давлений приведена в задачнике [3].
Значение ЭВМ при построении уравнений реального газа по экспериментальным данным
трудно переоценить. Длительная и громоздкая процедура статистической обработки экспери-
меиталып.1\ данных без ЭВМ оказалась бы практически неосуществимой.
Вопросы | Какие области состояния вещества разделяют нижняя и верхняя пограничные кривые?
2. Какое состояние вещества называется критическим?
3. Изобразите в координатах у, р изотермы реального газа с температурой выше и ниже
критической, а также соответствующие изотермы Ван-дер-Ваальса.
4. Почему нельзя осуществить сжижение газа при температурах выше критической?
Глава 11
ПАРЫ
§11.1. Получение пара
В современной технике в качестве рабочих тел широко применяются пары различных
веществ. Так, например, рабочим телом в паровых турбинах служит, как правило,
водяной пар. Кипение (получение пара) используется также в первичных контурах
атомных электростанций, в холодильной и криогенной технике, испарительное охлаждение
применяется в доменных печах и т. д.
Пар может быть получен не только в результате кипения, но и путем
непосредственного перехода вещества из твердого в газообразное состояние (сублимация).
Если в объеме, занимаемом жидкостью, быстро сбросить давление (осуществить
декомпрессию), то парообразование начнется в объеме жидкости, причем при
определенных условиях этот процесс имеет взрывообразный характер. Однако наиболее
часто в технике используется процесс кипения — получение пара из жидкости при
постоянном давлении.
Если подводить теплоту к жидкости начиная с состояния в точке с (рис. 11.1) при
некотором постоянном давлении, то температура ее будет расти, а объем — несколько
увеличиваться. По достижении состояния, характеризуемого точкой Ьу свойства
жидкости при продолжении подвода теплоты меняются иначе. При постоянном давлении
температура, соответствующая точке 6, остается постоянной, а объем увеличивается,
но не за счет равномерного увеличения всего объема жидкости (как на участке cb), a
за счет перехода части жидкости в пар. Температура Ть в точке Ъ называется
температурой насыщения, а соответствующее ей давление — давлением
насыщения. Точка Ь и соответствует началу процесса кипения. Кипение
характеризуется парообразованием в объеме жидкости в отличие от испарения, которое
происходит лишь со свободной поверхности жидкости при условии, что парциальное
Пары
129
Щласть сублимации Линия десубШац
К
Линия сублимации
Рис. 11.1. ир-диаграмма реального вещества
давление пара над жидкостью меньше давления насыщения. По мере подвода теплоты
все большее количество жидкости переходит в пар так, что парообразование закончится
в точке g.
Таким образом, процесс b-g в координатах v, p и s, T изображается изобарой
(p = const), одновременно являющейся изотермой (r = const).
Опыт показывает, что при более высоком давлении (выше рь) процесс кипения
начинается при большем, чем Vb, объеме, и заканчивается при меньшем, чем vs.
Разница между объемами, соответствующими началу й концу процесса кипения,
определяется индивидуальными свойствами вещества.
По мере приближения к критическому значению температуры Гкр пограничные
кривые, на которых располагаются точки b и g, постепенно сближаются и при Г=Гкр
сливаются в критической точке К.
Нижняя (левая) пограничная кривая является предельной для существования
пара. Правее верхней пограничной кривой все вещество, участвующее в процессе,
находится в парообразном состоянии. Необходимо при этом иметь в виду, что газ —
это всегда пар, но пар — это газ, состояние которого характеризуется близостью к
верхней (правой) пограничной кривой. Таким образом, принципиального различия между
газом и паром не существует.
В дальнейшем параметры состояния, относящиеся к нижней пограничной кривой,
снабжаются одним штрихом (р', vf и т. д.), относящиеся к верхней пограничной
кривой — двумя штрихами (р"у v" и т. д.). Линия, проведенная по точкам с, называется
линией затвердевания. Правее этой линии твердая фаза существовать
не может.
Линия парообразования bg в координатах Г, р представляется точками (см.
рис. 6.1), геометрическое место которых называется кривой упругости О К и
описывается дифференциальным уравнением Клапейрона—Клаузиуса. Одновременное
существование жидкой, твердой и газообразной фаз в Гр-диаграмме определяется
состоянием вещества в тройной точке О.
5 За к. 584
130
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Температура (К), соответствующая тройной точке, для некоторых веществ:
Азот 63,15 Дейтерий 18,73
Вода 273,16 Кислород 54,36
Водород 13,95 Неон 24,57
Единственным веществом, не имеющим тройной точки, является гелий (рис. 11.2).
Форма и протяженность кривой упругости отражают физические особенности
вещества (рис. 11.3). Если параметры состояния превышают критические, то
поверхность раздела фаз прекращает свое существование. Таким образом,
кипение возможно только в интервале параметров, определяющих тройную и
критическую точки.
Процесс парообразования весьма существенно отличается от процессов изменения
состояния идеального газа. Если в последних свойства вещества меняются постепенно,
то при фазовом превращении малое подведенное (или отведенное) количество теплоты
6q меняет свойства только малой части dm имеющегося вещества, причем эти свойства
меняются не монотонно, а скачком. Так, Ay = i/"— v' ■—скачок удельного объема,
As = .s"— s'— скачок удельной энтропии и т. д. Скачок удельного объема хорошо
виден на ур-диаграмме (см. рис. !11.1), скачок удельной энтропии — на sT-диаграмме
(рис. 11.4).
Процесс парообразования на sT-диаграмме также отображается горизонтальной
линией bg (значения Т и р постоянны). Область двухфазного состояния (влажного
пара) расположена ниже линии Т=Ткр. Точка а пересечения нижней пограничной
кривой с осью ординат соответствует параметрам тройной точки (точка О, см. рис. 6.1).
Принято считать, что в этой точке s = 0 и /г = 0. В жидкой фазе нижняя пограничная
кривая идет круче, чем изобара, так как термическая расширяемость жидкости
невелика, при малых и умеренных давлениях изобары почти совпадают с нижней
пограничной кривой.
Площадь под изотермой bg (рис. 11.4) представляет собой удельную теплоту
парообразования
Г=Г,(5"-5/), (ИЛ)
входящую в'уравнение (5.32). Здесь и далее Ть—Тн(Ти — температура насыщения).
р,МПа
i/
Твердый Не/
Ие(1)\не(1)
Критическая
точка
/ 2 J « 5 Т,К
Рис. 11.2. Гр-диаграмма гелия
50 100 150 100 250 300 350 400 М0Т,К
Рис. 11.3. Характеристики упругости
различных веществ: а — тройная точка; К —
критическая точка
Пары
131
Рис. 11.4. «^-диаграмма реального вещества
§11.2. Термодинамические свойства жидкости
Процесс с-Ь нагрева жидкости (см. рис. 11.1) до температуры насыщения в точке Ь
происходит при постоянном давлении. В соответствии с уравнением первого закона
термодинамики удельное количество теплоты, расходуемое на нагрев жидкости,
составит
Точка Ь принадлежит нижней пограничной кривой, поэтому удельная теплота,
затрачиваемая на нагрев жидкости от промежуточного состояния в точке с до начала кипения
(точка Ь), определится разностью:
q = h' — h = u' — u + p{v' — v). (11.2)
Так как h' — u' + pv't то выражение для определения внутренней энергии жидкости
на линии насыщения будет иметь вид
u' = h' — pv'. (11.3)
При построении sT-диаграммы (рис. 11.4) было принято, что в тройной точке О
удельная энтропия жидкости равна нулю, поэтому удельная энтропия кипящей
жидкости (точка Ь)
н н
5'= f dq/T= \ с AT/Т.
132
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Если удельную теплоемкость с' принять постоянной, то s'= с'\п(Тн/Та).
Теплоемкость жидкости незначительно изменяется с повышением давления, например для
воды:
p.
c\
МПа . .
кДж/(кг-
К)
1
4,214
4
10
,194
20
4,173
30
4,153
40
4,135
50
4,117
Исключение составляет гелий. При Г = 2,18 К теплоемкость жидкого гелия резко
возрастает, затем интенсивно уменьшается. При повышении давления точка разрыва
сдвигается в область более низких температур. Зависимость теплоемкости гелия
от температуры напоминает букву А,, поэтому появилось название «Х-переход» (см.
также § 6.7), который как бы разделяет гелий на состояния Не(1) и Не (II)
(рис. 11.5).
В состоянии II гелий обладает свойствами сверхтекучести и сверхпроводимости.
Сверхпроводимость гелия выражается в том, что при озлаждении ниже Х-точки он
перестает кипеть; благодаря высокой теплопроводности жидкой фазы пузырьки не
образуются, испарение происходит только с поверхности. При температуре А,-точки у
жидкого гелия наблюдается резкий максимум плотности жидкости. Немонотонно меняется
с изменением температуры и плотность воды: максимальная ее плотность наступает
при Т = 276,98 К.
В энергетике в качестве высокоэнтальпийных теплоносителей используют не
только водяной пар, но и жидкие металлы. Если cv жидких металлов с ростом
температуры монотонно убывает, то ср щелочных металлов сначала убывает, а затем
резко увеличивается (рис. 11.6), что необходимо учитывать при выборе рабочего
тела. '
Перспективным рабочим телом в энергетике является водород. В жидкой фазе
плотность водорода имеет две модификации, обусловленные ориентацией спинов: паро-
водород и ортоводород (нормальный водород). Следует иметь в виду, что при полном
переходе ортоводорода в пароводород выделяется 525 кДж/кг, что превышает удельную
теплоту испарения (455 кДж/кг).
10
1
,
I
i
' 3
Рис. 11.5. Зависимость удельной
теплоемкости гелия от температуры
Рис. 11.6. Зависимость удельной
теплоемкости щелочных металлов от
отношения T/Tk
35
25
>
/
V
V/
/На
ICS
1
0 0J Ц
0,6 Т/Тк
Пары 133
§11.3. Термодинамические свойства поверхности раздела фаз
Каждое вещество в зависимости от условий существования может находиться в трех
агрегатных состояниях: газообразном, жидком и твердом. Разделяются эти состояния
(они же — фазы) под действием сил поверхностного натяжения и гравитационных.
Поверхностное натяжение разделяет жидкую и газообразную фазы; под влиянием
гравитационной силы жидкая фаза из-за большей плотности опускается вниз.
Фазы могут сосуществовать вместе и при определенных физических условиях
переходить друг в друга — взаимопревращаться; Агрегатное превращение — всегда
фазовое превращение.
Межмолекулярные силы, существенно зависящие от расстояния между
молекулами, сильнее проявляются в жидком состоянии вещества и значительно слабее —
в газообразном. Для частицы, находящейся в объеме жидкости, результирующая сила
межмолекулярного взаимодействия равна нулю. Но при выходе частицы на
поверхность равновесие сил нарушается, так как со стороны газа на молекулы почти нет
воздействия. Следовательно, на частицу, находящуюся на поверхности, действует
результирующая сила, направленная по нормали к поверхности внутрь жидкости.
Под действием этой силы любая молекула стремится уйти с поверхности внутрь
жидкости. Это «внутреннее» давление, называемое когезией, чрезвычайно велико
(при р= 101,325 кПа и Г = 373 К внутреннее давление воды составляет примерно
580 МПа), поэтому внешнее давление мало «ощущается» жидкостью, в связи с чем
создается впечатление о ее несжимаемости.
Поверхностный слой толщиной в несколько молекул составляет
поверхностную фазу жидкости, основное свойство которой заключается в том, что она
стремится отдавать свои молекулы объему жидкости. Поэтому
равновесным состоянием поверхностной фазы оказывается такое, при котором число
молекул, находящихся в ней, минимально.
Любые изменения термодинамической системы, приводящие к изменению объема,
должны сопровождаться работой, пропорциональной изменению объема.
Одновременно с изменением объема изменяется площадь Q поверхности раздела фаз на dQ,
что также связано с работой. Для оценки поверхностных явлений целесообразно
использовать одну из характеристических функций. Возможность термического
равновесия между фазами определяется условием одинаковости температуры (r = idem).
Так как у характеристических функций — внутренней энергии и энтальпии —
основным фиксированным параметром является энтропия, а не температура, следует
использовать свободную энергию или свободную энтальпию.
Если учесть соотношения (2.34) и (4.5), то выражение (4.9) можно представить
в виде суммы:
G = F + pV.
Объем поверхности раздела мал и может быть принят равным нулю. Поэтому
G^Fh, следовательно, для анализа поверхностных явлений можно использовать
свободную энергию F. Далее принимается: F\V\ T) — свободная энергия жидкости;
F"(V'\ Т) — свободная энергия пара; F'"(Qt T) — свободная энергия поверхностной
фазы.
В соответствии с формулой (4.7) элементарное изменение свободной энергии
поверхностной фазы
dF'"= (dF'"/dQ)TdQ+(dF'"/dT)QdT (11.5)
или в условиях постоянства температуры
dF'" = (dF'"/dQ)TdQ = odQ, (11.6)
и f
У
«/
2 3
л
г
134 РАЗДЕЛ З. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
где a = (dF"/dQ)T — поверхностное
натяжение (удельная свободная энергия
поверхности) — является физической константой
вещества. Из опыта известно, что значение а не
зависит от (Ш, т. е. от площади поверхности раздела
фаз, а зависит только от температуры.
Для определения зависимости о = о(Т)
процессы, происходящие на поверхности раздела фаз,
J2 можно представить в виде обратимого цикла
Рис. 11.7. Цикл на поверхности разде- (рис. 11.7). В этом цикле Q — поверхность плен-
ла Фаз ки, a — поверхностное натяжение.
Процесс 1-2 является изотермным растяжением пленки. Постоянство температуры
обеспечивает постоянство поверхностного натяжения. Опыт показывает, что
увеличение площади поверхности жидкой пленки ведет к ее охлаждению. Поэтому для
удовлетворения условия r = const в процессе 1-2 к пленке необходимо подвести количество
теплоты Q\. По достижении состояния 2 растяжение пленки продолжается до
состояния <?, но в адиабатных условиях. В результате температура пленки понизится на
d7\ а поверхностное натяжение возрастает на da. Затем площадь пленки сокращается
при постоянной температуре T—dT. Для обеспечения изотермных условий в процессе
3-4 от пленки необходимо отводить количество теплоты Q2. Цикл завершается
адиабатным сокращением поверхности пленки в процессе 4-1.
Работу такого цикла можно определить площадью 1234, равной (Q2— Qi)da, а
выражениям (2.46) и (2.49) придать вид
(Q2— Qi)da/Qi = d777\ или da/dr= — Q,/|T(Q2 — Qi)].
Сомножитель Qi/(Q2 — Qi) представляет собой теплоту образования поверхности
(г*), поэтому
do/dT=-r*/T. (11.7)
Так как г* по своей природе больше нуля, то da/dT<0. Следовательно,
поверхностное натяжение с ростом температуры уменьшается.
Это происходит вследствие увеличения кинетической энергии молекул, в связи с чем
они легче проникают в поверхностный слой. Отрицательное значение производной
do/dT говорит также о том, что при положительной работе, совершаемой во время
сокращения площади пленки, теплота от нее должна отводиться. Положительная
(подведенная) теплота поглощается пленкой при отрицательной работе — работе
растяжения под действием внешних сил (что подтверждено опытом).
Для определения термодинамических свойств поверхности раздела фаз можно
воспользоваться выражением (10.3). При отсутствии работ немеханического характера
в соответствии с третьим уравнением (4.15)
dF'"=—S'"dT + odQ. (11.8)
Сопоставление выражений (11.5) и (11.8) показывает, что
(dF'"/dT)Q=—S'"\ (dF'"/dQ)T = a. (11.9)
Если воспользоваться соотношениями взаимности, то можно получить
* (dS//7dQ)r=-(da/d7i)Q> (11.10)
но s'" = S"7Q> поэтому
da/dr=-s///. (11-11)
Пары . 135
Полученное соотношение характеризует связь между деформационными и
тепловыми свойствами поверхностного слоя. Так как da/dr<0, то s'"> 0. Если учесть, что
S"/ = s"'Q, а s'"— — da/dr, то зависимость (11.8) можно представить в виде
d(aQ), откуда
удельная свободная энергия поверхностного слоя является функцией только
температуры, так как она равна поверхностному натяжению.
В соответствии с формулой (4.5) внутренняя энергия поверхностного слоя
определяется суммой: U"r = F'" + TSf". С учетом (11.11) и (11.12) i/'" = aQ — TQdo/dT=
= Q(a — Tdo/dT), или
u'"=U'"/Q = o-Tdo/dT; (11.13)
удельная внутренняя энергия поверхностного слоя больше его свободной энергии
(и!"> /'"), а разница определяется температурой.
Таким образом, термодинамические характеристики поверхностного слоя могут
быть выражены через поверхностное натяжение а, которое действительно является его
основной характеристикой. Так как для большинства веществ а зависит от температуры
линейно, то
a = a0 — aT\ do/dT = a. (11.14)
Если сравнить этот результат с (11.11), то можно прийти к выводу:
удельная энтропия поверхностного слоя постоянна в широком диапазоне температур
(s'" = a).
Подстановка соотношения (11.14) в формулу (11.13)
и'" — ао — аТ + аТ = Оо = const
показывает, что внутренняя энергия поверхностного слоя постоянна, так же как и его
энтропия. Удельная свободная энергия f" = f'o" — аТ = о — аТ является линейно
убывающей функцией температуры.
Свойства поверхностного слоя показывают, что не все условия равновесия
двухфазной системы сохраняются. Чтобы выяснить, какие условия не сохраняются,
воспользуемся характеристической функцией — свободной энтальпией (10.4), в которой
р — внешнее давление, V=V"-f-V". В процессе парообразования dV">0, dK'<0,
а объем поверхностного слоя мал и его можно не учитывать.
Условием термодинамического равновесия является уравнение
0. (11.15)
В соответствии с уравнениями (4.15) для фаз имеем
dF'=-S'dT-p'dV'\ dF"=-S"dT-p"dV"; d/r///
В последнее выражение входит Q" — площадь поверхности раздела фаз, определяемая
количеством паровых пузырей (сама жидкость может иметь и другую поверхность).
Если учесть, что внешнее давление и температура постоянны, то в соответствии с
(11.14) Q//da = 0,~S/dr=-S//dr = 0 и d(pV) = pdV = p(dV' + dV"). Поэтому dG =
= -p/dl//-p//dl/// + adQ// + pdl// + pdl///, или dG=(p-p')dV + {p-p" + odQ"/dV")X
XdV". Если допустить, что dV' и dV" независимы, то dG = 0 только в том случае, если
каждая из скобок равна нулю: (р — р') = 0\ р" — p = adQ"/dУ". Следовательно, давление
р' в жидкой фазе равно внешнему давлению р.
Пусть образующаяся вторая фаза (паровая) имеет форму сферы радиуса /?ш,
136 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
где dQ
p"-p = 2o/RWt (11.16)
т. е. давление в пузыре пара определяется не только давлением в жидкости, но и
действием поверхностного натяжения.
Уравнение (11.16) называется уравнением Лапласа.
Условия равновесного взаимодействия двух фаз можно представить в
координатах ер, Т, где ф = ф(р, Т) — удельная свободная энтальпия. Для выявления вида
зависимости ф = ф(Г) при p = const можно воспользоваться последним уравнением (5.3), тогда
с1ф=—sdT + vdp. Так как dp = O, то (ду/дТ)р=—s<cO. Следовательно, по мере роста
температуры свободная энтальпия уменьшается. Вторая производная (д2у/дТ2)р —
= — (ds/dT)p= — ср/Г<0, т. е. характеристика ф = ф(Г) при p = const расположена
выпуклостью вверх (рис. 11.8).
Пусть кривая фр соответствует жидкости, а кривая фр' — пару. Тогда при
взаимодействии фаз в области Т<Ть будет происходить конденсация, так как неравенство
Фр<Фр' свидетельствует о большей устойчивости жидкой фазы. При Т> Ть фР> фр', т. е.
более устойчивым оказывается парообразное состояние (происходит кипение).
Равновесное состояние может быть лишь при Т—Ть, так как при выбранном давлении только
при этой температуре выполняется условие равновесия фр = фр/. При более высоком
давлении обе кривые переместятся вверх, а точка пересечения (равновесия) сместится
вправо (точка Ь').
В двухфазной однокомпонентной системе каждое давление соответствует одному
значению температуры.
Для определения зависимости р = р(Г) можно воспользоваться последним
уравнением (5.3). В условиях равновесия для обеих фаз температура и давление одинаковы,
а энтропия и объем различны. Поэтому с1ф' = — s'dT + v'dp и с1ф" = — s"dT-\-v"dp.
Так как при равновесии с1ф' = (1ф", то дифференциальное уравнение кривых фазового
равновесия получит вид
(11.17)
Процесс фазового перехода сопровождается нарушением непрерывности
изменения координат состояния.
При агрегатных превращениях (при переходе из твердого в жидкое, из жидкого
в газообразное состояние) энтропия растет всегда, а объем растет только при переходе
из жидкого в газообразное. Иногда удельный объем жидкости меньше, чем удельный
объем твердой фазы. Таким свойством обладают вода, чугун, висмут.
Удельная теплота парообразования определяется интегралом
r= \ THds=THAs,
s,(7'=const)
подставив который в уравнение (11.17) получим
dp/dT = r/(THkv). В процессе перехода из
жидкого состояния в газообразное Ду;> О, Тн> 0, г> О,
поэтому dp/dr>0. Это значит, что точка
пересечения кривых ф/ = ф/(Г) и ф" = ф"(Г) в коорди-
J ^ натах ф, Т по мере увеличения давления пере-
\ Ть> Т мещается вверх и вправо.
Рис. 11.8. Зависимость свободной эн- Если при наличии пузырьков повысится
тальпии от температуры давление при той же температуре, то (ду/др)т~> 0.
Пары 137
Так как изменение давления Др = 2а//?ш, то чем меньше радиус /?ш пузырька, тем выше
давление и температура Ть>> 7Y Перегрев Ть> — Ть — кТ обеспечивает получение
пузырька радиуса /?ш. Для увеличения радиуса пузырька перегрев необходимо увеличивать.
Для того чтобы паровой пузырь мог развиваться, его первоначальный радиус
должен превышать некоторое значение, удовлетворяющее условиям термодинамического
равновесия фаз. Такой радиус называется критическим и определяется
следующим образом.
При v"^>vf уравнение Клапейрона—Клаузиуса (5.31) в форме конечных
разностей можно записать как
р"-р = (Ть,-Тн)гр"/Тн. (11.18)
Решив (11.18) совместно с (11.16), получим
/?5Г = 2аГ„/[гр"(Г6,-Г„) ]. (11.19)
При радиусе пузыря R~> Rm он будет расти, в противном случае —
сконденсируется.
§11.4. Характерные состояния пара
Количество теплоты, необходимое для перевода при постоянном давлении 1 кг
жидкости, нагретой до температуры насыщения, в сухой насыщенный пар, называется
удельной теплотой парообразования г. В соответствии с уравнением
первого закона термодинамики для изобарного (и изотермного) процесса
парообразования
— v'\ (11.20)
или
r = h"-h', (11.21)
где и", v" — соответственно внутренняя удельная энергия и удельный объем сухого
насыщенного пара.
Часть ри удельной теплоты парообразования г расходуется на изменение
внутренней удельной энергии, на преодоление сил внутреннего сцепления между молекулами,
т. е. на перевод жидкости в пар: совершается работа дисгрегации — изменение
агрегатного состояния, поэтому
ри = и"-и'. (11.22)
Оставшаяся часть -ф удельной теплоты парообразования обеспечивает совершение
работы расширения, поэтому
♦ = p(w//-w/). (11.23)
Следовательно,
(11.24)
где ри -г- внутренняя удельная теплота парообразования (кинетическая энергия
молекул сохраняется, так как температура парожидкостной смеси постоянна), г|э —
внешняя удельная теплота парообразования. Значения ри, -ф, г являются функциями
температуры (давления). При критической температуре они равны нулю, так как в этом
случае v' = v"y u' = u"y h' = h".
Пар может быть влажным, сухим насыщенным и перегретым.
Термодинамические свойства влажного пара. Смесь кипящей жидкости и, сухого
насыщенного пара, находящихся между собой в термодинамическом равновесии, на-
138 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
зывается влажным паром. На рис. 11.1, б это область состояния, ограниченная
верхней и нижней пограничными кривыми. Для однозначного определения состояния
влажного пара необходимо знать соотношение в нем масс жидкости и пара. Масса
тх влажного пара (масса смеси) определяется суммой масс т" сухого насыщенного
пара и т! жидкости так, что
тх = т" + т'. (11.25)
Отношение массы т" сухого насыщенного пара к массе тх смеси называется
степенью сухости пара:
= т"/тх. (11.26)
Следовательно, содержание жидкости в смеси можно охарактеризовать степенью
влажности пара в виде соотношения
1 — х = т''/(/л" + т') = т'/тх. (11.27)
На vp- и sT-диаграммах (см. рис. 11.1, б) значение х = 0 соответствует нижней,
а х=\ —верхней пограничной кривой.
Объем, энтропия, внутренняя энергия и энтальпия подчиняются закону
аддитивности, поэтому удельные значения этих величин для влажного пара определяются
соотношением vx = v'(\ — x) + v"x> или
vx = v' + x(v"-v'yy (11.28)
s'); (11.29)
-и')\ (11.30)
-h'). (11.31)
Приведенные соотношения позволяют определять степень сухости пара через
отношения
х = (vx - v')/(v" - v') = (sx - s')/(s" - s') = (ux - и')I{и" - и')=(Л, - Л')/(Л" - К). (11.32)
Эти выражения позволяют определить положение линий постоянной степени сухости
на любой диаграмме состояния.
В области двухфазной смеси (влажного пара) при испарении сохраняются
постоянными давление и температура, поэтому
(dp/dv)T = 0; (dT/dv)p = 0. (11.33)
Построенные по точным измерениям vp- и sT-диаграммы показывают, что при
переходе через пограничную кривую изотермы на ур-диаграмме (см. рис. 11.1) имеют
излом. Следовательно, значение производной (dp/dv)T в точке пересечения изотермы
с пограничной кривой оказывается различным в зависимости от того, из какого
состояния приближаться к этой кривой. В одном случае величина (11.21) равна нулю, в другом
имеет некоторое значение. Таким образом, при переходе через пограничную кривую
производная (dp/dv)T испытывает разрыв. Излом имеет и изохора при пересечении с
пограничной кривой в координатах s, Т.
Причины этих изломов можно выяснить путем сопоставления теплоемкостей
жидкой и паровой фаз рабочего тела на пограничных кривых. В изобарном процессе
dq = rdx = cpdT. Но изменения температуры при испарении не происходит (с1Г=0),
поэтому ср= оо. Такой вывод свидетельствует о том, что внутри двухфазной области
понятие удельной теплоемкости ср не имеет смысла. Удельная изохорная
теплоемкость cv при переходе состояния рабочего тела через пограничную кривую изменяется
скачкообразно. Чтобы выявить это изменение cv при переходе через пограничную
кривую, следует рассмотреть ряд состояний пара, приближаясь по изохоре к состояниям
Пары 139
х — 0 или х—\. Придя в эти точки с разных сторон, можно получить разные значения
удельной теплоемкости, что и будет свидетельствовать о наличии скачка удельной
теплоемкости на пограничной кривой (верхней-и нижней).
Пусть c'V2 и cj, — удельная теплоемкость на нижней пограничной линии
соответственно для двухфазной среды и жидкости, а с"2 и с", — удельная теплоемкость на верхней
пограничной кривой соответственно двухфазной среды и пара. Чтобы выявить скачок
удельной теплоемкости, воспользуемся уравнением (4.43), представив его для
рассматриваемых условий в форме
cx = cv+T(dp/dT)v(dv/dT)x. (11.34)
При х = 0 c'v является удельной теплоемкостью при постоянном объеме на нижней
пограничной кривой при подходе к ней со стороны однофазной области. В этом случае
в соответствии с уравнением (11.34)
с' = c'Vi + T(dp/dT)vAv /dT. (11.35)
Здесь (dv/дТ)х==0= dv'/dT, a (dp/dT)v,— термическая упругость жидкости.
Для двухфазной области в уравнение (11.34) следует подставить производную
dp/dT вместо (dp/dT)v,y что соответствует, уравнению (5.31) Клапейрона—Клау-
зиуса:
с = cV2 + T(dp/dT) (dv/dT). (11.36)
Вычтем из уравнения (11.35) уравнение (11.36). Это покажет скачок удельной
теплоемкости при переходе состояния рабочего тела через нижнюю пограничную
кривую:
c'V2 - S = Г[ (dp/6T)v. - dp/dT\ (dv/dT). (11.37)
Здесь Т и производная dv'/dT больше нуля, так как на нижней пограничной кривой
с ростом температуры увеличивается и объем. Термическая упругость жидкости
(dp/dT)v> больше, чем термическая упругость двухфазной среды dp/dT, поэтому
алгебраический знак скобки в выражении (11.37) также положителен. Следовательно, при
переходе жидкости в двузфазную область скачок удельной теплоемкости положителен:
c'V2> c'V{\ она возрастает.
Аналогично, для верхней пограничной кривой
c'V2- c^ = T\{dp/dT)v,. - &р/АТ\ {Av"/AT). (11.38)
На верхней пограничной кривой с ростом температуры объем уменьшается:
dv"/dT<cO. Знак скобки также отрицателен, так как термическая упругость сухого
насыщенного пара меньше влажного. При переходе в двухфазную область через
верхнюю пограничную кривую происходит положительный скачок удельной
теплоемкости: c"2 — c'v\> 0.
Удельные теплоемкости cv в двухфазной области можно определить по
выражению CVx = Cv2(\ — X) + C'V'2X, ИЛИ
4=s+*(4-s)- (1L39)
Термодинамические свойства сухого насыщенного пара. При окончательном
испарении жидкости из двухфазной смеси влажный пар становится сухим насыщенным
(точка g, см. рис. 11.4). Его состояние определяется положением верхней пограничной
кривой х—\. Сухой насыщенный пар характеризуется или давлением насыщения, или
НО РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
температурой насыщения. Из уравнения (11.21) следует, что
Л" = Л' + г. (11.40)
Внутренняя энергия сухого насыщенного пара
u" = h" — pv". (П.41)
В процессе парообразования энтропия возрастает на величину As" = /-/7V
Таким образом, энтропия 1 кг сухого насыщенного пара определится суммой:
r«) + r/rH. (11.42)
Значения v"\ v\ h", h', г, s", s' приводятся в таблицах термодинамических свойств
паров жидкостей на линии насыщения.
Необходимо отметить, что состояние сухого насыщенного пара является крайне
неустойчивым.
Термодинамические свойства перегретого пара. При переходе состояния вещества
через верхнюю пограничную кривую образуется перегретый пар. Это
газообразное состояние вещества возникает при температурах, превышающих температуру
насыщения Т„. Область / (см. рис. 11.1) существования перегретого пара расположена
правее верхней пограничной кривой KN. Разность температуры перегретого пара ГН1.,
находящегося под давлением р, и температуры насыщения Тн при том же давлении
называется степенью перегрева. Свойства перегретого пара значительно
отличаются от свойств насыщенного пара. Чем больше степень перегрева, тем ближе
свойства перегретого пара к свойствам идеального газа. Отклонение этих свойств
объясняется конечными объемами молекул пара и наличием сил взаимодействия между
ними.
Предложено несколько уравнений состояния перегретого пара воды, основой
которых является характеристическое уравнение идеального газа, например для
водяного пара — уравнение Линде (1905)
pv = 47M — p{\—2p- 10~6)[0,031 (373/Г)3-0,052],
или уравнение Молье (1925)
pv = 47,\T- 2p/(7yi00)I()/3 - 190(p/100)3/(7yi00)4
Эти уравнения показывают, что отклонение поведения перегретого пара от идеально-
газового состояния тем больше, чем меньше перегрев и выше давление.
Удельная теплота qne для перевода сухого насыщенного пара при постоянном
давлении в перегретый называется теплотой перегрева и определяется в виде
интеграла:
гпс
Qne= \cp(T)dT, (11.43)
7\„ р = с
где ср — удельная теплоемкость перегретого пара при р = const.
В соответствии с первым законом термодинамики удельные внутренняя энергия
и энтальпия перегретого пара выражаются соотношениями
-v"); (11.44)
(11.45)
Удельная теплоемкость перегретого пара при p = consi является функцией не
только температуры, но и давления, что установлено опытным путем (рис. 11.9, а).
Пары
141
Рис. 11.9. Зависимость удельной теплоемкости
водяного пара от температуры: а — при р = const;
б — к определению средней удельной
теплоемкости
Рис. 11.10. s/i-диаграмма реального вещества
h'
Эмпирические зависимости ср = ср(ру Тпе) очень сложны и пользоваться ими трудно.
Для упрощения расчетов используют таблицы средней удельной теплоемкости.
Пл. a!abb' под кривой ср = ср(р, Тпе) (рис. 11.9, б) при постоянном давлении опре-
деляет удельную теплоту перегрева qne= \ cpdT. Средней удельной теплоемкостью при
т „
р — const является высота прямоугольника mnb'a с основанием Тпе — Тн, площадь
которого равна площади под изобарой, т. е.
cPm = qne/(Tne-TH)y (11.46)
(11.47)
и тогда
qne = cPm(Tne-TH).
Удельная энтропия перегретого пара определяется в виде интеграла:
=s"+ \cPm{AT/T).
Если в заданном интервале Тпе — Тн принять сРт неизменной, то
(11.48)
/ТН). (11.49)
В таблицы перегретого пара включаются значения удельной энтропии,
подсчитанные на основе дифференциальных уравнений термодинамики, и значения теплоемко-
стей, полученные экспериментальным путем.
§ 11.5. з/г-диаграмма
Молье в 1904 г. предложил s/i-диаграмму (рис. 11.10), которая получила широкое
применение в теплотехнике, так как удобна при практических расчетах. Использование
vp- и sT-диаграмм всегда связано с определением площадей, т. е. планиметрированием:
s/i-диаграмма дает возможность вместо площадей измерять отрезки, что гораздо
удобнее.
142
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Рассмотрим, как на s/i-диаграмме построены изолинии, характеризующие
параметры состояния влажного и перегретого пара и пограничные кривые. Положение
пограничных кривых на диаграмме может быть определено с помощью второго
уравнения (5.3). В соответствии с этим уравнением для нижней (х = 0) и верхней (х=1)
пограничных кривых {dh/ds)x-o=T + v'(dp/ds') и (dh/ds)=T + v"(dp/ds"). Так как в
критической точке dp/ds = 0, то (dh/ds) кр=ГКр. Таким образом, тангенс угла наклона
касательной к критической точке пограничной кривой на s/i-диаграмме равен ГКр.
В области влажного пара изобары в координатах s, h совпадают с изотермами и
представляют собой прямые линии, имеющие угол наклона, тангенс которого
определяется температурой (dh/ds)p=T. Чем выше температура, тем круче должна идти
изобара. На sT-диаграмме (см. рис. 11.4) изобары жидкости почти сливаются с
нижней пограничной кривой. Аналогичное положение и на s/i-диаграмме: нижняя
пограничная кривая является огибающей линией изобар. Наиболее крутой подъем этой
линии находится в критической точке. Затем наклон уменьшается, линии проходят
через максимум и снова снижаются. Рост энтропии жидкости и перегретого пара при
постоянном давлении приводит к увеличению температуры Т. Следовательно, изобары
жидкости (область //) и перегретого пара (область /) имеют постепенно
увеличивающуюся крутизну. Положение изотерм в области / перегретого пара можно установить
из выражения (dh/ds)T = T + v(dp/ds)T, дающего тангенс угла наклона изотермы. Угол
наклона изотермы отличается от угла наклона изобары на слагаемое v(dp/ds)T. Если
учесть соотношение (4.14), то
(dh/ds\ = T- v(dT/dv)p. (11.50)
Здесь (dT/dv)p — величина, обратная термической расширяемости. В выражении (11.50)
из Т вычитается положительная величина, поэтому на пограничной кривой изотерма
и изобара расходятся. Чем выше температура, тем ближе состояние пара к состоянию
идеального газа, для которого
(dT/dv)p=T/v. (11.51)
Рис. 11.11. h—lg р-диаграмма реального вещества
Пары
143
Сопоставление выражений (11.50) и (11.51) показывает, что тангенс угла наклона
изотермы стремится к нулю. Следовательно, и изотерма становится все более пологой,
приближаясь к горизонтали.
Удельная энтальпия идеального газа при постоянной температуре неизменна,
поэтому зависимость h — h(s) для идеального газа представляет собой горизонтальную
линию.
Для любой точки на s/i-диаграмме можно найти величины р, v, Г, /i, s и х, значения
которых нанесены на соответствующие характерные линии. Удельная теплота
парообразования определяется разностью r = h" — h\ а внутренняя удельная энергия —
соотношением и = к— pv.
В некоторых случаях удобнее использовать координаты, в которых изобары
горизонтальны на всем поле диаграммы, например на к — lgp-диаграмме (рис. 11.11).
§11.6. Термодинамические процессы
Исследование и расчет процессов изменения состояния пара могут быть выполнены как
аналитическим путем, так и графически с помощью диаграмм. При аналитическом методе
расчета каждый процесс приходится рассматривать отдельно в области /// (рис. 11.1, б)
двухфазного состояния вещества и в областях I и II однофазного состояния. При
графическом методе, например по s/i-диаграмме (см. рис. 11.10), расчет сводится к
определению значений начальных и конечных параметров, определяющих состояние пара.
Для анализа работы теплотехнических установок существенное значение имеют
процессы: изохорный cb = 0 (рис. 11.12, а—в), изобарный dp = O (рис. 11.13, а—в),
изотермный dT = O (рис. 11.14, а—в) и изоэнтропный ds = 0 (рис. 11.15, а—в).
Ь)
/А
ЬТ
Рис. 11.12. Изохорное изменение состояния пара в координатах: а — у, р\ б — s, T\
в — s, h
/к:
и*
Рис. 11.13. Изобарное изменение состояния пара в координатах: а — и, р\ б —
s, Т\ в — s, к
144
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Рис. 11:14. Изотермное изменение состояния пара в координатах: а — и, р\ б — s, Г;
в — s, h
К 1
5-Const
Рис. 11.15. Изоэнтропное изменение состояния пара в координатах: а — и, р; б —
s, Г; в — s, h
Для применения графического метода расчета процессов изменения состояния
пара необходимо прежде всего нанести на диаграмму исследуемый процесс. После
этого значения всех тепловых величин находят непосредственно по s/i-диаграмме по
положению начальной и конечной точек линии процесса. Изменение удельной
внутренней энергии пара в процессе определяется по формуле
(11.52)
при всех термодинамических процессах. Количество теплоты, сообщаемое пару в
процессе, может определяться по формулам:
для изохорного процесса q = h2 — h\—v(p2 — p\)', (11.53)
для изобарного процесса q = h2 — h\\ (11.54)
для изотермного процесса q = T(s2 — s\). (11.55)
Удельная работа пара в этих процессах, согласно первому закону термодинамики,
l = q — ^ (11.56)
с учетом алгебраического знака входящих в нее величин.
При расчете изоэнтропного изменения состояния можно использовать уравнение
изоэнтропы pvk — const, которое дает лишь приближенное значение искомой величины.
Связано это с тем, что для паров k=£cp/cv(k — эмпирическая величина,
соответствующая данному веществу и данному давлению). Например, для влажного водяного пара
во многих (но не во всех) случаях справедливо соотношение Цейнера k= l,035 + 0,lx;
для перегретого водяного пара k =1,3.
Пары
145
Ввиду сложности уравнений состояния реальных газов термодинамические
параметры состояния обычно сводятся в таблицы. При разработке таких таблиц
используются надежные экспериментальные данные.
Две таблицы составлены для определения теплофизических свойств жидкости
и пара на линии насыщения. Так как давление и температура насыщения связаны
между собой однозначно, то в одной таблице в качестве аргумента приведена
температура насыщения, в другой — давление. В каждой из этих таблиц даны
функциональные значения удельных объемов, энтальпии и энтропии на нижней и верхней
пограничных кривых, а также удельной теплоты парообразования. По ним можно определить
все параметры состояния влажного пара.
Составлена таблица для однофазной области, в которой параметры состояния
у(м3/кг); /*(Дж/кг); $(Дж/(кг-К)) приведены по изобарам в зависимости от
температуры / °С).
На примере табл. 11.1 рассмотрим, как пользоваться таблицами для однофазной
области. Под цифрой, указывающей нужную изобару (в данном случае 100 кПа),
показаны значения параметров жидкости (v\ h\ s') и сухого насыщенного пара (v"', h", s"),
соответствующие температуре насыщения /Н = 99,63°С и выбранному давлению.
Таблица 11.1
/°, с
70
80
90
100
ПО
120
Р =
100 кПа
/,, = 99,63°С
и' = 0,0010434 и" = 1,6946
/i/ = 417,51 Л" = 2675,7
5'= 1,3027 $" = 7,3608
V
0,0010228
0,0010292
0,0010361
1,696
1,745
1,793
h
293,0
335,0
377,0
2676,5
2676,7
2716,8
s
0,9548
1,0752
1,1925
7,3628
7,4164
7,4681
В зависимости от температуры / параметры жидкости находятся над, параметры
перегретого пара — под горизонтальной чертой.
Параметры критического состояния воды:
Давление 22,1 МПа
Температура 374,12 °С (647,12 К)
Удельный объем 0,003147 м3/кг
Удельная энтальпия 2095,2 кДж/кг
Удельная энтропия 4,4237 кДж/кг
Наиболее распространенным рабочим телом в энергетике является вода. Таблицы
термодинамических свойств воды и водяного пара, разработанные советскими
учеными М. П. Вукаловичем, В. В. Сычевым, С. Л. Ривкиным, А. А. Александровым,
легли в основу рекомендаций по составлению уравнений состояния для воды и водяного
пара по всей области параметров состояния.
146 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Вопросы I. Чему равна теплота парообразования в критической точке?
2. Есть ли разница между давлением внутри парового пузыря и в окружающей его
жидкости? Если да, то где оно меньше?
3. Какое состояние пара является наименее устойчивым: влажный, сухой
насыщенный, перегретый?
4. Что называется степенью сухости пара?
Глава 12
ВЛАЖНЫЙ ВОЗДУХ
§ 12.1. Параметры влажного воздуха
Атмосферный воздух- всегда смешан с водяным паро.м. Такая смесь сухого воздуха с
водяным паром называется влажным воздухом. Однако количество водяного
пара в газовой смеси не может быть произвольным.
В зависимости от температуры и полного давления смеси количество водяного
пара во влажном воздухе не может превышать определенной величины.
Так как в процессах изменения физического состояния влажного воздуха состав
сухого воздуха не изменяется, его можно считать одним из компонентов
паровоздушной смеси, несмотря на то что в действительности он сам является смесью газов.
Вторым компонентом влажного воздуха является водяной пар. Возможность фазового
перехода у одного из компонентов смеси (воды) отличает влажный воздух от
обычной газовой смеси.
Кроме водяного пара влажный воздух может содержать мельчайшие капельки
воды (в виде тумана) или кристаллики льда. Водяной пар во влажном воздухе может
быть в перегретом или насыщенном состоянии. Парциальное давление водяного
пара рп во влажном воздухе не может быть выше давления насыщения рн при
данной температуре влажного воздуха (рп< Рн). Наибольшее значение парциального
давления водяного пара во влажном воздухе рн определяется только температурой
смеси и не зависит от давления смеси р.
Смесь сухого воздуха с перегретым водяным паром называется ненасыщенным
влажным воздухом. Для такой смеси справедливо условие рп<рн. Смесь
сухого воздуха с насыщенным водяным паром называется насыщенным влажным
воздухом. В насыщенном влажном воздухе р„ = рн-
Понижая температуру насыщенного влажного воздуха при постоянном давлении,
можно охладить воздух до такой температуры, при которой парциальное давление
водяного пара будет соответствовать состоянию насыщения, и при дальнейшем
понижении температуры из воздуха начнет выделяться влага. Так, например, понижение
температуры атмосферного воздуха часто приводит к появлению тумана (т. е. к
конденсации пара).
При давлениях, близких к атмосферному, газовая смесь, состоящая из воздуха и
водяного пара, по своим свойствам мало отличается от свойств идеального газа.
Парциальное давление водяного пара в воздухе обычно мало, поэтому и водяной
пар при этих условиях можно считать идеальным газом*.
Абсолютная и относительная влажность воздуха. Масса водяного пара,
содержащегося в 1 м3 влажного воздуха, называется абсолютной влажностью.
Так как влажный воздух представляет собой газовую смесь, то объем водяного
* При изучении процессов, протекающих во влажном воздухе, обычно не учитывается
растворимость воздуха в воде, а также присутствие в воздухе веществ, которые могут
повлиять на давление насыщения.
Влажный воздух 147
пара в смеси равен объему всей смеси и, следовательно, абсолютная влажность
равна парциальной плотности пара рп в смеси при своем парциадьном давлении рп
и температуре смеси:
9n=rnJV = pn/{RnT). (12.1)
Отношение абсолютной влажности воздуха р{, к максимально возможной
абсолютной влажности pi при данной температуре называется относительной
влажностью. Так как для идеальных газов в условиях T = const отношение
плотностей можно заменить отношением давлений, то относительная влажность
Ф==Рп/Рн=Рп/Рн, (12.2)
где рп и /?н — парциальные давления водяного пара во влажном воздухе и
насыщенного пара при температуре влажного воздуха.
Относительная влажность обычно выражается в процентах и изменяется в
пределах 0<ф<100%, так как пределы изменения парциального давления пара
0<рп<рн. Для сухого воздуха ф = 0, для насыщенного ф= 100 %. Для определения
содержания пара во влажном воздухе помимо относительной влажности ф необходимо
знать температуру влажного воздуха, по которой (из паровых таблиц) определяется
давление насыщенного пара рн. Абсолютная влажность воздуха рп = фр(,.
Влагосодержание и степень насыщения. Отношение массы т„ водяного пара,
содержащегося во влажном воздухе, к массе тв сухого воздуха называется
влагосодержанием d влажного воздуха:
d = mn/mB = p'n/pB, (12.3)
где рп и pi — парциальные плотности водяного пара и воздуха.
В некоторых случаях оказывается более удобным иметь дело с молярным
влагосодержанием. Отношение количества водяного пара, содержащегося во влажном
воздухе, к количеству сухого воздуха называется молярным
влагосодержанием х влажного воздуха:
х = {тп/Мп)/(тл/Мл), (12.4)
где индексами «п» и «в» отмечены массы и молярные массы водяного пара и сухого
воздуха соответственно.
В процессах изменения физического состояния влажного воздуха количество
сухого воздуха остается неизменным, поэтому все удельные величины, характеризующие
состояние влажного воздуха, целесообразно относить к количеству сухого, а не влажного
воздуха. С учетом того, что молярные массы водяного пара Мп и воздуха Мъ
равны 18,016 и 28,96 кг/кмоль соответственно, получим следующую связь молярного
влагосодержания х с влагосодержанием воздуха x=l,61d кмоль/кмоль или d =
= 0,622* кг/кг.
Так как влажный воздух рассматривается как смесь идеальных газов, отношение
количеств различных газов в киломолях равно отношению парциальных давлений этих
газов. Следовательно,
х = ра/(р-рп) (12.5)
или
£/ = 0,622р„/(р-р„), (12.6)
где р — давление влажного воздуха; р — рп — парциальное давление сухого воздуха.
Эти формулы применимы только для условий, при которых влага в воздухе содержится
в виде пара. При этих условиях относительная влажность и влагосодержание
148 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
d --= 0,622Фрн/(р - фр„); ф = pd/[(d + 0,622)рн].
Используя соотношение (12.6), получим
pn = d-p/(0fi22 + d)\ (12.7)
pB = 0,622p/(0,622 + d). (12.8)
В том случае, когда значение парциального давления водяного пара равно давлению
насыщенного пара при данной температуре, влагосодержание достигает наибольшего
значения. Из формул (12.5) и (12.6) для насыщенного влажного воздуха
получим
*.. = Рн/(р —Рн); (12.9)
dH = 0,622pH/(/?-pH) (12.10)
— значение влагосодержания зависит от давления и температуры влажного воздуха.
Чем выше температура влажного воздуха, тем больше значения хн и d», так как с
ростом температуры увеличивается давление насыщенного пара. В обычных условиях,
когда давление влажного воздуха равно барометрическому, по мере приближения
температуры влажного воздуха к 100 °С влагосодержание влажного воздуха стремится
к бесконечности, так как давление насыщенного пара в этих условиях приближается
к барометрическому. В предельном случае (d = 0) парциальное давление водяного пара
во влажном воздухе равно нулю, a pa = p. Из формул (12.7) и (12.8) следует,
что при d=oo парциальное давление водяного пара равно давлению влажного
воздуха, а рв = 0. Если влагосодержание поддерживается постоянным, а температура
влажного воздуха растет, относительная влажность воздуха уменьшается, поскольку с
ростом температуры увеличивается значение р„.
В некоторых случаях в качестве относительной меры влагосодержания
используется степень насыщения -ф:
(12.11)
С учетом выражений (12.6), (12.10) и (12.2) соотношение (12.11) примет вид
— Рп)]=ф(р — Рн)/(р — рп). (12.12)
Для умеренных температур влажного воздуха, при которых парциальное давление
пара мало по сравнению с давлением влажного воздуха, можно принять, что
*|з = ф. (12.13)
Кажущаяся молярная масса, газовая постоянная и плотность влажного воздуха.
Объемные доли сухого воздуха и пара во влажном воздухе могут быть определены,
если известны парциальные давления пара и сухого воздуха, отношениями
/-в = рв/р = (р — р„)/ругп = рп/р, где в соответствии с законом Дальтона р = рв + рп.
При известных объемных долях кажущаяся молярная масса влажного
воздуха может быть вычислена по формуле (8.16):
р. (12.14)
Если учесть, что рп = фр„, и принять водяной пар, находящийся во влажном воздухе, в
качестве идеального газа, то
М = 28,96 — 10,94фр„/р. (12.15)
При заданном давлении влажного воздуха кажущаяся молярная масса влажного
воздуха зависит от температуры и относительной влажности воздуха.
Так как, согласно формуле (8.13), газовая постоянная смеси газов /? = 8314/М,
газовую постоянную воздуха можно определить отношением
Влажный воздух И9
/? = 8314/(28,96 — 10,94рп/р) = 8314/(28,96 — 10,94фр„/р). (12.16)
При ср = О (соответствует сухому воздуху) /? = /?в = 287 Дж/(кг-К). В другом
предельном случае при ф= 1 (соответствует чистому водяному пару) рн = Р, а /? = /?„ =
= 461 Дж/(кг./С).
Газовая постоянная влажного воздуха всегда больше газовой постоянной сухого
воздуха.
Массовые доли сухого воздуха и пара во влажном воздухе могут быть выражены
через влагосодержание так:
gn = (mB/m) = тв/(тв + тп)= 1 /(1 +d)\ gn = (mn/m) = mn/(mB + mn) = d/(\ + d).
Используя зависимость (8.9), для газовой постоянной влажного воздуха
можно получить формулу
(12.17)
С учетом (12.16) уравнение состояния влажного воздуха может быть записано в
следующей форме: р/р = 83147/(28,96— 10,94рп/р), откуда плотность влажного
воздуха
р = (28,96р-10,94рп)/(8314Г). (12.18)
Из полученной формулы следует, что с увеличением парциального давления пара
(т. е. с увеличением влажности воздуха) плотность влажного воздуха уменьшается.
Поэтому влажный воздух всегда легче, чем сухой.
Так как плотность влажного воздуха равна сумме парциальных плотностей
сухого воздуха и водяного пара, а влагосодержание d = pn/p£, то
(12.19)
Парциальная плотность водяного пара может быть вычислена по уравнению
состояния. С учетом формулы (12.7)
9'n = (mJV) = pn/(RJ) = d.p/[(Ofi22 + d)RJ]. (12.20)
Подставляя значения р„ в выражение (12.19), окончательно получим
]. (12.21)
Теплоемкость и энтальпия влажного воздуха. Теплоемкость влажного
воздуха ср обычно относят к (\+d) кг влажного воздуха (или, что то же самое, к
1 кг сухого воздуха). Она равна сумме теплоемкостей 1 кг сухого воздуха и d кг
водяного пара:
fmt (12.22)
где срв и срп — массовые изобарные теплоемкости сухого воздуха и водяного пара
соответственно. В приближенных термодинамических расчетах, связанных с влажным
воздухом, можно принимать срвж\ кДж/(кг-К) и срп«1,93 кДж/(кг-К).
Энтальпия влажного воздуха определяется как энтальпия газовой
смеси, состоящей из 1 кг сухого воздуха и d кг водяного пара, поэтому
ny (12.23)
где ha — энтальпия сухого воздуха, hn — энтальпия водяного пара. При определении
энтальпии газовой смеси необходимо, чтобы энтальпии компонентов смеси имели одно и
то же начало отсчета. Энтальпия сухого воздуха hB = cpBt = t, так как срл=\. Водяной
пар в первом приближении можно принять в качестве идеального газа, энтальпий
которого не зависит от давления. Если кроме того, учесть, что в условиях измене-
150 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
ния физического состояния влажного воздуха интервал изменения температур мал, то
можно принять теплоемкость водяного пара постоянной. При этих упрощающих
предположениях энтальпия водяного пара может быть вычислена по формуле
hn = r + cpnt, (12.24)
где г — скрытая теплота парообразования при 0 °С. Так как /- = 2501 кДж/кг, то
/in = 2501 + 1,93/. Таким образом, формуле (12.23) можно придать вид
/1 = / + (2501 + 1,93/К (12.25)
Используя соотношения (11.2) и (11.6), установим зависимость энтальпии
влажного воздуха от относительной влажности:
(р —ФРн). (12.26)
В общем случае,- когда влажный воздух помимо водяного пара содержит воду
(туман) и лед (снег), в правой части формулы (12.25) появятся еще два слагаемых
йжИж и dThTy в которых с1жн dT — содержание жидкой и твердой фазы во влажном воздухе;
/гж = сж/ = 4,19/ и hT=2y\t — 335 — энтальпия воды и льда соответственно. В этом случае
формула для расчета энтальпии влажного воздуха получит вид
(12.27)
При наличии жидкой или твердой фазы влагосодержание d — dH.
§ 12.2. Температура мокрого термометра
Процессы тепло- и массообмена между открытой поверхностью воды и потоком влажного
воздуха распространены в природе и технике. С этими процессами приходится
иметь дело в системах охлаждения электростанций, системах кондиционирования
воздуха, системах жизнеобеспечения космических летательных аппаратов, а также в
сушильных и вентиляционных установках.
В общем случае температура поверхности воды может быть как ниже, так и выше
температуры окружающего ее влажного воздуха. Однако рассмотрим процесс испарения
жидкости при условии, что в начале процесса температура воды равна температуре
окружающего влажного воздуха, а слой жидкости достаточно тонкий (т. е. температура
жидкости одинакова по толщине слоя). Количество же воздуха неограниченно. Из
опыта известно, что парциальное давление пара в тонком слое, прилегающем к
поверхности жидкости, равно давлению насыщенного пара рн при температуре
поверхности жидкости. Если при этом во влажном воздухе, окружающем поверхность воды,
парциальное давление пара рп окажется меньше давления насыщенного пара рн, вода
начнет испаряться.
По мере испарения воды температура поверхности жидкости понижается, в то
время как разность температур окружающего воздуха и поверхности жидкости, а
также количество теплоты, поступающее от воздуха к жидкости, возрастают.
Понижение температуры воды прекратится только тогда, когда количество внутренней
энергии, расходуемое жидкостью на испарение, окажется равным количеству теплоты,
получаемому жидкостью от окружающего воздуха.
Температура поверхности жидкости, достигнутая в результате рассматриваемого
процесса установления равновесия, называется температурой мокрого
термометра (/„). Эта температура измеряется термометром, чувствительный элемент
которого обернут влажной тканью.
Температура мокрого термометра зависит от соотношения между коэффициентами,
характеризующими интенсивность процессов тепло- и массообмена, протекающих между
поверхностью воды и влажным воздухом. Следует подчеркнуть, что для условий, в
которых обычно протекают процессы во влажном воздухе, она близка к температуре
Влажный воздух
151
адиабатного насыщения воздуха. Последняя устанавливается при насыщении
ограниченного количества воздуха, находящегося в контакте с водой, если испарение воды
происходит только за счет количества теплоты, передаваемого из воздуха. В отличие
от температуры мокрого термометра температура адиабатного насыщения зависит
от начального состояния воздуха.
Уравнение теплового баланса влажного воздуха, находящегося в контакте с водой,
можно представить в форме
/i2-/i. =СжЛ.(£/2-4|), (12.28)
где индекс 1 соответствует начальным значениям энтальпии и влагосодержания,
а индекс 2 — конечным. Правая часть этого уравнения определяет также изменение
энтальпии испарившейся воды, приходящейся на 1 кг сухого воздуха, содержащегося
во влажном воздухе. В пределе воздух в конечном состоянии будет насыщенным.
Учитывая значение теплоемкости воды и принимая начальное влагосодержание
равным нулю, получим
Л, = Л2 — 4,19Ы2, (12.29)
где tM — температура мокрого термометра.
§ 12.3. rf/г-диаграмма влажного воздуха
Наиболее просто и быстро можно определять параметры влажного воздуха, а также
проводить исследования термодинамических процессов с влажным воздухом с помощью
d/i-диаграммы.
Впервые d/i-диаграмма для влажного воздуха была предложена профессором
Л. К. Рамзиным (1918) и нашла широкое применение в расчетах систем
кондиционирования, сушки, вентиляции и
отопления. В d/i-диаграмме (рис. 12.1) по
оси абсцисс откладывается влагосо-
3 10 11 12
d} б/кг
Рис. 12.1. dh—диаграмма влажного воздуха; а — схема построения; б- изображение процессов,
происходящих во влажном воздухе
152 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
держание d (г/кг сухого воздуха), а по оси ординат — удельная энтальпия h влажного
воздуха (кДж/кг). По делениям на оси абсцисс проведены вертикальные прямые
постоянного влагосодержания (d = const). За начало отсчета удельных энтальпий
принята точка 0, в которой / = 0°С, d = 0 и, следовательно, Л = 0 кДж/кг.
При построении d/i-диаграммы использована косоугольная система
координат, так как в такой системе область ненасыщенного воздуха занимает
значительно большую площадь диаграммы. Через точки на оси ординат проводят
линии /i = const под углом а=135° к линиям d = const. После нанесения сетки
линий d = const и /i = const на диаграмму наносят изотермы (/ = const) и кривые
cp = const. Уравнение (12.25) показывает, что изотермы в d/z-диаграмме — прямые
линии.
Из уравнения (12.25) следует, что /z = 0 кДж/кг, если / = 0 °С и d = 0.
Следовательно, изотерма / = 0°С проходит через начало координат. По уравнению (12.10) при
ф= ЮО % находят значение dH для заданной температуры. Энтальпию воздуха при
/ = 0°С и dH (в точке Ь) находят по формуле (12.26). Прямая, проведенная через
точки 0 и Ь, дает изотерму при / = 0°С. Для других значений (Ф0 строят изотермы
аналогично. Так, для построения изотермы при /=10°С, проходящей через точки
а\ и Ь\, по уравнениям (12.10) и (12.26) предварительно определялись значения
hud.
Соединив точки с одинаковыми значениями ф (например, точки b, b\ и другие
для ф=100%), получим кривую cp = const. Любая точка этой кривой ф=Ю0%
характеризует состояние насыщенного воздуха; точка, лежащая выш/кривой ф= 100 %,
характеризует состояние ненасыщенного воздуха, в котором водяной пар находится в
перегретом состоянии, а точка, лежащая ниже кривой ф=100%, характеризует
состояние так называемого пересыщенного воздуха (область тумана). При условии
Ф^ 100 % кривые ф = сопз1 строятся по тем же уравнениям, что и ранее.
Предварительно определяют значения влагосодержания для данного ф = сопя! при различных
температурах влажного воздуха. Затем находят точки, соответствующие парным
значениям d и /, соединение которых и дает кривую ф = согЫ. Например, таким
образом построена кривая для ф = 90 % (рис. 12.1, а), проходящая через точки
Си С2 И С3.
В нижней части d/i-диаграммы, используя расчеты по формуле (12.6), наносят
линию парциальных давлений водяного пара рп, содержащегося в воздухе. Для
этого на кривой насыщения ф=100% отмечают точки пересечения ее с изотермами
и из этих точек проводят вертикальные прямые (на схеме показаны пунктиром). На
этих вертикалях в определенном масштабе для парциальных давлений пара
откладывают отрезки O|/?i, O2k2, O3&3 и т. д., соответствующие парциальным давлениям
водяного пара в состоянии насыщения при заданных температурах (эти значения
определяют из таблиц водяного пара). Соединение плавной кривой точек ku &2, &з
и т. д. дает зависимость p,, = /(d).
На d/i-диаграмме строят изотермы мокрого термометра, т. е. линии /M = const.
Для их построения необходимо иметь аналитическую зависимость между величинами
/м, hud. Эта зависимость устанавливается уравнением (12.28).
Линии /м = const на d/z-диаграмме строят исходя из следующих соображений. При
адиабатном увлажнении воздуха, имеющем до начала увлажнения влагосодержание
d = 0, приращение энтальпии воздуха происходит за счет энтальпии испарившейся
воды (12.29). Пусть на d/z-диаграмме (рис. 12.1, а) состояние насыщенного воздуха
соответствует точке е. Чтобы определить параметры начального состояния, следует
найти точку, в которой d = 0 и h — he.
В соответствии с выражением (12.29) he^h2 — cAitMdMj поэтому из точки е
необходимо провести прямую /i2 = const до пересечения ее с осью ординат h и отложить
вниз от этой точки в масшабе энтальпии отрезок, равный сжгыйн. Это даст точку /.
Влажный воздух 153
Прямая ef и является искомой изотермой tM = const. На d/i-диаграмме линии tM = const
располагаются более полого, чем линии h = const.
На d/i-диаграмме линии /M = const наносят пунктирными линиями. При температуре
/ = 99,4 °С, соответствующей температуре насыщения при давлении р = 99,3 кПа (для
этого давления построена данная d/i-диаграмма), кривые ф = const круто поднимаются
вверх.
Обычно d/z-диаграмму строят для какого-то среднего атмосферного давления.
Чтобы выяснить, можно ли пользоваться данной d/i-диаграммой для других давлений,
необходимо найти зависимость основных параметров влажного воздуха от атмосферного
давления. Однако линия насыщения ф=100%, а также другие линии относительной
влажности (ср<<100%) при различных атмосферных давлениях не одинаковы.
Объясняется это тем, что при различных давлениях в данном объеме воздуха
содержится различное количество пара, т. е. d = f(p) в соответствии с формулой
(12.6).
Несмотря на это, по d/i-диаграмме, построенной для заданного атмосферного
давления, можно рассчитать параметры влажного воздуха и для других давлений.
В этом случае формулу (12.6) следует представить в виде d = 0,622/[(p/<p)(l/pH)— 1].
Из такой записи формулы вытекает, что любая кривая cp = const на данной d/z-диаграмме
может быть использована для любых атмосферных давлений, однако значения
относительной влажности будут различными и определятся отношением р/ср.
Для теплотехнических расчетов с влажным воздухом широко используются
d/i-диаграммы. Так, например, в процессе сушки воздух предварительно подогревается
в устройстве, называемом калорифером. При нагревании в калорифере влагосодержание
воздуха не изменяется (d\ = const), поэтому процесс нагревания на d/i-диаграмме
изображается вертикальной прямой (прямая 1-2 на рис. 12.1, б). Процесс охлаждения
воздуха происходит при постоянном влагосодержании, т. е. линия dz = const также
вертикальная прямая 3-4. В точке 4 ненасыщенный воздух становится насыщенным
(ф=100%), а водяной пар оказывается сухим насыщенным. При дальнейшем его
охлаждении происходит конденсация, которая приводит к уменьшению влагосодержания
во влажном воздухе. Условно процесс конденсации 4-5 принимается происходящим при
Ф=Ю0%.
Количество влаги Ad, выпавшей в процессе конденсации пара, определяется
разностью: Ad = d3 — d*>. Если принять, что энтальпия воды равна нулю, то процесс
испарения воды можно считать происходящим при постоянном значении энтальпии
влажного воздуха (прямая 3-6). Действительно, если энтальпия воды равна нулю, то
теплота воздуха, затраченная на испарение воды, возвратится в воздух вместе
с испарившейся влагой, поэтому энтальпия влажного воздуха в процессе испарения —
величина постоянная.
На d/i-диаграмме (рис. 12.1, б) дана схема определения точки росы. С
уменьшением температуры ненасыщенного влажного воздуха при d — const (процесс 3-4)
увеличивается ф. При ф=100% имеем состояние насыщенного влажного воздуха
(точка 4). Температуру, при которой ф=100%, называют точкой росы.
§ 12.4. Смешение потоков влажного воздуха
Смешение потоков влажного воздуха также можно анализировать с помощью d/i-диаг-
раммы. Пусть в смесительную камеру поступают два потока влажного воздуха с
расходами воздуха т\ и т2, соответствующими влагосодержаниями d\ и d<i,
температурами t\ и h и энтальпиями h\ и /гг- При анализе принимается, что в смесительной
камере оба потока перемешиваются при р = const без теплообмена с внешней средой.
В результате из смесительной камеры выходит поток воздуха (тт) с параметрами
dM, tm и hM.
154
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Запишем уравнения материального баланса для воздуха mi + m2 = mm и для воды
= tnmdm. Таким образом,
Уравнение энергетического баланса смешения в камере имеет вид mi/ii+m2A2 =
= mmhm, откуда
Соотношение поступающих з камеру масс влажного воздуха a = m2/mi;
следовательно, в соответствии с формулой (12.30) dm = (d\ +ad2)/(l +a), откуда
a = {dm — di)/(d2 — dm). (12.32)
Перепишем формулу (12.31) с учетом этого соотношения, тогда /im = (Ai+a/i2)/(l +a),
откуда
а = (Ат-Л,)/(А2-Л«).
(12.33)
Сопоставляя выражения (11.32) и (11.33), имеем (dm — d\)/(d2 — dm) —
= (Am — h\)/(fl2 — hm) , ИЛИ
Следовательно, точка m, характеризующая состояние влажного воздуха после
смешения, должна находиться на прямой, соединяющей точки / и 2, которые
характеризуют на d/i-диаграмме начальные потоки воздуха т\ и т2 (рис. 12.2, а).
Положение точки т на этой прямой может быть определено при известных массовых
долях смешиваемых потоков воздуха. Так как gx = m\/(m\ +m2) и £2 = т2/(я
а gi+g2=l, то с учетом формулы (12.32) g\—(d2 — dm)/(d2 — d\) и g2 = (dm — c
— d\). Из этих формул и следует, что точка т (рис. 12.2, а) делит прямую смешения
1-2 в отношении gi'.g2-
Из d/i-диаграммы видно, что перед смешением могут быть взяты такие два
состояния двух ненасыщенных потоков воздуха (точки V и 2'), которые при смешении
приведут к образованию тумана (точки т' на рис. 12.2, а).
а)
Рис. 12.2. Определение состояния влажного воздуха по rf/i-диаграмме: а— после
смешения; б — по температуре сухого и мокрого термометров
Влажный воздух 155
§ 12.5. Определение влажности воздуха по температурам
мокрого и сухого термометров
Относительная влажность воздуха является одним из основных его параметров,
используемых в различных технических расчетах (например, выбор режима вентиляции
и др.).
Применяют четыре способа определения относительной влажности воздуха:
химический, точки росы, волосяного гигрометра и психрометрический. Наиболее
распространенным способом является психрометрический.
Психрометр состоит из двух одинаковых термометров. Один из них называется
сухим термометром, а его показания — температурой воздуха по сухому
термометру. Второй термометр обернут мокрой лентой, обеспечивающей непрерывный
подвод воды к ртутному шарику, для того чтобы его поверхность была всегда
влажной. Этот термометр называют мокрым термометром. Испарение влаги
с поверхности шарика приводит к его охлаждению, поэтому мокрый термометр
всегда показывает более низкую температуру, чем сухой.
Разность показаний термометров называется психрометрической разностью. Однако
температура tMy показываемая мокрым термометром, вследствие теплопередачи к
термометру извне не равна истинной температуре мокрого термометра /£,(/*>/С). Для
уменьшения разности &t — tM — t'M шарик мокрого термометра обдувается воздухом,
движущимся с достаточной скоростью. Это уменьшает влияние возможного излучения
окружающих предметов на термометр. В современных психрометрах оба термометра
заключены в заградительные кожухи, поверхности которых полированы. Воздух через
кожухи продувается специальным вентилятором, имеющим механический или
электрический привод.
Показания психрометра дают возможность по d/i-диаграмме определить относитель^
ную влажность и влагосодержание влажного воздуха. Для этого необходимо
определить точку / пересечения изотермы tM (мокрого термометра) с изотермой tc
(сухого термометра), как это показано на рис. 12.2, б. Эта точка на d/i-диаграмме
и определит состояние влажного воздуха в помещении.
Если имеются показания психрометра, то определить относительную влажность ср
и влагосодержание d можно также по специальным психрометрическим таблицам.
§ 12.6. Кондиционирование воздуха
Деятельность современного человека протекает в самых разнообразных условиях: в
космических аппаратах, подводных лодках, глубоких шахтах, на фабриках и заводах,
наконец, дома — и везде человек должен находиться в определенных условиях.
Атмосферный воздух представляет смесь сухих газов и водяного пара, т. е. является
влажным воздухом. Практически неизменной остается лишь сухая часть состава воздуха.
Давление воздуха у поверхности Земли равно 90,6...108 кПа, температура 203...333 К,
относительная влажность 10... 100 %. В воздухе постоянно содержится пыль. Даже за
городом после дождя в 1 л атмосферного воздуха содержится до 100 частичек пыли
(в городе —до 200 000).
Во многих отраслях промышленности практически нельзя работать без создания
изолированного климата, без применения так называемого кондиционирования
воздуха. Под кондиционированием воздуха обычно понимают совокупность
технических средств и способов воздействия на температуру и влажность воздуха. Термин
«кондиционирование» происходит от латинского слова «condicio», что означает
«условие». Путем создания систем кондиционирования необходимо обеспечить определенные
значения параметров воздуха, подаваемого в кондиционируемое помещение.
Работа прямоточной системы кондиционирования воздуха протекает при различных
состояниях наружного воздуха, подаваемого в помещение. Поэтому при настройке
156
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Рис. 12.3. Схема определения параметров влажного
воздуха при кондиционировании: а — на летнем, б —
на зимнем режиме
г
6
/
\
-^—
2
\
J
Rk-
\
4(1
У
1
D
?
Рис. 12.4. Схема кондиционера
системы кондиционирования предусматривается обычно несколько режимов: летний,
зимний, промежуточный и др.
Для расчета параметров кондиционирования можно воспользоваться d/i-диаграм-
мой. Пусть, например, система кондиционирования настроена на летний режим, а точка
/ на диаграмме (рис. 12.3, а) отражает состояние наружного влажного воздуха с
параметрами t\ и d\, точка 2 — состояние подаваемого в помещение приточного
воздуха с параметрами t2 и d2, точка 3 — состояние воздуха в помещении с параметрами
/з, d3. Если при кондиционировании применяются прямоточная схема, то весь
приточный воздух поступает снаружи. Наружный воздух (точка /) обладает большими
влагосодержанием d\ и температурой t\. Следовательно, для получения приточного
воздуха с параметрами d2 и t2 необходимо уменьшить температуру наружного
воздуха от t\ до t2 и влагосодержание от d\ до d2. Это означает, что наружный воздух
надо охладить на А/ и осушить на Ad. Воздух, поданный в помещение с параметрами
t2 и d2, в процессе 2-3 достигает параметров воздуха в помещении (точка 3 с параметрами
/з и d3). Таким образом, линия 2-3 изображает процесс изменения состояния воздуха
в самом помещении.
Для зимнего режима работы также можно использовать прямоточную схему.
На d/i-диаграмме (рис. 12.3, б) точка / изображает состояние наружного влажного
воздуха с параметрами t\ и d\, а точка 3 — состояние воздуха в помещении с
параметрами /3 и d3. Так как h> t\ и d3> d\y то приточный воздух, подаваемый в помещение,
необходимо нагреть на At = t2 —1\ и увлажнить на I±d = d2 — d\ с таким расчетом, чтобы
конечные параметры воздуха в помещении стали /3 и d?, (точка 3). Следовательно,
линия 2-3 на d/i-диаграмме изображает процесс изменения состояния воздуха в
помещении.
Таким образом, для поддержания заданных параметров воздуха в помещении
необходимо при летнем режиме его охлаждать и осушать, а при зимнем режиме —
нагревать и увлажнять. Указанные процессы при кондиционировании осуществляются
в аппаратах, называемых кондиционерами.
Прямоточная схема кондиционирования приведена на рис. 12.4. Наружный
воздух массой т\ поступает в кондиционер /, в котором, проходя через фильтр (на
схеме не показан), очищается от пыли, а затем подвергается тепловой (в калориферах
подогрева 2) и влажностной (в оросительных камерах 3) обработке, после чего
Плазма 15Z
нагнетается вентилятором 4 в помещение 5. Одновременно из помещения с помощью
вытяжной системы 6 удаляется отработавший воздух. При этом соблюдается
материальный баланс: масса приточного воздуха равна массе удаляемого воздуха.
Вопросы 1. Что называется абсолютной и относительной влажностью воздуха?
2. Что называется влагосодержанием влажного воздуха?
3. Каким соотношением связаны относительная влажность и влагосодержание
влажного воздуха?
4. Как определить энтальпию влажного воздуха?
Глава 13
ПЛАЗМА
§ 13.1. Плазма в природе и технике
Плазмой называется состояние частично или полностью ионизованного вещества,
состоящего из совокупности большого числа положительно и отрицательно заряженных
частиц в такой пропорции, что общий заряд единицы объема равен нулю.
Следовательно, плазма — это электрически нейтральная в макроскопическом
масштабе смесь, в каждом кубическом сантиметре которой содержится пе электронов,
щ положительных ионов, а в низкотемпературной плазме еще и па нейтральных
атомов или молекул. Плазму часто называют четвертым состоянием вещества, так как
ее свойства резко отличаются от свойств тех же веществ, находящихся во всех других
известных состояниях.
Если обозначить через £прит энергию притяжения между атомами и молекулами
вещества, через Екол и EKiiH энергию колебаний и кинетическую атомов и молекул и через
Еион энергию ионизации вещества (энергию связи электронов с ядром), то с
энергетической точки зрения для конкретных состояний вещества можно отметить следующие
соотношения: твердое состояние существует при £кОЛ<£прит> Екши жидкое состояние —
при £прит~£кин, газообразное состояние—при Еион> Екин> £прит, плазменное
состояние — При £Кин> £ион-
Переход вещества из одного состояния в другое определяется количеством теплоты,
подведенным к веществу. При сообщении твердому телу достаточного количества
теплоты оно плавится и превращается в жидкость, при продолжении подвода теплоты
образуется пар (газ). Дальнейшее нагревание и рост температуры приводят вначале к
диссоциации сложных молекул, а затем к ионизации вещества, т. е. к образованию
плазмы.
Плазма является не только нормальной формой существования вещества при
температурах, больших 104 К, но и самым высокоэнергетичным состоянием, в котором
средняя кинетическая энергия в расчете на одну частицу больше энергии ионизации.
Возможный диапазон кинетической энергии для плазмы очень велик и составляет
1 эВ^Екин^ Ю6 эВ, тогда как всем другим состояниям вещества (твердое, жидкое,
газообразное) соответствует узкий диапазон энергии 0<£Кин<1эВ.
По своей распространенности во Вселенной плазма занимает первое место
(более 99%)—это вещество звезд, Солнца, газов межзвездного и межпланетного
пространства. Сравнительно недавно учеными обнаружены совершенно экзотические
объекты Вселенной — нейтронные звезды, или пульсары, с плотностью вещества
~1013...1014 г/см3. Это новое, еще не известное нам состояние вещества академик
Л. Д. Ландау назвал нейтронным. На Земле из-за низкой температуры и высокой
плотности земного вещества и нижних слоев атмосферы естественной плазмы
практически нет и ее приходится создавать искусственно.
158
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Получение плазмы низкотемпературной и особенно высокотемпературной связано с
большими техническими трудностями.
Для получения низкотемпературной плазмы широкое применение получили
электродуговые и высокочастотные генераторы плазмы, или плазмотроны, плазменные пушки,
ускорители, инжекторы.
В электродуговых плазмотронах (рис. 13,1, а, б) электрический ток от источника
питания / подводится к стержневому катоду 2 и цилиндрическому аноду 5, между
которыми горит электрический разряд (дуга) 6. Рабочее вещество 3 в газообразном
состоянии подается тангенциально в камеру 4 и, проходя через зону разряда,
стабилизирует электрическую дугу, нагревается до высоких температур и переходит в
плазменное состояние. В плазмотроне с комбинированной стабилизацией дуги
(рис. 13,1, б) магнитная катушка 7, установленная на аноде, создает внутри анода
небольшое магнитное поле (обычно 1,0... 10 А/м), взаимодействие которого с
электрическим полем разряда обеспечивает дополнительное вращение и стабилизацию дуги.
Такие плазмотроны обеспечивают получение максимальных температур на уровне
(5...8)104 К, а средних ~104 К.
В ВЧ (высокочастотных)- и СВЧ (сверхвысокочастотных)-плазмотронах электроды
отсутствуют (рис. 13.2). Плазмообразующее рабочее вещество /, поступающее в
разрядную камеру 2, нагревается вихревыми токами с частотой 1О4...1О7 Гц.
Вихревые токи создаются с помощью индуктора 3> подключенного к СВЧ-генератору 4 с
источником питания 5. ВЧ- и СВЧ-плазмотроны обеспечивают получение чистой
плазмы (без примеси материалов электродов) с температурой до 106 К.
Все возрастающий интерес ученых, инженеров и технологов к плазме связан с
необходимостью решения ряда важнейших фундаментальных и прикладных задач, в
которых плазме отводится сложная роль и высокотемпературного рабочего вещества, и
Рис. 13.1. Электродуговой
плазмотрон постоянного тока:
а — с вихревой газовой, б—
с комбинированной (вихревой
и электромагнитной)
стабилизацией электрической дуги
Рис. 13.2. Безэлектродный
индукционный высокочастотный
плазмотрон
п,см
ю6
/
-г
1
1
ш-а\
1
1
1
1
■
I
[ш
т
1 /
J
ш
1
1
1
7
0,1 1 Ю 10z 0 W*
Ю* W7
Е, эВ/</аст.
Рис. 13.3. Диаграмма «энергия частицы Е-
плотность частиц л»
Плазма 159
носителя электрических зарядов, и источника электромагнитных излучений в широком
диапазоне длин волн, и электромагнитной силовой динамической системы, и активной
среды с инверсной населенностью. К таким задачам относится создание управляемых
термоядерных реакторов, магнитогидродинамических преобразователей тепловой
энергии в электрическую, электрореактивных плазменных двигателей для космических
аппаратов, мощных лазеров на основе плазмы сложного состава в качестве активной
среды, плазмохимических реакторов, плазменно-технологических установок для плавки,
резки, сварки и пайки металлов, нанесения различных покрытий и др.
Перспективность плазмы как рабочего вещества для различных энергетических
и энерготехнологических процессов и устройств (уже известных и еще не разработанных)
хорошо видна из диаграммы (рис* 13.3), на которой в координатах Е, п (Е—
энергия частицы, п — плотность газа или плазмы) показана совокупность всех
устройств, используемых для ускорения вещества. В течение многих веков человечество
продвигалось только вдоль «берегов» (координат), осваивая области / и //, не имея
необходимых знаний и средств для проникновения в области /// — V этой диаграммы.
В самом деле, область / включает в себя все механические и газодинамические
устройства, созданные за всю историю человечества, а область // — все ускорители
заряженных частиц, даже самые гигантские.
Первоначальное освоение этих областей вполне понятно, так как всегда проще
создавать устройства с экстремальными значениями только одного из параметров. Так,
механические и газодинамические устройства (область /) характеризуются широким
диапазоном плотности рабочего вещества и низкими значениями энергии частиц, тогда
как в ускорителях заряженных частиц (область //) плотность рабочего вещества
чрезвычайно мала, а энергия частиц велика.
Плазма, как четвертое состояние вещества, на этой диаграмме занимает область
///. Чтобы еще раз подчеркнуть уникальность и огромные возможности плазмы как
рабочего тела, отметим, что все термоядерные системы занимают на диаграмме
небольшой «островок» 7\ а дуговые и высокочастнотные установки и генераторы
низкотемпературной плазмы укладываются в узкую область \ll-A. Пути освоения и
использования областей IV и V еще ждут своего решения. Различные плазмодинами-
ческие системы, обладая уникальными параметрами рабочего вещества (высокие
плотности и энергии частиц), обеспечат научно-технический прогресс во многих областях
науки, техники и технологии.
§ 13.2. Свойства и классификация плазмы
Процесс образования плазмы — это процесс ионизации нейтральных атомов и процесс
последующей ионизации уже имеющихся ионов.
Для превращения нейтрального атома в ион необходимо затратить определенную
энергию, называемую энергией ионизации £,, которая обычно выражается в электрон-
вольтах (1 эВ «1,6-10~19 Дж). Если электрон, проходя в электрическом поле с
какой-то разностью потенциалов, приобретает энергию, равную энергии ионизации
данного элемента, то такая разность потенциалов называется потенциалом
ионизации.
Энергия (потенциал) ионизации атомов любого вещества зависит от химической
природы вещества и энергетического состояния атомов. Слабее всего связаны электроны
в атомах ^одновалентных щелочных металлов, у которых один внешний электрон
находится на далекой, орбите. Прочнее всего связаны электроны в атомах инертных
газов, так как у них электроны образуют замкнутые электронные оболочки. В общем
случае энергия ионизации атомов тем меньше, чем больше их атомная масса. Это
объясняется_тем, что в тяжелых атомах много внутренних электронов, экранизирующих
160 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
поле ядра. При ионизации атомов с большим числом электронов (Z~> 1) возможен
процесс последовательности ступенчатой ионизации с образованием многозарядных
ионов: если однозарядный ион потеряет следующий электрон, то он превращается
в двухзарядный ион, и т. д. При этом энергия каждой последующей ионизации
больше предыдущей. Значения энергии однократной ионизации изменяются в пределах
от 3,87 эВ (цезий) до 24,5 эВ (гелий).
Существует несколько методов образования плазмы, наиболее распространенными
из которых являются термическая ионизация, ионизация электрическим разрядом и
ионизация излучением (фотоионизация).
Если ионизация атома идет с основного уровня, то во всех случаях энергия,
подводимая к нейтральному атому, должна быть равна или больше его энергии
ионизации. Это условие запишется для термической ионизации в виде неравенства
для ионизации электрическим разрядом е1Ен^Ег, для фотоионизации
i. Здесь к и h — постоянные Больцмана и Планка соответственно; Т —
температура плазмы; / — длина свободного пробега электрона в электрическом разряде;
Ен — напряженность электрического поля; v — частота излучения. При ионизации с
возбужденного уровня необходимая энергия будет меньше на величину энергии
возбуждения.
Для дальнейшего анализа процесс ионизации удобнее записывать в элементарной
форме как результат взаимодействия частиц. В этом случае ионизацию атома А с
основного уровня при взаимодействии с электроном е (независимо, за счет чего электрон
получил необходимую энергию) можно представить в следующей форме:
(13.1)
при фотоионизации
A + hv-+A + +e. (13.2)
Эти же процессы ионизации, но с возбужденного уровня Ан имеют вид
и
В плазме в результате электростатического взаимодействия атомов и заряженных
частиц, окружающих атом, происходит снижение энергии (потенциала) ионизации
на какую-то величину Д£. Объясняется это тем, что электростатическое
взаимодействие приводит к ослаблению связи электронов внешних электронных оболочек
атома с ядром и они могут в принципе оказаться даже свободными. Таким образом,
действительная, или, как принято называть, эффективная, энергия (потенциал)
ионизации в плазме определяется разностью:
£эф = £,_££. (13.3)
Величина Д£ наиболее просто вычисляется по формуле ДЕ = 7- \0~7л]пе,
предложенной А. Унзольдом. Г. Эккер предложил определять Д£ более точно с учетом
не только электростатического взаимодействия, но и теплового движения заряженных
частиц:
ДЕ = 6,7 • \0-7л[пе + 0,37 . \0~Wne/Te. (13.4)
И. Брюннер для этих целей рекомендовал использовать выражение
Д£= 12,1 . 10-7V/i\ + 2,5 - 10-6V"e/7V (13.5)
Здесь пе (1/см3) и Те (К) —соответственно плотность и температура электронов.
Одним из важнейших свойств плазмы является ее стремление к сохранению
Плазма 161
равенства плотностей положительно и отрицательно заряженных частиц, т. е. к
сохранению электронейтральности.
Это происходит не только потому, что заряженные частицы образуются в
равных количествах (по величине зарядов) из нейтральных атомов, но и потому, что
для получения хотя бы незначительного разделения зарядов в плазме потребовались
бы слишком большие силы. В общем случае условием электрической нейтральности
Z-кратно ионизованной плазмы, имеющей в своем составе ионы с различными зарядами
/*/г, является сумма:
«e=2z«jZ, (136)
где Z = l, 2, ..., k — кратность ионизации. Для низкотемпературной, однократно
ионизованной плазмы это условие принимает простой вид: гсе = Я/ = п.
Условием электронейтральности является также равенство парциальных давлений
электронного и ионного компонентов плазмы. Однако это условие справедливо только
для достаточно больших объемов, и с его помощью нельзя найти условия нарушения
электронейтральности плазмы.
Пусть плазма имеет плотность частиц /ге = п, = п. Если в этой плазме произойдет
полное разделение электронов и ионов на расстояние XR, то это вызовет появление
электрического поля напряженностью E = 4nneXR и каждый электрон получит энергию
Еэл = Аппе2Х\. При отсутствии внешних воздействий разделение зарядов произойдет
только в том случае, если тепловая энергия частиц Ет будет больше или равна
энергии электростатической ЕЭЛу т. е. при kT^4nne2X2R. Отсюда
XR = ^kT/Ылпе2) = 7£л[т/п. (13.7)
Величина XR характеризует максимально возможное расстояние, на котором
может нарушиться электронейтральность плазмы при данных значениях ее температуры
и плотности. Эта величина имеет размерность длины и называется дебаевским
радиусом экранирования или пространственным масштабом разделения
зарядов.
Дебаевский радиус — одно из основных понятий и параметров плазмы, что и
отражается в самом точном определении плазмы, данном И. Лэнгмюром:
плазмой называется такой ионизованный газ, дебаевский радиус которого мал по
сравнению с размерами объема, занимаемого этим газом.
Следовательно, в плазме всегда должно выполняться условие
L^>XR, (13.8)
где L — характерный линейный размер области, занятой ионизованным газом.
Электрическая нейтральность плазмы должна соблюдаться не только в
пространстве, но и во времени. Время
т = XR/wT = Ут/(4:гше2), (13.9)
за которое самые быстрые частицы плазмы (электроны), движущиеся со средней
тепловой скоростью wTt проходят расстояние, равное дебаевскому радиусу, называется
временным масштабом разделения зарядов.
Квазинейтральность плазмы может нарушаться только за время, меньшее т,
что приводит к появлению быстрых колебаний плотности зарядов. Обычно это колебания
электронов, как более легких и подвижных частиц, около ионов, в которых
возвращающая сила обусловлена электростатическим (кулоновским) взаимодействием, а
инерция — массой электронов.
6 За к 584
162 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Эти колебания, обычно называемые плазменными или электростатическими,
являются специфичными и обязательными только для плазмы.
Поэтому за характерный параметр плазмы принимается не временной масштаб
разделения зарядов т, а круговая частота плазменных колебаний:
©0= 1/т = лАляе2/™ = 5,6 • 104V^. (13.10)
Анализ выражений (13.7), (13.9) и (13.10) показывает, что чем выше плотность
плазмы, тем меньше масштабы декомпенсации зарядов и в пространстве, и во времени.
При увеличении температуры дебаевский радиус увеличивается, что связано с
подавлением эффекта поляризации зарядов тепловым движением частиц.
Изменение потенциала около любого заряда в плазме подчиняется закону
r/XR),
где г — текущее расстояние от заряда; XR — дебаевский радиус; vo — Ze2/r —
кулоновский потенциал заряда. Следовательно, потенциальное поле любого заряда в
плазме на расстоянии, равном дёбаевскому радиусу, практически полностью
экранируется пространственным зарядом. Поэтому дебаевский радиус характеризует также
расстояние, на котором в плазме осуществляется электростатическое взаимодействие
между заряженными частицами. Если в нейтральном газе расстояние взаимодействия
между частицами всегда меньше среднего расстояния между ними (/?ВЗ<С/'), то в
плазме — всегда больше (XR^>r). В обычном газе частицы взаимодействуют друг с
другом только при очень коротком сближении (соударениях), а основную часть времени
они находятся вне силового взаимодействия. В плазме характерным масштабом
взаимодействия между заряженными частицами является дебаевский радиус, который
в широком диапазоне температур и давлений составляет 10~6...10~2 см. Если взять
в плазме условную сферу с радиусом, равным дёбаевскому, то число частиц в этой
сфере будет достаточно велико. Следовательно, любая частица в плазме практически
постоянно испытывает силовое взаимодействие со стороны других частиц. Именно это
дало основание известному советскому физику А. А. Власову утверждать: «Плазма —
это не газ, а своеобразная система, стянутая далекими силами».
Основной количественной и качественной характеристикой равновесного процесса
ионизации является степень определенной кратности ионизации az,
равная отношению плотности ионов данной кратности ионизации к полной плотности
атомов и ионов:
az=/W2n/Zie. (13.11)
Z,a
Степень однократной ионизации плазмы с учетом электронейтральности принимает
вид
a, = rt/(/i + nfl), (13.12)
где пе = щ = п — плотность ионов и электронов; па — плотность нейтральных атомов.
В полностью однократно ионизованной плазме ои~1,0, а в слабоионизованной плазме
Как показывает анализ, приои< 10~4 подвижность электронов в плазме
определяется в основном электронно-атомными столкновениями. Такая плазма называется
слабоионизованной, и ее свойства в основном определяются химической природой
газа.
При а\> 10~3 подвижность электронов ограничивается главным образом дально-
действующими кулоновскими взаимодействиями с ионами. Такая плазма считается
Плазма
163
с и ль но ионизованной, ее свойства
подчиняются законам полностью
ионизованной плазмы и слабо зависят от
химической природы газа.
Степень ионизации любого вещества
в зависимости от температуры и
давления (рис. 13.4) с ростом давления
уменьшается, т. е. равновесие смещается в
область более высоких температур.
Классифицировать плазму можно
также в зависимости от температуры и
плотности частиц.
Пс температуре обычно различают
низкотемпературную (kT~~Et, или
5
<105 К) и высокотемпературную (kTy
Рис. 13.4. Принципиальная зависимость
степени ионизации от температуры и давления
£if или Т> И)6 К) плазму.
Низкотемпературная плазма может иметь в своем составе электроны, ионы (в
основном однозарядные), а также нейтральные атомы. Высокотемпературная плазма
состоит только из электронов и многозарядных ионов.
По плотности (см 3) частиц различают плазму разреженную
|217 17
Ю12), средней
( ) р
лотности (10|2</г<с1017) и плотную (/г>1017).
Общие свойства плазмы справедливы для всех названных типов, однако каждый
из них имеет и свои специфические особенности, которые приходится учитывать в
термодинамических расчетах.
§ 13.3. Идеальная и неидеальная плазма
В термодинамическом отношении плазму можно рассматривать как идеальный газ,
если средняя энергия электростатического взаимодействия между частицами мала по
сравнению с кинетической (тепловой) энергией частиц, т. е.
2 (13.13)
где Z — зарядовое число ионов; го — расстояние между частицами
Критерий г)к.-, обычно называют классическим параметром неидеальности
плазмы, а соотношение (13.13) — неравенством Кирквуда — Онсагера.
Параметр неидеальности является одним из важнейших безразмерных параметров
плазмы. Он показывает, в какой степени коллективные эффекты в плазме преобладают
над одиночными. В большинстве случаев параметр неидеальности мал и условие (13.13)
выполняется с большим запасом, особенно для разреженной плазмы и плазмы средней
плотности. Так, например, в ионосферной плазме Лкл^Ю""4, а в термоядерной
Лкл^Ю"2. Вместе с тем даже при г)кл<С1 (когда полная энергия плазмы практически
совпадает с ее тепловой энергией) непосредственное использование формул теории
идеальных газов для определения термодинамических параметров плазмы не
рекомендуется. По своим термодинамическим свойствам плазма превращается в идеальный газ
только в пределе при т]кл-^0. Однако на практике при rjo'Cl давление плазмы обычно
находится по уравнению состояния идеального газа (1.6), которое для частично
ионизованной и полностью ионизованной плазмы принимает соответственно вид
и p = 2nkT. (13.14)
Такой подход оправдывается тем, что расчеты по формулам (13.14) дают хорошее
совпадение с практикой.
С увеличением плотности плазмы параметр г\КЛ растет и уже в умеренно плотной
164 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
плазме г\кл~ 1. В этом случае в плазме электроны могут локализоваться флуктуациями
плотности. В результате в плазме возникают специфические квазичастицы — кластеры,
состоящие из электрона и избыточного числа атомов вокруг него. Это приводит к
уменьшению эффективного числа частиц, и уравнение состояния для такой плазмы по
предложению И. Т. Якубова следует записывать в виде
, (13.15)
где ср — избыточное число атомов вокруг электрона (число атомов в кластере);
п — полная плотность электронов (свободных и связанных); пс — плотность электронов,
связанных в кластерах. Если параметр г\кл приравнять единице, то можно определить
критическую плотность пкр, выше которой плазма перестает быть идеальной:
nKp = [kT/(Ze2)ftt3- 106Г3. С увеличением плотности плазмы взаимодействие между
частицами может возрасти настолько, что наступает вырождение плазмы и тогда ее
свойства будут определяться в основном квантовыми эффектами. Вырождение плазмы
является прямым следствием одного из основных принципов квантовой физики —
принципа Паули, согласно которому в каждом квантовом состоянии может находиться
не более одного электрона. Квантовое состояние занимает в шестимерном фазовом
пространстве элементарную ячейку объемом ~h\h — постоянная Планка), в котором
может поместиться не более двух электронов, отличающихся друг от друга только
направлением собственного вращения. При небольшой плотности плазмы число
элементарных ячеек значительно больше числа электронов. С увеличением же плотности
можно достигнуть такого состояния, когда все ячейки будут заполнены, и тогда
дальнейшее увеличение плотности приводит к вырождению.
Предельные формулы термодинамики плазмы получаются из условия заполнения
электронами всех элементарных ячеек. Объем плазмы в шестимерном фазовом
пространстве равен (4/3)np3mV, где V— координатный объем; рт — максимальный
импульс. Тогда число элементарных ячеек в этом объеме и полное число электронов
равны соответственно b = 4np3mV/(3h3) и Ne = (b/3)np3mV/h3y а плотность электронов в
единице V объема n = Ne/V = 8np3m/(3h3). Из последовательного выражения можно
определить максимальную энергию, соответствующих предельному случаю:
x f3, (13.16)
и давление плазмы
p = (2/5)rt£max = U2/(5m)] [3/(8я)]2/3л5/3. (13.17)
Эти выражения являются предельными формулами термодинамики плазмы при
очень больших плотностях (давлениях). Энергия £ГП.1Х называется энергией
вырождения или энергией Ферми.
При плотности плазмы ниже /г~1020 см"3 и температуре Г^ 104 К эффекты
вырождения приводят к небольшим поправкам. В вырожденной плазме понятие
температуры как меры энергии среднего хаотического движения частиц теряет смысл. Эту
роль в вырожденной плазме играет энергия Ферми, которая является функцией только
плотности и не зависит от температуры.
Отношение
l = Emax/(kT) (13.18) -
является параметром вырождения. Чем больше А,, тем больше вырожденным
является газ. При А,= 1 можно найти плотность
п = {2kTm/h2)3/2(Sn/3) « 1016Га/2, (13.19)
Плазма
165
выше которой плазма будет вырожденной,
или квантовой.
По аналогии с классической плазмой
можно ввести параметр неидеальности и для
вырожденной плазмы
х) = ЛкЛА. (13.20)
25
20
Условием идеальности вырожденной
плазмы будет неравенство г|кв<С 1 - Анализ
выражения (13.20) показывает, что вырожденная
плазма тем более идеальна, чем выше ее
плотность.
Из условия г|кв= 1 определяется
критическая плотность электронов
/
ш
/
Ькл '
Ш
I
/2 = 7-1024 см"
(13.21)
1дт[т,к]
Рис. 13.5. Логарифмическая диаграмма
термодинамических состояний плазмы
разделяющая вырожденную плазму на идеальную и неидеальную.
Различные термодинамические состояния плазмы (идеальная и неидеальная,
вырожденная и невырожденная, идеально вырожденная и неидеально вырожденная)
можно представить графически в координатах Ig7\ lg/г (рис. 13.5).
С помощью линий, соответствующих условиям Лкл=1, А,= 1 и т]кв=1,
диаграмма термодинамического состояния плазмы разделяется на несколько
характерных областей. Область / соответствует параметрам классической идеальной плазмы
со слабым взаимодействием (г|кл*< 1 и А,<<1). Сюда относятся межзвездный и
ионосферный газ, плазма газового разряда, термоядерная плазма и др. Область //
соответствует классической неидеальной, невырожденной плазме с сильным
взаимодействием (лкл> 1, A,<Il). Такими параметрами может обладать очень плотная плазма
некоторых электрических разрядов, плазма ударно-волновых устройств. Область ///
соответствует неидеальной вырожденной плазме (r\7> I, t1kb>1), а область IV —
идеальной вырожденной плазме (А,;> 1, т]<<1). Этим условиям удовлетворяют газ в
металлах, металлоаммиачные растворы, сильнолегированные полупроводники, ядерная
жидкость в сверхплотных звездах.
С позиций использования плазмы в различных энергетических и
энерготехнологических устройствах наибольший интерес в настоящее время представляют области
/ и //, т. е. области идеальной и неидеальной классической плазмы.
§ 13.4. Термодинамическое и термическое
равновесие в плазме
Плазма как смесь частиц с различными зарядами и массами может находиться в
термодинамическом равновесии, если в ней соблюдаются газокинетическое, диссоциаци-
онное и ионизационное равновесия, а процесс излучения подчиняется законам
излучения абсолютно черного тела.
Такое состояние устанавливается при детальном равновесии, которое обычно
реализуется в закрытых системах с запертым излучением при протекании прямых и
обратных процессов по одому и тому же пути с одинаковыми скоростями. Так, при
ионизации электронным ударом А + е^^А + + е + е обратный процесс (рекомбинация)
должен происходить при тройных соударениях, а фотоионизации А + hv^A + + е
должна соответствовать рекомбинация с излучением.
В открытых системах условия детального равновесия выполняются лишь при
большой плотности частиц, так как в плотной плазме ионизация и рекомбинация
всегда идут по одному пути.
]66 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
С уменьшением давления падает вероятность соударений между частицами,
уменьшается оптическая толщина плазмы и электроны практически свободно уходят
на стенки сосуда, не успевая передать ионам и нейтральным атомам энергию,
полученную ими бт внешнего источника. Это приводит к температурному расслоению
плазмы, при котором ее состояние характеризуется двумя температурами: электронной
Те и ионной Ti (при этом обычно Te>Ti). В силу того что массы нейтральных
атомов и ионов- близки, температура атомов Та не будет существенно отличаться от
температуры ионов, т. е. Га«7У Изменение температуры электронов, «онов и атомов в
зависимости от давления для всех веществ имеет одинаковый характер, однако
значение критического давления ркр, при котором начинается температурное расслоение,
зависит от природы вещества. Так, для лития ркр~4 кПа, для аргона ркр«6,7 кПа,
для ртути ркр«9,3 кПа. Следовательно, при больших давлениях плазма обычно
термически равновесна, а при низких давлениях — термически неравновесна. Условием
термического равновесия в плазме является неравенство
<1. (13.22)
Выравнивание температур между электронным и ионным компонентами плазмы
происходит за счет обмена энергией между электронами и ионами при их соударениях
друг с другом. Если электрон, движущийся со скоростью we, в результате
взаимодействия сионом отклоняется на угол 6, то импульс, переданный им иону, будет
Ap = 2mwesin(6/2) = 2p0sin(6/2). Под действием этого импульса ион приобретает
кинетическую энергию AE = (Ap)2/(2Mi) = (2p20/M)s\n\6/2) или при 6 = 90°Д£==р2,/М. Для
определения энергии, передаваемой ионам в единицу времени, необходимо Д£
умножить на частоту соударений электронов и ионов:
ei. (13.23)
В этих выражениях: пг и М — массы электрона и иона; 0et« \0~9Z2/Tel— эффективное
сечение соударений электронов и ионов в плазме; Z — заряд иона.
Энергию, передаваемую электроном к ионам в единицу времени, можно определить
также в виде
£=(£.- £,)/тр = -|* {Т. - Г,)/тр. (13.24)
Здесь Ее и Ei — средние кинетические энергии электронов и ионов, а
величина тр характеризует интенсивность энергообмена между электронами и ионами и
является временем релаксации, или временем термализации плазмы.
Если в начальный период в плазме 7\,»7\, то, сравнивая выражения (13.23) и
(13.24), получим время релаксации
тр~6А\07Т3е/2/пу (13.25)
где Л — атомная масса вещества.
Из полученного выражения видно, что время установления температурного
равновесия в плазме Te=Ti тем больше, чем больше атомная масса вещества и ниже
плотность частиц. Это объясняется тем, что доля энергии, передаваемой при
соударениях, пропорциональна отношению масс сталкивающихся частиц, т. е. m/М, и поэтому
чем тяжелее ион, тем меньше эта энергия и тем больше число соударений
требуется для выравнивания температур. С уменьшением плотности плазмы падает
число соударений, а время термализации возрастает. Выражение (13.25) можно
использовать для определения тр в очень широком диапазоне температур, так как оно
остается справедливым при условии Te^>mTi/M.
Проведенные оценки времени установления температурного равновесия в плазме
являются, конечно, приближенными, так как все рассуждения относились к случаю,
Плазма 167
когда запас энергии в плазме сохранялся постоянным, т. е. подвод и потери
энергии были равны. Поэтому при рассмотрении конкретных процессов плазму можно
считать изотермной, если тр<тпр, где тпр — характерное время процесса.
Соотношение Ti^>Te выполняется в сильноионизованной плазме только при
некоторых специальных условиях, например при кратковременных импульсных разрядах
большой мощности, приводящих к образованию и кумуляции ударных волн в
плазме.
Однако, несмотря на достаточно частое отсутствие температурного равновесия
между электронами и ионами в плазме, очень большой круг практических задач
можно рассматривать с позиций равновесной термодинамики. Так,
при температурном расслоении возможно частичное-термодинамическое равновесие,
при котором температура одного рода частиц в ллазме отличается от температуры
другого рода частиц, но для каждого из них распределение энергии (скоростей)
подчиняется максвелловскому.
Для многих прикладных задач часто используется так называемое
локальное термодинамическое равновесие (ЛТР) — состояние, при котором внутри
каждого малого объема плазмы имеет место полное термодинамическое равновесие,
но темпе он. гура является медленно меняющейся функцией координат.
При этом должны выполняться условия L>/ и T/(dT/dL)^>Ly где L —
характерный размер объема плазмы; / — длина свободного «пробега частиц в плазме. Важность
использования понятий частичного и локального термодинамических равновесий
заключается в том, что при соблюдении в плазме условий, характеризующих эти
состояния, можно с достаточно высокой степенью точности использовать любые
термодинамические функции, рассчитанные в предположении полного
термодинамического равновесия.
§ 13.5. Состав равновесной плазмы
При установлении термодинамического равновесия степень ионизации зависит только от
температуры и давления. Индийский физик М. Саха применил для анализа
термодинамически равновесного процесса ионизации закон химического равновесия
(закон действующих масс). Если ионы и электроны рассматривать в качестве
химических веществ, а процесс ионизации — как обратимую химическую реакцию, то
константу равновесия, характеризующую степень завершенности этой реакции,
можно представить в виде отношения
(13.26)
где ре, Pi и ра — парциальные давления электронов, ионов и нейтральных атомов.
Если не полностью ионизованная плазма имеет в своем составе электроны,
ионы и нейтральные атомы с плотностью соответственно пеу щ и ппУ то с учетом
условий электронейтральности (ne = rii = n) и N — ni + na можно найти значения
парциальных давлений компонентов плазмы:
п а N — п 1 — а
Ре = Р> = ТГТ^р = Т+^р' Р"=1Г+1Гр==Т+^р-
где р — общее давление плазмы, определяемое либо экспериментально, либо по
уравнению состояния; а — степень ионизации. Подстановка значений реу р, и ра в формулу
(13.26) приводит к уравнению Саха, связывающему константу равновесия со
степенью ионизации плазмы:
/С = а2р/(1-а2). (13.27)
Полученное выражение может быть использовано для определения степени ионизации
плазмы при различных давлениях и температурах:
]68 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
p). (13.28)
М. Саха и Э. Р. Эггерт методами статистической физики определили константу
равновесия при условии термодинамического равновесного состояния. Эта формула
имеет вид
К = ^^fl{kT)^ exp (- i±), (13.29)
где Zk и Zk-\ —статистические суммы по электронным состояниям k- и (k— 1)-кратно
ионизованных ионов; £Эф — эффективная энергия ионизации; m, e — масса и заряд
электрона; h и k — постоянные Планка и Больцмана.
Для практических расчетов выражение (13.29) удобнее представить в виде
^ \\fi2. (13.3Q)
Здесь давление выражается в Па, а температура — в К-
Ионизация в смеси газов протекает несколько сложнее, но основные положения
не меняются. Пусть ионизуется смесь одноатомных газов. В этом случае степень
ионизации у-го компонента плазмы а/ = /г,//(/га/ + /г//), а степень ионизации всей смеси
aCM==2ayAy, (13.31)
/
где Xj — относительная доля /-го компонента, а щ определяются по формулам
(13.28) и (13.30).
Например, в магнитогидродинамических генераторах для получения
необходимой электропроводимости в рабочую камеру обычно вводится небольшое количество
легкоионизирующейся присадки, потенциал ионизации которой значительно меньше
потенциала любого компонента продуктов сгорания. В этом случае степени ионизации
присадки anp и степени ионизации всего рабочего вещества асм определятся
соответственно отношениями
апр = ninp/{nanp + ninp) ~ Л/пр/ЛОпр'»
v
., . ч Гф
асм = ^«пр/^Огаз ~Г ^Опр) = 1 _|_ v anp»
I пр
где п/Пр, пОпр, п0 Газ — плотности ионов присадки, самой присадки и рабочего газа;
ХПр = пОпр/«о газ— массовая или молярная доля присадки в рабочем газе. Если A^p^l
и Е/пр^С/^-газ, то степень ионизации рабочего вещества в канале МГД-генератора
асм^аПрХпр. На практике обычно берется Хпр = 0,01...0,02.
Полученные выше формулы и рассмотренные примеры относились к случаю
установления теплового равновесия между электронами и ионами. Наличие в
низкотемпературной плазме нейтральных частиц не приводит к каким-либо изменениям
полученных выводов, так как их температура близка к температуре ионов. Не
учтенные здесь процессы возбуждения, тушения и перезарядки лишь улучшают условия
равновесия.
Однако в плазме не всегда соблюдается термодинамическое равновесие. При
температурном расслоении для неизотермной двухтемпературной плазмы уравнение
Саха в обычном виде использовать нельзя, а для случая, когда энергия подводится к
электронам (т. е. при Те~> Т{), его следует модифицировать. Учитывая, что электроны
имеют значительно большую скорость, чем ионы и атомы, и играют главную роль в
процессах ионизации и рекомбинации, в уравнениях Саха—Эггерта (13.30) можно
Плазма
169
заменить общую температуру Т на электронную Те. Экспериментальная проверка
такой подмены подтверждает ее правомерность, и этот метод широко применяется на
практике.
В случае неравновесной, неизотермной, но стационарной плазмы, когда энер1ия
ее частиц не подчиняется максвелловскому распределению, уравнение Саха становится
неприменимым. Степени ионизации в этих условиях можно получить из анализа и
сравнения скоростей процессов ионизации и рекомбинации.
Пусть, например, в достаточно разреженной стационарной плазме ионизация
происходит электронным ударом, рекомбинация сопровождается излучением, а само
излучение свободно выходит из объема плазмы. При этих допущениях можно пренебречь
ионизацией под действием излучения и рекомбинацией при тройных соударениях.
Тогда скорости процессов ионизации Wi и рекомбинации Wp будут равны
Wi = Kitiena и №Р= KPtieniy где Ki и Кр— константы скоростей ионизации и
рекомбинации. Из условия стационарности, т. е. равенства U7,= UPp, можно найти /<с = /(///(р =
= П{/пау где Кс—константа равновесия. Так как na = N — n и n = ne = rii, то степень
ионизации для неравновесной стационарной плазмы определится соотношением
а = Кс/(1+Кс). (13.32)
Выражение (13.32) часто называют формулой Эльверта. Константу
равновесия Кс нельзя найти из законов термодинамики, ее определить чрезвычайно
сложно и только при большом числе допущений.
Для определения степени ионизации, парциальных давлений и плотностей
(состава) компонентов термодинамически равновесной плазмы в общем виде необходимо
совместно рассматривать уравнения констант равновесия всех протекающих в плазме
реакций, Саха — Эггерта для всех реальных ступеней ионизации, электронейтральности
плазмы, баланса давления (закон Дальтона), состояния плазмы и всех входящих в нее
компонентов.
Решение этой системы уравнений при заданных значениях давления р и
температуры Т позволяет определять состав равновесной плазмы любого рабочего вещества
(рис. 13.6). Расчет выполняется методом последовательных приближений, так как для
вычисления эффективной энергии ионизации £Эф необходимо знать значение плотности
электронов в плазме пе.
Так, например, система уравнений для расчета состава равновесной
низкотемпературной плазмы, в которой протекают однократная и двукратная ионизация,
имеет вид
0,01
J
1
к
\
Рис. 13.6. Диаграмма состава плазмы: а — фторопласта; б — индия
170 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
K\=PePi\/Pa> K2= PePi2/Pi\>
ре = рп + 2pi2, или пе = Пц + 2ла;
Р = Ра + Ре + Pi\ + Pi2, ИЛИ N = Па + Пе+ Пп + Па\
p=NkT\ pa = nakT\ pe=nekT\
Pi\ = ni\ kT\ pl2 = tli2kT.
Решение этой системы уравнений можно представить в виде
_ [{{-а\)/а\]Р _ ' (* + аг) Р
- Z -|- 1*2 ( * — OL | J / OL | -\- Z -\- Оь.2
Р» - 1+а1 + За2/(1-а2); Р'2 ~ (1 - а,)/а, + 2 + а2'
где Ра(па)> Ре(пе), Рл(лл), р^Щ2) — парциальные давления (и плотности) нейтральных
частиц, электронов, однократно и двукратно ионизованных ионов соответственно;
он и о&2 — степени однократной и двукратной ионизации. При расчете состава
неидеальной плазмы константу равновесия следует записывать с учетом сильного
кулоновского взаимодействия: K = (pePi/Pa)/exp(r\KJl)y где г\кл — классический параметр
неидеальности плазмы.
§13.6. Термодинамические параметры плазмы
При определенных условиях (см. § 13.3) плазму можно рассматривать в качестве
идеального газа. Однако даже при этих условиях в плазме действуют (пусть
незначительные) силы электростатического притяжения, вызывающие отклонение
плазмы от идеальности, что следует учитывать при определении термодинамических
параметров плазмы.
Внутренняя энергия плазмы U складывается из кинетической энергии гг. отипеского
движения ее частиц (Уид, средней энергии их электростатического вза содействия
иэл и энергии излучения UH3Ji:
и=ит+иэл+иизл. (13.33)
Значения слагаемых уравнения (13.33) определяются опытным путем или находятся
методами статистической термодинамики. В идеальном газе инл^>иэл + и^л и
поэтому U =UHA=CVT+1/(0). Для равновесной плазмы уравнение (13.33) получит вид
U= Um + Ze2N/r + 4oT4V/wci (13.34)
где N — nV — число заряженных частиц в объеме V\ r — расстояние взаимодействия
между частицами; Z — зарядовое число иона; а — постоянная Стефана — Больцмана;
wc — скорость света.
Так как характерным расстоянием взаимодействия между частицами в плазме
является дебаевский радиус XRt то выражение для внутренней энергии плазмы получит
вид
^^^ /wc. (13.35)
Функция (13.35) не является характеристической функцией при переменных S и
V, так как зависит от температуры.
Свободная энергия, или энергия Гельмгольца (5.5), для плазмы сохраняет
свойство характеристической функции. В самом деле, так как
Плазма
171
df= —SdT — pdV,
то S=—(dF/dT)v\ P=-(dF/dV)T\ Cv= - T(d2 F / dT2)
(13.36)
Из (13.36) видно, что при изотермных процессах работа совершается не за счет
убыли внутренней энергии, а .за счет убыли свободной энергии. Так как
U = F + Ts = F—T(dF/dT) v——T2-^dF/T), то свободная энергия плазмы
AT _J_ Л*Т / 1 Q О7\
-а/ -у- С/. (13.37)
С помощью теоремы Нернста (см. § 17.5) можно доказать, что константа
интегрирования С = 0, тогда подстановка (13.35) в выражение (13.37) приводит последнее
к виду
Ze2N_^ UnZe2N
или после интегрирования
{13.38)
С помощью выражения свободной энергии плазмы F можно определить и остальные
термодинамические параметры плазмы:
давление
ftnzJW , , „, (1339)
энтропию
5= —(dF/dT)v--
теплоемкость при V = const
Cv=-T{d2F/dT2)v =
теплоемкость при р = const
энтальпию
(13.40)
(13.41)
(13.42)
(13.43)
В этих формулах SHA, Яид, Сунл и Срнл определяются по соответствующим уравнениям
идеального газа.
Для двух-, трех- и более компонентной плазмы термодинамические параметры
определяются суммированием по всем компонентам, имеющимся в плазме. Так,
например, энтальпия и энтропия многокомпонентной плазмы определяются
зависимостями
172 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
где Мир — молярная масса и давление плазмы; ру, Я/ и S; — величины,
определяемые по уравнениям (13.39), (13.40) и (13.43) для каждого компонента плазмы.
В общем случае термодинамические параметры плазмы отличаются от параметров
идеального газа также за счет снижения потенциала ионизации, вызванного
электростатическим взаимодействием между частицами в плазме. Однако для
низкотемпературной плазмы эти отклонения оказываются незначительными и поэтому, как
правило, не учитываются.
Полученные выражения для термодинамических параметров в зависимости от
температуры и плотности заряженных частиц хотя и удобны для расчетов, но
недостаточно наглядно характеризуют зависимость этих параметров от степени
ионизации. Для низкотемпературной не полностью ионизованной плазмы можно определить
термодинамические параметры, если известны соответствующие параметры идеального
газа и степень ионизации плазмы. Плотности плазмы, ионов и электронов в этом
случае определяются соотношениями
в которых Аа> А{ и Ае — относительные атомные массы атомов, ионов и электронов
соответственно. При этих условиях, а также с учетом Л,»Ла и пе = П/ можно получить
выражения для:
уравнения состояния плазмы
(13.44)
удельных теплоемкостей плазмы
p = (\ +a)cVa\ (13.45)
= (l +а)сРа\ (13.46)
внутренней энергии и энтальпии плазмы
+a)cVaT + aEi; (13.47)
i = (\+a)cpaT+aEi. (13.48)
В этих выражениях а — степень ионизации, £,- — энергия ионизации.
Теплоемкость плазмы при практических расчетах можно определить не только по
уравнениям (13.41), (13.42), (13.45) и (13.46), но и графическим дифференцированием,
если известны зависимости // = /(Г) и U = f(T), так как
р\ Cv=(dU/dT)v&(M//bT)v.
На рис. 13.7, а, б показаны зависимости теплоемкости плазмы аргона и водорода
от температуры и давления. В областях диссоциации и ионизации при поглощении
большого количества теплоты теплоемкость плазмы резко возрастает, а затем снова
снижается. При вторичной ионизации на кривой появляется новый пик и т. д.
Изменение показателя изоэнтропы к по температуре и давлению (рис. 13.8)
показывает, что от величины х = 5/3, характерной для идеального газа, показатель
изоэнтропы резко падает в областях диссоциации и ионизации. С ростом давления
характер изменения теплоемкости и показателя изоэнтропы несколько сглаживается.
Молярная масса и газовая постоянная плазмы изменяются в процессе ионизации,
так как каждый атом расщепляется по крайней мере на две частицы: электрон
и ион. При многократной ионизации количество электронов соответственно увеличивает-
Плазма
173
96
5/3
7/4
г)
CPIR
20
18
16
14
12
14 '16 18T-1fitK
J
ж
II
и
1
А
V
р=1(Г7МПа
I f^
1
ь-
р*0,1М(1а
\
6/5
1,0
\\
I
г^
.
I
К /
и4-
Л
\f
I
у
1ч-
/I
/
lp=O,l МПа
1
1
1
j
'рчо~7мпа
Ю5 2 ♦ 6 610й 2 * б 6W5 2 4 6 Т,К
Рис. 13.7. Зависимость теплоемкости плазмы
от температуры и давления: а — аргона; б —
водорода
W3 2 k 6 810* 2 4 Ь 810* 2 Т
Рис- 13-8- Изменение показателя изоэнтропы
плазмы водорода
ся. Если рассматривать плазму как смесь электронов, ионов и нейтральных атомов, то ее
относительная атомная масса
Т К
Am =
j = reAe + riAi
где re = pe/p = a/(l+a); /-, = р,/р = а/(1 +а) и га = ра/р = (1 — а)/(1+а)—молярные
или массовые доли электронов, ионов и атомов соответственно. С достаточной
степенью точности можно принять, что Ае + А[ = Аа, тогда
Ат = Аа/{\+а). (13.49)
Аналогичное выражение можно получить и для вторичной ионизации, приняв
первую ионизацию за основное состояние, и т. д. При многократной ионизации в
общем виде относительная атомная масса
Л щ = Aa/(k + а*), (13.50)
где к — кратность ионизации (fc=l, 2, ..., k)\ ak — степень /г-кратной ионизации.
Если в плазменное состояние переведена смесь газов, то для у-го компонента
смеси /г-кратной ионизации относительная атомная масса выразится как
(13.51)
(13.52)
а относительная молекулярная масса плазмы определится суммой:
Ат = 2Х,А, = Hx,Aa,/(k + a*,),
где Xj — относительная плотность частиц /-го компонента.
Вместе с изменением молекулярной массы изменится и газовая постоянная плазмы
так, что
(13.53)
где Ro — универсальная газовая постоянная.
174
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
а)
Л
35
30
5
V
v ^v ^ч!
WV
-WS
VrSOO
\
ЙЙ
\
*
^^
N
15
10
4 6 8 10 12 П 16 18
W5 TtK
Рис. 13.9. Изменение параметров плазмы аргона: а — относительной
атомной массы; б — газовой постоянной
Зависимость относительной массы и газовой постоянной плазмы от температуры и
давления можно представить серией кривых (рис. 13.9).
Все соотношения для термодинамических параметров получены для идеальной
плазмы, у которой т]кл<!1- В случае сильно неидеальной вырожденной плазмы
(Лкл^1) внутренняя энергия плазмы совпадает с энергией Ферми (13.16), а уравнение
состояния описывается уравнением (13.17). При г|кл~ 1 система не содержит малого
параметра и получить аналитические выражения для термодинамических параметров
такой плазмы не представляется возможным. В этом случае следует как можно дальше
продвигаться в область г)Кл~1 как со стороны низких, так и со стороны высоких
плотностей плазмы, а там, где это не удается, определять параметры плазмы методом
интерполяции.
При расчетах различных процессов, в которых плазма играет роль рабочего тела,
можно использовать также специальные s/z-диаграммы. На рис. 13.10 показана
s/i-диаграмма аргона, на которой нанесены также линии постоянной скорости звука а
и линии постоянной плотности ре, а на рис. 13.11 представлена s/z-диаграмма водорода.
а • 105, м/с
10 -
200
400 600 800 1000 1200
Рис. 13.10. s/г-диаграмма плазмы аргона
Плазма
175
Ью5}Дж1кг
100
200
При заданных значениях давления и темпе-
ратуры плазмы определение значений s и /г
по имеющимся диаграммам трудностей не
представляет.
В приведенных s/i-диаграммах аргона и
водорода не учитывается внутреннее
излучение, что допустимо для разреженной плазмы.
Для плотной плазмы необходимо вводить
поправку на излучение.
§13.7. Свойства замагниченной плазмы
Плазма, помещенная в сильное магнитное
поле, по своим свойствам отличается от
незамагниченной плазмы. Ее свойства
различны в разных направлениях, так как такая
плазма является веществом анизотропным. Это
объясняется тем, что магнитное поле не влияет
на движение заряженных частиц (электронов
и ионов) вдоль поля, но значительно
ограничивает их движение в поперечном
направлении. В связи с этим
в замагниченной плазме скорости движения
заряженных частиц вдоль и поперек
магнитного поля различны и такую плазму следует
характеризовать двумя температурами:
продольной (Гц) и поперечной (Т±). Каждой из этих
температур будет соответствовать и свое давление р„ и рх.
Анизотропия свойств замагниченной плазмы особенно сильно проявляется в
разреженной плазме. С увеличением плотности плазмы облегчается обмен энергией между
разными степенями свободы и анизотропия свойств плазмы сглаживается.
Пусть, например, напряженность магнитного поля В направлена вдоль оси z, a
электрического Е (ток плотностью /) — вдоль оси х. Известно, что на проводник с током,
текущим поперек магнитного поля, со стороны этого поля действует сила F = jB/wc,
направленная перпендикулярно векторам у и Б. В соответствии с уравнением
Максвелла напряженность магнитного поля в направлении, перпендикулярном векторам
В и / (т. е. вдоль оси у), должна меняться по закону dB/dy = 4nj/wc, откуда
j = [ws/(4n)](dB/dy). Тогда сила F определится выражением
(13.54)
(13.55)
Рис. 13.11. s/i-диаграмма плазмы
водорода
dyj dy\ 8л/"
Если магнитное поле изменяется только в поперечном направлении, то
F=—grad[B2/(8n)] = — grad/v
Сила F по своему виду аналогична силе давления. При этом роль давления рм,
называемого магнитным, играет величина рм = В2/(8л). Это давление в статическом
магнитном поле действует на поверхность плазмы, ограничивающую магнитный
поток.
Таким образом, полное давление и полная внутренняя энергия плазмы в попе[>еч-
ном магнитном поле определяются суммами:
2 (13.56)
176 РАЗДЕЛ 3. СВОЙСТВАМИ ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
2 (13.57)
где р и U—кинетическое давление и внутренняя энергия незамагниченной плазмы;
р — плотность плазмы. Обычно плазма является-ди а магнетиком и поэтому выталкивает
наружу приложенное к ней магнит+юе поле. -Условием- удержания плазмы магнитным
полем является равенство кинетического и магнитного давлений на границе плазма -
магнитное поле: £2/(8л) = k(neTe + nJi).
Увеличением магнитного поля, а следовательно^^ магнитного давления можно
обеспечить рост плотности и температуры плазмы. Если принять, что изменение
напряженности магнитного поля пропорционально изменению плотности (т. е. В/р =
= const), то изменения внутренней энергии и энтальпии плазмы определяются
выражениями
dUn=dU + [В2/(8лр2)} dp и d//n= dtf
Дифференцируя полученные соотношения с учетом уравнения состояния p = pkl,
получим
(dUn/dp)T = (dU/dp)T + JL.- В2/(8лр2)- (13.58)
(дНп/д9)т = (дН/др)т + В2/(4яр2) = В2/ (4яр2) (13.59)
— удельные внутренняя энергия и энтальпия плазмы при наличии ма1нитною поля
зависят от ее плотности.
В идеальных газах и идеальной незамагниченной плазме такой зависимости не
наблюдается.
Если изменение энтропии при отсутствии магнитного поля определяется соотноше
нием dS = [d(7 + pd(l/p)J/7\ то при наличии магнитного поля — соотношением
dSn = [d(/n + pnd(l/p)]/7\ Анализ этих соотношений показывает, что энтропия плазмы не
зависит от магнитного поля и dS = dSn.
Не зависит от магнитного поля и удельная теплоемкость плазмы при постоянном
объеме:
Cvn = (dUJdT)y = (dU/dT)v=cv. (13.60)
Для случая постоянства кинетического давления р
) \^(
или с учетом р =
cpn = cp-2RB2/(8np)=cp-2RpM/p. (13.61)
Тогда выражение для показания адиабаты будет иметь вид
к = ■£=-= с p/cv - 2RB2/(cv8np) = x - 2RpJ(cvp). (13.62)
CVn
Полученные выражения показывают, что срп замагниченной плазмы уменьшается
с ростом отношения магнитного и кинетического давлений плазмы. Показатель адиабаты
замагниченной плазмы также зависит от отношения магнитного и кинетического
давлений плазмы.
Вопросы 1. Оценить характерные значения частоты плазменных колебаний для разреженной
плазмы, плазмы средней плотности и плотной плазмы.
2. Определить условия термического равновесия для плазмы г-ле.ккжческ заряда,
Элементы статистической термодинамики 177
если напряженность электрического поля разряда равна Е, а длина свободного пробега
электронов в плазме 1е.
3. При каких условиях энергия Ферми становится в плазме определяющей?
4. Чем объясняется отличие термодинамических параметров замагниченной плазмы от
таковых для незамагниченной плазмы?
Глава 14
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
§ 14.1. Задачи статистической термодинамики
Техническая термодинамика рассматривает энергию и вещество в качестве непрерывных функций
определенных параметров (давление, температура, объем и др.). которые характеризуют их в целом
и не имеют смысла в применении к отдельным частицам, составляющим вещество.
Термодинамические методы исследования тепловых процессов наглядны и дают достоверные
результаты, подтверждаемые многочисленными опытами. Вместе с тем эти методы из-за своей
макроскопичности не могут раскрыть физической, молекулярной сущности тепловых процессов,
так как рассмотрение вещества в виде непрерывной функции с какими-то едиными параметрами
не соответствует реальной действительности: вещество является совокупностью огромного числа
частиц, каждой из которых приписывается определенный вес. Совокупность частиц можно
называть ансамблем или системой, а каждая частица может рассматриваться в качестве подсистемы.
Макроскопические свойства веществ в своей основе определяются микроскопическими
процессами взаимодействия (столкновениями) между частицами ансамбля, а также процессами
взаимодействия частиц с различными внешними силовыми полями. Для описания свойств таких
ансамблей можно использовать динамические процессы многих тел, их составляющих; при этом каждое
тело можно считать либо точечной частицей, либо микрочастицей, обладающей лишь небольшим
числом внутренних степеней свободы Вместе с тем ясно, что свойства ансамбля нельзя представить
в виде простой суммы динамических и энергетических характеристик всех отдельных частиц.
Установление характера связей макроскопических свойств системы с микроскопическими
явлениями, протекающими в ней постоянно, является главной задачей статистической физики.
Задачей статистической термодинамики как составной части статистической физики
является изучение особенностей и макроскопических характеристик различных тепловых и
энергетических процессов на основе молекулярно-кинетического подхода к изучаемым явлениям. Так
как движения молекул, атомов, ионов и электронов из-за постоянных столкновений друг с другом
происходят хаотично, то характер этих движений следует рассматривать не индивидуально, а
только усредненно, т. е. статистическими методами.
При изучении тепловых и энергетических свойств макроскопических систем, состоящих из
большого числа частиц и находящихся в состоянии статистического равновесия или близком к нему,
техническая и статистическая термодинамика дополняют друг друга.
§ 14.2. Функции распределения
В термодинамике рассматривается усредненное движение, так как всем частицам объема dV
приписывается одинаковая скорость перемещения. В действительности же движение частиц является
беспорядочным, они постоянно сталкиваются друг с другом и поэтому имеют скорости, различные
по модулю и направлению. С помощью статистических методов можно определить закон
распределения частиц по скоростям, который оказывается вполне определенным (несмотря на хаотичность
движения частиц).
Распределение частиц по скоростям определяется функцией распределения /(до),
показывающей среднее по времени число частиц данного вида в данном элементе объема, которые имеют
скорости, лежащие в заданном интервале.
Практическое значение функции распределения /(до) состоит в том, что любая величина, явно
зависящая от скорости частиц и, следовательно, от /(до), представляет собой некоторую среднюю
характеристику газа. Действительно, полное число частиц всех скоростей в элементе объема
определяется интегралом
n=\f(w)dw, (14.1)
с помощью которого можно вычислить среднюю скорость частиц в элементе объема
w = —\wf(w) 6w = \wf (w) 6w/\f(w) day, (14.2)
а следовательно', и среднюю кинетическую энергию частиц с одинаковой массой m
178 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
\w2f(w)dw\ (14.3)
2 2л
среднюю плотность вещества
р(г, t) = m\f(w)dw\ (14.4)
среднюю плотность электрического тока (для плазмы)
j = ZZie\wifi(w)dw, (14.5)
где w, — скорость ионов; Z,e — заряд иона; г — координата; / — время. Таким образом, при
известной функции распределения все макроскопические характеристики среды определяются
однозначно. При этом следует учитывать, что для среды, имеющей в своем составе несколько видов
частиц, функции распределения необходимо определять отдельно для каждого из этих видов.
Для рассмотрения многих теоретических и прикладных задач очень важным является
распределение совокупности частиц, находящихся в тепловом равновесии.
Если большое число частиц находится в ограниченном пространстве, в котором не действуют
какие-либо дополнительные силы, и каждая из частиц взаимодействует с другими в течение
продолжительного времени, то в системе установится равновесное состояние и соответствующее ему
распределение частиц по скоростям. В этом состоянии число частиц, скорость которых при
столкновениях увеличивается, будет равно числу частиц, скорость которых в результате столкновений
уменьшается. Выражение для функции распределения частиц по скоростям в системе, находящейся
в тепловом равновесии, было получено Дж. К. Максвеллом.
В равновесном стационарном состоянии число частиц с данными значениями скорости,
несмотря на столкновения друг с другом, остается в системе неизменным. Следовательно, в этом
случае можно принять, что столкновения между частицами не влияют на вид функции распределения.
Обычно такое состояние называют состоянием статистического равновесия.
При этих условиях в соответствии с теорией вероятности
(14.6)
где f(w\) и /(кУг) — число частиц со скоростями W\ и дог до столкновения друг с другом; /(доз) и
ftw*) — число частиц со скоростями Доз и w* после столкновения. Если в качестве аргумента функции
распределения взять квадрат скорости, то выражение (14.6) получит вид
К процессу столкновения этих частиц применим закон сохранения энергии. В этом случае
w2i + wl = wl + wl (14.8)
С учетом выражений (14.7) и (14.8) имеем
\nf(wb+\nf(wi)= lnfttt>§)+ ln/
После дифференцирования по w2 и w\ получим
Скорости w\ и W2 были выбраны произвольно, в связи с чем можно сделать выводы о
постоянстве выражения (14.9), т. е.
"4-dw2=-f$, (14.10)
f(w
или после интегрирования
f(w2) = Aexp( — $w2). (14.11).
Постоянную интегрирования А можно найти с помощью выражений (14.1) и (14.11),
записанных вдоль одной из координатных осей, например х:
+ ОО
п = А \ w2exp( — &W2) dwr.
Так как
+ °°
\ ку2ехр(-рау2) dwx= л/л/р,
— оо
то Л =я(р/л)|/2. Если при этом учесть три степени свободы, то
3/
(14.12)
Элементы статистической термодинамики
179
Значение р можно найти, если применить
уравнение, определяющее давление газа на
стенки сосуда, в который он заключен. Так
как pV = NkTy то p = nkTt где n = N/V. С
другой стороны, давление р можно подсчитать
в виде интеграла произведения числа частиц,
ударяющихся о стенку, на значение импульса,
передаваемого при этих столкновениях в
единицу времени:
р =
)
2тдо exp( — рдо2)дос1до.
Следовательно,
(14.13)
равновесная максвелловская
иГ
Рис. 14.1. Изменение максвелловской функции
распределения по скоростям при различных
температурах (ГГ)
функция распределения частиц-
С учетом полученных выражений
по скоростям принимает вид
fo(w) = n[m/{2nkT)\ 2w2exp\ — mw2/{2kT)}. (14.14)
График (рис. 14.1) показывает, что при некоторых значениях скорости доН| и до,,2 функции
распределения частиц по скоростям при разных температурах имеют свои максимумы. Эта скорость до„'
называется наивероятнейшей, так как частицы со скоростью, близкой к дон, чаще всего встречаются
в массе частиц. При этом следует заметить, что число частиц с очень большими и очень малыми
скоростями оказывается сравнительно небольшим, но они тем не менее всегда имеются в любой
системе. Для определения наивероятнейшей скорости до,, необходимо приравнять нулю
производную от fo(w), т. е.
1 г 2т / 2\
-j—/оС^) = 2до 1 ехР( ) — О,
откуда
(14.15)
до,,
т.
Средняя до скорость частиц ансамбля определяется соотношением
+ ОО
w = — ( wfQ (до) dw = -JSkT/(nm).
(14.16)
T
Так как
-2 1 Г
до =— V
п J
w2 /0 (до) dw = 3kT/m, то среднеквадратическая скорость
(14.17)
Сравнение полученных выражений показывает, что относительные значения трех характерных
скоростей близки между собой:
- / -V/2
дон: до :(w ) =1 : 1,13 : 1,22.
Максвелловское распределение частиц по скоростям справедливо для случая, когда полная
энергия частиц совпадает с их кинетической энергией поступательного движения.
иднпко на практике на ансамбль частиц часто действуют также внешние силовые
потенциальные поля. В этом случае полная энергия частиц E = Ek-\-En0Tt где Ek = mw2/2 — кинетическая
энергия поступательного движения; £Пот — потенциальная энергия во внешнем силовом поле,
зависящая от координат. С учетом этих обстоятельств выражение (14.14) получит вид
-mw2/(2kT) - Еат/{2кГ)
= n[m/(2nkT)}
3/2
(14.18)
Распределение частиц, удовлетворяющее этому выражению и называемое распределением
Максвелла — Больцмана, можно рассматривать в качестве произведения вероятностей
двух независимых событий: вероятности данного значения скорости
)
(14.19)
180 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
и вероятности, отвечающей данному значению потенциальной энергии,
f2 (w) = п0 е~Е"от/{2кТ\ (14.20)
ГД€" АГ() — ПЛОТНОСТЬ ЧЗСТИЦ В ПЛОСКОСТИ Г = 0.
Выражение (14.19) оаисывает распределение частиц в пространстве скоростей и является уже
известным распределением -Макс вел л а. Выражение (14.20), описывающее распределение ласти ц в
силовом потенциальном поле, называется- распределением Больцмана.
Одним из наиболее часто встречающихся случаев больцманского распределения является
распределение частиц в поле сил тяготения En0T = mgh. При этом n = noe~mgh/(2kT). Полученное
выражение называется барометрической формулой.
§_ 14.3. Кинетическое уравнение Больцмана
Зависимость изменения функции распределения от времени, координат и скорости определяется
кинетическим уравнением.
Так как в реальных системах взаимодействия между частицами очень многообразны, то для
описания таких систем обычно используются приближенные методы, среди которых наибольшее
распространение получило кинетическое уравнение Больцмана. Оно описывает поведение функции
распределения в приближении дискретного парного взаимодействия между частицами системы.
В этом случае df(w)/dt = fCT, где />т — так называемый интеграл столкновений, который
учитывает изменение функции распределения (числа частиц) в результате парных соударений.
При отсутствии столкновений движение частиц и изменение функции распределения определяются
только внешними полями и значениями /Ст = 0. Тогда
= f(w + dw,r+ dr,/ + dt)—f(w,r,t)=O.
dt
Учитывая, что dw/dt = F/M и dr/dt = w, получаем
df{w)/dt = df/dt+ wdf/dr + -L-df/dw = 0, (14.21)
где F — сила, действующая на частицу массой Af; r — координата; /— время.
Это бесстолкновительное кинетическое уравнение, или, как часто называют, кинетическое
уравнение без правой части. Динамика всей системы в этом случае определяется силой F.
Если же столкновения между частицами существенны, то правая часть кинетического
уравнения должна отражать скорость изменения функции распределения, вызываемую столкновениями,
поэтому
df/dt + wdf/dr + £jdf/dw = /ст. (14.22)
Это и есть кинетическое уравнение Больцмана, или кинетическое уравнение с правой частью.
Известно, что столкновения стремятся перевести систему в некоторое квазиустойчивое
равновесное состояние. Поэтому интеграл столкновений приближенно можно представить в виде
fn = W/ )ст = [/(иО-/о] *• (14.23)
Здесь f(w) и f{) — начальная и установившаяся функции распределения; т — характерное время
установления функции распределения, по порядку величины равное времени свободного пробега
частиц.
Решение уравнения Больцмана представляет немалые трудности. При современном состоянии
теории функцию распределения f(w) удалось найти только для некоторых предельных случаев.
Пусть, например, направленные скорости частиц и много меньше хаотических (тепловых)
скоростей до, т. е. «<С«у. В этом случае можно считать, что внешние поля на систему практически не
действуют и df/dt = —\f(w) — f о\/т. Решение этого уравнения имеет вид
f(w)=fa + [f{wfl)—fo] e~l/\ (14.24)
где f(w, 0) — функция распределения частиц по скоростям в начальный момент времени; fo —
максвелловская функция распределения. Из (14.24) видно, что система стремится к равновесному
максвелловскому состоянию за время, близкое по порядку времени между соседними соударениями
частиц.
Если же длина свободного пробега частиц / много больше характерного размера системы
L (/»/.), то это случай бесстолкновительной системы, для которой справедливо кинетическое урав-
Элементы статистической термодинамики 181
нение без правой части (14.21). Случай, когда /<CL, характерен для сплошной среды, в которой
времена свободного пробега частиц т малы, и в системе достаточно быстро устанавливается макс-
велловское распределение.
§ 14.4. Квантовая статистика
В классической механике состояние любой системы однозначно определяется координатами и
импульсами всех ее частиц, если для какого-то момента времени эти параметры заданы. В квантовой
механике дело обстоит значительно сложнее, так как координата и импульс, энергия и время, а
также другие пары динамических величин, характеризующих состояние любой микрочастицы, не могут
одновременно иметь строго определенные значения.
Эта ситуация называется принципом неопределенности Гейзенберга, смысл которого
характеризуется соотношением ДрАх> h и Д£Дт> И, где h — постоянная Планка; Др, Л*, Д£ и Дт — меры
неопределенности импульса, координаты, энергии и времени соответственно. Следовательно,
в квантовой механике определяется лишь вероятность нахождения системы в каком-то одном
состоянии из числа многих возможных, что отражает дискретный характер энергетических состояний
системы.
Пусть, например, в большой системе, состоящей из N подсистем, осуществляется обмен
различными формами энергии. В этом случае каждая из подсистем может принимать свое,
индивидуальное значение энергии И, и тогда полная энергия системы £ = 2 £,- Однако из-за принципа
неопределенности макросостояние любой подсистемы, а следовательно, н всей системы в целом в
каждым момент времени не может характеризоваться каким-то определенным значением энергии Е.
Поэтому можно только утверждать, что энергия подсистемы (или системы) определяется каким-то
достаточно узким интервалом между Е и £-f-A£, где £>Д£\ Кроме того, все состояния с различной
энергией характеризуются и различными вероятностями. Если нескольким различным состоянием
системы отвечает одна и та же энергия, то такие состояния называются вырожденными,
а число состояний с одной и той же энергией называют кратностью вырождения или
статистическим весом.
Величина \Е достаточно мала, поэтому в интервале энергий Е-\-\Е все состояния системы
могут быть приняты равновесными. Пусть Qm — вероятность нахождения системы в определенном
энергетическом состоянии. Эта вероятность равна отношению числа возможных состояний, при
которых система имеет энергию в интервале |£„, —(£,M±A£), к общему числу состояний системы
Qm = [r\(Em;bE)]/r\(E\ A£)] = exp[lnri(£«)-lnr|(£)], или
g. ехр ( — BE ,) р:
е--*;, »р(-Р£" НН^- (14-25)
где v
Z = ZH,e-"" = Zg,e-^L'":>> +E-> (14.26)
— статистическая сумма термодинамической системы, определяемая суммированием по
всем энергетическим состояниям; £|, £?, •••, Е,— энергии, соответствующие различным степеням
свободы системы.
В общем случае энергия атома или молекулы состоит из энергии поступательного движения £„
и анергии внутренних степеней свободы £„„:£ = £„ + £,,»♦
а статистическая сумма по состояниям имеет вид
Z= ZHZ№n = Zg.-e^*" *F'm). (14.27)
Статистическая сумма по состояниям энергии поступательного движения для газа объемом V
Z = ( 2лткТ) ""2 V=N( —) ( 2ят,кТ) (14.28)
Для определения статистической суммы по состояниям внутренней энергии необходимо знать, из
чего складывается энергия внутренних степеней свободы. Пусть, например, система состоит из
атомов и двухатомных молекул. У атомов энергия внутренних степеней свободы складывается из
энергии возбужденных электронных состояний /;0, £|, ..., Е,„ч соответствующих различным
электронным конфигурациям. Статистическая сумма но возбужденным электронным состояниям в этом
случае буде-i иметь вид
Z,,,, = g0 е~ Р"° + .<>, с ■*> + ... + В,,, е-"'". (14.29)
Для многих задач можно ограничиться /только первым членом, соответствующим основному
состоянию Е = 0. В этом случае
182
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Тогда для одноатомных газов
3/2
3/2
(14.30)
Здесь N — число атомов в системе; h и к — постоянные Планка и Больцмана; m — относительная
атомная масса.
В отличие от атомов, обладающих энергетическими состояниями только одного типа, энергия
внутренних степеней свободы двухатомных молекул складывается из энергии возбужденных
электронных состояний* £,-, энергии- колебания ядер атомов относительно друг друга £м энергии
вращения ядер относительно центра тяжести молекулы £вр.
В этом случае
Z = Z1( ZBM = Zn Z. ZK ZBp = Zg, е-р(
где
z,=
z =
exp
hv \
~"2kf)
(14.33)
где У — момент инерции молекулы; v — частота колебаний.
Таким образом, для вычисления статистической суммы по состояниям любой системы
необходимо знать допустимые состояния и уровни энергии. При вычислении этой суммы каждое состояние
рассчитывается отдельно, поэтому статистическая сумма состояний N систем может быть получена
из параметров, определенных для одной молекулы путем возведения в степень N:
Z = Z?/N\ = -L.(ZnZ.nZ«Z)" (14.34)
Распределение вероятностей, как следует из определения, должно быть при этом равно единице:
2Qm= 1. Пусть взаимодействуют друг с другом две системы, которые находятся в тепловом равно-
m
весии и, следовательно, обладают одинаковой температурой. Из анализа выражений (14.25) и
(14.26) видно, что у таких систем одинаковы значения параметра р. Можно показать, что параметр р
является функцией температуры и равен р= \/(kT). Это дает возможность представить
распределение любых систем (молекул, атомов, ионов и др.) по энергетическим состояниям в виде
Nm=Ngie-E"/m/Zgle-E^kT) (14.35)
Выражения (14.25) и (14.35) являются различными формами записи квантового
канонического распределения Гиббса, которое характеризует распределение вероятностей
различных состояний систем, находящихся в статистическом равновесии.
Распределение Гиббса позволяет определять среднее значение любого физического параметра,
явно зависящего от состояния системы. Так, если какой-то параметр при энергии Ет имеет
значение Qm, то выражение для определения его среднего значения получит вид
Для систем с большим числом частиц распределение Гиббса имеет резкий максимум при
некотором значении энергии. Состояние, отвечающее этому максимуму, является наиболее вероятным,
и именно оно вносит основной вклад в среднее значение любого параметра. Если систему
составляют молекулы идеального газа, то распределение Гиббса переходит в распределение Больцмана
(14.20).
§ 14.5. Определение термодинамических параметров
статистическими методами
Статистическая термодинамика позволяет определить значения термодинамических параметров
любой системы с использованием полученных зависимостей и статистических характеристик. Как
уже отмечалось, одной из важнейших характеристик термодинамических систем является статисти-
Элементы статистической термодинамики 183
ческая сумма по состояниям Z, значения котором зависят исключительно от молекулярных свойств
системы, а именно: возможных энергетических состояний, температуры Т и давления р. Это дает
основание использовать статистическую сумму для определения значений любых
термодинамических параметров.
Свободная энергия F является функцией состояния системы. Поэтому статистическая сумма
по состояниям может быть представлена в виде
(14.36)
Отсюда
F=—kT\nZ. (14.37)
Это выражение является основным для определения термодинамических параметров
статистическими методами, с помощью которых, учитывая известные связи свободной энергии с
термодинамическими параметрами, можно найти:
уравнение состояния системы
= ~7~Л w) ; (1438)
энтропию
= (If),-
дТ
внутреннюю энергию
энтальпию
теплоемкость при постоянном объеме
теплоемкость при постоянном давлении
изобарно-изотермный потенциал
[(|^)] (14.44)
Таким образом, при известном выражении для статистической суммы Z любой системы ее
термодинамические параметры определяются выражениями (14.37) — (14.44) однозначно.
В предыдущем параграфе было показано, что статистическая сумма по состояниям любой
системы Z = ZnZBH, при этом статистическая сумма по состояниям энергии поступательного
движения Zn определяется выражением (14.28), а внутренней энергии Z8H — выражениями (14.29),
(14.30), (14.33). Поэтому для получения расчетных выражений формулу (14.37) свободной энергии
следует записать в виде
F= - kT(\nZa + lnZniI), (14.45)
F=Fn + F. + F., = - trto^"1""' - kTlnZM, (14.46)
/2
где слагаемое Fn= — kT[\nV(2jitnkT) /Л3] соответствует поступательному движению, а слагаемое
/7BH= —krinZBll — энергии внутренних степеней свободы атомов или молекул. Тогда [см. (14.46)
и (14.38) — (14.44) ] выражения для основных термодинамических параметров примут вид:
уравнение состояния
184 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
внутренняя энергия
' dZ... .
(14.48)
энтальпия
5 kT2 / dZB \
Н= //° + "2"/jr + "z~(~d7r"/; (14.49)
энтропия
s = k\n I V -3 1 + -y-k -\- ^lnZBI1 + -у—( . j J; (14.50)
теплоемкость при постоянном объеме
3 kT / d
Г* :== h I О / —
теплоемкость при постоянном давлении
изобарно-изотермный потенциал
(14.53)
Определяя термодинамические параметры статистическими методами, следует помнить, что
для одноатомных газов ZBH = go, но для двухатомных молекул выражение ZBM гораздо сложнее [см.
соотношения (14.33)].
§ 14.6. Основы теории Онсагера
Классическая термодинамика не в состоянии предсказать поведение термодинамических систем
в неравновесных превращениях, например предсказать скорость протекания этих процессов. В
качестве необратимых процессов можно рассматривать такие процессы, как теплопроводность,
электропроводность, диффузия и некоторые другие. Эти процессы необратимы по своей природе, так
как протекают под воздействием конечных разностей потенциалов: температуры, электрического
потенциала, концентрации и т. д.
Если исключить из рассмотрения такие крайние случаи, как перенос ггод воздействием больших
градиентов температур и концентраций, для которых применение понятий температуры, энтропии
и т. п. сомнительно, то, как показывает опыт, названные выше процессы подчиняются линейным
феноменологическим законам переноса градиентного типа. Для теплопроводности это закон Фурье
q=-lgradT, (14.54)
где q — плотность теплового потока; к — теплопроводность; Т — температура;
для электропроводности — закон Ома
/= — xgradcp, (14.55)
где / — поток электрического заряда; <р — электрический потенциал; х — электропроводность.
И наконец, для описания процессов диффузии используется закон Фика
/,-=—Degrade, (14.56)
где У, —- поток массы /-го компонента; Dik — диффузия /-го компонента относительно /г-го
компонента; ct — массовая концентрация /-го компонента.
Эти законы, полученные на основе опыта, носят название феномено логических.
Теперь предположим, что два или несколько явлений переноса происходят одновременно.
Известно, что в результате взаимодействия этих явлений могут возникать новые физические явления.
Так, например, взаимодействие теплопроводности и электропроводности в цепи, составленной из
двух однородных (но различных) проводников электричества, спаи которых поддерживаются при
различных температурах, сопровождается двумя термоэлектрическими эффектами: эффектом Зее-
бека и эффектом Пельтье. Другой пример: взаимодействие процессов теплопроводности и диффузии
в газах приводит к термической диффузии, т. е. возникает поток массы вещества под действием
градиента температуры.
Элементы статистической термодинамики 185
Математически эти эффекты учитываются добавлением новых членов в феноменологические
законы переноса. Так, например, если через /| и /г обозначить потоки теплоты и вещества, а через
Х\ и Х2 градиенты температуры и концентрации, которые в дальнейшем мы будем называть
движущими сила ми или сокращенно силами, то феноменологические законы принимают вид
чгде коэффициенты Ln, L12, называются феноменологическими (или кинетическими).
В настоящее время статистическая и кинетическая теории газов в состоянии предсказать
числовые значения этих коэффициентов. Вместе с тем, как будет показано ниже, термодинамика
необратимых процессов вне зависимости от особенностей молекулярного строения вещества также
в состоянии указать методы вычисления этих коэффициентов.
Как было показано выше [см. (14.54) — (14.56)], силы X", являются первопричиной
возникновения необратимых процессов переноса. В общем случае можно записать п уравнений
в виде
п
/,= 2 LikX,t, (14.58)
k=\
имея в виду, что любой поток /, может быть вызван всеми силами.
Однако вначале в теории Онсагера существование уравнений (14.58) рассматривалось как
опытный факт, т. е. сначала необходимо было убедиться на опыте, что уравнения (14.58) описывают
исследуемое явление, и только после этого использовать аппарат термодинамики необратимых
процессов. Однако можно показать, что уравнения (Н.58) могут быть получены из анализа
уравнения состояния для связанных внутренних степеней свободы термодинамической системы. При
этом для доказательства единственным необходимым условием является справедливость
уравнения переноса градиентного типа для каждой из связанных внутренних степеней свободы в
отдельности (при отсутствии остальных потоков)*.
Теория Онсагера подразумевает, что матрица феноменологических коэффициентов L,k
является матрицей симметричной. Таким образом, соотношение
/г=1, 2,..., п) (i4.59)
представляет собой так называемые соотношения взаимности Онсагера.
Для доказательства соотношения (14.59) Л. Онсагером был использован принцип
микроскопической обратимости, смысл которого заключается в том, что все микрофизические законы
движения частиц инвариантны к трансформации времени (t—>—/), т. е. предполагается, что не существует
сил, действующих на частицы, которые являлись бы нечетными функциями.
Соотношения взаимности Онсагера (14.59) представляют собой величайшее достижение
термодинамики необратимых процессов, так как позволяют на макрофизическом уровне описать
сложные процессы переноса, возникающие под воздействием разнородных сил, лучше чем любая
другая феноменологическая теория. Исключение составляют химические реакции, так как при
исследовании химических реакций, имеющих практический интерес, область существования линейных
законов переноса весьма ограничена.
Например, при л = 2 выражения для потоков имеют вид
]\=L\\X\-\-L\2X2\ /2 = ^21X1 -\-L22X2,
откуда следует, что L\2 = L2\. А это означает, что, например, в случае сложного процесса переноса,
в котором участвует теплопроводность совместно с диффузией, коэффициент, связанный с переносом
теплоты под воздействием градиента концентрации, будет в точности равен коэффициенту,
связанному с переносом вещества под воздействием градиента температуры.
Остается указать правило выбора потоков и сил. Потоком некоторой физической величины
домазывают количество этой величины, протекающей через единицу поверхности в единицу времени:
/,.= cU/(dFdT). (14.60)
Так, например, тепловой поток q [Дж/(м2-с)], согласно соотношению (14.60), будет равен
а поток массы вещества / [кг/(м2-с)]
В общем случае, согласно Онсагеру, в качестве потока принимается величина
* Вейник А. И. Термодинамика. Минск, 1961.
186 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
, (14.61)
где х,—термодинамический параметр, представляющий собой координату состояния.
Как уже указывалось, в качестве силы принимается градиент соответствующего
термодинамического потенциала. Действительно, опыт показывает, что во всех без-исключения
самопроизвольных процессах поток субстанции направлен в сторону убывания соответствующего
термодинамического потенциала.
Так, например, жидкость течет сверху вниз, теплота самопроизвольно переходит от нагретого
тела к холодному, движение газа направлено в сторону убывания давления и т. п., но никто и никогда
не наблюдал обратного. Таким образом, направление переноса субетанвггги- противоположно
положительному градиенту соответствующего термодинамического потенциала.
Конкретные выражения для потоков У, и сил X, Онсагер предложил определять из анализа
выражения для скорости возникновения энтропии в неравновесных процессах
п
as=ds/dx= S/,X., (14.62)
1
полученного в результате анализа поведения развивающейся адиабатно изолированной
термодинамической системы. Это выражение можно также получить из следующих соображений*.
Элементарное количество внешних воздействий в любом неравновесном процессе может бы и.
представлено в следующем виде:
dQi=peidxi, (14.63)
где dQ,= — dL, — элементарное количество внешних воздействий; dL, — элементарная работа
данного рода; Pf — внешний термодинамический потенциал; ь—-координата состояния.
Связь между внешним Pi и внутренним Pt потенциалами следует из соотношения Pf =
= Р,-f dP,. Таким образом, уравнение (14.63) принимает вид
dQi =(P, + dP/)djcI- = fidx,-+ dP.-dx/. (14.64)
В случае протекания равновесных процессов (при равенстве внешнего и внутреннего
потенциала) второй член в (14.64) стремится к нулю и выражение для количества внешних воздействий,
равное и обратное по знаку элементарной работе, записывается в виде
dQ/=—dLi = P/dx/.
Дополнительное слагаемое dP,d*,, появляющееся в (14.64), представляет собой потери,
связанные с неравномерностью. Опыт показывает, что преобразование любых форм движения материи,
связанное с необратимыми потерями, всегда происходит в одном направлении, т. е. в конечном счете
все формы движения преобразуются в теплоту диссипации, что, в свою очередь, согласно второму
закону термодинамики, приводит к росту энтропии термодинамической системы:
. (14.65)
Из соотношения (14.65) следует, что
Из последнего равенства нетрудно получить выражение для скорости возникновения энтропии в
единице объема в виде
dS1HC I dxt dP, i
^4 ]Х О4-66)
T dFdx d£, T
где dV = dFd^i — элементарный объем; F — площадь поперечного сечения; £, — координата,
совпадающая с направлением потока; Jl = dXi/(dFd%) —поток величины х,\ X/=dP,/d£, — движущая
сила в направлении оси /.
Если термодинамическая система обладает п связанными степенями свободы, то суммарная
скорость возникновения энтропии определяется выражением
*Вейник Л. И. Термодинамика. Минск, 1961.
Элементы статистической термодинамики
187
Os = T^j JiXi> (14.67)
практически совпадающим с выражением (14.62), полученным Л. Онсагером.
Следует заметить, что уравнение (14.67) предоставляет некоторую свободу выбора потоков У,
и сил Л",-. Однако, несмотря на это, феноменологические коэффициенты в уравнении (14.58) будут
подчиняться соотношениям взаимности (14.60) Онсатера.
Ниже нриведены некоторые наиболее часто используемые выражения для потоков У, и
обобщенных сил Хг.
Процессы переноса
Теплопроводность
Диффузия
Электропроводность
Потоки У,
Я
У,
У
Силы X,
сплошная среда
grad(l/r), или — (gradr)/r2
graddi/Г)
—grad(4)/r)
неоднородная среда
Л Т/ Т2
А(И/П
Дф/Г
Выражения для потоков У, и сил Xt в каждом конкретном случае могут быть получены из
анализа зависимости для скорости производства энтропии (см. §14.7).
§ 14.7. Применение теории Онсагера к анализу процессов
теплопроводности
Рассмотрим цилиндр из материала с изотропными свойствами, в котором вдоль направления
оси х имеется градиент температур. Предположим, что задача одномерная, тогда направление
теплового потока совпадает с градиентом температуры (рис. 14.2).
Выделим элементарный цилиндрический объем длиной dx с единичной площадью поперечного
сечения. Согласно первому началу термодинамики, изменение внутренней энергии элемента должно
быть равно разности входящего и покидающего элементарный объем тепловых потоков за единицу
времени:
pdxdu= — dqdx, (14.68)
где и — удельная внутренняя энергия, Дж/кг; р — плотность, кг/м3; q — тепловой поток,
Дж/(м2«с); т — время, с.
Имея в виду, что для данного случая, согласно второму началу термодинамики,
запишем уравнение (14.68) в виде
Так как
jd_/ q\ = dq q at
dx \ T) T dx T2 dx '
pds/dx=-dq/{Tdx).
dT
окончательно получим
P17=-
T2 dx
(14.69)
— выражение для скорости возникновения энтропии. Первый член соответствует потоку энтропии
]s = q/T, поступающему в элементарный объем извне, в то время как второй член связан с
производством (скоростью возникновения) энтропии в объеме за
счет необратимости процессов переноса теплоты.
Таким образом, скорость производства энтропии
где gradr=dr/dA:.
Согласно уравнению (14.62), соотношение (14.70) можно
представить в виде
os = JqXq, Рис. 14.2. Теплопроводность
неограниченного цилиндра
188 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
где J,, = q\ X(f= — graAT/T2. При таком определении потока и силы феноменологический закон
переноса теплоты примет вид
J4=- LgradT/T'2. (14.71)
Если сопоставить уравнение (14.71) с законом Фурье t/=— ^gradT, то феноменологический
коэффициент L можно выразить через теплопроводность в следующем виде:
h=L/T*.
Если принять в качестве выражения для производства энтропии уравнение (14.66), то в этом
случае полечим следующее выражение для силы:
В случае стационарного процесса теплопроводности энтропия сохраняет постоянное значение
в любой точке цилиндра, а суммарное производство энтропии равно нулю, т. е.
/Ач
\ 7 )
Ах у 7 ) ' Г Ах "'
Однако в этом случае поток энтропии Js = q/T не остается постоянным вследствие уменьшения
температуры вдоль оси х. Соотношение (14.72) свидетельствует лишь о том,что поток энтропии,
покидающий элемент, равен ее производству в элементарном объеме за счет неравновесности
процесса переноса теплоты.
§ 14.8. Применение теории Онсагера к анализу
термоэлектрических эффектов
У. Томсон (Кельвин), применяя законы термодинамики равновесных процессов, создал в 1854 г.
теорию термоэлектрических явлений, которая приводит к результатам, подтверждаемым опытом.
Однако в своих рассуждениях Томсон предложил разделить необратимые эффекты (эффект
тепловыделения Джоуля и эффект теплопроводности) от эффектов, которые он считал обратимыми
(эффекты Зеебека и Пельтье), так как последние меняют свой знак при изменении направления
электрического тока и теплового потока. Эти рассуждения в настоящее время не являются
обоснованными, так как не представляется возможным произвольно отделить необратимые эффекты от
обратимых и применять к последним законы классической термодинамики.
Термодинамика необратимых процессов позволяет не только предсказать термоэлектрически'.,
эффекты, возникающие при взаимодействии процессов переноса электричества и теплоты в цепи,
состоящей из двух однородных, по различных проводников электричества, и найти соотношение
между ними, но и получить связь между феноменологическими коэффициентами переноса
[уравнение (14.58)] с теплопроводностью и электропроводностью.
Применим методы термодинамики необратимых процессов к анализу термоэлектрических
явлений. Допустим, что имеется замкнутая электрическая цепь, состоящая из двух однородных, но
различных проводников электричества А и В; концы этих проводников спаяны и поддерживаются
при постоянных температурах Т и Т-\-АТ с помощью двух источников теплоты: si и s2 (рис. 14.3).
Предположим также, что электрическая цепь, за исключением спая, помещенного в источник s?,
поддерживается при постоянной температуре Т. В этом случае, согласно Зеебеку, под воздействием
разности температур спаев возникает термоэде ф. Для такой термодинамической системы первое
начало термодинамики записывается в виде.
TAs = Au — ц>Ав, (14.73)
где е — электрический заряд, Кл; — фde— работа по переносу электрического заряда, Дж.
Из уравнения (14.73) можно получить общее выражение для суммарного изменения энтропии:
As = Au/T — ц)Ае/Т. ,
Предположим теперь, что источники s\ и s2 обмениваются количеством энергии Аи и
одновременно по цепи переносится электрический заряд Ае под действием разности потенциалов Лф;
состояние проводников при этом не меняется. Тогда полное изменение энтропии системы (рис. 14.3) будеа
равно
btpde/T. (14.74)
Если пренебречь величиной ЛГ по сравнению с Г, то
выражение для скорости производства энтропии принимает вил
Рис. 14.3. Схема электричес- Аи ДГ Лф Ае ,,л^г^
кой цепи "• = - Тт Т5 Т "Г' (|475)
Элементы статистической термодинамики 189
Из выражения (14.75), согласно (14.62), следуют выражения для потоков и сил:
Ju = du/dx — поток энергии;
Je=de/dj — поток электрического заряда;
Хи=— А Т/Т2 — термическая сила;
Хе= — Дф/Г — электрическая сила.
Получены выражения для потоков и сил, в точности совпадающие с общепринятыми (см.
табл. в § 14.6).
Выражение для скорости возникновения энтропии можно записать в форме уравнения (14.62):
os = ds/dT = JuXu + JeXe. (14.76)
В этом случае феноменологические законы переноса будут иметь вид
Je=z L\ \Xe-
у _ / ДФ
J е— ~ Ь\\ ~f
Проанализируем зависимости (14.78) для некоторых частных случаев.
Рассмотрим сначала стационарный случай: AT = const, Je = 0 (de = 0) [например, измерение
электродвижущей силы (эдс) термопары компенсационным методом]. Из (14.78) следует
^-_i2i_L ( 4 79)
т. е. получили эффект Зеебека, откуда зависимость эдс термопары от температуры
Дф = аД7\ (14.80)
где а=—т^2-=- коэффициент Зеебека.
L\\ 1
Рассмотрим теперь второй случай, когда температуры спаев одинаковы (Г = 0), а к местам
спаев приложена постоянная разность электрического потенциала Дф = сопз1. Тогда из (14.78)
следует
Ja/Je = L2i/Ln=n, (14.81)
где П = ПАВ —коэффициент, характеризующий эффект Пельтье, представляющий собой
количество теплоты, выделяющееся в единицу времени при циркуляции тока в цепи. Электрический
заряд в металле переносится под действием разности электрического потенциала за €чет свободных
электронов. Эти же электроны переносят под воздействием градиента температуры кинетическую
энергию микроскопического движения, которая представляет собой не что иное, как теплоту.
Обращаясь к рис. 14.3, заметим, что количество теплоты QA = ПА Je протекает по проводнику
А, в то время как теплота QB = Пв Je^- по проводнику В. Коэффициенты ПА и Пв могут быть
как положительными, так и отрицательными, а это означает, что направление теплового потока
может и не совпадать с направлением тока.
На спаях имеем разрыв в значениях тепловых потоков
(ПА-Пв)]е = ПАВ Je, (14.82)
представляющий собой поглощенное или выделенное количество теплоты за счет эффекта Пельтье.
Таким образом, электрический ток переносит теплоту от одного спая к другому.
На этом принципе работает термоэлектрическая холодильная машина. Эффект Пельтье
принципиально отличается от эффекта Джоуля» так как, во-первых, эффект Джоуля пропорционален
Je, а не Je, и, во-вторых, в случае эффекта Джоуля отсутствует определенное направление переноса
теплоты.
Решая совместно (14.79) и (14.86) и. учитывая соотношение Онсагера L\2 = L2\, получим
•-' .Да>- L2\ \ П
(483>
190 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
а=—П/Т. (14.83)
— соотношение между эффектами Зеебака и Пельтье, т. е. первое соотношение Томсона.
Предположим теперь, что спаи находятся при различных температурах и что, например,
коэффициент ПА ветви А зависит от температуры. В этом случае теплота, поглощенная на одном из
спаев, не будет равна теплоте, выделившейся на другом. Эта разность, возникающая при
циркуляции тока в проводнике при наличии градиента температуры, представляет собой третий
термоэлектрический эффект — эффект Томсона.
Пусть величина JeTAdT характеризует тепловой эффект Томсона, где тА — коэффициент
Томсона. Примем температуры спаев равными Т и T-\-dT. В этом случае суммарное количество
теплоты Пельтье и Томсона будет равно
]е(П-(П + 6П)) + (тв -тА )JedT.
Тогда для единичного заряда первое начало термодинамики запишется в виде
-dtf + Ofr -тл )dr = dq>. (14.84)
Здесь мы пренебрегли эффектом Джоуля (dq>2//?) как величиной 2-го порядка малости. С учетом
d(p/dr=— П/Т уравнение (14.84) принимает вид
т--т--4г-г (|485)
Это второе соотношение Томсона. Выражение (14.85) можно Переписать в виде % — тА =Т6(П/Т).
Имея в виду первое соотношение Томсона d(p/dT= —П/Т, получим третье соотношение Томсона:
*.-** =-т&=т Ж Ci4.ee)
А это означает, что эде термопары не может изменяться линейно в зависимости от температуры,
так как тв фтА .
Феноменологические коэффициенты LN, L\2 = L2\, L22 могут быть связаны с физическими
свойствами системы. Мы уже видели [см. (14.81)], что
Коэффициент L\\ связан с электропроводностью в стационарном состоянии (ДГ = 0):
где х = /,ц/Г — электропроводность.
Теплопроводность в стационарном состоянии (/«, = ()) можно определить из соотношений,
вытекающих из уравнений (14.78):
Дф ДГ Дф ДГ
откуда следует, что
L\\
(14-87)
Следовательно, теплопроводность X, входящая в закон Фурье, может быть связана с
феноменологическими коэффициентами уравнений переноса (14.78) следующим образом:
Таким образом, с помощью аппарата термодинамики необратимых процессов мы не только
получили соотношения (14.83), (14.85), (14.86) между термоэлектрическими эффектами, но и
зависимости, связывающие феноменологические коэффициенты LMf L)2, ... уравнений переноса (14.78)
с электропроводностью и теплопроводностью.
Вопросы 1- Что такое функция распределения?
2. Как определяются усредненные параметры газа или плазмы (скорость, плотность,
энергия) по известной функции распределения?
3. Что такое статистическая сумма по состояниям и чем она определяется для одно- и
двухатомного газов?
Элементы термодинамики твердого тела 191
Глава 15
ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ ТВЕРДОГО ТЕЛА
§ 15.1. Напряженное и деформированное состояние твердого тела
Твердое тело рассматривается как термодинамическая система в виде совокупности
материальных точек (континуум), расстояния между которыми изменяются в процессе
движения (деформации). В свободном же состоянии твердое тело в отличие от жидкости
и газа способно сохранять свои размеры и форму.
Изменение состояния твердого тела как термодинамической системы представляет
собой термодинамический процесс, который является следствием взаимодействия тела
с окружающей средой в форме теплообмена и работы; оно сопровождается изменением
свойств тела (температуры, механических параметров и др.)> определяющих
термопрочность материала, работоспособность и долговечность конструкции.
Особенностью термодинамического анализа состояний твердых тел и процессов,
в них происходящих, является необходимость использования представлений
неравновесной термодинамики с учетом специфики определения механической работы, т. е.
работы деформации.
На частицы твердого тела действуют инерционные и гравитационные силы и в общем
случае поверхностные силы (силы давления, трения и пр.). Совокупность поверхностных
сил определяет напряженное состояние тела. Под действием приложенных к телу сил
твердое тело деформируется, т. е. принимает состояние с отклонением (увеличением или
уменьшением) его геометрических размеров от их значений в отсутствие внешних сил.
Используя трехмерное евклидово пространство с декартовой прямоугольной системой
координат, напряженное и деформированное состояние тела в любой момент времени
можно определить заданием составляющих тензоров второго ранга zkK для напряжений
(z — p) и деформаций (z = e), где
/г, /(= 1, 2, 3; zkK =zKk ; ге(р, е), (15.1)
т. е. заданием шести числовых значений (или функций координат) в каждом случае.
Здесь первый k и второй К индексы последовательно указывают две координатные оси:
перпендикулярную плоскости действия составляющей zkK и параллельную направлению
действия zkK .
Величины гкК безразмерны и определяются соотношениями
Чк =(Y>.g +Ук.*-)/2; У* = у*-у*. (15.2)
которые получены для случаев задания мгновенных координат ук индивидуальных
частиц в виде функций их начальных координат yk и времени т. Здесь и в дальнейшем
будут использоваться общие обозначения типа Yk, Yk гл — dYk/dz^ (х= K\z=y\ х=К|г=^);
?k соответственно для компонентов вектора ? и их производных — частных по
координатам и полных по времени т.
В выражениях (15.2) Yk представляет собой составляющую вектора перемещения.
При этом величины ekK могут быть равными относительным локальным удлинениям
(при k = K) ребер элемента тела (рис. 15.1) в направлении соответствующей оси
координат yk или в два раза меньшими соответствующих углов сдвига (при кфК), т. е.
изменений углов между ребрами элемента, первоначально параллельными осям yk и ук . На
рис. 15.1, а показано удлинение VijAi/i ребра cd длиной Аг/i, вызванное смещением
Y\(y\) вдоль оси у\\ на рис. 15.1,6 — угловая деформация, вызванная смещениями
Y\(t)2) и Уг(«/1) и характеризуемая отклонением крайних точек / и d ребер на расстояния
У|,2Д«/2 и V^.iAi/i от осей t/2 и у\ соответственно. Относительное изменение объема тела
(15.3)
192
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Рис. 15.1. Примеры деформации элемента твердого тела: а —
чистое удлинение ребра cd\ б — угловая деформация с
отклонением точек / и d ребер
где
=2 de***
(15.4)
В (15.1) величины ркК имеют размерность силы, отнесенной к единице площади;
они характеризуют нормальные (при k = K) или касательные (k=^K) силы, локально
действующие на выделенный внутри тела элемент. С учетом изложенного уравнения
состояния твердых тел можно представить в виде
PkK =PkK(Z* le/L»; 2ё(7\ s)- /, L = l, 2, 3; *, /(е(1, 2, 3), (15.5)
где s—удельная энтропия; Т—температура.
Неизменное совпадение во всех точках тела значений как составляющих тензора
деформаций гкК , так и температуры Т является определяющей характеристикой так
называемых основных термодинамических систем. Состояние каждой такой системы
может быть однозначно задано совокупностью значений
(Z, ekK}\ Z<=(T, s); ky K=l, 2, 3, (15.6)
содержащей не более семи (с учетом s или Т) независимых числовых значений или
функций времени.
Если же несколько основных систем расположены так, что между ними возможен
обмен энергией, то говорят о составной системе, состояние которой
описывается набором совокупностей типа (15.6) для всех входящих в нее основных систем.
Любое тело конечной массы М и объема V в общем случае можно рассматривать как
составную систему в указанном смысле — с элементарными массами или объемами в роли
основных систем. Конфигурация тела и состояние его материала характеризуются
заданием величин (15,6), а также удельного объема и, в случае его неравномерности —
как функций времени и координат.
Для любой основной термодинамической системы уравнение первого закона
термодинамики можно представить в форме
6q = du-\-6a\ 6а= — vpkK dzkK , (15.7)
где 6q и 6а — элементарные количества теплоты и работы деформации;, du — диффе-
* В дальнейшем всюду, как и в (15.4), символ суммирования типа X по индексу, дваждн
k=i
использованному в записи суммируемых выражений, будет опускаться.
Элементы термодинамики твердого тела 193
ренциал внутренней энергии. Знак минус указывает на то, что при совпадении знаков
pkK и dzkK (например, при pkK >» 0, de^ >» 0 в случае растяжения) работа производится
над твердым телом и поэтому остается отрицательной. Уравнению (15.7) можно придать
также вид
e^K , (15.8)
где
Р*к =PkK \кфк ; Р*к =(PkK +P)k=K •
Использование уравнения в форме (15.8) целесообразно в тех случаях, когда pk*K =0
для каких-либо двух значений £ = /( (растяжение стержня или пружины) или даже для
всех трех значений k = K (как для газа или жидкости, лишенной трения).
С учетом (15.7) или (15.8) объединенное уравнение первого и второго законов
термодинамики для обратимых процессов принимает вид
Tds — du=— sdT — d/ = 6/ — vzkK dzkK , (15.10)
где &l^((pdv)z==p* , 0|z==p ); / — свободная энергия (энергия Гельмгольца). Наряду с
(15.10) справедливо также, что
Tds-dh*=-sdT-dg* = EkK d(vpkK), (15.11)
где
h* = u-vpkK EkK , g* = h*-Ts. (15.12)
В этих выражениях h* н g* — полная энтальпия [8] и полная энергия Гиббса
соответственно. Для необратимых процессов в силу второго закона термодинамики как в (15.10),
так и в (15.11) правая часть всегда меньше двух равных частей слева, если для pkK
использовать те же уравнения состояния, что и в обратимых процессах.
Деформации тел могут быть остаточными, т. е. не исчезающими после
прекращения нагрузки, или упругими. Упругостью называют свойство тел после прекращения
нагрузки восстанавливать свою форму и объем (для твердых тел) или только объем
(для жидкостей и газов). Процессы с остаточной, или, как говорят, пластической,
деформацией являются существенно необратимыми. Процессы с упругой деформацией
часто можно считать близкими к обратимым.
§ 15.2. Термодинамические соотношения для системы
с упругими деформациями
При условии взаимной независимости величин ekK , применяя уравнение (15.10) при
г = р с учетом однозначности выражений полного дифференциала для функций и или /,
а также независимости смешанных частных производных этих функций от порядка
дифференцирования, получим
vpx=(dz/dzx)z^ ; Z = {dz/dZU z<=(u\z=s , flz-г); (15.13)
(дгх /dZ)z-t,=-(dZ/d(vpx ))r; Zg(7, -s); (|Z|, Z) = (Tt s); x = MC, (15.14)
где нижний индекс е определяет условие постоянства всех величин e/L , кроме, может
быть ekK . Выражения (15.14) представляют собой уравнения Максвелла. Из (15.13)
следует, что при задании величин (15.6) и аналитических зависимостей
«=«(s,(e,J)nra/=/(r,(e/t)) (15.15)
могут быть вычислены все термодинамические свойства твердого тела. И потому
задание величин (15.6) действительно определяет состояние основной системы. Следует
отметить, что соотношения (15.13) имеют лишь принципиальное значение, так как для кон-
7 Зак. 584
194
РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
кретизации взаимосвязей между {plL) и { zlL } они почти не используются, в связи с тем
что зависимости (15.15) экспериментально не выявляются.
Выражение (15.15) можно прлучить на основе зависимостей (15.13), если
взаимосвязи (15.5) уже выявлены экспериментально (в форме соответствующих уравнений
состояния). Последние для системы с упругими деформациями можно представить
в виде [6]
7-1
,0
ьфк)'
где
ГД=Г— Го; Р = Я""1Д///ГД«const; £ = £(Г); v«const.
(15.16)
(15.17)
Здесь Го — температура системы в исходном недеформированном состоянии; Д// —
изменение линейного размера системы вследствие изменения ее температуры от Го до
Г; Е — изотермный модуль упругости (модуль Юнга); v — изотермный коэффициент
поперечной деформации (коэффициент Пуассона). Для большинства материалов v =
= 0,26...0,30. Последнее слагаемое выражения (15.16) для термически изотропного
тела одинаково во всех направлениях — это составляющая так называемого
шарового тензора деформаций, характеризующего тепловое расширение (сжатие) тела при
изменении его температуры на Гд . Остальные слагаемые выражают обобщенный закон
Гука. В тех случаях, когда модуль Юнга не зависит от тензора деформаций, выражение
(15.16) отражает зависимость типа
ETb, (15.18)
где сомножители AlL и QkK являются константами. Правая часть этого выражения
содержит лишь первые (линейные относительно e/L ) слагаемые из разложения pkK ({e/L }, Г)
в ряд по степеням e/L , в связи с чем уравнение (15.18) принципиально применимо лишь
при относительно малых e/L . Однако это обстоятельство не вносит заметной ошибки,
так как в случае упругих деформаций это условие выполняется для большинства
материалов.
Модуль упругости £ — характеристика упругих свойств материалов (чем больше
значение £, тем меньше при том же напряжении деформируется система). При
комнатных температурах для многих металлов £«10и Па, для гранита — 4,9• 1010 11а, для
бетона —2-105 Па, для каучука — 8 Па. Для некоторых материалов значения £
различны при растяжении и сжатии. Однако во многих случаях это различие можно не
учитывать. С ростом температуры значение £ уменьшается (чем выше температура, тем
легче деформируется материал). Для стали £• 10^"== 2,2; 2,12; 1,88 Па соответственно
при / = 0; 200; 450 °С; в интервале температур от
—50 до +50 °С зависимость £(Г) весьма слабая,
ею можно пренебречь или (в более точных расчетах)
полагать, что
Рис. 15.2. Диаграмма состояния
упругодеформируемого стержня при
Т = const
(£ т =—4,4*107 Па/К для стали). Здесь
производная считается полной, так как с достаточной
степенью точности можно пренебречь зависимостью
£ от [e[L }.
Уравнения (15.16) пригодны для построения
диаграмм состояния конкретных систем, например
упругодеформируемого стержня при заданном
давлении р — const в координатах ри, //, где абсцисса
Pw — растягивающая сила, отнесенная к единице
Элементы термодинамики твердого тела 195
площади сечения, ордината Я— длина стержня (рис. 15.2). Как следует из (15.16), для
стержня принимается
PkK
0; Н/Н
— 1
= 1 + е; е = е„ = (р„ + 2pv) E~l + рГд. (15.19)
р=0
При этом изотермы прямолинейны и тем выше на диаграмме, чем выше температура
(так как вследствие термического расширения большей температуре соответствует
большая длина стержня). С ростом температуры увеличивается и наклон изотерм к
оси рп, что связано с отрицательностью величины Ет.
§ 15.3. Выражения для калорических свойств и функций процесса
Величины (15.6), а также pkK и Yk [см. (15.2)] заранее не известны (их не больше 16).
Они могут быть определены расчетным путем на основе решения соответствующей
системы уравнений при заданных условиях однозначности. Такая система может
включать до 12 алгебраических уравнений (15.16) и (15.2), а также до 4 дифференциальных
уравнений [уравнение энергии, представляющее преобразованный вариант одного из
соотношений (15.10), и до трех уравнений, получаемых из векторного уравнения
движения, отражающего закон сохранения импульса, в проекциях на координатные оси]. В
случае неравномерной плотности материала системы добавляется уравнение
неразрывности, отражающее закон сохранения массы.
Если же необходимая часть из названных выше величин определена или задана,
то для системы возможен и расчет калорических свойств (энтропии, свободной и
внутренней энергии, энергии Гиббса и др.) и термодинамических функций процесса
(количеств работы и теплоты). Необходимость такого расчета возникает при решении ряда
прикладных задач термомеханики — при анализе поведения конструкционных
материалов в условиях интенсивных тепловых или динамических воздействий, оценке степени
поврежденности материала (энтропийный критерий плотности), оценке диссипативных
свойств материалов и т. д.
Рассмотрим некоторые возможности расчета применительно к упругодеформируе-
мому стержню при p = const. При этом используем соотношения (15.10) —(15.12) и
(15.14). В соответствии с (15.19)
р,,+р = Её; ё=е-рГд —p(2v— 1)£—'. < 15.20)
Дифференцирование в (15.20) приводит к результату
(г-$Ть)Е,т -рЕ. (15.21)
Выражение (15.16) при /г = /(е{2, 3) после подстановки ри из (15.20) принимает вид
e*K = Pv + prA(l+v)-ve; pv = p(2v2 + v- l)E~l. (15.22)
После дифференцирования в (15.22) получаем
dekK =<pdr-vde; <р = Р(1 +v)-pv Ej /E. (15.23)
Как простое следствие выражений (15.3) и (15.23) имеем:
); v = v(T, г)=г>[\ +е(1 — 2v)]; v = v(T; 0);.. (4.5-24)
o = v(To, 0); pv^p^T)-py(To)Г{\Ъ.2Ь)
В этом параграфе кроме введенных в (15.20) — (15.24) использованы обозначения
—vo/v)\ ГД1 =Г2-Г,;
I—2v); Dw = p(l — 2v)w; D=l+2pv. (15.26)
Вычисление калорических свойств проводится с точностью до значений при отсутствии
7*
196 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
деформирующей силы, кроме р, т. е. при
р„ = -р, ё = 0, в = Н(Т,р)/ЩТь О)-1=РГД -D.E"1
[как видно из (15.20)], до значений «нулевых» функций, которые одними лишь
термодинамическими методами вычислены быть не могут.
Методика вычислений сводится к следующему.
1. В связи с выражениями (15.1СЦ и (15.23) справедливы зависимости
= - (d(vp,, + 2pvv)/dT%.
С учетом (15.24), (15.21) и этих зависимостей имеем:
dsT =dE(ds/de)T =[ — (d(vpn)/dT)t — 2pyvo]dE = v(Eyl> + l)dE\ s(7\ e) = s(7\ 0) +
+ ь:е/2); (15.27)
s(T, e) = s(7\ 0) + еМ^д +N-e[(E + Ej Гд ) (1+4v) + £, p-'(l-2pv0)]/2};
, (15.28)
где -ф, £, 6 — см. (15.26). В (15.27) и последующих формулах отброшены слагаемые,
содержащие величины е3 и е3, в связи с их относительной малостью.
2. Подставив в (15.10) выражение dv в соответствии с (15.24), получим
df + (s + 2(ppy)dr= v(p*u —Dj) dE = v(Ee —D,)de;
/(7\ё) = /(Г0) + w[ (£ - D2) e/2 - D,].
3. Если учесть (15.10), (15.27) и последнее соотношение, то
и(Т,д = (/ + Ts)r - = и (ГО) + иё[ ё(Е - D2 + Щ/2 + П- D,]. (15.29)
4. Подставив в (15.12) соотношения (15.29), (15.22) и (15.20), имеем:
h* — и = v (2рг22 — р,,е) = рр — еу (рп + 2pv) = рр — у (ё + рГд — D,/£) (£ё — D,);
Pfi = 2pv(px + РГД(1 + v)); А'(7\в) = А'(Г,0) + иё[ ё((Г6 - £ + D2)/2 -
- TlDJp) + П + Dx - р£Гд]. (15.30)
5. Подставив в (15.12) соотношения (15.30) и (15.27), получим
ё\тЛ) = /(Г0) + v'e[(D2 - Е) ё/2 + D, - РЕГД]. (15.31)
С учетом выражений (15.20) в соотношениях (15.27) —(15.31) возможна замена е,
например
[l ] Е~\ (15.32)
6. По аналогии с ср и cv можно ввести понятие теплоемкости материала стержня
при постоянных р и деформирующей силе (сР)Р — аналог ср) или при постоянной длине
(сн р —аналог с„), а именно: cPiP=T(ds/dT)pu\ cH p —T(ds/dT)H. Расчеты с
использованием соотношений (15.27) и (15.32) показывают, что упругие деформации не
оказывают сколько-нибудь заметного влияния на теплоемкость материала стержня (cPiP«
&сНр ъср).
7. Для количеств работы деформации и теплоты в изотермном процессе упругой
деформации стержня получено
6
2~l +(1 — 2v)e/3];
Элементы термодинамики твердого тела 197
Величина q\2 относительно мала. Так, для стального стержня ^,2 = 84 Дж/кг при рц =
= 2-108 Па>р.
8. Для процесса рц = const, т. е. термического расширения стержня под неизменной
нагрузкой, в силу соотношений (15.16), (15.7), (15.25) и (15.11) можно получить
dep = pdT; aI2 = — j (pn vde) = — pu v{pT^ [D -\- (1 + v) РГД1]; v{ = (Th pn)
(15.24), (15.20). Из (15.11), (15.25), (15.16) следует:
&q = Tds = dh + (2pe22 — Рце) dvp; dvp = 2vx P(l + v) dT\
Q\2 = h*2 — h\ + 3^v{ ГД1/(2ре22 — pne) r _ Г( + (p — p,,/2) рГдЛ ;
•*/"п ч (m=l,2).
Для /г^ применимо выражение, получаемое из (15.30) заменой е в соответствии с (15.20).
9. Для процесса е = const, в котором сжатие (растяжение) стержня одновременно
сопровождается его подогревом (охлаждением), с тем чтобы уменьшение (увеличение)
длины стержня в результате упругой деформации компенсировалось увеличением
(уменьшением) длины стержня вследствие его термического расширения (сжатия), в
соответствии с выражениями (15.7), (15.28), (15.10) и (15.29) имеем:
2
а,2 = — \ vpn de = 0; bq = du -\- 2pvde22\ de22 = Pq>dT;
l
</i2 = "2-w,+2p(prAI[(l+v)prAI +\+2pv]v(Tu e); um = u(Ty г)\т_Тт.
10. Если процесс адиабатный, т. е. деформация осуществляется настолько быстро,
что заметный теплообмен между стержнем и средой не успевает произойти, то при
условии его обратимости с учетом (15.7), (15.25) и (15.20) справедливы соотношения
= const; <7i2 = O; щ2== — [ (vpu de)s= —vo[ {[e(l — 2v) + D +
l (15.33)
Зависимость Гд = Гд (e)|n==const, т. е. изменение температуры стержня в процессе
его деформации, называется эластокалорическим эффектом. При П =
= T = const эффект отсутствует, а для П = 5 (адиабатный эластокалорический эффект,
или эффект Джоуля) его оценка наиболее интересна с практической точки зрения.
Из (15.28), пренебрегая слагаемыми с е2, получим соотношение
Е2 (дг/дТ) s + ed£2/d Т= - ср/ (Tvo$); Е2 = G Гл + N,
интегрируя которое имеем
е = cp(£v0E2)-' 1 п(Т/Т0) (15.34)
или, заменяя логарифмическое выражение его приближенным значением,
Т-То=-/Се/Р; К = voE2To$2/cp. (15.35)
Из (15.35) видно, что эффект Джоуля не зависит от длины и сечения стержня. Так
как выражение v0T0E2/cp'> 0, то знак изменения температуры определяется
алгебраическими знаками величин е и р. Для большинства твердых тел значения р положительны,
поэтому при значениях е> 0, т. е. при растяжении, стержень охлаждается и, наоборот,
нагревается при сжатии, В частности, при быстром растяжении стальной проволоки с
198 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
напряжением рм = 2-108 Па температура ее снижается на 0,16 °С, что без труда можно
измерить. В 80-х годах прошлого века эксперименты по адиабатному расширению
серебряной и стальной проволок были использованы для вычисления механического
эквивалента теплоты. В настоящее время адиабатное расширение проволоки в принципе можно
использовать для экспериментального определения теплоемкости ср ее материала. В
редких случаях (например, для несильно растянутой резины) р<0 и тогда алгебраический
знак изменения температуры оказывается противоположным.
Подставив зависимость (15.35) в (15.33), имеем
Полученные результаты подтверждают эффективность изложенной методики
расчета.
§ 15.4. Пластические деформации и диссипативная функция
В каждом из соотношений (15.10) и (15.11) при z = p для необратимых процессов
(пластические деформации и др.) правая их часть всегда меньше двух равных частей слева
[если для pkK использовать уравнения типа (15.13) или (15.16), выведенные для случаев
упругих деформаций]. Р. Клаузиус предложил соотношения такого типа записывать
всегда со знаком равенства, но в правую часть формально добавлять величину bqH ^0,
названную им некомпенсированной теплотой. В действительности теплота
6<7Н к деформируемому телу из окружающей среды не подводится. Однако ее включение
в правую часть выражения (15.7), соответствующее допущению, что эта теплота
дополнительно поглощалась бы в обратимом процессе, обеспечивает в (15.10), (15.11) условия
равенства. При этом с учетом размерности q и структуры выражений (15.10) можно
записать
0 < 6qH = TdsH = 2 6a2; baq = Tdsq\ дар = - vpu deih (15.36)
z=p,q
где [ги } — {ekK } [см. (15.10)]; знак равенства слева относится только к обратимым
процессам; dsH — элементарное порождение энтропии в системе вследствие необратимости
протекающих в ней процессов; 26аг — элементарная работа диссипации. Последнюю
2
можно разбить на две группы слагаемых и рассматривать одну из них (z — p) в качестве
элементарной работы необратимых сил механического характера, определяемых
тензорами типа (15.1). Вторая группа слагаемых (z — q) рассматривается только для
элементов составной системы и обусловлена возможной необратимостью переноса теплоты
вследствие различия температур в системе.
Уравнения, которые с учетом соотношений (15.36) представляют собой точные
равенства для необратимых процессов [вотличиеот (15.10) и (15.11) с pkK по (15.13) или
(15.16)], можно записать в форме, близкой к выражениям (15.10), (15.11). Например,
Tds — du=— sdT — df= — vpkK dekK +Tdsq\ pkK = prR +pu , (15.37)
где /г, КУ г, /?, /, / — индексы суммирования с одинаковыми пределами (от 1 до 3 каждый),
но подчеркивающие различный смысл соответствующих величин. А именно ри , prR , pkK
называют соответственно необратимыми, обратимыми и фактическими составляющими
напряжений (или силами). При этом prR во всех случаях определимы как функции Т
(или s) и {гкК } по соотношениям типа (15.13) или (15.16) с логической заменой kK на
rR для р. Но только при обратимых процессах эти величины [prR } по смыслу равны
величинам [pkK } в выражениях (15.37); тогда ри =0. В необратимых процессах ри ф0,
поэтому для обеспечения возможности использования формул (15.37) необходимо
получить формулы для расчета ри и конкретизации выражения Tdsq.
Необратимые процессы в связи с их конечной скоростью рассматриваются в рамках
неравновесной термодинамики с учетом времени т. В частности, учитывается, что для
Элементы термодинамики твердого тела 199
конечной области тела объемом V, ограниченной поверхностью Я, справедливо
выражение
- $ = \T-lqktkdV = \ {Як/Т),к dV + \ = \ qk*k X T~l АН + |; \ = \ qk T~2T,kAV,
V Н V
(15.38)
где (Xk — компонента единичного вектора внешней нормали к элементу поверхности;
qk — компонента вектора плотности теплового потока qy имеющего локальное
(например, в точке Р) направление переноса теплоты в сторону понижения температуры,
причем абсолютная величина
1^1= lim (AQt/(A#costi));
Д# — площадь элемента поверхности (содержащего точку Р)\ г\ — угол между
направлениями (в точке Р) вектора q и нормали к элементу поверхности; AQT — количество
теплоты через этот элемент в единицу времени. Отметим, что ( — qktk), т. е. дивергенция
вектора qy взятая с обратным знаком, представляет собой приток теплоты в единицу
объема за единицу времени; это и объясняет исходное выражение для $ в соотношении
(15.38). В конечном выражении для 5, полученном посредством математического
преобразования с применением теоремы Гаусса—Остроградского, первое слагаемое дает
приращение энтропии, обусловленное потоком теплоты через поверхности Н из
окружающей среды. Отношение к величине Tdsqy обусловленной не непосредственным
подводом (отводом) теплоты, а лишь необратимым характером процесса теплообмена,
имеет только второе слагаемое £. По структуре £, особенно в сопоставлении с исходным
выражением для 5, видно, что именно оно представляет приращение энтропии внутри
элемента, обусловленное неравномерностью температуры в системе; при равенстве
температур в системе было бы 7\Л = £ = 0. Поэтому выражения
- T,kqJ-2 = $q и - T,kqkvT~2 = sq (15.39)
представляют составную часть скорости порождения энтропии единичных объема и
массы системы соответственно, что следует из выражения для £ в (15.38).
Имея конечной целью получение формул для необратимых составляющих
напряжений (ри ) и конкретизацию выражения Tdsqy перейдем в (15.36) от элементарных
изменений физических величин к их производным по времени:
где 5„ — скорость порождения энтропии; 2 аг — скорость работы диссипации. По ана-
z
логии с выражением для составляющей скорости ар механического характера
i/Pe{e,p}; (15.41)
составляющую aq скорости, обусловленную необратимостью переноса теплоты
вследствие различия температур в системе, с учетом размерности представляем в виде суммы
произведений компонентов обобщенной силы и обобщенной скорости (£/<7 и Xiq)y где
{%}=Ы; U)={-T,kv/T\. (15.41а)
На роль обобщенных скоростей компоненты вектора плотности теплового потока
подходят по размерности и по физическому смыслу; выражения же для t,iq вытекают из
соотношений
(15.42)
представляющих собой следствие выражений (15.36), (15.39), (15.40).
200 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Как правило, считают, что на любом участке процесса скорость работы диссипации
аг представляет собой некоторую функцию от соответствующих скоростей (с пределами
суммирования по (15.40)), так что
0 < az = liki = Dz ({*,}) = Tsz; Ь = ye& у = (ЬЬ) °'5 > 0; (ef-ef-)c = 1. (15.43)
Следуя Рэлею, выражение Dz ({xi}) называют диссипативной функцией системы. При
этом DZ = D зависит не только от компонент обобщенной скорости, но и от состояния
и предыстории системы. Значение диссипативной функции D можно определить и без
использования компонент скорости — через энтропию. Ранее было подчеркнуто, что
температура (или энтропия) и обратимые силы prR [или обратимые.составляющие
для pkK в (15.37)] можно представить через соответствующие частные производные от
внутренней или от свободной энергии. Необратимые характеристики в конечном счете
удается связать с диссипативной функцией, которая поэтому так же важна для
характеристики необратимой части процесса, как внутренняя или свободная энергия для
характеристики его обратимой части.
§ 15.5. Необратимые силы и экстремальные принципы
неравновесной термодинамики
Ближайшей задачей рассмотрения является поиск взаимосвязи между величинами
{*/} и {£,-}, совместно удовлетворяющими выражениям типа (15.43) для диссипативной
функции Dz. После этого с учетом обозначений (15.41) окажется возможным и
достижение ранее поставленной цели, подчеркнутой в связи с переходом от (15.36) к (15.40),—
получение формул для необратимых составляющих напряжений ри и конкретизация
выражения Tdsq.
В (15.43) для представления необратимых сил {£,-} использовано
вспомогательное множество значений {е^} с единичной суммой квадратов, каждое из
которых, например е^ пропорционально соответствующему значению £/ (при том же /)
с коэффициентом у3 общим для всего множества. Для выявления связи между
\хс] и {£,) принято, что необратимые процессы рассматриваемого типа удовлетворяют
принципу минимальных необратимых сил (принципу МНС). А именно: если в (15.43) заданы
только что введенное вспомогательное множество [е^\ и значение F = const>0 для
диссипативной функции D, то величины {i/} таковы, что обеспечивают в (15.43) возможный
минимум коэффициента пропорциональности у, следовательно, возможный максимум
выражения вцХи т. е. суммы произведений каждой из величин (е%) вспомогательного
множества на значение соответствующей (т. е. с тем же индексом /) обобщенной
скорости.
Доказано, что для большинства систем, представляющих практический интерес,
а именно при выполнении условия
dD/d/?>D/#(D>0); R = (iti,)°'5, (15.44)
принцип МНС эквивалентен принципу максимальной скорости работы диссипации
(принципу МСРД). Согласно утверждению последнего, истинное множество значений
{Xi} для заданных величин {&} дает максимум скорости работы диссипации £,•*,-,
удовлетворяющий дополнительному условию
FUxl})=D{\xi))-bii = 0. (15.45)
Из (15.43) видно, что в формулировке принципа МСРД выражение «скорость работы
диссипации» можно заменить на «скорость порождения энтропии». Это дает
формулировку принципа максимальной скорости порождения энтропии (принцип МСПЭ);
последний можно рассматривать как более точную версию второго закона
термодинамики: в системе с выполнением (15.44) и с заданными необратимыми силами скорость
Элементы термодинамики твердого тела 201
возрастания энтропии максимальна. Названные принципы были сформулированы
Г. Циглером в 1961 — 1962 гг.
Применение принципов МНС или МСРД приводит к задачам на условный
экстремум, решение которых получается на основе уравнений
Cx,- = 0, или dfcM-vLFUtM/dx^O (15.46)
соответственно, где \i — множитель Лагранжа. Из (15.46) следуют, по существу,
эквивалентные соотношения
en = \idD/dxi или ^kdD/дхг, Х= (\i~l + I)"1. (15.47)
Подставляя, например, £,- из (15.47) в (15.43), можно получить
Z>iXi = kxidD/dxi = D; X=D/(XidD/dxi). (15.48)
Наконец, используя для X в (15.47) его выражение по (15.48), имеем
. (15.49)
Доказано, что при выполнении как принципа МНС, так и принципа МСРД, помимо
(15.49) справедливы соотношения
Cii/. (15.50)
В частности, (15.50) применимо для систем, удовлетворяющих (15.44); при этом
оба принципа, как уже отмечено, эквивалентны. Применение (15.49) или (15.50),
конечно, предполагает непрерывность функций D({jc,-}) и Ь'({У) вместе со своими частными
производными. Известны и другие доказательства выражений (15.49) и (15.50) с интересной
геометрической интерпретацией [10].
Значительный интерес представляют частные случаи — с квазиоднородными, а
также с однородными (степени г) диссипативными функциями, т. е. соответственно с
выполнением условий
xidD/dxi=bi{D) или xidD/dxi=rD, (15.51)
где r = const; со— произвольная функция. В первом случае верны выражения,
определяющие некоторое преобразование Лежандра:
Ь=ду/дхг, х, = дФ/0Ь; ф((*})+Ф(К,-})=Сл, (15.52)
где функции <p({ii}) и Ф({У) удовлетворяют условиям
Г DdD ^ Г DdD | ^
ф = \ —ПгГ> Ф = \ frk.\ ;ф = Ф
= 0,
о'=о
a n(D') — произвольная функция.
А для случаев с однородными диссипативными функциями получено, что
г>1; cp = D/r; Ф=(г— \)D/r\ & = г-1д0/дхг, (15.53)
n = rD/(r—\)=tyidD'/dt>i. (15.54)
Из сопоставления выражений (15.54) и (15.51) видно, что если функция D однородна
степени г, то D' — однородная функция степени г/(г— 1); если г = 2, то D({xi}) и
— однородные функции второй степени.
Важным частным классом однородных функций являются полиномы степени г вида
2,»,.= г
202 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Здесь коэффициенты dp/ могут зависеть от мгновенного состояния и предыстории
системы. Так как D^O, они должны удовлетворять определенным условиям и обязательно
значение г должно быть четным. В случае двух механических координат (х\, хг) при
г = 4 имеем:
4 4 4
D = 2 (i[i*2di*)x=4_r £, = 0,25 2 (/ii"1 X ^/х)х=4_,; £2= 0,25 2 (к^Г' X
/=0 /=1 х=1
х <U=4_X.
Простейший частный случай (15.55) —квадратичная форма с положительно
полуопределенной матрицей (dn ):
D = rf/fi/Xf; d// = du или rf/f. ^ du. (15.56)
Любой из двух вариантов представляется возможным. Но в первом варианте (с
равенством) подстановка (15.56) в (15.53) приводит к линейным соотношениям
= 2), (15.57)
удовлетворяющим условиям симметрии [с равенством в (15.56)]. Если же исходить из
(15.57), т. е. считать связь между {х,} и £, линейной, но без обязательного равенства
в (15.56), то из (15.43) следует выражение для D по (15.56), после подстановки
которого в (15.49) получается
С* = 0,5 К,+ <*„);,. (15.58)
Из сравнения с (15.57) следует, что матрица (dn) симметрична. Обращение системы
(15.57) также линейно, оно выражается соотношениями
д&=Ы/; ьа=вп/в\ d ({&})=*/££.
где B—\dn | —определитель исходной матрицы; Вп —дополнение (адъюнкт) ее
элемента dn . Из симметрии матрицы (dn ) вытекает, что Вп =Ви и Ъп —Ьи .
Простейшие возможные соотношения между скоростями и необратимыми силами
впервые рассмотрел Л. Онсагер. Исходя из двух постулатов, касающихся
микроскопического поведения системы, он установил условия симметрии [равенства в (15.56)],
называемые сейчас соотношениями взаимности Онсагера (см. §14.6). При
вышеизложенном подходе с использованием принципа МНС или его эквивалентов исследования
не ограничивались линейными соотношениями между скоростями и необратимыми
силами, однако в линейном случае соотношения Онсагера подтвердились.
Ни один из рассмотренных подходов не свободен от тех или иных предположений.
И принцип МНС — гипотеза; однако то, что эта гипотеза подтверждает теорию
Онсагера в линейном случае, а также физическая естественность принципа НСПЭ вселяют
уверенность в справедливости и соответствии гипотезы физическим свойствам
исследуемых систем.
Известны и другие формулировки принципов [принцип наименьшей диссипации
Онсагера, принцип минимума скорости порождения энтропии (принцип Био), принцип
минимального порождения энтропии Пригожина и некоторые другие], но при
внимательном анализе они оказываются взаимосвязанными с рассмотренными выше.
Чтобы получить структуру уравнений состояния для системы с пластическими
деформациями, достаточно учесть конкретный смысл использованных выше обобщенных
обозначений, указанный в (15.41) применительно к двум составляющим скорости
работы диссипации. Для немеханических переменных ( — T,kv/T) и qk используются
только выражения типа (15.49), а именно:
T,k=-T(vqKdD/dqK)-lDdD/dqk\ D = Dq (15.59)
Элементы термодинамики твердого тела 203
и их частные варианты. Если принять в соответствии с (15.56), что D — vdkK qkqK /T\
dkK = dKk, то подстановка этих выражений в (15.59) приводит к линейной версии
(15,59) в форме
Tk= —dkKqK или даже qk— — AT*. (15.60)
Выражения (15.60) представляют закон Фурье для анизотропной и для изотропной
среды соответственно; А, — теплопроводность среды. В качестве механических
переменных в (15.41) указаны величины
(—vpu) и ги = 0,Ь(уиуп1 + уиуп$ wl%m% (15.61)
где wi = dyi/dT==w({yi}} т) — компонента скорости как функция времени и положения
точки в пространстве; сомножитель в скобках симметричен относительно индексов / и пг\
сомножитель wi,m можно заменить его симметричной частью Wim и тогда получается, что
^и = УцУт.1^ш\ Wlm = 0,5(wlM + wmJ). (15.62)
Величины типа Wit тоже называют составляющими тензора скорости деформации
(по Прагеру); эти величины также-можно использовать в роли компонент
обобщенной скорости, вместо ги и совместно с компонентами ои ({*//}, г), описывающими, как
говорят, эйлерово поле напряжений [10], в роли компонент обобщенной силы £,.
Итак, на роль компонент силы и скорости (£,-, jc,-) пригодны как компоненты (pih
ги ), так и компоненты (ои , Wu ). Для обеих комбинаций переменных применимы
выражения как типа (15.49), так и типа (15.50) вместе со всеми их частными вариантами.
В частности, во втором случае, по аналогии с (15.49), (15.52), (15.53), (15.57),
получается
^1 DdD/dWu\ ou= D (иы)'1 dD/dWu\
ou=v-1 dq>/dWu\ ф = $DdD/a>; ou = (vr)~l dD/dWu; (15.63)
°u = dillLWlL; dulL = dlLil (15.64)
соответственно. При этом значения dulL не зависят от скоростей деформации, а второе
соотношение в (15.64) равносильно соотношениям взаимности Онсагера. Следует еще
раз подчеркнуть, что уравнения типа (15.63), (15.64) связывают скорости деформации
в сплошных средах различных типов с необратимой частью тензора напряжений.
Соотношения типа (15.63) выше получены путем поиска условного экстремума
на основе уравнений (15.46). Однако, известен и другой способ их обоснования. В
частности при
\ N (15-65)
можно интерпретировать Wi и at как компоненты векторов в /г-мерных евклидовых
пространствах с декартовой прямоугольной системой координат (п = 9). Тогда
[е-ш]—компоненты единичных векторов (функций координат) и
D({lF,))=r = const>0; elaWi = r/y— (15.66)
соответственно уравнения гиперповерхности 6Г и гиперплоскости Л- Положения
поверхностей вместе с выражением D как функции только координат предполагаются
известными для любого конкретного этапа процесса.
Соответствие между (^ и о по ПМНС — не обязательно однозначно; пусть Р —
точки, представляющие решения в пространстве скоростей для заданных значений
D и {eia}. Все они — при общем минимуме у для {а,-} в (15.43) — должны удовлетворять
обоим уравнениям в (15.66), т. е. принадлежать как 6Г, так и Л- При этом Л всегда
ортогональна еа (обобщение факта, хорошо известного при /г = 3) и с каждой стороной Л
можно связать определенный знак так, чтобы скалярное произведение etaWi возрастало
204 РАЗДЕЛ 3. СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
при переходе через Д с отрицательной стороны на положительную. По ПМНС решение
Ф максимизирует e,-aUP,- на 6Г и потому все ее точки, кроме Р, лежат с отрицательной
стороны от Л- Очевидно, что каждая точка 6Г лежит хотя бы на одной плоскости типа
Л, а это означает, что поверхность 6Г выпуклая.
Определим внешнюю сторону поверхности 6Г так, чтобы ей принадлежали точки,
лежащие с положительной стороны хотя бы одной из плоскостей Л; другая сторона —
внутренняя. При заданных Г и еа решение W соответствует максимуму величины
eiaWi не только на поверхности Вг (согласно ПМНС), но и по всему объему с
внутренней стороны, так как внутренность 6Г расположена на отрицательной стороне
Л- Поэтому ПМНС можно выразить неравенством
или oiWi—Wi*)^ (15.67)
после умножения на у. Здесь Й^— истинная скорость, а W* — любая другая скорость,
соответствующая точкам на поверхности 8Г или внутри нее. В случаях (15.67) знак
равенства возможен только в тех случаях, когда другая скорость W* также
удовлетворяет ПМНС, а знак равенства во втором соотношении — и при D = 0.
Если функция D({Wi}) непрерывна со своими частными производными, то D-поверх-
ности — гладкие и в каждой их точке существует единственная внешняя нормаль.
Тогда в силу (15.67), полученного на основе ПМНС, а имеет направление этой
нормали в соответствующей точке Р, т. е.
Oi = \)dD/dWi\ \)ф\з{1)\ v>0 (15.68)
— коэффициент пропорциональности. Подстановка в (15.68) выражения для v на
основе (15.43), (15.68) дает
что с учетом (15.65) совпадает с первым из соотношений (15.63).
Итак, для компонент необратимых тепловых или механических сил применимы
выражения типа (15.59), (15.60) или типа (15.63), (15.64) соответственно. При этом
оказывается возможной конкретизация выражений (15.37) объединенного уравнения
первого и второго законов термодинамики с включением некомпенсированной теплоты.
Эти выражения по форме почти тождественны аналогичным выражениям (15.12)
объединенного уравнения для обратимых процессов; значит, их использование возможно
подобно тому, как это показано в § 15.3 с учетом (15.12).
Вопросы 1- Почему твердое тело считают составной термодинамической системой?
2. Применяя объединенное уравнение первого и второго законов термодинамики,
получите соотношения для систем с упругими деформациями. Возможно ли их использование
для систем с пластическими деформациями?
3. Напишите уравнения состояния, используя которые можно построить диаграмму
состояния упругодеформированного стержня в координатах «растягивающая сила —
длина стержня». Охарактеризуйте общий вид таких диаграмм.
4. Что такое эластокалорический адиабатный эффект? Как получено выражение для
его оценки?
Наука только тогда
достигает совершенства, когда ей
удается пользоваться математикой.
К. Маркс
В<ОДЕЛ
СИСТЕМЫ
С ХИМИЧЕСКИМИ
ПРЕВРАЩЕНИЯМИ
Нередко в тепловых машинах их состава и тепловыми эффектами.
и установках используются Количественное соотношение
неоднородные рабочие тела между веществами
с химическими превращениями в них — при химическом равновесии в системе
реакциями. с неоднородным рабочим телом
Изменение состояния таких систем определяется
сопровождается изменением законом действующих масс.
206 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Глава 16
ОСНОВНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ
§ 16.1. Характеристики состава сложной системы.
Основное уравнение термодинамики
Состав сложной термодинамической системы может быть представлен не только
количеством вещества Nk каждой ее составляющей, но и молярными долями
rk=Nk/iNk, (16.1)
где 2/Vfe — количество вещества в системе (молярные доли идеального газа численно
равны объемным долям).
Если составляющие системы находятся в газообразном состоянии и обладают
свойствами идеального газа, то система может быть задана парциальными давлениями
составляющих
Pk = rkpt (16.2)
где р — давление смеси газов.
Иногда системы задаются концентрациями компонентов
ck = Nk/V, (16.3)
где V — объем системы.
Указанные величины связаны между собой соотношениями
Pb^rup^Nkp/ZNk^CkpV/ZNk. (16.4)
Любая из этих величин может быть использована для выражения состава сложной
системы, и поэтому все величины, зависящие от состава системы, могут быть выражены
через каждую из них. Величины, характеризующие состав системы, являются наряду с
давлением, температурой и объемом параметрами состояния сложной системы.
Основное уравнение термодинамики для неоднородных систем имеет вид (6.10).
Изменение химической энергии системы, учтенное членом I>\ikdNk, может быть
представлено в виде немеханической работы, т. е.
d(A = 2MW*==-(L4max, (16.5)
Основные понятия и уравнения 207
где cL4max — максимальное количество немеханической работы, а знак минус означает,
что положительной полагается работа, совершаемая системой, энергия системы при
этом уменьшается.
Сложная термодеформационная система при химическом взаимодействии часто
получает третью внешнюю степень свободы. Например, в гальваническом элементе
внутреннее химическое взаимодействие сопровождается внешним электрическим
взаимодействием. Следовательно, уравнения (6.10) путем подстановки в них (16.5) могут
быть представлены в виде уравнения для системы с тремя внешними степенями свободы.
Из полученных уравнений следует, что при постоянстве двух термодеформационных
независимых переменных максимальное количество немеханической работы
определяется изменением соответствующей характеристической функции. Так, при постоянных
S и V dA™y* =—d/7; при постоянных Sup cL4™pax =—d//; при постоянных Т и V
dA^x = -d/7; при постоянных Тир dA?pax = —dG.
Так как Максимальное количество немеханической работы соответствует изменению
химической энергии сложной системы, то и изменение характеристической функции при
постоянстве двух соответствующих независимых переменных выражает изменение
химической энергии.
§ 16.2. Химический потенциал
Химический потенциал (6.11) чистого вещества представляет собой молярную
свободную энтальпию и определяется отношением
VL = (dG/dNk) TtPtN¥t Nk = G/Nk = G.
С помощью уравнения состояния вещества можно выразить химический потенциал
через измеряемые величины. Действительно, при условии постоянства температуры на
основании последнего уравнения (6.11) d\i=Vdp, после интегрирования имеем
ji = ji° + \Vdp, (16.6)
где \i° — постоянная интегрирования — зависит от природы вещества и температуры.
Интеграл в (16.6) можно вычислить при наличии уравнения состояния (1.5).
Определим, воспользовавшись уравнением (1.6), молярный объем; подставим его выражение
в уравнение и проинтегрируем при Т = const, тогда химический потенциал идеального
газа
|х = |х°(Г, p=\) + RT\np. (16.7)
Здесь (i°(7\ р— 1) представляет собой химический потенциал газа при данной
температуре и давлении, равном единице.
Если имеется смесь идеальных газов, то каждая составляющая этой смеси
характеризуется своим парциальным давлением. Поэтому уравнение (16.7) для k-и
составляющей смеси получит вид
ILk=ni + RT\npk. (16.8)
Если воспользоваться соотношением (16.4) и уравнением (6.9) состояния смеси
идеальных газов, то химический потенциал составляющей можно выразить через другие
характеристики состава смеси. Так, например, химический потенциал можно
определить, если известна концентрация с* составляющей. В этом случае
(16.9)
где n°k = f(T). Если известна молярная доля г* составляющей, то
(16.10)
208 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Здесь постоянная \к% зависит от температуры и давления смеси и определяется суммой:
\*>rk = \ik + RT\np. Можно также найти химический потенциал зная количество вещества
Nk составляющей смеси. В этом случае
(16.11)
где постоянная \i°Nk. = \ik + RT\n(RT/V) зависит от температуры и объема.
§ 16.3. Мера реакции
При химических превращениях вещества реагируют друг с другом в строго
определенных отношениях, характеризуемых стехиометрическими коэффициентами компонентов
реакции:
(v,Я, + v2B2 + ...)н s (v,Я, + vlB2 + ...)к; (vB)H = 2 (vB)K. (16.12)
Здесь В\у Бг, ...— символы реагирующих веществ; vi, V2, ...— стехиометрические коэф
фициенты компонентов. Индекс «н» относится к начальным веществам реакции (левая
сторона уравнения реакции), а индекс «к»— конечным веществам или продуктам
реакции (правая сторона уравнения реакции).
При химических превращениях изменения количеств реагирующих компонентов
пропорциональны их стехиометрическим числам:
(16.13)
Величина d£ характеризует степень изменения состава системы при химической
реакции и называется мерой реакции (иногда числом пробегов реакции).
Отсюда изменение количества вещества может быть получено через меру реакции:
d/V* = v*d£ или &Nk = Vk&t (16.14)
Уравнения химических реакций записываются так, чтобы в левой части равенства
стояли вещества, количество которых уменьшается в ходе реакции, а в правой части —
вещества, возникающие в результате реакции.
Мера реакции положительна, поэтому
стехиометрические коэффициенты компонентов левой части уравнения реакции
необходимо считать отрицательными* а правой части уравнения — положительными*, т. е.
vH<0, vk>0.
§ 16.4. Изменение функций состояния
при химических превращениях
Уравнения Гиббса—Гельмгольца. Химические превращения принято рассматривать
при условиях постоянства температуры и давления (Т = const, р — const) и постоянства
температуры и объема (T = const, K = const). Поэтому в химической термодинамике
используются только две характеристические функции, для которых данные параметры
входят в число независимых переменных. К этим функциям относятся свободная
энергия F и свободная энтальпия G, но используется чаще свободная энтальпия, так как в
подавляющем большинстве случаев реакции рассматриваются при условии Т = const
и р = const. Эти условия наиболее удобны для анализа, так как в этом случае любая
экстенсивная функция состояния (например, Z) сложной системы, представляющей
собой смесь идеальных газов, может быть представлена в виде суммы
' (16.15)
* Иногда для стехиометрических коэффициентов принимается противоположное правило
знаков.
Термохимия 209
а ее изменение при этих же условиях
AZ = 2Z*AN*. (16.16)
Здесь Z отражает экстенсивное свойство системы; Zk — молярное значение функции
для k-й составляющей системы при определенных Т и р; N'k — количество вещества /г-й
составляющей в системе.
Изменение функции состояния при химических превращениях обычно относят к мере
реакции. Подставив уравнение (16.14) в выражение (16.16) и разделив изменение
функции на меру реакции, получим
AZ = 2Z*v*. (16.17)
При необходимости определить молярное изменение функции относительно одного из
веществ, участвующих в реакции, например вещества А, нужно полученное выражение
разделить на стехиометрический коэффициент v^ этого компонента в уравнении
реакции &Z — 2,Zk{vk/vA )• Молярные изменения функции состояния при химических
превращениях приведены в справочных таблицах. Табличное значение относится одновременно
и к другим количествам веществ, участвующим в данной реакции. Количества веществ
равны соответственно стехиометрическим коэффициентам этих веществ в уравнении
реакции при условии, что стехиометрический коэффициент компонента, относительно
которого дается молярное изменение функции, в этом уравнении равен единице.
Сказанное свидетельствует о том, что мера реакции зависит от абсолютного
значения стехиометрических коэффициентов компонентов, принятых в уравнении реакции.
Обычно уравнение реакции записывается так, что стехиометрический коэффициент по
крайней мере одного из веществ в нем равен единице. В таком случае изменение функции
состояния, отнесенное к мере реакции и определяемое уравнением (16.17), является
молярным относительно веществ, стехиометрические коэффициенты которых в
уравнении реакции равны единице.
В соответствии с условиями, при которых рассматриваются химические
превращения, в химической термодинамике используются два уравнения. Одно уравнение
связывает внутреннюю энергию U со свободной энергией F, а другое — энтальпию Н со
свободной энтальпией G. Подставив S=—(dF/dT)v и S=—(dG/dT)p в соотношения
(4.5) и (5.9) соответственно, получим
U = F-T(dF/dT)v; (16.18)
H=G-T{dG/dT)p. (16.19)
Уравнения (16.18) и (16.19) называются уравнениями Гиббса — Гельм-
гольца, так как были получены ими независимо друг от друга в разное время.
Вопросы !• Какими величинами характеризуется состав сложной системы?
2. Что является мерой реакции?
3. Какие величины связывают между собой уравнения Fn66ca—Гельмгольца?
4. Объяснить правило знаков для стехиометрических коэффициентов.
Глава 17
ТЕРМОХИМИЯ
§ 17.1. Тепловые эффекты реакций
Химические реакции часто протекают с выделением или поглощением теплоты, т. е.
сопровождаются тепловыми эффектами. Как и химические превращения, тепловые
эффекты рассматриваются при условиях 7\ V = const или Г, p = const.
Используя первое из уравнений (5.10) для обратимых процессов с учетом уравне-
210 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
ния (14.5), в котором изменение химической энергии представлено в виде максимальной
немеханической работы (знак max далее опущен), можно для условия Г, V — const
записать MJTV — Qtv —ATV » гДе Qtv— количество теплоты, которым система
обменивается с окружающей средой в равновесном процессе перераспределения массы при
7\ V = const, отнесенное к мере реакции; ЛTV — максимальное количество
немеханической работы, которое может быть получено от системы при равновесном процессе
перераспределения массы, отнесенное к мере реакции.
Если процесс перераспределения массы необратимый, то в соответствии со вторым
законом термодинамики немеханическая работа превратится в теплоту и в этом случае
количество теплоты будет равно изменению внутренней энергии AL/'TV сложной системы.
Это количество теплоты называется тепловым эффектом реакции при
условии 7\ V — const:
В процессе Г, V== const количество немеханической работы выражается через
изменение свободной энергии, поэтому разницу между тепловым эффектом &UTV и
количеством теплоты в равновесном процессе Г, V — const можно представить в виде
/SLJjy —^cTV == —™TV == ^* TV ■
Используя второе уравнение [см. (5.10)] с учетом (16.5) для равновесных
процессов, можно по аналогии с предыдущим для условия Г, p = const получить ЬНТр =
= Qtp —Атр » гДе Qtp и Атр — соответственно количество теплоты и максимальная
немеханическая работа в равновесном процессе при Т, P = const, отнесенные к мере
реакции. Если процесс перераспределения массы необратимый, то немеханическая работа
превратится в теплоту и количество теплоты в этом случае будет равно изменению
энтальпии &НТр сложной системы. Это также тепловой эффект реакции &НТр = QP, но
при условиях Г, Р = const. Разницу между тепловым эффектом &НТр и количеством
теплоты в рассматриваемом процессе можно представить в виде ДЯ7р — Qjp ——АТр =
= AG,P;
под тепловым эффектом реакции понимается количество теплоты, выделяемое или
поглощаемое системой при наличии в ней химических реакций при постоянных
температуре и объеме (7\ V— const) или температуре и давлении (7\ р = const).
При этом между системой и окружающей средой кроме теплового возможно только
механическое взаимодействие. Это значит, что процесс химического взаимодействия
внутри системы протекает необратимо. В результате химическая энергия, которая в
случае равновесности процесса перераспределения массы могла бы быть передана
системой в форме немеханической работы, превращается в теплоту.
Молярные тепловые эффекты реакций, приводимые в справочных таблицах,
относятся к одному из веществ, участвующих в реакции. Это значение теплового эффекта
(изменение функции состояния) одновременно относится и к другим количествам
веществ, численно равным их стехиометрическим коэффициентам в уравнении реакции
при условии, что стехиометрический коэффициент табличного компонента в уравнении
равен единице. Например, молярный тепловой эффект реакции Нг+ '/202 = НгО,
приведенной в таблице на 1 кмоль Н2О, одновременно относится к '/г кмоль СЬ.
Следует заметить, что часто в термохимии для количества теплоты принимают
противоположное правило знаков по сравнению с принятым в технической
термодинамике, а именно: теплота, подведенная к системе, рассматривается как отрицательная, а
отведенная — как положительная. Если тепловые эффекты с таким правилом знаков
обозначить Qv и Qp соответственно условиям Г, V = const и Г, р — const, то
Wtv =Qv=~ Qv\ ЬНТр = Qp = - Qp.
Химические реакции, которые сопровождаются выделением теплоты (А£/<0 или
\//<<0), т. е. при которых теплота должна быть отведена от системы, для того чтобы
Термохимия 2JJ_
конечные продукты имели ту же температуру, что и начальные, называются
экзотермическими. Реакции, сопровождающиеся поглощением теплоты, называются
эндотермическими.
При записи изменений характеристических функций в химических процессах
часто опускают все индексы, так как разные характеристические функции
соответствуют различным условиям, а именно: U и F при Г, V = const и Я и G при Г, p = const.
Тепловые эффекты реакций часто называют в соответствии с типом реакции, например
тепловой эффект образования, сгорания, диссоциации и т. п.
Связь между молярным тепловым эффектом Д(/ реакции при постоянном объеме и
молярным тепловым эффектом ДЯ при постоянном давлении в соответствии с формулой
H—U + pV можно представить в виде ДЯ = Д(/ + Д(рК). Свойства идеального газа
дают возможность представить связь между Д/7 и ДЯ в более простом виде.
Действительно, из уравнения состояния смеси идеальных газов pV'=2Л/kRT следует, что в любом
процессе при Т = const в сложной системе соблюдается равенство
где SdiV* — изменение количества газообразных веществ в процессе реакции. С учетом
уравнения (14.17) d(pV) = RTfLvkdl или A(pV) = #r2v*Ag. Относя это уравнение к мере
реакции, получим
(17.1)
Так как в правой части этого уравнения нет других параметров, кроме температуры,
то оно справедливо для обоих процессов. Действительно, для 7\ V — const Д(рК) =
= V&p = RTI,Vk и для Г, p = const Д(рК) = рДК = /?Г2^*. С помощью уравнения (17.1)
связь между величинами ДЯ и Д/7 можно представить в виде
bH = bU + RT2vk. (17.2)
Уравнение (17.2) связано с использованием уравнения состояния идеального газа,
поэтому
выражение 2v^ включает только стехиометрические коэффициенты газообразных
составляющих реакции.
Для всех реакций, для которых 2v* = 0, тепловые эффекты Д(/ и ДЯ
одинаковы.
Важное практическое значение^равнения (17.2) заключается в том, что оно
позволяет определить тепловой эффект ДЯ для многих реакций горения, для которых тепловые
эффекты обычно находят при постоянном объеме. Так как фазовые превращения, так
же как и химические, сопровождаются выделением или поглощением теплоты, то при
оценке тепловых эффектов химических реакций необходимо учитывать фазовые
состояния веществ, поэтому термохимические уравнения должны содержать указания на
агрегатное состояние реагентов и продуктов реакции, а для твердых веществ —
указание на модификацию (если эти вещества существуют в различных кристаллических
модификациях).
§ 17.2. Закон Гесса
Тепловой эффект реакции выражается через изменение функции состояния, поэтому
определяется только начальным и конечным состояниями системы и не зависит от
промежуточных химических состояний, через которые система проходит. Следовательно,
если из определенных реагентов (определенного начального состояния) с помощью
различных промежуточных химических реакций получены определенные конечные
продукты, то можно утверждать, что независимо от рода промежуточных реакций
суммарный тепловой эффект этих превращений одинаков.
212
РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
°)
Продукты реакции
Рис. 17.1. К определению теплового эффекта реакции: а — С+1/2О2 = СО;
б — на основе тепловых эффектов образования веществ, принимающих участие
в реакции; в — на основе тепловых эффектов сгорания веществ,
принимающих участие в реакции
Независимость теплового эффекта реакции от промежуточных реакций, через
которые проходит система, называется законом Гесса (установлен впервые
Г. И. Гессом в 1840 г.).
Этот закон справедлив для реакций, протекающих как при условиях Г, V = const,
так и Т, p = const.
На основании закона Гесса термохимические уравнения можно складывать и
вычитать подобно алгебраическим и вычислять тепловые эффекты таких реакций, для
которых они непосредственно не могут быть измерены. Например, тепловой эффект АНХ
реакции С+ 0,502 = СО нельзя определить непосредственным измерением, так как
одновременно с этой реакцией всегда идет реакция образования СО2. Для вычисления
теплового эффекта Д//х следует использовать тепловые эффекты реакций СО + 0,5О2=СО2,
при которой Д//|=— 284 000 Дж/моль, и С + О2 = СО2, при которой Д#2 =
= -394 000 Дж/моль.
В соответствии с законом Гесса (рис. 17.1, а)
Л/Ух = Д//2 — ДЯ, = —394 000 + 284 000= — 110 000 Дж/моль.
Запись химической реакции с указанием теплового эффекта реакции получила
название термохимического уравнения.
Например, термохимическое уравнение сгорания оксида углерода
СО + 0,5О2 = СО2 + ДЯ, или СО + 0,5О2 = СО2—284 000.
Это уравнение показывает, что при образовании количества вещества диоксида
углерода 1 кмоль выделяется количество теплоты 284 000 кДж.
§ 17.3. Тепловые эффекты образования
и сгорания веществ
Тепловой эффект реакции зависит от физического состояния реагирующих веществ и от
условий, в которых протекает реакция, поэтому для сравнения и систематизации
тепловых эффектов реакций введено понятие стандартного состояния (стабильное состояние
вещества при температуре Г = 298 К и давлении р = 0,1013 МПа).
Определяя тепловой эффект образования веществ, полагают, что элементы реакции
находятся в стандартных состояниях. Величины, относящиеся к стандартному
состоянию, обычно помечают индексами, например S298.
В термохимии принято считать энтальпии всех элементов при стандартных условиях
равными нулю. Так как теплота образования соединения представляет собой разность
между энтальпией соединения и энтальпией элементов, из которых оно состоит, то,
следовательно, теплоту образования можно полагать равной энтальпии соединения.
Используя закон Гесса, можно определить тепловой эффект реакции через
молярные тепловые эффекты образования реагентов и продуктов реакции (рис. 17.1,6) так,
что Q = 2(vQo6P)k — 2(vQo6P)h, где Q — тепловой эффект реакции 2(v£)H = 2(v£)K;
Термохимия 213
(Qo6P)k — молярный тепловой эффект образования продукта (конечное вещество).
С учетом знаков стехиометрических коэффициентов, принятых выше, уравнение
Q = 2vQo6P (17.3)
дает тепловой эффект реакции безотносительно к веществу, т. е. тепловой эффект
реакции получается отнесенным к мере реакции и, следовательно, это тепловой эффект v
количеств веществ (моль), принимающих участие в реакции в соответствии с
уравнением. Для получения молярного теплового эффекта определенного вещества реакции
необходимо тепловой эффект реакции разделить на стехиометрический коэффициент v
этого компонента в уравнении реакции.
Уравнение (17.3) можно представить также в виде A(/ = 2vA#O6P при Г, V=const
и A// = 2vA//o6p при 7\ p = const.
Горение представляет собой процесс быстрого окисления вещества,
сопровождающийся высвобождением значительной химической энергии и, как следствие,
существенным повышением температуры веществ в реакции. Горючими элементами топлив
являются углерод, водород и сера. Так как содержание серы в топливе незначительно, то в
качестве горючих элементов можно рассматривать практически лишь углерод и водород.
Молярный тепловой эффект, сопровождающий полное сгорание соединения при
температуре Т =298 К и давлении р = 0,1013 МП а, называется стандартным
тепловым эффектом сгорания.
Значения стандартной теплоты сгорания органических соединений приведены в
таблицах и могут быть использованы для определения тепловых эффектов реакций.
Тепловой эффект сгорания зависит от условий, при которых он получен (7\ V — const
или Г, р = const), и может быть определен на основе молярных тепловых эффектов
сгорания реагентов и продуктов этой реакции с помощью закона Гесса (рис. 17.1, в) в виде
Q = 2(vQcr)H — 2(vQcr)K, где (QCr)n—молярный тепловой эффект сгорания реагента;
(Qcp)k — молярный тепловой эффект сгорания продукта реакции. С учетом знаков
стехиометрических чисел
(17.4)
Это выражение можно записать так: Д(/= — 2vA(7cr при Г, V = const и А//= — 2vA#cr
при 7\ p = const.
§ 17.4. Зависимость теплового эффекта от температуры
В соответствии с выражением (5.34) зависимость теплового эффекта А// реакции от
температуры можно представить в дифференциальной форме:
(дД///дГ)р = АСр, (17.5)
где АСР — изменение теплоемкости сложной системы.
Это уравнение называется уравнением Кирхгофа. Правая часть
уравнения (17.5) представляет собой изменение теплоемкости сложной системы в
химической реакции. При условии Г, p = const изменение теплоемкости (экстенсивное свойство)
на основании уравнений (16.16) и (16.14) можно представить через молярные
теплоемкости веществ: ДСр=2Ср*АЛ^ = 2Ср^Д£. Если отнести к мере реакции, то в
соответствии с уравнением (16.17) получим ACp = 2Cp*v*.
Таким образом, зависимость теплового эффекта А// реакции от температуры,
отнесенная к мере реакции,
(17.6)
где Crk — молярная теплоемкость вещества.
214 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
По аналогии с предыдущим, (dU/dT)v=Cv, поэтому зависимость теплового
эффекта Д[/ реакции при Г, K = const от температуры может быть представлена в виде
{дЫ!/дТ)у = ДС\,. (17.7)
Для реакции вещества в идеально-газовом состоянии это выражение может быть
представлено через молярные теплоемкости веществ, так как теплоемкость Cv
идеальных газов (как и Ср) не зависит от давления и объема, а зависит только от
температуры, поэтому молярные теплоемкости Cv составляющих не изменяются в обоих
процессах (7\ p = const и Г, V=const). Следовательно, для реакции с идеальными газами
зависимость теплового эффекта от температуры может быть представлена аналогично
выражению (17.6) в виде
(дЬО/дТ)у = 2C^v*. (17.8)
Используя общее обозначение Q для тепловых эффектов Л0 и Д//, уравнения
(17.6) и (17.8) для идеального газа можно объединить:
(17.9)
Из уравнения (17.9) следует, что знак производной dQ/dT определяется знаком
разности теплоемкостей ДС: при ДС>0 dQ/dT>0 и наоборот. Отсюда — характер
зависимости теплового эффекта от температуры.
Если суммарная теплоемкость продуктов реакции больше суммарной теплоемкости
реагентов (АС>0), то тепловой эффект этой реакции увеличивается с повышением
температуры. Если суммарная теплоемкость продуктов реакции меньше суммарной
теплоемкости реагентов (ДС<0), то тепловой эффект такой реакции уменьшается с
увеличением температуры.
И наконец, если продукты реакции и реагенты имеют одинаковую суммарную
теплоемкость, то тепловой эффект реакции не зависит от температуры.
Интегрирование уравнения (17.9) в пределах температур от Т\ и Т2 позволяет
определить тепловой эффект реакции при одной температуре, если известен эффект при
другой температуре:
т2 т2
Q2=Q{ + \ ACd7= Q, + $2Cd7\ (17.10)
где Qi и Q2 — тепловые эффекты реакции при двух разных температурах. Для
интегрирования уравнения (17.10) необходимо располагать зависимостями теплоемкости от
температуры для всех веществ, участвующих в реакции. Зависимость молярных
теплоемкостей С£ и Cv от температуры для многих веществ может быть представлена в виде
суммы: C — a + fiT + yT2. Поэтому изменение молярной теплоемкости системы
\ (17.11)
где Aa
Подставив выражение (17.11) в (17.10) и интегрировав, получим
W/b. (17.12)
Интегрируя уравнение (17.9) с учетом выражения (17.11) в пределах температур
0—Г, можно получить выражение для теплового эффекта при любой температуре:
$ = $0 + /±аТ + Ь$Т2/2 + /±уТ3/3. (17.13)
Здесь Qo — постоянная интегрирования, не являющаяся тепловым эффектом при
какой-либо температуре; ее можно было бы рассматривать как тепловой эффект при
абсолютном нуле, если бы зависимости теплоемкости от температуры для всех веществ,
участвующих в реакции, входящие в выражение (17.11), были справедливы вплоть до
Термохимия 2[5
абсолютного нуля; Qo можно определить с помощью выражения (17.13), если известно
значение теплового эффекта при какой-либо температуре.
Уравнения (17.12) и (17.13) одинаково справедливы как для условия 7\ V = const,
так и 7\ P = const. В первом случае Q = Qy =Д{7, a C=CVy во втором Q — Qp = kH,
я С — С
a. \~i — v-« р.
Тепловой эффект может быть определен с помощью значений средних теплоемко-
стей, как это следует из выражения
То
^(Г2-Г,), гдеДС
§ 17.5. Зависимость теплового эффекта
от агрегатного состояния веществ
Фазовые превращения сопровождаются выделением или поглощением скрытой теплоты
превращения, представляющей собой разность молярных энтальпий двух
рассматриваемых фаз при соответствующих температуре и давлении. Часто при оценке тепловых
эффектов реакции возникает необходимость учитывать скрытую теплоту фазовых
превращений. Например, часто требуется знать тепловой эффект реакции, когда одно (или
более) вещество находится в агрегатном состоянии, отличном от стандартного. Можно
получить уравнение, учитывающее влияние агрегатного состояния реагентов на
тепловой эффект. Для этого проведем реакцию при постоянных Тир между веществами в
жидком состоянии (процесс /—4, рис. 17.2) следующим образом. Сначала испарим
реагенты при давлении, соответствующем давлению насыщения при данной температуре
(процесс 1-2). Затем проведем реакцию между газообразными веществами при данных
температуре и давлении (процесс 2-3). После этого сконденсируем пары продуктов
реакции при давлении насыщения, соответствующем данной температуре (процесс 3-4).
Учитывая, что энтальпия является функцией состояния, получим
где Д#ж и Д//г — тепловой эффект реакции между жидкими и газообразными
веществами соответственно; Д#1-2 = (Д//исп)н — тепловой эффект испарения исходных веществ;
Д#з_4 =(Д//конд)к — тепловой эффект конденсации продуктов реакции. Тепловые
эффекты испарения и конденсации можно представить через скрытые теплоты
парообразования так, что ДЯ,.2==(Я// — Я/)н = 2^г)„ и ДЯ3.4 = — (Я"--Я') = — 2(vr)K. Отсюда общий
тепловой эффект, связанный с испарением и конденсацией веществ, участвующих в
реакции, Д//фП = ДЯ|.2 + ДЯ3.4 =-[S(vr)K-S(vr)H].
С учетом правила знаков для стехиометрических чисел ДЯфп=—2vr.
Следовательно,
Анг
ДЯж^ДЯг-Svr. (17.14) *<Г f
Таким образом, тепловой эффект реакции между | I
жидкими веществами может быть представлен через Щ T,p=const f^st
тепловой эффект между газообразными веществами. J I
Вопросы !• ^то называется тепловым эффектом реакции? 217?
2. Какой из тепловых эффектов, А/? или А#, больше,
если реакция сопровождается расширением? Рис. 17.2. К определению ха-
3. Объясните физический смысл закона Гесса. рактера зависимости теплово-
4. Как изменяется тепловой эффект реакции с го эффекта от агрегатного
увеличением температуры, если теплоемкость сие- состояния участвующих в ре-
темы или реакции увеличивается? акции веществ
216 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Глава 18
ХИМИЧЕСКОЕ РАВНОВЕСИЕ И СРОДСТВО
§ 18.1. Условия химического равновесия. Закон действующих масс
Любая химическая реакция в зависимости от условий может протекать самопроизвольно
как в прямом, так и в обратном направлении и поэтому является обратимой с химической
точки зрения. К условиям, которые могут влиять на направление химического процесса,
относятся начальные концентрации реагирующих веществ (исходных веществ и
продуктов реакции), температура и давление. Реакция самопроизвольно протекает до тех
пор, пока не будет достигнуто химическое равновесие между реагирующими веществами,
при котором состав смеси с течением времени при неизменных условиях не меняется.
Таким образом,
химическое равновесие является динамическим* равновесием.
На примере реакции H2 + l2 = 2HI при Т = 7\7 К (рис. 18.1) видно, что независимо
от того, что взято в качестве исходных продуктов (смесь водорода и иода или йодистый
водород), примерно через 2 ч система придет в одно и то же состояние равновесия с
количеством реагирующих веществ, определяемым соотношением 78 %Н1, 11%Н2 и
1 1 %Ь. Многие химические реакции при соответствующих условиях протекают до
фактического завершения, т. е. практически получаются только продукты реакции. Однако
даже в этих реакциях достигается состояние равновесия и обратные реакции протекают,
хотя и с весьма малой степенью превращения.
Средствами термодинамики на основе второго закона можно найти условия
химического равновесия, выразить их через величины, определяющие состояние системы, и
выяснить влияние на них температуры и давления.
Условие химического равновесия можно получить используя уравнение (6.16)
равновесия сложной системы совместно с условием перераспределения массы при
химических превращениях (стехиометрическим уравнением реакции). Изменение
количеств веществ реагентов при этом выражается уравнением (16.14).
Подставляя (16.14) в уравнение равновесия (6.16) и относя к мере реакции, можно
получить условие химического равновесия:
2v4|i4=0. (18.1)
k
Число таких уравнений в условиях химического равновесия сложной системы равно
числу химических реакций, которые одновременно могут протекать в ней.
Условия химического равновесия позволяют свести проблему равновесия к
определению химического потенциала (стехиометрические коэффициенты
известны из уравнения реакции).
Количественное соотношение между веществами в момент равновесия носит
название закона действующих масс, впервые установленного норвежскими
учеными Гульдбергом и Вааге (1864) на основе кинетического рассмотрения идеальных
газов. Аналитическое выражение закона действующих масс может быть получено, если
подставить выражение (16.8) для химического потенциала составляющей смеси
идеальных газов в условие химического равновесия (18.1): Zv^rinpfe + 2v/f(j,?=0, откуда
y,vk\npk= — 2v*p,g /(RT). Учитывая, что \i% является функцией температуры, выражение
закона действующих масс можно представить в виде
1п/СР=Ф(Г), (18.2)
где
/Ся-=(р?^-)к/(р1'Р22-)н=Пр?; (18.3)
ф(Т)= — 2,Vk\ik/(ftT); pk — парциальные давления составляющих систем в момент
равновесия.
Химическое равновесие и сродство
217
Так как изменение характеристической
функции, отнесенное к мере реакции,
выражается в виде AG = 2vjx, то можно записать
ф (Г) = -
(18.4)
где Д<5°= — I,Vk\ik — уменьшение свободной
энтальпии системы при переходе ее из
состояния, в котором каждая из составляющих
находится при парциальном давлении, равном
принятой единице, в состояние равновесия
(так называемое стандартное
химическое сродство)
Из уравнения (18.2) следует, что при
постоянной температуре КР—величина
постоянная. Эта постоянная, получившая
название константы равновесия реак-
60
о
РпбноЗесие
25
50
100
Рис. 18.1. Динамическое равновесие в
реакции между Н», 1-2 и HI при температуре
7 = 717 К
ции, связывает между собой парциальные давления веществ в системе. Константа
равновесия может быть выражена и через другие характеристики состава — молярные
концентрации с*, молярные доли г/,, количества веществ Nu- С помощью уравнения (16.4)
можно получить соотношение между этими константами равновесия:
Kp=Kt
*v=Kyv=KN(RT/vfv =
Здесь /(c = ricJfe; /О = Пг£А; KN=nNlk—константы равновесия, выраженные
соответственно через молярные концентрации, молярные доли и количества веществ. Константа
равновесия КР является функцией только температуры, поэтому из соотношений (18.5)
можно заключить, что константа равновесия Кс также зависит только от температуры:
/(С = ДГ); Кг зависит от температуры и давления (или объема): /(г = ср(Г, р); Кц зависит
от температуры и объема (или давления): Км =f(T, V).
Выражение (18.5) показывает, что КР= Кс — Кг — Км в тех случаях, когда реакция
не сопровождается изменением количества газообразных составляющих (2vfe = 0).
Константа равновесия КР является величиной безразмерной, хотя ее значение и
зависит от выбора единицы давления*
Закон действующих масс, полученный выше, справедлив только для реакций с
веществами, подчиняющимися законам идеальных газов. Для реальных веществ закон
действующих масс может быть использован, если в выражениях для констант
равновесия применены летучести или активности составляющих смеси. Однако при решении
многих теплоэнергетических задач нет необходимости использовать понятия летучести и
активности, так как большинство газообразных веществ могут считаться
подчиняющимися законам идеальных газов. На практике обычно пользуются константами
равновесия КР и Кс-
Форма записи констант равновесия связана с правилом знаков для стехиометри-
ческих коэффициентов и формой записи уравнения реакции. Для одной и той же реакции
в зависимости от формы записи уравнения реакции константа равновесия имеет
совершенно различные числовые значения.
Например, при температуре Г = 723К:
для реакции V2H2+ 72N2 = NH3 К\ = сынз/^н^л/,7" ) = 0,00649;
для реакции 3H2 + N2 = 2NH3 /С2 = /С? = 0,421 • 10~\
Это следует учитывать при использовании в расчетах значений констант равновесия.
Константы равновесия сложных реакций можно выразить через константы
равновесия простых реакций, из которых может быть скомбинирована сложная. Пусть,
например, имеются константы равновесия
218 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
К = Рнс\/(Рн2Рс\2) реакции Н2 + С12 = 2НС1;
К = Рн2Ро2/Рн2о реакции 2Н2О = 2Н2 + 02.
Тогда с их помощью можно определить константу равновесия
КР = Рн2о Pci2/(Phci Ро2) реакции 4НС1 + О2 = 2С12 + 2Н2О
в виде отношения КР= \/[{К'Р)2К'£\.
Если же известны константы равновесия
Кр = Рн2о/(Рн2Ро2*) реакции Н2 + 1/2О2 = Н2О;
К = Pco2/(PcoPof) реакции СО + 1/2О2 = СО2,
то можно найти константу равновесия
КР = Рсо2Рн2/(Рн2оРсо) реакции Н2О + СО = СО2 + Н2,
в виде КР=К?/К'Р.
Константа равновесия реакции может быть выражена через константы
равновесия реакций образования веществ, участвующих в реакции. Действительно, из
выражений (18.2) и (18.4) видно, что величина 1п/Ср представляет собой изменение
функции состояния и поэтому определяется только начальным и конечным состояниями
системы и не зависит от промежуточных состояний, через которые проходит система.
Следовательно, \пКР реакции можно выразить через \пКР реакций образования веществ,
участвующих в реакции таким же образом, как тепловой эффект реакции выражается
через тепловые эффекты образования реагентов и продуктов реакции ln/Cp=2vln/C06p
или 1п/С=1пП/СобР. Отсюда следует, что
/С=П/СовР- (18.6)
Примеры, рассмотренные выше, могут служить иллюстрацией к данному
уравнению. Так, выражения для констант равновесия реакций образования 1 кмоль НС1 и Н2О
имеют вид
1/2Н2+ 1/2С12= НС1, Киа = Рна/(р1{
Н2 + 1 /2О2 = Н2О, КЩо = Рн2о/( Рн2 Р
В соответствии с уравнением (18.6) константа равновесия реакции
+ 2НгО находится через константы равновесия реакций образования НС1 и ЬЬОтак, что
о2 п2
„ -*- й -* \ I * * i ИН2°
л = •
Рна / Рна Ро2
При выводе закона действующих масс предполагалось, что все составляющие
реакции находятся в газообразном состоянии. В гетерогенной системе некоторые вещества
находятся в жидком или твердом состоянии. Однако в химической реакции принимают
участие только пары твердых и жидких веществ, которые в состоянии равновесия
находятся при давлении насыщения, соответствующем температуре реакции.
Парциальные давления сухих паров, сосуществующих с конденсированными фазами
этих веществ, не зависят от давления других веществ реакции и остаются
постоянными до тех пор, пока полностью не исчезнут конденсированные фазы. При
исчезновении в ходе реакции некоторого количества этих паров это количество
немедленно восстанавливается в результате испарения или сублимации конденсированных
веществ. Следовательно, парциальные давления насыщенных паров конденсированных
Химическое равновесие и сродство 2Н)
веществ остаются постоянными и не зависят от наличия или отсутствия химической
реакции. При этом
выражение для константы равновесия гетерогенной реакции содержит только
парциальные давления (или концентрации) веществ, находящихся в газообразном состоянии.
Например, константу равновесия реакции Fe(T)+НгО(г) ==FeO(T)+Нг(г) можно
представить в виде KP = pnJpHi0 или Kc = cHJcHi0.
Сказанное справедливо для тех случаев, когда константы равновесия КР не зависят
от давления, т. е. это справедливо для паров веществ, подчиняющихся законам
идеальных газов.
§ 18.2. Степень полноты реакции и состав равновесной смеси
Степень полноты, или завершенности, реакции характеризует изменение состава
сложной системы при реакции. С ее помощью может быть определен состав
равновесной смеси. Степень полноты реакции можно выразить мерой реакции, степенью
превращения или степенью диссоциации. В соответствии с выражением (14.13) мера
реакции
bt = bNk/vk=(Nk-NkH)/vk, (18.7)
где Nk и Nkn — количество вещества /г-й составляющей в равновесной смеси и в исходной
смеси перед реакцией. Отсюда количество вещества /г-й составляющей в равновесной
смеси
Nk = NkH + vkM (18.8)
Значение меры реакции связано со значениями стехиометрических коэффициентов
в уравнении реакции.
Степень превращения представляет собой прореагировавшую часть
любого реагента, например А (составляющая, находящаяся в левой стороне уравнения
реакции). Если степень превращения вещества А обозначить хА, то
XA = {NA*-NA)INA*=-bNA/NAK (18.9)
где ДЛ/Л — изменение количества вещества A; NA» — количество вещества А перед
реакцией.
Из соотношения \NA/vA = ... = &Nk/vk — &l следует, что &Nk = &NAVk/vA.
Подставляя ДЛ/Л в уравнение (18.8) и учитывая уравнение (18.9), можно представить количество
вещества /г-й составляющей в равновесной смеси в виде
Nk = NAH(Gk-gkxA), (18.10)
где Gk = Nk/NA», gk = vk/vA.
Степень диссоциации ад представляет собой отношение количества
вещества, которое диссоциирует к моменту равновесия, к количеству данного вещества
перед диссоциацией, т. е. это доля вещества, которая продиссоциирована к моменту
равновесия: ад=—&NA/NAH. При реакции диссоциации левая часть уравнения реакции
имеет один член А — диссоциирующее вещество. Следовательно, степень диссоциации
является степенью превращения диссоциирующего вещества в реакции диссоциации
(aR — xA). Поэтому, по аналогии с уравнением (18.10), количество вещества любой /г-й
составляющей в равновесной смеси
Nk = NAH(Gk-gkaA). (18.11)
Стахиометрические коэффициенты веществ в уравнениях (18.8), (18.10) и (18.11)
должны браться в соответствии с правилом знаков. Понятие мера реакции не связано
с определенным веществом, участвующим в реакции, и может рассматриваться как
более общее.
220 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Величины Д£, хА, ад, выражающие степень завершенности реакции, связаны
между собой. Характер связи можно установить, если уравнение (18.7) отнести к
веществу А и сравнить с уравнением (18.9):
Система в состоянии химического равновесия представляет собой равновесную
смесь, которая в общем случае может содержать все вещества, участвовавшие в
реакции. Количественное соотношение между веществами в равновесной смеси
определяется константой равновесия: чем больше константа равновесия, тем больше в
равновесной смеси веществ, стоящих в правой части уравнения реакции. При /(->оо в
равновесной смеси есть только продукты реакции и, следовательно, реакция завершится
полностью. Таким образом, значение константы равновесия определяет степень
завершенности реакции.
Зависимость между константой равновесия КР или Кс и величинами Д£, х, ад может
быть найдена с помощью соотношений (18.5), если представить константы равновесия
КР и Кс через количества вещества в равновесной смеси в виде
Кр=ПМУк(р/2Ык)^=п№к($Т/У)^; (18.12)
Kc=UNvkk[p/(RTItNk) ]lv = UNk/Vlv. (18.13)
В соответствии с выражениями (18.8), (18.10) и (18.11) количество вещества любой
составляющей в равновесной смеси Nk может быть выражено через одну из величин
Д£, х или ад. Сумму количеств веществ составляющих в равновесной смеси 2/V* также
можно выразить через Л£, х и ад. Подставляя выражения для Nk и UNk в уравнения
(18.12) и (18.13), получаем уравнения для константы равновесия КР или Кс в одной из
следующих форм:
Так как константы равновесия КР и Кс зависят только от температуры (для
идеальных газов) и не зависят от давления и объема, полученные выражения дают
возможность, во-первых, определить степень полноты (Д£, х и ад) реакции, протекающей при
определенной температуре и давлении (объеме); во-вторых, они позволяют
установить влияние давления и объема на степень полноты реакции (Д£, х, ад) при
постоянной температуре (константа равновесия постоянна). Зная степень полноты реакции,
определяем количества веществ, т. е. состав равновесной смеси.
§ 18.3* Влияние давления и объема на степень диссоциации
Многие вещества при нагревании до высоких температур диссоциируют. Поэтому
степень диссоциации часто используют в инженерных расчетах, связанных с горением.
Чтобы установить зависимость степени диссоциации от давления и объема, рассмотрим
пример в общем виде.
Пусть уравнение реакции диссоциации имеет вид 2А(г)->-2С(г) +D(r). Для нее
Zv = (c + d) —а= 1. Это общее уравнение справедливо для многих реакций, например
2Н2О(г)+2Н2(г)+О2(г) или 2СО2(г)+2СО(г) +О2(г).
Обозначим степень диссоциации вещества А через ад, а его количество вещества
перед диссоциацией — через NH. Положим, что вещества С и D в начальном состоянии
(перед диссоциацией) отсутствуют. В соответствии с уравнением (18.11) количества
веществ в равновесной смеси следующие: NА = Nn(\ — ад), Nc = NHaAy ND = -^-N»a:l.
Общее количество вещества 2Л/* = УУ„(1 +ад/2).
Химическое равновесие и сродство 22Х
Уравнение для константы равновесия Кс (18.3) в применении к данной реакции
может быть представлено в виде Л^ = /(ад,К)> так чт0
Kc = a3aNH/[2(l-al)V}. (18.14)
Если степень диссоциации а мала по сравнению с единицей (что чаще всего и бывает), то
/Сс«аХ/(2Ю. О8-15)
Используя уравнение (18.12), можно получить зависимости /СР = Дал,К)и Kp = f(a1,p)
в виде
^[2] 2£ (18.16)
(18.17)
С помощью уравнения (18.13) константа равновесия /С,. = Дад,р) определяется в
виде отношения
Кс= alp/[(\ - a2R) (2 + ал) RT\ ^a,p/(2RT). (18.18)
Ha основе полученных выражений можно установить влияние объема и давления
на степень диссоциации для данной реакции. Из уравнений (18.15) и (18.16), имея
в виду, что величины КР(КС) постоянны при постоянной температуре, видно, что с
увеличением объема (dK;>0) степень диссоциации увеличивается (с1ад:>0) —реакция
смещается вправо. Уменьшение объема смещает реакцию влево. Влияние давления
может быть установлено на основе уравнений (18.17) или (18.18). Если давление
увеличивается (dp>0), то степень диссоциации уменьшается (с1ад<;0).
В выражения (18.15) и (18.16) входит исходное количество вещества Л/„, влияющее
на степень диссоциации. Это влияние аналогично влиянию давления, так как изменение
NH в системе при постоянном объеме равносильно изменению давления (pV = NRT).
Если исходное значение Ntl равно стехиометрическому коэффициенту
диссоциирующего вещества в уравнении реакции (в данном случае v = 2), то выражения (18.15) и
(18.16) будут иметь более простой вид.
По рассмотрении только одного типа реакции можно сделать заключение о
влиянии суммы стехиометрических коэффициентов 2v на зависимость степени диссоциации
от объема и давления. Для этого необходимо иметь в виду, что местоположение
объема и давления — в числителе или знаменателе полученных выше выражений
(18.15) — (18.17), (18.18) —зависит от знака изменения количества газообразных
веществ в реакции Zv. Действительно, как следует из уравнений (18.12) и (18.13),
константа равновесия пропорциональна (l/V)Iv. Так как всегда имеются выражения:
в числителе ад\ в знаменателе (1—aA)2v", а также ад<1,—то Кс (или КР) ~
) где 2v>0, 2vK>0.
Давление р системы находится в числителе исходных выражений для КР (18.12)
и Кс (18.13) в степени 2v. Следовательно, Кс (или /(р)~ад кр~^ , где Zv^O, Z
Полученные выражения позволяют сделать заключение о том, что
характер зависимости степени диссоциации от давления и объема определяется знаком
суммы стехиометрических коэффициентов газообразных веществ 2v,
и поэтому возможны следующие случаи:
2v;>0 при dp;>0 daa<<0, т. e. равновесие смещается влево;
при dV;>0 dafl>0, т. e. равновесие смещается вправо;
2v<cO при dp!>0 daa;>0, т. e. равновесие смещается вправо;
при dV:>0 dau<c0, т. е. равновесие смещается влево;
2v = 0 — объем и давление не входят в выражение для константы равновесия и,
следовательно, не влияют на степень диссоциации. Таким образом,
222 РАЗДЕЛ 4, СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
для каждой конкретной реакции может быть получено выражение, связывающее
константу равновесия с мерой реакции (степенью превращения, степенью диссоциации) и
объемом или давлением. Эти выражения дают возможность оценить влияние объёма и
давления на положение равновесия, а также определить меру реакции (степень
превращения, степень диссоциации), если известна константа равновесия и, следовательно,
равновесный состав смеси, что очень важно для практики.
§ 18.4. Химическое сродство
Химическим сродством называется способность различных химических веществ
реагировать друг с другом. Критерий, который мог бы служить мерой химического
сродства, был найден не сразу. Предлагалось выражать меру химического сродства
скоростью химической реакции. Однако это предложение было отвергнуто, потому что
скорость химической реакции зависит не только от состава и состояния реагирующих
веществ (концентрации, температуры), но и от других факторов, например от
присутствия катализаторов. Предложение П. Бертло (1867) принять в качестве меры
химического сродства положительный тепловой эффект реакции также оказалось
неудачным, так как наряду с экзотермическими реакциями известно много
самопроизвольно и энергично протекающих эндотермических реакций.
Первым правильную точку зрения на меру химического сродства высказал
Дж.В.Гиббс (1878), предложив оценивать химическое сродство максимальной работой,
которую силы, заставляющие вещества взаимодействовать, способны произвести.
Позже нидерландский ученый Я. Вант-Гофф (1885) сделал независимо от Гиббса такое
же предположение.
В сложной системе при Г, V = const и 7\ p = const могут протекать только такие
химические реакции, которые ведут к уменьшению свободной энергии (ATV——Л/7)
или свободной энтальпии (ЛТр=—AG) системы, а величина этого уменьшения при
переходе системы из неравновесного состояния в равновесное является мерой
химического сродства реагирующих веществ.
Максимальная немеханическая работа, равная изменению функции состояния
системы при соответствующих условиях, удовлетворяет всем требованиям, которые могут
быть предъявлены к величине, характеризующей химическое сродство: она не зависит
от пути, по которому протекает реакция, а определяется только начальным и
конечным состояниями системы; знак ее однозначно определяет направление течения
реакции.
Уравнение изотермы реакции связывает изменение характеристической функции,
являющейся мерой химического сродства, с парциальными давлениями или
концентрациями веществ, участвующих в реакции. Это уравнение позволяет установить
возможность или направление протекания реакции при данных исходных условиях
(парциальных давлениях или концентрациях веществ) и определить химическое сродство.
Уравнение можно получить следующим образом. Молярное изменение характеристической
функции свободной энтальпии Д<5 в условиях Тур = const можно записать в
соответствии с уравнением (16.17) в виде AG = 2jiKvK.
Выражая химический потенциал \i через парциальное давление из уравнения (16.8)
и подставляя в выражение для AG, получим
Л б = Ъфк + &ТШР1к = Ф(Т) +ЯГ21пЯ2*, (18.19)
где Pk — парциальные давления в неравновесном состоянии системы. Относя
уравнение (18.19) к состоянию равновесия (AG = 0), можно получить Ф(Т) = —RTl,\nplk =
= —RT\nKp, где pk — парциальные давления в равновесном состоянии. После
подстановки Ф(Т) в уравнение (18.19) получим
Химическое равновесие и сродство 223
. (18.20)
Это уравнение определяет химическое сродство в условиях Г, р = const и
называется уравнением изотермы реакции.
Выражая химический потенциал \i через концентрацию и подставляя в уравнение
для Д/7, можно аналогично получить уравнение изотермы для условий 7\ V = const:
/±F=RT(X\nClk — ln/Cc), (18.21)
где Сие обозначают концентрации вещества соответственно в неравновесном и
равновесном состояниях системы (входят в выражение для константы равновесия Кс)-
Уравнения изотермы реакции (18.20) и (18.21) впервые были получены Вант-
Гоффом (1886). С помощью уравнения изотермы реакции определяют возможность или
невозможность реакции в данных условиях. Самопроизвольный процесс при 7\ p = const
сопровождается уменьшением свободной энтальпии. Следовательно, для того чтобы
химическая реакция произошла, значение Д<5 должно быть отрицательным; если
значение Д<5 положительно, реакция не может протекать. Из уравнений (18.20) и (18.21)
следует, что знак AG(AF) зависит от соотношения между величинами
и 1п/С.
Если условия таковы, что 21nP^ft> ln/Cp, то реакция не идет. Для того чтобы реакция
происходила, необходимо изменить условия: либо при постоянной температуре
изменить парциальные давления веществ (или концентраций) так, чтобы значение 1>\пР1к
(или 21пС£*) оказалось меньше значения \пК (это значит, что парциальные давления
продуктов реакции в смеси должны быть уменьшены, или же должны быть увеличены
парциальные давления реагентов, или то и другое вместе), либо изменить температуру
таким образом, чтобы увеличить КР данной реакции, а именно чтобы стало КР7>ПР1к.
Уравнение изотерму реакции позволяет также определить направление реакции.
Действительно, если Дб<0 (Лр>0), то реакция протекает вправо (величина Дб при
этом выражает химическое сродство между веществами, находящимися в левой части
уравнения реакции); если же Д(5;>0 (Ар<С0)У то реакция протекает влево (величина
Дб при этом выражает химическое сродство между веществами, находящимися в
правой части уравнения реакции); если Дб = 0, то система равновесна.
Выражения (5.5) и (5.9) показывают, что при T = const AG = A// — FAS; \F =
= &U — T\S. Следовательно, при низких температурах (Г-^ОК) изменение
энтальпии или внутренней энергии может служить мерой химического сродства. Другими
словами. „ g g
при низких температурах тепловой эффект реакции можно рассматривать как меру
химического сродства.
Отсюда, имея в виду условия протекания реакции AG<<0 (AF<:0), следует, что
при низких температурах химические реакции всегда протекают в направлении
уменьшения энтальпии (внутренней энергии), т. е. сопровождаются выделением теплоты.
Таким образом,
при низких температурах самопроизвольно протекают только экзотермические реакции.
Это положение впервые было высказано Бертло, поэтому носит название
принципа Бе ртл о.
Как видно из уравнений (18.20) и (18.21), химическое сродство в одной и той же
реакции при одной и той же температуре может быть различным, так как зависит
от исходных парциальных давлений или концентраций веществ. Для оценки и сравнения
сродства различных веществ введено понятие стандартного химического сродства.
Стандартным (нормальным) химическим Сродством называется
сродство, когда «исходные парциальные давления всех веществ, принимающих участие
в реакции, равны принятой единице.
224 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
В этом случае член 21пЯ^ уравнения (18.20) становится равным нулю и
выражение для стандартного химического сродства получает вид
AG°=—RT\nKP. (18.22)
Можно рассматривать стандартное сродство, полагая исходные концентрации всех
веществ равными принятой единице. В таком случае член 21nQ* уравнения (18.21)
становится равным нулю и выражение для стандартного химического сродства
получает вид
AF°=-RT\nKc- (18.23)
То обстоятельство, что стандартное химическое сродство AG° и (AF°) зависит только
от конечного состояния (начальное определено) и не зависит от характера
промежуточных процессов, в результате которых конечное состояние достигнуто, говорит о
том, что стандартное химическое сродство, совершенно так же как тепловой эффект
реакции (закон Гесса), может быть найдено алгебраическим суммированием величин
AG°(AF°). Например, реакцию
С(т) + 72О2(г)=СО(г), (18.24)
для которой имеются значения К\ и AG?, можно рассматривать состоящей из
следующих реакций: С(т) +СО2(г) = 2СО(г)(К2 и AGS); Н2(г) + [/202{т) = Н2О(ж) (Кз и
AG§); СО(г)+Н2О(ж)==СО2(г)+Н2(г)(К4 и G4°).
Сложение этих ураинений дает уравнение (18.24), поэтому AG° = AG2 + AG3 + AG?.
При этом все вещества, которые есть более чем в одном уравнении, должны находиться
при одинаковых температуре, давлении и агрегатном состоянии.
Так как величина AG° зависит только от начального и конечного состояний
системы, то ее значение может быть найдено (подобно тепловому эффекту) с помощью
свободных энтальпий образования веществ. Стандартные свободные энтальпии
образования соединений при Г = 298 К приведены в таблицах.
Выражение для изменения свободной энтальпии реакции (стандартное химическое
сродство) через свободные энтальпии образования веществ, принимающих участие в
реакции, по аналогии с соответствующим выражением для теплового эффекта (17.3),
записывается в виде
AG° = 2vAGoV (18.25)
Стандартные свободные энтальпии реакций могут быть определены на основе
экспериментального определения констант равновесия и использования выражения
(18.22), стандартных свободных энтальпий образования и уравнения (1й.2о),
определения теплового эффекта АИ реакции и изменения энтропии в соответствии с
уравнением
д<5?98 = Д//&в — 298ДЙ98. (18.26)
Изменение энтропии реакции может быть определено из выражения AS298 =
= 2vS298, если известны энтропии в стандартных состояниях всех веществ,
участвующих в реакции.
С помощью уравнений (16.18) — (16.19) Гиббса—Гельмгольца можно связать
химическое сродство с тепловым эффектом реакции. Так, для начального и конечного
состояний в изотермном процессе уравнение (16.18) имеет вид FH = UH+T(dFH/dT) v и
FK=UK + T(dFK/dT)v. Их разность AF = FK-FH = (UK- UH) + T[{dFK/dT) v-(dFH/dT) v]
или AF = AU + T{dAF/dT)v. Аналогично, на основе уравнения (16.19)
AG = ДЯ + T(dAG/dT)p. (18.27)
Химическое равновесие и сродство 225
Уравнение (18.27) позволяет записать в дифференциальном виде зависимость
химического сродства от температуры. Производная AG/Г по температуре имеет вид
1 д^G AG
дТ ~~ Т дТ Т2
для процесса р = const
yd(AG/T) = J_ / dAG_ , _ AG
L аг J, г ( дт ),> т2'
Если учесть в полученном выражении уравнение (18.27), то
[д(ЬО/Т)/дТ\р= -Д///Г2. (18.28)
Таким образом, зависимость химического сродства от температуры определяется типом
реакции (экзотермическая или эндотермическая). В экзотермической реакции (Л//<:0)
(dAG/дТ)р~>0 и, следовательно, химическое сродство с увеличением температуры
увеличивается. В эндотермической реакции (Д//;>0) производная оказывается
отрицательной и химическое сродство с увеличением температуры уменьшается.
В интегральной форме уравнение (18.28) имеет вид
Д<5 = - Г$(ДЯ/Г2) dT+TIy (18.29)
где / — константа интегрирования. Подставив в полученное уравнение зависимость
теплового эффекта реакции от температуры (17.13), после интегрирования
получим
Й * Т*1. (18.30)
Определение изменения свободной энтальпии (свободной энергии) связано с
необходимостью располагать значением энтропии при абсолютном нуле. Отсюда следует,
что константа интегрирования / является функцией энтропии So при абсолютном нуле,
значение которой определяется третьим законом термодинамики.
§ 18.5. Зависимость константы равновесия от температуры.
Принцип Ле Шателье — Брауна
Уравнение (18.20) можно записать в виде
Подставив полученное уравнение в (18.28) с учетом того, что /?1пР^ = const, получим в
дифференциальном виде зависимость константы равновесия от температуры:
. (18.31)
Так как константа равновесия КР идеальных газов не зависит от давления, то
d\nKP/dT = /±H/(RT2). (18.32)
Соотношения (18.5) и (17.2) дают возможность получить для идеальных газов
зависимость от температуры константы равновесия Кс в виде
= bU/ (RT2). (18.33)
Уравнение (18.32) устанавливает связь между константой равновесия, температурой
и тепловым эффектом реакции при условии Г, р = const и называется уравнением
изобары реакции. Уравнение (18.33) относится к условиям 7\l/ = const и
называется уравнением изохоры реакции. Используя общее обозначение для константы
8 За к. 584
226 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
равновесия (К) и для теплового эффекта (Q), уравнения (18.32) и (18.33) можно
объединить в виде уравнения изобары-изохоры:
d\nK/dT=Q/(RT2), (18.34)
где К = Кр, если Q = Qp = kH; К=КС, если Q = Qv=kU.
Уравнение (18.34) свидетельствует о том, что характер зависимости константы
равновесия от температуры определяется типом реакции (экзотермическая или
эндотермическая).
Для экзометрической реакции (Q<<0) в соответствии с уравнением (18.34)
dln/(/dr<0. Отсюда следует, что при повышении температуры (dT>0) константа
равновесия уменьшается (d/C<0) и, следовательно, уменьшается степень превращения в
реакции. Реакция смещается влево. При понижении температуры (dT<<0), наоборот,
константа равновесия увеличивается (d/C>-0), степень превращения увеличивается—
реакция смещается вправо.
Для эндотермической реакции (Q>0) dln/C/dr>0. Отсюда dT>0 приводит к
dK>0 и, следовательно, к смещению реакции вправо и увеличению степени
превращения. Уменьшение температуры приводит к противоположному результату.
Анализируя характер влияния температуры на константу равновесия и степень
превращения, можно заметить, что увеличение температуры всегда смещает
равновесие в эндотермическом направлении. Это значит, например, что если реакция
экзотермическая, то при dT;>0 равновесие смещается влево, т. е. в направлении, когда
выделение теплоты уменьшается. И наоборот, если реакция эндотермическая, то
увеличение температуры смещает равновесие вправо, т. е. в направлении, когда поглощение
теплоты увеличивается. Это заключение представляет собой частный случай так
называемого прин.ципа Ле Шатель е—Б р а у н а. Этот принцип определяет реакцию
равновесной термодинамической системы на внешнее влияние и дает возможность во
многих случаях предвидеть направление процессов, возникающих в системе.
По принципу Ле Шателье—Брауна,
любая физико-химическая система, находящаяся в состоянии равновесия, стремится
удержать состояние равновесия и на любое влияние извне отвечает процессом, который
стремится противостоять изменениям,
и смещает систему в новое состояние равновесия. Например, если увеличить давление в
равновесной системе, то в ней должны возникнуть процессы, стремящиеся
противостоять этому увеличению. Увеличению давления противостоит уменьшение объема
системы, поэтому равновесие должно сместиться в том направлении, в котором происходит
уменьшение объема.
С помощью анализа выражений для КР применительно к реакции 2A(r)^t 2С(г) +
+ D(r) было установлено (см. § 18.3) влияние давления на равновесие. Этот же анализ
можно провести и на основании принципа Ле Шателье—Брауна. Так, если увеличить
давление, то, согласно этому принципу, объем должен уменьшиться, а равновесие —
сместиться по верхней стрелке, так как этому направлению соответствует уменьшение
значения суммы стехиометрических коэффициентов 2(v)H<C2(v)K, а значит, и уменьшение
объема. Таким образом, увеличение давления в системе, приводящее к уменьшению
объема, смещает реакцию влево. При этом степень диссоциации уменьшается, а выделение
теплоты увеличивается. Это полностью совпадает с предыдущим выводом.
Зависимость константы равновесия от температуры может быть получена на
основе интегрирования уравнения изобары-изохоры реакции. Рассмотрим только
интегрирование изобары реакции (18.32):
\пКР=][ЬН/ (RT2) ] d7 + A (18.35)
где / — константа интегрирования.
Проинтегрируем (18.35) при условии, что тепловой эффект не зависит от температу-
Химическое равновесие и сродство
227
ры, тогда имеем \пКР= — &H(RT) + J или \gKP= — Д///(19,15Г) +/, где 19,15=2,ЗЛ.
График зависимости \nKP = f(\/T) представляет собой прямую линию с тангенсом угла
наклона к оси (1/Г), равным (-&H/R). Интегрирование уравнения изобары реакции
в пределах температур Т\ — Т2 в предположении, что A# = const, дает выражение
2). (18.36)
Это уравнение может быть использовано для оценки теплового эффекта реакции, если
известны константы равновесия этой реакции при двух температурах. Соответственно
если известны тепловой эффект и константа равновесия при одной какой-либо
температуре, то может быть определена константа равновесия при любой другой температуре.
Рассмотренные зависимости являются приближенными, так как не учитывают
зависимости теплового эффекта реакции от температуры. Подставляя в уравнение (18.35)
зависимость теплового эффекта реакции от температуры (17.13) и интегрируя, получаем
\nKp=—i
(18.37)
Константа интегрирования / может быть найдена, если известны значения Д#о,
Да, Др, Ду и константа равновесия КР при одной температуре.
Константа равновесия, найденная из (18.37), также как и химическое сродство,
найденное из уравнения (18.30), относятся к реакции, записанной в такой форме, которой
соответствуют стехиометрические коэффициенты, используемые при определении Да, Др,
Ду. Это необходимо иметь в виду, так как значения констант равновесия и
соответственно стандартного химического сродства зависят от стехиометрических
коэффициентов уравнения реакции.
Константа интегрирования /, а также / имеют связь с изменением энтропии,
сопровождающим реакцию, и могут быть определены, если Д5 известно. Это можно видеть
в общем виде, сравнивая уравнение (18.30) с уравнением AG = A#— T&S.
§ 18.6. Тепловая теорема Нернста
Уравнения для константы равновесия (18.37) и стандартного химического сродства
(18.30) в функции от температуры содержат константу интегрирования. Поэтому
для определения константы равновесия и химического сродства необходимо кроме
теплового эффекта и теплоемкостей знать константу интегрирования. Из рис. 18.2, а
видно, что, в то время как зависимость теплового эффекта от температуры Д// = /(Г)
определена полностью [см. (17.13)], положение кривой &G° = f(T) [см. (18.29) и (18.30) ]
зависит от значения константы /. Известно только, что эта кривая пересекает ось ординат
в точке, соответствующей значению Д#о.
В двух случаях химическое
сродство определяется просто, так как
равно тепловому эффекту реакции [см. а' J)
(18.27)] при Г = 0 и при {dSG/dT)p= л" *
= 0, т. е. когда химическое сродство п1т~ "'^VV АН
не зависит от температуры. s' / Д(хс
Таким образом, определение
констант равновесия и химического
сродства с помощью данных о тепловых
эффектах и теплоемкостях (обычно
известных), имеющее большое
практическое значение, связано с
определением константы интегрирования, для
а)
*>*
4^
^■■^
7т
ч
чего первого и второго законов
термодинамики оказывается недостаточно.
Т Т
Рис. 18.2. Положение кривой зависимости
химического сродства от температуры: а —
неопределенное; б — в соответствии с теоремой Нернста
228 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Сопоставление тепловых эффектов реакций со стандартными изменениями
свободной энтальпии при различных температурах показывает, что в области низких температур
(когда Т-+0) в конденсированных системах (при Г->-0 все вещества находятся в
конденсированном состоянии) они сближаются. Это дало основание В. Нернсту
предположить, что кривые Д// = ДГ) и &G° — f(T) не только сходятся при Г = 0К, но имеют
общую касательную вблизи абсолютного нуля. Аналитически это выражается
равенством \\m(dhH/dT)T==0 = \\m(dAG° /dT)T==0. Кроме того, эксперименты показывают,
что свойства твердых и жидких веществ вблизи абсолютного нуля перестают зависеть
от температуры. Отсюда следует, что общая касательная к кривым параллельна оси
температур (рис. 18.2,6), т. е.
Wm(dbH/dT)T==o=\\m(dbG°/dT)T==o = O. (18.38)
Таким образом, из бесчисленного множества кривых &G° — f(T) реальной является
та, которая имеет горизонтальную касательную у оси ординат. Положения, относящиеся
к конденсированным системам, получили название тепловой теоремы Нернста.
Впервые они были высказаны в форме гипотез, но затем подтвердились
экспериментально. Отсюда вытекает ряд важных следствий. Так, дифференцируя уравнение
Д# = /(Г) (17.13), можно записать dbH/dT = ba + A$T + /iyT2.
Так как эта производная равна нулю при Т = 0 К, то из уравнения следует, что
Да = 0. (18.39)
Условие (18.39) позволяет определить константы интегрирования. Действительно,
дифференцируя уравнение (18.30), с учетом уравнения (18.39) получаем d&G°/dT =
= — ДрГ — (Av/2) Г2 — RT. Так как при Г = 0 К dAG°/dr = 0, то, зная, что &ф0у
получим / = 0 (соответственно/=—RJ = 0). Это значит, что для конденсированной системы
уравнение стандартного химического сродства принимает вид
Следует помнить, что теорема Нернста относится только к конденсированным
системам. Для газообразных систем константа интегрирования может быть и не равной нулю.
Таким образом, с помощью теоремы Нернста можно определить константу
интегрирования и, следовательно, константу равновесия и химическое сродство, зная ранее
названные данные.
§ 18.7. Третий закон термодинамики
Значение тепловой теоремы Нернста оказывается шире, чем только условие для
определения константы интегрирования (см. § 18.6). Анализ показал, что тепловая теорема может
быть представлена в форме общего утверждения, важность которого дает основание
рассматривать его как новый закон — третий закон термодинамики.
Из условия lim {d\G/dT)p= lim UdG2/dT) —(dGJdT) 1 =0, даваемого
тепловой теоремой, и (dG/dT)p——S следует, что lim (— AS) = 0.
•/•-►о
Это значит, что при Г-^0 AS-^0, S-+Sq = const. Планк предложил считать при
абсолютном нуле So = O.
Постоянство энтропии при абсолютном нуле означает, что изотермный процесс
вблизи абсолютного нуля является в то же время адиабатным. Так как все процессы
теплообмена сопровождаются изменением энтропии, то, следовательно, вблизи
абсолютного нуля система не обменивается теплотой. Поэтому третий закон часто
формулируется как принцип недостижимости абсолютного нуля, а иногда как принцип невозмож-
Химическое равновесие и сродство
229
ности вечного двигателя третьего рода, т. е.
невозможности создания машины, с помощью
которой можно было бы охладить тело до
абсолютного нуля.
Третий закон термодинамики определяет
начало отсчета энтропии и тем самым
позволяет вычислить абсолютное значение энтропии
веществ при различных температурах, если
известны теплоемкости этих веществ при всех
температурах от абсолютного нуля до
необходимой температуры, а также тепловые эффекты
и температуры всех фазовых превращений,
происходящих в этом интервале
температур.
Энтропия любого вещества при температуре Т и определенном давлении при
отсутствии фазовых переходов может быть представлена в виде
Ti
0
5=0
К-,
Г
т„Л
А»„
ASM
<лЛ 'пап \Jr
"А
шнНМшт
ZlSnap
^s
> 5
Рис. 18.3. К определению абсолютного
значения энтропии
= \CP (dT/T) + So =
Ср d \пТ
(18.40)
Изменение энтропии при фазовых превращениях определяется отношением
теплового эффекта Л//фП фазового превращения к температуре, при которой оно происходит:
Д5фп = ДЯф„/ГфП. С учетом фазовых переходов абсолютное значение энтропии
- S £;
К
S £p(d7yr).
(18.41)
где Га^р и Д//а^р — температура и тепловой эффект перехода вещества из одной
кристаллической модификации а в другую Р; Тп.ч, Тпа[)у ДГпл, ДГпар — температура и
тепловой эффект плавления и парообразования; Ср, С% С*, Сгр — зависимости молярных
теплоемкостей соответствующих фаз вещества от температуры.
Полученная зависимость может быть представлена на sT-диаграмме (рис. 18.3).
Если вещество имеет только одну кристаллическую модификацию, уравнение
упростится, и, наоборот, при наличии у вещества более чем двух твердых модификаций при
данном давлении число членов уравнения увеличивается.
§ 18.8. Расчеты с помощью таблиц стандартных величин
и таблиц полных энтальпий и энтропии
В таблицах обычно приводятся следующие величины при стандартных условиях (Г =
= 298 К, р = 0,1013 МПа); Д//298 — изменение молярной энтальпии образования
(тепловые эффекты образования) вещества; Дбгэв — изменение свободной молярной
энтальпии образования (химическое сродство) вещества; S298 — абсолютное значение
молярной энтропии вещества. Все расчеты с помощью таблицы стандартных величин
основываются на аддитивном свойстве величин Д//, ДС, S и поэтому сводятся к простому алге-
браичесхому суммированию по аналогии с расчетами, основанными на законе Гесса.
Напомним, что значения АН и AG элементарных веществ приняты равными нулю.
Таблицы дают возможность, используя уравнение реакции, определить значения
230 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
ЛЯ, Д<5, Д5, К при стандартных условиях. Определение этих величин при других
температурах связано с использованием зависимостей величин от температуры, которые
содержат коэффициенты а, р, у, из зависимостей теплоемкостей веществ от температуры.
Поэтому обычно вместе с таблицами стандартных величин в литературе приводятся
таблицы, содержащие коэффициенты а, р и у для различных веществ.
Ранее полученные выражения позволяют определить все необходимые величины с
использованием таблиц стандартных величин.
Тепловой эффект реакции при стандартных условиях [в соответствии с уравнением
(17.3)]
(18.42)
При температуре Г [в соответствии с уравнением (17.12)]
ДЯГ = Д//298 + Да(Г - 298) + (Др/2) (Г2 - 2982) + (Д?/3) (Г3 - 2983). (18.43)
Абсолютная величина энтропии вещества при температуре
т
298
Используя зависимость для теплоемкости, после интегрирования получим
ST = S298 + aln (Г/298) + Р(Г - 298) + (у/2) (Г2 - 2982). (18.44)
Если агрегатное состояние вещества при стандартных условиях отличается от его
агрегатного состояния при определяемой температуре Г, то необходимо учесть изменение
энтропии в соответствующих фазовых превращениях Д5фП = (Д#/Г)фП, где Д#фП и Гфп —
соответственно скрытая теплота и температура фазового превращения.
Изменение энтропии системы в реакции при стандартных условиях
При температуре Т
j
298
Используя зависимости для теплоемкости веществ от температуры, после
интегрирования получаем
Д5°г = Д5298 + Aaln (Г/298) + Др (Г — 298) + (Д?/2) (Т2 — 2982). (18.46)
Нормальное химическое сродство при стандартных условиях [в соответствии с
уравнением (18.25)]
AG298=2vAG298o6p. О8'47)
Используя выражение AG = A//— ГД5, справедливое для процесса Т—const, можно
нормальное химическое сродство Дб&в выразить формулой
AGggg = Д//298 — 298Д5298, (18.48)
Химическое равновесие и сродство 23_[
где ДЯ298 и Д5°298 определяются соответственно выражениями (18.42) и (18.45). При
температуре Г
Подставляя соответствующие выражения для &Н°Т (18.43) и &S°T (18.46), получим
Д<5°г = Д//298 — ГД$298 — даГ1п (Г/298) + (Т — 298) (Да — Д0Г) +
+ 1/2 (Г2 — 2982) (Др — ДуГ) + Л? (Т3 — 2983)/3. (18.49)
Константу равновесия реакции при стандартных условиях определяем используя
уравнение (18.22):
Кр = ехр[ - Дб^98/(298Л)] . (18.50)
При температуре Г
/Ср=ехр[-Абв7./(ГЛ)]. (18.51)
Если таблицы стандартных величин содержат только величины ДЯгэв и Sfa%, то
Дбгэв находится, как указывалось выше, из выражения (18.48).
В теплотехнических расчетах широко используют таблицы полных энтальпий
веществ. Законы термодинамики определяют начало отсчета только для одной из
экстенсивных функций состояния, неподдающихся непосредственному измерению,— энтропии.
Поэтому на основе законов термодинамики может быть вычислено только абсолютное
значение этой функции. Определение абсолютного значения других функций, в частности
энтальпии, связано с установлением (произвольным) начала отсчета функции, т. е.
состояния, в котором значение функции принимается равным нулю.
Так как в расчетах приходится иметь дело с изменениями функций, значения
которых не зависят от начала отсчета, то начало отсчета при определении
абсолютного значения энтальпии не имеет принципиального значения. При создании таблиц
полных энтальпий за начало отсчета энтальпий элементов было принято их стандартное
состояние, наиболее распространенное в природе (Ог, Н2, N2, СЬ, F2 и т. д. в газообразном
состоянии, С в форме графита, металлы — твердые кристаллы), при температуре Го
и давлении /?о = О,1О13 МПа, т. е. H°Tq (элемент) =0.
Энтальпию химических соединений при стандартных параметрах (Го и р0)
полагаем равной тепловому эффекту образования их из элементов при этих параметрах,
т. е. Й°пТо = ЬЙ%.
В соответствии с принятым началом отсчета полная энтальпия химического
соединения (вещества) при температуре Г
где &Н°т0—тепловой эффект образования вещества из элементов при Го и ро =
= 0,1013 МПа (он должен определяться с учетом фазовых превращений); Н°т и HoT(j —
энтальпия вещества при температуре Г и Го соответственно.
За температуру начала отсчета полных энтальпий обычно принимают одно из
значений: 293,15; 298,15; ОК. В таблицах полных энтальпий веществ принято Го = 293,15 К.
Полная энтальпия вещества НпТ при температуре Г в таком случае
НПТ=1ЬН293+(НТ-Н293). (18.52)
232 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Изменение энтальпии вещества при изменении его температуры от стандартного
значения (Г0 = 293 К) до температуры Т определится разностью
т
Нт — #293= 3 CpdT,
293
где Cp = f(T) — зависимость теплоемкости вещества от температуры.
При наличии таблиц полных энтальпий определить необходимые величины при
температуре Т можно с помощью следующих уравнений:
тепловой эффект реакции
SHt=^h[t (18.53)
[это уравнение находится в соответствии с уравнением (18.43) и может быть сведено
к нему с использованием уравнения (18.52)];
изменение энтропии системы
(18.54)
химическое сродство на основании уравнения &Gt=&H°t—T&S°T
° ° (18.55)
константа равновесия—из уравнения (18.51).
Сравнивая соответственно уравнения (18.43) и (18.53), (18.46) и (18.54), (18.49)
и (18.55), можно заметить, что при наличии таблиц полных энтальпий и абсолютных
энтропии веществ при различных температурах расчеты по определению тепловых
эффектов, изменений энтропии и констант равновесия реакций существенно
упрощаются.
§ 18.9. Определение параметров состояния
и состава рабочих тел и продуктов сгорания.
В тепловых машинах в качестве рабочего, тела часто используются смеси реальных
газов. Такие машины работают обычно при сравнительно низких давлениях и
высоких температурах. Поэтому во многих случаях с достаточной степенью точности для
расчетов можно использовать уравнение состояния идеального газа и учитывать
зависимость теплоемкости от температуры. Целесообразно при этом вместо параметров
состояния р, vy T применять калорические величины и, A, s, обладающие свойством
аддитивности (изменение энтропии при смешении обычно не учитывается), а их
значения для отдельных компонентов находятся по таблицам.
При определении энтальпии пользуются соотношением (2.34). Для смеси газов
hm= 2 gkhk\ 5m= 2 gksk\ um=hm — pmvmJ (18.56)
k=\ 6=i
где gk — массовая доля k-то компонента.
Свойство аддитивности калорических параметров позволяет рассчитывать
процессы рабочего тела переменного состава.
Аналитический расчет параметров процессов начинается с предварительного
определения по начальным условиям и характеру самого процесса параметров
состояния в начальной (pi, v\, T\y h\y Si) и конечной (pi, V2> T2, hi, 52) точках процесса.
Затем по общей для всех процессов и любых агрегатных состояний зависимости
определяется изменение внутренней удельной энергии рабочего тела: Aw = A/i — Д(р^).
Теплота зависит от характера процесса и определяется для: изохорного процесса
Химическое равновесие и сродство
233
(y = const) —по формуле (9.4) или q = h2 — h\—pov + p\V] изобарного процесса (р =
= const) — по формуле (9.1 1); изотермного процесса (r = const) — по формуле (9.16);
адиабатного процесса — q = 0.
Для определения теплоты в политропном процессе необходимо воспользоваться
дополнительными условиями, например условиями теплообмена. С точностью ±5%
удельную теплоту политропного процесса можно определить по приближенной
зависимости (9.60).
Затем вычисляются по общим для всех процессов формулам удельная работа
процесса l = q — Au и располагаемая удельная работа l{) = q — A/z.
При расчетах процессов и параметров реальных рабочих тел часто используют
специально составленные для этих целей 5//-диаграммы. В этом случае для каждого
состава смеси газов должна быть разработана отдельная такая диаграмма. Однако
практика расчетов показывает, что достаточно располагать лишь несколькими
диаграммами для наиболее употребительных топлив и для нескольких значений
коэффициентов избытка окислителя а.
В качестве примера на рис. 18.4, а приведена универсальная молярная 5//-ди а
грамма (построена на кафедре газовых турбин Казанского авиационного института),
пригодная как для воздуха, так и для продуктов сгорания различного состава. Средняя
часть этой диаграммы построена в прямоугольной системе координат (энтальпия Н —
по ординате, энтропия § — по абсциссе). На диаграмме нанесены сетки изобар, изохор
и изотерм.
Рис. 18.4. s/г-диаграмма; а — для
воздуха и продуктов сгорания; б —
определение адиабатного теилоисрепада
234 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Коэффициент р, учитывающий отклонение свойств продуктов сгорания топлива
состава 85 % С, 15 % Н от свойств чистого воздуха, определяется по формуле
Р=1+(рг—1)/а, где рг — постоянная величина; а — коэффициент избытка воздуха.
Для продуктов сгорания топлива рг=1,5 при а=1, а для чистого воздуха рг=1. Для
газовой смеси произвольного состава Лютц и Вольф предлагают использовать
формулу p = 0,96rN2+1,23/-О2+2,72/-Н2о+4гСо2, где rk — объемная доля компонента.
Пусть, например, необходимо определить адиабатный перепад энтальпии и построить
на S/Z-диаграмме процесс расширения продуктов сгорания нефти при снижении
давления от 0,5 до 0,1 МПа, если в камере сгорания турбины коэффициент избытка воздуха
а = 2,65 и температура 873 К. Для этого следует определить коэффициент р (получаем
Р=1,2) и из точки пересечения изобары 0,5 МПа и изотермы 873 К (А\ на рис. 18.4, б)
провести адиабату А\Ач параллельно лучу р=1,2 с левой стороны диаграммы до
пересечения с изобарой 0,1 МПа. Температура в конце адиабатного расширения составляет
578 К. Затем, проецируя точки А\ и Лг на вертикальный луч р = 1,2 (в правой части
диаграммы), получаем Н— 18 980 Дж/моль (точка Аз) и // = 9218 Дж/моль (точка Л4).
Следовательно, адиабатный перепад энтальпии ДЯ= 18 980 — 9218 = 9762 Дж/моль.
Каждая составленная подробным образом диаграмма предусматривает определенные
условия ее применения. Нарушение этих условий может привести к заметным
погрешностям.
При анализе рабочих процессов теплового двигателя большое значение имеет
определение состава и температуры продуктов сгорания. Для многих тепловых
двигателей (дизелей, газовых турбин и т. д.) сгорание можно считать полным, так как
отношение действительного количества окислителя к теоретически необходимому для
полного окисления горючего больше единицы (а> 1). В таком случае без учета
диссоциации для 1 кг углеводородного топлива можно записать химические реакции окисления
отдельных составляющих его (С и Н) в виде С + О2 = СО2 и 2Н2 + О2 = 2Н2О. Учитывая,
что 1 кмоль С соответствует 12 кг, а 1 кмоль Н2 — 2 кг, получим при сгорании С кг
углерода и Н кг водорода С/12 кмоль СО2 и Н/2 кмоль Н2О соответственно.
Кроме того, в продуктах сгорания останутся азот и неиспользованный кислород
(кмоль): N2 = 0,79aL0; O2 = 0,21 Lo(a—1), где Lo — необходимое количество воздуха
для сгорания 1 кг топлива, кмоль/кг. Последние соотношения справедливы для воздуха,
содержащего по объему 21 % кислорода и 79 % азота.
Расчет состава продуктов сгорания с учетом диссоциации проводится в
предположении достижения химического равновесия, т. е. при выполнении условий
обратимости протекания реакций (dS = 0) и равенства химических потенциалов реагирующих
компонентов.
Система уравнений для определения состава и температуры продуктов сгорания
топлива (1 кг горючего+ v кг окислителя), состоящего из углерода, водорода,
кислорода и азота, характерного для тепловых двигателей, может быть записана в следующем
виде:
СО2*=СО+1/2О2; КР1=
pH2p^2/p
?H2o=h (Г);
N2+CW2NO; КР<=
Химическое равновесие и сродство 235
KPt =p2o/po=fs(T);
Значения констант равновесия в зависимости от температуры находят по таблицам.
Семь приведенных реакций сгорания топлива являются наиболее вероятными. В
уравнениях для констант равновесия содержится 11 неизвестных парциальных давлений
элементов: рсо<1, pH<lO> рсо, р^ рН2, р0<£ pN(> рон, рн, Ро pN, а также температура Ткс
сгорания, которая определяет значение констант равновесия.
Давление рт смеси газов вычисляем по формуле (8.1). Количество продуктов (моль)
пт
сгорания пт может быть определено в виде отношения
где Мт — кажущаяся молярная масса смеси; М* — молярная масса /г-го элемента.
Из уравнений баланса элементов в топливе и продуктах сгорания получают еще
четыре зависимости, дополняющие систему уравнений:
где /zN, Л/т, Л/г, No— количество вещества азота в продуктах сгорания, топливе,
горючем, окислителе соответственно, кмоль; v — отношение масс горючего и окислителя;
rN — объемная доля азотсодержащих газов.
Таким образом,
NT = (Nr + vN0 )/(l + v) = 14 (пт /рт) (2pN2 + pN + pN0 ).
По аналогии с азотом, для других составляющих элементов топлива
Ст = (Сг + vC0)/(l + v) = 12 {пт/рт) (рСо2 + Рсо);
Нт = (Нг + vH0)/(1 + v) = (пт/рт) (2рн2о + 2рн2 + Рон + Ри);
От = (Ог + vOo)/(1 + v) = 16 (пт/рт) (2ро2 + 2рсо2 + Рн2о + Рсо + Рон + Pno + Ро )•
Последним уравнением в рассматриваемой системе является уравнение первого
закона термодинамики, которое для p = const в изолированной системе может быть
записано в виде q — kh = 0 или
k—n k=n k — n
£пТ = [#пс] TKC = (njPm) 2 ялрй='2 /W2 MkPk-y
ft)v), (18.57)
где Япт, Япс — полная молярная энтальпия соответственно топлива и продуктов
сгорания, Дж/моль; Hk — полная молярная энтальпия /г-го компонента, Дж/моль; Гкс —
температура в камере сгорания, К; Япг, Нпо — полная молярная энтальпия
соответственно горючего и окислителя, Дж/моль.
С помощью таблиц полных энтальпий компонентов можно для данного состава
продуктов сгорания найти полную энтальпию смеси.
В полученную систему из 14 уравнений для определения состава и температуры
продуктов сгорания топлива, состоящего из 1 кг горючего (Cr, Hr, Or, Nr) и v кг
окислителя, входит 14 неизвестных величин: 11 парциальных давлений газов, составляющих
236
РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
смесь, и пт, рт> Ткс. Поэтому принципиально система
может быть решена. Доказано, что она имеет только одну —
единственную систему корней, каждый корень которой
имеет действительное положительное значение.
Решение рассматриваемой системы может быть
осуществлено на ЭВМ или графоаналитическим методом.
Для этого следует задаться несколькими значениями V,
Г", V" в области ожидаемой температуры, определить
состав продуктов сгорания, Н'пс, //"с, //"с и построить
график зависимости // = /(Г) (рис. 18.5).
Для правильного выбора значения температуры надо
воспользоваться уравнением (18.57), подсчитать значение
//||Т, отложить его на оси ординат и полученную точку b
спроецировать на построенную кривую. Проекция
полученной таким образом точки а на ось абсцисс и даст искомую
температуру Ткс.
При сгорании топлива в камере с V= const аналогичная система уравнений
записывается через константу равновесия Kv:
h
Со
-с:
-с;
ПС <
^w
^J
К
Г
ткс T"TtR
Рис. 18.5. Графоаналитичес-
кий метод определения темпе-
ратуры сгорания
O= f\(T); KV2= VH2Vlo/
= Vh/4= ftW; 4= У%/Уо,= f'6{T);
k=n
VkMk;
k=\
k n
NT=14(2VN2+VNO+VN)/2
*1
OT = 16(21/o2
/2 мк
k=n k=n
,= 2 Mkvk/vm- vm= 2 vk,
k=\ k=\
где Vk — парциальный объем компонента (объем /г-го компонента при давлении смеси
газов); и11Ту м|К.— полная удельная внутренняя энергия топлива и продуктов сгорания,
Дж/кг.
Энтальпия и внутренняя энергия связаны между собой зависимостью (2.34).
Вопросы!. Напишите условие химического равновесия.
2. Объясните, почему константа равновесия является безразмерной величиной.
3. Что является мерой химического сродства?
4. Можно ли изменением температуры изменить направление течения реакции в смеси
реагирующих веществ?
5. Что называется стандартным химическим сродством?
6. Что утверждает третье начало термодинамики?
Растворы 237
Глава 19
РАСТВОРЫ
§ 19.1. Состав и парциальные свойства
Раствором называется гомогенная смесь веществ, в которой все составляющие
находятся в молекулярно-дисперсном состоянии.
Поэтому раствор нельзя разложить на составляющие части с помощью чисто
механических средств, без затраты работы. Растворы могут быть твердыми, жидкими и
газообразными. Составляющие раствор вещества называются компонентами Если
содержание одного из компонентов в растворе значительно больше, чем суммарное
содержание всех других компонентов, то этот компонент называется растворителем,
а остальные — растворенными веществами.
Состояние раствора определяется двумя термодинамическими параметрами
(обычно температурой и давлением) и концентрацией.
Способность веществ образовывать друг с другом растворы характеризуется их
взаимной растворимостью. Вещества, находящиеся при температурах выше критической
термодинамической температуры (газообразные), обладают неограниченной
растворимостью, т. е. смешиваются в любых соотношениях при не слишком высоких давлениях.
Вещества, находящиеся в жидком или твердом состоянии, могут обладать как
неограниченной, так и ограниченной взаимной растворимостью.
Раствор с максимально возможной в данных условиях концентрацией вещества
называется насыщенным.
При образовании раствора происходит перестройка молекулярной структуры как
растворимого вещества, так и растворителя. Это связано с изменением взаимного
расположения и ориентации молекул (а иногда и с изменением химического строения) и,
следовательно, с изменением энергии молекулярного взаимодействия. Перестройка
структуры приводит к тому, что зависимость термодинамических свойств растворов от
состава становится весьма сложной и эти свойства, вообще говоря, не могут быть получены из
термодинамических свойств компонентов.
Примерами растворов служат морская вода, воздух, металлические сплавы и т. д.
Растворимость жидкостей и твердых тел часто лимитирует работу энергоустановок
при сверхвысоких и сверхнизких параметрах.
Состав раствора характеризуется массовыми gk или молярными Xk долями
компонентов, определяемыми в виде отношений
k=n k—n
gk=mk/'Z mk\ xk = nk/Ti (19.1)
*=i k=\
Процесс растворения вещества обычно сопровождается поглощением теплоты.
Раствор, получающийся без изменения объема и теплового эффекта, называется
идеальным.
Для компонентов раствора справедливы те же уравнения, что и для чистого
вещества, однако в этом случае должны использоваться парциальные молярные
величины. Так, если к конечному количеству раствора добавить бесконечно малое
количество растворенного вещества dNk, то свойства всего раствора изменяются. Например,
объем Vy раствора изменится на
Производную Vk = {dV^/dNk)рj<N. в этом случае называют парциальным
молярным объемом. Аналогично определяются парциальные молярные
энтропия Sfe, энтальпия /*, свободная энергия /•* и т. д. Впервые понятие
парциальные молярные свойства растворов было введено Д. И. Менделеевым в 1885 г.
238 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
§ 19.2. Уравнение Ван-дер-Ваальса для бинарных систем
В тех случаях, когда раствор состоит из одного растворителя и одного
растворенного вещества, он называется бинарным раствором или бинарной
системой.
Изучение свойств бинарной системы имеет существенное практическое значение,
так как, с одной стороны, бинарные растворы часто встречаются как в природе, так и
в процессах производства, а с другой стороны, закономерности, выявленные при их
изучении, могут быть обобщены для многокомпонентных растворов.
Экспериментальные законы бинарных растворов могут быть установлены теоретически с единых
позиций из анализа уравнения Ван-дер-Ваальса.
Сумма молярных долей компонентов (19.1) бинарной смеси равна единице. Если
П2 — х — молярная доля растворенного вещества, то доля растворителя лгi = 1—х.
Для растворов характеристической функцией является свободная энтальпия G. В
соответствии с последней зависимостью (6.10) для бинарного раствора имеем
dG — vdp— sdT + M'id(l —x) + \i2dx,
или
dG = vdp — sdT + (\i2— \ii)dx. (19.2)
Последующие преобразования связаны с заменой химического потенциала \i более
известными величинами. Используя преобразование Лежандра, получим
dG = vdp — sdT — xd(\L2—\Li) + d[x(\L2 — \L\)]. (19.3)
Выражение, стоящее в квадратных скобках, является химическим потенциалом
растворителя (ii.
Действительно, при р, T = const и условии равновесия бинарной системы,
учитывая (6.18), имеем
2 \iknk = 0 = Мч (1 — х) + \i2 х,
k=\
откуда
M.i=*(|A2-|ii). (19.4)
Выражение (19.2) представляет собой полный дифференциал, поэтому
(dG/dp)T,x = v, (dG/dT)PiX=-s; (вС/вх)р,г = |1,-|1|. (19.5)
Из (19.5) следует xd(\i2 — \i\) — xd(dG/dx)pT и тогда
) dP(^) dT + ^
]
(19.6)
При r = const из уравнения (5.14) dG = ^dp. Так как для идеального газа pv = RT>
то dG — RTdp/p, или после интегрирования
G = RT\np+ G(T) (19.7)
Для бинарной смеси в соответствии с выражением (8.4) р1 = гр^=п\р1=
=(1—х)р2; р2 = хр2, поэтому свободная энтальпия такого раствора определяется
суммой:
Растворы 239
= RT\npz + RT[(\ — х) +xlnx] + GX(T) + G2(T).
После двойного дифференцирования
= Т7гЦг- (19-8)
Таким образом, с учетом (19.4), (19.5), (19.6) и (19.8) зависимость (19.3) получит
вид
Если предположить, что бинарный раствор находится в двух фазах в состоянии
равновесия (G = Gmin;dG = dG, + dG2 = 0; \l'\ = \i" \ dM.i = O), то
dx.
(19.10)
Уравнение (19.10) связывает термодинамические параметры раствора с концентрацией
и позволяет получить все основные закономерности бинарных растворов. Оно было
получено Ван-дер-Ваальсом на основе соотношения Гиббса—Дюгема для систем с
переменным числом частиц. При применении уравнения (19.10) к той или иной фазе
раствора необходимо параметры, оставшиеся без индексов, снабдить индексом,
соответствующим рассматриваемой фазе.
§ 19.3. Законы Рауля и Генри
Наиболее простые термодинамические соотношения получаются для разбавленных
растворов, т. е. таких, в которых содержание растворенного вещества мало по
сравнению с содержанием растворителя.
Свойства бесконечно разбавленных растворов сохраняются и при конечных
концентрациях, причем предельные концентрации можно определить лишь опытным путем.
Экстраполяция свойств реальных растворов, найденных экспериментально, до
бесконечно малых концентраций является методом проверки и обобщения
экспериментальных данных.
Для разбавленных растворов можно пренебречь изменениями объема и энтропии
раствора в зависимости от доли растворенного вещества и принять dy/dx = 0; ds/dx = 0.
Если объем v" пара определить по уравнению состояния идеального газа и учесть, что
удельный объем жидкости v' мал по сравнению с объеморт~Пяра v"', то v' = 0 и v" =
= /?цГ/р. Предполагая, что растворенное вещество нелетучее (х" = 0), уравнение
(19.10) для процесса Т — const можно записать в виде dp/p= — dx'/(l—xf). После
интегрирования (при р==ро и х' — О) имеем \п(р/ро) = \п(\ — х'), откуда
' (ро-р)/ро = х'. (19.11)
Полученное соотношение показывает, что
относительное понижение давления пара раствора пропорционально молярной деле
растворенного вещества.
240 РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Выражение (19.11) является математической формулировкой экспериментального
закона Рауля.
Из выражения (19.11) также следует, что при изменении температуры в
небольших пределах относительное понижение давления пара раствора не зависит от
температуры.
Уменьшение давления пара над раствором по сравнению с чистым растворителем
подтверждает принцип Ле Шателье. Так, например, при добавлении соли в систему
вода — пар часть пара переходит в жидкость, его давление падает, а доля растворенного
вещества уменьшается. Закон Рауля используется для экспериментального
определения молярной массы различных веществ. Действительно, если nt\ и т2 — соответственно
массы растворителя и растворенного вещества (m2<^im\)y то
т2М\ .. Ро т2 жл
х М М
При -J7=O; -J7=°; v=0\ v" = —\ x" = 0\ x«\ уравнение (19.10)
для процесса p = const имеет вид (s" — s')dT = RTdx и может быть
записано в конечных разностях:
RT2bx. (19.12)
Так как T(s" — s') — M\r — молярная теплота фазового перехода (для 1 кмоль), а
Дх = т2Л4|/(т|М2), то зависимость (19.12) можно использовать для определения
изменения ДГ температуры кипения и температуры замерзания раствора по сравнению
с чистым растворителем:
Д7-=«ИД* = ^1. (19.13)
Явление изменения температуры фазового перехода при образовании раствора
широко используется на практике (например, в зимнее время при поливке улиц
раствором солей, для создания охлаждающих смесей и т. д.).
В тех случаях, когда в жидкости растворяется газ, для процесса T = const
выполняются условия dy/dx = 0; ds/dx = 0; у' = 0; v" = RT/p и уравнение (19.10) при
х"=1 получит вид dp/p^dx' /х' или
х' = Ср, (19.14)
где С — постоянная величина.
Соотношение (19.14) утверждает, что
количество растворенного в жидкости газа прямо пропорционально его давлению.
Это закон Генри, знание которого имеет большое практическое значение.
Достаточно напомнить о кессонной болезни, связанной с выделением газов из крови при
понижении внешнего давления, разгерметизации кабин самолетов и т. д.
§ 19.4. Закон осмотического давления Вант-Гоффа
Избирательная диффузия через полупроницаемые перегородки (пропускающие
растворитель и задерживающие растворенное вещество) носит название осмоса.
Так как часть объема в растворе занята молекулами растворенного вещества,
то число молекул растворителя, встречающихся со стенкой со стороны чистого
растворителя, больше, чем со стороны раствора. Поэтому при р, T = const молекулы
растворителя проникают в раствор. Равновесие наступит тогда, когда избыток давления
со стороны раствора (осмотическое давление) при Г = const или избыток температуры
(осмотическая температура, с ростом которой растет интенсивность движения молекул)
при р = const компенсируют избыточный поток молекул растворителя.
Растворы 241_
Если пренебречь изменением объема раствора с изменением молярной доли
(cb/djt = O), то при равновесии (dG = 0; djx = O) и при T=const уравнение (19.9) для
однофазной бинарной системы получит вид vdp = [RT/ (1—x)]dx. После интегрирования
(y = const) и введения осмотического давления (росм = р— р0) имеем
Ро« = -^-1п(1—х). (19-15)
Если в полученном выражении логарифм разложить в ряд, т. е. (рОсм^ = ^
2/2+х3/3 + ...), и затем ограничиться только первым членом разложения, то
получим уравнение
PocmV==RTx (19.16)
— закон осмотического давления Вант-Гоффа. Уравнение (19.16) по
форме совпадает с уравнением состояния идеального газа и показывает, что
осмотическое давление равно тому давлению, которое имело бы растворенное вещество, если бы
оно в виде идеального газа занимало тот же объем при той же температуре.
Если воспользоваться уже изложенной методикой преобразования уравнения
(19.9), т. е. принять p = const, и считать, что теплообмена с окружающей средой не
происходит (система адиабатна и s = const), ввести осмотическую температуру Тосм —
= Г—Го, а также (dG/dT)p,x = — s, ln(l + T0CM/T) = (R/s)\n(\ — x)y то
T0CM = Rx/(dG/dT)p,x (19.17)
— одностороннего тока растворителя через полупроницаемую перегородку не будет
только при создании соответствующей разницы температур Госм между раствором и
растворителем.
Наличие избытка давления в виде рОсм приводит к тому, что при введении в раствор
новой порции растворителя Ami (при разбавлении раствора) объем раствора
изменяется на AV\ при этом затрачивается работа, превращающаяся затем в теплоту
разбавления, а именно: А, = рОсмА1//Дт1 =росму. При конденсации пара растворителя,
полученного при испарении из раствора, та же работа в виде теплоты добавится к теплоте
испарения го = г + Х.или А,= г0 —г, где г — удельная теплота испарения. Разность
удельных теплот испарения находят по уравнению (19.10), которое при dv/dx = 0y ds/dx = 0
превращается в уравнение Клапейрона—Клаузиуса: dp/dT = M\r/ [T(v" — v') ]. Если
пренебречь объемом жидкой фазы и принять у// = /?Г/р, то интегрирование в пределах
от р до ро приведет к уравнению
&(1"?). (19.18)
справедливому для любых растворов. Уравнение (19.18) дает возможность определить
теплоту разбавления по изменению упругости пара.
§ 19.5. Первый и второй законы Коновалова
При исследовании растворов применяют диаграммы состояния, на которых по оси
абсцисс откладываются доли компонентов, а по оси ординат — давление (рис. 19.1, а)
или температура (рис. 19.1, б) раствора. Характер граничных кривых на этих
диаграммах устанавливается с помощью законов Коновалова.
Рассмотрим двухфазную систему из двух жидкостей и их паров. При постоянной
температуре T = const уравнение (19.10) с учетом формулы (19.8) для жидкой и паро-
242
РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Рис. 19.1. Диаграмма свойств бинарной системы: а — при
образной фаз соответственно примет вид
XX 1 X
p = const; б — при T = const
v -v -(х -
Щ
дх
\v — v —{х — х )—- dp = {x — х )[ г
dx;
dx .
(19.19)
(19.20)
При температурах, превышающих критическую, в квадратных скобках уравнений
доминирует объем пара и"'. При равновесии имеет место G=Gmin и, следовательно,
(d2G/dx2)p r>0. Деление уравнения (19.19) на уравнение (19.20) приводит к условию
dxfldx"~> 0, свидетельствующему о том, что при повышении молярной доли
компонента в жидкой фазе увеличивается его доля и в парообразной.
Из уравнения (19.20) следует, что
Это выражение при х"> х' и предположениях, указанных выше, приводит к выводу,
что
dx"
(19.22)
— давление пара смеси растет с увеличением доли того компонента, которого больше
в парообразной фазе, или что пар бинарной смеси в большем количестве, чем жидкость,
содержит тот компонент, с увеличением доли которого растет давление пара смеси.
Этот вывод составляет первый закон Коновалова.
Анализ диаграмм состояния показывает, что жидкость и пар имеют разный состав
х' и х" при одном и том же давлении (рис. 19.1, а) или одной и той же температуре (рис.
19.1, б), т. е.
линии кипения жидкости и конденсации пара не совпадают.
На этом основаны процессы перегонки и ректификации, имеющие большую роль в
производстве моторных топлив и масел. Из первого закона Коновалова также следует,
что
кривая кипения жидкости и кривая конденсации пара одновременно или опускаются,
или поднимаются.
Пусть точка Ь (рис. 19.1, б) характеризует смесь состава х. Область между кривыми
принадлежит гетерогенной смеси (пар состава х" и жидкость состава xf). Если 1 кг смеси
образует m кг пара и (1— пг) кг жидкости, то х—пгх" + (\ — пг)х\ откуда
X
х"
— х
-X
1 -
т
т
ос
ас
X
X
1
- х
X
т ■
X
х"
~аЬ
be
— х
— X
ах
ас
Растворы
т =
Полученное соотношение часто называют
правилом рычага.
Так как (d2G/dx2)pT> О и знаменатель
принимает конечное значение, то из уравнения (19.21)
следует, что при х" = х'
^ = 0. (19.23).
dx v ;
Этот вывод составляет второй закон
Коновалова:
если кривая давления пара бинарной смеси проходит
через экстремум (рис. 19.2), то пар и жидкость
в точке экстремума имеют одинаковый состав
243
Рис. 19.2. Фазовая диаграмма с азе-
отропной точкой
Состав смеси в точке экстремума называется азеотропным. Знание точек
экстремума имеет большое практическое значение, так как при достижении их из-за
равного состава х"=х' кончается процесс ректификации. Те же закономерности
справедливы для твердых растворов, причем область пара занимает на диаграмме
состояний жидкий расплав, а область жидкости — смешанные кристаллы.
§ 19.6. Реальные и многокомпонентные растворы
Растворы, образуемые сходными по химическому составу и физическим свойствам
веществами, считаются идеальными. Отклонения от поведения идеальных растворов
вызываются как химическими эффектами (ассоциацией, сольватацией и т. д.), так и
физическими (различием молярных объемов, межмолекулярных сил и т. д.).
Отклонения первого вида с ростом температуры уменьшаются, а второго — возрастают. Однако
многие растворы ведут себя практически как идеальные. Учитывая простоту
закономерностей для идеальных растворов и сложность реальных систем, часто сознательно
допускают некоторую неточность, считая реальный раствор идеальным. Ответ на вопрос,
до каких концентраций и с какой степенью
точности поведение данного раствора подчи- -
няется законам идеального раствора, может
дать только эксперимент.
Растворы, для которых зависимость
парциальных и общего давления от состава
выражается прямыми линиями [закон Рауля
(19.11) на рис. 19.3], представляют тот
предел, к которому приближаются реальные
растворы. Исходя из этого реальные
растворы и соответствующие им графики
классифицируют по характеру отклонений от закона
Рауля. Кривые, построенные по эксперимен- д
тальным данным при г\-+\ и гг-*1, должны
быть касательными к прямым, выражающим рис ig 3 зависимость парциальных и об-
закон Рауля (разбавленный раствор), а при щего давлений пара от состава для идеаль-
Г]-+0 и г2->-0 иметь касательные прямые, соот- ного и реального растворов
Рид
244
РАЗДЕЛ 4. СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Рис. 19.4. л:Г-диаграмма кипения раствора; а—ЫНз в воде; б—КОН в воде
ветствующие закону Генри (19.14). Обычно оба компонента имеют отклонения одного
знака от закона Рауля. С увеличением отклонений от этого закона прямолинейные
отрезки изотерм на диаграмме состояний «давление—состав» сокращаются и может
появиться экстремум. В точках экстремума растворы обладают предельными
отклонениями от закона Рауля.
Для всех реальных растворов сохраняются законы Коновалова. Трех- и
многокомпонентные растворы являются более сложными системами. При изучении таких
систем основное значение имеет эксперимент.
Реальные растворы часто используются в качестве рабочих тел в теплотехнических
установках. Так, например, в абсорбционных холодильных машинах применяются
растворы H2SO4, КОН, NaOH в воде. Так как аммиак лучше других веществ растворяется
в воде (1 объем воды при О °С растворяет 1000 объемов Nbb), он используется наиболее
часто. В генераторе такой машины за счет подведенной извне теплоты испаряется водо-
аммиачный раствор, температура кипения которого на величину ДГ (19.13) ниже
температуры кипения чистого растворителя при том же давлении (рис. 19.4, а). Согласно
(19.22), состав полученного пара отличается от состава раствора и содержит в большем
количестве аммиак, который имеет меньшую температуру кипения при данном давлении
(рис. 19.4, а). Так как, согласно (19.15), давление чистого растворителя больше
давления растворителя в растворе, то при одинаковом внешнем давлении пар из раствора
имеет большую температуру, чем пар, полученный при испарении чистого NFb, т. е. пар
из раствора будет перегретым. Как и любой процесс парообразования, процесс
получения пара из раствора связан с затратой теплоты, т. е. эндотермичен, а процесс
поглощения пара (конденсации) экзотермичен. Для термохимических трансформаторов
теплоты используются водные растворы КОН, кипящие при более высокой температуре, чем
вода (рис. 19.4, б).
Таким образом, указанные свойства растворов создают возможность замены
компрессора генератором и абсорбером, не имеющими подвижных деталей, что
повышает надежность такой машины.
Вопросы1. Что такое идеальный раствор?
2. Какая разница между компонентом и фазой?
3. В чем заключается преобразование Лежандра?
4. Чем отличается химический потенциал от термодинамического?
5. Объясните, что такое осмотическое давление.
Книга природы написана на языке
математики.
Г. Галилей
ТЕЧЕНИЕ
ГАЗОВ И ПАРОВ
Рабочие процессы многих тепловых
машин и установок связаны
с интенсивным движением (потоком)
рабочих тел — носителей энергии.
В связи с этим в термодинамике
рассматриваются закономерности
истечения идеальных и реальных
рабочих тел из сосудов
ограниченных и неограниченных
размеров под воздействием
различных перепадов давлений.
Методики расчета процессов течения,
в том числе и с преодолением
препятствий (дросселированием),
основываются на допущении
неразрывности среды
и предусматривают применение
тепловых диаграмм и таблиц.
246 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Глава 20
ИСТЕЧЕНИЕ ИЗ СОСУДА НЕОГРАНИЧЕННОГО ОБЪЕМА
§ 20.1. Основные уравнения
Течение газов и паров рассматривается в термодинамике как внутренне равновесный
процесс, при котором для любой части потока значения термодинамических
параметров определяются однозначно. Это относится как к установившемуся, так и
неустановившемуся движению. Принятое допущение равнозначно рассмотрению одномерной
модели процесса.
Основным уравнением, определяющим движение газового потока, является
уравнение первого начала термодинамики в форме (2.39). Если учесть в этом уравнении d/xp —
работу трения, то уравнению (2.39) можно придать вид
(20.1)
Полученное соотношение позволяет проанализировать способы воздействия на
поток рабочего тела. С этой целью предварительно рассмотрим уравнение состояния
среды в виде функциональной зависимости p = cp(p,s), дифференцирование которой
приводит к выражению
pds. (20.2)
По аналогии с уравнением (5.17) запишем
(dp/ds)p=-(dp/dp)s(d9/ds)p.
В последнем равенстве
поэтому
(dp/ds)p= -(T/cp) (dp/dT)p(dp/dp)s.
Сопоставление полученного выражения с уравнением (20.2) показывает, что
производная (dp/dp)s дважды входит в это уравнение. Она иллюстрирует связь изменения
давления и плотности в адиабатных условиях при малых значениях изменения
давления и плотности по сравнению с общим уровнем этих величин. Слабые
возмущения в сплошной среде могут возникнуть, например, при перемещении в ней твердого
тела. При этом перед телом создается небольшое избыточное давление,
распространяющееся в среде в виде звуковой волны. Таким образом,
скорость перемещения фронта слабого возмущения есть скорость звука в данной среде.
Истечение из сосуда неограниченного объема 247
Значение скорости звука зависит от термодинамических параметров среды. Связь
между ними можно установить из рассмотрения перемещения газа в трубе
(поперечного сечения f) под действием медленно движущегося поршня со скоростью dw.
Это перемещение вызовет повышение давления в прилегающей к поршню области на
dp и плотности среды на dp. Фронт возмущения перемещается в среде со скоростью а,
в то время как скорость перемещения фронта возмущения относительно поршня
определяется разностью а — dw. Следовательно, масса среды, захваченная фронтом
распространения возмущения, за время dx составит dG = p/adx. Эта же масса, попадая
в область между поршнем и фронтом возмущения, приобретает параметры возмущенной
среды (p + dp; p + dp) и может быть выражена соотношением
(a — dw)dx.
Вследствие свойства неразрывности сплошной среды полученные выражения для dG
равны. В результате, пренебрегая членами второго порядка малости, имеем
adp — pdw.
Для определения входящих в данное выражение скоростей а и dw можно
воспользоваться уравнениями импульсов. Действительно, изменение количества движения
массы dG (скорость меняется от 0 до dw) составит dGdw = dwpfadT, а импульс силы,
действующей на эту массу, fdpdx. Из равенства этих величин следует, что
dp — padw.
Полученное выражение совместно с выражением adp = pdw позволяет получить формулу
для скорости звука:
Вследствие кратковременности процесса распространения возмущений в сплошной
среде процесс изменения параметра может быть принят адиабатным. Учитывая это,
следует записать a2 = (dp/dp)s, тогда уравнение (20.2) приобретает вид
dp = a2 [dp - T{dp/dT)pds/cp]. (20.3)
Расход газа G при движении в канале (площадь поперечного сечения /)
определяется соотношением G = /pw. При постоянстве расхода газа dG = d(pfw) = 0. Если
принять, что величины /, р, w переменны по длине канала, то, дифференцируя выражение
для dG, получим
dp= —p(df/f + dw/w). (20.4)
Дифференциал энтропии в уравнении (19.2) можно представить в виде
суммы:
(20.5)
где dqaH— теплота за счет внешнего теплообмена; dqTp — теплота трения.
Подстановка полученных выражений (20.4), (20.5) в (20.3) и затем полученного
результата в уравнения (20.1) с учетом соотношения v=\/p приводит к равенству вида
LPW +~) +\эт) ^ L^ = pwdw + pgdy + pdlT + pdlTp.
После деления обеих частей равенства на pa2 и введения обозначения M = w/a, где
М — число Маха, последнее уравнение может быть представлено в форме
V ' « f g a' a2 a2 + рсД дт)р + {Рср Д дТ
248 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Уравнение (20.6) называется уравнением обращения воздействий. Левая
часть уравнения определяет основные показатели потока (число Маха, изменение
скорости течения). В его правой части представлены члены, отражающие различные
воздействия на течение среды: изменение поперечного сечения потока, высоты, совершение
технической работы, работы трения, теплообмена с внешней средой.
Уравнение (20.6) показывает, например, что при дозвуковом течении среды (М< 1)
знак суммарного воздействия противоположен знаку изменения скорости. При
сверхзвуковом течении (М;> 1) знак суммарного воздействия совпадает со знаком изменения
скорости. Следовательно, для случая дозвукового движения среды (М<с\) увеличение
скорости потока (dw> 0) может быть обеспечено либо за счет уменьшения площади
поперечного сечения потока (df<cO), либо за счет увеличения высоты (dt/;>0), либо
за счет совершения технической работы (d/T>0). При сверхзвуковом течении (М~> 1)
картина будет обратной: увеличение скорости потока (dw~> 0) может быть обеспечено
при d/>0, dt/<0, d/T<0.
Воздействие на поток подвода теплоты и трения определяется дополнительно
физическими свойствами среды, которые выражаются конкретной формой уравнения
состояния. Если ограничиться рассмотрением сред, для которых выполняется условие
(др/дТ)р<:0, то подвод теплоты (наличие трения) приводит к увеличению скорости
дозвукового потока и к уменьшению скорости сверхзвукового потока.
В большинстве технически важных задач движение среды (газа или пара)
происходит практически без теплообмена с внешней средой, т. е. адиабатно (d^BH = 0). Если
дополнительно пренебречь изменением потенциальной энергии потока (di/ = 0),
допустить отсутствие технической работы (d/T = 0), то с учетом указанных условий
уравнение (2.39) приводится к виду
dh= — wdw, (20.7)
или после интегрирования
/г, — h2 = (w22 — ш?)/2. (20.8)
Таким образом, изменение кинетической энергии потока материальной среды в
адиабатных условиях происходит за счет уменьшения его энтальпии.
Из уравнения (20.8) следует, что скорость в произвольном сечении потока
w2 = Л/2 (Л, - h2) + w\. (20.9)
Здесь w\ — начальная скорость потока. Если до,=0, то
w = ^j2(hl — h2). (20.10)
Следует подчеркнуть, что уравнения (20.9), (20.10) справедливы для движения
как с трением, так и при отсутствии трения, как для идеальных, так и для реальных
газов (паров). В последнем случае изменение энтальпии определяется либо по sh-
диаграмме (см. рис. 11.10), либо по таблицам для данной среды.
Зависимость скорости потока от термодинамических параметров определяется
уравнением (20.1), которое для рассматриваемых условий (и при отсутствии трения)
принимает вид
wdw = — vdp. (20.11)
Следовательно, отрицательный градиент давления (dp<0) соответствует
ускоренному движению среды (dw> 0).
Интегрирование уравнения (20.11) приводит к выражению
Истечение из сосуда неограниченного объема 249
Р2
w\/2 — w2/2 = — $ vdp,
Р\
откуда
(20.12)
Полученная формула справедлива для любого случая течения без трения, поскольку
исходное уравнение (20.1) справедливо для любых процессов. Выражение (2.45)
показывает, что величина С v^p в формуле (20.12) представляет собой располагаемую работу
/о процесса, в связи с чем w2 = V w\ + 2/0 или w = ~\/2l0
при w\=0, что соответствует выражению (2.42). Для реальных газов эта работа
вычисляется по экспериментальным данным численными методами, а для идеальных
газов — по уравнению, связывающему параметры р и v в процессе, например в
адиабатном давление и объем связаны уравнением (9.22):
Сопоставление выражений (20.7) и (20.11) показывает, что d/i = ydp, или в
интегральной форме
hx — h2= $ vdp. (20.13)
Pi
Последнее выражение указывает на возможность определения располагаемой
работы по s/i-диаграмме или с помощью таблиц для рассматриваемой среды.
Если движущаяся среда является несжимаемой жидкостью, для которой cb = 0,
то при адиабатном течении внутренняя энергия потока не изменяется (сШ = 0). При
этих условиях уравнение (20.8) приобретает вид уравнения Бернулли
pl+Pw2l/2 = p2 + 9wl/2y (20.14)
где рш2/2 представляет собой динамический напор (давление); р — статическое
давление; р — плотность несжимаемой среды.
§ 20.2. Параметры торможения
Уравнение (20.8), справедливое при обратимом адиабатном течении среды, можно
представить в виде
/i, + w2i/2 = h2 + w22/2 = const, (20.15)
из которого следует, что уменьшение кинетической энергии потока (т. е. уменьшение
скорости) приводит к равновеликому возрастанию энтальпии.
При полностью заторможенном потоке энтальпия достигает своего максимального
значения, называемого энтальпией адиабатного торможения или полной
энтальпией:
h* = h + w2/2. (20.16)
Если движущаяся среда является идеальным газом, теплоемкость которого не зависит
от температуры, а энтальпия определяется выражением (9.11), то уравнение (20:16)
принимает вид
250 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Г* = Г + ш7(2ср), (20.17)
где Т* — температура адиабатного торможения; Т —
термодинамическая температура (температура движущейся среды).
Для идеального газа формула а= \{dp/dp)s с учетом выражения (9.21) и
соотношения dp— —dv/v2 может быть приведена к виду
a = ifov = ^kljf. (20.18)
Полученное таким образом выражение (20.18) с учетом (7.35) дает возможность
привести формулу (20.17) к виду
T* = 1\\+(k—\)M2/2]t (20.19)
которое наряду .с понятием температуры адиабатного торможения (20.17) позволит
ввести понятия давления и плотности адиабатного торможения.
С учетом соотношений (9.21) и (9.25) давление и плотность адиабатного
торможения определятся соотношениями
/ k — 1 9\ *А*-1)
Р =р(1+-^-М2) ; (20.20)
(*~l); (20.21)
Давление р* называют также полным давлением.
§ 20.3. Адиабатное течение идеального газа в каналах
Каналы, в которых движущийся газ увеличивает скорость с одновременным
уменьшением давления, называются соплами; каналы, в которых скорость газа
уменьшается, а давление возрастает, называются диффузорами.
В стационарном адиабатном процессе движения газа и при воздействии на
скорость только изменения площади сечения канала уравнение обращения (20.6)
принимает вид
(M2-l)i^=^. (20.22)
w f ч '
Используя уравнения (20.4) и (20.11), нетрудно получить соотношения,
связывающие изменение площади сечения канала с термодинамическими параметрами потока
идеального газа:
Уравнение (20.22) определяет соотношения между скоростью потока среды и
площадью поперечного сечения канала:
Ускоренное движение (dw> 0) Замедленное движение (dw<0)
M<l\ df<0 M<1, d/>0
M = l, d/ = 0 M=l, df = O
М> 1, d/>0 M> 1, d/<0
Истечение из сосуда неограниченного объема
251
Рис. 20.1. Изменение параметров потока в суживающихся и расширяющихся
каналах: а — М<1, day> 0; б — М<1, dw<0\ в — M>1, doy<O; г— М> 1,
dw<0
На рис. 20.1 представлен принципиальный характер изменения скорости, давления,
местной скорости звука вдоль сопл и диффузоров для рассмотренных выше случаев.
Изложенное свидетельствует о том, что в суживающемся сопле нельзя достичь
сверхзвуковой скорости газового потока, а суживающийся диффузор не может быть
использован для торможения дозвукового потока. В любом случае (ускоренное или
замедленное движение) непрерывное изменение скорости газового потока с переходом
от дозвукового к сверхзвуковому режиму (или наоборот) возможно лишь при перемене
знака воздействия df. При М = 1 (скорость течения равна местной скорости
распространения звука) канал должен иметь минимальное сечение (d/ = 0), которое называется
критическим.
Возможность создания дозвукового или сверхзвукового течения зависит от
располагаемого перепада давления.
В качестве примера рассмотрим процесс обратимого адиабатного истечения газа
из емкости, в которой параметры газа р\, T\ остаются неизменными. Истечение
происходит через суживающееся сопло в окружающую среду, давление в которой рн может
меняться от значения р\ до нуля.
Очевидно, что при равенстве давлений рн — р\ истечения не происходит, расход
газа равен нулю. При возникновении перепада давлений возникает поток рабочего
тела с определенной скоростью в выходном сечении (устье) сопла. Данная скорость
определит и расход вещества. Давление внутри сопла при этом изменяется от р\ на
входе в сопло до давления рч на выходе из него.
Как показывают результаты измерений, давление в устье сопла рг сохраняется
равным внешнему давлению рн до тех пор, пока скорость истечения не достигнет
значения, равного местной скорости звука (а-b на рис. 20.2). Дальнейшее
уменьшение внешнего давления не сказывается на распределении
давления внутри сопла и в том числе на значении р2 на срезе сопла
(Ь-с на рис. 20.2). Это явление связано с тем, что, как уже
отмечалось ранее, возмущения, происходящее во внешней среде (в
данном случае уменьшение давления), распространяются только со
скоростью звука. Следовательно, при достижении в устье сопла
скорости течения, равной скорости звука, возмущения внешней
среды не могут проникнуть внутрь сопла и таким образом вызвать
изменение режима течения за счет перераспределения давления.
Перепад давлений p2/pi = P, при котором устанавливаются
скорость истечения, равная скорости звука, скорость истечения
Рг
"кр
Рн
Рис. 20.2.
Зависимость давления в
выходном сечении
су ж и ва ющегося
сопла от внешнего
давления
252 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
и сечение сопла, в котором образуется такая скорость, называются критическими и
обозначаются соответственно ркр, wKp и /кр.
Как следует из выражения (20.22), скорость истечения для идеального газа
определяется по уравнению (20.12), которое при адиабатном процессе приобретает вид
w2 = -y[2kplvl/(k- 1)][ 1 -{p2/Pif l)/k] +wl (20.25)
При незначительной начальной скорости (в емкости) ею можно пренебречь и принять
до,=0. При этом условии
w = -\l[2kpxvj{k— 1)] | 1 — (Р2/Р1 )(/e-I)/fe ]. (20.26)
Из выражения (20.26) следует, что уменьшение перепада давления должно всегда
приводить к росту скорости. Однако на практике это не подтверждается и связано с
тем, что, как указывалось ранее, в суживающемся сопле скорость течения газа не
может превышать местную скорость звука. В связи с этим предельное значение
скорости течения в выходном сечении суживающегося сопла должно быть равно
местной скорости звука, определяемой по формуле (20.18). Если принять в формуле
(20.18) температуру Т\ газа в емкости равной температуре торможения, определяемой
формулой (20.19) при М=1, то критическая скорость истечения (скорость в
критическом сечении сопла) определится выражением
(k+ 1), (20.27)
или
;,/(&+1). (20.28)
Путем сопоставления формул (20.26) и (20.28) можно получить
значение критического перепада давления, т. е. перепада, при котором устанав
ливается критическая скорость истечения. Действительно, из равенства (Г_р(к*р~|)/А:)/
/(/г— 1)= 1/(6+ 1) следует, что
р 1). (20.29)
Расход газа через сопло
(20.30)
где fc — площадь сечения устья суживающегося сопла; w и v —
соответственно скорость и удельный объем газа в этом сечении.
Если выразить удельный объем через начальные параметры газа в
емкости, то уравнение (20.30) с учетом (20.26) можно привести к виду
На рис. 20.3 в соответствии с уравнением (20.31) представлена
зависимость расхода газа через суживающееся сопло от перепада давления. Приведенная
зависимость свидетельствует о том, что расход газа увеличивается при изменении
перепада давлений р от единицы до ркр (участок а-b) и затем остается неизменным
(при р<сркр), равным критическому расходу GKp (участок b-с); пунктирный участок,
определяемый формулой (20.31), не имеет физического смысла. Постоянство расхода
Истечение из сосуда неограниченного объема
253
при р<сркр объясняется тем, что в выходном сечении суживающегося сопла
устанавливается критическая скорость.
Значение критического расхода можно получить путем подстановки ркр (20.29) в
формулу (20.31), в результате чего имеем
G
кр
_f -л/ 2k РЧ
'КР V *+l vx\
М
k+\
(20.32)
— при истечении идеального газа через суживающееся сопло из емкости
неограниченных объемов расчет скорости истечения и расхода следует вести по формулам
(20.26) и (20.31) при условии р> рКр и по формулам (20.28) и (20.32) при Р<ркр
Наличие перепада давлений, превосходящего критический (Р<ркр), позволяет
получить и сверхзвуковую скорость истечения, но для этого необходимо использовать
так называемое сопло Лаваля (рис. 20.4). Это сопло представляет собой комбинацию
суживающегося и расширяющегося каналов. При этом в самом узком сечении при
Р^Ркр всегда устанавливается критическая скорость и тогда в расширяющейся части
происходит увеличение скорости в соответствии с выражением (20.22). Для
предотвращения отрыва потока от стенок сопла в сверхзвуковой его части конусность
расширяющегося участка рекомендуется выбирать в пределах от 8 до 12°.
Площадь выходного сечения сопла Лаваля выбирается из условия
достижения в этом сечении давления газа, равного давлению окружающей среды. При
соблюдении этого условия сопло называется расчетным. Скорость в выходном
сечении определится формулой (20.26), а площадь при сохранении постоянства расхода,
равного критическому, равна
Если расчетный режим сопла Лаваля заранее не определен, но задана площадь
выходного сечения, то скорость течения газа в этом выходном сечении доВых
определяется при известном критическом расходе газа GKp. При этом из равенства выражений
(20.31) и (20.32) определяется значение р, а затем по формуле (20.36) скорость в
выходном сечении сопла.
В ряде случаев истечение из сопла Лаваля может оказаться
нерасчетным. Так, например, сопло реактивного двигателя летательного аппарата, будучи
Рис. 20.3. Зависимость расхода газа от
перепада давления
Рис. 20 4 Сопло Лаваля
254
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
расчетным на одной высоте полета, окажется нерасчетным на других высотах. При этом
давление в выходном сечении может быть либо больше давления окружающей среды
(сопло недорасширенное), либо меньше (сопло перерасширенное). В последнем случае
возможно возникновение так называемого скачка уплотнения в сечении, находящемся
внутри сверхзвуковой части сопла Лаваля, при этом скорость на выходе из сопла
оказывается дозвуковой. Подробнее такие явления рассматриваются в курсе газовой
динамики.
§ 20.4. Движение газа при наличии теплообмена
с внешней средой
Выявление влияния подвода теплоты на характер движения среды
представляет определенный практический интерес при рассмотрении многих
процессов, в частности происходящих, например, в камерах сгорания
различных теплоэнергетических машин. При установившемся движении газа в
камере сгорания цилиндрической формы (d/ = 0), отсутствии трения d/Tp = 0 и без
совершения механической работы (d/T = 0), а также при dy = O уравнение (20.6)
получит вид
(2033)
Так как для газов (ф/дГ)р<0, то подвод теплоты к дозвуковому потоку (М<1)
приводит к увеличению скорости. Ускорение газа имеет своим пределом достижение
критической скорости (М=1). Дальнейшее ускорение возможно только при изменении
знака теплового воздействия, т. е. ускорение сверхзвукового потока можно обеспечить
при отводе теплоты. Таким образом,
подвод теплоты к потоку газа позволяет создать так называемое тепловое сопло,
в котором принципиально возможен непрерывный переход от дозвукового движения газа
к сверхзвуковому за счет изменения знака теплового воздействия (подвод заменяется
отводом теплоты при М=1).
На рис. 20.5 представлена принципиальная схема теплового сопла и
распределения термодинамических параметров в нем. Следует при этом отметить что теплота
может подводиться и отводиться не только путем теплообмена с внешней средой (через
стенки камеры), но и за счет теплоты,, например, химических реакций, происходящих в
самом потоке газа.
Изменение термодинамических параметров потока газа
определяется уравнениями, получающимися из (20.6) путем
преобразований, использованных при выводе уравнений
(20.23), (20.24). В результате получим следующие
соотношения:
иГ
с„Т'
(20.34)
\«
Рис. 20.5. Схема теплового
сопла
Из уравнений (20.34) следует, что давление и плотность в
тепловом сопле (имеющем дозвуковой и сверхзвуковой
участки) непрерывно падают, а температура растет в
дозвуковой части, достигает максимального значения
при M=^]cv/Cp, начинает уменьшаться в конце дозвуковой
Истечение из сосуда неограниченного объема 255
части, а затем уменьшение продолжается и в сверхзвуковой части теплового сопла.
Следует при этом подчеркнуть, что максимум температуры торможения (и энтальпии
торможения) достигается в критическом сечении, т. е. при М=\.
Закономерность подвода внешней теплоты может быть принята соответствующей
политропному процессу. В этом случае dQ = cnd7\ где сп — теплоемкость политропного
процесса, и уравнение (20.33) для идеального газа примет вид
Уравнения, аналогичные уравнениям (20.34), можно получить и для политропного
процесса.
§ 20.5. Движение газа при наличии трения
Движение потока газа при наличии трения о стенки канала является частным случаем
движения газового потока с подводом теплоты, так как в процессе трения выделяется
теплота, поглощаемая потоком.
Пусть, например, из всех возможных воздействий на поток имеется лишь работа
трения. Это воздействие равноценно подводу теплоты к рабочему телу, так как d/Tp =
— dqTp. Указанным условиям соответствует течение газа по трубе постоянного сечения,
неизменного уровня (dy = O)> при постоянном массовом расходе (dG = 0) и при
отсутствии взаимодействия с внешней средой (d/T = 0; d^BH = 0).
В случае движения идеального газа уравнения обращения воздействия (20.6) и
(20.34) примут следующий вид:
(М2- \)dw/w= -fcd/Tp/a2; (20.35)
= k[M\k-\)+\\dlT[)/a2; (20.36)
p = fcd/Tp/a2; (20.37)
= kM(k-\)dlTp/a2. (20.38)
Скорость w, давление p и плотность р под влиянием трения изменяются однозначно,
так как наличие трения всегда эквивалентно только подводу теплоты. Направления этих
изменений иллюстрируются следующими неравенствами:
если М<с1, то dw~> 0; dp<<0; dp<<0,
если Mz> 1; то dw<§\ dp~> 0; dp> 0.
Таким образом, особенностью влияния трения на поток газа является
односторонность воздействия, так как для изолированного процесса работа трения d/Tp =
= d<7Tp = 7"ds> 0. В связи с этим для дозвукового течения возможно лишь ускорение
потока, а для сверхзвукового — только замедление. Непрерывный переход через
критическую скорость при этом невозможен.
Так как принято условие d^BH = 0, то изменение параметров потока газа для двух
сечений трубы можно получить из условия постоянства температуры торможения
Tf = T$. Подстановка в это равенство выражения (20.19) приводит к соотношению
(20.39)
показывающему, что в дозвуковом потоке температура газа уменьшится (скорость
увеличится), а в сверхзвуковом — увеличится (скорость уменьшится).
Постоянство температуры торможения означает постоянство критической скорости:
256 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
wKp = \2kRT* I (k + 1) = const. Отношение скорости w движения потока к
критической скорости шкр называется коэффициентом скорости l = w/wK?.
Коэффициент скорости связан с числом Маха соотношением
— 2
Отношение скоростей в двух сечениях канала (трубы) определится выражением
(20.40)
Из условия постоянства плотности потока у = piWi =рг^2 можно получить отношение
плотностей рабочего тела в виде
<20-41»
Так как при у = const отношение M2/M\ = W2P\/{w\p2)> то отношение давлений в
двух выбранных сечениях определится выражением
(2042)
а для параметров торможения — выражением
Важно отметить, что при неизменной температуре торможения (T* = const) отношение
давлений торможения равно отношению плотностей заторможенного потока:
р*2 /р* = р* /р*. (20.44)
С учетом (20.42) отношение (20.43) получит вид
(*+!)/[ 2(*-1)|
Данное соотношение дает возможность рассчитать необратимые потери для движения
потока газа в трубе при наличии трения.
Для оценки длины трубы, в конце которой скорость потока газа достигает скорости
звука, работу трения следует связать с гидравлическим сопротивлением так, что
d/Tp = (gw2/2)(dx/D), (20.46)
где | — коэффициент гидравлического сопротивления, значения которого
определяются экспериментально; D — диаметр трубы. Подстановка (20.46) в (20.35) приводит
последнее к соотношению
(М2- \)dw/w= -ktw2dx/(2a2D). (20.47)
Так как
то уравнение (20.47) можно преобразовать к виду
Истечение из сосуда неограниченного объема 257
U~2- \)dX/X = [k/(k + О) Ш/D. (20.48)
Коэффициент гидравлического сопротивления £ зависит от режима течения газа
(ламинарный, переходный, турбулентный), поэтому точное решение уравнения (20.48)
практически невозможно, в связи с чем для решения используются различные
численные (приближенные) методы.
Если принять коэффициент гидравлического сопротивления постоянным, равным
некоторому среднему значению по каналу, то, интегрируя уравнение (20.48) от х — 0 до х,
получим
*«* - *~2 + Цй А2) = 12*/(* + 1)1 lefX/D. (20.49)
Правая часть уравнения (20.49) представляет собой так называемую приведенную
длину трубы х, тогда уравнение (20.49) можно представить в виде
(Х~2 + \пХ2вх) - (х~2 + \пХ2) = х. (20.50)
Последнее соотношение показывает, что приведенная длина трубы имеет
максимум при А,= 1, т. е.
*тах=Ьв~х2+1пХ2х-1. (20.51)
Длина трубы, которой соответствует значение приведенной длины хтах,
называется критической. На выходе из трубы, имеющей критическую длину,
устанавливается скорость, равная местной скорости звука. Это справедливо как для
дозвукового, так и сверхзвукового потока на входе в такую трубу.
Если известны параметры газа на входе в трубу, то по уравнению расхода можно
определить предельно допустимый расход газа.
В заключение следует подчеркнуть, что на поток сплошной среды можно
воздействовать технической работой. Действительно, если в уравнении (20.6) учесть лишь
воздействие на поток технической работой и пренебречь всеми остальными
воздействиями, то уравнение получит вид
(М2 — 0 dw/w = — d/T /a2 (20.52)
— совершение технической работы d/,> 0 дозвуковым потоком (М< 1) приводит к
ускорению потока. Для сверхзвукового потока результат противоположен.
Отсюда вытекает принципиальная возможность осуществления механического
сопла, представляющего собой теплоизолированную трубу постоянного сечения, в
которой поток, движущийся без трения, совершает работу на ряде турбин в дозвуковой
части. При достижении скорости звука (М = 1) воздействие меняется и поток газа может
продолжить ускорение за счет работы внешнего источника (d/T<0), передаваемой
сверхзвуковому потоку системой лопаточных машин (компрессоров).
§ 20.6. Истечение реальных газов и паров
Для расчета скорости истечения и расхода реальных газов и паров удобно пользоваться
s/i-диаграммами этих веществ (см. рис. 11.10). В этом случае должны быть заданы
начальное давление pi, температура Т\ и перепад давлений p = p2/pi. Точка / (рис.
20.6, а), характеризующая начальное состояние вещества, определяется пересечением
изобары pi = const и изотермы Т\= const. При адиабатном (изоэнтропном) истечении
процесс изображается вертикальной линией 1-2, причем точка 2, характеризующая
конечное состояние рабочего тела, располагается на изобаре /?2 = const.
Для определения скорости истечения по формуле (20.10) необходимо с помощью
s/i-диаграммы определить перепад энтальпий Д/г = Л|— hi. Теоретический расход веще-
9 Зак. 584
258
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
h
Сч
-с:
i
•«5
%
f
1
J-
/У
7
'Iм- ,
Рис. 20.6. Адиабатное истечение пара: а —в дозвуковой области из суживающегося сопла; г —
в дозвуковой области из сопла Лаваля; б — в сверхзвуковой области из суживающегося сопла; д —
в сверхзвуковой области из сопла Лаваля; в — с учетом начальной скорости; г — с учетом трения
ства GT через сопло определяется по формуле (20.30) при известной площади /
проходного сечения сопла. Удельный объем или плотность вещества на срезе сопла, (точка 2)
также определяется по s/i-диаграмме.
В зависимости от перепада давлений р и формы сопла скорость истечения может
быть дозвуковой, звуковой и сверхзвуковой. Если истечение вещества (например,
пара) происходит в дозвуковой области (Р>Ркр) из суживающегося сопла (см.
рис. 20.6, а), то давление пара на срезе сопла равно давлению рч среды, куда происходит
истечение. Скорость истечения при этом определяется по формуле (20.10). Если в этих
условиях вместо суживающегося используется сопло Лаваля (см. рис. 20.4), то
результат не изменится (рис. 20.6, г).
В сверхзвуковой области истечения применение суживающегося сопла обеспечит
на срезе сопла критическое давление, определяемое по значению ркр (рис. 20.6, б).
Для определения области сверхзвукового истечения необходимо
предварительно ~ определить значение коэффициента ркр. При этом для водяного пара
можно принять: рКр = 0,546для перегретого и ркр== 0,577 для сухого насыщенного пара.
Критические скорости истечения и расход определяются соответственно по
формулам
/кр^крРкР; (h — в кДж/кг).
Для определения ркр и /гкр необходимо, подсчитав ркр, найти точку 2' (рис. 20.6, д)
пересечения изобары ркр = const с адиабатой 1-2. Таким образом, в суживающемся
Истечение из сосуда неограниченного объема
259
сопле скорость истечения определяется только перепадом энтальпий (h\—Лкр),
составляющим лишь часть полного располагаемого перепада энтальпий.
Если при выбранном перепаде давлений (сверхзвуковая область) использовать
сопло Лаваля, то скорость истечения определяется по формуле (20.10) с учетом всего
располагаемого перепада энтальпий (рис. 20.6, г). Расход пара ограничивается
наименьшим сечением сопла Лаваля (/mjn==/rKp) и равен критическому, vKp определяется по
s/i-диаграмме, как указывалось выше.
Иногда при определении скорости истечения приходится учитывать начальную
скорость потока w\. В этом случае скорость истечения определяется по формуле
(20.9). Этот случай соответствует рис. 20.6, в.
Трение при истечении пара учитывается с помощью коэффициента потерь сопла
фс в соответствии с выражением wR = ycw. В этом случае потеря кинетической энергии
в сопле из-за трения определится по разности кинетических энергий пара,
соответствующих теоретической и действительной дод скоростям истечения. В соответствии с
выражением (20.10) при w\—0 потеря энтальпии за счет трения составит
\ ? (20.53)
Отложив от точки 2 (рис. 19.6, е) вверх значение ДЛТ, на изобаре p2 = const получим
точку 2', соответствующую состоянию пара на срезе сопла при наличии трения.
Найденное значение энтальпии hT дает возможность определить действительную скорость
истечения по формуле (20.10).
На рис. 20.6, е линия 1-2' условно представляет собой процесс истечения пара при
наличии трения (необратимая адиабата), As—увеличение энтропии, вызванное
необратимым выделением теплоты за счет трения.
§ 20.7. Процессы в эжекторах
Эжекторами называют аппараты, предназначенные для получения газа или пара
повышенного давления путем смешения двух потоков. Сжимаемый газ или пар с
давлением р2 поступает в камеру смещения 4 через патрубок 2 (рис. 20.7). Для увеличения
давления вещества используется энергия высоконапорного потока газа или пара с
давлением pi, подаваемого в камеру смешения через патрубок /. За счет турбулентного
смешения высоко- и низкоскоростных потоков в камере смешения 4 происходит
увеличение скорости сжимаемого газа при одновременном уменьшении скорости
высоконапорного потока. В диффузоре 3 кинетическая энергия движения потока переходит
в энергию давления так, что давление потока получает значение р, причем р\> р> Р2-
Эжектор может использоваться и в качестве эксгаустера для создания пониженного
давления в некотором объеме, например в конденсационных системах паросиловых
установок.
Термодинамический расчет эжектора состоит в
определении расхода массы вещества
высоконапорного потока через патрубок /, необходимого для
получения результирующего потока с расходом
1 кг/с и заданным давлением р в патрубке 3. Такой
расход (1 кг/с) вещества в потоке с давлением р
можно получить из G кг/с высоконапорного газа, /?,
поступающего через патрубок /, и (1 — G) кг/с
низконапорного газа, поступающего через патрубок 2.
Для этих составляющих смешанного потока должны
быть заданы начальные параметры давления pi, рг и
удельные энтальпии /**, А*
Процесс смешения потоков в эжекторе можно
рассматривать как адиабатный, протекающий без Рис. 20.7. Схема эжектора
260
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
потерь. В этом случае скорость w\
высоконапорного потока на срезе
сопла / может быть найдена в
соответствии с выражением (20.26) в
виде разности:
hf -/i, = w,2/2, (20.54)
где /if, hi — удельные энтальпии
соответственно торможения потока
в сопле / и высоконапорного
потока газа на срезе сопла /.
Аналогично определяется
скорость w смешанного потока
(смеси):
h* — h = w2/2, (20.55)
I
-«Г
nc:
1
04
E
' .
! ^
" \
0^
C"
yS
Й
Рис. 20.8. Процесс эжектора на s/i-диаграмме
где А* и h — удельные энтальпии соответственно торможения смеси и смеси.
Удельная энтальпия торможения смеси в сечении эжектора перед диффузором
определяется уравнением
Gf (20.56)
Если пренебречь малой скоростью низконапорного потока через патрубок 2, то в
соответствии с законом сохранения количества движения Gw\ = w. Подстановка этого
соотношения в уравнение (20.54) приводит последнее к виду
f-/i,). (20.57)
Полученное уравнение содержит две подлежащие определению величины: h*
и G. Их определение осуществляется методом последовательных приближений с
помощью s/i-диаграммы (рис. 20.8). Положение точек / и 2 на диаграмме находят по
заданным значениям р\у /if, рг, hi (задано и давление смеси р). Затем следует задаться
произвольным значением G, по уравнению (20.56) определить h* и по уравнению
(20.57)—/i. Тем самым находят положение точки Зп при давлении р2 и энтальпии hn.
От точки Зп по вертикали (адиабатный процесс) следует отложить G2(hf — h\) и таким
образом определить положение точки 4п. Если она окажется выше изобары р = const
(для смеси), то расход G выбран завышенным, если ниже (точка 4п'), то слишком
малым. При правильном выборе G точка 4 должна оказаться на изобаре p = const.
Если бы процесс смешения был обратимым, то положение точки 4 можно
было бы определить как точку пересечения изобары p = const и прямой 1-2 (точка а),
для которой справедливо соотношение (/i* — /if)/(/if —/if) = (sa — s\)/(s\ —s2). В этом
случае^ асход. высоконапорного потока был бы равен отношению GT = (h* — h$)/(hf — /ij) =
= а2/12. Однако из-за неравенства скоростей потоков процесс смешения в эжекторе
необратим, поэтому точка 4 лежит правее точки а и, следовательно, действительное
значение G больше теоретического GT.
Отношение действительного расхода газа к теоретическому r\3=G/GT обычно
называют кпд эжектора.
Вопросы 1. Укажите, при каких воздействиях дозвуковой поток газа будет ускоряться, а при
каких — замедляться.
2. Поясните, какие параметры называются параметрами торможения.
3. Дайте определения и приведите выражения для расчета критического перепада
давления и критической скорости потока газа.
4. При каких условиях целесообразно использовать сопло Лаваля?
5. Как определяется массовый расход при движении газа через сопло Лаваля?
Истечение из сосуда ограниченного объема
261
Глава 21
ИСТЕЧЕНИЕ ИЗ СОСУДА ОГРАНИЧЕННОГО ОБЪЕМА
§ 21.1. Основные уравнения
Истечение газа из сосуда ограниченного объема встречается в технике весьма часто.
К такого рода явлениям относятся, например, процессы, происходящие в цилиндре
ДВС (рис. 21.1) в периоды газообмена (выпуск из цилиндра продуктов сгорания через
выпускные отверстия 2 и наполнение цилиндра свежим зарядом через отверстия /).
При этом происходит истечение через отверстие либо постоянного, либо переменного
по времени сечения. Такого же типа задачи возникают при расчете процессов
истечения из емкостей в системах энергообеспечения летательных и космических аппаратов.
В общем виде задача состоит в определении либо времени, необходимого для
падения давления внутри сосуда от начального до конечного, либо в определении скорости
истечения в любой момент времени, термодинамических параметров в сосуде через
заданный промежуток времени и количества газа, вытекающего из сосуда. При
рассмотрении перетекания газа из одного сосуда в другой возникает необходимость в
определении термодинамических параметров в каждом сосуде в заданные моменты
времени.
Действительный мгновенный расход в момент времени т,- определяется уравнением
где / — площадь проходного сечения отверстия в момент т,-; \i — коэффициент расхода
отверстия; ри щ — соответственно давление и удельный объем внутри сосуда в момент
г/; г|5/ — коэффициент, получаемый из формулы (20.26) при р2 = ру, причем ру —
давление в устье отверстия.
Масса газа, истекающего из сосуда за время dx, составит
Если принять процесс расширения газа в сосуде политропным с показателем я, то
параметры газа в момент т,- можно выразить через начальные р\у v\ (в момент ti) так, что
Тогда
Суммарный расход газа из сосуда за
промежуток времени Дт = т/ —ti можно
определить в виде разности:
= G, - G,=
(21.3)
где G\ и d — массы вещества в сосуде
в моменты времени х\ и xt; V\ —
первоначальный объем сосуда (в момент ti);
Vi — объем сосуда в момент т,.
Дифференцируя выражение (21.3) с
учетом (21.1), получим
ч(л+1)/(2л)
(21.1)
(21.2)
Рис. 21.1. Схемы газообмена двухтактных
двигателей: а — прямоточная с противоположно
движущимися поршнями; б — прямоточная клапан-
но-щелевая; в — петлевая
262
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Сопоставление выражений (21.4) и (21.2) приводит к равенству
откуда
(1 - п)/п
Умножим полученное уравнение на
получим
d (£) = -
Обозначив (p//pi)"(/I~l)/(2n) = X, получим
л(у-(п-1)/2у\= П- 1
т. (21.5)
Проинтегрируем уравнение (21.5) в интервале времени от xi до xt, в течение
которого объем изменяется от V\ до V,-, а величина X — от Х= 1 до X/ = (p//pi)~(fI~l)/(2ll), тогда
dr.
Разделив все члены уравнения на V\ (л |)/2, получим
(тг)
iH^/lf dT- (21-6)
В качестве предела интегрирования
можно выбрать любой момент времени, например
момент, когда давление в сосуде станет
равным наружному давлению рг. Если при этом
истечение происходит со сверхзвуковой
скоростью, то i|?t = t|3 = const. При истечении
с дозвуковой скоростью коэффициент -ф,
является величиной переменной.
При истечении газа из сосуда
ограниченного объема давление в нем уменьшается,
jg 1,0 J=p2/pL а наружное давление рч остается постоянным.
Следовательно, отношение Р2/р/=Р является
Рис. 21.2. Изменение давления внутри переменным и возрастает со временем. На
сосуда \р\ и в устье отверстия |ру| в рис. 21.2 зависимость р2 = ф(Р) представляет
зависимости от р собой прямую, параллельную оси Р; р, = ф(р) —
Истечение из сосуда ограниченного объема 263
равнобокая гипербола (так как ppt = p2 = const), причем при р,=р2 (точка а) р = 1,0. При
сверхзвуковой скорости р = ркр, поэтому р« = р2/РкР (на гиперболе соответствует точке Ь).
Давление ру в устье отверстия при дозвуковом истечении равно давлению р2
окружающей среды, а в сверхзвуковой области при истечении через цилиндрический
или сужающийся насадок становится критическим: ру = ркр, а р/ = ру/ркр. При этом
P = p2/p/==p2pKp/py = const/py, поэтому зависимость ру = ф(Р) также изображается равно-
бокой гиперболой, проходящей через точку с при Р = ркр.
В дозвуковой области (при р> ркр) коэффициент -ф, по мере увеличения р будет
уменьшаться. Для этой области уравнение (21.6) имеет вид
Р.\("~1)/(2Л)/^.\(Л"1)/2 1
т) (V") "Ч
2К, Г/Р.\/^.\ 1
\() (V) (217)
В сверхзвуковой области при г|5, = const
Полученные уравнения дают возможность рассмотреть более детально частные
случаи истечения газа из сосуда ограниченного объема.
§ 21.2. Истечение из сосуда ограниченного постоянного
объема через отверстие постоянного сечения
Сверхзвуковая область. При V/=Ki=const и / = const интегрирование уравнения
(21.8) приводит к формуле
Дт = Т/ _ т, = 2V, [ (р, /р,)'"-1^2"» - lj /(ф/(п - 1) (хл/рТ^) , (21.9)
по которой можно определить время истечения Дт, если задано конечное давление р,,
или, наоборот — pi к концу заданного отрезка времени Дт. Так, например, для опреде-
|гиия момента времени ткр, соответствующего окончанию сверхзвукового режима ис-
кчения, в уравнение (21.8) следует подставить р/==ру==/72/Ркр и тогда
Дткр == 21/, [ (р, ркр /р2)(п-"/(2п> - 1] /(yf(n - 1) m-VpT^i) • (21-10)
В частном случае, если /г=1, формула (21.9) приводит к неопределенности типа
Дт = 0/0, которая раскрывается по правилу Лопиталя:
(21.11)
Дозвуковая область. Если истечение целиком протекает в дозвуковой области, то
при Vt = Vi=const и f = const формула (21.7) приводится к виду
") (21.12)
264
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Так как вид функций р, = ср(т) неизвестен, то аналитическое интегрирование
формулы (21.12) невозможно, в связи с чем целесообразно использовать метод
графического интегрирования. Для этого следует выражение (21.12) продифференцировать
по {pi/pi):
Умножив числитель и знаменатель отношения
на р2, получим
Отсюда
Интегрирование дает
Vl{Pl/P2)
Дт = -
Хт)
2/Pl / л \ Г /л ч(«+1)/(2л)-|
$ '(Ы*(т) ]
Для выполнения графического интегрирования зависимость -ф = ф(Р) рассчитывается по
формуле (19.24) и наносится на график (рис. 21.3) в виде кривой /, а функция
(+1)/(2) определяется прямой 2.
(п+1)/(2л)
Полученные зависимости дают возможность построить кривую 3 ^(рг/Р/У
затем подынтегральную функцию [/ф,(р2/р/)("+|)/(2п)]~|=(р(Р) в виде кривой 4. Площадь
под кривой 4 (кривая 5) в пределах от p2/pi до p2/pi численно равна интегралу в
выражении (21.3). Если ординаты кривой 5 обозначить через z, то формулу (21.13) можно
представить в виде
где Zi — ордината интегральной кривой для значения р = р2/р/ (в момент времени т,);
Z\ — то же, для р = р2/р\ (для момента времени xi).
При истечении, начинающемся в сверхзвуковой и заканчивающемся в дозвуковой
области, общее время процесса должно определяться суммированием Дткр и Дт,
найденных по формулам (21.11) и (21.12), причем в последней формуле надо положить Zi = 0, a
вместо p\Vi подставить произведение p\v\, относящееся к границе между сверх- и
дозвуковой областями. Очевидно, р{ = р2/Ркр,
а удельный объем v\ определяется из урав-
нения политропы р\Vn\ = p\(v\)nу где pi и ui —
параметры в начале истечения, т. е. в
сверхзвуковой области. Следовательно, v\ =
= {P\/P'\)X/nv\ = v\{p\$Kv/p2)x/n и тогда p\v\ =
= pip\$Kv/p2)~nV\/$w После подстановки
Ри v'\, Рч и некоторых преобразований
формула (21.14) получит вид
Рис. 21.3. К графическому определению
интеграла в выражении (21.13)
Ат = Vx (р2 /р, )(1 - п)/(2л)
Таким образом, суммарное время истечения
Истечение из сосуда ограниченного объема
265
("-1)/(2п)
п-\)/{2п)
Если л=1, то суммироваться должны выражения (21.11) и (21.14). При п=\ и
г, = 0 это дает
SAT=[l/,/(f|xVpT^)] [(Цр^р/рОУф + г,]. (21.16)
§ 21.3. Истечение из сосуда ограниченного постоянного
объема через отверстие переменного сечения
Сверхзвуковая область. Для определения времени истечения в этой области
используется уравнение (21.8), в котором принимается У,-=У = const. В этом случае после
деления выражения (21.8) на площадь /0 полного открытия отверстия получаем
fo(n—
Tl
Отношение f/f0 называют относительным открытием, а интеграл в левой части
уравнения — относительным время-сечением.
Для решения поставленной задачи надо знать закон относительного открытия
отверстия по времени. Часто он дается в виде графика. На рис. 21.4 показан один
из возможных графиков, горизонтальный участок 1-2 которого при f/fo=[ означает
время полного открытия отверстия. Заштрихованная площадь представляет собой
относительное время-сечение для интервала времени Дт = т,-— xi. Если построить
интегральную кривую х,- = ф(т) площади под линией ///0, то заштрихованная площадь, а
значит и левая часть последнего уравнения, определится разностью ординат xt — х\
и уравнение примет вид
^_х,^2К1[(р1/р0(л~1)/{2л)-1]/(/о^(/г-1)^Л^). (21.17)
Искомыми в этом уравнении могут быть время Дт, необходимое для снижения давления
внутри сосуда до заданного значения р„ или, наоборот, может быть определено
давление Pi через заданный промежуток времени Дт, отсчитываемый от известного начального
момента ti. Обе эти задачи решаются с помощью формулы (21.17) и графика на
рис. 21.3.
Дозвуковая область. Уравнение (21.7) после подстановки в него условия
K/=Ki=const получит вид
, dx = 2V,[ (р,
- 1] /[ (п -
в котором коэффициент -ф/ = (р(р2/Р1) = £(т). Вид
этой функции в общем случае неизвестен.
Дифференцируя последнее уравнение, получим
fa,- dx = 21/, d (p, /p, )O-l>/(2"V[ (n - 1)
Так как
(21.18)
Рис. 21.4. Процесс относительного
открытия отверстия во времени
266 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
то
./ / / ч(«-1)/(2я)
После деления на f0 и интегрирования получим
f
(л + 0/(2л)
Интеграл в левой части уравнения может быть найден по интегральной кривой
х = ф(т) на рис. 20.3, а в правой части — по интегральной кривой 5 на рис. 20.2. Поэтому
результат можно представить в виде
(1)/(2)(Wpi^i). (21.19)
Формула (21.19) и две указанные интегральные кривые позволяют решать задачу
в обоих ее вариантах.
§ 21.4. Истечение из сосуда ограниченного переменного
объема через отверстие переменного сечения
Эта задача может быть решена при условии, когда известны взаимосвязанные законы
изменения объема сосуда [например, цилиндра 3 (см. рис. 21.1) при перемещении
поршня (поршней) 4] и относительного открытия отверстия по времени, т. е. когда
имеются уравнения ///0=ф|(т) и У/ = ф2(т), в частности в виде соответствующих
графиков.
Сверхзвуковая область. После деления уравнения (21.8) на /0 получим
Так как начальный объем V\ должен быть известен, то члены уравнения можно
разделить на И|"+1)/2. При этом условии
Для определения левой части выражения (21.20) можно прибегнуть к графическому
интегрированию (рис. 21.5). На рисунке кривая /—зависимость относительного
открытия отверстия от времени ///0 = ф(т), линия 4 — величина 1/Ил+|)/2. Путем
перемножения ординат линий / и 4 для отдельных моментов времени на график наносятся
ординаты произведения (f/fo)/V(in+l)/2 (кривая 2), площадь под которой определяет ин-
Истечение из сосуда ограниченного объема
267
теграл в формуле (21.20). В пределах
времени т./ и т\ указанный интеграл на
рис. 21.5 изображается заштрихованной
площадкой. Если на график нанести
дополнительно интегральную кривую 3 площади
под линией 2, то левая часть в формуле
(21.20) определится по разности ординат yt
—ух интегральной кривой. Поэтому
уравнение (21.20) может быть представлено в
виде
h
J
У1
4
I
L-У;
A
r
6У
л
J
с
(п-
Рис. 21.5. Процесс относительного
открытия отверстия и изменения объема
резервуара во времени
(21.21)
Если задано значение Дт=т,— xi, то по рис. 21.5 можно найти разность yi-—y\,
т. е. левую часть уравнения (21.21). Давление р, может быть определено, если
предварительно по отрезку с будет найдено отношение \/V\n~l)/2 = c<<n~^n+2-\ Если же
задано pi и требуется найти время Дт = т, — ti, то задача может быть решена, если
одновременно известен и объем V/. В этом случае определяется правая часть уравнения
(21.21), а по ней и у( — у\у что при известном объеме V\ (соответствующем начальному
моменту ti) позволяет найти К/, а стало быть, и Дт = т/--Т|.
Дозвуковая область. Данная задача усложнена переменностью коэффициента
г)?, по времени. Приближенное решение ее возможно, если процесс истечения разбить
на участки, в пределах которых значение -ф, принимать постоянным. Для каждого
такого участка решение сводится к случаю, разобранному для сверхзвуковой области.
При определении Дт необходимо суммировать время по участкам. Конечное давление
Pi окажется известным после решения задачи для последнего участка.
§ 21.5. Истечение реальных газов и паров
Расчет скорости истечения и расхода реального газа или пара из сосуда ограниченного
объема должен производиться с помощью s/i-диаграммы для данного вещества. Расчет
является приближенным. Его результат тем точнее, чем на более мелкие участки
делится процесс (рис. 21.6, а). В пределах каждого промежутка времени скорость
и расход считаются постоянными и рассчитываются методом, изложенным в
предыдущих параграфах главы.
В качестве примера рассмотрим случай истечения пара из сосуда ограниченного
постоянного объема V через отверстие постоянного сечения /. Известными исходными
данными являются начальные параметры пара в сосуде pit T\, pi, G\ и давление р^
окружающей среды. Если процесс изменения параметров принять адиабатным, то
положения точек 1 и 2У соответствующих начальному и конечному состояниям пара
в сосуде, определяются на s/i-диаграмме (рис. 21.6, а).
В соответствии с рекомендациями, изложенными ранее* определяется значение
критического перепада давлений рКр- В том случае, если задан перепад (рг/pi)<Сркр,
существует два участка протекания процесса: сверхзвуковой и дозвуковой.
Сверхзвуковое истечение будет осуществляться до тех пор, пока давление р, в сосуде не станет
равным критическому ркр. На рис. 20.6, а этому давлению соответствует точка к'. На
участке 1-к' скорость равна критической, определяемой выражением
268
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Рис. 21.6. К расчету истечения пара из сосуда ограниченного
объема: а — адиабатный процесс; б — политропный процесс
где hi — значение энтальпии, соответствующее изменяющемуся давлению pt; /iKp/ —
значение энтальпии, соответствующее давлению рКр|=Р2/Ркр. На участке k'-2 скорость
для любого промежуточного значения pt определяется по уравнению
Для расчета времени протекания процесса и определения расхода весь процесс
1-2 разбивается на участки, границам которых соответствуют определенные значения
р„ Г/, р„ hi. Расчет ведется последовательно от точки /. Первому участку 1-а
соответствуют параметры нижней границы pat Ta, va. Так как объем неизменен, то масса пара
в конце первого участка Ga=Vpa, а масса, истекшая за этот период, AG| = G| — Ga.
Время процесса на первом участке Дт.| =AGi/(/wipcpi), где рср1=(р, +ра)/2 — средняя
плотность пара в сосуде на первом отрезке; скорость определяется положением
отрезка 1-а относительно точки к'.
Для последующих участков процесса расчет повторяется и определяется все
значения Дт*. Затем определяются время процесса ЕДт и суммарный расход.
Описанный метод расчета может быть использован и при решении задачи
истечения пара из сосуда переменной емкости через отверстие переменного сечения. Для
этого случая, как уже отмечалось, должны быть известны законы изменения объема
сосуда и площади отверстия по времени. И в этой задаче весь процесс истечения
1-2 разбивается на отдельные участки. В пределах каждого участка объем сосуда и
площадь отверстия считаются постоянными, равными соответствующим значениям
для начала каждого участка.
Для повышения точности в качестве постоянных значений объема сосуда и площади
отверстия на каждом участке могут быть приняты средние значения, определяемые по
начальным и конечным значениям на каждом участке, при этом приходится
использовать метод последовательных приближений. Так, для первого отрезка (рис. 21.6, а)
объем и площадь отверстия должны быть приняты неизменными и рассчитывается.
время Дт|. Для полученного момента времени находятся значения V, и /,-, а затем и
средние значения, для которых расчет повторяется до тех пор, пока не будет достигнута
требуемая точность.
Графические методы решения задач, приведенные в данной главе, достаточно
наглядны и хорошо иллюстрируют физическую сущность явления. Однако их
практическое использование всегда дает результат приближенный. Точность решения и быстро-
Дросселирование 269
та получения результатов могут быть существенно повышены за счет использования
ЭВМ.
В том случае, когда к газу, заключенному в сосуде, подводится (отводится)
теплота, процесс расширения носит характер политропного. Поэтому на каждом участке
(кроме первого, где скорость истечения считается постоянной) начальные параметры
будут определяться количеством теплоты, подведенным к рассматриваемому участку.
Расчет для этих условий иллюстрируется рис. 21.6, б.
Так же как и при отсутствии подвода теплоты, выделяется участок адиабаты
1-2, на котором скорость истечения и расход газа приняты постоянными. Параметры
газа в сосуде после завершения процессов на первом участке определяются на
диаграмме точкой 2', являющейся пересечением изохоры y2 = const с изоэнтропой, отстоящей
от исходной адиабаты 1-п на расстоянии Asi =*7|/Г|Ср, где 7"1Ср = (7"i + Гг)/2.
Точка 2Г является исходной для дальнейшего расчета (определяется новый теп-
лоперепад kh'— hT — hn,). Откладывая по адиабате отрезок 2'-Зг, рассчитывают
скорость истечения и расход и вновь определяют параметры в сосуде, для чего находят
точку 2" на пересечении изохоры v3, с изоэнтропой, расположенной правее линии
2'-3' на расстоянии As2 = <72/7"2cP, где Т2ср = (Т2, + Тг,)/2.
Описанные операции повторяются и на последующих этапах.
Вопросы 1. Как меняется скорость истечения из емкости ограниченных размеров?
2. Как меняется расход при истечении из емкости ограниченных размеров?
3. Какими расчетными формулами следует пользоваться при расчете скорости и расхода
для случая истечения идеального газа из сосуда ограниченных размеров?
4. Укажите метод расчета для определения времени истечения реального газа из сосуда
ограниченных размеров.
5. Можно ли использовать уравнение политропы py" = const для расчета скорости
истечения реального газа?
Глава 22
ДРОССЕЛИРОВАНИЕ
§ 22.1. Условия возникновения дросселирования
Дросселированием называется процесс понижения давления в движущемся
стационарном потоке газа или пара при прохождении его через препятствие. Препятствия
в проточных каналах встречаются в виде клапанов, диафрагм, вентилей, заслонок,
шиберов и т. п.
Любые препятствия, встречающиеся на пути движения потока, в том числе и не
указанные, приводят к необратимости протекающих в нем процессов, к частичной потере
работоспособности системы и, как следствие, к уменьшению коэффициента полезного
действия двигателей.
Эффект изменения параметров при дросселировании широко используется в
холодильной технике для получения низких температур, в паротехнике для получения
перегретого пара.
Рассмотрим дросселирование газа на примере течения потока по каналу с
диафрагмой (рис. 22.1). Параметры потока до сечения /—/ и после сечения //—// постоянны
по длине канала, течение по каналу происходит без совершения внешней работы, а
приращение скорости за контрольной поверхностью (сечение //—//), равное Ддо =
= 102 —До|, незначительно.
В самой же диафрагме и в непосредственной от нее близости скорость изменяется
заметно, вначале увеличиваясь, а затем уменьшаясь. Поток не производит полезной
работы.
270
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Энергия потока тратится на его проталкивание в пределах контрольной
поверхности, т. е. на преодоление внутренних сил сопротивления в пределах сечений от
/—/ до //—//. Если же дополнительно принять, что процесс дросселирования протекает
без теплообмена с окружающей средой и пренебречь отличием скорости t,y2 в сечении
//—// от скорости W\ в сечении /—/ (т. е. допустить, что Ддо = 0), то, согласно
уравнению (20.7),
d/i = 0, или h\ =/i2 = const (22.1)
— с достаточной степенью точности можно принять, что в результате дросселирования
энтальпия газа не изменяется, хотя вблизи диафрагмы энтальпия не остается
постоянной величиной, в связи с чем процесс дросселирования нельзя отождествлять с
обратимым изоэнтальпийным процессом.
Условие (22.1) справедливо только для сечений, удаленных от сужения, и
применимо как для идеального, так и реального газа.
Изменение энтальпии идеального газа в любых процессах связано с изменением
температуры соотношением dh — cpdTy поэтому процесс дросселирования идеального
газа, для которого ср = const, происходит без изменения температуры (dT — О).
Температура же реальных газов в процессе дросселирования по результатам опытов может
как уменьшаться, так и возрастать. Действительно, при расширении реальных газов
увеличивается расстояние между молекулами, совершается работа по преодолению сил
молекулярного взаимодействия. Кроме того, вследствие разной сжимаемости газов
различна и работа проталкивания, равная произведению pv. Эти работы практически
и предопределяют изменение внутренней энергии и температуры.
В зависимости от начальных параметров и физических свойств реальных газов
при дросселировании значение dT может быть и меньше и больше нуля. Явлению
дросселирования дали научное обоснование Дж. Джоуль и У. Томсон (Кельвин),
вследствие чего явление получило наименование эффекта Джоуля—Томсона.
Как уже отмечалось, процесс дросселирования относится к необратимым
процессам. Для идеального газа дросселирование — предельно необратимый процесс.
Дросселирование реального газа частично обратимо, так как возникающая разность
температур создает возможность совершить работу.
Физическую сущность эффекта Джоуля—Томсона можно выявить проведя анализ
течения газа по каналу малого диаметра (рис. 22.2), соединяющему два участка трубы.
В общем случае скорости потока в левой и правой частях трубы могут быть
различными. Пусть, например, w\~> w^. В сечениях трубы /—/ и //—// с помощью невесомых
поршней можно поддерживать постоянство давлений р\ в левой и р2 в правой частях.
ur;h;Pi
Рис. 22.1. Дросселирование газа или пара
при течении в канале с диафрагмой
Рис. 22.2. Схема установки для
определения физической
сущности эффекта Джоуля—Томсона
Дросселирование 271
При перемещении без трения поршни совершают работу p\V\ в сечении /—/ и p2v2 в
сечении II—II, причем p\v\ — работа внешней среды над рабочим телом, a p2v2 —
работа, затраченная рабочим телом на вытеснение внешней среды. При дросселировании
конечное давление р2 всегда меньше начального давления pi, а удельный объем
V2> v\, поэтому разность указанных работ p\V\ — p2v2 в зависимости от конкретных
свойств рабочего тела может быть положительной, отрицательной или равной нулю.
Трубка малого диаметра (рис. 22.2), через которую перетекает газ из левой части
трубы в правую, представляет собой некоторое сопротивление. На его преодоление
затрачивается работа, равная MKpv) — p\V\ — p2v2, которая целиком преобразуется в
теплоту и, следовательно, изменяет внутреннюю энергию газа. Изменение внутренней
энергии произойдет также за счет уменьшения скорости потока на величину Д(до2/2) =
= w?/2 — wl/2.
Так как в условиях адиабатного дросселирования отсутствует тепловое
воздействие и не совершается внешняя работа, то, согласно уравнению (2.43), с учетом
(2.42)
Дм = Д(/п;) + Д(ш2/2). (22.2)
Внутренняя энергия и есть сумма внутренней кинетической К и внутренней
потенциальной Я энергий, т. е.
(22.3)
Внутренняя кинетическая энергия прямо пропорциональна температуре газа, а
потенциальная — его удельному объему, поэтому последняя в процессе дросселирования
всегда возрастает на величину, зависящую от сжимаемости газа.
Если сумма внешних воздействий, всегда равная изменению внутренней энергии
системы Дм, больше приращения потенциальной энергии (ДЯ), то в соответствии с
уравнением (22.3) избыток внешнего воздействия (энергии) расходуется на увеличение
кинетической энергии Д/С и температура газа в этом случае повышается. Если затрата
внешнего воздействия равна приращению внутренней потенциальной энергии ДЯ, то
внутренняя кинетическая энергия и температура газа при дросселировании остаются
неизменными. Если же Дм<ДЯ (это соответствует случаю, когда совершается
значительная работа на преодоление сил притяжения между молекулами при существенном
увеличении объема v2), то разность между ними компенсируется уменьшением
внутренней кинетической энергии (Д/С). Температура газа за дроссельным устройством
при этом уменьшается. Изменение температуры газа в процессе адиабатного
дросселирования оценивается либо дифференциальным дроссель-эффектом (давление и
температура меняются на бесконечно малые величины), либо интегральным
дроссель-эффектом (давление и температура меняются на конечную величину).
Дифференциальный дроссель-эффект Джоуля—Томсона характеризуется
производной
ah = (dT/dp)h, (22.4)
определяющей изменение температуры газа при бесконечно малом падении давления
в процессе адиабатного дросселирования (h — const). Изменение температуры dT
в общем случае может иметь различные алгебраические знаки, а величина dp всегда
отрицательна. Поэтому дифференциальный дроссель-эффект может быть как
положительным (при с1Г<<0), так и отрицательным (при dr>0). Его величину и знак для
любого вещества (в том числе для реальных газов и паров) можно найти из
дифференциального уравнения (4.35).
В результате с учетом (22.4) имеем
= [T(dv/dT)p-v\/cp. (22.5)
272 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Из уравнения (22.5) следует, что алгебраический знак дроссель-эффекта, а
следовательно, и величины с!Г определится алгебраическим знаком разности T(dv/dT)p — v,
так как теплоемкость ср всегда величина положительная. Если T(dv/dT)p~> v, то
(при dp<O)dr<O. Если же T(dv/dT)p<v, то dT> 0 и, наконец, при T(dv/dT)p =
= v dr = O. Таким образом, в первом случае дроссель-эффект будет
положительным (ах>0), во втором — отрицательным, в третьем — равен нулю.
Состояние системы, в котором дроссель-эффект меняет знак, называется точкой
инверсии. Из уравнения (22.5) следует, что существует множество точек
инверсии, определяемых уравнением
T(dv/dT)p—v = 0. " (22.6)
Геометрическое место точек инверсии представляет собой непрерывную кривую,
называемую к р и в о й инверсии.
Для нахождения уравнения кривой инверсии в явном виде необходимо знать
уравнение состояния для данного вещества. В качестве примера на рис. 22.3
представлена кривая инверсии азота. Из графика следует, что в определенном диапазоне
для фиксированного давления существует два значения температуры инверсии; одна
из них (точка а) относится к газообразному состоянию вещества (перегретый пар),
вторая (точка Ь) — к жидкости.
Кривая инверсии в системе координат Г, р делит поле диаграммы на две области.
Во внутренней области дроссель-эффект положителен (а,-> О, <1Г<<0), во внешней —
отрицателен (а,<<0, dT:>0). Определение температуры инверсии можно
проиллюстрировать с помощью ^Г-диаграммы, построенной для реального вещества (рис. 22.4).
Величины, входящие в уравнение (22.5), определяются следующим образом. Проводя
касательные к изобаре в области перегретого пара, получаем ряд подкасательных:
ВС для точки р\ В\С\ для точки р' и т. д.
Из АСрВ следует, что СВ = СО + ОВ = TtgP, а так как tg$ = (dv/dT)p и OB = v,
то CO — T(dv/dT)p—v. Поскольку температуре инверсии соответствует значение ал = 0,
этому условию отвечает значение Го, соответствующее точке р0, касательная из которой
направлена в начало координат. Этому же условию соответствуют параметры точки
Fo (для жидкой фазы при том же давлении), касательная из которой также направлена
в начало координат. Для других значений давления (pi, P2) значения температур
инверсии определятся параметрами в точках рб, р'о'> найденными из указанных выше
условий.
Как следует из рис. 22.3 кривая инверсии имеет точку максимума, в которой
давление и температура равны соответственно р/тах и Г/тах.
Координаты этой точки могут быть определены, например, из уравнения (22.6),
в котором давление следует рассматривать как функцию температуры.
Дифференцирование этого уравнения по температуре Т дает:
В точке максимума инверсионной кривой dp/dT = 0, следовательно и (d2v/dT2)p = 0.
Если считать, что свойства вещества описываются уравнением Ван-дер-Ваальса,
то в точке максимума кривой инверсии объем равен критическому (^тах^кР), давление
Р;тах = 9ркР, температура Г/тах = ЗГкр.
Правая ветвь инверсионной кривой пересекает ось температур в точке Г = 6,75Гкр,
а левая — в точке Г = 0,75Гкр.
Таким образом, отрицательный дроссельный эффект для газов, подчиняющихся
уравнению Ван-дер-Ваальса, будет иметь место при температурах либо свыше 6,75 Ткр,
либо ниже 0,75 Гкр. Для охлаждения такого газа при дросселировании его температура
должна быть меньше 6,75 Гкр, но не больше 0,75 Гкр, а давление р меньше 9 ркр. Следует
Дросселирование
273
\/
\l
l
I
I
/77
4
\
к
-\
a
\
\\
w
№
300
200
100
r
200 Щ WJ,K
Рис. 22.3. Кривая инверсии
Рис. 22.4. уГ-диаг-
рамма гомогенного
вещества
однако отметить, что экспериментальные данные по определению кривой инверсии,
например для кислорода, азота, лишь приблизительно согласуются с приведенными
теоретическими оценками.
На практике дросселирование происходит при значительном перепаде давлений;
изменение температуры в этих условиях называется интегральным
дроссель-эффектом и вычисляется по соотношению
-Tl = \(dT/dp)hdp=\(l/cp){T(dv/dT)p-V}<ip.
(22.7)
Для вычисления интегрального дроссель-эффекта по уравнению (22.7) требуется
иметь достаточно точное уравнение состояния реального вещества. Более удобным
оказывается определять интегральный адиабатный дроссель-эффект с помощью sh- или
sT-диаграмм. На рис. 22.5 показан пример определения изменения температуры при
дросселировании, для чего использованы линии диаграммы, соответствующие процессу
/г = const. Максимальное значение ДГ=Г2— Т\ будет в том случае, когда начальное
давление при дросселировании равно давлению, соответствующему температуре
инверсии (расширение из точки а в точку Ь). При этом следует иметь в виду, что
положительный дроссель-эффект (охлаждение газа) получается в том случае, если исходная
температура дросселируемого газа ниже верхней температуры инверсии: Г<СГ„.В.
Следует также заметить, что уменьшение начальной температуры газа перед
дросселированием и, как следствие, увеличение интегрального дроссель-эффекта при одном
и том же перепаде давлений (процессы 1-2 и 3-4 на рис. 22.5) не означают увеличения
холодопроизводительности. Для ее увеличения необходимо предварительное охлаж-
274
РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
Рис. 22.5. Процессы дросселирования в
яГ-ди а грамме
1 2 3
5 6 1 8 9 10 11 11
o= v/vK9
Рис. 22.6. Безразмерная
оуу-диаграмма для
расчета интегрального
дроссель-эффекта
Дросселирование
275
дение газа, т. е. создание теплового резервуара с температурой более низкой, чем
температура окружающей среды.
В случае отсутствия тепловых диаграмм для дросселируемого газа по известным
его критическим параметрам можно получить приближенное значение интегрального
дроссель-эффекта по диаграмме, представленной на рис. 22.6, построенной по уравнению
Ван-дер-Ваальса (10.1). При использовании диаграммы следует определить
безразмерные параметры л\ — р\/ркр; Л2 = р2/РкР; vi = ri/rKp, где р\— начальное, а р%—
конечное давления газа, Т\ — начальная температура.
Пересечение изобары л\ и изотермы vi дает точку / на диаграмме. Линия
/i = const, проходящая через точку /, пересекает изобару лг в точке 2, соответствующей
состоянию воздуха после дросселирования. Изотерма V2, соответствующая точке 2, дает
возможность подсчитать температуру Тч и найти интегральный дроссель-эффект:
§ 22.2. Дросселирование водяного пара
Процессы дросселирования водяного пара и реального газа принципиально протекает
одинаково, т. е. при /i = const.
В современной паротехнике дросселирование встречается при движении водяного
пара в паропроводах, имеющих местные сопротивления, например в виде вентиля
(открытого или полузакрытого). Практически при существующих в
теплоэнергетике параметрах водяного пара при его дросселировании возможен только
положительный дроссель-эффект, так как температура инверсии очень велика (Гн.в = 4370 К).
Процесс дросселирования водяного пара удобно исследовать с помощью s/i-диаг-
раммы.
На рис. 22.7 изображен процесс дросселирования Di = D2 = D3 = D4, начинающийся
из области перегретого пара (точка D\). Для выбранных параметров дросселирование
приводит перегретый пар в сухой насыщенный (точка 1)г), затем во влажный (область
D2-D3), далее снова в сухой насыщенный (точка D$) и, наконец, в перегретый
(точка D4).
При оценке работы паросиловых установок существенным является тот факт, что
дросселирование пара снижает его работоспособность. На рис. 22.7 рассмотрен случай
расширения пара в турбине от начального давления р\ (точка /) до конечного рк
(точка 3). Работа в этом процессе l\—h\ — /13; если же пар перед турбиной предвари-
и
У
Г
i -С
У
^г
V
^г
' А1\
Рис. 22.7. К расчету параметров
дросселирования пара по s/i-диаг-
рамме
276 РАЗДЕЛ 5. ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
тельно дросселируется (процесс 1-2) до давления ръ (точка 2), то при расширении
до того же конечного давления рк работа окажется равной /2 = /i2 — h$, т. е. меньше, чем
в первом случае. Потеря работы составит Д/ = /г4 — /*з-
Вопросы 1- Является ли дросселирование обратимым процессом?
2. Что называется дифференциальным дроссель-эффектом?
3. Чему равен дифференциальный дроссель-эффект для идеального газа?
4. Как определяется интегральный дроссель-эффект?
5. Что такое температура инверсии?
6. Что будет происходить с температурой разреженного газа при его дросселировании?
7. Можно ли при дросселировании влажного водяного пара получить перегретый пар?
Жизнь не спросит, что ты учил,
но сурово спросит, что ты знаешь,
К Маркс
ПРОЦЕССЫ
В ТЕПЛОВЫХ
МАШИНАХ
Термодинамический расчет тепловых
машин и установок показывает
пути повышения
эффективности использования
подводимой к ним энергии.
Термодинамическому анализу
доступны процессы
как в широко используемых сегодня
теплоэнергетических машинах
и установках (газовые и паровые
двигатели и турбины, компрессоры,
холодильные машины),
так и в перспективных
энергопреобразующих установках
(магнитогидродинамические, термо-
и термоэлектронные генераторы,
топливные элементы и др.),
еще не нашедших широкого применения
из-за непреодоленных технических
трудностей.
278 РАЗДЕЛ в. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Глава 23
ЦИКЛЫ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
С ГАЗООБРАЗНЫМ РАБОЧИМ ТЕЛОМ
§ 23.1. Обобщенный цикл тепловых двигателей
В реальных тепловых машинах превращение теплоты в работу связано с комплексом
сложных физико-химических, газодинамических и термодинамических процессов,
поэтому изучение циклов достаточно сложно и основано в большей части на результатах
эксперимента. Циклы тепловых двигателей называют действительными.
Стремление выявить основные факторы, влияющие на экономичность работы
теплоэнергетических установок, оценить совершенство процессов, происходящих в них,
принуждает в первом приближении отбрасывать второстепенные факторы. Это
необходимо для того, чтобы по возможности полнее отождествить процессы, происходящие
в теплоэнергетических установках, с обратимыми термодинамическими процессами,
допускающими применение при их изучении термодинамических методов исследования.
Итак, чтобы рассматривать термодинамические циклы, состоящие из обратимых
термодинамических процессов, необходимо работу тепловых машин в определенной
степени идеализировать и принять, что:
процессы в идеальных термодинамических циклах протекают во всех своих
стадиях с постоянным количеством рабочего тела;
сгорание топлива не происходит, в связи с чем химический состав рабочего
тела принимается постоянным на всех стадиях термодинамического цикла; процесс
сгорания при этом заменяется подводом теплоты к рабочему телу от некоторого
фиктивного горячего источника теплоты;
процессы сжатия и расширения рабочего тела принимаются адиабатными;
удаление отработавшего рабочего тела не учитывается и заменяется отводом
теплоты от рабочего тела к так называемому холодному источнику теплоты (холодильнику);
теплоемкости рабочих тел не зависят от температуры;
рабочим телом является идеальный газ.
Термодинамические циклы (см. рис. 2.4, б или 2.6, б) состоят из обратимых
термодинамических процессов, протекающих последовательно так, что в совокупности
составляют замкнутый термодинамический процесс, или цикл. Отдельные процессы цикла
сопрягаются между собой узловыми точками (например, 1, 2, 3 на рис. 2.4, б),
число которых равно числу составляющих цикл термодинамических процессов. Каждый
из этих процессов характеризуется одним уравнением с двумя переменными (напри-
Циклы с газообразным рабочим телом
279
мер, р н v в цикле на рис. 2.4, б или 5 и Т в цикле на рис. 2.6, б). Значит, узловая точка
определяется одним термодинамическим параметром (так как второй можно
определить с помощью соответствующего уравнения процесса). Таким образом, при п
термодинамических процессах число независимых параметров составит п. Если при этом
учесть, что параметры начальной точки цикла обычно заданы (например, равными
соответствующим параметрам окружающей среды), то число независимых параметров
цикла окажется равным п — 2. Эти параметры иногда называются определяющими.
При оценке эффективности различных циклов на определяющие параметры
накладываются различные условия, вытекающие, например, из условий равных
значений термических кпд, равного количества подведенной к рабочему телу теплот,
равной произведенной работы, равных габаритов теплоэнергетической установки, равных
соотношений между отдельными параметрами и т. п. Однако эти условия не могут
быть произвольными. Полезность их оказывается тем выше, чем ближе они
соответствуют действительным техническим возможностям реальных теплоэнергетических
установок (ограничениям по давлению, температуре, мощности, приходящейся на единицу
рабочего объема, и т. п.). Число таких условий не может превысить п — 2.
Анализ термодинамических циклов различных тепловых двигателей показал, что
все они могут рассматриваться как частные случаи некоторого условного цикла,
показанного на vp- и sT-диаграммах (рис. 23.1, а, б). Далее этот цикл называется
обобщенным.
Сжатие 1-2 (рис. 23.1, а) рабочего тела принимается адиабатным. Подвод теплоты
в количестве q\ происходит вначале в изохорном процессе 2-3, а затем в количестве
q" в изобарном процессе. Далее происходит адиабатное расширение 4-5, после чего
теплота отдается холодному источнику вначале в изохорном процессе 5-6 {qi), а затем
в изобарном процессе (qi').
Параметрами, характеризующими обобщенный цикл, являются: e = v\/v2 — степень
сжатия; А, = рз/Р2 — степень повышения давления; pv = va/v2— степень
предварительного расширения; кр^рь/рь — степень падения давления при расширении; ev = ve/v\—
степень предварительного сжатия.
Таким образом, удельное количество теплоты q\, подведенное в обобщенном цикле
от горячего источника теплоты, и удельное количество теплоты q2y отдаваемое в цикле
холодному источнику теплоты, определяются суммами q\ — q\-{-qY и <72 = <72 + <72', Так как
v2 (вмт)
Рис. 23.1. Обобщенный термодинамический цикл теплоэнергетических
машин: а — на ир-диаграмме; б — на яГ-диаграмме
280 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
то
qi=Cv(T,-T2) + cp(T,-T3); (23.1)
q2 = Cv(Tb-Tb) + cn(L,-Ti). (23.2)
Подведенное и отведенное количества теплоты в цикле могут быть подсчитаны
через параметры цикла. Для этого температуры шч*\ точек цикла следует выразить
через температуру одной из точек цикла (например, Т\) и соответствующие параметры
цикла. Так, процесс 1-2 является адиабатным, поэтому Т2/Т\ =(у,/у2)л~' = е*-',
откуда
Т2=Тхгк~\ (23.3)
Процесс 2-3 — изохорный, в связи с чем Тз/Т2 = Рз/Р'2 = Х, откуда Тз=Т2Ху или с
учетом формулы (23.3)
Тз=Т{гк-1к. (23.4)
В изобарном процессе 3-4 Г4/Г3=У4/Уз = рУ, поэтому TA=T^V, или с учетом
формулы (23.4)
Т< = Т&ригк-1. (23.5)
Процесс отвода теплоты 5-6 — изохорный, поэтому Ть/Т& = рь/рь = Хр, откуда
Тъ=ТьХР. (23.6)
Процесс отвода теплоты 6-1 — изобарный, поэтому Te/Ti = Vb/v\ = e,v, откуда
Г6=Г,е,. (23.7)
С учетом выражения (23.7) формула (23.6) получает вид
(23.8)
Соотношения (23.3), (23.5), (23.7) и (23.8) дают возможность записать
выражения (23.1) и (23.2) в следующем виде:
kl[( (23.9)
е„- 1)]. (23.10)
Значения количества теплоты, подведенного и отведенного от рабочего тела в
цикле, позволяют определить термический кпд цикла r\t и работу цикла /ц.
Термический кпд цикла определяется по формуле (2.46), которая с учетом
выражений (23.9) и (23.10) приводится к виду
„-!*-!' '-^-Ц +*('■- О (231П
Удельная работа цикла определяется разностью
U = q\-q*\ (23.12)
с учетом выражений (23.9) и (23.10) после некоторых преобразований формуле
(23.12) можно придать вид
U = cJ\zk -1 [Х- 1 +kX(9v- l)r\t=qir\,. (23.13)
Здесь ц( определяется выражением (23.11).
Формулы (23.11) и (23.13) позволяют определять r\t и /„ для каждого конкретного
цикла.
Циклы с газообразным рабочим телом
281
§ 23.2. Циклы поршневых двигателей
внутреннего сгорания
Двигатели внутреннего сгорания (ДВС) подразделяют на двигатели с принудительным
воспламенением, работающие с подводом теплоты при постоянном объеме, и двигатели,
работающие по смешанному циклу или с подводом теплоты при постоянном давлении.
При движении поршня 5 (рис. 23.2) от верхней мертвой точки (ВМТ) вниз при
открытом впускном клапане 2 совершается такт всасывания / (рис. 23.3). В нижней
мертвой точке (НМТ) впускной
клапан 2 закрывается и поршень 5,
перемещаясь вверх, совершает такт
//, называемый тактом сжатия.
Вблизи ВМТ топливо
воспламеняется и давление вследствие
выделяющейся теплоты резко
поднимается. После завершения сгорания
совершается такт ///, называемый
рабочим тактом (или тактом
расширения). Вблизи НМТ
открывается выпускной клапан, давление
падает и при движении поршня от
НМТ к ВМТ (такт IV)
отработавшие газы выталкиваются из
цилиндра (такт выхлопа).
Эти четыре такта и
составляют действительный цикл ДВС.
Записывается этот цикл
экспериментальным путем с помощью
прибора, называемого индикатором, и
называется индикаторной
диаграммой (рис. 23.3).
В термодинамических циклах
ДВС такты впуска и выпуска (/ и
IV на рис. 23.3) не
рассматриваются. Сжатие газа 1-2 (рис. 23.4, а)
принимается адиабатным, а
процесс подвода теплоты q\=q\ + q\' в
смешанном цикле происходит
вначале по изохоре 2-3, а затем по
изобаре 3-4. Расширение 4-5, как и
сжатие, принимается адиабатным.
Отвод теплоты q% к холодному
источнику теплоты происходит по
изохоре 5-1.
Сравнение обобщенного цикла
(см. рис. 23.1) с рассматриваемым
(рис. 23.4) показывает, что в
смешанном термодинамическом цикле
£„=1. В этом случае параметр Рис. 23.2. Схема поршневого ДВС:
А.р=рв/Р1 МОЖет бЫТЬ преобраЗО- ' -впускной коллектор; 2 - впускной клапан; 3- фореун-
р po/fi P v ка; 4 — цилиндр; 5— поршень; 6 — шатун; 7 — коленчатый
ван. Действительно, вал
282
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
— ZiZi— Л^У — — /Zi i!i\k — —
~~ Pa Р\ ~\vb) Pi \уз yi/ P2 Pi,"
Так как
В связи с этим термический кпд
Ра Рч
К
I* — **-
= K то A,p =
*"1 А,- 1
H(Pt>- 1)'
(23.14)
а работа цикла /ц определяется формулой (23.13), в которой r\t должен подсчитываться
по формуле (23.14).
Одним из важнейших показателей работы ДВС является среднее цикловое
давление ри определяемое в виде отношения работы цикла /ц к удельному рабочему
объему цилиндра двигателя (рис. 23.4, а):
V2). (23.15)
Подставив /ц из формулы (23.13) в выражение (23.15) и проведя преобразования, имеем
*- (*-!)(■-о *» (23Л6)
где r\t определяется формулой (23.14).
В ДВС с принудительным воспламенением рабочей смеси (около ВМТ) от
электрической искры время сгорания очень мало, в связи с чем допустимо принять, что весь
процесс сгорания, (т. е. процесс подвода теплоты) осуществляется при постоянном
объеме. Такой цикл,, называемый циклом с подводом теплоты при постоянном объеме,
показан на рис. 23.5, а, б.
Сравнение циклов, изображенных на рис. 23.4 и 23.5, свидетельствует о том, что
в рассматриваемом цикле ри=1. Поэтому формула (23.14) получает вид
Л|=1-4т (23.17)
Л
— термический кпд цикла с подводом теплоты при постоянном объеме зависит от
свойств рабочего тела (k) и конструкции двигателя (е).
Это иллюстрируется графиком (рис. 23.6), который показывает, что термический
кпд двигателя увеличивается по мере увеличения степени сжатия и показателя
адиабаты. Этим объясняется тот факт, что по мере совершенствования таких двигателей
их степень сжатия постепенно возрастала.
Кпд цикла можно также подсчитать с помощью sT-диаграммы в виде отношения
площади 12351 к площади под процессом
2-3 (см. рис. 23.5, б).
Нагрузка на двигатель в
термодинамическом цикле характеризуется количеством
теплоты, подводимым к рабочему телу от
горячего источника. Для цикла с подводом
теплоты при постоянном объеме q\ =
= сиГ2(Я,—1). Следовательно, нагрузка при
заданных значениях cv и Тч пропорциональна
степени повышения давления А, и не зависит
от степени сжатия. Это свидетельствует о
том, что термический кпд рассматриваемого
цикла при изменении нагрузки не меняется.
Рис. 23.3. Индикаторная диаграмма ДВС: На Рис- 23'5 пунктирными кривыми показа-
/ — всасывание; // — сжатие; /// — расшире- ны процессы расширения рабочего тела при
ние; IV — выхлоп снижении нагрузки.
Циклы с газообразным рабочим телом
283
I)
Рис. 23.4. Смешанный термодинамический цикл ДВС: а — на ур-диаграм-
ме; б — на sT-диаграмме
а)
Рис. 23.5. Термодинамический цикл ДВС с подводом теплоты при
постоянном объеме: а — на ур-диаграмме; б—на sT-диаграмме
В соответствии с формулой (23.16) среднее
давление цикла при рУ=1
Л/,
(г— \)(k— 1)
где r\t определяется формулой (23.17);
с увеличением подводимого количества теплоты
(увеличивается к) среднее давление цикла также
увеличивается.
В цилиндрах ДВС с воспламенением от
сжатия при такте сжатия сжимается чистый воздух.
Вблизи от ВМТ в цилиндр двигателя через
форсунку 3 (см. рис. 23.2) впрыскивается
распыленное топливо, которое в среде горячего воздуха
самовоспламеняется и сгорает. Процесс подвода
0,5
0,4
0,^
0,2
-
t
>
V
<f\>
.—■—'
Рис. 23.6. Зависимость термического
кпд цикла с подводом теплоты при
постоянном объеме от степени
сжатия и показателя адиабаты
284
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.7. Термодинамический цикл ДВС с подводом теплоты при
постоянном давлении: а — на ир-диаграмме; б— на sT-диаграмме
теплоты к рабочему телу принимается в этом случае изобарным. Такой цикл, называемый
циклом с подводом теплоты при постоянном давлении, показан на v p- и sT-диаграммах
(рис. 23.7, а, б).
Сравнение циклов, показанных на рис. 23.4 и 23.7, свидетельствует о том, что в
цикле с подводом теплоты при постоянном давлении А,= 1, поэтому выражение (23.14)
получает вид
Ц( = 1 --^" Wp^-iy (23Л8)
термический кпд рассматриваемого цикла увеличивается при возрастании степени
сжатия е и уменьшается при возрастании степени предварительного расширения pv
(рис. 23.8).
Термический кпд цикла можно также подсчитать с помощью sT-диаграммы в виде
отношения площади 1245 к площади под процессом 2-4 (см. рис. 23.7, б). При
увеличении нагрузки двигателя, т. е. при увеличении подводимого количества теплоты,
увеличивается ру и не изменяется е. Следовательно,
по мере увеличения нагрузки термический кпд такого цикла уменьшается (рис. 23.8).
Это подтверждается и sT-диаграммой (см. рис. 23.7), показывающей, что по мере
увеличения подвода теплоты выигрыш в работе цикла от дополнительных количеств
теплоты постепенно уменьшается.
Среднее давление цикла определяется формулой (23.16), если принять А,= 1.
В этом случае
р< =
где r\t определяется формулой (23.18).
"Л/,
0,40
Ю
12
Рис. 23.8. Зависимость термического кпд цикла с подводом теплоты при постоянном давлении от
степени сжатия е и степени предварительного расширения р (при /е=!,35)
Циклы с газообразным рабочим телом 285
§ 23.3. Цикл двигателя Стирлинга
Двигатель Стирлинга имеет внешний подвод теплоты через теплонроводящую стенку*.
Количество рабочего тела (им может быть воздух), заключенного в рабочем объеме
двигателя, постоянно и несменяемо. В этом заключается одно из преимуществ такого
двигателя перед двигателями внутреннего сгорания, так как в качестве горячего
источника теплоты в этих условиях могут использоваться кроме продуктов сгорания
органических топлив ядерная энергия, солнечная батарея и др.
При подводе теплоты через теплопроводящую поверхность в замкнутый объем
двигателя рабочее тело расширяется (поршень совершает рабочий ход). Затем теплота
отбирается холодным источником теплоты, рабочее тело сжимается и таким образом
возвращается в исходное состояние, завершая рабочий цикл. Однако практическая
невозможность частой смены температуры теплопроводящей стенки при подводе и отводе
теплоты привела к необходимости усложнения конструкции двигателя — создания в нем
постоянных горячей Г и холодной X полостей. В связи с этим рабочее тело во время
цикла должно последовательно перемещаться из горячей полости в холодную и
наоборот.
Такие перемещения рабочего тела в двигателях Стирлинга обеспечиваются
вытеснителем У и поршнем Зу движущимся по определенному закону в одном цилиндре
(рис. 23.9). Двигатель Стирлинга может иметь и два сообщающихся между собой
цилиндра. В этом случае в одном цилиндре перемещается вытеснитель, в другом —
поршень.
Работа двигателя Стирлинга может быть условно разделена па четыре стадии
(рис. 23.10). На I стадии все количество рабочего тела находится в холодной
полости X. На II стадии поршень 3, перемещаясь вверх, сжимает рабочее тело в холодной
полости. Температура рабочего тела при этом сохраняется постоянной за счет отвода
теплоты через стенки цилиндра холодному источнику теплоты (изотермный процесс
сжатия 1-2; рис. 23.11). На III стадии вытеснитель / (рис. 23.10), перемещаясь вниз,
вытесняет рабочее тело (рис. 23.11) из холодной полости X в горячую Г при постоянном
объеме: V2=v-6. Особенностью двигателя Стирлинга является полная регенерация
теплоты изохорных процессов. С этой целью перемещение рабочего тела из холодной
в горячую полость осуществляется через регенератор 2 (см. рис. 23.10). Регенератор,
отдавая теплоту рабочему телу, охлаждается, а рабочее тело нагревается до
температуры Гз (изохорный процесс 2-3 на рис. 23.11). В горячей полости Г двигателя нагретое
до температуры Г3 рабочее тело расширяется, сохраняя свою температуру за счет
подвода теплоты от горячего источника теплоты через поверхность верхней крышки
цилиндра (изотермный процесс 3-4 на рис. 23.11). Затем вытеснитель / (см. рис. 23.10)
перемещается вверх, вытесняя при постоянном объеме v* = V\ рабочее тело (рис. 23.11)
из горячей полости в холодную через регенератор 2 (IV стадия). Регенератор
нагревается, отбирая теплоту от рабочего тела и охлаждая его в изохорном процессе 4-1
до температуры 7V Стенки холодной полости X сохраняют постоянную температуру Т\ за
счет отбора теплоты холодным источником теплоты. В изотермном процессе 1-2,
замыкающем рабочий цикл, сжатие рабочего тела происходит при более низкой
температуре Т\у чем расширение в процессе 3-4, поэтому в цикле совершается полезная
работа (23.12).
Все эти движения вытеснителя и поршня обеспечивают изменение объемов
горячей и холодной полостей в соответствии с графиками 4 и 5 на рис. 23.10. В
действительности ромбический механизм 4 (см. рис. 23.9) плавно перемещает вытеснитель / и
поршень 3 в соответствии с кривыми 6 и 7 на рис. 23.10. Изменение объема горячей
полости опережает по фазе изменение объема холодной полости.
* Двигатель Стирлинга//Сборник статей под редакцией В. М. Бродянского.—М.: Мир, 1975.
286
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
i i
V J- i1 -
S\ \
| ]
N:*>r
i
^. i ^»
j4
i
4^
I
1
Рис. 23.9. Схема двигателя Рис. 23.10. Схема изменения объемов горячей Vr и холодной
Стирлинга: Кх полостей двигателя Стирлинга при повороте коленчатого
/ — вытеснитель; 2 — регенера- вала:
гор; 3 — поршень; 4 — ромби- /_ вытеснитель; 2 — регенератор; 3 — поршень; 4,5 — условное из-
ческий механизм менение объемов; 6,7 — действительное изменение объемов
9
т\
t3
2
3 .
I
II
h
Js,.,
) ^ 1
/^
s
T,
Рис. 23.11. Цикл двигателя Стирлинга в координатах:
а — v, р\ б — s, T
Циклы с газообразным рабочим телом 287
Удельная теплота q\ подводится к рабочему телу при изохорном процессе 2-3
от регенератора в количестве q\ и при изотермном процессе 3-4 от внешнего источника
теплоты в количестве q". В связи с этим q\ = q'\ + qY. Теплота отводится вначале при
изохорном процессе 4-1 в регенератор в количестве qi и затем при изотермном процессе
1-2 в холодной полости двигателя в количестве qi'. Следовательно, q2 = q2-\-q%.
Подстановка полученных выражений в формулу (23.12) показывает, что U = q'\ + qi" — q'2 — q<{'.
Известно, что изменение энтропии в изотермных процессах определяется
соотношениями
Так как v\=vt и У2 = ^з, то As3.4s=Asi.2 = As7'» т. е. изохбрные процессы
эквидистантны в яГ-диаграмме. Следовательно, q\==q'2, т. е.
регенератор двигателя Стирлинга в идеальном случае (без учета потерь) осуществляет
полную передачу т&плоты в изохррных процессах 4-1 и 2-3 от горячего рабочего
тела (q'\) к холодному (q'2).
С учетом сказанного lXi = q\f — q'2={Tz — T\)\sT. Удельная теплота, передаваемая
рабочему телу от внешнего источника теплоты, составляет q\'=Tzksr поэтому
термический кпд цикла Стирлинга
/„ /„ (То — Т,) AsT T,
__ j _L
Термический кпд цикла Стирлинга равен термическому кпд цикла Карно.
В этом второе существенное положительное свойство цикла Стирлинга. Следует
при этом заметить, что аналогичный результат можно получить в любых обратимых
термодинамических процессах 2-3 и 4-1 при условии полной регенерации теплоты, т. е.
при условии эквидистантности этих процессов в sT-диаграмме.
Отмеченные положительные свойства цикла Стирлинга обусловили расширение
в последние годы исследований и конструкторских проработок двигателей, работающих
по циклу Стирлинга.
§ 23.4. Циклы газовых турбин
Газотурбинная установка (ГТУ) (рис. 23.12, а—в) состоит из собственно газовой
турбины, имеющей две основные части: вращающийся диск с радиальными
лопатками 11, называемый ротором, и корпус 2, называемый статором. На общем валу с
ротором располагаются потребитель энергии / и турбокомпрессор 5, сжимающий воздух
и подающий его по трубопроводу 8 в камеру сгорания 9. В эту же камеру по
трубопроводу 6 топливным насосом 5 из бака 4 подается топливо, которое через форсунку
(клапан) 7 впрыскивается в камеру сгорания 9. Газ, образующийся в результате
сгорания топлива в камере 9, подается в сопловый аппарат 10, в котором скорость его
движения увеличивается. После соплового аппарата газ, имеющий высокую
кинетическую энергию, попадает в канал между лопатками ротора, где и совершается работа
вследствие образующегося давления газа на вогнутую поверхность лопаток (рис.
23.12, в). Давление создает силу, вращающую ротор. Отработавшие газы выпускаются
через патрубок 12. Цикл ГТУ состоит из термодинамических процессов, проходящих в
турбокомпрессоре 3, камере сгорания 9 и в самой турбине 11.
Имеются два основных типа ГТУ: с подводом теплоты при постоянном давлении
и с регенерацией.
ГТУ с подводом теплоты при постоянном давлении. В ГТУ этого типа сгорание
рабочей смеси (подвод теплоты к рабочему телу) происходит при постоянном давлении
(p==const) (рис. 23.12).
288
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Ю ft 12
Рис. 23.12. Газотурбинная установка со сгоранием топлива при постоянном давлении: а — схема;
б — общий вид: в — разрез по Л—Л:
1 — потребитель энергии; 2 — статор; 3 — турбокомпрессор; 4 — бак; 5 — топливный насос; 6,8 —
трубопровод; 7 — форсунка; 9 — камера сгорания; /0 — сопловой аппарат; //—лопатки турбины; 12 — патрубок
На рис. 23.13, а, б изображен термодинамический цикл газотурбинной установки,
показанной на рис. 23.12, на vp- и sT-диаграммах. Рабочее тело вначале сжимается
в компрессоре по адиабате 1-2, затем к нему подводится теплота q\ при постоянном
давлении (изобара 3-4), после чего рабочее тело расширяется без теплообмена с внешней
средой (адиабата 4-5) до давления окружающей среды. Изобарный процесс 6-1
является процессом отдачи теплоты холодному источнику теплоты (окружающей среде).
Сравнение циклов, изображенных на рис. 23.1 и 23.13, показывает, что в
рассматриваемом цикле Хр = Х=\, Формула (23.11) в этом случае получает вид
1 Iе--1
1
в*"' Р„- Г
Но параметр ev = vQ/v\ — v5/v\ может быть преобразован. Действительно,
Циклы с газообразным рабочим телом
289
Рис. 23.13. Термодинамический цикл ГТУ с подводом теплоты при
постоянном давлении: а — на ур-диаграмме; б — на яГ-диаграмме
l/k
i/k
Таким, образом, для рассматриваемого цикла термический кпд определяется
формулой (23.17).
При рассмотрении термодинамических циклов газовых турбин часто вместо
степени сжатия е пользуются параметром o) = p2/pi, показывающим увеличение давления
воздуха при сжатии в компрессоре. Так как о> = еЛ, то г|/ = 1 — 1 /со(Ле ')/Ле.
Следовательно, термический кпд цикла ГТУ с изобарным подводом теплоты при равных
значениях е и к совпадает с термическим кпд цикла ДВС с изохорным подводом теплоты.
Формула (23.17) показывает, что
термический кпд рассматриваемого цикла зависит от работы компрессора,
сжимаемого воздуха и природы рабочего тела (показателя адиабаты k). Чем выше показатель
адиабаты к и чем больше сжимается воздух компрессором, чем выше р (или <о), тем
выше г\< (см. рис. 23.6).
Термический кпд цикла можно также определить по sT-диаграмме в виде
отношения площади 1245 к площади под процессом 2-4 (рис. 23.13). При изменении нагрузки
ГТУ, т. е. при изменении подводимого количества теплоты к рабочему телу (например,
при уменьшении), процесс расширения новых циклов показан пунктирными кривыми
на рис. 23.13, а, б. Степень сжатия и показатель адиабаты при этом не изменяются.
Это свидетельствует о том, что
изменение нагрузки на термический кпд цикла не влияет.
В соответствии с формулой (23.13) при Л,р = Л, = 1 и е„ = р0 удельная работа
рассматриваемого цикла может быть подсчитана по формуле
_ Ри_- 1)Ы,, (23.19)
где r\t определяется формулой (23.17).
ГТУ с регенерацией. Газ, прошедший через рабочие органы турбины и отведенный
в окружающую среду, имеет более высокую температуру, чем воздух, поступающий в
камеру сгорания после сжатия в компрессоре. Это дает возможность
усовершенствовать работу установки путем использования теплоты уходящих газов для
предварительного подогрева воздуха перед подачей его в камеру сгорания. Процесс этот
10 Зак. 584
290
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
6 7
Ю //
Рис. 23.14. Схема ГТУ с регенерацией и
изобарным подводом теплоты:
/ — компрессор; 2 — бак; 3 — потребитель; 4 —
насос; 5,7 — трубопровод; 6 — форсунка;
8—камера сгорания; 9 — лопатки турбины; 10 —
теплообменник: // — патрубок
Рис. 23.15. Термодинамический цикл ГТУ с
регенерацией и изобарным подводом теплоты:
а — на ур-диаграмме; б—на sT-диаграмме
5; 6
называется регенерацией. В схеме ГТУ с регенерацией (рис. 23.14) воздух,
сжатый в компрессоре /, подается в теплообменник 10, где подогревается газами,
отработавшими на лопатках турбины 9 и уходящими через патрубок П. Подогретый в
теплообменнике воздух по трубопроводу 7 поступает в камеру сгорания 8. В эту же камеру
через форсунку 6 насосом 4 подается топливо по трубопроводу 5 из топливного бака 2.
Выработанная установкой энергия используется потребителем 3.
Цикл ГТУ с регенерацией и изобарным подводом теплоты (рис. 23.15) состоит
из следующих термодинамических процессов: в компрессоре воздух сжимается адиа-
батно (процесс 1-2), после чего поступает в теплообменник, где подогревается
уходящими газами при постоянном давлении (изобара 2-8). Подогретый воздух подается в
камеру сгорания, где подогрев рабочего тела продолжается при постоянном давлении
за счет теплоты q\, поступающей от горячего источника теплоты, т. е. за счет теплоты,
выделяющейся при сгорании топлива (изобара 8-4). Затем газ расширяется адиабатно в
газовой турбине (процесс 4-5), попадает в теплообменник и отдает теплоту воздуху
при постоянном давлении в изобарном процессе 5-7. Дальнейшее изобарное
охлаждение 7-1 происходит вне установки за счет передачи теплоты окружающей среде
(рис. 23.15, а).
При полной регенерации теплоты T^—Ti и Гб = Г8 (пунктирными линиями на
рис. 23.15 показаны изотермы), поэтому Ть—Т7=Тг — Т2. Удельная теплота,
подведенная при наличии регенерации к рабочему телу в камере сгорания, равна q\ —ср(Т4 — Г8),
отданная холодному источнику теплоты q2 — cp(T7—T\), поэтому термический кпд
цикла с полной регенерацией
Г5). (23.20)
Циклы с газообразным рабочим телом 291^
Так как T2=T\ek~l; Г4= Tip^e*"1; Г5=Г1р„, то формула (23.20) получает вид r\t —
= 1— 1/ру. В рассматриваемом цикле ри=Г5/Г1, поэтому
Следовательно, чем выше температура Тъ и ниже Т\, тем выше термический кпд
цикла с изобарным подводом теплоты и полной регенерацией. Однако действительные
теплообменники имеют конечные размеры. Поэтому теплообмен с полной регенерацией
теплоты осуществляться не может: воздух в теплообменнике нагревается лишь до
температуры rg/ (рис. 23.15, б), а газ в том же теплообменнике охлаждается до температуры
Т1,>Тт. Это свидетельствует о том, что в действительности регенерация не может
быть полной. Ее степень приближения к полной регенерации оценивается степенью
регенерации.
ар = (Г8,-Г2)/(Г8-Г2). (23.21)
При полной регенерации ор—\.
Степень регенерации может быть учтена при выводе формулы термического кпд
цикла с регенерацией. Действительно, при наличии неполной регенерации q\ =cp(Ti — Г8/),
или q{=cp{TA — Т2 + Т2 — Г8,). С учетом формулы (23.21)
qi
Аналогично,
q2
Следовательно,
— при понижении температуры (в конце адиабатного сжатия) эффективность
применения регенерации увеличивается.
Об этом свидетельствует и сам цикл, изображенный на sT-диаграмме (рис. 23.15, б).
Действительно, чем ниже Г2, тем больше участок изобары 2-8, на котором может
осуществляться процесс регенерации.
Термический кпд ГТУ можно также повысить введя ступенчатый подогрев рабочего
тела и ступенчатое сжатие воздуха в компрессоре с охлаждением его между ступенями.
Схема такой ГТУ, также имеющей регенерацию, показана на рис. 23.16. Как видно из
схемы, установка имеет один промежуточный подогрев рабочего тела и одно
промежуточное охлаждение сжимаемого воздуха.
Термодинамический цикл установки показан на рис. 23.17, а, б. Воздух,
всасываемый из атмосферы, сжимается адиабатно (/-/') в первой ступени компрессора 8 (см.
рис. 23.16). Затем он подается в теплообменник-холодильник 9, где охлаждается при
постоянном давлении (/'-/") до первоначальной температуры. После теплообменника 9
сжатие воздуха продолжается по адиабате 1"-2 во второй ступени компрессора 7.
Сжатый таким образом воздух по воздухопроводу 6 поступает в
теплообменник-регенератор 5, где подогревается по изобаре 2-8. Подогретый в регенераторе воздух через
воздухопровод 4 попадает в камеру сгорания 3, в которой подогревается дополнительно
за счет подвода теплоты q\ (по изобаре 8-4) от горячего источника теплоты (за счет
сгорания топлива, поданного насосом 14 по трубопроводу 2). Рабочее тело с
параметрами точки 4 (рис. 23.17) подается в первую ступень газовой турбины 13, где
происходит адиабатный процесс расширения 4-4'. Отработавшее в первой ступени рабочее
тело вновь подается в камеру сгорания 12 и по изобаре 4'-4" подогревается до
температуры в точке 4 за счет подвода теплоты q". Подогретое таким образом рабочее
тело поступает во вторую ступень газовой турбины //, где расширяется по адиабате
4"-5. Отработавшее в турбине рабочее тело по выхлопному трубопроводу 10 поступает
10*
292
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.16. Схема ГТУ со ступенчатым подогревом, ступенчатым
сжатием в компрессоре и регенерацией (подвод теплоты при
постоянном давлении):
/ — потребитель; 2,10 — трубопровод; 3 — камера сгорания; 4,6 —
воздухопровод; 5 — теплообменник-регенератор; 7,8 — компрессор; 9 —
теплообменник-холодильник; 11.13—газовая турбина; А2 — камера
сгорания; 14 — насос
в теплообменник-регенератор 5, там оно отдает теплоту проходящему по змеевику
воздуху по изобарному процессу 5-7. После этого рабочее тело выпускается в атмосферу
и охлаждается по изобаре 7-1, отдавая теплоту в количестве цъ Выработанная
установкой энергия используется потребителем /.
Чем больше промежуточных ступеней подогрева и охлаждения, тем выше
термический кпд цикла. Действительно, если представить, что в цикле (рис. 23.18) в процессе
2-3 теплота подводится к рабочему телу только за счет охлаждения рабочего тела в
процессе 4-1, то в силу эквидистантности процессов эти количества теплоты не
должны учитываться при определении термического кпд цикла. Если приближенно
оценить теплоту, подведенную к рабочему телу в совокупном процессе 3-4, в виде
произведения ^| = ГзА534 и теплоту, отданную холодному источнику в процессе 1-2, в
виде произведения ^2=7"iAsi2, то Ti/ = 1 — Цч/ц\ = 1 — Г|Д5|2/(7"зА5з4). Так как
процессы 2-3 и 4-1 эквидистантны, то Asi2 = As34, поэтому т|/^= 1 — 7"i/7"3, т. е. термический
5)
%(г
2 6%J(
F\\
!\\ \ V
\\ \\
V \ А
\ \ ч)
\ \
<yh
In"
fb
w
\
4 \
i>
\\
\
n'l
Kfli
7
U"
Л
N.
Yz
i *
V
V
X/ ' 1
V
s5 s
Рис. 23.17. Термодинамический цикл ГТУ с регенерацией,
промежуточным охлаждением сжимаемого воздуха и промежуточным
подогревом рабочего тела (подвод теплоты при постоянном
давлении): а — на ур-диаграмме; б — на sT-диаграмме
Циклы с газообразным рабочим телом
293
кпд такого цикла оказывается равным кпд
цикла Карно. Однако сказанное справедливо лишь
применительно к циклу с большим количеством
промежуточных ступеней подогрева и
охлаждения.
Надо иметь в виду при этом, что по мере
увеличения числа промежуточных ступеней
интенсивность увеличения термического кпд
цикла постепенно понижается при
одновременном увеличении стоимости такой установки.
В связи с этим количество промежуточных
ступеней подобных ГТУ выбирается на основе
экономического анализа, учитывающего как
термодинамические, так и конструктивные и
экономические факторы
Схема ГТУ, имеющей цикл с изохорным
подводом теплоты, показана на рис. 23.19.
Рабочая смесь (топливо с воздухом) воспламеняется с помощью электрической
свечи зажигания 14, а газ из камеры сгорания периодически выпускается клапаном 13.
На рис. 23.20 а, б дан сам цикл на vp- и sT-диаграммах.
Сравнение циклов, изображенных на рис. 23.1 и 23.20, показывает, что в
рассматриваемом цикле Хр= 1 и ри=1. Так как б этом случае, кроме того,
— J!l _ i!i i!i — (!-±\/k — — (— fi\l/* — — x]/k
tV~ V\~ VA V\ \P5/ V\ ~\P2 Pb) V\ ""
Рис. 23.18. Термодинамический цикл
ГТУ с большим количеством
промежуточных ступеней подогрева и
охлаждения рабочего тела и подводом теплоты
при постоянном давлении
то формула (23.11) получает вид
<n'== ~~^IT х-1 ;
с увеличением степени повышения давления к и степени сжатия
цикла ГТУ с изохорным подводом теплоты увеличивается.
Зависимость r\t = f(k, e) при
fc = const(fc= 1,4) показана на
рис. 23.21.
Термический кпд цикла
можно определить, если
воспользоваться изображением
цикла на sT-диаграмме в виде
отношения площади 12351 к
площади под процессом 2-3
(рис. 23.20, б).
Формула (23.13) дает
возможность определить работу
рассматриваемого цикла. При
\р= 1; ро= 1 и еу =
(23-22)
термический кпд
к- 1
к — 1
■Л/. (23.23)
где x\i определяется выражением
(23.22).
Рис. 23.19. Схема ГТУ со сгоранием топлива при постоянном
объеме:
/ — потребитель; 2 — статор; 3 — турбокомпрессор; 4 — бак;
5 — топливный насос; 6 — трубопровод; 7,8 — форсунки; 9 —
камера сгорания; 10 — сопловой аппарат; // — лопатки турбины;
12— патрубок; 13 — клапан; 14 — свеча зажигания
294
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.20. Термодинамический цикл ГТУ и пульсирующего
воздушно-реактивного двигателя с изохорным подводом теплоты:
а — на ур-диаграмме; б — на sT-диаграмме
Зная параметры цикла, показатель адиабаты, а также давление и удельный объем
рабочего тела в конце процесса сжатия, можно подсчитать термический кпд и работу
цикла.
В ГТУ, имеющих цикл с изохорным подводом теплоты, также используется
регенерация (рис. 23.22). Процесс регенерации 2-8 в этом цикле, так же как и в цикле с
изобарным подводом теплоты, осуществляется по изобарному процессу, что связано со
стремлением не усложнять конструкцию теплообменника-регенератора. В связи с этим
воздух, сжатый адиабатно в компрессоре (1-2), а затем подогреваемый при р = const
(2-8) в теплообменнике-регенераторе, с параметрами точки 8 поступает в камеру
сгорания. За счет сгорания топлива к рабочему телу в изохорном процессе 8-4 подводится
теплота q\, после чего в газовой турбине происходит адиабатное расширение (4-5)
до давления окружающей среды р$. Перед выбросом в окружающую среду
отработавший газ проходит теплообменник-регенератор, где, отдавая теплоту сжатому воздуху,
охлаждается при р — const (5-7). Дальнейшее охлаждение (7-1) отработавших газов
происходит в окружающей среде.
Термический кпд цикла с изохорным подводом теплоты и полной регенерацией
можно определить по формуле
и е
ать через параметры цикла, необходимо
е ввести параметр ут=Тг/Т2У который можно
регенерацией. При полной регенерации Y^^
Так как
то
Для того чтобы эту формулу записать через параметры цикла, необходимо
кроме уже известных параметров к
назвать степенью подогрева
= Ть/Т2.
М
V
¥
0,5
0,2
2 *t 6 в 10Ъ В действительности процесса полной реге-
Рис. 23.21. Зависимость термическо- нерации получить не удается, поэтому практи-
в°одГ ГГт™ СсТИе3пеХи°„РНпЫовГ: ческ" осуществляемые циклы с подводом теплоты
ния давления и степени сжатия е ПРИ v =const и регенерацией имеют термические
при fc=l,4 = const кпд, меньшие подсчитанных по формуле (23.24).
'- 1
Циклы с газообразным рабочим телом
295
5c 5
Рис. 23.22. Термодинамический цикл ГТУ с изохорным подводом теплоты
и регенерацией: а—на ир-диаграмме; б — на sT-диаграмме
§ 23.5. Циклы реактивных двигателей
Реактивные двигатели подразделяются на две группы. К первой группе относятся
двигатели, в которых в качестве окислителя используется кислород атмосферного
воздуха. Поэтому такие двигатели, называемые воздушно-реактивными,
используются в авиации. Воздушно-реактивные двигатели, в свою очередь,
подразделяются на компрессорные (турбореактивные) и бескомпрессорные
(прямоточные и пульсирующие).
Ко второй группе относятся все реактивные двигатели, для работы которых
необходим окислитель, находящийся на борту летательного аппарата. Такие двигатели,
не связанные в работе с атмосферой, устанавливаются в основном на ракетах и поэтому
получили название ракетных. Ракетные двигатели подразделяются на
жидкостные и твердотопливные.
Основным показателем работы реактивных двигателей является тяга — усилие,
используемое для перемещения летательного аппарата. Тяга является силой реакции
струи газообразных продуктов сгорания, получающих ускорение в сопловом аппарате
двигателя и вытекающих в окружающую среду.
В корпусе 6 турбореактивного двигателя (рис. 23.23) в подшипниках укреплен
ротор, передняя часть которого является турбокомпрессором 5. На другом
конце ротора укреплено рабочее колесо 2 газовой турбины, предназначенной для вращения
компрессора. Воздух, поступающий в двигатель через диффузор 7, сжимается
компрессором 5 и подается в камеры сгорания 3. В эти же камеры по трубкам 4 поступает
топливо, при сгорании которого образуются газообразные продукты, являющиеся
рабочим телом.
Основная работа совершается газом в сопле /. Термодинамические процессы,
составляющие цикл турбореактивного двигателя, осуществляются в нескольких
элементах двигателя.
В двигателях с дозвуковыми скоростями полета первоначальное адиабатное
сжатие воздуха (процесс /-/' на рис. 23.24) происходит в диффузоре 7 (см. рис. 23.23)
вследствие набегающего потока воздуха. Затем адиабатное сжатие продолжается в
компрессоре (1'-2). Сжатый до давления рг воздух подается в камеры сгорания, где
при постоянном давлении к нему подводится теплота q\. Из камер сгорания газ —
рабочее тело — попадает на лопатки газовой турбины, где частично расширяется
(4-4') без теплообмена с внешней средой. При этом турбина совершает
положительную работу (пл. 344'4" на рис. 23.24, а), расходуемую компрессором на сжатие свежего
296
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.23. Схемы турбореактивных двигателей: а — с центробежным
компрессором; б — с осевым компрессором:
/ — сопло; 2—колеса газовой турбины; 3 — камера сгорания; 4 — трубка; 5 —
турбокомпрессор; 6 — корпус; 7—диффузор
а)
Рис. 23.24. Термодинамический цикл турбореактивного двигателя: а
на и/7-диаграмме; б — на sT-диаграмме
Циклы с газообразным рабочим телом 297
воздуха (пл. 1"1'23). Дальнейшее расширение газов (4'-5) происходит в реактивном
сопле адиабатно до давления окружающей среды (точка 5). Покинувшие двигатель
горячие выхлопные газы затем охлаждаются при давлении окружающей среды,
отдавая ей теплоту q<i (процесс 5-/).
Сравнение термодинамических циклов, показанных на рис. 23.13 и 23.24, а, б,
свидетельствует об их полном совпадении, поэтому термический кпд цикла
турбореактивного двигателя определяется формулой (23.17), а удельная работа цикла — формулой
(23.19).
По мере увеличения скорости полета летательного аппарата предварительное
поджатие воздуха увеличивается настолько, что при определенной скорости полета
необходимость в компрессоре, а следовательно, и в турбине отпадает.
Как уже отмечалось, подобные двигатели, относящиеся к числу бескомпрессорных
воздушно-реактивных двигателей, подразделяются на прямоточные и пульсирующие.
Схема прямоточного двигателя показана на рис. 23.25. При большой скорости
поступательного движения двигателя воздух, попадая в диффузор /, тормозится обтекателем 2\
динамический напор превращается в статическое давление (кривая 10). Сжатый таким
образом воздух проходит через турбулизирующие решетки 3, 4 и ъ камере сгорания 6
вместе с топливом, поданным форсунками 5, образует горючую смесь. Газы,
образующиеся в результате сгорания этой смеси, через стабилизатор 7 попадают в сопло 8.
При движении в сопле газы расширяются и получают большую скорость истечения
(график изменения скорости воздуха в зависимости от площади / сечения двигателя
показан кривой 9). Тяга двигателя, как и в предыдущем случае, создается в виде
прямой реакции вытекающей струи.
Двигатель (рис. 23.25) предназначен для полета с дозвуковыми скоростями.
При работе на скоростях, больших скорости звука, необходимо специально
приспособить форму диффузора и сопла для получения потоков рабочего тела со
сверхзвуковыми скоростями.
При сверхзвуковых скоростях полета воздух попадает во входной канал двигателя
со сверхкритической скоростью. Для снижения скорости движения воздуха до
критической сечение воздушного канала и передней части делают суживающимся и лишь
затем расширяющимся (рис. 23.26). Такая форма канала дает возможность плавно
снижать скорость воздуха и повышать его давление до уровня, необходимого для
сжигания определенных доз топлива в камере сгорания (см. кривые 3 и 4).
Таким образом, в прямоточных воздушно-реактивных двигателях сжатие воздуха
происходит либо полностью в диффузоре / (в двигателях с дозвуковой скоростью входа
воздуха, см. рис. 23.25), либо последовательно во входном конфузоре и диффузоре
(в двигателях со сверхзвуковой скоростью воздуха, рис. 23.26).
В идеальном цикле это сжатие (процесс 1-2, см. рис. 23.24, а, б) принимается
адиабатным. Подвод теплоты q\ происходит в камере сгорания при постоянном
давлении (процесс 2-4), после чего в реактивном сопле осуществляется адиабатное
расширение (4-5) до давления окружающей среды. Изобара 5-1 является процессом
отдачи теплоты от рабочего тела окружающей среде. Следовательно,
цикл прямоточного воздушно-реактивного двигателя по форме совпадает с циклом
турбореактивного двигателя. Поэтому термический кпд и работа цикла определяются
по формулам (23.17) и (23.19).
Изменение нагрузки (изменение q\) не влияет на значение термического кпд, но
соответственно изменяет работу цикла.
В бескомпрессорном пульсирующем воздушно-реактивном двигателе (рис. 23.27)
камера сгорания 6 отделена от диффузора / с обтекателем 2 решеткой 3 с клапанами
(на схеме справа пунктиром показаны клапаны в открытом состоянии,
обеспечивающем поступление воздуха в камеру сгорания из диффузора). Воздух, сжатый в
диффузоре, открывает клапаны в решетке 3 и заполняет камеру сгорания 6. В этот же
298
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.25. Схема прямоточного воздушно-реактивного двигателя для
дозвуковых скоростей полета:
/ — диффузор; 2 — обтекатель; 3,4 — турбулизирующие решетки; 5 —
форсунки; 6 — камера сгорания; 7 — стабилизатор; 8 — сопло; 9 — график
изменения скорости; 10— график изменения давления
Рис. 23.26. Схема прямоточного воздушно-реактивного двигателя для
сверхзвуковых скоростей полета:
/ — диффузор; 2 — сопло; 3 — график изменения скорости; 4 — график изменения
давления
/ 2 3
Рис. 23.27. Схема пульсирующего воздушно-реактивного двигателя:
/—клапаны открыты; // — клапаны закрыты:
/ — диффузор; 2 — обтекатель; 3 — решетка; 4 — форсунки; 5 — свеча зажигания;
6 — камера сгорания; 7 — конфузор; 8 — выхлопная труба
Циклы с газообразным рабочим телом 299
объем впрыскивается форсунками 4 топливо, которое, смешиваясь с воздухом, создает
рабочую смесь. Зажигание рабочей смеси осуществляется электрической свечой
зажигания 5. При воспламенении рабочей смеси давление в камере сгорания поднимается и
клапаны решетки 3> закрывая проход, изолируют объем камеры сгорания от диффузора.
Конфузор 7 и выхлопная труба 8 подобраны таким образом, что при сгорании в
камере сгорания рабочей смеси объемы их заполнены газами, образовавшимися при
сгорании предыдущей порции топлива. Таким образом, сгорание рабочей смеси
осуществляется в изолированном объеме. Расширение газов (продуктов сгорания)
происходит при движении в конфузоре и выхлопной трубе. Это приводит к увеличению
скорости истечения и образованию тяги двигателя. Газ, движущийся в выхлопной
трубе, обладает определенной инерцией, которая способствует образованию в камере
сгорания в конце процесса расширения некоторого разрежения, обеспечивающего
открытие клапанов решетки 3 и заполнение объема камеры сгорания свежим
воздухом. Следовательно, пульсирующие воздушно-реактивные двигатели работают
циклично, чем отличаются от остальных типов реактивных двигателей. Частота циклов
достигает нескольких тысяч в минуту.
В идеальном цикле (см. рис. 23.20, а, б), пульсирующего воздушно-реактивного
двигателя процесс подвода теплоты принимается изохорным (2-4). Затем газ
расширяется в конфузоре и выхлопной трубе адиабатно до давления окружающей среды
(4-5), после чего происходит изобарный процесс охлаждения — отдача теплоты от
рабочего тела окружающей среды (5-1).
Термический кпд цикла пульсирующего воздушно-реактивного двигателя
определяется по формуле (23.22), а удельная работа цикла — по формуле (23.23), поэтому
увеличение нагрузки двигателя (увеличение q\) приводит к увеличению как
термического кпд, так и работы цикла.
В жидкостном ракетном двигателе (рис. 23.28) основной частью является камера
сгорания // с соплом 10 и охлаждающей рубашкой 9. В камеру сгорания специальными
насосами 5 и 15 турбонасосного агрегата подаются жидкое горючее из бака 2 по
трубопроводам 16 и 14 через форсунку 12 и жидкий окислитель из бака / по трубопроводам 3
и 6 через форсунки 13. Эти два вещества являются двумя компонентами жидкого
ракетного топлива. Бак 8 предназначен для рабочего тела турбины, которое, проходя через
реактор 7, приводит турбину 4 в движение.
Объем жидкого топлива пренебрежимо мал по сравнению с объемом продуктов
сгорания. Кроме того, топливо, являясь жидкостью, практически не сжимается в
интервале давлений от р\ до рч. С учетом отмеченных обстоятельств при описании
идеального термодинамического цикла жидкостного ракетного двигателя объемом
подаваемого в камеру сгорания топлива, так же как и работой сжатия (при нулевом объеме),
пренебрегают. В связи с этим процесс 1-2 сжатия и подачи жидкого топлива в камеру
сгорания в идеальном цикле условно можно считать изохорным, совпадающим с осью
ординат (1-2 на рис. 23.29, а).
В камере сгорания топливо сгорает при постоянном давлении (2-3) и рабочее
тело получает теплоту q\. Образовавшиеся газообразные продукты сгорания затем
при движении по соплу расширяются по адиабате 3-4 (рис. 23.29, а, б).
При работе ракетного двигателя на так называемом расчетном режиме давление
газов на срезе сопла оказывается равным (в точке 4) давлению окружающей среды.
Поэтому отдача теплоты окружающей среде (холодному источнику теплоты)
происходит при давлении p4 = const.
Для определения термического кпд цикла следует определить подведенную
удельную теплоту q\ рабочего тела и удельную работу цикла /ц. Полезная внешняя
удельная работа цикла /ц = /1з — h\. Удельная теплота, подводимая к рабочему телу, q\ —
— кз — hi. Подстановка /ц и q\ в формулу (2.46) приводит последнюю к виду r\t = (fi3 —
— h\)/(hz — /12). Процесс адиабатного расширения 3-4 цикла на рис. 23.29, а является
300
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
ТТЛ t t t
Рис. 23.28. Жидкостный ракетный двигатель: а — схема; б — внешний
вид:
/ — бак окислителя; 2 — бак горючего; 3, 6, 14, 16 — трубопроводы; 4 —
турбина; 5, 15 — насосы; 7 — реактор, 8 — бак; 9 — охлаждающая рубашка; 10 —
сопло; // — камера сгорания; 12, 13 — форсунки
1ГА V
3 /
«V
У
.v
Рис. 23.29. Термодинамический цикл жидкостного ракетного
двигателя: а — на ир-диаграмме; б — на яТ-диаграмме
Циклы с газообразным рабочим телом 301
одновременно и процессом адиабатного истечения рабочего тела из камеры сгорания //
(см. рис. 23.28) в окружающую среду через сопло 10. Следовательно, площадь цикла на
рис. 23.29, а определяет не только удельную работу цикла /ц, но и располагаемую
удельную работу /о, т. е. в рассматриваемом случае /ц=/о. В соответствии с полученным
равенством и формулой (2.39) /ц=ш2/2 (где w — скорость истечения рабочего тела из
сопла). Полученное выражение дает возможность выражение (2.46) представить в виде
7
В ракетных двигателях твердого топлива шашки с топливом находятся
непосредственно в камере сгорания. Горючее и окислитель, содержащиеся в твердом топливе,
до воспламенения не вступают в реакцию между собой. При воспламенении твердого
топлива (при запуске двигателя) образуются газы — продукты сгорания, которые через
сопло покидают двигатель с большой скоростью и создают реактивную тягу.
В качестве идеального цикла такого двигателя, как и в предыдущем случае, может
быть принят цикл, показанный на рис. 23.29, а.
Реактивный двигатель предназначен для создания движущей силы, используемой
для перемещения в пространстве летательного аппарата (самолета или ракеты).
Эта движущая сила называется силой тяги или просто тягой Р. Тяга Р представляет
собой осевую равнодействующую сил давления, распределенных по всей поверхности
камеры сгорания 11. Неуравновешенная сила давления газа, действующая на
внутреннюю поверхность камеры (см. рис. 23.28), дает составляющую Р. Если учесть силу
давления на срезе сопла площадью /с, равную fc(pa — p), то результирующая сила
определится в виде разности Р — fc(pa — p) (здесь ра — давление в газовом потоке на срезе
сопла, р — давление окружающей среды). Импульс этой силы за время d/Bp равен
изменению количества движения газа dG, ушедшего за это время из двигателя со
скоростью w, т. е. [Р — fc(pa — p)]d/Bp =— wdG, откуда
P = fc(pa-p)-(dG/dtBp)w.
Производная dG/d/Bp представляет собой расход газа МГ. Для реактивных двигателей
dG/d/Bp<CO, поэтому —(dG/d/Bp) = wMr. Следовательно,
P = Mrw + fc{pa-p).
Внешнее давление окружающей среды зависит от высоты полета летательного
аппарата. В этом случае р = рл. При полете за пределами атмосферы ph~0.
Иногда при определении тяги двигательной установки за пределами атмосферы
используется понятие эффективной скорости истечения we, определяемой соотношением
we=w-\-fcpa/Mr. В этом случае P=we. Действительная скорость истечения w от расхода
газа не зависит, а давление ра в потоке газа на срезе сопла пропорционально расходу
газа Мг. В связи с этим значение we практически не зависит от расхода газа. Обычно
we>w на 10...15 %.
§ 23.6. Сравнительный анализ циклов тепловых двигателей
При анализе и сопоставлении между собой различных термодинамических циклов
наибольший интерес представляют их экономичность и значение термического кпд.
Чем выше значение т}/, тем более благоприятны исходные условия для обеспечения
высокой экономичности соответствующей реальной теплоэнергетической
машины—теплового двигателя.
Эталонным циклом для всех тепловых двигателей является цикл Карно, имеющий
тот же температурный перепад, что и сравниваемый с ним цикл. Так как термический
кпд цикла Карно, определяемый выражением (2.49), является наибольшим при
выбранных Тъ и Г|, то качество любого другого цикла, протекающего в этом же интервале
302 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
температур, будет тем большим, чем ближе значение термического кпд исследуемого
цикла к термическому кпд цикла Карно.
Вместе с тем во многих случаях возникает необходимость сравнивать различные
циклы между собой (а не с циклом Карно). Для того чтобы провести это сравнение,
необходимо выбрать условия, при которых проводится это сравнение. Такими условиями
могут быть равенства подведенных количеств теплоты, степеней сжатия, степеней
повышения давления и т. п. Циклы в этом случае изображаются на sT-диаграмме и
проводится сравнение их площадей.
В 1939 г. В. С. Мартыновским был разработан новый метод сопоставительного
анализа циклов, полностью основанный на втором начале термодинамики с
определением среднепланиметрических температур*. Его метод основывается на нахождении
для исследуемых циклов эквивалентных циклов Карно и последующем сравнении
между собой этих эквивалентных циклов. Этот метод анализа является более
определенным, поэтому целесообразно рассмотреть его несколько подробнее.
Как известно, термический кпд любого цикла тепловой машины определяется
выражением (2.46). Если Тъ — текущая температура процессов, в которых отводится
теплота, а Т\ — текущая температура процессов, в которых подводится теплота, то
Каждый цикл тепловой машины протекает в определенном интервале изменения
удельной энтропии As, поэтому всегда можно определить некоторые изотермные
процессы подвода и отвода теплоты, протекающие в этом интервале так, чтобы удельные
количества теплоты, подведенные и отведенные в этих изотермных процессах, были
равны соответственно q\ и q2 анализируемого цикла. В этом случае
^,==r,cpAs; <72=Г2срД5, (23.25)
откуда
Г,ср=$ Tids/bs; Т2с?=\ T2ds/ks. (23.26)
Подставив выражение (23.25) в формулу (2.46), получим
л,= 1_Г2ср/Г1ср. (23.27)
Сравнение формулы (23.27) с формулой (2.49) показывает их идентичность.
Следовательно, формула (23.27) определяет термический кпд некоторого эквивалентного
цикла Карно, равный термическому кпд исследуемого цикла. Таким образом,
любой цикл тепловой машины может быть заменен эквивалентным циклом Карно с
температурами Ги,, и 7\><р, называемыми среднепланиметрическими (часто эти температуры
называются среднетермодинамическими).
Такое их название связано с тем, что при наличии sT-диаграммы эти температуры
могут быть определены планиметрированием площадей закрашенных треугольников
(рис. 23.30). Средняя температура процесса должна быть подобрана так, чтобы
площади закрашенных треугольников были равны друг другу.
Если же теплота подводится или отводится от рабочего тела в некотором поли-
тропном процессе с постоянной удельной теплоемкостью с, то средняя планиметрическая
температура может быть подсчитана аналитическим путем. Действительно, в этом случае
* Мартыновский В. С. Термодинамическое сравнение образцовых циклов двигателей
внутреннего сгорания//Дизелестроение, 1939; № 12; Мартыновский В. С. Анализ действующих
термодинамических циклов,— М.: Энергия, 1972.
Циклы с газообразным рабочим телом
303
а)
Рис. 23.30. Определение средней планиметрической температуры
процесса: а —в одинаковом интервале изменения температуры;
б — в одинаковом интервале изменения удельной энтропии
поэтому в соответствии с формулами (23.26)
2
ГСР =
откуда
ср с1п(Г2/Г|) 1п(Г2/Г,)"
Следовательно, любой термодинамический политропный процесс, протекающий в
заданном интервале температур Гг и Т\, имеет одну и ту же среднюю температуру Гср
(рис. 23.30, а). Если же сравниваемые процессы протекают в одинаковых интервалах
изменения энтропии (рис. 23.30, б), то наибольшую среднюю температуру имеет
процесс с меньшей теплоемкостью.
Действительно, чем меньше теплоемкость процесса, тем меньше длина подкаса-
тельной к процессу на sT-диаграмме, тем интенсивнее изменяется температура
рабочего тела в процессе. Поэтому rcpi2> 7"cpi3> 7"cPi4, где
т,-
Гср14 —
1п(Г4/Г,
Для того чтобы воспользоваться указанным методом, необходимо анализируемые циклы
изобразить на sT-диаграмме в одинаковых границах температур Гтах и Tmin. Однако
для определенности сравнения циклов это единственное условие является
недостаточным, так как изменение, например, степени сжатия может в широких пределах изменить
термический кпд цикла без изменения температурных границ. Следовательно, для того
чтобы при рассматриваемом методе сравнения анализ циклов сделать определенным,
необходимо одновременно с выбором температурных границ принять дополнительные
условия. Такими условиями могут быть одинаковые количества теплоты, подведенные
за цикл к рабочим телам; равенство отдельных параметров (например, степени
сжатия) и т. д.
Так, при анализе циклов ДВС наибольший интерес представляет сравнение
между собой циклов с изохорным и изобарным подводом теплоты. Пусть в выбранных
циклах кроме равенства верхней и нижней температур (рис. 23.31, а) равны между
собой максимальное и минимальное давления (рис. 23.31, б). При выбранных условиях
отвод теплоты в обоих циклах происходит по одной и той же изохоре, поэтому темпера-
304
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 23.31. Сравнение циклов ДВС с подводом теплоты при v = const
и p = const, одинаковых ТтаХу pmax, TmtTb ртт: a — на яТ-диаграмме;
б — на ур-диаграмме
тура Г2ср обоих циклов одна и та же. Подвод теплоты в обоих циклах происходит
после адиабатного сжатия, но степень сжатия в цикле с изохорным подводом теплоты
меньше, чем в цикле с изобарным подводом теплоты. Этим и обусловливается большая
средняя температура Т\ср изобары 3-4, чем Т\ср изохоры 2-4. Поэтому
цикл ДВС с изобарным подводом теплоты при выбранных условиях сравнения
более экономичен (термический кпд выше), чем цикл ДВС с изохорным подводом
теплоты.
Аналогично можно сравнивать между собой, например, циклы ГТУ с подводом
теплоты по изохоре и изобаре и с одинаковыми степенями сжатия в компрессоре
(процесс 1-2 на рис. 23.32, б). Подвод теплоты в обоих циклах осуществляется в
процессах, протекающих в одинаковых пределах температуры с постоянными теплоем-
костями (рис. 23.32, а). Поэтому средние планиметрические температуры этих
процессов в обоих циклах одинаковы. Средняя планиметрическая температура процесса 5-1
отвода теплоты в цикле с изобарным подводом теплоты Г^р выше средней
планиметрической температуры Г2Ср процесса 6-1. В связи с этим
при выбранных условиях сравнения термический кпд цикла ГТУ с изохорным
подводом теплоты выше термического кпд цикла ГТУ с изобарным подводом
теплоты.
Изложенный метод сравнения циклов может быть использован для сопоставления
циклов разнородных теплосиловых установок, например ДВС й ГТУ. На рис. 23.33
a) i)
Рис. 23.32. Сравнение циклов ГТУ с подводом теплоты при v = const,
p = const, одинаковых Гтах, Гт1п и е: а — на sT-диаграмме; б — на vp-
диаграмме
Циклы с газообразным рабочим телом
305
Ь)
Рис. 23.33. Сравнение циклов ДВС и ГТУ при одинаковых Гтах, Гт1п и
Ртах> Pmin: а ~ на «Г-диаграмме; б — на ир-диаграмме
изображены циклы с подводом теплоты при р — const ДВС и ГТУ, имеющие
одинаковые температуры Гтах и Tmin (рис. 23.33, а). Кроме того, принимаются одинаковыми
значения ртах и р„т (рис. 23.33, б). Средняя планиметрическая температура Г|Ср
процессов подвода теплоты в обоих циклах одна и та же. Более того, в этих циклах одина-
козое количество подведенной к рабочему телу удельной теплоты (пл. 8247 на рис.
23.33, а). Средняя планиметрическая температура процесса изохорного отвода теплоты
Ггср выше, чем у процесса изобарного отвода теплоти Ггср, что свидетельствует о том, что
при выбранных условиях сравнения термический кпд ГТУ выше, чем термический
кпд ДВС.
Этот же вывод подтверждается сравнением площадей циклов на sT-диаграмме,
если имеется в виду, что подведенная теплота в обоих циклах одинакова. Площадь
цикла ДВС меньше площади цикла ГТУ на значение пл. 156, что также свидетельствует
о большем термическом кпд цикла ГТУ.
Приведенные примеры сравнительного анализа циклов показывают, что введение
понятия средних планиметрических температур термодинамических процессов подвода
и отвода теплот в циклах, т. е. замена исследуемых циклов эквивалентными циклами
Карно, в значительной степени облегчает анализ, делает его наиболее наглядным.
Вместе с тем при использовании этого метода необходимо правильно с инженерной
точки зрения выбирать дополнительные условия сравнения. Так, например, при
сравнении циклов ДВС с подводом теплоты при р = const и v = const при одинаковых Гтах и
Гт|п вряд ли целесообразно принимать равные степени сжатия в обоих циклах. Такой
анализ имеет незначительный практический интерес. Действительно, в двигателях с
воспламенением от сжатия более высокие степени сжатия, чем у двигателей с
воспламенением от электрической свечи. Больший интерес представляет дополнительное
условие в виде подвода к рабочему телу одинакового количества теплоты.
Вопросы 1- Назовите параметры, характеризующие обобщенный термодинамический цикл.
2. В каких циклах значение термического кпд увеличивается по мере увеличения
подводимого количества теплоты и в каких, наоборот, уменьшается?
3. Какой процесс называется регенерацией и в каких циклах он используется?
4. Какая температура называется среднепланиметрической и для чего она
применяется?
306
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Глава 24
ЦИКЛЫ ПАРОСИЛОВЫХ УСТАНОВОК
§ 24.1. Цикл Карно
Основным рабочим телом в паросиловых установках является водяной пар,
используемый как в перегретом, так и насыщенном состояниях.
Если рабочим телом установки является насыщенный пар, то возможно
осуществить цикл Карно и получить максимальный термический кпд. Действительно,
постоянство температуры в изобарном процессе 4-1 (рис. 24.1) подвода теплоты и в
процессе 2-3 отвода теплоты можно обеспечить только за счет испарения и конденсации.
Процесс 1-2 в цикле Карно является процессом адиабатного расширения пара в
машине, а процесс 3-4 — адиабатным сжатием рабочего тела. Осуществить такой цикл
возможно в паросиловой установке (рис. 24.2), состоящей из парогенератора-котла /,
паровой машины 2, конденсатора 3 и компрессора 4. В конденсаторе 3 пар частично
конденсируется до состояния влажного пара (точка 3), а теплота q2 при этом отводится
в окружающую среду. Влажный пар поступает в компрессор 4 и адиабатно сжимается
до полной конденсации (точка 4 на рис. 24.1), конденсат подается в
парогенератор /.
На адиабатное сжатие влажного пара тратится работа
4
/сж = — [vdp,
3
численно равная площади п43гп (рис. 24.1, а). Работа сжатия тем больше, чем выше
исходные параметры цикла, например, в точке 4 (см. цикл, изображенный пунктиром
на рис. 24.1, а). С увеличением начальных параметров рабочего тела возрастает и
термический кпд цикла, но его рост отстает от роста затрат на сжатие. Общий кпд
паросиловой установки в связи с этим падает, а эффективность использования теплоты
в паросиловой установке уменьшается. Таким образом,
преимущества паровой установки, работающей по циклу Карно (максимальный
термический кпд), теряются из-за большой работы, затрачиваемой на сжатие влажного
пара.
Рис. 24.1. Цикл Карно для насыщенного пара паросиловой Рис. 24.2. Схема паросиловой ус-
установки в координатах: а — и, р; б — s, T тановки:
/ — парогенератор; 2 — паровая
машина; 3 — конденсатор; 4 —
компрессор
Циклы паросиловых установок
307
§ 24.2. Цикл Ренкина
Недостаток, присущий паровому циклу Карно (большая работа, затрачиваемая на
сжатие влажного пара), устраняется, если процесс конденсации отработанного в машине
пара довести до полного его превращения в воду (2-3 на рис. 24.3, а), а затем насосом
подать ее в парогенератор-котел (процесс 3-4). Впервые такой цикл с полной
конденсацией отработанного пара предложил У. Дж. Ренкин, заменив в схеме паросиловой
установки компрессор 4 на водяной насос.
В паровом цикле Ренкина вода (конденсат) сжимается до давления р\ не по изохо-
ре 3-4, а по адиабате. Поэтому ее удельный объем несколько уменьшается, а
температура возрастает, вследствие чего происходит термическое расширение воды и
адиабатный процесс сжатия практически сливается с нижней пограничной кривой. Паровой
цикл Ренкина представляется круговым процессом 1-2-3-4-1. Отрезок 4"-4 на ур-диа-
грамме соответствует подогреву конденсата в парогенераторе-котле при р — const.
С учетом принятых допущений работа, затрачиваемая насосом на сжатие
конденсата до давления р\, на ур-диаграмме может быть представлена площадью п4"3т и
определена выражением /Нас = ^з(р1—Рз). Сравнение работы, подсчитанной по данной
формуле, с работой адиабатного сжатия в цикле Карно показывает, что работа,
затраченная в цикле Ренкина на сжатие конденсата до давления в парогенераторе-котле,
значительно меньше работы, затраченной в цикле Карно на сжатие до того же давления
влажного пара. Кроме того, в цикле Ренкина за счет полной конденсации отработанного
пара удается получить более глубокий вакуум, чем в цикле Карно. В современных
конденсаторах с полной конденсацией пара абсолютное давление составляет от 0,004 до
0,006 МПа, что при исходном давлении пара 10 МПа и выше позволяет получить
работу в цикле Ренкина, в 1,5 раза большую, чем в цикле Карно. Таким образом,
работа цикла Ренкина значительно больше работы цикла Карно как за счет
уменьшения работы, затрачиваемой на сжатие конденсата, так и за счет более глубокого
расширения пара. Однако термический кпд цикла Ренкина все же остается меньшим
кпд цикла Карно при одинаковых параметрах, что связано с большей затратой теплоты
q\ в цикле Ренкина.
Действительно, в цикле Карно теплота расходуется только на процесс
парообразования (qi = r), а в цикле Ренкина расходуется дополнительное количество теплоты на
подогрев питательной воды в процессе 4"-4.
Кпд цикла Ренкина определяется также по формуле (2.46), где q\ —подводимая
в цикле теплота, характеризуемая на sT-диаграмме (рис. 24.3, б) площадью //' 3' 3 4;
Ц2 — отводимая теплота (пл. /' 3' 3 2). Поэтому удельная работа цикла определяется
разностью площадей: /ц=пл. Oa41V — пл. Оа32Г'. Так как площадь Оа411' на sT-диаг-
рамме является удельной энтальпией h\ точки /, а площадь ОаЗ 2 V — удельной
энтальпией h<i точки 2> то удельная работа цикла определяется разностью:
т
Рис. 24.3. Теоретический цикл паросиловой установки (цикл Ренкина) в
координатах: а — у, р\ 6 — s,T\ e — s,h
308
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
lll = hi—h2. (24.1)
Так как подведенную теплоту q\ (пл. //' 3' 34) можно определить разностью площадей
</1 = пл. Оа4П' — пл. ОаЗЗ\ то
q\=hi —
(24.2)
где /i3 — удельная энтальпия питательной воды на входе в парогенератор.
Следовательно,
— (h h \ J(h Ai \ t ОА. *\\
Полученные формулы (24.1) — (24.3) говорят о том, что для расчетов целесообразно
использовать s/i-диаграмму. Например, кпд цикла по,s/i-диаграмме определится
отношением отрезков 72 и 75 (рис. 24.3, в).
Если представить /гз = *кСк, где tK — температура конденсата—питательной воды, а
сч = 4,1868 кДж/(кг-К) —ее теплоемкость, то формула (24.3) получит вид
,— 4,1868/к).
Экономичность парового цикла характеризуется также расходом пара d
(кг/МДж), определяемым из расчета на единицу работы в соответствии с формулой
(24.3) отношением
d = 1000//ц = 1000/(Л 1 — Л2), (24.4)
где h — в кДж. Знание расхода пара d необходимо для определения площади сечения
проточной части установки (трубопроводов, каналов, лопаток и т. д.). Так как удельный
расход теплоты на единицу работы (кДж/МДж) q = d{h\ — 4,1868/K), то с учетом (24.4)
получим
(24.5)
Обычно термический кпд цикла Ренкина равен 30...40 %.
t
А
и
As и»
§ 24.3. Расширение пределов рабочего процесса
Кпд паросиловых установок может быть повышен за счет увеличения температуры
подводимого и уменьшения температуры отработавшего пара.
В цикле Ренкина (рис. 24.3) рабочим телом является насыщенный пар, что
создает возможность сопоставления этого цикла с циклом Карно. Если же представить
цикл Ренкина контуром а-Ь-3-4 (рис. 24.4), состоящим из двух циклов (1-2-3-4 и t-a-b-2),
то один из них цикл Ренкина с кпд rtf, а другой цикл
Карно с т]?. Так как всегда т)?>т|?, то r\t суммарного
цикла Ренкина а-Ь-3-4 должен иметь какое-то
среднее значение л?^1!/^1!?- Следовательно,
термический кпд цикла Ренкина r\t при использовании в каче-
j/ I 41 стве рабочего тела перегретого пара становится боль-
3JL-^ .с^ j^ ше кпд ^р того же цикла ПрИ работе с насыщенным
/ \^ паром.
Если, кроме того, увеличить температуру
перегрева при сохранении давления насыщенного пара,
то кпд цикла возрастет дополнительно.
Действительно, по s/i-диаграмме (рис. 24.5) видно, что кпд
цикла в соответствии с формулой (24.3) определится
значениями энтальпий /ii, /i2, Лз, которые являются
функциями температур и давлений. Таким образом,
3'
Рис. 24.4. Цикл Ренкина с
перегретым паром на sT-диаграмме
циклы паросиловых установок
309
Рис. 24.5. Пути повышения кпд цикла Ренкина: а — за счет увеличения
начального давления; б — за счет увеличения начальной температуры;'
в — за счет понижения конечного давления; г — за счет повторного
перегрева пара
термический кпд цикла зависит в основном от значений р\у р<± и Т\. Увеличение начального
давления пара от р\ до р\ и р" (p\<.p'\<.pY) при постоянной температуре Т\
(рис. 24.5, а) и конечном давлении р2 приводит к увеличению теплоперепада h = h\ — /*2,
т. е. к увеличению числителя формулы (24.3) при уменьшающемся значении
знаменателя и, следовательно, к увеличению кпд цикла.
Существенным недостатком повышения кпд цикла за счет увеличения начального
давления пара р\< при сохранении постоянных значений температуры Т\ и давления рг
является рост влажности пара в конце процесса расширения. Так, при давлении 10 МПа
и довольно большой температуре перегрева (830 К) степень сухости при конечном
давлении 0,005 МПа адиабатно расширенного пара будет всего 0,79, а при 20 МПа—
0,74. Это может привести к разрушению поверхности лопаток последних ступеней
проточной части ротора турбины.
Избежать этого недостатка при одновременном увеличении кпд цикла Ренкина
можно за счет повышения температуры рабочего агента Т\, поступающего в турбину
(рис. 24.5, б). По мере роста температуры перегретого пара Т\'~>Т\~>Т\
увеличивается теплоперепад в турбине h">h'>h. Из трех приведенных на рис. 24.5, б
случаев кпд оказывается наибольшим при температуре Г", Повышение значения кпд цикла
происходит за счет роста средней температуры подвода теплоты. Следует при этом
заметить, что при увеличении начальной температуры пара Т\ одновременно
увеличивается и средняя температура отвода теплоты. Однако это увеличение идет менее
интенсивно, в связи с чем термический кпд цикла Ренкина при увеличении начальной
температуры пара Т\ увеличивается. Этот путь увеличения кпд паросиловых установок
используется на практике наиболее часто.
В настоящее время осваиваются установки с температурой перегрева пара,
достигающей 900...950 К- Дальнейшее ее увеличение ограничивается жаропрочностью
применяемых материалов.
310 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Существенное увеличение кпд цикла может быть достигнуто за счет понижения
конечного давления пара при его расширении (давление рч в конденсаторе). Падение
давления р2 соответственно до давления р£ и р</ (рис. 24.5, в) приводит к уменьшение
средней температуры отвода теплоты и к увеличению полезно используемого теплопере-
пада от h до W и h". В результате происходит увеличение кпд цикла, но и увеличение
влажности пара в конце процесса расширения, что нежелательно.
Проведенный анализ влияния отдельных параметров на кпд паровых циклов
показал, что
рабочие тела современных паросиловых установок должны иметь высокие температуры
насыщения при сравнительно небольших давлениях, низкие температуры насыщения в
конце процесса расширения (примерно равные температуре окружающей среды) при
легко осуществимом в энергетической технике вакууме и, наконец, малые
теплоемкости жидкости и большие теплоемкости перегретого пара.
§ 24.4. Цикл с промежуточным перегревом пара
Повышение начального и уменьшение конечного давлений пара приводит в цикле Рен-
кина к нежелательному явлению увеличения влажности пара в конце процесса
расширения. Устранить этот недостаток можно за счет повторного (промежуточного)
перегрева пара после его частичной отработки в первых ступенях паросиловой
установки (турбины).
Сущность этого способа заключается в том, что перегретый пар (точка / на
рис. 24.5, г), поступивший из пароперегревателя в турбину, расширяется в ней до
некоторого промежуточного давления (точка 2), совершая при этом работу l^2==h\—h%
затем направляется в пароперегреватель для повторного перегрева (процесс 2-3),
обычно осуществляемого при постоянном давлении р\. Повторно перегретый пар
(точка 3) направляется во вторую ступень турбины и совершает работу /_3_4 = /1з— h\.
Точка / соответствует начальному состоянию пара, поступившего из
пароперегревателя, точка 4 — состоянию пара в конце процесса расширения в турбине после
вторичного перегрева, при этом влажность пара (1— х4) мала. Если вторичный перегрев
отсутствует, то влажность пара в точке 2' составит (1—x2,)Z>{\—х4).
Повторный перегрев пара при определенных условиях приводит к повышению
кпд установки на 2...3 %. Для этого цикл надо организовать так, чтобы средняя
температура подвода теплоты в цикле с промежуточным перегревом была выше, чем
средняя температура подвода теплоты в цикле с однократным перегревом.
При давлениях, близких к критическому и сверхкритическому значениям, можно
применять (и применяют) два (и более) промежуточных перегрева работающего пара.
Термический кпд цикла с одним промежуточным перегревом (рис. 24.5, г) определится
по формуле
з —Л2)], (24.6)
где (h\—Лг) и (Нз— п4) — адиабатный теплоперепад соответственно в первой и второй
ступенях турбины; (h\—/15) —теплота, подведенная к пару в котле и в первом
пароперегревателе; (Из — h,2) —теплота, подведенная к пару во втором пароперегревателе.
Числитель формулы (24.6) представляет собой удельную работу 1 кг пара в
установке с одним промежуточным перегревом пара: /i = (/ii—/*2) + (^з — п*)- Она больше
удельной работы пара /u = /ii—hT без промежуточного перегрева, так как отрезок
34 на s/i-диаграмме больше отрезка ~22. Расход пара на 1 МДж работы при наличии
вторичного перегрева составит df — 1000//^. Так как /i>/u, то расход пара в установке
с промежуточным перегревом df меньше, чем d без повторного перегрева. Удельная
теплота, израсходованная на получение 1 кг пара в установке с повторным его перегревом
(рис. 24.5, г), определяется суммой q\—(h\— ^) + (пз— /*г), а в установке без перегрева
Циклы паросиловых установок 311
qx = h\—hb. Следовательно, q\>q\. Так как одновременно /i>/u, то сделать
однозначный вывод о направлении изменения кпд невозможно. Как уже отмечалось,
направление изменения кпд определится средней температурой подвода теплоты в цикле. Таким
образом,
экономичность установок с промежуточным перегревом зависит от состояния
(температуры) начала перегрева во втором пароперегревателе (точка 2) и температуры конца
перегрева (точка 3).
Помимо экономичности (кпд) большое значение имеют также конечные значения
параметров пара: влажность (1—ха) не должна превосходить допустимых значений.
Расход теплоты на 1 МДж работы в установках с промежуточным перегревом
пара определится отношением q' = d'q\ — 1000'т|<, а без промежуточного перегрева q —
§ 24.5. Бинарные циклы
Наибольшее значение термического кпд цикла может быть получено при максимально
высоких температурах подвода теплоты. Однако для создания реальных циклов и
реализации указанных преимуществ требуются особые природные свойства рабочего
тела, так как в отличие от цикла Карно свойство рабочего тела в цикле Ренкина
существенно влияет на термический кпд установки. Наиболее часто в качестве рабочего тела
в современных энергетических паровых установках используется водяной пар.
Однако вода имеет низкую критическую температуру (Гкр = 647,15 К) при достаточно
большом критическом давлении (ркр = 22,219 МПа). При таких-физических свойствах воды
и водяного пара с ростом температуры перегрева Т\ не удается существенно
повысить среднюю температуру подвода теплоты. Вода имеет слишком большую удельную
' н
теплоемкость, а это, как следует из формулы As = \ (с/Г) d7\ приводит к
сущего
ственному росту энтропии (см. рис. 24.4), что уменьшает заполняемость цикла Карно
(As3.4"<As3-4)- ^ конИе расширения при низких рабочих давлениях пар имеет слишком
большую удельную энтальпию /i2, т. е. отработанный пар уносит с собой большое
количество теплоты q2.
К недостаткам воды и водяного пара следует также отнести и неблагоприятное
соотношение между температурами насыщения и соответствующими им давлениями
(медленное увеличение температуры при существенном росте давления).
Действительно, рост температуры в 3 раза приводит к росту давления в 200 раз. Эти физические
особенности воды существенно ограничивают термический кпд паровых циклов,
увеличивают металлоемкость оборудования, удорожают его и затрудняют эксплуатацию.
Указанные недостатки воды как рабочего тела привели к необходимости поиска
других рабочих тел для паросиловых установок. В качестве рабочего тела может быть
использована ртуть, имеющая высокую температуру насыщения при сравнительно
небольшом давлении. Однако для охлаждения ртути (срабатывание теплоперепада в
турбине) до температуры, примерно равной температуре окружающей среды (Гк =
= 303 К), в конденсаторе необходимо обеспечить почти полный вакуум, так как давление
насыщения паров ртути, сответствующее этой температуре, составляет всего 0,33 Па.
Получить такое разрежение практически невозможно. Если же закончить расширение
паров ртути при возможно осуществимом давлении, например рк = 0,004 МПа, то
температура в конце расширения окажется равной 500 К. Такая высокая температура
отработавшего рабочего тела существенно увеличивает теплоту q<i и значительно
уменьшает термический кпд парового цикла.
Таким образом, рассмотренные рабочие тела (вода и ртуть) каждое в отдельности
не удовлетворяют требованиям, предъявляемым к рабочим телам паровых
турбин. Поэтому появилась идея создания сложного цикла, где вместо одного рабочего
312
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
тела используются два. Одно из рабочих тел (ртуть) имеет высокую критическую
температуру при сравнительно низком давлении и должно использоваться в зоне цикла
с высокими температурами. Другое рабочее тело (вода) имеет высокое давление
насыщения при температуре окружающей среды и должно использоваться в зоне цикла,
осуществляемого в области низких температур. Соединение этих двух циклов
значительно расширяет температурный перепад и приводит к увеличению общего
термического кпд по сравнению с обычным пароводяным циклом. Такой цикл называется
бинарным (рис. 24.6, б).
На схеме (рис. 24.6, а) сплошными линиями показан так называемый ртутный
контур, а пунктирными — водяной. Ртутный пар образуется в специальном
ртутном котле / и направляется для работы в ртутную турбину 3. После расширения в
турбине пары ртути поступают в конденсатор-испаритель 2, где пары ртути,
конденсируясь, отдают теплоту парообразования для получения водяного пара. Ртуть из
конденсатора-испарителя направляется вновь в ртутный котел, а образовавшийся водяной
пар после дополнительного перегрева в перегревателе 7 поступает в паровую
турбину 4. После расширения в ней отработанный пар направляется в конденсатор 5.
Образовавшаяся вода насосом 6 подается в конденсатор-испаритель 2.
В бинарном цикле на каждый 1 кг водяного пара приходится т кг паров ртути,
что обусловлено разностью значений удельных энтальпий насыщенных паров ртути в
конце процесса расширения в ртутной турбине и водяного пара в
конденсаторе-испарителе. Следовательно, для получения 1 кг водяного пара в конденсаторе-испарителе
(при практически отсутствующем температурном перепаде между насыщенным
ртутным паром и насыщенным водяным паром) требуется т кг ртути, т. е. m = (h%—hi)/
/(Л? — hi), где /i?—удельная энтальпия пара за ртутной турбиной; /г§ —удельная
энтальпия ртути за конденсатором-испарителем; h\ — удельная энтальпия водяного
пара на выходе из конденсатора-испарителя; h\ — удельная энтальпия воды,
поступающей в конденсатор-испаритель.
Расчеты показали, что на 1 кг водяного пара требуется от 10 до 12 кг ртути.
Обычно в бинарных установках применяют сухой насыщенный ртутный пар (точка 8
на рис. 24.6, б) при давлении 0,1... 15 МПа, что соответствует температурам насыщения
790...820 К. Расширение паров ртути в турбине (процесс 8-7) допускается до давления
Рт, равного 0,01...0,004 МПа. Этим давлениям соответствуют температуры насыщения
ртути 520...500 К- Если принять температурный перепад между ртутным и водяным
парами в конденсаторе-испарителе равным 10...15 К, то температура насыщенного водяного
В)
7 Ю 9
I/
;>j
3
в
V
5
1
1
Рис. 24.6. Бинарная ртутно-водяная теплоэнергетическая установка:
а — схема; б — цикл в координатах s, T:
1 — ртутный котел; 2 -- конденсатор-испаритель; 3 — ртутная турбина; 4 —
паровая турбина; 5 — конденсатор; 6 — насос
Циклы паросиловых установок 313
пара (точка 5) составит 505...490 К. Такой температуре соответствует давление
3,3...2,5 МПа. Об эффективности бинарного цикла можно судить по так называемому
коэффициенту заполняемости аБ — отношению полезной теплоты бинарного
цикла (<7пол) к аналогичной величине цикла Карно. Площади на sT-диаграмме подсчи-
тываются при одинаковых температурах Ттах—Т\0 и Гт1п=Гз. При этих условиях
а*=(пл. 6987 + пл. 12345)/пл. 123,10>ап\
где апв — коэффициент заполняемости одного пароводяного цикла Ренкина.
Если кпд цикла Карно при одинаковых температурных перепадах принять за
100 %, то кпд бинарного цикла составит 85...90 %, а цикла Ренкина — не более 70 %.
Термический кпд бинарного цикла без регенерации определится отношением
где Lp — работа пг кг ртутного пара; /в— работа 1 кг водяного пара; /i§ — энтальпия
ртутного пара за ртутным котлом; /if — энтальпия перегретого водяного пара за
пароперегревателем; h\ — энтальпия водяного пара за турбиной.
Практическая выгодность бинарных циклов была подтверждена созданием ряда
установок мощностью от 1,8 до 20 тыс. кВт. При эксплуатации они показали хорошую
надежность и безопасность и соответственно высокую экономичность. Их медленное
внедрение объясняется ядовитостью паров ртути и высокой стоимостью установок
(особенно повышенной мощности), требующих ртуть в больших количествах.
§ 24.6. Регенеративный цикл паротурбинной установки*
В тепловых схемах современных электрических станций часто подогрев питательной
воды, поступающей в парогенератор, производят паром, частично отбираемым из
паровой турбины. В пределе температура подогреваемой воды может быть получена
равной температуре насыщения в парогенераторе. Такой способ подогрева питательной
воды называется регенеративным, а цикл, по которому осуществляется работа всей
паротурбинной установки,—р егенеративным циклом.
В регенеративных циклах средняя температура, при которой подводится теплота к
рабочему агенту, получается большей, чем в циклах без регенерации, что и ведет к
повышению кпд.
Для получения регенеративного цикла следует заменить процесс адиабатного
расширения пара 1-2 (см. рис. 24.3, б) на политропный 1-5 так, чтобы линия политропного
процесса 1-5 была эквидистантной линии 3-4. В этом случае теплота, отведенная в
процессе 1-5 (пл. IV5'51), может быть полностью использована для нагревания воды в про
цессе 3-4 (пл. 44'3'34). В действительности создать установку с такими условиями
передачи теплоты возможно только с некоторым приближением. Пар, полученный в
парогенераторе / (рис. 24.7, а), направляется в паровую турбину 2, где основная его
часть расширяется до давления в конденсаторе 3 (рис. 24.7, б). После совершения
работы в отдельных ступенях турбины часть пара в количествах пгс и rrid отводится и
направляется в подогреватели питательной воды 5. Подогревая воду, пар конденсируется,
а затем совместно с основным конденсатом насосом 4 направляется в парогенератор /.
Процесс расширения пара в турбине и отвод теплоты с отобранным паром условно
(различные количества пара) изображаются ступенчатой линией 1-2-3-4-5-6 (рис.
* Общий анализ регенеративных циклов впервые в учебной литературе по термодинамике
был дан проф. И. А. Вышнеградским в его учебнике «Механическая теория теплоты» (1871).
Проблемы использования регенерации теплоты в паровых машинах были исследованы А. В.
Гречаниновым (1893).
314
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 24.7. Паротурбинная энергетическая установка с регенеративным циклом:
а — схема; 6 — цикл с перегревом пара:
/ — парогенератор; 2 — паровая турбина; 3 — конденсатор; 4 — насос; 5 —
подогреватель
24.7, б) так, что линии 1-2, 3-4 и 5-6 соответствуют процессу расширения, а линии
2-3 и 4-5 — процессу отдачи теплоты паром в подогревателях 5. Переданное таким
образом количество теплоты определяется площадью 21'5'5432. Площадь эта может
быть увеличена при увеличении количества отборов. Ломаная линия по мере увеличения
количества отборрв пара из турбины приближается к линии расширения пара,
эквидистантной линии подогрева питательной водой 7-8. Однако стоимость установки по мере
увеличения количества отборов пара значительно возрастает, в связи с чем количество
отборов пара для целей регенерации ограничено.
Так как в турбине в процессе расширения участвует не весь пар, то работу цикла
паросиловой установки следует подсчитывать по участкам. На участке а-с (рис. 24.7, а)
/, = /г, —/ic; на участке c-d /2 = (/ic — /id)/(l — тс); на участке d-b /3 = (/^— h?) (1 —тс—ntd).
Полная удельная работа цикла определится суммой:
С= /i + к + /з. или С = (Л, -h2)-{hc-h2)mc- (hd - h2)md.
Если в цикле Ренкина участвует весь пар, то работа цикла lfl==hi—/12. Следовательно,
при регенерации /Кег<С/ц. Однако расход теплоты в регенеративном цикле меньше,
чем в цикле Ренкина, температура питательной воды t%lr=ts за счет подогрева
отобранным паром больше, чем температура питательной воды в цикле Ренкина
(t%B—t7). Так как /8> t7i то q\=z{h\ — h%)<Cq\—{h\ — hi). Если при этом учесть, что отвод
теплоты в обоих циклах происходит при одинаковой температуре, а средняя температура
подвода теплоты в регенеративном цикле при одинаковых верхних температурах
больше, чем в цикле Ренкина, то iifer:>iiP- Уменьшение работы /£ег в регенеративном цикле
происходит медленнее, чем уменьшение расхода теплоты на получение пара.
Расход пара для регенеративного цикла dper== 1000//!Гг и для цикла Ренкина
</р=1ООО//р. Так как /Еег</Е, то d**r>d?.
Расход теплоты на 1 МДж для регенеративного цикла можно определить
произведением <7per = dper<7?er или <7рег=1ООО/т1рег. Для цикла Ренкина q? = d?q\ = 1000/лР.
Сопоставление полученных выражений показывает, что qp*r<Cqp.
В пределе, когда количество отборов пара стремится к бесконечности, кпд такого
регенеративного цикла стремится к значению кпд цикла Карно (рис. 24.8, а—в).
Паровой цикл с частичной регенерацией помимо указанного преимущества по эко-
Циклы паросиловых установок
315
Рис. 24.8. Регенеративный цикл на sT-ди а грамме с подогревом питательной воды
всем паром, проходящим через турбину: а — двумя отборами теплоты от пара;
б — равноэкономичный циклу Карно; в — цикл Карно
номичности благоприятно влияет на эксплуатацию и конструкцию паросиловой
установки в целом, так как приводит к уменьшению загрузки парогенератора и улучшению
работы последних ступеней паровой турбины.
§ 24.7. Циклы ядерных энергетических установок
Комплекс агрегатов установки, обеспечивающий преобразование тепловой энергии
ядерного реактора в другие его виды, называется ядерной энергетической
установкой. Конструктивные особенности таких установок, тепловые схемы и
термодинамические циклы определяются прежде всего их назначением, типом ядерного
реактора, применяемым топливом и теплоносителями. Существенное влияние на выбор
конструктивных решений оказывает и требование создания безопасных условий работы
для обслуживающего персонала.
В качестве ядерного топлива обычно используют уран и плутоний, а
теплоносителем являются вода, газы (гелий, азот, углекислый газ), металлы (калий, натрий)
и органические жидкости (углеводороды, дифенил, изопропилдифенил, нафталин и др.).
Схемы ядерных энергетических установок. Наиболее простой схемой ядерной
энергетической установки является одноконтурная (рис. 24.9, а), в которой отбор
теплоты в реакторе и получение работы производится одним и тем же рабочим телом.
Теплоноситель на выходе из реактора в таких схемах может содержать радиоактивные
продукты деления, поэтому весь контур (в том числе и потребитель) должен иметь
либо наружную биологическую защиту, либо не применяться там, где в принципе не
исключена возможность радиоактивного загрязнения (в том числе и в аварийных
ситуациях).
Чтобы полностью устранить указанные недостатки вместо одноконтурной схемы
применяют двухконтурные (рис. 24.9, б) и трехконтурные (рис. 24.9, в) схемы. В них
отвод теплоты из реактора и передача ее внешнему потребителю происходят с помощью
двух или трех, непосредственно не контактирующих между собой теплоносителей.
Так, в двухконтурной схеме (рис. 24.9, б) теплоноситель из ядерного реактора /
поступает в теплообменник 2, где отдает теплоту рабочему агенту второго контура, а из
него насосом 7 вновь возвращается в реактор. Рабочее тело второго контура (как
правило, вода и водяной пар) совершает работу в турбине 3, затем проходит
конденсатор 4 и насосом 5 возвращается в парогенератор. С целью безопасности второй контур
отделен от первого специальной биологической защитой 6.
Трехконтурная тепловая схема (рис. 24.9, в) осуществляется в тех случаях,
когда в качестве теплоносителя применяются металлы. При этом полностью
исключается возможность проникновения водяных паров и воздуха в циркуляционный контур
с повышенной радиацией. Тепловая мощность реактора может изменяться в широких
316
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
/6
/7
Рис. 24.9. Схемы ядерных энергетических установок: а — одноконтурной;
б — двухконтурной; в — трехконтурной:
/ — реактор; 2 — теплообменник; 3 — турбина; 4, 15 — конденсаторы; 5, 7, 8, 16, 18,
20—насосы, 6 —биологическая защита; 9, 10, 11, 19 — парогенераторы; 12 —
турбина высокого давления; 13 — турбина среднего давления; 14 — турбина низкого
давления; 17 — регенеративные подогреватели
пределах. Этот диапазон значительно больше, чем в обычных котельных установках.
Однако производительность установки определяется не только тепловой мощностью
реактора, но и рядом других факторов и, в частности, интенсивностью отвода теплоты
с поверхности тепловыделяющих элементов (твэлов). Определенные ограничения на
параметры ядерных реакторов (а следовательно, на их экономичность и
производительность) накладывают и физические свойства ядерного топлива, например термическая
стойкость.
В энергетических реакторах в качестве топлива чаще всего применяется диоксид
урана UO2(II), имеющий высокую температуру плавления (3073 К). £>н химически
не реагирует с водой и углекислым газом, имеет хорошую термическую и радиационную
стойкость. С применением диоксида урана стало возможным поддерживать
температуру теплоносителя в пределах 1070... 1270 К. При этих условиях кпд
термодинамического цикла установки достигает 55% (а всей станции — 45%). Основным
недостатком диоксида урана является ее низкая теплопроводность и, как следствие,
резкий перепад температур от центра твэлов к поверхности.
Ядерные установки с использованием воды в качестве теплоносителя бывают
двух типов. В установках первого типа (кипящего) пар' получается непосредственно
в самом реакторе. В установках второго типа (некипящего) реактор нагревает воду
до температуры насыщения. В таких реакторах давление рабочего тела допускается
до 10...20 МПа, что соответствует температуре насыщения 550...620 К. Такие параметры
первого контура дают возможность в парогенераторе и на входе в турбину получить
насыщенный или немного перегретый пар с давлением 3...6 МПа и температурой
530...550 К.
Циклы паросиловых установок
317
При определенных упрощениях двухконтурный цикл ядерной энергетической уста
новки можно свести к рассмотрению обычного цикла Ренкина с небольшим перегревом
пара (рис. 24.10, а). Площадь аЬ67 численно равна удельной теплоте, отдаваемой
теплоносителем первого контура в парогенераторе. Эта же теплота воспринимается
рабочим телом второго контура по изобаре 4-1 (пл. 5417). Процесс 1-2 в этом цикле
представляет собой работу пара в турбине, процесс 2-3 — конденсацию отработанного
пара в конденсаторе, процесс 3-4 — сжатие питательной воды.
Удельную теплоту q\, расходуемую на цикл 1-2-3-4, можно определить в виде
разности: qi = h\ — h4. Удельная работа цикла определяется разностью работы пара в
турбине и удельной работы, израсходованной на сжатие питательной воды, поэтому
/ц = (/г, — /г2) — (hi — hz). Полученные соотношения дают возможность определить
термический кпд цикла:
Теплоносители. Как уже отмечалось, в энергетических установках атомных
электростанций в качестве теплоносителей используются органические и жидкометаллические
вещества. Органические теплоносители при нагревании в реакторе приобретают на
столько незначительную радиоактивность, что создают возможность использовать для
энергетических установок одноконтурную тепловую схему (см. рис. 24.9, а). В этом
случае исключается промежуточный парогенератор и повышается кпд всей станции.
Однако большая температура конденсации (например, у дифенилоксида при давлении
0,015 МПа температура конденсации 470 К) не создает условий для полного
использования указанного преимущества органического теплоносителя. Поэтому такие тепло
носители используются в одноконтурной схеме только с турбинами высокого давления,
а отработанный в турбине пар используется для целей теплофикации. При
органическом теплоносителе в двухконтурной схеме парогенератор второго контура дает
возможность получить перегретый пар с перегревом в 320...370 К.
Жидко металлические теплоносители (в основном калий и натрий) дают
возможность за счет своих теплофизических свойств резко увеличить начальную
температуру рабочего тела, поступающего в турбину. При этом значительно возрастает
кпд цикла и установки в целом. Однако такие теплоносители обладают высокой
радиоактивностью, воспринятой в реакторе, и могут привести к взрыву при контакте с водой
и кислородом. Эти обстоятельства приводят к необходимости использовать трехкон-
турную тепловую схему (см. рис. 24.9, в). В первом контуре с реактором /,
парогенератором 9 и насосом 8 циркулирует металлический теплоноситель (обычно натрий), во
56
7 5
т\
750К
Рис. 24.10. Циклы ядерных энергетических установок: а— Ренкина;
б — с натриевым теплоносителем и промежуточным перегревом пара
318
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
втором—либо натрий, либо натриево-калиевый сплав. В третьем контуре
теплоносителем и рабочим телом является вода. Второй и третий контуры нерадиоактивны и не
требуют биологической защиты. Пар в третьем контуре после первичного перегрева в
парогенераторе 10 имеет давление 10 МПа и температуру 750 К. Вначале он
используется в турбине высокого давления 12 и расширяется до 2,2 МПа (d-e на рис. 24.10, б),
а затем поступает во второй пароперегреватель 11 и вновь перегревается до тех же
750 К (е-/) • Дальше пар используется в ступенях среднего 13 и низкого 14 давлений.
Высокий термический кпд станции можно получить, если осуществить с указанными
теплоносителями бинарный цикл.
Термически и радиационно более стойкими рабочими телами являются газовые
теплоносители. При прохождении через реактор они приобретают незначительную
радиоактивность и в принципе могут использоваться в одноконтурных тепловых схемах.
Однако в целях большей надежности в настоящее время такие теплоносители
применяются в двухконтурных схемах, причем теплоносителем второго контура является
водяной пар. В установках с газовым теплоносителем приходится затрачивать
значительно больше энергии на прокачку газа через реактор, так как теплоемкость газа
значительно меньше теплоемкости воды: в во до-водяных эти затраты составляют
1...3 % от мощности турбин, а в реакторах с газовым теплоносителем — 10...15%.
Чтобы снизить количество газов, проходящих через реактор, и таким образом
уменьшить расход энергии на его циркуляцию, создают большую разность температур
теплоносителя на входе в реактор и выходе из него. Для углекислоты эта разность
составляет, как правило, от 430 до 520 К, а для гелия — 550...750 К. Температура
теплоносителя на выходе из реактора в зависимости от его особенностей и температуры
поверхности твэлов может быть равна 620...1373 К. Применение бинарных циклов с
газотурбинной ступенью в ядерных энергетических установках (рис. 24.11) впервые
предложено в СССР Е. Ф. Ратниковым. Термический кпд такого цикла при
максимальной температуре в газовом цикле Т\ — 1076...1276 К (и при г|Р== 0,4 парового цикла
во втором контуре) составляет 0,5...0,62. Значение результирующего кпд бинарного
цикла не соответствует оптимальным значениям кпд отдельных (верхнего и нижнего)
/J7J/T
S13K
Рис. 24.11. Бинарная гелиево-пароводяная установка: а —схема; б — цикл:
/ — генераторы; 2 — компрессор; 3 — гелиевая турбина; 4 — паровые турбины; 5 —
конденсатор; 6 — насос; 7 — регенеративные подогреватели; 8 — экономайзер; 9 —
парогенератор; 10 — реактор
Циклы паросиловых установок
319
Рис. 24.12. Одноконтурная атомная энергетическая установка с газовым
теплоносителем и газовой турбиной: а — схема; б — цикл на sT-диаграмме:
1,8,12 — охладители; 2— насос; 3,4,10—компрессоры; 5 — турбина высокого
давления; 6 — реактор; 7 — регенеративный подогреватель; 9 — турбина низкого давления;
// — потребитель энергии
циклов, взятых при тех же параметрах газотурбинной и паротурбинной установок,
из-за дополнительных потерь при теплообмене и большей сложности конструкции
самой установки.
Наиболее перспективным направлением развития ядерных энергетических
установок с газовым теплоносителем остается создание все же одноконтурных систем с
газовой турбиной. Установка оказывается в этом случае более компактной (рис. 24.12).
В процессе а-Ь осуществляется подогрев гелия, причем а-а' в регенеративном
подогревателе 7 и а'-Ь — в реакторе 6. Сжатие гелия до давления 10 МПа производится
компрессорами 3, 4, 10. Так как температура поверхности твэлов составляет примерно
970 К, то подогрев в реакторе осуществляют до 870...920 К. Процесс Ь-с изображает
расширение газа в турбинах высокого 5 и низкого 9 давлений. Расширение газа
заканчивается при температуре, превышающей температуру гелия на входе в реактор на
10... 15 К, так как отработанный газ является греющим теплоносителем в
регенеративном подогревателе 7. Процесс c-d представляет собой изобарное охлаждение
отработанного газа в регенераторе 7, d-e — в охладителе-предохранителе 8 перед
поступлением его в компрессор низкого давления 10. Процессы е-\\ 1-2; 2-3; 3-4 и 4-а изображают
соответственно адиабатное сжатие и изобарное охлаждение в компрессорах 3 и 4 и
охладителях 12 и /. Кпд цикла при указанных параметрах достигает 42 % при
регенеративном подогреве и всего 31 % без регенеративного подогрева.
§ 24.8. Циклы парогазовых установок*
Кпд газовых турбин ограничивается температурой рабочего тела (не выше 1000...
1100 К) и единичной мощностью — из-за возрастающих затрат энергии на собственные
нужды. Если первое ограничение из-за отсутствия термически прочных и стойких
металлов в настоящее время практически неустранимо, то второе ограничение может
быть устранено полностью или частично, если в турбину вместо низкоэнтальпийного
подавать высокоэнтальпийный рабочий агент при той же температуре.
Последний можно получить путем добавки к продуктам сгорания присадки высо-
коэнтальпийного вещества, приводящего к общему увеличений энтальпии рабочего
тела. Чаще всего к продуктам камеры сгорания ГТУ добавляют воду. ГТУ, работаю-
* Одной из первых книг, посвященных парогазовым установкам, была книга проф.
Г. А. Михайловского «Термодинамические расчеты процессов парогоазовых смесей» (1962).
320 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
щие с рабочими телами, состоящими из смесей паров воды и газа или использующие
в тепловой схеме газ и пар, называются парогазовыми установками,, а их
циклы — парогазовыми.
Впервые идея создания энергетической установки с двумя рабочими телами
(водяной пар и продукты сгорания), смешиваемыми перед подачей в турбину, была
высказана в конце прошлого столетия русским инженером П. Д. Кузьминским. Сжатый
воздух в таких установках из компрессора / (рис. 24.13, а) направляется в камеру
сгорания 2, куда насосом 5 через регенеративный подогреватель 4 подается химически
очищенная вода. В камере сгорания 2 происходит смешение горячих продуктов
сгорания (газов) с подогретой водой, в связи с чем камера сгорания 2 выполняет следующие
функции: сжигание топлива, испарение воды и смешение продуктов сгорания с паром.
Образовавшаяся при этом парогазовая смесь из камеры сгорания 2 поступает в
турбину Зу а затем через регенеративный подогреватель 4 либо выбрасывается в атмосферу,
либо направляется в специальный конденсатор. Впрыск воды в продукты сгорания
камеры 2 снижает температуру газов до приемлемых значений и повышает удельную
энтальпию рабочего тела. Энтальпия парогазового агента для (\-\-d) кг
составляет
Лпгс=Ср|ТПгс + [Св7'н+/' + Сп(7'пгс— TH)]dt
где d — количество воды (кг) на 1 кг газа; срг, св, сп — соответственно теплоемкости
газа, воды, пара; Гпгс, Тн — температура пара газовой смеси и насыщения воды. Так
как св и сп существенно больше срг, то при одинаковых температурах hnrc>hr.
Парогазовый цикл можно представить в виде совокупности двух циклов
газовоздушного и парового (рис. 24.13, б). Полезная удельная работа всей установки
определяется суммой площадей парового a-b-c-d-e-k (/п) и газового 1-2-3-4 (7Г) циклов.
Указанные циклы построены для 1 кг продуктов сгорания и d кг водяного пара. Если твп —
масса водяного пара, а тг — масса продуктов сгорания, то их отношение d' = mBn/mr
называется относительным расходом пара. Обычно в таких схемах в регенеративном
подогревателе вода нагревается до температуры кипения. Необходимая для этого
теплота на схеме (рис. 24.13, б) представляется площадью abmn\ она отбирается от
отработавшего рабочего тела, состоящего из пара и газа. На sT-диаграмме удельная теплота,
отданная газовой составляющей парогазового рабочего агента, изображается
площадью 2578 и паровой составляющей — площадью efhg. В сумме они равны площади
abtnn, т. е. теплоте, затраченной на подогрев воды, подаваемой в камеру смешения.
Общая подведенная теплота в парогазовом цикле слагается из теплоты, подведенной
к газовой составляющей q\r (пл. 1564) и паровой составляющей q\n (пл. mbdf).
Термический кпд парогазового (двойного) цикла можно определить отношением
где /г и /п — соответственно работа газового и парового циклов; q\r и q\n — теплота,
затраченная на подогрев рабочего агента в газовом и паровом циклах.
В период освоения циклов с раздельными рабочими телами было опробовано
и осуществлено несколько различных тепловых схем. Наиболее эффективной все же
оказалась схема, в которой паровой цикл по отношению к газовому явился полностью
утилизационным. В такой схеме паровая часть установки работает без дополнительной
затраты топлива. Установка (рис. 24.14, а) состоит из высокотемпературной газовой
турбины <?, котла-утилизатора 4 и паровой турбины 5. Из компрессора / сжатый воздух
подается в камеру сгорания 2, где в результате сгорания топлива образуется рабочее
тело со средней температурой 1370... 1570 К. Такая высокая температура рабочего тела,
поступающего в турбину 3, требует охлаждения лопаточного аппарата. В приведенной
на рис. 24.14, а схеме оно осуществляется вторым рабочим агентом, т. е. водяным паром.
Охлаждающее устройство в газовой турбине является пароперегревателем паровой
Циклы паросиловых установок
321
/
1
1
It
л
/ 8У
k
М
I!
1ч
!
-Qd
К
*i
i
i
i
7/7 5/77
Рис. 24.13. Парогазовая энергетическая установка со смешанным рабочим
телом: а — схема; б— цикл на sT-диаграмме:
/ — компрессор; 2 — камера сгорания; 3 — турбина; 4 — регенеративный
подогреватель; 5 — насос
части комбинированной парогазовой схемы. В нем охлаждается газ газовой турбины
за счет перегрева пара, поступающего из котла-утилизатора 4.
Из пароперегревателя пар идет в паровую турбину 2, которая, как и газовая,
совершает полезную работу. Отработанный пар из турбины 5 через конденсатор 6
насосом 7 вновь подается в котел-утилизатор 4. Электрический кпд парогазовой установки,
работающей по такой схеме, достигает 50 % и более.
Подводимая теплота в рассматриваемом цикле (рис. 24.14, б) определяется только
удельной теплотой газовой части цикла (пл. 6238). Полезная работа всей установки
определяется суммой полезной работы газового цикла (пл. 1234) и работы парового
цикла (пл. abed). Подведенная теплота парового цикла (пл. fbee) в рассматриваемой
схеме складывается из теплоты уходящих газов, поступающих в котел-утилизатор
(пл. 4'7f5), и теплоты, затраченной на перегрев пара при охлаждении лопаток
турбины (пл. 4874').
Термические потери теплоты цикла изображены пл. 15f6 (теплота уходящих газов
7 в
Рис. 24.14. Парогазовая энергетическая установка с разделенным
рабочим телом: а — схема; б—цикл на sT-диаграмме:
/ — компрессор; 2 — камера сгорания; 3 — газовая турбина; 4 —
котел-утилизатор; 5 — паровая турбина; 6 — конденсатор; 7 — насос
1 1 Зак. 584
322 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
из котла-утилизатора) и пл. fade (теплота, теряемая паром в конденсаторе). С учетом
рассмотренного термический кпд цикла определится отношением
где d — относительный расход пара, кг/кг.
§ 24.9. Сравнительный анализ работы тепловых машин
Анализ циклов тепловых машин, сделанный при ряде упрощающих предпосылок, дал
возможность получить простые аналитические зависимости и выявить влияние
факторов, определяющих экономичность и эффективность работы тепловых машин. Такой
анализ представляет собой один из методов термодинамического исследования —
метод круговых процессов. Исторически этот метод возник из необходимости
анализа работы поршневых машин, но может быть применен для решения практически
любой термодинамической задачи, если составлен соответствующий цикл. Точность
решения задачи зависит от выбора цикла.
Стремление учесть в термодинамическом расчете зависимость теплоемкости от
температуры, изменение состава рабочего тела и наличие потока вещества (что имеется
практически в каждой тепловой машине) привело к тому, что для термодинамического
анализа работы тепловых машин стал достаточно широко применяться другой
метод— метод термодинамических функций.
Работу всех типов тепловых машин можно проанализировать с единых позиций,
если использовать свойства открытой неизолированной системы, способной
обмениваться с окружающей средой теплотой и работой.
Уравнение первого закона термодинамики для этих условий может быть записано
в виде
или (так как h — u + pv)
где 6Q — бесконечно малый теплообмен рассматриваемой системы с окружающей
средой; £2, Е\ — энергия системы в конечном и начальном состояниях; h — удельная
энтальпия; w2/2 — удельная кинетическая энергия движения рабочего тела; z —
удельная потенциальная энергия рабочего тела; 6m, 6L — бесконечно малые
взаимодействия рассматриваемой системы с окружающей средой в виде массообмена и
работы.
В общем случае энергия такой системы складывается из кинетической энергии
движения системы в целом, потенциальной энергии, обусловленной положением
системы в каком-либо внешнем поле (сумму указанных энергий иной раз называют
внешней энергией), и внутренней энергии, являющейся суммой кинетической энергии
молекулярного движения, межмолекулярной энергии взаимодействия частиц,
составляющих систему, внутримолекулярной химической энергии, энергии электронного
возбуждения, внутриядерной лучистой энергии, гравитационной энергии и т. д. Если
учитываются все перечисленные слагаемые внутренней энергии (энтальпии), то она
называется полной внутренней энергией (полной энтальпией).
При установившемся состоянии внутренняя энергия системы не меняется (Ег =
— Е\), поэтому для удельных величин
1 ? (24.7)
Полученное уравнение может применяться и в том случае, когда состояния
рабочего тела во всех точках открытой системы периодически и одновременно становятся
идентичными предшествующим состояниям в тех же точках. Таким образом, уравнение
Циклы паросиловых установок
323
(24.7) применимо как к турбинам, так и к поршневым двигателям. С его помощью можно
также анализировать работу отдельных агрегатов тепловой установки (рис. 24.15).
Производство теплоты для промышленных и бытовых целей в большинстве
случаев основано на процессе горения, т. е. на химической реакции между
окислителем и горючим. Для оценки такого теплового источника необходимо определить
максимальное количество теплоты, которое может быть получено в результате сгорания
топлива.
Потоки воздуха и топлива входят в установку практически при давлении и
температуре атмосферы и покидают ее при атмосферном давлении. Изменение состояния,
претерпеваемое потоком воздуха и топлива, когда они служат источником теплоты,
является установившимся процессом, в ходе которого работа через границы потока
обычно не передается (/ = 0). Скорость на входе в установку примерно равна скорости
на выходе из нее (До| = до2), а изменением потенциальной энергии можно пренебречь
(zi = Z2), поэтому в соответствии с уравнением (24.7)
— q — ho— /ii,
где ho — полная удельная энтальпия входящего потока; h\ — полная удельная
энтальпия уходящего потока.
Для того чтобы q было максимальным, температура в сечениях 0—0 и / — /
(рис. 24.15) должна быть одинаковой, а удельная энтальпия уходящего потока —
минимальной. Это соответствует состоянию полного сгорания топлива. На основании
изложенного процесс получения теплоты можно оценить отношением
r\q=\q\/\ho — /iminl,
где r\q — кпд установки для получения теплоты; q — удельная теплота,
от рабочего тела.
Эффективность получения работы оценивается отношением
полученная
где г\е — кпд теплового двигателя; / — удельная работа установки, полученная от
рабочего тела. На практике разность ho— /imin часто заменяют теплотой сгорания топлива.
Максимальная удельная работа установки (рис. 24.15) при сгорании топлива может
быть выражена в виде разности:
y4max= Go— Gmiw
где Go — удельная свободная энтальпия (5.9) потока горючего и окислителя при
давлении и температуре окружающей среды; Gmin— минимум величины G = h — Ts при тех
же давлении и температуре.
Система является вполне стабильной при заданных давлении и температуре,
если величина G минимальна. Как известно, наиболее стабильным состоянием
рассматриваемой системы, состоящей из
смеси окислителя и горючего (при
давлении и температуре атмосферы),
является состояние, при котором весь углерод
топлива входит в состав СОг, а весь
водород топлива — в состав НгО при условии,
что в системе имеется достаточное
количество окислителя^, обеспечивающего
полное сгорание топлива. Для этого
состояния системы по имеющимся
таблич^Продукты
сгорания
)ота
ным значениям G и составу продуктов
сгорания подсчитывают Gmin. Вычитая
11*
Окислитель
Рис. 24.15. Схема теплосиловой установки
324 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
^min из значения Go, соответствующего первоначальному состоянию, определяют
максимальную удельную полезную работу.
Паросиловая установка. Удельная работа /т турбины паросиловой установки (см.
рис. 24.2) определяется уравнением 1Т — Н\ — А2, которое является универсальным и
пригодным для необратимых процессов и может применяться для определения работы
реальных машин. Удельную работу /н, расходуемую на питательный насос (с удельным
объемом воды у4), определим по формуле
dp = v (р4 — Рз) = ДА3_4.
Полезная удельная работа установки /у представляет собой разность работы
паровой турбины /т и питательного насоса: /у = /т—|/н| =Ai — Н2 — ДА3.4.
В большинстве случаев /н мала по сравнению с /т и поэтому значением /н обычно
пренебрегают.
Удельная теплота, сообщаемая пару в котле и пароперегревателе, q\=h\—/i4,
где hi—удельная энтальпия перегретого пара при р\ и Т\\ /i4 — удельная энтальпия
конденсата после насоса.
Удельная теплота, отдаваемая в конденсаторе, определяется разностью: q2=
=Н2 — Из (где Нъ — удельная энтальпия конденсата до насоса; Нч — удельная
энтальпия отработанного пара).
Термический кпд установки определяется отношением
Л/ = (<7| — q2 — ln)/q\:=(hi — А2 + А3 — А4)/(А| — /z4).
Газотурбинная установка. Анализ с использованием тепловых свойств реального
рабочего тела можно провести для любого типа тепловой машины, будь то двигатель,
компрессор или холодильная установка. Так, например, если совершенство процесса
сжатия в компрессоре 3 газотурбинной установки (см. рис. 23.19) оценивается
адиабатным кпд компрессора т]ад=0,80...0,85, показывающим отношение работы
адиабатного сжатия /ад к действительной работе компрессора /к, то удельная работа
компрессора /к=/ад/Лад= (Al—А2)/Лад.
Процесс подвода теплоты q\ в камере сгорания оценивается коэффициентом
полноты сгорания £кс = 0,96...0,98, поэтому q\ =(/1, — /12)ДКС. Действительная удельная
работа расширения газа в турбине /T = (/i4— Нь)г\и, где г\и — 0,85...0,90 — относительный кпд
турбины, являющийся отношением действительной работы турбины к адиабатной
работе расширения.
Таким образом, эффективная удельная работа ГТУ равна разности удельных
работ турбины /т и компрессора /к:
/у = /т — /к = (Л4 — A5)t1u — (А2 — А1 )/т|ад,
а ее эффективная мощность
= МВ[(А4 — А5)Ли — (А2 —А,)/лаД]/3600,
где Мъ — расход воздуха через двигатель, кг/ч.
Эффективный кпд ГТУ
Жидкостный ракетный двигатель. Удельная работа насоса (см. рис. 23.28)
lH = v(p2, — py) = /i2, — hv,
где v — удельный объем топлива; р2, — давление топлива после насосов; р,, — давление
Сжатие газов в компрессоре 325
топлива на входе в насосы; /i2,, hy — удельные энтальпии топлива после и до насоса
соответственно.
Удельная теплота, подведенная к рабочему телу в камере сгорания при р — const,
Q\ = Qh£kc = /*3 — h2<,
где QS — удельная теплота сгорания топлива (горючее + окислитель); £Кс = 0,9...0,95—
кпд камеры сгорания; /г3 — полная удельная энтальпия топлива при температуре в
камере сгорания Гкс; h2, — полная удельная энтальпия продуктов сгорания при Гкс.
Если wi«0 (скоростью впрыска топлива можно пренебречь), то скорость рабочего
тела на выходе из сопла в соответствии с уравнением (20.3) для изоэнтропного
расширения (sz — Sa) может быть определена по соотношению (20.5).
На основании теоремы импульсов суммарный (полный) импульс ракетного
двигателя равен / = Pt = mw2—mw\, поэтому при w\&0 теоретическая тяга
где т — масса топлива в баках; t — время работы двигателя. Удельная тяга составляет
pyR=w2. Реальная удельная тяга Яруд=Рудф, где ф = 0,9...0,95 — коэффициент
удельной тяги.
Двигатель внутреннего сгорания. Аналогично проведен анализ с помощью
уравнения (24.7). Пренебрегая теплопередачей через стенки цилиндра и изменением
кинетической и потенциальной энергий во впускном и выхлопном трубопроводах, имеем
/ул = /ii — /г2, где /уд — удельная работа установки за цикл; h\ и /г2 — полные удельные
энтальпии рабочей смеси во впускном и выпускном трубопроводах, подсчитанные в
виде суммы, _ у *,для состава смеси: С/|2 кмоль СО2; Н/2кмольН2О; 0,79а£0кмоль
N2; 0,21L0(a— 1)*кмоль О2.
Подведенная теплота обычно отождествляется с теплотой сгорания топлива,
поэтому термический кпд т|/ = (Лгi — h,2)/qpH.
Таким образом, используя термодинамические функции и свойства открытой
системы, можно проанализировать работу всех основных типов тепловых машин.
Вопросы 1. В чем отличие цикла Ренкина паросиловой установки от цикла Карно?
2. Как определить термический кпд цикла Ренкина?
3. Каковы методы повышения кпд паросиловых установок?
4. Для чего применяется промежуточный перегрев пара в цикле паросиловой установки?
5. Какова цель применения бинарных циклов?
Глава 25
СЖАТИЕ ГАЗОВ В КОМПРЕССОРЕ
§25.1. Одноступенчатый компрессор
Одноступенчатый компрессор (рис. 25.1, а) представляет собой цилиндр / с
охлаждающей рубашкой «?, внутри которого движется поршень 2. К цилиндру компрессора
подведены воздушные каналы с впускными 4 и нагнетательными 5 клапанами, через
которые сжатый воздух по каналу 6 подается потребителю. Поршень 2 имеет два крайних
положения, называемых верхней и нижней мертвыми точками (ВМТ и НМТ).
Расстояние между этими положениями, умноженное на площадь поршня, называется
рабочим объемом Vh цилиндра компрессора. Объемы между поршнем и
крышками цилиндра в крайних положениях поршня (правом и левом) называются
вредными пространствами W Обычно Vo = (O,O4...O,lO)W Действительная ин-
326
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 25.1. Одноступенчатый компрессор:
а — схема; б — индикаторная диаграмма:
/ — цилиндр; 2 — поршень; 3 — охлаждающая
рубашка; 4 — впускные клапаны; 5 —
нагнетательные клапаны; 6 — канал
5 J
дикаторная диаграмма компрессора для рабочего объема слева от поршня
показана на рис. 25.1, б.
При движении поршня 2 от НМТ влево впускной клапан 4 закрывается и воздух,
имеющийся в цилиндре, сжимается. В точке 2 давление в цилиндре компрессора
оказывается равным давлению воздуха в нагнетательном патрубке. Однако затем давление
в цилиндре повышается дополнительно, что обеспечивает открытие клапана 5 и
выталкивание воздуха в нагнетательный патрубок 6 (в воздушный ресивер с давлением рг).
По мере приближения поршня к крайнему левому положению скорость его движения
уменьшается, перепад давлений между цилиндром и ресивером также уменьшается и
при достижении поршнем ВМТ (точка 3) давления в цилиндре и ресивере
сравниваются. При движении поршня в обратном направлении давление в цилиндре падает,
клапан 5 закрывается и воздух, сжатый в объеме Vo вредного пространства,
расширяется (процесс 3-4). В точке 4 давление в цилиндре оказывается равным давлению р\
окружающей среды, после чего в цилиндре образуется некоторое разрежение,
обеспечивающее открытие впускного клапана 4 и всасывание воздуха в цилиндр / из
окружающей среды. В точке / впускной клапан закрывается, и при обратном движении поршня
сжимается новая порция воздуха.
Кроме приведенного рабочего процесса и действительной индикаторной диаграммы
компрессора в теории компрессоров рассматривается идеальный рабочий
процесс. При этом пренебрегают влиянием клапанов и принимают, что процесс
нагнетания 2-3 осуществляется при давлении рг, равном давлению в ресивере, а всасывание —
при давлении pi, равном давлению окружающей среды. Таким образом, идеальной
индикаторной диаграммой компрессора является диаграмма 1-2-3-4 (рис. 25.1, б),
учитывающая наличие в компрессоре лишь вредного пространства Vo. При всасывании
часть рабочего объема заполняется расширяющимся воздухом вредного пространства,
в связи с чем вводится понятие объемного кпд компрессора
** = {Vi-Va)/{Vi-V0). (25.1)
По мере увеличения р2 (рис. 25.2) объемный кпд уменьшается. Действительно,
при давлениях нагнетания p2i и Р22
поэтому ек2<СеК|. Кроме того, при высоких давлениях нагнетания сильно увеличивается
Сжатие газов в компрессоре
327
температура сжатого воздуха, понизить которую не
удается ниже при интенсивном охлаждении. Это
может вызвать вспышку масла и привести к аварии
установки.
В связи с вышесказанным в одноступенчатых
компрессорах давление нагнетания обычно не
превышает 8... 10 МПа. Формула, (25.1) показывает, что на
объемный кпд существенно влияет объем вредного
пространства W Чем меньше Vo, тем выше ек.
Именно поэтому при конструировании компрессора
стремятся уменьшить Vo. В идеальном компрессоре
этот объем принимается равным нулю (У0 = 0),
поэтому идеальная индикаторная ур-диаграмма имеет
вид, представленный на рис. 25.3, а: На этой
диаграмме процессы 1-2, 1-2] и 1-2г являются различными
термодинамическими процессами сжатия, процесс 2-3 — процессом нагнетания,
процесс 4-1 — процессом всасывания свежего заряда. Если Ко = О, то при завершении
процесса нагнетания 2-3 давление р падает до р\ окружающей среды, так как ВМТ поршня в
этом случае совпадает с осью ординат.
Удельная работа, расходуемая на сжатие воздуха в компрессоре (рис. 25.3, а),
Рис. 25.2. Изменение теоретического
цикла одноступенчатого
компрессора при повышении давления
нагнетания
где I2_3 =
Сжатие в компрессоре осуществляется обычно по политропному процессу. В этом
случае /,.2 определяется выражением (9.44), при адиабатном сжатии — выражением
(9.30), при изотермном сжатии — выражением (9.15). Подстановка (9.44), (9.30) или
(9.15) в (25.2) дает формулы для подсчета абсолютного значения удельной работы
одноступенчатого компрессора:
при политропном сжатии
(25.3)
п— 1
при адиабатном сжатии
(25.4)
S)
рг' const /
V, V
Рис. 25.3. Сжатие газа в одноступенчатом компрессоре: а — на ур-диаграм-
ме; б — на яГ-диаграмме
328 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
при изотермном сжатии
/
p\). (25.5)
Удельная работа компрессора при адиабатном сжатии может быть подсчитана
и иным путем. Действительно, подстановка формулы (9.30) в выражение (25.2)
приводит последнее к виду
/k = [*/(*-1)](P202-Pi0i), (25.6)
или lK — [kR/{k—\)\T2—T\). Так как k = cp/cv и R = cp — cVy то 1к = ср(Т2—Т\) и,
следовательно,
/К = А2-А,. (25.7)
На рис. 25.3, а совмещены для сравнения три термодинамических процесса
сжатия воздуха в одноступенчатом компрессоре; адиабатный 1-22у политропный 1-2,
когда воздух в процессе сжатия охлаждается, но так, что температура его все-таки
увеличивается, и изотермный 1~2\, когда в процессе сжатия температура воздуха
сохраняется неизменной за счет интенсивного охлаждения стенок цилиндра компрессора
охлаждающей жидкостью (см. рис. 25.1). Сравнение процессов сжатия показывает, что
за счет повышения интенсивности охлаждения можно уменьшить работу, расходуемую
на сжатие газа в компрессоре. Однако на практике не удается обеспечить охлаждение
настолько интенсивное, чтобы температура сжимаемого воздуха не повышалась, поэтому
сжатие, как правило, является политропным с показателем политропы k>n>\.
Для определения удельной теплоты, отводимой от сжимаемого газа к охлаждающей
воде, можно при политропном процессе воспользоваться формулой (9.48), при
изотермном процессе — формулой (9.15). При адиабатном процессе сжатия теплообмен
с внешней средой отсутствует (q = 0). Сопоставление рис. 2.4, б и 25.3, а показывает,
что удельная работа одноступенчатого компрессора численно равна
располагаемой:
/к = /о, (25.8)
поэтому для определения удельной работы, затрачиваемой на сжатие газа в
одноступенчатом компрессоре, можно воспользоваться уравнением (2.39), но представить его в виде
(25.9)
где Д/i — изменение удельной энтальпии в процессе сжатия; q — удельная теплота,
идущая на теплообмен газа с окружающей средой в процессе сжатия.
На sT-диаграмме q — площадь под процессом. График на рис. 25.3, б показывает,
что при адиабатном сжатии q — О (так как площадь под процессом 1-22 равна
нулю). При политропном сжатии 1-2 теплообмен характеризуется площадью
с12Ь, поэтому приближенно
/2. (25.10)
При изотермном сжатии Т2—Т\, поэтому
q = t(s2l-si). (25.11)
Как известно, на sT-диаграмме площадь под изобарой дает числовое значение
удельной энтальпии, поэтому при адиабатном сжатии изменение Д/i выражается
площадью с222\а. Приближенно при адиабатном сжатии
(25.12)
При политропном сжатии изменение удельной энтальпии выражается площадью
Ь22\а, поэтому приближенно
Сжатие газов в компрессоре
329
АЛ = Л2-А|«(5|-52|Х712+Г,)/2 (25.13)
и тогда с учетом формул (25.9) и (25.10)
/2. (25.14)
А-А
При изотермном сжатии /i2i=/ii,
поэтому в соответствии с выражениями (25.9) и
(25.11)
s2l). (25.15)
Рис. 25.4. Схема одноступенчатого
центробежного компрессора:
/ — рабочее колесо; 2 — лопатки
Полученные формулы дают возможность
использовать sT-диаграмму для расчета
процесса сжатия газа в одноступенчатом
компрессоре.
Часто для сжатия газа используются центробежные (рис. 25.4) или осевые
турбокомпрессоры. При вращении рабочего колеса /, снабженного лопатками 2, воздух,
находящийся между лопатками, отбрасывается в улитку. Сжимаемому газу при
этом сообщается на выходе скорость w2 движения, большая скорости w\ газа на
выходе в турбокомпрессор. Поэтому часть работы, потребляемая турбокомпрессором,
расходуется на изменение кинетической энергии газа.
Если пренебречь разницей уровней (по высоте) сечений канала движения газа в
турбокомпрессоре на входе и выходе и принять ее равной нулю, то уравнение (2.36)
для рассматриваемого случая получит вид
или после интегрирования
Техническая работа /т расходуется турбокомпрессором на сжатие газа, поэтому
/т=/к. В связи с этим
где q — удельная теплота, отводимая от рабочего тела в процессе сжатия.
Если теплообменом с внешней средой пренебречь (адиабатный процесс сжатия),
то qzzO и тогда в дифференциальной форме
2/2). (25.16)
Если же скорость на выходе из турбокомпрессора приблизительно равна скорости
газа на входе, кинетическая энергия не изменяется: d(w2/2) — 0, тогда d/K = dA, что
соответствует работе сжатия газа в поршневых одноступенчатых компрессорах
[см. (25.7)] без теплообмена с внешней средой.
§25.2. Многоступенчатый компрессор
Анализ работы одноступенчатых компрессоров выявил их непригодность для
получения воздуха, сжатого до высокого давления. Для получения такого воздуха
используются многоступенчатые компрессоры (рис. 25.5), представляющие собой несколько
последовательно включенных одноступенчатых компрессоров. Между ступенями
устанавливаются теплообменники 4У обеспечивающие охлаждение воздуха, сжатого в
предыдущей ступени.
Атмосферный воздух через впускной клапан засасывается в цилиндр первой
ступени (процесс 4-11 на рис. 25.6, а). Затем сжимается политропно (1\-2\) и
перегоняется в холодильник (2\-3\). При движении по змеевику холодильника, омываемому
330
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
10 11 П 9
Рис. 25.5. Двухступенчатый компрессор: а — общий вид; б — схема:
/ — цилиндр первой ступени; 2, 11 — охлаждающая рубашка; 3, 10— поршень; 4 —
холодильник; 5,7—впускной клапан; 6, 8—нагнетательный клапан; 9 —
нагнетательный патрубок; 12 — цилиндр второй ступени
Сжатие газов в компрессоре
Рис. 25.6. Сжатие газа в двухступенчатом компрессоре: а — на ир-диаграм-
ме; б — на sjT-диаграмме
водой, воздух охлаждается до прежней температуры (2\-1<2 на рис. 25.6, б) и
впускается в цилиндр второй ступени (Зг/г на рис. 25.6, а). Так как температура
воздуха при неизменном давлении уменьшилась, соответственно уменьшился и его
удельный объем от и2, до V\2. Затем охлажденный воздух сжимается во второй
ступени (/2-^2) и нагнетается в ресивер (22-Зг).
Промежуточное охлаждение воздуха в холодильнике дает существенный выигрыш
в работе (пл. 2\h222 на рис. 25.6, а). Удельная теплота, отданная воздухом в
холодильнике, определяется площадью под процессом 2\-h (рис. 25.6; б) и подсчитыва-
ется по формулам
q = cp(Th-Tl2); (25.17)
q = li2l — hi2 (25.18)
или по sT-диаграмме она же может быть определена приближенно по формуле
^«(s,2-s2l)(r2l + r,2)/2. (25.19)
Для обеспечения экономичной работы (т. е. наименьшей затраты работы,
расходуемой на сжатие газа) необходимо при проектировании многоступенчатых компрессоров
выполнить следующие два условия:
предусмотреть равенство температур газа на входе во все ступени компрессора и на
выходе из ступеней (последнее обеспечивает необходимые условия для качественной
работы системы смазки);
определенным образом распределить работу между ступенями.
Пусть, например, в двухступенчатом компрессоре jc = p2/pi; *i=P2,/pi;
*2 = /02/Р2,; тогда
х = х\х2. (25.20)
Отношение давлений х задается при проектировании компрессора. При адиабатном
сжатии воздуха в обеих ступенях компрессора
k —
fv(*-D/*.
(25.21)
(25.22)
332
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Если выполняется первое условие (равенство температур), то
Удельная работа, затрачиваемая на сжатие газа,
1 , , I k пт, / (b—\)/k ,
k- I "' 'И
$-Х)1к-2),
или с учетом выражения (25.20)
(25.23)
Работа (25.23) окажется минимальной при выполнении условия d/K2:/clxi = 0,
откуда
k — 1 (*-i)/fc-i k — i r(k-\)/k -{k-\)/k-\ _ n
7 Aj X X\ — U,
или
JCi =
(25.24)
В соответствии с соотношением (25.20) Х2 — л[х. Так как pi,ui, =Pi2yi2 и xi=x2, то
в соответствии с формулами (25.21) и (25.22) /к, = /к2 = /к и тогда
Аналогичные рассуждения показывают, что если в компрессоре не две, а т ступеней
(рис. 25.7, а), то распределить давления между ступенями необходимо так, чтобы
выполнялось условие
х\ = Х2 = ••• = Хт == Vх-
Таким образом, задавшись начальным р\ и конечным рг давлениями воздуха,
сжимаемого в компрессоре, по формулам (25.22) или (25.23) можно определить х и
подсчитать давления сжатия в каждой ступени, с тем чтобы общая работа, расходуемая
на сжатие воздуха при заданных условиях, оказалась минимальной. По мере увеличения
конечного давления газа количество ступеней в многоступенчатых компрессорах
возрастает. На vp- и sT-диаграммах (рис. 25.7) показан процесс сжатия газа в
пятиступенчатом компрессоре. Вследствие охлаждения воздуха в четырех
промежуточных холодильниках общий процесс сжатия 1-2, 3-4, 5-6 и т. д. приближается к
изотермному сжатию 1-3-5-7 и т. д. (рис. 25.7, а), что дает дополнительную экономию
в работе.
Количество теплоты, отобранное от воздуха промежуточными холодильниками,
может быть найдено по si-диаграмме при подсчете суммарной площади,
заштрихованной на рис. 25.7, б.
10' 9* 8' Г 6' 5' V 3' Г S'
Рис. 25.7. Сжатие газа в многоступенчатом компрессоре: а — на vp-
диаграмме; б — на sT-диаграмме
Обратные циклы 333
В m-ступенчатом компрессоре р2 = хр\\ р* — хръ\ рь = хрь\ pg — xp7 и т. д. Так как
р2 = рз; Ра==Ръ\ Рв —р7 и т. д., то последовательно подставляя, получаем р2 — хр\\
p4 = x2p,; р6==х3р\ и т. д. Выбранные таким образом давления сжатия всех
промежуточных ступеней многоступенчатого компрессора дают возможность определить
суммарную удельную работу /к2, расходуемую на сжатие воздуха от начального до
конечного давления, в виде произведения:
где т — число ступеней; /к — удельная работа одной ступени.
Диаметры цилиндров ступеней компрессора постепенно уменьшаются при одном и
том же ходе поршней по мере увеличения давления сжимаемого воздуха.
Соотношения рабочих объемов цилиндров нетрудно получить, так как точки /, 3, 5 и т. д. (рис.
25.7, а) располагаются на одной изотерме. В связи с этим plvl=
И Т. Д., ПОЭТОМУ V3—V\Pi/p3=V\/x; Vb = VzPz/Pb—Vz/X—V\/x2 И Т. Д.
Вопросы!. Что ограничивает значение давления рабочего тела, сжимаемого одноступенчатым
компрессором?
2. Почему при помощи интенсивного охлаждения сжимаемого рабочего тела можно
уменьшить работу, затрачиваемую на это сжатие?
3. С какой целью в многоступенчатых компрессорах используются промежуточные
теплообменники?
4. Как необходимо распределить давление сжатия между ступенями многоступенчатого
компрессора и с какой целью?
Глава 26
ОБРАТНЫЕ ЦИКЛЫ ТЕПЛОВЫХ МАШИН
§26.1. Понятие об обратных циклах.
Обратный цикл Карно
Обратными называются термодинамические циклы, в которых подвод теплоты к
термодинамической системе происходит при более низкой температуре рабочего тела,
чем отвод теплоты (рис. 26.1, а—в). Для осуществления обратного цикла необходимо
иметь в окружающей среде по крайней мере два тела с различными температурами:
тело с низкой температурой служит источником теплоты для термодинамической
системы, а тело с высокой температурой воспринимает теплоту от рабочего тела и
служит приемником теплоты. Процессу подвода теплоты к рабочему телу на
sT-диаграмме соответствует линия процесса А-В-С, в ходе которого энтропия рабочего
тела возрастает на kSAC. Температура источника теплоты, вообще говоря, может
изменяться в процессе, оставаясь, однако, все время выше температуры рабочего тела
на бесконечно малую величину (чтобы процесс А-В-С был равновесным).
Линия C-D-A изображает процесс отвода теплоты от рабочего тела к приемнику
теплоты в окружающей среде, температура которого должна быть в течение всего
этого процесса ниже температуры рабочего тела также на бесконечно малое значение.
Количество теплоты, полученное рабочим телом от источника, эквивалентно
площади А'АВСС на sT-диаграмме, а количество теплоты, отданное рабочим тело
приемнику,— площади AfADCC. Так как абсолютные изменения энтропии в процессах
отвода и подвода теплоты должны быть одинаковыми, а отвод происходит при
более высокой температуре, то количество теплоты, отведенное от рабочего тела,
оказывается в обратном цикле больше подведенного количества теплоты.
Если обозначить абсолютное значение отведенной теплоты Q", абсолютное
значение подведенной теплоты Q' и суммарное (итоговое) количество теплоты за весь цикл
Qu, то Q'<Q" и QU=Q' —Q"<0. Таким образом,
334
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
А
А1
с
D
/1
~&sCB
С
~~f
С'
в)
Г
5 V 5
Рис. 26.1. Схема обратного
термодинамического цикла:
а — на яГ-диаграмме; б — на ир-диаграмме; в—обратный цикл Карно:
/—температура источника теплоты; 2—температура приемника теплоты
I
/
/'
'<Г
4 ,
«' Ц 2'
7
2
3'
термодинамическая система, совершающая обратный цикл, отдает в окружающую
среду энергию в форме теплоты.
Согласно первому закону термодинамики, записанному для кругового процесса,
A(/U = QU—Lu = 0, откуда Lll = Qll и Lu<c0. Это значит, что
термодинамическая система, совершающая обратный цикл, потребляет из окружающей
среды энергию в форме работы.
Вследствие этого в обратных циклах процессы расширения рабочего тела должны
происходить при более низком давлении, чем процессы сжатия (рис. 26.1, б).
Так как |£сж| > |£Расш1, то недостаток количества работы, равный |LJ, должен быть
восполнен от внешнего источника работы.
Важнейшей особенностью обратных циклов является отнятие с помощью
термодинамической системы теплоты в количестве Q' от менее нагретого тела в окружающей
среде и передача теплоты в количестве Q" более нагретому телу. При этом более
нагретое тело получает теплоты больше, чем отдает менее нагретое, на суммарную работу
цикла:
В соответствии со вторым законом термодинамики такой процесс, невозможный
при непосредственном тепловом контакте тел с различными температурами, становится
возможным лишь за счет затраты механической или немеханической работы либо
перехода необходимого количества теплоты с высокого температурного уровня на более
низкий, как, например, при работе абсорбционных машин.
Как и в случае прямых циклов, термодинамически наиболее совершенным
обратным циклом является обратый цикл Карно, т. е. цикл, состоящий из двух
равновесных изотермных и двух равновесных адиабатных процессов (рис. 26.1, в).
В обратном цикле Карно рабочее тело термодинамической системы в процессе 1-2
получает количество теплоты Q' от источника теплоты, имеющего температуру Т.
Полученное количество теплоты эквивалентно площади V122'. В результате адиабатного
сжатия в процессе 2-3 температура тела повышается до температуры, на бесконечно
малое значение превышающее температуру Т" приемника теплоты в окружающей среде.
Это создает возможность отвода теплоты от рабочего тела к приемнику теплоты в
равновесном изотермном процессе 3-4. Количество теплоты Q", передаваемое при
этом окружающей среде, эквивалентно площади V432'. В процессе равновесного
адиабатного расширения рабочего тела 4-1 его температура вновь понижается до
температуры низшего источника теплоты V', после чего цикл повторяется. В процессах
4-1 и 1-2 рабочее тело совершает некоторую работу, а в процессах 2-3 и 3-4 требуется
Обратные циклы
335
подвод работы для сжатия рабочего тела. Итоговое количество энергии, подводимое
в цикле в форме работы, эквивалентное площади 1234, передается приемнику теплоты
в форме теплоты вместе с энергией, полученной в форме теплоты от источника теплоты:
§ 26.2. Показатели эффективности обратных циклов
В зависимости от назначения обратных циклов приемниками и источниками теплоты
в окружающей среде являются различные конкретные тела, а для оценки
эффективности циклов используются различные показатели.
Назначением холодильного цикла является отвод теплоты от тела, имеющего
температуру более низкую, чем температура самого холодного тела в окружающей
среде. Такой процесс называется искусственным охлаждением.
Искусственный холод уже с середины XIX в. широко применяется для длительного хранения
пищевых продуктов. В современной технике искусственное охлаждение используется
для получения сжиженных газов, замораживания водонасыщенных грунтов при
земляных работах, термической обработки материалов, находит применение в медицине и т. д.
Холодильными машинами называют устройства, в которых обратный цикл
используется для искусственного охлаждения. На рис. 26.2 показан холодильный цикл
Карно (/) 1-2-3-4 применительно к случаю, когда приемником теплоты является
естественная окружающая среда, имеющая температуру Го. Полезным эффектом
холодильного цикла является количество теплоты QXK, которое рабочее тело холодильной
машины (хладоагент) отбирает от охлаждаемых предметов (от холодильной камеры),
имеющих температуру Гх.к<СГ0. Это количество теплоты называют холодопроиз-
водительностью цикла.
Энергия, равна сумме холодопроизводительности и затраченной работы цикла, т. е.
Q" = QXK-j-1LJ, передается окружающей (естественной) среде (в конечном счете
атмосферному воздуху), температура которой Г/ = Г0>Гх.к.
Эффективность холодильного цикла выражается холодильным
коэффициентом— отношением полезного эффекта (холодопроизводительности) к
затраченному эффекту, в данном случае работе цикла:
-QXK). (26.1)
По сравнению со всеми другими циклами равновесный обратный цикл Карно
обладает наибольшим значением
холодильного коэффициента в заданном
интервале температур холодильной камеры
Гх.к и окружающей среды Го:
(26.2)
Холодильный коэффициент резко
уменьшается при увеличении перепада
температур между окружающей средой и
охлаждаемым объектом. Так, например,
расчеты показывают, что отнятие от
охлаждаемого объекта теплоты при темпе-
7"
'/7
Тот
пом
то
и
у
_£
3 5
2 L%
'Ж * ^
г
lAs^
9
7
В
' Ш -7
//
10
S
Рис. 26.2. Разновидности обратных
термодинамических циклов:
/ — холодильный цикл Карно; // — цикл Карно для
отопительного теплового насоса; /// — цикл
теплового насоса для утилизации низкотемпературной
теплоты
336 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
ратуре жидкого гелия требует теоретической затраты работы в 700 раз больше, чем при
температурах, близких к комнатным (например, при кондиционировании воздуха в
бытовых и производственных помещениях).
В действительных холодильных циклах (характеризующихся большей или меньшей
неравновесностью термодинамических процессов, а также наличием потерь от трения в
механизмах машины, несовершенства тепловой изоляции и др.) холодопроизводитель-
ность всегда меньше, а затраты работы больше, чем в равновесном обратном цикле
Карно. Действительный холодильный коэффициент любого реального холодильного
цикла, как правило, значительно ниже теоретического холодильного коэффициента.
Тепловым насосом называют машину, работающую по обратному
термодинамическому циклу и предназначенную для передачи более нагретому телу теплоты,
отбираемой от менее нагретого (за счет затраты работы цикла).
В этом случае полезным эффектом является теплота, передаваемая на более
высокий температурный уровень. Примером использования теплового насоса может
служить так называемое динамическое отопление, предложенное У. Томсоном
(Кельвином) еще в 1852 г., но реализованное лишь в 30-е годы XX в. В этом случае
источником теплоты при низкой температуре служит естественная окружающая среда,
например наружный воздух, имеющий температуру Т' — То, более низкую, чем
температура отапливаемого помещения ГПОм- Приемником теплоты при более высокой температуре
является воздух в отапливаемом помещении. За счет затраты работы цикла |LJ,
выражаемой площадью 5678 (рис. 26.2), отапливаемому помещению передается теплота,
равная сумме теплоты Q' = Qo, отнятой у наружного воздуха, и работы цикла |LJ.
Эффективность обратного отопительного цикла характеризуется значением
отопительного коэффициента, представляющего собой отношение полезного
эффекта — теплоты, передаваемой отапливаемому помещению,— к затраченному
эффекту — работе цикла:
г\" Л t I ( Г\ I I/ 1\/1/ I /ОЛ Q\
ф/ == **с I и-"и == \ ^0 ~Т~ М-" и 1 / IJL»„I. I ZD.o)
В случае равновесного обратного цикла Карно теоретический отопительный коэффи-
цинет выражается соотношением
Ф//с = 7г—— т \ Ias—Г=Т—— т = 1 — т it—' (26.4)
^ пом 0) | 5-6| пом 0 0 / ^ пом
Так как предполагается, что То<.Тпом, то отопительный коэффициент положителен
и всегда больше единицы. Например, при температуре наружного воздуха 0 °С и
температуре помещения 25 °С отопительный коэффициент обратного цикла Карно
составляет около 12. Практические значения отопительного коэффициента за счет отличия
реальных циклов от цикла Карно и наличия разного рода потерь равны 2...7.
Другим применением тепловых насосов является утилизация так называемой
отбросной теплоты различных технологических и силовых установок (цикл Карно
9-10-11-12 на рис. 26.2). При этом теплоту Q' = Q0T, отбираемую при охлаждении
готового продукта, уходящих дымовых газов и других теплоносителей, имеющих
температуру ТОТ>Т0, передают с помощью теплового насоса потребителю, имеющему
несколько более высокую температуру TnZ> T0T, например в реактор, где идет химическая
реакция получения продукта. Потребитель получает теплоту Q" = Qn = QoT+1LJ.
В этих случаях для коэффициента эффективности цикла вместо термина отопительный
коэффициент применяют термин коэффициент преобразования.
Термотрансформаторами (или трансформаторами теплоты) называют устройства,
предназначенные для переноса теплоты с одного уровня на другой и сочетающие в себе
прямой и обратный термодинамические циклы. Если циклы составлены из равновесных
Обратные циклы
337
процессов, то такой перенос осуществляется обратимо, т. е. без потери
работоспособности переносимой теплоты.
В общем случае термотрансформатор (рис. 26.3) может работать с двумя
источниками теплоты: «силовой» источник / с температурой Г„ служит для совершения
прямого цикла и получения работы, а «тепловой» источник 4 с температурой Г„2
поставляет основное количество теплоты, подлежащее трансформации, т. е. переносу
на другой температурный уровень. В конкретных схемах источник 4 может
отсутствовать, в этих случаях трансформируемая теплота отбирается от силового источника
(Ти2=Т\) или от окружающей среды (Г„2=Г0).
Во всех случаях трансформации теплоты полезным эффектом является теплота
Qn, полученная потребителями, а затраченным эффектом — количества теплоты QH
и <Э„2, подведенные к термотрансформатору от источников, имеющих температуры
Г„ и Ти2 более высокие, чем температура окружающей среды Го-
Эффективность циклов термотрансформатора характеризуется значением
коэффициента преобразования теплоты
-ф = Qn/(QH+ Qh2) . (26.5)
Если вторым источником теплоты служит окружающая природная среда, то
отбираемая от нее теплота Qo не учитывается в затратах.
Наибольшая термодинамическая эффективность циклов термотрансформации
достигается в том случае, когда как прямой, так и обратный циклы
термотрансформатора являются обратимыми циклами Карно (рис. 26.4). Чтобы определить
значение коэффициента преобразования для этого случая, необходимо теплоты выразить
через абсолютные значения изменения энтропии в прямом Д5пр и обратном Д5Об циклах
и через соответствующие температуры. В этом случае Qn = Tn&S06', <Зи = 7\,Д5пр;
б. Тогда
Qm r"AS"" Г" =г-. (26.6)
^Sn
np /ASo
Так как работа /ц в прямом и обратном циклах одинакова по абсолютному
значению, то
-То). (26.7).
\и\
<?„2ТГ «
Рис. 26.3. Принципиальная схема
термотрансформатора:
/—«силовой» источник теплоты;
2—двигатель (источник работы); 3 — окружающая
природная среда; 4 — источник трансформируемой
теплоты; 5 — тепловой насос (потребитель
работы); 6— потребитель теплоты
ASnp ^
I \
Рис. 26.4. Циклы Карно для повыситель-
ного трансформатора
338 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Подставив отношение (26.7) в (26.6), получим
тп тн-т0 1 — го/ги
тнт0 1 го/ги
*к = Т7тп-тя2т0/тя = \-т0ти2/(титп) • (26-8)
Если трансформируемая теплота отбирается от окружающей среды и не входит в
знаменатель,-выражения (26.6), то
цк = Т„(Т„ - То)/[ТДТа -То)]. (26.9)
При ТН2<.ТП происходит трансформация температурного потенциала ГИ2 теплоты к
более высокому значению Гп, в результате чего за счет затраты низкопотенциальной
теплоты можно получить теплоту более высокого температурного потенциала, хотя и в
меньшем количестве. Трансформатор, передающий теплоту на более высокий
температурный уровень, называется повысительным трансформатором. Коэффициент
преобразования повысительного трансформатора меньше единицы.
Имеются также расщепляющие термотрансформаторы*, с помощью которых
за счет теплоты источника, имеющего некоторую среднюю температуру, снабжаются
теплотой различные потребители, из которых одни имеют температуру выше (повыси-
тельная часть), а другие — ниже, чем температура источника (понизительная часть
термотрансформатора).
Техническая реализация термотрансформаторных схем окзывается экономически
наиболее целесообразной, если имеются источники дешевой теплоты при температуре
лишь немного более низкой, чем температура потребителя теплоты. Такими
источниками являются, например, отходящие газы технологических печей или двигателей,
горячая, но загрязненная в производстве вода (так называемые вторичные тепловые
ресурсы), геотермальные воды и т. п. Обычно в этих случаях располагаемый
температурный перепад между таким источником теплоты и окружающей средой недостаточен
для создания экономичного теплового двигателя. Поэтому как прямой, так и обратный
циклы термотрансформатора целесообразнее всего осуществлять в так называемых
абсорбционных установках.
§ 26.3. Циклы газовой холодильной машины
Одним из первых типов холодильных установок была газовая (воздушная)
холодильная машина (рис. 26.5, а), состоящая из холодильной камеры /, компрессора //,
теплообменника /// и пневматического двигателя (детандера) IV. В теплообменнике ///
газ, сжатый в компрессоре //, охлаждается проточной водой, температура которой
при этом повышается от 7"£ (на входе) до Т" (на выходе). Компрессор // всасывает
газ из холодильной камеры / и после адиабатного сжатия 1-2 (рис. 25.6, а, б, в) подает
его в теплообменник ///. В процессе 1-2 температура рабочего тела возрастает на
Т2—Т\. При этом работа, затраченная на привод компрессора, эквивалентна площади
а12Ь (рис. 26.6, б), а Т2>Т! (рис. 26.5, в).
В изобарном процессе 2-3 газ отдает охлаждающей воде удельную теплоту q\. Его
температура и удельный объем падают, достигая значений Т3 и v3. В детандре IV после
адиабатного расширения 3-4 температура рабочего тела падает до Г4 более низкой,
чем температура холодильной камеры Гхк. Совершаемая при этом работа эквивалентна
* Несмотря на сходство названий, между трансформатором электрического напряжения и
трансформатором теплоты имеется принципиальное различие: повышение электрического
потенциала в идеальном трансформаторе происходит без затраты работы, в то время как повышение
температурного потенциала теплоты даже в идеальном термотрансформаторе требует
обязательной затраты работы.
Обратные циклы
339
I Охлаждающая
ь с гА
S)
Рис. 26.5. Газовая холодильная машина: а — схема; б — цикл
в координатах и, р; в — цикл в координатах s, T:
I — холодильная камера; // — компрессор; /// — теплообменник;
IV — детандер
площади Ь34а. Работа детандера отдается внешнему потребителю, например
электрогенератору.
В холодильной камере протекает изобарный процесс 4-1, в котором газ воспринимает
от окружающей среды теплоту q%. В этом процессе температура и удельный объем
рабочего тела возрастают до значений Т\, Vi, после чего цикл повторяется.
Затраченная на цикл удельная работа эквивалентна площади 12341. Переданная
охлаждающей воде удельная теплота q\ измеряется площадью c32d и равна
/ц. Следовательно, холодильный коэффициент рассмотренного цикла
Я х- 42
(Т2 -
- Т4) -
Так как для адиабатных процессов 1-2 и 3-4
T,/Tx={Pi/Pxf-xyk; T3/TA=(p2/Piyk-l)/k- T2/Tt=T3/T4,
то выражение для гх можно представить в следующей форме:
«*= 14(7*2/7*,) - 1] = 1/[(7"з/7*4) - 1] = 1/[ (Р2/Р,)(*"0/*- 1] ■ (26.10)
340 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Таким образом, чем ближе к единице отношение абсолютных температур Тч/Т\ или
Г3/Г4, тем выше экономичность цикла газовой холодильной машины.
Понижение уровня температуры охлаждающей воды в теплообменнике ///
(гп-п на рис. 26.5, в) при неизменных прочих условиях приводит к увеличению
гх. Более низкие значения температур Т'ъ и Т'1 (например, в зимнее время) позволяют
понизить давление /?2, которое необходимо поддерживать на выходе из компрессора, а
это приводит к уменьшению работы, затрачиваемой на привод компрессора. С
понижением давления р2 уменьшаются отношения Г2/Г1 и Гз/Г4. Чем выше требуемая
температура в холодильной камере (7\к), тем выше температуры Т\ и Г4, больше q<i, меньше
/ц и, следовательно, больше холодильный коэффициент гх.
Холодильный коэффициент гх газовой холодильной машины существенно отличается
от холодильного коэффициента обратного цикла Карно. Цикл Карно можно было бы
осуществить обратимо отнимая теплоту в холодильной камере при Т\ = ТХК и обратимо
отдавая теплоту охлаждающей воде при Гз=Гв.
На рис. 26.5, в обратный цикл Карно 1-2'-3-4'-1 показан пунктиром. Сопоставляя
площади c4'ld, c41d и \2'34f с площадью 1234, легко убедиться в том, что
экономичность реального цикла газовой холодильной машины значительно ниже экономичности
соответствующего цикла Карно. Сравним эти циклы для следующих условий: пусть
циклы осуществляются в интервале температур от 291 до 265 К, при этом в цикле
газовой холодильной машинй Г3 = 291 К\ рз = 0,490 МПа; р4 = 0,098 МПа. В обратном
цикле Карно 1-2'-3-4'-1 (рис. 26.5, в) Г3 = 291 К; Г4=Г, = 265 К. Принимая /г=1,4,
находим температуру в цикле газовой холодильной машины: Г4 = Г3(р4/рз)(*~1)/* =
= 291(98/490)(|<4~|)/|>4 = 183,7 К. В цикле газовой холодильной машины в соответствии
с формулой (26.10) гх=Т4/{Тз — Г4) = 183,7/(291 — 183,7)= 1,71; в обратном цикле Карно
ex=Ti/(Tz— Г,) = 265/(291 — 265)= 10,2.
Из полученных результатов следует, что в рассматриваемых условиях при одной и
той же затрате работы холодопроизводительность газовой холодильной машины в шесть
раз ниже холодопроизводительности машины, в которой осуществляется обратный
цикл Карно. Вследствие низкой экономичности для газовых холодильных машин
характерны большие расходы рабочего тела. В связи с этим в настоящее время
получили распространение газовые (воздушные) холодильные машины с
турбокомпрессорами. Экономичность этих машин можно повысить применением цикла с регенерацией.
§ 26.4. Циклы парокомпрессионной холодильной машины
В качестве рабочего тела (хладоагента) можно использовать влажный пар какой-либо
жидкости с температурой кипения, не превышающей 0 °С (при атмосферном давлении).
В этом случае холодильный цикл можо осуществить с изотермным подводом и
отводом теплоты и тем самым приблизить его к обратному циклу Карно.
На рис. 26.6, а приведена схема такой компрессионной холодильной машины.
Хладоагент в виде влажного или сухого насыщенного пара при отрицательной
температуре и давлении выше атмосферного (точка /) из испарителя /// поступает в компрессор
//. После адиабатного сжатия в компрессоре // (процесс 1-2 на рис. 26.6, б) температура
пара становится выше температуры охлаждающей воды Г", которая в рассматриваемых
условиях играет роль окружающей среды. Сжатый пар поступает в охладитель
(конденсатор) IV, где за счет отдачи теплоты охлаждающей воде при р = const
происходит конденсация пара. Из sT-диаграммы следует, что в том случае, если
хладоагент, поступающий в конденсатор, является влажным паром, отвод теплоты
(парообразования) будет происходить полностью в изотермных условиях. В более
общем случае в охлаждающую воду в процессе 2-3-4 отводится не только теплота
парообразования, но и теплота перегрева пара. В точке 4 пар полностью
конденсируется. Далее в процессе 4-5, протекающем при h = const, конденсат проходит через
Обратные циклы
i
1
- ™-П
г
?
шштттшшт
\
н
(
1
\
(к
^рВ?"
VsY
%5 т'
н1
1 'р
1 'Р
^1 Q
^ z
г
^;
а<
0
'А
7ffr&
/ It*
г*/ jVi^-
Г|^
г 1
1
1
l
\5*
i
с0 е'с
ЪлУ
'Л
h
А
\
^с
341
г
т
-fr -
d
5
Рис. 26.6. Парокомпрессионная холодильная машина: а — схема; б —
парокомпрессионный цикл в координатах s, T:
I — охлаждаемая камера; // — компрессор; /// — испаритель;
IV—конденсатор; V — регулирующий (дроссельный) вентиль
регулирующий вентиль V, в котором дросселируется до давления испарения.
(Необратимый процесс 4-5 изображен на sT-диаграмме условно.) Процесс
дросселирования в двухфазной области всегда протекает с понижением температуры. В
испарителе /// происходит процесс испарения 5-1 и хладоагент снова поступает в компрессор,
после чего цикл повторяется.
Теплота от веществ, хранящихся в холодильной камере, передается к испарителю
с помощью какого-либо незамерзающего жидкого теплоносителя, циркулирующего
между камерой / и испарителем ///.
В конечном счете после завершения рассмотренного цикла теплота, отбираемая в
холодильной камере при низкой температуре, вместе с теплотой, соответствующей
работе, затрачиваемой на привод компрессора, при более высокой температуре
передается охлаждающей воде, проходящей через конденсатор.
Рассмотренная холодильная машина называется парокомпрессионной, так
как сжатие пара осуществляется в ней с помощью компрессора.
При использовании влажного пара цикл, совершаемый в такой машине, отличается
от обратного цикла Карно только тем, что процесс расширения в парокомпрессионной
машине протекает по необратимой адиабате 4-5 (рис. 26.6, б), с чем и связано некоторое
уменьшение холодопроизводительности в парокомпрессионном цикле по сравнению
с обратным циклом Карно.
Работа адиабатного сжатия хладоагента в компрессоре (пл. 1234b) h^ = h<i — h\.
Теплоте ^2, отведенной из холодильной камеры и затраченной на испарение
хладоагента, на sT-диаграмме соответствует площадь 51dc. Следовательно, холодильный
коэффициент рассматриваемой парокомпрессионной машины
Ex = nA-51dc/nA-1234b = (hl — hb)/(h2 — hi). (26.11)
Таким образом, для повышения экономичности такой холодильной машины
необходимо стремиться к увеличению площади 51dc на sT-диаграмме и уменьшению
площади 1234b. Размер площади 51dc зависит от температуры 7\к, которую требуется
поддерживать в холодильной камере. Из соотношения (26.11) следует, что
экономичность холодильной машины понижается по мере пойижения Гхк, линии температур
Fp-Гр' и линии испарения 5-1. Площадь 1234b, в свою очередь, зависит от положения
линии 2-3-4, которое связано с температурой охлаждающей воды (линия Гв-Гв0-
Экономичность холодильной машины будет возрастать при понижении температуры ох-
342
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
лаждающей воды, так как при этом уменьшается работа /ц, затрачиваемая на сжатие
хладоагента в компрессоре. Повышение экономичности установки может быть достигнуто
также путем переохлаждения хладоагента на выходе из конденсатора.
Переохлаждение можно получить в специальном теплообменнике-переохладителе или в самом
конденсаторе. В случае переохлаждения площадь, соответствующая количеству теплоты
<72, увеличится, достигнув площади 5'tdc'. На дГ-диаграмме процесс переохлаждения
4-4' практически совпадает с нижней пограничной кривой. Увеличивая глубину
дросселирования путем прикрытия регулирующего вентиля, можно понизить температуру
хладоагента перед испарителем (см. процесс 5"-V на рис. 26.6, б) и, следовательно,
температуру в холодильной камере. Приоткрывая вентиль, добиваются повышения
температуры Тхк.
В рассматриваемой холодильной машине в отличие от газовой вместо детандера
применяется дросселирующей вентиль. Это позволяет существенно упростить
конструкцию. С другой стороны, использование детандера вместо вентиля привело бы к замене
необратимого процесса дросселирования 4-5 процессом адиабатного расширения 4-5
в детандере, повышению экономичности холодильной машины за счет увеличения q2
до значения, определяемого площадью 5'" Ыс", и уменьшению затрачиваемой работы
на величину работы детандера (пл. Ъ45'"). Однако создание детандера на жидком (а
не газообразном) рабочем теле представляет собой технически трудную задачу.
Парокомпрессионная холодильная машина при малом температурном перепаде
термодинамически более совершенна, чем газовая. При большом температурном
перепаде более экономичной оказывается газовая холодильная машина. Парокомпрес-
сионные машины обычно применяют для получения температур 7\к в пределах от 273
до 153 К. Расчет парокомпрессионного цикла удобно выполнять пользуясь sT-диаграм-
мой с нанесенными на ней линиями /i = const. Наряду с sT-диаграммой применяются
также hp- или h—lgp-диаграммы. Так, с помощью h—lgp-диаграммы (рис. 26.7, а)
можно определить холодильный коэффициент гх без вычисления площадей (рис. 26.7, б)
в виде отношения: zx — a/b = (h\ — hb)/{h2 — h\).
Хладоагенты для парокомпрессионных установок должны удовлетворять
определенным требованиям. Необходимо, чтобы в выбранном интервале температур цикла
хладоагент мог существовать в состоянии влажного пара. Давление насыщенных
паров хладоагента в этом интервале температур не должно быть слишком низким или
слишком высоким (нарушение этого требования привело бы к значительному
усложнению конструкции холодильной установки). Теплота парообразования хладоагента г
Рис. 26.7. h — lgp-диаграмма: а — схема диаграммы; б — парокомпрессион-
ный цикл на h—lgp-диаграмме
Обратные циклы
343
при температуре Гз должна быть достаточно высокой. Последнее требование связано с
тем, что количество теплоты q2y отбираемое из охлаждаемого объема, зависит от
разности энтропии s\ — S5 (рис. 26.6, б), а разность S3 — $5 тем больше, чем больше
разность энтропии s3 — s4, при этом s3 — s4 = /'/7Y
Из этого соотношения видно, что при одном и том же расходе хладоагента
холодопроизводительность цикла тем выше, чем больше величина г. Одним из лучших
хладоагентов является аммиак, используемый широко в промышленных установках.
В бытовых холодильных установках аммиак не применяется из-за токсичности и
коррозионной активности. Широкое распространение в качестве хладоагентов
получили фторхлорпроизводные простейших предельных углеводородов. Они отличаются
химической стойкостью, нетоксичны и не взаимодействуют с материалом конструкции.
Температура кипения этих жидкостей изменяется в широких пределах. Установки
с такими низкокипящими жидкостями по величине гх мало уступают аммиачным,
однако из-за малой теплоты парообразования расход этих хладоагентов по сравнению
с аммиаком значительно выше.
§ 26.5. Цикл абсорбционной холодильной машины
Одним из видов холодильных машин, потребляющих в процессе своей работы
тепловую энергию, являются абсорбционые холодильные машины. Рабочим телом в таких
машинах служит влажный пар. Цикл абсорбционной холодильной машины отличается
от цикла парокомпрессионной только способом сжатия пара.
В абсорбционных холодильных машинах используется явление абсорбции пара
раствором. Абсорбцией называется способность некоторых тел при определенных
условиях поглощать другие тела. Например, пар чистого вещества может быть поглощен
(сконденсирован) этим же веществом в жидком состоянии при условии, что температура
жидкости ниже температуры пара. В отличие от этого растворы обладают
способностью абсорбировать пар раствора одного состава жидким раствором другого состава
даже при нарушении этого условия. Это
свойство раствора и используется в
рассматриваемых холодильных машинах (рис. 26.8).
Испарение водоаммиачного раствора с
концентрацией аммиака хк происходит в
парогенераторе / при давлении рк и температуре Т\.
При этом на процесс испарения затрачивается
количество теплоты q\> которое подводится
горячим теплоносителем.
Низкокипящим компонентом раствора
является аммиак. Так как парциальное
давление водяного пара над раствором при
температурах, имеющих место в парогенераторе,
очень мало, из раствора практически
выделяется почти чистый аммиачный пар. В
конденсаторе 2 при постоянном давлении pK = const и
температуре Т\ полученный пар превращается
в жидкость, а выделившаяся в процессе
конденсации теплота воспринимается
охлаждающей водой. В редукционном вентиле 3
давление жидкого аммиака снижается до давления в
абсорбере 6 ра<СрКу в котором концентрация
раствора поддерживается на уровне ха>хк.
Этот процесс сопровождается пониже-
xa,Pa -=Г-гГгС>:
Рис. 26.8. Схема простейший
абсорбционной холодильной машины:
/ — парогенератор; 2 — конденсатор; 3 —
редукционный вентиль; 4 — испаритель; 5 —
холодильная камера; 6—абсорбер; 7—насос;
8 — редукционный вентиль
344 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
нием температуры от Т\ до Т2. После этого образовавшийся влажный пар аммиака
поступает в испаритель 4, где его степень сухости увеличивается до единицы. Количество
теплоты q2, необходимое для протекания процесса испарения, подводится к испарителю
от тел, находящихся в холодильной камере 5. Затем полученный в испарителе сухой
насыщенный пар при температуре Т2 и давлении ра поступает в паровое пространство
абсорбера 6. Абсорбер заполнен раствором аммиака. Полученный из этого раствора пар
находится под давлением ра и имеет более высокую температуру, чем пар, поступивший
из испарителя. Поэтому в соответствии с четвертым свойством растворов холодный
пар поглощается раствором. Выделяющаяся при этом теплота абсорбции отводится
охлаждающей водой.
При работе холодильной машины в парогенераторе и абсорбере поддерживается
некоторый постоянный уровень концентрации растворов. С этой целью из абсорбера 6
обогащенный аммиаком раствор с помощью насоса 7 в определенном количестве
подается в парогенератор /. Одновременно раствор аммиака, обедненный вследствие
выпаривания, из парогенератора / направляется в редукционный вентиль 8, дросселируется
от давления рк до давления ра и поступает в абсорбер 6. Этот обедненный раствор
по своим свойствам близок к воде, поэтому его температура в процессе
дросселирования остается практически постоянной и равной температуре в парогенераторе Т\.
Давление в парогенераторе рк соответствует температуре охлаждающей воды в
конденсаторе, в то время как давление ра в абсорбере соответствует температуре в холодильной
камере.
В отличие от парокомпрессионной установки роль компрессора здесь выполняет
абсорбционный узел. Он состоит из парогенератора /, абсорбера 6, насоса 7 и
редукционного вентиля 8. Таким образом, вместо механической работы, необходимой на
привод компрессора, в абсорбционной машине используется разность температур
горячего (в парогенераторе) и холодного (в абсорбере) источников теплоты. Если
пренебречь незначительной работой, затрачиваемой на привод насоса, то коэффициент
£а, характеризующий экономичность абсорбционной холодильной машины, можно
представить в виде отношения: Zia = q2/qu где q2 — количество теплоты, отнятое в
холодильной камере (полезный эффект), a q\ — количество теплоты, затраченное в
парогенераторе. Величину £а называют коэффициентом теплоиспользования.
Несмотря на относительную простоту конструкции абсорбционных холодильных
машин, их целесообразно применять в тех случаях, когда для работы парогенератора
имеется возможность использовать теплоносители низкого потенциала (например,
отработавший водяной пар).
§ 26.6. Цикл теплового насоса.
Термохимический трансформатор теплоты
Тепловой насос, применяемый для отопления зданий с использованием теплоты
окружающей (природной) среды (рис. 26.9), состоит из компрессора /, конденсатора 2,
регулирующего вентиля 3 и испарителя 4. Эти элементы составляют обычную
компрессионную холодильную установку, например паровую (см. рис. 26.6).
При испарении хладоагента в испарителе 4 он воспринимает теплоту q2 от воды,
подаваемой насосом 5 из водоема 8. В конденсаторе 2 холодильной установки
теплота q\ от нагретого в результате сжатия хладоагента передается «обратной»
воде системы отопления 9 здания 7. Если работа, затраченная в компрессоре /,
равна /ц, то в соответствии с выражением (26.3) и рис. 26.6
Я\
Ф' = ТГ
Поскольку qK = q2-\- |/ц| > |/ц|, всегда отопительный коэффициент ср,> 1. Реально дости-
Обратные циклы
345
Рис. 26.9. Схема теплового масоса:
/ — компрессор; 2 — конденсатор; 3 — вентиль; 4 — испаритель; 5,6 —
насос, 7 — потребитель; 8 — водоем; 9 — отопительная система
жимые значения составляют 3...5. Это означает, что, расходуя единицу электроэнергии
на привод компрессора теплового насоса, можно получить для целей отопления
в 3...5 раз большее количество теплоты, чем при прямом использовании того же
количества электроэнергии в электрических нагревательных приборах. В тепловых
насосах могут использоваться и другие типы холодильных машин, в частности
пароструйные и абсорбционные.
Работа термохимических трансформаторов теплоты основана на свойствах
растворов. В используемых для этих целей растворах растворителем является вода, а
растворенным веществом — гидрат оксида калия КОН или едкий натр NaOH.
Температура кипения чистой воды ниже температуры кипения раствора при том-же
давлении. На рис. 19.4 изображена зависимость температуры кипения водяного
раствора КОН от концентраций хКОн и *н2о при различных давлениях. При давлении
10 кПа чистая вода кипит при температуре 372,64 К, а 90 %-ный раствор КОН —
при 643 К.
Когда нужно повысить потенциал теплоты (например, получить пар более высокого
давления и температуры, чем имеющийся в наличии греющий пар),
термотрансформаторы работают по повысительной схеме, когда же необходимо средний потенциал
теплоты трансформировать и в более высокий, и в более низкий, трансформаторы
работают по расщепительной схеме.
На рис. 26Л0, а изображена схема расщепительного термохимического
трансформатора теплоты. Такая установка предназначена для получения за счет теплоты пара
среднего давления р\ (и соответственно средней температуры Т\) двух потоков пара: при
давлении р2 более высоком (р2~> р\) и при давлении р3 более низком (p3<Pi), чем
исходное давление.
Часть пара среднего давления р\ с температурой Т\ направляется в абсорбер
/ и часть — в испаритель VII. В абсорбере при давлении р\ происходит поглощение
пара раствором, концентрация которого поддерживается на уровне ха (рис. 26.10, б).
Абсорбция пара сопровождается выделением теплоты абсорбции, благодаря чему в
абсорбере устанавливается температура Т27>Т\. Основное количество теплоты
абсорбции непрерывно отводится из абсорбера благодаря циркуляции раствора под
действием насоса // через генератор пара высокого давления ///. В генераторе
теплота используется для испарения воды при температуре Т2~>Т\ и давлении насыщения
P2>Pi, соответствующем этой температуре.
Получение пара с температурой Т2 эквивалентно передаче теплоты от менее
нагретого тела к более нагретому. В соответствии со вторым законом термодинамики это
сопровождается переносом теплоты с более высокого температурного уровня Т\ на
346
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
х„ л
Рис. 26.10. Расщепительный термохимический трансформатор теплоты:
а — схема установки; б — процесс в координатах х, Т:
I — абсорбер; /// — генератор пара высокого давления; IV— теплообменник;
V — редукционный клапан; //, VI, VIII — насосы; VII—испаритель
более низкий Гз, что происходит в результате процессов, совершающихся в
испарителе VII. Раствор, непрерывно обедняющийся в абсорбере при поглощении пара,
направляется в испаритель VII, где за счет теплоты подаваемого туда пара из него
выпаривается вода и образуется пар низкого давления рз<.р\ с температурой Тз<С.Т\.
При этом концентрация раствора повышается до значения хи (рис. 26.10, б).
Циркуляция раствора между испарителем VII и абсорбером /, давление в которых
различно, осуществляется с помощью насоса VIII, а регулировка перепада давления —
с помощью редукционного клапана V. Теплообменник IV играет роль регенератора,
в котором теплота горячего обедненного раствора используется для подогрева
концентрированного раствора, возвращаемого в абсорбер.
Конденсат греющего пара из испарителя поступает в генератор пара высокого
давления ///, для чего устанавливается насос VI. При отсутствии потерь суммарное
количество пара высокого и низкого давлений равно расходу пара среднего
давления.
§ 26.7. Получение сжиженных газов
Область применения сжиженных газов необычайно широка. Она включает в себя многие
отрасли народного хозяйства.
Для получения сжиженных газов могут быть использованы дросселирование
(эффект Джоуля — Томсона), расширение газа, охлаждение рабочего тела
специальными хладоагентами, вакуумирование сжиженного газа, вихревой эффект Ранка, явление
Пельтье, адиабатное размагничивание и др.
В идеальном цикле, состоящем из обратимых процессов изотеркного сжатия в
компрессоре, изоэнтропного расширения в детандере и изобарного процесса передачи
теплоты от сжижаемого газа рабочему телу, работа цикла /ц (минимальная работа
сжижения) определится разностью: U = q2 — Q\, где q\ — теплота, отнятая рабочим телом
от сжижаемого газа; цч — теплота, отдаваемая рабочим телом окружающей среде.
Ниже приведены данные о минимальной удельной работе, необходимой для сжижения
Обратные циклы
347
некоторых газов при р = 0,1 МПа и Г = 300 К, и указана температура Т5 кипения
сжиженного газа при атмосферном давлении:
Газ
Водород
Гелий
/ц, кДж/кг
11900
6850
Т., К
20,4
4,2
Газ
Кислород
Воздух
/ц, кДж/кг
637
738
7",, К
90,2*
80
Основными методами сжижения газов считаются каскадный метод,
представляющий собой совокупность нескольких парокомпрессионных холодильных
циклов; метод Линде, в котором для сжижения используется адиабатное
дросселирование предварительно охлажденного газа, и метод Клода, в котором
помимо адиабатного дросселирования газа используется адиабатное расширение с
отдачей работы в детандере.
Холодильные установки (рис. 26.11, а), в основе которых лежит метод Линде,
наиболее просты и компактны. Детандерные ожижители сложнее по конструкции,
но более совершенны с термодинамической точки зрения. После сжатия в компрессоре
/ до давления рг (рис. 26.11, б) газ поступает в холодильник //, в котором с помощью
вспомогательного хладоагента температура газа понижается до уровня Т2{Т2—Т\).
Затем в противоточном теплообменнике /// газ в процессе 2-3 охлаждается при
постоянном давлении рч до еще более низкого уровня, соответствующего температуре
7Y
Роль охлаждающего агента в теплообменнике играет холодный газ низкого
давления, который движется в обратном направлении, показанном на схеме пунктиром
(рис. 26.11, а). В дроссельном вентиле IV давление и температура газа падают,
достигая значений р\ и Ts> соответствующих состоянию влажного пара. (Здесь
рассматривается установившийся режим работы установки; предполагается также, что
состояние газа перед дросселированием соответствует точке, лежащей внутри области,
ограниченной кривой инверсии.) Образующаяся при этом двухфазная смесь поступает
в сосуд V. В холодильных установках, предназначенных для получения сжиженных
as
Рис. 26.11. Холодильная установка с дросселированием предварительно
охлажденного газа: а — схема; б — цикл в координатах s, T:
I — компрессор; // — холодильник; /// — теплообменник; IV — дроссельный вентиль; V —
сосуд; VI — вентиль
348
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 26.12. Процесс изотермного сжатия
газа (в координатах s,h)
газов, жидкая фаза отделяется и отводится
из сосуда через вентитль VI. При этом цикл
не является полностью замкнутым. Так как
в процессе 4-5 к сосуду V подводится
некоторое количество теплоты qly то влажный
пар становится сухим. Сухой насыщенный
пар поступает в теплообменник ///,
подогревается до уровня Т\ и в перегретом
состоянии возвращается в компрессор. При
этом для возобновления цикла в
компрессор необходимо непрерывно подавать
дополнительное количество газа, равное массе
полученного жидкого продукта.
Удельное количество теплоты,
необходимое для перевода газа в жидкое
состояние, равно разности энтальпий h\—/i5, что
эквивалентно площади al5sc на sT-диаграмме (рис. 26.11, б). Величина h\ — /15 зависит
от температуры Т\ и физических свойств рабочего тела. При закрытом вентиле VI
(рис. 26.11, а) цикл становится замкнутым. В этом случае количество теплоты q\
(эквивалентное пл. 44'5'5) определяет холодопроизводительность цикла и должно
подводится к сосуду от охлаждаемых тел. Это количество теплоты определяется
разностью энтальпий Л5 —/*4, а работа, затраченная на свершение цикла, lK = qK — q\>
где qK — количество теплоты, отведенное в холодильнике и компрессоре. Так как
процессы теплообмена 2-3 и 5-1 протекают при постоянном давлении, то из теплового баланса
теплообменника /// следует, что h2— /i3 = Ai—/i5. В это уравнение вместо значения Нъ
можно подставить энтальпию /i4, так как в процессе дросселирования 3-4 энтальпия
рабочего тела не изменяется (/i3 = /i4). Следовательно, ^,=/г5 — /i4 = /*i — h2. Таким
образом, холодопроизводительность рассматриваемого цикла численно равна
понижению энтальпии газа при его изотермном сжатии. Следует иметь в виду, что величина
q\ не зависит от температуры перед дроссельным вентилем, однако предварительное
охлаждение сжатого газа в теплообменнике /// позволяет понизить температурный
уровень получаемого холода.
Учитывая, что в теоретическом цикле работа /к равна работе изотермного
сжатия газа в компрессоре (см. процесс 1-2 на рис. 26.11, б), получим lK = qK — (hi — h2) =
= Г|(5| — s2) — (h\ — h2). Это выражение дает возможность определить холодильный
коэффициент теоретического цикла с дросселированием предварительно охлажденного
газа:
Некоторые данные, характеризующие рассмотренный теоретический цикл при
pi = 0,1 МПа, Т\ = 293 К и различных давлениях р2, приведены в табл. 26.1. В качестве
рабочего тела выбран воздух. Из таблицы видно, что эффективность рассмотренного
цикла низка. В связи с этим цикл с дросселированием, несмотря на его простоту,
не может быть рекомендован для крупных установок.
По мере повышения давления р2 холодопроизводительность цикла возрастает
и достигает максимума при р2у равном давлению инверсии р„. Это объясняется тем,
что при р2 = Ри изотермы в системе координат s, h имеют минимум (рис. 26.12), а
минимум энтальпии соответствует условию (dh/ds)T=T—v(dT/dv)p = 0. Из s/i-диаграм-
мы следует, что максимальная холодопроизводительность теоретического цикла
определяется разностью энтальпий hi — /г„. Эффективность рассмотренного цикла может
быть повышена различными путями, например с помощью двойного дросселирования
и введения промежуточного охлаждения газа.
Обратные циклы
349
Циклы, основой которых является процесс дросселирования рабочего тела,
применяются для получения низкотемпературного холода, получения сжиженных
газов, а также разделения газовых смесей.
Таблица 26.1
Данные, характеризующие цикл
Холодопроизводительность q\, кДж/кг
Изотермная работа сжатия /к, кДж/кг
Холодильный коэффициент ех-Ю2
Наиболее низкая температура, которую можно получить в
цикле Ts, К
Давление р2, МПа
6
13,4
344
3,91
82
10
21,6
387
5,58
82
20
37,5
446
8,40
82
40,5
46,5
503
9,25
82
§ 26.8. Общие принципы и способы достижения
сверхнизких температур
Получение низких температур в термомеханических обратных циклах основано на
способности рабочих тел уменьшать свою температуру при изменении объема в
адиабатных процессах с совершением работы (в детандере), при дросселировании, испарении
в вакуум, при растворении.
Однако в области сверхнизких температур (ниже 4 К) уже не остается рабочих
тел, обладающих подходящими свойствами. (Если использовать кипение жидкого
изотопа гелия 3Не в вакууме, то можно получить температуру порядка 0,3 К.) Для получения
еще более низких температур применяются термодинамические системы, в которых для
изменения температуры и энтропии используются процессы, связанные с
немеханической работой. При этом общий принцип понижения температуры рабочего тела остается
тем же, что и в термодеформационной системе. На первой стадии процесса над
телом совершается работа при одновременном отводе теплоты к имеющемуся
приемнику теплоты возможно более низкой температуры. В идеальном случае
температура рабочего тела остается постоянной и равной температуре приемника теплоты,
а энтропия рабочего тела уменьшается. На второй стадии осуществляется адиабатный
процесс, в котором происходит возвращение системы к первоначальному значению
того параметра, который изменялся на первой стадии процесса при подводе работы.
При этом температура рабочего тела отпускается ниже температуры использованного
приемника теплоты. Эффект понижения температуры оказывается наиболее сильным,
если процессы на обеих стадиях проводятся
обратимо.
Для получения сверхнизких температур
используют термомагнитную систему, рабочим
телом которой являются кристаллы парамагнитной
соли, содержащей ионы трехвалентных металлов
гадолиния, железа, хрома или церия. Благодаря
наличию незаполненной внешней электронной
оболочки эти ионы обладают некоторым
магнитным моментом, поэтому их энергия может
изменяться под воздействием внешнего
магнитного поля. Напряженность магнитного поля
можно использовать в качестве параметра,
характеризующего нетепловое (магнитное) воздействие
на систему при рассмотрении происходящих
процессов в энтропийной диаграмме (рис. 26.13).
Рис. 26.13. Процесс охлаждения
вещества путем адиабатного
размагничивания парамагнетика
350 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
При отсутствии внешнего поля (//0 = 0) магнитные диполи ориентированы хаотически,
а кристалл в целом не обладает результирующим магнитным моментом (точка А). При
увеличении напряженности поля до значения Н\ происходит поворот диполей по
направлению поля, что приводит к увеличению внутренней энергии системы. При отсутствии
теплообмена это вызвало бы повышение температуры кристалла. Если же кристалл
находится в тепловом контакте с приемником теплоты, имеющим температуру Го, то
намагничивание происходит изотермно (процесс А-В), а энтропия кристалла уменьшается на
величину ДЗ^.д.
На следующей стадии кристалл изолируют от теплообмена с окружающими
телами и размагничивают уменьшением магнитного поля до нулевого значения (процесс
В-С). Температура кристалла уменьшается до значения Tc<cTq. Охлажденный таким
образом кристалл либо сам служит для изучения свойств вещества при низких
температурах, либо используется для охлаждения образцов других веществ, которые не
обладают магнитными свойствами и потому не могут быть охлаждены непосредственно
описанным способом. Применяя охлажденный кристалл в качестве приемника теплоты
с температурой Тс для другой термомагнитной системы, можно получить еще более
низкую температуру охлаждения ТЕ (процесс A-B-C-D-E).
Значение понижения температуры ДГ= То— Тс может быть рассчитано по известным
магнитным свойствам применяемой парамагнитной соли с помощью дифференциальных
термодинамических соотношений, записанных для термомагнитной системы.
С учетом выражения (2.7) уравнение первого закона термодинамики для
термомагнитной системы получит вид
duTM = dq — d/M = Tds + HdMMar.
При выборе алгебраических знаков в уравнении учтено, что увеличение
намагниченности (dMMar;>0) соответствует увеличению внутренней энергии, т. е. подводу
энергии к системе в форме магнитной работы. Изменение энтальпии термомагнитной
системы
dft™ = d(uTM - НМТЫ) = Tds - Mm&H.
Отсюда следует отношение Максвелла
(dT/dH)s= -(dMM}ir/ds)H, (26.12)
показывающее, что при обратимом изменении напряженности магнитного поля в
теплоизолированной системе (s — const) будет происходить изменение температуры.
Заменяя в (26.12) производную по энтропии через производную по температуре,
получим выражение для магнитокалорического дифференциального эффекта, дающего
относительное падение температуры при размагничивании:
aM=(dT/dH)s= -(дМмаг/дТ)н(дТ/д8)н.
В свою очередь,
(dT/ds)H = (TdT/Tds)H=T(dT/dq)H = T/cH,
где сн — теплоемкость парамагнитной соли при постоянной напряженности внешнего
магнитного поля. Тогда
аы=-(Т/си№Мылг/дТ)и. (26.13)
Для количественной оценки изменения температуры при адиабатном
размагничивании необходимо располагать уравнением состояния парамагнитного вещества в
переменных (//, ММаг, Г), а также сведениями о зависимости теплоемкости сн от температуры
и напряженности магнитного поля. Намагниченность парамагнетика выражается
законом Кюри
Обратные циклы 351
Ммаг = СН/Ту (26.14)
который справедлив при Я/Г<7000 А/(м-К). Постоянная Кюри С определяется
экспериментально или же рассчитывается методами квантовой статистики. При этом
(дМмаг/дТ)н=-СН/Т2. (26.15)
Теплоемкость парамагнитных солей при температурах выше 0,1 К подчиняется
зависимости
сн = (А + СН2)/Т\ (26.16)
где Л — постоянная, определяемая или из опыта, или по квантово-статистическим
соотношениям.
Подставив выражения (26.15) и (26.16) в формулу (26.13), получим
ам = СН/(снТ) = СНТ/(Л + СН2).
Интегрирование последнего выражения в пределах от начального значения
напряженности Н\ до конечного значения #о приводит к формуле, выражающей температуру
в конце процесса адиабатного размагничивания (интегральный магнитокалорический
эффект):
С помощью адиабатного размагничивания, используя в качестве приемника теплоты
ванну жидкого гелия 3Не, кипящего под вакуумом (Г0 = 0,35 К), удалось достичь
температур порядка 0,01 К. Используя, в свою очередь, охлажденную парамагнитную
соль в качестве приемника теплоты в термомагнитной системе ядерных спинов,
оказалось возможным получить температуру всего на 10~6 К выше абсолютного нуля.
§ 26.9. Поведение термодинамических систем при температуре,
стремящейся к абсолютному нулю
Получение температур, всего лишь на доли кельвина превышающих абсолютный нуль,
дало возможность экспериментально исследовать термодинамические свойства веществ
при таких экстремальных условиях.
При приближении температуры к абсолютному нулю в поведении
термодинамических систем обнаруживаются новые свойства, не известные при более высоких
температурах. С микрофизической точки зрения это объясняется тем, что при низких
температурах на поведении термодинамических систем начинают все больше
сказываться квантово-механические эффекты, поскольку средняя кинетическая энергия теплового
движения частиц (равная величине kT, где k= 1,381 • 10~~23 Дж/К — постоянная Больц-
мана) становится соизмеримой с разницей между энергиями соседних разрешенных
энергетических состояний частиц.
Применение дифференциальных соотношений, вытекающих из первого и второго
законов термодинамики, позволило теоретически объяснить, а в ряде случаев и
предсказать большое число закономерностей, связывающих различные физические свойства
веществ. Однако многие свойства не могут быть описаны с использованием только
этих законов. Так, например, остается неопределенным значение постоянной
интегрирования при вычислении энтропии, остается открытым вопрос о зависимости теплоемкостей
от температуры, об абсолютном значении констант равновесия химических реакций и
ряд других.
В 1906 г. немецкий физик В. Нернст, исходя из имевшихся к тому времени
экспериментальных данных о зависимости тепловых эффектов химических реакций от
температуры, высказал гипотезу об особых, не известных ранее и не вытекающих из
352 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
первого и второго законов термодинамики свойствах веществ при температурах,
приближающихся к абсолютному нулю. Последующий анализ следствий из теоремы
Нернста показал, что первоначальная ее формулировка, относившаяся к
энергетическим эффектам химических реакций, является следствием некоторого более общего
принципа, устанавливающего поведение равновесных термодинамических систем при
стремлении температуры к абсолютному нулю. Этот принцип, не вытекающий из
закона сохранения энергии (первого закона термодинамики) и из факта существования
и свойств энтропии (второго закона термодинамики), получил название третьего
закона термодинамики.
Одна из современных формулировок третьего закона термодинамики утверждает,
что
в любом равновесном изотермном процессе в конденсированной системе при
температуре, стремящейся к абсолютному нулю, изменение энтропии стремится к нулю
(формулировка Нернста — Симона). !
Математически это может быть представлено и следующем виде:
lim (AS)r = lim (S, — S2)T= 0. (26.17)
или
lim {dS/dx)T = 0, (26.18)
т — о
где S\ и $2 — значения энтропии, получающиеся при приближении температуры к
нулю с помощью двух различных процессов; х — обозначение любого параметра
состояния, изменяющегося в изотермном процессе при Т-+0.
Из выражения (26.17) следует, что при Т — 0 К переход от состояния / к состоянию
2 не сопровождается изменением энтропии, т. е. при Г->-0 энтропия системы во
всех состояниях одинакова:
о 1 = о2 = »Ь0
Т + 0 Т + 0 Т -* 0
В соответствии с третьим законом термодинамики линии всех процессов на sT-диаг-
рамме должны сходиться в одну точку на оси 5 при Г->-0. М. Планк показал, что
можно считать энтропию при абсолютном нуле температуры равной нулю, т. е. можно
положить S0 = 0 и начало координат энтропийной диаграммы совместить с этой точкой
(рис. 26.14).
Третий закон термодинамики позволяет сделать ряд важных заключений об
изменении термодинамических свойств веществ при температуре, стремящейся к
абсолютному нулю.
1. При Г->-0 К все вещества теряют термическую упругость и способность к
термическому расширению. Соотношение Максвелла связывает термическую упругость
вещества (dp/dT)v с зависимостью энтропии от объема (dS/dv)T. С учетом третьего
закона термодинамики в форме (26.18)
lim y= lim ([/р)(др/дТ)0 = 0. (26.19)
т -+о т + о И
Согласно соотношению Максвелла (5.14), термическая расширяемость (ди/дТ)р
связана с зависимостью энтропии от давления (ds/dp)T. В соответствии с (26.18)
имеем
lim oc= lim (\/v)(dv/dT)D =0.
т-+о т^ о
2. При Г->-0 К парамагнитные вещества должны обнаруживать принципиальные
отклонения от закона Кюри (26.14). Из соотношения Максвелла для термомагнитной
системы (ds/dH)T= — (дН/дТ)Ммаг и из (26.18) следует, что
Обратные циклы
353
lim (дН/дТ)м = 0. (26.20)
г — о маг
Однако, согласно закону Кюри (26.14),
lim (дН/дТ)Мыаг= lim (Ммаг/С) = const Ф 0.
Это противоречит условию, полученному
на основе третьего закона термодинамики,
и означает, в частности, что оценка
понижения температуры при адиабатном
размагничивании, сделанная в предыдущем параграфе,
при Г->-0 недействительна. При этом надо иметь
в виду, что третий закон термодинамики не
устанавливает, при какой именно температуре
его действие начинает влиять заметно на
физические свойства веществ.
3. Теплоемкости конденсированных, т. е.
твердых или жидких, тел в любых
процессах при температуре, близкой к
абсолютному нулю, равны нулю. Для изохорной
теплоемкости это можно показать, если воспользоваться определением свободной
энергии (5.5) и дифференциальными соотношениями (5.8):
S=(F-U)/T=-(dF/dT)v.
Предел полученного выражения Г->-0 К:
limS = — lim (dF/дТ) v= (UmF—UmU) /WmT = 0/0.
Раскрытие неопределенности в правой части полученного выражения по правилу
Лопиталя приводит к условию
Рис. 26.14. sT-диаграмма к пояснению
принципа недостижимости абсолютного
нуля
lim {dF/dT)v - lim {dU/dT)v
lim (dF/dT)v=— —
lim {dT/dT)v
7—0
= lim {dF/dT)v— lim V.
T + 0 T -» 0
Так как производная (dF/dT)v=—S ограничена (не стремится к бесконечности
при Г->-0), то, ее значения в правой и левой частях последнего уравнения
уничтожаются и тогда \\mcv = 0. Это условие практически не опирается на третий
закон термодинамики, так как при получении использовалось лишь предположение
об ограниченности значения энтропии при Г->-0, но не предположение об отсутствии
изменений энтропии в любых процессах при абсолютном нуле.
lim с =?.Q и lim сх = 0,
Аналогично можно показать, что
, где х — любой
параметр, остающийся постоянным в некотором процессе.
Эксперименты по определению удельной теплоемкости cv для кристаллических тел
при низких температурах показали, что cv~ Г3, т. е. она быстро убывает с
приближением температуры к абсолютному нулю. Так же изменяется теплоемкость не только
кристаллических тел, но и всех других равновесных термодинамических систем,
например электронного газа в металлах, жидкого гелия и др.
4. При температуре, стремящейся к нулю, обычная статистическая модель
идеального газа становится непригодной для описания поведения системы
невзаимодействующих частиц, поскольку получающееся при этом уравнение состояния, т. е. уравнение
12 Зак'..584 \
354 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Клапейрона (1.6), приводит к противоречию с третьим законом термодинамики.
В самом деле, из дифференциального соотношения (7.10) и уравнения (1.6) следует, что
для идеального газа (ds/dv)T — R/v = p/T. При Г-^0 эта производная принимает
бесконечно большое значение, в то время как третий закон термодинамики (26.18)
требует, чтобы она была равна нулю.
Квантовая теория показывает, что при весьма низких температурах, когда
кинетическая энергия поступательного теплового движения частиц соизмерима с интервалом
между разрешенными квантовыми уровнями энергии, независимое поведение частиц в
совокупности становится невозможным и происходит так называемое «вырождение»
идеального газа, когда его поведение описывается особым, квантовым, уравнением
состояния.
Рассмотренные свойства тел при температурах, близких к абсолютному нулю, а
также и ряд других свойств, следующих из третьего закона термодинамики, тщательно
изучались во многих экспериментах, проведенных при температурах вплоть до
предельно низких, получение которых оказалось возможным к настоящему времени (порядка
10~6 К). Эти эксперименты полностью подтверждают правильность положений третьего
закона термодинамики.
Изображая энтропийную диаграмму процессов охлаждения методом адиабатного
размагничивания до значения температуры Г = 0 (рис. 26.14) в соответствии с
требованиями третьего закона о неизменности энтропии при Г = 0, легко показать справедливость
следующего утверждения:
за конечное число процессов, сколь угодно близких к идеальным, невозможно охладить
термодинамическую систему до абсолютного нуля.
Это утверждение известно как формулировка третьего закона термодинамики в
виде принципа недостижимости абсолютного нуля (формулировка
Фаулера и Гугенгейма).
В самом деле, рассматривая последовательность процессов изотермного
намагничивания и адиабатного размагничивания 1-2-3-4-5-..., видим, что каждый следующий
шаг приводит ко все меньшему понижению температуры. Приближение к точке Г=0 и,
следовательно, 5 = 0 оказывается асимптотическим, а после любого конечного числа
операций температура все еще остается выше абсолютного нуля.
Однако законы термодинамики не устанавливают никаких пределов того, насколько
близко можно подойти к абсолютному нулю температуры.
Вопросы|. Укажите различия между холодильной машиной, тепловым насосом и термотрансфор-
ма юром.
2. Какие величины характеризуют термодинамическую эффективность обратных циклов?
3. Какие свойства растворов используются при создании абсорбционных холодильных
машин?
4. Определить холодильный коэффициент теоретического цикла сжижения газа, в
котором используется метод адиабатного дросселирования предварительно охлажденного
газа.
5. Что такое термомагнитные термодинамические системы и для чего они применяются?
Глава 27
БЕЗМАШИННОЕ ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ
§27.1. МГД-генератор
Наряду с повышением кпд обычных тепловых электростанций в последнее время
получили развитие новые методы получения электроэнергии без превращения тепловой
энергии в механическую и механической в электрическую. Этим достигается
уменьшение потерь и повышение максимальной рабочей температуры. Такие методы получили
Безмашинное преобразование энергии
355
\
Рис. 27.1. Энергетическая установка с МГД-генератором: а —схема; б — цикл в координатах
s, T:
1 — подача газа; 2 — камера сгорания; 3 — подача присадки; 4 — электроды; 5 — МГД-генератор; 6 —
паровая турбина; 7 — конденсатор; 8 — насос; 9 — парогенератор; 10—регенератор; // — компрессор
название безмашинного преобразования энергии. Одним из таких методов является
создание магнитогидродинамического (МГД) генератора (рис. 27.1, а). Газ /,
используемый как рабочее тело, подается в камеру 2, нагревается за счет подвода теплоты и
частично ионизируется. Обычно к газу добавляют легкоионизирующиеся присадки
(например, калий или натрий). Полученная таким образом слабоионизированная
плазма, имеющая температуру 2000...2200 К, расширяется в сопле, приобретая высокую
скорость (до 1000 м/с), и затем поступает в канал МГД-генератора 5, находящийся в
магнитном поле, которое создается специальной магнитной системой. Силовые линии
магнитного поля перпендикулярны оси канала. При пересечении проводником (которым
является ионизированный поток газа) магнитных силовых линий в этом проводнике
возникают ЭДС и электрический ток.
Ток течет в направлении, перпендикулярном плоскости, проходящей через векторы
скорости газа и индукции магнитного поля. Генерируемый в объеме МГД-генератора
электрический ток отводится с электродов 4, подключаемых к внешней нагрузке.
Основное преимущество использования МГД-генератора состоит в возможности
более эффективно использовать теплоту высокого температурного потенциала благодаря
отсутствию движущихся частей (подобных имеющимся в паро- и газотурбинных
установках). В канале МГД-генератора энтальпия потока уменьшается за счет совершения
полезной работы преодолевания электромагнитных сил. Одновременно газ нагревается
за счет джоулевой теплоты, вызванной протеканием тока через проводящий газ.
Выделение джоулевой теплоты приводит к снижению кпд МГД-генератора, поэтому всегда
стремятся к ее уменьшению.
Кпд преобразования МГД-генератора определяется отношением полезной
электрической мощности к энтальпии потока на входе в канал: r\( = IU//iM, где / — сила тока;
U — напряжение; /г„ — энтальпия потока на входе в канал.
Так как электрическая мощность представляет собой работу, производимую газом,
то IU — hH — /iK, где /iK— энтальпия потока газа на выходе из канала МГД-генератора.
Процесс истечения можно принять адиабатным, тогда, используя среднее
значение теплоемкости в диапазоне температур от Тн (на входе в канал) до Тк (на выходе
из канала), кпд определим отношением
r\t = (hH-hK)/hH=\-TK/TH=\-{pK/pH){k-{)/k. (27.1)
12*
356 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
значения hH и hK определяются выражениями
где m,h = Sw-hP/h/Ph; М"к = 2(1/кр/-к/Рк; М-у; Р\\ hj — соответственно молярная масса, давление
и молярная энтальпия компонентов плазмы.
Для определения температуры на выходе из канала МГД-генератора можно
исходить из постоянства энтропии потока sH = sK, считая истечение равновесным. Это
означает, что изменение состава ионизированного газа следует за изменением давления и
температуры.
Энтропия газа на входе в канал МГД-генератора определяется выражением
H), (27.2)
где Sj — табличные значения энтропии компонентов плазмы, определяемые по Тн и
отнесенные к давлению ро. Поправка на давление производится для изотермного процесса
(плазма принимается идеальным газом), тогда ds = pdv/T\ As = /?ln(pi/p2)= — /?Х
Xln(p2/Pi).
Выделение джоулевой теплоты приводит к уменьшению полезно используемой
разности энтальпий при том же перепаде давлений. При этом эффективность
преобразования в МГД-генераторе определяется внутренним кпд r\BH = (hH — /i'K)/(/*„ —
— /iK), где h'K— энтальпия потока для неизоэнтропного процесса.
МГД-генераторы могут использоваться в теплосиловых энергетических установках,
выполняемых по открытому или замкнутому циклу. МГД-установка (рис: 27.1)
предназначена для работы по открытому циклу. Атмосферный воздух сжимается в
компрессоре 11, попадает затем в камеру сгорания 2, куда подаются также топливо и
ионизирующие присадки; сгорание происходит при р„ = const. Для использования теплоты
газов, выходящих из МГД-генератора (имеющих температуру~2000 °С), имеется
регенеративный теплообменник 10, где подогревается воздух, подаваемый в камеру
сгорания. После прохождения регенератора 10 газы имеют еще достаточно высокую
температуру.
Для использования высокотемпературного потенциала обычно предусматривается
устройство пароводяного цикла. После регенератора 10 газ поступает в парогенератор 9,
полученный в нем пар поступает в паровую турбину 6, где производит работу. Затем
пар конденсируется в конденсаторе 7 и насосом 8 вновь подается в парогенератор 9.
Газ, охладившись примерно до 150 °С, выбрасывается в атмосферу.
Цикл установки с МГД-генератором (рис. 27.1, б) состоит из процесса 1-2 сжатия в
компрессоре, изобарного подвода теплоты 2-3-4 (участок 2—3 соответствует подводу
теплоты в регенеративном воздухоподогревателе, а участок 3-4 — подводу теплоты в
камере сгорания), адиабатного процесса 4-5 совершения работы в МГД-генераторе и
изобарного процесса 5-6-7-1 (участок 5-6 соответствует процессу в регенеративном
теплообменнике 10, участок 6-7— передаче теплоты воде в парогенераторе 9> участок
7-1 — отводу теплоты в атмосферу).
В пароводяном цикле процесс a-b-c-d — подвод теплоты в парогенераторе, d-e —
адиабатное расширение пара с совершением полезной работы в турбине, е-а — отвод
теплоты в конденсаторе.
Циклы на рис. 27.1, б построены для различных количеств рабочего тела —
пароводяной цикл для 1 кг воды, цикл с МГД-генератором — для G кг рабочего тела.
Значение G можно определить по sT-диаграмме. Действительно, теплота,
передаваемая воде в парогенераторе, отводится от газа на участке 6-7; следовательно,
G(/i6 — hT)r\Tn — hd — hat где т]тп — кпд пароперегревателя. Следовательно,
G = (hd-ha)/[(he-h7)r]Tn)]. (27.3)
Термический кпд цикла МГД установки
Безмашинное преобразование энергии
357
(27.4)
где /Мгд и 'в — работа, производимая соответственно в МГД-цикле и паротурбинном
цикле; q\ — теплота, подводимая к 1 кг рабочего тела в МГД-цикле.
С учетом обозначений, принятых на sT-диаграмме (рис. 27.1,6), уравнение (27.4)
можно представить в виде
т1/мгд= [ G(h4 — h5 — h2 + hx) —(hd— he)]/[ G (h4 — h3)]. (27.5)
Значения энтальпий соответствуют точкам на рис. 27.1.
§27.2. Термогенератор
Работа термогенератора (рис, 27.2) основывается на физическом эффекте Зеебека,
состоящем в том, что в разомкнутой электрической цепи, составленной из двух
разнородных проводников, возникает электродвижущая сила (эдс), если спаи проводников
помещены в среды с разными температурами.
Как следует из (14.80), эта эдс пропорциональна разности температур спаев:
d£ = a,.2d7\ (27.6)
где а,_2 — коэффициент термоэдс, зависящий от материалов ветвей, составляющих
термоэлемент. В общем случае ах_2 зависит также от температуры, но незначительно,
поэтому в дальнейшем эта зависимость не учитывается. Индексы 1 и 2 относятся к
горячему и холодному спаям. Если замкнуть концы термоэлектрического элемента (рис.
27.2) через нагрузку R или через батарею, то в замкнутой цепи потечет ток.
Работа термогенераторов основывается также на эффекте Пельтье, заключающемся
в том, что если через цепь, составленную из двух разнородных проводников, пропускать
ток от внешнего источника, то один из спаев цепи будет поглощать, а другой — выделять
теплоту. Количество теплоты dQ, поглощаемое или выделяющееся в спае, оказывается
пропорциональным силе тока dQ = /7,.2d/, где Я12— коэффициент Пельтье, связанный,
как это следует из (14.83), с термоэлектрическим коэффициентом ах_2 соотношением
Я,.2=а1.2Г.
Эффект Томсона состоит в том, что при наличии температурного градиента вдоль
доводящего материала происходит выделение (или поглощение) теплоты, значение
оторой пропорционально силе тока, проходящего через проводник:
dQ = xI(dT/dx)dx. (27.7)
Положительной величине dQ соответствует поглощение тепло-
из окружающей среды. Коэффициент т Томсона связан с коэффи-
^нтом термоэдс а соотношением . h ,
-А
ты
циентом термоэдс
(27.8)
Кроме рассмотренных выше эффектов при протекании тока в цепи
термоэлемента в единицу времени выделяется джоулева теплота
<3Дж = /2/?, где R — сопротивление в цепи из двух последовательно
соединенных термоэлементов.
Происходит также передача теплоты от горячего источника к
холодному за счет теплопроводности по двум электродам:
(27.9)
V
где Я.1, Я,2 — теплопроводности материалов термоэлектродов; / —
длина термоэлектродов; f\y /2 — площади поперечных сечений.
При наличии в цепи термогенератора внешнего потребителя
.J.U
Рис. 27.2.
Схема термоэлемента
358 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
мощности с сопротивлением R полезная внешняя работа Lll==I2R. Сила тока / = £(/-
где г — внутреннее сопротивление элемента, определяемое отношением r = (pi/i + p2f2) /I.
Здесь pi и р2 — удельные электрические сопротивления электродов.
Отношение m — R/r называется параметром нагрузки.
Если принять среднее значение коэффициента а в интервале температур от Т\
до Г2, т. е. а = (а, + а2)/2, то в соответствии с (27.6) Е = а(Т\ — Т2) и 1 =
/[r(m+ 1)], тогда
Термический кпд генератора определяется отношением
Tl,= W2Q3aTp, (27.10)
где SQaarp — теплота, отбираемая от горячего источника:
(27.11)
где Qn — теплота Пельтье; QT — теплота за счет теплопроводности; <3Дж — джоулева
теплота; QTm — теплота Томсона.
Теплота Пельтье определяется выражением
QT определяется по формуле (27.9).
Для джоулевой теплоты принято, что вся выделяющаяся теплота распределяется
поровну между горячим и холодным источниками.
Теплота Томсона
г, тх тх
Д<?Тм = /j Т2 df - / j Т, df = / j (t2 - Т, ) d7\
т2 т2 т2
В соответствии с (27.7), считая а(Г1) = а(Г2) = аср, имеем
-da=0,
'2 Т2
т. е. отвод теплоты Томсона по одному электроду компенсируется подводом
теплоты по другому электроду.
Таким образом,
_ а2(Г,- Т2)2 m/[r{m+ I)2]
N[ а2Г,(Г1-Г2)/[г(т+1)] + (X, /, + l2f2) (Г, - Т2)// + а2 (Г, - Т2 f / [2г (т + I)2 ]
= (Г'2~Г2)/Г' • (27.12)
1 +(Mi +^2/2) ^(^+ 0 /(7', т/а2) +(Г,_Г2)/(2Г,т)
Из полученного выражения следует, что термический кпд термоэлектрогенератора
зависит от температур горячего и холодного источников, параметра нагрузки m и свойств
термоэлектродных материалов (А,, г, а). Сомножитель в правой части (7"i — Т2)/Т\
представляет собой термический кпд цикла Карно для заданного интервала температур.
Второй сомножитель всегда меньше единицы, поскольку учитывает необратимые потери
вследствие теплопроводности и выделения джоулевой теплоты. Значение (A,i/i +
+ А,2/2)/'/(/а2) зависит только от свойств материала и размеров термоэлектродов.
Обозначив
Безмашинное преобразование энергии
359
можем сказать, что r\i тем больше, чем больше z. Максимальные значения z зависят
от соотношения /1/^2- Экстремум уравнения (27.13) имеет вид
При pi«p2 и A,i«A,2 zmax=a2/(4pA,). Исследование влияния параметра нагрузки т на
термический кпд показывает, что r\t достигает максимального значения при
m =
В этом случае
= Л/К/[ 1+2(1
(27.14)
(27.15)
Выражая z из (27.14), имеем
r\t=i\?(m -V{m + Г2/Т,). (27.16)
Материалами, обладающими сравнительно высоким значением параметра г,
являются полупроводники на основе теллура, такие, как В1гТез(2: = 3-10 3... 1 • 10~3К~'),
PbTe(z = 2-10~3...0,5- 10~3К~'), в пределах температур 200...700 °С. Недостатком этих
материалов является их невысокая термическая стойкость.
В перспективе предстоит еще большая работа по созданию новых
термоэлектрических материалов, обладающих как высоким значением параметра г, так и большой
термостойкостью.
§27.3. Термоэлектронный генератор
Действие термоэлектронного генератора основано на способности металлов в нагретом
состоянии испускать электроны со своей поверхности. Для испускания (эмиссии)
электронов необходима затрата работы, называемой работой выхода.
Термоэлектронный преобразователь простейшей формы состоит из двух
металлических поверхностей, разделенных вакуумным зазором (рис. 27.3, а). На поверхности /
(катод) поддерживается температура Т\, поверхность 2 (анод) имеет температуру Гг,
причем Т\>Т2.
Обозначим работу выхода для катода q>i, для анода фг- Вследствие разности
температура от катода к аноду будет уходить больше электронов, чем в обратном
Рис. 27.3. Термоэлектронный преобразователь: а — схема; б —
распределение электрических потенциалов между его
пластинами:
/ — катод; 2 — анод
360 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
направлении. Процесс на катоде можно условно рассматривать как «испарение», на
аноде — как «конденсацию» электронов. Если замкнуть пластины на внешнее
сопротивление, то в цепи возникает электрический ток. Если электроны, испускаемые
катодом, свободно рассеиваются в окружающем разреженном объеме, то плотность тока
эмиссии определяется формулой Ричардсона:
2 • (27.17)
где ср — работа выхода электронов; А=\20 А/(см2-К) —постоянный множитель;
к — постоянная Больцмана.
Работа выхода для различных материалов меняется (в пределах от 1 до 5 эВ) и
зависит от состояния поверхности электродов. В том случае, если электроны, испускаемые
катодом, накапливаются на аноде, работа выхода ф уже не будет обеспечивать попадание
электронов с катода на анод, так как потребуется преодолевать дополнительную
разность потенциалов Va, появившуюся между пластинами. Из схемы распределения
потенциалов между пластинами (рис. 27.3, б) ясно, что потенциальный барьер для
электронов катода равен (ф2+ Va)- Поэтому плотность тока между катодом и анодом
определяется выражением
ik = AT\w[-{<v2+Va)/{kTx)]=AT]e-^'(kT)e-*{kT\ (27.18)
где Д = ф2+ Va — ф|. Так как Д ;>0, то величина е~*^кТ) показывает, какая доля
электронов, преодолевших потенциал ф|, достигнет анода.
Одновременно с током эмиссии от катода к аноду протекает противоположно
направленный ток от анода к катоду, величина плотности которого определяется .
выражением
ja = ATkxp [-ф2/ (кТ) ]. (27.19)
Из-за малой плотности электронов в межэлектродном пространстве плотности
токов jk и \а не оказывают заметного противодействия друг другу.
Для электрической цепи с термоэлектронным преобразователем в соответствии с
законом Кирхгофа
]. (27.20)
Если / — площади поверхностей катода и анода, то сила тока / = //, а полезная внешняя
работа Lli = I2R = JVa.
Термический кпд термоэлектронного преобразователя подсчитывается обычным
способом:
t|i=WQi. (27.21)
где Q\ — количество теплоты, подведенное от горячего источника к катоду.
§ 27.4. Топливные элементы
Топливный элемент представляет собой электрохимическое устройство, в котором
химическая энергия горючего превращается непосредственно в электрическую энергию
(рис. 27.4).
Использование водорода и кислорода определяется их большой активностью и
доступностью, а продукт реакции (вода) легко выводится из системы. В
рассматриваемом элементе водород и кислород (поступающие под давлением через пористые
платиновые электроды / и 2) подаются к анодной и катодной сторонам элемента
соответственно. Обе стороны элемента разделяются ионообменной мембраной, которая
пропускает ионы водорода Н + , но не пропускает атомы водорода. В качестве такой
Безмашинное преобразование энергии
361
Суммарная реакция
Н20
мембраны используются электролиты,
например концентрированный раствор
щелочи КОН.
Реакции, происходящие в
элементе, можно представить в
следующем виде:
2Н2+4Н++4е;
Е +Q + L,
из которой следует, что кроме
химических изменений происходит
высвобождение электрической энергии АеЕ,
выделяется теплота Q и совершается
работа L, причем работа L
затрачивается, так как водород и кислород
а вода — в жидком.
Процесс, происходящий в топливном элементе, с большой степенью точности можно
считать обратимым изобарно-изотермным. Поэтому с учетом уравнения Гиббса—
Гельмгольца можно записать:
SGpJ=bHpJ + T{dbGpJldT)p. (27.22)
Изменение изобарно-изотермного потенциала AGp T равно работе переноса
электрического заряда пФА, где п — валентность; 0^ = 96500 Кл/моль — постоянная Фара-
дея. Следовательно,
\GpT=—n<PAE= —96 500/гЕ, (27.23)
где Е — эдс элемента. Знак минус показывает, что положительное значение эдс
соответствует убыли потенциала &GpT.
Подставив уравнение (27.22) в (27.23), получим
Рис. 27.4. Схема топливного элемента:
1,2 — платиновые элементы
находятся в газообразном состоянии,
или
Д GpT = - 96500/г£ = Д//рГ - 96500/г Т(дЕ/дТ)
Е=- A//Pi7./96500 + Т(дЕ/д Т)р.
(27.24)
(27.25)
Изменение энтальпии в изобарном процессе есть теплота реакции, т. е. &HpT=Qp.
Температурный коэффициент эдс определяется выражениями (27.23) и (27.25), в связи
с чем
(dE/dT)p=—(dbGPmT/dT)p/{96b00n).
(27.26)
Соотношение между AGp>7. и ЬНр%т определяет знак производной (дЕ/дТ)р. Так,
если (дЕ/дТ)р = Оу то &GPtT = &Hpj, т. е. топливный элемент работает без теплообмена.
При (дЕ/дТ)р<с0 &Gpj<kHpj\ следовательно, работа меньше теплового эффекта и
избыток теплоты либо отдается в окружающую среду, либо идет на нагревание самого
элемента. При (дЕ/дТ)р>0 теплота отбирается от окружающей среды (&HpT<:&GpT).
Работа топливного элемента оценивается коэффициентом эффективности,
определяемым отношением напряжения элемента к значению эдс при отсутствии внешней
нагрузки.
362 РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Напряжение на клеммах топливного элемента зависит от плотности тока и рабочей
температуры, что определяется экспериментально.
Вопросы 1. Опишите принцип работы МГД-генератора.
2. Чем определяется кпд МГД-генератора?
3. На каком принципе основана работа термогенератора?
4. В чем состоит эффект Томсона, используемый при расчете термогенератора?
5. Опишите принцип работы термоэлектронного генератора.
6. Поясните устройство топливного элемента.
7. Укажите характер процессаа, происходящего в топливном элементе.
Глава 28
РАБОТОСПОСОБНОСТЬ
ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
§28.1. Эффективность преобразования энергии
Главной задачей технической термодинамики является анализ условий
преобразования одних видов энергетического воздействия в другие, т. е. условий превращения
энергии. Это необходимо во всех случаях, когда имеющиеся источники первичной
энергии отдают ее не в той форме, какая нужна потребителю, или же когда потенциал
источника энергии (температура, давление, электрическое напряжение и т. д.) не
соответствует потенциалу потребителя. В общем случае преобразователь энергии может
получить первичную энергию в различных формах и количествах от нескольких
источников и отдавать энергию различным потребителям, также в различных формах и
количествах. Преобразователь может сам являться источником энергии для потребителя.
В этом случае отдаваемая им энергия равна уменьшению его внутренней энергии.
В большинстве случаев преобразователь получает первичную энергию в какой-либо
одной форме, а отдает энергию потребителям в нескольких формах, причем одна (или
немногие) из этих форм является полезной, а остальные — побочными и составляют так
называемые «потери» энергии. Эффективность преобразования энергии в общем случае
характеризуется отношением количества полезной энергии, отдаваемой потребителям,
к количеству первичной энергии, полученной преобразователем от источника.
Если первичная энергия является работой любого вида, то с помощью идеального
преобразователя, в котором отсутствуют неравновесные, необратимые процессы (трение,
электрическое сопротивление, диффузия и тому подобные процессы диссипации), она
может быть полностью преобразована в энергию любого иного вида.
Максимальная теоретическая эффективность преобразования работы в любую иную
форму энергии (т. е. наибольший кпд преобразователя работы) равна единице. В
реальных преобразователях имеются процессы диссипации, которые переводят часть энергии,
подведенной в форме работы, в энергию хаотического теплового движения микрочастиц
тел, участвующих в процессе преобразования, в связи с чем эффективность
преобразования снижается. Такое снижение эффективности вызвано наличием необратимых
процессов, поэтому для характеристики эффективности преобразователей работы
необходимо воспользоваться вторым законом термодинамики и следствиями из него.
Если первичная энергия подводится к преобразователю в форме теплоты, то,
согласно второму закону термодинамики, полное превращение ее в работу в принципе
невозможно.
Если преобразователь (тепловой двигатель) работает по замкнутому циклу, то
эффективность преобразования теплоты в работу в идеальном, обратимом тепловом
цикле характеризуется значением термического кпд цикла, имеющим максимальное
Работоспособность термодинамических систем 363
значение для цикла Карно. Однако понятия термического кпд цикла недостаточно для
полной характеристики эффективности процессов и устройств для преобразования
энергии.
Действительно, термический кпд цикла не отражает потерь, вызванных
необратимостью реальных процессов, необходимых для преобразования энергии. Понятие кпд
непригодно для характеристики таких преобразователей, в которых полезно
используемая потребителями энергия отдается им не только в виде работы, но и в виде теплоты
(например, в теплофикационных установках).
Для учета конкретных потерь в реальных машинах в практику были введены
дополнительные показатели эффективности преобразования, такие, как индикаторный,
относительный, электрический, эффективный и другие кпд машин и отдельных их
элементов. Разнородность этих коэффициентов затрудняет сравнительный анализ
эффективности тепловых двигателей. Кроме того, термический кпд цикла не может служить
показателем эффективности обратных термодинамических циклов и машин, работающих по
таким циклам, не может быть непосредственно использован для оценки эффективности
преобразования энергии в разомкнутых термодинамических процессах (например, при
анализе работы отдельных элементов двигательной установки).
В ходе развития термодинамических методов анализа было установлено, что
эффективность преобразования энергии следует оценивать сопоставлением
фактической работы, отдаваемой потребителю, с максимальным количеством работы, которое
мог бы получить потребитель от данной термодинамической системы за счет ее
внутренней энергии и подводимой к ней первичной энергии.
Если рассматриваемая система является лишь элементом (узлом) преобразователя,
ее эффективность характеризуется тем влиянием, которое оказывает необратимость в
нем на итоговый эффект преобразования энергии. Если полезная энергия отдается в
форме теплоты, то для оценки эффективности используют максимально возможную
работу, которую можно получить за счет этой теплоты.
Эффективность обратных термодинамических циклов и процессов, когда работа не
производится, а затрачивается (холодильные машины, процессы разделения газовых
смесей и т. п.), оценивается сравнением работы цикла (процесса) с минимальной
работой, необходимой для получения полезного эффекта при полной обратимости
всех процессов.
В зависимости от вида термодинамической системы, источников первичной
энергии и условий протекания процессов в системе максимальное количество работы
выражается различными соотношениями, получившими общее название функций
работоспособности.
При получении выражений этих функций для системы, находящейся в некотором
начальном состоянии или совершающей некоторый термодинамический цикл,
необходимо установить ее конечное состояние и оговорить условия перехода из одного состояния
в другое.
Система может производить полезную работу лишь при отсутствии равновесия
между ней и окружающей средой, поэтому за конечное состояние системы в случае
разомкнутого процесса принимается состояние равновесия системы с окружающей
естественной средой (например, с атмосферой), температура Го и давление р0 которой
принимаются постоянными.
Согласно второму закону термодинамики, работа будет максимальна, если при
переходе системы в состояние равновесия с окружающей средой все процессы будут
полностью обратимыми (равновесными). Если при этом система получает первичную
энергию от источников, то эти процессы также должны быть равновесными. Из условия
обратимости следует, что теплообмен с окружающей средой может происходить только
в равновесном изотермном процессе при температуре Го. Процесс обмена работой
также должен быть равновесным, но при этом нужно учесть, что не вся работа, совершае-
364
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
мая системой, может быть отдана потребителю: часть ее должна быть затрачена на
вытеснение соответствующего объема окружающей среды с противодавлением ро-
Поэтому при вычислении функций работоспособности учитывается только полезная работа
/п, равная разности работы деформации системы /,.о и работы по вытеснению объема
окружающей среды:
0 о
/п= \pdv-\ podv=ll.o-po(vo-vl). (28.1)
1 i
Полезной работой проточной системы является располагаемая работа /0, так как
при выводе уравнения (2.43) работа вытеснения окружающей среды (работа
проталкивания) была учтена.
§28.2. Функции работоспособности. Эксергия
Функция работоспособности рабочего тела в проточной термодинамической системе
может быть получена при рассмотрении процессов, в результате которых рабочее
тело, поступая в систему с начальным состоянием / (рис. 28.1) при давлении р\ и
температуре Г|, не равными давлению р0 и температуре Го окружающей среды, изменяет
свое состояние до состояния 0, соответствующего равновесию с окружающей средой.
Так как все процессы должны быть равновесными, то вначале проводится адиабатный
процесс 1-2, в результате которого температура рабочего тела становится равной
температуре источника теплоты. При этом рабочее тело обменивается с окружающей средой
(с потребителем) некоторым количеством работы.
В процессе 2-3 рабочее тело получает от источника теплоту в количестве q так,
что температура рабочего тела все время равна температуре источника (для выполнения
условия обратимое i!« При этом также происходит обмен работой.
В адиабатном ■ . а ссе 3-4 рабочее тело изменяет свою температуру до температуры
окружающей среды, совершая работу. Если при достижении температуры Го давление
рабочего тела оказалось не равным давлению окружающей среды, то для достижения
равновесия совершается изотермный процесс 4-0, в котором рабочее тело отдает
окружающей среде некоторое количество теплоты qo.
Суммарные количества располагаемой работы и теплоты, которыми обменивается
рабочее тело с источником теплоты, потребителем работы и окружающей естественной
средой при переходе от состояния / к состоянию О, связаны уравнением первого закона
термодинамики для проточной системы
qo. (28.2)
Суммарное изменение энтропии определяется
суммой изменений энтропии рабочего тела Asp.T,
источника теплоты AsH и естественной окружающей
среды Aso:As2=Asp.t + Ash + Aso. Изменение
энтропии рабочего тела Asp.T = s0— S\, где So — энтропия
рабочего тела при температуре Го и давлении ро,
соответствующих равновесию с окружающей средой;
si — энтропия рабочего тела в исходном состоянии.
Изменение энтропии источника теплоты
3
получающей теплоту от источни-
ка., с переменной температурой
пРичем интегРал
теплоты к рабочему телу. Знак минус перед интегра-
лом учитывает тот факт, что энтропия источника в
Работоспособность термодинамических систем 365
результате отдачи теплоты убывает. Изменение энтропии окружающей среды с учетом
постоянства ее температуры
о
Д$о = s4 — Sq = \ dq0 /То = q0 /То .
4
Здесь q0 — алгебраическая величина. Если в процессе 4-0 окружающая среда
получает теплоту от рабочего тела (как в примере на рис. 28.1), то энтропия среды
возрастает и величина qo положительна; если же изотермный процесс происходит с
поглощением теплоты рабочим телом из окружающей среды, то энтропия среды убывает и
количество теплоты qo отрицательно.
Таким образом,
з
As2 = (s0 — s\)~ \ dq/T + Qo/To>
2
откуда
3
\ (28.3)
Подставляя (28.3) в (28.2), получаем количество располагаемой полезной работы,
совершаемой рабочим телом в проточной системе:
з ^
- То bsz . (28.4)
При полной обратимости всех процессов суммарное изменение энтропии всех
участвующих тел равно нулю: Д5х = 0, а работа максимальна. Опуская индексы начального
состояния рабочего тела, которое может быть произвольным, получаем из (28.4)
выражение для функции работоспособности проточной системы:
/у«= {h-h0) - T0(s -So)+(q- T{)\dq/T). (28.5)
При отсутствии источников первичной теплоты работа может совершаться только
за счет энергии рабочего тела, проходящего через проточную систему.
Максимальное количество располагаемой работы, которое может быть получено от
рабочего тела в проточной системе в результате перехода рабочего тела в состояние
равновесия с окружающей средой при условии, что окружающая естественная среда
является единственным источником (или приемником) теплоты, называется эксер-
ги е й.
Выражение для эксергии (Э) получается из (28.5) при условии, что d^ = ^ = 0:
Э = (А— ho) — To(s — So). (28.6)
При фиксированных значениях параметров конечного состояния То и р0,
определяемых температурой и давлением окружающей среды, значение эксергии рабочего тела
зависит только от его начального состояния. Поэтому
эксергия является функцией состояния рабочего тела при заданных условиях в
окружающей среде.
Функция работоспособности теплоты используется в том случае, когда начальное
состояние рабочего тела совпадает с его конечным состоянием (рис. 28.2). При этом
совершение работы возможно только за счет первичной теплоты, получаемой рабочим
телом от источника. Это эквивалентно получению работы в термодинамическом цикле
2-3-4-5, когда рабочее тело периодически проходит через одни и те же состояния и его
собственная энергия не расходуется на совершение работы. При таких условиях h\ =
366
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
— ho и s\—so. Следовательно, ДЛР.Т = О и Asp.T = 0,
а уравнение (28.5) дает функцию
работоспособности теплоты, которую называют также
эксергией теплоты:
3Q = q-T0\dq/T. (28.7)
Эксергия теплоты характеризует
превращение теплоты в работу в цикле, поэтому для ее
выражения не используются параметры
состояния рабочего тела, совершающего цикл, а сама
эксергия теплоты не является функцией состояния
системы.
Функция работоспособности рабочего тела в
непротонной системе может быть получена на
основе уравнения первого закона термодинамики
для закрытой системы (2.29). В этом случае
выражение для максимальной работы закрытой
системы при наличии подвода теплоты к ней от
источника теплоты имеет вид / тах = (и — и0) — ro(s — So) + (q— T0\dq/T).
Подстановка полученного выражения в формулу (28.1) дает функцию
работоспособности закрытой системы (максимальной полезной работы):
po(v-Vo). (28.8)
Рис. 28.2. Определение
работоспособности теплоты, получаемой
от источника с переменной
температурой
При отсутствии подвода теплоты от источника dq — q — O, поэтому функция
работоспособности рабочего тела в закрытой системе Эс (которую иногда называют эксергией
закрытой системы) может быть выражена как
Эс = (и — и0) — T0(s — So) — po(v — vo). (28.9)
Как и эксергия, эта функция является функцией состояния при фиксированных
параметрах окружающей среды.
Как правило, рабочее тело, покидающее тот или иной элемент преобразователя
энергии (теплосиловой установки, холодильной машины и т. п.), не находится в
состоянии равновесия с окружающей средой и поэтому сохраняет некоторую
работоспособность. При этом работа, совершаемая рабочим телом в данном элементе установки,
меньше максимально возможной, т. е. меньше, чем "значение соответствующей функции
работоспособности системы, на величину эксергии рабочего тела, покидающего систему.
Чтобы выразить наибольшее количество работы, которое в этом случае можно получить
От системы, следует из функции работоспособности системы (28.5) вычесть эксергию
уходящего рабочего тела и прибавить то количество первичной энергии /„, которое
система может получить от источников в форме работы, и превратить в полезную работу
(или использовать для увеличения работоспособности рабочего тела).
С учетом сказанного, а также выражений (28.6), (28.7) уравнение для определения
максимального количества полезной работы, которое может быть получено от системы,
имеет вид
/omax=3i — Э2 + Э, + /„, (28.10)
где Э| и Э2 — эксергии рабочего тела соответственно на входе в систему и на выходе
из нее.
§ 28.3. Эксергетические диаграммы
Эксергия рабочего тела и эксергия теплоты допускают их наглядное представление на
диаграммах состояния. Для идеального газа изменение энтальпии, входящее в формулу
(28.6), изображается площадью 2'21Г под изобарой pi = const (рис. 28.3, а), а коли-
Работоспособность термодинамических систем
367
чество теплоты в изотермном
процессе А-0 площадью
VA00'. Таким образом, эксер-
гия идеального газа в
проточной системе изображается
на sT-диаграмме
алгебраической суммой площадей под
соответствующими
участками изобары р\ и изотермы То
с учетом их знаков. Эксергия
рабочего тела представляет
собой располагаемую работу,
поэтому на ру-диаграмме
(рис. 27.3, б) ей
соответствует площадь V'lAOO". Эк-
сергии рабочего тела в
закрытой системе на ур-диаграмме
Р1
Pi
"о
1"
0"
V
л
в
,'
\
V.
Рис. 28.3. Определение эксергии рабочего тела: а —
с помощью sT-диаграммы; б — с помощью ир-диаграм-
мы для проточной и закрытой систем
соответствует площадь 1А0В, представляющая
собой разность работы расширения (пл. 1ЧА00') и работы вытеснения окружающей
среды (пл. VB'OO'). Определение эксергии на ур-диаграмме возможно не только для
идеального газа, но и для реальных рабочих тел, если линии адиабатного 1-А и изо-
термного А-0 процессов будут нанесены на поле диаграммы в соответствии с уравнениями
этих процессов для рабочих тел.
Эксергия теплоты (28.7) изображается на sT-диаграмме (рис. 28.2) площадью
цикла 2-3-4-5.
Графически определить эксергию рабочего тела для реальных веществ можно с
помощью s/i-диаграммы (рис. 28.4). Уравнение (28.6) для этой цели следует
представить в виде 3 = (h — Tos).— (ho—7Vo)- Состояниям с нулевой эксергией соответствует
прямая //, проходящая через точку 0> характеризующую состояние рабочего тела в
равновесии с окружающей средой (т. е. при s = s0 и h = h0) и имеющую угловой коэффициент
То. Это прямая является касательной к изобаре р — ро в точке 0, так как в соответствии
с формулой (5.4)
= (dh/ds)p=Po=To.
Э, кДж/кг
51 50 5
Рис. 28.4. Изображение эксергии рабочего тела
на s/i-диаграмме:
/ — линия 3 = const; // — линия окружающей
среды при То и р0; /// — линия окружающей среды
при Т'о и p'd
200
-50
О 200 W0 11,кДж/кг
Рис. 28.5. Эксергетическая диаграмма
368РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Из рис. 28.4 ^дно^ что lb = hi—ho\ bc = bOtga=To(so — s\) и 3i=(/i| —/i0)+
s\)=lb + bc=lc. Следовательно, эксергия рабочего тела в проточной системе
изображается длиной вертикального отрезка 1с между точкой /, соответствующей
состоянию рабочего тела, и точкой с на прямой окружающей среды Эо = О. На s/i-диаграмму
можно нанести линии постоянной эксергии 3 = const, которые идут параллельно линии
окружающей среды, например линия / (3i = const) на рис. 28.4.
Были предложены также диаграммы, на которых эксергия выбрана в качестве одной
из координат (энтропия — эксергия, энтальпия — эксергия и др.). Пример такой
диаграммы приведен на рис. 28.5, где показана диаграмма энтальпия — эксергия для
воздуха в области температур до 400 К. При построении этой диаграммы принято,
что давление окружающей среды равно 0,1 МПа, а температура равна 293 К.
Однако каждая из таких диаграмм действительна только при одних определенных
параметрах окружающей среды р0, То, что значительно ограничивает их применение.
В этом отношении s/i-диаграмма более удобна, так как для определения эксергии при
изменении условий окружающей среды р0, То на ро, То достаточно провести новую линию ///
окружающей среды при ро и То. Значение эксергии рабочего тела Э{ в состоянии / в
новых условиях изображается отрезком прямой 1с'.
§ 28.4. Эксергетическме потери и эксергетический кпд
Любая необратимость процессов преобразования энергии приводит к уменьшению
фактической работы, отдаваемой потребителю, по сравнению с максимально возможной
работой, определяемой уравнениями (28.4) и (28.7). Потери возможной работы при этом
выражаются через изменения энтропии, вызванные необратимостью процессов.
Как известно, уравнение первого закона термодинамики в форме (2.38)
справедливо как для равновесных, так и неравновесных процессов, если под /0 и q
понимаются соответственно количества внешней работы и внешней теплоты, т. е. количества
энергии, переходящие между системой и телами окружающей среды. Поэтому выражение
для работы проточной системы пригодно не только для равновесных, но и
для.неравновесных необратимых процессов. Различие состоит в том, что при наличии необратимых
(индекс «н») процессов As^;> 0. Поэтому фактическая работоспособность системы
уменьшается по сравнению с максимальной на величину
n = TQbsly (28.11)
которая получила название эксергетических потерь. В этом случае
/o = /omax_roAsH2. (28.12)
Уравнение (28.11) выражает закон Гюи — Стодолы и свидетельствует о том, что
уменьшение полезной работы, вызванное наличием необратимых процессов, равно
произведению температуры окружающей среды на приращение энтропии всех участвующих
в процессах тел.
Использование понятия эксергии дает возможность количественно определить
влияние неравновесности термодинамических процессов на эффективность преобразования
энергии. Уравнение (28.11) показывает, что необратимость уменьшает количество
энергии, которое может быть получено в форме работы. Уравнение (28.10) позволяет найти
эти потери. Установки, работающие полностью обратимо, не обладают такими
потерями и являются с термодинамической точки зрения идеальными.
Степень термодинамического совершенства реальных установок определяется тем,
насколько велики в этих установках эксергетические потери, вызванные
необратимостью.
В настоящее время для оценки влияния необратимости используются два метода:
метод эксергетических потоков и метод эксергетических потерь.
Работоспособность термодинамических систем 369
В основу метода эксергетических потоков положен подсчет потоков
эксергии рабочих тел, входящих в систему, подводимой теплоты и потоков эксергии,
покидающих систему. При этом учитываются эксергия потока рабочего тела по
уравнению (28.5), эксергия потоков теплоты по уравнению (28.6), а также подводимая и
отводимая организованная энергия /„, т. е. работа всех видов. Для определения эксергии
рабочих тел и теплоты удобно использовать эксергетические диаграммы. Если рабочее
тело, покидающее систему, имеет ненулевую эксергию, то она учитывается только в
тех случаях, когда рабочее тело предназначено для получения от него работы в каких-
либо других установках (например, сжатый воздух от компрессора, предназначенный
для привода пневматических машин). При наличии необратимых процессов в системе
суммарный поток отводимой эксергии всегда меньше суммарного потока подводимой
эксергии на величину эксергетических потерь. Термодинамическое совершенство
системы характеризуется эксергетическим кпд
Лэ = Эп/Э3, (28.13)
определяемым в виде отношения полезно используемой эксергии, пересекающей
границу системы, к затрачиваемой эксергии.
Метод эксергетических потерь основан на подсчете эксергетических
потерь в пределах каждого участка (узла) системы по уравнению (28.11). Для этого
требуется определить увеличение энтропии под действием необратимости в каждом
узле. Вследствие аддитивности энтропии и постоянства температуры Го общая потеря
эксергии в системе равна сумме эксергетических потерь в отдельных узлах.
Относительное влияние необратимости процессов в отдельном узле на снижение общей
термодинамической эффективности системы характеризуется коэффициентом
эксергетических потерь, представляющим собой отношение потерь эксергии на данном участке к
полной эксергии, вводимой в систему: &;=П//ЭВх. Можно также рассматривать
коэффициент эксергетических потерь, отнесенный к эксергии, входящей в данный узел
установки: £2/=П;/ЭВх|. Коэффициент эксергетических потерь системы связан с ее полным
эксергетическим кпд простым соотношением т]э=1— 2Q,-.
§ 28.5. Эксергетический анализ работы тепловых машин
Для иллюстрации применения в термодинамике методов эксергетического анализа
ниже приводится ряд примеров оценки термодинамических процессов или работы
элементов тепловых установок с использованием понятия эксергии.
Адиабатное расширение рабочего тела. Процессы адиабатного расширения
рабочего тела с совершением работы, происходящие в реальных устройствах, например при
ускорении потока газа в соплах, при расширении газа или пара в турбинах, детандерах
и т. п., всегда характеризуются наличием некоторой необратимости, вызванной трением
в потоке. Это приводит к возрастанию энтропии рабочего тела и к уменьшению
фактической работы в процессе. Таким образом, реальный адиабатный процесс не является
изоэнтропным процессом. Потерю работы, вызванную необратимостью, можно
определить с помощью s/i-диаграммы, если начальное и конечное состояния рабочего тела
являются равновесными и могут быть изображены на диаграммах состояния. Линия
самого процесса может быть изображена на диаграммах лишь условно, так как
промежуточные состояния рабочего тела в ходе процесса не являются равновесными.
Рассмотрим адиабатное расширение рабочего тела от начального р\ до конечного
/?2 давления. При отсутствии необратимости процесс 1-2' на рис. 28.6 является
изоэнтропным.
Располагаемая работа в этом случае равна разности энтальпий начального и
конечного состояний рабочего тела и одновременно разности эксергии в этих же
состояниях. Следовательно, /0I_2, = /i,—/i2, = 3i — Э2/. Наличие необратимости, вызванной
действием трения в потоке, приводит к возрастанию энтропии рабочего тела на величину
370
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
Рис. 28.6. Потери эксергии при
необратимом адиабатном расширении
Рис. 28.7. К определению эксер-
гетических потерь в теплообмен-
ном аппарате
AsH, в результате чего конечное состояние рабочего тела изобразится точкой 2,
расположенной на изобаре конечного давления р2. Располагаемая работа в реальном процессе
по-прежнему равна разности энтальпий начального и конечного состояний /0 i_2 = /ii —/12 и
изображается длиной отрезка 1а. Вследствие роста энтропии процесс сопровождается
эксергетическими потерями, которые подсчитываются по формуле (28.11). Так как
линия 32 = const параллельна линии 3o = 0 = const, а тангенс угла наклона этих линий к
оси абсцисс равен Го, то _из треугольника 2ab определяется потеря
работоспособности в виде отрезка аЬ. Изменение эксергии между_начальным и конечным
состояниями рабочего тела характеризуется длиной отрезка 1Ь. Таким образом,
П = T0AsH = tgap2a = ab\
При определении эксергетического кпд процесса адиабатного расширения за
полезную эксергию принимают фактическую располагаемую работу процесса 1-2.
Учитывая, что эксергия уходящего рабочего тела обычно используется в последующих узлах
установки, в качестве затрат эксергии принимают разность между_эксергиями рабочего
тела в начальном и конечном состояниях: Лэ = /о 1-2/(^1 — Э^=1а/1Ь.
В теории расширительных машин влияние трения обычно характеризуют так
называемым внутренним относительным изоэнтропным кпд т]о/, который равен отношению
фактической располагаемой работы /0 ,_2 реального процесса 1-2 к располагаемому
перепаду энтальпии, т. е. к располагаемой работе процесса изоэнтропного расширения
101_<2>. Следовательно,
Разность между теоретической и фактической работой процесса расширения
представляет собой работу трения /тр = /г2 — h2, и изображается длиной отрезка аТ. Из сравнения
длин отрезков 1Ь и 12' видно, что потеря работоспособности рабочего тела при наличии
трения меньше, чем затрата работы на трение, а эксергетический кпд имеет более
высокое значение, чем внутренний относительный кпд. Это объясняется тем, что работа
трения не является полностью потерянной: будучи воспринята рабочим телом в форме
теплоты, эта энергия увеличивает работоспособность тела и впоследствии частично
может быть все-таки возвращена в форме работы.
Дросселирование. Процесс адиабатного дросселирования, протекающий без
совершения работы, изображается на s/z-диаграмме условной линией 1-3 (рис. 28.6).
Энтальпия рабочего тела при этом в начальном и конечном состояниях одинакова (h\ =
Работоспособность термодинамических систем 371
= /1з). Так как работа в процессе 1-3 равна нулю, то равны нулю внутренний
относительный кпд и эксергетический кпд, если рассматривать процесс дросселирования
лишь как предельный случай адиабатного расширения. Однако из рис. 28.6 видно, что
эксергия рабочего тела после дросселирования не равна нулю, т. е. рабочее тело
сохраняет определенную работоспособность, хотя и пониженную по сравнению с начальным
состоянием.
Снижение работоспособности рабочего тела при дросселировании нередко
используется при регулировании поточных машин с целью снижения их мощности. Если
рассматривать эксергию рабочего тела после дросселирования как полезную, а эксергию
до дросселирования — как затраченную, то_эксе£гетический кпд процесса
дросселирования выразится отношением т\1§ = Эз/Э\ = Зе/1с1.
Теплообмен при конечной разности температур. Передача теплоты в теплообменных
аппаратах происходит при конечной разности температур между греющим и
обогреваемым теплоносителями, т. е. является неравновесным процессом. В результате
теплообмена происходит уменьшение работоспособности греющего и возрастание
работоспособности обогреваемого теплоносителя. Наличие необратимости (конечной
разности температур) приводит к возникновению потерь работоспособности (эксерге-
тических потерь). На рис. 28.7 показаны схема противоточного теплообменника и
характер изменения температур теплоносителей в нем. Считая, что теплоемости
теплоносителей постоянны, а давление каждого из потоков неизменно, т. е. пренебрегая
гидравлическими сопротивлениями, запишем эксергии теплоты, отдаваемой греющим и
получаемой обогреваемым теплоносителями:
=Q -Tom cp\n^
Та
m"c'p'dT" „ „ „ Т4
h ?3
где Q' и Q" — количества теплоты; m! и m" — расходы теплоносителей; ср и с'р'— их
теплоемкости.
Эксергетическая потеря выразится в виде разности эксергии теплоты:
П = Э^ - Э » =( Q - Q") - То (пг ср ln-2-+ m" cp ln-^-V
Эксергетический кпд теплообменного аппарата определится отношением эксергии
теплоты, полученной обогреваемым теплоносителем, к эксергии теплоты, отданной
греющим теплоносителем:
•^ q ' q
В простейшем случае m' = m" = my cp = c'p=cp, Q'^Q". Если Г2 =
Т4 = Т\—ДГГ, то эксергетические потери
П = То пгср In
Г'Г' _r I Z7*' 1-АГг/7-,\
M7-r°mC"lnVn-l+Ar,/r2/
Эта формула показывает влияние конечной разности температур при теплопередаче
на потерю работоспособности рабочих тел.
Газотурбинная установка. На рис. 28.8, а показана схема простейшей замкнутой
ГТУ без регенератора, а на рис. 28.8, б — идеальный и реальный (с учетом
необратимости процессов расширения и сжатия) циклы на яГ-диаграмме. При определении
372
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
эксергетических потерь в целях упрощения часто принимается, что рабочее тело
является идеальным газом, а теплоемкость не зависит от температуры и отсутствуют потери
ма трение в трубопроводах, нагревателе и холодильнике (т. е. процессы 1-2 и 3-0 счита-
отся изобарными).
Полезная работа цикла /п находится в виде разности между работой турбины /т
и работой привода компрессора /к:
где г\т и r\K — внутренние относительные кпд соответственно турбины и компрессора,
а
/; = А2 - А3. = ср (Г2 - Гз,г);. lT = h2-h3 = cp(T2 - Г3); (28.14)
|//к1=Аг-Ао = Ср(Гг-Го); |/к| = Л, — /г0 = ср (Г, — Го). (28.15)
Эксергетические потери в турбине вычисляются по формуле (28.11): nT=710(s3 —5г)
- и изображаются площадью cbgd на sT-диаграмме. Эти потери можно выразить через
степень повышения давления в цикле и внутренний кпд турбины, определив
температуру в конце расширения из (28.14):
Т3=Т2[ 1 —
=Г2[1-Лт (*-
п = р2/рз и l=
k. Тогда
Следовательно, эксергетическая потеря в турбине
Пт = СрГ01п[А, —Лт(Я,—1)].
Потери эксергии в охладителе газов обусловлены тем, что эксергия охлаждающей
среды, как правило, не используется, хотя ее средняя температура после
охладителя заметно выше температуры окружающей среды. Термодинамически это
равносильно полностью необратимому процессу теплообмена уходящих из турбины газов
(температура которых при этом снижается с Г3 до Го) с окружающей средой, имеющей
т
h
То
1'
^6
е
1с
/1
А
1
1
р/
\\/
/
ir
a b
f
1
\
\
1
\<
\
/
с
W
\у
9
d ,
Охлаждающая
среда Y3/1 °* °/=эз' ^s D
Рис. 28.8. Эксергетический анализ замкнутой ГТУ: а —
схема; б — sT-диаграмма циклов:
К — компрессор; Т — турбина
Работоспособность термодинамических систем 373
постоянную температуру 7V Таким образом, потери эксергии в охладителе равны эксер-
гии отходящих газов, т. е.
о
Похл = Э„зо = <73-о - То\ dq/T=(h3-h0) - T0(s3-s0),
з
и изображаются площадью 03g. Потери эксергии в компрессоре UK = T0(si — s0)
изображаются площадью eOaf.
По формуле (28.15) мож^о найти температуру Т\ через повышение давления и
внутренний кпд компрессора:
Так как
то
При определении эксергетического кпд цикла полезную работу относят к
приращению эксергии рабочего тела Эг — Э| в нагревателе. Поэтому
Лэц= In/ (32-3i) = [(32-3i) -211,] /(Э2-Э,)=1-2П,/(Э2-Э|),
где 2П/ — сумма эксергетических потерь во всех элементах установки, за исключением
нагревателя.
Увеличение эксергии рабочего тела в нагревателе равно эксергии теплоты,
полученной рабочим телом:
2
Э2-Э, = 3^ = ^.2-rojd<7/r=(A2-Л,)-ro(*2-*i)-
1
Эта величина на sT-диаграмме изображается площадью а12Ь. Температура газов Гг
перед ту*рбиной выбирается по условиям прочности деталей турбины и является, таким
образом, заданной. Если ввести обозначение т = Г2/Г0, то
Таким образом, эксергетический кпд цикла можно представить в виде
пт+похл + пк /т_|/к|
или
Коэффициенты эксергетических потерь для отдельных элементов установки
составят:
турбины
От=
компрессора
374
РАЗДЕЛ 6. ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
охладителя
При определении эксергетического кпд установки в целом полезную работу (с
учетом механических потерь, расхода работы на привод вспомогательных механизмов
и др.) следует относить к изменению эксергии первичных источников энергии, которые
применяются для получения теплоты. Если нагревателем служит камера сгорания, то
вводимая в установку эксергия равна эксергии топлива Эт, значение которой близко
к значению так называемой высшей теплоты сгорания топлива.
При сжигании органических топлив в камерах сгорания происходят большие
потери эксергии, доходящие до 50 %. Это вызвано тем, что по условиям прочности
деталей установок допускаемая максимальная температура рабочего тела значительно
ниже максимальной теоретической температуры горения топлив. Эта вынужденная
разница температур эквивалентна (в смысле влияния на работоспособность)
необратимому теплообмену между источником теплоты и рабочим телом при такой же разности
температур.
Газовая холодильная машина. Схема простой газовой холодильной машины с про-
тивоточным теплообменником-регенератором показана на рис. 28.9, а. В качестве хладо-
агента выбран идеальный газ с постоянной теплоемкостью, а падение давления из-за
трения в трубопроводах и теплообменных аппаратах не учитывается. Далее
принимается, что в компрессоре К происходит адиабатное, но не изоэнтропное, сжатие газа,
теплообмен в концевом холодильнике происходит при постоянной температуре
охлаждающей среды, равной Го, и при переменной температуре хладоагента, а в холодильной
камере (ХК) — при постоянной температуре холодильной камеры 7\.к и также при
переменной температуре хладоагента. Соответствующие температурные разности
обусловливают внешнюю необратимость цикла и эксергетические потери. Внутренняя
необратимость вызвана возрастанием энтропии в процессах сжатия в компрессоре (процесс
1-2 на рис. 28.9, б) и расширения в детандере Д (процесс 4-5), а также наличием
конечной разности температур между прямым и обратным потоками хладоагента в проти-
воточном теплообменнике.
'ХК
<
А
У
ssst
Рис. 28.9. Эксергетический анализ холодильной машины: а —
схема; б — яГ-диаграмма циклов:
К — компрессор; X — холодильник; Т — противоточный теплообменник-
регенератор; Д — детандер; ХК — холодильная камера
Работоспособность термодинамических систем 375
Эксергетическая эффективность холодильной машины характеризуется отношением
минимальной работы, затрачиваемой в полностью обратимом обратном цикле для
переноса теплоты (равной холодопроизводительности) от холодильной камеры (с
температурного уровня Гх.к) к окружающей естественной среде (на температурный уровень
Го), к фактической затрате работы в реальном необратимом цикле. Минимальная
работа холодильного цикла равна работоспособности теплоты, отводимой от
холодильной камеры: 1т\п—Яо(То— Тх^)/Тхк. Работа в реальном цикле равна разности между
работой компрессора |/к| и работой детандера /д:/дейст = UkI—Лм/д.
Механические потери учтены через механический кпд детандера т|м. Эксергетиче-
ский кпд холодильной машины можно представить в виде отношения:
ЛЭ = 'min /'дейсг = [<70 (То — 7\.к) /7\.к ]//дейст■.
Работа компрессора в реальном процессе 1-2
-г.У^^
где л = р2/Р1 и X=T2,/
Работа детандера
Холодопроизводительность реального цикла равна количеству теплоты,
получаемому хладоагентом в процессе 5-6:
<7о= fee = ср(Т6- Т5) = ср{Т .к+ ЛГ - Т5 - А7) = ср[ 1\Л{ТХЛ+ А7) (Л - 1)Д - Д7].
Таким образом, эксергетический кпд
где
Из рис. 28.9, б видно, что работа детандера составляет небольшую долю работы,
необходимой для привода компрессора. Поэтому в машинах небольшой мощности
детандер нагружается тормозом и его работа передается окружающей среде в форме
теплоты трения, что равносильно значению г|м = 0. Это уменьшает эксергетическую
эффективность машины, но позволяет упростить машину за счет отказа от механизма
передачи работы от детандера к компрессору.
Вопросы 1. Что называется функцией работоспособности?
2. Как выражается полезная работа в закрытой и в проточной термодинамической
системе?
3. Как выражается функция работоспособности проточной системы, получающей теплоту
от внешнего источника?
4. Как изменяется эксергия в равновесных и в неравновесных процессах?
б. Как зависят потери эксергии в необратимых процессах от параметров окружающей
среды?
Список литературы
1. Андрющенко А. И. Основы термодинамических циклов теплоэнергетических установок.
М., 1985.—319 с.
2. Базаров И. П. Термодинамика. М., 1986.— 272 с.
3. Задачник по технической термодинамике и теории тепломассообмена/^. Н. Афанасьев,
С. И. Исаев, И. А. Кожаное и др.; Под ред. В. И. Крутова и Г. Б. Петражицкого. М.,
1986.— 383 с.
4. Исаев С. И. Курс химической термодинамики. М., 1986.— 272 с.
5. Кириллин В. А., Сычев В. В., Шейндлин А. Е. Техническая термодинамика.— М.,
1983.— 385 с.
6. Коваленко А. Д. Основы термоупругости. Киев, 1970.— 308 с.
7. Лабораторный практикум по термодинамике и теплопередаче/Б. Н. Афанасьев, А. А.
Афонин, С. И. Исаев и др.; Под ред. В. И. Крутова, Е. В. Шишова. М., 1988.— 216 с.
8. Сычев В. В. Сложные термодинамические системы. М., 1980.— 208 с.
9. Теплотехника/Л. М. Архаров, С. И. Исаев, И. А. Кожинов и др.; Под общ. ред.
В. И. Крутова. М., 1986.— 432 с.
10. Циглер Г. Экстремальные принципы термодинамики необратимых систем. М., 1966.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсорбция 343
Анализ эксергетический 369
Величина интенсивная 24
— калорическая 24
— молярная 25
— объемная 25
— термическая 24
— удельная 25
— экстенсивная 24
Влагосодержание 147
Влажность воздуха абсолютная 146
— — относительная 147
Влажный воздух 146
— — насыщенный 146
— — ненасыщенный 146
— — пересыщенный 152
Время релаксации плазмы 166
Второй закон термодинамики 17, 49
Газовая постоянная влажного воздуха 149
— — плазмы 173
смеси 94
— — универсальная 84, 207
Давление 24, 25
— абсолютное 25
— атмосферное 25
— избыточное 25
— насыщения 128
— осмотическое 241
— парциальное 91
— полное торможения 250
— среднее цикла 282
Двигатель внутреннего сгорания 281
— Стирлинга 285
— реактивный 295
Дебаевский радиус 161
Деградация энергии 54
Декомпрессия 128
Диаграмма индикаторная 281
— vp 28
— dh 151
— sT 35
— sh 141
— фазовая 80
— эксергетическая 366
Диффузор 250
Доля компонента массовая 91
молярная 92
объемная 92
Дросселирование 269
Дроссель-эффект 271, 272
Жидкость перегретая 125
Закон Вант-Гоффа 241
Закон Генри 240
— Гесса 212
— Гюи — Стодолы 368
— Дальтона 91
— действующих масс 216
— Коновалова 242, 243
— парциальных давлений 91
— Рауля 240
Идеальный газ 84
Изображающая точка 28
Кажущаяся молярная масса 93
Когезия 133
Компонент 73, 237
Компрессор многоступенчатый 329
— одноступенчатый 322
Кондиционирование 155
Константа равновесия 217
— — плазмы 167
Контрольная поверхность 20
Коэффициент заполняемости 313
— гидравлического сопротивления 256, 257
— избытка воздуха 234
— изотермной сжимаемости 66
— отопительный 45, 336
— преобразования теплоты 337
— скорости 256
— теплоиспользования 344
-- термического расширения 66
— термической упругости 66
— холодильный 45, 335
— эксергетических потерь 369
— эффективности топливного элемента 361
Кпд цикла термический 44, 45
Карно 46
эксергетический 369
Кратность ионизации 161
Кривая инверсии 272
— плавления 80
— сублимации 80
— упругости 129
Круговая частота плазменных колебаний 162
Линия Бойля 123
— затвердевания 129 '
— процесса 28
МГД-генератор 354
Мера реакции 208
Метод каскадный 347
— Клода 347
— круговых процессов 322
— Линде 347
— термодинамических функций 322
— характеристических функций 62
— эксергетических потерь 369
— — потоков 369
378
Предметный указатель
Неравенство Кирквуда — Онсагера 163
Объем 23, 25
— парциальный 92
Окружающая среда 20
Осмос 240
Основное уравнение термодинамики 38
Отношение теплоемкостей 88
Пар влажный 122, 138
— перегретый 121, 140
— пересыщенный 125
— сухой 121
Параметр вырождения 164
— неидеальности плазмы 163
Параметры состояния 22
Первый закон термодинамики 16, 29
Плазма 157, 161
— вырожденная 165
— высокотемпературная 158, 163
— замагниченная 175
— низкотемпературная 158, 16&
— равновесная 166
— сильноионизованная 163
— слабоионизованная 162
Плотность влажного воздуха 149
— парциальная 95
Поверхность состояний 27
Поверхностное натяжение 134
Поверхностная фаза жидкости 133
Пограничная кривая 121
Показатель адиабаты 90
— политропы 110
Потенциал Гиббса 64
— ионизации 159
— термодинамического взаимодействия 24
— химический 24, 72, 207
Правило рычага 243
— фаз Гиббса 77, 78
Принцип Бертло 223
— возрастания энтропии 49, 50—52
— Ле Шателье-Брауна 226
— микроскопической обратимости 185
— недостижимости абсолютного нуля 354
— неопределенности Гейзенберга 181
— существования энтропии 49
Процесс термодинамический 27
— — адиабатный 28
— — изобарный 28
— — изотермный 28
— — изохорный 28
— — круговой 43
неравновесный 27, 50, 51
— — нестационарный 40
— — политропный 109
равновесный 28
стационарный 40
Работа 19, 31, 32
— ввода 39
— вывода 39
— дисгрегации 137
Работа магнитная 33
—, механическая 33
— проталкивания 39
— располагаемая 42
— техническая 39, 41
Распределение Гиббса 182
— Максвелла — Больцмана 179
Раствор 237
— бинарный 238
— идеальный 237, 243
— насыщенный 237
— реальный 244
Растворитель 237
Растворенное вещество 237
Реакция экзотермическая 211
— эндотермическая 211
Регенерация 290
Род взаимодействия 20
Сечение канала 250
— — критическое 251, 252
Система термодинамическая 20
адиабатная 21
— — гетерогенная 73
гомогенная 73
закрытая 21
— — изолированная 53
" открытая 21, 39
— — проточная 21
расширенная 29
— — термодеформационная 21
— — термомагнитная 349
Смесь газовая 91
Соотношения взаимности Онсагера 185
Сопло 250
— Лаваля 253
— механическое 257
— расчетное 253
— тепловое 254
Состав смеси азеотропный 243
Состояние термодинамической системы 21
безразличное 70
— — — неустойчивое 70
— равновесное 22
— стационарное 22
— устойчивое 70
Статистический вес 181
Степень влажности пара 138
— диссоциации 219
— ионизации 162
— перегрева 140
— полноты реакции 219
— превращения 219
Сублимация 128
Тело макроскопическое 18
— рабочее 20
Температура адиабатного торможения 250
— Бойля 123
— мокрого термометра 150
— насыщения 128
— сухого термометра 155
— термодинамическая 24, 25
Теорема Карно 46, 59—62
Предметный указатель
379
— Нернста 228
Тепловой насос 336
Теплоемкость 36, 37
— газовой смеси 95
— идеального газа 86—90
— изобарная 37
— изохорная 37
— истинная 36, 37
— молярная 36
— объемная 36
— средняя 36, 38
— удельная 36
Теплоноситель газовый 318
— жидкометаллический 317
— органический 317
Теплообмен 19
Теплота 20, 34
— некомпенсированная 198
— парообразования удельная 137
— приведенная 61
— фазового перехода 78
Термическая расширяемость 65
— упругость 65
Термогенератор 357
Термотрансформатор 336
Термоэлектронный генератор 359
Термодинамика плазмы 157
— статистическая 17, 177
— твердого тела 191
— техническая 16
— физическая 16
— химическая 16
Третий.закон термодинамики 13, 228, 352
Точка инверсии 272
— росы 153
Тройная точка 80
Уравнение состояния Клапейрона —
Менделеева 84
Майера — Боголюбова 27
— — термическое 26
— сохранения энергии 29
— термохимическое 212
— Максвелла 64
Условия равновесия 70—72
— — фазового 77
химического 216
— устойчивости равновесного состояния 66
Установка абсорбционная 338
— газотурбинная 287
— парогазовая 320
— паросиловая 306
— ядерная энергетическая 315
Фаза 73
Фазовый переход 78
— — 1-го рода 78
— — 2-го рода 81
Формула Эльверта 169
Формулировки второго закона термодинамики
55
— первого закона термодинамики 30
Формы движения материи 18
— обмена энергией 20
Функции состояния 22
Функция работоспособности 363
Характеристические функции 64
Химическое сродство 222
стандартное 217, 223
Хладоагент 340
Холодильная машина 335
Холодопроизводительность 335
Цикл термодинамический 43
бинарный 312
Карно 46, 306
— — обратимый 46
обратный 45, 333
Карно 334
прямой 44
Ренкина 307
— — холодильный 45, 335
Уравнение Бернулли 249
— Больцмана 180
— Ван-дер-Ваальса 123
— Гиббса — Гельмгольца 209
— изобары реакции 225
— изотермы реакции 223
— изохоры реакции 225
— Кирхгофа 213
— Клапейрона — Клаузиуса 80
— Лапласа 136
— обращения воздействий 248
— Саха 167
— состояния 26
— — Ван-дер-Ваальса 27
— — Клапейрона 26
Шкала термодинамической температуры 25,
47
Эжектор 259
Эксергия 365
Элемент топливный 360
Энергия 18
— внутренняя 22, 23, 38, 63
— вырождения 164
— кинетическая 22
— потенциальная 22
— свободная 63
— — поверхностного слоя 101
Энтальпия 41, 63, 64
— идеального газа 85
— полная 231
— свободная 63, 222
Энтропия 24, 25, 56
— идеального газа 86
— изолированной системы 29
— смешения 98
Эффект образования 210
— реакции 210
— сгорания 213
— эластокалорический 197
Оглавление
Предисловие
Ввведение •
Раздел 1
ОСНОВНЫЕ ПОНЯТИЯ, ЗАКОНЫ И УРАВНЕНИЯ
Глава 1
ПОНЯТИЯ
И ОПРЕДЕЛЕНИЯ
Глава 2
ПЕРВЫЙ ЗАКОН
ТЕРМОДИНАМИКИ
§ 1.1. Предмет термодинамики 16
§ 1.2. Виды энергии и формы обмена энергией 18
§ 1.3. Термодинамические системы, окружающая среда и
взаимодействия между ними * 21
§ 1.4. Состояние термодинамической системы, параметры и
функции состояния 21
§ 1.5. Внутренняя энергия термодинамической системы ... 22
§ 1.6. Кординаты термодинамического состояния и потенциалы
взаимодействий 23
§ 1.7. Единицы термодинамических величин 24
§ 1.8. Уравнения состояния 26
§ 1.9. Термодинамические процессы 27
§ 2.1. Первый закон термодинамики как форма закона
сохранения энергии при ее превращениях 29
§ 2.2. Работа. Свойства работы как формы обмена энергией 31
§ 2.3. Теплота. Свойства теплоты как формы обмена энергией 34
§ 2.4. Теплоемкость 36
§ 2.5. Основное уравнение термодинамики 38
§ 2.6. Особенности открытых систем 39
§ 2.7. Уравнение первого закона термодинамики для открытых
систем 39
§ 2.8. Уравнение первого закона термодинамики для
стационарной проточной системы. Энтальпия и располагаемая работа . 41
Глава 3
ЗАМКНУТЫЕ
ТЕРМОДИНАМИЧЕСКИЕ
ПРОЦЕССЫ
§ 3.1. Прямой цикл 43
§ 3.2. Обратный цикл 45
§ 3.3. Цикл и теорема Карно 46
§ 3.4. Цикл Карно как инструмент для построения шкалы
термодинамической температуры 47
§ 3.5. Условия равновесной передачи энергии между телами
с разной температурой и взаимопревращения теплоты и работы 48
Глава 4
ВТОРОЙ ЗАКОН
ТЕРМОДИНАМИКИ
§ 4.1. Принцип существования энтропии 49
§ 4.2. Принцип возрастания энтропии 50
§ 4.3. Энтропия изолированной системы и деградация энергии 53
§ 4.4. Формулировки второго закона термодинамики .... 55
§ 4.5. Энтропия и вероятность состояния 56
§ 4.6. О доказательстве существования энтропии ..... 59
Глава 5
ХАРАКТЕРИСТИЧЕСКИЕ
ФУНКЦИИ
И ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
§ 5.1. Основные характеристические функции 6S
§ 5.2. Свойства характеристических функций 6^
§ 5.3. Дифференциальное уравнение состояния 6(
§ 5.4. Дифференциальные уравнения внутренней энергии,
энтальпии и энтропии 6"/
§ 5.5. Дифференциальные уравнения удельных теплоемкостей
cv и ср 6t-
Глава 6 § 6.1. Общие условия термодинамического равновесия . . . 7и
§ 6.2. Основное уравнение термодинамики для неоднородных
ТЕРМОДИНАМИЧЕСКОЕ систем 72
РАВНОВЕСИЕ ^ g 3. Условия термодинамического равновесия неоднородных
систем 715
§6.4. Условия фазового равновесия 77
§ 6.5. Фазовые переходы 1-го рода 78
§ 6.6. Фазовая Гр-диаграмма &0
§ 6.7. Фазовые переходы 2-го рода 81
Раздел 2
СВОЙСТВА И ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
Глава 7 § 7.1. Термодинамические характеристики 84
§ 7.2. Внутренняя энергия, энтальпия и энтропия 85
ТЕРМОДИНАМИЧЕСКИЕ § 7.3. Теплоемкость 86
СВОЙСТВА § 7.4. Основы кинетической теории теплоемкости 89
И ТЕПЛОЕМКОСТЬ
Глава 8
СМЕСИ
ИДЕАЛЬНЫХ ГАЗОВ
§ 8.1. Парциальные давления компонентов смеси 91
§ 8.2. Состав газовой смеси 91
§ 8.3. Свойства идеальных газовых смесей 92
§ 8.4. Кажущаяся молярная масса 93
§ 8.5. Соотношения между массовыми, объемными и молярными
долями компонентов газовой смеси. Плотность газовой смеси 94
§ 8.6. Теплоемкость газовой смеси 95
§ 8.7. Внутренняя энергия, энтальпия и энтропия газовой смеси 96
Глава 9
ОСНОВНЫЕ
ТЕРМОДИНАМИЧЕСКИЕ
ПРОЦЕССЫ
§ 9.1. Задачи изучения термодинамических процессов ... 9Ь
§ 9.2. Изохорный процесс 100
§ 9.3. Изобарный процесс 102
§ 9.4. Изотермный процесс Ю4
§ 9.5. Адиабатный процесс 106
§ 9.6. Политропный процесс Ю9
Раздел 3
СВОЙСТВА И ПРОЦЕССЫ РЕАЛЬНЫХ ГАЗОВ
Глава 10
РЕАЛЬНЫЕ ГАЗЫ
Глава 11
ПАРЫ
§ ЮЛ. Качественные особенности реальных газов 118
§ 10.2. Уравнение Ван-дер-Ваальса 123
§ 10.3. Уравнение состояния в вириальной форме .... 126
§ 11.1. Получение пара 128
§ 11.2. Термодинамические свойства жидкости 131
§ 11.3. Термодинамические свойства поверхности раздела фаз 133
Глава 12
ВЛАЖНЫЙ ВОЗДУХ
Глава 13
ПЛАЗМА
Глава 14
ЭЛЕМЕНТЫ
СТАТИСТИЧЕСКОЙ
ТЕРМОДИНАМИКИ
Глава 15
ЭЛЕМЕНТЫ
ТЕРМОДИНАМИКИ
ТВЕРДОГО ТЕЛА
§ 11.4. Характерные состояния пара 137
§ 11.5. sh-диаграмма 141
§ 11.6. Термодинамические процессы 143
§ 12.1. Параметры влажного воздуха 146
§ 12.2. Температура мокрого термометра 150
§ 12.3. rf/г-диаграмма влажного воздуха 151
§ 12.4. Смешение потоков влажного воздуха 153
§ 12.5. Определение влажности воздуха по температурам
мокрого и сухого термометров 155
§ 12.6. Кондиционирование воздуха 155
§ 13.1. Плазма в природе и технике 157
§ 13.2. Свойства и классификация плазмы 159
§ 13.3. Идеальная и неидальная плазма 163
§ 13.4. Термодинамическое и термическое равновесие в плазме 165
§ 13.5. Состав равновесной плазмы 167
§ 13.6. Термодинамические параметры плазмы 170
§ 13.7. Свойства замагниченной плазмы 175
§ 14.1. Задачи статистической термодинамики 177
§ 14.2. Функции распределения 177
§ 14.3. Кинетическое уравнение Больцмана 180
§ 14.4. Квантовая статистика 181
§ 14.5. Определение термодинамических параметров
статистическими методами 182
§ 14.6. Основы теории Онсагера 184
§ 14.7. Применение теории Онсагера к анализу процессов
теплопроводности 187
§ 14.8. Применение теории Онсагера к анализу
термоэлектрических эффектов 188
§ 15.1. Напряженное и деформированное состояние твердого
тела 191
§ 15.2. Термодинамические соотношения для системы с упругими
деформациями 193
§ 15.3. Выражения для калорических свойств и функций
процесса 195
§ 15.4. Пластические деформации и диссипативная функция . 198
§ 15.5. Необратимые силы и экстремальные принципы
неравновесной термодинамики 200
Раздел 4
СИСТЕМЫ С ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ
Глава 16
ОСНОВНЫЕ ПОНЯТИЯ
И УРАВНЕНИЯ
§ 16.1. Характеристики состава сложной системы. Основное
уравнение термодинамики 206
§ 16.2. Химический потенциал 207
§ 16.3. Мера реакции 208
§ 16.4. Изменение функций состояния при химических
превращениях 208
Глава 17
ТЕРМОХИМИЯ
Глава 18
ХИМИЧЕСКОЕ
РАВНОВЕСИЕ
И СРОДСТВО
Глава 19
РАСТВОРЫ
§ 17.1. Тепловые эффекты реакций 209
§ 17.2. Закон Гесса 211
§ 17.3. Тепловые эффекты образования и сгорания веществ . 212
§ 17.4. Зависимость теплового эффекта от температуры . . . 213
§ 17.5. Зависимость теплового эффекта от агрегатного
состояния веществ 215
§ 18.1. Условия химического равновесия. Закон действующих
масс 216
§ 18.2. Степень полноты реакции и состав равновесной смеси 219
§ 18.3. Влияние давления и объема на степень диссоциации . 220
§ 18.4. Химическое сродство 222
§ 18.5. Зависимость константы равновесия от температуры.
Принцип Ле Шателье—Брауна 225
§ 18.6. Тепловая теорема Нернста . ., 227
§ 18.7. Третий закон термодинамики 228
§ 18.8. Расчеты с помощью таблиц стандартных величин и
таблиц полных энтальпий и энтропии 229
§ 18.9. Определение параметров состояния и состава рабочих
тел и продуктов сгорания 232
§ 19.1. Состав и парциальные свойства 237
§ 19.2. Уравнение Ван-дер-Ваальса для бинарных систем . . 238
§ 19.3. Законы Рауля и Генри 239
§ 19.4. Закон осмотического давления Вант-Гоффа .... 240
§ 19.5. Первый и второй законы Коновалова 241
§ 19.6. Реальные и многокомпонентные растворы .... 243
20
ИСТЕЧЕНИЕ ИЗ СОСУДА
НЕОГРАНИЧЕННОГО
ОБЪЕМА
Глава 21
ИСТЕЧЕНИЕ ИЗ СОСУДА
ОГРАНИЧЕННОГО
ОБЪЕМА*-
Глава 22
ДРОССЕЛИРОВАНИЕ
Раздел 5
ТЕЧЕНИЕ ГАЗОВ И ПАРОВ
§ 20.1. Основные уравнения 246
§ 20.2. Параметры торможения 249
§ 20.3. Адиабатное течение идеального газа в каналах . . . 250
§ 20.4. Движение газа при наличии теплообмена с внешней
средой 254
§ 20.5. Движение газа при наличии трения 255
§ 20.6. Истечение реальных газов и паров 257
§ 20.7. Процессы в эжекторах 259
§ 21.1. Основные уравнения 261
§ 21.2. Истечение из сосуда ограниченного постоянного объема
через отверстие постоянного сечения 263
§ 21.3. Истечение из сосуда ограниченного постоянного объема
через отверстие переменного сечения 265
§ 21.4. Истечение из сосуда ограниченного переменного объема
через отверстие переменного сечения 266
§ 21.5. Истечение реальных газов и паров 267
§ 22.1. Условия возникновения дросселирования . . . . ' . 269
§ 22.2. Дросселирование водяного пара- 275
Раздел 6
ПРОЦЕССЫ В ТЕПЛОВЫХ МАШИНАХ
23
ЦИКЛЫ
ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
С ГАЗООБРАЗНЫМ
РАБОЧИМ ТЕЛОМ
§ 23.1. Обобщенный цик. 1 тепловых двигателей 278
§ 23.2. Циклы поршневых двигателей внутреннего сгорания . 281
§ 23.3. Цикл двигателя Стирлинга 285
§ 23.4. Циклы газовых турбин 287
§ 23.5. Циклы реактивных двигателей 295
§ 23.6. Сравнительный анализ циклов тепловых двигателей . 301
Глава 24
ЦИКЛЫ
ПАРОСИЛОВЫХ
УСТАНОВОК
§ 24.1. Цикл Карно 306
§ 24.2. Цикл Ренкина 307
§24.3. Расширение пределов рабочего процесса 308
§ 24.4. Цикл с промежуточным перегревом пара 310
§24.5. Бинарные циклы 311
§ 24.6. Регенеративный цикл паротурбинной установки ... 313
§ 24.7. Циклы ядерных энергетических установок 315
§ 24.8. Циклы парогазовых установок .... ... 319
§ 24.9. Сравнительный анализ работы тепловых машин . . . 322
Глава 25
СЖАТИЕ ГАЗОВ
В КОМПРЕССОРЕ
§ 25.1. Одноступенчатый компрессор .
§ 25.2. Многоступенчатый компрессор
325
329
Глава 26
ОБРАТНЫЕ ЦИКЛЫ
ТЕПЛОВЫХ МАШИН
Глава 27
БЕЗМАШИННОЕ
ПРЕОБРАЗОВАНИЕ
ЭНЕРГИИ
Глава 28
РАБОТОСПОСОБНОСТЬ
ТЕРМОДИНАМИЧЕСКИХ
СИСТЕМ
§ 26.1. Понятие об обратных циклах. Обратный цикл Карно . 333
§ 26.2. Показатели эффективности обратных циклов .... 335
§ 26.3. Циклы газовой холодильной машины 338
§ 26.4. Циклы парокомпрессионной холодильной машины . . 340
§ 26.5. Цикл абсорбционной холодильной машины 343
§ 26.6. Цикл теплового насоса. Термохимический
трансформатор теплоты 344
§ 26.7. Получение сжиженных газов 346
§ 26.8. Общие принципы и способы достижения сверхнизких
температур 349
§ 26.9. Поведение термодинамических систем при температуре,
стремящейся к абсолютному нулю 351
§ 27.1. МГД-генератор 354
§ 27.2. Термогенератор 357
§ 27.3. Термоэлектронный генератор 359
§ 27.4. Топливные элементы 360
§ 28.1. Эффективность преобразования энергии 362
§ 28.2. Функции работоспособности. Эксергия 364
§ 28.3. Эксергетические диаграммы 366
§ 28.4. Эксергетические потери и эксергетический кпд . . . 368
§ 28.5. Эксергетический анализ работы тепловых машин . . 369
Список литературы
Предметный указатель
376
381