Основы теории тепловых ракетных двигателей. Теория, расчет и проектирование - Дорофеев А.А.

Часть I. Теория идеального теплового ракетного двигателя
Глава 3. Основы теории сверхзвукового сопла
Глава 5. Высотная характеристика ракетного двигателя
Глава 6. Усилия, действующие на проточную часть ракетного двигателя
Глава 7. Составляющие тяги. Место приложения тяги ракетного двигателя
Глава 8. Дроссельные характеристики двигательной установки, состоящей из нескольких идентичных автономных ЖРД, при синхронном и последовательном дросселировании камер
Глава 9. Элементы внутренней баллистики РДТТ и твердотопливных газогенераторов. Совместная работа камеры сгорания и сопла
Глава 10. Идеальный ядерный ракетный двигатель
Глава 11. Ракетный двигатель со скоростной камерой сгорания. Полутепловое сопло
Глава 12. Камера сгорания ракетного двигателя с распределенным подводом рабочего тела. Полурасходное сопло
Глава 13. Классификация ракетных двигателей. Из истории ракетных двигателей
Часть II. Теория неидеального теплового ракетного двигателя
Глава 15. Система коэффициентов учета потерь в ракетном двигателе. Удельный импульс камеры ракетного двигателя и двигательной установки
Глава 16. Химические реакции и понятие о равновесном составе гетерогенной смеси. Основы термодинамического расчета
Глава 17. Термодинамический расчет. Запись закона сохранения массы вещества через элементный состав топлива и парциальные давления компонентов продуктов сгорания
Глава 18. Закон сохранения энергии в системе уравнений термодинамического расчета
Глава 19. Система уравнений термодинамического расчета с использованием констант равновесия
Глава 20. Принцип максимума энтропии и его использование при термодинамическом расчете
Глава 21. Модели течения в соплах. Термодинамический расчет состава продуктов сгорания в произвольном сечении сопла
Глава 22. Влияние давления в камере сгорания и степени расширения рабочего тела в сопле на термодинамические характеристики продуктов сгорания типовых ракетных топлив
Глава 23. Термодинамический расчет термокаталитического разложения гидразина и водных растворов пероксида водорода
Глава 24. Особенности и результаты термодинамического расчета при большом различии между соотношением компонентов и их стехиометрическим соотношением. Задача балластировки
Глава 25. Камеры сгорания, их параметры и оценка совершенства рабочих процессов
Глава 26. Сопла ракетных двигателей. Понятия, термины и определения. Потери в соплах
Глава 27. Расчет потерь в соплах ракетных двигателей
Глава 28. Профилирование сопл. Задачи выбора профиля сопла
Глава 30. Штыревое сопло: основы профилирования и особенности работы при переменном давлении окружающей среды
Глава 31. Тарельчатое сопло: основы профилирования и особенности работы при переменном давлении окружающей среды
Глава 32. Состояние и перспективы развития теории ракетных двигателей
Часть III. Методические указания и контрольно-измерительные материалы
1.2. Особенности методик изложения материала, его преподавания и изучения
1.3. Состав контрольно-измерительных материалов и курсовых заданий
2. Контрольно-измерительные материалы к части I
3. Контрольно-измерительные материалы к части II
4. Примерное содержание курсового домашнего задания
5. Примерное содержание курсового проекта
7. Примеры к разделу «Термодинамические расчеты»
8. Контрольные вопросы к защите лабораторных работ по курсу «Общая теория ракетных двигателей»
Лабораторная работа № 2 «Исследование влияния соотношения компонентов топлива на основные показателии характеристики ракетного двигателя»
Лабораторная работа № 3 «Экспериментальное определение дроссельной характеристики ЖРД»
Лабораторная работа № 4 «Работа сопла Лаваля при больших степенях перерасширения»
9. Типовые вопросы к защите курсового проекта
Приложение 1. Параметры стандартной атмосферы по ГОСТ 4401-81
Приложение 2. Параметры экстремального контура сопла
Author: Дорофеев А.А.
Tags: тепловые двигатели (кроме паровых машин и паровых турбин) междупланетные соединения (междупланетные полеты) космонавтика (аэронавтика) учебник для вузов ракетные комплексы и космонавтика тепловые ракетные двигатели расчет и проектирование
ISBN: 978-5-7038-3746-7
Year: 2014
Similar
Жидкостные ракетные двигатели. Основы проектирования
Сборник задачи и вопросов по основам теории и расчета ракетных двигателей
Основы теории и расчета жидкостных ракетных двигателей. Книга 2
Основы теории и расчета жидкостных ракетных двигателей
Text
                    А.А. Дорофеев
Основы теории
тепловых ракетных
двигателей
Теория, расчет и проектирование
Издание 3-е, переработанное и дополненное
Рекомендовано Учебно-методическим объединением вузов
по университетскому политехническому образованию
в качестве учебника для студентов высших учебных заведений,
обучающихся по направлению подготовки бакалавров
и магистров 160400.62.68 «Ракетные комплексы
и космонавтика» и инэюенеров по специальности 160700.65
«Проектирование авиационных и ракетных двигателей»
Москва
Издательство МГТУ им. Н.Э. Баумана
2014

УДК 621.455(075.8)
ББК 39.65
Д69
Рецензенты:
кафедра «Ракетные двигатели» Московского авиационного
института (национального исследовательского университета)
(зам. зав. кафедрой канд. техн. наук, проф. А.И. Коломейцев);
советник президента Ракетно-космической корпорации
«Энергия» им. С.П. Королева д-р техн. наук, проф. Е.А. Соколов
Дорофеев А. А.
Д69 Основы теории тепловых ракетных двигателей. Теория, расчет
и проектирование : учебник / А. А. Дорофеев. - 3-е изд., перераб.
и доп. - М. : Изд-во МГТУ им. Н.Э. Баумана, 2014.-571, [5] с. : ил.
ISBN 978-5-7038-3746-7
Содержание учебника, состоящего из трех частей, соответствует
курсу лекций, которые автор читает в МГТУ им. Н.Э. Баумана. В ч. I
представлены общие основы и понятийный аппарат теории идеальных
тепловых ракетных двигателей, а также их классификация.
В ч. II изложены физико-химические механизмы реальных рабочих
процессов, протекающих в тепловых ракетных двигателях, и методики
количественной оценки их влияния на выходные параметры двигателя
при отличии этих процессов от идеальных. Приведены методики решения
задач термодинамического расчета состава продуктов сгорания и
изменения их параметров при движении по соплу как химически активного
потока. В ч. III представлены методические указания и полный комплект
контрольно-измерительных материалов по блочно-модульным
образовательным технологиям.
Для студентов технических вузов авиационного и ракетного профилей
в качестве пропедевтического курса программ подготовки
дипломированных инженеров, магистров и бакалавров, также может представлять
интерес для инженерно-технических работников в области проектирования
и эксплуатации ракетной техники.
УДК 621.455(075.8)
ББК 39.65
В оформлении обложки использовано фото жидкостного
ракетного двигателя с дожиганием генераторного газа РД170 разработки
НПО «Энергомаш» им. академика В.П. Глушко
© Дорофеев А.А., 1999
О Дорофеев А.А., 2014, с
изменениями
© Оформление. Изд-во МГТУ
ISBN 978-5-7038-3746-7 им. Н.Э. Баумана, 2013

Оглавление
Предисловие к первому изданию 6
От автора (ко второму изданию) 9
Предисловие к третьему изданию 13
Основные условные обозначения 15
Сокращения 19
Введение 20
Часть I. Теория идеального теплового ракетного двигателя ... 23
Глава 1. Введение в дисциплину. Терминология. Виды ракетных
двигателей 25
Глава 2. Тяга ракетного двигателя 38
Глава 3. Основы теории сверхзвукового сопла 50
Глава 4. Режимы работы сверхзвукового сопла. Дроссельные
(расходные) характеристики идеального ракетного
двигателя 59
Глава 5. Высотная характеристика ракетного двигателя 69
Глава 6. Усилия, действующие на проточную часть ракетного
двигателя 79
Глава 7. Составляющие тяги. Место приложения тяги ракетного
двигателя 91
Глава 8. Дроссельные характеристики двигательной установки,
состоящей из нескольких идентичных автономных ЖРД,
при синхронном и последовательном дросселировании
камер 100
Глава 9. Элементы внутренней баллистики РДТТ и твердотопливных
газогенераторов. Совместная работа камеры сгорания
и сопла 107
Глава 10. Идеальный ядерный ракетный двигатель 121
Глава 11. Ракетный двигатель со скоростной камерой сгорания.
Полутепловое сопло 129
Глава 12. Камера сгорания ракетного двигателя с распределенным
подводом рабочего тела. Полурасходное сопло 139
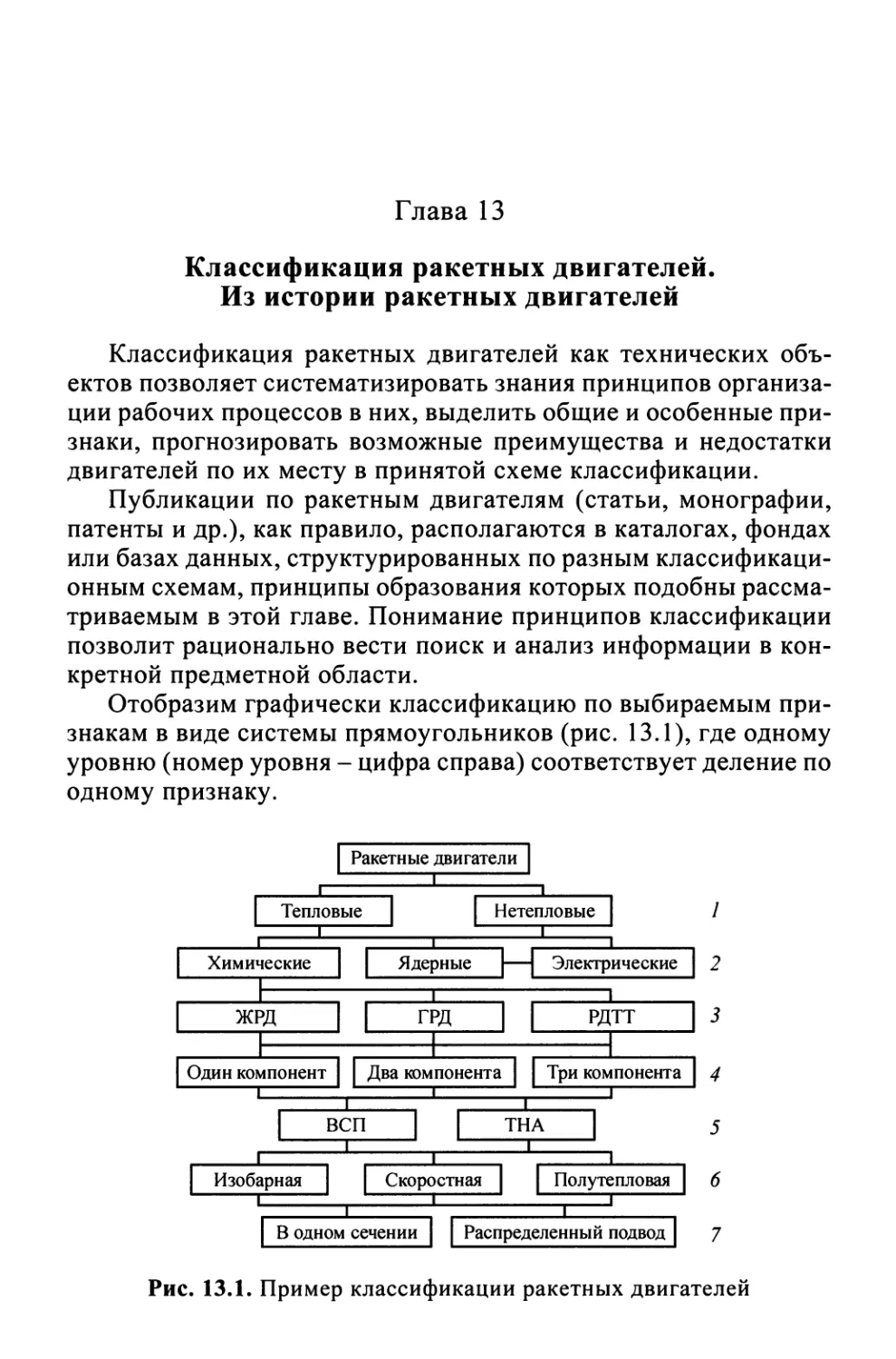
Глава 13. Классификация ракетных двигателей. Из истории ракетных
двигателей 154
Часть И. Теория неидеального теплового ракетного двигателя 167
Глава 14. Основные различия между реальными рабочими
процессами и их идеальным представлением в теории
ракетного двигателя 169

4
Оглавление
Глава 15. Система коэффициентов учета потерь в ракетном
двигателе. Удельный импульс камеры ракетного двигателя и
двигательной установки 177
Глава 16. Химические реакции и понятие о равновесном составе
гетерогенной смеси. Основы термодинамического расчета. . . 192
Глава 17. Термодинамический расчет. Запись закона сохранения
массы вещества через элементный состав топлива и
парциальные давления компонентов продуктов сгорания ... 212
Глава 18. Закон сохранения энергии в системе уравнений
термодинамического расчета 223
Глава 19. Система уравнений термодинамического расчета с
использованием констант равновесия 243
Глава 20. Принцип максимума энтропии и его использование при
термодинамическом расчете 251
Глава 21. Модели течения в соплах. Термодинамический расчет
состава продуктов сгорания в произвольном сечении сопла. . . 270
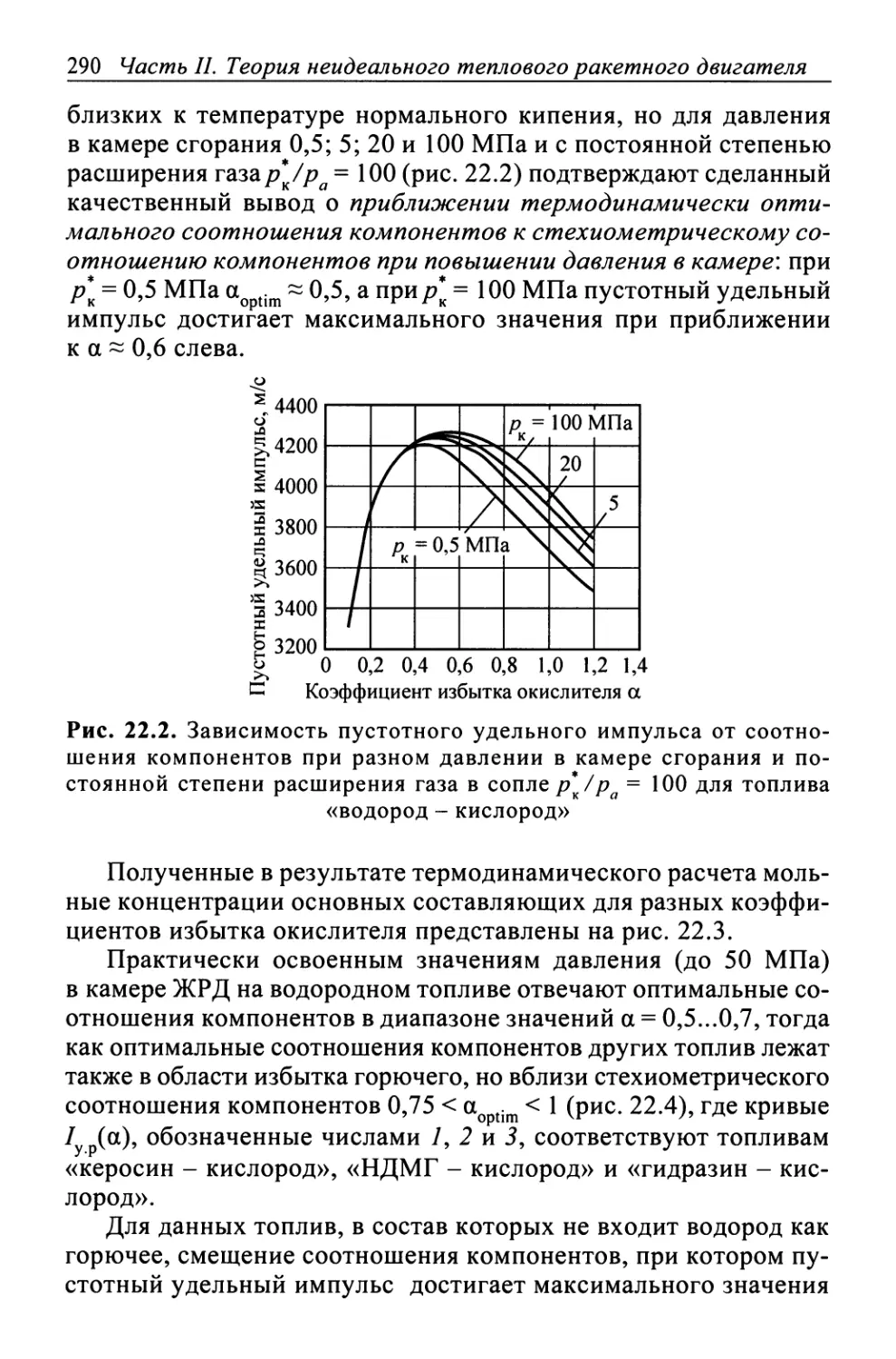
Глава 22. Влияние давления в камере сгорания и степени расширения
рабочего тела в сопле на термодинамические
характеристики продуктов сгорания типовых ракетных топлив. . . . 286
Глава 23. Термодинамический расчет термокаталитического
разложения гидразина и водных растворов пероксида водорода ... 301
Глава 24. Особенности и результаты термодинамического расчета
при большом различии между соотношением компонентов
и их стехиометрическим соотношением. Задача
балластировки 314
Глава 25. Камеры сгорания, их параметры и оценка совершенства
рабочих процессов 328
Глава 26. Сопла ракетных двигателей. Понятия, термины и
определения. Потери в соплах 346
Глава 27. Расчет потерь в соплах ракетных двигателей 350
Глава 28. Профилирование сопл. Задачи выбора профиля сопла . . 384
Глава 29. Работа сопл на режимах перерасширения при больших
степенях нерасчетности. Дроссельные (расходные) и
высотные характеристики ракетных двигателей 400
Глава 30. Штыревое сопло: основы профилирования и особенности
работы при переменном давлении окружающей среды ... 413
Глава 31. Тарельчатое сопло: основы профилирования и особенности
работы при переменном давлении окружающей среды . . . 427
Глава 32. Состояние и перспективы развития теории ракетных
двигателей 433

Оглавление
5
Часть III. Методические указания и контрольно-измерительные
материалы 443
1. Методические указания 445
1.1. Дидактические функции учебной дисциплины и их
отражение в учебнике 446
1.2. Особенности методик изложения материала, его
преподавания и изучения 450
1.3. Состав контрольно-измерительных материалов и
курсовых заданий 456
2. Контрольно-измерительные материалы к части I 463
2.1. Рубежный контроль 1 463
2.2. Рубежный контроль 2 469
3.3. Вопросы к зачету по части I 476
3. Контрольно-измерительные материалы к части II 485
3.1. Рубежный контроль 3 485
3.2. Рубежный контроль 4 501
3.3. Вопросы к зачету по части II 515
4. Примерное содержание курсового домашнего задания 534
5. Примерное содержание курсового проекта 537
6. Вопросы экзаменационных билетов 542
7. Примеры к разделу «Термодинамические расчеты» 545
8. Контрольные вопросы к защите лабораторных работ по курсу
«Общая теория ракетных двигателей» 548
Лабораторная работа № 1 «Изучение лабораторного
комплекса. Запуск стендовой жидкостной ракетной двигательной
установки (ЖРДУ)» 548
Лабораторная работа № 2 «Исследование влияния
соотношения компонентов топлива на основные показателии
характеристики ракетного двигателя» 549
Лабораторная работа № 3 «Экспериментальное определение
дроссельной характеристики ЖРД» 551
Лабораторная работа № 4 «Работа сопла Лаваля при больших
степенях перерасширения» 552
9. Типовые вопросы к защите курсового проекта 554
Литература 559
Электронные источники информации 561
Предметный указатель 562
Именной указатель 569
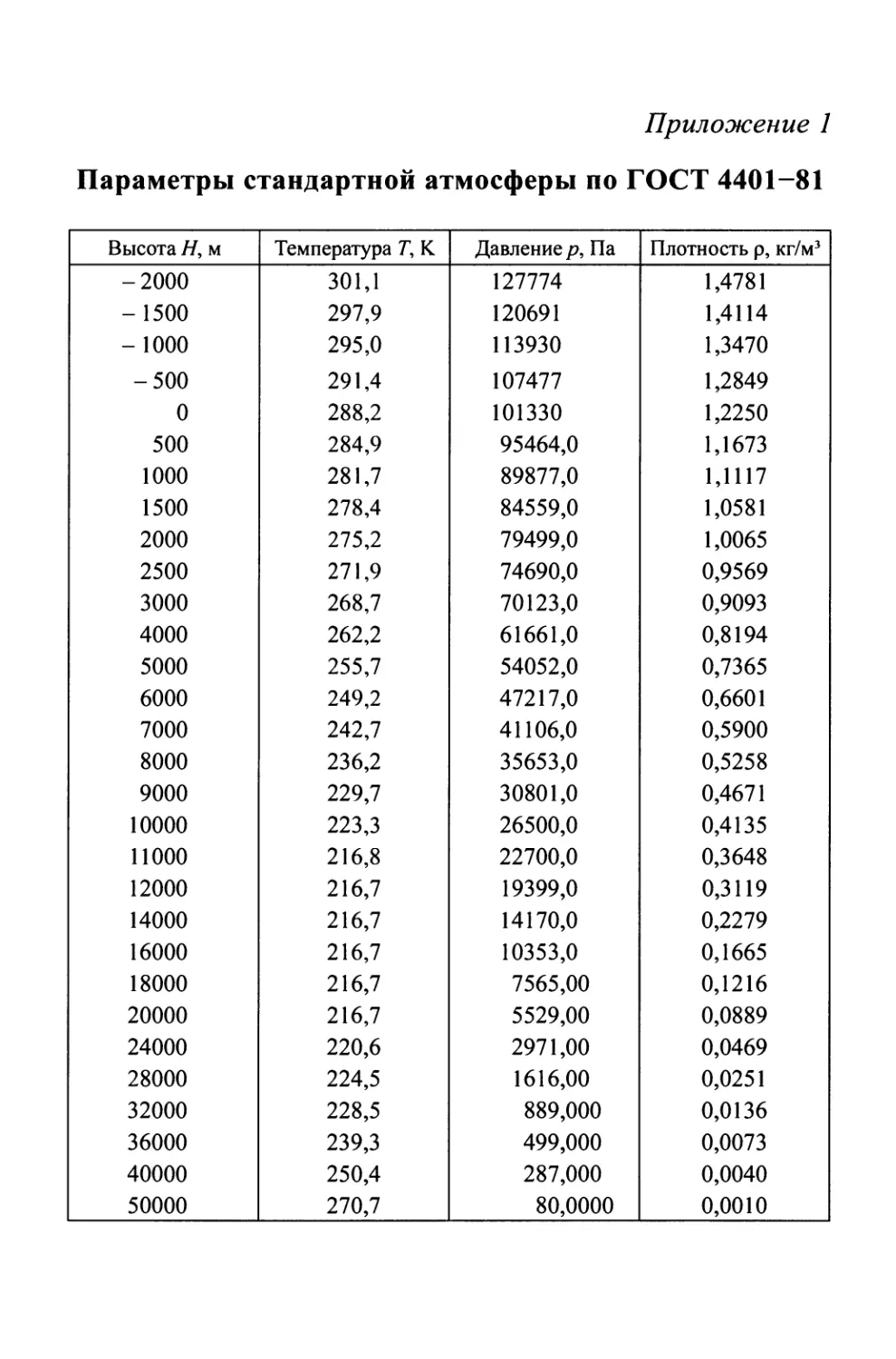
Приложение 1. Параметры стандартной атмосферы
по ГОСТ 4401-81 572
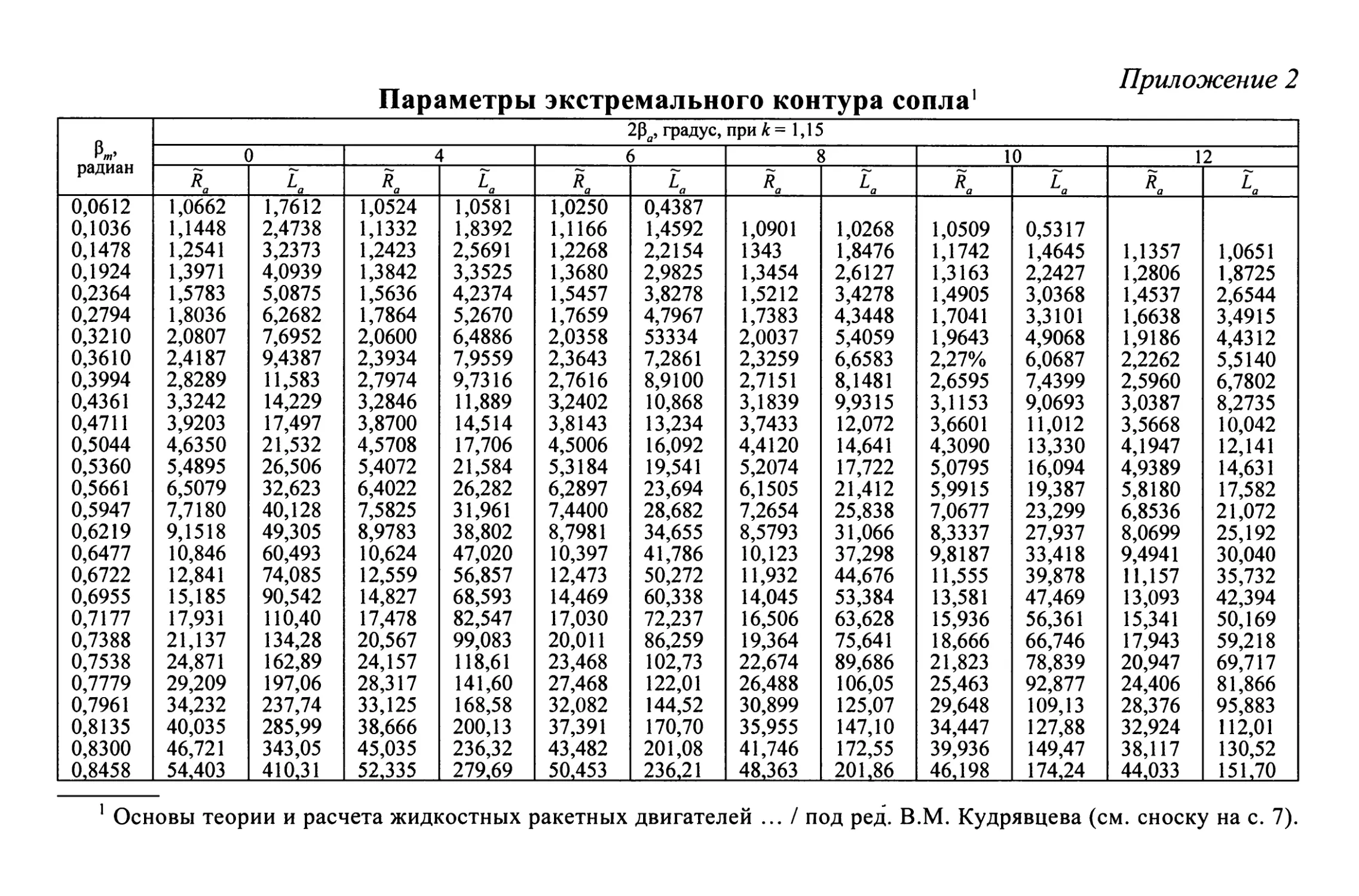
Приложение 2. Параметры экстремального контура сопла 573

Предисловие к первому изданию
Более чем полувековой опыт отечественной высшей школы
в подготовке специалистов в области конструирования,
производства и применения ракетных двигателей, закрепленный в
последние годы соответствующими образовательными стандартами,
говорит о рациональности построения профилирующей части
учебного плана на базе двухсеместровой дисциплины «Общая
теория ракетных двигателей».
Целью преподавания дисциплины является формирование у
студента-двигателиста, впервые приступающего к изучению дисциплин
специальности, целостного научно обоснованного представления
о принципах реактивного движения и их эффективной реализации
в ракетных двигателях, использующих различные источники
энергии. При этом имеется в виду изучение предельно достижимых
параметров и характеристик ракетных двигателей независимо от
конкретного типа источника энергии. В курсе обосновывается
необходимость понимания физической картины и адекватного, но
относительно простого математического описания особенностей
рабочих процессов конкретных видов и назначений.
Таким образом, обозначаются научная проблематика и место
в учебном плане последующих дисциплин специальности,
рассматривающих узлы, агрегаты ракетного двигателя и рабочие
процессы в них.
Близкая по содержанию дисциплина представляется
целесообразной и в учебном плане подготовки бакалавра по
специальности «Авиа- и ракетостроение», так как курс бакалавриата
предусматривает изучение общих основ конкретного направления
науки и техники. При этом требуется определенная унификация
содержания этой дисциплины, вытекающая из необходимости
обеспечить возможность для бакалавра продолжать образование в
любых высших учебных заведениях с целью получения как степени
магистра, так и квалификации дипломированного специалиста.
Необходимость интенсификации учебного процесса наряду
с унификацией содержания методически базовых дисциплин,
к которым можно отнести дисциплину «Общая теория ракетных
двигателей», является обоснованием выпуска представляемой
книги, раскрывающей дисциплину.
Основным предметом изданных до настоящего времени и
вполне апробированных учебных пособий являются, как правило,
ракетные двигатели конкретного вида, например ЖРД, РДТТ или

Предисловие к первому изданию
1
ЯРД, причем их общие свойства рассматриваются без полного
учета приведенных выше требований и не настолько подробно,
чтобы рекомендовать эти пособия в качестве основных для
изучения дисциплины «Общая теория ракетных двигателей».
Предлагаемый учебник «Основы теории тепловых ракетных
двигателей» написан с учетом изложенных выше требований и
представляет собой результат решения современной
учебно-методической задачи с использованием опыта, накопленного кафедрой
«Ракетные двигатели» МГТУ им. Н.Э. Баумана и другими
родственными кафедрами, а также достижений в области методики
подготовки по специальностям «Ракетные двигатели» и
«Ракетостроение», отраженных во многих известных учебных пособиях
и учебниках, прежде всего в таких, как написанные В.И. Фео-
досьевым, Г.Б. Синяревым, М.В. Добровольским, А.В. Квасниковым,
Т.М. Мелькумовым и соавторами, авторскими коллективами под
редакцией В.П. Глушко, В.М. Кудрявцева.
Состав, структура и объем книги в основном отвечают
образовательному стандарту по специальности «Ракетные двигатели»
и программе дисциплины «Общая теория ракетных двигателей»,
содержание и принципы изложения материала которой постоянно
уточнялись в процессе ее преподавания в разные годы
профессорами и доцентами МГТУ им. Н.Э. Баумана, главным образом А.П.
Васильевым, М.В. Добровольским, В.М. Кудрявцевым, В.М. Поляевым,
М.А. Поповым, В.А. Чернухиным и другими.
Следуя традициям преподавания этой дисциплины на
кафедре «Ракетные двигатели», отраженным в учебнике1,
выдержавшем четыре издания и отмеченном Государственной
премией, автор в рамках объема дисциплины отдает предпочтение
формам представления материала, которые обеспечивают его
ясную физическую интерпретацию, помогают и понять, и
усвоить. При этом студент получит возможность изучить уже в
основном освоенный заинтересовавший его вопрос на развернутой
теоретической основе в других дисциплинах применительно
к двигателям конкретного типа.
В основу содержания представляемой книги положен конспект
лекций, читаемых автором в МГТУ им. Н.Э. Баумана с 1980 г.
Основы теории и расчета жидкостных ракетных двигателей:
учебник для авиац. спец. вузов: в 2 кн. / А. П. Васильев, В.М. Кудрявцев,
В.А. Кузнецов и др.; под ред. В.М. Кудрявцева. 4-е изд., перераб. и доп.
М.: Высш. шк., 1993.

8
Предисловие к первому изданию
В связи с ограничениями объема книги часть материала
представлена в сжатом виде, в частности сведения, касающиеся истории
ракетных двигателей. Интересующимся читателям предлагается
обращаться к изданиям, приведенным в списке литературы.
Отсутствие в учебнике необходимых для закрепления
изученного материала задач объясняется ориентацией учебной
дисциплины на вышедший в 1995 г. сборник задач, указанный в списке
литературы, который следует рассматривать как минимально
необходимый при изучении дисциплины, хотя при написании
книги имелось в виду большинство из известных отечественных
и зарубежных учебников и монографий по ракетным двигателям.
Предлагаемый учебник имеет прямое предназначение —
дисциплина «Общая теория ракетных двигателей». Целесообразно
использовать книгу и при преподавании и изучении аналогичных
по целям курсов, но меньшего объема.
Книга также может быть полезна и инженерно-техническим
работникам предприятий, занимающимся разработкой,
производством и эксплуатацией ракетной техники.
Профессор I \j\^ y\ В.М.Кудрявцев
25 июня 1998 г.
Кудрявцев Вадим Михайлович (1925-1998) — д-р техн. наук,
профессор, заслуженный деятель науки и техники РСФСР, лауреат
Государственной премии СССР, заведующий кафедрой «Ракетные
двигатели» МГТУ им. Н.Э. Баумана (1962-1994), крупный специалист
в области проектирования и отработки реактивных и ракетных
двигателей на гидрореагирующем топливе, один из основателей московской
научно-педагогической школы подготовки специалистов по ракетным
двигателям, соавтор и редактор четырех изданий учебника «Основы
теории и расчета жидкостных ракетных двигателей»; работал в МГТУ
им. Н.Э. Баумана в 1949-1998 гг.

От автора (ко второму изданию)
Предусмотренная государственным образовательным
стандартом дисциплина «Теория, расчет и проектирование ракетных
двигателей» структурирована традиционно для МГТУ им. Н.Э.
Баумана и преподается по многозвенной схеме: вначале изучаются
основы общей теории тепловых ракетных двигателей, т. е. то, что
свойственно двигателям независимо от вида используемого
источника энергии (топлива), а затем - особенное, присущее
жидкостным, твердотопливным или другим ракетным двигателям. В
настоящем учебнике основы общей теории ракетных двигателей
представлены в виде учебной дисциплины.
Задача дисциплины - заложить общие, совпадающие основы
теории ракетных двигателей, использующих нехимические и
химические источники энергии и топлива разного агрегатного
состояния, т. е., по существу, дать в компактной и математически
простой форме систематическое изложение представления о
физической картине основных процессов преобразования энергии
в тепловых ракетных двигателях и их математическое
количественное описание. Рассмотрены принципы разработки моделей
основных рабочих процессов. Большинство моделей
дополняется реализующими их расчетными методиками.
Предлагаемая книга представляет собой второе издание
учебника, написанного на основе расширенных и дополненных
конспектов лекций, которые автор читает в МГТУ им. Н.Э. Баумана
с 1980 г. При этом автор ставит перед собой задачу сохранения
положительного опыта преподавания этой дисциплины в МГТУ
им. Н.Э. Баумана ведущими профессорами и доцентами кафедры
«Ракетные двигатели», прежде всего В.М. Кудрявцевым, В.М. По-
ляевым, М.В. Добровольским, В.А. Чернухиным, которых автор
с благодарностью считает своими учителями, а также
собственного опыта преподавания, чем можно объяснить отражение
отчасти субъективных представлений о предпочтительности тех или
иных методик изложения материала некоторых разделов.
Первое издание учебника (1999) нашло применение как в
учебном процессе, так и в среде разработчиков и исследователей
ракетных двигателей. Полное распространение тиража не вызвало
затруднений. На эту книгу сохраняется устойчивый спрос.
Выпущенные одновременно с книгой компьютерные аналоги
первого издания (программисты С.Ф. Никитина, канд. техн. наук
Д.Ю. Юдин), в том числе размещенный на сайте МГТУ им. Н.Э. Бау-

10
От автора (ко второму изданию)
мана (www.bmstu.ru/) мультимедийный вариант (www.engineer.
bmstu.ru/res/dorofeev/MAIN.HTM), существенно расширили круг
пользователей учебника, что с учетом отзывов позволяет считать
апробированной принятую концепцию изложения материала, его
методическую структуру и когнитивный инструментарий.
Теоретическое обоснование дидактических характеристик учебника
выполнено автором в процессе научно-педагогических
исследований, результаты которых приведены в монографии1.
С позиции автора изучение дисциплины «Общая теория
ракетных двигателей» и настоящий учебник должны сформировать
у студента основы профессиональной компетентности: обеспечить
целостное и системное представление о тепловом ракетном
двигателе, понимание сути и роли частных задач теории расчета
и проектирования, которые рассматриваются в последующих
дисциплинах специальности. Освоение этой дисциплины должно дать
студенту ориентиры для поиска нужных сведений в
профессиональном информационном поле.
За время, прошедшее с выхода в свет первого издания
учебника, при продолжающемся накоплении знаний и углублении
понимания сложнейших рабочих процессов новых
фундаментальных результатов в общей теории тепловых ракетных двигателей
не получено и методологические основы ее сохранились. Остались
в основном прежними программа дисциплины и предметное
содержание учебника. Однако происходящие существенные
изменения в отечественной высшей школе обусловили не только
новое представление профессиональной подготовки специалиста
в виде системы приобретенных профессиональных компетенций,
но и деление учебного плана на федеральную, региональную и
вузовскую компоненты (постоянную и вариативную части), что
находит отражение в учебных программах и должно быть учтено
в учебнике.
Получают распространение образовательные технологии,
предусматривающие блочно-модульное структурирование учебного
плана, допускающего изучение ряда дисциплин как по
традиционной жестко детерминированной лекционно-семинарской
модели, так и в индивидуальном, оптимальном для студента темпе.
Эти нововведения требуют ориентированных на такие технологии
Дорофеев А.А. Дидактические основы проектирования учебной
литературы по дисциплинам специальности технического
университета. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.

От автора (ко второму изданию)
11
новых учебников, включения в них специальных методических
и контрольных материалов, которые допускают их применение
как в комплексе (что предпочтительнее), так и выборочно, причем
в порядке, который представляется преподавателю или студенту
наиболее близким к оптимальному.
Кроме того, внедренный в промышленность новый
основополагающий ГОСТ 17655—89 «Двигатели ракетные жидкостные.
Термины и определения», заменивший сразу три стандарта
(ГОСТ 17655-80, ГОСТ 22396-85 и ГОСТ 22763-77), является
обязательным и для применения в учебной литературе по
ракетным двигателям. Одновременно появились новые сетевые
информационные ресурсы, например база данных «Термические
Константы Веществ» (www.chem.msu. su/cgi-bin/tkvl.pl?show=
welcome.html) и т. п., а также такие новые программные
продукты, входящие в профессиональную информационную среду
специалиста по ракетным двигателям и используемые
изучающими общую теорию ракетных двигателей, как разработанный
в МГТУ им. Н.Э. Баумана профессором Б.Г. Трусовым
программный комплекс «Terra»1 (trusov@iu7-head.bmstu.ru) и др.
Совокупность этих факторов указывает на целесообразность
второго издания учебника, переработанного, исправленного
и дополненного. По авторскому замыслу настоящее издание
представляет собой так называемый модульный учебник. Он
включает как собственно учебный материал с полным
комплектом вопросов и заданий для текущего, рубежного,
семестрового и итогового контроля, так и методические указания и
рекомендации по изучению и преподаванию дисциплины по
гуманизированным деятельностно-ориентированным
образовательным технологиям.
При этом в учебник помещен материал преднамеренно и
заведомо избыточный для выделенного на дисциплину ресурса
времени (если иметь в виду возможности среднего студента). Но
этот избыточный материал необходим для обеспечения
оптимально напряженной индивидуальной образовательной работы
способных студентов. Поэтому в методических указаниях даны
рекомендации преподавателям по ранжированию информации для
разных уровней освоения дисциплины.
Trusov B.G. Program system TERRA for simulation phase and chemical
equilibrium // Proc. of the XIV Intern, symp. on Chemical Thermodynamics,
St-Petersburg. Russia, 2002. P. 483.

12
От автора (ко второму изданию)
При освоении дисциплины будет полезно использовать еще
не вошедшие в учебник ввиду ограниченности его объема
материалы по курсовому проектированию, представленные в
апробированном учебно-методическом издании1.
Автор внимательно проанализировал и с благодарностью учел
отзывы и замечания коллектива кафедры «Ракетные двигатели»
Московского авиационного института (технического
университета), коллег-преподавателей, научных сотрудников и
специалистов из промышленности, а также студентов, выявивших ряд
опечаток, которые исправлены в настоящем издании.
Автор признателен рецензенту - одному из патриархов
отечественного ракетного двигателестроения - д-ру техн. наук, проф.
Б.А. Соколову, д-рам техн. наук, проф. А.В. Воронецкому,
В.К. Чванову, Д.А. Ягодникову, д-ру хим. наук, проф. В.А. Ба-
тюку и канд. техн. наук, доц. В.А. Буркальцеву, В.А. Гостеву,
А.И. Коломенцову и Л.В. Кудрявцевой за критику и ценные
рекомендации, направленные на улучшение книги.
С замечаниями и предложениями, которые будут с
благодарностью приняты и учтены автором в дальнейшей работе, просьба
обращаться по адресу Издательства МГТУ им. Н.Э. Баумана:
105005, Москва, 2-я Бауманская ул., д. 5.
Дорофеев А.А. Проектирование и расчет параметров и
характеристик камеры ракетного двигателя: учеб. пособие. 2-е изд., испр. М.:
Логос, 2004.

Предисловие к третьему изданию
При сохранении основы и структуры предметного содержания
предыдущих изданий учебника его материал значительно
дополнен. За время, прошедшее с выхода в свет первого и второго
изданий учебника, основы теории тепловых ракетных двигателей
не претерпели существенных изменений, также остались
практически прежними объем соответствующей учебной дисциплины
и ее место в учебном плане подготовки специалистов по ракетным
двигателям в МГТУ им. Н.Э. Баумана.
При этом следует отметить продолжающееся накопление
знаний и углубление понимания сложнейших рабочих процессов,
в частности теории пульсирующих детонационных двигателей,
применения жидкостных ракетных двигателей с раздвижным
соплом, а также со свободной границей потока (с тарельчатым
соплом). Нанодисперсные порошки металлов используются в качестве
специфических компонентов горючих ракетных топлив, что
необходимо учитывать в методиках расчета их термодинамических
характеристик. Однако выявлен некоторый недостаток
информации, касающейся условных названий и специфических
характеристик отечественных и зарубежных ракетных топлив,
применение которых расширилось в последние годы.
Отсутствие практической апробации относительно новых
сведений и положений теории позволяет уточнить их, включив в
учебник более сложные методики описания характерных рабочих
процессов. Приведенные ссылки на источники информации, в том
числе сетевые, позволят заинтересованным читателям получить
дополнительные детальные сведения.
Отличие третьего издания учебника от предыдущих в
основном и заключается в наличии дополнительных сведений.
Активное внедрение в учебный процесс отечественной высшей школы
инновационных образовательных методик, ориентированных на
блочно-модульное структурирование с рейтинговым способом
оценки усвоения материала, потребовало также
соответствующего дополнения контрольно-измерительных материалов,
приведенных в части III.
Кроме того, в учебник включены полезные сведения из
зарубежных публикаций, сохранены и объединены атрибутивные
признаки отечественных московской и казанской
научно-педагогических школ подготовки специалистов по ракетным двигателям.

14
Предисловие к третьему изданию
Первым звеном в генезисе учебной литературы стал курс лекций
«Основы устройства реактивных двигателей на жидком топливе»,
прочитанных основоположником отечественного ракетного дви-
гателестроения В.П. Глушко в МВТУ им. Н.Э. Баумана на Высших
инженерных курсах (ВИК) в 1947-1948 гг.
Понимая возможности дальнейшего совершенствования
материала, автор с благодарностью примет замечания и
предложения читателей, которые можно направлять по адресу: a.a.dorofeev@
bmstu.ru или через Издательство МГТУ им. Н.Э. Баумана.
Обложка курса лекций В.П. Глушко - первого
отечественного учебного пособия по ракетным
двигателям
Дорофеев А.А. Учебная литература по инженерным дисциплинам:
системная дидактика, методика и практика проектирования. М.: Изд-во
МГТУ им. Н.Э. Баумана, 2012.

Основные условные обозначения
а - скорость звука
А, В - константы
с* - характеристическая скорость
с - массовая концентрация; массовая доля
С - теплоемкость
С, - коэффициент трения
с - удельная теплоемкость при постоянном давлении
cv - удельная теплоемкость при постоянном объеме
d - диаметр
Еп - полная энергия
F - площадь; сила
F" - удельная площадь потока
F(x),j{x) - функции аргумента х
g - ускорение; массовая доля; коэффициент балластировки
h - глубина погружения; глубина хода
Н - высота полета; термодинамическая энтальпия
/ - удельный импульс тяги; удельный импульс
1п - полная энтальпия, полное энергосодержание
к - показатель адиабаты, к = с lcv\ коэффициент в
уравнении для скорости химической реакции
К - коэффициент тяги; константа равновесия; соотношение
компонентов топлива (по массе)
К' - мольное соотношение компонентов топлива
/ - линейный размер
L - длина
М - число Маха
т - масса
М - количество вещества, выражаемое в молях
т - секундный расход
т - относительный расход
п - показатель изоэнтропы; кратность ионизации
N - мощность
р - давление
Р - тяга; сила тяги; реактивная сила
q - тепловой эффект растворения; тепловой поток;
плотность теплового потока
Q - теплота; энергия
г - объемная доля; объемная концентрация; скрытая
теплота парообразования

16
Основные условные обозначения
R - газовая постоянная; равнодействующая сил; усилие;
радиус
s - поверхность
5 - энтропия
/ - время
Т - абсолютная температура
U - скорость химической реакции; внутренняя энергия
v - удельный объем
V - объем
w, W - скорость
х - степень разложения
x,y9z - прямоугольные координаты
Z - массовая доля конденсированной фазы
а - коэффициент избытка окислителя ракетного топлива;
угол
Р - расходный комплекс; угол; вириальный коэффициент
в уравнении состояния
а, р, у, п - виды излучения (в уравнениях ядерных реакций)
у, ф, 6, со - углы
6 - малое приращение; линейный размер
г|/ - термический КПД
X - приведенная скорость, X = WlaK
\i - коэффициент расхода сопла; атомная масса;
молекулярная масса
v - показатель степени в законе горения твердого
ракетного топлива; число грамм-атомов вещества в реальной
или условной молекуле
§ - коэффициент потерь
п(Х, к), г(Х, к), т(Х, к), fiX, к), q(X, к), Z(X) - газодинамические
функции изоэнтропийного адиабатного потока
тс(М, к), 7Г*(М, к), jI(M, к), 7(М, к), е(М, к) - газодинамические
функции неизоэнтропийного адиабатного потока
р - плотность; радиус кривизны
о - коэффициент отношения давления; коэффициент
восстановления давления; коэффициент сужения струи
т - время; напряжение трения
Ф - коэффициент, связанный с соответствующим
коэффициентом потерь соотношением ф = 1 - §
\|/ - значение функции тока
ф - обобщенный параметр
ф* - полный приведенный изобарно-изотермический
потенциал Гиббса

Основные условные обозначения
17
Нижние индексы
б - бак
бал - балластный
вн - внутренний
вх - вход
вых - выход
г - горючее
г.с - головка смесительная
д - действительный
докр - докритический
д.у - относящийся к ДУ
и - идеальный
к - камера
кр - критический
к.с - камера сгорания
н - номинальный
нар - наружный
нер - неравновесный
о - окислитель
обрат - относится к обратному направлению
отн - относительный
охл - охлаждение, охладитель
п - пустотный, полный
пер - периферийный
под - при параметрах подачи
пр - продукты термокаталитического разложения
прям - относится к прямому направлению
п.с - относящийся к продуктам сгорания
р, расч - расчетный
расш - расширяющаяся часть канала
с - сопло
ск - относящийся к скачку уплотнения
ср - средний
ст - стенка, на стенке
суж - сужающаяся часть канала
т - топливо, относящаяся к тяге величина
табл - табличный
ТНА - относящийся к ТНА
тр - трение
у - удельный

18
Основные условные обозначения
ус - условный
ф - фазовый
я - ядро
а - выходное сечение
а-Ъ - действующий между сечениями а-Ъ
f - при параметрах точки отсчета
g - газ
h - соответствующий высоте h
hQ - соответствующий уровню моря
т - массовый
max - максимальный
min - минимальный
О - значение в тупике; соответствующее нулевому
значению характерного параметра
optim - оптимальный
s - полученный при предположении равновесия;
отнесенный к поверхности; относящийся к пристеночному
слою
х - в сечении с координатой х; проекция на ось х
Е - суммарный; относящийся к смеси
1, 2, 3,...- номер (индекс) сечения
Верхние индексы
(I) - номер приближения
- параметр торможения
- параметр при стандартном давлении, равном 1 атм
- параметр, усредненный в некотором диапазоне
значений
- параметр, отнесенный к характерному значению
- вектор
*

Сокращения
AT - азотный тетраоксид
ВРД - воздушно-реактивный двигатель
ВСП - вытеснительная система подачи
ГДЛ - газодинамическая лаборатория
ГДФ - газодинамическая функция
ГИРД - группа по изучению реактивного движения
ГРД - гибридный ракетный двигатель
ДВС - двигатель внутреннего сгорания
ДПуВРД - детонирующий пульсирующий воздушно-реактивный
двигатель
ДУ - двигательная установка
ЖГГ - жидкостный газогенератор
ЖРД - жидкостный ракетный двигатель
ЖРДМТ - жидкостный ракетный двигатель малой тяги
КПД - коэффициент полезного действия
ММГ - монометилгидразин
НДМГ - несимметричный диметилгидразин
ПВРД - прямоточный воздушно-реактивный двигатель
ПуВРД - пульсирующий воздушно-реактивный двигатель
ПуПВРД - пульсирующий прямоточный воздушно-реактивный
двигатель
РДТТ - ракетный двигатель на твердом топливе
РИТ - радиоизотопный источник теплоты
РН - ракета-носитель
ТВС - тепловыделяющая сборка
ТНА - турбонасосный агрегат
ТРД - турбореактивный двигатель
ТРТ - твердое ракетное топливо
УВГ - углеводородное горючее
ЯРД - ядерный ракетный двигатель

Введение
Высокоскоростные летательные аппараты - самолеты, ракеты,
ракетопланы, искусственные спутники Земли, межпланетные и
орбитальные станции и др. - обеспечивают контролируемое,
преимущественно управляемое, движение для доставки груза в заданную
точку пространства и (или) движение по заданной траектории при
заданных скоростях (поступательной и вращательной) и
сохранении параметров движения. Например, самолет при ограничениях
длины взлетной полосы осуществляет набор скорости, достаточной
для взлета и устойчивого полета, сохранение управляемости при
эволюциях на траектории или выход на посадочную траекторию
с заданными стабильными скоростью, углом атаки и допустимым
креном. Ракетоноситель выводит полезный груз на заданную
траекторию при заданной ориентации вектора скорости.
Оснащенный солнечными батареями искусственный спутник
Земли, находящийся на геостационарной орбите, ориентируется
в пространстве относительно Солнца, а приближающаяся к
Венере межпланетная станция, передающая наблюдаемые из
космоса изображения на Землю, должна находиться в пространстве
в таком положении, чтобы передающая радиоантенна была
направлена в сторону приемника с заданной точностью. Для
сближающихся на стыковку космических аппаратов существенны все
характеристики их относительного движения - расстояние,
угловые и поступательные скорости и ускорения, взаимная
относительная ориентация.
Изменить параметры движения можно, прикладывая к
летательному аппарату силу и/или момент силы относительно его
центра масс. Если летательный аппарат движется в среде,
оказывающей детерминированное и случайное сопротивление, - в поле
сил гравитации, в атмосфере, в воде, - то не только изменение,
но и поддержание постоянными параметров движения требует
преодоления силы сопротивления. Это возможно, если
летательный аппарат снабжен устройством, работа которого вызывает
появление силы, совершающей механическую работу.
Машина (устройство), преобразующая какой-либо вид энергии
в механическую работу, называется двигателем. Существует
множество различных форм движения материи и соответственно
множество различных видов энергии. Однако известны лишь два
принципиально различающихся способа передачи энергии
(формы обмена энергией) - работа и теплообмен.

Введение
21
Из множества видов двигателей для летательных аппаратов
нашли применение преимущественно тепловые двигатели,
системным атрибутивным признаком которых является
преобразование тепловой энергии в механическую. Причем для
относительно малых скоростей полета в атмосфере применяются
двигатели с воздушным винтом - движителем, а для больших
скоростей - двигатели, называемые реактивными, в которых
движитель не используется. Сила тяги реактивного двигателя
возникает непосредственно в двигателе за счет реакции элементов
его конструкции на давление рабочего тела - вещества,
выбрасываемого в окружающую среду.
Реактивный двигатель, в котором используются только
источник энергии и рабочее тело, размещаемые на борту
предназначенного для движения аппарата {omnia mea mecum porto1),
называется ракетным двигателем. При близких габаритах
ракетный двигатель по сравнению с другими тепловыми
реактивными двигателями имеет максимальную мощность (уникально
большую мощность, приходящуюся на единицу массы) или для
заданной мощности - минимальную массу при наименьшей
зависимости от параметров окружающей среды. В частности,
только ракетный двигатель может обеспечить необходимый уровень
тяги, превышающий аэродинамическое сопротивление среды
при ускоренном движении в плотных слоях атмосферы, и
только ракетный двигатель может автономно работать в космическом
вакууме.
Достижения человечества в освоении космоса обусловлены
развитием ракетного двигателестроения. Баллистическая ракета
с ракетным двигателем на жидком топливе стала первым
летательным аппаратом, способным выходить за пределы земной
атмосферы. Более совершенная ракета, созданная в СССР под
руководством СП. Королева, 4 октября 1957 г. вывела на орбиту
первый в мире искусственный спутник Земли. В истории
человечества была открыта космическая эра.
Орбитальный космический полет 12 апреля 1961 г. первого
в мире космонавта гражданина СССР Ю.А. Гагарина, положил
начало дерзновенному проникновению человека в космос.
Широкомасштабные работы по становлению и развитию
ракетно-космической промышленности США позволили успешно
«Все мое ношу с собой» - изречение греческого философа Бианта.

22
Введение
осуществить полет к Луне: в 1969 г. впервые человек ступил на
поверхность ближайшего к Земле небесного тела.
Достижения мировой космонавтики последующих лет стали
возможными в результате успехов в области ракетного двигате-
лестроения. Высокие требования к безопасности при
значительном возрастании стоимости экспериментальной отработки
ракетной техники обусловливают совершенствование теории ракетных
двигателей как необходимое условие успешного развития
ракетного двигателестроения и космонавтики в целом.
Морфологически тепловой ракетный двигатель является
результатом совершенствования и развития тепловых машин,
и в частности тепловых реактивных двигателей. Как реактивный
двигатель и частный случай тепловой машины ракетный двигатель
можно рассматривать на основе достаточно общих
термодинамических подходов. Вместе с тем особенности ракетных
двигателей конкретного назначения требуют выделения специфических
аспектов, а для этого необходимо использовать уже изученный
материал, но на более высоком теоретическом уровне. Сочетание
общего и особенного лежит в основе системного подхода к теории
теплового ракетного двигателя. В рамках этой теории сначала
излагается теория идеального ракетного двигателя, позволяющая
оценить предельно достижимые параметры, далее
рассматриваются отличия реальных рабочих процессов от их идеального
представления при неизбежном использовании положений теории
идеального двигателя.
Предельная напряженность и сложность рабочих процессов
ракетного двигателя требуют их глубокого изучения. Теория
тепловых ракетных двигателей (независимо от вида используемого
топлива или источника энергии) - пропедевтическая, т. е. вводная,
одновременно является базовой, структурообразующей
дисциплиной при изучении полного курса теории и проектирования
ракетных двигателей.

ЧАСТЬ I
ТЕОРИЯ ИДЕАЛЬНОГО ТЕПЛОВОГО
РАКЕТНОГО ДВИГАТЕЛЯ

Глава 1
Введение в дисциплину. Терминология.
Виды ракетных двигателей
Двигатель - устройство, создающее силу или момент,
прикладываемые к объекту, вектор количества движения которого
нужно изменить (ускорить или замедлить поступательное или
вращательное движение, изменить ориентацию или направление
движения) или поддерживать постоянным. В последнем случае
двигатель преодолевает сопротивление окружающей среды, т. е.
компенсирует действие внешних сил.
В двигателе происходит преобразование энергии различных
видов в механическую энергию объекта, оснащенного двигателем.
Механическая энергия объекта изменяется в результате действия
на него системы сил, в которую входят и силы, образующиеся при
работе двигателя. Например, в автомобиле с двигателем
внутреннего сгорания (ДВС) химическая энергия топлива (горючее -
бензин, окислитель - воздух) переходит в камере сгорания и цилиндре
в тепловую энергию продуктов сгорания, которые, расширяясь,
преобразуют часть своей тепловой энергии в механическую
энергию звеньев кривошипно-шатунного механизма, передаваемую
колесу. Колесо, взаимодействуя с опорной средой (землей),
действует с некоторой силой на автомобиль, сообщая ему
механическую энергию. Между двигателем и опорной средой в качестве
движителя используется промежуточный элемент - колесо.
Воздушный винт (пропеллер) также выступает в роли
движителя - промежуточного элемента между подвижным объектом и
опорной средой (воздухом) при полете самолета с поршневым
ДВС.
Если двигатель выполняет свои функции без использования
движителя, то он называется двигателем прямой реакции или
реактивным двигателем. В реактивном двигателе сила
возникает как реакция элементов конструкции двигателя на действие
протекающего в нем газообразного или жидкого вещества,
отбрасываемого для создания тяги, так называемого рабочего тела.
Отбрасывание массы рабочего тела возможно только с некоторой
относительной скоростью. Следовательно, рабочее тело при

26 Часть I. Теория идеального теплового ракетного двигателя
движении в двигателе ускоряется, его кинетическая энергия
увеличивается за счет преобразования располагаемой (максимально
возможной) энергии других видов в кинетическую энергию
направленного движения. Устройство, в котором рабочее тело
ускоряется относительно двигателя, называется пропульсивным
устройством или пропульсивным аппаратом. Располагаемая
энергия рабочего тела, часть которой в пропульсивном устройстве
переходит в кинетическую энергию, может быть увеличена за
счет подвода к рабочему телу энергии от некоторого источника
в энергообменном устройстве.
Таким образом, реактивный двигатель как техническая
система (рис. 1.1) содержит следующие функциональные элементы:
источник энергии, рабочее тело, энергообменное устройство,
пропульсивное устройство.
Рабочее
тело
1—»•
Источник
энергии
Энергообменное
устройство
««—1
Пропульсивное
устройство
Рис. 1.1. Схема ракетного двигателя как технической системы
Если в реактивном двигателе в качестве рабочего тела
используется воздух, то такой двигатель называется воздушно-
реактивным двигателем (ВРД). Известно несколько схем ВРД,
в которых используется химическая энергия топлива и
реализуются описанные выше принципы.
В состав прямоточного воздушно-реактивного двигателя
(ПВРД) (рис. 1.2) входят входной диффузор 7, в котором
кинетическая энергия потока переходит в энергию давления в камере
сгорания 2, где химическая энергия переходит в тепловую
энергию продуктов сгорания; сопло 3, в котором продукты сгорания
ускоряются; устройство подачи горючего в камеру - коллектор
горючего 4 - и систему инициирования и поддержания горения
в камере сгорания - стабилизатор горения 5.

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 27
Г 5
Рис. 1.2. Схема ПВРД:
/ - диффузор; 2 - камера сгорания; 3 - сопло;
4 - коллектор горючего; 5 - стабилизатор горения
В соответствии с системным подходом в ПВРД источник
энергии (см. рис. 1.1) - топливо, энергообменное устройство -
камера сгорания, рабочее тело - продукты сгорания и непрореагиро-
вавшая часть воздуха, сопло - пропульсивное устройство.
Используя уравнение сохранения импульса (количества
движения) за малое время At и полагая, что давление на наружной
поверхности двигателя и во входном и выходном сечениях равно
атмосферному, получаем выражение для тяги Р этого двигателя:
AtP = (Am + Am )W - AmW ,
v г' а вх'
(l.l)
где Am - некоторая малая масса воздуха, поступившая в двигатель
за время At; Amr - некоторая малая масса горючего, поданная
в двигатель за время At; WBx - скорость входа воздуха, близкая
или равная скорости полета; Wa - скорость истечения продуктов
сгорания, причем
Атт«Ат. (1.2)
Тогда, разделив (1.1) на Д^ и выполнив предельный переход
(1.3)
с учетом (1.2) получим следующую формулу:
P=m(Wa-WJ. (1.4)
Отметим, что вывод (1.4) не связан с конкретной
конструкцией двигателей и справедлив для любого двигателя, если
принятые допущения соблюдаются достаточно точно. Поскольку
скорость истечения продуктов сгорания зависит от их темпера-
Ат
hm = w,
Д/->0 Д/

28 Часть L Теория идеального теплового ракетного двигателя
туры и давления в камере сгорания, которое определяется в
основном скоростью полета, особенностью двигателя является
зависимость его характеристик от скорости полета. Характерные
недостатки такого двигателя - отсутствие стартовой тяги и
низкая экономичность на малых скоростях - обусловлены малым
давлением в камере сгорания, не превышающим полного
давления набегающего потока. Одним из путей повышения давления
является организация горения в камере сгорания постоянного
объема. Поскольку для создания тяги после сгорания топлива
обязательно истечение продуктов сгорания, работающие по
такому принципу двигатели относятся к нестационарно работающим,
или пульсирующим, двигателям.
Конструктивная схема пульсирующего ВРД (ПуВРД)
приведена на рис. 1.3, где показаны (в отличие от схемы на рис. 1.2)
новые агрегаты: обратный клапан 6, пропускающий воздух в
камеру сгорания 2 и закрывающийся, когда давление в камере
сгорания выше, чем давление набегающего потока; сопло 3 с резо-
наторной трубой, которое кроме функций собственно сопла
служит каналом, где продукты сгорания выполняют функции
газового поршня. Поршень по инерции проходит положение
равновесия и приводит к понижению давления в камере сгорания
ниже равновесного. При этом частота пульсаций давления в
камере сгорания согласуется с собственной частотой камеры
сгорания с соплом и резонаторной трубой.
6 4 5 7
фф! +
/ 2 3
Рис. 1.3. Схема ПуВРД:
1 - входной диффузор; 2 - камера сгорания; 3 - сопло; 4 - коллектор
горючего; 5 - устройство инициации горения; 6 - обратный клапан;
7 - резонаторная труба
ПуВРД обеспечивает тягу за счет истечения продуктов
сгорания. При этом давление в камере сгорания может достигать
высоких значений, тяга слабо зависит от скорости полета и
развивается даже при ее нулевом значении. Но тяга создаетс*Гтоль-
ко при истечении продуктов сгорания, время которого
составляет около 10% продолжительности цикла работы. В остальное

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 29
время работы двигатель играет роль дополнительного
аэродинамического сопротивления, тормозящего движение объекта,
поэтому экономичность ПуВРД невысока.
Частным вариантом рабочего процесса пульсирующего
прямоточного воздушно-реактивного двигателя (ПуПВРД) является
циклический рабочий процесс со сгоранием топливной смеси
в режиме детонации, при котором скорость перемещения фронта
горения в воздухе (волны детонации) превышает скорость
звука в этой смеси. Такой двигатель называют детонирующим
пульсирующим ВРД (ДПуВРД). Высокая скорость выделения
тепловой энергии приводит к тому, что образующиеся продукты
сгорания остаются на месте исходной топливной смеси и
сохраняют удельный объем, т. е. процесс идет при подведении энергии
по адиабате Гюгонио (цикл Гемфри) со значительным
повышением (в несколько раз) давления по сравнению с давлением в
камере сгорания ПуВРД, где горение топлива идет с гораздо
меньшими скоростями и сопровождается одновременным истечением
продуктов сгорания и непрореагировавшего топлива, т. е.
только приближается к изохорному процессу. Высокий уровень
давления в волне детонации и ее сверхзвуковая скорость позволяют
использовать камеру (см. рис. 1.3) без сопловой части и резона-
торной трубы, которые должны быть весьма прочными, а
следовательно, массивными. Отличную от обратного клапана 6
конструкцию должны иметь и устройства для ввода воздуха
в камеру ДПуВРД, как и устройство инициации горения 5 (в
режиме детонации - детонатор).
Высокое давление в камере сгорания ДПуВРД обеспечивает
большую, чем у ПуВРД, тягу в импульсе, но меньшую долю
времени действия тяги в рабочем цикле, что требует объединения
в единую двигательную установку (ДУ) нескольких работающих
синхронно камер с детонационным режимом работы на частотах
50...500 Гц. Современные представления о процессах и
характеристики ДПуВРД приведены в сборнике работ1 и в других
отечественных и зарубежных публикациях.
Давление в камере сгорания можно повысить по отношению
к полному давлению набегающего потока, применяя компрессор
для нагнетания в нее воздуха. По такой схеме работают
турбореактивные двигатели (ТРД) (рис. 1.4), где агрегаты /, 3, 5 и 6
Импульсные детонационные двигатели / под ред. СМ. Фролова.
М.: ТОРУС ПРЕСС, 2006.

30 Часть I. Теория идеального теплового ракетного двигателя
выполняют те же функции, что и в ПВРД (см. рис. 1.2). Но
воздух в камеру сгорания подается после повышения его давления
в осевом лопаточном компрессоре 2, который приводится в
движение газовой турбиной 5, установленной между камерой
сгорания 3 и соплом 6. Этим достигаются меньшая зависимость
экономичности двигателя от скорости и высоты полета,
возможность развивать стартовую тягу (после раскрутки ротора)
и большая, чем у ПВРД, эффективность при работе на
относительно малых скоростях.
Рис. 1.4. Схема ТРД:
1 - диффузор; 2 - осевой компрессор; 3 - камера сгорания;
4 - коллектор горючего; 5 - газовая турбина; 6 - сопло
Покажем принципиальную возможность повышения тяги
реактивного двигателя путем перераспределения располагаемой
кинетической энергии рабочего тела на большую массу. Пусть
воздух не поступает в камеру и тяга P = mWa создается
истечением продуктов сгорания рабочего тела. Тогда вносимая в
камеру за 1 с кинетическая энергия рабочего тела
Е = ГИ^. (1.5)
Допустим, что масса рабочего тела увеличена в п раз. При
этом исходная кинетическая энергия Екин перераспределяется
с некоторыми потерями С, равномерно. Тогда кинетическая
энергия рабочего тела увеличенной массы составит (1 - Q долю
кинетической энергии, вычисляемой по уравнению (1.5), т. е.
(1 Q™Wl S^Wta (16)
Из (1.6.) следует, что

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 31
W2a=}—^Wa. (1.7)
V п
Тяга реактивного двигателя с увеличенным расходом
рабочего тела
Р2 = rhnA^Wa = />>(!" О- (1.8)
V п
Из (1.8) следует, что если массовый расход рабочего тела будет
существенно (в п раз) увеличен, то при низких потерях
кинетической энергии возможно повышение тяги реактивного
двигателя приблизительно в чп раз.
Одной из схем, реализующих этот принцип, является схема
двухконтурного ТРД (рис. 1.5), где второй контур образован
дополнительной турбиной 6, вращающей кроме дополнительной
ступени 9 компрессора еще и лопастную машину 7, передавая
таким образом энергию дополнительной массе воздуха. При этом
повышается экономичность двигателя в большем, чем у
одноконтурного ТРД, диапазоне значений скорости.
Рис. 1.5. Схема двухконтурного ТРД:
1 - диффузор; 2 - ступени высокого давления компрессора; 3 - камера сгорания;
4 - коллектор горючего; 5 - газовая турбина ступени высокого давления
компрессора; б - турбина ступени низкого давления компрессора и лопастной
машины второго контура; 7 - лопастная машина второго контура; 8 - обечайка
второго контура; 9 - ступень низкого давления компрессора
Общее для всех ВРД свойство - зависимость тяги от скорости
и высоты полета, поскольку воздушная атмосфера используется
и как компонент топлива (окислитель), и как рабочее тело. Если

32 Часть I. Теория идеального теплового ракетного двигателя
1
Рис. 1.6. Схема камеры
ракетного двигателя:
1 - камера сгорания; 2 - сопло;
3 - смесительная головка
же все компоненты топлива и рабочее тело транспортировать на
борту летательного аппарата, оснащенного двигателем, то такой
реактивный двигатель будет менее зависим от окружающей среды.
Реактивный двигатель, при работе которого используются
только вещества и источник энергии, имеющиеся в запасе на
аппарате, предназначенном для перемещения, называется
ракетным двигателем.
Основной агрегат ракетного
двигателя (рис. 1.6) - ракетная камера, или
просто камера, представляющая собой
объединенные камеру сгорания 1 и
сопло 2. В камере сгорания происходит
преобразование химической энергии
топлива в тепловую энергию
продуктов сгорания (камера сгорания
выполняет функции энергообменного
устройства), сопло играет роль про-
пульсивного устройства.
Если источником энергии
являются окислитель и горючее или
химическое соединение, переходящее в другое состояние электронных
оболочек атомов с выделением теплоты и газообразного
рабочего тела, то ракетный двигатель называется двигателем с
химическим источником энергии или химическим ракетным двигателем.
Двигатель, в котором используется энергия, высвобождающаяся
в результате изменения состояния ядер атомов, называется
ядерным ракетным двигателем (ЯРД). Двигатель, при работе
которого используется энергия, накопленная в виде разности
электрических зарядов, называется электрическим ракетным двигателем.
Необходимой составляющей рабочего процесса приведенных
реактивных двигателей, в том числе ракетных, является
преобразование тепловой энергии рабочего тела в кинетическую
энергию истекающего потока. По этому существенному
атрибутивному признаку такие двигатели относят к тепловым.
В настоящем курсе в основном рассматриваются ракетные
двигатели с химическим источником энергии. Эти двигатели
различаются по агрегатному состоянию топлива и подразделяются
на ракетные двигатели на твердом топливе (РДТТ) (рис. 1.7);
жидкостные ракетные двигатели (ЖРД) (рис. 1.8-1.11) и
гибридные ракетные двигатели (ГРД), у которых компоненты
топлива находятся в разных агрегатных состояниях (рис. 1.12).

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 33
/ /
шшшшшшшш
иииии
Рис. 1.7. Схема РДТТ:
1 - заряд твердого ракетного топлива; 2 - корпус камеры;
3 - утопленное сопло; 4 - воспламенитель
Рис. 1.8. Схема ДУ с ЖРД с вы-
теснительной системой подачи
топлива:
/ - камера; 2,8- клапаны окислителя
и горючего; 3 - газовый редуктор;
4 - шар-баллон сжатого газа; 5 -
разделитель; 6,7 - баки окислителя и
горючего; О - окислитель; Г - горючее
Рис. 1.9. Схема ДУ с ЖРД с турбо-
насосной системой подачи топлива
без дожигания генераторного газа:
/ - камера; 2,3- баки горючего и
окислителя; 4,5 - насосы окислителя и
горючего; б - газовая турбина; 7 -
газогенератор; 8 - сопло выхлопа ТНА;
9 - шар-баллон сжатого газа; 10 -
газовый редуктор; О - окислитель;
Г - горючее

34 Часть I. Теория идеального теплового ракетного двигателя
к
Рис. 1.10. Схема ДУ с ЖРД с турбонасосной системой подачи топлива
с дожиганием генераторного газа:
1 - камера; 2, 3 - баки горючего и окислителя; 4, 5 - насосы окислителя и
горючего; б - газогенератор; 7 - газовая турбина; 8 - подкачивающий насос
горючего; 9 - шар-баллон сжатого газа; 10 - газовый редуктор; О - окислитель;
Г - горючее
По схеме подачи топлива ЖРД подразделяют на два вида:
с вытеснительной системой подачи (см. рис. 1.8), когда
компоненты топлива подают в камеру путем их вытеснения из баков,
и с насосной системой подачи (см. рис. 1.9 и 1.10), которые, в свою
очередь, подразделяют на ЖРД без дожигания продуктов
газогенерации после их использования для привода турбонасосного
агрегата (ТНА) (см. рис. 1.9) и с дожиганием их в камере
(см. рис. 1.10).
Если в качестве рабочего тела турбины используется
подогретый в трактах охлаждения камеры один из компонентов
топлива, например водород, то возможна безгенераторная схема
ЖРД (см. рис. 1.11).

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 35
Рис. 1.11. Схема ДУ с
безгенераторным ЖРД:
1 - камера; 2,3- баки горючего и
окислителя; 4 - насос окислителя; 5 -
ступень низкого давления насоса
горючего; 6 - тракт испарительного
газогенератора; 7 - газовая турбина;
8 - ступень высокого давления насоса
горючего; 9 - шар-баллон сжатого газа;
10 - газовый редуктор; О - окислитель;
Г - горючее
Рис. 1.12. Схема ГРД:
1 - заряд твердого горючего; 2 - бак
окислителя; 3 - форсунка окислителя;
4 - сопло; 5 - шар-баллон сжатого газа;
6 - газовый редуктор; О - окислитель
Отметим, что ДУ содержит не только собственно двигатель
(камеру и систему подачи), но и баки и систему наддува. Для
РДТТ и ГРД понятия «двигатель» и «двигательная установка»
эквивалентны.
Ракетный двигатель характеризуют следующие основные
параметры.
Тяга - равнодействующая газо- и гидродинамических сил,
действующих на внутренние поверхности двигателя при исте-

36 Часть I. Теория идеального теплового ракетного двигателя
чении из него вещества (реактивная сила), и сил давления
окружающей среды, действующих на его внешние поверхности, за
исключением сил внешнего аэродинамического сопротивления.
Диапазон значений тяги 10-2... 106 Н.
Удельный импульс тяги {удельный импульс) - отношение тяги
двигателя к массовому расходу топлива двигателем. Численно
удельный импульс близок к скорости истечения рабочего тела из
сопла и составляет 1 000... 10 000 м/с.
Масса двигателя - масса конструкции, или масса двигателя
и масса топлива, находящегося в его полостях (0,1...105 кг).
Удельная масса - отношение масс двигателя и находящегося
в его полостях топлива к наибольшей тяге двигателя при работе
на основном режиме.
Время работы двигателя составляет 10~3... 104 с при
продолжительности непрерывного включения до 300 с.
Давление в камере - среднее по времени статическое давление
продуктов сгорания вблизи стенки камеры, противоположной
соплу (0,1...30,0 МПа).
Температура сгорания в камере - температура торможения
продуктов сгорания на выходе из камеры сгорания (до 4 000 К).
Ракетный двигатель является самым энергонасыщенным из
известных двигателей при одних и тех же массах и габаритах
конструкций. Основные свойства ракетных двигателей:
• слабая зависимость характеристик от параметров
окружающей среды, вплоть до возможности работы под водой, и
независимость характеристик от скорости полета;
• большие абсолютные значения тяги;
• минимальные значения удельной массы;
• повышенная опасность, в том числе экологическая, и
вытекающие отсюда высокие требования к надежности.
Контрольные вопросы и задания
1. Назовите виды реактивных двигателей. Дайте сравнительную
характеристику двух любых реактивных двигателей различного вида.
2. Перечислите преимущества ракетного двигателя по сравнению с
воздушно-реактивным двигателем.
3. Перечислите виды ракетных двигателей, различающихся по
агрегатному состоянию топлива.
4. Назовите типы систем подачи компонентов топлива в камеру ЖРД.

Глава 1. Введение в дисциплину. Терминология. Виды двигателей 37
5. Перечислите функции основных агрегатов реактивных двигателей:
камеры сгорания, смесительной головки, сопла, газовой турбины,
газового редуктора, насоса, газогенератора, шар-баллона.
6. Каково соотношение между значениями давления в баках и камере
сгорания ЖРД с вытеснительной системой подачи топлива?
7. Каково соотношение между значениями давления в баках и камере
сгорания ЖРД с насосной системой подачи топлива?
8. Назовите атрибутивный признак ЖРД с насосной системой подачи
топлива с дожиганием (без дожигания) рабочего тела турбины.
9. Обоснуйте преимущества и укажите недостатки ЖРД с дожиганием
по сравнению с ЖРД без дожигания рабочего тела турбины.
10. Назовите атрибутивный признак ЖРД с безгенераторной системой
подачи топлива.

Глава 2
Тяга ракетного двигателя
Для выполнения рабочих функций двигатель должен создавать
тягу - усилие, прикладываемое к объекту, оснащенному этим
двигателем. Ракетный двигатель - частный случай реактивного
двигателя, создающего тяговое усилие за счет реактивной силы,
т. е. реакции отбрасываемой массы - рабочего тела. Если рабочее
тело находится в жидком или газообразном фазовом состоянии,
то оно отбрасывается, истекая с некоторой скоростью истечения
в окружающую среду, относительно объекта, оснащенного
реактивным (в частности, ракетным) двигателем.
Реактивная сила - равнодействующая газо- и
гидродинамических сил, действующих на внутренние поверхности ракетного
двигателя при истечении из него вещества (внутренняя
составляющая тяги Рт)-
На наружную поверхность ракетного двигателя оказывает
силовое действие условно неподвижная относительно этой
поверхности окружающая среда - континуум с известным
давлением - скалярной величиной р . Абсолютное значение (модуль)
давления/? = \р\ = lim (AP/AF) не зависит от ориентации
площадки АР, на которую действует сила давления АР (закон
Паскаля), причем вектор силы давления АР направлен по нормали
к площадке AF.
Это действие предусматривает отсутствие гравитационных,
электростатических, магнитных, электромагнитных и иных пон-
деромоторных (действующих бесконтактно, т. е. дистанционно,
на расстоянии, существенно большем характерного размера
рассматриваемого объекта, в частности камеры ракетного двигателя)
сил, как и сил трения, влияние которых проявляется в
аэродинамическом сопротивлении движению летательного аппарата в
атмосфере. Поскольку чаще всего давление среды, окружающей
двигатель, равно атмосферному давлению, значение которого
зависит в основном от высоты h (или Н) над уровнем моря,
наружное давление обозначают рИ. Очевидно, что в вакууме ph = О
и силовое действие окружающей среды исчезает.

Глава 2. Тяга ракетного двигателя
39
Выражение для вычисления наружной составляющей тяги Р
нар
следует из определения ее как интегральной векторной суммы
сил давления, распределенных по наружной поверхности dF
ракетного двигателя:
^нар = J PnpdF,
(2.1)
где р - давление окружающей среды - вектор, направленный
по нормали к dF; F - наружная часть поверхности конструкции
двигателя, не находящаяся в контакте с рабочим телом и не
участвующая в образовании внутренней составляющей тяги.
Таким образом, тяга ракетного двигателя представляет
собой равнодействующую реактивной силы и сил давления
окружающей среды, действующих на его наруэюную поверхность, за
исключением сил внешнего аэродинамического сопротивления.
Для определения тяги через основные параметры ракетного
двигателя представим ее в виде суммы векторов:
Р=Р +Р .
нар вн
(2.2)
На рис. 2.1 приведена расчетная схема, на которой отражено
произвольное течение рабочего тела в некотором объеме V, огра-
Рис. 2.1. К выводу расчетного выражения для внутренней
составляющей тяги

40 Часть L Теория идеального теплового ракетного двигателя
ничейном замкнутой поверхностью L (обозначена штриховой
линией). В состав этой поверхности входит перпендикулярная
оси х плоскость, совпадающая с выходным сечением сопла
площадью Fq9 с равномерным распределением по сечению
плотности ра, давления ра и скорости Wa (одномерное течение слева
направо) рабочего тела. Это позволяет в дальнейших выкладках
опустить обозначение сил как векторов, учитывая только их
проекции на направление оси х.
Часть поверхности L (поверхность L без плоскости Fa,
совпадающей с выходным сечением сопла, т. е. внутренняя поверхность
камеры Fbh, обозначенная контуром / на рис. 2.1) располагается
сколь угодно близко от внутренней поверхности ракетного
двигателя и в пределе совпадает с ней. Другие ограничения на
свойства контура, форму камеры и природу, сущность и особенности
рабочих процессов в ней (в объеме V) не накладываются.
К множеству т. материальных точек, образующих рабочее
тело, находящееся в объеме V, ограниченном поверхностью L,
применим основную теорему динамики, известную из курса
теоретической механики как закон сохранения количества движения,
в дифференциальной форме:
т
=Е^> с2-3)
где / - число материальных точек, каждая из которых движется
со скоростью W., i = 1,..., n;j- число всех внешних сил,
действующих на систему материальных точек,у = 1, ..., т.
Сумма внешних сил, действующих на заключенную в
выбранном объеме V систему материальных точек, может быть
представлена как результат сложения сил, распределенных по
ограничивающей этот объем поверхности L, и массовых сил,
действующих извне на систему точек:
• равнодействующей сил с внутренней поверхности камеры
двигателя Fbh (контур /), равной по модулю силе Рвн, но
направленной в противоположную сторону (по третьему закону
Ньютона), т. е. слева направо;
• силы Fap 9 направленной справа налево, возникающей как
компенсация остающегося вне рассмотрения рабочего тела,
пересекшего границу поверхности L через плоскость выходного
сечения сопла F ;
d_
dt
£(тД)
/ = 1

Глава 2. Тяга ракетного двигателя
41
• силы тяжести Mncgx, действующей на массу Мп с продуктов
сгорания в объеме V, где gx - проекция ускорения силы тяжести
g на ось ОХ.
В выбранной системе координат сумму этих сил можно
записать в виде равенства
УР, =Р -F p +M g.
LmU J вн аг а п.с^х
(2.4)
Полную производную в координатах Лагранжа в (2.2) запишем
как сумму частных производных:
d_
dt
IMO
/=i
dt
5>д)
dt
2>д)
i = \
(2.5)
где слагаемое 1 - стационарная составляющая полной
производной в случае, когда скорость изменения во времени любого
параметра в любой точке равна нулю, но параметр изменяется при
движении точки по траектории (эту составляющую можно назвать
конвективной или переносной); слагаемое 2 - нестационарная
составляющая полной производной, учитывающая только
изменение во времени параметра в фиксированной точке пространства,
она обращается в нуль при работе в стационарном режиме.
Строгое и подробное обоснование такой записи полной
производной можно найти в книге Л.Г. Лойцянского1. Пусть для
стационарно работающего ракетного двигателя за малое время А/
внутрь объема, ограниченного контрольной поверхностью L,
вошла масса Am со скоростью Wx. Тогда через плоскую часть Fа
этой поверхности за это же время вышла такая же масса Am, но
со скоростью Wa, т. е.
dt
Z(^/)
./=i
AmWa -AmWx
A^
Выполняя предельный переход при At —► 0, получаем
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1974.

42 Часть I. Теория идеального теплового ракетного двигателя
= \xm^{Wa-Wx) = rh(Wa-Wx), (2.6)
где Wa, Wx - проекции на ось х скоростей проходящего через
контур рабочего тела, секундный массовый расход которого
равен т, кг/с.
Для второй составляющей полной производной при переходе
от системы дискретных точек к континууму запишем
Ё1
dt
2>Д)
/=1
4ffe<^}
dt
(2.7)
где р.9 Wt - плотность и скорость рабочего тела в некоторой
произвольной точке объема V, ограниченного контуром L; dv -
элементарный объем.
Подставляя (2.3), (2.5) и (2.6) в (2.2) и решая уравнение
относительно Р , получаем
Рвн = m(Wa- Wx) + ЩрРМ + FaPa~ K,SX- (2.8)
Следует отметить, что Рш - вектор, направленный
противоположно вектору скорости Wa, т. е. справа налево. Знак минус здесь
опущен.
Сущность реактивной тяги в таком представлении состоит
в реакции истекающего из сосуда потока. Особенность реакции
втекающего потока - ее значение близко к нулю, а не к значению
реакции истекающего потока, но с другим знаком, как кажется
на первый взгляд. Для подтверждения нетривиальности этого
утверждения отметим, что еще в конце XIX в. оно привлекло
внимание выдающегося русского ученого-механика Н.Е.
Жуковского, профессора Московского университета (ныне МГУ
им. М.В. Ломоносова) и Императорского технического училища
(ныне МГТУ им. Н.Э. Баумана). Вначале он приближенно
показал, что реакция втекающей в сосуд жидкости очень мала, а затем
посредством достаточно сложных выкладок доказал строго, что

Глава 2. Тяга ракетного двигателя
43
она равна нулю . Слабость обратной реакции можно
проиллюстрировать опытом с сегнеровым колесом, которое вращается как
турбина при истечении жидкости из его сопл и остается
неподвижным при втекании ее через эти же сопла с тем же расходом.
Для расчета наружной составляющей тяги учтем, что в
соответствии с принятыми допущениями, камера двигателя
находится в неподвижной невесомой среде. Это физически эквивалентно
пренебрежению силами Архимеда или соответствует
одинаковому для всех точек наружной поверхности камеры давлению ph
в любой точке на наружной поверхности F двигателя. Причем
наружная поверхность FHa охватывает внутреннюю поверхность
камеры, находящуюся в контакте с рабочим телом. При этом
расстояние между этими поверхностями в любой точке произвольно,
что можно интерпретировать как произвольную толщину стенки
или форму наружной поверхности камеры, не зависящую от
формы проточной части камеры.
Поскольку интеграл сил давления, взятый по произвольной
замкнутой поверхности, в частности по поверхности FL,
охватывающей контрольный объем V снаружи (т. е. вне его граничной
поверхности L, например F2 = F + Fa)9 должен быть равен нулю:
то при ph = const справедливо очевидное равенство
Ph J "»apdF + FaPh=0,
1 нар
из которого следует уравнение наружной составляющей тяги
4ф = J PmPdF = Ри\ >LpdF = -FaPh* (2-9)
F F
' нар ' нар
где п - единичный вектор, задающий ориентацию поверхности
интегрирования F .
Отметим возможность применения выражения Рш = -Faph
(направление слева направо) только в тех случаях, когда каждая
Жуковский Н.Е. Полное собрание сочинений: в 16 т. Т. 3.
Гидродинамика. М.; Л.: Гостехиздат, 1949.

44 Часть I. Теория идеального теплового ракетного двигателя
точка наружной поверхности двигателя контактирует со средой
с одним и тем же давлением ph = const.
Конкретизируем этот вывод для наиболее применяемых камер,
форма наружной поверхности которых осесимметрична и
представляет собой произвольное сочетание поверхностей вращения
с произвольной же образующей, но с одним и тем же постоянным
значением площади Fa и произвольным значением
максимального (миделевого) поперечного сечения наружного контура FK
камеры (рис. 2.2).
Дополним осесимметричную наружную поверхность камеры
цилиндрическими и плоскими торцовыми поверхностями так,
чтобы наружная поверхность была образована только
сочетанием соосных цилиндрических и перпендикулярных оси
поверхностей. Появившиеся дополнительные объемы (см. рис. 2.2,
заштрихованные сечения) будем считать заполненными
неподвижной и невесомой окружающей средой.
ЕЕ 1(/г«-£>
Рис. 2.2. К выводу расчетного выражения
для наружной составляющей тяги

Глава 2. Тяга ракетного двигателя
45
Силы, действующие на поверхности этих неподвижных
заштрихованных объемов, взаимно уравновешиваются
(равнодействующая равна нулю), а сила действия окружающей среды на
находящуюся с ней в контакте поверхность камеры равна по
модулю и противоположна по направлению силе, с которой эта
поверхность действует на окружающую среду (по третьему закону
Ньютона).
Это означает, что без влияния на результирующую наружную
составляющую тяги наружная поверхность камеры может
достраиваться до цилиндрической, при которой равнодействующая сил
не создает давления на боковую поверхность осевой
составляющей (давление нормально к поверхности, а значит, и к оси
симметрии ОХ), а равнодействующие на торцовых поверхностях F
параллельны оси ОХ и равны phF' .
Тогда для каждого из трех представленных на рис. 2.2
сочетаний размеров рассматриваемой камеры можно записать
очевидное соотношение для наружной составляющей тяги:
Р^ = ~Рьра при FK = Fa; (2.10)
raap = -Pd(Fa-FK) + FK]=-PhFa при FK<Fa; (2.11)
Pmp = -P^K-{FK-Fa)\=-phFa при Fa<FK, (2.12)
т. е. для всех рассмотренных случаев справедливо (2.9).
Подставляя (2.8) и (2.9) в (2.2) и принимая знак реактивной
силы положительным, получаем полное уравнение тяги
P=m(Wa-WJ + Fa(pe-pJ+ IffawM -Mncgx. (2.13)
В частном случае, когда нет притока массы в камеру извне,
т. е. Wx = 0, или все отбрасываемое для создания тяги вещество
размещено в камере до начала работы двигателя, для РДТТ из
(2.13) следует точное уравнение:
P = mWa + Fa(pa-ph)+ jj^JpWdv^ -Mncgx. (2.14)

46 Часть I. Теория идеального теплового ракетного двигателя
Для ЖРД, если рассматривать внешнюю границу камеры,
проницаемую в плоскости подачи компонентов топлива во входные
патрубки насосов, со скоростью потока в этом сечении Wx « Wa
и с учетом небольшой площади поперечных сечений входов
в насосы по сравнению с площадью выходного сечения сопла
AFbx « Fa, уравнение тяги также можно записать с достаточной
для практики точностью (2.14).
Если же жидкие компоненты топлива подают в камеру с
произвольной (по модулю) скоростью, но под прямым углом к
направлению вектора скорости Wq9 to уравнение (2.14) становится
точным и для ЖРД, и для ГРД.
Отметим, что для большинства случаев нестационарная
составляющая тяги не превышает 0,5... 1,0 % стационарной
составляющей, а член Мп cgx не превышает 0,1 %, что с достаточной для
практики точностью позволяет использовать квазистационарный
подход к расчету тяги:
P=mWa + Fo(pa-ph) = PBH-FaPh.
Следует отметить, что в этой часто применяемой форме
уравнение для внутренней составляющей тяги
Р =mW +F р (2.15)
вн а а^ a v '
справедливо независимо от устройства, состава и конструкции
камеры (т. е. от всего того, что находится внутри контрольной
поверхности) и от характера рабочих процессов в ней (адиабат-
ность, изоэнтропность, одномерность или отсутствие этих свойств,
закономерность подвода массы по длине или по сечению камеры,
наличие или отсутствие трения на стенке и др.). Другими
словами, (2.15) применимо как к ЯРД, ЖРД, РДТТ и ГРД, так и к
комбинированным ракетным ДУ. При этом требуется только
выполнение допущения о равномерных распределениях параметров
потока (скорости Wa, давления/^ и плотности ра) по всей
площади Fa выходного сечения сопла.
К специальным случаям, когда целесообразно использовать
полное уравнение тяги (2.13), следует отнести расчет тяги
практически не имеющих установившегося режима работы
импульсных ракетных двигателей, время работы которых менее 0,1 с,
а также расчет тяги двигателей, работающих в поле ускорений

Глава 2. Тяга ракетного двигателя
47
с gx > 50...100 м/с2. Например, расчет двигателей антиракет, за
время выхода которых на номинальный режим, составляющее
около 0,1 с, тяга возрастает от 0 до 6 000 кН (~ 600 тс), при
полном времени работы до 3 с и ускорении ракеты до 500 g
(~ 4 900 м/с2).
Отметим принципиальную возможность расчета внутренней
составляющей тяги не только по уравнениям (2.7) - (2.15) или их
математическим эквивалентам, полученным в виде интеграла
уравнения движения при одномерном потоке в выходном сечении
сопла, но и непосредственно интегрированием давления,
действующего на стенки ракетной камеры. При этом распределение
давления должно быть предварительно найдено в результате решения
уравнений нестационарного движения химически активных
компонентов топлива и продуктов сгорания в пространстве с
границей в виде стенок камеры. Современное математическое,
алгоритмическое и программное обеспечение для решения
аналогичных задач численными методами на ЦВМ
каталогизировано и доступно (многоцелевые конечно-элементные
программные средства типа ANSYS (http:///www.ansys.msk.ru), Cobra и др.,
аналогичные по возможностям и назначению) и требует для
своего применения адекватного отображения начальных, граничных
и других условий однозначности, задающих решаемую задачу.
Примером такого решения является расчет тяги
цилиндрической камеры детонирующего пульсирующего воздушного
реактивного двигателя (ДПуВРД), выполненный путем численного
интегрирования конечно-разностного аналога уравнений Эйлера
на нестационарных фазах заполнения камеры топливной смесью,
распространения детонационной волны и истечения продуктов
сгорания с помощью отечественного программного продукта
Cobra1. При этом кроме собственно значений переменной по
времени и среднеинтегральной тяги получены параметры рабочего
процесса, необходимые для проектирования двигателя.
К особым случаям расчета тяги двигателя относятся варианты
испытания двигателей на стендах, оборудованных барокамерами
или другими специальными вакуумирующими устройствами
(рис. 2.3, где/?Л1 ФрИ2 ^Pho'Pho ~ атмосферное давление на
уровне моря). При этом типовые практические задачи включают или
Гаранин И.В., Фролов В.Н. Методический подход к расчету тяги
камеры сгорания пульсирующего детонационного двигателя для решения
задач формирования облика // Вестник МАИ. 2009. Т. 16; № 4. С. 22-26.

48 Часть L Теория идеального теплового ракетного двигателя
определение ожидаемых показании
силоизмерительного устройства,
или на основе результатов,
полученных на стенде (показания сило-
измерителя, значения давления
в характерных объемах стендовой
установки), расчет тяги,
развиваемой двигателем в других условиях,
например в пустоте.
Возможны различные варианты
размещения разделяющих
перегородок: на цилиндрической части
камеры, вблизи минимального
сечения сопла, вблизи выходного
сечения сопла или на наружной
поверхности дозвуковой либо
сверхзвуковой части сопла. Принято
считать, что такие перегородки не
имеют существенной силовой связи
с камерой двигателя в месте стыка,
но при этом герметично разделяют
пространства1. Отметим, что параметры потока в выходном
сечении сопла от этого не зависят и их можно рассчитать по (2.15).
Причем уравнение наружной составляющей тяги в общем случае
отличается от уравнений (2.9) - (2.12) и записывается как
равнодействующая сил давления на наружную поверхность камеры с
учетом положения перегородки.
Например, для условий испытания, соответствующих
рис. 2.3, а, показания силоизмерителя 3 рассчитывают по
уравнению
Рис. 2.3. К расчету тяги
ракетного двигателя:
1 - барокамера; 2 - газовод;
3 - силоизмеритель
P=mWa + Fa(pa-phl) = PBH-FaPhr
поскольку давление ph2 в газоводе 2 не влияет на распределение
давления по наружной поверхности ракетной камеры,
находящейся в барокамере 1 с давлением средыphv а значение
внутренней составляющей тяги вычисляют по (2.15).
1 Волков В. Т., Ягодников Д. А. Исследование и стендовая отработка
ракетных двигателей на твердом топливе. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2007.

Глава 2. Тяга ракетного двигателя
49
При расположении перегородки согласно рис. 2.3, б, где
площадь сечения камеры в области стыка приблизительно равна FaV
показания силоизмерителя можно рассчитать по уравнению
P=[mWa + FaPa] - [Fa]Phi + (F -FJpJ,
в котором выражения в квадратных скобках представляют собой
модули внутренней и наружной составляющих тяги соответственно.
Контрольные вопросы и задания
1. Дайте определение тяги ракетного двигателя.
2. Что такое ракетная камера и что входит в ее состав?
3. Перечислите функции составных частей ракетной камеры.
4. Что такое внутренняя составляющая тяги ракетного двигателя?
5. Что такое наружная составляющая тяги ракетной камеры?
6. Что такое реактивная сила?
7. Какие допущения принимались при выводе формулы тяги?
8. Применимо ли полученное уравнение для тяги ракетной камеры,
если из нее в качестве рабочего тела вытекает жидкость?
9. Как изменится тяга работающей в пустоте ракетной камеры, если
рабочее тело - продукты сгорания водорода и кислорода - заменить
подогретой смесью водорода с гелием, а значения скорости,
плотности и давления рабочего тела в выходном сечении сопла не
изменились?
10. Как влияет на развиваемую реактивную силу температура рабочего
тела в выходном сечении сопла, если скорость, плотность и
давление в выходном сечении сопла остаются неизменными?

Глава 3
Основы теории сверхзвукового сопла
Известно, что поток газа может быть ускорен при движении
по соплу - конфузорно-диффузорному каналу. Такое сопло
называют соплом Лаваля по имени его изобретателя. Причем, если
перепад (отношение) давления на входе в сопло и в среде, куда
происходит истечение, достаточный, в минимальном сечении
сопла устанавливается скорость движения газа, равная местной
скорости звука, а в расширяющемся раструбе сопла поток
ускоряется до сверхзвуковых значений. При известных параметрах
на входе в сопло независимым аргументом, определяющим
местное значение параметров потока (скорость, статические давление,
температура, плотность), является геометрическая степень
расширения потока, равная отношению площадей потока в текущем
сечении и в критическом (т. е. минимальном), где скорость
потока газа равна местной скорости звука.
Пусть камера сгорания настолько больших размеров по
сравнению с размерами минимального проходного сечения, что
скорость потока газа в ней близка к нулю. Тогда во всех точках ее
объема давление газа одинаковое, т. е. камера изобарная. Для
изобарной камеры ракетного двигателя параметры на входе в
сопло суть известные параметры в камере, т. е. вблизи ее
смесительной головки. Определение параметров потока в выходном сечении
сопла и есть задача теории сопла, а вместе с тем и теории
ракетных двигателей. Одна из задач этой теории - определение
зависимости между параметрами потока в камере и развиваемой тягой
и удельным импульсом.
Для решения этой задачи примем ряд допущений.
1. Контур проточной части гладкий, углы наклона контура
настолько малы, что течение газа в нем безотрывное и
одномерное, т. е. эпюры распределения всех параметров по сечению -
прямоугольники.
2. Течение стационарное, т. е. значения всех параметров не
изменяются во времени.
3. Рабочее тело - идеальный, не проявляющий вязкости газ
с постоянными, не зависящими от давления и температуры

Глава 3. Основы теории сверхзвукового сопла 5J_
молекулярной (мольной) массой ц и газовой постоянной R,
теплоемкостью при постоянном давлении с и показателем адиабаты
k = cp/cv. (3.1)
При этом справедливы уравнения состояния
p/p = RT, (3.2)
скорости звука
и соотношение Майера
а = 4Ш (3.3)
cp-cv = R. (3.4)
4. Течение в сопле адиабатное, т. е. без обмена теплотой с
окружающей средой, и изоэнтропийное, т. е. без диссипации энергии
и соответственно при постоянной энтропии. Такой процесс
можно описать уравнением
p/pk = const, (3.5)
при этом параметры торможения р* = pK = const, T* = Тк = const.
Уравнение сохранения энергии при таких допущениях
имеет вид
W2
Т =Т + —. (3.6)
2ср
Разделив (3.6) на Г и введя критерий Маха М, получим
М.= W.la. (3.7)
как отношение местной скорости потока газа Wt к местной
скорости звука а.. С учетом (3.3) и (3.4) найдем
7"=7^т-? <38>
1 1 + М

52 Часть I. Теория идеального теплового ракетного двигателя
где к- показатель адиабаты, определяемый по (3.1).
Если М = 1, то в этом сечении, называемом критическим, где
местная скорость потока равна скорости звука,
термодинамическую (статическую) температуру можно вычислить по формуле
2_
Jt + Г
Гкр=Гт-т. (3.9)
Известно, что при ускорении потока газа в сопле происходит
переход кинетической энергии хаотичного движения молекул
(тепловой энергии) в направленную кинетическую энергию
потока. Таким образом, при полном переходе тепловой энергии
в кинетическую энергию потока его температура стремится к
абсолютному нулю, 7=0 (см. соотношение (3.2)), также к нулю
стремится и скорость звука в потоке (см. уравнение (3.3)), М —► оо.
Таким образом, критерий Маха - неограниченная величина,
что затрудняет его использование.
Введем приведенную, т. е. безразмерную, скорость,
называемую также коэффициентом скорости,
ХГ1¥/акр, (3.10)
равную отношению местной скорости W. к местной критической
скорости, т. е. к скорости звука в критическом сечении а (по
уравнению (3.3)).
С учетом (3.9) получим
2k_
к + 1
aKP=Jl-7RT • (З.Н)
Далее покажем, что введенная безразмерная скорость X. =
= W./a является ограниченной сверху положительной величиной.
Уравнения, связывающие термодинамические (статические)
параметры р, 7, р и параметры торможения потока (параметры
в камере сгорания рк, 7к) через промежуточный аргумент X,
называются газодинамическими функциями (ГДФ).
Определим основные ГДФ:
*{Кк) = у; (3.12)

Глава 3. Основы теории сверхзвукового сопла 53
я(я,,*)=4;
р
б(А.,*) = 4
Р
и получим их явные выражения через аргументы.
Разделив (3.6) на Т*, найдем
(3.13)
(3.14)
1 = т(Х,*) +
W2
2срТ
(3.15)
Учитывая следующее из (3.4) равенство
к
С» = к-1
R,
получим из (3.15) для ГДФ приведенной температуры,
определяемой по формуле (3.12), следующее выражение:
х(Х,к) = 1-—Х2.
(3.16)
Выражая константу в уравнении процесса (3.5) через
параметры торможения
Р__ Р
Р- (р-)"
с учетом уравнения состояния (3.2) получим соотношение
(3.17)
_Р_= Р_
* *
Р КР
к Г
pI(rt)
p/(rt>).
_г V-i
Г
позволяющее рассчитать между ГДФ приведенного давления
п(к,к), определяемой по (3.13), и ГДФ приведенной температуры
т(А,, £), рассчитываемой по (3.16):
к
,(U) = (l-bJx2)H=[t(U)p.

54 Часть I. Теория идеального теплового ракетного двигателя
т. е.
г ~\к
Из (3.14) и (3.17) непосредственно следует п(к,к) = \г(Х9к)\ ,
ИЛИ
г(Х,к) = \\-^У =[,(Ккф.
(3.18)
Графики ГДФ х (X., к), п (к, к)ие (к, к) для к = 1,15
представлены на рис. 3.1.
1,01
g0,8
•!о,6
х 0,4
1 0,2
СП
'Ve (X, к)
■я (А,
Fi vs.
' Xv
\гЧМ)
\<?(>
*Д)
0 0,5 1,0 1,5 2,0 2,5 3,0
Приведенная скорость X
Рис. 3.1. Графики основных ГДФ изоэнтропийного
адиабатного потока идеального газа
Отметим, что ГДФ т (А,, к), к (К, к) и е (к, к) в соответствии
с (3.12) - (3.18) обращаются в нуль только при равенстве нулю
выражения в скобках в основании степени, откуда следует
ограниченность положительной по физическому смыслу приведенной
скорости X сверху, а именно 1 Х^ах =0, или
к + 1
£ + 1
к-\
Из (3.6) с учетом (3.14) можно получить выражение для
расчета скорости истечения потока газа:

Глава 3. Основы теории сверхзвукового сопла 55
Подставив в (3.19) значение термического коэффициента по-
Т
лезного действия (КПД) л, =1—-, получим
Т
W = ^RT\. (3.20)
т к~х
Учитывая связь т(Х9к) = —? = [п(Х9к)] к , запишем выражение
для скорости истечения потока газа через реализуемое
соотношение местного статического давления и давления торможения
потока:
'к-1
к-\
1
' Р )
(3.21)
Из (3.19) - (3.21) следует ограниченность скорости истечения
при расширении до/? = 0 и Т= 0, когда л, = 1. Максимально
возможная скорость потока при заданных параметрах торможения
Т*,р* данного газа, характеризующегося значениями газовой
постоянной R и показателем адиабаты к, может быть вычислена по
формуле
Wmm=^xRT\ (3.22)
Отметим, что выражения (3.1) - (3.22) были получены без
определения ограничений (только для дозвукового или
сверхзвукового потока газа), следовательно, они применимы, если
только выполняются принятые допущения. Однако приведенная
скорость X используется только как промежуточный аргумент,
так как она не может быть измерена непосредственно и ее
независимость неочевидна.
К очевидно независимым переменным можно отнести
геометрическую степень расширения сопла F/F или обратную ей
величину, определяемую в ГДФ в виде
Я(АД) = %. (3.23)

56 Часть I. Теория идеального теплового ракетного двигателя
Учитывая уравнение сохранения массы т = const, запишем
для критического (1) и произвольного (2) сечений
соответственно соотношение
^крРкрЯкр=^Р^-
2
Из уравнения состояния (3.2) с учетом (3.10) и (3.18) получим
я(Кк)^[1-^р[^)к-1. (3.24)
График функции q(k,k) при к = 1,15 представлен на рис. 3.1.
Отметим, что для всех к ГДФ q(k,k) = 1.
Для всех к ГДФ т (к, к), к (к, к), е (к, к), q (к, к) равны нулю при
X-JL 'k + i
max л/ » -,
к-\
Отметим также, что q (A,max, к) = 0 интерпретируется как
необходимость увеличения до бесконечности площади выходного
сечения сопла Fa для получения скорости истечения
W=W = I—RT*.
max ^_j
Из анализа уравнений (3.16), (3.18) и (3.24) следуют
распределения температуры Г, скорости W и давления р по длине
проточной части камеры, представленные на рис. 3.2. Таким образом,
геометрическая степень расширения сопла выступает в качестве
естественного аргумента. Изменение термодинамических
параметров потока по длине сопла монотонно: давление р,
температура Г и плотность р газа уменьшаются, а скорость W, число Маха
М и приведенная скорость к растут. При этом значение скорости
приближается к предельному максимальному значению:
W =W = l-^-RT*
rr" "max \\ i 1 1K±

Глава 3. Основы теории сверхзвукового сопла 57
Рис. 3.2. Распределения основных
параметров рабочего тела по длине камеры
ракетного двигателя
что соответствует горизонтальной асимптоте. Распределение
приведенной скорости X является равномерно сжатой по оси ординат
функцией скорости Ww также имеет горизонтальную асимптоту:
^ ~ ^тах ~
к + \
к-\
Контрольные вопросы и задания
1. Перечислите основные допущения теории сопла.
2. Чему равен показатель изоэнтропы для процесса расширения
в сопле?
3. Дайте определение основных газодинамических функций.

58 Часть I. Теория идеального теплового ракетного двигателя
4. Какова область определения газодинамических функций,
выраженных через число Маха?
5. Какова область определения газодинамических функций,
выраженных через приведенную скорость X,?
6. Какова область изменения основных газодинамических функций?
7. Какие преимущества имеют расчетные выражения для
газодинамических функций, где в качестве аргумента используется приведенная
скорость потока X, а не число Маха?
8. Применимо ли уравнение для скорости истечения (3.21) при
дозвуковых скоростях потока в выходном сечении?
9. Какой параметр сопла можно рассматривать в качестве
естественного аргумента (независимой переменной) теории сопла?
10. На всем протяжении сопла с сопряженными сужающейся и
расширяющейся частями установилось безотрывное изоэнтропийное
течение потока газа со скоростями выше скорости звука. Какие из
приведенных в гл. 3 расчетных выражений применимы к такому
течению и что при этом следует учитывать?

Глава 4
Режимы работы сверхзвукового сопла.
Дроссельные (расходные) характеристики
идеального ракетного двигателя
Известно, что слабые возмущения распространяются в газе
со скоростью звука. Следовательно, если в расширяющейся части
сопла установилось одномерное сверхзвуковое течение, то
изменение давления окружающей среды ри (противодавления), в
которую происходит истечение, не влияет на параметры потока
в сопле, включая выходное сечение сопла Fa и давление газа ра
в нем, а соответственно, и в камере сгорания.
Таким образом, для сверхзвукового сопла в общем случае
можно реализовать режимы работы, на которых ра Ф ph, причем
режим, при котором ра < ph, называется режимом
перерасширения, режим, при которомра >ph, -режимом недорасширения,
режим, при котором ра = рИ, - расчетным режимом. Отсюда
следует независимость внутренней составляющей тяги Рвн и
скорости истечения газа Wa от противодавления рИ для идеального
ракетного двигателя с заданными размерами проточной части,
если поток в выходной части сопла сверхзвуковой.
Покажем, что при постоянных параметрах режимов в камере
сгорания, а следовательно, и в дозвуковой и сверхзвуковой частях
сопла, при геометрической степени расширения сопла FQ/ F
(сопло работает в расчетном режиме) развиваются наибольшие
тяга и удельный импульс.
Рассмотрим эпюры давления газа на стенки сверхзвуковой
части сопла вблизи выходного сечения (рис. 4.1) на участке
стенки сопла а\ - а, если сечение а соответствует расчетному
режиму работы сопла, т. е. в этом сечении ра = рИ.
С наружной стороны участка стенки сопла а\ - dl давление
постоянное и равно ph. Следовательно, равнодействующая сил
давления, приложенных к этому участку стенки сопла,
направлена снизу вверх и наклонена влево, а ее проекция АРх на ось
симметрии есть положительная составляющая тяги камеры. И если
сопло выполнить с выходным сечением FaX < Fа, то раХ > рИ,
и камера двигателя будет развивать тягу, меньшую чем при F 9

60 Часть I. Теория идеального теплового ракетного двигателя
АРа-а2
а\ а ей
Pa\>Ph Pa=Ph Pa2<Ph
Рис. 4.1. К обоснованию оптимальности
расчетного режима работы сопла
при котором ра = ph, на величину исключенной составляющей
АРх, т. е. недорасширенное сопло развивает меньшую тягу, чем
расчетное сопло.
Снабдим расчетное сопло с выходным сечением Fа дорасши-
рительным насадком с площадью выходного сечения Fa2 > F .
Тогда ра2 < ph и при постоянном давлении с наружной стороны
стенки насадка на ее внутренней стороне эпюра давления будет
нисходящей, а равнодействующая сил давления на участке а-а2
будет направлена вниз вправо с осевой проекцией, направленной
против тяги камеры с расчетным соплом.
Таким образом, камера с перерасширенным соплом развивает
меньшую тягу, чем камера с расчетным соплом. Другими
словами, камера с расчетным соплом развивает наибольшую тягу по
сравнению с тягами других камер, отличающихся только
геометрической степенью расширения сверхзвуковой части сопла.
К такому же результату можно прийти при определении
значения аргумента ра, при котором функция
P(P0) = ™Wa{pa) + Fa{pa){pa-ph)
достигает максимума при постоянном давлении в камере и
сохранении звуковой скорости потока в минимальном сечении.
Отметим, что между внутренними составляющими тяги
каждого из рассмотренных двигателей устанавливается следующее
соотношение: Рвн аХ < Рвн а < Рвн aV т. е. при работе двигателя
в пустоте, где рИ = О, чем больше геометрическая степень
расширения F/F' тем больше тяга и удельный пустотный импульс:
у.п а\ у.па у.п я2*
Но давление в любом сечении F сопла зависит не только от
местной геометрической степени расширения F/FK , но и от

Глава 4. Режимы работы сопла. Дроссельные характеристики 61
давления в камере сгорания /?*. Изменение давления в камере
сгорания связано с расходом топлива, подаваемого в нее, а именно:
Л = Pkp^VV
(4.1)
но
WKp = акр = JkRT]~P = JkRfy(l,k) = ^K (4.2)
P«p=P»e(U) =
( * А
Рщ>
KR7i;
A:-l4,V-i
(4.3)
Здесь и далее выражения под и над горизонтальными фигурными
скобками эквивалентны. Подставив (4.2) и (4.3) в (4.1), получим
т
Р F
\jRTKp
где
A(k) = yfk
k+\
2 >(*-!)
ifc + 1
(4.4)
(4.5)
Зависимость коэффициента А от показателя адиабаты к
приведена на рис. 4.2.
А
0,68
0,67
0,66
0,65
0,64
0,63
0,62
\^^
г
4 (Ъ\
Л\ч^^^
^Л
^^
1,1 1,2 1,3 1,4
Показатель адиабаты к
Рис. 4.2. Зависимость коэффициента А
от показателя адиабаты А:

62 Часть I. Теория идеального теплового ракетного двигателя
Отметим следующую из (4.4) линейную зависимость расхода
газа от давления торможения в критическом сечении сопла. Но
поскольку в рамках принятых допущений давление и
температура торможения в любом сечении проточной части камеры одни
и те же, вместо параметров торможения в критическом сечении
можно подставить параметры торможения в камере сгорания.
Тогда можно записать
rh=P^A{k) (4.6)
Выражение
Л(к) Р
называется расходным комплексом, или комплексом р, который
в рамках принятых допущений характеризует температуру и
свойства продуктов сгорания ракетного топлива и не зависит от
других параметров.
Для решения ряда задач ракетной техники эффективным
является применение ракетных двигателей с переменной во
времени тягой. Из уравнения тяги
P=mWa + Fa(pa-ph) (4.7)
следует, что, изменяя расход топлива, можно изменять
развиваемую двигателем тягу. Расход топлива можно изменять,
дросселируя поток топлива в камеру сгорания. При изменении
расхода топлива изменяются и другие параметры и характеристики
двигателя.
Введем понятие дроссельной (расходной) характеристики.
Под дроссельной, или расходной, характеристикой
ракетного двигателя понимается зависимость тяги и удельного
импульса от расхода топлива при постоянных давлении окруэюающей
среды, размерах камеры двигателя и свойствах топлива.
Получим расчетные выражения для тяги и удельного
импульса идеального ракетного двигателя, отражающие условия,
приведенные в определении. Подставив в (4.7) выражение для
расхода (4.6) и ра = р*к к (X, к), с учетом Wa = const получим

Глава 4. Режимы работы сопла. Дроссельные характеристики 63
P=p^lWa+Fa^AKfk)_Ph^
v<
=л
?***lwa + Fa*{K.k)
J*Z
FaPh-
(4.8)
Из (4.6) следует, что
♦ _ rhyJRT*
Рк =
F^AikY
(4.9)
тогда, подставляя (4.9) в (4.8), получаем уравнение
* I рт*
P = mWa+FXK,k)yL^-FaPh =
m
Wa+Fan{\a,k)
FKpA(k)
~Faph.
(4.10)
Значению ph = 0 соответствует тяга двигателя в пустоте
(пустотная тяга) Рп. С учетом равенства Рвн = Рп = I m уравнение
расходной характеристики по тяге можно записать в виде
P=ml -F p..
у.п а?п
(4.11)
Сопоставив (4.11) с выражением в квадратных скобках в (4.10),
получим формулу для определения развиваемого в пустоте
удельного импульса:
7>" Wa+ A(k) q(Xa,k) C°St'
(4.12)
значение которого зависит от свойств продуктов сгорания
топлива, характеризующихся параметрами R, к, Гк*, и от геометрической

64 Часть I. Теория идеального теплового ракетного двигателя
степени расширения сопла ——, так как из равенства q (k , к) =
= —— однозначно следует значение безразмерной скорости X для
F" P
сверхзвукового сопла, а отношение давлений —т = пСка,к) также
А
однозначно определяется безразмерной скоростью Ха.
Сомножитель в квадратных скобках в (4.8) также зависит только от тех же
параметров, что и удельный импульс, определяемый по
уравнению (4.12).
Таким образом, расходная характеристика для тяги
(определяемой по уравнениям (4.8) и (4.12)) представляет собой линейную
зависимость общего вида (рис. 4.3, прямая), причем tg (а) = I п.
Смещение наклонной прямой вниз пропорционально давлению
окружающей среды ph, при котором определяется
характеристика идеального ракетного двигателя.
Используя определение удельного импульса и уравнение
расходной характеристики по тяге (4.11), получим
Wy.n-— РИ-
(4.13)
т
На рис. 4.3 приведены дроссельные (расходные)
характеристики идеального ракетного двигателя при разных давлениях
окружающей среды. График зависимости I (т) имеет
горизонтальную асимптоту I п, к которой она приближается снизу при
1у\Р-
Of
1
Of
h?,
'0
Г"
[
/г/
'И
А 1
///
У ' У
/is ri
'у2
m;pK
риг<ры
Рис. 4.3. Дроссельные (расходные) характеристики идеального
ракетного двигателя при разных давлениях окружающей среды

Глава 4. Режимы работы сопла. Дроссельные характеристики 65
т —► оо. Из линейной связи расхода и давления в камере (4.4)
следует, что по оси абсцисс можно откладывать и расход, и давление.
При этом изменится только масштаб.
Уравнение для / =f(p*K) с учетом (4.6) и (4.13) можно записать
в виде
7У^"-#^^ (4Л4)
FKppKA(k)
Из анализа (4.13) и (4.14) следует, что дросселирование
двигателя в пустоте не приводит к снижению его эффективности.
Если же противодавление не равно нулю, то увеличение или
уменьшение расхода топлива вызывает соответствующее
увеличение или уменьшение тяги и удельного импульса, причем
относительное изменение удельного импульса тем меньше, чем
больше давление в камере.
Если расходные характеристики получены для одного и того
же ракетного двигателя, но при разных противодавлениях,
причем ph2 < phv то зависимость характеристики по тяге Р2(т;рк)
может быть получена из зависимости Рх(т;рк) путем ее
параллельного переноса вверх на расстояние, соответствующее в
масштабе произведению Fa(phl - ph2)- Кривая / 2 будет проходить
левее и выше кривой / х (см. рис. 4.3).
Представляет интерес взаимное положение расходных
характеристик двух ракетных двигателей, камеры которых
различаются только площадями выходных сечений сопл. Примем для
конкретности Fа1 > FaX (рис. 4.4).
Крутизна (угол наклона а) зависимости Р2(т) будет больше
крутизны зависимости Рх(т), так как внутренняя составляющая
тяги Рш2 > PBliV что обусловлено соотношением геометрических
степеней расширения сопла Fa2/F > Fal /F . Соотношение
между ординатами кривых вблизи нулевых значений расхода
l^i^J < \^a2Ph\ есть следствие того, что Fa2 > Fal по условию.
Кривые расходных характеристик будут иметь точку
пересечения при некотором расходе т0. При этом расходе будут
пересекаться попарно кривые, относящиеся к тяге для первого и
второго двигателей, и кривые удельных импульсов. Асимптотами
кривых I хи12 будут горизонтали / п1 и / п2, взаимное
расположение которых следует из соотношений Рвн2 > Рвн{ и т = idem.

66 Часть I. Теория идеального теплового ракетного двигателя
1' 2'
Рис. 4.4. Дроссельные (расходные) характеристики
идеальных ракетных двигателей, различающихся
только геометрической степенью расширения сопла
Из анализа рис. 4.4 следует, что при дросселировании
двигателя по отношению к точке расчетного режима работы сопло
переходит на режим перерасширения и целесообразным
является уменьшение его геометрической степени расширения. И
напротив, при увеличении давления по отношению к расчетному
сопло переходит на режим недорасширения и целесообразно
увеличить его геометрическую степень расширения, увеличив
площадь выходного сечения сопла.
Вследствие крайней технической сложности таких изменений
задача носит в основном методический характер как вариант
получения оценки сверху характеристик двигателя с идеально
регулируемым соплом.
Определим характеристики Р(т), I (т) для двигателя с
постоянными размерами камеры сгорания, дозвуковой и
трансзвуковой частями сопла и изменяющейся сверхзвуковой частью
сопла, выходная площадь которого при каждом значении
расхода позволяет обеспечить равенство ра= ph = const.
Известно, что на расчетном режиме работы сопла значения
удельного импульса и скорости истечения численно совпадают:
/ =w = ' 2k
у а Ч*-1
RTV
k-\
It
Рк
(4.15)

Глава 4. Режимы работы сопла. Дроссельные характеристики 67
Тогда для тяги двигателя, работающего на расчетном режиме,
можно записать
р=Тщ=Ш
p*KFKpA(k)
Jrtk
ИЛИ
р=р1
к-\
1-
PkJ
VWJni-
(4.16)
Выражения (4.15) и (4.16) есть уравнения характеристик
/у =/j (р*К) и Р =f2 (р*к) двигателя с постоянными размерами
сужающейся части сопла и идеально регулируемой площадью
выходного сечения сопла, при которых при всех давлениях в
камере в выходном сечении соблюдается равенство р = ph.
Очевидно, что, используя уравнение связи расхода и давления
в камере (4.6), можно записать уравнения этих же характеристик
для аргумента - секундного расхода топлива т, а именно:
'у(*К|£<
k-\ *d
m
iK
(4.17)
\к-\
1-
V rh
к-\ *zl
fFKpA(k)^ *
л/<
(4.18)
Графические зависимости, построенные по уравнениям (4.17)
и (4.18), представляют собой огибающие семейства прямых -
расходных характеристик двигателей, отличающихся друг от друга
только площадями выходного сечения сопла. Поскольку на
расчетном режиме работы сопла двигатель будет развивать
наибольшую из возможных тягу, огибающие будут являться
мажорантами поля всех возможных характеристик.
Исследование зависимостей, соответствующих уравнениям
(4.15) - (4.17) и (4.21), может быть предметом самостоятельной
внеаудиторной работы студентов.

68 Часть I. Теория идеального теплового ракетного двигателя
Контрольные вопросы и задания
1. Какие параметры называются номинальными?
2. Какой режим работы сопла называется расчетным?
3. Охарактеризуйте условия, для которых справедливо утверждение
«при работе сопла на расчетном режиме двигатель развивает
максимальную тягу (максимальный удельный импульс)».
4. Раскройте кажущееся противоречие утверждения «на расчетном
режиме двигатель развивает максимальный удельный импульс, но
удельный импульс продолжает расти при увеличении расхода
топлива (давления в камере) на дроссельной (расходной)
характеристике».
5. Дайте определение дроссельной (расходной) характеристики
ракетного двигателя.
6. Какие одинаковые допущения приняты и соблюдаются при выводе
всех расчетных соотношений в гл. 4?
7. Обоснуйте энергетически (на основе уравнения сохранения энергии)
существование конечного максимального значения удельного
импульса (см. рис. 4.3 и 4.4).
8. Какие из полученных в гл. 4 расчетных выражений применимы
к двигателям, рабочее тело которых существенно отличается от
идеального газа?
9. Какие из полученных в гл. 4 расчетных выражений применимы
к двигателям, процесс течения рабочего тела в которых
существенно неизоэнтропийный?
10. Какие из полученных в гл. 4 расчетных выражений применимы
к двигателям, процесс течения рабочего тела в которых
сопровождается существенной потерей полного давления?

Глава 5
Высотная характеристика
ракетного двигателя
Ракетный двигатель как автономная система может работать
в различных средах: в атмосфере, под водой, в вакууме. В общем
случае траектория летательного аппарата с ракетным двигателем
может включать участки подводного старта и движения под водой,
полета в атмосфере с набором высоты полета до нескольких
десятков километров и полета на высоте 100 км и выше, где
окружающая среда представляет собой почти вакуум. Высота 100 км
считается условной границей атмосферы и космоса (так
называемая линия Кармана). Давление окружающей среды при такой
программе полета может изменяться в пределах от нуля до
нескольких мегапаскалей (десятков атмосфер).
При подъеме от уровня моря до высоты Н (~ 11 км) - границы
приземного слоя атмосферы, называемого тропосферой, -
температура уменьшается с почти постоянным градиентом 6,5 °С / км,
и соответственно давление ph также уменьшается от значения
давления на уровне моря/?ло, принимаемого равным 0,101325 МПа
(1 бар) по уравнению, близкому к экспоненте (частный случай
так называемой барометрической формулы):
ph=Ph0exp(-0MH).
Закономерность изменения атмосферного давления на больших
высотах иная, так как в следующих слоях атмосферы -
последовательно в тропопаузе и стратосфере - с увеличением высоты
прекращается уменьшение температуры воздуха и она начинает
возрастать. Изменение давления с увеличением высоты
незначительно зависит от погодных условий, географического положения
и других факторов. Для исключения неопределенности при
расчетах принимаются стандартизованные табличные зависимости

70 Часть I. Теория идеального теплового ракетного двигателя
так называемой стандартной атмосферы1. Приближенно
зависимость давления от высоты, соответствующая стандартной
атмосфере, описывается следующими уравнениями:
для высоты Н ^ 11 000 м
( н V'256
Pk=p»V-um) ' (5Л)
где/?ло - давление на уровне моря;
для высоты Н ^ 11 000 м
(Я-ПООСЛ
Ph=Phn^P- ————
V 6300 )
(5.2)
где/?ш - давление на высоте Я, рассчитанное по (5.1).
Зависимость давления от глубины погружения в воду по
отношению к уровню моря описывается законами гидравлики и
увеличивается примерно на 0,0981 МПа (1 бар) с каждым
увеличением глубины погружения на 10 м.
Тяга ракетного двигателя описывается интегралом давления
окружающей двигатель условно неподвижной среды по наружной
поверхности двигателя. При изменении давления этой среды
изменяется значение интеграла давления на наружную поверхность
двигателя и, следовательно, развиваемые тяга и удельный импульс.
Поскольку в выражения для расчета тяги
P-P--FaPk (5-3)
и удельного импульса
1у=-{Рт-РаРь) (5-4)
т
1 Атмосфера стандартная. Параметры (ГОСТ 4401-81). Настоящий
стандарт устанавливает числовые значения основных параметров
атмосферы для высоты от -2 000 м (ниже уровня моря) до 1 200 000 м.
Предназначен для использования при расчетах и проектировании
летательных аппаратов, а также при приведении результатов испытаний
летательных аппаратов и их элементов к одинаковым условиям (не
применяется при баллистических расчетах искусственных спутников
Земли (см. прил. 1).

Глава 5. Высотная характеристика ракетного двигателя 71
входят слагаемые, учитывающие давление окружающей среды
как фактор наружной составляющей тяги, тяга и удельный
импульс ракетного двигателя являются функциями противодавления.
А поскольку противодавление - это давление окружающей среды,
зависящее от высоты полета или заглубления двигателя ниже
уровня моря (под воду), поэтому и тяга, и удельный импульс
изменяются при движении по траектории с переменной высотой.
Высотной характеристикой ракетного двигателя
называется зависимость тяги и удельного импульса от высоты (или
давления окруэюающей среды) при постоянных параметрах в камере
сгорания и размерах двигателя. Аналитические выражения для
высотных характеристик следует записывать, используя в
качестве аргумента давление ph. А при необходимости при известных
взаимосвязях между высотой (глубиной) и давлением получение
характеристик в зависимости от высоты или глубины становится
математической задачей, алгоритм решения которой известен.
Рассмотрим в качестве аргумента высотной характеристики
противодавление ph. Из сравнения (5.3) и (5.4) следует, что
зависимости Р и Iу от ph линейные. Причем, выбрав масштаб при
общем нуле (совпадении начала координат), обе зависимости
можно отображать одной и той же прямой. При общем нуле и
произвольных масштабах по оси ординат кривые в общем случае
совпадать не будут, но обязательно пересекутся в точке с
абсциссой (противодавление), в которой тяга двигателя при соблюдении
принятых допущений равна нулю (рис. 5.1).
Переходя к аргументу - высоте полета (определяемой,
например, в километрах по (5.1) и (5.2)), получим зависимости,
представленные на рис. 5.2. В приведенных координатах кривые
■р(ри)
Рис. 5.1. Высотные характеристики
идеального ракетного двигателя (в
зависимости от давления окружающей среды)

72 Часть I. Теория идеального теплового ракетного двигателя
Рис. 5.2. Высотные характеристики идеального
ракетного двигателя (в зависимости от высоты
полета и глубины погружения) при Fa2 > FaX
Р и I имеют горизонтальные асимптоты: Рп - пустотная тяга
и / п - пустотный удельный импульс. При увеличении давления
по отношению к давлению на уровне моря, т. е. при заглублении
двигателя под воду, тяга и удельный импульс уменьшаются и
теоретически могут стать отрицательными (см. рис. 5.2, левая
полуплоскость).
При линейной шкале рИ (см. рис. 5.1) тангенс угла наклона
(tg а) пропорционален площади выходного сечения сопла Fa,
a tg р — величине Fa/m9 т. е. чем больше Fa, тем интенсивнее
уменьшается тяга с ростом противодавления ph и чем больше
FJm или чем меньше т при заданном Fa, тем интенсивнее
уменьшается удельный импульс при увеличении противодавления.
Высотные характеристики двигателей
с одинаковыми размерами камер,
работающих при разных расходах (давлениях в камере)
Соотношение между высотными характеристиками в этом
случае удобно рассматривать, исходя из уравнений для тяги
P = Pn~PhFa (5-5)
И
P = Iy>-PkF* (5-6)
Но поскольку I n = const, то из (5.6) следует, что увеличение
расхода в п раз (при этом давление в камере также увеличится

Глава 5. Высотная характеристика ракетного двигателя 73
в п раз) приведет к пропорциональному в п раз увеличению
значения тяги в пустоте Рп, а угол наклона характеристик
сохранится (рис. 5.3).
Рис. 5.3. Высотные характеристики
идеального ракетного двигателя при разных
давлениях в камере (в зависимости от
давления окружающей среды) при
0<п<\;рк2<рк1
Для анализа высотных характеристик I = f( ph)
предпочтительно записать уравнение для удельного импульса в виде
1у _А.п Ри~г-
т
(5.7)
В связи с тем, что значение удельного импульса в пустоте не
зависит от давления в камере, зависимости / (ph) для одного и того
же двигателя, но работающего при разных расходах, будут
исходить из одной точки ph = О, / = I п. Наклон прямой будет
большим (снижение удельного импульса интенсивнее) для случая
меньшего расхода, а следовательно, меньшего давления в камере,
и 12 < I . везде, кроме точки с абсциссой ph = 0.
Высотные характеристики камер с соплами,
отличающимися только площадями выходного сечения
Рассмотрим ракетный двигатель с соплом, снабженным до-
расширительным насадком (рис. 5.4), установка в рабочее
положение которого обеспечивает увеличение выходной площади

74 Часть I. Теория идеального теплового ракетного двигателя
сопла от F , до F ~
> F .. Такое
Рис. 5.4. Схема камеры
ракетного двигателя с составным
(раздвижным) соплом:
1 - камера с исходным соплом; 2 -
дорасширительный насадок в
транспортном положении
сопло называется раздвижным или
составным.
Обозначим двигатель с
соплом без насадка индексом «1»,
а с насадком - индексом «2». Из
Fa2/FKP>Fal/FKP СЛеДУеТ 7у.п2 >7y.nl
и р^>раг Поскольку Fal>FaV то
темп снижения тяги и удельного
импульса для двигателя с насадком
будет выше, чем для двигателя без
насадка, и кривые характеристик
пересекутся при некотором
давлении
/Ъ=/>лпР(Рис-5-5)-
Рис. 5.5. Высотные характеристики идеальных
ракетных двигателей, отличающихся степенью
геометрического расширения сопла (в
зависимости от давления окружающей среды)
На высотах с давлением ph < ph большую тягу развивает
двигатель с дорасширительным насадком, а на меньших
высотах - двигатель без насадка. При движении по траектории вверх
по достижении высоты, на которой ph = ph , насадок
целесообразно перевести из транспортного положения в рабочее. Если
ракета с таким двигателем снижается, то на больших высотах
насадок должен находиться в рабочем положении, а при снижении
до высоты, на которой атмосферное давление равно рИ , насадок

Глава 5. Высотная характеристика ракетного двигателя 75
должен быть переведен в транспортное положение, т. е.
необходимо перевести сопло из одного режима в другой, т. е.
переключить сопло. Поэтому давление, при котором становится
целесообразным переключение, называют давлением
переключения, а соответствующую этому давлению высоту - высотой
переключения.
Отметим, что сопло с насадком только при одном давлении
ph, когда ph2 = ph 2, будет работать на расчетном режиме. Сопло
без насадка также будет работать на расчетном режиме при одном
давлении ph] = ph .. Очевидно, что рИ > phT И при таких
давлениях окружающей среды двигатели будут развивать наибольшую
тягу по сравнению с тягой других двигателей, отличающихся от
рассматриваемых только площадями выходного сечения сопла.
Если представить множество ракетных двигателей,
отличающихся друг от друга только площадями выходного сечения
сопла F ^ Fа ^ оо (рис. 5.6), то для любого ры из диапазона
значений 0^ph ^p можно найти в этом множестве такой /-й
двигатель, сопло которого при данном ph будет работать на
расчетном режиме, т. е. при ph = ра.
И на высотных характеристиках
(см. рис. 5.5) для этого множества
двигателей на прямой,
соответствующей выбранному /-му двигателю,
есть точка, выше которой не может
располагаться никакая другая
характеристика, так как сопло
именно этого двигателя имеет
оптимальную для данного ph геометрическую
степень расширения, при которой
сопло работает на расчетном
режиме и развивается максимальная
тяга.
Совокупность таких точек, мажоранта, и она же огибающая
мноэюества характеристик, является зависимостью тяги от
давления окружающей среды для двигателя, сверхзвуковая часть
сопла которого регулируется путем изменения площади
выходного сечения сопла так, что при любом О ^ ph ^ p в выходном
сечении сопла достигается равенство ра = ph.
Аналитическое выражение для этой кривой можно получить,
исходя из уравнения тяги с учетом ра = ph для всех рИ из
диапазона значений 0 ^ ph ^ /?кр, а именно:
Рис. 5.6. К обоснованию вида
высотной характеристики
камеры с идеально регулируемым
соплом

76 Часть I. Теория идеального теплового ракетного двигателя
P = mWa + Fa{pa-ph) = mWa =
тА
г ~ \
Ph
\гк;
(5.8)
откуда
т Mk-l
л;
к-\
(5.9)
Равенство нулю второго слагаемого Fa(pa - ph) в уравнении
тяги (5.8) не очевидно для/?Л = 0 и соответствующего
предельного значения Fa = оо, так как в этом случае имеем неопределенность
вида произведения нуля и оо. Равенство нулю этого произведения
следует из преобразований, в которых используется подстановка
к + \
\/(к-\)
к-\
к + \
f-~{pJpTHpJp:)
{к-\)1к
Выразив отсюда Fа и выполнив предельный переход, получим
lim (FaPa)= lim^^FKppK=Z lim %Ш== = 0, (5.10)
/7л->°°
P°-*°FkPPk
Ра^Ъ
где Z = const Ф 0.
Как и высотные характеристики, зависимости для тяги (5.8)
и удельного импульса (5.9) имеют постоянный для данного
двигателя множитель т, поэтому могут совпадать в декартовой
системе координат при соответствующем выборе масштаба, или
в общем случае при любом значении давления ph их ординаты
будут различаться в т раз.
График зависимости тяги (или - в другом масштабе -
удельного импульса) от давления окружающей среды, построенный по
уравнениям (5.8) или (5.9), приведен на рис. 5.5.

Глава 5. Высотная характеристика ракетного двигателя 11
Применение дорасширительного соплового насадка,
образующего в сочетании с основным соплом так называемое
раздвижное сопло, рассматривалось для одного из вариантов маршевого
двигателя центрального блока ракеты-носителя (РН),
работающего при запуске с земной поверхности до высоты более 40 км.
Если использовать ЖРД НК-33 или другой двигатель с
давлением на срезе сопла, оптимизированным для полета в составе
первой ступени РН, то увеличение геометрической степени
расширения его сопла привело бы не только к нежелательному
увеличению габаритов двигателя на старте, но и к значительным
потерям тяги и удельного импульса на относительно малых
высотах, соответствующих работе на траектории полета первой
ступени. Поэтому одним из путей повышения эффективности РН
с таким двигателем является использование раздвижного двух-
позиционного сопла, у которого геометрическая степень
расширения увеличивается от 25...27 до 75...80 с помощью
выдвижного соплового насадка. В этом случае на участке полета РН
приблизительно до высоты 10 км (высота или точка
переключения) будет работать исходное сопло, а на больших высотах - это
же сопло, но с подключенным выдвижным дорасширительным
сопловым насадком.
Известно также применение раздвижного сопла или
подвижного дорасширительного насадка NEA (Nozzle Extension Assembly)
на двигателях RL 10A-4-2 и RL 10B-2, используемых на верхних
ступенях РН, а также на отечественном керосин-кислородном
ЖРД космических разгонных блоков 11Д58М и др. Раздвижные,
так называемые телескопические, сопла широко применяются
(см., например, http://www.npoiskra.ru/ и др.) при ограничении
осевых габаритов летательных аппаратов, обусловленном,
например, размерами транспортно-пусковых контейнеров.
Контрольные вопросы и задания
1. Дайте определение высотной характеристики ракетного двигателя.
2. Что такое стандартная атмосфера?
3. От чего зависит давление на наружной поверхности камеры
двигателя, работающего под водой?
4. Что такое раздвижное сопло?
5. В чем состоят преимущества камер с раздвижным соплом перед
камерами с соплом неизменяемых размеров?
6. Что такое точка переключения?

78 Часть I. Теория идеального теплового ракетного двигателя
7. Где именно - в атмосфере или под водой - градиент давления
окружающей среды будет выше?
8. На графиках высотной характеристики (зависимость удельного
импульса от давления окружающей среды) двух камер, отличающихся
только геометрической степенью расширения сопла, нанесите девять
точек, соответствующих характерным режимам: удельные
импульсы в пустоте; давление окружающей среды, при котором камеры
развивают тягу, равную нулю; точки расчетных режимов; точки
переключения; удельные импульсы камер при номинальном
давлении окружающей среды.
9. Почему область существования высотной характеристики для
камеры сгорания с идеально регулируемым соплом (см. рис. 5.5) не
включает давление окружающей среды, большие давления в
критическом сечении камеры?
10. Найдите значения тяги и удельного импульса, которые развивает
камера с идеально регулируемым соплом (см. рис. 5.5) в пустоте.

Глава 6
Усилия, действующие на проточную часть
ракетного двигателя
Равнодействующая газо- и гидродинамических сил,
приложенных к внутренней поверхности проточного тракта при течении
по нему рабочего тела, является реактивной силой. Природа
появления реактивной силы - изменение вектора количества
движения потока.
Пусть поток безотрывно протекает по криволинейному
каналу произвольной формы (рис. 6.1). При этом параметры потока
во входном 1 и выходном 2 сечениях канала стационарны и
распределены равномерно по сечению.
Выберем ось х плоской системы
координат, совпадающей с
направлением скорости потока в сечении 7.
Ограничим поток сечениями 1 и 2
поверхностью, сколь угодно близко
отстоящей от поверхности канала. Пусть
R - равнодействующая всех сил,
действующих со стороны стенок канала
на объем газа, ограниченный этими
поверхностями. Тогда по третьему
закону Ньютона R = -Р, где Р -
реактивная сила.
Используя уравнение сохранения количества движения в
форме Эйлера, получим
►
/ \У
i ^N *
°| 4rV2
Рис. 6.1. К расчету
реактивной силы
R = (mWa + pF)2-(mWa+pF\,
(6.1)
где выражения в скобках - полный импульс в сечениях 2 и 1
соответственно.
Запишем уравнение (6.1) в проекциях:
на ось х
Rx = (m2Wa cosot + p2F2 cosa) - (mJVa + pxFx);

80 Часть I. Теория идеального теплового ракетного двигателя
на ось у
Ry = (m2Wasma + p2F2sma).
Отметим, что если при движении по каналу полный импульс
потока возрастает по модулю, то на поток действует сила в
направлении вектора скорости истечения газа, и соответственно
реактивная сила будет действовать в противоположном
направлении, т. е. для реактивной силы справедливо соотношение
Кг = -[(mWe+PF)2 -(mWa + PF\]. (6.2)
Рассмотрим примеры использования уравнения (6.2) в частных
случаях, когда поток в канале только меняет направление,
сохраняя абсолютные значения расхода, скорости и давления. При
этом площади входных и выходных сечений газовода (канала)
равны между собой, а параметры потока при переходе от сечения а
к сечению 1 не изменяются и F = F*.
а 1
Пример 1 (рис. 6.2). С какой силой (без учета наружного
давления) будет действовать на опору газовод, если известна
пустотная тяга двигателя Рп?
Рис. 6.2. К расчету реактивной силы, действующей
на газовод с поворотом потока на 90°
Решение:
/>_2=[(m2^2cos90° + F2p2cos90°)-(m^+^Fj],
но Рп = тх Wa +paFa, \P{_2\ = Рп9 т. е. газовод будет прижат к
опоре силой, равной по модулю пустотной тяге двигателя.

Глава 6. Усилия, действующие на проточную часть двигателя 81
Пример 2 (рис. 6.3). С какой силой R (без учета наружного
давления) будет действовать газовод на опору, если известны
показания Р силомерного устройства?
Рис. 6.3. К расчету реактивной силы,
действующей на газовод с поворотом
потока на произвольный угол
Решение:
^_2=-[(w2^2cos(90o-a) + p2F2cos(90°-a))-(w1^1+jr?1F1)] =
= (rhlWl+plFl)(l + cos(90°-a)),
но
тЖ + p}F. = mW+pF=P.
1 1 * 1 1 а Г а а вн
Тогда с учетом Р = Рвн - Faph получим
/? = (P + F^)(l+cos(90o-a)).
Расчет реактивной силы, возникающей при движении
сжимаемого рабочего тела по каналу.
Осевые усилия в стенках ракетной камеры
Если необходимо рассчитать усилия, действующие на
расширяющийся или сужающийся канал, по которому течет
сжимаемое рабочее тело, то во многих случаях полный импульс потока

82 Часть I. Теория идеального теплового ракетного двигателя
в сечении канала удобно выражать в одномерном приближении
через ГДФ.
Получим выражение для полного импульса потока с учетом
тех же допущений, что и при выводе соотношений для ГДФ. При
этом не имеют значения процессы, происходящие между
контрольными сечениями, так как при выводе используется связь
между параметрами потока в одном сечении или, что в рамках
принятых допущений эквивалентно, в точке. Тогда можно записать
rhW + pF = max
кр
rhW pF
+ ——
vwaKp maKVJ
(6.3)
где W/a = X. При этом
a^ = ^9^4kRT\{\,k)^^kRr^=^RT\ (6.4)
Упростим соотношение pF/(m a ), используя выражения для ГДФ
и расхода:
к(Х,к)-
F
к-\,
'к + 1
к-\
к + 1
к-\
Х\ 1
■ *±1х'
к-\
1
Аг—1
. pLF„A{k)
т= '*2^"\ A(k) = xlk\ 2
к+\
4-1
Из равенства
pF _
4W '
pF^Kf
vifc + 1.
(6.5)
(6.6)
(6.7)
п(Х,к) jk + l
ma.
* p'FMk)
2k DT,. q(X,k)A(k)\ 2k
k + l
RT
подстановкой (6.5), (6.6) и (6.7), выполнив приведение подобных
членов и сокращения, получим
pF
= 1
та
кр
к + 1
к + 1
2кХ
(6.8)

Глава 6. Усилия, действующие на проточную часть двигателя 83
Подставим (6.4) и (6.8) в (6.3) и, проведя упрощения, получим
(6.9)
mW + pF = —maKDZ(X),
"кр^
где
г(х)=-(х+-Л
2К X.
График ГДФ Z(X) представлен на рис. 6.4.
Приведенная скорость X
Рис. 6.4. Изменение ГДФ Z(X)
и/(Х, к) в зависимости от
приведенной скорости X
Из (6.1) и (6.9) с учетом свойств ГДФ Z(X) следует, что на
сужающуюся часть сопла действует сила, стремящаяся оторвать
ее от камеры сгорания, расширяющаяся же часть прижимается
реактивной силой к сужающейся части сопла.
Для решения некоторых задач удобно представить полный
импульс движущегося потока через произведение давления
торможения р* и площади F потока, а именно:
к + \
та Z(X) = p*Ff(X,k)9
где/(А,, к) - ГДФ, зависящая только от приведенной скорости X
и показателя адиабаты к.
Приведем следующие преобразования:

84 Часть I. Теория идеального теплового ракетного двигателя
-j-matpZ(X) = — Z(X)pKpFKpaKpaKp =
т
= *±1z(x)J^Wvlrt* =
k RTn F Jt + 1
KP v v '
<
= (k + i)Z(X)p*Fn(\,k)q(X,k) =
: p*F{(k + l)Z(X)n(\,k)q(X,k)} = p*Ff{X,k)
при —??- = n(\,k)=> ркр = p*n(\,k); -^- = q(X,k). Здесь введена ГДФ
^ = n(l,k)^pKp=pn(l,k);^
/(A,, k) = (k + 1)Z(A,) 7i(l Д) #(A,, А:), график которой приведен на
рис. 6.4.
Покажем, что эта функция имеет смысл полного импульса
одномерного потока в данном сечении с площадью F,
приведенного к параметрам торможения этого же потока в этом же сечении.
Согласно уравнению (6.9), где левая часть представляет собой
импульс одномерного потока, записанный в форме Эйлера, имеем
mW + pF = pWFW + pF = pW2F + pF = p*Ff(X,k).
m
Отсюда следует соотношение, примененное при аналитическом
решении ряда практических задач:
р F р
Это соотношение позволяет выражать пустотную тягу ракетного
двигателя через известные параметры потока в выходном сечении
сопла вне зависимости от особенностей конструкции и
протекания рабочих процессов в камере, т. е. и для случаев, когда течение
в камере неизоэнтропийное ир* </?*, например, в общем случае
рп = "Л + Ра Fn = РУЛК *)>
п а а * а а * а aj \ а? /»
тогда как для идеального ракетного двигателя р* = р* и Р =

Глава 6. Усилия, действующие на проточную часть двигателя 85
Используя уравнение (6.9) для записи полного импульса
потока, рассчитаем осевые усилия в стенках камеры от действия
реактивной силы, учитываемые при расчетах на прочность.
Рассмотрим четыре варианта крепления камеры:
• вариант А (рис. 6.5) - сила тяги передается упором наружной
торцовой поверхности камеры;
• вариант Б (рис. 6.6) - сила тяги передается через опоры,
установленные на камере сгорания между смесительной головкой
камеры сгорания и входом в сопло;
• вариант В (рис. 6.7) - опоры установлены вблизи сечения
минимальной площади;
0 j
I"
Ч
К
о = 0 ^•""
^
Kh У^
*0
^-вх
0
/
/
IF
,
X
~ г, i
* X
а
Рис. 6.5. Эпюра осевых усилий от внутренней составляющей тяги
при закреплении камеры в сечении вблизи смесительной головки
Рис. 6.6. Эпюра осевых усилий от внутренней составляющей тяги
при закреплении камеры в произвольном сечении камеры сгорания

86 Часть I. Теория идеального теплового ракетного двигателя
• вариант Г (рис. 6.8) - камера закреплена за периферийную
часть расширяющейся части сопла.
Расчеты удобно проводить, начиная с сечения, в котором
известна нагрузка или ее изменение. Такими сечениями являются
Рис. 6.7. Эпюра осевых усилий от внутренней составляющей тяги
при закреплении камеры вблизи сечения минимальной площади
Рис. 6.8. Эпюра осевых усилий от внутренней составляющей тяги
при закреплении камеры в сечении вблизи среза сопла
сечения крепления - здесь осевое усилие или претерпевает скачок
на величину реактивной силы (для вариантов Б и В), или равно
реактивной силе (для варианта Г). Усилие известно также и для

Глава 6. Усилия, действующие на проточную часть двигателя 87
Рис. 6.9. К определению условий равно- ^^ф
весия участка камеры сгорания вблизи
смесительной головки
свободного конца - оно равно нулю вблизи выходного сечения
сопла для вариантов А-В.
Для графического отображения результатов расчетов вверх
от оси Ох будем отображать в выбранном масштабе сжимающие
усилия, вниз - растягивающие. Поскольку расширяющаяся часть
сопла для вариантов А-В работает в одинаковых условиях,
усилие вблизи минимального сечения (справа) будет одним и тем
же. Значение его рассчитываем по уравнению
Рассмотрим условие равновесия смесительной головки для
варианта А (рис. 6.9):
где Т - растягивающее усилие; Рвн - реакция опоры,
воспринимающей реактивную силу, т. е. пустотную тягу камеры; р*, Frc -
давление в камере и площадь смесительной головки, равная
площади камеры сгорания FK c.
Из (6.10) следует
причем Т - растягивающее усилие, сохраняющееся до сечения
входа в сопло. Отметим, что направление усилия Г
(сжимающего или растягивающего) зависит от соотношения размеров и
параметров двигателя.
Поскольку на участке от входа в сопло до критического
сечения (вх - кр) нет приложенных местных сил, эпюра нагрузки
переходит через нулевой уровень, т. е. меняет знак.
Покажем принципиальную возможность существования
сечения Fx0, где осевое усилие равно нулю, а именно:
(W
-^/
т*т

88 Часть I. Теория идеального теплового ракетного двигателя
^_e=^wo4)[z(A,e)-Z(XJt0)] = 0. (6.11)
Из (6.11) следует равенство
Z(\) = ZQ,J, (6.12)
ИЛИ
1 ! -1 1
Ка Кх0
Квадратное относительно \х0 уравнение (6.12) имеет два
корня: тривиальное решение Хх0 = Ха, не удовлетворяющее условию
, 1
задачи, и решение Ах0 =—.
Если Хвх < XxQ, то сечение Fx0 находится на сужающемся
участке сопла и эпюра в точке, соответствующей этому сечению,
проходит через нуль (усилие равно нулю или меняет знак).
Отметим, что из идентичности условий работы сопла для
вариантов А и Б следует идентичность эпюр осевых усилий, по
крайней мере, в стенках сопла, т. е. для варианта Б часть эпюры
(на участке правее сечения закрепления камеры сгорания)
определена.
Записав уравнение равновесия смесительной головки камеры
для вариантов Б-Г аналогично (6.10), получим
max rK г.с'
где Гтах - растягивающее усилие, направленное вправо. Причем
скачок осевой нагрузки в сечении закрепления камеры для
вариантов Б и В должен быть равен реактивной силе Рви. Практически
это равенство будет приближенным, так как вследствие
конечности площади камеры статическое давление на входе в сопло не
равно давлению вблизи смесительной головки.
Из идентичности условий нагружения прилежащих к
смесительной головке участков камеры сгорания для вариантов Б-Г
следует идентичность соответствующих эпюр, тогда (см. рис. 6.7)
Т2+Т,=РВп-

Глава 6. Усилия, действующие на проточную часть двигателя 89
1,5...2,0ДКС
Т
1
¥
««—
»-
2ав^Г
Рис. 6.10. Схема построения примерного
контура камеры ракетного двигателя
Для варианта крепления Г все характерные ординаты известны.
Отметим, что способом проверки правильности построения
эпюр является расчет ординат эпюр, начиная с противоположных
свободных концов камеры. Проверка заключается в расчете
разности ординат справа и слева от сечения крепления камеры и
сопоставлении со значением пустотной тяги.
При решении учебных задач на построение эпюр осевых
нагрузок камеры рекомендуется построить приближенный контур
камеры (контур камеры - линия пересечения внутренней
поверхности камеры со стороны потока продуктов сгорания с плоскостью,
проходящей через его ось симметрии) в соответствии с
приведенной на рис. 6.10 схемой, где
К, = 0,5DKC, Л, = (0,8...1,2)Якс, R2 = Л3 = (0,8...1,2)*кр,
DKC 5* (1,8...2ДОкр, 2Рвх = 50°...80<\ 2Рвых = 25°...30°.
Контрольные вопросы и задания
1. Запишите уравнение (в форме Эйлера) импульса потока в сечении
с равномерным распределением параметров с использованием
газодинамических функций Z(X) uf(k, к).
2. При каких допущениях справедливо каждое из полученных в гл. 6
расчетных выражений?
3. В чем противоречивость (приближенность) допущений, принятых
при выводе расчетных выражений применительно к изобарной
камере сгорания?
4. Какие газодинамические функции изменяются немонотонно в
области существования?
5. Чему равняется изменение осевой силы в сечении закрепления
камеры?

90 Часть I. Теория идеального теплового ракетного двигателя
6. При каком расположении сечений закрепления камеры развивается
максимальное (минимальное) осевое усилие в ее стенках?
7. При каком расположении сечения закрепления камеры осевое
усилие не меняет знака?
8. Возможно ли такое сочетание размеров и рабочих параметров
камеры с конечной площадью поперечного сечения проточной части,
при котором будут развиваться только сжимающие или только
растягивающие осевые усилия?
9. Если сопло или его часть крепится к камере сгорания, то как найти
сечение закрепления, в котором осевое усилие равно нулю?
10. Что такое контур камеры?

Глава 7
Составляющие тяги.
Место приложения тяги ракетного двигателя
Цель этой главы - определить, из каких составляющих
складывается тяга камеры ракетного двигателя, для оценки
целесообразности совершенствования того или иного узла камеры с
учетом его вклада в основной показатель, характеризующий ракетную
камеру, - тягу при заданном расходе топлива. Тем более что из
материала гл. 6 следует, что равнодействующая сил давления на
сужающуюся часть сопла направлена против направления
суммарной силы тяги, т. е. налицо формальный парадокс: неизменно
присутствующий в конструкции современных ракетных
двигателей участок камеры уменьшает ее тягу. В дальнейшем мы
должны убедиться в том, что сформулированный выше парадокс
кажущийся.
Введем стандартизованные определения.
Коэффициент расхода сопла есть отношение
действительного расхода газа через сопло к идеальному расходу,
определенному при тех же значениях температуры и давления торможения
в минимальном сечении сопла, газовой постоянной и местного
показателя адиабаты:
ЦС= **т\(У\> (7Л)
Таким образом, коэффициент расхода топлива цс позволяет
учитывать сужение струи (минимальная площадь потока меньше,
чем минимальная площадь проходного сечения сопла) и различия
распределений параметров потока и одномерного в сечении

92 Часть I. Теория идеального теплового ракетного двигателя
минимальной площади потока. Для рассматриваемого
идеального ракетного двигателя цс = 1.
При сравнительном анализе тяговых (импульсных)
характеристик камеры ракетного двигателя применяется
стандартизованный показатель - коэффициент КТ, определяемый как
коэффициент тяги, равный отношению тяги камеры к произведению
давления торможения в минимальном сечении сопла, площади
этого сечения и коэффициента расхода сопла.
Если при расчете КТ используется значение пустотной тяги,
то и коэффициент тяги называется коэффициентом пустотной тяги
или, другими словами, коэффициентом тяги в пустоте и
обозначается Кт п. Поскольку Рп = Рвн, то Кт п характеризует внутреннюю
составляющую тяги, или, что то же самое, реактивную силу.
В связи с тем что реактивная сила есть равнодействующая сил,
приложенных к внутреннему контуру камеры, можно представить
реактивную силу как сумму трех слагаемых:
Р =Р +Р +Р ,
вн кр суж расш'
(7.2)
где Р - составляющая от действия сил давления, приложенных
к смесительной головке на площади ортогональной проекции
минимального (для идеального двигателя - критического) сечения
сопла на обращенную вовнутрь камеры сгорания поверхность
смесительной головки; Рс ж - равнодействующая сил давления,
приложенных к внутренней поверхности сужающейся части
сопла и к части поверхности смесительной головки, на которую
ортогонально проецируется внутренняя часть поверхности
сужающейся части сопла; Р асш - равнодействующая сил давления,
приложенных к внутренней поверхности расширяющейся части
сопла (рис. 7.1).
При этом равнодействующая Р асш приложена к
расширяющейся части сопла непосредственно, Р приложена непосред-
Рис. 7.1. К определению и анализу вклада
составляющих силы тяги ракетной камеры

Глава 7. Составляющие тяги. Место приложения тяги 93
ственно к смесительной головке камеры - к приосевои ее части
площадью F , аРсж- векторная сумма двух слагаемых:
• силы, действующей на периферийную кольцевую часть
смесительной головки площадью Fr с - F ,
Лсольц^К^с-^кр); (7-3)
• силы, действующей на сужающуюся часть сопла на участке
от входа в сопло до его минимального (критического) сечения,
Пх-кр = -(^.с-^Р)^ (7-4)
где р - некоторое усредненное по площади сужающейся части
сопла давление, для которого по теореме о среднем справедливо
неравенство
PV<P<P\- (7-5)
Отсюда следует, что равнодействующая тяги направлена в
сторону смесительной головки:
Р =Р -Р . (7.6)
суж кольц вх-кр ч '
Разделив уравнение (7.2) nap*KF с учетом справедливых для
идеального двигателя соотношений р*к = р*р, Fmin = FKp, цс = 1,
получим
*т.п =^Г = 1 + ЛКт.„.сУ» + ДКт.п.расш. (7-7)
Выведем расчетные соотношения для коэффициентов АКТ п суж
и АКт п ш, используя уравнение сохранения импульса в форме
. pKFKpA(k) m^Ri:
Эйлера с учетом т = ." и pKF = ] :

94 Часть I. Теория идеального теплового ракетного двигателя
Jt + 1
АК.
k m%
чю-
-^maKpZ(l)
т.п.расш
рЛ
к' кр
1
-я^Х*.)-']-
(7.8)
Вследствие ограниченности значения приведенной скорости,
К ^ ^тах "
а именно:
к + \
к-\
, ограниченно также слагаемое Л^тп ш,
o^a/W,^
2 V-1
к + 1
1 -1Ч
^
(7.9)
Оценим вклад сужающейся части сопла в создание тяги:
р \ _ п* F Р \
nh =1 Л^кр 'пк =1
АК.
т.п.суж
к + 1
рЛ
maKpZ(l)
А(к)
кр
-1 = 2
ДЛ
-1 =
кЛ кр
2 V-i
к + \)
(7.10)
npnZ(l)=l, a =
2£
к + \
RZ
Рассчитаем максимально возможное значение коэффициента
пустотной тяги. Аналогично выводу соотношения (7.10) получим
К,
Jt + 1
Р (mW + pF)
_ птах _ V г /птах _
k ~ma*p
Z(^ax)
рЛ
■ = 2
кр
Jt+1.
к+\
4к^\
(7.11)

Глава 7. Составляющие тяги. Место приложения тяги 95
Зависимость вклада составляющих в создание суммарной тяги
от показателя адиабаты к (расчеты по соотношениям (7.8), (7.10)
и (7.11)) иллюстрируют данные табл. 7.1 и рис. 7.2.
Таблица 7.1. Доля участков камеры в создании тяги
(по отношению к основной составляющей тяги)
в зависимости от показателя адиабаты рабочего тела
Параметр
Максимальная тяга
Доля тяги от расширяющейся
части сопла
Доля тяги от сужающейся
части сопла
Показатель адиабаты к
1,1
2,947
1,719
0,228
1,2
2,247
1,005
0,242
1,3
1,964
0,709
0,255
Согласно данным табл. 7.1, доля составлющей тяги от
сужающейся части сопла составляет 23,0...25,5 % так называемой
основной составляющей тяги, причем зависимость от показателя
адиабаты слабая.
3,0
§1.5
|1,0
го
0,5
0
1,10 1,15 1,20 1,25 1,30
Показатель адиабаты к
Рис. 7.2. Соотношение между долями
составляющих тяги в зависимости от показателя адиабаты
при постоянной степени расширения рабочего тела
Доля составляющей тяги от расширяющейся части сопла при
предельно возможной степени расширения, напротив,
превышает основную составляющую тяги на 70 % при к = 1,1, равна ей
при к= 1,2 и составляет 70 % ее значения при к= 1,3.
В первой строке табл. 7.1 приведены максимально возможные
значения коэффициента тяги, реализуемые при расширении газа
в сопле до нулевых значений давления в выходном сечении сопла.
к^
'
1 ,
1
V
i
<
к***
г
1
1
пах
71. ..172%
\
lN23...25% V
1. докр J
L_J

96 Часть I. Теория идеального теплового ракетного двигателя
Очевидно, что суммарная тяга двигателя может превысить
основную составляющую тяги в 2-3 раза.
В действительности степень расширения газа в сопле
конечна и приведенная скорость Ха не достигает максимально
возможного значения.
Оценим влияние степени расширения газа на распределение
тяги по составляющим тяги для £= 1,15и -£-*- = 10...1 000.
Ра
Получим выражения для коэффициента тяги в виде, удобном
для анализа:
v _ *п к
mavZ(Xa)A(k)
рЛ
кЛ кр
тфа?
= 2
2 V-i 1 k + \
Jfc + 1
2\k-\
k-\
\-rf
.A
k-\
a+oji-
f ~ \
k-\
Pa
V-fK/
ИЛИ
К, =2
k + \.
k-\
O(Wa)-
Введем функцию
ф.^/лЦ^.м
k-\
'PaV'
A.
1 + -
k-\
k-\
a+oji- [Ц
\P*J
, (7.12)
которая также ограничена сверху и принимает наибольшее
значение при расширении газа в сопле до нулевого давления. Оценим
эту границу, выполнив предельный переход:
lim a(k9pJPl)^Jj^(1+777) = Т?=-

Глава 7. Составляющие тяги. Место приложения тяги 97
Анализируя (7.12), отметим, что Ктп для конкретного k = с /cv
определяется только степенью расширения рабочего тела и не
зависит от абсолютных значений давления.
Зависимость Кт п от р*к/ра для к= 1,15 иллюстрирует рис. 7.3.
Видно, что при степенях расширения рабочего тела, равных 10...20,
характерных для двигателей 1940-50-х годов, большую, т. е.
основную, часть тяги создает неуравновешенная составляющая сил
давления на проекцию критического сечения на поверхность
смесительной головки камеры. Отсюда и термин, все еще
встречающийся в книгах прошлых лет, «основная составляющая тяги».
Для современных же двигателей при степенях расширения
рабочего тела в диапазоне значений 60... 1 000 сопло может обеспечить
вклад в создание реактивной силы такой же и даже больший, чем
так называемая основная составляющая тяги.
3,0
2,5
^2,0
§1,0
го
0,5
0
10 30 90 270 810 2430
Степень расширения
Рис. 7.3. Соотношение между долями
составляющих тяги в зависимости
от степени расширения рабочего тела
- ^Т.П
/
^Т.П1
К / ' 1
Лт.п. докр
iax
*т
р- р
а h
При решении ряда практических задач и анализе влияния
параметров камеры на развиваемую пустотную тягу
рационально выразить коэффициент пустотной тяги Ктп (7.7) через ГДФ
f(k, k) и q(X, к) с учетом (6.9):
к + \
Pn=mWa+paFa=-—maKpZ(XJ = plFa(Xa9k^
К^
ПРИ Ра=Р*р> ~^ =
Рп =P:Faf(Xa9k) = f(Xa9k)
Ркр"кр Ркр"кр
1
^кр я(К>к)

98 Часть I. Теория идеального теплового ракетного двигателя
Для изобарической идеальной ракетной камеры ра = р =
Для сопла с бесконечно большой геометрической степенью
расширения коэффициент тяги принимает конечное максимальное
значение:
г,
к
Если при расчете коэффициента тяги рассматривать тягу при
ненулевом противодавлении, т. е.
Y - ^ - ^п "" FgPh _ у FgPh fl Л1\
Ат " *р ~ Г^ -\n 5Г—, (/-l^j
Рк"кр Рк"кр Рк"кр
то, как следует из (7.12) и (7.13), коэффициент тяги будет зависеть
от абсолютных значений противодавления ph и давления в
камере/?*, а также, как и Ктп, от степени расширения газа р*к/ра и
однозначно определяемой для ее конкретного значения
геометрической степени расширения сопла FJF . При этом проявляются
две противоположные тенденции: возрастание Ктп с
увеличением р*к /ра и возрастание вычитаемого в (7.13) с увеличением
FJF' соответствующим росту р*к/ра.
Взаимодействие этих тенденций обусловливает существование
максимума Кт при степени расширения газа в сопле,
соответствующей расчетному режиму работы сопла при конкретных
значениях/^ и/?*, на которому =ph (см. рис. 7.3).
Контрольные вопросы и задания
1. Что такое коэффициент расхода сопла?
2. По каким причинам значение коэффициента расхода сопла
отличается от единицы?
3. Дайте определения коэффициента тяги и коэффициента пустотной
тяги (или, другими словами, коэффициента тяги в пустоте).
4. Какие две противодействующие тенденции обеспечивают
существование максимального коэффициента тяги (см. рис. 7.3)?
5. Чем можно объяснить применение термина «основная составляющая
тяги»?

Глава 7. Составляющие тяги. Место приложения тяги 99
6. Если развиваемую пустотную тягу принять за 100 %, то какую долю
составляет основная составляющая тяги, тяга расширяющейся части
сопла и вклад его сужающейся части?
7. При каких ограничениях доля основной составляющей тяги
превышает 50 %, т. е. можно считать ее вклад преобладающим?
8. Какие параметры определяют доли сужающейся и расширяющейся
частей сопла в создании пустотной тяги?
9. Возможны ли в принципе ракетные камеры с соплом без
сужающейся части?
10. С позиций теории ракетного двигателя определите возможные
положительные и отрицательные факторы, проявляющиеся при
переходе от изобарных камер сгорания к камерам, не имеющим
сужающейся части.

Глава 8
Дроссельные характеристики двигательной
установки, состоящей из нескольких
идентичных автономных ЖРД,
при синхронном и последовательном
дросселировании камер
Если ДУ состоит из нескольких идентичных автономных ЖРД,
дроссельная характеристика каждого из которых есть дроссельная
характеристика идеального ЖРД, то возможно несколько
вариантов дросселирования ДУ, отличающихся порядком (все
одновременно или последовательно) дросселирования камер и
кратностью дросселирования каждой камеры.
Все возможные варианты представляют собой сочетание двух
предельных возможных режимов дросселирования:
• первый режим - синхронное дросселирование всех камер ДУ
одновременно и с одинаковой скоростью изменения расхода',
• второй режим - последовательное дросселирование
единичных камер ДУ с остановом дросселируемой камеры при
достижении нулевого значения развиваемой тяги и с сохранением
номинального режима работы недросселируемых камер.
Второй режим формально может быть реализован и при
останове дросселируемой камеры путем снижения расхода топлива
через нее до нуля. В данном случае камера при ненулевом
давлении окружающей среды должна развивать отрицательную тягу,
что не имеет практического смысла. Такой режим может
представлять только методический интерес.
Сравнительную оценку режимов синхронного и
последовательного дросселирования можно провести на основе
сопоставления дроссельных характеристик, построенных для одинаковых
ДУ, дросселируемых в разных режимах.
Примем, что дроссельная характеристика единичной ракетной
камеры известна (рис. 8.1, кривая А). По оси абсцисс отложены
значения относительного расхода топлива через ДУ т0ТН =——,
равного отношению текущего суммарного расхода топлива через
ДУ к номинальному расходу топлива через одну камеру, т. е.

Глава 8. Дроссельные характеристики ДУ с ЖРД 101
Относительный расход т{
Рис. 8.1. Дроссельные характеристики ДУ при
дросселировании единичных камер до нулевого расхода топлива
расходу топлива, при котором камера работает на номинальном
режиме. Пусть расход т0, при котором тяга одной
дросселируемой камеры становится равной нулю, составляет известную часть
х от номинального расхода т1н, т. е. т0 = хт1н.
На рис. 8.1 по оси ординат на шкале справа отложены
значения развиваемой ДУ тяги, отнесенной к тяге единичной ракетной
Ру
камеры, работающей на номинальном режиме, Рду =—^-. По оси
ординат на шкале слева также отложены значения безразмерного
удельного импульса ДУ I ду - отношения развиваемого ДУ
удельного импульса / дУ к удельному импульсу единичной камеры на
номинальном режиме /.:
7 _ 7у-ду
2у-ДУ ~ г
Отметим, что эти шкалы проще представлять как размерные,
но в качестве единицы измерения расхода через ДУ использовать
расход через единичную камеру на номинальном режиме работы,
в качестве единицы измерения тяги - тягу единичной камеры на
номинальном режиме, а удельного импульса - удельный импульс
одной камеры на номинальном режиме. В такой трактовке
проанализируем дроссельные характеристики ДУ, представленные
на рис. 8.1.

102 Часть I. Теория идеального теплового ракетного двигателя
Рассмотрим режим синхронного дросселирования. При
произвольном значении расхода через единичную камеру 0 < т] < т]н
развивается тяга
Л = ™xWa + FaX{pa -ph) = РХп - FaXph = Iynmx - Fa[Ph.
Если все п камер, входящих в ДУ, одновременно работают на
одинаковом расходе, ДУ развивает тягу
Рду = nPx = n(IynX mx - FaXph) = IynX(nmx) - (nFaX)ph.
Поскольку тъ = nmv то при/?* = idem, FK x = idem, FaX = idem
из условия одновременности работы камер и равенства расходов
следует, что зависимость тяги ДУ от расхода отражается
уравнением, записанным для тяги некоторого эквивалентного
однокамерного двигателя, у которого площади проходных сечений
камеры FK и Fа в п раз превышают соответствующие площади
единичной камеры. Следовательно, дроссельная характеристика
Ръ{ т) будет такой же, как для эквивалентного однокамерного
ЖРД (см. рис. 8.1, штрихпунктирные прямые).
Зависимость удельного импульса от расхода для ДУ при
синхронном дросселировании камер следует из определения
удельного импульса:
^.ДУ ~ . ~ ^у.экв.ЖРД*
тхп
На рис. 8.1 ее отображают штрихпунктирные кривые,
представляющие собой растянутую по оси абсцисс в п раз кривую А -
удельный импульс единичной ракетной камеры.
Для режима последовательного дросселирования
целесообразно ввести кроме обозначения числа камер п в ДУ еще и число
камер (ин), работающих на номинальном режиме. Очевидно, что
0 ^ пн ^ (п - 1). Причем, когда ни одна из п камер не работает
на номинальном режиме, т. е. пн = 0, характеристики ДУ
вырождаются в характеристики единичной камеры (см. рис. 8.1,
кривые А). Если пн Ф 0, то для тяги ДУ запишем уравнение
= /,l"„ + /y.->i-F0.n>

Глава 8. Дроссельные характеристики ДУ с ЖРД 103
которому соответствуют отрезки прямой В или С,
представляющие собой часть кривой А, суммированную с увеличенным в п раз
номинальным уровнем тяги единичной камеры.
Отрезки А, В и С параллельны, так как в соответствующих
уравнениях коэффициенты перед аргументом т одинаковы и
равны / п1. Смещение кривой вниз при т = О соответствует
ординате Falph(nH + 1), как это следует из уравнения
Р^ = Р,п +1 ,m.-F,p,=(I .m,-F.p.)n + / .m.-F.pL =
I 1н н y.nl 1 ям A v y.nl 1 a\rh> и y.nl 1 a\^h
= 1 An т. +m,)-F.p,(n + 1).
y.nlv н 1н 1' al-г/Л ii '
Таким образом, зависимость Р^(т) для ДУ с работающими
(пн + 1) двигателями, из которых дросселируется один,
совпадает с зависимостью Р(т) для эквивалентного однокамерного
двигателя ДУ, состоящей из п = пн + 1 синхронно дросселируемых
автономных одинаковых камер.
Ввиду взаимной идентичности дроссельных характеристик
Р(т) будут попарно идентичными и зависимости для / (т) (см.
режим синхронного дросселирования и соответствующие
зависимости на рис. 8.1 - участки кусочно-возрастающих кривых В
и С для пн = 1 и пн = 2 соответственно).
Рассмотрим ординаты характерных точек зависимости / ду(ая)
(см. рис. 8.1).
Справа от точек разрыва
™ДУ = ™1н + 0> Пн=1>
т мн ~Fa\Ph j FaXph
2у . iy.lH
w,„ mu.
j _ 2Mh ~ Fa\Ph _ j FaXph
y 2mlH yUl 2m]H '
J _ ^lH ~Fg\Ph _J FalPh
y 3< ylH 3mlH '
(8.1)
(8.2)
(8.3)

104 Часть I. Теория идеального теплового ракетного двигателя
Очевидно, что и для других пн будут справедливы соотношения
тду
'у =
=
'у.
"и
1н
,< + °;
FalPh
пнт]н'
Слева от точек разрыва (камеры работают на номинальном
режиме)
^ду^.н-0; /y = /y.iH;
'«ДУ = 3^.н - О? /у = /у.1н-
Точки обнуления тяги дросселируемых камер:
/v= —= 0; (8.4)
у
хты
7 = ^1н+0 =/у.1н,
у w1h(1 + jc) 1 + *'
",ДУ = 2",1н + *»,1н' "н = 2'
7 = 2^н+0 =7у1н
у 2/wlH+x/wlH 1 + х'
(8.5)
(8.6)
2
Очевидно, что для других ин # 0 справедливо соотношение
/..
'у _'
у _ У-'н
1 + ^

Глава 8. Дроссельные характеристики ДУ с ЖРД 105
Для сравнения режимов последовательного и синхронного
дросселирования рассчитаем значения удельного импульса ДУ,
двигатели которой дросселируются синхронно, в характерных
точках:
mnw = 3m- Pnw = 3P' I
ЗР
'ду
ДУ
1н'
'у.ДУ
1н
Зт
= 1
т
ДУ
Зхт- Pnv = 0; /
ду
у.ДУ
1н
0;
у.н'
^nv = 2^i„; pi
•ду
1н' 'ДУ
'-m]HWa+Fa]
'2 ^
PaU-Ph
\з-
j
(8.7)
(8.8)
(8.9)
'у.ДУ
'ДУ
2тЛи
2 (2
-m]HWa+Fa^-pa]H-ph
2т
= 1
Fa\Ph
у.н
1и
2т
1н
Если дросселирование каждой камеры ДУ ведется до
обнуления тяги (снижения тяги до нулевого значения), а не расхода, то
такому режиму дросселирования соответствуют зависимости,
представленные на рис. 8.2.
Характерным для такого режима дросселирования является
наличие интервалов по оси абсцисс, где тяга и удельный импульс
не определены как функции, т. е. изменение расхода топлива
становится кусочно-дискретным. При этом тяга изменяется
монотонно и без скачков, а удельный импульс - с меньшими скачками,
'"у.ДУ ^У
1,0 г 3,0
0,5 [- 1,5
Ob 0
-0,5
-1,5
"J'?n» = 0
0 0,5 1,0 1,5 2,0 2,5 3,0
Относительный расход тОТН
Рис. 8.2. Дроссельные характеристики ДУ при
дросселировании единичных камер до нулевой тяги

106 Часть!. Теория идеального теплового ракетного двигателя
чем при дросселировании камер ДУ до обнуления расхода (см.
рис. 8.1).
Из сравнения выражений (8.1) - (8.6) и (8.7) - (8.9) следует,
что режим последовательного дросселирования предпочтительнее
режима синхронного дросселирования, причем выигрыш в
удельном импульсе возрастает с увеличением числа камер в ДУ. Это
преимущество подтверждается и иллюстрируется зависимостями,
представленными на рис. 8.1 и 8.2.
Выбор режима дросселирования для реальных ДУ
проводится с учетом большого числа факторов, и удельный импульс -
только один из них, хотя, как правило, существенный.
Контрольные вопросы и задания
1. Какой режим работы камеры называется номинальным?
2. Дайте определения двух предельно возможных режимов
дросселирования.
3. Почему один из возможных вариантов режима последовательного
дросселирования, как правило, не имеет технического смысла?
4. В чем состоит преимущество режима последовательного
дросселирования перед режимом синхронного дросселирования всех камер
двигательной установки?
5. Проанализируйте предельный вариант дросселирования
двигательной установки путем последовательного отключения камер, каждая
из которых до отключения работает только на номинальном режиме.
6. От чего зависит изменение тяги и удельного импульса при
отключении дросселируемой камеры?
7. От чего зависит предельное снижение расхода одной камеры (во
сколько раз можно уменьшить расход одной камеры по отношению
к номинальному) при ее отключении по достижении нулевого
значения тяги?

Глава 9
Элементы внутренней баллистики РДТТ
и твердотопливных газогенераторов.
Совместная работа камеры сгорания и сопла
Основной рабочий процесс в РДТТ (см. рис. 1.7) заключается
в преобразовании химической энергии находящегося в камере
сгорания твердого ракетного топлива в тепловую энергию
продуктов его сгорания (или разложения), которая в сопле переходит
в кинетическую энергию истекающих, преимущественно
газообразных, продуктов сгорания, выполняющих функцию
рабочего тела.
Твердое ракетное топливо (ТРТ) - гомогенное твердое
вещество или объединенная в твердое тело гетерогенная смесь
нескольких веществ, способных к химическим превращениям с
образованием газообразных продуктов и выделением теплоты.
Твердое топливо размещается в камере сгорания РДТТ.
Твердое тело - твердое ракетное топливо, предназначенное
для сжигания в камере сгорания газогенератора или ракетного
двигателя, называется зарядом ТРТ. Таким образом, заряд
твердого ракетного топлива представляет собой часть РДТТ,
обеспечивающую требуемый режим газообразования.
Известно, что ТРТ горит (газифицируется с выделением
теплоты) с поверхности эквидистантными слоями (если поверхность
горения плоская, то параллельными слоями), причем скорость
горения есть скорость перемещения горящей поверхности заряда
ТРТ вдоль ее собственной нормали и описывается в некоторых
диапазонах значений переменных уравнением
u = kwkTHu{p\ (9.1)
где и - скорость горения ТРТ (скорость перемещения горящей
поверхности заряда ТРТ) при текущем значении давления р
газообразных продуктов реакции; v - безразмерная величина,
постоянная для данного ТРТ (для большинства ТРТ 0 < v < 1); их -
постоянный для данного ТРТ коэффициент при некоторой
заданной стандартной температуре топлива, например при

108 Часть I. Теория идеального теплового ракетного двигателя
температуре 298 К; кТ - коэффициент, отражающий влияние
начальной температуры топлива Гн, увеличивается при ее
повышении и уменьшается при ее снижении (кт = 1 при стандартной
температуре); kw- коэффициент, учитывающий влияние на
скорость горения скорости потока W, обтекающего горящую
поверхность. Если скорость потока ^ниже некоторого порогового
значения, то kw = 1, в противном случае kw > 1. Причем, если
давление р = 1 МПа (1 бар), то и, приобретает смысл так
называемой единичной скорости горения, т. е. некоторой условной
скорости горения, с которой горело бы данное топливо при этом
давлении. Условность такой трактовки определяется тем, что не
все ТРТ горят при таком давлении. При этом значение
коэффициента их зависит от выбора единиц измерения длины (м/с, см/с
или мм/с) и давления р (Па, бар или атм), сомножитель pv
считается безразмерным, но значение его зависит от принятых единиц
измерения давления. Например, если р измеряется в паскалях
(Па), уравнение (9.1) приобретает математически эквивалентный,
но более удобный для практического применения вид:
/у
U = Kii/Kn* U\ ,
w 7н \98066,5j
где число в знаменателе дроби соответствует значению
стандартного атмосферного давления в паскалях.
Принципиально возможны, но в данном учебнике не
рассматриваются РДТТ, в которых топливо горит в объеме, а не по
поверхности, а также так называемые детонационные двигатели,
в которых преобразование химической энергии топлива в
тепловую энергию продуктов реакции происходит в детонационной
волне и имеет характер взрыва, т. е. рабочий процесс существенно
нестационарен.
Если известна форма заряда ТРТ, то при предположении
эквидистантности перемещения горящей поверхности можно
построить зависимость площади горящей поверхности Fr от
толщины е сгоревшего слоя топлива, называемого сводом горения,
х
e-\udx, а следовательно, и от времени 0 ^ т ^ тк (рис. 9.1, где
о
плоская горящая поверхность F, является торцом
цилиндрического заряда ТРТ 7, горящего только по одному из торцов). На
другие поверхности заряда нанесено препятствующее горению
покрытие 2, называемое бронировкой.

Глава 9. Элементы внутренней баллистики РДТТ и ТГ 109
Рис. 9.1. К понятию скорости горения ТРТ:
1 - заряд ТРТ торцового горения; 2 - бронировка поверхности заряда ТРТ
Свойства продуктов сгорания ТРТ характеризуются
параметрами Л, Т и к = с /cv, а также массовой концентрацией
конденсированной (жидкой или твердой) фазы Z и практически не
зависят от давления и других переменных параметров. Основное
уравнение, описывающее связь между законом горения и
свойствами продуктов сгорания ТРТ, текущим значением площади
горящей поверхности и размером минимального проходного
сечения сопла, называется уравнением внутренней баллистики. При
этом площадь горящей поверхности определяется размерами
и формой заряда ТРТ.
Получим уравнение для некоторого РДТТ или газогенератора
на ТРТ, которое можно условно назвать идеальным. Для
идеального РДТТ или газогенератора на ТРТ справедливы следующие
допущения:
• свойства ТРТ и его начальная температура Тн постоянны во
всех точках заряда ТРТ;
• скорость потока, обтекающего горящую поверхность заряда
ТРТ, мала и не влияет на скорость горения, т. е. W ~ О и kw = 1,
и тогда для скорости горения справедливо соотношение и = kT uxpv,
а давление в любой точке камеры сгорания равно/?;
• продукты сгорания - идеальный газ, не содержащий
конденсированной фазы, т. е. Z= 0, с известными постоянными R, к
и температурой торможения Г*, равной температуре горения ТРТ;
• камера сгорания идеально теплоизолирована и снабжена
соплом Лаваля, в котором реализуется безотрывное одномерное
адиабатное и изоэнтропийное течение с сохранением на всех
режимах скорости звука в минимальном сечении сопла;
• плотность ТРТ существенно больше плотности продуктов
сгорания в камере сгорания, т. е. расход продуктов сгорания,

ПО Часть I. Теория идеального теплового ракетного двигателя
идущий на заполнение объема, освободившегося от сгорания ТРТ,
мал по сравнению с массой образовавшихся за единицу времени
(с приходом) продуктов сгорания этого ТРТ;
• камера сгорания работает на квазистационарном режиме.
Уравнение внутренней баллистики получим из уравнения
сохранения массы, записанного в виде равенства секундного
прихода газа, обусловленного сгоранием топлива, секундному
расходу газа через сопло:
Чрих = Часх> (9*2)
с учетом уравнения сохранения энергии для адиабатного процесса
Г = Г = Г = const.
Уравнение сохранения импульса можно не включать в
решаемую систему уравнений, так как в рамках принятых допущений
продукты сгорания в камере сгорания неподвижны ирк=р* =р*к.
Выразим секундный приход газа через скорость горения и
топлива (9.1), площадь /^горящей поверхности и плотность рт
топлива при и = kT uxpv ир = р*к = рк:
Чрих = FrWPT = FrpTkTHUlPl' С9'3)
Уравнение расхода продуктов сгорания запишем через
параметры потока в критическом сечении сопла:
РЛрА(к)
тхжх = Г= • С9'4)
расх ^—Г
Приравняв правые части уравнений (9.3) и (9.4), получим
FrpTkTuxpK = —j^=^. (9.5)
Решая уравнение (9.5) относительно^, получаем

Глава 9. Элементы внутренней баллистики РДТТ иТГ 111
Л
FrpTkTux4Kf
KpA(k)
1
1-V
(9.6)
Уравнение (9.6) называется основным уравнением внутренней
баллистики РДТТ или газогенератора на ТРТ.
Из анализа уравнения (9.6) следует взаимосвязь параметров
заряда (площадь Fr горящей поверхности), характеристик ТРТ
(коэффициент кт , отражающий влияние начальной температуры
заряда ТРТ, плотность рт, единичная скорость и{ и показатель
степени v в законе горения), свойств продуктов сгорания (газовая
постоянная R, температура Г*, показатель адиабаты к) и
основного параметра сопла - площади критического сечения F .
Взаимосвязь непосредственно проявляется при совместной работе
камеры сгорания и сопла как части РДТТ, определяющей
параметры в камере сгорания и числовое значение развиваемой тяги.
Получим уравнения, отражающие эту существенную
взаимосвязь. При принятых допущениях в любой точке камеры сгорания
до сечения входа в сопло соблюдается равенство р = рк = р* =
= р*к = const (в любом сечении сопла р* = р*к = const), что
позволяет записать уравнение тяги ракетного двигателя в виде
P = P^KT,-FaPh, (9.7)
где Кт п - коэффициент тяги в пустоте - функция геометрической
(F Л
степени расширения сопла и показателя адиабаты, Ктп =/ ——9k .
F
V кр )
Р
С учетом выражения для удельного импульса / = —- и
расти
. р*Лр Q л/лг7 „ /Л^Ч
хода гп-—-—, где р = —--^- - расходный комплекс, из (9.7)
р Лук)
получим выражение для определения пустотного удельного
импульса:
Р ^т.пР
£у.п * у-,
рКр
А.„ = ?" -РК,.,,, (9.8)
а также три эквивалентных выражения для определения
удельного импульса при ненулевом давлении окружающей среды ph > 0:

112 Часть L Теория идеального теплового ракетного двигателя
/ =/ -^ = / -^Р = рГ^тп-А4\ (9.9)
т FkPPk { FkPPk)
Уравнения (9.6) - (9.9) позволяют анализировать совместную
работу камеры сгорания и сопла. Основной фактор, определяющий
связь между ними, - зависимость давления в камере сгорания
р*к = р* от соотношения площадей минимального сечения сопла
F и горящей поверхности Fr для данной формы и размеров
заряда конкретного ТРТ.
Уменьшение FK при сохранении других размеров ведет,
согласно (9.6), к увеличению скорости горения топлива и,
следовательно, к увеличению прихода и равного ему расхода рабочего
тела - продуктов сгорания (см. (9.3)). Поскольку пустотный
удельный импульс / п зависит для данных продуктов сгорания
(данного ТРТ с известным значением к = с /cv) только от геометрической
степени расширения сопла (см. (9.8)), то уменьшение F при
неизменности других размеров приведет к росту ЛГтп, что при
постоянном значении расходного комплекса р обеспечит
увеличение / . Поскольку возросли расход рабочего тела т и / .
уменьшение FK ведет к увеличению пустотной тяги Рп двигателя
или газопроизводительности газогенератора на ТРТ.
Из аналогичных рассуждений следует, что увеличение F
приводит к снижению Рп и расхода рабочего тела - газообразных
продуктов сгорания. Очевидно, что изменение Fa не влияет на
внутрикамерные процессы и изменение характеристик РДТТ в этом
случае связано только с изменением КТП.
Влияние параметров в камере сгорания на тягу двигателя или
расход продуктов газогенерации описывается уравнением (9.7).
Например, выполняя заряд ТРТ с переменной по толщине
сгоревшего слоя топлива е (свода горения) площадью горящей
поверхности Fr, можно получить заданное изменение во времени
тяги РДТТ или количества газа, генерируемого газогенератором
на ТРТ, так как изменение во времени е, а следовательно, и Fr,
ведет к изменению во времени прихода газа и давления в камере.
Взаимосвязь формы и размеров заряда ТРТ с реализуемым
законом изменения во времени площади горящей поверхности
и, как следствие, соответствующее изменение тяги являются
существенной качественной особенностью РДТТ или
газогенератора на ТРТ. Проектируя заряд ТРТ, т. е. выбирая его форму,

Глава 9. Элементы внутренней баллистики РДТТ и ТГ 113
соотношение размеров, защищая (бронируя) поверхности
топлива от контакта с продуктами сгорания, можно получить требуемый
закон изменения во времени тяги или прихода газа.
На рис. 9.1 схематично показан заряд ТРТ с постоянной во
времени площадью горящей поверхности, Fr(x) = const, на
рис. 9.2 - заряд ТРТ с прогрессивной, т. е. с увеличивающейся
во времени, Fr(x), а на рис. 9.3 - заряд ТРТ с дегрессивной Fr(x),
5Fr(x) Л dFr(e)
чему соответствует неравенство
5т
<0 и
де
<0.
Рис. 9.2. Схема заряда ТРТ в виде полого цилиндра,
горящего с внутренней поверхности:
1 - заряд ТРТ; 2 - бронировка поверхности заряда ТРТ
Рис. 9.3. Схема заряда ТРТ в виде сплошного
цилиндра, горящего по всей поверхности

114 Часть I. Теория идеального теплового ракетного двигателя
В общем случае заряд ТРТ (рис. 9.4, поз. 7) имеет сложную
форму, включающую дегрессивные и прогрессивные участки
горящей поверхности, сочетание которых обеспечивает задаваемый
закон изменения тяги РДТТ или прихода газа в газогенераторе
на ТРТ. При этом заряд 1 ТРТ (см. рис. 9.4) размещен в полости
камеры 2, которая служит камерой сгорания и одновременно
емкостью для хранения топлива.
Рис. 9.4. Схема РДТТ:
1 - заряд ТРТ; 2 - камера; 3 - сопло; 4 - воспламенитель
Камера снабжена частично размещенным в ней так
называемым утопленным соплом 3. Нагруженная внутренним давлением
камера сгорания является базовым элементом конструкции
ракеты с РДТТ и составляет с ней единое целое, во многом определяя
массогабаритное совершенство летательного аппарата и
обеспечивая давление до 5... 10 МПа.
Специфическим устройством РДТТ и газогенератора на ТРТ
является воспламенитель 4 - заряд специального топлива с
системой инициирования горения, создающий в камере условия для
воспламенения и устойчивого горения основного заряда ТРТ.
В целом РДТТ и газогенератор на ТРТ при относительной
простоте конструкции (отсутствуют система подачи, подвижные

Глава 9. Элементы внутренней баллистики РДТТ и ТГ 115
части) и высокой надежности требуют минимального времени на
подготовку к запуску.
Требуемая надежность РДТТ может быть достигнута только
при обеспечении стабильности размеров, свойств, прочности
и устойчивости к детонации заряда ТРТ как твердого тела.
Нередко эти требования не позволяют выбирать состав твердого
топлива, при котором достигаются максимально возможные
удельные термодинамические характеристики. Этим можно объяснить
относительно низкий (по сравнению с ЖРД) удельный импульс
тяги РДТТ, но его в целом положительные качества обусловили
широкое применение РДТТ в ракетно-космической технике.
Элементы теории устойчивости работы
камеры РДТТ или газогенератора на ТРТ
Параметры и характеристики работы РДТТ или газогенератора
на ТРТ определяются условиями баланса прихода и расхода
газообразных продуктов сгорания. Поскольку в общем случае все
существенные факторы могут изменяться во времени, говорят
о динамическом равенстве прихода и расхода газа. Одной из
характеристик динамических процессов является их реакция на
слабое внешнее воздействие, вызывающее кратковременное
нарушение установившегося ранее баланса, т. е. состояния равновесия.
Изменение площади выходного сечения сопла не влияет на
внутрикамерные процессы, так как в соответствии с принятым
допущением в области минимального сечения сопла
сохраняются критические параметры потока. Газогенератор на ТРТ и РДТТ
различаются только геометрической степенью расширения сопла.
Следовательно, с позиций изучения протекания во времени
балансовых процессов в камере газогенератор на ТРТ и РДТТ
эквивалентны, поэтому достаточно исследовать в этом аспекте
только одно из этих устройств.
Рассмотрим идеальный РДТТ, сопло которого в
расширяющейся части имеет участок развитого сверхзвукового течения газа,
а в минимальном сечении на всех режимах работы сохраняются
критические параметры, в частности скорость потока равна
местной скорости звука, т. е. А, = М = 1.
Под устойчивостью в малом будем понимать состояние
рабочего процесса в камере РДТТ или газогенератора на ТРТ, при
котором во время работы на первоначально стационарном
номинальном режиме при воздействии случайных малых возмущений
давления в камере в системе возникают ответные отклики -

116 Часть I. Теория идеального теплового ракетного двигателя
реакции, возвращающие рабочий процесс к исходному
стационарному номинальному состоянию.
При принятых допущениях суть стационарного режима
работы состоит в равенстве прихода газообразных продуктов горения
и их расхода через сопло при сверхкритическом перепаде
давления. Как следует из (9.4), расход пропорционален давлению в
камере сгорания, см. соответствующий участок прямой, исходящей
из начала координат (рис. 9.5).
Рис. 9.5. К определению условий устойчивости работы РДТТ и
газогенератора на ТРТ при сверхкритическом перепаде давления в сопле
(светлые стрелки соответствуют исходному возмущению - росту расхода,
темные - реакции системы):
a-0<v<l;6-v= 1; e-v> l
Вид зависимости прихода газа как функции давления
определяется числовым значением показателя степени v в законе горения
ТРТ (9.1). Для большинства применяемых ТРТ v > 0. Рассмотрим
три случая: 0<v< l,v= 1 hv> 1, где точка v = 1 соответствует
линейной зависимости скорости горения от давления.
В случае 0 < v < 1 (рис. 9.5, а) точка пересечения зависимостей
расхода и прихода является точкой стационарного режима при

Глава 9. Элементы внутренней баллистики РДТТ и ТГ 117
рк = ркн. Здесь и далее нижний индекс «н» обозначает значение
переменной при работе на номинальном режиме.
Пусть случайно рк увеличится на Арк. При этом/?к =рк н + Арк,
но расход возрастает больше, чем приход, т. е. Д/w > Атп их,
что соответствует большему наклону кривой прихода (см.
рис. 9.5, а, участок 1-2) по сравнению с наклоном кривой
расхода (участок 1-3). Из свободного объема в камере в целом будет
уходить газа больше, чем приходить в него, т. е. масса газа в
камере будет уменьшаться, следовательно, давление в ней также
будет уменьшаться, поскольку температура продуктов сгорания
остается постоянной на всех режимах.
Таким образом система реагирует на возмущение для
компенсации внешнего возмущения (прирост давления Арк) и возврата
в исходное равновесное состояние. Если внешнее возмущение по
давлению в камере имеет отрицательный знак (-Арк), реакция
системы (ломаная 1-4-5-1) содействует возвращению двигателя
на исходный номинальный режим.
При v = 1 кривые расхода и прихода (рис. 9.5, б) вблизи
точки равновесия (рк =ркн) практически совпадают. Случайное
незначительное повышение давления ± Арк (участки 7-2, 1-3, 1-5)
не вызывает дисбаланса расхода и прихода, и, следовательно, не
проявляется реакция системы, стремящаяся изменить ее
состояние. Система находится в безразличном равновесии, что не
отвечает требованиям, предъявляемым к газогенераторам и
ракетным двигателям: в такой ситуации невозможно предсказать, при
каком давлении в камере установится равновесие прихода и
расхода при запуске двигателя и на какой режим он перейдет под
воздействием случайных малых отклонений параметров.
В диапазоне значений v > 1 (рис. 9.5, в) случайное отклонение
давления вызывает повышение скорости горения, в результате
чего увеличивается приход газа, причем превышение прихода
газа больше превышения его расхода (участок 1-3). Это приводит
к увеличению массы газа в объеме камеры и, как следствие, к
росту давления в камере, если случайное возмущение давления было
положительным, причем происходит дальнейший неограниченный
рост давления, приводящий к разрушению камеры. Аналогично
увеличение случайного возмущения давления приводит к гашению
заряда ТРТ, если случайное возмущение давления отрицательное
(участки 1-4, 7-5, 5-5\ 4-4').
Таким образом, с точки зрения обеспечения устойчивой
работы РДТТ при малых отклонениях давления от равновесного

118 Часть I. Теория идеального теплового ракетного двигателя
в камере необходимым условием является 0 < v < 1. Причем
меньшие значения показателя v соответствуют слабой зависимости
давления в камере, а значит, и тяги или прихода (для
газогенераторов на ТРТ), от отклонений размеров заряда ТРТ и
критического сечения сопла, что предпочтительно для нерегулируемых
двигателей.
Напротив, если необходимо в значительных пределах изменять
тягу двигателя, то обеспечить заданный диапазон ее значений
при небольшом относительном изменении площади
критического сечения сопла можно, применяя топливо с показателем
степени в законе горения, приближающимся к единице.
Пример анализа совместной работы
камеры сгорания и сопла
РДТТ с зарядом ТРТ в виде горящего с внутренней
поверхности полого цилиндра с забронированными торцами имеет
следующие размеры: dmin = d, £>max = D, Did = 2 (см. рис. 9.2). Закон
горения топлива и свойства продуктов сгорания известны и
заданы через значения параметров /?, Т*, к = с /cv, uv a kw = kT =1
и v = 0,5. Тогда площадь горящей поверхности Fr(i) = nd(x)l9 где
d(i) - текущее значение диаметра канала в момент времени т.
Во сколько раз изменятся значения основных параметров
двигателя за время его работы?
1. Давление в камере - отношение начального давления к
конечному:
Л/о _
Рк. кон 1
Ft.kohPtU\4RTk
FKpA(k)
1
l-v
1
]l-v
=
( F Л
F
V г. кон /
4)
i
l-v 1
4
Здесь и далее нижние индексы «ДО» и «кон» обозначают
начальное и конечное значения переменных (давления в камере,
площади горящей поверхности заряда ТРТ и др.).
Из приведенного соотношения следует, что давление в
камере сгорания возрастает в 4 раза.
2. Расход продуктов сгорания - отношение начального
расхода к конечному:

Глава 9. Элементы внутренней баллистики РДТТ и ТГ 119
Що = РЛюЩРкЮ =d( Ркю \ _}_(]_
Кои РЛкон^Рк.кон D
Расход продуктов сгорания также возрастает в 4 раза.
3. Пустотная тяга и пустотный удельный импульс -
отношения пустотных тяг и пустотных удельных импульсов, развиваемых
в начальный и в конечный моменты времени.
Отношение пустотных тяг:
PntO = Л/О^кр^т.п = PKlQ = 1
Р п F К п 4
п. кон гк.кон кр т.п .гк.кон
Пустотная тяга также возрастает в 4 раза.
Отношение пустотных импульсов:
у.п.кон т.пР
В данном случае пустотный удельный импульс от давления
в камере не зависит.
4. Температура продуктов газогенерации (рабочего тела) в
выходном сечении сопла - отношение температур:
Та10 _ Тк10тСка9к) _^
*акон *кконНя' /
F
при Т = const, —2- = const, k = const, Xa = const, та(ка9 k) = const.
Температура рабочего тела в выходном сечении сопла Та
остается постоянной, так как не изменяется температура торможения
в камере Т* (она определяется только свойствами топлива), и ГДФ
т(ка, к) остается постоянной, для данного значения показателя
адиабаты к она зависит только от геометрической степени
расширения сопла.
Контрольные вопросы и задания
1. Что такое ТРТ?
2. Дайте определение заряда ТРТ и перечислите его функции.
3. Дайте определение бронировки как элемента заряда ТРТ.

120 Часть I. Теория идеального теплового ракетного двигателя
4. Объясните термин «эквидистантно» и равносильный ему для плоских
поверхностей термин «параллельно» применительно к эволюции
горящей поверхности заряда ТРТ.
5. Что такое скорость горения ТРТ и от каких параметров она зависит?
6. Что такое закон горения ТРТ и какая математическая зависимость
его, как правило, отражает?
7. Перечислите допущения, принятые при выводе основного уравнения
внутренней баллистики РДТТ.
8. Дайте определения видов зарядов ТРТ в зависимости от характера
изменения во времени площади горящей поверхности (по толщине
свода горения).
9. Дайте определения типов режимов работы РДТТ в зависимости от
их устойчивости к слабым отклонениям параметров.
10. Почему рекомендуется снабжать камеру сгорания
твердотопливного газогенератора критическим соплом?

Глава 10
Идеальный ядерный ракетный двигатель
Ядерный ракетный двигатель (ЯРД) - это ракетный двигатель
с ядерным источником энергии. Ниже рассмотрены так
называемые тепловые ЯРД, в которых ядерная энергия (энергия связи
частиц, составляющих ядра атомов) преобразуется в кинетическую
энергию продуктов ядерной реакции, переходящую в процессе
торможения продуктов ядерной реакции в тепловую энергию
тормозящей среды. В таком представлении и радиоактивный
распад можно условно рассматривать как ядерную реакцию.
Тепловая энергия тормозящей среды передается рабочему телу ЯРД,
т. е. температура рабочего тела повышается. Тепловая энергия
рабочего тела в сопле Лаваля переходит в кинетическую энергию
истекающего потока рабочего тела.
Вариант обобщенной структурной схемы ракетного
двигателя как технической системы (см. рис. 1.1) применительно к ЯРД
представлен на рис. ЮЛ, а, где пропульсивное устройство - сопло 3;
Рабочее тело -
водород
\
Энергообменное
устройство
ГР2—^ Т2.
Пропульсивное
устройство -
сопло
/уГ/>
V
а б
Рис. 10.1. Структурная схема (а) и условный термодинамический цикл (б)
идеального теплового ЯРД как технической системы:
1 - рабочее тело (жидкий водород); 2 - ядерный реактор или радиоизотопный
источник теплоты; 3 - сопло
L
Источник
энергии
2351
II 235и
т
I 2

122 Часть!. Теория идеального теплового ракетного двигателя
энергообменное устройство - нагреватель; источник энергии -
ядерный реактор или радиоизотопный источник теплоты; рабочее
тело - вещество (например, водород 7), нагреваемое в
энергообменном устройстве 2 и ускоряемое в сопле 3. Реализуется
термодинамический цикл идеального теплового ракетного двигателя
(рис. 10.1, б), где изобара 1-2 отражает нагрев рабочего тела
в ядерном источнике теплоты от температуры Г, до температуры
Т2 = Гк*, кривая 2-3 - адиабатное расширение от рк= р* = р2 до
ра=р3в сопле Лаваля.
Поскольку торможение продуктов ядерной реакции или
радиоактивного распада происходит в основном непосредственно
вблизи их возникновения, например в твердом материале,
содержащем делящийся изотоп, источник энергии и энергоообмен-
ное устройство, как правило, представляют собой единую
конструкцию - источник энергии входит в состав энергообменного
устройства.
Конструктивная схема ЯРД, в котором используется реакция
деления изотопа урана 235U, представлена на рис. 10.2.
Основной параметр, характеризующий экономичность
ракетного двигателя, - удельный импульс на расчетном режиме -
численно равен скорости истечения рабочего тела. Тогда в рамках
принятых допущений для ЯРД как идеального теплового
ракетного двигателя справедливы следующие соотношения:
Рис. 10.2. Конструктивная схема ЯРД с твердой активной зоной:
1 - теневая радиационная защита; 2 - активная зона; 3 - сопло; 4 - боковой
отражатель

Глава 10. Идеальный ядерный ракетный двигатель 123
7у-р = ^=а1^Г<
к-\
\ГК J
= ЬсХц^уЩл (юл)
//_,
npncp-cv = R, cp=-j^R, срТ;*Нвх, Л, =1-5г.
Для заданного отношения давлений pjph (10.1) удельный
импульс может быть повышен при переходе на высокоэнтальпийное
рабочее тело. При этом значение температуры Т* ограничено
тугоплавкостью материалов и трудностью охлаждения
конструкции двигателя при больших температурах. Этим обусловлены
рекомендации к выбору рабочего тела ЯРД - максимальное
значение газовой постоянной R или, что то же самое, минимальное
значение молекулярной массы в условиях предсоплового объема
и сопла.
Очевидно, что лучшее рабочее тело - водород или вещества,
диссоциирующие с образованием водорода (например, аммиак
NH3). Энергосодержание рабочего тела на входе в сопло
оценивается термодинамической энтальпией #вх, а на входе в
энергообменное устройство - энтальпией рабочего тела в баке Яб.
Энергия радиоизотопного источника теплоты или ядерного реактора
с тепловой полезной мощностью NT затрачивается на повышение
энтальпии рабочего тела от #б до #вх.
Оценим требуемую тепловую мощность NT ядерного
источника энергии ЯРД с тягой Р, развивающего на расчетном режиме
удельный импульс I , численно равный скорости истечения Wa
(см. уравнение (10.1)). Поскольку ЯРД - изолированная от
окружающей среды система, опишем ее системой уравнений
сохранения.
Уравнение сохранения массы
m = const, (10.2)
т. е. расход рабочего тела через сопло равен расходу
транспортируемого на борту летательного аппарата компонента. Причем
компонент инертен, а изменение массы делящегося вещества
в ядерном реакторе или в радиоизотопном источнике теплоты
несоизмеримо мало по сравнению с расходом рабочего тела.

124 Часть I. Теория идеального теплового ракетного двигателя
Уравнение сохранения энергии
NT=m(HBx-H6X (10.3)
причем предполагается, что вся тепловая мощность источника
энергии затрачивается только на повышение энтальпии рабочего
тела, проходящего через источник энергии и охлаждающего его.
Уравнение сохранения импульса с учетом (10.1) и (10.2)
можно записать в трех эквивалентных формах:
P = mWa=myj2HmT\l=mI„. (10.4)
Из (10.4) следует выражение для расхода рабочего тела и
удельного импульса и требуемой для его достижения энтальпии
рабочего тела на входе в сопло #вх:
Р Р Р
т = — = . Г =—; (10.5)
wa Щ~^{ iy
ур
#вх=^. (Ю.6)
Подставим (10.5) и (10.6) в (10.3) и после очевидных
упрощений получим уравнение связи между заданными параметрами
двигателя (тягой и удельным импульсом) и тепловой мощностью
источника энергии:
N. =Р
(I н Л
[-*L-ilS- . (10.7)
2Л, /у
'урУ
На рис. 10.3 приведена зависимость (10.7) требуемой тепловой
мощности NT ядерного источника энергии от заданной тяги Р
и удельного импульса / . Наклонная асимптота - прямая,
исходящая из начала координат, где абсцисса и ордината равны нулю.
Уравнение наклонной асимптоты
NT=P^. (10.8)

Глава 10. Идеальный ядерный ракетный двигатель 125
Согласно (10.8), для разных значений тяги асимптоты будут
исходить из начала координат под разными углами, а ордината
/ 0, соответствующая нулевой требуемой тепловой мощности Nj9
сохранится. На рис. 10.3 NTl и Nt2 соответствуют соотношению
тяг Рх <Р2.
0 Удельный импульс А
Рис. 10.3. Зависимость требуемой
тепловой мощности ядерного реактора от
удельного импульса теплового ЯРД
Из (10.3) следует, что увеличение тепловой мощности,
подводимой к рабочему телу при его постоянном расходе, приводит
к повышению Нвх и, следовательно, к увеличению удельного
импульса I . Это означает (при недиссоциирующем рабочем теле),
что необходимо повышение температуры торможения на входе
в сопло для увеличения удельного импульса. При постоянстве
номинального удельного импульса на расчетном режиме переход
от тяги Рх к тяге Р2 возможен в случае увеличения тепловой
мощности от N . до N ~ .
т1н ^ т2н
Ракетные двигатели, в которых используется энергия,
высвобождающаяся в результате изменения состояния ядер атомов,
можно классифицировать по типу ядерных превращений.
1. Ракетные двигатели с радиоизотопными источниками
теплоты (РИТ), в которых теплота выделяется в результате
реакции распада нестабильных радиоактивных изотопов,
записываемой условно в общем виде:
*'л-»ЙД + а + Р + у + л,
a b i-i7
где А - исходный радиоактивный изотоп, превращающийся в
результате распада в изотоп В; верхние и нижние индексы слева av

126 Часть I. Теория идеального теплового ракетного двигателя
Ьх и я2, Ь2 - заряд и массовые числа ядра соответственно; а, Р, у,
п - виды излучения, которым сопровождается распад изотопа.
Для конкретного изотопа, как правило, можно указать наиболее
вероятные вид излучения и значение энергии, которой обладает
излучаемая частица или квант электромагнитного излучения.
Торможение продуктов распада приводит к нагреву среды, где
они теряют энергию. При этом каждый акт распада приводит к
выделению некоторой, в среднем постоянной, тепловой энергии.
Число актов распада убывает во времени по экспоненте,
следовательно, и тепловая мощность во времени уменьшается по закону
ВД = V",
где Nj0 - тепловая мощность в начальный момент времени т = 0;
а - константа, обратно пропорциональная периоду полураспада
изотопа; т - время, отсчитываемое от начального момента
времени т = 0.
Реакция радиоактивного распада неуправляема,
следовательно, также невозможно управление ракетным двигателем с
радиоизотопным источником теплоты путем изменения тепловой
мощности источника теплоты.
2. ЯРД, в которых используется реакция термоядерного
синтеза. Возможный вид реакции ядерного синтеза:
2D + 3Т _, 4Не + ^
где в левой части уравнения реакции отображены вступающие
в реакцию ядра изотопов водорода - дейтерий ^D и тритий *Т,
а в правой части - продукты идущей при высоких температурах
реакции термоядерного синтеза: более тяжелого ядра гелия *Не
и высвобождающегося свободного нейтрона я. Продукты реакции
обладают значительной энергией, которая может быть передана
рабочему телу.
Поскольку управление реакцией термоядерного синтеза в
настоящее время еще не освоено даже на стационарных установках,
применение таких ЯРД в ближайшее десятилетие представляется
проблематичным.
3. ЯРД, в которых используется управляемая цепная реакция
деления тяжелых ядер, например 235U, вызываемая
взаимодействием делящегося ядра изотопа урана и нейтрона. Примерная
схема ядерной реакции деления:

Глава 10. Идеальный ядерный ракетный двигатель 127
235U + п -> А + В + (2...3)л + а + Р + у,
где А, В - осколки, на которые делится ядро изотопа урана при
взаимодействии с нейтроном; п - нейтроны, высвобождающиеся
при делении одного ядра 235U (в среднем 2,75 нейтрона на один
акт деления ядра); а, |3, у - виды излучения, сопровождающего
деление ядер изотопа урана. Более 80 % высвобождающейся при
этом энергии проявляется в виде кинетической энергии осколков
деления ядра урана. Один акт деления 235U приводит к выделению
тепловой энергии около 190 МэВ.
Этот вид реакции освоен как в стационарных ядерных
реакторах на атомных электростанциях и в транспортных реакторах
на кораблях, подводных лодках и в космических ядерных
энергетических установках, так и в реакторах, входящих в состав ЯРД,
разработанных в США (ЯРД «Нерва») и в СССР (РД-0410).
Конструктивная схема ЯРД с твердой активной зоной
приведена на рис. 10.2. Управление ядерной реакцией
осуществляется путем изменения числа нейтронов в единице объема
активной зоны - пространстве, где находится материал, содержащий
делящиеся изотопы 235U.
Введение в активную зону материала - поглотителя нейтронов
(например, борсодержащих материалов) приводит к поглощению
нейтронов, которые вызывают деление ядер 235U. Следовательно,
число актов деления ядер в единице объема в единицу времени
уменьшается, что приводит к снижению тепловой мощности и, как
следствие, при сохранении расхода рабочего тела - к снижению
его температуры перед соплом и уменьшению удельного импульса.
Применение в качестве рабочего тела водорода при
достигнутой температуре его нагрева в ядерном реакторе 2 000...3 400 К
позволило приблизиться к значению пустотного удельного
импульса 10 000 м/с.
Большие требуемые массы собственно реактора и
радиационной защиты и требования максимальной надежности ЯРД
вследствие повышенной экологической опасности ядерных реакторов
затрудняют их применение.
Высокие, не достижимые ракетными двигателями с
химическими источниками энергии значения удельного импульса
обеспечивают применение ЯРД в качестве двигателей космических
кораблей для межпланетных перелетов Земля - Марс с
возвращением корабля на Землю, а также и для более дальних
межпланетных перелетов.

128 Часть I. Теория идеального теплового ракетного двигателя
В настоящее время перспективным признается применение
тепловых ЯРД, входящих в состав космических ядерных
энергетических установок двойного назначения, вырабатывающих
электрическую энергию и подогревающих рабочее тело теплового
ЯРД, например водорода, до температуры около 2 000 К.
Освоенные тепловые мощности позволяют развивать в
пустоте тягу до 10 Н в течение нескольких часов или суток,
достаточных для перевода спутника с опорной орбиты на геосинхронную
или геостационарную1 орбиту.
Контрольные вопросы и задания
1. Какой тепловой ракетный двигатель называют ядерным?
2. Сформулируйте функции рабочего тела, энергообменного и про-
пульсивного устройств ЯРД.
3. Составьте схему последовательной трансформации энергии - от
энергии связи нуклонов в атомном ядре до полезной кинетической
энергии истекающего рабочего тела.
4. Перечислите характерные особенности ЯРД с радиоизотопными
источниками теплоты.
5. Каковы характерные особенности ЯРД, в которых используется
энергия, высвобождающаяся при делении ядер?
6. Перечислите преимущества и недостатки ЯРД по сравнению с
тепловыми ракетными двигателями с химическими источниками энергии.
7. Какие допущения приняты при получении уравнения связи между
параметрами камеры двигателя и тепловой мощностью реактора?
8. Сформулируйте требования к рабочим телам ЯРД, вытекающие из
закономерностей теории идеального теплового ракетного двигателя.
9. Выделите общее и особенное в ЖРД, РДТТ и ЯРД, рассматриваемых
в качестве тепловых машин и двигателей.
10. Предложите принципиальную схему ЯРД, в котором используется
энергия, высвобождающаяся при импульсных реакциях
термоядерного синтеза.
Космос на страже Родины: Первые научные чтения по военной
космонавтике памяти М.К. Тихонравова. М.: КОСМО, 1998.

Глава 11
Ракетный двигатель со скоростной камерой сгорания.
Полутепловое сопло
Если площадь поперечного сечения цилиндрической камеры
сгорания FK превышает площадь минимального сечения сопла
F
Fmin = FK более чем в 4 раза, т. е. —*-^4, то камера сгорания на-
зывается изобарной. Для нее характерно распределение
параметров потока рабочего тела по длине камеры, представленное за-
F
висимостями / на рис. 11.1. Если —— <4, камера сгорания
FkP
называется скоростной.
Предельный случай скоростной камеры - камера с
полутепловым соплом, когда FK = F и нет сужающейся части сопла.
Рабочее тело ускоряется до скорости звука за счет подвода
теплоты сгорания топлива в цилиндрическом канале. Камера сгорания
функционально и конструктивно совмещена с докритической
частью сопла, поэтому в составе ракетной камеры (камеры)
невозможно выделить собственно камеру сгорания и собственно
сопло, которое выявляется частично как расширяющаяся
сверхзвуковая часть. Для скоростных камер характерно распределение
параметров по длине проточной части камеры, представленное
на рис. 11.1 зависимостями II. Различия в характере зависимостей
/ и // обусловлены особенностями протекания термодинамических
энергообменных процессов в камерах.
В изобарных камерах сгорания это изобарный подвод
теплоты к неподвижному потоку, так как из условия —*-^4 следует
WK« WK , т. е. в изобарных камерах сгорания скорость движения
рабочего тела (газа) WK на участке от смесительной головки до
входа в сопло мала по сравнению со скоростью в критическом
сечении W и может быть приближенно приравнена к нулю
(WK ~ WT ~ 0). Давление торможения рабочего тела одно и то же
во всех точках камеры сгорания и не изменяется до входа в сопло,

130 Часть I. Теория идеального теплового ракетного двигателя
Ра
t—\
о
w4
wu
>I
a
1 .
1 /S*
&>
i
9 1
o^^
1 ^
B>
0
к кр
Рис. 11.1. Распределения параметров потока по длине
изобарной и скоростной камер сгорания:
/, /- изобарная камера и распределение параметров по ее
длине соответственно; 2, II - скоростная камера и распределение
параметров по ее длине соответственно
и при заданном давлении ра, например ра = ph, в сопле
реализуется максимально возможное расширение газа, степень которого
равнар*/ра. Соответствующий максимальный для данного
двигателя КПД преобразования тепловой энергии в кинетическую
энергию в сопле

Глава 11. Ракетный двигатель со скоростной камерой сгорания 131
л,=1-
к
( Р ^
l/max*
Деление камер на изобарные и скоростные условно, так как
скорость потока в реальных камерах сгорания даже при —^^4
обязательно имеет ненулевое значение, пусть и значительно
меньшее, чем скорость в критическом сечении сопла. Поэтому в
камере сгорания происходит не только переход химической энергии
в тепловую (прямое функциональное назначение), но и ускорение
потока, т. е. частично выполняется функция сопла.
В скоростных камерах выделяющаяся при горении топлива
теплота подводится к ускоряющемуся потоку газа (продуктам
сгорания) при 0«WK< W . При этом скорость газа вблизи
смесительной головки может быть близка к нулю, Wrc ~ 0, но до
входа в сопло (в его сужающуюся дозвуковую часть) скорость
потока существенно возрастает. Температура торможения также
увеличивается до известного максимального значения Т*, но
давление торможения снижается. Таким образом, во входном сечении
соплар*вх ^р* и Г*х = Т*. Причем в идеальном рабочем процессе
в сопле при течении в нем давление торможения потока не
изменяется: /?*х = р* = const. При этом расширение газа в сопле
реализуется не полностью, степень расширения не равнар*/ра,
гР*вх^Ра <Рк//Ра- Поэтому соответствующий КПД преобразования
тепловой энергии в кинетическую энергию в сопле уменьшится
по сравнению с его максимальным значением Л/тах' достигаемым
при изобарном подводе теплоты:
л,=1-
'ач
к
к-\
<Л/
max*
Ч^вхУ
Физическую причину снижения полного давления,
называемого тепловым сопротивлением, можно представить как
реализацию термодинамического процесса - подвода теплоты
к расширяющемуся (ускоряющемуся, снижающему давление)
рабочему телу, т. е. по стадиям: расширение, подогрев, сжатие.
Этот процесс входит в условный термодинамический цикл,
обратный циклу теплового ракетного двигателя с идеальной
изобарной камерой. Термодинамическая противоположность циклов

132 Часть I. Теория идеального теплового ракетного двигателя
обеспечивает обратный эффект: в скоростной камере часть
полной энергии, выраженная в полном давлении, идет на повышение
статической температуры.
Другая интерпретация «теплового сопротивления»
базируется на неизбежности роста энтропии S при подводе теплоты Q для
л/л)
реальных процессов: dS = — >0. Рост энтропии отражает
диссипацию, т. е. «снижение качества» энергии, которое
выражается в снижении полного давления, что неизбежно и происходит.
Следует обратить внимание на то, что для данного рабочего
тела с заданной температурой торможения при постоянном
минимальном давлении в цикле (в выходном сечении сопла)
именно полное давление определяет качество энергии как возможную
степень преобразования тепловой энергии в кинетическую
энергию истекающего потока. Подробно эти вопросы изложены в
монографии1.
Для количественного описания термо- и газодинамических
процессов в двигателе со скоростной камерой сгорания
используем принятое ранее допущение, что рабочее тело - нагреваемый
в камере сгорания газ с неизменяющимися параметрами Л, с ,
к = с /су9 для которого справедливо уравнение состояния
идеального газа
£ = RT.
Р
Для корректности сравнения ЖРД с изобарной и скоростной
камерами сгорания примем следующие допущения:
• используется одно и то же топливо, т. е. для сравниваемых
двигателей 7^ах, R, с , к = idem;
• давление в камере (вблизи смесительной головки) рк= ргс =
= р* равно давлению торможения (скорость рабочего тела
вблизи смесительной головки Wrc ~ 0) и они одинаковы для
сравниваемых двигателей;
• давление в выходном сечении сопла сравниваемых
двигателей одно и то же и равно давлению окружающей среды ра =
Абрамович Г.Н. Прикладная газовая динамика. 3-е изд., перераб.
М.: Наука, 1969.

Глава 11. Ракетный двигатель со скоростной камерой сгорания 133
= ph = idem, т. е. сопла обоих двигателей работают в расчетном
режиме.
Рабочие процессы в цилиндрической камере сгорания опишем
следующими уравнениями сохранения в одномерном
стационарном приближении.
Уравнение сохранения массы:
т = const (11.1)
в любом сечении проточной части камеры, т. е. все рабочее тело
подается в сечение смесительной головки.
Уравнение сохранения энергии:
Т*=Дх), (11.2)
означающее, что горение топлива заменяется подогревом
поданного через смесительную головку рабочего тела и его
температура торможения есть функция координаты с известным
максимальным значением в выходном сечении камеры сгорания,
совпадающем с сечением входа в сопло: Т* = Т* = Т*
ГПаХ ВХ К
Уравнение сохранения количества движения при
предположении отсутствия трения на стенке:
pF+ mW = ^-mamZ(X) = const (11.3)
k
Анализируя уравнение (11.3) с учетом (11.1) и (11.2), покажем,
что подвод теплоты к ускоряющемуся потоку ведет к диссипации
энергии, выражающейся в падении давления торможения.
Приравняем количества движения в сечении вблизи
смесительной головки и в произвольном /-м сечении:
^mZiX)axp=plFlf{Kk). (И.4)
К
В правой части этого уравнения использована введенная ранее
(см. гл. 6) ГДФ/(А,/5 к), связывающая значение полного
импульса потока с его давлением торможения и площадью поперечного
сечения (см. рис. 6.4).
Конкретные значения f(k.9 к) и р* можно вычислить при
известной безразмерной скорости А,., которую, в свою очередь, можно

134 Часть I. Теория идеального теплового ракетного двигателя
получить путем решения уравнения (11.3) при известном
значении температуры торможения в сечении (см. (11.2)). Для этого
приравняем, согласно (11.3), выражения для расчета импульса
потока вблизи смесительной головки (нижний индекс «г.с»)
и в произвольном /-м сечении (нижний индекс «/»):
* + 1 .
mZ(XrJ^rc^(U*)=^AZ(A./)>/«?7;4(l,*). (11.5)
к к
Из (11.5) получим
Z{\,) = Z{K.X
(П.6)
Согласно (11.6), увеличению температуры торможения Т* по
длине цилиндрической камеры сгорания соответствует снижение
значения ГДФ Z(X{), а значит (см. ГДФ Z(l) на рис. 6.4), рост
безразмерной скорости X. с приближением ее к единице и
абсолютной скорости Wp стремящейся к местной скорости звука. При
этом увеличивается значение ГДФ/(А,, к) и, согласно (11.4),
снижается полное давление потока.
Если на v-p-диаграмме условный термодинамический цикл
ЖРД с изобарной камерой сгорания изображается замкнутой
ломаной кривой 1-2-3-4-1 (рис. 11.2), то цикл ЖРД с полутепловым
соплом - предельный вариант ЖРД со скоростной камерой
сгорания - можно изобразить ломаной кривой 1-7-У-4-1. При этом
Удельный объем V
Рис. 11.2. К сопоставлению термодинамических
циклов тепловых ракетных двигателей с
изобарной и скоростной камерами сгорания

Глава 11. Ракетный двигатель со скоростной камерой сгорания 135
форма кривой на участке 1-2' зависит от закона теплоподвода по
длине камеры сгорания. Поскольку из условия сравнения
следует одинаковость Т* с = idem, т. е. Т* = Т* = idem, то отсюда
ГПаХ р К ГПаХ
следует равенство температур продуктов сгорания в критических
сечениях сравниваемых двигателей: Т = 7^ахт(1, k) = idem, т. е.
точки, соответствующие критическим параметрам, лежат на
одной изотерме.
Известно, что значения удельного импульса и скорости
истечения газа на расчетном режиме численно совпадают. Значение
скорости истечения пропорционально квадратному корню из
площади, ограниченной замкнутой кривой, отображающей
условный термодинамический цикл в координатах v-p. Поскольку
КПД сопла изобарной камеры выше, чем у скоростной, т. е.
л,=1-
PcL
/С
к
к-\
постольку и ограниченная замкнутой кривой 1-Т-У-4-1 площадь
на рис. 11.2 должна быть меньше площади, соответствующей
ракетному двигателю с изобарной камерой и циклом 1-2-3-4-1.
Оценим соответствующее снижение удельного импульса
количественно, учитывая, что для принятых условий сравнения
давление торможения потока при его движении по соплу не
изменяется, т. е.р*х -р*~ const, но при этом для изобарной камеры
Р\х =Рк =РК> а для скоростной камеры/?*х <рк прир* =рк.
Для расчетного режима работы сопла
I=W=t
2k
\k-\
RTl
1-
'A^
k-\
\Ркр;
= CA\-
'iO
A:—1
(11.7)
V^KPy
где С рассчитывается только по характеристикам топлива и будет
одинаковой для сравниваемых вариантов, С = const.
Из (11.4) следует, что
Ркс =
/(*«.*)
= Pi
кр'
(11.8)
где р*к с Дк с - давление торможения и безразмерная скорость
потока на выходе из камеры сгорания, т. е. на входе в сопло, при

136 Часть I. Теория идеального теплового ракетного двигателя
движении по которому давление торможения потока не
изменяется. Наибольшие потери давления торможения реализуются при
ХГ = 0 и Хкс = 1, т. е. при равенстве FK = FK и ускорении потока
до звуковой скорости за счет подвода теплоты. Тогда потери
полного давления можно оценить по уравнению (11.8), зная значения
f(Uk).
Значения ГДФ/(1Д) при различных значениях показателя
адиабаты к приведены ниже:
к 1,15 1,П 1,19 1,25 1,40
Д1Д) 1,235 1,238 1,240 1,249 1,268
Другими словами,/?* = р*к/(1,235... 1,268), что равнозначно
уменьшению реализуемой в сопле степени расширения потока
при ра = ph в 1,235 раза при FK = FKp.
Fv
Для "тг-^! уменьшение реализуемой степени расширения (р
кр
кр
/ph) по отношению к располагаемой степени (p*K/ph)
иллюстрирует рис. 11.3. Видно, что при относительной площади камеры
сгорания —*-^3 потери полного давления о до входа в сопло
^кр
практически не влияют на значение реализуемого соотношения
давлений. Поскольку влияние уменьшения степени расширения
потока в сопле на удельный импульс (реализуемое отношение
давлений р* /рИ при располагаемом, т. е. принципиально
возможном для изобарной камеры, р*к /ph) зависит от абсолютного
значения отношения р*к /ph, потери удельного импульса будут
разными для разных значений отношенияp*K/ph и показателя
адиабаты к = с /с.
1,U
0,9
0,8
п п
Ft-FJF*
Рис. 11.3. Зависимость коэффициента
восстановления полного давления от
относительной площади камеры сгорания

Глава 11. Ракетный двигатель со скоростной камерой сгорания 137
В табл. 11.1 представлены значения коэффициента ср = / JI ,,
где I v I x - удельные импульсы на расчетном режиме для
камеры сгорания с полутепловым соплом и изобарной камеры
сгорания соответственно, рассчитанные для приведенных выше
условий сравнения.
Таблица 11.1. Значения коэффициента <р в зависимости
от показателя адиабаты к и отношения давлений p*K/ph
Показатель
адиабаты к
1,15
1,4
Располагаемое отношение давлений р*К/рИ
2
0,830
0,836
10
0,960
0,964
100
0,980
0,988
2 000
0,980
0,990
Значения располагаемых степеней расширения рабочего тела
современных ракетных двигателей соответствуют данным,
приведенным в 4-й и 5-й графах табл. 11.1. Уровень максимально
возможных потерь удельного импульса при этом составляет 1...2 %.
Поскольку современные реальные двигатели, как правило, имеют
камеры сгорания, у которых Fk/Fk > 2,5, потери в них меньше
приведенных в табл. 11.1.
Из изложенного следует, что ракетные двигатели со
скоростной камерой по сравнению с двигателями с изобарной камерой
могут иметь меньшие радиальные размеры камеры сгорания, но
при одном и том же топливе и одинаковых давлениях в камерах
и выходных сечениях сопла будут уступать в удельном
импульсе. Для работающих в пустоте двигателей эти потери удельного
импульса можно компенсировать уменьшением давления/^ в
выходном сечении сопла.
Контрольные вопросы и задания
1. Дайте определение ракетного двигателя со скоростной камерой
сгорания.
2. Дайте определение ракетного двигателя с полутепловым соплом.
3. Какие физические процессы присущи ЖРД со скоростной камерой
и определяют его особенности по сравнению с ЖРД с изобарной
камерой сгорания?
4. Что такое «тепловое сопротивление» и в чем количественно оно
проявляется?

138 Часть I. Теория идеального теплового ракетного двигателя
5. Какие преимущества и недостатки имеет ракетный двигатель со
скоростной камерой сгорания по сравнению с ракетным двигателем
с изобарным подводом теплоты к рабочему телу?
6. От чего зависит коэффициент потери полного давления рабочего
тела в камерах с полутепловым соплом?
7. При каких условиях сравнения особенности рабочего процесса ЖРД
со скоростным соплом не влияют на значение развиваемого
удельного импульса, в частности в пустоте?
8. При каких условиях сравнения особенности рабочего процесса ЖРД
со скоростным соплом проявляются в снижении развиваемого
удельного импульса, в частности в пустоте?
9. Изменяя какие параметры камеры ракетного двигателя, можно
обеспечить равенство пустотных импульсов ЖРД с изобарной и
скоростной камерами сгорания, если тяга, расход топлива и давление
в камере должны сохраняться неизменными?
10. Примените соотношения (11.4) - (11.8) к анализу ЯРД, в котором
нагрев рабочего тела сопровождается его ускорением еще до входа
в сопло.

Глава 12
Камера сгорания ракетного двигателя
с распределенным подводом рабочего тела.
Полурасходное сопло
Компоненты жидкого топлива подаются не только в плоскости
смесительной головки, но и со стенок цилиндрической
поверхности камеры сгорания «по потоку» под острым углом к боковой
поверхности, но чаще всего радиально, т. е. под прямым углом
к ее оси симметрии (рис. 12.1). Аналогичная схема течения
реализуется также в РДТТ с зарядом ТРТ, горящим по внутренней
поверхности цилиндрического канала (рис. 12.2, я), и в ЯРД с
радиальным течением рабочего тела через активную зону с
центральным осевым каналом (рис. 12.2, б).
Если считать, что компоненты жидкого топлива
взаимодействуют вблизи точки их подачи, то течение в камере сгорания,
как и в центральных цилиндрических каналах РДТТ и ЯРД,
можно рассматривать как течение идеального газа в канале
постоянного сечения с распределенным по длине подводом массы того
же газа, с теми же одинаковыми свойствами (с;, су, Л, Т* = idem).
Предельным вариантом ракетного двигателя с расходной
камерой сгорания является РДТТ или ЖРД с полурасходным соплом,
когда поток ускоряется за счет подвода массы в цилиндрической
части до скорости звука. Этому случаю соответствует равенство
площадей сечения канала в заряде РДТТ или камеры сгорания
ЖРД вблизи смесительной головки, площади в сечении перехода
камеры в сопло FK и площади критического сечения F , т. е. для
конкретности анализа ЖРД Frc = FK = F и сужающаяся часть
сопла отсутствует (рис. 12.3).
Механизм ускорения потока при распределенном подводе
массы состоит в поджатии ранее сформированного потока массой,
поданной ниже по течению нормально к оси симметрии. При этом
образуются непроницаемые в среднем трубки тока,
уменьшающегося по течению сечения. Интенсивный сопряженный тепло-
массоперенос между струями приводит к выравниванию
параметров потока в сечении с неизбежными потерями полного давления
(диссипацией энергии) и ростом энтропии, что обусловливает

140 Часть I. Теория идеального теплового ракетного двигателя
к кр
Рис. 12.1. Распределения параметров потока по длине камер ракетных
двигателей с локальным и распределенным подводом топлива:
1,1- изобарная камера с локальным подводом топлива и распределение
параметров по ее длине соответственно; 2, II- камера с распределенным подводом
топлива и распределение параметров по ее длине соответственно
отличие рассматриваемого ЖРД от идеального ЖРД с изобарной
камерой сгорания.
Снижение полного давления потока можно рассматривать как
«потери на удар», если иметь в виду исходную разность векторов
скоростей потока вблизи оси симметрии камеры и продуктов
сгорания, подаваемых с боковой поверхности. Выравнивание

Глава 12. Камера сгорания ракетного двигателя 141_
Рис. 12.2. Схемы ракетных двигателей с распределенным подводом
рабочего тела в канале постоянного сечения:
а - РДТТ; б - ЯРД; 1 - заряд TPT, горящий с внутренней поверхности; 2 -
центральный цилиндрический канал; 3 - сопло; 4 - дорасширительный насадок;
5 - сопло-решетка; б - пористая зона нагрева рабочего тела; 7 - центральный
цилиндрический канал ТВС; # - корпус реактора ЯРД; полужирные стрелки -
преимущественные направления движения рабочего тела
Рис. 12.3. Картина течения в камере с полурасходным соплом:
1 - камера сгорания; 2 - форсунки; 3 - линии (поверхности) тока
скоростей, в процессе которого «теряемая часть» кинетической
энергии переходит в тепловую, происходит под действием сил
внутреннего трения. При этом на твердой стенке трение может
не проявляться, а в остальном продукты сгорания ведут себя как
идеальный газ. Температура торможения как мера полной энергии
не изменяется.

142 Часть I. Теория идеального теплового ракетного двигателя
Уравнение сохранения массы:
Л =/(*), (12.1)
т. е. считаем известным закон распределения подводимой
нормально к оси симметрии массы. Функция/(х) задана.
Уравнение сохранения энергии:
Т* = const (12.2)
в любой точке камеры.
Следствием для совершенного, подчиняющегося уравнению
состояния идеального потока газа с постоянными параметрами
с , cv, R будет уравнение связи между термодинамической
(статической) температурой Г, температурой торможения Т* и
скоростью потока W в произвольных точке или сечении:
W2
Т =Т + —. (12.3)
Уравнение сохранения импульса потока в канале
постоянного сечения F запишем по Эйлеру при предположении отсутствия
потока в тупиковой части канала - сечении х = О (рис. 12.4) -
и пренебрегая трением о стенки канала:
p*F = pF+mW, (12.4)
где нижний индекс «О» соответствует значению параметра с этим
индексом в тупике, величины без индекса соответствуют значе-
Рис. 12.4. Расчетная схема:
/ - камера; 2 - форсунки; 3 - линии (для плоского течения) или
поверхности (для осесимметричного течения) тока; 4,5-
действительное и идеальное распределение параметров соответственно

Глава 12. Камера сгорания ракетного двигателя 143
ниям параметров в некотором удаленном от тупика произвольном
сечении, в котором известен расход т.
Учитывая, что для одномерного приближения справедливо
выражение т = pWF, и разделив уравнение (12.4) на FФ О,
получим закон сохранения импульса в канале постоянного сечения
в следующем виде:
P;=p + Pw2.
Решение системы уравнений (12.1) - (12.4) удобно искать
в виде выражений для некоторых ГДФ для потока с подводом
массы. Полученные ГДФ отметим верхней волнистой чертой ~
(знаком «тильда»), отличающей их от ГДФ для изоэнтропийного
адиабатного потока идеального газа. Поскольку поток можно
ускорить подводом массы только до скорости звука (М = 1), то
полученное решение будет соответствовать изменению числа
Маха в диапазоне значений 0 ^ М ^ 1.
Учитывая простую запись газодинамических соотношений
через критерий Маха, получим решение системы уравнений в
функции от М и показателя адиабаты к.
Определим ГДФ приведенной температуры:
х(М,*) = -р, (12.5)
Т* W2
Разделив (12.3) на Г, получим уравнение — = 1 + , пре-
Т 2срТ
образовав которое с учетом справедливых для идеального газа
соотношений
W
c-c=R\ a2 = kRT\ M = —, (12.6)
приходим к расчетному выражению для ГДФ (12.5):
х(М,*) = —г±- . (12.7)
1 + ^м2
2
2
При этом х{\,к) = х(\,к) =
к + \

144 Часть I. Теория идеального теплового ракетного двигателя
Определим ГДФ приведенного статического давления:
я(М,*) = 4.
(12.8)
Разделив (12.4) на/>, с учетом соотношений (12.6) получим
1
я(М,*) = :
,2 -
l + kMz
Определим ГДФ приведенного полного давления:
й-(м,*)=4.
Ро
(12.9)
(12.10)
Используем ГДФ изоэнтропийного адиабатного потока для
связи статического и полного давлений в точке (сечении) л(к, к) =
Р * Р
= —5г => Р = —г.—г и подставим выражение для давления тормо-
р к(Х,к)
жения/?* в (12.10).
С учетом (12.9) получим
п(М,к) =
п(М,к)
п(М9к)'
(12.11)
Определенные таким образом ГДФ потока с распределенным
подводом массы для к = 1,15 в диапазоне значений чисел Маха
0 ^ М ^ 1 представлены на рис. 12.5.
1,0 f
0,8
.0,6fcr
0,4
03
X
m
0,2
0
—►
Р(М,
/ >
//
\1/
* г
п
Л
/
/
ч
/
V*
А
/ SU, k)\
/\^
гМ,к)
0,2 0,4 0,6 0,8 1,0
Число Маха М
Рис. 12.5. Графики ГДФ для неизоэнтропийного адиабатного потока

Глава 12. Камера сгорания ракетного двигателя 145
Таким образом, если известны параметры потока в тупикер*,
Т* и свойства газа (Л, с ), а также число Маха М в текущем
сечении, то из уравнений (12.5) - (12.11) можно найти значения всех
параметров потока/?,/?*, W, р, Г в этом сечении.
Если в ГДФ для изоэнтропийного адиабатного потока
естественным независимым аргументом, определяющим состояние
потока, является отношение площади критического сечения к
площади канала (безразмерная площадь, численно равная ГДФ q(k, к)),
то в ГДФ неизоэнтропийного адиабатного потока таким
аргументом может служить безразмерный расход - отношение расхода
в текущем сечении к расходу, который надо подать через боковые
стенки этого же канала с этими же параметрами потока в тупике,
чтобы в выходном сечении получить скорость потока, равную
звуковой, т. е. М = 1 и F = F .
В соответствии с этим определением
«МЛ-ЭД--!^.^. 02..2)
m{U) Ркр^/^р pKpWKp
Здесь в числителе m =f(x) - известная функция (см. (12.1)).
Покажем, что знаменатель (12.12) однозначно
рассчитывается по параметрам в тупике:
р^_ р0п(\,к) .
RTKP RT HU)
^p=*«p=>/^ = ^7'*^_. (12-14)
Таким образом, ГДФ ц(МД) однозначно рассчитывается при
известном распределении расхода (12.1) и параметрах в тупике.
Если можно выразить ГДФ jx (M, к) только через М и £, то,
зная значение ГДФ jl (M, к) при заданном к, определяют местное
значение числа Маха М.
Для числителя правой части уравнения (12.12) получим
Л_= р0п(Ы,к)
RT RTx(M,k)

146 Часть I. Теория идеального теплового ракетного двигателя
Подставим (12.13) - (12.16) в (12.12) и после выполнения
упрощающих преобразований получим
I2U + 1)
Д(М,*) = М-
1 £-1,_2
1 + Nr
1 + Ш2
Зависимость ГДФ ц(МД) приведена на рис. 12.5 для
показателя адиабаты k= 1,15.
Если требуется определить параметры потока на входе в сопло
ЖРД с камерой сгорания с распределенным подводом топлива по
площади смесительной головки и цилиндрической поверхности,
то задача сводится к расчетной схеме, приведенной на рис. 12.4.
1. Поскольку закон распределения расхода до текущего
сечения при принятых допущениях не оказывает влияния на
параметры потока в сечении, условно продлим камеру сгорания влево
с образованием виртуального тупика, полагая, что поток в
сечении смесительной головки образован радиальной подачей
компонентов топлива на участке от виртуального тупика до
действительного сечения смесительной головки.
2. Зная параметры потока в сечении смесительной головки,
рассчитаем параметры потока в виртуальном тупике.
В результате переходим от задачи, соответствующей рис. 12.1
и 12.3, к задаче, алгоритм решения которой известен.
Таким образом можно оценить предельные потери полного
давления для камеры с полурасходным соплом при Frc = FK = FK ,
а именно:
1
Отметим, что п*(19к) =—-—-, т. е. снижение полного давле-
AU)
ния на участке от смесительной головки до критического сечения
одно и то же для камер с полутепловым и полурасходным
соплами (см. гл. 11). И соответствующее уменьшение удельного
импульса на расчетном режиме при заданном давлении ph в
результате снижения располагаемой степени расширения газа от
р*/рИ пор* /р. будет одинаковым.

Глава 12. Камера сгорания ракетного двигателя 147
Для оценки уменьшения удельного импульса численными
методами можно выполнить те же преобразования, что и при
оценке потерь удельного импульса двигателя с полутепловым
соплом (см. гл. 11).
Итак, ЖРД с расходной камерой сгорания может иметь
камеру сгорания с меньшими радиальными размерами и более
защищенными от тепловых потоков поверхностями, чем у идеального
ЖРД с изобарным подводом теплоты. При этом первый будет
уступать последнему в удельном импульсе при работе на
расчетном режиме и иметь большую площадь критического сечения
сопла. Площадь выходного сечения изменится незначительно.
Отметим, что потери полного давления в камере сгорания
с распределенным подводом топлива существенны только в тех
случаях, когда скорость потока на входе в газодинамическое
сопло сопоставима с местной скоростью звука. Оценки дают
минимальное отношение площадей камеры сгорания и критического
сечения сопла, равное 4. При более высоком его значении эффект
от распределенного подвода топлива настолько незначителен, что
им можно пренебречь даже в теоретических расчетах. По
существу, из этого следует, что для изобарных камер сгорания схема
подачи топлива в камеру не имеет значения.
Проведем количественное сравнение ракетных двигателей
с изобарной и скоростной камерами сгорания для разных схем
подачи топлива:
• с торцовой поверхности;
• с боковой цилиндрической поверхности;
• частично с торцовой поверхности и частично с боковой
цилиндрической поверхности.
Схемы ракетных двигателей или ракетных камер (что в данном
случае эквивалентно, так как не указано фазовое состояние
топлива и тип системы его подачи) приведены на рис. 12.6, где 1 -
изобарная камера сгорания двигателя № 1; 2, 5, 6 - камеры
сгорания двигателей № 2; 5, 6 - скоростные, с заданным отношением
площади камеры сгорания к критическому сечению сопла, равным
1,6636; 3,4- камеры сгорания двигателей № 3, 4, не имеющие
сужающейся части. Совместно со сверхзвуковыми частями сопл
они представляют собой ракетные камеры с полутепловым и
полурасходным соплом соответственно.
В камере сгорания двигателя № 6 большая часть расхода
топлива (80 %) подается с торцовой поверхности, а оставшаяся часть
(20 %) - с боковой цилиндрической поверхности камеры сгорания.

148 Часть I. Теория идеального теплового ракетного двигателя
Рис. 12.6. Схемы ракетных камер с цилиндрической камерой сгорания
При этом ракетные двигатели (ракетные камеры) следует
проектировать так, чтобы каждый из них, работая на уровне моря (ph =
= 0,1 МПа) при давлении в камере (в сечении камеры сгорания
вблизи торцовой поверхности рк = 10 МПа, при расчетном режиме
работы сопла, при ра = рИ = 0,1 МПа), развивал тягу Р = 1 000 000 Н =
= 1 МН(100тс)в.
Свойства продуктов сгорания топлива одинаковы для всех
двигателей: температура торможения Т* = 3 700 К; показатель
адиабаты к= 1,15; кажущаяся молекулярная масса \х = 24.
Расчеты удельного импульса / , расхода топлива т,
располагаемого соотношения давленийph/p* и площадей критического
FK и выходного Fа сечений сопла будем выполнять в
одномерном приближении с использованием ГДФ для изоэнтропийного
адиабатного потока при описании течения в геометрическом
сопле. Для получения уравнений связи между параметрами
торможения и статическими параметрами в произвольной точке
потока применим ГДФ для неизоэнтропийного адиабатного
потока с распределенным подводом массы. Эти же ГДФ используем
при описании течения в камере сгорания с радиальной подачей
топлива через боковые поверхности и для получения уравнений
связи между параметрами торможения в действительном или
виртуальном тупике и статическими параметрами в произвольной
точке потока в камере сгорания.
Для удобства сравнительного количественного анализа
результаты расчета сведем в табл. 12.1.
Предваряя расчеты, относящиеся к конкретному варианту
двигателя, вычислим значения параметров, общих для всех
вариантов двигателей, а именно:
скорость потока в критическом сечении
^.CE^.Jlbli.Hliijwo., 171м/с;
* U + l VU5 + 1 24

Глава 12. Камера сгорания ракетного двигателя 149
расходный комплекс
р = ^ = 1773м/с
Вычислим некоторые параметры, одинаковые для нескольких
вариантов двигателей.
1. Безразмерные параметры потока во входном сечении
сопла Лаваля двигателей № 2, 5 и 6: из условия задачи значение ГДФ
^«•*>=шг0-60"-
Решив численными методами уравнение q (А,вх, к) = 0,6011 в
дозвуковой области относительно безразмерной скорости, получим
Хвх = 0,4 и вычислим ГДФ потока во входном сечении сопла Лаваля:
я (X, Л) = я (0,4; 1,15) = 0,9175;
М(Х,к) = М(0,4; 1,15)-0,388;
f(K к) =/(0,4; 1,15) =1,0764.
2. Безразмерные параметры потока в выходном сечении
камеры сгорания, совпадающем со входным сечением сопла
двигателей № 5 и 6:
я (МД) =£(0,388; 1,15) = 0,85242;
ц (МД) = ц (М; к) = 0,68969.
Рассчитаем параметры двигателя № 1. Располагаемое
отношение давленийph/p* определяет термодинамическую
эффективность ракетного двигателя как тепловой машины, т. е. скорость
истечения или, что в данном случае то же самое, удельный импульс.
Решением уравнения п(ка; 1,15) = 0,01 в общем виде будет
соотношение
подстановка значений в которое дает Ха = 2,541 и
соответствующие значения ГДФ, в частности qr (2,541; 1,15) = 0,076.

150 Часть I. Теория идеального теплового ракетного двигателя
Удельный импульс Iy=Wa = Xaa = 2,541 • 1171=2 976 м/с.
Требуемый расход топлива т = P/I =106/2 976 = 336,02 кг/с.
Площадь критического сечения F определим из соотношений
т = ^ и р = —т~т? а именно: FKn =—J- = 0,0595763 м .
ЛГ Ж*) кр рк
Площадь выходного сечения рассчитаем по полученному
значению F и известному значению ГДФ ^(2,541; 1,15) = 0,076:
Fa = Fa/q(\,k) = 0,7839 м2.
Рассчитаем параметры двигателя № 2, учитывая, что именно
отношение статического давления в выходном сечении к давлению
торможения в критическом сечении определяет скорость
истечения. Для заданного по условию расчетного режима работы сопла
особенность расчета сводится к определению давления
торможения в критическом сечении сопла.
Поскольку р*к/р*кр =/(0,4; 1,15), то р*кр= 10/1,0764 = 9,29 МПа
и располагаемое отношение давленийph/p*K = 0,010764.
Так же, как для двигателя № 1, находим для двигателя № 2
безразмерную скорость истечения Ха = 2,526 и зависящие от нее
значения параметров:
^(2,526; 1,15) = 0,081;
/ = W =2,526-1 171 =2 958 м/с;
у а ' 7
т - 338,1 кг/с;
FKp = 0,64527 м2;
F = 0,79663 м2.
Различия в расчитанных значениях параметров двигателей
№ 2 и 3 обусловлены безразмерной скоростью потока на входе
в геометрическое сопло, которое представлено в двигателе № 3
только сверхзвуковой частью, что упрощает опеделениер* :
4»=1=>я(1;1,15) = 0,5744 =Р:р/ркр,
/(1; 1,15)= 1,2349 =рк/ркр,
откуда следует

Глава 12. Камера сгорания ракетного двигателя 15_[
р =10/1,2349 = 8,09782.
Г кр ' '
Располагаемое соотношение давленийp*h/p*K для двигателя № 3
п(Ха; 1,15) = 0,1/8,09782 = 0,012349, что соответствует
безразмерной скорости Ха = 2,498, определяющей так же, как и для двух
других двигателей, значения I ,m9FK и Fa, а именно: 1=2 925 м/с;
т = 342 кг/с; F = 0,07488 м^; F =К(),832 м2.
7 кр ' 7 я '
Принципиальное различие расчетов параметров двигателей
№ 4-6 и расчетов параметров двигателей № 1-3 заключается в
отражении потерь полного давления при распределенном подводе
массы к ускоряющемуся потоку сжимаемого рабочего тела,
описываемому специальными ГДФ.
Среди методик расчетов параметров двигателей № 4-6
наиболее простой является методика расчета параметров
двигателя № 4, представляющего собой камеру с полурасходным соплом,
где все параметры на входе в сверхзвуковую часть сопла звуковые,
т. е. соответствуют критическим, где X = М = 1. Для двигателя
№ 4 в критическом сечении
й(1; 1,15) = Ркр/Рк = Ркр/Р0 = 0,4651;
й*(1; 1,15) = 0,8097.
Значение/(1; 1,15) соответствует значению обратной функции
я*(1; 1,15), т. е./(1; 1,15)= 1/я*(1; 1,15). Отсюда следует равенство
давлений торможения в критических сечениях камер двигателей
№ 3 и 4. Тогда равны и располагаемые степени расширения
рабочего тела в сопле и соответственно остальные параметры и
размеры, зависящие для данного топлива только от степени
расширения (см. третью и четвертую строки в табл. 12.1).
Расчет параметров двигателя № 5 следует начинать с
определения давления торможения на входе в сопло Лаваля.
Безразмерная скорость в его входном сечении определена ранее и
равна 0,4, а соответствующее ей число Маха Мвх = 0,388. Отметим
очевидное для однозначно определенного числа Маха
соотношение Д0,4; 1,15)= 1/й*(0,388; 1,15).
Таким образом, давления торможения в критических
сечениях двигателей № 2 и 5 одинаковы, следовательно, одинаковы
и остальные одноименные размеры и параметры (см. вторую и
пятую строки в табл. 12.1).

152 Часть I. Теория идеального теплового ракетного двигателя
Таблица 12.1. Результаты расчета основных параметров
и размеров ракетных двигателей
Номер

двигателя
1
2
3
4
5
Параметры
Pk'Pwt
0,01
0,010764
0,012350
0,012350
0,010764
/у,м/с
2976
2958
2925
2925
2958
т, кг/с
336,02
338,10
342,00
342,00
338,10
Размеры
F. -102,m2
кр
5,9576
6,4530
7,4880
7,4880
6,4530
F102,m2
а '
78,39
79,66
83,20
83,20
79,66
^С^.р
4,0
1,6636
1,0
1,0
1,6636
Из сопоставления данных табл. 12.1 следует:
• снижение удельного импульса при переходе от изобарных
камер сгорания к скоростным при заданном соотношении
давлений в камере и в окружающей среде составляет 1...3 %;
• при заданном постоянном соотношении площадей камеры
сгорания и минимального сечения сопла схема подвода топлива
в камеру сгорания не влияет на уровень потерь удельного импульса;
• площади характерных сечений сопла у двигателя со
скоростной камерой сгорания больше, чем у двигателя с изобарной
камерой сгорания, причем для площадей критического сечения
такое соответствие не зависит от соотношения давлений в
камере и в окружающей среде, тогда как площадь выходного сечения
сопла у двигателя со скоростной камерой сгорания во многом
определяется именно этим соотношением и может быть как
несколько больше, так и несколько меньше соответствующей
площади двигателя с изобарной камерой сгорания.
Расчет параметров двигателя № 6 принципиально не
отличается от приведенных выше расчетов, но может быть отнесен к
задачам повышенной сложности. Рекомендуемый методический
прием, с помощью которого можно учесть ввод преобладающей
части топлива через торцовую поверхность, заключается в
переходе к расчетной схеме двигателя № 5, но при этом тупик будет
виртуальным, с параметрами потока в нем, в общем случае
отличными от параметров в камере.
Рекомендуется расчеты двигателя № 6 провести
самостоятельно при разных допущениях, принимаемых при расчете параметров
потока в виртуальном тупике на базе заданных параметров в камере
ракетного двигателя. Результаты можно представить в виде
дополнительных строк в табл. 12.1.

Глава 12. Камера сгорания ракетного двигателя 153
Контрольные вопросы и задания
1. Приведите примеры схем ракетных двигателей (ЖРД, РДТТ, ЯРД)
с распределенным подводом массы в дозвуковой области камеры.
2. Дайте определение ракетной камеры с полурасходным соплом.
3. Какие физические процессы присущи камере ЖРД с распределенным
подводом массы и определяют его особенности по сравнению с ЖРД
с изобарной камерой сгорания?
4. Что такое диссипация энергии и в чем количественно она
проявляется?
5. Какие преимущества и недостатки имеет ракетный двигатель с
распределенным подводом массы по сравнению с ракетным двигателем
с изобарным подводом теплоты к рабочему телу?
6. От чего зависит коэффициент потери полного давления рабочего
тела в камерах с распределенным подводом массы?
7. Какие допущения приняты при выводе газодинамических функций
для потока с распределенным подводом массы? Сравните эти
допущения с теми, которые были приняты при описании изоэнтропий-
ного адиабатного течения в идеальном сопле (см. гл. 3).
8. При каких условиях сравнения особенности рабочего процесса ЖРД
с распределенным подводом массы не влияют на значение
развиваемого удельного импульса, в частности в пустоте?
9. При каких условиях сравнения особенности рабочего процесса ЖРД
(РДТТ) с распределенным подводом массы проявляются в снижении
развиваемого удельного импульса, в частности в пустоте?
10. Примените соотношения для газодинамической функции неизоэн-
тропийного потока к анализу ЯРД, в котором нагретое до заданной
температуры Т* рабочее тело подается через боковую поверхность
канала, где ускоряется еще до входа в сопло (см. рис. 12.2, б).

Глава 13
Классификация ракетных двигателей.
Из истории ракетных двигателей
Классификация ракетных двигателей как технических
объектов позволяет систематизировать знания принципов
организации рабочих процессов в них, выделить общие и особенные
признаки, прогнозировать возможные преимущества и недостатки
двигателей по их месту в принятой схеме классификации.
Публикации по ракетным двигателям (статьи, монографии,
патенты и др.), как правило, располагаются в каталогах, фондах
или базах данных, структурированных по разным
классификационным схемам, принципы образования которых подобны
рассматриваемым в этой главе. Понимание принципов классификации
позволит рационально вести поиск и анализ информации в
конкретной предметной области.
Отобразим графически классификацию по выбираемым
признакам в виде системы прямоугольников (рис. 13.1), где одному
уровню (номер уровня - цифра справа) соответствует деление по
одному признаку.
Ракетные двигатели
-Г
Тепловые
I
Химические
х:
Нетепловые
I
Ядерные
Электрические
ЖРД
ГРД
Один компонент
ZL
рдтт
Два компонента Три компонента
X
всп
—I—
THA
—г~
Изобарная
-ц
Скоростная
I :
Полутепловая
I
В одном сечении
Распределенный подвод
Рис. 13.1. Пример классификации ракетных двигателей

Глава 13. Классификация ракетных двигателей 155
Объединяющий рассмотренные двигатели признак состоит
в том, что их работа соответствует условному циклу
тепловой машины. Необходимой составляющей рабочего процесса
является преобразование тепловой энергии рабочего тела в
кинетическую энергию истекающего потока, происходящее в про-
пульсивном устройстве - сопле. По этому признаку
рассмотренные ракетные двигатели относятся к тепловым (рис. 13.1,
уровень /).
Отметим, что представляющийся необходимым с точки зрения
семантики тепловой процесс - нагрев рабочего тела от
температуры хранения в баке до температуры на входе в сопло - на самом
деле не определяет необходимый признак и может вообще
отсутствовать в рабочем процессе теплового ракетного двигателя.
Следовательно, к тепловым ракетным двигателям относится и
ракетный двигатель, в котором в качестве рабочего тела
используется сжатый газ, хранящийся на борту и истекающий через сопло
в окружающую среду с созданием тяги. Причем источники
энергии и рабочего тела совмещены, а энергообменное устройство
отсутствует за ненадобностью.
В общем случае нагрев рабочего тела присутствует как
составляющая рабочего процесса теплового ракетного двигателя.
Наличие источника теплоты - нагревателя - формально
обязательно (в частном случае его тепловая мощность может
равняться нулю). Его тип можно характеризовать видом энергии,
переходящей в теплоту. Таким образом, признаком
классификации тепловых ракетных двигателей является вид исходной
энергии, преобразуемой в тепловую энергию рабочего тела. По
этому признаку тепловые ракетные двигатели делятся на
электрические, ядерные (см. рис. 10.1) к химические (рис. 13.1,
уровень 2).
Схема, конструкция и достижимые параметры ракетного
двигателя с химическим источником энергии во многом
определяются агрегатным состоянием ракетного топлива. Ракетные
двигатели на химическом топливе (в зарубежной литературе их
иногда называют химическими ракетными двигателями) по
этому признаку подразделяются:
• на жидкостные ракетные двигатели (ЖРД), компоненты
топлива которых в состоянии хранения на борту являются жидкими
(рис. 13.1, уровень 3);
• ракетные двигатели твердого топлива (РДТТ) (см. рис. 1.7,
9.4);

156 Часть I. Теория идеального теплового ракетного двигателя
• гибридные ракетные двигатели (ГРД), компоненты
топлива которых находятся на борту в разных агрегатных состояниях
(см. рис. 11.2).
Очевидным признаком классификации ракетных двигателей
на химическом топливе является число компонентов ракетного
топлива, например: ЖРД на одно- или двухкомпонентном
топливе, ГРД на трехкомпонентном топливе (по зарубежной
терминологии - на трибридном топливе) (рис. 13.1, уровень 4).
По конструктивным признакам ракетные двигатели можно
классифицировать по десяткам рубрик, но основные различия
в выполнении целевой функции определяют схемой подачи
компонентов топлива в камеру сгорания. Наиболее часто
используется классификация ЖРД именно по этому признаку.
По схеме подачи компонентов топлива принято подразделять
ЖРД на следующие виды (рис. 13.1, уровень 5):
• с вытеснительной системой подачи (ВСП) компонентов
топлива (см. рис. 1.8);
• с насосной системой подачи топлива (см. рис. 1.9, 1.10).
В зависимости от способа генерации и использования
рабочего тела привода насосов ЖРД с насосной системой подачи
топлива относятся к ЖРД:
• без дожигания генераторного газа (см. рис. 1.9);
• с дожиганием генераторного газа в камере двигателя (см.
рис. 1.10);
• безгенераторным (см. рис. 1.11).
Как следует из теоретического анализа достижимых удельных
характеристик камер ЖРД, существенным является не только
соотношение площадей проходного сечения камеры сгорания и
минимального сечения сопла (предельные случаи - изобарная
камера сгорания и камера с полутепловым соплом - см. рис. 11.1),
но и схема распределения подаваемого в камеру сгорания
топлива по контуру камеры: в сечении вблизи переднего торца
(см. рис. 11.1) или по боковой поверхности камеры сгорания
(см. рис. 12.3). В камере с полутепловым соплом рабочее тело
ускоряется до скоростей звука за счет распределенного подвода
теплоты, а при сгорании топлива в изобарной камере сгорания
поток ускоряется в сужающейся части сопла. При распределенном
по длине камеры сгорания подводе топлива поток рабочего тела
ускоряется за счет последовательного подвода массы.
Существенным при этом является именно схема подачи компонентов
топлива в камеру.

Глава 13. Классификация ракетных двигателей 157
И в первом, и во втором случае конструктивные параметры
определяют смену преобладающего физического механизма
рабочего процесса, т. е., по существу, принципа работы.
Представляется логичной классификация ЖРД формально по
соотношению размеров камеры, г по сути - по принципу
ускорения рабочего тела в дозвуковой области камеры при подводе
топлива в одном сечении камеры (рис. 13.1, уровень 6). В
соответствии с этим свойством выделяют следующие виды ЖРД:
• с изобарной камерой сгорания;
• со скоростной камерой сгорания;
• с полутепловым соплом.
В схеме классификации можно выделить ЖРД по совпадению,
сочетанию или комбинации нескольких признаков. Например, если
убрать ограничение - подвод топлива в одном сечении, то каждая
разновидность камеры ЖРД может выполняться в двух предельных
вариантах (рис. 13.1, уровень 7), а именно: с подводом топлива
только в одном сечении камеры; с подводом топлива только по
боковой поверхности камеры (распределенный подвод).
В качестве учебного примера применения классификации
ракетных двигателей для прогнозирования возможных схемных
решений двигателей проведем следующий анализ.
Из структуры ракетного двигателя как
технической системы (см. рис. 1.1) с
учетом принципов классификации (см.
рис. 13.1) следует формальная возможность
создания теплового ракетного двигателя
с электрическим источником энергии,
схема которого приведена на рис. 13.2. Здесь
заряженный конденсатор (источник
энергии) 1 ключом 2 подключает источник
энергии к проводнику 3, нагревающемуся
и испаряющемуся под действием
протекающего через него электрического тока
разрядки конденсатора. Образовавшиеся
нагретые пары в качестве рабочего тела
истекают через сопло с созданием тяги.
Сочетание турбонасосной подачи жидкого компонента
топлива (см. рис. 1.9) с размещенным в камере твердым компонентом
топлива (см. рис. 1.12) позволяет получить синтезированную
схему ГРД, приведенную на рис. 13.3.
Рис. 13.2. Схема
теплового ракетного
двигателя с электрическим
источником энергии:
1 - конденсатор; 2 - ключ;
3 - проводник тока

158 Часть I. Теория идеального теплового ракетного двигателя
Рис. 13.3. Схема ГРД с турбонасосной подачей жидкого
компонента:
/ - заряд твердого горючего; 2 - камера; 3 - центробежный
насос подачи окислителя в камеру; 4 - бак жидкого
окислителя; 5 - газовый редуктор; 6 - емкость сжатого газа наддува;
7 - газогенератор на гибридном топливе; 8 - газовая турбина
Очевидно, что синтезированная схема двигателя в большей
или меньшей степени наследует как преимущества, так и
недостатки, свойственные составляющим ее фрагментам. При этом
возможно появление новых свойств, не проявлявшихся у
фрагментов при их использовании в другой совокупности.
В рамках приведенного подхода, используя рассмотренные
схемы, можно синтезировать более 10 различных схем ракетных
двигателей.
Рекомендуем читателю самостоятельно проверить усвоение
учебного материала, рассмотрев приведенные в книгах из списка
литературы схемы ЖРД, отличающиеся принципом образования
газа наддува баков, и предложив признаки, по которым то или
иное техническое решение можно отнести к конкретной рубрике
системы классификации ракетных двигателей.
В зарубежных и отечественных учебниках по ракетным
двигателям можно найти несколько различных систем
классификации ракетных двигателей, различающихся признаками, по
которым классифицируют двигатели, детализацией
классификаций, выделением в качестве самостоятельных таких рубрик,
которые у других авторов рассмотрены как соподчиненные,

Глава 13. Классификация ракетных двигателей 159
и т. п. Нередки различия в терминологии. Предлагаемые
разными авторами схемы классификации ракетных двигателей
в большинстве случаев различаются незначительно, и
обосновать преимущества какой-либо одной из них не
представляется возможным.
Принятые системы классификации ракетных двигателей,
как правило, определены государственными или отраслевыми
стандартами. Например, ГОСТ 17655-89 «Двигатели ракетные
жидкостные. Термины и определения» основан на
подразделении ЖРД на 21 вид. При этом признаками классификации
выступают:
• схема подачи топлива (с насосной или с вытеснительной
системой подачи);
• схема использования рабочего тела турбины ТНА (с
дожиганием или без дожигания);
• число камер ракетного двигателя (одно- или многокамерный);
• сила тяги (ЖРД малой тяги выделяют в отдельный вид);
• число использований (одно- или многократное);
• число включений (одно- или многократное);
• число основных режимов работы (одно- или многорежимный);
• функции на траектории (маршевый, коррекции, рулевой,
тормозной, стартовый, ориентации, стыковки).
Вследствие отсутствия или ограниченной доступности
других нормативных документов, определяющих терминологию
и классификацию в области ракетных двигателей, при
дальнейшем изложении курса в основном используется схема
классификации ракетных двигателей и терминология, установленные
ГОСТ 17655-89.
Более подробные схемы классификаций, учитывающие
существенно большее число конструктивных, схемных и режимных
признаков, могут быть рассмотрены по результатам изучения
ракетных двигателей конкретных типов и видов.
Ознакомимся с историей ракетного двигателестроения.
Принято считать, что ракетный двигатель был изобретен практически
одновременно с изобретением пороха. Вероятно, при
изготовлении пороха возникали случаи его воспламенения и при горении
пороха в сосуде истекающие продукты сгорания создавали тягу,
вызывающую перемещение сосуда.
Впервые упоминание о том, что в настоящее время
называется ракетным двигателем, встречается в древнейших китайских
документах, относящихся к VIII в. до н. э. («огненная стрела»).

160 Часть I. Теория идеального теплового ракетного двигателя
В документах европейских стран сведения о ракетных двигателях
появились в середине XIII в. Но, по мнению некоторых историков,
«греческий огонь», применявшийся в X в. при осаде русскими
войсками Константинополя, представлял собой простейший
снаряд с твердотопливным ракетным двигателем.
Достаточно широкое применение ракеты нашли в XVHI-XIX вв.
Это сигнальные и боевые зажигательные ракеты, а также ракеты
как элементы фейерверков. Можно отметить сигнальную ракету
массой около 0,4 кг, поднимавшуюся на высоту более 700 м и
стоявшую на вооружении российской армии в годы правления Петра I.
Не исключено, что производили эту ракету в Москве в
Лефортово, вблизи Коровьего брода, где сейчас расположен МГТУ
им. Н.Э. Баумана.
Предпосылки теории реактивных и в частности, ракетных
двигателей сформировались уже в XIX в. в результате
разработки проблем общей теории тепловых машин на основе
термодинамического подхода. Значительный вклад в развитие этой
теории внесли работы таких иностранных и отечественных ученых,
как И. Ван-дер-Ваальс, Л. Вантцель, Н.Л.С. Карно, Б. Клапейрон,
Д.И. Менделеев, входивший в педагогический совет
Императорского технического училища (ИМТУ) (информацию в Интернете,
связанную с именем Д.И. Менделеева, можно найти на сайте
www.chem.msu.su/eng/misc/mendeleev/), А. Навье, Л. Прандтль,
А. Сен-Венан, А. Стодола, Г. Цейнер, академик Российской
академии наук Л. Эйлер и другие.
К началу XX в. в технической термодинамике и ее прикладных
разделах рассматривались задачи, впоследствии составившие
основу теории ракетных двигателей как тепловых машин.
Основы ракетной техники на уровне принципов и схем были
заложены в трудах К.Э. Циолковского, хотя в рабочих тетрадях
российского ученого-изобретателя С.С. Неждановского (1850-1940)
с опережением в несколько лет были впервые изложены многие
из имевших принципиальное значение и опередивших свое
время идей, касающихся устройства и расчета ракетных двигателей,
значительно позднее предложенных и развитых независимо от
него другими учеными и инженерами. Остается только сожалеть
об отсутствии их публикаций в свое время. Многие идеи
создания и развития ракетных двигателей были предложены Н.И.
Кибальчичем, Ю.В. Кондратюком, Ф.А. Цандером, который
довел идеи до инженерного воплощения в чертежах и опытных
образцах.

Глава 13. Классификация ракетных двигателей Ш
Научные основы теории реактивного движения были
созданы профессором Императорского Московского технического
училища (ИМТУ, ныне МГТУ им. Н.Э. Баумана) и
Московского университета (ныне МГУ им. М.В. Ломоносова) Н.Е.
Жуковским и развиты позднее учеными и преподавателями ИМТУ
Ю.А. Победоносцевым, Б.С. Стечкиным, С.А. Чаплыгиным и
другими.
Несколько позднее К.Э. Циолковского профессор Г. Оберт
(Германия, 1923 г.) развил теорию ракетных снарядов.
Технические вопросы создания ракетных двигателей рассматривались
также в трудах инженера Е. Зенгера (Австрия, 1933 г.).
С 1915 г. и до 1940-х годов в США были выполнены
технические и конструкторские работы в области ракетной техники
профессором Р. Годдардом. Работы в области создания ракет
и ракетных двигателей в Германии в 1930-1940-е годы
завершились созданием под руководством В. фон Брауна баллистической
ракеты V-2 с ЖРД.
Планомерные теоретические и экспериментальные
исследования в области создания ракетных двигателей в СССР были
начаты в 1929 г. в газодинамической лаборатории (ГДЛ) в
Ленинграде под руководством В.П. Глушко. В 1930 г. в ГДЛ были
впервые предложены в качестве окислителей азотный тетраоксид,
азотная кислота и их растворы, пероксид водорода и другие
вещества, а в качестве горючего - бериллий, трехкомпонентное
топливо (кислород, водород и бериллий), порох с
диспергированным в нем металлом и др. В 1930-1933 гг. в ГДЛ было
создано семейство ЖРД-ОРМ (от ОРМ-1 до ОРМ-52).
В 1931 г. в Москве и Ленинграде были организованы группы
по изучению реактивного движения (ГИРД). В МосГИРДе
работали такие известные ученые, как Ф.А. Цандер (первый
руководитель), СП. Королев и другие, в ЛенГИРДе - Н.А. Рынин,
Я.И. Перельман и другие. В 1932 г. была создана
научно-исследовательская и опытно-конструкторская организация, также
именовавшаяся ГИРДом. Ее начальником был назначен СП. Королев,
выпускник МВТУ им. Н.Э. Баумана (ныне МГТУ им. Н.Э. Баумана),
впоследствии академик, генеральный конструктор ракетных
систем, преподававший в МВТУ им. Н.Э. Баумана.
В 1933 г. в СССР был организован Реактивный
научно-исследовательский институт - первая в мире
научно-исследовательская и опытно-конструкторская организация,
объединившая различные направления теоретической и практической

162 Часть I. Теория идеального теплового ракетного двигателя
разработки ракетной техники, в том числе ракетного двигате-
лестроения.
В нашей стране были созданы РДТТ (для установок
«Катюша»), ГРД для первой отечественной ракеты ГИРД-09 (1933) на
жидком кислороде и бензине, сгущенном путем растворения в нем
канифоли; ЖРД на различных высоко- и низкокипящих топливах,
в том числе для крылатой ракеты конструкции СП. Королева,
для ракетопланов и вспомогательных двигательных устройств
самолетов.
Качественно новый этап развития ракетных двигателей
начался после Второй мировой войны. Научные предпосылки
создания ЖРД разрабатывались в 1940-1950-е годы одновременно
с освоением экспериментальных ракетных двигателей.
Становление и затем интенсивное развитие отечественной
космонавтики непосредственно обусловлено достижениями в
области разработки ЖРД. В 1957 г. в СССР мощной
ракетой-носителем с ЖРД был запущен первый в мире искусственный спутник
Земли, открывший эру освоения космоса человечеством. В 1961 г.
осуществлен первый в мире полет человека в космос. Ю.А.
Гагарин - первый космонавт планеты Земля.
В 1960-е годы крупных успехов достигло ракетное двигате-
лестроение в США, результатом которых были полеты
американских астронавтов на Луну (первый полет - в 1969 г. на
космическом корабле Аполлон-П).
Среди крупных отечественных достижений следует отметить
запуск долговременных орбитальных станций «Салют» и «Мир»,
полеты автоматических кораблей-зондов к Венере и Марсу.
Выдающиеся советские конструкторы ракетных двигателей,
основатели отечественного ракетного двигателестроения - В.П. Глуш-
ко, A.M. Исаев , С.А. Косберг, М.В. Мельников, И.Н. Садовский
и другие. Их дело продолжили Е.П. Селезнев1, В.Н. Богомолов,
СП. Изотов, А.Д. Конопатов, Н.Д. Кузнецов, Б.Н. Лагутин,
Н.И. Леонтьев, А.И. Люлька, А.Д. Надирадзе, В.П. Радовский,
В.Г. Степанов и другие.
В настоящее время разработка ракетных двигателей в России
ведется под руководством крупных конструкторов - Б.И. Катор-
Селезнев Евгений Петрович (1943) - генеральный конструктор-
генеральный директор КБ ХИММАШ им. A.M. Исаева (2001-2006),
заслуженный конструктор РФ; выпускник МВТУ им. Н.Э. Баумана.

Глава 13. Классификация ракетных двигателей 163
гина1, Е.Г. Ларина2, B.C. Рачука, Ю.С. Соломонова, Б.А. Соколова,
А.П. Сухадольского3, И.А. Смирнова и других.
Качественно новым достижением ракетного двигателестрое-
ния стало создание ЯРД в США и в СССР. Причем отечественный
ЯРД развивал существенно больший удельный импульс, чем
американский. Двигатели прошли основные стендовые наземные
испытания.
В СССР и США были разработаны и испытаны, в том числе
в полете, плазменно-ионные электрические ракетные двигатели.
Созданные крупногабаритные РДТТ нашли применение в
основном в военной технике, за исключением стартовых
ускорителей комплекса «Спейс Шаттл» и ракетоносителей «Ариан».
В последние годы лучшие образцы отечественных ракет
с РДТТ - ракеты семейства «Старт» (ОАО «Корпорация
«Московский институт теплотехники» (МИТ)», www.roscosmos.ru/) -
используют в модернизированном варианте для запуска
искусственных спутников Земли с мобильных стартовых комплексов.
Значительные успехи в ракетном двигателестроении
достигнуты Китаем, Японией и Европейским космическим агентством.
Если для разработанных до начала 1960-х годов двигателей
были характерны схемы с выбросом отработавшего на
турбине рабочего тела в окружающую среду, то создание ЖРД с
дожиганием генераторного газа можно считать началом
современного периода ракетного двигателестроения (например,
«Самарский научно-технический комплекс им. Н.Д. Кузнецова»,
сайт www.ssau.ru/partners/sntk/), (ОАО КБХА, Воронеж, сайт
www. kbha.ru/). Давление в камере сгорания при этом возросло
с 1,5 МПа (ЖРД ракеты V-2, Германия) до 27,5 МПа (один из
Каторгин Борис Иванович (1934) - генеральный директор (1991—
2005 гг.), генеральный конструктор ОАО «НПО Энергомаш им.
академика В.П. Глушко» (2005-2008 гг.), член-корреспондент (2000 г.),
академик РАН, заслуженный деятель науки РФ. Лауреат премии
Правительства России, Государственной премии РФ; выпускник МВТУ
им. Н.Э. Баумана.
Ларин Евгений Григорьевич (1931) - главный конструктор ФГУП
«Научно-исследовательский институт машиностроения» (г. Нижняя
Салда); выпускник МВТУ им. Н.Э. Баумана.
3 Сухадольский Александр Петрович (1948) - генеральный
конструктор корабельного комплекса ОАО «Корпорация «Московский институт
теплотехники», заслуженный конструктор РФ; выпускник МВТУ
им. Н.Э. Баумана.

164 Часть I. Теория идеального теплового ракетного двигателя
ЖРД разработан в СССР, в ОАО КБХА «НПО Энергомаш им.
академика В.П. Глушко» (сайт www.npoenergomash.ru/). Близкие к
термодинамически предельным показатели эффективности при не
достигнутой другими конструкторским бюро надежности имеют
разработанные в КБ ХИММАШ им. A.M. Исаева ЖРД на высоко-
кипящих компонентах (http://www.kbhmisaeva.ru/main.php?id=21).
Освоены экологически чистые криогенные компоненты топлива -
кислород и водород.
Примером современных достижений ракетного двигателестро-
ения можно считать твердотопливные и жидкостные двигатели
SSME американского ракетоплана «Спейс Шаттл» (Pratt & Whitney
Rocketdyne, сайт www.pw.utc.com/) и российского комплекса -
корабля «Буран» и ракеты-носителя «Энергия», разработанного
Ракетно-космической корпорацией «Энергия» им. СП. Королева
(сайт www.energia.ru/).
Не имеет аналога в мире по своим параметрам работающий
на топливе «углеводородное горючее - кислород» двигатель
РД-170 ракеты-носителя «Энергия», развивающий тягу 8 000 кН
при давлении в камере около 25 МПа, давлении в газогенераторе
60 МПа, мощности турбины газогенератора 220 МВт и
температуре окислительного газа на входе в турбину 780 К.
Самые высокие показатели эффективности у входящих в состав
объединенной ДУ орбитального корабля «Буран» двух двигателей
орбитального маневрирования с тягой по 80 кН и у 46 импульсных
двигателей систем управления и ориентации, из которых 38
имеют тягу 4 кН, а восемь - тягу 200 Н; в их разработке принимали
участие ученые и инженеры МГТУ им. Н.Э. Баумана.
За сравнительно короткий срок ракетные двигатели достигли
значительного совершенства и весьма высоких, близких к
пределу, параметров, превысить которые можно, только применяя
принципиально новые схемы энергопреобразования, материалы
и технологии.
В настоящее время продолжается развитие и
совершенствование ракетных двигателей в направлении повышения
надежности, удельного импульса, уменьшения удельной массы, снижения
стоимости, снижения или устранения вредного экологического
воздействия на окружающую среду.
Надежность и экологическая безопасность стали основными
показателями качества проектируемых двигателей. При этом
разрабатываются двигатели с большими запасами
работоспособности. Из схемных решений предпочтение отдается тем, в которых

Глава 13. Классификация ракетных двигателей 165
минимизируется число потенциально опасных агрегатов и
увеличивается доля хорошо отработанных и показавших на
практике высокую надежность технических решений с ориентацией на
современные материалы и технологии. Предусматривается
применение систем оперативной диагностики и аварийной защиты.
Большое внимание уделяется снижению стоимости
выполнения задачи летательным аппаратом с ракетным двигателем: в
одних случаях более эффективным может оказаться двигатель
однократного применения, изготовленный из относительно дешевых
материалов по типовым технологиям и развивающий
относительно невысокий удельный импульс, в других случаях предпочтение
отдается многотопливному многорежимному двигателю
многократного применения.
Более подробные сведения об истории создания и развития
ракетных двигателей содержатся в трудах Института истории
естествознания и техники им. СИ. Вавилова РАН (www.ihst.ru/).
Их также можно найти в литературе, рекомендованной к ч. I
учебника.
Несколько иное представление истории ракетных двигателей
отражено в книгах зарубежных авторов, в частности в работах
Д. Саттона1.
Контрольные вопросы и задания
1. Приведите пример классификации ракетных двигателей по виду
энергии, преобразуемой в полезную кинетическую энергию
истекающего потока, создающего тягу.
2. Приведите пример классификации ракетных двигателей по
агрегатному состоянию химического топлива.
3. Приведите пример классификации ракетных двигателей по числу
компонентов топлива.
4. Приведите пример классификации ракетных двигателей по типу
системы подачи топлива.
5. Приведите пример классификации ракетных двигателей по способу
использования рабочего тела турбины ТНА.
Sutton G. Rocket propulsion elements an introduction to the engineering
of rockets. Second printing. N. Y.; L., 1949. Перевод на русский язык
книги с изменениями в очерке истории: СаттонД. Ракетные двигатели,
основы теории и конструкции ЖРД : пер. с англ. М.: Изд-во иностр.
лит., 1952.

166 Часть 1. Теория идеального теплового ракетного двигателя
6. Приведите пример классификации тепловых ракетных двигателей
по принципу ускорения рабочего тела до входа его в геометрическое
сопло.
7. Каким веком датируются первые упоминания об использовании
принципа ракетного движения («огненная стрела», «греческий
огонь»)?
8. Перечислите фамилии иностранных и отечественных ученых и
инженеров, в том числе выпускников МГТУ им. Н.Э. Баумана (ИМТУ,
МММИ, МВТУ), внесших крупный вклад в разработку ракетных
двигателей.
9. Назовите эпохальные свершения человечества в освоении космоса,
которые не могли бы состояться без применения
высокоэффективных ракетных двигателей.
10. Подтвердите ведущие позиции в мировом ракетном двигателестро-
ении отечественных предприятий - разработчиков ракетных
двигателей. Охарактеризуйте решающую роль отечественных достижений
в освоении космоса человечеством.

ЧАСТЬ II
ТЕОРИЯ НЕИДЕАЛЬНОГО ТЕПЛОВОГО
РАКЕТНОГО ДВИГАТЕЛЯ

Глава 14
Основные различия между
реальными рабочими процессами
и их идеальным представлением
в теории ракетного двигателя
Изложенная в ч. I данного учебника теория идеального
ракетного двигателя позволяет рассчитать в первом приближении
основные размеры сопла ракетной камеры, получить значения
удельного импульса, выявить свойства дроссельных (расходных)
и высотных характеристик проектируемого двигателя и на этой
основе оценить выполнимость технического задания и определить
конкретный вид удовлетворяющего установленным
ограничениям ракетного двигателя.
Достоверность количественных параметров и характерных
показателей ракетного двигателя, полученных в рамках допущений
об идеальности рабочего процесса, недостаточна для принятия
обоснованного инженерного решения. Количественное
рассогласование полученных таким образом расчетных и действительных,
достигаемых на практике данных объясняется тем, что теория
идеального ракетного двигателя отражает только основные
взаимосвязи без учета имеющих место существенных неидеальностей.
Различия между реальными рабочими процессами в ракетном
двигателе и их идеальным представлением формируются в
результате проявления реальных свойств рабочего тела при течении
его по соплу, контур которого имеет конечные размеры, а стенки
выполнены из теплопроводных материалов. При этом
идеальному процессу подвода теплоты к идеальному рабочему телу в
действительности отвечает сложный параллельно-последовательный
процесс преобразования химической энергии топлива в тепловую
энергию рабочего тела, сохраняющего возможность внутренних
химических превращений за тысячные доли секунды при
движении по трактам ракетной камеры.
Проанализируем указанные различия на примере ЖРД, многие
составляющие совокупного рабочего процесса которого
свойственны и ракетным двигателям на топливах другого
агрегатного состояния.

170 Часть II. Теория неидеального теплового ракетного двигателя
Поскольку ЖРД является тепловой машиной, полезно
рассмотреть условный термодинамический цикл его работы как
компактное и наглядное отображение качественных соотношений
между реальными рабочими процессами и их идеальными
моделями (рис. 14.1). С методической целью на рисунке утрированно
показаны изменения в реальном цикле по сравнению с идеальным.
Р
Р*
п*
V
Рис. 14.1. К сопоставлению условных
циклов идеального и реального ЖРД
В координатах v-p площадь, ограниченная отражающей цикл
ломаной кривой, пропорциональна удельной работе цикла.
Термодинамически удельной работе цикла соответствует квадрат
скорости истечения, т. е. квадрат удельного импульса на
расчетном режиме. Вследствие такого соответствия изменение
площади в результате деформирования графика процесса по отношению
к идеальному отражает влияние конкретной неидеальности на
удельный импульс. При этом введение в состав условного цикла
роста давления компонента от давления в баке до давления
подачи в камеру отражает удельные затраты располагаемой энергии
топлива на подачу компонентов.
На рис. 14.1 точки 1-4 соответствуют циклу идеального
ракетного двигателя. Идеальный и реальный двигатели
сопоставляются:
• при одинаковом давлении в камере р*к, т. е. вблизи
смесительной головки;
• одинаковом давлении в выходном сечении сопла ра, равном
давлению окружающей среды ph, т. е. ра = ph\
• одном и том же составе топлива, т. е. при одинаковых для
идеального и реального рабочих тел усредненных по сечению
молекулярных массах ц и показателях адиабаты к = с /cv до

Глава 14. Различия между реальными и идеальными процессами 171
входа в сопло и температурах топлива на входе в головку
смесителя.
Для подачи топлива в камеру давление перед смесительной
головкой должно быть больше, чем в камере (см. рис. 14.1,
точка /').
Собственно горению, идущему при высокой температуре с
образованием газообразных продуктов реакции и выделением
теплоты, предшествуют:
• исходное распределение компонентов по сечению камеры
сгорания и их первичное диспергирование, задаваемое
конструкцией и параметрами режимов работы смесительной головки;
• вторичное диспергирование жидкой фазы за счет
взаимодействия с заполняющей камеру многофазной средой;
• испарение компонентов;
• смешение компонентов в газовой и жидкой фазах;
• химические реакции, идущие без значительного повышения
температуры;
• воспламенение.
Этим процессам соответствует кривая 7-2'
термодинамического цикла.
Физико-химические превращения происходят во времени
частично последовательно, частично параллельно. При этом
локализация процессов также неоднозначна.
Конечность скоростей превращений при ограниченности
времени пребывания компонентов в камере приводит в общем случае
к незавершенности преобразования химической энергии топлива
в тепловую энергию продуктов сгорания.
Если камера сгорания не охлаждается либо охлаждается
аккумуляцией теплоты или излучением теплоты в окружающую
среду, то из-за отвода теплоты происходит снижение
температуры вблизи стенок камеры.
В результате распределение параметров рабочего тела в
выходном сечении камеры сгорания существенно отличается от
равномерного, принятого в качестве основного в теории
идеального ракетного двигателя. При этом усредненная по времени
и площади потока температура рабочего тела на входе в сопло
Т*' (точка 2') будет несколько меньше, чем для того же топлива
в идеальном представлении (точка 2), т. е. Т*' < Т*.
Движение сжимаемого рабочего тела по камере сгорания в
любом сечении идет с ненулевой скоростью и сопровождается
внутренним тепловыделением, внутренним трением и трением о стенки

172 Часть II. Теория неидеального теплового ракетного двигателя
камеры сгорания, что ведет к потере полного давления - от
давления р*к до давления торможения на входе в сопло /?*х.
Давление торможения в критическом сечении р* =р*вх,
определяющее для заданного рабочего тела пропускную способность
сопла, снижается, что при сохранении р*к и расхода топлива
требует увеличения площади критического сечения F . При этом
статическое давление в критическом сечении реального двигателя
будет меньше, чем у его идеального прототипа, т. е. р''/ркр < 1.
Располагаемое отношение давлений в сопле в результате
уменьшается отp*K/ph доp*BX/ph, при этом и в случае идеального
процесса в сопле скорость истечения Wa (удельный импульс на
расчетном режиме / ) будет ниже, чем у идеального двигателя,
вследствие снижения температуры торможения Г* < Т*' и тер-
к-Л
мического КПД л, =1-Та/т^=\-(ра/' p*Kp) k .
Идеальному процессу расширения в сопле газа постоянного
состава и с постоянными свойствами 2-3 в реальном двигателе
отвечает кривая 2'-3'. Предполагая теплоизолированное течение
в сопле, учитываем химическую активность рабочего тела,
приводящую к внутреннему тепловыделению в потоке за счет идущих
при понижении температуры экзотермических реакций
рекомбинации, частично возвращающих теплоту, затраченную на
термическую диссоциацию в камере сгорания. Опишем процесс
несколькими следующими друг за другом изоэнтропами
с показателем п < к, постоянным для каждой изоэнтропы, при
этом справедливо неравенство п > 1, так как п = 1 соответствует
изотермическому процессу. Таким образом, действительная
зависимость 2'-3" будет некоторой средней между изотермой и изо-
энтропой с показателем п = к для идеального газа с постоянными
свойствами (кривая 2'-3').
Отметим, что скорость истечения химически активного
потока, судя по площади под кривой 2'-3"9 будет выше скорости
истечения химически инертного газа (кривая 2'-3'), если не
учитывать неидеальности другой природы. При этом точка 3' может
располагаться на графике правее или левее точки 3.
Действующими ГОСТами выделяются следующие
особенности реального процесса в сопле: скоростная, температурная
и химическая неравновесность течения, неодномерность и мно-
гофазность потока. Причем две последние не отображаются на
v-p-диаграмме, приведенной на рис. 14.1.

Глава 14. Различия между реальными и идеальными процессами 173
В отличие от повышения давления идеального
несжимаемого компонента по изохоре 4-1 реальный компонент сжимаем,
и требуется затратить энергию на его подачу в камеру. Если
ЖРД работает по схеме с дожиганием (см. рис. 1.10), то
затраченная на подачу компонентов энергия возвращается в камеру,
т. е. имеет место перераспределение энергии внутри цикла.
Пренебрегая незначительной регенерацией в цикле, отразим этот
внутренний энергообмен путем уменьшения площади кривой цикла
на площадь криволинейного треугольника 5-4'-4 (см. рис. 14.1)
и увеличения на площадь криволинейного треугольника Г-1-5,
приблизительно равновеликого треугольнику 5-4'-4, что
отражает качественно возврат затраченной на подачу топлива энергии
в камеру сгорания.
Если жидкое топливо подается в камеру насосным агрегатом
с приводом от внешнего источника мощности, то это
соответствует подводу энергии к рабочему телу и отображается на
v-p-диаграмме, приведенной на рис. 14.1, дополнением площади
под ломаной кривой Г-1-2'-3" площадью криволинейного
треугольника Г-1-4 слева от изохоры 4-1.
Обратим внимание на то, что охлаждение сопла
компонентами топлива представляет собой регенерацию теплоты -
использование низкопотенциальной теплоты исходящего
низкотемпературного потока (в сопле) для нагрева топлива, поступающего
в камеру сгорания и возвращающего теплоту в зону с
максимальной температурой цикла. Теория тепловых машин указывает на
возможность повышения эффективности преобразования
теплоты в кинетическую энергию рабочего тела, т. е. повышения
удельного импульса камеры, благодаря введению регенерации
теплоты. Реализуемые практически в современных двигателях степени
регенерации теплоты (доля подогрева компонента в тракте
охлаждения в суммарном повышении температуры от температуры
в баке до температуры сгорания) не дают существенного
прироста удельного импульса, но перспектива перехода к созданию
космических двигателей на криогенных компонентах с
давлением в камере около 100 МПа ведет к существенному повышению
степени регенерации теплоты и, как следствие, к необходимости
учета регенерации теплоты в методиках расчета. Разработка таких
методик является пока нерешаемой задачей общей теории
тепловых ракетных двигателей, требующей дальнейшего развития.
Важным представляется то, что температура и состав
рабочего тела, считающиеся в теории идеального ракетного двигателя

174 Часть II. Теория неидеального теплового ракетного двигателя
заданными через известные значения ц, к, Гк*, в действительности
являются рассчитываемыми величинами.
Определение значений кажущейся молекулярной массы ц,
показателя адиабаты к и температуры Т* продуктов сгорания
топлива заданного состава при заданном давлении является
основной задачей термодинамического расчета, которому будет
посвящено несколько последующих глав.
Затраты энергии на подачу компонентов топлива принято
учитывать, различая удельные импульсы камеры и ДУ. Другие
различия реальных рабочих процессов и их идеального
представления стандартом рекомендуется описывать в виде системы
коэффициентов, отражающих локализацию - в камере сгорания или
в сопле - и физическую природу неидеальности.
Поскольку современный ракетный двигатель представляет
собой термодинамически совершенную тепловую машину,
проявление какой-либо одной неидеальности дает, как правило, вклад
в суммарное отклонение значения выходного параметра от
идеального значения не более 1,5 %. При этом взаимное влияние
неидеальностей пренебрежимо мало. Отсюда следует
рекомендуемое стандартом суммирование потерь при расчете их
суммарного эффекта - потери удельного импульса и др.
Вводятся коэффициенты потерь некоторого параметра ф из-за
влияния /-й неидеальности:
£, = Дф,/ф, (14.1)
где Аф. - уменьшение значения параметра ф по отношению к его
невозмущенному данной /-й неидеальностью значению.
Уменьшение значения параметра (потери) в результате
совместного действия нескольких неидеальностей Афх
вычисляется по соотношению
Дф,=ХАф,., (14.2)
/ = 1
где п - число учитываемых факторов (неидеальностей).
Тогда с учетом (14.1) справедливо равенство
АФ1=ФЕ^. (14-3)
/ = 1

Глава 14. Различия между реальными и идеальными процессами 175
Вводятся также коэффициенты, представляющие собой
отношение реального значения параметра ф, установившегося при
совместном действии нескольких неидеальностей, к его
идеальному значению:
cPi = /71 ■ (14.4)
ф
Нижний индекс коэффициента (pz для упрощения может быть
опущен, если рассматриваются конкретный агрегат или процесс
при заданном числе учитываемых неидеальностей.
Коэффициент, учитывающий влияние одной i-й
неидеальности, записывается аналогично (14.4):
Ф/=^М = 1-^, (14.5)
Ф
Поскольку значения коэффициентов потерь %., как правило,
не превышают нескольких сотых и, следовательно,
соответствующие коэффициенты (р. близки к единице, справедливо
приближенное равенство
ф-2Хф .
ф!= ф' =ГО< (14-6)
Погрешность при замене вычислений по (14.4)
произведением коэффициентов по (14.6) в реальном диапазоне значений ф.
и £. не превышает долей процента и считается для практики
приемлемой.
Представление итогового коэффициента фЕ (или ф) в виде
произведения учитывающих отдельные неидеальности
коэффициентов ф. упрощает математическое описание реального
совокупного рабочего процесса в рамках заданного государственным
стандартом порядка оценки совершенства ракетного двигателя.
Отметим также, что подобный метод учета влияния
неидеальностей принимается в большинстве публикаций, касающихся
технических вопросов.

176 Часть II. Теория неидеального теплового ракетного двигателя
Контрольные вопросы и задания
1. Перечислите факторы, обусловливающие различия реальных
рабочих процессов в камере ракетного двигателя и их идеального
представления.
2. При условии постоянства каких параметров сравнивают идеальный
и реальный ракетные двигатели?
3. Каким образом на v-p-диаграмме (см. рис. 14.1) отражаются
затраты энергии на повышение давления сжимаемого компонента в ЖРД
с дожиганием генераторного газа?
4. Каким образом на у-/?-диаграмме (см. рис. 14.1) отражается процесс
подвода энергии к компонентам топлива при повышении давления
сжимаемого компонента в ЖРД с ТНА без дожигания рабочего тела
турбины?
5. Следствием каких допущений (и соответствующих ограничений на
коэффициенты потерь £. как положительные величины,
существенно меньшие единицы) является возможность вычисления
коэффициентов фх, учитывающих совместное влияние на некоторый
параметр нескольких (например, п) потерь или неидеальностей, как
п
произведение, т. е. cpz =П(1-£/) ?

Глава 15
Система коэффициентов учета потерь
в ракетном двигателе.
Удельный импульс камеры ракетного двигателя
и двигательной установки
Различия реальных процессов и их идеального представления
находят отражение в различии значений параметров, получаемых
в действительности, и их идеальных значений.
Под идеальным значением параметра камеры понимается
значение параметра, соответствующего равновесному
одномерному потоку продуктов сгорания (газогенерации) при отсутствии
трения и отвода теплоты.
Термин «равновесное» означает, что в каждой точке потока
существует энергетическое, химическое и фазовое равновесие.
Основной параметр, характеризующий совершенство рабочих
процессов в двигателе, - коэффициент удельного импульса
камеры ф , определяемый как отношение действительного
удельного импульса камеры в пустоте I к идеальному удельному
импульсу в пустоте Iупи, вычисленному при тех же значениях
соотношения компонентов, давлении в камере и геометрической
степени расширения сопла:
1у.пм
Как показано в гл. 14, следствием применимости принципа
суперпозиции в реальных диапазонах отклонения от идеальности
является представление коэффициента ф в виде произведения:
Фу = ФкФс>
где фк, фс - коэффициенты, учитывающие процессы,
происходящие соответственно в камере сгорания и в сопле.
Потери удельного импульса также можно подразделить по
месту проявления порождающих их неидеальностей:

178 Часть II. Теория неидеального теплового ракетного двигателя
в камере сгорания
А/у.пк = (1-СРк)/у.п.и;
в сопле
А/у.пс = (1-(Рс)/у.п.и;
в целом по камере
Д/ = (2 - ф - ф V .
у.п v тс тк/ у.п.и
Помимо уже названных различий идеальных и реальных
процессов, приводящих к потере полноты перехода одной формы
энергии в другую, реализуются неидеальности, которые
непосредственно влияют только на кажущееся изменение размеров
проточной части камеры. Если такое следствие неидеальностей
не учтено при расчете требуемых размеров и параметров
двигателя, то развиваемый удельный импульс будет существенно
меньше идеального.
Учет требует количественной оценки такого проявления
неидеальностей, и особенно вблизи минимального проходного
сечения камеры, определяющего не только геометрическую степень
расширения сопла, но и зависимость между расходом топлива
и давлением в камере.
В идеальном случае (равномерные распределения всех
параметров потока по сечению и одномерное течение вблизи этого
сечения) минимальное сечение канала практически совпадает
с критическим сечением (Fmin = F ), и расход рассчитывается по
соотношению
. р* FminA(n)
m= РГ\ , (15.1)
\jRTKP
где п - показатель изоэнтропы, усредненный по процессу в
диапазоне значений давления р*к...рк . Для изоэнтропийного
адиабатного течения инертного идеального газа показатель
изоэнтропы п равен показателю адиабаты &, а/?* = р*к и R = RK.
Кажущееся изменение размеров проточной части вызывают
существенная неодномерность потока и загромождение
проходного сечения сопла пограничным слоем (так называемое вытес-

Глава 15. Учет потерь в ракетном двигателе 179
нение). В наиболее явной форме результатом действия этих
факторов является сужение струи от площади канала Fmin до
минимальной площади струи в с раз при отрыве потока от стенок
(рис. 15.1 и 15.2, на которых в утрированном с методической
целью виде изображены возможные схемы камер с разным
профилем входа в сопло).
Рис. 15.1. Схема течения в камере с входом в
сопло типа «отверстие в тонкой плоской стенке»:
1 - контур камеры; 2 - поверхность тока, образующая
границу струи; 3 - отрывная зона потока
Рис. 15.2. Схема течения в камере с входом в
сопло типа «насадок Борда»:
1 - контур камеры; 2 - поверхность тока, образующая
границу струи; 3 - отрывная зона потока
В этом случае минимальное сечение Fmin канала не совпадает
с критическим сечением F для камеры, для нее критическим
является минимальное сечение струи.
Известны теоретические расчеты сужения струи несжимаемой
идеальной жидкости, истекающей из отверстия в плоской стенке
(аналог см. на рис. 15.1) о ~ л/(я + 2) ~ 0,611 и из насадка Борда
(аналог см. на рис. 15.2) о ~ 0,5. Эти значения могут быть в пер-

180 Часть II. Теория неидеального теплового ракетного двигателя
вом приближении использованы для оценки ожидаемого сужения
потока газа вблизи минимального сечения сопла.
Сужение струи и неодномерность течения на практике
сопряжены с потерей полного давления потока. Для численных
характеристик влияния всего комплекса описанных различий реального
и идеального потоков вводится коэффициент расхода сопла:
тИ
Расчет идеального значения расхода т ведется по формуле
(15.1).
Отметим, что ц < а, так как коэффициент расхода сопла ц
учитывает не только уменьшение площади струи в сопле в а раз,
но и другие неидеальности, ограничивающие пропускную
способность сопла.
Для оценки совершенства рабочих процессов в двигателе
обычно вводится ряд параметров, вычисляемых при предположении
одномерного потока.
Характеристическая скорость с* в камере - произведение
давления торможения в минимальном сечении сопла, площади
этого сечения и коэффициента расхода сопла, отнесенное к
массовому расходу топлива камерой:
* F
т
Значение характеристической скорости зависит для данного
топлива только от совершенства преобразования полной энергии
топлива в тепловую энергию продуктов сгорания в камере на
участке от смесительной головки до минимального сечения. При
этом влияют и прямые потери через теплопроводные стенки
камеры, если камера не охлаждается регенеративно.
Расходный комплекс камеры Р - произведение давления в
некотором сечении камеры сгорания и площади минимального
сечения сопла, отнесенное к массовому расходу топлива:
pF ■
р=/^лшь (153)
т
Расходный комплекс камеры удобно использовать для
анализа стабильности характеристик камер при их эксплуатации или

Глава 15. Учет потерь в ракетном двигателе Ш
при производстве, так как расходный комплекс оценивает
совокупный рабочий процесс в камере сгорания и сопле, включая
дополнительно по отношению к неидеальностям, учитываемым
характеристической скоростью, потери полного давления потока,
кажущееся снижение проходных сечений и др.
В качестве давления в характерном сечении р. рекомендуется
статическое давление в начальном сечении камеры вблизи
смесительной головки.
Вследствие различной локализации неидеильностей рабочего
процесса стандарт рекомендует оценивать совершенство
рабочего процесса в камере коэффициентом камеры фк, определяемым
по формуле
*
Фк=%> (15.4)
где действительное с* и идеальное с* значения характеристической
скорости определяются при одинаковых соотношениях
компонентов и давления в камере сгорания. Причем идеальное значение
определяется путем расчета при предположении равновесного
одномерного потока продуктов сгорания при отсутствии трения,
теплообмена и других необратимых явлений, т. е. с*
вычисляется по (15.2) при \i = 1 для расхода, задаваемого выражением
т = Щ^. (15.5)
Из (15.5) с учетом (15.1) получаем
А(п) т
т. е. расчетное выражение для теоретического определения
идеальных параметров с* и ри, если р. = /?*, имеет вид
Ри и А(п)'
Реальный процесс смесеобразования и горения
сопровождается снижением давления торможения на участке «смесительная
головка - минимальное сечение камеры» от давления в камере р*

182 Часть II. Теория неидеального теплового ракетного двигателя
до давления торможения в критическом сечении р* в основном
вследствие теплового сопротивления (подвода теплоты к
сжимаемому ускоряющемуся потоку) и трения. Оставаясь в рамках
принятых допущений о суперпозиции влияния совместно
действующих неидеальностей, запишем
р* = р* ого ,
где о, - коэффициент снижения давления из-за теплового
сопротивления; ос - коэффициент снижения давления из-за трения.
Коэффициенты о, и сс могут быть рассчитаны по известным
универсальным методикам. Тогда действительное значение
характеристической скорости с* можно определить, используя рас-
четно-экспериментальный метод, по уравнению
где Рд рассчитывается по результатам испытания камеры путем
подстановки в (15.3) измеренных действительных значений
расхода тд, давления в камере/?* д и площади минимального сечения
камеры Fmin. При этом
С\ С\ ^а/асРд
С* Ри Ри
где введен коэффициент
Коэффициент фр используют для анализа стабильности
характеристик двигателя одной и той же конструкции или для
сравнения вариантов двигателя, различающихся, например,
конструкцией смесительной головки.
Для сравнения камер различных конструкций следует
применять коэффициент фк.
Отметим, что если в двигатель, рассчитанный по
соотношениям для идеальных процессов, т. е. в идеальном приближении,
подать теоретически необходимый для создания давления в
камере р*к расход топлива тн, то в результате потерь теплоты

Глава 15. Учет потерь в ракетном двигателе 183
и неидеальности процесса горения даже при идеальном течении
газа по соплу получим в ц>{ раз меньшее давление в камере ивф,2
раз меньшую температуру торможения газа на входе в сопло Гк*,
а именно:
о = ЛсиФ^тт . (156)
Ри = Рки. тш . (15.7)
Разделим (15.6) на (15.7) и получим
Фк=Фр=Ф,=%. (15.8)
Рки
Таким образом, коэффициент фк приближенно показывает, во
сколько раз действительное давление в камере реального
двигателя будет меньше рассчитанного в идеальном приближении при
совпадении идеального и действительного расходов. Поэтому
коэффициент фк называют коэффициентом полноты давления.
Если предположить, что неполнота сгорания и потери теплоты
через стенки камеры приводят только к снижению температуры
торможения при сохранении состава и свойств продуктов
сгорания, а остальные процессы идеальны, то
Фк*<
или
*
Фк*Фр = ^- (15-9)
К. И
Другими словами, действительная температура в камере будет
ниже ожидаемой теоретически в ф^ раз.
Оценим идеальные и действительные значения параметров на
примере.

184 Часть II. Теория неидеального теплового ракетного двигателя
Пусть при расчетном давлении в камере/?* и = 10,0 МПа и
идеальной температуре сгорания Т*И = 3 300 К при испытании
двигателя и расходе топлива, равном идеальному, получено
действительное давление в камере р*к = 9,5 МПа.
На сколько ниже расчетной идеальной температуры Т*и была
действительная температура продуктов сгорания Т* ? Во
сколько раз следовало бы увеличить расход топлива, чтобы давление
в камере стало равным расчетному?
При тех же допущениях, при которых получены приведенные
выше преобразования, справедливы приближенные равенства
9 5
Фк ~Фв = —1—= 0,95;
Vk Ур 10,0
Т*
ф2«^ = 0,952 =0,9025.
к. и
Тогда, согласно (15.9), действительная температура
Г* =ф2Г* =0,9025-3 300 = 2 978,25 К.
К.Д тк к.и ' ?
Искомое уменьшение температуры в камере
АГ= Т*м - Г*д = Ги (1 - ф2) = 3 300(1 - 0,9025) = 321,75 К.
Трактуя фк как коэффициент полноты давления в камере,
рассчитаем требуемое для достижения заданного давления в камере
увеличение расхода:
тЛ=^ = 1,053тИ.
Фк
Обратим внимание на значительные различия идеального
и действительного значений температуры при практически
приемлемом снижении давления.
Поскольку физическая природа потерь в камере сгорания и в
сопле, как и целевые функции этих частей ракетной камеры,
различаются, для оценки влияния неидеальностей в сопле вводят
коэффициенты.

Глава 15. Учет потерь в ракетном двигателе 185
Коэффициент тяги КТ - отношение тяги камеры к
произведению давления торможения в минимальном сечении сопла,
площади этого сечения и коэффициента расхода сопла:
Kr^-r-j • (15.10)
Р min minM'
Умножив числитель и знаменатель в (15.10) на массовый
расход продуктов сгорания или топлива т, получим уравнение
связи между удельным импульсом и характеристической скоростью:
_ Р т _ /у
Ат - Г— ~ —•
т PmmFmmV C
Отсюда следует возможная трактовка характеристической
скорости как удельного импульса тяги, создаваемой
равнодействующей сил давления на проекцию критического сечения на
поверхность смесительной головки камеры.
Если требуется оценить влияние нескольких неидеальностей
и при этом не рассматривать несовпадение критического и
минимального сечений, то задача решается анализом тяговых
комплексов.
Тяговый комплекс К s - отношение тяги камеры к
произведению давления в некотором сечении камеры сгорания и площади
минимального сечения сопла:
Kps=-^-- 05.11)
Тяговый комплекс удобно использовать для анализа
стабильности характеристик камеры при ее серийном производстве, при
этом рекомендуется рассчитывать К s по статическому давлению
в начальном сечении камеры сгорания.
Умножив и разделив (15.11) на массовый расход топлива или
продуктов сгорания w, получим уравнение связи между
расходным комплексом р и удельным импульсом / :
К =Р ™ = 7у
Р" ™ PiFmm Р '
Степень приближенности реальных рабочих процессов в сопле
к идеальным рабочим процессам оценивается коэффициентом

186 Часть II. Теория неидеального теплового ракетного двигателя
сопла фс, который определяется отношением действительного
коэффициента тяги в пустоте Ктпдк идеальному
коэффициенту тяги в пустоте КТ п и, вычисленным при одинаковых
значениях соотношения компонентов топлива, давления в камере
сгорания и геометрической степени расширения сопла:
т.п.и
Влияние неидеальностей рабочих процессов на достижимые
параметры ракетного двигателя приводит к необходимости
изменения размеров камеры и увеличения расхода топлива. Оценим
эти изменения при следующих условиях сравнения: пустотная
тяга, давление в камере и геометрическая степень расширения
сопл двигателей с идеальным и реальным рабочими процессами
равны между собой, т. е.
Р = Р , р* =р* ; Ли_ = Л^.
п.д п.и' ^к.д *к.и' |-. г*
кр.и кр.д
Полагая известными и близкими к единице коэффициенты
камеры фк и сопла фс реального двигателя, для которого
справедливо равенство
/ =фф/ , (15.12)
у.п.д Чс Чк у.п.и' y±~s.±^s
воспользуемся соотношением ри = с*, записанным для двигателя
с идеальными рабочими процессами.
Расход для идеального двигателя
тп=у^- (15-13)
у.п.и
Поскольку действительные удельный импульс и расход
связаны соотношением
Р
т= °
Д ФсФЛ.пи '
то из сопоставления (15.12) с (15.13) получаем искомое
соотношение для действительного (тд) и идеального (/ии) расходов топлива:

Глава 15. Учет потерь в ракетном двигателе 187
т,ж
тД =
ФсФк
Из (15.2) для определения характеристической скорости
следует значение площади критического сечения для двигателя с
идеальным рабочим процессом:
F = c»rh»
^кр.и * *
Л
Из определения коэффициента камеры в соответствии с (15.4)
можно рассчитать действительную характеристическую скорость:
< = ФЛ- (15-14)
Рассчитав по (15.14) значение с*, из (15.2) для
действительного расхода тд и давления торможения в камере /?*, равного
заданному идеальному давлению, определим требуемую
действительную площадь критического сечения:
КР,=^ О5'15)
Фс
Из заданного по условию равенства геометрических степеней
расширения сопл идеального и реального двигателей с учетом
(15.15) следует, что
F
Таким образом, определение параметров и размеров
ракетного двигателя с учетом неидеальностей рабочих процессов может
быть представлено в виде трех этапов.
1. Расчет параметров, размеров и характеристик ракетного
двигателя при предположении идеальных рабочих процессов.
2. Расчетно-теоретическое определение коэффициентов
потерь, отражающих неидеальное протекание рабочих процессов.
3. Расчет параметров, размеров и характеристик ракетного
двигателя с учетом определенных коэффициентов потерь.
Специфика учета потерь, а точнее, затрат энергии на подачу
компонентов топлива в камеру, состоит в условном подразделении

188 Часть II. Теория неидеального теплового ракетного двигателя
рабочих процессов на процессы в камере и процессы в органах
подачи, которые являются неотъемлемой частью двигателей с
дожиганием рабочего тела турбины (см. рис. 1.10) или автономны
и выступают как внешняя по отношению к камере система для
двигателей без дожигания (см. рис. 1.9).
Как следует из приведенного выше анализа условных
термодинамических циклов для двигателей с дожиганием, процессы
повышения давления происходят внутри системы с полной
регенерацией энергии, т. е. собственно потери энергии отсутствуют.
Для двигателей без дожигания генераторного газа
дополнительные затраты топлива на подачу его большей части в камеру
учитывают, исходя из следующих понятий:
удельного импульса камеры
расход топлива через
где Рк -
h
ЛК . >
тк
тяга, развиваемая камерой; тк
камеру;
удельного импульса ДУ
^у.ДУ ~
^к+АРТНА
Ч+А%НА
(15.16)
где АРТНА - тяга, развиваемая выхлопным устройством турбины
THA; AwTHA - расход топлива газогенератора рабочего тела
турбины ТНА.
Камера работает при соотношении компонентов топлива,
близком к тому, при котором развивается максимальный пустотный
удельный импульс. При этом температура в камере сгорания
может превышать 3 000 К, что считается в большинстве случаев
допустимым, так как можно применить охлаждение стенок камеры.
Особенности работы лопаток турбины под дополнительной
нагрузкой от центростремительных ускорений и практическая
невозможность их эффективного охлаждения ограничивают
допустимую температуру рабочего тела в пределах 1 000... 1 500 К,
что достигается применением для выработки рабочего тела
турбины компонентов основного топлива, но при существенно
неоптимальном их соотношении, или использованием
вспомогательного топлива с допустимой для лопаток турбины
температурой горения.

Глава 15. Учет потерь в ракетном двигателе 189
Следствием различия свойств и параметров рабочего тела
камеры и турбины является соотношение удельных импульсов
камеры / к и сопла выхлопного патрубка турбины ТНА / ТНА:
7У-ТНА - _ \RTlHh ^ МТНА
С учетом соотношения
Р=т1у
преобразуем (15.16), подставив вместо развиваемых тяг их
значения, определенные через расход и удельный импульс, и получим
/
• . -у.ТИА А •
т + —Т Д^ТНА --
j _j 7ук , 1 + Фу.ТНА^ТНА
mK+AmTUA 1 + ^ТНА
п . _ AwTHA
Здесь АтТНА = -^^ -соотношение расходов топлива, подава-
тк
емого в газогенератор ТНА АтТНА и в основную камеру тк.
Введем коэффициент относительного снижения удельного
импульса ДУ:
Фу.ду = -^ = /(футна> А^тна)-
у.к
Практически реализуемые относительные расходы топлива
в газогенераторе и соотношение удельных импульсов камеры
и сопла выходного патрубка турбины ТНА располагаются в
следующих диапазонах значений:
• для расходов 0 ^ AmTHA ^ 0,15, где левая граница
соответствует схеме ДУ с дожиганием, правая - может достигаться
на некоторых режимах работы ЖРД без дожигания;
• для удельных импульсов 0 ^ ф ТНА ^ 0,7, где нулевое
значение соответствует направлению истечения рабочего тела из
сопла выхлопного патрубка турбины ТНА перпендикулярно
скорости в выходном сечении сопла основной камеры.

190 Часть II. Теория неидеального теплового ракетного двигателя
Зависимость относительного снижения удельного
импульса ДУ фду (фу ТНА, ДтТНА) иллюстрирует рис. 15.3, где по оси
абсцисс откладывается Am ТНА, по оси ординат - Ф ду, а Ф ТНА -
параметр.
О 0,05 0,10 AwTHA
Рис. 15.3. Зависимость относительного снижения
удельного импульса ДУ без дожигания генераторного газа
от параметров системы подачи топлива
Уменьшение удельного импульса есть следствие неполного
использования располагаемой химической энергии части
топлива при существенно неоптимальном соотношении его
компонентов в газогенераторе рабочего тела турбины ТНА. Рост
относительного расхода топлива, подаваемого в газогенератор ТНА,
например при повышении давления в камере, приводит к
существенному уменьшению удельного импульса ДУ, не
компенсируемому увеличением удельного импульса основной камеры. Это
является одной из главных причин ограничения давления в
камере для ДУ ЖРД без дожигания генераторного газа.
Контрольные вопросы и задания
1. Что понимается под идеальным значением параметра камеры?
2. Дайте определение коэффициента удельного импульса камеры.
Обратите внимание на то, какие параметры идеальной и реальной
камер принимаются одинаковыми.
3. Что представляет собой коэффициент расхода сопла? Обратите
внимание на физические причины отличия значения этого
коэффициента от единицы.
4. Дайте определение характеристической скорости в камере и
рекомендации по ее применению.
5. Дайте определение расходного комплекса и рекомендации по его
применению.

Глава 15. Учет потерь в ракетном двигателе \9\_
6. Дайте определение коэффициента тяги и рекомендации по его
применению.
7. Дайте определение тягового комплекса и рекомендации по его
применению.
8. В чем суть коэффициента сопла? Обратите внимание на то, какие
параметры идеального и реального сопл принимаются одинаковыми.
9. Назовите причины различий значений удельного импульса камеры
и двигательной установки.
10. Как изменится (увеличится, уменьшится или не изменится)
пустотный удельный импульс двигательной установки с насосной системой
подачи, если привод насосов от газовой турбины заменить
электрическим приводом с тем же самым КПД?

Глава 16
Химические реакции и понятие
о равновесном составе гетерогенной смеси.
Основы термодинамического расчета
В ракетных двигателях на химическом топливе основной
и одновременно исходной составляющей в последовательности
энергопреобразований является выделение теплоты, которое
происходит в камере сгорания в результате химических превращений
и сопряженных с ними физических явлений тепло- и массопере-
носа. Понятие «химические превращения» включает химические
реакции и другие преобразования, при которых изменяется
состояние электронных оболочек атомов и не изменяются состав
и состояние ядер химических элементов. При этом в общем
случае образуется неравновесная гетерогенная, химически
активная, претерпевающая фазовые переходы среда - рабочее тело,
свойство и состояние которого характеризуются по меньшей мере,
минимальным набором величин: давлением /?*, температурой Т*,
кажущейся молекулярной массой |iK, показателем изоэнтропы п
или, в приближении идеального газа постоянного состава,
показателем адиабаты к.
Целью термодинамического расчета является получение
характеризующих рабочее тело количественных данных,
необходимых и достаточных для выполнения расчетов по определению
параметров и характеристик ракетных двигателей.
Предметом термодинамического расчета в общем случае
являются процесс и результат перехода некоторой среды от
начального состояния равномерно распределенных по объему
компонентов ракетного топлива к конечному состоянию в виде
находящихся в заданной степени динамического равновесия
нагретых до относительно высокой температуры гетерогенных
составляющих с преобладанием газовой фазы. В такой трактовке
косвенно содержится допущение, что химические реакции идут
в кинетическом режиме.
Одно из основных положений химической термодинамики
определяет зависимость результата превращений в химически
активной среде только от ее исходного состава и параметров

Глава 16. Основы термодинамического расчета 193
начального и конечного состояний. Причем наличие и
последовательность промежуточных стадий значения не имеют.
В связи с этим предмет термодинамического расчета можно
представить и без процесса перехода от одного относительно
устойчивого состояния к другому, т. е. оставив только
равновесную химически активную гетерогенную среду как результат
завершения всех возможных химических превращений. При этом
становится неважным, достаточно ли велико выделяемое на их
реализацию время или химические превращения протекают со
скоростями, близкими к бесконечно большим скоростям.
Другими словами, время может быть исключено как аргумент, и из
описания совокупного рабочего процесса исключается
собственно кинетика химических процессов.
В основе представлений о процессах, протекающих в
высокотемпературных химически активных средах, лежит газофазная
химическая реакция (как преобладающая).
Только часть относительно простых по составу химических
соединений можно рассматривать как результат элементарной
химической реакции, т. е. реакции, протекающей за одно
столкновение реагентов, например
ОН + О -► 02 + Н
Образование воды из молекул кислорода и водорода
2Н2 + 02^2Н20 (16.1)
проходит, напротив, ряд стадий с образованием таких
промежуточных продуктов реакции, как О, Н, ОН, Н02. При этом
возможно протекание преобразований не последовательно, а в
режиме параллельных реакций, расчет кинетических характеристик
которых в настоящее время не вполне достоверен для условий,
характерных для ракетных камер.
Кроме того, многие соединения образуются в результате
столкновения трех и более частиц-реагентов, одна из которых
выполняет функцию катализатора и в итоге не изменяет своего состава.
Причем одно и то же соединение может быть результатом разных
реакций. Например, молекула воды может образоваться как
результат по меньшей мере трех разных процессов:
Н + ОН + Н2 -> Н20 + Н2

194 Часть II. Теория неидеального теплового ракетного двигателя
н + он + о2 -► н2о + о2
н + он + н2о -> н2о + н2о
где Н2, 02, Н20 выступают как каталитические частицы.
Возможны, хотя и менее вероятны, также реакции при
столкновении четырех частиц.
Большинство химических превращений может протекать в
направлении, обратном обозначенному стрелкой в уравнении
реакции. Такие реакции называются обратимыми. Например,
обратимой является реакция диссоциации - рекомбинации молекулы
воды, которую, если опустить промежуточные продукты и
каталитические частицы, можно записать в виде
Н2О»Н2 + 0,5О2 (16.2)
Отметим в качестве полезной справочной информации
следующее.
Отсутствие знака равенства между частями уравнения с
двойной стрелкой делает, вообще говоря, необязательным равенство
числа грамм-атомов одноименных элементов в левой и правой
частях уравнения (которое формально не является уравнением).
Если коэффициенты перед слагаемыми выбраны исходя из
сохранения числа грамм-атомов одноименных элементов, то
такая запись называется стехиометрическим уравнением или просто
уравнением химической реакции. По сути, это уравнение
однонаправленной реакции, по завершении которой концентрация
элементов, отображенных в его левой части, становится близкой
к нулю, а концентрация элементов правой части установится в
соответствии с их стехиометрическими коэффициентами и
молярными массами.
В частности, как следует из методики расчета свойств газовых
смесей в приближении идеального газа, коэффициент перед
обозначением молекулы (атома) соответствует числу молей данного
газа в смеси, а отношение этого коэффициента к сумме
коэффициентов перед всеми слагаемыми правой части уравнения равно
объемной или, что то же самое, мольной доле данной составляющей
в смеси продуктов реакции. По существу, используя уравнения
связи, мы принимаем допущение: компоненты смеси имеют
одинаковую температуру, а газообразные составляющие
подчиняются уравнению состояния идеального газа.

Глава 16. Основы термодинамического расчета 195
Более подробные, необходимые для усвоения принципов и
методик термодинамического расчета сведения о соотношении
массовых, объемных (мольных) долей компонентов и кажущихся
свойствах газовых смесей приведены в написанном
преподавателями МГТУ им. Н.Э. Баумана учебнике по технической
термодинамике1.
Поскольку реагенты, обладающие разными энергиями,
участвуют в хаотичном движении, то и столкновение, результатом
которого является химическая реакция, и образование продукта реакции
имеют вероятностный характер и, следовательно, могут быть
описаны некоторыми средними наиболее вероятными
величинами, изменяющимися во времени с приближением каждой из них
к своему значению, соответствующему стационарному состоянию.
По достижении стационарного состояния скорости прямых и
обратных реакций выравниваются. И хотя реакции идут,
усредненные по объему концентрации компонентов не изменяются.
Это состояние называется динамическим равновесием химически
активной системы {Vita mota constat)2.
Поскольку процессы рассматриваются вне связей с внешними
воздействиями, естественным предположением является подход
к анализу поведения системы как изолированной и ограниченной.
Тогда в соответствии со вторым законом термодинамики
энтропия S рассматриваемой системы в процессе установления
равновесия должна возрастать до некоторого значения,
соответствующего стационарному состоянию.
Если химическая реакция протекает без воздействия
катализатора, то время т, необходимое для установления химического
равновесия для конкретной обратимой реакции, зависит от температуры
и давления, но наиболее существенно - от температуры вследствие
экспоненциального характера взаимосвязи скорости U и
температуры Г химической реакции, отражаемой зависимостью Аррениуса:
_в_
U = Ae~T9
где А, В - константы для конкретной химической реакции.
Техническая термодинамика: учебник для машиностроительных
специальностей вузов / В.И. Крутов, СИ. Исаев, И.А. Кожинов и др.;
под ред. В.И. Крутова. 3-е изд., перераб. и доп. М.: Высш. шк., 1991.
2 «Жизнь подвижная стабильна» - изречение древнегреческого
философа Аристотеля.

196 Часть II. Теория неидеального теплового ракетного двигателя
Например, для реакции С02 + Н2 <=> СО + Н20 при постоянном
давлении около 0,4 МПа и росте поддерживаемой подводом
теплоты извне температуры в зоне реакции от 1 000 до 1 500 К
т уменьшается от 0,63110~6 до 0,925 10"8 с, тогда как идущая
преимущественно с разложением реакция 2NH3 => N2 + 3H2 при
этих же условиях требует для своего завершения времени от
нескольких часов при температуре 1 000 К до нескольких
миллисекунд при температуре 1 500 К.
Как правило, большие значения времени установления
равновесия имеют реакции, идущие с образованием конденсированной
фазы. Например, термическое разложение метана с образованием
водорода и сажи при температуре 1 000 К в основном
завершается за 10 ч, а при температуре 1 500 К - за 12 мс.
Описанные процессы применительно к реакции (16.1),
проходящей в газовой фазе, иллюстрирует рис. 16.1, где
представлено предполагаемое изменение во времени объемных долей
(концентраций) водорода, кислорода и водяного пара при
предположении отсутствия диссоциации водяного пара-реакция (16.3)
идет только справа налево:
Н20-Н2 + 1о2 (16.3)
Система из начального неравновесного состояния (объемные
доли водяного пара, водорода и кислорода составляют 0; 66,6
и 33,3 % соответственно) переходит в конечное равновесное
состояние за некоторое время т,, достаточное для завершения про-
Рис. 16.1. Изменение во времени объемных долей (концентраций)
водорода, кислорода и водяного пара при образовании воды из стехио-
метрической смеси по условно необратимой реакции (16.3)

Глава 16. Основы термодинамического расчета 197
межуточных и конечной реакций образования воды, содержание
паров которой достигает 100 %.
Если бы реакция шла только по схеме
Н20-+Н2 + 1о2 (16.4)
объемные доли составляющих смеси изменялись бы во времени
(рис. 16.2), и система пришла бы в состояние равновесия за
время т2 Ф ij в общем случае. Начальные концентрации для случая,
иллюстрируемого рис. 16.1, совпадают с итоговыми для
варианта, представленного на рис. 16.2.
Рис. 16.2. Изменение во времени объемных долей (концентраций)
водорода, кислорода и водяного пара при термической диссоциации воды
по условно необратимой реакции (16.4)
~Asl
У' ^^тах |
(0,661 ^г
(о.ззУ/ "^
Дь
\h^-~^\
у^г\кго
^
*»
Т
Рис. 16.3. Изменение во времени объемных долей (концентраций)
водорода, кислорода и водяного пара при образовании воды из стехиометри-
ческой смеси кислорода и водорода и одновременной термической
диссоциации воды по обратимой реакции диссоциации-рекомбинации (16.5)

198 Часть II. Теория неидеального теплового ракетного двигателя
В отличие от вариантов, приведенных на рис. 16.1 и 16.2 как
предельных из всех возможных, наиболее вероятен некоторый
промежуточный вариант Н20 <=> Н2 + 02, когда одновременно
с образованием воды происходит диссоциация некоторой ее
массовой доли на газообразные водород и кислород по реакции (16.4).
Этот вариант показан на рис. 16.3.
Число х, равное массовой доле диссоциирующей воды от всей
воды, которая образовалась бы, если диссоциации воды не было,
т. е. по реакции (16.3), называется степенью диссоциации,
зависящей в общем случае от температуры и давления.
Рис. 16.3 иллюстрирует объемные доли для х = 0,5:
Н2 + |02-(1-1)Н20 + 1(Н2 + 102) (16.5)
При этом объемные доли водорода и кислорода уменьшаются
от начальных 66,6 и 33,3 % до 40 и 20 % соответственно, а
концентрация водяного пара увеличивается от нуля до равновесной
концентрации 40 %. Время перехода от начального состояния
к состоянию динамического равновесия равно ту
Отметим, что если результат реакции задан в виде суммы
молекулярных формул с определенными коэффициентами перед
каждой суммой, как в реакции (16.5), то это означает задание
массового и объемного составов среды. Исходные реагенты в
общем случае всегда должны находиться в продуктах реакции, но
в концентрациях, существенно отличных от начальных.
Коэффициенты перед молекулярными формулами соединений
означают число молей этих соединений в смеси, а сумма этих
коэффициентов равна числу всех молей в продуктах реакции для
заданных исходного состава и количества реагентов.
Применительно к реакции (16.5) с учетом принятого
допущения о газообразной составляющей как идеальном газе это
означает следующее. В результате сгорания двух массовых частей
(например, 2 кг) водорода в 16 массовых частях (16 кг)
кислорода при некоторой температуре в продуктах реакции установятся
мольные доли и численно равные им объемные концентрации:
водорода
гн = 0,5/(0,5 + 0,5 + 0,25) = 0,4;

Глава 16. Основы термодинамического расчета 199
кислорода
r0i = 0,25/(0,5 + 0,5 + 0,25) = 0,2;
сухого или перегретого водяного пара
rHiQ = 0,5/(0,5 + 0,5 + 0,25) = 0,4.
Соответствующие массовые концентрации в долях или
процентах составят:
для водорода
СН2 = 0,5-2/(2 + 16) = 1/18 = 0,055 (5), т. е. 5,5 (5) %;
для кислорода
С02 = 0,25-32/(2 + 16) - 8/18 = 0,44 (4), т. е. 44,4 (4) %;
для водяного пара
СНз0 = 0,5 • 18/(2 + 16) = 0,5, т. е. 50 %.
Массовые концентрации в молях на 1 кг смеси:
для водорода
СН2 = 0,5-1 000/(2 + 16) = 27,77 (7);
для кислорода
С02 = 0,25-1 000/(2 + 16) = 13,88 (8);
для водяного пара
СНз0 = 0,5-1 000/(2 + 16) = 27,77 (7).
Поскольку равновесному состоянию соответствует
максимальное значение энтропии S системы, за это же время т3 энтропия
возрастает и достигает максимального значения S = Smax.
Если считать, что начальная концентрация компонентов во
всех трех рассмотренных случаях возникала мгновенно и являлась
как бы возмущением предшествующего равновесного состояния,

200 Часть II. Теория неидеального теплового ракетного двигателя
то характерные значения времени т,, т2 и т3 представляют собой
значения времени реакции системы, необходимого для перехода
в новое равновесное состояние, т. е. так называемые значения
времени релаксации.
Поскольку для заданного суммарного давления существует
очевидная однозначная, хотя и строго справедливая только для
смесей идеальных газов, связь между парциальными
давлениями газообразных компонентов и относительной объемной
(мольной) долей, состав газовой смеси, в том числе и ее динамически
равновесное состояние, можно определить или задать через
парциальные давления. В общем случае подобная реакции (16.2)
сопряженная реакция диссоциации-рекомбинации при
произвольной степени диссоциации может быть представлена как
комбинация прямой реакции диссоциации сложной молекулы
по схеме
*1-АаВьСс -*2-Аа1Вы +*3-ВЬ2Сс1 (16.6)
где XI, Х2, ХЪ - стехиометрические коэффициенты
соответствующего уравнения реакции полной диссоциации, и обратной по
направлению реакции рекомбинации
*2-AaIBbl +^3-Bb2CcI -*l-AaBbCc (16.7)
записанной по тем же правилам, что и (16.6).
Скорость прямой реакции U, выраженной (16.6), по закону
действующих масс имеет вид
^прям^ЛААС/1, (16-8)
где [АаВьСс] - концентрация диссоциирующего компонента АаВьСс,
выраженная, например, в молях на килограмм; XI - стехиоме-
трический коэффициент в (16.6); к м - коэффициент скорости
этой реакции при данной температуре.
Скорость обратной реакции £/об по (16.7) в соответствии
с законом действующих масс
^браТ = ^обраТ[Аа1ВЬ1Р[ВЬ2Сс1]" (16.9)

Глава 16. Основы термодинамического расчета 20J_
где в квадратных скобках приведены концентрации реагентов
в тех же единицах, что и в (16.8); Х2, ХЪ - показатели степени,
численно равные стехиометрическим коэффициентам (16.7); ко6 -
коэффициент скорости реакции образования соединения АаВьСс
по реакции (16.7) при данной температуре.
Состоянию, в котором концентрации всех реагентов не
изменяются во времени, отвечает равенство скоростей идущих
одновременно прямой (16.6) и обратной (16.7) реакций, т. е.
^прям = ^обрат' что можно записать с учетом (16.8) и (16.9) в
следующем виде:
^прям^а^^с] — ^обрат L^al^bl J L^b2^cl J •
Перенеся в одну часть сомножители, содержащие только
концентрации реагентов, и обозначив отношение коэффициентов
скоростей прямой и обратной реакций К, значение которого для
данной сопряженной реакции зависит только от температуры,
получим
^(г) = [Аа,Вы] [ВЬ2Сс|]
[A.BbCcf
Отметим произвольность расположения в правой или левой
части (16.10) концентраций продуктов прямой или обратной
реакции и следующую из этого допустимую произвольность
записи для К(Т). Однако первоначально выбранный произвольно
порядок концентраций должен соблюдаться и в дальнейшем для
сохранения однозначности выводов.
Выражая молярные концентрации реагентов через их
парциальные давления и преобразуя (16.10) так, чтобы в правой части
остались только парциальные давления, получим выражение для
константы равновесия:
хг хъ
Кр = "УBb,Ccl , (16.11)
/\вьСс
где нижний индекс «р» означает, что данная, зависящая только
от температуры, константа равновесия реакции однозначно
определяет связь между парциальными давлениями составляющих
химически активной газовой смеси, находящейся в динамическом

202 Часть II Теория неидеального теплового ракетного двигателя
равновесии. Например, для реакции (16.4) константа равновесия
К. согласно (16.11), имеет вид
Рн2У[р^
кр= •
Рн2о
Отметим, что аналогично константам равновесия,
связывающим парциальные давления реагирующих составляющих
химически активных газов, вводятся и используются константы
равновесия, характеризующие состав таких газовых смесей через
объемные (мольные) доли составляющих. Но по ряду причин чаще
используются константы равновесия, связывающие стационарное
динамическое состояние и соотношение парциальных давлений.
Выражениям (16.10) и (16.11) соответствует следующая
физическая интерпретация: в состоянии динамического равновесия
концентрации всех соединений, составляющих химически
активную систему, должны находиться в однозначно определенном
соотношении, зависящем от температуры. При этом соотношении
между составляющими систему соединениями энтропия всей
системы принимает максимальное значение.
Обратим внимание на то, что логика введения константы
равновесия обусловливает следующие выводы:
• значение константы зависит от единицы измерения
подставляемых в расчетное выражение парциальных давлений;
• возможная с точки зрения закона сохранения массы вещества
произвольность записи сопряженных химических реакций
требует использования известных значений К только для той
химической реакции, только при той же записи условно исходных
и получаемых веществ и только при тех же, а не при кратных
значениях стехиометрических коэффициентов, при которых
обрабатывались используемые данные зависимости константы
равновесия К от температуры.
Например, неэквивалентными в данном смысле являются
реакции
н2о = н2 + 1о2 и н2 + 1о2 = н2о
так как записанные для них константы равновесия будут взаимно
обратными величинами.
В данном контексте неэквивалентны записи одного и того же
процесса:

Глава 16. Основы термодинамического расчета 203
Н20»Н2 + -02 и 2Н2Оо2Н2 + 02
поскольку в (16.11) используются разные стехиометрические
коэффициенты.
Очевидна также зависимость числового значения константы
равновесия от абсолютных значений парциального давления, т. е.
от выбора единиц его измерения, поскольку разные
стехиометрические коэффициенты перед слагаемыми в разных частях
уравнения реакции дают разные степени в числителе и знаменателе, не
приводящие к сокращению и масштабированию значений давлений.
Зависимости констант равновесия основных химических
реакций от температуры приводятся в большинстве литературных
источников в виде таблиц, полученных по сложным расчетно-
теоретическим методикам или обработкой экспериментальных
данных, где парциальные давления выражаются в физических
атмосферах.
Поскольку при выводе (16.11) не учитывались особенности
рассмотренной в качестве базовой именно сопряженной реакции
диссоциации-рекомбинации в газовой смеси, введенные понятия
о константах равновесия можно формально относить и
использовать при описании динамического равновесия химических
превращений, определенных в начале этой главы.
К таким превращениям относится термическая ионизация -
вероятностное явление исхода электрона при высокой
температуре из электронной оболочки электрически нейтрального атома
или молекулы и превращение потерявшего электрон атома
(молекулы) в положительно заряженный ион, идущее одновременно
с образованием из свободных электронов так называемого
электронного газа с некоторым парциальным давлением/?.
Присоединение электрона к электронной оболочке приводит к
восстановлению электрической нейтральности атома или молекулы. В этом
смысле говорят о сопряженных реакциях
ионизации-нейтрализации, например:
ионизация атома
Li <^> Li+ + e~
ионизация молекулы
N0 о NO+ + e~
(16.12)

204 Часть II. Теория неидеального теплового ракетного двигателя
Число ставших свободными электронов определяет заряд иона,
например:
А1«АГ+ + 2*Г (16.13)
или
А1 <=> АГ++ + Зё~ (16.14)
В связи с этим вводят также понятие кратности ионизации:
А1++ - двукратно ионизированный атом алюминия, А1+++ -
трехкратно ионизированный атом алюминия.
Очевидно, что для электрически изолированной системы
суммарный электрический заряд при этом не изменяется. Это
утверждение представляет собой формулировку закона сохранения
электрического заряда.
Технически существенная степень термической ионизации
продуктов сгорания ракетного топлива достигается, как правило,
при температурах, при которых ионизируемые компоненты
находятся в газовой фазе, что позволяет для описания состояния
динамического равновесия сопряженных реакций
ионизации-нейтрализации применять аппарат констант равновесия, косвенно
принимая допущение о применимости уравнения состояния
идеального газа и к электрически заряженным частицам.
Для реакции (16.12) константа равновесия запишется как
К _Рт+Ре~
Р Pno
Для реакций (16.13) и (16.14), различающихся степенью
ионизации атомов алюминия, константы равновесия имеют
соответственно следующий вид:
к = Ptf+P)-
Р Рм
и
К =РМ^Р1-
Р Рм
Поскольку энергия (потенциал) ионизации определяется в
условиях камеры сгорания ракетного двигателя в основном темпе-

Глава 16. Основы термодинамического расчета 205
ратурой, то и соответствующая константа равновесия
рассматривается как зависящая непосредственно только от температуры, т. е.
условия, установленные для химических реакций, не нарушаются.
Отметим, что степень ионизации рабочего тела ракетного
двигателя обычно настолько незначительна, что возникающим
механизмом электрического взаимодействия между
заряженными частицами пренебрегают без заметного влияния на точность
расчетов. В специальных случаях при описании процессов
исходят из представления о рабочем теле как о плазме, но это не
является предметом изучения настоящего курса.
Аппарат констант равновесия, введенный для описания
равновесия в газовых смесях, может быть условно распространен и на
гетерогенные системы, в которых конденсированная
составляющая занимает в смеси газов пренебрежимо малую объемную долю
и не вносит существенного вклада в давление потока
непосредственно, но определяет слагаемое в суммарном давлении за счет
давления паров конденсированного компонента. Причем
считается, что динамическому химическому равновесию
соответствует и межфазное равновесие, т. е. за давление паров принимается
давление насыщенного пара жидкой или твердой составляющей ps
при данной температуре Т. При этом сохраняется такая же форма
записи, как для константы равновесия, и не нарушаются
зависимость значения аналога константы равновесия только от
температуры и соответствие принципу максимума энтропии.
Например, для реакции
С02 <=> С + 02
где диоксид углерода и кислород - газы, а углерод находится в
твердом состоянии (сажа), аналог константы равновесия
*^ps насыщ ?
Рсог
или, если ввести давление насыщенных паров углерода, зависящее
только от температуры, в значение аналога константы равновесия,
" Рсо2'

206 Часть II. Теория неидеального теплового ракетного двигателя
При этом К s насыщ и К не являются, строго говоря,
константами равновесия гетерогенной реакции и характеризуют ее
только в первом приближении. Приемлемость такого приближенного
описания равновесия гетерогенной реакции подтверждается
практикой термодинамических расчетов и удовлетворительным
согласованием экспериментальных и расчетных данных.
Обратим внимание на весьма важное соображение:
представление о состоянии динамического равновесия химически активных
систем с помощью констант равновесия по результатам при-
менения эквивалентно представлению о максимальном значении
энтропии изолированной системы, находящейся в стационарном
состоянии. При этом описываемая находящаяся в динамическом
равновесии химически активная среда реагирует на внешние
возмущения (изменение температуры или давления) в соответствии
с принципом Ле Шателье - Брауна. Согласно этому принципу,
внешние возмущения вызывают в системе процессы,
стремящиеся компенсировать внешние воздействия и перевести систему
в новое состояние равновесия.
Следует иметь в виду, что при совместном воздействии
изменений температуры и давления более интенсивно действует
температура, чем давление, так как влияние температуры на
скорость химических реакций проявляется через экспоненциальную
зависимость (по закону Аррениуса). По крайней мере, при
одновременном снижении давления и температуры при движении по
соплу реакция системы определяется именно превалирующим
действием снижения температуры. Противоположное действие -
понижение давления - не влияет существенно на реакцию системы.
Применение принципа Ле Шателье - Брауна в сочетании с
аппаратом констант равновесия позволяет качественно, т. е. на
уровне выявления тенденции, анализировать априори влияние
внешних факторов на состав и свойства таких химически
активных сред, как продукты сгорания ракетных топлив.
Проанализируем, например, зависимость кажущейся
молекулярной массы продуктов сгорания кислородно-водородного
топлива от давления и температуры в камере сгорания при
постоянном заданном исходном соотношении компонентов.
Запишем стехиометрическую реакцию горения в виде
2 -л 2 2

Глава 16. Основы термодинамического расчета 207
Константа равновесия для данной реакции
Кр= Р"2° (16.15)
Ри2у1Ро2
Состав продуктов сгорания выражается при этом уравнением
реакции, аналогичным (16.5), но при переменном параметре X-
степени диссоциации молекул воды:
Н2 + 1-02 - (1 -*)Н20 + Х(Щ + 1-02) (16.16)
Обратим внимание на то, что отражающее закон сохранения
вещества уравнение (16.16) является тождеством при всех
имеющих физический смысл значениях степени диссоциации X из
диапазона значений 0 ^ X ^ 1. Но стабильному динамически
равновесному состоянию соответствует единственное значение
степени диссоциации.
Кажущаяся молекулярная масса
Шс = "
\-Х + Х\ 1 + -
откуда следует увеличение кажущейся молекулярной массы при
повышении степени диссоциации молекул воды или, что то же
самое, при повышении массовой доли воды.
Повышение давления должно вызвать изменения в системе,
компенсирующие повышение давления, т. е. при той же массе
продуктов сгорания значение |ик должно увеличиться, а число
молей - уменьшиться, что соответствует увеличению массовой
доли недиссоциированных молекул воды (уменьшится значение X)
и росту парциального давления водяного парарн 0. Как ответ на
внешнее воздействие кратковременно возрастет интенсивность
(скорость) прямой реакции
н2 + 1о2^н2о
при неизменности скорости обратной реакции
н,о-»н, + -о,
2 2^2

208 Часть II. Теория неидеального теплового ракетного двигателя
Затем несколько возрастет и скорость обратной реакции, а
скорость прямой реакции снизится настолько, что скорости
сопряженных - прямой и обратной - реакций сравняются. Система
придет в новое состояние динамического равновесия при новом
давлении и при новой увеличенной (по сравнению с прежним
равновесным состоянием) массовой концентрацией водяного пара
и уменьшенной степени диссоциации X.
Отметим отсутствие влияния давления на равновесный состав
реагентов, если состояние равновесия обеспечивается балансом
прямой и обратной реакций, проходящих без изменения числа
молей газообразных компонентов, например аналогично
реакциям N2 + 02 <-» 2NO или С02 + Н2 <-► СО + Н20
Исследуем влияние температуры на равновесный состав
химически активных продуктов сгорания на примере среды,
содержащей водяной пар и продукты его термической диссоциации,
по уравнению реакции (16.2).
Пусть в состоянии исходного равновесия за счет подвода
теплоты извне повысилась температура. Рассмотрим ответные
изменения как реакцию системы.
Согласно принципу Ле Шателье - Брауна, в системе должны
интенсифицироваться процессы, идущие с поглощением теплоты,
например должна ускориться эндотермическая реакция
диссоциации молекулы водяного пара и увеличиться степень
диссоциации X. При этом уменьшится концентрация водяного пара
(снизится парциальное давление рн 0) и несколько уменьшится
скорость прямой реакции; система перейдет в новое положение
динамического равновесия, соответствующее новым измененным
внешним условиям.
На качественном уровне можно сформулировать следующие
выводы:
• повышение температуры приводит к увеличению степени
термической диссоциации, а снижение температуры ведет к
подавлению диссоциации и уменьшению ее степени;
• рост давления, напротив, вызывает уменьшение степени
диссоциации, тогда как понижение давления способствует
увеличению степени диссоциации.
Аналогично изменяется состав продуктов сгорания топлива.
Например, если изменять суммарное давление/^ продуктов
сгорания 2 кг водорода в 16 кг кислорода при сохранении их
температуры, равной 3 200 К, то будут изменяться суммарное число
молей М1? парциальные давления р. и число молей М. газообразных

Глава 16. Основы термодинамического расчета 209
составляющих в зависимости от суммарного давления. Численно
для преобладающих составляющих эту зависимость отражают
данные, представленные в табл. 16.1.
Таблица 16.1. Влияние давления на состав продуктов сгорания
МПа
0,02
0,1
1,0
19,0
Число молей на 1 кг
продуктов сгорания
мн2о
12,614
19,855
25,174
27,720
К
"2
5,6315
3,4369
1,2549
0,3019
%
11,400
12,485
13,322
13,985
Щ
65,069
53,559
47,401
45,145
Парциальное давление, МПа
Рщо
0,003877
0,037072
0,531094
11,66570
Рн2
0,001731
0,006417
0,026476
0,127082
Ро2
0,003504
0,023311
0,281041
5,885460
Данные, иллюстрирующие изменение состава преобладающих
составляющих продуктов сгорания того же топлива, но при
постоянном суммарном давлении 0,101325 МПа (1 атм) в
зависимости от температуры Г (в Кельвинах), приведены в табл. 16.2,
в девятой графе которой указаны значения константы равновесия
К реакции диссоциации-рекомбинации воды (16.2), вычисленные
по формуле К =———-, где парциальные давления измерены
Рщо
в атмосферах.
Таблица 16.2. Влияние температуры на состав продуктов сгорания
г, к.
3200
3400
3600
5000
Число молей на 1 кг
продуктов сгорания
мн2о
19,90
15,11
9,857
0,0189
К2
3,419
4,991
6,113
0,670
м02
12,49
11,58
10,24
0,571
"i
53,50
60,26
69,79
115,1
Парциальное давление, МПа
Рн2о
0,03769
0,02540
0,01431
1,6710-
5
Рн2
0,00648
0,00839
0,00887
59-Ю-5
Ро2
0,02366
0,01948
0,01486
50,28-10"5
К
р
0,0828
0,1444
0,2368
2,4812
Отметим, что при температуре 5 000 К существенный вклад
в суммарное давление вносят продукты диссоциации воды и
двухатомных молекул водорода и кислорода, поэтому данные табл. 16.2

210 Часть II. Теория неидеального теплового ракетного двигателя
можно оценивать как ориентировочные и отражающие
закономерности только качественно.
Приведенное представление об идущих в камере сгорания
завершающих процессах преобразования химической энергии
топлива в тепловую энергию продуктов сгорания позволяет
сформулировать принципы создания математической модели этих
процессов. Поскольку предметом термодинамического расчета
является результат этих процессов, то их свойства должна
отражать математическая модель собственно термодинамических
расчетов. Базовый термодинамический расчет выполняется для
продуктов полного сгорания, образующихся в стационарных
условиях в энергоизолированной изобарной камере сгорания в
результате завершения всех процессов взаимодействия компонентов,
приводящих систему в равновесное состояние.
Математическая модель энергоизолированного явления
должна включать как функционально обязательную часть уравнение
сохранения энергии, учитывающее все виды энергии,
существенные в описываемом процессе. В данном случае это химическая,
тепловая и механическая энергии. Причем энергия единицы
массы введенного в камеру топлива сохраняется, перераспределяясь
между ее различными видами. При этом для изобарной камеры
сгорания кинетическая энергия пренебрежимо мала вследствие
равенства нулю скорости продуктов сгорания.
Закон сохранения массы вещества в рамках принятой
математической модели процессов выражается явно в соотношениях
постоянства содержания химических элементов в одном и том
же количестве топлива и продуктов сгорания. Ионизация, хотя
и уменьшает массу химических элементов, одновременно на то
же значение увеличивает массу электронного газа в смеси.
В этих рассуждениях учитывается очевидное для
изолированных (энергетически, а значит, и электрически) систем условие
электронейтральности системы в целом.
При допущении возможности описания свойств газовых
составляющих смеси уравнением состояния идеального газа без
учета объемной доли конденсированной фазы справедлив закон
Дальтона.
Поскольку отвечающая перечисленным законам химически
активная система может находиться во многих состояниях, из
которых стационарным является только одно, математическая
модель обязательно дополняется соотношениями, отражающими
принцип стационарности или равновесности. Это могут быть или

Глава 16. Основы термодинамического расчета 211
соотношения, отражающие условия максимума энтропии либо
экстремума других, включающих энтропию термодинамических
комплексов, или эквивалентные в данном контексте зависимости
для констант равновесия.
Математическое выражение составляющих основу
математической модели законов сохранения с учетом конкретных
представлений об отражаемых физических явлениях рассмотрено
в следующих главах.
Контрольные вопросы и задания
1. Что общего у диффузионного и кинетического режимов химической
реакции и в чем их различие?
2. Какие химические реакции называются обратимыми?
3. Какое состояние химически активной среды называется
динамическим равновесием?
4. От чего зависит время, необходимое для установления
динамического равновесия (время релаксации) смеси химически активных
газов, нарушенного, например, скачкообразным изменением
температуры или давления?
5. Дайте определение константы равновесия обратимой химической
реакции.
6. Какие допущения следует принять для описания состояния смеси
химически активных газов с помощью констант равновесия?
7. Для выбранной химической реакции приведите пример расчетного
выражения константы равновесия через парциальные давления
компонентов или через их молярные (объемные) концентрации.
8. От каких основных параметров зависит значение константы
равновесия? Сформулируйте принцип Ле Шателье - Брауна и на его
основе объясните эти зависимости.
9. Обоснуйте возможность приближенного описания гетерогенных
химических реакций и термической ионизации (которые могут быть
формально отнесены к химическим превращениям) с
использованием аппарата констант равновесия, записанных через парциальные
давления газов.
10. Как изменяется энтропия смеси химически активных компонентов
в течение времени релаксации, т. е. при переходе из
неравновесного состояния к равновесному стационарному состоянию?

Глава 17
Термодинамический расчет.
Запись закона сохранения массы вещества
через элементный состав топлива
и парциальные давления компонентов
продуктов сгорания
Один из фундаментальных законов - закон сохранения массы
вещества - входит в систему связей, описывающих в
термодинамическом расчете результат преобразования химической энергии
топлива в тепловую энергию продуктов сгорания. Выбор
конкретных форм записи этого закона из множества эквивалентных
обусловлен особенностями термодинамических процессов в ракетных
двигателях и отражающего их математического аппарата,
применяемого при термодинамических расчетах. В частности, высокая
температура в камере сгорания позволяет не учитывать при
термодинамических расчетах непосредственно исходный состав
компонентов топлива: химические молекулярные и структурные
формулы, степень полимеризации, гидратации, взаиморастворимости,
фракционный и фазовый состав и другие физико-химические
особенности, во многом определяющие эксплуатационные свойства
топлива. Это обусловлено тем, что в процессе преобразования
химической энергии в тепловую компоненты топлива
претерпевают нагрев от низких температур (20...400 К) хранения в баке до
высоких температур (1 500...4 000 К) в зоне пламени. При высоких
температурах результат химических процессов определяется
балансом химически активных составляющих, в большинстве своем
не существующих при хранении топлива. При этом
физико-химические свойства компонентов топлива не проявляются
непосредственно, но косвенно влияют на достижимую равновесную
температуру за счет вносимой химической энергии.
Такая особенность позволяет представить закон сохранения
массы вещества как идентичность элементного состава топлива
и продуктов его сгорания, т. е. число грамм-атомов конкретных
химических элементов в 1 кг топлива и в 1 кг образующихся
продуктов сгорания одно и то же, что можно записать в виде
системы уравнений

Глава 17. Термодинамический расчет. Закон сохранения массы 213
L yJ 1 кг топлива L у-" 1 кг продуктов сгорания' ^ ' '
где х. - входящий в состав топлива химический элемент; [х] -
число грамм-атомов этого элемента в 1 кг топлива и 1 кг
продуктов сгорания.
При этом 1 ^ j ^ я, где п - число химических элементов,
входящих в состав топлива, и число уравнений. Левые части
уравнений системы (17.1) выражаются через известные параметры
топлива, правые - через известные и неизвестные, определяемые
термодинамическим расчетом параметры продуктов сгорания.
Система уравнений (17.1) представляет собой условную
формулу состава топлива, записанную в виде, аналогичном
молекулярной химической формуле, но с произвольной условной
молекулярной массой. Если условная молекулярная масса выбирается
равной 1 000, то такая условная формула называется удельной
формулой. Например, молекулярной формуле гидразина N2H4 с
молекулярной массой (j^ H ~ 32 соответствует удельная формула
N625H125 с условной молекулярной массой \л ~ 1 000.
В обозначениях, принятых при записи (17.1), удельная
формула гидразина имеет вид системы равенств
[N] = 62,5;
[Н] = 125.
Поскольку состав топлива принимается известным,
содержание конкретных химических элементов в нем является частью
условий однозначности задачи термодинамического расчета. Для
конкретной записи левой части каждого уравнения системы (17.1)
требуется методика расчета элементного состава топлива,
задаваемого через состав и соотношение его компонентов.
Из приведенного примера следует, что если топливо -
индивидуальное вещество, молекулярная или условная формулы
которого известны, то переход к удельной формуле заключается
в умножении ее коэффициентов на постоянный множитель с,
вычисленный по формуле
1000
с = - >
5>7V7

214 Часть II. Теория неидеального теплового ракетного двигателя
где ц. - атомная массау'-го элемента, кг/кмоль (или г/моль); v. -
числоу-х грамм-атомов в реальной или условной молекуле
топлива; п - число разноименных атомов в молекуле.
Отсюда следует задача получения условной формулы
многокомпонентного топлива, сводимой затем по приведенным
правилам к удельной формуле топлива. Очевидно, что удельная
формула отражает соотношение химических элементов в топливе и их
абсолютное содержание в 1 кг топлива, поэтому возможно
применение предлагаемой записи химических реакций для расчета
удельных формул. Например, получим удельную формулу
окислителя, содержащего 27 % тетраоксида азота N204, 72 % азотной
кислоты HN03 и 1 % воды.
Запишем условную химическую реакцию:
^N204 + Л2НЖ)3 + АъЩО = HhNnOo (17.2)
где А19А2,А3- коэффициенты, определяющие заданное
соотношение веществ, из которых состоит окислитель, в виде числа
молей составляющих в условном моле компонента; HhNnOo -
удельная формула компонента с условной молекулярной массой
|х = 1 000.
Очевидно, что при известных коэффициентах Ар А2 и Аъ
число грамм-атомов водорода, азота и кислорода определяется
соотношениями
h = A2\ +АЪ2\
п = Ах2+А2\\
о = А14 + А23 +АЪ\.
Значения коэффициентов А19 А2, А3 определим с учетом
исходных данных. Масса тетраоксида азота в 1 кг окислителя со-
270
ставляет 27 %, т. е. 270 г, тогда Ах = = 2,9348. Аналогично
^N204
720 10
А2 = = 11,43 и А3 = = 0,5555. Удельная формула окис-
ИНЖ>3 ^Н20
лителя примет вид H1254N1730O4658 или [Н] = 12,54, [N] = 17,30,
[О] = 46,58. Другими словами, если компонент задан массовыми
долями g. нескольких веществ, а для каждого /-го вещества
известна химическая или условная формула с известной молеку-

Глава 17. Термодинамический расчет. Закон сохранения массы 215
лярной массой ц/5 это означает, что число молей данного вещества
в условном моле компонента с условной молекулярной массой
ц = 1 000
М,-=1000^. (17.3)
По этой методике, исходя из состава воздуха (% об.): 78,09
азота, 20,95 кислорода, 0,93 аргона, 1,6*10"3 неона и 0,03
углекислого газа и соответствующей массовой доли (%) каждого
компонента: 75,53; 23,15; 1,28; 0 и 0,04 получена удельная формула
воздуха1: N53 91O1448Ar03204C001045, широко применяемого в
качестве окислителя.
Поскольку никаких ограничений на состав и химическую
природу реагентов условной химической реакции (17.2) не
накладывалось, аналогично можно получить удельную формулу топлива,
если известны соотношение компонентов и их химические или
условные (в том числе и удельные) формулы. Например,
рассчитаем коэффициенты удельной формулы ракетного топлива на
основе окислителя, состав которого задан в предыдущем примере, и
горючего, состоящего из 50 % (по массе) гидразина N2H4 и
несимметричного диметилгидразина (НДМГ) (CH3)2N2H2, если
расходы окислителя и горючего относятся как 2:1. Получим удельную
формулу горючего из уравнения условной химической реакции
AN2H4 + ^2(CH3)2N2H2 = CcrHh,Nn,
Согласно (17.3),
Л, = 1 000-0,5/(2-14+ 4-1)= 15,625;
А2= 1 000-0,5/(2-12 + 2-14+ 1-8) = 8,3333,
откуда по аналогии с примером для условной химической
реакции (17.2) получим
[Сг] = 16,666; [Нг] = 129,16; [Nr] = 47,916.
Термодинамические и теплофизические свойства продуктов
сгорания: в X т. Т. III. Справочник // под ред. В.П. Глушко. М.: ВИНИТИ
АН СССР, 1973. С. 482.

216 Часть II. Теория неидеального теплового ракетного двигателя
Тогда условная химическая реакция для топлива примет вид
г*^ 16,66^129,16^ 47,92 о*112,54^ 17,3^46,58 ~~
Cc,Hh.TNn.TOo.T
а коэффициенты условной (удельной) формулы при вычисленных
по (17.3) для массовых долей окислителя (0,6666) и горючего
(0,3333) в условных мольных долях Ао = 0,66 (6) и АГ = 0,33 (3)
составят
[Ст] = 5,555; [Нт] = 51,371; [NJ = 27,505; [От] = 31,1055.
Соотношение расходов компонентов топлива принято задавать
или в виде массового соотношения компонентов
кг -™°
тг
где то и тг - секундные массовые расходы компонента -
окислителя и горючего соответственно, или как произведение
т /я0'
где а - коэффициент избытка окислителя; Кт0 - стехиометриче-
ское (теоретическое) соотношение компонентов.
Стехиометрическое, или теоретическое, соотношение
компонентов Кт0 есть расчетное количество окислителя в килограммах,
необходимое и достаточное для окисления всех горючих
элементов, находящихся в 1 кг горючего и в самом окислителе, с
образованием оксидов при проявлении стандартных максимальных
валентностей химических элементов. Стандартные валентности
элементов А. приведены в табл. 17.1, где валентностям элементов
условно приписывается знак: например, валентностям элементов,
действующих в качестве горючего, приписывается знак «-»
(минус), а валентностям элементов, действующих как окислитель, -
знак «+» (плюс). Азот и гелий считаются инертными.
Приведенное в скобках в табл. 17.1 значение валентности
азота соответствует соединениям азота с бором BN, где азот
выступает в качестве окислителя. Валентность +2 серы как окислителя
проявляется по отношению к водороду в соединении H2S.
Из определения стехиометрического соотношения
компонентов следует, что горючие элементы окисляются до высших,

Глава 17. Термодинамический расчет. Закон сохранения массы 217
согласно табл. 17.1, стандартных валентностей: С02, Н20, MgO,
А1203, BeO, B203, S03, SF6, HF, HC1 и т. д.
Таблица 17.1. Стандартные валентности А. наиболее часто
входящих в состав ракетных топлив химических элементов
(в порядке возрастания атомной массы)
Элемент
Н
Не
Li
Be
В
С
N
Валентность
-1
0
-1
-2
-3
-4
0(+3)
Элемент
О
F
Mg
А1
Р
S
С1
Валентность
+2
+ 1
-2
-3
-5
-6 (+2)
+1
Стехиометрическому соотношению отвечает условная
химическая реакция окисления, например:
Н2 + К'т0О2 = Н20 (17.4)
N2H4 + ^'ЛЛо = 2Н20 + |N2 (17.5)
(CH3)2N2H2 + ^'moH7,94N19,84039,68 - 2C02 + (...) H20 + (...)N2
(17.6)
Здесь H2,02, N2H4, (CH3)2N2H2 - химические формулы; N20O40 -
условная формула, a H7 94N19 84039 68 - условная формула компонентов.
Оставляя перед формулой горючего коэффициент 1 и
подбирая коэффициенты перед другими слагаемыми так, чтобы
уравнять число грамм-атомов в левой и правой частях уравнения,
получим условные стехиометрические уравнения. Причем
коэффициент перед формулой окислителя имеет смысл мольного сте-
хиометрического коэффициента (1 моль окислителя/1 моль
горючего), зависящего не только от соотношения элементов
в компонентах, но и от формы записи их химических
молекулярных или условных (удельных) формул.
Если известно мольное стехиометрическое соотношение К'т0,
то стехиометрическое массовое соотношение может быть
рассчитано по формуле

218 Часть II. Теория неидеального теплового ракетного двигателя
Кто - Кт0
(17.7)
где |io - молекулярная масса окислителя; цг - молекулярная
масса горючего, соответствующая формулам, для которых
определено мольное стехиометрическое соотношение К'т0.
Отметим возможность применения в одном уравнении
условной химической реакции и химических и удельных (условных)
формул компонентов, как, например, в (17.4) - (17.6). Но, как
следует из определения стехиометрического соотношения
компонентов, при этом обязательным является баланс стандартных
валентностей элементов, действующих в качестве окислителя
и в качестве горючего. Например, для левых частей уравнений
(17.4) и (17.5) баланс выражается равенством
Iv,
+ КтО
ч/ = 1
( п Л
IV,
-о,
(17.8)
/о
где А;. - стандартная валентность /-го химического элемента; v. -
число грамм-атомов /-го элемента в условной или химической
формуле горючего, в которую входят т элементов; Д., v. и п - те
же величины для окислителя.
Из (17.8) следует расчетная формула для стехиометрического
мольного соотношения компонентов (число молей окислителя /
1 моль горючего):
Sv,
V — —
Л/я0 _ /
7 = 1
IV,
(17.9)
Из (17.9) с учетом (17.7) получим расчетную формулу для
стехиометрического соотношения компонентов (1 кг окислителя /
1 кг горючего):
Г т \
^о
к,
/wO
Цг
(17.10)
IV,
и-»
/о

Глава 17. Термодинамический расчет. Закон сохранения массы 219
Очевидно, что формулы (17.9) и (17.10) неприменимы в
случаях, когда окислитель представляет собой оксид, например воду,
у которой сумма стандартных валентностей входящих в нее
элементов равна нулю.
Однако вода выступает в качестве окислителя по отношению
к таким металлам, как алюминий, магний и др., и реагирует с ними
с образованием оксида металла и свободного водорода:
Me + K'm0H2O^...MevlOv2 + ... + ...H2
Здесь Me - обобщенное обозначение металла, валентность
которого определит конкретное число грамм-атомов металла (vl)
и кислорода (v2) в формуле оксида металла MevlOv2 и значение
мольного стехиометрического соотношения К'т0. Коэффициенты
в правой части уравнения рассчитываются для конкретных
металла и окислителя. В таких случаях стехиометрическое
соотношение компонентов рассчитывается непосредственно по
уравнению условной химической реакции. Например, для реакции
алюминия с водой
А1 + -Н90 = -АЦХ + -Н,
2 2 2 2 3 2 2
мольное стехиометрическое соотношение K'mQ = 1,5 моль/моль,
а массовое стехиометрическое соотношение компонентов,
согласно (17.7), рассчитывается по формуле
Hai 27
Из приведенных математических выкладок следует
возможность расчета содержания входящих в состав топлива химических
элементов в грамм-атомах на килограмм и однозначная
определенность левых частей системы уравнений (17.1).
Поскольку в математическую модель термодинамических
процессов в камере сгорания входит уравнение Дальтона
т
/ = 1
как равенство давления продуктов сгорания/^ сумме парциальных
давлений т газообразных составляющих р., представляется

220 Часть II. Теория неидеального теплового ракетного двигателя
целесообразным правые части системы уравнений (17.1) также
записать через парциальные давления:
Щ=АРх>Р2> —>Рр •••>/>«)•
Пусть известно содержание составляющих (моль/кг),
записанное как результат химической реакции, например:
100Н2 + 2502 = 10Н2О + 90Н2 + 20О2
где множители перед слагаемыми в правой части равны числу
молей воды, водорода и кислорода соответственно в 1 кг
продуктов сгорания. Тогда содержание водорода и кислорода в грамм-
молях на килограмм будет выражено в виде
[Н] = 10-2 + 90-2 = 200 и [О] = 101 + 20-2 = 50.
В общем виде содержание у'-го элемента в грамм-атомах на
килограмм
т
[Х]у=£м,у,.у, (17.11)
1 = 1
где М. - число молей /-го вещества в 1 кг продуктов сгорания;
vi . - число грамм-атомов у-го элемента в одном моле /-го
вещества; т - количество веществ (соединений), содержащих в своем
составеу-й элемент.
Выразим число молей в 1 кг /-го компонента М. с
молекулярной массой \л. через его парциальное давление р. при известном
суммарном давлении рГ Для смеси к идеальных газов
кажущаяся молекулярная масса ^ определяется соотношением
к
fe= — , (17.12)
Ръ
а объемное содержание /-го газа г. выражается числом молей
(мольной концентрацией) М. и парциальным давлением р.:
г,--*--*-. (17.13)

Глава 17. Термодинамический расчет. Закон сохранения массы 221
Число молей всех веществ в 1 кг
И;--1-™. (17.14)
Hz
С учетом (17.12) и (17.14) из (17.13) определим
M = pi—k . (17.15)
Подставив (17.15) в (17.11), получим
г^п 1000 А
1 = 1
5>,А ' =
/ = 1
Уравнения (17.16) (их число определяется максимальным
значением индексау, т. е. числом химических элементов, входящих
в состав топлива) представляют собой закон сохранения вещества,
выраженный через известный элементный состав топлива и
неизвестные парциальные давления газообразных составляющих,
которые определяют состав продуктов сгорания.
Число этих уравнений равно числу химических элементов,
входящих в состав топлива, а число неизвестных парциальных
давлений газообразных составляющих в общем случае равно
числу всех возможных химических соединений, которые могут
образовывать химические элементы, входящие в состав топлива.
Контрольные вопросы и задания
1. Перечислите законы сохранения, которые описывают произвольное
состояние не обменивающегося массой с окружающей средой
постоянного количества энергетически изолированной смеси
химически активных гетерогенных компонентов. Запишите математические
выражения этих законов в общем виде.
2. Предполагая, что в системе происходят химические превращения,
не затрагивающие состав ядер химических элементов, запишите
закон сохранения массы вещества, учитывающий постоянство числа
грамм-атомов химических элементов.
3. Дайте определения химической, условной и удельной формул
компонентов топлива и многокомпонентного топлива в целом.

222 Часть IL Теория неидеального теплового ракетного двигателя
4. Дайте определение стехиометрического (теоретического)
соотношения компонентов топлива.
5. Что такое соотношение компонентов двухкомпонентного топлива
и коэффициент избытка окислителя?
6. Каким образом может быть задан состав многокомпонентного
топлива?
7. Каким образом может быть записан состав гетерогенных продуктов
сгорания, если их газообразный компонент представляется в виде
смеси идеальных газов?
8. Запишите состав продуктов сгорания через массовые доли
компонентов.
9. Запишите состав продуктов сгорания через объемные (мольные)
доли компонентов.
10. Составьте расчетное выражение для числа грамм-атомов
произвольного химического элемента в 1 кг газообразных продуктов сгорания,
полагая, что известны парциальные давления всех компонентов.

Глава 18
Закон сохранения энергии
в системе уравнений термодинамического расчета
Камера ракетного двигателя при принятых допущениях
рассматривается как ограниченная система, не обменивающаяся
с окружающей средой ни массой, ни энергией. Вследствие этого
полная энергия единицы массы топлива, поступившего в камеру
сгорания, (Еп){ кгтоплива преобразуется в такую же по величине
полную энергию единицы массы образовавшихся продуктов
сгорания (Еп\ кгпродуктовсгорания, т. е. исходная форма уравнения
сохранения энергии имеет вид
^ п'1 кгтоплива ^ п'1 кг продуктов сгорания' ^ * '
При этом, если камера сгорания изобарная, скорость топлива
и образовавшихся продуктов сгорания, а следовательно, и их
кинетическая энергия равны нулю и происходит только
преобразование большей части химической энергии топлива в тепловую
энергию продуктов сгорания.
Полное энергосодержание /п единицы массы, учитывающее
все виды энергии, кроме кинетической, определяется
относительно некоторого произвольно задаваемого уровня энергии и
численно характеризуется полной энтальпией, вводимой как
термодинамический параметр уравнением
1п(Т) = дшм + ]ср(Т)сИ + АНфп\Тг , (18.2)
ту f
где Г-температура, для которой рассчитывается полная
энтальпия; Tf- начальная температура выбранной системы отсчета, при
которой полная энтальпия равна химической энергии; с (Г) -
зависимость удельной теплоемкости при постоянном давлении от
температуры; £?хим - химическая энергия, под которой
понимается количество выделившейся (знак «-») или поглощенной (знак
«+») теплоты при образовании единицы количества вещества из

224 Часть II. Теория неидеального теплового ракетного двигателя
элементов, находящихся в стандартных состояниях, в пересчете к
начальной температуре выбранной системы отсчета; ЛЯфп -
\7f
изменение полной энтальпии при фазовых переходах или
полиморфных превращениях, претерпеваемых при изменении
температуры от Т, до Т. При этом поглощению энергии при фазовом
переходе или полиморфном превращении соответствует
увеличение полной энтальпии (например, при плавлении или кипении),
а выделению энергии (например, при конденсации или
кристаллизации, переходе из жидкого состояния в твердое) - уменьшение
полной энтальпии.
Сумма второго и третьего слагаемых в (18.2) представляет
собой термодинамическую составляющую полной энтальпии.
Отметим, что из теории идеальных газов следует независимость
термодинамической энтальпии от давления. Реакция образования
атомарного электрически нейтрального газообразного водорода Н
(свободных радикалов) из молекулярного Н2 - диссоциация -
также идет с подводом энергии, поэтому его полная энтальпия при
давлении 1 атм и температуре 298,15 К равна 217,978 кДж/моль
или 217,978 МДж/кг, а если при этом атом теряет электрон
(совершается дополнительно работа ионизации), то для Н+ полная
энтальпия составляет 1 536,20 кДж/моль = 1 536,20 МДж/кг.
Отметим, что хранение газов в атомарном состоянии
представляет собой нерешенную в настоящее время задачу, успешная
техническая реализация которой обеспечила бы повышение
удельного энергосодержания вещества примерно в 10-20 раз. В таком
веществе атомы активных элементов (свободные радикалы)
сохраняются в условиях, предотвращающих их рекомбинацию,
например, в топливном баке.
В настоящее время в большинстве литературных источников
принимается Tf= 298,15 К (25 °С).
В качестве стандартных состояний элементов с нулевой
химической энергией в стандартных условиях при температуре
298,15 К и давлении 1 атм принимают:
• газы 02, Н2, N2, F2, Cl2, He, Ne и др.;
• твердые вещества А1, В, Be (в стабильном кристаллическом
состоянии, а если таких состояний несколько, то указывается
конкретная характеристика, например: а-железо
кристаллическое, сера S кристаллическая ромбическая, углерод С в форме
Р-модификации графита);
• жидкий бром Вг и др.

Глава 18. Термодинамический расчет. Закон сохранения энергии 225
Следует отметить, что при стандартных давлениях и
температурах твердые вещества могут находиться в метастабильном
состоянии, не соответствующем стабильному кристаллическому
состоянию. При этом важно, какая именно кристаллическая
структура вещества принята за исходную или стандартную в начальной
точке системы отсчета. Например, для углерода это графит,
полная энтальпия которого при температуре 298,15 К принимается
равной нулю, тогда как при этой же температуре полная
энтальпия алмаза составляет 1,897 кДж/моль или 158,08 кДж/кг.
Имеет значение также и абсолютный размер частиц
конденсированного (твердого или жидкого) вещества, находящегося при
давлении и температуре, соответствующих точке отсчета полной
энергии. Для металлов полная энтальпия принимается равной
нулю, если они находятся в твердом состоянии с размерами
частиц, при которых число атомов, располагающихся на
поверхности, незначительно по сравнению с числом атомов в объеме
каждой частицы и их энергетическое состояние не влияет на
физические свойства частиц.
В составе ракетных топлив металлы применяются как в виде
порошков с характерным размером частиц более нескольких
микрометров (10"6...10~4 м), так и в виде частиц нано- и
ультрадисперсного размера 1 ...500 нм (Ю-9...0,5-10"6 м) для повышения
действительных энергетических характеристик и плотности
топлива, а также для придания его компонентам требуемых
технологических и эксплуатационных свойств. При размерах на-
нодиапазона удельная поверхность частиц может достигать
30-103 м2/кг и вклад поверхностной энергии в полную энтальпию
компонента может стать существенным.
Для нано- и ультрадисперсных порошков металлов,
характерный размер частиц которых не более 100 нм, т. е. 10~7 м,
некоторые термодинамические характеристики зависят от размера частиц.
В частности, уменьшение радиуса поверхности твердой частицы
приводит к изменению температур фазового перехода. Например,
температура плавления платины в частицах диаметром 50 нм
снижается на 137 К, а сферическая частица твердой воды (льда)
того же диаметра плавится при 4,7 °С (277,85 К).
Влияние абсолютного размера частиц можно объяснить тем,
что у крупнодисперсных (больших) частиц доля атомов на
поверхности крайне невелика (для «кубика» графита со стороной
10"2 м на поверхности и вблизи нее располагаются не более
10"5...10~4 % атомов углерода), тогда как у наночастиц она пре-

226 Часть II. Теория неидеального теплового ракетного двигателя
вышает несколько процентов (у наночастицы углерода с
характерным размером 10 нм или 10~8 м на поверхности находятся уже
около 10 % атомов), что соответствует энергии приповерхностных
слоев, сравнимой с полной внутренней энергией вещества частицы.
Всю совокупность эффектов, зависящих от размера
конденсированных частиц вещества, можно учитывать интегрально
путем введения некоторой положительной удельной энтальпии
дисперсного вещества при стандартной температуре и давлении
в точке отсчета. Например, для ультрадисперсных частиц
углерода с характерными размерами 10... 100 нм при стандартных
условиях удельная энтальпия графита повышается до уровня
примерно 20 кДж/моль (~1 670 кДж/кг) соответственно для
алмазного порошка - приблизительно 28 кДж/моль (~2 350 кДж/кг),
тогда как для фуллеренов С60 - примерно 42,5 кДж/моль
(-59 кДж/кг) и для С70 - около 40 кДж/моль (~48 кДж/кг).
Приведенные данные характеризуют только суммарный
масштаб наноэффектов. Конкретные характеристики
ультрадисперсных порошков определяются их дисперсным составом,
распределением частиц по размерам, состоянием кристаллической
решетки или структурой связей между атомами (фуллерены, на-
нотрубки и т. п.), состоянием поверхности и др.
Например, согласно теоретическим оценкам1, для частиц
алюминия радиусом 1 и 10 нм (10~9...10~8 м) полная энтальпия при
температуре 298,15 К составляет 1 014 и 95,56 кДж/кг
соответственно, тогда как для частиц с радиусом не менее 1 мкм (10~6 м)
ее значение близко к нулю. При том что значение удельной
теплоты плавления алюминия сопоставимо с поверхностной
энергией (~ 400 кДж/кг), влияние вклада поверхностной энергии на
расчетное значение удельного импульса существенно (примерно
1 %) только для частиц радиусом менее 10 нм (10* Ю-9 м). Это
позволяет не учитывать поверхностную энергию при задании
полной энтальпии металла, входящего в состав топлива в виде
частиц большого размера. Данное условие с приемлемой для
термодинамических расчетов ракетных топлив точностью
соблюдается практически для всех твердых веществ.
Ягодников Д.А., Антонов Ю.В., Пырлин СВ. Использование на-
нодисперсных компонентов в ракетных топливных композициях и
пиротехнических составах // Вестник МГТУ им. Н.Э. Баумана. Сер.
Приборостроение. Спец. выпуск «Наноинженерия». М.: Изд-во МГТУ
им. Н.Э. Баумана. 2010. С. 110-117.

Глава 18. Термодинамический расчет. Закон сохранения энергии 227
Если ультрадисперсные частицы входят в состав компонента
топлива (например, углерод, металлы и их соединения и сплавы
и др.), то, как правило, их энергосодержание учитывается
интегрально в теплоте образования или полной энтальпии компонента
топлива, определяемых чаще всего экспериментально без
дифференциации вкладов ингредиентов и задаваемых в составе
стандартных данных для топлива или его компонента. При этом важны не
только дисперсный состав, но и технология получения и хранения
этих частиц, а также способ их введения в состав топлива.
Например, при давлении 1 атм и температуре 298,15 К полное
энергосодержание металла в виде полученного методом теплового
электровзрыва ультрадисперсного порошка1 с диаметром частиц
до 10"7 м (менее 100 нм) может достигать пяти-шестикратного
значения теплоты плавления, но при этом £?хим = 0.
С учетом такого определения химической энергии QxiiM из (18.2)
следует, что при стандартных условиях, соответствующих
начальной точке отсчета полных энтальпий с температурой Т= 0,
полная энтальпия вещества численно равна его химической
энергии или теплоте образования. Если же Tf= 298,15 К, то £?хим есть
лишь мера химической энергии. Например, при образовании воды
из взятых при стандартных условиях газообразных кислорода
и водорода выделяется теплота 68,3149 ± 0,0096 ккал/моль (или
285,8 кДж/моль воды), соответствующая в пересчете на 1 кг воды
теплоте 15879,8 кДж, и £?хим = -15 879,8 кДж/кг. Для безводной
азотной кислоты QxiiM = -2 756 кДж/кг.
Образование гидразина N2H4 идет с подводом теплоты извне,
(Q = +1 559,3 кДж/кг), так же как и дициклобутила С8НИ
(условное название при использовании в качестве ракетного горючего -
боктан), полная энтальпия которого при температуре 20 °С равна
+334,72 кДж/кг.
В термодинамических расчетах рекомендуется применять
теплоту образования и другие термические константы, приведенные
в виде табличных данных в справочниках или в компьютерных
базах данных, например в находящихся в свободном доступе в сети
Интернет справочнике «Термические Константы Веществ» (на
сайте МГУ им. М.В. Ломоносова http://www.chem.msu.su/cgi-bin/
tkv2.pl?show=welcome.html) или в электронной базе данных
Иванов Г.В., Сурков В.Г. Наноразмерные электровзрывные
порошки - перспективные компоненты энергетических материалов // Физика
горения и взрыва. 1998. Т. 34; № 6.

228 Часть II. Теория неидеального теплового ракетного двигателя
ИВТАНТЕРМО (http://www.chem.msu.su/rus/handbookyivtan).
Значимость достоверных данных о термодинамических
характеристиках компонентов ракетных топлив подтверждается тем, что
начиная с 1950-х годов исследованиями в этом направлении
руководил крупнейший ученый в области ракетного двигателе-
строения академик В.П. Глушко. Полученные данные постоянно
уточняются и дополняются учеными разных стран. Например,
термохимические данные для 5 000 неорганических веществ
можно найти в справочной книге Института стандартов и
технологии США CHEMINFO на указанном выше сайте МГУ
им. М.В. Ломоносова.
Информацию о сайтах, содержащих сведения о
термодинамических данных и программах расчета свойств химических
соединений, можно найти по адресу http://www.uic.edu/~mansoori/
Thermodynamic/Data.and.Propertyhtml.
В качестве примера значения полной энтальпии и некоторых
других характеристик применяемых и перспективных
компонентов жидких ракетных топлив приведены в табл. 18.1.
Ряд компонентов ракетных топлив имеет сокращенные для
удобства применения условные или торговые названия,
встречающиеся в публикациях без расшифровки: несимметричный
диметилгидразин (НДМГ) - гептил, монометилгидразин (ММГ) -
амидол, тетраоксид диазота N204 - амил или атин, азотный
тетраоксид (АТ)и др. (www.export.fstec.ru). Углеводороды: ди-
циклобутил С8Н14 имеет название боктан; С7Н8 - квадрициклан;
1-метил-1,2-дициклопропилциклопропан С10Н16 - синтин
(плотность 851 кг/м3, Тш ия = 158 °С, полная энтальпия при 1 атм
и 25 °С равна +980 кДж/кг) или циклин и т. п. Отметим, что одной
и той же формуле углеводорода СМИ может отвечать несколько
различных веществ с существенно различающимися свойствами.
Например, задающая соотношение атомов углерода и водорода
формула С10Н16 описывает не только компонент ракетного
топлива - горючее циклин, но и получаемые переработкой древесины
смеси углеводородов, такие как скипидар (техническое название)
и его компоненты терпены, компоненты янтаря, компонент
нефти полиметиленовый углеводород адамантан, легкоплавкий
твердый углеводород камфен и ряд других углеводородов, получаемых
выделением из природного сырья или синтезируемых из
различных исходных веществ.
Горючее ТГ-02 (ГОСТ 17147-89, сокращение от «Топливо
ГИПХ-02», где ГИПХ - сокращенное название Государственного

Таблица 18.1. Значения характеристик компонентов
жидких ракетных топлив
Компонент
Формула

Молярная
масса

Температура
кипения,
Т, К, при
р = 1 атм
Теплота

испарения,
кДж/кг
Плотность,
кг/м3
Полная

энтальпия,
кДж/кг
При температуре, К
Жидкий окислитель
Кислород
Фтор
Азотный
тетраоксид
Азотная
кислота
(100%-ная)
Пероксид
водорода,
(100%-ный)
о2
F2
N204
HN03
НА
31,999
37,97
92,011
63,013
34,015
90,188
85,02
294,30
355,8
423,35
212,85
1135
-398,3
90,188
172,22
1507
-339,3
85,02
414,26
1442
-212,5
294,3
626,3
1503,5
-2756
298,15
1516,6
1442
-5520,4
298,15
Жидкое горючее
Водород
Аммиак
Гидразин
Метан
Дицикло-
бутил
(боктан)
ММГ
НДМГ
Аэрозин-50
Керосин
Т-1
н2
NH3
N2H4
сн4
С8Н14
CH3N2H3
(CH3)2N2H2
-
CHI,956
(условная)
2,016
17,030
32,04
16,047
ПО
46,08
60,10
-
-
20,27
239,73
386,65
111,66
407,15
360,65
336,25
343,25
423...553*
446,0
70,76
^1353,9
20,27
1732
681,9
^185,0
239,73
1397,6
1004
1559,3
298,15
510,94
424
-5566,0
111,66
-
828
334,72
293
876,54
874
1155,9
298,15
582,68
786
823,6
298,15
989,55
884
1198,8
298,15
267**
832
-1958
298,15
* Температура начала кипения 423 К; 50 % испаряется при температуре
498 К и 98 % - при температуре 553 К.
** Теплота испарения при температуре 293...323 К.

230 Часть II. Теория неидеального теплового ракетного двигателя
института прикладной химии; http://www.giph-design.ru/) в ряде
публикаций упоминается как самим и по составу близко к
немецкому горючему «Тонка-250», представляющему собой смесь
равного по массе количества триэтиламина N(C2H5)3 или C6H15N
(ц = 101,19 г/моль) и изомерных ксилидинов (CH3)2C6H3NH2 или
C8HUN (\i = 121,18 г/моль) с примесью воды до 0,20 %. Для
безводного горючего удельная формула С62 6552Hj 19 504N9 06718 и полная
энтальпия 1п 29815 = -774,2 кДж/кг.
В ряде работ ракетное криогенное горючее - жидкий
водород - условно называется винилом, г. люминалом-А (без указания
конкретных характеристик) в некоторых публикациях называют
экспериментальное горючее, представляющее собой тиксатроп-
ную взвесь дисперсного алюминия в сгущенном гидразине, т. е.
вещество, не имеющее ничего общего с одноименным
лекарственным препаратом. Окислитель на основе раствора азотного
тетраоксида в азотной кислоте с остаточным содержанием воды
и добавками ингибитора, например Ак-27и или Ак-20 и т. п.,
называют меланжем, причем в некоторых ранних публикациях
меланжем называлась смесь азотной и серной кислот, а
некоторым другим названиям соответствуют химические соединения
совсем другой природы и состава. Таким образом, для каждого
конкретного случая условному или торговому названию должен
быть поставлен в соответствие компонент топлива
определенного состава.
Действительный состав компонента топлива не
ограничивается основными химическими соединениями и с учетом добавок
и примесей по их массовым долям и дисперсному составу
регламентируется государственными, отраслевыми стандартами и
техническими условиями. Наличие добавок и примесей в
компоненте существенно, иногда решающим образом оказывает влияние
на его эксплуатационные качества, но, как правило, практически
не влияет на термодинамические свойства компонента (например,
на значение его полной энтальпии, на развиваемый удельный
импульс и т. п.) и может не учитываться при термодинамических
расчетах, не касающихся определения токсичности и
экологической безопасности продуктов сгорания топлива.
Например, приводится1 состав типичного высококипящего
сложного (составного) окислителя на основе азотной кислоты
1 Термодинамические и теплофизические свойства продуктов
сгорания... Т. V / под ред. В.П. Глушко... С. 262 (см. сноску на с. 215).

Глава 18. Термодинамический расчет. Закон сохранения энергии 231
HN03 (71,15 %) и азотного тетраоксида N204 (27 %) с
содержанием воды 1,6 % и HF 0,25 %, значение полной энтальпии
которого 1п 29815 = -2 377,3 кДж/кг весьма близко к учитывающей
массовую концентрацию сумме энтальпий составляющих (см.
базу данных www.chem.msu.su/cgi-bin/tkvl.pl7show). А в
качестве примера сложного компонента топлива ЖРД приведен
состав горючего НДМГ (%): 97,1 (CH3)2N2H2; 1,8 (CH3)2N2CH2 и
1,1 (CH3)2NH с примесью воды до 0,5 %. Для этого горючего
1п 29815 = +823,6 кДж/кг, что также примерно равно взвешенной
сумме энтальпий составляющих.
Аналогичные сведения о составе компонентов жидких
ракетных топлив, применяемых в США (аэрозин-50, водород, гидразин,
керосин RP-1, монометилгидразин, тетраоксид азота, кислород),
приводятся на официальном сайте http://propellants.ksc.gov/.
Например, в состав горючего аэрозин-50 (Aerozine-50),
получившего свое название по приближенному составу из смеси
приблизительно одинакового количества (~ 50 %) гидразина N2H4
и несимметричного диметилгидразина (НДМГ) N2H2(CH3)2, на
самом деле входят два основных компонента: 51 ± 0,8 N2H4 и
минимум 47 N2H2(CH3)2, которые в сумме с другими примесными
аминами составляют не менее 98,2 %, и не более 1,8 % воды.
Используя полную энтальпию как меру энергосодержания,
уравнение сохранения энергии (18.1) с учетом (18.2) можно
записать для произвольного сечения камеры в виде
^ гктопливо ^ гкпродукты сгорания -л ' V • /
где второе слагаемое в правой части уравнения соответствует
доле полной энергии топлива, перешедшей в кинетическую
энергию продуктов сгорания. Очевидно, что для изобарной камеры
скорость потока близка к нулю и W2I2 ~ 0.
Полная энергия продуктов сгорания (правая часть уравнения
(18.3)) должна быть выражена через параметры в камере в общем
случае с учетом температуры Гк, давления рк и состава продуктов
сгорания, например массовой концентрации конденсированных
компонентов, молярных концентраций или парциальных
давлений/?, газообразных составляющих.
В зависимости от выбранных аргументов назначается
единица измерения полной энтальпии - джоуль на килограмм или джоуль

232 Часть II. Теория неидеального теплового ракетного двигателя
на моль. Соотношение между ними для z'-го вещества с
молекулярной атомной массой \i. в граммах имеет вид
/[Дж/кг] = /[Дж/моль] ^^. (18.4)
И/
Записанная в левой части уравнения (18.3) полная энтальпия
единицы массы топлива рассчитывается непосредственно на
основе табличных данных для компонентов топлива (при
характерных для данного компонента температуре и давлении в баке)
с учетом соотношений расхода, давления и температуры всех
компонентов в условиях входа в систему.
Полная энтальпия компонентов топлива представляется в
качестве справочных (табличных) данных /птабл чаще всего при
стандартном давлении р = 1 атм для типичных значений
температуры:
• при Т= 298,15 К для твердых или высококипящих
компонентов;
• при температуре кипения при указанном давлении для низ-
кокипящих компонентов.
В действительности компонент топлива может быть
переохлажденным или нагретым на AT и поступает в камеру при
давлении подачи /?под, существенно превышающем нормальное
давление.
Уравнение (18.2) позволяет получить значение полной
энтальпии вещества при температуре и давлении, отличных от
стандартных, для которых известна теплота образования.
Если изменение состояния компонента (повышение давления
на Ар от р= 1 атм до давления подачи рпод) и изменение
(увеличение или уменьшение) температуры на AT происходит без
использования энергии самого компонента, то полная энтальпия
компонента в условиях подачи /п под
7ЧА7' д
',под=',Табл(7»+ J ср(ШТ + АНфп\Г;АГ+-^, (18.5)
Т Рср
где при вычислении приращения энергосодержания в результате
повышения давления плотность компонента топлива усреднена
(р ) в диапазоне значений давления р...(р + Ар)- Для газов с
достаточной для практики точностью Ар/рс =R(T+AT)\n [(p + Ар)/р].

Глава 18. Термодинамический расчет. Закон сохранения энергии 233
Если в диапазоне значений температуры Т.. AT вещество
претерпевает фазовые переходы или полиморфные превращения, то
Пусть при достижении температуры Г1ф, находящейся в
диапазоне значений Т<Т{,<(Т+ ДГ), компонент претерпевает
полиморфное превращение или фазовый переход (например,
переходит из жидкого состояния в газообразное), который
сопровождается удельными энергозатратами Д//1ф (например,
АЯ]ф = р1ф, т. е. удельной теплоте парообразования), тогда
целесообразно вычислять интеграл и изменение энергосодержания
в результате повышения давления в (18.5) в диапазонах значений
температуры Т...Т{, и 7^.... (Г+ AT) для теплоемкостей и
плотностей при конкретном фазовом состоянии, а теплоту фазового
перехода учитывать путем прибавления Д#1ф, если полиморфное
превращение требует подвода энергии, и путем вычитания Д#1ф,
если при изменении фазового состояния происходит передача
энергии в окружающую среду. В общем случае таких фазовых
переходов может быть несколько, например т. При этом в правой
т
части (18.5) записывается сумма VA//1(b учитывающая суммар-
/ = 1
ный тепловой эффект фазовых переходов и полиморфных
превращений.
В качестве примера рассчитаем полную энтальпию /п/25
гипотетического ракетного горючего - шугаобразного водорода с
содержанием твердого водорода («водородного льда») в жидком
водороде 25 % при температуре подачи, равной равновесной
температуре плавления (кристаллизации) Тпл = 13,957 К (-259,19 °С),
при предположении равновесного соотношения пара- и ортово-
дорода. Термодинамические свойства водорода выбираем по
данным сайта http://www.chem.msu.ru/, полагая исходное состояние
водорода в газовой фазе при давлении 0,1 МПа и температуре
298,15 К с полной энтальпией, равной нулю.
Исходя из свойств аддитивности энтальпии, запишем
/„,0=0,25 7 +0,75/ ,
п/25 % ' п.тв ' п.ж'
где значения полных энтальпий твердого /п тв и жидкого /п ж
водорода рассчитаем по (18.5) в диапазоне значений температуры

234 Часть II. Теория неидеального теплового ракетного двигателя
Гпл(кРист) ^ Т7^ 298,15 К (13,957 К ^ Т ^ 298,15 К) при
постоянной удельной теплоемкости водорода:
^п тв = ^ — Сг (^"°>1 ^ — ^кип(конденс)) ~ ^^кип(конденс) ~~
Охлаждение газообразного водорода
до температуры кипения (конденсации)
Полная энтальпия жидкого водорода
~~ ^ж \/кип (конденс) ~~ пл(крист)/ — ^Г2пл(крист) —
v
Охлаждение жидкого водорода
до температуры плавления (кристаллизации)
= 0 - 14,301(298,15 - 20,38) - 454,365 -
- 9,53(20,38 - 13,957) - 58,036= -4 504,1 кДж/кг.
Тогда /пж = -4 383,85 кДж/кг и 1п/25% = -4 413,91 кДж/кг.
Отметим, что рассчитанное таким образом значение полной
энтальпии жидкого водорода отличается от приведенного в
справочнике по ракетным топливам1, так как в расчетах не учитывалась
зависимость удельной теплоемкости водорода от температуры.
Вследствие практической несжимаемости жидких высококипя-
щих компонентов увеличение энтальпии при повышении давления
компонента в системе подачи незначительно и его целесообразно
учитывать только при давлении более 5 МПа. Для газообразных
компонентов и для жидкого водорода, отличающегося высокой
сжимаемостью, повышение энергосодержания в насосе А/нас
необходимо учитывать и при меньших значениях давления.
Если известна потребляемая мощность Nn0R насоса подачи при
секундном расходе компонента т, то увеличение энтальпии А/нас
вследствие повышения давления и температуры компонента
в насосе
_Nn,
'нас ~"
Л/нас=—• (18-6)
т
Если значение Nnojx неизвестно, то вычисления ведут по (18.5)
с учетом существенных особенностей компонента. Причем если
мощность насоса не дана, но известно значение его КПД л,
Термодинамические и теплофизические свойства продуктов
сгорания... Т. I / под ред. В.П. Глушко... (см. сноску на с. 215).

Глава 18. Термодинамический расчет. Закон сохранения энергии 235
повышение давление Л/?нас и среднее значение плотности
компонента в насосе р , то увеличение энтальпии компонента в насосе
А/нас можно рассчитывать с учетом диссипации энергии и,
следовательно, подогрева компонента по формуле А/нас =——.
РЛ„ас
Для ЖРД с дожиганием генераторного газа увеличение
энергосодержания компонентов топлива в насосах происходит с
использованием энергии самих компонентов, вследствие чего
полная энтальпия компонента при термодинамическом расчете
процессов в камере берется при параметрах входа в насосы, а при
расчете газогенераторов - с учетом энергии, сообщенной
компоненту в насосах, т. е. при параметрах на входе в газогенератор.
Если для компонента топлива, представляющего собой смесь
известных п компонентов, отсутствуют данные по полной
энтальпии, то ее можно вычислить по выражению
п т
'„=2>Л/+х;&&' (18.7)
где g. - массовая доля /-го компонента; /п/ - полная энтальпия
/-го компонента при одной и той же температуре для всех
компонентов смеси; q. - тепловой эффект растворения /-го
компонента, выражаемый в джоулях на килограмм растворяемого
вещества; т - число компонентов, растворение которых
сопровождается поглощением или выделением теплоты; п - число
смешиваемых компонентов.
Тепловые эффекты растворения, которые проявляются при
получении компонента (окислителя или горючего жидких
ракетных топлив или составляющей твердого ракетного топлива) как
смеси веществ, могут дать существенный вклад в полную
энтальпию топлива. Это происходит за счет того, что при
эндотермических процессах растворения температура раствора понижается,
а затем возвращается к исходной в результате теплообмена с
окружающей средой - подвода теплоты, а следовательно, увеличения
полного энергосодержания и соответственно полной энтальпии.
Например, при растворении в 1 л воды 0,750 кг нитрата натрия
NaN03 температура понижается на 18,5 К; при растворении 0,300 кг
хлористого аммония (нашатыря) NH4C1 - на 18,4 К, тогда как
растворение 0,600 кг нитрата аммония NH4N03 приведет к
снижению температуры на 27,2 К, что может обусловить образование
твердой фазы. Особенно велико снижение температуры при

236 Часть II. Теория неидеального теплового ракетного двигателя
растворении одновременно нескольких веществ1. Например, при
растворении в 1 л воды 1 кг нитрата аммония NH4N03 и 1 кг
углекислого натрия Na2C03 температура раствора уменьшится
на 35 К. Затем охлажденная смесь нагревается до температуры
окружающей среды и ее энергосодержание повышается.
Если же растворение идет с выделением теплоты
(экзотермический процесс, например, растворение серной кислоты или
этилового спирта в воде), т. е. раствор нагревается, а затем
охлаждается до начальной температуры, отдавая тепловую энергию
окружающей среде, то полная энтальпия раствора в результате
уменьшается на величину, пропорциональную теплоте
растворения. При этом имеется в виду, что полученная смесь до подачи
в камеру приходит в тепловое равновесие с окружающей средой,
т. е. принимает ту температуру, которую имели компоненты до
их перемешивания.
В общем случае тепловой эффект растворения изменяется
в зависимости от соотношения растворяемого вещества и
растворителя. Например, растворение 0,1 моля воды в 1 моле
этилового спирта, т. е. получение водного раствора этилового спирта
С2Н5ОН0,1Н2О с массовой концентрацией 96,2 %,
сопровождается выделением теплоты 74,4 кДж на 1 кг воды, тогда как
разбавление этилового спирта водой до концентрации 73,95 %
(С2Н5ОН-0,9Н2О) приводит к выделению 47,037 кДж на 1 кг
растворенной воды. Причем при дальнейшем разбавлении спирта
водой до концентрации не менее 40 % (С2Н5ОН*4Н20) теплота
растворения воды изменяется незначительно, возрастая
приблизительно до 50 кДж/кг.
Основные физико-химические закономерности растворения
этилового спирта и других веществ в воде были установлены
русским ученым Д.И. Менделеевым2.
1 Данные специфические количественные характеристики процессов
(www.2x2business.ru/oxlad.htm) приведены в методических целях, и не
относятся непосредственно к ракетным топливам.
2 Менделеев Дмитрий Иванович (1834-1907) - русский химик,
открывший периодический закон и разработавший периодическую систему
химических элементов, разносторонний ученый, педагог и общественный
деятель, чл.-кор. Петербургской академии наук (1876). В 1865 г. защитил
докторскую диссертацию «О соединении спирта с водой». Свои взгляды
на природу растворов изложил в монографии «Исследование водных
растворов по удельному весу» (1887). Входил в попечительский совет
Императорского технического училища (ныне МГТУ им. Н.Э. Баумана).

Глава 18. Термодинамический расчет. Закон сохранения энергии 237
Водные растворы этилового спирта применялись в качестве
горючего первых баллистических ракет, в настоящее время
рассматривается их применение в качестве высококипящего, долго-
хранящегося и малотоксичного, экологически безопасного
компонента ракетного топлива для пилотируемых летательных аппаратов.
Когда нет возможности получить значение энтальпии
образования в зависимости от концентрации растворяемого вещества,
приводится некоторое усредненное по всему интервалу
концентраций значение, которое применяют ко всем концентрациям
с учетом допустимой при этом погрешности. Так, в базе данных
для растворов ацетилена СНСНиСН3ОН, СНСНиСН3СОСН3
и CHCH«NH3 приводятся усредненные значения энтальпий
образования 206,982 ± 2,092 кДж/моль соответственно, тогда как
для чистого жидкого ацетилена теплота образования равна
219 кДж/моль. Отметим, что раствор ацетилена в аммиаке
рассматривается в качестве перспективного ракетного горючего
с условным названием ацетам.
Экспериментально измеренные тепловые эффекты при
растворении могут отражаться в снижении или увеличении полной
энтальпии растворителя в зависимости от доли растворяемого
вещества, чаще всего воды (http://www.chem.msu.su/cgi-bin/tkv2.
pl?show= welcome.html)). Эти результаты представлены в табл. 18.2,
где в первой строке приведены полные энтальпии этилового
спирта в килоджоулях на 1 кг безводного спирта при температуре
285,15 К в зависимости от его массовой доли gx в водном
растворе, указанной во второй строке. В третьей и четвертой строках
приведены те же данные для безводной азотной кислоты и ее
водных растворов. Значения, приведенные в седьмой графе,
относятся к так называемым «бесконечно разбавленным» растворам
(с содержанием спирта или азотной кислоты менее 3 %), для
которых теплота растворения практически не изменяется.
Если даны энтальпии растворителя в зависимости от его
массовой доли gx (см. табл. 18.2), полная энтальпия раствора
рассчитывается как аддитивная величина (только первая сумма
в (18.7)). При этом подставляется энтальпия воды как
индивидуального вещества, а значение полной энтальпии другого вещества
(этилового спирта или азотной кислоты) берется в соответствии
с его массовой долей.
Например, полная энтальпия горючего (76,2 % раствора
этилового спирта в воде) рассчитывается как сумма: 0,762(-6 032,9) +
+ 0,238 (-15 879,8) = -8 376,46 кДж/кг.

238 Часть II. Теория неидеального теплового ракетного двигателя
Таблица 18.2. Значения полных энтальпий, кДж/кг, этилового
спирта и азотной кислоты в водных растворах в зависимости от^
Безводное
вещество
-6020,4
g, = i,o
-2764,1
Водный раствор
хО,1Н20
-6023,3
g,= 0,962
х0,8Н2О
xl,0H2O
х2,0Н2О
Этиловый спирт
-6032,9 -6039,2 -6058,6
g, =0,762 g, =0,719 g, =0,561
Азотная кислота
1 -2978,9 1 -3088,8
- |g, =0,778 |g, =0,636
х4,0Н2О
-6100,9
g,= 0,390
-3192,8
g,= 0,467
xooH20
-6237,8
0<g,<0,03
-3292,1
0<g,<0,03
Если компонент топлива получается смешением п
компонентов в теплоизолированном баке, т. е. без обмена энергией с
окружающей средой, то тепловые эффекты растворения не изменяют
полного энергосодержания смеси, полную энтальпию которой
вычисляют только по (18.7) при присвоении нулевых значений
всем тепловым эффектам ^.растворения. Например, полная
энтальпия гипотетической смеси жидкого гелия и атомарного
водорода (свободных радикалов), полученной в идеально
теплоизолированном баке подачей в жидкий гелий с температурой
Т= 4,214 К газообразного атомарного водорода, не зависит от
возможных изменений температуры и фазового состояния
компонентов и вычисляется как аддитивная сумма. В частности,
для массовых долей водорода 5 и 13,6 % она равна 9 466,5 и
28 422,1 кДж/кг соответственно.
Первая сумма в (18.7) отражает свойство аддитивности полной
энтальпии для не взаимодействующих между собой компонентов.
На основании этого свойства вычисляется полная энтальпия
топлива / , если известно массовое соотношение компонентов
п. т'
Кт = —- = Кт0а и полные энтальпии окислителя / и горючего
тГ по
/п г при параметрах подачи в камеру сгорания или газогенератор:
^n,=-^-L+-T-/,r. (18.8)
т0 +тг т0+ тг
Здесь множители в первом и втором слагаемых выражают
массовые доли компонентов. Полные энтальпии компонентов
берутся в общем случае при неодинаковых давлениях и температурах.

Глава 18. Термодинамический расчет. Закон сохранения энергии 239
Разделив числители и знаменатели дробей в (18.8) на то и
перейдя к соотношению компонентов Кт = Кт0а, получим
j =In.r+aKmOIu.o
\ + аК
(18.9)
/wO
Если камера сгорания и сужающаяся часть сопла
охлаждаются регенеративно компонентами топлива, то допущение об
изолированности системы выполняется, и при расчетах можно
использовать значение полной энтальпии топлива, рассчитанное по
(18.9). Но в ряде случаев камера охлаждается сторонним
охладителем (рис. 18.1), который при расходе тохп нагревается на ДТ^
от температуры входа в тракт охлаждения Гвх до температуры
выхода Гых = Гх + ДГохл, повышая
собственную энтальпию на Д/п охл и снижая
при этом полную энтальпию продуктов
сгорания на Д/пт. Расчетами и
экспериментами доказано, что данный подход
справедлив и в случаях охлаждения по
такой схеме и камеры сгорания, и
сужающейся части сопла.
Поскольку расходы продуктов
сгорания и топлива равны, т. е. тп с = wT,
учесть этот энергообмен можно,
соответственно уменьшив энтальпию
топлива, рассчитанную по (18.9), исходя из
уравнения равенства уменьшения
энергии продуктов сгорания тп сД/п т и увеличения энергии
охладителя тохлД/п охл в единицу времени для схемы, представленной на
рис. 18Л:
Рис. 18.1. К учету
изменения полной энтальпии
продуктов сгорания при
охлаждении камеры сторонним
охладителем
Д/п.т=Д/п.охл
тп
т^.
(18.10)
Таким образом, соотношения (18.5) - (18.10) позволяют
получить значение левой части уравнения сохранения энергии (18.3)
как одно из условий однозначности математической модели
термодинамического расчета.
Отметим, что при регенеративном охлаждении камеры
сгорания и сужающейся части сопла компонентами топлива, когда они,
повысив температуру в трактах охлаждения, поступают в камеру

240 Часть II. Теория неидеального теплового ракетного двигателя
сгорания нагретыми, потерь полной энергии компонентов нет,
как нет и повышения термодинамического КПД цикла из-за
низкой степени регенерации.
Если предположить, что точное для смесей идеальных газов
свойство аддитивности полной энтальпии приближенно
справедливо и для находящейся в динамическом равновесии химически
активной смеси продуктов сгорания, то для принятой ранее
модели идеального газа полная энтальпия продуктов сгорания
т
'„,с=1>Л„ (18-11)
/ = 1
где gf - массовые доли /-х компонентов; /п. - полные энтальпии
z'-x компонентов, Дж/кг. Причем массовые доли gi косвенно, а
энтальпии компонентов индивидуальных веществ /п.
непосредственно и однозначно зависят от равновесной температуры продуктов
сгорания Т= Т., т. е. In. = Ini(T). При этом в приближении
идеального газа полная энтальпия компонента /п. не зависит от его
парциального давления р., а неидеальность компонента может
учитываться использованием при расчетах экспериментально
полученных значений энтальпий индивидуальных веществ для
различных температур (в виде аппроксимирующих зависимостей,
таблиц или электронных баз данных).
Если в используемых зависимостях Ini(T) полная энтальпия
измеряется в килоджоулях на килограмм, то массовые доли g.
выражают через парциальные давления р. следующими
соотношениями из теории идеального газа:
= А И,
Si „ 9
/=1
и (18.11) примет вид
п
4,с-^—7 • (18-12)
Если /п ;(Г) даны в килоджоулях на моль, то вместо массовых
долей, как в (18.11), в суммировании энтальпий In (T) i-x компо-

Глава 18. Термодинамический расчет. Закон сохранения энергии 241
нентов используется число их молей М. в 1 кг продуктов сгорания,
т. е.
4п.с=5>лД7'>- (18.13)
/=1
Выражая число молей М. через парциальные давления;?., как
для смеси идеальных газов,
ы 100°
Z^/A
/=i
преобразуем (18.13) к виду
/„,с=4^-1М,(П (18.14)
/ = 1
Одно из эквивалентных уравнений (18.12) и (18.14) входит
в систему уравнений, решение которой определяет результат
термодинамического расчета. Неизвестные величины в этих
уравнениях - парциальные давления/?, и температура Т. В левой части
уравнений записывается в качестве константы значение полной
энтальпии данного топлива, вычисленное для условий подачи
в камеру по соотношениям (18.5) - (18.10).
Контрольные задания и вопросы
1. В какой системе отсчета и в каких единицах измеряется полная
энтальпия вещества?
2. Запишите соотношение, по которому, зная значение полной
энтальпии в джоулях на моль в жидком состоянии, можно рассчитать
полное энергосодержание 1 кг этого же вещества в газообразном
состоянии при температуре кипения.
3. Какое состояние газов и твердых веществ отвечает нулевому
значению их химической энергии? Приведите примеры для газов и
металлов.
4. В чем состоит кажущееся противоречие результатов экспериментов
по определению полной энтальпии нанопорошков металлов?
5. Какие виды энергии учитывает полная энтальпия вещества?
6. Что является мерой химической энергии вещества?

242 Часть II. Теория неидеального теплового ракетного двигателя
7. Для каких условий полная энтальпия вещества численно равна
теплоте образования?
8. Увеличивается или уменьшается полное энергосодержание топлива,
если его отдельные компоненты, имеющие температуру окружающей
среды, заранее смешиваются в баке, причем процесс взаимного
растворения экзотермический, но затем температура раствора
равняется температуре окружающей среды?
9. Как можно интерпретировать положительное значение полной
энтальпии?
10. Как рассчитать полную энтальпию топлива, если известны полные
энтальпии его компонентов, находящихся в баках при разных
температурах и давлениях, когда до подачи в камеру сгорания давление
компонентов повышается в насосах, причем один из компонентов
нагревается в тракте охлаждения камеры сгорания? Рассмотрите
особенности ответа на этот вопрос применительно к ЖРД с
дожиганием генераторного газа и к ЖРД без дожигания.

Глава 19
Система уравнений термодинамического расчета
с использованием констант равновесия
Полученные при принятых допущениях уравнения сохранения
массы, энергии и следствие закона сохранения импульса
(уравнение Дальтона) составляют математическую основу
термодинамического расчета при известном составе топлива,
предположении отсутствия в продуктах сгорания конденсированных веществ
и заданном давлении в камере сгорания ръ и являются системой
алгебраических уравнений:
Г1г1 1000 А
\Х\Г~ 2>v^ (19.1)
^.=4^-2>А,(г); (19.2)
/ = 1
a=Za- (19-3)
Здесь [X]. - обозначение химического элемента, причем
1 ^у ^ К, где К- число химических элементов, входящих в
состав топлива; ц - число индивидуальных веществ, в состав
которых входиту-й химический элемент; п - число индивидуальных
веществ с молекулярной массой \ij9 входящих в состав продуктов
сгорания как составляющие смеси газов;р. - парциальное
давление /-го газа; vi . - число грамм-атомову-го элемента в одном моле
/-го индивидуального вещества.
В (19.1) число уравнений равно К, т. е. по одному уравнению
для каждого у-го входящего в состав топлива химического
элемента. Неизвестными величинами здесь являются: jer-
парциальные давления п газов - индивидуальных веществ; Г-
температура смеси газов, равная температуре каждого компонента, т. е.
всего п + 1 неизвестных.

244 Часть II. Теория неидеального теплового ракетного двигателя
Поскольку всего из К = 2 элементов (например, кислорода
и водорода) даже без учета ионизации может быть образовано не
менее шести индивидуальных веществ (О, 02, Н, Н2, Н20, ОН),
т. е. п > К + 4, то число уравнений в (19.1) - (19.3), равное К + 2,
меньше числа неизвестных п + 1. Это означает, что ряд
неизвестных может принимать произвольные значения, но при этом
сохраняется необходимость однозначного соотношения между
значениями всех переменных. Возможная физическая интерпретация
такого соответствия заключается в вероятностном составе смеси
газов в продуктах сгорания, т. е. возможны различные
количественные соотношения между составляющими, но наиболее
вероятны только вполне определенные, однозначно задающие состав
и температуру продуктов сгорания.
Наиболее вероятному, т. е. устойчивому, состоянию
термодинамической системы соответствует состав, для которого при
заданных суммарном давлении, температуре и полной энтальпии
энтропия будет максимальной.
Такому состоянию отвечает соотношение парциальных
давлений газообразных компонентов, задаваемое значениями констант
равновесия возможных обратимых химических реакций, идущих
равновесно между всеми входящими в продукты сгорания
индивидуальными веществами.
В общем виде для реакции
Х\ AaBbCcO*2AalBbl +^3Bb2Cc, (19.4)
где XI9 XI, ХЗ - стехиометрические коэффициенты
соответствующего химического уравнения, константа равновесия
wr) = [Aa,Bbl] [Bb2Ccl]
V } AaBbC/'
Здесь в квадратных скобках приведены молярные концентрации
или парциальные давления веществ, участвующих в реакциях.
Числовое значение константы равновесия для одной и той же
реакции различно для разных способов ее выражения - через
парциальные давления или через молярные концентрации.
Число уравнений для констант равновесия вида (19.5) будет
равно числу идущих в смеси обратимых химических реакций,
описываемых уравнениями, аналогичными (19.4). В общем случае

Глава 19. Термодинамический расчет. Константы равновесия 245
число независимых уравнений констант равновесия равно
разности числа рассматриваемых химических соединений и числа
химических элементов, входящих в состав топлива.
Математическими методами можно доказать для общего
случая существование и однозначность решения системы уравнений
(19.1)-(19.3) и (19.5).
Поскольку большинство ракетных топлив в качестве основы
компонентов содержат химические вещества, в состав которых
в различных сочетаниях входят три-пять разноименных
химических элементов, покажем однозначность состава продуктов
сгорания, получаемого в соответствии с математической моделью
(19.1) - (19.3) и (19.5), на примере так называемого четырехэле-
ментного топлива, содержащего в своем составе только четыре
химических элемента: Н, С, О и N, а в продуктах сгорания -
только газообразные соединения этих элементов.
Ограничимся следующими наиболее вероятными в условиях
камеры сгорания ЖРД 11 соединениями: С02, СО, Н20, 02, О,
Н2, Н, ОН, N2, N, NO.
Предположим, что эти индивидуальные вещества
получаются в результате следующих реакций диссоциации-рекомбинации:
1.С09»СО + -09
2 2 2
2. Н20»Н2 + -02
3. Н20<^ОН + -Н2 (19.6)
4. N2 + 02 о 2NO
5. Н2 <z> 2H
6. 02 о 20
7. N2 <=> 2N
Укажем на произвольность при выборе химических реакций
в том смысле, что компоненты продуктов сгорания могут
получаться в результате различных химических реакций, в том числе
и той, которая выбрана в качестве единственной. Каждой
выбранной реакции соответствует константа равновесия с известной
зависимостью от температуры. Причем предполагается, что

246 Часть II. Теория неидеального теплового ракетного двигателя
зависимости сохраняются и в случаях, когда реакция идет в
присутствии реагентов, участвующих в других реакциях.
Это предположение соответствует правдоподобной гипотезе:
динамическое равновесие смеси всех газов достигается при
установлении динамического химического равновесия для каждой из
перечисленных реакций.
Таким образом, в математическую модель включаются
следующие семь уравнений:
Kp]{T) = PcoJp^_; (19?)
Рсо,
Кр2{Т) = ^^; (19.8)
Рн,о
Кр3(Т) = *ф±.; (19.9)
Рн,о
Pno
К (т) = -2**-; (19.10)
Pn2Po2
М^Ь—; (19Л1>
Рн2
Кр6{Т) = -^; (19.12)
Ро2
Кр1{Т) = -&-. (19.13)
Рщ
Для рассмотренного случая число неизвестных равно 12:11
парциальных давлений и температура в камере Т. Причем в
математическую модель кроме семи уравнений констант равновесия
(19.7)- (19.13) входят еще семь уравнений и 11 нестрогих
неравенств, которые приведены далее.
Четыре уравнения сохранения количества вещества - грамм-
атомов водорода, азота, углерода и кислорода, согласно (19.1):

Глава 19. Термодинамический расчет. Константы равновесия 247
г-, 1000 / ч
lCJ = -Tl [Рсо2+Рсо)>
(19.14)
Е^А
; = 1
1000
[Н] = ~п {2Рн2о + Рн2+Рон+РнУ> (19-15)
(=i
1000
[О] = 71 {2Рсо2 + Рсо + Рн2о + Ран + 2Аэ2 + Ргю+Ро)> (19.16)
&А
»=1
Гхт1 1000 и „ \
lNJ = Ti (2An2+2Ano + An)>
(19.17)
где Ёй/А = 44Аю2 + 28Рсо + ™Рнго + 2Рн2 + Пр<т + 28An2 +
+ 32р0г + 30рио +рн+\6р0+ \4pN. (19.18)
/=i
(19.19)
Знак приближенного равенства в (19.8) отражает применение
приближенных значений молекулярных масс компонентов продуктов
сгорания.
Уравнение сохранения энергии, записанное по (19.2):
fh со2 (Т) Рсо2 + h со (т) Рсо + Л
+1пН2о(Т)Рн20 + /пН2 {Т)Рн2 +
+1пон(Т)Рон+1пк2{Т)р»2 +
+W7>o2+W7>no +
+1пн(Т)Рн+1по(Т)Ро +
где знаменатель соответствует (19.18).
Уравнение Дальтона, согласно (19.3):
Pz=P,= Рсо2 + Рсо + Рн2о + Рн2 + Рон + Рн2 +
+ Рон + Рщ + Ро2 + Рио + Рн + Ро + /V
Г
П.ПС
1000
п
Х^а
/=1
(19.20)

248 Часть II. Теория неидеального теплового ракетного двигателя
Следствие из представления продуктов сгорания как смеси
идеальных газов, подчиняющихся уравнению состояния
идеального газа:
и
Hi=- • (19-21)
Ръ
При этом из физического смысла следуют ограничения на знак
неизвестных величин - парциальных давлений и температуры:
р.^0 и Г>0. (19.22)
Имеется в виду, что зависимости от температуры констант
равновесия для каждой из химических реакций (К (Г)) и полных
энтальпий для каждого индивидуального вещества (Inj(T))
известны и представлены для констант равновесия безразмерными
величинами, соответствующими выбранной размерности
давления, а для энтальпий - в джоулях на моль, например в виде таблиц
или электронной базы данных. При этом условии
соответствующая математической модели для четырехэлементного топлива
система уравнений (19.7) - (19.20), содержащая как линейные,
так и нелинейные уравнения и неравенства (19.21) и (19.22),
может быть решена численными методами.
Отметим, что к переменным величинам кроме 11 парциальных
давлений и температуры относятся также и неизвестные в общем
случае суммарное давление р19 полная энтальпия /п и кажущаяся
молекулярная масса p,L продуктов сгорания. Таким образом,
число неизвестных 15, а число уравнений 14.
Задание одной неизвестной величины, например полной
энтальпии, приводит систему в состояние, при котором решение,
если оно существует, является единственным. Укажем на то, что
превышение числа переменных над числом уравнений в
рассмотренном примере позволяет произвольно выбираемой переменной
присваивать постоянное значение, определенное внешними
условиями. В случае расчета состава продуктов в камере сгорания
полная энтальпия задается постоянной. Давление в камере как
суммарное давление (формально неизвестная величина) также
можно задавать произвольно. Физически возможность задания
суммарного давления означает произвольный выбор плотности
продуктов сгорания. Для камеры сгорания это отвечает соотно-

Глава 19. Термодинамический расчет. Константы равновесия 249
шению расхода и площади критического сечения при конкретном
значении расходного комплекса (3.
Можно также определить состав продуктов сгорания при
произвольных температуре и давлении. При этом полная энтальпия
становится неизвестной величиной.
Результатом реализации математической модели является
решение задачи термодинамического расчета. Достаточная для
практики точность расчетов подтверждена многочисленными
экспериментальными данными для широко применяемых топлив.
Вместе с тем изложенный подход к решению задачи
термодинамического расчета трудно реализовать для топлив, в
продуктах сгорания которых происходят еще мало изученные
химические реакции, для которых неизвестны зависимости констант
равновесия от температуры.
Кроме того, произвольный выбор химических реакций при
записи уравнений для констант равновесия ставит под сомнение
правильность их выбора для новых топливных композиций, тем
более что в камере сгорания значительная часть химических
превращений происходит в виде многостадийных разветвленных
реакций.
Решение системы уравнений позволяет прямыми
вычислениями рассчитать энтропию продуктов сгорания Sn с, т. е. система
дополняется еще одним уравнением и при этом добавляется
формальная переменная Sn c, что не препятствует разрешимости
полученной новой системы уравнений:
1000
>,р, '■'
S?(70-^lnA
А>.
Pi- (19.23)
/ = 1
Здесь S®(T) - известная зависимость энтропии (Дж/(мольК))
каждого компонента от температуры при стандартном давлении
р0 = 0,1 МПа. Отметим, что если давление р. измеряется в
физических атмосферах, тор0 в соотношении (19.23) и в аналогичных
соотношениях равняется единице и при записи формул для
вычисления энтропии в выражении под знаком натурального
логарифма можно опускать знаменатель и записывать только
давление р., что в общем случае не вполне корректно.
Вместе с тем на уровне современных международных
соглашений представление изученных свойств индивидуальных веществ
принято выражать в виде зависимости их энтропии и полной

250 Часть 2. Теория неидеального теплового ракетного двигателя
энтальпии от температуры в единой системе отсчета. Поскольку
одним из фундаментальных принципов физики является следующий
из второго закона термодинамики принцип максимума энтропии
для стационарного состояния, которому в частном случае для
конкретной реакции соответствует фиксируемое константой
равновесия соотношение парциальных давлений, то имеется возможность
решать задачи термодинамического расчета на более общих
принципах, не требующих выбора системы химических реакций.
Контрольные вопросы и задания
1. Вследствие каких допущений уравнение Дальтона может быть
введено в систему уравнений, описывающих стационарное равновесное
состояние продуктов сгорания?
2. Какое уравнение или условие может характеризовать стационарное
равновесное состояние смеси химически активных гетерогенных
компонентов продуктов сгорания?
3. Какие индивидуальные вещества (газообразные соединения), как
правило, входят в состав продуктов сгорания четырехэлементного
ракетного топлива?
4. В каких семи наиболее вероятных обратимых реакциях
диссоциации-рекомбинации участвуют индивидуальные вещества
(газообразные соединения), которые, как правило, входят в состав продуктов
сгорания четырехэлементного ракетного топлива? Запишите
уравнения этих реакций.
5. Запишите выражения для констант равновесия наиболее вероятных
обратимых реакций диссоциации-рекомбинации, проходящих
равновесно в условиях камеры сгорания и сопла ракетного двигателя.
6. Применяя принцип Ле Шателье - Брауна, выявите тенденцию
изменения (возрастает, убывает, не изменяется или недостаточно
данных для выполнения задания) значения константы равновесия
реакции диссоциации-рекомбинации углекислого газа при повышении
температуры.
7. Какие ограничения входят в математическую модель
термодинамического расчета, дополняя систему уравнений и условия
стационарности? Обоснуйте эти ограничения.
8. В каком виде в математическую модель термодинамического
расчета входят зависимости полных энтальпий индивидуальных веществ
от температуры?
9. В каком виде в математическую модель термодинамического
расчета входят зависимости энтропии индивидуальных веществ от
температуры при стандартном давлении 1 атм?
10. Каким образом учитывается изменение энтропии индивидуального
вещества, обусловленное различиями его парциального давления
и стандартного давления?

Глава 20
Принцип максимума энтропии и его использование
при термодинамическом расчете
Рассмотренное идеализированное представление продуктов
сгорания как системы ограниченной, т. е. конечных размеров, и
изолированной, т. е. не обменивающейся с внешней средой веществом
(содержание химических элементов не может изменяться) и
энергией (полная энтальпия постоянна), позволяет применять для описания
ее состояния химического и фазового равновесия вместо аппарата
констант равновесия следующий из второго закона термодинамики
принцип максимума энтропии, или экстремального значения
(максимума или минимума) других содержащих энтропию
термодинамических функций, например минимума изобарно-изотер-
мического или изохорно-изотермического потенциала.
Использование той или иной термодинамической функции
принципиально равнозначно. Наиболее общим и методически
обусловленным представляется подход с использованием
непосредственно энтропии iS, отнесенной к единице количества вещества,
т. е. джоуль на килограмм-кельвин или джоуль на моль-кельвин.
Свойство аддитивности энтропии как термодинамической
функции позволяет записать для расчета энтропии 1 кг продуктов
сгорания соотношение
*,с = 1>Ал(^)> (20-1)
к = \
где Мк - количество к-то компонента, моль/кг; S£' - энтропия
А>го компонента (Дж/(мольК)) при температуре Г при его
парциальном давлении р., если этот компонент - газ, и при давлении
ps, если компонент конденсированный; К - число компонентов
продуктов сгорания - индивидуальных веществ, газообразных
и конденсированных, электрически нейтральных и
ионизированных. При этом К = п + /?, где R - число конденсированных
компонентов, а п - число /-х газообразных компонентов, в молях,
выражается через парциальные давления и давления смеси
соотношением

252 Часть II. Теория неидеального теплового ракетного двигателя
М.=р,—
1000
(20.2)
Ya^iPi
1=1
Следуя принятому допущению об описании свойств
газообразных компонентов как идеальных газов, для которых
известны зависимости S®(T) (Дж/(моль*К)), т. е. значения энтропии при
разных температурах, но при стандартном давлении р0 = 0,1 МПа,
определим значение энтропии /-го газообразного компонента при
той же температуре Т, но при его парциальном давлении р. по
формуле
S?(T) = S?(T)-R0ln^-,
Ро
(20.3)
где R0 - универсальная газовая постоянная.
Для конденсированного компонента (для упрощения примем,
что он единственный) вследствие незначительной его
сжимаемости не учитываем влияние давления:
S^(T) = Sr(T\
(20.4)
где Sr(T) - известная зависимость энтропии от температуры для
данного конденсированного компонента.
Тогда уравнение (20.1) примет вид
v nc/max J
1000
S?{T)-Rob
El
Po
Pi
■S?(T)Mr
(20.5)
где Mr - число молей конденсированного вещества в 1 кг
продуктов сгорания; индекс «max» означает, что парциальные
давления газообразных компонентов соответствуют таким
концентрациям и фазовым состояниям всех компонентов, при которых
для данного суммарного давления р^9 температуры Т и полной
энтальпии продуктов сгорания 1ппс энтропия продуктов сгорания
S принимает максимальное значение.

Глава 20. Термодинамический расчет. Принцип максимума энтропии 253
Термодинамический расчет с использованием принципа
максимума энтропии математически сводится к задаче поиска
условного экстремума Sn c как функции многих аргументов: парциальных
давлений газов р., концентраций конденсированных
компонентов Afr, температуры Г, принимающих значения в области,
определенной некоторыми ограничениями (условиями): сохранением
концентраций химических элементов, постоянством полной
энтальпии или внутренней энергии, равенством суммы парциальных
давлений ръ внешнему давлению при сохранении
неотрицательности значений температуры и парциальных давлений газов.
Ниже приведены уравнения, описывающие эти условия.
Уравнения сохранения элементного состава топлива:
[П=4^1>,,, (20.6)
ЪьРг '■'
1 = 1
причем число уравнений равно числу химических элементов,
входящих в состав топлива.
Уравнение сохранения энергии'.
/„пс=4^1>Л,(Г). (20.7)
&/>,' = '
/ = 1
Уравнение Дальтона:
л=2>/- (20-8>
/=1
Условия неотрицательности давлений
р, 5* 0 (20.9)
и положительной температуры
Г>0. (20.10)
Дополнительным ограничением является также условие
электрической нейтральности системы:

254 Часть II. Теория неидеального теплового ракетного двигателя
1Х,М,.=0, (20.11)
/7 = 1
где пе.. - кратность ионизации //-го компонента, концентрация
которого М.. (моль/кг), причем для отрицательно заряженных
веществ кратности ионизации присваивается знак минус, для
положительно заряженных - знак плюс, а Я - число электрически
заряженных компонентов.
Таким образом, в математическую модель помимо
соотношения (20.5) входят уравнения (20.6) - (20.8), (20.11) и неравенства
(20.9) и (20.10).
Возможны два основных подхода к реализации математической
модели, в частности, для определения температуры и
равновесного состава химически активной смеси газов: применение
стандартных универсальных алгоритмов нахождения максимума
функции многих переменных или разработка специализированных
алгоритмов, использующих стандартные процедуры, но
учитывающих особенности задачи. Чаще всего именно второй подход
позволяет создавать более эффективные программы.
Рассмотрим основы одной из реализаций второго подхода.
Соответствующие термодинамическому (химическому,
фазовому и энергетическому) равновесию состав и температура
продуктов сгорания в рамках полученной модели могут быть
определены методом неопределенных множителей Лагранжа, следуя
которому задачу сводят к решению трансцендентной системы
уравнений численным методом.
Отметим, что число учитываемых индивидуальных веществ
К здесь ограничивается только располагаемыми данными об их
свойствах - зависимостях от температуры энтальпии /п .(Т) и
энтропии S?(T) - в форме, которая позволяет использовать их при
реализации математической модели и не требует перечислять
предположительно существенные химические реакции, что
необходимо при расчете на основе констант равновесия.
Вывод более полной системы уравнений, метод ее решения,
описание реализующих алгоритмов и программного комплекса
«Астра-4» и его современной реализации «Терра» (E-mail: trusov@
iu7-head.bmstu.ru) приведены в монографии1. В этой работе,
Применение ЭВМ для термодинамических расчетов
металлургических процессов / Г.Б. Синярев, Н.А. Ватолин, Б.Г. Трусов, Г.К.
Моисеев. М.: Наука, 1982.

Глава 20. Термодинамический расчет. Принцип максимума энтропии 255
в основу которой положены выполненные в МГТУ им. Н.Э. Баумана
многолетние исследования профессоров Г.Б. Синярева, Б.Г. Тру-
сова и их учеников, приведена система уравнений, описывающая
свойства и состав многокомпонентной, многофазной и
электрически нейтральной смеси химически активных веществ в
стационарном состоянии при фиксированном задаваемом удельном
содержании химических элементов и постоянной полной энергии.
К неизвестным характеристикам смеси как рабочего тела
относятся: содержание газообразных компонентов М.\ числа молей
веществ, образующих несмешивающиеся конденсированные фазы
и конденсированные растворы; давление р\ температура Г;
удельный объем v; энтропия S\ полная энтальпия /; внутренняя
энергия U. Причем превышение числа неизвестных над числом
уравнений на два позволяет задавать в качестве известных два
термодинамических параметра, определяющих равновесие
описываемого рабочего тела с окружающей средой. Например, в
качестве известных можно задавать следующие пары
термодинамических параметров: давление и полная энтальпия; давление
и энтропия; полная энтальпия и удельный объем; давление и
температура; температура и удельный объем.
При расчетах используются апробированные зависимости
свойств индивидуальных веществ от температуры в виде
подключенных к программному комплексу электронных баз данных.
Методика допускает:
• присвоение постоянного в пределах одних исходных данных
значения содержанию (фиксацию абсолютного количества)
одного или нескольких индивидуальных веществ, в том числе
равного нулю, причем последнее соответствует исключению
возможности образования этого вещества;
• фиксацию фазового состояния индивидуального вещества,
например: конкретное индивидуальное вещество может
рассматриваться как жидкое даже при температуре ниже точки
плавления или как газообразное при температуре ниже температуры
конденсации.
Результаты расчета позволяют установить состав и
концентрацию продуктов сгорания как в числах молей индивидуальных
веществ, так и в их объемных и массовых долях или через
парциальные давления газообразных компонентов.
Выводятся также значения всех запрашиваемых переменных,
например внутренней энергии, удельного объема, полной
энтальпии, энтропии и др.

256 Часть II. Теория неидеального теплового ракетного двигателя
В рамках рассмотренных моделей химически активное
рабочее тело, подчиняющееся уравнению состояния идеального газа,
рассматривается как неподвижное. Однако при движении
рабочего тела по соплу снижаются давление и температура и в
соответствии с законом сохранения энергии повышается скорость
потока и изменяется полное энергосодержание потока,
характеризуемое полной энтальпией, т. е. изменяются условия, от
которых, как следует из анализа рассмотренных моделей, зависят
состав и свойства рабочего тела.
Необходимостью учета этих характеристик объясняется
создание методик термодинамического расчета для определения
параметров рабочего тела в произвольной точке проточной части
ракетной камеры.
Методику термодинамических расчетов, основанную на
принципе максимума энтропии относительно термодинамических
степеней свободы, рассмотрим применительно к жидкому
ракетному топливу «кислород - водород» с избытком горючего, когда
уровень температуры, с одной стороны, позволяет пренебречь
термической ионизацией и диссоциацией молекулярных газов,
а с другой стороны, делает невозможным появление
конденсированных компонентов продуктов сгорания.
Пусть для конкретности соотношение компонентов
соответствует коэффициенту избытка окислителя а = 0,5 (стехиометри-
ческое соотношение Кт0 = 7,937), а давление в камерерк = 2 МПа.
При известных полных энтальпиях компонентов в состоянии
подачи - окислителя (жидкого кислорода, /п = -398,3 кДж/кг при
Т= 90,188 К) и горючего (жидкого водорода, /п = -4 353,9 кДж/кг
при Т = 20,27 К) - однозначно определяется полная энтальпия
топлива 1п т = -1 194,44 кДж/кг, приближенно равная внутренней
энергии, т. е. /пт = Unr.
Удельная формула топлива 049 9226^i99 69* Совокупность полной
энтальпии, удельной формулы и давления в камере представляют
собой условия однозначности для задачи расчета состава и
температуры продуктов сгорания.
Стехиометрическая реакция горения водорода в кислороде
Н7 + - О = Н90
2 2 2 2
откуда следует, что при принятых допущениях в составе
продуктов сгорания как наиболее вероятные компоненты могут быть
водяной пар и газообразные водород и кислород.

Глава 20. Термодинамический расчет. Принцип максимума энтропии 257
Но в общем случае два химических элемента - водород и
кислород - могут образовывать гораздо большее число
индивидуальных веществ: электрически нейтральные О, 02, Н, HL, ОН,
Н02, Н20, Н202, 03, ионы 0+\ О"1, О*1, О"1, H+1, H"1, Щ\ Щ\
ОН+1, ОН"1, H02_1, H20+1, H30+1 и свободные электроны, так
называемый электронный газ. Равновесная концентрация каждого
индивидуального вещества в этой совокупности может быть
разной, в том числе и нулевой. И в общем случае нет необходимости
до выполнения расчетов предполагать отсутствие каких-либо
веществ. Приведенные выше предположения (ограничение
состава тремя возможными соединениями - Н2,02 и Н20) сделаны
только с методической целью для снижения числа неизвестных и
упрощения задачи. При этом состав продуктов сгорания задан только
тремя концентрациями в молях на килограмм: М., / = 1, 2, 3, или
м м02, мНг0.
Тогда термодинамические степени свободы будут включать
в себя кроме молярных концентраций водяного пара и
газообразных кислорода и водорода только температуру Т. В таком случае
уравнение (20.5) для принимающей максимальное значение
энтропии продуктов сгорания S (Дж/кг) будет иметь относительно
простой вид:
/=i / = iv Pov J
м, => s„
или
s2(r)-^in
Pov
Мн +
Sb(T)-*o In
RqTM0i
P0v
5°i0(r)-^ln
PqV
M,
н,о»
^o +
(20.12)
где Sfl(T) - энтропия /-го компонента (Дж/(мольК)) при
парциальном давлении/?/5 которое будет соответствовать равновесному
содержанию компонента М{ в продуктах сгорания, имеющих
температуру Г; S?(T) - известное табличное стандартное значение
энтропии /-го компонента (Дж/(моль-К)) при стандартном
давлении^ = 0,1 МПа и температуре Г., равной температуре
продуктов сгорания Т\ v - удельный объем продуктов сгорания.

258 Часть II. Теория неидеального теплового ракетного двигателя
Исходя из принятого в термодинамике определения
парциального давления, удельные объемы продуктов сгорания v и их
газообразных составляющих v. равны, т. е. v = v.. Тогда выраже-
ние R0ln— L = R0mJ-L отражает изменение энтропии z-ro ком-
Pov Ро
понента при его изотермическом сжатии (при температуре Т = Г.)
от давления pQ = 0,1 МПа до соответствующего парциального
давления рг
Формально в уравнении (20.12) шесть неизвестных:
температура Г (К); энтропия S (Дж/кг); удельный объем v (м3/кг) и
концентрации Мн , М0 , МП20 (моль/кг). Причем энтропия S = Smax
может быть получена непосредственно расчетом при известных
соответствующих равновесному состоянию температуре Г,
удельном объеме v и концентрациях газообразных компонентов.
При этом энтропия достигает максимального значения при
ограничениях вида ф(хр х2, х3, ..., хп) = 0, отражающих законы
сохранения, приведенные ниже.
Закон сохранения энергии как равенство полных энтальпий
топлива и продуктов сгорания:
/ = 1
где 1п т - полная энтальпия 1 кг продуктов сгорания, равная
полной энтальпии 1 кг топлива, формально это новая переменная,
значение которой для данной задачи входит в заданные условия
однозначности; Ini(T) - полная энтальпия одного моля /-го
компонента (Дж/моль), вычисляемая по известным интерполяционным
формулам или определяемая по таблицам базы данных для
температуры Т без учета давления, так как для идеального газа
полная энтальпия зависит только от температуры.
Запишем этот закон в виде, принятом для выражения
ограничений:
ф,(г, мН2, м02, мНг0) =
= /Н2(Г)МН2 + уГ)М02 + /Н20(Г)МН20 - 1пя = 0. (20.13)
Отметим, что закон сохранения энергии может быть записан
аналогично и через полную внутреннюю энергию Un в виде

Глава 20. Термодинамический расчет. Принцип максимума энтропии 259
^,т=2>„,(^- (20-14)
/ = 1
Правую часть уравнения (20.14) запишем с учетом
приближенного равенства полной энтальпии и полной внутренней энергии
для конденсированных веществ:
In(T) = Un(T). (20.15)
Для газообразных компонентов, подчиняющихся уравнению
состояния идеального газа, если энтальпия и энергия выражены
в джоулях на килограмм, справедливо соотношение
Ini(T) = Uni(T) + RT, (20.16)
а если энтальпия и энергия выражены в джоулях на моль, то
Л(Г) = [/п,.(Г)+Д0Г (20.17)
Запись уравнения сохранения энергии через полную
внутреннюю энергию (20.14) позволяет существенно упростить систему
уравнений. В дальнейшем преимущественно будем использовать
запись аналогично (20.14).
Закон сохранения массы вещества в виде сохранения
содержания химических элементов в топливе и в продуктах сгорания
для рассматриваемой задачи:
для грамм-атомов водорода
[Н] = 2МН2 + 2МНг0,
или в принятой форме
ср2(МН2, МНг0) = [Н] - 2МН2 - 2МНг0 = 0; (20.18)
для грамм-атомов кислорода
%Шо2, МН20) = [О] - 2М02 - МНз0 = 0. (20.19)

260 Часть II. Теория неидеального теплового ракетного двигателя
Уравнение состояния газовой фазы:
pv^RJ^M,
i=\
ИЛИ
Ф4(Г, М02, МН20, МН2) = RT(M02 + МНз0 + Мщ) -pv = 0. (20.20)
Таким образом, математически задача сводится к нахождению
координат максимума - значений неизвестных Г, М0 , Мн 0, Мн ,
р, v, /п т или Un т, при которых достигается максимальное значение
5, и самого значения функции 5тах, заданной уравнением (20.12)
при ограничениях, описанных уравнениями (20.14), (20.18) - (20.20).
При решении задачи в такой формулировке представляется
целесообразным применять метод Лагранжа (см. разд. 11.3 - 4
«Условные экстремумы»)1, согласно которому система, состоящая
из уравнения (20.12) и определяющих ограничения уравнений
(20.14), (20.18) - (20.20), дополняется приравненными к нулю
частными производными некоторой вспомогательной функции
Лагранжа L по независимым переменным - координатам:
(20.21)
(20.22)
(20.23)
(20.24)
(20.25)
8L
8р~
dL _
дТ~
dL
дм0г
dL
дМщ
dL
0;
:0;
= 0;
= 0;
— П
дМН0
Корн Г., Корн Т. Справочник по математике для научных
работников и инженеров. М.: Наука, 1970.

Глава 20. Термодинамический расчет. Принцип максимума энтропии 261
Здесь функция Лагранжа задана выражением
L = S„
ZVp/s
(20.26)
/=i
где / = 1 ... 4 - номер (индекс) для условия, при котором
достигается экстремум S ; <р, - математическое выражение этого
условия (в нашем случае таких условий четыре и заданы они
уравнениями (20.14), (20.18) - (20.20)); X, - неопределенные
множители Лагранжа.
Выполним дифференцирование функции Лагранжа L, заданной
(20.26), и проведем упрощение полученных выражений.
Подставив в выражение (20.26) соответственно (20.12), (20.14),
(20.18) - (20.20), получим
L =
S°H(T)-J^ln
RJM»
5°2(Г)-^1п
мн +
■C^b^ln
Pov
RJMHfi
Pov
Mo +
M,
н,о
> +
+*ч{ианЛТ)Мнг +Un02{T)M02 +UnHi0{T)MHi0-U„.T}i +
+Х2{[Н]-2МЩ -2MH20}2+^{[0]-2M02 -2МН2о}з +
+ 14{rot(mH2 +M0i +MH20)-pv)4. (20.27)
Выполним дифференцирование (20.21), учитывая, что
давление р как аргумент входит только в сомножитель А,4:
|j = ^-[x,{Rj(MQi +MH2 +МН2О)-ру}] = Х4у = 0. (20.28)
Поскольку продукты сгорания содержат только газовую фазу,
то очевидно, что р Ф 0 и v Ф 0. Отсюда следует равенство нулю
множителя Х4, что существенно упростит выводы выражений для
других частных производных функции Лагранжа.

262 Часть II. Теория неидеального теплового ракетного двигателя
Производная функции Лагранжа по температуре имеет вид
дТ
Ми
+х,
ми
дТ °2 дТ
+м,
н,о
мпН(т)
дТ
+ми
дТ
+ М,
н,о
Ко(Т)
дТ
SUnuAT)
дТ
л
= 0.
(20.29)
Здесь выражение в скобках [ ]{ есть результат
дифференцирования группы слагаемых в фигурных скобках с нижним индексом
«S» выражения (20.27), а сомножитель [ ]2 получен путем
дифференцирования группы слагаемых в фигурных скобках с
индексом «1» того же выражения. Причем частные производные
функции Лагранжа по температуре берутся при постоянном объеме,
что соответствует условиям равновесия, т. е. для каждого
газообразного компонента
дТ
(20.30)
где cv. - удельная теплоемкость при постоянном объеме /-го
газообразного компонента.
При этом частные производные полной внутренней энергии
по температуре для каждого газообразного компонента
дТ
= сЛ>
(20.31)
Подставив выражения (20.30), (20.31) в (20.29), с учетом
следующего из (20.28) равенства Х4 = 0 получим значение для
первого неопределенного множителя Лагранжа:
.,=-1.
(20.32)
Выражения для частных производных функции Лагранжа по
числам молей водорода (/ = 1) МН2, кислорода (/ = 2) MQi и
водяного пара (/ = 3) Мн 0 с учетом Х4 = 0 и Хх = — после
упрощения запишем в виде

Глава 20. Термодинамический расчет. Принцип максимума энтропии 263
*..т-*.-<Ш-*.ъ*г±.±х^.
dMf ' Т p0v
7 = 2
где индексы / = 1, 2, 3 - обозначения составляющего
газообразного вещества, причем суммирование ведется по номерам
(индексам) химических элементов: j = 2 соответствует водороду,
а у = 3 - кислороду; ni . - число атомову-го химического
элемента в /-м компоненте; X. - неопределенные множители Лагранжа.
Используем известные из термодинамики идеального газа
соотношения
^(^)4-^=^(r)-v+^(r)=^(r)-^^;,(r),
где ty*ni(T) - полный приведенный изобарно-изотермический
потенциал Гиббса /-го вещества, представляющий собой известную
функцию температуры в виде базы данных или
аппроксимирующих зависимостей.
Введя потенциал Гиббса ф*п/(Г), получим выражение для
частных производных функции Лагранжа по числу молей в общем виде:
^ = Ф;дг)-/г>^^+^ (2033)
дМ, p0v pi
Выражение (20.33) запишем конкретно для каждого из
возможных компонентов, а именно:
для молекулярного водорода
8L . , ч RJMH
^^иХт)-^п— — + 2Х2+0-Х3=0; (20.34)
дмщ 2 Pov
для молекулярного кислорода
—— = ф (Г)-^1п-2—^- + 0.Я.2 + 2^=0; (20.35)
дМ0 p0v
для водяного пара
-^— = Фп н2о (Т) - ^ In *°™Hfi + 2X2 + Щ = 0. (20.36)

264 Часть II. Теория неидеального теплового ракетного двигателя
Используя (20.28) - (20.36), запишем полную систему
уравнений, связывающую равновесные состав и температуру продуктов
сгорания, удельную формулу и полное энергосодержание
топлива. При этом будем иметь в виду, что по аналогии с
использованием аппарата констант равновесия целесообразно считать
формальными переменными также энтропию (см. уравнение (20.12)),
полную энтальпию (см. уравнение (20.13)), полную внутреннюю
энергию (см. уравнение (20.14)) и суммарное давление р.
Система уравнений примет следующий вид:
1. -S +
(
Sl\T)-R,\*
RqTMh Л
Pov
мН2 +
М0,+
S°(r)-*0ln
*оГМН;0
Pov
^н,о=о;
2.1нтмн +i0(T)m0 +i„jt)m.
'h2v
н2 'о2
о2 h2ov
'Н20 п.т
0;
3- -ипя + UnH2(T)MH2 + Un02(T)M02 + UnH20(T)MH20 = 0;
4.R0T(MO2 + MH2O + MH2)-pv = 0;
5. [Н]-2МНгО-2МН2 = 0;
6. [О] - 2М0о - 2МН,0 = 0;
7
02 ~J"H20
^Л^)-^#|-^1п^^ + 2Я2=0;
8.
9.
&(7)-
илт)
\
-Ло1п
Pov
RqTMQ2
Pov
+ 2Х3 = 0;
Slo(T)-
*пнАТ)
■Rob— ^- + 2Х2+Х3=0.
Pov
(20.37)
В системе уравнений (20.37) уравнение 1 связывает значение
энтропии 1 кг продуктов сгорания с энтропией составляющих их

Глава 20. Термодинамический расчет. Принцип максимума энтропии 265
газов. Уравнения 2 и 3 представляют собой запись закона
сохранения энергии через полную энтальпию и полную внутреннюю
энергию соответственно. Уравнение 4 - это уравнение состояния
идеального газа. Уравнения 5 и 6 - уравнения сохранения
содержания грамм-атомов водорода и кислорода соответственно.
Уравнения 7, 8 и 9 - частные производные функции Лагранжа по
числу молей водорода, кислорода и водяного пара
соответственно. Здесь переменные: температура Г; давление/?; удельный
объем v; полная внутренняя энергия Un; полная энтальпия /п;
энтропия S; состав: как неизвестные - числа молей водяного пара Мн 0,
молекулярных двухатомных водорода Мн и кислорода MQ ;
неопределенные множители Лагранжа Х2 и Ху
Число неизвестных 11, а число уравнений 9. Превышение
числа неизвестных над числом уравнений на два требует
обязательного задания двух характеристик топлива или продуктов сгорания,
которые наряду с удельной формулой топлива определяют условия
однозначности конкретной задачи термодинамического расчета.
Если не делать предположений о возможных составляющих
продуктов сгорания, то в уравнениях 1-3 системы (20.37) число
слагаемых с множителями М. будет равно числу всех возможных
химических веществ, содержащих только атомы, входящие в
состав топлива. Кроме того, вместо уравнений 5 и 6 можно записать
систему т уравнений, где т - число различных химических
элементов (атомов), входящих в состав топлива. При этом число
уравнений, аналогичных уравнениям 7-9 (приравненные к нулю
частные производные функции Лагранжа по числу молей
каждого из возможных соединений - газообразных, индивидуальных
конденсированных или их растворов), будет равно числу
возможных компонентов продуктов сгорания.
В случае, когда число компонентов продуктов сгорания
ограничивается только соответствующими базами данных,
превышение числа переменных над числом уравнений на два сохраняется.
Решение системы уравнений (20.37) дает следующие результаты:
температура в камере сгорания Т= 3 014 К, число молей кислорода
М0 = 0,01084, водорода - Ми = 49,94, водяного пара - Мн Q = 49,90;
газовая постоянная продуктов сгорания R = 830,26 Дж/(кгК).
Тогда как расчет, учитывающий возможность образования всех
известных соединений водорода и кислорода, приводит к
несколько отличающимся результатам: Т= 2 893 К; М0 = 0,004748;
Мн = 49,32; Мн 0 = 49,36, причем в состав продуктов сгорания

266 Часть II. Теория неидеального теплового ракетного двигателя
входят также газообразные атомарные кислород (М0 = 0,01199)
и водород (Мн = 1,777), соединение ОН (Мон = 0,5376) в
концентрациях менее 10"4, соединения Н02 и Н202, чему соответствует
другое значение газовой постоянной продуктов сгорания: R =
= 839,94 Дж/(кгК). При этом не требовались предположения
о преобладании тех или иных компонентов, а рассматривались
все возможные компоненты - девять электрически нейтральных
и 13 ионов и свободные электроны (электронный газ).
Типичные задачи термодинамического расчета - определения
состава и свойств продуктов сгорания топлива в камере - можно
представить в виде двух групп (табл. 20.1):
• для изохорного горения (нагрева) (горение в работающем на
импульсном режиме ракетном двигателе или в пульсирующем
воздушно-реактивном двигателе, когда скорость образования
продуктов сгорания существенно больше их расхода в окружающую
среду, или горение в камере ракетного двигателя на одном из
этапов запуска в период, следующий за задержкой
воспламенения), в РДТТ горение до вскрытия сопловой заглушки;
Таблица 20.1. Характерные задачи и параметры
термодинамического расчета
Задача
Состав и свойства
продуктов сгорания топлива
заданного состава или
нагреваемого рабочего
тела при V= const
Состав и свойства
продуктов сгорания топлива
заданного состава или
нагреваемого рабочего
тела при р = const
Задаваемые условия
однозначности
Состав
Удельная
формула топлива
или рабочего
тела-[О], [С],
[Н]...

Термодинамические
параметры
'„.*
U«v
T,v
Ър
ил>р
Т,Р
Определяемые
параметры
>Г9 '"'п.С' П.П.С
состав
^'А^п.с'^п.п.с
состав
Р> \.с> п.п.с'
^п.п.С С0СТаВ
состав
^' V' ^п.с' п.п.с
состав
п.п.с' V' *Vc'
U .состав
п.п.с'

Глава 20. Термодинамический расчет. Принцип максимума энтропии 267
• для изобарного горения (нагрева), когда рассчитывается
результат идущего при постоянном давлении совокупного
рабочего процесса преобразования располагаемой энергии топлива
в тепловую энергию продуктов сгорания в камере сгорания
теплового двигателя на химическом топливе или в канале нагрева
рабочего тела теплового ракетного двигателя, использующего
теплоту, высвобождающуюся при ядерных реакциях, или
электрический источник теплоты.
Все уравнения математической модели приводят к одному
виду. Система уравнений является трансцендентной с числом
неизвестных, достигающим нескольких сот, и решается после
линеаризации итерационным методом Ньютона. При этом начальное
приближение задается автоматически и не требует
корректировки. Расчет считается завершенным, когда максимальная
относительная погрешность станет меньше 10_6.
Приведенный алгоритм достаточно эффективен при решении
большого числа задач термодинамического расчета ракетных
двигателей. Разработаны, прошли широкую апробацию и
применяются реализующий этот алгоритм программные комплексы
«Астра-4» и «Терра» с подключенной базой данных теплофизи-
ческих свойств индивидуальных веществ. Причем база данных
может быть расширена и уточнена как автором - разработчиком
программного комплекса, так и пользователем с учетом
особенностей решаемой задачи.
Простота и очевидность физического обоснования первичных
предпосылок, использованных при разработке метода, наряду
с универсальностью полученной системы уравнений позволяют
решать не только задачи теории тепловых ракетных двигателей,
но и многие задачи из смежных областей теплотехники. На
современной компьютерной технике задача расчета для
многоэлементной топливной композиции решается за весьма малое время,
что позволяет включать описанное программное обеспечение
в оптимизирующие программные комплексы систем
автоматизированного проектирования технологических процессов и
тепловых энергетических установок с максимальным диапазоном
значений давления 15...25 МПа.
При больших значениях давления отличия параметров
состояния реального и идеального газов (коэффициент сжимаемости
1,05 ^zb уравнении pv = zRT) превышают 5 %. И это влияет на
результаты расчета, нередко существенно отличающиеся от
результатов, полученных экспериментально, чем и обусловлены

268 Часть II. Теория неидеального теплового ракетного двигателя
работы, где описанный термодинамический метод
распространяется на такие «неидеальные» системы.
Так, в монографии Г.В. Белова1 обобщены результаты
термодинамического моделирования, которым автор занимался в
период работы в МГТУ им. Н.Э. Баумана и позднее в организациях
РАН. Приведены модели и описаны реализующие их алгоритмы
и программы расчета состава продуктов сгорания топлив при
повышенном давлении с учетом реальных свойств газовой фазы.
Показано, что для работающего при давлении более 30 МПа
газогенератора ЖРД с дожиганием генераторного газа (топливо
«кислород - керосин» при соотношении расходов компонентов
в газогенераторе 0,03 <Кт< 65) учет отличия уравнения
состояния реального газа от уравнения состояния идеального газа
приводит к значительным изменениям расчетного значения скорости
истечения - на 10...20 м/с.
Аналогичные по назначению программные продукты
имеются и в нашей стране, и за рубежом, причем ряд из них доступен
пользователям Интернета (обзор представленных в Интернете
программ термодинамического расчета приведен в указанной
выше монографии Г.В. Белова).
При единстве общих фундаментальных принципов
термодинамических расчетов большинства программных комплексов
среди них нет полностью универсальных. Поэтому полученные
с их помощью результаты следует критически анализировать,
сопоставляя расчетные и достоверные экспериментальные данные
и корректировать на этой основе как математические модели, так
и значения термодинамических констант. Реальная возможность
эффективного применения программных продуктов такого
назначения доказывается достигнутой эффективностью современных
ракетных двигателей, создание которых было бы невозможно без
привлечения методов термодинамики к оптимизации и анализу
результатов основного рабочего процесса - преобразования
располагаемой химической энергии топлива в полезную кинетическую
энергию истекающего из сопла потока.
Белов Г.В. Термодинамическое моделирование: методы,
алгоритмы, программы. М.: Научный мир, 2002.

Глава 20. Термодинамический расчет. Принцип максимума энтропии 269
Контрольные вопросы и задания
1. Сформулируйте принцип максимума энтропии и конкретизируйте
его применительно к решению задачи термодинамического расчета:
определению состава и температуры продуктов сгорания при
заданном суммарном давлении и полной энтальпии топлива.
2. Перечислите преимущества методики решения задачи
термодинамического расчета на основе принципа максимума энтропии по
сравнению с методикой решения этой же задачи с использованием
аппарата констант равновесия обратимых химических реакций.
3. В чем состоит метод неопределенных множителей Лагранжа
применительно к определению сочетания координат, при котором
функция многих переменных принимает максимальное значение?
4. Какие уравнения сохранения выступают в качестве ограничений?
5. Что представляет собой функция Лагранжа?
6. Почему равна нулю частная производная функции Лагранжа по
давлению?
7. Почему полную энтропию можно рассматривать как независимую
переменную?
8. Перечислите возможные сочетания исходных данных в качестве
условий однозначности решения задачи термодинамического
расчета применительно к изобарной камере сгорания.
9. Перечислите возможные сочетания исходных данных в качестве
условий однозначности задачи термодинамического расчета
применительно к изохорному горению (в непроточной камере сгорания
постоянного объема, в которой сжигается известное количество
топлива).
10. Сформулируйте условия однозначности задачи определения
состава рабочего тела, получаемого путем нагрева ракетного топлива
с известной условной формулой до заданной температуры при
заданном постоянном давлении.

Глава 21
Модели течения в соплах.
Термодинамический расчет
состава продуктов сгорания
в произвольном сечении сопла
В случае энергоизолированного адиабатного движения
химически активного потока продуктов сгорания происходит
перераспределение энергии потока:
• химическая энергия составляющих продуктов сгорания
переходит в тепловую энергию;
• тепловая энергия продуктов сгорания переходит в
кинетическую энергию потока.
При этом происходит изменение температуры и давления
в потоке химически активного рабочего тела, в результате чего
изменяются концентрации составляющих, появляются новые
компоненты, может изменяться фазовое состояние некоторых
индивидуальных веществ. Вследствие различной скорости разных
типов химических реакций и фазовых переходов изменения идут
с конечной, переменной по длине сопла скоростью. Время
пребывания рабочего тела в зоне с конкретными значениями
давления и температуры мало и может оказаться недостаточным для
перехода потока как стремящейся к стационарному состоянию
системы к динамическому химическому равновесию.
Если представить, что скорости всех возможных превращений
в потоке продуктов сгорания столь велики (близки к
бесконечности), что в любом сечении потока устанавливается химическое,
фазовое и энергетическое равновесие, то говорят о равновесном
течении в сопле. Энергетическое равновесие - это такое
равновесное распределение атомов и молекул по энергетическим
состояниям, которое соответствует равенству температур каждой
фазы и каждого компонента одной фазы, например, температура
всех составляющих смесь газов одна и та же.
Течение в сопле, при котором не соблюдается хотя бы один
из видов равновесия (энергетическое, химическое или фазовое),
называется неравновесным. Частным случаем химически
неравновесного течения в сопле, когда химический состав продуктов

Глава 21. Термодинамический расчет. Модели течения в соплах 271
сгорания (рабочего тела) не соответствует местной температуре
и давлению, является химически замороженное течение^ при
котором в каждой точке потока предполагается постоянство
химического состава. Область химически замороженного течения
может составлять часть всего потока, ограниченную некоторым
сечением с одной стороны и простирающуюся ниже по течению
до выхода из проточной части. О такой картине течения говорят
как о внезапном «замораживании» в сечении, которое, как
правило, может задаваться значением в нем одного из параметров
из совокупности давления, температуры, геометрической
степени расширения потока.
Если в процессе приближения к равновесному состоянию
потока (к равновесному течению) снижение температуры вызывает
преобладание экзотермических реакций рекомбинации в потоке
и смещение состава рабочего тела в сторону образования сложных
молекул с относительно большой молекулярной массой, то
происходит внутренняя регенерация - потери тепловой энергии на
диссоциацию в камере сгорания возвращаются в виде
выделяющейся теплоты при реакциях рекомбинации в сопле. При
химически замороженном течении такого возврата энергии нет. Если
на части сопла течение равновесное, то имеет место и частичный
возврат энергии, затраченной на диссоциацию продуктов
сгорания в зоне высоких температур. Влияние этих процессов
проявляется в значительной разнице между максимально возможными
удельными импульсами, достигаемыми при равновесном и
замороженном течении в сопле ракетного двигателя.
На рис. 21.1 представлены рассчитанные для трех различных
видов течения в сопле зависимости пустотного удельного
импульса от соотношения компонентов топлива «НДМГ - кислород»
для двигателя с давлением в камере 15 МПа и давлением в
выходном сечении сопла 0,01 МПа.
Соотношение максимальных значений удельного импульса
подтверждает существенность влияния описанного физического
процесса внутреннего энергообмена на достижимые
характеристики двигателя.
Дополним предположение о постоянстве химического
состава допущением энергетического равновесия внутри составляющих
одной фазы, т. е. равенства температур всех составляющих смесь
газов, равенства температур всех составляющих раствор
жидкостей, тогда как температуры веществ, находящихся в разных
фазовых состояниях, могут быть разными в одной и той же точке.

272 Часть II. Теория неидеального теплового ракетного двигателя
3700
| 3650
2 3600
| 3550
| 3500
5 3450
J 3400
3350
0,6 0,8 1,0 1,2
Коэффициент избытка окислителя а
Рис. 21.1. Зависимости пустотного удельного импульса от соотношения
компонентов топлива «НДМГ - кислород»:
1 - равновесное течение на всем протяжении проточной части; 2 - химически
замороженное течение на всем протяжении проточной части; 3 - локально
неравновесное течение, т. е. равновесное течение на дозвуковом участке и
химически замороженное течение на сверхзвуковом участке сопла (приближение Брея)
Такая ситуация соответствует скоростному и температурному
отставанию, когда при многофазном течении в сопле разнятся
скорости и температуры частиц конденсированной фазы и
окружающей ее газообразной среды.
Если некоторое индивидуальное вещество при течении по
соплу не претерпевает фазовых переходов, которые должны бы
произойти при достаточном времени нахождения вещества в
каждом сечении или при весьма высоких скоростях фазовых
переходов, то говорят о фазовом неравновесии в потоке.
Представляющим практический интерес примером такого неравновесия
может служить отсутствие кристаллизации жидкой фазы в сопле
в области течения, где температура газовой фазы ниже
температуры ее плавления.
Максимальной полноте преобразования располагаемой
энергии топлива в кинетическую энергию рабочего тела
соответствует идеализированная модель одномерного равновесного течения
в энергетически изолированном канале при отсутствии трения,
а следовательно, и диссипации энергии на стенке канала и внутри
потока. Значение любого параметра, рассчитанного в таком
приближении, называется идеальным значением параметра, а
полученные характеристики двигателя представляют собой
мажоранту поля возможных характеристик, достигаемых при реализации
других, отличных от идеальной моделей течения в сопле.
Y з
2 !
0,7sJ i7o,73
\/
^0,92 |

Глава 21. Термодинамический расчет. Модели течения в соплах 273
Такому идеальному представлению поставим в соответствие
идеальную же математическую модель, описывающую состояние
продуктов сгорания как термодинамическую систему,
находящуюся в полном равновесии в любой точке.
Поскольку течению в сопле предшествует процесс горения,
то результат последнего будет начальным состоянием для
описания изменений в потоке.
Полагая, что химические реакции и фазовые переходы
происходят в потоке при близких к нулю перепадах температур и
концентраций реагентов, можем считать их обратимыми и
идущими при практически неизменной энтропии, т. е. можем
рассматривать их как изоэнтропийные процессы.
В математическую модель термодинамического расчета в
произвольной точке потока помимо полученных ранее (см. гл. 19,
20) уравнений сохранения содержания у химических элементов
г -, 1000 А
[Х1=- 2>'vu (21.1)
/=i
включается уравнение для расчета энтропии (20.5) в виде
1000
Ё^-л
/=1
5?(Г)-^1пА
Pi
+ S*(T)Mr
/ = 1
(21.2)
где значение *Snc в левой части есть константа для всех точек
течения (расчетных сечений), равная энтропии, рассчитанной для
параметров в камере сгорания.
Поскольку действует допущение об идеальности свойств газа,
то справедливо и уравнение Дальтона
/ъ=Ёл>
(21.3)
/=i
где ръ - давление в расчетном сечении, и ограничения для
парциальных давлений
р.^0
(21.4)
и для температуры

274 Часть II. Теория неидеального теплового ракетного двигателя
Г>0. (21.5)
Химическое и энергетическое равновесие продуктов сгорания
достигается в расчетном сечении относительно степеней свободы
по температуре Г и концентрациям индивидуальных веществ,
выражаемым через парциальные давления рг При этом равновесию
соответствует максимальное значение энтропии. Математически
это отражается или путем введения в математическую модель
уравнений констант равновесия, аналогичных уравнениям (19.7) -
(19.13), или путем включения функции Лагранжа с
соотношениями для расчета одноименных неопределенных множителей.
Справедливо также уравнение для расчета полной энтальпии
продуктов сгорания:
где в отличие от уравнений (19.2) и (20.7) для расчетов параметров
в камере сгорания энтальпия /п п c(r,/?z) есть неизвестная
величина, вычисляемая непосредственно для конкретных парциальных
давлений pi и температуры Т.
Адиабатные процессы описываются уравнением сохранения
энергии для одномерного течения:
',т = '„.„,(^)+^р (21-6)
где 1ПТ- полная энтальпия топлива в условиях подачи в камеру
сгорания; Г, /?s, W - температура, давление и скорость потока
в расчетном сечении.
Отметим различия математических моделей
термодинамического расчета для изобарной камеры сгорания и для произвольной
точки (произвольного сечения - при одномерном течении)
потока в проточной части камеры.
Математическая модель дополнена уравнением сохранения
энергии (21.6), но при этом введены дополнительные неизвестные:
W - скорость потока и 1п п с(Г, pL) - полная энтальпия в расчетном
сечении, значения которых можно задавать произвольно.
Задаваемое как константа суммарное давление в камере
сгорания (формально являющееся переменной величиной) стало

Глава 21. Термодинамический расчет. Модели течения в соплах 275
определяемой неизвестной переменной в произвольном расчетном
сечении, что, однако, не изменило числа переменных в системе
уравнений. Таким образом, произошло формальное увеличение
числа неизвестных на единицу и к системе добавилось одно
уравнение, причем свойства математической модели сохранились,
а именно: так же как и при термодинамическом расчете для
изобарной камеры сгорания, при термодинамическом расчете для
произвольного сечения сопла можно задавать значения двух
термодинамических параметров, например давления и энтропии. При
этом энтропия задается обязательно.
Значение энтропии выбирается не произвольно. Энтропия S
вычисляется для известных параметров: давления в камере
сгорания рк, элементного состава [X]. и полной энтальпии топлива 1п т
в результате решения задачи термодинамического расчета для
изобарной камеры сгорания. Здесь постоянство энтропии
отражает допущение обратимости всех элементарных процессов,
включая и химические превращения.
Постоянство энтропии соблюдается и в том случае, когда
химические превращения отсутствуют, т. е. для химически
замороженного течения, для которого сохраняются неизменными
мольные концентрации компонентов при всех значениях давления во
всех точках или сечениях потока.
Задаваемое давление определяет условия расширения потока
до расчетного сечения. Далее будет показано, что условия
расширения потока можно задавать и через другие параметры.
Таким образом, задача термодинамического расчета для
произвольного сечения потока сводится к той же самой
математической задаче, что и при термодинамическом расчете для изобарной
камеры сгорания, но при этом задают:
• условия, определяющие параметры расчетного сечения, или
значение полной энтальпии, вычисляемой для выбранного
значения скорости по уравнению (21.6) вместо полной энтальпии
топлива, или непосредственно давление в сечении, для которого
выполняется расчет, вместо давления в камере сгорания;
• значение энтропии, рассчитанное предварительно в
результате решения задачи термодинамического расчета для камеры
сгорания.
Следовательно, задаче расчета состава, свойств и скорости
в произвольном сечении сопла предшествует термодинамический
расчет для условий камеры сгорания, где скорость потока равна
нулю.

276 Часть II. Теория неидеального теплового ракетного двигателя
Существование и однозначность решения обосновываются
математической эквивалентностью математических моделей
расчета для изобарной камеры сгорания и для произвольного сечения
потока. И в том и в другом случае для топлива данного
элементного состава состав и температура продуктов сгорания
определяются однозначно, если заданы значения любых двух
термодинамических параметров, выбранных из следующих шести:
давления, удельного объема, температуры, энтропии, энтальпии,
внутренней энергии. Для расчета в некотором сечении
обязательно задают энтропию, другой параметр выбирают из оставшихся
пяти произвольно.
В результате решения задачи для потока в сечении, где
скорость движения рабочего тела W, а давление/?, получаем: состав
(например, в виде значений парциальных давлений
индивидуальных химических веществ/?, с молекулярной (мольной) массой \i.9
а значит, и удельные теплоемкости с . и газовую постоянную
рабочего тела /?z); температуру Т; плотность рабочего тела р;
полную энтальпию 1ппс (Г, /?z).
Покажем, что этих данных достаточно для расчета удельной
площади потока F", т. е. площади сечения сопла при расходе
рабочего тела 1 кг/с.
Для одномерного течения со скоростью ^рабочего тела
плотностью р (удельным объемом v), с секундным массовым расходом
m в сечении площадью F уравнение неразрывности имеет вид
m = pWF. (21.7)
Разделив уравнение (21.7) на m и учитывая определение для
F
удельной площади потока F" = —, получаем
m
F" = — = —
pW W*
Известность значения удельной площади потока F" в сечении
с давлением р позволяет определить площадь F, а значит, и
размеры сопла для конкретного расхода топлива т.
Задавая значения давления потока, находящиеся в пределах
от значения давления в камере рк до значения давления в
выходном сечении ра, и решая задачу термодинамического расчета для
каждого значения давления потока, получаем распределение

Глава 21. Термодинамический расчет. Модели течения в соплах 277
давления, температуры, плотности и скорости потока по длине
проточной части камеры, если задано изменение площади
нормального сечения сопла.
При этом значение развиваемого удельного пустотного
импульса / п, зависящего для данного топлива и от давления в
камере сгораниярк, и от давления^, удельной площади потока F'J
и скорости в выходном сечении сопла Wq9 определяется
однозначно по соотношению
j =™Wa+FgPa=W +vF„
-*у.п . "а ' УаЛ
т
Здесь влияние давления в камере сгорания проявляется при
расчете скорости истечения через рассчитанное для условий камеры
сгорания значение энтропии, используемое при расчете полной
энтальпии в выходном сечении сопла.
Свойства потока во многом зависят от его сжимаемости, кри-
W.
терием которой служит число Маха Mf. = —, где а. - скорость
ai
звука, определяемая в том же сечении, что и скорость потока W..
Представляет интерес расчет местной скорости звука в
каждом сечении, в том числе и в критическом, где местная скорость
потока WK равна местной скорости звука ак , а число Маха
и приведенная скорость потока X равны единице, т. е. WK = a
иМ =Х =1. КР
кр кр
Под скоростью звука а в находящемся в динамическом
равновесии потоке будем понимать скорость распространения слабых
возмущений, определяемую соотношением
(21.8)
где частная производная давления по плотности вычисляется при
предположении, что равновесные процессы в волне возмущений
изоэнтропийные. Определенная таким образом скорость звука
называется равновесной.
Если период колебаний давления в волне возмущений мал по
сравнению с временем релаксации состава смеси, то скорость
распространения таких возмущений ближе к так называемой
замороженной скорости звука, обозначаемой а' и определяемой
уравнением (21.8). В этом случае частная производная вычисля-

278 Часть II. Теория неидеального теплового ракетного двигателя
ется для неизменного химического состава среды.
Соответственно и параметры, вычисляемые с использованием замороженной
скорости звука, отмечают штрихом и этим они отличаются в
обозначениях от таких же параметров, рассчитанных по равновесной
скорости звука.
В рамках настоящего курса, кроме особо оговариваемых
случаев, используется равновесная скорость звука.
Для получения значения расходного комплекса Р определим
состав (газовую постоянную RK ), давление р , температуру Т
и удельную площадь потока F" в критическом сечении из условия
равенства WK = ак , применяя математическую модель
термодинамического расчета для произвольного сечения и результаты
термодинамического расчета в изобарной камере сгорания.
Вследствие неизвестности параметров потока, кроме
постоянной для всех точек потока энтропии S, процесс расчета ведем
итерационно.
Этап 1. Через ГДФ, принимая показатель адиабаты таким же,
что и в камере сгорания, рассчитываем давление;? в первом
приближении.
Этап 2. Для известной энтропии S и полученного значения
давления выполняем термодинамический расчет, определяя
дополнительно местные скорости потока и звука.
Этап 3. Сравнивая значения Wna, определяем необходимость
корректировки значения давления р в большую или меньшую
сторону и повторяем расчет, начиная с этапа 1, до тех пор, пока
не будет выполнено с заданной точностью равенство W = а .
Описанный итерационный процесс, как правило, является
сходящимся, а полученное решение - единственным. Ускорить
сходимость можно применением известных итерационных
методик, основанных, например, на методах половинного деления,
методе Ньютона и др.
Укажем на то, что в общем случае не доказано совпадение
критического и минимального сечений, рассчитанных по
рассмотренной математической модели. Однако многочисленные
расчеты критических параметров (как исходя из равенства W = а ,
так и при предположении минимальности удельной площади
потока) дают практически совпадающие результаты в
диапазонах значений параметров, характерных для ракетных двигателей.
Это позволяет с приемлемой погрешностью отождествлять
минимальное и критическое сечения, которые при протекании в
сопле необратимых процессов могут не совпадать (критические

Глава 21. Термодинамический расчет. Модели течения в соплах 279
условия достигаются в потоке ниже по течению минимального
сечения).
Значительный практический интерес представляет расчет
параметров ракетного двигателя с заданными относительными
размерами проточной части камеры, т. е. с заданной геометрической
степенью расширения сопла или относительной площадью вы-
F
ходного сечения F =—g-. Покажем однозначность результатов
термодинамического расчета для сопла с заданной геометрической
степенью расширения, учитывая известность результатов
термодинамического расчета для камеры сгорания и для критического
сечения.
Для сечения с площадью Fa рассчитывают удельную площадь
потока по следующему из уравнения неразрывности соотношению:
F" = F"F . (21.9)
а кр отн v '
Далее может быть образован следующий итерационный цикл.
Этап 1. По соотношениям газодинамики идеального потока,
например через ГДФ, определяют значение давления р(а1) и
решают задачу термодинамического расчета для двух задаваемых
термодинамических параметров: давления, равногоp{J\ и энтропии S,
значение которой берется равным значению энтропии в камере
сгорания.
Этап 2. По результатам термодинамического расчета
вычисляют значение удельной площади потока F"{]) при давлении//1}
и сравнивают полученное значение F'J{X) со значением FJ',
рассчитанным по соотношению (21.9).
Этап 3. Если рассогласование не отвечает требуемой
точности, то корректируют значение давления в расчетном сечении
и повторяют расчет по этапам 1 и 2 до тех пор, пока не будет
выполнено равенство F"(1) = F".
Таким образом, задание условий расширения рабочего тела
в сопле через параметры в камере сгорания и относительную
площадь потока приводит к задаче термодинамического расчета,
имеющей однозначное решение, поскольку заданы два
термодинамических параметра - давление и энтропия.
В качестве корректируемой величины итерационного
процесса может рассматриваться не только давление, но и другие
параметры, выбор которых зависит от особенностей алгоритма решения

280 Часть II. Теория неидеального теплового ракетного двигателя
задачи термодинамического расчета, но достижимость заданной
точности оценивается сравнением значений удельных площадей
потока.
Типичное сочетание задаваемых и рассчитываемых величин
для этих задач представлено в табл. 21.1.
Таблица 21.1. Характерные задачи и параметры
термодинамического расчета для расширяющегося потока
Задача
Состав, температура
и скорость рабочего
тела, расширяющегося
равновесно от
давления рк в камере до
давления р
Га
Состав, температура
и скорость рабочего
тела, расширяющегося
равновесно от
давления рк в камере до
сечения, превосходящего
критическое в Fqth раз
Температура и
скорость рабочего тела
известного постоянного
состава,
расширяющегося от давления рк в
камере до давления ра
* Значение определяв
ского расчета для условир
Задаваемые условия
однозначности
Состав
Удельная
формула топлива
или рабочего
тела-[С], [Н],
[0],Мит.д.
Состав
рабочего тела - М*
гея с помощью пр(
i в изобарной кам<

Термодинамические и
геометрические
параметры
P,ST
Fm>?
P.?
^дшествующего
гре сгорания.
Определяемые
параметры
T,v,I„,Un,
W,F",
состав - Мг
F
отн
7>,/„,£/„,
F" F"
1 ' Л кр'
состав - М.
Т.*>Ъип>
W, F"
термодинамиче-
Вследствие изменения свойств и состава рабочего тела при
его течении по соплу таким образом, что энтропия остается
постоянной величиной, можно связать параметры продуктов
сгорания в изобарной камере сгорания (например, параметры

Глава 21. Термодинамический расчет. Модели течения в соплах 281
торможения: давление/7 , плотность р ) и в произвольном сечении
сопла через уравнение изоэнтропы, записываемое для
некоторого усредненного по процессу показателя изоэнтропы п в
общепринятом виде:
"' -" (21.10)
И"
Р
Усредненный по процессу в диапазоне значений давления
р"... р показатель изоинтропы п может быть рассчитан по
следующему из (21.10) уравнению:
п--
. р . RT
In — + ln
дГ
При выводе этого уравнения использовалось уравнение
состояния идеального газа.
Идущие в расширяющемся потоке при снижении
температуры как преобладающие экзотермические реакции рекомбинации
обеспечивают внутренний теплоподвод, что как бы приближает
процесс к изотермическому, и показатель процесса п
уменьшается по сравнению с показателем адиабаты к идеального газа
с параметрами продуктов сгорания (7?*, с и др.) в изобарной
камере. При этом устанавливается соотношение \ <п < к.
Значение показателя изоэнтропы п или, что то же самое,
показателя процесса, для конкретной ракетной камеры зависит от
выбранного диапазона значений давления, в котором
выполняется усреднение. Значение показателя адиабаты к продуктов
сгорания в разных точках сопла будет разным вследствие
переменности состава и теплоемкости по длине проточной части камеры.
Полученное значение показателя процесса п при усреднении
в диапазоне значений давления/Л../?, гдер* - давление в камере
сгорания, а р - текущее давление, позволяет использовать
аналитические соотношения одномерной газовой динамики
идеального газа для связи параметров продуктов сгорания в камере
сгорания, т. е. параметров торможения, и параметров потока в
сечении с давлением р, что в ряде случаев существенно упрощает
методики расчета.

282 Часть II. Теория неидеального теплового ракетного двигателя
Значение показателя процесса п можно найти и
непосредственно из уравнений ГДФ, записанных для п = к через число Маха Мв,
которое получено термодинамическим расчетом для заданного
соотношения давлении — = —-, г или для геометрической
Ра я(Мв,л)
?а 1
степени расширения сопла —— = —, г-.
FKp q(Ua,n)
Например, для соотношения давлений имеем уравнение связи
b-=(]+t±Mlf, pi.ii)
где давление в камере рк есть давление торможения, одно и то же
для любой точки области течения.
Отметим, что значения показателя процесса п = к9 полученные
из соотношений (21.10), (21.11) или из аналогичных соотношений,
следующих из ГДФ q(Ma, я), т(Мд, и), в(Мв,я), будут различаться,
а каждое из них будет точнее описывать распределение той
величины, которая положена в уравнение связи: F9p9 Гили р. Если
же требуется использовать одно и то же значение показателя
процесса п для расчета распределений нескольких параметров,
например р и р, то в этом случае предпочтительнее находить его из
соотношения (21.10).
Как отмечалось ранее, постоянство энтропии при течении
рабочего тела по соплу характерно не только для
рассмотренного случая условно обратимых равновесных процессов (скорость
химических реакций близка к бесконечности), но и для
процесса течения газа постоянного химического состава, так
называемого химически замороженного течения, когда скорость
химических реакций близка к нулю и отличие от течения идеального
газа состоит только в зависимости удельной теплоемкости от
температуры.
Задача термодинамического расчета для произвольных
сечений потока в таком неравновесном приближении математически
существенно проще, чем задача расчета по математической
модели равновесного течения, так как абсолютные концентрации
(мольные доли) газов (индивидуальных химических веществ)
в любом сечении те же, что и в изобарной камере сгорания, и
система уравнений и неравенств (21.1) - (21.5) математической

Глава 21. Термодинамический расчет. Модели течения в соплах 283
модели упрощается и приближается по свойствам к системе
уравнений одномерной газовой динамики идеального газа. Отличия
в результатах расчета по этим близким математическим моделям
обусловлены только учетом зависимости с от температуры Т.
Специфика задачи термодинамического расчета одномерной
скоростной камеры (в пределе - камеры с полутепловым соплом)
состоит в отсутствии в камере зоны, где горение происходит в
неподвижном относительно ее границ потоке, и поэтому в общем
случае невозможно однозначно выявить сечение, которое
является выходным для камеры сгорания и входным для сопла.
Энтропия в таком течении растет на участке от начального
сечения камеры, в котором подводятся компоненты топлива, вплоть
до сечения, где горение завершается. Здесь полное
энергосодержание продуктов реакции (полная энтальпия в сумме с
кинетической энергией) становится равным полной энтальпии топлива.
Полное давление потока в этом сечении, очевидно, будет меньше
давления в камере - в начальном ее сечении. Таким образом,
уравнение сохранения энергии для одномерного течения (21.6),
как и включающая его математическая модель изоэнтропийного
течения химически активного потока, применимо только на
участке от входа в сопло до его выходного сечения. При этом условия
однозначности, позволяющие реализовать эту модель
математически, неполные, так как неизвестно давление торможения
потока, поэтому невозможно рассчитать значение энтропии
продуктов сгорания на входе в сопло, а значит, и его проектные
размеры, развиваемый удельный импульс и другие искомые
параметры и характеристики двигателя.
Если предположить, что на участке от входного до
выходного сечения цилиндрической камеры сгорания с площадью
поперечного сечения FK горение заменяется подводом теплоты к
одномерному потоку изменяющегося по составу идеального газа,
поступившему в камеру сгорания в ее входном сечении при
давлении рк с близкой к нулю скоростью W~ О и расходом т, то для
этого участка описанная выше математическая модель может быть
дополнена уравнением сохранения количества движения в форме
Эйлера:
pFK + mW = pKFK, (21.12)
где/?к, FK, m - постоянные величины. Причем уравнение (21.6)
также входит в математическую модель и связывает параметры

284 Часть II. Теория неидеального теплового ракетного двигателя
потока в произвольном сечении камеры сгорания, где полная
энтальпия заторможенного потока - текущая переменная, а также
параметры потока в произвольном сечении сопла и
неизменяющиеся параметры торможения на входе в сопло.
Поскольку при движении продуктов сгорания от входного
сечения камеры сгорания до входа в сопло снижается давление
и растет температура, то, следовательно, монотонно
уменьшается плотность продуктов сгорания. Эти предположения позволяют
записать систему уравнений и неравенств, имеющую получаемое
численными методами решение в виде распределения состава,
давления, температуры, скорости, энтальпии и энтропии на
участке камеры от входного сечения камеры сгорания до входного
сечения сопла. При этом линейные координаты расчетных
сечений фиксированы только для смесительной головки (входное
сечение камеры сгорания) и входа в сопло, а промежуточные
сечения только упорядочены, т. е. располагаются в заданной
последовательности, но расстояния между сечениями не
определены. Как показали расчеты, для двигателя с камерой с
полутепловым соплом значения параметров потока могут на 40...50 %
отличаться от значений, полученных для эквивалентного по тяге
и топливу двигателя с изобарной камерой. Таким образом,
описанная методика может быть востребована при проектировании
современных ракетных двигателей, большинство из которых
имеют камеру сгорания, близкую к скоростной камере1.
Применение полной математической модели для сквозного
расчета параметров потока во всех сечениях - от выходного
сечения камеры сгорания до среза сопла - позволяет в основном
сохранить алгоритм, трансформируя при этом математическую
модель так, чтобы в расчетных сечениях учитывались физически
обоснованные допущения о скоростях химических реакций -
бесконечность или нуль. При конечности скоростей химических
реакций реальное течение может рассматриваться как некоторое
среднее между предельными: равновесным течением и химически
замороженным течением. Зависимости параметров реального
течения будут принадлежать ленте решений с верхней (мажоранта)
и нижней (миноранта) границами, соответствующими
равновесному и химически замороженному течениям.
Дорофеев А.Л., Розинский СМ. Расчет состава и свойств
газообразных продуктов сгорания топлива в скоростной камере // Известия
вузов. Машиностроение. 2003. № 4. С. 49-52.

Глава 21. Термодинамический расчет. Модели течения в соплах 285
В результате анализа многочисленных термодинамических
расчетов для равновесных течений можно выявить некоторые
качественные зависимости принципиально достижимых
показателей совершенства ракетных двигателей от основных факторов.
Контрольные вопросы и задания
1. Какое течение в сопле ракетного двигателя называется равновесным?
2. Какое течение в сопле ракетного двигателя называется
неравновесным? Что такое фазовое неравновесие?
3. Как рассчитывается условный усредненный по процессу показатель
изоэнтропы nl
4. Какое течение в сопле ракетного двигателя называется химически
замороженным?
5. Почему рассчитанная при предположении равновесного течения
в сопле температура в его выходном сечении будет существенно
выше, чем рассчитанная при предположении течения, химически
замороженного на всем протяжении проточной части?
6. Какое течение называют локально неравновесным (например, так
называемое приближение Брея)?
7. Какие допущения являются общими для моделей равновесного и
химически замороженного течений? Перечислите и подтвердите их
выполнение на основе распечатки результатов
термодинамического расчета, выполненного с использованием программных
комплексов «Астра-4» или «Терра».
8. Какие допущения являются особенными для моделей равновесного
и химически замороженного течений? Перечислите и подтвердите
их выполнение на основе распечатки результатов
термодинамического расчета, выполненного с использованием программных
комплексов «Астра-4» или «Терра».
9. В какой форме записывается уравнение сохранения полной энергии
для одномерного адиабатного течения (для произвольного сечения
сопла)?
10. Обоснуйте справедливость утверждения: решению задачи
термодинамического расчета состава, температуры и скорости рабочего
тела в произвольном сечении сопла необходимо предшествует
расчет состава и температуры продуктов сгорания топлива в выходном
сечении камеры сгорания.

Глава 22
Влияние давления в камере сгорания
и степени расширения рабочего тела в сопле
на термодинамические характеристики
продуктов сгорания типовых ракетных топлив
Значения давления, температуры, скорости движения
рабочего тела в характерных сечениях проточной части камеры во
многом обусловливают облик конструкции двигателя, задавая
требования к применяемым материалам и системе охлаждения
камеры. Параметры потока в критическом F и выходном Fа
сечениях сопла непосредственно определяют интегральные
параметры качества двигателя как тепловой машины, создающей
реактивную тягу - расходный комплекс:
v F С
Р - —:— - АрЛср - Ркх
т
'кр" кр
-кр
V
кр
_ У^р^кр
= АЛ")'
(22.1)
П+\
где Акр(п) = л/п
; п = п - значение условного показа-
_V("-o
теля изоэнтропы, усредненного в диапазоне значений давления
*
р ... р .
*к *кр
Если потерь полного давления при течении рабочего тела по
сужающейся части сопла нет, то справедливо равенство/?* =/?*,
а удельный импульс на расчетном режиме работы сопла /
численно равен скорости истечения
W=<
2п
\п-\
*£
1-
п-\
(22.2)
где показатель изоэнтропы п усреднен по процессу в диапазоне
значений давления /?*... ра, причем в общем случае значения
показателя изоэнтропы п в (22.1) и (22.2) разные.
Введение усредненных по процессу показателей изоэнтропы
позволяет выявлять на качественном уровне зависимости между

Глава 22. Термодинамический расчет. Влияние параметров в камере 287
выходными параметрами двигателя и основными аргументами -
соотношением компонентов Кт или коэффициентом избытка
окислителя а, давлением в камере сгорания р*, степенью
расширения газа в сопле р*/ра или геометрической степенью
расширения сопла F /F .
а кр
В частности, усреднение показателя изоэнтропы п = паъ
диапазоне значений давления/?*... ра позволяет использовать
соотношения газовой динамики для выражения пустотного
удельного импульса:
'уп = И*.Рк) KlPjPs "J = Ко.P.) KrJFJFKp, na), (22.3)
где па - функция и коэффициент избытка окислителя а для
данного двухкомпонентного топлива и (через влияние давления на
степень диссоциации продуктов сгорания) абсолютного значения
давления в камере.
Отметим, что значение атах р, при котором достигается
максимум комплекса Р, в общем случае не совпадает со значением
a im, при котором достигается максимум произведения
сомножителей в (22.3), причем значение пустотного удельного
импульса I п определяет вся совокупность условий однозначности
задачи термодинамического расчета: состав компонентов, их
температура и давление в условиях подачи в камеру, соотношение
компонентов, давление в камере, давление в выходном сечении
сопла и реализуемый режим течения в сопле (равновесный,
химически замороженный или локально-неравновесный).
Удельный импульс как отношение тяги к массовому расходу
топлива или рабочего тела, при котором создается эта тяга -
один из основных, но не единственный показатель эффективности
двигателя.
Для ряда случаев, когда габаритные ограничения более важны,
чем массовые, предпочтительнее камеры и топлива с наибольшим
объемным удельным импульсом
/ =1.
mv
где mv - объемный секундный расход топлива, м3/с.
Комплексную оценку двигателя и топлива можно провести
по формуле Циолковского с учетом плотности топлива по
приращению скорости объекта при расходовании топлива.

288 Часть II. Теория неидеального теплового ракетного двигателя
Для потенциально экологически опасных компонентов
топлива оптимальным может быть режим с полным сгоранием
токсичного компонента при обеспечении минимальных отрицательных
экологических последствий, пусть даже при меньшем удельном
импульсе, чем на расчетном режиме.
Для твердого ракетного топлива соотношение компонентов,
соответствующее максимальному удельному импульсу, в
большинстве случаев реально недостижимо, так как при этом не
обеспечиваются необходимые прочностные характеристики заряда
ТРТ или топливо имеет склонность к детонации. Следовательно,
понятие оптимальности соотношения компонентов топлива
всегда условно и конкретизируется по отношению к достигаемой
целевой функции.
Если двигатель рассматривается вне конкретной связи с
летательным аппаратом, то как основной показатель эффективности
или качества ракетного двигателя используют удельный импульс,
исследуемый при работе на расчетном режиме (У ) или в
пустоте (/ ). В таком случае вводят понятие термодинамически
оптимального соотношения компонентов, т. е. такого соотношения
расходов выбранных окислителя и горючего, при котором
достигается максимальное значение расчетного удельного
импульса / или пустотного удельного импульса / п для заданных
давлений в камере сгорания /?*ив выходном сечении сопла ра или
давления в камере сгорания р*к и геометрической степени
расширения сопла Fa/FK . Именно такое понятие оптимальности
соотношения компонентов имеется в виду в следующих главах,
если иное не оговорено специально.
Из уравнений для расходного комплекса (22.1) и скорости
истечения (22.2) следует, что основное влияние на удельный импульс
оказывает значение произведения RT, тогда как при изменении
значений показателя изоэнтропы п в пределах 1,10... 1,25
значения Р и / могут изменяться не более чем на 15 %.
Покажем существование оптимального соотношения
компонентов для топлива, молекулярные массы компонентов которого
существенно отличаются от молекулярных масс продуктов
полного сгорания. К таким топливам можно отнести двухкомпонент-
ные топлива:
«кислород - водород» (цН2 ~ 2, \iUiQ ~ 18, |и0г ~ 32);
«фтор - водород» (|iH2 ~ 2, |iHF ~ 20, ^F2 ~ 38).
Поскольку максимум температуры должен соответствовать
близкому к стехиометрическому соотношению компонентов, где

Глава 22. Термодинамический расчет. Влияние параметров в камере 289
а ~ 1, значение газовой постоянной R будет тем больше, чем
большим будет избыток горючего - водорода. При этом максимум
произведения R Т будет достигаться в области а « 1.
Если предположить полную диссоциацию оксидов, то
кажущаяся молекулярная масса продуктов сгорания уменьшится
незначительно, но температура заметно понизится вследствие затрат
теплоты на диссоциацию весьма стабильных оксидов, а максимум
произведения RT сместится дальше от а - 1 влево. Отсюда
следует смещение максимума произведения RTпо оси абсцисс
вправо, ближе к а ~ 1, при увеличении давления в камере сгорания,
так как повышение давления подавляет термическую диссоциацию.
Из анализа представленных на рис. 22.1 зависимостей -
изменения Л, Г, р, RT и расчетного удельного импульса / для
топлива «водород - кислород» при постоянном давлении в
камере сгорания р* = 10 МПа и на срезе сопла ра = 0,1 МПа - следует,
что максимумы произведения RTn расчетного удельного
импульса / достигаются при разных соотношениях компонентов. Это
объясняется изменением термического КПД процесса расширения
газа в сопле при изменении коэффициента избытка окислителя.
Очевидно, что полнота перехода химической энергии в тепловую,
4000
3500
3000
2500
2000
1500
1000
500
0
0,1 0,3 0,5 0,7 0,9 1,1 1,3
Коэффициент избытка окислителя а
Рис. 22.1. Зависимости температуры, газовой постоянной, произведения
RT, расходного комплекса и расчетного удельного импульса от
коэффициента избытка окислителя для топлива «водород - кислород»
а тепловой энергии в кинетическую энергию потока зависит от
реальной степени равновесности: между предельными
состояниями - равновесным и химически замороженным.
Полученные расчетным путем зависимости / п(а) для этого
же топлива при температурах компонентов на входе в камеру,

290 Часть II. Теория неидеального теплового ракетного двигателя
близких к температуре нормального кипения, но для давления
в камере сгорания 0,5; 5; 20 и 100 МПа и с постоянной степенью
расширения газар*к/ра = 100 (рис. 22.2) подтверждают сделанный
качественный вывод о приближении термодинамически
оптимального соотношения компонентов к стехиометрическому со-
отношению компонентов при повышении давления в камере', при
р*к = 0,5 МПа a im - 0,5, а при/?* = 100 МПа пустотный удельный
импульс достигает максимального значения при приближении
к а ~ 0,6 слева.
,4400
4000
3800
3 3400
х
S 3200
с
1
1
/
I
Рк
г^Щ
= 0,5
5$v
мп<-
р =100 МПа
1 >
20
5
/
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4
Коэффициент избытка окислителя а
Рис. 22.2. Зависимость пустотного удельного импульса от
соотношения компонентов при разном давлении в камере сгорания и
постоянной степени расширения газа в сопле р*к/ра = 100 для топлива
«водород - кислород»
Полученные в результате термодинамического расчета
мольные концентрации основных составляющих для разных
коэффициентов избытка окислителя представлены на рис. 22.3.
Практически освоенным значениям давления (до 50 МПа)
в камере ЖРД на водородном топливе отвечают оптимальные
соотношения компонентов в диапазоне значений а = 0,5...0,7, тогда
как оптимальные соотношения компонентов других топлив лежат
также в области избытка горючего, но вблизи стехиометрического
соотношения компонентов 0,75 < a im < 1 (рис. 22.4), где кривые
/ (а), обозначенные числами /, 2 и J, соответствуют топливам
«керосин - кислород», «НДМГ - кислород» и «гидразин -
кислород».
Для данных топлив, в состав которых не входит водород как
горючее, смещение соотношения компонентов, при котором
пустотный удельный импульс достигает максимального значения

Глава 22. Термодинамический расчет. Влияние параметров в камере 291
М, моль/кг
О 0,3 0,5 0,7 0,9 1,1
Коэффициент избытка окислителя а
Рис. 22.3. Состав продуктов сгорания топлива «водород - кислород»
при различных соотношениях компонентов и давлении в камере
сгорания 10 МПа
(ао tim), от стехиометрического соотношения (а = 1) в сторону
избытка горючего (0 < а < 1) не столь значительно, как для
водородных топлив, и объясняется явлениями диссоциации при
высоких температурах, соответствующих стехиометрическому
соотношению горючего и окислителя. При этом в продуктах
сгорания снижается содержание молекул оксидов, например С02
и Н20, и возрастает содержание продуктов их диссоциации СО,
02 и Н2 с соответствующим снижением кажущейся молекулярной
массы продуктов сгорания, т. е. некоторое уменьшение
температуры при снижении коэффициента избытка окислителя
сопровождается ростом газовой постоянной продуктов сгорания.
Влияние этих процессов, как и смещение значения a im от
а = 1 в сторону уменьшения, наиболее заметно для топлив, в
продуктах сгорания которых большую долю составляет углекислый
газ, причем степень термической диссоциации последнего
значительно превышает этот же показатель для водяного пара при
одинаковых температуре и давлении. При этом влияние
температуры и давления можно анализировать на основе принципа Ле
Шателье - Брауна, который иллюстрируют результаты расчета
степени равновесной термической диссоциации (доля
диссоциировавших молекул) углекислого газа и водяного пара,
представленные в табл. 22.1. и 22.2.
В частности, смещение значения a im от а = 1, обусловленное
влиянием термической диссоциации, уменьшается при
увеличении давления в камере рк. Вследствие этого для топлив, в продуктах

292 Часть II. Теория неидеального теплового ракетного двигателя
сгорания которых не содержится углекислый газ, а диссоциация
водяного пара при давлении около 5... 10 МПа незначительна,
например N2H4 и N204, при дальнейшем увеличении давления
значение a im приближается к единице и практически
становится стехиометрическим, т. е. lim a tim =1.
Таблица 22.1. Зависимость равновесной степени диссоциации
оксидов от температуры Г при постоянном давлении/? = 5 МПа
Г, К
1000
2000
3000
4000
*ССЬ' °/°
0
0,41
15,18
62,26
хн,0' °/о
0
0,19
6,61
37,87
Таблица 22.2. Зависимость равновесной степени диссоциации
оксидов от давления р при постоянной температуре Т= 3000 К
р, МПа
0,5
5,0
10
50
*С02' %
30,00
15,18
12,24
0
*н2о> °/о
14,20
6,61
5,24
3,07
Влияние рассмотренных процессов в целом приводит к тому,
что для кислородных топлив, различающихся составом горючего,
например для водорода (1), керосина (2), НДМГ (3), гидразина (4),
при одинаковых давлениях в камере и степенях расширения
рабочего тела в сверхзвуковом сопле оптимальные коэффициенты
избытка окислителя находятся в соотношении a timl < а im2 <
< aoptim3 < ао tim4 ~ * (для ПРИНЯТЫХ обозначений топлив). Такое
соотношение используется практически для всех отечественных
и иностранных ЖРД, в качестве основного критерия
эффективности которых выбран пустотный удельный импульс (см.,
например, рис. 22.4 и 22.5).
Переохлаждение жидкого кислорода с целью снижения его
потерь на испарение при длительном хранении или уменьшения
требуемой массы теплоизоляции кислородных баков приводит
к снижению удельного импульса. Например, охлаждение жидкого

Глава 22. Термодинамический расчет. Влияние параметров в камере 293
<s
I
S
3
3500
3000
2750
2500
2250
2^
-1
аи
V
/
а2
/
а3
/
3
2000
0,1 0,3 0,5 0,7 0,9 1,1
Коэффициент избытка окислителя а
Рис. 22.4. Зависимости расчетного удельного импульса от
коэффициента избытка окислителя для разных топлив при постоянном давлении в
камере сгорания/7* = 10 МПа и в выходном сечении сопла ра = 0,1 МПа:
/ - «керосин - кислород»; 2 - «НДМГ - кислород»; 3 - «гидразин - кислород»
5000
:4500
*4000
)5
£3500
« 3000
3
я
£2500
о
'iL
1
-2а
/2
0 0,2 0,4 0,6 0,8 1,0 1,2
Коэффициент избытка окислителя а
Рис. 22.5. Зависимости пустотного удельного импульса от
коэффициента избытка окислителя для разных топлив при постоянном давлении в
камере сгорания и различных геометрических степенях расширения сопла:
топливо «водород - кислород»: / -
«керосин - кислород»: 2
F /F
а кр
-F /F ■■
д кр
I0;la-FJFV,
10; 2а -FJF„
500; топливо
= 500
кислорода от температуры нормального кипения 90,188 К до
температуры около 63 К при использовании его как окислителя с
горючим, близким по свойствам к керосину, в двигателе с
давлением в камере 10 МПа и давлением в выходном сечении сопла
около 0,005 МПа обеспечило уменьшение максимально возможного

294 Часть II. Теория неидеального теплового ракетного двигателя
для этих условий пустотного удельного импульса
приблизительно на 1 % при сохранении соотношения компонентов.
Предварительное испарение и подогрев кислорода до температуры 300 К,
напротив, приводит к увеличению удельного импульса на
1,0...1,5%.
Покажем, что для этих топлив, как и для водородных топлив,
a im приближается к единице слева при повышении давления
в камере сгорания. При отсутствии термической диссоциации
максимальная температура соответствовала бы стехиометриче-
скому соотношению компонентов, однако даже при больших
значениях давления в камере сгорания, когда диссоциация
практически подавлена, максимум удельного импульса достигается
при а, несколько меньших единицы. Для горючих, содержащих
углерод, это можно объяснить тем, что молекулярная масса
продуктов неполного окисления углерода, оксида углерода СО,
значительно меньше молекулярной массы диоксида углерода С02,
и некоторое снижение температуры в результате недоокисления
углерода в области а < 1 компенсируется ростом кажущейся
газовой постоянной продуктов сгорания со значительной долей
недоокисленного углерода. Кроме того, молекула С02 заметно
диссоциирует в основном на оксид углерода СО и кислород 02.
При температурах, характерных для сгорания топлива при сте-
хиометрическом соотношении компонентов (например, при
давлении 10 МПа и температуре 3 200 К), равновесная степень
диссоциации молекулы С02 приближается к 25 %, т. е. газовая
постоянная равновесной смеси в 1,1 раза превышает значение
этого параметра для молекулы С02. Причем молекула СО более
устойчива к термической диссоциации, чем молекула С02, и
далее не диссоциирует. По этим же причинам значения
произведения RT и удельного импульса при а < 1 больше, чем при а = 1.
Для топлива «гидразин - кислород» (см. рис. 22.4, кривая 3),
не содержащего углерод и, следовательно, его диоксида в
продуктах сгорания, a im находится ближе к стехиометрическому
соотношению компонентов (a im —1 = 1— А), чем для топлива
«керосин - кислород» (см. рис. 22.4, кривая 7). Это можно
объяснить большей, чем у молекулы С02, устойчивостью молекул
водяного пара Н20 к термической диссоциации. Так, при давлении
10 МПа и температуре 3 200 К диссоциирует только около 12 %
молекул Н20, и значение газовой постоянной равновесной смеси
увеличивается только на 4,5 % (для молекулы С02 при тех же
условиях - соответственно 25 и 10 %) (см. табл. 22.1 и 22.2).

Глава 22. Термодинамический расчет. Влияние параметров в камере 295
Отметим, что среднее по отношению к топливам «керосин -
кислород» и «гидразин - кислород» относительное содержание
углерода в топливе «НДМГ - кислород» объясняет расположение
a im для этого топлива (см. рис. 22.4, кривая 2).
Влияние повышения давления в камере на смещение
максимума удельного импульса к стехиометрическому соотношению
компонентов проявляется для всех рассмотренных топлив аналогично,
что обусловлено подавлением реакции термической диссоциации
и повышением вследствие этого температуры (см. рис. 22.2).
Обратим внимание на то, что затраченная на диссоциацию
энергия может быть возвращена в поток и преобразована в
полезную кинетическую энергию рабочего тела при равновесном
течении последнего, когда в области низких температур идут
экзотермические реакции рекомбинации, что возможно в соплах
с большой степенью расширения.
Подтверждением этого предположения может служить
смещение a im к единице при увеличении геометрической степени
расширения от 10 до 500 для постоянного давления в камере
р*к = 5 МПа (см. рис. 22.5).
Основным фактором, влияющим на значение достижимого
пустотного удельного импульса для данного топлива при
заданном давлении в камере сгорания и на срезе сопла, является
коэффициент избытка окислителя. Влияние проявляется через
температуру и состав продуктов сгорания в камере сгорания.
Покажем изменение содержания основных (преобладающих)
составляющих продуктов сгорания в зависимости от значения а
для топлива «гидразин - кислород» при давлении в камере 10 МПа
(рис. 22.6). При а < 1 преобладают продукты неполного
окисления горючих элементов, тогда как в области а ~ 1 основные
компоненты - водяной пар и продукты его термической
диссоциации. С удалением от стехиометрического соотношения
компонентов снижается температура, почти прекращается
термическая диссоциация и увеличивается содержание термически
стабильных индивидуальных веществ: при а » 1
стабилизируется абсолютное количество воды как продукта окисления
всего водорода горючего и появляются оксиды азота, при а « 1 -
свободный азот.
Изменение состава продуктов сгорания в рассмотренном
случае есть результат совместного действия изменения элементного
состава топлива и температуры. При движении продуктов сгорания
по соплу элементный состав не изменяется, а химический состав

296 Часть II. Теория неидеального теплового ракетного двигателя
Ъ4 Коэффициент избытка окислителя а
Рис. 22.6. Состав продуктов сгорания топлива «гидразин - кислород»
при разных соотношениях компонентов для давления в камере
сгорания 10 МПа
изменяется, реагируя на совместное снижение давления и
температуры, задаваемое геометрической степенью расширения сопла.
Пусть в качестве естественного аргумента рассматривается
текущая геометрическая степень расширения сопла,
возрастающая от 1 до 256, а состав топлива соответствует соотношению
расходов жидкого кислорода 02 и условного синтетического
углеводорода со свойствами, подобными свойствам керосина,
с условной формулой С10Н20 при а = 0,8. Изменение давления,
температуры и молярных концентраций индивидуальных веществ
представлено на рис. 22.7.
Из анализа кривых на рис. 22.7 следует, что при движении
рабочего тела по соплу преобладающее влияние оказывает
снижение температуры: например, равновесные концентрации таких
продуктов диссоциации, как СО, ОН, О, Н, снижаются, но
возрастает концентрация оксидов С02, Н20, т. е. преобладают
экзотермические реакции рекомбинации. Согласно принципу Ле Шателье,
это соответствует реакции системы на снижение температуры,
тогда как ответом на снижение давления должно быть увеличение
концентрации веществ с меньшей молекулярной массой
(увеличение числа молей в 1 кг продуктов сгорания). При этом
принципиально возможна конденсация веществ с низкой температурой
насыщенных паров или температуры кипения (конденсации) при
конкретных значениях давления, а при дальнейшем движении по
соплу - кристаллизация (затвердевание). Состав рабочего тела

Глава 22. Термодинамический расчет. Влияние параметров в камере 297
МПа
с£
'кг;
моль/
5?
100
10
1
0,1
0,01
L-
н^
7^ч
Ъ<6
\5>^ч
3
чГУ
^ЧГ2
3500
3000
2500 &
I
2000 ё
1500
0,0011 " 1 L_^ 1 Ю00
1 10 100 1000
Геометрическая степень расширения сопла Fa IF
Рис. 22.7. Изменение давления, температуры и молярных концентраций
индивидуальных веществ по длине проточной части сопла:
1 - температура, К; 2 - давление, МПа; 3 - Н20; 4 - С02; 5 - Н2; 6 - Н;
7-ОН;8-02
в произвольном сечении есть результат равновесного перехода
химически активной среды из состояния, задаваемого для
данного топлива (состав компонентов, коэффициент избытка
окислителя а) только давлением в камере сгорания, в состояние
внутреннего равновесия при паре параметров давление/^
-температура Г., задаваемой местной относительной площадью сопла
F . = F./F .
отн / / кр
Если состав продуктов сгорания в камере сгорания
соответствует существенным отклонениям соотношения компонентов
топлива от стехиометрического соотношения, то в продуктах
сгорания возможно появление паров компонентов или продуктов
их разложения, но такие режимы работы характерны для
газогенераторов, а не основных камер сгорания и будут рассмотрены
в других главах.
В зависимости от условий эксплуатации ракетного двигателя
температура компонентов топлива может отличаться от
номинальной температуры. Изменение температуры компонента
приводит к изменению его полной энтальпии и в общем случае к
изменению оптимального соотношения компонентов. Отметим, что
для топлива «кислород - водород» охлаждение водорода ниже
температуры кипения (при нормальном давлении 0,1 МПа) вплоть
до появления взвеси твердого водорода в жидком (шугаобразном)
водороде приводит к уменьшению значения пустотного удельного

298 Часть II. Теория неидеального теплового ракетного двигателя
импульса на несколько единиц, но при этом увеличивается
плотность топлива и снижаются потери водорода на испарение или
уменьшается требуемая масса теплоизоляции баков. Оптимальное
(по максимальному пустотному удельному импульсу при
заданной геометрической степени расширения сопла) соотношение
компонентов изменяется незначительно.
Напротив, предварительный подогрев водорода, например
в активной зоне бортовой ядерной энергетической установки, не
только увеличивает максимальный удельный импульс, но и
уменьшает соответствующее значение коэффициента избытка
окислителя: при температуре водорода около 1 000 К максимальный
удельный импульс достигается при а ~ 0,15, а при подогреве
водорода до больших температур добавление кислорода приводит
только к уменьшению удельного импульса, так как прирост
температуры продуктов сгорания сопровождается одновременным
уменьшением газовой постоянной вследствие образования
«тяжелых» молекул водяного пара.
Переохлаждение, вплоть до температуры появления твердого
кислорода, как и испарение и подогрев кислорода до
температуры около 1 000 К, не приводит к заметному изменению
максимальных значений пустотного удельного импульса и
соответствующих соотношений расходов компонентов.
Иллюстрирующие эти выводы результаты расчетов для
постоянных давления в камере 20 МПа и геометрической степени
расширения сопла 77,5 представлены на рис. 22.8 в виде
трехмерных диаграмм.
Действительное, т. е. определяемое при проектировании,
соотношение компонентов топлива может отличаться и, как правило,
Рис. 22.8. К оценке влияния температуры компонентов ракетного
топлива на достижимый удельный импульс

Глава 22. Термодинамический расчет. Влияние параметров в камере 299
отличается от термодинамически оптимального соотношения
в основном по следующим причинам:
• увеличение расхода одного из компонентов в целях
повышения плотности топлива и увеличения прироста скорости
летательного аппарата (скорости Циолковского) или для сохранения
положения центра масс летательного аппарата с заданной
точностью при расходовании компонентов топлива или объемные
(одинаковые массовые расходы компонентов);
• увеличение расхода одного из компонентов топлива в целях
снижения до приемлемых значений температуры продуктов
сгорания и (или) тепловых потоков в конструкцию камеры;
• увеличение расхода одного из компонентов топлива,
используемого для создания относительно низкотемпературного
пристеночного слоя (внутреннего завесного охлаждения);
• существенное отличие режимов течения в сопле от
равновесных;
• увеличение расхода одного из компонентов топлива в целях
уменьшения токсичности продуктов сгорания или ликвидации
остатков наиболее токсичного или экологически опасного
компонента в баках, а также иными причинами, например
исключением отложения сажи на поверхностях оптических приборов либо
солнечных батарей или минимизацией помех радиосвязи.
Задача выбора оптимального для конкретной целевой функции
соотношения расхода компонентов ракетного топлива является
одной из основных задач, определяющих эффективность
летательного аппарата.
Контрольные вопросы и задания
1. Какие расчеты могут быть проведены с приемлемой точностью и по
упрощенным соотношениям, если известно значение условного
показателя изоэнтропы, и чем объясняется приблизительность
полученных таким образом результатов?
2. Какое соотношение компонентов называется термодинамически
оптимальным?
3. Чем объясняется существенный избыток горючего (0,5 < а < 0,7)
при термодинамически оптимальном соотношении компонентов
топлива «водород - кислород»?
4. Почему для большинства ракетных топлив термодинамически
оптимальное соотношение компонентов незначительно отличается от
стехиометрического соотношения (0,75 < a { < 0,95)?

300 Часть II. Теория неидеального теплового ракетного двигателя
5. Предложите объяснение результатов математического
эксперимента по оптимизации соотношения компонентов ракетных топлив при
заданной постоянной степени расширения газа в сопле: при
повышении давления в камере оптимальное соотношение компонентов
приближается к стехиометрическому соотношению.
6. Дайте объяснение результатов термодинамических расчетов для
топлив, у которых окислителем является кислород: если горючее
не содержит углерод (например, гидразин), то термодинамически
оптимальное соотношение компонентов практически равно
стехиометрическому соотношению (a im ~ 1); применение углеродсодер-
жащего горючего (например, керосина) приводит к уменьшению
относительного содержания окислителя (a im ~ 0,8).
7. Предложите объяснение результатов термодинамических расчетов
по определению термодинамически оптимального соотношения
компонентов для постоянного давления в камере и переменной
геометрической степени расширения сопла при предположении
равновесного течения в сопле: с увеличением степени расширения
термодинамически оптимальное соотношение компонентов
приближается к единице.
8. Почему с ростом температуры одного из компонентов
термодинамически оптимальное соотношение компонентов смещается в
сторону избытка этого компонента (особенно явно это проявляется при
подогреве водорода (см. рис. 22.8))?
9. По каким причинам действительное соотношение компонентов
ракетного топлива, например жидкого двухкомпонентного, можно
выбирать отличным от термодинамически оптимального соотношения?
10. С использованием программных комплексов «Астра-4» или «Терра»
проведите математический эксперимент по исследованию влияния
фазовой неравновесности (отсутствие кристаллизации, т. е.
затвердевание жидкой фазы) на значение пустотного удельного импульса
при оптимальном соотношении компонентов. Дайте возможное
объяснение полученных результатов.

Глава 23
Термодинамический расчет
термокаталитического разложения гидразина
и водных растворов пероксида водорода
Гидразин N2H4 и водные растворы пероксида водорода Н202
можно рассматривать как типичные однокомпонентные
энергоносители, термодинамический расчет разложения которых
характеризуется всеми основными особенностями расчетов и
других однокомпонентных топлив, свойства которых в известном
приближении являются промежуточными между свойствами
гидразина и пероксида водорода.
Являясь эффективным горючим ракетных топлив, гидразин
достаточно широко применяется как однокомпонентное топливо
ЖРД малой тяги и газогенераторов рабочего тела турбин ТНА,
бортовых источников питания и других потребителей
газообразного рабочего тела. В основе такого применения гидразина лежит
его способность к экзотермическому самоподдерживающемуся
разложению, инициируемому первичным тепловым импульсом,
и к термокаталитическому разложению при контакте с
веществами-катализаторами, содержащими в качестве каталитически
активных составляющих платину, иридий, другие металлы
платиновой группы или некоторые их соединения. При температуре
выше 675 К реакция термического разложения идет как
самоподдерживающаяся и без воздействия катализатора. При этом на
выходе из камеры, в которой расположен катализатор (аналог
камеры сгорания), температура продуктов разложения может
достигать 1 200... 1 600 К. Разлагается 100 % молекул гидразина.
Относительно низкая температура не приводит ни к ионизации,
ни к термической диссоциации устойчивых молекул водорода Н2
и азота N2, но при этом происходит разложение молекулы
аммиака NH3. Продукты разложения содержат три молекулярных
газа: Н2, N2 и NH3.
В целом экзотермическая реакция разложения гидразина
может быть представлена как двухстадийная. Первая
экзотермическая стадия идет по схеме

302 Часть II. Теория неидеального теплового ракетного двигателя
N2H4 = |nH3 + |n2 (23.1)
Причем важно, что гидразин в продуктах реакции отсутствует.
Вторая стадия - эндотермическая. На этой стадии аммиак NH3
под действием катализатора разлагается, т. е. диссоциирует по
уравнению
NH3 = ^N2 + |h2 (23.2)
Здесь и аммиак, и азот, и водород могут одновременно
присутствовать как компоненты равновесной или неравновесной смеси
газов. При этом первая реакция идет с большей скоростью, чем
вторая. В действительности в зависимости от температуры,
активности (типа) катализатора и времени нахождения продуктов
первичного разложения гидразина в зоне действия катализатора
разлагается только часть аммиака, оцениваемая параметрически
долей или степенью диссоциации:
(NH3/
х\ зу«_ (233)
где 0 ^ X ^ 1; (NH3)'w - масса диссоциировавшего аммиака;
(NH3)w- масса исходного количества аммиака по уравнению (23.1).
Очевидно, что при наличии катализатора время установления
равновесных концентраций будет существенно меньшим, чем при
его отсутствии.
Зависимость1 равновесной доли продуктов диссоциации
аммиака от температуры Т при давлении около 2 МПа приведена
ниже:
Температура нагрева, К 400 500 600 700 800
Степень диссоциации, % 5 25 60 88 96
Умножив обе части уравнения (23.2) на параметрами прибавив
полученное произведение к уравнению (23.1) с учетом снижения
числа молей аммиака в (1 -X) раз, получим обобщенное
параметрическое уравнение разложения гидразина:
Беляев Н.М. Системы наддува топливных баков ракет / под ред.
В.М. Ковтиненко. М.: Машиностроение, 1976.

Глава 23. Термодинамический расчет для N2H4 и Н2Р2 303
N2H4 =|(1-*)NH3 +^N2 + |*(|n2 + |h2 j (23.4)
4 1
где первые два слагаемых —(l-X)NH3+—N2 представляют собой
продукты первичного разложения гидразина с остаточным
количеством неразложившегося аммиака, а вторая пара слагаемых
-;t[-n2+-h2
3 12 2 2
Л
4 v
продукты разложения -а молей аммиака по
уравнению (23.2).
Выполнив суммирование в правой части уравнения (23.4),
получим вариант параметрического уравнения разложения
гидразина при частичном разложении аммиака (параметр, доля или
степень X разложения аммиака):
N2H4 = f О -*)NH3 + ± (1 + 2ХЩ2 + 2Ш2 (23.5)
Тепловой эффект реакции (23.5) будет меньше, чем реакции (23.1),
4
за счет затрат теплоты на разложение - X молей аммиака по
эндотермической реакции (23.2).
Следовательно, при сопоставимых близких удельных тепло-
емкостях температура продуктов реакции (23.5) будет ниже, чем
продуктов реакции (23.1), но кажущаяся молекулярная масса
продуктов реакции (23.5) будет меньшей, чем продуктов реакции
(23.1). Другими словами, проявляются две противодействующие
тенденции:
• первая - увеличение степени ^разложения аммиака приводит
к уменьшению кажущейся молекулярной массы продуктов
разложения на выходе из камеры, где расположен катализатор, т. е.
Цы2н4 96
!(i-jr)+-(i + 2;r)+2jr 5+4*'
и, следовательно, к росту кажущейся газовой постоянной RK смеси;
• вторая - повышение степени разложения аммиака ведет
к снижению температуры Т* разложения.
Рабочий процесс термокаталитического разложения
гидразина (при давлении 0,1 МПа температура кипения равна 387 К,

304 Часть II. Теория неидеального теплового ракетного двигателя
температура самоподдерживающегося термического разложения
составляет 675 К) локализован в камере термокаталитического
газогенератора, в которой установлен проницаемый массив
катализатора в виде засыпки дискретных элементов или пакета
металлических сеток. Схема рабочего процесса такого
газогенератора приведена на рис. 23.1, где процессу разложения аммиака
предшествует условно полное разложение гидразина (нисходящая
кривая N2H4). При этом разложению аммиака соответствует
снижение его объемной доли г NH3 от максимального значения 0,8
до нуля (нисходящий участок кривой NH3) при уменьшении
температуры Гот 1 650 до 850 К, тогда как объемные доли водорода
Рис. 23.1. Схема рабочего процесса
термокаталитического газогенератора, работающего на гидразине
(стрелками обозначено направление движения рабочего тела)
и азота возрастают до 0,666 и 0,333 соответственно (кривые Н2
и N2). В действительности разложение аммиака начинается
с момента его образования, что учитывается при выборе времени
контакта гидразина и продуктов его разложения с катализатором
на основании экспериментальных данных, исходя из получения
заданной концентрации аммиака или степени X его разложения
в выходном сечении газогенератора (кривые на рис. 23.1 соот-

Глава 23. Термодинамический расчет для N2H4 и Н202 305
ветствуют полному разложению аммиака, т. е. X возрастает от
нулевого значения в сечении максимальной температуры до
единицы в выходном сечении блока катализаторов).
Поскольку работоспособность продуктов разложения
пропорциональна произведению RKT*9 а удельный импульс - корню
квадратному из этого произведения, может существовать условно
оптимальная степень разложения аммиака Хо tim, при которой
достигается максимальная работоспособность продуктов
разложения гидразина. Причем при изменении степени разложения
аммиака в пределах 0 ^ X ^ 0,8 произведение RKT* изменяется
примерно на 5 %, а температура снижается существенно - от 1600
до 850 К.
Отсюда следует целесообразность проектирования камеры
термокаталитического разложения гидразина, исходя из
получения максимальной концентрации аммиака и отсутствия его
разложения на катализаторе, т. е. время контакта гидразина и
продуктов его разложения при контакте с катализатором, а значит,
и длина каталитического пакета должны соответствовать
максимальной объемной доле аммиака rNH - 0,8. Вне действия
катализатора время, требуемое для термического разложения аммиака,
составляет от нескольких единиц до нескольких десятков секунд,
что в сотни раз превышает время пребывания рабочего тела в
трактах ЖРД. Поэтому аммиак в качестве компонента рабочего
тела в сопле можно рассматривать как термически стабильное
вещество.
Поскольку термодинамически равновесному состоянию
(максимальное значение энтропии) соответствует полное разложение
аммиака (разложение гидразина по (23.5) при X = 1), расчет при
предположении полного термодинамического равновесия будет
соответствовать именно значению параметра X = 1. Частичное
разложение аммиака можно учесть параметрически, задав
фиксированное неизменное при итерациях значение концентрации
аммиака. В мольных долях на 1 кг продуктов разложения это зна-
4 1000
чение может изменяться от 0 до моль/кг (расчет по (23.5)).
3 1Чн4
При расчете состава продуктов разложения с использованием
констант равновесия соответствие заданной степени разложения
аммиака будет достигаться автоматически, если использовать
константы, описывающие разложение аммиака при заданной
температуре и постоянной энтальпии гидразина как компонента.

306 Часть II. Теория неидеального теплового ракетного двигателя
и
| 1650
* 1450
^1250
^ 1050
^ 850
*, 650
| 450(
Рис. 23.2. Зависимости некоторых параметров,
характеризующих свойства продуктов разложения
гидразина, от содержания недиссоциированного аммиака
На рис. 23.2 приведены зависимости Гк*, /?к, RKT* от молярной
концентрации аммиака в 1 кг продуктов разложения гидразина,
рассчитанные с использованием энтропийного подхода к
определению условий равновесия. Максимального значения
произведение RKT* достигает при диссоциации около 50 % аммиака
(Х~ 0,5). Значения удельного пустотного импульса/ } и / 2
соответствуют давлению в камерер* = 1,5 МПа и расширению газа
в сопле соответственно до раХ = 0,1 МПа и ра2 = 0,01 МПа. При
этом возрастающим от нуля до 40 моль/кг значениям молярной
концентрации аммиака поставлена в однозначное соответствие
степень разложения аммиака, уменьшающаяся от 1 до 0,04.
Следует обратить внимание на то, что при движении
продуктов разложения гидразина по соплу степень разложения аммиака
увеличиваться не может, так как термическое бескаталитическое
разложение аммиака идет с заметной скоростью при
температуре выше 2 000 К. Поэтому расчет удельного импульса
проводится обязательно при предположении неизменного состава
рабочего тела при течении по соплу (химически замороженное течение).
В результате совместного проявления двух противоположных
тенденций удельный импульс для малых степеней расширения
(см. рис. 23.2, для / . р*/ра = 15) достигает максимума при
концентрации аммиака около 35 моль/кг. А для больших степеней
расширения (для 12 при р*/ра - 150) удельный импульс
монотонно увеличивается при снижении степени диссоциации аммиака.
Для закрепления изученного материала рекомендуется
рассчитать температуру Т* и газовую постоянную /?к, если задано
2500
32400
42300
-12200
2100,
7?7ll900
1800
NH3, моль/кг

Глава 23. Термодинамический расчет для N2H4 и Н202 307
значение константы равновесия реакции разложения аммиака
(23.2) до выхода из камеры, где размещен катализатор. При этом
представляется полезным из методических соображений
определить значение степени разложения аммиака.
Большинство горючих, содержащих в своем составе гидрази-
ноподобные соединения, в той или иной мере подвержены
экзотермическому термокаталитическому разложению. Особенности
расчета состава таких горючих и параметров, характеризующих
свойства продуктов их разложения, по сравнению с
относительно простым расчетом для гидразина обусловливаются наличием
в их составе углерода и возможностью его высвобождения в виде
сажи. Например, в продуктах разложения НДМГ (CH3)2N2H2
помимо паров самого диметилгидразина и смеси, состоящей из
метана, азота, водорода и аммиака, может содержаться до 10 % (по
массе) сажи.
Отметим, что при термическом разложении НДМГ в целях
уменьшения сажеобразования, согласно принципу Ле Шателье -
Брауна, в роли теплового аккумулятора в зоне термического
разложения используют так называемый «сварочный уголь» -
засыпку графитовых шариков или цилиндров из материала,
аналогичного материалу неплавящихся инертных сварочных
электродов. Причем до начала работы газогенератора засыпку
нагревают продуктами сгорания твердого ракетного топлива (например,
бездымного пороха) до температуры около 700 К, достаточной
для инициации самоподдерживающейся реакции термического
разложения НДМГ. Ориентировочно можно считать, что до
температуры 400 К (127 °С) НДМГ находится в камере в виде паров.
Продукты термокаталитического разложения однокомпонент-
ных топлив гидразинной группы представляют собой
газифицированное химически активное горючее, активно вступающее
в реакцию с большинством химических веществ, содержащих
атомы окислительных элементов. Наряду с другими факторами
это ограничивает возможности применения таких горючих в
качестве однокомпонентных топлив.
Окислительными свойствами обладают продукты разложения
ряда окислителей, среди которых вполне освоены как
экологически безопасное однокомпонентное топливо пероксид
водорода Н202 и его водные растворы, содержащие 1...35 % воды.
Несмотря на значительное снижение удельного энергосодержания
по сравнению с безводным пероксидом водорода практическое
применение находят только его водные растворы. Это объясняется

308 Часть II. Теория неидеального теплового ракетного двигателя
тем, что температура их замерзания существенно ниже, чем у
безводного пероксида водорода, а его водные растворы при
добавлении стабилизирующих компонентов приобретают свойства
малотоксичных, экологически безвредных, относительно
стабильных и умеренно взрыво- и пожароопасных технологических
жидкостей. Соотношение температуры замерзания водного раствора
пероксида водорода и его содержания в водном растворе
приведено ниже.
Содержание
пероксида
водорода, % 20 30 40 70 80 90 100
Температура
замерзания, °С...-14,6 -25,7 -41,4 -37,0 -22,2 -7,80 -1,70
С повышением концентрации пероксида водорода
значительно увеличивается его термокаталитическая нестабильность, что
существенно повышает опасность несанкционированного
разложения, например под действием света, радиации, загрязнений
или неконтролируемых примесей, а также при контакте с
острыми кромками или нанодисперсными частицами конструкционных
материалов (например, интенсивное разложение
концентрированного пероксида водорода может вызвать стружка
коррозионно-стойкой стали с цветами побежалости, а безводный пероксид
водорода разлагается со скоростью, близкой к скорости детонации,
при контакте с острыми кромками стекла).
Сильным каталитическим действием отличаются серебро Ag,
перманганат калия КМп04 и перманганат натрия NaMn04.
Принято считать, что выделяющийся из молекулы пероксида
водорода атом кислорода обладает крайне высокой окислительной
активностью до тех пор, пока он непосредственно вблизи точки
отделения не образует с таким же атомом стабильную
двухатомную молекулу кислорода. Продукты разложения пероксида
водорода Н202 в итоге содержат только молекулярный кислород и воду,
не диссоциирующие даже в контакте с катализаторами при
характерной максимальной температуре продуктов разложения
пероксида водорода, равной 1 100... 1 270 К.
Реакция каталитического разложения необратима и для
чистого безводного пероксида водорода идет как экзотермическая,
т. е. с выделением теплоты:
Н202 = Н20 + 1о2 (23.6)

Глава 23. Термодинамический расчет для N2H4 и Н202 309
Причем при параметрах, характерных для газогенераторов и
ракетных двигателей на однокомпонентном топливе, пероксид
водорода разлагается полностью и в генерируемом рабочем теле не
содержится даже его паров. Выделяющаяся при разложении
молекулы Н202 теплота идет на нагрев образующегося кислорода
02 и перегрев водяного пара до температуры около 1 000 К.
Если в водном растворе на один моль пероксида водорода
приходится g молей воды - H202gH20, это соответствует
массовой доле
Мн2о2
сн,о, -
" * ^н2о2+^н2о
Тогда для водных растворов пероксида водорода реакция
разложения с учетом (23.6) имеет вид
Н202 +gH20 = Н20 + ± 02 + gH20 (23.7)
Массовая доля водяного пара в продуктах этой реакции
сно = 2-—, (23.8)
^н2о2+£Ин2о
где цн 0, |iH202 - молекулярные массы воды и пероксида водорода
соответственно.
При этом массовая доля кислорода в продуктах разложения
определяется соотношением
4=1- Чо- (23-9)
Для кажущейся молекулярной массы продуктов разложения
водного раствора пероксида водорода в камере, где размещен
катализатор, справедливо следующее из (23.7) выражение:
_ )%2о2 + g^H2o _ 0 + g)fa2o + °>5Vo2
1,5 + g 1,5 + g
'1 + 0,38(8)^
v
1 + g
(23.10)
Из анализа (23.10) следует, что в результате увеличения доли
более легких по сравнению с молекулами кислорода 02 молекул
воды Н20 в продуктах разложения по уравнению (23.7) снижение

310 Часть II Теория неидеального теплового ракетного двигателя
содержания пероксида водорода Н202 в исходном растворе ведет
к уменьшению кажущейся молекулярной массы |iK и, как
следствие, к увеличению газовой постоянной RK (рис. 23.3). Здесь
приведены кривые для расходного комплекса |3, рассчитанного
для давления в камере рк = 2 МПа, а для пустотного удельного
импульса - для расширения в сопле до ра = 0,1 МПа. Очевидно,
что при этом температура продуктов разложения будет
снижаться вместе с увеличением содержания воды вследствие увеличения
ее доли в исходном растворе, так как на испарение воды
затрачивается теплота. Другими словами, проявляются две
противоположные тенденции: увеличение газовой постоянной и снижение
1800
| 1600
с£1400
.« 1200
*1000
^ 800
£г 600
« 400
^ 200
0
Рис. 23.3. Зависимости некоторых параметров,
характеризующих свойства продуктов каталитического
разложения пероксида водорода, от содержания воды
температуры продуктов разложения с увеличением содержания
воды в водном растворе пероксида водорода.
Значение температуры продуктов разложения водного
раствора пероксида водорода в зависимости от массовой доли
пероксида в растворе получим, решая уравнение сохранения энергии,
записанное через значения полных энтальпий:
• раствора пероксида водорода /пН20 при условиях подачи;
• водяного пара /п н Q при некоторой температуре Г, равной
искомой температуре продуктов разложения;
• кислорода /п0 при некоторой температуре Г, равной искомой
температуре продуктов разложения, т. е.
J 1 1360
10 20 30
Содержание воды, %
W = cH2oWr) + co2Wr)' <23Л1)

Глава 23. Термодинамический расчет для N2H4 и Н202 3_П
где коэффициенты сн 0, с0 - массовые доли водяного пара и
кислорода, рассчитанные по соотношениям (23.8) и (23.9); /пН 0(^)»
/п0 (Г) - известные функциональные зависимости (Дж/кг),
представленные в виде таблиц, графиков или в иной форме.
Решая уравнение (23.11) относительно единственной
неизвестной величины - искомой температуры Г для ряда значений g
как параметра, получим зависимости температуры продуктов
разложения водных растворов пероксида водорода от массовой доли
воды (см. рис. 23.3). Из анализа зависимостей на рис. 23.3
следует, что, несмотря на присутствие двух противоположных
тенденций (при увеличении содержания пероксида водорода в водном
Вход Н202
Вход N2H4
Рис. 23.4. Схема гипотетического трехтопливного ЖРД на двухкомпо-
нентном топливе:
/ - каталитический газогенератор или камера разложения пероксида водорода
Н202; 2 - каталитический генератор или камера разложения гидразина N2H4;
3 - камера сгорания с соплом Лаваля
растворе происходит уменьшение газовой постоянной смеси и рост
температуры), работоспособность продуктов разложения,
принимаемая пропорциональной произведению RT, монотонно
растет и достигает максимального значения 465 кДж/кг при 100 %-ной
концентрации Н202, так как увеличению температуры более чем
в 2 раза противодействует относительно небольшое, менее 20 %,
уменьшение газовой постоянной.
В качестве однокомпонентного топлива может применяться
также такой окислитель, как закись азота N20, отличающаяся от
пероксида водорода большей стабильностью в условиях бака и при
100 %-ной концентрации. Продукты термокаталитического
разложения закиси азота представляют собой смесь молекулярных
азота и кислорода при объемном соотношении 2:1 и температуре
до 1600...1900К.

312 Часть II. Теория неидеального теплового ракетного двигателя
Для закрепления изученного материала рекомендуется
рассчитать соотношения между пустотными тягами гипотетического
трехтопливного ЖРД на двухкомпонентном топливе,
работающего на основном режиме по схеме газ - газ при коэффициенте
избытка окислителя а = 0,85 на предварительно подвергнутых
каталитическому разложению компонентах Н202 и N2H4. Схема
двигателя представлена на рис. 23.4.
На вспомогательных режимах работы сохраняется расход
одного из компонентов и отключается расход другого, при этом
термокаталитическое разложение расходуемого компонента
остается полным. Давление в изобарной камере на основном режиме
5 МПа, геометрическая степень расширения сопла равна 100.
Относительно небольшая работоспособность продуктов
разложения однокомпонентных топлив ограничивает их
использование, поэтому представляют практический интерес
газогенераторы, работающие на основном двухкомпонентном ракетном
топливе, но при соотношениях компонентов, существенно
отличных от соотношений, характерных для камер сгорания.
В качестве высокоэффективного перспективного
гипотетического однокомпонентного топлива можно рассматривать
квазистабильную в условиях бака взвесь микрочастиц атомарного
водорода (активных радикалов) в жидком гелии1, переходящую при
частичной рекомбинации водорода в состояние равновесной
смеси газов в камере разложения с преобразованием в теплоту
энергии, затраченной на образование атомарного водорода Н из
молекулярного водорода Н2 (см. гл. 18). В частности, согласно
термодинамическим расчетам, в равновесном приближении для
массовых долей атомарного водорода 5 и 13,6 % в жидком гелии
при давлении 10 МПа температура в ракетной камере достигает
1 957 и 3 892 К и при расширении в сопле до давления 0,1 МПа
на расчетном режиме развивается удельный импульс, равный 4 303
и 6 970 м/с соответственно. Отметим, что задача хранения
топлива с активными радикалами и организации рабочего процесса
в камере рекомбинации до настоящего времени не решена, хотя
перспективность ее признается.
Черный И. NASA исследует новое топливо / Электронный журнал
«Новости космонавтики». 1999. № 11 (http://www.novosti-kosmonavtiki.
ru/content/numbers/203/42.shtml), дата обращения 04.01.2012.

Глава 23. Термодинамический расчет для N2H4 и Н202 3J_3
Контрольные вопросы и задания
1. Какие металлы являются катализаторами разложения гидразина?
2. Какие металлы и химические соединения являются катализаторами
разложения пероксида водорода?
3. Температура в зоне термокаталитического разложения и гидразина,
и пероксида водорода не превышает 1 600 К. Каким образом это
учтено в частных методиках термодинамического расчета?
4. Реакция разложения гидразина идет практически как необратимая.
Как это учтено в методике термодинамического расчета?
5. Изменяя какой конструктивный параметр газогенератора, можно
получить заданную степень разложения аммиака?
6. Каким образом учтено существенное различие скоростей
разложения гидразина и аммиака в предложенной частной методике
термодинамического расчета?
7. Каким образом можно учесть существенное различие скоростей
разложения гидразина и аммиака, если термодинамический расчет
вести с использованием программных комплексов «Астра-4» или
«Терра»?
8. Будет ли влиять на состав и температуру продуктов разложения
гидразина и пероксида водорода давление в камере? Подтвердите
вывод математическим экспериментом с использованием
программных комплексов «Астра-4» или «Терра».
9. Реакция разложения пероксида водорода идет как необратимая. Как
это учтено в методике термодинамического расчета?
10. Почему при наличии двух противодействующих тенденций не
реализуется максимум удельного импульса в области
работоспособности пероксидводородных парогазогенераторов?

Глава 24
Особенности и результаты
термодинамического расчета при большом различии
между соотношением компонентов
и их стехиометрическим соотношением.
Задача балластировки
На переходных неустановившихся режимах работы при запуске
или при останове ЖРД, в частности, когда предусматривается
возможное полное дожигание наиболее токсичного или
экологически опасного компонента, соотношение расходов окислителя
и горючего может значительно отклоняться от номинального
соотношения, как правило, близкого к стехиометрическому.
В состав некоторых ДУ, например в объединенную ДУ
орбитального корабля «Буран»1, входит газификатор жидкого
кислорода, используемого в газообразном состоянии как компонент
топлива двигателей малой тяги. Газификация производится в
газогенераторе балластировкой продуктов сгорания горючего в
кислороде большим количеством жидкого кислорода.
В некоторых ракетных ДУ в качестве рабочего тела
используются вырабатываемые в газогенераторе газы с заданными
свойствами: окислительными (коэффициент избытка окислителя о^ для
газогенератора в целом достигает 30); восстановительными (о^ « 1
или aL ~ 0); нейтральными (az - 1) при относительно невысокой
температуре 300...2 000 К, получаемой вводом балластного
нейтрального в смысле окислительно-восстановительных свойств
компонента, например воды. По такой схеме организован рабочий
процесс жидкостного газогенератора (ЖГГ) разработки ГДЛ 1935—
1936 гг., ЖГГ двигателей «Викинг-5» и «Викинг-6», ЖГГ наддува
баков современных западноевропейских ракет семейства «Ариан».
Рабочее тело газовых турбин ТНА также вырабатывается в
газогенераторах, в которых соотношение компонентов,
отличающееся от стехиометрического соотношения, выбирается исходя
Многоразовый орбитальный корабль «Буран» / Ю.П. Семенов,
Г.Е. Лозино-Лозинский, В.Л. Лапыгин и др.; под ред. Ю.П. Семенова.
М.: Машиностроение, 1995.

Глава 24. Термодинамический расчет газогенераторов 315
из температуры, допустимой для лопаточного аппарата турбины:
600...900 К, если газ окислительный, и 1 000... 1 250 К-для
восстановительного рабочего тела.
Таким образом, первой особенностью газогенераторов
является значительное различие между соотношениями компонентов
и их стехиометрическим соотношением.
Полученные расчетным путем в приближении термической и
химической равновесности зависимости температуры и газовой
постоянной продуктов газогенерации от коэффициента избытка
окислителя az для разных топлив представлены на рис. 24.1. Из
анализа приведенных зависимостей следует, что параметры,
характеризующие свойства продуктов газогенерации, изменяются
в весьма широких пределах, затрудняющих применение одних и
тех же допущений во всем диапазоне значений коэффициента аГ
3500
3000 £
25001
2000 5
х
X
1500 §
о
с
1000 §
со
0,01 0,1 1 10
Коэффициент избытка окислителя a
Рис. 24.1. Зависимости температуры (кривые 1-3) и газовой
постоянной продуктов газогенерации (кривые R]9 Rv R3) от суммарного
соотношения компонентов топлива (р = 10 МПа):
1 - «водород - кислород»; 2 - «гидразин - тетраоксид азота»;
3 - «керосин - пероксид водорода»
Выработка низкотемпературного газа с заданным балансом
окислительных и горючих элементов (az ~ 0, az - 1 или aL » 1)
может производиться в газогенераторах на двухкомпонентном
ракетном топливе при соотношении компонентов с существенным
избытком одного из них или с использованием балластного
нейтрального компонента, например гелия, воды, жидкого азота.
4VVV

316 Часть II. Теория неидеального теплового ракетного двигателя
Отметим, что если для газогенератора на двухкомпонентном
топливе суммарный коэффициент избытка окислителя (для
газогенератора в целом) az « 1, то в зоне 1 (рис. 24.2)
устанавливают соотношение компонентов с а, < 1, а при az » 1 -
соответственно с ах > 1. Такие соотношения устанавливают с тем, чтобы
при переходе из зоны 1 в зону 2 исключить образование
промежуточной местной высокотемпературной области с локальным
значением a ~ 1. Сжигание компонентов при a2 ~ 1 может
обеспечить минимальное содержание токсичных и экологически
опасных составляющих, а балластировка нетоксичным
компонентом сохраняет эти свойства продуктов сгорания.
Рабочий процесс газогенераторов должен обеспечить, во-
первых, устойчивое воспламенение и горение, для которых
характерна температура, равная нескольким тысячам Кельвинов, и,
во-вторых, испарение и нагрев избыточного компонента с
образованием низкотемпературного газа (перегретого пара).
Такой рабочий процесс реализуют в большинстве случаев
по двухзонной схеме (см. рис. 24.2): в зоне 1, так называемой
зоне горения, соотношение компонентов незначительно
отличается от стехиометрического соотношения, а в зоне 2, или зоне
смешения, происходит смешение продуктов сгорания топлива,
поступивших из зоны 1, с подаваемым в зону 2 избыточным
балластным компонентом, создающим в продуктах
газогенерации заданный баланс элементов, действующих в качестве
окислителя и в качестве восстановителя, и (или) снижающим
температуру до заданного значения.
Подобное протекание рабочих процессов имеет место и в
газогенераторах с подачей всех компонентов через смесительные
элементы, расположенные в одном сечении, например в
смесительной головке (формально такие газогенераторы относятся
Ввод балластного
/ компонента
Зона 1 Зона 2
Рис. 24.2. Схема газогенератора с двухзонной
организацией рабочего процесса

Глава 24. Термодинамический расчет газогенераторов ЗГ7
к однозонным). Но устойчивые воспламенение и горение
возможны только в зоне с соотношением компонентов,
незначительно отличающимся от стехиометрического соотношения, т. е.
при а ~ 1 ± А, тогда как для всего газогенератора az » 1 или
О < о^ « 1. Деление камеры газогенератора на зоны горения и
балластировки по площади проходного сечения реализуется
конструкцией смесительной головки, а по длине камеры -
применением смесительных элементов разной дальнобойности. Таким
образом, совокупный рабочий процесс и в этом случае
подразделяется на составляющие - горение и балластировку,
происходящие последовательно в разнесенных в пространстве объемах.
Двухзонная организация рабочего процесса является второй
особенностью газогенераторов.
Термодинамические процессы в зоне 1 подобны процессам
в камере сгорания ракетного двигателя, соответственно и
термодинамический расчет можно вести по тем же методикам, что и для
камеры сгорания, в приближении теплового и химического
равновесия. В зоне 2 в результате подачи большого количества
балластного компонента интенсивно охлаждаются продукты
сгорания, поступившие из зоны 1, их состав «замораживается», т. е.
фиксируется, и затем ниже по течению происходит
распределенный по длине камеры, сопряженный межфазный тепломассообмен
при уменьшении содержания жидкой фазы и незначительном
снижении температуры, который завершается образованием
однофазной термически равновесной смеси. При этом при низкой
температуре и сбалансированности окислительных и горючих
элементов в зоне 1 (а ~ 1 ± Д) скорость химических реакций
между балластным компонентом и продуктами сгорания топлива,
поступившими из зоны 1, замедляется настолько, что продукты
сгорания могут сохранять свой состав в дальнейших обменных
процессах и становиться инертными по отношению к
избыточному компоненту.
Поскольку термодинамические рабочие процессы в зонах 1
и 2 существенно разнятся, методику термодинамического
расчета для таких газогенераторов целесообразно рассматривать как
двухстадийную.
В зависимости от термической и термокаталитической
стабильности избыточного компонента возможны следующие
результаты процесса балластировки в зоне 2.
Если избыточный компонент, например Н2, 02, F2, H20, N2
и т. п., стабилен в условиях зоны 2 камеры газогенератора, то

318 Часть II. Теория неидеального теплового ракетного двигателя
рабочий процесс в зоне 2 сводится к смешению продуктов
сгорания топлива, поступивших из зоны 1, с подаваемым в зону 2
компонентом и испарению последнего. При этом к продуктам
сгорания топлива в зоне 1 добавляются пары избыточного
балластного компонента, а химический состав каждого компонента
сохраняется.
Как аддитивная величина кажущаяся газовая постоянная
гомогенных продуктов газогенерации RK может быть определена
непосредственно по формуле
*к=^Лбал+-!-*,, (24.1)
где 7?бал - газовая постоянная химически стабильного
балластного компонента, определяемая его молекулярной формулой в
условиях подачи в газогенератор; Rl - газовая постоянная
продуктов сгорания топлива, поступающих из зоны 1, которую можно
рассчитать в приближении химического равновесия; g -
коэффициент балластировки, равный отношению расхода балластного
компонента тбал и расхода топлива в зону 1 газогенератора т{9
т. е. g = ——; , - массовые доли продуктов сгорания
топлива и избыточного компонента в продуктах газогенерации,
определяемые соотношением расходов топлива в зоне \ тх =
= т , + т . при соотношении компонентов Кт1 = аКт0 = —— и рас-
хода балластного компонента /w6ajl. При этом суммарный расход
через газогенератор
тъ = то1 + тг2 + тбал (24.2)
складывается из расходов окислителя то1 и горючего тг1,
подаваемых в зону 1, и расхода балластного компонента тбал.
Если соотношение компонентов в зоне 1 соответствует
коэффициенту избытка окислителя 0ц (в частном случае равно стехио-
метрическому соотношению компонентов, т. е. оц = 1), то с
учетом (24.1) и (24.2) получаем соотношения коэффициентов az ng,
а именно:
для области генерации газа, действующего в качестве
окислителя, где az » 1,

Глава 24. Термодинамический расчет газогенераторов 3_19
(Ху -а,
а, +
для восстановительных газогенераторов с 0 < az « 1
az
g = .
Согласно принятой физической модели и (24.1), предельный
переход к большим значениям коэффициента g » 1 дает
приближенное значение для газовой постоянной смеси:
lim /?K «/?Гпи1(т;).
g-»CO
При балластировке окислителем, когда ах » 1,
lim^*/?o(rK).
При балластировке горючим для az ~ 0 справедливо
приближенное равенство
lim 7^*^(7;).
g->00
Отметим, что одним из ограничений на максимально и
минимально допустимые значения а является появление в продуктах
газогенерации или твердой фазы (сажи, оксидов и др.), или
жидкости. На рис. 24.1 соотношению компонентов, при котором
начинает появляться сажа в продуктах газогенерации, на зависимости
температуры 3 соответствует характерный излом в области
a -0,25...0,50.
Для топлива «водород - кислород» характерна близость или
практическое совпадение значений газовых постоянных
равновесных смесей, рассчитанных по (24.1), и газовых постоянных
паров избыточного компонента при больших отличиях az от 1.
В области избытка горючего, в частности для az ~ 0,038,
соотношение (24.1) дает значение RK = 3 192,1 Дж/(кг*К), а
равновесное приближение с учетом химических реакций во всех сечениях
газогенератора - незначительно меньшее значение - 3 178 Дж/(кгК).
При этом для чистого водорода RH = 4 127 Дж/(кгК).

320 Часть II. Теория неидеального теплового ракетного двигателя
При недостатке горючего в диапазоне значений
коэффициента избытка окислителя 8 < as < 16 расчетом по (24.1) получаем
RK = 295...278 Дж/(кгК), а в равновесном приближении с учетом
химических реакций - 288...274 Дж/(кгК). В пределе с
увеличением значения az значение газовой постоянной продуктов
газогенерации RK приближается к газовой постоянной кислорода
R0i = 260 Дж/(кгК).
Газовая постоянная избыточного компонента в общем случае
зависит от температуры, и только в частном случае для
стабильных инертных компонентов, например Н2, 02, F2, H20, He, N2,
такая зависимость отсутствует или несущественна в условиях
рабочего процесса газогенератора. Тогда задача
термодинамического расчета сводится или к расчету равновесной, т. е. конечной,
температуры продуктов газогенерации Тк в выходном сечении
зоны 2, если задано значение g, или к определению соотношения
расходов балластного компонента и топлива g в зону 1 при
известной заданной температуре продуктов газогенерации Тк.
Соотношение расходов g и температуры Тк можно выразить,
используя уравнение сохранения энергии
iu№ ~ **№ = rfW*;) - W^)], (24-3)
в левой части которого записано уменьшение полной энтальпии
1 кг продуктов сгорания при охлаждении в зоне 2 газогенератора
от температуры сгорания Тх до равновесной температуры
продуктов газогенерации 7\
В правой части уравнения (24.3) отражена передача энергии
от 1 кг продуктов сгорания g килограммам балластного
компонента, температура которого (и одновременно полная энтальпия)
повышается от температуры подачи Гпод до равновесной
температуры в выходном сечении камеры газогенератора Тк.
Если задана температура Тк, то искомый необходимый для ее
получения расход балластного компонента, задаваемый
коэффициентом g, рассчитывается по (24.3):
/ (т\-1 (т V
■*п.бал\ к/ п.бап V под/
Укажем на то, что полная энтальпия продуктов сгорания в зоне 1
равна полной энтальпии топлива при условиях подачи в
газогенератор, а для химически инертного избыточного компонента

Глава 24. Термодинамический расчет газогенераторов 321
вместо полных энтальпий в правую часть уравнения (24.3)
можно подставлять термодинамические энтальпии с учетом
изменения фазового состояния балластного компонента при заданном
давлении в газогенераторе.
Если же балластный компонент в зоне 2 газогенератора
подвергается термическому и термокаталитическому разложению,
то в (24.1) газовая постоянная Лбал не только определяется
составом компонента в состоянии подачи, но и зависит от его
химических свойств. Например, если балластный компонент - те-
траоксид азота N204, термически диссоциирующий уже при
температуре, равной нескольким сотням градусов по шкале
Кельвина, с образованием диоксида азота
N204 -> 2N02
то отличие значения /?бал от значения, рассчитанного по
молекулярной массе N02, определится степенью завершенности реакции
диссоциации диоксида азота
N0, <=> N0 + - 09
2 2 2
Разложение N02 в газогенераторе идет существенно
медленнее, чем практически необратимая реакция диссоциации тетра-
оксида азота N204 —► 2N02, поэтому в первом приближении для
расчета давления в газогенераторе или площади его
критического сечения можно принимать значение 7?бал, определяемое по
молекулярной массе N02.
На рис. 24.1 для топлива «гидразин - тетраоксид азота»
балластировке тетраоксидом азота соответствует область а ^ 10, где
равновесное значение газовой постоянной продуктов
газогенерации вблизи а = 15... 16 RK = 271 Дж/(кгК), а при степени
диссоциации N02 около 40 % \ = 219 Дж/(кгК).
Для более точных данных следует определить степень
диссоциации N02 или в результате расчетов кинетических характеристик
процесса, или задавая эту величину как параметр на основании
экспериментальных данных. Действительные характеристики
рабочего тела будут находиться между значениями, полученными
путем расчетов при равновесном приближении и при
предположении полного отсутствия диссоциации молекул N02.
Рекомендуется для закрепления изученного материала
получить формулы для расчета кажущейся молекулярной массы

322 Часть II. Теория неидеального теплового ракетного двигателя
продуктов разложения тетраоксида азота N02, NO и 02, если доля
диссоциирующего диоксида азота N02 задана. Представляется
полезным использовать подход, принятый при анализе
разложения гидразина N2H4.
Если в качестве балластного компонента рассматривается
гидразин N2H4, то методика расчета двухзонного газогенератора
будет подобна предложенной выше для тетраоксида азота,
только молекулярная масса балластного компонента цбал для расчетов
7?бал в первом приближении принимается в соответствии с
необратимой реакцией разложения гидразина с образованием азота
и аммиака как стабильного компонента:
N2H4-^NH3 + |n2 (24.4)
Разложение аммиака на азот и водород не учитывается, так
как этот процесс с технически существенными скоростями
протекает только при температуре выше 2 000 К.
На рис. 24.1 описанным особенностям соответствует область
а ^ 0,25 для кривых 2 и Rr
Пероксид водорода как балластный компонент в двухзонных
газогенераторах претерпевает полное разложение по практически
необратимой реакции
H202-H20 + i02 (24.5)
задающей соотношение между водяным паром и кислородом,
а следовательно, и значение /?бал. Наличие воды как составляющей
балластного компонента учитывается по методике расчета,
принятой для смесей идеальных газов.
Соответственно в области а ^ 2 для кривой 3 расчет по
уравнению (24.1) с учетом (24.3) дает значение газовой постоянной,
практически совпадающее с равновесным значением: по
уравнению (24.1) RK = 366,67 Дж/(кгК), а в равновесном приближении
в диапазоне значений 2 ^ а ^ 64 RK = 362,0...365,5 Дж/(кгК).
Если в качестве балластного применяется углеродсодержащий
компонент, то расчеты в равновесном приближении при
суммарном для газогенератора соотношении компонентов дают
содержание сажи как углерода, избыточного по отношению к
элементам, действующим в качестве окислителя. Так, согласно расчетам,
для топлива С7 21Н13 29 - Н202 (углеводородное горючее, например,

Глава 24. Термодинамический расчет газогенераторов 323
керосин и пероксид водорода) при давлении 10 МПа сажа составляет
заметную долю при а « 0,25. При этом расчет показывает
содержание сажи существенно большее, чем фиксируется при
экспериментах с двухзонными газогенераторами.
Следовательно, принятая двухзонная схема рабочего
процесса и в случае углеродсодержащих избыточных компонентов
обеспечивает химически неравновесное содержание компонентов
смеси в выходном сечении газогенератора, что позволяет
рекомендовать к применению описанную выше двухстадийную
методику термодинамического расчета.
В наиболее явной форме химическая неравновесность в зоне
балластировки характерна для газогенераторов на кислородно-
метановом топливе, работающем при значительном избытке
горючего. Экспериментально доказана возможность горения
метана при недостатке окислителя без образования конденсированной
фазы: твердого углерода в форме сажи. Это объясняется
большими значениями времени установления равновесия реакции
разложения метана СН4 —► Ств + 2Н2: до 10... 15 с при температуре
1 100... 1 200 К, характерной для таких газогенераторов. При этом
время пребывания компонентов в зоне 2, как правило, не
достигает и 0,1 с. Отсутствие сажи математически моделируется
или исключением из числа возможных составляющих
конденсированного углерода, или фиксацией концентрации
углеродсодержащих компонентов, в том числе метана (в молях на 1 кг
продуктов газогенерации). Особенности применения методик
термодинамического расчета к определению проектных
параметров двухзонных восстановительных газогенераторов
рассмотрены в учебном пособии1.
Существенно, что применение уравнения сохранения энергии
(24.3) в случае определения температуры при заданном
коэффициенте балластировки и решения обратной задачи для
экзотермически разлагающихся компонентов возможно только для
имеющих физический смысл соотношений энтальпий и температур.
В частности, при балластировке продуктов сгорания их
минимальная температура не может быть ниже температуры
разложения балластного компонента, достигаемой при заданном давлении
Буркалъцев В.А., Дорофеев А.А., Новиков А.В. Проектные и
поверочные расчеты камеры и газогенератора жидкостного ракетного
двигателя: Метод, указания к курсовому проектированию по дисциплине
«Проектирование ЖРДУ». М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.

324 Часть II. Теория неидеального теплового ракетного двигателя
при реализуемой степени диссоциации, если в потоке не образуется
жидкая фаза одного из компонентов. Наличие жидкой фазы
означает, что при фазовом равновесии давление ее паров
соответствует температуре насыщения Гнас для давления, равного
давлению в газогенераторе рг г. Для этих условий справедливы
предельные переходы для газогенератора с балластировкой
окислителем МтТк =Г 0(/?гг), горючим ИтГк =Т г(ргг) или
g—>оо г \ / g—>°°
а-»оо а-»0
сторонним химически и термически стабильным компонентом,
например водой lim Тк =Ттс н 0(ргг), т. е. снижение темпера-
g—>00 F 2 \ • /
туры в зоне балластировки ограничено температурой насыщенных
паров. Эта особенность может использоваться при тестировании
программ расчета.
Если избыточный (балластирующий) компонент подвержен
термическому разложению, то при температурах, меньших
температуры начала разложения, он ведет себя как термически
стабильный, т. е. приведенные выше предельные переходы
применимы и к газогенераторам на термически нестабильных
компонентах, например с балластировкой НДМГ при
температурах генераторного газа ниже 400 К, или гидразином при
температурах ниже 675 К.
Если продукты газогенерации представляют собой только
равновесную смесь газов, то это соответствует следующим
утверждениям:
• невозможно при балластировке продуктов сгорания
топлива гидразином получить равновесную температуру
генерируемого потока газа ниже температуры разложения гидразина (~ 1 600 К);
• невозможно при балластировке продуктов сгорания перок-
сидом водорода получить равновесную окислительную среду
температурой ниже 1 000 К.
При этом значения температуры, достигаемые в реальных
газогенераторах, зависят от давления в камере газогенератора и
степени приближения состава к равновесному. Поэтому в общем
случае результаты расчетов, полученные в равновесном
приближении, следует рассматривать как оценочные с точностью,
достаточной для первого приближения.
Результаты расчетов по описанной двухстадийной методике
и по методике, разработанной для расчетов равновесных
процессов, практически не различаются, если расчет для коэффици-

Глава 24. Термодинамический расчет газогенераторов 325
ента az проводить по равновесной методике, но задавать значения
термодинамических характеристик основных компонентов
фиксированными и равными их абсолютным значениям,
предварительно полученным при расчете горения в зоне 1.
Если концентрация сохраняющих свое количество веществ
Ст задается в молях вещества на 1 кг продуктов сгорания, то при
балластировке от a = 1 до az Ф 1 концентрация /-го компонента
однозначно рассчитывается или по концентрации в зоне 1, или
исходя из уравнения соответствующей химической реакции.
Например, если требуется отразить отсутствие второй стадии
реакции разложения гидразина N2H4 (реакция диссоциации аммиака
NH3 не идет) в зоне смешения, то для произвольного значения az
концентрация аммиака определится соотношением
С^=Г^Г' (24-6)
где множитель 4/3 - число молей аммиака, образующихся при
разложении 1 моля гидразина по (23.1); Ц^ Н4 - молекулярная
масса гидразина, г/моль; Кт0 - стехиометрическое соотношение
компонентов.
Если фиксируемая составляющая образуется при диссоциации
окислителя, например диссоциация тетраоксида азота идет без
разложения диоксида азота, т. е. N204 —► 2N02, то для
произвольного значения az фиксируемая концентрация
1000
CNG2=2-i^-, (24.7)
1 +
Кт0а1
где множитель 2 - число молей N02, образующихся при
диссоциации 1 моля N204 по выбранному уравнению; М^ 0 -
молекулярная масса N204, г/моль.
Множители в уравнениях (24.6) и (24.7), как и в уравнениях,
записываемых аналогично для других веществ, могут быть
заданы, исходя из выбранных реакций образования вещества,
содержание которого фиксируется.
Для большинства инженерных задач, касающихся рабочих
процессов в ракетных двигателях, подход к описанию продуктов

326 Часть II. Теория неидеального теплового ракетного двигателя
газогенерации как смеси идеальных газов ограничен диапазоном
значений давления 20...30 МПа.
Газогенераторы некоторых современных ЖРД с дожиганием
рабочего тела турбины работают при давлении 60...65 МПа.
Высокие давления определяют третью особенность газогенераторов.
Для упрощенных методик это позволяет в первом
приближении исключить продукты диссоциации, которые практически
отсутствуют при характерных для газогенераторов низких
температурах (менее 1 500 К) и подавлении диссоциации высоким
давлением.
Для более точных методик отражение этой особенности
состоит во включении в методику термодинамического расчета
вместо уравнения состояния идеального газа/?у = RT других
соотношений параметров реального газа, учитывающих внутреннее
давление, появляющееся вследствие наличия сил сцепления
между молекулами, и объем, занимаемый молекулами.
В общей форме уравнение состояния идеального газа (в так
называемой вириальной форме) имеет вид
pv = RT\l-kf/ *Р* .1
где р^ - вириальные коэффициенты, зависящие от температуры
рабочего тела.
Выбор достаточного числа слагаемых п в этом уравнении
зависит от абсолютного значения давления смеси и необходимой
точности расчетов. Для наиболее изученных экспериментально
двухкомпонентных топлив возможно применение эмпирических
уравнений состояния продуктов сгорания. В общем случае
особенности термодинамических расчетов процессов в двухзонных
газогенераторах состоят:
• в учете отличий свойств продуктов газогенерации от их
идеального представления;
• в отражении химической неравновесности рабочего тела
в зоне 2.
Для повышения достоверности расчетных данных
необходимо привлечь эмпирические уравнения состояния или
экспериментальные данные о достигаемых степенях диссоциации
нестабильных компонентов либо использовать весьма сложные методики
кинетических расчетов, также основанных на экспериментальных
данных.

Глава 24. Термодинамический расчет газогенераторов 327
Методики термодинамического расчета, учитывающие
существенные отличия уравнения связи параметров реального газа от
уравнения состояния идеального газа, описаны в работе1.
Практический опыт расчета газогенераторов систем наддува топливных
баков ДУ ЖРД отражен в монографии2.
Контрольные вопросы и задания
1. Перечислите общее и особенное в рабочих процессах
газогенераторов и камер сгорания.
2. Чем обусловлена двухзонная схема рабочего процесса в
газогенераторах на двухкомпонентном топливе с большим избытком
одного из компонентов?
3. Чем обусловлены преимущества двухзонной схемы рабочего
процесса в газогенераторах на трехкомпонентном топливе с большим
избытком балластного компонента, например воды или азота?
4. Почему для газогенераторов на трехкомпонентном топливе с
инертным (сбалансированным по составу элементов, действующих в
качестве окислителя и в качестве горючего, т. е. с нулевой суммой
валентностей) балластным компонентом горение в зоне 1 может
протекать как с избытком горючего, так и с избытком окислителя?
5. Почему для газогенераторов рабочего тела с избытком окислителя
для газогенератора в целом (Кт0 « Кт1) коэффициент избытка
окислителя в зоне 1 должен превышать единицу (а, > 1)?
6. Почему для газогенераторов рабочего тела с избытком горючего
для газогенератора в целом (Кт1« Кт0) коэффициент избытка
окислителя в зоне 1 должен быть меньше единицы (а] < 1)?
7. Какие факторы ограничивают избыток горючего в продуктах
газогенерации?
8. Почему при подаче в зону 2 газогенератора в качестве балластного
компонента азотного тетраоксида N204 в составе продуктов
газогенерации практически отсутствуют пары N204 и такие продукты его
термического разложения, как N0 и 02?
9. Каким образом можно учесть низкую скорость термического
разложения углеводородов при избытке горючего, например метана,
если выполнять термодинамический расчет с использованием
программных комплексов «Астра-4» или «Терра»?
10. Каким образом можно учесть низкую скорость термического
разложения аммиака в зоне балластировки, если термодинамический
расчет выполнять с использованием программных комплексов
«Астра-4» или «Терра»?
Белов Г.В. Указ. соч.
2 Беляев Н.М. Указ. соч.

Глава 25
Камеры сгорания, их параметры и оценка
совершенства рабочих процессов
Решение задачи термодинамического расчета дает
характеристики продуктов сгорания как результат сложного
параллельно-последовательного процесса преобразования химической
энергии топлива в тепловую энергию рабочего тела,
происходящего в камере сгорания ракетного двигателя при движении
топлива в ней по некоторой траектории.
Стандарт определяет камеру сгорания как часть ракетной
камеры, в которой в основном завершаются процессы
смесеобразования и сгорания.
Это же определение распространяется и на камеру сгорания
газогенератора.
Рабочий процесс в камере сгорания представляет собой
совокупность происходящих в ней процессов превращения
компонентов топлива в продукты сгорания - рабочее тело сопла или
генерируемую газовую среду, если имеется в виду газогенератор.
В ЖРД и ГРД собственно горению топлива предшествуют
(рис. 25.1):
• исходное распределение компонентов топлива по сечению
камеры сгорания и их первичное диспергирование и распыление
(области 7 и 7 для окислителя и горючего соответственно),
задаваемые конструкцией и параметрами режимов смесительной
головки и камеры;
• вторичное диспергирование за счет взаимодействия с
заполняющей камеру многофазной средой;
• испарение компонентов (области 2 и 6 для окислителя и
горючего соответственно);
• перемешивание компонентов в жидкой (область 3) и газовой
(область 4) фазах;
• (предпламенные) гомогенные и гетерогенные химические
реакции, предшествующие воспламенению (область 5);
• воспламенение ракетного топлива.
Конечность скоростей химических превращений при
ограниченном времени пребывания компонентов в камере приводит

Глава 25. Камеры сгорания и их параметры 329
Си
а
о
О Tv т
Рис. 25.1. Укрупненная
функциональная структура совокупного рабочего
процесса в камере сгорания ЖРД
в общем случае к незавершенности преобразования химической
энергии топлива в тепловую энергию продуктов сгорания.
Физико-химические превращения происходят во времени частично
последовательно, частично параллельно. При этом локализация
процессов также неоднозначна, но может рассматриваться как
распределенный по линии тока или траектории движения
топлива в камере сгорания совокупный рабочий процесс (см. рис. 25.1),
для завершения которого с заданной полнотой необходимо
известное время xs. Очевидно, что время движения топлива по
траектории от момента входа в камеру сгорания до пересечения
выходного сечения камеры сгорания, т. е. действительное время
пребывания в камере сгорания т , должно быть не меньше, чем
время т1# Время пребывания топлива в камере сгорания
определяется как средней скоростью движения топлива по линии тока,
так и длиной траектории, зависящей при заданных габаритах от
картины течения в камере сгорания, а следовательно, и от ее формы.
При многообразии форм, обусловленных множеством
конструктивных, технологических и эксплуатационных требований
(рис. 25.2), камеры сгорания можно условно подразделить на две
группы по структуре течения:
• камеры сгорания с преимущественно однонаправленным
одномерным потоком (варианты а-ж)\
• камеры сгорания с возвратно-циркуляционным течением
(варианты з и и), где течение или трехмерное с возвратным
вихрем в меридиональном сечении (вариант з), или вращательно-по-
ступательное (вариант и).

330 Часть II. Теория неидеального теплового ракетного двигателя
Рис. 25.2. Схемы камер ракетных двигателей:
а - цилиндрическая; б - коническая расширяющаяся; в - коническая
сужающаяся; г - цилиндрическая камера сгорания как часть полутеплового сопла;
д - сферическая; е - кольцевая с плоским критическим сечением; ж - кольцевая
с коническим критическим сечением; з - камера сгорания с трехмерной
рециркуляционной структурой течения; и - цилиндрическая с
поступательно-вращательным движением продуктов сгорания; 1 - собственно камера сгорания;
2 - смесительная головка, распылительные устройства; 3 - траектории
компонентов топлива и продуктов сгорания
Характерное почти одномерное течение в камерах вариантов
а-эю позволяет, переходя к обобщенной схеме, приведенной на
рис. 25.3, оценить время пребывания топлива в камере т
интегрированием по траектории от входного х = 0 до выходного
х = /к с сечения камеры сгорания
ТПР L С 7
о о W\x)

Глава 25. Камеры сгорания и их параметры ЪУ\_
u«—
vw
1*0
<pU4
о
I
-
*■
K.C
»•
y-W(x)
/
—►
I
Увеличено
Рис. 25.3. Схема течения в камере сгорания. К расчету среднего времени
пребывания в камере сгорания:
1 - линии тока в зоне с преимущественно осевым течением; 2 - зона рециркуляции
где W(x) - усредненная по сечению в одномерном приближении
скорость потока, зависящая от координаты х (удаления от
начального сечения камеры сгорания); dx = ——— - время прохождения
Wyx)
расстояния dx со скоростью W(x)\ /кс - длина камеры сгорания.
Записав уравнение неразрывности для произвольного сечения
камеры сгорания т{х) = р(х) W(x)F(x) и приравняв расход
продуктов сгорания т(х) к расходу топлива тт, т. е.
т(х) = тт = const,
получим скорость в произвольном сечении камеры
W(x) = -
m^
p(x)F(xY
подстановка которого в (25.1) дает соотношение
Тпр =
WT
*к.с
\ p(x)F(x)dx
dx
My
= ^S (25.2)
где F(x)dx - элементарный объем dv; произведение p(x)dv -
элементарная масса dm, а интеграл от p(x)dv по объему камеры
сгорания VK c равен суммарной массе продуктов сгорания и топлива
ML, находящейся в объеме камеры сгорания.

332 Часть II. Теория неидеального теплового ракетного двигателя
Полученное значение тп называется средним временем
пребывания в камере сгорания, которое в соответствии с ГОСТ 17655-89
«Двигатели ракетные жидкостные. Термины и определения»
определяется как отношение массы продуктов, находящихся в
камере сгорания, к массовому расходу ею топлива.
Для большинства известных конструкций камер сгорания ЖРД
с преимущественно поступательным одномерным потоком
среднее время пребывания в камере сгорания 0,001 < т < 0,005 с.
ГОСТ 17655-89 позволяет, рассчитав среднее время пребывания
для разных камер (см. рис. 25.2), сравнивать их по этому параметру.
Отметим также обусловленную аналогичностью рабочих
процессов в камерах сгорания ЖРД и ГРД возможность оценки
времени пребывания газообразных и диспергированных
конденсированных компонентов в области горения камеры ГРД по (25.2),
если под массой Мъ понимать массу компонентов топлива,
находящихся в свободном от заряда ТРТ объеме. При этом даже на
стационарном режиме значение массы Ms будет изменяться во
времени, тогда как для ЖРД на таком режиме Мъ = const.
Покажем зависимость среднего времени пребывания т в
камере сгорания ЖРД от соотношения размеров камеры сгорания
и состава топлива.
Пусть продукты сгорания - идеальный газ, состав, давление
р*к и температура Т* которого одинаковы во всех точках объема
Vkc камеры сгорания и определены термодинамическим расчетом.
Тогда из уравнения состояния газа следует соотношение
PV
Mz=^. (25.3)
Расход топлива запишем для известного из
термодинамического расчета расходного комплекса Ри или соответствующей ему
при принятых в расчете допущениях теоретической
характеристической скорости с*:
tk[=ElLs. = El^S., (25.4)
Ри си
Подставив (25.3) и (25.4) в (25.2), получим

Глава 25. Камеры сгорания и их параметры 333
где А(п) - функция усредненного по процессу в диапазоне
значений давленияр*к...р показателя изоэнтропы п в соотношении
для расходного комплекса.
Отметим, что, как следует из анализа влияния давления на
результаты термодинамического расчета, комплекс в квадратных
скобках в (25.5) от давления в камере практически не зависит
и характеризует конкретное двухкомпонентное топливо при
заданном соотношении компонентов.
Отношение объема камеры сгорания к площади критического
V
сечения -^ имеет размерность длины и называется приведенной
длиной камеры сгорания Ln .
Поскольку в реальных камерах сгорания скорость продуктов
сгорания во входном сечении сопла не равна нулю, т. е. реальные
камеры являются, строго говоря, скоростными, и переход
химической энергии в тепловую происходит и в сужающейся части
сопла, то для сохранения возможности применения (25.5) при
расчете среднего времени пребывания т в скоростных камерах
сгорания приведенную длину рассчитывают для суммарного
объема камеры сгорания и сужающейся части сопла. При этом с
достаточной для практики точностью принято считать справедливым
приближенное равенство действительного тд и среднего тп
времени пребывания.
Из сопоставления (25.2) и (25.5) следует эквивалентность
приведенной длины камеры сгорания и среднего времени пребывания
при оценке условий достаточности для завершения в основном
преобразования химической энергии в тепловую энергию
продуктов сгорания, так как для одного и того же топлива значения
L и т отличаются постоянным размерным множителем.
Соответственно достаточность объема камеры сгорания можно
оценивать и по приведенной длине, и по времени пребывания.
Причем данные апробированных конструкций камер могут
отличаться и для одного и того же топлива, если значительно
отличались конструкции и параметры режимов (например,
перепады давления) смесительных элементов. При этом требуемые
значения времени пребывания для одного того же двухкомпо-
нентного топлива, как правило, будут уменьшаться:
• с ростом давления в камере сгорания, так как с повышением
давления увеличивается плотность, т. е. концентрация реагентов,
и, следовательно, увеличивается интенсивность процессов тепло-

334 Часть II. Теория неидеального теплового ракетного двигателя
массопереноса, в том числе скорости химических реакций по
закону действующих масс;
• с повышением температуры компонентов до подачи их в
смесительное устройство (например, из системы регенеративного
охлаждения), так как снижается вязкость, улучшается распыление,
интенсифицируются процессы испарения и перемешивания,
повышается скорость химических реакций (по закону Аррениуса);
• при введении в компоненты присадок, придающих
несамовоспламеняющимся двухкомпонентным топливам свойства
самовоспламеняющегося топлива;
• при подаче одного менее летучего компонента или обоих
компонентов в камеру сгорания после предварительного
испарения (испарение компонента в трактах охлаждения или в
газогенераторах-подогревателях в ЖРД с дожиганием).
В частности, для работающих на одном и том же топливе
и при одном и том же давлении в камере ЖРД, схемы пневмо-
гидросистем которых представлены на рис. 25.4, максимальное
значение требуемого времени пребывания будет для варианта я,
когда компоненты имеют температуру, близкую к температуре
их хранения в баках. Охлаждение камеры ЖРД без дожигания
генераторного газа одним из компонентов (схема жидкость -
жидкость, вариант б) и соответственно повышение его
температуры до подачи в камеру снижает необходимое время на нагрев
этого компонента до температуры кипения. По этой же причине
охлаждение камеры двумя компонентами (вариант в) приводит
к дополнительному снижению требуемого времени пребывания
топлива.
Для схем ЖРД с дожиганием генераторного газа полная
газификация одного из компонентов - окислителя в
газогенераторе (схема жидкость - газ, вариант г) исключает затраты времени
на нагрев и испарение окислителя в камере сгорания, тогда как
горючее необходимо проходит эти фазы, пусть и за меньшее
время. При этом повышенная скорость газообразного окислителя
интенсифицирует процессы смешения компонентов и распыления
жидкого горючего, а температура уменьшает время его испарения.
Для схемы ЖРД с газификацией и горючего, и окислителя
(схема газ - газ, вариант д), когда в камере сгорания не
происходят предшествующие горению нагрев и испарение компонентов,
затраты времени на эти процессы исключаются.
Таким образом, устанавливается следующее качественное
соотношение между требуемыми значениями времени пребывания

Глава 25. Камеры сгорания и их параметры 335
топлива в камере сгорания ъд<хг<1в<тб< та при прочих равных
условиях.
Вход Вход
К ОХЦЦ ОХЦД \А К/ Е>ХиД ИХУД А I К DXU>U
КГ ТЧТУТ ТЧТУТ
&
Вход Вход
1
Вход
а
ГМ
W
Вход
Вход Вход
ХОД А I К ХЭХОД ОХОД А I
Jj
Рис. 25.4. Схемы пневмогидросистем ЖРД, определяющие различия
значений требуемого времени пребывания компонентов в камере сгорания:
1 - камера сгорания; 2 - газовая турбина; 3 - насос окислителя; 4 - насос
горючего; 5 - газогенератор; 6 - газогенератор, работающий с избытком
окислителя; 7 - газогенератор, работающий с избытком горючего; О - окислитель;
Г - горючее
Для качественной (не количественной) оценки изменения времени
пребывания [т ] топлива в камере сгорания, требуемого для полного

336 Часть II. Теория неидеального теплового ракетного двигателя
сгорания топлива при малых изменениях значений существенных
параметров вблизи их некоторого значения, можно составить следующее
соотношение пропорциональности:
Гх -I Zrfe?v?v>T4d?d?
пр т» т/2 д^3 Ар? г;5 р? (Wr f'
где нижние индексы «о» и «г» означают, что величина с этим индексом
характеризует окислитель или горючее соответственно; индекс «я»
относится к параметрам ядра потока в камере сгорания; а - коэффициент
поверхностного натяжения для жидкого компонента; Z - константа,
характеризующая топливную пару; jcI ...х6иу\ ... yl - показатели
степени; v - кинематическая вязкость; d- характерный диаметр отверстия
форсунки; Г-температура компонента на входе в смесительный элемент;
А/? - перепад давления на смесительном элементе; рк - давление в
камере сгорания; ^т - степень турбулентности, усредненная по зоне
смешения, характеризующая конструкцию и режим работы смесительной
головки и влияющая на процессы перемешивания.
Причем х^0ну^0,у6~ 0,5, а значение у5, как правило,
наибольшее из значений всех показателей, что отражает степенную
зависимость скорости химических реакций от температуры по закону
Аррениуса. Следует учитывать также противоположный характер
зависимости вязкости от температуры для жидкостей и газов: с
повышением температуры вязкость жидкостей снижается, тогда как вязкость
газов возрастает.
При этом для Z справедливо соотношение
7 ^7 ^7 ^7 ^7
z^| z^2 ^з 4 5'
где индекс «1» соответствует самовоспламеняющимся термически
разлагающимся в условиях камеры сгорания топливным парам
(компонентам) окислителя и горючего; индекс «2» - паре
самовоспламеняющихся компонентов, один из которых термически разлагается
в условиях камеры сгорания; индекс «3» - несамовоспламеняющимся
парам окислителя и горючего, оба компонента которых термически
неустойчивы (разлагаются) в условиях камеры сгорания; «4» -
несамовоспламеняющимся топливным парам (компонентам) окислителя и
горючего, один из которых термически неустойчив в условиях камеры
сгорания; «5» - несамовоспламеняющимся парам окислителя и
горючего, оба компонента которых термически устойчивы в условиях
камеры сгорания.
Равенство показателя степени нулю означает отсутствие
существенного влияния этого параметра на время пребывания топлива в камере

Глава 25. Камеры сгорания и их параметры 337
сгорания (например, поверхностное натяжение жидкости и
соответственно его влияние исчезают при давлениях и температурах, превышающих
критические для данного компонента значения, что отражается
равенствами х2 ~ О или хЗ ~ 0). Это может быть учтено также малым, а в
пределе нулевым, значением весового коэффициента g в выражении
5
для требуемого времени пребывания: I тпр J « ^g/T, =g1T, (распыление)
+ g2x2 (испарение) + g3x3 (смешение в газовой фазе) + g4x4 (смешение
в жидкой фазе) + g5x5 (химические реакции, включая предпламенные
реакции и собственно горение), где продолжительности распыления или
диспергирования х, и испарения х2 вычисляют для компонента, у
которого эти значения больше, чем у другого компонента, а значения
весовых коэффициентов g. учитывают как последовательное, так и
частично одновременное (параллельное) протекание рабочих процессов (см.
рис. 25.1).
Как правило, для одного и того же топлива переход от схемы
без дожигания к схеме с дожиганием генераторного газа
обеспечивает снижение значений требуемого времени пребывания т
в 1,5-1,8 раза.
Для одного и того же топлива при одной и той же конструкции
смесительного устройства требуемая минимальная приведенная
длина камеры L обратно пропорциональна корню квадратному
из значения давления в камере:
Аф(л)*-т='
VA
где Cj - коэффициент, зависящий от рода топлива, конструкции
и режимных параметров смесительного устройства.
Ориентировочные значения требуемых приведенных длин L
камеры сгорания, полученных обработкой параметров известных
ЖРД для семи топливных пар, представлены в табл. 25.1, где
в правом столбце приведены значения полученного пересчетом
по (25.5) соответствующего времени хп пребывания топлива в
камере сгорания.
В представленных в табл. 25.1 ориентировочных диапазонах
значений Ln меньшие значения соответствуют большим
значениям давления в камере и схемам двигателей с предварительной
газификацией либо подогревом одного или двух компонентов,
а также, при прочих равных условиях, с более совершенными
смесительными головками камер ЖРД. Минимальные значения

338 Часть II. Теория неидеального теплового ракетного двигателя
приведенной длины, как правило, свидетельствуют о
конструктивном совершенстве камеры сгорания в целом.
Таблица 25.1. Требуемая приведенная длина камеры сгорания
и время пребывания в камере сгорания ракетного топлива
№ п/п
1
2
3
4
5
6
7
Топливо
Водород - кислород
Керосин - кислород
НДМГ - кислород
HAMr-N204
НДМГ-АК
Керосин - АК
Аммиак - фтор
Vм
0,25...0,6
1,08...2,0
1,4...2,1
1,0...2,0
1,5...2,25
1,5...2,5
1,0...1,5
V мс
0,26...0,62
1,50...2,78
1,88...2,82
1,44...2,88
2,24...3,35
2,35...3,90
1,10...1,65
Примечание: АК - окислитель на основе азотной кислоты и тетра-
оксида азота, например аналог*
1чный Ак-27.
Из сопоставления данных (см. табл. 2.51), например для топлив
«водород - кислород» и «керосин - кислород» (строки 1 и 2),
следует, что наличие в топливе хотя бы одного высококипящего
стабильного, а значит, и требующего большего времени на
диспергирование и испарение, т. е. менее летучего, компонента (в
данном случае керосина), приводит к увеличению требуемой
приведенной длины камеры сгорания. И напротив, криогенный
компонент топлива (жидкий кислород, применяемый вместо
окислителя, состоящего из двух криогенных компонентов при
одинаковом горючем, строки 2 и 6) способствует уменьшению
требуемой приведенной длины камеры сгорания, что косвенно
качественно подтверждается минимальными значениями L для
топлива «водород - кислород» АК (строка 1).
Оставаясь в рамках приведенной модели, можно утверждать,
что если действительная приведенная длина не меньше
минимально необходимой, xs ^ т , то процесс преобразования
химической энергии топлива в тепловую энергию продуктов сгорания
завершается с достаточной полнотой. Тогда значение
коэффициента камеры, учитывающего возможное незавершение
преобразования энергии, близко к единице. Для современных ракетных
двигателей этот уровень косвенно оценивается коэффициентами
Фк1 ~ фр1 - 0,995...0,998, причем приведенные длины камер
значительно меньше, чем у ЖРД разработки 1955-1980 гг.

Глава 25. Камеры сгорания и их параметры 339
Рассчитать только эти весьма малые потери на основании
данных измерений практически невозможно, так как одновременно
проявляются и потери другой физической природы,
обусловленные, например, неадибатностью процесса.
Термодинамический расчет дает идеальные параметры -
характеристическую скорость с* и совпадающий с ней в рамках
расчетной модели расходный комплекс Ри, соответствующие
полному, т. е. идеальному, завершению всех рабочих процессов в
камере сгорания в адиабатных условиях. В отличие от модели
идеального адиабатного рабочего процесса реальные камеры не
обеспечивают идеальной теплоизоляции.
Если камера сгорания охлаждается аккумуляцией теплоты,
излучением теплоты в окружающую среду или протекающим по
ее трактам охладителем (регенеративное или автономное
нерегенеративное охлаждение), то отвод теплоты приводит к
снижению температуры вблизи стенок камеры. Здесь формируется
менее нагретый пристеночный слой потока, отличающийся от ядра
потока - центральной, приосевой, части потока - не только
температурой, но и скоростью, а в общем случае - химическим и
фазовым составом. При этом пристеночный слой потока
практически не влияет на рабочие процессы в ядре потока.
Приближенный учет потерь тепловой энергии при
нерегенеративном наружном охлаждении камеры возможен, если
известны суммарные теплопотери или распределение плотности
теплового потока qs по наружной поверхности s камеры.
Принимая процесс потери теплоты усредненным по объему
камеры и учитывая закон сохранения энергии в виде равенства
суммарных теплопотерь \qsds секундному снижению полного
s
энергосодержания продуктов сгорания, т. е.
S
где Д/п т - уменьшение полной энтальпии топлива; тт - массовый
расход топлива, определим уменьшение удельного
теплосодержания топлива Д/п т по сравнению с исходным, задаваемым при
термодинамическом расчете в адиабатном приближении.
Выполняя термодинамический расчет для камеры сгорания
в адиабатном приближении, но для уменьшенной полной
энтальпии 1=1пт- А1пт (см. (18.10)), получим значение характеристической

340 Часть II. Теория неидеального теплового ракетного двигателя
скорости с*2 с учетом неадиабатности. Коэффициент,
позволяющий учитывать таким образом усредненные потери на неадиабат-
ность, с учетом (15.2) и (15.3)
*
Фк2*Фр2=^Г-
В большинстве случаев тепловой поток в стенки камеры
сгорания снижается путем создания защитного пристеночного слоя
жидкости или газа (так называемое внутреннее охлаждение). В ЯРД
защитный пристеночный слой создается подачей по периферии
камеры водорода, испаренного и нагретого до меньшей
температуры, чем в основных тепловыделяющих сборках (ТВС),
расположенных вблизи оси симметрии ядерного реактора и сопла.
В высоконапряженных РДТТ пристеночный слой образуется
продуктами сгорания низкотемпературного твердого топлива,
размещаемого вблизи периферии входной части сопла.
Пристеночный слой может образовываться продуктами
сгорания с расходом ms при соотношении компонентов Kms
(соответствующие Kms значения газовой постоянной Rs, усредненного
показателя изоэнтропы ns, температуры Ts, расходного
комплекса и равной ему характеристической скорости |35 - с*), отличном
от соотношения компонентов в ядре потока Ктяс расходом тя
(известные из термодинамического расчета для Кт я параметры
ядра /?я, «я, Гя, Ря ~ с*я) и от усредненного по всей камере
суммарного соотношения компонентов Къ при суммарном расходе через
камеру:
тъ = тя + ms. (25.6)
Следует иметь в виду, что, как правило, соотношение
компонентов в ядре потока соответствует идеальному и |Зя - с* ~ с*.
В результате распределения параметров рабочего тела в
выходном сечении камеры сгорания существенно отличаются от
равномерного распределения, принятого как основное в идеальном
приближении, по отношению к которому рассчитывают
коэффициенты, учитывающие особенности реальных рабочих процессов.
Предполагая отсутствие тепломассобмена между ядром и
пристеночным слоем потока, рассмотрим кусочно-равномерные
распределения параметров потока по сечению камеры вблизи
минимального (критического) сечения (рис. 25.5).

Глава 25. Камеры сгорания и их параметры 34Л
Рис. 25.5. Схема течения в камере сгорания с
внутренним охлаждением:
1 - условная граница раздела ядра и пристеночного слоя
потока; 2 - кусочно-равномерные распределения
параметров потока вблизи минимального сечения камеры
В этом случае в минимальных сечениях пристеночного слоя
и ядра потока установятся состав, температура и давление
топлива, задаваемые соотношениями его компонентов -
соответственно в пристеночном слое и в ядре потока - и давлением в камере
сгорания. Поскольку в рамках настоящего анализа неравномерные
распределения по сечению камеры параметров, характеризующих
свойства продуктов сгорания, рассматриваются как единственное
отклонение от идеальной модели, значения характеристической
скорости и расходного комплекса совпадают и выбор
характеристической скорости в качестве параметра сравнения обусловлен
ГОСТ 17655-89.
Примем следующие допущения:
• давления в камерах идеального и реального двигателей
равны между собой;
• в любом сечении потока давления в ядре и в пристеночном
слое потока равны между собой;
• минимальные, они же критические, сечения пристеночного
слоя Fs min и ядра Fe min потока располагаются в одной плоскости
с минимальным, являющимся также критическим, сечением ка-
МеРЫ Fmin = FKp«
Из этих допущений следует
F ■ =F . +F . .
mm я mm s mm
(25.7)
В рассматриваемом случае характеристическая скорость с
в камере - произведение давления торможения в минимальном
сечении сопла и площади этого сечения, отнесенное к
суммарному массовому расходу топлива камерой:
р ■ F ■
У min min
ГПу
(25.8)

342 Часть II. Теория неидеального теплового ракетного двигателя
Такие же соотношения можно записать для периферийной
зоны (пристеночного слоя потока):
р,«*,=
р. . F
и для приосевой части (ядра) потока:
р F
тя
(25.9)
(25.10)
Выразив площади минимальных сечений из (25.8) - (25.10)
и подставив их в (25.7), после упрощения получим
9кЗ='
тя | csms
т т cm,
(25.11)
Используя следствие из (25.6) тя = тъ -ms, преобразуем (25.11)
к виду
ФкЗ=ФР3=1
т.
т,
i-^
V
= \-тк
"я J
1-
ск
"я J
(25.12)
где ms
т<
относительный расход топлива, подаваемый
тя+т&
для создания пристеночного слоя.
Согласно (25.12), с учетом очевидных неравенств ms < тъ
и с] < с* коэффициент камеры фк может значительно отличаться
от единицы. В частности, для ЖРД фк ~ 0,70...0,95, где меньшие
значения относятся к двигателям малой тяги.
Если расчет коэффициента камеры фк ведется на этапе, когда
известны основные параметры смесительной головки, то более
точные, чем по (25.12), значения можно получить, используя
расчетное соотношение для расходного комплекса камеры в
многозонном (число зон или, что то же самое, ячеек, равное п)
приближении:
Ь=1^-Р„
(25.13)
где mj - расход топлива через г-ю ячейку, занимающую некоторую
часть проходного сечения проточной части камеры, с некоторым

Глава 25. Камеры сгорания и их параметры 343
соотношением компонентов Кт . и соответствующим значением
Р;.; mz - суммарный расход топлива через камеру.
Для двухзонной модели (см. рис. 25.5) значения расходного
комплекса р или характеристической скорости с* в ядре потока (Ря ~ с*) и в
пристеночном слое (Pv ~ с*), как и относительный расход топлива ms,
подаваемого для создания пристеночного слоя, определяют
распределением расхода компонентов топлива между центральной и
периферийной частями камеры. К типовым задачам проектного расчета относится
распределение расходов окислителя то и горючего тг между ядром
потока с выбранным соотношением компонентов
171
К„,я=-^> (25.14)
по возможности приближающимся к условно оптимальному, и
относительно низкотемпературным пристеночным слоем с соотношением
компонентов
*„,s=—> (25.15)
для заданного соотношения расходов топлива для камеры в целом
^mi=^ = const- (25.16)
тТ
Для таких исходных данных с учетом (25.6), (25.14) - (25.16) и
равенств, выражающих очевидные балансы то = mos + я?оя, тг = mrs + тгя
и расходы окислителя mos и горючего mrs в пристеночный слой в долях
хп и х„ от расходов тп и т в ядро потока т = х т и т =
О S Г S г <~« О.Я Г.Я *^~ О Л О S О.Я Г Л
= xrs ^гя' относительный расход топлива ms, подаваемого для создания
пристеночного слоя, рассчитывается однозначно по одному из пяти
приведенных эквивалентных выражений:
тг + т0 тг(\ + Кт1) (mTS +тгя)(\ + Кт1)
= (y + Kms)(Km*-Kml) = XrsO + Kms) (25 17)
(\ + KmL)(Kmsi-Kms) (*rs+l)(l + *wS)'
При этом справедливы соотношения связи:

344 Часть II. Теория неидеального теплового ракетного двигателя
Кт,=Ктя^; (25.18)
хо*=-7Г^*г*'> (25.19)
хГЯ= тя~ wZ. (25.20)
Рассчитанное по (25.17) значение ms позволяет количественно
оценивать потери в камере сгорания, обусловленные наличием
относительно холодного пристеночного слоя, например по (25.12), а соотношения
(25.18) - (25.20) наряду с балансовыми выражениями, отражающими
закон сохранения массы, можно использовать для контроля
правильности вычисленных значений.
Завершившиеся рабочие процессы в камере сгорания
определяют параметры потока во входном сечении сопла и в этом
смысле задают условия его работы. Результаты расчета процессов
в камере сгорания представляют собой исходные данные для
расчета течения в сопле.
Контрольные вопросы и задания
1. Дайте определение камеры сгорания через выполняемые ею функции.
2. Какое время принимается за условное время пребывания
компонентов топлива в камере сгорания?
3. Перечислите схемы камер сгорания ЖРД, различающиеся
структурой течения.
4. Какое условие принимается в качестве необходимого при расчете
требуемого объема камеры сгорания?
5. Почему по условному времени пребывания можно достаточно
достоверно оценить ожидаемую полноту сгорания для камер с
преимущественно осевой структурой течения, но достоверность
аналогичных оценок проблематична для камер ЖРД малой тяги с трехмерной
вихревой схемой течения?
6. Будут одинаковыми или разными (количественно и качественно)
соотношения между условным временем пребывания и приведенной
длиной одной и той же камеры сгорания для различных топлив?
7. Перечислите допущения, принятые при выводе уравнения для
расчета коэффициента камеры, учитывающего наличие пристеночного
слоя потока с соотношением компонентов, отличным от
соотношения компонентов в ядре потока.

Глава 25. Камеры сгорания и их параметры 345
8. В каких случаях в расчетном выражении (25.12) отношение
характеристических скоростей можно заменить отношением расходных
комплексов р?
9. Почему условное время пребывания топлива в камере сгорания для
ЖРД малой тяги, как правило, выше, чем для двигателей больших
тяг, работающих на тех же топливах?
10. Дайте объяснение известному факту: условное время пребывания
топлива в камере сгорания для ЖРД, разработанных или
модернизированных в 1980-2000 гг., нередко значительно меньше (в
некоторых случаях на 30...50 %), чем у двигателей, спроектированных
в середине XX в.

Глава 26
Сопла ракетных двигателей.
Понятия, термины и определения.
Потери в соплах
Если камера сгорания обеспечивает основное для ракетных
двигателей на химическом топливе преобразование химической
энергии топлива в тепловую энергию продуктов сгорания, то
функция сопла как части ракетной камеры состоит в
использовании продуктов сгорания как рабочего тела, в котором тепловая
энергия преобразуется в кинетическую энергию истекающей струи.
Другими словами, функционально сопло является пропулъсивным
аппаратом.
Отметим также, что протекание в химически активном
рабочем теле реакций рекомбинации обеспечивает переход химической
энергии рабочего тела в тепловую энергию в процессе
расширения. При этом затраченная на диссоциацию в камере сгорания
тепловая энергия возвращается в виде тепловой энергии,
выделяющейся при экзотермических реакциях.
Сопло в составе ракетной камеры наряду с основной
составляющей целевой функции - пропульсивного аппарата - работает
в качестве агрегата, задающего в совокупности с другими
параметрами давление в камере сгорания.
Точность числовых значений и характерных показателей
ракетного двигателя, полученных на основе решения задачи
термодинамического расчета в произвольном сечении сопла в
одномерном равновесном приближении, не всегда достаточна для
практики. Количественное рассогласование расчетных и
действительных данных объясняется тем, что принятая модель течения
в сопле отражает только основные идеализированные процессы
без учета проявляющихся существенных неидеальностей.
Отличия реальных рабочих процессов в сопле ракетного
двигателя от их идеального представления формируются в
результате совокупного действия ряда факторов: неравномерности
распределения характеристик потока в начальном сечении сопла;
проявления реальных свойств рабочего тела (вязкости,
несжимаемости конденсированных составляющих, конечности скоростей

Глава 26. Сопла. Потери в соплах
347
физико-химических процессов) при течении его по соплу, контур
которого имеет конечную кривизну, а стенки выполнены из
негладких теплопроводных материалов.
Здесь и далее контур сопла есть линия пересечения
поверхности сопла со стороны потока продуктов сгорания с плоскостью,
проходящей через ее центральную ось.
Поскольку целевые функции камеры сгорания и сопла
различны, вводится рекомендованная ГОСТ 17655-89 и
распространяемая на сопла других видов ракетных двигателей система
коэффициентов фс для оценки влияния неидеальностей в сопле.
Коэффициент сопла фс определяется как отношение
действительного коэффициента тяги в пустоте Ктт]д к идеальному
Ктпи, вычисленное при одинаковом соотношении компонентов
топлива при одном и том же давлении в камере сгорания и
геометрической степени расширения сопла, где коэффициент тяги
КТ - отношение тяги камеры к произведению давления
торможения в минимальном сечении сопла, площади этого сечения
и коэффициента расхода сопла.
При этом с достаточной для практики точностью коэффициент
сопла представляют в виде произведения п сомножителей:
п
Фс=Фс1<Рс2- Фс^ЕК,' (26.1)
/ = 1
где каждый из сомножителей (рс. - это коэффициент сопла,
учитывающий влияние только одного из п факторов проявления
неидеальности при предположении идеального протекания
рабочего процесса вне влияния учтенного фактора.
Определенный таким образом коэффициент сопла косвенно
относит влияние неидеальностей в сужающейся части сопла к
потерям в камере сгорания, что дополняет аргументацию в пользу
условного включения объема сужающейся части сопла в объем
камеры сгорания.
Из сказанного следует, что идеальный и реальный рабочие
процессы в сопле будем сопоставлять при одинаковых параметрах
рабочего тела в минимальном сечении, отождествляемом при
принятых для термодинамического расчета допущениях с
критическим сечением. При этом примем, что идеальное и реальное
течения безотрывны.
Что касается задания параметров расширения потока в сопле,
то в зависимости от задачи сравнительного анализа условиями

348 Часть II. Теория неидеального теплового ракетного двигателя
сравнения могут быть или одинаковые давления в выходных
сечениях сопла, или, что предпочтительнее, одинаковые
геометрические степени расширения, как это установлено ГОСТ 17655-89.
В данном учебнике рассматриваются потери удельного
импульса, проявляющиеся в сопоставимой мере в соплах ЖРД, ЯРД,
РДТТ и ГРД. К ним будем относить уменьшение удельного
импульса вследствие:
• химической неравновесности течения срс1;
• неравномерности свойств потока в минимальном сечении
сопла фс2;
• рассеяния, понимаемого как неравномерность потока в
выходном сечении сопла, фс3;
• трения и вытеснения, т. е. загромождения проходных
сечений сопла пограничным слоем, фс4;
• многофазности рабочего тела фс5.
Что касается влияния неадиабатного течения рабочего тела
в сопле, то теплоотвод на сужающейся части сопла учитывается
при расчете камеры сгорания, а для сопл с неохлаждаемой
расширяющейся частью влияние неадиабатного течения мало по
сравнению с действием факторов другой физической природы.
В большинстве ракетных двигателей сопла охлаждаются
регенеративно. При этом следует иметь в виду, что охлаждение
сопла компонентами топлива представляет собой регенерацию
теплоты - использование низкопотенциальной теплоты
исходящего низкотемпературного потока (в сопле) для нагрева топлива,
поступающего в камеру сгорания и возвращающего теплоту в зону
с максимальной температурой цикла.
Из теории тепловых машин следует возможность повышения
эффективности преобразования теплоты в кинетическую энергию
рабочего тела, т. е. повышения удельного импульса камеры в
результате регенерации. Реализуемые практически в современных
двигателях степени регенерации (доля подогрева компонента
в тракте охлаждения в суммарном повышении температуры от
температуры в баке до температуры сгорания) не дают
существенного прироста удельного импульса, но перспектива перехода
к созданию космических двигателей на топливе, состоящем из
криогенных компонентов с давлением в камере до 100 МПа ведет
к существенному повышению степени регенерации и, как
следствие, к необходимости учета регенерации в методиках расчета.
Задача разработки таких методик в настоящее время не
актуальна и тем более не рассматривается в настоящем курсе общей

Глава 26. Сопла. Потери в соплах
349
теории тепловых ракетных двигателей, но относится к ряду
перспективных проблем.
Контрольные вопросы и задания
1. Дайте определение сопла через выполняемые им функции.
2. Что такое контур сопла?
3. Сформулируйте определение коэффициента сопла. Обратите
внимание на условия, при удовлетворении которых ведется сравнение
идеального и реального сопл.
4. При каких ограничениях (условиях) справедлива методика расчета
коэффициента сопла как произведения коэффициентов,
учитывающих отдельные факторы, влияющие на различия реального
рабочего процесса и его идеального представления?
5. Какие процессы, происходящие в сужающейся части сопла,
условно отнесены к камере сгорания и учитываются при оценке качества
рабочих процессов в ней?
6. Перечислите основные факторы (неидеальности), определяющие
различия реальных процессов в соплах и их идеального
представления и, как следствие, способствующие уменьшению значения
удельного импульса по отношению к возможному максимальному
значению для конкретного ракетного топлива.

Глава 27
Расчет потерь в соплах ракетных двигателей
Рассмотрим стандартизованные определения потерь
удельного импульса, обусловленных различием между реальными
рабочими процессами в сопле и их идеальным представлением.
Количественные оценки потерь, рассчитываемые по
приведенным зависимостям, отражают влияние основных физических
механизмов проявления неидеальностей, но представляют собой
только первое приближение. Рекомендуемые стандартами
существенно более сложные методики расчета потерь значительно
точнее учитывают реальную структуру течения рабочего тела
в сопле, и достоверность получаемых по ним данных достаточна
для их применения при проектировании ракетных двигателей.
При этом методики, как правило, ориентированы на ракетные
двигатели конкретных видов и учитывают их особенности.
Рассмотрим методики количественной оценки потерь,
характерных для двигателей разных видов.
Потери удельного импульса
из-за химической неравновесности течения
(коэффициент сопла фс1 = <рн)
Потери удельного импульса вследствие химической
неравновесности течения (коэффициент сопла фс1) и неравномерности
свойств потока в минимальном сечении сопла (срс2) имеют
термодинамическую природу: цикл расширения рабочего тела
реализуется так, что часть располагаемой полной энергии
химического топлива не переходит в тепловую энергию рабочего тела и не
преобразуется в кинетическую энергию истекающей струи.
Расчет потерь удельного импульса, обусловленных химической
неравновесностью течения (коэффициента сопла (рс1),
проводится на основе следующих представлений.
Протекание в химически активном рабочем теле реакций
рекомбинации обеспечивает распределенный по длине сопла
переход химической энергии рабочего тела в тепловую энергию в
процессе расширения. При этом затраченная на диссоциацию
в камере сгорания часть высвобождающейся при химических

Глава 27. Сопла. Расчет потерь
351
реакциях тепловой энергии возвращается в виде тепловой энергии,
подводимой изнутри к ускоряющемуся в сопле потоку1.
Существенными факторами, действие которых обеспечивает
реально достижимую степень равновесности процесса, является
ограниченность скоростей физико-химических процессов, идущих
в рабочем теле при течении его по соплу. Будем считать, что
рабочее тело - газ, а возможная неравновесность, свойственная
гетерогенным рабочим телам, учитывается как составляющая
потерь вследствие наличия в потоке газа конденсированных
(твердых или жидких) частиц.
Коэффициент сопла фс1, характеризующий рассматриваемую
неидеальность, определяется как отношение действительного
коэффициента тяги в пустоте Кт при реализующейся степени
химической неравновесности течения к идеальному
коэффициенту тяги в пустоте АГтпи, вычисленному в рамках допущения
о полном равновесии в потоке:
Ат.п.и
При этом свойства рабочего тела в критических сечениях
считаются одинаковыми и геометрические степени расширения сопла
будут также одинаковыми.
При таких условиях сравнения равны тяги, создаваемые
камерами на участках от смесительной головки камеры сгорания
до минимального сечения сопла, а отношение коэффициентов
тяги равняется отношению развиваемых пустотных удельных
импульсов:
v F I
Упи ''у.п.и
крЛ кр
При этом считаем, что идеальное и реальное течения одномерны
и безотрывны (поток занимает все проходное сечение сопла).
1 Одна из возможных трактовок процессов трансформации энергии
в сопле ракетного двигателя представлена в кн.: Гостев В.А. Параметры
и характеристики камеры ЖРД. Методология исследования: учеб.
пособие. 2-е изд., перераб. М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.

352 Часть II. Теория неидеального теплового ракетного двигателя
В рамках настоящей дисциплины рассматриваются потери
удельного импульса вследствие химической неравновесности
течения (фс1), проявляющейся в сопоставимой мере в соплах ЖРД,
ЯРД, РДТТ и ГРД.
Термодинамический расчет дает значения удельного
пустотного импульса как результат перехода рабочего тела из
произвольного состояния топлива до входа в камеру к состоянию
продуктов сгорания параметрах в камере при заданной модели
процесса в сопле для конкретной степени расширения газа в сопле
—- или геометрической степени расширения сопла ——.
Ра КР
Модель идеального процесса в сопле - адиабатное и
равновесное изоэнтропийное расширение.
Реальный процесс идет с возрастанием энтропии, что
отражает необратимость явлений переноса при конечных градиентах
концентраций реагентов в потоке и, как следствие, при конечных
значениях скоростей химических реакций. Однако конечная, но
равная нулю скорость всех возможных химических реакций в
потоке (модель химически замороженного течения) соответствует
случаю полного отсутствия возврата затраченной на диссоциацию
энергии и, следовательно, минимальному значению
коэффициента сопла фс1.
Учет реальной степени завершенности химических реакций
требует привлечения аппарата описания химической кинетики
превращений. В рамках настоящего курса рассматриваются
только численные оценки первого приближения на основе так
называемых локально предельных допущений: равновесное течение
в дозвуковой области и химически замороженное течение (скорость
химических реакций равна нулю, состав рабочего тела постоянен)
в сверхзвуковой части сопла. Все анализируемые расчетные
данные для оценки влияния химической неравновесности получены
сравнением идеальных параметров двигателя с результатами
расчета при предположении локальной предельной химической
неравновесности.
Оценим влияние давления в камере на потери пустотного
удельного импульса вследствие химической неравновесности при
17 Fa
разных геометрических степенях расширения сопла F = —*- = var
FkP
на примере двигателя на кислородно-водородном топливе
(коэффициент избытка окислителя а = 0,8). Причем для каждого

Глава 27. Сопла. Расчет потерь
353
давления рк принимается такая геометрическая степень
расширения сопла, чтобы давление в выходном сечении сопла
сохранялось одинаковым: ра = 0,07 МПа.
Расчеты проведены в равновесном и локально-неравновесном
приближении. Под локально-неравновесным приближением
понимается равновесное течение в сужающейся части сопла и
химически замороженное течение в расширяющейся части сопла
(так называемое приближение Брея1).
Результаты расчетов приведены в табл. 27.1.
Таблица 27.1. Зависимость потерь пустотного удельного импульса
от давленния в камере
рк, МПа
5
10
15
20
25
30
35
Равновесное течение
!у^ы1с
4200
4340
4420
4460
4500
4520
4545
п
1,200
1,210
1,217
1,220
1,223
1,225
1,227
Локально-неравновесное
течение
'у.,,'1^
4140
4290
4370
4420
4460
4480
4510
п
1,220
1,225
1,228
1,230
1,232
1,233
1,234
"Pel
0,985
0,987
0,989
0,990
0,991
0,991
0,992
Расчеты показывают, что с повышением давления в камере
с 5 до 35 МПа и увеличением удельного импульса с 4 200 до
4 545 м/с абсолютное значение потерь уменьшается с 6 до 3 м/с,
что отражается в увеличении коэффициента сопла с 0,985 до
0,992.
Сравним значения условных показателей изоэнтропы п в
равновесном п вн и локально предельно неравновесном (химически
замороженном) пн вариантах протекания процессов
расширения рабочего тела в сопле. Во всем рассмотренном диапазоне
значений давления выполняется неравенство п авн < пн авн, что
отражает приближение равновесного процесса к
изотермическому, для которого п = 1. При этом в потоке внутренний теплопод-
вод осуществляется за счет протекания реакций рекомбинации
Тимнат И. Ракетные двигатели на химическом топливе: пер. с англ.
М.:Мир, 1990.

354 Часть II. Теория неидеального теплового ракетного двигателя
•5 0,995 | 1 1 1 1
0 10 20 30 40
Давление в камере /?к, МПа
Рис. 27.1. Влияние давления в камере и геометрической степени
расширения сопла на уровень потерь вследствие химической неравновесности:
1-3 - для сопла с геометрической степенью расширения соответственно 1 000,
500 и 250; 4 - для сопла с постоянным давлением в выходном сечении
ра = 0,07 МПа и переменной геометрической степенью расширения
и соответствующего выделения теплоты. В составе рабочего тела
возрастает концентрация компонентов с относительно большой
молекулярной массой - С02, Н20 и др. - и уменьшается
содержание СО, ОН, Н и др. При этом возвращается тепловая энергия,
затраченная в камере сгорания на температурную диссоциацию,
температура равновесного потока возрастает по сравнению с
температурой потока, в котором химические превращения не идут.
На рис. 27.1 представлены зависимости коэффициента сопла
Фс1 от давления в камере, полученные путем решения задачи
термодинамического расчета для двух вариантов течения,
равновесного на всем протяжении камеры и локально-неравновесного
течения, у которого неравновесность распространяется на всю
сверхзвуковую часть сопла. Сплошным кривым 1-3
соответствуют расчетные данные для постоянных геометрических степеней
расширения сопла, кривой 4 - для постоянного давления в
выходном сечении сопла ра = 0,07 МПа и переменной
геометрической степени расширения. Видно, что при увеличении давления
в камере относительный уровень потерь в сопле на химическую
неравновесность снижается.
Стремление значения коэффициента (рс1 к единице при росте
давления в камере отражает уменьшение влияния возвращения
затраченной на диссоциацию в камере сгорания теплоты, так как
при повышенных давлениях в камере сгорания диссоциация в
значительной степени подавляется (согласно принципу Ле Шателье -
Брауна).

Глава 27. Сопла. Расчет потерь
355
При постоянном давлении в камере увеличению степени
расширения сопла соответствует рост потерь на химическую
неравновесность, поскольку в соплах с большой степенью
расширения имеется возможность большей внутренней регенерации
теплоты, т. е. возвращения рабочему телу большей доли тепловой
энергии, поглощенной в результате эндотермических процессов
термической диссоциации в камере сгорания.
Эта выявляемая расчетом и подтверждаемая практикой
тенденция усиливается в соответствии с увеличением скорости
химических реакций с ростом давления вследствие увеличения
концентрации реагирующих веществ и температуры в камере.
Приближение значения удельного импульса к его идеальному
равновесному значению с ростом давления наряду с другими
факторами обусловливает преимущества ракетных двигателей
с повышенным давлением в камере.
Конечность скоростей реакций рекомбинации определяет
влияние абсолютных значений размеров двигателя на потери
вследствие химической неравновесности, так как при одних и тех же
скоростях движения потока время пребывания в сопле будет
большим у болынеразмерного двигателя и соответственно
возникает возможность более полного завершения реакций
рекомбинации и снижения потерь. В связи с этим при прочих равных
условиях потери на химическую неравновесность больше у
ракетных двигателей малых тяг (например, у ЖРД малой тяги), чем
у двигателей с уровнем тяг 5 кН и более.
Таким образом, потери удельного импульса вследствие
химической неравновесности в основном связаны с неполнотой или
отсутствием возврата теплоты, затраченной на диссоциацию
продуктов реакции горения в камере теплоты при «замораживании»
(незавершенности) в сопле экзотермических химических реакций
рекомбинации, каждая из которых отличается значением
теплового эффекта, составом и свойствами продуктов реакции и
другими параметрами. В свою очередь, вероятность тех или иных
химических реакций в основном определяется химическим
составом топлива. Отсюда следует зависимость потерь удельного
импульса вследствие химической неравновесности течения в
сопле от состава топлива, а для заданного двухкомпонентного
топлива - от соотношения расходов горючего и окислителя.
Очевидно, что при низких температурах (больших отличиях
соотношения компонентов от стехиометрического соотношения),
когда реакции термической диссоциации в камере сгорания

356 Часть II. Теория неидеального теплового ракетного двигателя
практически не идут, невозможен и возврат теплоты при
равновесном течении рабочего тела в сопле. Соответственно не будет
и потерь на химическую неравновесность.
Поскольку значения параметров, характеризующих свойства
продуктов сгорания различных топлив, изменяются в
достаточно широких пределах, выявить однозначную зависимость
уровня потерь от состава топлива не представляется возможным.
Связь состава топлива и потерь на химическую неравновесность
проявляется при определении условно оптимального
соотношения компонентов Kjo tim - значения соотношения расходов
окислителя и горючего, при котором достигается максимальное
значение пустотного удельного импульса для заданной степени
расширения.
На рис. 27.2 представлены зависимости пустотного
удельного импульса / п от соотношения расходов компонентов
топлива «углеводородное горючее - кислород» (коэффициента
избытка окислителя а при KmQ = 3,4119) при давлении в камере
р*к = 5,2 МПа и давлении на срезе сопла ра = 0,034 МПа. При
этом кривая 1 получена при предположении равновесного
течения на всем протяжении камеры, кривая 2 -
кусочно-равновесного течения (равновесного - до критического сечения
сопла и химически замороженного - на участке сверхзвукового
потока), а кривая 3 - химически замороженного течения продуктов
|3400
l
о
с 3200
CQ
а
С
I 3000
«
х
А
|*2800
^ 0,55 0,65 0,75 0,85 0,95 1,05
Коэффициент избытка окислителя,а
Рис. 27.2. К оценке влияния соотношения компонентов топлива на
потери удельного импульса вследствие химической неравновесности
/
\/
/
/^
г-~
1
4
^2
3^
\
ТКЛ
3700
3600
3500
3400
3300
3200

Глава 27. Сопла. Расчет потерь
357
сгорания в сопле от входного до выходного сечений. Кривая 4
отражает изменение температуры в камере сгорания.
Максимальный удельный импульс / п1 = 3 350 м/с,
рассчитанный в равновесном приближении, достигается при ат о timl =
= 0,81; при полностью химически замороженном течении при
a tim3 = 0,68 развивается удельный импульс I ъ = 3 112 м/с,
промежуточному случаю (кусочно-равновесное приближение)
соответствуют ат im2 = 0,725 и / п2 = 3 166 м/с.
Смещение условного оптимального соотношения компонентов
от a iml = 0,81 в сторону избытка горючего при учете потерь на
химическую неравновесность, т. е. с приближением к модели
реального течения, можно объяснить снижением температуры
(кривая 4 на рис. 27.2) и соответствующим уменьшением степени
диссоциации.
Реальные процессы течения в сопле могут быть представлены
как некоторые промежуточные между предельными
рассмотренными вариантами: мажорантой - равновесным течением и
минорантой - химически замороженным течением на всем протяжении
сопла. Приближенным к реальному течению вариантом может
быть, например, равновесное течение в сужающейся части сопла
и предельно неравновесное (химически замороженное) течение
на расширяющемся участке сопла.
При этом, сопоставляя время прохождения выбранного
участка Axj 2 = х{ - х2 сопла со средней для этого участка скоростью
Wx_v рассчитываемое как Aij_2 = Axl2/Wl2, и требуемое время
установления химического равновесия т (время релаксации),
согласно принятому уравнению химической реакции, можно
фиксировать содержание компонентов смеси - реагентов этой реакции,
т. е. «замораживать» менее скоростные реакции на участках
сопла, где Aij 2 « т. Если справедливо неравенство т « ATj_2, to
течение близко к равновесному. В первом приближении значения1
требуемого времени для нескольких характерных химических
реакций можно определять по табл. 27.2.
Практически значимая точность расчета потерь на химическую
неравновесность достигается только решением сопряженной
задачи о течении химически активного рабочего тела в канале с
учетом кинетики химических превращений.
Беляев Н.М. Указ. соч.

358 Часть II. Теория неидеального теплового ракетного двигателя
Таблица 27.2. Значения времени, с, необходимого для
установления химического равновесия при разных температурах
Реакция
СН4~Ств + 2Н2
С2Н4~2Ств + 2Н2
С2Н6~2Ств + ЗН2
2NH3 <-> N2 + ЗН2
С02 + Ств <r+ 2CO
со2 + н2 «-> со + н2о
Примечание. Ств -
реагента.
Температура, К
700
5,28'Ю12
1,02-102
1,59-107
3,54-Ю12
1,59-108
1,45-10"5
1000
3,55-104
2,16-10"2
99,0
1,11104
7,20-102
6,31 10"7
1200
17,74
9,24-10^
8,00-10"2
6,31
0,3
1,41-Ю"7
обозначение твердого углерода (
1500
1,24-10"2
2,50-10"5
2,50-10"4
5,02-10"3
1,00-10"3
9,25-10"9
сажи) как
Потери удельного импульса из-за неравномерности
потока в минимальном сечении сопла
(коэффициент сопла <рс2 = <рвх)
Если для расширяющейся части сопла выбирается профиль
при предположении равномерных по сечению распределений
свойств одномерного потока с плоской поверхностью перехода
через скорость звука в минимальном сечении сопла, то отличие
реального потока от такой его модели приводит к отличиям
удельного импульса от расчетного, т. е. к потерям.
В отличие от течения в минимальном сечении сопла
одномерное течение ведет к формированию неплоской, выпуклой
в сторону выходного сечения сопла поверхности перехода через
скорость звука, а следовательно, к местному повышению
давления вблизи оси симметрии сопла, возникновению малых
возмущений в сверхзвуковой части потока, к отличиям в геометрической
степени расширения сопла для приосевых и периферийных частей
потока. При этом уменьшается скорость истечения ядра потока.
Поток становится неодномерным в выходном сечении сопла,
и проявляются дополнительные потери на рассеяние. Однако для
сопл с профилем сужающейся части, выбранным, согласно
принятым для ЖРД рекомендациям, эти потери, как правило, не
превышают 0,5 % и могут быть в первом приближении оценены этим
числом.

Глава 27. Сопла. Расчет потерь
359
При одномерных распределениях скорости и давления
рабочего тела в минимальном сечении сопла состав, а следовательно,
и свойства потока могут быть различными для пристеночного
слоя и ядра потока. Такая картина течения представляет собой
результат проявления неидеальности, как правило, объективно
необходимой и часто создаваемой преднамеренно.
Создаваемое с целью организации внутреннего охлаждения
камеры сгорания неравномерное распределение соотношения
компонентов по сечению камеры вплоть до минимального
сечения сопла в той или иной мере сохраняется и при течении
рабочего тела в расширяющейся части сопла (рис. 27.3). Причем в
процессе течения в сверхзвуковой зоне происходит взаимный
тепломассообмен между пристеночным слоем и ядром потока,
обусловленный градиентами концентраций, температур и
скоростей. В результате зона контакта пристеночного слоя и ядра
потока размывается, термодинамические свойства рабочего тела
усредняются в слое смешения и, хотя занимаемые пристеночным
слоем и ядром потока доли площади проходного сечения
изменяются, сохраняется равномерное распределение давления по
радиусу потока. Эта особенность позволяет оценить потери
удельного импульса вследствие неравномерности течения в
минимальном сечении сопла, если принять ряд качественно обусловленных
допущений, а именно:
• степени расширения в сопле пристеночного слоя и ядра
потока одинаковы, т. е. одинаковы давления в выходном
сечении сопла (рая = pas) и давления торможения в критическом
сечении (р* = р* );
Рис. 27.3. К оценке влияния неравномерности распределений параметров
потока на входе в критическую часть сопла на потери удельного импульса:
/ - условно непроницаемая граница раздела ядра и пристеночного слоя
потока; 2 - кусочно-равномерные распределения параметров потока в
критическом сечении; 3 - кусочно-равномерные распределения параметров потока
в выходном сечении сопла

360 Часть II Теория неидеального теплового ракетного двигателя
• свойства рабочего тела в пристеночном слое и в ядре
потока при течении в расширяющейся части сопла изменяются, как
при адиабатном равновесном изоэнтропийном расширении,
задаваемом соотношением давлений, т. е. тепломассообмен между
пристеночным слоем и ядром потока пренебрежимо мал.
Следствием допущений является представление пустотной
тяги Рп двигателя как суммы тяг, создаваемых пристеночным
слоем Ps и ядром Ря потока, рассчитываемых через известные
расходы в пристеночном слое ms и ядре тя и удельные импульсы
I nsnl п я, которые определяются термодинамическим расчетом
для одних и тех же давлений торможения, равных давлению в
камере р*9 и давлений в выходном сечении ра, но разных для ядра
и потока сотношений компонентов:
Р = Р + Р = I m +I т .
п ns п.я y.ns s у.п.я я
Тогда коэффициент фс2 = фвх, учитывающий коэффициент по-
pF
терь как единственную неидеальность, прирк aF = idem, m = к кр
Ри.Д Р„.,
ф,
с2
*т.п.д _ Рк.Лр _ ^дРд _
к.
/Уи Рп.»
Рк.дКр *нРи
mJy.nS+тя1упи
Рд /-
фр
= 1--
у.п.и
/и.
Щ+тя\ Ри
J_
фр
i_jl
т„
т1 +та
1 —
mv
y.ns
V у п и J
( I
1 Упл
mv + ma
V уп.и у
тк
т^ +та
Подставив / п = Ш п, -*^-= ^ТПЛ^Л
^ у.П г Т. П' Г ^" О
у.п.и
получим

Глава 27. Сопла. Расчет потерь
361
т
ms +mi
Фс2= Г Г „ Л
^тп.иРи
W,
тя+тяК
Ри
При расчете коэффициентов пустотной тяги принимается, что
давления в ядре и в пристеночном слое потока в выходном
сечении сопла равны номинальному давлению: рая= pas ~ Рапот> так
как свойства потока незначительно влияют на степень
расширения газа в данном сопле.
Если коэффициент пустотной тяги Kjns, рассчитанный для
потока с параметрами пристенного слоя, превышает этот же
коэффициент, но определенный для рабочего тела с параметрами
ядра потока КТ п я, т. е. Kjns> Ктп я, то потери удельного
импульса вследствие рассматриваемой неравномерности потока
отсутствуют и даже может иметь место некоторый незначительный
прирост удельного импульса. В этом случае принимается Фс2 ~ 1-
В противном случае, когда Кт ns < Кт п я, различие усредненных
показателей изоэнтропы пристеночного слоя и ядра потока
(ns Ф пя) приводит к отклонению давления в выходном сечении
сопла от номинального:Рад¥1Рапот- Причем и при равенстве
давлений рая = pas ввиду различия свойств (температуры Ts < Тя,
кажущейся газовой постоянной Rs Ф /?я, усредненного показателя
изоэнтропы ns Ф пя) скорость истечения пристеночной части
рабочего тела будет меньше скорости истечения ядра потока:
Was < Waj{. Это наряду с отличием давления от номинального
приводит к снижению удельного импульса. Действительный
удельный импульс будет меньше условного идеального удельного
импульса / и, который развивала бы камера без пристеночного слоя
в сопле и с заданным номинальным давлением в его выходном
сечении, т. е. срс < 1.
В реальных течениях граница раздела ядра и пристеночного
слоя потока проницаемая. Через нее происходят перенос
импульса и сопряженный тепломассообмен, ведущие к выравниванию
параметров и свойств потока, в том числе к перераспределению
располагаемой избыточной кинетической энергии ядра потока
на массу, движущуюся в пристеночном слое. Для достаточно
длинных сопл радиальные распределения параметров потока
в выходном сечении сопла приближаются к равномерным
распределениям.

362 Часть II. Теория неидеального теплового ракетного двигателя
Расчетные оценки показывают, что, как правило, в
характерном для тепловых ракетных двигателей диапазоне значений
параметров потери удельного импульса вследствие
неравномерности распределения свойств рабочего тела по сечению сопла не
превышают 0,5 %, т. е. 0,995 ^ Фс2 ^ 1>0 и их можно не учитывать
на этапе предварительного расчета основных характеристик
проектируемого двигателя.
Потери удельного импульса из-за рассеяния
(коэффициент сопла (рс3 = <р )
Техническая невозможность выполнения сопла с одномерным
течением потока в выходном сечении приводит к тому, что вектор
скорости истечения Wa имеет помимо осевой компоненты Wax
еще и радиальную компоненту War, переменную по радиусу, т. е.
распределения параметров потока в выходном сечении сопла
отличаются от принятых в идеальном представлении равномерных
распределений параметров, что приводит к потерям удельного
импульса вследствие рассеяния, понимаемого как
неравномерность потока в выходном сечении сопла.
Учитывающий эти потери коэффициент сопла фс3 = ср
определяется из соотношения
где КТ п д, Кт п и - коэффициенты тяги в пустоте, рассчитанные для
сопл, имеющих идентичные сужающиеся и околокритические
части и равные площади выходных сечений, но разные контуры
расширяющихся частей:
• одно сопло обеспечивает равномерное распределение всех
параметров в выходном сечении и коэффициент тяги Кт п и такой,
как в идеальном случае, рассмотренном в качестве базового^ (27.1);
• в выходном сечении другого сопла скорость газа Wa равна
по модулю скорости, принятой в идеальном представлении, но
на разном удалении от стенки сопла радиальная компонента ее
вектора War Ф 0, т. е. ненулевой угол наклона к оси симметрии
сопла - угол наклона вектора скорости р - изменяется от р = 0 на
оси симметрии сопла до Р = Ра у стенки сопла.
Для наиболее применяемых осесимметричных сопл ракетных
двигателей вблизи выходного сечения сопла поток в первом

Глава 27. Сопла. Расчет потерь
363
приближении может рассматриваться как часть сферически
симметричного течения, ограниченная телесным углом 2§а.
Схема течения для конического сопла с радиусами
критического R и выходного Ra сечения и углом наклона $а образующей
в приближении сферической симметрии представлена на рис. 27.4,
где р - радиус сферы с центром в точке О; Р - произвольный угол
наклона вектора скорости в точке Д лежащей на сферической
поверхности и удаленной от оси симметрии сопла на
расстояние Rd; AB - срез сопла, перпендикулярный оси симметрии; dl -
ширина (хорда) сферического кольца, соответствующая малому
приросту угла наклона <ф.
Рис. 27.4. К расчету потерь удельного импульса
в сопле вследствие рассеяния
По условиям симметрии, все параметры потока в точках,
лежащих на сферической поверхности одного и того же радиуса,
равны по модулю. При этом векторные величины направлены по
радиусу сферы.
Запишем соотношение для расчета реактивной силы dP9
создаваемой расходом рабочего тела mdF, проходящего через часть
сферической поверхности - кольцо площадью dF ~ 2nRdl, в
одномерном приближении:
dP = mdF ^cos P + padFcos p. (27.2)
Выразим расход mdF через параметры потока в точке D с
учетом следующих из малости приращения угла <ф равенств sin dp ~
~ */р и pdp ~ dl как произведение известных величин:
mdF=paWa2nRpd^.
dF

364 Часть II. Теория неидеального теплового ракетного двигателя
Для прямоугольного треугольника ОАВ (см. рис. 27.4) спра-
ведливо равенство —- = sinPa, а для треугольника ODC - равен-
Р
ство —— = sinp, из сопоставления которых следует соотношение
Р
sinp
Kd-Ra-T-Z--
sinp.
Подставив соотношения для расхода mdF и текущего радиуса R
в (27.2) и выполнив очевидные упрощения, получим выражение
dP = PaWa22nRa -^f pcos p^P + д^тфД, ^-cos р<ф,
sinp0 sinpa
интегрируя которое по переменной р от р = 0 до Р = Ра, получаем
формулу для определения внутренней составляющей тяги сопла:
Р„
P=\dP =
о
R2 Рг Л2 Рг
р1^а22я—f— [ sin Pcos р</р + ра2я—a- f sinpcospJp.
sin P. о ^T Sinp" о ^T
Выполнив подстановку sin2 p = 1 - cos2 P,
0 Sin Pa
получ]
/г
"* сфер
дм
=/
1 + COS
= 2
EL
l-cospa=1
sin2pa
2 -.,0...1,017 дляО^ р« 15°,
1 _1_ cos В
т
откуда следует расчетная формула
Ф„ = исо^. (2?4)
Оценим погрешность расчета по приближенному равенству
(27.3), обусловленному подстановкой f= 1 в выражение для расчета

Глава 27. Сопла. Расчет потерь
365
внутренней тяги в одномерном приближении. Запишем расчетное
выражение в одномерном (в данном контексте это идеальный
вариант) приближении:
Р =mW+pF=pF(\+ кМ2\
п.и а г а а га а\ а/>
где «статическая»paFa и «динамическая»/^/^кМ2а составляющие
тяги соотносятся как 1 : кМ2.
В диапазоне значений степеней расширения рк /ра = 10...200
для к= 1,15...1,20 число Маха Ма изменяется в пределах 2,5...3,5,
т. е. доля «статической» составляющей в тяге не превышает
6... 15 %. Тогда максимальная погрешность 1...2 %, вносимая
заменой /= 1,017 на/= 1, приведет к погрешности при замене
уравнения, учитывающего сферичность контрольной поверхности,
уравнением для плоского течения не более 0,1...0,3 %, что
значительно ниже уровня потерь вследствие рассеяния.
Следовательно, принятые допущения приемлемы.
Потери из-за трения и вытеснения
(коэффициент сопла <рс4 = <р )
Реальное рабочее тело обладает вязкостью, и при течении
вблизи стенки сопла в пограничном слое в результате трения
возникает сила, приложенная к стенке сопла в направлении,
противоположном скорости потока, т. е. уменьшающая тягу сопла.
Кроме того, наличие пограничного слоя оказывает на поток
действие, эквивалентное уменьшению поперечных размеров
проточной части на некоторую величину, называемую толщиной
вытеснения, что обусловливает различие геометрической степени
расширения потока и геометрической степени расширения сопла.
Из определения коэффициентов сопла с учетом точного
равенства давлений торможения в минимальных сечениях
действительного и идеального сопл и при предположении
приближенного равенства F д = F и следует выражение для коэффициента
сопла с учетом потерь на трение:
р f P P -АР АР
m -m _ гкр.д* кр.д _ *п.д _ 'п.и ^ тр _ t ^ тр Щ *\
Фс4-Фтр- р "Б р ~ р~' ^ }
IJLi! гпи Лги г"
пи
Р F
Укъ.п* к
кр.и" кр.и

366 Часть II. Теория неидеального теплового ракетного двигателя
где АРТ - проекция на ось симметрии сопла суммарной силы
трения, действующей на стенки сопла; Рп и - пустотная тяга,
развиваемая этим же соплом при отсутствии трения.
При расчете коэффициента сопла по (27.5) предположим, что
кажущееся уменьшение проходного сечения сопла вследствие
загромождения пограничным слоем происходит таким образом,
что сохраняется геометрическая степень расширения сопла, а
сужение минимального сечения сопла не влияет на потери на трение
и может быть учтено коэффициентом расхода сопла |ic < 1. Тогда
вводимый (27.5) коэффициент (рс4 не будет учитывать часть
потерь на вытеснение, связанных с изменением геометрической
степени расширения потока вследствие эффекта вытеснения.
Отметим, что масштаб (или порядок) толщины вытеснения для
течения в соплах ракетных двигателей - до нескольких миллиметров,
а такое уменьшение размеров заметно повлияет на изменение
геометрической степени расширения сопл с характерными
диаметрами до десятков миллиметров, т. е. двигателей малых тяг,
специфика теории которых не рассматривается в настоящем курсе.
На рис. 27.5 представлена схема течения в сопле.
Рис. 27.5. К расчету потерь
удельного импульса в сопле на трение
Проекция на ось симметрии сопла суммарной силы трения,
действующей на стенки сопла (АРт ), вычисляется как
интегральная сумма проекций на ось симметрии х напряжений трения тт,
приложенных к элементарным коническим участкам площадью as,
составляющим контур сопла R(x):
APTp=lxTpcosPJCds, (27.6)
s
где $х - угол наклона образующей контура R(x) в точке с осевой
координатой х и радиусом Rx.

Глава 27. Сопла. Расчет потерь
367
Напряжение тт выражается через коэффициент трения С,
и скоростной напор , рассчитанные для сечения сопла с
координатой х:
Коэффициент трения находят по известным формулам,
например по соотношению Авдуевского:
cf ~ с/о
(j V°-3V lr-^ Л"0'55
1 + 0,88—M
f2
где С,0 - коэффициент трения, определенный без учета
сжимаемости для параметров потока вне пограничного слоя; Гст, Т -
температура стенки и рабочего тела вне пограничного слоя; М -
значение числа Маха; к - показатель адиабаты. Здесь через
соотношение температур на стенке и в потоке учитывается
восстановление давления в пограничном слое и неадиабатное
течение, а введением числа Маха - сжимаемость потока.
Коэффициент 0,88 отражает характерное для большинства газов повышение
температуры на идеально непроводящей теплоту (адиабатной)
стенке в пограничном слое с исчезающей молекулярной
вязкостью1 при типичном соотношении между вязкостью и
температуропроводностью (критерий Прандля Рг ~ 0,7). Таким образом
проявляется неадиабатность течения, т. е. теплопроводность
стенки сопла и наличие системы охлаждения независимо от ее
типа: автономная или регенеративная. Причем очевидны
тенденции: возрастание напряжений трения с увеличением
интенсивности охлаждения (ростом радиальной неизотермичности) и
снижение влияния неизотермичности по длине сопла.
Коэффициент трения Cf0 рассчитывается, как правило, по
полуэмпирическим соотношениям, имеющим вид
с - а
/0 Re"
1 Соотношения, связывающие параметры идеального течения и
реального потока с трением и теплообменом, приведены в монографии:
Кутателадзе С. С, Леонтьев А.И. Тепломассообмен и трение в
турбулентном пограничном слое. М.: Энергия, 1972.

368 Часть II. Теория неидеального теплового ракетного двигателя
где Re - число Рейнольдса, определенное по параметрам потока
вне пограничного слоя; а, т - константы, задаваемые для
конкретных диапазонов значений чисел Рейнольдса. Причем для
больших чисел Рейнольдса, когда течение автомодельное,
показатель степени уменьшается до т ~ 0, константа а
приближается к коэффициенту трения С,0, который можно считать
постоянным. Для предварительных расчетов Cf0 можно принимать
равным 0,002 для полированных и 0,003...0,005 для технически
гладких поверхностей, имея в виду, что уже на первых секундах
работы первоначально полированная поверхность сопла по
характеристике шероховатостей приближается к технически гладкой.
Отметим, что характерное для РДТТ термохимическое и
эрозионное взаимодействие рабочего тела и стенки сопла сопровождается
значительным ростом шероховатости по отношению к исходной
и свойства течения рабочего тела при этом могут значительно
отклоняться от описанных выше закономерностей еще и из-за
сочетания двух противоположных факторов: вдува газа в
пограничный слой и изменения шероховатости1.
При практических расчетах определенный интеграл (27.6)
находят, как правило, численно. При этом существенным является
шаг разбиения проточной части сопла на участки, на протяжении
которых параметры и свойства рабочего тела можно принять
постоянными.
Отметим, что основное влияние на значение потерь на трение
оказывает длина расширяющейся части сопла, тогда как вид
профиля образующей - парабола, совокупность участков окружностей
или полученный решением вариационной задачи полином общего
вида - практически не влияет на суммарные потери удельного
импульса на трение. Это с приемлемой для расчетов первого
приближения точностью позволяет принимать равными значения
коэффициентов потерь на трение для сопл с отличающимися, но близкими
к геометрически подобным (аффинно-подобными) образующими
расширяющейся части, т. е. с почти одинаковыми значениями
тангенса наклона хорды образующей (Ra -RK) / (La-LK) = idem.
Вследствие квадратичной зависимости напряжения трения от
скорости потока потери на трение на сужающемся участке сопла
ниже, чем на расширяющемся участке, и пренебрежение ими
приводит к погрешности расчета суммарных потерь на трение не
Шишков А.А., Панин С.Д., Румянцев Б.В. Рабочие процессы в ракетных
двигателях твердого топлива: справочник. М.: Машиностроение, 1988.

Глава 27. Сопла. Расчет потерь
369
более десятых долей процента. Это позволяет, введя
дополнительные допущения об одномерности течения, при постоянстве
свойств рабочего тела и коэффициента трения получить,
используя ГДФ приведенного скоростного напора J0(X), расчетное
выражение для оценки уменьшения удельного импульса камеры
с коническим соплом:
*--.^-
-c/Ctgp/(xe,*)
(27.7)
ПРИ РПИ = РЛрКг.п = РЛ
кр
к + \
к-\\2+\
•'„(*■) =
2Л '
Переходя от интегрирования напряжений трения тт по боковой
поверхности s к интегрированию по сечению потока F, а затем по
приведенной скорости X и проводя упрощающие математические
преобразования, получаем выражение для интегрального
газодинамического комплекса:
/(*..*)=
(Ц>-£^
к + \
Х+-
_1_
X2
dX
(27.8)
Значение входящего в (27.8) определенного интеграла зависит
от геометрической степени расширения сопла. При изменении
геометрической степени расширения сопла Foth = FJF от 10 до
2 000 приведенная скорость в выходном сечении сопла
возрастает с Ха = 2,19 до Ха = 3,10 и соответственно значение интеграла
из (27.8) при к= 1,17 изменяется с 0,86 до 2,69. Числовые
значения определенного интеграла из (27.8) приведены в табл. 27.3.
Физический смысл комплекса f(Xa,k) в (27.8) можно
определить как долю потерь на трение, пропорциональную боковой
поверхности сопла, на которой проявляются напряжения трения.
Вид зависимости от угла наклона образующей конического
сопла $а позволяет прогнозировать тенденции изменения потерь
на трение в зависимости от основных параметров сопла -
геометрической степени расширения Fa/FK и угла $а.

370 Часть II. Теория неидеального теплового ракетного двигателя
Таблица 27.3. Данные для оценки потерь на трение
Параметр
X
а
1
f(KJ)
Геометрическая степень расширения сопла
10
2,1934
0,864
0,176
100
2,7179
1,707
0,298
1000
3,025
2,47
0,397
2000
3,0875
2,69
0,425
Представленная на рис. 27.6 возрастающая кривая ф^
построена для сопла с Fa/FK = 10 и отражает тенденцию,
следующую из конечного выражения (27.7): уменьшение угла
наклона образующей ведет к увеличению боковой поверхности и,
следовательно, к росту абсолютных потерь на трение.
Следствием этого факта является увеличение оптимального угла наклона
образующей конического сопла с ростом его геометрической
степени расширения (при прочих равных или близких по
значению существенных параметрах).
Более точные предпроектные оценки потерь удельного
импульса вследствие трения можно сделать на основе теории
пограничного слоя, позволяющей рассчитать толщину вытеснения
при течении сжимаемого потока вдоль гладкой поверхности.
~ 1,00
V0,99
§ 0,98
о 0,97
3 0,96
5 0,95
| 0,94
% °'93
S 0,92
* 0,91
0,90
/ х^***
^ CW
ФГ
V4)
Yc
V!>
(2)
%
5-=^>
^
^TD Cl>(,#)-
тр ^с
0 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16
Угол наклона образующей конического сопла ра, рад
Рис. 27.6. К оптимизации конического сопла (верхние
индексы коэффициентов сопла (р*;) соответствуют постоянной
геометрической степени расширения сопла Foth = FJF' ):
/-F =10;2-F =100; 3-F= 1000; 4-F* =2000

Глава 27. Сопла. Расчет потерь
371
Методика таких расчетов и необходимые табличные данные
содержатся в руководстве для конструкторов по проектированию
ракетных сопл1, а примеры - в учебном пособии2.
Потери удельного импульса из-за многофазности
рабочего тела (коэффициент сопла <рс5 = q>5)
Наличие в продуктах сгорания конденсированных
составляющих - жидких или твердых частиц - свойственно, как правило,
или ракетным двигателям, сопло которых обеспечивает снижение
температуры газообразного в условиях камеры сгорания
рабочего тела до уровня температуры конденсации его составляющих,
или двигателям, работающим на металлизированном топливе,
когда в продуктах сгорания содержатся относительно тугоплавкие
оксиды металлов.
Коэффициент фс5 = ф^ учитывает потери удельного импульса
вследствие многофазности, т. е. вызванные несжимаемостью
конденсированной фазы, скоростным и температурным отставанием
конденсированных частиц от газообразной составляющей
рабочего тела и изменениями в пристеночном, в частности в
пограничном, слое проточной части камеры, где реализуется силовое
взаимодействие потока и границы канала.
Движение полидисперсной конденсированной фазы может
сопровождаться как слиянием жидких частиц (коагуляцией), так
и их дроблением (диспергированием). Рассогласование параметров
конденсированных частиц и газа вызывается тем, что
конденсированная фаза практически несжимаема, имеет плотность, более
чем на порядок превышающую плотность газовой фазы, и
теплоемкость, изменяющуюся неравномерно - со скачкообразными
фронтами вблизи фазовых переходов.
Ускорение в сопле газообразной составляющей рабочего тела
связано с высокоскоростным снижением давления и
температуры в несколько раз, тогда как снижение давления среды,
окружающей конденсированную частицу, не приводит к ее ускорению
и уменьшению температуры. Появляется скоростное и
температурное отставание частиц. Причем вместе с температурным
Руководство для конструкторов по проектированию сверхзвуковых
осесимметричных круглых сопел реактивных двигателей / Д.А.
Мельников и др.; ГКАТ СССР. НИИ № 1. М., 1964.
Буркалъцев В.А., Дорофеев А.А., Новиков А.В. Указ. соч.

372 Часть II. Теория неидеального теплового ракетного двигателя
рассогласованием возникает и фазовое неравновесие, связанное
с ограничением интенсивности теплопередачи и, следовательно,
с конечным требуемым временем образования, охлаждения и
затвердевания (кристаллизации) частиц конденсированной фазы,
а также с недостаточностью для этих процессов времени
контакта частицы и газа при течении по соплу.
Развиваемая пустотная тяга однозначно определяется
параметрами потока в выходном сечении сопла. Следуя принятым
принципам анализа неидеальностей без учета их взаимного
влияния, рассмотрим уравнение для пустотной тяги сопла, рабочее
тело которого в выходном сечении представляет собой газ с
известными параметрами ра , Та , ра , Wa и конденсированные
частицы, движущиеся со скоростью Was < W и имеющие
температуру Tas > Та . Причем массовая доля конденсированных частиц
в потоке равна Z, а векторы скоростей частиц и газа направлены
параллельно оси симметрии сопла.
В ракетных топливах содержание конденсированной фазы
в продуктах сгорания может достигать 80 % (гибридные метал-
лосодержащие топлива), тогда как в топливах РДТТ - 25...35 %,
а в продуктах сгорания жидких ракетных топлив, как правило,
не превышает 3...5 %. Коэффициент (рс5 может быть априори
довольно точно оценен количественно для случаев с относительной
массовой долей конденсированной фазы Z не более 5 %, когда
можно влиянием конденсированной фазы на газообразные
компоненты рабочего тела пренебречь или рассматривать его как
слабое.
Если удельный импульс, рассчитанный в идеальном
приближении без учета влияния конденсированной фазы, принять
приближенно равным скорости газа (/ пи-^)ив выходном
сечении сопла скорость конденсированных частиц Was Ф Wa известна,
а других отличий от идеального рабочего тела нет, то потери
можно приближенно оценить по соотношению
Фс5* : *x~z
'у.п.и^т
(
1-
w„.
w
(27.9)
где / п и - пустотный удельный импульс, рассчитанный для
газовой фазы в равновесном приближении для заданного отношения
давлений в камере сгорания и в выходном сечении сопла.

Глава 27. Сопла. Расчет потерь
373
Такие допущения соответствуют отсутствию теплообмена
между фазами и известному скоростному отставанию
конденсированных частиц от газа, что близко к реальной картине при
содержании конденсированной фазы Z < 0,02. При этом
максимально возможным потерям из-за скоростного отставания
конденсированной фазы (Was « Wa или Was ~ 0) соответствует
минимальный коэффициент сопла
cp^l-Z.
Если предположить полное тепловое равновесие между
частицами и газом, но не пренебрегать скоростным отставанием,
то среднюю скорость потока в выходном сечении сопла Wa
можно определить, приравняв кинетическую энергию
эквивалентного потока при усредненной скорости Wa и сумму кинетической
энергии газа (скорость Wa ) и частиц (скорость Was):
W2 = (l-Z)Wz +ZW1 .
a v ' a g as
Отсюда следует выражение для расчета средней скорости
эквивалентного потока с учетом влияния конденсированной фазы при
скорости конденсата, близкой к нулю:
wa = wagM-z
w
w„
ag J
w„t
w.
«1
ag
= WagyTTz. (27.10)
После преобразований соотношения (27.10) получим
расчетное выражение для коэффициента сопла, в котором реализуется
равновесный теплообмен между фазами, а скорость конденсата
близка к нулю:
9^)«>/r^Z*l-Z/2.
Если при полном равновесии фаз по скорости теплообмен
между фазами пренебрежимо мал, т. е. тепловая
неравновесность максимальна, то коэффициент сопла, отражающий
возникающие при этом потери удельного импульса, можно
вычислять по формуле

374 Часть II. Теория неидеального теплового ракетного двигателя
Т -Т
1 + ln-*-
Т
к
V Ла J
(27.11)
где Cs - удельная теплоемкость конденсированной фазы; WQ -
скорость потока в выходном сечении сопла; Гк*, ^-температуры
потока в камере и в выходном сечении сопла.
Согласно (27.11), коэффициент сопла ф^ = 0,98...0,99 при
параметрах, соответствующих продуктам сгорания типичного
твердого смесевого ракетного топлива с содержанием алюминия
около 10%.
Наряду с температурной неравновесностью между газовой
и конденсированной фазами (АТ= Tqs-Tq ) при течении жидкой
фазы по соплу может возникать и фазовое неравновесие -
существование переохлажденной жидкости при температуре ниже
температуры завердевания (кристаллизации) или наличие паров
при сочетании температуры и парциального давления и ниже
точки равновесной конденсации.
Причина связанных с такой неравновесностью потерь
состоит в выносе тепловой энергии со скрытой теплотой
кристаллизации или конденсации, которая могла бы пойти для подогрева
рабочего тела и увеличения его скорости в выходном сечении
сопла, что происходит при сохранении полного равновесия в
рабочем теле в любом сечении сопла.
Количественные оценки показывают существенность (более
1 %) потерь удельного импульса вследствие фазового
неравновесия - переохлаждения жидкости и отсутствия кристаллизации
(затвердевания) - только при массовой доле конденсированной
фазы более 50 %.
Для характерных содержаний конденсированной фазы в
продуктах сгорания твердого ракетного топлива (Z до 30 %) и гид-
рореагирующих топлив (Z до 60 % и более) расчеты срс5
представляют собой самостоятельную весьма трудную задачу. Таким
же трудным является учет потерь другой природы, например
из-за изменения профиля сопла при его эрозии или в
результате налипания конденсированной фазы на стенки, называемых
прочими потерями, которые в рамках настоящего курса не
рассматриваются.
Отметим следующее из численных оценок потерь
соотношение: скоростная неравновесность влияет на уровень потерь
удельного импульса сильнее, чем температурная.

Глава 27. Сопла. Расчет потерь
375
Изменение удельного импульса
из-за неадиабатности течения в сопле
Что касается влияния неадиабатности течения рабочего тела
в сопле, то теплообмен на сужающейся части сопла учитывается
при расчете параметров камеры сгорания соответствующим
изменением полной энтальпии топлива (см. гл. 18), если
охлаждение автономное. Для регенеративных схем охлаждения камеры
сгорания и сужающейся части сопла1 регенеративный эффект
(отвод теплоты от рабочего тела при малых давлении и
температуре, т. е. в зоне ускоряющегося потока, и возвращение теплоты
в зоне максимальных давлений и температур, т. е. в камере
сгорания) пренебрежимо мал.
Для сопл с неохлаждаемой (а по сути, с неадиабатной,
охлаждаемой излучением или аккумуляцией теплоты) или с
охлаждаемой проточным охладителем расширяющейся частью влияние
неадиабатности, как правило, относительно мало (суммарный
отвод теплоты не превышает 1 % полной энтальпии продуктов
сгорания в выходном сечении сопла) по сравнению с суммарным
действием факторов, учитываемых коэффициентами срс1 - срс5. Но
в ряде случаев его вполне можно сравнить с действием отдельных
факторов из рассмотренных выше. Например, значительно более
интенсивно, чем сопла ЖРД в составе летательного аппарата
(летные варианты), могут охлаждаться сопла ЖРД, исследуемые
в стендовых условиях. Возникает задача интерпретации
результатов, полученных на ЖРД со стендовой автономной системой
охлаждения, и перерасчет их на условия работы летных
вариантов ракетных двигателей с регенеративной системой охлаждения.
Представляет интерес неадиабатность процесса при
регенеративном охлаждении, когда охлаждающие расширяющуюся часть
сопла компоненты топлива, нагреваясь в зоне относительно
низких температур, переносят теплоту в зону максимальных
температур и давлений термодинамического цикла. Причем отведенная
от пристеночного слоя теплота равномерно подводится по всему
сечению камеры сгорания.
Известно, что такие процессы повышают термодинамическую
эффективность преобразования располагаемой полной энергии
Каторгин Б.И., Станкевич Д.Б., Стернин Л.Е. О влиянии
регенерации тепла в ЖРД на удельный импульс // Труды НПО «Энергомаш»
им. академика В.П. Глушко. 2005. Т. 23. С. 57-75.

376 Часть II. Теория неидеального теплового ракетного двигателя
топлива в полезную кинетическую энергию рабочего тела, т. е.
могут увеличить удельный импульс.
В одномерном приближении влияние отвода или подвода
теплоты на параметры потока идеального газа в сопле Лаваля
можно рассмотреть на основе анализа известного
дифференциального соотношения, сформулированного Л.А. Вулисом при
предположении отсутствия взаимного влияния бесконечно малых
геометрического (±dF) и теплового (±dQ) воздействий:
(M»-l)^-£-.S,
v ' W F cpT
Согласно этому уравнению, отражающему условия обращения
воздействия на поток, переходящий критические параметры, отвод
теплоты должен приводить к увеличению скорости потока по
сравнению со скоростью, соответствующей адиабатному процессу.
Однако, как показали многочисленные расчеты для рабочих
тел с параметрами, характерными для ракетных двигателей (в
зависимости от температуры и давления изменяются состав и
удельные характеристики смеси химически активных газов), при
одновременном геометрическом и тепловом воздействии на поток этот
вывод справедлив только до достижения таких значений числа
Маха, которые существенно меньше значений этого критерия
в выходном сечении сопла ракетных двигателей. Причем, если
по сравнению с адиабатным течением число Маха увеличивается
везде, то скорость потока растет только на относительно коротком,
примыкающем к критическому сечению сверхзвуком участке,
а затем монотонно уменьшается, при этом давление потока и
соответствующий удельный импульс также монотонно снижаются
на всем протяжении проточной части сопла.
Отвод теплоты от рабочего тела через теплопроводную
стенку сопла приводит к снижению удельного импульса по отношению
к случаю адиабатного течения не только в результате повышения
напряжения трения в низкотемпературном пристеночном слое,
но и вследствие уменьшения скорости истечения.
Отвод теплоты от расширяющегося потока можно описать
увеличением условного показателя изоэнтропы п с по отношению
к идеальному показателю изоэнтропы яи, т. е. п > пи.
Пусть сопло рассчитано на заданное соотношение давлений
р*к/ра и показатель изоэнтропы пи при предположении, что
течение адиабатное, а газ идеальный равен показателю адиабаты к.

Глава 27. Сопла. Расчет потерь
377
При этом геометрическая степень расширения сопла (Fa/F )и =
= l/q(ka,k) = const. Пусть при неизменности параметров в
камере сгорания при движении по соплу вследствие неадиабатности
течения (отвода теплоты через стенки сопла) рабочее тело
расширяется как идеальный газ, но с показателем п с. Очевидно, что
п > к. Тогда из выражения для геометрической степени
расширения \lq (Ха, к) = const как из уравнения с одним параметром п
(вместо к) и неизвестной \а однозначно определяется приведенная
скорость истечения и, следовательно, коэффициент тяги в
пустоте Ктп, развиваемый соплом при степени неадиабатности,
заданной косвенно неравенством n c > к.
Для количественной оценки изменения коэффициента тяги
используем (после очевидных преобразований) ГДФ
приведенного импульса:
Р ?аРЛр ЛЛр Fa
Приравнивая исходное и конечное выражения, получаем
соотношение для вычисления коэффициента тяги по
предварительно найденным значениям приведенной скорости Ха с и заданного
параметрически показателя изоэнтропы п :
*тп=^^. (27.12)
Пусть первоначально сопло рассчитано для показателя
адиабаты к = 1,15, а с учетом теплоотвода через поверхность сопла
показатель процесса увеличился до п = 1,25. Результаты
расчетов фс для трех значений геометрической степени расширения
сопла Foth = FJF = 3, 10 и 100 поместим в табл. 27.4, где
влияние неадиабатности выражается коэффициентом
Фс а ~
K^FjF^k) q{K,k)
Такая методика приближенной оценки потери удельного
импульса требует априорной или полученной в эксперименте оценки
снижения температуры потока в выходном сечении сопла Та по

378 Часть II. Теория неидеального теплового ракетного двигателя
отношению к температуре Та, рассчитанной в адиабатном
приближении фг= Та /Та, где 0,9 < фг< 1,0. Далее необходимо
последовательно выполнить следующие расчеты:
• для заданной геометрической степени расширения сопла
Fa/F = l/q(ka,k) и полученного термодинамическим расчетом
значения показателя адиабаты к рассчитать значение ГДФ т(ка, к);
• по известному значению (рт и неизменному известному
значению температуры в камере сгорания рассчитать значение ГДФ
т(к, к) с учетом снижения температуры в выходном сечении
вследствие неадиабатности процесса в сопле:
• определить значение нового условного показателя изоэн-
тропы п , решая численными методами уравнение,
представляющее собой выражение ГДФ q(Xa,k) (3.24) через известное
значение т(Ха с,п с) (3.16) и условный показатель изоэнтропы п с:
j_ 1
F ( -А_ "Ус+1Ъ
l/f^+lfw^+lV*-1
*ус
'ус
• найти значение приведенной скорости по соотношению,
полученному из (3.16),
Kyc-Jl-*(Kyc>^)-^-^'.
• по значению X „ . .
а ус ^ г ус
коэффициент уменьшения пустотного удельного импульса по
соотношению
_/(^аус»Лус)
Например, для исходного сопла с геометрической степенью
расширения Fa/FK = 125, т. е. q(ka,k) = 0,008, при адиабатном
течении рабочего тела с к = 1,122, т(ка, к) = 0,4589 и Ха = 3,068.
Если вследствие неадиабатности течения в расширяющейся части
сопла среднемассовая температура в выходном сечении
уменьшится на 10 % по отношению к исходному варианту, то значение

Глава 27. Сопла. Расчет потерь
379
показателя изоэнтропы п с увеличится до 1,137 при уменьшении
значения приведенной скорости Ха с до 3,026, что соответствует
уменьшению пустотного удельного импульса на 1 %.
Таблица 27.4. Данные для оценки влияния неадиабатности
течения в сопле
Параметр
X
а
К
тп
тс<7
F .L.
отн р
кр
3
10
100
3
10
100
3
10
100
Расчетные значения для показателей
изоэнтропы
и = Аг= 1,15
2,050
2,467
2,945
1,460
1,650
1,800
1
1
1
V=l,25
1,973
2,313
2,650
1,375
1,530
1,700
0,942
0,927
0,944
Из сопоставления помещенных в табл. 27.4 данных следует,
что изменение показателя процесса п с от 1,15 до 1,25 приводит
к потерям удельного импульса, составляющим 6...8 %. Согласно
численным оценкам, изменение показателя изоэнтропы при
параметрах реальных двигателей, как правило, не превышает
нескольких сотых и соответствующие таким изменениям потери
удельного импульса не достигают 1 %. Поскольку двигатели
с большой степенью расширения в основном охлаждаются
регенеративно, то термодинамическая эффективность ракетного
двигателя как тепловой машины повышается, что практически
полностью компенсирует рассмотренные потери на неадиабатность
течения в сопле. Но при этом сохраняются потери на трение,
увеличенные в результате снижения температуры потока в
пограничном слое. Отметим, что переход к давлениям в камере,
достигающим нескольких десятков мегапаскалей (нескольких сот
бар), и увеличение в связи с этим размеров сопл может сделать
существенными именно процессы регенерации. И достоверность
результатов их теоретического расчета может стать необходимым
условием проектирования, что потребует составления теоретических

380 Часть II. Теория неидеального теплового ракетного двигателя
моделей, учитывающих значительно больше особенностей, чем
в рассмотренной выше методике.
Совместное одновременное действие нескольких
характеризующих неидеальность рабочих процессов факторов, в том числе
оказывающих противоположное по знаку влияние на удельный
импульс, существенно усложняет оценку их суммарного эффекта.
Например, охлаждение стенок сопла увеличивает потери на
трение, но одновременно повышает термодинамическую
эффективность цикла двигателя вследствие регенерации теплоты, а
применение полированных стенок сопла ведет к уменьшению
коэффициента трения, но при этом одновременно снижает
плотность теплового потока.
Совокупное влияние нескольких факторов может
отличаться от суммы последствий действия каждого фактора отдельно,
даже если каждое из них весьма мало.
Примером такого сверхсуммарного (системного) воздействия
может служить влияние неадиабатности течения в сверхзвуковой
части сопла, оснащенного регенеративной системой охлаждения,
на развиваемый пустотный удельный импульс.
В упомянутых выше трудах НПО «Энергомаш» описаны
несколько методик учета эффекта регенерации и для наиболее
характерных исходных данных приведены результаты оценок,
полученных численными методами, согласно которым величина
регенеративного эффекта всегда положительная, но не
превышает 0,25 % для топлива «водород - кислород» (и только не более
0,15 % для топлива «углеводородное горючее - кислород») от
пустотного удельного импульса, рассчитанного при
предположении равновесного изоэнтропийного адиабатного течения в
сопле. Показано, что можно оценивать положительный эффект от
регенеративной системы охлаждения расширяющейся части
сопла как равный по модулю приблизительно 40 % (максимум 50 %,
когда Ма стремится к бесконечности) от снижения удельного
импульса вследствие отбора теплоты, который имел бы место
при охлаждении сторонним охладителем. Учитывая, что
регенеративный эффект весьма мал, точность таких оценок можно
считать приемлемой для расчетов первого приближения.
Совокупное влияние не зависящих непосредственно друг от
друга факторов (потерь удельного импульса с радиальной
скоростью вследствие ненулевого угла наклона вектора скорости
истечения и потерь на трение) на характеристики сопла рассмотрим
на примере конического сопла - осесимметричного круглого сверх-

Глава 27. Сопла. Расчет потерь
381
звукового сопла, расширяющаяся часть которого, начиная с
сечения, близкого к минимальному, имеет прямолинейный контур.
Как показали результаты многочисленных расчетов, потери
на трение в сужающейся части сопла сохраняются
приблизительно на одном и том же уровне и практически не влияют на
потери на трение в расширяющейся части сопла, что позволяет
анализировать влияние на коэффициент сопла только угла
наклона образующей Рд. При изменении угла наклона образующей
проявляются совместно два противодействующих фактора или
реакции:
• уменьшение угла Ра ведет к снижению потерь на рассеяние,
что выражается увеличением коэффициента фс3;
• уменьшение угла §а приводит к увеличению площади
боковой поверхности s6oK сопла, на которой проявляется трение, и
увеличению потерь на трение, отражаемому уменьшением
коэффициента фс4.
Коэффициент сопла, учитывающий основные потери на трение
и рассеяние, согласно (26.1),
ТС ~ т с3 Тс4 Тр Тур*
Это означает, что при монотонном изменении сомножителей
(уменьшении значения фс3 и увеличении значения фс4)
коэффициент сопла фс изменяется с переходом через абсолютный
максимум, что отражается графиками на рис. 27.6. При расчетах
принимали коэффициент трения С,~ const ~ 0,005, а показатель
адиабаты рабочего тела к = 1,17.
Из анализа формулы для расчета потерь на трение следует
зависимость фс4 от абсолютного значения площади боковой
поверхности 5бок сопла. Поэтому потери на трение у сопл,
отличающихся только геометрической степенью расширения, будут
разными, следовательно, разными будут и оптимальные значения
угла Ра im, при которых достигает максимума коэффициент
сопла фс. Причем с увеличением геометрической степени
расширения сопла оптимальное значение угла $а im смещается
в сторону больших значений: от Р tim ~ 6° для сопла с Foth = 10
Д° К op,im s 8° Д™ сопла с Foth = 2 000.
Для большинства применяемых в ракетной технике конических
сопл характерен диапазон значений угла наклона образующей
15°<2Ро<50°.

382 Часть II. Теория неидеального теплового ракетного двигателя
Полирование поверхности сопл для уменьшения трения не
приводит к заметному увеличению коэффициента фс4, так как
в процессе работы под действием высокой температуры и
скорости поверхность сопла приобретает шероховатость, уровень
которой слабо зависит от начального состояния.
Следовательно, если учитывающие трение и рассеяние
сомножители ограничены сверху, то ограничены потери удельного
импульса в коническом сопле.
Уменьшение потерь на рассеяние сопряжено с существенным
увеличением продольных габаритов конического сопла, а
следовательно, и его массы, что может снизить эффективность такого
технического решения.
Это противоречие может быть разрешено применением не
конического, а профилированного сопла, расширяющаяся часть
которого имеет криволинейный контур, спрофилированный для
увеличения эффективности сопла, оцениваемой в первом
приближении коэффициентом сопла фс.
Контрольные вопросы и задания
1. Какие потери удельного импульса имеют термодинамическую
природу?
2. Почему с ростом давления в камере (геометрическая степень
расширения увеличивается так, что давление в выходном сечении
сопла не изменяется) относительные потери удельного импульса на
химическую неравновесность уменьшаются?
3. Охарактеризуйте механизм внутренней регенерации теплоты в
соплах с равновесным течением.
4. Почему реальное течение в сопле ЖРД космических летательных
аппаратов или верхних ступеней ракетоносителей точнее отражает
модель локально-неравновесного течения (приближение Брея), чем
модель равновесного течения или модель химически
замороженного течения на всем протяжении сопла?
5. Почему для одного и того же сопла значение усредненного
показателя изоэнтропы зависит от координаты сечения, начиная от
которого течение становится химически замороженным?
6. Дайте объяснение следующим результатам математического
эксперимента: максимально возможное значение пустотного
удельного импульса и соответствующие соотношения компонентов
топлива зависят от принятой модели течения в сопле (см. рис. 21.1).
7. Каким образом загромождение проходного сечения сопла
пограничным слоем может привести к различию между действительной
геометрической степенью расширения потока и геометрической

Глава 27. Сопла. Расчет потерь
383
степенью расширения сопла? Почему эти различия, как правило,
несущественны для сопл двигателей больших тяг?
8. Дайте объяснение известному результату: с увеличением
геометрической степени расширения конического сопла уменьшается угол
наклона его образующей, при котором коэффициент сопла,
учитывающий потери на трение и рассеяние, принимает максимальное
значение.
9. Перечислите физические факторы, объясняющие снижение
удельного импульса вследствие наличия в потоке кроме газа
конденсированной фазы.
10. В чем состоит кажущееся противоречие между уменьшением
удельного импульса при отводе теплоты от стенки расширяющейся части
сопла (см. табл. 27.4) и способом ускорения сверхзвукового потока
отводом теплоты, следующим из уравнения Вулиса?

Глава 28
Профилирование сопл.
Задачи выбора профиля сопла
Из анализа уравнения тяги следует, что при прочих равных
условиях максимальную тягу при заданных параметрах рабочего
тела в камере сгорания развивает сопло, контур расширяющейся
части которого обеспечивает в выходном сечении сопла
параллельный поток с одним и тем же значением скорости в любой
точке этого сечения. Контур такого сопла называется контуром
с равномерной характеристикой.
Увеличение удельного импульса при уменьшении до нуля
радиальной компоненты вектора скорости в выходном сечении
сопряжено с увеличением продольных габаритов и массы сопла,
а также потерь тяги на трение. Поэтому реальные сопла
выполняют так, что вектор скорости истечения Wa имеет помимо осевой
компоненты Wax еще и радиальную компоненту War9 переменную
по радиусу.
С помощью методов газовой динамики значения всех
параметров реального неодномерного потока можно рассчитать для
сопла известного профиля - так называемая прямая задача.
В реальных соплах распределения параметров потока в
выходном сечении сопла отличаются от принятых в идеальном
представлении равномерных распределений параметров, что приводит
к потерям удельного импульса вследствие рассеяния,
понимаемого как неравномерность потока в выходном сечении сопла.
В гл. 27 приведен вывод соотношения для расчетной оценки
учитывающего эти потери коэффициента сопла срс3:
l+cosP„
где Рд - угол наклона вектора скорости в наиболее удаленной
точке выходного сечения сопла, задаваемый контуром
сверхзвуковой части сопла.
Потери удельного импульса на трение и вследствие
вытеснения, т. е. загромождения проходных сечений сопла пограничным

Глава 28. Сопла. Выбор профиля сопла из семейства известных 385
слоем (фс4), как следует из приведенной в гл. 27 методики, также
зависят от контура расширяющейся части сопла.
Задача профилирования - построение контура сопла, исходя
из достижения некоторой целевой функции (максимум тяги,
минимум потерь, минимальная масса и т. п.) при заданных
ограничениях на переменные величины (габариты, площадь боковой
поверхности, давление в выходном сечении и т. п.) - относится
к вариационным задачам, а полученный в результате ее решения
контур сопла называется экстремальным.
Если известны требуемые распределения параметров потока
в выходном сечении сопла при заданных ограничениях и
расчетным путем определяется контур обеспечивающего эти
распределения сопла, то такая задача называется обратной задачей
газовой динамики. Если при этом должен минимизироваться один
из определяющих задачу параметров, то задача будет относиться
к классу экстремальных, а поскольку контур сопла задается
некоторой неизвестной до решения задачи функцией, то задача
может быть отнесена к вариационным.
Математически экстремальную задачу для осесимметричного
сопла можно представить в достаточно общем виде:
Рп= J (p(x)+x(x))2nR(x)dR,
где Рп - пустотная тяга; р(х)9 т(х) - соответственно проекции на
ось симметрии векторов давления и напряжения трения в текущей
точке контура сопла с текущим радиусом R(x) и линейной
координатой х, отсчитываемой по оси симметрии от характерного
сечения, например входного сечения сопла, в котором радиус
проточной части R = /?j(x0), до выходного сечения сопла с
максимальными радиусом R = R2(xmax) и линейной координатой
х = хтах. В общем случае задающие габариты сопла радиусы Rx(x0)9
R2(xmax) и осевая координата выходного сечения х = хтах так же
как и собственно контур сопла R(x), находят в результате решения
вариационной задачи. Здесь R(x) - описывающая контур сопла
искомая функция, обеспечивающая максимальное значение
выбранного параметра, например пустотной тяги, при заданных
ограничениях, длине расширяющейся части сопла или его максимальном
диаметре.
Если контур сопла должен обеспечить минимальное значение
площади боковой поверхности s6oK сопла, находящейся в контакте

386 Часть II. Теория неидеального теплового ракетного двигателя
с потоком, то при этом чаще всего задают постоянной внутреннюю
составляющую тяги и ограничивают диаметр сопла. Эти и
аналогичные вариационные задачи можно решить для конкретных
условий и ограничений, как правило, численными методами,
требующими больших затрат вычислительных ресурсов, что не
вполне оправданно на этапе предварительного проектирования. Тем
более, что вблизи оптимального решения параметры изменяются
незначительно, что позволяет с достаточной точностью оценить
характеристики двигателя с контуром сопла, близким к
экстремальному и полученному на основе решения задачи построения
контура сверхзвуковой части сопла, являющейся упрощенным
аналогом вариационной задачи.
Одним из путей снижения сложности решения вариационной
задачи является сведение ее к выбору исходного контура из
семейства известных контуров, рассчитанных на степень
геометрического расширения, большую, чем у сопла с оптимизируемым
контуром. Затем проводится и его укорочение - определение длины
его начального участка, удовлетворяющей вариационной задаче.
Особенность контура сужающейся части сопла
обусловливается ее специфическими функциями - обеспечением устойчивого
по отношению к акустическим колебаниям протекания рабочего
процесса в камере сгорания, безотрывного течения и заданного
распределения параметров потока в трансзвуковой зоне при
стабильной форме и положении поверхности перехода через скорость
звука и минимальных потерях на трение.
В результате многочисленных расчетов и экспериментов
близкий к оптимальному контур сужающейся части сопла
камеры ЖРД с достаточной для практики точностью можно
представить как сочетание (рис. 28.1, а) участка окружности
Рис. 28.1. Схема течения в сопле при разных радиусах образующей
вблизи минимального сечения:
а - сопло с угловым входом, R3 ~ 0; б - R3 ~ 1,25/? ; / - область дозвукового
течения; 2 - область разворота потока с ускорением; 3 - область разворота
потока без увеличения скорости; 4 - область равномерного потока

Глава 28. Сопла. Выбор профиля сопла из семейства известных 387
радиусом Rv участка окружности радиусом R2 и прямой,
касательной к этим окружностям. Такой профиль сужающейся части
сопла называется радиусно-коническим. В зависимости от
соотношения радиусов Rv R2 и угла Рвх длина конического
участка может уменьшаться до нуля. Таким образом, радиусно-кони-
ческая сужающаяся часть сопла вырождается в радиусную,
применяемую чаще всего в современных ЖРД с камерами,
близкими к скоростным.
Рекомендуемое соотношение радиусов образующей
сужающейся части сопла: R] ~ (0,8...1,2)/?кс, R2 ~ (0,8... 1,2)/? при
2Рвх ~ 50°...80°. Выбор конкретных значений определяется
анализом условий компоновки камеры, обеспечением в ней
устойчивости рабочего процесса, а также организацией охлаждения
стенки сопла и уровнем давления в камере. Эти вопросы в
настоящем учебнике не рассматриваются.
Многочисленными расчетами показано, что неравномерность
распределений потока, сформированного сужающейся частью
сопла и ускоренного в ней до звуковой скорости, практически не
влияет на форму образующей оптимальной расширяющейся части
сопла. Поэтому для расширяющейся части сопла в первом
приближении в качестве исходных могут рассматриваться
рассчитываемые с помощью известных методов газовой динамики
контуры, совпадающие с меридиональными сечениями поверхностей
потока, свободно расширяющегося в пространство с заданным
давлением ph. Параметры этого потока в минимальном сечении
совпадают с параметрами потока на входе в расширяющуюся часть
проектируемого сопла (см. рис. 28.1). Траектории частиц газа
и соответствующие трубки тока устанавливаются
самопроизвольно, не претерпевая ограничений (рис. 28.2). Известно, что
полученный таким образом контур может рассматриваться в качестве
приближения экстремального контура, так как свободно идущие
процессы реализуются стационарно в вариантах, связанных с
минимальным приростом энтропии, т. е. протекают с минимальной
диссипацией энергии.
Отметим, что контур, образованный внешней (граничной)
поверхностью тока, имеет максимальный угол наклона сотах,
меньший, чем угол разворота потока при обтекании тупого
двугранного угла (течение Прандтля - Майера) с расширением
и ускорением потока до числа Маха М^, соответствующего
степени расширения потока/?*/рл:

388 Часть II. Теория неидеального теплового ракетного двигателя
^max
i /FT!
где Amax = J максимально возможное значение приведенной
V к-\
скорости А, при расширении потока с показателем адиабаты к
в пустоту.
Рис. 28.2. Структура течения и поверхности тока свободно
расширяющегося потока с плоской поверхностью перехода ОМ через скорость звука:
MAV MA2, MAV MA4 - характеристики потока;
\|/,, \|/2, \|/3, \|/4 - поверхности тока
Любая из выбранных поверхностей тока может
рассматриваться как стенка сопла (см. рис. 28.2), для каждого сечения
которого можно рассчитать значение коэффициента потерь,
учитывающего рассеяние и трение.
Если в качестве семейства известных контуров
рассматриваются контуры профилированного сопла с равномерной
характеристикой и выбирается его начальный участок в качестве
контура реального сопла, то полученный таким образом контур сопла
называется укороченным, а использованный контур с равномерной
характеристикой - исходным. Причем, если контур сопла имеет
излом (обычно либо непосредственно вблизи критического
сечения сопла, либо в сечении стыка частей, выполняемых из разных
материалов, или секций раздвижного сопла), то его называют
контуром сопла с угловой точкой. Если излом контура
совпадает по координате с минимальным сечением сопла, то такое сопло
называют соплом с угловым входом.
Исходные контуры сопл с равномерной характеристикой
можно рассчитывать известными методами и представлять в виде массива

Глава 28. Сопла. Выбор профиля сопла из семейства известных 389
безразмерных величин, отнесенных, например, к радиусу
критического сечения координат или соответствующих графиков.
На рис. 28.1 изображена условная схема течения в сопле при
разных радиусах образующей вблизи минимального сечения. Если
радиус R3 ~ О (сопло с угловым входом), то течение в сопле
можно представить как следующие друг за другом сопряженные
области: 1 - область дозвукового течения; 2 - область разворота
потока при обтекании угла (3w с ускорением потока до скорости
Wa числа Маха Ма, соответствующего располагаемой степени
расширенияр*к/ра', 3 - область разворота потока без увеличения
скорости, т. е. изменяется только наклон вектора скорости к оси
симметрии сопла, уменьшаясь до нуля; 4 - область
равномерного потока.
По окончании разворота потока вокруг точки входа на угол
Pw в области 2 характеристика с числом Маха Ма будет
наклонена по отношению к стороне угла Pw под углом Маха аа = arcsin ,
при этом осевая протяженность области 2 (размер L0l) будет
наименьшей по сравнению с протяженностью области 2 сопла
с R3 ~ 1...1,57? (см. рис. 28.1, б). Замыкающая характеристика
на правой границе области 3 будет составлять с осью симметрии
. 1
сопла угол ап = arcsin .
ма
Несколько отличается от описанной картина течения в сопле
с плавным переходом от сужающейся части к расширяющейся
(радиус R3 ~ 1,25/J ). Здесь область 2 включает участок
плавного роста скорости справа от поверхности перехода через скорость
звука М = 1 при незначительном развороте вектора скорости и
постепенном увеличении угла наклона характеристик, что требует
увеличения осевой протяженности сопла от минимального
сечения до сечения окончания разворота с ускорением.
Из сопоставления схематичных картин течения следует
неравенство Z,*, > L01, т. е. осевые размеры расширяющейся части
сопла с угловым входом меньше, чем у сопла с плавным контуром
вблизи минимального сечения.
Используя известные методы газовой динамики, можно
рассчитать контуры расширяющихся частей сопл с равномерной
характеристикой для произвольно задаваемой геометрической
степени расширения.

390 Часть II. Теория неидеального теплового ракетного двигателя
На рис. 28.3 схематично представлено семейство контуров,
рассчитанных для разных геометрических степеней расширения
и постоянного значения усредненного показателя изоэнтропы,
исходя из равномерного поля параметров потока в критическом
сечении.
Рис. 28.3. К выбору экстремального контура расширяющейся части
сопла из известного семейства контуров
Отметим, что, как показали многочисленные расчеты, от
параметров химически активного рабочего тела с реакциями между
его компонентами можно перейти к модели идеального газа с
заменой переменных значений показателей изоэнтропы одним
постоянным значением, усредненным в диапазоне значений
давления от критического давления до давления в выходном сечении.
Таким образом, методика, составленная для газа с постоянными
свойствами, распространяется на реальные рабочие тела сопл
ракетных двигателей.
Для рабочего тела с известным постоянным показателем
изоэнтропы для каждой заданной геометрической степени
расширения Foth = Fq/Fk строится свой контур, для каждой точки
которого рассчитывается значение пустотного коэффициента тяги КТ п
с учетом потерь на трение и рассеяние. При этом для каждого
контура определяется максимальное значение Кт п, достигаемое
при некоторой геометрической степени расширения, которую
нецелесообразно превышать, так как дорасширение потока в сопле
и увеличение осевой компоненты вектора скорости истечения
компенсируется увеличением потерь тяги на трение.

Глава 28. Сопла. Выбор профиля сопла из семейства известных 391
Соединив точки построенных для разных геометрических
степеней расширения исходных контуров с одинаковыми
значениями АГтп, получим линии постоянной тяги. Таким образом для
каждой точки плоскости определяются: координаты контура
сопла от критического сечения до данной точки и рассчитанные для
этого контура коэффициент пустотной тяги и значение боковой
поверхности расширяющейся части сопла.
Работа с такими массивами может проводиться с
использованием алгоритмов, реализуемых на компьютерах. Однако
логические основы решения задач выбора оптимального контура из
семейства исходных контуров с равномерной характеристикой
яснее представляются в виде построений на плоскости,
представленных на рис. 28.3.
Рассчитав для выбранных точек исходных контуров сопл
значения относительной поверхности расширяющейся части S =
= s6ok/F' где s6ok - площадь боковой поверхности, a F -
площадь критического сечения сопла, и соединив точки с
одинаковыми значениями, получим линии, ограничивающие контуры сопл
cS= const.
Задача оптимизации контура сопла сводится к выявлению
в известном семействе кривых такого контура сопла, при котором
сопло обеспечивает максимальное или минимальное значение
некоторого заданного параметра при заданных ограничениях на
другие параметры. Сопло с таким контуром, представляющим
собой близкую к решению вариационной задачи кривую, также
может называться экстремальным.
В зависимости от задачи проектирования задается конкретный
критерий экстремальности, но можно рассмотреть наиболее часто
встречающиеся критерии и соответствующие типовые задачи.
К типовым задачам оптимизации можно отнести следующие.
Выбор сопла, развивающего при заданной длине наибольшую
пустотную тягу. Как следует из рис. 28.3, из всех
различающихся исходными контурами сопл, имеющих одну и ту же длину
расширяющейся части, только одно развивает максимальную
пустотную тягу. Решение задачи начинаем с построения
вертикали, соответствующей заданной безразмерной длине
сверхзвуковой части сопла Ьу Оптимальным будет контур, проходящий
через точку ах касания вертикали Lx и кривой КТ п = 1,8. При этом
ордината точки ах задает радиальные габариты сопла
экстремального профиля.

392 Часть II. Теория неидеального теплового ракетного двигателя
Выбор сопла, развивающего при заданной геометрической
степени расширения наибольшую пустотную тягу, состоит в
определении на соответствующей заданной геометрической степени
расширения горизонтали точки горизонтали R2 с максимальным
значением Кт п. Этой точке а2 соответствует касание горизонтали
R2 и кривой Ктп = 1,85. Профиль сверхзвуковой части искомого
экстремального сопла образован начальным участком контура
сопла с равномерной характеристикой, построенного для
максимальной геометрической степени расширения Fa/FK = 120.
Выбор сопла, развивающего при заданной боковой поверхности
наибольшую пустотную тягу. Очевидно, что на каждой кривой
s6ok/Fk = const есть единственная точка с максимальным
значением Ктп, т. е. существует и оптимальный профиль,
обеспечивающий наибольшую тягу. Решим задачу графически для s6ok/F = 20.
Кривые s6ok/F = 20 и Ктп= 1,7 имеют одну общую точку av
через которую и проходит контур экстремального сопла,
отвечающий поставленной задаче, тогда R3 и Z3 - безразмерные радиус
и длина сверхзвуковой части этого сопла.
Выбор развивающего заданную пустотную тягу сопла с
минимальной боковой поверхностью представляет собой задачу,
аналогичную предшествующей, но с заменой ограничения и
минимизируемой величины. Пусть задан КТП = 1,8 и требуется
найти контур имеющего этот коэффициент тяги сопла, если боковая
его поверхность s6ok минимальна. Касание кривой Ктп = 1,8 с
линией s6ok/Fk = 40 определяет проходящий через точку а4 контур
экстремального сопла. Отметим близость профилей сопл
минимальной боковой поверхности (контур \-а4) и максимальной тяги
при заданной длине (контур 1-я,), что объясняется близкой к
прямо пропорциональной зависимостью между боковой поверхностью
сопла и потерями на трение.
Выбор развивающего заданную пустотную тягу сопла с
минимальной длиной расширяющейся части представляет собой
задачу, обратную задаче выбора контура сопла заданной длины,
развивающего максимальную пустотную тягу. Порядок
соответствующих построений: строится вертикальная касательная к
заданной кривой (например, Ктп = 1,85), выбирается контур,
проходящий через точку касания ау Этот контур - искомый.
Практически описанные построения не проводят, но
реализуют эквивалентные этим построениям алгоритмы выбора
наибольших или наименьших значений из массивов данных (баз
данных).

Глава 28. Сопла. Выбор профиля сопла из семейства известных 393
Отметим, что в контексте описанных методик не имеют
значения методы расчета исходных контуров. Они могут быть или
получены решением более общих вариационных задач для
широкого набора параметров, или, как было рассмотрено,
определены как поверхности тока свободно расширяющегося потока
при конкретных распределениях параметров потока в начальном
сечении: в неподвижной бесконечной среде или в сечении, где
число Маха М = 1 и равномерные распределения всех параметров,
как в выходном сечении сопла Витошинского.
Решение задач, аналогичных рассмотренным, но в случае
задания тяги при ненулевом давлении окружающей среды,
усложняется необходимостью расчета сетки постоянных значений
коэффициентов тяги при заданном давлении. В остальном логика
выбора экстремальных контуров сохраняется.
Область поиска решения может быть сужена классом
описывающих экстремальные профили зависимостей,
предположительно соответствующих физическим и техническим ограничениям.
Например, вследствие конечной точности выполнения
профиля сопла представляется возможным ограничиться кривыми
второго порядка общего вида, а, как правило, неизвестный
априори закон изменения давления окружающей среды на траектории
делает невозможным строгую оптимизацию геометрической
степени расширения сопла, вследствие чего давление ра или угол
наклона контура в выходном сечении (За приходится задавать на
основании предварительных оценок.
Учитывая близость профилей сопл минимальной боковой
поверхности (см. контур \-аЛ на рис. 28.3) и максимальной тяги при
заданной длине (см. контур \-а] на рис. 28.3), можно упростить
задачу поиска экстремального контура сверхзвуковой части
сопла, заменяя оптимальный контур сопла в трансзвуковой части,
т. е. вблизи минимального сечения, дугами окружностей
радиусами в сужающейся части R2 = (0,8... 1,2)/? и в расширяющейся
части /?3 = 0...1,5Я , а на последующем участке вплоть до
выходного сечения - параболой второго порядка общего вида, т. е.
в том числе и с осью симметрии, не параллельной осям координат
(рис. 28.4). Причем в этом диапазоне значений радиус R3
практически не влияет на картину течения и, как следствие, не
отражается существенно на потерях тяги, что позволяет выбирать
значение этого радиуса, в основном исходя из требований
организации охлаждения стенки сопла вблизи его минимального
сечения. Экстремальный профиль можно приближенно заменить

394 Часть II. Теория неидеального теплового ракетного двигателя
Рис. 28.4. Схема приближенного построения экстремального
контура сопла
дугой окружности радиусом /?4, имеющей в характерных точках
те же углы наклона касательных (3w и Ра, что и заменяемый контур.
Радиус и центр окружности радиусом ЯЛ находят при построении
на пересечении нормалей к касательным к контуру в точках
стыка с дугой радиусом R3 (точка В, угол наклона касательной Рт)
и точкой в выходном сечении сопла (точкам, угол наклона
касательной Рд).
Таким образом, сводим задачу к определению двух параметров
из четырех: углов Pw и Ро, безразмерных длины расширяющейся
L R
части сопла La = -JL- и радиуса выходного сечения Ra =——.
Отметим, что именно длина расширяющейся части сопла в
основном задает уровень потерь удельного импульса вследствие
трения, которые практически не зависят от профиля образующей
и составляют 70...80 % суммарного значения, а оставшиеся 20...30 %
потерь связаны с неравномерностью потока в выходном сечении,
т. е. с профилем образующей.
Если при этом использовать выявленные при решении
вариационных задач мало изменяющиеся вблизи оптимальных решений
соотношения между максимальными и минимальными углами
наклона контура (рис. 28.5) или соответствующие числовые массивы,
то конкретная задача профилирования сопла может быть решена
упрощенно, но с точностью, достаточной для оценки габаритов
и массы двигателя и расчета параметров системы охлаждения.
Если нет других оценок, то можно применить приближенное
соотношение между степенью расширения рабочего тела в сопле
рк/ра и углом наклона контура в выходном сечении сопла рй,

Глава 28. Сопла. Выбор профиля сопла из семейства известных 395
4 6 8 10 12 14 16 18 20-5-^
Якр
Рис. 28.5. К построению экстремального контура сопла
приближенными методами. Зависимости между угловыми и линейными параметрами
контура сопла (см. прил. 2)
значения которых получены перерасчетом параметров сопл
многих современных ракетных двигателей и представлены ниже:
рк/ра 50 100 500 1000 2 000
р ...! 9° 9°30' 10° 1Г30' 12°
Возможность такой обработки объясняется тем, что контуры,
соответствующие разным критериям оптимизации, близки к аф-
финно-подобным, а их координаты отличаются друг от друга в
пределах ± 10 %, причем тенденция увеличения угла наклона (Зя
с ростом степени расширения рабочего тела сохраняется для сопл
с реально приемлемыми относительными (т. е. выраженными
через диаметр критической части) длинами расширяющейся части
сопла. При этом потери вследствие вязкости (1,5...2,5 %), в
несколько раз превышающие потери вследствие непараллельности
потока в выходном сечении (менее 1 %), зависят в основном от
относительной длины сопла и в меньшей степени от формы
контура. В частности, замена экстремального контура образующей
параболой или дугой (двумя дугами радиусами R3 и R4)
окружности приводит к уменьшению коэффициента сопла на 0,5... 1,5 %,
что обосновывает возможную замену экстремального профиля
сопла кривой второго порядка в расчетах предпроектного этапа
создания ракетного двигателя.
Ограничение минимального значения 9° ^ Ра (иногда априори
все же принимают $а = 8°) также соответствует современным

396 Часть II. Теория неидеального теплового ракетного двигателя
методикам профилирования и реализуемым точностям
выполнения контура и достигаемого качества поверхности сопл.
В условиях некорректного задания на проектирование сопла
для связи радиуса выходного сечения сопла Ra (давления в
выходном сечении ра), угла $а и давления окружающей среды рИ
можно использовать соотношение, полученное решением
вариационной задачи для развивающих максимальную тягу сопл
заданной относительной длины (в радиусах выходного сечения
сопла L /R ~ const):
а а '
sin2Pfl =^_^ctgQa =Ь^ф^Ги (28.1)
рК рК
2 2
где Qa - угол Маха, для которого sin Qa = 1/Me; ph - давление
окружающей среды; ра, р, Wa, Me- давление, плотность, скорость
и число Маха рабочего тела в выходном сечении сопла.
Отметим, что оптимальный угол наклона образующей
контура сопла в выходном сечении может быть другим, если учесть
его влияние на донное разрежение при обтекании двигательного
отсека при движении в атмосфере.
Для сопл, работающих в пустоте, в результате преобразований
(28.1) получим расчетное выражение
sin2P0=-^_9 (28.2)
к Ма
где к - показатель адиабаты для рабочего тела в выходном
сечении сопла.
Монотонное уменьшение значения угла обратно
пропорционально числу Маха и приближенно отвечает движению конечной точки
образующей не только вверх, но и вправо на рис. 28.3, так как
сохраняется постоянным значение отношения длины
расширяющейся части сопла к радиусу его выходного сечения {La/Ra ~ const).
Для сопл, спроектированных для работы в пустоте, как правило,
Ма = 4...5 и полученные по (28.2) значения р^ ~ 8...11°
соответствуют параметрам сопл реальных ракетных двигателей
космического назначения. В связи с существенным увеличением
габаритов сопла при уменьшении угла Ра практически
нецелесообразно выполнение сопл с меньшим значением угла
наклона контура в выходном сечении сопла.

Глава 28. Сопла. Выбор профиля сопла из семейства известных 397
Построение экстремальных контуров с использованием
зависимостей, представленных на рис. 28.5, выполняется в
порядке, который зависит от набора заданных параметров. При этом
находят контур, близкий к контуру сопла, которое развивает
максимальную пустотную тягу с рабочим телом, расширяющимся по
изоэнтропе (адиабате) с постоянным показателем п.
В системе координат длина - радиус нанесена сетка
пересекающихся тонких и утолщенных кривых, каждой из которых
соответствует постоянное значение характерного угла наклона
контура, для тонких - угла наклона в выходном сечении, для
утолщенных - угла наклона контура в начальной точке
параболического участка Рш. Таким образом, каждой паре координат
соответствует пара углов, т. е. каждая точка диаграммы
однозначно задает близкий к оптимальному параболический контур
сопла.
Порядок выбора конкретного контура заключается в
определении двух неизвестных величин при двух известных, задаваемых
из сторонних по отношению к данной методике соображений.
Рассмотрим применение методики (см. рис. 28.5) на примерах.
В общем случае значение $а может быть рассчитано при
оптимизации летательного аппарата и двигателя с учетом
динамики его движения по траектории в атмосфере или по
соотношениям, аналогичным (28.1) и (28.2).
Для предпроектных расчетов, как правило, значения угла fia
выбирают из типичного для сопл ракетных двигателей с
однофазным рабочим телом диапазона значений 8... 12° по аналогии
с контурами сопл известных двигателей с той же степенью
расширения рабочего тела в сопле, что и у проектируемого двигателя.
Задача выбора экстремального контура сводится к
определению двух параметров: безразмерной длины L/RK
расширяющейся части сопла и начального угла наклона контура в точке стыка
дуги окружности и параболы Pw. Проводится горизонталь с
известной ординатой Ra/RK до пересечения с линией постоянных
углов наклона контуров в выходном сечении. Проходящая через
эту точку полужирная линия задает значение угла рт, а
ордината - длину расширяющейся части сопла.
По координатам и углам наклона касательных в крайних
точках кривой строится заменяющая контур парабола, например
с помощью геометрического метода касательных (см. рис. 28.4).
В ряде случаев можно задавать площадь выходного сечения
сопла, т. е. RJR , и ограничивать или задавать длину сопла. Тогда

398 Часть II. Теория неидеального теплового ракетного двигателя
определяют только характерные углы §а и рт контура,
обеспечивающего при заданных ограничениях максимальную тягу.
Задачи выбора экстремального контура, аналогичные
рассмотренной, решаются точнее, если вместо диаграмм, представленных
на рис. 28.5, используют их аналоги в виде таблиц. При этом, если
массивы чисел представлены, например, на магнитных носителях,
целесообразно применять компьютеризированые технологии.
Современный уровень развития вычислительных методов
газовой динамики позволяет решать большинство вариационных
задач расчета сопла в достаточно общей постановке с учетом
практически всех существенных взаимосвязей и неидеальностей.
В частности, в некоторых научно-исследовательских
учреждениях и организациях России наряду с оптимизацией образующей
контура расширяющейся части сопла были решены задачи
совместного профилирования сопла в целом - его дозвуковой,
трансзвуковой и сверхзвуковой частей - при ограничениях на
суммарную длину сопла и заданных расходе, параметрах реального газа
и давлении окружающей среды. При этом была показана
возможность существенного повышения тяги при замене постепенно
сужающегося канала дозвуковой части его внезапным сужением.
Таким образом, показано, что экстремальные сопла, профиль
которых определен на основе решения вариационной задачи,
имеют наименьшие значения потерь удельного импульса.
Однако оптимальные размеры сопла следует определять с
учетом массогабаритных характеристик сопла и соотнесения
положительного эффекта (уменьшение потерь удельного импульса)
с отрицательными последствиями (увеличение массы сопла)1.
Поэтому задача выбора основных параметров сопла - диаметра
и длины - чаще всего является не вполне корректной
математически и имеет конструкторский характер, т. е. решается по
неопределенному, субъективно ощущаемому критерию оптимальности.
Неопределенность условий на начальном этапе
проектирования двигателя делает нецелесообразными сложные, продолжи-
Верещака Л.П., Стернин Л.Е. Результаты расчетов потерь из-за
рассеяния в сверхзвуковых реактивных соплах // Труды НПО «Энерго-
маш» им. академика В.П. Глушко. 2004. Т. 22. С. 15-21; Руководство
для конструкторов по проектированию сверхзвуковых осесимметричных
круглых сопел реактивных двигателей / Д. А. Мельников, У .Г. Пирумов,
В.М. Семичастнов и др. М:. Госкомитет по авиац. технике СССР.
НИИ № 1. Отдел науч.-техн. информ., 1964.

Глава 28. Сопла. Выбор профиля сопла из семейства известных 399
тельные и дорогостоящие расчеты, тогда как применение
описанных в данной главе ускоренных приближенных методов
позволяет обосновывать выбираемые принципиальные решения
с заданной точностью, имея в виду проведение точных
оптимизационных расчетов на близких к заключительным этапах
проектирования, тем более что для большинства типовых случаев
расчетные характеристики спрофилированных по упрощенным
методикам сопл уступают экстремальным не более чем на 1 ...2 %.
Такие расхождения, как правило, приемлемы на начальном этапе
проектирования двигателя.
Контрольные вопросы и задания
1. Какой контур сопла называется исходным, экстремальным,
укороченным, контуром с равномерной характеристикой, контуром с
угловой точкой, в частности с угловым входом? Дайте определение этим
контурам.
2. В чем состоит методика приближенного построения
экстремального контура расширяющейся части сопла, если определены углы
наклона касательных на минимальном и максимальном радиусах
(см. рис. 28.4 и 28.5)?
3. Дайте объяснение утверждению: из совокупности сопл с одной и той
же относительной длиной расширяющейся части, но с разными
геометрическими степенями расширения только одно обеспечивает
максимальную пустотную тягу (см. рис. 28.3).
4. Дайте объяснение утверждению: из совокупности сопл с одной и той
же геометрической степенью расширения только одно
обеспечивает максимальную пустотную тягу (см. рис. 28.3).
5. Дайте объяснение утверждению: из совокупности сопл с одной и той
же площадью боковой поверхности расширяющейся части, но с
разными геометрическими степеням расширения только одно
обеспечивает максимальную пустотную тягу (см. рис. 28.3).
6. Предложите методику выбора профиля сверхзвуковой части сопла,
отвечающего одному из пяти рассмотренных в гл. 28 критериев,
если семейство профилей и соответствующих значений
относительных площадей и коэффициентов тяги представлено в виде
многомерного массива данных.

Глава 29
Работа сопл на режимах перерасширения
при больших степенях нерасчетности.
Дроссельные (расходные) и высотные характеристики
ракетных двигателей
При эксплуатации ракетных двигательных установок
возможны режимы работы, когда давление окружающей среды ph в 5-10 раз
превышает рассчитанное для безотрывного течения давление р
в выходном сечении сопла. Такие степени нерасчетности
достигаются при старте ракет из шахт или транспортно-пусковых
контейнеров либо на режимах запуска и при работе двигателей
высотных ступеней одновременно с двигателями первых ступеней
ракет. Например, маршевый двигатель SSME
воздушно-космического самолета «Спейс Шаттл» начинает работать на старте на
уровне моря и продолжает работу при необходимости маневра
на орбите в пустоте. Кроме того, высока степень нерасчетности
сопла в первые моменты времени на режимах плавного
нарастания давления в камере до номинального.
Наличие в реальном течении пограничного слоя в
расширяющейся части сопла обусловливает помимо трения также и
воздействие окружающей среды на течение сверхзвукового потока.
Это воздействие происходит через область пограничного слоя
с дозвуковой скоростью течения, в результате чего на режимах
перерасширения может произойти отрыв потока от стенки сопла.
Область отрыва для сверхзвукового потока является
препятствием, обтекание которого происходит с возникновением
сопряженных зон значительных градиентов давлений и системы скачков
уплотнения (далее - скачков).
Для таких режимов работы тяга как равнодействующая сил
давления не может быть вычислена через определяемые в
одномерном приближении скорость и давление в выходном сечении
сопла, для ее расчета требуется применение методик,
учитывающих существенные особенности течения.
Укрупненная структура течения при отрыве потока в
сверхзвуковой части сопла представлена на рис. 29.1, где распределение

Глава 29. Сопла. Режимы значительного перерасширения 401
давления р. на стенке сопла построено в относительных единицах
Л Р
d
кр Мск2 Мск, Мск
Рис. 29.1. Структура течения при отрыве потока
в сверхзвуковой части сопла
При значительной степени перерасширения потока на срезе
сопла возникает мостообразная система скачков уплотнения,
включающая косые скачки а-Ъ, b-с, с-а и b-d. Если
расположение скачка в сопле определять по сечению, где начинается резкий
рост давления, то это сечение можно приближенно задавать
рассчитанными в одномерном приближении числом Маха Мск и
давлением рск невозмущенного потока в этом же сечении. Тогда для
описанной системы скачков на срезе сопла М = М и р = р .
Г ск а Г ск ~ а
При росте противодавления до/?Л1 скачок перемещается внутрь
сопла и останавливается в состоянии равновесия в сечении Мск1,
начиная от которого давление на стенке сопла возрастает от
значения рск1 до значений, близких к значению phv При этом система
скачков изменяется афинноподобно, т. е. с сохранением формы и
характерных свойств. Следствием этой выявленной в
экспериментах закономерности является возможность описания
количественных соотношений между основными параметрами течения
математическим выражением, единым для диапазона значений давления,
в котором система скачков проникает в глубь сопла вплоть до
сечения с числом Маха, где участок скачка b-d практически
исчезает. В первом приближении сечение предельного углубления
системы скачков можно определить равенством М . ~ 1,4.

402 Часть II. Теория неидеального теплового ракетного двигателя
При изучении условий отрыва турбулентного пограничного
слоя в сверхзвуковом потоке при взаимодействии с областью
отрыва с ростом давления от рск ДО рск + Ар выявлена зависимость
необходимой для отрыва потока степени повышения давления
(рск + Ар) /рск от числа Маха Мск в потоке, соответствующем
давлению рск:
^±^ = 1 + 0,2 *<, (29.1)
K-i)
0,25 :
где к - местный показатель адиабаты.
При этом способ формирования положительного градиента
давления не оказывает влияния на процесс отрыва, если
турбулентный пограничный слой развит и стационарен.
В случае возникновения отрыва пограничного слоя в сопле
положительный градиент давления создается давлением
окружающей среды ph, распространяющимся с некоторым снижением
по пограничному слою вверх по потоку до некоторого сечения,
и давлением невозмущенного потока вблизи этого сечения. Если
при этом создаются условия, достаточные, согласно (29.1), для
отрыва пограничного слоя, то формируется представленная на
рис. 29.1 мостообразная система скачков.
Давление ниже по потоку за сечением отрыва рск + Ар
определяется в основном противодавлением ph, но устанавливается
на меньшем уровне в зависимости от профиля сопла, а для
конического сопла - от угла раскрытия сопла 2ра вследствие эффекта
эжекции. Причем с увеличением угла раскрытия снижение
давления за областью отрыва по отношению к противодавлению/^
практически исчезает. Для конических сопл с углом раскрытия
2$о > 30° этим влиянием можно пренебречь и считать давление
за скачком равным ph. Обработка данных экспериментов,
проведенных в МВТУ им. Н.Э. Баумана под руководством В.М.
Кудрявцева, для конических сопл с углом раскрытия 2$а ^ 30° дает
следующее соотношение между противодавлением ph,
вызывающим отрыв потока в сечении, где 1,4 < Мск < 5,0, и давлением
невозмущенного потока в сечении отрыва рск:
рИ=рск (0,39 + 0,73 Мск), (29.2)
описывающее для к~ 1,4 соотношение (29.1) с погрешностью не
более ±5 %. Если для известного сопла имеется, например,

Глава 29. Сопла. Режимы значительного перерасширения 403
рассчитанное в результате решения задачи термодинамического
расчета распределение по длине сопла значений давления р( и
чисел Маха М/5 то давление окружающей среды ph, при котором
отрыв потока происходит в расчетном сечении Fck = F.9
непосредственно определяется по (29.2) прирск =р. и Мск = М..
Угол раскрытия конических сопл 2ро < 30° существенно
влияет на снижение давления за скачком рск + Ар по отношению
к противодавлениюph, что влияет и на положении системы
скачков в потоке. Для таких сопл соотношение, аналогичное (29.2),
имеет вид
Рн =Дж(0>39 + 0,73МСК)
1 +
0,192-
1
sinpa
0,7 ,-М»
м
и J
(29.3)
где выражение в квадратных скобках в целом отражает влияние
угла раскрытия сопла, а в нем сомножитель (1 - Мск/М J
учитывает усиление этого влияния при перемещении сечения отрыва
в сторону минимального сечения сопла, т. е. при уменьшении
значения Мск. Из (29.3) следует, что конические сопла с
меньшими углами наклона образующей могут работать без отрыва
потока при больших степенях перерасширения, чем сопла с большими
углами.
Отражающие общие закономерности отрыва пограничного
слоя применительно к коническим соплам (29.2) и (29.3) можно
использовать для оценок первого приближения и для
профилированных сопл, если профилированному соплу поставить в
соответствие эквивалентное коническое сопло с той же самой
геометрической степенью расширения, но с образующей, соединяющей
точку отрыва с выходной точкой контура профилированного
сопла. Схема построения конического сопла, эквивалентного
профилированному соплу, представлена на рис. 29.2, где при положении
Рис. 29.2. Схема построения конического сопла,
эквивалентного данному профилированному соплу

404 Часть II. Теория неидеального теплового ракетного двигателя
скачка в сечении с числом Маха невозмущенного потока Мск1
угол наклона образующей эквивалентного конического сопла (Jal
определяется как угол наклона секущей ВХА. Аналогично для
числа Маха Мск2 угол наклона образующей эквивалентного
конического сопла fia2 определяется как угол наклона секущей В2А.
Современные методики решения численными методами
прямой задачи газовой динамики для осесимметричного течения
вязкого газа позволяют рассчитать тягу сопла при отрыве
перерасширенного потока, но это связано как с обязательным
привлечением экспериментальных данных, так и с большими
затратами вычислительных ресурсов, не всегда оправдываемыми на
этапе предварительных расчетов, для которых достаточно
результатов первого приближения. Такие результаты можно получить,
применяя соотношения (29.2) и (29.3).
Используя уравнение ГДФ я(М.,к) =р/р*9 выразим давление
в сечении скачка рск через давление в камере р* и, подставив его
в (29.2), получим
к
\к-\
Л.
Ри
1 + -
-Mi
0,39 + 0,73МС
(29.4)
Графики на рис. 29.3 построены для разных показателей
адиабаты в диапазоне значений 1,10 < к < 1,4.
1,5 2,0 2,5 3,0 3,5 4,0
Число Маха в сечении скачка М ск
Рис. 29.3. Связь числа Маха в сечении отрыва потока
с давлением в камере и давлением окружающей среды
По (29.4) можно определять давление окружающей среды ph
(или соответствующую высоту полета), при котором скачок будет
находиться в сечении, задаваемом числом Маха Мск. При
заданном постоянном значении ph по (29.4) однозначно определяют

Глава 29. Сопла. Режимы значительного перерасширения 405
Мск и положение сечения отрыва потока при переменном
медленно меняющемся давлении в камере, например при запуске
двигателя или при его дросселировании. Аналогично могут быть
решены и другие задачи, сводимые к решению уравнения (29.4)
относительно одного неизвестного.
Умножив знаменатель правой части (29.4) на выражение в
квадратных скобках из (29.3), учтем влияние угла наклона
образующей конического сопла. Согласно термодинамическим расчетам,
значения числа Маха ML и относительного давления pf/pK = л,
в одном и том же сечении сопла слабо зависят от абсолютного
давления в камере рк. Это позволяет считать, что рассчитанные
для конкретного давления в камере распределения М;. и 7г
справедливы для всех значений давления рк на полной дроссельной
характеристике (рис. 29.4) при заданном значенииph = const.
Тогда давление в сечении рск = р., при котором на дроссельной
характеристике сечение скачка давления совпадает с конкретным
сечением F = F. с известными М. = М и относительным давле-
ск / / ск
нием 7Г, можно вычислить по (29.2), а соответствующее давление
в камерерк=рск/кг
Рис. 29.4. К расчету тяги сопла при отрывном течении в расширяющейся
части. Схема для сопл с углами раскрытия:
я-2Ра>30°;б-ра« 15°
Рассматривая тягу как равнодействующую сил, приложенных
к соплу, представим внутреннюю составляющую тяги Рвн как
сумму тяги Рх = Рм < м , создаваемой суммой сил на участке
безотрывного течения до сечения с числом Маха М = Мск, и тяги
Р2 = Рм < м < м , складывающейся из сил давления, приложенного
на участке от сечения отрыва потока до выходного сечения сопла:

406 Часть II. Теория неидеального теплового ракетного двигателя
р = р + Р = Р + Р
вн Г\ Г2 ^М<МСК г\
На участке безотрывного течения справедливо записываемое
в одномерном приближении соотношение:
^м<мск = ^ск+^Лк> (29-5)
где т - расход рабочего тела; Wa ск, рск, FcK - соответственно
скорость, давление и площадь потока, рассчитанные для
безотрывного течения невозмущенного потока в сечении, где М = Мск.
Используя следствие теоремы о среднем, запишем для
расчета составляющей Р2 равенство
РМСК < М < Me = (Fck " Fa>Pcp> (29-6)
где Fa - площадь выходного сечения сопла;/? - среднее давление
на участке стенки сопла от сечения скачка, в котором М = Мск,
до выходного сечения сопла.
Для конических сопл с углом раскрытия 2$а > 30° (рис. 29.4, а)
давление на стенке сопла непосредственно за областью отрыва
интенсивно возрастает почти до давления/^ и его значение
остается неизменным вплоть до выходного сечения, т. е.
РсР=Рн-
На рис. 29.4, а такому усреднению соответствует
обозначенный штриховой линией участок графика, где в сечении Мск
давление скачком - вертикальная прямая - возрастает от значения
рск до значения давления окружающей среды ph.
Если сопло профилированное или коническое, но с малым
углом наклона образующей, т. е. fia « 15°, то в области за
скачком на стенке сопла давление возрастает почти линейно от
давления за скачком р2 до давления окружающей среды ph. В этом
случае с достаточной для предварительных оценок точностью
справедливо равенство
Р^1^- (29.7)
В первом приближении, когда приемлемы заниженные
оценки тяги, можно принимать р2 ~рск (рис. 29.4, б), тогда как более

Глава 29. Сопла. Режимы значительного перерасширения 407
точные расчеты должны выполняться по методике, приведенной
в учебнике1, с учетом того, что/?ск <р2 <ph.
На рис. 29.4, б приведено изменение давления на стенке
сопла, отличающееся от предствленного на рис. 29.4, а только
меньшим углом раскрытия. При одном и том же давлении окружающей
среды скачок размещается в сечении сопла с большим числом
Маха, т. е. М'ск > Мск. Давление в области за скачком
восстанавливается постепенно, не достигая в выходном сечении сопла
давления окружающей среды ph. Отражающий рост давления участок
графика можно аппроксимировать прямой в виде штриховой
наклонной линии.
Поскольку при определении тяги двигателя не учитывается
обтекание наружной стенки сопла, на которое в некоторых
случаях может повлиять изменение картины течения при вхождении
скачков в сопло, то расчет наружной составляющей тяги Рна
проводится по известному соотношению:
Р = -F р..
нар а^п
Отрыв потока и вхождение скачков уплотнения в
расширяющуюся часть сопла приводит к нелинейности дроссельной и
высотной характеристик при больших степенях перерасширения
потока в сопле.
На рис. 29.5 приведены полные, т. е. включающие все
характерные участки, высотные характеристики ракетных двигателей,
работающих на одном и том же топливе, но различающихся
только геометрическими степенями расширения сопл, где двигатели
имеют сопла / и 2, у которых FaX < FaY
На рис. 29.5 прямые линии - высотные характеристики,
соответствующие безотрывному течению потока во всем
диапазоне значений давления окружающей среды. Обозначены точки
характеристики, начиная с которых при увеличении ph в потоке
появляются области отрыва и скачки уплотнения. На этих
участках тягу и удельный импульс рассчитывают с учетом вхождения
скачка в сопло по (29.5) и (29.6) влияния угла раскрытия для сопл
с 2§а < 30°. При этом сплошные кривые соответствуют соплам
с углом раскрытия расширяющейся части 2fia > 30°, штриховые
кривые - соплам с углом раскрытия 2$а < 30°. При расчете
1 Основы теории и расчета жидкостных ракетных двигателей. Кн. 1 /
под ред. В.М. Кудрявцева... . С. 96-102 (см. сноску на с. 7).

408 Часть II. Теория неидеального теплового ракетного двигателя
h п h ск2 h ск1 h max h
Рис. 29.5. Полные высотные характеристики ракетных двигателей,
различающихся геометрической степенью расширения сопл
характеристик двигателей принимались одинаково
пренебрежимо малыми (и соответственно не учитывались) потери тяги и
удельного импульса с радиальной скоростью.
Продолжение высотной характеристики двигателя с соплом 1
совпадает с соответствующим участком характеристики
двигателя с соплом 2, если 2$а > 30°. Такого совпадения для высотных
характеристик нет для двигателей с углом раскрытия сопла
2$а < 30°. Укажем на то, что максимальное значение
противодавления ph, для которого определены точки высотной
характеристики, соответствует положению системы скачков уплотнения
вблизи сечения потока с числом Маха М ~ 1,4.
На рис. 29.6 представлены полные дроссельные
характеристики - зависимости удельного импульса / и тяги Р от давления
в камере/?* (расхода топлива т) - ракетных двигателей, высотные
характеристики которых приведены на рис. 29.5.
При расчетах принимались одни и те же допущения, а при
построении дроссельных характеристик сохранены те же
условные обозначения, что и при построении высотных характеристик.
Параметры ракетных двигателей и давление окружающей среды
подобраны так, чтобы давление в камере/?* ск1, при котором
скачок входит в сопло первого двигателя, было меньше, чем
давление, при котором равны тяги, развиваемые первым и вторым
двигателями при бесскачковом течении в сопле, - точка
пересечения прямолинейных участков характеристик двигателей. Это
во многом определяет вид и взаимное положение характеристик.

Глава 29. Сопла. Режимы значительного перерасширения 409
Рис. 29.6. Полные дроссельные характеристики ракетных двигателей,
различающихся геометрической степенью расширения сопл
Количественное соотношение между координатами
характерных точек - давлений, при которых скачок начинает двигаться
от среза в расширяющуюся часть того или иного сопла, - зависит
от конкретного соотношения углов наклона образующих сопл,
но обусловливают это соответствующие физические механизмы,
причем те же, что описаны при анализе высотных характеристик.
Общим для высотных и дроссельных характеристик является
то, что значения развиваемых на режимах перерасширения при
отрывном течении тяг и удельных импульсов превышают
соответствующие значения, рассчитанные при приближении
безотрывного течения, и уступают только значениям параметров
ракетного двигателя с соплом, идеально регулируемым по степени
расширения так, чтобы режим работы сопла всегда был расчетным,
С этой позиции при работе сопла на режимах перерасширения
отрыв потока и вызванное им течение со скачками уплотнения
являются более эффективными и более предпочтительными, чем
режим перерасширения при безотрывном течении.

410 Часть II. Теория неидеального теплового ракетного двигателя
Практически отрыв потока не обладает осевой симметрией,
что приводит к возникновению случайных по величине и
направлению боковых усилий, затрудняющих управление летательными
аппаратами. Кроме того, в области отрыва нередко
интенсифицируется теплопередача от рабочего тела к стенке сопла, что
усложняет охлаждение.
Заметные значительные поперечные вибрации сопла
двигателя SSME на этапе работы на старте до подъема со стартового
стола можно объяснить именно несимметричным отрывным
течением вблизи выходного сечения сопла при малых давлениях в
камере на режиме плавного выхода на номинальные расходы
топлива.
Эти особенности реальных отрывных течений учитывают,
определяя целесообразность проектирования сопл, которые будут
работать и на режимах с отрывом потока.
Работа сопла на режимах с отрывом потока обусловливает
повышение значений тяго-импульсных характеристик ДУ с
поочередно дросселируемыми автономными камерами при
уменьшении расхода топлива до перемещения сечения отрыва в зону
сопла с числом Маха около 1,4. Пример полных дроссельных
характеристик такой ДУ приведен на рис. 29.7.
Рекомендуется сравнить эти характеристики с
аналогичными, построенными при предположении безотрывного течения
у.ДУ гду
;| L 1 1 1 1 1 1
О 0,5 1,0 1,5 2,0 2,5 3,0
Относительный расход т0ТН
Рис. 29.7. Дроссельные характеристики ДУ при поочередном
дросселировании автономных камер, работающих при больших степенях
перерасширения (А, В, С - см. рис. 8.1, 8.2)
1,U
0,5
_л *

Глава 29. Сопла. Режимы значительного перерасширения 411
и дросселирования камер до нулевой тяги или нулевого расхода
(см. рис. 8.1 и 8.2).
Отметим, что рациональное с позиций увеличения тяги
ракетного двигателя устранение перерасширения рабочего тела
в сопле (нередко называемое регулированием высотности сопла)
может быть реализовано внесением изменений в его
конструктивную схему. Расширяющаяся часть сопла может иметь ломаную
образующую контура, в том числе вариант с удаляемой вставкой
(рис. 29.8, а), или гладкий профиль с узкими кольцевыми щелями
а б
Рис. 29.8. Схемы сопл, авторегулируемых по степени расширения:
а - с ломаной образующей контура расширяющейся части; б - с кольцевыми
щелями с клапанами / и коллекторами 2 щелей
с клапанами, коллектор щели сообщается с областью
повышенного давления - так называемое щелевое сопло (рис. 29.8, б).
В щелевом сопле повышенное давление (например, из атмосферы)
через щели воздействует на поток, принудительно отрывая его
от стенки сопла и препятствуя его перерасширению с
образованием отрицательной составляющей тяги. Работа таких, по сути,
авторегулируемых сопл может быть исследована на основе
современных методик описания осесимметричных отрывных
течений вязкого сжимаемого газа.
Контрольные вопросы и задания
1. В каких случаях реализуются режимы работы сопла с большими
степенями перерасширения?
2. Какой вид имеет система скачков уплотнения вблизи области
отрыва потока от стенки сопла?
3. От каких факторов зависит форма эпюры давления на участке
сопла от области отрыва потока до выходного сечения сопла?
4. От каких параметров зависит степень перерасширения потока, при
которой инициируется отрыв потока вблизи выходного сечения
сопла?

412 Часть II. Теория неидеального теплового ракетного двигателя
5. От каких параметров зависит положение области скачков
уплотнения в проточной части конического сопла?
6. Для конкретного известного ракетного двигателя оцените
максимально возможное давление окружающей среды, при котором оно
не оказывает влияния на давление в камере сгорания.
7. Каким образом можно применить зависимости, полученные для
конических сопл, к профилированным соплам?
8. Предложите методику определения возможности испытания
ракетного двигателя с раздвижным соплом при атмосферном давлении
(см. рис. 29.5). В каком положении - транспортном или рабочем -
может находиться дорасширительный насадок?
9. Предложите методику определения требуемого давления в области
за срезом сопла испытуемого ракетного двигателя с дорасширитель-
ным насадком или без него, если режимы работы сопла с отрывом
потока недопустимы.
10. Для заданного давления окружающей среды предложите методику
определения минимально возможного давления в камере
испытуемого ракетного двигателя с дорасширительным насадком или без
него, если режимы работы сопла с отрывом потока недопустимы.

Глава 30
Штыревое сопло: основы профилирования
и особенности работы при переменном давлении
окружающей среды
Продольные габариты сопла Лаваля в основном
определяются длиной расширяющейся части. Сокращение длины сопла при
сохранении качества рабочих процессов в нем обусловливает
уменьшение габаритов ракетного двигателя и способствует росту
эффективности летательного аппарата, оснащенного ракетным
двигателем.
Из свойств геометрически подобных тел следует, что
выполнение вместо одного сопла с заданными геометрической степенью
расширения сопла и площадью FK минимального сечения
соплового блока из нескольких, например из п одинаковых сопл
с геометрически подобным контуром и суммарной площадью
минимальных сечений, равной FK , приведет к снижению длины
сопловой части ракетного двигателя приблизительно в Vtt раз.
Аналогичное сокращение продольных габаритов сопловой части
ракетного двигателя можно получить, применяя сопла, проточная
часть которых представляет собой поверхность тела,
образованного вращением вокруг оси некоторой плоской фигуры, например
меридионального сечения сопла Лаваля. Схема такого сопла
представлена на рис. 30.1, а. Нормальное, т. е. перпендикулярное оси
симметрии, сечение этого сопла представляет собой кольцо, и по
этому признаку такое и аналогичные сопла называются кольцевыми.
Выбирая плоскую фигуру, ориентируя ее контур
относительно оси вращения, можно получить семейство кольцевых сопл,
в том числе и имеющих контуры с участками, параллельными
оси вращения. Равнодействующая сил давления на этих участках
перпендикулярна оси симметрии сопла и не дает вклада в
создание тяги, что позволяет на данных участках выполнять сопла без
твердых стенок (см. рис. 30.1). При этом уменьшается масса
сопла и потери на трение. Кроме того, свободная, находящаяся в
контакте с окружающей средой, поверхность тока обеспечивает соплу
специфические свойства авторегулирования при работе на
нерасчетных режимах.

414 Часть II. Теория неидеального теплового ракетного двигателя
б в
Рис. ЗОЛ. Схемы кольцевых сопл:
а - кольцевое сопло Л аваля; б - штыревое сопло; в - тарельчатое сопло;
1 - внешний участок контура; 2 - внутренний участок контура
При отрывном течении в расширяющейся части круглого
сопла на режимах перерасширения тяга и удельный импульс
превышают соответствующие значения, рассчитанные в приближении
безотрывного течения, и уступают только параметрам двигателя
с соплом, идеально регулируемым по степени расширения.
Отрывное течение проявляет свойства авторегулирования за счет
воздействия давления окружающей среды, находящейся в области
отрыва, на сверхзвуковой поток в поперечном направлении к
неограниченной стенкой сопла свободной периферийной
поверхности тока. Подобное воздействие на свободную границу
истекающей из сопла перерасширенной сверхзвуковой струи
приводит к изменению ее поперечных размеров таким образом, что,
проходя через систему самопроизвольно возникающих скачков
уплотнения и изменяя распределение скоростей, поток
приближается к состоянию равновесия с окружающей средой.
Этот эффект - установление близкого к расчетному режима
течения в сверхзвуковом потоке со свободной границей - объясняет

Глава 30. Штыревое сопло
415
потенциальную возможность авторегулирования кольцевых сопл,
сверхзвуковая область течения рабочего тела в которых
ограничивается стенкой сопла только частично: у штыревого сопла
(рис. 30.1, б) - по внутренней замыкающей поверхности тока, у
тарельчатого сопла (рис. 30.1, в) - по периферийной поверхности
тока. Соответственно свободная граница сверхзвуковой области
потока для штыревого сопла - периферийная поверхность тока ф ,
а для тарельчатого сопла - внутренняя поверхность тока фвн.
Рассмотрим схему течения в штыревом сопле, представленную
на рис. 30.2.
Рис. 30.2. Схема расчета габаритов и профиля
центрального тела (штыря) штыревого сопла
Предположим, что рабочее тело - идеальный газ. Полагаем
заданными: давление в камере/?*; давление окружающей среды ph\
показатель адиабаты для рабочего тела к. На представленной на
рис. 30.2 схеме течения в штыревом сопле прямая С С- ось
симметрии сопла, АЕ - свободная поверхность тока, параллельная
оси симметрии сопла С С, кривая МС - образующая штыря,
совпадающая с поверхностью тока потока рабочего тела,
ускоренного в сужающейся части сопла до звуковой скорости W .
Контур стенки дозвуковой части сопла и штыря заштрихован.
Пусть течение в сужающейся части сопла такое, что
поверхность перехода через скорость звука коническая с образующей
МА, т. е. вектор скорости W перпендикулярен образующей МА
и направлен по прямой АА'.
Поток, разворачиваясь на кольцевой кромке (точка А на
рис. 30.2) на угол оо^ - угол между прямыми АА' и АЕ, ускоряется

416 Часть II. Теория неидеального теплового ракетного двигателя
от М = 1 до М = М . При этом угол наклона вектора скорости Wa
к оси симметрии сопла уменьшается от (оа до нуля.
В характерном для ракетных двигателей диапазоне параметров
потока радиусы кривизны поверхностей тока в меридиональном
сечении существенно меньше радиусов кривизны поверхностей
тока в нормальном сечении, что позволяет с приемлемой
точностью рассматривать поток как течение Прандтля - Майера, т. е.
обтекание тупого двугранного угла с разворотом вектора
скорости по отношению к исходному направлению АА' на угол сод,
соответствующий соотношению давленийp*K/ph, давлению
окружающей среды рн =ра, показателю адиабаты для рабочего тела к.
При таком представлении течения связь между текущим углом
разворота со^ вектора скорости Wb и соответствующим этой
скорости значением числа Маха М^ описывается соотношением
Прандтля - Майера:
СО;
= ^^ arctg ^_i(M,2-l)-arctg ф^1. (30.1)
Пусть термогазодинамическим расчетом определены
площади критического FK и выходного Fa сечений сопла и параметры
потока ра, Та, ра и Ма в одномерном приближении, причем все
необходимые параметры потока можно определить и для любого
F F
значения геометрической степени расширения 1 <—-<——.
F F
кр Л кр
На расчетном режиме работы сопла поток в выходном сечении
одномерный, т. е. рассматриваем сопло с равномерной
характеристикой АС, в каждой точке которой вектор скорости Wa
параллелен прямым С'С и АЕ. Тогда угол САЕ = аа есть угол Маха
a =arcsin . Радиальная координата точки Е совпадает с ра-
диальной координатой точки А, т. е. R = СЕ рассчитываем по
W
известной площади выходного сечения сопла F как R - \\—-•
а V л
Вследствие этого и с учетом соотношения (30.1) в дальнейшем
будем считать известными углы аа, соа и радиус Ra.
Характеристика для произвольного угла ш^ разворота потока
будет также отображаться прямой АВ, наклоненной по отношению
к направлению вектора скорости Wb на угол Маха а^, = arcsin .

Глава 30. Штыревое сопло
417
Соответствующая углу разворота соь и числу Маха М^ площадь
потока Fb представляет собой площадь усеченного конуса с
образующей ВР, перпендикулярной прямой АР. Точка В
принадлежит образующей контура центрального тела сопла - штыря.
Направление вектора скорости Wb в точке В совпадает с
направлением касательной контура штыря, т. е. построенный таким
образом контур соответствует замыкающей поверхности тока, а в
меридиональном сечении в принятом приближении плоского
течения - линии тока, что обеспечивает плавное, без скачков,
течение потока с разворотом и ускорением.
При принятых допущениях профилирование штыря может
быть сведено к расчету для выбранного ряда произвольных чисел
Маха 1 ^ Mh ^ Ма угла фЛ и радиуса Rb, однозначно задающих
положение составляющих контур множества точек В,
расположенных между точками М и С.
Характерные точки сопла А и С являются вершинами
прямоугольного треугольника АСЕ, который может быть однозначно
построен по известным катету СЕ = Ra и противолежащему углу аа.
Как следует из рис. 30.2, задающий наклон отрезка МА /ЕАМ
вычисляется по соотношению/£'^М= сод + я/2. Проектируя
равную F боковую поверхность усеченного конуса с образующей
МА на плоскость его основания, перпендикулярную оси симметрии
С'С, получим уравнение
FKpcosn = n(R2a-R2J, (30.2)
где Q - угол между образующей МА и нормальной к оси
плоскостью основания.
Если/ЕАМ = юа + я/2, из рис. 30.2 следует
Q. = /ЕАМ- я/2 = со + я/2 - я/2 = со .
*— а а
Тогда, поскольку Q = соа, радиальную координату точки М
определим из (30.2):
Г~? ^oCosco^
К=^а- ' п • (30.3)
Таким образом определяются задающие габариты контура
штыревого сопла: длина АЕ и радиусы Ra и Rm. Профиль
центрального тела (штыря) для ориентировочных оценок можно

418 Часть II. Теория неидеального теплового ракетного двигателя
построить как дугу окружности или отрезок параболы, задаваемые
графически положением двух крайних точек Ми С и направлений
касательных в них (прямые М'Ми С'С соответственно). Большая
точность достигается построением профиля как огибающей
множества точек. Последовательность расчета координат каждой
точки покажем для ранее введенной произвольной точки В,
которой соответствуют число Маха Мь, площадь потока Fb и
рассчитанный по соотношению (30.1) угол поворота потока со6.
Из вершины А прямоугольного треугольника АСЕ проведем
прямую АА' под известным рассчитанным по (30.1) для^М = Ма
углом соа, задав таким образом наклон вектора скорости W в
критическом сечении. Направление вектора скорости потока Wh в
точке В зададим, проведя из этой же точки прямую под углом со^
к прямой АА'. Тогда исходящая из точки А прямая, составляющая
с направлением вектора скорости Wb угол Маха ab =arcsin ,
будет задавать направление характеристики потока. Искомая
точка В будет принадлежать этой прямой.
Задача сводится к расчету удаления точки В от оси
симметрии Rm.
Известная площадь потока Fb представляет собой площадь
боковой поверхности конуса с образующей ВР. Площадь Fb
является проекцией площади FАВ конической поверхности с
образующей АВ, составляющей угол аь с образующей ВР, т. е.
или
^*=^-- (30.4)
sina6
Проекция площади FАВ на плоскость, нормальную оси
симметрии СС\ есть площадь кольца, радиусы которого Rb и Ra, т. е.
FABsmq>B = n(R2a-R2b),
или
Fab=^ -■ (30-5)

Глава 30. Штыревое сопло
419
Приравнивая правые части выражений (30.4) и (30.5),
получаем уравнение с одним неизвестным Rb, решение которого
имеет вид
Y л sin ab
где, как следует из рис. 30.2,
Ф* = Шя + К - Ю*)- (30-7)
Подстановка (30.7) в (30.6) дает расчетную формулу для
прямого вычисления радиуса Rb:
fr=Jjg-F'gto(*-+a'-4 (30.8)
у 7i sin aA
Последовательность построения контура центрального тела
штыревого сопла при известных координатах точек А9 Ми С включает:
• задание произвольного значения числа Маха М^ из
диапазона значений 1 < М, < М ;
• вычисление угла разворота вектора скорости (оь по
соотношению Прандтля - Майера (30.1) и построение луча (прямой) АР\
• вычисление угла Маха по формуле ab = arcsin и постро-
ение луча АВ\
• вычисление радиуса Rb и нахождение положения точки В
контура центрального тела на луче АВ.
Огибающая построенных таким образом точек дает искомый
контур.
Схема течения в штыревом сопле с сохранением обозначений
характерных точек приведена на рис. 30.3.
На рисунке параллельная оси симметрии сопла прямая АЕ
представляет собой границу сверхзвукового потока, на
поверхности которого статическое давление^ равно давлению
окружающей среды ph, что соответствует расчетному режиму
работы сопла и положению равновесия границы потока. При этом
слабые возмущения, представляющие собой действие давления
окружающей среды, направлены нормально границе, т. е. под
прямым углом к направлению вектора скорости сверхзвукового
потока, таким образом, имеется возможность влияния давления

420 Часть II. Теория неидеального теплового ракетного двигателя
С" С
Рис. 30.3. Схема изменения параметров течения при
работе штыревого сопла на нерасчетных режимах
окружающей среды на параметры течения, а следовательно, и на
развиваемую камерой тягу.
Рассмотрим возможные изменения картины течения для
постоянного давления в камере/?* = const при отклонении давления
окружающей среды от ph = ра.
Пусть давление уменьшается до/?Л1 <ph, т. е. сопло от работы
на расчетном режиме переходит к работе на режиме недорасши-
рения, когдара >phv Тогда поток, свободно расширяясь при
развороте на кромке А (точка А в сечении), дополнительно
ускоряется до числа Маха МаХ > Ма, соответствующего соотношению
давлений —т- < ~т- При этом на свободной границе потока уста-
А А
новится равенство давленийраХ =phv уменьшится и угол Маха ааГ
Согласно соотношению Прандтля - Майера (30.1), угол
разворота потока увеличится, т. е. соо1 > соа, и внешняя граница
потока будет отображаться прямой АЕу Соответствующая числу
Маха Мд1 характеристика займет положение А С", а
характеристика А С, соответствующая числу Маха Мд, сохранит положение,
так как сохраняется площадь Fa, соответствующая этому числу
Маха. Это означает, что течение в области, ограниченной
поверхностью центрального тела и цилиндрической поверхностью
с образующей АЕ, также не претерпевает изменений.
Соответственно сохраняется и распределение давления по поверхности
центрального тела.

Глава 30. Штыревое сопло
421
Тяга Р камеры со штыревым соплом, как и камеры с соплом
Лаваля, представляет собой алгебраическую сумму наружной
Р = -Faph и внутренней Рвн составляющих тяги камеры Р =
Внутренняя составляющая тяги Рвн складывается из
равнодействующей сил давления потока на внутренний контур камеры
сгорания и сужающейся докритической части сопла Рвн с ж
(контур МА) и интеграла сил давления по поверхности центрального
тела с криволинейной образующей контура МС сопла Рвн , т. е.
Р =Р +Р .
вн вн.суж вн.ц.т
Для тяги справедливо равенство Р = Рвнсуж + РШЛ1Т - Faph.
На расчетном режиме работы штыревого сопла и на
анализируемом режиме недорасширения часть потока, находящаяся в
контакте с центральным телом, расширяется до соответствующего
расчетному режиму числа Маха М = Мд, а поток в выходном
сечении будет одномерным. При этом сохраняются распределение
давления на стенке камеры, а следовательно, и сумма сил
давления, определяющая значение внутренней составляющей тяги.
Эти условия соответствуют допущениям, принятым при
выводе уравнения тяги, имеющего вид
P = mWa+FaPa-FaPh. (30.9)
v /
Р
1 вн
Тогда из уравнения (30.9), описывающего высотную
характеристику ракетного двигателя, следует, что при работе на режимах
недорасширения авторегулируемость штыревого сопла не
проявляется, и представленные на рис. 30.3 графики характеристик
двигателей с соплом Лаваля и со штыревым соплом на этом
режиме совпадают.
Из проведенного анализа следует, что авторегулируемость
может проявиться только при изменении распределения давления
на стенке центрального тела, т. е. при возникновении зон натека-
ния потока на твердую стенку под углом к ее местной касательной.
Рассмотрим работу сопла при постоянном давлении в камере
на режимах перерасширения, когда давление окружающей среды
ph увеличивается по отношению к расчетному^ =ра и достигает
Ph2>Pa
В соответствии с уменьшением располагаемой степени
расширения p\/phl уменьшаются максимальное число Маха Ма2 и угол
соо2 < ыа разворота вектора скорости W 2 при обтекании кромки А

422 Часть II. Теория неидеального теплового ракетного двигателя
(точка в сечении А). На рис. 30.3 свободная поверхность тока
будет отображаться прямой АЕ'\ а соответствующая
характеристика - прямой А С", причем угол Маха аа2 > аа. При этом
непосредственно в точке С" направление вектора скорости Wa2
совпадает с направлением касательной профиля центрального тела,
но на участке дальнейшего течения наклон профиля
центрального тела уменьшается и поток становится набегающим на твердую
стенку под ненулевым углом атаки. Возникают взаимосвязанные
системы косых скачков, происходит отрыв пограничного слоя
и вследствие этого образуется зона местного незначительного
повышения статического давления по сравнению с давлением при
безотрывном обтекании (см. рис. 30.3, участок кривой С"С). В
системе скачков давление повышается, но одновременно за счет
эжекции рабочего тела из области отрыва оно уменьшится и в
результате сохранится на уровне, несколько меньшем давления
окружающей среды.
Если бы сохранилось безотрывное течение, то давление на
участке С"С должно было уменьшаться, что в сочетании с
направленной противоположно наружной составляющей тяги Faph2
привело бы к уменьшению тяги двигателя. Однако описанное
повышение давления частично компенсирует отрицательное
влияние окружающей среды, и высотная характеристика двигателя
со штыревым соплом (рис. 30.4) будет располагаться выше
Рис. 30.4. Высотные характеристики ракетных двигателей с соплами
различных видов:
/ - двигатель с нерегулируемым круглым соплом Лаваля при безотрывном
течении; 2 - двигатель с нерегулируемым круглым соплом Лаваля при отрывном
течении на режимах перерасширения; 3 - двигатель с идеально регулируемым
соплом Лаваля за счет изменения геометрической степени расширения сопла
так, что при сохранении сверхзвукового течения для всех значений рИ сопло
работает на расчетном режиме, т. е. прира =ph\4- двигатель с нерегулируемым
кольцевым, тарельчатым или штыревым соплом; р. - давление окружающей
среды, соответствующее расчетному режиму работы сравниваемых сопл;/?Лск2 -
давление окружающей среды, при котором сечение отрыва потока в сопле
Лаваля близко к выходному сечению сопла

Глава 30. Штыревое сопло
423
высотной характеристики двигателя с нерегулируемым соплом
Лаваля при безотрывном течении в нем, но несколько ниже
высотной характеристики идеально регулируемого сопла. Таким
образом, проявляется свойство авторегулируемости штыревого
сопла на режимах перерасширения.
Анализ результатов многочисленных расчетов по
профилированию штыревых сопл, в том числе и по более сложным и
точным методикам, показывает, что осевые габариты этих сопл
получаются недопустимо большими. Отметим, что роль концевой
части центрального тела (штыря) в создании тяги незначительна,
поскольку давление потока на этих участках потока невелико
и равнодействующая сил давления проецируется на направление
действия тяги под углом, близким к прямому, тогда как доля этих
участков в длине центрального тела превышает 40 %. Это
позволяет заменить полный профиль центрального тела (осевые
размеры которого, как правило, технически нереальны)
укороченным при приемлемом уровне потерь тяги, одновременно
существенно снижая осевые габариты сопла и двигателя в целом.
Например, замена профилированного концевого участка
коническим, начиная с углов наклона касательной профиля 30°,
приводит к уменьшению длины центрального тела1 приблизительно на
40...60 % при потерях удельного импульса до 1 %.
Авторегулируемость при работе на режимах перерасширения
является существенным преимуществом штыревого сопла перед
соплом Лаваля.
Для большеразмерных ракетных двигателей появляется
возможность использования пространства внутри укороченного
центрального тела для размещения агрегатов ДУ, что снижает
габариты и способствует повышению массового совершенства
летательного аппарата.
Отметим, что наряду с большей конструктивной сложностью
поверхность штыревого сопла, обтекаемая рабочим телом со
сверхзвуковой скоростью, будет меньше, чем у круглого сопла, тогда
как поверхность докритической части - существенно большая.
Это приводит к росту потерь на трение и суммарного теплового
потока в систему охлаждения. С одной стороны, это требует
больших расходов охладителя или большего его нагрева при постоянном
Добровольский М.В. Жидкостные ракетные двигатели: основы
проектирования: учеб. для вузов / под ред. Д.А. Ягодникова. 2-е изд., пере-
раб. и доп. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005.

424 Часть II. Теория неидеального теплового ракетного двигателя
расходе, что повышает массу двигателя. Но, с другой стороны,
такая особенность может обеспечить энергетический баланс
безгенераторного ЖРД при больших давлениях в камере и в сочетании
со свойством авторегулируемости при движении в атмосфере с
изменением высоты полета повысить показатели эффективности ДУ
в целом.
Профиль проточной части и габариты камеры ЖРД со
штыревым соплом определяются заданным давлением окружающей
среды рИ, которому при известном давлении в камере рк однозначно
соответствуют число Маха Ма =fl(k,pK/ph) и скорость истечения
^а ^f^PjPi) СТРУИ в выходном сечении сопла. В свою очередь,
от значения числа Маха зависит угол поворота потока со звуковой
скоростью WK, ускоряющегося при этом до скорости Wa, и Ма (угол
Прандтля - Майера соа). Эта зависимость соо(Ма, к), (30.1) при
к= 1,13 представлена кривой 1 на рис. 30.5, на котором кривой 2
соответствуют значения угла Маха аа, задающего наклон
замыкающей характеристики одномерного сверхзвукового потока
(см. рис. 30.2), а следовательно, и длину сверхзвуковой части сопла.
(йа;аа, градус
160
140
120
100
80
60
40
20
0
1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 М
Рис. 30.5. Зависимость углов Прандтля - Майера
соо (7) и Маха а (2) от числа Маха М при к =1,13
Отметим, что для диапазона значений 1 < Ма < 3,5 угол
поворота остается острым, т. е. 0 < соа < 90°. Этому диапазону
соответствует профиль проточной части камеры со штыревым соплом,
представленный на рис. 30.6, а, где свободная граница
сверхзвукового потока 2 параллельна оси симметрии сопла и
центрального тела в виде штыря 7, а геометрическая степень расширения
потока равна отношению FaX /FK , причем поверхность
выходного сечения плоская, а критического сечения - коническая.

Глава 30. Штыревое сопло
425
Для значений Ма ~ 3 угол поворота соа ~ 90°, камера с такими
параметрами представлена на рис. 30.6, б. В этом случае
поверхность перехода через скорость звука F - цилиндрическая с
радиусом, равным радиусу выходного плоского сечения FaV
Для больших чисел Маха, Ма > 3, поток, ускоряющийся в
течении Прандтля - Майера, поворачивается на тупой угол а > 90°
в г
Рис. 30.6. Профиль проточной части камеры ЖРД:
а - в - камеры со штыревым соплом при 1 < Ыа < 3, Ма ~ 3 и Мо > 3 (Мо ~ 5)
соответственно; г - камера с сочетанием признаков штыревого и тарельчатого
сопл при Ма > 3 (Мо ~ 5); / - штыревое центральное тело; 2 - свободная
граница сверхзвукового потока; 3 - обечайка

426 Часть II. Теория неидеального теплового ракетного двигателя
(см. (30.5)), т. е. разворачивается. Этому случаю соответствует
камера, приведенная на рис. 30.6, в, где осевая компонента
вектора скорости в критическом сечении WK направлена
противоположно вектору скорости потока в выходном сечении Wa. Причем
для F = idem и одного и того же топлива соотношение 1 < MtfI <
< Ма2 < Ма3 задает существенное для проектирования двигателя
соответствие между площадями выходных плоских сечений
Fal < Fa2 < Fa2 и косвенно - для радиальных габаритов камеры.
Отметим, что при размещении кольцевой камеры сгорания не
на периферии, а на оси симметрии (см. рис. 30.6, г)иМд>3 (Me ~ 5)
камера сохраняет признаки штыревого сопла (см. рис. 30.6, в)
(наличие центрального тела, разворачивающего поток с ускорением)
и приобретает обязательный дополнительный элемент - обечайку J,
завершающую разворот и доускорение потока до максимального
значения скорости (см. рис. 30.6, до Ма ~ 5). Обечайка является
атрибутивным элементом кольцевых сопл, относящихся к так
называемым тарельчатым соплам, которые будут рассмотрены в гл. 31.
Решение о целесообразности применения штыревого сопла
принимается с учетом всего комплекса его особенностей
применительно к конкретному летательному аппарату.
Контрольные вопросы и задания
1. Какие сопла называются кольцевыми?
2. Перечислите преимущества и недостатки штыревого сопла по
сравнению с круглым соплом Лаваля.
3. Проведите сравнительный анализ (перечислите потенциальные
преимущества и недостатки) круглого и кольцевого сопл Лаваля.
4. Каким образом изменение давления окружающей среды влияет на
параметры сверхзвукового потока?
5. Какие допущения приняты при составлении методики
профилирования центрального тела штыревого сопла?
6. За счет каких физических эффектов осуществляется повышение
давления на концевом участке штыря при авторегулировании?
7. Почему не проявляется свойство авторегулирования штыревого
сопла на режимах недорасширения?
8. Возможен ли разворот потока на угол более 90° в штыревом сопле
при ускорении рабочего тела от скорости звука до заданной
скорости, направленной параллельной оси симметрии сопла?
9. Каким образом может быть использован объем внутри штыря?
10. Предложите объяснение эффекта авторегулирования в кольцевом
сопле с укороченным штырем.

Глава 31
Тарельчатое сопло: основы профилирования
и особенности работы при переменном давлении
окружающей среды
При полете ракеты, оснащенной ЖРД с камерой со штыревым
соплом с ненулевым углом атаки нарушается симметрия
воздействия набегающего потока на свободную границу потока, что
приводит к эксцентриситету тяги - появлению радиальной
составляющей тяги и нарушению авторегулирования на режимах
перерасширения.
Кроме того, длина сверхзвуковой части штыревого сопла
с равномерной характеристикой однозначно связана с площадью
выходного сечения сопла и не может быть существенно
уменьшена по сравнению с длиной сопла Лаваля, что может быть
необходимым при строгом ограничении длины двигателя.
Отмеченных отрицательных особенностей лишены так
называемые тарельчатые сопла (рис. 31.1) - кольцевые сопла с
центральным телом в виде тарели 7, часть контура которой является
сужающейся частью сопла, а другая часть контура, как правило,
нормальная (перпендикулярная) оси симметрии. Сопло имеет
обечайку 2, ограничивающую периферийную часть
сверхзвукового потока рабочего тела, внутренняя граница которого
представляет собой цилиндрическую поверхность, сообщающуюся с
окружающей средой.
Рассмотрим схему течения в тарельчатом сопле,
представленную на рис. 31.1. Пусть течение в сужающейся части сопла такое,
что поверхность перехода через скорость звука коническая с
образующей AM. Расширение потока от давления в критическом
сечении/? до давления окружающей средыph при ускорении от
числа Маха М = 1 до М = М^ происходит при развороте потока
около острой кромки тарели (точка А) на угол соа, т. е. вектор
скорости Wa становится параллельным оси симметрии сопла ее'.
Значение угла сод для рабочего тела с показателем адиабаты к при
предположении одномерного течения Прандтля - Майера
однозначно определяется располагаемым соотношением давлений и
может быть рассчитано по соотношению Прандтля - Майера (30.1).

428 Часть II. Теория неидеального теплового ракетного двигателя
Рис. 31.1. Схема расчета габаритов и контура обечайки
тарельчатого сопла:
1 - тарель; 2 - обечайка
Очевидно, что в идеальном случае при работе на расчетном
режиме поток в выходном сечении одномерный, т. е.
рассматриваем сопло с равномерной характеристикой - прямая А С под углом
Маха ос = arcsin к горизонтали АЕ, параллельной оси симме-
М«
трии сопла 88'. Радиус центрального тела (тарели) Ra выбирается
из конструктивных соображений и, как правило, сопоставим с
радиусом выходного сечения сопла Лаваля. Будем считать
радиус Ra известным.
Принимая те же допущения, что и при расчете контура
штыревого сопла, выполним математические преобразования,
позволяющие получить расчетные соотношения для основных размеров
тарельчатого сопла.
Определяющая осевые габариты длина катета
прямоугольного треугольника АЕС (см. рис. 31.1)
АЕ =
СЕ
tg arcsin —
= ^-^ = {Rc-Ra)^KI'h (31.1)
Ч^а
где Rc - неизвестная величина.
Сравним габариты кольцевого тарельчатого и штыревого сопл,
рассчитанных для одного и того же двигателя, т. е. при одинаковых

Глава 31. Тарельчатое сопло
429
площадях критического F и выходного Fа сечений сопл и
одинаковых числах Ма и углах Маха аа.
Из равенства выходных сечений тарельчатого и штыревого сопл
где Ra ш - радиус выходного сечения штыревого сопла, следует,
что радиальные габариты тарельчатого сопла
*с=>1*£ш+*£- (31-2)
Из сопоставления Rcn Ram следует увеличение радиальных
габаритов тарельчатого сопла по сравнению со штыревым в
зависимости от выбранного радиуса тарели Ra.
Пусть задано соотношение Ra = nRa ш, где п ^ 1. Тогда с
учетом (31.1) и (31.2), получим:
для радиальных габаритов увеличение в
R [л 2
= \11 + п раз;
аш
для осевых размеров уменьшение в
АЕШ 1
—= ; = Ра3-
АЕ yj\ + n2-n
Наряду с меньшей зависимостью эксцентриситета тяги от угла
атаки при движении в атмосфере сокращение осевых габаритов
является одним из преимуществ тарельчатого сопла перед
штыревым и перед соплом Лаваля. Так же как и для штыревого
сопла, профиль насадка МС строится как профиль поверхности тока
в одномерном течении Прандтля - Майера. Согласно принятым
допущениям, произвольному числу Маха Мь соответствуют
однозначно рассчитываемые углы со6, ab, (pb и площадь потока Fb,
равная площади боковой поверхности усеченного конуса с
образующей ВР.
Луч АВ строится по известным углам, а радиальная
координата Rb точки В рассчитывается по выводимому аналогично (30.8)
соотношению

430 Часть II. Теория неидеального теплового ракетного двигателя
у sina6
Свободная поверхность тока, цилиндрическая на расчетном
режиме (прямая АЕ на рис. 31.3) и находящаяся в контакте с
частью окружающей среды, прилегающей к торцовой поверхности
тарели /, обеспечивает соплу специфические свойства при
работе на нерасчетных режимах. При этом за счет эффекта эжекции
давление вблизи торца тарели будет несколько ниже давления
окружающей среды.
Если сопло рассчитано на давление окружающей среды ph, то
увеличение высоты полета (уменьшение давления до рИ < ph)
приведет к дополнительному доразвороту потока на угол Асо, но
при этом характеристика потока АС сохранит положение и,
следовательно, не изменится распределение давления на стенке
обечайки 2, а внутренняя составляющая тяги сохранится такой же,
как и у двигателя с соплом Лаваля.
Таким образом, тарельчатое кольцевое сопло при работе на
режимах недорасширения не проявляет свойства
авторегулируемости и высотная характеристика двигателя с таким соплом
не будет отличаться от высотных характеристик двигателей с
соплом Лаваля или со штыревым кольцевым соплом.
Росту противодавления Д,орн <рИ2 соответствует уменьшение
числа Маха Ма2 < Ма и, следовательно, уменьшение угла
разворота вектора скорости до соа2 и наклона характеристики потока.
При этом правее общей точки встречи поверхности обечайки
и характеристики потока течение становится набегающим на
твердую стенку под острым углом с возникновением зоны
местного повышения давления до давления, близкого к/?Л2, т. е.
реализуется авторегулирование режима работы сопла. Кривая
высотной характеристики (см. рис. 30.4) будет практически
совпадать с соответствующим участком характеристики
штыревого сопла.
В некоторой степени свойство авторегулируемости присуще
и течению в сопле Лаваля, когда при значительных степенях
перерасширения происходит отрыв потока от стенки сопла с
формированием ниже по потоку зоны увеличения давления
(см. рис. 30.4, кривая 2). При отрывном течении в
расширяющейся части круглого сопла Лаваля, работающего на режимах
перерасширения, значения тяги и удельного импульса превышают

Глава 31. Тарельчатое сопло
431
соответствующие значения, рассчитанные в приближении
безотрывного течения (см. рис. 30.4, прямая 7), но не превышают
значений, получаемых для кольцевых штыревых или тарельчатых
сопл (см. рис. 30.4, кривая 4), выше которых только значения
параметров двигателя с соплом, идеально регулируемым по
степени расширения, так, что при всех противодавлениях ра = ph
(см. рис. 30.4, кривая 3).
Отметим, что пространство внутри тарельчатого
центрального тела кольцевых сопл может быть использовано для размещения
агрегатов ДУ, например ТНА, вывод выхлопа турбины которого
на торцовую поверхность центрального тела может повысить
качество авторегулирования, в том числе компенсировать
уменьшение эффективности, связанное с эжекционным снижением
донного давления.
Главной особенностью реальных рабочих процессов является
существенно неодномерное течение с большими местными
градиентами параметров, в котором проявляются эффекты
неидеальности газа, локализующиеся в пограничном слое. Это
подтверждается некоторыми экспериментами с кольцевыми соплами,
размеры которых близки к размерам реальных сопл, т. е.
характерны для сопл двигателей ракетоносителей. Приведенная
методика профилирования позволяет определить габариты и профиль
образующей обечайки тарельчатого сопла только в первом
приближении.
Научно-практические основы современного подхода к
проектированию кольцевых сопл приведены в работах специалистов
ведущего российского предприятия по разработке мощных ЖРД
НПО «Энергомаш» им. академика В.П. Глушко1 и в трудах
сотрудников других научно-исследовательских и конструкторских
организаций и предприятий.
Как и для штыревого сопла, решение о выборе именно такой
схемы сопла принимается с учетом всей совокупности факторов,
характерной именно для конкретного летательного аппарата с
конкретными параметрами ДУ.
Тяговые характеристики ЖРД со штыревыми соплами / Б.И. Ка-
торгин, А.С. Кисилев, И.А. Клепиков и др. // Труды НПО «Энергомаш»
им. академика В.П. Глушко. 2001. Т. IX. С. 18-37; Кисилев А.С., Стер-
нин Л.Е. Экстремальные осесимметричные кольцевые сопла
тарельчатого типа. Там же. С. 38-52.

432 Часть II. Теория неидеального теплового ракетного двигателя
В ОАО КБХА разработан и испытан на стенде
безгенераторный кислородно-водородный ЖРД РД-126Э с кольцевой камерой
и тарельчатым соплом, в котором поток разворачивается на угол
около 90° по отношению к вектору его скорости в критическом
сечении. Относительно малые габариты при высокой степени
расширения рабочего тела и безотрывном течении потока в сопле на
режимах значительного перерасширения обеспечивают
возможность эффективного использования этого двигателя в составе
кислородно-водородных разгонных блоков и ступеней
ракетоносителей, работающих при изменяющемся давлении окружающей
среды.
Представляется обоснованным предположить
преимущественное применение кольцевых сопл для летательных аппаратов,
предназначенных для полетов в атмосфере планет с большой
плотностью и большими градиентами давления по высоте, где наиболее
эффективно проявятся свойства авторегулируемости.
Контрольные вопросы и задания
1. Что такое характеристика поля течения сверхзвукового потока?
2. Какие допущения приняты при составлении методики
профилирования обечайки тарельчатого сопла?
3. Проведите сравнительный анализ (перечислите преимущества и
недостатки) штыревого и тарельчатого кольцевых сопл.
4. Каковы функции обечайки тарельчатого сопла при движении
летательного аппарата в атмосфере под углом атаки?
5. Объясните, за счет каких физических эффектов происходит
повышение давления на стенке обечайки при работе сопла при больших
степенях перерасширения.
6. Каким образом может быть компенсирован недостаток
тарельчатого сопла, связанный со снижением давления на наружной
поверхности тарели по отношению к атмосферному давлению?
7. Возможно ли в принципе тарельчатое сопло, у которого осевая
компонента вектора скорости потока в минимальном сечении сопла
направлена вперед, т. е. против тяги двигателя?
8. Перечислите преимущества и недостатки кольцевых сопл по
сравнению с круглыми соплами Лаваля.
9. Почему не проявляется свойство авторегулирования кольцевых сопл
на режимах недорасширения?
10. При каких номинальных степенях расширения рабочего тела в
кольцевых соплах поверхность перехода через скорость звука из
конической становится цилиндрической?

Глава 32
Состояние и перспективы развития
теории ракетных двигателей
Часть теории ракетных двигателей, описывающая рабочие
процессы и соотношения параметров, присущих ракетным
двигателям разных видов, относится к общей теории ракетных
двигателей, в которой рассматриваются следующие взаимосвязанные
базовые вопросы:
• термодинамические расчеты процессов горения и течения
химически активного рабочего тела по трактам ракетного
двигателя;
• газодинамические расчеты неадиабатного течения
сжимаемого химически активного рабочего тела по трактам известной
формы (прямая задача) и вариационная задача профилирования -
определение формы канала, обеспечивающей заданное
распределение параметров потока (обратная задача) или достижение
экстремального значения характерного параметра;
• расчет развиваемых тяги и удельного импульса двигателей
и ДУ конкретных схем, а также определение путей их
термодинамического совершенствования и повышения функциональной
надежности;
• расчет статических внешних дроссельных и высотных
характеристик двигателей.
Вследствие существенного взаимного влияния
физико-химических процессов, рассматриваемых в общей теории ракетных
двигателей, их целостное описание можно представить в виде
объектно-ориентированной интегральной математической
модели ракетного двигателя, включающей математическое описание
отдельных определяющих процессов. Ракетный двигатель
является тепловой машиной, поэтому целесообразной является
композиция его интегральной модели на основе
термодинамического анализа с учетом регенерации теплоты, которая значительно
влияет на эффективности двигателя.
Усложнение схем энергообмена в современных ракетных
двигателях с формальной возможностью реализации множества
вариантов перераспределения потоков массы и энергии обусловливает

434 Часть II. Теория неидеального теплового ракетного двигателя
возможность разработки некоторого общетеоретического
подхода к анализу ракетного двигателя как тепловой машины.
Развитие ракетной техники, и в частности ракетного двигате-
лестроения, обусловливает актуальность проблем, пути решения
которых может дать общая теория ракетных двигателей. К таким
проблемам относится создание многотопливных ракетных
двигателей, работающих на первых ступенях ракет на топливе с
большей плотностью, а на последующих, верхних ступенях, - на
топливе, на котором развивается больший удельный импульс.
Причем для того и другого топлива может использоваться один
и тот же окислитель, например жидкий кислород, а горючее -
разное: углеводородное на первых ступенях и жидкий водород
на последующих ступенях (рис. 32.1, 32.2).
Рис. 32.1. Возможная схема камеры
перспективного двухтопливного ЖРД:
/ - внешняя камера (камера первой ступени);
2 - внутренняя камера, составляющая в сочетании
с внешней камеру второй ступени
Как показали проведенные исследования, использование
комбинации двух горючих с одним окислителем для сопоставимых одинаковых
условий применения топлива приводит к уменьшению массы и
габаритов одноступенчатого летательного аппарата с ЖРД приблизительно на
15 %, а с двухступенчатым ЖРД - на 10 %, или к эквивалентному
увеличению массы полезной нагрузки, что может быть экономически
существенным для ряда актуальных и перспективных задач практической
космонавтики. При этом наибольшая эффективность достигается при
применении сопл со степенью расширения, увеличивающейся при
снижении давления окружающей среды.
При анализе возможных схем трехкомпонентных ЖРД учитывалось,
что уникальные теплофизические характеристики водорода
обеспечивают возможность его эффективного использования и в качестве
охладителя, и как основы рабочего тела турбин для привода насосов. Один
из рассмотренных возможных вариантов трехкомпонентных двигателей
предусматривал использование конструктивно единой камеры,
состоящей из двух коаксиальных соосных камер (см. рис. 32.1), работающих
на режиме первой ступени совместно: одна - внешняя камера
(периферийная) 7, - например на керосине или другом более плотном, чем жидкий
водород, углеводородном горючем (УВГ) и кислороде; другая - внутренняя

Глава 32. Перспективы развития теории ракетных двигателей 435
Рис. 32.2. Схема двухтопливного ЖРД:
/ - бак первого горючего; 2, 11 - клапаны; 3 - газогенератор ТНА первого
горючего; 4 - насос первого горючего; 5 - турбина ТНА первого горючего;
6 - ракетная камера; 7 - насос окислителя; 8 - турбина ТНА второго горючего;
9 - насос второго горючего; 10 - газогенератор ТНА второго горючего; 12 - бак
второго горючего; 13 - бак окислителя; О - окислитель; Гр Г2 - первое и
второе горючее
камера 2 - на водороде и кислороде. На режиме второй ступени ракеты
углеводородная камера отключается. При работе водородной камеры
на втором режиме возрастает геометрическая степень расширения
сопла без механической трансформации конструкции камеры.
Общий вид принципиальной схемы газожидкостных систем
варианта двухтопливного ЖРД с двумя ТНА представлен на рис. 32.2, где
для упрощения не показаны агрегаты обеспечения регулирования. Этот
двигатель относится к ЖРЛ с полной газификацией компонентов
топлива до их подачи в камеру сгорания ракетной камеры 6 - так
называемая схема с дожиганием типа газ - газ. Согласно этой схеме,
газогенератор 3 работает с избытком кислорода. Вырабатываемое им
рабочее тело подается на турбину 5 ТНА первого горючего, вращающую
насосы окислителя (кислорода) 7 и первого горючего (УВГ) 4.
Газогенератор 10 ТНА второго горючего вырабатывает рабочее тело
с избытком водорода, подаваемое на турбину 8 ТНА второго горючего

436 Часть II. Теория неидеального теплового ракетного двигателя
насоса 9 второго горючего. При этом первое горючее вырабатывается
до опорожнения бака 1 на участке траектории, соответствующей
полету первой ступени ракеты.
Ряд иностранных фирм (например, Pratt & Whitney Rocketdyne, http://
www.pw.utc.com/ и др.1), отечественных организаций и предприятий
ведут практическую разработку многотопливных ЖРД с испытанием
их в наземных стендовых условиях. Например, НПО «Энергомаш»
им. академика В.П. Глушко разрабатывает трехкомпонентные двухре-
жимные ЖРД. При этом на режиме максимальной тяги
предусматривается одновременное использование трех компонентов топлива -
кислорода, водорода и УВГ - при полете ракеты на траектории первой
ступени. На режиме максимальной экономичности (при пониженной
тяге приблизительно до 40 % максимального значения, как на
траектории второй ступени) расходуются только два компонента - кислород
и водород. Трехкомпонентные смесительные элементы находятся в
одной камере сгорания ракетной камеры, работающей на обоих режимах.
Для обеспечения большего удельного импульса при полете на уровне
Земли и на большой высоте камера сгорания выполняется с
подключаемым дорасширительным сопловым насадком. В отличие от
представленной на рис. 33.2 схемы двухтопливного ЖРД с дожиганием типа
газ - газ, т. е. с газификацией всех компонентов топлива до их подачи
в камеру сгорания, в разрабатываемом двухтопливном ЖРД ТНА
отдельные для каждого компонента, а единая камера сгорания не имеет
коаксиальных секций в отличие от камеры на рис. 32.1. В качестве
рабочего тела турбин ТНА принят окислительный газ с дожиганием его
в основной камере при наиболее высоком давлении в камере сгорания
(до уровня около 35 МПа на режиме максимальной тяги). В
газогенераторы подается весь жидкий кислород и часть УВГ, необходимая для
выработки окислительных продуктов сгорания, поступающих на привод
турбин ТНА. Оставшаяся часть УВГ и весь жидкий водород поступают
в камеру сгорания (схема с дожиганием типа газ - жидкость). На втором
режиме УВГ в камеру сгорания не подается. Это решение основано на
многолетнем опыте разработки отечественных ЖРД, выполненных по
схеме с дожиганием окислительного рабочего тела турбин ТНА.
В разработках ОАО КБХА трехкомпонентного ракетного двигателя
и двухтопливных ЖРД НПО «Энергомаш» им. академика В.П. Глушко
используется качественно различный состав рабочих тел турбин ТНА:
НПО «Энергомаш» приняло традиционную схему с избытком
окислителя ОАО КБХА с избытком горючего на основе
кислородно-водородного ЖРД РД-0120 собственной разработки с его минимальной
модификацией.
Тимнат И. Указ. соч.

Глава 32. Перспективы развития теории ракетных двигателей 437
Отметим, что для многоразовых ЖРД с увеличенным ресурсом
вариант с окислительным рабочим телом ТНА менее надежен из-за
возможности возгорания в «горячем» тракте, которое в принципе
невозможно при использовании восстановительного газа. Кроме того,
энергетические возможности генераторного газа с избытком горючего
выше примерно в 1,3 раза, чем у трехкомпонентного двигателя с
газогенератором, работающем с избытком окислителя. Это позволяет в
некотором диапазоне тяг для кратности применения ЖРД, равной 20...25,
и ресурсе до 10 тыс. с, когда температура восстановительного
генераторного газа не должна превышать 800 К, достигать давления в камере
приблизительно на 4...5 МПа больше, чем в двигателе с окислительным
рабочим телом турбин ТНА. Выбор оптимального схемного решения
для многотопливных ЖРД остается к настоящему времени нерешенной
в общем виде актуальной задачей системного характера, как и задача
оптимального распределения соотношения расходов трех компонентов
топлива при движении летательного аппарата по заданной траектории
(по высоте полета).
К этой проблеме относится, в частности, разработка ракетных
двигателей, дросселируемых по оптимальному закону,
определяемому для конкретных летательных аппаратов, выполняющих
конкретное полетное задание (так называемое оптимальное
управление). При этом возможно изменение не только давления в
камере, но и соотношения компонентов топлива в ней. Движение
летательного аппарата (например, воздушно-космического
самолета) в атмосфере обеспечивает возможность использования ее
в качестве окислителя, например, путем глубокого охлаждения
и сжижения воздуха за счет хладоресурса бортового
криогенного компонента ракетного топлива. В этом случае ДУ становится
комбинированной. Приблизиться к максимально возможной
эффективности таких ДУ можно за счет оптимизации
термодинамического цикла и конструкции воздушно-реактивной и ракетной
частей. Общим для данных проблем является их совместная
сопряженная постановка и необходимость комплексного решения
с учетом характеристик летательного аппарата.
Перспектива перехода на высокие (до 100 МПа) давления
в камере и соответствующего увеличения располагаемой степени
расширения рабочего тела в сопле до 104...105 наряду с
приближением эффективности ракетных двигателей как тепловых машин
к термодинамически предельной эффективности требует
разработки методик анализа двигателя с учетом регенерации теплоты
в системе охлаждения. Актуальной становится реализация одной
из первых схем ДУ с ЖРД с замкнутым контуром привода турбины

438 Часть II. Теория неидеального теплового ракетного двигателя
и охлаждением камеры ракетного двигателя автономным
теплоносителем.
Рост масштабов воздействия ракетной техники на окружающую
среду ставит в первый ряд экологические проблемы создания и
эксплуатации ракетных двигателей. Экология наряду с требованием
повышения экономической эффективности ракетной техники
диктует переход к разработке ракетных двигателей разового и
многократного использования с учетом полного жизненного цикла и
возможности и целесообразности реновации как восстановления
работоспособности двигателя на разных фазах его жизненного
цикла. При этом главной задачей становится повышение
надежности двигателя. Перспективой решения этих проблем
обусловлены исследования в области использования сжиженного
природного газа или метана в качестве горючего ЖРД.
Решение отмеченных проблем связано с получением ответов
на конкретные вопросы, входящие в общую теорию ракетных
двигателей, что стимулирует ее развитие. Постоянно
совершенствуется один из базовых разделов общей теории ракетных
двигателей - термодинамические расчеты.
Многократное повышение производительности компьютерной
техники за последние годы сделало второстепенной задачей
упрощение алгоритмов и повышение скорости сходимости
итерационных процессов. Весьма совершенные современные методики
решения задач термодинамических расчетов в основном
сохраняются, и их развитие связывается с использованием все более
точных уравнений состояния реального газа. При этом
достоверность результатов возрастает благодаря использованию
постоянно уточняемых термодинамических характеристик
индивидуальных веществ и расширению перечня рассматриваемых
компонентов продуктов сгорания. При таком пути
совершенствования целесообразно учитывать значительно разнящиеся
скорости образования или разложения некоторых химических веществ
с тем, чтобы обоснованно задавая химическую неравновесность,
не рассматривать компоненты, применение которых нереально
в условиях ракетного двигателя.
Если химическая кинетика, как правило, незначительно
влияет на требуемое время пребывания топлива в камере сгорания,
то при движении рабочего тела по соплу определяющим
является кинетический режим химических реакций. Причем именно
скорость химических превращений может ограничить полноту
преобразования энергии в соплах современных и перспективных

Глава 32. Перспективы развития теории ракетных двигателей 439
ракетных двигателей с большой степенью расширения.
Кинетические процессы определяют также взаимодействие продуктов
сгорания с окружающей средой с образованием загрязняющих
вредных веществ. Этим обусловлено совершенствование методик
термодинамических расчетов в части учета кинетики химических
реакций. Вместе с известными представлениями об образовании
индивидуальных веществ в результате последовательно
протекающих химических реакций разрабатываются методики, не
требующие таких допущений и использующие наиболее общие
законы термодинамики необратимых процессов. Первый
практически освоенный и вполне апробированный подход требует
привлечения множества кинетических констант, получаемых
экспериментально в условиях, существенно отличающихся от
реализуемых в ракетном двигателе. Причем предполагается
конкретная линейная последовательность химических реакций, тогда как
в действительности велика вероятность протекания разветвленных
реакций, требующих для описания принципиально другого
математического аппарата.
Такой подход к методикам расчета перспективных ракетных
двигателей в отличающемся от освоенного диапазоне значений
параметров требует расширения перечня рассматриваемых
химических реакций и большого объема дополнительных исследований.
Использование законов термодинамики необратимых
процессов, например таких, как теорема Пригожина о наибольшей
вероятности протекания процесса по пути с наименьшим
производством энтропии, напротив, позволяет получить теоретическое
решение с точностью до неопределенного множителя без
привлечения дополнительных экспериментальных данных. При этом
не требуется принимать допущения о схеме химических
превращений. И в этом смысле более общая теоретическая модель
ближе к реальной физической картине. Развитие такого
перспективного подхода доведено до практических результатов пока только
для реакций в газовой фазе, и учет гетерогенных процессов
требует разработки их адекватного математического описания и
существенной доработки математической модели в целом1.
Задача описания термодинамических процессов в
кинетическом приближении неизменно сопряжена с газодинамическими
расчетами течений рабочего тела с переменными свойствами.
Трусов Б.Г. Применение вариационного принципа для решения
задачи химической кинетики // Докл. РАН. 1994. Т. 339; № 6.

440 Часть II. Теория неидеального теплового ракетного двигателя
Современные требования интегрального системного
проектирования летательного аппарата и ракетного двигателя могут
быть удовлетворены при совместном расчете газодинамических
и термодинамических процессов. Заданная точность достигается
при трехмерном описании картины течения сжимаемого газа
с учетом кинетики изменения свойств рабочего тела, в том числе
в скачках уплотнения и в пограничном слое на охлаждаемых
поверхностях. При этом непосредственно учитываются как
регенерация теплоты, так и потери удельного импульса вследствие
неидеального протекания рабочих процессов.
Проектирование летательных аппаратов с двигателями,
работающими в диапазоне противодавлений от давления на уровне
моря до космического вакуума, ставит задачу расчета кольцевых
сопл (штыревых, тарельчатых) и аналогичных им, обладающих
свойством авторегулирования при изменении давления
окружающей среды.
Таким образом, общей характеристикой актуальных и
прогнозируемых проблем и задач теории тепловых ракетных
двигателей является их комплексный характер, что обусловливает
тенденцию развития различных разделов теории в части
системного подхода к описанию и анализу рабочих процессов с учетом
их реального протекания. Это позволит не только предложить
эффективные методики расчета, не требующие рассмотрения
большого числа вариантов, но и выявить пути дальнейшего
совершенствования ракетных двигателей.
Контрольные вопросы и задания
1. За счет каких особенностей рабочих процессов можно достичь более
высоких показателей эффективности импульсных детонационных
ракетных двигателей?
2. Какие специфические условия следует учитывать при оптимизации
соотношения компонентов топлива многотопливных ракетных
двигателей или комбинированных ДУ, использующих атмосферу?
3. Каковы недостатки двухтопливных ЖРД по сравнению с разными
ЖРД и топливами для первой и второй ступеней ракет?
4. Может ли быть реализован в принципе двухтопливный ЖРД,
схема которого отличается от представленной на рис. 32.2, без
клапанов 2 и 77?
5. Какие преимущества дает применение раздвижных сопл в
многотопливных ЖРД?

Глава 32. Перспективы развития теории ракетных двигателей 441
6. Какие преимущества может обеспечивать применение составных
камер двухтопливных ЖРД (см. рис. 32.1)?
7. В чем может состоять задача оптимизации размеров и параметров
составной камеры, аналогичной представленной на рис. 32.1?
8. Предложите критерии оптимизации составной камеры
двухтопливного ЖРД.
9. В чем может состоять задача оптимизации раздвижного сопла для
двухтопливного ЖРД?
10. Предложите критерии оптимизации раздвижного сопла для
двухтопливного ЖРД.

ЧАСТЬ III
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ
МАТЕРИАЛЫ

1. Методические указания
Консервативность педагогических систем, и особенно
продемонстрировавших высокие общественно признанные
результаты, относится к их объективным, имманентным свойствам. МГТУ
им. Н.Э. Баумана и его основанные более 150 лет назад научно-
педагогические школы в области тепловых машин и процессов,
в частности возникшая в середине XX в. на их базе московская
научно-педагогическая школа (МВТУ - МАИ)1 подготовки
специалистов по ракетным двигателям, относятся именно к таким
системам. Однако традиционная для большинства отечественных
технических университетов лекционно-семинарская модель
организации учебного процесса обязательно дополняется курсовым
проектированием, активизирующим познавательные действия
студентов и переводящим их активность из области получения
знаний в область их творческого применения. Наиболее
эффективно эти процессы происходят тогда, когда курсовой проект
выполняется во время научно-производственной практики
студента на базовом предприятии с использованием не только
учебной, но и профессиональной инженерной научно-технической
и нормативной документации, особенно если тема курсового
проекта связана с реальной производственной проблематикой, а
консультант - крупный специалист, работающий в промышленности.
У студента появляется необходимость оценки, осмысления
собственных знаний и способностей, т. е. рефлексия. На ее основе
формируется запрос на личностно-ценные новые знания и умения,
возникает стимул к их приобретению.
Таким образом, необходимая, но недостаточная традиционная
составляющая образования - передача и приобретение знаний -
дополняется (но не заменяется) усвоением знаний до уровня
творческого применения, что, собственно, и входит в основу
профессионально значимых характеристик и качеств будущего
инженера, заключающихся в выраженной готовности и
способности применять для решения актуальных профессиональных
В настоящее время МГТУ им. Н.Э. Баумана и Московский
государственный авиационный институт (технический университет).

446 Часть III. Методические указания и КИМ
задач свои приобретенные в учебном процессе знания и умения,
т. е. то, что в современной терминологии называется
«профессиональной компетентностью» (ГОСТ Р ИСО 9000-2001).
Представленные методические указания и полный комплект
контрольно-измерительных материалов (КИМ) ориентированы
именно на деятельностные гуманизированные образовательные
технологии, обеспечивающие достижение таких качественных
показателей.
1.1. Дидактические функции учебной дисциплины
и их отражение в учебнике
Государственный образовательный стандарт подготовки
дипломированного инженера по ракетным двигателям
предусматривает преподавание комплексной учебной дисциплины «Теория,
расчет и проектирование ракетных двигателей». Ее составная
часть - «Общая теория ракетных двигателей», которой
соответствует настоящий учебник, - является пропедевтической (вводной
и системообразующей, задающей структуру) для блока дисциплин
специальности и специализации, т. е. формирует структуру
учебного плана в части этих дисциплин, определяет основы
понятийного аппарата, тезауруса и системы представления знаний в
профессиональной области.
В структуре и содержательной части программы дисциплины
«Общая теория двигателей» отражен опыт ее преподавания в 1950—
2005 гг. на кафедре «Ракетные двигатели» и место в современном
учебном плане специальности «Ракетные двигатели» с учетом
содержания других, в том числе предшествующих (по времени
включения в учебный план), дисциплин, в общем цикле
подготовки инженера-механика в традициях теплотехнической школы
МГТУ (МВТУ) им. Н.Э. Баумана и ее подсистемы - московской
научно-педагогической школы подготовки специалистов по
ракетным двигателям.
При этом имеется в виду, что преподавание или
самостоятельное изучение дисциплины ведется на основе деятельностного
подхода, когда ее освоение студентами сопряжено с оперативным
практическим применением получаемых знаний на уровне,
позволяющем не только продолжать изучение ракетных двигателей
конкретных видов, но и осуществлять конкретно-предметную
деятельность в моделируемой профессиональной области, что
обусловливает формирование профессиональной компетентности
инженера.

1. Методические указания
447
Двуединая целевая функция дисциплины включает основные
дидактические компоненты:
• системозадающий (системообразующий) - формирование
у студента системного подхода к ракетному двигателю как к
тепловой машине, интегрального представления о взаимосвязях
параметров и характеристик теплового ракетного двигателя,
наиболее общих физических моделях рабочих процессов в нем;
формирование интуитивно-логического образа ракетного двигателя,
доступного творческому осмыслению, в том числе в процессе
дальнейшего изучения; восприятие ракетного двигателя как
изучаемого системного объекта, когнитивное представление
которого обусловлено его системной моделью как тепловой машины;
• конкретно-предметный - введение в профессиональную
предметную область понятийного аппарата и тезауруса, приобретение
студентом декларативных знаний теоретического типа, процедурных
знаний и навыков решения задач из профессиональной области.
При этом реализуется также имманентно присущая
информационно-коммуникативная, когнитивная (по целям) функция
дисциплины, конкретизируемая с учетом ее места в учебном плане:
с одной стороны, коммуникация (смысловое системное
объединение) профилирующих дисциплин через формулировку
предмета и задачи их изучения, а с другой - отражение (или
предопределение) структуры учебного плана и отчасти последовательности
его реализации, а также формирование в целом
когнитивно-ориентированного контекста.
Интегральная цель обучения - профессиональная
компетентность - на данном этапе выполнения учебного плана
формируется путем приобретения студентами знаний, умений и навыков,
необходимых как для продолжения образования, так и
непосредственно для компетентной деятельности в профессиональной
области, если студент приступит к практической профессиональной
деятельности после получения высшего образования,
соответствующего степени бакалавра.
Изучивший дисциплину студент приобретает основные знания
по теории ракетных двигателей, использующих источники
энергии, в том числе топлива разных видов, и на этой основе
представляет место и роль последующих дисциплин в системном
знании о ракетном двигателе как объекте изучения.
По окончании изучения дисциплины студент на уровне
репродуктивной и комбинаторной деятельности с творческой
компонентой должен уметь:

448 Часть III. Методические указания и КИМ
• анализировать последовательность преобразования энергии
в тепловых ракетных двигателях различных принципиальных схем;
• рассчитывать основные параметры камер ракетных
двигателей с учетом реальной эффективности рабочих процессов,
задаваемой параметрически значениями соответствующих
коэффициентов;
• рассчитывать и строить газодинамический профиль камер
ракетных двигателей с коническими или профилированными
соплами, работающими на однофазном рабочем теле;
• рассчитывать и комплексно анализировать высотные и
дроссельные характеристики камер ракетных двигателей и
двигательных установок при задаваемых параметрически соответствующих
коэффициентах, характеризующих различие реального рабочего
процесса и его идеального представления;
• выполнять термодинамические расчеты сгорания и
истечения в зоне высоких температур для различных топлив
применительно к тепловым машинам и технологическим устройствам
различных видов и типов и творчески анализировать результаты
по отношению к проблемно-сформулированной цели.
Студент должен освоить методики расчета: 1) параметров
однофазного рабочего тела в различных сечениях сопла при
одномерном течении;
2) расхода продуктов
сгорания через сопло при
сверхкритических перепадах
давления;
3) полной энтальпии
вещества, в том числе рабочих
тел для различных схем
ракетных двигателей;
4) тяги и удельного
импульса на различных режимах
работы сопла;
5) близких к оптимальным
контуров профилированных
сопл на однофазном рабочем
теле;
6) термодинамических характеристик процессов сгорания и
истечения в камерах ракетных двигателей.
Реализация большинства когнитивных и коммуникативных
компонент целевой функции дисциплины должна обеспечить
ость
имативн
нфор
~
Рубеж 4 Курсовой проект
г
Рубеж 3 /
г
Рубеж 2 Семестровое домашнее
* у^ задание
*7^ Н
-тг Главы или темы (укрупненные
дидактические единицы)
> • i
3 5 7 111315
Цикл 1
19 23 27
Цикл 2
31

7. Методические указания
449
системный эффект - формирование у студента осознанной
потребности в изучении и усвоении дисциплин специальности
и смежных с ними в качестве социально- и личностно-значимых
способов и методов действия, причем не только в предметной
профессиональной области.
Содержание учебника структурировано в соответствии с блоч-
но-модульным принципом: цикл 1 - «Теория идеального
теплового ракетного двигателя»; цикл 2 - «Теория неидеального
теплового ракетного двигателя».
Когнитивно-дидактическая структура учебника отражена на
приведенном рисунке в виде графиков качественного изменения
информативности и сложности модели по главам, которые
представляют собой укрупненные дидактические единицы.
Деятельностный контекст первой части задается домашним
заданием, а контекст второй части - курсовым проектом, которые
выполняются параллельно лекционному курсу. При этом
дидактически обусловленное усложнение материала отражает рост
информативности дисциплины за счет дискретного дополнения
и углубления отражения реальности в модели рабочего процесса
в камере теплового ракетного двигателя.
Это позволило снабдить каждую главу комплектом
контрольных вопросов и заданий, а в учебнике выделить четыре рубежа
и предложить для каждого рубежа комплект контрольных заданий,
которые в сочетании с семестровым домашним заданием и
курсовым проектом позволяют оценить методом рейтинга как
текущую успеваемость (рубежный контроль), так и качество усвоения
студентом дисциплины в целом. Для интегральной семестровой
оценки усвоения учебного материала, например в виде зачета,
предлагаются комплекты вопросов, разработанных с учетом
выявления усвоенных знаний как на репродуктивном, так и отчасти
на творческом уровне.
Учебник ориентирован в основном на традиционную по
структуре образовательную технологию: лекционный курс -
последовательно изучаемые разделы или темы (укрупненные
дидактические единицы) с прохождением текущего контроля на четырех
рубежах: практические занятия (семинары), дополняемые
лабораторным практикумом, домашним заданием, курсовым проектом.
Но модульные характеристики учебника позволяют изучать
дисциплину также и по индивидуальному графику с большей долей
самостоятельной работы в индивидуально (субъективно)
оптимальном темпе.

450 Часть III. Методические указания и КИМ
1.2. Особенности методик изложения материала,
его преподавания и изучения
Основные положения теории излагаются в соответствии с
реализуемыми совместно дидактическими принципами возрастания
сложности и цикличности при чередовании подходов «от общего
к частному» - дедукции - и «от частного к общему» - индукции.
Традиционный для теплотехнической школы МВТУ (МГТУ)
им. Н.Э. Баумана условный термодинамический цикл теплового
ракетного двигателя в координатах v-p приводится как
наглядное графическое отображение взаимосвязей факторов. Это
позволяет ускорить усвоение нового материала
(транслингвистическая когнитивная карта). При этом для дисциплины в целом
в качестве когнитивных шаблонов (неоднократно применяемых
логических схем и последовательностей, устойчивых выражений,
понятий или формул, отражающих важные для процесса познания
взаимосвязи и усвоенные обучающимся до уровня навыков)
выделяются и фиксируются:
• основные аналитические выражения наружной и внутренней
(реактивной силы) составляющих тяги;
• соотношения параметров потока в сопле идеального
теплового ракетного двигателя - через ГДФ изоэнтропийного
адиабатного одномерного потока, где геометрическая степень
расширения канала вводится в качестве естественного аргумента;
• соотношения параметров для камер с распределенным
подводом рабочего тела через ГДФ для неизоэнтропийного потока,
для которого естественным аргументом является локальный
относительный расход рабочего тела.
Отвечающая последнему для настоящего времени ГОСТ 17665-89
«Двигатели ракетные жидкостные. Термины и определения»
основа тезауруса и понятийного аппарата теории ракетных
двигателей формируется по дедуктивной схеме «от частного к общему».
Основное уравнение теории ракетного двигателя - уравнение
тяги - выводится на базе непосредственного применения теоремы
динамики, изучаемой в предшествующем курсе теоретической
механики в сочетании с использованием дифференциального
исчисления многих переменных и сведений из раздела
«Гидростатика» механики жидкости и газа, что способствует реализации
ретроспективных междисциплинарных связей. Причем выбранная
методика в достаточно общей постановке позволяет, если это
целесообразно, ограничиться квазистационарным приближением

1. Методические указания
451
или получить соотношение с нестационарной составляющей, т. е.
допускается диверсификация рабочих программ дисциплины.
Изложение основ понятийного аппарата и базовых элементов
теории идеальных ракетных двигателей в первых пяти главах
позволяет уже на этом этапе изучения дисциплины выдавать
семестровые домашние задания «Расчет основных параметров и
характеристик теплового ракетного двигателя». Требование его
обязательного выполнения одновременно с изучением
дисциплины способствует формированию у студента актуальной
потребности в изучении последующего материала, приобретающего
субъектную ценность не только в качестве цели, но и как средства
обязательной контролируемой и оцениваемой деятельности.
По окончании изложения теории идеального сопла Лаваля
целесообразно провести рубежный контроль 1.
При изложении методик расчета осевых усилий в стенках
ракетной камеры, закрепляемой в разных сечениях (см. рис. 6.5-6.8),
реализуются и подчеркиваются междисциплинарные связи:
рассчитываются усилия, необходимые для оценки несущей
способности корпуса камеры (курс сопротивления материалов), и
допустимые толщины стенки как элемент системы охлаждения (курс
теплопередачи).
Ракетный двигатель твердого топлива рассматривается как
частный случай идеального теплового ракетного двигателя. При
таком же методически эквивалентном подходе рассматривается
идеальный тепловой ядерный ракетный двигатель, выводятся
уравнения связи тепловой мощности реактора и параметров
ракетного двигателя (тяга, удельный импульс, КПД сопла).
Изучение примерно 85 % материала первой части учебника
целесообразно завершить проведением рубежного контроля 2.
В гл. 11 и 12 в методически единой постановке излагаются
основы теории ракетных двигателей со скоростной и расходной
камерами сгорания. При этом применяются вводимые впервые
для студента ГДФ для неизоэнтропийного потока. Эта часть
дисциплины (и учебника) состоит из двух блоков-модулей, причем
каждый из них или оба сразу могут быть изъяты и (или)
заменены (в зависимости от ресурса времени назначены для
самостоятельного изучения) другими блоками без ущерба для изучения
обязательного материала части II дисциплины.
Очерк истории ракетного двигателестроения (в нем
характеризуются место и ведущая роль отечественных достижений
в ракетном двигателестроении и в развитии мировой ракетно-

452 Часть III. Методические указания и КИМ
космической техники и космонавтики), завершающий часть I
учебника, кроме информационной выполняет также
воспитательную функцию.
Интегральное усвоение части I дисциплины можно оценить
в форме зачета, вопросы к которому (билеты) приведены в разд. 2.
Отметим, что вопросы сформулированы так, что от отвечающего
требуется понимание основных взаимосвязей, в том числе
неявных. Это способствует усвоению материала на уровне,
приближающемся к творческому.
Часть II учебника, соответствующая второму дидактическому
циклу, содержит основы теории учета различий реальных рабочих
процессов и их идеального представления. Причем эти различия
рассматриваются в соответствии с ГОСТ 17665-89, определяющем
термины и определения, касающиеся ЖРД. При этом основы
теории реального ракетного двигателя излагаются при сочетании
моделей рабочих процессов и реализующих их методик учета
различий реального протекания энерго- и массообменных
процессов и их идеального представления. Эти различия
обусловлены проявлением реальных свойств топлива, конструкционных
материалов и рабочего тела, а также конечностью размеров
конструкции и времени протекания того или иного компонента
преобразования исходной энергии топлива в полезную кинетическую
энергию истекающего потока, создающего тягу.
После изучения первых глав второго цикла учебника
представляется дидактически обоснованным выдать задания на
курсовое проектирование. Разъяснение содержания курсового
проекта, выполняемого одновременно с изучением дисциплины,
способствует созданию когнитивного контекста изучения всего
последующего материала.
Теоретические основы термодинамического расчета
представлены с использованием как аппарата констант равновесия
обратимых реакций диссоциации-рекомбинации, так и наиболее общих
принципов термодинамики необратимых процессов (по Г.Б. Си-
няреву и Б.Г. Трусову). Причем эти подходы анализируются в
комплексе с выделением общих и особенных признаков,
преимуществ и недостатков. Показана эквивалентность такого
представления состояния динамического равновесия химически активных
систем. Подчеркивается мировоззренческая сущность этого
термодинамического и одновременно дидактического положения.
Таким образом, устанавливается связь между общепринятым для
учебников предшествующих изданий представлением и совре-

1. Методические указания
453
менным подходом, что с позиций современной педагогики
содействует бесконфликтному восприятию нового в связи, а не
в противостоянии с апробированным и привычным.
Реакция высокотемпературного рабочего тела ракетного
двигателя на внешние возмущения рассматривается в соответствии
с принципом Ле Шателье - Брауна, применение которого должно
быть освоено студентами до уровня умений при изучении
предшествующего курса химии.
Математическая модель термодинамического расчета
отражает закон сохранения энергии в виде равенства полной
энтальпии некоторой постоянной величине. Закон сохранения массы
вещества выражается в равенстве содержания химических
элементов в топливе и в продуктах сгорания, а допущение
идеальности газообразных компонентов - в непосредственной
применимости закона Дальтона и уравнения состояния идеального
газа. Подчеркивается фундаментальный характер и
мировоззренческая сущность принципа максимума энтропии и
уравнений сохранения массы, энергии и количества движения. При
этом методика расчета состава топлива и его стехиометрических
характеристик излагается с использованием формализма (правил
записи формул химических веществ и соединений, их
качественной и количественной интерпретации), усвоенного студентами
при изучении химии на младших курсах до уровня навыков.
Таким образом, непосредственно реализуются актуальные и
ретроспективные дидактические междисциплинарные связи и
снижаются затраты времени на изучение прикладных вопросов
теории двигателей.
Часть дисциплины, касающаяся термодинамического расчета
с использованием констант равновесия (методически описана так,
как в апробированных учебниках, авторы которых - профессора
МВТУ им. Н.Э. Баумана Г.Б. Синярев, М.В. Добровольский,
В.М. Поляев и другие представители московской
научно-педагогической школы подготовки специалистов по ракетным
двигателям), представляет собой модуль, т. е. этот материал может быть
опущен при изучении дисциплины без ущерба для его
продолжения или рекомендован для самостоятельного изучения.
Далее приводится дидактически переработанный,
опубликованный ранее только в научных изданиях материал, касающийся
непосредственного использования принципа максимума энтропии
в методиках термодинамического расчета. Этот метод разработан
принадлежащими к московской научно-педагогической школе

454 Часть III. Методические указания и КИМ
учеными МВТУ им. Н.Э. Баумана профессорами Г.Б. Синяревым
и Б.Г. Трусовым и представляется наиболее дидактически
обоснованным. Важно, что разработанное профессором Б.Г. Трусовым
реализующее данный метод программное обеспечение
апробировано многолетней практикой, входит в профессиональную
информационную среду разработчиков ракетной техники и
доступно студентам в качестве учебного материала. Это программное
обеспечение будет применяться ими в дальнейшей
профессиональной деятельности как компонент реальной производственной
информационной среды.
Причем если в научной монографии авторы метода и
реализующего его программного комплекса описывали его сущность,
излагая материал по схеме математической дедукции «от
общего к частному», то в учебнике для этих же целей выбрана более
доступная для восприятия студентов индуктивная схема «от
частного к общему». Получены и преобразованы к виду,
удовлетворяющему выбранному методу решения задачи поиска
экстремума (изученный в курсе высшей математики метод
неопределенных множителей Лагранжа), уравнения, составляющие
разрешимую систему. Выбранное из дидактических соображений
топливо «кислород - водород» и условные ограничения на состав
продуктов сгорания позволили привести систему уравнений к виду,
доступному для качественного анализа при выделении не более
трех попарно противодействующих факторов, обеспечивающих
существование оптимума некоторого параметра.
Впервые обоснована методика расчета и анализируется
зависимость условно (термодинамически) оптимального
соотношения компонентов топлива от их температуры (переохлаждение
вплоть до образования «льда» или «шуги» либо подогрев
избыточной теплотой бортовой ядерной электростанции бимодальных
ядерных установок).
Неуниверсальная методика термодинамических расчетов
разложения пероксида водорода и гидразина приводится так, как и в
учебниках представителей казанской научно-педагогической
школы, но в соответствии с атрибутивными признаками
московской школы, т. е. с явным выделением в анализе двух
противоположных тенденций, взаимодействие которых обеспечивает
существование оптимальных режимов работы. Блок глав,
касающихся термодинамических расчетов, завершается анализом
работы газогенераторов при больших различиях соотношения
компонентов и стехиометрического соотношения и представляет

1. Методические указания
455
собой дидактически законченный фрагмент. Это позволяет
провести рубежный контроль 3.
В следующих главах приводятся основы методик
профилирования сопл (в том числе в форме, принятой в Московском
государственном авиационном институте как в одном из
субъектов московской научно-педагогической школы подготовки
специалистов по ракетным двигателям) и учета различия
протекания реальных процессов и их идеального представления
в соответствии с последовательным дискретным дополнением
и усложнением целостной модели изучаемого объекта (агрегата,
процесса).
Известная методика (разработана М.В. Добровольским),
примененная при выводе соотношения, учитывающего радиальную
компоненту вектора скорости в выходном сечении сопла,
дополнена не проводимой ранее оценкой погрешности в результате
замены сферической поверхности плоскостью. Оценку этой
погрешности можно или проводить на лекции, или задавать
студентам для самостоятельного выполнения. При дефиците времени
этот материал может быть опущен.
Коэффициенты, учитывающие потери вследствие наличия
конденсированной фазы при ее относительно малом содержании
в газообразном рабочем теле, вводятся по методике,
разработанной учеными, представляющими казанскую
научно-педагогическую школу (профессора В.П. Глушко, В.Е. Алемасов, А.П. Тишин
и другие).
Методика приближенного профилирования излагается как
задача выбора близкого к оптимальному профиля из семейства
известных профилей, что представляется дидактически более
обоснованным, чем формализованное описание профилирования как
вариационной задачи, которая может рассматриваться в
последующих дисциплинах учебного плана.
Методика учета отрывных течений в сопле при больших
степенях перерасширения потока основывается на
экспериментальных данных, полученных на кафедре «Ракетные двигатели» МГТУ
им. Н.Э. Баумана под руководством профессора В.М. Кудрявцева -
одного из основателей московской научно-педагогической
школы подготовки специалистов по ракетным двигателям. Причем
подробно анализируется только вариант с большим углом
наклона образующей расширяющейся части конического сопла
(более 15°), поскольку влияние угла наклона образующей будет
рассмотрено в последующих учебных курсах (дисциплинах).

456 Часть III. Методические указания и КИМ
Впервые (в виде, позволяющем сравнивать и анализировать)
представлены полные, т. е. включающие все возможные режимы,
высотные и дроссельные характеристики камер. Этот материал
касается дроссельной характеристики многокамерной ракетной
ДУ с автономными двигателями, дросселируемыми по различным
законам изменения расхода топлива. При курсовом
проектировании обращается внимание на практическую применимость
рассчитанных полных характеристик для определения возможности
испытания двигателей в условиях стенда и требуемых параметров
вакуумирующих агрегатов.
Основы профилирования штыревого и тарельчатого сопл
излагаются без использования специальных теорем стереометрии,
что при сохранении корректности вывода обеспечивает большую
доступность материала, изучение которого завершает
дидактически законченный фрагмент. Его усвоение целесообразно
завершить проведением рубежного контроля 4.
Приведенный в разд. 3 материал может быть использован для
итогового контроля усвоения материала части II дисциплины
методом зачета по билетам.
Содержание последних глав учебника - проблемная
постановка актуальных, но не решенных пока задач теории тепловых
ракетных двигателей с учетом как достижений собственно
ракетного двигателестроения, так и его научной базы.
1.3. Состав контрольно-измерительных материалов
и курсовых заданий
Приведенные материалы для курсового задания, рубежного
контроля и курсового проектирования ориентированы на деятель-
ностные методики обучения. Такая направленность выражается
в получении обучающимся совокупности знаний, умений и
навыков, достаточных для понимания и суждения, в презентации
знания, качественного или количественного ответа, в принятии
технического решения, в готовности и способности к усвоению
нового из области будущей профессиональной деятельности.
Примеры для практических (семинарских) занятий приведены
в рекомендуемом сборнике задач и вопросов, где также имеются
ответы или решения. Задания разработаны как инструмент
контроля и самоконтроля усвоения знаний и формирования навыков
их применения в моделируемой профессиональной деятельности,
а также как средство активизации познавательной репродуктивной
и креативной (в идеальном случае - творческой) деятельности.

1. Методические указания
457
Типовые задачи для каждого из предусмотренных четырех
рубежей контроля приведены в настоящем учебнике и,
следовательно, известны студентам еще до начала изучения дисциплины.
Это позволяет проводить тренинг и осуществлять самоконтроль,
придает получаемым знаниям субъектную ценность,
активизирует познавательную деятельность студентов и повышает ее
результативность.
В один вариант входят задания нескольких уровней:
преобразование словесного описания в символьную форму и анализ ее
в качестве модели; анализ типовой ситуации, сводимый к
процедуре попарного сравнения или ранжирования физических
величин; формализация сложной проблемной ситуации, выделение
в ней типовых соотношений и их анализ. При этом допускается
некорректность задачи (избыточность или недостаточность данных),
приближающая ее к творческому уровню, поскольку учебная
деятельность базируется не только на репродуктивной основе
(действия по известным правилам, комбинаторные решения), но и на
субъективно-продуктивной основе (эвристические приемы).
Предлагаемые формулировки вопросов для рубежного
контроля исключают нахождение в учебнике прямых ответов.
Разрешение или запрет пользоваться учебником при прохождении
рубежного контроля наряду с возможностью уменьшать число
вопросов в задании понижает или повышает уровень трудности
заданий для студентов. Изменяя объем задания и время на его
выполнение (от одного до двух академических часов),
преподаватель может адаптировать их к актуальному уровню готовности
студентов.
Все пять заданий одного варианта приблизительно одной
трудности, однако один из четырех вопросов задания объективно
труднее остальных. Текстовая формулировка заданий и вопросов
требует от студента как минимум актуализации приобретенного
тезауруса, усвоение которого особенно важно при изучении
пропедевтических дисциплин. Причем деятельностное содержание
вопроса - обосновать правильность или неправильность каждого
из представленных утверждений либо установить наиболее
точное соответствие между величинами (выразить его одним из
следующих шести знаков: <,=,>, Ф, =^, ^), либо показать
невозможность его однозначной оценки - снижает вероятность
угадывания хотя бы одного правильного ответа до 1/7, что
обеспечивает результатам рубежного контроля достаточную
достоверность. Поскольку предполагается, что вопросы имеют равную

458 Часть III. Методические указания и КИМ
трудность, каждый обоснованный правильный и максимально
точный ответ оценивается одинаковым максимальным баллом,
а правильный, но не мотивированный ответ может оцениваться
1/2 от максимального балла, другими словами, «угадывание»
может расцениваться как проявление формирующейся
профессиональной интуиции. Экспертной корректировкой итоговой
суммарной оценки преподаватель может учесть фактическую
неэквивалентность заданий по трудности и нелинейность шкалы
оценки.
Начиная с рубежного контроля 2, каждый вариант заданий
прямо или косвенно включает вопросы, ответить на которые
можно только с использованием знаний, полученных при изучении
предшествующих глав и тем. Тексты вариантов, представляемых
для рубежного контроля, могут быть составлены как комбинация
неизмененных или незначительно отредактированных заданий из
опубликованных и известных студентам.
В заданиях рубежного контроля 3 и 4 сочетаются как
теоретические, т. е. требующие качественного обоснования, задания,
так и практические вопросы, требующие ответа или в виде
математических выражений, или в числовом виде. При этом
вычисления можно проводить и на калькуляторе. Если у студента есть
возможность в процессе рубежного контроля использовать
компьютер с программой для термодинамических расчетов
(комплексы «Астра-4», «Терра» и т. п.), то задания можно усложнить
дополнительным условием: решить задачу на компьютере и сравнить
полученные на калькуляторе приближенные результаты с
«точными» компьютерными решениями. В учебном процессе более
полно моделируется ситуация актуализации профессиональной
компетентности в современной ракетно-космической отрасли.
Выдача семестрового домашнего задания в первые недели
семестра и известность его содержания формируют дидактический
контекст изучения материала части I дисциплины, т. е. для
студента усвоение нового знания из цели становится средством,
необходимым для выполнения задания, в результате появляется
объективная потребность в новом знании, которое приобретает
субъектную ценность.
Выбранная структура задания позволяет выполнять его
поэтапно и одновременно с изучением дисциплины. При заданном
объеме и трудоемкости задание может быть успешно
выполнено как на калькуляторе, так и с использованием компьютерных
программ для выполнения расчетов и оформления пояснительной

1. Методические указания
459
записки (MathCAD, Microsoft Word и т. п.). Материал,
касающийся камеры с полутепловым соплом, может исключаться из
задания, если соответствующий модуль был изъят из лекционной
части курса.
Выполненное домашнее задание сдается преподавателю на
проверку. Если задание выполнено в полном объеме и без
принципиальных ошибок, то оно допускается к защите. Целью
защиты является выяснение уровня знаний и понимания студентом
примененных методик, его умения аргументировать выбор
формул и методик, а также выявление навыков сравнительной
количественной оценки ожидаемых и полученных результатов
расчета и представления их в графической форме.
Защита домашнего задания состоит в ответе на вопросы
преподавателя по тексту расчетно-пояснительнои записки, а при
необходимости - в решении простых качественных задач,
требующем применения полученных при выполнении домашнего задания
знаний, умений и навыков в качественно новой информационной
ситуации. При этом студент может пользоваться только самой
расчетно-пояснительнои запиской.
Уровень усвоения материала части I дисциплины может быть
оценен также и в форме зачета, вопросы к которому (в виде
билетов) приводятся в разд. 2. Вопросы сформулированы так, что
от студента требуется понимание основных взаимосвязей, в том
числе опосредованных. Причем ответы на такие вопросы не
содержатся в явном виде ни в учебнике, ни в конспекте лекций.
Студентам разрешается пользоваться этими источниками
информации непосредственно при подготовке к ответу.
Когнитивный контекст части II дисциплины задает курсовой
проект «Проектирование и расчет параметров и характеристик
камеры двигателя», моделирующий профессиональную задачу
предпроектной оценки выполнимости технического задания с
использованием прототипа или определения основных параметров
и габаритов ЖРД, отвечающего поставленным требованиям.
Выдача задания на курсовое проектирование на первых занятиях по
изучению теории реального двигателя и выполнение проекта
одновременно с изучением дисциплины создают у студента
мотивацию к изучению нового материала. Примерное оглавление
расчетно-пояснительнои записки к курсовому проекту приведено
в разд. 5.
Требования к структуре, содержанию и методические
указания по выполнению проекта приведены в книге: Дорофеев А.А.

460 Часть III. Методические указания и КИМ
Проектирование и расчет параметров и характеристик камеры
ракетного двигателя: учеб. пособие. 2-е изд., испр. М.: Логос, 2004.
При необходимости материал, приведенный в разд. 3, может
быть использован для итогового контроля усвоения части II
дисциплины методом зачета на основе ответов на вопросы
билетов. При этом вопросы относятся к двигателю, параметры
которого те же, что получены студентом при курсовом
проектировании.
Полный комплект контрольных материалов по дисциплине
(контрольные вопросы и задания к каждой главе, четыре
рубежных контроля, комплекты вопросов к зачетам по обеим частям
курса, курсовое домашнее задание и курсовой проект) позволяет
применять рейтинговую оценку освоения дисциплины в целом,
что может быть дополнено и традиционным экзаменом, комплект
вопросов к которому приведен в разд. 6.
Разработана и апробирована почти двадцатилетней практикой
методика рейтинговой оценки усвоения материала студентами
на основе применения приведенных контрольно-измерительных
материалов (КИМ) и формирования интегрирующей оценки -
показателя рейтинга студента, преобразуемого в традиционную
четырехбалльную итоговую оценку успеваемости по двухсеме-
стровой дисциплине «Общая теория ракетных двигателей»,
программе которой соответствует настоящий учебник. Блочно-мо-
дульная структура программы предусматривает в завершающем
семестре три равнозначных по трудоемкости лабораторных
работы, два рубежных контроля в виде двух письменных
контрольных работ, рассчитанных на один академический час каждая
(см. разд. 3), курсовой проект (см. разд. 5) и экзамен (см. разд. 6).
При этом обязательно сдают экзамен студенты, набравшие
рейтинговую сумму, не достаточную для получения оценки
«удовлетворительно» без сдачи экзамена, или же студенты, желающие
повысить полученную рейтинговую оценку.
Максимальная рейтинговая сумма 100 баллов получается
взвешенным сложением оценок по шести показателям: от 0 до 5
баллов по каждой из трех лабораторных работ; суммы оценок от 0
до 5 за каждую из двух рубежных контрольных работ,
умноженных на весовой коэффициент; оценки за курсовое проектирование
с назначенным весовым коэффициентом.
По выбору преподавателя в зависимости от объективной
сложности вариантов рубежных контрольных работ возможно иное
распределение весовых коэффициентов: равного 4 для оценки

1. Методические указания
461
первого рубежного контроля; 5 - для оценки на втором рубеже
и 8 - для оценки курсового проекта. При этом по каждому из
показателей оценка должна быть зачетной, а граница зачета
определяется преподавателем по результатам проверки всей
совокупности оцениваемых работ.
Установлено, апробировано и рекомендуется следующее
соответствие между рейтинговой суммой S и традиционной оценкой:
«неудовлетворительно» для набравших менее 60 баллов,
«удовлетворительно» при 60 ^ S < 70, «хорошо» при 70 ^ £ ^ 84
и «отлично» для набравших более 84 баллов.
Применение такой рейтинговой методики требует замены
традиционной оценки лабораторной работы по типу
«зачет/незачет» на оценку в баллах, что возможно с достаточной
объективностью в случае, когда задача каждой лабораторной работы
диагностируема и задана студентам в виде совокупности заранее
сообщаемых студентам вопросов, ответы на которые необходимо
включать в защиту выполненной лабораторной работы. Пример
таких вопросов приведен в разд. 9.
Больший удельный вес в рейтинговой сумме оценки по
курсовому проектированию (около 50 %) обусловливает повышенные
требования к методике формирования этой оценки по нескольким
аспектам, как правило, от 5 до 9 баллов. Например, курсовой
проект по настоящей дисциплине целесообразно оценивать не
менее чем по пяти аспектам или позициям:
• по соответствию оформления расчетно-пояснительной
записки, чертежей и иллюстративных материалов действующим
нормативам (ГОСТам, ОСТам, стандартам предприятия и т. п.);
• пониманию студентом особенностей работы комплектующих
агрегатов выбранной схемы газожидкостных систем подачи
компонентов топлива в камеру;
• сущностному соответствию требованиям расчетно-теорети-
ческого обоснования определенных параметров испытания
спроектированного двигателя (на основе анализа рассчитанных и
построенных высотных и/или дроссельных характеристик);
• умению научно обосновывать результаты проектирования
и выявлять на этой базе существенные взаимосвязи режимных
параметров и характеристик рабочих процессов
(преимущественно по материалам к иллюстрации научно-исследовательской
части курсового проекта);
• знанию теоретических основ выполненных базовых газо- и
термодинамических расчетов и умению обосновывать выполнимость

462 Часть III. Методические указания и КИМ
принятых допущений по результатам расчетов (распечаток),
помещенных в расчетно-пояснительнои записке.
При этом на рубежах, когда определяются компоненты
рейтинговой оценки, студенту разрешается пользоваться
собственными протоколами (при защите лабораторной работы),
конспектами лекций (на рубежных контрольных работах), а при защите
курсового проекта - расчетно-пояснительнои запиской к проекту.
Пример типовых вопросов к защите курсового проекта
приведен в разд. 10.

2. Контрольно-измерительные материалы к части I
2.1. Рубежный контроль 1
Общее условие для всех вариантов:
• рассматривается идеальный тепловой ракетный двигатель;
• рабочее тело и топливо одинаковы, т. е. Г*, R Д = idem;
• когда говорится об изменении каких-то параметров,
имеется в виду, что значения остальных параметров, по возможности,
не изменяются, если иное не оговорено специально.
Общее задание для всех вариантов: обосновать правильность
или неправильность каэюдого из представленных утверэюдений
или показать невозможность его однозначной оценки.
Вариант 1/1
1. Увеличение давления в камере сгорания приводит к увеличению:
1.1. Скорости рабочего тела в минимальном сечении сопла.
1.2. Числа Маха в выходном сечении сопла.
1.3. Плотности рабочего тела в критическом сечении сопла.
1.4. Произведения плотности рабочего тела и его скорости
в минимальном сечении сопла.
2. Увеличение площади выходного сечения сопла вызывает:
2.1. Уменьшение плотности рабочего тела в выходном сечении.
2.2. Рост давления в критическом сечении.
2.3. Увеличение разности значений давления в камере
сгорания и в минимальном сечении сопла.
2.4. Снижение температуры рабочего тела в выходном
сечении сопла.
3. Уменьшение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:
3.1. Рост скорости рабочего тела в минимальном сечении сопла.
3.2. Увеличение плотности рабочего тела в камере сгорания.
3.3. Неизменности соотношения давлений в камере сгорания
и в критическом сечении сопла, т. е. рк/ркр = const.
3.4. Снижение температуры рабочего тела в выходном сечении.
4. При увеличении площадей критического сечения и
выходного сечения сопла в 2 раза:

464 Часть III. Методические указания и КИМ
4.1. Скорость истечения увеличится.
4.2. Соотношение давлений в камере сгорания и в выходном
сечении сопла не изменится, т. е. рк/ра = const.
4.3. Разность значений температуры в камере сгорания и в
выходном сечении сопла увеличится.
4.4. Приведенная скорость (коэффициент скорости) Ха в
выходном сечении сопла не изменится.
5. Увеличение диаметра критического сечения сопла в 2 раза
при одновременном уменьшении расхода топлива в 2 раза
вызывает:
5.1. Увеличение давления в камере сгорания.
5.2. Увеличение давления в выходном сечении сопла.
5.3. Снижение скорости истечения.
5.4. Уменьшение числа Маха рабочего тела в выходном
сечении сопла.
Вариант 1/2
1. Увеличение давления в камере сгорания приводит к
увеличению:
1.1. Приведенной скорости рабочего тела (коэффициента
скорости) X в минимальном сечении сопла.
1.2. Температуры рабочего тела в сечении сопла, где число
Маха М = 0,5.
1.3. Плотности рабочего тела в выходном сечении сопла.
1.4. Скорости звука в рабочем теле в критическом сечении
сопла.
2. Увеличение площади выходного сечения сопла приводит к
увеличению:
2.1. Давления в выходном сечении.
2.2. Температуры в выходном сечении сопла.
2.3. Разности значений давления рабочего тела в камере
сгорания и в выходном сечении сопла (рк -ра).
2.4. Числа Маха в выходном сечении сопла.
3. Уменьшение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:
3.1. Неизменность соотношения значений скорости рабочего
тела в выходном сечении сопла и в минимальном сечении
сопла.
3.2. Неизменность соотношения давлений в камере сгорания
и в критическом сечении сопла.

2. Контрольно-измерительные материалы к части I 465
3.3. Уменьшение разности значений температуры рабочего
тела в камере сгорания и в выходном сечении сопла.
3.4. Неизменность скорости рабочего тела в критическом
сечении сопла.
4. При увеличении площадей критического сечения и
выходного сечения сопла в 2 раза:
4.1. Скорость истечения не изменится.
4.2. Соотношение значений плотности рабочего тела в
камере сгорания и в выходном сечении сопла не изменится.
4.3. Разность числа Маха и значения приведенной скорости
(коэффициента скорости) Ха в выходном сечении сопла
может поменять знак.
4.4. Число Маха в выходном сечении сопла не увеличится.
5. Увеличение диаметра критического сечения сопла в 2 раза
при одновременном уменьшении расхода топлива в 2 раза
вызывает:
5.1. Увеличение давления в камере сгорания.
5.2. Изменение давления в выходном сечении сопла.
5.3. Возрастание скорости истечения.
5.4. Изменение температуры рабочего тела в критическом
сечении сопла.
Вариант 1/3
1. Увеличение расхода рабочего тела приводит к увеличению:
1.1. Скорости рабочего тела в выходном сечении сопла.
1.2. Скорости звука в выходном сечении сопла.
1.3. Плотности рабочего тела в критическом сечении сопла.
1.4. Давления рабочего тела в минимальном сечении сопла.
2. Уменьшение площади выходного сечения сопла приводит
к увеличению:
2.1. Давления в выходном сечении сопла.
2.2. Температуры в выходном сечении сопла.
2.3. Разности значений давления в камере сгорания и в
выходном сечении сопла.
2.4. Числа Маха в выходном сечении сопла.
3. Увеличение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:
3.1. Неизменность соотношения скоростей в выходном и в
минимальном сечениях сопла.

466 Часть III. Методические указания и КИМ
3.2. Неизменность значения скорости в минимальном сечении
сопла.
3.3. Увеличение соотношения давлений в камере сгорания
и в выходном сечении сопла.
3.4. Уменьшение разности значений температуры рабочего
тела в камере сгорания и в выходном сечении сопла.
4. При уменьшении диаметров критического сечения и
выходного сечения сопла в 2 раза:
4.1. Соотношение значений плотности рабочего тела в
камере сгорания и выходном сечении сопла не изменится.
4.2. Соотношение давлений в камере сгорания и в
минимальном сечении сопла не изменится.
4.3. Разность значений температуры в камере сгорания и в
минимальном сечении сопла увеличится.
4.4. Скорость истечения уменьшится.
5. При уменьшении диаметра критического сечения сопла в 2 раза
и одновременном уменьшении расхода топлива в 2 раза:
5.1. Давление в камере сгорания не увеличивается.
5.2. Скорость в выходном сечении сопла растет.
5.3. Температура в критическом сечении не снижается.
5.4. Плотность в минимальном сечении сопла увеличивается.
Вариант 1/4
1. Уменьшение расхода топлива приводит к увеличению:
1.1. Скорости рабочего тела в выходном сечении сопла.
1.2. Скорости звука в сечении сопла, где число Маха М = 0,5.
1.3. Плотности рабочего тела в критическом сечении сопла.
1.4. Давления в минимальном сечении сопла.
2. Уменьшение площади выходного сечения сопла вызывает:
2.1. Рост давления в критическом сечении.
2.2. Увеличение разности значений давления в камере
сгорания и в выходном сечении сопла.
2.3. Рост температуры рабочего тела в выходном сечении
сопла.
2.4. Уменьшение плотности рабочего тела в выходном
сечении сопла.
3. Увеличение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:

2. Контрольно-измерительные материалы к части I 467
3.1. Уменьшение давления в камере сгорания.
3.2. Неизменность соотношения давлений в выходом сечении
сопла и в критическом сечении сопла.
3.3. Уменьшение числа Маха рабочего тела в выходном
сечении сопла.
3.4. Увеличение произведения плотности рабочего тела и его
скорости в выходном сечении сопла.
4. При уменьшении площадей критического сечения и
выходного сечения сопла в 2 раза:
4.1. Скорость истечения не увеличится.
4.2. Соотношение температур в камере сгорания и в выходном
сечении сопла не уменьшится.
4.3. Разность числа Маха и значения приведенной скорости
(коэффициента скорости) Ха рабочего тела в выходном
сечении сопла не изменит знак.
4.4. Число Маха в выходном сечении сопла не изменится.
5. Уменьшение диаметра критического сечения сопла в 2 раза при
одновременном снижении расхода топлива в 2 раза вызывает:
5.1. Увеличение давления в критическом сечении сопла.
5.2. Увеличение скорости истечения.
5.3. Уменьшение плотности рабочего тела в выходном
сечении сопла.
5.4. Увеличение числа Маха рабочего тела в выходном
сечении сопла.
Вариант 1/5
1. Уменьшение давления в камере сгорания приводит к
уменьшению:
1.1. Приведенной скорости рабочего тела (коэффициента
скорости) Ха в выходном сечении сопла.
1.2. Плотности рабочего тела в выходном сечении сопла.
1.3. Скорости звука в критическом сечении сопла.
1.4. Температуры рабочего тела в сечении, где число Маха
М= 1.
2. Увеличение площади выходного сечения сопла вызывает
увеличение:
2.1. Температуры рабочего тела в выходном сечении.
2.2. Разности значений температуры в камере сгорания и в
выходном сечении сопла (Тк - Та).
2.3. Скорости истечения.
2.4. Числа Маха в выходном сечении сопла.

468 Часть III. Методические указания и КИМ
3. Уменьшение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:
3.1. Уменьшение давления в камере сгорания.
3.2. Неизменность соотношения значений давления рабочего
тела в выходном сечении сопла и в критическом сечении
сопла, т. е. р /р = const.
7 г а г кр
3.3. Увеличение числа Маха в выходном сечении сопла.
3.4. Увеличение произведения плотности рабочего тела и его
скорости в выходном сечении сопла (pW)a.
4. При уменьшении площадей критического сечения и
выходного сечения сопла в 2 раза:
4.1. Скорость истечения уменьшится.
4.2. Разность значений давления в камере сгорания и в
выходном сечении сопла не изменится, т. е. р*-ра - const.
4.3. Соотношение температур в камере сгорания и в выходном
сечении сопла не изменится, т. е. Т* /Та = const.
4.4. Число Маха в выходном сечении сопла не изменится.
5. При увеличении площади критического сечения сопла в 2 раза
и одновременном увеличении расхода топлива в 2 раза:
5.1. Давление в камере сгорания не увеличивается.
5.2. Разность значений температуры в камере сгорания и в
выходном сечении не изменяется т. е. Г*- Та = const.
5.3. Плотность рабочего тела в минимальном сечении
увеличивается.
5.4. Скорость истечения уменьшается.
Вариант 1/6
1. Увеличение расхода рабочего тела приводит к уменьшению:
1.1. Скорости рабочего тела в минимальном сечении сопла.
1.2. Температуры в выходном сечении сопла.
1.3. Давления рабочего тела в выходном сечении сопла.
1.4. Произведения плотности рабочего тела и его скорости
в выходном сечении сопла.
2. Увеличение площади выходного сечения сопла вызывает:
2.1. Снижение температуры торможения рабочего тела в
выходном сечении сопла.
2.2. Увеличение разности значений температуры в камере
сгорания и в выходном сечении сопла.
2.3. Рост скорости истечения.

2. Контрольно-измерительные материалы к части I 469
2.4. Уменьшение произведения плотности рабочего тела и его
скорости в выходном сечении сопла.
3. Уменьшение площади критического сечения сопла при
неизменности площади его выходного сечения для одного и того
же расхода топлива обусловливает:
3.1. Увеличение плотности рабочего тела в камере сгорания.
3.2. Неизменность отношения давлений в камере сгорания
и в критическом сечении сопла.
3.3. Уменьшение температуры рабочего тела в выходном
сечении сопла.
3.4. Рост скорости рабочего тела в минимальном сечении сопла.
4. При увеличении площадей критического сечения и
выходного сечения сопла в 2 раза:
4.1. Скорость истечения не изменится.
4.2. Соотношение давлений в камере сгорания и в выходном
сечении сопла изменится.
4.3. Разность числа Маха и значения приведенной скорости
(коэффициента скорости) Ха в выходном сечении сопла
не увеличится.
4.4. Приведенная скорость Ха в выходном сечении сопла не
увеличится.
5. Увеличение площади критического сечения сопла в 2 раза при
одновременном уменьшении расхода топлива в 2 раза вызывает:
5.1. Увеличение давления в камере сгорания.
5.2. Уменьшение плотности рабочего тела в выходном
сечении сопла.
5.3. Изменение скорости истечения.
5.4. Изменение скорости рабочего тела в минимальном
сечении сопла.
2.2. Рубежный контроль 2
Вариант 2/1
1. При известной снятой на уровне моря дроссельной
характеристике тяга - расход идеального ракетного двигателя
построить дроссельную характеристику тяга - расход работающей на
уровне моря ДУ, состоящей из трех таких же ракетных
двигателей, дросселируемых до нулевого значения тяги поочередно.
2. При известной снятой в пустоте дроссельной
характеристике тяга - давление в камере идеального ракетного двигателя

470 Часть III. Методические указания и КИМ
построить дроссельную характеристику тяга - расход
работающей в пустоте ДУ, состоящей из трех таких же ракетных
двигателей, дросселируемых до нулевого значения расхода топлива
поочередно.
3. Идеальный РДТТ с зарядом ТРТ с постоянной площадью
горящей поверхности регулируется уменьшением критического
сечения сопла в 2 раза при неизменности площади выходного сечения.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения ТРТ v ~ 0,5.
3.1. Как изменится тяга?
3.2. Как изменится пустотный удельный импульс?
3.3. Как изменится удельный импульс?
3.4. Как изменится скорость истечения?
3.5. Как изменится скорость в минимальном сечении сопла?
4. Идеальный тепловой ЯРД работает на двух режимах. На
первом режиме температура торможения рабочего тела -
молекулярного водорода - перед соплом равна 2 000 К.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при переходе на второй режим, на котором
не изменяется расход рабочего тела, а температура торможения
рабочего тела увеличивается в 2 раза, причем 50 % водорода
переходит в атомарное состояние при неизменности значения
показателя адиабаты рабочего тела?
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Давление перед соплом.
4.2. Температура в критическом сечении.
4.3. Скорость истечения.
4.4. Пустотный удельный импульс.
4.5. Тяга двигателя.
Вариант 2/2
1. При известной снятой в пустоте дроссельной
характеристике тяга - расход идеального ракетного двигателя построить
дроссельную характеристику тяга - расход работающей в
пустоте ДУ, состоящей из трех таких же ракетных двигателей,
дросселируемых до нулевого значения тяги поочередно.
2. При известной снятой на уровне моря дроссельной
характеристике тяга - давление в камере идеального ракетного двига-

2. Контрольно-измерительные материалы к части I 471
теля построить дроссельную характеристику тяга - расход
работающей в пустоте ДУ, состоящей из трех таких же ракетных
двигателей, дросселируемых до нулевого значения расхода
топлива поочередно.
3. В идеальном РДТТ площадь горящей поверхности заряда
ТРТ уменьшается в 2 раза.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения ТРТ v ~ 0,5.
3.1. Как изменится тяга?
3.2. Как изменится пустотный удельный импульс?
3.3. Как изменится удельный импульс?
3.4. Как изменится расход топлива?
3.5. Как изменится скорость истечения?
4. Идеальный тепловой ЯРД работает на двух режимах. На
первом режиме температура торможения рабочего тела -
молекулярного водорода - перед соплом равна 2 000 К.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при переходе на второй режим, на котором
не изменяется расход рабочего тела, а температура торможения
рабочего тела увеличивается в 2 раза, причем 100 % водорода
переходит в атомарное состояние при неизменности значения
показателя адиабаты?
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Пустотная тяга.
4.2. Давление в критическом сечении сопла.
4.3. Температура в выходном сечении сопла.
4.4. Удельный импульс.
4.5. Скорость в минимальном сечении сопла.
Вариант 2/3
1. При известной снятой в пустоте дроссельной
характеристике тяга - расход идеального ракетного двигателя построить
дроссельную характеристику тяга - расход работающей на
уровне моря ДУ, состоящей из трех таких же ракетных двигателей,
дросселируемых до нулевого значения тяги поочередно.
2. При известной снятой на уровне моря дроссельной
характеристике тяга - давление в камере идеального ракетного двига-

472 Часть III Методические указания и КИМ
теля построить дроссельную характеристику тяга - расход
работающей в пустоте ДУ, состоящей из трех таких же ракетных
двигателей, дросселируемых до нулевого значения расхода
топлива поочередно.
3. В идеальном РДТТ площадь горящей поверхности заряда
ТРТ за время работы увеличивается в 2 раза.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения ТРТ v ~ 0,5.
3.1. Как изменится тяга?
3.2. Как изменится пустотный удельный импульс?
3.3. Как изменится удельный импульс?
3.4. Как изменится расход топлива?
3.5. Как изменится скорость в выходном сечении сопла?
4. Система регулирования идеального теплового ЯРД
поддерживает постоянную температуру рабочего тела на входе в сопло.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при замене рабочего тела - молекулярного
водорода Н2 (ц ~ 2) - гелием Не (ц - 4) при неизменности
расхода и значения показателя адиабаты?
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Пустотная тяга.
4.2. Давление в критическом сечении.
4.3. Температура в выходном сечении.
4.4. Удельный импульс.
4.5. Скорость в минимальном сечении сопла.
Вариант 2/4
1. При известной снятой на уровне моря дроссельной
характеристике тяга - расход идеального ракетного двигателя
построить дроссельную характеристику тяга - расход работающей в
пустоте ДУ, состоящей из трех таких же ракетных двигателей,
дросселируемых до нулевого значения тяги поочередно.
2. При известной снятой в пустоте дроссельной
характеристике тяга - давление в камере идеального ракетного двигателя
построить дроссельную характеристику тяга - расход
работающей в пустоте ДУ, состоящей из трех таких же ракетных
двигателей, дросселируемых до нулевого значения расхода
топлива поочередно.

2. Контрольно-измерительные материалы к части I 473
3. В идеальном РДТТ с двухсоставным зарядом ТРТ
торцового горения последовательно установленные друг за другом
полузаряды выполнены из ТРТ, законы горения которых различаются
только отношением сомножителей 1 : 2, учитывающим влияние
начальной температуры, а продукты сгорания имеют одинаковый
состав и температуру. Причем полузаряды имеют одинаковую
начальную температуру, а ближе к соплу установлен полузаряд
с меньшей скоростью горения, чем у другого полузаряда.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения ТРТ v - 0,5.
3.1. Как за время работы изменится тяга?
3.2. Как при этом изменится пустотный удельный импульс?
3.3. Как при этом изменится удельный импульс?
3.4. Как за время работы изменится расход продуктов сгорания?
3.5. Как за время работы изменится скорость в выходном
сечении сопла?
4. При работе идеального теплового ЯРД используется в
качестве рабочего тела гелий Не (ц - 4). Причем при увеличении
расхода рабочего тела на 10 % температура торможения
рабочего тела на входе в сопло уменьшается в 1,21 раза.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при переходе на режим увеличенного
расхода рабочего тела, если справедливо допущение о неизменности
значения показателя адиабаты?
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Статическое давление в сечении сопла, где число Маха
М = 0,5.
4.2. Температура в выходном сечении сопла.
4.3. Скорость в критическом сечении сопла.
4.4. Пустотный удельный импульс.
4.5. Внутренняя составляющая тяги двигателя.
Вариант 2/5
1. При известной снятой в пустоте дроссельной
характеристике тяга - расход идеального ракетного двигателя построить
дроссельную характеристику тяга - расход работающей на
уровне моря ДУ, состоящей из трех таких же ракетных двигателей,
дросселируемых до нулевого значения тяги поочередно.

474 Часть III. Методические указания и КИМ
2. При известной, снятой на уровне моря дроссельной
характеристике тяга - давление в камере идеального ракетного
двигателя построить дроссельную характеристику тяга - расход
работающей на уровне моря ДУ, состоящей из трех таких же
ракетных двигателей, дросселируемых до нулевого значения
тяги поочередно.
3. В идеальном РДТТ с двухсоставным зарядом ТРТ
торцового горения последовательно установленные друг за другом
полузаряды выполнены из ТРТ, законы горения которых отличаются
только относящимися как 1 : 2 сомножителями, учитывающими
влияние начальной температуры. Причем ближе к соплу
установлен полузаряд с большей скоростью горения, чем у другого
полузаряда.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения v ~ 0,5.
3.1. Как за время работы изменится тяга?
3.2. Как при этом изменится пустотный удельный импульс?
3.3. Как при этом изменится удельный импульс?
3.4. Как за время работы изменится секундный расход топлива?
3.5. Как за время работы изменится скорость истечения?
4. При работе идеального теплового ЯРД используется в
качестве рабочего тела молекулярный водород Н2 (ц ~ 2). Причем
при уменьшении расхода рабочего тела в 1,21 раза температура
торможения рабочего тела на входе в сопло увеличивается на
21 % и водород сохраняет молекулярное состояние.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при переходе на режим уменьшенного
расхода рабочего тела, если справедливо допущение о неизменности
значения показателя адиабаты?
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Пустотная тяга.
4.2. Пустотный удельный импульс.
4.3. Число Маха в выходном сечении сопла.
4.4. Давление в критическом сечении сопла.
4.5. Давление в выходном сечении сопла.

2. Контрольно-измерительные материалы к части I 475
Вариант 2/6
1. При известной снятой в пустоте дроссельной
характеристике тяга - расход идеального ракетного двигателя построить
дроссельную характеристику тяга - расход работающей на
уровне моря ДУ, состоящей из трех таких же ракетных двигателей,
дросселируемых до нулевого расхода топлива поочередно.
2. При известной снятой на уровне моря дроссельной
характеристике тяга - давление в камере идеального ракетного
двигателя построить дроссельную характеристику тяга - расход
работающей на уровне моря ДУ, состоящей из трех таких же
ракетных двигателей, дросселируемых до нулевого значения
тяги поочередно.
3. Идеальный РДТТ с зарядом ТРТ с постоянной площадью
горящей поверхности регулируется одновременным увеличением
в 2 раза площадей минимального и выходного сечений сопла.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или докажите невозможность
однозначного ответа, если показатель в законе горения ТРТ v ~ 0,5.
3.1. Как изменится тяга?
3.2. Как изменится удельный импульс?
3.3. Как изменится пустотный удельный импульс?
3.4. Как изменится расход топлива?
3.5. Как изменится скорость в выходном сечении сопла?
4. Система регулирования идеального теплового ЯРД
поддерживает постоянной температуру торможения рабочего тела
на входе в сопло.
Как изменятся (или не изменятся) некоторые параметры
(п. 4.1-4.5) двигателя при замене рабочего тела - молекулярного
водорода Н2 (ц, ~ 2) - гелием Не (ц - 4), если при этом расход
рабочего тела не изменится, а влиянием различий в значениях
показателей адиабаты можно пренебречь.
Дайте обоснованный ответ на поставленный вопрос с
максимально возможной точностью или покажите невозможность
однозначного ответа:
4.1. Давление торможения на входе в сопло.
4.2. Тяга двигателя.
4.3. Пустотный удельный импульс.
4.4. Температура в минимальном сечении сопла.
4.5. Скорость истечения.

476 Часть III. Методические указания и КИМ
2.3. Вопросы к зачету по части I
Билет № 1. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 2. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 3. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
•/y.nl
fy.pl
к.р!

2. Контрольно-измерительные материалы к части I 477
Билет № 4. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 5. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза площадями
критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 6. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза площадями
критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 7. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза площадями
критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.

478 Часть III. Методические указания и КИМ
Билет № 8. Дроссельные характеристики
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза площадями
критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 9. Дроссельные характеристики
Камеры идеальных ЖРД 1 и ЖРД 2 идентичны,
но двигатели работают на разных топливах при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)r
Билет № 10. Дроссельные характеристики
Камеры идеальных ЖРД 1 и ЖРД 2 идентичны,
но двигатели работают на разных топливах при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)y
Билет №11. Дроссельные характеристики
Камеры идеальных ЖРД 1 и ЖРД 2 идентичны,
но двигатели работают на разных топливах при
одном и том же давлении окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2{RKT*)y
Л
'y.pl
-/y.nl
/VPi

2. Контрольно-измерительные материалы к части I 479
Билет № 12. Дроссельные характеристики
Камеры идеальных ЖРД 1 и ЖРД 2
идентичны, но двигатели работают на разных то-
пливах при одном и том же давлении
окружающей среды.
При известной дроссельной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)y
Билет № 13. РД с РИТ. Высотная характеристика
Известна высотная характеристика РД с РИТ.
При работе используется на первом режиме в
качестве рабочего тела гелий (на рисунке графики
удельного импульса и тяги совпадают). При
работе на втором режиме в качестве рабочего тела
используется водород, а система регулирования
поддерживает постоянными температуру и
давление торможения на входе в сопло.
Построить высотную характеристику этого
двигателя, работающего на втором режиме.
Билет № 14. РД с РИТ. Высотная характеристика
Известна высотная характеристика РД с РИТ,
использующего на первом режиме гелий в
качестве рабочего тела (см. рисунок). При работе
на втором режиме в качестве рабочего тела
используется водород, а система регулирования
поддерживает постоянными температуру и
давление торможения на входе в сопло.
Построить высотную характеристику этого
двигателя, работающего на втором режиме.

480 Часть III. Методические указания и КИМ
= 1у
У1
0 Д
Лр1
Билет № 15. РД с РИТ. Высотная характеристика
Известна высотная характеристика РД с РИТ,
использующего на первом режиме гелий в
качестве рабочего тела (на рисунке графики
удельного импульса и тяги совпадают). При работе
на втором режиме в качестве рабочего тела
используется водород, а система регулирования
поддерживает постоянными расход рабочего тела
и температуру торможения на входе в сопло.
Построить высотную характеристику этого
двигателя, работающего на втором режиме.
Билет № 16. РД с РИТ. Высотная характеристика
Известна высотная характеристика РД с РИТ,
использующего на первом режиме гелий в
качестве рабочего тела (см. рисунок). При работе
на втором режиме в качестве рабочего тела
используется водород, а система регулирования
поддерживает постоянными расход рабочего тела
и температуру торможения на входе в сопло.
Построить высотную характеристику этого
двигателя, работающего на втором режиме.
Билет № 17. Высотная характеристика РДТТ
Два РДТТ с зарядами ТРТ с постоянной
площадью горящей поверхности различаются
только площадью критического сечения сопла,
причем FKp2 = 0,5FKpl.
Построить высотные характеристики
второго РДТТ, если характеристики первого РДТТ
известны (см. рисунок).
Билет № 18. Высотная характеристика РДТТ
Два РДТТ с зарядами ТРТ с постоянной
площадью горящей поверхности различаются
только площадью выходного сечения сопла, причем
FKP2 = 0,5FKpV
Построить высотные характеристики
второго РДТТ, если характеристики первого РДТТ
известны (см. рисунок).

2. Контрольно-измерительные материалы к части I 4%\_
Билет № 19. Высотная характеристика РДТТ
Два РДТТ с зарядами ТРТ с постоянной
площадью горящей поверхности различаются
только площадями критического и выходного
сечений сопла, причем FKp2 = 0,5FKpl и Fa2 = 0,5FaV
Построить высотные характеристики
второго РДТТ, если характеристики первого РДТТ
известны (см. рисунок).
Билет № 20. Высотная характеристика РДТТ
Два РДТТ с зарядами ТРТ с постоянной
площадью горящей поверхности различаются
только площадями критического и выходного
сечений сопла, причем FKp2 = 0,5,Ркр1 и Fa2 = 0,5FaV
Построить высотные характеристики
второго РДТТ, если характеристики первого РДТТ
известны (см. рисунок).
Билет № 21. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 22. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.

482 Часть III. Методические указания и КИМ
Билет № 23. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 24. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенной в 2 раза площадью
критического сечения. Двигатели работают на
одном и том же топливе при одном и том же
расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 25. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза
площадями критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе
при одном и том же давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 26. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза
площадями критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе
при одном и том же давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.

2. Контрольно-измерительные материалы к части I 483
Билет № 27. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза
площадями критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе
при одном и том же расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 28. Высотная характеристика
Идеальный ЖРД 2 отличается от идеального
ЖРД 1 только уменьшенными в 2 раза
площадями критического и выходного сечений сопла.
Двигатели работают на одном и том же топливе
при одном и том же расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2.
Билет № 29. Высотная характеристика
Камеры идеальных ЖРД 1 и ЖРД 2
идентичны, но двигатели работают на разных топливах
при одном и том же давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)V
Билет № 30. Высотная характеристика
Камеры идеальных ЖРД 1 и ЖРД 2
идентичны, но двигатели работают на разных топливах
при одном и том же давлении в камере.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)r

484 Часть III. Методические указания и КИМ
Билет №31. Высотная характеристика
Камеры идеальных ЖРД 1 и ЖРД 2
идентичны, но двигатели работают на разных топливах
при одном и том же расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)V
Билет № 32. Высотная характеристика
Камеры идеальных ЖРД 1 и ЖРД 2
идентичны, но двигатели работают на разных топливах
при одном и том же расходе топлива.
При известной высотной характеристике
ЖРД 1 (см. рисунок) построить такую же
характеристику ЖРД 2, если при одинаковом
показателе адиабаты (RKT*)2 = 2(RKT*)V

3. Контрольно-измерительные материалы к части II
3.1. Рубежный контроль 3
Вариант 3/1
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. При постоянном соотношении компонентов тяга
двигателя в пустоте изменяется почти линейно по отношению
к давлению в камере при постоянной геометрической
степени расширения сопла.
1.2. С ростом давления в камере для заданной степени
расширения в сопле при постоянном коэффициенте избытка
окислителя удельный импульс в пустоте увеличивается.
1.3. С увеличением давления в камере температура
торможения возрастает.
Какие из этих выводов верны?
2. Чем объясняется увеличение степени диссоциации
продуктов сгорания с увеличением температуры путем подвода теплоты?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
с катализатором имеет вид 3N2H4 = 2NH3 + 3H2 + 2N2
Рассчитайте парциальные давления образовавшихся газов,
если давление в камере разложения равно 10 МПа.
4. Определите теоретически необходимое количество
окислителя и Кт0 для топлива «НДМГ - АК-35», если за 1 с сгорает
7 кг НДМГ. Содержанием воды в окислителе пренебречь.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «кислород -
водород» при а = 5,0 ирк = 15 МПа.

486 Часть III. Методические указания и КИМ
Вариант 3/2
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. При постоянном соотношении компонентов тяга
двигателя в пустоте изменяется линейно по отношению к
расходу топлива при постоянной геометрической степени
расширения сопла.
1.2. С увеличением расхода топлива для заданной степени
расширения газа в сопле при постоянном коэффициенте
избытка окислителя удельный импульс в пустоте
увеличивается.
1.3. С увеличением расхода топлива температура торможения
на входе в сопло возрастает.
Какие из этих выводов верны?
2. Чем объясняется снижение степени диссоциации продуктов
сгорания при движении по соплу?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
4 1
с катализатором имеет вид N2H4 = - NH3 + - N2
Рассчитайте парциальные давления образовавшихся газов,
если давление в камере разложения равно 1 МПа.
4. Определите теоретически необходимое количество
окислителя и Кт0 для топлива «НДМГ - АК-27», если за 1 с сгорает
7 кг НДМГ. Содержанием воды в окислителе можно пренебречь.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «пероксид
водорода - водород» при а = 0,1 ирк = 15 МПа.
Вариант 3/3
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. Тяга двигателя с постоянной геометрической степенью
расширения сопла, определенная для соответствующего
каждому расходу расчетного режима, изменяется
линейно по отношению к расходу.

3. Контрольно-измерительные материалы к части II 487
1.2. С увеличением расхода для заданной степени расширения
газа в сопле удельный импульс в пустоте увеличивается.
1.3. С увеличением расхода температура торможения на
входе в сопло возрастает.
Какие из этих выводов верны?
2. Чем объясняется снижение степени диссоциации продуктов
сгорания при увеличении давления в камере?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
с катализатором имеет вид 3N2H4 = 2NH3 + 3H2 + 2N2
Рассчитайте степень разложения аммиака.
4. Определите теоретически необходимое количество
окислителя - кислорода - и Кт0 для горючего, представляющего собой
смесь равных по массе частей гидразина и НДМГ, если за 1 с
сгорает ЮкгНДМГ.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «тетраоксид
азота - жидкий водород» при а = 0,1 ирк = 15 МПа.
Вариант 3/4
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. Тяга двигателя с постоянной степенью расширения газа
в сопле, определенная для соответствующего каждому
давлению расчетного режима, изменяется линейно по
отношению к расходу.
1.2. С ростом давления для заданной геометрической степени
расширения сопла удельный импульс в пустоте увеличивается.
1.3. С увеличением давления в камере температура
торможения на входе в сопло возрастает.
Какие из этих выводов верны?
2. Чем объясняется увеличение степени диссоциации
продуктов сгорания в камере при дросселировании (уменьшении
расхода топлива) идеального ЖРД?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
4 1
с катализатором имеет вид N2H4 = - NH3 + - N2
Рассчитайте степень разложения аммиака.

488 Часть III. Методические указания и КИМ
4. Определите теоретически необходимое количество
окислителя - тетраоксида азота N204 - для горючего,
представляющего собой смесь равных по массе частей гидразина и НДМГ
(C2H3)2N2H2, если за 1 с сгорает 7 кг топлива.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «тетраоксид
азота - жидкий водород» при а = 5,0 и/?к = 15 МПа.
Вариант 3/5
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. При постоянном давлении в камере удельный импульс
в пустоте увеличивается при увеличении геометрической
степени расширения сопла.
1.2. С ростом давления в камере для заданной степени
расширения газа в сопле температура потока в выходном
сечении сопла снижается.
1.3. С увеличением давления в камере работоспособность
продуктов сгорания (произведение RT) в выходном
сечении камеры сгорания возрастает.
Какие из этих выводов верны?
2. Чем объясняется снижение массового содержания
продуктов полного окисления углерода при движении по соплу
продуктов сгорания топлива «керосин - кислород»?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
с катализатором имеет вид 3N2H4 = 2NH3 + 3H2 + 2N2
Рассчитайте массовые доли образовавшихся газов, если
давление в камере разложения равно 1 МПа.
4. Определите теоретически необходимое количество воды
как окислителя и Кт0 для горючего в виде сплава равных по
массе частей алюминия и магния, если за 1 с сгорает 7 кг горючего.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «пероксид
водорода - водород» при а = 5,0 и рк = 15 МПа.

3. Контрольно-измерительные материалы к части II 489
Вариант 3/6
1. По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделаны выводы:
1.1. Закономерность изменения тяги двигателя в пустоте
отклоняется от линейной по отношению к давлению в
камере при постоянной геометрической степени расширения
сопла.
1.2. Закон изменения пустотного удельного импульса в
зависимости от расхода отличается от линейного при
постоянной степени расширения газа в сопле.
1.3. С увеличением расхода топлива кажущаяся
молекулярная масса продуктов сгорания на входе в сопло
уменьшается.
Обоснуйте правильность или ошибочность каждого вывода.
2. Чем объясняется увеличение степени диссоциации
продуктов сгорания с приближением к стехиометрическому
соотношению компонентов топлива «газообразные водород и кислород при
нормальных условиях»?
3. В двигателе малой тяги, работающем на гидразине,
суммарная экзотермическая реакция разложения при взаимодействии
с катализатором имеет вид 3N2H4 = 4NH3 + N2
Рассчитайте объемные доли образовавшихся газов, если
давление в камере разложения равно 1 МПа.
4. Определите теоретически необходимое количество
окислителя - 25 % (масс.) раствора воды в пероксиде водорода - и Кт0
для горючего - абсолютного этилового спирта, если за 1 с
сгорает 7 кг горючего.
5. Напишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «кислород -
водород» при а = 5,0 и рк = 15 МПа.

490 Часть III. Методические указания и КИМ
Вопросы для студентов,
не получивших зачет на рубежном контроле 3
Вопрос 3/1
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении его компонентов
с учетом диссоциации сделан вывод: при постоянном давлении
в камере удельный импульс в пустоте растет при увеличении
геометрической степени расширения сопла.
Запишите файл исходных данных для количественного
обоснования справедливости этого вывода с помощью
программного комплекса «Астра» и теоретически обоснуйте его.
Вопрос 3/2
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении его компонентов
с учетом диссоциации сделан вывод: с ростом расхода топлива
для заданной степени расширения газа в сопле температура
потока на входе в сопло увеличивается.
Запишите файл исходных данных для количественного
обоснования справедливости этого вывода с помощью
программного комплекса «Астра» и дайте теоретическое объяснение этому
выводу.
Вопрос 3/3
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении его компонентов с
учетом диссоциации сделан вывод: при двукратном уменьшении
пустотной тяги камеры кажущаяся молекулярная масса продуктов
сгорания в выходном сечении камеры сгорания уменьшится.
Запишите файл исходных данных для количественного
обоснования справедливости этого вывода с помощью
программного комплекса «Астра» и дайте теоретическое объяснение этому
выводу.
Вопрос 3/4
Чем объясняется увеличение температуры в камере сгорания
ЖРД при синхронном увеличении в 2 раза расходов газообразных
кислорода и водорода?
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

3. Контрольно-измерительные материалы к части II 491
Вопрос 3/5
Чем объясняется снижение температуры в камере сгорания
ЖРД при синхронном уменьшении в 2 раза расходов газообразных
кислорода и водорода?
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/6
Чем объясняется снижение температуры в камере сгорания
ЖРД при уменьшении в 2 раза расхода газообразного кислорода
и сохранении расхода водорода?
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/7
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- скорость истечения;
- пустотный удельный импульс.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/8
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- объемная доля кислорода в рабочем теле на входе в сопло;
- массовая доля кислорода в рабочем теле на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

492 Часть III. Методические указания и КИМ
Вопрос 3/9
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- объемная доля кислорода в рабочем теле в выходном
сечении сопла;
- массовая доля кислорода в рабочем теле в выходном сечении
сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/10
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- объемная доля водяного пара в рабочем теле на входе
в сопло;
- массовая доля водяного пара в рабочем теле на входе
в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/11
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- массовая доля водяного пара в рабочем теле в выходном
сечении сопла;
- массовая доля водяного пара в рабочем теле на входе
в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

3. Контрольно-измерительные материалы к части II 493
Вопрос 3/12
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- температура рабочего тела на входе в сопло;
- температура рабочего тела в выходном сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/13
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменились
(увеличились, уменьшились, не изменились или недостаточно
данных для суждения):
- кажущаяся молекулярная масса рабочего тела на входе
в сопло;
- кажущаяся молекулярная масса рабочего тела в выходном
сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/14
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидкого аммиака и продуктов разложения
пероксида водорода.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/15
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких аммиака и пероксида водорода.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».

494 Часть III. Методические указания и КИМ
Вопрос 3/16
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидкого кислорода и продуктов разложения
гидразина.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/17
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких кислорода и гидразина.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/18
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких кислорода и абсолютного этилового
спирта.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/19
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = ОД и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/20
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = 1,0 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/21
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = 10 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».

3. Контрольно-измерительные материалы к части II 495
Вопрос 3/22
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при Кт ~ 0,14 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/23
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при Кт ~ 1,4 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/24
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при Кт ~ 14 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/25
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделан вывод: при постоянном давлении в
камере удельный импульс в пустоте растет при увеличении
геометрической степени расширения сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра» и дайте теоретическое объяснение этому выводу.
Вопрос 3/26
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов с
учетом диссоциации сделан вывод: с ростом расхода топлива для
заданной степени расширения газа в сопле температура потока
на входе в сопло увеличивается.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра» и дайте теоретическое объяснение этому выводу.

496 Часть III. Методические указания и КИМ
Вопрос 3/27
По результатам термодинамических расчетов процесса
сгорания топлива при постоянном соотношении компонентов
с учетом диссоциации сделан вывод: при двукратном
уменьшении пустотной тяги камеры кажущаяся молекулярная масса
продуктов сгорания в выходном сечении камеры сгорания
уменьшится.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра» и теоретически обоснуйте его.
Вопрос 3/28
Чем объясняется увеличение температуры в камере сгорания
ЖРД при синхронном увеличении в 2 раза расходов газообразных
кислорода и водорода?
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/29
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) скорость истечения.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/30
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменился
(увеличился, уменьшился, не изменился или недостаточно данных
для суждения) пустотный удельный импульс.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

3. Контрольно-измерительные материалы к части II 497
Вопрос 3/31
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) объемная доля кислорода в рабочем теле
на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/32
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) массовая доля кислорода в рабочем теле
на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/33
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) объемная доля кислорода в рабочем теле
в выходном сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/34
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) массовая доля кислорода в рабочем теле
в выходном сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

498 Часть III. Методические указания и КИМ
Вопрос 3/35
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) объемная доля водяного пара в рабочем
теле на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/36
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) объемная доля водяного пара в рабочем
теле на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/37
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) массовая доля водяного пара в рабочем
теле в выходном сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/38
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) массовая доля водяного пара в рабочем
теле на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

3. Контрольно-измерительные материалы к части II 499
Вопрос 3/39
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) температура рабочего тела на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/40
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) температура рабочего тела в выходном
сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/41
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) кажущаяся молекулярная масса рабочего
тела на входе в сопло.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».
Вопрос 3/42
В ЖРДМТ, работающем в пустоте на продуктах
каталитического разложения пероксида водорода, при переходе с 50 %-ного
раствора пероксида водорода в воде на 75 %-ный изменилась
(увеличилась, уменьшилась, не изменилась или недостаточно
данных для суждения) кажущаяся молекулярная масса рабочего
тела в выходном сечении сопла.
Запишите файл исходных данных для количественного
обоснования ответа на этот вопрос с помощью программного
комплекса «Астра».

500 Часть III. Методические указания и КИМ
Вопрос 3/43
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидкого аммиака и продуктов разложения
пероксида водорода.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/44
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких аммиака и пероксида водорода.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/45
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидкого кислорода и продуктов разложения
гидразина.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/46
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких кислорода и гидразина.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/47
Определите теоретически необходимое соотношение
подаваемых в камеру ЖРД жидких кислорода и абсолютного этилового
спирта.
Запишите файл исходных данных для расчета этого
соотношения с помощью программного комплекса «Астра».
Вопрос 3/48
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = 0,1 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».

3. Контрольно-измерительные материалы к части II 501
Вопрос 3/49
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = 1,0 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
Вопрос 3/50
Запишите систему уравнений для приближенного
термодинамического расчета процесса сгорания топлива «жидкий
кислород - жидкий аммиак» при а = 10 и давлении в камере,
практически исключающем термическую диссоциацию.
Запишите файл исходных данных для расчета с
использованием программного комплекса «Астра».
3.2. Рубежный контроль 4
Вариант 4/1
1. При работе ракетного двигателя во время движения
летательного аппарата из стратосферы до уровня моря при постоянном
давлении в камере площадь выходного сечения сопла
изменяется так, что на всех высотах ра =phn течение рабочего тела в сопле
одномерное безотрывное с постоянной звуковой скоростью в
минимальном сечении.
Получите расчетное соотношение для тяги двигателя в
зависимости от ph.
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одном и том же давлении в
изобарной камере, и с соплами, имеющими одинаковые
геометрические степени расширения, развивают в пустоте различающиеся
в ТУраз тяги.
Для этих двигателей получите соотношения диаметров
критических сечений.
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющейся части
сопла дополнили дорасширительным коническим насадком с тем же
углом наклона образующей.
Как изменились (увеличились, уменьшились, не изменились
или для ответа недостаточно данных) при этом абсолютные
потери удельного импульса (тяги) на трение?

502 Часть III. Методические указания и КИМ
4. Некоторый исходный идеальный ЖРД (фк = фс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 500 м/с
при коэффициенте пустотной тяги Ктп = 1,85. При подаче 20 %
окислителя в периферийную часть камеры, занимающую 10 % ее
проходного сечения, при неизменности равномерного
распределения горючего по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,05 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз изменилась пустотная тяга, если суммарный
расход топлива, коэффициент пустотной тяги и размеры
двигателя не изменились?
5. Два двигателя работают на одном и том же топливе при
одном и том же давлении в камере, но по разным схемам: а) без
дожигания (схема жидкость - жидкость); б) с дожиганием (схема
газ - газ).
Укажите соотношение значений необходимого времени
пребывания топлива в камере.
Вариант 4/2
1. При работе ракетного двигателя во время движения
летательного аппарата из стратосферы до уровня моря при постоянном
давлении в камере площадь выходного сечения сопла
изменяется так, что на всех высотах pa=ph и течение в сопле одномерное
безотрывное с постоянной звуковой скоростью в минимальном
сечении.
Получите расчетное соотношение для удельного импульса
двигателя в зависимости от значения/?Л.
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одном и том же давлении в
изобарной камере, сопла имеют одинаковые геометрические
степени расширения и развивают в пустоте различающиеся в N раз
тяги.
Для этих двигателей получите соотношения площадей
критических сечений.
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющейся части
сопла дополнили дорасширительным коническим насадком с тем же
углом наклона образующей.

3. Контрольно-измерительные материалы к части II 503
Как изменился (увеличился, уменьшился, не изменился или
для ответа недостаточно данных) при этом коэффициент сопла,
учитывающий потери удельного импульса на трение вследствие
неодномерности течения в выходном сечении сопла с радиальной
скоростью?
4. Некоторый исходный идеальный ЖРД (срк = фс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 200 м/с
при коэффициенте пустотной тяги Ктп = 1,85. При подаче 15 %
окислителя в периферийную часть камеры, занимающую 10 % ее
проходного сечения, при неизменности равномерного
распределения горючего по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,05 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз изменился пустотный импульс, если осталились
неизменными расходы компонентов топлива, размеры двигателя
и значение К ?
т.п
5. Двигатели работают на одном и том же топливе при одном
и том же расходе, но по разным схемам: а) без дожигания (схема
жидкость - жидкость); б) с дожиганием (схема газ - газ).
Укажите соотношение реализуемых значений условного
времени пребывания при одинаковом объеме практически изобарных
камер этих ЖРД.
Вариант 4/3
1. При движении летательного аппарата с ракетным
двигателем из стратосферы до уровня моря при постоянном давлении
в камере площадь выходного сечения сопла изменяется так, что
на всех высотах ра = ph и течение в сопле одномерное
безотрывное с постоянной звуковой скоростью в минимальном сечении.
Получите расчетное соотношение для минимального
удельного импульса, развиваемого двигателем при таких условиях.
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одинаковом давлении в камере
и имеющие геометрически подобные контуры сопл, развивают
в пустоте различающиеся в N раз тяги.
Для этих двигателей получите соотношения диаметров
выходных сечений сопл.
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющейся части сопла

504 Часть III. Методические указания и КИМ
дополнили дорасширительным коническим насадком с тем же
углом наклона образующей.
Как изменилась (увеличилась, уменьшилась, не изменилась
или для ответа недостаточно данных) при этом относительная
доля потерь тяги с радиальной скоростью?
4. Некоторый исходный идеальный ЖРД (фк = (рс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 200 м/с
при коэффициенте пустотной тяги Kjn = 1,85. При подаче 15 %
окислителя в периферийную часть камеры, занимающую 10 % ее
проходного сечения, при неизменности равномерного
распределения горючего по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,05 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз увеличится (уменьшится) давление в камере,
если расходы компонентов топлива и размеры двигателя не
изменились?
5. Ракетные двигатели работают при одинаковых расходах
на одном и том же топливе, но по разным схемам: а) без
дожигания (схема жидкость - жидкость); б) с дожиганием (схема
газ - газ).
Укажите соотношение реализуемых значений условного
времени пребывания топлива при одинаковом объеме камер этих
ЖРД, если у первого и второго двигателей сопла полутепловые.
Вариант 4/4
1. При движении летательного аппарата с ракетным
двигателем из стратосферы до уровня моря при постоянном давлении
в камере площадь выходного сечения сопла изменяется так, что
на всех высотах ра = ph и течение в сопле одномерное
безотрывное с постоянной звуковой скоростью в минимальном сечении.
Получите расчетное соотношение для минимальной тяги,
развиваемой двигателем при таких условиях.
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одинаковом давлении в изобарной
камере и имеющие геометрически подобные контуры сопл,
развивают в пустоте различающиеся в Мраз тяги.
Получите для этих двигателей соотношения площадей
выходных сечений сопл.

3. Контрольно-измерительные материалы к части II 505
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющей части сопла
дополнили дорасширительным коническим насадком с тем же
углом наклона образующей.
Как изменился (увеличился, уменьшился, не изменился или
для ответа недостаточно данных) коэффициент сопла,
учитывающий потери тяги с радиальной скоростью?
4. Некоторый исходный идеальный ЖРД (фк = Фс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 500 м/с
при коэффициенте пустотной тяги Ктп = 1,75. При подаче 25 %
горючего в периферийную часть камеры, занимающую 10 % ее
проходного сечения, при неизменности равномерного
распределения окислителя по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,21 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз нужно увеличить (уменьшить) расход топлива,
чтобы давление в камере оставалось постоянным, если размеры
двигателя не изменились?
5. Двигатели работают на одном и том же топливе «жидкий
кислород - керосин», но по разным схемам: а) без дожигания
(схема жидкость - жидкость); б) с предварительной
газификацией в газогенераторе ТНА кислорода (схема газ - жидкость).
Укажите соотношение значений необходимого времени
пребывания топлива в камере.
Вариант 4/5
1. При движении летательного аппарата с ракетным
двигателем из стратосферы до уровня моря при постоянном давлении
в камере площадь выходного сечения сопла изменяется так, что
на всех высотах ра = ph и течение в сопле одномерное
безотрывное с постоянной звуковой скоростью в минимальном
сечении.
Получите расчетное соотношение для предельно возможного
максимального удельного импульса, развиваемого двигателем
при таких условиях.
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одном и том же давлении в
камере, с соплами, имеющими одинаковые геометрические степени

506 Часть III. Методические указания и КИМ
расширения, развивают в пустоте различающиеся в N раз тяги.
При этом приведенные длины камер сгорания одинаковые.
Оцените соотношение значений условного времени
пребывания топлива в этих двигателях.
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющей части сопла
дополнили дорасширительным коническим насадком с тем же
углом наклона образующей.
Как изменились (увеличились, уменьшились, не изменились
или для ответа недостаточно данных) при этом абсолютные
суммарные потери тяги в результате трения и с радиальной скоростью?
4. Некоторый исходный идеальный ЖРД (срк = фс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 000 м/с
при коэффициенте пустотной тяги Ктп = 1,75. При подаче 20 %
горючего в периферийную часть камеры, занимающую 5 % ее
проходного сечения, при неизменности равномерного
распределения окислителя по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,05 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз увеличилось (уменьшилось) давление в
камере, если расход топлива и размеры двигателя не изменились?
5. Двигатели работают на одном и том же топливе «кислород -
водород», но по разным схемам: а) с дожиганием
предварительно испаренного и подогретого в газогенераторе водорода (схема
газ - жидкость); б) с дожиганием (схема газ - газ).
Укажите соотношение значений необходимого времени
пребывания топлива в камере.
Вариант 4/6
1. При движении летательного аппарата с ракетным
двигателем из стратосферы до уровня моря при постоянном давлении
в камере площадь выходного сечения сопла изменяется так,
что на всех высотах ра = ph и течение в сопле одномерное
безотрывное с постоянной звуковой скоростью в минимальном
сечении.
Получите расчетное соотношение для предельно
возможной максимальной тяги, развиваемой двигателем при таких
условиях.

3. Контрольно-измерительные материалы к части II 507
2. ЖРД одной и той же принципиальной схемы, работающие
на одном и том же топливе при одинаковом давлении в камере
и имеющие геометрически подобные контуры камер, развивают
в пустоте различающиеся в N раз тяги.
Получите для этих двигателей соотношения значений
условного времени пребывания.
3. Работающее в пустоте исходное коническое сопло с
оптимальным углом наклона образующей расширяющей части сопла
дополнили дорасширительным коническим насадком с тем же
углом наклона образующей. Как изменилась (увеличилась,
уменьшилась, не изменилась или для ответа недостаточно данных) при
этом относительная доля потерь тяги на трение?
4. Некоторый исходный идеальный ЖРД (фк = фс = 1)
работает при Кт = 8 и развивает пустотный удельный импульс 3 000 м/с
при коэффициенте пустотной тяги Kjn = 1,75. При подаче 20 %
горючего в периферийную часть камеры, занимающую 10 % ее
проходного сечения, при неизменности равномерного
распределения окислителя по сечению камеры характеристическая скорость
в ядре потока уменьшилась в 1,05 раза, а расходный комплекс
газа завесы стал меньше в 1,69 раза, чем расходный комплекс
ядра потока исходного идеального двигателя.
Во сколько раз следует увеличить (уменьшить) площадь
критического сечения сопла, чтобы при неизменности расхода
топлива давление в камере также не изменилось?
5. Двигатели с соплами со сверхзвуковой скоростью
продуктов сгорания в выходном сечении работают на одном и том же
топливе при одинаковом давлении в равновеликих по площадям
критических сечениях, но по разным схемам: а) без дожигания
(схема жидкость - жидкость); б) с дожиганием (схема газ - газ).
Укажите соотношение объемов камер этих ЖРД, если
реализуемые значения условного времени пребывания топлива в них
равны.

508 Часть III. Методические указания и КИМ
Вопросы для студентов,
не получивших зачет на рубежном контроле 4
Вопрос 4/1
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе
летательного аппарата, снижающегося из стратосферы до уровня моря
и опускающегося под воду на максимально возможную
глубину при постоянном давлении в камере с удаляемой
расширяющейся частью сопла и геометрической степенью расширения,
равной 30.
Во сколько раз уменьшится развиваемая тяга? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/2
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе
летательного аппарата, снижающегося из стратосферы до уровня моря
и опускающегося под воду на максимально возможную
глубину при постоянном давлении в камере с удаляемой
расширяющейся частью сопла и геометрической степенью расширения,
равной 30.
На какую глубину может погрузиться летательный аппарат?
Запишите файл исходных данных для программы «Астра» для
получения количественного ответа на этот вопрос.
Вопрос 4/3
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе
летательного аппарата, снижающегося из стратосферы до уровня моря
и опускающегося под воду на максимально возможную
глубину при постоянном давлении в камере с удаляемой
расширяющейся частью сопла и геометрической степенью расширения,
равной 30.
Как изменится скорость истечения рабочего тела? Запишите
файл исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.

3. Контрольно-измерительные материалы к части II 509
Вопрос 4/4
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся частью
сопла и геометрической степенью расширения, равной 30.
Как изменится удельный импульс? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.
Вопрос 4/5
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается до 1 атм.
Во сколько раз уменьшится развиваемая тяга? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/6
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается до 1 атм.
На какую глубину может погрузиться летательный аппарат?
Запишите файл исходных данных для программы «Астра» для
получения количественного ответа на этот вопрос.
Вопрос 4/7
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается до 1 атм.
Как изменится скорость истечения рабочего тела? Запишите
файл исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.

510 Часть III. Методические указания и КИМ
Вопрос 4/8
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается до 1 атм.
Как изменится удельный импульс? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.
Вопрос 4/9
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается в 100 раз.
Во сколько раз уменьшится развиваемая тяга? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/10
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается в 100 раз.
На какую глубину может погрузиться летательный аппарат?
Запишите файл исходных данных для программы «Астра» для
получения количественного ответа на этот вопрос.
Вопрос 4/11
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла, в котором давление потока уменьшается в 100 раз.
Как изменится скорость истечения рабочего тела? Запишите
файл исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.

3. Контрольно-измерительные материалы к части II 511
Вопрос 4/12
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при Кт = 1 и давлении в камере 1,5 МПа в составе
летательного аппарата, снижающегося из стратосферы до уровня моря
и опускающегося под воду на максимально возможную
глубину при постоянном давлении в камере с удаляемой
расширяющейся частью сопла, в котором давление потока уменьшается
в 100 раз.
Как изменится удельный импульс? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.
Вопрос 4/13
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при а = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла и геометрической степенью расширения,
равной 30.
Во сколько раз уменьшится развиваемая тяга? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/14
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при а = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла и геометрической степенью расширения,
равной 30.
На какую глубину может погрузиться летательный аппарат?
Запишите файл исходных данных для программы «Астра» для
получения количественного ответа на этот вопрос.

512 Часть III. Методические указания и КИМ
Вопрос 4/15
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при а = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла и геометрической степенью расширения,
равной 30.
Как изменится скорость истечения рабочего тела? Запишите
файл исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/16
ЖРД работает на топливе «гидразин + азотный тетраоксид»
при а = 1 и давлении в камере 1,5 МПа в составе летательного
аппарата, снижающегося из стратосферы до уровня моря и
опускающегося под воду на максимально возможную глубину при
постоянном давлении в камере с удаляемой расширяющейся
частью сопла и геометрической степенью расширения,
равной 30.
Как изменится удельный импульс? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.
Вопрос 4/17
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при
Кт = 1 и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении
размеров камеры и расходов компонентов топлива в ядре потока
в периферийную часть камеры подают дополнительно окислитель
и горючее при соотношении компонентов, соответствующем
Кт = 10. При этом суммарный расход топлива увеличивается на
10%.
Как изменится давление в камере? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.

3. Контрольно-измерительные материалы к части II 513
Вопрос 4/18
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при
Кт = 1 и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении
размеров камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель
и горючее при соотношении компонентов, соответствующем Кт=10.
При этом суммарный расход топлива увеличивается на 10 %.
Как изменится пустотный удельный импульс? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/19
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при
Кт = 1 и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении
размеров камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель
и горючее при соотношении компонентов, соответствующем Кт = 10.
При этом суммарный расход топлива увеличивается на 10 %.
Во сколько раз нужно уменьшить расходы всех компонентов
топлива при сохранении их соотношений, чтобы давление в
камере не изменилось? Запишите файл исходных данных для
программы «Астра» для получения количественного ответа на этот вопрос.
Вопрос 4/20
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при
Кт = 1 и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении
размеров камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель
и горючее при соотношении компонентов, соответствующем Кт= 10.
При этом суммарный расход топлива увеличивается на 10 %.
Во сколько раз нужно уменьшить расходы всех компонентов
топлива при сохранении их соотношений, чтобы развиваемая
в пустоте тяга не изменилась? Запишите файл исходных данных
для программы «Астра» для получения количественного ответа
на этот вопрос.

514 Часть III. Методические указания и КИМ
Вопрос 4/21
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при а = 1
и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении размеров
камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель и
горючее при соотношении компонентов, соответствующем а = 10.
При этом суммарный расход топлива увеличивается на 10 %.
Как изменится давление в камере? Запишите файл исходных
данных для программы «Астра» для получения количественного
ответа на этот вопрос.
Вопрос 4/22
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при а = 1
и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении размеров
камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель и
горючее при соотношении компонентов, соответствующем а = 10.
При этом суммарный расход топлива увеличивается на 10 %.
Как изменится пустотный удельный импульс? Запишите файл
исходных данных для программы «Астра» для получения
количественного ответа на этот вопрос.
Вопрос 4/23
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при а = 1
и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении размеров
камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель и
горючее при соотношении компонентов, соответствующем а = 10.
При этом суммарный расход топлива увеличивается на 10 %.
Во сколько раз нужно уменьшить расходы всех компонентов
топлива при сохранении их соотношений, чтобы давление в
камере не изменилось? Запишите файл исходных данных для
программы «Астра» для получения количественного ответа на этот вопрос.

3. Контрольно-измерительные материалы к части II 515
Вопрос 4/24
Некоторый исходный идеальный (фк = фс = 1) ЖРД рассчитан
для работы на топливе «гидразин + азотный тетраоксид» при а = 1
и давлении в камере 10 МПа с геометрической степенью
расширения сопла, равной 50, при равномерном распределении
компонентов топлива по сечению камеры. При сохранении размеров
камеры и расходов компонентов топлива в ядре потока в
периферийную часть камеры подают дополнительно окислитель и
горючее при соотношении компонентов, соответствующем а = 10.
При этом суммарный расход топлива увеличивается на 10 %.
Во сколько раз нужно уменьшить расходы всех компонентов
топлива при сохранении их соотношений, чтобы развиваемая
в пустоте тяга не изменилась? Запишите файл исходных данных
для программы «Астра» для получения количественного ответа
на этот вопрос.
3.3. Вопросы к зачету по части II
Построить получаемую на уровне моря
(ph] = 0,1 МПа) дроссельную
характеристику Рх ЖРД с Т-образной камерой, размеры
сопл которой те же, что и у сопл камеры
спроектированного ЖРД, а давление^ в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла
с насадком, близко к нулю и поддерживается
постоянным (см. рисунок).
/?Л1 = 0,1 МПа
Я]
Построить график изменения во времени
суммарной тяги Р^ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в
герметичной барокамере равно атмосферному
давлению на уровне моря рИХ = 0,1 МПа
(см. рисунок).

516 Часть III. Методические указания и КИМ
Построить график изменения во времени
суммарной тяги Ръ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в
герметичной барокамере равно атмосферному
давлению на высоте около 20 км (см. рисунок).
= 0,1 МПа
РИ2=0\
Построить получаемую на уровне моря
(phl = 0,1 МПа) дроссельную характеристику
Ръ ЖРД с Т-образной камерой, размеры сопл
которой те же, что и у сопл камеры
спроектированного ЖРД, а давление рИ2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла без
насадка, близко к нулю и поддерживается
постоянным (см. рисунок).
= 0,1 МПа Г
Построить получаемую на уровне моря
(phl = 0,1 МПа) дроссельную характеристику
Pz ЖРД с Т-образной камерой, размеры сопл
которой те же, что и у сопл камеры
спроектированного ЖРД, а давление ph2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла
с насадком, близко к нулю и поддерживается
постоянным (см. рисунок).
ЪС£УИ
РИ2=0
Построить получаемую на уровне моря
(phl = 0,1 МПа) дроссельную характеристику
Pz ЖРД с Т-образной камерой, размеры сопл
которой те же, что и у сопл камеры
спроектированного ЖРД, а давление ph2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла без
насадка, близко к нулю и поддерживается
постоянным (см. рисунок).
/?Л1=0,1 МПа

3. Контрольно-измерительные материалы к части II 517
= 0,1 МПа =
rs,/ 5* \уЛ
1^Л Щ T4J
Ры\
Построить график изменения во времени
суммарной тяги Ръ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла с
насадком, равно атмосферному давлению на
уровне моря/>Л2 =phl = 0,1 МПа и с течением
времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).
= 0,1 МПа = const
М|
Построить график изменения во времени
суммарной тяги Ръ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла без
насадка, равно атмосферному давлению на
уровне моря ph2 =phl = 0,1 МПа и с течением
времени снижается практически до нуля:
рИ2 = 0,00001 МПа (см. рисунок).
= 0,1 МПа = const
М
Построить график изменения во времени
суммарной тяги Р^ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла без
насадка, равно атмосферному давлению на
уровне морярИ2 =phl = 0,1 МПа и с течением
времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).

518 Часть III. Методические указания и КИМ
А =0,1 МПа = const
Ksxd
IXSX]
Построить график изменения во времени
суммарной тяги Ръ ЖРД с работающей при
номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла с
насадком, равно атмосферному давлению на
уровне моря/^ =phx = 0,1 МПа и с течением
времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальном расходе топлива двух ЖРД, размеры сопл
которых те же, что и у сопла
спроектированного ЖРД, а начальное давление в
герметичной барокамере равно атмосферному
давлению на уровне моря рИ] = 0,1 МПа
(см. рисунок).
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальном расходе топлива двух ЖРД, размеры сопл
которых те же, что и у сопла
спроектированного ЖРД, а начальное давление в
герметичной барокамере равно атмосферному
давлению на высоте около 20 км (см. рисунок).
/?Л1=0,1 МПа = const Г
УН
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальных расходах топлива двух ЖРД, размеры
сопл которых те же, что и у сопла
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем
барокамере, куда поступает рабочее тело из
сопла с насадком, равно атмосферному давлению
на уровне моря/?^ = phx = 0,1 МПа и с
течением времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).
|М

3. Контрольно-измерительные материалы к части II 519
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальных расходах топлива двух ЖРД, размеры
—i ">-__ ^1 сопл которых те же, что и у сопла спроекти-
^Л2|!ХЖ/н] рованного ЖРД, а начальное давление в не
*LL связанной механически с двигателем
барокамере, куда поступает рабочее тело из
сопла без насадка, равно атмосферному давлению
на уровне моря ph2 = ph] = 0,1 МПа и с
течением времени снижается практически до нуля:
Phi = 0,00001 МПа (см. рисунок).
/?Л1=0,1 МПа = const
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальных расходах топлива двух ЖРД, размеры
сопл которых те же, что и у сопла
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем
барокамере, куда поступает рабочее тело из
сопла без насадка, равно атмосферному давлению
на уровне моря ph2 = phx = 0,1 МПа и с
течением времени снижается практически до нуля:
Phi = 0,00001 МПа (см. рисунок).
О^Я]
Построить график изменения во времени
суммарной тяги Ръ работающих на
номинальных расходах топлива двух ЖРД, размеры
сопл которых те же, что и у сопла
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем
барокамере, куда поступает рабочее тело из
сопла с насадком, равно атмосферному давлению
на уровне моря/?Л2 = phx = 0,1 МПа и с
течением времени снижается практически до нуля:
Phi = 0,00001 МПа (см. рисунок).
&C3D3]
1М.

520 Часть III. Методические указания и КИМ
' Й1 ' I
г^/—**—\Л\
1^\_и*_уЧ]
РкГ*
Построить получаемую на уровне моря
(рИ = 0,1 МПа) дроссельную характеристику
/ (рк) ЖРД с Т-образной камерой, размеры
сопл которой те же, что и у сопл камеры
спроектированного ЖРД, а давление ph2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла
с насадком, близко к нулю и поддерживается
постоянным (см. рисунок).
Построить график изменения во времени
удельного импульса / ЖРД с работающей
при номинальном давлении Т-образной
камерой, размеры сопл которой те же, что
и у сопл камеры спроектированного ЖРД,
а начальное давление в герметичной
барокамере равно атмосферному давлению на
уровне морярИ = 0,1 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса / ЖРД с работающей
при номинальном давлении Т-образной
камерой, размеры сопл которой те же, что
и у сопл камеры спроектированного ЖРД,
а начальное давление в герметичной
барокамере равно атмосферному давлению на
высоте около 20 км (см. рисунок).
Построить получаемую на уровне моря
(Ph\ = 0»! МПа) дроссельную характеристику
РИ2=°
0,1 мпа L(pK) ЖРД с Т-образной камерой, размеры
сопл которой те же, что и у сопл камеры
спроектированного ЖРД, а давление ph2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла без
насадка, близко к нулю и поддерживается
постоянным (см. рисунок).

3. Контрольно-измерительные материалы к части II 52J_
/?Л1=0,1 Mflaf
К^Х]
РН7=0
Построить получаемую на уровне моря
(Ри\ = 0,1 МПа) дроссельную характеристику
I (рк) ЖРД с Т-образной камерой, размеры
сопл которой те же, что и у сопл камеры
спроектированного ЖРД, а давление ph2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла
с насадком, близко к нулю и поддерживается
постоянным (см. рисунок).
Построить получаемую на уровне моря
(рИ = 0,1 МПа) дроссельную характеристику
1(рк) ЖРД с Т-образной камерой, размеры
яА2=о
сопл которой те же, что и у сопл камеры
спроектированного ЖРД, а давление рИ2 в не
связанной механически с двигателем
барокамере, куда истекает рабочее тело из сопла без
насадка, близко к нулю и поддерживается
постоянным (см. рисунок).
РиГо,\ мп
0CXIXQ
Построить график изменения во времени
удельного импульса / ЖРД с работающей
при номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла с
насадком, равно атмосферному давлению на
уровне морярИ2 =phl = 0,1 МПа и с течением
времени снижается практически до нуля:
Phi = 0,00001 МПа (см. рисунок).
';„2|

522 Часть III. Методические указания и КИМ
Построить график изменения во времени
удельного импульса / ЖРД с работающей
при номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
рН]= 0,1 мпа = const те же, что и у сопл камеры спроектирован-
N/^*~vr1 ного ЖРД, а начальное давление в не связан-
|||^ ной механически с двигателем барокамере,
*™* куда поступает рабочее тело из сопла без
насадка, равно атмосферному давлению на
уровне моря ph2 = ph] = 0,1 МПа и с течением
времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса I ЖРД с работающей
при номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла без
насадка, равно атмосферному давлению на
уровне моря ph2 = рИ = 0,1 МПа и с течением
времени снижается практически до нуля:
ph = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса I ЖРД с работающей
при номинальном давлении в камере сгорания
Т-образной камерой, размеры сопл которой
те же, что и у сопл камеры
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
куда поступает рабочее тело из сопла с
насадком, равно атмосферному давлению на
уровне моря ph2 =phx = 0,1 МПа и с течением
времени снижается практически до нуля:
ph2 = 0,00001 МПа (см. рисунок).
0,1 МПа = const
/? =0,1 МПа = const
ссгзз]
ы

3. Контрольно-измерительные материалы к части II 523
КЖХ1
1ХЖХ]
/?Л1 = 0,1 МПа = const Г
tc
X]
|М_
р. = 0,1 МПа = const
М
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальном расходе
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в герметичной барокамере
равно атмосферному давлению на уровне
моря^Л1 = 0,1 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальном расходе
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в герметичной барокамере
равно атмосферному давлению на высоте около
20 км (см. рисунок).
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальных расходах
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в не связанной механически
с двигателем барокамере, куда поступает
рабочее тело из сопла с насадком, равно
атмосферному давлению на уровне моря ph2 =
~Ри\ = ®->' МПа и с течением времени
снижается практически до нуля: ph2 = 0,0001 МПа
(см. рисунок).
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальных расходах
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в не связанной механически
с двигателем барокамере, куда поступает
рабочее тело из сопла без насадка, равно
атмосферному давлению на уровне моря рИ2 =
-phx = 0,1 МПа и с течением времени
снижается практически до нуля: ph2 = 0,0001 МПа
(см. рисунок).

524 Часть III. Методические указания и КИМ
= 0,1 МПа = const
Ml
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальных расходах
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в не связанной механически
с двигателем барокамере, куда поступает
рабочее тело из сопла без насадка, равно
атмосферному давлению на уровне моря рИ2 =
=phl = 0,1 МПа и с течением времени
снижается практически до нуля: ph2 = 0,0001 МПа
(см. рисунок).
Построить график изменения во времени
удельного импульса / ДУ, состоящей из двух
работающих на номинальных расходах
топлива ЖРД, размеры сопл которых те же, что
и у сопла спроектированного ЖРД, а
начальное давление в не связанной механически
с двигателем барокамере, куда поступает
рабочее тело из сопла с насадком, равно
атмосферному давлению на уровне моря ph2 =
=phl=09l МПа и с течением времени
снижается практически до нуля: ph2 = 0,0001 МПа
(см. рисунок).
рн = 0,1 МПа = const
язи
phx = 0,1 МПа = const
Построить график изменения во времени
суммарной тяги Ръ ДУ, состоящей из
работающих на номинальных расходах топлива
двух ЖРД, размеры сопл которых те же, что
и у спроектированного ЖРД, а начальное
давление в не связанной механически с
двигателем барокамере, куда поступает рабочее
тело сопла без насадка, равно атмосферному
давлению на уровне моря/?Л2 =phl = 0,1 МПа
и с течением времени снижается практически
до нуля: ph2 = 0,00001 МПа (см. рисунок).
о г» п г» J

3. Контрольно-измерительные материалы к части II 525
Ph2
Построить график изменения во времени
удельного импульса I yZ ДУ, состоящей из
работающих на номинальных расходах
топлива двух ЖРД, размеры сопл которых те же,
Phx = 0,1 мпа = const что и у спроектированного ЖРД, а начальное
~Т^~| гт-\^<1 давление в не связанной механически с дви-
Ua >ГТк /^J гателем барокамере, куда поступает рабочее
^ | && тело сопла без насадка, равно атмосферному
давлению на уровне морярН2 = phl= 0,1 МПа
и с течением времени снижается практически
до нуля: ph2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
суммарной тяги РЕ ДУ, состоящей из
работающих на номинальных расходах топлива
Phl = o,i мпа = const двух ЖРД, размеры сопл которых те же, что
/-—] f~IZr~3j и у спроектированного ЖРД, а начальное
£^_>M<_ysJ Phi\ давление в не связанной механически с дви-
^ | ^ гателем барокамере, куда поступает рабочее
тело сопла с насадком, равно атмосферному
давлению на уровне моря/?/;2 =ph] = 0,1 МПа
и с течением времени снижается практически
до нуля: ph2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса / z ДУ, состоящей из
работающих на номинальных расходах топли-
Phx = o,i мпа = const ва двух ЖРД, размеры сопл которых те же,
^-^ rZT~~^j что и у спроектированного ЖРД, а начальное
[X цТн /CJ рм\ давление в не связанной механически с дви-
^ о^о, ^ гателем барокамере, куда поступает рабочее
тело сопла с насадком, равно атмосферному
давлению на уровне ыорярИ2 = phx= 0,1 МПа
и с течением времени снижается практически
до нуля: ph2 = 0,00001 МПа (см. рисунок).

526 Часть III. Методические указания и КИМ
phx = 0,1 МПа = const
о о о о т4
Риг\
NWNW WXWN
ph] = 0,1 МПа = const
оо оо т41
^^Я ^Я^Я
phl = 0,1 МПа = const
оо оо Р I
^^^ ^^^
рЛ1 = 0,1 МПа = const
&GHD4R
оо оо Т |
\\N\W 4WNW
Построить график изменения во времени
суммарной тяги PL ДУ, состоящей из
работающих на номинальных расходах топлива
двух ЖРД, размеры сопл которых те же, что
и у спроектированного ЖРД, а начальное
давление в не связанной механически с
двигателем барокамере, куда поступает рабочее
тело сопла с насадком, равно атмосферному
давлению на уровне морярЛ2 =phl = 0,1 МПа
и с течением времени снижается практически
до нуля: рИ2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса/ z ДУ, состоящей из
работающих на номинальных расходах
топлива двух ЖРД, размеры сопл которых те же,
что и у спроектированного ЖРД, а начальное
давление в не связанной механически с
двигателем барокамере, куда поступает рабочее
тело сопла с насадком, равно атмосферному
давлению на уровне моря/?А2 =рИ = 0,1 МПа
и с течением времени снижается практически
до нуля: рИ2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
номинальном расходе топлива ЖРД, размеры
сопл которых те же, что и у
спроектированного ЖРД, а начальное давление в
барокамере равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
номинальном расходе топлива ЖРД, размеры
сопл которых те же, что и у
спроектированного ЖРД, а начальное давление в
барокамере равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).

3. Контрольно-измерительные материалы к части II 527
Построить график изменения во времени
I ДУ, состоящей из двух работающих на но-
phl = 0,1 мпа=const минальном расходе топлива ЖРД, размеры
| ук_, ^—^^л сопл которых те же, что и у спроектирован-
\Ph21^\ Ц—[< /^ч[ ного ЖРД, а начальное давление в барокаме-
ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
ры = У МПа = const номинальном расходе топлива ЖРД, размеры
К гчУ^а R~V-<1 сопл К0Т0РЫХ те же> что и У спроектирован-
iP/,2Uvj N AvlJ ного ЖРД, а начальное давление в барокаме-
I J&S &§? ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на но-
Phi = 0>] мпа = const минальном расходе топлива ЖРД, размеры
| Г1 ^^^^л сопл которых те же, что и у спроектирован-
^2СХ Н—к A^L ного ЖРД, а начальное давление в барокаме-
I Ig^ ^gj ре равно атмосферному давлению на уровне
моря и с течением времени возрастает (см.
рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
Ри = o,i мпа = const номинальном расходе топлива ЖРД, размеры
| ~1 ^_^^ ^л сопл которых те же, что и у спроектирован-
tP/,2LX >|—K_XsL ного ^^Д'а начальное давление в барокаме-
1 T-gg о^ ^ ре равно атмосферному давлению на уровне
моря и с течением времени возрастает (см.
рисунок).

528 Часть III. Методические указания и КИМ
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
Ph] = од мпа = const номинальном расходе топлива ЖРД, разме-
JH ~Z | ры сопл которых те же, что и у спроектиро-
Г^( D—С XT \PhA ванного ЖРД, а начальное давление в баро-
igjO ^o, ^^ I камере равно атмосферному давлению на
ровне моря и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
Phx =0,1 мпа = const номинальном расходе топлива ЖРД, разме-
ХЦ j—ч ^л | ры сопл которых те же, что и у спроектиро-
\^\ >|—[< ^лЦ \Ph2\ ванного ЖРД, а начальное давление в
барсук ^ | камере равно атмосферному давлению на
уровне моря и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на но-
Pfll = o,i мпа = const минальном расходе топлива ЖРД, размеры
Г" ~~~^ | сопл которых те же, что и у спроектирован-
Г^ D—С XJ гh2\ ного ЖРД, а начальное давление в барокаме-
TOjg, о^о, ^^ I ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на но-
Phl = o,i мпа = const минальном расходе топлива ЖРД, размеры
. I | сопл которых те же, что и у спроектирован-
j^^u—С>СГ| рп\ ного ЖРД, а начальное давление в барокаме-
^^ V^o oi/ I ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).

3. Контрольно-измерительные материалы к части II 529
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
Ри = o,i мпа = const номинальном расходе топлива ЖРД, размеры
|s. J~ ZT | сопл которых те же, что и у спроектирован-
\^( Ц—С )С^ Ph2\ ного ЖРД, а начальное давление в барокаме-
•^ j^ c^g, I ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
Рнх = o,i мпа = const тяги Ду> состоящей из двух работающих на
I 1 номинальном расходе топлива ЖРД, разме-
Г^^-Я_^^-^| ^Л2| ры сопл которых те же, что и у спроектиро-
1^^%о о oV^"^^ I ванного ЖРД, а начальное давление в баро-
1 ' камере равно атмосферному давлению на
уровне моря и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
р.. =0,1 МПа = const у г-л ? «-» j г-
^ номинальном расходе топлива ЖРД, разме-
|^л~р [ГЛ^гЯп v ры сопл которых те же, что и у спроектиро-
^V^T~c_/^J hl | ванного ЖРД, а начальное давление в баро-
г*** ^^ 1 камере равно атмосферному давлению на
уровне моря и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
Phx = o.iMna^const номинальном расходе топлива ЖРД, разме-
Р^^П 1 E~"Vi J Ры сопл которых те же, что и у спроектиро-
\\^\ И~т~к А^Г^. ванного ЖРД, а начальное давление в баро-
^ I ^ I камере равно атмосферному давлению на
уровне моря и с течением времени
возрастает (см. рисунок).

530 Часть III. Методические указания и КИМ
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
Рн] = о,1мпа = const номинальном расходе топлива ЖРД, разме-
Г>\Л~>]1 R~~V-i J Ры сопл которых те же, что и у
спроектировал >ГТк гЛРн^ ванного ЖРД, а начальное давление в баро-
£& I ^ | камере равно атмосферному давлению на
уровне моря и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на но-
Рм = o,i мпа = const минальном расходе топлива ЖРД, размеры
р-^л~ЯП~\^\ ^ сопл которых те же, что и у
спроектированную n К /^ P/'2' ного ЖРД, а начальное давление в барокаме-
т 4& ^г I ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
phl = 0,1 МПа = const -ТЛГ| -л-
j. _ номинальном расходе топлива ЖРД, размеры
рь^Л^|_р~Л^| J сопл которых те же, что и у спроектирован-
[J^Vj Ь_У^1 Л2'. ного ЖРД, а начальное давление в барокаме-
I ^—s 1 ре равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
Построить график изменения во времени
I ДУ, состоящей из двух работающих на но-
Phl = o,i мпа = const минальных расходах топлива ЖРД, размеры
р^_, р--> | сопл которых те же, что и у спроектирован-
]х\ И—к /Cr*2t ного ЖРД, а начальное давление в не связан-
т ^ && | ной механически с двигателем барокамере,
куда поступает рабочее тело сопла без
насадка, равно атмосферному давлению на
уровне морярЛ2 =phl = 0,1 МПа и с течением
времени возрастает (см. рисунок).

3. Контрольно-измерительные материалы к части II 531
/?Л1 = 0,1 МПа = const
1
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
номинальных расходах топлива ЖРД, размеры
сопл которых те же, что и у спроектирован-
р>^л~д р~Л^| * ного ЖРД, а начальное давление в не связан-
\)^\Jn П—/^ Л2 | ной механически с двигателем барокамере,
—^—^ 1 куда поступает рабочее тело сопла без
насадка, равно атмосферному давлению на
уровне моря/?Л2 =phl = 0,1 МПа и с течением
времени возрастает (см. рисунок).
Построить график изменения во времени
суммарной тяги Ръ ДУ, состоящей из
работающих на номинальных расходах топлива
двух ЖРД, размеры сопл которых те же, что
/>А1 = o,i мш = const и у спроектированного ЖРД, а начальное
Г^к^^з с~л^<1 давление в не связанной механически с дви-
\\^\ И И /^J гателем барокамере, куда поступает рабочее
^ ^ I тело сопла с насадком, равно атмосферному
давлению на уровне моря/?Л2 =phl = 0,1 МПа
и с течением времени снижается практически
до нуля: рИ2 = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса ДУ, состоящей из
работающих на номинальных расходах топлива
Pkl = o,i мпа = const ДВУХ жрД> размеры сопл которых те же, что
•f и у спроектированного ЖРД, а начальное
Г^НЗ—-Е~^| phi\ давление в не связанной механически с дви-
^jTo oo^l гателем барокамере, куда поступает рабочее
тело сопла с насадком, равно атмосферному
давлению на уровне моря/?Л2 =phx = 0,1 МПа
и с течением времени снижается практически
до нуля: ph2 = 0,00001 МПа (см. рисунок).
www www

532 Часть III. Методические указания и КИМ
оо оо ^
SSSS NSSSSS'
Построить график изменения во времени
суммарной тяги Pz ДУ, состоящей из
работающих на номинальных расходах топлива
двух ЖРД, размеры сопл которых те же, что
и у спроектированного ЖРД, а начальное
давление в не связанной механически с
двигателем барокамере равно атмосферному
давлению на уровне моря/?Л = 0,1 МПа и с
течением времени снижается практически до
нуля: рИ = 0,00001 МПа (см. рисунок).
Построить график изменения во времени
удельного импульса / z ДУ, состоящей из
работающих на номинальных расходах
топлива двух ЖРД, размеры сопл которых те же,
что и у спроектированного ЖРД, а начальное
давление в не связанной механически с
двигателем барокамере равно атмосферному
давлению на уровне моря/?А = 0,1 МПа и с
течением времени снижается практически до
нуля: ph = 0,00001 МПа (см. рисунок).
оо оо ^
.YftYtt .4VSW>
JmI
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
номинальном расходе топлива ЖРД, размеры
сопл которых те же, что и у
спроектированного ЖРД, а начальное давление в
барокамере равно атмосферному давлению на высоте
около 20 км и с течением времени
возрастает (см. рисунок).
оо оо ^
.\4SSNS' ,N4SSS\
JmI
Построить график изменения во времени
удельного импульса ДУ, состоящей из двух
работающих на номинальном расходе
топлива ЖРД, размеры сопл которых те же, что
и у спроектированного ЖРД, а начальное
давление в барокамере равно атмосферному
давлению на высоте около 20 км и с
течением времени возрастает (см. рисунок).
оо о о ^

3. Контрольно-измерительные материалы к части II 533
JMl
о о о о ^
SSSS SSSS
JmI
оо оо ^
SSSS SSSS2
Построить график изменения во времени
тяги ДУ, состоящей из двух работающих на
номинальных расходах топлива ЖРД,
размеры сопл которых те же, что и у
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем
барокамере равно атмосферному давлению на
уровне моря/?^ = 0,1 МПа и с течением
времени возрастает (см. рисунок).
Построить график изменения во времени
/ ДУ, состоящей из двух работающих на
номинальных расходах топлива ЖРД, размеры
сопл которых те же, что и у
спроектированного ЖРД, а начальное давление в не
связанной механически с двигателем барокамере,
равно атмосферному давлению на уровне моря
ph = 0,1 МПа и с течением времени
возрастает (см. рисунок).

4. Примерное содержание
курсового домашнего задания
«Расчет основных параметров
и характеристик идеального теплового
ракетного двигателя»
Для заданного значения тяги камеры при номинальных
условиях для известных параметров камеры и рабочего тела
(температура торможения продуктов сгорания Т*, кажущаяся
молекулярная масса продуктов сгорания ц, показатель адиабаты к,
давление в камере р*9 давление в выходном сечении сопла ра
и давление окружающей среды ph, кратность увеличения или
уменьшения площади выходного сечения сопла за счет
соплового дорасширительного насадка^нас) выполнить:
• расчеты площадей и диаметров поперечных сечений
проточной части (камера сгорания, критическое сечение, выходное
сечение сопла), удельного импульса и расходов топлива для
изобарной камеры и камеры с полутепловым соплом;
• построение приближенного контура проточной части
двигателя с изобарной камерой сгорания;
• построение приближенного контура проточной части
камеры с полутепловым соплом;
• расчет и построение дроссельных характеристик двигателя
с изобарной камерой сгорания с дорасширительным сопловым
насадком и без него при трех значениях давления окружающей
среды: заданном номинальном, уменьшенном и увеличенном в 2 раза;
• расчет и построение высотных характеристик двигателя с
изобарной камерой сгорания с дорасширительным насадком и без него
при заданном, увеличенном и уменьшенном в 2 раза давлении
в камере;
• расчет и построение эпюры осевых усилий для работающих
на номинальном режиме двигателей с изобарной камерой
сгорания и с камерой с полутепловым соплом для каждого из четырех
вариантов закрепления (в упор, в сечении между смесительной
головкой камеры сгорания и входом в сопло, в области
критического сечения, в области выходного сечения сопла).

4. Примерное содержание курсового задания 535
При этом обязательно рассчитываются и наносятся на все
графики координаты всех характерных точек, в том числе точки
пустотных, номинальных и расчетных режимов, точки равенства
тяг и удельных импульсов нулю, точки одинаковых тяг камер
с дорасширительным насадком и без него (точки переключения).
Оглавление расчетно-пояснительной записки
к домашнему заданию
Исходные данные
1. Расчет параметров и размеров камеры с изобарной
камерой сгорания
1.1. Расчет параметров и размеров камеры
1.1.1. Расчет параметров и размеров камеры без
соплового насадка
1.1.2. Расчет параметров и размеров камеры с сопловым
насадком
1.2. Расчет и построение дроссельных характеристик
1.2.1. Камера без соплового насадка (для трех значений
давления окружающей среды)
1.2.2. Камера с сопловым насадком (для трех значений
давления окружающей среды)
1.2.3. Дроссельные характеристики камер,
различающихся только наличием или отсутствием соплового
насадка, при номинальном давлении окружающей
среды
1.3. Расчет и построение высотных характеристик
1.3.1. Камера без соплового насадка (для трех значений
давления в камере)
1.3.2. Камера с сопловым насадком (для трех значений
давления в камере)
1.3.3. Высотные характеристики камер, различающихся
только наличием или отсутствием соплового
насадка, при номинальном давлении в камере
1.4. Расчет и построение эпюр осевых усилий изобарной
камеры, работающей в пустоте при номинальном расходе
2. Расчет параметров и размеров камеры с полутепловым
соплом без соплового насадка
2.1. Расчет параметров и размеров камеры. Построение
приблизительного контура проточной части камеры
2.2. Расчет и построение эпюр осевых усилий камеры,
работающей в пустоте при номинальном расходе

536 Часть III. Методические указания и КИМ
3. Сравнение размеров и параметров камер с изобарной
камерой сгорания и с полутепловым соплом
Примерные исходные данные к курсовому домашнему заданию
приведены в таблице.
Исходные данные к курсовому домашнему заданию
Номер
варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Параметры
раб
С к
2500
2800
3000
3200
3400
2500
2800
3000
3200
3400
2500
2600
2800
3000
3200
3500
3600
3800
3600
3200
очего тела
Ц
28
29
30
29
28
24
26
30
32
34
18
18
16
8
2
30
28
26
24
24
к
1,10
1,15
1,20
1,25
1,20
1,15
1,25
1,25
1,25
1,15
1,15
1,15
1,15
1,15
1,15
1,20
1,25
1,20
1,25
1,15
камеры
Р,кН
800
820
840
860
880
107,6
107,6
107,6
107,6
107,6
250
250
250
250
250
500
500
500
600
600
р'К, МПа
8,0
8,0
8,0
8,0
8,0
8,5
8,5
8,5
8,5
8,5
6,5
7,0
7,5
8,5
9,0
6,0
6,5
7,0
7,5
8,0
р ,МПа
г СУ
0,07
0,07
0,07
0,07
0,07
0,06
0,06
0,06
0,06
0,06
0,001
0,001
0,001
0,001
0,001
0,07
0,07
0,07
0,07
0,07
ph, МПа
0,10
0,10
0,10
0,10
0,10
0,02
0,02
0,02
0,02
0,02
0,002
0,002
0,002
0,002
0,002
0,10
0,10
0,10
0,10
0,10
F
мае
1,5
1,8
2,0
2,2
2,4
0,8
0,5
1,5
1,25
1,25
0,5
0,6
0,7
0,7
0,7
1,25
1,3
1,35
1,4
1,45

5. Примерное содержание
курсового проекта
Курсовое проектирование заключается в выполнении
технического задания (см. примерные исходные данные), что можно
представить как последовательность следующих действий:
• выбор прототипа проектируемого двигателя,
предварительная проработка схемы ДУ и описание ее работы на
установившемся режиме;
• расчет стехиометрического соотношения компонентов
топлива, условная (по пустотному удельному импульсу)
оптимизация соотношения компонентов при предположении
равновесного, неравновесного и локально-неравновесного течения в сопле;
• расчет и построение графиков Л, Гк, р, / для равновесного
течения в сопле и / для неравновесного и
локально-неравновесного течения в зависимости от а и К ;
• проектирование проточной части сопла с конической
сверхзвуковой частью и оптимальным по удельному импульсу углом
и сопла с профилированной сверхзвуковой частью;
• расчет основных параметров двигателя и размеров камеры
с профилированным соплом с учетом потерь;
• расчет и построение характеристик спроектированной
камеры (дроссельных характеристик единичной камеры при
давлении окружающей среды 0,1 МПа, дроссельной характеристики
ДУ при поочередном дросселировании камер при давлении
окружающей среды 0,1 МПа, высотных характеристик в зависимости
от противодавления и высоты полета и (или) глубины хода);
• расчет и построение графиков распределения параметров
р, Г, р, М, X, W, pW и состава продуктов сгорания в массовых
долях по длине сопла;
• выполнение индивидуального или типового
учебно-научного задания по исследованию частных вопросов с получением
субъективно новой научной информации.
По результатам расчетов обосновываются и
формулируются выводы о выполнимости технического задания. Если
известны параметры двигателя-прототипа (он может быть указан
при формулировке задания на проектирование), их сравнивают

538 Часть III. Методические указания и КИМ
с полученными при проектировании и приводят обоснование
различий.
Рассматривая режимы работы сопла со скачками уплотнения
как недопустимые, определяют возможность или невозможность
испытания спроектированного двигателя (с дорасширительным
насадком или без него) в земных условиях без применения
стендовых вакуумирующих устройств. Если они необходимы, то
указывается требуемое значение давления, которое должно
обеспечить вакуумирующие устройства.
Расчетно-пояснительная записка к курсовому проекту
оформляется в соответствии с требованиями ГОСТ 7.32-91 (ИСО 5966-82),
предъявляемыми к отчетам по научно-исследовательским работам.
Объем записки (без приложений) в знаках приблизительно равен
объему одного печатного листа.
Графическая часть проекта выполняется на стандартных листах
чертежной бумаги общей площадью не менее трех листов
формата А1.
На листы обязательно выносят:
• контур проточной части камеры с профилированным и
коническим соплом с необходимыми номинальными размерами;
• высотные характеристики в зависимости от высоты (глубины);
• высотные характеристики в зависимости от противодавления;
• расходные характеристики камеры и ДУ при поочередном
дросселировании камер;
• распределения параметровр, Т, р, М, X, W, pWn массовых
концентраций основных составляющих рабочего тела (продуктов
сгорания) по длине сопла при равновесном истечении;
• графики зависимости Л, Гк, р, / п для равновесного течения
в сопле и / при частично равновесном течении от а и Кт;
• схему газожидкостных систем двигателя;
• графическую иллюстрацию выполнения научно-учебного
задания.
При этом характеристики рассчитывают и строят для сопл
с подключенным и с отключенным дорасширительным насадком.

5. Примерное содержание курсового проекта 539
Исходные данные к курсовому проектированию

Номер

варианта
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Окислитель
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
N204
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
02(ж)
АК-27
АК-27
АК-27
АК-27
Горючее
Керосин
Керосин
Керосин
Керосин
НДМГ
НДМГ
Керосин
НДМГ
НДМГ
НДМГ
НДМГ
УВГ
Н2(ж)
НДМГ
Н2(ж)
Н2(ж)
УВГ/Н2
Н2(ж)
Керосин
Керосин
NH3 (ж)
НДМГ
НДМГ
НДМГ
НДМГ
/>п,кН
627,8
645,5
1000
941,8
101,6
105,6
1628
1089
1138
1654
1726
7776
1023
1635
2090
66,72
3466/3779
103,5
8060
1500
250
1095
1140
1666
1730
Ло
МПа
5,89
5,89
5,86
5,1
7,75
7,9
7,85
14,72
14,72
14,72
14,72
7,78
5,38
14,7
20,5
2,76
20
3,7
25
3,75
4,12
15,0
15,0
15,0
15,0
р.МПа
(W
0,059
0,039
0,039
0,033
0,01
0,0062
0,059
0,049
0,0098
0,0677
0,0157
0,05(16)
0,01 (27,5)
0,061
0,0175(77,5)
0,004 (57)
(35)
(8,48)
0,07
(8)
-
0,048
0,095
0,061
0,014
Р» МПа
"ол
0,05
0,05
0,04
0,005
0,001
0,08
0,07
0,005
0,1
0,006
I
II, III
I
0,1.0
II, IV
II, III
II
I
I
-
I
II, III
I
II, III
F
нас
~?J~
1,5
1,5
1,5
0,5
0,5
2,5
2,8
0,5
1,5
0,5
0,5
0,5
1,5
0,5
4,0
5,71
16,5
1,5
1,5
1,5
0,5
0,25
0,8
0,35
N
1
1
4
4
1
1
4
4
4
1
1
1
1
1
1
1
1
1
4
2
1
1
1
1
1
Примечание. Римские цифры - номера ступеней ракеты-носителя.
Обозначения: ж - жидкий; УВГ - углеводородное горючее;
АК-27 - окислитель на основе азотной кислоты (70 %) и тетраоксида
азота (27 %) с остаточным содержанием воды (3 %).

540 Часть III. Методические указания и КИМ
Примерное оглавление расчетно-пояснительной записки
к курсовому проекту
Введение
1. Задание на проектирование. Исходные данные
2. Выбор прототипа проектируемого двигателя.
Предварительная проработка схемы ДУ и описание ее работы на
установившемся режиме
3. Условная оптимизация соотношения компонентов
топлива по пустотному удельному импульсу
3.1. Расчет стехиометрического соотношения компонентов
3.2. Подготовка данных. Расчет и построение графиков
зависимости / п от а и Кт при разных допущениях о
равновесности процесса
4. Проектирование проточной части сопла
4.1. Сопло с конической сверхзвуковой частью с оптимальным
углом раскрытия
4.2. Сопло с профилированной сверхзвуковой частью
5. Расчет основных параметров двигателя и размеров
камеры двигателя с учетом потерь
6. Расчет и построение характеристик камеры
6.1. Дроссельные характеристики
6.1.1. Характеристика единичной камеры
6.1.2. Характеристика ДУ при поочередном
дросселировании
6.2. Высотные характеристики
6.2.1. Высотные характеристики в зависимости от ph
6.2.2. Высотные характеристики в зависимости от высоты
полета летательного аппарата и глубины
погружения под воду (см. рис. 5.2)
7. Расчет и построение распределений параметров/;, Г, р, М,
X, W, pfVu массовых концентраций основных
составляющих рабочего тела по длине сопла в равновесном
приближении
8. Научно-исследовательская часть проекта (типовой
вариант): математическое моделирование предельного влияния
скорости химических реакций в рабочем теле
8.1. Расчет и построение распределений параметров
рабочего телар, Г, р, W, pWno длине профилированного сопла
при различных допущениях о скоростях химических
реакций в потоке

5. Примерное содержание курсового проекта 541
8.1.1. Равновесная модель течения
8.1.2. Неравновесная модель течения
а) Равновесная модель течения на дозвуковом
участке и неравновесная модель (химически
замороженное течение) на сверхзвуковом участках сопла
б) Неравновесная модель (химически замороженное
течение) на всем протяжении проточной части
камеры
8.2. Анализ особенностей распределений параметров
рабочего тела по длине проточной части камеры при разных
моделях течения
8.3. Оценка возможных потерь на неравновесность течения
в сопле двигателя
Выводы
Приложения
A. Результаты расчетов по условной оптимизации соотношения
компонентов
Б. Результаты расчетов распределений параметров потока по
длине проточной части камеры в равновесном приближении
B. Результаты расчетов распределений параметров
равновесного течения на дозвуковом участке камеры и химически
замороженного течения в расширяющейся части сопла
Г. Результаты расчетов распределений параметров потока по
длине проточной части камеры в приближении химически
замороженного течения на всем протяжении камеры

6. Вопросы экзаменационных билетов
1. Различие рабочих процессов в реальном и идеальном ракетных
двигателях. Термодинамический подход.
2. Различие рабочих процессов в реальном и идеальном ЖРД.
Потери нетермодинамической природы. Удельный импульс
камеры и ЖРД без дожигания рабочего тела ТНА.
3. Показатели совершенства рабочего процесса в камере
сгорания. Характеристическая скорость. Расходный комплекс.
4. Анализ результатов термодинамических расчетов. Влияние
давления при а = const на Гк, Р, Л, I п.
5. Оценка совершенства рабочего процесса в сопле. Система
коэффициентов. Физическая природа потерь.
6. Особенности рабочего процесса в камере ЖРД по сравнению
с рабочими процессами в других тепловых ракетных двигателях.
7. Термическая диссоциация, рекомбинация и ионизация
рабочего тела. Принцип Ле Шателье - Брауна. Влияние давления
и температуры на эти процессы.
8. Равновесное и замороженное расширение как предельные
варианты протекания реальных процессов. Приближение Брея.
Показатель изоэнтропы.
9. Определение теоретических соотношений компонентов топлив
Особенность расчета для гидрореагирующих горючих.
Условные формулы двухкомпонентных топлив.
10. Уравнение сохранения массы вещества в системе уравнений
термодинамического расчета. Число уравнений.
11. Уравнение сохранения энергии, записанное через полную
энтальпию для ДУ различных схем. Расчет скорости истечения
химически активного газа. Расчет скорости истечения для
равновесного и химически замороженного потоков.
12. Уравнение констант равновесия. Число независимых
уравнений. Зависимость констант равновесия от температуры.
13. Система уравнений термодинамического расчета для четырех-
элементного топлива. Допущения. Существование и
единственность решения. Анализ результатов, влияние давления и
коэффициента избытка окислителя.
14. Особенности термодинамического расчета для выходного
сечения сопла. Расчет изоэнтропийного расширения. Расчет

6. Вопросы экзаменационных билетов
543
скорости истечения, пустотного удельного импульса и
показателя изоэнтропы при известных параметрах (свойствах)
рабочего тела в камере сгорания.
15. Полная система уравнений для термодинамического расчета.
Неуниверсальные методы решения. Пример для пероксида
водорода и гидразина.
16. Система уравнений термодинамического расчета без
использования констант равновесия. На примере комплексов «Астра-4»
и (или) «Терра»: исходные данные, однозначность решения,
система допущений, формы задания исходных данных и их
эквивалентность.
17. Профилирование сверхзвуковой части круглого сопла.
Конические и профилированные сопла. Оптимальный угол
конусности. Оптимальные и укороченные профилированные сопла.
18. Расчет тарельчатого кольцевого сопла. Работа сопла при
переменном противодавлении. Сравнение кольцевых штыревого
и тарельчатого сопл.
19. Особенности термодинамического расчета для
газогенераторов на двухкомпонентном ракетном топливе. Характерный
состав продуктов сгорания.
20. Система уравнений термодинамического расчета ЖГГ на
гидразине и пероксида водорода.
21. Особенности термодинамического расчета при наличии
конденсированной фазы в продуктах сгорания.
22. Особенности термодинамического расчета с учетом
ионизации (в том числе рассмотреть в качестве рабочего тела
водород).
23. Анализ результатов термодинамических расчетов. Влияние
коэффициента избытка окислителя на температуру, расходный
комплекс, кажущуюся молекулярную массу, пустотный
удельный импульс. Выбор и объяснение существования оптимума
соотношения компонентов при заданных значениях давления
в камере и в выходном сечении сопла.
24. Профилирование сужающейся части сопла.
25. Система отсчета полных энтальпий. Полная энтальпия
окислителя, горючего, топлива, продуктов сгорания.
26. Расчет потерь удельного импульса вследствие рассеяния.
27.Расчет потерь на трение и вытеснение в сопле ракетного
двигателя.
28. Расчет характеристик камеры с учетом внутреннего завесно-
го охлаждения.

544 Часть III. Методические указания и КИМ
29. Расчет основных параметров штыревого сопла. Работа сопла
при переменном противодавлении.
30. Круглые и кольцевые сопла. Виды сопл. Качественный
сравнительный анализ.
31. Основы методик определения размеров камеры сгорания.
Приведенная длина. Время пребывания. Формы камер сгорания.
32. Полная высотная характеристика реального ракетного
двигателя, в том числе с авторегулируемым соплом.
33. Дроссельная (расходная) характеристика реального
ракетного двигателя с соплом Л аваля.
34. Работа круглого сопла на режимах значительного
перерасширения. Тяга и удельный импульс при вхождении мосто-
образного скачка уплотнения в сопло.
35. Оценка влияния наружного охлаждения камеры на
достижимые характеристики камеры сгорания и сопла.
36. Уравнение Дальтона и уравнение электронейтральности
ионизированных продуктов сгорания в системе уравнений
термодинамического расчета.
37. Константы равновесия основных химических реакций в
системе уравнений термодинамического расчета. Зависимость
от температуры. Условная запись для реакций, идущих с
образованием конденсированной фазы.
38. Оценка совершенства рабочего процесса в камере сгорания
и в сопле с внутренним завесным охлаждением.
39. Расчет основных характеристик и радиальных размеров
проточной части камеры идеального и реального ракетных
двигателей.

7. Примеры к разделу «Термодинамические расчеты»
Записать файлы исходных данных для решения следующих
задач с использованием программных комплексов «Астра» или
«Терра»1:
1. Эквивалентные формы задания состава рабочего тела:
химические и (или) условные (удельные) формулы, коэффициенты
удельной формулы топлива, соотношение компонентов,
коэффициент избытка окислителя.
2. Расчет состава и свойств продуктов термического разложения
смеси веществ при ее нагревании до заданной температуры
при постоянном давлении.
3. Задача оптимизации соотношения расходов горючего и
окислителя двухкомпонентного топлива в равновесном
приближении.
4. Задача оптимизации соотношения горючего и окислителя
двухкомпонентного топлива в приближении замороженного
течения на всем протяжении прочной части сопла.
5. Задача оптимизации соотношения расходов горючего и
окислителя двухкомпонентного топлива при предположении
равновесного течения в сужающейся части сопла и
неравновесного (замороженного) в расширяющейся части сопла
(приближение Брея).
6. Эквивалентные формы задания условий расширения
рабочего тела в сопле: критические параметры, давление в выходном
сечении, геометрическая степень расширения сопла.
7. Расчет свойств продуктов сгорания твердого ракетного
топлива с заданной условной или удельной формулой и
теплотой образования и параметров РДТТ для разных температур
заряда.
Значительная часть этих задач может быть решена также с
использованием разработанного специалистами NASA программного
комплекса СЕА2 - Chemical Equilibrium with Applications v.2 (http://
www.grc.nasa.gov/WWW/CEAWeb/) или другого доступного
программного обеспечения термодинамических расчетов, например Rocket
Propulsion Analysis (http://www.propulsion-analysis.com/) или TDC -
TermoDynamic Calculation for LRE (http://www.mai202.ru/ENG/tools.htm).

546 Часть III. Методические указания и КИМ
8. Расчет параметров РДТТ и свойств продуктов сгорания сме-
севого твердого ракетного топлива с заданным массовым
содержанием компонентов и известной теплотой образования.
9. Моделирование расширения рабочего тела в сопле при
отсутствии кристаллизации жидких компонентов.
10. Расчет константы равновесия обратимой реакции
диссоциации-рекомбинации при разных температурах раствора.
11. Расчет степени диссоциации в зависимости от температуры
и давления.
12. Расчет каталитического разложения пероксида водорода (при
разной концентрации воды в ее составе) и удельного
импульса ЖРДМТ, работающего на этом топливе.
13. Расчет термокаталитического разложения гидразина (для
фиксированной степени разложения аммиака) и удельного
импульса ЖРДМТ, работающего на этом топливе.
14. Расчет изменения параметров РД с РИТ вследствие замены
рабочего тела при сохранении температуры на входе в сопло
и расхода рабочего тела.
15. Расчет изменения параметров РД с РИТ вследствие замены
рабочего тела при сохранении тепловой мощности
нагревателя и давления торможения на входе в сопло.
16. Расчет изменения параметров РД с РИТ вследствие замены
рабочего тела при сохранении его расхода для постоянной
тепловой мощности нагревателя.
17. Расчет параметров РД с РИТ для данного рабочего тела при
известной тепловой мощности нагревателя.
18. Расчет требуемой тепловой мощности нагревателя (ядерного
реактора или РИТ) для заданной температуры, давления на
входе в сопло с известными геометрической степенью
расширения и размером минимального сечения.
19. Расчет требуемой тепловой мощности нагревателя (ядерного
реактора или РИТ) РД с известными значениями пустотной
тяги при заданных температуре и давлении на входе в сопло
с известной геометрической степенью его расширения.
20. Термодинамический расчет для камеры сгорания ПуВРД при
предположении изохорного процесса сгорания топлива.
21. Термодинамический расчет для продуктов сгорания
заряда воспламенителя РДТТ в свободном постоянном объеме
камеры.

7. Примеры к разделу «Термодинамические расчеты» 547
22. Термодинамический расчет двухзонного ЖГГ с
балластирующим инертным (условно инертным) компонентом для
заданного коэффициента балластировки.
23. Термодинамический расчет двухзонного ЖГГ с
балластирующим инертным компонентом для заданной температуры
в выходном сечении камеры смешения.
24. Термодинамический расчет двухзонного ЖГГ с
балластирующим углеродсодержащим компонентом (например, метаном)
при отсутствии сажи в продуктах газогенерации.
25. Термодинамический расчет двухзонного ЖГГ с аммиаком
в качестве балластирующего компонента при отсутствии его
разложения и инертности по отношению к другим
компонентам продуктов газогенерации.

8. Контрольные вопросы к защите лабораторных работ
по курсу «Общая теория ракетных двигателей»
Лабораторная работа № 1 «Изучение лабораторного
комплекса. Запуск стендовой жидкостной ракетной
двигательной установки (ЖРДУ)»
1. Перечислите основные потенциально опасные факторы
(высокое электрическое напряжение в системе запуска, высокое
давление, высокая температура, свойства чистого кислорода,
свойства технического этилового спирта, высокий уровень
шума).
2. Перечислите вентили, входящие в состав стендовой
установки, и охарактеризуйте их функции и принцип работы.
3. Перечислите клапаны, входящие в состав стендовой
установки, и охарактеризуйте их функции и принцип работы.
4. Перечислите редукторы воздушные, входящие в состав
стендовой установки, и охарактеризуйте их функции и принцип
работы.
5. Перечислите дроссели, входящие в состав стендовой
установки, и охарактеризуйте их функции и принцип работы.
6. Перечислите датчики давления, входящие в состав стендовой
установки, и охарактеризуйте их функции и принцип работы.
7. Перечислить датчики перепада давления, входящие в состав
стендовой установки, и охарактеризуйте их функции и
принцип работы.
8. Укажите на схеме агрегаты и подсистемы, установленные для
повышения безопасности эксплуатации стендовой установки
(предохранительные клапаны, фильтры, блокировки,
продувка камеры).
9. Укажите на схеме одну из основных систем стендовой
установки (система пневмоавтоматики, подачи окислителя,
горючего, охладителя) и объясните принцип ее работы.
10. Охарактеризуйте назначение, состав и функционирование
системы измерения одного из параметров (давление в камере,
расход горючего, расход окислителя, тяга).

8. Контрольные вопросы к лабораторным работам 549
11. Охарактеризуйте назначение, состав и порядок
функционирования одной из систем стендовой установки (системы
пневмоавтоматики, подачи окислителя, горючего, охладителя) на
одном из режимов (заправка, запуск, останов).
12. Охарактеризуйте методику расчета соотношения компонентов
(коэффициент избытка окислителя), удельного импульса,
пустотного удельного импульса.
13. Перечислите причины различия результатов измерений и
истинного значения измеряемой величины.
14. Перечислите причины различия результатов измерений и
вычисленного значения измеряемой величины.
15. Чем объясняется существование границ допустимого
изменения соотношения компонентов для стендового ЖРД?
Лабораторная работа № 2 «Исследование влияния
соотношения компонентов топлива на основные
показатели и характеристики ракетного двигателя»
1. Перечислите основные потенциально опасные факторы
(высокое электрическое напряжение в системе запуска, высокое
давление, высокая температура, свойства чистого кислорода,
свойства технического этилового спирта, высокий уровень
шума).
2. Перечислите входящие в состав стендовой установки
агрегаты (вентили, клапаны, редукторы, дроссели, датчики,
манометры) и охарактеризуйте их функции и принцип работы.
3. Чем объясняется существование границ допустимого
изменения соотношения компонентов для стендового ЖРД?
4. Перечислите причины различия результатов измерений и
истинного значения измеряемой величины.
5. Перечислите причины различия результатов измерений и
вычисленного значения измеряемой величины.
6. Охарактеризуйте назначение, состав и функционирование
системы измерения одного из параметров (давление в камере,
расход горючего, расход окислителя, тяга).
7. Какова последовательность операций и параметры режимов
(методика) при определении дроссельной характеристики
лабораторного ЖРД?
8. Перечислите причины расхождения расчетных и
экспериментальных данных на графике зависимости удельный импульс
в пустоте - коэффициент избытка окислителя.

550 Часть III. Методические указания и КИМ
9. Перечислите причины расхождения расчетных и
экспериментальных данных на графике зависимости расходный комплекс -
коэффициент избытка окислителя.
10. Дайте качественное объяснение влияния системы
охлаждения на полученные результаты для расходного комплекса
топлива.
11. Объясните правомерность оценки эффективности рабочего
процесса в камере сгорания по отношению
экспериментального и расчетного значений расходного комплекса топлива,
а не характеристических скоростей.
12. Как можно количественно оценить возможный диапазон
изменения коэффициента камеры (рк = фр? Какие для этого
потребуются измерения и расчеты?
13. Приведите пример расчета расходного комплекса топлива по
результатам измерений.
14. Объясните причины немонотонной зависимости
(существование максимума) расходного комплекса топлива от
соотношения его компонентов.
15. Объясните причины немонотонной зависимости
(существование максимума) пустотного удельного импульса от
соотношения компонентов топлива.
16. Объясните причины несовпадения ординат («оптимальных»
соотношений компонентов) максимальных значений для
расходного комплекса топлива и пустотного удельного
импульса.
17. Объясните причину различия соотношения компонентов
топлива в реальных ракетных двигателях и соотношения, при
котором пустотный удельный импульс принимает
максимальное значение.
18. Предложите объяснение различий полученных значений
Фк = фр на разных режимах работы по соотношению
компонентов топлива.
19. Дайте возможное объяснение различному виду истекающей
из сопла двигателя газовой струи при работе двигателя на
разных режимах.
20. Предложите изменения в конструкцию двигателя, которые
могут повысить эффективность работы камеры сгорания.

8. Контрольные вопросы к лабораторным работам 551
Лабораторная работа № 3 «Экспериментальное определение
дроссельной характеристики ЖРД»
1. Перечислите основные потенциально опасные факторы
(высокое электрическое напряжение в системе запуска, высокое
давление, высокая температура, свойства чистого кислорода,
свойства технического этилового спирта, высокий уровень
шума).
2. Перечислите входящие в состав стенда агрегаты (вентили,
клапаны, редукторы, дроссели, датчики, манометры) и
охарактеризуйте их функции и принцип работы.
3. Чем объясняется существование границ допустимого
изменения давления в камере для стендового ЖРД при определении
дроссельной характеристики?
4. Перечислите причины различия результатов измерений и
истинного значения измеряемой величины.
5. Перечислите причины различия результатов измерений и
вычисленного значения измеряемой величины.
6. Охарактеризуйте назначение, состав и функционирование
системы измерения одного из параметров (давление в камере,
расход горючего, расход окислителя, тяга).
7. Дайте отвечающее государственному стандарту определение
дроссельной (расходной) характеристики ракетного двигателя.
8. Охарактеризуйте схему измерения тяги двигателя (силовая
схема, принцип действия, градуировка, первичная обработка
показаний, причина погрешности измерений).
9. Охарактеризуйте подсистему измерения расхода окислителя
(схема, принцип действия, первичная обработка показаний,
расчет расхода по результатам измерений, причина
погрешности измерений).
10. Охарактеризуйте подсистему измерения расхода горючего
(схема, принцип действия, расчет расхода по результатам
измерений, причина погрешности измерений).
11. Дайте объяснение малых отклонений расчетных и измеренных
значений тяги в координатах давление в камере - тяга.
12. Оцените количественно возможный диапазон изменения
коэффициента сопла фс.
13. Приведите пример расчета пустотной тяги по результатам
измерений.
14. Приведите пример расчета коэффициента тяги в пустоте по
результатам измерений.

552 Часть III. Методические указания и КИМ
15. Перечислите потенциально опасные факторы, которые имеют
место при проведении лабораторной работы.
16. Манометры с какими шкалами применялись при проведении
эксперимента?
17. Охарактеризуйте компоненты ракетного топлива, на котором
работает лабораторный ракетный двигатель.
18. Предложите мероприятия, направленные на повышение
точности данных, получаемых в процессе проведения этой
лабораторной работы.
19. Предложите изменения в конструкции двигателя, которые
могут повысить эффективность работы камеры сгорания.
20. Предложите изменения в конструкции двигателя, которые
могут повысить эффективность работы сопла.
Лабораторной работы № 4 «Работа сопла Лаваля
при больших степенях перерасширения»
1. Перечислите основные потенциально опасные факторы
(высокое давление, высокий уровень шума).
2. Охарактеризуйте назначение, состав и функционирование
системы измерения давлений и расхода рабочего тела.
3. Перечислите причины различия результатов измерений и
истинного значения измеряемой величины.
4. Объясните назначение агрегатов и характерных узлов пнев-
мосхемы экспериментальной установки.
5. Охарактеризуйте методику проведения эксперимента.
6. Охарактеризуйте методику первичной обработки результатов
измерений.
7. Какие размеры сопла существенны по отношению к цели
экспериментального исследования?
8. Какие характеристики рабочего тела существенны по
отношению к цели экспериментального исследования?
9. Какие допущения приняты при разработке методики расчета
положения системы скачков уплотнения?
10. Что является причиной расхождения экспериментальных и
расчетных данных?
11. Охарактеризуете влияние пограничного слоя на
возникновение системы скачков уплотнения.
12. Какие различия реальных рабочих процессов в исследованном
сопле и их идеального представления существенны по
отношению к цели экспериментального исследования?

8. Контрольные вопросы к лабораторным работам 553
13. Какие параметры (размеры) можно рассматривать в качестве
«естественного аргумента» теории идеального сопла?
14. Дайте определение газодинамических функций, применяемых
при обработке результатов эксперимента.
15. Дайте определение числа Маха и относительной скорости X.
16. Дайте определение показателя к.
17. Опишите возможный механизм влияния угла наклона
образующей расширяющейся части сопла на положение сечения
отрыва потока.
18. В чем заключается механизм эжекции и каким образом он
влияет на параметры течения потока в сопле?
19. Что такое «импульсная трубка» и как ее параметры влияют
(или не влияют) на погрешности измерения?
20. Какие размеры сопла не влияют на координаты характерных
точек на эпюре давления?
21. Предложите методику эксперимента по исследованию работы
сопла при больших степенях перерасширения при постоянном
давлении рабочего тела перед соплом.
22. Объясните причины включения (или отсутствия) осушителя
воздуха в схему экспериментальной установки.
23. Охарактеризуйте примененную методику проведения
эксперимента.
24. Какие допущения приняты в методике расчета давления на
стенке сопла на участке безотрывного течения?
25. Объясните назначение агрегатов и характерных узлов пнев-
мосхемы экспериментальной установки.
26. Что входит в систему измерений? Какие факторы влияют на
погрешности измерений?

9. Типовые вопросы к защите курсового проекта
1. Влияет ли значение расхода топлива на удельный пустотный
импульс I п для данной камеры ракетного двигателя при
постоянном соотношении компонентов топлива?
2. Какие параметры камеры не зависят или слабо зависят от
режима работы камеры по давлению?
3. Почему (и когда?) удельный импульс камеры растет с ростом
расхода топлива?
4. Как изменятся (или не изменятся) параметры камеры
(пустотная тяга, давление в камере, удельный пустотный импульс,
скорость истечения продуктов сгорания), если расход
топлива будет снижен от действительного номинального до иде-
ального значения т = 1 ?
Ри
5. Изменится ли температура продуктов сгорания топлива во
входном сечении сопла, если вместо жидкого кислорода
подать в камеру сгорания кислород, газифицированный в
регенеративной системе охлаждения, а горючее и соотношение
компонентов оставить прежними?
6. Изменится ли температура продуктов сгорания топлива во
входном сечении сопла, если вместо жидкого кислорода
подать в камеру сгорания кислород, газифицированный с
использованием стороннего источника теплоты, а горючее и
соотношение его компонентов оставить прежними?
7. Почему с ростом давления в камере увеличивается
температура продуктов сгорания топлива, а кажущаяся газовая
постоянная снижается?
8. При течении рабочего тела по соплу химическая энергия
отдельных газов остается постоянной, химическая энергия
рабочего тела изменяется, а полная энтальпия рабочего тела
уменьшается. Верны ли эти заключения?
9. Нужно ли стремиться к повышению термического КПД при
выборе параметров камеры ракетного двигателя?
10. Что такое условно оптимальное соотношение компонентов
топлива ракетного двигателя?

9. Типовые вопросы к защите курсового проекта 555
11. Чем определяется максимальное значение удельного
пустотного импульса для заданной топливной пары?
12. Зависит ли скорость истечения рабочего тела от давления
в камере при одном и том же соотношении компонентов
одного и того же топлива?
13. Зависит ли наружная составляющая тяги ракетной камеры от
закона распределения давления по корпусу летательного
аппарата?
14. Зависит ли наружная составляющая тяги ракетной камеры от
наличия или отсутствия отрывного течения в сверхзвуковой
части сопла?
15. Оцените снижение тяги спроектированного двигателя при
удалении расширяющейся части сопла.
16. Равен ли рассчитанный по внутренней составляющей тяги
удельный импульс удельному пустотному импульсу камеры
на всех рассчитанных режимах?
17. Зависит ли значение расходного комплекса и (или)
характеристической скорости от профиля сужающейся (трансзвуковой,
сверхзвуковой) части сопла?
18. На какие параметры и характеристики камеры ракетного
двигателя может повлиять коррозия внутренней поверхности
сопла?
19. Что произойдет с тягой камеры, если вследствие изменения
соотношения компонентов топлива и расхода давление в
камере сгорания, кажущаяся молекулярная масса и усредненный
по процессу показатель изоэнтропы останутся постоянными,
а температура продуктов сгорания возрастет на 20 %? Как
изменятся (или не изменятся) при этом значения удельного
импульса, удельного пустотного импульса, скорости
истечения продуктов сгорания?
20. Чему равен удельный импульс камеры с идеально
регулируемым соплом, у которого площадь выходного сечения сопла
изменяется так, что давление в выходном сечении становится
равным давлению окружающей среды?
21. В каком случае развиваемый удельный импульс камеры будет
выше, чем на расчетном режиме?
22. Как следует изменить диаметры камеры сгорания,
критического и выходного сечений сопла, объем камеры сгорания
спроектированного двигателя, если в исходных данных будет
увеличено давление в камере?

556 Часть III. Методические указания и КИМ
23. Как следует изменить диаметры камеры сгорания,
критического и выходного сечений сопла, объем камеры сгорания
спроектированного двигателя, если схема двигательной
установки изменится на схему с дожиганием (на схему без
дожигания)?
24. Обоснуйте возрастание удельного импульса при увеличении
расхода от номинального значения.
25. Как следует изменить диаметры камеры сгорания,
критического и выходного сечений сопла, объем камеры сгорания
спроектированного двигателя, если при сохранении
соотношения компонентов топлива их температура возрастает за счет
теплоподвода от стороннего источника энергии?
26. Как следует изменить диаметры камеры сгорания,
критического и выходного сечений сопла, объем камеры сгорания
спроектированного двигателя, если при сохранении
соотношения компонентов топлива они подаются в камеру сгорания
нагретыми в системе охлаждения двигателя?
27. Для каких схем двигательных установок с ЖРД дроссельные
характеристики камеры и двигательной установки совпадают?
28. Каким образом можно регулировать геометрическую степень
расширения сопла спроектированной ракетной камеры?
29. Приведите общее и особенное в системе допущений, принятых
при расчетах параметров камер в равновесном, химически
замороженном и кусочно-равновесном приближениях, а также
при использовании аппарата газодинамических функций.
30. Дайте физическое обоснование применимости допущений
идеальности газа и адиабатности и изоэнтропности процесса.
31. Установите соответствие между значениями показателя изо-
энтропы и адиабаты для равновесной и замороженной моделей
течения рабочего тела и подтвердите его результатами
термодинамических расчетов.
32. Укажите пределы изменения концентраций компонентов
рабочего тела, давления, температуры, плотности, скорости
истечения рабочего тела, чисел Маха и приведенной скорости X
при неограниченном увеличении площади выходного сечения
сопла. Как при этом будут изменяться тяга и удельный
пустотный импульс?
33. В каких случаях вытеснительная система подачи компонентов
жидкого ракетного топлива эффективнее систем подачи
других видов?

9. Типовые вопросы к защите курсового проекта 557
34. В каких случаях турбонасосная система подачи компонентов
жидкого ракетного топлива эффективнее систем подачи
других видов?
35. В каких случаях наиболее эффективна турбонасосная система
подачи компонентов жидкого ракетного топлива без
дожигания рабочего тела турбины?
36. В каких случаях наиболее эффективна турбонасосная система
подачи компонентов жидкого ракетного топлива с
дожиганием рабочего тела турбины?
37. Установите и обоснуйте соответствие (больше, меньше,
равно или однозначно не определено) между температурами,
давлениями, коэффициентами избытка окислителя
(окислительных элементов для однокомпонентного топлива) в
указанных точках схемы двигательной установки, например,
в камере сгорания, в газогенераторе, в полости наддува баков
и др.
38. Дайте сравнительную оценку изобарной и скоростной камер.
Как изменятся размеры характерных сечений проточной
части камеры и ее характеристики при переходе от изобарной
камеры к скоростной камере? Приведите сравнительную
характеристику профилированного и конического сопл (на
примере сопл, спроектированных при выполнении
курсового проекта).
39. Приведите сравнительную характеристику профилированных
сопл с угловым и радиусным входом в расширяющуюся часть
(на примере сопла, спроектированного при выполнении
курсового проекта).
40. На чертеже спрофилированного методом парабол сопла
постройте контур сверхзвуковой части, аппроксимированный
дугой окружности.
41. Объяснить смысл термина «точка переключения» высотной
характеристики.
42. Установите и обоснуйте соответствие между значениями
скорости истечения, удельного пустотного импульса и
удельного импульса на номинальном и расчетном режимах.
Используйте результаты термодинамических расчетов.
43. Установите и обоснуйте соответствие между значениями
скорости истечения, удельного пустотного импульса и
удельного импульса на номинальном и расчетном режимах,
полученными термодинамическим расчетом при различных
допущениях.

558 Часть III. Методические указания и КИМ
44. Как (в сторону увеличения концентрации продуктов реакций
диссоциации или рекомбинации) смещается динамическое
равновесие при перемещении рабочего тела к выходному
сечению сопла? Обоснуйте и проиллюстрируйте ответ
результатами термодинамических расчетов.
45. Расшифруйте обозначения и назовите размерности величин,
приведенных в распечатке результатов термодинамического
расчета.
46. По результатам термодинамического расчета вычислите
константу равновесия приведенной химической реакции.
47. Рассчитайте скорость потока, используя данные, приведенные
в распечатке результатов термодинамических расчетов.
48. Сформируйте исходные данные для термодинамического
расчета при различных допущениях о наличии химического
равновесия в потоке. Используя полученные результаты
термодинамических расчетов, подтвердите реализацию принятых
допущений.
49. Обоснуйте принципиальные ограничения на применение
использованной методики термодинамического расчета при
проектировании перспективных ЖРД.

Литература
Часть I
Алемасов В.Е., Дрегалин А.Ф., Черенков А.С. Основы теории физико-
химических процессов в тепловых двигателях и энергетических
установках: учеб. пособие для вузов. М.: Химия, 2000.
Виницкии A.M. Ракетные двигатели на твердом топливе: учеб. пособие
для вузов. М.: Машиностроение, 1973.
Добровольский М.В. Жидкостные ракетные двигатели: Основы
проектирования: учеб. для вузов / под ред. Д.А. Ягодникова. 2-е изд.,
перераб. и доп. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005.
Дорофеев А.А. Ядерные ракетные двигатели и энергетические
установки. Введение в теорию, расчет и проектирование: учеб. пособие /
под ред. чл.-кор. РАН И.И. Федика. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2012.
Импульсные детонационные двигатели / под ред. СМ. Фролова. М.:
ТОРУС ПРЕСС, 2006.
Максимов А.И. Космическая одиссея, или Краткая история развития
ракетной техники и космонавтики / под ред. A.M. Хохлова.
Новосибирск: Наука. Сиб. отд-ние, 1991.
Основы теории и расчета жидкостных ракетных двигателей: учеб. для
авиац. спец. вузов: в 2 кн. / А.П. Васильев, В.М. Кудрявцев, В.А.
Кузнецов и др.; под ред. В.М. Кудрявцева. 4-е изд., перераб. и доп. М.:
Высш. шк., 1993.
Ракетно-космические двигатели и энергетические установки: науч.-техн.
сб. Вып. 4 (142). Общие вопросы ракетного двигателестроения. М.:
НИИ ТП им. академика М.В. Келдыша, 1993.
Ракетные двигатели / Т.М. Мелькумов, Н.И. Мелик-Пашаев,
П.Г. Чистяков и др. М.: Машиностроение, 1976.
Сборник задач и вопросов по основам теории и расчета ракетных
двигателей: учеб. пособие для вузов / Е.Л. Березанская, В.А. Буркальцев,
В.Г. Волков и др.; под ред. В.М. Кудрявцева, А.А. Дорофеева. М.:
Изд-во ЦНИИНТИ КПК, 1995.
Ядерные ракетные двигатели / Ю.Г. Демянко, Г.В. Конюхов,
А.С. Коротеев и др. М.: ООО «Норма-Информ», 2001.
Часть II
Алемасов В.Е., Дрегалин А.Ф., Тишин А.П. Теория ракетных двигателей:
учеб. для втузов / под ред. В.П. Глушко. М.: Машиностроение,
1989.
Азов В., Воронцов Д. Последний бой углеводородов // Новости
космонавтики. 2008. № 2 (301). Т. 18. С. 44-46.
Основы теории и расчета жидкостных ракетных двигателей: учеб. для
авиац. спец. вузов: в 2 кн. /А.П. Васильев, В.М. Кудрявцев, В.А. Куз-

560
Литература
нецов и др.; под ред. В.М. Кудрявцева. 4-е изд., перераб. и доп. М.:
Высш. шк., 1993.
Применение ЭВМ для термодинамических расчетов металлургических
процессов / Г.Б. Синярев, Н.А. Ватолин, Б.Г. Трусов, Г.К. Моисеев.
М.: Наука, 1982.
Рабочие процессы в жидкостном ракетном двигателе и их
моделирование / Е.В. Лебединский, Г.П. Калмыков, СВ. Мосолов и др.; под
ред. академика РАН А.С. Коротеева. М.: Машиностроение, 2008.
Сборник задач и вопросов по основам теории и расчета ракетных
двигателей: учеб. пособие для вузов / Е.Л. Березанская, В.А. Буркальцев,
В.Г. Волков и др.; под ред. В.М. Кудрявцева, А.А. Дорофеева. М.:
Изд-во ЦНИИНТИ КПК, 1995.
Термодинамические и теплофизические свойства продуктов сгорания:
Справочник: в 10 т. / под ред. В.П. Глушко. М.: ВИНИТИ АН СССР,
1971-1979.
Термодинамические свойства индивидуальных веществ: Справочник:
в 4 т. / под ред. В.П. Глушко. М.: Наука, 1978-1982.
Техническая термодинамика: учеб. для машиностроит. спец. вузов /
В.И. Крутов, СИ. Исаев, И.А. Кожинов и др.; под ред. В.И. Круто-
ва. 3-е изд., перераб. и доп. М.: Высш. шк., 1991.

Электронные источники информации
(www.chem.msu.su/cgi-bin/tkvl.pl?show=welcome.html) - база данных
«Термические Константы Веществ» на сайте МГУ им. М.В.
Ломоносова
http://www.chem.msu.su/rus/handbook/ivtan - электронная база данных
ИВТАНТЕРМО
http://www.uic.edu/~mansoori/Thermodynamic/Data.and.Property_html -
информация о сайтах, содержащих сведения о термодинамических
данных и программах расчета свойств химических соединений
www.bmstu.ru/ - официальный сайт МГТУ им. Н.Э. Баумана
www.chem.msu.su/eng/misc/mendeleev/- информация в Интернете,
связанная с именем Д.И. Менделеева
www.energia.ru/ - сайт РКК «Энергия» им. СП. Королева
www.engineer.bmstu.ru/res/dorofeev/MAIN.HTM. - полнотекстовый
мультимедийный сетевой онлайн-учебник
www.ihst.ru/ - сайт Института истории естествознания и техники РАН
им. СИ. Вавилова
www.kbha.ru/ - сайт ОАО КБХА (Воронеж)
www.kerc.msk.ru/ipg/development/development.shtml - сайт ФГУП
«Исследовательский центр имени М. В. Келдыша»
www.novosti-kosmonavtiki.ru/ - электронное издание журнала «Новости
космонавтики»
www.npoenergomash.ru/ - сайт НПО «Энергомаш» им. академика
В.П. Глушко
http://www.npoiskra.ru/index.php?main=production&id_parent=9 - сайт
ОАО «НПО «Искра»
www.pw.utc.com/ - сайт Pratt & Whitney Rocketdyne
www.roscosmos.ru/ - сайт Федерального космического агентства
Российской Федерации (РОСКОСМОС)
www.ssau.ru/partners/sntk/ - сайт Самарского научно-технического
комплекса им. Н.Д. Кузнецова

Предметный указатель1
Агрегат турбонасосный 19, 33, 34, 158, 435
Адиабата 51, 122, 178,233
Азот 217,224
Алмаз 226
Аммиак 123,229, 301
Аппарат пропульсивный 26, 346
Баки топливные 33, 302, 327
Балластировка 316,320
Бронировка 108
Валентность 217
Вода 227
Водород 224, 229
Водорода пероксид 229, 307
Воспламенение ракетного топлива
жидкого 316, 328
твердого 33, 114
Время пребывания в камере среднее 332
- работы двигателя 34
- релаксации 196
Газ идеальный 50, 123, 194
Газовод 80
Газогенератор на ракетном топливе
жидком 314
многозонный 316
однозонный 316
твердом 109, 115
Гелий 126,224
Гидразин 215,227,229
Головка камеры (газогенератора) смесительная 32, 316, 328
Горение 316,328
Горючее ракетных топлив 161, 225
жидкое 228
твердое 107, 225
Курсивом выделены термины, определения которых приведены
в тексте.

Предметный указатель
563
Давление
- в камере 36, 164
сгорания (в газогенераторе) 164, 326
-парциальное 201,219
- статическое 50, 55
Давление полное (торможения) 51, 131
Двигатель 25
- воздушно-реактивный 26, 28, 30
- идеальный 22
-ракетный 32
- - жидкостный (ЖРД) 19, 32, 154, 155
коррекции 159
малой тяги 159
маршевый 159
многокамерный 159
многократного
запуска 159
использования 159
многорежимный 159
однокамерный 159
однократного
запуска (включения) 159
использования 159
однорежимный 159
ориентации 159
рулевой 159
с вытеснительной системой подачи 33, 156, 159
стартовый 159
с турбонасосной системой подачи 33, 156
безгенераторный 34, 156
без дожигания генераторного газа 33, 156
с дожиганием генераторного газа 34, 156
стыковки 159
тормозной 159
- - многокамерный 159
--однокамерный 159
- - твердого топлива (РДТТ) 19, 32, 155
- - ядерный тепловой 32, 121
- реактивный 25
- тепловой 21

564
Предметный указатель
Детонация 29, 47
Диметилгидразин несимметричный (НДМГ) 215, 228
Диссипация энергии 131,139
Диссоциация 198, 321
Длина камеры приведенная 333, 338
Заряд твердого ракетного топлива 33, 107
Значение параметра камеры (газогенератора) идеальное \11,
272
Импульс удельный номинальный 36,64
- - пустотный 63
- - расчетный 66
- - тяги 36
Камера
- газогенератора на ТРТ 107
- ракетная 32, 328
-РДТТ 33, 107
- сгорания ракетной камеры (газогенератора) 32, 328
Керосин 229
Комплекс камеры расходный 180
-тяговый 185
Компонент ракетного топлива 229
Константа равновесия 201
- скорости химической реакции 200
Контур камеры 89
- сопла ЪА1
- - исходный 388
- - с равномерной характеристикой 384
угловой точкой 388
--укороченный 388
--экстремальный 385,391
Коэффициент
- избытка окислителя 216
- камеры 181
- расхода сопла 91, 180
- сопла 186, 347
- тяги 93,98, 185
- - пустотный 93, 97
- удельного импульса камеры \11

Предметный указатель
565
Масса двигательной установки 35
- двигателя 36
Металлы 161,217,219,224,230
- наноразмерные 225
Метан 229
Насос
- горючего 33, 435
- окислителя 33, 435
- подкачивающий 34, 35
Окислитель жидкий ракетный
азотнокислотный 229, 203, 230
азоттетраоксидный 229, 230
фторный 229
Отставание в сопле
скоростное 371,373
температурное 371,374
Охлаждение внутреннее 359
- -завесное 359
- емкостное 171, 339
- наружное 239, 339
- - проточное 239,339
автономное сторонним компонентом 239, 339
- регенеративное 239, 339
Перманганат калия 308
- натрия 308
Плотность топлива 110
Показатель адиабаты 51, 170
- изоэнтропы 281
Полнота сгорания 183,338
Потери в сопле из-за
многофазности 371
незавершенности кристализации 374
рассеяния 362
трения 365
химической неравновесности течения 350
Продукты газогенерации 301, 314, 328
- сгорания 286,328

566
Предметный указатель
Процесс в камере сгорания ЖРД (газогенератора) рабочий
- распыление 328
- смесеобразование 328
--- РДТТ рабочий 107
устойчивость 115
Радикалы активные 224,312
Расход массовый 27, 56, 62
- - горючего 216
- - окислителя 216
- - продуктов сгорания 62, ПО, 178, 186, 239
- - топлива ПО, 239
Реакции
-диссоциации-рекомбинации 172, 194
-обратимые 194,350,353
- радиоактивного распада 125
-химические 194
- - экзотермические 172, 271, 281,354
- - эндотермические 207, 302,354
-ядерные 126
--деления 127
- - синтеза 126
Режим работы сопла расчетный 59, 421, 422
при отрыве потока в системе скачков 400
с недорасширением 59, 422
с перерасширением 59, 400, 421
Рекомбинация 194
Сечение сопла выходное 39, 385
- - критическое 52, 277
--минимальное 91,278
- - начальное 385
Сила реактивная 38
Скорость истечения 27, 36, 46, 55, 277
- потока 51, 274
- характеристическая 180
--в камере 180
Слой потока пристеночный 340
Смесеобразование в камере 171, 328

Предметный указатель
567
Соотношение компонентов массовое стехиометрическое
(теоретическое) 216
действительное 216
Сопло 27,30-32,346
-кольцевое 413,427
- коническое 363, 370
- круглое 50
- Л аваля 50
- осесимметричное 363
- профилированное 382
- раздвижное 74
- регулируемое 74
- с угловым входом 386,388
-тарельчатое 413,427
Сопло утопленное 33
- штыревое 413
Степень расширения газа в сопле 131, 352
- - сопла геометрическая 55, 352
Тело рабочее 25
Температура компонента 232, 297
- потока 51, 276
- продуктов разложения однокомпонентного топлива 301
- сгорания в камере (газогенераторе) 36, 289, 315
- - твердого ракетного топлива 108
Тетраоксид азота 214,228,229
Течение в сопле двухфазное 371
неравновесное 270
равновесное 270
химически замороженное 271
- изоэнтропийное 51,273
Топливо ракетное жидкое 32, 155, 229
- - металлосодержащее 161,225,371
- - твердое 107, 225
закон горения 108
- - шугаобразное 233, 297
Тракт охлаждения камеры (газогенератора) 239, 375
Турбина газовая 30, 31, 33, 34
Тяга двигателя ракетного, внутренняя составляющая 35, 38
наружная составляющая 43

568
Предметный указатель
Установка двигательная жидкостная 35, 100, 410
Устройство пропульсивное 26, 121
Фаза конденсированная 205, 351, 371
Фуллерены 226
Функции газодинамические адиабатного потока изоэнтропий-
ного 19, 52
неизоэнтропийного 143
Характеристика двигательной установки дроссельная (расходная)
при дросселировании синхронном 100, 410
последовательном 100, 410
- двигателя ракетного высотная 69, 407, 422
дроссельная 62, 400, 409
Часть сопла расширяющаяся 89, 384, 390, 394
- - сужающаяся 89, 386, 387
Энтальпия полная 223, 229
- - в условиях подачи 232
стандартных 229
- - компонента 232
- - система отсчета 224
- - топлива 239
- термодинамическая 123, 224
Энтропия идеального газа 251, 252, 263
- система отсчета 249, 252
Ядро потока 339, 359

Именной указатель
Абрамович Г.Н. 132
Авдуевский B.C. 367
Алемасов В.Е. 455
Аристотель 195
Аррениус С. (S. Arrhenius) 195, 206, 334, 336
Белов Г.В. 230,268,327
Беляев Н.М. 302,327,357
Богомолов В.Н. 162
Борда Жан Шарль (Borda J.C.) 179
Браун В. фон (Braun W. von) 161
Браун К. (Braun К.) 206, 208, 291, 307, 453
Васильев А.П. 7
Витошинский Ч.М. (Witoszynski CM.) 393
ВулисЛ.А. 376
Гагарин Ю.А. 21, 162
Гемфри Д. (Humphrey D.) 29
Гиббс Дж.В. (Gibbs В.) 263
ГлушкоВ.П. 7, 161,431,455
Годдард P. (Goddard R.) 161
Гюгонио Пьер-Генри (Hugoniot P.-H.) 29
Дальтон Дж. (Dalton J.) 210, 219, 243, 247
Добровольский М.В. 7, 9, 423, 453, 455
Жуковский Н.Е. 42, 161
Зенгер Е. (Sanger E.) 161
Изотов СП. 162
Исаев A.M. 162
Карман Т. фон (Karman T. von) 69
КаторгинБ.И. 162,375,431
Квасников А.В. 7
Кибальчич Н.И. 160
Кондратюк Ю.В. 160

570
Именной указатель
Конопатов А.Д. 162
Королев СП. 21, 161
КосбергС.А. 162
Кудрявцев В.М. 8, 9, 402, 455
Кузнецов Н.Д. 162
Кутателадзе С.С. 367
Лаваль К.Г. (Laval C.G.) 50, 413, 422, 427
Лагранж Ж. (Lagrange J.) 41, 254, 261, 263
Лагутин Б.Н. 162
Ларин Е.Г. 163
Леонтьев А.И. 367
Леонтьев Н.И. 162
Ле Шателье A. (Le Chatelier H.) 206, 208, 291, 307, 453
Лойцянский Л.Г. 41
Люлька А.И. 162
МайерЮ.Р. (Mayer J.R.) 51,387,416
Max E. (Mach E.) 51, 277, 367, 376, 387
Мелькумов Т.М. 7
Мельников М.В. 162
Менделеев Д.И. 160, 236
Надирадзе А.Д. 162
Неждановский С.С. 160
Ньютон И. (I. Newton) 40, 45, 79, 267
Оберт Г. (Oberth H.) 161
Перельман Я.И. 161
Победоносцев Ю.А. 161
ПоляевВ.М. 7,9,453
Попов М.А. 7
Прандтль Л. (Prandtl L.) 160, 367, 387, 416
Пригожий И.P. (Prigogine I.R.) 439
Радовский В.П. 162
РачукВ.С. 163
Рейнольде О. (Reynolds О.) 368
РынинН.А. 161

Именной указатель
571
Садовский И.Н. 162
Саттон Д. (Sutton G.) 165
Селезнев Е.П. 162
СиняревГ.Б. 7,254,453
Смирнов И.А. 163
Соколов Б.А. 12, 163
Соломонов Ю.С. 163
Степанов В.Г. 162
СтернинЛ.Е. 375,398,431
Стечкин Б.С. 161
Сухадольский А.П. 163
Трусов Б.Г. 11,254,439,454
Феодосьев В.И. 7
Цандер Ф.А. 160
Циолковский К.Э. 160,287,299
Чаплыгин С.А. 161
Чернухин В.А. 7, 9
Эйлер Л. (Euler L.) 79, 84, 93, 142, 160, 283

Приложение 1
Параметры стандартной атмосферы по ГОСТ 4401-81
Высота Н, м
-2000
- 1500
- 1000
-500
0
500
1000
1500
2000
2500
3000
4000
5000
6000
7000
8000
9000
10000
11000
12000
14000
16000
18000
20000
24000
28000
32000
36000
40000
50000
Температура Т, К
ЗОЦ
297,9
295,0
291,4
288,2
284,9
281,7
278,4
275,2
271,9
268,7
262,2
255,7
249,2
242,7
236,2
229,7
223,3
216,8
216,7
216,7
216,7
216,7
216,7
220,6
224,5
228,5
239,3
250,4
270,7
Давление р, Па
127774
120691
113930
107477
101330
95464,0
89877,0
84559,0
79499,0
74690,0
70123,0
61661,0
54052,0
47217,0
41106,0
35653,0
30801,0
26500,0
22700,0
19399,0
14170,0
10353,0
7565,00
5529,00
2971,00
1616,00
889,000
499,000
287,000
80,0000
Плотность р, кг/м3
1,4781
1,4114
1,3470
1,2849
1,2250
1,1673
1,1117
1,0581
1,0065
0,9569
0,9093
0,8194
0,7365
0,6601
0,5900
0,5258
0,4671
0,4135
0,3648
0,3119
0,2279
0,1665
0,1216
0,0889
0,0469
0,0251
0,0136
0,0073
0,0040
0,0010

Приложение 2
Параметры экстремального контура сопла1
р-
радиан
0,0612
0,1036
0,1478
0,1924
0,2364
0,2794
0,3210
0,3610
0,3994
0,4361
0,4711
0,5044
0,5360
0,5661
0,5947
0,6219
0,6477
0,6722
0,6955
0,7177
0,7388
0,7538
0,7779
0,7961
0,8135
0,8300
1 0,8458
0
R
а
1,0662
1,1448
1,2541
1,3971
1,5783
1,8036
2,0807
2,4187
2,8289
3,3242
3,9203
4,6350
5,4895
6,5079
7,7180
9,1518
10,846
12,841
15,185
17,931
21,137
24,871
29,209
34,232
40,035
46,721
54,403
L
а
1,7612
2,4738
3,2373
4,0939
5,0875
6,2682
7,6952
9,4387
11,583
14,229
17,497
21,532
26,506
32,623
40,128
49,305
60,493
74,085
90,542
110,40
134,28
162,89
197,06
237,74
285,99
343,05
410,31
L
R
а
1,0524
1,1332
1,2423
1,3842
1,5636
1,7864
2,0600
2,3934
2,7974
3,2846
3,8700
4,5708
5,4072
6,4022
7,5825
8,9783
10,624
12,559
14,827
17,478
20,567
24,157
28,317
33,125
38,666
45,035
52,335
К
1,0581
1,8392
2,5691
3,3525
4,2374
5,2670
6,4886
7,9559
9,7316
11,889
14,514
17,706
21,584
26,282
31,961
38,802
47,020
56,857
68,593
82,547
99,083
118,61
141,60
168,58
200,13
236,32
279,69
:
2ра, градус,
6
R
а
1,0250
1,1166
1,2268
1,3680
1,5457
1,7659
2,0358
2,3643
2,7616
3,2402
3,8143
4,5006
5,3184
6,2897
7,4400
8,7981
10,397
12,473
14,469
17,030
20,011
23,468
27,468
32,082
37,391
43,482
50,453
L
а
0,4387
1,4592
2,2154
2,9825
3,8278
4,7967
53334
7,2861
8,9100
10,868
13,234
16,092
19,541
23,694
28,682
34,655
41,786
50,272
60,338
72,237
86,259
102,73
122,01
144,52
170,70
201,08
236,21
при к = 1,15
8
К
1,0901
1343
1,3454
1,5212
1,7383
2,0037
2,3259
2,7151
3,1839
3,7433
4,4120
5,2074
6,1505
7,2654
8,5793
10,123
11,932
14,045
16,506
19,364
22,674
26,488
30,899
35,955
41,746
48,363
L
а
1,0268
1,8476
2,6127
3,4278
4,3448
5,4059
6,6583
8,1481
9,9315
12,072
14,641
17,722
21,412
25,838
31,066
37,298
44,676
53,384
63,628
75,641
89,686
106,05
125,07
147,10
172,55
201,86
10
1
1,0509
1,1742
1,3163
1,4905
1,7041
1,9643
2,27%
2,6595
3,1153
3,6601
4,3090
5,0795
5,9915
7,0677
8,3337
9,8187
11,555
13,581
15,936
18,666
21,823
25,463
29,648
34,447
39,936
46,198
L
а
0,5317
1,4645
2,2427
3,0368
3,3101
4,9068
6,0687
7,4399
9,0693
11,012
13,330
16,094
19,387
23,299
27,937
33,418
39,878
47,469
56,361
66,746
78,839
92,877
109,13
127,88
149,47
174,24
12 I
К
1,1357
1,2806
1,4537
1,6638
1,9186
2,2262
2,5960
3,0387
3,5668
4,1947
4,9389
5,8180
6,8536
8,0699
9,4941
11,157
13,093
15,341
17,943
20,947
24,406
28,376
32,924
38,117
44,033
К
1,0651
1,8725
2,6544
3,4915
4,4312
5,5140
6,7802
8,2735
10,042
12,141
14,631
17,582
21,072
25,192
30,040
35,732
42,394
50,169
59,218
69,717
81,866
95,883
112,01
130,52
151,70
Основы теории и расчета жидкостных ракетных двигателей ... / под ред. В.М. Кудрявцева (см. сноску на с. 7).

Окончание таблицы
радиан
0,1924
0,2364
0,2794
0,3210
0,3610
0,3994
0,4361
0,4711
0,5044
0,5350
0,5661
0,5947
0,6219
0,6477
0,6722
0,6955
0,7177
0,7388
0,7588
0,7779
0,7961
0,8135
0,8300
0,8458
0,8609
0,8754
0,8892
1 0,9024
16 1
К
1,1895
1,3628
1,5666
1,8102
2,1017
2,4501
2,8651
3,3580
3,9418
4,6312
5,4428
6,3958
7,5116
8,8142
10,331
12,091
14,130
16,484
19,194
22,307
25,872
29,945
34,587
39,863
45,845
52,613
60,250
68,850
К
1,1303
1,9133
2,6986
3,5464
4,4974
5,5879
6,8542
8,3348
10,072
12,113
14,511
17,324
20,619
24,470
28,959
34,181
40,239
47,248
55,335
64,643
75,327
87,558
101,53
117,44
135,52
156,01
179,19
205,34
18
R
а
1,1338
1,3090
1,5104
1,7485
2,0320
2,3694
2,7702
3,2453
3,8068
4,4686
5,2467
6,1589
7,2253
8,4687
9,9146
11,591
13,530
15,767
18,339
21,290
24,667
28,521
32,910
37,893
43,539
49,921
57,117
65,213
К
0,7579
1,5538
2,3226
3,1339
4,0306
5,0478
6,2191
7,5799
9,1679
11,025
13,197
15,737
18,701
22,156
26,171
30,830
36,220
42,441
49,604
57,830
67,252
78,018
90,288
104,24
120,06
137,97
158,19
180,97
:
ZPo, градус,
20
К
1,0713
1,2500
1,4496
1,6826
1,9580
2,2845
2,6713
3,1285
3,6679
4,3026
5,0476
5,9197
6,9381
8,1241
9,5015
11,097
12,940
15,065
17,506
20,304
23,503
27,151
31,301
36,011
41,343
47,365
54,151
61,781
L
а
0,3842
1,2011
1,9500
2,7396
3,5885
4,5405
5,6274
6,8816
8,3373
10,032
12,006
14,307
16,984
20,094
23,701
27,874
32,693
38,243
44,619
51,928
60,285
69,817
80,664
92,977
106,92
122,68
140,44
160,43
прик= 1,15
22
R
а
1,0018
1,1859
1,3844
1,6127
1,8804
2,1961
2,5689
3,0086
3,5262
4,1342
4,8469
5,6801
6,6519
7,7823
9,0939
10,612
12,364
14,381
16,698
19,351
22,382
25,836
29,763
34,217
39,256
44,943
51,349
58,546
К
0,0092
0,8549
1,6072
2,3622
3,1692
4,0633
5,0749
6,2341
7,5723
9,1229
10,923
13,013
15,438
18,248
21,500
25,254
29,579
34,552
40,255
46,781
54,231
62,715
72,356
83,285
95,646
109,60
125,30
142,95
24
R
а
1,1167
1,3151
1,5391
1,7994
2,1047
2,4638
2,8862
3,3825
3,9646
4,6458
5,4413
6,3680
7,4450
8,6935
10,137
11,802
13,718
15,916
18,432
21,305
24,578
28,295
32,509
37,274
42,650
48,702
55,498
L
а
0,5148
1,2666
2,0006
2,7710
3,6135
4,5580
5,6325
6,8658
8,2885
9,9338
11,838
14,042
16,589
19,530
22,919
26,816
31,289
36,411
42,263
48,935
56,523
65,134
74,883
85,897
98,313
112,28
127,95
26 1
R
а
1,0426
1,2419
1,4622
1,7154
2,0106
2,3564
2,7620
3,2376
3,7944
4,4451
5,2042
6,0875
7,1132
8,3013
9,6741
11,256
13,076
15,162
17,549
20,273
23,374
26,895
30,885
35,895
40,480
46,202
52,626
К
0,1806
0,9363
1,6537
2,3923
3,1891
4,0734
5,0721
6,2117
7,5204
9,0282
10,768
12,776
15,092
17,759
20,828
24,352
28,390
33,007
38,275
44,274
51,089
58,813
67,550
77,410
88,514
100,99
114,99

ри.
радиан
0,0573
0,0960
0,1355
0,1745
0,2123
0,2484
0,2827
0,3151
0,3456
0,3743
0,4012
0,4264
0,4501
0,4723
0,4932
0,5128
0,5312
0,5485
0,5648
0,5802
0,5947
0,6084
0,6214
0,6337
0,6453
0,6563
0,6668
0,6768
0,6863
1 0,6953
2Ро, градус, при к = 1,25
0 1
1
1,0616
1,1328
1,2290
1,3508
1,4997
1,6778
1,8876
2,1322
2,4149
2,7396
3,1102
3,5312
4,0074
4,5435
5,1451
5,8175
6,5667
7,3987
8,3200
9,3337
10,457
11,687
13,036
14,509
16,116
17,865
19,764
21,823
24,050
26,455
К
1,7324
2,4167
3,1351
3,9201
4,8018
5,8107
6,9794
8,3427
9,9388
11,809
13,999
16,558
19,540
23,006
27,016
31,643
36,963
43,056
50,012
57,925
66,898
77,041
88,470
101,13
115,69
131,17
149,67
169,58
191,65
216,07
Z
X
1,0470
1,1208
1,2169
1,3377
1,4850
1,6609
1,8678
2,1087
2,3868
2,7056
3,0689
3,4809
3,9460
4,6888
5,0541
5,7071
6,4330
7,2376
8,1264
9,1057
10,181
11,360
12,648
14,053
15,581
17,240
19,037
20,980
23,076
25,334
К
0,9913
1,7639
2,4541
3,1716
3,9545
4,8310
5,8271
6,9692
8,2846
9,8021
11,552
13,556
15,880
18,528
21,550
24,985
28,877
33,271
38,215
43,759
49,954
56,858
64,526
73,020
82,402
92,737
104,09
116,53
130,14
144,99
6
К
1,0153
1,1030
1,2007
1,3211
1,4670
1,6406
1,8445
2,0814
2,3545
2,6670
3,0227
3,4253
3,8791
4,3882
4,9572
5,5909
6,2941
7,0720
7,9298
8,8730
9,9073
11,038
12,272
13,615
15,073
16,652
18,360
20,203
22,187
24,320
К
0,2793
1,3579
2,0852
2,7917
3,5410
4,3659
5,2919
6,3432
7,5437
8,9179
10,491
12,315
14,342
16,676
19,322
22,312
25,680
29,459
33,686
38,399
43,636
49,439
55,850
62,912
70,670
79,172
88,466
98,600
109,62
121,59
8
К
1,0738
1,1768
1,2976
1,4421
1,6131
1,8133
2,0454
2,3123
2,6172
2,9635
3,3548
3,7949
4,2877
4,8375
5,4485
6,1253
6,8724
7,6947
8,5970
9,5846
10,662
11,836
13,110
14,492
15,986
17,598
19,334
21,200
23,202
L
а
0,8822
1,6950
2,4077
3,1338
3,9158
4,7813
5,7531
6,8528
8,1017
9,5215
11,134
12,962
15,029
17,359
19,977
22,910
26,184
29,828
33,869
38,339
43,267
48,687
54,629
61,128
68,219
75,936
84,316
93,396
103,21
10
R
а
1,0294
1,1443
1,2671
1,4105
1,5788
1,7749
2,0016
2,2615
2,5578
2,8936
3,2723
3,6972
4,1722
4,7009
5,2873
5,9356
6,6498
7,4344
8,2938
9,2325
10,255
11,366
12,571
13,875
15,282
16,797
18,427
20,176
22,049
К
0,3194
1,2817
2,0194
2,7324
3,4801
4,2935
5,1958
6,2071
7,3464
8,6323
10,083
11,718
13,557
15,619
17,924
20,494
23,349
26,512
30,005
33,852
38,076
42,701
47,754
53,259
59,242
65,731
72,752
80,333
88,503
12 1
К
1,1020
1,2292
1,3724
1,5382
1,7301
1,9509
2,2034
2,4904
2,8150
3,1801
3,5891
4,0952
4,5519
5,1128
5,7317
6,4123
7,1585
7,9744
8,8640
9,8314
10,881
12,017
13,244
14,566
15,988
17,515
19,151
20,901
К
0,8430
1,6263
2,3366
3,0577
3,8270
4,6688
5,6025
6,6456
7,8144
9,1252
10,593
12,236
14,069
16,109
18,373
20,877
23,641
26,681
30,016
33,665
37,647
41,982
46,690
51,791
57,305
63,254
69,660
76,543

Учебное издание
Дорофеев Анатолий Александрович
ОСНОВЫ ТЕОРИИ
ТЕПЛОВЫХ РАКЕТНЫХ ДВИГАТЕЛЕЙ
Теория, расчет и проектирование
Редактор Л.Т. Мартыненко
Технический редактор Э.А. Кулакова
Художник О.В. Левашова
Корректор О. В. Калашникова
Компьютерная графика Н.П. Новиковой, О.В. Левашовой
Компьютерная верстка И.Д. Звягинцевой
Оригинал-макет подготовлен
в Издательстве МГТУ им. Н.Э. Баумана.
Сертификат соответствия
№ РОСС RU. AE51. Н 16228 от 18.06.2012
Подписано в печать 29.09.2013. Формат 60x90/16.
Усл. печ. л. 36. Тираж 1500 экз. (1-й з-д 1-500). Заказ №629
Издательство МГТУ им. Н.Э. Баумана.
105005, Москва, 2-я Бауманская ул., д. 5, стр. 1.
http://www.baumanpress.ru
E-mail: press@bmstu.ru
Отпечатано в типографии МГТУ им. Н.Э. Баумана.
105005, Москва, 2-я Бауманская ул., д. 5, стр. 1.
baumanprint@gmail.com